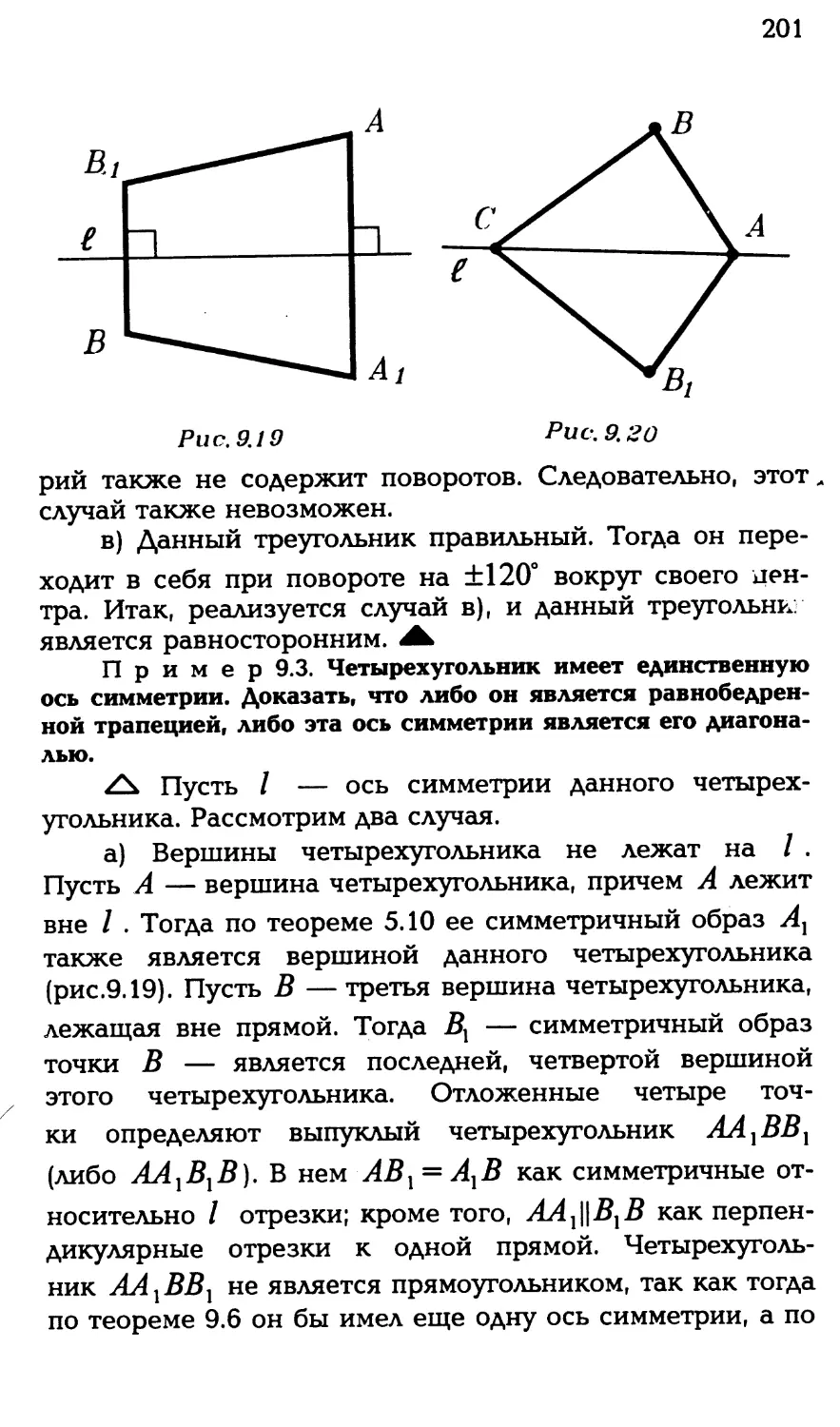
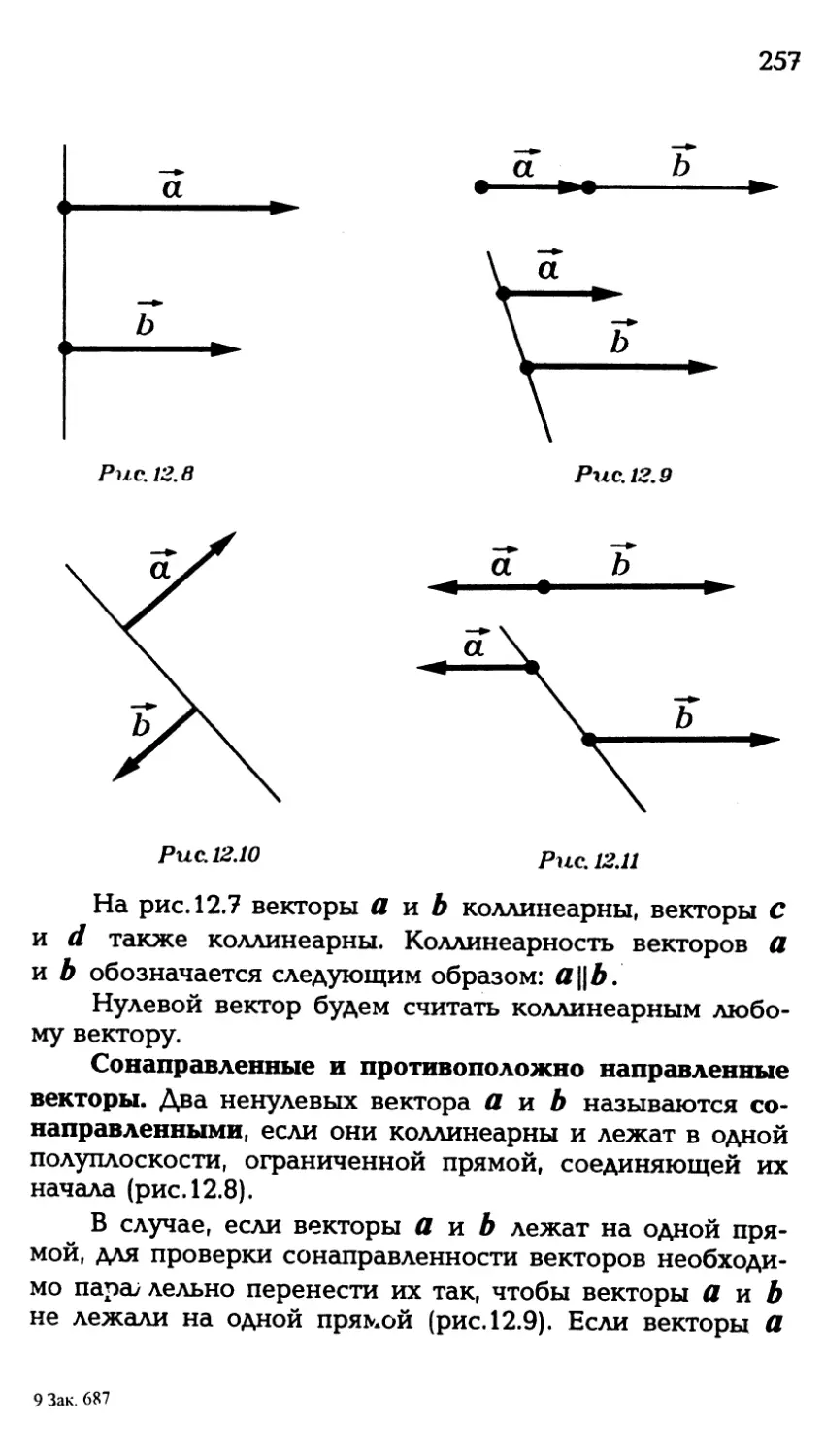
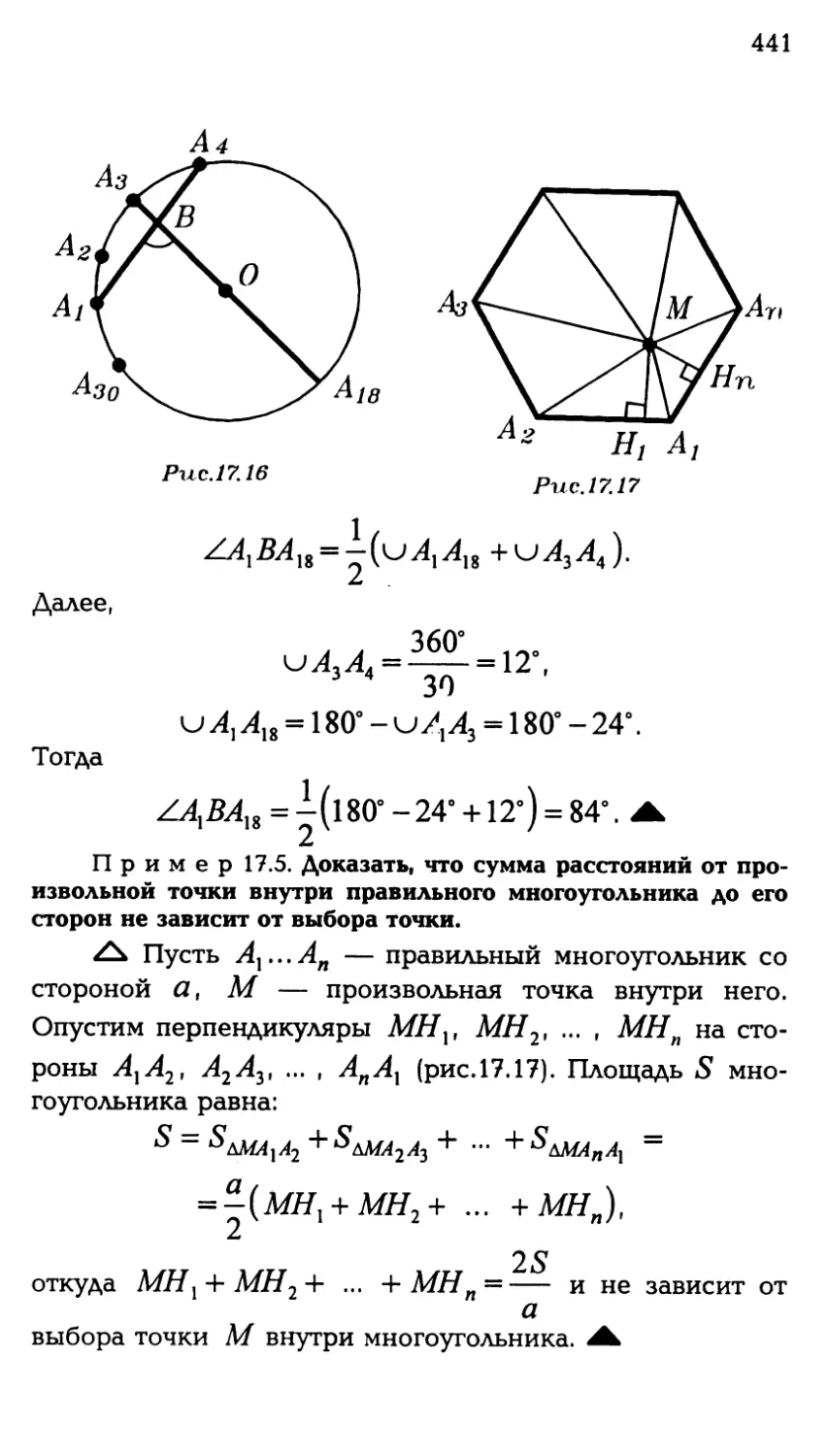
Автор: Никулин А.В.
Теги: геометрия программирование учебное пособие планиметрия
ISBN: 9986-582-54-7
Год: 1998
Текст
УДК 514.112
ББК 32.973
Н65
Серия основана в 1996 году
Охраняется законом об авторском праве. Воспроизведение всей
( книги или любой ее части преследуется в судебном порядке.
РЕЦЕНЗЕНТЫ:
Ядренко Михаил Иосифович —
член-корреспондент Национальной Академии Наук Украины,
заведующий кафедрой теории вероятностей и математической
статистики Национального Киевского университета
им. Тараса Шевченко.
Кириченко Владимир Васильевич —
доктор физико-математических наук, заведующий кафедрой
геометрии Национального Киевского университета им. Тараса Шевченко.
Ушаков Рудольф Петрович —
заслуженный учитель Украины, учитель-методист средней
школы № 173 города Киева, «Соросовский учитель средней школы».
Никулин А. В. и др. I
Н 65 Планиметрия. Геометрия на плоскости: Уч. пос. / Под общ. ред.Я
Ю. С. Татаренко. — Висагинас: Альфа, 1998. — 592 с. — (Библиотека!
школьника). I
ISBN 9986-582-54-7.
В книге содержится подробный теоретический и практический материал поЛ
планиметрии за курс средней школы. Пособие рассчитано для учащихся школ, аби-Я
туриентов, студентов младших курсов педагогических университетов, преподавателей. Я
П 5140112000
ББК 32.973
ISBN 9986-582-54-7
© Издательство «Альфа», 1998
ОГЛАВЛЕНИЕ
От издательства ........... И
Предисловие ...............13
Г л а в а 1. Основные понятия
§ 1.1. Расположение точек и прямых.
Лучи................................ 15
§ 1.2. Измерение отрезков и углов . . 22
§ 1.3. Отображения, движения и
наложения. Равные фигуры ... 23
§ 1.4. Аксиомы движений и наложе-
ний. Биссектриса угла................ 25
§ 1.5. Примеры с решениями......... 28
§ 1.6. Задачи для самостоятельного
решения....................... 32
Г л а в а 2. Треугольники
§ 2.1. Треугольник и его элементы . . 35
§ 2.2. Два признака равенства
треугольников................. 38
§ 2.3. Примеры с решениями 40
§ 2.4. Задачи для самостоятельного
решения 42
Г л а в а 3. Параллельные и перпендикулярные
прямые
§3.1. Смежные и вертикальные углы 43
§ 3.2. Аксиома параллельных........ 45
§3.3. Свойства параллельных прямых 46
§3.4. Сумма углов треугольника .... 49
§ 3.5. Выпуклые многоугольники.
Сумма углов выпуклых много-
угольников ................... 51
§3.6. Существование и единствен-
ность перпендикуляра к прямой 53
4
§ 3.7. Расстояние между параллель-
ными прямыми.......................... 54
§ 3.8. Примеры с решениями........ 55
§ 3.9. Задачи для самостоятельного
решения....................... 61
Г л а в а 4. Виды треугольников
§ 4.1. Медиана, биссектриса и высота
треугольника................. 65
§ 4.2. Равнобедренный треугол! ник . 67
§ 4.3. Третий признак равенства тре-
угольников .......................... 69
§ 4.4. Признаки равенства прямо-
угольных треугольников.............. 71
§ 4.5. Сравнение сторон и углов тре-
угольника ........................... 76
§ 4.6. Перпендикуляр и наклонная . . 77
§ 4.7. Неравенство треугольника .... 79
§ 4.8. Примеры с решениями........ 80
§ 4.9. Задачи для самостоятельного
решения...................... 87
Г л а в а 5. Движения на плоскости
§ 5.1. Основные виды движений .... 90
§ 5.2. Свойства движений. Группа
движений на плоскости...... 98
§ 5.3. Движения и наложения........ 101
§ 5.4. Теорема Шаля о структуре
группы движений............ 105
§ 5.5. Примеры с решениями........ 108
§ 5.6. Задачи для самостоятельного
решения..................... 116
Г л а в а 6. Окружность и описанные много-
угольники
§ 6.1. Окружность и круг. Касатель-
ная к окружности ................... 119
§ 6.2. Свойство биссектрисы угла ... 120
§ 6.3. Окружность, вписанная в
многоугольник....................... 122
§ 6.4. Углы, связанные с окружностью 125
§ 6.5. Окружности, касающиеся друг
друга............................... 132
§ 6.6. Примеры с решениями........ 135
§ 6.7. Задачи для самостоятельного
решения............................. 142
Г л а в а 7. Вписанные многоугольники
§ 7.1. Серединный перпендикуляр к
отрезку..................... 145
§ 7.2. Окружность, описанная около
многоугольника.............. 146
§ 7.3. Вневписанная окружность .... 151
§ 7.4. Примеры с решениями........ 152
§ 7.5. Задачи для самостоятельного
решения..................... 160
Г л а в а 8. Четырехугольники
§ 8.1. Параллелограмм.............. 164
§ 8.2. Прямоугольник............... 166
§ 8.3. Ромб и квадрат.............. 168
§ 8.4. Трапеция.................... 170
§ 8.5. Примеры с решениями........ 177
§ 8.6. Задачи для самостоятельного
решения..................... 183
Г л а в а 9. Группы симметрий фигур
§ 9.1. Группа симметрий фигуры .... 186
§ 9.2. Группы симметрий треуголь-
ника ............................... 188
§ 9.3. Группа симметрий четырех-
угольника .......................... 192
§ 9.4. Группа симметрий круга 194
§ 9.5. Магические треугольники и
квадраты.................... 196
§ 9.6. Примеры с решениями........ 199
6
§ 9.7. Задачи для самостоятельного
решения.............................. 204
Глава 10. Пропорциональность отрезков и
подобие фигур
§ 10.1. Теорема Фалеса............... 206
§ 10.2. Средние линии треугольника и
трапеции.................... 207
§ 10.3. Гомотетия. Преобразование
подобия..................... 209
§ 10.4. Примеры с решениями.... 213
§ 10.5. Задачи для самостоятельного
решения................................ 219
Глава 11. Свойства подобных фигур
§ 11.1. Признаки подобия треугольни-
ков ........................ 222
§ 11.2. Метрические соотношения в
прямоугольном треугольнике.
Теорема Пифагора................. 225
§ 11.3. Окружность, описанная около
прямоугольного треугольника . 226
§ 11.4. Окружность, вписанная в
прямоугольный треугольник . . 227
§ 11.5. Метрические соотношения в
окружности................ 228
§11.6. Свойство медиан треугольника 230
§ 11.7. Метрические соотношения в
правильном треугольнике..... 231
§ 11.8. Параллельные отрезки в трапе-
ции ................................ 232
§ 11.9. Теорема Птолемея......... 236
§ 11.10. Примеры с решениями 237
§ 11.11. Задачи для самостоятельного
решения.................. 246
7
Г л а в a 12. Векторы
§ 12.1. Декартовы координаты....... 251
§ 12.2. Координаты середины отрезка 253
§ 12.3. Расстояние между двумя точ-
ками ............................... 254
§ 12.4. Понятие вектора............. 256
§ 12.5. Действия над векторами..... 259
§ 12.6. Разложение вектора по базису 265
§ 12.7. Векторы в прямоугольной сис-
теме координат....................... 269
§ 12.8. Скалярное произведение векто-
ров ................................ 270
§ 12.9. Свойства скалярного произведе-
ния ................................. 273
§ 12.10. Применение векторов........ 278
§12.11. Примеры с решениями....... 283
§ 12.12. Задачи для самостоятельного
решения...................... 319
Г л а в а 13. Прямая и окружность в декартовых
координатах
§ 13.1. Уравнение прямой............. 302
§ 13.2. Углы между прямыми......... 307
§ 13.3. Расстояние от точки до прямой 309
§ 13.4. Уравнение окружности....... 310
§13.5. Примеры с решениями........ 311
§ 13.6. Задачи для самостоятельного
решения..................... 319
Г л а в а 14. Метрические соотношения в
треугольниках
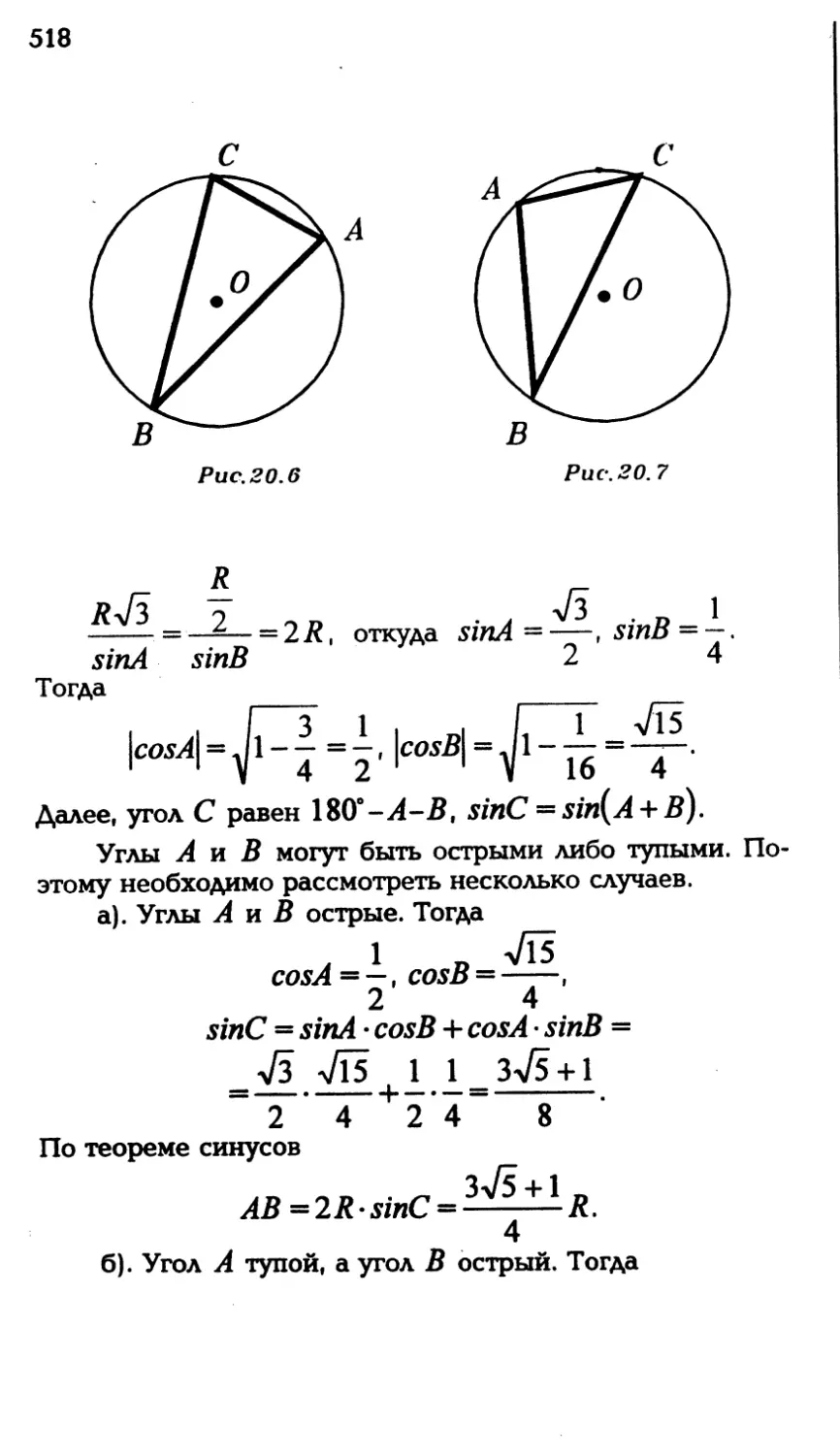
§14.1. Теорема косинусов........... 323
§ 14.2. Теорема синусов............. 327
§ 14.3. Свойства биссектрисы угла
треугольника................ 330
§ 14.4. Примеры с решениями........ 335
§ 14.5. Задачи для самостоятельного
решения..................... 349
8
Г л а в a 15. Площади
§ 15.1. Площадь прямоугольника...... 352
§ 15.2. Площадь параллелограмма .... 355
§ 15.3. Площадь треугольника.
Формула Герона............ 356
§ 15.4. Другие формулы площади тре-
угольника 360
§ 15.5. Площадь трапеции.......... 363
§ 15.6. Площадь четырехугольника. . . . 365
§ 15.7. Площади подобных фигур .... 368
§ 15.8. Ортоцентрический треугольник 369
§ 15.9. Примеры с решениями........ 374
§ 15.10. Задачи для самостоятельного
решения..................... 393
Г л а в а 16. Геометрия масс
§ 16.1. Центр масс системы материаль-
ных точек................ 398
§ 16.2. Центр масс треугольника.
Теорема Чевы............. 401
§ 16.3. Применения теоремы Чевы . . . 403
§ 16.4. Тождества Лагранжа и Якоби . 406
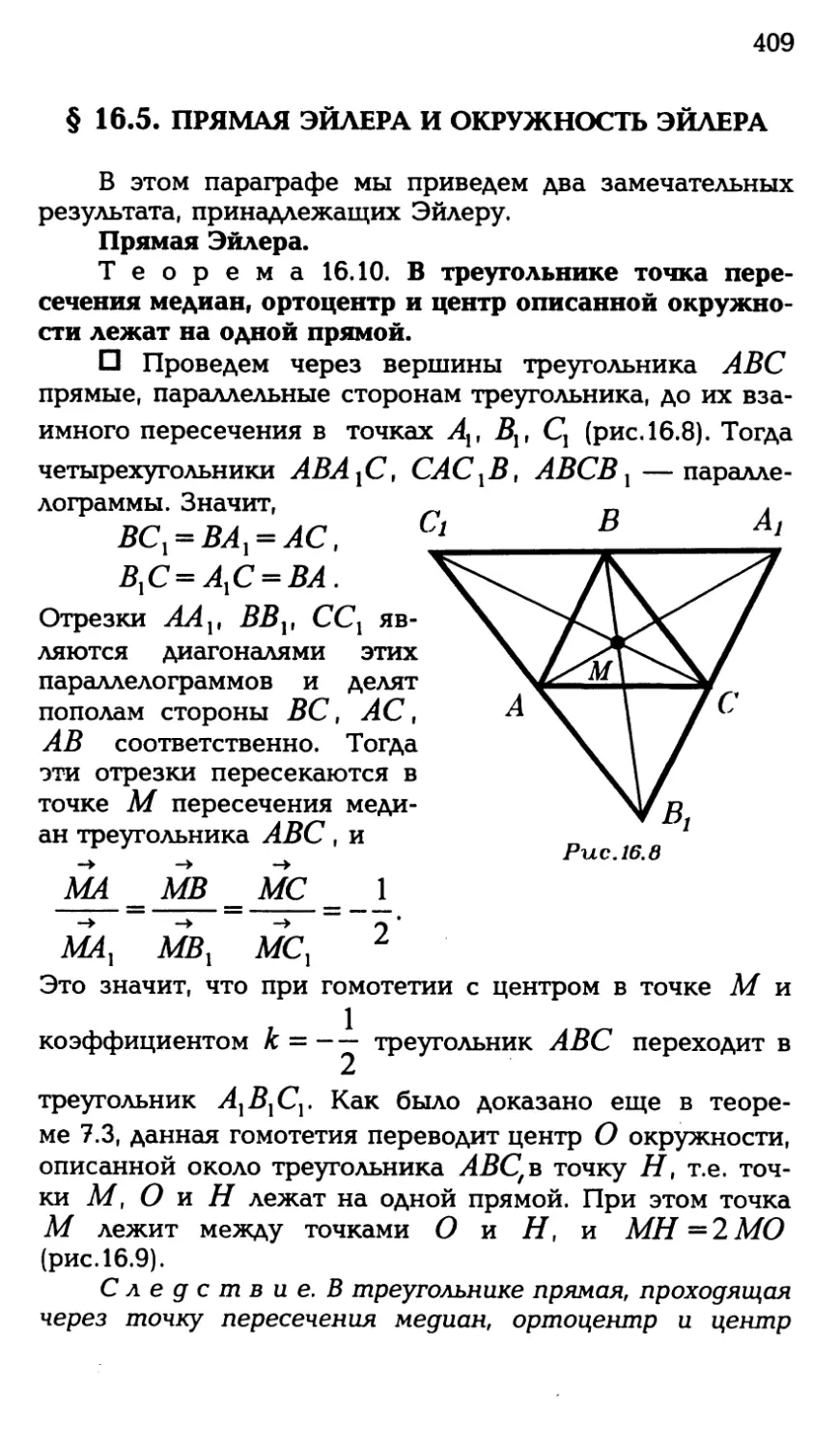
§ 16.5. Прямая Эйлера и окружность
Эйлера................... 409
§ 16.6. Расстояния между замечатель-
ными точками треугольника .. 411
§ 16.7. Примеры с решениями........ 415
§ 16.8. Задачи для самостоятельного
решения.................. 421
Глава 17. Правильные многоугольники
§ 17.1. Свойства правильных много-
' угольников ................... 425
§ 17.2. Построение правильных
П -угольников циркулем и ли-
нейкой ...................... 432
§ 17.3. Подобие правильных много-
угольников ........................... 436
§ 17.4. Примеры с решениями...... 437
9
§ 17.5. Задачи для самостоятельного
решения................................. 446
Г л а в а 18. Длина окружности и площадь круга
§ 18.1. Длина окружности.............. 448
§ 18.2. Радианная мера дуги и угла . . 451
§ 18.3. Площадь круга и его частей . . 452
§ 18.4. Примеры с решениями........... 456
§ 18.5. Задачи для самостоятельного
решения....................... 466
Г л а в а 19. Полярные координаты и золотое
сечение
§19.1. Полярные координаты........ 469
§ 19.2. Связь полярных координат с
декартовыми координатами ... 471
§ 19.3. Уравнение окружности в поляр-
ных координатах......................... 472
§ 19.4. Уравнение прямой в полярных
координатах.................... 478
§ 19.5. Спираль Архимеда............... 481
§ 19.6. Логарифмическая спираль .... 484
§ 19.7. Золотое сечение................ 490
§ 19.8. Золотое сечение и спирали . . . 496
§ 19.9. Примеры с решениями........ 503
§ 19.10. Задачи для самостоятельного
решения........................ 513
Г л а в а 20. Задачи по всему курсу планиметрии
§ 20.1. Примеры с решениями......... 514
§ 20.2. Задачи для самостоятельного
решения.................... 526
10
Приложения:
1. Предел числовой последователь-
ности ............................. 530
2. Доказательство теоремы Фалеса .... 535
3. Вычисление длины окружности
и площади круга....................... 539
Указания к решению задач.............. 545
Ответы к задачам...................... 581
Список использованной литературы .... 589
11
ОТ ИЗДАТЕЛЬСТВА
Уважаемые читатели!
Книга "Геометрия на плоскости"
написана
группой
опытных преподавателей и рассчитана на школьников и
преподавателей.
В этой книге геометрия рассматривается как часть
математики, и поэтому математические методы широко
используются для доказательства многих теорем. В книге
изложены многие известные геометрические фаюы, ко-
торые изучаются в общеобразовательных школах в не-
достаточном объеме. Все утверждения сопровождаются
строгими доказательствами. И хотя это сделало кишу
более сложной, системное изложение материала помо-
жет учащимся расширить свое представление о гео-
метрии. В учебном пособии содержится около 200 задач с
решениями, в которых подробно изложены способы и
методы применения теории на практике. Более 500 задач
для самостоятельного решения позволят учащимся закре-
пить свои знания и проверить степень усвоения матери-
ала.
Издательство надеется, что данное пособие будет по-
лезно как для учащихся так и для преподавателей школ,
лицеев, колледжей.
Вторая книга по геометрии "Геометрия в прост-
ранстве", написанная известными авторами А Александ-
ровым А. Вернером и В. Рыжиком, в настоящее время го-
товится к изданию и выйдет в свет в 1996 г.
СВЕДЕНИЯ ОБ АВТОРАХ:
Никулин Александр Вильевич — кандидат
физико-математических наук, учитель-методист средней
школы N 223 г. Киева.
К у к у ш Александр Георгиевич — доктор физико-
математических наук, доцент кафедры математического
анализа Национального Киевского университета им. Та-
раса Шевченко.
Татаренко Юрий Семенович — учитель мате-
матики, член Московского математического общества,
работает в Литве.
12
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
— начало решения задачи.
— конец решения задачи.
□ — начало доказательства.
— конец доказательства.
о
— группа основных задач.
о
— группа более сложных задач.
13
ПРЕДИСЛОВИЕ
Геометрия — это раздел математики, который изуча-
ет пространственные отношения и формы реального ми-
ра. Термин "геометрия" происходит от греческих слов
уеа — "земля" и gSTpeiv — "измерение". По свидетель-
ству древнегреческого историка Геродота египетская гео-
метрия началась с измерения земельных участков. Егип-
тяне были вынуждены постоянно производить такие из-
мерения из-за разливов Нила.
Эта книга посвящена планиметрии (от латинского
planum — "плоскость") — разделу геометрии, в котором
изучаются свойства плоских фигур. В книге с единых по-
зиций изложены вопросы школьного курса планиметрии.
По сравнению с другими учебными пособиями, данное
пособие включает значительно больше теоретического
материала, оно содержит более 200 теорем. Традицион-
ные вопросы, изучаемые в школьном курсе, рассматрива-
ются более подробно, что способствует повышению ква-
лификации учителя и углублению знаний учащихся. Ав-
торы стремились изложить материал так, чтобы его мог-
ли использовать в учебной работе как учащиеся, так и
учителя.
В книге содержится интересный материал для фа-
культативных занятий, в частности: группы движений,
группы симметрий фигур, магические квадраты и тре-
угольники, геометрия масс, полярные координаты, спира-
ли, золотое сечение.
В каждой главе помещены примеры с решениями,
иллюстрирующие применение теоретического материала,
а также задачи для самостоятельного решения. Эти за-
дачи делятся на две группы. Задачи группы "А" иллюст-
рируют определения и теоремы соответствующей главы.
В группе "Б" содержатся более сложные задачи, при ре-
шении которых необходимо использовать несколько гео-
метрических фактов, возможно, из различных глав посо-
14
бия. Ко всем задачам даются ответы, а к наиболее труд-
ным — указания к решению. В пособии приводятся исто-
рические сведения, разъясняется происхождение геомет-
рических терминов. Авторы считают, что при введении
нового математического термина полезно давать инфор-
мацию о его происхождении. Это способствует более
глубокому усвоению этого понятия, иллюстрирует нераз-
рывность математики с окружающим миром.
При изложении аксиоматики авторы не стремились
ограничиться минимальным количеством аксиом. Счита-
ем, что при доказательстве теорем школьного курса гео-
метрии нет необходимости концентрировать внимание
на аксиомах, так как это приводит к смещению акцентов
с развития геометрической интуиции на формальное со-
вершенство приведенных доказательств. Поэтому лишь в
самом начале в доказательствах делаются ссылки на со-
ответствующие аксиомы. В дальнейшем широко исполь-
зуются геометрические построения, возможность выпол-
нения которых можно обосновать с помощью приведен-
ных аксиом.
В книге систематизирован обширный материал о за-
висимостях между элементами различных фигур. Изло-
жение материала основано на понятии движения, ко-
торое, по мнению авторов, является центральным в
современной геометрии. Это понятие связывает геомет-
рию с другими разделами математики и позволяет реа-
лизовать единый подход при изучении геометрии.
Авторы выражают глубокую благодарность учителю
математики средней школы №264 г. Киева Л. Дольной за
рад ценных замечаний, позволивших значительно улуч-
шить изложение материала, преподавателю Русаковского
лицея №182 г. Киева М. Рожковой за помощь при подбо-
ре задач, а также А. Теплинскому и В. Никулину за
участие в подготовке рукописи.
А.Никулин
А.Кукуш
Ю. Татаренко
15
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ
§ 1.1. РАСПОЛОЖЕНИЕ ТОЧЕК И ПРЯМЫХ. ЛУЧИ
Как и всякая строгая математическая наука, геомет-
рия имеет свои объекты исследования. Это геометричес-
кие фигуры. Основными понятиями в геометрии являют-
ся точка, прямая и плоскость. Мы также будем активно
использовать понятие множества. Эти основные понятия
не определяются, их свойства формулируются в аксио-
мах — утверждениях, считающихся истинными без дока-
зательства.
Термин "аксиома" впервые встречается у Аристотеля
(384—322 г.г. до н.э.) и пришел в математику от древне-
греческих философов. Греческое слово a^io переводит-
ся как "важность", "уважение", "авторитет".
В дальнейшем будем считать, что все точки принад-
лежат некоторой плоскости.
Определение.
Фигурой на плоскости назы-
вается всякое множество . „
точек этой плоскости, со- t t
держащее хотя бы одну
точку.
Термин "фигура" проис-
ходит от латинского слова D , ,
Рис. 1.1
figura — образ, вид. Точки в
геометрии будем обозначать большими буквами латин-
ского алфавита. Следующие четыре аксиомы описывают
взаимное расположение точек и прямых на плоскости.
Аксиома 1.1. Существует бесконечное множест-
во точек, принадлежащих данной прямой, и бесконечное
множество точек, не принадлежащих данной прямой.
Аксиома 1.2. Через две различные точки мож-
но провести прямую и притом только одну.
16
На рис. 1.1 изображена прямая, проходящая через
точки А и В.
Аксиома 1.3. Всякая точка О на прямой делит
эту прямую на два луча так, что любые две точки одно-
го луча лежат по одну сторону от точки О, а любые две
точки разных лучей лежат по разные стороны от точ-
ки О. Точка О принадлежит при этом обоим лучам.
На рис. 1.2 точки At
и А2 лежат по одну сторо-
ну от точки О, а точки А2
и А3 — по разные стороны
от точки О. Словосочета-
ния "лежат по одну сторо-
ну от точки’’ и "лежат по
разные стороны от точки"
будем считать основными
понятиями, не требующи-
ми специального определе-
ния.
Рис.1.2
Точки прямой, лежащие по одну сторону от некото-
рой точки О этой прямой, вместе с точкой О образуют
луч. Точку О будем называть началом луча. Лучи обоз-
начаются двумя большими буквами, первая из которых
указывает начало луча. Например, на рис. 1.3 изображен
луч ОА. Здесь О — начало луча, А — произвольная
точка луча. Кроме того, лучи можно обозначать малень-
кими буквами. На рис. 1.4 изображен луч ТП.
Рис. 1.4
Рис. 1.3
Аналогично обозначаются и прямые, однако порядок
букв в обозначении прямой может быть произвольным.
На рис. 1.5 изображена прямая АВ (или ВА), Эта же
прямая обозначена через а.
17
Пусть А и В — две точки прямой а. Если третья
точка С лежит одновременно на лучах АВ и ВА, то го-
ворят, что точка С лежшп между точками А и В
(рис. 1.5).
Аксиома 1.4. Из трех различных точек прямой
одна и только одна лежит между двумя другими.
Множество, состоящее из
точек А и В, а также точек,
лежащих между ними, называ- г д
ется отрезком (рис. 1.5). Такой А I в
отрезок обозначим через АВ CL
или ВА. Точки А и В называ-
ются концами отрезка, а все
другие точки отрезка называ- Рис.1.5
ются его внутренними точками.
Параллельные прямые. Две прямые, не имеющие
общих точек и лежащие в одной плоскости, называются
параллельными.
На рис. 1.6 изображены
и b. Если прямые а nb па-
раллельны, то пишут: а ||Ь.
Термин "параллельная" про-
исходит от греческого слова
яараХА/г|Хо£, т.е. "идущая
рядом" или "проведенная ря-
дом". Это слово употребляет-
ся как математический тер-
мин уже более 2500 лет, еще
со времен Пифагора.
Пересечение прямых.
Две различные прямые пере-
секаются, если они имеют
только одну общую точку.
На рис .1.7 показаны
прямые а и b, пересекаю-
щиеся в точке С. Предполо-
жим, что две различные пря-
мые а и b имеют по край-
ней мере две общие точки.
Однако это предположение
параллельные прямые а
а
b
PUC.1.6
Рис. 1.7
18
в
Рис. 1.8
Рис.1.9
противоречит аксиоме 1.2. Таким образом, наше допуще-
ние ложно. И мы строго доказали следующее утвержде-
ние:
Теорема 1.1. Две различные прямые на плоско-
сти либо пересекаются, либо параллельны.
Эта теорема доказана методом от противного. Этот
метод состоит в том, что мы делаем допущение о ложно-
сти утверждения теоремы и путем логических рассужде-
ний приходим к противоречию. Он широко распростра-
нен в математике, и мы будем часто использовать его в
дальнейшем.
Далее изучается взаимное расположение отрезка и
прямой, что позволяет ввести понятие полуплоскости, а
также изучается взаимное расположение лучей, на осно-
вании чего вводится понятие угла.
Рассмотрим прямую а и две точки А и В, не лежа-
щие на этой прямой. Говорят, что точки А и В лежат по
одну сторону от прямой а, если отрезок АВ не пересе-
кает прямую а (рис. 1.8), и лежат по разные стороны от
прямой а, если отрезок АВ пересекает эту прямую
(рис. 1.9).
Множество, состоящее из точек прямой а и точек,
лежащих по одну сторону от прямой а, называется по-
луплоскостью, ограниченной прямой а. Прямая а назы-
вается границей полуплоскости, а точки, не лежащие на
прямой а, называются внутренними точками полуплос-
кости (рис. 1.10).
Аксиома 1.5. Всякая прямая а делит плоскость
на две части (полуплоскости). При этом точки прямой а
и только они являются общими точками этих полуплос-
костей.
19
Рис. 1.10 Рис. 1.11
Развернутый угол. Пусть точка О лежит на гра-
нице полуплоскости. Множество точек полуплоскости с
фиксированной точкой О называется развернутым уг-
лом.
Точка О называется вершиной развернутого угла.
Лучи а} и а2, на которые граница полуплоскости де-
лится точкой О, называются сторонами развернутого
угла (рис.1.11).
Дополнительные лучи. Два различных луча, ле-
жащие на одной прямой и имеющие общее начало, на-
зываются дополнительными.
Дополнительные лучи ах и а2 изображены на
рис. 1.11. Луч b лежит между дополнительными лучами
ах и а2, если все три луча имеют общее начало и при
этом луч b отличен от лучей ах и а2. Заметим, что в этом
случае луч Ъ принадлежит некоторому развернутому
углу со сторонами ах и а2. Пусть лучи ах и а2 не яв-
ляются дополнительными и имеют общее начало О.
Рассмотрим луч b с началом в точке О, не совпадаю-
щий с лучами а} и а2, такой, что:
1) лучи ах и b лежат в одной полуплоскости, ог-
раниченной прямой, содержащей луч а2;
2) лучи а2 и b лежат в одной полуплоскости, ог-
раниченной прямой, содержащей луч аг
20
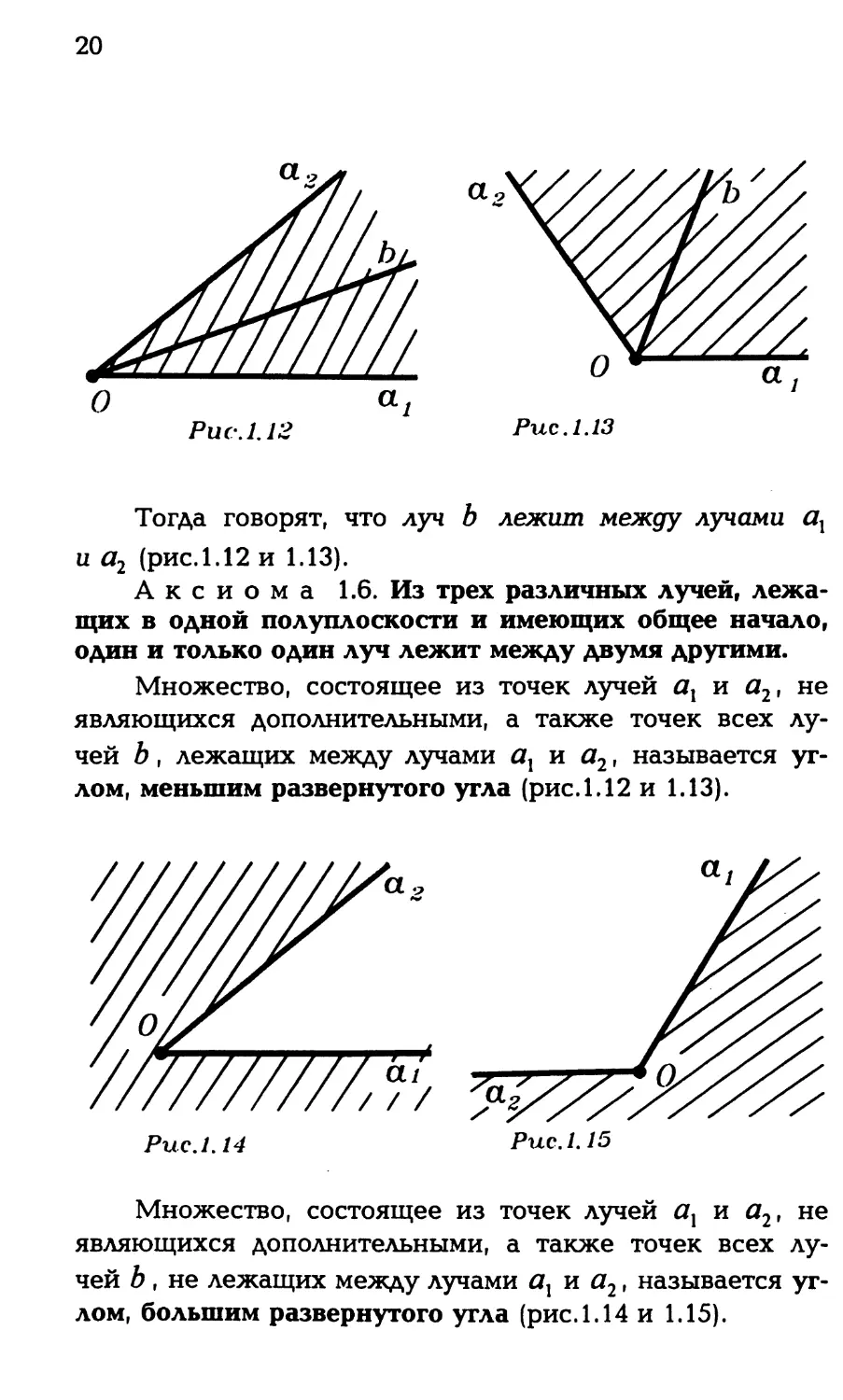
Рис.1.12 Рис.1.13
Тогда говорят, что луч b лежит между лучами а}
и а2 (рис. 1.12 и 1.13).
Аксиома 1.6. Из трех различных лучей, лежа-
щих в одной полуплоскости и имеющих общее начало,
один и только один луч лежит между двумя другими.
Множество, состоящее из точек лучей ах и а2, не
являющихся дополнительными, а также точек всех лу-
чей b, лежащих между лучами ах и а2, называется уг-
лом, меньшим развернутого угла (рис.1.12 и 1.13).
Рис. 1.14 Рис. 1.15
Множество, состоящее из точек лучей ах и а2, не
являющихся дополнительными, а также точек всех лу-
чей b , не лежащих между лучами ах и а2, называется уг-
лом, большим развернутого угла (рис. 1.14 и 1.15).
21
Пусть а — луч с на-
чалом в точке О. Множество
всех точек плоскости, на
которой зафиксированы точ-
ка О и луч а, называется
полным углом (рис. 1.16).
Точка О в каждом из
рассмотренных случаев на-
зывается вершиной угла; лу-
чи ар а2 или луч а для пол- Рис.1.16
ного угла называются сторо-
нами угла.
Мы дали определения углов различных видов. На
рисунках 1.17—1.20 приведены различные варианты изо-
бражения и обозначения углов.
Точки, принадлежащие углу, но не лежащие на его
сторонах, называются внутренними точками угла.
Рис.1.17
Рис. 1.18
Рис.1.19
22
Puc.l .23
Пусть луч b не совпадает со сторонами угла (ара2),
а его начало совпадает с вершиной угла и все точки лу-
ча b принадлежат углу. Тогда говорят, что луч Ъ лежит
внутри угла (рис. 1.21—1.24). Отметим, что на рис. 1.24
луч b лежит внутри полного угла.
§ 1.2. ИЗМЕРЕНИЕ ОТРЕЗКОВ И УГЛОВ
Аксиома 1.7. Каждый отрезок имеет положи-
тельную длину. Длина отрезка равна сумме длин двух
частей, на которые он делится некоторой точкой.
Аксиома 1.8. Каждый угол имеет положитель-
ную градусную меру. Градусная мера угла равна сумме
23
градусных мер двух углов, на которые он делится неко-
торым лучом, лежащим внутри угла.
Латинское слово gradus означает "шаг". Как заметили
вавилонские жрецы, солнечный диск укладывается на пу-
ти, проходимым солнцем за день, 180 раз, т.е. солнце
как бы делает 180 шагов. Обозначения градусов, напо-
минающие современные, были введены Птолемеем око-
ло 100—178 г.г. Иллюстрацией аксиомы 1.8 могут слу-
жить рисунки 1.21—1.24, на которых градусная мера изо-
браженного угла равна сумме градусных мер тех двух уг-
лов, на которые данный угол делится лучом b .
Аксиома 1.9. Каково бы ни было положитель-
ное число, существует отрезок, длина которого равна
этому числу.
Аксиома 1.10. Каково бы ни было положитель-
ное число, не превышающее 360, существует угол, гра-
дусная мера которого равна этому числу.
Прямой угол. Перпендикулярные прямые. Угол, гра-
дусная мера которого равна 90°, называется прямым уг-
лом. Прямые, содержащие стороны прямого угла, назы-
вают перпендикулярными.
§ 1.3. ОТОБРАЖЕНИЯ, ДВИЖЕНИЯ И НАЛОЖЕНИЯ.
РАВНЫЕ ФИГУРЫ
плоскости на
ставится в со-
Взаимно-однозначное отображение
себя. Пусть каждой точке А плоскости
ответствие некоторая точка /(л) этой плоскости, при-
чем для различных точек А и В точки /(л) и /(в)
также различны. Кроме того, пусть для всякой точки Y
плоскости существует такая точка X этой плоскости,
что Y = f(x). Тогда говорят, что задано взаимно-одно-
значное отображение f плоскости на себя.
Рассмотрим некоторые примеры.
1. Для каждой точки А плоскости положим
f(A) = A. Тогда f является взаимно-однозначным ото-
бражением плоскости на себя (убедитесь в этом само-
24
Рис. 125
стоятельно). Такое отображение называется тождествен-
ным. Обозначим его греческой буквой 8 .
2. Пусть О — фиксированная точка плоскости. Для
произвольной точки А плоскости, отличной от точки О,
проведем отрезок АО. На луче, дополнительном к лу-
чу ОА, отложим отрезок ОАХ той же длины, что и отре-
зок ОА. Будем считать, что f(A)= Ах и f(O) = О. Такое
соответствие f называется центральной симметрией и
является взаимно-однозначным отображением плоскости
на себя (рис. 1.25).
3. Пусть а — некоторая прямая. Если точка А ле-
жит на этой прямой, то положим f[A) = A. Если же
точка А не лежит на этой прямой, то перпендикулярно к
ней через точку А проведем другую прямую и на ней от-
ложим отрезок РА^, имеющий ту же длину, что и отре-
зок РА. Положим, что f(A}= Ах (рис. 1.26). Такое соот-
ветствие называется осевой симметрией и также являет-
ся взаимно-однозначным отображением плоскости на се-
бя.
Заметим, что эти примеры мы рассматриваем только
для того, чтобы проиллюстрировать определение взаим-
но-однозначного отображения. Для строгого обоснования
нам не хватает некоторых определений и аксиом.
Движения и наложения. Взаимно-однозначное ото-
бражение f плоскости на себя называется движением,
если для любых точек А и В плоскости расстояние меж-
25
ду этими точками равно расстоянию между точками
f(A) и f(B). Очевидно, что тождественное отображе-
ние 8 является движением. В двух последних примерах
отображение f также является движением, что будет
доказано позднее.
Наложением фигуры Ф на фигуру Oj называется
такое движение f, при котором для всякой точки В
фигуры Oj существует точка А фигуры Ф такая,
что f (А) = В и для всякой точки А фигуры Ф точ-
ка f (А) принадлежит фигуре Ф1. В этом случае точка А
определяется однозначно заданием точки В. Будем пи-
сать /(Ф)= Ф! и говорить, что наложением f мы фигу-
ру Ф совместили с ФР
Равные фигуры. Две фигуры называются равными,
если их можно совместить некоторым наложением. Ра-
венство фигур Ф1 и Ф2 обозначается так: Ф1 = Ф2.
Замечание. Для трех произвольных фигур Фр Ф2,
Ф3 из равенств Ф, = Ф2, Ф2 = Ф3 следует равенство Ф, = Ф3.
Это утверждение будет доказано позднее с помощью так назы-
ваемой композиции движений.
§ 1.4. АКСИОМЫ ДВИЖЕНИЙ И НАЛОЖЕНИЙ.
БИССЕКТРИСА УГЛА
Аксиома 1.11. Если при некотором движении
две точки одной прямой совмещаются с двумя точками
другой прямой, то данное движение является наложени-
ем, которое совмещает одну прямую с другой.
Аксиома 1.12. Отрезки, имеющие равные дли-
ны, равны.
Аксиома 1.13. Равные углы имеют равные гра-
дусные меры и, наоборот, углы, имеющие равные гра-
дусные меры, равны.
Аксиома 1.14. На луче h с началом в точке О
существует и притом единственная точка А такая, что
отрезок ОА имеет заданную длину.
26
Рис. 1.2 7
Аксиома 1.15. В полуплоскости, ограниченной
прямой, содержащей луч ОА, существует и притом
единственный луч ОВ такой, что ЛВОА имеет задан-
ную градусную меру, меньшую 180°.
Нетрудно понять, что если при некотором движении
совмещаются начала двух лучей и еще две точки этих
лучей, то данное движение является наложением, совме-
щающим эти лучи. Кроме того, если при некотором дви-
жении совмещаются концы отрезков, то данное движе-
ние является наложением, совмещающим эти отрезки.
Рассмотрим некоторый угол ВАС, меньший развер-
нутого (рис. 1.27). Проведем луч AD в той полуплоскости,
ограниченной прямой АС, которая содержит луч АВ,
так, чтобы градусная мера угла DAC была равна полови-
не градусной меры угла ВАС. Это можно сделать со-
27
Рис. 1.31
гласно аксиоме 1.15. По аксиомам 1.6 и 1.8 луч AD ле-
жит внутри угла ВАС. Аналогичное построение можно
выполнить для развернутого угла и углов, больших раз-
вернутого. Сделайте это самостоятельно, рассмотрев
рис. 1.28—1.30.
Биссектриса угла. Луч, лежащий внутри угла и об-
разующий с его сторонами два равных угла, называется
биссектрисой угла.
Термин "биссектриса" происходит от латинского
слова bissectrix — "делящая пополам".
Аксиома 1.16. Всякий угол (а,б) можно совме-
стить с равным ему углом (лр двумя способами:
1) так, чтобы луч а совместился с лучом av а
луч Ь — с лучом Ьх;
2) так, чтобы луч а совместился с лучом bv а
луч b — с лучом
Отметим, что любое движение, при котором выпол-
няется условие 1) или 2), является наложением угла (a,b)
на угол
Аксиома 1.17. Пусть /ЛОА меньше разверну-
того, a /ВХОХАХ равен /ВОА. Если при некотором дви-
жении луч ОА совместился с лучом OXAV а лучи ОВ
и ОХВХ лежат в одной полуплоскости, ограниченной
прямой OXAV то луч ОВ совмещается при этом движе-
нии с лучом ОХВХ (рис. 1.31).
28
§ 1.5. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1.1. Из четырех точек Л, В, С, D точки А,
В, С лежат на одной прямой и точки В,С, D также лежат
на одной прямой. Доказать, что все четыре точки лежат на од-
ной прямой.
ZS Пусть через точки At Bt С проходит прямая I ,
а через точки В, С, D — прямая т. Обе прямые прохо-
дят через точки В и С, и по аксиоме 1.2 прямые I и ТП
совпадают. Следовательно, все четыре данные точки ле-
жат на прямой / . Ж
Пример 1.2. Могут ли три точки А, В, С лежать на
одной прямой, если длина отрезка АВ меньше суммы длин
отрезков АС и ВС, причем отрезок А В длиннее каждого из
этих двух отрезков?
ZS Докажем, что три данные точки не лежат на од-
ной прямой. Доказательство проведем методом от про-
тивного.
Допустим, что заданные точки А, В, С лежат на
прямой / . По аксиоме 1.4 одна из них лежит между дву-
С
Рис.1.32
Рис. 1.3 3
мя другими. Если это точка А (рис. 1.32), то по аксио-
ме 1.7 длина отрезка ВС равна сумме длин отрезков В А
и АС, следовательно, отрезок АВ короче, чем отре-
зок ВС. Получили противоречие с условием примера,
поэтому точка А не лежит между точками В и С. Ана-
логично можно доказать, что точка В не лежит между
точками А и С.
Осталось рассмотреть случай, когда точка С лежит
между точками А и В (рис. 1.33). В этом случае по аксио-
ме 1.7 длина отрезка АВ равна сумме длин отрез-
ков АС и ВС, что тоже противоречит условию приме-
ра. Значит, наше предположение ложно, и заданные
точки не могут лежать на одной прямой. Ж
29
Пример 1.3. Изобразить полуплоскость и точку О,
не лежащую в этой полуплоскости. Изобразить полуплос-
кость, симметричную данной относительно точки О.
Zs На рис. 1.34 изображены полуплоскость а, огра-
ниченная прямой а, и точка О, не лежащая в полуплос-
кости а. Сначала построим прямую av симметричную
прямой а относительно точки О. Прямая а} состоит из
всех точек, симметричных точкам прямой а относитель-
но точки О. Поэтому возьмем произвольную точку В на
прямой а, проведем луч ВО и отложим на нем отрезок
ОВ} = ОВ (рис. 1.34). Точки Вх и В симметричны относи-
тельно точки О. Затем возьмем другую точку С на пря-
мой а и построим точку Ср симметричную ей относи-
тельно точки О. Через точки В} и С} проведем прямую.
Это и есть искомая прямая ах. Искомая полуплоскость
otj изображена на рис. 1.34. Она ограничена прямой а}.
Пример 1.4. Отрезок длиной 24 см разделили на
четыре неравные части. Длина отрезка между серединами
крайних частей равна 20 см. Найти длину отрезка между се-
рединами средних частей.
Zs Данный отрезок АЕ , разделенный на четыре
части, изображен на рис. 1.35. Пусть Л, b, С, d —длины
отрезков АВ, ВС, CD, DE соответственно. По аксио-
ме 1.7 сумма их длин a + b + c + d равна 24 см. По той
же аксиоме
30
Искомое расстояние равно
Пример 1.5. Даны четыре точки Л, Bt С, D, не ле-
жащие на одной прямой. Известно, что прямая АВ пересека-
ет отрезок CD, а прямая CD пересекает отрезок АВ. Дока-
зать, что отрезки АВ и CD пересекаются.
Z2s Обозначим прямую АВ через Z , а прямую CD
— через Ш. Поскольку точки А, В, С, D не лежат на
Рис. 1.37
одной прямой, прямые I и т не совпадают. Тогда по
теореме 1.1 они либо пересекаются, либо параллельны.
Параллельными они быть не могут, так как прямая I пе-
ресекает отрезок CD, лежащий на прямой т. Следова-
тельно, I и Ш пересекаются, т.е. имеют одну общую
точку. Эта точка принадлежит отрезку CD, поскольку I
пересекает отрезок CD. Однако эта точка принадле-
жит также отрезку АВ, поскыхжу т пересекает отре-
зок АВ. Следовательно, эта точка принадлежит одновре-
менно обоим отрезкам, и отрезки АВ и CD пересекают-
ся. Возможные расположения данных отрезков показаны
на рис. 1.36 и 1.37. Ж
Пример 1.6. Из точки О исходят четыре луча: ОА,
ОВ, ОС, OD, которые следуют друг за другом в том порядке,
в каком они перечислены. Градусная мера угла АОВ равна
градусной мере угла COD, а градусная мера угла ВОС равна
градусной мере угла DOA. Доказать, что лучи ОА и ОС яв-
31
ляются дополнительными, а лучи ОВ и OD также являются
дополнительными.
Обозначим /ЛОВ — ZCOD = а, ZBOC =
= ZAOD =Р (рис. 1.38). Лучи ОА и ОС определяют два
угла: угол у, внутри которого лежит луч ОВ, и угол 5,
з'тутри которого проходит луч OD. По аксиоме 1.8 име-
ем:
T = ZAOB + ZBOC = a + p;
8 = ZCOD + ZDOA = a + p.
Следовательно, у = 5. Если бы лучи ОА и ОС не
были дополнительными, то один из этих двух углов был
бы больше 180°, а другой —
меньше 180°, и они бы не име- . /
ли одинаковую градусную ме- d I / ?
ру. Значит, лучи ОА и ОС— , \ / /
доп лнительные. Аналогично \ / / у
устанавливается, что лучи ОВ \ I / с
и OD также являются допол- у 7 /
нительными. JL \
Пример 1.7. Лучи С \ CL
и d &елзп угол (а,Ь) на три рав- ..
ные части. Доказать, что биссек-
триса угла (c,d) является также Рис. 1. 39
биссектрисой угла (а,Ь).
ZS, Пусть луч I является биссектрисой угла (ctd)
(рис. 1.39). По аксиоме 1.8
Z (6, Z) = Z (b, d) + Z (d, I); Z(a,l) = Z (a, c) + Z (c, I).
32
Однако по условию
Z(M)=Z(a,c); Z(rf,Z) = Z(c,Z).
Следовательно, Z (Ь, /) = Z- (а, /).
Так как луч / лежит внутри угла (а, Ь), то он является
биссектрисой этого угла.
§ 1.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
1.01. Сколько прямых можно провести через одну
точку плоскости?
1.02. Могут ли две различные прямые иметь только 5
общих точек?
1.03. Сколько точек пересечения могут иметь два отрезка,
не лежащие на одной прямой?
1.04. Четыре точки А, В, С, D лежат на одной прямой,
причем точка В лежит между точками А и С, а точка С ле-
жит между точками В и D. Доказать, что точки В и С лежат
между точками А и D.
1.05. Точка М лежит на прямой CD между точками С
и D. Найти длину отрезка CD, если:
а) СМ = 2,5 м, MD = 4,6 м;
б) СМ = 7,2 дм, MD = 5— дм;
4
в) СМ = 2,1 м, MD =8,2 м.
1.06. Точки М, N, Q лежат на одной прямой. Известно,
что
a) MN = 5,3 м, MQ = 8 м;
б) NQ = 9,1 см, MQ = 8,2 м.
Может ли точка N лежать между точками М и Q1
1.07. Лежат ли точки А, М и S на одной прямой, если:
а) AM =7,3 м, MS =2,8 м, AS =4,5 м;
б) AM = 81,2 см, MS = 39,4 см, AS = 1,205 м?
1.08 . Точка С лежит на отрезке АВ. Какой из отрезков
длиннее: АВ или АС?
1.00 . Точка С лежит на отрезке АВ. Известно, что
АВ = 8,6 м и АС = ЗВС. Найти длину отрезков АС и ВС.
33
1.10. На отрезке MN взята точка Р, причем длина отрез-
ка МР на 9,6 см меньше длины отрезка NP, а длина отрез-
ка NP составляет 80% длины отрезка МР . Найти длины отрез-
ков MP , NP, MN .
1.11. Существует ли точка, делящая длину отрезка попо-
лам? Ответ объясните.
1.12. Отрезок АВ пересекает прямую U, а отрезок ВС не
пересекает эту прямую. Пересекает ли прямую Q отре-
зок АС?
1.13. Сколько отрезков данной длины можно отложить на
прямой а от заданной на ней точки О?
1.14. Луч X ложзкт внутри угла (а,й). Найти этот угол, ес-
ли:
a) Z(a,x) = 30°, Z(i,x) = 42°;
б) градусная мера Z(a,x) в четыре раза больше градус-
ной меры Z(Z\x), а их разность составляет 18°.
1.15. Попытайтесь построить на глаз углы, градусная мера
которых составляет 30°, 32°, 40°, 60°, 90°, 160°, 180°, 250°.
Проверьте точность построения транспортиром.
1.16. Между сторонами угла (а,Ь), градусная мера которо-
го составляет 60°, проходит луч С. Найти углы (а, с) и (й, с), ес-
ли:
а) угол (а, с) на 30° больше угла (Ь,с);
б) градусные меры углов (а, с) и (й,с) относятся как 2:3.
1.17. Луч С лежит между сторонами угла {а,Ь). Градусная
мера какого угла больше: (а,с) или (а,Ь)?
1.18. Объясните, почему у всякого угла существует бис-
сектриса этого угла.
1.19. Нарис'чпе некоторую прямую U и угол, стороны ко-
торого лежат в одной полуплоскости, ограниченной этой пря-
мой. Изобразите угол, симметричный данному относительно
прямой а.
1.20. Доказать, что при всяком движении полуплос-
кость переходит в полуплоскость.
1.21. Сумма градусных мер углов АОВ и BOD рав-
на 252°. Найти их градусные меры, если луч, дополнительный к
лучу ОА , делит угол BOD пополам.
2 Зак. 687
34
1.22. Найти число прямых, которыми можно соединить
попарно 4 точки, из которых никакие 3 не лежат на одной
прямой. Каково будет число таких прямых в случае 5, 6, 7
точек?
1.23. Отрезки SAJt SA2, SA* пересекают прямую а,
причем точки S, Ах, ..., Ак не лежат на одной прямой. До-
казать, что всякий отрезок, соединяющий какие-либо две точки
Aj и Ар не пересекает прямую а.
1.24. На плоскости заданы пять точек и прямая, не со-
держащая ни одной из них. Известно также, что из этих точек
три точки лежат в одной полуплоскости, ограниченной этой
прямой, а две точки — в другой полуплоскости, ограниченной
этой прямой. Каждую пару точек соединили отрезком. Сколько
отрезков пересекает прямую? Ответ объясните.
1.25. Доказать, что если концы отрезка АВ лежат в одной
полуплоскости, то хотя бы один из лучей АВ или ВА также
лежит в этой полуплоскости.
1.26. Заданы четыре прямые а, Ь, с, d. Известно, что
прямые а, Л, С пересекаются в одной точке и прямые Л, с, d
также пересекаются в одной точке. Доказать, что все четыре
прямые проходят через одну точку.
1.27. Даны три точки А, В, С, не лежащие на одной
прямой. Доказать, что всякая прямая, не проходящая через точ-
ки А, В, С, либо не пересекает никакой из отрезков АВ , ВС,
/ 7, либо пересекает только два из них.
1.28. Пусть точки Ах и А^ лежат на прямой а, а точки Вх
и В2 — на прямой b , параллельной прямой а. Доказать, что
среди отрезков АХВ2, A1Bxt найдутся два отрезка,
которые пересекаются в точке, не принадлежащей прямым а
и Ь.
1.29. Полосой называется множество точек, не являюще-
еся полуплоскостью и состоящее из точек, содержащихся од-
новременно в двух полуплоскостях, ограниченных параллель-
ными прямыми. Доказать, что если точки А и В принадлежат
некоторой полосе, то и весь отрезок АВ лежит в этой полосе.
35
ГЛАВА 2
ТРЕУГОЛЬНИКИ
§ 2.1. ТРЕУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Если не оговорено противное, то под словом "угол"
будем подразумевать развернутый угол либо угол, мень-
ший развернутого.
Треугольник. Вершины, углы и стороны треуголь-
ника. Пусть точки А, В, С не лежат на одной прямой.
Множество, состоящее из точек, принадлежащих одно-
временно углам ВАС, АВС, АСВ, называется тре-
угольником. Обозначается: ДАВС.
На рис.2.1 изображен треуголь-
ник АВС.
Точки А, В, С называются вер-
шинами треугольника АВС, отрезки
АВ, ВС, СА — сторонами тре-
угольника АВС, Стороны АВ, ВС,
СА называются противолежащими
углам ВСА, CAB, АВС соответст-
венно, и наоборот, указанные углы
будем называть противолежащими соответственным сто-
ронам.
Длины этих сторон обозначаются так: ВС = а (сто-
рона а, противолежащая углу А), СА= b (сторона Ь,
противолежащая углу В}, АВ =с (сторона с, противоле-
жащая углу С).
Углы САВ и АВС являются прилежащими к сто-
роне АВ, углы АВС и ВСА — прилежащими к сторо-
не ВС и углы ВСА и САВ — прилежащими к сторо-
не СА.
Точки треугольника, не лежащие на его сторонах,
называются внутренними точками треугольника.
Периметр и полупериметр треугольника. Сумма
длин всех сторон треугольника АВС называется пери-
Pvlc. 2.1
36
метром этого треугольника и обозначается через Р.
Употребляются также такие обозначения: Р^вс ?авс-
Половина периметра треугольника называется его полу-
периметром. Полупериметр треугольника обычно обоз-
начается буквой р. Если a, b, С — длины сторон тре-
а + 6 + с
угольника, то р =------. Периметр треугольника ра-
^2*
вен 2р.
Слово Л8р1|18ТрО^ образовано из греческих слов
"Kept" — "около" и "|i8Tp8tv" — "измерять". Оно встре-
чается в трудах древнегреческих математиков Архимеда,
Герона, Паппа.
Равные треугольники. Два треугольника называ-
ются равными, если они совмещаются некоторым нало-
жением.
Аксиома 2.1. Существует такое наложение f
треугольника АВС на равный ему треугольник
AXBXCV при котором точки /(Л), f(B}t явля-
ются вершинами треугольника АХВХСХ.
Пусть треугольники АВС и А^С^ равны и f —
такое наложение треугольника АВС на треугольник
АХВХСХ, что
4=/(Л),д=/(в),с;=/(С).
Отрезки АВ и АС и АХСХ, ВС и ВХСХ совмеща-
ются. Также совмещаются лучи АВ и АХВХ, ВС и ВХСХ,
АС и АХСХ. Согласно аксиоме 1.16
Z АВС = Z АХВХСХ, Z ВСА = Z ВХСХАх и
А САВ = А СХАХВХ.
Это значит, что в равных треугольниках соответственные
стороны равны и соответственные утлы, противолежа-
щие этим сторонам, также равны (рис.2.2).
Теорема 2.1. Если f — наложение фигуры,
состоящей из точек Л, В, С, на фигуру, состоящую из
точек Ах, Вх, Ср и точки А, В, С не лежат на одной
37
Рис.2.2
прямой, то f является наложением треугольника АВС
на треугольник АХВХСХ.
□ Пусть при наложении f имеет место равенство
/(Л) = 4,/(Б) = В1,/(С) = С1.
Тогда отрезки АВ и AXBV ВС и BXCV АС и АХСХ со-
вмещаются, лучи АВ и АХВХ, ВС и ВХСХ, АС и АХСХ
также совмещаются. Согласно аксиоме 1.16
Z АВС = Z АХВХСХ, Z ВАС = Z ВХАХСХ,
ЛАСВ = ААХСХВХХ и /(ZZBQ = ZZ1B1C1,
' f (X. ВАС) = ZJBXAXCV f(XACB) = XAxCxBv
т.е. соответственные углы при наложении f совмещают-
ся.
Произвольная внутренняя точка Мх треугольни-
ка АХВХСХ является внутренней точкой одновременно для
углов АХВХСХ, ВХАХСХ, АХСХВХ. Поскольку стороны уг-
лов АВС, ВАС, АСВ при наложении f переходят со-
ответственно в стороны углов AXBXCV ВХАХСХ, АХСХВХ,
то Мх = f(M), где М — внутренняя точка углов АВС ,
ВАС, АСВ, т.е. М является внутренней точкой тре-
угольника АВС. Аналогично для произвольной внутрен-
ней точки М треугольника ABC f(M) является внут-
ренней точкой треугольника АХВХСХ. Таким образом, f
является наложением треугольника АВС на треуголь-
ник . и
38
§ 2.2. ДВА ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Первый признак равенства треугольников. Этот
признак мы сформулируем следующим образом.
Теорема 2.2. Если две стороны и угол, за-
ключенный между ними, одного треугольника соответ-
ственно равны двум сторонам и углу, заключенному ме-
жду ними, другого треугольника, то такие треугольники
равны.
Рис, 2.3
□ Пусть заданы треугольники АВС и AXBXCV в ко-
торых AB=AXBV АС=АХСХ, АА = ААХ (рис.2.3). Рас-
смотрим наложение f угла ВАС на угол ВХАХСХ такое,
что f(AB) = AxBv f(AC) = AxCx для лучей АВ и АС.
Такое наложение существует в силу аксиомы 1.16. Так
как f — движение, то расстояние между точками f(A}
и f(B) равно длине отрезка АВ. Из равенства
f(A) = Ax следует, что расстояние между точками Ах
и f{B) равно длине отрезка АХВХ. Согласно аксиоме 1.14
точки /(В) и Вх совпадают, т.е. /(В) = В1. Аналогичным
образом получаем, что f(C) = Сх. Отсюда, по теореме 2.1
следует, что f является наложением треугольника АВС
на треугольник АХВХСХ.
Второй признак равенства треугольников. Об этом
признаке говорится в следующей теореме.
Теорема 2.3. Если сторона и два прилежащих к
ней угла одного треугольника соответственно равны
39
стороне и двум прилежащим к ней углам другого тре-
угольника, то такие треугольники равны.
□ Пусть для треугольников АВС и АХВХСХ вы-
полняются равенства А В = Ах Вх, ХА = ХАх, ХВ = ХВх
(рис.2.4).
Рассмотрим такое наложение f угла А на угол Ах,
что f(AB) = AxBx, f(AC)=AxCx для лучей АВ и АС.
Это можно сделать согласно аксиоме 1.16. Как и в
предыдущей теореме, согласно аксиоме 1.14 име-
ем: f(B) = Вх. По аксиоме 1.17 лучи ВС и ВХСХ совмеща-
ются, т.е. для них выполняется равенство f(BC] = ВХСХ.
Аналогично совмещаются лучи АС и АХСХ. Согласно
теореме 1.1 лучи f(AС) и f(BC) пересекаются в един-
ственной точке Ср т.е. f(C) = Сх. Отсюда по теореме 2.1
имеем, что f является наложением треугольника АВС
на треугольник АХВХСХ. Значит, ДЛВС = ДЛ^Ср
Рис.2.4
Об аксиомах. В первой и настоящей главах мы при-
вели систему аксиом, которые описывают свойства точек
и прямых на плоскости. При идеальном построении сис-
темы аксиом она должна удовлетворять следующим
трем условиям: 1) независимости; 2) непротиворечивости;
3) полноты.
Прокомментируем эти требования применительно к
введенной системе аксиом.
1) Мы не ставили своей целью ввести независимые
аксиомы. Некоторые из них можно рассматривать как
теоремы и доказать с помощью других аксиом. Это ус-
40
ложнило бы доказательство теорем, которые рассматри-
ваются в этой главе. Но именно этого мы хотели избе-
жать.
2) Рассмотренные аксиомы непротиворечивы в том
смысле, что, пользуясь ими, мы не придем к противо-
речию. Доказательство этого утверждения мы приводить
не будем.
3) Требование полноты означает, что система акси-
ом содержит достаточно много аксиом, с помощью кото-
рых можно было бы доказать основные теоремы геомет-
рии на плоскости. Некоторые аксиомы планиметрии мы
не будем формулировать, хотя фактически будем ими
пользоваться, так как мы считаем, что построение пол-
ной системы аксиом может значительно усложнить изло-
жение геометрии. Построение системы аксиом планимет-
рии будет продолжено в последующих главах.
§ 2.3. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 2.1. Стороны треугольника пропорциональ-
ны числам 5, 6, 7. Сумма двух меньших сторон на 12 см
больше третьей стороны. Найти периметр треугольника.
ZX Предположим, что а, b , С — длины сторон дан-
ного треугольника и а < b < с. Положим при к>0:
а = 5к, Ь = 6к, с = 1к и а + Ь = 5к + 6к = \\к.
По условию задачи
(а + 6)-с = 12.
Значит,
1 \k-lk = 12,
откуда
к = 3.
Следовательно,
а = 15 см, 6 = 18 см, с = 21 см.
Имеем:
Р = а + 6 + с = 15 + 18 + 21 = 54 (см). ▲
Пример 2.2. На сторонах угла, меньшего развернуто-
го, от его вершины отложены равные отрезки. Их концы со-
единены отрезком. Доказать, что этот отрезок делится биссек-
трисой угла пополам.
41
Zs Пусть на сторонах а
и Ь данного угла (а, 6) отло-
жены равные отрезки АВ
и AC t I — биссектриса уг-
ла (а,6) (рис.2.5). Она пере-
секает отрезок ВС в некото-
рой точке D. Рассмотрим
треугольники ABD и ACD.
У них AD — общая сторо-
на, АВ = АС по условию
и Z.BAD = ACAD по опре-
делению биссектрисы угла. По первому признаку равен-
ства треугольников &ABD = 1SACD. Отсюда следует ра-
венство отрезков BD и DC.
Пример 2.3. В треугольниках АВС и АХВХСХ углы А
и Ах равны и углы В и Вх также равны. Сторона АВ равна
Рис. 2.5
А
стороне АХВХ. Точки М и Мх — соответственно середины сто-
рон ВС и ВХСХ. кт/аз&гь, что отрезки AM и АХМХ равны.
Рис. 2. 6
ZS Данные треугольники изображены на рис.2.6. По
условию
ab = axbv AA = AAv zb = zbx.
Значит, по второму признаку равенства треугольни-
ков АЛ ВС = ЛАХВХСР Отсюда следует, что ВС = ВХСХ,
откуда ВМ = ВХМХ. Далее рассмотрим треугольники
АМВ и АХМХВХ. В этих треугольниках
AB = AXBV ВМ = ВХМХ и ZB = ZBp
42
По первому признаку равенства треугольников эти тре-
угольники равны. Значит, AM = АХМХ.
§ 2.4. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
2.01. В треугольнике одна сторона втрое длиннее дру-
гой и на 2 см длиннее третьей стороны. Периметр треугольни-
ка равен 26 см. Найти стороны треугольника.
2.02. В треугольниках АВС и АХВХСХ
АА — ААХ । АВ = АВХ, АВ — АХВХ.
Точки М и Мх лежат соответственно на сторонах ВС и ВХСХ,
причем
АМАС = АМАВ , АМХАХСХ = АМХАХВХ.
Доказать, что AM = АХМХ.
2.03. В треугольниках АВС и АХВХСХ известно, что
АВ = АХВХ, АС = АХСХ, АА = ААХ.
Точки D и Dx являются серединами сторон ВС и BjC, соответ-
ственно. Точки К и Кх — середины сторон АВ и АХВХ соответ-
ственно. Отрезки AD и СК пересекаются в точке М, отрез-
ки AXDX и СХКХ пересекаются в точке Мх. Доказать, что тре-
угольники АСМ и АХСХМХ равны.
2.04. На стороне угла А отложим последовательно отрез-
ки АВ и ВС, а на другой стороне этого угла отложим после-
довательно отрезок АВХ, равный АВ, и отрезок ВХСХ, рав-
ный ВС. Доказать, что отрезки ВСХ и ВХС равны.
43
ГЛАВА 3
ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ
ПРЯМЫЕ
§ 3.1. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ
Смежные углы. Два уг-
ла, у которых одна сторона
общая, а две другие являются
дополнительными лучами, на-
зываются смежными.
На рис.3.1 углы АВС
и ABD — смежные. Следст-
вием аксиомы 1.8 является
следующая теорема.
Теорема 3.1. Сумма
смежных углов равна 180°.
Если смежные углы не рав-
ны, то градусная мера одного
гого — больше 90°.
На рис.3.1 угол АВС
меньше 90°, а угол ABD
больше 90°.
Острые и тупые углы.
Угол, градусная мера которо-
го меньше 90°, называется
острым. Если градусная ме-
ра угла больше 90° и мень-
ше 180°, то такой угол назы-
вается тупым.
Если ZABC = Z.ABD ,
из них меньше 90°, а дру-
Рис.З. 2
то градусная мера каждого из них составляет 90°
(рис.3.2).
44
- j Напомним, что угол,
\ л В градусная мера которого
уА уГ составляет 90°, называется
((\ /\\ прямым.
(( Ju) ) / Вертикальные углы. Два
Vz угла называются вертикаль-
ными, если стороны одного
/ \ D угла являются дополнитель-
С 9 у ными лучами к сторонам
z другого.
Рис.3.3 На рис.3.3 изображены
две пары вертикальных уг-
лов: /АОВ и /COD, а
также /АОС и /BOD. Для вертикальных углов спра-
ведливо следующее утверждение.
Теорема 3.2. Вертикальные углы равны.
□ Рассмотрим углы АОВ и COD. Так как уг-
лы АОВ и АОС смежные, то согласно теореме 3.1
/АОВ =180°-ЛАОС.
Аналогично
/COD =180°-ЛАОС.
Следовательно,
/АОВ =/COD.*
Термин "вертикальный" происходит от латинского
слова "verticalis”, которое в свою очередь образовано от
слова "vertix” — "вершина".
Пересечение прямых. Перпендикулярные прямые.
При пересечении двух прямых возможны два случая:
а) образуются два равных острых и два равных ту-
пых угла;
б) образуются четыре прямых угла.
Согласно §1.2 в случае, когда прямые С1 и Ъ при пе-
ресечении образуют четыре прямых угла, эти прямые яв-
ляются перпендикулярными.
Перпендикулярность прямых а и Ъ обозначается
так: alb. Угол между этими прямыми равен 90°. Такит*
образом, если alb, то /{а, Ь) = 90°.
Будем называть перпендикулярными также отрезки
или лучи, лежащие на перпендикулярных прямых.
45
§ 3.2. АКСИОМА ПАРАЛЛЕЛЬНЫХ
Напомним, что две прямые, лежащие в одной плос-
кости и не имеющие общих точек, называются парал-
лельными (рис.3.4).
Аксиома 3.1. На плоскости через точку, лежа-
щую вне заданной прямой, можно провести прямую, па-
раллельную этой прямой, и притом только одну.
Построенная система аксиом определяет привычную
нам геометрию, результаты
которой широко использу- А
ются в повседневной прак- ' -..........
тике. Эту геометрию так- а
же называют евклидовой в ___________
честь древнегреческого уче- £
ного Евклида. В первой по-
ловине XIX в. русский мате-
матик Н.И.Лобачевский, не- Рис.З.
мецкий математик К.Ф.Га-
усс и венгерский математик Я.Бойаи независимо друг
от друга построили новую геометрию, в которой аксио-
ма 3.1 параллельных прямых была заменена следующей:
на плоскости через точку вне данной прямой можно
провести бесконечно много прямых, параллельных этой
прямой.
Геометрию, в которой выполняется такая аксиома,
назвали неевклидовой геометрией. Открытие неевклидо-
вой геометрии было выдающимся событием в истории
науки. Приведем краткие сведения о математиках, внес-
ших определяющий вклад в создание геометрии:
Евклид (ок.365—ок.ЗОО до н.э.) один из первых
начал изучать логические основы математики. Автор вы-
дающегося труда ’’Начала”, в котором были систе-
матизированы сведения по геометрии на плоскости и в
пространстве.
Гаусс Карл Фридрих (1777—1855) — математик,
астроном, геодезист, физик. Ему принадлежат некоторые
46
идеи неевклидовой геометрии, хотя с изложением своих
взглядов в этой области он никогда не выступал. Создал
теорию поверхностей, исследовал возможность построе-
ния правильных многоугольников циркулем и линейкой.
Лобачевский Николай Иванович (1792—1856)
в 1823 г. завершил труд "Геометрия", где впервые была
выделена так называемая абсолютная геометрия, содер-
жащая утверждения, которые не зависят от аксиом па-
раллельных прямых.
Б о й а и Янош (1802—1860) еще до 1825 г. владел
основами неевклидовой геометрии, однако напечатал
труд по геометрии лишь в 1832 г. как дополнение
("Appendix") к учебнику своего отца.
§ 3.3. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
Теорема 3.3. Две различные прямые, парал-
лельные третьей прямой, параллельны между собой.
□ Пусть различные прямые а и b параллельны пря-
мой С. Допустим, что пря-
мые а и b пересекаются в
точке М. по аксио-
ме 3.1 эти прямые должны
совпадать, что противоречит
условию.
Рис.3.5
Рассмотрим две раз-
личные прямые а и b, пере-
секаемые третьей прямой. На
рис.3.5 цифрами обозначены
образованные при этом углы.
Эта углы в геометрии имеют
специальные названия:
47
внутренние накрест лежащие:
внешние накрест лежащие:
внутренние односторонние:
внешние односторонние:
соответственные:
Z3 и Z5,
Z4 и Z6;
Z1 И Z7,
Z2 и Z8;
Z3 и Z6,
Z4 и Z5;
Z2 и Z7,
Z1 и Z8;
Z1 и Z5,
Z2 и Z6,
Z3 и Z7,
Z4 и Z8.
Таким образом, на рис.3.5 представлено изображе-
ние четырех пар соответственных углов и по две пары
углов других четырех типов.
Теорема 3.4. Следующие равенства являются
равносильными:
1) Z3 = Z5,
2) Z4 = Z6,
3) Z1 = Z7,
4) Z2 = Z8,
5) Z1 = Z5,
6) Z4 = Z8,
7) Z2 = Z6,
8) Z3 = Z7,
9) Z4 + Z5 = 180°,
10) Z3 + Z6 = 180°,
11) Z2 + Z7 = 180°,
12) Zl + Z8 = 180°.
□ Докажем, например, что из равенства 8) следует
равенство 12). Действительно, пусть Z3 = Z7. Из теоре-
мы 3.2 следует, что Z3 =Z1, а из теоремы 3.1 получаем:
Z8 = 180°-Z7.
Отсюда
Zl + Z8 = Z3 +180°-Z7 = Z3 +180°-Z3 = 180°.
В качестве упражнения попробуйте доказать, что из
какого-либо условия теоремы 3.4 следует другое условие
этой теоремы.
Условия параллельности прямых. Выясним условия
параллельности прямых а и b.
48
Теорема 3.5. Две различные прямые а и b па-
раллельны тогда и только тогда, когда при пересечении
этих прямых третьей прямой выполняется одно из усло-
вий 1)—12) теоремы 3.4, а, следовательно, и все другие
условия этой теоремы.
□ Пусть при пересечении прямых а и b прямой с
выполняется одно из условий 1)—12). Тогда по теоре-
ме 3.4 все условия 1)—12) выполняются.
Обозначим через В и С соответственно точки пере-
сечения прямой С с прямыми а и b. Допустим, что пря-
мые а и b пересекаются в некоторой точке А (рис.3.6).
Отложим от точки С в сторону, противоположную точ-
ке А, отрезок CD, равный ВА . Так как условия 1)—12)
выполнены, то Z1 = Z2. По теореме 3.1
ZABC = 180°-Z2, ZBCD = 18O°-Z1,
откуда ZABC = Z.BCD. По первому признаку равенства
треугольников lOsABC = i±BCD, значит, ZA — Z.DBC.
Отсюда следует, что ADBC = Z2, а это невозможно со-
гласно аксиоме 1.8. Допущение о пересечении прямых а
и b привело к противоречию. Таким образом, а\\Ь .
Докажем вторую часть теоремы.
Допустим, что а\\Ь, однако Z1^Z2 (рис.3.7). Про-
ведем через точку В прямую Ь} так, чтобы Z.ABM = Z1.
Из первой части теоремы 3.5 следует, что ftjla. По аксио-
ме 3.1 прямые b и Ь{ совпадают, поэтому
Z.2 = AABM =Z1,
49
что противоречит принятому
допущению.
Следствие 1. Две
различные прямые, перпен-
дикулярные к одной и той
же прямой, являются парал- & “П
лельным и.
Следствие 2, Ес-
ли одна из двух параллель-
ных прямых перпендикуляр-
на прямой а, то и другая
прямая перпендикулярна пря- Рис. 3.8
мой а (рис.3.8).
Доказательства этих следствий проведите самостоя-
тельно.
§ 3.4. СУММА УГЛОВ ТРЕУГОЛЬНИКА
Выясним, чему равна сумма всех углов треугольни-
ка. Для этого рассмотрим следующую теорему.
Теорема 3.6. Сумма
углов треугольника равна 180°. ______2L
□ Проведем через верши- Г77\fJ/
ну В треугольника АВС пря- у
мую а, параллельную АС /
(рис.3.9). Это можно сделать со- /
гласно аксиоме параллельных /
прямых. Тогда по теореме 3.5 А /________[( С
ZZ = Z1, ZC = Z2. -------- ----
Значит, по аксиоме 1.9
Рис.3.9
ZZ + ZB + ZC = Z1+ ZB + Z2 = 180°.
Внешний угол треугольника. Угол, смежный с од-
ним из внутренних углов треугольника, называется
внешним углом треугольника.
На рис.3.10 изображен внешний угол BAD тре-
угольника АВС, смежный с внутренним углом ВАС
этого треугольника.
50
Рис.З.13
Т е о р е м а 3.7. В треугольнике внешний угол ра-
вен сумме двух внутренних углов, не смежных с ним.
□ В самом деле, согласно теореме 3.1
A.BAD =\№-АВАС.
По теореме 3.6 имеем:
ABAC = \Ю-АВ-АС,
значит,
ABAD = \%Q°-(\$Qa-AB-AC] = АВ + АС.
Следствие 1. Для треугольника выполняется
одна из трех возможностей:
1) все углы треугольника острые (рис.3.11);
2) один из углов треугольника прямой, а два дру-
гие — острые (рис.3.12);
3) один из углов треугольника — тупой, а два дру-
гие — острые (рис.3.13).
51
Отметим, что в первом случае треугольник называ-
ется остроугольным, во втором случае — прямоуголь-
ным, а в третьем случае — тупоугольным.
Следствие 2. Сумма двух острых углов пря-
моугольного треугольника равна 90°.
Доказательство следствий 1 и 2 проведите само-
стоятельно.
§ 3.5. ВЫПУКЛЫЕ МНОГОУГОЛЬНИКИ. СУММА
УГЛОВ ВЫПУКЛЫХ МНОГОУГОЛЬНИКОВ
Рассмотрим различные точки A2,.,.,An_vAnt ни-
какие 3 из которых не лежат на одной прямой. Соеди-
ним их последовательно отрезками Д Л2, Л2Л3,..., Л^Д,
ДА
Допустим, что для каждого из этих отрезков выпол-
няется следующее условие: все другие отрезки лежат в
одной полуплоскости, ограниченной прямой, содержащей
данный отрезок. Тогда фигура, состоящая из точек от-
резков А{А2,А2А3,..чАп_хАп,АпАх, а также точек, принад-
лежащих всем указанным полуплоскостям, называется
выпуклым П-угольником. Точки А1,А2,...,Ап_11Ап назы-
ваются вершинами, отрезки A[A2,A2A3,..4An_}An,AnAi —
сторонами, а углы А^А^, Л^Лз, ..., А^А^ — внут-
ренними углами (или просто углами) выпуклого П-
угольника Л^.-.Д.
Две вершины П —угольника, соединенные стороной,
называются соседними.
Отрезок, соединяющий несоседние вершины вы-
пуклого п -угольника, называется диагональю.
На рис.3.14 изображен пятиугольник ABCDE . Точ-
ки AtB'CiD'E — его вершины; АВАЕ .AAED,
AEDC 'ADCB 'Z.CBA — его углы; АВ ,ВС tCD ,DE,
ЕА —его стороны; AC ,AD tBE ,BD tCE —диагонали
этого пятиугольника.
На рис.3.15 и 3.16 изображены многоугольники, не
являющиеся выпуклыми. В дальнейшем, если не оговоре-
52
Рис.З.14
Рис. 3.15
Рис.3.16
Рис.3.17
но противное, будем рассматривать только выпуклые
многоугольники.
Теорема 3.8. Сумма углов выпуклого П-уголь-
ника равна 180° (п —2).
□ Рассмотрим выпуклый и-угольник АхА2...Ап
(рис.3.17). Проведем диагонали А1А3, А^4, .... A}An_v
Получим (и-2) треугольника А}А2А3, АХА3А4, ....
АхАп_хАп. Сумма всех углов этих треугольников, соглас-
но теореме 3.6, равна . 180° ‘(12 — 2). Эта сумма, очевидно,
равна сумме углов данного И -угольника. И
Следствие. Сумма углов выпуклого четырех-
угольника равна 360°.
На рис.3.18 изображены невыпуклые четырехуголь-
ники ABCD и MNP К. Убедитесь самостоятельно, что
53
Рис. 3.18
сумма углов четырехугольника ABCD равна 360°, а сум-
ма углов четырехугольника MNP К меньше 360°.
§ 3.6. СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ
ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ
Теорема 3.9. Через всякую точку плоскости
можно провести прямую, перпендикулярную к данной
прямой, и притом только одну.
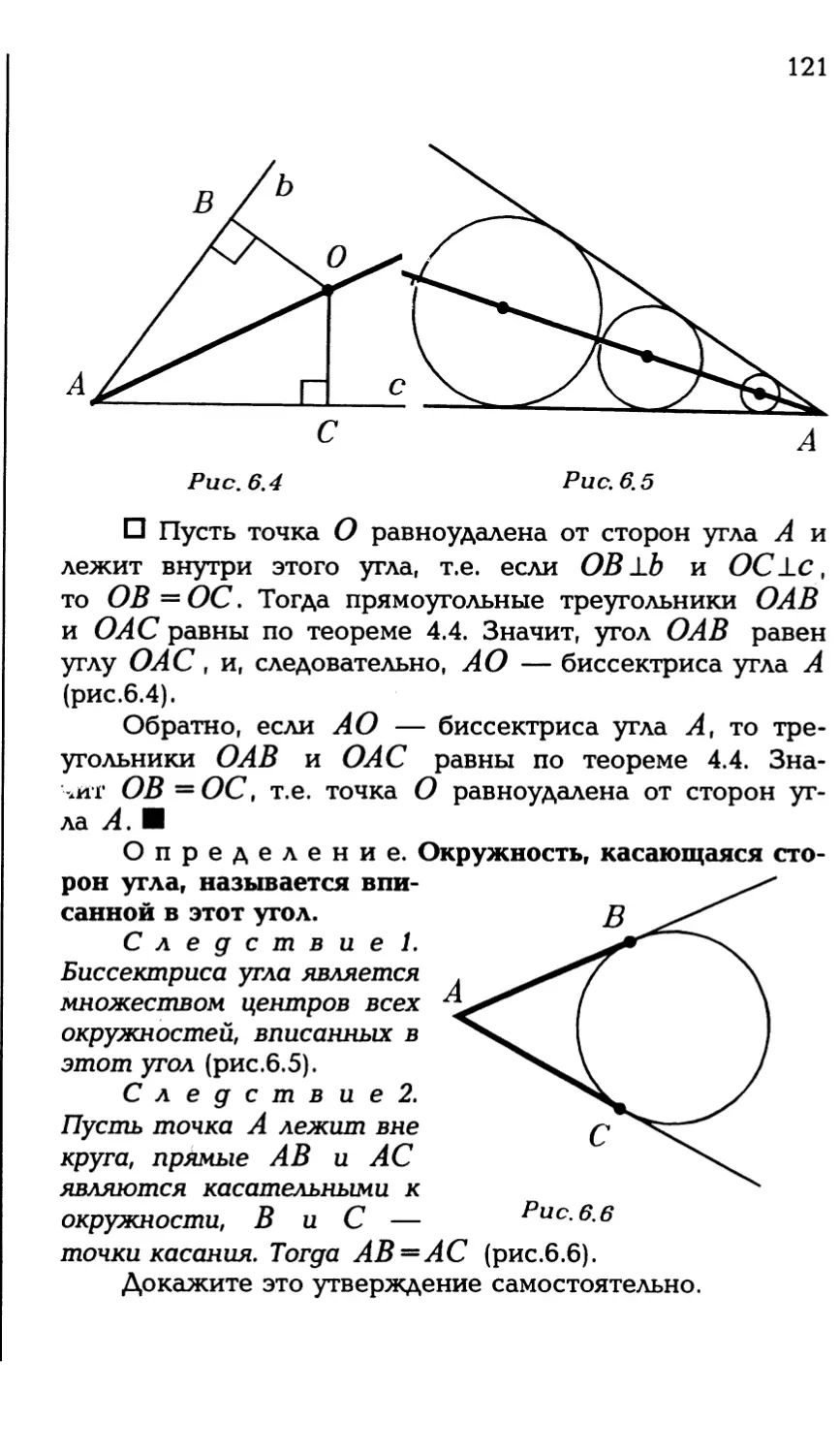
□ Пусть точка А не ле-
жит на прямой а (рис.3.19).
Выберем произвольные точ-
ки В и D на прямой а таким
образом, чтобы Z.DBA был
острым. Построим угол DBA2,
равный углу DBA, и отложим
на стороне ВА2 этого угла от-
резок ВАХ, равный ВА. Со-
единим точку А с точкой Ах.
Тогда ААВК = ААХВК по
Рис.З. 19
первому признаку равенства треугольников,
чит, Z.BKA = АВКАХ. По теореме 3.1
Зна-
ЛВКА = АВКАХ =
180°
= 90°.
54
A
Рис.З. 20
Значит, прямая AAx.La,
Докажем единственность
такой прямой. Пусть прямые
АТ и АК перпендикулярны
прямой а. Тогда в треуголь-
нике АТК (рис.3.20) два угла
прямые, что противоречит
следствию 1 теоремы 3.7.
Случай, когда точка А
лежит на прямой Л, рассмот-
рите самостоятельно. И
§ 3.7. РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ
ПРЯМЫМИ
Расстояние от точки до прямой. Пусть точка А не
лежит на прямой а. Проведем через точку А прямую,
перпендикулярную к прямой а. Она пересекает эту пря-
Рис. 3.22
мую в некоторой точке В (рис.3.21). Длину отрезка АВ
будем называть расстоянием от точки А до прямой.
Пусть прямые а и Ъ параллельны. Докажем, что
расстояние от точки, лежащей на прямой Л, до пря-
мой b не зависит от выбора этой точки (рис.3.22).
□ Пусть А и В — точки прямой а и Ах, Вх —
точки прямой Ь, для которых ААХ1.Ь, ВВХ1Ь. Согласно
следствию 2 из теоремы 3.5 имеем: ААх1.а, ВРЛ.а. Про-
ведем отрезок АХВ. В треугольниках АВАХ и АХВВХ сто-
55
рона АХВ является общей. Углы 1 и 2 равны по теоре-
ме 3.5. Далее, по следствию 1 из теоремы 3.5 AAX\\BBV и
поэтому Z3 = Z4. По второму признаку равенства тре-
угольников треугольники АВАХ и АХВВХ равны. Зна-
чит, ААХ = ВВХ. И
Назовем расстоянием между параллельными пря-
мыми а и b расстояние от произвольной точки пря-
мой а до прямой b.
§ 3.8. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 3.1. Сумма градусных мер двух углов, обра-
зованных при пересечении двух прямых, равна 80°. Найти
градусные меры всех четырех образовавшихся углов.
Zs. Пусть данные прямые пересекаются в точке О
(рис.3.23). Обозначим лучи одной прямой, исходящей из
точки О, через av а2, а лучи другой — через bv b2. Об-
разовались четыре пары смежных углов:
чЬ, аг/ ZfapZjJ и Z(61(a2),
/ A\ia2) И Аа2’Ь2)<
/ Z(a2rh2) и Z(b21ax)
у. / и две пары вертикальных уг-
О лов:
а / M’s ДауЬ2) и Да^).
f X Так как по теореме 3.1 сумма
Рис. 3,23 1ОЛо
смежных углов равна lol) ,
то можно считать, например,
что Z\avbx] + Z(a2,62) = 80°. Тогда по теореме 3.2
А^ЬХ} = ^(а2Д) = 80°:2 = 40°,
а затем по теореме 3.1
Z(a, r b2) = Z(a2 , Ьх) = 180° - 40° = 140°.
56
Итак, градусная мера двух углов равна 40°, а двух
других углов — 140°. Ж
Пример 3.2. Разность двух внешних односторонних
углов при двух параллельных прямых и секущей равна 44°.
Найти градусные меры всех об-
/ разевавшихся углов.
/ Рассмотрим две па-
1 / 2 & раллельные прямые а и b,
4 / $ которые пересекает третья
/ прямая. Образовавшиеся при
/ этом углы обозначены на
5 /6 Ь рис.3.24 цифрами. Углы 2
Q /7 и 7 являются внешними од-
/ посторонними, и по условию
' Pvlc.3.24 Z7-Z2 = 44°.
По теореме 3.5
Z2 + Z7 = 180°.
Пусть Z2 = х, тогда Z7 = 44° + х, и поэтому
44° + х+х = 180°,
откуда 2х = 136°, х = 68°.
Имеем:
Z2 = 68°, Z7 = 180o-68° = 112°.
По теореме 3.5
Z2 = Z4 = Z6 = Z8 = 68°, Z1=Z3 = Z5 = Z7 = 112°.
Таким образом, градусная мера каждого из четырех об-
разовавшихся углов равна 68°, а каждого из четырех
других углов — 112° Ж
Пример 3.3. В треугольнике ABC Z4=af ZJ5=p.
Биссектрисы углов А и В пересекаются в точке I. Най-
ти ZAIB.
Пусть биссектрисы AL} и BL2 треугольни-
ка АВС пересекаются в точке I (рис.3.25). Тогда
Л1АВ = ±(ZBAC) = ^-, ZIBA =|(ZC&4)«|.
По теореме 3.6
57
Рис. 3.25
AAIB = \ЫГ-Л1АВ-А1ВА = 180°-—-—.
2 2
Итак,
AAIB =180°-^Д ▲
2
Замечание. Из рассмотренной задачи легко по-
ZC
лучить, что AAIB = 90°Ч-, т.е. ZAIB всегда является тупым
углом.
Пример 3.4. Какое наибольшее количество острых
углов имеет выпуклый четырехугольник?
Согласно следствию из теоремы 3.8, сумма углов
выпуклого четырехугольника равна 360°. Так как сумма
четырех величин, каждая из которых меньше 90, будет
меньше 360, то выпуклый четырехугольник не может
иметь четырех острых углов.
Построим выпуклый четырехугольник, три утла ко-
торого острые. Отложим на некоторой прямой отре-
зок АВ. Далее отложим в одну полуплоскость, огра-
ниченную прямой АВ, лучи ВС и АС так, что-
бы Z.CAB =40°, ААВС =51°, а в другую полуплоскость
отложим лучи АС} и ВСХ так, чтобы ЛС}АВ =40°,
ААВС t =5Г (рис.3.26). Тогда в четырехугольнике
АСВС,
ACAQ =80°, ZCBCj = 102°.
58
По теореме 3.6
КАСВ = ЛАСХВ = 180°-40°-51° = 89°.
Читателю предоставляется возможность проверить,
что четырехугольник АСВСХ выпуклый.
Итак, наибольшее число острых углов в выпуклом
четырехугольнике равно 3 . А
Пример 3.5. Доказать, что две прямые d и Ь, пер-
пендикулярные параллельным прямым X и у, отсекают на
прямых X и у равные отрезки.
ZS На рис.3.27 прямые а и Ь, перпендикулярные
прямым х и у, отсекают на них отрезки АВ и АХВХ.
Проведем прямую ABV Длины отрезков ААХ, ВВХ явля-
ются расстояниями между параллельными прямыми X
Рис. 3. 2 7
и у. Значит, ААХ = ВВХ, По
следствию 1 из теоремы 3.5
ААХ\\ВВХ. Рассмотрим тре-
угольники ААХВХ и АВВХ.
Сторона АВХ у них общая,
AAX = BBV ХАхАВх = ААВхВ
как внутренние накрест ле-
жащие при параллель-
ных прямых а и b и секу-
щей АВХ. По первому при-
знаку равенства треугольни-
ков ЛААХВХ = ЛАВВХ. Значит, АВ = АХВХ. Ж
Пример 3.6. Точки А, В, Ct D лежат на одной пря-
мой. Точки L и К лежат по разные стороны от этой прямой,
причем \ABL-\ABK и AL=AK, BL-BK. что тре-
угольники CLD и CKD равны.
Пусть на прямой а последовательно расположе-
ны точки А, В, С, D (рис.3.28). Тогда из условия следу-
ет, что AABL = ZABK. Рассмотрим углы LBC и КВС .
Они являются смежными соответственно углам ABL
и АВК и поэтому по теореме 3.1 также равны. В
треугольниках BCL и ВСК сторона ВС — об-
щая, BL = ВК, ALBC = Z.KBC. По первому признаку
равенства треугольников эти треугольники равны. Следо-
вательно, Z.LCB = Z.KCB и LC = КС. Вновь по теоре-
59
ме 3.1 /.LCD = AKCD. Далее аналогично по пер-
вому признаку равенства треугольников получа-
ем: &CLD = kCKD.
Другие случаи расположения точек А, В, С, D на
прямой а рассмотрите самостоятельно. Ж
Пример 3.7. Прямая пересекает отрезок АВ в его се-
редине. Доказать, что точки А и В лежат на одинаковом рас-
стоянии от этой прямой.
ZS Пусть прямая а
пересекает отрезок АВ в А
точке О, причем АО — ОВ.
Проведем AAx_La, ВВхХ.а q В; I
(рис.3.29). Согласно теоре- д
ме 3.9 это можно сделать 1
единственным образом. По
следствию 1 из теоремы 3.5 В
ААХ\\ВВХ. Рассмотрим тре-
угольники АОАХ и ВОВХ, В Рис.З. 2 9
них АО=ОВ, углы АОАХ
и ВОВХ равны как вертикальные, углы АХАО и ВХВО
равны как внутренние накрест лежащие при параллель-
ных прямых ААХ, ВВХ и секущей АВ . По второму при-
знаку равенства треугольников эти треугольники равны.
Следовательно, ААХ = ВВХ. А
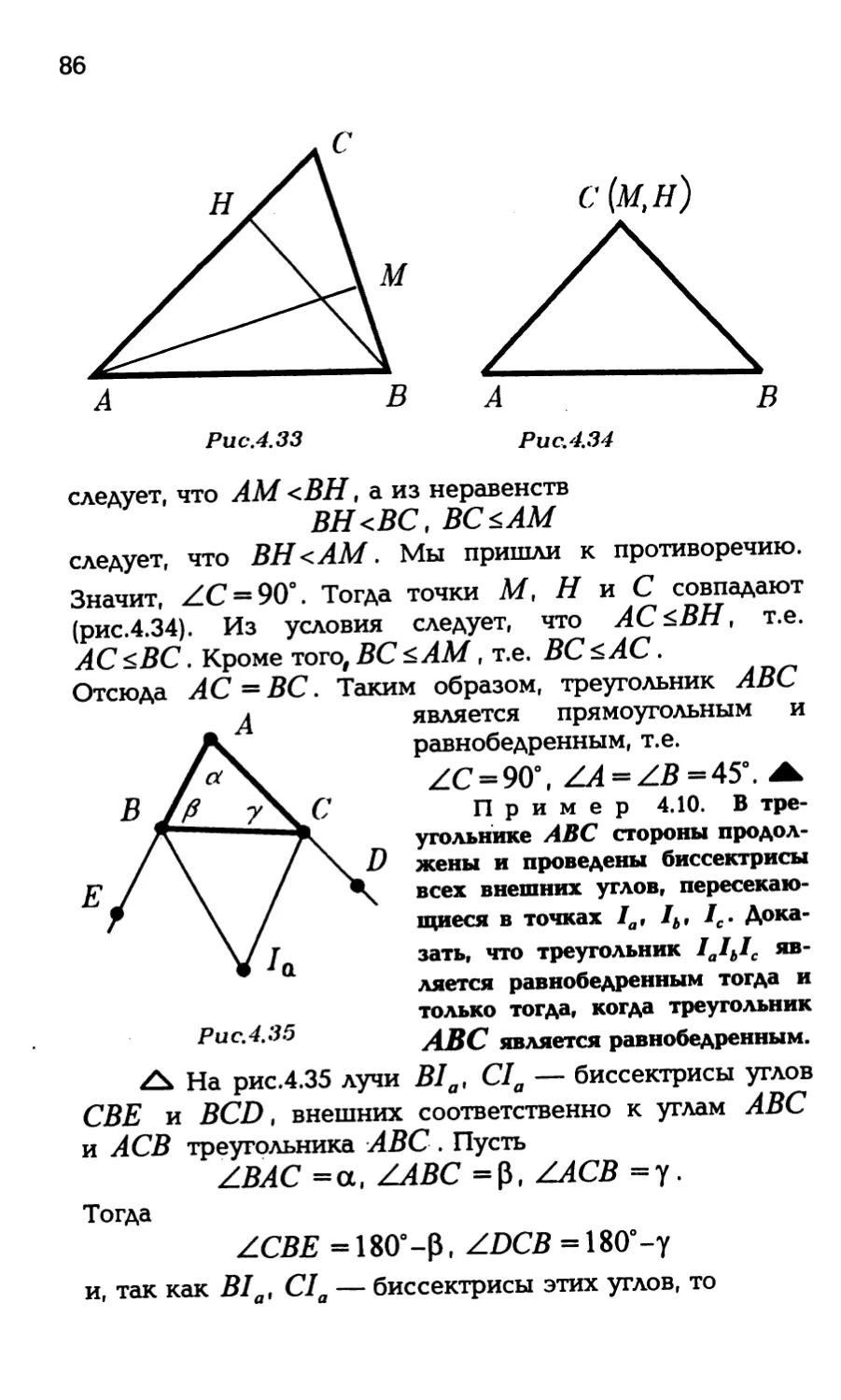
Пример 3.8. Внутри треугольника АВС взята точ-
ка О, Доказать, что угол АВС меньше угла АОС.
60
На рис.3.30 О — внутренняя точка треугольни-
ка АВС . Тогда эта точка является внутренней точкой уг-
лов ВАС и ВСА, и следовательно,
ZOAC<ZBAC,
ZOCA<ZBCA.
По теореме 3.6
ЛАОС = 180°-ZOAC-ZOCA,
ZABC = 180°-ZBАС-ЛВСА.
Таким образом, ЛАВС <ЛАОС.
Пример 3.9. Доказать, что при пересечении диагона-
лей выпуклого П -угольника можно получить выпуклый мно-
гоугольник не более, чем с И сторонами.
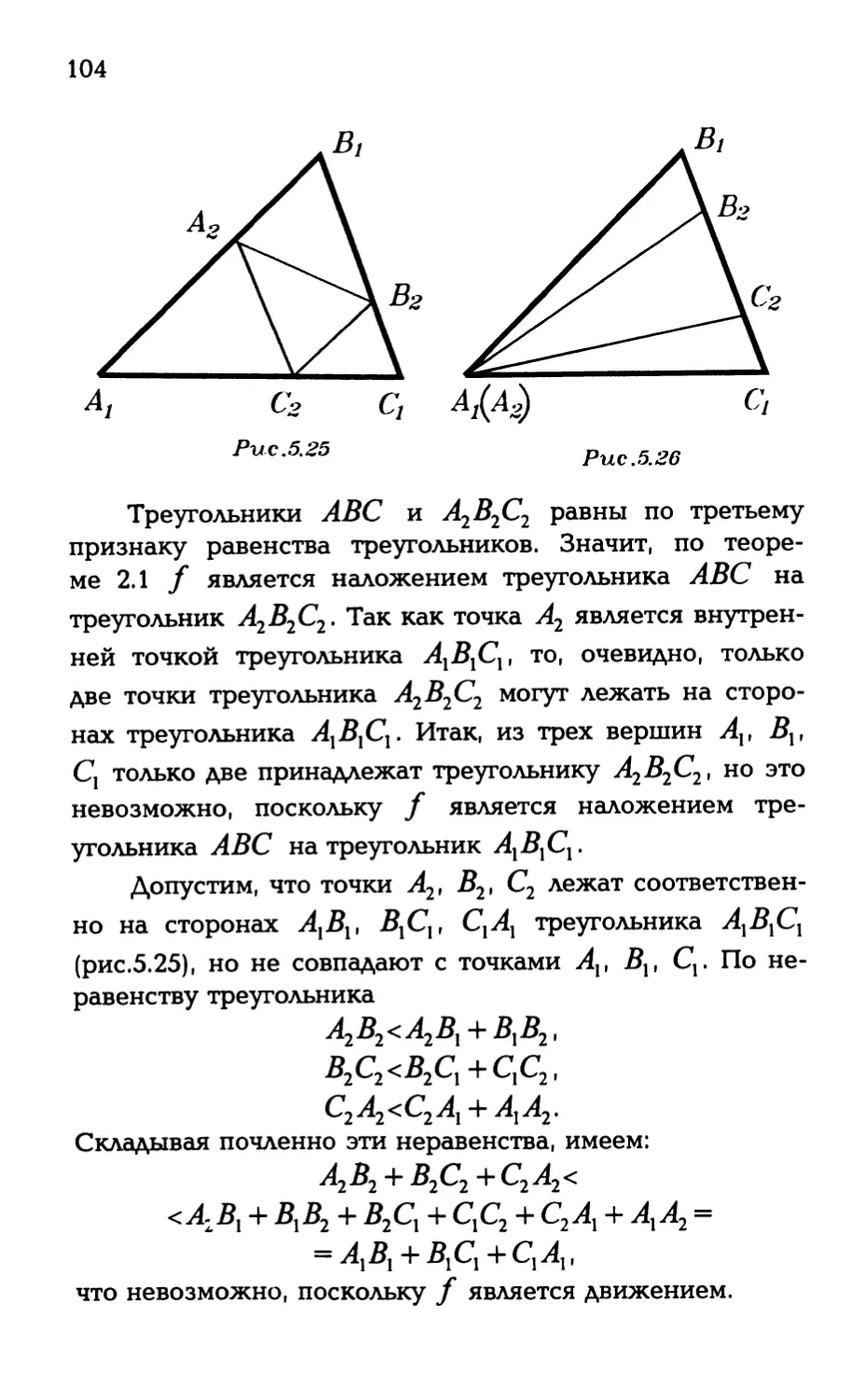
Л± Докажем вначале, что в выпуклом многоугольни-
ке не более двух прямых, содержащих его стороны, пе-
ресекаются в одной точке.
Прежде всего отметим, что по определению выпук-
лого многоугольника никакие три прямые, содержащие
стороны, две из которых имеют общую вершину, не мо-
гут пересекаться в одной точке. Предположим, что для
вершин А, В, С, D, Е, F прямые АВ, CD, EF, содер-
жащие соответственно стороны АВ, CD, EF, пересека-
ются в точке М. Так как многоугольник выпуклый, то
точки С, D, Е, F лежат по одну сторону от пря-
мой АВ, и значит, углы АМС, АМЕ меньше разверну-
того (рис.3.31). Тогда по аксиоме 1.6 один из лучей, на-
пример МС, лежит между двумя другими лучами МА
и ME. Но в этом случае точки А и Е лежат по разные
61
стороны от прямой CD, что противоречит выпуклости
многоугольника.
Рассмотрим произвольный выпуклый Ш-угольник,
образованный в результате проведения диагоналей
данного выпуклого П -угольника. Каждой стороне b
/И-угольника соответствуют две вершины И-угольника,
через которые проходит прямая, содержащая сторону b.
Кроме того, из сказанного выше следует, что каждая вер-
шина Л-угольника соответствует не более двум сторо-
нам ТП-угольника. Значит, 2ди < 2п, откуда т < п. Ж
§ 3.9. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
3.01. Могут ли два смежных угла быть одновременно:
а) острыми? б) тупыми? в) прямыми?
3.02. Найти градусную меру углов, смежных с углами, гра-
дусная мера которых равна:
а) 70°; б) 8ПЗ';в) 124’27'.
3.03. Градусная мера одного из смежных углов в 5 раз
меньше градусной меры другого. Найти градусные меры этих
углов.
3.04. Разнссть градусных мер смежных углов равна 54°.
Найти эти градусные меры.
3.05. Сумма градусных мер трех углов, образованных при
пересечении двух прямых, равна 270°. Доказать, что эти пря-
мые перпендикулярны.
3.06. Найти градусную меру угла, смежного с углом ВАС,
если биссектриса этого угла делит угол ВАС на две части, гра-
дусные меры которых равны 35°.
3.07. Найти градусную меру угла между биссектрисой дан-
ного угла (а,Ь) и продолжением одной из его сторон, если:
а) Х(а,Ь) = 60°; б) Х(а,Ь) = 130°.
3.08 . Из вершины развернутого угла (a,Z>) в одной полу-
плоскости проведены два луча С и d так, что Z(Z>, d) = 120°,
Z(a,c) = 140°. Найти углы (a,d), (c,d), (b,c).
3.09 . От прямой MN в различных полуплоскостях отложе-
ны углы: Z.NMP =42°, ANMK=\C. Среди образовавшихся
62
при этом углов найдите те из них, которые больше развернуто-
го угла.
3.10. Доказать, что если прямая пересекает одну из двух
параллельных прямых, то она пересекает и другую прямую.
3.11. Два отрезка АВ и CD пересекаются в точке О и де-
лятся этой точкой пополам. Доказать, что AD = ВС, BD = АС
и AC\\BD, BC\\AD,
3.12. Отрезки АВ и CD пересекаются в точке О. Дока-
зать, что ЛАСО = ЛОВО, если известно, что ZACO = Z.DBO
и ВО = СО.
3.13. Могут ли биссектрисы двух углов треугольника быть
перпендикулярными ?
3.14. Градусная мера одного из углов, образованных при
пересечении двух параллельных прямых секущей, равна 68°.
Найти градусные меры всех других углов.
3.15. Даны три параллельные прямые Cl, b, С, причем
прямая b находится на одинаковом расстоянии от прямых а
и С. Доказать, что при пересечении этих прямых некоторой
секущей прямой образуются два равных отрезка.
3.16. В треугольнике биссектрисы двух внешних углов об-
разуют с продолжениями сторон треугольника углы а и р.
Найти углы треугольника.
3.17. В треугольнике АВС биссектрисы углов А и В пе-
ресекаются в точке К. Доказать, что угол ААКВ — тупой.
3.18. В прямоугольном треугольнике градусные меры ост-
рых углов относятся как 2:3. Найти градусные меры этих уг-
лов.
3.19. В выпуклом семиугольнике все углы имеют одинако-
вую градусную меру. Найти эту градусную меру с точностью
до градуса.
3.20. Доказать, что при пересечении двух параллельных
прямых секущей образуются четыре острых равных угла и
четыре тупых равных угла или восемь прямых углов.
^^3.2 1. Треугольники АВС и BAD равны. Точки С
и D лежат по разные стороны от прямой АВ . Доказать, что
либо AC\\BD и AD\\BC , либо CD.LAB .
3.22. Доказать, что биссектрисы двух смежных углов пер-
пендикулярны .
3.23. Доказать, что биссектрисы двух вертикальных углов
являются дополнительными друг к другу.
63
3.24. Доказать, что биссектрисы двух тупых углов, образо-
ванных при пересечении двух параллельных прямых секущей,
параллельны.
3.25. При пересечении двух параллельных прямых секу-
щей прямых углов не оказалось. Доказать, что биссектриса лю-
бого острого угла перпендикулярна биссектрисе любого тупого
угла.
3.26. Найти множество точек, равноудаленных от двух
данных параллельных прямых.
3.27. Доказать, что прямая, проведенная через произволь-
ную точку на стороне острого угла перпендикулярно к этой
стороне, пересекает другую сторону этого угла.
3.28. Пусть прямая а перпендикулярна одной стороне уг-
ла, а прямая b перпендикулярна другой стороне угла. Доказать,
что прямые U и b пересекаются, если стороны угла не лежат
на одной прямой.
3.29. Найти с точностью до минут градусные меры углов
треугольника, если известно, что градусная мера одного из них
на 25% меньше градусной меры другого и на 20% больше гра-
дусной меры третьего.
3.30. Доказать, что точка пересечения биссектрис двух уг-
лов треугольника лежит внутри треугольника.
3.31. Биссектрисы углов А и В треугольника АВС пере-
секаются в точке / . Найти угол АСВ , если ZAIB = 120°.
3.32. Доказать, что угол, дополнительный к меньшему из
двух смежных углов до прямого, равен разности смежных уг-
лов.
3.33. Даны два угла с общей вершиной, не имеющие дру-
гих общих точек. Стороны одного угла перпендикулярны к сто-
ронам другого. Найти каждый из этих углов, если один из них
вдвое больше другого.
3.34. Доказать, что два острых угла с соответственно пер-
пендикулярными сторонами равны.
3.35. Пусть острый, a Z-(c,d) тупой, причем ale,
bl-d. {^оказать, что Z(a,Z>) + Z(c,af) = 180°.
3.36. В треугольнике АВС углы А и В равны. Доказать,
что биссектриса внешнего угла при вершине С параллельна
стороне АВ.
3.37. На сторонах угла выбраны две точки, находящиеся
на одинаковых расстояниях от вершины. Через каждую из них
проведена прямая, перпендикулярная соответствующей сторо-
не угла. Доказать, что эти прямые пересекаются на бис-
сектрисе угла.
64
3.38. Отрезки АВ и CD имеют одинаковую длину и пере-
секаются в точке О так, что АО — OD. Доказать, что треуголь-
ники АВС и DCB равны.
3.39. Внутри выпуклого 1000-угольника лежат 500 точек,
каждые 3 из которых не лежат на одной прямой. Многоуголь-
ник разрезают на треугольники, вершинами которых являются
данные 1500 точек. Определить число образовавшихся тре-
угольников.
65
ГЛАВА 4
ВИДЫ ТРЕУГОЛЬНИКОВ
§ 4.1. МЕДИАНА, БИССЕКТРИСА И ВЫСОТА
ТРЕУГОЛЬНИКА
Медиана треугольника. Отрезок, соединяющий вер-
шину треугольника с серединой противоположной сторо-
ны, называется медианой треугольника.
Слово "медиана" происходит от латинского слова
"medius" — средний.
В треугольнике АВС можно провести три медиа-
ны: AAV BBV СС{ (рис.4.1). В дальнейшем будет доказа-
но, что медианы пересекаются в одной точке.
Точка пересечения медиан треугольника называется
центром масс треугольника. Обычно центр масс тре-
угольника обозначается через М.
Свойства центра масс будут рассмотрены в гла-
вах И и 12. В главе 16 будет установлена связь точки пе-
ресечения медиан треугольника с понятием центра масс
системы трех материальных точек, откуда станет ясным
происхождение термина "центр масс".
Биссектриса треугольника. Отрезок биссектрисы уг-
ла треугольника, который соединяет вершину с точкой
3 Зак. 687
66
на противоположной стороне, называется биссектрисой
треугольника.
В дальнейшем будет доказано, что три биссектри-
сы ALV BL2, CL3 пересекаются в одной точке (рис.4.2).
Точка пересечения биссектрис треугольника называется
инцентром треугольника. Обычно инцентр треугольника
обозначается через I.
Высота треугольника. Рассмотрим отрезок, один ко-
нец которого совпадает с вершиной треугольника, а дру-
гой лежит на прямой, содержащей противоположную
сторону. Такой отрезок называется высотой треугольни-
ка, если он перпендикулярен этой прямой.
На рис.4.3—4.5 AHV ВН2> СН3 — высоты треуголь-
ника АВС. Позже мы докажем, что три прямые, содер-
Рис.4.5
жащие высоты треуголь-
ника, пересекаются в од-
ной точке.
Точка, в которой пе-
ресекаются прямые, содер-
жащие высоты треуголь-
ника, называется ортоцен-
тром треугольника. Обыч-
но ортоцентр треугольника
обозначается буквой Н. В
остроугольном треугольни-
ке ортоцентр Н лежит
внутри треугольника (рис.4.3). В прямоугольном треуголь-
нике ортоцентр Н совпадает с вершиной прямого угла
67
треугольника (рис.4.4). В тупоугольном треугольнике ор-
тоцентр Н лежит вне треугольника (рис.4.5).
§ 4.2. РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Равнобедренный треугольник. Треугольник, в кото-
ром какие-либо две стороны равны, называется равно-
бедренным (рис.4.6). Равные стороны равнобедренного
треугольника называются боковыми сторонами, а третья
сторона — его основанием.
Теорема 4.1. Равнобедренный треугол ьник об-
ладает следующими свойствами:
1) углы при основании равны;
2) биссектриса, медиана и высота, проведенные к
основанию, совпадают;
3) биссектрисы углов при основании равны;
4) медианы, проведенные к боковым сторонам, рав-
ны;
5) высоты, проведенные к боковым сторонам, рав-
ны.
□ Пусть в треугольнике АВС стороны АВ и ВС
равны. Проведем биссектрису BD (рис.4.7). Тогда сторо-
ны АВ и BD, а также угол ABD треугольника ABD
равны соответственно сторонам ВС, BD и углу CBD
треугольника CBD. По первому признаку равенства тре-
угольников &ABD = &CBD . Следовательно, Z.A = ZC, и
утверждение 1) доказано.
68
Рис.4.8
Рис.4.9.
Кроме того, отрезки AD и DC равны. Значит,
биссектриса BD является также медианой треугольника
АВС. Так как углы ADB и BDC равны и являются
смежными углами, то согласно теореме 3.1
1 40°
AADB = ABDC = — - 9 У
2
Отсюда следует, что биссектриса f D перпендикулярна
основанию AD треугольника АВС . Значит, биссектриса
BD — высота треугольника АВС . Таким образом, ут-
верждение 2) доказано.
Докажем утверждение 3). Пусть ALX и С£3 —
биссектрисы треугольника АВС (рис.4.8). В треуголь-
никах ALXC и CL3A имеется общая сторона АС. Уг-
лы LyAC и LXCA равны как углы при основании
треугольника АВС. Углы ЦСА и LyAC равны как по-
ловины равных углов ВСА и ВАС соответственно. По
второму признаку равенства треугольников &ALXC =
= &CL3A, откуда следует, что ALX = CL3, что и требо-
валось доказать.
Докажем свойство 4). Пусть ААХ и ССХ — медианы
треугольника АВС (рис.4.9). Тогда треугольники ААХС
и ССХА равны (докажите самостоятельно), следо-
вательно, медианы ААХ и ССХ равны.
69
Докажем, наконец, свой- д
ство 5). Пусть АНХ и СН3 —
высоты треугольника АВС / \
(рис.4.10). В прямоугольных
треугольниках АНХС и СН3А / \
сторона АС является общей;
углы АСНХ и САН3 равны д С
как углы при основании рав- Рис.4.10
нобедренного треугольника
АВС ; по следствию 2 из теоремы 3.7
ЛНХАС = 90°-ZA СНХ = 90°-АСАН 3 = АН3СА.
Тогда треугольники АНХС и СН3А равны по второ-
му признаку равенства треугольников. Отсюда получа-
ем, что высоты АНХ и СН3 равны. М
Равносторонний треугольник. Треугольник, все
стороны которого равны, называется равносторонним.
Другое название равностороннего треугольника —
правильный треугольник. Каждый правильный тре-
угольник является равнобедренным, причем за основание
его можно принять любую сторону.
Справедливо следующее утверждение.
Теорема 4.2. Равносторонний треугольник
обладает следующими свойствами:
1) все его углы равны 60°;
2) биссектриса, высота и медиана, проведенные из
одной вершины, совпадают;
3) три биссектрисы равны между собой.
Докажите эту теорему самостоятельно.
§ 4.3. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ
Этот признак устанавливает следующая теорема.
Теорема 4.3. Если три стороны одного тре-
угольника соответственно равны трем сторонам дру-
гого треугольника, то такие треугольники равны.
□ Пусть для треугольников АВС и АХВХСХ выпол-
няется равенство
70
AB = A}BV AC = AXCV BC = B}CX.
Отложим угол BAC2, равный углу Al треугольника
AXBXCV так, чтобы точки С и С2 лежали в различных по-
луплоскостях, ограниченных прямой АВ. Это всегда
можно сделать согласно аксиоме 1.15. Точку С2 выберем
так, чтобы АС2 = АХСХ. Это возможно по аксиоме 1.16.
Тогда ДЛВС2 = по первому признаку равенства
треугольников. Возможны следующие случаи:
1) луч СС2 лежит внутри угла АСВ (рис.4.11);
2) луч СС2 лежит вне угла АСВ (рис.4.12);
3) луч СС2 совпадает с лучом С А (рис.4.13);
4) луч СС2 совпадает с лучом СВ (рис.4.14).
Рассмотрим случаи 1) и 2).
71
Очевидно, что АС2 = АС, ВС2 = ВС, значит тре-
угольники АСС2 и ВСС2 равнобедренные. Отсюда сле-
дует, что
Z1 = Z2, Z3 = и ZACB = ZAC2B,
Поэтому ХЛСВ = ZAlClBv По первому признаку равен-
ства треугольников ДАВ С =ЛА1В1С].
Случаи 3) и 4) рассмотрите самостоятельно. И
§ 4.4. ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ
В прямоугольном треугольнике стороны, образую-
щие прямой угол, называются катетами. Третья сторона,
лежащая против прямого угла, называется гипотенузой.
На рис.4.15 стороны АС и ВС — катеты, а сторона
АВ — гипотенуза прямоугольного треугольника АВС , в
котором угол С прямой.
Греческое слово %осОето^ переводится как "опущен-
ный перпендикулярно", "отвес". В средние века словом
"катет" называли высоту прямоугольного треугольника. В
современном смысле эти
слово употребляется с XVII
века.
Следующая теорема ус-
танавливает пять основных
признаков равенства прямо-
угольные, треугольников.
Т е о р u л а 4.4. Два
прямоугольных треугольни- —।
ка равны, если выполняется —
одно из следующих уело- С В
вий: Рис.4.15
1) катеты одного треугольника соответственно рав-
ны катетам другого;
2) катет и прилежащий к нему острый угол одного
треугольника соответственно равны катету и прилежа-
щему к нему острому углу другого треугольника;
72
Рис,4.16
3) катет и лежащий против него острый угол одно-
го треугольника соответственно равны катету и лежа-
щему против него острому углу другого треугольника;
4) гипотенуза и острый угол одного треугольника
соответственно равны гипотенузе и острому углу друго-
го треугольника;
5) гипотенуза и катет одного треугольника соответ-
ственно равны гипотенузе и катету другого треугольни-
ка.
□ Рассмотрим прямоугольные треугольники АВС
и АХВХСХ (рис.4.16).
Пусть условие 1) выполнено, т.е.
AC = AXCV ВС = ВХСХ.
Так как АС = АСХ = 90°, то согласно первому признаку
равенства треугольников ДЛВС = A/ljВХСХ.
Если выполнено условие 2), то
АС = АХСХ и АА = ZAX,
тогда &АВС = &АХВХСХ по второму признаку равенства
треугольников.
При выполнении условия 3) имеем:
АС = АХСХ, ZB = ZB},
По следствию 2 из теоремы 3.7 углы А и Ах равны. Та-
ким образом, условие 2) выполнено, и треугольники рав-
ны.
Далее, при выполнении условия 4), когда
АВ = АХВХ, ЛА = ЛАХ,
73
получим, что АВ = и тре-
угольники равны по второму при-
знаку равенства треугольников.
Наконец, пусть выполняется
условие 5):
ЛС = ДСр АВ = АХВХ.
Расположим эти треугольники так,
чтобы равные катеты АС и АХСХ
совпадали, а точки В} и В лежа-
В, CfCJ в
Рис.4.17.
ли в разных полуплоскостях, ог-
раниченных прямой А С (рис.4.17). Это осуществляется
так же, как и при доказательстве теоремы 4.3. Поскольку
АВХСА = ААСВ = 90°, то АВСВХ = 1Ю,
а это значит, что точки Вх, С и В лежат на одной пря-
мой. Треугольник АВВХ является равнобедренным, от-
куда следует, что АВ = АВГ Значит, &АВС =
согласно условию 4). И
Теорема 4.4 позволяет доказать теоремы 4.5—4.7,
обратные утверждениям 1), 2) теоремы 4.1.
Теорема 4.5. Если два угла треугольника рав-
ны, то такой треугольник является равнобедренным.
□ Пусть BD — высота треугольника АВС (рис.4.18).
Если АА = АС, то &ABD = &CBD согласно п.З) теоре-
мы 4.4. Тогда АВ = СВ. Значит, треугольник АВС —
равнобедренный. Теорема 4.5 доказана.
Теорема 4.6. Если в треугольнике высота и
биссектриса, выходящие из одной вершины, совпада-
ют, то такой треугольник является равнобедренным.
С Если высота BD — биссектриса треугольника
АВС, то треугольники ABD и BDC равны согласно
п.2) теоремы 4.4. И мы вновь получаем, что АВ = СВ,
т.е. треугольник АВС — равнобедренный. Теорема 4.6
доказана. И
Теорема 4.7. Если в треугольнике высота и
медиана, выходящие из одной вершины, совпадают, то
такой треугольник является равнобедренным.
74
щие утверждения.
A D
Рис.4.18
□ Пусть высота BD — медиана треугольника АВС .
Тогда AD = DC, и треугольники ABD и CBD равны
согласно п.1) теоремы 4.4. Следовательно, АВ = СВ, и
треугольник АВС — равнобедренный. Теорема 4.7 до-
казана. И
Из теоремы 4.5 непосредственно вытекают следую-
Следствие 1. Если в
треугольнике все углы равны, то
такой треугольник является рав-
носторонним.
Докажите это следствие са-
мостоятельно.
Следствие 2. Катет
прямоугольного треугольника, ле-
жащий против угла с градусной
мерой 30°, равен половине гипо-
тенузы.
□ Пусть в треугольнике ABD
AD = 90°, АВ =30°. На продолжении катета AD отло-
жим отрезок DC, равный отрезку AD, и соединим
точки В н С (рис.4.18). Прямоугольные треугольники
ABD и CBD равны согласно п.1) теоремы 4.4. Отсюда
следует, что
ABAD = ABCD, AABD = ACBD = 30°.
Тогда
ЛАВС = 60°, ABAC = АВСА = |(180° -60°) = 60°.
По следствию 1 треугольник АВС равносторонний,
высота BD является также и его медианой. Значит,
AD=-AC =-АВ.Ъ
2 2
Докажем теперь обратное утверждение.
Следствие 3. Если в прямоугольном треуголь-
нике катет вдвое меньше гипотенузы, то он лежит про-
тив угла, градусная мера которого равна 30°.
75
□ Пусть в треугольнике ABD угол D — прямой
и AD = — АВ . На продолжении отрезка AD отложим
отрезок DC, равный отрезку AD (рис.4.18). Тогда
AC=2AD = АВ.
Кррме того, в треугольнике АВС отрезок BD является
одновременно высотой и медианой. По теореме 4.7 за-
ключаем, что треугольник АВС равнобедренный с осно-
ванием АС, т.е. АВ = ВС. Но так как АВ = АС, то
этот треугольник — равносторонний, все утлы которого
равны 60°. Поскольку BD — высота этого треугольника,
то она же является его биссектрисой. Значит,
Рис.4,19
ZABD =^(ХАВС)=^~ = 30°.
Теорема 4.8. Если в треугольнике биссектриса
и медиана, выходящие из од-
ной вершины, совпадают, то
такой треугольник является
равнобедренным.
□ Пусть в треугольни-
ке АВС отрезок BD являет-
ся одновременно биссектри-
сой и медианой. Отложим на
луче BD отрезок DBX, рав-
ный отрезку BD, и соединим
точку Вх с точками А и С
(рис.4.19). Тогда
&ADB = &CDBX и
по первому признаку равенства треугольников. Значит,
Z1 = Z4, Z2 = Z3.
Однако Zl = Z2, откуда следует, что
Z1 = Z2 = Z3 = Z4.
Кроме того, из равенства треугольников следует, что
ВС = ABV
В треугольнике АВВХ Zl =Z3, и из теоремы 4.5 следу-
ет, что он равнобедренный. Таким образом,
АВ = АВХ = ВС.Ъ
76
Теоремы, обратные к утверждениям 3), 4), 5) теоре-
мы 4.1, будут доказаны позднее.
§ 4.5. СРАВНЕНИЕ СТОРОН И УГЛОВ
ТРЕУГОЛЬНИКА
Теорема 4.9. В треугольнике против большей
стороны лежит больший угол, и наоборот, против боль-
шего угла лежит большая сторона.
□ Пусть в треугольнике АВС известно,
что АВ>АС. Отложим на стороне АВ отрезок AD,
равный АС (рис.4.20). Тогда, так как AD<AB, то точ-
Рис. 4.20
ка D лежит между точка-
ми Л и В, и поэтому
луч CD лежит внутри уг-
ла АСВ . Очевидно, что тре-
угольник ADC — равнобед-
ренный, значит Z1=Z2.
Однако угол 1 — часть угла
АСВ, Значит, угол 2 мень-
ше утла АСВ . Угол 2 явля-
ется внешним для треутоль-
ника BDC. По теореме 3.7
имеем:
Z2 = Z3+ZB, т.е. Z2>ZB.
Таким образом,
ЛАСВ>АВ,
Второе утверждение теоремы докажем методом от
противного.
Допустил, что ZACB>Z.B и АВ<АС. Если АВ =
= АС, то Z2? = ААСВ по теореме 4.1. Если же АВ <АС,
то из доказанного выше следует, что АВ>ААСВ. В
каждом случае получили противоречие с услови-
ем, что ААСВ >АВ. Значит, наше допущение о том,
что АВ<АС, ложно. Следовательно, из неравенства
ZACB >ЛВ вытекает неравенство АВ>АС. И
Следствие 1. В тупоугольном треугольнике
против тупого угла лежит наибольшая сторона.
77
Следствие 2. Гипотенуза прямоугольного тре-
угольника больше катета.
Докажите эти следствия самостоятельно.
Пусть г! — конец этого
В
Рис. 4.21
§ 4.6. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Перпендикуляр. Проекция точки на прямую. Пусть
точка А не лежит на прямой а. Проведем отрезок АН,
перпендикулярный прямой а.
отрезка, лежащий на пря-
мой а (рис.4.21). Точка Н
называется проекцией точ-
ки А на прямую Л, отре-
зок АН — перпендикуля-
ром, опущенным из точки А
на прямую а. Точка Н на-
зывается также основанием
перпендикуляра АН.
Напомним, что длина
перпендикуляра АН являет-
ся расстоянием от точки А до прямой а.
Проекцией точки Т, лежащей на прямой а, на эту
же прямую считается сама точка Т.
По теореме 3.9 из точки А можно опустить на пря-
мую а лишь один перхтэндикуляр.
Наклонная. Проекция наклонной на прямую. Отре-
зок АВ, для которого точка А не лежит на прямой а, а
точка В лежит на прямой а, называется наклонной,
проведенной из точки А на прямую а, если отрезок АВ
не перпендикулярен прямой а. Точка В в этом случае
называется основанием наклонной АВ. Отрезок ВН
называется проекцией наклонной АВ на прямую а, со-
держащую этот отрезок.
Очевидно, что треугольник АВН — прямоугольный.
Тогда справедливо следующее утверждение, которое не-
посредственно вытекает из следствия 2 теоремы 4.9.
Теорема 4.10. Наклонная, проведенная к пря-
мой из произвольной точки, не лежащей на прямой,
78
всегда больше перпендикуляра, опущенного из этой же
точки на прямую, и всегда больше проекции наклонной.
В этой теореме утверждается, что АВ >АН и
АВ >ВН (рис.4.21). Докажите это самостоятельно.
Следующая теорема устанавливает связь между на-
клонными, проведенными из одной точки, и их проек-
в2 Bi н
Рис. 4.23
Теорема 4.11. Если из одной точки проведены
две наклонные к прямой, то большая наклонная имеет
большую проекцию, а меньшая наклонная — меньшую
проекцию. Равные наклонные, проведенные из одной
точки к прямой, имеют равные проекции.
О Пусть точка А лежих вне прямой а и АН JLa
(рис.4.22). Для произвольной наклонной АВ рассмотрим
наклонную АС такую, что НВ = НС и точки В и С яв-
ляются различными. Так как АН является одновременно
высотой и медианой треугольника АВС, то по теоре-
ме 4.7 имеем: АВ = АС. Значит, для всякой наклон-
ной АВ существует равная ей наклонная АС, причем
основания наклонных лежат по разные стороны от точ-
ки Ht а проекции этих наклонных равны. Поэтому в
дальнейшем можно считать, что основания наклонных
лежат по одну сторону от точки Н.
Пусть АВ} и АВ2 — такие наклонные, для кото-
рых НВХ<НВ2 (рис.4.23). Тогда точка Вх лежит на от-
резке НВ2. Очевидно, что ААВХН — острый, значит,
ХАВуВ^ — тупой. Согласно следствию 1 из теоремы 4.9,
79
в треугольнике ЛВ^ сторона АВ2 является наиболь-
шей, следовательно, АВХ<АВ2.
Допустим теперь, что АВ2>АВХ и HB2<HBV Тогда,
если НВХ = НВ2, то точки Вх и В2 совпадают, а значит,
совпадают и наклонные АВХ и АВ2. Если же HB2<HBV
то из доказанного следует, что АВ2<АВХ. В каждом слу-
чае получили противоречие с условием, что АВ2>АВХ.
§ 4.7. НЕРАВЕНСТВО ТРЕУГОЛЬНИКА
Т е о р е м а 4.12. Во &
всяком треугольнике каждая Лч
сторона меньше суммы двух / \Х.
других сторон. / у х.
□ Отложим на про- / I X.
должении стороны АС в / \
треугольнике АВС отрезок / 1_____< х
CD, равный СВ (рис.4.24). А С D
Тогда BCD — равнобедрен-
ный треугольник, в котором Рис. 4.24
Z1 = Z2, значит, Z.2<ZABD. По теореме 4.9 в тре-
угольнике ABD имеем:
AB<AD.
Однако
AD = AC +CD = AC + СВ.
Отсюда получаем, что
АВ<АС + CB.U
Можно доказать, что в любом треугольнике АВС
справедливо неравенство:
|ЛС-ВС|<ЛБ.
Докажите это самостоятельно.
Следствие 1. Для любых точек А, В, С, не
лежащих на одной прямой, имеют место неравенства:
АВ<АС+СВ, АС<АВ+ ВС, ВС<ВА+АС.
80
Каждое из этих неравенств называется неравенст-
вом треугольника. Напомним также, что если точка С
лежит на отрезке АВ, то АВ = АС + СВ.
Следствие 2. Во всяком многоугольнике каж-
дая сторона меньше суммы всех других сторон.
□ Пусть АхА2 ... А*— некоторый Л-угольник, тогда
из неравенства треугольника имеем, что
л’
Аналогично
откуда
т л2л3 ’ УА3УАн
Продолжая эти рассуждения, получим:
Следствие 3. Если для трех точек А, В, С
выполняется равенство AC =АВ +ВС, то эти точки
лежат на одной прямой, причем точка В лежит между
точками А и С.
Докажите это самостоятельно.
§ 4.8. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 4.1. Доказать, что угол при основании рав-
Рис.4.25
нобедренного треугольника
равен углу между биссектри-
сами внешних углов треуголь-
ника, прилегающих к основа-
нию.
ZS Пусть АС — осно-
вание равнобедренного тре-
угольника АВС, углы CAD
и АСЕ — внешние углы
при основании, биссектри-
сы которых пересекаются в
точке М (рис.4.25). Обоз-
начим угол ВАС через а.
По теореме 4.1 угол ВСА также равен а. Значит,
ZCAD = ZACE = 180°-а.
81
Рис. 4.26
Так как AM и СМ — биссектрисы этих углов, то
180°-а
Z.MAC = Z.MCA =--------.
2
По теореме о сумме углов треугольника имеем:
АМ = \Ю-АМАС-ЛМСА =
1ОЛ. 180’-а 180’-а
= 180-----------------= а . ▲
2 2
Пример 4.2. Доказать равенство треугольников АВС
и АХВХСХ1 если высота АН одного треугольника равна высо-
те АХНХ другого треугольника и ZB=ZBlr ZC=ZCj.
ZS Данные треугольники изображены на рис.4.26. Рас-
смотрим прямоугольные треугольники АСН и АХСХНХ.
По условию АН = AXHV ZC = ZCP По теореме 4.4 эти
треугольники равны по катету и противолежащему ост-
рому углу. Тогда АС = АХСХ. Аналогично равны прямо-
угольные треугольники АВН и АХВХНХ, откуда следует,
что АВ = АХВХ. Из теоремы о сумме углов треугольни-
ка следует также, что ABAC = АВХАХСХ. Таким образом,
треугольники АВС и АХВХСХ равны по первому призна-
ку равенства треугольников. Ж
Пример 4.3. Отрезок АВ соединяет вершину А тре-
угольника АВС с точкой D на стороне ВС. Доказать, что
длина AD меньше большей из сторон треугольника АВС.
ZX Из теоремы о сумме смежных углов следует, что
один из углов ADC или ADB не является острым. Пред-
82
положим, что угол ADC больше или равен 90°
(рис.4.27). Тогда из следствий 1 и 2 теоремы 4.9 по-
лучаем, что в треугольнике ADC AC>AD. Таким обра-
зом, AD меньше и наибольшей стороны треугольни-
ка АВС. А
Пример 4.4. На каждой стороне выпуклого много-
угольника выбрано по одной точке и они последовательно со-
единены. Доказать, что периметр образовавшегося много-
угольника меньше периметра данного многоугольника.
Пусть на сторонах АХА2, А2А3, Ап^Ап, АпАх
выпуклого многоугольника АхА2...Ап взяты точки Д,
В2, .... В„_р Вп соответственно (рис.4.28). Применим не-
равенство треугольника для каждого из треугольни-
ков BiB2A2, В2В3А3, .... Вп_}ВпАп, ВпВхАх. Получаем:
В, В, <В, А2 + А, В2,
В2В3<В2А3 + А3В3,
Л J Ла О J J
Складывая почленно эти неравенства, имеем:
<( Д Л2 "I" В1А1) 4- (А2В2 4- В2А3) 4- (А3В3 4- В3А4) 4-... 4-
Пример 4.5. В равностороннем треугольнике АВС
на сторонах АВ, АС, ВС выбраны точки М, Р, N так,
83
что AM '.MB=BN *NC=CP :РЛ=2 :3 . Доказать, что треуголь-
ник MNP также равносторонний.
Zs Очевидно, если АВ = ВС = АС = а, то
AM = BN =СР = -а,
5
ВМ = NC = AP=-a
5
(рис.4.29). По теореме 4.2
Z4 = ZB =ZC = 60°.
Рассмотрим треугольни-
ки АМР , BMN и CNP. В
них
AP=BM=CNt
АА = ЛВ = Х.С.
Рис.4.29
По первому признаку равенства треугольников эти тре-
угольники равны. Значит, MN = NP = РМ. Ж
Рис.4.30
Пример 4.6. Доказать, что если основание, высота и
медиана, проведенные к этому основанию, одного треугольни-
ка соответственно равны основанию, высоте и медиане, про-
веденным к этому основанию, другого треугольника, то такие
треугольники равны.
Zs На рис.4.30 в треугольниках АВС и АХВХСХ рав-
ны основания ВС и ВХСХ, медианы АМ и AXMV высо-
ты АН и АХНХ (случаи, когда точки Н, Нх совпадают с
одной из вершин треугольников или лежат на продолже-
84
ниях оснований ВСt ВХСХ9 рассмотрите самостоятельно).
В прямоугольных треугольниках АНМ и АХНХМХ имеем:
АН = АХНХ, АМ=АХМХ.
Значит, эти треугольники равны по гипотенузе и катету
по теореме 4.4. Отсюда следует, что МН = МХНХ, Так
как СМ =СХМХ, то НС = НХСХ. Аналогично, посколь-
ку МВ = МХВХ, то НВ = НХВХ,
Рассмотрим далее прямоугольные треугольники АНВ
и АХНХВХ. В этих треугольниках
AH~AXHV НВ = НХВХ.
Значит, они равны по двум катетам. Отсюда следует,
что АВ — АХВХ. Треугольники АНС и АХНХСХ равны, от-
куда следует, что АС = АХСХ. Таким образом, в треуголь-
никах АВС и АХВХСХ выполняются условия
AB = AXBV АС = АХСХ, ВС = ВХСХ.
т.е. они равны по третьему признаку равенства треуголь-
ников.
Пр и м е р 4.7. Доказать равенство треугольников по
двум углам и биссектрисе одного из них.
Пусть в треугольниках АВС и АХВХСХ отрез-
ки AL и AXLX являются биссектрисами, причем
(рис.4.31). По теореме о сумме углов треугольника
85
ZALB = 1W°-ZLAB -ZB = 18O°--ZA-ZB
2
АД = 180°--ZZ-ZA.
Значит,
ЛАЬВ = ЛАХ Lx Вх.
Рассмотрим треугольники ALB и AXLXBV В них
AL = AXLX, Z.LAB -AL.AXBV AALB ^ZAXLXBX.
Значит, эти треугольники равны по второму признаку ра-
венства треугольников. Отсюда следует, что АВ — АХВХ.
Тогда ДАВС = ЛАХВХСХ также по второму признаку ра-
венства треугольников. Ж
Пример 4.8. Пусть две высоты АНХ и ВН2 треуголь-
ника АВС пересекаются в точке Н. Известно, что АНХ—ВН2.
Доказать, что треугольник АНВ
равнобедренный.
Рассмотрим прямо-
угольные треугольники АНХВ
и АН2В (рис.4.32). В них ги-
потенуза АВ — общая, а кате-
ты АНХ, ВН2 равны. Следова-
тельно, эти треугольники рав-
ны по гипотенузе и катету. От-
сюда следует, что
ZHAB = ZHBA .
По теореме 4.5 треугольник АВН равнобедренный. ▲
Пример 4.9. В треугольнике АВС высота AM не
меньше стороны ВС, а высота ВН не меньше стороны АС.
Найти градусные меры углов треугольника АВС.
ZS Предположим сначала, что угол С треугольника
АВС не является прямым (рис.4.33). Рассмотрим прямо-
угольные треугольники АМС и ВНС. По следствию 2
теоремы 4.9 имеем:
АМ<АС, ВН<ВС.
По условию ВС <АМ, АС <ВН. Из неравенств
86
следует, что AM <ВН, а из неравенств
ВН<ВС, ВС<АМ
следует, что ВН<АМ. Мы пришли к противоречию.
Значит, ZC = 90°. Тогда точки М, Н и С совпадают
(рис.4.34). Из условия следует, что АС<ВН, т.е.
АС <ВС. Кроме того, ВС <АМ, т.е. ВС <АС.
Отсюда АС—ВС. Таким образом, треугольник АВС
является прямоугольным и
равнобедренным, т.е.
ZC = 90°, ZZ = ZB=45°. ▲
Пример 4.10. В тре-
угольнике АВС стороны продол-
жены и проведены биссектрисы
всех внешних углов, пересекаю-
щиеся в точках Ia, 1Ь, 1С. Дока-
зать, что треугольник IaIbIc яв-
ляется равнобедренным тогда и
только тогда, когда треугольник
АВС является равнобедренным.
На рис,4.35 лучи В1а. С1а — биссектрисы углов
СВЕ и BCD. внешних соответственно к углам АВС
и АСВ треугольника АВС. Пусть
Тогда
ZCBE =180°-р, ZDCB = 180°-у
и, так как В1а, С1а — биссектрисы этих углов, то
87
ZIBC = 90°-—, Z/ CB = 90°-—.
2 2
По теореме о сумме углов треугольника имеем:
Zl = 180°-(90°-—)-(90°-—) = ^ +1 = 90°-—.
2 2 2 2 2
Аналогично
ZL = 90°-—, ZZ. = 90°-—.
ь 2 с 2
Очевидно, условие а = Р равносильно условию
откуда и следует утверждение задачи. Ж
§ 4.9. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
4.01. В равнобедренном треугольнике основание вдвое
меньше боковой стороны, а периметр равен 50 см. Найти сто-
роны треугольника.
4.0 2. В равнобедренном треугольнике АВС с основани-
ем ВС проведена медиана ААХ. Найти ее длину, если периметр
треугольника АВС равен 32 см, а периметр треугольни-
ка АВАХ равен 24 см.
4.0 3. В равнобедренном треугольнике величина угла при
основании на 30° меньше величины угла при вершине. Найти
углы треугольника.
4.0 4. Может ли угол при основании равнобедренного тре-
угольника быть: а) тупым? б) прямым?
4.0 5. Доказать, что два прямоугольных треугольника рав-
ны, если равны их высоты, опущенные на гипотенузу, и ост-
рый угол одного треугольника соответственно равен острому
углу другого.
4.0 6. Доказать, что каждая точка на биссектрисе равнобед-
ренного треугольника, проведенной к основанию, равноудалена
от концов этого основания.
4.0 7. Всегда ли два прямоугольных треугольника равны,
если катет одного треугольника соответственно равен катету
другого и острый угол одного треугольника соответственно ра-
вен острому углу другого?
88
4.0 8. В равнобедренном треугольнике АВС сторона АВ
— основание, а точки Л, и Д — середины боковых сторон. До-
казать, что треугольник AtBjC — равнобедренный.
4.0 9. Доказать, что если в равнобедренном треугольнике
градусная мера одного из углов равна 60°, то этот треугольник
— равносторонний.
4.10 . Пусть Р — периметр выпуклого четырехугольни-
ка, L —сумма его диагоналей. Доказать, что L<P<2L.
4.11 . В треугольнике АВС на сторонах ВС, СА и АВ вы-
браны точки Av Ди Сх так, что
ВАХ _ СВ} _ACj_2
АХС ВХА СХВ
Доказать, что
ААХ +ВВх + ССх<-^->
где р — полупериметр треугольника АВС .
4.12 . В треугольнике длины двух сторон равны 5,12
и 0,63. Найти длину третьей стороны, если известно, что она
является целым числом.
4.13 . Доказать, что в треугольнике каждая сторона меньше
его полупериметра.
4.14 . Доказать, что сумма высот треугольника меньше его
полупериметра.
4.15 . В равнобедренном треугольнике АВС с основани-
ем ВС проведены высоты ВН2 и СН3. Доказать, что
АН2 = АН3.
4.16 . В равнобедренном треугольнике АВС с основани-
ем ВС проведены биссектрисы BL2 и CL3. Доказать, что
AL2 = AL3.
^^4.17. Если две стороны и медиана, проведенная к
третьей стороне треугольника, соответственно равны двум сто-
ронам и медиане, проведенной к третьей стороне другого тре-
угольника, то такие треугольники равны. Доказать.
4.18. Доказать равенство треугольников по медиане и уг-
лам, на которые она делит угол треугольника.
4.19. Доказать равенство треугольников по двум углам и
высоте, выходящей из вершины одного из них.
89
4.20. Могут ли длины сторон треугольника образовывать
геометрическую прогрессию? Какие значения может прини-
мать знаменатель этой прогрессии?
4.21. Доказать, что в любом треугольнике медиана тс
удовлетворяет неравенству
4.22. Доказать, что в любом треугольнике выполняется не-
равенство
3 _ а + Ь + с
— р<та+ть + тс<2р, где р =----------.
4.23. Доказать, что расстояние между двумя произвольны-
ми точками, взятыми на сторонах треугольника, не превышает
его наибольшей стороны.
4.24. Отрезки АВ и АХВ} равны. Найти такую точку С,
чтобы треугольники АВС и А}ВХС были равны между собой.
4.25. В треугольнике АВС известно, что
ZJ =ZC = 50°.
Из точки С под углом 30° к основанию АС проведен во внеш-
нюю сторону отрезок CD; Z.CBD = 20°. Найти X.CAD .
4.26. В одной полуплоскости, ограниченной прямой а, за-
даны внутренние точки полуплоскости А и В. Найти на пря-
мой С1 такую точку X, чтобы сумма АХ 4- ВХ была наимень-
шей.
4.27. На данной прямой / найти такую точку X, чтобы
для двух данных точек А и В величина АХ - ВХ была наи-
меньшей. Всегда ли задача имеет решение?
4.28. На стороне АС треугольника АВС задана точка D.
Проведен отрезок BD. Доказать, что
АВ + BC<2BD + АС .
90
ГЛАВА 5
ДВИЖЕНИЯ НА ПЛОСКОСТИ
§5.1. ОСНОВНЫЕ ВИДЫ ДВИЖЕНИЙ
Движением называется такое взаимно-однозначное
отображение плоскости на себя, при котором сохраняет-
ся расстояние между точками. Пусть f — движение, а А
и В — произвольные точки плоскости. Если Ах = f(A)
и ^=/(5), то А.В^АВ.
В главе 1 мы рассмотрели примеры движений только
для того, чтобы проиллюстрировать определение движе-
ния. Теперь же мы имеем возможность провести подроб-
ное исследование.
Центральная симметрия. Напомним определение
этого понятия. Пусть О — некоторая фиксированная
точка плоскости. Соединим ее с произвольной, отличной
от нее точкой А и отложим на луче АО отрезок OAV
равный отрезку ОА (рис.5.1). Определим отображение f
следующим образом:
Ал)=Л,. f(p) = o.
s' А Так как точка А — произ-
вольная точка плоскости, то
отображение f задано на
y'Ai всей плоскости. Это отобра-
жение называется симмет-
рией относительно точки О
(центральной симметрией).
^ис-5,/ Точка О называется цен-
тром симметрии, а точки А и А1 называются симмет-
ричными относительно точки О.
Докажем, что симметрия f относительно точки О
является движением.
91
□ Пусть f(A) = Av f(B) — Bx (рис.5.2) и точки А,
В, О не лежат на одной
прямой. Тогда треугольни-
ки АОВ и АХОВХ равны по
первому признаку равенства
треугольников. Значит,
АХВХ = АВ.
Предположим теперь, что
точки А, В, О лежат на од-
ной прямой. Тогда в зависи-
мости от того, лежит ли
точка О между точками А
и В или нет, имеем:
Рис.5.2
АХВХ = ОВХ — ОАХ\ = ОВ — ОА = АВ (рис.5.3)
или
АХВХ = АХО + ОВХ = ОА + ОВ = АВ (рис.5.4).
Следовательно, f является движением.
Рис.5.3
Рис. 5.4
Фигуры Ф1 и Ф2 называются симметричными отно-
сительно точки О, если симметрией относительно этой
точки фигура Ф1 переводится в Ф2, а фигура Ф2 — в
фигуру ФР Для центральной симметрии существует
только одна точка, а именно точка О, для которой
ЛоЬо.
92
Рис.5.7
Рис.5.6
Рис.5. в
Каково бы ни было отображение f плоскости на се-
бя, точку О, для которой f(d) = О, будем называть не-
подвижной.
На рис.5.5 и 5.6 изображены центрально-симмет-
ричные фигуры.
Если некоторая фигура при симметрии относительно
точки О переходит в себя, то точка О называется цен-
тром симметрии этой фигуры, а фигура называется сим-
метричной относительно точки О. На рис.5.7 и 5.8 изо-
бражены такие фигуры.
Осевая симметрия. Рассмотрим прямую CL и опреде-
лим отображение f плоскости на себя следующим обра-
зом: проведем через произвольную точку А, не лежащую
на прямой а, перпендикуляр АН и продолжим его
на отрезок НА}, равный длине этого перпендикуляра
93
Рис. 5.9
Рис.5.10
(рис.5.9). Положим /(Л) = Ах. Для всякой точки М пря-
мой а будем считать, что /(Л/) = М.
Такое отображение f называется симметрией от-
носительно прямой d (осевой симметрией). Прямая а
называется осью симметрии, а точки А и Ах — сим-
метричными относительно прямой И.
Докажем, что при осевой симметрии AxBx = ABt
где Л, -/(Л). B,-f(B). т.е. осевая симметрия явля-
ется движением.
□ Пусть точки А и В лежат в одной полуплос-
кости, ограниченной прямой а. Проведем АК _L ВВХ,
АХКХА^ВВХ. Согласно следствию 1 теоремы 3.5 ААХЦВВХ
(рис.5.10). Тогда АК = AXKV так как длины этих отрезков
равны расстоянию между параллельными прямыми ААХ
и ВВХ. Аналогично
АН = КНХ, АХН = КХНХ.
Тогда
ВК = ВНХ-КНХ и ВХКХ=ВХНХ-КНХ.
Но ВНХ = НХВХ, KHX = KXHV значит, ВК — ВХКХ.
Тогда треугольники АВК и АХВХКХ равны согласно п.1
теоремы 4.4. Таким образом, АВ = АХВХ.
Случай, когда одна из точек А и В или они обе ле-
жат на прямой а, предлагаем рассмотреть самостоятель-
94
a
Рис.5.12
Рис.5.14
нс. Рассмотрите также случай, когда точки А и В лежат
пс разные стороны от прямой а.
Итак, отображение f является движением. Я
На рис.5.11 и 5.12 изображены фигуры, симмет-
ричные относительно прямой.
Заметим также, что неподвижными точками при
симметрии относительно прямой являются точки этой
прямой и только они.
Если некоторая фигура при симметрии относительно
прямой а переходит в себя, то прямая Л называется
осью симметрии этой фигуры, а фигура называется сим-
метричной относительно прямой а.
На рис.5.13 и 5.14 изображены такие фигуры.
Параллельный перенос. Рассмотрим луч а с началом
в точке О и отрезок ООХ на этом луче. Определим ото-
бражение f плоскости на себя следующим образом.
95
1) Через точку А вне прямой ООХ проведем пря-
мую АО. Рассмотрим полуплоскость, ограниченную этой
прямой, в которой лежит луч а. В этой полуплоскости
через точку А проведем луч, параллельный а, и отложим
на нем отрезок AAV равный ООХ (рис.5.15). Положим
/(Л) = Л,.
2) Для точки А на прямой
OOV отличной от точки О,
построим такую точку Ах,
для которой ААХ = ООХ, при-
чем множество всех общих
точек лучей ООХ и ААХ яв-
ляется некоторым
(рис.5.16 и 5.17).
/W-4-
з)/(о) = о,.
лучом
Положим
Oi
О
Рис.5.16
Такое отображение называется параллельным пере-
носом вдоль луча а на длину отрезка ООХ.
Докажем, что параллельный перенос является дви-
жением.
□ Пусть А и В — некоторые точки, не лежащие на
прямой, параллельной лучу Л, и не лежащие на прямой,
содержащей луч а (рис.5.18).
96
Рис. 5.18
Рис.5.19
о
а
Положим f(A) = Alt /(в) = Вх. Соединим точку В
с точками A, Av Вх, а точку Ах — с точками А и Вг То-
гда в треугольниках АВАХ и АХВВХ имеем:
ААХ = ВВХ = ООХ,
АВ — общая сторона, Zl = Z2 согласно теореме 3.5.
Значит, эти треугольники равны по первому признаку
равенства треугольников. Таким образом, АХВХ = АВ.
Допустим теперь, что точки А и В лежат на пря-
мой, параллельной ООг, Тогда АА} = ВВ} = ОО}. Если од-
на из точек А и В, например, точка В (рис.5.19), лежит
между А и Av то
-----• А} Д = ВВ} - Д в,
о Oj AB = AAi-AJB,
откуда АХВХ = АВ.
Если же точка В не ле-
* * • жит на отрезке AAV а точка
А А/ В В [ А г>г>
А не лежит на отрезке ВВХ,
то
Рис.5.20 АВ = ААХ + АХВ,
АХВХ = АХВ + ВВХ
и вновь АХВХ = АВ (рис.5.20).
97
Рис.5.21
Рис.5.22
Аналогичные рассуждения проводятся также в
случае, когда точки А и В лежат на прямой ООХ. Таким
образом, отображение f является движением. И
Поворот. Пусть О — фиксированная точка плоско-
сти. Для произвольной точки А плоскости определим
отображение f плоскости на себя таким образом: отло-
жим от луча ОА по (против) часовой стрелке луч, обра-
зующий с лучом ОА угол ф, и на этом луче отложим
точку А так, чтобы выполнялось равенство: ОАХ = ОА.
Положим (рис.5.21). Такое ото-
бражение называется поворотом вокруг точки О по
(против) часовой стрелке на угол ф.
Очевидно, что при повороте на угол ф (^5*0°,
^5*360°) точка О и только эта точка является непод-
вижной. Если ^=180°, то f —симметрия относительно
точки О.
Докажем, что поворот f вокруг точки О на угол ф
является движением.
О Пусть f(A) = Ах, f(B) = В, и точки А, В не сов-
падают с точкой О. Пусть луч ОВ лежит внутри уг-
ла АОАХ (рис.5.22). Тогда
ZBOA = ZAXOA -АВОА j = ф- АВОАХ,
ЛВХОАХ = АВОВХ-АВОАХ = ф-ЛВОАх.
4 Зак. 687
98
Значит, ZAOB = ZAXOBX. Кроме того, ОА=ОАХ,
ОВ = ОВХ по определению поворота. Треугольники
О АВ и ОАХВХ равны по первому признаку равенства
треугольников, значит, АХВХ = АВ.
Другие возможные варианты расположения лучей
ОА, ОАХ, ОВ, ОВХ, а также случай, когда одна из то-
чек А, В совпадает с точкой О, рассмотрите самостоя-
тельно.
Заметим также, что центральная симметрия является
поворотом на угол 180°.
Объединяя полученные результаты, можно сформу-
лировать следующее утверждение.
Теорема 5.1. Центральная симметрия, осевая
симметрия, параллельный перенос и поворот являются
движениями.
§ 5.2. СВОЙСТВА ДВИЖЕНИЙ.
ГРУППА ДВИЖЕНИЙ НА ПЛОСКОСТИ
Теорема 5.2. Точки А, В, С, лежащие на пря-
мей, при движении переводят в точки А}, В}, Сх, лежа-
щие также на некоторой прямой. При этом, если точ-
ка В лежит между точками А и С, то точка Вх также
лежит между точками Ах и Сх.
□ Пусть точки А, В, С лежат на одной прямой,
причем точка В лежит между точками А и С. Тогда
АС=АВ+ВС.
Так как f — движение, то
АХСХ = АС, АХВХ = АВ, ВХСХ=ВС.
Значит, АХСХ = АХВХ + ВХСХ. Тогда согласно следствию 3
теоремы 4.12 точки Ах, Вх, Сх лежат на одной прямой,
причем точка Вх лежит между точками Ах и Сх. Я
Следствие. При движении прямые переходят в
прямые, лучи — в лучи, а отрезки — в отрезки.
99
Из аксиомы 1.16 следует также, что при движении
сохраняются углы между лучами.
Композиция движений. Рассмотрим два движения f
и g. Пусть для произвольной точки А
f(A) = Av g(j]) = ^2.
Определим отображение плоскости h= gof равенст-
вом: Ji(a) = А2.
Определение. Отображение go f называется
композицией движений g и f.
Для композиции движений g и f справедливо сле-
дующее утверждение.
Теорема 5.3. Композиция движений g и f яв-
ляется движением.
□ Очевидно, что для произвольных точек А и В от-
резки А2В2, AxBv АВ равны, где Ах= f(A), A2 = g(Ax),
Вх= f(B), B2 = g(Bx). Кроме того, если А и В — раз-
личные точки, то точки А2 и В2 также различны.
Пусть теперь А2 — некоторая точка плоскости. То-
гда, так как g —движение, то А2 = g(Ax), где Ах — так-
же некоторая точка плоскости. Поскольку f является
движением, то Ах = f(A) для некоторой точки А плоско-
сти. Значит, A2 = (g° f)(A), т.е. отображение g°f яв-
ляется взаимно-однозначным отображением плоскости
на себя. И
Следствие. Пусть Фр Ф2, Ф3 — произволь-
ные фигуры. Тогда, если Ф!=Ф2 и Ф2=Ф3, то Ф^Фз .
□ По условию существуют наложение f фигуры Ф1
на Ф2 и наложение g фигуры Ф2 на Ф3. Эти наложе-
ния являются движениями. Рассмотрим композицию
h = go f. По предыдущей теореме h также является
движением. Проверим, что h является наложением фи-
гуры Ф1 на фигуру Ф3. В самом деле, для каждой точки
100
А фигуры Ф| имеем: f(A) = Av где А} принадлежит
фигуре Ф2, g(Ax) = A2, где Л2 принадлежит фигуре Ф3,
откуда следует, что h(A) = g(Ax) является точкой фигуры
Ф3. Наконец, для каждой точки С фигуры Ф3 найдется
такая точка В фигуры Ф2, что g(B) = C, а для точки В
найдется точка А фигуры Фр для которой /(Л)-в.
Значит h(А) = g(B) = С.
По определению наложения движение h является
наложением фигуры Oj на фигуру Ф3. И
Напомним, что отображение 8 , для которого е(л) =
= А для каждой точки А плоскости, называется тожде-
ственным. Это отображение является движением,
причем 8 ° У* = f о s = f для всякого движения f.
Определение. Отображение называется
обратным к движению f, если /’~1(Л1)=Л при выпол-
нении равенства /’(Л)=Л1.
Сформулируем еще один результат, доказательство
которого рекомендуется провести самостоятельно.
Теорема 5.4. Обратными движениями для цен-
тральной и осевой симметрий, параллельного переноса
и поворота являются соответственно центральная и осе-
вая симметрии, параллельный перенос и поворот.
Теорема 5.5. Для операции композиции движе-
ний справедлив сочетательный закон, т.е. для любых
движений f, g, h имеет место равенство
(/og)oA = /o(goA).
□ Для произвольной точки А положим, что
Й(Л) = ЛР g(Ai')=A2, f(A2) = A3.
Тогда:
(f°g)o^) = (f°g)(Al) = f(g(Al)) = f(A2) = A3
И
101
/ “ (g »/>Х л) = /((g « А)( л)) = /(g(A( Л))) -
=/(«(л,))-/(4)-л,.и
Понятие о группе. Группа движений плоскости. Мы
показали, что для операции композиции на множестве G
всех движений плоскости выполняются следующие свой-
ства:
1) множество G замкнуто относительно операции
композиции движений, т.е. для всяких элементов f
и g, принадлежащих G, элемент f°g также принад-
лежит G\
2) для операции композиции движений имеет место
сочетательный закон;
3) во множестве G существует единичный эле-
мент 8 относительно операции композиции движений;
4) для всякого элемента f множества G существует
обратный элемент У”1, принадлежащий G.
Множество, обладающее свойствами 1)—4) относи-
тельно какой-либо операции, называется группой.
Множество всех движений плоскости относительно
операции композиции образует группу, которая называ-
ется группой движений плоскости.
§ 5.3. ДВИЖЕНИЯ И НАЛОЖЕНИЯ
Установим связь между понятиями движения и на-
ложения для треугольников.
Теорема 5.6. Всякое движение является нало-
жением данного треугольника на некоторый треуголь-
ник.
□ Пусть f — произвольное движение плоскости.
Рассмотрим произвольный треугольник АВС и поло-
жим:
4=/(л),в,=/(в),с,=/(с).
Тогда f является наложением фигуры, состоящей из то-
чек А, В, С, на фигуру, состоящую из точек Av В}1 С}.
102
По теореме 2.1 f является наложением треугольника
АВС на треугольник АХВХСХ.
Мы доказали, что при движении треугольник пере-
ходит в равный ему треугольник.
Рассмотрим теперь произвольную фигуру Ф и дви-
жение Составим фигуру Ф! из образов f(A) всех
точек фигуры Ф. Непосредственно из определения нало-
жения следует, что f является наложением фигуры Ф
на ФР Таким образом, доказано следующее утвержде-
ние:
Теорема 5.7. При движении всякая фигура пе-
реходит в равную ей фигуру.
Теорема 5.8. Пусть даны два равных треуголь-
ника АВС и ДДС] с соответственно равными сторо-
нами АВ и AXBV АС и АХСХ, ВС и ВХСХ. Тогда суще-
ствует единственное движение f , для которого:
/(Л)=Д, /(в)=д, /(с)=с,.
□ Существование такого движения следует из ак-
сиомы 1.18. Пусть g — движе-
ние, при котором также
g(A) = Л„ g(B) = В„
g(C) = C,.
Докажем, что g = f.
Допустим противное. Тогда
существует такая точка М, для
которой
= g(M)=M2
Рис.5.23 и точки А/р М2 — различные.
Так как fug являются движениями, то
'AM •AM,, АМ = А.М2,
Д 1 Д
откуда
АХМХ = АХМ2,
Значит, либо точка Ах — середина отрезка Мх М2, либо
треугольник АХМХМ2 равнобедренный (рис.5.23).
103
Во втором случае проведем высоту АХТ треугольни-
ка МХАХМ2. Тогда АХТ также является медианой. Таким
образом, в обоих случаях точка Ах лежит на прямой а,
перпендикулярной отрезку МХМ2 и проходящей через
середину этого отрезка.
Аналогично доказывается, что на прямой а лежат
точки j?j и Ср
Значит, точки Ах, Вх, Сх лежат на одной прямой, что
невозможно. Таким образом, совпадение движений f
и g доказано.
Теорема 5.9. Пусть треугольники АВС и
АХВХСХ равны и f является наложением треугольни-
ка АВС на треугольник АХВХСХ. Тогда /(л), /(в),
/(С) являются вершинами треугольника АХВХСХ.
Рис.5.2 4
□ Обозначим Л2 = /’(Л), B2=f(B), C2 = f(C).
Предположим, что какая-нибудь из точек А2, В2, С2, на-
пример, точка А2, является внутренней точкой треуголь-
ника ДВ]С] (рис.5.24). Точки В2 и С2 либо лежат на сто-
ронах треугольника А^С^, либо являются также внут-
ренними точками треугольника Так как f явля-
ется движением, то АВ = А2В2, ВС = В2С2, АС = А2С2.
104
Треугольники АВС и А2В2С2 равны по третьему
признаку равенства треугольников. Значит, по теоре-
ме 2.1 f является наложением треугольника АВС на
треугольник А2В2С2, Так как точка А2 является внутрен-
ней точкой треугольника AXBXCV то, очевидно, только
две точки треугольника А2В2С2 могут лежать на сторо-
нах треугольника Л^Ср Итак, из трех вершин Лр Вх,
С1 только две принадлежат треугольнику А2В2С2, но это
невозможно, поскольку f является наложением тре-
угольника АВС на треугольник АХВХСХ.
Допустим, что точки А2, В2, С2 лежат соответствен-
но на сторонах 4BP BjCp СХАХ треугольника АХВХСХ
(рис.5.25), но не совпадают с точками Лр Вх, СР По не-
равенству треугольника
А2В2<А2Вх 4- ВХВ2,
£ <£ л» 1 1 £
Складывая почленно эти неравенства, имеем:
что невозможно, поскольку f является движением.
105
Наконец, допустим, что одна из точек А2, В2, С2,
например, точка А2, совпадает с вершиной Av а точ-
ки В2 и С2 лежат на стороне В}СХ (рис.5.26). Тогда:
Л1В2<ДВ1 4- ВХВ21
1 11 IX»
Отсюда
и мы снова приходим к противоречию.
Итак, точки А2, В2, С2 должны совпасть с вершина-
ми А}, В}, С,.
Приведем без доказательства более общее утвержде-
ние:
Теорема 5.10. Пусть f — наложение много-
угольника АхА2...Ап на многоугольник ВхВ2...Вп. Тогда
точки /(4). /(4)........ /(4.) являются вершинами
многоугольника В} В2... Вп.
§ 5.4. ТЕОРЕМА ШАЛЯ О СТРУКТУРЕ ГРУППЫ
ДВИЖЕНИЙ
В §5.1 было установлено, что тождественное отобра-
жение, параллельный перенос, осевая и центральная
симметрии, а также поворот являются движениями (тео-
рема 5.1).
Оказывается, что все движения на плоскости фак-
тически исчерпываются приведенными выше. В этом па-
раграфе мы докажем теорему Шаля о структуре группы
движений.
Мишель Шаль (1793—1880) — французский мате-
матик, создал новое направление в математике — вычис-
лительную геометрию.
Теорема 5.11. (теорема Шаля). Всякое движе-
ние на плоскости является одним из следующих отобра-
жений:
106
1) поворот (включая центральную симметрию и то-
ждественное отображение);
2) параллельный перенос;
3) осевая симметрия;
4) композиция поворота и параллельного переноса;
5) композиция осевой симметрии и параллельного
переноса.
Для доказательства этой теоремы нам потребуется
несколько вспомогательных утверждений, называемых
леммами. Термин "лемма" происходит от греческого
Лтщца, встречается уже в трудах Архимеда, где приоб-
ретает современный смысл как "вспомогательная теоре-
ма".
Лемма 5.1. Пусть А и В — различные точки
плоскости, a f — некоторое движение, при котором
/’(л)=Л, /*(в)=В. Тогда либо /=£( либо f — осевая
симметрия.
□ Проведем через точку А прямую а, перпендику-
лярную прямой АВ. Пусть
с,-7(c). по теореме 5.7
Z.BAC х = Z.BAC = 90°,
поэтому точка Q лежит на
прямой С1. Так как
AC = ACV
то либо точки С и Q совпа-
дают, либо А — середина
отрезка ССХ. В первом слу-
чае
7(л)-л,/(5) = р,
7(c) = с.
Тогда по теореме 5.8 f = s .
Во втором случае (рис.5.27)
7М-л./(в)-в,7(с)=с,.
107
Но для осевой симметрии g относительно прямой АВ
выполняются условия g{A) = A, g(B) = B, g(C)=Cr
; н г.
Значит j —g-
Лемма 5.2. Композиция поворота вокруг точки О
и осевой симметрии относительно прямой, проход
через точку О, является осевой симметрией.
Доказательство этой леммы проведите самостоя-
тельно.
Лемма 5.3. Пусть
для некоторого движения t
и точки О выполняется ра-
венство t{O)=O. Тогда либо
t =8, либо t — осевая сим-
А
Рис.5.28
метрия с осью, проход
через точку О, либо t —
поворот вокруг точки О.
□ Если для движения t
все точки неподвижны, то
t = 8. Пусть А — такая точка, для которой At = /(л), и
точки А1 и А — различные.
Рассмотрим поворот g вокруг точки О на угол АХОА
такой, что g(A1) = A (рис.5.28). Тогда для движения
Л = got имеем:
А(О) = О, A(j)-g(<(4)-g(4)-J.
По лемме 5.1 либо h = 8, либо Л — осевая симмет-
рия относительно прямой ОА.
В первом случае gof = 8, т.е. t =g~\ и из теоре-
мы 5.4 следует, что t — поворот.
Во втором случае t — g~X °й, где g} — поворот во-
круг точки О, h — осевая симметрия относительно пря-
мой, проходящей через точку О. По лемме 5.2 t — осе-
вая симметрия с осью, проходящей через точку О.
Рассмотрим доказательство теоремы Шаля.
□ Пусть f — произвольное движение на плоскости.
Если все точки при этом движении являются неподвиж-
108
ными, то тогда f = 8. Пусть А — такая точка, для кото-
рой /(Л) = И„ и точки А и Aj — различные. Рассмот-
рим параллельный перенос g вдоль луча А}А на отре-
зок Ах А. Тогда для движения h=g°t имеем:
h(A) = g{f{ J)) = g( Д) = A.
Согласно лемме 5.3 возможны следующие случаи:
1) h = 8 . Тогда f = g~x — параллельный перенос;
2) h — осевая симметрия, тогда f = g1 ° Л — ком-
позиция осевой симметрии и параллельного переноса;
3) h — поворот, тогда f = g1 о h — композиция по-
ворота и параллельного переноса.
При доказательстве теоремы Шаля мы лишь один
раз использовали лемму 5.2, а именно при доказательстве
леммы 5.3. Сформулируем теперь следствие из теоремы
Шаля, доказательство которого можно осуществить ана-
логичным образом, однако без использования леммы 5.2.
Следствие. Всякое движение на плоскости яв-
ляется композицией следующих движений:
1) поворот;
2) параллельный перенос;
3) осевая симметрия.
§ 5.5. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 5.1. Известно, что для двух различных то-
чек А и В при преобразовании плоскости f справедливы ра-
венства а все остальные точки плоскости
остаются неподвижными. Будет ли f движением ?
Напомним, что движение — это преобразование
плоскости, сохраняющее расстояние между точками. Вы-
ясним, сохраняет ли расстояние между точками заданное
в условии преобразование f. Для этого проведем
прямую АВ и отложим на ней от точки В отрезок
ВС — АВ (рис.5.29). При преобразовании f образы от-
меченных точек будут такими:
4 = 5, Вх = А, С} = С.
109
Однако
AC =2 АВ,
HjQ = ВС = AB,
следовательно,
А}С!<АС,
и У не сохраняет расстоя-
ние между точками А и С,
Значит, f не является дви-
жением. Ж
Пример 5.2. Дока-
зать, что при центральной
симметрии прямая, не прохо-
дящая через центр симметрии,
прямую.
Рис.5.2 9
переходит в параллельную
Рис. 5.31
Л О А
Рис.5.30
Пусть Z — данная прямая, О — центр симмет-
рии, 1Х — образ Z при центральной симметрии.
Прямые I и Zj не совпадают. Действительно, если
бы они совпали, то произвольная точка А прямой Z пе-
решла бы в точку той же прямой. Однако тогда отре-
зок ААХ лежал бы на Z , и точка О как середина этого
отрезка также принадлежала бы Z (рис.5.30). Получили
противоречие с условием примера.
Нужно доказать, что Z ||Zr Допустим противное:
пусть эти прямые пересекаются в некоторой точке В
(рис.5.31). Эта точка не может совпасть с точкой О, Рас-
смотрим точку Bv в которую переходит точка В при
110
центральной симметрии. Точка Вх одновременно принад-
лежит прямой 7, как образу I и прямой 7 как образу 1Х
при центральной симметрии (каждая точка прямой 1}
при центральной симметрии возвращается назад на пря-
мую I). Тогда различные прямые 7 и 7, имеют две об-
щие точки В и Вх, что противоречит аксиоме 1.2. Зна-
чит, допущение ложно, и I Ц/j. Ж
Пример 5.3. Пусть А и В — различные точки,
причем при осевой симметрии f точка А переходит в точ-
ку В. Как построить ось этой симметрии?
Соединим точки А и В (рис.5.32). Ось симмет-
рии 7 перпендикулярна этому отрезку и делит его попо-
лам. Для построения 7 строим произвольный равнобед-
ренный треугольник АВС с основанием АВ, и через
вершину С проводим прямую 11АВ (это можно сделать
М
по теореме 3.9). Она пересе-
кает отрезок АВ в некото-
рой точке М. Отрезок СМ
является высотой треуголь-
ника АВС, и по свойству
равнобедренного треуголь-
ника отрезок СМ также яв-
ляется и медианой. Значит,
точка М — середина АВ, и
построенная прямая — ис-
комая. Ж
Рис. 5.3 2
Пример 5.4. Точка А
при повороте вокруг точки О
переходит в точку В. Какую линию представляет собой мно-
жество всех возможных точек О?
По определению поворота ОА = ОВ. Через
точку О проведем прямую 11.АВ (рис.5.33), и
пусть М — точка пересечения прямых I и АВ. По
теореме 4.11 равные наклонные ОА и ОВ имеют равные
проекции AM и МВ. Значит, М — середина отрез-
ка АВ, и точка О лежит на прямой I , перпендикуляр-
ной отрезку АВ и проходящей через его середину.
Ill
Рис. 5,34
Обратно, для любой точки С прямой I имеем:
ЛС=СВ,
и точка А переходит в точку В при повороте вокруг
точки С на угол АСВ ,
Таким образом, искомое множество точек есть пря-
мая, перпендикулярная отрезку АВ и проходящая через
его середину. Ж
Пример 5.5. Выполняется ли переместительный за-
кон для композиции двух симметрий относительно двух па-
раллельных прямых?
ZSk Пусть I и т — заданные параллельные прямые,
a S, и Sm — симметрии относительно этих прямых. Нам
надлежит проверить, справедливо ли равенство
SloSm = Sm oSz .
Для этого выберем произвольную точку А на
прямой I и рассмотрим точки A^ — S^Al), A2 = S/(Al)
(рис.5.34). Тогда точка А2 есть образ точки А под дейст-
вием композиции S[°Sm. Однако S^A)^ A, Sm(A) = Av
и точка Ах есть образ точки А под действием компози-
ции SmoSt. Следовательно, движения Sf°Sm и Sm °Sj пе-
реводят точку А в разные точки, и Sl°Sm^SmoSl.
Значит переместительный закон для заданных симмет-
рий не выполняется. Ж
Пример 5.6. Внутри острого угла дана точка А. По-
строить треугольник АВС наименьшего периметра, верши-
ны В и С которого лежат на сторонах угла.
112
Z\ Пусть острый угол образован лучами /и ТП,
точка А лежит внутри угла. Возьмем призвольную точ-
ку В на луче I и точку С на луче ТП (рис.5.35). Построим
Рис.5.3 5
точки Ах и А2, симметричные точке А относительно пря-
мых / и ТП. Тогда по свойствам симметрии:
АВ = АХВ, АС = А2С.
Периметр треугольника АВС равен
Р = ЛВ + ВС + СЛ = 4В + ВС + СЛ2,
т.е. периметр равен длине ломаной АХВСА2. Эта длина
наименьшая в том случае, когда точки В и С лежат на
отрезке АХА2.
Отсюда вытекает такое построение (рис.5.36). Точ-
ку А отображаем симметрично относительно прямых I
и ТП. Получаем точки Ах и А2, Соединяем эти точки. От-
резок АХА2 пересекает луч / в точке В, а луч ТП — в
точке С. Треугольник АВС — искомый, т.к. его пери-
метр
Р= АВ + ВС +СА = АХВ + ВС +СА2 = АХА2,
а это и есть наименьшая возможная длина ломаной, со-
единяющей точки Ах и А2.
Задача всегда имеет единственное решение. А
Пример 5.7. В каком месте следует построить
мост MN через реку, разделяющую деревни А и В, так, что-
бы дорога AMNB между деревнями была самой короткой?
(Берега реки считаются параллельными, а мост перпендику-
лярным к ним).
113
Рассмотрим произвольное положение моста
(рис.5.37). Из точки А проведем луч I , перпендикуляр-
ный берегам реки. Перенесем точку А вдоль Z на длину
отрезка MN (длина MN есть ширина реки d и не зави-
сит от расположения моста). Получим точку Аг Длина
дороги между деревнями равна
Z = AM + MN + NB = AxN + d + NB.
Мы воспользовались тем, что точка М при рассмотрен-
ном параллельном переносе переходит в точку N и рас-
стояние AM равно расстоянию между образами Ахи N
точек А и М. Итак, L есть сумма ширины реки и длины
ломаной AXNB, Длина дороги минимальна, когда точ-
ка N лежит на отрезке АХВ.
Отсюда вытекает такое построение (рис.5.38). Про-
водим из точки А луч Z , перпендикулярный берегам ре-
ки. Этот луч пересекает берега в точках Р и Q. Перено-
сим точку А вммъ I на расстояние PQ. Для этого на
луче Z откладываем отрезок ААХ = PQ. Соединяем точ-
ки Ах и В. Отрезок АХВ пересекает дальний от точки А
берег в точке N. Из нее опускаем перпендикуляр NM
на противоположный берег. Отрезок MN задает иско-
мое положение моста, поскольку длина дороги между де-
ревнями
L = AM + MN +NB = AxN+d + NB = AxB + d,
114
на заданных прямых. При
точка А переходит в
Рис. 5.39
а это и есть наименьшее возможное значение длины пу-
ти.
Задача всегда имеет единственное решение. Ж
Пример 5.8. Прямые I и Ш пересекаются в точке О.
Доказать, что композиция симметрий относительно прямых /
и т есть поворот вокруг точки О.
ZX Рассмотрим произвольную точку А, не лежащую
симметрии относительно Z
Симметрия относительно т
переводит точку Ах в А2,
Итак, при композиции сим-
метрий точка А переходит
в А2.
Поскольку симметрии
сохраняют расстояния, име-
ем ОА = ОАХ = ОА2. Далее,
пусть AQOP =(Х (рис.5.39).
Тогда по свойствам симмет-
рий
ZAOP=ZPOAX,
zaxoq=z.qoa2.
Отсюда
ААОА 2 = а + ХЛОР + XQOA2 = а + ХРОАх + XAxOQ =
= а + а = 2а.
Следовательно, АО = А2О, ЛАОА2=2а и от выбо-
ра точки А не зависит. Проверьте самостоятельно, что
эти соотношения выполнены и тогда, когда точка А ле-
жит на одной из заданных прямых. Значит, композиция
осевых симметрий задает поворот вокруг точки О на
угол 2а. Jk
Пример 5.9. Дан правильный треугольник. Для ка-
кой точки плоскости сумма расстояний от этой точки до вер-
шин треугольника принимает наименьшее значение?
ZX Рассмотрим равносторонний треугольник АВС
и произвольную точку Р плоскости (рис.5.40). Повернем
треугольник и точку Р на угол 60° вокруг точки А. При
этом точка С перейдет в точку В, точка В — в точку Вх,
а точка Р — в точку Рх\ треугольники АВВХ и АРРХ яв-
115
Рис.5.41
Рис. 5.40
ляются правильными. Тогда сумма расстояний от точки
Р до вершин исходного треугольника будет равна
Lp = РВ + РА + РС = РХВХ + РХР + PC,
т.е. Lp есть длина ломаной ВХРХРС. Эта длина будет
наименьшей, когда ломаная вырождается в последова-
тельные отрезки прямой.
Найдем, для какого расположения точки Р это про-
исходит. Отметим, что точка Вх лежит на высоте CD
правильного треугольника АВС (рис.5.41). Для построе-
ния искомой точки следует расположить равносторонний
треугольник АРРХ так, чтобы точки Р и Рх находились
на отрезке СВХ. Для этого из точки А проведем два луча
под углом 30° к лучу АВ. Эти два луча пересекают отре-
зок СВХ в точках Р и Рх, где точка Р лежит внутри тре-
угольника АВС . Эта точка искомая, поскольку для нее
Lp = РВ + РА + PC = Рх Вх + Рх Р + PC = Вх С,
а это и есть наименьшее возможное значение суммы
расстояний от точки Р до вершин. Здесь РВ = РХВХ, по-
скольку при повороте вокруг точки А на 60° точка Р
переходит в точку Рх, а точка В — в точку Вх.
Отметим, что построенная точка Р есть центр тре-
угольника АВС. Действительно,
АРАС = ADAC-ADAP = 60°-30° = 30° = ADAP.
116
Значит, точка Р есть точка пересечения биссектрис пра-
вильного треугольника АВС, проведенных из вершин А
и С. А это и есть центр треугольника АВС . А
§ 5.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
^^5.01. Постройте отрезок, симметричный данному от-
резку АВ относительно центра О, если:
а) точка О лежит на прямой АВ ;
б) точка О не лежит на прямой АВ ;
5.02. Изобразите отрезок АВ и точку О вне этого отрез-
ка. Начертите отрезок, образованный поворотом отрезка АВ
вокруг точки О на угол:
а) 60° против часовой стрелки;
б) 120е по часовой стрелке;
в) 180е.
5.03. Изобразите луч ОА и точку А на этом луче; нари-
суйте произвольный треугольник. Сделайте параллельный пере-
нос этого треугольника вдоль луча ОА на отрезок ОА .
5.04. Расстояние между любыми двумя точками одной фи-
гуры меньше 10 см, а расстояние между некоторыми двумя
точками другой фигуры больше 10 см. Могут ли эти фигуры
быть симметричными относительно точки?
5.05. Точка А симметрична точке Ах относительно оси /.
Верно ли, что точка Л, симметрична точке А относительно той
же оси?
5.06. Четырехугольник ABCD симметричен относительно
прямой АС. Найти стороны ВС и AD, если АВ = 1, CD = 2.
5.07. В какую фигуру перейдет полуплоскость при симмет-
рии относительно:
а) границы полуплоскости;
б) прямой, лежащей в полуплоскости и параллельной гра-
нице этой полуплоскости?
5.08 . При симметрии f относительно прямой, проходя-
щей через вершину А треугольника АВС, /(в) = С. Доказать,
что треугольник АВС — равнобедренный.
5.09 . В какую фигуру отображается полуплоскость при па-
раллельном переносе в направлении, параллельном границе по-
луплоскости?
117
5.10. На плоскости заданы точки М и О. Построить точку,
в которую переходит точка М при повороте на 30° против ча-
совой стрелки вокруг точки О.
5.11. Стороны АО и ВО треугольника ЛОВ равны.
Угол АОВ равен а. Построить образ этого треугольника при
повороте вокруг точки О на угол а по часовой стрелке.
5.12. Точка А называется неподвижной при движении f,
если /(л) = Я. Определить неподвижные точки, если движе-
ние f является:
а) центральной симметрией;
б) поворотом;
в) осевой симметрией;
г) параллельным переносом.
5.13. Выполняется ли переместительный закон для движе-
ний f и g, если:
a) f и g — осевые симметрии?
б) f — поворот, g — параллельный перенос?
5.14. Доказать, что для осевой симметрии f выполняются
равенства
f ° /о f ...of = f,
2л+1
f ° f ° f'“°f =
2n
где И — произвольное натуральное число.
5.15. Скользящей симметрией называется композиция
осевой симметрии и параллельного переноса в направлении,
параллельному оси симметрии. Укажите скользящую симмет-
рию и постройте образ заданного треугольника АВС при этом
движении.
м^5.16. Дана окружность с центром в точке О, и точ-
ки Р и Q, не лежащие на ней. Найти на окружности такие
точки А и В, для которых АЛОВ =180° и АР ||ВО.
5.17. Построить треугольник АВС, если известны точ-
ки Л и В и прямая, содержащая биссектрису угла С.
5.18. Прямоугольный треугольник А}В}С (ZC = 90°) сим-
метричен прямоугольному треугольнику АВС относительно
прямой, содержащей биссектрису угла С. Доказать, что медиа-
на СМ треугольника АВС перпендикулярна прямой А}В}.
118
5.19. Движение f каждую прямую переводит либо в себя,
либо в параллельную прямую. Доказать, что это движение яв-
ляется параллельным переносом.
5.20. Построить равносторонний треугольник с вершина-
ми на трех данных параллельных прямых.
5.21. Какие движения на плоскости удовлетворяют усло-
вию f о f = £ ?
5.22. Доказать, что композиция двух симметрий относи-
тельно параллельных прямых и /2 есть параллельный пере-
нос.
5.23. Найти нетождественное движение /, для которого
выполняется условие f о f о f = £, где п — заданное
'--------------------------*-----'
натуральное число.
5.24. Подгруппой группы G называется непустое мно-
жество, состоящее из некоторых элементов группы G и также
являющееся группой.
Доказать, что множество всех поворотов вокруг фикси-
рованной точки образует подгруппу группы всех движений на
плоскости.
5.25. Доказать, что всякое движение можно представить в
виде композиции двух или трех осевых симметрий.
5.26. Доказать, что f~l является движением и
° / = / о / = &
5.27. Доказать, что если фигура Ф, равна фигуре Ф2, то
фигура Ф2 равна фигуре Ф,.
5.28. Доказать, что композиция двух параллельных пере-
носов является параллельным переносом.
5.29. Пусть f— осевая симметрия. Доказать, что f ° f = 8.
119
ГЛАВА 6
ОКРУЖНОСТЬ И ОПИСАННЫЕ
МНОГОУГОЛЬНИКИ
§6.1. ОКРУЖНОСТЬ И КРУГ. КАСАТЕЛЬНЫЕ К
ОКРУЖНОСТИ
Окружность. Множество точек плоскости, равноуда-
ленных от некоторой точки О этой плоскости, называет-
ся окружностью (рис.6.1). Точка О называется центром
окружности. Отрезки, соединяющие точки окружности с
центром, называются радиусами окружности.
Рис.6.1
Рис.6.2
Очевидно, все радиусы равны между собой. На
рис.6.1 изображена окружность с центром в точке О.
Отрезки ОМ, ОС, ОЕ, OF — радиусы этой окружно-
сти.
Отрезок, соединяющий две точки окружности, назы-
вается хордой. На рис.6.1 изображена хорда АВ.
Хорда, проходящая через центр окружности, назы-
вается диаметром. Очевидно, что диаметр окружности
равен удвоенному радиусу. На рис. 6.1 изображен диа-
метр EF.
120
Круг. Пусть а — произвольное положительное чис-
ло. Множество точек плоскости, удаленных от точки О
на расстояние, не превышающее а, называется кругом
(рис.6.2).
Аналогично тому, как это было определено для ок-
ружности, вводятся понятия радиуса, диаметра и хорды
для круга.
Термин "радиус" происходит от латинского слова
radius — луч, термин "хор-
Р да" — от греческого слова
/^\- %ор6т|— струна, тетива, тер-
/ \ мин "диаметр" — от гречес-
I \ кого слова бгарьтро^— по-
I и I перечник. У древнегреческих
\ / математиков последний тер-
\ / мин употреблялся и в значе-
нии "диагональ".
Касательная к окружно-
Рис 6 3 сти. Рассмотрим окружность
с центром в точке О и точ-
ку Р на ней. Касательной к окружности с центром О,
проведенной через точку Р, называется прямая, перпен-
дикулярная радиусу ОР этой окружности (рис.6.3).
Теорема 6.1. Касательная имеет с окружностью
омиу общую точку.
□ Допустим, что касательная имеет с окружностью
две общие точки Р и Q. Тогда ОР и OQ — радиусы ок-
ружности. Отсюда следует, что треугольник OPQ— рав-
нобедренный. Значит, в треугольнике OPQ имеем:
Z2 = ZP = 90°,
что противоречит следствию 1 теоремы 3.7.И
Общая точка окружности и касательной называется
точкой касания.
§ 6.2. СВОЙСТВО БИССЕКТРИСЫ УГЛА
Теорема 6.2. Множество точек утла, равноуда-
ленных от его сторон, является биссектрисой данного
угла.
121
□ Пусть точка О равноудалена от сторон угла А и
лежит внутри этого угла, т.е. если ОВ Х~Ь и ОС±С,
то ОВ = ОС. Тогда прямоугольные треугольники ОАВ
и ОАС равны по теореме 4.4. Значит, угол ОАВ равен
углу ОАС , и, следовательно, АО — биссектриса угла А
(рис.6.4).
Обратно, если АО — биссектриса угла А, то тре-
угольники ОАВ и ОАС равны по теореме 4.4. Зна-
чит ОВ =ОС, т.е. точка О равноудалена от сторон уг-
ла А. М
Определение. Окружность, касающаяся сто-
рон утла, называется впи-
санной в этот угол.
Следствие!.
Биссектриса угла является
множеством центров всех
окружностей, вписанных в
этот угол (рис.6.5).
Следствие 2.
Пусть точка А лежит вне
круга, прямые АВ и АС
являются касательными к
окружности, В и С —
точки касания. Тогда АВ=АС (рис.6.6).
Докажите это утверждение самостоятельно.
122
§ 6.3. ОКРУЖНОСТЬ, ВПИСАННАЯ В
МНОГОУГОЛЬНИК
Определение. Окружность, касающаяся всех
сторон многоугольника, называется вписанной в этот
многоугольник.
В этом случае говорят также, что многоугольник
описан около данной окружности.
На рис.6.7 изображена окруж-
ность, вписанная в пятиугольник.
^1 Центр вписанной окружности обоз-
ж начается обычно через 1. Если в
Ч I многоугольник вписана окружность,
\ У1 то ее центр равноудален от всех сто-
рон многоугольника. Значит, центр
вписанной окружности лежит на
пересечении биссектрис углов мно-
Рис. 6.7 гоугольника.
Окружность, вписанная в тре-
угольник. О существовании и един-
ственности такой окружности говорится в следующей
теореме.
Теорема 6.3. Для всякого треугольника суще-
ствует одна и только одна вписанная окружность.
Центр вписанной окружности лежит на пересечении
биссектрис треугольника.
□ Пусть ALV BL2, CL3 — биссектрисы углов А, В,
С треугольника АВС, I — точка пересечения биссек-
трис ALX и ВЬ2. По теореме 6.2 точка I равноудалена
от сторон АВ и АС треугольника АВС, а также от
сторон В А и ВС этого треугольника. Тогда точка 1
равноудалена от всех сторон треугольника АВС , т.е. она
является центром окружности, вписанной в треуголь-
ник АВС.
Так как прямые ALX и ВЬ2 пересекаются в одной
точке, а точка I должна лежать на этих прямых согласно
теореме 6.2, то вписанная в треугольник АВС окруж-
ность единственна.
123
Наконец, биссектриса CL3 — это множество точек,
равноудаленных от сторон СА и СВ. Значит, точка I
лежит также на биссектрисе CL3.
Следствие. Три биссектрисы треугольника пе-
ресекаются в одной точке (рис.6.8).
Напомним, что точка I пересечения биссектрис на-
зывается инцентром треугольника.
Теорема 6.4. Пусть F, К и Т — точки касания
вписанной окружности соответственно со сторонами
АВ, ВС и СА треугольника АВС. Тогда
AF = АТ = р-а,
BF = BK = p-b,
СК = СТ = р-с,
где p = ВС-а, АС = Ь, АВ = с
(рис.6.9).
□ Пусть AF = X. Тогда согласно следствию 2 из
теоремы 6.2 имеем:
AT = AF=X,
Аналогично
BF = ВК = с-х
и
СК = СТ = а-ВК = а-(с - х) = а-с + х.
Так как АТ + ТС = АС, то получим:
х + (а- с + х) = Ь,
124
2x=b + с -a = (a + b + c)-2a = 2p-2a,
т.е.
x = p-a.
Теперь легко найти отрезки BF и СК. Сделайте
это самостоятельно. И
Окружность, вписанная в четырехугольник. Усло-
вие, при котором такая окружность существует, устанав-
ливает следующая теорема.
Теорема 6.5. В четырехугольник можно вписать
окружность тогда и только тогда, когда суммы его про-
тивоположных сторон равны.
□ Пусть М, N, Р, Q — точки касания вписанной в
четырехугольник ABCD окружности (рис.6.10). Тогда из
следствия теоремы 6.3 имеем:
AM = AQ=a\ BN=BM=b; CN=CP=c-
DP = DQ = d.
Отсюда
AB+CD = a + b + c+d = BC + AD.
Пусть теперь в четырехугольнике ABCD выполне-
но условие АВ -F CD == ВС -F AD. Докажем, что в четы-
рехугольник ABCD можно вписать окружность. Прове-
дем биссектрисы углов А и В. Они пересекаются в
точке I, равноудаленной от сторон АВ, ВС и AD
(рис.6.11). Проведем окружность, касающуюся сторон
АВ, ВС и AD. Допустим, что расстояние IT от центра
окружности до прямой CD меньше радиуса этой окруж-
ности, а отрезок IK = Г . Проведем через точку К отре-
зок CjDp перпендикулярный IK, причем точка Сх ле-
125
жит на прямой ВС, а точка D} — на прямой AD. Тог-
да C}D} — касательная к окружности, и эта окружность
вписана в четырехугольник ABC^D^ (рис.6.11). Значит,
AB+C}D}=BC} + ADV
Далее имеем:
АВ +C}DX = ВС +СС} + AD + DD},
и, следовательно,
AB+CD+QDi =
= CD + В С + СС, + DD. + A D.
Так как
AB+CD = BC + AD, то CXD} = CD + СС, + DDV
Однако, по следствию 2 теоремы 4.12
C}D}<CD + CC} + DDV
т.е. отрезок IT не может быть меньше Г .
Аналогично доказывается, что отрезок IT не может
быть больше Г (сделайте это самостоятельно). Значит,
/Г=г,
т.е. окружность вписана в четырехугольник ABCD .
§ 6.4. УГЛЫ, СВЯЗАННЫЕ С ОКРУЖНОСТЬЮ
Центральный угол. Угол с вершиной в центре ок-
ружности называется центральным.
На рис.6.12 центральным углом является угол АОВ
(заштрихованная часть пло-
скости). Он образован лу-
чами ОА и ОВ, исходящи-
ми из центра окружнос-
ти О и пересекающими ок-
ружность в точках А и В
соответственно.
В этом параграфе мы
вновь рассмотрим углы,
большие развернутого. На
рис.6.12 это угол, который
дополняет угол АОВ до
Рис. 6.12
полного угла. Обозначим его так: Z АОВ . Каждому цен-
126
тральному углу соответствует множество точек, лежащих
на окружности и принадлежащих этому углу.
Дуга окружности. Градусная мера дуги. Множество
точек окружности, принадлежащих центральному углу,
называется дугой окружности (рис.6.12). Дуга, соот-
ветствующая центральному углу ЛОВ (хАОв), обоз-
начается так: иАв(иАб). Говорят, что центральный
угол ЛОВ \AAOB ) опирается на дугу AB{<JAB ).
Градусной мерой дуги называется градусная мера
центрального угла, опирающегося на эту дугу. Градусную
меру дуги АВ обозначим, как и саму эту дугу, че-
рез иАВ.
Рис. 6.14
Рис. 6.13
Вписанный угол. Угол, вершина которого лежит на
окружности, а стороны пересекают эту окружность, на-
зывается вписанным. На рис.6.13 вписанными углами яв-
ляются углы АВС и DFE. Они опираются на дуги АС
и DE.
Теорема 6.6. Вписанный угол имеет градусную
меру, равную половине градусной меры дуги, на кото-
рую он опирается.
□ Рассмотрим три возможных случая.
1) Одна из сторон вписанного угла А проходит
через центр окружности (рис.6.14).
127
Рис. 6.15
Рис. 6.16
Рис. 6.17
Проведем радиус ОВ. Тогда в образовавшемся тре-
угольнике АОВ угол А равен углу В, так как треуголь-
ник АОВ — равнобедренный. По теореме 3.7
АВОС = 2(аа).
значит,
zS4-l(Z5OC)=l(uBC).
2) Центр О окружности лежит внутри вписанного
угла ВАС (рис.6.15).
Проведем диаметр AD. Тогда, учитывая п.1), имеем:
ABAC = ABAD + ACAD =-(uBD + uCD) = -(uBC).
2 2
3) Центр О окружности лежит вне вписанного уг-
ла ВАС (рис.6.16).
Доказательство проведите самостоятельно. И
128
Следствие!. Вписанные углы, опирающиеся на
дуги с одинаковой градусной мерой или на общую дугу,
равны (рис.6.17).
Следствие 2. Вписанный угол, опирающийся на
диаметр, является прямым (рис.6.18).
Докажите эти следствия самостоятельно.
Следствие 3. Равные дуги окружности стягива-
ются равными хордами.
□ Рассмотрим случай, когда дуги АВ и CD имеют
равную градусную меру, меныпую 180°. Пусть О —
центр окружности. Тогда треугольники АОВ и COD
равны по первому признаку равенства треугольни-
ков, поскольку
Рис. 6.19
АО = ВО = СО = DO и центральные
углы АОВ и COD равны.
Значит, АВ = CD. Случай, ко-
гда градусная мера равных дуг
больше либо равна 180°, рас-
смотрите самостоятельно. И
Угол между двумя пересе-
кающимися хордами. Рассмот-
рим окружность и точку М
внутри этой окружности. Про-
ведем хорды AD и ВС через
точку М (рис.6.19). Тогда угол
CMD — внешний угол тре-
угольника АСМ . По теореме 3.7 имеем:
ACMD =ZA + ZC = -(uCD) + -(<jAB) =
=—(uCD+<jAB).
Таким образом, угол между двумя пересекающими-
ся хордами имеет градусную меру, равную полусумме
градусных мер тех дуг, на которые опирается этот угол
и угол, вертикальный к нему.
Угол, образованный двумя секущими. Пусть А
и С — две точки, лежащие на окружности. Всякая пря-
мая, имеющая с окружностью две общие точки, называ-
ется секущей этой окружности. Очевидно, каждая хорда
129
Рис. 6.20
Рис. 6.21
окружности определяет некоторую секущую этой окруж-
ности, и каждая секущая содержит хсрду.
Допустим , что точка М лежит вне круга. Проведем
две секущие МС и MD, пересекающие окружность со-
ответственно в точках А, С и В, D (рис.6.20). Эти секу-
щие высекают на окружности дуги АВ и CD. Опреде-
лим величину угла CMD, опирающегося на дугу CD
этой окружности и содержащего дугу АВ этой окружно-
сти. Для этого соединим точки В и С. Тогда Z.CBD—
внешний угол треугольника МВС , и
ACBD=AMCB + ZM,
откуда
ZM = ZCBD-ZMCB =—(\jCD -оАВ).
Таким образом, угол между двумя секущими, пере-
секающимися в какой-либо точке вне круга, имеет гра-
дусную меру, равную половине разности градусных мер
большей и меньшей дуг, высекаемых этими секущими
на окружности и заключенными между ними.
Угол, образованный касательной и хордой, прове-
денной через точку касания. Пусть DA — касательная к
окружности, АВ — хорда, проходящая через точку ка-
сания А. Проведем диаметр АС и соединим точки В
и С (рис.6.21).
1) Рассмотрим сначала случай, когда хорда является
диаметром и угол DAC — прямой. Тогда
5 Зак. 687
130
ADAC = AABC =|(оЛС),
где <jAC — дуга, заключенная между сторонами AD
и АС угла DAC.
2) В случае, когда ADAB — острый, имеем:
ADAB = ADAC-ABAC.
Но
ADAC = AABC =-{yjAC\a ABAC = -(uBC).
2 2
Значит,
ADAB = -(иЯС)--(оВС) = -(иЛС-оВС) =
2 2 2
~^ЛВ\
Но дуга АВ — это дуга, заключенная между сторонами
угла DAB.
3) В случае, когда угол, образованный касатель-
ной AM и хордой АВ, — тупой, получаем:
АМАВ =АВАС + АСАМ = -(иВС) + -(иЛС) =
2> 2
= -(uBC +и АС) = -(и Ав).
Но дуга АВ — это дуга, заключенная между сторонами
тупого угла МАВ . Таким образом, угол, образованный
касательной и хордой, прове-
денной через точку касания,
имеет градусную меру, равную
половине градусной меры ду-
ги, заключенной между сторо-
нами этого угла.
Угол, образованный каса-
тельной и секущей. Пусть М
— точка, лежащая вне круга.
Проведем секущую МС, пере-
секающую окружность в точ-
ках А и С, и прямую MD, ка-
сающуюся окружности в точ-
Рис. 6.22
131
ке D (рис.6.22). Соединим точки D и А. Получим тре-
угольник MAD , для которого угол DAC является внеш-
ним углом. По теореме 3.7 имеем:
ADAC = AMDA + AM,
откуда
AM = ADAC - AMDA = -(yjDC) --(<jAD) =
= -(uDC-uAD).
Таким образом, угол, образованный касательной и
секущей, имеет градусную меру, равную половине раз-
ности градусных мер большей и меньшей дуг, высекае-
мых сторонами этого угла и
заключенными между ни-
ми.
Угол, образованный дву-
мя касательными. Пусть АВ
и АС — две касательные к
окружности, В и С — точки
касания (рис.6.6). Нетрудно
доказать, что
ZJ = -(oBC-u5cl.
2' 7
Сделайте это самостоятель-
но.
Найдем теперь для дан-
ного отрезка АВ и острого
угла а множество точек М,
для которых ААМВ =а.
Построим равнобедрен-
ные треугольники АОХВ и А
' Рис. 6. 23
2 В по разные стороны от
прямой АВ, в которых О] А = В = О2А = О2В, и, кро-
ме того,
АОХАВ = АО}ВА = АО2АВ = АО2ВА = 90°-а
(рис.6.23). Очевидно, что ААОХВ = ААО2В = 2а.
Проведем две окружности с центрами в точках Ох
и О2 и одинаковым радиусом, равным ОХА. Тогда гра-
дусная мера дуги АВ в каждой окружности равна 2а.
132
Пусть точка М отлична от точек А, В и лежит на ду-
ге АВ какой-либо из этих окружностей. По теореме 6.6
угол АМВ равен а. Рассмотрим теперь точкуX, лежа-
щую вне кругов Ох и О2. Без ограничения общности до-
пустим, что точки X и Ох лежат в одной полуплоскости,
э L раниченной прямой АВ.
Пусть Ах, Вх — точки пересечения соответственно
отрезков ХА и ХВ с окружностью, имеющей центр в
точке Ох. (Они могут совпадать с точками А, В). Тогда
ZAXB =-(иЛВ-оЛ1В1)<а.
Аналогично доказывается, что для точки Хх, лежащей
внутри какого-либо из этих кругов, имеет место нера-
венство: ХАХхВ> а. Мы доказали, что множество то-
чек М, для которых Z-АМВ =а, состоит из двух
дуг АВ, симметричных относительно прямой, содержа-
щей отрезок АВ, причем точки А и В в это множество
не входят. Оно изображено на рис.6.23.
§ 6.5. ОКРУЖНОСТИ, КАСАЮЩИЕСЯ ДРУГ ДРУГА
Касание окружностей. Внешнее и внутреннее каса-
ние. Пусть заданы две окружности. Говорят, что они ка-
саются друг друга или имеют общее касание, если эти
Рис. 6.24
Рис. 6.25
133
окружности имеют единственную общую точку. Эта
точка называется точкой касания окружностей.
При этом возможны два случая:
а) каждая из окружностей располагается вне другой
(рис.6.24).
б) одна из окружностей лежит внутри другой
(рис.6.25).
В первом случае говорят, что окружности имеют
внешнее касание или касаются друг друга внешним обра-
зом. Во втором случае говорят, что окружности имеют
внутреннее касание или касаются друг друга внутрен-
ним образом. Отрезок, соединяющий центры двух окруж-
ностей, будем называть их линией центров.
Условие внешнего касания. Это условие формулиру-
ется в следующей теореме.
Теорема 6.7. Две окружности имеют внешнее
касание тогда и только тогда, когда расстояние между
их центрами равно сумме радиусов. При этом точка ка-
сания окружностей лежит на линии центров.
□ Рассмотрим две окружности: одну с центром Ох и
радиусом Rx и другую с центром О2 и радиусом
Пусть сначала ОХО2 =/?1 + 7?2. Докажем, что окружности
имеют внешнее касание. Соединим центры окружностей.
На отрезке ОХО2 отложим отрезок ОХА, равный Rx
(рис.6.26). Тогда
ao,=o.o2-o.a=(r. + r2 )-/?,=r7.
Лв I 1 * Ж Лв * 1
Точка А принадлежит обеим окружностям, поскольку
расстояние от А до центра Ох первой окружности рав-
но радиусу Rx этой окруж-
ности, а расстояние от А до R
центра О2 второй окружно- »- < е
сти равно радиусу R2 этой ®2
окружности. Покажем да-
лее, что окружности не име-
ют больше общих точек. Рис. 6. 26
Действительно, на пря-
мой ОХО2 других общих то-
чек окружности иметь не могут. Допустим, что существу-
134
Рис.6.27 Рис.6.28
ет точка Ах вне прямой ОХО2, принадлежащая обеим
окружностям (рис.6.27). Тогда О2Д = R2, и в
треугольнике О1О2Л1 сторона ОХО2 равна сумме сто-
рон О} Ах и О2 Aj. Получили противоречие с допущением
о существовании общей точки Ах данных окружностей.
Значит, точка А — единственная общая точка окруж-
ностей, и она лежит на отрезке ОХО2. Окружности каса-
ются друг друга. Мы имеем здесь случай внешнего каса-
ния, поскольку для любой точки М второй окружности
справедливо неравенство:
МО}> IOXO2 —О2М= + R2 — J?2| = R}.
1 I 1 X X I X X | 1
Значит, точка M либо лежит вне первой окружности,
когда MOX>RV либо принадлежит обеим окружностям,
когда МОХ = Rx. Но в этом случае М есть точка А обще-
го касания окружностей. Итак, вторая окружность рас-
положена вне первой; аналогично доказывается, что пер-
вая окружность также находится вне второй. Значит, мы
доказали, что окружности имеют внешнее касание.
Обратно, пусть две окружности касаются друг друга
внешним образом. Обозначим через Rx и R2 их радиусы,
пусть Ох и О2 — соответственно их центры, А — точка
касания. Докажем сначала, что эта точка лежит на отрез-
ке О|О2. Допустим противное: что точка А находится
вне линии центров. Ясно, что при внешнем касании она
135
не может находиться на продолжении линии центров.
Итак, пусть точка касания А лежит вне прямой OtO2
(рис.6.28). Тогда О}А = Лг и О2А = Л2. Пусть точка А}
симметрична точке А относительно прямой О{О2. Тогда
О. А, = О.А = Л., О2А,=О2А = Л2,
и точка Ах принадлежит обеим окружностям. Значит, ок-
ружности имеют две общие точки А и Ах и не касаются
друг друга. Получили противоречие. Значит, точка каса-
ния А действительно находится на отрезке ОХО2.
Докажем теперь, что ОХО2 = Rx + R2. Действительно,
для точки А отрезка ОХО2 (рис.6.26) имеем:
ОХО2 = Ох А + АО2 = Rx + R2.
Теорема полностью доказана. И
Условие внутреннего касания. Об этом условии го-
ворится в следующей теореме.
Теорема 6.8. Две окружности имеют внутреннее
касание тогда и только тогда, когда расстояние между
их центрами равно модулю разности радиусов. При
этом точка касания лежит на продолжении линии цен-
тров.
Докажите эту теорему самостоятельно.
§ 6.6. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 6.1. В окружно-
сти проведены две параллельные
хорды. Доказать, что градусные
меры дуг, заключенных между
ними, равны.
zS Пусть АВ и CD —
параллельные хорды окружно-
сти с центром в точке О. Про-
ведем хорду AD (рис.6.29).
По теореме 3.5 углы DAB
и ADC равны. Но эти углы
являются вписанными в ок-
ружность. Значит, по теореме 6.6
Рис. 6.29
136
uAC =2(AADC), <jBD =2(ZDAB)t
откуда ясно, что kJ AC = kjBD. A
Пример 6.2. Доказать, что все хорды данной окружно-
сти, имеющие заданную длину, касаются некоторой окружно-
сти.
ZS Пусть АВ и CD — равные хорды данной дли-
ны а, проведенные в окружности с центром в точке О.
Проведем радиусы ОА, ОВ, ОС, OD и радиусы ОМ
и ON, пересекающие хорды АВ и CD соответственно
в точках Т и 5 и перпендикулярные этим хордам
(рис.6.30). Треугольники АОВ и COD — равнобедрен-
ные, и поэтому отрезки ОТ и OS являются их медиана-
ми, т.е. AT =CS =—. Тогда прямоугольные треугольни-
М
Рис. 6.30
ки АОТ и COS равны по гипотенузе и катету, откуда
ОТ — OS. Мы доказали, что
расстояния от центра окруж-
ности до хорд данной длины
равны между собой. Значит,
все хорды длины а касаются
окружности с центром в
точке О и радиусом, равным
длине отрезка ОТ. А
Пример 6.3. Пусть М,
N, Т — точки касания вписан-
ной окружности соответствен-
но со сторонами АВ, ВС, АС
треугольника АВС. Доказать,
что биссектрисы этого
треугольника перпен-
дикулярны соответст-
венным сторонам тре-
угольника АВС. Выра-
зить углы треуголь-
ника MNT через углы
треугольника АВС.
Zs Пусть в тре-
q угольник АВС впи-
сана окружность с
центром в точке I ;
М, N, Т — точки
137
касания этой окружности соответственно со сторона-
ми АВ, ВС, АС (рис.6.31). Тогда по теореме 6.3 отрез-
ки AAV BBV CQ — биссектрисы треугольника АВС.
Кроме того, по следствию 2 теоремы 6.2 имеем:
AM = АТ, BM = BN, CN=CT,
т.е. треугольники АМТ , BMN , CNT — равнобедрен-
ные. Следовательно, по теореме 4.1
АА.1МТ, BB.1MN, CC^lNT.
Из теоремы о сумме углов треугольника имеем:
ZAMT
180° -А
ZJ3MN
180° -В
откуда
ATMN =180°
180°-А 180°-В А + В пло С
----------------------— ------
2 2 2 2
Аналогично Z.NTM = 90°- —, Z.MNT = 90°- — .
2 2
Пример 6.4. Через точку Л*
вне окружности проведены два луча,
пересекающие окружность соответст-
венно в точках А и В, С и D
(рис.6.32). Градусные меры дуг АС,
CD, DB и ВА в указанном порядке
находятся в отношении 2:3:5:8. Най-
ти угол между лучами.
При некотором к>0° име-
ем:
u AC = 2к, uCD = 3k,
<jDB — 5k, <jBA = 8к.
Рис.6.32
Градусная мера всей окружности составляет 360°, по-
этому
2 к + Зк + 5 к +8 к = 360°,
откуда £=20°. Тогда uZ)B = 100°, <JAC =40°. Из ре-
зультатов §6.4 следует, что
^S = -(uDB-uAC) =-(100° -40°) =30°. Ж
2V ' 2V 7
138
Рис. 6.33
Пример 6.5. В четырехугольник с параллельными сто-
ронами AD и ВС вписана окружность. Под каким углом вид-
ны из центра этой окружности две другие стороны?
Пусть I — центр впи-
санной окружности четырех-
угольника ABCD , AD || ВС.
Тогда лучи DI, CI — биссек-
трисы углов ADC и BCD
(рис.6.33). По теореме 3.5
ABCD 4- AADC = 180°,
откуда
Z/CP + ZZDC = 90°.
Из теоремы о сумме углов
треугольника следует, что
ZCZD = 180°-90° = 90°,
т.е. сторона CD видна из точки I под прямым углом.
Аналогично доказывается, что сторона АВ видна из
точки I также под прямым углом. Ж
Пример 6.6. Из точки Р проведены к окружности две
касательные РА и РВ, а через точку В — диаметр ВС. Дока-
зать, что СА ||ОР f где О — центр окружности.
Так как РВ и РА —
касательные к окружности, то
РВ = РА, АРВО = АРАО = 90°
(рис.6.34). Треугольники РОА и
РОВ равны по двум катетам,
значит,
АРОА = АРОВ.
Очевидно, АЛОВ является вне-
шним углом треугольника АОС.
По теореме 3.7 имеем:
ААОВ = АОАС + АОСА .
Но
АЛОВ =2(ХАОР),
Рис. 6.34
а
АОАС = АОСА,
так как треугольник АОС равнобедренный. Следова-
тельно, А_АОР ~ АОАС. По теореме 3.5 прямые АС
и ОР параллельны. Ж
139
Рис. 6.35
Рис. 6.36
Пример 6.7. Найти множество точек, из которых каж-
дая сторона данного равностороннего треугольника видна под
тупым утлом.
ZS Вначале найдем множество точек, из которых
данный отрезок виден под тупым углом. Построим ок-
ружность с центром О в середине отрезка АВ и радиу-
сом ОА (рис.6.35). Тогда для любой точки X на этой ок-
ружности ZAXB =90° по следствию 2 теоремы 6.6. Рас-
смотрим произвольную точку Y вне данной окружности,
не лежащую на прямой АВ. Тогда из §6.4 следует, что
ZAYB =-(иАТВ -оСО) = -(180°-uCd)<90°.
2 2
В случае, если точка Y лежит на прямой АВ, то
ZAYB =0°. Наконец, рассмотрим произвольную точ-
ку Z, лежащую внутри круга, но не лежащую на диамет-
ре АВ. Тогда из результатов §6.4 следует, что
ZAZB =—(иEF + АТВ ) =—(иEF + 9Q°)>9Q°
2 2
и
ZAZB >90°.
В случае, если точка Z лежит на диаметре АВ, ZAZB =
= 180°. Таким образом, множество точек, из которых от-
резок АВ виден под тупым углом, совпадает с множест-
вом всех внутренних точек круга, исключая точки диа-
метра АВ.
140
Предположим теперь, что треугольник —
равносторонний. Построим на сторонах этого треуголь-
ника, как на диаметрах, три равные окружности
(рис.6.36). Так как данный треугольник равносторонний,
то эти окружности будут попарно пересекаться в верши-
нах Av А2, А3, а также в точках О2, О3, которые яв-
ляются серединами сторон треугольника (проверьте это).
Поэтому искомым
Рис. 6.37
множеством точек будет множество,
состоящее из внутренних точек
общей части построенных кру-
гов. А
Пример 6.8. Точка С дви-
жется по дуге окружности, кото-
рую стягивает хорда АВ. Найти
траекторию движения точки I, яв-
ляющейся центром вписанной ок-
ружности треугольника АВС.
ZS Рассмотрим вначале тре-
угольник АВС и описанную
около него окружность. Прове-
дем лучи, которые являются бис-
и С и пересекаются в точке I;
сектрисами углов А
пусть луч CI пересекает окружность в точке S
(рис.6.37). Углы S и В являются вписанными, опираю-
щимися на дугу АС. По следствию 1 теоремы 6.6 углы S
и В равны. Аналогично
ABAS = ABCS = ^AACB).
Так как луч AI является биссектрисой угла ВАС , то
AIAB = -(АВАС\
Значит,
AIAS = ASAB + AIAB = -(ААСВ) + -(АВАС) =
= ^(ААСВ + ABAC ) = 90°-Цав).
Далее, в треугольнике AIS имеем:
141
AAIS = 180’-ZS-ZZ4S =
180°-ZB- 90°- — (ZB)j = 90’-—(ZB).
Таким образом, AIAS = AAIS , откуда следует, что тре-
угольник AIS — равнобедренный, и SA = SI. Проведем
окружность с центром в точке S и радиусом SA. Эта
окружность пройдет и через точку В, Тогда точка I ле-
жит на дуге этой окружности, лежащей в той же полу-
плоскости, ограниченной прямой АВ, в которой лежит
точка С. Очевидно, точка I не совпадает с точками А
и В,
Обратно, пусть точка I лежит на указанной дуге.
Проведем прямую SI, пересекающую данную в условии
задачи окружность в точке С. Так как точка S делит ду-
гу АРВ пополам, то по следствию 1 теоремы 6.6
AACS = ABCS.
Далее,
AIAS = ABAS + AIAB ,
откуда
AIAB = AIAS-ABAS = AIAS -ABCS = AIAS -ACS
и
AIAC = (180° - AAIC )-AACS = AAIS -AACS .
Но поскольку SA =SI, то треугольник SAI — равно-
бедренный, откуда следует, что AIAS = AAIS . Значит,
AIAB = AIAC, т.е. луч Al является биссектрисой уг-
ла ВАС. Таким образом, точка I является точкой пере-
сечения биссектрис углов САВ и АСВ , и значит, явля-
ется центром вписанной окружности треугольни-
ка АВС . Мы доказали, что точка I описывает дугу (без
ее концов) окружности с центром в точке S, делящей
пополам дугу, которая дополняет указанную в условии
дугу до окружности. Радиус искомой дуги равен SA,
причем эта дуга лежит с точкой С в одной полуплоско-
сти, ограниченной прямой АВ. Ж
П р и м е р 6.9. Через общую точку двух окружностей
провести прямую так, чтобы окружности отсекали на ней рав-
ные хорды.
142
ZX Пусть окружности
на искомой прямой отсе-
кают равные хорды АВ
и АС (рис.6.38). Тогда точ-
ки 5 и С симметричны от-
носительно точки А.
Отсюда вытекает такое
построение. Строим сим-
метричный образ одной из
окружностей относительно
точки А. Это будет окруж-
ность того же радиуса,
центр которой симметричен
центру О} взятой окружно-
сти относительно точки Л.
Этот образ пересекает вто-
рую окружность в точках А и В. Прямая В А является
искомой.
Задача имеет единственное решение, когда окруж-
ности пересекаются в двух точках; не имеет решений,
когда окружности разных радиусов касаются друг друга;
имеет бесконечное множество решений, когда окружно-
сти касаются и имеют равные радиусы (выясните, по-
чему). Лк
§ 6.7. ЗАДАЛИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
^^6.01. Из точки на окружности проведены диаметр и
хорда, равная радиусу окружности. Найти угол между ними.
6.02. Из точки А на окружности проведены хорды АВ
и АС, равные радиусу. Найти величину угла ВАС.
6.03. Пусть две окружности имеют общее касание. Через
точку касания проведена прямая, перпендикулярная линии цен-
тров. Доказать, что зга прямая является общей касательной к
6.04. Определить градусную меру дуги АМВ , если пер-
акуляр, проведенный из конца хорды, делит дополнитель-
6.05. Доказать, что всякая хорда окружности не превыша-
ет ее диаметра.
143
6.06 . Две окружности пересекаются под прямым углом,
т.е. радиусы этих окружностей, проведенные через их общую
точку, перпендикулярны. Найти градусные меры частей, на ко-
торые разделились эти окружности общей хордой, если раз-
ность углов, под которыми эта хорда видна из их центров, рав-
на 30°.
6.07 . Три стороны четырехугольника, в который можно
вписать окружность, относятся как 1:2:3 (в порядке следова-
ния). Определить стороны четырехугольника, если его пери-
метр равен 24 м.
6.08 . Точка М лежит вне круга с центром в точке О, Пря-
мая МО пересекает окружность в точках А и В (МА <МВ).
Пусть X— произвольная точка окружности, отличная от то-
чек А и В. Доказать, что МА < MX < МВ .
6.09 . Доказать, что касательная в точке пересечения двух
взаимно перпендикулярных окружностей (см. задачу 6.06), про-
веденная к одной из окружностей, проходит через центр дру-
гой.
6.10. Через точку М вне круга с центром в точке О про-
ведены две касательные, А и В — точки касания. Доказать,
что угол АМВ вдвое больше угла ОАВ .
6.11. Доказать, что если прямая пересекает две окружно-
сти, имеющие общий центр, то отрезки этой прямой, лежащие
между окружностями, равны.
6.12. В треугольник вписана окружность. Точки касания
делят его стороны на три пары
равных отрезков, суммы кото- . „
рых относятся как 1:2:3. Пери- *
метр треугольника равен 2,4 см. у
Найти стороны треугольника. / уС \
6.13. Точки касания окруж- / / \
ности, вписанной в равнобедрен- I /
ный треугольник, делят одну из I / Т
боковых сторон на отрезки дли- \ / /
ной 3 см и 4 см, считая от осно- \ / у
вания. Найти периметр треуголь- "С
ника. и ----------
6.14. Доказать, что из лю-
бой точки вне круга его диаметр Рис. 6.39
виден под острым углом.
6.15. Сформулировать и решить задачу, аналогичную зада-
че 6.14, для точки, лежащей внутри круга.
6.16. Через точку внутри круга проведены две прямые, пе-
ресекающие окружность соответственно в точках А и В, С
и D (рис.6.39). Градусные меры дуг АС, СВ, BD и DA в ука-
144
занном порядке находятся в отношении 1:2:3:4. Найти острый
угол, образованный этими прямыми.
V6.17. Четыре точки окружности следуют в порядке А,
В, С, D. Продолжения хорды АВ за точку В и хорды CD за
точку С пересекаются в точке Е, причем угол AED равен 60°.
Угол ABD в три раза больше угла ВАС. Доказать, что AD —
диаметр окружности.
6.18. Из произвольной точки М внутри данного угла с
вершиной А опущены перпендикуляры МР и MQ на стороны
угла. Из точки А опущен перпендикуляр АК на отрезок PQ,
Доказать, что углы РАК и MAQ равны.
6.19. Доказать, что множество центров окружностей, ка-
сающихся прямой в данной точке А, есть другая прямая, из ко-
торой удалена точка А.
6.20. Пусть точка А лежит вне круга, АВ и АС — каса-
тельные к кругу, причем В и С — точки касания. Будем гово-
рить, что окружность видна из точки А под углом ВАС . Найти
множество точек, из которых данная окружность видна под уг-
лом 60°.
6.21. Окружность отсекает на сторонах четырехугольника
равные хорды. Доказать, что в этот четырехугольник можно
вписать окружность.
6.22. Среди точек окружности, лежащих в фиксированной
полуплоскости относительно некоторой хорды, найти ту точку,
сумма расстояний от которой до концов хорды является наи-
большей.
6.23. Угол при вершине равнобедренного треугольника ра-
вен 40°. Одна из боковых сторон его является диаметром полу-
окружности, которая делится двумя другими сторонами на три
части. Найти градусные меры этих частей.
6.24. Доказать, что в треугольнике АВС угол А является
а
острым тогда и только тогда, когда та>~'
6.25. На стороне ВС треугольника АВС выбрали точ-
ки В} и С,. Оказалось, что ВВ} = СС} и ЛВАВ} = ЛСАС}. Дока-
жите, что треугольник АВС равнобедренный.
145
ГЛАВА 7
ВПИСАННЫЕ МНОГОУГОЛЬНИКИ
§7.1. СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР К ОТРЕЗКУ
Определение. Прямая, перпендикулярная к
отрезку и проходящая через его середину, называется
серединным перпендикуляром к данному отрезку.
На рис.7.1 изображена прямая а — серединный
перпендикуляр к отрезку АВ.
Важное свойство серединного перпендикуляра от-
мечается в следующей теореме.
Теорема 7.1. Серединный перпендикуляр к от-
резку представляет собой множество точек, равноуда-
ленных от концов данного отрезка.
□ Пусть точка М лежит на серединном перпенди-
куляре а к отрезку АВ (рис.7.2). Тогда МС — медиана
и высота треугольника АМВ . По теореме 4.7 треуголь-
ник АМВ — равнобедренный, следовательно, AM =
= МВ. Это равенство остается верным и в том случае,
когда точки М и С совпадают.
Обратно, пусть АМ = МВ, тогда треугольник
АМВ — равнобедренный. Если МС — высота тре-
угольника АМВ , то МС является также и медианой
146
этого треугольника. Следовательно, точка М лежит на
серединном перпендикуляре к отрезку АВ,
Следствие. Диаметр, перпендикулярный к хор-
де, делит ее пополам, и наоборот, диаметр, делящий хор-
ду пополам, перпендикулярен к этой хорде.
Докажите это следствие самостоятельно.
§ 7.2. ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО
МНОГОУГОЛЬНИКА
Определение. Окружность называется опи-
санной около многоугольника, если все вершины много-
угольника лежат на этой окружности (рис.7.3).
Многоугольник в этом случае называется вписан-
ным в окружность. Центр окружности, описанной около
многоугольника, будем обозначать через О. Этот центр
равноудален от вершин многоугольника, а значит, и рав-
ноудален от концов всех его сторон. Таким образом,
если около многоугольника можно описать окружность,
----------------А 2 то центр этой окруж-
А ности лежит на пере-
/7^ Хч сечении серединных пер-
II Л л пендикуляров к сторо-
и нам многоугольника. Об-
д К • О /I ратно, если все середин-
X // ные перпендикуляры к
\Х If сторонам многоугольни-
XX ка пересекаются в од-
ной точке, то около не-
го можно описать окруж-
Рис.7.3 ность.
Рассмотрим вопрос о существовании описанной ок-
ружности для треугольника и четырехугольника.
Теорема 7.2. Для всякого треугольника сущест-
вует описанная окружность и притом только одна.
Центр описанной окружности лежит на пересечении се-
рединных перпендикуляров, проведенных к сторонам
треугольника.
□ Пусть в треугольнике АВС прямые а и Ъ — се-
рединные перпендикуляры к сторонам ВС и АС. Тогда
147
P^lC.7.4 Рис.7.5
точка О их пересечения равноудалена от концов В и С
отрезка ВС и от концов А и С отрезка АС (рис.7.4),
откуда следует, что ОА = ОВ = ОС.
Таким образом, точка О является центром окружно-
сти, описанной около треугольника АВС, и такая ок-
ружность существует.
Так как прямые а и b пересекаются в одной точке,
и точка О согласно теореме 7.1 должна лежать на пря-
мых а и b, то описанная окружность единственна. Кро-
ме того, серединный перпендикуляр С к отрезку АВ —
это множество точек, равноудаленных от точек А и В,
Поскольку точка О также равноудалена от точек А и В,
то прямая С проходит через точку О. И
Следствие. Три серединных перпендикуляра к
сторонам треугольника пересекаются в одной точке.
Рассмотрим теперь равносторонний треугольник
АВС . Тогда, как известно, биссектриса, высота и медиа-
на, выходящие из одной вершины этого треугольника,
совпадают и лежат на серединном перпендикуляре, про-
веденном к противоположной стороне треугольника
(рис.7.5). Следовательно, точка О пересечения высот рав-
ностороннего треугольника АВС является одновремен-
но центром описанной окружности и центром вписанной
окружности этого треугольника. Эту точку называют так-
же центром равностороннего треугольника АВС. Если
треугольник АВС — прямоугольный (угол С = 90°), то
угол С опирается на диаметр АВ описанной окружно-
сти, поскольку дуга АВ равна 180° (см. следствие 2 тео-
148
Рис.7.6 Рис.7. 7
ремы 6.6). Таким образом, гипотенуза АВ прямоугольно-
го треугольника АВС является диаметром описанной
окружности. Центр О этой окружности лежит на сере-
дине гипотенузы (рис.7.6). Отрезки ОА, ОВ и ОС явля-
ются радиусами этой окружности.
Воспользуемся результатом следствия теоремы 7.2
для доказательства следующего утверждения.
Теорема 7.3. Три прямые, содержащие высоты
треугольника, пересекаются в одной точке.
□ Проведем через вершины А, В, С треугольни-
ка АВС прямые, параллельные соответственно сторо-
нам ВС, АС, АВ, до их взаимного пересечения в
точках Ах, Вх, Q (рис.7.7). Пусть АНХ, ВН2, СН3 —вы-
соты треугольника АВС . В треугольниках АВС и АХВС
сторона ВС является общей, угол АСВ равен уг-
лу АХВС и угол АВС равен углу АХСВ как внутренние
накрест лежащие при параллельных прямых АС, АХСХ
и АВ, АХВХ (см. теорему 3.5). Тогда по теореме 2.3 тре-
угольники АВС и АХВС равны, и, следовательно,
АВ=АХС, АС = АХВ.
Аналогично
АС=ВСХ, АВ=ВХС, ВС = ВХА, ВС = АСХ.
Таким образом, точки А, В, С являются серединами
отрезков ВХСХ, АХСХ, АХВХ соответственно. Значит, пря-
мые, содержащие высоты АНХ, ВН2, СН3 треугольни-
ка АВС, являются серединными перпендикулярами к
149
Рас.7.8 Puc.7.9
сторонам ВХСХ, АХСХ и АХВХ треугольника АХВХСХ. Со-
гласно следствию теоремы 7.2 эти прямые пересекаются
в одной точке. И
Напомним, что точка пересечения прямых, содержа-
щих высоты треугольника АВС, называется ортоцен-
тром этого треугольника.
Отметим, что эта точка может лежать вне треуголь-
ника (рис.7.8). Этот случай имеет место для тупоугольно-
го треугольника, у которого две высоты находятся вне
треугольника. Для прямоугольного треугольника орто-
центр совпадает с вершиной прямого угла. В остроуголь-
ном треугольнике ортоцентр находится внутри треуголь-
ника.
Теперь выясним при каких условиях около четы-
рехугольника можно описать окружность? Для этого рас-
смотрим теорему 7.4.
Теорема 7.4. Около четырехугольника можно
описать окружность тогда и только тогда, когда суммы
его противолежащих углов равны 180°.
□ Пусть около четырехугольника ABCD описана
окружность (рис.7.9). Тогда по теореме 6.6 имеем:
ZA + Z.C =—(<jBCD) +—(\jBAD ) =
2 2
= - (<JBCD + и BAD) = - • 360° = 180°.
2 2
Так как сумма всех углов четырехугольника равна 360°,
то сумма 4- Z.D также равна 180°.
150
Обратно, пусть Z_A 4 ZC = ZB 4- ZZ) = 180°. Опи-
шем окружность около треугольника АВС. Если точ-
ка D лежит вне круга (рис.7.10), то
АВ + ZD = - (и АМС) + - (u ABC -vMN) =
2 2
~-(иАМС +<jABC)--(uMN) =
2 2
= 180°-|(иЛ/У)<180°,
что противоречит условию ZB 4- ZZ) = 180°.
Аналогично, если точка D лежит внутри круга
(рис.7.11), то
AB + AD = -(uAMC) + -(uABC +uW) =
2 2
= -(vAMC +uABC) + -(<JMN) =
2 2
= 180°+-(иМУ)>180°,
2
что привело к противоречию.
151
§ 7.3. ВНЕВПИСАННАЯ ОКРУЖНОСТЬ
Рассмотрим треугольник АВС и продолжим две его
стороны АВ и АС, Проведем биссектрису угла А
(рис.7.12). Тогда всякая ее точка равноудалена от лу-
чей АС и АВ. Проведем также биссектрису угла, смеж-
ного с углом В треугольника АВС. Точка 1а пере-
сечения этой биссектрисы и биссектрисы угла А равно-
удалена от стороны ВС и продолжения сторон АВ
и АС. Значит, точка 1а лежит на биссектрисе угла,
смежного с углом С треугольника АВС .
Пусть 1аТ1АС, 1аК1ВС, IaLkAB. Тогда
IaT = IaK = IaL (рис.7.12).
Значит, точка 1а является цен-
тром окружности, касающейся
стороны ВС = а и продолже-
ния двух других сторон АВ
и АС. Эта окружность назы-
вается вневписанной окружно-
стью треугольника АВС.
Теорема 7.5. Точка ка-
сания вневписанной окружно-
сти треугольника делит его пе-
Рис.7.12
риметр пополам.
□ Действительно, согласно следствию 2 теоремы 6.2
имеем (рис.7.12):
СК = СТ, BK = BL, AT = AL.
Тогда
2AT=AT + AL = AC+СТ + АВ + BL =
= AC + CK + AB + BK = AC + AB + BC =2p,
значит, AT = p. Однако,
AT = AC+CT = AC+CK.
Итак, AC 4- СК = p.
152
Рис.7.13
Следствие. СК=р-Ь; ВК—р-С.
Для всякого треугольника можно построить три вне-
вписанных окружности. Это показано на рис.7.13.
§ 7.4. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример?.1. В четырехугольнике два противополож-
ных угла прямые. Доказать, что около такого четырехугольни-
ка можно описать окружность, причем одна из диагоналей
четырехугольника является диаметром этой окружности.
ZS Пусть в четырехугольнике ABCD углы В
и D — прямые. Тогда ZS+ZjD = 180° (рис.7.14). По
теореме 7.4 около этого четырехугольника можно опи-
сать окружность. Далее, по теореме 6.6 имеем:
\jABC = 2(ZZ>) = 2-90° = 180°,
т.е. диагональ АС —диаметр этой окружности. Ж
153
Рис. 7.14
Рис.7.15
Пример 7.2. Диагонали вписанного в окружность
четырехугольника ABCD пересекаются в точке О. Известно
также, что ОВ=ОС, AO=OD. Определить углы четырехуголь-
ника, если AAOD =140° и ^ЛР=200°.
ZS Данный четырехугольник изображен на рис.7.15.
Рассмотрим случай, когда <jABD =160°, а дополнитель-
ная к ней дуга составляет 200°. Тогда по теореме 6.6:
ZACD =|(uJD) = 100°.
Так как треугольник AOD равнобедренный и AAOD =
= 140°, то AOAD = AODA =20°. Аналогично получим:
АОВС = АОСВ =20°.
Следовательно,
ABCD = AACD + АОСВ = 100° + 20° = 120°.
По теореме 7.4
ABAD = 180°-120° = 60°.
По этой же теореме
/LABD =|(иЛГ>) = 100°,
откуда ААВС =120° и AADC —60°. Случай, когда
<JABD =200°, рассмотрите самостоятельно.
Таким образом, углы А, В, С, D четырехугольника
равны 60°, 120°, 120°, 60° либо 80°, 100°, 100°, 80°. ▲
П р и м е р 7.3. Продолжения высот, проведенных из вер-
шин А и В остроугольного треугольника АВС, пересекают
154
окружность, описанную около треугольника, в точках D и Е.
Доказать, что вершина С делит дугу DE пополам.
Пусть в треугольнике АВС высоты АНХ и ВН2
пересекают описанную окружность в точках D и Е
(рис.7.16). Рассмотрим прямоугольные треугольники
АСНХ и ВСН2. По следствию 2 теоремы 3.7:
ЛСАНХ = АСВН2 = 90°-ZC.
Значит, по теореме 6.6:
u ЕС = uCD = 2 • (90° - ZC),
т.е. точка С делит дугу DE пополам. Ж
П р и м е р 7.4. Доказать, что если в четырехугольни-
ке ABCD углы ABD и ACD равны, то этот четырехугольник
является вписанным в некоторую окружность (рис.7.17).
ZS Опишем окружность около треугольника ABD
(это можно сделать по теореме 7.2). Из § 6.4 следует, что
если точка С лежит вне окружности, то AACD меньше
половины дуги AD, а значит, и меньше угла ABD, а
в случае, если точка С лежит внутри окружности,
то AACD больше половины дуги AD, т.е. ZACD боль-
ше ZABD. Однако углы ACD и ABD равны по усло-
вию. Таким образом, точка С лежит на окружности,
кбторая является описанной вокруг четырехугольни-
ка ABCD. ▲
Пример 7.5. На данной прямой найти точки, равно-
удаленные от двух заданных точек.
Пусть данная прямая а неперпендикулярна от-
резку АВ, соединяющему данные точки А и В. Про-
ведем серединный перпендикуляр Ъ к отрезку АВ
155
Рис. 7.18 Рис. 7.19
(рис.7.18). По теореме 7.1 любая точка этого перпендику-
ляра равноудалена от точек Л и В, и наоборот, если
точка равноудалена от точек А и В, то она лежит на
прямой b. Так как прямые а и АВ неперпендикулярны,
то прямые а и b пересекаются в некоторой точке X со-
гласно следствию 2 теоремы 3.5. Эта точка равноудалена
от точек Л и В и лежит на прямой а. В случае, если а
перпендикулярна АВ, то по этому же следствию пря-
мые а и Ъ либо параллельны, либо совпадают. В первом
случае задача не имеет решений (рис.7.19), а во втором
случае любая точка прямой b равноудалена от точек А
П р и м е р 7.6. Найти углы выпуклого четырехугольни-
ка ABCD, в котором :
ZR4C =30°, AACD =40°, ХЛРЛ=50°, Z.CBD =60°
и Z4BC+Z4DC>180°.
Прежде всего докажем две леммы.
А е м м а 1. Пусть диаметр окружности делит неко-
торую дугу пополам. Тогда этот диаметр делит пополам
хорду, стягивающую эту дугу, и перпендикулярен к ней.
□ Действительно, пусть диаметр ST делит дугу MN
пополам (рис.7.20). Тогда по определению центрального
угла имеем:
/МОЕ = /NOE.
В треугольниках МОЕ и NOE сторона ОЕ — общая,
ОМ = ON, /МОЕ = /NOE . Значит, эти треугольники
равны по первому признаку равенства треугольников, от-
куда ME = NE и /МЕО = /NEO = 180°:2 = 90°.
156
Л е м м a 2. Пусть диаметр ST делит хорду MN по-
полам, и Р — произвольная точка этого диаметра, не
лежащая на хорде MN. Проведем хорды ММХ и NNX
через точку Р. Тогда диаметр ST делит хорду MXNX по-
полам (рис.7.21).
□ По следствию из теоремы 7.1 имеем: ST1MN,
т.е. прямая ST является серединным перпендикуляром к
отрезку MN. По теореме 7.1 треугольник MPN равно-
бедренный с основанием MN . Значит,
Z.PMN =APNM.
Но по следствию 1 теоремы 6.6 имеем:
Z.PMN = ZPNXMX, a APNM = ^PMXNV
откуда
Z.PMXNX = APNXMV
Следовательно, треугольник PMXNX равнобедренный. Да-
лее, углы NPE и NXPEX, а также углы МРЕ и МХРЕХ
равны как вертикальные. Но так как РЕ — биссектриса
угла MPN, то и ее продолжение РЕХ также будет бис-
сектрисой угла MXPNX. Значит, биссектриса РЕ} будет и
медианой треугольника Мх PNX. Я
Перейдем теперь к решению примера.
Пусть ABCD — данный в условии примера
четырехугольник (рис.7.22). Опишем окружность около
треугольника АВС. Так как ZABC + ZADC> 180°, то
точка D лежит внутри этой окружности. По теореме 6.6
иВС = 60°, иСЖ = 120°, \jMA =80°.
157
Из §6.4 следует, что
и АВ + uW =2(ZADB) = 100°,
а так как ВК — диаметр, то
uMK + vMA +VAB =180°,
откуда получаем, что
<jMK +\jAB +80° = 180° и \jMK +<jAB =100°.
Следовательно,
UMK =uNK,
По лемме 1 BKLMN и ME = NE, а по лемме 2 имеем:
AF —FC. По следствию из теоремы 7.1 ВК1АС. Та-
ким образом, В К — серединный перпендикуляр к от-
резку АС. Значит, по тео-
реме 7.1 имеем:
АВ=ВС, AD = DC.
Треугольники АВС и ACD
равнобедренные, а отрезки
BF и DF — их биссектри-
сы. Значит,
АВСА =АВАС =30°,
AABF =ACBF = 60°,
AFAD=AFCD= 40°,
ZCZ)^ = ZZDF=50°.
Отсюда ААВС =120°, Z.BCD =70°,
Z.CDA = 100°, Z.DAB =70°. ▲
Пример 7.7. В треугольнике АВС угол В равен 60°,
биссектрисы AD и СЕ пересекаются в точке I. Доказать,
что ID-IE.
Пусть биссектрисы AD, BF, СЕ треугольни-
ка АВС пересекаются в точке 1, и угол АВС равен 60°
(рис.7.23). Тогда по теореме о сумме углов треугольника
имеем:
AAIC = 180°-| {ABAC + АВСА) =
= 180°-—(180°-60°) = 120°.
2V ’
Так как углы EID и АТС вертикальные, то
158
Z£ZD = 120°.
В четырехугольнике BDIE
ZDBE + ZEID = 60° +120° = 180°.
Значит, около этого четырехугольника можно описать
окружность. Но ZIBE равен углу ZDBI, поэтому по
теореме 6.6 получим: kjEI =<jDI. Из следствия 3 теоре-
мы 6.6 вытекает, что IE = ID. Ж
Пример 7.8. Пусть Т — точка пересечения биссектри-
сы /гла А треугольника АВС с описанной около него окруж-
ностью. Доказать, что ТВ =ТС =Т1 =Т1а.
ZS На рис.7.24 изображен треугольник АВС с опи-
санной около него окружностью, I — центр вписанной в
него окружности, Т — точка пересечения биссектрисы
угла А с окружностью, 1а — центр вневписанной окруж-
ности треугольника АВС. Из § 7.3 следует, что В1а —
биссектриса угла, смежного с углом АВС. Значит, В1а
и BI перпендикулярны. Пусть ZBAC = а, ZABC = р,
ZACB =у. Тогда ZIBC По следствию 1 теоре-
мы 6.6 имеем:
Z.CBT = Z.CAT , ZITB =ХАСВ =у.
2
Значит,
ZZBT = —+ —= 90°-—.
2 2 2
По теореме о сумме углов треугольника имеем:
159
ABIT =Ш°-А1ВТ-AITB = 180°-(90°-р-у = 90°-^-.
Таким образом, в треугольнике IBT углы IBT и BIT
равны. Значит, TI =ТВ. Аналогично доказывается, что
TI = ТС. Далее, в прямоугольном треугольнике TBI а
угол ВП а равен (90° —-). Значит,
2
All В = 90°-ZB//_ = 90°-(90° - = V
° а 2 2
Наконец,
ATBI = AIBI-AIBT = 90’-(90° -
° ° 2 2
Таким образом, в треугольнике TBI а углы TIаВ и TBI а
равны, откуда 1аТ = ТВ. Ж
Пример 7.9. Дан четырех- 7t\
угольник ABPQ. Для некоторой / / \ \
точки С на стороне PQ и точ- / / \ \
ки R на стороне АВ треугольни- ( / / \ \ ]
ки АВС и PQR — равносторон- \ -----/
ние. Доказать, что BP || AQ. R jCz'
Так как /1 \\
ААВС = AQPR = 60°
и A Q
ABAC =RQP =60°, Рис. 7.25
то из примера 7.4 следует, что около четырехуголь-
ников ARCQ и RBPC можно описать окружности
(рис.7.25). По следствию 1 теоремы 6.6 имеем:
ACAQ = ACRQ , а АРВС = APRC.
Но
ACRQ +APRC =60°, ABAC = АСВА =60°.
Значит,
ААВР + ABAQ = АРВС + АСВА + ARAC + ACAQ =
= APRC + АСВА + ARAC + ACRQ =
= (APRC + ACRQ ) + АСВА + ARAC .
Но АСВА = ARAC =60°. Поэтому
160
ЛАВР + АВА Q = 60° + 60° + 60° = 180°.
По теореме 3.5 прямые ВР и AQ параллельны. Ж
Пример 7.10. В угол с
У вершиной М вписана окруж-
/ ность, касающаяся сторон угла
в точках К и N, находящихся
\ на расстоянии 8 см от верши-
77 \ ны М (рис.7.26). К окружности
АЛ I J проведена касательная, пере-
С / I секающая стороны угла МК
/ / и MN в точках А и В соответ-
S ственно. Найти периметр тре-
• угольника АВМ, если центр ок-
Л» В N ружности находится вне треу-
Рис. 7. 26 голышка.
Пусть С — точка
касг.ния окружности со стороной АВ треугольника. По
условию МК = MN = 8 см. Так как отрезки касательных
к окружности, проведенные из одной точки, равны
между собой, то для периметра треугольника АВМ
имеем:
МА + АВ+ВМ = МА + АС+СВ + ВМ =
= MA+AK + BN + BM = MK + MN =
= 8+8=16.
Таким образом, периметр треугольника АВМ ра-
вен 16 см. А
§ 7.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
В
^^7.01. Доказать, что окружность имеет лишь один
центр.
7.02. Можно ли описать окружность около четырехуголь-
ника, углы которого в последовательном порядке относятся как:
а) 2:4:5:37 б) 5:7:8:97
7.03. Три угла вписанного четырехугольника (в последова-
тельном порядке) относятся как 1:2:3. Найти эти углы.
7.04. Хорда АВ стягивает четверть окружности. Диа-
метр CDt перпендикулярный к хорде, проведен так, что точ-
ка С лежит на меньшей дуге окружности. Найти угол CAD .
161
7.05 . Диагонали четырехугольника ABCD , вписанного в
окружность, пересекаются в точке М, а прямые АВ и CD пе-
ресекаются в точке N. Известно, что угол AMD равен 108°, а
угол AND равен 24°. Найти углы ABD и BDC.
7.06 . В треугольнике АВС точки 1а, 1Ь, 1С — центры вне-
вписанных окружностей. Доказать, что стороны треугольни-
ка IaIbIc перпендикулярны соответствующим биссектрисам
треуголт ника АВС.
7.07 . Доказать, что радиус окружности, описанной около
равностороннею треугольника, вдвое больше радиуса вписан-
ной окружности.
7.08 . В четырехугольнике ABCD известно, что ZB =
= Z.D — 90°, острый угол между его диагоналями равен 80°, гра-
дусная мера дуги DC равна 60°. Найти углы А и С.
7.09 . В окружности диаметр ААХ перпендикулярен хор-
де ВВХ. Доказать, что градусные меры дуг АВ и АВХ,
мены
полуокружности, равны.
7.10. Из одной точки, лежащей на окружности, проведены
две перпендикулярные хорды, расстояния от которых до цен-
тра окружности равны соответственно 6 см и 10 см. Найти
длины хорд.
7.11. Окружности с радиусами 30 см и 40 см касаются
друг друга. Найти расстояние между центрами этих окружно-
стей в случаях их внешнего и внутреннего касания.
7.12. Лежат ли точки А, 1 и 1а на одной прямой, ес-
ли 1а — центр вневписанной окружности треугольника АВС ,
I — центр вписанной окружности этого треугольника?
7.13. Один из острых углов прямоугольного треугольни-
ка равен 25°. Под каким углом виден каждый катет этого тре-
угольника из центра описанной окружности?
7.14. Вершины четырехугольника ABCD лежат на окруж-
ности, причем АВ — диаметр, а сторона CD равна радиусу.
Найти угол между продолжениями двух других сторон.
7.15. Доказать, что биссектриса угла А треугольника АВС
делит пополам ду.у описанной окружности, которую стягивает
сторона ВС.
7.16. Доказать, что биссектриса треугольника лежит
между медианой и высотой, проведенными из той же верши-
ны.
6 Зак. 687
162
7.17. Во вписанном четырехугольнике диагонали перпен-
дикулярны. Доказать, что прямая, проходящая через точку пе-
ресечения диагоналей перпендикулярно к одной из сторон, де-
лит противоположную сторону пополам.
7.18. В четырехугольнике ABCD, вписанном в окруж-
ность, через вершины А, В и точку Р пересечения диагоналей
проведена окружность, пересекающая сторону ВС в точке Е.
Кроме того, известно, что АВ = AD. Доказать, что CD = СЕ.
7.19. Три окружности проходят через точку Р и попарно
пересекаются в точках Я, В и С. Из произвольной точки М
первой окружности через точки В и С проведены прямые, пе-
ресекающиеся с другими окружностями в точках S и Т. Дока-
зать, что отрезок ST проходит через точку А.
7.20. Доказать, что если в треугольнике центры вписанной
и описанной окружностей совпадают, то этот треугольник явля-
ется равносторонним.
7.21. Доказать, что если в треугольнике ортоцентр совпа-
дает с центром описанной окружности, то этот треугольник яв-
ляется равносторонним.
7.22. Доказать, что если в треугольнике ортоцентр совпа-
дает с инцентром, то этот треугольник является равносторон-
ним.
7.23. Дан треугольник АВС . Доказать, что около четырех-
угольника AIBI с мякло описать окружность, центр которой
лежит на окружности, описанной около треугольника АВС .
7.24. В треугольнике АВС на сторонах АВ , ВС и АС
выбраны соответственно точки Ср А} и Bv отличные от вер-
шин треугольника АВС . Доказать, что три окружности, прохо-
дящие через соответствующие тройки точек А, В}, Ср* А}, В,
Ср Л,, Вр С, имеют общую точку.
7.25. В остроугольном треугольнике АВС угол В ра-
вен 60е, AM и CN — его высоты, a Q — середина сторо-
ны АС, Рркжжь, что треугольник MNQ является равносто-
ронним.
7.26. Две окружности пересекаются в точках А и В.
Через точку В проведена прямая, пересекающая окружности в
точках С и D, Затем через точки С и D проводятся касатель-
ные к этим окружностям. Доказать, что точки А, С, D и точ-
ка Р пересечения этих касательных лежат на одной окружно-
сти.
7.27. На гипотенузе АВ прямоугольного треугольни-
ка АВС во внешнюю сторону от него построен квадрат с цен-
163
тром в точке О. Доказать, что СО — биссектриса прямого угла
треугольника.
7.28. Две непересекающие окружности вписаны в угол. К
этим окружностям проведена общая внутренняя касательная.
Обозначим точки пересечения этой касательной со сторонами
угла через А1 и A2t а точки касания — через Вх и В2. Доказать,
что А}В} = ^B2.
7.29. Стороны треугольника равны 8 см, 16 см и 20 см. Из
вершин этого треугольника, как из центров, описаны окруж-
ности так, что каждая из них касается внешним образом двух
других. Найти радиусы этих окружностей.
7.30. Два круга имеют одну общую точку. Доказать, что
внутренняя касательная этих кругов делит пополам отрезок
внешней касательной, заключенный между точками касания.
7.31. На отрезке АВ, как на диаметре, построена окруж-
ность С,. BD — хорда. Окружность С2 касается окружности С}
в точке А и отрезка BD в точке К. Доказать, что АК — бис-
сектриса угла DAB.
164
ГЛАВА 8
ЧЕТЫРЕХУГОЛЬНИКИ
§ 8.1. ПАРАЛЛЕЛОГРАММ
Напомним, что многоугольник, имеющий 4 верши-
ны, называется четырехугольником. В этой главе мы рас-
смотрим следующие четырехугольники: параллелограмм,
прямоугольник, ромб, квадрат, трапецию.
Параллелограмм. Четырехугольник, у которого про-
тивоположные стороны параллельны, называется парал-
лелограммом.
На рис.8.1 изображен параллелограмм, у которо-
го AB\\CD, AD\\BC. Углы BAD и BCD принято на-
зывать противоположными. Вторая пара противополож-
ных углов — углы АВС и ADC . Отрезок, соединяющий
вершины противоположных углов, называется диагона-
лью параллелограмма. Отрезки АС и BD являются
диагоналями параллелограмма.
Высотой параллелограмма называется отрезок, пер-
пендикулярный противоположным сторонам, концы ко-
торого лежат на прямых, со-
держащих эти стороны.
На рис.8.1 отрезок MN
— высота параллелограмма.
Все высоты, проведенные ме-
жду двумя противоположны-
ми сторонами параллелограм-
ма, равны.
Свойства параллелограм-
ма. Рассмотрим пять свойств
параллелограмма.
1. Диагональ параллело-
грамма делит его на два равных треугольника.
□ Пусть BD — диагональ параллелограмма ABCD
(рис.8.2). Тогда в треугольниках ABD и BDC отре-
зок BD является общей стороной, Zl= Z2 как внутрен-
165
Ри,с.&2
P1JLC.&3
ние накрест лежащие углы при параллельных пря-
мых AD и ВС и секущей BD. Аналогично доказывает-
ся, что Z3 = Z4. Следовательно, треугольники ABD
и BDC равны. И
2. Противоположные стороны параллелограмма рав-
ны.
3. Противоположные углы параллелограмма равны.
Эти свойства следуют непосредственно из равенства
треугольников ABD и BDC.
4. Диагонали тараллелограмма в точке пересечения
делятся пополам.
□ В треугольниках AOD и ВОС стороны AD
и ВС равны по свойству 2; Zl = Z2, Z3 = Z4 как внут-
ренние накрест лежащие (рис.8.3). Следовательно, тре-
угольники AOD и ВОС равны. Отсюда получаем, что
АО = ОС, ЭО = ОВ.Я
5. Точка пересечения диагоналей является центром
симметрии параллелограмма.
□ Согласно свойству 4 при симметрии f относи-
тельно точки О имеем:
f(A)-C. f(c) = A, f(D) = B.
Отсюда следует, что при симметрии f треуголь-
ник ABD переходит в треугольник BCD. Значит, точ-
ка С? — центр симметрии параллелограмма ABCD . Я
Признаки параллелограмма. Рассмотрим теперь три
признака параллелограмма.
166
1. Если в четырехугольнике диагонали в точке пе-
ресечения делятся пополам, то такой четырехугольник
— параллелограмм.
□ Пусть в четырехугольнике ABCD диагонали АС
и BD пересекаются в точке О, причем АО = ОС,
DO = OB
равны как
о
Рис. 84
(рис.8.4). Очевидно, что углы AOD и ВОС
вертикальные. Значит, треугольники AOD и
ВОС равны. Отсюда следует,
что Z1 = Z2. Тогда по теоре-
ме 3.5 имеем: AD\\BC. Анало-
гично из равенства треуголь-
ников COD и АОВ имеем:
Z3 = Z4, и поэтому CD\\AB.
Итак, четырехугольник ABCD
— параллелограмм.
Следующие признаки до-
кажите самостоятельно.
2. Если в четырехугольни-
ке противоположные стороны
равны, то такой четырехугольник — параллелограмм.
3. Если в четырехугольнике две противоположные
стороны равны и параллельны, то этот четырехуголь-
ник — параллелограмм.
§ 8.2. ПРЯМОУГОЛЬНИК
Параллелограмм, у которого все углы прямые, назы-
вается прямоугольником (рис.8.5).
Из свойства 2 параллелограмма и теоремы 3.5 следу-
ет, что если у параллелограмма один угол прямой, то и
все другие углы также прямые, откуда ясно, что данный
параллелограмм является прямоугольником.
Свойства прямоугольника. Прямоугольник обладает
всеми свойствами параллелограмма. Кроме того, он име-
ет также и свои характерные свойства.
1. Диагонали прямоугольника равны.
О В самом деле, в прямоугольных треугольни-
ках ABD и ACD отрезок AD является общим кате-
том, АВ = CD по свойству 2 параллелограмма. По теоре-
167
Рис.8.6
ме 4.4 треугольники ABD и ACD равны, откуда следу-
ет, что АС = BD. И
2. Точка пересечения диагоналей прямоугольника
является центром окружности, описанной около этого
прямоугольника.
□ Из свойства 4 параллелограмма и свойства 1 пря-
моугольника следует, что О А = ОВ = ОС = OD. Значит,
точка О равноудалена от вершин А, В, С, D прямо-
угольника и поэтому является центром описанной окруж-
ности. И
3. Прямая, соединяющая середины противополож-
ных сторон прямоугольника, является его осью симмет-
рии.
□ Пусть точки М и N — середины сторон ВС
и AD прямоугольника ABCD (рис.8.6). В четырехуголь-
нике ABMN имеем: BM\\NA. По признаку 3 паралле-
лограмма четырехугольник ABMN — параллелограмм, а
так как /Л =90°, то ABMN — прямоугольник. Значит,
AANM=ABMN =90°.
Аналогично имеем:
Z.CMN 90°.
Очевидно, что
ВМ = МС, AN =ND.
Поэтому для симметрии f относительно MN получаем:
168
По теореме 2.1 при симметрии f относительно прямой
MN треугольник АВМ переходит в треугольник CMD ,
треугольник AMN — в треугольник DMN , а прямо-
угольник ABMN переходит в прямоугольник CMND .
Значит, прямая MN является осью симметрии прямо-
угольника ABCD.
Пусть К и L — сере-
дины сторон АВ и CD со-
ответственно в прямоуголь-
нике ABCD . Тогда прямая
L KL — ось симметрии пря-
моугольника ABCD . Дока-
зательство этого факта про-
водится аналогично приве-
А N D денному выше для оси сим-
метрии MN. Сделайте это
Рис. 8.7 самостоятельно.
Заметим также, что оси
симметрии АСУ и KL прямоугольника ABCD являются
серединными перпендикулярами, проведенными к проти-
воположным сторонам, и поэтому пересекаются в точке
пересечения диагоналей (рис.8.7).
§ 8.3. РОМБ И КВАДРАТ
Ромб. Параллелограмм, у которого все стороны рав-
ны, называется ромбом.
На рис.8.8 изображен ромб ABCD , диагонали АС
и DB которого пересекаются в точке О,
Из признака 2 параллелограмма следует, что четы-
рехугольник является ромбом тогда и только тогда, когда
все его стороны равны.
Свойства ромба. Ромб обладает всеми свойствами
параллелограмма, однако имеет также и собственные ха-
рактерные свойства.
1. Диагонали ромба делят его на четыре равных
прямоугольных треугольника.
□ Из свойства 4 параллелограмма имеем АО = ОС,
DO —ВО (рис.8.8). Значит, треугольники АОВ , ВОС,
169
Рис. 8.8 Рис. 8.9
OCD и DOA равны согласно третьему признаку равен-
ства треугольников.
Отсюда следует, что углы АОВ и AOD равны, и
так как эти углы являются смежными, то они прямые. А
это значит, что треугольники ABO, ВСО, CDO, ADO
— прямоугольные. И
2. Диагонали ромба взаимно перпендикулярны и
делят углы ромба пополам.
3. Диагонали ромба являются его осями симметрии.
4. Точка пересечения диагоналей ромба является
центром вписанной в этот ромб окружности.
Свойства 2—4 следуют непосредственно из свойст-
ва 1.
На рис.8.9 изображен ромб ABCD , в который впи-
сана окружность с центром в точке О. Точки М, N, Р,
Q являются точками касания этой окружности соответ-
ственно со сторонами АВ, CD, ВС и AD. Отрез-
ки ОМ, ON, ОР и OQ — ее радиусы. Точки М, О, N
лежат на одной прямой. Отрезок MN является высотой
ромба. Аналогично отрезок PQ также является высотой
ромба, и точка О лежит на этом отрезке.
Докажите эти утверждения самостоятельно.
Квадрат. Ромб, у которого все углы прямые, называ-
ется квадратом.
Квадрат ABCD изображен на рис.8.10. Квадрат об-
ладает всеми свойствами параллелограмма, прямоуголь-
ника и ромба. Ниже сформулированы свойства квадрата.
170
Рис. в. 11
Рис. & 10
D
1. Диагонали квадрата делят его на четыре равных
прямоугольных треугольника.
2. Стороны квадрата равны.
3. Диагонали квадрата равны.
4. Диагонали квадрата в точке пересечения делятся
пополам.
5. Диагонали квадрата взаимно перпендикулярны и
делят углы квадрата пополам.
6. Точка пересечения диагоналей квадрата является
его центром симметрии.
7. Точка пересечения диагоналей квадрата является
центром окружности, описанной около квадрата.
8. Точка пересечения диагоналей квадрата является
центром окружности, вписанной в квадрат.
9. Прямые, проходящие через середины противопо-
ложных сторон квадрата, являются его осями симмет-
рии.
10. Диагонали квадрата являются его осями симмет-
рии.
Квадрат с осями симметрии АС, BD, MN и PQ, а
также с вписанной и описанной окружностями, пред-
ставлен на рис.8.И.
§ 8.4. ТРАПЕЦИЯ
Четырехугольник, в котором две противоположные
стороны параллельны, а две другие — непараллельны, на-
зывается трапецией.
171
Трапеция ABCD представлена на рис.8.12.
Параллельные стороны трапеции называются осно-
ваниями, а непараллельные — боковыми сторонами.
Перпендикуляр, опущенный &
из точки, лежащей на од- f " 1
ном основании, на прямую, / Лг I
содержащую другое осно- / 1
вание, называется высотой / 1
трапеции. На рис.8.12 отре- / 1
зок MN — высота тра- / 1
пеции ABCD. / ।— I
Как правило, высоту ^wi И 1
можно провести так, чтобы A N D
она проходила между осно- Рмс.я./<?
ваниями. Однако иногда это
осуществить нельзя (рис.8.16). Отметим также, что все
высоты трапеции равны.
Прямоугольная трапеция. Трапеция называется пря-
моугольной, если одна из ее боковых сторон перпецди-
кулярна к основаниям.
В дальнейшем в трапеции ABCD основание AD бу-
дет большим, а основание ВС — меныпим, как показано
на рисунках 8.12—8.16.
Равнобедренная трапеция и ее свойства. Трапеция
называется равнобедренной, если ее боковые стороны
равны (рис.8.14).
Рассмотрим четыре свойства равнобедренной трапе-
ции ABCD с диагоналями АС и BD и высотами BF
и СЕ (рис.8.17).
1. Углы при основании равнобедренной трапеции
равны, т.е. Z.BAD=Z.CDA; /АВС=АОСВ.
□ В прямоугольных треугольниках ABF и DCE
имеем: BF=CE, АВ—CD. Значит, эти треугольники
равны по теореме 4.4. Отсюда следует, что углы BAD и
CDA равны. Так как
ZABC = W-ABAD,* ZDCB=lW-ZCDAt
то
ЛАВС =ZDCB.*
172
Рис. 8 15
Рис.8.16
2. Пусть BF и СЕ — высоты, опущенные на осно-
вание AD равнобедренной трапеции ABCD. Тогда
AF=DE=
AD-BC
AE=DF=
□ Из равенства треугольников ABF и DCE следу-
ет, что AF = ED. Очевидно также, что BCEF — прямо-
угольник, значит, FE = ВС. Тогда
AD-FE AD-BC
AF = DE =-------=---------.
Кроме того,
173
АЕ = AD-DE = AD-AF=DF = AF+FE =
AD-ВС
AD-BC + 2BC
AD + BC
2
3. Диагонали равнобедренной трапеции равны,
т.е. AC=BD.
□ Так как BF = СЕ и FD = АЕ , то треугольни-
ки АСЕ и BFD равны согласно теореме 4.4. Отсюда
следует, что AC =BD.
4. Пусть О — точка пересечения диагоналей АС
и BD равнобедренной трапеции ABCD. Тогда
AO = OD, ВО = ОС
□ Из равенства треугольников АСЕ и BDF следует
также, что угол 1 равен углу 2 (рис.8.17). Значит, тре-
угольник AOD— равнобедренный. Отсюда имеем:
АО = OD. Следовательно, ВО = ОС.
Трапеция, в которую можно вписать окружность.
Выясним, когда в трапецию можно вписать окружность.
Ответ на этот вопрос дает следующая теорема.
Теорема 8.1. В тра-
пецию можно вписать ок-
ружность тогда и только то-
гда, когда сумма ее основа-
ний равна сумме боковых
сторон. При этом боковые
стороны видны из центра
вписанной окружности под
углом 90°, т.е. отрезки, со-
единяющие центр вписан-
ной окружности с концами
боковой стороны, перпен-
Рис.8.17
дикулярны.
□ По теореме 6.5 в трапецию ABCD можно впи-
сать окружность тогда и только тогда, когда
AD + BC = AB+CD,
174
Рис.8.19 рис в. 18
т.е. когд сумма ее оснований равна сумме боковых сто-
рон. Пусть в трапецию ABCD вписана окружность с
центром в точке I (рис.8Л 8). Проведем радиусы IM,
IN , IP , IQ в точки касания этой окружности со сторо-
нами трапеции. Тогда треугольники ABI и CDI — пря-
моугольные. В самом деле, сумма углов CDA и BCD
равна 180е как внутренних односторонних при парал-
лельных прямых AD и ВС. Однако DI и CI — биссек-
трисы этих углов, значит, Z.CDI +Z.DCI =90°, откуда
следует, что Z.CID = 90е.
Трапеция, около которой можно описать окруж-
ность. Выясним теперь, когда около трапеции можно
описать окружность. Об этом говорится в следующей
теореме.
Теорема 8.2. Около трапеции можно описать
окружность тогда и только тогда, когда трапеция явля-
ется равнобедренной.
□ Пусть ABCD — равнобедренная трапеция. Тогда
ZA = ZD и ZD + ZC=ZZ + ZC = 180°.
По теореме 7.4 около трапеции ABCD можно описать
окружность (рис.8.19).
Обратно, если около трапеции ABCD описана ок-
ружность, то по теореме 7.4 имеем:
Z4 + ZC = 180е.
Но и
ZD + ZC = 180°.
175
Значит, углы А и D равны. Докажем, что трапеция
ABCD— равнобедренная. Проведем СК\\АВ. Тогда
АВСК — параллелограмм. Значит, АВ = СК. Так как
АВ\\СК, то углы ВАК и CKD равны как соответствен-
ные при параллельных АВ и СК и секущей AD. Отсю-
да следует, что углы CKD и CDK равны, т.е. тре-
угольник KCD — равнобедренный и СК = CD. Итак,
АВ = СК = CD, а это значит, что в трапеции ABCD
боковые стороны АВ и CD равны. Таким образом,
ABCD — равнобедренная трапеция.
Связь между свойствами отдельных видов четырех-
угольников показана на схеме (стр. 176).
Полезно ознакомиться с происхождением названий
некоторых четырехугольников.
Евклид называл параллелограмм "параллельно-линей-
ной площадью". Слово лараХХ^Хсгураццоу — "парал-
лельнолинейный" составлено из слов лараХХ^Хо^ и
урацц^ —линия.
По одной версии термин "ромб" происходит от
греческого роцРо^ — бубен, поскольку ромб похож на
четырехугольный бубен. Существует и другое объясне-
ние: слово роцР означало "вращающееся тело", "верете-
но", и в геометрию данный термин вошел потому, что
сечение, проведенное в обмотанном веретене, действи-
тельно имеет форму ромба.
Название квадрата происходит от латинского
quadratus — четырехугольный.
Термин "трапеция" восходит к греческому
трале^ШУ — маленький стол. Это слово и русское "тра-
пеза" имеет общий корень.
176
СВОЙСТВА НЕКОТОРЫХ ВИДОВ
ЧЕТЫРЕХУГОЛЬНИКОВ
ПАРАЛЛЕЛОГРАММ
AB\\CD, BC\\AD; AB=CD, BC=AD ;
ZA = ^C, ZB=/D; BO=OD, A 0=/
AB=BC=CD=AD;
ПРЯМОУГОЛЬНИК
РОМБ
А
О A =OB=OC=OD=R.
ZDAO=ZBAO=
=ZDCO-ZBCO;
ZADO=ZCDO=
=ZABO=ZCBO;
С OM=OR=ON=OQ=r;
177
§ 8.5. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 8.1.В параллелограмме ABCD точка М де-
лит сторону AD в отношении AM :MD=2 :3, а точка N де-
лит сторону ВС в таком же отношении BN :NC=2 :3 . Дока-
зать, что четырехугольники ABNM и MNCD являются парал-
лелограммами.
Пусть ABCD — заданный параллелограмм
(рис.8.20). По свойству 2 параллелограмма AD =ВС. От-
сюда
AM = — AD=—BC = BN.
5 5
Кроме того, AM\\BN. Тогда в четырехугольнике
ABNM противоположные стороны AM и BN равны и
параллельны. Следовательно, по признаку 2 параллело-
грамма этот четырехугольник — параллелограмм. Отсюда
следует, что MN \\АВ, значит, MN\\CD, кроме то-
го, MD || NC. Тогда четырехугольник MNCD удовлетво-
ряет определению параллелограмма. 4k
Пример 8.2. Доказать, что биссектрисы углов прямо-
угольника при пересечении образуют квадрат.
ZS Пусть ABCD — заданный прямоугольник, и
биссектрисы его углов при пересечении образуют четы-
рехугольник EFGH (рис.8.21).
Докажем сначала, что у четырехугольника EFGH
все углы прямые. Действительно, в треугольнике CGD
имеем:
178
90° 90°
Z£>CG= —=45°, ZGDC = —= 45°,
2 2
откуда следует, что внешний угол FGC этого треуголь-
ника равен 90°. Следовательно, FG1.GH. Аналогично ус-
танавливается перпендикулярность других соседних сто-
рон четырехугольника EFGH.
Докажем теперь, что EFGH — ромб. Действитель-
но, EF = AF-AEf FG = FD-GD. Однако в равнобед-
ренном треугольнике AFD боковые стороны AF и FD
равны. Далее, из равенства прямоугольных треугольни-
ков АВЕ и DCG следует, что АЕ = GD. Тог-
да EF = FG. Аналогично FG = GH = НЕ. Таким обра-
зом, у четырехугольника EFGH все стороны равны, сле-
довательно, он является ромбом.
Однако ромб, у которого все углы прямые, есть
квадрат. Значит, EFGH — квадрат. Ж
Пример 8.3. Доказать, что если на сторонах квадра-
в одном направлении равные отрез-
ки AM, BN, СР, DQ, то точ-
ки М, N, Р, Q «ваяются вер-
шинами квадрата.
Zs На рис.8.22 изобра-
жен квадрат ABCD . Пусть а
— стороны квадрата
ABCD , b— длина каждого
из отложенных равных отрез-
ков. В прямоугольных тре-
угольниках BMN и CNP
имеем:
BN=CP, BM=a-b=CN.
Значит, эти треугольники равны, откуда MN = NP. Ана-
логично в четырехугольнике MNPQ равны между собой
и другие соседние стороны. Значит, MNPQ — ромб.
Далее, из равенства рассмотренных треугольников
следует, что Z.BNM = Z.NPC. Тогда
AMNP =\NT-(Z.BNM + APNC) =
= 180° -(ZWPC + ZPNC) =
та ABCD отложены
м
= 180°-90° = 90°.
179
A D
Рис*. 8.23
Puc.8.24
В ромбе MNPQ другие углы также прямые, и
ромб MNPQ является квадратом. Ж
Пример 8.4. Меньшее основание равнобедренной тра-
пеции равно боковой стороне, а диагональ перпендикулярна
боковой стороне. Найти углы трапеции.
ZS Пусть ABCD — данная трапеция, в кото-
рой АВ = ВС = CD, AC LCD (рис.8.23). Обозначим
угол CAD через а. Углы ВСА и CAD равны как внут-
ренние накрест лежащие при параллельных прямых ВС
и AD и секущей АС. Из равнобедренного треугольни-
ка АВС имеем:
ABAC = АВСА = а,
откуда
ABAD = АВАС + ACAD =2а.
По свойству 1 равнобедренной трапеции имеем:
ACDA = ABAD = 2а.
В прямоугольном треугольнике ACD справедливы ра-
венства:
ACAD -h AADC = а + 2а = За = 90°,
откуда а = 30°. Тогда углы трапеции равны: 60°, 60°,
120°, 120°. ▲
Пример 8.5. Прямоугольная трапеция делится диаго-
налью на равносторонний и прямоугольный треугольники.
Большее основание трапеции равно U. Найти меньшее осно-
вание.
Пусть ABCD — прямоугольная трапеция,
АС = CD = AD = а (рис.8.24). Опустим перпендику-
180
ляр СЕ на основание AD. Высота СЕ в правильном
треугольнике является медианой, поэтому АЕ ==~^' В
четырехугольнике АВСЕ имеем: ВС\\АЕ, АВ\\ЕС как
д”а перпендикуляра к одной прямой AD. Тогда АВСЕ
— параллелограмм (точнее, прямоугольник), и по свойст-
ву 2 параллелограмма получаем:
ВС = АЕ =—. Ж
2
Пример 8.6. Вершины А, В, Ct D параллелограм-
ма ABCD лежат соответственно на сторонах АХВХ1 BxC}t C}D}I
A} параллелограмма AxB}C} D}. Доказать, что центры этих па-
раллелограммов совпадают.
На рис.8.25 изображен указанный в условии па-
раллелограмм на сторонах которого лежат вер-
шины параллелограмма ABCD . Рассмотрим треугольни-
ки AXAD и СХСВ. В этих треугольниках AD = CB как
противоположные стороны параллелограмма, углы Ах AD
и СХСВ равны как углы с соответственно параллельными
сторонами, аналогично ZADAX = Z-CBCX. Значит, эти
треугольники равны по второму признаку равенства тре-
угольников. Отсюда ЛГ1) = СГВ. Изобразим эти отрезки
и параллелограмм AXBXCXDX на отдельном чертеже
(рис.8.26).
181
Отрезки JjCj и DB пересекаются в некоторой
точке О. Докажем, что точка О является серединой каж-
дого из этих отрезков. Для этого рассмотрим треугольни-
ки AXDO и СХВО, В этих треугольниках стороны AXD
и СХВ равны, и AOAXD = Z.OCXB как внутренние на-
крест лежащие при параллельных прямых AXDX и BXCV
точно так же Z.ODAX = ZX)BCx. Треугольники равны по
второму признаку равенства треугольников, откуда
= оах = осх.
Точка О есть центр параллелограмма AXBXCXDV по-
скольку она является сере-
диной диагонали АХСХ. Эта В г С
же точка есть центр парал- / /
лелограмма ABCD как се- / /
редина диагонали BD .А / /
Пример 8.7. В трапе- / /
ции ABCD с основаниями AD / /
и ВС угол А острый, а угол D / /
тупой. Доказать, что разность L
проекций боковых сторон тра--tX. Ilf f----------L
пеции на основание равна раз- А В[ D Cj
ности оснований.
Рис.8.27
Пусть ABCD — за-
данная трапеция (рис.8.27).
Опустим перпендикуляры ВВХ и ССХ на прямую AD.
При остром угле А и тупом угле В возможно располо-
жение точек А, Вх, D, Ср представленное на рисунке. В
этом случае
DC, - АВ, = (DC, + B,D}-(ЛВ, + В,D) =
= B£l-AD = BC-AD,
что и требовалось доказать. Возможно еще такое распо-
ложение четырех точек на прямой AD-. A, D, Вх, Сх.
Этот случай рассмотрите самостоятельно. Ж
Пример 8.8. Фигура имеет две перпендикулярные оси
симметрии. Доказать, что их точка пересечения является цен-
тром симметрии этой фигуры.
182
Z\ Пусть I , ТП — пер-
пендикулярные оси симмет-
рии фигуры, О — их точка
пересечения (рис.8.28). Возь-
мем произвольную точку А
фигуры, отличную от точ-
ки О. Тогда точки А1 и А2,
симметричные этой точке
относительно прямых I
и т, также принадлежат
фигуре. Отразим точку А2
Рис. 8.28
симметрично относительно
прямой I . Полученная точка А3 также принадлежит фи-
гуре.
Четырехугольник АА^А^ — параллелограмм, по-
скольку его противоположные стороны АА} и Л2Л3 рав-
ны и параллельны. Он является прямоугольником, по-
скольку все его углы прямые. Оси mt I являются его
осями симметрии (они проходят через середины проти-
воположных сторон), поэтому точка их пересечения О
есть точка пересечения диагоналей прямоугольни-
ка АА}А3А2 (см. §8.2). Тогда О есть середина диехюна-
ли АА3, и точка А3 симметрична точке А относите льно
центра О. Значит, фигура вместе с каждой своей точкой
содержит также и ее симметричный образ относительно
центра О. Это и означает, что точка О есть центр сим-
метрии данной фигуры. Ж
Пример 8.9. Точка Е лежит внутри квадрата ABCD,
причем Z£4D=Z£ZM=15°. Доказать, что треугольник ВЕС
правильный.
ZS Отметим, что точка Е однозначно задается усло-
виями примера. Действительно, для ее построения доста-
точно провести лучи из точек А и D под углом 15° к
стороне AD. Точка пересечения лучей и есть точ-
ка Е (рис.8.29).
Осуществим теперь другое построение. Внутри квад-
рата ABCD поместим правильный треугольник BFC
(рис.8.30). Найдем угол FAD. Имеем:
183
Рис. 8.29 Рис.8.30
ZFBC = 60°, ZABF = 90° - 60° = 30°.
Треугольник ABF равнобедренный, поэтому
ABAF =ABFA =-(180°-30°) = 75°.
2V 7
Тогда Z.FAD = 15°. Аналогично 27*7X4 = 15°. Итак, по-
строенная точка F обладает всеми свойствами точки Е
из условия примера. Поскольку точка Е однозначно за-
дается условиями примера, то точки Е и ^совпадают.
Значит, треугольник ВЕС равносторонний. ▲
§ 8.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
8.01. Сколько можно построить параллелограммов с
вершинами в трех заданных точках, не лежащих на одной пря-
мой?
8.02 . Боковая сторона равнобедренного треугольника рав-
на 5 см. Из точки на основании проведены прямые, параллель-
ные боковым сторонам. Найти периметр полученного паралле-
лограмма.
8.03 . Разность двух углов параллелограмма равна 36°. Най-
ти эти углы.
8.04 . Через точку пересечения диагоналей параллелограм-
ма проведена прямая. Доказать, что отрезок этой прямой, рас-
положенный внутри параллелограмма, делится этой точкой по-
полам.
8.05 . Доказать, что в параллелограмме диагональ меньше
полупериметра.
184
8.06 . Периметр параллелограмма равен 14,24 м. Диагональ
делит его на два треугольника, периметр каждого из которых
составляет 12,42 м. Найти длину этой диагонали.
8.07 . Доказать, что если две смежные стороны и угол меж-
ду ними одного параллелограмма соответственно равны двум
смежным сторонам и углу между ними другого параллелограм-
ма, то эти параллелограммы равны.
8.08 . Доказать, что параллелограмм с равными диагоналя-
ми -— прямоугольник.
8.09 . Расстояния от центра прямоугольника до двух его
сторон равны 15 см и 18 см. Найти периметр прямоугольника.
8.10. Доказать, что четырехугольник, все стороны которо-
го равны, является ромбом.
8.11. Доказать, что параллелограмм, диагонали которого
перпендикулярны, является ромбом.
8.12. Доказать, что все высоты ромба равны между собой.
8.13. Доказать, что середины сторон прямоугольника явля-
ются вершинами ромба.
8.14. Высота ромба, проведенная из вершины, делит его
сторону пополам. Найти углы ромба.
8.15. Сторона ромба образует с продолжениями диагона-
лей углы, относящиеся как 9:7. Найти углы ромба.
8.16. Доказать, что в параллелограмм можно вписать ок-
ружность тогда и только тогда, когда он является ромбом.
8.17. Сформулируйте и докажите утверждение, анало-
гичное указанному в предыдущей задаче, для окружности, опи-
санной около параллелограмма.
8.18. Каким должен быть параллелограмм, для которого су-
ществуют вписанная и описанная окружности?
8.19. В равнобедренной трапеции высота, опущенная из
вершины на большее основание, делит его на отрезки ТП и п.
Найти основания трапеции.
8.20. В равнобедренной трапеции боковая сторона равна
меньшему основанию, а диагональ — большему основанию.
Найти углы трапеции.
W^8.21. Доказать, что выпуклый четырехугольник явля-
ется параллелограммом, если его противоположные углы попар-
но равны.
8.22. Доказать, что сумма расстояний от какой-либо точки,
лежащей внутри параллелограмма, до его сторон не зависит от
выбора точки.
185
8.23. Доказать, что точки касания вписанной в ромб ок-
ружности со сторонами ромба являются вершинами прямо-
угольника.
8.24. Биссектрисы двух углов параллелограмма, прилежа-
щих к его большей стороне, делят противоположную сторону
на три части. Найти их длины, если стороны параллелограмма
равны 10 и 3 .
8.25. Доказать, что четырехугольник ABCD , для которого
прямые АС и BD являются осями симметрии, есть ромб.
8.26. Доказать, что прямые, соединяющие центры квад-
ратов, построенных на сторонах параллелограмма во внешние
от него стороны, также образуют квадрат.
8.27. Доказать, что сумма длин нижнего основания тра-
пеции и боковой стороны превышает сумму длин верхнего
основания и другой боковой стороны.
8.28. Сумма углов при основании трапеции равна 90°.
Доказать, что отрезок, соединяющий середины оснований
трапеции, равен их полуразности.
8.29. От параллелограмма осталось только три точки: вер-
шина и середины двух противоположных сторон. Восстановите
параллелограмм.
8.30. Доказать, что композиция двух осевых симметрий
относительно взаимно перпендикулярных осей является цен-
тральной симметрией.
8.31. В центре квадратного пирога находится изюминка.
От пирога можно отрезать треугольный кусок по линии, пере-
секающей в точках, отличных от вершин, две соседние сторо-
ны; от оставшейся части пирога можно отрезать следующий
кусок (таким же образом) и т.д. Можно ли отрезать изюминку?
8.32. Диагональ АС трапеции ABCD равна боковой сто-
роне CD, Прямая, симметричная BD относительно AD, пере-
секает прямую АС в точке Е. Докажите, что прямая АВ делит
отрезок DE пополам.
186
ГЛАВА 9
ГРУППЫ СИММЕТРИЙ ФИГУР
§ 9.1. ГРУППА СИММЕТРИЙ ФИГУРЫ
Напомним, что множество всех движений плоскости
образует группу относительно операции композиции, т.е.
операции последовательного применения двух движений.
Пусть Ф — произвольная геометрическая фигура.
Рассмотрим множество G таких движений, прк которых
фигура Ф накладывается на себя (т.е. множество всех
наложений фигуры Ф на себя). Последнее для движе-
ния f, содержащегося во множестве G, означает, что
для всякой точки М фигуры Ф, точка Мх = /(Л/) так-
же принадлежит Ф, причем всякая точка Мх фигуры Ф
является образом некоторой точки М фигуры Ф
(т.е. Мх = /(А/) для некоторой точки М фигуры Ф).
Например, ромб при симметрии относительно диаго-
нали накладывается на себя согласно свойству 3 ромба, а
прямой угол при параллельном переносе вдоль биссек-
трисы его угла сам на себя не накладывается.
Теорема 9.1. Множество G образует группу о г-
носительно операции композиции.
□ Для доказательства этой теоремы проверим, что
для множества G выполняются четыре свойства группы.
1. Если f e.G и g eG, то fQg^G.
Действительно, пусть М — произвольная точка фи-
гуры Ф. Тогда A/1 = g(Af) — также точка фигуры Ф,
и = — f(Mx) также является
точкой фигуры Ф.
Обратно, пусть М2 — произвольная точка фигу-
ры Ф, тогда существует такая точка Мх этой фигуры,
187
для которой /(Л/1) = Л/2. Кроме того, найдется точ-
ка М фигуры Ф, для которой g(M)= Мг Таким обра-
зом, для точки М2 фигуры Ф имеем: (/ ° g)(Af)= Л/2.
2. Если f, gt h — движения из множества (7,
то f °(g° h)—^f °g)Qh.
Это свойство является следствием теоремы о сочета-
тельном законе для операции композиции движений.
3. Существует такое движение 8 eGt что для вся-
кого движения f из множества G выполняются ра-
венства:
f ©б =8 ° f = f.
Действительно, таким движением 8 является тожде-
ственное движение плоскости.
4. Для всякого движения f, содержащегося во мно-
жестве G1 существует движение У*-1, обратное движе-
нию f.
Действительно, если точка Мх принадлежит Ф,
то найдется такая точка М фигуры Ф, для которой
/(м) = Мг Тогда для обратного движения имеем:
/"1(М1) = Л/. Очевидно, что у1 является движением,
принадлежащим множеству G, и /°/”1 = /”1о/ = 8.
Определение. Группа движений, наклады-
вающих фигуру Ф на себя, называется группой симмет-
рий фигуры Ф.
При фиксированном центре поворота обозначим по-
ворот на угол ф через 7^. Такое обозначение происходит
от первой буквы английского слова "torsion", означающе-
го "кручение". При ф = 0° условимся, что TQ. = 8. Так-
же условимся о том, что при положительных значени-
ях ф преобразование будет поворотом против часо-
вой стрелки, а при отрицательных значениях ф — пово-
ротом по часовой стрелке на угол ф .
188
Обычно угол ф изменяется от (—180°) до 180°. Ино-
гда угол ф будет принимать значения из промежут-
ков [180°;360°] и [—360°;—180°]. Заметим, что если
180° < ф < 360°, то Гф = 7"ф_360о, и фактически является
поворотом по часовой стрелке на угол ф — 360° . Если же
—360°<ф<—180°, то 7^ = 7^+360of и 7^ является поворотом
против часовой стрелки на положительный угол ф + 360°.
Очевидно также, что повороты 7Jg0. и Г . являются
центральной симметрией.
Обозначим через Sa осевую симметрию относитель-
но прямой а, а через So — центральную симметрию от-
носительно точки О.
§ 9.2. ГРУППЫ СИММЕТРИЙ ТРЕУГОЛЬНИКОВ
Группа симметрий разностороннего треугольника.
О группе симметрий такого треугольника говорится в
следующей теореме.
Теорем . 9.2. Группа симметрий треугольника с
неравными сторонами состоит лишь из тождественного
движения.
□ Пусть АхА2 А3 —треугольник с неравными сторо-
нами, и пусть f — такое движение, при котором тре-
угольник АХА2А3 накладывается на себя. По теореме 5.9
каждая вершина Я, треугольника перейдет в некоторую
вершину Aj (z,; = l,2,3). При этом возможны два слу-
чая:
а) все вершины остаются неподвижными, и тогда по
теореме 5.8 имеем: f = 8 ;
б) существует такая вершина Ait что Aj — f(Ai)t
причем i Ф j. Тогда стороны угЛа Л,- перейдут в стороны
189
угла Aj, откуда ZA^ ZAj, однако это противоречит то-
му, что треугольник является разносторонним.
Итак, единственное движение, при котором раз-
носторонний треугольник А^А2А3
бя — это тождественное дви-
жение. И
Группа симметрий равно-
бедренного треугольника. Рас-
смотрим равнобедренный тре-
угольник АВС с основанием
АВ, причем АВ*АС. Прове-
дем высоту СН, обозначим
через а прямую, содержащую
эту высоту (рис.9.1). Справед-
лива следующая теорема.
Теорема 9.3. Группа
симметрий равнобедренного треугольника АВС со-
стоит из тождественного движения 8 и осевой симмет-
рии Sa относительно прямой а.
□ Очевидно, что движения 8 и Sa накладывают
треугольник АВС на себя. Докажем, что других движе-
ний, накладывающих равнобедренный треугольник АВС
на себя, не сущэст^ует.
Пусть f принадлежит группе симметрий тре-
угольника АВС. Если /(с) = Л, то угол С перейдет в
угол А, и тогда ZC = ZA, что противоречит условию.
Аналогично доказывается, что случай, когда /(С) = В,
также невозможен. Значит, /(с) = С. Тогда точка А ли-
бо перейдет в точку В, либо останется неподвижной.
В первом случае /(Л)-В, f(B)=A, f(C) = C.
Однако это свойство выполняв".! и для Sa. По теоре-
ме 5.8 имеем: f = Sa.
Во втором случае f{A) = A, /(в) = В, /(с) = С.
Таким образом, в этом случае f = 8.
190
Рис. 9.2
Структуру группы симметрий удобно задавать с по-
мощью так называемых таблиц Кэли. В таблице Кэли в
строках и столбцах записываются все элементы группы.
На пересечении строки f и столбца g находится эле-
мент f о g. На рис.9.2 представлена таблица Кэли группы
симметрий равнобедренного треугольника.
Артур Кэли (1821—1895) — английский матема-
тик, заложивший основы современной алгебраической
геометрии, что дало возможность построить модель гео-
метрии Лобачевского. Он создал матричное исчисление,
ввел понятие абстрактной группы, занимался также сфе-
рической астрономией и астрофизикой.
Группа симметрий равностороннего треугольника.
Пусть АВС — равносторонний треугольник с цент-
ром О. Обозначим прямые А О, ВО, СО соответствен-
но через а, Ъ, С (рис.9.3). Справедлива следующая тео-
рема.
Теорема 9.4. Группа симметрий равносторонне-
го треугольника состоит из шести движений: s, Sa, Sb,
^120-' ^-120’’ где ^±120- — повороты относительно
центра О треугольника.
□ Самостоятельно проверьте, что перечисленные
движения накладывают треугольник АВС на себя. Дока-
жем, что других элементов в группе симметрий равносто-
роннего треугольника нет.
Пусть f — элемент этой группы симметрий. Рас-
смотрим следующие три случая:
191
ХУ г Т.12Г Т-120* •5О Sb %
г г Т120* Т-120* С? о» Sc
Т+120* Т120* Т-120* £ Sc sa
Т-120* Т-120* г Т120* с? С.* Sb
с* Sb г т.1го- Т120*
Sb S’b Sc Т120* г Т-120*
Sc Sc Sb Т-120* т.1го- г
Рис.9.4
а) все вершины треугольника АВС являются непод-
вижными, тогда очевидно, что f = 8 ;
б) в треугольнике АВС нет неподвижных вершин.
Тогда, если /(Л) = В, то /(В) = С, /(с) = Л. Яс-
но, что этим равенствам удовлетворяет поворот Т_ ,
т.е. / = Г120.. Если же f(A) = C, /(в) = A, f(c) = B.
™f = TW
в) в треугольнике АВС лишь одна вершина непод-
вижна.
усть /(Л) = Л, тогда /(в) = С, /(с) = В. Поэто-
му f = Sa, Аналогично, если то Ал)-с
и /(С) = Л, и тогда f = Sb. В случае, если /(С) = С,
/(л) = Ви /(в) = А, будем иметь f = SC.
Таблица Кэли группы симметрий правильного тре-
угольника приведена на рис.9.4.
192
С помощью таблицы Кэли удобно находить движе-
ния, обратные к данному. Например, Т и Т явля-
Д & tiyJ
ются взаимно обратными.
На рис.9.4 можно увидеть, что в каждой строке таб-
лицы Кэли содержатся все элементы группы. Это свойст-
во справедливо для всякой конечной группы. Наконец,
таблица Кэли группы симметрий правильного треуголь-
ника не симметрична относительно диагонали. Это
значит, что равенство f Q g — gQ f не всегда выполняет-
Р Р о +120 ^^+120“ °
§ 9.3. ГРУППЫ СИММЕТРИЙ ЧЕТЫРЕХУГОЛЬНИКА
Группа симметрий параллелограмма. Пусть ABCD
— параллелограмм с неравными смежными сторона-
ми АВ и AD и неравными смежными углами BAD
и АВС, О — точка пересечения диагоналей АС и BD
(рис.9.5).
Теорема 9.5. Группа симметрий параллелограм-
ма ABCD состоит из тождественного движения 8 и
центральной симметрии
Рис, 9.5
все вершины А, В, С и D
□ По свойству 5 па-
раллелограмма централь
С ная симметрия So являет
ся наложением паралле-
лограмма ABCD на се-
бя. Докажем, что других
элементов группы сим-
метрий параллелограмма,
кроме So и 8, нет.
Пусть f — элемент
группы симметрий парал-
лелограмма ABCD . Если
неподвижны, то f = 8 .
193
Допустим, что вершина А при наложении f пере-
ходит в вершину Лр При этом сторона АВ перейдет в
некоторую сторону АХВХ. Тогда возможны два случая:
а) АХВ\ совпадаете АВ\
б) АХВ\ совпадает с CD.
В случае а) точка А{ совпадает с В, точка В} совпа-
дает с А. Допустим, что точка С} совпадает с точкой С,
а точка D} совпадает с точкой D. Тогда
АС = А}С} = ВС, BD = BXDX = AD.
Один из углов параллелограмма, например, угол В тупой.
Тогда в тупоугольном треугольнике АВС име-
ем АС>ВС. Получили противоречие. Значит, точка Q
совпадает с точкой D, а точка Dx — с точкой С. При
этом угол BAD перейдет в угол равный уг-
лу АВС. Но по условию углы BAD и АВС не равны.
Таким образом, получаем, что случай а) невозможен.
Рассмотрим случай б). Аналогично случаю а) ника-
кая вершина не может перейти в смежную. Поэтому
f(A)=C, f{C) = А,
откуда
/ = 5О.И
Группа симметрий пря-
моугольника. Пусть ABCD
— прямоугольник с нерав-
ными сторонами АВ и AD,
О — точка пересечения диа-
гоналей АС и BD. Через
середины противоположных
сторон проведем прямые Ш
точке О (рис. 9.6).
Рис.9.6
и I . Они пересекаются в
Докажите самостоятельно следующее утверждение:
Теорема 9.6. Группа симметрий прямоугольни-
ка состоит из движений е, So, Sm, Sf.
' Зак. 687
194
Группа симметрий ромба. Пусть ABCD — ромб, не
являющийся квадратом. Через противоположные верши-
ны проведем прямые I и т, содержащие соответственно
диагонали АС и BD, пересекающиеся в точке О
(рис.9.7).
Докажите самостоятельно следующее утверждение:
Теорема 9.7. Группа симметрий ромба состоит
из движений 8, So, S/r Sw.
Группа симметрий квадрата. Пусть ABCD — квад-
рат с центром в точке О. Проведем через точку О четы-
ре прямые к, Ш, П, I (рис.9.8). Докажите самостоятельно
следующую теорему и постройте таблицу Кэли для груп-
пы симметрий квадрата.
Теорема 9.8. Группа симметрий квадрата состо-
ит из восьми движений: 8 г поворотов Т_^а t Г 90. вокруг
точки О и симметрий So, Skf S[t Smf Sn.
Отметим, что квадрат является параллелограммом,
ромбом и прямоугольником. Поэтому все элементы груп-
пы симметрий этих фигур являются элементами группы
симметрий квадрата. Специфическими для квадрата яв-
ляются лишь повороты Г+90о и Т90о вокруг центра.
§ 9.4. ГРУППА СИММЕТРИЙ КРУГА
Рассмотрим круг с центром О. Проведем через
точку О произвольную прямую (У (рис.9.9). Легко прове-
195
Рис.9.9
В
Рис. 9.10
рить, что поворот Ту вокруг точки О на произвольный
угол ф (—180° < ф < 180°) и осевая симметрия Sd явля-
ются наложениями круга на себя. Напомним также,
что при ф = 0° выполняется условие: = TQ„ = е , а при
ф = ±180° получаем: 7^ = — центральная симметрия
относительно точки О. Докажем, что других элементов
группа симметрий круга не имеет. Сначала рассмотрим
две вспомогательные леммы.
Лемма 9.1. Пусть f — наложение круга на себя.
Тогда для каждой точки А окружности точка Ai=f(A}
также является точкой окружности.
□ Допустим, что точка А} не лежит на окружности.
Тогда она лежит внутри круга, т.е. OAt<R. Проведем
диаметр АВ. Пусть Вх = /(в). Точка В} может лежать
на окружности или внутри круга. Значит, ОВ} < R
(рис.9.10). Так как f — наложение, то А}В} = АВ = 2R.
Согласно неравенству треугольника имеем:
АХВХ < ОА1 + OBX<R + R = 2R,
что приводит к противоречию. Следовательно, точка А}
лежит на окружности. И
Лемма 9.2. При наложении f круга с центром в
точке О на себя выполняется равенство
196
□ Пусть точки А, В, С лежат на окружности. Тогда
согласно лемме 9.1 точки А1=/(а), Bx = f{B), €\ =
= /(С) также лежат на окружности. Пусть Ох = f(O).
Так как f — движение, то
ОХАХ = ОХВ} = (\СХ = R.
Значит, треугольник АХВХСХ вписан в окружность с цен-
тром в точке Ох. По теореме 7.2 точки О и Ох совпада-
ют. И
Применим эти леммы для нахождения группы сим-
метрий круга.
Теорема 9.9. Группа симметрий круга состоит
из всех поворотов вокруг центра круга (в частности, то-
ждественного движения и центральной симметрии от-
носительно центра), а также всех симметрий относи-
тельно осей, проходящих через центр круга.
□ Пусть f — произвольное наложение круга с цен-
тром в точке О на себя. Тогда по лемме 9.2. имеем:
/(0) = 0.
Согласно лемме 5.3 движение f является либо поворо-
том вокруг точки О, либо осевой симметрией относи-
тельно прямой, содержащей диаметр.
§ 9.5. МАГИЧЕСКИЕ ТРЕУГОЛЬНИКИ И КВАДРАТЫ
Рис. 9.11
кую-либо цифру от 1 до 9
Магические треугольни-
ки. В правильном треуголь-
нике каждая сторона разде-
лена на три равные части, и
через каждую точку деления
проведены две прямые, па-
раллельные сторонам тре-
угольника. В результате тре-
угольник разбивается на де-
вять маленьких правильных
треугольников (рис.9.11). В
каждый из них впишем ка-
так, чтобы в разных треуголь-
197
Рис. 9.12
Рис. 9.13
никах стояли разные цифры. Подобную систему чисел
назовем магическим треугольником, если сумма чисел,
прилежащих к каждой из сторон, и сумма чисел вдоль
каждой медианы треугольника совпадают.
В частности, на рис.9.11 имеем:
а + р+ у= у+ 5+ е= уч-у + ф =
= а + е+ (р=а + т+ У = ф + ц + р.
Нетрудно установить, что каждая такая сумма в магичес-
ком треугольнике равна 15. Убедитесь в этом самостоя-
тельно, рассмотрев сумму чисел вдоль всех трех медиан.
Рассмотрим магический треугольник, изображенный
на рис.9.12. С помощью движений, накладывающих тре-
угольник на себя, можно получить из этого треугольника
новые магические треугольники. Рассмотрим, в частно-
сти, поворот вокруг центра треугольника на 120° против
часовой стрелки. При этом преобразовании каждый ма-
ленький треугольник перейдет в другой. Будем считать,
что написанные цифры также перемещаются в новые
маленькие треугольники. Таким образом, мы получим но-
вый магический треугольник (рис.9.13). Так как группа
симметрий правильного треугольника, кроме тождествен-
ного движения, содержит еще пять элементов, то изобра-
женный на рис.9.12 магический треугольник порождает
пять новых магических треугольников.
Существует еще одно преобразование, порождаю-
щее магические треугольники. Заменим каждую циф-
ру п на рис.9.12 на цифру (10 —л). Получим снова ма-
гический треугольник (рис.9.14). Обратим внимание на
198
Рис.9.14 Рис.9.15
то, что этот треугольник нельзя получить из данного с
помощью движения, так как при движениях цифра 9 ос-
тается прилежащей к стороне треугольника, а в новом
треугольнике на рис.9.14 это свойство нарушается.
Из треугольника, изображенного на рис.9.14, можно
построить еще пять новых магических треугольников с
помощью движений из группы симметрий правильного
треугольника. Таким образом, из магического треуголь-
ника, изображенного на рис.9.12, мы построили еще 11
магических треугольников.
Магические квадраты. Перейдем к рассмотрению
магического квадрата. В квадрате разделим каждую сто-
рону на три равные части, и через каждую точку деле-
ния ^поведем прямую, параллельную стороне квадрата.
Получим 9 квадратиков, изображенных на рис.9.15. В
каждый и » них запишем какую-либо цифру от 1 до 9
так, чтобь в разных квадратиках стояли разные цифры.
Подобную систему чисел назовем магическим квадра-
том, если умма трех цифр вдоль какой-либо прямой бу-
дет одина овой. В частности, на рис.9.15 имеем:
ос + р+ у=а + е+ ф = 5+ е+ т =
= ц + У4-ф=а + б+ ц =
= Р+ е+ у = у+ т+ ф = у+ 8+ ц.
Проверьте самостоятельно, что каждая такая сумма в ма-
гическом квадрате равна 15.
На рис.9.16, изображен магический квадрат. С помо-
щью группы симметрий квадрата он порождает еще 7
магических квадратов. Заметим, что замена всех цифр п
199
Рис.9.16
на (10 —л) не порождает
так как это преобразование в данном случае равносильно
центральной симметрии.
новых магических квадратов,
§ 9.6. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 9.1. Найти множество всех центров симмет-
рии фигуры, составленной из двух параллельных прямых.
ZS Пусть заданная фигура состоит из параллельных
прямых 1Х и /2, О — некоторый центр симметрии фигу-
ры. Ясно, что точка О лежит между прямыми 1Х и Z2.
Опустим перпендикуляры ОР и OQ на прямые 1Х и /2
соответственно (рис.9.17). Эти перпендикуляры лежат на
одной прямой. Точка Р при симметрии относительно
центра О должна перейти в некоторую точку Pv принад-
лежащую прямой 12. Такой точкой Р} может быть только
точка Q: ведь Р должна лежать на прямой РО, а един-
ственной точкой пересечения прямых РО и /2 является
точка Q. Итак, точки Q и Р симметричны относительно
точки О. Тогда OP = OQ, и точка О равноудалена от за-
данных прямых. Следовательно, она лежит на прямой Ш,
параллельной этим прямым и равноудаленной от них.
200
Обратно, пусть точка О — произвольная точка пря-
мой Ш (рис.9.18). Опустим перпендикуляры ОР и ОРХ на
прямые Zj и 12 соответственно. Точки Р, О, Рх лежат на
одной прямой, причем OP =OPV Пусть А — произволь-
ная точка прямой отличная от точки Р. Проведем
прямую АО до пересечения с /2 в точке Ах. В прямо-
угольных треугольниках АОР и АХОРХ катеты ОР
и ОРХ равны, углы АОР и АХОРХ равны как вертикаль-
ные. Тогда эти треугольники равны, следовательно,
О A = ОАХ, и точка А1 есть образ точки А при симмет-
рии относительно центра О. Точно так же доказывается,
что для произвольной точки В прямой 12 ее симмет-
ричный образ Вх попадает на прямую 1Х. Итак, при сим-
метрии относительно точки О каждая точка фигуры пе-
реходит в некоторую дру-
А Р £ 1 гую точку фигуры. Значит,
" \ 1 | ..... " произвольная точка пря-
\ мой Ш есть центр симмет-
X О т рии фигуры.
—-----------^1— —------- Таким образом, мно-
\ жество всех центров сим-
\ метрии фигуры, составлен-
~П \ 2 ной из двух параллельных
р . прямых, — это прямая, па-
1 раллельная заданным пря-
Р и с. 9.18 мым и равноудаленная от
них. А
Пример 9.2. Рассмотрим некоторый поворот,
отличный от тождественного движения. Пусть треугольник
при этом повороте переходит в себя. Доказать, что этот
треугольник равносторонний.
ZX Рассмотрим несколько случаев.
а) Данный треугольник имеет неравные стороны.
Тогда по теореме 9.2 его группа симметрий состоит толь-
ко из тождественного движения, и накладываться на се-
бя при повороте он не может.
б) Данный треугольник является равнобедренным,
но неравносторонним. По теореме 9.3 его группа симмет-
201
рий также не содержит поворотов. Следовательно, этот А
случай также невозможен.
в) Данный треугольник правильный. Тогда он пере-
ходит в себя при повороте на ±120° вокруг своего цен-
тра. Итак, реализуется случай в), и данный треугольна
является равносторонним. Ж
П р и м е р 9.3. Четырехугольник имеет единственную
ось симметрии. Доказать, что либо он является равнобедрен-
ной трапецией, либо эта ось симметрии является его диагона-
лью.
ZS Пусть Z — ось симметрии данного четырех-
угольника. Рассмотрим два случая.
а) Вершины четырехугольника не лежат на Z .
Пусть А — вершина четырехугольника, причем А лежит
вне Z . Тогда по теореме 5.10 ее симметричный образ Аг
также является вершиной данного четырехугольника
(рис.9.19). Пусть В — третья вершина четырехугольника,
лежащая вне прямой. Тогда Вх — симметричный образ
точки В — является последней, четвертой вершиной
этого четырехугольника. Отложенные четыре точ-
ки определяют выпуклый четырехугольник АА}ВВ}
(либо АА}В}В). В нем АВХ = АХВ как симметричные от-
носительно Z отрезки; кроме того, ААХ\\ВХВ как перпен-
дикулярные отрезки к одной прямой. Четырехуголь-
ник АА}ВВ} не является прямоугольником, так как тогда
по теореме 9.6 он бы имел еще одну ось симметрии, а по
202
условию такая ось единственная. Итак, данный четырех-
угольник — равнобедренная трапеция.
б) Хотя бы одна вершина четырехугольника лежит
на I . Пусть такой вершиной будет А. Все вершины не
могут лежать на / . Пусть В — вершина, лежащая вне
оси симметрии / , тогда Вх — симметричный образ точ-
ки В — также является вершиной четырехугольни-
ка(рис.9.20). Четвертая вершина его не может лежать
вне / , поскольку в противном случае ее симметричный
образ был бы пятой вершиной данного четырехугольни-
ка. Итак, четвертая вершина С лежит на оси симмет-
рии / , и для четырехугольника ВАВХС ось симметрии /
является его диагональю. А
Пример 9.4. Пусть фигура обладает осью симметрии и
единственным центром симметрии. Доказать, что центр сим-
метрии принадлежит оси симметрии фигуры.
Допустим, что центр симметрии О данной фигу-
ры Ф не лежит на ее оси симметрии / (рис.9.21).
Пусть А — произвольная точка фигуры Ф, лежащая вне
прямой I (случай, когда А лежит на / , рассмотрите са-
мостоятельно). Отразим точку А симметрично относи-
01 А
А з
тельно I , получим точку Ах фигуры. Отразив Ах симмет-
рично относительно центра симметрии О, получим точ-
ку А2 фигуры. Наконец, отразим А2 симметрично отно-
сительно прямой I , получим
точку А3 фигуры Ф. От-
разим затем весь отрезок
Ах А2 симметрично относи-
тельно прямой I . По след-
ствию из теоремы 5.2 он
перейдет в отрезок АА 3,
причем середина О отрез-
ка АхА2 перейдет в середи-
ну Ох отрезка АА3, так как
при центральной симметрии сохраняются расстояния ме-
жду точками, и АОХ = АХО = ОА2 = О}А3. Тогда точка А3
симметрична точке А относительно О}. В силу произ-
203
Рис. 9,22
вольности выбора точки А фигуры можно заключить,
что Ох — еще один центр симметрии фигуры Ф. При-
шли к противоречию с условием примера. Значит, допу-
щение неверно, и центр симметрии данной фигуры обя-
зан лежать на ее оси симметрии. Ж
Пример 9.5. Построить группу симметрий выпуклого
четырехугольника с перпендикулярными диагоналями, кото-
рый имеет две равные смежные стороны и не является ром-
бом.
Рассмотрим выпуклый четырехугольник ABCD
с перпендикулярными диаго-
налями АС и BD, который
имеет равные стороны АВ
и AD и не является ромбом
(рис.9.22). Пусть О — точ-
ка пересечения диагоналей.
Прямоугольные треугольники
АОВ и AOD имеют общий
катет АО и равные гипоте-
нузы АВ и AD. Следова-
тельно, треугольники АОВ
и AOD равны. Отсюда сле-
дует, что ВО = OD, и точки В и D симметричны от-
носительно прямой АС. Тогда стороны ВС и DC сим-
метричны относительно этой прямой и равны. Поскольку
данный четырехугольник не является ромбом, то
ВС* АВ.
Перейдем к построению группы симметрий четы-
рехугольника ABCD . Пусть f — наложение данного
четырехугольника на себя. Обозначим через Ах, Bv Cv
Dx образы вершин А, В, С, D при наложении f. Тогда
точка А является неподвижной. Действительно, если Ах
не совпадает с Л, то равные смежные стороны АВ
и AD перейдут в другие равные смежные стороны, а это
есть пара сторон ВС и DC, имеющих другую длину.
Значит, при таком отображении f получим: А{ВХ*АВ, и
наложение f не является движением. Получили проти-
204
воречие. Значит, А}=А. Аналогично доказывается, что
С} = С. Далее рассмотрим два случая:
а) Вх = В, тогда по теореме 5.8 движение f является
тождественным;
б) Bx — D, тогда DX = B, и f —симметрия относи-
тельно прямой АС.
Итак, искомая группа симметрий состоит из тожде-
ственного движения и симметрии относительно одной из
диагоналей четырехугольника. А
§ 9.7. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
^^9.01. Доказать, что если у четырехугольника есть
центр симметрии, то этот четырехугольник — параллелограмм.
9.02 . Доказать, что прямая, содержащая биссектрису угла,
является осью симметрии этого угла.
9.03 . Сколько осей симметрии имеет отрезок, прямая, луч?
9.04 . Может ли у треугольника быть центр симметрии?
9.05 . Доказать, что разносторонний треугольник не имеет
осей симметрии.
9.06 . Доказать, что группа симметрий многоугольника с
неравными сторонами состоит лишь из тождественного движе-
ния.
9.07 . Доказать, что группа симметрий многоугольника с
неравными углами состоит л*
ИНГ
из тождественного движения.
9.08 . Построить таблицу Кэли группы, состоящей из двух
элементов: 1 и (-1), относительно операции умножения. Срав-
ните эту таблицу с таблицей Кэли для группы симметрий рав-
нобедренного треугольника.
9.09 . Составьте таблицу Кэли группы симметрий ромба и
группы симметрий прямоугольника.
9.10. Докажите, что группа симметрий неравнобедренной
трапеции состоит только из тождественного движения 8 .
9.11. Из каких движений состоит группа симметрий рав-
нобедренной трапеции?
9.12. Противоположные стороны выпуклого шестиугольни-
ка попарно равны и параллельны. Доказать, что он имеет центр
симметрии.
9.13. Доказать, что если фигура имеет две перпендикуляр-
ные оси симметрии, то она имеет и центр симметрии.
205
9.14. Сколько осей симметрии имеет каждая из следую-
щих фигур:
а) полоса, ограниченная двумя параллельными прямыми;
б) круг;
в) полуплоскость;
г) полукруг?
9.15. Может ли фигура иметь более одного центра симмет-
рии?
М^9.16. Придумайте фигуру, имеющую бесконечное
множество осей симметрии, но не имеющую ни одного центра
симметрии.
9.17. Придумайте фигуру, имеющую бесконечное множе-
ство центров симметрии, но не имеющую ни одной оси сим-
метрии.
9.18. Доказать, что существует только 24 магических тре-
угольника.
9.19. Доказать, что в каждом магическом квадрате в цен-
тре стоит цифра 5 .
9.20. Доказать, что существует только 8 магических г:
патов.
9.21. Постройте подгруппу поворотов груши. симметрий
равностороннего треугольника.
206
ГЛАВА 10
ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ и
ПОДОБИЕ ФИГУР
§ 10.1. ТЕОРЕМА ФАЛЕСА
Определение. Пусть прямые АВ и CD пере-
секаются прямыми аг и п2г причем aJIOj (рис.10.1). От-
резки и M2N2, образующиеся на прямых АВ
и CD г назовем соответственными.
Свойства соответственных отрезков описывает сле-
дующая теорема.
Теорема 10.1 (Фалеса). Пусть прямые АВ
и CD пересекаются параллельными прямыми. Тогда от-
ношение каких-либо отрезков прямой АВ равно отно-
шению соответственных отрезков прямой CD.
PucJO. 1
Фалес Милете
Доказательство теоре-
мы Фалеса использует опе-
рацию предельного перехо-
да и содержится в прило-
жении 2.
Следствие. Если
на стороне угла отложены
равные отрезки и через их
концы проведены параллель-
ные прямые, то и на другой
стороне угла образуются
равные между собой отрез-
ки.
кий (ок. 625—547 гг до н.э.)
— древнегреческий математик и астроном. Предсказал
солнечное затмение. Доказал, что круг делится диамет-
ром пополам. Фалесу приписывают также способ опреде-
ления высот разных предметов, в частности, пирамид, по
тени, когда солнце поднимается по горизонтали на 45°.
207
§ 10.2. СРЕДНИЕ ЛИНИИ ТРЕУГОЛЬНИКА И
ТРАПЕЦИИ
Средняя линия треугольника. Отрезок, соединяю-
щий середины двух сторон треугольника, называется
средней линией треугольника.
РисЛО. 2
РисЛО. 3
На рис. 10.2 изображен треугольник АВС . С} — се-
редина стороны АВ, А} — середина стороны ВС.
С\А} — средняя линия треугольника АВС. О свойствах
средней линии треугольника говорится в следующей тео-
реме.
Теорема 10.2. Средняя линия треугольника па-
раллельна третьей стороне треугольника и равна ее по-
ловине.
□ Пусть С1А1 — средняя линия треугольника АВС
(рис. 10.3). Проведем через точку At прямую А^ЦАВ
(точка Вх лежит на стороне АС). Из следствия теоре-
мы 10.1 имеем:
АВ,=В,С = — АС.
1 1 2
Прямая, проходящая через точку С\ и параллельная АС,
пересекает согласно следствию теоремы 10.1 сторо-
ну ВС в точке Аг, т.е. эта прямая содержит среднюю ли-
нию С}А} треугольника АВС . Таким образом, С1А1ЦАС t
208
Puc.10.4
A DE
Puc.10.5
откуда ясно, что ACXAXBX — параллелограмм. Отсюда
следует, что
CtAt = ABt=^AC. Ш
Средняя линия трапеции. Отрезок, соединяющий
середины боковых сторон трапеции, называется средней
линией трапеции. На рис. 10.4 изображена трапе-
ция ABCD . Точки М и N — середины ее боковых сто-
рон АВ и CD соответственно. Отрезок MN — средняя
линия трапеции ABCD . Утверждения о свойствах сред-
ней линии трапеции содержит следующая теорема.
Теорема 10.3. Средняя линия трапеции парал-
лельна основаниям трапеции и равна полусумме осно-
ваний.
□ Пусть отрезок MN — средняя линия трапе-
ции ABCD (рис. 10.5). Докажем вначале, что MN \\AD.
Проведем через точку М прямую MNX, параллельную
AD, где точка Nx лежит на стороне CD. По теореме
Фалеса Nx — середина CD, и тогда прямые MNX
и MN совпадают. Значит MN \\AD. Проведем пря-
мую BN до пересечения ее с прямой AD в точке Е. По
теореме Фалеса точки Т, К, N являются серединами
отрезков АС, BD и CD соответственно. Итак, отрезки
MN, МТ, TN и KN являются средними линиями тре-
угольников АВЕ , АВС, ACD и BCD соответственно.
По теореме 10.2 имеем:
209
MN= — AE, MT = KN =—BC, TN= — AD.
2 2 2
Кроме того, треугольники NDE и NCB равны (докажи-
те это). Итак,
АЕ = AD + DE = AD + ВС.
Имеем:
mn=Uad + bc), тк=TN -KN =^(ad - вс).
Попутно мы доказали следующую теорему.
Теорема 10.4. Отрезок средней линии трапеции,
расположенный между ее диагоналями, равен полураз-
ности оснований.
§ 10.3. ГОМОТЕТИЯ. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ
Рассмотрим еще одно преобразование плоскости.
Гомотетия. Преобразование f плоскости, ставящее
в соответствие каждой точке М точку МХ = /\М),
лежащую на прямой ОМ, по правилу ОМх—\куОМ,
где к — постоянное, отличное от нуля число, а О —
фиксированная точка, называется гомотетией.
М
0
Mt
О М
Рис.10.6 Рис. 10.7
При к>0 точки О, М, лежат на одном луче с
„ ОМ. ,
центром в точке О, при этом = к (рис. 10.6).
210
Если £<0, то точки О, М, лежат на одной пря-
мой, но точка О лежит между точками М и М} и
ОМ. I I
~ОМ == (рис.10.7). Будем считать также, что для точ-
ки О выполняется условие: f(O) = О,
Число к называется коэффициентом гомотетии, а
точка О — центром гомотетии.
Если фигура Fx образовалась в результате примене-
ния гомотетии ко всем точкам фигуры F, то эти фигуры
называются гомотетичными.
Термин "гомотетия" составлен из греческих слов
и 0ето^ — "расположенный". Его буквальный
смысл — "одинаковое расположение”, "одинаковое поло-
жение".
Подобие. Преобразованием подобия называется та-
кое отображение f фигуры F, при котором
АХВХ = к • АВ,
где А, В —любые точки фигуры F,
к — некоторое фиксированное положительное число.
Фигура Fp образованная в результате применения
преобразования подобия к фигуре F, называется подоб-
ной этой фигуре. Число к называется коэффициентом
подобия.
Пусть Fx, F2, F3 — некоторые фигуры. Нетрудно ус-
тановить выполнение следующих свойств:
1. Фигура F} подобна фигуре
2. Если фигура подобна фигуре F2, то фигура F2
подобна фигуре Fv
3. Если фигура подобна фигуре F2, а фигура F2
подобна фигуре F3f то фигура F} подобна фигуре F3.
Сделайте это самостоятельно.
Так же, как и для движения, доказывается, что при
преобразовании подобия три точки А, В, С, лежащие
211
на одной прямой, переходят соответственно в точки Л,,
Bv Ср которые также лежат на одной прямой. При этом,
если точка В лежит между точками А и С, то точка Вх
лежит между точками А1 и СР
Таким образом, при преобразовании подобия пря-
мые переходят в прямые, лучи — в лучи, отрезки — в от-
резки. Кроме того, преобразование подобия также
сохраняет углы между лучами. Мы докажем это,
предварительно установив связь между преобразованием
подобия и гомотетией.
Теорема 10.5. Гомотетия с коэффициентом к яв-
ляется преобразованием подобия с коэффициентом |Аг|.
□ Доказательство про-
ведем только для случая
к>\ . Пусть f — гомоте-
тия с центром О и коэф-
фициентом к>\ . Возьмем
на плоскости произволь-
ные точки Л и В, отлич-
ные от центра О. На сто-
ронах угла АОВ располо-
жены точки 4=/U) И
Bj = /(В) (рис.10.8). Дока-
жем, что А}ВХ = к • АВ .
Проведем через точку
ОВ, до пересечения с отрезком АХВХ в точке М. Тогда
АМВХВ — параллелограмм, следовательно, МВХ = АВ.
Далее,
AA1 = OAj-OA=k-OA-OA=(k-l)-OA.
По теореме Фалеса имеем:
ДЛ/ А,А ,
_:__ =__i_ = к — I
МВХ АО
О В Bj
Рис.10.в
А прямую, параллельную
Отсюда
AxM = (k-l)-MBv
212
Рис. 10.9
Рис. 10.10
АХВХ = АхМ+МВх=(к-\)-МВХ + МВХ =
= к-МВх = к-АВ.
Значит, преобразование f увеличивает расстояния
между точками в к раз, и f является преобразованием
подобия с коэффициентом £|.
Случаи 0<£<1 и к<0 рассмотрите самостоятельно.
А теперь перейдем к доказательству следующего
утверждения.
Теорема 10.6. Преобразование подобия сохра-
няет углы между лучами.
□ Пусть f — преобразование подобия с коэффици-
ентом к. Рассмотрим угол с вершиной в точке А
(рис. 10.9). Пусть /(j) = Аг Тогда угол ВАС (точки В
и С лежат на сторонах угла А) переходит в некого-
рый угол ВХАХСХ, где Bx = f(B), Сх = f(C), причем
АхВ} = к • АВ t AjC^k-AC, В^ — к-ВС (рис.10.10).
Рассмотрим гомотетию g с центром в точке Ах и коэф-
1
фициентом —. Тогда
к
= = -®2’ £>(С])=С2,
причем
213
А,В7 = — А,В,= — -к- АВ = АВ
12 к 1 1 к
и аналогично получаем, что АХС2 = АС. Кроме того, из
теоремы 10.5 следует, что В2С2 = ВС. Значит, треуголь-
ники АВС и АхВ2С2 равны по третьему признаку ра-
венства треугольников. Итак, ZA = AAV И
§ 10.4. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 10.1. Проекции двух сторон остроугольного
треугольника АВС на прямую АС имеют длины 6 см и 4 см.
Какую длину имеют проекции медиан этого треугольника на
эту же прямую?
Пусть в треугольнике ЛВС отрезки AAV BBV
CCi — медианы, ВН1. AC, АН = 4 см, НС = 6 см
Рис. 10.11
т.е. проекция НВ} медианы
Фалеса
AF = FH,
Но
(рис. 10.11). Опустим пер-
пендикуляры CjF и АХЕ
на прямую Л С. По следст-
вию 1 теоремы 3.5 и теоре-
ме 3.3 прямые ВН, C}F,
А}Е параллельны. Очевид-
но,
НВХ = НС-ВХС =
= НС-—АС =
2
= 6 —5 = 1(см),
ВВ} равна 1см. По теореме
НЕ=ЕС.
Я£=-ЯС=--6=3(см), HF =-НА= — -4 = 2(см).
Найдем теперь проекции АЕ и FC медиан ААХ и СС,
соответственно:
214
АЕ = НА + НЕ =4 + 3 = 7 (см),
FC = HF + ЯС=2 + 6 = 8(см).
Итак, АЕ = 7 см, НВХ = 1 см, FC = 8 см. Ж
Пример 10.2. Доказать, что середины сторон ромба
являются вершинами прямоугольника.
Пусть ABCD — ромб, Е, F, G, Н — середины
его сторон (рис.10.12). Диагонали ромба АС и BD вза-
имно перпендикулярны. Отрезок ЕН есть средняя линия
треугольника АВС, и по теореме 10.2 ЕН\\АС. Анало-
гично EF\\BD. Тогда по следствию 2 теоремы 3.5 име-
ем: EF 1 АС, откуда по тому же следствию EF 1.ЕН.
Аналогично устанавливается, что остальные углы четы-
рехугольника EFGH также прямые. Противоположные
стороны его параллельны, и параллелограмм EFGH яв-
Рис. 10.12
Рис. ю. 13
Пример 10.3. Отрезок средней линии трапеции, за-
ключенный между ее диагоналями, вдвое короче этой средней
линии. Найти отношение оснований трапеции.
ZX Пусть MN — средняя линия трапеции ABCD
(рис. 10.13). Е, F —точки пересечения этой средней ли-
нии с диагоналями АС и BD соответственно. По теоре-
ме 10.4 получаем:
EF =
AD-BC
а по теореме 10.3 имеем:
MN =
AD + BC
2
215
По условию
EF
MN
1
= -, откуда
MN = 2EF,
AD + ВС A AD- ВС
= 2 ,
2-----------2
AD + BC = 2AD-2BC,
AD
3BC = AD и—= 3. A
BC
Пример 10.4. Доказать, что в равнобедренную трапе-
цию можно вписать окружность тогда и только тогда, когда
боковая сторона равна средней линии трапеции.
zCs Пусть а и Ь — длины оснований равнобедрен-
ной трапеции, С — длина ее боковой стороны, а т —
а + Ь
длина средней линии. По теореме 10.3 ТП =----. Если в
^2
трапецию можно вписать окружность, то по теореме 6.5
имеем:
= 7И.
Обратно, пусть С = т. Тогда
Рис. 10.14
Значит, по теореме 6.5 в тра-
пецию можно вписать ок-
ружность. А
угольника остались три точки
— основания медиан. Восста-
новить данный треугольник.
Предположим, что
треугольник восстановлен и
точки А, В, С — его вер-
шины. Пусть точки Ах,
С — основания медиан
AAV BBV ССХ треугольника АВС (рис. 10.14). Соединим
эти точки отрезками. Тогда AXBV BXCV АХСХ — средние
линии треугольника АВС. По теореме 10.2 ЛВ||ДВр
216
м
м
Рис. 10.15
ВС ||ВхСр JCllJjCp Таким образом, треугольник АВС
можно восстановить так:
1) построить треугольник АХВХСХ\
2) через точки Ах, Вх, Сх провести прямые, парал-
лельные соответственно прямым ВХСХ, АХСХ, АХВХ.
Точки пересечения этих
прямых и являются верши-
нами треугольника АВС.
Пример 10.6. Пусть О
центр гомотетии f с коэффи-
циентом к * 0, g — симметрия
относительно прямой, проходя-
щей через точку О. Доказать,
что f °g=g° f.
Пусть точка М при
гомотетии с центром в точке О и коэффициентом к пе-
реходит в точку Мх (рис. 10.15). Проведем прямые, пер-
пендикулярные прямой а, через точки М и Мх и отло-
жим на них отрезки SN и SXNX, равные соответствен-
но SM и SXMX. Тогда точки Ot N и Nx лежат на одной
прямой (докажите это самостоятельно). Прямые MN
и Мх Nx параллельны, и по теореме Фалеса
ONX _ ОМ. _ ;,
ON ОМ b
Следовательно,
f(g( М)) - fW = JV, и g(/( Л/)) = g( М,) = Д',.
Пример 10.7. Доказать, что любое преобразование по-
добия может быть представлено в виде композиции гомотетии
и некоторого движения.
ZS Докажем вначале, что композиция fx ° f2,
где fx — преобразование подобия с коэффициентом к,
2 — гомотетия с коэффициентом —, является движени-
217
ем. Очевидно, f\° f2 — взаимно однозначное отображе-
ние плоскости на себя. Пусть
Л(л)=л,,/2(в)=г,.
Тогда
А.В. = — АВ,
1 1 к
Далее, предположим, что
fl(А ) = Д' f\(д) = Д •
Тогда
А1В, = кА.В, = к--АВ = АВ.
22 11 к
Таким образом,
/,(Л(л))=4. /,(/2(в))=д и л2вг=лв.
т.е. fx ° f2 является движением.
Пусть теперь F — данное в условии задачи преоб-
разование подобия с коэффициентом к. Рассмотрим
произвольную гомотетию f с коэффициентом к. Тог-
да f~\ очевидно, является гомотетией с коэффициен-
Т X Г"* ~ 1
том —. Из доказанного выше следует, что г о J являет-
к
ся движением. Но тогда lF°У”1)0 f = F, т.е. преобра-
зование подобия F пред-
ставлено в виде компози-
ции движения F о f~} и го-
мотетии f. А
Пример 10;8. С помо-
щью циркуля и линейки вос-
становить треугольник АВС
по его вершине А, середи-
не М стороны ВС и основа-
нию перпендикуляра, опущен-
ного из точки В на биссектри-
Рис.10.16 СУ Угла ВАС.
ZS Пусть треугольник
АВС восстановлен. Проведем в треугольнике АВС пря-
218
мую ВК, перпендикулярную биссектрисе AL, до пере-
сечения со стороной АС в точке Вх и соединим отрез-
ком точки К и М (рис. 10.16). Треугольник АВВ} —рав-
нобедренный, так как АК является его биссектрисой и
высотой. Значит, точка К делит отрезок ВВХ пополам.
Таким образом, КМ является средней линией треуголь-
Таким образом, восстановление треугольника АВС
осуществляется так:
1) проводится отрезок КМ;
2) проводится прямая АК;
3) через точку К проводится прямая I , перпендику-
лярная прямой АК;
4) через точку А проводится прямая ТП, параллель-
ная КМ',
5) от точки Вх пересечения прямых ТП и I отклады-
вается отрезок ВХС = 2КМ так, чтобы точки А и С ле-
жали по разные стороны от точки Вх;
6) проводится прямая СМ.
Точка пересечения этой прямой и прямой I являет-
ся искомой вершиной В треугольника АВС. Ж
Пример 10.9. Назовем
фигуру ограниченной, если она А Ао Аз
лежит в некотором круге. До- \ у ж
казать, что ограниченная фигу- \ /
ра не может иметь более одно- \ /
го центра симметрии. \ /
Допустим, что огра-
ниченная фигура Ф имеет
два центра симметрии —
Q
точки Р и Q (рис.10.17).
Пусть А — произвольная
точка фигуры, причем А не
Рис.10.17
лежит на прямой PQ (случай, когда А находится на пря-
мой PQ рассмотрите самостоятельно). Отразим точку А
симметрично относительно центра Р, Тогда получим
точку Ах, принадлежащую фигуре Ф. Отразим теперь А}
219
симметрично относительно центра Q. Тогда получим
точку J2, также принадлежащую фигуре Ф. Отметим,
что в треугольнике АА}А2 отрезок PQ есть средняя ли-
ния, поэтому
ЯЛ2||Р0, AA2 = 2PQ.
Точка А2 получается из точки А параллельным перено-
сом L вдоль луча PQ на расстояние 2 • PQ. Итак, каж-
дая точка фигуры Ф, лежащая вне прямой PQ, под дей-
ствием движения L переходит в новую точку фигуры Ф.
Тогда J3 = £(J2) принадлежит фигуре Ф, Я4 = £(Л3)
также принадлежит фигуре Ф и т.д. На луче АА2 по-
лучаем бесконечное множество точек фигуры Ф. Это та-
кие точки ЯЛ+1, для которых
ААЛ+1 = пАА2=2п- PQ, п > 1.
Расстояние от точки Ап+1 до точки А может быть боль-
ше любого заданного числа, поэтому фигура Ф не поме-
щается целиком ни в каком круге и не является огра-
ниченной. Ж
§ 10.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
А
10.01. С помощью циркуля и линеики разделить дан-
ный отрезок на П равных частей.
10.02. Доказать, что середины сторон выпуклого четырех-
угольника являются вершинами параллелограмма.
10.03. Доказать, что если на каждой стороне угла последо-
вательно отложить отрезки равной длины и через соответст-
вующие концы отрезков, считая от вершины, провести прямые,
то эти прямые будут параллельны.
10.04. Построить отрезок длины X, если:
ab
а) Х= —;
с
а2
6) Х=—,
и
где а, b , С —- длины заданных отрезков.
220
10.05 . Стороны треугольника равны a, b , С. Найти пери-
метр треугольника, вершины которого находятся в серединах
сторон данного треугольника.
10.06 . Основания трапеции относятся как 3:2, а средняя
линия трапеции равна 20 см. Найти основания трапеции.
10.07 . Концы диаметра удалены от касательной к окруж-
ности на 1,4 см и 0,6 см. Найти длину диаметра окружности.
10.08 . Средняя линия треугольника делит его на треуголь-
ник и трапецию. Найти отношение их средних линий.
10.09 . Пусть /р f2 — гомотетии с центром в точке О
и коэффициентами кх и к2 ( ^*0, Л2^0). Доказать, что
/j о/2 = Л °/1» и определить, каким будет преобразование
f\ ° fi*
10.10. Какими преобразованиями являются гомотетия с ко-
эффициентами 1 и (-1)?
10.11. Пусть f — поворот вокруг точки О, a g — гомоте-
тия с центром в точке О. Доказать, что f оg = go f.
10.12. Доказать, что любые две окружности подобны.
10.13. Доказать, что при преобразовании подобия полу-
плоскость переходит в полуплоскость.
10.14. В круге проведены две хорды ССХ и DDV пер-
пендикулярно диаметру АВ . Доказать, что отрезок MMV кото-
рый соединяет середины хорд CD и CXDV также перпендикуля-
рен к АВ.
10.15. Точки А и В стягивают на окружности с центром в
точке О дугу, градусная мера которой равна 60°. На этой дуге
выбрана точка М. Доказать, что прямая, проходящая через се-
редины отрезков МА и ОВ, перпендикулярна прямой, прохо-
дящей через середины отрезков МВ и ОА .
10.16. Доказать, что отрезки, соединяющие середины про-
тивоположных сторон выпуклого четырехугольника, в точке пе-
ресечения делятся пополам.
10.17. Доказать, что середины двух противоположных сто-
рон и середины двух диагоналей выпуклого четырехугольника
либо являются вершинами параллелограмма, либо лежат на
одной прямой.
10.18. Если отрезок, соединяющий середины двух проти-
воположных сторон выпуклого четырехугольника, равен полу-
сумме двух других сторон, то такой четырехугольник является
параллелограммом или трапецией. Доказать это.
221
10.19. На плоскости даны две непараллельные прямые и
точка М, лежащая вне этих прямых. Найти на одной из пря-
мых такую точку X, для которой отрезок MX делится второй
прямой пополам.
10.20. На плоскости заданы окружность S, прямая I и
точка М на ней. Для каждой окружности Т, касающейся пря-
мой / в точке М, строим точку X —- точку пересечения об-
щих внешних касательных к окружностям S и Т (если они су-
ществуют). Доказать, что множество точек X принадлежит
двум прямым.
10.21. На биссектрисы внешних углов, смежных углам В
и С треугольника АВС, из его вершины А опущены пер-
пендикуляры AM и AN. Точки М и N соединены между
собой. Доказать, что MN = р, где р — полупериметр данного
треугольника.
222
ГЛАВА 11
СВОЙСТВА ПОДОБНЫХ ФИГУР
§ 11.1. ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
Из определения преобразования подобия и теоре-
мы 10.6 следует, что в подобных треугольниках стороны
пропорциональны и соответствующие углы равны, т.е.
если треугольники АВС и АХВХСХ подобны и при преоб-
разовании подобия f выполняются равенства
А С At Ct
Рис.11.1
а}-Аа).вх~/(в),сх=/(с),
AtBt = BtC, _ АХСХ
AB ~ ВС AC '
XA = AAV ZB = ZBP ZC = ZC1 (рис. 11.1).
Эти равенства справедливы и для равных треуголь-
ников АВС и АХВХСХ, причем
АХВХ _В&_АХСХ
АВ ВС АС
Очевидно, что равные треугольники являются подобны-
ми с коэффициентом подобия к = 1.
223
Рассмотрим теперь три признака подобия треуголь-
ников, которые аналогичны соответствующим признакам
равенства треугольников.
ТеоремаИ.1. (первый признак подобия тре-
угольников). Если две стороны одного треугольника про-
порциональны двум сторонам второго треугольника и
углы между этими сторонами равны, то такие треуголь-
ники подобны.
□ Пусть АВС и 4 AG — два треугольника и
44 _ 4G. / л — / л
, Z-A — Z А* •
АВ АС 1
Пусть к = . Применим к треугольнику АВС пре-
образование подобия с коэффициентом к. Тогда треу-
гольник АВС перейдет в треугольник J2B2C2, причем
Тогда имеем:
44 = 44» 4G = 4G»= ^-А *
По первому признаку равенства треугольников
и поэтому треугольники А2В2С2 и А}В}С} подобны. Из
§10.3 следует, что треугольники AiBlCl и АВС подобны.
Те орема 11.2. (второй признак подобия тре-
угольников). Если два угла одного треугольника равны
соответственно двум углам второго треугольника, то та-
кие треугольники подобны.
□ Пусть в треугольниках АВС и АХВХС} дано:
ZZ=ZJP ZB = ZB1.
Обозначим так же, как и при доказательстве теоре-
4Д
мы 11.1 отношение через к. Применив к треуголь-
нику АВС преобразование подобия с коэффициен-
том к, получим треугольник А2В2С2, в котором
Тогда получим:
224
А& = AXBV ZJ, = Z^, ZB, = ZB2.
По второму признаку равенства треугольников
ДЛ2В2С2 =
и поэтому треугольники и АХВХСХ подобны. Но
тогда из §10.3 следует, что треугольники АХВХСХ и АВС
подобны. И
Теорема 11.3. (третий признак подобия треуголь-
ников). Если три стороны одного треугольника пропор-
циональны трем сторонам второго треугольника, то та-
кие треугольники подобны.
Теорема 11.3 доказывается аналогично. Сделайте это
самостоятельно.
Puc.ii. г
Al В,
Рис.11.3
Следствие 1. Пусть прямая, параллельная сто-
роне АВ треугольника АВС, пересекает стороны АС
и ВС в точках Ах и Вх (рис. 11.2). Тогда треугольники
АХВХС и АВС подобны.
□ Углы САХВХ и С АВ равны как соответственные
углы при параллельных прямых АХВХ и АВ и секу-
щей АС. Аналогично равны углы АХВХС и АВС. Тогда
треугольники АХВХС и АВС подобны по второму при-
знаку подобия. Й
Следствие 2. Если острый угол одного прямо-
угольного треугольника равен острому углу другого пря-
моугольного треугольника, то такие прямоугольные тре-
угольники подобны (рис. 11.3).
225
□ Это утверждение следует из второго признака по-
добия.
§ 11.2. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В
ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ. ТЕОРЕМА
ПИФАГОРА
Пусть в прямоугольном треугольнике АВС АС = b,
ВС = а, Z.C = 90°, АВ = с, CD = h — высота треуголь-
ника АВС. Она делит гипотенузу АВ на отрезки
BD = ac, AD =bc, являющиеся проекциями катетов
ВС = а, АС = b на гипотенузу АВ = с (рис. 11.4).
Треугольники АВС , ACD , BCD подобны, посколь-
ку Z.DCA = Z.B, Z.DCB =АА (по следствию 2, §11.1). Из
подобия треугольников АВС и BCD следует, что
— =—, т.е. b2 = cb ,
ь ъс
а из подобия треугольников
АВС и ACD получаем^
что
— = —, т.е. а2 =с а. А
а ас
Из подобия треугольников
ACD и BCD следует, что
h Ъс
a h '
V
Рис. 11.4
h2 = а.Ь..
V V
т.е.
2 2 *
Складывая равенства а =с-ас, b =с-Ьс, получим:
a2 +b2 = c-(ar+br)=c-c = c2.
\ V V *
Таким образом, нами доказаны следующие три утвер-
ждения.
Теорема11.4 (теорема Пифагора). В прямо-
угольном треугольнике квадрат гипотенузы равен сум-
ме квадратов катетов.
Те орема И.5. В прямоугольном треугольни-
ке квадрат катета равен произведению гипотенузы на
проекцию этого катета на гипотенузу.
8 Зак. 687
226
Теорема 11.6. В прямоугольном треугольнике
квадрат высоты, проведенной из вершины прямого угла
на гипотенузу, равен произведению проекций катетов
на гипотенузу.
Пифагор Самосский (около 570—около 500
до н.э.) — древнегреческий математик и философ-идеа-
лист. Создал свою школу, во многом благодаря которой
геометрия приобрела характер науки. Особенностью ме-
тода Пифагора было сочетание геометрии и арифметики.
Теорема 11.7. В прямоугольном треугольнике
произведение катетов равно произведению гипотенузы
на высоту, опущенную на гипотенузу.
□ Обратимся к рис. 11.4. По теореме 11.5 и 11.6 име-
ем:
с2Л2=с2 -ас - Ь=(с • ас) 4с - Ьс) = а2Ь2,
откуда
а&=сй.И
Следствие 1. Гипотенуза равнобедренного
прямоугольного треугольника в 42 раз больше катета
(рис. 11.5).
□ В самом деле, согласно теореме Пифагора
АВ = 4 а2 + а2 = 42а2 = aл/2.
Следствие 2. Диагональ квадрата в 42 раз
больше его стороны.
Докажите это самостоятельно.
§ 11.3. ОКРУЖНОСТЬ, ОПИСАННАЯ ОКОЛО
ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
Пусть около прямоугольного треугольника АВС
(ВС=а, АС =Ь, АВ=с, А_С = 90°) описана окруж-
ность. Тогда по теореме 6.6
ZC = |(oJ5), т.е. =180°.
Значит, гипотенуза АВ является диаметром описанной
окружности. Середина О гипотенузы АВ является цен-
тром этой окружности (рис. 11.6). Обозначим радиус опи-
227
санной около треугольника АВС окружности через R.
Тогда СО — медиана треугольника АВС, т.е. СО = тс.
с
Таким образом, тс = R = —, т.е. медиана, проведенная к
гипотенузе прямоугольного треугольника, является ра-
диусом описанной окружности и равна половине гипо-
тенузы. Кроме того, треугольники АОС и ВОС равно-
бедренные, и поэтому ААСО = АЛ, АВСО = АВ,
§ 11.4. ОКРУЖНОСТЬ, ВПИСАННАЯ В
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Рассмотрим теперь окружность, вписанную в прямо-
угольный треугольник АВС.
Пусть I — центр этой окружности. М, N, Р —
точки касания этой окружности соответственно со сторо-
нами bf а, с (рис.И.7). Тогда IM1AC, INU3C,
IP1AB, и по следствию 1 теоремы 3.5 IN || МС,
IM\\CN. Значит, CMIN —параллелограмм, и
ZC = ZM = ZW = 90°.
Итак, AMIN = 90°. Но IM = IN , где г — радиус ок-
ружности, вписанной в треугольник АВС . Таким обра-
зом, CMIN — квадрат ( IM = СМ = CN = IN = г).
Из следствия 2 теоремы 6.2 имеем:
AM = АР = АС-СМ = Ь-г,
228
Рмс.11.7 Рис.11.8
BP = BN = ВС-CN = а-г.
Так как АР + ВР = АВ, то а-г + Ь -г =с, откуда
. ь о а+Ь-с
а + Ь — 2г = с и г =--.
2
Мы получили формулу для вычисления радиуса окружно-
сти, вписанной в прямоугольный треугольник с катета-
ми а и Ь и гипотенузой с.
§ 11.5. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В
ОКРУЖНОСТИ
Рассмотрим окружность и две ее хорды АВ и CD,
пересекающиеся в точке М (рис. 11.8).
Теорема 11.8. Произведения отрезков хорд, пе-
ресекающихся внутри круга, равны.
□ Треугольники MAD и МСВ подобны, так как
AAMD = АСМВ, АА = AC = ^-(\jBD)
по теореме 6.6. Значит,
AM МВ =СМ DM.Ъ
СМ ВМ
Пусть точка А находится вне круга, и прямая, про-
ходящая через точку А, пересекающая окружность в
точках В и С, — секущая. Будем называть отрезок АС,
где АС>АВ, — отрезком секущей, а отрезок АВ —
229
внешней частью этого отрезка. Проведем через точку А
касательную к окружности. Пусть D — точка касания.
Отрезок AD будем называть отрезком касательной к
окружности (рис. 11.9). Справедлива следующая теорема.
Теорема 11.9. Квадрат отрезка касательной,
проведенной из точки, лежащей вне круга, равен произ-
ведению какого-либо отрезка секущей на его внешнюю
часть.
□ 1) Пусть сначала АС — отрезок секущей, прохо-
дящий через центр окружности, AD — отрезок каса-
тельной (рис. 11.10). Треугольник AOD — прямоуголь-
ный, поэтому
AD2 = AO2-OD2 = (AC-R)2 -R2,
где R — радиус окружности. Отсюда,
AD2 = АС2-2АС • R = АС(АС -2R) = АС-АВ.
2) Пусть теперь АС2 и АС} — два отрезка секу-
щих, АВ2 и АВ} — их внешние части (рис.11.11). Так
как четырехугольник СХС2В2В} вписан в окружность, то
ZC, =180°- Z5,В.С., т.е. ZC, = ХАВ,В2.
л» л» 1 1 X IX
Аналогично ZC] = ХАВ 2ВХ. По второму признаку подо-
бия треугольники АС2СХ и АВ2ВХ подобны. Тогда
АС2 _ АСХ
АВХ АВ2
откуда
230
Рис.11.11 Рис.11.12
АСг • АВ , = АС2 АВ2.
Это значит, что произведение отрезка секущей, проходя-
щего через точку А, на его внешнюю часть есть ве-
личина постоянная. Учитывая результат, доказанный
в п.1) получаем, что это произведение равно квадрату от-
резка касательной к окружности, проведенной из точ-
ки А.
Т е о р е м а 11.10. Квадрат перпендикуляра, опу-
щенного из точки окружности на диаметр, равен произ-
ведению отрезков, на которые этот перпендикуляр де-
лит диаметр.
□ Пусть CD ХАВ, АВ — диаметр окружности с
центром в точке О (рис. 11.12). Тогда
ЛАСВ = |(иЛВ) = 90°,
и CD — высота треугольника АСВ . По теореме 11.6
имеем:
cd2 = ad db.
§ 11.6. СВОЙСТВО МЕДИАН ТРЕУГОЛЬНИКА
Теорема 11.11. Три медианы пересекаются в од-
ной точке. Эта точка делит каждую из медиан в отно-
шении 2:1, считая от вершины.
231
Рис.11. 13 Рис.11.14
□ Пусть ААХ, ВВХ — две медианы треугольни-
ка АВС , пересекающиеся в точке М; А2, В2 — середи-
ны отрезков AM и ВМ (рис. 11.13). Тогда А2В2 —сред-
няя линия треугольника АМВ , АХВХ — средняя линия
треугольника АВС . По теореме 10.2 имеем:
A^WAB > ДД||ЛВ и А2В2= — АВ ; АХВХ = — АВ.
2> 2>
Итак, А2В2ЦАхВх и А2В2 = АхВх, значит, АХВХА2В2 —па-
раллелограмм. Поэтому точка М делит его диагона-
ли АхА2 и ВхВ2 пополам. Это значит, что
АМ-.МАХ = 2-Л, ВМ:МВХ = 2:1.
Таким образом, точка М, делящая какую-либо ме-
диану треугольника АВС в отношении 2:1, считая от
вершины, делит в таком же отношении и две другие ме-
дианы. Итак, медианы ААХ, ВВХ, ССХ пересекаются в
точке М и делятся этой точкой в отношении 2:1, считая
от вершин треугольника. И
§ 11.7. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В
ПРАВИЛЬНОМ ТРЕУГОЛЬНИКЕ
Пусть треугольник АВС — равносторонний, О —
его центр (рис. 11.14), АВ = ВС = АС = а. По теоре-
232
ме 4.2 высоты AAV ВВХ, ССХ являются его медианами и
поэтому
АО = 2АХО, ВО=2ВХО, СО=2СХО.
Обозначим отрезки AAV ВВХ, ССХ через h, радиусы
описанной окружности ОА, ОВ, ОС через R, а радиу-
сы вписанной окружности ОАХ, ОВХ, ОСХ через г .
По теореме Пифагора из треугольника АВВХ по-
лучим:
откуда
значит
Мы доказали следующие формулы для правильного
треугольника:
7? = 2г.
§ 11.8. ПАРАЛЛЕЛЬНЫЕ ОТРЕЗКИ В ТРАПЕЦИИ
Рассмотрим трапецию ABCD с основаниями AD =
= а и ВС = b . Мы знаем, что средняя линия этой трапе-
а + Ъ
ции равна —и параллельна основаниям.
1) . Пусть MXNX\\AD и отрезок MXNX делит АВ (а
по теореме Фалеса делит также и отрезок CD) в отно-
шении 5: t, считая от основания AD, т.е.
233
AMX _DNX _ £
МХВ~ NXC~ t
Проведем BT\\CD (рис.11.15). Тогда
MXNX=MXL + LNX,
LNx=BC = b, AT = AD-BC = a-b
(докажите это самостоятельно). Треугольники MXBL
и АВТ подобны по следствию 1 §11.1. Поэтому
MXL _ МХВ
АТ ~ АВ
АМХ s
Так как ----= —, то суще-
МХВ t
ствует такое положительное
число X, для которого
AMX = SX, a MxB = tx,
откуда
AB=(s + t)x.
Таким образом,
Pnc.il. 15
Тогда
MXNX
(a-b)t at + bs
-------+ о =
s + t-s + t
Итак,
at+bs
s + t
(1)
В частности, если s = t = 1, то MXNX =------ и MXNX —
средняя линия трапеции ABCD .
2) . Проведем через точку О пересечения диагоналей
трапеции ABCD отрезок PQ, параллельный основани-
ям (рис. 11.16). Тогда треугольники AOD и ВОС подоб-
ны, т.к. Z^l = z^2, Z3 = z^4. Поэтому
234
Рис. и. 16
Рис.11.17
АО DO а
ОС ~ ОВ b
По теореме Фалеса
АР _ DQ _ АО _ а
РВ QC ОС b
Из формулы (1) при S = а, t = Ъ имеем:
D/n _ ab + ab _ 2ab
“х ~ ~ ГТ'
a+b а+Ь
(2)
3) . Рассмотрим, наконец, отрезок FE, параллельный
основаниям AD и ВС, который делит трапецию на две
подобные трапеции FBCE и AFED (рис. 11.17).
Тогда
AD FE
FE ВС'
откуда
FE2 = ab.
Таким образом,
FE = Jab. (3)
„ 2аЬ
Полученное в п.2) число ----- можно представить
а + Ь
так:
235
2
В математике числа
называются соответственно средним квадратичным,
средним арифметическим, средним геометрическим и
средним гармоническим чисел а и b Известно также,
что для положительных чисел а и b справедливы нера-
венства:
причем в каждом их этих
неравенств равенство дости-
гается тогда и только тогда,
когда а = Ь.
В трапеции основа-
ния AD = а и ВС = b раз-
личны. Пусть а >Ъ , тогда от-
резки MN, FE, PQ распо-
лагаются так, как показано > у Л п
на рис. 11.18. При этом длина 71 а
отрезка MN — среднее
арифметическое длин осно- Puc.ii.i8
ваний трапеции, длина от-
резка FE — среднее геометрическое длин оснований
трапеции, а длина отрезка PQ — среднее гармоническое
длин оснований трапеции.
Позднее при изучении площади трапеции мы дока-
жем, что отрезок XY, который делит площадь трапеции
1а2+Ь2
пополам и параллелен основаниям, равен л-------- —
среднему квадратичному длин оснований трапеции.
236
§ 11.9. ТЕОРЕМА ПТОЛЕМЕЯ
Вписанный четырехугольник обладает замечатель-
ным свойством, найденным древнегреческим астрономом
и математиком Клавдием Птолемеем (около 100 —
178). Он составил первую таблицу синусов, заложил ос-
новы учения о стереографической проекции и о сол-
нечных часах. Впервые ввел три прямоугольные оси —
прообраз современной координатной системы.
Теорема 11.12 (теорема Птолемея). Во всяком
четырехугольнике, вписанном в окружность, произве-
дение диагоналей равно сумме произведений его про-
тивоположных сторон.
□ Пусть ABCD — вписанный четырехугольник
(рис. 11.19). Из вершины А
проведем отрезок АК так,
р чтобы конец К этого отрезка
к лежал на диагонали BD и
) чтобы угол ВАК был равен
I углу CAD . Рассмотрим снача-
ла треугольники ВКА и CDA .
В них углы АВК и ACD
равны как вписанные, опи-
рающиеся на общую дугу AD.
Кроме того, угол ВАК равен
углу CAD в силу выбора
точки К. Треугольники ВКА и CDA имеют по два
равных утла и, следовательно, подобны. Отсюда за-
ключаем, что
AC CD
В
Рис. 11.19
АВ ВК
или
АС ВК = АВ CD.
(1)
Рассмотрим теперь треугольники AKD и АВС . В
них углы АСВ и ADK равны как вписанные, опираю-
щиеся на общую дугу. Кроме того, из равенства уг-
лов ВАК и CAD следует равенство углов ВАС
237
Рис.11.20 Рис.11.21
и KAD . Треугольники AKD и АВС имеют по два рав-
ных угла и, следовательно, подобны. Тогда
АС ВС
AD DK'
откуда
ACDK = ADBC.
(2)
Складывая равенства (1) и (2), получим:
AC (BK + DK) = AB CD + AD ВС,
следовательно,
AC BD = АВ CD + AD ВС.
§ 11.10. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1.1. В равнобедренном треугольнике АВС с
основанием АС и углом при вершине 36° проведена биссек-
триса AD. Доказать, что треугольники АВС и CAD подобны.
В треугольнике АВС дано: АВ = ВС, АВ = 36°,
AD — биссектриса (рис. 11.20). Тогда
АС = ABAC
180°-36°
откуда
238
ZDAC = ZBAD =^ZBAC) =36°.
В треугольниках ЛВС и CAD угол С — общий и уг-
лы В и CAD равны. По второму признаку подобия тре-
угольников треугольники АВС и CAD подобны. Ж
Пример И.2. Основания трапеции равны 2 м и 8 м, а
боковые стороны — 6 м и 9 м. Прямая, параллельная основа-
ниям, делит трапецию на две подобные трапеции. Найти их
стороны.
Пусть в трапеции ABCD известно, что
AD — 8 м, ВС =2м, АВ = 6м, CD —9м, MN\\AD, а
трапеции MBCN и AMND подобны (рис. 11.21). Из
формулы (3) §11.8 следует, что
MN = V АО • ВС = VT2 = 4 (м).
Далее из подобия трапеций имеем:
AM DN АР
MB ~ CN~ MN'
т.е.
AM _DN Z
MB ~ CN ~ 4 ~
Значит,
AM =2 MB. DN = 2CN.
Следовательно,
А/В =-ЛВ = —-6 = 2(м), ЛЛ/=4(м),
CN =-СР=--9 = 3(м), ZW = 6(m).
Таким образом, образованные прямой MN, параллель-
ной основанию, подобные трапеции имеют такие сторо-
ны: 8 м, 4 м, 4 м, 6 м и 4 м, 2 м, 2 м, 3 м. Ж
Пример 11.3. В угол 60° вписаны две окружности, ка-
сающиеся друг друга внешним образом. Найти отношение их
радиусов.
На рис. 11.22 окружности с центрами Ох и О2,
касающиеся друг друга внешним образом, вписаны в
угол с вершиной в точке А, равный 60°. По следствию 1
теоремы 6.2 луч АО} является биссектрисой данного
239
Рис.11. 22 Рис.11.23
угла, откуда ЛОХАВХ = 30°. Пусть ОХВХ и О2В2 перпен-
дикулярны лучу а, тогда отрезки ОхВх и О2В2 — радиу-
сы этих окружностей. Введем следующие обозначе-
ния:
ОхВх = г, О2В2 = R, тогда ОхО2 = г + R.
Ж Я Л» Лл < Лл
Так как — катет, лежащий против угла в 30°, то
АОХ = 2ОХВХ = 2г,
откуда
АО2 = АОХ + OxO2=2r + r + R = 3r + R.
Так как угол ОХАВХ является общим для прямоугольных
треугольников ОХАВХ и О2АВ2, то по следствию 2 §11.1
эти треугольники подобны. Значит,
ОХВХ ОХА г 2г
-----=------, откуда — =--------.
О2В2 О2А R Зг + Я
Имеем далее:
R
3r + R = 2R, отсюда R = Зг и — = 3.
Таким образом, радиусы относятся как 3:1. Ж
Пример 11.4. В прямоугольном треугольнике один из
катетов равен 4 см, а проекция другого катета на гипотену-
зу — 1,8 см. Найти расстояние от вершины прямого угла тре-
угольника до инцентра.
Известно, что в треугольнике ABC ZACB =
= 90°, АС =4см, CD —высота, /)В = 1,8см (рис.И.23).
240
Обозначим длину отрезка AD через X. Тогда АВ =
= х + 1Г8. По теореме 11.4 имеем:
ЛС2 = ABAD,
откуда
(х + 1г8)х = 16 или х2 + 1г8х —16 = 0.
Решая это уравнение, получаем х1 =3Г2, Х2 = —5. Зна-
чение Х2 не удовлетворяет условию примера. Таким об-
разом, AD = 3,2, откуда
ЛВ = ЯР + £В = 3Г2 + 1Г8 = 5.
По теореме Пифагора
ВС2 = АВ2-АС2 = 52-42 =9, т.е. ВС = 3.
Пусть I— центр окружности, вписанной в заданный тре-
угольник, a N, М, Р — точки касания ее со сторонами
треугольника. Тогда из §11.4 следует, что CNIM — квад-
рат, причем
riz ВС + АС - АВ 4 + 3-5 t
IM = r =-------------=---------= 1.
2 2
Тогда
С1=1М 41=41.
Итак, расстояние от вершины прямого угла до инцентра
равно V2cm. Zk
Пример 11.5. В прямоугольном треугольнике радиусы
описанной и вписанной окружностей соответственно равны
R и Г. Найти катеты этого треугольника.
ZS Пусть АВ — гипотенуза прямоугольного тре-
угольника АВС , I — центр вписанной окружности, М,
N, Р — точки касания этой окружности со сторона-
ми АС, ВС, АВ соответственно (рис.11.7). Из §11.3 сле-
дует, что AB=2R. Предположим, что АС < ВС
и АР =х. Тогда BP = 2R — х. Из §11.4 следует, что
АМ = АР=х, BN =BP=2R-x,
откуда
АС = AM + МС=х + г, ВС = BN + CN =2R-x + r.
Так как АС2 + ВС2 = АВ2, то
(х + г)2 + (2 R - х + г)2 = 4Л2,
После упрощения получаем уравнение
241
x2 -2Rx +r2 + 2Rr = 0,
откуда
X'=R- Jr2 -r2 -2Rr, x2=R + у/r2 -r2 -2Rr .
Легко проверить, что условию АС <ВС удовлетворяет
только значение Xj. Значит,
AC=R + r-^R2-г2-2Rr ,
BC=2R-(r-4r2-г2-2Rr) + r =
X ГТ аЬ
Пример 11.6. Построить отрезки: a) yiab, б) -===
где d и b — данные отрезки.
а) Рассмотрим прямоугольный треугольник
АВС. Пусть CD — его высота, О — центр описанной
окружности, AD=a, DB — b —проекции катетов АС
и ВС на гипотенузу (рис. 11.24). По теореме 11.6 имеем:
Построение отрезка АВ осуществляется так:
1) Проводим окружность с центром в произвольной
п “ а + Ь
точке О, радиус которой равен —;
2) Проводим в этой окружности произвольный диа-
метр АВ и на нем откладываем отрезок AD = а, тогда
BD=b\
3) Через точку D проводим луч, перпендикулярный
диаметру АВ, пусть С — точка пересечения этого луча с
окружностью. По теореме 6.6 ZACB =90°. По теоре-
ме 11.6 имеем: CD = y[cib. Отрезок CD является иско-
мым.
б) Отрезок c = yla2+b2 является гипотенузой
прямоугольного треугольника с катетами а и b. Иско-
мый отрезок а = —. Его построение осуществляется на
242
Рис.11. 24
Рис.11.25
d b
основании теоремы Фалеса, исходя из пропорции — = —,
а с
следующим образом:
1) строим прямоугольный треугольник АВС с кате-
тами ВС = а и АС =Ь. Его гипотенуза
АВ = у/а2 +Ь2 = С;
2) строим произвольный угол О и на его сторонах
откладываем отрезки OD} = а и OD = С (рис. 11.25) ;
3) на луче OD откладываем отрезок DE = Ь и про-
водим прямую EEX\\DDX до пересечения с лучом в точ-
ке Ev Отрезок DXEX — искомый, поскольку по теореме
Фалеса
д.д. » А
а с
Пример 11.7. Какую
линию описывает середина от-
резка данной длины /И, концы
которого скользят по сторонам
данного прямого угла?
Zs Пусть Z(a,d) —
данный прямой угол с вер-
шиной С и АВ — отрезок
данной длины /И; О — его
середина (рис. 11.26). Тогда
243
из §11.3 следует, что О — центр описанной окружности
треугольника ЛВС и
со=—=—
Таким образом, длина отрезка СО не зависит от положе-
ния точек А и В.
Обратно, пусть точка О лежит внутри угла (а,б)
тп
и СО = —. Тогда АВ = 2СО = ТП. Очевидно также, что
если одна из точек А или В занимает положение точ-
1 тп
ки С, то и в этом случае СО = — АВ = —. Значит, сере-
дина отрезка описывает дугу окружности с центром в
тп
вершине угла и радиусом —, причем эта дуга принадле-
Рис.11.27
жит данному углу (рис. 11.26).
Пример 11.8. В пра-
вильный треугольник вписан
квадрат так, что две его верши-
ны лежат на одной стороне
треугольника, а две другие вер-
шины — на двух других сторо-
нах треугольника. Найти отно-
шение их периметров.
Пусть MNPQ —
квадрат, вписанный в пра-
вильный треугольник АВС,
BD — высота этого тре-
угольника (рис.11.27). Обоз-
начим через О, сторону треугольника АВС, а через X —
сторону квадрата. Так как NP\\AC, то по теореме 3.5
ZBNP = ZBPN = ZA = ZC = 60°,
т.е. треугольник BNP — равносторонний. Очевид-
но, BE — высота этого треугольника и DE = MN = X.
Из §11.7 следует, что BD = ——, откуда
244
BE=BD-DE = ?^L-x.
2
По следствию 1 §11.1 треугольники BNP и ВЛ С подоб-
ны. Далее имеем:
NP _ВЕ
AC BD
или
I
откуда
2
-а
Таким образом, отношение периметра треугольника к пе-
риметру квадрата MNPQ равно
За _ За 2>/3 + 3
4а(2>/3-з) 4
Пример 11.9. В окружности проведены два радиуса.
Провести хорду, которая этими радиусами делится на три
равные части.
ZS Пусть О — центр данной окружности, ОА
и ОВ — ее радиусы. Проведем прямую АВ и отложим
отрезки АС и BD, равные АВ. Соединим точки С и D
с центром О и обозначим через М и F точки пере-
сечения соответственно отрезков ОС и OD с окружно-
стью. Проведем отрезок MF и обозначим через N и Е
точки пересечения его соответственно с отрезками ОА
и ОВ (рис. 11.28). Так как треугольник АОВ — равно-
245
бедренный, то углы ОАВ и ОВА равны, откуда следует,
что углы САО и DBO также равны. В треугольниках
ОАС и OBD имеем:
ОА=ОВ, AC=BD,
ZCAO = ZOBD.
Значит, эти треугольники
равны по первому признаку
равенства треугольников.
Отсюда ОС = OD т.е. тре-
угольник OCD — равно-
бедренный. Тогда
ZC = ZD=W~ZCTD
2
Но треугольник OMF так-
же равнобедренный, и сле-
PuLC.ll. 2 8
довательно,
ZOMF = ZOFM =
180°-ZWF
2
Таким образом,
ZC = ZOMF = ZD = ZOFM.
По второму признаку подобия треугольники OMF
и OCD подобны, а по теореме 3.5 MF ||DC. Тогда по
следствию 1 §11.1 имеем: треугольник ONE подобен тре-
угольнику ОАВ, треугольник OEF подобен треуголь-
нику OBD, треугольник OMN подобен треугольнику
ОСА . Следовательно, имеем:
MN _ON _NE _ОЕ _EF
СА ~ ОА~ АВ ~ ОВ~ BD'
откуда
MN _NE _EF
СА ~ АВ ~ BD
Так как
AC = AB = BD,
MN=NE=EF.±
Пример 11.10. В параллелограмме ABCD середины Е
и F сторон ВС и AD соединены с вершинами (рис. 11.29). До-
246
A F D
Ри.с. и.2 9
казать, что диагонали параллелограмма точками пересечения
делятся на три равные части.
Доказательство проведем для диагонали АС.
Обозначим через М и N точки пересечения диагона-
ли АС с прямыми BF и DE соответственно. Так как
AF =FD = -AD,
2
ВЕ=ЕС=-ВС,
2
то, учитывая, что ВС = AD,
получаем:
BE=FD.
Но BE ||FD, и значит, по
третьему признаку паралле-
лограмма BEDF является
параллелограммом. Отсюда
следует, что BF\\DE. Учи-
тывая, что AF = FD, по теореме Фалеса имеем:
AM = MN.
Таким же образом из равенства СЕ = BE следует, что
CN = MN.
Итак,
AM = MN = CN.
Рассуждения для диагонали BD проводятся анало-
гично. Ж
§ 11.11. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
11.01. В трапеции ABCD с основаниями AD и ВС
диагонали пересекаются в точке О. Доказать, что треугольни-
ки AOD и ВОС гомотетичны, Чему равен коэффициент гомо-
тетии, если AD = а, ВС = 5?
11.02. Длина стороны ВС треугольника ЛВС равна 6 см.
Чему равна длина отрезка, параллельного этой стороне, с кон-
цами на сторонах АС и АВ , проходящего через точку пере-
сечения медиан треугольника АВС 1
11.03. а) Подобны ли два равносторонних треугольника?
247
б) Подобны ли два равнобедренных треугольника?
11.04. Подобны ли треугольники АВС и АХВХСХ, если:
а) АВ = 2м, ВС = Зм, АС = 1,5м; Л1В1=4м, ^С^бм,
АХСХ = 3,1 м?
б) АВ = 5м, ВС = 8м, АС =9,2м; АХВХ = 35м, ВХСХ= 56м,
АХСХ = 64,4 м?
11.05 . Доказать, что отношение периметров подобных тре-
угольников равно отношению их соответственных сторон.
11.06 . В треугольнике АВС известно, что ЛВ=15м,
АС = 20м. На стороне АВ отложен отрезок AD = 8 м, а на
стороне АС — отрезок АЕ =6м. Подобны ли треугольни-
ки АВС иADE?
11.07 . Из вершины прямого угла С треугольника АВС
проведены медиана СЛ/ и высота С/7. Точка Н находится
между точками А и М. Найти отношение АН'.АМ,
если ОИ:СЯ = 5:4.
11.08 . Высота прямоугольной трапеции равна 2 , а боковая
сторона равна 4 . Найти длину средней линии трапеции, если
ее диагональ равна боковой стороне.
11.09 . В равнобедренном треугольнике отношение высоты,
опущенной на основание, к основанию этого треугольника рав-
но 3:4, а боковая сторона равна 2л/39дм. Найти высоту и осно-
вание этого треугольника.
11.10. В прямоугольном треугольнике катет равен 6 см, а
его проекция на гипотенузу равна 3,6 см. Найти радиусы впи-
санной и описанной окружностей.
11.11. В прямоугольном треугольнике гипотенуза рав-
на 20 м, а высота, опущенная на гипотенузу, равна 9,6 м. Найти
периметры образованных при этом треугольников.
11.12. Найти отношение радиусов описанной и вписанной
окружностей для равнобедренного прямоугольного треугольни-
ка.
11.13. В ромб, диагональ которого делит его на два равно
сторонних треугольника, вписана окружность, радиус которой
равен 1 м. Найти сторону ромба.
11.14. Основание равнобедренного треугольника рав-
но 60 см, а высота, опущенная на боковую сторону, рав-
на 48 см. Найти периметр треугольника.
11.15. Прямые, содержащие боковые стороны равнобед-
ренной трапеции, перпендикулярны. Меньшее основание тра-
пеции равно 2 см, а боковая сторона равна 2,2 см. Найти боль-
шее основание трапеции.
248
11.16. В трапеции с основаниями а и b параллельно осно-
ваниям проведены прямые, которые делят боковые стороны на
три равные части. Найти отрезки, образовавшиеся на этих пря-
мых.
11.17. С помощью циркуля и линейки построить отрезки:
\ / -2 1.2 \ i_ __
a) yla +Ь ; б) ---, где а,Ь — заданные отрезки.
а + Ь
11.18. Задан единичный отрезок. С помощью циркуля и
11.19. Из точки, лежащей вне окружности проведены: от-
резок секущей длиной 12см и отрезок касательной, длина кото-
рого составляет — внутреннего отрезка секущей. Наити длину
отрезка касательной.
11.20. Точка Р удалена на 7 см от центра окружности ра-
диуса 11см. Через эту точку проведена хорда длиной 18 см.
Найти длины отрезков, на которые хорда делится точкой Р.
11.21. Из точки проведены к окружности два отрезка каса-
тельных длиной 12 см. Расстояние между точками касания рав-
но 14,4 см. Найти радиус окружности.
11.22. Диагонали выпуклого четырехугольника ABCD пе-
ресекаются в точке Л/. Доказать, что если
AM* CM = BM-DM,
то около этого четырехугольника можно описать окружность.
11.23. Точки Яр Вх, Сх — середины медиан •треуголь-
ника АВС . Найти отношение периметров треугольников АВС
и АХВХСХ.
11.24. Точки Яр Вх, С, лежат на сторонах ВС, АС и АВ
соответственно некоторого треугольника АВС . Доказать, что
стороны треугольника АХВХСХ соответственно параллельны сто-
ронам треугольника АВС и только тогда, когда точки Ах,
Вх, С, —середины сторон ВС, АС, АВ .
11.25. Доказать, что середины оснований трапеции, точка
пересечения диагоналей и точка пересечения продолжений бо-
ковых сторон лежат на одной прямой.
11.26. Две окружности, радиусы которых равны R и Г ,
касаются внешним образом. Найти расстояние от точки каса-
ния этих окружностей до их общей внешней касательной.
11.27. Через точку, лежащую внутри окружности, провес-
ти хорду наименьшей длины.
249
11.28. Построить треугольник по периметру и двум углам.
11.29. Центр окружности, вписанной в прямоугольную
трапецию, удален от концов боковой стороны на расстоя-
ния 8 см и 4 см. Найти длину отрезка, параллельного основани-
ям, концы которого лежа^ на боковых сторонах и проходящего
через точку пересечения диагоналей.
11.30. Теорема Архимеда. Если две пересекающиеся хор-
ды круга взаимно перпендикулярны, то сумма квадратов длин
отрезков этих хорд равна квадрату длины диаметра круга. До-
казать.
11.31. Доказать, что если в треугольнике длина медианы
равна половине длины стороны, к которой она проведена, то
такой треугольник — прямоугольный.
11.32. Доказать, что в прямоугольном треугольнике выдол-
л . г _ .
няется неравенство: 0,4 < — < 0, .
11.33. Доказать, что в прямоугольном треугольнике сумма
катетов равна сумме диаметров вписанной и описанной окруж-
ностей.
11.34. Доказать, что в прямоугольном треугольнике бис-
сектриса прямого угла делит пополам угол между медианой и
высотой, опущенными на гипотенузу.
11.35. Медиана, опущенная на гипотенузу, разбивает пря-
моугольный треугольник на два треугольника с периметрами 8
и 9 . Найти длины сторон этого
треугольника.
11.36. В квадрате каждая
сторона поделена на три рав-
ные части и через точки деле-
ния проведены прямые, парал-
лельные сторонам квадрата.
Проведены отрезки AF, EF
и DG так, как показано на
рис. 11.30. Доказать, что углы
AFE и GDC равны.
11.37. Длина хорды ок-
ружности равна 10. Через один
конец хорды проведена каса-
тельная к окружности, а через
другой — секущая, параллель-
ная касательной. Найти радиус
окружности, если внутренний отрезок секущей равен 12.
11.38. Окружность, диаметр которой равен V10, проходит
через соседние вершины Л и В прямоугольника ABCD . Дли-
на касательной, проведенной из точки С к окружности, рав-
А Е В
250
на 3, АВ = 1. Найти все возможные значения, которые может
принимать длина стороны ВС.
11.39. В трапеции ABCD боковая сторона АВ перпенди-
кулярна основанию ВС. Окружность проходит через точки С
и D и касается прямой АВ в точке Е. Найти расстояние от
точки Е до прямой CD, если AD = 4, ВС = 3.
11.40. В треугольнике АВС угол С — тупой. D — точка
пересечения прямой DB, перпендикулярной к АВ, и пря-
мой DC, перпендикулярной к АС. Высота треугольника ADC,
проведенная из вершины С, пересекает АВ в точке М. Из-
вестно, что AM = а, ВМ = Ъ . Найти АС .
11.41. Построить отрезки: a) Va2 + ft2 + с2 ; б) yla2 +ab + b2;
в) tfabcd , где а, b , С, d — заданные отрезки.
11.42. Из вершины тупого угла А треугольника АВС опу-
щена высота AD. Из точки D радиусом, равным AD, описана
окружность, пересекающая стороны треугольника АВ и АС в
точках М и N соответственно. Вычислить длину стороны АС,
если заданы длины отрезков АВ = с, AM = и, AN = т.
11.43. На данной окружности выбрали точку А, а внутри
круга — точку D. Пусть М — центр масс треугольника АВС ,
где ВС — хорда, проходящая через точку D. Какую линию
описывает точка М, если хорда ВС вращается вокруг точ-
ки D?
11.44. Доказать, что в любом треугольнике выполняется
неравенство:
3
ma+mb+mc>-pt
а + Ь + с
где р =------.
11.45. Доказать, что в прямоугольном треугольнике бис-
сектриса прямого угла не превосходит по длине половины про-
чи гипотенузы на прямую, перпендикулярную к биссектри-
се.
251
ГЛАВА 12
ВЕКТОРЫ
§ 12.1. ДЕКАРТОВЫ КООРДИНАТЫ
Декартова прямоугольная система координат. Коор-
динаты точки на плоскости. Проведем через произволь-
ную точку О плоскости две взаимно перпендикулярные
прямые ОХ и OY. Назовем их осями координат. Пря-
мую ОХ будем называть осью абсцисс, а прямую OY —
осью ординат. Точку О бу-
дем называть началом коор-
динат. Эта точка делит каж-
дую ось на два луча. На каж-
дой оси один из этих лучей
примем за положительную
полуось и обозначим это на
рис. 12.1 с помощью стре-
лок. Вторую полуось назовем
отрицательной. Кроме того,
примем некоторый отрезок
за единичный, т.е. имеющий
длину, равную 1.
Рис.12.1
Введем координаты точки на плоскости. Опустим
из произвольной точки А перпендикуляры AAxLOX и
AAyl.OY. Точки Ах и Ау являются проекциями точ-
ки Л на оси ОХ и OY (рис.12.1). Если точка А лежит
на оси ОХ, то Ау совпадает с точкой О. Считаем тогда,
что точка Ах совпадает с точкой А. Аналогично для
точки А на оси OY точка AY совпадает с точкой О, а
точка Ау — с точкой А. Наконец, проекциями точки О
на обе оси будем считать точку О.
Абсциссой точки А назовем такое число X, для ко-
торого выполняются условия:
а) х = 0, если Ах и О совпадают;
252
б) X совпадает с длиной отрезка ОАХ, если точка Ах
лежит на положительной полуоси и не совпадает с
точкой О.
в) число X равно отрицательному числу, модуль ко-
торого равен длине отрезка ОАХ, если точка Ах лежит на
отрицательной полуоси и не совпадает с точкой О.
Аналогично через длину отрезка ОАу определяется
вторая координата точки А, которая называется ордина-
той этой точки. Тот факт, что точка А имеет абсциссу X
и ординату у, записывают так: А(х;у).
Точки, лежащие на оси ОХ, имеют ординату, рав-
ную нулю, а точки, лежащие на оси OY, имеют абсцис-
су, равную нулю. Точка О имеет обе нулевые координа-
ты. Введенные таким образом координаты точки называ-
ются декартовыми. Плоскость с осями ОХ и OY назы-
вают декартовой (прямоугольной) системой координат.
Оси координат делят плоскость на четыре части — I, II,
III, IV четверти. В пределах
каждой четверти знаки коор-
динат распределяются так,
как показано на рис. 12.2. При
этом строгие неравенства со-
ответствуют внутренним точ-
кам каждой четверти.
Нетрудно
установить,
что декартовы координаты
задают взаимно-однозначное
соответствие между точками
плоскости и парами чисел:
каждой точке плоскости со-
ответствует некоторая пара чисел (х;у), и каждой паре
чисел (х;у) соответствует некоторая точка плоскости —
Л(х;у). Сделайте это самостоятельно.
Декартовы координаты точки называются так в
честь Рене Декарта (1596—1650) — французского
философа, математика, физика и физиолога. Он впервые
ввел понятие переменной величины и функции, предло-
жил общепринятые теперь обозначения для переменных,
253
буквенных коэффициентов и степеней, создал метод пря-
моугольных координат.
Термин "координата” произошел из латыни. При-
ставка "со" обозначает объединение, общность, ordinatus
— упорядоченный. Термин "абсцисса" восходит к латин-
скому abscissa — отрезанная. Латинское ordinatus оз-
начает "расположенный в порядке".
§ 12.2. КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА
Ах Мх Вх
Пусть в некоторой декартовой системе координат
XOY задан отрезок / В,
где Aix^yi) и В(х2;у2).
Пусть М\х;у) — середина
этого отрезка (рис. 12.3).
Допустим, например,
что Xj<x2. По теореме Фа-
леса Мх — середина отрез-
ка АХВХ. Координаты то-
чек AY и Вх таковы:
Лх(хрО), Вх(х2;0). Кроме
того,
ЛхЛ/х = х-х1,
Из равенства АХМХ = Л/ХВХ
х - Xj = х2 - х,
откуда
Рис. 12.3
МуВ=хэ-х.
Л Л Лл
получаем
Аналогично рассматривается случай, когда хг>х2.
Если же Х! = х2, то AB\\OY, и тогда точки Ах,
МХ,ВХ совпадают. В этом случае также
254
Аналогично доказывается, что у ==-----.
2
Таким образом, координаты середины Af(x;y) от-
В(х2;^2) вычисли-
резка с концами в точках
ются по формулам:
Х1 + Х9
х= ....
§ 12.3. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Пусть ^(xp-yi) и В(х2;У2 ) — некоторые две точки
в декартовой системе координат. Расстоянием между
точками А и В будем называть длину отрезка АВ, если
точки А и В различны, и число 0, если точки А и В
совпадают.
Обозначим длину отрезка АВ через d. Выразим зна-
чение d через координаты точек ^Хр^) и в(х2;^2)
(рис.12.4).
Допустим сначала, что Хх*Х2 и ух^у2, т.е. отрезок
АВ непараллелен осям ко-
ординат. Проведем через
точки А и В прямые, па-
раллельные осям коорди-
нат; N — их точка пере-
сечения. Тогда
AN = АХВХ = х2-хх ,
BN = ^Л? = |у2 -yj.
По теореме Пифагора из
Рис, 12,4
прямоугольного треугольни-
ка ABN получим
откуда
-*1)2 +(у2 -У1)
255
Это и есть формула расстояния между двумя точками.
Пусть теперь какие-либо две координаты этих то-
чек совпадают. Если, например, х1=х2, а У1*У2,
т.е. АВ ||ОГ, то формула расстояния дает значение
^ = 1^2 “ J1I- с другой стороны, АВ = АуВу=[у2 -у^
(рис. 12.5), т.е. формула, полученная ранее, справедлива и
в этом случае. Наконец если хх = х2 и ух = у2, то точ-
ки Л и В совпадают, наша
стояние между ними, что и
должно быть получено со-
гласно формулы расстояния.
Отметим, что расстоя-
ние ОА, где О — начало ко-
ординат, Л(х;у) — произ-
вольная точка, вычисляется
по формуле:
дает нулевое рас-
Р'ис.12.5
Легко доказать, что рас-
стояние d —d[A,B) между
точками А и В на плоскости
обладает следующими свойствами:
1) для любых точек А и В d(A,B)>(y пря-
чем б/(Л,В)=0 тогда и только тогда, когда А и В сов-
падают;
2) для любых точек А и В справедливо равенст-
во d(A,B} = d(B,A)-,
3) для любых точек А, В и С выполняется неравен-
ство:
d(A;C)<d(A;B) + d(B-,C).
Сделайте это самостоятельно.
256
§ 12.4. ПОНЯТИЕ ВЕКТОРА
Определение вектора. Модуль вектора. Направлен-
ный отрезок называется вектором.
а
К
Рис. 12.6
Рис.12.7
На рис. 12.6. изображены векторы АВ и Ш. Точка А
называется началом, а точка В — концом вектора АВ;
направленность отрезка означает, что у него фиксирова-
ны начало и конец. Длина отрезка АВ называется моду-
лем этого вектора и обозначается так:
АВ
Модуль
вектора Ш обозначается так: \т. Вектор также характе-
ризуется направлением, на которое указывает стрелка.
Нулевой вектор. Вектор, начало и конец которого
совпадают, будем называть нулевым и обозначать че-
рез 0.
Будем считать, что
и что он не имеет направ-
ления. Его общим началом и концом может быть произ-
вольная точка плоскости.
Коллинеарные векторы. Два ненулевых вектора на-
зываются коллинеарными, если они лежат на одной пря-
мой или на параллельных прямых.
257
Рис. 12.10
Рис. 12.11
На рис. 12.7 векторы а и b коллинеарны, векторы С
и d также коллинеарны. Коллинеарность векторов а
и b обозначается следующим образом: Л||А.
Нулевой вектор будем считать коллинеарным любо-
му вектору.
Сонаправленные и противоположно направленные
векторы. Два ненулевых вектора а и b называются со-
направленными, если они коллинеарны и лежат в одной
полуплоскости, ограниченной прямой, соединяющей их
начала (рис. 12.8).
В случае, если векторы а и b лежат на одной пря-
мой, для проверки сонаправленности векторов необходи-
мо пара? лельно перенести их так, чтобы векторы а и b
не лежали на одной прямой (рис. 12.9). Если векторы а
9 Зак. 687
258
Рис. 12.12
Рис.12.13
и Ь сонаправлены, то это обозначают следующим обра-
зом: а ТТЛ.
Векторы Л и b называются противоположно на-
правленными, если они коллинеарны и лежат в разных
полуплоскостях, ограниченных прямой, соединяющей их
начала (рис. 12.10). Как и в случае сонап>авленных векто-
ров, если векторы лежат на одной прямой, то проверка
того, что они противоположно направлены, осуществля-
ется так. Необходимо параллельно перенести векторы а
и b так, чтобы они не лежали на одной прямой
(рис. 12.И). Если векторы а и b противоположно направ-
лены, то это обозначают следующим образом: лТФЛ.
Равные векторы. Противоположные векторы. Два
ненулевых вектора называются равными, если они сона-
правлены и их модули равны (рис.12.12).
Проверьте самостоятельно справедливость следую-
щего утверждения:
АВ = Afix тогда и только тогда, когда существует
параллельный перенос, при котором точка А переходит
в точкуД, а точка В — в точку Вх .
Два ненулевых вектора называются противополож-
ными, если они противоположно направлены и их моду-
ли равны (рис. 12.13).
Термин "вектор" происходит от латинского vector —
несущий, термин "модуль" — от латинского modulus —
259
мера, термин "коллинеарен" — от латинского слова con
— вместе и Ипеа — линия.
§ 12.5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
Сложение векторов. Правило многоугольника. По-
нятие равенства векторов позволяет отложить вектор,
равный данному, от произвольной точки плоскости.
Пусть л2, ..., ап — ненулевые векторы. Отложим
от произвольной точки Ах вектор А^А^Оу затем от
точки А2 — вектор А2А3—а2 и т. д. Наконец, отложим
от точки Ап вектор АпАп+х:=ап. Соединим точки Ах
и Ап+Х. Вектор AiAn+x будем называть суммой векторов
Лр а2, ..., ап и обозначать
(рис.12.14). Следующее ут-
через ах +а2 + ... + ал
верждение показывает, что
данное определение не явля-
ется противоречивым.
Теорема 12.1. Сум-
ма векторов не зависит от
выбора точки, от которой
мы начинаем откладывать
векторы.
□ Допустим, что кроме
векторов Ах Л2, Л2 А3.....
АпАп+х, мы отложим также
векторы ВХВ2= ах, В2В3=а2, ..., ВпВп+х—ап. Рассмотрим
параллельный перенос, переводящий точку з точку
Вх, а точку А2 в точку В2. Согласно §12.4 такой парал-
лельный перенос существует. Из определения параллель-
ного переноса следует, что вектор Я2Л3 переходит в рав-
260
ный ему вектор с началом в точке В2, т.е. в вектор В2В3,
и т.д. Наконец, вектор переходит в вектор
ВЛ2?Л+1. Таким образом, точка А1 переходит в точку а
точка Д,+1 —в точку Bn+V Следовательно, вектор AtA„+l
переходит в вектор ВхВп+х. Из §12.4 следует, что
Приведенный способ нахождения суммы векторов
называется правилом многоугольника. Для всякого век-
тора а будем считать, что 04-0 = 0+ 0 = 0.
Сложение векторов. Пра-
вило параллелограмма. Сум-
му двух векторов можно най-
ти также другим способом.
Пусть векторы а и b некол-
линеарны. Отложим эти век-
торы от произвольной точ-
ки А. Проведем через концы
екторов а и b прямые, па-
раллельные прямым, на кото-
рых лежат соответственно
вэкторы b и а. Получим па-
раллелограмм ABCD (рис. 12.15). Вектор АС является
суммой векторов а и Ь, так как по правилу многоуголь-
нк.;. АС = АВ + ВС, что совпадает с суммой АВ + AD.
Отданный способ сложения двух векторов будем назы-
вать правилом параллелограмма.
Вычитание векторов. Вектор X называется разно-
стью векторов а и Ь, если = и обозначается
^ак: X = а~Ь.
Рис. 12.15
На рис. 12.15 изображен вектор BD = b-Cl. Вектор
DB противоположен вектору BD, поэтому DB=a-b.
261
Рис. 12.16
Из правила многоугольника следует, что сумма двух
противоположных векторов равна 0, поэтому для каждо-
го вектора а разность 0-а — это вектор, противопо-
ложный вектору а.
Умножение вектора на число. Пусть а — произ-
вольный ненулевой вектор и X — произвольное число,
отличное от нуля. Будем считать при X >0 вектор Ха со-
направленным с вектором а (рис.12.16), а при Х<0 —
противоположно направленным с вектором а (рис.12.17),
причем в обоих случаях |Хл| =|Х|'|л|. Кроме того, будем
считать, что 0 • а = 0 и X • 0 = 0.
Очевидно, с помощью операции умножения ненуле-
вого вектора а на число X мы можем получить любой
вектор, коллинеарный вектору а. При этом |Х| = -t-J,
|а|
т.е. модуль числа X указывает на отношение модулей
векторов, а знак числа X — на то, будут ли векторы а
и Ха сонаправлены или противоположно направлены.
Замечание. Если Х = 1, то Ха = 1*а = а. Если же
X = -1, то вектор (~1)а будет противоположным к вектору а.
Вектор, противоположный вектору а, обозначается
так: -а.
262
Теорема 12.2. Пусть
М — середина отрезка АВ.
Для произвольной точки О
справедливо равенство:
ом=-\6л+ов .
2k )
□ Рассмотрим паралле-
лограмм ОАСВ , построен-
ный на векторах ОА и ОВ.
Рис. 12.1в Диагонали параллелограмма
ОС и АВ в точке пере-
сечения М делятся пополам (рис. 12.18). Поэтому
ом=-ос
2
ОА + ОВ
Деление коллинеарных векторов. Пусть а и b —
коллинеарные векторы, причем а 0. Тогда при некото-
ром % имеет место равенство: b = Ха. Будем считать, что
а
Свойства действий над векторами. Для любых век-
торов а, b, С справедливы следующие равенства:
1) а + д = д + а.
2) (а + b) + c = а + (д + с).
3) а + 0 = а.
4) Для любого вектора АВ выполняется равенст-
во ВА = — АВ.
5) Для любого вектора а существует единственный
вектбр b, для которого а + b = 0.
Для произвольных векторов а, b и чисел Хр Х2, X
справедливы следующие равенства:
6) (Х, + Х2)а = Х1а + Х2а.
263
Рис. 12.19 Рис. 12.20
7) Х(я +б) = Ха+ Х6.
8) Х1(Х2а) = (к1Х2)а.
Приведем доказательство свойств 1—8 для неколли-
неарных векторов Л и b.
1) □ Пусть на рис. 12.19 изображены векторы а
и д, а также их сумма а + b. Очевидно, что ес
ли AD = ВС = 6, то ABCD — параллелограмм. Поэто-
му, если АВ = О, то DC = а. Значит,
2) □ По теореме 12.1 можно считать, что вектор а
отложен от некоторой точки А, вектор b отложен от
конца В вектора а, вектор С — от конца С векГора b
(рис. 12.20). По правилу многоугольника имеем:
(a + b) + c = AC+CD = AD,
a + (b + c)= AB+BD = AD.
Таким образом,
(a + b) + c = a + (b + c}.
3) □ Свойство 3 вытекает из определения сум-
мы а + 0.
264
4) □ Пусть сначала АВ — ненулевой вектор.
Очевидно,
Кроме того,
векторы АВ и ВА противоположно направлены, поэ-
тому векторы ВА и
сонаправлены. Значит,
ВА = — АВ. Если же АВ = 0, т.е. точки А и В совпада-
ют, то ВА = 0, и равенство 0 = — 0 справедливо, по-
скольку — 0 = (—1) -0 = 0. И
5) □ Очевидно, что для вектора а таким векто-
ром b будет вектор (—а). Докажем единственность век-
Рис./2.2/
тора b. Пусть Ьх и Ь2 — два
таких вектора, для которых
0 + ^ = 0 и а +1*2 = 0.
Тогда
а + 6| = я + ^,
откуда
(-я) + (я +fy) = (-а) + (а +62).
По свойству 2 имеем далее:
(-а + а) + Ьх = (-а + а) + Ь2,
откуда bx = b2. Таким образом, единственность вектора b
доказана и, следовательно, доказано свойство 5). И
6) □ Пусть Xj>0, Х2>0, а^О. Изобразим сумму
векторов 'кха + 'к2а так, как показано на рис. 12.21. В
этом случае
265
и векторы + Х2а и (X1+XJа сонаправлены. Поэтому
Xjfl + Х2а =(Xj + k2)a. Доказательство свойства 6 в дру-
гих случаях выполните самостоятельно. И
7) □ Пусть Х>0. На рис. 12.22 изображены векто-
ры АВ = а, BD = b, АС = Ха, СЕ = ХЬ. Тогда
AD=a + b, АЕ = Ха + ХЬ.
Треугольники ABD и АСЕ подобны, т.к.
АВ _ВР \
АС СЕ X
и углы ABD и АСЕ равны. Значит, углы BAD и САЕ
также равны, т.е. точки A, D и Е лежат на одной пря
мой. Кроме того,
AD _ 1
АЕ X'
откуда АЕ =XAD. Таким
образом, Ха + ХЬ = Х(а 4- b).
Доказательство свойст-
ва 7 в других случаях выпол-
ните самостоятельно. И
А
8) □ Это свойство сле-
дует из сочетательного зако- Рис. 12.22
на умножения чисел. Прове-
дите подробное рассуждение самостоятельно.
§ 12.6. РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСУ
Базис вектора. Координаты вектора. Будем гово-
рить, что всякие два неколлинеарных вектора а и b об-
разуют базис. Если для вектора С и для некоторых чи-
сел X и у выполняется равенство С = xa + yb, то гово-
рят, что вектор С разложен по базису, составленному из
векторов а и b, а числа Хну называются координата-
ми этого вектора в данном базисе.
Справедлива следующая теорема.
266
о Ь в D
Рис. 12.23
Теорема 12.3. Вся-
кий вектор можно разло-
жить по заданному базису и
притом единственным обра-
зом.
□ Пусть векторы а и b
образуют базис, С — произ-
вольный вектор. Отложим
эти векторы от некоторой
точки О. На рис. 12.23
ОА=а, ОВ=Ь, ОС = с.
Проведем через точку С
прямые, параллельные прямым ОА и ОВ, до пере-
сечения с ними соответственно в точках Е и D. Тогда
по правилу параллелограмма
e = 6c=dk+6b.
Однако, вектор ОЕ коллинеарен вектору Л, и поэтому
существует число X такое, что вектор ОЕ = ха. Анало-
гично из коллинеарности векторов OD и b ясно, что су-
ществует число у такое, что вектор OD = yb. Значит,
с = ха + yb.
Возможны различные варианты положения вектора С в
зависимости от знаков чисел X и у. Кроме того, необхо-
димо рассмотреть случай, когда Х = 0 и у = 0. Рассмот-
рение этих различных случаев проведите самостоятель-
но.
Докажем теперь единственность разложения векто-
ра С. Допустим, что существует два различных разложе-
ния вектора С по базису векторов а и Ь. Тогда будут
выполняться равенства:
с = ха + yb и с = хха + у}Ь.
Пусть, например, x*xv Тогда
ха + yb-(x}a + yb) = 0,
откуда
267
(x-xjn = (<y1 -y)b и a = ———bt
x-x}
т.е. векторы а и b коллинеарны. Однако это невозмож-
но, поскольку они образуют базис. Итак, наше предполо-
жение о существовании двух различных разложений век-
тора С по базису векторов а и b является ложным. И
Действия над векторами в координатах.
Теорема 12.4. Пусть Хи — координаты век-
тора с, а х2, у2 — координаты вектора d в базисе, со-
ставленном из векторов а и Ь. Тогда
координаты вектора c + d в этом базисе, a Xj—х2,
У\— У 2 — координаты вектора c — d в этом базисе.
□ В самом деле, пусть
с = xxa + yxb, d = х2а +у2Ь.
Тогда
с + d = х}а + у}Ь + х2а + у2Ь = (х, + х2)а + (у, + y2)b;
Доказательство для разкости C — d аналогично. И
Теорема 12.5. Если X, у — координаты векто-
ра с в некотором базисе, то Ах, Ху — координаты век-
тора X с в этом базисе.
Эта теорема доказывается аналогично предыдущей.
Пропорциональность координат векторов. Пусть
ненулевой вектор С имеет координаты хр а ненуле-
вой вектор d — координаты х2, у2 в базисе, составлен-
ном из векторов U и b. Будем говорить, что координаты
векторов С и d пропорциональны, если выполняется од-
но из следующих условий:
X] и
1) числа Хр х2, yv у2 отличны от нуля И — ;
*2 У2
2) х, = х2 = 0, причем ух 0 и у2 Ф 0;
3) ух = у2 = 0, причем Xj Ф 0 и х2 Ф 0;
268
Условие коллинеарности ненулевых векторов.
Справедливо следующее утверждение об условии колли-
неарности ненулевых векторов.
Теорема 12.6. Для того, чтобы ненулевые векто-
ры с и d были коллинеарными, необходимо и доста-
точно, чтобы их координаты в каком-либо базисе были
пропорциональны.
□ Зафиксируем некоторый базис Д, Ь, Пусть Xj
и ух — координаты вектора С, а х2 и у2 — координаты
вектора d в этом базисе. Допустим, что С, d — коллине-
арные векторы. Тогда какой-нибудь из них, например d,
можно представить в виде d = Хс. Так как хр ух — ко-
ординаты вектора С, то Ххр *кух — координаты векто-
ра d. По теореме 12.5 имеем:
^2 = ^1-
Если числа хр yv х2, у2 отличны от нуля, то Х#0 и
1
х1:х2 = у1:^2 = 7
Л.
и пропорциональность координат векторов доказана.
Допустим далее, что х1 = 0. Тогда и х2 = 0. Если
же х2 = 0, то либо Xj = 0, либо Л, = 0. В первом случае
выполняется условие 2 пропорциональности координат
векторов. Во втором случае у2 = 0 и поэтому d = 0, что
противоречит условию теоремы. Аналогично рассматри-
вается случай, когда = 0 и у2 = 0. Итак, во всех
случаях для коллинеарных векторов пропорциональность
координат установлена.
Обратно, пусть координаты ненулевых векторов С
и d пропорциональны. Тогда, если хр ур х2, у2 — чис-
ла, отличные от нуля, получаем:
где Л. — некоторое число, отличное от нуля. Зна-
чит, х2 = Ххр у2 = ХуР Таким образом, вектор
269
d = Xxjfl + \yxb = + yxb} = Xc,
откуда следует, что векторы С и d коллинеарны. Если
же, например, Xj =х2 = 0, то С = yxb, d = угЬ и коллине-
арность векторов С и d очевидна.
Аналогично доказывается следующее утверждение.
Теорема 12.7. Для того, чтобы ненулевые векто-
ры end были сонаправлены (противоположно на-
правлены), необходимо и достаточно, чтобы их коорди-
наты были пропорциональными и отношение ненуле-
вых соответствующих координат было положительным
(отрицательным).
§ 12.7. ВЕКТОРЫ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ
КООРДИНАТ
Рассмотрим вектор АВ в прямоугольной систе-
ме координат. Пусть — начало вектора АВ
и В(х2,у2) —конец этого вектора (рис. 12.24). Тогда
АВ = АС+СВ.
Пусть i и j — векто-
ры, направление которых
совпадает с направлением
осей ОХ и OY соответст-
венно. Будем считать также,
что длины этих ве. торов
равны 1, т.е. |i| = j =1. На-
зовем эти векторы основ-
ным базисом прямоугольной
системы координат на плос-
кости. Очевидно, что
СВ=(у2-у^.
270
Таким образом,
АВ =(хг- х, )< + (уг - yt )j,
т.е. координатами вектора АВ в основном базисе будут
числа х2 — и у2 — Уг. В этом случае принято писать
так: ЛВ(х2-х1;у2-у1), либо АВ = (х2-Хру2-yj. В
частности, если точка А совпадает с началом О системы
координат XOY, то вектор ОВ в основном базисе име-
ет координаты (х2 ;у2 ).
Радиус-вектор точки. Французский математик
О.К оши (1789—1857) в 1853 г. ввел новое понятие —
радиус-вектор точки.
Пусть Af(x;y) — произвольная точка плоскости.
Вектор ОМ, начало которого совпадает с началом декар-
товой прямоугольной системы координат, называется ра-
диусом-вектором точки М. Так как О(0;0) — начало де-
картовой прямоугольной системы координат, то коорди-
наты радиус-вектора точки М совпадают с декартовыми
координатами точки М — конца этого вектора. Найдем
координаты базисных векторов / и j. Так как
i =bi + O j, а у = 0-< + 1- J,
то получим:
< = (1;0), / = (0;1).
$ 12.8кСКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Угол между векторами. Пусть а и b — два произ-
вольных ненулевых вектора, МА и МВ — два направ-
ленных отрезка, для которых МА = а, МВ = b. Углом
271
между двумя ненулевыми векторами а и b называется
угол, образованный лучами МА и МВ.
В частности, если лучи МА и МВ совпадают, то
угол между векторами а и b считается равным 0°. Угол
между векторами а и b обозначается так: Этот
угол не зависит от выбора точки М.
Скалярное произведение векторов. Пусть а Ф 0,
b Ф 0. В этом случае скалярным произведением векто-
ра а на вектор b называется число, равное произведе-
нию
О и
а|- bcosZ(a,b).
Скалярное произведение Векторов а и b обозначает-
ся через ab или а-b. Будем считать также, что
а• 0 = Оп = 0 для произвольного вектора а. Таким обра-
зом, скалярное произведение определено для произволь-
ных векторов а и Ь. Подчеркнем, что скалярное произ-
ведение а • b — это число, так как сомножители |а , b\ и
cosZ(atb) — это числа. Если угол между ненулевыми
векторами а и b — острый, то
со$Х(а,Ь)>0, значит в этом случае скалярное произведе-
ние положительно, т.е. а-Ь>0. Если же угол между не-
нулевыми векторами С и b тупой, то |а >0, |b| > 0 и
cos^(at b)<Q , значит в таком случае скалярное произве-
дение отрицательно, т.е. а-Ь<0. Если векторы Л и b
сонаправлены, т.е. то угол Z(ard) между ними
равен 0° и а • b = a -\b , так как cos0° = 1. Если же векто-
ры а и b противоположно направлены, то угол
Z(a, b) = 180° и cos\ 80° = —1. Тогда ab = — a - \b .
Перпендикулярность векторов. Два ненулевых век-
тора называются перпендикулярными, если угол между
272
ними равен 90°. Нулевой вектор считается перпендику-
лярным любому вектору. Перпендикулярность векто-
ров а и b обозначается так: a Lb. Справедливо следую-
щее утверждение.
Теорема 12.8. Два вектора а и b перпендику-
лярны тогда и только тогда, когда их скалярное произ-
ведение равно нулю.
Докажите эту теорему самостоятельно.
Скалярный квадрат вектора. Найдем скалярное про-
изведение ненулевого вектора а на вектор а. Получим
a a = |a|-|a|-co5Z(ara).
Так как векторы а и а сонаправлены, то Z(ara) = 0°
и cos0° = 1, значит,
Illi I |2
а-а = |а|-|а| = |а|
Очевидно, 0-0 = 0.
Произведение а • а обозначается а2 и называется
скалярным квадратом вектора.
Мы доказали, что скалярный квадрат вектора а ра-
вен квадрату его длины. Итак
|2
а а = а| .
Из определения скалярного произведения ненулевых
векторов следует, что
cos/{a, b) =
1а1 г
Так как со$Л(а, b) < 1, то
ab
<1,
откуда
\ab\ < л|-|б|.
Это неравенство выполняется также в случае, когда хотя
бы один из векторов а и b является нулевым.
273
Термин "скалярный" происходит от латинского
scalaris — ступенчатый. Создавая свою алгебру, француз-
ский математик Виет рассматривал не только длины, пло-
щади, объемы, но и величины, лишенные геометрическо-
го содержания и соответствующие возрастающим степе-
ням длины. Эти степени образуют шкалу — ступеньки, а
соответствующие величины Виет назвал "скалярами" —
ступеньками. Современный смысл термину "скалярная
величина" (т.е. не векторная) придал ирландский матема-
тик Гамильтон.
§ 12.9. СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
J е о р е м а 12.9. Пусть а, Ь, с— векторы и X —
некоторое число. Тогда выполняются следующие свой-
ства:
1) ab- Ьа.
6) cosZ a,b
, если а * 0 и b 0.
а b
274
□ 1) Пусть сначала а Ф 0, О. Тогда
а • b = |а • |Л cosZ(a, b) = |Л| • ]a\cosZ(t>f а)=Ь а,
так как
cos -COS ДЬ,а).
Пусть далее один из векторов, например, вектор а—
нулевой вектор, тогда 0- b = b • 0 = 0.
2) Пусть а и Ь — ненулевые векторы и X 0. Тогда
(Ха)-Л = |Ха|- b\ •cos Z.{Xa,b) =
= |Х| • |а| • |б| • cos/.(а, Хй) =
= |а|- |Хб|-со5/(а,ХЛ) = а-(ХЛ).
Если % '0, то (Хв)-Л =l|a|-|6|casZ(%a,h) =
= 1|л| • $cosZ(a, b) = 1(а, Ь).
Если X < 0, то
(Хд) • b = |Х||д| • |ft|cosZ(Xfl r b) =
= -Х|д • [А[со5г(1 80° - Z(a, Л)) =
= -X • |д| • |б| • (-cayZ(a, б)) =
= Х(д-Л).
Доказательства для случаев, когда один из векто-
ров а или b является нулевым, а также в случае, ког-
да X = 0, проведите самостоятельно.
3) Докажем, что (а4-b)c =а-с + Ь-с. Ограничимся
t *
случаем, когда векторы а и b неколлинеарны, а век-
тор С отличен от нулевого. Обозначим У =а + Ь. Пусть
векторы Д, b, С и 5 отложены от некоторой точки О
(рис. 12.25).
Возможны следующие случаи расположения этих
векторов:
275
а) Проекции Av Bv SI
точек A, Bf S на прямую,
содержащую вектор С, ле-
жат по одну сторону от
точки О, причем векторы а
и b образуют острые углы с
вектором С (рис. 12.25).
Представим, опираясь
на определение скалярного
произведения векторов, ис-
комое равенство в следую-
Pvlc.12.25
щем виде:
Тогда
s| • |с| • cosZ(s, с) =
= a |c| cayZ(arc)+ b -|с -cosZ(b,c)
или после сокращения на с :
у| • cosZ(s,c) = |а| • cosZ(a,c) + |Л| • cosZ(btc).
Но
s -cosZ(s,c) = OSV - cosZ(atc) = СЩ
и
\b\ cosZ.(b,c) = OB} = A^.
Отсюда
OS} =OAX + A{S} = OA} + OB},
что равносильно искомому соотношению.
б) Проекции Av Вр iS\ точек А, В, S на прямую,
содержащую вектор С, лежат по одну сторону от точ-
ки О, причем векторы а, b образуют тупые углы с
вектором С (рис. 12.26). Тогда, учитывая равенство
соя 180° — а) = -cosa, легко убедиться, что
S
cos
1»
b\-cosZ.(b,c) =-ОВ} =-A}S}
276
и далее имеем равенство: -OS} = -OA1-A]Sl, которое
верно л равносильно искомому соотношению.
в) Проекции Av В} и точек А, В и S на прямую,
содержащую вектор С, лежат по разные стороны от точ-
ки О (рис.12.27). Тогда, если точки О, Av Bv S} располо-
жены так, как показано на рис. 12.27, что можно вполне
допустить без ограничения общности, то
^•co5Z(^rc) = O51,
a\cosZ.{a1c) = OAv
b 'CosZ(bfc)=-OB} =-AxSr
Имеем: OS} = OA1-AlSl. Это равенство верно и рав-
носильно равенству 3).
Случаи, когда какая-нибудь из точек Alt Вр сов-
падает с точкой О, а также случаи, когда а\\Ь или С = О,
рассмотрите самостоятельно.
Свойства 4)—6) были доказаны ранее.
7) a + b < а + b\.
Это неравенство равносильно следующим неравен-
ствам:
|а + А|2 <|а|2+2|а|-|б| + |б|2,
a2+2ab + b2 <а2+2\a\\b\ +Ь2,
277
откуда ab< а • b , Получили верное равенство согласно
свойству 4). И
Скалярное произведение в координатах. Докажем
следующее утверждение:
Теорема 12.10. Если fl=(xI;j1) и b = (x2;j2)r
то ai = x1x24-j1j2.
□ Рассмотрим векторы д=(х1;>’1) и Л = (х2; _у2) в
декартовой прямоугольной системе координат. Тогда
a = x1i + y1j, b = x2i + y2j.
Согласно свойствам 1) и 3) из теоремы 12.9f получим:
а • b = (x,i + yj) (x2i + y2j) =
= x,x2 • i2 + yxy2 • J2 + xxy2 i-J + x2yx ij.
Так как i ij, to i • j = 0. Кроме того,
fl=M=1
Следовательно,
ab = xxx2 + yxy2-
Следствие!.
2 2,2 II I 2 I 2. 2
a — xx 4-^,; \a\ = yla =y]xx 4-^ .
Следствие 2.
cosj/(a,b}= -r__U_2L_•^1^2 ... -г если а Ф 0 и 6^0.
I 2 2 I 2 .2
Vх! +^1 ЧХ2 +У2
Следствие 3.
+ yxy2 )2 < (xf + y2 )(x22 + y2).
□ Если Л = (х1;<у1), b =(x2;<y2), то из свойства 4)
скалярного произведения векторов имеем:
Х\У\ + Х2У2 I >1х1 +У1 • +У2
откуда и следует^данное неравенство. И
278
§ 12.10. ПРИМЕНЕНИЕ ВЕКТОРОВ
Применим векторы к решению геометрических за-
дач. Некоторые из этих задач были решены ранее други-
ми методами.
Теорема о медианах.
Теорема 12.11. Пусть А(х}
С(х3 ;у3) — вершины треугольника АВС. Тогда
три медианы пересекаются в одной точке
них в отношении 2:1 считая от вершины.
, которая делит каждую из
□ Пусть Ах — середина
стороны ВС треугольни-
ка АВС (рис. 12.28) и точка
Л/(х;у) — такая точка ме-
дианы АА}, что
АМ:МА\ = 2:1.
Ясно, что
AM = (х-х1;^-^1),
динаты
а вектор 2 МАХ имеет коор-
или после уп-
рощения: 2 МА{ = (х2 + х3 - 2х; у2 + у3 - 2у). Значит,
х-х1 =х2+х3-2х, у-у} =у2 + у3-2у,
откуда
Повторяя такие же рассуждения и для медиан ВВ}
и СС}, получим, что точка с координатами
279
принадлежит всем медианам треугольника АВС и делит
их в отношении 2:1, считая от вершины. Я
Т е о р е м а 12.12. Пусть AAV ВВХ, СС, — медиа-
ны треугольника АВС и М — точка пересечения меди-
ан. Тогда справедливы следующие равенства:
1) ЛЛ1 + ЛВ1 + О71 = 0.
2) МАх + МВ' + МСу =0.
3) МА+МВ+МС =
□ Прежде всего заметим, что
= л7С1=|сС1.
M4=--Xli, МВ=--ВВх,
3 3
л7с=-|сС1.
Поэтому для доказательства теоремы достаточно устано-
вить только первое свойство. Рассмотрим первую коор-
динату вектора АА\+ ВВ\ + СС\. Она равна сумме пер-
вых координат векторов АА\, ВВ\, СС\, т.е. равна
Аналогично и вторая координата этого вектора рав-
на нулю, т.е. АА\ + jBBi + CCi = 0. Доказательства для
равенств 2) и 3) проведите самостоятельно.
280
Деление отрезка в данном отношении.
Теорема 12.13. Пусть А(хх;Jj)r В(х2;J2) — кон’
цы отрезка АВ и точка Т(х;у) делит отрезок АВ в
отношении АТ:ТВ =ш:п. Тогда
у^пУх+™У2.
т+п ’ т + п
А. Т ТУ1 ~
□ Очевидно, что —— =—, или и-АТ — т-ТВ. Но
ТВ п
п-АТ = (п(х - хх );п(у - ух))
и
т-ТВ = (т(х2-х},т(у2 -у)).
Отсюда получаем систему двух уравнений с переменны-
ми X и у:
n(x-Xj) = ти(х2 -х)
п(у-У\) = т(у2-у)<
решая которую получим требуемые равенства.
Свойства некоторых четырехугольников.
Т е о р е м а 12.14. Диагонали прямоугольника рав-
ны.
□ Пусть ABCD — прямоугольник. Тогда AB1AD и
скалярное произведение АВ- AD = 0. Отсюда
= АВ2+2АВ-AD + AD2 =
=ab2 + ad2-,
BD2 =\ AD-AB] = АВ2-2АВ AD + AD2 =
= АВ2 + AD2.
281
Значит AC = BD . I
Теорема 12.15. Диагонали ромба перпендику-
лярны.
□ Пусть ABCD — ромб. Тогда
АС= АВ+ AD; BD = AD-AB.
Вычислим скалярное произведение векторов AC -BD.
AC-BD = АВ + AD | | AD-АВ = AD2- АВ2 =
2
2
= AD - АВ =0,
так как стороны ромба равны. Мы доказали, что скаляр-
ное произведение векторов А С и BD равно нулю,
значит, согласно теореме 12.8, векторы АС и BD пер-
пендикулярны.
Т е о р е м а 12.16. (о сумме квадратов всех сторон
четырехгольника). Сумма квадратов всех сторон четы-
рехугольника равна сумме квадратов его диагоналей
плюс квадрат удвоенного расстояния между серединами
диагоналей.
□ Рассмотрим произ-
вольный четырехугольник
ABCD и точку О вне его
(рис.12.29). Обозначим через
a, b, С, d векторы ОА,
ОВ, ОС, OD соответствен-
но. Тогда разности b-а, С-
—b, d-C, a-d есть векторы
АВ, ВС, CD, DA, направ-
0
Рис, 12.29
ленные вдоль сторон четырехугольника, а разности С-а
и d-b есть векторы АС и BD, направленные вдоль его
282
диагоналей. Пусть М и N — середины диагоналей АС
и BD соответственно. Имеем далее по теореме 12.2:
= — (b+d-а-с); 1- MN = b + d-а-с.
Искомое равенство
АВ2 + ВС2 + CD2 + DA2 = АС2 + BD2 +(2MN)2
равносильно соотношению
Представляя в каждом случае квадрат модуля вектора
как скалярный квадрат, получаем равносильное равенст-
во:
2(а2 + Ь2 + с2 + d2 -ab-bc-cd-da)^
-а2 + b2 + с2 + rf2 -2a-c-2b-d +\b + d-a-cf,
или
|AW-a-c|2 =a2 + A2+c2+rf2 +
+ 2(ac + Arf - ab- be - cd - da). (2)
Для доказательства соотношения (2) снова представим
квадрат модуля вектора как скалярное произведение век-
тора на себя:
+ а-с| = (b + d-a-c)\b + d-а-с) =
= b2 +d2 +а2 +c2 + 2(bd -ba-be-da- de-ас).
Отсюда следует равенство (2), а из него вытекает иско-
мое соотношение (1). Итак равенство
АВ2 + ВС2 + CD2 + DA2 = AC2 + BD2 + (2 MN )2
доказано. M
Так как в параллелограмме ABCD точки М и N
совпадают, то имеет место следующее утверждение.
Т е о р е м а 12.17. Сумма квадратов всех сторон
параллелограмма равна сумме квадратов его диагона-
лей.
283
§ 12.11. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 12.1. Доказать, что середина отрезка с конца-
ми в точках л(5;7) и В(8;-7) лежит на оси ОХ,
Пусть М(х;у) — середина отрезка АВ. Тогда
из §12.2. следует, что
откуда ясно, что точка М лежит на оси ОХ. А
Пример 12.2. Найти точку, равноудаленную от осей
координат и точки
Пусть А(х;у) — искомая точка. Так как эта
точка равноудалена от осей координат, то ААХ = ААу,
где Ах, Ау — проекции точки А соответственно на
оси OX, OY. Эти проекции имеют следующие коор-
динаты: Ах(х;6), Ay(tyy). Вычисляя длины отрезков
ААХ и ААу, имеем:
yj(x-x)2 + G-0)2 = -J(x-0)2 +(у-у)2,
т.е. [j/ = |х , откуда следует, что либо у = х, либо у = — X.
Пусть вначале у = х, тогда
AM = - х)2 + (-6 - х)2.
По условию получаем:
х2 + 18х + 45 = О,
откуда X! = —3, х2 = —15.
Таким образом, точки (—3;—3) и (—15;—15) равноудале-
ны от осей координат и точки ЛА.
Рассмотрим теперь случай, когда у = —х. Имеем:
284
AM =у/(-3-х)2 +(-6 + х)2 =
Рис. 12.30
х2 -6х + 45 = 0.
Последнее уравнение корней не имеет. Значит, ус-
ловию задачи удовлетворяют только найденные ранее
точки (-3;-3) и (-15;-15). ▲
Пример 12.3. Найти множество точек (х;у) коорди-
натной плоскости, удовлетворяющих условию ху > 0.
Условие ху > 0 равносильно тому, что х > 0,
у > 0 или х < 0, у < 0. Множество точек, удовлетворяю-
щих условиям х > 0, у>0,
совпадает с множеством всех
точек первой четверти ко-
ординатной плоскости, ис-
ключая точки, лежащие на
осях координат. Аналогич-
но множество точек, удовле-
творяющих условиям х < 0,
у<0, совпадает с множест-
вом точек третьей четверти
координатной плоскости, ис-
ключая точки, лежащие на
осях координат. Объединение этих множеств и является
искомым множеством. Оно изображено на рис. 12.30 за-
штрихованными точками. А
Пример 12.4. В параллелограмме ABCD известно,
что АВ = а, AD=b. Точки М и N лежат соответственно на
отрезках АВ и CD, причем AM:MB=CN:ND=2:1. Найти век-
тор MN.
ZS По правилу многоугольника получим
AM =MB+BC+CN
(рис. 12.31). Так как векторы МВ и АВ сонаправлены и
AM: МВ = 2:1, то
285
MB =-АВ =-а.
Аналогично, так как векто-
ры CN и АВ противопо-
ложно направлены и
CN:ND-2A,
то
CN =— DC = — АВ =
Учитывая также, что
ВС = AD = b,
имеем:
Пример 12.5. Доказать, что векторы а(5;-1), £(-4;3)
образуют базис и разложить вектор с(б;1) по этому базису.
ZS. Составим отношения координат векторов а и b:
I
2
Очевидно,----Ф—. Тогда по теореме 12.6 векторы а
и b неколлинеарны, т.е. образуют базис. Будем искать
такие чис/ka X
ха + yb имеет координаты (5х — 4у;—х 4- Зу)
теоремам 12.4.
уравнений:
[5x-4j/= 6
< откуда
и у, для которых ха + yb = С. Вектор
согласно
и 12.5. Получаем следующую систему
Таким образом, С = 2а + b.
286
Пример 12.6. Известно, что точка М делит отре-
зок АВ в отношении АМ\МВ=2'.5. Найти координаты точ-
ки М, если Л(5;-1), В(2;4).
Пусть (х;у) — координаты точки М. Тогда
ЛЛ/ 2 - п
из §12.5 следует, что ---.- = —, откуда зАМ=ШЬ.
МВ 5
Очевидно, что
AM =(х-5;у + 1), МВ = (2-х;4-у),
откуда
5ЛЛ/=(5х-25;5у + 5), 2 МВ = (4-2х;8-2у).
Получаем следующую систему линейных уравнений:
f5x-25 = 4-2x
(5^ + 5 = 8-2^г
29 3
решая которую получим: х = —, у = у. А
Пример 12.7. Доказать, что треугольник АВС,
где Л(4;-2), Б(5;-1), С(0;2), является прямоугольным.
ZX Найдем координаты векторов АВ и АС. Полу-
чим: АВ = (1;1), АС = (—4;4). Вычислим скалярное про-
изведение этих векторов:
АВ ЛС = 1-(-4) + 1-4 = 0.
По теореме 12.8. векторы АВ и АС перпендикулярны, а
это значит, что в треугольнике АВС угол А — прямой.
Пример 12.8. Пусть при гомотетии с центром в начале
координат точка Л(1, -2) переходит в точку ЛД-5; 10). Найти
коэффициент гомотетии. В какую точку переходит точ-
ка при этой гомотетии?
287
Пусть О — начало координат. Тогда векто-
ры ОА=(1; — 2) и ОА]=(—5;10) противоположно на-
правлены. Очевидно, что коэффициент гомотетии к от-
рицателен и
2 V125
ОА
Далее, ОВ =(-1;7). Пусть — координаты
точки В}, в которую перейдет точка В при гомотетии с
коэффициентом к = — 5. Тогда X и у пропорциональны
числам (—1) и 7 и ОВ}=5ОВ. Значит, для некоторого
числа t выполняется: х = — t, у = ъ поэтому
ОВ1 = л/^Г+49?’ = 5л/2|г|.
Учитывая, что
получаем:
5л/2 г[ = 25л/2, откуда t =5 .
Так как при отрицательном коэффициенте гомотетии
векторы ОВ и ОВХ проти-
воположно заправлены, то
t = — 5, откуда х = 5, у =
= —35. Таким образом, полу-
чили, что к = — 5, и точка В
Пример 12.9. В тре-
угольнике АВС дано: Z.C=90°,
ЛС=6, ВС=8. Точки О, It
М — центр описанной окруж-
ности, центр вписанной ок-
Рис. 12.32
288
ружности, точка пересечения медиан соответственно. Найти
расстояния OI t MIr МО.
Выберем систему координат так, как показано
на рис.12.32. Проведем ООХ±СВ, ООу±АС, ПХ±СВ,
Пу1АС. Так как О — середина АВ и ООХЦАС,
ООуЦВС, то по теореме Фалеса СОХ = ОХВ и
СОу — ОуА. Значит, точка О имеет координаты х0=4,
у0 = 3 . Четырехугольник IIуС1х — квадрат, причем сто-
рона его равна радиусу Г вписанной в треуголь-
ник АВС окружности. По теореме Пифагора
ЛВ2 = ЛС2 + ВС2 = 62 + 82 =100, откуда ЛВ=10.
а + Ь-с
По формуле Г =-------имеем:
6 + 8-10
Г 2
Таким образом, 1(2; 2). По теореме 12.11 координаты
(х;у) точки М находятся так:
0+0+8 8 0+6+0 n ,/8^
х =--------= -; у =-------= 2, т.е. М — ;2 .
3 3 3 U )
По формуле расстояния между двумя точками имеем:
OI = 7(2-4)2 +(2-3)2 = 75,
M7=^2-|J+(2-2)2=|,
= +(3-2)2 = Jf-1 +1 =-. Ж
vl з; vl3J 3
Пример 12.10. Пусть Alt Blr С, — середины сто-
рон ВС, AC t АВ соответственно в треугольнике АВС. Дока-
зать, что точки пересечения медиан треугольников АВС
и А^ВХСХ совпадают.
Решим этот пример двумя способами.
Первый способ.
289
Пусть заданы вершины треугольника
В(х2;у2). Тогда из §12.2 получим координаты точек Лр
Обозначим через М(х',у) и точки пересечения
медиан треугольников ЛВС и соответственно.
По теореме 12.11 имеем:
*2 +х3 t xt +х3 t Х} + х2
2 2 2 _х1+х2+х3
откуда X = W, у = V, т.е. точки М и N совпадают.
Второй способ.
Пусть М — точка пересечения медиан треугольни-
ка АВС. Проведем медиану АА j. Она пройдет через
точку М треугольника АВС и пересечет отрезок ВХСХ в
некоторой точке А2 (рис. 12.33). Этот отрезок есть сред-
няя линия треугольника АВС, поэтому BjCjjCB. Тогда
А2С1ЦА1В, АСх = СхВ и в треугольнике ААХВ отре-
зок А2С} есть средняя линия. Поэтому
290
Ри.с.1233
Рис.12.34
а2с.=—а.в=—св.
2 1 2 1 4
Аналогично ВХА2 — средняя линия треугольника ACAV
откуда
В.А2 = -СА. = -СВ.
1 2 2 1 4
Итак, ВХА2 = А2Сх и АхА2 — медиана треугольни-
ка АХВХСХ. Тогда точка М лежит на прямой АХА2. Ана-
логично точка М лежит на прямых ВХВ2 и СХС2, где В2,
С2 — середины отрезков АХСХ и АХВХ. Следовательно,
точка М есть точка пересечения медиан треугольни-
ка АХВХСХ. А
Пример 12.11. Доказать, что OA+OB+OC+OD =0,
где О — точка пересечения отрезков, соединяющих середины
противоположных сторон четырехугольника ABCD.
Пусть Е, F, G, Н — середины сторон АВ,
ВС, CD, DA, а отрезки EG и FH пересекаются в
точке О (рис. 12.34). Четырехугольник EFGH — паралле-
лограмм, поскольку EF\\GH как средние линии тре-
угольников АВС и CAD , аналогично EH\\FG. Тогда
диагонали этого параллелограмма в точке О делятся по-
полам.
291
Продолжим отрезок ОЕ и на его продолжении от-
ложим отрезок EEV равный ОЕ. По первому признаку
параллелограмма четырехугольник ОАЕ j В — параллело-
грамм, и по правилу параллелограмма сложения векторов
ОА+ОВ =ОЕХ=2ОЕ .
Аналогично,
6c + 6b=2OG.
Тогда
oa^ob^oc^od^oe+og}^,
поскольку векторы ОЕ и OG противоположны. Ж
Пример 12.12. Вычислить косинус острого угла между
медианами равнобедренного прямоугольного треугольника,
проведенными к его катетам.
ZS, Для прямоугольно?)
треугольника АОВ с пря-
мым углом О и равными ка-
тетами ОА и ОВ введем
прямоугольную систему ко-
ординат так, как показано на
рис. 12.35. Если
ОА = ОВ = а,
то координаты вершин А
и В таковы:
Л(0;а), В(а;0).
Рис. 12.35
Проведем медианы АА} и ВВ}. Тогда имеем: Ах
По следствию 2 теоремы 12.10
292
Острый угол ф между прямыми АА} и ВВХ ра-
вен 180°-Z AAVBBX , откуда coscp = .
Пример 12.13. Доказать, что сумма квадратов расстоя-
ний от любой точки окружности до вершин вписанного в нее
равностороннего треугольника есть величина постоянная, не
зависящая от положения точки на окружности.
ZS Через центр О равностороннего треугольника
АВС проведем две взаимно перпендикулярные оси ОХ
и OY так, чтобы ось ОХ была параллельна АС
(рис.12.36). Пусть АВ = АС — ВС = а. В правильном тре-
угольнике легко находятся отрезки
Пусть М(х',у) — произвольная точка описанной окруж-
ности. По формуле расстояния между двумя точками по-
лучим:
МО2=х2 +y2 = R2 =—.
3
По этой же формуле имеем:
293
Тогда
МА2 + МВ2 + МС2 =
Таким образом, величина МА 2 + МВ2 + МС2 не зави-
сит от положения точки М
на окружности. Ж
Пример 12.14. В прямо- j
угольном треугольнике АВС
точка М делит катет АС в от-
ношении ЛЛГ:ЛГС=3:1, а точ- v
ка N делит гипотенузу АВ в
отношении AN: NB=2:3. Най-
ти длину отрезка MN, ес-
ли ЛС=4 см, ВС = Зсм.
ZS Выберем прямоуголь-
ную систему координат так,
как показано на рис. 12.37. По
теореме Пифагора
ав=4ас2
294
Точка М имеет координаты (0;1). Проведем NNX1CB,
NN у1АС. По теореме Фалеса
AN CNX AN 2
J Л «аж
nvc~~njT NB ~3'
Z л
Тогда
CN =-АС =--4 =—, CNx = -BC = — -3-—.
у 5 5 5 х 5 5 5
Значит точка N такова:
. По формуле расстоя-
ния между двумя точками получаем:
Рис.12.38
А
Пример 12.15. Пусть
ААХ, ВВ}, ССХ — высоты тре-
угольника АВС. Доказать, что
треугольник АВС рг посто-
ронний тогда и только тогда,
когда ААХ+ВВХ+ССХ=О.
ZS Пусть треуголь-
ник АВС — равносторон-
ний; AAV BBV ССХ — его
высоты. Тогда они являются
также и медианами. По тео-
реме 12.12 имеем:
Д+Д+ccj = o.
Обратно, пусть в треугольнике АВС выполнено ус-
ловие
Д + ВВ}+СС}=0.
Докажем, что в этом случае треугольник АВС —
равносторонний (рис. 12.38). Для этого умножим обе час-
ти этого равенства скалярно на вектор АВ. Так как
О- АВ = 0, то получим:
295
= AB- AAX + ABBBX + AB-CCX =
= AB - AAxcosZ.BAA j + AB • BBxcos{\ 80° — Z.ABBX) +
+ AB CCxcos9Q° =
= AAX-AB-BBxcosZABBx = AAX -BBX.
Мы воспользовались здесь свойствами скалярного
произведения (теоремы 12.8 и 12.9), а также тождест-
вом соу(180°— а) = - cosa. Далее имеем:
ААХ=ВВХ, ААх = ВВх,— = —,
1 1 1 1 ВС АС
следовательно,
ВС = АС,
Аналогично, умножая исходное равенство скалярно
на вектор AC t получим: АВ = ВС. Значит,
ВС = АС = АВ,
и данный треугольник рс вносторонний. Ж
Пример 12.16. Медианы,
проведенные к сторонам АВ и р
АС треугольника АВС, перпенди-
кулярны. Доказать, что угол между 1
этими сторонами меньше 45°. Ciх / i
Пусть в треугольнике у'чА 1
АВС стороны АС = Ь, АВ=с
и медианы ВВХ и ССХ перпен-
дикулярны (рис. 12.39). Введем A В] С
векторы АВ = С и АС = b и
выразим через них векторы Рис.12.39
В}В и CjC, направленные вдоль медиан. Имеем:
анало! лчно
296
Поскольку ВХВ±С\С, то скалярное произведение этих
векторов равно 0, т.е.
свойствам скалярного произведения
2 2
—Ьс--—— = 0; l{b2 +c2) = 5b‘C =5bc-cosA;
cosA =------
5bc
Покажем, что cosA > cos45° =—j=, откуда в силу
убывания функции косинуса на промежутке от 0°
до 90° будет следовать утверждение задачи. Действитель-
но, по неравенству между средним арифметическим и
средним геометрическим имеем:
cosA >
Однако, — >
что равносильно очевидно-
2 1
му неравенству 16-2 >5 . Итак, cosA>—и утвержде-
ние задачи доказано.
§ 12.12. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
в
12.01. Найти точки, симметричные точкам Я(5;-3),
В(-7;б), С(0;4) относительно координатных осей и начала ко-
ординат.
297
12.02. Найти координаты середин отрезков АВ , ВС и АС
по данным задачи, если >4(5;-3), В(-7;б), С(0;4) — вершины
трегольника АВС .
12.03. Доказать, что четырехугольник ABCD с вершинами
в точках >4(1;3), В(0;2), С(1;1), £>(2;2) — параллелограмм. Бу-
дет ли этот четырехугольник
а) ромбом?
б) прямоугольником?
в) квадратом?
12.04. Вычислить расстояние между точками координатной
плоскости:
а) >4(0:0), В(2;4);
б) >4(2:4), В(1;-3).
12.05. Доказать, что четырехугольник ABCD с вершинами
в точках >4(4:1), В(0;4), С(-3;0), £>(1;-3) — квадрат.
12.06. Один из концов отрезка находится в точке (1;3), а
его середина — в точке (2;2). Найти второй конец отрезка.
12.07. Найти множество точек D(x;y) координатной плос-
кости, удовлетворяющих условию:
а) х = 5,
б) у = 4,
в) |х| = 3,
г) ху <0,
д) AADC < 30е,
е) ZBDC - ZADC > 60°,
если >4(1:0), В(-1;0), С(3;0).
12.0 8. Пусть f — параллельный перенос координатной
плоскости. Тогда для любой точки А(х;у) выполняется усло-
вие f(A) = Av где Я1(хр-у|), причем х} = х+а, ух = у + Ь
и а, b — постоянные числа. Доказать.
12.0 9. При параллельном переносе точка А переходит в
точку В. В какую точку переходит середина отрезка АВ , если:
а) >4(5;-7), В(2;7);
б) >4(4:1), Б(0;8)?
12.10 . Существует ли параллельный пере юс, при котором
точка Я(5;-7) переходит в точку 2?(8;0), а точка С(3;2) — в
точку £>(б;9)?
298
12.11 . Доказать, что векторы АВ и АХВХ противоположны
тогда и только тогда, когда существует центральная симметрия,
при которой точка А переходит в точку Ах, а точка В перехо-
дит в точку В}.
12.12 . Изобразить образ треугольника АВС при парал-
лельном переносе, если точка А переходит в начало координат,
а вершины треугольника имеют координаты Л(2;-3), В(4;1),
С(8;0).
12.13 . На оси абсцисс найти точку, равноудаленную от
точек И(1;2) и В(-3;4).
12.14 . Четырехугольник ABCD — параллелограмм. Пе-
речислите все пары равных и все пары противоположных век-
торов, построенных на сторонах параллелограмма.
12.15 . На прямой а даны точки А, В, С, D, причем точ-
ка В лежит между точками А и С, а точка С лежит между
точками В и D. Укажите все пары сонаправленных и все пары
противоположно направленных векторов.
12.16 . Даны векторы л = (5;-7) и £ = (-1;4). Найти век-
тор 2а - ЗЬ и его модуль.
12.17 . При каких значениях ТП векторы а = (5т;2) и
b = (1;2m} сонаправлены?
12.18 . Доказать, что треугольник АВС с вершинами
Л(2;1), В(3;0), С(1;5) тупоугольный, и найти косинус тупого
угла.
12.19 . Известно, что |а| = 2, |^| = 3, = 120е. Найти:
a) (2а + 5д)-(5а-б);
б) |2а + 5^|;
12.20 . Лежат ли точки Л(2;7), В(4;9), С(0;5) на одной
прямой?
12.21 . Вычислить длины диагоналей параллелограмма, по-
строенного на векторах й = 5р + 2q, b-p~3q, если И = 2>/2.
|»| = 3, Z(p,«)=45".
12.22 . Доказать, что для произвольных точек А, В и О
выполняется равенство АВ = ОВ-ОА.
12.23 . При каком значении ТП векторы а=(5;-7) и
b = (m -1; 3) перпендикулярны?
299
12.24 . Найти единичный вектор, сонаправленный векто-
ру р = (3;-4).
12.25 . Доказать, что для ненулевого вектора Л век-
t 1
тор о является единичным вектором, противоположно
|а|
направленным вектору Л.
12.26 . Изобразите два неколлинеарных вектора X, у и по-
стройте векторы:
12.27 . Изобразите попарно неколлинеарные векторы Q,
b , С. Постройте вектор 2а-ЗЬ+±с.
12.28 . Точка О — середина медианы AM треугольни-
ка АВС . Выразите векторы АО и ОМ через векторы АВ
12.29 . Точки М и N — середины диагоналей АС и BD
четырехугольника ABCD . что
MN =-( AD+CB |.
2\ J
12.30 . Найти вектор, длина которого равна V5, образую-
щий с осью ОХ тупой угол и перпендикулярный векто-
РУ а = (1;2).
12.31 . Найти вектор, длина которого равна 26, образую-
щий с вектором b =(1;3) острый угол и коллинеарный векто-
РУ а = (5;-12).
12.32 . Даны координаты двух вершин треугольни-
ка АВС: Я(2;-1), В(-3;5) и координаты точки пересечения
медиан Л/(1; 1). Найти координаты вершины С.
12.33 . Даны две вершины равностороннего треугольни-
ка АВС : А(-2;2), В(-2;-4). Найти координаты третьей вер-
шины.
12.34 . Найти координаты вершин С и D квадрата ABCD,
если заданы вершины А(2; 1) и В(4;О).
300
12.35 . Даны четыре точки: Л(1;1), В(б;б), С(5;4), £>(2;1).
Доказать, что ABCD — трапеция и вычислить косинус угла ме-
жду ее диагоналями.
12.36 . Даны три вектора 0, b, С. Доказать, что век-
тор (b c)a-(a-c)b перпендикулярен вектору С .
12.37 . При каких значениях ТП векторы (т2 -т-2)-Ь
и т3 b противоположно направлены, если b 0.
12.38 . В прямоугольном треугольнике АВС угол С = 90°,
—> ♦
СВ = a, CA-b, CD — &tq высота. Найти вектор CD.
12.39 . Пусть f — гомотетия с коэффициентом к и цен-
тром в начале координат. Доказать, что для произвольной точ-
ки А(х;у) точка А} = /(л) имеет координаты х}- кх, у{ = ку.
12.40 . Пусть f— поворот против часовой стрелки на
угол а вокруг начала координат. Доказать, что для произволь-
ной точки Л(х;у) точка Ах = /(л) имеет координаты:
х, = х • cosa - у • sina,
ух = x-sina+y-cosa.
12.41 .-Доказать, что для произвольной точки М и прямо-
угольника ABCD выполняется равенство
МА-МС = MBMD.
12.42 . Даны два вектора ОА = а и ОВ = Ь. Точка М делит
отрезок АВ в отношении АМ:МВ=ТП\П. Выразить век-
тор ОМ через векторы CL и b .
12.43 . Пусть М — точка пересечения медиан треугольни-
ка АВС . Доказать, что МА2 + МВ2 + МС2 = 0, где А2, В2, С2 —
середины медиан ЛЛР ВВЛ, ССГ
12.44 . Найти единичный вектор, коллинеарный вектору,
направленному по биссектрисе угла Л треугольника АВС, ес-
ли Л(1;1), В(3;0), С(0;3).
12.45 . Пусть Л, В, С, D — произвольные точки плоско-
сти. Доказать что
АВ • DC + ВС • DA + СА • DB = 0.
12.46 . Используя результат предыдущей задачи, доказать,
что высоты треугольника пересекаются в одной точке.
12.47 . Доказать, что для произвольных векторов а и b
выполняется равенство
301
I > |2 I . |2 _ 21 -|.|2
|a + ft| +|a-d| = 2a | + 2|£| .
Каков геометрический смысл этого равенства?
12.48 . Доказать неравенство
7(^|+Х2)2+и+У2)2 < 7X|2+J12 + +^2 •
12.49 . Теорема Гамильтона. В треугольнике АВС выполня-
ется равенство: ОН = ОА 4- ОВ 4- ОС, где Н — ортоцентр тре-
угольника АВС , О — центр описанной около него окружно-
сти. Доказать это.
12.50 . Доказать, что векторы а и b неколлинеарны тогда
и только тогда, когда из равенства ХЛ 4- yb = 0 следует, что
х = у = 0.
12.51 . В треугольнике АВС на сторонах АВ и АС во
внешние от треугольника стороны построены квадра-
ты AMNB и ATSC . Доказать, что прямая, содержащая медиа-
ну АА} треугольника АВС , перпендикулярна прямой МТ.
302
ГЛАВА 13
ПРЯМАЯ И ОКРУЖНОСТЬ В ДЕКАРТОВЫХ
КООРДИНАТАХ
§ 13.1. УРАВНЕНИЕ ПРЯМОЙ
PULCJ3.1
Уравнение прямой,
проходящей через точку
(хо»^о)» перпендикулярно
вектору п = (а; Ь). Спра-
ведлива следующая теоре-
ма:
Теорема 13.1.
Пусть точка ^(x0;j0) ле-
жит на прямой Ш, пер-
пендикулярной к ненуле-
вому вектору л=(а;Ь). Точка А(х;у) лежит на пря-
мой т тогда и только тогда, когда выполняется равен-
ство:
a(x-xo) + ft(j-jo) = O. (1)
□ Пусть в прямоугольной системе координат задан
ненулевой вектор Л = (л;й) и точка Д)С*(н Уо) на пря-
мой т, перпендикулярной вектору Л. Пусть Я(х;у) —
произвольная точка этой прямой (рис. 13.1). Тогда векто-
ры Л=(а;б) и А$А = (х—х0;у — у0) перпендикулярны. А
это значит, что скалярное произведение этих векторов
равно нулю, т.е. Л-АцА =0, или
а(х-хо)+б(у-уо)=О.
303
Обратно, пусть точка А(х;у) удовлетворяет урав-
нению я(х-х0) 4-б(у — у0) =0 • Тогда левую часть этого
уравнения можно представить как скалярное произведе-
ние вектора Л = (я;б) на вектор AqA. Получим
л-= 0.
Тогда векторы И = (а;Ь) и А0А = (х — х0;у — у0) перпен-
дикулярны. А это значит, что прямая AqA перпендику-
лярна прямой, на которой лежит вектор Л, и следова-
тельно, прямая AqA совпадает с прямой Ш. Таким обра-
зом, точка А(х\у) лежит на прямой Ш.
Уравнение (1) — это уравнение прямой, проходя-
щей через точку ^(xqJJq) и перпендикулярной ненуле-
вому вектору л=(а;^).
Общее уравнение прямой. Представим уравнение
я(х — х0 ) 4- б(у — Уо ) = 0 в следующем виде:
ах 4- by -ах0 - 6у0 = 0.
Обозначим число (—axQ — byQ) через с, Тогда мы по-
лучим уравнение
ах+by + с =0. (2)
Его называют общим уравнением прямой на плос-
кости.
Таким образом, всякая прямая в прямоугольной сис-
теме координат может быть задана линейным уравнени-
ем ах 4- by 4- с = 0 . Числа а и b одновременно не обра-
щаются в нуль, т.е. а2 +62^0, так как вектор Л = (а;б)—
ненулевой. Кроме тл о, прямая ах + Ьу 4-с =0 и вектор
Л = (а;б) перпендикулярны.
Уравнение прямой, проходящей через точку
(*о; л) • параллельно вектору 5=(/, Л1) с ненуле-
выми координатами. Пусть $=(/;#:) вектор, имеющий
304
ненулевые координаты, а точка Д)(х0;у0) лежит на пря-
мой, параллельной этому вектору. Если точка Л(х;у)
также лежит на этой прямой, то векторы А$А и S кол-
линеарны. Следовательно, их координаты пропорцио-
нальны и справедливо равенство:
(3)
Уравнение (3) и есть уравнение искомой прямой.
Угловой коэффициент прямой. Пусть в уравнении
ах + by + С = 0 коэффициент 6^0, т.е. эта прямая не-
параллельна оси OY. Тогда получим
Обозначим
Получим уравнение
у=кх+1. (4)
Число к называется угловым коэффициентом пря-
мой (4). Числа к и I в уравнении (4) имеют следующий
геометрический смысл, о чем утверждает следующая тео-
рема.
Теорема 13.2. В уравнении у — кх-\-1 число к
Рис.13.2
— это тангенс угла а, обра-
зованного этой прямой с по-
ложительным направлени-
ем оси OX. I — ордината
точки пересечения этой пря-
мой с осью OY.
□ Если X = О, то из
уравнения (4) следует, что
У~1, т.е. точка А пере-
сечения прямой с осью OY
имеет ординату, равную / .
Пусть 0°<а<90°. Тогда пря-
305
мая пересекает оси координат в точках Я(0;/)
В------;0 , и при I >0 имеем: ОА —I, ОВ = — (рис.13.2),
поэтому
ОА
ОВ
Если I <0
(рис.13.3), то ОЛ = —7, ОВ — —
вновь tga— к.
Наконец, при 7 = 0 (рис. 13.4) рассмотрим на прямой
точку Из треугольника OMN находим:
MN ,
tga=-----= к.
6 ON
Случаи, когда 90°<а<180° (рис.13.5—13.7) и а = 0°
(рис. 13.8), рассмотрите самостоятельно.
Уравнение прямой с угловым коэффициентом к,
проходящей через точку (x0;j0). Уравнение прямой с
угловым коэффициентом к записывается в таком виде:
у = кх +7. (а)
Поскольку прямая проходит через точку (х0;yQ), то
306
Рис.13.7 Рис.13.8
у0=кх0+1. (б)
Вычитая из уравнения (а) равенство (б), получим:
У-Уо = к(х-хо). (5)
Уравнение (5) — это уравнение прямой с угловым
коэффициентом к, проходящей через точку (x0;j0).
Уравнение прямой, проходящей через две заданные
точки. Пусть заданы две точки А(х^ух) и В(х2;у2),
причем хг&х2 и У1=^У2. Составим уравнение пря-
мой АВ , проходящей через эти точки.
Воспользуемся уравнением (3). Рассмотрим век-
тор S = АВ , Согласно §12.7 имеем:
307
Искомая прямая проходит через точку Л(х1;>'1) и парал-
лельна этому вектору. Значит в уравнении (3) следует по-
ложить х0 = х,, у0 ~ У1 < I- х2 -х1- т = Уг ~У1 • Получим:
Х . (6)
Х2~Х1 У1-У1
Уравнение (6) называется уравнением прямой, про-
ходящей через две заданные точки и в(х2‘, у2).
Случаи, когда: а)Х] = х2, УХ*У2\ б) хх*х2, ух=у2,
рассмотрите самостоятельно.
Уравнение прямой в отрезках. Пусть Л/(а;0) и
nM — точки на осях координат, не совпадающие с
началом координат, т.е. 6^0. Составим уравнение
прямой MN , используя уравнение (6). Получим:
х -а _ у-0
откуда
(7)
Уравнение (7) называется уравнением прямой в от-
резках.
§ 13.2. УГЛЫ МЕЖДУ ПРЯМЫМИ
Пусть цх + 1\у + с, = 0 и а^х + 1\у + с2 = 0 — уравне-
ния двух прямых в прямоугольной системе координат.
Тогда вектор перпендикулярен прямой
цх + l\y + q = 0, вектор = (а2; Ь2) перпендикулярен
прямой с^х + Ь^у + Cj = 0.
Нетрудно доказать, что угол ф между этими прямы-
ми равен углу между прямыми, на которых лежат векто-
ры щ и /ij- В качестве угла ф между прямыми берется:
острый угол, если прямые неперпендикулярны и непа-
308
раллельны; угол 0°, если прямые параллельны; угол 90°,
если прямые перпендикулярны. Во всех случаях выпол-
няется неравенство cos(p>0.
Следовательно,
/( . - *4'14 |а1а2
COSCP = COsZX^t^) = ; -j Г--7 = . о -7- * —.
Итак:
а^а2+ЬхЬ2\
c°s<$ = / , , /, (1)
7а, +ЬХ -^а2 +Ь2
Из формулы (1) следует, что прямые
fljX + Ajj + q = 0 и я2х ++ с2 = 0
перпендикулярны тогда и только тогда, когда
а1а2 + ААг = (2)
Условие перпендикулярности прямых J=A1x+/1 и
j = A2x + /2. Пусть теперь прямые заданы уравнениями
и y = fc2x+4- Преобразуем их к общему
уравнению прямой на плоскости:
кхх - у+ 4 =0i к2х -J/ + 4 =0.
Условие перпендикулярности этих прямых получается из
равенства (2), если положить = kv а^ — к2, й| = /^ = —1.
Имеем:
кхк2 +1 = 0,
откуда следует, что прямые j = A1x + /1 и у = к2х + 12
перпендикулярны тогда и только тогда, когда
Aj£2 = —1. (3)
Мы получили условие перпендикулярности прямых с
угловыми коэффициентами кх и к2.
Условие параллельности прямых у=кхх+1х и
у = к2х + 12. Рассмотрим две различные прямые
у = кхх + Z, и у = &2х + 4. Условие их параллельности вы-
текает из теоремы 13.2. У параллельных прямых углы ОЦ
и а2, образованные этими прямыми с положительным
направлением оси ОХ, одинаковы. Поэтому прямые па-
309
параллельны тогда и только тогда, когда tgax = tga2, а
это по теореме 13.2 выполнено в том и только в том
случае, когда кх = к2. Таким образом, прямые у = к}х + 1х
и у = к2х +12 параллельны тогда и только тогда, когда
к2 . (4)
Мы получили условие параллельности прямых с уг-
ловыми коэффициентами кх и к2.
§ 13.3. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Пусть А(х0;у0) — данная точка и / — прямая,
уравнение которой имеет вид:
ах Л-by + с = 0.
Обозначим через d расстояние от точки А до этой пря-
мой. Тогда справедливо следующее утверждение:
Теорема 13.3. Расстояние d от точки
Л(хо;^о) до прямой ах + by + с = 0 вычисляется по
формуле:
j _ |ах0 4- Ьу„ + с|
/_2 , д2
\а + b
□ Пусть точка 4Wo) не
принадлежит прямой I . Опус-
тим перпендикуяр AM на
прямую / (рис. 13.9). Пусть хх и
ух — координаты точки М.
Тогда ненулевой вектор
Рис, 13.9
коллинеарен
ЛЛ/ = (х1 -х0;у' -у0)
вектору П = (a;b}, перпендикулярному
прямой / . Значит, существует такое число %, для кото
рого хх — xQ = Xzz и ух — у0 = kb. Тогда
xx = xQ + *ka-t y} = yQ + M.
310
Так как точка М лежит на прямой / , то выполняется ус-
ловие:
а(х0 + Azz)+b(y0 + Хб) + с = О,
откуда
Так как AM = (х, - х0; у, - у0) = (Ха; XZ>), то
AM = д/(Ха)2 + (XZ>)2 = + A?Z>
В случае, когда точка А(х0;у0) лежит на прямой
ах + Ьу + с = 0, расстояние d считается равным нулю.
Проверьте самостоятельно, что формула для вычисле-
ния d в этом случае также дает правильный результат.
§ 13.4. УРАВНЕНИЕ ОКРУЖНОСТИ
Окружность с центром в точке P(xo;yoj и радиу-
сом R. Точка А(х',у) (рис. 13.10) лежит на окружности
тогда и только тогда, когда расстояние между точками
А(х;у) и R(x0;y0) равно радиусу R этой окружности,
т.е.: дДх - х0)2 + (у-у0)2 = R, или
(х-х0)2+(у-у0)2 = Л2.
(1)
Уравнение (1) — это уравнение окружности с цен-
тром в точке Р(х0;у0) и радиусом R. Если центр ок-
ружности совпадает с началом координат, т.е. хо=О и
>>0 =0, то уравнение (1) принимает вид:
311
(2)
Пересечение прямой и
окружности. Для нахожде-УЙ
ния точек пересечения пря-
мой ах + Ъу 4- с = 0 и окруж-
ности
Рис.13.10
необходимо найти решения—
системы уравнений: О
Пусть для определенности 6^0. Из первого урав-
а с
нения у =----х----. Подставляя это значение у во вто-
b b
рое уравнение, мы получим квадратное уравнение вида
Ах2 + Вх 4- С = 0. Пусть D = В2 —^АС — дискриминант
этого квадратного уравнения. Тогда возможны следую-
щие 3 случая:
a) D>0. Квадратное уравнение имеет два корня. В
этом случае прямая и окружность пересекаются в двух
точках.
б) D = 0. Квадратное уравнение имеет один корень.
В этом случае прямая и окружность имеют одну общую
точку, т.е. прямая ах + Ьу 4-С =0 — это касательная к
окружности (х — х0)2 4- (у — у0)2 = R2.
в) D<0. Квадратное уравнение не имеет корней. В
этом случае прямая и окружность не пересекаются.
§ 13.5. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 13.1. Записать уравнения сторон ромба с диа-
гоналями 10 и 6, если большая диагональ лежит на оси OX ,
а меньшая — на оси OY.
312
ZS Пусть ABCD — заданный ромб, диагональ АС
лежит на оси абсцисс, а диагональ BD — на оси ординат
Рис.13.11
(рис. 13.И). Тогда
ЛО = ОС = 5,
Точки С, В, At D имеют ко-
ординаты
С(5;0), В(0;3),
Л(-5; 0), £>(0;-3).
Для записи уравнений
сторон ромба воспользуемся
уравнением прямой в отрез-
ках. Тогда прямая ВС имеет
уравнение —h —=1 ; прямая
АВ —уравнение----h —=1 , прямая AD —уравнение
—— Ч—— = 1 , прямая DC — уравнение у Ч—— = 1 .
После упрощения уравнения этих прямых примут
следующий вид:
для прямой ВС: Зх + 5у —15 = О,
для прямой АВ: Зх — 5у +15 = О,
для прямой AD-. Зх + 5^ + 15 = О,
для прямой DC\ Зх — 5у —15 = О.А
Пример 13.2. Дан треугольник АВС, где Л(-2;0),
В(1;4), С(4;0). Записать уравнения прямых, на которых ле-
жат : а) медиана ВВ} , б) высота СН3.
Точка Вх является серединой отрезка АС .
ордината yQ равна нулю, а абсцисса
х0— —1 .
Согласно уравнению (6) §13.1, уравнение прямой ВХВ за-
писывается в виде:
313
РисЛ3.12 Рис.13.13
Далее найдем координаты вектора АВ, перпендикуляр-
ного высоте СН3 (рис.13.12). Исходя из координат то-
чек А и В, имеем:
JB=(2-(-2);4-0) = (4;4).
По теореме 13.1 уравнение прямой СН3 записывается в
виде 4(х-4)+4(у-0) = О, откуда у = 4— х,
Таким образом, медиана В}В лежит на прямой
у = 4х —4, а высота СН3 — на прямой у = 4— х. Ж
Пример 13.3. Построить окружность х2 +у2 +5х = С и
прямую х + у = 0. Найти их точки пересечения.
ZS Приведем уравнение окружности к виду
(х - х0)2 + (у - Jo)2 = R2.
Имеем:
314
Это
окружность с центром в точке Р----;0 и радиу-
сом
- (рис. 13.13).
Прямая у = —х есть биссектриса первого и третьего
координатных углов.
Для нахождения точек пересечения окружности и
прямой решим систему уравнений
Подставляя у из второго уравнения в первое, получаем
Искомые точки пересечения есть начало коорди-
нат (?(0;0) и точка М ——|. Ж
прямую
Пример 13.4. Найти радиус R, при котором прямая
х 4- у = 1 является касательной к окружности х2 + у2 = R2 ?
е решение. Изобразим данную
(рис.13.14). Она проходит через точки
Л(1;0) и С(0;1). Пусть В —
точка касания прямой АС с ис-
комой окружностью. Тогда ра-
диус ОВ окружности перпен-
дикулярен касательной АС . Из
равнобедренного прямоугольно-
го треугольника АОВ находим
искомый радиус:
R=OB=OA
315
Za Второе решение. Этот пример можно
решить способом, описанным в §13.4. Составим систему
уравнений:
1х + у = 1
[х2 + у2 = R2.
Из первого уравнения находим у = 1—х и подстав-
ляем во второе уравнение:
х2+(1-х)2 = R2,
откуда
2х2-2х+(1-Я2) = 0.
Касание произойдет, когда это уравнение имеет единст-
венное решение, т.е. при
Отсюда
j=1-2(1-J?2) = 0.
М(?0-.у0)
Рис.13.15
Пример 13.5. Составить
уравнение касательной к ок-
ружности
преходящей через точку (х0;у0)
эт< I окружности.
Пусть М(х0;у0) —
точка на данной окружности
с центром в начале координат и радиусом R (рис. 13.15).
Касательная / , проведенная через точку М, перпенди-
кулярна вектору ОМ = (х0;у0). Этот вектор ненулевой,
поскольку его длина равна R>0. По теореме 13.1 уравне-
ние прямой / имеет вид:
xo(x-xo)+^o(j-j/o) = O
ИЛИ
хх0+уу0 =X2+J2.
Однако, точка М лежит на данной окружности, поэтому
316
Рис.13.16
V2 -L I,2 - P2
XQ + Уо ~ К '
Следовательно, искомое уравнение касательной таково :
ХХо+УУо =r2- ж
Пример 13.6. Найти образ прямой 2х-Зу + 5 = 0 при
гомотетии с центром в точке Л(1;2) и коэффициентом 2 .
ZS Пусть т — данная прямая, М(х0',у0) — произ-
вольная точка на прямой
(рис. 13.16). Найдем коорди-
наты (xyyj точки —
образа точки М при гомо-
тетии с центром А и коэф-
фициентом 2. Так как
АМ =(х0-1;у0-2),
ТО
^=(2х0-2;2Л-4) =
Отсюда
X, = 2х0-1, у, = 2у0-2.
Координаты точки М удовлетворяют равенству
2х0 +5 = 0
и выражаются через координаты точки так:
Тогда координаты точки удовлетворяют соотноше-
нию
2^iil-3^L^ + 5=0
2 2
ИЛИ
2х1 -Зу} +6 = 0.
Таким образом, точка Л/, лежит на прямой
2х -Зу + 6 = 0.
Из §10.3 следует, что гомотетический образ заданной
прямой есть некоторая прямая. Значит, все точки прямой
317
Л (а: о)
2х — Зу + 6 = 0 являются гомо-
тетическими образами некото-
рых точек прямой т. Ж
Пр и м е р 13.7. Найти мно-
жество точек М, для которых
МА2 + МВ2 = 2МС2, где треуголь-
ник АВС — прямоугольный с
прямым углом С.
ZS Направим ось абтдисс,
вдоль катета СА , а ось орди-
нат — вдоль катета СВ. Вер-
шина С является началом ко- Рие.гз.гг
ординат. Пусть Л(а;0) и В(0;б) — две другие вершины
треугольника (рис. 13.17). Рассмотрим произвольную точ-
ку М(х,у) искомого множества. Имеем:
МА2 = (х-а)2 4-у2,
MB2 =x24-(<y-Z>)2,
МС 2 =х2 +У.
Коор^ инаты точки М связаны соотношением
МА2 + МВ2 =2МС2,
откуда
х2-2ох 4- а2 4- у2 +х2 +у2-2Ъу 4-62 =2х2 +2у2,
значит,
2(ах +Ьу) = с2,
где С — длина гипотенузы данного треугольника. По-
лучили уравнение прямой, которая и есть искомое мно-
жество точек. Середина гипотенузы Сх лежит на этой
прямой, поскольку
СХА2 +СХВ2 =2СХС2 =2R2,
где R — радиус окружности, описанной около тре-
угольника АВС. Таким образом, искомое множество
точек — прямая, проходящая через середину гипотенузы.
пример 13.8. Пусть А и В — фиксированные точ-
ки, к — данное положительное число, не равное 1 . Дока-
318
1} М{х-.у)
Рш .13.18
зать, что все точки М, для которых
= к , образуют ок-
МА
МВ
ружность (окружность Аполлония ).
Направим вдоль прямой АВ ось абсцисс, а вдоль
серединного перпендикуляра к отрезку АВ — ось орди-
нат (рис13.18). Пусть длина отрезка АВ равна 2а,
где а>0. Рассмотрим произвольную точку М(х\у) та-
кую, ч со
— = к, или МА2 = к2МВ2.
МВ
Поскольку А(-а; 0), В(а;0), то имеем отсюда:
/ , V I 2 1 2 / \2 J 2 2
(x + aj + у =к \х-а) + к у
или
(1 - к2 )(х2 + у2) + 2ах (1 + к2) + а2 (1 - к2) = 0.
Разделим обе части последнего равенства на число 1 — к2,
не равное нулю по условию. Получим:
•2ах + а2 = 0.
Обозначим
£2 + 1
—----= X, тогда имеем:
к 1
х2 -2акх + у2 +а2 = 0
или
319
Отсюда
2ak
Получили уравнение окружности с центром в точ-
2ак
—-----------------------------. Это и есть искомое
ке Z(aX;0) и радиусом R =
множество точек, называемое окружностью Аполлония.
Циркулем и линейкой эта окружность строится так.
С помощью теоремы Фалеса находим на отрезке АВ та-
кую точку Р, для которой
РВ
а также, такую точку Q на продолжении этого отрезка,
для которой
(выполните подробное построение самостоятельно,
считая, что заданы единичный отрезок и отрезок дли-
н ( к) Далее строим середину L отрезка PQ и радиу-
сом LP проведем окружность Аполлония.
Построенное геометрическое место точек названо в
честь Аполлония Пергского (около 260—170
до н.э.) — древнегреческого математика, который пер-
вым рассмотрел эллипс, параболу и гиперболу как пло-
ские сечения круговых конусов.
§ 13.6. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
13.01. Составить уравнение прямой, проходящей че-
рез начало координат и образующей с осью ОХ угол:
а) 45°, б) 60°, в) 90°, г) 120°.
13.02. Найти точку пересечения прямых, заданных уравне-
ниями:
320
a) x + 2y+ 3 = 0, 4x + 5y + 6 = 0;
6) 3x-y-2 = 0, 2x4-y-8 = 0.
13.03. Доказать, что три прямые х4-2у = 3, 2х-у = 1 и
Зх + у = 4 пересекаются в одной точке.
13.04. При каких к прямые Зх-Лу 4-5 = 0 и 2х4-5у-7 = 0
перпендикулярны ?
13.05. Даны координаты вершин четырехугольника
ABCD \ Я(-3;1), В(-2;2), С(7;7), D(3;l). Написать уравнение
прямой, содержащей среднюю линию этого четырехугольника.
13.06. Дана окружность х24-у2=25 и две точки Л(3;4)
и В(4;-3). Доказать, что АВ — хорда этой окружности.
13.07. Найти длину хорды при пересечении:
а) прямой х - у 4-1 = 0 и окружности
х2 -2x4- у2 — 2у4-1 = 0;
б) прямой 8x4-у-5 = 0 и окружности
х2 4-у2 4-2x4-4у- 35 = 0.
13.08 . Доказать с помощью декартовых координат, что две
различные окружности либо имеют две общие точки (т.е. пере-
секаются), либо имеют одну общую точку (т.е. касаются друг
друга), либо не имеют ни одной общей точки.
13.09 . Построить множество точек (х;у), удовлетворяю-
щих уравнению И+2Ы=1-
13.10. Найти центр и радиус окружности:
а) х24-у2-6х4-4у-23 = 0;
б) х2 4-у2 4-5х-7у 4-2,5 = 0.
13.11. При каком условии пересекаются окружности с ра-
диусами и и расстоянием d между центрами?
13.12. Найти угол между прямыми 2х-у4-5 = 0 и
х4-2у4-6 = 0.
13.13. Найти тангенс острого угла, образованного прямы-
ми у = 5х-1 и у = -4x4- 2.
13. К. Написать уравнение прямой, перпендикулярной к
прямой Ъ: 4- 4у 4- 5 = 0 и проходящей:
а) ерез начало координат;
б) через точку (-1;2).
321
13.15. Составить уравнение окружности, вписанной в
треугольник, стороны которого лежат на осях ОХ и OY и на
прямой Зх + 4у-12 = 0.
13.16. Две стороны квадрата лежат на прямых
х - 2 у + 2 = 0 и х - 2у - 5 = 0. Найти диагональ квадрата.
13.17. Пересекает ли прямая 7х + 11у = 3 отрезок АВ,
если координаты точек А и В таковы:
а) л(11;-7), В(-6;4);
б) Л(5;-3), В(-4;3)?
13.18. Найти центр и радиус окружности, описанной около
треугольника АВО с вершинами Л(а;0), 2?(0; />), О(0;0), и
составить уравнение этой окружности.
13.19. Дан ромб ABCD , диагонали которого равны 2а
и ЗЬ. Найти множество всех точек М таких, что
AM2 + DM2 = ВМ2 + СМ2.
13.20. Даны точки А и В. Найти множество точек М та-
ких, для которых МА2 + МВ2 есть величина постоянная.
13.21. В треугольнике АВС на стороне АС выбрана точ-
ка D так, что окружности, вписанные в треугольники ABD
и DBC, касаются. Известно, что AD = 2, CD = 4, BD = 5.
Найти радиусы окружностей.
13.22. В равнобедренной трапеции ABCD известно, что
AD = 14, ВС = 2. Окружность касается сторон АВ, ВС
и CD, причем боковая сторона делится точкой касания в от-
ношении 1:9, считая от меньшего основания. Найти радиус
окружности.
13.23. Две окружности пересекаются в точках А и В.
Через точку А проведены хорды АС и AD, касающиеся дан-
ных окружностей. Доказать, что АС2 • BD = AD2 • ВС.
13.24. Найти координаты точки А, симметричной точке
В(2; -1) относительно прямой х - 2у + 5 = 0.
13.25. Как прямая х 4- у = 0 расположена относительно
окружности (х -1)2 + (у -1) = 2 ? Написать уравнение образа
данной окружности при симметрии относительно прямой
х + у = 0.
13.26. Точка (х;у) лежит в круге х2+у2<2. Доказать,
что 1x1 + |у| < 2. Для каких точек круга выполняется равенство:
322
13.27. Написать систему трех линейных неравенств, опи-
сывающую множество всех внутренних точек треугольника с
вершинами Л(2;5), В(-1;-2), С(-3;4).
13.28. Найти множество точек (х;у), образующихся при
параллельном переносе окружности
х2 - у2 - 2х -2 у + 1 = 0
вдоль биссектрисы III координатного угла на расстояние V2 .
13.29. Написать уравнение прямой, проходящей через
точку Л/(-1;2):
а) параллельно прямой у = ^-х-4;
б) перпендикулярно этой прямой .
13.30. Длина хорды равна 10. Через один конец хорды
проведена касательная к окружности, а через другой — секу-
щая, параллельная касательной. Найти радиус окружности, ес-
ли отрезок секущей, заключенный внутри окружности, ра-
вен 12.
323
ГЛАВА 14
МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В
ТРЕУГОЛЬНИКАХ
§ 14.1. ТЕОРЕМА КОСИНУСОВ
Теорема 14.1. В тре-
угольнике квадрат стороны
равен сумме квадратов двух
других сторон минус удвоен-
ное произведение этих сторон
на косинус угла между ними.
□ Рассмотрим в треуголь-
нике АВС векторы АВ, АС и
Рис. 14.1
ВС (рис. 14.1.). Очевидно, что
откуда
ВС = АС-АВ.
Тогда
ВС2 = [аС-АВ\ = АС2-2 АС-АВ + АВ2,
следовательно,
ВС2 = АС2 + АВ2 -2 AC- АВ cosA.
Следствие!. Если ВС =а, AC =b, АВ =С , то
2Ьс
Докажите самостоятельно.
Следствие 2. (Теорема, обратная теореме
Пифагора). Пусть в треугольнике АВС дано, что
324
Рис. 14.2
c? + b2 = с2.
Тогда угол С —прямой.
□ По теореме косинусов
с2 = а2 + b2 -2аЬ • cosC, откуда
2аЬ • cosC = 0, т.е. cosC = 0,
значит, угол С — прямой. И
Докажем иным спосо-
бом, независимо от теоре-
мы 12.17., следующее свой-
ство параллелограмма.
Теорема 14.2. Сумма квадратов диагоналей па-
раллелограмма равна сумме квадратов всех его сто-
рон.
□ Рассмотрим параллелограмм ABCD (рис. 14.2). По
теореме косинусов из треугольников АВС и ABD по-
лучаем:
А С2 = АВ2 + ВС 2-2АВ • ВС cosAABC ,
BD2=AB2+AD2 -2АВ • AD cos ABAD.
Ho
AABC = \%tf-ABAD ,
поэтому
cos Z-ABC =-cosABAD .
Значит,
A C2 = AB2 + BC2 + 2 AB • BC • cos ABAD.
Отсюда имеем:
BD2+A C2 = 2AB2 + AD2 + BC2 =
=AB2 + BC2+CD2+AD2.
Итак,
AC2 + BD2 = AB2 + BC2+CD2 + AD2.
Теорема 14.3. Если a, b, С — стороны тре-
угольника ABC, ma, mb, mc — его медианы, прове-
денные к соответствующим сторонам, то справедливы
формулы:
2 2Ь2+2с2-а2
325
2 2а2 + 2с2 - b2
2 2а2+2Ь2-с2
□ На продолжении медианы АА । треугольника
АВС отложим отрезок AtD, равный отрезку ААХ
(рис.14.3). Тогда по теореме 14.2 имеем:
AD2+ВС2 = 2АВ2+2АС2,
ИЛИ
4 wa2 = 2Ь2+2с2-а2,
откуда
2 2Ь2+2с2-а1
Остальные формулы дока- I 1 /
зываются аналогично. И ></
Следствие!. Вс-
ли a, b, С — стороны
треугольника АВС , та, ть, Рис.14.3
тс — его медианы, прове-
денные к соответствующим сторонам, то справедлива
формула:
2 . 2 . 2
та + ть + тс
cf+tf+c1 4
Следствие 2. Если а, b, С — стороны тре-
угольника АВС , та, ть, тс — его медианы, проведен-
ные к соответствующим сторонам, то справедливы
формулы, выражающие стороны треугольника через его
медианы:
а2 = |(2»%2+2тс2-^).
Ь2 = (2т2 + 2т2 -п^\
(? = ~(^та2 + ~тс)-
а Т> с ]
326
Следствия 1 и 2 докажите самостоятельно.
Следствие 3. В треугольнике ЛВС угол С ра-
вен 90е тогда и только тогда, когда т^-\-т^=5тс .
□ Пусть ZC = 90°, тогда с2 = с? +Ь2. Согласно след-
ствию 2 получим:
—(2т2 + 2ть2 -т2) =
= | (W + 2тс - 1 f2™/ + 2т/ - mf ),
откуда после сокращения и приведения подобных членов
2 , 2 с 2
имеем: тп + mh .
с/ V
Обратно, если т2 + т^ = 5тс2, то по теореме 14.3
получим:
2Ъ2 +2С2 -а2 2а2 +2с2 - Ь2 2а2+2Ь2 ~2
4 + 4 4
ИЛИ
d2 + b2 = c2.
Из теоремы, обратной теореме Пифагора, заключаем, что
угол С — прямой.
Следствие 4. Если а, b, С — стороны тре-
угольника АВС , та, ть, тс — его медианы, проведен-
ные к соответствующим сторонам, то неравенства
□ Пусть а<Ь. Для доказательства этого следствия
достаточно показать, что та > ть. В самом деле, кмеем:
ol2 . п_2 2 о^2 . nJ /2
Следствие 5. Если в треугольнике две медианы
равны, то этот треугольник — равнобедренный.
□ Пусть a, b, С — стороны треугольника и
та=ть. Тогда ш2 = ^. Отсюда согласно теореме 14.3
получаем равенство:
327
откуда a—b2. Следовательно, a=b и рассматриваемый
треугольник — равнобедренный.
§ 14.2. ТЕОРЕМА СИНУСОВ
Теорема 14.4. Для всякого треугольника АВС
справедливо равенство
sinA sinB sinC
где R — радиус описанной окружности.
□ Рассмотрим 3 случая.
а) Угол А — острый. Проведем ОКХЛС (рис. 14.4).
Тогда АВОС =2(ZA), а треугольник ВОС — равнобед-
ренный. Значит, углы ВОК и А равны. Из треугольни-
ка ВОК имеем:
----= sinZ.BOK,
ВО
откуда
sinA
Таким образом,
—-—=Л или ———=2R.
2 sinA sinA
328
б) Угол А — прямой. Гипотенуза ВС является диа-
метром, т.е. ВС = 2R . С другой стороны,
ВС
sin9Q°
= ВС
= 2R
и формула--------=2R верна (рис.14.5).
sinA
в) Угол А — тупой. Тогда
Z.BOC = 360°-2(Z/f),
откуда
АВОК = 180°-ZA
Из треугольника ВОК имеем:
= sin(\ 80° - а) = sinA.
ВО V '
Рис. 14.6
Таким образом, — = sinA,
22?
а
откуда------= 2л (рис.14.6).
sinA
Во всех случаях мы до-
лг _ п
казали, что -----= 2л. По-
sinA
вторяя те же рассуждения
для стороны b и угла В,
стороны С и угла С, по-
лучим:
-^—=2R, —^— = 2R.
sinB sinC
Тогда
a _ b
sinA sinB
sinC
Следствие!. Во всяком треугольнике ABC
a=2RsinA, b=2RsinB, c=2R-sinC.
Следствие 2. 2Rhd=bc, 2Rhb=ac, 2Rhc—ab,
где ha, hb, hc — высоты треугольника ABC , проведен-
ные к сторонам a, b, С соответственно.
329
Докажем, что 'lRha = be для остроугольного тре-
угольника (другие случаи рассмотрите самостоятельно).
□ Пусть АН ] — высота треугольника АВС
(AHi = ha). Из треугольника АНХС имеем (рис. 14.7):
— = sinC,
b
откуда
ha = bsinC.
Однако, из теоремы
синусов следует, что
sinC =—.
2R
1 be
Тогда па=—, откуда по-
2л
лучаем 2R -ha = bc.
С помощью теоремы синусов можно получить дру-
гое доказательство теоремы 4.9.
Следствие 3. (Теорема 4.9), В треугольни-
ке против большей стороны лежит больший угол, а про-
тив меньшей стороны — меньший угол, т.е. неравенст-
ва а <Ь< с и А < В <С равносильны.
□ Пусть треугольник АВС не является тупоуголь-
ным. Тогда вследствие возрастания функции f(x) = sinx
на промежутке 0; 90° неравенство А < В < С равно-
сильно неравенству: sin Л < sin В < sinC, которое по тео-
реме синусов равносильно неравенству
а b с
2R~2R~2R'
a<b<c.
Допустим теперь, что угол С тупой и А < В <С. Тогда по
доказанному выше имеем: а<Ь, поскольку углы А и В
острые. Кроме того,
Л+В = 180°-С, и Л<180°-С, В<180°-С.
Угол, равный 180° -С является острым, и
sinC = sin(l 80° - с).
330
Из следствия 1 имеем:
a = 2R-sinA,b = 2R-sinB,
с =2R- sinC = 2R- sin(\80° - с).
Значит, a <C, b <C.
Следствие 4. Для всякого треугольника нера-
венства a<b<c и ha>hb>hc равносильны.
□ Из следствия 2 имеем:
, Ьс t ас t Ьа
п =—. ЛА =—, п =—.
а 2R 2R с 2R
Тогда неравенство а<Ь<с равносильно неравенст-
ву bc>ac>ab. Последнее неравенство равносильно не-
равенству ha>hb>hc, что и требовалось доказать.
Следствие 5. Если в треугольнике две высоты
равны, то такой треугольник равнобедренный.
§ 14.3. СВОЙСТВА БИССЕКТРИСЫ УГЛА
ТРЕУГОЛЬНИКА
Теорема 14.5. Бис-
./'д сектриса угла треугольника
/уЧ делит противоположную сто-
/ \ рону на отрезки, пропорцио-
/ \ нальные соответствующим
/ \ боковым сторонам.
/ \ □ По теореме синусов из
С £_В треугольника AL ХС (рис. 14.8)
получаем:
Рис.ы.в АС _ CL}
sinZAL}C s in AC AL}
откуда
AC _ sinZAL}C
CL} sinZCAL^
Аналогично по теореме синусов из треугольника
ALXB имеем:
331
AB _ sinAALxB
BLX sin ABAL j
Так как углы CAL 1 и BAL !, равны, то
sinACAL, = sinABAL j.
Далее AAL XC = 180° - ABLX A , поэтому
sinAALxC = sinABLxA.
Тогда
AC _AB
и поэтому
Следствие. Пусть ALX — биссектриса угла А
треугольника АВС. Тогда отрезки CLX и LXB находятся
по формулам:
□ Так как
которого
Отсюда имеем:
= —, то существует число Х>0, для
а
Ь + с
Значит,
Ьх +СХ=а, т.е.
Теорема 14.6. Пусть в треугольнике АВС из
вершины угла А проведена биссектриса которая
делит сторону СВ на отрезки CLX = mt LxB — n. Тогда
справедливо равенство:
12л = Ьс-тп.
332
□ Опишем окружность около треугольника АВС и
продолжим биссектрису AL1 до пересечения с окружно-
стью в точке Р. Соединим точки С и Р (рис. 14.9). Обоз-
Рис.14.9
начим LxP=d. По свойству
отрезков хорд, пересекающих-
ся внутри круга, имеем:
lA -d = mn.
В треугольниках AL ХВ и
АСР имеется по два равных
угла: углы САР и LXAB рав-
ны, поскольку AL j — биссек-
триса; углы СРА и LXBA рав-
ны как вписанные, опираю-
щиеся на дугу АС . Следовательно, эти треугольники по-
добны. Тогда
откуда имеем:
7^ + /, -d = bc , lA = bc-lA-d.
Так как по доказанному выше
/. d-mn,
Л
то
1гА = bc-тпп.
Теорема 14.7. Для всякого треугольника АВС
справедливы равенства:
7р(р-®)-
у1р(р-ь),
Jp(p-c),
333
где
а + Л + с
— полупериметр треугольни-
ка АВС.
□ Применяя теорему 14.6. и следствие из теоре-
мы 14.5, получаем:
l2 = bc-CL.L,B=bc
Л 11
Ьс -((&+с)2 -а2)
(& + с)2
ab ас , а2Ьс
---------- be-------
Ь+с Ь+с (Ь+с)
Ьс-\Ь+с + а)(Ь + с-а)
(b + с)2
Ьс-2р(2р-2а) 4Ьср -(р-а)
„ J 2jbc [—7-------?
Следовательно, 1А =------J рур — а)
Ь + с v
Аналогично
получаются формулы для 1В и 1С.
Напомним, что буквой I мы обозначаем точку пере-
сечения биссектрис треугольника, т.е. инцентр.
Имеет место следующее утверждение.
Теорема 14.8. Расстояние от инцентра тре-
угольника до его вершин вычисляется по формулам:
ub
□ В треугольнике АВС отрезок CLX =-- соглас-
6 + с
но следствия из теоремы 14.5, отрезок CI — биссектри-
са треугольника ACLX (рис.14.10). По теореме 14.5 по-
лучим:
334
РнеММ
Тогда при некотором
Х>0 имеем:
Так как
<jp(p-a)
или
2>1Ьс rj-----г
2рх =-----^р{р-а),
Ь~¥С
Следовательно,
Аналогично находятся расстояния BI и С7. И
Теорема 14.9. Для углов А, В, С и биссектрис
/Л, 1Л, 1С треугольника АВС неравенства А<В<С и
1с равносильны.
О Достаточно доказать, что из вершины меньшего
угла выходит большая биссектриса.
Пусть А < В. Тогда а < Ь, Докажем, что 1Л>1В.Ъ са-
мом деле, искомое неравенство равносильно следующему
неравенству:
335
(a + c\lb(p-a) > (b + c)yja(p-b),
(a + c)2 b(p -a)>(b + cf a(p -b).
Разделим обе части этого неравенства на
(р~a)(p~~b)’ Используя равенства а + С =2р-Ь и
b 4- С « 2р-а, получим:
b(2p-b)2 а(2р-а)2
(1)
р — Ь р-а
Чтобы доказать неравенство (1), рассмотрим функ-
цию:
=-t2-pt 4- р24- —.
С возрастанием t функция g(/) убывает. Однако
= p-а = Р~Ь • Поэтому g(/j) <g(/2), и неравенст-
во (1) доказано.
Из неравенства (1) следует теперь неравенст-
во 1А >1В. Мы доказали, что из вершины меньшего угла
треугольника выходит большая биссектрисса. Отсюда
следует утверждение теоремы.
§ 14.4. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 14.1. Две силы величиной Р и Q, угол между
которыми равен a(0° <а < 180°), приложены к материальной
точке. Найти величину равнодействующей силы.
336
ZS Пусть силы вели-
чиной Р и Q приложены к
точке А (рис. 14.И). Тогда
длина диагонали АС па-
раллелограмма ABCD вы-
ражает величину равнодей-
ствующей этих сил. Если
угол BAD равен а, то
ZABC = 180°-а,
Рис.14. и причем
cos/.АВС =сау(180°-а) =-cosa.
По теореме косинусов из треугольника АВС имеем:
АС2 = АВ2 + ВС 2-2АВ ВС cosZА ВС =
=Р2 + Q2 + IPQcosa.,
откуда
AC = ^Р2+Q2+2PQcosa.
Это и есть величина равнодействующей силы. Ж
Пример 14.2. Доказать, что треугольник с медианами
у/52, у/тЗ и 5 является прямоугольным.
ZX Согласно следствию 4 из теоремы 14.3zbo всяком
треугольнике наименьшая медиана проведена к наиболь-
шей стороне. В прямоугольном треугольнике такой сто-
роной является гипотенуза. Поэтому из трех заданных
медиан на гипотенузу может быть опущена лишь наи-
меньшая медиана длиной 5 .
По следствию 3 теоремы 14.3 для доказательства то-
го, что данный треугольник является прямоугольным,
достаточно проверить выполнение равенства
от2 + т2ь = 5т2,
где С—гипотенуза, а и b —катеты.
В нашем случае имеем:
(>/52)2 + (л/73 )2 = 5 • 52
Это равенство верно. Отсюда следует, что треуголь-
ник с заданными медианами прямоугольный.
Пример 14.3. Стороны равностороннего треугольника
равны Л. На этих сторонах построены квадраты во внешние
стороны от треугольника. Вершины этих квадратов, которые
337
не являются вершинами данного треугольника, последова-
тельно соединены. Найти периметр полученного шестиуголь-
ника.
ZS Пусть квадраты АВА 3А2, ВА4А5С, СА6А}А
построены на сторонах равностороннего треугольника
АВС (рис.14.12), и АВ —ВС = АС — а, Тогда
^1^6 = ^2^3 = ^4^5 = & ’
Кроме того,
ЛА.АА 2 = = ЛА'СА. = 360°-90о-60о-90° = 120°.
Очевидно, треугольники АХАА2, А3ВА4, А5СА6 равны по
первому признаку равенства треугольников. По теореме
косинусов
АХА2 — АА ,2 + АА 2-2АА, • АА 2 -cosZA,AA7 =
1 * * Д л» 1 м
= а2 + а2-2а2со5120° = 2а2 + 2а2 - = За2,
2
338
Рис.14.13
откуда АХА2 = Chj3. Значит,
периметр шестиугольника
АХА2А$А4А5А6 равен
За+Зл-Уз =3а(л/3+1). Ж
Пример 14.4. Точ-
ка D лежит на стороне АВ
треугольника АВС. Доказать,
что отношение радиусов ок-
ружностей, описанных около
треугольников ACD и BCD,
не зависит от выбора точ-
ки D.
Z\ Пусть Rx и R2 —
радиусы окружностей, описанных около треугольников
ACD и BCD соответственно (рис.14.13).
По
теореме синусов имеем:
2RX
АС
sinZADC'
2R2 =
ВС
sin ZB DC
Поскольку ZADC + ZBDC =180°, то синусы этих
углов равны. Поэтому
Rx = АС ВС = АС
R, sinZADC sin ZB DC ВС
R}
Таким образом, отношение —- не зависит от Выбо-
рг
ра точки D на стороне АВ . Ж
Пример 14.5. В треугольнике АВС известно, что
Z4=a , Z5=P, радиус описанной окружности равен R. Най-
ти: а) стороны треугольника, б) медианы треугольника.
Пусть Ctt b, С — стороны треугольника АВС .
тд, ть, тс — медианы, проведенные к этим сторонам
соответственно. По следствию 1 из теоремы 14.4 имеем:
a = 2Rsina, b = 2Rsin$, с =2Лпи(180°-а-р) =
= 2Rsin(a + р).
Далее, по теореме 14.3 получаем:
339
2( 4 R2 sin2 p + 4J?2jf«2(a + p)j - 4/?25i«2a
-
= R2 (2sin2p + 2sin2 (a + p) - sin2a),
откуда
ma = Rdlsin2^ + 2sin2 (a + p) - sin2a .
Аналогично
mb = RJ2sin2a + 2sin2 (a + P) - sin2$
и
mc = Rd2sin2a + 2sin2$ - sin2 (a + p) . Jk
Пример 14.6. В прямо-
угольном треугольнике катеты
равны б см. и 8 см. Найти наи-
большую биссектрису. р
Пусть в прямоугольном
треугольнике АВС дано: _____
АС =6 см, ВС =8 см. Тогда с В
АС — наименьшая сторона рис
треугольника, и по теореме 14.9
биссектриса BD является наибольшей (рис. 14.14). По
теореме Пифагора АВ = \ 62 + 82 =10. По теореме 14.5
имеем:
СР ВС СР_8_4
AD АВ ' Т‘е‘ AD 10 5'
откуда
CD=4k, AD =5fc
для некоторого положительного числа к. Так как
CD + AD = АС, то 4к+5к = 6 ик = ~
3
Значит, CD = —. По теореме Пифагора
340
BD = JCD2+BC2 = J^ +82 (см). Ж
Пример 14.7. В прямоугольном треугольнике АВС из-
вестно! что угол С — прямой, а угол А равен 30е. Найти от-
ношение AI\ BI.CI г где / — инцентр треугольника АВС.
ZS Пусть ВС = а, тогда по теореме о катете, лежа-
щем против угла в 30°, имеем: АВ =2ВС = 2а. По тео-
реме Пифагора
АС = у1аВ2-ВС2 = -Ucf-a2 = ал/з.
Далее,
341
окончательно, что
Л7:5/:С7 =(3 + л/3):7б:7з =(л/3+1):л/2:1. Ж
Пример 14.8. В треугольнике АВС т*+т1>5т*. Ка-
ким должен быть угол С: тупым или острым?
Преобразуем неравенство, заданное в условии,
применяя формулы из теоремы 14.3. Получим:
2Ь2 +2с2 -а2 2а2 +2с2 -b2 &аг+2Ьг - с2)
4 + 4 4
откуда 9с2>9а2 + 962 или а2 + &2<с2. По следствию 1 из
теоремы 4.1 имеем:
л2 + Ь2 - с2
cosC =---------<0
2ab
I
т.е. угол С является тупым. А
Пример 14.9. В треугольнике АВС угол А больше уг-
ла В. Какой отрезок длиннее: AI или BI1
ZS По следствию 3 из теоремы 14.4 получаем,
что а>Ь. Рассмотрим разность А12-В12. Имеем:
..2 Dr2 bc(p-a) ac(p-b)
Л1 —JD1 =---------------------
р
р
= -(b(p-a)-a(p-b)) =
Р
342
Рис. 14.15
Р Р
Значит, В1>А1, т.е. отрезок BI длиннее. Ж
Пример 14.10. В тре-
угольнике АВС дано: ЛВ=13,
1?С =14, ЛС=15. Через центр
вписанной окружности прове-
дена прямая, параллельная АС,
пересекающая стороны АВ
и ВС соответственно в точ-
ках М и N. Найти длину от-
резка MN.
ZS Пусть I — центр
вписанной окружности тре-
угольника АВС ; ALV BL2,
CL3 — биссектриссы тре-
если MN \\АС (рис.14.15), то
угольника АВС . Тогда,
треугольники BMN и АВС подобны, откуда
MN BI
2
BI
Найдем отношения--. Имеем по теореме 14.7:
ВЬ2
2 a+cV ’ 14+13 9
а по теореме 14.8 получаем:
^=2ЛЗ.
21
ЛСУ = ВС • — = -4'2^J = 9. А
BL2 28V13
BI =
Таким образом,
9
Пр им ер 14.11. В параллелограмме со сторонами 2
и 4 проведена диагональ, равная 3. В каждый из образован-
ных треугольников вписана окружность. Найти расстояние
между центрами этих окружностей.
343
Рис, 14.16
Za В параллело-
грамме ABCD дано:
АВ = 2, AD =4. По-
ложим для определен-
ности, что угол BAD
— острый (рис. 14.16).
Тогда, так как тре-
угольник АВС тупо-
угольный, по следст-
вию 3 из теоремы 14.4
имеем:
АС >ВС =4.
Значит, BD = 3 . Проведем биссектрисы AM , BS , DP
треугольника ABD , пересекающиеся в точке /р и бис-
сектрисы CN , BQ , DT треугольника BCD , пересекаю-
щиеся в точке 12. По формулам из теоремы 14.8 имеем:
DT Iabbd(p-ad) Ibc-bd(p-cd)
BIX = I------------ и Bl 2 = -------------
V P V P
где p — полупериметр каждого из равных треугольни-
ков ABD и BCD . Значит,
Очевидно, что AIXDB = AI2BD, AIXBD = ZJ2DB. Зна-
чит, по теореме 3.5 получаем: B1X\\DI2, т.е. D1X\\BI2 и
BIxDI2 — параллелограмм. Применяя теорему 14.2, по-
лучим:
откуда
344
Рис. 14.17
Пример 14.12. Доказать, что в треугольнике АВС:
6) Л/= 1^.
11, Л1, \Ь(р-а) V-.
a) ZX Пусть в треугольнике ЛВС точки 1, 1а, 1Ь —
центр вписанной окружности и центры вневписанных
окружностей соответственно (рис.14.17). Из теоремы 6.3
и §7.4 следует, что
точки /, 1а лежат на
биссектрисе угла А, а
точки 1, 1Ь — на бис-
сектрисе угла В. Из
точки 1а опустим пер-
пендикуляры 1аЕ1АВ,
IaNXAC, а из точки 1Ь
опустим перпендикуля-
ры, ^SJLBC, ЦТ1АВ.
Точка 1а лежит также
на биссектрисах углов
BCN и СВЕ, а точка
\ 1Ь — на биссектрисах
2? углов CAT и ACS .
Так как углы САВ
и CAT смежные, то
А11АЦ. Аналогично,
В1а1В1. Тогда по вто-
рому признаку подобия
треугольники В1а1 и
А1Л подобны. Имеем далее:
IIb AIb AI
ас(р-Ь) Ьс(р-а) _
РУР
345
IaM — радиусы вневписанной
а, IK — радиус впи-
а(Р~Ь) А
V Ь(Р-а)
б) Zib Проведем перпендикуляры 1аМ13С и
IK1AB. Тогда 1аЕ,
окружности с центром в точке It
санной окружности треугольника АВС . Из следствия 2
теоремы 6.2 имеем:
АК = p-а,
а из теоремы 7.6 и того же следствия получаем:
Далее, прямоугольные треугольники AIаЕ и AIK по-
добны по второму признаку подобия треугольников.
AIa АЕ
Следовательно, —у = > откуда
ВЕЗ
° АК у р
п р и м е р 14.13. Прямая,
проходящая через вершину
прямого угла треугольника, обра-
зует с меньшим катетом угол 30°
и пересекает гипотенузу в точке,
которая делит ее в отношении 1:2.
Найти длину гипотенузы, если
длина меньшего катета равна ^3.
Пусть в треугольнике
АВС угол АСВ прямой, ме-
ньший катет ВС равен л/З и прямая CD проведена так,
что ZDCB = 30°
ZB = 90°-а и 0
угольников ACD
(рис14.18). Пусть также Z4 = а, тогда
<а<45°. По теореме синусов из тре-
и BCD получаем:
CD АР
sinA sinZACD
346
CD _ BD
sinB sinZ.DCВ '
откуда
_ AD sinA _ ADsin a _ 2ADsina
sinZACD sin6Q° 7з
CD = BDsinB = BD' Sir^9Qi
sinZDCB
Следовательно,
2 ADsin a.
------------------;=— = 2BDcosa
sin30°
— 2BDcosa.
и значит,
rga =
у/ЗАР
BD
0’<a<45°, to /ga<l , откуда отношение
не может быть равно 2. Таким образом,
Так как
AD.BD
AD 1 .. „
---= —. Итак, tga. = . Значит,
BD 2 2
По теореме Пифагора
ав =>1ас2+вс2 =
=^22+(>/з)2 =77. ж
Пример 14.14. В треугольнике АВС перпендикуляр,
опущенный из центра описанной окружности на биссектрису
угла В, проходит через точку пересечения медиан. Найти ве-
личину угла В.
Докажем вначале следующее вспомогательное утвер-
ждение.
Лемма. Пусть в треугольнике MNP дано,
что MN=MP, MS — высота, точка L лежит на сторо-
не MN, причем прямая PL пересекает высоту MS в
347
точке F и PF'.FL=2'.l. Тогда PL — медиана треуголь-
ника MNP.
□ Из точки L опустим перпендикуляр LD на осно-
вание NP (рис.14.19). Тогда LD\\FS, и по следст-
вию 1 §11.1 треугольники FSP и LDP подобны. Имеем
тогда:
DP LP
SP FP'
откуда
DP 3
SP 2
и DS=-SP.
2
Таким образом, DS = ND .
NL = LMf т.е. PL является
ка MNP .
По теореме Фалеса
медианой треугольни-
Перейдем к решению примера.
ZS Пусть в треугольнике АВС АВ ^ВС, О —
центр описанной окружности, ВВЛ — медиана, М —
точка пересечения медиан, BR — биссектриса треуголь-
ника АВС (рис. 14.20). По условию перпендикуляр OL ,
опущенный на BR , проходит через точку М. Так как
ZABR = Z-CBR , то по теореме 6.6 прямая BR пересе-
кает окружность в точке К, делящей дугу АС пополам.
По следствию теоремы 7.1 прямая OBV содержащая
диаметр данной окружности, перпендикулярна сторо-
348
не AC . Кроме того, эта прямая делит дугу АС пополам,
т.е. проходит через точку К. В треугольнике ОВК
ОВ = ОК, OL — высота. По теореме 11.11
ВМ: MB j = 2:1. Тогда в равнобедренном треугольнике
ОВК высота OL пересекает отрезок ВВХ в точке М и
делит его в отношении 2:1, считая от вершины В. Тогда
в силу доказанной леммы точка Bt — это середина бо-
ковой стороны ОК равнобедренного треугольника
ОВК, откуда
ОВ.=-ОК = -ОА.
1 2 2
Тогда по следствию 3 §4.4 имеем: АОАВ j = 30°. Значит,
ААОК = 90о~ХОЛВ1 = 90о-30о = 60°.
Но угол АОК является центральным. Следовательно,
градусная мера дуги iK также равна 60°, откуда по тео-
реме 6.6 имеем: ААВК =30°. Таким образом,
ААВС =2(AABK) = 6Q°.
Если же в данном треугольнике АВС стороны АВ
и ВС равны, то центр О
описанной окружности ле-
жит на биссектрисе ВВ},
которая совпадает с медиа-
ной. Прямая ON, перпен-
дикулярная ВВ,, пройдет
через точку пересечения
медиан только тогда, когда
медианы пересекаются в
точке О. Пусть К — сере-
дина дуги АС (рис. 14.21).
\вв,-,
В}К = ОК -ОВ. = - ВВ. -- ВВ. = - ВВ. = ОВ..
3 3 3
в
Рис. 14.21
Тогда
ОВ
349
В треугольнике AOK высота АВ} совпадает с медианой,
поэтому АО = АК. Однако АО = КО, и треугольник
АОК — равносторонний. Тогда
ЛАОК = 60°, ЛАОС =2-60°, ЛАВС = ZZ-C- =60°.
2
Значит, во всех случаях Z.ABC =60°. А
§ 14.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
14.01. Пусть Cl, b , С — стороны треугольника. Дока-
зать, что угол С острый тогда и только тогда, когда а2 + Ь2>с2.
Доказать также, что угэл С — тутмж и только тогда, когда
а2+Ъ2<с2.
14.02. Определить является ли треугольник прямоуголь-
ным, остроугольным или тупоугольным, если его стороны рав-
ны:
а) 15, 18, 23; б) 12, 5, 13; в) 7, 9, 13.
14.03. В параллелограмме сторона и две диагонали соответ-
ственно равны 5 см, 7 см и V73 см.
Найти периметр параллелограмма.
14.04. Найти стороны параллелограмма, если его диагонали
равны 4 и 6 , а угол между ними равен 60°.
14.05. В треугольнике две стороны равны а и b , а угол
между ними равен а. Найти медианы этого треугольника.
14.06. В треугольнике АВС известно, что АВ = 3 , АС =
= 5 , угол ВАС =120°. Найти: а) длину стороны ВС, б) длину
биссектрисы угла В, в) медиану, опущенную на сторону ВС.
14.07. В треугольнике АВС известны длины сторон:
АВ = 6 , ВС = 5 , АС = 3 . Найти расстояние между точками
касания окружности, вписанной в этот треугольник, лежащими
на сторонах АВ и АС.
14.08. В квадрате ABCD точки М и N— середины сто-
рон АВ и AD. Найти косинус угла MCN .
14.09. Каким должен быть угол при вершине равнобедрен-
ного треугольника, чтобы его основание было больше боковой
стороны?
350
14.10. Две стороны треугольника равны 6 и 7 , а медиана,
проведенная к меньшей из них, равна 5 . Найти третью сторо-
ну треугольника и две другие его медианы.
14.11. Сторона и две медианы, проведенные к двум другим
сторонам треугольника, равны 8 см, 6 см и 9 см соответст-
венно. Найти две другие стороны и третью медиану.
14.12. Пусть AD и ВС — основания равнобедренной тра-
пеции ABCD . Доказать, что АС2 = AD *ВС + АВ2.
14.13. Диагонали параллелограмма относятся как
V19: д/з9 , а стороны его равны 2 см и 5 см. Найти углы парал-
лелограмма.
14.14. В равнобедренном треугольнике центр вписанной
окружности делит его высоту в отношении 12:5, а боковая сто-
рона равна 60 см. Найти основание треугольника.
14.15. Острый угол ромба равен 30°. Вершина тупого угла
соединена с серединами двух его сторон. Найти косинус угла
между этими отрезками.
14.16. Две стороны треугольника и биссектриса угла меж-
ду ними соответственно равны (2, b , I . Найти третью сторону
треугольника.
14.17. Найти отношение биссектрис равнобедренного пря-
моугольного треугольника.
14.18. В равнобедренном треугольнике основание рав-
но (2, а угол при вершине равен а. Найти биссектрису угла
при основании и радиус вписанной окружности.
14.19. Доказать, что произведение квадратов диагона-
лей параллелограмма, в котором острый угол равен 45°, равно
сумме четвертых степеней двух его смежных сторон.
14.20. Пусть (2, b — основания трапеции, С , d —ее боко-
вые стороны. Найти отрезок, соединяющий середины основа-
ний трапеции.
14.21. В равнобедренном остроугольном треугольнике
АВС дано: АВ = ВС и угол А больше 60°. Какой отрезок
больше: АО или AI ? Здесь О — центр описанной окружно-
сти, I — центр вписанной окружности треугольника АВС .
14.22. В треугольнике АВС дано: АВ = 1 см, Z_A = 60°. Ка-
кой должна быть сторона АС, чтобы сторона ВС была наи-
меньшей?
14.23. В прямоугольном треугольнике расстояния от цен-
тра вписанной окружности до концов гипотенузы АВ рав-
ны y[s и л/То . Найти гипотенузу АВ .
351
14.24. В треугольник вписана окружность, которая касает-
ся сторон АВ , ВС, АС треугольника АВС соответственно в
точках М, D, N. Определить длину отрезка MD , если извест-
но, что NA = 2 , NC = 3 , угол ВСА равен 60°.
14.25. В треугольнике АВС медианы, проведенные к сто-
ронам АС и ВС, пересекаются под прямым углом. Найти сто-
рону АВ , если АС = b , ВС = а.
14.26. Одна из диагоналей четырехугольника, вписанного в
окружность, является диаметром. Доказать, что проекции двух
противоположных сторон четырехугольника на другую диаго-
наль равны.
14.27. Найти косинус угла между медианой и биссектри-
сой, проведенными к двум катетам равнобедренного прямо-
угольного треугольника.
14.28. Дан угол и его биссектриса. Окружность, проходя-
щая через вершину угла, отсекает на сторонах угла и его бис-
сектрисе соответственно отрезки а, b , С. Доказать, что отно-
а + Ь
шение не зависит от положения окружности.
с
14.29. Отрезки AAV ВВХ, ССХ — биссектрисы углов тре-
угольника АВС . Доказать, что равенство
ААХ+ВВХ +CCj = 0
выполняется тогда и только тогда, когда треугольник АВС —
равносторонний.
14.30. Вершины треугольника АВС имеют координаты:
А(~3;0), Z?(0;4), С(3;0). Биссектриса угла А пересекает сторо-
ну ВС в точке D. Найти координаты точки D и уравнение
прямой AD.
14.31. Две стороны треугольника равны CL и b . Найти тре-
тью сторону треугольника, если угол, противолежащий этой
стороне, вдьое больше угла, противолежащего стороне b .
14.32. На гипотенузе КМ прямоугольного треугольни-
ка KLM находится центр О окружности, касающейся кате-
тов KL и LM в точках А и В соответственно. Найти АК, ес-
23
ли ВМ АКх АС =5:23 и точка С является точкой пере-
сечения окружности с КМ и лежит между точками О и М.
14.33. Около равнобедренного треугольника АВС с уг-
лом В при вершине, равным 30°, описана окружность S, ради-
ус которой R. AD — диаметр этой окружности. Найти радиус
окружности, касающейся стороны АС этого треугольника, диа-
метра и окружности S.
352
ГЛАВА 15
ПЛОЩАДИ
В настоящей главе существенно используются свой-
ства предела числовой последовательности, изложенные
в приложении 1.
§ 15.1. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Простые фигуры. Фигура называется простой, если
ее можно разбить на конечное число треугольников.
Примером простой фигуры является выпуклый мно-
гоугольник. Он делится на треугольники диагоналями,
Ап
Рис.15.1
проведенными из одной вер-
шины (рис. 15.1).
Аксиомы площади. Сле-
дующие утверждения явля-
ются аксиомами площади
простой фигуры.
Аксиома 15.x. Каж-
дая простая фигура имеет
площадь S>0.
Аксиома 15.2. Рав-
ные простые фигуры имеют
равные площади.
Аксиома 15.3. Если
простую фигуру разделить на несколько простых фи-
гур, то площадь этой фигуры равна сумме площадей ее
частей.
Аксиома 15.4. Площадь квадрата со стороной 1
равна 1.
Нетрудно доказать, что если простая фигура F явля-
ется частью простой фигуры G, то площадь фигуры F
не превышает площади фигуры G. Для этого необходимо
дополнить фигуру F до фигуры G некоторой простой
фигурой Н. Проведите это доказательство самостоятель-
но.
353
Рис.15.3
В дальнейшем площадь фигуры F будем обозначать
через SF.
Теорема 15.1. Площадь прямоугольника равна
произведению двух его смежных сторон.
□ Пусть длины смежных сторон а и b прямоуголь-
к
ника выражаются рациональными числами, т.е. а= —,
, р 7 7
b = —, где к, I , р, q — натуральные числа. Разделим
Я
эти две смежные стороны на равные части длиной — ка-
ждая и проведем через точки деления прямые, парал-
kq
лельные соответствующим сторонам. Так как а = —,
Iq
, pl ,
b =—, то сторона а делится на kq равных частей, а
Ql
сторона b — на pl равных частей (рис. 15.2). Образуется
1 г 1
kq • pl равных квадратов со стороной —. Найдем пло-
1<1
щадь Q одного такого квадрата (на рис. 15.3 один из та-
ких квадратов заштрихован). Квадрат со стороной 1
можно разбить на Гq таких квадратов, которые показа-
354
ны на рис. 15.3. Тогда согласно аксиомам 15.3 и 15.4, име-
ем: /V 0=1 , откуда ^ = -т-у. Наконец, площадь дан-
/<?
ного прямоугольника
S = kqpl ~г =—-— = аЬ.
I q
Пусть теперь хотя бы одно из чисел а или b являет-
ся иррациональным. Рассмотрим для числа а последова-
тельности (ал) и (ал) рациональных чисел, для которых
выполняются следующие условия (см. приложение 1):
1) (аЛ) —возрастающая последовательность, (ал) —
убывающая последовательность;
2) 1ппаЛ = а, 1ппал = а.
Л->оО Л—>00
Тогда для любого натурального числа П имеем:
а < а< а„.
Л Л
Аналогичные последовательности (бЛ) и (бл) рацио-
нальных чисел построим для числа b. Так как последова-
тельности (ал) и (Ьл) возрастают, а последовательнос-
ти (ал) и (бл) убывают, то
Из доказанного ранее
следует, что площади 5Р Sn,
S}, Sn прямоугольников
соответственно со сторона-
ми и 1\, ап и Ьп, и bv
ап и Ьп равны:
5i 5И = пп&Л, 51
$п ~ апК •
Кроме того, легко по-
лучить, согласно §15.1, что
355
Все эти прямоугольники изображены на рис. 15.4. Таким
образом, последовательность (5Л) возрастает и огра-
ничена сверху числом S, а последовательность (Sn) убы-
вает и ограничена снизу числом S. По теореме Вейершт-
расса (см. приложение 1) существуют пределы:
1пп5Л, 1ип5л,
л—>00 Л—>оо
причем
lim Sn = lim(anbn) = (lim an) • (lim bn) = ab.
Л->00 Л->00 Л->00 Л->00
Аналогично limS'n=aZ>. Таким образом, мы получи-
Л->00
ли, что одновременно ab<S и ab>S. Значит, S =ab.
Итак, мы доказали,что площадь прямоугольника со
сторонами а и b вычисляется по формуле:
S=ab.
Следствие, Площадь S квадрата со сторо-
ной а равна квадрату его стороны, т.е,
S=d.
§ 15.2. ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА
Теорема 15.2. Площадь параллелограмма равна
произведению его стороны на
эту сторону.
□ Проведем высоты ВТ
и СК параллелограмма
ABCD (рис. 15.5). Ограничим-
ся лишь случаем, когда точ-
ка Т лежит на стороне AD , а
не на ее продолжении. Прямо-
угольные треугольники АВТ
и CDK равны. Значит,
$ ABCD =$МВТ +$BCDT =
= S&CDK ^^BCDT =$ВТКС ’
Кроме того, отрезки AD и ТК
высоту, опущенную на
356
равны. Так как четырехугольник ВТКС — прямоуголь-
ник, то
Sabcd = Sbtkc =ТК ВТ =AD ВТ .
Итак, площадь параллелограмма со стороной а и
высотой h, опущенной на эту сторону, вычисляется по
формуле: 5 = ah.
Следствие. Площадь S параллелограмма равна
произведению двух его смежных сторон а и b на синус
угла А между ними, т.е. S=ab-sinA.
□ SABCD = a-h = ab-sinA (рис. 15.5).
§ 15.3. ПЛОЩАДЬ ТРЕУГОЛЬНИКА. ФОРМУЛА ГЕРОНА
Теорема 15.3. Площадь S треугольника АВС
вычисляется по формулам:
1) S=-ah=-bhb=-chc.
2 ‘ 2 * 2 с
s 2) S=—ab sinC=—ac sinB=—bc sinA.
2 2 2
3) S=---, S=2R2 sinA-smB-sinC.
4R
4) S=pr.
5) S=y/p(p-a)(p- b)(p-c).
Отметим, что равенст-
C D во 5) называется формулой
A В
Рис.15.6
Герона.
Перейдем к доказатель-
ству этой теоремы.
□ Всякий треугольник
можно достроить до паралле-
лограмма (рис. 15.6). Так как
параллелограмм разбит на два
равных треугольника, то пло-
щадь треугольника равна по-
ловине площади параллело-
грамма. Отсюда вытекают
357
формулы 1) и 2). Далее из теоремы синусов имеем:
а =2R'sinA, b =2R-sinB, с =2R-sinC.
Тогда
5 = ^ab- sinC = -^(2R - sinA}(2R • sinB)(sinC) =
= 2R2 • sinA sinB sinC.
Кроме того,
Рис.15.7
S =—ab • sinC = —ab--=
2 2 2R
abc
то есть формулы 3) доказа-
ны. Пусть I— центр окруж- А
ности, вписанной в треуголь-
ник АВС (рис. 15.7). Тогда
= $ЬАВ1 $&ВС1 “И °АЛС/ ~
и формула 4) доказана.
Докажем теперь формулу Герона.
По теореме косинусов имеем:
а2 = Ь2 + с2-2Ьс • cosA.
Согласно формуле 2),
45 = 2Ьс • sinA.
Из этих равенств получаем:
. bl + с1 -cf . . 45
cosA =----------, sinA =----
2bc 2bc
Поскольку sin A + cos A =1 , to
2bc
Отсюда
358
= (b + с + a)(b + c-a)(a +b- c)(a-b + c) =
= 2 p(2 p - 2a)(2 p - 2c)(2 p - 2b) =
= 16p(p-a)(p-b)(p-c).
Окончательно получаем:
S2 = p{p-a){p-b){p-c),
S=^p(p- а)(р - b)(p -с) Я
Следствие. В треугольнике АВС угол С —
прямой тогда и только тогда, когда —г Ч—у =—у. В этом
ha hb hc
случае S=-hahb.
□ Пусть высоты треугольника удовлетворяют усло-
вию:
Тогда по формуле 1) имеем:
откуда
2 л2 . т 2
с =а +0 .
По теореме, обратной теореме Пифагора, заключаем, что
угол С — прямой.
Обратно, пусть угол С равен 90°. Докажем, что
1 1 1
—уЧ-—у= —. Действительно, по формуле 1) и теореме
4 Ч #
Пифагора имеем:
359
,2
2 (2S)2 (2S)2
Ч'
что и требовалось доказать.
Наконец, если угол С — прямой, то Cl — hbt b —ha,
Теорема 15.3 позволяет получить полезные формулы
для вычисления радиусов описанной и вписанной окруж-
ностей. Действительно, из формулы 3) теоремы 15.3 име-
_ аЬс
ем: К = -^-, а из формулы 4) теоремы 15.3 заключаем,
что Г = — . Последняя формула справедлива для произ-
вольного многоугольника, в который можно вписать ок-
ружность. Кроме того, из теоремы синусов имеем:
2?=—^— = —^—=-^—.
2sinA IsinB 2sinC
Напомним также, что в прямоугольном треугольни-
ке R = тг
, а в правильном треугольнике
со стороной а
справедливы равенства:
R =
,R =2г.
Теорема 15.4. Радиусы ra, rb, гс вневписанных
окружностей треугольника АВС вычисляются по фор-
мулам:
а
р-а
p-b
360
Рис.15.9
□ Пусть 1а — центр вневписанной окружности тре-
угольника АВС ; IaK, IaT, IaL — ее радиусы, прове-
денные в точки касания этой окружности соответственно
со стороной ВС =а ис продолжениями сторон АС
и АВ (рис. 15.8). Тогда
- $ЬАВС
~ 8&лв1а 8&ва„
= —АВ -г +-АС -г-—ВС -га =
2 2 2
=—ra(AB + АС -ВС) =—(а + Ь + с-2а)га =
2 2
= |(2р-2а)га = (р-а)га.
S
Итак, га =--. Радиусы гь и гс вычисляются анало-
р-а
гично.
§ 15.4. ДРУГИЕ ФОРМУЛЫ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Определение. Фигуры с одинаковой площа-
дью называются равновеликими.
Теорема 15.5. Медианы треугольника делят его
на шесть равновеликих частей.
361
□ Пусть в треугольнике АВС точка М является
точкой пересечения медиан ААХ, ВВХ и ССХ (рис. 15.9).
Треугольники ВМА j и СМА j имеют равные основания
и общую высоту. Поэтому их площади равны. Обозначим
это общее значение площади через X. Аналогично обоз-
начим:
$ЛАМВ j “ S&CMB J = У1 ^ЛАМС j = S&BMC
Однако треугольники САС х и СВСХ также равновелики,
поскольку имеют равные основания ЛС, и ВСХ и общую
высоту, опущенную из вершины С на прямую АВ . Сле-
довательно, — Z +2х, откуда X = у. Аналогично из
равенства площадей треугольников АВА, и АА ХС по-
лучаем: у = Z . Итак, X = у = Z .
Следствие/. Отрезки, соединяющие центр
масс треугольника с его вершинами, делят треугольник
на три равновеликие части.
Следствие 2. Медиана треугольника делит его
площадь пополам.
Оба эти следствия по существу доказаны при дока-
зательстве теоремы 15.5.
Теорема 15.6. Площадь треугольника, стороны
которого равны медианам данного треугольника, со-
ставляет три четверти его площади.
□ Отложим отрезок ВХК,
равный отрезку МВХ, на про-
должении медианы ВВХ. Че-
тырехугольник АМСК явля-
ется параллелограммом, так
как его диагонали в точке Вх
делятся пополам. Значит,
Рис.15.10
SММК $ММВ j + 8ЛАВ
~$ЛАМВ 1 =
~ $ЛАМС $ЛАВС
Кроме того,
(см. следствие 1 из теоремы 15.5).
362
AM = — mQl MK=-mb, AK=CM=-mc.
Проведем А{Г\\МК (рис.15.10). Тогда треугольники
АА}Т и АМК подобны и АА}= — AM = Из подо-
бия треугольников получаем: АТ = тпс, А}Т = mb, т.е. сто-
роны треугольника АА}Т равны медианам данного тре-
угольника. Далее,
СМ ХТ
-AM --АК -sinZMAK =
- - AM • АК • sin ZМАК
ЬАМК
ЛЛВС Л °ДЛВС •
Теорема 15.7. Площадь S треугольника АВС
вычисляется по формуле:
где ma, mb, mc — его медианы.
□ Из теоремы 15.6 имеем: S = — т .
Применяя формулу Герона для вычисления площади
треугольника АА {Г, получим искомое равенство. И
Теорема 15.8. Площадь S треугольника АВС
вычисляется по формуле:
I
\\ha Ч hc)\ ha Ч hc
где ha, hb, hc — его высоты.
□ По формуле Герона имеем:
К he
ha hb hc
363
Из формул S = —aha = — bhb = —chc получаем:
2 2 2
a=~T'
ha
hC
Тогда
5 =—4S2-
4 N\ha h h
у \ a T> <
откуда и следует утверждение теоремы.
h h. h.
a T> c
ht ht Г
§ 15.5. ПЛОЩАДЬ ТРАПЕЦИИ
Теорема 15.9. Пло-
щадь трапеции равна произ-
ведению полусуммы ее осно-
ваний на высоту.
□ Пусть BE — высота
трапеции ABCD, AD —
большее основание трапеции.
Проведем BK\\CD (рис.15.11).
Четырехугольник BCDK —
параллелограмм, поэтому
KD = BC<AD,
и точка К принадлежит от-
РысЛ5.11
резку AD. Далее,
^ABCD
S&ABK + $bcdk
-АК BE + KDBE =
2
= ^AD -BQBE + BCBE = ^(AD + BC)BE.
T e о p e м a 15.10. Пусть а и b — основания тра-
пеции. Длина отрезка с концами на боковых сторонах,
параллельного основаниям и делящего площадь трапе-
ции пополам, равна
2
364
□ Пусть в трапеции ABCD основания AD и ВС
равны соответственно а и b, отрезки LK и AD парал-
лельны и SLBCK = SALKD (рис. 15.12). Опустим перпендику-
S-^a + W + hJ.
Л*
Имеем систему уравнений
{(x + afa =(x + b)h2
2(х + а)^ = (а + б)(Л, + ),
равносильную системе:
Отсюда получаем:
2(x + a)(x+b)hl=(a + b)((x+b)hl+(x + a)hl),
2(x + a)(x+b) = (a + b)(2x + a+b),
2x2+2bx +2ах +2ab = 2ax +а*+ ab+2bx +ab + b2,
2x2 = a2 + b2,
l^+b2 _
2
365
§ 15.6. ПЛОЩАДЬ ЧЕТЫРЕХУГОЛЬНИКА
Теорема 15.11. Площадь четырехугольника рав-
на половине произведения его диагоналей на синус угла
между ними.
□ Согласно аксиоме 15.3 имеем (рис. 15.13):
$ABCD = S&AOB + + *$ACOD + $\AOD =
= — АО ОВ sirup + — ВО ОС-5/л(180°-(
+ - СО • OD -sintp + — AO OD -sin(l 80° - <р) =
= - 5 in ф (ОА • ОВ + ОВ • ОС + ОС • OD + OD • О А) =
*2*
= -simp (ОВ(ОА + ОС) + OD(pC + ОА)) =
= -5Шф(ОВ AC + ODAC) =
= ^АС - sirup (ОВ + OD) = ~ЛС BD sirup. U
Следствие. Площадь ромба равна половине
произведения его диагоналей.
a + b + c + d
Пусть р =------------ — полупериметр четырех-
угольника.
Рис. 15.13
Рис. 15.14
366
Т е о р е м a 15.12. Площадь четырехугольника
ABCD со сторонами 0, Ь, с , d вычисляется по фор-
муле:
S^(P-а)(Р-Ь)(Р-с)(Р-d>-abed-cos'
□ По аксиоме 15.3 имеем (рис. 15.14):
S = $МВС + S^ADC = ” (^ • sinB + cd • sinD),
откуда:
4!У2=а2^2 -sin2В + Zabcd sinB sinD + c2d2 sin2D =
= c?l?-(i& cos2B + c2d2-c2d2 cos2D Л-Zabcd -sinB sinD.
Далее,
c?l? cos2B + c2d2 cos2D =
= c?b2 + c2d2 + Zabcd sinB sinD-452.
С другой стороны, по теореме косинусов из тре-
угольников АВС и ADC получаем:
АС 2 = a2 +b2-Zab*cosB = с2 + d2-Zcd cosD,
откуда
Z( ab • cosB-cd • cosD )-a2 + b2 -c2-d2.
Возведя в квадрат обе части этого равенства, имеем:
4(а2£2 • cos2В - Zabcd • cosB • cosD + c2d2 • cos2D] =
, т2 2 12 У
= \а +b —с —а ) .
Тогда
A^b2 +c2d2-4S2 +
+2abcd -sinB -sinD -2abcd -cosB -cosD) =
= +b —c —a ) .
Отсюда
16S2 =4^b2 + 4c2d2-(a2 +b2-c2-d2)2 +
iabed (sinB sinD - cosB cosD) =
=4a2b2 + Zabcd +4c2d2-(a2 +b2 —c2 -d2) -Zabcd-
367
-Zabcd • cos(B + D) = 4(ab + cd)2-(a2 + b2 — c2 -d2>) -
-Sabcd (1 + cos(B + D)) = (2ab+2cd-c?-
-b2 + c2 + d2) (2ab + 2cd + a2+ b2-c2-d2) -
-I6abcd cos2 B + D = ((c+d)2-(a-b)2)((a+b)2-
z _r\2x iz l j 2 В D
-(c-d))-\6abcd-cos —-— =
= (c + d - a + Z>)(c + d + a - 6)(a + b-c + d)(a + b + c-d)~
1 z > j 2 B + D
-loabcd-cos ----=
2
= (2p -2a) (2p-2b) (2p - 2c) (2p- 2d)~
1 z I j +
-loabcd-cos -----=
2
=16(p-a) (p-b) (p-c) (p-d)-16abcd cos2
Окончательно получаем:
S = -J(p - a)(p - b)(p - c)(p - d) - abed • cos2 . I
Следствие!. Площадь четырехугольника, впи-
санного в окружность, вычисляется по формуле:
S = J(p- а\р - b)(p - с)(р - d) .
О Это утверждение вытекает из того, что в ука-
занном случае В + D = 180°, т.е. —-— = 90° и
cos2
= 0 .
Следствие 2. Площадь четырехугольника, в ко-
торый можно вписать окружность, определяется по
формуле:
368
S2 = abed -sin2 .
2
□ По теореме 6.5 имеем: a + С = b + d. Поэтому
Аналогично p-b = d, p-C — a, p-d = b. Значит,
О о
5 = abed—abed-cos
= abcd \-cos2
= abed -sin2
Следствие 3. Площадь четырехугольника, впи-
санного в окружность и около которого можно описать
окружность, вычисляется по формуле:
S = >Jabcd.
§ 15.7. ПЛОЩАДИ ПОДОБНЫХ ФИГУР
Напомним, что две фигуры называются подобными,
если отношение их соответствующих линейных размеров
является постоянной величиной. Число к, равное этому
отношению, называется коэффициентом подобия. Ино-
гда для подобных фигур F и G коэффициент подобия
обозначается через
Т е о р е м а 15.13. Отношение площадей простых
подобных фигур F и G равно квадрату отношения их
соответствующих линейных размеров, т. е. равно к2,
где к — коэффициент подобия.
□ Рассмотрим сначала два подобных треугольни-
ка АХВ}С\ и А2В2С2, в которых
Тогда ЛА} = ZA2, и
369
дл2в2с2 _ В2 • Л2С2 • sinZA2
Пусть теперь F и G — две простые подобные фи-
гуры с
= к . Разобьем
фигуру F на треугольники Fv F2, ... , Fn. Преобразова-
ние подобия переводит эти треугольники в подобные им
треугольники Gp G2, ... , Gn соответственно. Эти тре-
угольники образуют
получаем:
разбиение фигуры G. Очевидно,
i =1, 2, ..., п. По аксиоме 15.3
Однако SF = к2 -SG , где i =1, 2, ...г п.
Значит,
откуда
§ 15.8. ОРТОЦЕНТРИЧЕСКИЙ ТРЕУГОЛЬНИК
В §7.2. было доказано, что прямые, содержащие
высоты треугольника, пересекаются в одной точке. Далее
в этом параграфе мы будем считать, что треуголь-
ник АВС — остроугольный. Все результаты, которые
будут доказаны, легко перенести на случай прямоуголь-
ного и тупоугольного треугольников.
Напомним, что точка Н пересечения высот тре-
угольника АВС называется ортоцентром.
370
РисЛб.15 Pvlc.15. 16
Треугольник НаНьНс с вершинами в основаниях
высот треугольника АВС называется ортоцентрическим
(рис.15.15).
Установим несколько свойств ортоцентрического
треугольника.
Т е о р е м а 15.14. Если Н— ортоцентр треуголь-
ника АВС, то
ZAHHb = ZC, АВННС = АА> АСННа = АВ
□ Треугольники АННь и АН аС прямоугольные
(рис. 15.16). Отсюда следует, что
AAHHb + AHAHb = ZACB 4- Z.HaAC = 90°.
так как АНАНь = Х.НаАС, то ААННЬ = ЛАСВ.
Остальные два равенства доказываются аналогично.
Т е о р е м а 15.15. Точка, симметричная ортоцентру
относительно прямой, содержащей сторону треугольни-
ка, лежит на окружности, описанной около этого тре-
угольника.
□ Пусть в треугольнике АВС точка D лежит одно-
временно на луче ВНЬ и на окружности, описанной око-
ло треугольника АВС (рис.15.17). По теореме 15.14 име-
ем:
ZAHHb = ZC,
откуда следует, что
Z.HAC = 90°-ZC.
371
Рис. 15.17 Рис.15.18
Углы CAD и СВНЬ равны, так как опираются на ду-
гу CD . Однако Z.CBHb = 90°-ХС. Значит,
AHAHb=ADAHb.
В треугольнике HAD отрезок АНЬ является одновре-
менно биссектрисой и высотой. Поэтому треуголь-
ник HAD равнобедренный. Значит, АНЬ — медиана
этого треугольника. Следовательно, точка D симмет-
рична точке Н относи-
тельно прямой АС. Оче-
видно также, что всякая
другая точка луча ВНЬ не
симметрична точке Н от-
носительно прямой АС.
Поэтому точка, симмет-
ричная ортоцентру Н от-’
носительно прямой АС,
совпадает с точкой D, ле-
жащей на описанной ок-
ружности. И
Т е о р е м а 15.16. Ес-
ли На, Нь, Нс — вершины ортоцентрического тре-
угольника в треугольнике АВС (рис. 15.18), то справед-
ливы равенства:
ZA = АННВ = ЛСНаНь ,
АВ = АНаНьС = ААНЬНС ,
Рис.15.19
372
ZC = XBHcHa = XHbHcA .
□ В четырехугольнике АНСННЬ углы АНСН
и ННЬА — прямые. Их сумма равна 180°. Значит, около
этого четырехугольника можно описать окружность
(рис.15.19). Так как ХАНЬН = 90° , то АН —диаметр
этой окружности. Углы АНСНЬ и АННЬ опираются на
дугу АНЬ этой окружности. Вследствие теоремы 15.14,
XAHcHb = XAHHb = Z-C. Остальные равенства доказы-
ваются аналогично.
Следствие. Высоты треугольника лежат на
биссектрисах ортоцентрического треугольника.
□ В самом деле,
ЛИНН=90°-ХАНСНЬ = 90°-ZC
О С V О
и
АН НН = 9W-ABHH = 90°-ZC,
С* С* I* с*
откуда
АННН=АННН.
w w с*
Т е о р е м а 15.17. Треугольники АНЬНС, НаВНс,
НаНьС и треугольник АВС подобны, причем коэффи-
циенты подобия определяются по формулам:
= cosB,
□ Так как углы треугольника АНЬНС равны соот-
ветственно углам треугольника АВС, то треугольни-
ки ЛНЬНС и АВС подобны. Поэтому
к( мщ А _ ля,
I ЛЛВС J с
Однако из треугольника АВНЬ получаем, что
АНЬ
= cosA .
с
Остальные равенства доказываются аналогично. И
373
Следствие. Стороны ортоцентрического тре-
угольника находятся по формулам:
НЬНС= a-cosA, НсНа = b• cosB, НаНь = с• cosC .
Т е о р е м а 15.18, Углы ортоцентрического тре-
угольника НаНьНс связаны с углами треугольни-
ка АВС следующими равенствами:
АНа = 180 -2Л, AHb = 180 -2В, АНС = 180°-2С.
□ Это утверждение немедленно следует из теоре-
мы 15.16. И
Теорема 15.19. Радиус окружности, описанной
около ортоцентрического треугольника НаНьНс, вдвое
меньше радиуса окружности, описанной около тре-
угольника АВС.
□ Пусть RH — радиус окружности, описанной около
треугольника НаНьНс. По теореме синусов, из треуголь-
ника НаНьНс имеем:
2„ _ НаНь _ с-cosC _ccosC _
н sinAHc szn(180° -2С) sin2C
с • cosC с D
=------------=------=к.
2sinC • cosC 2sinC
Теорема 15.20. В треугольнике АВС расстоя-
ния от ортоцентра до вершин вычисляются по форму-
лам:
АН = J4R2-а2 = 2R cosA ,
ВН = ^4R2 - b2 = 2R cosB ,
CH = y/4R2-с2 = 2R cosC.
□ Из треугольника АННЬ по теореме 15.14 по-
лучаем:
АНЬ
smC =--- ,
АН
откуда
АН
sinC
374
Из теоремы 15.17 имеем: AHb=c-cosA. Таким образом,
АН = С Однако по теореме синусов —-— = 27?.
sinC sinC
Значит, АН = 2R- cos А. Далее,
cosA = *J\-sin2A
и тогда
АН = 2R>11-sin2 А = >l4R2-4R2sin2A = >l4R2-c? .
Расстояния ВН и СН находятся аналогично.
§ 15.9. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 15.1. Прямоугольник со сторонами 8 см
и 34 см разделен на два подобных и неравных прямоугольни-
ка. Найти их площади.
ZS Пусть ABCD
ник, АВ — 8 см, ВС = 34 см
BE С
X 34 -X
A F D
Рис,15.20
— данный прямоуголь-
(рис. 15.20). Описанное в
условии разбиение пря-
моугольника осуществля-
ется отрезком EF, па-
раллельным стороне АВ
(убедитесь самостоятель-
но, что отрезок, парал-
лельный большему ос-
нованию, не разбивает
ABCD должным обра-
зом). Обозначим BE = Х,
тогда ЕС = 34-х. Мож-
но считать, что ЕС < EF.
Из подобия прямоуголь-
ников ABEF и CEFD
имеем пропорцию:
х __ 8
8 ~ 34-х ’
откуда
х2-34х + 64 = 0.
Решая это уравнение, получим: X = 2 или X = 32.
При X = 2 имеем: ЕС = 32 > EF = 8 , что противоречит
375
Рис. 15.21
условию ЕС < EF. При х = 32 имеем: ЕС = 2 < EF.
Итак, X = 32. Тогда
SMEE = 32-8 =25б(см2), SCEFD =8-2 = 1б(см2). Ж
п р и м е р 15.2. Острый угол параллелограмма ра-
вен 45°, а диагонали равны 1 см и 3 см . Найти площадь па-
раллелограмма.
ZX Пусть ABCD— параллелограмм, Z.DAB =45°.
Обозначим AD = а, АВ = b. Проведем отрезок СЕ па-
раллельно BD (рис.15.21.). Точка D есть середина АЕ,
AEDC = ADAB =45\
Докажем сначала, что AC >BD. Рассмотрим тре-
угольники ACD и DCE (рис.15.22). Отметим, что
ZADC = 180’-45° = 135°, a cosAADC =-cos45°=-—.
2
По теореме косинусов имеем:
АС2 = а2 + b2-2ab cosZADC = a2 + b2 + abjl;
ЕС2 = а2 + b2 -2аЬ • cos45° = а2 + b2 -abj2.
Значит, АС >СЕ = BD, откуда следует, что АС — боль-
шая диагональ, равная 3, BD — меньшая диагональ,
равная 1 . Имеем систему уравнений:
a2 +b2 +ab42 = 9
a2 +b2 - ab-j2 = 1.
По следствию из теоремы 15.2 имеем:
376
, ab-J2
abcd =ab-sin45° =------
AdCU
Вычитая из первого уравнения второе, получим:
ctbyH
2аЬ^2 = 8 (см); =-------= 2 (см2). Ж
4^
Пример 15.3. Две стороны треугольника равны 25 см
и 30смг а его площадь составляет 300 см2. Найти третью сто-*
рону.
Рассмотрим треугольник ABC, в котором
СВ = а = 25см, СА = Ь = 30см, 5 = 300см2.
Тогда
5 =—ab-sinC,
2
откуда
300 = — • 25 • ЗОл/иС; sinC = —.
2 5
Отсюда
„ а. А a. /i . 3
cosC = ±v 1 - sin С = +, 1-=±-.
V 25 5
Необходимо рассмотреть два случая:
a) cosC = . Тогда угол С — острый, и
АВ2 = с? + b2-2ab-cosC=252+302-2-25-30-~=252,
5
т.е. АВ =25(см).
б) cosC =—. Тогда угол С —тупой, и
ЛВ2=252 + 302+2-25-30--= 2425;
5
АВ = л/2425 = 5л/97 (см).
Таким образом, для третьей стороны возможны два
значения: 25 см или 5>/97 СМ.
Пример 15.4. Медианы треугольника равны 12, 15
и 18 см. Найти площадь треугольника.
377
Найдем сначала площадь So треугольника, со-
ставленного из медиан та, ть, тс. Его полупериметр
12 + 15 + 18
Ро =-----"-----
= 22,5;
р-та = 22,5-12 = 10,5,
р0-ти4 = 22,5-15 = 7,5,
р0-тс = 22,5-18 = 4,5.
По формуле Герона
So = д/22,5-10,5-7,5-4,5 =
= — V225-105-75-45 = - V45-21-15-9 = — V7.
100 4 4
По теореме 15.6 искомая площадь равна:
5=-50=45д/7 (см2). Ж
Пример 15.5. Катеты
прямоугольного треугольника S.
равны 6 см и 8 см. Внутри тре-
угольника дана точка, удален- \ р
ная на 2 см от каждого катета. 6 \
Найти расстояние от этой \ Z z
точки до гипотенузы. q —
Пусть ЛВС — дан- ** / 2
ный прямоугольный тре- /
угольник, катеты АС = 6 см, р L 8 В
СВ = 8 см, для точки М
внутри треугольника рас- Рис. 15.23
стояния MQ = ML = 2 см
(рис. 15.23). Опустим перпендикуляр МР на сторону АВ.
Отрезки МА, МВ и МС разбивают треугольник ЛВС
на три треугольника. Имеем:
ВАВС =^АМВ + ВАМС + $ВМС
или
И=И 2*6 мр АВ
2 2 + 2 + 2
откуда
МР АВ =48-16-12 = 20.
378
Рис. 15.24 Рис.15.25
Далее, по теореме Пифагора АВ = л/б2 + 82 =10,
20
следовательно, МР = — = 2 (см). Ж
В разобранном примере точка М оказалась центром
вписанной окружности. Это можно было установить
сразу, вычислив С = 10см и убедившись, что
а+Ь-с _
г =-------------------------= 2 см,
что совпадает с заданным расстоянием от точки М до
катетов.
Пример 15.6. Основания трапеции равны 89 и 142, а
диагонали — 120 и 153. Найти площадь трапеции.
ZX Рассмотрим трапецию ABCD, основания кото-
рой равны Л£) = 142, ВС =89, а диагонали равны
АС =120, В£> = 153 (рис.15.24). Проведем CE\]BD.
Четырехугольник BCED — параллелограмм, поэтому
DE = ВС = 89. В треугольнике АСЕ имеем:
ЯС =120, CB=BD = 153,
АЕ = AD+£)E = 142 4-89 = 231.
Площади заштрихованных на рисунке треугольников
равны, поэтому
&ABCD =$АВС + &ACD =^CDE + ACD = АСЕ •
Воспользуемся формулой Герона. Полупериметр р тре-
угольника АСЕ равен:
379
120 + 153 + 231
2
p- AC =132,
р-СЕ =99,
р-АЕ =21.
Тогда
SACE = V252-132-99-21 =8316 = SABCD . Ж
П р и м е р 15.7. Доказать, что в трапеции треугольники,
образованные отрезками диагоналей и боковыми сторонами,
имеют одинаковые площади.
ZX Рассмотрим трапецию ABCD, диагонали кото-
рой пересекаются в точке О (рис. 15.25). Нужно доказать,
что заштрихованные треугольники имеют равные площа-
ди. Треугольники ABD и ACD имеют одинаковые пло-
щади, так как у них общее основание AD и равные вы-
соты, опущенные на AD. Тогда
^ABD = $АОВ + ^AOD = ^ACD = $COD + AOD '
Отсюда
$АОВ 8COD -
Пример 15.8. На сторо-
нах прямоугольного треугольни-
ка вне его построены квадраты.
Вершины квадратов, не совпа-
дающие с вершинами треуголь-
ника, последовательно соедине-
ны. Найти площадь образован-
ного шестиугольника, если кате-
ты треугольника равны 5 и 12. ^'^у // С & В \1
zS Пусть АВС— дан- V/ \]
ный треугольник, АА}С2С, у' у
ВВ2СХС, АА2ВХВ — постро- X I/в
енные квадраты. Нужно най-
ти площадь S шестиугольни-
Рис. 15.26
ка АХА2ВХВ2СХС2 (рис. 15.26).
Обозначим ВС=а = 12, ЛС=&=5, АВ=С. По тео-
реме Пифагора
с=л/52 +122 =13.
380
Шестиугольник составлен из треугольника АВС, трех
квадратов и трех заштрихованных треугольников. Опус-
тим перпендикуляры A2D на прямую АХА и ВХЕ на пря-
мую В2В, как показано на рисунке. В треугольни-
ке AA2D гипотенуза ЛЛ2 = С, углы AA2D и АВС рав-
ны как углы со взаимно перпендикулярными сторонами.
Значит, треугольники AA2D и АВС равны, откуда
A,D = а. Тогда
Ля
Аналогично треугольники ВВХЕ и ВАС равны, и
ВХЕ = b, откуда
8 мм = -ab.
2 о * О
= -ab. Тогда
Очевидно, что
S =al+b2 +с2 +4--аЬ=
2
= (а+Ь)2 + с2 =
= 172+132 = 458. Ж
Пример 15.9. На сторо-
нах прямого угла С выбирают-
ся точки А и В так, что пло-
щадь треугольника АВС рав-
на 2. Какую линию описывает
середина отрезка АВ ?
Направим вдоль сто-
рон прямого угла С оси ко-
ординат. Пусть СА = b , СВ = а. Тогда точки А и В та-
ковы: Л(0;б), В(а; О) и середина М отрезка АВ имеет
координаты
Оч-а 6 + 0
(рис.15.27).
381
По условию SMBC =2=—, откуда ab = 4. Далее,
«2
аб - .,
xQ-yQ =— =1 • Значит, точка М лежит на ветви гипер-
4
1
болы у = —, лежащей в первой четверти.
Обратно, каждая точка M(xQ;yQ) этой ветви гипер-
болы является серединой отрезка АВ, где Л(О;2>уо),
В(2хо;О), причем х0 >0, >0, хоуо=1 . Тогда
S&abc СА *СВ • 2x0*2^ 2х0у0 2
и для точек А и В выполнены условия данного примера.
Значит, искомой линией является ветвь гиперболы
П р и м е р 15.10. В треугольнике АВС дано, что
1 1 1
*; к; <
Каким должен быть угол С: тупым или острым?
ZS Пусть S — площадь данного треугольника. Тогда
7 2S 1 а
’ 1 по'
a ha 2S
Аналогично выражая остальные высоты, получаем:
или
d + b2>c2.
По теореме косинусов имеем:
а2 4- b2-2аЬ • cosC = с2.
Тогда
а2 + b2 >а2 + b2-2аЬ • cosC; cosC>0.
Значит, угол С острый. Ж
Пример 15.11. К вневписанной окружности тре-
угольника АВС, центр которой находится в точке 1а, прове-
382
дена касательная, параллель-
ная ВС. Найти длину отрез-
ка этой касательной, содержа-
щегося внутри угла Л, если
ЛВ=5, ВС =6, ЛС=7.
ZS Пусть DE — отре-
зок данной касательной, со-
держащийся внутри угла А.
Вневписанная окружность с
центром 1а и радиусом га
является вписанной в тре-
РмсЛ5.28 угольник ADE, подобный
треугольнику АВС (рис. 15.28). Пусть Г — радиус впи-
санной в треугольник АВС окружности. Тогда
DE - г° DF - аг°
--------, или Ulh-------.
ВС г г
Для нахождения радиусов найдем сначала площадь S
треугольника АВС. Имеем:
Далее, по теореме 15.4 получаем:
S б4б „
a
Окончательно
DE =6-2л/б= 18.
Пример 15.12. Пусть Д, Д, L3 — основания биссек-
трис треугольника АВС со сторонами Я, b, С. Доказать, что
отношение площадей треугольника и треугольника
2abc
ABC равно
(рис Л 5.29).
383
ZS Найдем сначала от-
S ML 3L2 __
ношение ----По своист-
$МВС
ву биссектрисы треугольника
= AL2+L2C=b.
L2C а 22
Отсюда AL 2 =--b. Анало-
с+а
п Ь
гично AL 3 =-С . Тогда
Ъ+а
о — AL2 • AL3 • sinA Рис. 15.29
faALyl^ _ 2 __
С 1
_ be • sinA
2
_AL 2 -AL3 _ be
be (a + b)(a + e)
При вычислении отношения ------ нужно в выра-
$мвс
жении (1) заменить а на b, b на а. Имеем:
ML —аС
$мвс + <0
При нахождении отношения
^ACZiZ2
$мвс
следует в выра-
жении (1) заменить а на С и С на а. Имеем:
_ ab
S&ABC
Искомое отношение равно:
^SLxL2L3 —$МВС —8 ML3L2~S MLxL3~~S lclxl2
мве
ДЛВС
384
SbCLiLj _
к S&ABC $ЬАВС 8&ЛВС )
be ас ab _
(a + b}(a + c) (a+b)(b + c) (b + c)(a + c)
(a+b)(b + c)(a+c) - bc(a + c) - ac(a + c) - ab(a + b) _
(a+&)(6 + c)(a + c)
_ 2abc
(a + b)(a + c)(/>+c)
Пример 15.13. Доказать, что из всех треугольников с
заданным периметром наибольшую площадь имеет равносто-
ронний.
z2s По формуле Герона имеем:
S2 = p(p-a)(p-b)(p-c),
^- = ^(p~a)(p-b)(p-c). (1)
Как известно из алгебры, для положительных чи-
сел Л, В, С, D справедливо неравенство Коши:
\Jabcd <a+b+c+d (2)
4
/—^Х+У
Действительно, согласно неравенству Jxy <- для
двух неотрицательных чисел имеем:
и неравенство (2) доказано. Отметим, что равенство в не-
равенстве (2) достигается только при А = В = С = D.
I— х + У
Действительно, в неравенстве у]ху < —-— равенство
возможно только для совпадающих чисел, поэтому в
385
выражении (3) равенство будет только тогда, когда
А = В, С = D,-------=-------, т.е. когда А = В = С = D.
2 2
Перейдем к оценке площади S при фиксированном
полупериметре р. Имеем из равенства (1) согласно нера-
венству (2):
= 4^у(р-а)(р-&)(р-с) <
откуда
Равенство достигается только тогда, когда
_ = р_а = р-Ь=р-с,
т.е. а = b = С и р = ~а — по-
лупериметр правильного тре-
угольника. Итак, из всех тре- >
угольников с заданным полу- /
периметром наибольшую пло- /
щадь имеет равносторонний /(
треугольник. Ж / \
Пример 15.14. В рав- / У
нобедренной трапеции ради-
ус вписанной окружности ра- д
вен Г, а угол при большем ос- 24
новании равен а. Найти пло-
Рис. 15.30
щадь трапеции.
ZS Пусть ABCD— дан-
ная равнобедренная трапеция, в нее вписана окружность
с центром О и радиусом г, Z.BAD = а (рис. 15.30). Най-
дем основания грапеции. Пусть Р и Q — середины ос-
нований трапеции. Тогда PQ — диаметр окружности.
386
Рис. 15.31
Рис. 15.32
Точка О равноудалена от сторон угла BAD , поэтому она
а
лежит на биссектрисе этого угла, и АО АР =—. Отсюда
АР = r-ctg —
AD = 2rctg—.
Далее,
°-ос =90 —
Площадь трапеции
S= -(AD + BC)-PQ =r( tg-+
2г =
2г2-2 4г2
sina sina
Итак,
sina
Пример 15.15. Найти выпуклый пятиугольник наи-
большей площади, два угла которого прямые, а длина каждой
стороны равна 1 . Определить площадь этого пятиугольника.
Рассмотрим 2 случая.
а) У пятиугольника два соседних угла прямые. На
рис.15.31 изображен выпуклый пятиугольник со сторона-
387
ми, равными 1 , Z.BAE = AAED =90°. Очевидно, что та-
кой пятиугольник единственный. Его площадь равна:
_ VI
= ^ABDE + S&BCD = 1 +
б) У пятиугольника два несоседних угла прямые. На
рис. 15.32 изображен выпуклый пятиугольник со сторона-
ми, равными 1 , Z.BAE = Z.BCD =90°. В этом пятиуголь-
нике диагонали BE и BD равны у[2. Такой пятиуголь-
ник также единственный. Его площадь равна:
82 $ЬАВЕ +S&BCD +S&BDE $ &BDE *
В равнобедренном треугольнике BDE проведем вы-
соту ВК. Тогда
Значит,
S2=l +—>s,.
4
Пятиугольник наибольшей площади представлен на
рис. 15.32. Таким образом,
наибольшую площадь имеет
пятиугольник, у которого
два несоседних угла прямые.
Площадь его равна 1 Ч----.
4
Пример 15.16. Высота
равнобедренной трапеции рав-
на ht а ее боковая сторона
видна из центра описанной ок-
ружности под углом 60°. Най-
ти площадь трапеции, если оба
Рис. 15.33
388
ее основания находятся по одну сторону от центра описанной
окружности.
Пусть ABCD — равнобедренная трапеция,
вписанная в окружность с центром О, Z-AOB =
= Z.COD = 60°, высота трапеции BL = h. Обозначим
через R радиус окружности, а угол BAD — через а
(рис. 15.33). Тогда
АВОС = uBC=uB£>-60° = 2a-60°.
Далее,
AAOD = 120° + Z.BOC = 2a + 60°.
Площадь трапеции равна:
MOB ^^SBOC MOD
R
„ . 2a - 60° - 2a - 60°
2 sin-------------------cos
R
cos2a
Выразим отрезок BL через введенные величины R
и а. Треугольник АОВ равносторонний, поэтому
АВ = R, h = BL = АВ • sina = R -sina. Следователь-
но, 5 = h2y/3.
Пример 15.17. Стороны треугольника АВС равны 5;
6; 7. Найти периметр ортоцентрического треугольника.
ZS В треугольнике АВС а = 5 , Ъ = 6, С = 7. Най-
дем косинусы углов треугольника. По теореме косинусов
имеем:
Ь2+с2-с? = 36+49-25 = 60 = 5
2Ьс 2-6-7 2-6-7 7'
с?+с2-Ь2 = 25+49-36 = 38 = 19
2ас 2-5-7 “ 2-5-7 35'
389
12
cosC =------
2ab
По следствию из теоремы 15.17 периметр
трического треугольника равен:
Рн-a cosA + b cosB + с• cosC =
_ 5-5 649 7 1_288 __ 8
ортоцен-
Пример 15.18. Дока-
зать, что отношение площадей
ортоцентрического треугольни-
ка и данного треугольника
АВС равно 2cosA cosB cosC.
ZS Пусть S— площадь
тео-
Pue. 15.34
треугольника АВС. Из
ремы 15.17 следует, что
^шьнс = Seos А,
$ьвнаНе ~S COS В,
“SCHaHb
Тогда искомое отношение равно (рис. 15.34):
ЬНаНъН
SAHbHe ^ЬВНаНс ^ыснань
=1 - cos2 А + cos1 В + cos1 В) =
l + cos2A l + cos2B
= 1-----cos2 А------cos2B - cos2 С =
— (cos2A + cos2B)-cos1C =
= — cos(A + B) cos(A - B)-cos2C =
= cosC cos{A - B)-cos2C =
= cosC\cos(А -В)-cosC) =
390
= cosC\-2sin(9Q° - B)sin( A - 90°)) =
Рис. 15.35
= 2cosCcosBsin(90° - A) =
= 2 cosA cosB cosC.
Итак, искомое отношение
равно 2 cosA cosBcosC. Ж
Пример 15.19. Высоты
AD. BE. CF остроугольного
треугольника АВС пересека-
ются в точке Н. Известно, что
площади четырехугольников
AEHF и HECD равны. Дока-
зать, что треугольник АВС
равнобедренный (рис. 15.35).
Обозначим площа-
ди треугольников АНЕ,
СНЕ. AHF. CHD соот-
ветственно через iSj , S2, S3.
S4. По условию 5j 4- = S2 + S4.
Докажем, что AB = ВС. Доказательство проведем
методом от противного. Допустим, что АВ>ВС. Срав-
ним площади Sj и S2; S3 и S4. Большая наклонная имеет
большую проекцию, поэтому АЕ >СЕ, Тогда
Далее,
-sinA)(AC-cosA) =—AC 2-sin2A,
2 4
= 2 -sin2C.
4
Рассмотрим разность
391
~^лАсп ~ —АС2 (sin2A - sin2C) =
£viC/* ZxhGl/ y| \ /
AC 2
= ^=— sin(A - C) cos( A + C) =
= sin(A - C) co.s{l80’ - в) = - sin(C- A) cosB.
Эта разность положительна, T.K.ZB — острый угол и
cosB>0, а из неравенства АВ >ВС следует:
С>А, 0°<С-Л<90’, sintC-A)>0.
Тогда S&ACF ^3 >$&ACD *^4' ОТКуда
S3>54.
Далее, имеем по доказанному:
**^3^2 ’ *^4'
что противоречит условию. Значит, неравенство АВ>ВС
невозможно; аналогично невозможно неравенство
АВ<ВС. Итак, АВ = ВС, и треугольник АВС равно-
бедренный.
Пример 15.20. Две прямые I и fit разбивают квадрат
на четыре фигуры одинаковой площади. Доказать, что точки
пересечения этих прямых со сторонами квадрата являются
вершинами нового квадрата.
ZS Доказательство про-
ведем в три этапа.
а) Докажем, что пря-
мые проходят через центр Г
квадрата. 1
Каждая прямая делит I
площадь квадрата пополам. I
Допустим, что какая-нибудь I
из этих прямых Z не прохо- I
дит через центр О квадрата
(рис. 15.36). Проведем через
точку О прямую I' \\1 . Пря- Рис.15.36
мая 1} разделит квадрат на
две части, симметричные относительно точки О, поэтому
эти части имеют одинаковые площади. Однако тогда I
делит квадрат на фигуры неравной площади: площадь од-
392
ной части больше половины площади квадрата на ве-
личину, равную площади заштрихованной фигуры, а пло-
щадь другой части — меньше половины площади квадра-
та на эту величину. Итак, допущение ложно, и каждая
прямая проходит через центр квадрата.
б) Докажем, что данные прямые I и ТП взаимно
перпендикулярны.
Допустим, что это не так (рис. 15.37). Проведем через
точку О прямую lx _L I . В силу допущения прямые 1Х
и ТП не совпадают. Прямые 1Х и I делят квадрат на
четыре равные фигуры, поскольку эти фигуры наклады-
ваются друг на друга при повороте на 90° вокруг точ-
ки О (убедитесь в этом самостоятельно). Тогда, напри-
мер, площадь части S на рисунке меньше четвертой час-
ти площади квадрата на величину, равную площади за-
штрихованного зазора между прямыми ТП и 1Х. Значит,
прямые / и тп не делят квадрат на фигуры одинаковой
площади. Вновь получили противоречие с допущением.
Значит, прямые I и тп перпендикулярны.
в) Прямая I пересекает стороны квадрата в точках
А и С, прямая ТП — в точках В и D (рис.15.38). Дока-
жем, что ABCD — квадрат.
Рассмотрим поворот Т квадрата вокруг центра О
на 90° против часовой стрелки. При этом сторона EF
перейдет в сторону НЕ, а прямая I — в перпендикуляр-
ную прямую ТП. Следовательно, точка А перейдет в
393
точку пересечения прямой ТП и отрезка НЕ, т.е. в точ-
ку В. Поворот является движением, поэтому ОА = ОВ .
Аналогично доказывается равенство отрезков ОВ, ОС
и OD. По признаку 1 параллелограмма получаем, что
ABCD — параллелограмм. Его стороны равны (они пере-
ходят друг в друга при повороте Т), поэтому ABCD —
квадрат. Ж
§ 15.10. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
©
15.01. Найти стороны прямоугольника, периметр ко-
торого равен 24 см, а площадь — 35 см2.
15.02 . Стороны прямоугольника равны 2 см и 24 см. Найти
стороны равновеликого прямоугольника, если его стороны от-
носятся как 3:4.
15.03 . Даны два квадрата, диагонали которых равны 5
и 3 . Площадь третьего квадрата равна разности площадей дан-
ных квадратов. Найти диагональ третьего квадрата.
15.04 . Площадь ромба вдвое меньше площади квадрата с
таким же периметром. Найти острый угол ромба.
15.05 . Определить сторону ромба, если отношение его диа-
гоналей равно 2:3, а площадь ромба равна 36 см2.
15.06 . Определить площадь треугольника по трем сторо-
нам:
а) 6 ; 25; 29, б) 5 ; Ц; 12^.
15.07 . Правильный треугольник со стороной а и ромб,
а
сторона которого равна —?=• и внутренний угол которого ра-
V2
вен 60°, равновелики. Доказать.
15.08 . Найти площадь треугольника, две стороны которого
равны 27 см и 29 см, а медиана, проведенная к третьей сторо-
не, равна 26 см.
15.09 . Найти площадь треугольника, высоты которого рав-
ны 12, 15 и 20.
15.10. Найти площадь прямоугольного треугольника с ги-
потенузой С и острым углом 15°.
394
15.11. Найти площадь прямоугольного треугольника, если
радиус описанной около него окружности равен 5 , а радиус
вписанной в него окружности равен 2 .
15.12. Найти площадь прямоугольного треугольника, если
радиус описанной около него окружности равен 5 , а радиус
вневписанной окружности, касающейся гипотенузы, равен 12.
15.13. Основания трапеции равны 6 и 20, а боковые сто-
роны 13 и 15. Найти площадь трапеции.
15.14. Высота трапеции равна 12 см, а длины ее диагона-
лей — 20 см и 15 см. Найти площадь трапеции.
15.15. В равнобедренной трапеции длина средней линии
равна 10 см, а диагонали — перпендикулярны. Найти площадь
трапеции.
15.16. Центр окружности, вписанной в прямоугольную
трапецию, удален от концов ее боковой стороны на расстоя-
ния 3 дм и 9 дм. Найти площадь трапеции.
15.17. Доказать, что площадь трапеции равна произведе-
нию длины боковой стороны на длину перпендикуляра, опу-
щенного на нее из середины другой боковой стороны.
15.18. Прямая, параллельная основанию треугольника, де-
лит его площадь в отношении 2:3, считая от вершины. В каком
отношении делятся этой прямой его боковые стороны?
15.19. В каком отношении, считая от вершины, необходи-
мо разделить боковую сторону треугольника тремя прямыми,
параллельными основанию, чтобы площадь треугольника разде-
лилась на четыре равные части?
15.20. Стороны треугольника равны 10, 10, 16. Найти ра-
диусы описанной и вписанной окружностей и расстояние меж-
ду их центрами.
15.21. Отрезок длиной 10 см соединяет боковые стороны
трапеции. Он параллелен основаниям трапеции и делит ее пло-
щадь пополам. Найти среднюю линию трапеции, если длины
оснований относятся как 1:7.
15.22. В трапецию можно вписать окружность и около нее
можно описать окружность. Найти площадь трапеции, если ее
основания равны 2 см и 6 см.
15.23. В равнобедренной трапеции основания равны 21
и 9 , а высота ее равна 8 . Найти радиус описанной окружно-
сти.
15.24. Найти площадь трапеции, если радиус описанной
около нее окружности равен R, острый угол равен а, а угол
между ее диагоналями равен р .
15.25. В треугольнике АВС стороны равны 12, 10 и 18.
Найти радиусы вневписанных окружностей.
395
15.26. Найти площадь прямоугольника, вписанного в пра-
вильный треугольник, если сторона треугольника равна Л, а
стороны прямоугольника относятся как 2:3, причем меньшая
из них лежит на стороне треугольника.
15.27. Точка касания окружности, вписанной в прямо-
угольный треугольник, делит его гипотенузу на отрезки а и b .
Найти площадь треугольника.
15.28. Найти площадь параллелограмма, меньшая диаго-
наль которого равна 5 см, а высоты — 4,8 см и 4 см.
15.29. Доказать, что если диагонали четырехугольника рав-
ны, то его площадь равна произведению отрезков, соединяю-
щих середины противоположных сторон.
15.30. В треугольнике ЛВС проведена медиана AD. Из-
вестно, что АВ = 5 , ВС = 6 , АС = 7 . В треугольники ABD
и ADC вписаны окружности с центрами в точках 1Х и /2. Най-
ти площадь треугольника DIXI2.
15.31. В остроугольном треугольнике АВС проведены вы-
соты АНХ и СН2. Известно, что площадь треугольника АВС
равна 18, а площадь треугольника ВНХН2 равна 2 . Длина от-
резка НХН2 равна 2^2. Найти радиус окружности, описанной
около треугольника АВС .
15.32. Через вершину А и центр О окружности, опи-
санной около треугольника АВС, проведен диаметр, пересе-
кающий сторону ВС в точке D. Доказать, что площа-
ди образовавшихся треугольников ABD и ACD относятся
как sin2B\sin2C.
15.33. Пусть М и N — точки касания окружности, впи-
санной в треугольник АВС , лежащие соответственно на сторо-
нах АВ и АС. Доказать, что
MN = (р- a) J------------.
V Ьс
15.34. Расстояния от точки Л/, расположенной внутри уг-
ла 60°, до сторон этого угла равны 41 и 241. Найти расстоя-
ние от точки Л/ до вершины этого угла.
15.35. Доказать, что из всех четырехугольников, вписан-
ных в данную окружность, наибольшую площадь имеет квад-
рат.
15.36. Доказать, что в остроугольном треугольнике сумма
расстояний от центра описанной окружности радиуса R до его
сторон равна R + г, где Г — радиус вписанной окружности.
396
15.37. Около равностороннего треугольника описана ок-
ружность. Доказать, что сумма расстояний от произвольной
точки окружности до двух ближайших вершин треугольника
равна расстоянию от этой точки до третьей вершины.
15.38. Доказать,что площадь 5 произвольного четырех-
угольника ABCD удовлетворяет неравенству
S <-(АВ +CD)(BC + AD).
4
15.39. Доказать, что из всех четырехугольников с данными
сторонами наибольшую площадь имеет тот, около которого
можно описать окружность.
15.40. В окружность вписан четырехугольник, три после-
довательные стороны которого равны 2>/5 см, 2л/5см, 6 см, а
четвертая сторона является диаметром окружности. Найти ра-
диус окружности.
15.41. Доказать, что из всех треугольников с данным осно-
ванием а и углом при вершине а наибольшую площадь имеет
равнобедренный.
15.42. Доказать, что из всех прямоугольников с данным
периметром наибольшую площадь имеет квадрат.
15.43. Доказать, что если в треугольнике АВС выполняет-
ся неравенство а < b < с и стороны образуют арифметическую
прогрессию, то Г = -
15.44. Каждая сторона равностороннего треугольни-
ка АВС разделена на три равные части. Через середину АС
и ближайшую к вершине С точку деления стороны ВС прове-
дена прямая /,. Через середину ВС и ближайшую к верши-
не В точку деления стороны АВ проведена прямая /2. Через
середину АВ и ближайшую к вершине А точку деления сто-
роны АС проведена прямая /3. Найти площадь треугольника,
образованного в результате попарных пересечений прямых 1Х,
12 и /а, если площадь треугольника АВС равна 5.
15.45. Найти площадь треугольника АВС , если известно,
что медиана AM равна ТП и угол В равен р, а угол С ра-
вен у .
15.46. В треугольнике АВС известно, что АВ = 5 ,
ВС = 7 , АС = 8 , AM— биссектриса, ВК — высота этого тре-
угольника. Найти площадь треугольника СКМ .
15.47. В трапеции, вписанной в окружность, диагонали
перпендикулярны и одно основание в 7 раз короче другого
397
основания. Найти площадь трапеции, если ее периметр ра-
вен 18 см.
15.48. В трапеции большее основание равно а, прилежа-
щие к основанию углы равны а и р , а меньшее основание
равно b . Найти площадь трапеции.
15.49. В равнобедренной трапеции основания равны а
и , а угол между диагоналями равен а. Найти площадь трапе-
ции.
15.50. Каждая из боковых сторон и меньшее основание
трапеции равны 10 см. Каким должно быть большее основание,
чтобы площадь трапеции была наибольшей?
15.51. Диагонали АС и BD трапеции ABCD пересекают-
ся в точке О. Найти площадь трапеции, если площадь треуголь-
ника AOD равна S,, а площадь треугольника ВОС равна S2,
15.52. Через точку внутри треугольника проведены пря-
мые, параллельные сторонам треугольника. Площади трех обра-
зованных треугольников равны Sp 52, 53. Найти площадь дан-
ного треугольника.
15.53. Построить треугольник, зная его высоты ha, 7^, hc.
15.54. Диагонали выпуклого четырехугольника делят его
на четыре треугольника. Доказать, что произведение площадей
двух противолежащих треугольников равно произведению пло-
щадей двух других треугольников.
15.55. Найти площадь выпуклого шестиугольника, три угла
которого прямые, а длина каждой стороны равна 1 .
15.56. В треугольнике АВС известно, что (2 = 15, b =14,
С = 13. Вычислить площадь треугольника, ограниченного высо-
той и биссектрисой, проведенными из точки В.
15.57. Точка М удалена от сторон угла в 60° на расстоя-
ния 3 и 9 , причем основания перпендикуляров, опущенных из
точки М на стороны угла, лежат на сторонах, а не на их про-
должениях. Прямая, проходящая через точку М, пересекает
стороны угла и отсекает треугольник, периметр которого ра-
вен 12>/з . Найти площадь этого треугольника.
15.58. Доказать, что если 5— площадь равнобедренного
треугольника с боковой стороной b и углом при вершине 10°,
то выполняется равенство:
(4£?
. b1 J 4S
398
ГЛАВА 16
ГЕОМЕТРИЯ МАСС
§ 16.1. ЦЕНТР МАСС СИСТЕМЫ МАТЕРИАЛЬНЫХ
ТОЧЕК
Рассмотрим известное в физике архимедово правило
рычага. На рис. 16.1 показаны две материальные точ-
ки Ах и А2 с массами тх и т2 соответственно, соеди-
ненные невесомым стержнем, имеющим точку опо-
ры М. Система будет находиться в равновесии тогда и
т2 МАХ
только тогда, когда -=------, что равносильно равен-
тх МА2
ству: пц • МАх = т2МА2 или МА1+т2 МА2 = 0, Точ-
ка М в механике называется центром масс систе-
At М As мы материальных точек Ах
Д* 1. I и А2. Далее приведем стро-
гие математические опреде-
ления.
I Материальной точкой бу-
дем называть пару (А;т),
т*9 Где А — некоторая точка
.. — плоскости, т — положитель-
I 9 ное число (масса точки А).
Системой материаль-
ных точек будем называть
множество, состоящее из конечного числа материальных
точек.
Центром масс системы материальных точек (Ах; тх),
(Я2;т2), ... , (А^;т^) называется такая точка М, для
которой выполняется равенство:
399
тц MA^+rn^ МА2+ ... + mkMAk = Q.
Для рассмотренной на рис. 16.1 системы, находящей-
ся в равновесии, точка М — центр масс точек (A^mj),
(A2;m2).
Будем считать в дальнейшем, что в плоскости задана
прямоугольная декартова система координат. Имеет ме-
сто
Теорема 16.1. Для данной системы материаль-
ных точек существует центр масс и притом только
один.
□ Пусть точки системы имеют координаты:
>£ 2 (х2»«У 2 )' ••• ' ^к(хк^Ук)^ и эти материаль-
ные точки имеют массы mv т2, ... , тк соответственно.
Найдем координаты точки Л/(х;у), удовлетворяющей
определению центра масс системы материальных точек.
Векторы MAit где i = 1, 2, ... , к имеют координаты
(х, -x;yt - у). Тогда вектор
МАу+щ МЛ2 + ... + тк МАк
имеет такие координаты:
Условие, что точка М является центром масс равносиль-
но системе уравнений:
- х) 4- тг(х2 ~ *) + ••• +7W*(x£~x) = 0
^(У1-У) + ^2(У2-У)+ - + тк(ук - у) = О,
откуда
/=1
/=1
/=1
400
Таким образом, центр масс
существует и притом
только один.
Теорема 16.2 (основное свойство центра масс).
Пусть дана система материальных точек
Тогда центр масс этой системы совпадает с центром
масс системы материальных точек
где М — центр масс системы материальных точек
, (Ак;тк).
□ Пусть точки Ах, А2, ... , Ак имеют такие коорди-
наты: А2(х2;у2), ... . Ак(хк;ук), а точки Bv
В2, ... , Bt — соответственно такие координаты:
B2(a2;Z>2), ... , Тогда, если
Vj) — центр масс данной системы точек, то
kt kt
Ymixi+H njaj E м+ X njbj
i=l j=\ i=l J=\
Щ=—---------------, V1=—---------------•
Z^+Z^ Z^+Z",
'=1 >=1 i=l j=\
С другой стороны, пусть Af2(u2;v2) — центр масс сис-
темы материальных точек
(М; тх + т2 +...+тк), (В2;и2), ..., (В,;и,).
Тогда
( к \ / ( к \ /
I JX4- I 1У +
Vj=i ✓ /=1 \/-1 7 /=1
U2 =---*-----------• V2 =--------к--J-----.
4- 4- Z«,
Ml j=l Ml J=1
Отсюда получаем:
401
к
к ^miXi t
У т< • -<=1-, - .—+Z »jaj
71 mi+m2+...+mk %
u2 =----------k------t-----------= Щ
i=l j=\
Аналогично v2 = v1, т.е. точки Mx и М2 совпадают.
§ 16.2. ЦЕНТР МАСС ТРЕУГОЛЬНИКА. ТЕОРЕМА ЧЕВЫ
Поместим в вершинах
треугольника АВС три рав-
ные массы ТП (рис. 16.2). То-
гда по теореме 16.2 центр
масс М треугольника АВС
будет центром масс систе-
мы точек (Ср 2m) и (С;т),
где С, — середина сторо-
ны АВ. Итак,
2пг-МСх+тМС = О,
Рис. 16.2
СМ о
откуда ----= 2. Мы доказали, что точка М лежит на
МСа
медиане CCj треугольника АВС и делит ее в отноше-
нии 2:1, считая от вершины. Учитывая единственность
центра масс, мы можем утверждать, что центр масс тре-
угольника, в вершинах которого сосредоточены равные
массы, совпадает с точкой пересечения медиан этого тре-
угольника.
Рассмотрим теорему Чевы, которая обобщает по-
следний результат.
Ч е в а Джованни (1648—1734) — итальянский ин-
женер, гидравлик и геометр. Построил учение о секу-
щих, которое положило начало синтетической геометрии.
402
Теорема 16.3 (теорема Чевы). Пусть точки Ах, Вх,
Сх лежат соответственно на сторонах ВС, АС, АВ
треугольника АВС. Отрезки ААХ, ВВХ, СС} пересека-
ются в одной точке М треугольника тогда и только то-
гда, когда
АВХ САХ ВСХ г
ВХС АХВ СХА ”
□ Введем такие обозначения:
(1)
САХ ВСХ
АХВ~ ’ СХА
В
рис. 16.3
Пусть сначала kin = 1. Дока-
жем, что отрезки ААХ, ВВХ,
ССХ пересекаются в одной
точке. Поместим в верши-
нах А, С, В соответствен-
но массы 1 , к, kl. Тогда
очевидно, что
ЬДЯ + Л-ДС = 0,
k-AxC + kl-AXB = Q,
т.е. точки Вх и Ах являются
центрами масс систем материальных точек соответствен-
но: (Л;1), (С;Л) и (С;Л), (jfykl). Тогда по теореме 16.2
центр масс М треугольника АВС лежит на отрез-
ках ААХ и BBV т.е. эти отрезки пересекаются в точ-
ке М (рис. 16.3). Затем докажем, что kl • СХВ 4-1 • СхА = 0.
Действительно, это равенство равносильно следую-
ВС
щему:
. Но — = и, и мы имеем верное равен-
kl
ство
ВСХ
СХА
= п. Таким образом, точка
Cj — центр масс
системы точек (В;#), (Л;1), и по теореме 16.2 точка Л/
403
лежит также на отрезке СС,. Значит, отрезки АА,, ВВ,
и СС, пересекаются в точке Л/.
Обратно, пусть отрезки АА,, В В,, СС, пересекают-
ся в точке М, Докажем равенство (1). Вновь обозначим
. . АВ, СА,
через к и / соответственно отношения ------ и ----.
В,С А,В
Пусть П — такое число, для которого kin = 1.
Доказательство проведем методом от противного.
ВС, АВ, СА, ВС, л
Допустим, что ----т.е.-------------------1. Выбе-
С,А В,С А,В С, А
ВС2
рем на отрезке ВА точку С2 такую, что----= п. Тогда
с2а
из доказанного выше следует, что отрезок СС2 проходит
через точку М. Значит, он совпадает с отрезком СС,, и
точки С, и С2 также совпадают. Таким образом,
АВ, СА, ВС, и
~В£ ~А^В qJ ~
§ 16.3. ПРИМЕНЕНИЯ ТЕОРЕМЫ ЧЕВЫ
Теорема Чевы позволяет доказать, что некоторые за-
мечательные отрезки в треугольнике пересекаются в од-
ной точке. Мы дадим также механическую интерпрета-
цию этим точкам. Отдельные приводимые ниже утвер-
ждения были уже установлены ранее, однако другим
способом.
Теорема 16.4. Три биссектрисы треугольни-
ка АВС пересекаются в одной точке I, которая являет-
ся центром масс системы материальных точек (Л;а),
(B;b), (С;с).
□ Пусть AL,, BL2, CL3 —биссектрисы треугольни-
ка АВС (рис. 16.4). По свойству биссектрисы имеем:
404
Рис. 16.4
Рис. 16. 5
AL3 _b BLX _ c CL2 _ a
L3B a' LXC b' L2A c
Перемножая эти равенства, получим
AL3 BLX CL2 _b c a _
L3B L,C L2A a b c
J A
Отсюда по теореме Чевы следует, что биссектрисы ALV
BL2, CL3 пересекаются в одной точке. Обозначим ее
через I.
Далее рассмотрим систему материальных точек
(Л;а), (В;б), (С;с). Центр масс этой системы лежит на
отрезке СК3, причем точка К3 лежит на стороне АВ
АК3 b
и -----= —. Таким образом, эта точка совпадает с
К3В а
точкой Z3, т.е. центр масс лежит на биссектрисе CL3.
Аналогично доказывается, что центр масс лежит также
на биссектрисах ALX и ВЬ2.
Теорема 16.5. Три высоты остроугольного тре-
угольника АВС пересекаются в точке Н, которая яв-
ляется центром масс системы материальных точек
(A;tgA\ (B;tgB), (C;tgC).
405
□ Пусть АНа, ВНЬ, СНс — высоты треугольни-
ка АВС (рис. 16.5). Из треугольника СНсА имеем:
АНс = hcCtSA •
Аналогично
ВНа = hactgB, ВНС = hcctgB, СНа = hactgC,
СНЬ = hbctgC, AHb = hbctgA.
Тогда:
АНС ВНа СНЬ _ hc ctgA ha ctgB hh • ctgC _ t
HCB HaC HbA hcctgB ha ctgC fy-ctgA
Таким образом, по теореме Чевы высоты АНа, ВНЬ,
СНс пересекаются в одной точке Н.
Далее рассмотрим систему материальных точек
(A-,tgA\ (B;tgB), (C;tgC). Ее центр масс лежит на от-
резке, соединяющем вершину С с точкой X на сторо-
не АВ, причем точка X делит отрезок АВ в отношении
АХ _ tgB _ ctgA
ХВ tgA ctgB
. Однако для точки Нс справедливо ра-
венство
АНС _ ctgA
НСВ ctgB
. Поэтому точки X и Нс совпадают.
Также совпадают отрезки СХ и СНс. Значит, центр
масс системы лежит на высоте СН. Аналогично доказы-
с*
вается, что центр масс системы лежит также на двух дру-
гих высотах. Н
Теорема 16.6. Отрезки, соединяющие вершины
треугольника с точками касания вписанной в этот тре-
угольник окружности, пересекаются в одной точке.
□ Пусть в треугольник АВС вписана окруж-
ность, К, N, М — точки касания этой окружности со
сторонами АВ, ВС, АС соответственно (рис. 16.6). Со-
гласно теореме 6.4 имеем:
AM = АК = р-а, BK = BN=p-b,
CM = CN =р-с.
Тогда
406
AK BN CM _ p-a p-b p-c _
KB NC MA p-b p-c p-a
и в соответствии с теоремой Чевы отрезки AN, ВМ
и СК пересекаются в одной точке Т.
Теорема 16.7. Отрезки, соединяющие вершины
треугольника с точками касания вневписанных окруж-
ностей со сторонами треугольника, пересекаются в од-
ной точке.
□ Пусть вневписанные окружности касаются сто-
рон АВ, ВС, СА треугольника АВС в точках F, К, D
соответственно (рис.16.7, 7.12). Согласно следствия из
теоремы 7.6 имеем:
AD = BK = p-c, CD = BF=p-a, CK = AF =p-b.
Далее,
AF BK CD _ p-b p-c p-a
FB КС DA p-а p-b p-c
И вновь из теоремы Чевы следует, что отрезки АК,
BD и CF пересекаются в одной точке N. И
§ 16.4. ТОЖДЕСТВА ЛАГРАНЖА И ЯКОБИ
Теорема 16.8. Пусть (Лр/nj), {А2*,т2)1 ... ,
) — некоторая система материальных точек
407
и М — ее центр масс. Тогда для произвольной точки Р
справедливо тождество Лагранжа:
к к
^т,РА2 = ^т,МА2 +(т}+... + тк)МР2.
/=1 /=1
□ Из правила сложения векторов следует, что для
каждого i = 1, 2, ... , к справедливо равенство:
откуда
А*Р2 = ДМ2 + 2 ДМ- МР + МР2
или
т,А,Р2 = т,А,М2 + 2т, А*М- МР + т, МР2. (1)
Складывая почленно все равенства вида (1), получаем:
/=1
к к _> _> к
= '£miAiM2 +2^т, А,М-МР + ^т>МР2 =
/=1 /=1 /=1
к _> к
= У^т,А,М2 -2 МР-^т, МА, +0^ + ... + тк}МР2.
/=1 Г=1
Поскольку М — центр масс системы точек (Д;^),
к -+ -+
(л2;^2 ).....(4 ',тк), то МА, = 0, откуда и следу-
/=1
ет требуемое равенство:
к к
т,РА2 =^т,МА2 +(тх +т2+...+тк)МР2.
/=1 /=1
Далее для совокупности чисел a,j, индексированных
двумя буквами / и j, под суммой ^^a,j будем пони-
l<j< j<k
мать сумму всех слагаемых вида a,j, где 1 < i < j < к.
408
Теорема 16.9. Пусть М — центр масс системы
материальных точек (Д ;»»]), (Д ;™2).(А!"»*). То-
гда выполняется тождество Якоби:
£ =-------------------- £ 4Д2 •
SM i ЯАА I 1 ллл лшяш J *
5=1 + • •• + ЖЛ
□ Рассматривая скалярный квадрат обеих частей ра-
венства
п\ МА} +nt2 МА2 +. . . + тк МАк = 0 ,
получим:
УХ МД2 =-2 ^m^MA^MAj .
5=1 К/< j£k
Тогда
к
(wi+mz-i- ... + mk)-^msMA2 =
5=1
= ^т2МА2 + ^пцт^МА2 + МА2)
s=l l<i<j<k
= У т.т. (МА 2 + МА / )-2 Упип, МА. МА. =
1 J \ 1 J ' 1 J 1 J
!&*</£& \<.i<j<k
У т.т. МА. - МА.
4—Л f J 1 J
откуда следует тождество Якоби.
Лагранж Жозеф Луи (1736—1813) — француз -
ский математик и механик, автор фундаментальных ра-
бот по математическому анализу; алгебре, теории диффе-
ренциальных уравнений и вариационному исчислению.
Участвовал в работе комиссии по разработке метричес-
кой системы мер.
Якоби Карл Густав Якоб (1804—1851) — немец-
кий математик. Ввел эллиптические функции, с помощью
которых выражается длина дуги эллипса, внес значитель-
ный вклад в разработку методов механики.
409
§ 16.5. ПРЯМАЯ ЭЙЛЕРА И ОКРУЖНОСТЬ ЭЙЛЕРА
В этом параграфе мы приведем два замечательных
результата, принадлежащих Эйлеру.
Прямая Эйлера.
Т е о р е м а 16.10. В треугольнике точка пере-
сечения медиан, ортоцентр и центр описанной окружно-
сти лежат на одной прямой.
□ Проведем через вершины треугольника АВС
прямые, параллельные сторонам треугольника, до их вза-
имного пересечения в точках Лр Вр С} (рис. 16.8). Тогда
четырехугольники АВА^С, CACxBt АВСВ х —паралле-
лограммы. Значит,
ВСХ = ВАХ = АС,
ВХС = АХС = ВА.
Отрезки ЛЛР BBV ССХ яв-
ляются диагоналями этих
параллелограммов и делят
пополам стороны ВС, АС,
АВ соответственно. Тогда
эти отрезки пересекаются в
точке М пересечения меди-
ан треугольника АВС, и
Ci В А1
Рис. 16. в
МА МВ МС 1
МА, МВ, МС, 2
Это значит, что при гомотетии с
центром в точке М и
коэффициентом к =---треугольник АВС
переходит в
треугольник AXBXCV Как было доказано еще в теоре-
ме 7.3, данная гомотетия переводит центр О окружности,
описанной около треугольника АВС/в точку Н, т.е. точ-
ки М, О и Н лежат на одной прямой. При этом точка
М лежит между точками О и Н, и МН =2 МО
(рис. 16.9).
Следствие. В треугольнике прямая, проходящая
через точку пересечения медиан, ортоцентр и центр
410
Рис, 16,10
описанной окружности, называется прямой Эйлера. В
треугольнике АВС справедливы равенства:
МН =2-МО, ОН = ЗМО.
Окружность Эйлера.
Теорема 16.11. В треугольнике основания меди-
ан, основания высот и середины отрезков, соединяющих
вершины треугольника с ортоцентром, лежат на одной
окружности.
□ Пусть в треугольнике АВС точки Ait Bv Q —
середины сторон ВС, АС, АВ соответственно, точ-
ки На, Нь, Нс — основания высот, точки Л2, В2, С2 —
середины отрезков АН, ВН, СН соответственно
(рис.16.10). Отрезки С\ВХ и С2В2 параллельны ВС как
средние линии треугольников АВС и НВС. Аналогично
отрезки В\С2 и С\52 параллельны АН, Кроме то-
го, АН и ВС перпендикулярны, следовательно, четы-
рехугольник В}СХВ2С2 — прямоугольник. Аналогично ус-
танавливается, что ClAiC2A2 — также прямоугольник.
Тогда три отрезка АХА2, ВХВ2 и С}С2 равны между со-
бой и делятся в общей точке пересечения пополам, т.е.
это три диаметра некоторой окружности. Диаметр АХА2
стягивает прямой угол AJ^A^, поэтому эта окружность
содержит точку На. Диаметр ВХВ2 стягивает прямой
угол В,НьВг, а диаметр СХС2 стягивает прямой угол
411
поэтому на этой окружности лежат также точ-
ки Нь и Нс.
В треугольнике окружность, проходящая через три
основания медиан, три основания высот и три середины
отрезков, соединяющих вершины с ортоцентром, назы-
вается окружностью девяти точек или окружностью Эй-
лера.
Эйлер Леонард (1703—1783) — математик, фи-
зик, механик и астроном. Много лет провел в России.
Почти во всех областях математики встречается имя Эй-
лера. Внес весомый вклад в математический анализ, ва-
риационное исчисление, ввел понятие функции ком-
плексной переменной. Применил математические методы
в теории чисел. Эйлер является одним из творцов совре-
менной дифференциальной геометрии.
§ 16.6. РАССТОЯНИЯ МЕЖДУ ЗАМЕЧАТЕЛЬНЫМИ
ТОЧКАМИ ТРЕУГОЛЬНИКА
Используя основные результаты геометрии масс, ус-
тановим формулы для расстояний между точками М, О,
I, Н треугольника АВС , стороны которого равны а, b ,
С; R — радиус описанной окружности, Г — радиус впи-
санной окружности.
Т е о р е м а 16.12. В треугольнике АВС справедли-
вы следующие равенства:
1) ОМ = -yl9R1-a1-b2-c1.
3
2) МН = —yl9R2-a2-b2-c2.
3______________
3) ОН = y/9R2-g2-b2-c2.____________
„ __ _ IЗаЬ + Зле + ЗЬс -а2 -Ь1 - с1 abc
4) IM = I--------------------------.
N___________?_______ р
I -> а3 4 5 + Ь3 +с3 +abc
5) IH = J4R2 --—-— .
V а+Ь+с
412
6) 10 = ylR2-2Rr.
□ Поместим в вершинах треугольника АВС еди-
ничные массы. Тогда точка М является центром масс
треугольника АВС. Используя формулу Лагранжа для
точки О, получим:
ОА2 + ОВ1 + ОС1 = МА2 + МВ2 + МС2 + ЗОМ2.
Однако
ОА = ОВ = ОС = R,
МА2+МВ2 + МС2 =-(та2 +ть2 +т2) =
4 3 / 9 ,2 2 I 2 . 1 2 2 \
------1а +6 +с21 = -1а*+Ь +с ).
9 4К 7 Зк 7
Мы использовали здесь также теорему 11.11 и следст-
вие 1 из теоремы 14.3. Итак,
ЗЯ2 = а2 + 62 + с2 + 2
или
9OM2 = 9R2-а2-Ъ2-с2,
откуда и следует формула 1).
Так как согласно следствию из теоремы 16.10
МН =2МО и ОН = ЗМО, то, используя формулу 1),
получим:
МН =^9R2-a2-b2-c21
OH = ^9R2-a2-b2-c2.
Формулы 2) и 3) доказаны.
Поместим далее в вершинах Л, В, С соответствен-
но массы а, 6, С. По теореме 16.4 центром масс тре-
угольника АВС является точка I пересечения биссек-
трис этого треугольника. Применяя формулу Лагранжа
для точки М получаем:
а-МА2 +b-МВ2 +с-МС2 =
= а!А2 +b-IB2 +с-1С2 +(a + b + c)lM2.
Согласно формуле Якоби, имеем:
а-1А2 +Ь1В2 +с-1С2 =
413
=--------(ab-AB2 + ас-AC2 + be ВС2) =
a + b + c
abc2 + ab2 c + a2 be
=----------------= abc.
a + b + c
Кроме того,
MA2 = --m2=-(2b2 +2c2-a2),
9 a 9' 7
MB2 = -(2a2 + 2c2 - b2), MC2 = ~(2a2 + 2b2 - c2
9' 7 9V
Тогда
(a + b + c)lM2 =
a(2b2 +2c2 -a2)+b(2a2 +2c2 -b2)
_ +
c(2a2 +2b2 — c2)
+----------------abc =
9
(2a2b + 2ab2 + 2abc) + (2ac2 + 2a2 c + 2abc)
= _ +
(2bc2 + 2b2c+2abc)-15abc-a3 -b3 -c3
+ _
2(ab + ac + bc)(a + b + c)-(a3 +b3 +c3 -3abc)
ISabc
9
Применяя формулу
a3 +b3 +c3 -3abc =
получим:
IM2 =
414
(a+Z> + c)(a2 +b2 +c2 - ab - ac - be) - liabc
9(a + b + c)
(a + b + с)(ЗаЬ + 3ac + 3bc - a2 -b2 -c2)-\%abc
9(a + b + c}
2р(ЗаЬ + Зас + ЗЬс-a2 -b2 -c2)-lSabc
Таким образом,
IM2
3ab + 3ac + 3bc-a2 -b2 -c2 abc
9 P
и формула 4) доказана.
Аналогично, используя формулу Лагранжа для точ-
ки Ht имеем:
а НА2+ Ь НВ2+ с-НС2 =
= а1А2+ЫВ2 + cIC2 + (a + b + c)lH2.
Однако из теоремы 15.20 следует, что
HA2=4R2-a2, HB2=4R2-b2, HC2=4R2-с2.
Значит,
(а + b + с)1Н2 = a(4R2-a2) + b(4R2-Ь2) +
+ c(4R2 -с2)-(а1А2 + ЫВ2+с1С2).
Как было доказано выше,
а1А2 + ЫВ2 + cIC2 = abc.
Тогда
(а + b + c}lH2 = 47?2 (а + b + c)-a3-b3-c3-abc,
откуда находим, что
IH2 = 4 R2
а3 +Ь3 + с3 +abc
а+Ь + с
Следовательно, формула 5) доказана.
Наконец, применяя формулу Лагранжа к точке О,
получим:
а-ОА2 +ЬОВ2+с-ОС2=
= а-1А2 +Ь1В2 +с1С2 +(а + Ь + с)Ю2.
415
Отсюда
R2(a + b + c) = abc + (a + b + c)lO2,
IO2 -(a + b + c) = R2 (a + b + c) - abc,
IO2 = R2= R2-4RS-. — = R2-2Rr .
2p r
Обозначим IO через d и запишем последнюю фор-
мулу доказанной теоремы 16.12 в виде
d2 = R2-2Rr.
Это равенство называется формулой Эйлера.
§ 16.7 ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 16.1. В тре-
АВС в верши-
угольнике
нах А, В, С помещены мас-
сы 1 , 2, 3 соответственно.
Построить центр масс образо-
ванной системы материальных
точек.
Найдем вначале
центр масс системы двух
материальных точек ( А; 1)
и (jB;2) (рис.16.11). Это бу-
дет такая точка L на сторо-
м
Рис. 16.11
не АВ, для которой 1 • LA 4- 2 • LB = 0, т.е. -= —. То-
LB 1
гда по теореме 16.2 центр масс М системы материаль-
ных точек (Л;1). (В;2), (С;3) совпадает с центром масс
системы материальных точек (Z;3), (С;3). Таким об-
разом, точка М делит пополам отрезок CL, при-
чем AL: LB =2:1. Ж
Пример 16.2. В вершинах трапеции ABCD помещены
равные массы. Доказать, что центр масс образованной систе-
мы материальных точек является серединой средней линии
трапеции.
416
Рис.16.13
Пусть в вершинах трапеции ABCD (рис. 16.12)
помещены равные массы ТП. Тогда центром масс системы
материальных точек (Л;ти), является середина
стороны АВ, а центром масс системы материальных то-
чек (C;zn)r (D;/n) является середина N стороны CD.
Отрезок MN является средней линией трапеции.
По теореме 16.2 центр масс системы материальных точек
(А;т), (В;т), (С;т), (D;m) совпадает с центром масс
системы материальных точек (М,2т), (N;2m), а зна-
чит, искомый центр масс S является серединой средней
линии MN. А
П р и м е р 16.3. Середины сторон выпуклого шести-
угольника соединены через одну. Доказать, что два образовав-
шихся треугольника имеют общую точку пересеченья медиан.
ZX Поместим в вершинах Ах, А2, А3, А4, А5, А6
данного выпуклого шестиугольника единичные массы
(рис. 16.13). Тогда точки Вр В2, В3 являются центрами
масс отрезков АХА2, А3А4, А5А6 соответственно, а точ-
ки Ср С2, С3 — центрами масс отрезков А6АХ, А2А3,
А4А5 соответственно. По теореме 16.2. центр масс дан-
ного шестиугольника совпадает как с центром масс тре-
угольника BxB2B3f так и с центром масс треугольни-
ка СХС2С3. При этом в вершинах каждого из треугольни-
ков помещены массы, равные 2. В силу единственности
417
центра масс шестиугольника центры масс треугольни-
ков ВХВ2В3 и CjC2C3 совпадают. Однако эти центры
масс являются точками пересечения медиан этих тре-
угольников. Значит, оба треугольника имеют общую
точку пересечения медиан. А
Пример 16.4. Найти такую точку плоскости, чтобы
сумма квадратов расстояний от нее до вершин данного тре-
угольника была наименьшей.
Zs Пусть X — произвольная точка плоскости, М —
точка пересечения медиан треугольника АВС. Помес-
тим в вершинах А, В, С единичные массы. Применяя
тождество Лагранжа, получаем:
ХА2 + ХВ2 + ХС2 = МА2 + МВ2 + МС2 + ЗМХ2,
откуда
ХА2 + ХВ2 + ХС2 > МА2 + МВ2 + МС2.
Следовательно, величина ХА2 + ХВ2 + ХС2 будет
наименьшей тогда и только тогда, когда точки X и М
совпадают. Поэтому сумма квадратов расстояний до вер-
шин треугольника будет наименьшей для точки пере-
сечения медиан треугольника. А
Замечание. Доказанное при решении примера ут-
верждение имеет интересную механическую интерпретацию.
Поместим в вершины треугольника равные массы. Спрашива-
ется: относительно какой точки момент инерции треугольника
будет наименьшим? Оказывается, такой точкой является центр
масс треугольника.
Пример 16.5. На ме- А
AD треугольника АВС
выбрана точка К такая, что У^ / \
АК: KD =4:1. В каком отноше- / / \
нии прямая ВК делит пло- / \
щадь треугольника АВС ? У^ / \
ZS Проведем через —\
точку К отрезки BL и СТ S \
(рис. 16.14). Поместим в вер-
шинах В и С единичные D В
массы. Тогда середина D
стороны ВС является цен- Рис. 16.14
тром масс системы матери-
альных точек
418
Поместим в точку А такую массу X, чтобы точка К ста-
ла центром масс системы материальных точек (Л;х),
(В;1), (С;1). По теореме 16.2 этот центр масс совпадает
с центром масс системы (Л;х), (D;2). Тогда для точ-
„ DK х
ки К должно выполняться равенство = откуда
имеем:
Из теоремы 16.2 и определения центра масс следует те-
перь, что точка
риальных точек
L является центром масс системы мате-
24;— I и (С;1). Отсюда
AL
Имеем далее:
S&ABL _ А.
5ДСВ£ cl 1 ’
Пример 16.6. Стороны треугольника АВС равны:
ЛВ=5, ВС =6, АС = ^, Пусть биссектриса AL и медиана
ВВХ пересекаются в точке К. Найти отрезки АК и ВК
(рис. 16.15).
ZS Из теоремы 14.3 следует, что
2
41
Найдем полупериметр треугольника АВС :
Р =
= 10.
По теореме 14.7 получаем:
„ 2-Jab-ас
419
30V2
Поместим в вершинах А и С единичные массы, тогда
точка В, является центром
масс системы материальных
точек (Я;1) и (С;1). По
свойству
угольника
биссектрисы тре-
BL АВ
имеем: ---=-----,
BL
—. Пусть L
центр масс системы матери-
альных точек (С; 1) и (В;х).
Рис, 16,15
Тогда
1 5 19
= —, откуда — = —, х = —. Из теоремы 16.2 и
определения центра масс следует, что центр масс систе-
(С;1) леж"т на
мы материальных точек
отрезках AL и BBV т.е. он совпадает с точкой К. Вновь,
по теореме 16.2 точка К является центром масс системы
и (Д;2). а также центром
материальных точек В; —
масс системы материальных точек
Да
э.9 rf 10 гп
= 2: — , откуда ВК = — KBV и значит,
вк=—вв}=—
19 ' 19
19
14
Аналогично
откуда
— = 14:1,
420
14
Следовательно,
14 .. 14 30л/2
Лл = — AL -------------
19 19 7
60л/2
19
Итак,
19 19
Пример 16.7. В треугольнике АВС известно, что
АВ =5, ВС = 6, ЛС=7. Найти ОМ, МН, ОН, IM, Ш, Ю,
где О — центр описанной окружности, I — инцентр, М —
точка пересечения медиан треугольника АВС, Н — орто-
центр.
По формуле Герона имеем:
S&ABC = ^1 р(р - а)(р - - с) .
Так как р = 9, то
SMBC =79(9-5)(9-б)(9-7) = 3-2Тб = бТб.
Тогда радиус описанной окружности равен:
R = АВ ВС АС = 5 6 7 = 35
4-бл/б 4л/б
а радиус вписанной окружности:
_ Здавс __ 6л/б _ 2-Уб
Г~ р ” 9 Г”’
Применяя формулы из теоремы 16.12, получим:
ОМ = - y/9R2-а2-Ь2-с2 =
> ^-25_36-49=^,
ЗУ 96 24
.т эплх V310 оллу л/зТо
МН = 1UM =--------, ОН = ЗОМ =-------,
_________12__________________8_
г,, 13аЬ + Зас + ЗЬс - а2 — b2 — с2 abc
У 9 Р
421
§ 16.8. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
А
16.01. Точка М является центром масс системы точек
(Л;т), (В;5) и делит отрезок АВ в отношении AM :МВ = 2:3.
Найти массу 7W.
16.02 . В треугольнике АВС биссектриса AL и медиа-
на ВВ} пересекаются в точке D. Известно, что АВ: АС =2:1. В
каком отношении, считая от вершины А, прямая CD делит от-
резок АВ 1
16.03 . Доказать, что если точки А}, А2, ... , лежат на
прямой / , то центр масс системы (Яр/иД ... , (Astms)
также лежит на прямой / .
16.04 . Пусть ABCD — параллелограмм, в вершинах кото-
рого находятся равные массы. Где находится центр масс систе-
мы точек Л, В, С, D1
16.05 . Дана трапеция ABCD с основаниями AD—at
ВС = Ь. Доказать, что центром масс системы точек (Л;б),
(В;а), (С;а). м является точка пересечения диагоналей.
16.06 . Теорема Менелая. Пусть в треугольнике АВС на
сторонах ВС, СА и АВ или на их продолжениях выбраны со-
ответственно точки Вр Ср не совпадающие с вершинами
422
треугольника. Доказать, что точки A,, В,, С, лежат на одной
прямой тогда и только тогда, когда выполняется равенство:
ВА, СВ, АС, _
- *
АХС ВХА СХВ
Менелай Александрийский (1в.) — древнегреческий
математик и астроном. Автор работ по сферической тригоно-
метрии.
16.07 . На сторонах АВ и АС треугольника АВС заданы
iz v AM CN 1
соответственно точки м и N, причем ------=-----= —. В ка-
МВ NA 2
ком отношении точка S пересечения отрезков BN и СМ де-
лит каждый из этих отрезков?
16.08 . В треугольнике АВС через середину медианы ВВХ
проведена прямая, параллельная медиане ССХ. В каком отноше-
нии делит эта прямая стороны АВ и ВС 2
16.09 . В треугольнике АВС на стороне АС выбрана точ-
ка М, а на стороне ВС выбрана точка N, причем АВ || MN .
Доказать, что точка пересечения отрезков AN и ВМ лежит на
медиане ССХ.
16.10. Доказать, что для произвольной точки О выполняет-
ся равенство
ОМ =-\ ОА, + ОА2+ ... + СИ„ |,
)
где М — центр масс системы точек (Л,; 1), ... , (Ап; 1).
16.11. Для произвольных точек А, В, С, X доказать ра-
венство:
МА2 + МВ2 + МС2 = ХА2 + ХВ2 + ХС2 + ЗАЛ/2,
где М — точка пересечения медиан треугольника АВС .
16.12. На сторонах АВ, ВС, СА треугольника АВС вы-
браны точки М, N, Р такие, что AMzMB^k, BN:NC = n,
СР:РА = 1, где к, П, I— некоторые положительные числа,
причем knl = 1 . Доказать, что прямые AN, BP, СМ пересека-
ются в одной точке. Найти отношение площади треугольни-
ков MNP и АВС.
16.13. В выпуклом четырехугольнике ABCD точки Е
и F — середины сторон ВС и AD, а точки G и Н — середи-
ны диагоналей АС и BD. Доказать, что отрезки EF и GH в
точке пересечения делятся пополам.
423
16.14. Пусть (А^щ), (Л^гъ), ... , (Л^б) — систе-
ма материальных точек. Р — центр масс первых двух из
них, Q — центр масс следующих двух точек, R — центр масс
оставшихся двух точек. Доказать, что центр масс данной систе-
мы совпадает с центром масс системы (Р;/И| ч-ти^), + /и4),
16.15. Теорема Ван-Обеля. Для прямых Чевы ААХ, ВВХ,
ССХ, пересекающихся в точке К, выполняется равенство:
АК_=АВ± AQ
КАХ “ В1С+С1В*
Доказать это.
В а н-О бель — бельгийский математик.
16.16. Теорема Жергонна. Если прямые AAV ВВХ, ССХ пе-
ресекаются в точке К, лежащей внутри треугольника АВС , то
выполняются равенства:
ХЛ, । । КСХ р
АХА + ВХВ + СХС ” '
КА КВ КС 2
АА । ВВХ ССХ
Доказать это.
Ж е р г о н н Ж.Д. (1771—1859) — французский астро-
ном и математик.
16.17. Доказать, что центр окружности Эйлера треугольни-
ка АВС — середина отрезка, соединяющего ортоцентр и центр
описанной около треугольника АВС окружности. Найти отно-
шение радиуса описанной около треугольника АВС окружно-
сти к радиусу окружности Эйлера.
16.18. Через вершины треугольника АВС параллельно
сторонам проведены прямые, пересекающиеся в точках Ах, Вх,
СР Доказать, что окружность Эйлера треугольника 4ДС] явля-
ется окружностью, описанной около треугольника АВС, а ок-
ружность Эйлера треугольника АВС является окружностью,
описанной около ортоцентрического треугольника НХН2Н3.
16.19. На сторонах ВС, СВ и АВ треугольника АВС вы-
браны точки Ах, Вх, Сх так, что прямые ААХ, ВВХ, ССХ пересе-
каются в одной точке. Доказать, что прямые, симметричные
этим прямым относительно соответствующих биссектрис, так-
же пересекаются в одной точке.
424
16.20. Доказать, что основания перпендикуляров, опущен-
ных из точки, лежащей на окружности, на прямые, содержа-
щие стороны вписанного в эту окружность треугольника, ле-
жат на одной прямой (эта прямая называется прямой Симеона).
Симеон Р. (1687—1768) — шотландский математик.
16.21. Даны два параллелограмма ABCD и AMPN ,
причем вершины М и N второго параллелограмма принадле-
жат сторонам АВ и AD первого. Прямые BN и DM пересе-
каются в точке О, Доказать, что точки С, Р и О лежат на од-
ной прямой.
16.22. Три окружности разных радиусов расположены на
плоскости так, что каждая из них не лежит в круге, ограничен-
ном другой окружностью. Для каждой пары окружностей по-
строим точку пересечения их двух общих внешних касатель-
ных. Доказать, что полученные три точки лежат на одной пря-
мой.
16.23. На сторонах АВ , ВС и АС данного остроугольного
треугольника АВС во внешнюю от него сторону построены как
на основаниях попарно подобные равнобедренные треугольни-
ки А}ВС, АВ}С, АВСХ. Докажите, что прямые АА}, ВВ} и СС}
пересекаются в одной точке.
425
ГЛАВА 17
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
§ 17.1. СВОЙСТВА ПРАВИЛЬНЫХ
МНОГОУГОЛЬНИКОВ
Правильные многоугольники. Основное свойство
правильного многоугольника. Разделим окружность с
центром в точке О и радиусом R точками А}, А2, .... Ап
на дуги равной градусной меры. Соединим последова-
тельно точки А}, А2, .... Ап и А} отрезками. В результате
образуется Л-угольник Л]Л2 .... Ап, который мы назовем
правильным. Точки Av А2, Ап являются его верши-
нами, отрезки JjH2, Л2Л3, ...,
Ап_1Ап, АпА} — его сторона-
ми, а углы А}А2А3, А2А3А4,
> Л-14.4- АпА1А2 — внут-
ренними углами многоуголь-
ника (рис. 17.1).
Теорема 17.1.В пра-
вильном многоугольнике все
стороны равны и все внут-
ренние углы равны.
□ Согласно первому при-
знаку равенства треугольни-
ков имеем:
&OAj А2 = ДОА2А3= ... =ЛОА„А1
1 Л» Л9 J fl 1
(рис.17.1). В самом деле, ОЛ1=ОЛ2= ... = ОАп как ра-
диусы окружности, ЛАХОА2 = ZL42CM3 = ... =ЛАпОА}
как центральные углы, опирающиеся на равные дуги.
Следовательно, стороны А}А2, А2А3, ... , АпА} рав-
ны как соответственные стороны равных треугольников.
Из равенства треугольников следует также, что углы
426
OA}A2, OA2A3, ... , ОАпАх равны между собой, и по-
этому углы AnAxA2t АХА2А3, ... , Ап_хАпА} также равны
как углы, составленные из двух равных углов. И
Признак правильного многоугольника. Рассмотрим
утверждение, обратное к утверждению теоремы 17.1.
Теорема 17.2. Если в многоугольнике все сто-
роны равны и все внутренние углы равны, то такой
многоугольник является правильным.
□ Пусть в многоугольнике АХА2 ... Ап выполняются
равенства:
Л1Л2 = Л2Л3= ... =ЛиЛр
zL41 = zL42= ...
Проведем биссектрисы уг-
лов А2 и А3. Пусть О — их
точка пересечения. Соединим
также все остальные вершины
многоугольника с точкой О
(рис. 17.2). В треугольниках
ОАХА2 и О42Л3 сторона ОА2
является общей, Ах А2 = А2А3 и
ХОА2Ах= ХОА2А3 как половины внутреннего угла А2.
Поэтому треугольники ОАХА2 и СМ2Л3 равны. Кроме
того, треугольник ОАХА2 — равнобедренный, так как
ХОА}А2 = ZOA2A{ =—. Значит,
ОА} — ОА2 = ОА3
Л Лг
и
ЛОА, А, = ЛОА.А, = ЛОА, А. =
IX J X J
т.е. ОА3 — биссектриса угла А3. Аналогично получаем,
что ДОЛ2Л3 = ДОЛ3Л4 = ДОЛ4Л5 = ... =ДО4ЛЛр Значит,
ZAXOA2 = ZA2OA3 = ... = ZAnOAv и тогда <jAxA2 =
= <jA2A3 = ... = иЛЛЛр а лучи АХО, А2О, ... , АпО яв-
427
В
Рис.17,3
В
D
Рис.17.4
ляются биссектрисами углов АпАгА2, АаА2А31 ... ,
Ап_х AnAv Таким образом, данный многоугольник являет-
ся правильным.
Центр правильного многоугольника. Центр О ок-
ружности, описанной около правильного многоугольни-
ка, называется центром этого многоугольника.
Центр О правильного П -угольника лежит на биссек-
трисах его внутренних углов, поэтому точка О является
также центром окружности, вписанной в этот много-
угольник.
Рассмотрим некоторые правильные многоугольники.
Правильный треугольник. Пусть АВ = ВС = АС =
= а,- AAV BBV СС} — высоты треугольника АВС.
Обозначим АА} = BB^CC^h, OA=OB—OC = Rt
ОАХ = ОВ} = ОС} = г, СС, — площадь треугольника
АВС (рис. 17.3). Тогда
ал/з aJl а4з аг4з
п =-----, R =-----, г =----, R = 2r, S =-----.
2 3 6 4
Правильный четырехугольник. В этом случае
АВ =ВС =CD = AD =а, AC = BD = d, d=aj2. R =
Правильный пятиугольник. Пусть Л]у42Л3Л4Л$ —
правильный пятиугольник. Обозначим его сторону че-
428
Рис.17.5
Тогда
= 72°. Найдем связь между ра-
диусом R описанной окруж-
ности и радиусом Г вписан-
ной окружности (рис. 17.5).
Если ОМ — высота тре-
угольника ОА1А2, то ом
одновременно является бис-
сектрисой и медианой этого
треугольника, а также радиу-
сом окружности, вписанной
в этот пятиугольник. Очевид-
но, что
72
Z.A.OM = 36°.
1 2
Ах М = OAxsinZAxOM = Rsin 36°,
ОМ = OA}cosAA}OM = Rcos 36°;
a = 2R sin36°, r = Rcos36°.
Чтобы вычислить sin36° и cos36°, найдем снача-
ла ли18°. Имеем: sin54° = sin(90° -36°) = СО5'36°. Далее
воспользуемся формулами тригонометрии:
sin3a = 3sina -4sin3а и с<м2а = 1 - 2sin2a.
Выражая sin54° и cos36° через 5ш18°, получим:
3«и18° -4«л318° = 1-25ш218°,
откуда имеем кубическое уравнение относительно вели-
чины у = 57и18°:
4/-2/-Зу + 1 = 0.
Так как сумма коэффициентов
4—-2-3 + 1 = 0,
то у = 1 — один из корней этого уравнения. Тогда
4j3 - 2у1 - Зу +1 = 4у3 - 4у2 + 2у2 - 2у2 - у +1 =
= 4/ (у -1) + 2у(у -1) - (у -1),
откуда имеем:
429
(y-l)(4/+2^-l) = 0.
Получаем:
Поскольку
О < sinl 8° < 1, то sin\8° =
или
sinl 8° = | ^(>/5 -1)2 = | д/б-2л/5 .
Тогда
cosl8° = Vl-5zn218° = J1 - 6~2л^ = -710 + 275 .
V 16 4
Таким образом,
sin36° = 2«и18°со$18° = 2--7б-275--710 +275 =
4 4
= | ^(з-75)(5 + 75) = 1710-275 = 75-75.
Значит, а =----Ryj5 — J5
2
Найдем соу36°. Имеем:
С 05 36° = СО5218° - sm218’ =^(10 + 275-6 + 275) =
R ( rz
Таким образом, г = “yVi +1/.
Замечание. Нахождение значений тригонометричес-
ких функций для углов 18° и 36° можно произвести иным спо-
собом — с использованием золотого сечения (см. §19.7).
Правильный шестиугольник. Рассмотрим правиль-
ный шестиугольник Л3Л4 Л5Л6. Очевидно, что
430
Рие.17.6 Рис.17.7
ZAlOA2 = zS42CM3 = ...=ZA6OAl = 60°,
т.е. шестиугольник делится радиусами OAV ОА2, .... ОА6
на шесть правильных треугольников (рис. 17.6). Значит,
R = a. Отрезок ОМ = г является высотой правильного
. а-/3
треугольника АУОА2, откуда Г =———. Наконец,
о А о & °2 о ^л/З 2
5 = 6-5^^ =6——, т.е.о=——- а.
“Т
Заметим, что ХА}ОАа = 3-60° = 180°, поэтому диаго-
нали AYA4, A2A5t А3А6 являются диаметрами описанной
окружности.
Правильный Л-угольник. Пусть А}А2 ... Ап — пра-
вильный многоугольник, ОМ — радиус вписанной в него
180°
окружности (рис. 17.7). Тогда AAXVM =-----. Из
п
угольника ОАХМ получаем:
04, =----„ т.е. R =-----------------.
‘ sinZA.OM „ . 180°
1 2sin----
п
тре-
Далее, ОМ = АХМ-ctgZAxOM> т.е. г = — ctg
180°
п
431
Теорема 17.3. Пусть ап и а2я — стороны пра-
вильного Л-угольника и правильного 2и-угольника,
вписанных в окружность ра-
диуса R. Тогда справедливо
равенство:
«,=2Л’-2Л^1-^.
□ Пусть АВ — сторона
правильного П -угольника и
точка С делит дугу АВ попо-
лам (рис. 17.8). Тогда АС —
сторона правильного 2 77-
угольника, вписанного в ту
же окружность. Таким обра-
зом, ОА =ОВ = R, АВ = ап, AC = а2п- Из треугольни-
ка АМС получаем:
МС = JAC2 - AM1 = Ja22n - .
Из треугольника АОМ имеем:
МО = Jao2-am2 = Jr2-^-.
У 4
Однако, МС + МО = R. Значит,
Г~2 ?
ja2„-—+Jr -— = r
V 4 V 4
и тогда
,U„ - = r - Jr2-—.
V 4 V 4
Возведем обе части этого равенства в квадрат. Получим:
9 я2 о I й а2" 9 а2
а2п —- = R -2RJR2 —0- + ri_2’Li
2" 4 V 4 4
откуда:
432
что и требовалось доказать.
Используя выведенную формулу, выразим через R
сторону а8 правильного 8-угольника. Поскольку
I d2
я4 = Ял/2, то a2s = 2R2-2R, Я2- —,
откуда
а8 = R^2-y[2 .
Аналогично имеем: а6 = R, тогда
a2 = 2R2 -2RJR2 - —
12 V 4
ИЛИ
а12 = R^2-y[3.
§ 17.2. ПОСТРОЕНИЕ ПРАВИЛЬНЫХ П-УГОЛЬНИКОВ
ЦИРКУЛЕМ И ЛИНЕЙКОЙ
Циркуль — это чертежный и измерительный инст-
румент, с помощью которого чертят окружности или от-
кладывают равные отрезки.
Линейку будем рассматривать без делений и исполь-
зовать как инструмент для проведения прямой через
две данные точки. Рассмотрим некоторые геометричес-
кие построения с помощью только двух этих инструмен-
тов. Такое ограничение ввел древнегреческий философ
Платон (427—347г.г. до н. э.). Построения циркулем и
линейкой сыграли большую роль в развитии геометрии.
Термин "циркуль" происходит от латинского слова
circulus — окружность, круг.
Построение прямого угла. С помощью циркуля
строим окружность с центром в точке О. Через эту
точку линейкой проводим диаметр АВ. Затем на окруж-
ности выбираем произвольную точку С, не совпадаю-
щую с концами диаметра. Далее линейкой соединяем
сначала точку А с точкой С, а потом точку В с точ-
433
Рис. 17.12
кой С. Тогда ЛАСВ =90° т.к. он опирается на диаметр.
Этот угол—искомый (рис.17.9).
Построение серединного перпендикуляра к данно-
му отрезку. С помощью циркуля проводим окружность с
центром в точке А, радиус которой R больше длины от-
резка АВ, а также окружность с тем же самым радиу-
сом и центром в точке В. Эти окружности пересекаются
в точках С и D (рис. 17.10). Четырехугольник ACBD —
ромб. Соединим линейкой точки С и D. Прямая CD яв-
ляется искомым серединным перпендикуляром к отрез-
ку АВ.
Построение правильного треугольника. Произволь-
ные точки А и В соединяем линейкой. Далее циркулем
делаем засечку радиусом R, равным длине отрезка АВ с
центром в точке А, а затем делаем засечку тем же ра-
диусом с центром в точке В, Пусть эти засечки Пересе-
434
каются в точке С. Тогда линейкой соединяем точки А
и С, а затем точки В и С. Полученный треуголь-
ник АВС — искомый (рис.17.11).
Построение квадрата. Циркулем проводим окруж-
ность с центром в точке О, Линейкой строим диаметр
АВ. Далее проводим прямую /И, являющуюся середин-
ным перпендикуляром к отрезку АВ. Пусть С и D —
точки пересечения прямой ТП с окружностью. Соединяем
их линейкой с точками А и В. Тогда ACBD — квадрат
(рис.17.12).
Построение правильного восьмиугольника. Постро-
им квадрат ACBD с центром в точке О (рис.17.13). По-
строим серединные перпен-
дикуляры к отрезкам АС,
СВ, BD и AD. Пусть А},
Вх, Ср Dx — их точки пере-
сечения с окружностью. То-
гда АА j СВХ ВСХ DDX — пра-
вильный восьмиугольник
(рис.17.13). Докажите по-
следнее утверждение само-
стоятельно.
Замечание. Если
правильный И -угольник по-
строен, то с помощью середин-
сторонам можно построить пра-
вильный 2 п -угольник.
Построение правильного десятиугольника. Сторо-
В,
Puc.17.13
ных перпендикуляров к его
на а10 правильного десятиугольника, вписанного в ок-
ружность радиуса R, равна
1R0’ л/s — 1 -i/s 1
л10 = 2Rsin — = 2Я$ш18° = ^—--R = — R --R.
10 2 2 2
Пусть задан отрезок длиной R. Поскольку
435
Рис.17.14
Рис.17.15
.45
то отрезок длиной —л является гипотенузой прямо-
2
п К
угольного треугольника с катетами R и —. Построение
отрезка а10 осуществляется следующим образом. Строим
прямой угол и на его сторонах откладываем отрезки R
R п R
и — (рис.17.14). Затем циркулем радиусом = СВ = —
проводим окружность с центром в точке С. Пусть она
пересекает гипотенузу АС треугольника АВС в точ-
ке D. Тогда AD — искомый отрезок.
Наконец, для построения правильного десятиуголь-
ника проведем окружность радиуса R, возьмем произ-
вольную точку А} на окружности и строим с помощью
циркуля такие точки А2, А3, ... , А10 на окружности, что-
бы А}А2 = А2А3 = ... = А9А10 = а10. Многоугольник
А} А2... Л10 является правильным десятиугольником
(рис.17.15).
Построение правильного пятиугольника. Сначала
строим правильный десятиугольник, затем соединяем
через одну вершины правильного десятиугольника. На-
пример, последовательно соединим отрезками точки А},
436
А3, А5, А1, А9, А}. Получаем правильный пятиугольник
А । А3 А5 А2 А9.
Немецкий математик Карл Гаусс (1777—1855) до-
казал, что правильный П -угольник можно построить с
помощью циркуля и линейки тогда и только тогда, когда
число п является степенью числа 2 или число п допус-
кает разложение на простые множители:
и = 2/р,р2...рт.
Здесь />0, т>1, а числа р}, р2, ... , рт являют-
.1
ся несовпадающими простыми числами вида 2 +1 , где
k>Q.
2к
Числа Fk = 2 +1 называются числами Ферма в
честь французского математика Пьера Ферма (1601—
1665). Наименьшими простыми числами Ферма являются
числа
Fq =3, Fx =5, F2 =17, F3 =257, F4 =65537.
Правильные многоугольники, имеющие такое количество
сторон, допускают построение с помощью циркуля и ли-
нейки. Простое число 7 не является числом Ферма, по-
этому правильный семиугольник циркулем и линейкой
построить невозможно. Правильный девятиугольник так-
же не допускает построения циркулем и линейкой, так
как в разложении 9 = 3-3 простое число Ферма FQ = 3
повторяется.
§ 17.3. ПОДОБИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Теорема 17.4. Правильные многоугольники,
имеющие одинаковое число сторон, подобны.
□ Пусть, ЛЛ-4 и в\В2...вп — два правиль-
ных П -угольника и
4^2
ДВ2
= к. Применим ко второму
многоугольнику преобразование гомотетии с коэффици-
ентом Л, приняв центр этого многоугольника за центр
437
гомотетии. Тогда он перейдет в многоугольник С]С2...СЛ
с тем же самым центром, при этом CjC2 = кВ}В2 = А}А2,
С2С3 = А2А3, ... , СпСх = АпА}, т.е. стороны и-угольни-
ков СхС2...Сп и АХА2... Ап будут равными. С другой сто-
роны, по свойству гомотетии И-угольник ВхВ2...Вп по-
добен П-угольнику С}С2...Сп. Далее, в треугольни-
ках СХС2С3 и АхА2А3 имеем: СХС2 = А}А2, С2С3 = А2А3,
ZCjC2C3 = ЛВХВ2В3 по свойству преобразования гомо-
тетии, откуда следует, что утлы СХС2С3 и АХА2А3 равны.
Значит, треугольники С}С2С3 и АхЛ2Л3 равны по перво-
му признаку равенства треугольников. Применим к мно-
гоугольнику С}С2...Сп такое движение, при котором эти
треугольники совместятся, причем так, чтобы точка Сх
перешла в точку Ах, точка С2 — в точку А2, точка С3 —
в точку А3. Поскольку при движении углы сохраняются,
то ZC2C3C4 = Х42Л3Л4. Учитывая, что С3С4 = Л3Л4, по-
лучаем, что точки С4 и А4 совпадают. Далее, таким же
образом получаем, что совпадают и точки С5 и А5, С6
и А6, ... , Сп и Ап. Значит, многоугольники С}С2...Сп
и АХА2... Ап совпадают, то есть они равны. Подобие мно-
гоугольников АхА2...Ап и ВхВ2...Вп доказано.
Следствие?. Правильные П -угольники с равны-
ми сторонами равны.
§ 17.4. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 17.1. Являются ли истинными утверждения:
а) если в выпуклом многоугольнике все стороны равны,
то он правильный;
б) если в выпуклом многоугольнике все углы равны, то
он правильный?
В ромбе с внутренним углом а 90° все стороны
равны, однако он не является правильным четырехуголь-
ником (квадратом); в прямоугольнике с неравными сосед-
438
ними сторонами все углы прямые, однако он также не
является квадратом.
Таким образом, оба утверждения ложны. Ж
Пример 17.2. Выразить радиус Г вписанной окружно-
сти правильного Л-угольника через радиус R его описанной
окружности, если п = 3, 4,5,6,8,10, 12.
ZS Пусть а — сторона правильного п -угольника.
При п = 3 имеем: R = 2г, г = —.
При П = 4
При п = 5
При п = 6
а а кЛ
имеем: г = —, R = —f=, откуда г =-
согласно §17.1 получаем: г =
ал/З _ яТз
имеем: Г =-----, К = а, откуда г =----
Для произвольного значения П из рис. 17.7 имеем:
180’
г = Rcos
п
180
Подсчитаем величину cos---
п
ях и =8, 10, 12.
При п = 8 имеем:
О
при оставшихся значени-
180
cos----
8
45
= cos
тогда
При п = 10 имеем:
cos = cosl 8° = — 710 + 2-J5 ,
10 4
439
г = -710 + 2^5.
4
Наконец, при п = 12 имеем:
откуда
Пример 17.3. Найти площадь правильного П угольни-
ка, вписанного в окружность радиуса R, если п = 3, 4, 5 , 6,
8,10, 12.
Пусть а — сторона правильного П -угольника.
При п = 3 имеем:
откуда
a = R43. S = — R2.
4
При п = 4 получаем:
S = a2, R =
I
откуда
а = R&, S = 2R2.
При п = 6 имеем:
£ = R = a,
откуда
440
s = ^.
2
Для произвольного значения П из рис. 17.7 имеем:
_ _ nR2 . nR2 . 360’
S = nSM 0A = — sin^AxOA2 = —- sin---.
1 2 2 2 n
. 360°
Подсчитаем величину sin-- при оставшихся зна-
п
чениях п.
При п = 5 получим:
. 360’
sin-----
= sin72° = cosl 8’ = - л/10 + 2д/5,
тогда
S = - R2 710 + 2^5 .
8
При п = 8 имеем:
. 360’ л/2 ГТ 2
sm-----— sin45 =—, S = 2\2R .
8 2
При П = 10 имеем:
. 360’ . 1 СТ о /т
sin---= 5ш36 = —л/10-2д/5,
10 ______4
S = -710-2>/5 J?2.
4
Наконец, при п = 12 имеем:
. 360° . _о 1 с , п2 ж
sin-----= 37иЗО = —, S = 3R .А
12 2
Пример 17.4. Дан правильный 30-угольник ДЛ2...Л30
с центром О. Найти угол между прямыми ОА3 и Л4.
z2s Нетрудно убедиться в том, что вершины А3
и Л18 лежат на одном диаметре. Пусть хорды АХА4
и А3А18 пересекаются в точке В внутри круга, описан-
ного около данного 30-угольника (рис. 17.16). Искомым
является острый угол А}ВА}8. Согласно §6.4 имеем:
441
Рис.17.16
Далее,
u А, А,. = 180’ - и А А. =180’- 24’.
1 I о 1 3
Тогда
ZJ1BJ]g = |(180’-24' + 12’) = 84’. Ж
Пример 17.5. Доказать, что сумма расстояний от про-
извольной точки внутри правильного многоугольника до его
сторон не зависит от выбора точки.
Пусть А}...Ап — правильный многоугольник со
стороной а, М — произвольная точка внутри него.
Опустим перпендикуляры MHV МН2, ... , МНп на сто-
роны А}А2, А2А3, ... , АпА} (рис.17.17). Площадь S мно-
гоугольника равна:
£ = $ЬМА}А2 + 5ДМ42Я3 + ••• =
-^мн, + мн2+ ... +мн„),
2S
откуда МНj + МН2 + ... + МНп =---- и не зависит от
а
выбора точки М внутри многоугольника. Ж
442
Пример 17.6. При каких П сторона правильного П-
угольника:
а) больше радиуса R описанной окружности?
б) равна R1
в) меньше R?
Согласно §1*7.1, сторона правильного И-угольни-
ка вычисляется по формуле:
ап = 2Rsin
180°
п
При п = 6 имеем: а6 = R.
Пусть 3 < п < 5. Тогда
0. < 180; < № < 90.
6 п
. 180° . 180°
sin---- <sin----,
6 п
откуда
оп . 180° „п . 180° _
а = 2Rsin-----> а6 = 2Rsin-----= R, т.е. ап > R.
п 6
Пусть теперь п > 7, тогда
0- < < 90°,
п 6
откуда
n п . 180° „ п . 180° „
ап = 2Rsin----< 2Rsin-----= R, т.е. ап < R.
п 6
Таким образом, сторона правильного п -угольника
больше радиуса описанной окружности при 3<и<5.
При п = 6 сторона правильного шестиугольника равна
радиусу описанной окружности. При п > 7 сторона пра-
вильного п -угольника меньше радиуса описанной окруж-
ности. А
Пример 17.7. Пусть Л^ ... Л,, — правильный десяти-
угольник, вписанный в окружность радиуса R. Доказать, что
Л, Л4 ~ A Ai —R.
Опустим перпендикуляр ОР на хорду А}А4
(рис.17.18). Тогда
443
Ри.с.17.18 Рис.17.19
ААХОР = -ZA}OA4 =-• 3 — = 54’.
1 2 1 4 2 10
Из треугольника А}ОР имеем:
Ах А4 = 2 А} Р = 2Rsin 54° = 2Rcos 36°.
Далее получаем:
АХА4-АХА2 = 2 Rcos 36°-2 /?л7п18о =
Пример 17.8. Пусть О — центр правильного /1-уголь-
ника А^А^.А^ Доказать, что Л41+ОЛ2+ ... +ОЛл=0 .
Пусть Т — поворот на угол а вокруг точ-
ки О, В — произвольная точка плоскости, В} = Т(в).
Положим
= ОАг. Мы определили действие дви-
жения Т
что 7] 0
на векторы с началом в точке О. Очевидно,
0 .
Докажем сначала следующую лемму.
Лемма. Пусть А и В — произвольные точки на
плоскости. Тогда 71 ОА+ОВ
=71 ОА | + 71 ОД
\ 7 \
7
444
□ Рассмотрим параллелограмм ОАСВ (рис.17.19).
По правилу параллелограмма имеем: ОС = ОА + ОВ.
Пусть А,, Bv С] — образы точек А, В, С при поворо-
те Т. Пусть Р — точка пересечения диагоналей АВ
и ОС, Р. — ее образ при повороте Т. Тогда Р] — точ-
ка пересечения отрезков А. В. и ОС., при-
чем ОР. = ОР=РС=Р.С., Л,Р,= АР = РВ = Р.В.. По
признаку параллелограмма четырехугольник ОА.С.В. —
параллелограмм. Следовательно,
или
что и требовалось установить. И
Перейдем непосредственно к решению примера.
Пусть вершины И-угольника занумерованы по часовой
360°
стрелке, То — поворот вокруг точки О на угол----про-
п
тив часовой стрелки. Тогда
То ОА. =Ш„, То\ ОА
= ОА., То ОА3 = ОА2,...,
п' ЛО1 ^^2
о
То ОА
п I ^^Л-1 •
По лемме имеем:
о
п
О
п
О
= ОАп + ОА.+... + ОАп_. = ОА.+... + .
445
Вектор h — 0А} +... + ОАп неподвижен под действи-
ем поворота То: To(h) — h Значит, конец этого вектора
остается на месте при действии поворота То. Это может
быть только тогда, когда неподвижен конец вектора Л,
т.е. конец вектора h совпадает с его началом О. <Утск>-
да А = О. Итак, OAt +... + ОАп = 0. Ж
Пример 17.9. Доказать, что сумма квадратов расстоя-
ний от произвольной точки окружности до вершин правиль-
ного И-угольника, вписанного в окружность, есть величина
постоянная, не зависящая от выбора точки.
Пусть А}А2...Ап — правильный И-уголь-
ник, О — центр описанной окружности, R — ее радиус,
точка М лежит на окружности. Тогда
п
п
п f -> -> -> \
= Е\OAi-OM \OA-OM =
= ^0Аг0А1-2^(0А10м} + ^0М-0М =
1=1 <=1 \ J i=l
По теореме 12.9 и согласно предыдущей задаче
£ ( OAi • ОМ ] = | б А• ОМ = 0 • ОМ = 0.
Итак,
п
^МА2 = 2nR2
/=1
и не зависит от выбора точки М на окружности. Ж
Пример 17.10. На сторонах правильного пятиугольни-
ка как на диаметрах построены пять кругов. Покрывают ли
они весь пятиугольник?
446
ZS Из центра О правильного пятиугольника каждая
360
его сторона видна под углом
= 72°, т.е. под острым
углом. Но из главы 6 следует, что из точек внутри круга
диаметр виден под тупым углом, а из точек окружнос-
ти — под прямым. Следовательно, точка О не принадле-
жит ни одному кругу, построенному на стороне пяти-
угольника как на диаметре. А это значит, что построен-
ные пять кругов не покрывают пятиугольник. Ж
§ 17.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
17.01. В окружность радиуса R вписаны правильный
шестиугольник и правильный пятиугольник. Найти отношение
их площадей.
17.02 . В окружность радиуса 6 см вписан правильный тре-
угольник, на стороне которого построен квадрат. Вычислить ра-
диус окружности, описанной около квадрата.
17.03 . Вычислить площадь правильного П -угольника, опи-
санного около окружности радиуса Г, если п = 3, 4, 5, 6, 8,
10, 12.
17.04 . Найти внутренние углы правильного Л-угольника,
если и = 3, 4, 5, 6, 8, 10, 12.
17.05 . Доказать, что если ... — правильный 2и-
угольник, то A^yAs ... ^2л-1 —правильный И- угольник.
17.06 . Доказать, что середины сторон правильного П-
угольника также образуют правильный П -угольник.
17.07 . Доказать, что центр правильного 2и-угольника явля-
ется его центром симметрии.
17.08 . Доказать, что прямая, соединяющая центр правиль-
ного П -угольника с его вершиной, является осью симметрии
этого И-угольника.
17.09 . Сторона правильного пятиугольника равна 1 . Найти
его площадь и диагональ.
17.10. Найти отношение периметров двух правильных
восьмиугольников, один из которых вписан в окружность, а
другой описан около этой окружности.
17.11. В правильный треугольник со стороной а вписана
окружность, а в эту окружность вписан правильный шести-
угольник. Найти его площадь.
447
17.12. Найти отношение площадей правильного пятиуголь-
ника и квадрата, стороны которых равны.
17.13. Чему равна сумма внешних углов правильного П-
угольника, если при каждой его вершине взято по одному
внешнему углу?
17.14. Доказать, что если ... А* правильный восьми-
угольник, то А^АуА^ — прямоугольник.
^^17.15. В окружность радиуса R вписан правильный
пятиугольник А}А2А3А4А5. Доказать, что
17.16. Доказать, что если в выпуклом (2 л +1)-угольнике,
вписанном в окружность, все углы равны, то этот (2 л+ 1)-
угольник — правильный.
17.17. Найти наименьшую и наибольшую диагонали пра-
вильного десятиугольника, сторона которого равна 1 .
17.18. Доказать, что площадь правильного П -угольника,
« 1 п п 180°
вписанного в окружность радиуса к, равна —rnKcos-----------,
2 п
где Рп — периметр данного П -угольника.
17.19. Диагонали AiA6 и правильного двенадцати-
угольника пересекаются в точке В. Доказать, что треугольни-
ки А^А^В и А6А9В — правильные и диагональ AtА6 равна диа-
метру вписанной в данный многоугольник окружности.
17.20. Найти площадь правильного двенадцатиугольника,
сторона которого равна С1.
17.21......Доказать, что центр О правильного П -угольни-
ка АуАг ... Ап является центром масс системы точек (Яу/и),
(^;т)......(Л;от)-
17.22. Пусть Bv В2, ... , Вп — середины сторон правильно-
го И -угольника А^.-.А” с центром О. Доказать равенство:
ОВ} 4- ОВ2 4- ... 4- ОВп = 0 .
17.23. Найти отношение площади правильного пятиуголь-
ника к площади треугольника, образованного стороной пяти-
угольника и двумя его диагоналями, выходящими из концов
этой стороны.
448
ГЛАВА 18
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ
КРУГА
§ 18.1. ДЛИНА ОКРУЖНОСТИ
В приложении 3 дано определение длины окруж-
ности. Доказано, что отношение длины окружности к
диаметру есть величина постоянная, не зависящая от ок-
ружности. Это число обозначается греческой буквой я.
я — это первая буква греческого слова яеркрерыа — ок-
ружность. Приближенное значение числа я таково:
я«3.14159.
Пусть I — длина окружности радиуса R. Тогда
I
---= я, откуда следует формула:
27?
/=2я-Я.
Аксиомы длины дуги. Длина дуги окружности.
Пусть каждой дуге АВ окружности радиуса R ставится
в соответствие положительное число 1АВ, обладающее
следующими тремя свойствами, называемыми аксиомами
длины дуги окружности:
Аксиома 18.1. Если дуга АВ равна дуге CD,
то ^в^св*
Аксиома 18.2. Если дуга АВ разделена на не-
сколько меньших дуг АА}, AiA1, А*В, то
^АВ =^ААх +lAxA2 •
Аксиома 18.3. Если дуга EF — полная окруж-
ность, то lEF — этой окружности, т.е. lEF=2nR.
Тогда число 1АВ называется длиной дуги АВ ок-
ружности.
449
Аксиомы 18.1—18.3 аналогичны аксиомам длины от-
резка (в роли эталона длины на этот раз выступает не
единичный отрезок, а длина окружности) и аналогичны
аксиомам площади.
Воспользовавшись аксиомой 18.2 длины дуги окруж-
ности, получим следующее следствие.
Следствие. Если дуга АВ является частью ду-
ги CD, то длина дуги АВ меньше длины дуги CD,
т.е.
Вычислим длину дуги окружности радиуса R с гра-
дусной мерой а °. Для этого сначала рассмотрим лемму
для случая, когда число а является рациональным чис-
лом.
Лемма. Пусть т — произвольное рациональное
число, удовлетворяющее неравенству 0<Ш<360. ’'дина
дуги окружности радиуса R, градусная мера которой
составляет т°9 равна:
/ . Я.
т 180 ~
□ Рассмотрим сначала дли- /
ну lr дуги с градусной мерой Г. / 0/^ 1
Окружность можно разбить на I ]
360 таких дуг, так как полный \ I
угол составляет 360° (рис.18.1). У
Тогда согласно аксиоме 18.1
эти дуги имеют одинаковую
длину По аксиоме 18.2 длина рис./Л/
окружности I равна 3607.» от-
куда
_ 2я • Я _ я • Я
г~360 Зб6""”Т80 ’
к
Далее, пусть ТП = — — положительное рациональное
п
число, причем Ш<360. Здесь к и П — натуральные чис-
ла. Разбивая дугу с градусной мерой Г на И равных час-
450
тей, получим, что n-l, .. — I.., или I, .. = — /,. =-. На-
(1) (Г) п' 180„
конец, откладывая на окружности последовательно к раз
дугу с градусной мерой
, получим:
kl
т
, _it-k-R _п-т
180-и "Ш) ’
Эту лемму мы используем для доказательства сле-
дующей теоремы.
Теорема 18.1. Пусть а — действительное чис-
ло, удовлетворяющее неравенству 0«Х<360. Длина ду-
ги окружности радиуса R v градусной мерой а ° равна:
рис. 18 2
ложим дуги АВ, ADn,
180 R
чисел а эта формула уже до-
иррационально. Рассмотрим
произвольную возрастающую
последовательность (ап) поло-
жительных рациональных чи-
сел, предел которой равен а,
а также убывающую последо-
вательность (/>„) рациональ-
ных чисел, предел которой
также равен а, причем такую,
что 6„^360 при каждом п. Та-
кие последовательности суще-
ствуют по теореме 7 приложе-
ния 1. Имеем: а <а</>„. Распо-
ЛСп, градусные меры которых
равны соответственно а°, а’, Ь°, так как показано на
рис. 18.2. Согласно следствию из аксиом длины дуги ок-
ружности, имеет место неравенство:
^AD„ -^АСЯ '
п . п
451
откуда вследствие рациональности чисел ап и Ьп, а также
доказанной выше леммы получаем, что
---^К<1ЛВ<------R.
180 АВ 180
Согласно теоремам из приложения 1, имеем:
, .. л а„ п it-R .. я а _
/ >lim----- R ------lim a„ =---R.
AB ™ 180 180 »->» " 180
Аналогично
1АИ <lim---R =-----R.
м 180 180
Значит,
lAB= — R
AB 180
§ 18.2. РАДИАННАЯ МЕРА ДУГИ И УГЛА
Радиан. Введем новую единицу измерения дуги и уг-
ла — радиан. Слово "радиан" происходит от латинского
"radius" — "спица", "луч". Суффикс "ап" означает "проис-
хождение". Таким образом, буквальное значение этого
термина — рожденный лучом.
Рассмотрим сначала ок- _____р
ружность, радиус которой ра-
вен 1. Будем называть ее еди- / 1 / у. ;
ничной окружностью. Цен- / / \
тральный угол единичной / ।
окружности, опирающийся на I О х ; 1 А
дугу длиной 1 , называется ра- \ /
дианом (рис. 18.3). Будем счи- \ /
тать также, что центральный
угол единичной окружности, ----
опирающийся на дугу длиной
а (0<а<2п), содержит а ра- Рислв.з
диан. Кроме того, будем гово-
рить, что дуга единичной окружности содержит а ради-
ан, если длина этой дуги равна а.
Связь между градусной и радианной мерами изме-
рения углов (дуг). Установим связь между градусами и
452
радианами. По теореме 18.1 дуга на единичной окружно-
сти с градусной мерой имеет длину - —. Поэтому эта
дуга содержит---• радиан. Итак, угол (дуга) в Р граду-
180
сов содержит радиан. В частности, углы в 0°, 30°,
45°, 60°, 90°, 120°, 135°, 150°, 180°, 270°, 360° имеют
соответственно такие радианные меры: О
2л Зл 5л 3 _
—, —, —( 2п, Очевидно, что угол, радианная
180а
мера которого равна а рад, содержит-------градусов.
§ 18.3. ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ
В приложении 3 доказано, что площадь круга радиу-
са R вычисляется по формуле: 5 = Л • R2. Рассмотрим не-
которые части круга и вычислим их площади.
Сектор. Площадь сектора. Назовем сектором часть
крута, содержащуюся между двумя радиусами.
Пусть соответствующий центральный угол сектора
содержит а° (рис. 18.4). Ис-
ходя из площади круга, мож-
но определить площадь этого
сектора подобно тому, как
мы определяем длину дуги,
исходя из длины всей окруж-
ности. Тогда получится, что
площадь этого сектора Sa.
пропорциональна числу а,
Рис.18.4 т.е. между S'. и а сущест-
вует линейная зависимость
453
вида: S ' — kct, где к — некоторый положительный чис-
ловой коэффициент пропорциональности, зависящий от
радиуса окружности.
Найдем этот коэффициент пропорциональности.
Площадь круга равна:
S = S =360fc,
откуда
2
л-Я2 = 36(Н, к = ——.
360
Окончательно имеем:
S .=——R2.
“ 360
Если же центральный угол сектора составляет [3 рад, то
180р п о
его градусная мера равна---градусов. Площадь со-
те
ответствующего сектора будет равна:
л 180₽ 2_Я2Р
" 360 Л 2
Таким образом,
Эта формула допускает интересную геометрическую
интерпретацию. Заметим, что длина соответствующей ду-
ги центрального угла равна: /р = 7?р. Тогда Sp = —-2JZp.
Это равенство похоже на формулу площади треугольни-
о 1 ,
ка S=—an. Сектор является криволинейным аналогом
треугольника, причем роль основания играет дуга секто-
ра, а роль высоты — радиус окружности. Если угол Р
достаточно мал, то сектор АОВ на рис. 18.5 незначитель-
но отличается от треугольника АХОВХ, в котором отре-
зок ОС, равный R, является высотой, а основание А}ВХ
равно:
454
Рис. 18.5
Рис. 18.6
АЛ = 2Rsin | = R 0 = lAB.
Мы воспользовались здесь приближенной формулой
sinx^X, где X — малое положительное число. Смысл
этого приближенного равенства состоит в том, что отно-
шение ----- близко к 1 для малых значении аргумен-
та X, вычисляемых, конечно, в радианах.
Подытожим доказанные соотношения в виде сле-
дующей теоремы.
Теорема 18.2. Площадь сектора с центральным
углом, опирающимся на дугу окружности радиуса R
длиной I, вычисляется по формуле:
с = А р/
° сект 2 ’
Площадь сектора круга радиуса R с центральным
углом, опирающимся на дугу, содержащую а °, вычисля-
ется по формуле:
_ ла • R2
се1ип 360
Площадь сектора круга радиуса R с центральным
углом, опирающимся на дугу, содержащую [3 радиан,
вычисляется по формуле:
455
$сект ~ j •
Слово "сектор” происходит от латинского sector —
рассекающий.
Сегмент. Площадь сегмента. Проведем отличную от
диаметра хорду АВ в круге радиуса R (рис.18.6). Она
разбивает круг на две части, которые называются сег-
ментами.
Греческий астроном Птолемей делил окружность
на 360 частей. Для этих частей он иногда применял на-
звание "отрезки". Это слово было буквально переведено
на латинский как segmentes.
Рассмотрим сначала меньший из двух сегментов,
заштрихованный на рис.18.6. Пусть его дуга содержит
а рад (0<а<тг). Тогда АЛОВ = а.
Будем считать по определению, что площадь -.его
сегмента равна разности площадей сектора ОАВ и тре-
угольника ОАВ . Следовательно, она равна:
_ R2a R2sina
&сегм Z
ИЛИ
R2
Sr--. -—(а - sina).
Рассмотрим теперь больший из двух сегментов. Он
показан на рис. 18.6 в виде незаштрихованной части кру-
га. Сегмент стягивается дугой, содержащей 0 рад,
где 0 = 2я-а, причем Ж0<271. Будем считать по опре-
Puc.ie. 7
делению, что площадь это-
го сегмента равна разно-
сти площадей круга и
меньшего сегмента. Само-
стоятельно докажите, что в
этом случае площадь сег-
мента равна -^-(р — 57ир).
Проведем в окружно-
сти диаметр CD (рис. 18.7).
Он делит круг на две рав-
456
ные части. Если принять, что их площади равны, то пло-
nR2
щадь полукруга равна —-—. Но полукруг также можно
рассматривать как сегмент с центральным углом a = 7t.
Как видим, формула для площади сегмента подходит и в
этом случае. Мы доказали такое утверждение:
Теорема 18.3. Пусть в круге радиуса R цен-
тральный угол имеет радианную меру, равную а,
где О <ос <2тс. Тогда площадь соответствующего сегмен-
та вычисляется по формуле:
R2
Srpr =—(a-sina).
§ 18.4. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 18.1. По данной длине дуги Ш найти ее хор-
Зк
дуг если дуга составляет- радиан.
4
с На рис. 18.8 изобра-
жена данная дуга АВ с цен-
\ тральным углом АОВ , рав-
I А ным —. R — радиус окруж-
1 0 R 1 Рис. 18.8 АВ1 = 2R2-2R2cos- = 2R2\\ + — k 2 4 ности, содержащей дугу АВ. Тогда Зл „ „ 4m т =—R, R =—. 4 Зя Из треугольника АОВ по теореме косинусов имеем: ?71 0 02^1 Зя А — = 2R 1-cos— = 4 V 4 J - =R2(2 + j2).
Отсюда
457
AB=R^2 + y[2
ИЛИ
Пример 18.2. Четыре
равных круга касаются внеш-
ним образом круга радиуса Г ,
причем каждый из этих четы-
рех кругов касается внешним
образом двух соседних. Найти
сумму площадей всех пяти
кругов.
Данные круги пред-
ставлены на рис. 18.9. Цен-
тры четырех равных кругов
лежат в вершинах квадрата
со стороной 2R. Центр 05 Рис.18.9
пятого круга лежит в центре
этого квадрата, причем
О5О2 = г + R,
где R — радиус каждого из четырех равных кругов
(рис.18.10). Мы воспользовались тем фактом, что при
внешнем касании двух ок-
ружностей точка касания
лежит на линии центров и
расстояние между центрами
равно сумме радиусов.
Тогда диагональ квадра-
та равна:
O.O, = 2Rj2,
О5О2 = Ryp2 = г + R,
J л»
Рис. 18.10
Найдем площадь пяти кругов:
S =4тс-7?2 4-7С-Г2 =471-Г2(л/2 4-1) 4-7С-Г2 =
458
= л-г2(4-(2 + 2>/2+1) + 1) =
= тгт2(13 + 8^). Ж
Пример 18.3. Общая хорда двух кругов стягивает ду-
ги 60° и 120°. Найти отношение площадей этих кругов.
На рис. 18.11 точки О1 и О2 — центры кру-
гов, АВ —общая хорда, , Z.BO2A = Y2ff.
На рисунке изображен случай, когда центры кругов
лежат по разные стороны от хорды. Пусть Ох А = С\В =
= Л, О2А = О2В = Г — радиусы данных кругов. В равно-
бедренном треугольнике
Рис. 18.11
АОХВ угол ВОХА равен 60°,
поэтому
ХС\АВ = =
= 1(180’-60°) = 60°,
следовательно, этот тре-
угольник равносторонний и
AB=R.
Пусть М — середина
хорды АВ. В равнобедрен-
ном треугольнике АО2В
медиана О2М является вы-
сотой и биссектрисой. По-
этому
1 19П°
аво2 м=~(хво2 А) -—=60°,
2 2
ВМ =rsinf>W = —, АВ=2ВМ=г4з.
2
Отсюда R = Гл/з. Пусть 5, и S2 — площади данных в ус-
ловии примера кругов. Тогда отношение площадей этих
кругов будет:
_ Л • Я2 _ Зг2
S2 л-r2 г2
459
В случае, когда точки Ох и О2 находятся по одну
сторону от прямой АВ, рассуждения проводятся анало-
гично, и мы снова получаем, что искомое отношение рав-
но трем.
Итак, площади кругов
относятся как 3:1. Ж &
Пример 18.4. В сектор,
дуга которого составляет — pa- /
диан, вписан круг. Найти отно- 1
шение площадей круга и секто-
ра. О Q А
Данный сектор изо-
бражен на рис. 18.12, угол Pxic.ie.i2
71
АОВ равен у рад, Р —
центр круга, вписанного в этот сектор. Он касается
сторон угла АОВ . Так как точка Р лежит на биссектри-
се угла АОВ , то
Z.POA = ХРОВ= — .
6
Пусть Q — точка касания
круга с отрезком ОА, тог-
да PQ.LOA. Вписанная ок-
ружность и окружность, ко-
торой принадлежит сектор,
касаются друг друга внут-
ренним образом, как пока-
зано на рис. 18.13. Поэтому
точка С касания кругов ле-
Рис.18.13
жит на продолжении отрез-
ка ОР, причем OP = R-r,
где ОА = R, PC = г — радиусы касающихся кругов.
Найдем связь между этими радиусами. В треуголь
нике OPQ угол POQ равен —, поэтому противолежа-
6
щий катет равен:
460
R-r
<хгкуы&.
R = 3r.
Площадь вписанного круга равна: SKp = Tt-г2, пло-
щадь сектора АОВ с центральным углом — равна:
- - 1 R2 П -n‘R2
сект л * о г
Тогда
5к₽ .b'2
--=5. -
С-11
° сект \ л
т.е. площади вписанного в
сятся как 2:3 . Ж
сектор круга и сектора отно-
Ot
Ог
Рис.1в.14
круга с радиусами 1 м. Рас-
стояние между их центрами
щадь общей части этих кругов.
Пусть Ох, О2 — цен-
тры данных кругов, М —
середина линии центров
ОХО2, В иС — точки пере-
сечения окружностей, огра-
ничивающих круги. Искомая
площадь равна 2ScerM, где
ScerM — площадь заштрихованного сегмента (рис.18.14).
Обозначим угол ВОХС через а. Найдем его. В прямо-
угольном треугольнике ОХВМ катет ОХМ равен:
ОХМ = -ОХО2 =
cosABO, М =
Z.BOX М = — рад,
461
Рис. IB. 15
Рис.1В.16
a = 2(ZBO]M) = y рад.
Тогда по теореме 18.3 искомая площадь будет:
сегм
Итак, площадь общей части кругов равна:
27C-3V3/ .
Пример 18.6. Фигура на рис.18.15 ограничена полуок-
ружностями, построенными на отрезках АВ, ВС, АС как на
диаметрах, причем DBA. АС. Доказать, что площадь фигуры
равна площади круга с диаметром DB (эту фигуру называют
фигурой Архимеда).
Для произвольного отрезка EF обозначим че-
рез SEF площадь полукруга, построенного на отрез-
ке EF как на диаметре. Предварительно докажем сле-
дующее вспомогательное утверждение.
Лемма. Пусть в треугольнике PQL угол Q пря-
мой. Тогда Spj^Spq^SqL (рис.18.16).
□ По теореме Пифагора имеем:
462
s^+s« -т(ре2+ei2)-7'Pi2-sfI-
* 4 4
ZS Дополним данную фигуру до полукруга с помо-
щью двух незаштрихованных полукругов (рис. 18.15).
Согласно лемме имеем:
$ АВ &BD “ '
8ВС + 8BD = $CD
Складывая эти равенства, получим:
8АВ 8ВС 2SbD “ &AD + &CD *
Угол ADC = 90°, так как он является вписанным,
опирающимся на диаметр АС. Тогда, согласно лемме,
SAD + $CD = 8АС •
поэтому
откуда площадь круга с диа-
метром BD равна:
Рис м. 17
$ вс '
т.е. площади фигуры Архи-
меда, заштрихованной на
рис. 18.15. Ж
Пример 18.7. Четыре
луночки образованы окружно-
стью, описанной вокруг квад-
рата, и полуокружностями,
построенными на сторонах
квадрата как на диаметрах
(рис.18.17). Доказать, что их
общая площадь равна площа-
ди квадрата (эти луночки на-
зывают луночками Гиппокра-
та).
ZS Пусть, как и в предыдущем примере, SEF обоз-
начает площадь полукруга, построенного на отрезке EF
как на диаметре. Дополним площадь заштрихованных лу-
ночек площадями сегментов 1 , 2, 3,4 большого круга.
Согласно лемме примера 18.9, имеем:
8АВ + Вс ~ $ ас •
8CD + $DA ~ S АС •
463
Ho SAC + SAC = SKp, где SKp — площадь круга с диа-
метром АС. Тогда
Пусть S — площадь фигуры, заштрихованной на
рис. 18.17, и ScerM — площадь каждого из четырех сегмен-
тов 1,2, 3,4.
Тогда
S = SAB
сегм
4* 8ВС 8сегм
&DA 8сегм
4" *^CD 8сегм
8кр~^8сегм 5abcd •
что и требовалось доказать. Ж
Рассмотренные луночки названы в честь Гиппок-
рата Хиосского (2-я половина V века до н.э.) — древ-
негреческого геометра, автора первого систематического
труда по геометрии.
Пример 18.8. Дан ромб со стороной Л и острым уг-
лом 60°. На его большой диагонали как на диаметре построен
круг. Что больше: площадь
ромба или площадь части кру-
га вне ромба?
ZS Рассмотрим ромб
ABCDt в котором АВ = а,
ZDHB=60° (рис.18.18). На
его большой диагонали АС
как на диаметре построен
круг. Его центр Э есть
точка пересечения диагона-
лей ромба. Из точки В диа-
метр АС виден под тупым
Рис, 18.18
углом, равным 180о-60° = 120°, и из §6.4 следует, что вер-
шина В лежит внутри круга. Аналогично, точка D также
находится в круге, и весь ромб ABCD принадлежит
кругу.
Площадь ромба равна:
.2
2
MBD
464
Мы воспользовались тем, что треугольник ABD равно-
. _ а-Уз
сторонний. Далее, АО —----- как длина высоты в пра-
вильном треугольнике. Тогда площадь круга равна:
, Зл-д2
SKp~n. АО2 =
а площадь 5, части круга вне ромба равна разности най-
денных площадей, поскольку ромб целиком лежит в кру-
ге:
о о Зя-а2 а2>13 а2 К /т\
= SkD~sd =-------------= —(Зя - 2V3I.
1 кр р 4 2 4 v 7
Сравним площади Sp
и Определим зьак разно-
сти Sj- Sp:
5, - S =—(зл - 2 л/з) - =
1 р 4 ' 7 2
= —(з-л-4>/з).
4
Далее выясним какое число больше 3-Я или 4^3.
Сравним квадраты этих чисел 9-я2 и 16-3. Ясно,
что 9-я2>9-9>48, значит 3-я>4^/з и 51-5р>0. Следо-
вательно, площадь части круга вне ромба больше площа-
ди ромба. А
Рис .18.19
Пример 18.9. Даны две
окружности с общим центром.
Проведена хорда большей окруж-
ности, которая касается меньшей
окружности. На хорде как на диа-
метре построен круг. Доказать,
что площадь этого круга равна
площади кольца между двумя ис-
ходными окружностями.
Пусть О — общий
центр двух окружностей. Хор-
да АВ большей окружности
касается меньшей окружности
465
в точке М (рис.18.19). Радиус ОМ перпендикулярен
хорде АВ, поэтому в равнобедренном треугольнике
АОВ высота ОМ является медианой, и точка М — се-
редина АВ. Тогда площадь круга, построенного на АВ
Рис. 18.20
как на диаметре, равна:
SK = я МВ2 = я • ВО2-п • МО2.
Правая часть этого равенства есть площадь кольца
между окружностями с радиусами ВО и МО.
Пример 18.10. Три рав-
ных окружности, которые по-
парно имеют внешнее касание,
касаются также внешним обра-
зом окружности радиуса Г.
Найти площадь каждого из
трех криволинейных треуголь-
ников, образованных четырьмя
окружностями.
На рис. 18.20 заштри-
хована площадь трех таких
криволинейных треугольни-
ков. Здесь Ov О2, О3 — цен-
тры больших окружнос-
тей; Р, Q, L — их точки по-
парного касания, лежащие
на отрезках, соединяющих
их центры. Пусть R — ради-
ус ролыпих окружностей.
Центр меньшей окружнос-
ти О4 удален от каждой из
точек Ov О2, О3 на расстоя-
ние R + г , поэтому О4 —
центр правильного треуголь-
ника ОХО2О3 со стороной
2R (рис.18.21).
Найдем R. В равносто-
роннем треугольнике ОХО2О3 отрезок ОХО4 есть радиус
описанной окружности, поэтому
466
откуда
2>/3-3
Из рис. 18.20 заключаем, что искомая площадь равна:
tsop-fiy
сект ^кр / ’
Здесь Scejan — площадь сектора O2PQ, SKp — пло-
щадь меньшего круга. Имеем:
= R2
- = w № 60 _K R2
сект 360 6
2
кр
Тогда
S = - R2
tz-R1
2
2
§ 18.5. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
А
18.01. Вычислить длину окружности и площадь круга
радиусом а) 10м; б) 15 м.
18.02. Как изменится длина окружности, если радиус:
а) уменьшить в три раза; б) увеличить на 1 мм?
18.03 . Найти длину дуги окружности радиуса б см, если ее
градусная мера равна 72°.
467
18.04 . Радиус окружности равен — км, а дл.*\*а дуги —
я
400 м. Найти градусную меру этой дуги.
18.05 . Каждую сторону квадрата разделили на три равные
части и через точки деления провели прямые, параллельные
сторонам квадрата. В каждый из образовавшихся девяти квад-
ратиков вписали круг. Что больше: общая площадь этих кругов
или площадь круга, вписанного в исходный квадрат?
18.06 . Квадрат со стороной а вписан в круг. Найти пло-
щадь этого круга.
18.07 . Вычислить площадь кольца, ограниченного окруж-
ностями с радиусами R} и и имеющими общий центр.
18.08 . В круг вписан равнобедренный треугольник со сто-
ронами 1,1, л/з. Найти площади четырех образовавшихся
при этом частей круга.
18.09 . Найти площадь меньшего сегмента, который стяги-
вается стороной вписанного в круг радиуса R правильного
шестиугольника.
18.10. По заданному радиусу R — 1 м найти длину дуги,
имеющей градусную меру, равную
Рис. 18.22
а) 45°; б) 150°36'.
18.11. По данной длине дуги / найти ее хорду, если дуга,
стягиваемая этой хордой, содержит:
я Зл
а) у рад; б) — рад.
18.12. Найти площадь круга, вписанного в равнобедрен-
ную трапецию, длина большего основания которой равна а, а
угол при меньшем основании pai
18.13. В круг вписан пря-
моугольный треугольник с кате-
тами 1 м и л/Зм. Найти пло-
щадь меньшей из четырех час-
тей круга, которые при этом
образовались.
18.14. Круг радиуса R де-
лится двумя концентрическими
с ним окружностями (т.е. все
три окружности имеют общий
центр) на три равновеликие
части. Найти радиусы этих двух
окружностей.
468
Рис.18.23
Рис.18. 24
18.15. Фигура Архимеда. Фигура на рис. 18.22 огра-
ничена полуокружностями, построенными на отрезках АВ,
ВС, CD, AD как на диаметрах, причем АВ — CD. Доказать,
что площадь фигуры равна площади круга с диаметром EF,
где Е и F — середины дуг AD и ВС соответственно.
18.16. Две луночки образованы полуокружностями, по-
строенными на сторонах прямоугольного треугольника как на
диаметрах (рис. 18.23). Доказать, что их общая площадь равна
площади прямоугольного треугольника АВС .
18.17. В прямоугольнике одна сторона вдвое больше дру-
гой. Фигура образована дугами трех окружностей с радиусами,
равными меньшей стороне (рис. 18.24). Доказать, что ее пло-
щадь равна площади прямоугольника.
18.18. Две окружности разных радиусов касаются в точ-
ке А одной и той же прямой и расположены по разные сторо-
ны от нее. Отрезок АВ — диаметр меньшей окружности. Из
точки В проведены две прямые, касающиеся большей окруж-
ности в точках М и N. Прямая, проходящая через точки М
и А, пересекает меныпую окружность в точке К. Известно,
что длина отрезка МК равна ^2 +л/з см, а угол ВМА ра-
вен 15е. Найти площадь фигуры, ограниченной отрезками каса-
тельных ВМ, BN и той дугой MN большей окружности, кото-
рая не содержит точку А.
469
ГЛАВА 19
ПОЛЯРНЫЕ КООРДИНАТЫ И ЗОЛОТОЕ
СЕЧЕНИЕ
§ 19.1. ПОЛЯРНЫЕ КООРДИНАТЫ
Полярная ось. Полюс. Рассмотрим луч Z с началом
в некоторой точке О. Назовем его полярной осью, а
точку О — полюсом. Слово "полюс” происходит от
греческого — ось. Это название в геометрии оз-
начало, что точка или конец диаметра на сфере является
центром окружности, проведенной на сфере.
Примем некоторый отрезок за единичный. Введем
так называемые полярные координаты на плоскости —
полярный радиус и полярный угол.
Полярный радиус. Пусть М — произвольная точка
плоскости, отличная от по-
люса. Соединим точки М м у
и О, Полярным радиусом
точки М назовем расстоя- т
ние МО от точки М до по-
люса. Полярным радиусом
точки О считать чис- в
ло 0. О
Обозначим полярный
радиус через Г . Число Г мо- Рис ig j
жет принимать произволь-
ные неотрицательные значе-
ния. При этом г = 0 тогда и только тогда, когда взятая
точка совпадает с полюсом.
Полярный угол. Полярным углом точки М назовем
угол ф между лучами I и ОМ, который отсчитывается
от полярной оси в положительном направлении, т.е. про-
тив часовой стрелки.
470
На рис. 19.1 этот угол является острым, а на рис. 19.2
он попадает в промежуток от — Л рад до 2 л рад. В боль-
шей части главы углы будем
измерять в радианах, причем
при указании величины угла
слово "рад" будет опускаться.
Будем пользоваться обоб-
щенным понятием угла, т.е.
полярный угол может изме-
няться не только от 0 до 2 л,
но может принимать произ-
вольные значения — как по-
ложительные, так и отрица-
тельные.
М задается с точностью до
О
Ml
Рис. 19.2
Полярный угол точки
числа, кратного 2тг, т.е. если ф — некоторый полярный
угол точки М, то при каждом целом значении П
угол ф + 2л-и также считается полярным углом этой
точки. Полярным углом точки О будем считать всякий
угол ф0.
В частности, для точек полярной оси, отличных от
полюса, полярный угол равен: ф = 2л-и, где П — произ-
вольное целое число. Для точки Mv изображенной на
рис. 19.2, отрицательный угол ф1 является полярным уг-
лом. Он отсчитывается от оси I в отрицательном направ-
лении, т.е. по часовой стрелке.
Полярные координаты. Положение точки М на
плоскости можно задавать двумя числами: Г и ф,
где Г — полярный радиус точки, а ф — полярный угол.
Эти числа будем называть полярными координатами
точки М. Если точка М имеет полярные координаты г
и ф, то это обозначают так: Л/(г;ф).
В частности, при произвольном угле ф0 для полю-
са О имеем: (?(О;фо). В отличие от декартовых коорди-
нат, полярные координаты не задают взаимно-одно-
471
значного соответствия между точками плоскости и мно-
жеством всех таких пар чисел (г;ф), для которых г > 0.
§ 19.2. СВЯЗЬ ПОЛЯРНЫХ КООРДИНАТ с
ДЕКАРТОВЫМИ КООРДИНАТАМИ
Пусть задана прямо-
угольная система коорди-
нат XOY . Примем точку О
за полюс, а луч ОХ — за
полярную ось Z . Тогда в
данной плоскости имеем од-
новременно две координат-
ные системы: декартову и
полярную (рис. 19.3).
Установим связь между
ними. Рассмотрим произ-
вольную точку М плоско-
Рис. 19.3
сти, не совпадающую с точ-
кой О. Напомним, что полярный радиус Г точки М —
это длина отрезка ОМ, а полярным углом ф этой точки
является угол, образованный отрезком ОМ с осью I .
Найдем декартовы координаты X, у точки М. По опре-
делению тригонометрических функций угла ф имеем:
С05ф = —, 5/«ф = —,
г г
откуда
Х = Г-СОУф, y = r-sinq>. (1)
Обратно, пусть заданы декартовы координаты X, у
точки М. Если точка М совпадает с точкой О, то г = 0,
а ф — произвольное число. Если же точка М не совпа-
дает с точкой О, то опустим перпендикуляры ММх
и ММу из точки М на оси координат (рис. 19.3). В пря-
моугольном треугольнике ОММ х гипотенуза ОМ = г, а
катетами являются отрезки ОМХ и МХМ, равный OMV.
Тогда
472
г2 = ОМхг + ОМ’=|х|2+И2=х!+/.
откуда
Далее из формулы (1) получаем:
cos® = .....—..., sin® = ,.....-....
/.J , .2 V /2 , ,.2
Заметим, что для определения угла ф недостаточно
задать значение только ЛШф или только содер. Формула
г = у]х2 + у2 справедлива для произвольного положения
точки М на плоскости.
§ 19.3. УРАВНЕНИЕ ОКРУЖНОСТИ В ПОЛЯРНЫХ
КООРДИНАТАХ
Рис. 19.4
Окружность с центром в
полюсе. Рассмотрим поляр-
ную систему координат и ок-
ружность радиуса R, центр
которой находится в полюсе
"(рис.19.4). Произвольная точ-
ка М лежит на этой окруж-
ности тогда и только тогда,
когда полярный радиус Г ра-
вен радиусу R окружности,
т.е. г = R. При этом поляр-
ный угол ф может быть
произвольным. В любом направлении можно провести
луч ОА, образующий угол ф с полярной осью I . И этот
луч пересечет окружность в некоторой точке с полярны-
ми координатами (/?;<[>).
Итак, уравнение окружности радиуса R с центром в
полюсе полярной системы координат имеет вид:
r = R.
Полюс находится на окружности. Предположим,
что центр окружности Р лежит на полярной оси I , а по-
473
люс О находится на окружности. Пусть ОК — диаметр
окружности (рис.19.5). Обозначим: OK = d.
Рассмотрим произволь-
ную точку М окружности, ____________ __
отличную от точек О и К.
Согласно теореме 6.6, тре- f
угольник ОМК — прямо- [ .s' Vk
угольный, и тогда \ ~ 1г
г = ОМ = d • сояр . Д р ] К
Если же точка М совпада- \ /
ет с точкой К, то ф = 0. И /
тогда
г = OK -d-d* cosb.
Таким образом, уравнение Рис.19.5
окружности принимает вид:
г — d-cosy.
В частности, для полюса О, лежащего на окружности,
имеем:
г = 0, ф = с.
Здесь С — любое число, так как полярный угол ф для
полюса может быть произвольным.
Проверим, что найденное уравнение не задает
точек, которые не принадлежат окружности. В самом де-
ле, пусть полярные координаты некоторой точки N
удовлетворяют уравнению г = d • cosy, где d — диаметр
окружности. Тогда г > 0, откуда находим, что соуф > 0, и
поэтому угол ф лежит либо в I четверти, либо в IV чет-
верти. Можно считать, что
имеем:
Значит, в этих случаях точка N — полюс.
Пусть теперь полярный угол ф удовлетворяет нера-
венству 0 < ф < — (рис. 19.6). Луч ON пересекает окруж-
ность в некоторой точке М, для которой из треугольни-
474
ка ОМК получим: ОМ = d • cos<p. Но тогда ON = г =
= d • cos(p — ОМ. Кроме того, точки N и М лежат на од-
ном луче с началом в точке О. Следовательно, точки N
и М совпадают, и точка N лежит на окружности.
Случай,
когда
О,
рассмотрите самостоя-
тельно. В этом случае луч ON расположен ниже диамет-
ра ОК.
Итак, уравнение окружности, содержащей полюс,
имеет вид:
r=d-cos<p.
Полюс находится вне круга. Пусть центр Р окруж-
ности лежит на полярной оси, а полюс О удален от цен-
тра Р на расстояние, большее радиуса окружности.
Через точку О проведем произвольную секущую
(рис. 19.7), и из центра Р опустим на нее перпендику-
ляр PQ. Отрезки секущей ОМх=гх и ОМ2=г2 являют-
ся полярными радиусами точек Л/, и М2. Составим
квадратное уравнение с корнями гх и г2. Пусть ОР = р,
R — радиус окружности. По свойству секущей имеем:
г,-r2 = OLOK = (р-Я)(р+ R) = р2 - R2.
По свойству хорды получаем, что точка Q — середина
хорды Мх М2 , поэтому
П + r2 = (OQ - М£)+(OQ + M2Q) = 2OQ = 2p- cost?.
475
Мы нашли сумму + г2 и произведение гхг2 корней не-
которого квадратного уравнения. Составим это уравне-
ние. Получим:
г2 -2гр-сояр + р2 -7?2 = 0.
Заметим, что при ф = 0 имеем: rx = OL, г2 = ОК. Эти
значения удовлетворяют условиям:
гх +г2 = 2рсау0 = 2р, гхг2 = р2 -7?2,
поэтому они также будут корнями полученного квадрат-
ного уравнения. Рассмотрим теперь предельное положе-
ние секущей, когда она превращается в касатель-
ную ОМ (рис. 19.7). По свойству касательной имеем:
г2 = OLOK = p2-R2.
Из треугольника ОРМ получаем:
гл/ = р-сшфл/,
где гм, фду — полярные координаты точки М. Для сов-
падающих чисел гх =г2 = г м имеем вновь:
rt + г2 = 2р cos(p м, rl-r2 = p2-R2,
поэтому они являются кратными корнями уравнения
г2-2rp'cosyм + р2 - R2 =0.
Таким образом, каждая точка окружности удовлетворяет
полученному квадратному уравнению. Проверим, не
удовлетворяют ли этому уравнению какие-либо точки, не
принадлежащие окружности.
Пусть полярные координаты (г;ф) некоторой точ-
ки N удовлетворяют нашему уравнению. Вычислим дис-
криминант D этого уравнения:
D = 4р2 • cos2!?-4(г2 - 7?2) = 4(р2 • cos2q> + R2 - р2) =
= 4(R2 - р2 • (1 - са^ф)) = 4(/?2 - р2 • 5/п2ф).
Корни этого уравнения и г2 существуют, если
R2 - р2 • sin2q > 0, т.е. р2 • sin2<p < R2 и sirup < —.
Р
Эти корни удовлетворяют уравнениям:
Г] + г2 = 2р • с05ф и г\г2 = р2 - R2.
476
Рис. 19.8
N
Рис. 19.9
Так как p = OL>PL = R, то г,г2>0. Если 2р-со5ф<0, то
оба корня отрицательны. Поэтому обязательно должно
выполняться условие: 2р-СО5ф>0, и угол ф должен ле-
жать в первой или четвертой четверти. Учитывая огра-
ничения на sin<p, получаем неравенство —а < ф < а,
R
где а —такой острый угол, для которого sma =—. Про-
Р
ведем из точки О лучи ОА и ОВ, касательные к окруж-
D
ности (рис. 19.8). Так как sinZAOP =—, то а. = ZAOP.
Р
Таким образом, точка ./У(г;ф) принадлежит углу АОВ .
Если ф = ±а, то D = 0 и уравнение имеет кратные
корни, равные p-COSCt. Тогда точка N является одной из
точек касания.
Пусть далее —а < ф < а. Из точки О проведем секу-
щую через точку N. Она пересечет окружность в неко-
торых точках Л/] и М2 (рис. 19.9). Расстояния ОМ{
и ОМ2 по доказанному выше являются корнями нашего
квадратного уравнения, поэтому либо г = OMt, ли-
бо г = ОМ2, и точка N — это одна из точек Мх и М2 •
Значит, точка N лежит на окружности.
Итак, составленное нами уравнение
г2 - 2rp-coscp + р2 - R2 = О
477
действительно является уравнением окружности.
Полюс находится в кру-
ге. Пусть центр окружнос-
ти Р лежит на полярной оси,
а полюс лежит в круге. До
сих пор мы находили уравне-
ния окружности, опираясь на
геометрические соображе-
ния. Далее мы пойдем иным
путем, применяя декартовы
координаты. Для этого нача-
Рис. 19. ю
ло системы декартовых пря-
моугольных координат О со-
вместим с началом системы
полярных координат, как по-
казано на рис.19.10. Пусть, как и прежде, <9Р = р,
РК = R, но на этот раз 7? > р. Уравнение окружности с
центром в точке Р(р; 0) и радиусом R в декартовых ко-
ординатах представляется в виде:
(х-р)2+/ = Я2
или иначе:
х2 +у2 -2р-х-(т?2 -р2) = 0.
Чтобы записать это уравнение в полярных координатах,
подставим в него вместо X и у их значения, выражен-
ные через полярные координаты Гиф.
Так как х2 + у2 = г2 и х = г -coscp, то имеем:
г2-2р-Г •СО5ф-(/?2 -р2) = 0.
Полученное уравнение окружности совпадает с уравне-
нием из предыдущего пункта, однако оно имеет несколь-
ко иной смысл. Прежде всего установим, что относитель-
но Г это уравнение всегда имеет единственный положи-
тельный корень. В самом деле, дискриминант этого урав-
нения равен:
D = 4(р2 • cos2(p + R2 - р2 )>0.
Это значит, что уравнение имеет два действительных
корня. Однако, произведение этих корней равно чис-
478
лу — (Л2 —р2), которое отрицательно, так как /?>р.
Значит, корни этого уравнения имеют разные знаки, и
один из этих корней является положительным. Геомет-
рический смысл этого утверждения состоит в том, что
всякий луч, проведенный из точки О, пересекает окруж-
ность в единственной точке (рис. 19.10).
§ 19.4. УРАВНЕНИЕ ПРЯМОЙ В ПОЛЯРНЫХ
КООРДИНАТАХ
Луч с началом в полюсе. Пусть луч ТП имеет начало
в точке О — полюсе полярной системы координат и об-
разует угол ф0 с полярной осью, причем угол отсчитыва-
ется против часовой стрелки. Тогда уравнение этого луча
представляется в виде:
В самом деле, для произвольной точки луча поляр-
ный угол можно взять равным ф0 (рис. 19.И). И наобо-
рот, произвольная точка Л/(г;ф0) лежит на луче ТП.
При г = 0 точка М является началом луча, а при Г >0
Z.MOL = и точка М принадлежит прямой ТП.
Прямая проходит через полюс. Рассмотрим пря-
мую <7, содержащую точку О. Проведем через эту точку
луч П, перпендикулярный к прямой а (рис. 19.12). Пусть
этот луч образует угол а с полярной осью I . Точка О
479
делит прямую а на два луча, образующие соответствен-
но углы а + — и а--с полярной осью. Уравнения этих
лучей имеют вид:
Л Л
Ф=а + — и ср=а-------.
Тогда прямая а задается совокупностью уравнений:
Л
Ф = а + -
, которая равносильна уравнению
л
Ф = а--
са$\ф —а) = 0. При этом мы учли то обстоятельство, что
полярный угол задается с точностью до числа, кратно-
го 2л.
Прямая не проходит через полюс. Пусть полюс О
не лежит на прямой а,
Опустим перпендикуляр ОР
на прямую а. Обозначим:
OP — d — расстояние от
точки О до прямой а
(рис. 19.13). Возьмем произ-
вольную точку Л/(г;ф) на
прямой, отличную от точ-
ки Р. В треугольнике РОМ
угол РОМ равен |ф —а|.
Для точки М на рис.19.13
этот угол равен а — ф. (Дру-
гие случаи рассмотрите самостоятельно). Тогда
г = _£_
со$|ф-а|
Учитывая то, что косинус — четная функция, получим:
г соу(ф-а) = J.
Если же точка М совпадает с точкой Р, то точка М
имеет координаты г ~d и ф = а, и эти координаты удов-
480
летворяют данному уравнению. Обратно, пусть для неко-
торой точки М(г;ф) выполняется равенство:
г соз(<р - а) = d.
Так как г > 0, то со$(ф — а) > 0, и можно считать, что
разующие
Рис. 19.14
параллельную
Точка
Проведем через полюс О
прямую b,
прямой а.
прямую b на два
О делит
луча, об-
а + у с полярной осью I .
Тогда луч ON образует угол
ф с осью I и обязательно
пересечет прямую а. Если
ф = а, то
NO = r =
и точка N совпадает с точкой Р.
Пусть а < ф < а + у. Тогда луч ON пройдет так, как
показано на рис. 19.14, и пересечет прямую а в некото-
рой точке М. Однако,
ON = —--------г, ОМ =-----—-----= —--------г.
со$(ф-а) cosZ.MOP со5(ф а)
Значит, ОМ = ON, и точки М и N совпадают. Случай,
когда а----< ф < а, рассмотрите самостоятельно. Таким
481
образом, точка N(r;<p) принадлежит прямой а. Итак,
мы получили следующее уравнение прямой:
Каждая точка прямой а удовлетворяет этому уравнению,
и всякая точка #(г;ф), координаты которой удовлетво-
ряют этому уравнению, принадлежит прямой а.
§ 19.5. СПИРАЛЬ АРХИМЕДА
Из условия г > 0 следует,
Пусть а — некоторое положительное число. Спи-
раль Архимеда — это кривая, задаваемая в полярных ко-
ординатах уравнением
Г = Яф.
Название "спираль Архимеда" происходит от латин-
ского слова "spira" — кольцо, образованного от греческо-
го ояетра — виток. Древнегреческий физик и матема-
тик Архимед (287—212 до н.э.) нашел способ по-
строения касательных к этой кривой, сумел вычислить
площадь сегмента, ограниченного дугой спирали.
Построим эту кривую,
что аф>0, и так как
а > 0, то ф > 0. Поэто-
му при построении
спирали Архимеда мы
будем вращать луч
против часовой стрел-
ки из начального поло-
жения, совпадающего
с полярной осью I .
При ф = 0 имеем:
г = 0, так что началь-
ная точка кривой сов-
падает с полюсом. При ф > 0 полярный радиус Г поло-
жителен, причем при возрастании ф радиус Г также
возрастает, т.е. расстояние от точки М на спирали до
полюса О будет увеличиваться. Мы получили кривую,
часть которой изображена на рис. 19.15. Она пересекает
16 Зак. 687
482
полярную ось в тех точках, где либо г = 0, либо
<р=2тг п, где П —натуральное число. Соответствую-
щие расстояния, обозначаемые через гп, вычисляются по
формуле: гп=а-2п-П. Значит, пересечение полярной
оси и спирали будет происходить последовательно в
точках О, Р., Р,, ... , Р_, ... Здесь ОР„ = 2тг аи, где п S1.
* * 99 99
С каждым новым оборо-
том луча мы получаем но-
вый виток спирали. Заме-
тим, что вблизи точки О
спираль будет касаться
полярной оси. Это значит,
что первый виток спирали
не может образовывать
острый угол с полярной
осью / : если бы вблизи
точки О имела бы место
ситуация, изображенная
на рис. 19.16, то луч, про-
веденный под достаточно
Рис.19.16
малым углом ф0<а, пере-
секал бы первый виток спирали лишь в полюсе. Однако
при <р = (р0 имеем: г = аф0>0, и поэтому даже при ма-
лых углах <р0 мы, кроме полюса, обязаны получить еще
одну точку пересечения луча Ш с первым витком спира-
ли.
Свойство спирали Архимеда. Следующая теорема
устанавливает важное свойство, которым обладает спи-
раль Архимеда.
Т еорема 19.1. Каждый луч, проведенный из по-
люса; имеет бесконечное множество точек пересечения
со спиралью Архимеда, причем расстояния от этих
точек до полюса образуют арифметическую прогрессию.
□ Проведем из точки О произвольный луч под уг-
лом ф0 к полярной оси, считая, что 0 < ф0 < 2п. При
значениях полярного угла ф„ = ф0 + 2п -п, где п > 0, мы
получим точки Мп (гп ;фЛ ) на спирали, где
483
rn = acpn = a(<p0 + 2л-и) = а<р0 + 2 л-an.
Все эти точки лежат на проведенном луче (рис. 19.15).
Расстояния гп обладают следующим свойством: при лю-
бом натуральном П разность гп-гп_х = 2тс-а и не зависит
от П. Такие последовательности, в которых каждый член
образуется из предыдущего путем сложения его с неко-
торой постоянной величиной, в алгебре называют ариф-
метической прогрессией. Значит, на рис. 19.15 расстояния
OMV ОМ2, ... , ОМп, ... образуют арифметическую про-
грессию. Геометрически это означает, что отрезки
МХМ2, М2МУ ... , Мп_хМп являются равными.
Оказывается, что спираль Архимеда — это единст-
венная кривая, обладающая
таким свойством. X
Увидеть спираль Архи-
меда можно, если вам пове-
зет, даже не выходя из X
квартиры. Представьте себе / О J \ Е
вращающуюся пластинку I 1------►
электропроигрывателя и му- \ 'JJq /
ху, которая ползет от цен- 7
тра по радиусу пластинки с -----------
постоянной скоростью. То-
гда мы увидим, ЧТО муха Рис.19.17
описывает спираль Архиме-
да. Действительно, пусть в начальный момент t = 0 муха
находится в центре пластинки. Затем она начинает дви-
гаться по радиусу с постоянной скоростью v0. Эта ско-
рость задана в системе отсчета, связанной с пластинкой.
Пластинка начинает вращаться против часовой стрелки с
угловой скоростью СО, измеряемой в радианах в секунду.
Выберем полярную ось так, как показано на рис. 19.17.
Тогда через t секунд положение мухи в системе отсчета,
связанной с наблюдателем, задается уравнениями:
откуда
484
Следовательно, муха движется по спирали Архимеда
г = а • <р, где а =
§ 19.6. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ
Перейдем теперь к рассмотрению новой кривой.
Пусть с > 0, а > 0, причем а 1. Логарифмическая
спираль — это кривая, задаваемая в полярных координа-
тах уравнением:
г = саф.
Такое название она получила потому, что некоторые ее
свойства напоминают свойства логарифмов.
Первое свойство логарифмической спирали. На
рис. 19.18 изображена лога-
Г= C Ct , CL>1 рифмическая спираль с ос-
нованием а > 1. Так как
X рЛ р р I g cP > 0 при любом показа-
/ Z3)212! ---------2 I »» теле степени, то угол ф
I Л/ДсОх / может быть произвольным
и полюс не лежит на
этой спирали. При ф =
= ф*=2л-£, где к —лю-
бое целое число, логариф-
мическая спираль пересе-
кается с полярной осью в
Рис. 19.18
точках РДгл;фл), где гк=оаь = с-а2пк =с-qk.
Мы обозначили здесь через q число а2п и восполь-
зовались свойствами степеней. Заметим, что для последо-
вательности расстояний ОРк отношение
485
ОРщ СЧЫ ,
OPt cqk
является постоянной величиной, большей 1 .
Последовательность таких чисел, у которой отноше-
ние последующего члена к предыдущему не изменяется
и отлично от 1, в алгебре называют геометрической про-
грессией, а само отношение, равное q, называется зна-
менателем этой прогрессии.
Итак, последовательность расстояний ... , ОР_п,
OP_nU....ОР_2, OP_V OPQ, OPV ОР2......ОРп,
... образует геометрическую прогрессию со знаменате-
лем q > 1.
Указанное свойство имеют точки пересечения дан-
ной логарифмической спирали с произвольным лу-
чом ТП, выходящим из точки О. Пусть угол между
лучами I и тп равен а0, где 0<а0<2я. Тогда при
ф=ал=а0+2я-£, где к— любое целое число, имеем
точки на луче ТП и, соответственно, получаем точки
Мк (dk ;а*) на спирали. Здесь к — целое число и
dk = C‘а*к = [с'аа° . При каждом значении к отно-
OMk+l c-aa°-qk+1
шение -------=-------—;— = q, и поэтому последова-
ОМк caa°qk
тельность расстояний ОМк образует геометрическую
прогрессию со знаменателем q. Этим мы фактически до-
казали следующее утверждение.
Теорема 19.2. Всякий луч, выходящий из полю-
са, пересекает логарифмическую спираль в бесконечном
множестве точек, причем их расстояния до полюса об-
разуют геометрическую прогрессию, знаменатель кото-
рой не зависит от направления луча.
Логарифмическая спираль является единственной
кривой, обладающей этим свойством. Чтобы хорошо
прочувствовать это, рассмотрим еще одно утверждение,
о котором нам говорит
486
Теорема 19.3. Пусть на луче с началом в точ-
ке О лежит бесконечное множество точек Mv М2,
... r Мп, ...» причем расстояния ОМ^ OMV ОМ2, ... ,
ОМп,... образуют геометрическую прогрессию. Тогда
точки Mv М2, ... , Мп, ... лежат на логарифмичес-
кой спирали.
□ Обозначим ОМп = гп, п >0. Примем данный луч
за полярную ось и рассмотрим логарифмическую спи-
раль г = с-а^. Подберем числа а и С так, чтобы эта
спираль прошла через точки Мк (гк; ф* ), где ф* = 2 я • к,
fc>0. Это будет выполнено лишь в том случае, если
с • a2nk = гк, где к > 0. Положим с = r0, а2п = q, откуда
1
а = q2nt
где q -— знаменатель прогрессии. Тогда c-a27lO=ro,
~ Э L 27С'(* - Ч
с-а2п =rQq = rv с-а2*' =с а q -q = rk.
Значит, логарифмическая спираль с заданными па-
раметрами действительно пройдет через точки Мк, где
£>о.а
Вернемся к рис. 19.18, на котором изображена лога-
рифмическая спираль при а > 1. Ее можно понимать как
результат вращения материальной точки вокруг полюса.
Представьте себе луч, совпадающий с осью I , и на нем
некоторую точку Ро(с;О). Луч начинает вращаться про-
тив часовой стрелки, образуя некоторый угол ф0 > 0 с
осью I , и на луче получаем соответствующую точ-
ку Л^0(саФо;ф0). С возрастанием ф0 расстояние до полю-
са г0 = с-лФо увеличивается, так как основание степе-
ни а > 1. Луч делает полный оборот, и при ф = 2 я по-
лучаем точку • а2*;2я).
При ф = 4я получаем точку /^(с-а471;4я) и т.д. Чис-
ло таких витков будет неограниченным, причем расстоя-
487
ние от точки на спирали до полюса будет неограниченно
возрастать. При очень больших значениях ф величи-
на с • аф будет также очень большой. Наша спираль явля-
ется неограниченной кривой, так как не существует кру-
га, в который ее можно было бы поместить. Однако это
еще не вся спираль. Вернем наш луч в начальное поло-
жение, совпадающее с полярной осью, а материальную
точку — в точку Ро. Начнем вращать луч в отрицатель-
ном направлении, т.е. по часовой стрелке. Тогда при
ф = -ф0, где ф0>0, получим точку О)(с-а~фо;-ф0) на
спирали. При этом с возрастанием величины ф расстоя-
ние OQ0=c-a-v<>= —
уменьшается. При каждом новом
обороте получим новые витки спирали (рис.19.18).
При очень больших значениях ф| расстояние (9<2о
будет очень маленьким, так как оно будет выражаться
дробью с большим знаменателем а~Фо. Спираль будет
приближаться к полюсу О, Она как бы наматывается на
него, при этом никогда его не достигая. Как видим,
при а > 1 спираль раскручивается против часовой стрел-
ки и закручивается по часовой стрелке.
Нетрудно понять, что при основании Ь, меньшем 1,
все происходит наоборот.
Действительно, пусть 0 < b < 1. Рассмотрим спи-
-ф. Пусть • а
-Ф j
. Обозначим а = —. При
про-
извольная точка на этой кривой. Рассмотрим точку NQ,
симметричную точке Л/о относительно полярной оси I .
Тогда ее полярные координаты будут такими:
ЛГ0(са’Фо;-ф0). Она будет лежать на спирали г = с-аф.
Действительно, при ф = —ф0 получим:
г =c-a~Vo =c-av.
488
Рис.19.19
Таким образом, все точки искомой спирали являются
симметричными образами точек спирали г = с*а^ отно-
сительно полярной оси. На рис. 19.19 изображена спи-
раль г = с-Ь^, где 0 < b < 1.
Второе свойство логарифмической спирали. Сле-
дующее неожиданное утверждение является следствием
свойства степени: Можно доказать, что
это утверждение справедливо лишь для логарифмических
спиралей.
Те.ор е м а 19.4. При повороте логарифмической
спирали вокруг полюса образуется логарифмическая
спираль, являющаяся образом данной спирали при го-
мотетии с центром, совпадающим с полюсом.
□ Пусть задана логарифмическая спираль г = с-лф.
Повернем ее против часовой стрелки вокруг полюса О.
Тогда точка Л/0(саФо;ср0) на данной спирали перейдет в
489
точку М[са*°; (р0 + а). Для новой кривой при ф = ф0 + а
получим полярный радиус г = саФо = (саф)а~а. По срав-
нению с точкой ЛЛсаф;ф) на данной спирали полярный
радиус г умножился на постоянное число ккото-
рое не зависит от выбора ф. Это и означает, что новая
кривая является образом данной спирали при гомотетии
с коэффициентом к и центром О. Новая кривая также
будет логарифмической спиралью, так как ее уравнение
имеет вид:
Ф —а м
г = q • ст, где сх = с • а .
При гомотетии с центром О и коэффициен-
том к = л"а, где а —любое число, логарифмическая спи-
раль г = с-лф поворачивается на угол а против часовой
стрелки вокруг точки О. Докажите это самостоятельно.
Пусть на плоскости задано бесконечное множество
точек О, MQt Mv ... , Мп, ... . Расстояния OMQf OMV
ОМ2.....ОМп, ... образуют геометрическую прогрессию,
a = ZMXOM2 = ... = ZMXOM =..., причем
при каждом целом значении п > 0 точка Л/Л+2 не лежит
на луче ОМп. Тогда точки Мо, Mv М2, ... лежат на лога-
рифмической спирали с полюсом О.
Докажите это самостоятельно. Для этого выберите в
качестве полярной оси луч ОМ$. Убедитесь, что искомая
ф
спираль имеет уравнение г = rQqa, где q — знаменатель
геометрической прогрессии расстояний OMQ, ОМХ,
ОМ2.....ОМп ... , а = ZMQOMX.
Логарифмическую спираль открыл Рене Декарт.
Швейцарский математик Якоб Бернулли (1654—
1705) пережил настоящее потрясение от того, что лога-
рифмическая спираль восстанавливает себя после раз-
личных преобразований (см., например, теорему 19.4).
Он завещал выбить на своем надгробии спираль и над-
пись на латыни: "Измененная, я вновь воскресаю".
490
Соцветия многих растений, в частности, подсол-
нечника, маргаритки, имеют форму логарифмической
спирали. На сосновой шишке чешуйки также расположе-
ны вдоль спирали. Некоторые пауки закручивают паути-
ну вокруг центра по спирали. Улитки также закручивают
раковину спиралью. Они выбирают именно логариф-
мическую, а не, скажем, архимедову спираль, ибо рост
тканей можно описывать гомотетическим преобразова-
нием, а при гомотетии логарифмическая спираль пово-
рачивается на некоторый угол. Поэтому улитке не нужно
досконально перестраивать свое жилище, и при его уве-
личении оно будет последовательно поворачиваться.
§ 19.7. ЗОЛОТОЕ СЕЧЕНИЕ
Пусть АВ — произвольный отрезок и точка С ле-
жит между точками А и В (рис.19.20). Говорят, что эта
точка С делит отрезок АВ в крайнем и среднем отно-
шении, если выполняется равенство:
АВ _ АС
АС ~ СВ
(1)
Вычислим это отношение. Обозначим: -
СВ
Тогда СВ = —, АВ = fl + —= 1 + — а. Равенство (1) вы-
полняется тогда и только то-
гда, когда
fl
Рис, 19.2 О
. При этом
отсюда х — х - 1 = 0. Это
уравнение имеет два корня
геометрическую интерпретацию
имеет лишь положительный корень. Мы доказали сле-
дующее утверждение.
491
Теорема 19.5. Точка заданного отрезка делит
его в крайнем и среднем отношении тогда и только то-
гда, когда отношение большей части отрезка к меньшей
1 + V5
его части равно —-—.
1 + V5
Число ------ называется золотым сечением и обоз-
2
начается греческой буквой ф. Число ф является ирра-
циональным, его приближенное значение таково:
ф« 1,61803398.
Буква ф, которой обозначается золотое сечение, — это
первая буква в имени древнегреческого скульптора Ф и-
д и я (начало V в до н.э.—около 430г до н.э.), который в
своих скульптурах часто использовал золотое сечение.
Золотой прямоугольник. Прямоугольник будем на-
зывать золотым, если отношение его сторон равно чис-
лу ф — золотому сечению.
Свойство золотого прямоугольника. Золотые прямо-
угольники широко использова-
лись архитекторами, художни-
ками и скульпторами. Свойст-
во, которым обладает золотой
прямоугольник, устанавливает
следующая теорема.
Теорема 19.6. Если от
золотого прямоугольника от- A F D
резать квадрат, то оставшийся
прямоугольник также является
золотым (рис.19.21). Рис .19.21
□ Пусть ABCD — золо-
той прямоугольник, ABEF —
квадрат. Обозначим АВ=а, тогда ВС = аф, BE =
= EF = а, ЕС = аф - а = а(ф — 1). Найдем отношения
сторон прямоугольника FECD:
EF а 1
492
Вспомним, что ф является корнем уравнения 14— = X,
X
, 1 1
поэтому ф —1 =—, откуда ф = ——. Значит---= ф.
ф ф-1 ЕС
Свойства золотого сечения. При доказательстве тео-
ремы 19.6 мы установили одно интересное свойство зо-
лотого сечения:
Ф
0,61803398.
Таким образом, —
Ф
Золотое сечение является также отношением радиу-
са R окружности к стороне а10 правильного десятиуголь-
ника, вписанного в эту окружность. Это утверждение
фактически было доказано раньше в главе 17.
Действительно,
а10 = 2R siril 8°, значит
7? = 1 = 1 = 75-1 =
а10 2ял18° л/5-1 2
^2 *
4
1 1
л/5 + 1 t Ф-1
2
В следующей теореме мы приведем геометрическое дока-
зательство, не использующее значение sinl8°.
Теорема 19.7. Для правильного десятиугольни-
ка, вписанного в окружность радиуса R, справедливо
равенство
R
— = ф.
вю
где а10 — длина его стороны, а ф — золотое
сечение.
493
□ Соединим центр окруж-
ности О с вершинами Ах и А2
правильного вписанного десяти-
угольника (рис. 19.22). В равно-
бедренном треугольнике АХА2О
угол при вершине О равен
360° ТА»
-----= 36 ,
10
а углы при основа-
нии равны
180°-36°
2
= 72°.
Про-
Рис .19.22
ведем биссектрису A2L. В тре-
угольнике AXLA2 имеем:
1Т
—= 36°,
1 2 2
]£Л2 = 180°-(зб° + 72°)
72°.
Тогда треугольники AtLA2 и АХА2О подобны. Обоз-
R
начим----= X. Из подобия треугольников получим:
AXL
откуда
AXL = ^~.
X
Далее,
LO = R- — = а10 -х~ — = а10 х- — .
X X у X J
По свойству биссектрисы угла треугольника ^jCM2
имеем:
LO _ R
A\L С1щ
или
494
ю
t
10
Рис.19.23
откуда х2—х —1 = 0. Но число ф является единственным
положительным корнем этого уравнения, поэтому х = ф.
Золотой треугольник. Равнобедренный треугольник
назовем золотым, если отношение боковой стороны к ос-
нованию равно числу ф.
В ходе доказательства теоремы 19.7 мы установили
следующее свойство золотого треугольника.
Теорема 19.8. Биссектриса угла при основании
золотого треугольника делит его на два треугольника,
один из которых является золотым. Меньший золотой
треугольник является прилежащим к основанию боль-
шего золотого треугольника.
Золотые треугольники
появляются при изучении
свойств правильного пяти-
угольника и его диагоналей.
Пусть около правильно-
го пятиугольника ABCDE
описана окружность с цен-
тром в точке О, Проведем
все диагонали пятиугольника
(рис. 19.23). Пусть F и G —
точки пересечения диагонали
АС соответственно с диаго-
налями BE и BD. Справед-
лива следующая теорема*
Теорема 19.9. Отно-
длины диагонали правильного пятиугольника к
его стороны равно золотому сечению ф. Кроме
шение
длине
того, точка F делит каждый из отрезков СА и AG в
крайнем и среднем отношении.
495
□ 1. В равнобедренном треугольнике АСЕ угол при
вершине С равен ^-(yjAE ) как вписанный, опирающий-
ся на дугу АЕ , т.е.
360’
Поэтому треугольник АСЕ является золотым, откуда
---= ф.
АЕ
2. Проведем прямую OD. Она является осью сим-
метрии правильного пятиугольника ABCDE . Поэтому
точка А симметрична точке В, а точка С симметрична
точке Е относительно OD. Тогда диагонали АС и BE
будут также симметричными, и точка их пересечения F
принадлежит оси симметрии. В треугольнике CFD име-
ем:
ZCDF^~(uHC\
ZCFD = -(yjAH + uCD) = -(yjHB + vBC) =
2 2
= -(vHC) = ZCDF.
Поэтому этот треугольник является равнобедренным, от-
куда CF = CD. Тогда по доказанному выше
ЛС _ЛС _ЛС _
CF CD АЕ Ф‘
Согласно теореме 19.5, точка F делит отрезок АС в
крайнем и среднем отношении.
3. В треугольнике AFE угол AEF =36°,
ZAFE =^>АЕ +<jBC) = U'uED + vDC) =
Поэтому этот треугольник золотой, откуда
496
AG АЕ
AF AF
= <₽•
Рис. 19.24
Рассмотрим ломаную ли-
нию, составленную из диаго-
налей правильного пятиуголь-
ника — звезду. По теоре-
ме 19.9 она обладает таким за-
мечательным свойством: лю-
бой отрезок в этой фигуре
находится в отношении
к наименьшему соседнему от-
резку.
Например, на рис. 19.24 имеем:
AF AG CF
Благодаря этому свойству звезда или пентаграмма была
символом школы древнегреческого математика Пифаго-
ра.
§ 19.8. ЗОЛОТОЕ СЕЧЕНИЕ И СПИРАЛИ
Существует интересная связь между золотым
сечением и логарифмическими спиралями.
Рассмотрим золотой прямоугольник ABCD
(рис. 19.25). Отрежем от него квадрат ABFE . Согласно
теореме 19.6 прямоугольник FCDE является также золо-
тым. Отрежем от него квадрат FCHG. Останется золо-
той прямоугольник EDHG. Продолжая неограниченно
эту процедуру, получим бесконечное множество вложен-
ных друг в друга золотых прямоугольников.
Отметим по одной вершине в этих прямоугольниках
и рассмотрим следующую последовательность вершин
золотых прямоугольников:' A, F, Н, К, L, М, ...
(рис. 19.25). Оказывается, что эти точки лежат на лога
497
В
PxLC.19.25
рифмической спирали и справедлива следующая теоре-
ма:
Теорема 19.10. Вершины вложенных золотых
прямоугольников A, Ff Н f К, L, Мf ... лежат на лога-
рифмической спирали с полюсом в точке О пере-
сечения диагоналей BD и ЕС двух золотых прямо-
угольников.
□ Доказательство проведем в несколько этапов.
1. Точка G лежит на диагонали BD. Действительно,
золотые прямоугольники ABCD и EGHD подобны, по-
этому
tgAGDE =
GE
ED
BA
AD
= tgZ-BDA,
откуда
AGDE = ABDA,
и точка G лежит на BD.
2. Аналогично диагональ ЕС проходит через верши-
ну Р третьего золотого прямоугольника. Таким образом,
точка О пересечения диагоналей BD и ЕС является
также точкой пересечения диагоналей ЕС и GD, диаго-
налей GD и ЕР и т.д. Для золотого прямоугольника, по-
498
строенного на п-м шаге, точка О является точкой пере-
сечения его диагонали с диагональю (и + 1)-го золотого
прямоугольника.
3. Прямоугольники ABCD и FCDE подобны, и
ZAOF = Z.FOH как соответственные углы в подобных
фигурах. Аналогично
AFOH = AHOK =ALOK = ALOM =...
Далее, АО и OF являются соответственными отрезками
в подобных фигурах, и поэтому
АО ,(ABCD\ AD
----= к ------- =----=ф.
OF k FCDE JFE
Аналогично
_FO _ОН OK OL _
9 ОН OK OL ОМ
Тогда расстояния АО, OF, ОН, OK, OL, ОМ, ...
образуют геометрическую прогрессию, и согласно §19.6
точки A, F, Н, К, L, М, ... лежат на логарифмичес-
кой спирали с полюсом в точке О,
Спираль можно построить также с помощью золото-
го треугольника.
Пусть треугольник АВС —золотой (рис. 19.26). Про-
ведем биссектрису CD. Со-
гласно теореме 19.8, тре-
угольник ACD — золотой.
Проведем его биссектри-
су АЕ, тогда треуголь-
ник DAE — золотой. Про-
ведем его биссектрису DF,
тогда треугольник FDE —
золотой, и т.д.
Оказывается, что все
вершины бесконечной по-
следовательности вложен-
ных золотых треугольников
лежат на спирали. Для дока-
зательства этого утвержде-
ния рассмотрим сначала
лемму.
499
Лемма. Пусть в золотом треугольнике АВС бис-
сектриса AN и медиана АК пересекают биссектрису
угла С соответственно в точках Е и R. Тогда точка R
делит отрезки CD и DE в одном и том же отношении
(рис. 19.27).
□ Первый способ.
Обозначим АС = Ь. Тогда DC = b,
b b
AD =—, DE = — . Рассмотрим векторы AC=b,
Ф Ф
AD = C. Тогда
= 1(ф2.с + б).
Вектор DR можно предста-
вить в виде:
Рис.19.27
DR = x-(b-c), где
0<х<1.
Для вычисления X рассмотрим вектор AR:
AR = AD +DR = с + х-(б-с) ==х-£ + (1™х)с.
По теореме 12.6 векторы AR и АК коллинеарны в том
и только том случае, когда — =
1-х 1
—г-, откуда Х=-т—
ф ф +1
Тогда
Далее,
500
c-b
2/ 2,1V
Ф VP +У
Следовательно,
|c-&| 2 X_CD
RE ср2 ф2(ф2 + 1) DR
Второй способ.
Рис.19.2в
Через точку К прове-
дем прямую, параллель-
ную DC, до пересечения с
прямой АВ в точке F и с
прямой AN в точке Р.
Имеем несколько равнобед-
ренных и подобных тре-
угольников: АСВ, ADC,
CNA, NPK.
Необходимо доказать,
что
DE DC DC DR
---=---- идп ---=----
RE DR DE RE
(рис. 19.28).
Из подобия треугольников АСВ и ADC имеем:
DC СВ
DE CN'
Далее,
_ fx cd kn -1 АС
RE КР KN 2 ’ 2 KN'
Осталось доказать, что
СВ 1 АС СВ CN
- = иди -=------
CN 2 KN---------AC 2KN
Но по свойству биссектрисы треугольника АСВ имеем:
501
CN =
вс =
ВС.
=вс —
KN =—ВС-CN =—ВС--------ВС =
2 АС + ВС
7_А АС + ВС-2 АС
ВС) ' 2(АС + ВС)
^ВС(ВС-АС)
2(АС + ВС)
и искомое равенство равносильно соотношению:
ВС = АС
АС ВС-АС'
Тогда
ВС-AC^ВС-AN =BC-BN = NC
и равенство
ВС _АС
AC ~ CN
следует из подобия треугольников АСВ и CNA .
Вернемся к вложенным
(рис. 19.29).
Теорема 19.11. В зо-
лотом треугольнике АВС
все вершины, а также осно-
вания последовательно про-
веденных биссектрис 27, Е,
F ... лежат на логариф-
мической спирали с центром
в точке О пересечения ме-
диан АК и DM треуголь-
ников АВС и DCA соот-
ветственно.
□ 1. В треугольнике
DEA проведем медиану ЕР
(рис. 19.29). Докажем, что медианы АК, DM, ЕР пере-
секаются в одной точке. Пусть DE и АК пересекаются
в точке R, a DM и АЕ — в точке G. В подобных тре-
угольниках ADC и САВ точке А соответствует точ-
золотым треугольникам
Рис. 19.2 9
502
ка С (вершина основания), а точке G — точка R (точка
пересечения медианы и биссектрисы), точке Е соответ-
ствует точка D (основание биссектрисы). Поэтому
AG . CR
GE RD'
Но согласно лемме
CR DR
RD RE
Составим произведение отношений
DR GE JP DB GE 1==
RE AG PD RE'AG-
DP,ЛС _ DP,СВ DRDR
RE' GE RERD RERE
Таким образом,
DR EG АР г
RE ' GA ' PD ~
Согласно теореме Чевы, прямые AR, DG и ЕР, а
значит, и прямые АК, DM и ЕР пересекаются в одной
точке — точке О.
2. Таким образом, в каждом вложенном золотом
треугольнике медиана, проведенная к боковой стороне,
проходит через точку О, Для каждого золотого тре-
угольника точка О является точкой пересечения такой
медианы и отрезка, соединяющего основание биссек-
трисы с серединой основания треугольника. Поэтому при
соответствии, устанавливаемом подобием треугольников
САВ и ADC, точка О как внутренняя точка треуголь-
ника САВ соответствует сама себе как внутренняя точка
треугольника ADC. И это будет выполняться для каж-
дой пары вложенных золотых треугольников. Устанав-
ливая соответствие между вершинами подобных тре-
угольников, получаем равенства:
ВО СО ЛО ОО ВО _
СО АО~ DO ЕО GO ’
т.е. расстояния ВО, СО, АО, DO, ЕО, GO, ... со-
ставляют геометрическую прогрессию. Из подобия тре-
угольников следует также равенство углов:
503
АВОС = ACOA = ZAOD = ADOE = AEOG =...
Из §19.6 следует, что точки В, С, A, D, Е, G лежат на
логарифмической спирали с центром в точке О
(рис. 19.26).
§ 19.9. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 19.1. Кривая задана в полярных координатах
уравнением Г=/(ф) • Каким свойством она обладает, если:
а) функция f является четной функцией;
б) функция f является периодической с периодом Т ?
Рис. 19.30
Ции f
— произвольная точка кри-
вой, т.е. фц принадлежит об-
ласти определения функ-
ции f и го = /(фо)- Тогда
точка Л<(г0; Фо) также ле-
жит на кривой. Действитель-
но, в силу четности функ-
значение ф = — ф§
также принадлежит области
определения функции /, причем /(“"Фо) = /(фо)=го»
координаты точки Мх удовлетворяют заданному урав-
нению. Точка Мх симметрична точке М относительно
полярной оси I (рис. 19.30), поэтому кривая симметрична
относительно полярной оси. Для построения кривой с
таким свойством достаточно построить ее при ф>§ и
полученную дугу отразить симметрично относительно
полярной оси. Jhk
2S. б) Пусть Л/(г0;ф0) — произвольная точка кри-
вой. Тогда точка М2 (г0;<р0 + Г) также лежит на кривой.
Действительно, в силу периодичности функции f
значение <р=ф0 + Т принадлежит области определения
функции f одновременно со значением <рй, причем
504
/(фо +г) = /(фо) = го, и координаты точки М2 удовле-
творяют заданному уравнению. Точка М2 получается из
точки М поворотом на угол Т против часовой стрелки
вокруг центра О (рис. 19.31). Поэтому при таком поворо-
те каждая точка кривой переходит в новую точку кри-
вой. Обратно, для каждой точки кривой М2(г2;ф2)
точка Л/(г2;ф2 — Г), лежащая на кривой, при указанном
повороте переходит в М2.
М2(г0-.<р0+Г) Ита^ поворот вокруг точ-
' ки и на угол 1 в положи-
тельном направлении осуще-
ствляет наложение кривой на
себя.
Пусть, например, функ-
ция f — периодическая с
Рис. 19.31
периодом Т = —, где п —
п
натуральное число, п > 2.
Построение достаточно осу-
ществить при 0<ф<—, а
п
затем полученную дугу (/7 — 1) раз последовательно пово-
рачивать на угол 1 = —.
п
Пример 19.2. Логарифмическую спираль г = 22к отра-
зили симметрично относительно полюса. Доказать, что по-
лученная кривая также является логарифмической спиралью,
уравнение которой г = V2-2271. Какова геометрическая интер-
претация появления множителя в уравнении спирали?
ZS Пусть Л/(г0;ф0) — произвольная точка данной
Фп
спирали, г0 = 22п. При симметрии относительно полюса
точка М переходит в точку M}(rQ9t(pQ — я) (рис. 19.32),
505
Рис.19.32
Рис. 19.33
О
поскольку симметрия относительно точки О совпадает с
поворотом вокруг этой точки на угол Л по часовой
стрелке. Найдем связь между полярными координатами
Фо-Я Л ф,
точки М}. Имеем: г0 = 2 2л -22к = V2 -22я, где —
полярный угол точки М}. Тогда координаты точек по-
лученной кривой удовлетворяют уравнению Г = V2 -22л.
Это — уравнение логарифмической спирали.
Таким образом, точка Л/(г0;ф0) исходной спирали
соответствует точке А/2(г0д/2;ф0) новой спирали. Пере-
ход от точки М к точке М2 осуществляется гомотетией
с центром О и коэффициентом к=^2 (рис.19.33).
Значит, при симметрии относительно полюса О исходная
спираль подвергается гомотетии с центром О и коэффи-
циентом у[2. Ж
Пример 19.3. Записать в полярных координатах урав-
нения кривых:
а) у = х;
б) х2 +у2 = ах, где а — положительное число.
a) ZS На плоскости задана система XOY прямо-
угольных декартовых координат. Свяжем с ней систему
полярных координат, приняв точку О за полюс, а
луч ОХ — за полярную ось I .
506
Рис. 19.34 с-193 5
Прямая у = х есть биссектриса первого и третьего
координатных углов. Точка О разбивает ее на два лу-
я ( Зя^
ча, которые образуют с осью / углы ~ и
(рис. 19.34). Учтем, что полярный угол задается с точно-
стью до числа, кратного 2я. Тогда данная прямая задает-
ся совокупностью уравнений
ф = ~Ч-2я-А, k gZ
п eZ
или sin ср--
= 0. Это и есть уравнение прямой у = х
в полярных координатах. Ж
б) ZS Согласно §19.2 декартовы и полярные коорди-
наты связаны соотношениями x = rcos^1 y^r-sintp.
Подставим их в уравнение кривой. Имеем:
(г • coscp)2 + (г • swep)2 = аг • со$ф или г2 = аг • сояр.
Это уравнение равносильно уравнению г =сгcosy,
поскольку значение г = 0 тут принимается, например,
при ф = —
507
Пример 19.4. Из конца С отрезка ВС проведен пер-
пендикуляр АС=~ВС f а из точки А как из центра описана
окружность радиусом АС, Секущая АВ пересекает окруж-
ность в точках Р и Е, причем BD<BE, Доказать, что точка
D делит отрезок BE в крайнем и среднем отношении.
Z2S По свойству секущей и касательной
BDBE = BC2. Однако по условию ВС =2 АС, значит
отрезок ВС равен диаметру окружности и ВС == ED
(рис.19.35). Тогда BD • BE = ED2 или = ——. Итак,
ED BD
точка D делит отрезок BE в крайнем и среднем отно-
шении. Ж,
Пример 19.5. Построить трехлепестковую розу — кри-
вую Г=5/лЗф. Доказать, что кривая состоит из 3 равных ле-
пестков, каждый из которых обладает осью симметрии.
Воспользуемся результатом примера 19.1 б).
Функция f (ср) = яшЗф является периодической с перио-
дом Т — —. Поэтому построение достаточно осущест-
л . 2л
вить при и < ф <- с дальнейшим применением поворо-
та на угол — вокруг полюса. Из этого промежутка толь-
ко значения (ре 0; —
входят в область определения
уравнения г = sin3(p, поскольку при фб —;— аргу-
мент Зф попадает в интервал (л;2л) и 5шЗф< 0, а это
недопустимо, так как для точек кривой необходимо, что-
бы выполнялось неравенство г = 57иЗф > 0.
Если ф меняется от 0 до у, то аргумент Зф изме-
няется от 0 до л. При этом полярный радиус г = 5шЗф
508
возрастает от 0 до 1 (при ф = —), а затем убывает от 1
до 0. Дуга кривой расположена при этом в угле Ют,
, и касается
т
/ ?Г\ обеих сторон этого угла
(рис. 19.36). Касание проис-
ходит потому, что при ф,
= sin3<f>
РисЛЭ.36
близких к 0 либо к —, зна-
чение г положительно и
близко к нулю. Наиболее
удаленной от полюса явля-
ется точка MQ 1;— .
Согласно примеру
19.16), вся кривая получается из
построенного лепестка двумя последовательными поворо-
тами вокруг полюса на угол
(рис. 19.36). Эта кривая
состоит из трех лепестков, расположенных в углах, соот-
ветствующих таким интервалам изменения ф:
я 2я . . 4я . 5я
Эти лепестки являются равными фигурами, поскольку
накладываются друг на друга при повороте на угол —
вокруг полюса.
Проведем биссектрису р угла Ют и покажем, что
она является осью симметрии первого лепестка.
Пусть М rQ; — + Д — произвольная точка на пер-
вом лепестке, где
509
= sin
= cos3lS. При Д = О точка М совпадает с
ТОЧКОЙ MQ
лежащей на р, и при симметрии отно-
сительно р остается неподвижной. При Д = ± — точ-
6
ка М совпадает с полюсом и также неподвижна под дей-
ствием отображения симметрии. Пусть теперь-<Д<—
и Д Ф 0. Точка Мх
также лежит на первом
лепестке, поскольку значение
и. совпадает с полярным радиусом точки
= cos3 Д = г0
Мх. Точки М
и Мх симметричны относительно р. Действитель-
но, ОМ = OMx=rQ, и треугольник ОММх — равнобед-
ренный. Пусть Q — точка пересечения луча р и отрез-
ка MMV тогда Z.MOQ — Z.QOMх = IS , отрезок OQ яв-
ляется биссектрисой, высотой и медианой треугольни-
ка ОММ р Отсюда MMxlp, MQ = QMV значит, точ-
ки М и Мх симметричны относительно р. Мы устано-
вили, что первый лепесток обладает осью симметрии —
лучом р. Каждый из остальных двух лепестков также об-
ладает осью симметрии. Эти оси получаются последова-
2я _
тельными поворотами р на угол -у- вокруг полюса. А
Пример 19.6. Построить кардиоиду г = 2(1 - coscp).
Название кривой составлено из греческих слов
XapSia — сердце и — вид, внешность.
Воспользуемся результатами примера 19.1. Функция
fM -2(1 — СОУ(р) является периодической с перио-
510
дом Т = 2л, поэтому доста-
Рис.19.37
точно рассматривать ф из
отрезка [—л; л]. Кроме то-
го, f— четная функция,
поскольку косинус являет-
ся четной функцией. По-
этому достаточно постро-
ить кривую при ф е[0;л] и
отразить построенную ду-
гу симметрично относи-
тельно полярной оси. Фун-
кция cosy убывает от 1 до
когда ф е 0;л .
Соответственно функция /(ф)
возрастает от
/(о)-о
до f ( Л ) = 4 . Несколько
значений функции представим в следующей таблице:
ф 0 Л У я 2 2л 3 Л
0 1 2 3 4
Найденным значениям /(ф) соответствуют точ-
ки О, Mv М2, А/3, Л/4 на рис.19.37. Соединяем их
плавной кривой. Дуга кардиоиды ОМХ касается
оси / , поскольку при малых положительных значени-
ях ф полярный радиус г = 2(1 —со5ф)>0 и близок к ну-
лю; при увеличении ф в пределах от 0 до Л точка на ду-
ге кардиоиды удаляется от полюса. Чтобы построить всю
кривую, отражаем дугу ОМ^М^ симметрично относи-
тельно оси I . Получим дугу O^^2V3A/4, где N2,
N3 — образы точек , М2, М3 при симметрии относи-
511
тельно I . Кардиоида состоит из двух симметричных дуг.
Пример 19.7. Построить лемнискату Бернулли
(х2 + у2)2=х2 -у1-
Согласно §19.2, декартовы и полярные координа-
ты связаны соотношениями X = г • саяр, у = г • sinq>.
Подставим их в уравнение кривой. Имеем:
((г • СО8<$ + (г • 57Иф)2 ) = (г • СОГф)2 -(г • 37Иф)2
ИЛИ
Г4=Г2СО52ф.
Это соотношение равносильно уравнению
г2 = cos2q или г = y]cos2(p .
Воспользуемся результатами примера 19.1.
ция /(ф) = yjcos2(p периодическая с периодом
Поэтому достаточно построить дугу кривой,
Функ-
когда
с последующим поворотом вокруг полюса
на угол я, т.е. с последующей центральной симметрией.
Кроме того, функция f — четная, поэтому достаточно
строить дугу при изменении ф от 0 до - с последую-
щей симметрией относительно полярной оси. Следова-
тельно, достаточно рассмотреть ф G 0; —
Так как
при ф е ——
аргумент 2ф принадлежит промежут-
512
При возрастании ср от 0 до — аргумент 2ф возрас-
тает от 0 до —, и cos2q> убывает от 1 до 0, а значит
и /(ф) также убывает от 1 до 0.
Вычислим значение f — = lcos— =
т z
Рис. 19. 38
лучаем соответственно точки Mlt М2, О на рис. 19.38.
Соединяем их плавной дугой МХМ2О. Дуга лемнискаты
будет касаться луча т, проведенного из точки О под уг-
7Г , л 71
лом — к оси / . При изменении ф от 0 до ~ точка на
кривой будет приближать-
ся к полюсу, поскольку
значение г — /(ф) умень-
шается.
Затем построенную ду-
гу отражаем симметрично
относительно I , получаем
дугу ON2Mv
ки М2. Вся
где N2 —
симметричный образ точ-
лемниската
строится присоединением к
петле ON2MxM2O ее образа при центральной симмет-
рии относительно полюса. А
Греческое слово означает "лента",
"бант", "повязка". Кривая действительно похожа на по-
вязку.
513
§ 19.10. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО
РЕШЕНИЯ
19.01. В правильном пятиугольнике AlA2A3A4As прове-
дены диагонали, попарно пересекающиеся в точках Вх, В2, В3,
В4 и В5. Доказать, что:
а) ВХВ2В3В4В5 — правильный пятиугольник;
б) центры обоих пятиугольников совпадают.
19.02. Выразить сторону пятиугольника ВХВ2В3В4В5 из пре-
дыдущей задачи через сторону пятиугольника АХА2А3А4А$.
п
19.03. Спираль Архимеда г = ф повернули на угол — про-
тив часовой стрелки вокруг полюса. Каким станет теперь ее
уравнение в полярных координатах?
19.04. Построить кривые:
а) Г = а, где #>0 ;
71
б) Ф=".
4
19.05. Записать в полярных координатах уравнения сле-
дующих кривых, если а > 0:
а) х2 -у2 =а2;
б) х2 + у2 = а2.
19.06. Построить кривую г = 1 - s/иЗф.
19.07. Построить кривую г = а • sin2<p.
19.08. Построить кривую г = а(1 + 2сауф) (улитка Паскаля).
19.09. Пусть И — нечетное натуральное число. Доказать,
что кривая г = sin п<$ (роза) состоит из И лепестков.
17 Зак. 687
514
ГЛАВА 20
ЗАДАЧИ ПО ВСЕМУ КУРСУ ПЛАНИМЕТРИИ
§ 20.1. ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 20.1. Рассмотрим цепочку из 32 равных ок-
ружностей, каждая из которых касается двух соседних и цен-
тры которых лежат на окружности С (подобная цепочка из 8
окружностей изображена на
рис.20.1). Что больше: длина
окружности С или сумма
длин диаметров окружностей
цепочки?
2^. Пусть d — диаметр
окружностей цепочки. Тог-
да центры двух соседних
окружностей цепочки нахо-
дятся на расстоянии d друг
от друга. Соединим после-
довательно центры окруж-
ностей цепочки. Получим
Рис. 20.1 правильный 32-угольник со
стороной d, вписанный в окружность С. Его периметр
Р32 равен сумме длин диаметров окружностей цепочки.
Покажем, что Р32 < /, где / длина окружности С. Вос-
пользуемся результатами из приложений 1 и 3.
Действительно, при п >6 имеем: Qn > Q6, где Qn —
2п
-угольника, вписанного в ок-
ружность С. Однако по определению / = и по
п—>00
теореме 8 приложения 1 I > Q*. Далее, Q6 > Qs, поэтому
I > Q. Следовательно, длина окружности С больше. 2lk
Пример 20.2. В окружности радиуса R проведены два
взаимно перпендикулярных радиуса ОА и ОВ. Центр второй
окружности такого же радиуса находится в точке В. Найти
радиус третьей окружности, касающейся радиуса ОА первой
515
Рис. 20.3
Рис. 20.2
окружности внутренним образом (точка касания принадле-
жит дуге АВ) и второй окружности внешним образом.
ZS Заданное расположение трех окружностей пред-
ставлено на рис.20.2. Здесь ОА = ОВ = R, ОА 1.ОВ .
Пусть С — центр меньшей окружности, Г — ее радиус.
Тогда
OC = R-r, BC = R + r.
Опустим из точки С перпендикуляры CD и СЕ на ра-
диусы ОА и ОВ соответственно (рис.20.3). Тогда
CD = £O = r, BE=R-r.
Из треугольников ВЕС и СЕО по теореме Пифагора
имеем:
ЕС2 =(R + r)2 -(Л-г)2=(/?-г)2-г2
или
4Rr = R2-2Rr,
откуда
= - ▲
6’
Пример 20.3. В правильном треугольнике АВС два
луча, проведенные из вершин А и С, пересекаются в точ-
ке D. Площади треугольника ADC и четырехугольни-
ка BEDF равны (рис.20.4). Найти меньший угол между этими
лучами.
Из условия получаем, что:
$bADC + S*ADE = $BEDF + $MDE’
откуда
S&AEC = $bABF •
516
Далее,
5 = 1 AC • АЕ • ««60°, S^bj, =-AB-BF- sinftf.
ZV1.CC IVIDr
Поскольку AC = AB , то AE = BF.
Рассмотрим поворот T вокруг центра О треугольни-
ка на 120° против часовой стрелки. При этом Т(л) = С;
сторона ВС перейдет в сторону АВ, значит, точка F
перейдет в такую точку Fx, для которой длины отрез-
ков BF и AFX равны. Однако для точки Е на сторо-
не АВ имеем: АЕ = BF, поэтому точки F} и Е совпа-
дают.
Следовательно, отрезок AF при повороте Т перехо-
дит в отрезок ЕС. Поворот осуществляется на угол 120°,
поэтому угол между отрезком AF и его образом ЕС
также равен 120°. Здесь мы опираемся на следующее ут-
верждение: при повороте прямой I на угол а угол меж-
ду прямой Z и ее образом 1Х также равен а. При пере-
сечении лучи AF и СЕ образуют две пары вертикаль-
ных углов, равных 120° и 60°. Меньший из них ра-
вен 60°. Ж
Пример 20.4. В равнобедренный треугольник АВС с
основанием АС вписана окружность. Прямая, параллельная
стороне АВ и касающаяся окружности, пересекает сторо-
2
ну АС в такой точке Л/, для которой МС=—АС. Найти ра-
517
диус окружности, если периметр треугольника ЛВС ра-
вен 20.
Пусть О — центр вписанной окружности; ВН—
высота; прямая, параллельная АВ и касающаяся окруж-
ности, пересекает сторону ВС в точке К; Q — точка ка-
сания окружности со стороной ВС (рис.20.5).
Рассмотрим треугольник МКС. Он подобен тре-
угольнику АВС, поэтому отношение периметров этих
треугольников равно:
?шкс _ ^7 _ 2 р _ па 2 _
— —- -—, откуда Гдджс — 20 • — - 8 .
*ЬАВС А'-' Э -*
С другой стороны, по свойству отрезков касательных
Лл/кс = МС + ML + LK + КС =
= МС + НМ + KQ + КС =СН + CQ = 2CH = АС.
Значит,
АС=8, АВ = ВС = -(20-%) = 6.
2
Далее,
ВН = 7б2 -42 =2л/5 .
В треугольнике АВН отрезок АО является биссектри-
сой, и по свойству биссектрисы
ОН _АН _4 _2
ОВ АВ 6 3 ’
Тогда искомый радиус равен:
ОН = -ВН = —. А
5 5
Пример 20.5. Три хорды окружности радиуса R обра-
зуют вписанный в эту окружность треугольник. Найти длину
третье, хорды, .,л„ д.. други, ра.иы и '
Пусть АВС — данный треугольник, ВС = R л/З,
С А Найдем синус и косинус углов А и В. По тео-
реме синусов имеем:
518
Рис. 20. в Рис. 20. 7
R
^- = -^- = 2R,
sinA sinB
откуда sinA = —, sinB = —.
Тогда
Далее, угол С равен 180°-Л-В, sinC = sin(A + В).
Углы А и В могут быть острыми либо тупыми. По-
этому необходимо рассмотреть несколько случаев.
а) . Углы А к В острые. Тогда
А 1 D V15
cosA= —, cosB —---,
2 4
sinC = sinA • cosB 4- cosA • sinB =
_Уз V15 1 1_Зл/5 + 1
2 ’ 4 +2 4 8
По теореме синусов
3>/5 + l
AB=2R sinC= ~ - R.
4
б) . Угол А тупой, а угол В острый. Тогда
519
cosA =—,
2
sinC =
ab.^Lix
8 4
в). Угол А острый, а угол В тупой. Тогда
а это невозможно для внутреннего угла С треугольника.
Значит, случай в) невозможен.
Случаи а) и б) представлены на рис.20.6 и 20.7.
Таким образом, данный пример имеет два решения:
Рис. 20. в
Пример 20.6. Четырехугольник со взаимно перпенди-
кулярными диагоналями вписан в окружность. Доказать, что
расстояние от центра окружности до стороны четырехуголь-
ника равно половине противоположной стороны.
ZS Пусть четырехугольник ABCD вписан в окруж-
ность с центром О, AC USD, Р — точка пересечения
диагоналей АС и BD (рис.20.8). Докажем, что расстоя-
ние от точки О до хорды АВ равно — СО.
2
Пусть дуга АВ равна 2а градусов. Тогда соглас-
но §6.4 имеем:
Рис. 20.9
520
90° = ZAPB
2a+uCD
т.е. vCD = 180’-2a.
Отсюда следует, что дуги АВ и CD не равны 180° и
хорды АВ и CD не являются диаметрами. Из центра О
опустим перпендикуляры ОЕ и OF на стороны четы-
рехугольника АВ и CD соответственно. Точки Е
и F — середины хорд АВ и CD (рис.20.9). Рассмот-
рим прямоугольные треугольники ОАЕ и ODF. В
гл:
; ОА = OD как радиусы окружности. Далее,
ZDOF = uCD_180--2a = 90._a;
2 2
2a
Z.OAE = 90°-Z£Q4 = 90°--= 90° - a = Z.DOF.
2
Тогда треугольники ОАЕ и ODF равны, откуда
OE = DF=-CD.
2
что и требовалось доказать.
Пример 20.7. На окружности единичного радиуса от-
мечены 11 точек. Доказать, что среди них можно найти такие
точки АяВ, для которых длина дуги АВ меньше —.
Ж Впишем в данную окружность правильный 10-
угольник Л2... Л10. Пусть множество М} — это множе-
ство точек дуги Д ^4 без точки А2, М2 — это множество
точек дуги без точки А3 и т. д. М9 — это множест-
во точек дуги АдЛ10 без точки Л10 и, наконец, Л/10 — это
множество точек дуги А10Аг без точки Аг Множест-
ва Mv ... , разбивают окружность на 10 частей. По
крайней мере две из данных 11 точек попадают в одно и
то же множество Мг Пусть это будут точки Ак и Ар
л л / 2я Л
Тогда длина дуги Ак А? меньше, чем — = = у,
где I — м&на. данной окружности. Ж
Пример 20.8. На сторонах АВ, ВС и AD параллело-
грамма ABCD взяты соответственно точки К, М и L так,
521
Рис.20.10
что АК: КВ =2:1, ВМ\МС-\'Л, AL: LD=1:3. Найти отноше-
ние площадей треугольников KBL и BML.
ZS Сравним площади треугольников с площадью па-
раллелограмма. Проведем высоту DF параллелограмма
(рис.20.10). Тогда
'-FD ВЫ
_ 2_________ £ о -1с
SABCD FD BC 4' 4 ABCD-
Далее,
'-ALFD
^\ABL _2_________£ c _±c
SABCD AD-FD 8’ MBL 8abcd'
— AK • AL • sinA
&AKL _ 2_______________
ABCD
AB • AD • sinA
12'
MKL ~ -2 ABCD'
&KBL
bABL
bAKL ~
8 12
ABCD ~ 24 ABCD ‘
Таким образом,
ДВМ1
CsKBL _aABCD .aABCD
24 ’ 4
522
Пример 20.9. Каждая диагональ выпуклого четырех-
угольника делит его на два равновеликих треугольника. Дока-
зать, что этот четырехугольник — параллелограмм.
z2s Пусть ABCD — выпуклый четырехугольник,
SbABC=ShACD> SbABD=SMCD (РИС.20.11). ОпуСТИМ Пер-
пендикуляры BE и DF на диагональ АС. Имеем:
Sm„c " • BE - SUDC = 1 AC DF,
откуда
BE = DF.
Пусть О — точка пересечения диагоналей данного четы-
рехугольника. Если BDAAC, то точки Е, О и F совпа-
дают, причем по доказанному ранее ВО = OD. Если
же BD не перпендикулярно АС, то точки Е, О и F —
это три различные точки. Именно этот случай изображен
на рисунке. В прямоугольных треугольниках ВОЕ
и DOF имеем: BE = DF, углы ВОЕ и DOF равны как
вертикальные. Значит, &ВОЕ = &DOF, откуда также по-
лучаем, что ВО = OD.
Аналогично из того, что диагональ BD разбивает
площадь четырехугольника ABCD на две одинаковые
части, имеем: АО = ОС. По признаку параллелограмма
четырехугольник ABCD является параллелограммом. Ж
П р и м е р 20.10. В выпуклом пятиугольнике ABCDE уг-
лы АВС и CDE равны по 90°, стороны ВС t CD и АЕ равны
по 1,а сумма AB+DE=1 . Доказать, что площадь пятиуголь-
ника равна 1 .
П _______ 1
Рис. 20.1 з
523
В прямоугольных треугольниках АВС и EDC
одинаковые высоты ВС и DC (рис.20.12). Приставим их
друг к другу вдоль высоты СВ, отложив на продолжении
стороны АВ отрезок ВЕХ, равный DE. Тогда
АЕХ = АВ + ВЕХ = АВ + DE = \
(рис.20.13), откуда
S&ABC + S&CDE = S&ACEX = 1 ’ = Z •
В треугольниках ЕСА и ЕХСА сторона С А общая,
АЕ =АЕ1 = 1 , ЕС = ЕХС, так как треугольники CED
и СЕХВ равны. Тогда по третьему признаку равенства
треугольники САЕ и САЕ, равны и
£дсле = ^дсяе, = 2 •
Наконец,
П р и м е р 20’11. Точка М
— середина стороны AD квадра-
та ABCD, точка Р — основание
перпендикуляра, опущенного из
вершины С на прямую ВМ. До-
казать, что DP -DC.
Пусть ABCD — за-
данный в условии задачи квад-
рат (рис.20.14). В четырех-
угольнике CPMD имеем:
Z.CPM + Z.MDC =
= 90°+ 90° = 180°, Pw.20.14
Z.PMD + ZPCD = 360°-(АСРМ + /АЖ) = 180°.
Значит,
ЛСРМ + Z.MDC = APMD + ZPCD
и вокруг этого четырехугольника можно описать окруж-
ность. Отрезок МС является ее диаметром, поскольку
вписанный угол СРМ — прямой. Значит, центр Q
окружности есть середина МС.
524
Пусть L — середина ВС. Поскольку М — середи-
на стороны квадрата AD, то четырехугольник MLCD
— прямоугольник. Его диагонали LD и МС в точке пе-
ресечения делятся пополам. Значит, они пересекаются в
точке Qt причем отрезки QL и QD равны между собой.
Эти же отрезки равны радиусу окружности, описанной
около четырехугольника PMDC, и поэтому точка L
также лежит на проведенной окружности.
В четырехугольнике BLDM противоположные сто-
роны BL и MD равны и параллельны, и по признаку
параллелограмма четырехугольник BLDM — параллело-
грамм, откуда BM\\LD. Однако CPUBM, значит,
CPLLD. В окружности диаметр LD , перпендикулярный
хорде СР, делит ее пополам. Пусть N — точка пе-
ресечения хорд СР и LD. Тогда NP = NC. Наклон-
ные DP и DC равны, поскольку равны их проекции NP
и NC на прямую PC, что и
требовалось доказать. Ж
П р и м е р 20.12. Сущест-
вуют ли треугольники, у кото-
рых длины двух медиан в це-
лое число раз меньше длин
С сторон, к которым эти медиа-
ны проведены?
Пусть в треугольни-
ке АВС — >2, —>2,
та ть
точка М — есть основание
медианы та. На луче МА
Л
отложим отрезок МАХ = — (рис.20.15). Поскольку по ус-
ловию МА = та< — = MAV то точка А принадлежит от-
2
резку МАХ.
Кроме того, МВ = МС = МА j = —, поэтому точ-
2
ки В, С, Aj лежат на окружности с центром М и ра-
525
диусом —. Вершина А лежит на радиусе МА,, поэтому
2
точка А лежит либо на окружности, либо в круге, огра-
ниченном окружностью. Из §6.4 следует, что угол ВАС
либо прямой, либо тупой.
b
Аналогично из неравенства — > 2 следует, что
угол АВС также либо прямой, либо тупой. Тогда
180° = ZJ + ZB + ZC > ZC + 90° + 90°>180°,
что невозможно. Итак, треугольники с указанным в усло-
вии задачи свойством не существуют,
526
§ 20.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
20.01. Докажите, что если повернуть катеты вокруг их
вершин так, чтобы они легли на гипотенузу, то длина их общей
части равна диаметру вписанной окружности.
20.02. В треугольнике АВС дано: АВ>АС t ZA — CL, Ах —
середина стороны ВС, а точка D делит длину ломаной ВАС
пополам. Пусть продолжения отрезков AXD и СА пересека-
ются в точке Е. Найти угол DEA.
20.03. Пусть А иВ — две окружности, лежащие по одну
сторону от прямой / . Постройте касательную к окружнос-
ти А, которая после отражения от прямой / также коснется и
окружности В.
20.04. Прямая касается окружностей О} и О2 внешним
образом, т.е. окружности лежат по одну сторону от прямой /,.
Расстояние между точками касания равно 24. Прямая /2 явля-
ется внутренней общей касательной, т.е. окружности лежат по
разные стороны от прямой /2. Расстояние между точками каса-
ния в этом случае равно 7 . Наименьшее расстояние между
точками окружностей О} и О2 равно 1 . Найдите радиусы дан-
ных окружностей.
20.05. Из вершины А параллелограмма ABCD с прямым
углом CAD опущен перпендикуляр АК на сторону CD, Из-
вестно, что AD = 2AK =12. Из точки Л/, лежащей на отрез-
ке КС, опущены перпендикуляры МР и MQ на стороны AD
и АВ соответственно. В четырехугольник MPAQ вписана ок-
ружность. Найдите ее радиус.
20.06. Окружности Q и С2 с радиусами 2 и 7 соответст-
венно касаются друг друга внешним образом. Прямая / прохо-
дит через центр окружности Сх и касается окружности С2. Оп-
ределить радиус большей из окружностей, которая расположе-
на по одну сторону от I с окружностью С2 и касается внеш-
ним образом окружностей Q, С2 и прямой I .
20.07. От квадрата отрезали прямоугольный треугольник,
сумма катетов которого равна стороне квадрата. Доказать, что
сумма углов, под которыми видна его гипотенуза из трех ос-
тальных вершин, равна 90е.
20.08. Окружность, проходящая через вершину С тре-
угольника ABC , касается стороны АВ в точке L и пересекает
стороны АС и ВС в точках Р и Q соответственно. Найди-
527
те АС и ВС, если йзвестно, что АР =3 , AL =6, LB =8 и
прямая PQ параллельна АВ .
20.09 . Окружность с центром в точке О и радиусом R =
= 6 + 4>/2 касается прямой в точке А. На окружности взята
точка В так, что угол АОВ равен 45°. Найдите радиус окруж-
ности, касающейся данной прямой и данной окружности в
точке В.
20.10. Доказать, что трапеция является прямоугольной то-
гда и только тогда, когда разность квадратов диагоналей равна
разности квадратов ее оснований.
20.11. В трапеции диагонали равны 2л/бТ и Зл/дТ, а ее ос-
нования равны 10 и 15. Найти площадь трапеции. Можно ли в
нее вписать окружность?
20.12. Отрезок AD является биссектрисой прямоугольного
треугольника ABC (ZC = 90°). Окружность радиусом V15 про-
ходит через точки А, С, D и пересекает сторону АВ в точ-
ке Е так, что АЕ:АВ=3:5. Найдите площадь треугольни-
ка АВС .
20.13. Высота трапеции ABCD равна 7 , а длины основа-
ний AD и ВС равны соответственно 8 и 6 . Через точку Е,
лежащую на стороне CD, проведена прямая BE , которая делит
диагональ АС в точке О в отношении АО:ОС = 3:2. Найдите
площадь треугольника ОЕС.
20.14. Внутри параллелограмма расположены две одинако-
вые окружности радиусом 6 , каждая из которых касается бо-
ковой стороны параллелограмма, обоих оснований и второй ок-
ружности. Боковая сторона делится точкой касания в отноше-
нии 9:4. Найдите площадь параллелограмма.
20.15. В трапеции ABCD основание AD равно 16, сумма
диагоналей АС и BD равна 36, а угол CAD равен 60°. Отно-
шение площадей треугольников AOD и ВОС, где О — точка
пересечения диагоналей, равно 4 . Найдите площадь трапеции.
20.16. В треугольнике АВС сторона АВ. равна 4 , угол А
равен 30е, угол В равен 130е. На стороне АВ как на диаметре
построена окружность. Найдите площадь части круга, лежащей
внутри треугольника.
20.17. Материальная точка движется по окружности ра-
диуса 1 против часовой стрелки, поворачиваясь каждую секун-
ду на угол а вокруг центра, где а — острый угол, измеряемый
иррациональным числом градусов. Пусть А^ — начальное поло-
жение точки. Доказать, что через некоторое целое число се-
528
кунд материальная точка займет такое положение А, что длина
дуги АА0 будет меньше .
20.18. В трапеции ABCD основание ВС вдвое меньше ос-
нования AD, а продолжения боковых сторон пересекаются в
точке К. Через точку О, взятую внутри треугольника ВКС , из
вершин В и С проведены две прямые, пересекающие отре-
зок СК в точке N, а отрезок ВК— в точке М. Площади тре-
угольников ВМО , ВОС и CON равны Д, S2 и S3 соответст-
венно. Найти площадь трапеции ABCD .
20.19. На сторонах АВ, ВС, CD, DA прямоугольни-
ка ABCD соответственно взяты точки К, L, М, N, отличные
от вершин. Известно, что KL || MN и КМ JJVZ. Докажите, что
точка пересечения отрезков КМ и LN лежит на диагона-
ли BD прямоугольника.
20.20. В треугольнике АВС расстояние от центра описан-
ной окружности до стороны АВ равно d, а угол АВС ра-
АВ
вен 60°. Точка D на стороне ВС такова, что BD = . Найди-
те длину отрезка CD.
20.21. Точки А и В лежат на сторонах выпуклого много-
угольника F, а точка Ах такова, что АВ = ВА}. Пусть F} — вы-
пуклый многоугольник наименьшей площади, содержащий мно-
гоугольник F и точку А{. Докажите, что его площадь не боль-
ше удвоенной площади многоугольника F.
20.22. Пусть АВС— произвольный треугольник. Через
точку К, взятую на стороне АВ , проведена прямая, параллель-
ная стороне АС и пересекающая сторону ВС в точке Д, и
прямая, параллельная ВС и пересекающая сторону АС в точ-
ке М. При каком положении точки К площадь треугольни-
ка KLM будет наибольшей? Чему равна эта площадь, если пло-
щадь треугольника АВС равна 5 ?
20.23. От пирога, имеющего форму выпуклого пятиуголь-
ника, можно отрезать треугольный кусок по линии, пересекаю-
щей в точках, отличных от вершин, две соседние стороны; от
оставшейся части пирога — следующий кусок (таким же обра-
зом) и т.д. В какие точки пирога можно воткнуть свечку, чтобы
ее нельзя было отрезать?
20.24. Пусть О9 — центр окружности Эйлера треугольни-
ка АВС . Доказать, что
529
9 4
20.25. Пусть Ia — центр вневписанной окружности тре-
угольника ABC , касающейся стороны а. Доказать, что
Ь + с-а
20.26. Пусть точку М наугад бросают на отрезок АВ .
J — некоторый отрезок, входящий в АВ . Назовем вероятно-
стью того, что точка Л/ попадет в отрезок J, отношение длины
отрезка J к длине отрезка АВ .
На плоскости задана окружность. На ее диаметре АВ вы-
берем произвольную точку Л/, через которую проведем хор-
ду DE, перпендикулярную диаметру АВ . Найти вероятность
того, что длина хорды DE больше или равна длине стороны
правильного треугольника, вписанного в окружность.
Замечание. Подобный эксперимент можно осущест-
вить следующим образом: нарисовать на асфальте окружность
и издалека закатывать круглую палку в эту окружность.
20.27. Пусть точку М наугад выбирают на данной окруж-
ности. Рассмотрим произвольную дугу I этой окружности. Бу-
дем называть вероятностью того, что точка М попадет на ду-
гу / , отношение длины дуги / к длине окружности.
Дана окружность и точка D на ней. Выберем наугад ка-
кую-либо точку Е на этой окружности. Найти вероятность то-
го, что длина хорды DE больше или равна длине стороны пра-
вильного треугольника, вписанного в окружность.
Замечание. Описанный эксперимент можно провес-
ти с помощью игральной рулетки.
20.28. Пусть точку М наугад бросают в данный круг, Ф —
произвольная фигура, содержащаяся в круге. Будем называть
вероятностью того, что точка М попадет в фигуру Ф, отноше-
ние площади фигуры Ф к площади круга (рассматриваются
лишь такие фигуры Ф, для которых площадь определена).
Выберем в данном круге произвольную точку Af, прове-
дем через нее диаметр АВ и хорду DE, перпендикулярную
диаметру АВ (если точка М совпадает с центром круга,
то АВ — произвольный диаметр). Найти вероятность того, что
длина хорды DE больше или равна стороне правильного тре-
угольника, вписанного в круг.
Замечание. Чтобы случайным образом выбрать
точку М в круге, можно намазать круг медом и выпустить му-
ху.
18 Зак. 687
530
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение. Если согласно какому-то пра-
вилу или закону каждому натуральному числу П ста-
вится в соответствие некоторое действительное чис-
ло ап, то говорят, что задана числовая последователь-
ность а2, ... , ап, ... Будем обозначать ее также че-
рез (ал).
Пусть, например, числу 1 соответствует число 1,
числу 2 — число —, числу 3 — число — и т.д. Таким
2* 3
^11
способом задается последовательность 1 , —, —, ... После-
довательности могут также задаваться формулами. На-
пример, ап-п2 —это последовательность 1 ; 4; 9; 16; ...
Такая формула называется формулой общего члена по-
следовательности. Еще один способ задания последова-
тельности — это указание рекуррентного соотношения,
при котором общий член последовательности выражает-
ся через некоторые ее предыдущие члены. Пусть, напри-
мер, ах =2, а2 =3, ап = ап_2+2ап_х. Тогда по формуле
для ап можно вычислить все остальные члены последова-
тельности, начиная с а3. Имеем:
а3 = а1+2а2=2 +2-3 = 8; а4 = а2+2а3 = 3 + 2-8 = 19;
а5 = а3 + 2а4 =8+2-19 = 46 и т.д.
Определение. Числовая последовательность
(ал) называется ограниченной сверху (снизу), если су-
531
ществует число Мут) такое, что для всякого натураль-
ного числа П неравенство ап<М (ап > т) истинно.
Например, последовательность, заданная формулой
ал = и2, ограничена снизу числом 1 , так как при любом
натуральном значении П неравенство п1 > 1 истинно.
Рассмотрим последовательность ап = ~. Она огра-
п
ничена сверху числом 1 . Кроме того, эта последователь-
ность ограничена также и снизу — числом 0 . Для после-
довательностей, обладающих подобными свойствами,
введем следующее определение.
Определение. Последовательность, огра-
ниченная и сверху, и снизу, называется ограниченной.
Пусть задана следующая последовательность:
1 ; -1; 2; -2; 3; -3; 4; -4; ... .
Очевидно, что эта последовательность не ограничена
снизу. Но она также не ограничена сверху.
Определение. Последовательность (ал) назы-
вается возрастающей, если яя<яя+1 для любого нату-
рального числа /1, и убывающей, если при всех нату-
ральных И справедливо неравенство: яя>яя+р
Например, последовательность ап = п — возрас-
1
тающая, а последовательность ап =-----убывающая.
п
Рассмотренная нами ранее последовательность
1 ; —1; 2; —2; 3 ; —3; 4; —4; ...
не возрастающая, но и не убывающая. Напомним,
что а — модуль числа а — это расстояние от начала
отсчета, т.е. от точки 0 на числовой прямой, до точки,
изображающей число а на этой прямой. Выраже-
ние
равно расстоянию между точками числовой
прямой, соответствующими числам а и b .
Определение. Пусть 8 — произвольное по-
ложительное число. Промежуток (а — 8;а + е) называет-
ся 8-окрестностью точки а (рис. 1).
532
Рассмотрим числовую последовательность, Я-й член
которой задается формулой an =--------. Она имеет вид:
п
I 13 2001
I I • • • I I • • • •
6 1000
Мы видим, что это убывающая
последовательность. Нетрудно
убедиться в том, что при неог-
раниченном увеличении чис-
ла П члены этой последова-
тельности неограниченно при-
ближаются к числу (точке)
(рис.2), т.е. расстояние ап —2
становится как угодно близ-
ким к нулю. Опишем этот про-
цесс подробнее. Возьмем не-
число 8 и рассмотрим произ-
которое положительное
вольную 8 -окрестность точки 2. Если выбрать число 8
достаточно большим, то можно увидеть, например, при
d10 CLs dj d>3
Рис. 2
8 = 2, что все члены последовательности содержатся
внутри 2-окрестности точки 2, т.е. на интервале (0;4).
Если взять 8 достаточно малым, то, например, при
8 = 0,01 часть членов последовательности будет нахо-
диться снаружи 0,01-окрестности точки 2, т.е. на проме-
жутке (1,99; 2,01). Это будут первые 100 членов последо-
вательности. В самом деле,
100 100
= 2,01, a101 =----------
101 101
533
203 n 1
=-----= 2 Ч----<2,01.
101 101
Это значит, что, начиная со 101-го члена последователь-
ности, все остальные ее члены меньше, чем al00 и содер-
жатся внутри 0,01-окрестности точки 2. Обобщая это
наблюдение, мы можем обнаружить, что для произволь-
ного сколь угодно малого положительного числа 8 всегда
найдется такое натуральное число к, что все члены по-
следовательности, номер которых больше числа к, будут
содержаться внутри 8 -окрестности точки 2, т.е. будет
выполняться неравенство: \ап — 2|<е . Решим его.
п
п
П
1 <пг
п 8
При 8 = 0,01 получим: И>100, т.е., начиная со 101-го
члена, все члены последовательности а101, а102, а103 ... со-
держатся внутри 8 -окрестности точки 2 радиу-
са 8 =0,01. Это свойство последовательности мы будем
выражать словами: последовательность ап =------ имеет
п
предел, равный 2. Приведенные рассуждения позволяют
нам дать определение предела последовательности.
Определение. Число а называется пределом
числовой последовательности (ля)г если для любо-
го 8 > 0 существует такое натуральное число к, что для
всякого натурального числа Я, удовлетворяющего нера-
венству П>к, выполняется неравенство: |пя — п| < 8.
Это определение можно сформулировать иначе: для
любого 8 >0 существует натуральное число к такое, что
все члены последовательности, номер которых больше
числа к, содержатся в 8 -окрестности числа а. Этот
факт записывается так: lima = а или а„-»а, и—>оо.
и-»ао
534
Говорят также: "последовательность (яЛ) имеет пре-
дел О" или "последовательность (аЛ) сходится к а".
Определение. Последовательность, имеющая
предел, называется сходящейся. Последовательность, не
имеющая предела, называется расходящейся.
Напомним некоторые важные теоремы о пределах
последовательностей.
Теорема! (о единственности предела). Всякая
сходящаяся последовательность имеет предел и притом
только один.
Теорема2 (теорема Вейерштрасса). Всякая огра-
ниченная и возрастающая (убывающая) последователь-
ность имеет предел.
Теорема 3. Если последовательности (ая) и (бЛ)
сходятся, то последовательности (ая + 6Л) и (ая — Ьп)
также сходятся и
1пп(аи + Ли)=Кш a„+lim b„,
Л->оо' П Я/ Л->00 П П-*Х> п
lim (а
Л->00
П
Теорема 4. Если последовательности (ая) и (бЛ)
сходятся, то последовательность (ап *Ьп) также сходится
и
lim anbn = lim ап • lim bn.
Л->ОО П П-+<Х)
Из теоремы 4 получаем
Следствие. Если последовательность схо-
дится, то для любого числа С последовательность
(с• ап) также сходится и
Птс-аЛ=с1ппаЛ.
Л—>00 Л—>00
Теорема 5. Если последовательности (аЛ) и (бя)
сходятся, причем b О при любом натуральном
535
значении П и lim/L^O, то последовательность
Л->оо
ап
Ь„
также сходится и
lim —= .
Л->°° b„ lim b„
п п-ж п
Теорема 6. Если последовательность (лЛ) схо-
дится, причем ап > 0 при любом натуральном значе-
нии Пг то lim ап >0 и последовательность \Ja„ I также
Л->00 \ V Л /
сходится, причем
lim Ja„ = .
П->О0 * V Л->ОО
Теорема?. Для всякого числа а существует
возрастающая (убывающая) последовательность (аЛ)
рациональных чисел таких, что lim ап = а.
Л->00
Теорема 8. Пусть lim ап = а и lim bn = 6,
Л->00 Л->СО
причем ап >с и bn<d. Тогда а >с и b<d.
ПРИЛОЖЕНИЕ 2
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФАЛЕСА
Теорема Фалеса. Пусть прямые АВ и CD
пересекаются параллельными между собой прямыми.
Тогда отношение каких-либо отрезков прямой АВ рав-
но отношению соответствующих отрезков прямой CD.
□ Достаточно доказать следующее утверждение:
если AD\\MN \\ВС (рис.1), то AM*. МВ = DN'.NC.
Рассмотрим два случая.
536
1) Пусть длины отрезков АМ и МВ выражаются
рациональными числами, т.е. AM ——, МВ где
п q
Ш, п, р, q —натуральные числа. Тогда
~ т(1 ud Рп
В __________ С AM =-----------, МВ = £—.
/ I qn nq
ML___________17V Разделим отрезок AM
I l на mq равных частей, а от-
T К 1 резок MB — на рп равных
q /\К___________\S[ частей. При этом длина каж-
/ I дой образовавшейся части
L----------------1 1
J) равна —. Через точки деле-
*• nq
Puc.i ния проведем прямые, па-
раллельные AD и ВС, а
через точку В и точки деления проведем прямые, парал-
лельные CD. На рис.1 изображены две прямые ТТХ
и iSS*!, параллельные AD и ВС, а также прямая ТК, па-
раллельная CD. Очевидно, что при этом образуется mq
треугольников типа треугольника TSK, у которых одна
сторона (вида TS) лежит на отрезке AM, и рп тре-
угольников типа треугольника TSK , у которых одна сто-
рона лежит на отрезке МВ . Все эти треугольники равны
по второму признаку равенства треугольников. Итак, сто-
роны этих треугольников, которые соответствуют сторо-
не ТК треугольника TSK, также равны. Кроме того, в
результате построения образуется mq + рп параллело-
граммов вида TTXSXK и mq + рп отрезков вида TXSV ко-
торые равны между собой, а также равны отрезку ТК.
При этом отрезок ND разобьется на mq отрезков ви-
да TXSV а отрезок NC — на рп отрезков вида TXSX. Зна-
чит,
ND = mqTxSv NC = pnTxSx
и тогда
537
ND _ mqTxSx _mq p _ AM
NC рп7\8х np n q MB
Отметим, что если длины AM и МВ рациональны,
то
AM МВ
DN CN
= к, где к за-
висит только от прямых АВ и
CD, но не зависит от выбора
точек на этих прямых.
2) Допустим теперь, что
длина хотя бы одного из от-
резков AM или МВ является
иррациональным числом.
Пусть AM = а, ВМ =
= Ъ. Тогда по теореме 7 при-
Рис .2
ложения 1 существуют возрастающие последовательно-
сти (ал) и (&л) рациональных чисел такие, что
limап = а, limb=b. Обозначим через
Л->00 Л->00
4(А.) такую
точку отрезка МА[МВ}, что МАп=ап (МВп=Ьп}
(рис.2). Тогда lim МАп = МА , lim МВп = МВ . Проведем
Л->00 Л-»00
AnXn\\AD, BnYn HAD. Так как длины МАп, МВп выра-
жаются рациональными числами, то согласно п.1)
NXn-.MAn = NYn-.MBn = k,
где к — некоторое постоянное число, которое зависит
только от четырехугольника ABCD . Согласно следствию
из теоремы 4 приложения 1 имеем:
lim NXn = lim кМАп = к lim МАп = ка
Л~»00 Л->00 Л->О0
и аналогично
limMY =1ппШВ =k\imMB=kMB = kb.
П->ао П-^оо П-*ао
Из п.1) также следует, что
NXn:MAn = NXn+l:MAn+l,
538
и так как МАп< МАп+^, то и NXn<NXn^t т.е. последо-
вательность [NXn} возрастает.
Допустим, что на отрезке ND существует такая
точка Z, отличная от точки D, что для произвольного П
выполняется неравенство NXn<NZ. Проведем ZF\\AD
и выберем номер т такой, что MAm>MF. Тогда точ-
ки Ат и Хт лежат в разных полуплоскостях, огра-
ниченных прямой FZ, и значит, прямые АтХт и FZ
пересекаются, что невозможно. Итак, на отрезке ND не
существует такой точки Z, отличной от D, чтобы для
какого-нибудь п выполнялось бы условие NXп < NZ.
Аналогично можно показать, что NXn < ND для
каждого П.
Пусть 8 — некоторое положительное число. Тогда
существует номер I такой, что NXpND — 8. Так как
последовательность (NX^) возрастает, то NXn>ND — 8
для всех п>1. В данном случае это значит, что
|АСГ„ - ЛЮ|<8 для всех п>1. Тогда по определению
предела последовательности (приложение 1) имеем:
lim ЛОГ= ND.
п-*<п
Аналогично
lim NY = NC.
Л->оо
Таким образом, получаем:
ND \™NXn ка а МА _
NC \imNYn kb b MB'
И->00
539
ПРИЛОЖЕНИЕ 3
ВЫЧИСЛЕНИЕ ДЛИНЫ ОКРУЖНОСТИ И ПЛОЩАДИ
КРУГА
Длина окружности. Рас-
смотрим квадрат — пра-
вильный четырехугольник
АХА2А3А4, вписанный в ок-
ружность радиуса R, Разде-
лим каждую из дуг, огра-
ниченных сторонами квад-
рата, пополам и соединим
точки деления с ближайши-
ми вершинами квадрата
(рис.1). В результате по-
лучим правильный восьми-
Л4
Рис. 1
угольник
АХВХА2В2А3В3А4В4. Повторив эту же опера-
цию с дугами, ограниченными сторонами этого восьми-
угольника, мы получим правильный шестнадцатиуголь-
ник и т.д.
Обозначим через Qn периметр правильного 2я - уголь-
ника, вписанного в окружность радиуса R. Введем сле-
дующее определение.
Определение. Длиной окружности называет-
ся предел последовательности (бл) периметров пра-
вильных 2я-угольников, вписанных в окружность ра-
диуса R.
Прежде всего докажем, что такой предел существу-
ет.
Сумма двух сторон ах и а2 правильного 2^-уголь-
ника, образовавшихся в результате соединения концов
2п
-угольника с серединои огра-
ниченной его дуги, больше а (рис.1). Поэтому £?Я+1>0Я.
Значит, последовательность ({?„) возрастающая.
540
Рис. 2
Далее рассмотрим пра-
2п
-угольники, опи-
санные около данной окруж-
ности. Вновь начнем с опи-
санного квадрата ТХТ2Т3ТА.
Пусть К, L,M, N — точки
касания окружности со сто-
ронами квадрата. Разделим
каждый из углов KON,
KOL, LOM, MON попо-
лам (рис.2) и построим бис-
сектрисы OSV OS2, OS3,
OS4 этих углов. Через точки
Sp S2, S3, S4 проведем каса-
тельные к окружности. В результате образуется правиль-
ный восьмиугольник FXF2F3F4F5F6F7F3, описанный око-
ло этой окружности. Имеем:
т.е. периметр правильного четырехугольника больше пе-
риметра правильного восьмиугольника. Повторяя эти по-
строения и проводя аналогичные рассуждения, мы по-
лучим убывающую последовательность (qJ периметров
2 и
-угольников, описанных около данной ок-
ружности. В частности, Q, < Q2 при всех п > 2.
Наконец, докажем, что 0Л<О,. В самом деле, пусть
АВ — сторона правильного 2”-угольника, вписанного в
окружность. Проведем касательную ДД||ЛВ (рис.З). То-
гда АХВХ — сторона правильного 2”-угольника, описан-
ного около данной окружности. Треугольники ОАВ и
ОАХВХ подобны и
АВ _ ОА
АХВХ ~ ОАХ < ’
541
откуда следует, что AB<A}BV Поэтому Qn<Qn. Мы дока-
зали, что
Qn<Q^Qv
Таким образом, возраста-
ющая последовательность
(бл) ограничена сверху.
По теореме Вейерштрасса
она имеет предел. Итак, су-
ществует предел последо-
вательности (бЛ), который
Рис. 3 мы назвали длиной окруж-
ности. Поскольку правиль-
ные многоугольники с фиксированным числом сторон
подобны, то при каждом конкретном значении П отно-
си
шение ---- является величиной, не зависящей от R. Та-
2R
ким образом, lim—— также существует и не зависит
от R. Этот предел мы обозначим через п (читается
"пи"). Число л является иррациональным числом. Его
приближенное значение таково: 7t«3r 14159. Тогда
Qn
lim----= 71. Обозначим длину окружности через Z , то-
"-»00 2R
гда HmQ, = Z. Из последнего равенства имеем:
Л—>СО
lim — = — • lim Q„ = — • I = п, откуда I = 2itR.
2R "-**> 2R
Мы доказали, что длина окружности радиуса R вычисля-
ется по формуле Z = 2tiR .
Площадь круга. Пусть тп — площадь правильно-
го 2п -угольника, вписанного в окружность радиуса R.
Введем следующее определение.
Определение. Площадью круга называется
предел последовательности (шЛ) площадей правиль-
542
ных 2я-угольников, вписанных
в окружность радиуса R.
Докажем, что этот предел
существует, и вычислим пло-
щадь круга радиуса R. Для это-
го сначала докажем следующее
вспомогательное утверждение.
Лемма. Пусть Ьп — сто-
рона правильного 2я-угольни-
ка, вписанного в круг радиу-
са R. Тогда lim b существует
П->оо
и равен нулю.
□ На рис.4 хорда АВ изображает сторону правиль-
ного 2п-угольника, т.е. АВ = Ъп, точка С — середина ду-
ги АВ. Итак, AC =ВС =bn+{t где П =2,3, ... . Докажем,
что угол АСВ — тупотл. В самом деле, угол АСВ — это
угол правильного 2n+1-угольника. Сумма всех углов этого
многоугольника равна 180° *(2n+I —2), поэтому
180°(2"+1-
= 180° 1-----
2"+1
При п > 2 имеем:
П
= 180°—>90°.
V 22
Из этого следует, что в тупоугольном треугольнике АСВ
справедливо неравенство АВ>АС, т.е. Ьп>Ьп^. Значит,
последовательность (bn ) — убывающая. Она ограничена
снизу числом 0, и по теореме Вейерштрасса существу-
ет lim b , который мы обозначим через Ь. Посколь-
Л->00
ку Ьп > 0, то по теореме 8 приложения 1 имеем,
что b > 0. Далее, из результатов §17.2 получаем, что сто-
2п
-угольника выражается через радиус
543
t
, 0J? . 180°
описанной окружности по формуле: bn=2R-sin---------.
п
Найдем связь между значениями Ьп и hn+1. Имеем по
формуле sin2a = 2sina • cosa:
180”
Z> =2 2R-sin
При возрастании
180°
значение cos-----г
пп+1
Тогда
Поскольку
180° 180°
•C0S^T = 2bn+iC0S^r-
180°
числа П дробь - —у уменьшается, а
увеличивается, поэтому
180° 180°
cos—~r>cos—т— = слу45 =
ОП+1
п+1
Л—>00
то по теореме 8 приложения 1 имеем:
О, от-
n
п
куда Ъ < 0. Однако выше было отмечено, что b > 0.
Значит, Ь = 0, и limZ>n существует и равен нулю. И
Л—>ОО
Теперь задача о нахождении площади круга сводит-
ся к решенной ранее задаче вычисления длины окружно-
сти.
Теорема 1. Площадь круга радиуса R равна
к R1.
□ Пусть АВ — сторона правильного 2”-угольника,
вписанного в окружность с центром в точке О, обоз-
наченная через Ьп. Проведем перпендикуляр ОМ на сто-
рону АВ (рис.4). При этом образуется прямоугольный
544
треугольник AMO , из которого по теореме Пифагора
находим:
OM=\R2-
Тогда площадь тп правильного 2”-угольника будет:
тп = 2" • 1 • Ьп • ОМ = 2" • Ьп • - • J R2 - .
Но 2" • Ьп — периметр правильного 2" -угольника, обоз-
начаемый через Qn. Поэтому
п2 Ь2
к-------
Тогда площадь круга S равна Иттии. Имеем:
И—>00
5=limw„ = -lim2n-
«—>оо / л->со
Но
limQI = 2^-7?,
«—>о0
2
и—>00
Так как согласно доказанной лемме lim&w = 0, то
И—>00
Мы доказали, что площадь круга радиуса 7? вычис-
ляется по формуле S = Л • R2,
545
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ДЛЯ
САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
ГЛАВА 1
1.11. Воспользуйтесь аксиомами 1.9 и 1.14.
1.12. Докажите, что точки Л и С лежат по разные
стороны от прямой (2.
1.14. Воспользуйтесь аксиомой 1.8.
1.16. Воспользуйтесь аксиомой 1.8.
1.17. Разбейте угол (a,Z>) на два угла и примените аксио-
му 1.8.
1.18. Воспользуйтесь аксиомами 1.8, 1.10 и 1.15.
1.20. Воспользуйтесь определением полуплоскости и акси-
омой 1.11.
1.21. Пусть ОА1 — луч, дополнительный к лучу ОА. Най-
дите угол Ах OD.
1.22. Каждая пара точек порождает одну прямую.
1.23. Точки Av А2, ... , А к лежат в одной полуплоскости,
ограниченной прямой (2.
1.25. Проведите прямую АВ и примените теорему 1.1.
1.27. Рассмотрите два случая: а) все три точки лежат по
одну сторону от прямой; б) две точки лежат по одну сторону от
прямой, а одна — по другую сторону от нее.
1.28. Если отрезки АХВХ и А2В2 не пересекаются, то
точки А} и В2 лежат по разные стороны от прямой A2BV
1.29. Воспользуйтесь определением полуплоскости.
ГЛАВА 2
2.02 . Примените второй признак равенства треугольников
к треугольникам АВМ и Ах Вх М{.
2.03 . Докажите равенство углов MA{J и МХАХС}, а так-
же углов MCA и МХСХАХ. Примените к треугольникам
АСМ и АХСХМХ второй признак равенства треугольников.
2.04 . К треугольникам АВС х и АВХС примените первый
признак равенства треугольников.
ГЛАВА 3
3.05 . Из этих трех углов два являются смежными.
3.10. Предположите противное и получите противоречие с
аксиомой 3.1.
3.11. Примените первый признак равенства треугольни-
ков, а затем теорему 3.5.
546
3.13. Допустите перпендикулярность биссектрис и с по-
мощью теоремы 3.6 получите противоречие.
3.15. Пусть некоторая прямая пересекает прямые U, Ь
и С в точках А, В и С соответственно. Опустите перпен-
дикуляры: АА} на прямую Ь и ВВХ на прямую С. Рассмотрите
треугольники АА}В и ВВХС.
3.17. Выразите угол АКБ через углы А и В. Убедитесь,
что угол АКБ можно выразить через угол С.
3.18. Воспользуйтесь следствием 2 из теоремы 3.7.
3.19. Примените теорему 3.8.
3.20. Рассмотрите два случая: а) секущая перпендикулярна
параллельным прямым; б) секущая перпендикулярна этим
прямым.
3.21. Пусть f — наложение треугольника АВС на тре-
угольник BAD . Рассмотрите три случая: a) f^A) = A, /(в) =
= В', б) /(в) = А, /(А) = В; в) f{AB) равно AD или BD.
3.24. Воспользуйтесь теоремой 3.5.
3.26. Проведите общий перпендикуляр к данным прямым
и через его середину проведите прямую, параллельную дан-
ным.
3.27. Предположите противное и с помощью теоремы 3.5
получите противоречие.
3.28. Если бы прямые С1 и b были параллельными, то и
стороны угла были бы параллельными.
3.30. Пусть биссектрисы проведены из вершин А и В
треугольника. Биссектрисы не являются параллельными, при-
чем биссектриса угла А лежит внутри угла А, а биссектриса
угла В— внутри угла В. Воспользуйтесь далее определением
треугольника.
3.31. Найдите сумму углов А и В.
3.33. Данные углы и два прямых угла образуют разбиение
полного угла.
3.34. Один и тот же угол дополняет каждый из двух ост-
рых углов до прямого.
3.35. Рассмотрите угол, смежный с углом (c,j), и вос-
пользуйтесь задачей 3.34.
3.37. Соедините точку пересечения перпендикуляров с
вершиной угла и рассмотрите два прямоугольных треу-
гольника.
3.38. Из рассмотрения треугольников АОС и DOB дока-
жите, что АС = BD, а затем примените третий признак ра-
венства к искомым треугольникам.
547
3.39. Сумма внутренних углов всех треугольников равна
сумме углов 1000-угольника плюс 500 х 360°.
ГЛАВА 4
4.02 . Сравните удвоенный периметр треугольника АВА j с
периметром треугольника АВС .
4.04 . И в случае а), и в случае б) сумма углов треугольника
будет больше 180°.
4.05 . Рассмотрите прямоугольные треугольники, образо-
ванные прилежащими катетами и проведенными высотами.
4.06 . Биссектриса является высотой и медианой данного
треугольника.
4.07 . Катет может быть как прилежащий, так и проти-
волежащий.
4.09 . Данный угол может быть как при вершине, так и при
основании равнобедренного треугольника.
4.10. Примените неравенство треугольника.
4.11. Для каждого из отрезков ААХ, ВВХ, ССХ записать
неравенство треугольника.
4.14. К каждой высоте примените теорему о перпендику-
ляре и наклонной.
4.17. Пусть в треугольниках АВС и АХВХСХ стороны АС
и АХСХ, АВ и АХВХ, медианы AM и АХМХ соответственно
равны. На продолжении медиан отложите отрезок MN, рав-
ный отрезку AM, и отрезок MXNX, равный отрезку АХМХ,
Треугольники АМС и NBM равны, откуда следует, что BN =
= АС. Аналогично докажите, что BXNX = AXCX. Далее рас-
смотрите треугольники ABN и AXBXNX.
4.18. Выполните вспомогательное построение из указания
к задаче 4.17.
4.19. Третьи углы треугольников также будут равны.
4.20. Можно считать, что знаменатель прогрессии q > 1.
Пусть С1 — меньшая сторона треугольника. Достаточно потре-
бовать, чтобы выполнялось условие aq <a + aq.
4.21. Первое неравенство получается из неравенств:
С ъ с
тс>а~—, тпс>Ь — — . Чтобы доказать второе неравенство, вы- ’
полните вспомогательное построение из указания к задаче 4.17.
4.22. Для каждой медианы примените неравенство из
примера 4.21.
4.23. Если отрезок проходит через вершину, то он меньше
одной йз двух сторон, между которыми он заключен. Пусть в
548
треугольнике АВС точка D лежит на стороне АВ, а точка Е
— на стороне ВС. Если Z.EDA >90°, то DE < АЕ .
4.24. Должен реализоваться один из двух случаев:
а) АС =А}С и ВС = В}С; б) АС = ВХС и ВС = ДС.
4.25. BD = ВС.
4.26. Пусть Aj— такая точка, что АА j LCI и точки А и Aj
равноудалены от прямой (Л. Докажите, что точка X является
пересечением отрезка АХВ и прямой С1.
4.27. Для каждой точки X прямой I справедливо нера-
венство АХ — ВХ [ < АВ.
4.28. BD>BC-AD, BD>BC-DC.
ГЛАВА 5
5.04 . При симметрии относительно точки сохраняются
расстояния.
5.08 . Проверьте, что АВ = АС .
5.13. а) Если оси симметрии параллельны, то У о
Если же оси симметрии перпендикулярны, то f о g = g о f.
б) Для центра О поворота проверьте, что
(/ 0 g)(o)*(g°
5.16. Прямые АР и BQ симметричны относительно точ-
ки О.
5.17. Пусть биссектриса лежит на прямой I . Прямая АС
симметрична прямой ВС относительно прямой Z .
5.18. Рассмотрите поворот на 90° вокруг точки С.
5.19. Воспользуйтесь теоремой Шаля.
5.20. Возьмите точку на прямой и поверните другую
прямую вокруг точки на 60°.
5.21. Воспользуйтесь теоремой Шаля.
5.22. При композиции двух симметрий каждая точка пере-
мещается на расстояние 2d t где d— расстояние между пря-
мыми Zj и Z2.
5.23. Рассмотрите два случая: а) И — четное число; б) П
— нечетное число и п > 3. Воспользуйтесь теоремой Шаля.
5.24. Композиция двух поворотов вокруг точки О также
является поворотом вокруг этой точки.
5.25. Докажите, что каждый паралллельный перенос и по-
ворот можно представить как композицию двух осевых сим-
метрий. Затем примените теорему Шаля.
549
ГЛАВА 6
6.01 . Рассмотрите треугольник, образованный хордой и
двумя радиусами.
6.02 . Проведите диаметр через точку А и воспользуйтесь
задачей'6.01.
6.04 . Прямой угол опирается на дугу с градусной ме-
рой 180°.
6.05 . В случае, когда хорда не является диметром, вос-
пользуйтесь неравенством треугольника.
6.06 . Рассмотрите четырехугольник, образованный четырь-
мя радиусами, проведенными к концам общей хорды.
6.08 . Углы ХАМ и ВХМ — тупые.
6.09 . Воспользуйтесь определением касательной к окруж-
ности.
6.10. Луч МО является биссектрисой угла АМВ .
6.11. Эти отрезки являются сторонами двух равных треу-
гольников.
6.13. Вторая боковая сторона делится точкой касания на
отрезки такой же длины.
6.14. Воспользуйтесь результатами §6.4.
6.15. Воспользуйтесь результатами §6.4 и докажите, что из
точки внутри круга диаметр виден под тупым углом.
6.16. Найдите градусные меры дуг и примените ре-
зультаты §6.4.
6.17. Докажите равенство: XAED = XABD-ABAC .
7 6.18. Точки At Р, Q, М лежат на одной окружности.
6.19. Искомая прямая перпендикулярна к данной прямой.
6.20. Пусть точка А принадлежит искомому множеству,
АВ — отрезок касательной, О — центр окружности. В
треугольнике АОВ катет ОВ лежит против угла в 30°.
6.21. Центр данной окружности равноудален от сторон
четырехугольника.
6.22. Пусть О — середина данной дуги, опирающейся на
хорду АВ. Опишите дугу с центром в точке О, опирающуюся
на хорду АВ и лежащую по одну сторону с данной дугой от
этой хорды. Пусть С — точка на данной дуге, D — точка
пересечения прямой АС со второй дугой. Тогда СВ = CD.
6.23. Два угла треугольника вписаны в полуокружность.
6.24. Опишите окружность, радиус которой равен —, а
2
центр находится в точке At — середине стороны ВС.
550
6.25. Около треугольника опишите окружность и про-
должите отрезки АВХ и АС1 до пересечения с ней в точках В2
и С2. Треугольники ВВХВ2 и ССХС2 равны.
ГЛАВА 7
7.01 . Рассмотрите произвольный треугольник, вписанный
в эту окружность.
7.05 . Заданные углы равны полусумме и полуразности дуг
AD и ВС.
7.06 . Биссектриса угла А перпендикулярна биссектрисе
угла, смежного с углом А.
7.08 . Воспользуйтесь результатами §6.4.
7.09 . Воспользуйтесь результатами §6.4.
7.12. Эти точки лежат на биссектрисе угла А.
7.13. Центр описанной окружности совпадает с середи-
ной гипотенузы.
7.14. Градусная мера дуги CD равна 60°.
7.16. Воспользуйтесь задачей 7.15.
7.17. Пусть ABCD— данным, вписанный четырехуголь-
ник, Е —точка пересечения диагоналей, EF 1.AD, точка G —
точка пересечения прямой EF со стороной ВС. Докажите, что
Z.GEC = ZGCE.
7.18. Докажите, что углы ЕРС и DPC равны. Далее
рассмотрите треугольники ЕРС и DPC.
7.19. Рассмотрите три вписанных четырехугольника и
докажите, что угол SAT — развернутый.
7.20. Соедините этот центр с вершиной треугольника и
опустите перпендикуляры на стороны, выходящие из этой
вершины. Далее рассмотрите два прямоугольных треугольника.
7.21. В таком треугольнике каждая высота является меди-
аной.
7.22. В таком треугольнике каждая высота является бис-
сектрисой.
7.23. Воспользуйтесь утверждением из примера 7.8.
7.24. Пусть М — точка пересечения первых двух окруж-
ностей. Тогда точки Alf Blf С, М лежат на одной окружности.
7.25. Точки М и N лежат на окружности с центром Q и
диаметром АС.
7.26. Сумма градусных мер дуг СВ А и ABD равна 360°,
поскольку сумма градусных мер дополнительных дуг также
составляет 360°. Тогда сумма углов АСР и ADP равна 180°.
7.27. Около четырехугольника АОВС можно описать
окружность.
551
7.28. Воспользуйтесь теоремой 6.4 и следствием теоре-
мы 7.5.
7.29. Воспользуйтесь тем, что расстояние между центрами
касающихся окружностей равно длине стороны треугольника.
7.30. Пусть окружности с центрами О1 и О2 имеют внеш-
нее касание в точке С, а внешняя касательная касается первой
окружности в точке А и второй окружности в точке В. Пусть
D — такая точка отрезка АВ, что DCA_C\O2. Тогда около
четырехугольника ADCO} можно описать окружность, откуда
следует, что AD = DC.
7.31. Пусть О2— центр окружности С2. Опустите перпен-
дикуляры KL1AB и O2PLAD. Рассмотрите треугольники
О2КЬ и АРО2.
Ла Ля
ГЛАВА 8
8.04 . Части отрезка входят в два равных треугольника.
8.05 . Дважды примените неравенство треугольника.
8.06 . Периметр треугольника равен сумме полупериметра
параллелограмма и длины диагонали.
8.07 . Рассмотрим параллелограммы ABCD и AXBXCXDX, у
которых АВ = AlBl, AD = AXDV Z.BAD = Z.BXAXDV Треуголь-
ники ABD и AXBXDX равны, поэтому существует наложение f
треугольника ABD на треугольник AyBxDx. Докажите, что
/(с)=/(с,). Для этого проведите также диагонали АС
и А^ и рассмотрите в каждом параллелограмме точку
пересечения диагоналей.
8.08 . В данном параллелограмме ABCD рассмотрите
треугольники ABD и DCA.
8.11. Стороны такого параллелограмма равны.
8.12. Воспользуйтесь свойством 2 ромба и рассмотрите две
высоты, опущенные из одной вершины.
8.14. Пусть в ромбе ABCD высота ВК делит сторону
AD пополам. Докажите, что треугольник ABD — равнобед-
ренный. Тогда Z.BAD = ZADB = Z.BDC.
8.15. Данные углы являются внешними углами
прямоугольного треугольника.
8.16. Примените теорему 6.5.
8.17. Воспользуйтесь теоремой 7.4.
8.18. См. задачи 8.16 и 8.17.
8.19. Воспользуйтесь свойством 2 равнобедренной трапе-
ции. Рассмотрите два случая: ТП>П и ТП<П.
552
8.20. Диагональ разбивает данную трапецию на два равно-
бедренных треугольника. Составьте систему уравнений отно-
сительно углов при основаниях этих треугольников.
8.21. Пусть в выпуклом четырехугольнике ABCD выпол-
няются равенства: ЛА = ZC = а, ЛВ = ЛЕ = Р. Докажите, что
а + р = 180°.
8.22. Эта сумма расстояний равна сумме двух высот парал-
лелограмма.
8.23. Воспользуйтесь свойством 4 ромба. Точки касания
образуют четырехугольник EFGH, диагонали которого явля-
ются диаметрами окружности, вписанной в ромб.
8.24. Биссектриса отрезает от параллелограмма равнобед-
ренный треугольник.
8.25. Две соседние стороны четырехугольника симметрич-
ны соответствующим диагоналям и потому равны.
8.26. Пусть Ор О2, О3, О4 — центры квадратов, постро-
енных на сторонах АВ , ВС, CD и DA данного параллело-
грамма. Рассмотрите треугольники С\О2А и О^Л.
8.27. Пусть в трапеции ABCD дано: AD > ВС. Через
точку С проведите прямую, параллельную стороне АВ, до
пересечения с основанием AD в точке Е. Рассмотрите
треугольник EDC.
8.28. Через вершину меньшего основания проведите пря-
мую, параллельную боковой стороне. Образуется прямоуголь-
ный треугольник.
8.29. Проведите прямую через вершину и середину отрез-
ка, соединяющего две другие точки.
8.30. Пусть две перпендикулярные прямые Q и b пересе-
каются в точке О, а точка А лежит вне этих прямых. Рас-
смотрим
точку Ах, симметричную точке А относительно пря-
мой П;
точку А2, симметричную точке относительно пря-
мой Ь ;
точку А3, симметричную точке А относительно пря-
мой Ь .
Докажите, что четырехугольник ЛЛ1Л2Л3 — прямоуголь-
ник с центром О.
8.31. После каждого отрезания остается выпуклый много-
угольник, у которого некоторые четыре стороны лежат на
сторонах данного квадрата. Поэтому всегда можно выбрать по
553
одной неотрезанной точке на каждой стороне квадрата. Эти
четыре точки определяют выпуклый четырехугольник,
содержащий центр квадрата.
8.32. Рассмотрите такую точку Е} внутри квадрата, чтобы
треугольник ВЕХС был правильным. Докажите, что угол EXAD
равен 15°.
ГЛАВА 9
9.01 . Воспользуйтесь признаком параллелограмма.
9.02 . Рассмотрим угол, меньший развернутого. Пусть I —
биссектриса этого угла. Докажите, что при симметрии Sf точка
на стороне угла переходит в точку на другой стороне угла, а
внутренняя точка угла также переходит во внутреннюю точку
угла.
9.04 . Допустим, что некоторая центральная симметрия
осуществляет наложение данного треугольника на себя. Тогда
при таком наложении каждая вершина должна переходить в
вершину треугольника.
9.05 . Примените теорему 9.2.
9.06 . Примените рассуждения, которые были сделаны при
доказательстве теоремы 9.2.
9.07 . См. указание к задаче 9.06.
9.12. Пусть А}А2• ••А6 —данный шестиугольник. Четырех-
угольник А}А3А4А^ — параллелограмм, и его диагонали в точке
пересечения делятся пополам. Затем рассмотрите четырех-
угольник
9.13. Пусть Ф — данная фигура, а перпендикулярные
прямые I и ТП пересекаются в точке О и являются осями
симметрии фигуры Ф. Пусть точка А фигуры лежит вне
прямых I и тп. Рассмотрим точки Л^ЗДл), А2 = Sm(Ах).
Докажите, что А2 = ^(л).
9.15. В качестве данной фигуры рассмотрите прямую
линию.
9.16. Примером такой фигуры является полуплоскость.
9.17. Рассмотрите параллелограмм ABCD и его парал-
лельные переносы вдоль луча АВ на расстояния п • АВ, а
также вдоль луча ВА на те же расстояния. Здесь И — произ-
вольное натуральное число.
9.18. Сначала докажите, что 1 и 9 не могут находиться в
углах а, у , ф магического треугольника, изображенного на
рис.9.11. Затем рассмотрите случаи, когда цифра 9 примыкает к
554
стороне треугольника и когда ни одна из цифр 1 и 9 не
примыкает к сторонам этого треугольника.
9.19. Рассмотрите сумму чисел вдоль диагоналей и вдоль
средних линий квадрата.
9.20. Докажите, что цифры 1 и 9 не могут находиться в
углах а, у , ф, Ц магического квадрата, изображенного на рис.
9.15.
9.21. Воспользуйтесь таблицей Кэли группы симметрий
равностороннего треугольника.
9.22. Допустите противное и воспользуйтесь теоремами 9.2
и 9.3.
ГЛАВА 10
10.01 . Из конца А данного отрезка АВ проведите луч I .
На этом луче отложите равные отрезки АА}, АХА2, ... , Ап_^Ап.
Через точки Av А2, ... , Ап_^ проведите прямые, параллельные
прямой АпВ.
10.02 . Отрезок, соединяющий середины соседних сторон,
является средней линией треугольника, образованного этими
сторонами и диагональю.
10.03 . Примените следствие из теоремы Фалеса.
10.04 . а) На стороне угла О последовательно откладываем
отрезки ОС = с, СВ = Ь. На другой стороне угла откладываем
отрезок ОА = а. Через точку В проводим прямую, парал-
лельную отрезку СА, до пересечения со стороной угла в точ-
ке D. Отрезок AD—искомый.
10.07 . Радиус, проведенный в точку касания, является
средней линией трапеции.
10.09 . Рассмотрите различные случаи относительно знаков
коэффициентов гомотетии.
Преобразование j\ о f2 является гомотетией с тем же
центром и коэффициентом кх • к2.
10.11. Пусть коэффициент гомотетии положителен и точ-
ка А отлична от центра О. Положим At=g(A), В = /(а),
Д = g(l?). Докажите, что д=/Ц)-
10.12. Пусть О1 и О2, Rx и Т?2 — центры и радиусы дан-
ных окружностей соответственно. Рассмотрим параллельный
перенос f вдоль луча ОХО2 на расстояние 0}О2 и гомотетию g
___ . Л
с центром (>2 и коэффициентом к = —. Докажите, что
555
преобразование подобия h — g^f переводит первую окруж-
ность во вторую.
10.13. Пусть а— полуплоскость, ограниченная прямой I ,
f— преобразование подобия. Согласно §10.3 прямая I
переходит в некоторую прямую 1Х, а луч ТП, перпендику-
лярный Z и принадлежащий а, переходит в луч перпен-
дикулярный 1Х. Пользуясь теоремой 10.6, докажите, что полу-
плоскость 01 переходит в полуплоскость, ограниченную пря-
мой 1Х и содержащую луч тпх.
10.14. Если точки С и D лежат по одну сторону от
диаметра АВ, то ММХ — средняя линия трапеции. Если же
точки С и D лежат по разные стороны от диаметра АВ, то
постройте параллелограмм CXI\DE и через точку М
проведите среднюю линию треугольника CDE.
10.15. Середины сторон четырехугольника А МВ О
являются вершинами ромба.
10.16. Воспользуйтесь задачей 10.02.
10.17. Примените теорему о средней линии треугольника.
10.18. Воспользуйтесь задачей 10.03 и докажите, что эти
две другие стороны параллельны.
10.19. Примените гомотетию с центром М и коэффици-
ентом к = 2. Существуют две искомые точки.
10.20. Окружности S и Т гомотетичны с центром гомо-
тетии в точке X.
10.21. Пусть прямые AM и AN пересекаются с продол-
жением стороны ВС в точках Р и Q соответственно. Дока-
жите, что треугольники АВМ и РМВ равны, а также тре-
угольники ACN и QCN равны. Отрезок MN— средняя
линия треугольника APQ.
ГЛАВА И
11.01 . Треугольники AOD и СОВ подобны и гомотетич-
ны с центром гомотетии О и отрицательным коэффициентом
гомотетии.
11.02 . Указанный отрезок отсекает от данного треуголь-
ника меньший треугольник, подобный данному. В подобных
треугольниках медианы пропорциональны соответственным
сторонам.
11.03 . У подобных треугольников соответственные углы
равны.
556
11.05 . Справедливы равенства:
Рх _ ах +l\ + q _ ка + kb + кс
Р a+b+с а+Ь+с
где к— коэффициент подобия треугольников.
АЕ AD
11.06 . Проверьте, что =
11.07 . Обозначим Cff = 4x, СМ = 5х. Тогда Л2? = 10х.
Воспользуйтесь теоремой 11.6.
11.08 . По теореме Пифагора найдите основания трапеции.
11.09 . Обозначьте высоту через Зх, а основание — через
4х.
11.10. Найдите высоту, опущенную на гипотенузу. Затем
из подобия найдите второй катет и гипотенузу прямоугольного
треугольника.
11.11. Используя теорему Пифагора и теорему 11.7, со-
ставьте систему уравнений относительно неизвестных катетов.
11.13. Центр окружности совпадает с центром ромба. Ра-
диус окружности равен половине высоты равностороннего тре-
угольника.
11.14. Найдите проекцию основания на боковую сторону.
Далее, опустите высоту на основание и найдите боковую
сторону из подобия прямоугольных треугольников.
11.15. Пусть ABCD — данная трапеция, ВС = 2см, а
продолжения боковых сторон пересекаются в точке О. По
теореме Фалеса ОВ = ОС.
11.16. Воспользуйтесь результатами §11.8.
11.17. а) Это гипотенуза прямоугольного треугольника с
катетами Q и b .
б) Воспользуйтесь результатами §11.8.
11.18. Отрезок у[2 — это гипотенуза равнобедренного
прямоугольного треугольника с единичными катетами. Два
других отрезка постройте, опираясь на указания к задаче 11.17.
Воспользуйтесь равенством VT1 = + З2 .
11.19. Обозначьте длину отрезка касательной через 2х, а
длину внутреннего отрезка секущей через Зх.
11.20. Проведите диаметр через точку Р.
11.21. Пусть АВ и АС— отрезки касательных, прове-
денных к окружности с центром О, а отрезки ВС и ОА пере-
секаются в точке D. Тогда прямоугольные треугольники АОВ
и ABD подобны.
557
11.22. Треугольники АМВ и DMC подобны. Тогда углы
ВАС и BDC равны. Значит, точки А и D принадлежат
множеству точек, из которых отрезок ВС виден под фик-
сированным углом. Кроме того, в силу выпуклости четы-
рехугольника точки А и D лежат по одну сторону от пря-
мой ВС.
11.23. Пусть Ах и Вх середины медиан та и т^, М—
центр масс треугольника. Треугольники АМВ и А}МВХ
подобны с коэффициентом подобия к =6.
11.24. Пусть стороны треугольника АХВХСХ соответственно
параллельны сторонам треугольника АВС . Тогда по теореме
ВАХ АВХ АСХ ВАХ
Фалеса имеем: ----=-----=-----L =---L.
11.25. Пусть в трапеции ABCD точки О, Е, F, G—
точки пересечения диагоналей, продолжений боковых сторон,
середина большего основания AD и середина основания ВС
соответственно. Треугольники AOD и сов гомотетичны с
центром гомотетии О, поэтому середина F основания AD
гомотетична середине G основания ВС с тем же центром
гомотетии. Значит, точки F, О, G лежат на одной прямой.
Прямая EG пересекает основание AD в ее середине.
11.26. Пусть Ох, О2 — центры данных окружностей
радиусов R и Г , Р — точка их внешнего касания, А и В —
точки касания этих окружностей их общей внешней
касательной. Пусть О — точка пересечения диагоналей
прямоугольной трапеции ОХО2ВА. Докажите, что прямая,
проходящая через точку О параллельно АОХ, проходит через
точку Р.
11.27. Проведите через данную точку диаметра произволь-
ную хорду. Для отрезков С1 и Ь этой хорды примените
> y[ab.
неравенство
11.28. Пусть Р— заданный периметр. Постройте произ-
вольный треугольник с двумя заданными углами. Пусть его
периметр — Ро. Примените гомотетию с центром в одной из
вершин и коэффициентом к = —. При гомотетии углы между
лучами сохраняются.
558
11.29. Пусть ABCD— данная трапеция, AD — большее
основание, угол А — прямой. Из центра О вписанной
окружности сторона CD видна под прямым углом. Найди-
те CD.
Вписанная окружность касается основания AD в точ-
ке Е и основания ВС в точке F. Обозначим: ED = х,
FC = у. Составьте систему уравнений: а) с помощью теоремы
Пифагора из треугольников OED и OFC\ б) представив CD
как сумму х + у.
11.30. Пусть О — центр окружности, АС и BD —
перпендикулярные хорды, не проходящие через центр.
Опустим перпендикуляры ОЕ и OF на стороны AD и ВС.
Треугольники АОЕ и OBF равны.
11.31. В таком треугольнике центр описанной окружности
лежит на середине стороны.
S ab гс
11.32. Поскольку г — — =----, то — =--------. За-
р a+b+c h a + b + c
мечание: первое неравенство можно уточнить: yf2 —1<—,
h
причем равенство достигается в случае равнобедренного пря-
моугольного треугольника.
а + Ь-с
11.33. Воспользуйтесь формулой г =---.
11.34. Пусть АВС — треугольник с прямым углом С, в ко-
тором угол А больше угла В. Проведем медиану СС}, бис-
сектрису CL3 и высоту СНЪ. Тогда ААСН^ = ZjB, AACL3 —
= 45°, ZACC} = ZA.
11.35. Медиана равна половине гипотенузы. Разность пе-
риметров равна разности катетов.
11.36. На отрезок AF опустите перпендикуляр ЕН и до-
кажите подобие треугольников EHF и GCD .
11.37. Соедините точку касания с концами хорды. Про-
ведите диаметр через точку касания. Отрезок этого диаметра
является медианой и высотой образовавшегося треугольника.
11.38. Возможны два случая: а) центр окружности лежит
вне прямоугольника; б) центр окружности находится внутри
прямоугольника.
11.39. Условию задачи удовлетворяют две окружности. До-
кажите, что их центры равноудалены от прямой CD .
559
11.40. Отрезок AD является диаметром окружности, опи-
санной около треугольников ACD и ABD. Треугольники
АСМ и АВС подобны.
11.41. а) Сначала постройте отрезок d = ylа2 + Ь2 . Иско-
мый отрезок равен yjd2 + с2 .
б) Сначала постройте отрезки d = л/п2 +Ь2 и f = y[ab.
Искомый отрезок равен ^d2 -F f2 .
в) Сначала постройте отрезки f — y/ab и g = y[cd. Иско-
мый отрезок равен у] fg .
11.42. Продолжите AD до пересечения с окружностью в
точке Е. Углы AMN и ACD равны. Треугольники АВС
и ANM подобны.
11.43. Пусть N— середина ВС. Найдите множество всех
возможных положений точки N и примените гомотетию с
центром А.
11.44. Пусть М— центр масс треугольника АВС . Для
каждого из треугольников АМВ , ВМС, СМА запишите
неравенство треугольника.
11.45. Пусть в треугольнике АВС угол В— прямой, BD
— биссектриса, ВА<ВС. Пусть Ах и Q— проекции точек А
и С на биссектрису. Треугольники AAXD и CCXD подобны;
поэтому AXD < DC}.
ГЛАВА 12
12.03 . Все стороны четырехугольника равны, а соседние
стороны перпендикулярны.
12.07 . д) Постройте множество точек, из которых отрезок
АС виден под углом 30°. Оно делит плоскость на внутреннюю
и внешнюю части. Внешняя часть является искомой.
е) Постройте множество точек, из которых отрезок ВА
виден под углом 60°. Для точек искомого множества угол BDA
больше 60°.
12.08 . Пусть f— параллельный перенос вдоль луча 7W на
расстояние d. Из начала координат проведем луч, сона-
правленный лучу ТП, и отложим на нем от точки О вектор ОМ
длины d. Пусть точка М имеет координаты М(а\Ь). Для этих
U и Ь докажите утверждение задачи.
560
12.09 . В такую точку С, что точка В является серединой
отрезка МС , где М— середина АВ .
12.10. Проверьте, что векторы АВ и CD равны.
12.11. Центр симметрии является серединой каждого из
отрезков ААХ и ВВХ.
12.12. К векторам ОВ и ОС прибавьте вектор АО.
12.13. Для точки М(х;6) запишите квадраты расстояний
до точек А и В.
12.17. Когда координаты векторов (1 и Ь пропорци-
ональны, причем первые координаты имеют одинаковые знаки.
12.18. Значение COS А находится через скалярное произ-
ведение векторов АВ и АС.
12.19. а) Векторы можно скалярно умножать, как мно-
гочлены.
б) |2а + 5*| = yl(2a + 5b) (2a + 5b).
12.20. Проверьте, являются ли векторы АВ и АС кол-
линеарными.
12.21. Длины диагоналей равны |л + б| и а — b\.
12.22. Проверьте, что вектор АВ удовлетворяет определе-
нию разности векторов ОВ и ОА, т.е. убедитесь в справед-
ливости равенства: ОВ = ОА 4- АВ .
12.23. Искомое значение находится из равенства: а • Ь = 0.
1
12.24. Это вектор —- • р.
Р\
12.25. Убедитесь, что b = 1.
12.27. Постройте сначала вектор d—'la — ЗЬ. Искомый
J 1
вектор равен а 4— с.
12.28. Справедливо равенство ААХ =— АВ 4- АС
12.29. Убедитесь, что
561
MN = MC +CN = —\ AD + Dc\ + —[СВ + Cd\.
2k J 2< )
12.30. Искомый вектор b имеет отрицательную ординату,
причем а • b = 0.
12.31. Для искомого вектора С выполнено неравенство
Ь-с>0.
12.32. Примените теорему 12.11.
12.33. Для искомой точки С(х; у) справедливы равенства:
са2=св2 = ав2.
12.34. Для искомой точки С\х;у) справедливы равенства:
СВ = АВ. СВАВ=0.
12.35. Найдите косинус угла между векторами АС и BD .
12.36. Если d = (b - с) • а — (а • с) - Ь, то d с = (b c)-(a-c)-
-(a-c)-(bc).
12.37. Когда множители т2—т — 2 и т3 имеют разные
знаки, т.е. (т2 — т — 2) w3 < 0.
12.38. Вектор CD представьте в виде а + Х(Ь — а). Чис-
ло X находится из условия CD- (Л — л) = 0.
12.39. Рассмотрите случаи, когда к>0 и k<Q. Вос-
пользуйтесь подобием прямоугольных треугольников.
12.40. Рассмотрите точки С(х 4- и, у -I- v), А(х;у) и
В{и, v). Убедитесь, что ОС = ОА 4- АВ . Пусть Ах(х,, ух),
Д (W1 ’ vi) и Q G1»z\) — образы точек А, В и С при заданном
повороте. Докажите, что tx = х} 4- их, zx = ух 4- Vj. Далее найдите
координаты образов точек Z)(x;0) и £(0;^).
12.41. Пусть О
МА-МС = МО + ОА
— центр прямоугольника. Тогда
МО-ОА |=ЛЮ2 -ОА2.
12.42. Выберите точку О за начало декартовой системы
координат и воспользуйтесь теоремой 12.13.
12.43. Примените правило многоугольника, откладывая
векторы от точки М.
19 Зак. 687
562
12.44. Треугольник симметричен относительно биссек-
трисы первого и третьего координатных углов. Возможны два
направления искомого вектора.
12.45. Выразите все векторы АВ = Л, ВС = b и CD = С.
12.46. Пусть D — точка пересечения высот, проведенных
из вершин А и В. Тогда АВ 1DC и BC1.DA,
12.47. Воспользуйтесь тем, что |а + 6| =(а + Ь)-(а + b).
Для геометрической трактовки постройте параллелограмм на
векторах (I и Ь.
12.48. Рассмотрите векторы (I = (xpJi) и Ь = (х2; у2).
Неравенство
можно доказать возведением в
квадрат.
12.49. Пусть D — такая точка, для которой ОА + ОВ +
+ ОС = OD. Докажите, что CD А-АВ . Для этого заметьте, что
CD = ОА + ОВ и точка О равноудалена от точек А и В.
12.50. Примените определение коллинеарных векторов.
12.51. Пусть АВ=Ь, АС=С, AM = rn, АТ = t .Тогда
ТМ = т — t, АА} = — (b +с). Рассмотрите скалярное произве-
дение этих векторов.
ГЛАВА 13
13.01 . а), б), г) — это прямые вида у = кх, где к = tgOL, а
— угол, образованный прямой с осью ОХ. в) это ось ординат.
13.02 . Составьте систему уравнений и решите ее.
13.03 . Решите систему из первых двух уравнений и убе-
дитесь, что решение удовлетворяет третьему уравнению.
13.04 . Воспользуйтесь условием перпендикулярности пря-
мых, записанных в общем виде.
13.05 . Четырехугольник имеет две средние линии.
13.06 . Точки А и В лежат на окружности.
13.07 . Найдите точки пересечения прямой и окружности.
13.08 . Начало координат совместите с центром одной из
окружностей.
13.09 . Постройте отрезок прямой х + 2у = 1, лежащий в
первой четверти. Искомое множество получается из этого от-
563
резка с помощью симметрий относительно осей координат и
симметрии относительно начала координат.
13.10. Приведите уравнения окружностей к виду
13.11. Пусть О1 и О2 — центры окружностей, А — одна
из двух точек пересечения. Точки Q, О2 и А лежат в
вершинах треугольника.
13.12. Воспользуйтесь формулой (1) из §13.2.
13.13. Рассмотрим две прямые: у = кхх + 1} и у = к2х + 12.
Пусть они образуют углы аир соответственно с положи-
тельным направлением оси Ох. Тогда кх =tgCL, к2 =(gP. Один
из углов между прямыми равен р —а. Если прямые непер-
пендикулярны, то
,g(P-a)='g|i-*a=Ask.
1 + fgP/ga 1 + k2kx
Тангенс меньшего угла, образованного такими прямыми,
равен
13.14. Пусть к} — угловой коэффициент данной прямой.
Искомые прямые имеют угловой коэффициент к2 =-----.
К
13.15. Найдите катеты и гипотенузу этого прямоугольного
треугольника, затем найдите Т* и координаты инцентра.
13.16. Сторона квадрата равна расстоянию от произ-
вольной точки А первой прямой до второй прямой. Вос-
пользуйтесь теоремой 13.3.
13.17. Прямая ax + Zry + c = 0 пересекает отрезок АВ в
его внутренней точке тогда и только тогда, когда выражение
ах + by + с в точках А и В имеет разные знаки.
13.18. Центр окружности есть середина отрезка АВ.
13.19. Выберите систему координат так, чтобы ось Ох
прошла по диагонали АС, а ось Оу— по диагонали BD.
Вершины имеют координаты:
Л(а;0), С(-а,0).
V у
. Возьмите
из искомого множества
564
Возьмите
квадраты
до точки
и составьте выражения для квадратов расстояний от нее до
вершин ромба.
13.20. Пусть середина отрезка АВ есть начало коорди-
нат, а ось абцисс проходит через этот отрезок. Если длина
отрезка АВ равна 2/ , то имеем: Л(/;0), В(—Z;0).
точку М(х',у) из искомого множества и выразите
расстояний от нее до концов отрезка.
13.21. Примите за X расстояние от точки D
касания окружностей друг с другом.
13.22. Треугольники АВС и ABD подобны.
13.23. Пусть Ох и Rx — центр и радиус первой окруж-
ности, О2 и Т?2 — центр и радиус второй окружности, АС —
хорда первой окружности, AD— хорда второй окружности. Из
AC Rx
равенства углов ОХАС и O2AD следует, что----= —.
AD R2
Пусть из центра Ох хорда АВ видна под углом 2а, а из
центра О2 — TLQ& углом 2р. Проверьте, что BD = 2R2 cos а,
BC = 2^cosp.
13.24. Составьте уравнение прямой, проходящей через
точку В и перпендикулярной данной прямой.
13.25. Точка О лежит на окружности, а радиус, прове-
денный в точку О, перпендикулярен данной прямой. Образом
окружности будет окружность того же радиуса, центр которой
симметричен точке (1,1) относительно прямой X + у — 0.
13.26. Проверьте, что данный круг лежит в квадрате, ко-
торый задается неравенством |х| +1 < 2.
13.27. Напишите уравнения прямых, содержащих сторо-
ны треугольника.
13.28. Приведите уравнение окружности к виду
(х — а)2 4- (j/ — Z>)2 = 7?2. Осуществите параллельный перенос
центра (a;Z>). Радиус окружности при параллельном переносе
не изменится.
13.29. В обоих случаях найдите угловой коэффициент к
искомой прямой. Ее уравнение запишите в виде: у — у$ =
= к(х — х0), где (х0;у0) — координаты точки М.
13.30. Соедините точку касания с концом второй хорды.
Образовался равнобедренный треугольник, вписанный в дан-
ную окружность.
565
ГЛАВА 14
2
14.01 . Выразите с по теореме косинусов.
14.02 . Пусть С— большая сторона треугольника. Сравните
числа а2 + Ь2 и с2. Воспользуйтесь задачей 14.01.
14.03 . Воспользуйтесь теоремой 14.2.
14.04 . Рассмотрите треугольник, образованный полови-
нами диагоналей, с внутренним углом 60°.
14.05 . Медианы, проведенные к данным сторонам, нахо-
дятся по теореме косинусов. Чтобы найти третью медиану,
достройте треугольник до параллелограмма.
14.06 . а) Найдите отрезки, на которые биссектриса делит
сторону АС , и примените теорему косинусов.
14.07 . Пусть окружность касается сторон АВ и АС в
точках Р и Q. Найдите отрезки АР и AQ, а также COS Л.
14.09 . Угол при вершине должен быть больше угла при
основании.
14.10. Воспользуйтесь теоремой 14.3.
14.11. Воспользуйтесь следствием 2 теоремы 14.3.
14.12. Примените теорему Птолемея.
14.13. Обозначьте меньшую диагональ за а боль-
шую — за V39X. С помощью теоремы 14.2 найдите эти диаго-
нали.
14.14. Центр вписанной окружности лежит на биссек-
трисе. К прямоугольному треугольнику примените теоре-
му 14.5.
14.15. Пусть U— сторона ромба. Найдите длины этих
отрезков и расстояние между их концами.
14.16. Воспользуйтесь теоремами 14.5. 14.6.
14.19. Квадраты диагоналей находятся по теореме коси-
нусов.
14.20. Через середину меньшего основания проведите от-
резки, параллельные боковым сторонам. Искомый отрезок
является медианой образованного треугольника.
14.21. Выразите эти отрезки через основание ВС и
угол А.
14.22. Обозначьте АС через X и примените теорему ко-
синусов.
14.23. Найдите угол AIB.
14.24. По теореме косинусов найдите отрезок МВ,
равный DB.
566
14.25. Пусть Ах и Вх — середины сторон ВС и С А соот-
ветственно. Выразите векторы ВВХ и ААХ через векторы
СВ и СА = b. Из условия ВВХ • ААХ = 0. Найдите cosC.
14.26. Пусть четырехугольник ABCD вписан в окруж-
ность. АС— ее диаметр; /.ВАС = а, ZACD = р. Докажите,
что проекция стороны ВС на диагональ BD равна
AC sina sinp.
14.27. Пусть АВС — равнобедренный треугольник с пря-
мым углом С. Проведем медиану ААХ и биссектрису BL. Вы-
разите векторы ААХ и BL через векторы С А = U и св = ь.
Воспользуйтесь свойством биссектрисы. Искомый косинус най-
дите через скалярное произведение ААХ- BL.
14.28. Выразите длины отрезков через радиус окруж-
ности R и соответсвующие центральные углы.
14.29. Воспользуйтесь основным свойством биссектрис и
выразите данные векторы через векторы, направленные вдоль
сторон треугольника.
14.30. Из точки D опустите перпендикуляр DDX на ось
ОХ. По основному свойству биссектрисы имеем:
AB BD _ ОРХ
AC~DC~DXC'
14.31. По теореме синусов имеем:
Ь _ а _ х
sinB sin3B sin2B’
где X — длина третьей стороны треугольника. Из первого
равенства находим sin В, используя формулу sin ЗВ =
= 3sinB-4sin3B .
14.32. Из треугольника АСК по теореме синусов найдите
отрезок СК.
14.33. Соедините центры окружностей и точку А.
ГЛАВА 15
15.05 . Площадь ромба равна половине произведения
диагоналей.
15.08 . Найдите третью сторону.
15.09 . Воспользуйтесь теоремой 15.8.
15.10. Воспользуйтесь формулой sin 2a = 2 sin a cosa.
567
15.11. В прямоугольном треугольнике
п с а+Ь-с
R = —, г —------------------------
Найдите катеты.
15.12. Выразите Гс по теореме 15.4. Составьте систему
уравнений относительно катетов.
15.13. Пусть ABCD — донная, трапеция, в которой
AD =20, ВС =6, АВ = 13, CD = 15. Проведите высоты ВВ}
и ССр Обозначьте АВХ через X, а СС{— через у. Тогда
132 - х2 = 152 - у2, х + у = 14.
15.14. Найдите проекции диагоналей на большее осно-
вание, а затем полусумму оснований.
15.15. Диагонали равнобедренной трапеции равны. Через
вершину верхнего основания проведите отрезок, параллель-
ный диагонали. Найдите диагональ. Площадь трапеции равна
площади образованного треугольника.
15.16. Пусть ABCD — трапеция. Вписанная ок-
ружность радиуса Г с центром О касается большего
основания в точке Е, меньшего основания в точке G и боль-
шей боковой стороны в точке Н. Обозначим: CG = CH = Х,
DH = DE = у. Из прямоугольного треугольника COD найди-
те х + у. Из прямоугольных треугольников DOE и COG
п2 ,,2 о2 2
имеем: 9 — у = 3 — х
15.17. Через середину боковой стороны проведите пря-
мую, параллельную другой боковой стороне, и сравните
площадь трапеции с площадью параллелограмма.
15.18. Площади подобных треугольников относятся как
квадраты линейных размеров.
15.19. Рассмотрите площади четырех подобных треуголь-
ников.
15.20. Это равнобедренный треугольник с основанием 16.
Найдите его высоту. Центры окружностей лежат на высоте.
Для нахождения их радиусов найдите площадь треугольника.
15.21. Примените теорему 15.10.
15.22. Если около трапеции можно описать окружность, то
трапеция является равнобедренной.
15.23. Найдите диагональ трапеции. Искомая окружность
описана около треугольника, образованного диагональю, ос-
нованием и боковой стороной.
15.24. Соедините центр окружности с вершинами данной
равнобедренной трапеции. Площадь трапеции выражается
568
через площади равнобедренных треугольников. Центральные
углы выражаются через а и Р.
15.25. Примените теорему 15.4.
15.26. Большая сторона прямоугольника равна высоте
правильного треугольника.
15.27. Пусть Г— радиус вписанной окружности. Тогда
катеты равны Г + а и г + Ь.
15.28. Рассмотрите треугольник, образованный меньшей
диагональю и двумя сторонами параллелограмма. Высоты
параллелограмма — это высоты этого треугольника. Найдите
синусы двух углов треугольника.
15.29. Четырехугольник с вершинами в серединах сторон
данного четырехугольника является ромбом.
15.30. Докажите, что угол I\DI2— прямой.
15.31. Из теоремы 15.17 следует, что
S&BAC
= cos2 В,
НХН2 D
причем -----= cos В.
15.32. По теореме синусов выразите стороны А С и АВ
через R и углы треугольника АВС .
15.33. Примените теорему Птолемея к четырехугольнику
AMIN.
15.34. Около образованного четырехугольника опишите
окружность.
15.35. Выразите площадь вписанного четырехугольника с
помощью теоремы 15.11 и оцените ее через диаметр окруж-
ности.
15.36. Выразите указанные расстояния и радиус V через
R и функции углов треугольника.
15.37. Воспользуйтесь теоремой Птолемея.
15.38. Проведите диагональ и оцените площади треуголь-
ников через произведения соответствующих сторон. То же
самое проделайте для второй диагонали.
15.39. Воспользуйтесь теоремой 15.12.
15.40. Пусть ABCD — данный вписанный четырехуголь-
ник, AD — диаметр, АВ = ВС = 2л/5 см, CZ) = 6 см, Обоз-
начим угол АОВ через 2а. Тогда Z.COD = 180°— 4а. Сос-
тавьте уравнение относительно неизвестной величины sin а.
15.41. Постройте множество точек, из которых основа-
ние АВ видно под углом а. Выясните, для какой точки С
этого множества высота hr максимальна.
569
15.43. Пусть d— разность прогрессии. Тогда CL=b—d,
15.44. Пусть D— середина АВ , точка Е лежит на АС
АЕ = — АС. Построенный треугольник также является пра-
вильным и имеет общий центр О с исходным треугольником.
Пусть ZADE = а. Радиус вписанной в построенный треу-
гольник окружности равен: = гcosa, где Г = DO— радиус
вписанной в треугольник АВС окружности. Чтобы найти
cosa, вычислите DE и воспользуйтесь теоремой косинусов.
15.45. Углы Р и у задают треугольник АВС с точностью
до подобия. Рассмотрите треугольник АХВХСХ с углами АВХ = Р,
АСх—у и стороной 5^ = 1. Найдите его площадь и
. 1 _ тп
медиану тпх — Ах Мх. Искомая площадь равна; —
15.46. Отношение площадей равно:
W мс КС
S^ABC ВС АС •
15.47. Обозначим меньшее основание данной равнобед-
ренной трапеции через X, а боковую сторону через I . Диа-
гональ трапеции равна 4хд/2(см. указание к задаче 15.14).
Через вершину меньшего основания проведите высоту. Из двух
прямоугольных треугольников имеем:
15.48. Найдите высоту треугольника с основанием Cl-b и
углами а и Р при основании.
15.49. Через вершину меньшего основания проведите пря-
мую, параллельную диагонали. Из образовавшегося равнобед-
ренного треугольника найдите диагональ.
15.50. Выразите площадь через угол а при большем осно-
вании.
15.51. Пусть угол между диагоналями равен а. Выразите
площадь каждого из четырех треугольников через отрезки
диагоналей и sina. Воспользуйтесь подобием треугольников
AOD и СОВ.
15.52. Образованные треугольники подобны данному.
570
15.53. Из равенств S = —aha=—bhb=—chc следует, что
стороны Cl, b и С пропорциональны величинам —, — и
ha hb
hc
Пусть I — произвольный отрезок. Постройте треугольник со
I2 I2 I2
сторонами —, — и —. Искомый треугольник гомотетичен
данному.
15.54. Пусть а — угол между диагоналями. Выразите
площади треугольников через отрезки диагоналей и sin а.
15.55. В шестиугольнике прямые углы идут через один.
Разбейте шестиугольник на равносторонний треугольник и три
прямоугольных треугольника.
15.56. Найдите высоту и биссектрису.
15.57. Рассмотрите два случая: точка М лежит внутри
угла и снаружи. Составьте систему уравнений относительно
отрезков, отсекаемых прямой на сторонах угла.
15.58. Сведите искомое равенство к тригонометрическому
тождеству.
ГЛАВА 16
16.01 . Справедливо равенство: тп • AM = 5 • МВ.
16.02 . Пусть К— точка пересечения отрезка АВ и
прямой CD. По свойству биссектрисы BL: LC = 2:1. Помес-
тите в точку В массу /И, а в вершину С массу 2m. Тогда L —
центр масс этих двух материальных точек. В вершину А по-
местите массу 2 m — тогда В} — центр масс системы матери-
альных точек (А;2тп), (С;2ти). Точка D — центр масс систе-
мы трех материальных точек, поэтому Е — центр масс
системы (А;2т), (В\тп). Отсюда следует равенство:
тп-ВК=2тКА.
16.03 . Пусть — координаты точки А^, где
1 < к < п, а прямая I задана уравнением ах + |3у + у = 0 .
Воспользуйтесь формулами координат (х0;у0) центра масс
(теорема 16.1) и проверьте, что ах0 4- Ру0 4- у = 0 .
16.04. Пусть О— точка пересечения диагоналей парал-
леллограмма, а в вершинах его находятся равные массы ТП.
Центр масс системы материальных точек (А;т), (С;т) —
571
точка (О; 2т). По теореме 16.2 искомый центр масс совпадает с
центром масс системы (0;2ти), (В;т), (Dtm).
16.05 . Пусть диагонали АС и BD пересекаются в точке
О, тогда АО:ОС = а:Ь. Поэтому центром масс системы
материальных точек (С; а) является точка (O;a + Z>).
По теореме 16.2 искомый центр масс совпадает с центром масс
системы (О: а + b), (В;а), (D;b).
16.06 . При доказательстве необходимости проведите
произвольную прямую I и спроектируйте на нее точки А, В,
С, Alt СР Воспользуйтесь теоремой Фалеса. Достаточность
доказывается так же, как и в теореме Чевы.
16.07 . Поместите в вершины А, В, С массы 2т, т, 4 m
соответственно. Тогда В— центр масс этой системы
материальных точек. Он совпадает с центром масс системы
материальных точек (В; т), откуда. следует равен-
ство т • BS = 6т • SN.
16.08 . Пусть М — точка пересечения медиан, D — сере-
дина медианы ВВр Найдите отношение BD.DM и восполь-
зуйтесь теоремой Фалеса.
16.09 . Пусть Р — точка пересечения отрезков AN
и ВМ, а С2 — точка пересечения прямых СР и АВ.
ЛС2 ,
Воспользуйтесь теоремой Чевы и докажите, что-----= 1.
С2В
16.10. Поскольку МА{ + Л£42 + ... 4- МА$ = О, то
+... +1 ОМ 4- MAS
16.11. Поместите в вершины А, В, С единичные массы и
воспользуйтесь тождеством Лагранжа.
16.12. Отношение площадей равно
। S& + + S&CNP
$ЬАВС
Кроме того,
АМАР АМ АР
S^bc ~ АВ АС АВ АС
16.13. Поместите в вершины А, В, С, D одинаковые
массы 1П. Общая середина есть центр масс системы
материальных точек (Atm), (В;гп),
16.14. Трижды примените теорему 16.2: искомый центр
масс совпадает с центром масс системы материальных точек
(Лтц+Шг), (А^гпз), (А5;т5), (А^; т6). Он же сов-
падает с центром масс системы материальных точек
(Р;тх + 7^), (б;^з + w4), (А^щ). Наконец, он сов-
падает с центром масс системы материальных точек Р, Q, R.
АСЛ 1 ВА. , СВХ
16.15. Пусть-1 = к, —i- = /,---L = п.
СХВ А£ ВХА
Поместите в вершинах А, В, С соответственно массы 1,
к, kl. Тогда К— центр масс данной системы, и он совпадает с
центром масс системы материальных точек (A;k + kl).
Отсюда
= k + kl.
16.16. Воспользуйтесь результатом задачи 16.15.
16.18. Пусть Р— точка окружности, описанной около
треугольника АВС , а точки Av Bv Q— основания перпен-
дикуляров, опущенных из точки Р на прямые ВС, АС и АВ
соответственно. Тогда
ВА
СА
ВР cos АР ВС
СР cos АРСВ
и
СВ.
Аналогично выразите отношение —~
АВХ
примените теорему Менелая (задача 16.06).
16.19. Пусть AD = 6lf АМ = а2,
смотрите систему материальных точек (А;с
(С; аД), (D; . Покажите, что точка Р является центром
АС.
затем
ВС.
AN —Ь2. Рас-
масс этой системы, а точка Q — центром масс системы
материальных точек ( АюА)- (В;аД), (£>;оД).
16.20. Соедините центры окружностей и к образованному
треугольнику примените теорему Менелая (задача 16.06).
Отметим, что задача имеет интересную пространственную ин-
573
терпретацию. Построим три шара так, чтобы заданные ок-
ружности были окружностями больших диаметров этих шаров.
Каждая пара шаров вписана в конус с образующими, сов-
падающими с двумя внешними касательными. Плоскость, каса-
тельная к шарам, будет касательной к конусам и пройдет через
их вершины.
16.21. Для движения f докажем утверждение методом
математической индукции по числу точек S. Пусть М2 —
центр масс системы материальных точек ),
N^ = Тогда точка М2 лежит на отрезке причем
А,М2 пи ..
-----= —. Однако для точки TV2 имеем:
М2А2 тх
B}N2 _ АхМ2 = п^
N2B2 М2А2 тх ’
причем точка N2 лежит на отрезке ВХВ2. Значит, N2— центр
масс системы материальных точек ( Bj; тх ), (В-^пи,}.
Предположим, что утверждение доказано при некоторых
S=k>2. Рассмотрим (& + 1) точек (Ах',тх ). (Л;»»г).....
(Ам;тк+1) и точки B„=f(An), где \<п<к + 1. Пусть Мк+1
— центр масс системы материальных точек Лр А2, ... , Ак+р
По теореме 16.2 точка Мк+Х— центр масс
системы материальных точек (М2\тх + (А3;т3), ... ,
(А^+1;т^+1). Тогда центр масс системы точек Вр В2, ... , В^+х
совпадает с центром масс системы материальных точек
(N2; тпх 4- ), (В3; тщ ), ... , (B^+1; , а это по предположе-
нию индукции есть точка . Шаг индукции выполнен.
При преобразовании подобия отрезок переходит в от-
резок, причем сохраняются отношения расстояний. Схема рас-
суждений остается без изменений и соответствующее утверж-
дение будет справедливо.
16.22. Примените теорему Чевы.
ГЛАВА 17
17.05 . Хорды АХА3 и равны, поскольку опираются на
равные дуги.
17.06 . Середины сторон правильного И-угольника рав-
ноудалены от центра.
574
17.07. Пусть О — центр правильного 2 Л-угольника. При
симметрии относительно точки О вершина 2«-угольника
на Л-угольника переходит в вер
111Я
этого же П -угольника.
17.09 . Найдите радиус R описанной окружности. Диа-
гональ равна 22?sin36°.
17.10. Пусть Г— радиус данной окружности. Опишем ок-
ружность около большего восьмиугольника. Если R — ее ра-
диус, то искомое отношение равно —.
R
17.13. Сумма внутренних углов выпуклого Л-угольника
17.14. Диагонали четырехугольника А3А4А7А% являются
диаметрами описанной окружности.
17.15. Выразите через R отрезок А^А3 из треугольника
OAiA3t где О —центр данной окружности.
17.16. Пусть А^А^... — данный многоугольник. Из
равенства углов А^ и А3 следует, что ^jAiA3 = kjA2A4t откуда
получаем, что ДЛ^ = ^jA3A4 . Тогда
^ДЛ2 = с?Л3Л4 =...=^Л2я_1Л2л ^^Azn+iA} =^jA2A3 = ...
^^2л^2л+1*
17.17. Наибольшая диагональ является диаметром
описанной окружности, а наименьшая диагональ — это сторона
правильного пятиугольника, вписанного в ту же окружность,
что и д анный десятиугольник.
17.18. Пусть О — центр правильного И -угольника
ДЛ^... А*, в котором Л1Л2 = б/. Докажите, что
о 1 п • 180°
SMio^2 = 2aRsm~lT
Площадь данного многоугольника равна сумме площадей И
таких треугольников.
*7" пр»„р..те. ™
= 60°. Выразите диагональ А^А^ через R и Г— радиусы
описанной и вписанной окружностей.
575
17.20. Найдите К — радиус описанной окружности,
выразите площадь треугольника ОА}А2 через R и примените
формулу из теоремы 17.3 для стороны а12.
17.21. Проверьте, что для точки О выполнено определе-
ние центра масс. Воспользуйтесь результатами примера 17.8.
17.22. Воспользуйтесь тем, что ОВХ = — ОА} + ОА2
, где
2?! — середина стороны А}А2.
17.23. Эти две диагонали равны и образуют угол, рав-
ный 36°. Выразите указанные площади через радиус R опи-
санной окружности.
17.24. Пусть ABCD— данный квадрат, AMN— вписан-
ный в него треугольник, в котором вершина М лежит на
стороне ВС, а вершина N — на стороне CD. Треугольники
АВМ и ADN равны, следовательно,
АВАМ = ADAN =^-(90°-60°) = 15°.
17.25. Рассмотрите два правильных треугольника, обра-
зованных вершинами данного шестиугольника. Воспользуйтесь
примером 5.9.
ГЛАВА 18
18.05 . Пусть сторона квадрата равна Q. Найдите коли-
чество меньших кругов, их радиусы, а также радиус большего
круга.
18.07 . Рассмотрите два случая: Rx > R2 и Rx < R2. Площадь
кольца равна разности площадей кругов.
18.08 . Найдите высоту треугольника, опущенную на осно-
вание, а также внутренние углы треугольника. Определите
дуги, стягивающие сегменты. По теореме синусов вычислите R
и воспользуйтесь формулой площади сегмента.
я
18.09 . Данный сегмент стягивает дугу, содержащую —рад.
18.11. Определите радиус окружности. Из равнобед-
ренного треугольника по теореме косинусов найдите хорду.
18.12. В данной трапеции суммы противоположных сто-
рон равны. Найдите высоту трапеции, равную диаметру круга.
18.13. Найдите меньший угол данного треугольника. Пло-
щадь сегмента тем меньше, чем меньше стягиваемая им дуга.
18.14. Площадь меньшего круга втрое меньше площади
круга радиуса R.
576
18.15. Пусть АВ—г, BC = R. Тогда ЛС = 7? + г,
__ R + r , nd2
EF =------- Площадь полукруга с диаметром а равна----.
2 8
18.16. Дополните каждую луночку до полукруга. Суммар-
ная площадь этих полукругов равна площади полукруга, пос-
троенного на гипотенузе как на диаметре.
18.17. Сторона прямоугольника разбивает фигуру на две
части. Сравните площадь нижней части с незаштрихованной
частью площади прямоугольника.
18.18. Пусть R и Г — радиусы большего и меньшего кру-
гов, О — центр большего круга. Искомая площадь есть удво-
енная сумма площадей треугольника МОВ и сектора MOD,
где AD — диаметр большего круга. Поскольку МВ2 =
2 R
= {R-\-2r} — R2, а, с другой стороны, МВ=г-\---------, то
2/
получаем соотношение между R и Г. Другое соотношение
находим из равенства МК • МА = МВ • ME .
18.19. Пусть О2, О3 — центры равных окружностей
радиуса X, О4 — центр четвертой окружности. В равно-
стороннем треугольнике сторона OjOj 2х, а
радиус описанной окружности О^4 равен (г + х). Найдите X.
Суммарная площадь трех криволинейных треугольников равна
-Gvs2), где aS\ — суммарная площадь трех
12 3
секторов, a S2 — площадь круга радиуса Г .
ГЛАВА 19
19.01. Пусть О — центр пятиугольника А1А2А3А4А5. При
повороте вокруг точки О на 72° пятиугольник ВХВ2В3В4В5
переходит в себя.
19.02. Примените теорему 19.9.
19.03. Точка Л/(г;ф) на спирали Архимеда перейдет при
повороте в точку Му (1\; ср j),
где г} = г, ф j = ф 4—. Найдите
связь между г\ и ф j.
19.04. а) При а<0 множество Г —а не содержит ни
одной точки. Рассмотрите случаи а = 0 и а > 0. Воспользуйтесь
результатом § 19.3.
б) Примените результат § 19.4.
577
19.05. а),в) Подставьте в уравнения кривых X = rcos(p,
у = rsirup.
б) Это окружность.г) Примените результат § 19.4.
19.06. Функция /(ф) — 1 — БтЗф является
периодичес-
кой с периодом Т =-----. Достаточно построить
кривую при
2 71
с последующими поворотами
построенной
вокруг полюса. Исследуйте на этом отрезке
функцию У(ф) на монотонность.
19.07. Функция /(ф) =Я8П12ф является периодической с
периодом Т = я. Достаточно построить кривую при (р G О,—
с последующей симметрией относительно полюса. Исследуйте
на этом отрезке функцию У(ф) на монотонность.
19.08. Функция /(ф) = а(1 + 2созф) является четной и
периодической с периодом Т = 2 я. Кривую достаточно по-
строить при ф G 0;
с последующей симметрией относи-
тельно полярной оси. На этом отрезке функция У(ф) убывает.
19.09. При нечетном натуральном И функция /(ф) =
= sin иф является периодической с периодом Т = —
п
с последующими
Кривую достаточно построить при ф G 0; —
L п
поворотами на углы тпТ, где ТП = 1,2, ... л —1. Функция /(ф)
возрастает при ф Е 0; —
2п
и убывает при ф G
Тп' п
ГЛАВА20
20.01. Радиус окружности, вписанной в прямоугольный
треугольник, равен
578
20.02 . На продолжении стороны ВА отложите отрезок
AD, равный АС. Отрезок DAX является средней линией
треугольника DBC. Искомый угол равен углу при основании
равнобедренного треугольника DCA, внешний угол которого
равен а.
20.03. Отразите окружность А симметрично относительно
прямой Z . К полученной окружности Ах и окружности В
проведите общую касательную. Таких касательных может быть
четыре. Поэтому задача имеет четыре решения. Общая
касательная к двум непересекающимся кругам строится так.
Пусть Ох и Rx — центр и радиус первого круга, О2 и R2 —
центр и радиус второго крута. Ограничимся случаем, когда
R} <R2. Строим прямоугольный треугольник ОХО2Р с гипо-
тенузой ОхО2 и катетом О2Р — R2 + RX. Прямая О2Р пересе-
кает вторую окружность в точке N, через которую проводим
прямую, параллельную ОХР, до пересечения с первой окруж-
ностью в точке М. Отрезок MN— искомая общая каса-
тельная.
20.04 . Пусть К и L точки касания первой прямой с
окружностями Ох и О2; М и N — точки касания второй
прямой с окружностями Ох и О2 соответственно. Пусть Rx
и /?2 — радиусы окружностей Ох и О2, Rx> R2. Опустите
перпендикуляры О2Р на ОХК и OXQ на O2N. Учитывая, что
О2 = 7?! 4- R2 4- 1, получите из прямоугольных треуголь-
ников ОХРО2 и OXQO2 следующие уравнения: 4J?17?2 4-
+ 2(Я,+/?,) = 575, Л + Я, = 24.
20.05 . Угол MAD равен 75°. Треугольник ADM равно-
бедренный.
20.06 . Проведите линии центров и по теореме Пифагора
составьте уравнение относительно искомого радиуса.
20.07 . Пусть на сторонах АВ и ВС квадрата ABCD
выбраны точки Ах и причем АхВ = х, ВВХ = у, х 4-у =
= АВ . Нужно доказать, что zLAxАВХ 4- ZAXDBX 4- ААХСВХ =
= 90°. Отложите на стороне CD отрезок ССХ =у и на
стороне DA отрезок DDx-y. Тогда АВХАСХ = zLAxDBx и
ACXAD = ЛСАХВХ.
20.08 . Отрезок CL является биссектрисой угла С.
579
20.09 . Пусть Ох— центр искомой окружности радиуса X.
Опустите перпендикуляр ОХС на отрезок ОА. В равно-
бедренном прямоугольном треугольнике ООХС имеем:
OOx = R + x, OC = R-x.
20.10. Пусть в трапеции ABCD дано: основания AD и
ВС равны а и b , диагонали BD и АС равны dx и d2,
Z.BAD — а, АВ = х, причем известно, что d2 -d2 — a2 —b2.
Докажите, что АВ 1AD . Из треугольников ABD и АВС по
теореме косинусов имеем: d2 — с^—х1 — 2 ax cos a, d\- b2 =
= х2 4- 2bxcosa. Заключите отсюда, что cosa = 0.
20.11. Воспользуйтесь задачей 20.10.
20.12. Угол AED—прямой.
20.13. Опустим перпендикуляры ON и КР на пря-
мую ВС. Пусть прямая ВК пересекает прямую AD в точ-
ке М. Из подобия треугольников ОВС и ОМА найдите
отрезки AM и ON, затем отрезок DM. Из подобия
треугольников КСВ и KDM найдите отрезок КР. Искомая
площадь равна
(KP-ON)BC
^ьвкс ~ ^лвос - 2 ’
20.14. Центр одной из окружностей соедините с двумя
ближайшими вершинами. Образуется прямоугольный тре-
угольник с высотой 6 и проекциями катетов 9х и 4х. Тогда
62 =(9х)(4х).
20.15. Составьте систему уравнений относительно длин
отрезков АО и OD.
20.16. Угол В является тупым. Поэтому искомая площадь
равна сумме площадей сектора и равнобедренного треуголь-
ника.
20.17. Пусть Ап— положение материальной точки че-
рез И секунд, где И — целое неотрицательное число. Все
точки Ап, являются различными. Найдутся по крайней мере
две такие точки Ап и An+k, что длина дуги AnAn+k меньше
Одна из точек Ап, А„+к, Ап+1к..Ап+тк. ... является
ИСКОМОЙ.
580
20.18. ПустьВС = а, Z.OBC = а, Z.OCB =р. Площадь52
выражается через а и c/ga + c7gp. Аналогично выражаются
суммы 5j + S2, 52 + S3 и площадь треугольника ВСК .
20.19. Пусть отрезки КМ и LN пересекаются в точке О.
Докажите равенство углов NOD и LOB с помощью ок-
ружностей, описанных около четырехугольников MDNO и
LOKB .
Замечание. Условие перпендикулярности отрезков
КМ и NL можно отбросить. Для доказательства этого нужно
установить, что два последних четырехугольника гомотетичны
с центром О.
20.20. Пусть О — центр окружности. Опустите перпен-
дикуляр ОЕ на сторону АВ. Треугольники АОЕ и ADC
подобны.
20.21. В многоугольнике F найдутся такие вершины С
и D, что отрезки АХС и AXD будут сторонами многоугольни-
ка Fx. При этом треугольники Aj ВС и Ах BD будут содержать
часть Fx, лежащую вне F. Сравните площади треугольников
АВС и АХВС -, ABD и AXBD.
20.22. Обозначьте АК — х • АВ . Четырехугольник KMCL
— параллелограмм.
20.23. Проведите все диагонали пятиугольника. Обра-
зуется меньший пятиугольник, который остается вместе с
пирогом при каждом отрезании.
20.24. Отрезок АО9 является медианой треугольни-
ка АОН.
20.25. В треугольнике точка О является центром
окружности Эйлера. Воспользуйтесь результатом задачи 20.24.
и формулами для длин IIaIct I^IC из задачи 14.34.
20.26. Впишите в окружность правильные треугольники
ААхА2 и ВВхВ2. Пусть С и D — точки пересечения хорд
Ах А2 и ВхВ2 с диаметром АВ. Найдите вероятность попа-
дания точки М на отрезок CD.
20.27. Впишите в окружность правильный треугольник
DAB . Найдите вероятность попадания точки Е на дугу А В .
20.28. Впишите в круг правильный треугольник, а в него
впишите круг. Найдите вероятность попадания точки М на
меньший круг.
581
ОТВЕТЫ
ГЛАВА 1
1.01. Бесконечное множество. 1.02. Нет. 1.03. Одну. 1.05. а) 7,1;
б) 12,45 дм; в) 2,24 м. 1.06. а) Да; б) Нет. 1.07. а) Да; б) Нет.
1.08. АВ. 1.09. 2,15м и б,45м. 1.10. 48см, 38,4см и 86,4см.
1.11. Да. 1.12. Да. 1.13. 2. 1.14. а)72°; б) 30°. 1.16. а) 45° и 15°;
б) 24° и 36°. 1.17. (а,А). 1.21. 108°; 144°. 1.22. 6; 10; 15; 21.
1.24. 6.
ГЛАВА 2
2.01. 12см, 4см, 10см.
ГЛАВА 3
3.01. а) Нет; б) Нет; в) Да. 3.02. а) 110°; б) 98°47’; в) 55°33’.
3.03. 30°, 150°. 3.04. 117°, 63°. 3.06. 110°. 3.07. а) 150°; б) 115°.
3.08. 60°, 80°, 40°. 3.09. 344°, 302°, 202°, 196°. 3.13. Нет. 3.14. 68°,
112°. 3.16. 180°-2а, 180°-2р, 2а + 2р-180°. 3.18. 36°, 54°. 3.19. 129°.
3.26. Прямая, параллельная данным прямым. 3.29. 48°39‘, 58°23‘,
72°58’ . 3.31. 60°. 3.33. 60°, 120°. 3.39. 1998.
ГЛАВА 4
4.01.10см, 20см, 20см. 4.02. 8см. 4.03. 50°, 50°, 80°. 4.04.а)нет;
V5-1 V5 + 1
б) нет. 4.07. Нет. 4.12. 5. 4.20. Да, -<q<------. 4.24. С —
точка пересечения серединных перпендикуляров к ААХ и ВВХ
или точка пересечения серединных перпендикуляров к АВХ и
ВАХ. 4.25. 10°. 4.26. Это точка пересечения отрезка АВХ с
прямой С1, где точка симметрична точке В относительно
прямой U.
4.27. Не всегда. Если АВ I, то решений нет. В
остальных случаях X— это точка пересечения прямых I
и АВ.
ГЛАВА 5
5.04. Нет. 5.05. Да. 5.06. 2; 1. 5.07. а) в другую полуплоскость с
той же границей I . б) в полуплоскость, ограниченную пря-
мой ТП, симметричной прямой I относительно оси симметрии.
Прямая ТП параллельна прямой I . Исходная и построенная
полуплоскости покрывают всю плоскость. 5.09. В себя.
5.12. а)Центр симметрии, б) Центр поворота, в) Точки оси
симметрии, г) Не существует неподвижных точек. 5.13. а) Не
всегда, б) Нет. 5.21. Центральная симметрия, осевая симметрия
и тождественное движение. 5.23. При четном Т1 это осевая
582
симметрия либо поворот на угол --. При нечетном п > 3 это
п
360°
поворот на угол ---.
п
ГЛАВА 6
6.01. 60°. 6.02. 120°. 6.04. 112°30 6.06. 60° и 300°; 120° и 240°.
6.07. Зм, 6м, 9м и 6м. 6.12. 0,6см, 0,8см и 1см. 6.13. 20см. 6.15. Из
точки внутри круга диаметр виден под тупым углом. 6.16. 72°.
6.20. Окружность вдвое большего радиуса с тем же центром.
6.22. Середина дуги, стягиваемой хордой. 6.23. 40° , 40 ° и 100°.
ГЛАВА?
7.02. а) Да. б) Нет. 7.03. 45°, 90° и 135°. 7.04. 90°. 7.05. 66° и 42°.
7.08. 70° и 110° либо 50°и 130°. 7.10. 12см и 20см. 7.11. 70см или
10см. 7.12. Да. 7.13. 50° и 130°. 7.14. 60°. 7.29. 14см, 6см и 2см.
ГЛАВА 8
8.01. 3. 8.02. 10см. 8.03. 108° и 72°. 8.06. 5,3м. 8.09. 132м. 8.14. 60°
и 120°. 8.15. 123°45’ и 56°15’. 8.17. Около параллелограмма
можно описать окружность тогда и только тогда, когда он
является прямоугольником. 8.18. Должен быть кв-дратом.
8.19. т+п , |/и-и|. 8.20. 72° и 108°. 8.24. 3; 4 и 3. 8.31.Нет.
ГЛАВА 9
9.03. 2, бесконечное число, 1. 9.04. Нет. 9.11. 8 и Sp где I —
прямая, проходящая через середины оснований трапеции.
9.14. а), б), в) бесконечное число, г) 1. 9.15. Да. 9.16. Например,
полуплоскость. 9.17. Фигура, составленная из сторон
параллелограмма ABCD и их образов при параллельных пе-
реносах вдоль луча АВ на расстояния П • АВ, а также при
параллельных переносах вдоль луча ВА на те же расстояния.
Здесь П— произвольное натуральное число; параллелограмм не
является прямоугольником.9.21. Подгруппа состоит из 8 , ^120°
и Т •, где повороты осуществляются вокруг центра
треугольника.
ГЛАВА 10
10.05. а + Ь + с , ю,об. 24см и 16см. 10.07. 2см. 10.08. 1:3. 10.09.
2
Гомотетией с тем же центром и коэффициентом к = • к2.
10.10. Тождественным преобразованием; центральной
симметрией.
583
ГЛАВА И
11.02. 4см. 11.03. Да; не обязательно.
11.04.а) Нет. б) Да. 11.06. Да. 11.07. 2:5. 11.08. Зд/З . 11.09.8д/3 дм
11.13.
4V3
------м. 11.14. 160см. 11.15. 6см. 11.16.
11.19. 6см. 11.20. 12см и 6см. 11.21. 9см. 11.23. 6:1. 11.26.
2Rr
11.27. Эта
хорда перпендикулярна диаметру. 11.29.
11.35. 3, 4
11.37. 6,25. 11.38.
11.39. 2д/3 .
11.40.
тп
ГЛАВА 12
12.01.
(0,-4).
(-7-6), (0;4),
Это квадрат.
11.01.
и
и
и
12.04. а) 2у[5\ б) 5л/2. 12.06. (3;1). 12.07. а) Вертикальная
прямая, б) Горизонтальная прямая, в) Две вертикальные пря-
мые. г) Точки второй и четвертой координатных четвертей без
осей координат, д) Внутренность фигуры, ограниченной двумя
дугами АС, симметричными относительно оси абсцисс,
е) Внешность фигуры, ограниченной двумя дугами АВ,
симметричными относительно оси абсцисс. 12.09. а) (0,5,14);
б) (-2;11,5). 12.10. Да. 12.13. (5;0). 12.14. АВ = DC, AD = ВС,
В А = CD, DA = СВ. Пары противоположных векторов: АВ
и CD, AD и СВ, ВА и DC, DA и ВС. 12.16. (13;-2б),
13-J5. 12.17.
5
. 12.18.---у=.
V34
12.19. а) 64. б) 7181. 12.20. Да.
584
2
2
2
12.35.
31
-т=. 12.37. ТП<-\ или 0<т<2. 12.38.
12.42.
па + mb
----------. 12.44.
или
f
Сумма квадратов диагоналей параллелограмма равна
12.47.
сумме квадратов всех его сторон.
ГЛАВА 13
13.01.
13.02. а) (1;-2),
б) (2;4). 13.04. к=-. 13.05. 7x-5j> + 5 = 0,
13.07. a) V2, б) 10V19. 13.09. Это ромб с
вершинами в
точках:
0; —
2
13.11. I-R] -Л2|<d<R} +R2. 13.12.
13.14. а) 4х - Зу = 0, б)
13.15. (х-1)2 +(у-1)2 = 1. 13.16. 7.1—
9
90°. 13.13. —.
19
4х-Зу + Ю = 0.
13.17. а) Да, б) нет.
13.18.
Уравнение окружности:
{2х-а)г +(2y-Z>)2 = а1 +Ь2.
13.19. Прямая, проходящая
через точку пересечения диагоналей ромба и перпен-
дикулярная стороне ромба. 13.20. Окружность с центром в
585
середине отрезка
13.24. (-1,6; 6,2).
АВ. 13.21. ------- и -------. 13.22. 2.
3 2
13.25. Прямая касается окружности;
(х + 1)2+(у + 1)2 =2.
13.26. (!; — !), (-!;!), (-1;- 1).
13.27.
Зу-7х-1>0
« Зх + у + 5 > О
О о
13.28. Окружность х — 2х + у =0.
5у-х-23<0
13.29. а) х - Зу + 7 = 0, б) Зх + у +1 = 0. 13.30. 6.25.
ГЛАВА 14
14.02. а) остроугольный, б) прямоугольный, в) тупоугольный.
14.03. 22. 14.04. 717 и 719. 14.05. — 7а2 + 4Z>2 — adcosa ,
2
— 74a2 + 62 -aZ>cosa,
2
,7 717
б) 1-, в) —-. 14.07.
о 2
— 7a2+Z>2-2a5cosa . 14.06. а) 7,
2
2^2
----. 14.08. 0.8. 14.09. Большим 60°.
3
14.10. 719, -ТбТ, -7151. 14.11. 2734 см, 2719см и
2 2
I— 10 — 9Тз
3710 см. 14.13. 60° и 120°. 14.14. 50см. 14.15. ---------. 14.16.
26
14.17. Биссектриса, проведенная к катету,
относится к биссектрисе, проведенной к гипотенузе, как
272 - 72:1 • 14.18.
а
a cos—
_______2
( 3a V 2
sin 45°+ —
14.21.Отрезок АО.
14.22. 0,5см. 14.23.10. 14.24.
5
586
14.27.
14.31.
710 + 72
2^5
jb(b + a) . 14.32.
14.30.
'15.24^
<1Г ПУ
x-2j + 3 = 0.
2 2(Тз - 1)я
14.33. -i-------.
3 3
ГЛАВА 15
15.01. 5см и 7см. 15.02. 6см и 8см. 15.03. 4. 15.04. 30°.
/-- 1 2
15.05. 739см. 15.06. а) 60, б) 17-. 15.Q8. 270см .
3
2 С2
15.09. 150см . 15.10. —. 15.11. 24. 15.12. 24. 15.13. 84.
8
15.14. 150см2 . 15.15. 100см2 . 15.16. 43.2дм2 . 15.18. 8316.
15.19. 1. (72-1). (7з-72). (2-7з). 15.20. —, 5. 15.21.
8см. 15.22. вТЗсм2 . 15.23. 10.625. 15.24. 2 R2 sin2 a sinfk 15.25.
472,
572
24см2
ИЛИ
7ТЗ
15.40.
2R2
sin Р sin у 5/л(Р + у)
и 20Т2. 15.26.
10см.
54—см2. 15.30.
-S.
31. 4.5.
15.28.
15.34.
15.45.
15.48.
. 15.46.
. 15.47. 1бсм2 .
\а2 -b2jsinasin$
2 sin(a + р)
15.51. (Т^Г + Т^)2-
15.56. 9. 15.57. 12ТЗ.
ГЛАВА 16
16.01. 7.5. 16.02. 1:2. 16.04. В точке пересечения диагоналей.
16.07. 1:6, 3:4. 16.08. 3:5, 1:3.
к(1 +1) + 1(п +1) + п(к +1)
(*+!Х/+1Х» + 1)
16.12.
16.17. 2.
587
17.01.
5л/5
ГЛАВА 17
. 17.02. Зу[2 см.
2
17.04. 60°,
90°, 108°, 120°, 135°, 144°, 150°.
17.09. — cZg36°,
17.10.
8
17.12. — Ctg36°.
17.13. 360°.
17.17.
17.23.
17.24. а2
ГЛАВА 18
20ям, ЮОям2 ; б) ЗОям, 225ям2 .
18.02. а) уменьшится в 3 раза, б) увеличится на 2Ямм.
12я
18.03. --см. 18.04. 72°.
18.01.
18.05. Эти площади равны. 18.06.
па2
18.07. яТ?2-/^2. 18.08.
Площадь треугольника равна
площади сегментов
равны:
12
J 12
251
. 18.09.
2
12
. 18.10. а) —м;
3/
18.11. а) —
300
2я-ЗТз
18.13. -----. 18.14.
12
Зя
_^2
па
18.12. -----
12
19.02.
ГЛАВА 19
полюс О, при а > 0 это окружность с центром О и радиусом
588
Cl. б) Это луч, исходящий из полюса, и образующий с полярной
я а
осью угол —. 19.05. а) г = —==; б)
4 7^2^
в) г = acostp; г) sin ср-=0.
ГЛАВА 20
а 31 17 о г- 7 „ „
20.02. —. 20.04. —, —. 20.05. 3 - л/3. 20.06. -. 20.08. 12 и 16.
2 2 2 2
48
20.09. 2.20.11. 150; можно. 20.12. 32. 20.13. —.
5
20.14. 300 . 20.15. 90-УЗ. 20.16. -У3+—.
3
3S2 + s2 )(s2 + s3) r
20.18. ----------------------. 20.20. d-Уз. 20.22. Если К—
S2 “ЗД
S
середина стороны AB] —. 20.23. В произвольную точку
4
выпуклого пятиугольника, ограниченного всеми диагоналями
1 1 1
данного пятиугольника. 20.26. —. 20.27. —. 20.28. —.
Учебное издание
Никулин Александр Вильевич
Кукуш Александр Георгиевич
Титаренко Юрий Семенович
ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Главный редактор В. Жабцев
Корректор М.Жабцева
Иллюстрации В. Бебенин
Компьютерный набор А. Хомчик
Подписано в печать с готовых диапозитивов 30.03.98.
Формат 60x90Vi6. Бумага офсетная. Гапнитура Тип Таймс.
Печать офсетная. Усл. печ. л. 37. Тираж 11 000 экз. Заказ 687.
Издательство «Альфа». Лицензия № 835. 4671, Литовская Республика,
г. Висагинас, ул. Тайкос, 44 — 8.
При участии ООО «Харвест». Лицензия ЛВ № 32 от 27.08.97.
220013, Минск, ул. Я. Коласа, 35 — 305.
Отпечатано с готовых диапозитивов заказчика
в типографии издательства «Белорусский Дом печати».
220013, Минск, пр. Ф. Скорины, 79.