Н.А.ГЛАГОЛЕВ,
А.А.ГЛАГОЛЕВ
- «
J н л е b Si
УЧЛЕДГИЗ-1958

Η. Α. ГЛАГОЛЕВ и Α. Α. ГЛАГОЛЕВ
ГЕОМЕТРИЯ
ЧАСТЬ 1
ПЛАНИМЕТРИЯ
УЧЕБНИК ДЛЯ 6—9 КЛАССОВ
СРЕДНЕЙ ШКОЛЫ
ИЗДАНИЕ ЧЕТВЕРТОЕ, ПЕРЕРАБОТАННОЕ
Под редакцией А. А. ГЛАГОЛЕВА
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
МОСКВА —1958

ОТ ИЗДАТЕЛЬСТВА
Книга Н. А. Глаголева .Элементарная геометрия*
(планиметрия) переработана А. А. Глаголевым и издаётся под
названием .Геометрия·, ч. 1, в качестве пробного учебника для
6—9 классов средней школы·
Все отзывы и замечания о возможности использования ее
в качестве стабильного учебника в средней школе просьба
направлять в Учебно-педагогическое издательство Министерства
просвещения РСФСР по адресу: Москва, 3-й проезд
Марьиной рощи, д. 41, редакция математики.

ПРЕДИСЛОВИЕ
Книга Η. А. Глаголева .Элементарная геометрия· выдержала три издания;
она широко известна учителям и получила положительную оценку в печати.
С целью приспособления указанной книги к действующей ныне программе
средней школы в четвёртом издании сделаны значительные изменения в
изложении материала и некоторые дополнения.
При изложении вопросов принципиального характера (измерения отрезков,
подобия фигур, измерения площади и др.) мной произведены значительные·
изменения по существу, вследствие чего можно считать, что соответствующие
разделы написаны заново.
В главе .Измерение отрезков" вводится отсутствующее в предыдущих
изданиях понятие о наибольшей общей мере двух отрезков, и на этой основе
приводится пример несоизмеримых отрезков, что даёт возможность наиболее
естественным путём прийти к понятию иррационального числа.
Мне представляется, что пример несоизмеримых отрезков важен ещё и
потому, что на этом примере мы показываем ценность чисто теоретических
исследований, так как на практике убедиться в существовании несоизмеримых
отрезков невозможно.
В шестой главе .Подобие фигур· дано современное строгое определение
подобия как прямолинейных, так и криволинейных фигур.
Мне представляется, что принятое у нас определение подобны^ фигур
как фигур» имеющих различные размеры, но одинаковую форму, не является
строгим математическим определением, ибо непонятно, как точно, а не на глаз
определить, имеют ли две фигуры одинаковую форму или нет.
Например, если мы начертим два прямоугольника со сторонами 3 см и
7 см и соответственно 3 см и 7,01 см, то вследствие несовершенства наших
органов зрения эти прямоугольники будут нам казаться не только имеющими
одинаковую форму, но даже и равными.
Между тем на самом деле данные прямоугольники будут не только не
равны, но даже и не подобны.
Так как определение подобных фигур, а также подобное преобразование
фигур и, в частности, гомотетия не могут быть изложены без применения
некоторых 'теорем о подобных треугольниках, то глава .Подобие фигур·
в отличие от прежних изданий начинается с изложения теории подобных
треугольников.
Кроме того, в настоящем издании гомотетия рассматривается как частный
случай общего подобного преобразования фигур.
3

Раздел «Измерение площадей" изложен мной по-новому, а именно: при
помощи понятия равновеликих фигур доказывается, что площадь прямоугольника
с основанием а и высотой Ь равна площади прямоугольника с основанием аЬ
и высотой 7. Таким образом, при помощи элементарных построений вопрос
об измерении площади прямоугольника сводится к вопросу об измерении
отрезка, что представляет собой большие удобства.
В связи с новой программой средней школы мне пришлось ввести новые
параграфы, например параграф об астролябии, об эккере, о съёмке местности
и составлении плана местности, масштабе и пр.
Параграф о построении корней квадратного уравнения как устаревший
и не имеющий ни теоретического, ни практического значения заменен мной
другим. Здесь я элементарным путём излагаю графический способ решения
квадратного уравнения, предложенный в 1922 г. Соро в его обширном труде
по номографии.
В заключение считаю своим долгом выразить глубокую признательность
доценту Т. В. Солнцевой и редактору Учпедгиза Н. И. Лепёшкиной,
оказавшим мне неоценимую помощь при подготовке четвёртого издания учебника
Н. А. Глаголева.
20 мая 1958 г.
А. Глаголев

ВВЕДЕНИЕ
1. Предмет геометрии
Наблюдая окружающие нас предметы, мы замечаем большое
разнообразие их внешнего вида и их свойств.
Предметы отличаются один от другого своим видом, весом,
свойствами вещества, из которого они состоят, и т. д. Но при
всём этом разнообразии можно заметить свойство, присущее вс$м
предметам без исключения, а именно: каждый предмет имеет свою
форму и свой размер.
При изготовлении различных предметов им придают форму и
размер, соответствующие их назначению. Например, кузову
легковой автомашины „Победа" придают обтекаемую форму с целью
уменьшения сопротивления воздуха; кузову корабля — форму,
которая даёт ему устойчивое положение на поверхности воды и
позволяет легче рассекать волны морской стихии.
Далее, мы замечаем, что каждый предмет занимает определённое
положение среди других предметов.
В практической жизни необходимо уметь определять расстояние
между предметами, размещать их должным образом на нужных
расстояниях. Так, на заводах важно правильно расставить станки,
при постройке новых населённых пунктов необходимо правильно
распланировать будущие улицы, точно разметить строительные
площадки воздвигаемых зданий.
Изучение форм и размеров предметов и их взаимного
положения составляет отдельную область знания. Наука, изучающая
формы, размеры и взаимное расположение предметов, называется
геометрией.
2. Происхождение геометрии
Уже первобытные люди на самой начальной ступени своего
развития должны были различать формы окружавших их предметов
и замечать места их расположения. Так, они запоминали места
охоты, места стоянок и селений. Люди постепенно научились
определять расстояния между отдельными предметами, размеры
отдельных участков местности и т. п.
5

По мере развития общественной жизни людей изучение форм
и размеров предметов и их взаимного расположения становилось
всё более нужным и требовало от человека всё больших знаний.
В древнем Египте весенние разливы огромной реки Нила смывали
границы между отдельными земельными участками. Нужно было
ежегодно их восстанавливать, что было связано с большими
измерительными работами на местности. Чтобы выполнять эти работы,
надо было иметь удобные правила для вычисления длин линий,
площадей участков земли, для выполнения планировок местности
и т. п. Эти правила были выработаны и записаны.
Греки, ведя торговлю с египтянами, ознакомились с этими
правилами, дополнили их и постепенно развили из них целую
науку, которую и назвали геометрией, что значит искусство
измерять землю.
Греческий учёный Евклид, живший в III в. до н. э., особенно
подробно разработал эту науку и изложил её вместе с
арифметикой в одиннадцати книгах, которые он назвал „Начала". По
ним и изучали геометрию в последующие века. По образцу этих
„Начал" составляются учебники геометрии и до нашего времени.
3. Основные геометрические понятия
Геометрическое тело. Когда изучается лишь форма и размер
предмета, то этому предмету дают название „геометрическое
тело", подчёркивая этим самым, что его физические свойства
просто не рассматриваются. Если взять два предмета одинаковой
формы и одинакового размера, но сделанные из разных материалов,
то они будут представлять собой два одинаковых геометрических
тела, хотя физические их свойства будут различны.
Например, небольшой резиновый мяч и мыльный пузырь того
же размера, совершенно различные по своим физическим
свойствам, представляют собой два одинаковых геометрических тела,
а именно шары.
Физическое тело при изменении его положения относительно
других тел, например при переносе его из одной среды в другую,
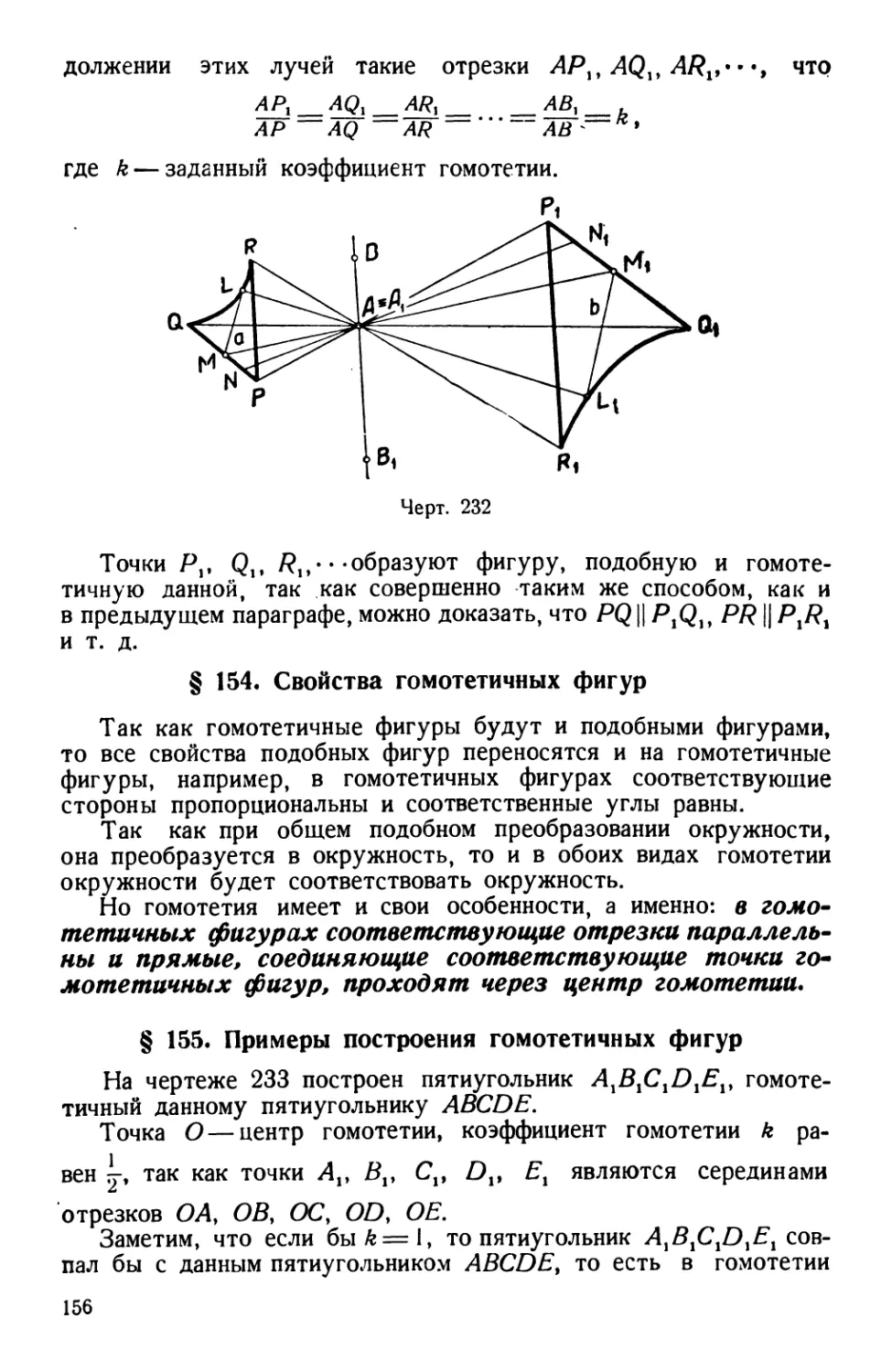
неизбежно, хотя бы и ничтожно мало, изменяет свои физические
свойства и даже свой размер под влиянием среды. Геометрическое
тело рассматривается независимо от физических свойств предмета.
Поэтому ему приписывают следующее свойство: геометрическое
тело может свободно перемещаться и изменять своё
положение среди других тел, неч1зменяя при этом ни своего раз-
мера, ни формы, ни взаимного расположения своих частей.
Поверхность. Всякое физическое тело отделяется от
прилегающих к нему других тел, например от прилегающих частиц
воздуха, поверхностью этого тела.
Поверхность тела можно представить себе отдельно от самого
тела. Такой отдельной поверхности в действительности не суще-
6

ствует. Мы создаём её в своём воображении. В природе можно
найти лишь грубое её изображение в виде, например, очень
тонкого листа бумаги или плёнки мыльного пузыря.
Геометрическую поверхность мы воображаем не имеющей толщины.
Линия. Иногда поверхности тел пересекаются. Например,
поверхность дымовой трубы пересекается с поверхностью крыши;
боковая грань куба пересекается с его основанием и т. п. При
таком пересечении поверхностей образуется линия.
Линию весьма часто представляют себе отдельно от
геометрических поверхностей в виде тончайшей нити, не имеющей ширины.
Геометрических линий в природе не существует. Мы создаём
их в своём воображении.
Точка. Две линии также могут пересекаться. При таком
пересечении образуется точка. Например, два ребра куба
пересекаются в вершине куба. Вершины куба — точки.
Точку также часто представляют себе отдельно от линии как
мельчайшее зёрнышко или прокол тонкой иглы на листе бумаги·
Точка не имеет никакого размера. Геометрической точки в
природе не существует.
4. Образование линий и поверхностей движением
Если точка будет как-либо перемещаться, то при своём
движении она опишет линию. Так, например, если провести остриём
карандаша по листу бумаги, то на бумаге образуется черта —
след, оставляемый остриём. Эта черта даёт представление о линии,
образуемой движением острия карандаша. Точно так же летящая
искра, быстро перемещаясь, образует светящуюся линию.
Интересно наблюдать, как от горящего ночью костра по ветру отлетает
множество искр, образующих целый поток огненных линий.
Если линия будет перемещаться из одного положения в
другое, то при таком перемещении она опишет поверхность.
Образование поверхности движением линии можно, например, видеть,
наблюдая вращение спиц велосипедного колеса. При быстром
вращении они как бы сливаются в один сплошной диск.
5. Простейшие линии и поверхности
Прямая линия. Простейшая из всех линий — прямая.
Представление о ней даёт туго натянутая на двух опорных точках
тонкая нить или луч света, выходящий из отверстия. Основное
свойство прямой следующее: через две любые точки молено
провести прямую и притом только одну.
Этим свойством прямой постоянно пользуются на практике.
Например, чтобы наметить на местности прямую линию, вбивают
в землю деревянную веху и на некотором расстоянии от неё —
вторую; эти вехи определяют на местности прямую.
7

Плоскость. Простейшей поверхностью является плоскость.
Представление о ней может дать поверхность жидкости в сосуде,
находящейся в покое, или поверхность хорошо отполированной
крышки стола, или поверхность хорошо отшлифованного зеркала.
Но это представление лишь приближённое. Как бы хорошо ни
был отполирован стол, на его ловерхности всегда останутся
мельчайшие шероховатости и неровности древесных волокон. Чтобы
представить себе плоскость, нужно отвлечься от всех этих
неровностей и вообразить, что поверхность стола абсолютно гладкая.
В геометрии плоскость мыслится неограниченно простирающейся
в пространстве.
Основное свойство плоскости следующее: если две любые
точки плоскости соединить прямой линией, то все точки
этой .прямой окажутся лежащими на плоскости.
Этим свойством плоскости пользуются при отшлифовке гладких
плит для проверки точности шлифовки, а именно: берут
металлический брусок с точно выверенным прямолинейным ребром и
этим ребром прикладывают его к данной поверхности. Если
шлифовка достаточно точна, то брусок будет во всех своих точках
одинаково плотно прилегать к поверхности, в каком бы
направлении и в каком бы месте его ни прикладывали.
6. Геометрические фигуры и способы их изучения
Любое сочетание точек, линий и поверхностей называется
геометрической фигурой.
Геометрические фигуры разделяются на плоские и
пространственные.
Плоской фигурой называется такая, все точки которой лежат
на одной плоскости. Представление о такой фигуре даёт всякий
рисунок, сделанный на гладком листе бумаги.
Фигура называется пространственной тогда, когда не все её
точки лежат на одной плоскости. Представление о такой фигуре
даёт всякое геометрическое тело.
В первой части геометрии изучаются плоские фигуры. Эта
часть геометрии называется планиметрией.
Непосредственных измерений и опытов, применяемых при
изучении физических тел, бывает иногда недостаточно для изучения
свойств и взаимного расположения геометрических тел. Так,
например, непосредственное измерение длины или высоты предмета
не всегда возможно. Легко измерить длину стола или высоту
комнаты, но значительно труднее измерить высоту растущего
дерева или определить высоту летящего самолёта.
Поэтому в геометрии не ограничиваются только одними
измерениями, а прибегают и к рассуждениям: заметив какое-либо
свойство изучаемого тела, по нему стараются правильными
рассуждениями обнаружить новые свойства этого тела.
8

Так, например, мы отметили свойство прямой линии: через
две точки можно провести прямую и притом только одну. Из
этого утверждения можно сделать следующий вывод: две прямые
линии не могут пересекаться более чем в одной точке.
В самом деле, если бы две прямые пересеклись в двух точках,
то через эти две точки стали бы проходить две прямые, а не
одна. Таким образом, путём правильного рассуждения мы
обнаружили новое свойство прямых линий: они могут пересекаться
не более чем в одной точке.
Точно так же путем правильного рассуждения можно
показать, что для совмещения одной прямой с другой прямой
достаточно совместить две какие-нибудь точки одной прямой с двумя
точками другой прямой.
В самом деле, если две точки одной прямой совпадают с двумя
точками другой прямой, то и данные прямые совпадают, так как
в противном случае через две точки проходили бы две различные
прямые, что невозможно.
Подобного рода правильные рассуждения и являются главным
средством изучения свойств геометрических фигур.

ГЛАВА ПЕРВАЯ
ПРЯМАЯ ЛИНИЯ
I. ПРЯМЫЕ, ЛУЧИ, ОТРЕЗКИ
§ 1. Аксиомы о прямой линии
Аксиомой называется утверждение, справедливость которого
принимается без доказательства. Слово „аксиома" — греческое,
в переводе на русский язык означает: истина, достойная признания.
Аксиомы, выражающие свойства прямых линий, следующие:
/· Через любые две точки можно провести прямую
линию и притом только одну.
2. Если две точки прямой лежат на плоскости, то и
все точки этой прямой лежат на той же плоскости.
§ 2. Изображение прямой линии
Прямую линию нужно представлять себе безгранично
продолженной в обе стороны. Прямая обозначается или двумя буквами,
обычно большими латинскими, поставленными при каких-либо
двух её точках, например прямая АВ (черт. 1), или одной малой
буквой, например прямая а (черт. 2). Для вычерчивания прямой
линии употребляется линейка.
Черт. 1 Черт. 2
Чтобы вычертить прямую, проходящую через две заданные
её точки, например А и В, придвигают край линейки вплотную
к данным точкам и остриём карандаша проводят вдоль края черту.
Если хотят проверить правильность линейки, то прикладывают
её тем же боком к тем же точкам, но с другой стороны и вновь
проводят черту вдоль края.
Если карандаш вычертит ту же линию, что и раньше, то это
значит, что линейка—правильная.
10

§ 3· Луч и отрезок
Часть прямой, ограниченная с одной стороны данной точкой
этой прямой и неограниченно простирающаяся в другую сторону,
называется лучом· Сама данная точка называется началом луча.
Часть прямой, ограниченная с обеих сторон, называется
отрезком этой прямой. Отрезок обозначается обычно двумя буквами,
а в „, ц * ,
ι- ■<
Черт. 3 Черт. 4
поставленными при его концах, например отрезок АВ (черт. 3),
или одной малой буквой, например отрезок а (черт. 4).
§ 4. Равенство и неравенство отрезков
Два отрезка называются равными, если эти отрезки можно
совместить так, что их концы совпадут. Если дан какой-либо
отрезок прямой, то на каждой прямой от любой её точки в
любую сторону можно отложить отрезок, равный данному. Для
этого служит прибор, называемый циркулем. Чтобы отложить на
прямой а от точки С (черт. 5) отрезок CD, равный АВ, сначала
Л В
Черт. 5 Черт. 6
помещают ножки циркуля так, чтобы острия их концов упирались
в точки Л и 5, а затем, не изменяя раствора циркуля, переносят
его так, чтобы один из его концов прошёл через точку С, а
другой находился на прямой а. Этот второй конец и определит
положение точки D.
Равенство двух отрезков, например АВ и CD, записывается
так:
AB=CD или CD = AB.
Если отложить на прямой от данной точки, например Л, в
одну сторону два отрезка АВ и АС и точка В окажется между
точками Л и С (черт. 6), то говорят, что отрезок АВ меньше
отрезка АС или что отрезок АС больше отрезка АВ. Это
записывают так:
АВ<АС или АС>АВ.
§ 5. Сложение и вычитание отрезков
Если на отрезке АВ взять какую-либо точку С (черт. 7), то
образуются два новых отрезка АС и СВ. Отрезок АВ называется
И

суммой отрезков АС и СВ. Каждый из отрезков АС и СВ
называется разностью отрезка АВ и другого отрезка. Это
записывают так:
АВ=АС+СВ; АС=АВ — СВ\ СВ=АВ — АС.
Чтобы сложить два отрезка, например А В и CD, продолжим
отрезок АВ за точку β и на этом продолжении отложим от
1 В Ε
А С В С ~ '
Черт. 7 Черт. 8
точки В отрезок BE, равный CD. Отрезок АЕ даёт сумму
отрезков АВ и BE или АВ и CD (черт. 8):
Д F В AE=AB-\-CD.
f О Чтобы вычесть из большего отрезка
меньший, например из отрезка АВ отре-
Черт. 9 зок CD, отложим на отрезке АВ от
конца А отрезок AF, равный CD (черт.9).
Отрезок FB и даст искомую разность отрезков АВ и CD:
FB=AB — CD.
§ 6· Длина отрезка
Для приближённого определения длин отрезков служит
измерительная линейка с нанесёнными на ней миллиметровыми
делениями и цифрами, находящимися друг от друга на расстоянии
1 см (10 мм).
Чтобы определить длину отрезка, прикладывают к нему
линейку так, чтобы нулевое деление линейки совпало с началом
отрезка, и отсчитывают число сантиметров и миллиметров,
содержащихся в данном отрезке.
0 12 3 4 5 6
lnillllllllllllllllllllllllllfll1inill|nillllllfl|lltll1llllH
А\ Ιβ
Черт. 10
На чертеже 10 показано, как производится измерение отрезка
при помощи измерительной линейки. Как видим, длина отрезка
АВ равна 4 см, длина АС равна 5,2 см, длина AD равна 6,5 см.
12

Черт. 11
Для определения длины отрезка на местности поступают
следующим образом. В конечных пунктах отрезка, который
необходимо измерить, вбивают в землю два деревянных шеста,
заострённых с одной стороны, называемых вехами (черт. 11).
Согласно основному свойству прямой эти две вехи определяют
на местности единственную прямую.
Для проверки того, что вехи
установлены в строго вертикальном
направлении, применяется отвес —
нить с подвешенным грузом.
Приблизив отвес к вбитой в землю вехе,
легко проверить, вертикально ли она
установлена (черт. 12).
Если расстояние между двумя
данными пунктахми большое, то между
двумя первыми вехами ставится третья
веха. При этом нужно приблизить глаз
к одной из крайних вех и
посмотреть, закрывает ли собой эта веха
две другие или нет. Затем ставится
ещё несколько промежуточных вех
таким образом, чтобы из трёх любых
вех всякая крайняя веха закрывала
собой две остальные.
Описанный выше процесс установки
вех называется провешиванием
прямой линии на поверхности земли.
13

После провешивания прямой линии между двумя конечными
пунктами измеряют расстояния между каждыми двумя вехами.
Для измерения расстояний служит специальная металлическая
лента (или шнур) длиной в 20 м с подразделением на дециметры.
При измерениях следят за тем, чтобы лента была туго натянута·
§ 7, Ломаная линия
Если на плоскости дано несколько точек, не лежащих на
одной прямой, например точки Д В, С, D, Ε (черт. 13), то их
можно последовательно в каком-либо порядке соединить отрезками
прямых линий, например АВ, ВС, CD,
DE. .
Совокупность этих отрезков
называется ломаной линией; отрезки АВУ
ВС, CD, DE называются звеньями
этой ломаной, а точки А, В% С, D и
Ε — её вершинами. Отрезок, равный
сумме всех звеньев ломаной линии, то
есть AB-\-BC-{-CD-\-DE называется её периметром.
Ломаная называется выпуклой, если все её звенья лежат по
одну сторону от каждого из них, неограниченно продолженного·
Такова, например, линия ABCDE (черт. 14).
Черт. 13
Линия ABCDE на чертеже 13, напротив, не является
выпуклой ломаной, так как звенья АВ и DE, а также ВС и DE лежат
по разные стороны от неограниченно продолженного звена CD.
Ломаная линия называется замкнутой, если ее начало и конец
совпадают. Такова, например, линия ABCDE А (черт. 15).
ВОПРОСЫ
1· Как проверить правильность линейки?
2. Что такое луч?
3. Что называется отрезком прямой?
4. Как построить отрезок, равный данному?
5. Как убеждаются в равенстве двух отрезков?
14

6. Как записать равенство двух отрезков?
7. Как сложить два отрезка?
8. Что называется ломаной линией?
9. Что такое периметр ломаной линии?
10. Какая ломаная называется замкнутой?
11. Какая ломаная называется выпуклой?
12. Почему трёхзвенная замкнутая линия всегда выпукла?
УПРАЖНЕНИЯ
1. На данной прямой от данной точки отложить отрезок, равный данному·
2. На данной прямой отложить от данной точки отрезок, равный сумме
двух данных.
3. Построить отрезок, равный разности двух данных отрезков.
4· По данной сумме двух отрезков и одному из них построить другой.
5. По данной разности отрезков и меньшему из них построить больший
отрезок.
6. По данной разности отрезков и большему из них построить меньший
отрезок.
7· Начертить ломаную линию, состоящую из пяти звеньев, и построить
отрезок, равный периметру этой ломаной.
8· Даны пять точек, из которых каждые три не лежат на одной прямой.
Через каждые две из них проводят прямую линию. Сколько всего таких
прямых можно провести? Отв. 10.
9. Сумма двух отрезков равна 15 см, а разность их равна 4 см. Чему
равен каждый отрезок? Отв. 5,5 см и 9,5 см.
10. Отрезок длиной 18 см разделён на две неравные части. Чему равно
расстояние между серединами этих частей? Отв. 9 см.
11. Отрезок длиной 24 см разделён на три равные части. Чему равно
расстояние между серединами первой и третьей части? Отв. 16 см.
И. УГЛЫ МЕЖДУ ПРЯМЫМИ
§ 8· Угол
Два луча, выходящие из одной точки, образуют фигуру,
которая называется углом· Лучи, образующие угол, называются
сторонами угла, а их общее начало — вершиной угла. Угол
обозначается или одной буквой, поставленной при его вершине,
например £А (черт. 16), или тремя буквами, из которых одна
В
fit— А^—С Л* /\'
Черт. 16 Черт. 17
ставится при вершине, а две — при каких-либо точках его сторон·
При записи буква, стоящая при его вершине, помещается между
двумя другими, например /_ВАС (черт. 16).
Иногда угол обозначают одной малой буквой или даже
цифрой, поставленной внутри угла, например ^а, £1 (черт. 17)
15

§ 9· Равенство углов
Два угла называются равными, если они могут быть
совмещены при наложении. Чтобы наложить один угол на другой,
нужно совместить их так, чтобы вершины углов совпали и одна
сторона первого угла совместилась со стороной второго, а
вторые стороны углов легли бы по одну сторону от совмещенных
С F
βΔ ή ε*- о
Черт. 18
лучей. Если вторые стороны углов также совместятся, то данные
углы равны. Равенство углов, например /_АВС и /_DEF
{черт. 18), записывается так:
/_ABC=/_DEF.
§10· Развёрнутый угол
Два луча, выходящие из одной точки и составляющие одну
прямую, образуют развёрнутый угол. Таков угол ЛВС (черт. 19).
а в с
о ε f
Черт. 19
Если даны два развёрнутых угла, например ABC и DEF
(черт. 19), то их можно совместить, наложив один на другой
так, чтобы точка В совпала с точкой Е. Следовательно,
все развёрнутые углы равны между собой.
§11· Прилежащие углы· Действия над углами
Два угла, имеющие общую вершину, одну общую сторону
и расположенные по разные стороны от этой общей стороны,
называются прилежащими углами. Таковы, например, углы ABC
и CBD (черт. 20)·
Угол ABD, образованный внешними сторонами BD и ВА двух
прилежащих углов ABC и CBD, называется суммой этих углов,
что записывается так:
^ABD = Z.ABC+Z.CBD.
16

Каждый из прилежащих углов, /_АВС и /_CBDy называется
разностью углов ABD и другого прилежащего, то есть:
Ζ АВС= Ζ ABD — Ζ CBD9
Z^CBD = /_ABD — ^ABC.
Для того чтобы сложить три угла,
нужно сначала сложить два угла, а затем к
полученному углу прибавить третий.
Пусть, например, нужно сложить три
угла: ^//, /_2, /_3 (черт. 21). Строим
сначала два прилежащих угла: /_АВС= /А и
/_CBD = /i2. Тогда J^ABD будет суммой /_\ и /2. Далее,
к Ζ ABD прибавляем /JDBE, равный £3. Угол ABE будет
суммой трёх данных углов: ^/, ^/2 и ^3.
Черт. 20
^
Черт. 21
Аналогично складываются четыре, пять и т. д. углов.
Если складываются несколько равных углов, например четыре,
то говорят, что угол был увеличен в четыре раза или что угол
был умножен на 4 (черт. 22).
Черт. 22
При сложении нескольких углов, а также при умножении угла
на некоторое число могут иметь место следующие случаи:
1. Сумма углов представляет собой развёрнутый угол. Так,
например, на чертеже 23 сумма ^/, /J2, ^3 и ^4
представляет собой развёрнутый угол АОВ.
17

2. Если к той же сумме Z^ + Z2 + Z5 + Z^ = Z^°^
мы прибавим ещё один ^/5, то получим /_АОЕ, равный сумме
развёрнутого угла и /_5 (черт."24).
3. Может случиться, что при сложении нескольких углов
сторона первого слагаемого угла совместится со стороной
последнего слагаемого угла. Например, на чертеже 25 сторона ОА
Черт. 24
/_1 совместилась со стороной ОН /_6. Угол, образованный двумя
совпавшими лучами и равный сумме нескольких углов, называется
полным.
4. Если к ^//, ^/2, Z.3* £4, /_5 и /_6 (черт. 25) мы
прибавим ещё один ^7, то полученная сумма будет равна сумме
полного угла и/7.
Из сказанного ясно, что два луча, выходящие из одной точки,
образуют не один, а два угла. Например, на чертеже 24 два луча
ОА и ОЕ образуют два угла — один угол, равный сумме ^//,
^2, ^/3, /_4 и ^£5, и другой угол, составляющий вместе
с первым полный угол.
§ 12. Внутренняя область угла
Обычно, говоря об угле АОЕ (черт. 24), разумеют только
тот из двух углов, образованных лучами АО и ОЕ, который
меньше развёрнутого угла.
Внутренней областью такого угла
(который меньше развёрнутого) называется та
часть плоскости, в которой целиком
помещается отрезок прямой, соединяющий две
любые точки, лежащие на сторонах угла.
На чертеже 26 изображена внутренняя
область угла ВАС. В ней целиком
помещается отрезок AfTV, соединяющий точки Μ и /V,
лежащие соответственно на сторонах АВ и
АС угла ВАС.
Черт. 26
18

§ 13. Сравнение углов
Угол ABC (черт. 27) считается большим каждого из
составляющих его прилежащих углов: /_ABF и Z.CBF. Это
записывается так: ^ABC>^ABF и ^АВС> ^CBF. Чтобы сравнить
два любых угла, например /_АВС и /_DEF (черт. 27), и
определить, какой из них больше, поступают так: накладывают угол
DEF на угол ABC так, чтобы
вершина Ε совпала с вершиной В,
луч ED совпал с лучом В А, а
лучи ВС и EF оказались по одну
сторону от совмещенных лучей
ВА и ED. Луч EF займёт
некоторое положение BF. Если BF
окажется внутри угла ABC, то
при вершине В образуются два
прилежащих угла: /_ABF и
Z.FBC, которые вместе составляют /^АВС. Так как /_АВС
больше каждого из составляющих его углов, то /_ АВС^> /^ABF,
но /_ABF=/_DEF, а потому /_АВС>/_DEF.
§ 14· Смежные углы. Прямой угол
Два прилежащих угла, несовпадающие стороны которых
составляют одну прямую линию, называются смежными углами.
Так, на чертеже 28 /_АВС и /_CBD — смежные углы.
Чтобы построить угол, смежный с данным углом, нужно одну
из сторон данного угла продолжить за вершину.
А
В
Черт. 28
В
Черт. 29
Если два смежных угла равны между собой, то каждый из
них называется прямым углом. Таковы, например, углы ABC
и CBD (черт. 29). Общая сторона ВС этих углов называется
перпендикуляром к прямой AD, а точка В — основанием
перпендикуляра.
Сумма двух прямых углов составляет развёрнутый угол. Так,
сумма углов ABC и CBD составляет развёрнутый угол ABD
(черт. 29). Следовательно, можно сказать:
прямой угол равен половине развёрнутого; развёрнутый
угол равен сумме двух прямых углов или, короче, двум
прямым углам.
Прямой угол обозначается буквой d.
19

§ 15. Сумма двух смежных углов
Всякие два смежных угла составляют в сумме развёрнутый
угол. Но развёрнутый угол, как мы видели, равен двум прямым
углам. Поэтому можно сказать, что
сумма двух смежных углов равна двум прямым углам.
Это записывается так: /_АВС-\-/_CBD = 2d (черт. 28).
Если сумма углов равна двум прямым, то говорят, что один
угол дополняет другой до двух прямых углов.
Если два угла ABC и CBD имеют общую вершину β,
расположены по разные стороны от общей стороны ВС (L ерт. 28) и в
сумме составляют 2d, то их две другие стороны АВ и BD
составляют продолжение одна другой, то есть такие углы будут
смежными. В самом деле, сумма указанных углов составляет угол
АВО, и если этот угол равен 2d, то это значит, что он есть
развёрнутый угол, то есть что АВ составляет с BD одну прямую.
§ 16· Построение прямого угла
Для построения прямых углов можно пользоваться угольником;
угольник — это прибор, изображённый на чертеже 30. Два из
его рёбер образуют прямой угол. Чтобы построить прямой угол,
когда даны его сторона АВ и вершина А, поступают так:
сначала прикладывают к прямой АВ линейку (черт. 31), затем при-
Черт. 30 Черт. 31 Черт. 32
ставляют к этой линейке угольник и заставляют его скользить
вдоль линейки до тех пор, пока вершина его прямого угла не
совпадёт с точкой А. В этом положении угольник останавливают
и проводят вдоль его ребра вторую искомую сторону прямого
углн.
Итак, мы видим, что для построения прямого угла по его
стороне АВ и вершине А нужно провести перпендикуляр в точке А
к прямой АВ.
§ 17. Проверка угольника
Чтобы проверить правильность угольника, прикладываем его к линейке
в какой-либо её точке одной из сторон прямого угла угольника и вдоль
другой черним прямую. Затем перевёртываем угольник (черт. 32), прикладываем
20

его к линейке с другой стороны от начерченной прямой и вновь чертим
прямую. При правильности угольника обе начерченные прямые должны
совпасть. Этот способ проверки угольника основан на свойстве смежных углов
(§ 15). -
§ 18. Взаимно перпендикулярные прямые
Две прямые линии, пересекаясь, образуют четыре угла. Так,
прямые АС и DE пересекаются в точке В (черт. 33) и образуют
4 угла: ^АВЕ, /_ABD, Z.DBC и /_СВЕ.
Если один из этих углов прямой, то остальные три также
должны быть прямыми.
В самом деле, допустим, что /_ABD — прямой (черт. 33).
Это значит, что он равен смежному с ним углу CBD и точно
так же равен смежному с ним углу ABE. Значит, углы CBD и
ABE — прямые. A /_CBD равен смежному с ним углу СВЕ.
Значит, /_СВЕ— прямой.
Таким образом, все четыре угла—прямые.
Прямые линии, образующие между собой прямой угол,
называются взаимно перпендикулярными. Таковы прямые АС и DE
на чертеже 33.
/7-
В
Ε
Черт. 33
С
Черт. 34
В
обозначается знаком J_, например:
(черт. 34) провести пер-
Перпендикулярность
AC±DE.
Задача. Через данную точку С
пендикуляр к данной прямой АВ.
Решение. К прямой АВ
прикладываем линейку и вдоль неё
передвигаем угольник до тех пор,
пока его второе ребро не пройдёт
через точку С (черт. 35). Затем
проводим вдоль этого ребра прямую-
линию CD, CD _[_ АВ. Из
приведённого построения вытекает, что через
точку С можно провести только один перпендикуляр к АВ.
Для того случая, когда точка С лежит на прямой АВ,
построение перпендикуляра см. в § 16.
Д-
т-в
Черт. 35
21

§ 19. Эккер
вбиваются вертикальные острия (в виде оу-
лавки или гвоздика) таким образа-, чтобы
прямые, соединяющие пР0ТИВ0П0Л°*"%°СрТ~
рия, были взаимно перпендикулярны. Эккер
помещается в намеченном месте так чтобы
штатив на котором помещен эккер, был уста
новлен в строго вертикальном направлении.
Затем провешивается (§ 6) в направлении
Черт· 36 двух остриёв одной планки одна прямая ли-
Угол ВСА — прямой.
Черт. 37
§ 20· Острые и тупые углы
Угол, меньший прямого, называется острым.Таков^например
ZC£Z/(черт. 38), меньший ^^J^J^/jSc] больший
прямого, называется тупым. Таков, например, ^.л
прямого угла ABE.
22

§21. Вертикальные углы
Если стороны одного угла служат продолжением сторон
другого, то такие углы называются вертикальными. Таковы углы ABC
и EBD, а также углы CBD и ABE (черт. 39).
В
Черт. 38
Чтобы построить угол, вертикальный с данным углом, следует
приложить линейку последовательно к каждой стороне данного
угла и продолжить каждую из них за вершину.
Докажем, что вертикальные углы равны между собой.
В самом деле, рассмотрим вертикальные углы ABC и DBE
(черт. 39). Углы ABC и CBD составляют вместе развёрнутый
угол ABD. Значит, /_АВС дополняет /_CBD до двух прямых.
Углы DBE и CBD составляют развёрнутый угол СВЕ. Значит,
/_DBE дополняет ^CBD до двух прямых. Таким образом, углы
ABC и DBE дополняют до двух прямых один и тот же угол CBD.
Значит, ^ABC^^DBE.
§ 22. Биссектриса угла
Луч, проходящий через вершину угла и
разделяющий его на два равных прилежащих
угла, называется биссектрисой угла или
его равноделящей.Так, луч BD (черт. 40)
служит биссектрисой угла ABC, Это
записывается следующим образом:
^ ABD = Ζ DBC. Черт. 40
§ 23. Угол как мера поворота луча
1. Допустим, что какой-либо луч, например АВ (черт. 41),
вращается вокруг своего начала А Сделав некоторый поворот
от исходного положения АВ, он займёт новое положение АС.
Это новое положение луча образует со старым ^ВАС.
23

Этот угол определяет меру поворота луча или меру его
отклонения от исходного положения.
2. Если продолжать вращение луча, то сначала этот угол
будет острым, затем станет прямым и при дальнейшем вращении
сделается тупым. Продолжая вращаться, луч достигнет такого
положения ΑΒλ (черт. 42), при котором он будет служить
продолжением исходного луча АВ.
fll·
-В
Чсрг. 41
Черт. 42
В;
Лучи АВ и АВХ образуют развёрнутый угол. Следовательно,
развёрнутый угол служит мерой поворота, при котором луч
меняет своё направление на противоположное.
3. Допустим, что луч АВ, достигнув развёрнутого угла,
продолжает вращаться в том же направлении и займёт положение АВ2
(черт. 43). Мерой этого поворота служит угол ВАВ2— сумма
развёрнутого угла ВАВХ и острого угла ΒλΑΒ2. Угол ВАВ2 больше
развёрнутого угла, то есть больше 2d.
Его внутренней областью считается та, по
которой скользил луч АВ. На чертеже 43
внутренняя область угла ВАВ2 заштрихована.
Если внутри этого угла через его верь-
шину провести луч, например АС, то
образуются два прилежащих угла: ^ВАС и
^/САВ^Угол ВАВ2булет суммой и этих углов.
То же положение АВ2 луч может занять,
вращаясь от исходного положения в
обратном направлении. Мерой этого поворота
меньший 2d; его внутренней областью служит
незаштрихованная часть плоскости.
Таким образом, два луча АВ и АВ2 определяют не один, а два
угла: один, меньший 2d, другой, больший 2d. Оба эти угла имеют
одни и те же стороны, но разные внутренние области.
Вместо того чтобы говорить о том, каким поворотом луча
образован данный угол, можно указать, какая часть плоскости
считается его внутренней областью.
Если же этого не указано, то внутренней областью угла, как
сказано выше (§ 12), считается та, в которой лежит отрезок
прямой, соединяющий две какие-либо точки на сторонах угла.
Допустим теперь, что луч АВ, сделав полный оборот
вокруг точки Л, возвратился в своё исходное положение АВ. Можно
Черт. 43
служит /_ВАВ2
24

считать, что он описал угол, внутренней областью которого
служит вся плоскость. Этот угол'называется полным углом (§ 11).
Обе его стороны совпадают в один луч АВ.
Продолжив луч АВ в противополож- г
ном направлении и проведя через точку А
прямую CD, перпендикулярную к АВ
(черт. 44), замечаем, что полный угол
равен сумме четырёх прямых углов, то й
есть 4d. B'
На чертеже 45 изображены все виды
углов, которые образует со своим
начальным положением АВ луч ВС, вращающийся
вокруг точки В. Внутренняя область
каждого угла отмечена дугой со стрелкой.
С
о
Черт. 44
ь С
z^
β А В А В АС В А
острый прямой тупой развернутый 7 больше
развернутого
С
Чсрг. 45
-В
§ 24· Понятие об окружности
Когда луч АВ (черт. 46) сделает полный оборот вокруг своего
начала А, каждая его точка, например 5, опишет линию, которая
называется окружностью· Отрезок АВ называется радиусом
окружности, а точка А — её центром (черт. 46). Все точки
окружности отстоят от центра на расстоянии, равном радиусу. Часть
плоскости, лежащая внутри окружности
вместе с точками самой окружности,
называется кругом. Часть окружности между
двумя её точками называется дугой· Дуга
обозначается знаком vj, например \j MN
(черт. 46). Две точки окружности выделяют
на ней две дуги, составляющие вместе
целую окружность.
Отрезок прямой, соединяющий концы
Черт. 4б дуги, называется хордой (например,
отрезок BN на черт. 46). Как видно из чертежа, хорда BN
разделяет окружность на две дуги: меньшую и большую.
Считается, что хорда стягивает меньшую дугу· Например,хорда BN
стягивает \j BCN. Хорда, проходящая через центр, называется
диаметром· Диаметр равен явум радиусам. Часть круга,
ограниченная двумя радиусами и дугой окружности, называется
сектором· Таков сектор MAN (черт. 46). Часть круга, ограниченная
25

дугой и проходящей через её концы хордой, называется
сегментом. Таков сегмент NCB (черт. 46), ограниченный дугой NCB
и хордой NB. Окружность вычерчивается при помощи циркуля.
§ 25. Центральный угол
Угол, образованный двумя радиусами одной окружности,
называется центральным углом. Таков, например, /^АОВ (черт. 47).
Дуга АВ, лежащая во внутренней^области угла АОВ, называется
дугой, соответствующей этому центральному углу. Прямому
углу соответствует дуга, равная -ξ части всей окружности;
развёрнутому углу — дуга, равная половине окружности; полному
углу — вся окружность.
D
Черт. 48
Величина центрального угла измеряется при помощи
соответствующей ему дуги. Это измерение основано на
следующих свойствах центральных углов:
/· Если β данной окружности два центральных угла
равны, то и соответствующие им дуги равны.
Чтобы убедиться в этом, возьмём какой-либо круг (черт. 48)
и в нём два равных центральных угла АОВ и COD. Им
соответствуют дуги: АВ и CD. Наложим сектор COD на сектор АОВ
так, чтобы прямая ОС совместилась с прямой ОА, а точка О
осталась на месте. При этом точка С совпадёт с А, так как
ОС=ОА. Прямая OD совпадёт с ОБ, так как /_COD = /_AOB.
Точка D совпадёт с В, так как OD = OB. Таким образом, концы
дуги CD совместятся с концами дуги АВ. Следовательно,
совместятся и дуги АВ и CD. Значит, \j AB=\j CD.
Совершенно так же можно убедиться, что:
2. Если β данной окружности две дуги равны, то и
соответствующие им центральные углы равны*
§ 26. Измерение центральных углов
Для измерения центральных углов всю окружность делят
на 360 равных частей, называемых дуговыми градусами; каждый
дуговой градус делят на 60 равных частей, называемых дуговыми
26

минутами; каждую дуговую минуту — на 60 равных частей,
называемых дуговыми секундами. Если точки деления, полученные
при первом разделении окружности, соединить с центром, то весь
полный угол при центре разделится на 360 равных центральных
углов. Они будут равны между собой, потому что соответствуют
равным дугам, а именно дуговым градусам. Эти углы называются
угловыми градусами· Полный угол содержит 360 угловых
градусов. Значит, угловой градус составляет ^ часть полного угла.
Каждой дуговой минуте соответствует центральный угол,
называемый угловой минутой. Все угловые минуты равны между
собой. Угловой градус содержит 60 угловых минут. Дуговой
секунде соответствует центральный угол, называемый угловой
секундой. Все угловые секунды равны между собой. Угловая
минута содержит 60 угловых секунд.
Центральный угол содержит столько же угловых
градусов, минут и секунд, сколько соответствующая ему
дуга содержит дуговых градусов, минут и секунд.
Градусы обозначают знаком (°), минуты знаком ('), секунды
знаком ("). Таким образом, угол в 30 градусов 25 минут и
15 секунд запишется так: 30°25'15".
Прямой угол содержит 90°. Развёрнутый угол —180°. Если
увеличить радиус окружности, то, очевидно, увеличится и сама
окружность, а следовательно, увеличится и ^ её часть, то есть
дуговой градус. Следовательно, величина дугового градуса
зависит от радиуса окружности.
Угловой же градус не зависит от длины радиуса. В самом
деле, при увеличении радиуса полный центральный угол не будет
изменяться. Значит, не будет изменяться и ^ его часть,
составляющая угловой градус.
§ 27. Транспортир. Измерение угла на местности
Для измерения дуг, а следовательно, и углов в простейших
случаях употребляется прибор, называемый транспортиром. Он
состоит из линейки и составляющей с ней одно целое
полуокружности, причём центр её отмечен на ребре линейки штрихом или
вырезом. Дуга полуокружности разделена на градусы от 0° до
180° (черт. 49).
Для измерения угла при помощи транспортира помещают
транспортир так, чтобы центр полуокружности совпал с
вершиной угла, а диаметр — с одной из его сторон. Вторая сторона
угла укажет на дуге транспортира точку, отмеченную числом
градусов, содержащихся в данном угле.
При помощи транспортира можно также строить угол,
имеющий данное число градусов.
27

Наконец, при помощи транспортира можно разделить
приближённо угол на несколько равных частей. Для этого нужно
сначала измерить транспортиром данный угол и разделить число
гралусов этого угла на данное число частей, а затем снова при
помоши транспортира построить последовательно внутри данного
угла равные углы, имеющие
каждый найденное число градусов и
составляющие в сумме
первоначальный угол.
Для измерения или построения
углов на местности служит
специальный прибор, называемый
астролябией.
Астролябия состоит из
металлического круга, на котором
нанесены деления — от 0° до 360°.
На концах диаметра, соединяющего деления 0° и 180°,
прикреплены две вертикальные пластинки А и В (черт. 50).
В центре металлического круга прикреплена горизонтальная
линейка CD (короче диаметра АВ), которая может вращаться по
Кругу и на концах которой установлены вертикальные пластинки
С и D. Во всех четырех вертикальных пластинках имеются
продольные разрезы, причём у пластинок В и D в эти разрезы
вставлены тонкие вертикальные волоски.
Черт. 49
Черт. 50
Черт. 51
Для того чтобы измерить угол с вершиной Μ на данной
местности нужно поставить астролябию так, чтобы прямая,
соединяющая центр её круга с точкой М, была вертикальна
(это достигается при помощи отвеса). При этом линейка АЬ
должна быть направлена по одной из сторон ML измеряемого
угла (черт. 51). Чтобы добиться этого, нужно, смотря через
вырез в пластинке Л, вращать круг астролябии до тех пор, пока
волосок противоположной пластинки В не покроется вехой,
установленной в точке L на земле. После этого при помощи
винта закрепляется металлический круг (вместе с диаметром Αΰ).
28

Далее, диаметр CD устанавливается в направлении другой
данной стороны MN измеряемого угла. Для этого нужно
смотреть через вырез в пластинке С и вращать линейку CD до тех
пор, пока волосок в пластинке D не покроется вехой,
установленной на земле в точке ЛЛ
Для определения величины угла NML нужно посмотреть,
против какого деления остановилась пластинка D.
§ 28· Понятие о теореме
В предыдущих параграфах были обнаружены свойства
некоторых геометрических фигур. Например, в § 15 мы заметили
свойство двух смежных углов, а именно: эти углы в сумме
всегда составляют 2d. В § 21 мы нашли свойство вертикальных
углов: всякие два вертикальных угла равны между собой. Эти
свойства углов мы установили путём правильных рассуждений,
опираясь на принятые вначале аксиомы. Всякая истина или
утверждение, которое выводится при помощи рассуждений из аксиом,
называется теоремой, а рассуждение, при помощи которого
убеждаются в правильности теоремы, называется ее
доказательством· Таким образом, найденные свойства вертикальных углов,
а также смежных углов следует назвать теоремами*.
Теоремы имеются не только в геометрии, но и в других
частях математики, например в арифметике. Так, свойство целых
чисел: „если сумма цифр числа делится на 3, то и всё число
делится на 3"—выражает одну из теорем арифметики.
В геометрии теоремы выражаются в форме отчётливо
высказанных математических предложений, которые следует запоминать
так же хорошо, как основные правила арифметики.
До сих пор мы доказали следующие теоремы:
1. Все развёрнутые углы равны между собой (§ 10).
2. Сумма двух смежных углов равна двум прямым углам
(§ 15).
3. Вертикальные углы равны между собой (§ 21).
4. Если в данной окружности два центральных угла равны,
то и соответствующие им дуги равны (§ 25).
5. Если в данной окружности две дуги равны, то и
соответствующие им центральные углы равны (§ 25).
6. Центральный угол содержит столько же угловых градусов,
минут и секунд, сколько соответствующая ему дуга содержит
дуговых градусов, минут и секунд (§ 26).
Каждую теорему обычно высказывают в форме условного
предложения. При этом первая часть предложения называется
условием теоремы, а вторая — её заключением·
* Слово „теорема" — греческое; в переводе на русский язык оно
означает: истина, доступная созерцанию.
2*

Так, в теореме § 25 первая часть: „Если в данной окружности
два центральных угла равны"—составляет условие теоремы, а
вторая: „...то и соответствующие им дуги равны"—составляет
её заключение.
В такой же форме можно высказать и другие доказанные
нами теоремы. Так, теорему § 15 можно высказать так: „Если
два угла смежные, то их сумма равна двум прямым углам".
Предложение, непосредственно вытекающее из теоремы,
называется её следствием·
ВОПРОСЫ
1. Что называется углом?
2. Какие углы называются прилежащими?
3. Как определить, какой из двух углов больше?
4. Какие углы называются смежными?
5. Какой угол называется прямым?
6. Как строится прямой угол?
7. Каким образом проверяется правильность чертёжного треугольника?
8. Сколько прямых, перпендикулярных к данной, можно провести через
данную точку на плоскости?
9. Какой угол называется тупым, острым и развёрнутым?
10. Какие углы называются вертикальными и каким свойством они
обладают?
11. Что называется биссектрисой угла и как её построить?
12. Что служит биссектрисой развёрнутого угла?
13. Что называется полным углом?
14. Сколько прямых углов содержит полный угол?
15. Что называется центральным углом и как он измеряется?
УПРАЖНЕНИЯ
1. Какой угол образуют стрелки часов в 6 час, в 12 час, в 3 часа,
в 5 час, в 9 час, в 8 час, в 10 час?
2. Сколько раз в промежуток от 2 до 5 час. стрелки часов образуют
развёрнутый угол? Отв. Три раза.
3. Который теперь час, если стрелки часов образуют угол в 105°, а
минутная стрелка указывает 6 час? Отв. 2 часа 30 мин. или 9 час. 30 мин.
4. Один из двух смежных углов на 30° больше другого. Чему равен
каждый из них? Отв. 105° и 75°.
5. Один из двух смежных углов в три раза больше другого. Чему равен
каждый из них? Отв. 135° и 45°.
6. Один из четырёх углов, образуемых двумя пересекающимися прямыми,
равен 0,6tf. Чему равен каждый из остальных трёх углов?
7. Какой угол образуют между собой биссектрисы двух смежных углов?
8. Доказать, что если два угла равны, то и смежные им углы также
равны.
III. ПРЯМЫЕ ПЕРЕСЕКАЮЩИЕСЯ И ПАРАЛЛЕЛЬНЫЕ
§ 29· Углы, образуемые при пересечении двух прямых третьей
Предположим, что две прямые АВ и CD (черт. 52) пересечены
третьей прямой EF. Назовём её секущей прямой. При
пересечении этих трёх прямых образуется 8 углов: 4 — с вершиной G
и 4 — с вершиной И.
30

Черт. 52
Обозначим эти углы цифрами, поставленными внутри каждого
угла.
Эти углы можно различным образом соединить в пары, беря
один угол с вершиной G, другой с вершиной //. Этим парам
углов дают различные названия, сообразуясь с их положением
относительно прямых АВ и CD и
секущей EF.
1) Углы /и 5, 2 и б, 4 и 8, 3 н 7
называются соответственными.
2) Углы / и 7, 2 и 8 называются
внутренними накрест лежащими.
3) Углы 3 и 5, 4 и 6 называются
внешними накрест лежащими.
4) Углы / и 8, 2 и 7 называются
внутренними односторонними.
5) Углы 4 и 5, 3 и 6 называются
внешними односторонними.
Все эти пары углов связаны между
собой соотношениями, выражаемыми следующей теоремой.
Теорема. Если какие-нибудь соответственные углы
равны, то:
1) внутренние накрест лежащие углы равны;
2) внешние накрест лежащие углы равны;
3) сумма внутренних односторонних углов равна 2d;
4) сумма внешних односторонних углов равна 2d.
1. Дано: Z.5= Z.1 (черт. 53). Требуется доказать, что
В самом деле: /_7=/_Ь как вертикальные, но /_5 = /_1>
следовательно, /_7= /_1. Также доказывается, что Ζ.2=Ζ-8-
2. Дано: Ζ5 = Ζ7 (чеРт· 53)ί
требуется доказать, что
^/5 = ^3 ϋΖ0 = Ζ*
В самом деле: Z^^ZA a
/_1 = /_3 как вертикальные,
следовательно, /_5 = /_3. Так же
доказывается, что Ζ-6 = Ζ-4-
3. Дано: /_5 =/_1 (черт. 53);
требуется доказать, что
Черт. 53
Z' + ZS = 2d и Ζ.ϊ + Δ7= 2^.
В самом деле: Z#+Z<5 —2d (§ 15), но /Jo ==Z ^
следовательно, £8-\- £l=2d. Так же доказывается, что Ζ2 + Ζ7=2ώ.
4. Дано: Z-^^^l (черт. 53); требуется доказать, что
Z^ + Z5=2d и Z<? + Z6=2d.
В самом деле: Ζ^+Ζ^ = 2ώ, но Ζ^ = Ζ^, следовательно,
Z^ + Z<5=2d. Далее, /_1 = Ζ~3 как вертикальные, но //-
31

= ,/5, следовательно, ζί<3=^5, но Z^5 + ^6= 2d,
следовательно, ^/_3-{- ^6=2d.
Совершенно такими же рассуждениями можно доказать, что
если равны внутренние или внешние накрест лежащие углы, то
соответственные углы также равны, и что если сумма внутренних
или внешних односторонних углов равна 2d, то соответственные
углы равны.
§ 30. Параллельные прямые. Признаки параллельности
прямых
Две прямые, лежащие в одной плоскости и непересекающиеся,
называются параллельными прямыми.
Параллельность прямых АВ и CD обозначается знаком || :
АВ || CD (черт. 54).
Теорема. Если внутренние накрест лежащие углы
равны, то прямые параллельны.
Дано: прямая EF пересекает
прямую АВ в точке TV, а
прямую CD — в точке Μ и пусть
при этом /_ 1 =,/ 2. Требуется
доказать, что АВ \\ CD.
Так как ^/ / = Ζ2, το
^/ 3= ,/ 4. Легко доказать, что
фигура BNMD может быть
совмещена с фигурой CMNA.
Черт. 54 В самом деле, будем
вращать фигуру BNMD в плоскости
чертежа вокруг точки О — середины отрезка MN по часовой
стрелке (черт. 54). Тогда фигура BNMD, вращаясь вокруг
точки О, займёт положение II, и при дальнейшем вращении
наступит такой момент, когда точка Μ совпадёт с точкой 7V,
а точка 7V —с точкой М. При этом луч ΝΒ совместится с
лучом МС, так как /.3 = Ζ.4> а ЛУЧ MD совместится с лучом ΛΛ4,
так как /.1 = Ζ.2· Таким образом, фигура BNMD совпадёт
с фигурой CMNA. Но отсюда следует, что прямые АВ и CD
пересечься не могут, так как если бы они пересеклись, например,
справа от секущей EF, то, совмещая фигуру BNMD с фигурой
CMNO, мы обнаружили бы, что они должны были бы пересечься
и слева от секущей EF, и тогда прямые АВ и CD пересекались бы
в двух точках, что невозможно.
Таким образом, мы доказали, что прямые АВ и CD
параллельны.
Следствия. 1. Если соответственные углы равны, или
внешние накрест лежащие углы равны, или сумма внутренних
или внешних односторонних углоз равна 2d, то прямые
параллельны, так как при каждом из этих условий равны внутренние
накрест лежащие углы.
32

2. Две прямые, перпендикулярные к третьей, параллельны
между собой, так как эти прямые образуют с третьей равные
соответственные углы.
3. Через каждую точку вне данной прямой можно провести
только одну прямую, перпендикулярную данЪой, так как два
перпендикуляра к одной прямой должны быть параллельны и,
следовательно, не могут исходить из одной точки.
§ 31. Построение прямой, параллельной данной
Задача. Через данную точку С вне прямой АВ (черт. 55)
провести прямую, ей параллельную.
Решение 1. При помощи чертёжного угольника проводим
через точку С прямую, перпендикулярную к АВ, так, как это
было указано в § 18. Она пересечёт прямую в некоторой точке D.
Затем через точку С проводим прямую СЕ, перпендикулярную
к CD (черт. 55). Эта прямая СЕ и будет искомой прямой,
параллельной АВ.
D В
Черт. 55
Черт. 56
Решение 2. Приложим чертёжный угольник ребром прямого
угла к данной прямой АВ. К его большому ребру прикладываем
равный ему второй чертёжный угольник, как указано на
чертеже 56, и передвигаем его вдоль первого до тех пор, пока
ребро его не пройдёт через точку С. Это ребро и определит
искомую прямую. Правильность построения следует из равенства
внутренних накрест лежащих углов, отмеченных на чертеже.
§ 32. Рейсмас. Малка
В строительном деле для нанесения прямых линий,
параллельных обстроганному ребру, употребляется инструмент,
который называется рейсмасом. Рейсмас
состоит из колодки а, в которую с А
вставлены два подвижных закрепляемых /
в требуемом положении деревянных
стержня £?, имеющих на одном из
концов по острию с (черт. 57). ь^г-_=| :_ | ■___ :_г.—\
Для того чтобы провести прямую, s
параллельную кромке какого-нибудь из- с о
делия, колодка а прижимается к боко- Черт. 57
±
u^
/
ΞΖ3
гз

вой стороне изделия и передвигается вдоль этой стороны (черт. 58).
При этом остриё прочерчивает на поверхности детали риску
(черту), параллельную кромке.
Для разметки углов и проведения на поверхности доски или
бруска прямых линий под заданным углом употребляется
инструмент, который называется малкой. Малка состоит из линейки а
Черт. 58
Черг. 59
и планки b одинаковой ширины, скреплённых шарниром с
(черт. 59). В планке имеется продольный прорез. Когда
инструмент сложен, линейка закрывает собой этот прорез.
Для того чтобы наметить на каком-нибудь изделии из дерева
прямую, к его кромке прикладывают планку & и на поверхности
изделия* проводят прямую по краю линейки а, заранее
установленной под определённым углом к планке.
§ 33· Аксиома о параллельных прямых
Построение прямой, параллельной данной, было сделано нами
в δ 31 двумя способами. Спрашивается, будет ли прямая,
полученная вторым способом, совпадать с прямой, полученной
первым способом. Если эти прямые окажутся различными, то через
точку С будут проходить две прямые, параллельные прямой АВ,
и можно будет спросить, нельзя ли каким-либо способом
провести через точку С ещё одну прямую, параллельную АВ, и
сколько всего прямых, параллельных данной, можно провести
через данную вне её точку. На опыте можно убедиться, что,
каким бы способом ни производить построение параллельной
прямой и как бы тщательно его ни выполнять, на чертеже
всегда получается одна и та же прямая.
В таком случае нельзя ли это доказать так же, как
доказываются все другие теоремы геометрии?
Этот вопрос на первый взгляд кажется очень простым. На
самом же деле он оказался одним из наиболее трудных
вопросов геометрии. В своих „Началах" Евклид принимал аксиому,
в силу которой такая прямая может быть только одна. Многие
34

геометры после него пытались это утверждение доказать. Эти
попытки продолжались более чем две тысячи лет, но были
безуспешны. И только в 1826 г. русский геометр профессор
Казанского университета Николай Иванович Лобачевский сделал
величайшее открытие, показав, что это утверждение никаким способом
доказать нельзя и что его нужно
принимать за новую аксиому
геометрии.
Эту аксиому принимают теперь
в следующей форме: через данную
точку вне данной прямой можно
провести только одну прямую,
параллельную данной.
Следствия. 1. Две прямые,,
параллельные третьей, параллель- '
ны между собой, так как если бы ЧеРт· w
эти прямые пересекались, то через
точку их пересечения проходили бы две прямые, параллельные
третьей.
2 Прямая, пересекающая одну из двух параллельных
прямых, пересекает а другую. Действительно, если прямая АВ
(черт 60) параллельна CD и прямая CD' пересекает прямую CD
в точке Я, то прямая CD' должна пересечь прямую АВ. В
противном случае через точку Η будут проходить две прямые: CD и
CD\ параллельные прямой АВ, что невозможно.
§ 34· Углы, образованные параллельными прямыми и секущей
Теорема. Если две прямые параллельны, то при
пересечении с третьей они образуют:
1) равные внутренние и равные внешние накрест
лежащие углы;
2) равные соответственные углы;
3) односторонние углы, такие, что сумма внутренних
односторонних углов равна 2d и сумма внешних
односторонних углов равна 2d.
Дано: прямая АВ \\ CD (черт. 60). Требуется доказать, что
Предположим, что /_7φ/_1. Тогда в точке Η можно постро-
ить >7'=//. Но тогда прямая CD' будет параллельна
прямой АВ (§ 30). Таким образом, через точку Η будут проходить
две прямые: CD и CD\ параллельные прямой АВ, что
невозможно в силу аксиомы о параллельных прямых.
Так же доказываются и остальные утверждения теоремы.
35

§ 35. Свойство углов с параллельными сторонами
Теорема. Углы с соответственно параллельными
сторонами или равны, если эти углы оба острые или оба
тупые, или сумма их равна 2d, если один из них острый,
а другой тупой.
Дано: АВ II А'В\ ВС || В'С (черт. 61). Требуется доказать, что:
1) /тАВС = /тАВ'С\
2) /_АВС + /_АВ'П = Ы.
1. Продолжим сторону ВС
первого угла до пересечения
в точке Ε со стороной А'В'
второго угла.
/mABC = /mA'EF как
соответственные при параллельных
прямых АВ и А'В' и секущей
DF; Z A'EF = Ζ А!ВС как
соответственные при
параллельных прямых ЕЕ и В'С и
секущей А'В'.
Следовательно, /_АВС = /_АВ'С\
2. /_АВ'С + /_D'B'A = U, но /_АВ'С = /_АВС, как было
только что доказано.
Следовательно, ^/ABC^/_D'B'A = 2d.
Чсрг. 61
§ 36. Свойство углов с взаимно перпендикулярными сторонами
Теорема. Если стороны одного угла перпендикулярны
сторонам другого, то эти углы или равны между собой,
если они оба острые или оба тупые, или сумма их равна 2d,
если один из них острый, а другой
тупой.
Рассмотрим отдельно два случая:
1) углы имеют общую вершину; ί
2) углы имеют различные вершины.
1. Дано: AB±AD, AC \_АЕ (черт.
62). Требуется доказать, что ^ВАС =
=ZDAE и /_BAF-^/_DAE=2d.
J/tBAD = ^mCAE как прямые углы.
Отнимая от прямого угла BAD угол
CAD, получим угол ВАС. Отнимая от
прямого угла САЕ тот же самый угол
CADy получим угол DAE. Следовательно, /_ВАС = /_DAE.
Далее: /_BAF-\-Ζ.ВАС = 2d. Но ZBAC = ZDAEy
следовательно, /_BAF' + /_DAE=2d.
2. Дано: AB±FD; AC±FE (черт. 63); требуется доказать,
что Z.BAC= £EFD и /_EFD-\-Z^AG=2d.
36

Проведём через вершину А прямые АЕ' и AD\
соответственно перпендикулярные прямым АС и АВ: АЕ' _[_ AC, AD' _[_ АВ.
JMbi замечаем, что АЕ' \\ EF (так как обе они перпендикулярны
к прямой АС) и AD' \\ FD
(так как обе они
перпендикулярны к прямой АВ).
Следовательно, /_ EFD =
= /_Е'AD' как углы с
параллельными сторонами.
Замечаем теперь, что
/.ВАС и Z-D'AE' имеют
попарно перпендикулярные
стороны и общую вершину А.
Следовательно, 2^ВАС =
= /_D'AE' и /_D'AE' +
-\-^BAG = 2d. Заменяя /_D'AE' равным ему Z.EFD, получим:
^BAC^^EFD и ZEFD + Z.BAG = 2d.
Черт. 63
УПРАЖНЕНИЯ
1. Прямая, пересекающая две параллельные прямые, наклонена к одной
2
из них под углом -=- d. Определить остальные углы, образуемые той же се-
5
кущей с параллельными прямыми.
Доказать, что:
2. Если развёрнутый угол разделить на три равные части, то
биссектриса средней из этих чгстей перпендикулярна к сторонам развёрнутого угла.
3. Если продолжить сторону АВ угла ABC
за вершину В (черт. 64) и по другую сторону
прямой провести луч BE так, чтобы £ DBE
был равен £АВС, то лучи ВС и BE составят
д одну прямую.
4. Биссектрисы двух вертикальных углов
составляют продолжение одна другой.
5. В вершине данного острого угла к
его сторонам восставлены перпендикуляры,
образующие тупой угол. Доказать, что этот
угол вместе с данным образуют "Id.
6. Биссектрисы двух внутренних или
внешних накрест лежащих углов при параллельных прямых параллельны
между собой.
7. Биссектрисы двух соответственных углов при параллельных прямых
параллельны между собой.
8. Биссектрисы двух внутренних или внешних односторонних углов при
параллельных прямых перпендикулярны между собой.
9. Биссектрисы двух углов с параллельными сторонами параллельны
или перпендикулярны между собой.
10. Биссектрисы двух углов с перпендикулярными сторонами параллельны
или перпендикулярны между собой.
11. Перпендикуляр к данной прямой пересекается с каждой прямой, не
перпендикулярной к данной.
12. Два перпендикуляра, восставленные к каждой из сторон угла,
пересекаются.
"Ъ
Черт. 64

ГЛАВА ВТОРАЯ
ТРЕУГОЛЬНИКИ
I. ОБЩИЕ СВОЙСТВА ТРЕУГОЛЬНИКОВ
§ 37· Понятие о многоугольнике
Часть плоскости, ограниченная замкнутой ломаной линией,
звенья которой не имеют других общих точек, кроме вершин, и
в каждой вершине которой сходятся лишь два её
последовательные звена, называется простым многоугольником. Таков
многоугольник ABCDEF (черт. 65). Вершины ломаной называются
вершинами многоугольника, а её звенья — сторонами
многоугольника. Углы, составленные каждыми двумя соседними
сторонами, называются внутренними углами многоугольника. Углы,
смежные с внутренними углами многоугольника, называются его
внешними углами. Таков угол GCD (черт. 65). Простой
многоугольник, образованный выпуклой ломаной линией,
называется выпуклым. Таков многоугольник ABCDE (черт. 66).
Черт. 65
На чертеже 67 дан пример замкнутой ломаной линии ABCDE,
не образующей простого многоугольника. Здесь звенья АЕ и DE
пересекают звено ВС в двух точках, отличных от вершин.
Многоугольник может иметь самое меньшее три стороны.
По числу сторон многоугольник называется треугольником,
четырёхугольником, пятиугольником и т. д.
Прямые, соединяющие две вершины, не прилежащие к одной
стороне, называются диагоналями многоугольника. Таковы
прямые AC, AD, BE, BD и СЕ (черт. 66) в пятиугольнике ABCDE.
38

Из каждой вершины можно провести диагонали ко всем другим
вершинам, кроме её самой и двух соседних с ней вершин, а
потому число диагоналей, выходящих из каждой вершины, на три
единицы меньше числа углов многоугольника. Эти диагонали
разделяют часть плоскости, ограниченную контуром выпуклога
многоугольника, на части, ограниченные треугольниками, число
которых на две единицы меньше числа углов. В самом деле,
Ε
С
Черт. 67
в два крайних треугольника войдёт по две стороны, а во все
остальные — по одной стороне многоугольника. Так,
семиугольник ABCDEFG (черт. 68) имеет семь сторон. Из вершины А
исходят четыре диагонали AC, AD, AE и AF, образующие вместе
со сторонами пять треугольников. Если многоугольник имеет η
углов, а следовательно, и η сторон, то число диагоналей,
исходящих из одной вершины, равно η — 3, а так как число вершин
равно я, то всего можно провести η (η — 3) диагоналей. Но при
этом каждая диагональ будет проведена два раза, а потому
η (η — 3)
число различных диагоналей равно —к—^—-.
§ 38· Треугольник и его элементы
Как было сказано выше, часть плоскости, ограниченная
замкнутой трёхзвенной ломаной (§ 7), называется треугольником.
Таков треугольник ABC (черт. 69). Вершины
ломаной называются вершинами треугольника,
а её звенья — сторонами треугольника. Так,
в треугольнике ABC точки Л, β и С —
вершины, отрезки АВ> ВС и АС — стороны.
Сторона АВУ лежащая против вершины С,
обозначается одноимённой малой буквой с,
точно так же сторона ВС обозначается буквой
я, сторона АС — буквой Ь.
Углы, образованные двумя сторонами треугольника,
называются углами треугольника. Углы и стороны треугольника
называются его элементами. Внутренней областью угла, образован-
39

ного двумя сторонами треугольника, считается та, в которой
лежит третья сторона треугольника. Углы, смежные с углами
треугольника, называются его внешними углами·
Перпендикуляр, опущенный из вершины треугольника на
противоположную сторону, называется высотой треугольника.
Таков отрезок BD (черт. 70). Высота треугольника может иногда
пересекать не сторону треугольника, а ее продолжение. Так, высота
BDтреугольника АВС(чертЛ) пересекает продолжение стороны АС.
Во всяком треугольнике можно провести три высоты.
Далее будет доказано, что три высоты треугольника
пересекаются в одной точке. Высота треугольника обозначается
буквой h со значком внизу, указывающим, на какую сторону
треугольника опущена высота: Afl, hby hc (черт. 72). Если в
треугольнике проведена одна высота, то сторона треугольника, на
которую она опущена, называется основанием треугольника.
В
В
Черт. 73
Прямая, делящая угол треугольника пополам, называется
биссектрисой или равноделящей угла треугольника. Отрезок
биссектрисы угла треугольника от вершины угла до точки встречи
с противоположной стороной называется биссектрисой
треугольника. Таков отрезок BE (черт. 70).
Во всяком треугольнике можно провести три биссектрисы.
Далее будет доказано, что три биссектрисы треугольника
пересекаются в одной точке. Биссектриса угла треугольника
обозначается буквой / со значком внизу, указывающим, какой угол
она делиг пополам: /л, /в, 1С (черт. 73).
40

Отрезок, соединяющий вершину треугольника с серединой
противоположной стороны, называется медианой треугольника.
Таков отрезок ВМ (черт. 70).
Во всяком треугольнике можно
провести три медианы. Далее
будет доказано, что три медианы
треугольника пересекаются в одной
точке. Медиана треугольника
обозначается буквой т со значком
внизу, указывающим, какую сто-
пополам: тп
mh
рону она делит
тс (черт. 74).
Для сокращения записи слово
иногда знаком Д. Так, символ /\АВС надо читать:
ник АВС\
„треугольник*1
заменяется
„треуголь-
§ 39. Виды треугольников
Треугольники различаются между собой, во-первых, по виду
углов, во-вторых, по соотношению длин сторон.
По виду углов треугольник называется:
1) остроугольным, если все его углы острые (черт. 75);
Черт. 75
Черт. 76
2) прямоугольным, если один из углов прямой; сторона,
лежащая против прямого угла, называется гипотенузой, а стороны,
образующие прямой угол, — катетами (черт. 76);
Черт. 77
Черт. 78
Черт. 79
3) тупоугольным, если один из его углов тупой (черт. 77).
По соотношению длин сторон треугольник называется:
1) разносторонним, если все его стороны имеют разную
длину (черт. 75);
41

2) равнобедренным, если две его стороны равны между
собой (черт. 78); сторона, неравная двум другим, называется его
основанием;
3) равносторонним, если все три его стороны равны между
собой (черт. 79).
§ 40. Сумма углов треугольника
Теорема. Сумма углов треугольника равна 2d.
Дан треугольник ABC (черт. 80). Требуется доказать, что
ZCAB + /_АВС + ^ВСА = Ж
Продолжим стороны АВ и ВС и проведём через точку В
прямую DE, параллельную стороне АС. Тогда /^САВ = /^GBE
как углы соответственные при парал-
' v - лельных прямых АС и DE и секущей
AG; ^ABC= /_FBG как углы
вертикальные; ^/тВСА = ^DBF как углы
соответственные при параллельных АС
и DE и секущей FC. Но углы DBF,
FBG и GBE образуют все вместе
развёрнутый угол DBE, а потому
Черт. 80 Ζ DBF' + /_FBG + /_GBE = 2d.
Заменяя в этом равенстве углы DBF, FBG и GBE
соответственно равными им углами АСВ, ABC, ВАС, получим:
/_АСВ + /_АВС + ZBAC=2d.
Теорема доказана.
Следствия. 1. Если один из углов треугольника прямой
или тупой, то оба другие его угла острые.
2. Внешний угол треугольника равен сумме двух
внутренних, с ним несмежных.
Возьмём внешний угол ABF (черт. 80). Имеем:
/_ABF=/_ABD + /_DBF, (1)
но ^ABD = Z ВАС (как внутренние накрест лежащие при
параллельных АС и DE и секущей AB),/^DBF= /_ ВС А (как
соответственные при параллельных АС и DE и секущей ВС), а потому,
заменяя в равенстве (1) углы ABD и DBF соответственно равными
им углами ВАС и ВСА, получим:
£ABF= ZBAC + £ВСА-
3. Внешний угол треугольника больше каждого
внутреннего, с ним несмежного, так как сумма больше каждого из
слагаемых.
42

4. Если два треугольника имеют по два равных угла, то
и третьи их углы равны между собой.
5. Сумма острых углов прямоугольного треугольника равна
прямому углу.
6. Сумма острых углов тупоугольного треугольника меньше
прямого угла.
Доказательства следствий 1, 3, 4, δ, 6 мы опускаем ввиду
их простоты. Эти доказательства учащиеся могут провести
самостоятельно.
§ 41. Сумма углов многоугольника
Теорема. Сумма внутренних углов выпуклого
многоугольника, имеющего η вершин, равна 2d(n — 2).
Взяв какую-либо точку О внутри выпуклого многоугольника
ABCDE (черт. 81) и соединив её с вершинами, получим η
треугольников. Сумма углов всех этих треугольников равна 2dn.
Но эта сумма состоит: 1) из углов при вершинах многоугольника»
Черт. 81
Черт. 82
составляющих сумму углов многоугольника, и 2) из углов при
точке О, составляющих 4d. Вычитая эту последнюю сумму из
всей суммы углов треугольников, равной 2d/z, получим в остатке
сумму углов многоугольника 2dn— 4d = 2d(/z — 2).
Теорема. Сумма внешних углов выпуклого
многоугольника, взятых по одному при каждой вершине, равна 4d.
Возьмём какую-либо точку О внутри многоугольника ABCDE
(черт. 82) и проведём через неё прямые, параллельные сторонам
многоугольника. При точке О образуются углы, соответственно
равные внешним углам многоугольника и в сумме составляющие
полный угол, то есть 4d.
§ 42. Равнобедренный треугольник
Теорема. В равнобедренном треугольнике углы при
основании равны.
Дан треугольник ABC; AB = BC (черт. 83). Требуется
доказать, что 2iCAB = ^ACB.
43

Проведём биссектрису BD угла ABC и перегнём плоскость
чертежа по прямой BD так, чтобы правая её часть совместилась
с левой. Прямая ВС совпадёт с прямой АВ, так как ^/ CBD=^ ABD.
Точка С совпадёт с точкой А, так как АВ = ВС. Следовательно,
угол BDC совместится с углом BDA, отрезок DC сольётся с
отрезком DA, а потому ^АСВ совместится с ^САВ\ следовательно,
/_АСВ = /_САВ.
Следствия. 1. В равнобедренном
треугольнике биссектриса угла при вершине
есть одновременно и медиана и высота.
В самом деле, так как AD = DC, то BD —
медиана, и так как ^/mBDC = ^/mBDA и оба
они смежные, то ^BDC — прямой, а потому
BD — высота.
2. Углы при основании равнобедренного
треугольника всегда острые; внешний угол
при основании равнобедренного треугольника всегда тупой.
3. В равностороннем треугольнике все три угла равны
между собой и каждый из них равен -^ d.
II. ОСЕВАЯ СИММЕТРИЯ ФИГУР
§ 43. Определение фигур, симметричных относительно оси
Две фигуры а и Ь, расположенные по разные стороны от
прямой АВ, называются симметричными относительно этой прямой,
если при вращении вокруг
прямой АВ части плоскости,
лежащей справа от прямой АВ,
до совмещения с частью
плоскости, лежащей слева от
прямой АВ, фигура Ъ
совмещается с фигурой а (черт. 84).
Прямая АВ называется
осью симметрии, а сама
симметрия фигур а и Ь
называется осевой симметрией.
Приведём несколько
примеров осевой симметрии:
1) Стороны угла
симметричны относительно его
биссектрисы, которая служит
осью симметрии
В самом деле, вращением вокруг биссектрисы мы можем
одну сторону угла совместить с другой (черт. Щ.
44

2) Высота BD, опущенная из вершины В равнобедренного
треугольника ABC на основание АС (черт. 83), будет осью
симметрии для треугольников ABD и DBC, потому что, как мы
видели выше (§ 42), вращением вокруг BD можно треугольник
ABD совместить с треугольником DBC.
3) Перпендикуляр CD, восставленный в середине О отрезка
АВ, будет осью симметрии для отрезков АО и ОВ и" точек Л и β,
так как вращением вокруг перпендикуляра CD отрезок АО
совмещается с отрезком ОВ и точка А совпадает с точкой В
(черт. 86).
Отсюда следует, что для построения точки А19 симметричной
данной точке А относительно данной оси я, следует провести через
точку А прямую, перпендикулярную к оси я, и продолжить
отрезок АО за точку О на расстояние OAv равное ОА. Точка Ах
будет точкой, симметричной А относительно оси а (черт. 87).
С
!
/К+$.
Черт. 85 Черт. 86 Черт. 87
§ 44. Построение фигуры, симметричной данной
относительно оси
Зная способ построения точек, симметричных относительно оси
я, легко построить фигуру, симметричную данной относительно
некоторой оси. Пусть, например, требуется построить
треугольник AXBXCV симметричный данному треугольнику ABC
относительно оси а (черт. 88).
Тогда строим точки Av Bi и С,, симметричные точкам А, В
и С относительно оси а.
Ясно, что если мы теперь повернём вокруг.оси а часть
плоскости, лежащую справа от оси я, до совмещения с частью
плоскости, лежащей слева от оси а, то точка А совместится
с точкой Αί9 точка В совместится с точкой ВХУ точка С — с
точкой С,, вследствие чего совпадут отрезки АВ и Aiβ,, ВС и
ВХС1У АС и А}С\, то есть треугольник ABC совместится с
треугольником a^bJc^
45

Нетрудно видеть, что каждой точке треугольника ABC
соответствует симметричная ей точка треугольника AiBiCi.
Если Ε— точка, лежащая на стороне АС треугольника ABC,
то симметричная ей относительно оси а точка £",, с одной
стороны, должна лежать на прямой ЕУЕ, перпендикулярной к оси я,
а с другой стороны,— на стороне Afi^ симметричной АС
относительно я, то есть точка Ελ будет
точкой пересечения прямых ΕλΕ и
Л, С,, следовательно, ЕМ = Е\М (§43).
Попутно мы доказали, что:
Если две точки одной прямой
симметричны двум точкам
другой прямой относительно
некоторой оси, то и все точки
первой прямой симметричны точкам
второй прямой относительно
той же оси.
Обратим внимание на
характерную особенность в расположении
двух симметричных относительно оси
треугольников ABC и AABlCi (черт. 88). Если мы будем
обходить вершины треугольника ABC против часовой стрелки, то
соответствующие вершины треугольника ΑλΒ£λ будут обходиться
по часовой стрелке.
Отсюда следует, что если не выводить треугольник ABC из
плоскости, то никаким перемещением в этой плоскости нельзя
совместить его с симметричным ему треугольником АхВ^и так
как при любом перемещении треугольника ABC направление
обхода его вершин остаётся неизменным.
Поэтому говорят, что треугольники ABC и ААВХС^
симметричные относительно оси я, неодинаково расположены на
плоскости.
То же самое можно сказать и про любые другие фигуры,
симметричные относительно оси, за исключением отрезка,
который всегда можно совместить, не выходя из плоскости, с
симметричным ему относительно оси отрезком.
Черт, 88
§ 45. Фигуры, имеющие ось симметрии
Если какая-либо фигура состоит из двух частей, которые
симметричны одна другой относительно некоторой оси, то
говорят, что данная фигура имеет ось симметрии.
Такие фигуры весьма часто встречаются в природе и в
обыденной жизни. Так, узорам на комнатных обоях, архитектурным
украшениям на фасадах зданий в виде плоских рисунков весьма
часто придают форму, симметричную относительно некоторой
оси. Листья деревьев и лепестки цветов имеют форму, симмет-
46

ричную относительно среднего стебля (черт. 89 — лист клёна).
Крылья бабочки и самый их рисунок имеют форму,
симметричную относительно её туловища (черт. 90).
Черт. 89.
Некоторые фигуры могут иметь и более одной оси
симметрии. Например, равносторонний треугольник имеет три оси
симметрии (три высоты), а окружность — бесконечно много осей
симметрии, так как любой диаметр служит её осью симметрии.
УПРАЖНЕНИЯ
1. В треугольнике один угол равен 42°35', другой — 85° 17'.
Определить третий угол. Отв. 52°8'.
2. Угол при вершине равнобедренного треугольника равен -д- d.
Определить угол при основании. Отв. y~d.
3. Определить углы равнобедренного треугольника, если каждый угол
при основании вдвое меньше угла при вершине. Отв. d, —, —.
4. Определить углы равнобедренного треугольника, если угол при
вершине на 30° меньше угла при основании. Отв. 40°, 70°, 70°.
5. Определить угол, образуемый биссектрисами острых углов в
прямоугольном треугольнике. Отв. -^d.
6. Определить угол, образуемый биссектрисами внешних тупых углов
прямоугольного треугольника. Отв. —.
2
7. Один из углов треугольника равен -^ d\ определить угол,
образованный биссектрисами двух других углов треугольника. Отв. -ςά.
8. В прямоугольном треугольнике один из его углов равен 40°.
Определить величину углов, образуемых перпендикуляром, опушенным из
вершины прямого угла "на гипотенузу, с катетами треугольника. Отв. 50° и 40°.
47

9. Найти сумму внутренних углов выпуклого 20-у гол ь ник а. Отв. 36*/.
10. Внутренние углы /4, £, С, Д Е, F выпуклого 6-угольника таковы,
что каждый следующий в два раза больше предыдущего, т. е. £В = 2 £ А.
8
^C = 2^fi и т. д. Определить эти углы. Отв. /_A = ~d.
ио
11. Сумма внутренних углов многоугольника равна 14rf. Сколько сторон
имеет многоугольник? Отв. 9.
12. Сколько диагоналей имеет выпуклый многоугольник, сумма углов
которого равна 20rf? Отв. 54.
Доказать теоремы:
13. Если один из углов треугольника равен сумме двух других, то
треугольник — прямоугольный.
14. Биссектриса внешнего угла при вершине равнобедренного
треугольника параллельна основанию.
15. Внутри треугольника ABC взята точка О и соединена с вершинами
треугольника. Доказать, что ^/ АОВ > /_ АСВ.
16. Если медиана какой-либо стороны треугольника равна половине этой
стороны, то треугольник — прямоугольный.
17. Доказать, что перпендикуляры, восставленные в серединах двух
симметричных относительно оси отрезков, симметричны между собой
относительно той же самой оси.
18. Доказать, что две прямые, проходящие через две точки А и АХУ
симметричные относительно оси MN и образующие равные углы с отрезком AAV
симметричны относительно оси MN.
19. Доказать, что если на двух симметричных прямых в обе стороны от
двух симметричных точек отложить отрезки, равные какому-либо данному
отрезку, то концы этих отрезков попарно симметричны.
20. Даны три точки Л, В и С, не лежащие на одной прямой. Доказать,
что оси симметрии трёх пар этих точек {А и В, В и С, С и А) пересекаются
в одной точке.
Указание. Построить точку пересечения осей симметрии точек В и
Л, С и β и доказать, что она лежит на оси симметрии точек А и С (при
этом следует воспользоваться следствием 1 § 42).
21. Доказать, что если из двух данных точек одинаковыми радиусами
описать две дуги, то прямая, соединяющая точки пересечения этих дуг,
служит осью симметрии данных точек.
III. РАСШИРЕНИЕ ПОНЯТИЯ О ТЕОРЕМЕ
§ 46. Прямая и обратная теоремы
В § 28 было указано, что каждую теорему можно высказать
в форме предложения, состоящего из двух частей: условия и
заключения.
Если в данной теореме переставить между собой условие и
заключение, то есть сделать условие заключением, а заключение —
условием, то получится новая теорема. Она называется теоремой,
обратной данной, а данная теорема по отношению к этой новой
называется прямой.
Например, для теоремы „если соответственные углы равны,
то прямые параллельны44 обратная будет такая: „если прямые
параллельны, то соответственные углы равны".
48

Если прямая теорема верна, то это ещё не значит, что всегда
будет верна и обратная. Так, например, для теоремы § 21
.вертикальные углы равны между собой" обратная была бы: .если
два угла равны между собой, то они вертикальные". Этр
неверно, так как два равных угла могут и не быть вертикальными
(например, два острых угла с перпендикулярными
сторонами).
Всякую теорему можно выразить в такой общей форме; ..если
есть Л, то есть иВ*.
Здесь под А подразумевается условие теоремы, а под В—
заключение.
Обратная теорема выскажется так: .если есть В, то есть и Л*.
§ 47. Примеры теорем
Прямая
Если центральные углы
равны, то и соответствующие им'
дуги равны.
(Верно.)
• Если соответственные углы
равны, то прямые параллельны.
(Верно.)
Если стороны двух острых
углов перпендикулярны, то эти
углы равны.
(Верно.)
Если прямые параллельны,
то внешние накрест лежащие
углы равны.
(Верно.)
Если два данных угла
смежные, то их сумма
равна 2d.
(Верно.)
Если стороны двух острых
углов параллельны, то эти
углы равны.
(Верно.)
Биссектриса угла служит
осью симметрии для его
сторон.
(Верно.)
Обратная |
Если две дуги окружности]
равны, то и соответствующие им
центральные углы равны. 1
(Верно.) 1
Если прямые параллельны, 1
то соответственные углы равны. 1
(Верно.)
Если два острых угла равны,
то их стороны
перпендикулярны.
(Неверно.)
Если внешние накрест
лежащие углы равны, то прямые
параллельны. 1
(Верно.)
Если сумма двух углов
равна 2d, то они смежные.
(Неверно.)
Если два острых угла равны,
то их стороны параллельны.
(Неверно.)
1 Ось симметрии двух сторон
угла служит биссектрисой этого
угла.
(Верно.)
49

ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что такое теорема, обратная данной?
Для следующих теорем составить все теоремы, обратные данным, и
проверить их правильность.
2. Если данные углы равны, то и смежные с ними углы равны.
3. Развёрнутый угол равен сумме двух прямых углов.
4. Вертикальные углы равны между собой.
5. Если сумма внутренних односторонних углов равна 2d, то прямые
параллельны.
IV. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ
И УГЛАМИ ТРЕУГОЛЬНИКА
§ 48. Соотношения между сторонами и углами одного
и того же треугольника
Теорема 1. В треугольнике против большей стороны
Лежит больший угол.
Дано: В треугольнике ABC сторона ВС больше АВ (черт. 91).
Требуется доказать, что угол А больше угла С.
Отложим на стороне ВС отрезок BD = AB и соединим
точкиА и D прямой линией. Треугольник ABD — равнобедренный,
так как AB=BD; следовательно, угол ADB равен углу DAB
(§ 42). Но угол ADB больше угла С (как внешний угол
треугольника ADC), следовательно, и угол DAB больше угла «С,
β а потому и подавно угол ВАС боль-
хч. ше угла С, или /_А> /_С.
/ ^ч. Теорема (обратная). В тре-
/ ^S^^^L угольнике против большего угла
^ ~~ ^^ лежит и большая сторона.
А С Дано: угол А больше угла С
Черт. 91 (черт. 91). Требуется доказать, что
ВС больше АВ: ВС> АВ.
АВ не может быть больше ВС, так как тогда в силу
прямой теоремы угол С был бы больше угла Л, что противоречит
условию теоремы. Точно так же сторона АВ не может быть
равна ВС, так как тогда треугольник ABC был бы
равнобедренным и в нём угол А и угол С были бы равны. Следовательно,
АВ меньше ВС или, что то же, ВС больше АВ.
Теорема (обратная теореме § 42). Если два угла
треугольника равны, то и стороны, лежащие против этих
углов, также равны.
Дано: ^ Л = ^С (черт. 92). Требуется доказать, что АВ = ВС.
Если бы сторона АВ была больше ВС, то в силу прямой
теоремы угол С был бы больше угла Л. Если бы сторона ВС была
больше стороны АВ, то угол Л был бы больше угла С.
Следовательно, АВ = ВС.
Из доказанных теорем легко вывести такие следствия:
50

1. Угол, лежащий против меньшей стороны треугольника,
всегда острый.
2. В тупоугольном треугольнике наибольшая сторона
лежит против тупого угла.
3. В прямоугольном треугольнике гипотенуза всегда больше
катета.
4. Если в треугольнике все три угла равны, то он
равносторонний.
Теорема 2. Если в прямоугольном треугольнике один
из острых углов равен 30°, то катет, лежащий против
него, равен половине гипотенузы.
Черт. 92
Дано: Д ABC— прямоугольный; ^/β = 30ο, ^C=9G°
(черт. 93). Требуется доказать, что АС=-к-.
К катету ВС пристраиваем угол CBD, равный 30°, и
продолжаем его сторону BD до пересечения в точке D с прямой АС.
Тогда мы получим равноугольный, а следовательно, и
равносторонний (следствие 4) треугольник ABD, то есть будем иметь:
AB = BD = AD.
Биссектриса СВ треугольника ABD делит сторону AD
поло
полам. Поэтому имеем: AC = CD = -^. Но AD = AB, следо*
вательно, АС = -^-.
§ 49· Соотношения между сторонами одного
и того же треугольника
Теорема 1. Каждая сторона треугольника меньше
суммы двух других его сторон и больше их разности.
Дан треугольник ABC (черт. 94). Требуется доказать, что
АС<АВ + ВС\ АВ>АС — ВС.
Продолжим сторону АВ и отложим на её продолжении от
точки β отрезок BD, равный ВС. Соединив точки С и D отрезком
прямой, получим треугольник CBD, в котором сторона BD = BC
51

и, следовательно, угол BCD равен углу BDC (§ 42), а потому
угол ACD больше угла ADC. Следовательно, в треугольнике
ACD сторона AD>AC, но AD = AB + BD, а таккакЯО = ВС,
то AD = АВ + ВС; следовательно,
О АВ-\-ВС>АС. Вычитая из обеих частей
ВС, получим: АВ>АС — ВС.
§ 50· Соотношения между сторонами
и углами двух треугольников с двумя
равными сторонами
Теорема. Если две стороны одного
треугольника равны двум сторонам
другого, а углы между ними не
Черт. 94 равны, то против большего угла
лежит и большая сторона.
Дано: АВ = АХВ19 ВС = В1С1 и Z.ABG> Z-Afifi^
Требуется доказать, что AC^>A1Ci (черт. 95).
Повернув треугольник ДВ,С1Э приложим его к /\АВС так,
чтобы сторона ВХСХ совместилась с ВС. Треугольник AiBlC1
займет положение АгВС (черт. 96). При этом А2В = АВ и
£А%ВС < /_АВС\ AtC=AlCl. Мы должны показать, что АС
А С 4, С, t с
Черт. 95 Черт. 96
больше АХСХ или что АС больше АгС. Соединив точки А и Аг,
получим равнобедренный треугольник АВАг. Биссектриса BD
угла АВАг при его вершине В пройдёт внутри треугольника ABC
(так как угол ABC больше угла СВАг) и, следовательно,
пересечёт сторону АС в некоторой точке Е. Кроме того, она будет
перпендикулярна к основанию ААг и разделит его пополам:
AD = DA2 (§ 42).
Следовательно, точки А и Аг симметричны относительно
прямой BE, и, поэтому, соединив точки Ε и Л2, будем иметь:
АЕ = АгЕ. В треугольнике АгЕС сумма двух его сторон больше
третьей, то есть AtE-\-EC>AtC. Заменив*отрезок АгЕ равным
ему отрезком АЕ, получим:
АЕ^ЕС>АгС, то есть АС>АгС или АС>АХСХ.
52

Из этой теоремы следует обратная теорема:
Если две стороны одного треугольника равны двум
сторонам другого треугольника, а третьи стороны у
них не равны, то против большей стороны лежит и
больший угол.
Предлагаем учащимся доказать эту теорему способом от
противного.
УПРАЖНЕНИЯ
1. Стороны треугольника выражаются целыми числами 1 и 7. Чему
равна третья сторона?
2. Одна из сторон треугольника равна 2 м, другая 8 м. Определить
третью сторону, зная, что она выражается целым числом, делящимся на 3.
3. Доказать, что каждая сторона треугольника меньше половины его
периметра.
4. Доказать, что сумма двух сторон треугольника больше двух отрезков,
соединяющих какую-либо точку, лежащую внутри треугольника, с концами
третьей стороны.
V. РАВЕНСТВО ТРЕУГОЛЬНИКОВ
§ 51. Предварительные замечания
Два треугольника называются равными, если их можно
совместить наложением. Но, чтобы не выполнять каждый раз
наложения, когда хотят убедиться в равенстве треугольников,
устанавливают некоторые признаки, по которым можно заранее
определить, совмещается ли один треугольник с другим или нет.
Эти признаки носят название признаков равенства треугольников·
§ 52. Первый признак равенства треугольников
Теорема. Два треугольника равны, если две стороны
и угол, заключённый между ними в одном треугольнике,
соответственно равны двум сторонам и \глу, заключён*
ному между ними в другом треугольнике.
В,
Даны треугольники ABC и А1В1С1 (черт. 97), причём
ΑΒ = Αβν AC = A1Clf /.Α = /_Αν
Требуется доказать, что &АВС = /\ Afifi^
53

Наложим AAiB1C1 на {\АВС так, чтобы точка Л,
совместилась с А и прямая Л ,5, совместилась с прямой АВ. Точка В ι
совместится с точкой В, так как AiB1 = AB. Сторона АЛСХ
пойдёт по стороне АС, так как Ζΐ^ι = ΖΜ· Точка С, совпадёт с
точкой С, так как А,СХ = АС. Стороны В]С1 и ВС окажутся
совмещёнными, так как совместились их концы. Таким образом,
треугольники совместятся.
§ 53· Второй признак равенства треугольников
Теорема. Два треугольника равны, если сторона и
два прилежащих к ней угла в одном треугольнике
соответственно равны стороне и двум прилежащим к ней
углам в другом треугольнике.
Даны треугольники ABC и AxBfilt причём АС = А1С1,
/_А = /_Ахъ /С=/_СХ (черт. 98).
Требуется доказать, что /\АВС=/\А1В1С1.
/Χ /χ
А С А,'"^С
Черт. 98
Наложим 1\АХВХСХ на /\АВС так, чтобы точка Ах совпала
с Л, сторона А1С1 пошла по АС. Точка Сх совпадёт с С, так
как AlCi=AC. Прямая Α1Βί пойдёт по прямой АВ, так как
^/Л1 = 4^/Л; прямая С1В1 пойдёт по прямой СВ, так как
Вершина Вх совпадёт с вершиной β, так как В и Βλ будут
служить точками пересечения одних и тех же прямых.
Следовательно, треугольники совместятся.
§ 54. Третий признак равенства треугольников
Теорема. Два треугольника равны, если три сто-
раны одного треугольника соответственно равны трём
сторонам другого треугольника.
Даны треугольники ABC и AlBlCl (черт. 99), причём
AB=AXBU BC=Bfiv AC=A1C1.
Требуется доказать, что /±ABC=AAiBlCi.
Приложим треугольники AiBlCl и ABC один к другому так,
чтобы их равные стороны АС и АХСХ совместились, причём
точка Ах совпала бы с точкой Л, точка Сх — с точкой С (черт. 99).
54

Треугольник АХВХСХ займёт положение АВгС, причём ЛВ=з
= Л/?а, CB — CB%. Соединив точки В и Bt, получим два
равнобедренных треугольника В%АВ и BtCB; в первом из них
^АВВг = /.АВгВ, во втором /тСВВ% = £СВгВ (как углы при
В
Черт. 99
основании). Следовательно, /_АВВг + Z.ctiBi = Z.AB1B-\-
+ Zc^iS» или ZmABC = ZmABtC. Таким образом, i\ABC и
ДАВгС равны по первому признаку равенства треугольников.
Следовательно,
ДАВС = ДАВаС или &ABC=&AlBlCl.
§ 55. Признаки равенства прямоугольных треугольников
Теорема 1. Два прямоугольных треугольника равны,
если их катеты равны.
Действительно, так как углы между катетами равны как
прямые, то треугольники будут равны по первому признаку
равенства треугольников (§ 52).
Теорема 2. Два прямоугольных треугольника равны,
если они имеют по равной гипотенузе и по равному
острому углу.
Действительно, два других острых угла треугольников будут
также равны, так как они в силу § 40 (следствие 5) дополняют
до прямого равные углы, а потому треугольники равны по
второму признаку равенства треугольников (§ 53).
Теорема 3. Два прямоугольных треугольника равны,
если они имеют по равному катету и равному
прилежащему или противолежащему углу.
В самом деле, в этом случае два других острых угла будут
равны между собой. Так как, кроме этого, данные треугольники
имеют ещё и по равному катету, то эти треугольники равны по
второму признаку равенства треугольников.
Теорема 4. Прямоугольные треугольники равны, если
катет и гипотенуза одного прямоугольного треугольника
соответственно равны катету и гипотенузе другого
прямоугольного треугольника.
Пусть даны два треугольника ABC и АХВХСХ1 у которых углы
В и Вх — прямые, катет СВ равен катету СХВ19 а гипотенуза АС
55

равна гипотенузе Afix (черт. 100). Требуется доказать, что
&ABC=&AlBlCl.
Повернём ДАВС вокруг катета ВС и приложим его к
Δ ЛАВ1С1 так, чтобы их равные катеты ВС и BlCi совместились,
причём точка В совпала
(черт· 101).
С с,
с точкой Bv точка С — с точкой Сх
Черт, ΐυο
Черт. 101
Так как углы В и Вх — прямые, то в сумме они составляют
2d, следовательно, АВАХ — прямая линия (§ 15). Таким образом,
мы получили /\ACXAV Так как по условию AC = AiCl, то
/\АСЛАХ — равнобедренный, а СВ — его высота. Следовательно,
СВ является и биссектрисой угла АСАА в ДИСД,. /\ABC =
— /\Bfi\Ax по первому признаку равенства треугольников.
§ 56. Элементы,, определяющие треугольник
Из доказанных теорем о равенстве треугольников следует,
что элементы, перечисленные в признаках равенства
треугольников, вполне определяют единственный треугольник. Так,
треугольник определяется:
1) стороной и двумя углами;
2) двумя сторонами и углом, лежащим между ними;
3) тремя сторонами.
Прямоугольные треугольники определяются:
1) двумя катетами;
2) катетом и одним острым углом;
3) гипотенузой и одним острым углом;
4) катетом и гипотенузой.
Таким образом, из трёх углов и трёх сторон для
определения произвольного треугольника нужно брать три данных, в
числе которых должна быть по крайней мере одна из его сторон.
§ 57. Общее определение равенства двух геометрических
фигур
В предыдущем изложении мы не раз встречались с понятием
о равенстве геометрических фигур. Вначале мы говорили о
равенстве отрезков (§ 4), затем о равенстве углов (§ 9) и,
наконец, о равенстве треугольников. Во всех этих случаях фигуры
назывались равными, если они совмещались при наложении.
66

Таким образом, мы приходим к общему определению
равенства двух геометрических фигур: две геометрические фигуры
называются равными, если их можно совместить одну с
другой taK, чтобы они совпали во всех своих точках. Таковы,
например, всякие две фигуры, симметричные относительно какой-
либо оси.
УПРАЖНЕНИЯ
Доказать, что два треугольника равны, если:
1. Высота одного треугольника равна высоте другого треугольника и
углы при основаниях равны.
2. Они имеют равные высоты и две боковые стороны одного, равные
двум боковым сторонам другого.
3. Основание, медиана основания и боковая сторона одного равны
основанию, медиане основания и боковой стороне другого.
4. Углы при основании и биссектриса угла при вершине в одном
треугольнике равны углам при основании и биссектрисе угла при вершине в
другом треугольнике.
5. Высота первого треугольника и отрезки, на которые она делит
основание, равны высоте и таким же отрезкам во втором треугольнике.
6. Боковая сторона, угол при вершине и биссектриса этого угла в
первом треугольнике равны боковой стороне, углу при вершине и биссектрисе
этого угла* во втором треугольнике.
Доказать, что:
7. В равнобедренном треугольнике перпендикуляры, опущенные из
концов оснований на боковые стороны, равны между собой.
8. Биссектрисы углов при основании в равнобедренном треугольнике
равны между собой.
9. Медианы боковых сторон в равнобедренном треугольнике равны
между собой.
10. Перпендикуляры, опушенные из концов какой-либо стороны на
медиану этой стороны, равны между собой.
11. Прямая, перпендикулярная к биссектрисе угла, отсекает на его
сторонах равные отрезки*
12. Треугольники равны, если основание, медиана основания и высота
одного треугольника соответственно равны основанию, медиане основания
и высоте второго треугольника.
13. Перпендикуляры, опущенные из двух каких-либо точек одной из двух
параллельных прямых на вторую, равны между собой.
14. Доказать, что сумма двух перпендикуляров, опушенных из какой-
либо точки основания равнобедренного треугольника на его боковые
стороны, равна перпендикуляру, опущенному из конца основания на боковую
сторону.
VI. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ
§ 58. Предварительные замечания
До сих пор для выполнения различных построений (§ 18, 23, 24)
мы пользовались тремя инструментами: линейкой, циркулем и
чертежным угольником. Доказанные теоремы о равенстве
треугольников позволяют выполнять те же построения при помощи лишь
двух инструментов — циркуля и линейки: циркуль — для
вычерчивания окружности и её дуги, линейка — для вычерчивания прямой
линии.
57

Греки времён Евклида считали прямую линию и окружность
основными линиями в геометрии и потому требовали, чтобы
всякое геометрическое построение выполнялось при помощи лишь
тех двух инструментов, которые вычерчивают эти линии. Умение
полностью использовать эти два основных инструмента — линейку
и циркуль — и в настояшее время представляется весьма важным.
В дальнейшем все построения будем выполнять лишь при помощи
циркуля и линейки.
§ 59. Основные задачи на построение
Задача 1. Через данную точку О на прямой провести
прямую, к ней перпендикулярную (черт. 102).
Решение. В обе стороны от точки О откладываем два
произвольных, но равных между собой отрезка ОА и ОВ. Из точек
g А и В одним и тем же радиусом описы-
ч-' ваем дуги, пересекающиеся в точке С.
Соединяем точки С и О. Полученная
линия СО— искомая.
Доказательство. Треугольники
АОС и ВОС равны между собой (§ 54),
-^—следовательно, ^COA = ^COB. А так
^ как эти углы смежные, то они прямые.
Черт. 102 Задача всегда имеет решение и притом
только одно, так как всякая другая
прямая, проходящая через точку О, образует с лучом ОА угол,
или меньший, или больший прямого.
Задача 2. Из данной тонки вне прямой опустить на эту
прямую перпендикуляр (черт. 103).
Решение. Из данной точки С описываем дугу, пересекающую
данную прямую в точках А и В; из точек А и В описываем равными
радиусами дуги, пересекаюшиеся в точке
D. Прямая CD, встречающая в точке F
прямуй) АВ,— искомая.
Доказательство. ДACD =/\,CDB
(§ 54). Поэтому ZACD = ZDCB.
В равнобедренном треугольнике АСВ
прямая CD есть биссектриса угла при
вершине, а потому CD J_ AB (§ 42,
следствие 1). Задача всегда возможна и имеет
одно решение.
Задача 3· Манный угол разделить
пополам (черт. 104).
Решение. Из вершины А данного угла ВАС произвольным
радиусом описываем дугу ВС. Из точек В и С одинаковыми
радиусами описываем дуги, пересекаюшиеся в точке L·. Прямая
АЕ—искомая биссектриса угла, так как Д Л5£ = Д ЛС£ (§ 54).
Задача всегда возможна и имеет одно решение.
58

Задача 4. Разделить данный отрезок АВ пополам (черт. 105)·
Решение. Из концов А и В произвольными, но равными
радиусами проводим дуги, пересекающиеся в точках С и D,
лежащих по разные стороны от отрезка АВ. Точки С и D
соединяем прямой линией. Точка F пересечения CD с АВ есть середина
отрезка АВ. q
Черт. 105
Доказательство. /\ACD = /\,BCD (§ 54), значит,
/_ACD = /_DCB. Следовательно, в равнобедренном треугольнике
АСВ прямая CD—биссектриса угла при вершине. А потому CF_[_AB
и AF=FB (§ 42, следствие 1).
Задача всегда возможна и имеет одно решение.
Задача 5. Через данную точку вне данной прямой
провести прямую, ей параллельную (черт. 106).
Решение. Из данной точки С произвольным радиусом
проводим дугу, пересекающую данную прямую. Пусть А—одна из
точек пересечения. Из точки А тем же
радиусом проводим дугу,
пересекающую данную прямую в точке В; из
точки В тем же радиусом проводим
дугу, пересекающую в точке D дугу,
проведённую из точки С. Соединяя
точки С и D, получим искомую
прямую.
Доказательство. Соединив
точки Л и С, 5 и О, С и В, получаем
два равнобедренных треугольника ABC и BCD,
имеющих общую сторону ВС и равные стороны: АС=АВ =
= CD = DB. Эти треугольники равны (§ 54), а потому /^АВС =
= ^BCD. Эти углы служат внутренними накрест лежащими для
прямых АВ и CD при секущей СВ. Следовательно, АВ
параллельна CD.
Задача всегда возможна и имеет одно решение в силу аксиомы
о параллельных прямых.
УПРАЖНЕНИЯ
1. Дан треугольник ABC. Построить медианы двух его сторон.
2. Построить высоту данного треугольника.
3. Построить угол, вдвое больший данного.
Черт. 106

4. Через вершину А данного треугольника ABC провести прямую,
параллельную биссектрисе угла ABC.
5. Через вершину В данного треугольника ABC провести прямую,
параллельную биссектрисе внешнего угла при вершине А.
6. Построить прямые, проходящие через вершчны данного тре угольника
и параллельные противоположным сторонам, и доказать, что кажда я сторона
этого нового треугольника в два раза больше параллельной ей стороны
данного треугольника.
7. Прямой угол разделить на три равные части (§ 42, следствие 3).
8. Циркулем и линейкой построить угол в 15°.
9. Через данную точку провести прямую, отсекающую на сторонах
данного угла равные отрезки.
10. Через данную точку провести прямую, наклонённую к данной прямой
под данным углом.
VII. ЗАДАЧИ НА ПОСТРОЕНИЕ ТРЕУГОЛЬНИКОВ
§ 60. Основные задачи на построение треугольников
Задача 1. Построить треугольник, равный данному
треугольнику ABC (черт. 107).
Решение. На произвольной прямой ММ от произвольной
точки Аг откладываем отрезок ΑλΒλ> равный АВ. Из точки Ах
как из центра описываем дугу
£ J£v радиусом, равным АС, а из
точки 5, описываем дугу радиусом,
равным ВС. Точку их
пересечения Сх соединяем с концами
отрезка Α ,Βλ. Треугольник
A1BiCi—искомый.
Доказательство.
Треугольник AlB}Ci и треугольник
ABC равны (по трём сторонам).
Задача всегда возуожна.
Задача 2. Построить угол, равный данному углу ABC,
имеющий данную вершину Вх и данную сторону ВЛСХ (черт. 108).
Решение. Из какой-либо точки С стороны ВС данного угла
описываем произвольным радиусом дугу, пересекающую сторону АВ
данного угла в точке А Соединив точки А и С, строим на прямой
Β£λ треугольник ΒλΟλΑλ> равный треугольнику ВС А (задача 1).
В этом треугольнике ZmBl будет равен /_В. Задача всегда имеет
решение.
60

Задача 3. Построить треугольник по трём данным его
сторонам: а, Ь9 с.
Решение. Отложив на произвольной прямой одну из заданных
сторон, например а, проводим из её концов радиусами, равными
отрезкам b и с, две дуги. Точку их пересечения соединяем
с концами.
Для решения задачи необходимо, чтобы наибольшая из данных
сторон была меньше суммы двух других (§ 49).
Задача 4. Построить треугольник по двум сторонам а
и b и углу между ними С (черт. 109).
Черт. 109
Решение. Строим угол, равный данному, и откладываем на
£го сторонах от вершины отрезки, равные данным. Соединяя их
концы, получаем искомый треугольник.
Правильность решения очевидна. Для построения необходимо,
чтобы заданный угол был меньше 2d. Задача имеет одно решение.
Задача 5. Построить треугольник по стороне с и двум
прилежащим к ней углам А и В (черт. ПО).
Черт. 110
Решение. Отложив на произвольной прямой отрезок АВ = с,
строим при его концах А и В данные углы и продолжаем их
стороны (не совпадающие с АВ) до пересечения в точке С.
Треугольник ABC — искомый.
Задача имеет единственное решение при условии, что сумма
двух данных углов меньше 2d.
61

§ 61. Общая схема решения задач на построение
Рассмотрим пример более сложной задачи на построение.
Задача. Построить треугольник, если даны два его угла А
и В и сумма двух его сторон Ь-\-с — АС-\-АВ.
Анализ. Чтобы отыскать способ решения задачи или, как
говорят, выполнить анализ задачи, предположим, что задача
решена и что Д ЛЯС (черт. 111) — искомый треугольник. Найдём
связь между искомыми элементами треугольника и данными задачи.
Отложим на продолжении стороны АВ за точку А отрезок
AD = AC и соединим точки Си D; &ACD — равнобедренный.
Следовательно, ^ΟΟΑ = /_DCA = γΖ-Α- Β треугольнике BCD
ι °+с , известны сторона BD = b-\-c
и углы СОВ и CBD. Этот
треугольник можно
построить и получить, таким
образом, две вершины В и С
искомого. Третья его
вершина А служит вершиной
равнобедренного
треугольника ACDy в котором известны
основание CD и углы при
основании.
Построение. На произвольной прямой откладываем
отрезок DB, равный данному отрезку Ь-\-с. При точке D строим угол,
равный -irZA а ПРИ точке в~ УГ0Л> Равный ДанН0МУ УГЛУ в-
Точку пересечения вторых сторон этих углов обозначим через С.
При точке С строим угол DCA, равный углу СОВ. Точка
пересечения второй стороны этого угла с отрезком DB будет третьей
вершиной А искомого треугольника ABC.
Доказательство. Угол В построенного треугольника равен
данному Z^B по построению. Угол CAB построенного треугольника
как внешний угол треугольника ACD равен ^ЛСО-(-^ЛОС =
—i-^/Л +4-^Л = ^/А Далее, треугольник ACD —
равнобедренный, так как по построению /_DCA —/_CDA = -^/_A и,
следовательно, AC = AD. Поэтому AC-\-AB = DA-\-AB = DB.
Треугольник ABC удовлетворяет всем условиям задачи.
Исследование. Задача имеет единственное решение при
условии, что сумма двух данных углов меньше 2d.
Из приведённого примера видно, что полное решение задачи
на построение состоит из следующих четырёх частей.
1. Отыскание способа решения задачи в тех случаях, когда
этот способ не ясен непосредственно (анализ).
2. Выполнение построения.

3. Доказательство того, что построенная фигура удовлетворяет
всем условиям задачи.
4. Исследование. Всегда ли возможна задача при заданных
её условиях и сколько решений она имеет.
УПРАЖНЕНИЯ
1. Обозначения
Во всём дальнейшем будем придерживаться следующих обозначений
элементов треугольника (черт. 112):
д, Ь% с —стороны треугольника; А% Вч С—углы треугольника; hw Н& Л,—
высоты, опушенные на соответственные сто.
роны треугольника; та, ть, тс— медианы
сторон a, by c\ lAy 1в% 1с — биссектрисы углов А,
А С ра% рь — отрезки, на которые высота hc
делит основание АВ% причём отрезок ра
прилежит к вершине В, отрезок рь прилежит
к вершине А\ qA% q* — отрезки, на которые
биссектриса угла С делит основание АВ,
причём qA прилежит к ^ Л, a qB — к
Δ в.
2. Простейшие задачи на построение треугольников
Построить треу го ль ник, если даны:
1. с, Ζ А и Ра- 2· Ра* Рь и L Β· 3· Рф Рь и тс
4. ра, Рь и Л*· 5· Ρω Рь ? α· 6· с, h€ и £ А.
7. с, Л^ и Ь. 8. he, а ъ £ А. 9. с, Л^ и т^
10. hc, а и т^. 11. с, Л^ и ЛЛ. 12. рд, Л^ и т^
13. с, Лд и ЛА. 14. с, тс н 2. Л. 15. а, Ь и Л^.
16. с, те и а. 17. Л^, а и ^ С. 18. a, b и 2.А-
Построить равнобедренный треугольник, если даны:
19. Основание и высота.
20. Основание и высота, опушенная на боковую сторону.
21. Основание и угол при основании.
22. Основание и угол при вершине.
23. Угол при вершине и высота, опушенная на боковую сторону.
24. Построить равносторонний треугольник по его высоте.
Построить прямоугольный треугольник (С — вершина нря-
мого угла), если даны:
25. he и Ζ А-
26. hc и ра.
27. hc и а.
3. Более сложные задачи на построение треугольников
Построить треугольник, если даны:
28. Ь + с, £А, а. 29. b + c, £A, h^
30. b + c, hc, a. 31. b + c, £B, h^

32· Построить треугольник, если даны разность его сторон а — Ь и два
угла А и В.
Анализ. На стороне ВС (черт. ИЗ) откладываем отрезок Си = о и
соединяем точки А и D.
Тогда: £ CAD = £ ADC=2d~3f' ° = d -^- .
Следовательно, £ADB = 2d—(d — ^-J=d + ^
Далее, DB = a — b. Следовательно, легко построить треугольник ABD н
определить, таким образом, положение вершин А и В. После этого вершина С
* определится как вершина равнобедренного
/ ^ треугольника ADC, для которого будут
/ ^г известны основание AD и ^/ ADC.
- °* ■ ■■ Построить треугольник, если
даны:
33. а — Ъ,с,£В. 34. α - b, с, £ А.
35. а — Ь,с,£С. 36. a — b,hc,£B.
37. α - &, Л,, /Л. 38. а - δ, Λα, ^ С.
39. α — с, Лв, ^ С.
40. Построить треугольник, если даны
его периметр и два угла А и В.
Черт. ИЗ Анализ. Продолжив в обе
стороны прямую АВ (черт. 114), отложим на
ней отрезки AD = b и ВЕ=а и соединим вершину С с точками D и Е. Тогда:
DE=a + b + c; £D=^£A> Δ^=^Δ^
Следовательно, Δ DCE можно построить. Этим определяется вершина С.
f . I
а+6+с
ZL L
А В
О A BE
Черт. 114
Вершины А и В найдутся так же, как в задаче § 61.
Построить треугольник, если даны:
41. a + b + c, £A, hr 42. а + Ь + с, hc, pa.
43. a + b+c, ра, £B.
VIII. О ПРОЕКЦИЯХ ТОЧЕК И ОТРЕЗКОВ
§ 62· Проекция точки· Проекция наклонной
Проекцией точки на прямую называется основание
перпендикуляра, опущенного из точки на эту прямую.
Например, проекцией точки А на прямую PQ (черт. 115)
служит точка β —основание перпендикуляра АВ, опущенного из
точки А на прямую PQ.
64

Длина отрезка АВ называется длиной перпендикуляра.
Соединив точку А (черт. 115) с какой-либо точкой С прямой PQ,
получим прямую АС, которая называется наклонной; длина
отрезка АС этой прямой называется длиной наклонной. Отрезок СВ
от точки С до основания
перпендикуляра В называется проекцией
наклонной АС.
§ 63. Сравнительная длина
перпендикуляра и наклонных
В приводимых ниже теоремах ' * С В D
под перпендикуляром и наклон- Черт. 115
ными подразумеваются их
длины; перпендикуляры и наклонные предполагаются проведёнными
из одной точки.
Теорема. Перпендикуляр короче наклонной.
Дано: АВ \_ PQ. Требуется доказать, что ЛС>ЛВ (черт. 115).
Наклонная АС является гипотенузой прямоугольного
треугольника ABC, перпендикуляр АВ служит катетом того же
треугольника, а потому АС>АВ.
Длина перпендикуляра АВ называется расстоянием точки А
от прямой PQ.
§ 64. Сравнительные длины наклонных и их проекций
Теорема. Если проекции двух наклонных равны, то
равны и сами наклонные, и обратно: равные наклонные
имеют равные проекции.
1. Если CB = BD (черт. 115), то /\ABC=/\ABD (по двум
катетам), следовательно, AC=AD.
2. Если ЛС=ЛД то {\ABC={\ABD (так как катет АВ —
общий и гипотенузы АС и AD равны по условию), следовательно,
CB=BD.
Теорема. Из двух наклонных больше та, которая
имеет большую проекцию, и обратно: большая наклонная
имеет большую проекцию.
1. Дано: FB>BD. Требуется доказать, что. AF>AD.
Отложим на отрезке FB от точки В отрезок BC = BD и
соединим С с Л. Наклонные АС и AD равны, так как равны их
проекции С В и BD. В треугольнике ACF угол ACF—тупой как
внешний угол прямоугольного треугольника ABC, следовательно,
AF>AC (§ 48) или AF>AD.
2. Дано: AF>AD. Требуется доказать, что FB>BD.
Действительно, если бы BD было больше FB, то и AD было бы
больше AF; если бы FB было равно BD, то и AF было бы
равно AD, следовательно, FB>BO.
65

IX· ГЕОМЕТРИЧЕСКИЕ МЕСТА ТОЧЕК
§ 65. Понятие о геометрическом месте точек
Рассматривая задачи на построение, которые мы решали до
сих пор, легко заметить, что решение их сводилось к отысканию
одной или нескольких точек.
Так, например, строя треугольник ABC по трём сторонам,
мы, имея данные вершины Л и β, отыскивали положение третьей
вершины С, которая удовлетворяла бы двум условиям: 1) точка С
должна была находиться на данном расстоянии от вершины А;
2) точка ,С должна была находиться на данном расстоянии от
вершины β.
Если же какая-нибудь точка удовлетворяет только одному
условию, то мы можем построить на плоскости бесчисленное
множество точек, удовлетворяющих этому условию. Совокупность
таких точек называется геометрическим местом точек·
Таким образом, геометрическое место точек — это
совокупность всех точек, каждая из которых удовлетворяет одному
определённому заданному условию.
Ниже мы приводим несколько задач, решение которых сводится
к отысканию геометрического места точек.
§ 66. Основные задачи на определение
геометрических мест точек
Задача 1. Найти точку, находящуюся от данной точки А
на расстоянии, равном длине данного отрезка ВС.
Решение. Проведём через точку А какую-либо прямую и
отложим на ней по обе стороны от точки А отрезки AM и AN,
равные ВС (черт. 116): АМ= AN = BC.
0 1С Точки Μ и N удовлетворяют
условию задачи. Таких точек, очевидно,
можно построить бесчисленное
множество: проведя через точку А вместо
прямой ΜΝ другую прямую и отложив
на ней от точки А отрезки АР и AQ>
равные ВС, получим новые точки Ρ и
Q, также удовлетворяющие условию
задачи. Легко заметить, что все
получаемые таким построением точки Λί,
Ny P, Q, ... лежат на окружности с
Черт. 116 центром в точке Лис радиусом, равным
ВС, и только на этой окружности.
Следовательно, геометрическое место точек,
находящихся на данном расстоянии от данной точки, есть
окружность с центром в данной точке и с радиусом,
равным данному расстоянию.
66

Задача 2. Найти точку, находящуюся на одинаковом рас-
стоянии от сторон данного угла.
, Решение. Воспроизведём построение, при помощи которого
мы разделим угол пополам, а именно: из вершины А данного
угла ВАС произвольным радиусом опишем дугу ВС. Затем из
точек В и С одинаковыми радиусами описываем дуги,
пересекающиеся в точке Ε (черт. 117).
Тогда, как мы знаем, прямая АЕ будет биссектрисой угла ВАС.
Докажем, что точка Ε удовлетворяет условию нашей задачи.
Для этого опустим перпендикуляры ED и EF соответственно
на стороны АС и АВ угла ВАС. Прямоугольные треугольники
AED и AEF равны, так как гипотенуза АЕ у них общая, а
острые углы (/ и 2) равны (черт. 117).
Следовательно, EF=ED.
Таким образом, точка Е, как и
всякая другая точка биссектрисы,
удовлетворяет условиюданнэй задачи.
Обратно, если точка Ε
удовлетворяет условию данной задачи, то
есть перпендикуляры ED и EF,
проведённые к АС и к АВ, равны, Г' ел
то точка Ε лежит на биссектрисе Черт. 117
АЕ угла ВАС.
В самом деле, в этом случае прямоугольные треугольники AED
и AEF равны, так как гипотенуза АЕ у них общая, а катеты ED
и EF равны. Следовательно, ^// =^ 2, а это значит, что точка Ε
лежит на биссектрисе АЕ угла ВАС.
Таким образом, все точки, удовлетворяющие условию задачи,
лежат на биссектрисе данного угла и только на этой биссектрисе.
Следовательно, геометрическое место точек,
находящихся на равном расстоянии от сторон угла, есть бис-
м сектриса этого угла.
а Задача 3. Найти точку, находящу-
*' ч юся на одинаковом расстоянии от концов
данного отрезка.
Решение. Пусть дан отрезок АВ
(черт. 118). Из точек А и β опишем
произвольными, но одинаковыми радиусами две дуги,
пересекающиеся в точке С. Точка С, оче-
Черт. 118 видно, удовлетворяет условию задачи.
Посмотрим, где лежат все такие точки.
Опустив из точки С перпендикуляр CD на прямую АВ,
получим два равных прямоугольных треугольника ACD и BCD, так
как они имеют равные гипотенузы АС и ВС и общий катет CD>
а потому AD = DB. Значит, точка С лежит на перпендикуляре
к прямой АВ, восставленном в середине отрезка АВ.
Покажем, что каждая точка этого перпендикуляра
удовлетворяет условию задачи. Пусть Μ—какая-либо его точка. Соеди-
67

нив М с А и 5, получим два равных прямоугольных
треугольника AMD и BMD, так как они имеют равные катеты AD = DB
и общий катет MDy а потому АМ = МВ.
Таким образом, все точки, удовлетворяющие условию задачи,
лежат на перпендикуляре, восставленном из середины данного
отрезка, и только на этом перпендикуляре.
Следовательно, геометрическое место точек,
находящихся на одинаковом расстоянии от концов отрезка, есть
перпендикуляр к отрезку, восставленный из его середины.
§ 67· Метод геометрических мест
На понятии о геометрическом месте точек основан особый
приём решения задач на построение, носящий название метода
геометрических мест· Сущность его состоит в следующем.
Задача на построение обычно сводится к определению
положения на плоскости одной или нескольких точек, которые должны
удовлетворять двум условиям. Если мы отбросим одно из
условий задачи, то задача станет
неопределённой и оставшемуся условию будет
удовлетворять бесчисленное множество
точек, образующих некоторое
геометрическое место. Если затем мы восстановим
отброшенное нами условие и отбросим
другое, то оставшемуся условию опять
будет удовлетворять бесчисленное
множество точек, образующих новое
геометрическое место.
Искомая точка должна удовлетворять
Черт. 119 обоим условиям задачи и, значит, должна
принадлежать обоим геометрическим
местам. Если построить каждое из найденных геометрических мест,
то точка их пересечения и будет искомой. Задача будет иметь
столько решений, сколько общих точек имеют найденные
геометрические места.
Приведём для примера решение двух задач методом
геометрических мест.
Задача 1. Найти точку, находящуюся на равных
расстояниях от двух данных точек Μ и N и на равном расстоянии
от сторон данного угла ВАС (черт. 119).
Решение. Искомая точка должна удовлетворять двум
условиям: 1) она должна находиться на равных расстояниях от точек
Μ и N и 2) она должна находиться на равных расстояниях от
сторон угла ВАС,
Отбросим второе условие. Тогда одному первому условию
будут удовлетворять все точки перпендикуляра ДА,
восставленного из середины отрезка ΛίΛΛ
68

Сохраним теперь второе условие и отбросим первое. Тогда
одному второму условию будут удовлетворять все точки,
лежащие на биссектрисе АЕ угла ВАС.
Точка Ε пересечения прямых KL и АЕ и есть искомая точка,
так как она удовлетворяет обоим условиям задачи.
Задача 2. Найти точку, находящуюся на данном
расстоянии а от точки С и на равном расстоянии от точек А и В.
Решение. Искомая точка должна удовчетворять двум
условиям:
1) она должна находиться на
расстоянии а от точки С и
2) она должна находиться на
равном расстоянии от точек А
и В. Отбросим второе условие.
Тогда одному первому условию
будут удовлетворять все точки
окружности, имеющей радиус а
и центр С (черт. 120).
Сохраним теперь второе
условие и отбросим первое. Тогда одному второму условию будут
удовлетворять все точки, лежащие на перпендикуляре ΛίΛΓ
(черт. 120), восставленном из середины D отрезка АВ.
Точки Ε и F пересечения окружности с центром С радиуса а
и перпендикуляра ΜΝ являются искомыми точками, так как обе
они удовлетворяют двум условиям задачи.
УПРАЖНЕНИЯ
Найти геометрические места точек:
1. Геометрическое место вершин треугольников с заданным основанием
и с заданной медианой, проведённой к этому основанию.
2. Геометрическое место середин параллельных отрезков, заключённых
между сторонами данного угла и одинаково наклонённых к этим сторонам.
3. Геометрическое место точек, равноудалённых от высоты и боковой
стороны данного треугольника.
4. Геометрическое место вершин равнобедренных треугольников с
заданным основанием.
5. Геометрическое место вершин треугольников: а) с заданным
основанием и с данным углом Л при основании; б) с данным при основании
отрезком ра\ в) с данным углом наклона медианы тс к основанию с.
X. УПРАЖНЕНИЯ К ГЛАВЕ ВТОРОЙ
1. Доказать, что в равнобедренном треугольнике перпендикуляры,
опущенные из концов основания на противоположные стороны, равны.
2. Доказать, что биссектрисы равных углов равнобедренных
треугольников равны.
3. Провести через вершину прямого угла прямоугольного треугольника
прямую, разделяющую этот треугольник на два равнобедренныч треугольника.
4. Доказать, что медиана гипотенузы прямоугольного треугольника равна
половине этой гипотенузы.
Черт. 120
69

5. Из вершины прямого угла прямоугольного треугольника- проведены:
биссектриса прямого угла, медиана гипотенузы и высота, опущенная на
гипотенузу. Доказать, что биссектриса делит пополам угол между высотой и
медианой.
6. Из вершины С треугольника ABC проведена прямая, параллельная
биссектрисе угла Д до пересечения в точке и с продолжением стороны АВ.
Доказать, что BD = BC.
7. Из точки, лежащей на стороне равностороннего треугольника со
стороной а, опущены перпендикуляры на две другие его стороны. Доказать, что
сумма отрезков, которые отсекают эти перпендикуляры от сторон
противоположного угла, начиная от его вершины, равна -^а.
8. Построить равнобедренный треугольник, если даны:
а) основание его и противолежащий угол и
б) основание и высота, опущенная на основание.
9. Если через какую-либо точку, лежащую на одной из сторон равно-
•стороннего треугольника, провести прямее, параллельные двум другим его
сторонам, то сумма отрезков, которые отсекают две стороны данного
треугольника от проведённых прямых, равна стороне равностороннего
треугольника.
10. Восставить перпендикуляр в начале данного луча, не продолжая его
за начало.
Указание. На данном луче от начала А луча отложить какой-либо
отрезок АВ и из его концов А и В описать произвольным радиусом две дуги,
пересекающиеся в точке С. Провести прямую ВС и на ней от точки С
отложить отрезок СД равный ВС Прямая AD — искомый перпендикуляр. Доказать.
И. Построить равносторонний треугольник, если дана его высота.
12. Построить треугольник, если даны:
а) Л„ 1с, Ζ с·
б) hc, lc, a.
в) hcy lc, Ζ Λ·

ГЛАВА ТРЕТЬЯ
ЧЕТЫРЁХУГОЛЬНИКИ
I. ОБЩИЕ СВОЙСТВА ЧЕТЫРЁХУГОЛЬНИКОВ
§ 68. Типы четырёхугольников
Часть плоскости, ограниченная замкнутой ломаной линией,
состоящей из четырёх звеньев, называется четырёхугольником.
Вершины ломаной называются вершинами четырёхугольника, а её
звенья — сторонами четырёхугольника.
Четырёхугольник называется простым, если
его стороны не имеют других обших точек,
кроме вершин. Таков четырёхугольник AECD
(черт. 121). Че тырёху гол ьник назыиается
непростым, если его стороны, кроме вершин,
имеют другие обшие точки. Таков
четырёхугольник MNPQ (черт. 122). Простой
четырёхугольник называется выпуклым, если он
образован выпуклой ломаной линией, то есть
если любые три его стороны лежат по одну сторону от
четвёртой, неограниченно продолженной в обе стороны. Таков
четырёхугольник ABCD (черт. 121).
Я N В противном случае четырёх-
Черт. 122 Черт. 123
угольник называется вогнутым. Таков четырёхугольник EFGH
(черт. 123). В нём стороны EF и GH лежат по разные стороны
от прямой GF. В дальнейшем будут* рассматриваться только
простые выпуклые четырёхугольники.
71

§ 69· Общие свойства выпуклых четырёхугольников
Углы, составленные каждыми двумя соседними сторонами
четырёхугольника, называются внутренними углами
четырёхугольника. Углы, смежные с углами четырёхугольника, называются его
внешними углами. Прямые, соединяющие
В противоположные (то есть несоседние)
вершины четырёхугольника, называются его
диагоналями.
С Четырёхугольник имеет две диагонали
АС и BD (черт. 124). Каждая диагональ
четырёхугольника разбивает его на два
треугольника. Так, диагональ АС
разбивает четырёхугольник ABCD на
треугольники ABC и ACD, а диагональ BD — на
Черт. 124 треугольники ABD и BCD. Сумма
внутренних углов четырёхугольника ABCD
равна сумме внутренних углов двух треугольников ABD и BCD
(черт. 124) и, следовательно, равна 4d. Стороны, углы и
диагонали четырёхугольника называются его элементами·
§ 70. Число данных, необходимых для построения
четырёхугольника
Чтобы построить четырёхугольник ABCD (черт. 124), нужно
уметь построить составляющие его треугольники ABD и BCD
{или ABC и ACD). Для построения &ABD нужно иметь три
данных, а для построения Д BCD только два, так как сторона BD
будет уже найдена при построении первого треугольника. Таким
образом, для построения четырёхугольника нужно иметь пять
данных, из которых должно быть не более трёх его углов (так
как четвёртый угол определится по трём остальным).
Таким образом, четырёхугольник вполне определится пятью
своими элементами, в числе которых должно быть не более трёх
его углов.
II. ПАРАЛЛЕЛОГРАММ
§ 71. Общие свойства параллелограмма
Параллелограммом называется четырёхугольник,
противоположные стороны которого попарно параллельны.
Параллелограмм обладает следующими свойствами:
1. Противоположные стороны параллелограмма равны
между собой.
Действительно, если АВ \\ DC и ВС \\ AD (черт. 125), то
/\ABD= Δ BCD, так как сторона BD у них общая, ^ABD =
==^BDC и ^/mADB = ^mCBD как внутренние накрест лежащие
при параллельных прямых.
^
72

Из равенства треугольников ABD и BCD следует и равенство
соответствующих сторон: AB = DC и AD = BC.
2. Углы, прилежащие к каждой стороне, составляют
в сумме 2d.
Действительно,
как внутренние односторонние при параллельных прямых.
v^^ 'с д о
Черт. 125 Черт. 12о
3. Противоположные углы параллелограмма равны
между собой.
Действительно,
/_А = /_С и /_B=/_D
как углы с параллельными сторонами.
4. Диагонали параллелограмма β точке их пересечения
делятся пополам.
Действительно, проведя диагонали АС и BD (черт. 126),
.получим два треугольника ВОС и ΑΟΩ, в которых
BC=AD9 Z.BCO=ZOAD и /.CBO = Z.ODA
как накрест лежащие при параллельных прямых. Следовательно»
/\BOC = AAuD, а потому
BO=OD и АО=ОС.
§ 72. Признаки параллелограмма
Когда хотят убедиться в том, что данный четырёхугольник—
параллелограмм, нет необходимости проверять наличие всех че-
тырёх свойств параллелограмма. Достаточно убедиться, что
четырёхугольник обладает одним из этих свойств. Тогда и три
остальные будут иметь место. Докажем это.
1. Допустим, что в данном четырёхугольнике ABCD
противоположные стороны равны: AB = CD и BC = AD.
Докажем, что этот четырёхугольник — параллелограмм, то есть
докажем, что АВ || DC и ВС \\ AD (черт. 125).
Проведя диагональ BD, получим два треугольника ABD и BCD,
имеющие общую сторону BD. Эти треугольники равны по трём
сторонам, следовательно,
/_CBD = Z.ADBy Z.ABD=ZBDC>
73

значит,
AD\\BC и АВ || CD.
Итак, мы доказали, что если противоположные стороны
четырёхугольника попарно равны, то этот
четырёхугольник— параллелограмм.
2. Пусть теперь дан четырёхугольник ABCD, в котором углы,
прилежащие к каждой стороне, в сумме составляют 2d:
Z^ + Z# = 2d и Z.B + ZC=M (черт. 125).
Углы А и В — внутренние односторонние для прямых ВС и
AD, а углы В и С — внутренние односторонние для прямых АВ
и DC. А потому из данных равенств следует: ВС \\ AD и АВ \\ DC.
Значит, четырёхугольник ABCD — параллелограмм.
Итак, если в четырёхугольнике углы, прилежащие
к каждой стороне, составляют в сумме 2d, то такой
четырёхугольник есть параллелограмм.
3. Допустим, что дан четырёхугольник ABCD, в котором
противоположные углы равны: /_А = /_С, /_В = /_D (черт. 126).
Мы знаем, что ^А-^-^В-^-^С-^^D = 4d. Заменяя здесь
углы С и D равньдми им углами Л и β, получим:
2Z^ + 2Z£ = 4rf, Или ZA + Z.B = 2d·
Но углы А и В — внутренние односторонние при прямых ВС и
AD и секущей АВ, следовательно, ВС || AD.
Заменяя в равенстве: Z^ + Z# + Zc+Z£* = 4d Углы в
и С соответственно равными углами D и Л, получим:
2Z^ + 2Z£> = 4d, или Z.A + Z.D = M.
Но углы Л и D — внутренние односторонние при прямых АВ и
DC и секущей AD> следовательно, АВ || DC. Значит, данный
четырёхугольник — параллелограмм.
Четырёхугольник, противоположные углы которого
равны, есть параллелограмм.
4. Допустим, что дан четырёхугольник ABCD, в котором
диагонали АС и BD при пересечении делятся пополам, то есть
АО = ОС и BO=OD (черт. 126). Докажем, что ABCD —
параллелограмм.
Углы AOD и ВОС равны как вертикальные, а потому Δ AOD =
= АВОС (§ 52). Следовательно, /_BCO = /_OADy а потому
ВС || AD. Так же доказывается, что АВ \\ DC.
Четырёхугольник, диагонали которого β точке
пересечения делятся пополам, есть параллелограмм.
5. Допустим теперь, что в данном четырёхугольнике ABCD
две противоположные стороны, например ВС и АО, равны и
параллельны, то есть BC=AD и BC\\AD (черт. 126).
Докажем, что четырёхугольник ABCD — параллелограмм.
Проведём диагональ BD; 4i/.CBD = 4</mADB как накрест
лежащие, а потому Д ABD = Δ CDB (§ 52). Следовательно, АВ = CD
74

и ^BDC=^DEtA; значит, AB\\CD9 то есть данный
четырёхугольник — параллелограмм.
Четырёхугольник, две противоположные стороны
которого равны и параллельны, есть параллелограмм.
§ 73. Число данных, необходимых для построения
параллелограмма
Известно (§ 70), что для построения четырёхугольника нужно
иметь пять данных, из которых должно быть не более трёх его
углов.
Но так как один угол параллелограмма определяет остальные,
то для построения параллелограмма нужно иметь лишь три
данных, в числе которых должно содержаться не более одного
из его углов.
III. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ФИГУР
§ 74· Определение центральносимметричных фигур
Две точки называются симметричными относительно третьей
точки, если последняя служит серединой отрезка прямой,
соединяющего две данные точки. Таковы точки Л и Л,, симметричные
относительно точки О (черт. 127). Точка О называется центром
симметрии данных точек, а сама симметрия называется
центральной симметрией в отличие от осевой
симметрии. А А*
Чтобы построить точку, симметричную ■ i L
с данной точкой Л относительно другой
данной точки О, следует соединить точки Черт. 127
Л и О отрезком прямой и продолжить его за
точку О на расстояние ОЛ,, равное ОА. Точка Л, будет искомой.
Если для каждой точки какой-либо фигуры построить точку,
симметричную ей относительно некоторого центра О, то все
построенные таким образом точки образуют новую фигуру,
которая называется симметричной данной относительно центра О,
или, коротко, центральносимметричной данной.
§ 75· Фигуры, имеющие центр симметрии
Если для каждой точки данной фигуры существует
симметричная ей относительно некоторого центра О точка той же самой
фигуры, то говорят, что фигура имеет
центр симметрии О.
Примером такой фигуры слу-
Черт 128 жит 0КРУЖН0СТЬ· Центром её
симметрии является её центр.
Фигуры, имеющие центр симметрии, весьма часто встречаются
в жизни. На чертеже 128 дано изображение пропеллера самолёта,
75

имеющего центром симметрии точку О. На чертеже 129 дано
изображение снежинки, имеющей центр симметрии (она, очевидно,
имеет также шесть осей симметрии).
§ 76. Центр симметрии параллелограмма
Теорема. Точка пересечения
диагоналей есть центр симметрии
параллелограмма.
Возьмём на одной из сторон
параллелограмма ABCD, например на ВС,
произвольную точку Ε (черт. 130) и
соединим её с точкой О пересечения
диагоналей АС и BD. Пусть прямая ОЕ
пересекает противоположную сторону AD
параллелограмма в точке F. Тогда треугольник
ВОЕ равен треугольнику DOF, так как BO = OD (§ 71), углы
ОВЕ и ODF равны как внутренние накрест лежащие при
параллельных и углы ВОЕ и DOF
равны как вертикальные. Следова- В Ε с
тельно, сторона ОЕ треугольника /V \ ^00^^Ί
ВОЕ и сторона OF треугольника / ^Х^*^^ /
DOF равны как лежащие против А-^^^^м44^ /
равных углов. д"0^^ ^. ^^
Так как точка Ε была взята
совершенно произвольно, то для каж- Черт. 130
дои точки параллелограмма ABCD
существует симметричная ей относительно центра О точка,
принадлежащая тому же параллелограмму, а потому параллелограмм
ABCD имеет в точке О центр симметрии.
Следствие. В центральной симметрии отрезку ВС со-
ответствует равный ему и параллельный отрезок AD.
УПРАЖНЕНИЯ
Доказать, что:
1. Две прямые, проведённые через концы какого-либо отрезка и
перпендикулярные к нему, симметричны относительно середины этого отрезка.
2. Две параллельные прямые, проходящие через две симметричные точки,
симметричны (относительно того же центра симметрии).
3. Две параллельные прямые симметричны относительно каждой точки
прямой, им параллельной и отстоящей на одинаковом от них расстоянии.
4. Две прямые, проходящие через центр симметрии, отсекают οι двух
симметричных прямых равные отрезки.
5. Если две данные прямые пересекаются, то и симметричные им прямые
пересекаются, и угол между ними равен углу между данными прямыми.
Черт. 129
76

IV. ЧАСТНЫЕ ВИДЫ ПАРАЛЛЕЛОГРАММА
§ 77· Прямоугольник
Прямоугольником называется параллелограмм, все углы
которого равны. Так как в сумме все углы прямоугольника
составляют 4д?, то каждый из них равен d. Прямоугольник обладает
всеми свойствами параллелограмма. Но, кроме того, он имеет и
собственные свойства, отличающие его от других
параллелограммов, именно диагонали прямоугольника равны между собой.
Докажем это.
Прямоугольные треугольники ABD и DC А (черт. 131) равны
по двум катетам (AD — общий катет и AB = DC, так как ABCD—
параллелограмм). Следовательно, AC=BD. ВМС
Легко видеть, что и обратно: если
в параллелограмме диагонали равны,
то этот параллелограмм есть пря- Ρ
моугольник.
Действительно, если дан параллело-
грамм ABCD, в котором AC = BD, то Д N О
/\ABD = l\DCA (по трём сторонам), Черт. 131
следовательно, ^/_BAD= /_CDA, а так
как £ BAD -f- /_ CD A = 2d (как внутренние односторонние), то
Z.BAD = Z.CDA = d.
Далее легко заметить, что прямоугольник имеет две оси
симметрии, а именно: прямые, проходящие через точку О
пересечения диагоналей и параллельные противоположным сторонам.
В самом деле, прямая /ИЛ/, проходящая через точку О (черт. 131)
и параллельная сторонам АВ и CD, составлена высотами
равнобедренных треугольников ВОС и AOD, а потому она делит
ВС и AD пополам (§ 42). Значит, точки β и С, а также точки А
и D симметричны относительно оси ΜΝ. То же самое можно
повторить и для прямой PQ.
Как мы увидим из следующего параграфа, последнее свойство
не является характерным признаком прямоугольника.
§ 78· Ромб
Ромбом называется параллелограмм, все стороны которого
равны между собой.
Кроме общих свойств параллелограмма, ромб имеет и свои
особые свойства, отличающие его от других параллелограммов,
а именно диагонали ромба взаимно перпендикулярны и
делят углы ромба пополам.
В самом деле, /\АВО= /\СВО (черт. 132) по трём сторонам.
Следовательно, /_АОВ = /_СОВ как углы, лежащие против
равных сторон АВ и ВС равных треугольников АОВ и ВОС. А так
а
77

как эти углы смежные — они прямые. Из равенства тех же
треугольников следует, что ^АВО = ^СВО. Значит, диагональ BD
делит угол ABC пополам. Сравнив треугольники AOD и COD,
убедимся, что BD делит пополам и
£ /_ ADC. То же можно повторить и для
диагонали АС.
Легко показать, что и обратно:
а) если диагонали параллелограмма
взаимно перпендикулярны, то
параллелограмм есть ромб; б) если
диагонали параллелограмма делят
его углы пополам, то
параллелограмм есть ромб.
Легко убедиться, что диагонали ромба служат осями
его симметрии. В сауом деле, так как АО=ОС и AC\_BD,
то точки А и С симметричны относительно оси BD. '
§ 79· Квадрат
Квадратом называется параллелограмм, все стороны и все
углы которого равны.
Квадрат можно рассматривать как прямоугольник с равными
сторонами или как ромб с равными углами.
Квадрат обладает всеми свойствами
параллелограмма, прямоугольника и ромба. Но он
имеет и своё особое свойство, отличающее
его от других видов параллелограмма.
Квадрат имеет четыре оси
симметрии: MN, PQ — как сси симметрии
прямоугольника и ACf BD — как оси симметрии
ромба (черт. 133). Черт. 133
V. НЕКОТОРЫЕ ТЕОРЕМЫ, ОСНОВАННЫЕ НА СВОЙСТВАХ
ПАРАЛЛЕЛОГРАММА
§ 80. Теоремы о средней линии треугольника
Теорема. Прямая, проходящая через середину одной
из двух сторон треугольника и параллельная третьей,
делит вторую сторону пополам, а отрезок этой прямой,
лежащий внутри треугольника, равен половине третьей
стороны.
Дано: AD = BD и DE || АС (черт. 134). Требуется доказать,
что 1) ВЕ=ЕС и 2) DE=^AC.
1. Проведём через точку Ε прямую EF, параллельную АВ.
78

Так как DE || AF по условию, a DA || EF по построению, то
четырёхугольник ADEF—параллелограмм, противоположные
стороны которого равны, а потому DE = AF и EF= AD,
следовательно, EF=DB. β
Далее, /_DBE=/_FEC как соответ- л.
ственные при параллельных АВ и EF и / >w
секущей ВС, /mBDE=/_EFC как углы с л/ \ ^
соответственно параллельными сторонами; чг т^
следовательно, /\DBE=&FEC. А по- / / \
тому ВЕ = ЕС. £ / \
2. Из равенства треугольников BDE ъ д /г ρ
FEC следует, что DE = FC, а так как
ι Черт. 134
DE = AF,to АС = 20Е9ши DE—AC.
Теорема (обратная). Прямая, соединяющая середины
двух сторон треугольника, параллельна третьей стороне,
а отрезок этой прямой, лежащий внутри треугольника,
равен половине третьей стороны.
Дано: AD=DB и ВЕ=ЕС (черт. *34). Требуется доказать, что
1) DE || АС и 2) DE—AC.
Если через точку D провести прямую, параллельную АС, то
она в силу прямой теоремы должна будет пройти через середину
стороны ВС, то есть через точку Е; следовательно, она совпадёт
с DE, так как через две точки нельзя провести двух различных
прямых. Значит, DE || АС и в силу прямой теоремы DE=-^ АС.
Отрезок прямой, соединяющий середины двух сторон
треугольника, называется средней линией треугольника.
§ 81· Теорема Фалеса*
Теорема. Если на одной стороне угла отложить ряд
равных отрезков и через их концы провести параллельные
прямые, то они отсекут на второй стороне угла также
равные между собой отрезки.
Дано: MN = NP = PQ и DM \\ EN \\ FP \\ GQ (черт. 135).
Требуется доказать, что DE = EF = FG.
Проводим прямые D/V,, ЯР,, FQi9 параллельные В А. Отрезки
D/V,, EPi9 FQi будут все равны между собой. В самом деле,
DNi=MNt EP1=NPt FQi=PQ как противоположные стороны
параллелограммов. А так как MN=NP=PQ, то DN1=:EPi=:FQi.
Сравним треугольники DENX и EFPV В них DNi=EPi9 ^EDNi=
= ^/mFEPl как соответственные и ^/mDNiE=^_EP1F как углы
с параллельными сторонами; следовательно, /\DEN1 = /\EFPlt
* Фалёс — древнегреческий учёный, жил в городе Милета в Малой Азии
(639—548 гг. до нашей эры). Ьго причисляют к группе .Семи мудрецов"
древности.
79

А потому DE=EF. Таким же образом убедимся в равенстве
треугольников EFPX и FGQ.. Следовательно, EF = FG, а потому
DE=EF=FG.
Теорема Фалёса имеет важные применения в геометрии. Одним
из её применений является решение следующей задали.
С
Μ Ν ft О
Черт. 135
Задача. Разделить данный отрезок на η равных частей.
Решение. Через конец А данного отрезка АВ (черт. 136)
проводим произвольную прямую АС и на ней от точки А
отложим равные между собой отрезки столько раз, на сколько частей
нужно разделить данный отрезок АВ. Допустим, нам нужно
разделить его на три равные части. В таком случае откладываем
три равных отрезка AD = DE = EF. Конец последнего отрезка
соединяем с β и из точек деления Dh E проводим прямые,
параллельные FB. Они пересекут отрезок АВ в искомых точках
деления Μ и /V.
Правильность решения непосредственно вытекает из теоремы
Фа леса.
УПРАЖНЕНИЯ
1. Данный отрезок разделить на пять равных частей.
2. Данный отрезок разделить на две части так, чтобы одна часть была
В четыре раза больше другой.
3. Между сторонами данного угла поместить отрезок данной длины так,
чтобы он составлял с одной из сторон угла угол
заданной величины. Всегда ли эта задача имеет
решение?
Указание. В какой-либо точке В одной
из сторон угла А (черт. 137) построить угол ABC,
равный заданному, и отложить на его стороне
отрезок ВС данной длины. Через точку С
провести прямую CD || АВ и через точку D —
прямую DH\\ ВС. Отрезок ОБ — искомый.
4. Между сторонами данного угла поместить
отрезок данной длины так, чтобы он был
параллелен данной прямой, проходящей через вершину
данного угла.
Указание. Прямая, проходящая через вершину данного угла, не должна
проходить через внутренние области данного и вертикального с ним угла.
δ. Через данную точку внутри угла провести прямую так, чтобы её
отрезок между сторонами данного угла делился в данной точке пополам.
80

6. Через данную точку внутри угла провести прямую так, чтобы её
отрезок между сторонами данного угла делился в данной точке на части, из
которых одна вдвое больше другой.
Указание. Воспользоваться теоремой Фалёса.
,7. Через точку, данную вне угла, провести прямую так, чтобы её отрезок
от данной точки до встречи с одной из сторон угла делился другой стороной
пополам.
8. Через данную точку провести прямую так, чтобы её отрезок,
заключённый между двумя данными параллельными прямыми, имел данную длину.
9. Доказать, что каждая из медиан треугольника меньше суммы двух
других и больше их разности.
10. Доказать, что та -\- tnb > -^ с.
VI. ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ В ТРЕУГОЛЬНИКЕ
§ 82· Свойства биссектрис углов треугольника
Теорема. Биссектрисы трёх углов треугольника
пересекаются в одной точке.
Проведём биссектрисы углов А и В треугольника ABC и
опустим из точки их пересечения F перпендикуляры FE, FGt FH на
стороны АВ, ВС и АС (черт. 138). Точка F должна одинаково
отстоять от сторон АВ и АС,
так как она лежит на
биссектрисе угла Л. Значит, EF=FH.
Точка F должна также
одинаково отстоять от сторон АВ и
ВС, так как она лежит на
биссектрисе угла Ву ' значит,
EF = FG. Из написанных
равенств следует: FG = FH. Это
равенство показывает, что точ- Черт. 138
ка F одинаково отстоит от
сторон ВС и АС, и, значит, она лежит на биссектрисе угла С
Следовательно, биссектрисы углов Л, β и С проходят через одну
и ту же точку F. Точка F одинаково удалена "от всех трёх
сторон треугольника.
Теорема. Биссектрисы двух внешних углов треугольника и
одного внутреннего, с ними несмежного, также пересекаются в одной
точке.
Так, биссектрисы внешних углов Ли С и внутреннего угла А
пересекаются в точке Λ, равноудаленной от сторон треугольника, продолженных
неограниченно. Учащиеся могут доказать это сами таким же способом.
§ 83. Свойства медиан треугольника
Доказанные в § 80 и 81 теоремы позволяют обнаружить весьма
важное свойство медиан треугольника. Это свойство выражается
следующей теоремой:
81

Теорема. Медианы трёх сторон треугольника
пересекаются в одной точке. Каждая медиана при
пересечении с другой медианой отсекает от неё третью часть,
считая от основания.
Из трёх медиан проводим любую, например медиану АЕ.
Докажем, что каждая из двух других медиан, например CD,
пересекает медиану ЕА в такой точке О, что ОЕ=\-АЕ.
о
В Для этого проводим в треугольнике
ABC среднюю линию DE, а через
точку Ε проводим прямую ΕΝ,
параллельную медиане DC (черт. 139).
Получаем параллелограмм DENC, в
котором DE=CN. Но DE = ±AC, сле-
М С N довательно, CN=-^AC и поэтому се-
Черт. 139 редина Μ стороны АС и точка С делят
отрезок AN на три равные части.
Проведя через точку Μ прямую ME || EN, а значит, и
параллельную ОС, получим согласно теореме Фалёса АЕ=ЕО=ОЕ9
то есть OE = -j AE.
Аналогично можно доказать, что медиана ВМ также отсечёт
от медианы АЕ тот же самый отрезок ОЕ. Следовательно, все
три медианы проходят через точку О. Точка пересечения медиан
треугольника называется центром тяжести·
§ 84· Свойство перпендикуляров, восставленных
из середин сторон треугольника
Свойство перпендикуляра, восставленного из середины отрезка,
даёт возможность вывести важное свойство перпендикуляров,
восставленных из середин сторон
треугольника. В
Теорема. Перпендикуляры к сто-
ранам треугольника, восставленные
в их серединах, пересекаются в одной
точке.
Первое доказательство.
Восставим перпендикуляры Ε К и FK из
середин сторон АВ и АС треугольника ABC
(черт. 140). Точку их пересечения К со- Черт. 140
единим со Есеми вершинами
треугольника. Точка К одинаково удалена от вершин Л и β, так как она
лежит на перпендикуляре ЕК, восставленном из середины АВ.
Следовательно, АК=КВ. Точка К также одинаково удалена от
вершин Л и С, так как она лежит на перпендикуляре FK, вос-
82
их
м,

ставленном из середины стороны С А, следовательно, АК=КС.
Из двух последних равенств следует: КВ = КС. Это равенство
показывает, что точка К лежит на перпендикуляре,
восставленном из середины стороны ВС. Значит, перпендикуляр,
восставленный из середины G стороны ВС, проходит через точку К.
Точка К одинаково удалена от всех вершин треугольника.
Второе доказательство. Перпендикуляр из середины АВ служит
осью симметрии для точек А и В, перпендикуляр из середины отрезка АС
служит осью симметрии для точек Л и С, а потому точка их пересечения К
одинаково отстоит от точек Л и β, а также от точек Л и С, а значит, и от
точек β и С. Следовательно, точка К лежит на оси симметрии точек В и С,
то есть на перпендикуляре, восставленном из середины отрезка ВС.
§ 85· Свойство высот треугольника
Теорема § 84 позволяет обнаружить интересную особенность
высот треугольника.
Теорема. Три высоты треугольника или их продол-
жения пересекаются в одной точке.
Проведём через вершины треугольника ABC прямые,
параллельные противоположным сторонам. Эти прямые образуют новый
треугольник DEF (черт. 141), для
которого Л, 5 и С служат серединами
сторон. В самом деле, СЕ = АВ и
ВА = DC как противоположные стороны
параллелограммов АВСЕ и ABDC.
Следовательно, CE = CD. Точно так же
докажем, что FB = BD и FA = AE.
Отсюда следует, что высоты
треугольника ABC являются перпендикулярами
из середин сторон треугольника DEF,
а потому они пересекаются в одной
точке.
Точка пересечения высот треугольника называется его
ортоцентром·
Точки пересечения биссектрис, медиан, высот треугольника и
перпендикуляров, восставленных из середин его сторон,
называются четырьмя замечательными точками треугольника·
УПРАЖНЕНИЯ
1. Доказать, что четыре замечательные точки равнобедренного
треугольника лежат на его высоте, а в равностороннем треугольнике они сливаются
в одну точку.
2. Через точку пересечения биссектрис углов А и С треугольника ABC
проведена прямая, параллельная стороне АС и пересекающая стороны АВ
и ВС соответственно в точках D и Е. Доказать, что DE=AD-\-EC.
3. Через точку пересечения биссектрис внешних углов А и В проведена
прямая, параллельная стороне АВ и встречающая продолжение сторон АС
и ВС соответственно в точках D и Е. Доказать, что DE = AD-\-BE.
83

4. Построить треугольник, симметричный данному относительно его центра
тяжести.
Построить треугольник, если даны:
5. тф тъ и угол между та и т^
6. та, тс, hc. 7. с, тф тс.
Указание. Построить сначала треугольник, стороны которого равны
1 1 2
у с, у тсп -jma.
8. α, b, mc.
Указание. Предположить задачу решённой, продолжить в искомом
треугольнике ABC медиану CD стороны АВ. за точку D на расстояние DE,
равное CD, и доказать, что /\ADC = /\BDE и, следовательно, ВЕ=АС.
Значит, в треугольнике СВЕ известны все три стороны и т. д.
9. а, тс, /_C 10. та, ть, тс.
Указание. В искомом треугольнике ABC провести все три медианы,
встречающиеся в точке М. Медиану CD стороны АВ продолжить за точку D
на расстояние DN = DM. Доказать, что Δ ADN^= Д BDM и что в треуголь-
2 2 2
нике AMN /Ш = -о- tna, AN=-^-mb, MN = -^-mc\ следовательно, в этом
треугольнике известны все три стороны и т. д.
VII. ТРАПЕЦИЯ
§ 86. Понятие о трапеции
Четырёхугольник, две противоположные стороны которого
параллельны, а две другие — не параллельны, называется
трапецией. Таков четырёхугольник ABCD, изо-
В С бражённый на чертеже 142.
Параллельные стороны трапеции
называются ее основаниями, а
непараллельные— её боковыми сторонами. Углы
^ D трапеции, прилежащие к одной боковой
Черт. 142 стороне, в сумме равны 2d (как
внутренние односторонние). Так (черт. 142):
^ВАО + ,/АВС = 2с1 и Z^DC + ZBCD = 2d.
Если один из углов трапеции — прямой, то трапеция
называется прямоугольной. Такова трапеция ABCD, изображённая на
чертеже 143. .
В С
А О
Черт. 143 Черт. 144
Если две боковые стороны трапеции равны между собой, то
трапеция называется равнобедренной. Такова трапеция ABCD,
изображённая на чертеже 144.
64
/ \
\

§ 87. Средняя линия трапеции
Отрезок, соединяющий середины боковых сторон трапеции,
называется средней линией трапеции.
Относительно средней линии трапеции можно доказать
следующую теорему:
Теорема. Средняя линия трапеции параллельна
основаниям трапеции и равна их полусумме.
Для доказательства теоремы
проводим диагональ BD (черт. 145)
и делим её пополам. Затем
соединяем середину G отрезка BD
с серединой Ε отрезка АВ и с
серединой F отрезка CD. Тогда
EG как средняя линия
треугольника ABD будет параллельна AD ni
AD * Л
и равна -у. Аналогично из тре- Черт. 145
угольника BCD находим, что
GF\\BC и GF=-^. Но через точку G можно провести только
одну прямую, параллельную основаниям AD и ВС, а потому EG
и GF лежат на одной прямой, и мы имеем: EF \\ ВС, EF \\ AD
ire en \ ru AD \ ВС AD4-BC
и EF = EG+GF = -2' + -2- = —f—.
§ 88· Число данных, необходимых для построения трапеции
Так как два угла трапеции, прилежащие к одной боковой
стороне, составляют 2d, то достаточно знать два угла трапеции,
не прилежащих к одной боковой стороне, чтобы определить два
других. А потому для построения трапеции нужно иметь не пять
данных, а лишь четыре, среди которых должно быть не более
двух углов трапеции.
§ 89. Свойства равнобедренной трапеции
Теорема. В равнобедренной трапеции углы при
основании равны.
Дано: в трапеции ABCD (черт. 146) AB = CD. Требуется
доказать, что /_ BAD = ^/ CD А.
Проведя прямую СЕ \\ АВ, имеем:
АВ==СЕ как противоположные стороны
параллелограмма АВСЕ. Но AB = CD,
д - -^ следовательно, CE = CD; значит, /\ECD
равнобедренный, а потому ^/mCED =
Черт. 146 /_CDE, но ^CED = Z.BAD (как
ответственные углы при параллельных
прямых АВ и ЕС и секущей АЕ). Следовательно, /_BAD — /_ADC.
85

Совершенно таким же способом доказывается и обратная
теорема:
Если углы при основании трапеции равны, то боковые
стороны её также равны.
Из доказанной теоремы вытекает ряд следствий,
доказательство которых ввиду их простоты мы предоставляем самим
учащимся:
1. Сумма противоположных углов равнобедренной трапе-
ции равна 2d.
2. В равнобедренной трапеции диагонали равны.
3. Перпендикуляр, восставленный из середины одного из
оснований равнобедренной трапеции, является её осью
симметрии и, следовательно, делит пополам другое основание.
§ 90· Общая схема подразделения всех четырёхугольников
Подразделение четырёхугольников можно представить в виде
следующей схемы (черт. 147).
Вогнутый, «выпуклый Чйёпростои!
нвадрат
Черт. 147
В настоящей схеме указаны частные виды выпуклого
четырёхугольника. Из этой схемы мы видим, что выпуклый
четырёхугольник имеет два частных вида: трапеция и параллелограмм.
Трапеция в свою очередь имеет два частных вида: равнобед-
8б

ренная трапеция и прямоугольная трапеция. Параллелограмм имеет
также два частных вида: прямоугольник и ромб. Наконец,
квадрат есть частный вид одновременно прямоугольника и ромба.
Выше мы подробно рассмотрели каждый из этих
четырёхугольников в отдельности, ограничившись лишь выпуклыми
четырёхугольниками.
VIII. МЕТОД ПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ
§ 91. Сущность метода параллельного перемещения
На свойствах параллелограмма основан особый приём решения
геометрических задач на построение, который носит название
метода параллельного перемещения. Сущность его заключается
в следующем:
Если какой-либо отрезок прямой перемещается по плоскости
так, что он остаётся параллельным своему первоначальному
положению, то говорят, что отрезок
смещается параллельно. После
такого перемещения новое положение
отрезка вместе с первоначальным
будет составлять пару
противоположных сторон параллелограмма. Так,
сместив отрезок АВ (черт. 148)
параллельно самому себе в положение Черт. 148
DC, получим параллелограмм ABCD.
Таким параллельным смещением отрезков бывает удобно
пользоваться при решении некоторых задач на построение. Именно,
иногда производя анализ задачи и отыскивая связь между
данными и искомыми элементами строимой фигуры, удаётся так
караллельно сместить отдельные отрезки, входящие в состав
этой фигуры, что эта связь обнаружится значительно быстрее,
чем без такого смещения.
Рассмотрим несколько примеров.
§ 92. Примеры применения метода параллельного
перемещения
Задача 1. Построить трапецию по четырём сторонам
я, Ъ% с, d.
Анализ. Пусть ABCD — искомая трапеция (черт. 149).
Сместим параллельно сторону ВС по направлению CD на длину Ь.
Сна займёт положение DBX. В полученном после смещения
треугольнике ADBX сторона АВх=а — b, DBx=:cy AD = d.
Следовательно, этот треугольник может быть построен по
трём сторонам. Построив его и сместив в нём сторону DBX ял
расстояние Ь, получим искомую трапецию.
87

Построение. Строим треугольник ABXD со сторонами
АВ1 = а— Ъу AD = dy DB1 = c. Продолжим сторону АВХ и
отложим на этом продолжении от точки Вх отрезок β,β = &.
Из точки D проводим прямую, параллельную АВ, и
откладываем на ней отрезок DC=b. Соединив точки β и С, получим
искомую трапецию.
Исследование. Чтобы
задача была возможна,
нужно, чтобы отрезки a, b, с,
d удовлетворяли
соотношениям c-\-d>a— b и
а — b>d—с.
Задача 2. Построить
равнобедренную трапецию
по двум её основаниям и
диагонали.
Решение. Пусть ABCD -г- искомая равнобедренная
трапеция (черт. 150). Сместим верхнее основание ВС в направлении
диагонали BD на расстояние BD. Тогда ВС займёт положение DE.
В полученном равнобедренном треугольнике АСЕ все три
стороны известны, так как АС и СЕ равны каждая данной
диагонали, а АЕ равно сумме верхнего и нижнего оснований.
Построив треугольник АСЕ, смещаем параллельно самому
себе отрезок DEy равный верхнему основанию, в направлении BD
на расстояние BD.
Задача 3. Построить четырёхугольник, если даны три
его угла и две противоположные стороны.
Указание. Четвёртый угол искомого четырёхугольника
сейчас же определится как дополняющий три первых до 4rf.
Сместим параллельно сторону ВС в направлении CD на длину CD.
Пусть DB' — смещённое положение этой стороны. Треугольник
ADB' легко построить (по двум сторонам и углу между ними)
и т. д.
УПРАЖНЕНИЯ
1. Дан угол ABC и прямая р.
Найти на прямой ρ точку л, расстояние которой от стороны АВ на
данную длину а больше её расстояния от стороны ВС.
Указание. Сместить параллельно сторону АВ в направлении, к ней
перпендикулярном, на длину а.
88

2. В плоскости данного треугольника ЛВС найти точку О, расстояние
которой от стороны АВ на данную длину а больше её расстояния от стороны
ВС и на данную длину Ь меньше её расстояния от стороны АС.
Указание. Параллельным смещением сторон ВС и АС свести задачу
к предыдущей.
3. Построить четырёхугольник по трём сторонам а, Ь, с и двум углам,
прилежащим к неизвестной стороне d.
4. Построить трапецию, если даны её диагонали, угол между ними и
боковая сторона.
5. Построить трапецию по двум параллельным сторонам и двум
диагоналям.
6. Построить трапецию по одному её углу, двум диагоналям и средней
линии.
7. Построить треугольник по высоте hc и медианам боковых сторон та и ть.
Указание. Параллельным смещением одной из медиан задача сводится
К
к построению треугольника по двум сторонам та и ть и высоте -у.
8. Построить треугольник по основанию с и медианам ρ и q его боковых
сторон.
9. Даны две точки А и В и две параллельные прямые/? и q,
пересекающие отрезок АВ. Найти на прямой ρ точку Μ и на прямой q точку N так,
чтобы отрезок MN имел данную длину, а периметр ломаной линии ΑΜΝΒ был
наименьшим.
Указание. Сместить точку А в направлении ΜΝ на длину ΜΝ.
10. Дана прямая ρ и две точки Л и β по разные стороны от неё.
Поместить на прямой ρ отрезок ΜΝ=α данной длины так, чтобы периметр
данной ломаной линии ΑΜΝΒ был наименьшим.
Указание. Сместить точку А параллельно прямой ρ на расстояние а
в положение А'. Прямая А'В пересечёт прямую ρ в точке Λί, служащей
концом искомого отрезка ΜΝ.
IX. УПРАЖНЕНИЯ К ГЛАВЕ ТРЕТЬЕЙ
А. Доказать теоремы.
1. Каждая из диагоналей четырёхугольника ^меньше его полупериметра.
2. Сумма противоположных сторон четырёхугольника меньше суммы его
диагоналей.
3. Сумма диагоналей четырёхугольника меньше его периметра и больше
полупериметра.
4. Середины сторон четырёхугольника суть вершины параллелограмма.
5. Если углы при большем основании трапеции оба острые, то сумма
проекций боковых сторон трапеции на её основание равна разности оснований.
6. Если углы при одном из оснований трапеции разноимённые (один
острый, а другой тупой), то разность проекций боковых сторон трапеции на
её основание равна разности оснований трапеции.
7. Если биссектрисы углов при одном из оснований трапеции
пересекаются на втором основании, то это второе основание равно сумме боковых
сторон трапеции.
8. Отрезок, соединяющий середины диагоналей трапеции, параллелен её
осионаниям и равен их полуразности.
9. В равнобедренной трапеции диагонали равны.
10. Прямая, соединяющая середины оснований равнобедренной трапеции,
служит осью её симметрии.
И. Треугольник, симметричный с данным относительно середины его
основания, вместе с данным треугольником образует параллелограмм.
12. Сумма расстояний любой точки, лежащей внутри параллелограмма, от
ьсех €Г0 продолженных сторон есть величина постоянная.
89

13. Продолженные параллельные стороны параллелограмма отсекают на
прямой, параллельной его диагонали, равные отрезки.
14. Биссектриса внешнего угла параллелограмма вместе с его
сторонами, не проходящими через вершину этого угла, образуют
равнобедренный треугольник, сумма боковых сторон которого равна периметру
параллелограмма.
15. Основания перпендикуляров, опущенных из точки пересечения
диагоналей ромба на его стороны, суть вершины прямоугольника.
16. Отрезки, отсекаемые нарами противоположных сторон квадрата на
двух перпендикулярных прямых, равны между собой.
17. Если на сторонах квадрата ABCD отложить равные отрезки (на
стороне АВ— отрезок AM, на стороне ВС — отрезок BN, на стороне CD
—отрезок СЯ, на стороне DA — отрезок DQ, AM — BN = СР = DQ), то точки
Α/, Ν, Ρ, Ο будут вершинами нового квадрата.
18. Если через две противоположные вершины квадрата провести
параллельные прямые, а через две другие вершины — прямые, перпендикулярные
к первым, то четыре проведённые прямые в пересечении образуют квадрат.
Б. Задачи на построение.
Элементы четырёхугольника будем обозначать так, как указано на
чертеже 151, а именно, стороны: АВ = a, CD = с, AD = d,BC = ft; диагонали: АС = е,
* BD=f\ углы: Л, В, С, Д угол между диагона-
- лями: М.
Построить выпуклый
четырёхугольник, если даны:
19. a, ft, с, е, /. 20. а, ft, с, е, £С.
21. а, ft, с, d, Ζ А. 22. а, ft, е, /, Ζ Μ.
23. а, с, е, /, Ζ Л. 24. а, ft, d, Ζ Л, Ζ В.
25. а, ft, f, LB> L Μ. 26. а, с, е, Ζ θ, Ζ Λ1
Черт. 151 27. а, ft, Ζ ^» Ζ ^ Ζ Λί· 28. а, с, Z^.ZftZ. Я.
29. Внутри данного четырёхугольника найти точку, сумма расстояний
которой от всех вершин четырёхугольника была бы наименьшей.
В трапеции ABCD основания AD и ВС обозначим соответственно буквами
α и ft, боковые стороны АВ и CD — буквами е и /, высоту трапеции — буквой
Λ, среднюю линию — буквой т, углы — буквами Л, В, С, Д угол между
диагоналями — буквой М.
Построить трапецию, если даны:
30. я, ft, с, е. 31. а, с, rf, е.
32. а, с, rf, Λ. 33. а, е, /, Λ. 34. а, ft, с, /?.
35. а, ft, *?, Λ. 36. а, с, rf, Ζ Α· 37· Λ> ^ с Ζ β·
38. α, Λ, Ζ Λ. Ζ Λ 39. α, Λ, Ζ Α Ζ Μ· 40. α, ft, Ζ Λ. Ζ 0.
41. m, Λ, с, rf. 42. /я, Λ, Ζ ^, Ζ D· 43· α> c> «. Ζ^·
Построить параллелограмм, если даны:
44. Две смежные стороны и одна диагональ.
45. Сторона и две диагонали.
46. Две смежные стороны и один из углов.
47. Две смежные стороны и высота.
48. Две диагонали и угол между ними.
49. Две диагонали и высота.
50. Диагональ, сторона и высота, опущенная на эту сторону.
51. Диагональ, сторона и высота, опущенная на другую сторону.
£0

Построить прямоугольник, если даны:
52. Две его смежные стороны.
53. Сторона и диагональ.
54. Диагональ и угол между диагоналями.
Построить ромб, если даны:
55. Сторона и один из углов.
56. Диагональ и один из углов.
57. Две диагонали.
58. Диагональ и высота.
59. Высота и угол.
60. Построить квадрат, если дана его диагональ.
61. Даны две точки А и В; провести прямую, наклонённую к прямой АВ
под данным углом так, чтобы сумма её расстояний от точек А и В была
равна данному отрезку а.
62. Построить квадрат, стороны которого проходят через четыре данные
точки.
Указание. См. упр. 16.
63. Построить пятиугольник, если дано положение середин его сторон.
Указание. Теорема §80 даёт возможность определить длину и
направление каждой диагонали искомого пятиугольника. Упражнение 4 позволяет
определить положение середины каждой диагонали.

ГЛАВА ЧЕТВЁРТАЯ
ОКРУЖНОСТЬ
I. ОБЩИЕ СВОЙСТВА ОКРУЖНОСТИ
§ 93. Число точек, определяющих окружность
Мы знаем, что для построения прямой нужно задать две её
точки. Посмотрим, сколько точек нужно задать, чтобы через них
можно было провести одну окружность. Возьмём на плоскости
сначала две точки Л и В (черт. 152) и будем искать центр
окружности, проходящей через эти точки. Этот центр должен находиться
на одинаковом расстоянии от точек Л и β и, следовательно, ле-
Черт. 152 Черт. 153
жать на перпендикуляре к прямой АВ, восставленном из середины
отрезка АВ (§ 66, задача 3). А так как любая точка С этого
перпендикуляра одинаково отстоит от концов отрезка АВ, то за
центр окружности, проходящей через точки Л и β, можно взять
любую точку этого перпендикуляра. Таким образом, можно
построить бесчисленное множество окружностей, проходящих через
взятые точки Л и β.
Возьмём теперь на плоскости три точки Л, В и С, не лежащие
на одной прямой (черт. 153). Будем искать центр окружности,
проходящей через эти точки. Этот центр должен находиться на
одинаковом расстоянии от всех трёх точек Л, В и С. В § 84 было
показано, что этим свойством обладает точка О пересечения
перпендикуляров, восставленных из середин сторон треугольника ABC,
и только она одна. Эта точка и служит искомым центром
окружности, проходящей через точки Л, β и С. Для построения этого
92

центра достаточно провести лишь два из этих трёх
перпендикуляров, например из середин отрезков АВ и ВС. Если точки А, В
и С будут взяты на одной прямой, то перпендикуляры из середин
отрезков АВ и ВС будут параллельны. Значит, через такие точки
окружность провести нельзя.
Итак:
Через всякие три точки плоскости, не лежащие на
одной прямой, можно провести окружность и притом
только одну.
§ 94· Симметрия окружности
Центр окружности служит центром её симметрии,
так как каждой точке окружности соответствует точка,
симметричная с ней относительно центра, а именно: второй конец
диаметра, проходящего через эту точку.
Любой диаметр окружности есть её ось симметрии.
В самом деле, проведём два взаимно перпендикулярных диаметра
АВ и CD (черт. 154) и перегнём плоскость чертежа по диаметру
CD так, чтобы правая её часть совместилась с левой. Точка В
совместится с Л, и вся правая часть окружности CBD совместится
с левой CAD, так как через три точки Л, С и D можно провести
лишь одну окружность. Следовательно, CD — ось симметрии
окружности.
Рассмотрим следующие свойства хорд и дуг окружности,
которые вытекают из симметрии окружности.
Теорема 1. Диаметр, перпендикулярный к хорде,
делит эту хорду и стягиваемую ею дугу пополам.
В самом деле, диаметр CD (черт. 154), делит хорду MN, к нему
перпендикулярную, и дугу MCN пополам, так как после
перегибания плоскости чертежа вокруг CD точка N совместится с Μ и,
следовательно, отрезок ΝΡ—с отрезком ΡΛί, а дуга CN — с
дугой СМ.
Предлагаем читателю доказать следующие две теоремы,
обратные первой:
93

Диаметр, проведённый через середину хорды,
перпендикулярен к этой хорде и делит стягиваемую ею дугу
пополам.
Диаметр, проведённый через середину дуги,
перпендикулярен к хорде, стягивающей эту дугу, и делит её пополам.
Теорема 2. Дуги, заключённые между параллельными
хордами, равны.
В самом деле, эти дуги симметричны относительно диаметра,
перпендикулярного к данным хордам. На чертеже 155 дуги АС и
HD симметричны относительно диаметра MN, следовательно,
kjAC=kjBD.
§ 95· Зависимость длин хорд от их расстояния от центра
Относительно хорд одной и той же окружности справедливы
следующие теоремы:
Теорема. Равные хорды равно отстоят от центра,
и обратно: хорды, равноотстоящие от центра, равны.
1. Дано: AB=CD, OE\_AB и OF±CD (черт. 156).
Требуется доказать, 4toOE = OF.
Прямоугольные треугольники ОБЕ и ODF равны, так как
Черт. 156 Черт. 157
OB=OD как радиусы; ВЕ= FD как половины равных хорд;
следовательно, OE=OF.
2. Если OE = OF, то прямоугольные треугольники ОВЕ и ODF
равны (по катету и гипотенузе), а потому BE = DFt или у АВ=
= —CD, следовательно, AB = CD.
На чертеже 157 изображены окружность и несколько хорд,
параллельных её диаметру. Докажем относительно них теорему:
В ряду всех хорд, параллельных диаметру, всегда можно
отыскать хорду, равную по длине любой хорде
окружности.
В самом деле, проведём, например, хорду MN (черт. 157) и
из центра окружности О опустим перпендикуляр ОК на хорду MN.
04

Затем на радиусе ОС отложим отрезок ОКг = О К- Тогда хорда
Λί,Ν,, перпендикулярная к отрезку О/С,, будет параллельна
диаметру АВ и согласно предыдущей теореме будет равна хорде ΜΝ.
Рассматривая параллельные хорды одной окружности, мы
убеждаемся, что большая из двух неравных хорд
расположена ближе к центру окружности, и наоборот, чем меньше
расстояние хорды от центра окружности, тем она больше.
Хорда, проходящая через центр, то есть диаметр, будет
наибольшей из хорд. Кроме того, имеют место следующие теоремы:
Большая дуга стягивается большей хордой, и наоборот,
большая хорда стягивает большую дугу.
Так как любым двум хордам соответствуют равные им хорды
в ряду параллельных хорд, то все высказанные нами теоремы
относительно параллельных хорд имеют место и для любых хорд
одной окружности.
II. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ОКРУЖНОСТИ И ПРЯМОЙ ЛИНИИ
§ 96. Прямая, не пересекающая окружности
Прямая может не иметь с окружностью ни одной общей точки.
Таковы все прямые, расстояния которых от центра больше
радиуса окружности. В самом деле, еслиОО±_ АВ и 0Д> ОС (черт. 158),
то точка D лежит вне окружности
и любая точка Μ прямой АВ также
лежит вне окружности, так как ОМ *>OD
(§ 63). Построить такую прямую не
представляет затруднений.
§ 97. Касательная к окружности
Прямая может иметь с
окружностью одну общую точку. В этом
случае она называется касательной к
окружности. Построить такую прямую
можно следующим образом. Проведя
произвольный радиус окружности О А ЧеРт· 158
(черт. 159), строим прямую Λί/V,
перпендикулярную к ОА в точке А Прямая MN и будет искомой
касательной. В самом деле, так как MN _]_ОЛ, то расстояние
всякой точки В прямой MN от центра больше радиуса ОА, то
есть ОВ>ОА (§ 63). А потому все точки прямой Λί/V, кроме
точки Л, лежат вне окружности, то есть прямая ММ имеет с
окружностью одну общую точку Л. Отсюда вытекает теорема:
Прямая, перпендикулярная к радиусу β конце его, есть
касательная.
Для этой теоремы верна и обратная:
Касательная перпендикулярна к радиусу, проведённому
в точку касания.
95

В самом деле, предположим, что МЫ—касательная к
окружности в точке Л. Докажем, что МЫ ±_ОА (черт. 159).
Все точки прямой МЫ, кроме точки Л, лежат вне окружности.
Поэтому для всякой точки В этой прямой ОВ>ОА. Значит,
радиус ОА есть наименьший из всех отрезков, соединяющих
центр О со всеми точками прямой МЫ, следовательно, ОА J_ МЫ
(§ 63).
Ещё одно свойство касательной выражается следующей
теоремой:
Если касательная параллельна хорде, то тонка^
касания делит пополам дугу, стягиваемую этой хордой.
Даны касательная CF и хорда АВ, причем CF\\AB (черт. 160).
Требуется доказать, что kjAC=vCB.
Так как CF— касательная, то С/7 JL ОС, а так как CF\\AB, то
АВ±ОС, следовательно, и kjAC=\jCB (§ 94).
§ 98. Секущая прямая
Прямая может пересекать окружность в двух точках. В этом
случае она называется секущей. Такова, например, всякая прямая
АВ, проходящая через конец радиуса ОА (черт. 161) и не
перпендикулярная к нему. В самом деле,
прямая АВ не может иметь с
окружностью лишь одну общую точку Л, так
как в этом случае она была бы
перпендикулярна к радиусу О А. Но более двух
общих точек прямая и окружность
иметь не могут, так как через три
точки, лежащие на одной прямой,
окружности провести нельзя. Следова-
Черт. 161 тельно, кроме точки Л, прямая АВ имеет
с окружностью ещё одну общую
точку С. Так так АО является наклонной к АВ, то перпендикуляр
OD меньше АО, то есть расстояние прямой АВ от центра О
меньше радиуса.
96

§ 99. Общий вывод
Рассмотренные выше три случая исчерпывают все возможные
виды взаимного расположения прямой и окружности. Таким
образом, прямая линия и окружность могут занимать следующие
положения одна относительно другой.
1. Прямая отстоит от центра на расстоянии, большем радиуса;
такая прямая не пересекает окружности.
2. Прямая отстоит от центра на расстоянии, равном радиусу;
такая прямая касается окружности и носит название касательной.
3. Прямая отстоит от центра на расстоянии, меньшем радиуса;
такая прямая пересекает окружность в двух точках и носит
название секущей.
III. УГЛЫ, ОБРАЗОВАННЫЕ ПРЯМЫМИ, ПЕРЕСЕКАЮЩИМИ
ОКРУЖНОСТЬ
§ 100. Вписанный угол
Вписанным углом называется угол, составленный двумя
хордами, пересекающимися в точке, лежащей на окружности. Таков
угол ABC (черт. 162). Принято говорить, что вписанный угол ABC,
а также центральный угол АОС опираются на одну и ту же
дугу АС (черт. 162).
Теорема. Вписанный угол измеряется половиной дуги,
на которую он опирается. й
Черт. 162 Черт. 163
Рассмотрим три возможных случая.
1. Одной из сторон угла служит диаметр окружности (черт. 163).
Соединив точку С с центром О, получим равнобедренный
треугольник ВОС, для которого ^АОС — внешний, а потому
/_АОС=2/ОВС (§ 40, следствие 2) или /тАВС=\/_АОС.
Но так как центральный угол АОС измеряется дугой АС, то
вписанный угол АВС9 равный его половине, будет измеряться
половиной дуги АС.
97

2. Центр О лежит внутри угла ABC (черт. 164). Проведя
диаметр 5D, мы разобьём /_АВС на сумму двух углов:
Ζ АВС= Ζ ABD + Ζ DBC.
Но так как угол ABD измеряется половиной дуги AD, a
угол DBC измеряется половиной дуги DC, то угол ABC
измеряется полусуммой дуг AD и DC, то есть половиной дуги АС.
Φ
Черт. 164 Черт. 165
3. Центр О лежит вне вписанного угла (черт. 165). Проведя
диаметр BD, заметим, что ^/ABC=/_DBC — /_DBA.
Но Ζ DBC измеряется у —DC, а ^05Л измеряется у ^-ОЛ,
следовательно, ^Л5С измеряется y^DC—y^DЛ, то есть
Следствия. 1. Вписанные углы, опирающиеся на одну и ту
же дугу, равны.
Так, ^/ ABC = £ADC= Z. AEC= /_ AFC (черт. 166), так как
все эти углы измеряются половиной одной и той же дуги АС.
Черт. 166 Черт. 167
2. Вписанный угол, опирающийся на диаметр (то есть на
полуокружность), прямой, так как он измеряется половиной дуги,
содержащей 180° (черт. 167).
98

§ 101. Угол между хордой и касательной
Теорема. Угол, образованный хордой и касательной,
измеряется половиной дуги, лежащей внутри этого угла.
Даны хорда АВ и касательная ВС. Требуется доказать, что
2
АМВ.
/_ ABC измеряется
Проведя прямую AD \\ ЕС
(черт. 168), получим /_ АВС =
= /_BAD как накрест лежащие
и - АМВ = — BND (§ 94).
/_ BAD измеряется -j —&VD,
следовательно, равный ему
/_АВС измеряется 1 — BND =
~ — АМВ.
В
Черт. 168
Отсюда следует, что дополнительный /_АВЕ как смежный
с /_АВС измеряется -к — ADB.
§ 102. Угол с вершиной внутри круга
Теорема. Угол, образованный двумя хордами,
пересекающимися внутри круга, измеряется полусуммой двух
дуг, заключённых: первая — между
сторонами угла, вторая — между их
продолжениями.
Даны хорды АВ и CD (черт. 169). Требуется
доказать, что /_AED измеряется ^
Проведя хорду ВК || CD, мы будем иметь:
~СЯ = —DAT (§ 94) и ^AED = Z.ABK
как соответственные. ^АВК измеряется
половиной дуги АК> Но — АК равна сумме дуг
AD и DK, или сумме дуг AD и ВС.
Таким образом, угол AEDt равный АВК, измеряется
~АР+~СВ
2
§ 103. Угол между двумя секущими
Теорема. Угол, образованный двумя секущими,
пересекающимися вне круга, измеряется полуразностью дуг,
заключённых между сторонами этого угла.
90

Даны секущие АВ и CD, пересекающиеся в точке Ε (черт. 170)·
Требуется доказать, что ^АЕС измеряется
*->AC—*->BD
2
Проведя прямую BK\\CD9 находим: /_АВК=/_АЕС и
^BD = ^KC9 (§ 94), но —АК=^АС — ^КС или ~ Л/С=
= — ЛС — — m
Черт. 170
Так как /_АВК измеряется у^-Д/С, то равный ему /_АЕС
измеряется ^ac — ^bd
2 ~~ ·
§ 104. Описанный угол
Угол между двумя касательными называется описанным углом.
Теорема. Описанный угол измеряется полу разностью
дуг, заключённых между сторонами угла.
Черт. 171
Даны две касательные: АВ и ВС. Требуется доказать, что
, яп„ ^ADC-^AEC
/_ ABC измеряется ^ .
Проведя АК\\ВС (черт. 171), находим: /mFAK=/^ABC и
w^c = ~ С К (§ 94). Но /_FAK измеряется -j — AK (§ 101) или
полуразностью дуг ADC и ЛЕС.
Следовательно, равный ему ^FBC также· измеряется
^ADC-~AEC
100

IV. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ОКРУЖНОСТЕЙ
§ 105. Линия центров
Неограниченно продолженная прямая, соединяющая центры
двух окружностей, называется их линией центров. Такова
линия ООх (черт. 172). Эта линия является неограниченно продол·
женным диаметром обеих
окружностей.
Так как диаметр
окружности есть ось её симметрии, то
линия центров служит осью
симметрии всей фигуры, образо- ·
ванной обеими окружностями.
§ 106. Пересекающиеся
окружности
Две окружности не могут ЧеРт· 172
пересекаться более чем в двух
точках, так как через три точки можно провести только одну
окружность.
Из симметрии окружностей относительно их линии центров
следует, что: 1) точки пересечения двух окружностей
расположены симметрично относительно их линии центров. Таковы точки
А и В (черт. 172); 2) общая хорда двух пересекающихся
окружностей перпендикулярна к линии центров и делится ею пополам;
АВ±001 и СА = СВ.
Углы между касательными к обеим окружностям в каждой из
точек их пересечения равны между собой. Каждый из них
называется углом между данными окружностями. Если этот угол
прямой, то окружности называются взаимно ортогональными.
Соединив точку А с центрами О и О,, получим
треугольник ОАО,, в котором ΟΟ^ΟΑ + Ο,Α и ΟΟλ>ΟΑ — ΟλΑ\
значит, расстояние между центрами пересекающихся окружностей
меньше суммы радиусов и больше их разности.
§ 107. Касающиеся окружности
Если две окружности имеют лишь одну общую точку, то
принято говорить, что они касаются одна другой.
Касание окружностей может быть двояким:
1) внешним, когда окружности расположены одна вне другой
(черт. 173), и 2) внутренним, когда одна окружность лежит
внутри другой (черт. 174). В обоих случаях точка касания
окружностей лежит на их линии центров, так как если бы окружности
имели общую точку не на линии центров, то они имели бы и
вторую общую точку, симметричную с первой относительно линии
101

центров. При внешнем касании OOl = OA-\-A01 (черт. 173), при
внутреннем ΟΟί = ΟΑ — О,А (черт. 174). Итак, если две
окружности касаются, то расстояние между их центрами равно сумме
Черт. 173
Черт. 174
радиусов, если касание внешнее, и разности радиусов, если каса-
ьие внутреннее.
§ 108· Непересекающиеся окружности
Если окружности не имеют общих точек, то они могут быть
двояко расположены одна относительно другой:
1) лежать одна вне другой (черт. 175) и 2) лежать одна внутри
Черт. 175
Черт. 176
так как
другой (черт. 176). В первом случае расстояние между их
центрами, очевидно, больше суммы радиусов:
ОО^ОА + О^,
OOi = OA + 01A1 + AA1.
Во втором — оно меньше разности
радиусов. В самом деле, из чертежа 176
находим: ΟΑ = 001 + 01Αί-\-ΑίΑ.
Вычитая из обеих частей по ΟλΑν
получим:
ОД — ОлА, = ООх +А% А.
Следовательно, О А — О, Д, > OOv
Если две окружности имеют общий центр,
они называются концентрическими (черт· 177).
Черт. 177
(02

§ 109. Общий вывод
Мы рассмотрели все (пять) возможные случаи расположения
двух не концентрических окружностей, а потому будут
справедливы утверждения, обратные доказанным.
Обозначая через d расстояние между центрами даух
окружностей радиусов R и R^iR^RJ, мы можем теперь утверждать
следующее:
1) если /? + /?! >d>/?— /?р то две окружности
пересекаются;
2) если R-\-Ri=d, то две окружности касаются одна
другой внешним образом;
3) если R — R^=d, то две окружности касаются одна другой
внутренним образом;
4) если RJ^R1<id, то две окружности расположены одна
вне другой;
5) если R — /?!>ί/, то окружность радиуса R1 лежит внутри
окружности радиуса R.
Найденные соотношения между радиусами окружностей и
расстоянием между их центрами позволяют, зная это расстояние и
радиусы окружностей, определить их взаимное расположение, не
вычерчивая самих окружностей.
Так, например, если расстояние между центрами d=7 см,
радиус первой окружности R = 5 см, радиус второй R1 = 3 смг
то окружности пересекаются, так как d^R-^-R^ d^>R — /?,,.
а ни при каком другом положении окружностей такого
соотношения не бывает.
Если d=3 см, R=\l см, /?j=4 см, то R — R1=7 см,
следовательно, d<iR — R^ — окружности не пересекаются и лежат
одна внутри другой.
Если d=lb cm, R = 9 cm, R1=Q см, то R-^R^ = 15 см,
следовательно, d = R-\-Rl — окружности касаются и лежат одна
вне другой.
V. ЗАДАЧИ НА ОКРУЖНОСТЬ
§ по
Задача 1. Определить центр дуги окружности.
Решение. Взяв на дуге три произвольные точки А, В и С
(черт. 178), будем искать центр окружности, проходящей через
эти точки. Для этого восставляем из середин хорд АВ и ВС
перпендикуляры к ним; точка их пересечения О и есть
искомый центр.
Задача 2. На отрезке АВ как на лорде построить дугу
окружности, вмещающую данный угол (то есть так, чтобы
вписанный угол, опирающийся на эту дугу, был равен данному).
Анализ. Предположим, что задача решена и С — есть центр
искомой дуги. Так как отрезок АВ (черт. 179) служит хордой
103

искомой дуги, то точка С лежит на перпендикуляре CD к
прямой АВ, восставленном из середины отрезка АВ. ^/_АСВ как
центральный угол должен быть в два раза больше данного
вписанного угла, a /_ACD должен быть равен данному. Отсюда
вытекает построение.
Построение. Из
середины D отрезка АВ восставляем
к нему перпендикуляр и при
какой-либо его точке К строим
Черт. 178
Черг. 179
угол, равный данному, одной стороной которого служит КО.
Из точки А проводим прямую, параллельную второй стороне
построенного угла. Она пересечёт прямую KD в точке С.
Из точки С как из центра радиусом СА описываем дугу АМВ.
Дуга ANB, симметричная с дугой АМВ относительно
прямой АВ, также удовлетворяет поставленному условию. Задача
имеет два решения.
Задача 3. Из данной точки вне
окружности провести к ней касательную.
Первое решение.
Анализ. Предположим задачу
решённой. ПустьЛ — данная точка и АХ—искомая
касательная, А' —точка её касания с данной
окружностью (черт. 180). Соединим точку Л
с центром О. Продолжим радиус ОХ и
отложим на нём от точки X отрезок
ХК=ОХ. Соединив затем точки А и К9
получим треугольник АКО, в котором
ОХ=ХК и АХ J_ OK, следовательно, этот
треугольник равнобедренный и АК=АО$
то есть точка К находится от точки А на расстоянии АК, равном
АО, и от центра О на расстоянии ОК> равном диаметру
окружности. Отсюда следует построение.
Построение. Радиусом, равным АО, описываем из точки А
как из центра дугу окружности. Радиусом, равным диаметру
данной окружности, описываем из центра О вторую дугу. Эти дуги
104

пересекаются в двух точках К и Кх (черт. 180). Соединим точку К
с центром О. Прямая ОК пересечёт окружность в точке X. Пря-г
мая АХ есть искомая касательная. Сделав такое же построение
для точки /Ср получим вторую касательную АХХ.
Доказательство. Так как отрезок ОК равен диаметру,
то есть двум радиусам, а ОХ есть радиус, то КХ = ХО;
следовательно, в равнобедренном треугольнике АКО отрезок АХ есть
медиана стороны ОК, а потому он служит и высотой. Значит,
AXJlOX, следовательно, АХ есть касательная (§ 97). То же
докажем и для прямой AXV Задача имеет два решения.
Из сделанных построений можно вывести такие следствия:
/\АХО = /\АХгО как прямоугольные треугольники с общей
гипотенузой АО и равными
катетами ОХ и ΟΧν А поэтому
АХ=АХХ и £ О АХ = Ζ ОАХ\.
Следовательно:
1. Касательные, проведённые из Д
одной точка к окружности, равны.
2. Прямая, соединяющая точку
пересечения двух касательных с
центром, делит пополам угол
между ними. 4ерт 181
3. Прямая, соединяющая точку
пересечения двух касательных с центром, делит пополам
угол между радиусами, проведёнными в точки касания.
Второе решение.
Соединив точку А с центром О, строим новую окружность,
для которой отрезок О А служит диаметром (черт. 181).
Эта окружность пересечёт данную в искомых точках
прикосновения X и Хх. В самом деле, углы ΑΧΟ и АХхО — прямые,
так как они опираются на диаметр АО в проведённой второй
окружности.
Следовательно, прямые АХ и АХХ перпендикулярны к
радиусам данной окружности ОХ и ОХх в точках X и Х1% а потому
они служат касательными к данной окружности (§ 97).
УПРАЖНЕНИЯ
А. Доказать теоремы.
1. Параллельные хорды, проведённые через концы одного диаметра,
равны между собой.
2. Если прямая пересекает две концентрические окружности, то отрезки
секущей между этими окружностями равны между собой.
3. Две хорды данной окружности, имеющие одинаковую длину, касаются
окружности, концентрической с данной.
4. Из всех хорд, проходящих через данную точку внутри круга,
наименьшую длину имеет та, которая перпендикулярна к радиусу, проходящему через
эту точку.
5. Из всех отрезков, соединяющих данную точку внутри круга с
различными точками окружности, наибольшим и наименьшим являются отрезки
диаметра. .
105

6. Вписанный угол вращается вокруг вершины, не изменяя величины.
Доказать, что хорда, стягивающая его дугу, скользит по плоскости, оставаясь
касательной к окружности, концентрической с данное.
7. Если точки С и D лежат по одну сторону от прямой АВ и
^/ АСВ = /_ ADB, то точки А, Д С и D лежат на одной окружности.
8. Диагонали АС и BD четырёхугольника ABCD пересекаются в точке М.
Дано, что касательная в точке Μ к окружности, проходящей через точки
А, В, Λί, параллельна стороне CD. Доказать, что сумма противоположных
углов четырёхугольника ABCD равна 2d.
9. Дана окружность с центром в точке О и точка Μ вне её. Чзрез
точку Μ проведены: диаметр МАВ и секущая MCD, такая, что её внешняя
часть МС равна радиусу окружности. Доказать, что £ BMD = -^-^BOD.
о
10. Угол между секущей и касательной равен полуразности центральных
углов, опирающихся на дуги, заключённые между сторонами угла.
И. Доказать, что касательная в точке пересечения двух взаимно
ортогональных окружностей к одной из них проходит через центр другой.
12. Доказать, что угол между двумя пересекающимися окружностями
равен углу между их радиусами, проведёнными в точку их пересечения.
13. Две окружности имеют внешнее касание. В точке их касания
проведена к ним общая касательная и, кроме того, проведена общая внешняя
касательная. Доказать, что отрезок этой второй касательной между точками
касания при пересечении с первой касательной делится пополам.
14. Две окружности касаются одна другой. Через точку их касания
проведена секущая. Доказать, что касательные к окружностям в точках их
встречи с секущей параллельны между собой.
15. Две касающиеся окружности отсекают на прямой, проходящей через
точку их касания, хорды, которые видны из центров окружностей под
равными углами.
16. Если даны две окружности, касающиеся одна другой изнутри, причём
меньшая проходит через центр большей, то хорды большей окружности,
проводящие через точку касания, делятся меньшей окружностью пополам.
17. Две окружности имеют внутреннее касание в точке С. В какой-либо
точке Μ внутренней окружности проведена к ней касательная, встречающая
внешнюю окружность в точках А н В. Доказать, что отрезки AM и ВМ
видны из точки С под равными углами.
Указание. Провести прямую СМ и продолжить её до встречи с
внешней окружностью. Далее см. упр. 14 и конец § 97.
18. Две окружности пересекаются в точках А и В. В точке А проведены
касательные к каждой из них. Доказать, что отрезки этих касательных,
лежащие внутри окружностей, видны из точки В под равными углами.
19. Две окружности пересекаются в точках А и В. Через точку А
.проведена секущая CAD. Доказать, что отрезок CD виден из точки Я под
постоянным углом.
Указание. В треугольнике BCD углы BCD и BDC имеют постоянную
величину.
20. Две окружности пересекаются в точках А и В. Через точку А
проведена секущая CAD. В точках С и D построены касательные к
окружностям. Доказать, что эти касательные пересекаются под постоянным углом.
Указание. При помощи теоремы § 101 задача сводится к упр. 19.
21. Из всех секущих, проведённых через точку пересечения двух
окружностей, наибольшую длину имеет та, которая параллельна линии центров (под
длиной секущей здесь понимается часть секущей, лежащая внутри обеих
окружностей).
Указание. Из центров окружностей опустить перпендикуляры на
произвольную секущую, проходящую через точку пересечения окружностей, и
рассмотреть получаемую при этом прямоугольную трапецию.
22. Из точки А вне окружности проведены к ней две касательные
АВ и АС. К какой-либо точке Λί на меньшей дуге ВС проведена третья
касательная, встречающая две первые в точках Ρ и Q. Доказать, что при переме-
i06

щении точки Μ по дуге ВС периметр треугольника APQ имеет постоянную
величину, равную АВ-\-ВС.
23. В точках А и В, произвольно взятых на окружности, проведены к ней
касательные АС и ВС, пересекающиеся в точке С. В какой-либо точке Μ
меньшей дуги АВ проведена третья касательная, пересекающая две первые.
Доказать, что отрезок этой третьей касательной, заключённый между двумя
первыми, виден из центра под постоянным углом (§ ПО, следствие 3).
24. Отрезок произвольной касательной к окружности, заключённый между
двумя параллельными касательными к той же окружности, виден из центра
под прямым углом (§ ПО, следствие 3).
25. Две окружности касаются одна другой внешним образом в точке С.
Проведённая к ним общая касательная касается их в точках А и В.
Доказать, что треугольник ABC— прямоугольный.
26. Доказать, что в равных треугольниках радиусы описанных
(вписанных) окружностей равны.
Б. Найти геометрические места точек.
27. Геометрическое место середин хорд данной длины в данной
окружности. Отв. Окружность, концентрическая с данной.
28. Геометрическое место середин параллельных хорд в данной
окружности. Отв. Диаметр, перпендикулярный к этим хордам.
29. Геометрическое место центров окружностей данного радиуса,
проходящих через данную точку. Отв. Окружность с центром в данной точке.
30. Геометрическое место центров окружностей, касающихся данной
прямой в данной точке. Отв. Прямая, перпендикулярная к данной.
31. Геометрическое место центров окружностей данного радиуса,
касающихся данной прямой. Отв. Две прямые, параллельные данной.
32. Геометрическое место центров окружностей данного радиуса,
касающихся данной окружности. Отв. Две окружности, концентрические с данной.
33. Геометрическое место центров окружностей, проходящих через две
данные точки. Отв. Перпендикуляр в середине отрезка, соединяющего
данные точки.
34. Геометрическое место центров окружностей данного радиуса,
пересекающих данную прямую под данным углом. (Угол, под которым окружность
пересекает прямую, называется угол между данной прямой и касательной:
к окружности в точке её пересечения с данной прямой.) Отв. Две прямые,,
параллельные данной.
35. Геометрическое место центров окружностей данного радиуса,
пересекающих данную окружность под прямым углом. Отв. Окружность,
концентрическая с данной.
36. Геометрическое место центров окружностей, касающихся двух
данных пересекающихся прямых. Отв. Две прямые линии, делящие пополам углы
между данными прямыми.
37. Геометрическое место концов равных касательных, проведённых
к данной окружности. Отв. Окружность, концентрическая с данной.
38. Геометрическое место веошин прямых углов, стороны которых
проходят через две данные точки. Отв. Окружность, диаметром которой служит
отрезок, соединяющий данные точки.
39. Геометрическое место середин хорд данной окружности, выходящих
из данной точки окружности. Отв. Окружность, диаметром которой служит
радиус данной окружности, проходящий через данную точку.
40. Геометрическое место центров окружностей, отсекающих на
сторонах данного угла равные хорды. Отв. Биссектриса данного угла.
41. Даны две концентрические окружности. Найти геометрическое место
вершин прямых углов, у которых одна сторона касается внешней
окружности, другая — внутренней. Отв. Окружность, концентрическая с данными.
42. Отрезок постоянной длины скользит по плоскости, оставаясь
параллельным самому себе, так, что один его конец перемещается по данной
окружности. Какую линию описывает второй конец этого отрезка? Отв.
Окружность, равную данной.
107

43. Отрезок АВ постоянной длины скользит по плоскости так, что его
концы А и В перемещаются по двум взаимно перпендикулярным прямым ОА
и ОВ. Какую линию описывает при этом середина этого отрезка? Отв. Окруж-
«ость с центром в точке О и радиусом -~-.
В. Задачи на построение.
Построить окружность данного радиуса:
44. Проходящую через две данные точки.
45. Касающуюся данной прямой и центр которой находился бы на другой
данной прямой. (Данные прямые не параллельны.)
46. Касающуюся данной прямой и отсекающую на другой данной прямой
.хорду данной длины. (Данные прямые не параллельны.)
47. Касающуюся данной прямой и данной окружности.
48. Касающуюся двух данных пересекающихся прямых.
49. Касающуюся двух данных окружностей.
50. Проходящую через данную точку и касающуюся данной прямой или
данной окружности.
51. Построить окружность, касающуюся данной прямой в данной её точке
и данной окружности.
Указание. Сместить параллельно данную прямую в направлении, к ней
перпендикулярном, на длину радиуса данной окружности.
52. Построить окружность, проходящую через данную, точку и
касающуюся двух данных параллельных прямых.
Указание. Построить какую-либо окружность, касающуюся данных
прямых, а затем сместить её параллельно так, чтобы она прошла через
данную точку.
53. Через точку, данную внутри круга, провести хорду так, чтобы она
в этой точке делилась пополам.
54. К данной окружности провести касательную параллельно данной
прямой.
55. Через точку, лежащую вне окружности, провести секущую так, чтобы
её часть, лежащая внутри окружности, имела данную длину.
56. Через точку, лежащую вне окружности, провести секущую так, чтобы
её внешняя часть была равна внутренней.
57. Даны прямая /, окружность О и на ней две точки А и В. Найти на
окружности точку С так, чтобы прямые СА и СВ в пересечении с прямой
образовали равнобедренный треугольник с основанием на прямой /.
Указание. Биссектриса угла С проходит через середину дуги АВ и
служит высотой искомого треугольника.
58. Построить вписанный угол данной величины так, чтобы его стороны
проходили через две данные точки внутри круга.
Построить треугольник, если даны:
59. с, £ С и hc. 60. с, £ С и а. 61. с, £ С и тс. 62. с, ha и hb.
63. Даны две окружности; построить угол данной величины, вписанный
в одну окружность и описанный около другой.
64. Построить отрезок данной длины и данного направления концы
которого лежали бы на двух данных окружностях (см. упр. 42).
65. Через данную точку провести прямую так, чтобы её отрезок,
заключённый между двумя данными окружностями, в этой точке делился пополам.
Указание. Построить окружность, симметричную с одной из данных
относительно данной точки, и найти точки её пересечения с другой данной
окружностью.
66. Через точку пересечения двух окружностей провести прямую так,
чтобы данные окружности отсекали от неё равные хорды.
Указание. См. задачу 65.
67. Построить общую касательную к двум данным окружностям.
Анализ. Пусть Ох и Ог — центры данных окружностей, г, и г, — их
радиусы· Если г, < г2, то смещаем параллельно общую касательную в направ·
108

лении, к ней перпендикулярном, на длину г,. Смещённая таким образом
прямая пройдёт через точку и будет касаться окружности с центром в точке О,
и радиусом, равным гг — г,. Такую прямую легко построить. После чего
обратным смещением на длину г, получим искомую общую касательную.
Задача имеет четыре решения, если окружности лежат одна вне другой.
Предоставляем учащимся рассмотреть и остальные случаи.
VI. ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ
И ЧЕТЫРЁХУГОЛЬНИКИ
§ 111. Вписанный треугольник
Задача. Построить окружность, проходящую через
вершины данного треугольника ABC (черт. 182).
Эта задача равносильна уже решённой задаче: провести
окружность через три данные точки (§ 93). Центр искомой окружности
лежит в точке пересечения перпендикуляров,
восставленных из середин сторон
треугольника.
Окружность, проходящая через вершины
треугольника, называется описанной около
треугольника, а треугольник — вписанным
в окружность.
Опираясь на свойства вписанных углов,
учащиеся сами могут доказать следующие
свойства описанной окружности.
1. Центр окружности, описанной около
остроугольного треугольника, лежит внутри
треугольника.
2. Центр окружности, описанной около прямоугольного
треугольника, лежит в середине гипотенузы.
3. Центр окружности, описанной около тупоугольного
треугольника, лежит вне треугольника.
Черт. 182
§ 112· Описанный треугольник
Задача. Построить окружность, касающуюся трёх сторон
данного треугольника ABC (черт. 183).
Мы видели, что биссектрисы углов
треугольника пересекаются в одной
точке и эта точка одинаково удалена
от всех трёх сторон треугольника
(§ 82). Поэтому, если из точки О
пересечения биссектрис опустить
перпендикуляры ОД ОЕ и OF на стороны
треугольника, то OD = OE = OF, и,
следовательно, окружность с центром в
точке О, проходящая через одну из точек D, Ен F, пройдёт и через
две другие и будет касаться всех трёх сторон треугольника.
Черт. 183
109

Так как другой точки, равноудалённой от сторон
треугольника, не существует, то задача имеет только одно решение.
Окружность, касающаяся трёх сторон треугольника, называется
вписанной в этот треугольник, а треугольник—описанным
около неё.
Из проведённых построений следует (см. также § 111):
Около всякого треугольника можно описать
окружность и во всякий треугольник можно вписать
окружность.
§ 113. Вневписанная окружность
Задача. Построить окружность, касающуюся трёх данных прямых,
попарно пересекающихся и не проходящих через одну точку (черт. 184).
Одна из искомых окружностей вписана в
треугольник ЛВС (черт. 184), образованный
данными прямыми. Если провести
биссектрисы внешних углов этого треугольника, то
получим ещё три точки Ох, 02, 03, также
равноудалённые от всех трёх прямых ВС,
АС, АВ (§ 82).
Они также служат центрами
окружностей, касающихся данных прямых. Эти
окружности называются вневписанными в
треугольник ABC.
Всего, таким образом, можно провести
четыре окружности, касающиеся трёх данных
попарно пересекающихся прямых, не
проходящих через одну точку.
§ 114· Вписанный четырёхугольник
Если через все вершины данного четырёхугольника проходит окружность,
то четырёхугольник называется вписанным в эту окружность, а окружность —
описанной около четырёхугольника.
Так как не через всякие четыре точки можно провести окружность, то
не для всякого четырёхугольника можно построить окружность, проходящую
через все его вершины. Чтобы такое построение
было возможно, нужно, чтобы четырёхугольник
удовлетворял некоторому условию. Это условие
выражено в следующих теоремах.
Теорема. Сумма противоположных углов
вписанного четырёхугольника равна 2d.
Дан четырёхугольник ABCD (черт. 185),
вписанный в окружность. Требуется доказать, что
£В+ £D=2d и £A + /mC = 2d.
Углы А и С — вписанные. Поэтому
/_ А измеряется — — BCD]
Черт. 185
/_ С измеряется -^ — BAD.
Сумма дуг BCD и BAD составляет окружность, следовательно, сумма
углов А и С измеряется половиной окружности, то есть
£A + /mC=2d.
110

Точно так же докажем, что
£В+ £П = 2о.
Теорема (обратная). Если сумма двух противоположных угло*
четырёхугольника равна 2d, то около этого четырёхугольника можно
описать окружность.
Дан четырёхугольник ABCD, в котором
£В + £D=2d.
Проведём окружность через точки Α, θ, С и
допустим, что она не пройдёт через D. Тогда она
пересечёт сторону AD (или её продолжение) в
некоторой точке Д (черт. 186).
Соединив точки С и Dv получим
четырёхугольник ABCDV в котором в силу прямой
теоремы *
а по условию Черт. 186
ΔΒ + LD = 2d.
Следовательно,
//)=^Д, или /_ADC=£ADXC,
что невозможно, так как в Д DXCD /_ ADXC — внешний, а / ADC —
внутренний, с ним несмежный.
Следовательно, окружность, проходящая через точки Л, В и С пройдёт и
через точку D.
§ 115. Описанный четырёхугольник
Если окружность касается всех четырёх сторон данного
четырёхугольника, то четырёхугольник называется описанным около этой окружности,
а окружность — вписанной в данный четырёхугольник.
Чтобы в данный четырёхугольник можно было вписать окружность, он
должен обладать свойством, выраженным в следующих теоремах:
Теорема. Во всяком описанном четырёхугольнике суммы
противоположных сторон равны между собой.
Дан четырёхугольник ABCD (черт. 187), стороны которого касаются
окружности в точках Е, Ft G, //.Требуется доказать, что АВ-\- CD= ВС + АЕ>·
Черт. 187 Черт. 188
Так как касательные, проведённые из одной точки к окружности, равны, то
АЕ = АН\ ВЕ = ВГ\
CG = CF; DO = DH.
ill
М>

Сложив эти равенства почленно, получим:
(АЕ+ BE) + (CG + DG) = АИ+ (BF + FQ + DH.
Но
АЕ + ВЕ=АВ; CG + DG = CD; BF+FC = BQ
AN + ND = AD.
Поэтому
AB + CD=BC+AD.
Теорема (обратная). Если β четырёхугольнике суммы
противоположных сторон равны, то в этот четырёхугольник можно
вписать окружность.
Дано: АВ -J- CD = ВС + AD (черт. 188). Проведём окружность,
касающуюся сторон АВ, ВС и CD. Допустим, что она не коснулась стороны AD.
Проведя из точки А касательную AD}, получим описанный четырёхугольник
ABCDlf в нём в силу прямой теоремы AB-\-CDx = BC-{- ADV Вычитая это
равенство почленно из данного, получим:
CD - CDX = AD- ADlt
или
DDl=AD-^ADly
что невозможно, так как третья сторона в треугольнике должна быть больше
разности двух других сторон.
Следовательно, окружность, касающаяся сторон АВ> ВС и СД касается
и стороны AD.
УПРАЖНЕНИЯ
А. Доказать теоремы.
1. Радиус окружности, вписанной в равносторонний треугольник, в два
раза меньше радиуса описанной окружности, а сумма обоих радиусов равна
высоте треугольника.
2. Сумма диаметров окружностей, вписанной в прямоугольный
треугольник и описанной около него, равна сумме его катетов.
3. Биссектрисы углов В и С при основании равнобедренного
прямоугольного треугольника ABC пересекаются в точке Ε и при продолжении
встречают окружность, описанную около этого треугольника, в точках D и F.
Доказать, что четырёхугольник EDAF — ромб.
4. Окружности, описанные на сторонах треугольника как на диаметрах,
пересекаются в точках, служащих основаниями высот треугольника.
5. Если на каждой стороне треугольника построить равный ему
треугольник, дополняющий его до параллелограмма, то центры окружностей,
описанных около этих трёх треугольников, служат вершинами треугольника, равного
данному.
6. Если в произвольном треугольнике одну из вершин соединить с
центром описанной окружности и из этой же вершины опустить высоту, то углы,
образованные высотой и радиусом описанной окружности с прилежащими
сторонами треугольника, равны.
7. Окружность, проходящая через ортоцентр треугольника и две его
вершины, равна окружности, описанной около треугольника.
8. Через вершину С треугольника ABC проведены: высота CD на
сторону АВ и прямая СО, соединяющая вершину С с центром описанной
окружности. Доказать, что /. OCD= L& — L&-
9. В треугольнике ABC проведены: высота CD из вершины С на
сторону АВ, биссектриса CF угла С и прямая СО, соединяющая вершину С
с центром описанной окружности. Доказать, что прямая CF делит пополам
угол OCD.
10. Высоты, проведенные из вершин А и В треугольника АВСУ при
продолжении встречают окружность, описанную около треугольника, в точке D
и Е. Доказать, что вершина С делит дугу DE пополам.
112

И. Высоты треугольника продолжены до встречи с описанной
окружностью. Доказать, что отрезки этих линий от ортоцентра до окружности делятся
соответственными сторонами пополам.
Указание. Каждый из этих отрезков служит основанием
равнобедренного треугольника, высота которого совпадает со стороной да иного
треугольника.
12. Касательные к окружности в вершинах вписанного прямоугольника
в пересечении образуют ромб.
13. Точки касания/сторон ромба к вписанной в него окружности служат
вершинами прямоугольника.
14. Если около данной трапеции можно описать окружность и в ту же
трапецию можно вписать окружность, то каждая боковая сторона трапеции
равна её средней линии.
15. Около всякой равнобедренной трапеции можно описать окружность,
и наоборот, если около трапеции можно описать окружность, то эта трапеция
равнобедренная.
16. Диагональ вписанного четырёхугольника образует со сторонами,
сходящимися в одном её конце, углы, равные углам, образуемым касательной в
другом конце диагонали с двумя другими сторонами.
17. Прямые, соединяющие середины дуг, стягиваемых противоположными
сторонами вписанного четырёхугольника, взаимно перпендикулярны.
Б. Задачи на построение.
Обозначения:
Я — радиус описанной окружности; г — радиус вписанной окружности; га,
гь, гс — радиусы вневписанных в треугольник окружностей, касающихся
соответственно сторон а, Ьу с и продолжений других" сторон.
Построить треугольник, если даны:
18. Я, с, а. 19. Я, с, / Л. 20. Я, £ Л, £ В.
21. Я, с, /L. 22./?, £С, hc. 23. Я, с, тс.
24. Я, £ С, /τν 25. Я, Лс, £ Л. 26. Я, Л„ а.
27. Я, Лс, ра. 28. Я, ра, рь. 29. ра, рь, £ С.
30. Я, qA, qB. 31 qA, qB £ С. ψ. Я, с, та.
33. Я, hc, lc. 34. с, £ С, та. 35. г, £ А, £ В.
36. г, с, ^ Л. 37. г, а, Лс. 38. г, Л„ /?а.
39. г, hci £ С. 40. с, гф Ζ Л. 41. га, ^ θ, / С.
42. га, Л„ ^ Л. 43. г, га, ^ Л. 44. гф гь, £ С.
Построить равнобедренный треугольник ABC, в котором
ВС=АВ, если даны:
45. Я, а. 46. Я, Ζ Л. 47. Я, А<-
48. &, г. 49. /\ ^ Л.
Построить вписанный четырёхугольник, если даны:
50. Я, я, Ь, с. 51. Я, а, Ь, /. 52. Я, я, е, /.
53. Я, е, /, /1 Λ1
Указание. Через любую точку одной диагонали провести хорду,
параллельную второй диагонали. Далее, провести диаметр данной окружности
перпендикулярно этой хорде и на расстоянии, равном половине второй
диагонали, провести две хорды, параллельные этому диаметру, что определит
остальные вершины четырёхугольника.
54. Построить ромб, если даны его сторона и радиус вписанной
окружности.
ПЗ

VII. МЕТОД СИММЕТРИИ
§ 116· Сущность метода
Один из методов решения задач на построение основывается на
•свойствах осевой симметрии фигур. Иногда, производя анализ задачи,
'чтобы обнаружить связь между искомыми и данными задачи, бывает удобно
или для всей фигуры, или для её части построить фигуру, ей симметричную
относительно какой-либо оси.
После такого построения иногда обнаруживается такая зависимость между
элементами фигур, которую раньше было трудно заметить.
Успех этого приёма зависит от характера самой задачи, а также и от
удачного выбора осей симметрии.
§ 117· Примеры применения метода симметрии
Задача 1. Дана прямая I и две точки А и В по одну сторону от неё
(черт. 189). Найти на прямой I точку X, такую, чтобы сумма АХ-\-ХВ
была наименьшей.
Решение. Построим точку Bv симметричную для точки В относительно
прямой I. Пусть А" —искомая точка, тогда ВХ = ВХХ и АХ-\- ХВ = АХ -\-ХВх\
следовательно, задача сводится к нахождению точки X, такой, что сумма
АХ-\-ХВх имеет наименьшую величину. Этому условию, очевидно,
удовлетворяет точка X, лежащая на отрезке прямой линии, соединяющей А и Βν
Отсюда вытекает такое решение данной адачи:
Данную точку А соединяем прямой линией с точкой Blt симметричной
с В относительно прямой I. Прямая АВУ· пересечёт прямую I в искомой
точке X.
Задача 2. Даны две окружности с центрами в точках О, и Ог и не
пересекающая их прямая АВ. Найти на прямой А В точку X, такую, чтобы
касательные из нее к данным окружностям были наклонены к АВ под
равными углами.
' Решение. Допустим, что задача решена. AT, и АТ2 — касательные к
данным окружностям (черт. 190), причём /mAX7\=/mBXTi. Построим
окружность 0\, симметричную с окружностью О, относительно прямой АВ.
Прямая ХТ[, симметричная касательной ХТХ1 будет касаться окружности 0[. При
этом так как ^ ЛАТ, = /_ АХТ[, то £ АХТ[ = ,/ ВХТ2\ следовательно,
линия ТгХТ\ — прямая. Она служит общей касательной к окружностям Ог
и О^. Отсюда вытекает такое построение. Строим окружность 0[,
симметричную О, относительно прямой АВ. Проводим общую касательную к
окружностям 0[ и 0%. Она пересечёт прямую АВ в искомой точке.
Ш

Задача имеет четыре решения, по числу общих касательных к двум
окружностям, если окружности Ох и Ог лежат одна вне другой, и меньшее
число решений в остальных случаях (см. стр. 108, упр. 67).
УПРАЖНЕНИЯ
1. Построить треугольник по двум сторонам а и Ь и разности углов:
Указание. Выбрать за ось симметрии высоту треугольника,
опущенную из вершины С, и построить прямую Л'С, симметричную АС.
Треугольник А'СВ определяется данными задачи.
2. Даны две прямые ρ и q и на прямой ρ точка А. Найти на той же
прямой точку Ху такую, что отрезок АХ равен расстоянию точки X от
прямой q.
Указание. Если ΑΎ—перпендикуляр из точки X на прямую q, то за
ось симметрии следует выбрать биссектрису угла АХУ.
3. Даны две точки А и В по одну сторону от прямой /. Найти на
прямой I такую точку X, чтобы прямые АХ и ВХ были наклонены к прямой /
под равными углами.
4. Дана прямая I и две точки А и В по одну сторону от неё. Найти на
прямой I две точки Μ и Ν, такие, чтобы отрезок ΜΝ имел данную длину,
а периметр ломаной ΑΜΝΒ был наименьшим.
5. Дан угол ABC и внутри него две точки Μ и N Найти на одной стороне
угла такую точку X и на другой такую точку К, чтобы периметр
ломаной ΜΧΫΝ был наименьшим.
6. Дан угол ABC и точка Μ внутри него. Найти на одной стороне угла
точку X и на другой—точку Υ так, чтобы периметр треугольника МХУ был
наименьшим.
7. Дана прямая АВ и две точки Μ и N по одну сторону от неё. Найти
на прямой АВ такую точку X, чтобы разность углов АХМ и ΒΧΝ имела
данную величину.
Указание. Построить точку Λί\ симметричную точке Μ
относительно АВ. /_ М'ХМ определяется через данную разность углов.
VIII. УПРАЖНЕНИЯ К ГЛАВЕ ЧЕТВЁРТОЙ
Построить треугольник, если даны:
1. Три точки, в которых продолжения высот треугольника встречают
описанную около него окружность.
Указание. Надо доказать, что высоты искомого треугольника являются
биссектрисами углов треугольника с вершинами в данных точках.
2. Три точки, в которых продолжения биссектрис углов треугольника
встречают описанную около него окружность.
3. Три точки, в которых проведённые из одной вершины высота, медиана
и биссектриса угла треугольника встречают описанную около него
окружность.
Указание. См. стр. 112, упр. 10.
4. а + Ь + с, hc, ^ С.
Указание. /, DCE=d-{- -^ /_ С (черт. 114, стр. 64).
5. a -j- b + с, г, га. 6. а + Ъ-\-с, га, /_ В. 7. а + b -f- с, ra, hc.
8. Дан угол ABC и точка Μ вне его. Провести через точку Μ прямую,
образующую в пересечении со сторонами данного угла треугольник данного
периметра.
Указание. См. стр. 106, упр. 22.
9. Внутри данного треугольника найти точку, из которой все три его
стороны видны иод равными углами.
115

10. В равносторонний треугольник вписать другой равносторонний
треугольник, стороны которого были бы перпендикулярны к сторонам данного.
11. В равносторонний треугольник вписать другой равносторонний
треугольник, стороны которого имеют данную длину.
12· Построить равносторонний треугольник, вершины которого лежали бы
на трёх данных параллельных прямых.
Указание. При анализе описать около искомого треугольника
окружность, вторые точки её пересечения с данными прямыми соединить с
вершинами треугольника и рассмотреть полученные при этом вписанные углы.
13. Построить квадрат, три вершины которого лежали бы н-а трёх данных
параллельных прямых.
Указание. См. указание к упр. 12.
14. В данный квадрат вписать другой квадрат с данной стороной.
15. Построить три окружности с центрами в трёх данных точках, попарно
касающиеся одна другой.
Указание. Каждая из сторон треугольника с вершинами в трёх
данных точках равна сумме двух радиусов искомых окружностей. Это позволит
определить радиусы всех трёх окружностей.
Даны три точки А, В, С. Через точку А провести.прямую так,
чтобы:
16. Сумма её расстояний от точек В к С была равна данной длине а.
17· Сумма её расстояний от точек В и С была наибольшей.
Указание. Искомая прямая перпендикулярна или к BQ или к В'С> где
В' — точка, симметричная В относительно точки А.
18. Разность её расстояний от точек В и С была равна данной длине а.
Указание. Строим окружность радиуса а с центром в точке В и из
точки С проводим к ней касательную и т. д.
19. На плоскости даны два равных не параллельных между собой
отрезка АВ и А'В'. Показать, что один можно совместить с другим одним
вращением вокруг некоторого центра.
Решение. Даны отрезки АВ и А'В\ причём АВ = А'В'. Построим оси
симметрии точек А и А' к точек В и В'. Пусть О—точка пересечения этих
осей. Соединим её с концами данных отрезков и рассмотрим треугольники
АОВ и А'ОВ'. Так как АО = А'0, ВО = В'0 и по условию АВ = А'В\ то
/\АОВ= £±А'ОВ'. Следовательно, /тАОВ=/яА'ОВ'. А поэтому, приняв
точку О за центр вращения и повернув весь Δ АОВ вокруг этого центра на
угол АОА', мы совместим отрезок АВ с отрезком А'В'.
20. Треугольник ABC скольжением по плоскости, без выхода из неё, был
переведён в положение А'В'С, причём А'В' не параллельна АВ. Показать,
что такое перемещение может быть произведено путём одного вращения
вокруг некоторого центра. Построить центр вращения и угол поворота.
21. Сложенная вдвое крышка стола имеет форму прямоугольника,
меньшая сторона которого в два раза короче большей. В сложеннОхМ виде крышка
лежит на стойке той же формы и того же размера. Нижняя часть крышки
прикреплена к стойке винтом, вокруг которого может вращаться. После
поворота вокруг этого винта на прямой угол верхняя часть крышки открывается
и вся крышка принимает форму квадрата, причём две его противоположные
стороны совпадают с короткими сторонами стойки, а две другие —
параллельны её сторонам и одинаково отстоят от них. Определить, в каком месте
крышки должен быть укреплён винт.
Отв. Центр вращения крышки находится на расстоянии -j а от стороны
крышки, где а — длина меньшей её стороны.
22· Произвольная точка окружности, описанной около равностороннего
треугольника, соединена с его вершинами. Доказать, что наибольшая из
полученных трёх хорд равна сумме двух других.
Указание. Через конец меньшей хорды провести хорду, параллельную
наибольшей. Соединить конец проведённрй хорды с концом второй меньшей
116

хорды. Последняя прямая пересечёт наибольшую хорду в точке, делящей эту
хорду на части, равные меньшим хордам.
23· Из произвольной точки X окружности, описанной около данного
треугольника ЛВС, опущены перпендикуляры ХСХ1 ХА1У ХВх на стороны АВ,
ВСУ АС» Доказать, что основания перпендикуляров Av Bv С, лежат на одной
прямой (называемой прямой Симеона).
Указание. Пусть точка X лежит на дуге, стягивающей сторону А В.
Соединив точку X с вершинами А, В, докажем, что £ АХХВ равен £ AXBV
Затем на хордах ХВ и ХА как на диаметрах описать окружности и доказать,
что угол АХСХВ равен углу ACXBV
24· Через произвольную точку Л", взятую на данной окружности,
проведены три произвольные хорды лА, ХВ и ХС, и на каждой из этих хорд как
на диаметрах построена окружность. Доказать, что три точки Av Bv Сх
попарного пересечения этих окружностей (кроме их четвёртой точки X,
лежащей на данной окружности) лежат на одной прямой.
Указание. Доказать, что эта теорема является лишь иной
формулировкой предшествующей теоремы (см. задачу 23), то есть доказать, что
прямая АХВХСХ будет прямой Симеона для Δ ABC.
25· Через конец А диаметра АВ данной окружности проведена
произвольная хорда AM и на ней, по обе стороны от точки Λί, отложены отрезки
MP и MQ, равные MB. Найти геометрическое месте точек Ρ и Q, когда
точка Μ перемещается по данной окружности.
Указание. Найдём сначала геометрическое место точек Р. Так как
MB=MPt то перпендикуляр MF из точки Μ на прямую РВ делит отрезок РВ
и угол BMP пополам; следовательно, BF = FP и £ΒΜΕ=£ FMP= у. Если
С —вторая точка встречи прямой FM с данной окружностью, то ^ AMC=z
= £FMP= — , Следовательно, дуга АС составляет -j- часть всей
окружности и, значит, точка С есть конец диаметра CD, перпендикулярного к АВ.
Следовательно, положение точки С не меняется.
26. На плоскости даны: окружность О и прямая/?. На окружности О взята
какая-либо точка А, а на прямой ρ — какая-либо точка В. Через точки А и В
проводят произвольную окружность Ох. Она встречает второй раз
окружность О в точке С и прямую ρ в точке D.
Доказать, что прямая CD пересекает второй раз окружность О в
постоянной точке Ρ (независимо от того, какая окружность О, проведена через
точки А и В).
Указание. Доказать, что /mACP=/ABD. Для этой цели провести
в точке С к окружности Ох касательную EF. Тогда ^/ АСР= /_ АСЕ 4- /_ ЬСР\
но / АСЕ= £ ABC и £ ЕСР= £ FCD=£ CBD и т. д.

ГЛАВА ПЯТАЯ
ОТНОШЕНИЕ И ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ
I. ОБЩИЕ ПОЛОЖЕНИЯ ОБ ИЗМЕРЕНИИ ОТРЕЗКОВ
§ 118. Аксиома Архимеда
Измерение отрезков основано на следующей истине, известной
под названием аксиомы Архимеда:
Если даны два любых отрезка А В и CD (AB>CD)
(черт. 191), то на прямой АВ можно отложить от точки А
отрезок CD последовательно
А , , , , ι ι - Г столько раз, что получится
отрезок AF, больший или равный
q л АВ. Значит, можно найти такое
целое ЧИСЛО /72, при КОТОРОМ будут
Черт. 191 верны неравенства:
m-CD^AB, a {m+l)CD>AB.
Число /72, показывающее, сколько раз возможно уложить
отрезок CD на отрезке АВ, даёт представление о размере отрезка АВ.
Отрезок, при помощи которого измеряется данный, называется
единицей измерения.
§ 119. Измерение отрезков
Измерение отрезков производится следующим образом.
Принимаем какой-либо отрезок CD за единицу измерения и откладываем
его на измеряемом отрезке АВ, начиная от точки Л,
последовательно столько раз, сколько это возможно.
Если отрезок CD уложится в отрезке АВ целое число раз,
например т раз, то в этом случае говорят, что отрезок АВ
содержит т единиц длины или что длина отрезка АВ равна т
единицам, и записывают это так: AB=m-CD.
Например, на чертеже 192 отрезок CD уложился на отрезке АВ
пять раз, и поэтому кы говорим, что длина АВ равна 5 единицам,
и пишем: AB=5-CD.
Если отрезок CD не укладывается целое число раз на
отрезке АВ, то отрезок CD делят пополам и укладывают половину
118

отрезка CD на отрезке АВ, начиная от точки А, последовательно
столько раз, сколько это возможно.
Если и половина отрезка CD не укладывается в отрезке АВ
целое число раз, то отрезок CD делят на три части и
укладывают -о- часть отрезка CD на отрезке АВ столько раз, сколько
это возможно. Если же и -^ часть отрезка CD не укладывается
в отрезке АВ целое число раз, то отрезок CD делят
последовательно на 4, на 5 и т. д. частей до тех пор, пока какая-нибудь
—я часть отрезка CD не уложится в отрезке АВ целое число
раз, например т. В этом случае говорят, что отрезок АВ содер-
* В й В
| 1 1 1 1 J , , , , ^^
CD CD
l 1 J 1 Η—*
Черг. 192 Черт. 193
жит Ш. единиц длины или что длина отрезка АВ равна —
единиц, и пишут: AB = — -CD.
Так как —я часть отрезка CD укладывается в отрезке АВ
целое число раз, а именно т раз, в то время как каждая из ча-
„111 1 1 ПТЛ
стей -тря, у-я, -^--я, ..., ^-—^ -я, п_ {-я отрезка CD не
укладывается целое число раз в отрезке АВ, то в рассматриваемом нами
случае я часть отрезка CD будет самым большим из всех
отрезков, укладывающихся целое число раз как в отрезке CD,
так и в отрезке АВ.
Самый большой отрезок из всех отрезков, укладывающихся целое
число раз как в отрезке АВ, так и в отрезке CD, называется
наибольшей общей мерой этих отрезков. Например, в нашем
случае наибольшей общей мерой отрезков АВ и CD будет —я
часть отрезка CD.
Если —я часть отрезка CD — наибольшая общая мера
отрезков АВ и CD и если она укладывается в отрезке АВ т раз, то
в равенстве АВ = — CD несократимая дробь. Если бы эта
дробь была сократимой, то —я часть отрезка CD не была бы
наибольшей общей мерой отрезков АВ и CD. Например, на
чертеже 193 изображены два отрезка АВ и CD, причём
-g-я часть отрезка АВ укладывается три раза в отрезке CD, в то
119

время как каждая из частей у-я, у-я, -^--я отрезка Л# не
укладывается целое число раз в отрезке CD. Отсюда мы заключаем,
что -^г-я часть отрезка АВ будет наибольшей общей мерой отрез-
3 3
ков АВ и CD и в равенстве CD = jr АВ убудет несократимой
дробью.
Существует, конечно, бесчисленное множество других
отрезков, укладывающихся целое число раз как в отрезке АВ, так и
в CD. Так, например, т~-я часть отрезка АВ укладывается шесть
раз в отрезке CD, ^-я—12 раз и т. д.
с. ι о
Но в соответствующих равенствах CD =γ0ΑΒ; CD = ^ AB
и т. д. дроби тп; 20 и т· Д· будут уже сократимыми дробями.
§ 120. Соизмеримые и несоизмеримые отрезки
Если найдётся такая —я часть отрезка CD (п= 1, 2, 3 ...),
которая укладывается целое число т раз в данном отрезке АВ,
то в этом случае говорят, что отрезок АВ соизмерим с
отрезком CD, принятым за единицу измерения. Это означает, что длину
отрезка АВ мы можем выразить дробью —, числитель и
знаменатель которой — целые числа. Дробь —, у которой знаменатель
β £ι с и числитель — целые числа, называют
числом, соизмеримым с единицей, или
рациональным числом.
Но может случиться, что на какие бы
части мы ни делили отрезок CD, никакая
ι
я часть его не укладывается целое число
раз в отрезке АВ. В таком случае отрезки
АВ и CD будут называться несоизмеримыми.
С первого взгляда может показаться, что
несоизмеримых отрезков не может быть, но
легко доказать, что такие отрезки существуют.
Для этой цели возьмём квадрат ABCD и разделим его на
четыре квадрата (черт. 194). Во всех четырёх полученных
квадратах проведём диагонали. Тогда квадрат ABCD будет составлен
из восьми равных равнобедренных прямоугольных треугольников.
Полученный четырёхугольник AlBlClDl (черт. 194) также
будет квадратом, так как его стороны будут равны как гипотенузы
равных равнобедренных прямоугольных треугольников, а четыре
угла его будут прямыми, так как каждый из них составлен из
двух углов по- 45°.
120

Из чертежа 194 видим, что квадрат AlBlClDl состоит из
четырёх равных равнобедренных прямоугольных треугольников.
Докажем, что сторона АВ квадрата ABCD несоизмерима со
стороной А1В1 квадрата Αβ^β^
Допустим, что отрезок АВ соизмерим с отрезком ΑλΒ19 τ. е.
допустим, что эти отрезки имеют наибольшую общую меру,
которая укладывается т раз в отрезке АВ и η раз в отрезке ΑγΒλ.
Тогда квадрат ABCD содержит тг квадратов со стороной,
равной наибольшей общей мере отрезков AJBl и АВ, а квадрат
A1B1C1Dl — пг таких же квадратов (черт. 1?5).
В
Черт. 195
Но так как, с другой стороны, квадрат ABCD составлен из
восьми равных равнобедренных прямоугольных треугольников, а
квадрат AlBlC1Dl — из четырёх таких же треугольников, то имеем:
т2 = 2п2, откуда ^- = 2.
Так как мы предположили, что отрезки АВ и А1В1 имеют
наибольшую общую меру, которая укладывается в отрезке АВ
т раз, а в отрезке ΑλΒΛ η раз, то, следовательно, — —
несократимая дробь (§ 119), квадрат которой не может равняться никакому
целому числу и, в частности, двум.
Таким образом, допустив, что стороны квадратов ABCD и
AlB]ClDl соизмеримы, мы пришли к неверному выводу.
Следовательно, отрезки АВ и А1В1 не имеют наибольшей
общей меры, то есть несоизмеримы.
§ 121. Приближённое вычисление длины отрезка,
несоизмеримого с единицей измерения
Если отрезок АВ несоизмерим с отрезком CD, принятым за
единицу измерения, то длину отрезка АВ нельзя выразить в виде
дроби —, где т и η — целые числа, и поэтому длину отрезка АВ
можно вычислить лишь приближённо следующим образом.
Отрезок CD делим на η равных частей, где η — произвольное
целое число. Затем —ю часть отрезка CD откладываем после-
121

довательно от точки А на отрезке АВ. Таким образом получаем
равные отрезки: AAl = AiA2 = ...==AmAm+i (черт*. 196). Согласно
аксиоме Архимеда, существует целое число т, что точка Ат
лежит левее точки В, а точка Am+i — правее точки В.
Тогда длина отрезка ААт будет равна — единиц длины, а длина
отрезка ААт+Л равна т "^ единиц длины. Так как точка В лежит
между точками Ат и Лт+1, то длина отрезка АВ будет
содержать 6<
длины.
r m m -4-1
жать больше, чем — единиц длины, и меньше, чем —— единиц
А *' ** ft ^-Л^Ди
l·—*—ι ι -j. ι ι ι | ι
Cc,D
1 ι ι Ι
Черт. 196
Поэтому говорят, что оба числа — и ~|~ определяют длину
ι m
отрезка АВ с точностью до —и, причём — определяет дли-
т I 1
ну АВ с недостатком, а —— с избытком.
Если мы будем неограниченно увеличивать число л, то число т
также будет увеличиваться и точки Ат и Ат+1 будут
приближаться к β, следовательно, длины отрезков ААт и ААт+1 будут
неограниченно приближаться к длине отрезка АВ. Но этот
процесс никогда не может закончиться, так как если бы он
завершился, то это означало бы, что какая-то точка Ат совпала с
точкой В и, следовательно, какая-то —я часть отрезка CD
уложилась в отрезке АВ т раз, что невозможно, так как по условию
АВ и CD несоизмеримы.
Так как при неограниченном увеличении числа η отрезки ААт
и ААт+1 по длине неограниченно приближаются к отрезку АВ,
то рациональные числа — и т "~ , равные длинам отрезков ААт
и ААт+1, будут стремиться к некоторому числу а, выражающему
длину отрезка АВ.
#Как мы показали выше, это число а не может быть
рациональным. Следовательно, кроме рациональных чисел, существуют
числа другого рода, которые называются иррациональными.
С этими числами учащиеся более близко ознакомятся в курсе
алгебры, где они узнают, что с иррациональными числами можно
обращаться так же, как и с рациональными.
122

Поэтому в случае, когда а — число иррациональное, мы снова
будем говорить, что длина отрезка АВ равна а единиц, и будем
писать:
AB = a-CD.
Таким образом, если АВ и CD — два произвольных отрезка,
то мы всегда можем написать:
AB = a-CD9
где а называется длиной отрезка АВ при условии, что отрезок CD
принят за единицу измерения. Если а — рациональное число, то
отрезки АВ и CD соизмеримы, а если а — иррациональное число,
то отрезки АВ и CD несоизмеримы.
Из алгебры известно, что всякое иррациональное число может
быть выражено бесконечной непериодической десятичной дробью.
Пусть, например, а = 5,6372086... Возьмём лишь несколько
десятичных знаков этой дроби. Например, оставим лишь один
десятичный знак, а остальные зачеркнём. Мы получим тогда дробь
с одним десятичным знаком: 5, 6. Она будет приближённой длиной
отрезка АВ с точностью до 0,1 с недостатком по той причине,
что отрезок длиной 5,6 единицы меньше данного отрезка и
разнится от него меньше, чем на 0,1 единицы. Отсюда следует, что
если мы будем делить отрезок CD сначала на 10 частей, а затем
на 100 частей и т. д. и будем вычислять указанным выше
способом число а или длину отрезка АВ с точностью до 0,1, 0,01
и т. д., то мы будем получать последовательно цифры после
запятой: 6, 3, 7, 2, 0, 8, 6, ... и этот процесс никогда не
закончится, если а есть бесконечная десятичная дробь. Причём если а
есть бесконечная непериодическая десятичная дробь 5,6372086...,
то данный отрезок АВ несоизмерим с отрезком CDy принятым за
единицу измерения.
Если же число а выражается десятичной бесконечной
периодической дробью, например а = 0,333 ..., то в этом случае число
я=у, то есть будет числом рациональным, и два данных
отрезка АВ и CD будут соизмеримыми.
Последний пример показывает, что при нахождении
наибольшей обшей меры двух отрезков мы должны придавать η
последовательно все целые значения, не пропуская ни одного. В
самом деле, как показывает последний пример, давая η лишь
значения 10, 100, ..., 10*, мы не найдём общей меры у двух отрезков,
из которых один равен -j единицы измерения. Между тем, мы
сразу обнаружили бы общую меру этих отрезков, полагая п = 3.
§ 122. Основные законы измерения отрезков
Длины отрезков при вычислении их установленным выше
способом обладают следующими свойствами;
123

1. При одной и той же единице измерения длины двух
равных отрезков равны.
Это очевидно, если два равных отрезка АВ и Л,β, соизмеримы
каждый с третьим отрезком CD, принятым за единицу
измерения.
Если же два отрезка АВ и Α1Βί несоизмеримы каждый с
отрезком CD, то прежде чем утверждать, что длина отрезка АВ
равна длине отрезка ААВи нужно доказать, что с какой бы
произвольной, но одинаковой степенью точности мы ни вычисляли
длины отрезков АВ и ΑλΒχ, всегда будем получать один и
тот же результат. Но это опять очевидно, если ΑΒ=ΑλΒλ.
2. Если данный отрезок разбить на несколько
произвольных частей, то длина всего отрезка будет равна сумме
длин этих частей.
Эти свойства называются основными законами измерения
отрезков.
§ 123. Изменение длины отрезка при переходе от одной
единицы измерения к другой
Если измерять один и тот же отрезок различными единицами,
то длина его будет выражаться различными числами. Так, если
длина отрезка АВ, измеренная единицей в 1 м, равна 5, то длина
того же отрезка, измеренная единицей в 1 дм, равна 50, а
измеренная единицей в 1 см, равна 500.
Поставим теперь задачу. Зная длину отрезка АВ, измеренную
единицей CD, найти его длину при новой единице измерения CXDX.
Мы знаем, что ьсегда можно написать:
ClDl = k-CD,
где k есть длина отрезка Cfi^, вычисленная при единице
измерения CD.
Допустим, что длина отрезка АВ равна а при единице
измерения CD, то есть AB = a-CD.
Примем теперь за единицу измерения новый отрезок CjD, =
= k-CD. Тогда, заменяя в равенстве AB=a-CD CD через
-t-'CjDj, получим:
AB=±.C1D1>
откуда видно, что длина отрезка АВ при новой единице
измерения равна -г-.
Например, если мы увеличиваем единицу измерения в три раза,
то длина отрезка уменьшается в три раза, если мы уменьшаем
единицу измерения в пять раз, то длина отрезка увеличивается
в пять раз, и т. д.
124

II. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ
§ 124. Отношение двух отрезков
Отношением двух отрезков называется отношение длин этих
отрезков, вычисленных при одной и той же единице измерения.
АВ
Отношение отрезка АВ к отрезку А1В1 записывается в виде -г-*
и равно у, где а — длина отрезка АВ, а Ь — длина отрезка ΑχΒλ.
Теорема. Отношение двух отрезков не зависит от
выбора единицы измерения.
Даны отрезки АВ и Л,В,. Пусть их длины при некоторой
единице CD равны соответственно а и Ь.
о АВ а
В таком случае j-g-=y-
Измерим те же отрезки новой единицей СгОи и пусть я, и Ьх
соответственно новые длины отрезков АВ и АХВХ. Требуется
доказать, что j±=—.
Обозначим через k длину отрезка CXD19 измеренного
единицей CD. Тогда C1D, = k-CD и c^f и ίι = {· (§ 123), сле-
а
a, k a
довательно, ^ = —=—.
k
Следствия. 1. Отношение отрезка АВ к отрезку А,5,
равно длине а отрезка АВ, когда отрезок AiBi принят за единицу
измерения.
В самом деле, мы имеем: ΑΒ = α·ΑιΒ19 ΑιΒι = 1·ΑιΒι.
Следовательно,
АВ _а__
АА~ 1 —β'
2. Отношение двух соизмеримых отрезков есть число
рациональное, отношение несоизмеримых отрезков — число
иррациональное.
3. Отношение -^ двух отрезков АВ к ΜΝ равно отношению
А В
двух других отрезков -тт-Л-, если, каково бы ни было п, значе-
ние первого отношения, взятое с точностью до ~, равно
значению второго отношения, взятого также с точностью до — .
125

§ 125· Понятие о пропорциональных отрезках
Мы будем говорить, что отрезки АВ, CD, BFy ..., LN
пропорциональны соответственно отрезкам ΑλΒλ, CXDV Я,/7,, ..., LxNl%
АХВХ ClDl EXFX LXNX
если отношения -Ъг, Т7Г» ~Е^"» " ·» ~7Ж соответствующих
отрезков будут равны некоторому числу k, называемому
коэффициентом пропорциональности или численным масштабом.
Например, если мы уменьшим в 5 раз каждый из данных
отрезков АВ, CD, EF, GH, то получим отрезки ΑλΒλ, C,D,, Я,/7,,
GXHX, пропорциональные данным. В этом случае коэффициент про-
1
порциональности равен -^.
В случае, если имеется две пары пропорциональных отрезков,
например АВ, CD и АХВХ, CiDv говорят, что эти отрезки
составляют пропорцию
АХВХ _ СХРХ
АВ ~ CD *
Αβλ и CD называются крайними членами пропорции, АВ и CXDX —
её средними членами.
Теорема 1. Если отрезка ряда АВ, CD, EF,..., LN
пропорциональны отрезкам ряда ΑλΒχ, C,D,, EJFX,... L^N^,
то отношение двух любых отрезков второго ряда равно
отношению соответствующих отрезков первого ряда, и
наоборот.
Пусть di*i—£А— — b*L — k
пусть АВ — со — LN—*"
Выберем произвольно из первого ряда два отрезка CD и LN.
Во втором ряду этим отрезкам соответствуют отрезки CXDX и LXNX.
π С\Д CD
Докажем, что -^=Ш-
Но условию теоремы, Y^==~hr==^y откуда получаем:
CxD, = k-CD и LxNx = k-LN.
~ CXDX k-CD CD
Следовательно, -Щ = ГШ = 7Т^
В случае, если отрезки АВ, CD и AXBV CXDX составляют
пропорцию ~ΐΓ = -ζΤΓ * то' пеРеставив средние члены, получим:
Ахвх _ав
CXDX~CD'
Теорема 2. Если отношения отрезков АВ, CD, ... LN
к одному и тому же отрезку MN соответственно равны
отношениям отрезков Αβλ, CXDX,..., ί,,ΛΓ, к одному
и тому же отрезку ΜλΝλ, то второй ряд отрезков
пропорционален первому ряду отрезков.
126

В самом леле, пусть имеем: 4? = ιττγ; S = t5tt;.-.;
* J MN MXNX' MN MXNX * *
AW = /¥77"' то есть мы имеем Ряд пропорции. Докажем, что
i4lJ3l С,Д _ _L,N,_MlN,
АВ CD ~ " · — LN ~ MN '
На основании теоремы 1 в применении к пропорции мы можем
написать:
ΑΧΒΛ ==ΜλΝι C,Di_MlNl L,N,_MlNl
Аи ~ MN ' CD ~ MN ' * * ·' LN~ MN '
Таким образом,
A±B1_CAD1_ _L,N,_M,NX
AB CD * * * LN ~ MN ·
то есть отрезки Αβ19 ^Dj, ..., Ζ^Λ/, пропорциональны
соответственно отрезкам АВУ CD, ..., LN.
Теорема 3. Если отрезка ряда АВ, CD, EF, ..., LN
пропорциональны соответственно отрезкам ряда ΑλΒλ,
CxDl9 ExFl9 ..., LXNX, то отношение суммы всех отрезков
второго ряда к сумме всех отрезков первого ряда равно
коэффициенту пропорциональности этих отрезков.
По условию теоремы, имеем:
A}BL_C1D1_E}F1_ — b^l—h
АВ ~ CD — EF ~~ ' * ' ~ LN ~ П>
откуда
AiBi = k-AB9 C1D1 = k-CD9 ..., L,N, = k*LN.
Складывая эти равенства почленно, найдём:
A1B1 + C1D1 + ... + LiN1 = k(AB + CD + ...-\-LN),
откуда получаем:
AlB1 + C1D1 + ...+LlNl_h
AB + CD + ... + LN ~к'
§ 126. Основная теорема о пропорциональных отрезках
Теорема. Ряд параллельных прямых отсекает на двух
произвольных прямых пропорциональные отрезки.
Пусть а и b — две произвольные прямые и пусть
параллельные прямые AAl9 BBl9...f ΚΚλ, ММ1У ΝΝλ отсекают на прямых
а ]\ Ь соответственно отрезки АВ, ВС,..., ΜΝ и ΑλΒν ВхСи ...,
ΜΧΝΧ (черт. 197).
Требуется доказать, что ряд отрезков, расположенных на
прямой я, пропорционален ряду соответствующих отрезков,
расположенных на прямой Ь% то есть
АВ _ ВС ___ _ ΜΝ
ΑγΒχ ~ В,С, ~'"~ Μ,Ν,'
127

Возьмём на прямой а два отрезка MN и АВ и будем
вычислять с точностью до —й (с недостатком) отношение отрезков
АВ
-ju^. Для этой цели разделим отрезок MN на η частей и будем
1
ΜΝ
откладывать
-ю часть отрезка ΜΝ на отрезке АВ. Пусть т—
наибольшее число отрезков, каждый из которых равен —й части
отрезка ΜΝ, укладывающихся в отрезке АВ. Тогда число —
будет выражать приближённо с
точностью до —й отношение
отрезка АВ к ΜΝ. Если через точки
деления отрезков ΜΝ и АВ
провести прямые, параллельные
данным параллельным прямым, то
отрезок M1Ni тоже разделится на
η равных частей и каждая из этих
частей уложится самое большее
т раз в отрезке А1В1 (§ 81).
Отсюда следует, что
отношения отрезков АВ к ΜΝ и ΑλΒχ
к Ai,iV,, вычисленные с
произвольной, но одинаковой степенью
точности, будут давать равные
результаты. А это означает, что
АВ
АХВХ
Черт. 197
MN MXNX'
какими бы ни были — соизмеримыми или несоизмеримыми —
рассматриваемые пары отрезков.
о .. АВ т
В самом деле, если при некотором η мы найдем, что д^у=х»
то из приведённого выше построения мы немедленно выведем
заключение, что -г~гг = — . Если же отрезки АВ и AW, а также
А1В1 и M1N1 несоизмеримы, то мы снова можем написать, что
АВ _ΑγΒγ
так как мы доказали выше, что, вычисляя эти отношения с
произвольной, но одинаковой степенью точности, мы будем получать
одинаковые результаты (§ 124, следствие 3).
ВС В,С, МК ΜχΚγ
Аналогично можно показать, что ^ = ^ρ-, ... >^=дЩ >
а потому, в силу теоремы 2 § 125, отрезки, лежащие на прямой
128

а, будут пропорциональны соответствующим отрезкам, лежащим
на прямой Ь, то есть
^ЛВ___ВС__ _ MN
А,В, ~ ВХС, ----- Mi/vr ·
Следствие. Отношение любых двух отрезков, лежащих
на прямой а, равно отношению двух соответствующих
отрезков, лежащих на прямой Ь.
ΒλΡχ ΛΚ _ А^
:VV вк~в1к1
Например: д^ =
7?Р=7Пг1 и т· д· (§ 125> теорема 1).
§ 127. Теорема о прямой, параллельной какой-нибудь
стороне треугольника
Теорема. Прямая, параллельная одной из сторон
треугольника и пересекающая две другие его стороны, делит
их на пропорциональные отрезки.
Пусть дан /\АВС и пусть прямая
DE\\ АС (черт. 198).
Проведя через точку В прямую FG,
параллельную АС, заметим, что три
параллельные прямые FU, DE и АС
отсекают на сторонах АВ и ВС
пропорциональные отрезки: AD, DB, АВ и
ЕС, BE, ВС (§ 126). А потому в силу
следствия § 126 мы можем записать:
Ав_#С AD СЕ АВ
DB~BE* DB BE9 AD~~
Черт. 198
ВС
СЕ'
С другой стороны, на основании теоремы § 126 мы можем
β написать:
АВ
ВС'
AD
'СЕ~~
BD
'BE'
Черт. 199
Теорема (обратная). Если прямая,
пересекая две стороны АВ и ВС
треугольника ABC, делит их на
пропорциональные отрезки, то она параллельна
третьей стороне АС.
π АВ ВС /1Ч АВ BD ,оч
Пусть, например, g^ = ^g(l), откуда следует, что ^,=^ (2).
Требуется доказать, что DE \\ АС.
Допустим, что не прямая DE, а другая прямая DF
параллельна АС (черт. 199). Тогда в силу прямой теоремы мы будем
иметь:
ВС~BF W"
129

Сравнивая пропорции (2) и (3), находим, что в них три члена
одинаковы, а следовательно, и четвёртые члены должны быть
равны, то есть BE = BF. А это значит, что DE совпадает с DF,
то есть, что DE \\ АС.
III. ПОСТРОЕНИЕ ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКОВ
§ 128· Основные задачи
Задача 1. Даны три отрезка a, b и с; построить
отрезок χ так, чтобы а:Ь = с:х.
Решение. На стороне произвольного угла от его вершины
откладываем отрезки ОА = а, ОВ=^Ь, а на второй
стороне—отрезок ОС = с (черт. 200). Соединив А и С, проводим прямую
ВХ\\АС. Отрезок ОХ=х.
Задача 2. Данный отрезок разделить β данном
отношении т\п, то есть на данном отрезке АВ найти точку X, та-
кую, что
АХ:ХВ = т:п.
Решение. Рассмотрим два случая.
1. Отношение т:п дано в виде отношения двух заданных
отрезков. Через конец А данного отрезка АВ (черт. 201) проводим
произвольную прямую и на ней от точки А откладываем
последовательно отрезки АС = т и CD = n. Соединив точки В и D,
проводим прямую СХ || BD. Точка X — искомая, так как АХ: ХВ=
= AC:CD.
2. Отношение т\п дано в виде отношения двух рациональных
чисел. Такое отношение всегда можно заменить отношением целых
чисел. Например,
52 С Л
т:п=Н: у = &:4.
Взяв произвольную единицу измерения е, строим отрезки
т = 5е и п = 4е
и для этих отрезков выполняем предыдущее построение.
130

Задача, очевидно, всегда имеет решение и притом только одно.
В самом деле, для всякой точки X' отрезка АВ, лежащей вправо от
Л (черт. 201), имеем: АХ' > АХ и Х'В<ХВ,
АХ' ^ АХ AXf ^ m
следовательно, -χΓβ>-χβ> то есть Ί^β^ΊΪ'
Точно так же для всякой точки Л", лежащей влево от А", имеем АХ"<АХ
ν»ο ^ νο АХ" ^ АХ АХ" ^ т
и X В>ХВ, следовательно, -чт»-5<-тг5> то есть -тггб< — ·
Л D AtS Л D П
Таким образом, на отрезке АВ, кроме точки X, нет другой
точки, которая разделяла бы отрезок АВ на части, находящиеся
в отношении — . Принято говорить, что точка X, лежащая на
отрезке АВ и удовлетворяющая
условию АХ:ХВ = т:п, делит отрезок АВ
в отношении т:п внутренним
образом.
Задача 3. Данный отрезок
разделить на несколько частей,
находящихся между собой β заданном
отношении m:n:p:q.
Решение. Через конец А данного
отрезка АВ (черт. 202) проводим
произвольную прямую и на ней от точки А откладываем
последовательно отрезки АМ = ту MN = n, NP = p, PQ = q.
Соединив точки Q и β, проводим прямые MX, NY, PZ,
параллельные QB. Точки Χ, Υ, Ζ — искомые, так как из теоремы
§ 126 следует, что
AX:XY:YZ:ZB = m:n:p:q.
§ 129· Внешнее деление отрезка
Задача. На продолжении данного отрезка найти точку, расстояния
которой от концов данного отрезка находятся в данном отношении т:п,
то есть на продолжении отрезка АВ найти
точку X, такую, что АХ:ХВ = т:п (черт.
203).
Решение. Проводим через точку А
произвольную прямую и на ней от точки А
откладываем отрезок АС = т, а от точки С
в сторону точки А — отрезок CD = n.
Соединив точки D и Bf проводим прямую
СХ || BD. Точка X — искомая, так как
АХ__АС_т_
ВХ~~ DC~ η '
Если отношение т\п дано как отношение двух чисел, поступаем так же,
как в § 128, задача 2.
Принято говорить, что точка X, лежащая на продолжении отрезка АВ и
удовлетворяющая условию АХ:ВХ = т:п, делит отрезок АВ в отношении
т\п внешним образом.
Задача внешнего деления отрезка имеет юлько одно решение.
Черт. 203
131

§ 130· Гармоническая группа точек
Если две точки X и Υ делят отрезок АВ одна внутренним, а другая
внешним образом в одном и том же отношении, то есть
ΑΧ:ΧΒ = ΑΥ:ΥΒ,
то говорят, что точки Χ, Υ разделяют гармонически точки А и В.
Теорема. Если точки X и Υ разделают гармонически точки
А и В, то и точки А и В разделяют гармонически точки X и Υ.
Дано (черт. 204): ΑΧ:ΧΒ=ΑΥ:ΥΒ. Требуется доказать, что ΧΒ:ΥΒ=ΑΧ:ΑΥ.
Переставляя в данной пропорции
д У средние члены, получим:
—■ι £—λ 1 ΑΧ\ΑΥ=ΧΒ\ΥΒ,
или, меняя местами правую и левую
Черт. 204 части:
ΧΒ:ΥΒ = ΑΧ:ΑΥ.
Группа точек Л, θ, Χ, К, лежащих на одной прямой и удовлетворяющих
пропорции ΑΧ:ΧΒ = ΑΥ:ΥΒ, называется гармонической группой точек.
В этой группе точки Χ, Υ называются гармонически сопряжёнными
относительно точек Л и θ, и наоборот, точки А, В гармонически сопряжёнными
относительно точек X и К.
§ 131. Построение четвёртой гармонической к трём
данным точкам
Задача. Даны три точки на одной прямой А, В и С. Построить
точку X, гармонически сопряжённую с одной из этих точек относительно
двух других (черт. 205).
Решение. Допустим, что В
лежит между Л и С. Построим точку,
гармонически сопряжённую с В
относительно Л и С. Для искомой точки
АХ АВ и
X должно быть ·™=^. Через
точку А проводим какую-либо прямую и
на ней от точки А откладываем
отрезок AD = AB, а от точки D в
обратную сторону — отрезок DE = BC. Соединяем точки Си£и проводим прямую
DX\\CE. Точка А'—искомая (§ 128, задача 1).
Задача возможна и имеет лишь одно решение, если АВ Φ ВС. Если
АВ = ВС, то задача не имеет решения, так как в этом случае точка Ε
совпадает с точкой А.
Подобным же образом строится точка, гармонически сопряжённая с С
относительно А и В, а также точка, гармонически сопряжённая с А
относительно В и С, причём для этих случаев задача всегда возможна и имеет
лишь одно решение.
IV. СВОЙСТВА БИССЕКТРИС УГЛОВ ТРЕУГОЛЬНИКА
§ 132· Свойство биссектрисы внутреннего угла треугольника
Теорема. Биссектриса внутреннего угла треугольника
делит противоположную сторону на части,
пропорциональные прилежащим сторонам треугольника.
132

Дано: /тАВЕ=/тСВЕ (черт. 206). Требуется доказать, что
АЕ
ЕС'
АВ
'ВС
Проведём через точку С прямую CD \\ BE до пересечения её
в точке D с продолжением стороны АВ. Замечаем, что ^/_АВЕ=
= /_ADC (как соответственные), /_CBE=/_BCD (как накрест
лежащие); но по условию
Z.ABE=ZCBE,
а потому
/mBDC=/mBCD.
Следовательно, Δ BCD — равнобедренный, в нём
BD=BC. В треугольнике ACD имеем (§ 127):
АЕ АВ
EC~BD' ш
Заменяя в этой пропорции отрезок BD равным £ ^ ^
ему отрезком ВС, получим: Черт. 206
АЕ_АВ
ЕС~ ВС
Теорема (обратная). Если прямая, проходящая через
вершину треугольника, делит противоположную сторону
внутренним образом в отношении, равном отношению
прилежащих сторон, то эта прямая служит
биссектрисой того угла треугольника, через вершину которого она
проходит.
Дано: -рг = вс (чеРт· 206). Требуется доказать, что прямая
BE делит пополам /_ ABC. Если бы не прямая BE, а другая пря-
АЕ АВ
мая ВЕХ делила пополам ^АВС, то мы имели бы: 2Г5=£С"
Значит, две точки Ε и Е1 делили бы отрезок АС в одном и
том же отношении, что невозможно (§ 128, задача 2).
§ 133. Свойство биссектрисы внешнего угла треугольника
Теорема. Биссектриса внешнего угла треугольника делит
противоположную сторону внешним образом в отношении, равном от-
ношению прилежащих сторон.
Дано: 2.CBD= /_DBE (черт. 207). Требуется доказать, что
AD_AB
CD" ВС
Проведём прямую CF\\BD.
Замечаем, что £ BFC= £ DBE (как соответственные), £ FCB== £ CBD
(как накрест лежащие). Но ^ CBD= £ DBE, следовательно, ^ BFC= £ FCB.
133

:ВС. В треугольнике
Значит, треугольник FBC равнобедренный, то есть BFz
ABD имеем:
CD~~BFf
а так как BF=BC, то
AD__AB
CD^BC
Имеет мзсто и обратная теорема;
формулировку и доказательство её
мы оставляем читателю.
Опираясь на определение
биссектрисы угла, учащиеся легко
могут убедиться, что биссектрисы
внутреннего и смежного с ним внешнего угла треугольника взаимно
перпендикулярны. D_
Заме чание. Биссектриса BG внутреннего угла ЛВС и биссектриса ВО
смежного внешнего угла СВЕ треугольника ABC (черт. 208) пересекают
прямую АС соответственно в точках G и Д образующих с точками А и С гар-
AG AD АВ _ т>г- \ t>r\
так как -^= —= —. При этом BG±BD как
GC~~DC ВС
Черт. 208
моническую группу точек
биссектрисы смежных углов.
Легко заметить, что справедливо и
обратное предложение, а именно:
если точки Л и С гармонически
сопряжены с точками G и D и из
какой-либо точки В вне прямой АС
проведены прямые В А, ВС, BG,
BD, причём оказалось, что BG^_BD,
то прямые BG и BD служат
соответственно биссектрисами угла
ABC и угла, с ним смежного.
В самом деле, если бы прямая
BG не была биссектрисой угла ABC,
то можно было бы построить угол ОВА', равный углу GBC. Прямая BU служила
бы биссектрисой угла А0ВС, а прямая BD как перпендикулярная BG была бы
биссектрисой смежного угла СВЕ' и точки G и D были бы гармонически
сопряжены с точками А' и С. Но для точек G, D и С можно построить лишь
одну точку Л, гармонически сопряжённую с С относительно G и D.
Следовательно, А' должна совпасть с Л, а прямая BG должна служить
биссектрисой угла ABC
§ 134· Окружность
Аполлония
Задача. Найти
геометрическое место точек, отношение
расстояний которых от концов
данного отрезка равно
отношению длин а и b данных отрезков
(а Ф b).
Дан отрезок АВ (черт. 209), два
отрезка а и Ь (а Ф b). Радиусами,
равными α и Ь (или радиусами, им пропорциональными), описываем из точек Л и
В как из центров две дуги. Точка X пересечения этих дуг будет одной из
искомых точек. Разделив угол АХВ и смежный с ним пополам прямыми АС
и XD, получим на примой АВ две точки С и Д также принадлежащие иско-
Черт. 209
134

мому геометрическому месту, так как АС\СВ=а:Ь и AD:BD = a:b (§ 132 и
§133), причём точки/4, В, С, D образуют гармоническую группу точек. Так как
£ CXD — прямой, то точка А'лежит на окружности, описанной на СД как
на диаметре. Покажем, что каждая точка этой окружности принадлежит
искомому геометрическому месту. Возьмём на этой окружности произвольную
точку Υ и соединим её с точками Л, θ, С и D. Пары точек Л, В и С, D
гармонически сопряжены, и, кроме того, угол DYC— прямой как опирающийся
на диаметр, а поэтому (§ 133, замечание)
£AYC=£BYC,
следовательно,
AY _AC_ a
YB~~ СВ~~ Ь '
Итак:
Геометрическое место точек, отношение расстояний которых
от концов данного отрезка равно отношению длин а и b данных
отрезков (а Ф b), есть окружность, описанная как на диаметре, на
отрезке между точками, делящими данный отрезок внутренним и
внешним образом в отношении -г-.
Эта окружность называется окружностью Аполлония, по имени впервые
открывшего её греческого геометра Аполлония Пергского, жившего
в III в. до н. э.
V. УПРАЖНЕНИЯ К ГЛАВЕ ПЯТОЙ
A. Доказать теоремы.
1. Лежащий внутри треугольника отрезок секущей, параллельной
основанию треугольника, при пересечении с медианой основания делится пополам.
2. Каждая диагональ трапеции при пересечении с другой диагональю
разбивается на части, находящиеся в одинаковом отношении для обеих диагоналей.
3. Лежащий внутри трапеции отрезок прямой, параллельный основаниям
трапеции и проходящий через точку пересечения её диагоналей, делится в
этой точке пополам.
4. Даны два треугольника ABC и АВСЛ с общим основанием АВ и
равными высотами CD и QD, и расположенные по одну сторону от основания
АВ. Прямая EF, параллельная АВ> пересекает стороны первого треугольника
в точках Μ и TV и стороны второго — в точках Λί, и Νν Доказать, что ΜΝ=ΜχΝλ.
Б. Геометрические места точек.
5. Найти геометрическое место точек, делящих в данном отношении
отрезки всех прямых, пересекающих две параллельные прямые, заключённые
между этими прямыми. Отв. Прямая, параллельная данным.
6. Найти геометрическое место точек, делящих в данном отношении
отрезки всех прямых, проведённых из общей точки О до встречи с данной
прямой АВ. Отв. Прямая, параллельная АВ.
7. Даны две параллельные прямые ρ и q. На прямой ρ даны две
неподвижные точки А и В. По прямой q перемешаются две точки Μ и N так, что
расстояние между ними ΜΝ остаётся неизменным. По какой линии
перемещается при этом точка пересечения прямых AM и BN? Отв. По прямой,
параллельной прямым ρ и q.
B. Задачи на построение.
8. Через данную точку внутри угла провести прямую так, чтобы её
отрезок, лежащий между сторонами угла, делился данной точкой в заданном
отношении т:п.
9. Через данную точку вне угла провести прямую, пересекающую стороны
угла так, чтобы данная точка делила отрезок этой прямой, лежащий между
сторонами этого угла, внешним образом в заданном отношении т.п.
135

10. Даны три луча ОА, ОВ и ОСУ выходящие из одной точки, и какая-
либо точка My не лежащая ни на одном из них. Провести через эту точку
прямую, пересекающую все три луча так, чтобы её отрезки, заключённые
между данными лучами, находились в данном отношении.
11. В данный треугольник вписать прямоугольник так, чтобы две его
вершины лежали на основании, а две другие — на боковых сторонах, и так,
чтобы диагональ этого прямоугольника имела наименьшую длину.
Указание. При помощи теоремы упражнения 4 свести задачу к случаю
прямоугольного треугольника. Отв. Из конца А основания АВ данного
треугольника ABC восставляем перпендикуляр к стороне АВ и откладываем на
нём отрезок ACV равный высоте данного треугольника: ACl = hc. Соединив
точки С, и Ву опускаем из точки А перпендикуляр AD на прямую СХВХ. Через
точку D проводим прямую, параллельную АВ. Эта прямая пересечёт стороны
АС и ВС в двух вершинах искомого прямоугольника.
12. В данный треугольник вписать прямоугольник так, чтобы его
диагональ имела данную длину.
См. указание к упражнению 11.
13. Ь данный треугольник вписать прямоугольный треугольник данного
периметра.
См. указание к упражнению 11.
14. Й данный четырёхугольник вписать ромб так, чтобы его стороны
были параллельными диагоналям четырёхугольника.
Указание. Вершины ромба делят стороны четырёхугольника в
отношении, равном отношению диагоналей четырёхугольника.
Построить треугольник, если даны:
15. а 4- by а\Ьу /_С.
16. /?, Су ра\рь. 17. a, hCy ра\рь.
Решение нижеследующих задач основано на изложенном в § 132—134.
Построить треугольник, если даны:
18. Су а:Ьу £А. 19. с, a:bt £C. 20. с, a:bf hc.
21. a.by qAy £A. 22. a:bt qAt /C. 23. qA:qB, at hc.
24. qA'QB> a> mc 25· Qa'Qb* Z>.
ΑΓ. Задачи на вычисление.
26. Дуги, стягиваемые сторонами вписанного четырёхугольника, относятся,
как 1:2:3:4; определить угол между диагоналями этого четырёхугольника.
Отв. 72°.
27. На какую длину следует продолжить отрезок Л£ = 20сж, чтобы
ΑΧ\ΒΧ = Ζ:2. Отв. 40см.
28. Через точку D стороны АВ треугольника ABC проведена секущая
DEy параллельная основанию АС. Определить длину DEy если АВ=\ЬЬсМу
АС =10 см и j4D = 31 см. Отв. Ъсм.
29. Отрезок секущей DE% проходящей через точку D стороны АВ
треугольника ABC параллельно основанию АСУ равен 7 см. Найти длину стороны
АСу если АВ = 24см и AD= 10 см. Отв. \2см.
30. Основания трапеции равны 15 см и 25 еж; определить отношения
отрезков, на которые разбивается каждая диагональ её при их взаимном
пересечении. Отв. 3:5.
31. Боковые стороны трапеции, продолженные до взаимного пересечения,
образуют вместе с меньшим основанием трапеции треугольник. Вычислить
его стороны, если основания трапеции равны \2см и 18слг, а боковые её
стороны 7 см и 9 см. Отв. 14 еж и \8 см.
32. Зная длины a, b и с сторон треугольника АВСу вычислить длины от-
_ ас be
резков qA и дв. Отв. ^я = ^р^, 4а=^гь-

ГЛАВА ШЕСТАЯ
ПОДОБИЕ ФИГУР
I. ПОДОБИЕ ТРЕУГОЛЬНИКОВ
§ 135. Основные определения
Два треугольника называются подобными, если углы одного
треугольника соответственно равны углам другого.
Примером подобных треугольников могут служить два любых
равносторонних треугольника, так как у этих треугольников все
углы равны.
Заметим, что как два любых равносторонних треугольника,
имея одинаковую форму, отличаются лишь своими размерами,
так и два любых подобных треугольника, имея одинаковую форму,
отличаются друг от друга лишь своими размерами.
В
а ^ Ас к /А/у *Г\ \с
Черт. 210 Черт. 211
В подобных треугольниках стороны, лежащие против равных
углов, называются сходственными сторонами.
На чертеже 210 изображены два подобных треугольника ABC
и KLM, у которых ΖΑ = Ζ.Κ> Ζβ = Ζ.Ι-' /C = /JA. Стороны
АС и КМ, АВ и ΛΧ, ВС и LM будут сходственными сторонами
треугольников ABC и KLM.
В дальнейшем вместо слов „треугольник ABC подобен
треугольнику KLM* мы будем употреблять знак подобия ел и
коротко записывать:
AABCcs>&KLM.
Из определения подобия треугольников вытекает следующая
теорема:
137

Прямая, параллельная какой-нибудь стороне
треугольника и пересекающая две другие его стороны, отсекает
от него треугольник, подобный данному.
В самом деле, из чертежа 211 видно, что если DE
параллельна АС, то углы А и D, а также С и Ε треугольников
ABC и DBE равны как соответственные при параллельных, а
угол В — общий. Следовательно, треугольник DBE подобен
треугольнику ABC по определению подобия треугольников.
§ 136. Основная теорема о подобных треугольниках
Теорема*. В подобных треугольниках сходственные
стороны пропорциональны.
Пусть даны два подобных треугольника ABC и ΑλΒ£λ, у
которых /_А = /Ах, Ζβ = Ζβ\* /β = Ζ£\ и» следовательно,
стороны АВ, ВС, АС сходственны сторонам АХВ„ В^С^ АХСХ
(черт. 212).
Τ * Β£ΐ ClAl ΛΑ
Требуется доказать, что -^ = -^■ = -^■.
На стороне АВ от вершины В отложим отрезок ВА\ равный
ВХА1% и из точки А' проведём прямую АС, параллельную
основанию АС треугольника ABC.
Тбгда углы А и А равны
как соответственные. Но по
условию теоремы /_А = /_А1%
следовательно, /А = /_АХ.
Кроме того, угол В равен
кл УГЛУ &1 по условию, а А'В =
1 =AiBJ по построению.
Следовательно, треугольники
ABC и А1В1С1 равны
согласно второму признаку равенства треугольников.
Проведём теперь прямую CD параллельно стороне АВ. Тогда
параллельные прямые АВ и CD отсекают на сторонах ВС и АС
угла С пропорциональные отрезки (§ 126), и мы будем иметь:
*£.-*£ m
ВС~ АС \Ч
Но в параллелограмме AACD противоположные стороны
равны, а потому AC = AD и, следовательно,
БС_Л1С
ВС — АС ' W
Аналогично параллельные прямые АС и АС отсекают на
сторонах угла В пропорциональные отрезки, и мы можем написать:
ВС _ В А1
ВС ~ ВА ·
* Эта теорема принадлежит Фалесу.
138

Итак, мы имеем:
ВС_ _ ВА^ JVC_
ВС~ ВА~ АС
Но так как треугольник ABC равен треугольнику АХВХС.%
то ΑΒ = ΑλΒλ, AC = AiCl и ВС = BlCli а потому окончательно
получаем:
ВХСХ B^Aj AJCi
ВС~ ВА~ АС
§ 137. Первый признак подобия треугольников
Теорема. Если два угла одного треугольника равны
двум углам другого треугольника, то треугольники
подобны.
В самом деле, если два угла одного треугольника равны двум
углам другого треугольника, то и третьи углы этих
треугольников равны, следовательно, согласно определению подобных
треугольников данные треугольники будут подобны.
§ 138. Второй признак подобия треугольников
Теорема. Если две стороны одного треугольника
пропорциональны двум сторонам другого треугольника и углы,
заключённые между этими сторонами равны, то
треугольники подобны.
A R R С*
Пусть даны два треугольника ABC и A1B1C1$-j^=-±-a t
/βλ = /β (черт. 213).
Требуется доказать, что
ДЛЯСсоДЛДС,.
Отложим на стороне АВ
отрезок BD = BlAl и на
стороне ВС отрезок BE = Bfix.
Тогда треугольник DBE
будет равен треугольнику А1ВХС1
по первому признаку равен- Черт. 213
ства треугольников. А β вс
По условию теоремы ~^ = -πγ? и по построению BD = BXAX
и BE = BiCl, следовательно, имеем:
BD_BE_
АВ~ВС'
Тогда согласно обратной теореме § 127 прямая DE
параллельна прямой АС и, следовательно, на основании теоремы § 135
треугольники ABC и DBE подсбны, а значит, и треугольник
АХВХСХ, кгк равьый ктреугольььку BDE, также подобен
треугольнику ABC.
139

§ 139. Третий признак подобия треугольников
Теорема. Если три стороны одного треугольника
пропорциональны трём сторонам другого, то
треугольники подобны.
Дано (черт. 213)
AA_B}C1_AJC1 т
АВ~ ВС~ АС · 1 '
Требуется доказать, что АА1В1С1оп ДАВС.
Снова откладываем на стороне АВ от вершины В отрезок
BD = A1B1 и проводим DE\\AC. Тогда согласно теореме § 135
получаем треугольник DBE, подобный треугольнику ABC. Из
подобия этих треугольников следует, что
ОВ_ВЕ DE (ζ).
ν АВ~ ВС~ AC (Z)
Но у рядов отношений (1) и (2) равны первые отношения,
следовательно, равны и остальные их отношения, а именно:
В}С1_ВЕ_ А,С, __РЕ
ВС ~~ ВС И АС ~АС>
откуда:
В£х = BE и A1Cl=DE.
Итак, треугольники DBE и A1BiC1 имеют по три
соответственно равные стороны, значит, они равны. Но /\DBE& ДЛ5С,
следовательно, l\AlBlCl с/э /\АВС.
§ 140. Признаки подобия прямоугольных треугольников
Из первого и второго признаков подобия треугольников
непосредственно вытекают следующие признаки подобия
прямоугольных треугольников.
Прямоугольные треугольники подобны, если:
1) имеют по равному острому углу;
2) катеты одного пропорциональны катетам другого.
Докажем третий признак подобия прямоугольных
треугольников, а именно:
Если катет и гипотенуза одного прямоугольного
треугольника пропорциональны катету и гипотенузе другого
прямоугольного треугольника, то такие треугольники
подобны*
Пусть в треугольниках ABC и AlBlCl ^/β = ^/β1 = 90° и
AlBl_AlCl
АВ~ АС ·
На стороне В А от точки В (черт. 214) отложим отрезок BDy
равный отрезку ΒχΑλ и через точку D проведём прямую DE па-
140

раллельно гипотенузе АС.Л Тогда ДОВ£соДАВС (§ 135), и
поэтому мы можем написать:
DE_BD
АС~ АВ*
Так как BD = A1B1, то полученную пропорцию можно
переписать таким образом: ,.
ΡΞ_ΑιΒι
АС~ АВ * ■
Сравнивая эту пропорцию с данной
пропорцией, мы убеждаемся, что
DE = A1Clt а потому треугольник BDE
равен треугольнику AxBfiv
Но так как ДОВЕсл /\АВСУ то и £*
равный ему треугольник А1В1С1 также
будет подобен треугольнику ABC. Черт. 214
§ 141· Сравнение признаков подобия треугольников
с признаками их равенства
Обозначим стороны двух треугольников через а, Ь, с н а19
bv clt а углы, лежащие против них, через Л, β, С и Л,, Ви С,.
Составим сравнительную таблицу условий равенства и подобия
треугольников.
Признаки равенства треугольников:
I. a = a1$ b = b1$ ZC=/CV
II. a = alt ΖΒ = Ζ&» Δβ=Δ^
III. a = alf b = b19 c = cr
Признаки подобия треугольников:
Эта таблица показывает, что для равенства треугольников
всегда нужно иметь на одно условие больше, чем для подобия.
§ 142. Свойство отрезков параллельных прямых,
пересекаемых пучком прямых
Теорема. Прямые, проходящие через одну точку,
отсекают на двух параллельных прямых пропорциональные
отпезки.
Пусть SAlt SBlf SClt SDi — прямые, проходящие через точку
tS\ пересекают две параллельные прямые AD и A1Dl соответственно
141

в точках Л, 5, С, D и Д, fit, С,, D, (черт. 215). Требуется
доказать, что
АА _ В^С, _ C,DY
АВ — ВС — CD *
Согласно теореме § 135 имеем:
ASABcnASAA,
Отсюда следует, что
a1b1_b1s. bas_b1c1_c2s9 cvs
АВ ~~ BS ' BS~ ВС ~ CS ' CS ''
: CD
Сравнив полученные равенства, будем иметь:
/!,£, ^С,
ЛЯ ~~ ВС
С,Д
: CD *
§ 143. Пропорциональный циркуль
Для изменения длины данных линий в заданном отношении
употребляется прибор, называемый пропорциональным циркулем»
Он состоит из двух равных по длине пластинок с остриями на
концах (черт. 216). Вдоль пластинок сделаны
прорезы, в которые вложены короткие
пластинки с отверстиями для винта, вокруг
которого пластинки могут вращаться. Когда
винт ослаблен, короткие пластинки могут
перемещаться в прорезах так, что длина
ножек циркуля может изменяться. В силу
подобия треугсльниксв расстояния между
остриями верхних ножек к расстоянию
между остриями нижних равно отношению длины
верхних ножек к длине нижних.
Для изменения отрезков в данном
отношении устанавливают центр винта так, чтобы
длины верхних и нижних ножек находились в
данном отношении. После этого, закрепив / \
винт, ставят концы нижних ножек на концы ** ^А
заданного отрезка и между верхними концами Черт. 216
получают изменённую длину отрезка.
Особенно удобно пользоваться пропорциональным циркулем, когда
приходится изменять длины большого числа отрезков в одном и
том же отношении.
142

§ 144· Масштаб
Различают численный и линейный масштабы. Под
численным масштабом подразумевают отношение расстояния между
двумя любыми точками на чертеже, плане или карте к
расстоянию между соответствующими двумя точками в натуре.
Например, если на карте расстояние между точками А1 и Βλ
равно 1 см, а в натуре расстояние между соответствующими
пунктами А и В равно 1 км, то численный масштаб этой карты
Α1Βλ___\
равен АВ— юооэо'
Вообще численный масштаб карт или планов выражают дробью,
в числителе которой стоит единица, а знаменатель есть число,
показывающее, во сколько раз уменьшаются расстояния на карте
по сравнению с соответствующими расстояниями в натуре.
Зная численный масштаб, строят линейный масштаб, который
представляет собой отрезок с нанесёнными на него равными
делениями и надписью, указывающей, что соответствует каждому
делению в натуре.
Например, если численный масштаб равен 1QQQQQ0, то это зна-
чит, что каждому миллиметру на карте соответствует 1000 000 мм
или 1 км в натуре. Поэтому одному сантиметру на карте
соответствует 10 км в натуре.
Основываясь на этих рассуждениях, вычерчиваем
соответствующий линейный масштаб (черт. 217).
Масштаб 1 :1 000 000
10 О Ю 20 30 40 50 60 Ю 80 90км
I I I I I I I I I I I
Черт. 217
Для определения расстояния по карте между двумя
определёнными пунктами А и В при помощи линейного масштаба нужно
поставить одну ножку измерительного циркуля в точку Л, а
другую— в точку В и, не меняя раствора циркуля, перенести
циркуль на линейный масштаб так, чтобы одна ножка находилась
справа на каком-нибудь крупном делении, а другая — слева на
мелких делениях первого отрезка.
Тогда по линейному масштабу мы сразу определим расстояние
между пунктами А и В в натуре.
Для более точного измерения по карте к линейному масштабу
пристраивают ещё так называемый поперечный масштаб.
В основе устройства поперечного масштаба лежит следующая
теорема: если катет ВС прямоугольного треугольника ABC
{черт. 218, β) разделить на 10 равных частей и через точки деления
ИЗ

провести прямые, параллельные другому катету АС, то мы
получим ряд параллельных отрезков MN, А77,..., 57", причём, если
длина катета АС равна 10, то длина AW = 9, AT7 =8,..., ST= 1.
В самом деле, это непосредственно вытекает из теоремы Фалёса
и из элементарных построений, приведённых на чертеже 218, а.
а)
В
к.
м/
ZL
/
/
/ 7
/ 8
9
1 1 L. 1 1-1
/А
Ю9876543210.
F
N
С
Черт. 218
Ясно, что если ЛС=1, то ΛίΝ = 0,9; AT7 = 0,8 и т. д. Обычно
прямоугольный /\АВС располагают иначе, а именно так, как
указано на чертеже 218, tf.
Для того чтобы лучше уяснить, что представляет собой
поперечный масштаб и как с ним работать, обратимся к чертежу 219,
где через точки с пометками
0,10,20, ..., 90 проведены
10 параллельных наклонных
таким образом, что прямая,,
проходящая через пометку 90
на горизонтальной шкале,
проходит через левую
верхнюю вершину
прямоугольника.
Из этого чертежа
непосредственно видно, что
отрезок MN равен сумме
отрезков МКи KN. Но МК = 30,
так как ОАМК—
параллелограмм, у которого МК =
= АО = 30, a /<7V согласно
доказанной выше теореме
равен 3, следовательно, ΜΝ =
цифру 3 без нанесения
единично 90 80 70 60 50 40 30 20 Ю
Черт. 219
= 33, причём мы получили
ных делений на горизонтальную шкалу.
Аналогично мы сразу находим по нашему чертежу, что £77=29
и т. д·
144

Для удобства пользования поперечным масштабом через точки
деления вертикальной шкалы проводят прямые, параллельные
горизонтальной шкале, и пристраивают поперечный масштаб к
линейному. В результате мы получим чертёж 220.
При измерениях при помощи поперечного масштаба поступают
так. Циркуль, перенесённый с карты, накладывается на масштаб
таким образом, чтобы обе его ножки лежали на одной горизон-
,Ν
вО 60 40 20 Q
100
200
300
400
Черт. 220
тали, причём стараются сделать это так, чтобы одна ножка
находилась на пересечении горизонтали с вертикалью, а другая —
на пересечении горизонтали с наклонной прямой.
Допустим, что после наложения циркуля одна его ножка
попала в точку 7V, а другая — в точку М. Тогда длина отрезка ΜΝ,
как это видно из чертежа, равна сумме трёх отрезков:
MN = MP + PQ + QN.
Но Q7V = 300, MP =50 и PQ = 8, следовательно, M/V=358.
II. ПОДОБИЕ РАЗЛИЧНЫХ ФИГУР
§ 145. Определение подобных фигур
На практике часто приходится из данной фигуры получать
другую фигуру путём увеличения или уменьшения расстояний
между всеми точками данной фигуры в одно и то же число раз.
Так, при составлении планов зданий и различных сооружений
или при составлении географических карт часто приходится
изготовлять эти планы и карты в различных масштабах, другими
словами, приходится изменять расстояния между всеми точками
данной фигуры в одно и то же число раз.
Чтобы показать, как это осуществляется, приведём следующий
пример.
На чертеже 221 изображена схема расположения Полярной-
звезды на небосклоне. Пусть нам нужно получить ту же схему,
но другого размера путём увеличения расстояний между всеми
точками данной схемы (фигуры) в два раза.
145

Тогда выбираем на плоскости два таких произвольных отрезка
А В
АВ и АЛВЛ% что -ттг = 2. Затем соединяем точки А и В с какой-
1 ι* АВ
либо точкой данной фигуры, например с точкой /?, и строим
углы BJAlRl и ΑχΒβχ, соответственно равные и одинаково
расположенные* с углами BAR и ABR
(черт. 222).
Будем считать точку R1
пересечения лучей И,/?, и Sj/?! точкой,
соответствующей точке R данной схемы.
* Из нашего построения следует, что
L м^ *Р AAiBiRi^AABR по первому приз-
Черт. 221
наку подобия, а потому будем иметь:
Α^_Ββ, =А,В,
AR ~ BR АВ
= 2.
Построив совершенно таким же способом точку Nlf
соответствующую другой произвольной точке N данной фигуры, мы
получим два новых подобных треугольника AlBlNl и ABN, а потому
будем иметь:
ΑλΝλ_ΑΛΒλ
AN
АВ
= 2.
Черт. 222
Но так как /BXAXRX = Z.BAR и /.Β,Α,Ν^ Ζ.ΒΑΝ,
то ^mRlAlNl = ^RAN. Кроме того, как мы нашли выше,
AR
AN
• Это означает, что если, двигаясь от А к В, мы видим лучи AR и BR
расположенными справа (или слева) от АВ, то, двигаясь от /4, к βρ мы будем
видеть лучи AXRX и BXRX также расположенными справа (или слева) от АХВХ.
146

следовательно, Л /?,Л,Л^,сл Δ RAN (§138), и из подобия этих тре -
угольников мы будем иметь:
AiRl_A,Nt_NlRl_Ci
AR~ AN~ NR ~ Ζ·
Отсюда мы видим, что расстояние между точками Νλ и /?,
вдвое больше расстояния между точками N и R. Но так как
N и R — произвольные точки первоначальной фигуры, то, построив
нашим способом все остальные точки Clf Eu Flt /С,,..., 5,,
соответствующие точкам С, Еу Fy /С,..., S данной фигуры, мы
получим новую фигуру, в которой расстояния между двумя любыми
её точками, например между Сх и Ei или между Я, и f, и т. д.„
будут вдвое больше расстояний между соответствующими точками
С и Ε или Ε и F и т. д. первоначальной фигуры.
Таким образом, вторая фигура Cjf,/7,/^,... Si получается из
первой CEFK... «S путём увеличения расстояний между всемь?
точками первой фигуры в два раза.
А В
Заметим, что если бы отношение -hr было равно к, то в этом
случае мы имели бы: #,/?, ,
и тогда вторая фигура получалась бы из первой путём изменения
расстояний между всеми точками первой фигуры в k раз.
Данная фигура CEFK... S и вновь построенная фигура
CjZr,/7,/^,... S, называются подобными фигурами.
Если, наоборот, мы примем фигуру C1EiD1Fi... S, за данную,
то тем же построением*, которое описано выше, мы получим
фигуру CEDF... S, подобную фигуре С^Д/γ... Sr
Из изложенного выше ясно, что каждой точке первой фигуры,
например точке F, соответствует определённая точка Fi второй,
фигуры, и наоборот, каждой точке второй фигуры, например
точке Llt соответствует определённая точка L первой фигуры.
Такое соответствие между точками двух фигур называется взаимно,
однозначным. Кроме того, расстояние между любыми двумя
точками первой фигуры в два раза меньше расстояния между
соответствующими точками второй фигуры, или, что то же самое*
расстояние между двумя любыми точками второй фигуры вдвое
больше расстояния между соответствующими точками первой
фигуры.
Таким образом, мы пришли к следующему определению
подобных фигур.
Две фигуры называются подобными, если между точками
этих фигур может быть установлено такое взаимно однозначное
соответствие, что отношение расстояния между двумя любыми
точками одной фигуры к расстоянию между двумя
соответствующими точками другой фигуры есть величина постоянная.
* Но только сначала мы будем строить треугольники АХВ&, Α^Ν^...,
а затем — подобные им треугольники ABR, ABN,....
147

§ J 46. Понятие о подобном преобразовании фигур
В § 145 мы дали построение, при помощи которого получили
фигуру, подобную схеме расположения Полярной звезды на
небосклоне.
Легко видеть, что если бы вместо схемы расположения
Полярной звезды мы взяли любую другую фигуру, то таким же
построением, которое описано в § 145, мы получили бы новую
фигуру, подобную данной.
В самом деле, произвольной точке /V первой фигуры при этом
построении соответствовала бы определённая точка /V, новой
фигуры, а именно: вершина Nl треугольника ΑλΒλΝ^ подобного
треугольнику ΑΒΝ, и наоборот. Кроме того, если N и R— две
произвольные точки данной фигуры, а Л^ и R^—
соответствующие им точки вновь
построенной фигуры, то буквально
так же, как и в § 145, можно
доказать, что
^,Я,
NR
АВ
к
Черт. 223
где k—- постоянная величина.
Таким образом, данная
фигура и вновь построенная
удовлетворяют определению
подобных фигур.
Приведённое нами построение, при помощи которого мы
из данной фигуры получаем ей подобную, называется
подобным преобразованием данной фигуры. Подобное
преобразование фигуры вполне определяется заданием двух отрезков АВ и
В качестве примера подобного преобразования фигуры приведём
построение фигуры подобной окружности.
Пусть дана окружность с центром в точке О и радиусом г
(черт. 223). Проведём произвольный диаметр АВ этой
окружности и возьмём на плоскости произвольный отрезок Л,В,. Пусть
R — произвольная точка данной окружности. Тогда, применяя
построение, данное в § 145, строим угол R^B^ равный углу
RAB9 и угол R&A^ равный углу RBA. Точка Rx пересечения
прямых A1Rl и B1Rl будет соответствовать точке /?. "
Когда точка R будет перемещаться по данной
окружности, то соответствующая ей точка R1 опишет окружность с
диаметром АХВ1% так как угол А^В1% равный углу ARBt будет
прямой.
Так как в результате построения, рассмотренного в § 145 и
в этом параграфе, получается фигура, подобная данной, то мы
заключаем, что фигура, подобная окружности, есть также
окружность.
на

§ 147. Коэффициент подобия двух подобных фигур
Когда рассматривают две подобные фигуры, то обычно одну
фигуру считают данной или первой, а другую — второй фигурой,
которая получена из первой фигуры при помощи определённого
построения (например, приведённого в § 145). При этом
отношение расстояния между любыми двумя точками второй фигуры к
расстоянию между двумя соответствующими точками первой
фигуры называют коэффициентом подобия двух подобных фигур
и обозначают его буквой k. Таким образом, если X и Υ — две
произвольные точки первой фигуры, а Л", и К, — две соответст-
X Υ
вующие им точки второй фигуры, то -yjr = £» где &—
коэффициент подобия.
Коэффициент подобия k показывает, во сколько раз нужно
изменить расстояния между всеми точками первой фигуры, чтобы
получить вторую фигуру.
Если k > 1, то вторая фигура будет больше первой, если k < 1,
то вторая фигура будет меньше первой, если, наконец, k=l9 то
вторая фигура будет равна первой, то есть равенство двух фигур
есть частный случай подобия.
§ 148. Свойства подобных фигур
Теорема 1. Отрез/су АВ данной фигуры
соответствует отрезок ΑιΒί подобной ей фигуры.
Пусть С—произвольная точка отрезка АВ и пусть точкам
Л, В, С первой фигуры соответствуют точки Al9 Blt Cx второй
фигуры.
В
В,
Черт. 224
Требуется доказать, что точка С, лежит на отрезке А1В1
(черт. 224).
Согласно определению подобных фигур имеем:
АХВХ _В1СХ АХСХ _ .
АВ — ВС ~ АС ~ *
149

или
А ХВХ = k. АВ, ВХСХ = k-BC, AlCl = k-ACi
где k — коэффициент подобия данных фигур.
Но так как АС + СВ = АВ, то k-AC-\-k-BC = k-AB или
Л1С1+В1С1 = Л1В1, а это означает, что точка Сх лежит на
отрезке ΑχΒλ.
Так как С — любая точка отрезка АВ, то и всем точкам отрезка
АВ будут соответствовать точки отрезка Л,В,, а это означает,
что отрезку АВ первой фигуры соответствует отрезок А1В1
второй фигуры.
Отрезки АВ и ΑίΒί подобных фигур называются
соответствующими отрезками.
Следствие. Прямой данной фигуры соответствует
прямая в подобной ей фигуре.
В самом деле, из доказанной теоремы следует, что трём
любым точкам Л, В, С, лежащим на прямой данной фигуры,
соответствуют в подобной фигуре три точки Л,, Blt Cif лежащие
также на прямой.
углы, не превышающие 180° и образо-
соответствующих отрезков, называют
соответственными углами.
Теорема 2. В подобных
фигурах соответствующие
отрезки пропорциональны, а
соответственные углы равны.
Даны две подобные фигуры
ABCDE и AlB1C1D1E1 (черт. 225).
Требуется доказать, что
АХВХ B1C1_C1D1 D& £И,
Черт. 225 АВ ВС CD DE ЕА
В подобных фигурах
ванные двумя парами
Ζ ЯΑ^ι = Z.BAE, Ζ Α,Β,Ο, = Ζ ABC, Ζ Д,СА = Ζ BCD,
/mClDlEl = /mCDE, /mDlElAl = /mDEA.
Согласно определению подобных фигур и теоремы 1 имеем:
Αβλ я,С,_
АВ
ВС
СХР, DJB, Е^ ,
DE fa '
CD
ЕА
где k — коэффициент подобия данных фигур.
Остаётся, следовательно, доказать, что соответственные углы
подобных фигур будут равны.
Для этой цели соединяем точку В с точкой Ε и точку В. с
А В
точкой £",. Тогда согласно определению подобных фигур -^г =
А Е BE
= -jrjf- = -±j£- = k и, следовательно, /\ABEcn/\AlBlE1 по третьему
признаку подобия треугольников, а поэтому углы ВАЕ и В1А1Е1
равны.
150

Совершенно таким же способом доказываются и равенства
остальных углов.
Заметим, что обратная теорема неверна, так как всегда можно
указать две фигуры, у которых соответственные углы равны и
соответствующие стороны пропорциональны, но тем не менее
эти фигуры не подобны. Например,
на чертеже 226 изображены две
фигуры ABCD и i^SjCjD,, у
которых
AB = BC=CD = AlBl = BlCl=C1D1
В
В
С,
= Z5,C1D1 = 909. /I1 /7,1 1д
Тогда в этих фигурах соответ- Черт 22б
ствующие отрезки пропорциональны,
А Я ВС CD
так как -χ§- = ^ζ- = -^ и соответственные углы равны, так как
£ABC = ZAiBfi» /.ΒΟΒ = /_ΒρλΏχ.
Между тем, эти фигуры не подобны, так как из чертежа
непосредственно видно, что отношение расстояний между точками
Л, и D, к расстоянию между точками А и D не равно отноше-
АХВХ
нию
АВ
§ 149· Подобие многоугольников
Теорема 1. В двух подобных многоугольниках
соответственные углы равны, а сходственные стороны про-
порциональны.
В подобных многоугольниках соответствующие отрезки
называются сходственными сторонами.
С
Черт. 227
Так как многоугольник ABCDEF подобен многоугольнику
ΑββιΡΑ^ι (чеРт· 227)> то согласно теореме 2 § 148
Δ& = ΔΚ ΔΒ=/_Βι% Z.C=AC„
AO=AD» Δ£=Δε„ Δ?=ΔΡ»
АВ
ВС
CD
DE
EF
FA
131

Теорема 2. Подобные многоугольника сходственными
диагоналями разделяются на подобные треугольники.
Проведём в подобных многоугольниках ABCDEFw AlBiClDlElFl
(черт. 227) диагонали из вершин Л и Л, и сравним
треугольники ABC и A.Bfi^ACD и Afi.D^ADE и Αβ,Ε,; AEFwA.E.F,.
Докажем, например, что /\ACD& /\AlClDl.
Согласно определению подобных фигур будем иметь:
-^£? = -£jy = -£jy = k , где k — коэффициент подобия, и,
следовательно, /\ACD c/d /\AlC1Dl πο третьему признаку подобия
треугольников.
Совершенно таким же способом ^доказывается и подобие
остальных пар треугольников.
Из изложенного выше вытекают два следствия.
Следствия. 1. В подобных многоугольниках отношение
сходственных диагоналей равно отношению сходственных сто-
рон.
2. Отношение периметров подобных многоугольников равно
отношению их сходственных сторон.
Действительно, из равенств
AJB, fiiCi CXDX_D,EX EJ\ FXAX
• АВ ~ ВС~ CD ~ DE ~ EF~ FA
в силу свойств пропорциональных отрезков (§ 125, теорема 3)
имеем:
АгВ, + В,СХ + С1Р1 + ΡχΕλ + E,F, + F,AX _ ΑλΒλ _B,CX _
АВ + ВС + CD + DE + EF + FA ~ АВ ~ ВС #
§ 150. Признак подобия многоугольников
Теорема. Два одноимённых многоугольника подобны,
если стороны одного пропорциональны сторонам другого,
а углы между пропорциональными сторонами равны.
Даны два многоугольника ABCDE и AlBiClDlEl (черт. 228),
причём
ZA = ZA Zfli=Z*.···. Z^i=Z£
И ΑλΒλ BlCl ΑχΕλ
АВ ~~ ВС ~ *" — АЕ ~*-
Требуется доказать, что данные многоугольники подобны.
Построим такой многоугольник A2B2C2D2E2f подобный
многоугольнику ABCDE (например, при помощи построения,
изложенного в § 145), чтобы коэффициент подобия многоугольников
A2B2C2D2Et и ABCDE был равен отношению сторон данных
многоугольников A1BlCiDlEl и ABCDE.
Тогда мы будем иметь:
А2В2 _ В2С2 _ С2Рг __ DtE2 __ еХ _
АВ ~ ВС ~ CD~ DE ~ ЕА~*Щ
152

Кроме того, мы знаем, что в подобных многоугольниках
соответственные углы равны, а поэтому
Но по условию теоремы мы имеем:
АХВХ ^С, С,Р1 ΡλΕλ ΕλΑλ _ .
АВ
ВС
CD
DE
ЕА
ZA = ZA Z*, = A
Следовательно,
AlBl=AtB%9 BlCl=BtCt9
C1Dl=CIDIfD1£1=DI£,lf
/ν
И Черт. 228
ZA = ΖΛ. Ζ*.=Z#2, Zc, = zc„ ZOi=Z#2> Z^ = Z*.·
Это означает, что многоугольники AlBlClDlEl и A2B2C2D2E2
равны, так как при наложении они совместятся.
Так как многоугольник A2Bfi2D2E2 по построению подобен
многоугольнику ABCDE, то и равный ему многоугольник AlBlClDlEi
подобен многоугольнику ABCDE.
III. ГОМОТЕТИЯ
§ 151. Предварительные замечания
В § 145 мы познакомились с общим приёмом подобного
преобразования данной фигуры при помощи двух отрезков АВ и
АХВХ, произвольно расположенных на плоскости.
Черт. 229
Черт. 230
Если же отрезки АВ и ΑίΒι мы расположим не произвольно,
а так, как это показано на чертеже 229 или на чертеже 230, то
153

получим частный вид подобного преобразования фигуры, который
называется гомотетией.
Различают два вида гомотетии. Если точки В, Βλ лежат по
одну сторону от точки Л,, совпадающей с точкой Л, то
гомотетия будет первого вида (черт. 229). Если же точки В, Βλ
лежат по разные стороны от точки Л, то гомотетия будет
второго вида (черт. 230).
§ 152· Центр и коэффициент гомотетии
Пусть дана фигура а (черт. 231) и требуется при помощи
гомотетии первого вида построить новую фигуру, подобную данной.
Тогда, следуя правилу построения соответствующих точек,
изложенному в § 145, берём произвольную точку К данной
фигуры, соединяем её с точками Л и β и строим углы ΒλΑλΚλ и
ΑγΒίΚχ* соответственно равные и одинаково расположенные с уг-
Черт. 231
лами ВАК и АВК. Так как при гомотетии точка Ах совпадает с
точкой Л и точки Л, В, Вх лежат на одной прямой, то точка Klt
соответствующая точке К, будет точкой пересечения прямой АК
с прямой β,ΛΊ, причём прямая ВХКХ параллельна прямой ВК, так
как ΖΑΒΚ=ΖΑΒ1Κ1.
Кроме того, мы видим, что прямая, соединяющая
соответствующие точки К и /С,, проходит через точку Л.
Параллельные прямые ВК и ΒλΚχ отсекают на сторонах
угла ΒιΑιΚί пропорциональные отрезки (§ 126), а потому
АК1_АВ1_.
АК~ЛВ —*·
Число k называется коэффициентом гомотетии, точка Л,
совпадающая с точкой Av называется центром гомотетии.
Коэффициент гомотетии не зависит от положения точки /С
Тем же способом, каким мы получили точку Ки мы можем
построить и другие точки фигуры b и тем самым получить
фигуру, подобную фигуре а (§ 145, 146).
Для этой цели соединяем точки Z,, Ж, 7V,... фигуры а с
центром гомотетии Л и, проведя прямые B1Li |] BL, В1М1 [\ ВМ,...,
154

получаем на лучах AL, ЛЛ1,··· такие отрезки ALl9- AMlt---9
что
AL1_AM1_ _ЛВ1_
AL ~АМ ~ АВ~ k>
где k — коэффициент гомотетии.
Тогда точки /С,, I,, Mlf Nlt- · -образуют новую фигуру Ь,
подобную данной (§ 145).
Это же можно доказать иначе.
В самом деле, каждой точке фигуры а соответствует
определённая точка фигуры Ь9 и наоборот.
Далее, если Ρ и Q — две любые точки фигуры а, Р1 и Qx—
соответствующие им точки фигуры Ь, то по построению:
AP1_AQ1_\ '
АР ~ AQ — *»
и согласно обратной теореме § 127 прямые PQ и PxQt
параллельны. Тогда /\APXQX<^/\APQ и мы имеем:
P£1_AP1_AQ1_b
PQ —АР ~AQ — *»
где k — постоянная величина.
Поэтому согласно определению подобных фигур фигура Ъ
подобна фигуре я, причём коэффициент подобия этих фигур
равен коэффициенту гомотетии.
Заметим, что фигуры α и & не только подобны, но и
определённым образом расположены на плоскости, так как прямая,
соединяющая две произвольные точки одной фигуры, параллельна
прямой, соединяющей соответствующие точки другой фигуры, и,
кроме этого, прямая, соединяющая соответственные точки обеих
фигур, проходит через центр гомотетии.
Подобные фигуры, расположенные таким образом на
плоскости, называются гомотетичными фигурами. Например, фигуры
а и b будут гомотетичными фигурами.
§ 153· Другой способ построения гомотетичных фигур
Применив данное в § 145 правило построения
соответствующих точек подобных фигур для случая второго вида гомотетии,
то есть когда точки β и β, лежат по разные стороны от
точки Л, совпадающей с точкой Л,, мы таким же путём, как и в
предыдущем параграфе, приходим к следующему второму
способу построения фигуры &, гомотетичной фигуре а (черт. 232). .
Соединяем точки Р, Q, /?,··-первой фигуры с центром
гомотетии Л = Л,, продолжаем лучи АР, AQ, AR,- · · за центр А и
при помощи построения, изложенного в § 145, получаем на про-
155

должении этих лучей такие отрезки APU AQlf ARl$···, что
АР, AQ, AR, /Ш,
АР ~AQ ~AR ~"' — AS-*9
где k — заданный коэффициент гомотетии.
Черт. 232
Точки Рр Q,, /?,,· · -образуют фигуру, подобную и
гомотетичную данной, так как совершенно таким же способом, как и
в предыдущем параграфе, можно доказать, что PQ \\ PXQU PR \\ PlRi
и т. д.
§ 154· Свойства гомотетичных фигур
Так как гомотетичные фигуры будут и подобными фигурами,
то все свойства подобных фигур переносятся и на гомотетичные
фигуры, например, в гомотетичных фигурах соответствующие
стороны пропорциональны и соответственные углы равны.
Так как при общем подобном преобразовании окружности,
она преобразуется в окружность, то и в обоих видах гомотетии
окружности будет соответствовать окружность.
Но гомотетия имеет и свои особенности, а именно: в
гомотетичных фигурах соответствующие отрез/си
параллельны и прямые, соединяющие соответствующие точки
гомотетичных фигур, проходят через центр гомотетии.
§ 155· Примеры построения гомотетичных фигур
На чертеже 233 построен пятиугольник A^Bfi^^^
гомотетичный данному пятиугольнику ABCDE.
Точка О — центр гомотетии, коэффициент гомотетии k
равен тг, так как точки А1У Bv Cp Dv Е1 являются серединами
отрезков ОЛ, ОВу ОС, OD, ОЕ.
Заметим, что если быД=1, то пятиугольник Л,B1C1DiE1
совпал бы с данным пятиугольником ABCDE, то есть в гомотетии
156

первого вида при k = \ гомотетичные фигуры совпадают друг с
другом.
На чертеже 234 построен треугольник AlBlCv гомотетичный
треугольнику ABC. Здесь мы имеем дело с гомотетией второго
вида, причём коэффициент гомотетии & = 2, то есть
Черт. 233
Черт. 234
Если бы А=1, то треугольник А1В1С1 был бы симметричен с
треугольником ABC относительно центра О, и, следовательно,
гомотетия второго вида при k = 1 превращается в центральную
симметрию.
§ 156· Пантограф
Дл я механического построения фигуры, гомотетичной данной,
служит прибор, называемый пантографом*.
Для того чтобы понять, как устроен пантограф, возьмём
параллелограмм ABCD, сторонами которого служат металлические
стержни, скреплённые
шарнирами, благодаря чему
стороны параллелограмма могут
вращаться вокруг его
вершин (черт. 235). д
Закрепим вершину Л и на
продолжении стержня ВС
отметим точку Я, после чего
проведём отрезок АЕ.
F — точка пересечения CD
и АЕ.
Пусть, далее, ABCD и ΑΒ£λΩχ—два положения
шарнирного параллелограмма.
После перемещения параллелограмма из положения ABCD в
положение AB1CiD1 точки β, С, D, Я, F займут новые
положения В1% Ср О,, Еи Fl9 причём длины сторон параллелограмма
Черт. 235
1 Слово пантограф — греческого происхождения; в переводе на русский
язык оно означает: .все описывать".
157

A BCD и длины отрезков СЕ, FC и FD не изменятся,
следовательно, будем иметь:
CE = ClEv FC=FlCv FD = F,Dl%
BE = B,Eiy ВС = В,СЛ иАО = АО>.
Так как AD\\CE, то {\CFEtsi/\AFD, а потому
AD_FD
СЕ~ FC
Но AD = ADi9 CE = CXEU FD = F1DV /ГС = /Г1С1,
следовательно, полученную пропорцию можно переписать так:
AD1_F\D1
Кроме того, /_АО£х = /_DXCXEX как накрест лежащие при
параллельных ADX и BiEi и секущей Dfix.
Таким образом, Д ADiFi с/о Д FiCiEl по второму признаку
подобия треугольников и, следовательно, /^AFiDi^/^CXFAEU a
это означает, что точки Л, /\, Я, лежат на одной прямой.
BE AE
В треугольнике ABE AB\\FCt а потому gQ=jp (§126) ·
Аналогично в треугольнике ABiE1 Afi^Ffi^ а потому
В1Е}_АЕ1
В,С, ~~ AFX ·
Но так как ВЕ — ВХЕХ, а ВС=В1С1У то имеем:
АЕ_АЕХ
AF~~AF/
Это значит, что точки Ε и £,,
F w F} соответствуют друг другу
в гомотетии с центром в точке А
Черт. 236
и с коэффициентом гомотетии
k_AF_BE
к~~~~~ AF~ ВС*
Отсюда следует, что если точка Ε опишет какую-либо
фигуру, то точка F опишет фигуру, гомотетичную ей," причём
ВЁ
коэффициент гомотетии равен отношению ^ (черт. 235).
158

Если в точке Ε укрепить остриё иглы, а в точке F — остриё
карандаша, то при обводе остриём иглы контура фигуры остриё
карандаша зарисует на бумаге контур фигуры гомотетичной. Для
изменения коэффициента гомотетии следует переместить точку Ε
по прямой ВС в ту или другую сторону.
На этом свойстве шарнирного параллелограмма и основано
устройство пантографа (черт. 236, а). Схема пантографа другого
устройства дана на чертеже 236, б. Прибор применяется при
перерисовке планов в различных масштабах.
§ 157· Метод подобия
Свойства подобных и гомотетичных фигур с успехом могут
быть применены при решении многих задач на построение. В
самом деле, во многих задачах на построение условия задачи
удаётся разделить на две такие части, что одна часть условий вполне
определяет фигуру, подобную искомой, а
другая определяет размер искомой фигуры.
Пусть, например, требуется построить
треугольник по двум данным его углам А1 и Bt
и биссектрисе /с.
Эти условия можно разделить на две
части: к первой отнести заданные углы Л, и Blt
ко второй — заданную длину биссектрисы /с.
Применение метода подобия состоит в ^/
том, что сначала по первой части условий
задачи строят фигуру, подобную искомой,
а затем придают ей тот размер, который Черт* 3
соответствует второй части условий задачи.
В нашем примере по двум углам Д и β, можно построить
треугольник АХВХС (черт. 237) произвольной величины, взяв,
например, произвольную длину стороны AXBV Этот треугольник
будет подобен искомому.
В построенном таким образом треугольнике мы проводим
биссектрису 1С угла С и от точки С откладываем на ней
отрезок CD, равный заданной биссектрисе /с. Через точку D
проводим прямую, параллельную A iBi, встречающую прямые Afi и ВХС
в точках А и S. Треугольник АСВ — искомый.
Решим ещё несколько задач методом подобия.
Задача 1. Построить треугольник, если даны а:Ь, </.Си/гс.
Решение. Первые два данных условия а\Ъ и /_С вполне
определяют форму искомого треугольника (§ 138). Возьмём
какие-либо два отрезка й, и ί„ отношение которых равно а:Ь,
и построим треугольник ААВХС (черт. 238) по двум сторонам
uj и 6, и углу между ними С. Этот треугольник будет подобен
искомому.
159

На высоте CD] треугольника ΑλΒλΟ (если нужно, продолжив её)
откладываем отрезок CD = hc и через точку D проводим прямую,
параллельную Αβν Эта прямая встретит стороны САХ и СВХ
(или их продолжения) в точках А и В.
Треугольник ABC — искомый.
Приведём теперь примеры задач,
которые легко решаются, если
воспользоваться свойствами гомотетичных фигур.
Задача 2. В данный треугольник
вписать квадрат так, чтобы две его
вершины лежали на основании
треугольника, а две другие — на его боковых
сторонах.
Решение. Строим произвольный квадрат MNPQ, две
вершины которого лежат на основании АС данного треугольника,
а третья — на стороне АВ (черт. 239). Далее, приняв А за центр
гомотетии и проведя луч АР до пересечения в точке Рх со
стороной ВС, строим квадрат ΜλΝχΡ^^ гомотетичный квадрату MNPQ.
Задача 3. В данный равносторонний треугольник вписать
другой равносторонний треугольник, стороны которого были бы
перпендикулярны сторонам данного.
Черт. 238
мм* а с,
Черт. 239
мм, с
Черт. 240
Решение. Взяв на стороне АВ (черт. 240) произвольную
точку Ν, опускаем из неё перпендикуляр ММ на сторону АС.
Затем через точки N и Μ проводим прямые, перпендикулярные
соответственно сторонам АВ и ВС, до пересечения в точке Р.
Далее, проводим прямую АР до пересечения со стороной ВС
в точке Р, и строим треугольник Pfl^M^ гомотетичный
треугольнику PNM.
§ 158. Применение подобного преобразования
к съёмке плана местности
Предположим, что при съёмке плана местности нам необ(одимо нанести
на план характерные точки местности (черт. 241).
Для этой цели измеряют лентой на местности расстояние между какими-
нибудь двумя точками, например между точками А и В.
160

Пусть оказалось, что это расстояние АВ= 300 м.
Пусть, далее, мы желаем построить план местности в каком-либо заранее
выбранном масштабе, например в масштабе ттгтШ'
Тогда точки А и В местности изображают на листе чертёжной бумаги
L
(черт. 242) точками Ах и Вх таким образом, чтобы ф^ = γ^τ^.
AtS 1U UUU
Черт. 241
Но так как Л£=300 м, то АХВХ = 3 см.
Далее, для нанесения на план какой-либо третьей характерной точки,
например точки /С, поступают следующим образом.
При помощи специальных угломерных инструментов измеряют на
местности углы ВАК и АВК и затем, пользуясь транспортиром, строят на листе
бумаги углы ВХАХК\ и АХВХКХ, соответственно равные и одинаково
расположенные с углами ВАК и АВК.
Черт. 242
Точку /С,, в которой пересеклись прямые ΑχΚι и BXKV принимают за
изображение на плане характерной точки К (черт. 242).
Совершенно таким же способом пегеносятся на план и другие
характерные точки Д Е, F, ..., L, М.
Так как треугольник АВК подобен и одинаково расположен с
треугольником ΑχΒχΚν то легко видеть, что приведённое нами построение точек
161

резков АВ и ΑλΒν причём -j^:
Kv Dv ..., Λί, является не чем иным, как подобным преобразованием фигур,
лежащих на местности, в фигуры плана (§ 145, 146).
Ясно также, что это подобное преобразование определяется парой от-
" 10 000*
Как и при есяком подобном преобразовании, здесь будут иметь место
теоремы, доказанные нами в § 148.
Например, согласно теореме 1 отрезок МК на местности преобразуется
в отрезок МХКХ плана, и мы будем иметь:
мхкх__. ι
МК 10 000*
Отсюда следует, что если, например, на плане отрезок МХК1 = 2,5 см,
то в натуре отрезок МК будет равен 250 м.
У
V
^
У
Ак'
к/
V-
-Л
Черт. 243
В
На практике угломерный инструмент обычно помещают сначала в точку А
и записывают результаты измерений углов ВАК, BAL, BAF, ..., ВАМ, затем
переносят угломерный инструмент в точку В и записывают результаты
измерений углов АВК, ABL, ABF, ..., АВМ.
Пользуясь полученными данными, строят на плане указанным выше
способом точки Κν С,, ..., Λί,. Ясно, что построение плана удобнее произвести
не в поле, а в помещении.
Но существует инструмент, называемый мензулой, который позволяет
строить план местности непосредственно на поле.
Основная особенность мензулы состоит в том, что, пользуясь ею, мы
можем на листе бумаги, прикреплённом к квадратной доске, входящей в
состав мензулы, чертить угол, равный углу, образованному какими-либо двумя
прямыми на местности.
Эта особенность мензулы освобождает от пользования угломерным
инструментом и приводит к довольно быстрому построению плана местности.
В самом деле, допустим, что нам нужно, пользуясь мензулой, нанести на
план характерные точки местности А, В, С, ..., Λί, которые упоминались
нами выше (черт. 241).
Тогда на листе бумаги, прикреплённом к квадратной доске мензулы,
заранее ориентированной при помощи компаса, руководствуясь выбранным
масштабом, отмечаем две точки Л, и Вх (черт. 243), которые соответствуют
характерным точкам А и В местности.
162

Затем, пользуясь мензулой, чертим на бумаге углы ΑλΒχΚλ и BiAiKv
равные и одинаково расположенные с углами АВК и ВАК на местности, тем
самым определяем треугольник ΑβχΚν подобный и одинаково
расположенный с треугольником АВК на местности.
и KF,... и построив на бумаге в том
же масштабе треугольники CxNxDxy CXBXEV DX0XCX1 ..., /(,Λί,Γ,,..., подобные
и одинаково расположенные с треугольниками CND, СВЕ, DOC, ..., KMF,...,
получим план земельного участка в требуемом масштабе (черт. 245).
Мы произвели подобное преобразование многоугольника ABELFMDNA
в многоугольник Λ,β,/ί',Ζ.,/^Λ^Ο,Λ^Λ,, определяемое парой соответствующих
отрезков АВ и AXBV
В самом деле, легко доказать, что при этом преобразовании Δ ABE
преобразуется в подобный Δ ΑλΒχΕν Δ ABL — в подобный Δ Αβ^ и т. д.
163

Ясно также, что, например, треугольник NOC преобразуется при этом
подобном преобразовании в подобный треугольник NxOxCx и т. д.
Отсюда следует, что мы можем различными способами строить план
земельного участка, смотря по тому, на какую систему треугольников мы
разобьём земельный участок на местности.
Рассмотренный метод съёмки плана называется способом
треугольников или триангуляцией.
УПРАЖНЕНИЯ
Доказать, что при подобном преобразовании:
1. Параллельные прямые переходят в параллельные прямые.
2. Квадрат преобразовывается в квадрат.
3. Трапеция преобразовывается в трапецию.
4. Средняя линия трапеции преобразовывается в среднюю линию трапеции.
5. Ромб преобразовывается в ромб.
6. Замечательные точки данного треугольника переходят в замечательные
точки преобразованного треугольника.
IV. УПРАЖНЕНИЯ К ГЛАВЕ ШЕСТОЙ
А. Доказать теоремы.
Треугольники ABC и А'В'С подобны, если:
1. a:b:hc = a':b':h'c. 2. a:c:he = a':c':h'c,
3. Pa-Pb-hc=P'a-P'b'h'c. 4. а:Ъ:те = а':Ь':т\.
5. c:ma:mb = c':m' :m^ 6. a:hc = a':h'cn £C= /_ С.
7. hc\lc = h'\Vc и а^А = ^А\ 8. с:Ла = с'://0 и £А = £А'.
9. ЯА'Яв = Яа'Яв и £С=£С.
10. Прямая, соединяющая середины оснований трапеции, проходит через
точку пересечения её диагоналей.
11· Высоты треугольника обратно пропорциональны его сторонам, то есть
и и и ! 1 *
па'.Пи\пе = — : -г : —.
а ° с а Ь с
Указание. Построить две высоты и рассмотреть подобные
треугольники, для которых эти высоты служат катетами.
Б. Задачи на построение.
Построить треугольник, если даны:
12. а, а:Ъ, £С.
14. а-\-Ь-{-с, а:Ь\с.
16. £А, £В, hr
18. a:b, /_ С, та.
20. pa:pb, £С, hc ш
22. α:ΛΓ, £ A, R. 23. а:1с, £ В, г.
24. hc:pa:pb, R. 25. дА:дв] £, С, 1С.
26. Построить ромб, если даны его сторона и отношение диагоналей.
Построить параллелограмм, если даны:
27. Отношение двух его сторон, угол и одна из диагоналей.
28. Высота, отношение диагоналей и угол между ними.
29. Сторона, отношение диагоналей и угол между ними.
30. Один угол, сторона и отношение другой стороны к высоте,
опущенной на эту сторону.
164
13.
15.
17.
19.
21.
а:Ьи
а.
а:Ь,
/ic:lc
:, а.
Δ в, ι0
Δ в, г.
Δ С, ιΑ.
, ΔΑ,η,

Построить равнобедренную трапецию, если даны:
31. Угол при основании, одна диагональ и отношение оснований.·
32. Один угол, одно из оснований и отношение другого основания к
боковой стороне.
Построить трапецию, если даны:
33. Отношение её оснований, диагональ и два её угла.
34. Отношение её оснований, два угла и высота.
35. Отношение одного основания к боковой стороне, два угла и средняя'
линия.
36. В данный треугольник вписать прямоугольник, угол между
диагоналями которого имел бы данную величину.
37. В данный ромб вписать квадрат, вершины которого лежали бы на
сторонах ромба.
38. В данный круг вписать прямоугольник с данным углом между
диагоналями.
39. Описать около данной окружности треугольник, углы которого даны.
Указание. Сначала построить треугольник с данными углами и
вписать в него окружность, а затем произвести гомотетичное преобразование-
40. В данный полукруг вписать квадрат так, чтобы две его вершины
лежали на окружности, а две другие — на диаметре.
41. В данный полукруг вписать равнобедренную трапецию, подобную
данной.
42. Построить треугольник, для которого даны три его высоты ha, hb и hc.
Указание. Пользуясь пропорциями a\b:c=.j- : j- : -г- (упр. 11),
опрела **b **c
делить отношение сторон искомого треугольника и т. д.
43. Дан угол ABC и какая-либо точка О в его плоскости. Провести через
эту точку прямые так, чтобы отрезки, отсекаемые ею на сторонах угла,
находились в заданном отношении т:п.
44. Найти геометрическое место точек, отношение расстояний которых
от сторон данного угла равно данной величине. Отв. Луч, проходящий череа
вершину угла.
45. Найти геометрическое место точек, делящих в данном отношении*
отрезки параллельных прямых, заключённые между сторонами угла. Отв. Луч„
проходящий через вершину угла.

ГЛАВА СЕДЬМАЯ
ЧИСЛОВЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОСТРОГО УГЛА
§ 159· Определение тригонометрических функций
острого угла
Прямоугольный треугольник, как мы знаем, вполне
определяется двумя его сторонами, например двумя катетами или
катетом и гипотенузой. Но если вместо двух сторон задать их
отношение, то можно построить бесчисленное множество
прямоугольных треугольников, удовлетворяющих условиям
задачи, то есть имеющих данное отношение двух
сторон. Все эти треугольники будут подобными
между собой и, значит, все они будут иметь
одинаковые углы. Таким образом, отношение двух
сторон прямоугольного треугольника вполне определяет
величину его острых углов.
Отсюда следует, что величину всякого острого
угла можно определить при помощи отношения двух
прямолинейных отрезков, а именно: сторон
прямоугольного треугольника, содержащего этот угол.
Определять величину угла при помощи отношения
отрезков оказывается весьма удобным при решении многих задач.
Для облегчения пользования этими отношениями им дают особое
название: отношение катета ВС к гипотенузе АВ (черт. 246)
называется синусом угла А и обозначается символом sin Л:
ВС . .
■325- = sin А;
отношение катета АС к гипотенузе АВ называется косинусом
угла А и обозначается символом cos A:
АС л
наконец, отношение катета ВС к катету АС называется
тангенсом угла А и обозначается символом tgi4:
ВС , л
166

AC
Отношение -ggr называется котангенсом угла Л и обозначается,
символом ctgi4:
АС * л
Из этих отношений имеем, что
sin A
ЧА=
cos Л
И Ct<?A:
cos Λ
sin Λ
Величины sin Л, cos Л, tgЛ и ctgA называются
тригонометрическими функциями угла Л.
АС
Легко заметить, что cos Л, то есть отношение -т^, является
в то же время синусом для угла β, то есть
АС
АВ
■ sin В.
Так как
ZB=90° — Z.A,
то можно написать, что
cos Л = sin (90° —Л).
Точно так же
А л АС
ctgA = -^
является тангенсом для угла В, то есть
с1£Л=^(90° — Л)
Если дан угол Л, то можно определить его
тригонометрические функции. Для этой цели опускаем из какой-либо точки В на
одной из его сторон перпендикуляр ВС на другую сторону
(черт. 247). Тогда отношения сторон образовавшегося
треугольника ABC и будут представлять искомые тригонометрические
функции угла Л:
ВС . л АС А ВС х .
АВ'
АВ'
Если вместо точки В взять другую точку Вх и опустить
перпендикуляр ВХС1$ то получится треугольник ABfi^ подобный
треугольнику ABC, и, следовательно, отношение его сторон будет
равно отношению сходственных сторон треугольника ABC. А
потому тригонометрические функции угла Л при выборе точки Вх
будут иметь ту же величину, что при выборе точки В; значит,
они не зависят от выбора точки В на стороне угла.
167

§ 160. Построение острого угла по какой-либо одной заданной
его тригонометрической функции
Зная одну из тригонометрических функций острого угла, легко
построить этот угол. Пусть, например, нам дано, что sirb4 = -T.
Тогда легко построить угол А. Для этого, выбрав какую-либо
единицу длины, строим прямоугольный треугольник, один катет
Черт. 248
Черт. 249
которого равен 2 единицам, а гипотенуза равна 3 единицам (черт. 248).
Угол, лежащий против катета, равного 2 единицам, и будет
искомым·
Точно так же, если дано, что tgB=-j, το этого достаточно,
чтобы найти угол В. Для этой цели, выбрав какую-либо единицу
длины, откладываем отрезки в 5 единиц и 4 единицы на сторонах
прямого угла (черт. 249) от его вершины — это будут катеты
искомого треугольника. Угол, лежащий против катета, равного
5 единицам, будет искомым.
§ 161· Изменение тригонометрических функций при изменении
угла от 0° до 90°
На чертеже 250 изображена -χ часть круга, радиус которого
равен единице длины.
Построим произвольный центральный
/_АОВ. Опустив из точки В перпендикуляр
ВС на радиус ОА, получим:
sin Ζ ΑΟΒ=^=^= ВС;
cos ^АОВ=щ = ^ = ОС.
С2 d Си
Черт. 250
Пусть теперь радиус ОБ вращается от
положения О А до положения ОК, в
направлении, противоположном вращению часовой
стрелки. Тогда центральный угол АОВ будет увеличиваться от 0°
до 90°, а следовательно, длина отрезка ВС будет увеличиваться
от 0 до 1, а длина отрезка ОС будет уменьшаться от 1 до 0.
168

Но так как sin ^ АОВ = ВС, a cos ^/АОВ= ОС, то,
следовательно, при возрастании угла от 0° до 90° синус его
увеличивается от О до 1, а косинус уменьшается от 1 до 0+
Выясним, как изменяется тангенс и котангенс при изменении
угла от 0° до 90°.
На чертеже 251 изображён прямоугольный треугольник АОВ,
у которого сторона ОА равна единице длины.
Мы знаем, что К|
Ч^АОВ = ^=^ = АВ.
Пусть луч ОА вращается вокруг точки О
в направлении, противоположном вращению
часовой стрелки, от положения ОА до
положения ОА'
Тогда /_АОВ изменяется от 0° до 90°.
Отметим на прямой АВ точку D. Луч ОА,
вращаясь, перейдёт через положение OD.
В это время длина отрезка АВ,
увеличиваясь от 0, станет больше, чем отрезок AD.
Так как точка D была выбрана нами произвольно, то при
изменении угла АОВ от 0° до 90° длина отрезка АВ становится
больше длины отрезка AD любой длины, то есть увеличивается от
нуля неограниченно.
Так как tg £АОВ=АВ, то мы заключаем, что при
возрастании угла от 0° до 90? тангенс этого угла увеличивается
от нуля неограниченно, или, как условились говорить,
изменяется от нуля до бесконечности.
Так как мы знаем, что котангенс есть величина, обратная
тангенсу, то при возрастании угла от О9 до 00° котангенс его
неограниченно уменьшается, то есть стремится к нулю*
Черт. 251
§ 162· Таблицы тригонометрических функций острого угла
Чтобы легче было пользоваться тригонометрическими функциями
различных острых углов, для них составлены таблицы. Таблицы
тригонометрических функций имеются в книге В. М. Брадиса
„Четырёхзначные математические таблицы· (стр. 19—25). Таблица
синусов (таблица VIII) содержит значения синусов углов от 0° до
90°. С левой стороны таблицы показано число градусов, а сверху —
число минут через каждую десятую долю градуса, то есть через
6 минут.
Например, чтобы найти sin38°24', находим слева число 38°, а
сверху число 24' и в пересечении соответствующих строки и
столбца находим значение синуса 0,6211.
Эта же таблица служит и для отыскания значений косинуса.
При этом надо помнить свойства функций дополнительных углов,
например: cos 37° = sin (90° — 37°) = sin 53° = 0,7986.
163

Но чтобы не прибегать каждый раз к таким вычислениям, в
этой же самой таблице справа и снизу указаны числа градусов
и минут для дополнительных углов. Поэтому, чтобы найти,
например, значение cos50°18', находим справа число 50°, а снизу
число 18' и в пересечении соответствующих строки и столбца
находим число 0,6388.
По такому же принципу построены таблицы IX и X для
тангенсов и котангенсов.
Как уже было показано выше, при помощи этих таблиц можно
для каждого острого угла находить приближённо его
тригонометрические функции, и обратно, по заданной
тригонометрической функции угла находить приближённо самый угол.
Пусть дано, что sin x = 0,5402. Чтобы найти угол х, ищем
в таблице синусов величину 0,5402. Слева и сверху против этого
числа читаем 32°42'.
Подробное руководство к пользованию таблицами дано в той
же книге В. М. Брадиса на странице 21.
§ 163. Соотношения между сторонами и углами
в прямоугольном треугольнике
т, ВС л АС λ ВС А . АС . я
Из равенств ^g = sin A; ^ = cos4; jc = t%A] #C = ctg A
(черт. 246) следует:
1) ВС=АВ- sin A; 2) AC = AB-cosA;
3) ВС = AC-tg A; 4) AC=BC-ctgA.
Словами эти равенства формулируют так:
/. Катет равен гипотенузе, умноженной на синус
противолежащего катету угла.
2. Катет равен гипотенузе, умноженной на косинус
прилежащего катету угла.
3. Катет равен другому катету, умноженному на
тангенс угла, противолежащего первому катету.
4. Катет равен другому катету, умноженному на
котангенс угла, прилежащего первому катету.
§ 164. Решение прямоугольных треугольников
Выведенными соотношениями можно пользоваться, чтобы по
заданному острому углу и одной из сторон прямоугольного
треугольника найти остальные его стороны. Такой способ отыскания
сторон называется решением прямоугольного треугольника.
Пусть, например, нам дано, что катет ВС = 4,5 ед. и ^/ А = 35°.
Из первого равенства находим:
4,5 = AB.sin35°.
170

По таблице находим:
sin 35° = 0,5736.
Следовательно,
4,5 = ЛБ-0,5736,
откуда:
АВ = 0^736 ^7'8·
Из третьего равенства находим:
4,5 = 4C.tg35°.
По таблице находим:
tg 35° = 0,7002,
следовательно,
4,5 = АС- 0,7002,
откуда:
АС— 4>5 =-6 4
ЛС — 0,7002^°'*·
К решению прямоугольных треугольников приходится
прибегать во многих практических задачах. Рассмотрим пример такой,
задачи.
Задача. Определить высоту дерева,
не поднимаясь на его вершину (черт. 252).
Решение. Отмеряем от дерева
какое-либо расстояние, например 10 л/, и
устанавливаем в этом месте угломерный
прибор. Далее, наводим трубку прибора
на вершину дерева и измеряем угол АСВ
наклона трубки к горизонтальной прямой
СВ. Допустим, что /_АСВ оказался
равным 62°. В прямоугольном треугольнике
ABC имеем:
AB=BC-tgC9 или AB=lO-tgQ2°. £ D "
Черт. 252
По таблице находим:
tg 62°= 1,881,
следовательно,
АВ= 1С 1,881 ^18,8.
Чтобы найти высоту дерева AD, нужно к найденной длине АВ
прибавить высоту прибора BD или СЕ. Допустим, что СЕ= 1,2 м.
Тогда
AD ъ ISfi м+1,2 м = 20 м.
171

II. ЧИСЛОВАЯ ЗАВИСИМОСТЬ МЕЖДУ ЭЛЕМЕНТАМИ
ТРЕУГОЛЬНИКОВ
§ 165. Свойство перпендикуляра, опущенного из вершины
прямого угла на гипотенузу
Теорема. Перпендикуляр, опущенный из вершины
прямого угла на гипотенузу, есть среднее пропорциональное
между проекциями катетов на гипотенузу, а каждый из
катетов есть среднее пропорциональное между всей
гипотенузой и проекцией этого катета
ji на гипотенузу.
/\\. 1 · Дан прямоугольныйДЛВС (черт. 253).
/ >v Опустив из вершины его прямого угла
/ N. С на гипотенузу перпендикуляр CD, по-
/ ! ν. лучим два прямоугольных треугольника
А о в ADC и CDB> пРичём
Черт. 253 Δ ADC С/Э /\CDB9
так как
^CAD = Z.DCB и £ACD = /_CBD
как углы с перпендикулярными сторонами.
А потому сходственные стороны этих треугольников
пропорциональны, то есть
AD_CD.
CD~DB*
Из написанной пропорции следует, что
CD2 = AD-DB, или CD = VAD-DB.
2. Рассмотрим теперь треугольники ACD и ABC. Они подобны,
то есть
AACD^AABC,
так как у них^Л— общий, a /^ADC=/^ACB.
А потому сходственные стороны этих треугольников
пропорциональны, то есть
АР_АС
АС~АВ *
Из этой пропорции следует:
AC* = AB-AD, или AC = VAB-AD.
Аналогично доказывается, что BC = VAB-DB.
Так как вписанный угол, опирающийся на диаметр, прямой
(§ 100, следствие 2), то из доказанной нами теоремы следуют
следующие следствия.
172

Следствия. 1. Перпендикуляр, опущенный из какой-либо
точки окружности на диаметр, есть среднее
пропорциональное между отрезками диаметра.
2. Всякая хорда в окружности есть средняя
пропорциональная между диаметром, проходящим через её конец, и
проекцией хорды на диаметр.
§ 166. Теорема Пифагора
Теорема. Квадрат гипотенузы равен сумме квадратов
катетов.
Дан прямоугольный треугольник ABC (черт. 253). Требуется
доказать, что АС*-\-ВС* = АВ\
Выше было доказано, что
AC* = AB.AD.
Точно так же
BC2 = AB-DB.
Сложив почленно эти равенства, получим:
AC + BC2 = AB-AD + AB.DB=AB(AD + DB) = AB-AB=AB\
Эта замечательная теорема была открыта греческим
геометром Пифагором (VI в. до н. э.).
Теорема Пифагора даёт возможность убедиться в
существовании отрезков, несоизмеримых между собой. В самом деле, если
взять прямоугольный треугольник, катеты которого равны
единице, то его гипотенуза будет несоизмерима с катетом.
Действительно, по теореме Пифагора гипотенуза этого треугольника
равна VV+l2 = V5.
Это число иррациональное, выражаемое бесконечной
непериодической десятичной дробью, и потому никакая десятичная доля
отрезка, равного единице, не может уложиться на гипотенузе
целое число раз без всякого остатка.
§ 167. Исторические сведения о теореме Пифагора.
Пифагорейские числа
Простейший случай этой теоремы для треугольника со сторонами 3, 4 и
5 единиц был известен египетским жрецам, а ещё ранее — китайским
учёным (около 11 000 лет до н. э.). Пифагор долго жил в Египте, специально
изучал науку египетских жрецов и ознакомился с искусством жрецов
строить на поверхности земли прямой угол при помощи верёвочного
треугольника со сторонами 3, 4 и 5 ед. Построив этот треугольник на
поверхности земли, они получали прямой угол против стороны длиной в 5 ед.
Пифагор обратил внимание на замечательное соотношение между числами
3, 4 и 5 :32-]-42 = 52 и обнаружил, что такое соотношение имеет место для
всякого прямоугольного треугольника. Как доказывал эту теорему сам
Пифагор — осталось неизвестным. Теорема была высказана Пифагором в
несколько иной форме, а именно как некоторое соотношение между площадями.
173

Из арифметики известно, что площадь всякого квадрата со стороной а равна а*.
Поэтому квадрат каждого катета выражает величину площади квадрата,
построенного на этом катете, а квадрат гипотенузы — величину площади
квадрата, построенного на гипотенузе. Таким образом, теорема Пифагора
выражает следующее соотношение между площадями: площадь квадрата,
построенного на гипотенузе, равна сумме площадей квадратов, по-
строенных на катетах. В этой
форме теорема и была высказана.
Пифагором и в такой форме
помещена в .Началах" Евклида, где
Евклид дал ей своё собственное
доказательство.
Геометрическое соотношение
между площадями для
треугольника со сторонами 3, 4 и 5 ед.
учащиеся могут проследить на
прилагаемом чертеже 254.
Геометрическое доказательство для
произвольного прямоугольного
треугольника будет дано в главе VIII
.Измерение площадей" (§ 193).
Целые числа, представляющие
длины сторон некоторого
прямоугольного треугольника, носят
название пифагорейских чисел.
Для получения всех таких чисел
можно вывести общие формулы.
Действительно, пусть α и β — целые
числа, причём α > β.
Тогда, полагая а = а2 — β2,
& = 2α·β, с = аг4-Ь2, получим,
+ Р2)2 = с*.
25
Черт. 254
что аг + Ьг = (α2 - β2)2 + 4α2β2 = (α2
А это означает, что формулы
α = α2-β2, & = 2α·β, £ = α2 + β2
(1)
являются общими формулами пифагорейских чисел.
Подставляя сюда вместо α и β произвольные целые числа, будем получать
для а, Ь и с тройки чисел, удовлетворяющие равенству (1), то есть тройки
пифагорейских чисел.
Так, при а = 2, β = 1 получим:
:3, Ь = 4, с = 5;
при α = 3, β = 2 имеем:
α = 5, £=12, с =13 и т. д.
Пифагорейские числа представляют собой интересную категорию чисел.
§ 168. Теоремы о квадрате стороны, лежащей против острого
и тупого угла в треугольнике
Теорема 1. Квадрат стороны, лежащей против
острого угла треугольника, равен сумме квадратов двух
других сторон без удвоенного произведения одной из этих
сторон на проекцию на неё другой стороны.
Дан /\ ABC (черт. 255). Опустив из вершины С на сторону
АВ перпендикуляр CD, получим два прямоугольных треугольника
174

ACD и BCD. Из треугольника BCD имеем:
BC2 = CD2 + BD2.
Вычислим отдельно CD2 и BD2.
Из треугольника ACD находим:
CD2 = AC2 — AD2.
Далее,
BD = AB — AD,
следовательно,
BD2 = (AB — AD)2 = AB2 + AD2 — 2AB-AD.
С
О)
Черт. 255
Подставляя выражения для CD2 и BD2 в равенство (1), получим:
ВС2 = АС2 — AD2 + АВ2 + AD2 — 2АВ- AD;
или:
ВС2 = АС2 + АВ2 — 2АВ- AD.
Это равенство и доказывает теорему, так как AD есть проекция
стороны АС на сторону АВ.
Теорема 2. Квадрат стороны, лежащей против тупого
угла тупоугольного треугольника, равен сумме квадратов
двух других сторон, сложенной с удвоенным произведением
одной из этих сторон на проекцию на неё другой стороны.
Дан тупоугольный треугольник ABC (черт. 256). Опустив из
Еершины С перпендикуляр CD на продолжение стороны АВ,
получим два прямоугольных треугольника BCD и ACD. Из
треугольника ACD имеем:
AC2 = CD2 + AD2. (2)
Вычислим отдельно CD2 и AD2.
Из треугольника BCD находим:
CD2 = BC2 — DB\
175

Далее,
Au = BD + AB,
следовательно,
AD2 = BD2 + AB2 + 2BD-ABf
Подставляя эти значения для AD2 и CD2 в равенство (2),
получим:
АС2 = ВС2 + АВ2 + 2AB-BD.
Все три доказанные теоремы о квадрате стороны
треугольника можно объединить в одну.
Во всяком треугольнике квадрат стороны меньше,
равен или больше суммы квадратов двух других сторон,
смотря по тому, будет ли угол, лежащий против этой
стороны, острый, прямой или тупой.
Пользуясь этой теоремой, можно, зная лишь длины сторон
треугольника, определить, будет ли этот треугольник
остроугольный, прямоугольный или тупоугольный. Допустим, например,
что стороны треугольника равны 6 ед., 8 ед. и 12 ед. Так как
прямой или тупой угол может лежать только против наибольшей
стороны, то достаточно определить вид угла против стороны
12 ед. Замечая, что 12*= 144, 62 = 36, 82 = 64 и, следовательно,
122>б2 + 82, заключаем, что этот угол тупой, так как при
другом виде угла имело бы место иное соотношение между
сторонами.
§ 169. Свойство диагоналей параллелограмма
Теорема. Сумма квадратов диагоналей
параллелограмма равна сумме квадратов всех его сторон.
Дан параллелограмм ABCD (черт. 257). Проведя диагонали
АС и BD, мы разделим его на треугольники, В треугольнике
ABD опустим перпендикуляр DE из точки
D на сторону АВ, тогда:
BD2 = АВ2 + AD2 — 2АВ- АЕ.
_ В тупоугольном треугольнике ABC
Я Ε or опустим перпендикуляр CF из точки С на
Черт. 257 продолжение стороны АВ; тогда:
АС2 = АВ2 + ВС2 + 2 АВ · BF.
Складывая эти равенства и замечая, что AE = BF (так как
&ADE = &BCF) и AB = DCt получим:
АС2 + BD2 = АВ2 + AD2 + ВС2 + CD2.
176

§ 170. Выражение высоты треугольника через три его стороны
Рассмотрим /\АВС (черт. 255 ил^ 256). Введём обычные
обозначения: AB = ct BC=^a и AC = b9 CD = hc. Из
треугольника ACD имеем:
hc* = b*-AD\ (1)
Но в силу теорем § 168:
аг = Ьг-\-сг — 2c-AD (или: а* = Ь*+ с2-\-2c-AD);
отсюда:
лгл Ь2+с2-а2 ( лгл ь2+с2 — а*
AD = -±Yc (или: AD= t_2c
Следовательно: AD>' = —L-^2- (в оооих случаях).
Подставляя это в равенство (1), получим:
, 2 _ ь2 Ф2 + с2 - а2)2 _ 4Ь2с2 - (Ь2 + с2 - а2)2
пс —° 4с2 — 4с2
Числитель последнего выражения есть разность квадратов
двух выражений 2Ьс и (Ьг -\-с2 — я2). Разлагая её на произведение
суммы на разность, получим:
, 2 _ [26с + (ft2 + с* - а2)] [2Ьс - (У + g* - я*)1
или
, 2 _ №2 + g2 + 2М - Д2] [Д2 - (У + сг — 2^)1
^ ~~ 4с2"
_ К* + с)2 - а2] [а2 - (Ь - с)2]
~~ 4с2
Выражения, заключённые в квадратные скобки, опять можно
разложить на произведение суммы на разность, следовательно:
t _ (Ь + с + а)(Ь + с-а){а + Ь-с)(а_ь + с)
пс -~4^2 · \Δ)
Полагаем: а^\- Ь-{-с = 2р. Вычитая из обеих частей по 2а,
получим: Ь-\-с — а = 2(р — а); вычитая по 2Ь, получим: а — fe-f"
-±-с = 2(р — Ь); вычитая по 2с, получим: а-\-Ь — с = 2(р — с).
Замещая в равенстве (2) множители в числителе равными им
величинами, получим:
и 2 _/> (Р — а)(р — Ь) (р — с) 1R
ас — 4с2" °'
kc = irVp(P — a)(p — b)(p — c) .
4с2
откуда:
_2
с
177

HI. ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В КРУГЕ
§ 171. Основные теоремы
Теорема 1. Любая хорда, проходящая через точку,
которая лежит внутри окружности, делится этой
точкой на два отрезка, произведение которых есть величина
постоянная (для данной точки).
Пусть даны точка Ж, лежащая внутри некоторой окружности О,
и две произвольные хорды АВ и CD, проходящие через точку Μ
(черт. 258).
Требуется доказать, что
AM-MB = CM-MD.
Соединяя точки Л и С и точки В и
D, получим два подобных треугольника
АМС и BMD.
В В самом деле, каждый из углов С
и В измеряется половиной дуги AD,
следовательно, эти углы равны.
Аналогично ^/A = 2lD> так как каждый из
них измеряется половиной дуги СВ.
Черт. 258 Поэтому Д АМС с/э Д BMD по первому
признаку подобия треугольников.
Так как сходственные стороны подобных треугольников
пропорциональны, то мы можем написать:
AM _CM
MD~ MB '
откуда будем иметь:
AM-MB = CM-MD.
На чертеже 259 проведена секущая МА. Отрезок MB этой
секущей называется её внешней частью.
Теорема 2. Если из точки, лежащей вне окружности,
провести к окружности секущую и касательную, то
произведение всей секущей на её внешнюю часть есть
величина постоянная, равная квадрату касательной,
проведённой к окружности из той же точки.
Пусть даны: точка Λί, лежащая вне окружности, две
произвольные секущие МА и МС и касательная МК Требуется
доказать, что MA-MB = MC-MD = MIC.
Соединяем точку К с точками А и В секущей МА (черт. 259).
Тогда треугольник МКВ будет подобен треугольнику МКА по
первому признаку подобия треугольников, так как ^/_ КМ А у них
общий, а углы ВКМ и КАМ, измеряемые половиной одной и
той же дуги KB, равны.
Из подобия треугольников МКВ и МКА имеем:
MB _МК
МК~МА 9
178

откуда:
ΜΑ·ΜΒ = ΜΚ2.
Таким же образом можно доказать, что и для секущей МС
МС-МО = МК2.
Следовательно:
MA-MB = MC-MD.
MB МК
Из пропорции ^ = 774 вытекает следствие:
Если из какой-либо точки вне окружности провести к ней
касательную и секущую, то касательная есть средняя
пропорциональная между всей секущей и её внешней частью.
Черт. 259
Черт. 260
Задача. Разделить данный отрезок АВ на две части АС
и СВ так, чтобы произведение их АС-СВ было наибольшим.
Решение. На отрезке АВ как на диаметре строим
окружность (черт. 260). Затем через произвольную точку С диаметра
проводим хорду DF, перпендикулярную к АВ.
Тогда будем иметь:
AC-CB = CF-CD = CD2.
Ясно, что, чем ближе точка С будет расположена к центру О,
тем больше будет CD2, и что произведение АС-СВ будет
наибольшим, когда АС-
:СВ = %.
§ 172· Деление отрезка в крайнем и среднем отношении
Задача. Данный отрезок разделить на две части так,
чтобы одна его часть была средней пропорциональной между
всем отрезком и другой его частью.
17£

Решение. Дан отрезок АВ (черт. 261). Из конца β
восставляем перпендикуляр ВС = ^АВ; из точки С радиусом, равным
ВС, описываем окружность; она коснётся АВ в точке В.
Соединив точки А и С, получим секущую АЕ. Dh E — точки
пересечения секущей с окружностью. Тогда:
АЕ
ΑΒΖ
отсюда:
АЕ—АВ
АВ
~'AD
AB-AD
Следовательно,
АВ ~
Заметим, что
АВ = 2ВС
а потому
-AE — DE = AD.
AB-AD
AD
• DE,
AD
и, значит, AD есть искомая большая часть отрезка АВ. Отложив
на АВ отрезок AX = AD и замечая, что
AB — AD = AB — AX=BX,
будем иметь:
АХ
АВ~~
ВХ
~'АХ'
Следовательно, X — искомая точка деления. Такое деление
отрезка называется делением в крайнем и среднем отношении.
Чтобы найти отношение частей АХ и ВХ, полагаем: АВ = а,
АХ = х. Внося эти значения в пропорцию, получим:
χ α — χ
отсюда:
хг = а{а — х) или х2-\-ах — а2
Решая это квадратное уравнение, найдём:
х = '-
= 0.
•а± Уа2 + 4а*
Так как x^>0f то перед корнем нужно брать знак плюс.
Выполняя действия, получим: _
х = а
0,618а,
то есть приближённо (с точностью до 0,1) я = 0,6 а.
180

Отношение 0,6... обладает весьма интересными свойствами.
Так, ещё в древности было замечено, что прямоугольник,
стороны которого являются частями отрезка, разделённого в крайнем
и среднем отношении, имеет наиболее приятную для глаза форму.
В других областях знания, как в живописи, архитектуре,
отношение 0,6... встречается всегда в связи с наиболее приятными
для глаза сочетаниями размеров частей предметов и
изображений. В музыке отношение длин струн, равное 0,6..., связано с
гармоническими аккордами. Поэтому делению отрезка в крайнем
и среднем отношениях в средние века придавали особенно
большое значение и называли его „золотым сечением".
IV. СТЕПЕНЬ ТОЧКИ ОТНОСИТЕЛЬНО ОКРУЖНОСТИ
§ 173· Определение степени точки
Степень точки относительно данной окружности определяется по-
разному, смотря по тому, лежит ли точка внутри или вне окружности.
Если точка А лежит внутри окружности, то степенью точки А
относительно данной окружности называется постоянное число, взятое со знаком
минус и равное произведению отрезков, на которые точка А делит
произвольную хорду, проходящую через неё.
Если же точка А лежит вне окружности, то степенью точки относительно
данной окружности называется постоянное число, взятое со знаком плюс,
равное произведению любой секущей,
проходящей через точку Л, на её
внешнюю часть, или квадрату касательной,
проведённой из Л к данной
окружности.
Наконец, если точка А лежит на
окружности, то её степень считают
равной нулю. ^
Таким образом, степени точек,
лежащих внутри окружности, отрицательны,
причём степень центра окружности,
равная (— /?2), будет меньше степени
любой другой точки плоскости (см. зада- Чеот. 262
чу в § 171).
Введение отрицательных степеней для точек, лежащих внутри
окружности, очень удобно, так как благодаря этому сильно упрощаются
формулировки некоторых теорем.
Теорема. Если две точки А и В находятся на одинаковом
расстоянии от центра, то степени этих точек относительно данной
окружности равны.
Предположим, что точки А и В лежат вне окружности. Тогда из чертежа 262
непосредственно видно, что если ОА = ОВ, то FA = DB и Л#=£С и,
следовательно, AE-AF=BC-DB, то есть степень точки А равна степени точки В.
Так же доказывается теорема и для случая, когда точки А и В лежат
внутри окружности.
Предлагаем учащимся доказать обратную теорему:
Если степени двух точек относительно данной окружности
равны, то эти точки одинаково удалены от центра окружности.
Заметим, что мы смогли сформулировать эту обратную теорему только
потому, что ввели отрицательные знаки для степеней точек, лежащих внутри
окружности.
181

§ 174. Радикальная ось двух окружностей
Радикальной осью двух данных не концентрических окружностей
называется прямая, перпендикулярная к их линии центров и пересекающая её в
точке, имеющей равную степень относительно обеих окружностей.
Например, если две окружности касаются друг друга в точке Μ (черт. 263),
то их общая касательная в точке Μ будет служить радикальной осью этих
окружностей, так как эта каса-
„ /V тельная перпендикулярна к линии
^ —~ '""—■" центров и пересекает её в точке
М, степень которой относительно
каждой из окружностей равна
нулю. Точно так же, если две
окружности пересекаются (черт. 264),
то их общая хорда ΆΒ
(продолженная в обе стороны) будет
служить радикальной осью этих
окружностей, так как эта хорда
перпендикулярна к линии центров и
пересекает её в точке, имеющей
одинаковую степень относительно
Л В2
обеих окружностей, а именно j-
Черт. 263
Теорема. Любая точка радикальной оси двух окружностей
имеет равную степень относительно каждой из данных окру ж-
ностей.
Эта теорема очевидна в двух случаях: 1) когда радикальная ось
совпадает с общей касательной двух касающихся окружностей, проведённой в
точку их касания (черт. 263), и 2) когда радикальная ось совпадает с общей
хордой двух пересекающихся окружностей (черт. 264).
Черт. 264
В самом деле, пусть К — произвольная точка радикальной оси в первом
случае (черт. 263). Тогда, проведя из точки К две касательные KL и KN,
мы будем иметь:
KL = KM и KN=KMy
следовательно,
/α=/ον,
и точка К имеет одинаковую степень относительно двух данных окружностей.
Пусть теперь К—произвольная точка радикальной оси во втором случае
(черт. 264). Тогда, проведя через К две секущие КМ и КО к двум данным
окружностям, мы будем иметь:
К1КМ = КА-КВ и КС-КО=КАКВ,
182

откуда:
KL.KM=KCKD.
Черт. 265
Следовательно, точка К имеет одинаковую степень относительно обеих
окружностей.
Докажем теперь теорему для того случая, когда две данные окружности
не пересекаются.
Пусть МК — радикальная ось двух данных окружностей с центрами в О
и О,. Требуется доказать, что степень любой точки радикальной оси,
например точки /С, одинакова по
отношению к каждой из данных
окружностей (черт. 265).
Другими словами,
требуется доказать, что EK-KE=z
=KN-KL, где Ей F— точки
пересечения прямой ОК с окруж- β/
ностью О, a Z, и N — точки
пересечения прямой ΟλΚ с
окружностью Ох (черт. 265).
Пусть линия центров ООх
пересекает окружность О в
точках А и В, а окружность
Ох — в точках С и D.
Так как точка Μ согласно
определению радикальной оси
имеет равную степень относительно окружностей О и 0„ то мы можем
записать следующее: МВ-МА =MD-MC или (черт. 265) ( ОМ + /?,)( ОМ — /?t) =
= (OlM-+-Rt)(OlM — /?2), где /?! и R2 — радиусы данных окружностей.
Полученное равенство можно переписать так:
OMi-Ri = OlMi-Rl
Аналогично из чертежа 265 будем иметь:
КЕ-KF= (OK + /?ι)(OK-/?,) = ОКг - Rl
KN-KL = (OlK + R2)(01K~Ri)=01K*-Rl
Но из прямоугольных треугольников ОКМ и Λί/CO, имеем: ΟΛ^ = ΟΛί2 +
+ МКг и 0,/С2 = ОхМг + МК2, а потому ΚΕ·ΚΕ=ζΟΚ* - R\ = ΛίΑ?-f
+СШ2-/?,2 и KN-KL = OlK2 - /?2 = Μ/^ + <W - Rl
Но по доказанному выше, ОМг — R\ = ОхМг — R\> а потому KE-KF =
z=KN-KL, то есть точка /С имеет одинаковую степень относительно обеих
окружностей.
Теорема (обратная). Если точка имеет одну и ту же
степень относительно двух данных окружностей, то она лежит на
радикальной оси этих окружностей.
Допустим, что точка /С, не лежащая на радикальной оси, имеет одну и
ту же степень относительно двух данных окружностей О и О, (черт. 266).
Тогда из центров О нОх данных окружностей мы всегда можем описать
две окружности С и Cv пересекающиеся в двух точках А и В радикальной
оси, причём одна из окружностей, например Q, проходит через точку К.
Условимся вместо слов .степень точки А относительно окружности О*
записывать кратко: ст. А (О).
Тогда будем иметь:
ст. Л(0) = ст. А(Ох\
так как А лежит на радикальной оси;
ст. /С(0) = ст. /С(0,),
183

по нашему предположению.
Но
Следовательно,
ст. Л(0,) = ст. К(Ох)у
так к^к А и К равноудалены от Ог
ст. /4(0) = ст. К (О).
Даны три окружности Q,
Точки Л и /С, имеющие одинаковую степень относительно окружности С,
будут равноудалены от точки О, и, следовательно, две окружности,
пересекающиеся в точках Л и В, пересекаются в третьей точке /С, что невозможно.
Таким образом, точки радикальной оси, и только они, имеют одинаковые
степени относительно двух данных окружностей.
§ 175. Радикальный центр трёх окружностей
Теорема. Три радикальные оси трёх окружностей, центры
которых не лежат на одной прямой, пересекаются в одной точке.
~ Q, С8, центры которых не лежат на одной
прямой. Если построить радикальные оси
для окружностей Q и С2, а также для
окружностей С2 и С8, то точка
пересечения этих прямых, очевидно, будет
иметь одинаковую степень как относи-
и
а
следовательно, и относительно
окружностей С, и С8. Значит, она лежит и на
радикальной оси окружностей Q и С8.
Точка пересечения трёх радикальных
осей трёх окружностей называется их
радикальным центром.
Радикальным центром удобно
пользоваться для построения радикальной
оси двух непересекающихся
окружностей.
Допустим, что нужно построить
радикальную ось окружностей с
центрами О, и 02 (черт. 267). Проведём две
какие-либо окружности с центрами О' и О", пересекающие обе данные, и
построим радикальный центр S окружностей Ор 02 и О' и радикальный
тельно окружностей Q и С2, так
относительно окружностей С2 и С8,
Черт. 267
окружности
радикальный
184

центр S' окружностей Ор Ог и О". Точки S и S\ очевидно, лежат на
радикальной оси окружностей О, и 02. Следовательно, прямая S'S — искомая
радикальная ось.
V. АЛГЕБРАИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ НА ПОСТРОЕНИЕ
§ 176. Сущность алгебраического метода
Формулы, выражающие одни элементы геометрических фигур
через другие, могут служить иногда средством для решения
задач на построение. Пользуясь этими формулами, можно величины
отдельных алгебраических выражений представлять в виде длин
некоторых отрезков. Так, например, выраж^рие
представляет длину отрезка, четвёртого пропорционального к
трём данным отрезкам a, b и с. Действительно, из формулы
следует:
*. — А
а с '
а потому, зная величины отрезков a, b и с, мы можем построить
отрезок χ (§ 128, задача 1), иначе говоря, можем построить зе-
ab
личину отношения —.
Точно так же выражение
х=У7Г\П>*
представляет длину гипотенузы прямоугольного треугольника,
катеты которого равны а и Ь, а потому по данным отрезкам
β и & мы можем построить отрезок, длина которого равна
Уаг-\-Ьгу то есть построить величину выражения ΐΛζ2-|-ί?2.
Если научиться, таким образом, строить величины различных
алгебраических выражений, то этим можно иногда с успехом
пользоваться при решении задач на построение, а именно: когда
требуется построить какую-либо фигуру по некоторым заданным её
элементам. Иногда можно выразить какой-либо из неизвестных
элементов фигуры через данные её элементы, то есть найти для
неизвестного отрезка алгебраическое выражение, дающее его
длину. Если удаётся построить величину этого выражения, то
тем самым будет найден ещё один отрезок, входящий в искомую
фигуру, и построение её может значительно облегчиться. В этом
состоит сущность алгебраического метода. Чтобы успешно
пользоваться этим методом, нужно уметь строить величины
различных алгебраических выражений.
185

§ 177. Построение простейших формул
- ab
1. л=— ·
с
Из этого равенства следует:
следовательно, χ есть четвёртая пропорциональная к трём
данным я, Ьу с. Построение её дано в § 128, задача 1.
2. х = т.
Из этого равенс^а находим:
х_ а_
a b >
следовательно, задача сводится к предыдущей. Кроме того, можно
дать другое решение задачи, а именно легко заметить, что если
построить прямоугольный треугольник, гипотенуза которого
равна Ь, а один из катетов равен я, то проекция этого катета
на гипотенузу будет равна χ (§ 165).
3. x = V~ab.
Отсюда:
x2 = ab.
Это равенство показывает, что χ есть длина перпендикуляра,
опущенного из вершины прямого угла на гипотенузу
прямоугольного треугольника, в котором проекции катетов на гипотенузу
равны а и b (§ 165). Отсюда непосредственно вытекает способ
построения отрезка х.
Можно также заметить, что χ есть длина катета
прямоугольного треугольника, гипотенуза которого равна большему из
отрезков а и Ьу а проекция катета на гипотенузу равна меньшему
из этих отрезков. Отсюда вытекает второй способ построения
отрезка х. Третий способ построения отрезка χ легко получить
на основании теоремы о длине касательной (§ 171).
4. х = Уаг + Ь\
Отсюда:
следовательно, χ есть гипотенуза прямоугольного треугольника,
катеты которого равны а и Ь.
5. х = УЯ~ъ*.
χ есть катет прямоугольного треугольника, гипотенуза
которого равна а, а другой катет Ь.
6. х = Уаг + Ь2 + с\
Полагаем:
а* + Ьг=у*.
186

Тогда отрезок у может быть построен как гипотенуза
прямоугольного треугольника, катеты которого равны а и Ь.
Построив уу будем иметь:
и тем же способом построим х.
§ 178. Графическое решение квадратного уравнения
Графическим решением квадратного уравнения хг -\-px-\-q = 0
называют такое построение, в результате которого получаются
два отрезка, по своей длине равные абсолютным значениям
корней данного уравнения.
Зная абсолютное значение корней и пользуясь тем, что
произведение корней равно q, а сумма—/?, мы легко определим их
знаки.
У\
М(р;д)
Черт. 268
Приведём графическое
решение данного
уравнения хг -(- рх-\- <7 = 0,
состоящее из следующих
трёх шагов:
1. Строим оси
координат и точки Л (0, 1),
5(0, — 1) и через точку В
проводим прямую /,
параллельную оси абсцисс
(черт. 268).
2. Строим точку Μ с
координатами ρ и q, где ρ
и q — коэффициенты данного уравнения, и из точки Μ как из
центра радиусом, равным МА, описываем окружность, которая
пересечёт прямую I в точках С и D.
3. Определяем числа аи ft, равные соответственно длинам от-
ВС BD
резков -γ и -ψ.
Тогда 05 = 1^,1 и b = \xt\, где хх и х2 — корни уравнения
хг-\- px-\-q = 0.
Это построение остаётся в силе при любых ρ и q, то есть
точка Μ может лежать в любом из четырёх координатных углов.
На чертеже 268 точка М(р\ q) оказалась в первом
координатном углу, а потому в этом случае р^>0 и <7>0.
Так как χλ -]Γχ% = — ρ<^0 и xix2 = q>0, то оба корня
отрицательны, и, следовательно \хх \-\-\х2\=р и \xx\-\xl\ = q.
Но | хх | = я, а | х21 = b и для доказательства правильности
приведённого выше графического решения квадратного уравнения
нам, следовательно, нужно доказать, что а-\-Ь=р и ab = q.
Для этой цели из точки Μ на прямую / опустим
перпендикуляр Λί/0
187

Тогда из чертежа 268 имеем:
ntr CD BD — ВС
CAV —-χ- =
p=BK=BC-\-CK=BC-\-
2 — 2
BD-BC _BC , BD
2 — 2 "Τ" 2 '
„ ВС , BD , . ВС . BD
Но ~2—1—2~ = β +&» так как а = ~2~ И & = ~2~·
Докажем теперь, что ab = q.
Для этой цели опустим перпендикуляр AN на прямую МК и
обозначим через Ρ точку пересечения Λί/C с осью ОХ.
Из прямоугольного треугольника ΑΜΝ имеем:
ΑΜ2 = ΑΝ* + ΝΜ2 или ЛуИ2 = Л^2 + (уИР — ΝΡ)2 =
= (a + b)* + (q-l)\
так как MP = q, NP=\y AN=BK=a-\-b.
Аналогично из прямоугольного треугольника МСК имеем:
МС2 = СК2 + МК*. Но так как ^- = ау то есть ВС=2а, то
CK=BK—BC = a-\-b — 2a = b — a\ кроме того, МК=МР-\-
+ PK=q+l.
А потому мы можем написать:
МСг = СК2-\-МК* = (а — Ь)2 + (? + 1)2.
Но АМ=МС как радиусы окружности, и поэтому
(α+&)2 + (<7-1)2 = (α-&)2 + («7+1)2,
откуда:
4яЬ = 4<7,
или
ab = q.
Совершенно таким же способом можно доказать правильность
приведённого выше графического решения квадратного
уравнения и в том случае, когда точка М(р; q) лежит в каком-нибудь
другом координатном углу, но только нужно учитывать знаки
корней.
Заметим, что если окружность радиуса МА с центром в
точке Μ не пересекает прямую /, то корни данного уравнения
будут мнимыми.
Чертёж 269, приводимый ниже, позволяет очень быстро и
просто определять корни квадратного уравнения. На этом
чертеже на осях координат нанесены равномерные деления с
пометками от 0 до 10 вправо и вверх и от 0 до—10 влево и вниз и
отмечены точки Л(0; 1) и #(0; —1). Через точку В проведена
так называемая шкала корней — прямая, параллельная оси ОХ, и
188

на ней нанесена равномерная шкала вдвое большего масштаба,
чем масштаб шкал, нанесённых на координатные оси, но точки с
отрицательными пометками расположены на этой прямой вправо,
а точки с положительными пометками — влево от точки В.
Допустим, нам нужно найти корни квадратного уравнения
хг— 5jc-f-6 = 0· Тогда мы отмечаем на плоскости точку
Λί,( — 5; 6) и радиусом, равным tylxAy проводим окружность с
центром в точке Ж,. Эта окружность пересечёт шкалу корней
в двух точках: 2 и 3. Числа 2 и 3 и будут корнями уравнения
*■ —5* + 6 = 0.
Черт. 269
На чертеже 269 показано, как определяются корни (2; —5)
уравнения хг + Зх — 10 = 0.
Способ определения корней квадратного уравнения при
помощи чертежа 269 является в сущности механизацией
графического способа решения квадратного уравнения, приведённого в
начале настоящего параграфа.
Предлагаем читателю выяснить, на какой кривой должны
располагаться точки М(р; ?), чтобы соответствующие этим точкам
квадратные уравнения хг -\-рх + Я = ° имели равные корни.
189

§ 179. Общее замечание о построении алгебраических выражений
Формулы, выражающие длину одного отрезка через длины
других, обладают одной особенностью, которая отличает их от
других алгебраических формул.
Допустим, что искомый отрезок χ входит в состав какой-либо
фигуры (например, является стороной или диагональю какого-
либо многоугольника) и его длина у выражена через длины
других отрезков а, Ь, с, ..., входящих в ту же фигуру
(например, через другие стороны и диагонали).
Если произвести подобное преобразование всей фигуры с
каким-либо коэффициентом подобия k, то все отрезки, входящие
в состав фигуры, изменятся в одном и том же отношении,
именно в отношении, равном коэффициенту подобия k.
Следовательно, отрезки х, а, Ь, с, ... преобразуются в отрезки kx,
ka, kb, kc, ... .
Новый отрезок kx, очевидно, будет выражаться через новые
отрезки ka, kb, kc, ... той же формулой, какой отрезок χ
выражается через старые отрезки а, Ь, с, . . . .
Отсюда следует, что" для получения новой величины отрезка
χ нужно в старой формуле заменить буквы а, Ь, с, ...
соответственно через ka, kb, kc, .... Так как длина отрезка χ равна
старой, умноженной на k, то отсюда заключаем, что если в
формуле, дающей х, заменить а, Ь, с, ... соответственно через ka,
kby kc, ... , то всё выражение умножится на k.
Например, гипотенуза прямоугольного треугольника с катетами
а и b равна У аг-\-Ь2. Заменив а через ka wb через kb, получим:
У{ка)г + {Щг = Укга2 + к2Ь2 = Укг{а2+Ьг) = кУ^Г+¥,
Таким образом, величина Уаг-\-Ьг получила множитель k.
Алгебраическое выражение, обладающее тем свойством, что
замена входящих в него величин я, Ь> с, ... величинами ka, kb,
kc, ... равносильна умножению всего выражения на k, называется
однородным выражением первой степени относительно этих
величин.
Следовательно, всякое выражение, представляющее длину
искомого отрезка через длины данных, должно быть однородным
первой степени относительно длин данных отрезков.
§ 180. Возможность выполнения построения при помощи
циркуля и линейки
Теперь возникает вопрос, всякое ли однородное выражение
первой степени можно изобразить отрезком прямой линии. Всякое
алгебраическое выражение имеет определённую величину, когда
даны значения входящих в него букв. Эту величину в каком-либо
масштабе всегда можно представить в виде отрезка прямой. Но
190

возникает вопрос, всегда ли можно этот отрезок построить, если
значения букв заданы в виде отрезков и если пользоваться лишь
циркулем и линейкой, то есть проводя только прямые линии и
окружности.
Подробное исследование этого вопроса, требующее знаний,
далеко выходящих за пределы элементарной математики, показало*
что, проводя только прямые линии и окружности, можно
получать лишь такие отрезки, длины которых получаются из длин
данных отрезков только при помощи конечного числа
рациональных операций и извлечения квадратных корней. Поэтому, если
задача сведётся к построению отрезка, представляемого более
сложным выражением, то такую отдачу при помощи циркуля и
линейки решить невозможно. Таковы, например, знаменитые
задачи древности, которые древние греки долго и безуспешно
старались решить при помощи циркуля и линейки:
1. Данный угол разделить на три равные части.
2. Построить ребро куба, объём которого был бы в два раза
больше объёма данного куба.
3. Построить квадрат, площадь которого была бы равна
площади данного круга.
Невозможность решения этих задач при помощи циркуля и
линейки была показана лишь в XIX в. нашей эры, когда был
решён общий вопрос о том, какие задачи на построение можно
решать при помощи циркуля и линейки.
VI. УПРАЖНЕНИЯ К ГЛАВЕ СЕДЬМОЙ
А. Доказать теоремы.
1. Отношение проекций катетов прямоугольного треугольника на
гипотенузу равно отношению квадратов катетов.
2. Произведение катетов прямоугольного треугольника равно
произведению гипотенузы на перпендикуляр, опущенный из вершины прямого угла на
гипотенузу.
3. Произведение двух сторон треугольника равно произведению высоты,
опущенной на третью сторону, на диаметр описанной окружности.
4. Квадрат медианы основания треугольника равен половине суммы
квадратов боковых сторон минус квадрат половины основания треугольника.
Указание. Продолжить медиану на равную ей длину, конец
полученного отрезка соединить с концами основания и рассмотреть полученный
параллелограмм.
5. Дан квадрат ABCD. Через его вершины А и В проведены две взаимно
перпендикулярные прямые, встречающие продолженную в обе стороны
прямую CD в точках Ε и F.
Доказать, что CD есть средняя пропорциональная между ED и СЕ.
6. Дан параллелограмм ABCD. Через его вершину А проведена
произвольная секущая, встречающая диагональ BD в точке Ё и стороны ВС и CD
соответственно в точках F и G. Доказать, что АЕ есть средняя
пропорциональная между EF и EG.
7. Если в равнобедренную трапецию можно вписать окружность, то
высота трапеции есть средняя пропорциональная между её основаниями.
8. Середины сторон равнобедренной трапеции служат вершинами
квадрата. Доказать, что боковая сторона трапеции больше среднего
пропорционального между её основаниями.
191

9. Произведение отрезков двух параллельных касательных к окружности,
измеренных от точек касания до точек пересечения с произвольной третьей
касательной, есть величина постоянная, равная квадрату радиуса окружности.
10. Доказать, что если две окружности касаются одна другой внешним
образом, то отрезок общей внешней касательной к этим окружностям,
заключённый между точками касания есть средняя пропорциональная между
диаметрами окружностей.
11. На плоскости дана окружность О и две какие-либо точки А и В. Через
точку А проведена произвольная секущая, встречающая окружность в точках
С и Ь. Доказать, что окружность, проведённая через точки В, Си Д при
любом положении секущей отсечёт на прямой АВ один и тот же отрезок.
12. Произвольная точка плоскости Μ соединена с вершинами треугольника
ABC, причём прямая AM встречает сторону ВС в точке АХ1 прямая ВМ—
сторону СА в точке Вх и прямая СМ— сторону АВ в точке Cv Доказать, что
АВХ САХ ВСХ_
ВХС' Ахв' СХА~~
Обратно, если для трёх точек Ах, Bv С,, лежащих на сторонах
треугольника АВСУ имеет место написанное равенство, то прямые ΑΑν ВВХ и ССХ
проходят через одну точку (теорема Чевы).
Решение. Дан треугольник ABC Пусть точка Μ лежит внутри него
(черт. 270). Из точки А проводим прямую AL || BBV Тогда:
АВХ_Ш
ВХС~~МС
Из точки С проводим прямую CN\\BBX.
Треугольники CMN и A ML подобны, а
потому
LM_AL
MC~~CN *
Сравнивая эти пропорции, получим:
О)
Черт.
Треугольники
270
CAXN и
АВХ
ВХС~
МАХВ подобны, следовательно,
САХ
АХВ~
СМ
" MB'
AL
'CN'
(2)
Треугольники ACXL и МСХВ подобны.
Отсюда:
ВСХ _ MB
СХА~AL *
Перемножив равенства (1), (2) и (3), получим:
АВХ САХ ВСХ _
ВХС' АХВ* СИ
Обратная теорема легко доказывается способом от противного.
13. Рассмотреть частные случаи теоремы Чевы, когда точки АХУ Вх, Сх
являются:
1) серединами сторон треугольника',
2) точками встречи сторон с биссектрисами противолежащих углов;
3) основаниями высот треугольника.
(3)
(4)
192

Показать, что во всех этих трёх случаях отрезки АВХ,ВХС, СА^АХВ,ВС^
СХА удовлетворяют равенству (4), и вывести отсюда теоремы о пересечении в
одной точке медиан треугольника, а также его высот и биссектрис его углов
как частные случаи теоремы Чевы.
Б. Задачи на построение.
Построить выражения:
t. abc .- a*b
14. х = —т. 15. х = —г-
ed cd
„з пг _μ μ
18. х = * K.X=-4-h.
20. χ = αγ2. 21. * = -£=.
Υ·ι
22. x = aYb. 23. x=-%=.
γ*
24. χ = αΫη , где η — целое число.
Указание, х есть среднее пропорциональное между а и па.
25. < = «^2-+уУ
а — Ь
26. Зная сумму а двух неизвестных отрезков χ и ^ и отрезок 6, длина
которого есть средняя пропорциональная между х и уУ построить каждый из
отрезков хну.
27. Построить равнобедренный треугольник по двум высотам hc и hb.
28. Построить равнобедренный треугольник, если даны его боковая
сторона b и расстояние q ортоцентра треугольника от концов основания.
29. Определить положение центров гомотетии взятых попарно
окружностей, вписанной и вневписанных в данный треугольник. Отв. Вершины
треугольника и точки пересечения биссектрис его внутренних и внешних углов
с противоположными сторонами.
В. Задачи на вычисление.
30. Проекции катетов прямоугольного треугольника на гипотенузу равны
9 еж и 16 см. Вычислить стороны треугольника. Отв. 15, 20, 25.
31. Гипотенуза прямоугольного треугольника на 8 см больше одного
катета и на 1 см больше другого. Вычислить стороны треугольника. Отв.
5, 12, 13.
32. Сумма катетов прямоугольного треугольника равна 17 см, а е^о
периметр 30 еж. Вычислить длину перпендикуляра, опущенного из вершины
прямого угла на гипотенузу. Отв. 4 у= см.
33. Гипотенуза прямоугольного треугольника равна 52 см, а отношение
его катетов равно 5:12. Определить длины катетов. Отв. 20, 48.
34. Радиус окружности, описанной около прямоугольного треугольника,
/?=10сж, радиус вписанной г = 4см Определить длину сторон
треугольника. Отв. 12, 16, 20.
35. Боковая сторона равнобедренного треугольника равна 25 см, высота,
опущенная на эту сторону, равна 24 см. Вычислить длину основания
треугольника. Отв. 30 см или 40 см.
36. В равнобедренном треугольнике даны: основание а = "^10 см и
медиана боковой стороны 3 см. Вычислить длины боковых сторон. Отв. Ь =
= с = 4 см.
37. Вычислить высоту hc треугольника, зная его стороны: α = 68 еж,
Ь = 87 см% с = 95 см. Отв. 60 см.
193

Задачи на решение прямоугольных треугольников.
Обозначения: а, Ъ — катеты, с — гипотенуза.
38. а = 25см; ^ = 17,5см;определить ^А не. Отв. с = 30,5см; £'А = 55°.
39. α = 15,6 еж; £А = 40°; & = ? с = ? Отв. b= IS J см; с = 24,3 см.
40. с = 26 еж; ^.#=35°; а = ? & = ? Отв. α = 21,3 еж; 6 = 14,9 еж.
41. Лс = 12 см; а =15 еж; £А = ? £Β=? с = ? Ome. ^£=53°10';
^Л = 36°50'; с = 25 еж.
42. тс = 8 еж; Л, = 5 еж; а = ? & = ? с = ? £А = 7 £В=? Отв. Ь =
= 15 еж; а = 5,5 см; с = 1б"еж; Ζ. # = 69°54'; ^Л = 20°6\

ГЛАВА ВОСЬМАЯ
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
I. ИЗМЕРЕНИЕ ПЛОЩАДЕЙ МНОГОУГОЛЬНИКОВ
§ 181. Равносоставленные и равновеликие фигуры
Всякая фигура занимает некоторую часть плоскости. Величина
части плоскости, занимаемая какой-нибудь фигурой, называется
площадью этой фигуры.
Нетрудно заметить, что, например, два многоугольника могут
быть различной формы и в то же время иметь одинаковые
площади. В этом легко убедиться, если взять два равных
прямоугольных треугольника ABC и DEF (черт. 271,а) и прикладывать
Черт. 271
их различным образом один к другому. Приложив их равными
катетами ВС и EF> мы получим или равнобедренный треугольник
(черт. 271,6), или параллелограмм (черт. 271,в); приложив их
гипотенузами, получим или прямоугольник (черт. 271,г), или
четырёхугольник, называемый дельтоидом (черт. 271,5).
Все эти четыре фигуры (б, в, г, д) различной формы, у о имеют
одну и ту же площадь, так как все они составлены из двух
равных прямоугольных треугольников.
В наших рассуждениях мы считали очевидными следующие два
положения:
1. Равные фигуры имеют равные площади.
2. Если фигура составлена из нескольких фигур, то её
площадь равна сумме площадей этих фигур.
Две фигуры называются равносоставленными, если они могут
быть разложены на одинаковое число попарно равных фигур.
195

Например, изображённые на чертеже 272 правильный
шестиугольник и параллелограмм — равносоставленные фигуры, так как
обе они составлены из шести равных равносторонних
треугольников.
Две фигуры называются равновеликими, если они имеют
одинаковую площадь.
Черт. 272
Две равных фигуры всегда равновелики, но не всякие две
равновеликие фигуры равны.
Обычно равновеликие фигуры получаются, когда от равно-
составленных фигур
отнимают равносоставленные
фигуры или, в частности, когда
от равных фигур отнимают
равные фигуры.
Например, если от двух
равных треугольников ABC
и FDH отнять один и тот же
треугольник DEC (черт. 273),
то получатся две
равновеликие, но не равные трапеции
ABDE и FECH.
Черт. 273
§ 182. Теорема о равновеликих прямоугольниках
Теорема. Если произведение основания на высоту в
одном прямоугольнике равно произведению основания на
высоту в другом прямоугольнике, то такие
прямоугольники равновелики.
Расположим данные прямоугольники ABCD и AEFH так, как
это показано на чертеже 274.
По условию теоремы
AB-AD = AH-AE. (1)
Требуется доказать, что прямоугольники ABCD и AEFH
равновелики.
196

Из равенства (1) выводим:
АВ_АН {ъ
АЁ—AD' У}
Соединив точки Ε и D, В и //, мы замечаем, что в силу
пропорции (2) прямые ED и ВИ параллельны (§ 127).
Из чертежа 274 непосредственно видно, что прямоугольник
ABCD состоит из трёх треугольников, обозначенных на чертеже
цифрами /, 2, 3, и трапеции МКВЕ, а прямоугольник AEFH
состоит из треугольников 1,2, 4 и трапеции MLHD.
Нетрудно видеть, что все четыре треугольника 1,2,3 к 4
равны между собой по гипотенузе и катету. Например,
треугольник 2 равен треугольнику 3, ибо катеты ЕМ и ВС равны как
D Η
Черт. 274
противоположные стороны прямоугольника ВСМЕ, а гипотенузы
ED и ВК равны как противоположные стороны параллелограмма
BKDE. Так же доказываются и равенства других треугольников.
Далее, прямоугольные треугольники BLE и KDH равны, ибо
катеты BE и KD равны как противоположные стороны
параллелограмма BEDK и катеты EL и DH равны как противоположные
стороны параллелограмма EDHL.
Отнимая от треугольника BEL треугольник ΑΧΛί, получим
трапецию ВЕМК, равновеликую трапеции HDML, которая может
быть получена вычитанием того же треугольника KLM из
треугольника KDH, равного треугольнику BLE. Отсюда следует, что
прямоугольник ABCD равновелик прямоугольнику AEFH.
§ 183. Понятие об измерении площадей фигур
Измерить площадь какой-нибудь фигуры — это значит узнать,
во сколько раз измеряемая площадь больше или меньше площади
другой фигуры, выбранной за единицу измерения площадей.
Другими словами, мы должны определить число, которым
характеризуется величина площади данной фигуры, когда за
единицу измерения принята площадь некоторой фигуры.
197

Обычно за единицу измерения площадей принимается площадь
квадрата со стороной, равной единице длины. Так, если за
единицу длины принят метр, то за единицу площади принимается
площадь квадрата, сторона которого равна одному метру
(квадратный метр).
При измерении площадей площади всяких двух равносостав-
ленных, а также и равновеликих фигур считаются одинаковыми
и, следовательно, должны измеряться одним и тем же числом.
§ 184. Измерение площади прямоугольника
Теорема 1. Площадь прямоугольника, высота
которого равна единице длины, содержит в себе столько
квадратных единиц, сколько единиц длины содержится в его
основании.
Случай 1. Пусть в основании прямоугольника ABCD
содержится целое число, например шесть единиц длины. Тогда из
чертежа 275 видно, что в прямо-
В
Й
угольнике ABCD будет
содержаться шесть единичных
квадратов. Следовательно, в этом
случае в прямоугольнике ABCD
содержится столько квадратных
единиц, сколько единиц длины
содержится в его основании.
Случай 2. Если основание прямоугольника ABCD измеряется
Черт. 275
рациональным числом-
то это означает, что—-я часть единицы
η
длины ΜΝ уложилась в основании AD m раз.
L
к
т раз
N
w+t
m+t
η
частей
η
частей
Черт. 276
Черт. 277
Если мы теперь разделим основание ММ единичного квадрата
на η равных частей, как это показано на чертеже 276, то
единичный квадрат разделится на η равных прямоугольников, причём
площадь каждого такого прямоугольника будет равна — -й части
площади единичного квадрата или — -й части единицы площади.
198

Так как в прямоугольнике ABCD содержится т таких
прямоугольников, то площадь прямоугольника ABCD будет равна —
квадратных единиц, то есть будет выражаться тем же числом,
которым выражается длина основания прямоугольника ABCD.
Случай 3. Пусть основание AD несоизмеримо с единицей
длины MN. В этом случае делим отрезок MN на η равных частей
и откладываем на AD —ю часть единичного отрезка ΜΝ. Тогда
согласно аксиоме Архимеда найдутся: такой отрезок ААт9
меньший AD, в котором —я часть отрезка ММ укладывается т раз,
и такой отрезок AAm+lf больший AD, в котором—я часть
отрезка MN укладывается (т-\-\) раз. Тогда из чертежа 277 видно,
что площадь прямоугольника ААтВтВ9 равная — квадратных
единиц (случай 2), будет меньше площади прямоугольника ABCD, a
площадь прямоугольника ААт+1Вт+1В9 равная т~*~ квадратных
единиц, будет больше площади прямоугольника ABCD. Итак, мы
имеем:
— кв. ед. <площади ABCD<m~*~ кв. ед.
Аналогично
^-ед. длины<длины AD< m „ ед. длины.
Это означает, что, вычисляя длину отрезка AD и площадь
прямоугольника ABCD при сколь угодно большом я, мы будем
получать одинаковые численные результаты.
Следовательно, если — при неограниченном возрастании η
будет стремиться к иррациональному числу а, выражающему длину
отрезка AD, то к тому же самому числу будет стремиться число
квадратных единиц, содержащихся в прямоугольнике ААтВтВ,
площадь которого стремится к площади прямоугольника ABCD.
Таким образом, если в отрезке AD содержится α единиц длины,
то в прямоугольнике ABCD содержится α квадратных единиц.
Теорема доказана и для случая 3.
Теорема 2. Площадь прямоугольника равна
произведению основания на высоту.
Дан прямоугольник ABCD.
Нам нужно доказать, что число, выражающее площадь
прямоугольника ABCD в квадратных единицах, равно произведению
чисел, выражающих длины основания и высоты прямоугольника.
На высоте АВ прямоугольника ABCD откладываем отрезок АЕ,
длина которого равна единице. Соединяем точку Ε с точкой D и
199

через точку В проводим прямую BF9_ параллельную ED. Затем
строим прямоугольник AEKF (черт. 278).
Параллельные прямые BF и DE отсекают на сторонах угла А
параллельные отрезки, а потому мы можем написать:
АВ
АЕ~
''AD1
откуда:
AB-AD = AE-AF.
Согласно теореме § 182 прямоугольник ABCD равновелик с
прямоугольником AEKF, и поэтому площади их измеряются
одним и* тем же числом квадратных единиц.
Но АЕ= 1, следовательно, AF=АВ- AD. Но согласно теореме 1
площадь прямоугольника AEKF с высотой, равной единице,
измеряется тем же числом, что и длина основания AF.
В
Г\.
1
с
^\|
1 F
Черт. 278
Но AF=AB-AD, а потому в прямоугольнике AEKF
содержится AB-AD квадратных единиц.
Следовательно, и в прямоугольнике ABCD, равновеликом
с прямоугольником AEKF, также содержится АВ- AD квадратных
^Приведённое выше построение отрезка, измеряющегося тем же
числом что и площадь данного прямоугольника с произвольными
высотой и основанием, имеет важное практическое значение.
В самом деле, вместо того чтобы измерять основание и высоту
прямоугольника, производить перемножение полученных чисел,
достаточно измерить длину отрезка, полученного при помощи простого
построения. Для построения отрезка, измеряющегося тем же
числом, что и площадь прямоугольника, удобно пользоваться калькой с
нанесёнными на ней параллельными прямыми.
В ряде случаев предложенный способ графического
определения площади прямоугольника даёт большую точность, чем
обычный способ. Поясним это примером. Пусть основание прямоуголь-
200

ника равно У*, а высота Ϋ2 (черт. 2/9); не зная заранее
значений высоты и основания, мы будем измерять их при помощи
масштабной линейки. Естественно, что большая точность при
этом невозможна и в результате измерений мы получим, что ос-
В С
швание равно 2,8 ед. длины, а высота- 1,4 ед. длины. Перемножив
эти числа мы получим приближённое значение площади
прямоугольника, равное 3,9 кв. ед. Решив же эту задачу графически, мы
получим более точный ответ, а именно, что площадь
прямоугольника равна 4 кв. ед. (черт. 279).
§ 185. Площадь параллелограмма и ромба
Дан параллелограмм ABCD (черт. 280). Построим
прямоугольник ABEF"имеющий то же основание АВ и ту же: высоту AF
(или BE). Треугольник AFD равен треугольнику ВЕС так как
AD = BC как противоположные стороны параллелограмма ADLB
и AF==B£ как противоположные стороны прямоугольника Attts.
О
а/ \о Хс
ΝΓ3
ЕВ F
Черт. 281
Вычитая из трапеции ABCF треугольник FAD, получим
параллелограмм ADCB, а вычитая из той же трапеции треугольник ВЬС,
оавный треугольнику AFD, получим прямоугольник ABEF.
Следовательно, прямоугольник ABEF имеет ту же площадь, что и
данный параллелограмм ABCD. Но площадь прямоугольника равна
АВ-ВЕ, а потому площадь параллелограмма ABCD равна АВ-BL·,
то есть приходим к такой теореме:
Площадь параллелограмма равна произведению его
основания на высоту.
201

В случае ромба можно указать и другое выражение для
площади. Пусть дан ромб ABCD (черт. 281). Проведём через
вершину В прямую, параллельную диагонали АС. Через вершины А
и С проведём прямые, параллельные диагонали BD, до их
пересечения в точках Ε и F с прямой, проведённой через вершину В.
Так как диагонали ромба взаимно перпендикулярны, то
четырёхугольники АЕВО, OBFC и AEFC, где О—точка пересечения
диагоналей ромба,— прямоугольники. Прямоугольные
треугольники AOD, COD, ΒΕΑ и ВЕС равны между собой, так как
AO=OC=BE=BF и DO=OB = AE=CF.
Следовательно, ромб ABCD равносоставлен с
прямоугольником ACFE. Поэтому площадь ромба ABCD равна АС-АЕ=
= yAC-BD, to есть мы доказали теорему:
Площадь ромба равна половине произведения его
диагоналей.
§ 186. Площадь треугольника
Дан треугольник ЛВС (черт. 282). Проведя через вершину В
прямую, параллельную стороне АС, а через середину D стороны
ВС—прямую DE, параллельную стороне АВ9 получим
параллелограмм ABFE, равновеликий с данным треугольником.
Действительно, треугольник ABC составлен из трапеции ABDE и
треугольника DCE; параллелограмм ABFE составлен из той же
трапеции ABDE и треугольника BDF. Но
/\BDF = /\CDE.
так как
BD = DC, /_BDF = £CDE и Z.DBF = /DCE.
В F
В Βι В2 Вз
А С
Черт. 282 Черт. 283
Следовательно, площадь треугольника ABC равна площади
параллелограмма ABFE. Основание АЕ этого параллелограмма равно
половине стороны АС треугольника ABC, а высота его ВН
служит в то же время и высотой треугольника ABC. А потому
площадь /\АВС равна -jAC-BH,
то есть имеет место теорема:
Площадь треугольника равна половине произведения
его основания на высоту.
202

Следствия. 1. Два треугольника, имеющие равные
основания и равные высоты, равновелики.
2. Если, оставляя неизменяемым основание треугольника,
перемещать его вершину по прямой, параллельной основанию,
то его площадь не будет изменяться. Так, все треугольники
ABC, АВХС, АВгС9 АВ3С, изображённые на чертеже 283, имеют
одно и то же основание АС и равные высоты.
§ 187· Площадь трапеции
Дана трапеция ABCD (черт. 284). Проведя через середину F
боковой стороны CD прямую GH, параллельную боковой стороне
АВ> и продолжив верхнее основание трапеции ВС, получим
параллелограмм ABGH, равновеликий с данной трапецией.
Действительно, трапеция ABCD состоит из пятиугольника ABCFH и
треугольника HFD. Параллелограмм
ABGH состоит из того же
пятиугольника ABCFH и треугольника
CFG. Но &CFG = ADFH, так
как CF = FD и /_CFG = /HFD>
a /mGCF=/_HDF. Следователь- ц1 и **
но, площадь трапеции ABCD равна к н
площади параллелограмма ABGH. Черт. 284
Основание АН этого
параллелограмма равно средней линии EF данной трапеции, 'а высота его
ВК служит в то же время и высотой трапеции ABCD, а потому
площадь трапеции ABCD равна EF-BK, то есть мы доказали
теорему:
Площадь трапеции равна произведению средней линии
на высоту, или в силу § 87, площадь трапеции равна
полусумме её оснований, умноженной на высоту.
Следствие. Две трапеции, имеющие равные средние ли-
нии и равные высоты, равновелики.
§ 188. Другие выражения площади треугольника
и параллелограмма
Площадь треугольника можно выразить не только через его
основание и высоту, но и через другие его элементы.
1. Если даны три стороны треугольника, то его площадь можно
найти следующим образом. Высоту треугольника мы уже
выразили через его стороны (§ 170):
he = ±V р[р-а)(р — Ъ){р — с).
А потому площадь S треугольника равна:
S = Lc.he= Vp{p-a){p-b)(p-c).
203

Эта формула, выражающая площадь треугольника через три
его стороны, была впервые найдена Г ероном (I—III вв. до н.э.)
и носит название формулы Герона.
2. Если даны две стороны треугольника и острый угол между
ними, то его площадь можно выразить и через эти элементы.
Пусть даны стороны b и с и угол А (черт. 285).
S = -jb-hb.
Из треугольника ABD находим:
hb = c-ur[ A,
Черт. 285 а потому
S = "2" b-c-sinA. (1)
Площадь треугольника равна половине произведения двух
его сторон, образующих острый угол, на синус угла между
ними.
3. Для площади параллелограмма также можно найти другие
выражения. Из формулы (1) для площади треугольника легко
получить следующие выражения для площади параллелограмма:
1) площадь параллелограмма равна произведению двух его
смежных сторон на синус его острого угла;
2) площадь параллелограмма равна половине произведения
его диагоналей на синус острого угла между ними;
3) площадь ромба равна квадрату его стороны,
умноженному на синус его острого угла.
§ 189. Площадь многоугольника
Для определения площади многоугольника, например ABCDEF
(черт. 286), его разбивают диагоналями, проведёнными из одной
вершины, на треугольники. Сумма площадей этих треугольников
называется площадью всего многоугольника.
§ 190. Отношение площадей подобных многоугольников
Теорема 1. Площади подобных треугольников
относятся как квадраты сходственных сторон.
Пусть /\АВС подобен ΔΑ^ι^ι (черт. 287). Строим высоты
этих треугольников ЕЮ и BXDV
Из подобия прямоугольных треугольников ABD и AlB1D1
(имеющих равные острые углы) следует:
BD _ АВ
β,ο,—λ,β/
204

Далее имеем:
пл. &ABC = ±AC.BD;
ι
пл. Д AXB1C1 = ^AXCX-B1D1.
Следовательно,
пл. Д ЛВС AC BD __ АС АВ АВ_ _АВ_
пл. Δ ΛΑ С, ~~~ АХСХ ' BXDX ~~~ АХСХ ' АХВХ АХВХ # ~АХ~ВХ
С
АВг
F " С; *,
Черт. 286 Черт. 287
Теорема 2. Площади подобных многоугольников
относятся, как квадраты их сходственных сторон.
Возьмём два подобных многоугольника ABCDE и AlBlClDiE1
(черт. 288). Сходственные диагонали разбивают их на подобные
треугольники (§ 149):
ААВС^ААХВХСХ;
AACD^AA^D,;
ΑΑΟΕ^ΑΑ,Ο,Ε,.
В
Следовательно,
Черт. 288
пл. Δ ЛВС ВС2
пл. Δ ЛХВХСХ
пл. Δ ACD
'вхс\>
CD2
пл. Δ AXCXDX
пл. & АРЕ
DE*
но
пл. £\AXDXEX
CD
а потому
ВС
вхсх
' DXE2 ;
1 1
DE
CXDX DXEX
пл. &АВС пл. &ACD пл. Δ ΑΡΕ
пл. Δ А&Сг ~
ВС1
" пл. Δ AfikDx пл. Δ А^А BXC['
205

По известному свойству пропорций:
пл. Д /ШС + пл. д ACD + пл. Д ЛРЯ _ЯС*
пл. Д АХВХСХ + пл. Д AlClDl + пл. Д /ЦД^ ВХС^'
ИЛИ
пл. ЛДС£>£ _ДС2
пл. AXBXCXDXEX~ВХС['
Мы видим, таким образом, что при переходе от данного
многоугольника к многоугольнику, ему подобному, площадь
многоугольника изменяется в отношении, равном квадрату числа,
характеризующего изменение его сторон.
Так, если сторона многоугольника увеличивается в три раза,
то его площадь увеличится в девять раз.
II. ПРЕОБРАЗОВАНИЕ МНОГОУГОЛЬНИКОВ БЕЗ
ИЗМЕНЕНИЯ ИХ ПЛОЩАДЕЙ
§ 191. Преобразование многоугольника в равновеликий
ему прямоугольник
Задача 1. Построить прямоугольник, равновеликий
данному выпуклому многоугольнику.
Решение. Пусть дан выпуклый пятиугольник ABCDE
(черт. 289). Построим сначала треугольник, равновеликий данному
пятиугольнику. Для этой цели из вершин В и Ε проводим
прямые ВК и EF, параллельные диагоналям АС и AD и
пересекающие прямую CD соответственно в точках К и F.
Черт. 289 Черт. 290
Тогда треугольник AKF будет искомым.
В самом деле, пятиугольник ABCDE, составленный из трёх
треугольников ABC, ACD, ADE9 равновелик треугольнику AKF,
составленному из того же самого треугольника ACD и двух
треугольников АКС и ADF, так как треугольник ABC равновелик
треугольнику АКС, а треугольник ADE равновелик
треугольнику ADF (§ 186, следствие 2).
206

Таким образом, пятиугольник ABCDE преобразован в
равновеликий ему треугольник AKF. Для треугольника AKF легко
построить равновеликий ему прямоугольник.
Приняв за основание треугольника сторону KF, строим
прямоугольник с основанием KF и высотой, вдвое меньшей высоты
треугольника AKF. Это построение выполнено на чертеже 290.
Таким образом, данный многоугольник ABCDE преобразован в
равновеликий ему прямоугольник KLMF.
Такое преобразование имеет следующее значение. При
вычислении площадей фигур прямоугольник является самой простой
фигурой, площадь которой определить легче всего. Площадь же
неправильного многоугольника определить довольно сложно.
Произведённое нами преобразование одними построениями, без
вычислений, сводит эту сложную задачу к простейшей.
§ 192. Преобразование прямоугольника в равновеликий
ему квадрат
Задача. Построить квадрат, равновеликий данному
прямоугольнику.
Решение. Пусть дан прямоугольник ABCD (черт. 291).
Требуется построить квадрат, равновеликий данному
прямоугольнику.
К L
в /
V
с \
■В I I шшЧШвШШшШ——— \ I ■ 1 W*—JL
ft О D F Μ
Черт. 291
Продолжаем основание AD прямоугольника ABCD и
откладываем на нём от точки D отрезок DF, равный высоте DC. Затем
на полученном отрезке AF как на диаметре описываем
полуокружность и продолжаем прямую DC до её пересечения с
полуокружностью в точке Я*. Тогда DK—сторона искомого квадрата.
В самом деле, построив на DK квадрат DKLM, мы на
основании § 165, следствия 1 будем иметь:
DK* = AD-DF,
или
DK* = AD-CD.
Отсюда следует, что площадь квадрата DKLM равна площади
прямоугольника ABCD.
207

Объединяя задачу, рассмотренную в § 191, с только что
решённой, мы можем теперь построить квадрат, равновеликий
данному выпуклому многоугольнику.
Числовые зависимости между элементами треугольников,
выведенные нами ранее, могут быть представлены в форме некоторых
соотношений между площадями фигур. Так, теорема:
перпендикуляр, опущенный из вершины прямого угла на гипотенузу, есть
среднее пропорциональное между проекциями катетов — может
быть выражена таким образом:
Квадрат, построенный на перпендикуляре, опущенном
из вершины прямого угла на гипотенузу, равновелик
прямоугольнику, имеющему сторонами проекции катетов на
гипотенузу.
Точно так же теоремы о пропорциональных линиях в круге
могут быть высказаны таким образом:
/· Прямоугольники, имеющие сторонами отрезки одной и
той же хорды, проходящей через данную точку внутри
окружности, равновелики.
2. Квадрат, построенный на касательной, проведённой
из внешней точки окружности, равновелик
прямоугольнику, имеющему сторонами всю секущую, проведённую
из той же точки, и её внешнюю часть.
В этой именно форме все эти теоремы и были найдены
древними греками, которые доказывали их геометрически построением
квадрата, равновеликого прямоугольнику.
§ 193. Теорема Пифагора
Допустим теперь, что мы имеем два квадрата. Поставим задачу: сложить
их площади, то есть построить квадрат, площадь которого равна сумме
площадей данных квадратов.
Решение этой задачи даётся знаменитой теоремой Пифагора.
Квадрат, построенный на гипотенузе прямоугольного
треугольника, равновелик сумме квадратов, построенных на катетах этого
треугольника.
С числовым выражением этой теоремы в виде соотношения между
длинами катетов и гипотенузы прямоугольного треугольника мы уже
встречались (§ 166).
Приведём теперь геометрическое доказательство этой теоремы, выражая
её как соотношение между площадями.
На гипотенузе ВС прямоугольного треугольника ABC построим
квадрат BCDE (черт. 292). Через точки D и Ε проводим прямые, параллельные
соответственно катетам АВ и АС до взаимного пересечения с продолжениями
этих катетов в точках L и Λί и до взаимного пересечения в точке N.
Четырёхугольник ALNM— квадрат, сторона которого равна сумме катетов данного
треугольника. Действительно, &ABC = &CMD, так как BC = CD как
стороны квадрата, £ ВАС=£ CMD как прямые углы, £ ABC'= £МСО как углы
с перпендикулярными сторонами. Следовательно,
СМ = АВ, АМ = АС + АВ, DM = AC.
Точно так же
Δ CMD = Д DNE=& ELB.
208

Следовательно,
значит,
LE=ND=CM = AB\ LB = EN=MD = AC\
AL = LN=MN=AM.
Построим теперь квадраты ABDE и ACFG на катетах АВ и АС (черт. 293).
Продолжив стороны DB и FC до взаимного пересечения в точке Η и стороны
DE и FG до пересечения в точке /С, мы получим квадрат DHFK, сторона
которого опять равна сумме катетов треугольника ABC. Соединив точки Ε
и (/, мы получим треугольники ОКЕ и ЕАиу причём
Δ KGE=&AEGz=/\HCB = &ABC
как имеющие равные катеты. Отнимая теперь от квадрата ALNM (черт. 292)
четыре равных треугольника, получим квадрат, построенный на гипотенузе,
а отнимая от квадрата KDHF (черт. 293), равного квадрату ALNM, четыре
В
Η
А
Черт. 292
Черт. 293
таких же треугольника, получим сумму квадратов, построенных на катетах.
Следовательно, квадрат, построенный на гипотенузе, равновелик сумме
квадратов, построенных на катетах.
Теорема Пифагора даёт возможность складывать геометрически площади
нескольких многоугольников. Пусть, например, требуется сложить
площади Pl} Р2, Я8 трёх многоугольников. Строим сначала квадраты, равновеликие
этим многоугольникам. Пусть стороны этих квадратов будут
соответственно alt аг и а8. Строим прямоугольный треугольник с катетами αλ и а2. Строим,
далее, новый треугольник, принимая гипотенузу построенного треугольника
за катет нового треугольника, а за второй его катет берём сторону третьего
квадрата а3.
Площадь квадрата, построенного на гипотенузе этого нового
треугольника, будет равна сумме площадей данных многоугольников.
III. УПРАЖНЕНИЯ К ГЛАВЕ ВОСЬМОЙ
А. Доказать теоремы.
1. Если через вершины четырёхугольника провести прямые, параллельные
его диагоналям, то площадь параллелограмма, образованного этими прямыми
в два раза больше площади'данною четырёхугольника.
2* Если два треугольника имеют по две равные стороны, а углы,
заключённые между ними, в сумме составляют 180°, то эти треугольники
равновелики.
3. На сторонах прямоугольного треугольника построены квадраты.
Соединив ближайшие вершины каждых двух соседних квадратов, получим три
треугольника.
Доказать, что каждый из них равновелик данному треугольнику.
4. Отношение периметра треугольника к одной из его сторон равно
отношению высоты, опущенной на эту сторону, к радиусу вписанного круга.
20Э

5. Если два треугольника имеют по равному углу, то их площади
относятся между собой, как произведения сторон, заключающих равные углы.
6. Внутри треугольника ABC взята какая-либо точка М, расстояния
которой от сторон треугольника равны х, у и г. Доказать, что сумма
ax-\-by + cz, где а, Ь, с — длины сторон треугольника, есть постоянная
величина, равная удвоенной площади треугольника.
7. Доказать, что если в каком-либо многоугольнике все стороны равны
между собой, то сумма расстояний точки, лежащей внутри многоугольника от
его сторон, есть величина постоянная.
8. Доказать, что площадь многоугольника, построенного на гипотенузе
прямоугольного треугольника, равна сумме площадей подобных ему
многоугольников, построенных на катетах как на сходственных сторонах.
Б. Задачи на построение.
9. Построить треугольник, равновеликий данному и имеющий то же
основание, одна из сторон которого имела бы данную длину.
10. Построить треугольник, равновеликий данному, имеющий основание,
в два раза меньшее основания данного, и данный угол при основании.
11. Построить треугольник, равновеликий данному, с тем же основанием,
высота которого была бы в три раза меньше высоты данного и угол при
вершине которого был бы равен заданному углу.
12. Построить треугольник, у которого площадь составляет — площади
1
данного, основание равно -=- основания данного и медиана одной из
боковых сторон имеет данную длину.
13. Построить треугольник, равновеликий данному и имеющий то же
основание, так, чтобы в построенном треугольнике отрезок основания qA имел
заданную длину.
14. Построить треугольник, у которого плошадь составляет — площади
1
данного, высота равна -«- высоты данного, а радиус описанной окружности
о
2
равен -^- радиуса окружности, описанной около данного,
о
15. Построить треугольник, равновеликий данному, с тем же углом при
основании, высота которого равна
данному отрезку Λ.
Указание. Из конца А
основания АС данного треугольника ABC
(черт. 294) восставляем перпендикуляр
AE — h. Через точку Ε проводим
прямую ЕХ || АС {X — точка её пересечения
с прямой АВ). Соединяем точки X и С
и через точку В проводим прямую
BD\\XC. Треугольник AXD — искомый.
16. Построить треугольник,
равновеликий данному, имеющий с ним
общий угол при основании и боковую
сторону данной длины I.
Указание. На стороне АВ
откладываем отрезок АХ = 1 и далее
поступаем так же, как при решении предыдущей задачи.
17. Построить треугольник, равновеликий данному и подобный другому
данному.
18. Данный треугольник разделить на три равновеликие части прямыми,
выходящими из вершины.
210

19. Данный треугольник разделить на три равновеликие части прямыми,
параллельными основанию.
Указание. Площадь треугольника, отсекаемая секущей, ближайшей
к вершине, равна -«г площади данного треугольника, а площадь треугольника,
2
отсекаемая второй секущей, равна -«- той же площади.
20. Данный треугольник разделить на три равновеликие части прямыми,
проходящими через точку, данную на стороне треугольника.
21. Данный треугольник разделить на две равновеликие части прямой,
перпендикулярной к основанию.
Указание. Искомая прямая отсекает от данного треугольника
прямоугольный треугольник, площадь которого равна -у площади данного. Кроме
того, этот треугольник подобен одному из тех треугольников, на которые
данный треугольник делится высотой.
22. Данный треугольник разделить прямой на две фигуры, имеющие
одинаковую площадь и "одинаковый периметр.
У к а з а и и е. Пусть ABC — данный треугольник, и искомая прямая XY
пересекает прямую СВ в точке Υ и прямую СА в точке X. На основании
упражнения 5 и условия задачи имеем:
пл. САВ_САСВ
пл. СХУ — СХ-СУ
откуда:
CX-CY=-^-CA.CB. (*)
Далее, по условию задачи, CX+CY+XY= XY+АХ + АВ+BY. Но
АХ=АС-СХ\ ВУ = ВС-СУ. Отсюда: СХ+ СУ = АС- СХ + АВ + ВС: —
— CYy или
СХ+СУ=±-(АС+АВ + ВС). (2)
Равенства (1) и (2) дают возможность построить отрезки СХ и CY.
23. Построить равносторонний треугольник, равновеликий данному
квадрату.
24. В данный треугольник вписать треугольник, равновеликий данному
квадрату.
25. Построить параллелограмм по двум данным его сторонам так, чтобы
он имел наибольшую площадь.
26. Данный прямоугольник преобразовать в прямоугольник, ему
равновеликий, имеющий одну из сторон, равную данному отрезку.
27. Построить квадрат так, чтобы его площадь относилась к площади
данного квадрата, как т.п.
Указание. Если а — сторона данного квадрата, χ — сторона искомого,
х2 т тг _ 2 ~ хг тг
то —, = — = . Строим отрезок р, такой, что pz = mn. Тогда —г = -=-,
аг η т-п v v r> r аг рг »
χ т
откуда — = —.
J а р
28. Данную трапецию разделить на две равновеликие части прямой,
параллельной её основаниям.
29. Прямой, перпендикулярной к основаниям трапеции, разделить её
площадь пополам.
В. Задачи на вычисление.
30. Площадь прямоугольника равна 150 кв. м, а отношение его сторон
равно 1,5. Определить его стороны. Отв. 10 ж, 15 лс.
211

31. Периметр прямоугольного треугольника равен 24 ж, его площадь
равна 24 кв. м. Определить его стороны. Отв. 6 Л£, 8 л*, 10 м.
32. Вычислить площадь параллелограмма, стороны которого равны 3 см,
8 см, а острый угол содержит 30°. Отв. 12 кв. см.
33. Две стороны треугольника равны 8 см и 14 см, а угол между ними
60°. Вычислить плоЛадь треугольника. Отв. 28 Ϋ'6 кв. см.
34. Стороны треугольника равны 61, 74 и 87. Вычислить его площадь.
Отв. 2 220.
35. Вычислить площадь равностороннего треугольника, сторона которого
η a2Y*
равна а. итв. —j
36. Диагонали ромба равны 48 см и 14 см. Определить его площадь.
Отв. 336 кв. ели
37. Высота треугольника равна 10 см. Определить высоту
прямоугольника, вписанного в этот треугольник, если отношение площади
прямоугольника к площади треугольника равно 8:25. Отв. 2 см и 8 см.

ГЛАВА ДЕВЯТАЯ
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
I. ОБЩИЕ СВОЙСТВА ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
§ 194. Правильный многоугольник
Равносторонний многоугольник (за исключением треугольника·),
вообще говоря, не будет равноугольным, и наоборот. Например,
ромб — равносторонний, но не равноугольный многоугольник, а
прямоугольник — равноугольный, но не равносторонний
многоугольник.
Если же многоугольник одновременно и равносторонний, и
равноугольный, то такой многоугольник называется правильным·
Таким образом, правильный многоугольник — это
многоугольник, у которого все стороны и все углы равны. Например,
равносторонний треугольник и квадрат — правильные многоугольники.
Так как во всяком /z-угольнике сумма углов равна 2dn—Ad
(§ 41), то каждый угол правильного я-угольника равен .
§ 195. Вписанные и описанные правильные многоугольники
Многоугольник, все вершины которого лежат на окружности,
называется вписанным в окружность·
Многоугольник, все стороны которого касаются
окружности, называется , описанным около
окружности·
Теорема. Около всякого
правильного многоугольника можно описать
окружность и во всякий правильный
многоугольник можно вписать
окружность.
1. Пусть ABCDE — правильный
многоугольник (черт. 295). Проведём биссектрисы Черт. 295
его углов А и В. Они пересекутся в
некоторой точке О. Соединим эту точку с остальными вершинами
и докажем, что AO=BO = CO = DO = EO.
213

Так как углы А и В равны, а прямые АО и ВО делят их
пополам, то
Z.ABO=^BAO
и, следовательно, Д АОВ — равнобедренный; значит,
АО = ВО.
Сравним треугольники АОВ и ВОС. Они имеют общую
сторону ОВ и, кроме того, АВ = ВС и /_АВО = /_СВО как
половины одного угла; следовательно,
ААОВ=&ВОС и АО=ОС.
Сравним, далее, треугольники ВОС и COD. Сторона ОС у
них общая, BC = CD. Кроме того, /_ВСО= /_ОВС, а этот угол
есть половина угла ABC; но /_АВС=/_BCD> следовательно,
^ВСО есть половина /_BCD, а потому
Z.bco=zocd.
Значит,
д ВОС = Д COD,
откуда следует, что
OB=OD.
Продолжая такое сравнение соседних треугольников, найдём:
AO = BO = CO = DO = EO.
Отсюда следует, что окружность с центром в точке О и
радиусом ОА пройдёт через все вершины данного многоугольника.
2. Опустив из точки О перпендикуляры на стороны АВ> ВС,
CD у ..., найдём:
OM=ON=OP=...
как катеты равных прямоугольных треугольников АОМ, BON
СОР, .... Следовательно, окружность с центром в точке О и
радиусом ОМ коснётся всех сторон данного многоугольника.
Следствия. 1. Биссектрисы внутренних углов
правильного многоугольника пересекаются в одной точке — центре
описанной окружности; та же точка есть центр вписанной
окружности.
2. Перпендикуляры, восставленные в серединах сторон
правильного многоугольника, пересекаются в одной точке — общем
центре вписанной и описанной окружности.
Общий центр вписанной и описанной окружности называется
центром правильного многоугольника. Длина перпендикуляра,
опущенного из центра правильного многоугольника на сторону,
называется апофемой многоугольника·
214

§ 196· Отношение периметров правильных многоугольников
Теорема. Отношение периметров правильных одно-
именных многоугольников равно отношению радиусов
описанных окружностей, а также отношению их апофем.
Согласно признаку подобия многоугольников (§ 150)
правильные одноимённые многоугольники подобны, а потому если даны
правильные многоугольники ABCDEF и AB'CD'E'F' и Ρ и Р'—
их периметры, то
-pf = jrg, (§ 149, следствие 2).
Далее (черт. 296),
ΔΑΟΒ<*>ΔΑΌ'Β
Черт. 296
АВ _ АО _R
А'В'~ А'О' ~ R"
Ρ _ АО
Р' А'О' '
Если ОН — апофема, опущенная на сторону АВ, то
ΔΑΟΗν>ΔΑΌΉ\
следовательно,
АО _ ОМ
АО' О'Н' '
Таким образом,
Ρ _ АО _ ОН
Р'~А'0'~0'Н"
§ 197· Площадь правильного многоугольника
Теорема. Площадь правильного многоугольника равна
половине произведения его периметра на апофему.
Дан правильный многоугольник (черт. 297). Соединив его
центр О со всеми вершинами, получим столько равных треуголь-
а потому
Следовательно,
215

ников, сколько сторон имеет данный многоугольник. Так, для
шестиугольника ABCDEF имеем:
/\AOB = /\BOC = /\COD=... .
Сумма площадей этих треугольников
называется площадью всего
многоугольника. Но
площадь /\АОВ равна γΑΒ-ΟΗ,
где ОН — апофема многоугольника,
ОН = а. Сумма площадей всех
полученных треугольников равна у АВ-ОН-п, где
η — число сторон многоугольника; но η · АВ
есть периметр Ρ многоугольника:
п-АВ = Р.
А потому площадь всего многоугольника ABCDEF равна
II. ВЫЧИСЛЕНИЕ СТОРОН ПРАВИЛЬНЫХ ВПИСАННЫХ
МНОГОУГОЛЬНИКОВ
§ 198· Квадрат
Построить квадрат, вписанный в данную окружность, можно
следующим образом. Проведём два взаимно перпендикулярных
диаметра АС и BD (черт. 298) и точки их
пересечения с окружностью Л, β, С и D
соединим между собой. Эти два диаметра
разделят окружность на четыре равные
части, и полученный вписанный
четырёхугольник — квадрат.
Сторону вписанного квадрата найдём
из треугольника АОВ:
АВ2 = АО2 + ВО2 = R2 + R2 = 2/?2,
откуда:
AB = RV2.
§ 199· Шестиугольник
Сторона АВ (черт. 299) правильного вписанного
шестиугольника является хордой, стягивающей дугу, равную -^ части
окружности. Следовательно, /_ АОВ = -g · 360° = 60°, а потому j/BAO=
216

Значит, /\АОВ— равносторонний, и потому AB = Rt то есть
сторона правильного вписанного шестиугольника равна радиусу
окружности.
Отсюда вытекает простой способ построения шестиугольника
путём откладывания от какой-либо точки А окружности дуг
радиусом, равным радиусу этой окружности.
§ 200· Треугольник
Соединяя через одну вершины
правильного вписанного шестиугольника ABCDEF
(черт. 299), получим правильный вписанный
треугольник АСЕ. Сторону АС этого тре-
угольника найдём из параллелограмма АВСО:
АС2 + ОВ2 = АВг + ВС2 + СО2 + ОА2,
или
отсюда:
ЛС2 + /?2 = /?2 + /?2 + /?2 + /?2
AC2 = 3R2; AC = RV3.
§ 201· Десятиугольник
Если АВ — х (черт. 300) — сторона правильно вписанного
десятиугольника, то
ΔΑΟΒ=^ = Ζ6°,
£ ВАО= L АВО = 18°° ~ 36° = 72°.
Проведём биссектрису AM угла ОАВ. Тогда
£МАВ=Щ- =36°; а так как £АВМ= 72°, то
/_ АМВ= 180° — 36° — 72° = 72°; следовательно,
треугольник МАВ равнобедренный и АМ=АВ.
Треугольник АМО также имеет два равных угла:
£ΜΑΟ=£ΑΟΜ = 36°,
АМ = ОМ.
/\АОВсп£±МАВ,
ОВ:АВ = АВ:ВМ,
AB-=r-AM = OM = x, OB = R
BM = OB-OM = R-xt
Черт. 300
следовательно,
Далее,
а потому
а так как
и
217

R:x = x:(R-x),
то есть искомая сторона десятиугольника равна большей части радиуса,
разделённого в крайнем и среднем отношении. Следовательно (§ 172), .
х = ^(]/5~-1)=^ 0,618/?.
§ 202. Общий случай
Для получения стороны любого правильного вписанного многоугольника
удобно пользоваться тригонометрическими функциями. Пусть АВ (черт. 301)—
сторона правильного вписанного /z-уголышка. Построив его апофему ОМ,
из треугольника ОАМ имеем:
Черт. 301
АМ = ОА sin/ А ОМ.
(1)
Обозначив сторону /z-угольника через ап, будем
иметь:
АМ = ^
Далее, заметим, что
глл η / лпал 360° 180°
OA = R и /АОМ—~-— =
2п η
Внося эти величины в равенство (1), получим:
ап _ . 180°
f = /?sin —,
откуда:
ап — 2R sin
180°
Из этой общей формулы можно получить как частный случай записанные
выше выражения для сторон вписанных квадрата, шестиугольника и
треугольника.
В самом деле,
VT -
a, = 2R s'm45° = 2R^- = RVt2;
а, = 2R sin 30° = 2R .i- = R;
аг = 2R sin 60° = 2Rl-£- = R ]/Ύ.
III. УПРАЖНЕНИЯ К ГЛАВЕ ДЕВЯТОЙ
1. Доказать, что все диагонали правильного пятиугольника при взаимном
пересечении образуют новый правильный пятиугольник.
2. Доказать, что правильный шестиугольник содержит три пары
диагоналей параллельных, три диагонали, к ним перпендикулярных, и две тройки
диагоналей, составляющих равносторонний треугольник.
3. Не прилежащие одна к другой стороны правильного шестиугольника
продолжены в обе стороны до взаимного пересечения. Доказать, что получен-
218

ный при этом треугольник — равиосторонний, со сторонами, в три раза
большими сторон шестиугольника.
4. На каждой стороне правильного шестиугольника, вне его, построен
квадрат. Ближайшие вершины соседних квадратов соединены прямыми.
Доказать, что полученный при этом 12-угольник — правильный.
5. Стороны правильного шестиугольника продолжены в одну и ту же
сторону на одну и ту же длину. Концы полученных отрезков соединены
прямыми в последовательном порядке. Доказать, что полученная фигура есть
правильный шестиугольник.
6. Построить правильный шестиугольник по данной его стороне.
7. Построить правильный шестиугольник по данной его меньшей диагонали.
8. Построить правильный восьмиугольник по данной его стороне.
9. В данном квадрате срезать углы так, чтобы образовался правил ьный
восьмиугольник.
Указание. Четыре стороны искомого восьмиугольника являются
отрезками сторон данного квадрата, а четыре другие стороны — отрезками
сторон квадрата, равного данному.
10. Зная сторону правильного шестиугольника, вычислить площадь
правильного 12-угольника, вершинами которого служат вершины квадратов,
построенных на сторонах шестиугольника.
Указание. См. упр. 4. Отв. За2 (2 -f V%)·
И. Две противоположные стороны правильного восьмиугольника и две
перпендикулярные к ним диагонали образуют прямоугольник. Вычислить его
площадь, если сторона восьмиугольника равна а. Отв. α*(\-\-γ~2).
12. Определить вписанный угол, образованный двумя хордами, из
которых первая равна стороне правильного вписанного шестиугольника, а
другая—стороне правильного вписанного десятиугольника. Отв. 1) 132°. 2) 12°.

ГЛАВА ДЕСЯТАЯ
ВЫЧИСЛЕНИЕ ДЛИНЫ ОКРУЖНОСТИ И ПЛОЩАДИ КРУГА
I. ДЛИНА ОКРУЖНОСТИ
§ 203. Предварительные замечания
Когда мы измеряли длину прямолинейного отрезка, мы
старались определить, сколько раз на данном отрезке можно
отложить отрезок, принятый за единицу длины. Этот приём нельзя
применить для вычисления длины окружности, так как какой бы
прямолинейный отрезок ни был принят за единицу длины, его
нельзя будет совместить с дугой окружности. Поэтому для
вычисления длины окружности стараются найти величины, которые
могли бы заменить собой длину окружности и в то же время
могли бы быть измерены обычным приёмом.
За такие величины берут периметры правильных вписанных
многоугольников. Чем больше вершин в таком многоугольнике,
тем больше он имеет общих точек с окружностью и тем более
по своему виду он похож на круг.
Поэтому периметр правильного вписанного многоугольника
принимается за приближённое значение длины окружности. Чтобы
перейти отсюда к точному определению длины окружности,
рассмотрим некоторые свойства периметров вписанных
многоугольников и периметров ломаных линий.
§ 204. Свойства периметров ломаных линий
Теорема. Отрезок прямой, соединяющий две точки,
короне всякой ломаной линии, проведённой между этими
же точками.
Даны: отрезок АВ и ломаная ACDEFB (черт. 302). Соединив
точку А с точками D, Еу /\ получим треугольники ACD,
ADE, AEF и AFB. Из этих треугольников имеем:
AC + CD>AD; AD + DE>AE;
AE + EF>AF; AF + FB>AB.
220

Сложив эти неравенства и приведя подобные члены, получим:
AC + CD + DE+EF + FB>AB.
Из двух ломаных линий с общим началом и общим концом
одна называется объемлющей по отношению к другой, если эта
другая лежит внутри многоугольника, образованного первой
ломаной и отрезком, соединяющим их концы.
Так, ломаная AEFGD — объемлющая
по отношению к ломаной ABCD
(черт. 303).
А ~ D
Черт. 302 Черт. 303
Теорема. Периметр выпуклой ломаной линии меньше
периметра всякой объемлющей её ломаной.
Даны две ломаные: выпуклая ABCD и объемлющая её AEFGD
(черт. 303).
Продолжим звенья АВ и ВС до пересечения с объемлющей
ломаной в точках И и /О В силу предыдущего имеем:
АЕ+ЕН>АВ + ВН%
BH+HF + FK>BC + CKt
CK+KG+GD>CD.
Складывая эти неравенства и приведя подобные члены, получим:
AE+EH + HF+FK+KG + GD>AB + BC + CD9
или:
AE + EF + FG+GD>AB + BC + CD.
§ 205. Свойства периметров вписанных многоугольников
Периметры вписанных многоугольников обладают свойствами,
выраженными в приведённых ниже теоремах.
Теорема 1. Периметр вписанного многоугольника при
удвоении числа его сторон возрастает.
221

В самом деле, при удвоении числа сторон вписанного
многоугольника сторона MN (черт. 304) заменяется двумя сторонами
МТ и TN нового многоугольника. Но MT-\-TN^>MN, а потому
Р2„>Р„, где Рп и Р2Л— периметры старого и нового
многоугольников.
Теорема 2. Периметр любого вписанного
многоугольника меньше периметра любого описанного многоугольника.
Это непосредственно вытекает из доказанных выше свойств
выпуклых ломаных линий.
В самом деле, обозначим периметр вписанного
многоугольника через Р, описанного — через Q. Соединим точку касания
одной из сторон описанного многоугольника Τ с ближайшими
к ней слева и справа вершинами Μ κ Ν вписанного
многоугольника (черт. 304). Заменяя хорду ΜΝ двумя хордами МТ и 77V,
мы получим новый вписанный многоугольник,
периметр которого Р' > Р. Но Р' есть
периметр замкнутой выпуклой ломаной линии,
начало и конец которой совпадают в точке
Т; Q есть периметр объемлющей ломаной с
теми же началом и концом, а потому Q> P'
и, следовательно, Q>Р.
Теорема 3. При неограниченном
удвоении числа сторон правильного
вписанного многоугольника
последовательна. 304 ность периметров Plf Рг, Р3, · · · Рп, · ·.
получающихся при этом
многоугольников имеет определённый предел.
В самом деле, если удвоить число сторон правильного
вписанного многоугольника, затем удвоить число сторон вновь
полученного многоугольника и продолжить этот процесс удвоения
неограниченно, то получится последовательность правильных
вписанных многоугольников со всё возрастающим числом сторон.
Периметры этих многоугольников образуют бесконечную
последовательность чисел:
Ρ Ρ Ρ Ρ
* 1> * 2» ·* 3> •••»J/|»····
Эта последовательность обладает такими свойствами: в силу
первой теоремы этого параграфа каждый член
последовательности больше предшествующего, то есть эта последовательность
возрастающая. В силу второй теоремы члены этой
последовательности меньше некоторого постоянного числа, именно меньше
периметра любого описанного многоугольника, например меньше
периметра описанного квадрата.
Как известно из алгебры, возрастающая последовательность
чисел, все члены которой меньше некоторого числа, имеет
определённый предел. А потому последовательность периметров Р19
Р2, Р3, ..., РпУ ... имеет определённый предел.
222

§ 206. Удвоение числа сторон правильного вписанного
многоугольника
Задача. Зная сторону ап правильного вписанного
многоугольника и радиус круга R, определить сторону а2п
правильного вписанного многоугольника, имеющего вдвое более сторон*
Дана сторона АВ = ап (черт. 305). Проводим радиус ОС у
перпендикулярный к АВУ и соединяем точку С с точками Л и β.
Хорды АС и ВС и будут сторонами искомого многоугольника:
АС=ВС=а2п. Из треугольника АОС имеем: q
АС2 = АО2 + ОС2 — 20С- ОМ, ^
или
a22n=R2 + R2-2R.OM;
но из треугольника АОМ:
R2
Следовательно,
4 *
Черт. 305
а\ч = 2R2 — 2R
V
R'-Ъ
отсюда:
a2n = -l/2R2-RV4R2
Ту же формулу можно получить иначе. Из треугольника
АОС имеем:
или
Но
АС2 = А02 + ОС2 — 2АО- ОС- cos Z АОС,
aln = R2±R*-2R-R-cos^ = 2R2(\-cosl-^y
180° Ί/"" "ΤΓδΟ5
cos = 1/ 1—sin
η У п
^~ = % (§ 202),
а потому:
следовательно,
агп = ^2R2-RV~4R2-tfn.
223

§ 207· Длина окружности· Число π
Предел периметров правильных вписанных в круг
многоугольников при неограниченном увеличении (путём удвоения)
числа их сторон называется длиной окружности.
Таким образом, вычисление длины окружности приводит к
нахождению предела периметров правильных вписанных
многоугольников при неограниченном возрастании числа их сторон.
Нахождение этого предела облегчается замечательным свойством
окружности, которое выражается следующей теоремой.
Теорема. Отношение длины окружности к диаметру
есть величина постоянная, то есть одна и та оке для
всех окружностей.
Возьмём две окружности и впишем в них одноимённые
правильные многоугольники. Их периметры Ρ и ρ относятся, как
радиусы R и г (§ 196), то есть
P:p = R:r,
отсюда:
L-L·
2R 2г'
При увеличении числа сторон многоугольников их периметры
стремятся, как к своим пределам, к длинам данных
окружностей Сиг.
Так как переменные величины ^ и %г остаются равными при
неограниченном удвоении числа сторон, то будут равны и их
пределы, то есть
£ — L
2R~2r>
что и доказывает теорему.
Постоянная величина ^ обозначается греческой буквой π (пи),
С
то есть 9© = π» отсюда
С=2тт/?.
Таким образом, задача вычисления длины окружности
сводится к вычислению некоторого постоянного числа π.
Когда это число будет найдено, то, умножив его на диаметр
круга 2/?, получим длину окружности.
Чтобы получить приближённую величину числа π, вписывают
в окружность какой-либо правильный многоугольник. Затем
вычисляют его периметр и делят его на диаметр круга. Чтобы
получить более точное значение ττ, удваивают число сторон
многоугольника и периметр нового многоугольника опять делят на
диаметр. Чем больше число сторон вписанного многоугольника,
тем более точное значение получается для числа π. Ниже даётся
224

таблица, в которой приведены приближённые значения чисел π,
соответствующие различным многоугольникам.
I Число сторон
12
24
48
96
192
384
768
Отношение периметра
вписанного многоугольника к
диаметру круга
3,10582854
3,13262861
3,13935020
3,14103195
3,14145247
3,14155761
3,14158389
Число сторон
1536
3072
6144
| 12 288
24 576
49 152
98 304
Отношение периметра вписан-1
ного многоугольника к диа- 1
метру круга 1
3,14159046
3,141592106
3,141592517
3,141592619
3,141592645
3,141592651
3,141592653
Точная величина отношения длины окружности к диаметру
представляется бесконечной непериодической десятичной дробью:
π = 3,14159265358979323846....
На практике берут часто приближённо
22
π =sr 3,14, или π =^ у .
Последнее значение π было найдено Архимедом и носит
название Архимедового числа. Оно даёт значение π с точностью
до 0,01.
§ 208· Длина дуги окружности
Дуговые градусы разбивают всю окружность на 360 равных
частей, а потому длина дуги в 1° должна составлять g™ часть
всей окружности, то есть должна измеряться числом:
2π/?_π/?
360 180 *
Длина s дуги в п° равна:
6— 180 ·
Если дуга s несоизмерима с дуговым градусом, то поступают
так же, как при измерении отрезков (§ 119), а именно: делят
дуговой градус на η равных частей и укладывают на данной
дуге —ю часть дугового градуса столько раз, сколько это
возможно. Таким образом, получают длину дуги, измеренную
дуговым градусом с точностью до —й части.
225

§ 209. Радианная мера углов
Деля обе части равенства s = -^ на /?, получим:
S ПК
Это равенство показывает, что отношение длины дуги к
радиусу вполне определяется числом градусов а/, содержащихся
в этой дуге (а следовательно, и в соответствующем ей
центральном угле), независимо от длины радиуса. Обратно, если известно
отношение ^-, то можно определить в градусах величину
центрального угла. В самом деле, из полученной формулы находим:
5 180
Отсюда следует, что величина отношения тг так же хорошо
определяет величину центрального угла, как и число
содержащихся в нём градусов, так как, зная величину -^, можно сейчас
же определить число градусов угла. Величина -β
непосредственно показывает, сколько раз радиус круга содержится в дуге,
соответствующей данному центральному углу, или сколько раз
в данном угле содержится угол, измеряемый дугой, по длине
равной радиусу. Таким образом, вместо прежнего градуса можно
ввести новую единицу измерения центральных углов, а именно:
угол, измеряемый дугой, длина которой равна радиусу круга.
Эта новая единица измерения углов носит название радиана,
а величина ^ — радианной мерой угла. Она показывает, сколько
к
радианов содержится в данном угле. Обозначим величину -^
одной буквой:
Связь между радианной и градусной мерой угла выражается
формулой:
ПК
По этой формуле, зная градусную меру η угла, можно найти
его радианную меру φ, и обратно — по радианной мере угла
вычислить число его градусов.
Найдём радианную меру прямого угла. Полагая η = 90°,
имеем:
90π π
*=ί80 = Τ·
226

ί
(?=^-
Найдём число градусов, содержащихся в одном радиане. Для
радиана s = Rt φ—1. Таким образом, для радиана имеем:
| ПК
откуда:
„ = 1^57° 1744".
π
Такова градусная мера одного радиана. Наконец, из формулы
"R
следует:
s = Rut
то есть длина дуги равна длине радиуса, умноженной на
радианную меру центрального угла.
II. ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ
§ 210· Площадь круга
Площадью круга называется предел площади правильного
вписанного в этот круг многоугольника при неограниченном
удвоении числа его сторон. -
Для вычисления площади круга радиуса R ^- ^^-°
находим сначала площадь «S правильного
вписанного многоугольника. Если Ρ — периметр
этого многоугольника и а— его апофема, то
Ρ·α
5 =-тт" (§197). При удвоении числа сторон
многоугольника его периметр Ρ имеет пределом „ ~Т1
длину окружности, то есть 2ττ/?. ерг'
Апофема я, как легко заметить, имеет пределом радиус
круга R, В самом деле, из треугольника АОМ (черт. 306) имеем:
АО—ОМ<АМ или R — а<^. Так как ап стремится к нулю
при возрастании я, то R есть предел переменной величины а,
а потому
P. a 2tzR.R пг
предел -γ- =—Т— = π/?2.
Итак, имеет место теорема:
Площадь круга радиуса R равна π/?2·
Следствие. Площади кругов пропорциональны квадратам
радиусов.
Если R и г — радиусы кругов, S w s — их площади, то
S = nR\ s = nr\
Отсюда:
s г2 ■
227

§ 211· Площадь сектора
Если разделить всю окружность на 360 дуговых градусов и
соединить точки деления с центром, то весь круг разобьётся на
360 равных секторов. Площадь каждого из них мы определим
1 π/?2
как щ часть площади круга и будем измерять её числом «йт ·
Площадь сектора в η градусов будем измерять числом ^^ .
Это число можно представить в форме η · щ · ~. Но ^ есть
длина s дуги сектора (§208), а потому
sR
пл. сектора равна -у·, (1)
то есть мы имеем теорему:
Площадь сектора равна длине дуги сектора,
умноженной на половину радиуса.
Если дуга s сектора несоизмерима с единицей длины, то
берут сначала приближённую величину дуги. Тогда формула (1)
будет давать приближённую величину площади сектора.
§ 212· Площадь сегмента
Площадь сегмента АМВ (черт. 307) определим как разность
площади сектора АОВ и площади треуголвника АОВ. Но пло-
щадь сектора АОВ равна —, где s — длина дуги АВ\ площадь
треугольника АОВ равна -тг АО-ВС, где
ВС — высота треугольника АОВ,
проведённая через вершину β, а потому
пл. сегм. AMB = ^-^=y(s-BC).
Легко заметить, что ВС есть половина
хорды BD, которая стягивается дугой
Черт. 307 BD(—BD = 2^AB). Таким образом, мы
доказали теорему:
Площадь сегмента равна половине радиуса,
умноженной на разность между дугой сегмента и половиной
хорды двойной дуги.
III. УПРАЖНЕНИЯ К ГЛАВЕ ДЕСЯТОЙ
1. Радиусы двух окружностей равны 8 см и \Ъсм. Расстояние между
их центрами равно 17 см. Определить длину их общей хорды. Отв. 14-^ см,
228

2. Основания равнобедренной трапеции равны 26 см и 30 см, а высота
3,5 см. Вычислить радиус окружности, описанной около этой трапеции.
Отв. 16,25 см.
3. Две окружности, радиусы которых равны 7 см и 24 см,
пересекаются под прямым углом. Определить расстояние между их центрами. Отв.
25 см.
4. Радиусы двух концентрических окружностей равны \0см и 26 см.
Определить длину наибольшего отрезка, лежащего в кольце между обеими
окружностями. Отв. 48 см.
5. Радиус окружности равен 6 см; из точки, отстоящей от центра на
расстоянии 10 см, проведена касательная к окружности. Вычислить её длину.
Отв. 8 см.
6. К окружности радиуса г проведены две перпендикулярные
касательные. Вычислить радиус окружности, касающейся обеих этих прямых и данной
окружности. Отв. х = г(3^:2>Л2).
7. К двум окружностям, имеющим внешнее касание, проведена общая
касательная, не перпендикулярная к линии центров. Вычислить длину отрезка
этой касательной между точками касания, если радиусы окружностей равны
8 см и \8см. Отв. 24 см.
8. Сторона вписанного в круг правильного десятиугольника равна 10 см.
Определить радиус г круга и длину 5 дуги окружности, стягиваемой этой
стороной. Отв. r = §Y§ -\-Ь, ί = π("|/"5" + 0·
9. Вычислить сторону правильного вписанного в круг радиуса R 12-уголь-
ника и 24-угольника. Отв. alt = R у 2 — Y% и a2A = R у 2 — Т^2-f-У"3".
10. Определить отношение дуги в 120° к хорде, стягиваемой этой дугой.
Отв. —g—.
11. Дуга окружности, содержащая 10°, имеет длину 0,5 см. Вычислить
радиус этой окружности. Отв. —см.
12. Доказать, что площадь круга, описанного как на диаметре на
гипотенузе прямоугольного треугольника, равна сумме площадей кругов,
описанных как на диаметрах на катетах.
13. Теорема Гиппократа. Сумма
площадей серпов (луночек Гиппократа), заключённых
между дугой полукруга, описанного на
гипотенузе прямоугольного треугольника как на диа*
метре, и дугами полукругов, описанных как на
диаметрах на катетах этого треугольника, равна
площади треугольника (черт. 308).
Указание. Если S — площадь большего
полукруга, S, и S2 — площади малых полукругов, Черт. 308
то S = S,-|-ί>2 (упр. 12). Вычитая из обеих частей
площади сегментов, ограниченных дугой большего полукруга и катетами
треугольника, получим слева площадь треугольника, а справа сумму площадей
серпов.
14. Около двух равных окружностей, касающихся извне в точке О,
описана окружность с центром в точке О, касающаяся первых двух окружностей.
Затем внутри большего круга вписаны две окружности, касающиеся первых
трёх окружностей. Центры четырёх окружностей, лежащих внутри большей,
служат вершинами ромба. Определить его площадь, если радиус большей
2
окружности равен R. Отв. -z-R2.
о
15. Вычислить площадь круга, если длина его окружности равна 15 см.
Отв. -г—кв. см.
4π
229

16. Вычислить площадь круга, описанного около равностороннего тре-
m гл 100π
угольника, сторона которого равна 10 см. Отв. —тг— кв. см.
о
17. Периметр сектора равен 20 см, а его площадь 25 кв. см. Определить
его радиус. Отв. 5 см.
18. Хорда АВ постоянной длины скользит своими концами по окружности
радиуса R. Точка С этой хорды, находящаяся на расстоянии а и b от концов
А и В этой хорды, описывает при полном обороте окружность. Вычислить
площадь кольца, заключённую между данной окружностью и окружностью,
описанной точкой С. Отв. r.ab. Площадь кольца не зависит от радиуса круга.
19. Три равные окружности попарно касаются одна другой. Вычислить
площадь фигуры, лежащей вне окружностей и ограниченной их дугами,
заключёнными между точками касания. Отв. -у (2 "^3 — π).
20. Из каждой вершины равностороннего треугольника радиусом, равным
его стороне, проведена дуга, концами которой служат две другие вершины
треугольника. Вычислить площадь криволинейного треугольника, образован-
2
ного этими дугами. Отв. — (π — Υ?> ).

ОГЛАВЛЕНИЕ
Предисловие 3
Введение
1. Предмет геометрии 5
2. Происхождение геометрии —
3. псновные геометрические понятия 6
4. Образование линий и поверхностей движением 7
5. Простейшие линии и поверхности —
6. Геометрические фигуры и способы их изучения 8
Глава первая
ПРЯМАЯ ЛИНИЯ
I. Прямые, лучи, отрезки
§ 1. Аксиомы о прямой линии 10
§ 2. Изображение прямой линии —
§ 3. Луч и отрезок 11
§ 4. Равенство и неравенство отрезков —
§ 5. Сложение и вычитание отрезков —
§ 6. Длина отрезка 12
§ 7. Ломаная линия 14
Вопросы —
Упражнения 15
II. Углы между прямыми
§ 8. Угол 15
§ 9. Равенство углов 16
§ 10. Развёрнутый угол —
§ 11. Прилежащие углы. Действия над углами —
§ 12. Внутренняя область угла 18
§ 13. Сравнение углов 19
§ 14. Смежные углы. Прямой угол —
§ 15. Сумма двух смежных углов 20
§ 16. Построение прямого угла —
§ 17. Проверка угольника —
§ 18. Взаимно перпендикулярные прямые 21
§ 19. Эккер 22
§ 20. Острые и тупые углы —
§ 21. Вертикальные углы 23
§ 22. Биссектриса угла —
§ 23. Угол как мера поворота луча —
§ 24. Понятие об окружности 25
§ 25. Центральный угол , . 26
§ 26. Измерение центральных углов —
231

§ 27. Транспортир. Измерение угла на местности 27
§ 28. Понятие о теореме 29
Вопросы 30
Упражнения —
III. Прямые пересекающиеся и параллельные
§ 29. Углы, образуемые при пересечении двух прямых третьей .... 30
§ 30. Параллельные прямые. Признаки параллельности прямых .... 32
§ 31. Построение прямой, параллельной данной 33
§ 32. Рейсмас. Малка —
§ 33. Аксиома о параллельных прямых 34
§ 34. Углы, образованные параллельными прямыми и секущей 35
§ 35. Свойство углов с параллельными сторонами 36
§ 36. Свойство углов с взаимно перпендикулярными сторонами .... —
Упражнения 37
Глава вторая
ТРЕУГОЛЬНИКИ
I. Общие свойства треугольников
§ 37. Понятие о многоугольнике 38
§ 38. Треугольник и его элементы 39
§ 39. Виды треугольников 41
§ 40. Сумма углов треугольника 42
§ 41. Сумма углов многоугольника 43
§ 42. Равнобедренный треугольник —
II. Осевая симметрия фигур
§ 43. Определение фигур, симметричных относительно оси 44
§ 44. Построение фигуры, симметричной данной относительно оси ... 45
§ 45. Фигуры, имеющие ось симметрии 46
Упражнения 47
III. Расширение понятия о теореме
§ 46. Прямая и обратная теоремы 48
§ 47. Примеры теорем 49
Вопросы и упражнения 50
IV. Соотношения между сторонами и углами треугольника
§ 48. Соотношения между сторонами и углами одного и того же
треугольника 50
§ 49. Соотношения между сторонами одного и того же треугольника . . 51
§ 50. Соотношения между сторонами и углами двух треугольников с двумя
равными сторонами 52
Упражнения 53
V. Равенство треугольников
§ 51. Предварительные замечания 53
§ 52. Первый признак равенства треугольников —
§ 53. Второй признак равенства треугольников 54
§ 54. Третий признак равенства треугольников —
§ 55. Признаки равенства прямоугольных треугольников 55
232

§ 56. Элементы, определяющие треугольник 56
§ 57. Общее определение равенства двух геометрических фигур ... 56
Упражнения 57
VI. Геометрические задачи на построение
§ 58. Предварительные замечания 57
§ 59. Основные задачи на построение 58
Упражнения 59
VII. Задачи на построение треугольников
§ 60. Основные задачи на построение треугольников 60
§ 61. Общая схема решения задач на построение 62
Упражнения. 63
VIII. О проекциях точек и отрезков
§ 62. Проекция точки. Проекция наклонной 64
§ 63. Сравнительная длина перпендикуляра и наклонных 65
§ 64. Сравнительные длины наклонных и их проекций —
IX. Геометрические места точек
§ 65. Понятие о геометрическом месте точек 66
§ 66. Основные задачи на определение геометрических мест точек . . —
§ 67. Метод геометрических мест 68
Упражнения 69
X. Упражнения к главе второй 69
Глава третья
ЧЕТЫРЁХУГОЛЬНИКИ
I. Общие свойства четырёхугольников
§ 68. Типы четырёхугольников 71
§ 69. Общие свойства выпуклых четырёхугольников 72
§ 70. Число данных, необходимых для построения четырёхугольника . . —
II. Параллелограмм
§ 71. Общие свойства параллелограмма 72
§ 72. Признаки параллелограмма 73
§ 73. Число данных, необходимых для построения параллелограмма . . 75
III. Центральная симметрия фигур
§ 74. Определение центральносимметричных фигур 75
§ 75. Фигуры, имеющие центр симметрии —
§ 76. Центр симметрии параллелограмма 76
Упражнения —
IV. Частные виды параллелограмма
§ 77. Прямоугольник 77
§ 78. Ромб —
§ 79. Квадрат 78
233

V. Некоторые теоремы, основанные на свойствах параллелограмма
§ 80. Теорема о средней линии треугольника 78
§ 81. Теорема Фалёса 79
Упражнения 80
VI. Четыре замечательные точки в треугольнике
§ 82. Свойства биссектрис углов треугольника 81
§ 83. Свойства медиан треугольника —
§ 84. Свойство перпендикуляров, восставленных из середин сторон
треугольника 82
§ 85. Свойство высот треугольника 83
Упражнения —
VII. Трапеция
§ 86. Понятие о трапеции 84
§ 87. Средняя линия трапеции 85
§ 88. Число данных, необходимых для построения трапеции —
§ 89. Свойства равнобедренной трапеции —
§ 90. Общая схема подразделения всех четырёхугольников 86
VIII. Метод параллельного перемещения
§ 91. Сущность метода параллельного перемещения 87
§ 92. Примеры применения метода параллельного перемещения . . . . —
Упражнения 88
IX. Упражнения к главе третьей 89
Глава четвёртая
ОКРУЖНОСТЬ
I. Общие свойства окружности
§ 93. Число точек, определяющих окружность 92
§ 94. Симметрия окружности 93
§ 95. Зависимость длин хорд от их расстояния от центра 94
II. Взаимное расположение окружности и прямой линии
§ 96. Прямая, не пересекающая окружности 95
§ 97. Касательная к окружности —
§ 98. Секущая прямая ' 96
§ 99. Общий вывод 97
III. Углы, образованные прямыми, пересекающими окружность
§ 100. Вписанный угол 97
§ 101. Угол между хордой и касательной 99
§ 102. Угол с вершиной внутри круга - —
§ 103. Угол между двумя секущими —
§ 104. Описанный угол 100
IV. Взаимное расположение двух окружностей
§ 105. Линия центров 101
§ 106. Пересекающиеся окружности -
§ 107. Касающиеся окружности -
§ 108. Непересекающиеся окружности 102
§ 109. Общий вывод 103
234

V. Задачи на окружность
§ 110 103
Упражнения 105
VI. Вписанные и описанные треугольники и четырёхугольники
§111. Вписанный треугольник 109
§ 112. Описанный треугольник —
§ ИЗ. Вневписанная окружность ПО
§ 114. Вписанный четырёхугольник —
§ 115. Описанный четырёхугольник 111
Упражнения 112
VII. Метод симметрии
§ 116. Сущность метода 114
§117. Примеры применения метода симметрии —
Упражнения 115
VIII. Упражнения к главе четвёртой 115
Глава пятая
ОТНОШЕНИЕ И ПРОПОРЦИОНАЛЬНОСТЬ ОТРЕЗКОВ
I. Общие положения об измерении отрезков
§ 118. Аксиома Архимеда 118
§ 119. Измерение отрезков —
§ 120. Соизмеримые и несоизмеримые отрезки 120
§121. Приближённое вычисление длины отрезка, несоизмеримого с
единицей измерения 121
§ 122. Основные законы измерения отрезков 123
§ 123. Изменение длины отрезка при переходе от одной единицы
измерения к другой 124
П. Пропорциональные отрезки
§ 124. Отношение двух отрезков 125
§ 125. Понятие о пропорциональных отрезках 126
§ 126. Основная теорема о пропорциональных отрезках 127
§ 127. Теорема о прямой, параллельной какой-нибудь стороне треугольника 129
III. Построение пропорциональных отрезков
§ 128. Основные задачи 130
§ 129. Внешнее деление отрезка 131
§ 130. Гармоническая группа точек 132
§ 131. Построение четвёртой гармонической к трём данным точкам . . . —
IV. Свойства биссектрис углов треугольника
§ 132. Свойство биссектрисы внутреннего угла треугольника 132
§ 133. Свойство биссектрисы внешнего угла треугольника 133
§ 134. Окружность Аполлония 134
V. Упражнения к главе пятой 135
235

Глава шестая
ПОДОБИЕ ФИГУР
I. Подобие треугольников
§ 135. Основные определения 137
§ 136. Основная теорема о подобных треугольниках 138
§"137. Первый признак подобия треугольников 139
§ 138. Второй признак подобия треугольников —
§ 139. Третий признак подобия треугольников 140
§ 140. Признаки подобия прямоугольных треугольников —
§ 141. Сравнение признаков подобия треугольников с признаками их
равенства 141
§ 142. Свойство отрезков параллельных прямых, пересекаемых пучком
прямых —
§ 143. Пропорциональный циркуль 142
§ 144. Масштаб 143
II. Подобие различных фигур
§ 145. Определение подобных фигур 145
§ 146. Понятие о подобном преобразовании фигур 148
§ 147. Коэффициент подобия двух подобных фигур 149
§ 148. Свойства подобных фигур —
§ 149. Подобие многоугольников 151
§ 150. Признак подобия многоугольников 152
III. Гомотетия
§ 151. Предварительные замечания 153
§ 152. Центр и коэффициент гомотетии 154
§ 153. Другой способ построения гомотетичных фигур 155
§ 154. Свойства гомотетичных фигур 156
§ 155. Примеры построения гомотетичных фигур —
§ 156. Пантограф " 157
§ 157. Метод подобия 159
§ 158. Применение подобного преобразования к съёмке плана местности 160
Упражнения 164
IV. Упражнения к главе шестой 164
Глава седьмая
ЧИСЛОВЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
I. Тригонометрические функции острого угла
§ 159. Определение тригонометрических функций острого угла 166
| 160. Построение острого угла по какой-либо одной заданной его
тригонометрической функции 168
§ 161. Изменение тригонометрических функций при изменении угла от 0°
до 90° —
§ 162. Таблицы тригонометрических функций острого угла' 169
§ 163. Соотношения между сторонами и углами в прямоугольном
треугольнике* 170
§ 164. Решение прямоугольных треугольников . . —
II. Числовая зависимость между элементами треугольников
§ 165. Свойство перпендикуляра, опущенного из вершины прямого угла
на гипотенузу 172
236

§ 166. Теорема Пифагора 173
§ 167. Исторические сведения о теореме Пифагора. Пифагорейские числа —
§ 168. Теоремы о квадрате стороны, лежащей против острого и тупого
угла в треугольнике ' 174
§ 169. Свойство диагоналей параллелограмма 176
§ 170. Выражение высоты треугольника через три его стороны .... 177
III. Пропорциональные отрезки в круге
§ 171. Основные теоремы 178
§ 172. Деление отрезка в крайнем и среднем отношении 179
IV. Степень точки относительно окружности
§ 173. Определение степени точки . * 181
§ 174. Радикальная ось двух окружностей 182
§ 175. Радикальный центр трёх окружностей 184
V. Алгебраический метод решения задач на построение
§ 176. Сущность алгебраического метода 185
§ 177. Построение простейших формул 186
§ 178. Графическое решение квадратного уравнения 187
§ 179. Общее замечание о построении алгебраических выражений . . . 190
§ 180. Возможность выполнения построения при помощи циркуля и линейки —
VI. Упражнения к главе седьмой 191
Глава восьмая
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ
I. Измерение площадей многоугольников
§ 181. Равносоставленные и равновеликие фигуры 195
§ 182. Теорема о равновеликих прямоугольниках 196
§ 183. Понятие об измерении площадей фигур 197
§ 184. Измерение площади прямоугольника 198
§ 185. Площадь параллелограмма и ромба 201
§ 186. Площадь треугольника 202
§ 187. Площадь трапеции 203
§ 188. Другие выражения площади треугольника и параллелограмма ... —
§ 189. Площадь многоугольника 204
§ 190. Отношение площадей подобных многоугольников —
II. Преобразование многоугольников без изменения их площадей
§ 191. Преобразование многоугольника в равновеликий ему прямоугольник 206
§ 192. Преобразование прямоугольника в равновеликий ему квадрат . . . 207
§ 193. Теорема Пифагора 208
III. Упражнения к главе восьмой 209
Глава девятая
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
I. Общие свойства правильных многоугольников
§ 194. Правильный многоугольник 213
§ 195. Вписанные и описанные правильные многоугольники —
§ 196. Отношение периметров правильных многоугольников 215
§ 197. Площадь правильного многоугольника —
237

II. Вычисление сторон правильных вписанных многоугольников
§ 198. Квадрат 216
§ 199. Шестиугольник —
§ 200. Треугольник . . . * 217
§ 201. Десятиугольник —
§ 202. Общий случай 218
III. Упражнения к главе девятой 218
Глава десятая
ВЫЧИСЛЕНИЕ ДЛИНЫ ОКРУЖНОСТИ И ПЛОЩАДИ КРУГА
I. Длина окружности
§ 203. Предварительные замечания 220
§ 204. Свойства периметров ломаных линий —
§ 205. Свойства периметров вписанных многоугольников 221
§ 206. Удвоение числа сторон правильного вписанного многоугольника 223
§ 207. Длина окружности. Число π 224
§ 208. Длина дуги окружности 225
§ 209. Радианная мера углов 226
II. Площадь круга и его частей
§ 210. Площадь круга 227
§ 211. Площадь сектора 228
§ 212. Площадь сегмента —
III. Упражнения к главе десятой 228

Нил Александрович Глаголев и
Александр Александрович ί лаголев
ГЕОМЕТРИЯ, ЧАСТЬ I
Редактор Н. //. Лепёшкина
Технический редактор Н. И. Махова и Г. Л. Татура
Корректор 3. И. Почаева
Сдано в набор 8 VII 1958. г. Подписано к печати 16/1Х 1958 г. 60χ92 >
15 п. л. Уч.-изд. л. 14,40. Тираж 10 000 экз. А08456. Заказ № 2089.
Цена без переплета 1 р. 85 к. Переплет 75 коп.
Учпедгиз. Москва, 3-й проезд Марьиной рощи, д. 41
Первая Образцовая типография имени А. А. Жданова
Московского городского Совнархоза. Москва, Ж-54, Валовая, 28.