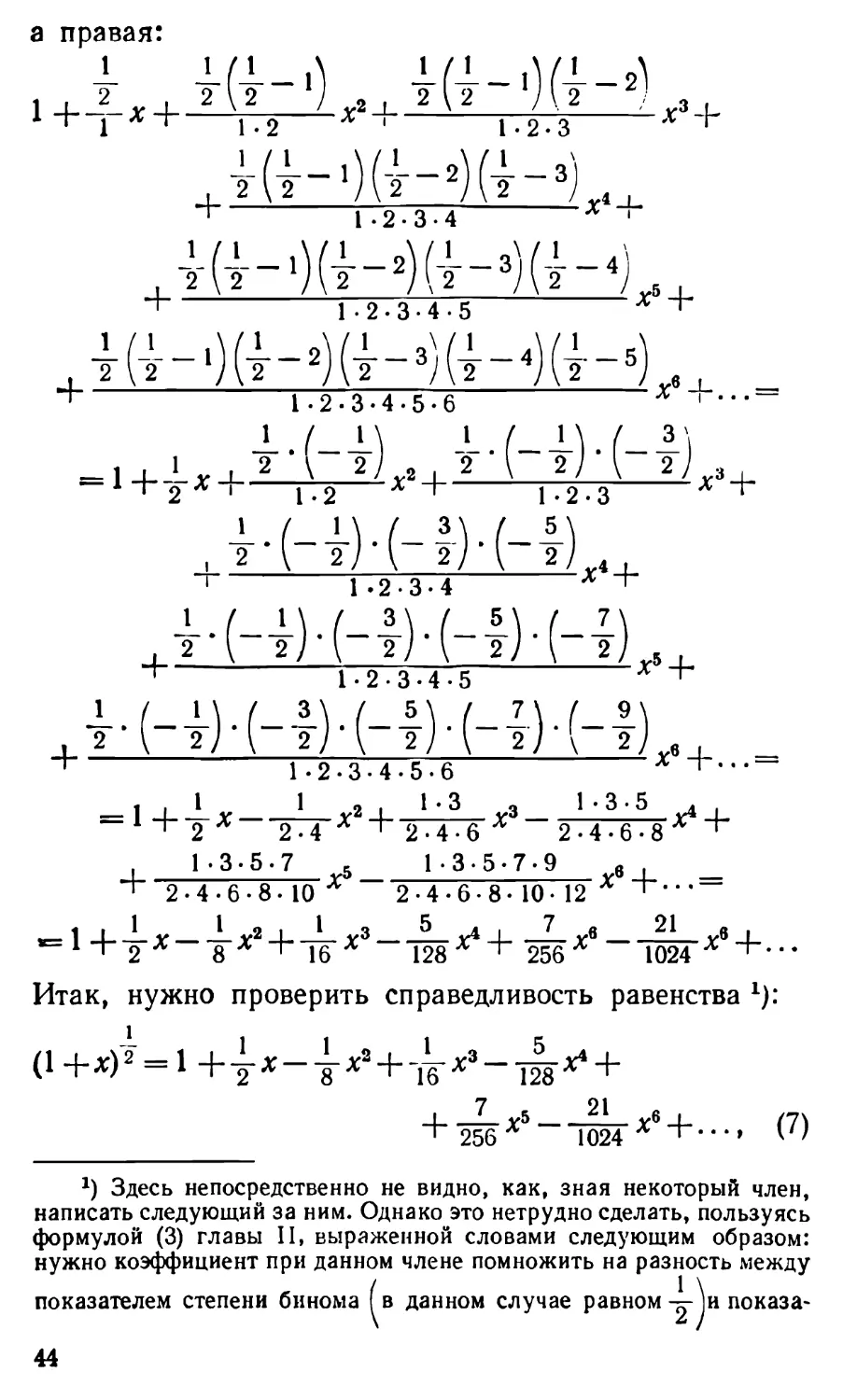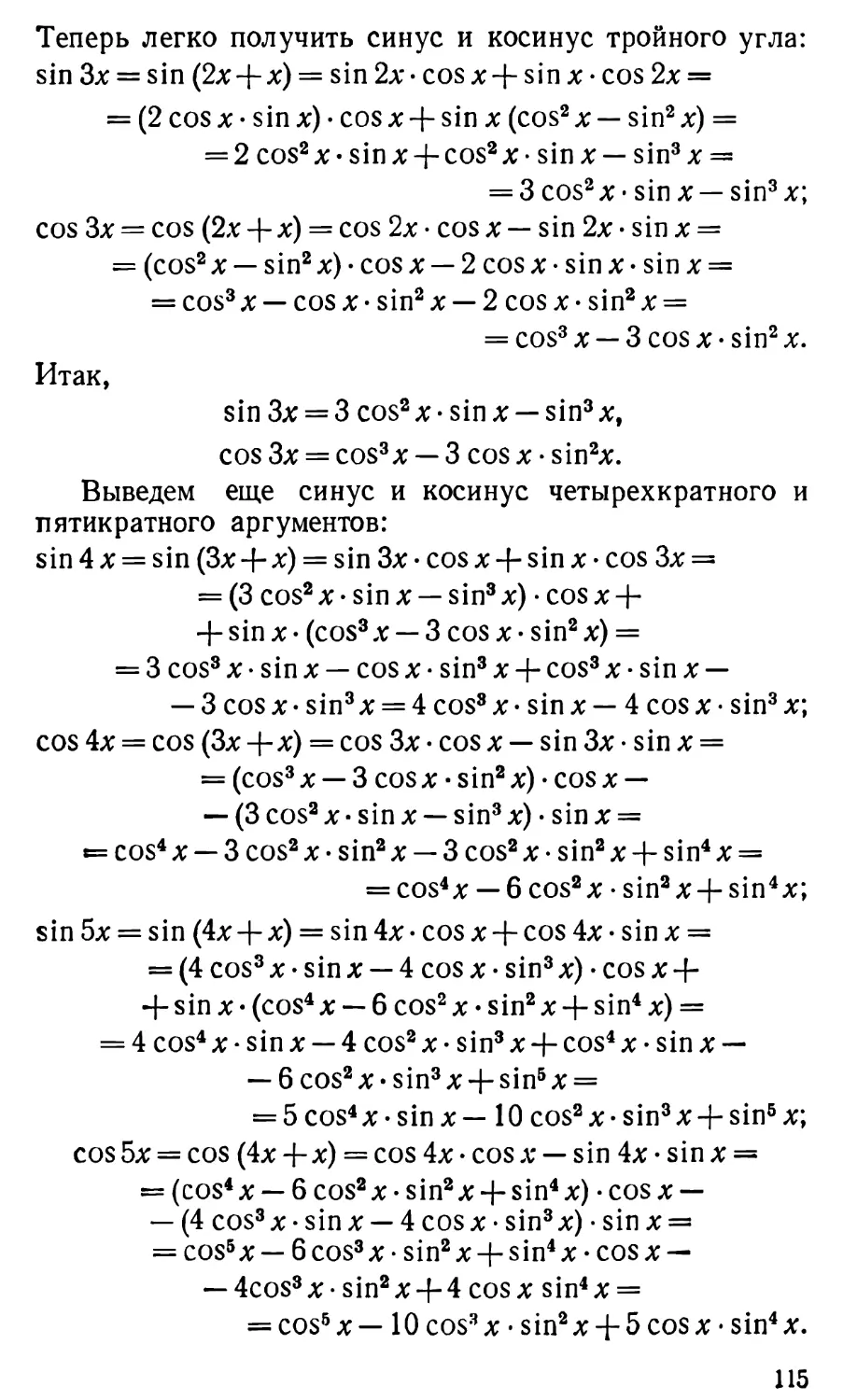А. И. МАРКУШЕВИЧ
РЯДЫ
ЭЛЕМЕНТАРНЫЙ ОЧЕРК
ИЗДАНИЕ ЧЕТВЕРТОЕ.
ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ
ш
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1979

22.16
M26
УДК 517
Маркушевич А. И.
М26 Ряды. —4-е изд. — М.: Наука.
Главная редакция
физико-математической литературы, 1979 —
192 с. 30 к.
Книга имеет целью в доступной и
свободной форме познакомить читателя, имеющего
математическую подготовку в объеме
примерно девяти классов средней школы, с
основными свойствами рядов и с задачей изображения
элементарных функций рядами (без помощи
формулы Тейлора). В книге содержится также
много поучительных сведений из истории
математики, способных заинтересовать также
учителей и других искушенных в математике
читателей.
20203-013 ББК 22.16
М 053(02)-79 88"79 517.2
9П9ПЧ fm © Главная Редакция
zu^uo—ul<3QO _Л 17ЛОПСПЛЛЛ физико-математической
лсо/лоч нг\ 88"'9 1702U5U000 литературы издательства «Наука»,
UoJ(Uz)-7y 1979, с изменениями

К ЧИТАТЕЛЮ
Эта книжка была издана впервые в 1936 г., с тех пор
она неоднократно переиздавалась и переводилась на
другие языки. Цель ее — в доступной и свободной форме
познакомить читателя, имеющего математическую
подготовку в объеме, примерно, девяти классов средней
школы, с отделом математики, который Коши называл
алгебраическим анализом. Речь идет о понятии ряда,
основных свойствах рядов, а также об изображении
элементарных функций рядами (без помощи формулы
Тейлора).
Книжка далека от того, чтобы служить учебником.
Мы, как правило, не даем в ней развернутых
определений и формулировок теорем и довольствуемся в
некоторых доказательствах как бы неполной индукцией. Однако
мы прилагали старания к тому, чтобы существо дела
передавалось правильно и точно, а неполная индукция
всюду построена так, что стоит только ввести в выкладку
пресловутое «я» вместо 2, 3, 4 и т. д., чтобы убедиться
в полной общности проводимых рассуждений и выводов.
Автор хотел помочь молодому читателю,
интересующемуся математикой и не боящемуся выкладок,
проследовать путями, которые проложили Ньютон и Эйлер,
много сделавшие для того, чтобы приучить математиков
обращаться с бесконечными рядами так же свободно
и легко, как и с многочленами. Мы не упускаем, однако,
случаев показать читателю, что ряды — это не
многочлены и что осмысленное и безошибочное их
употребление основывается на развитой Коши теории пределов.
Автор пытался строить все изложение в виде более
или менее связного математического повествования,
главным героем которого является биномиальный ряд.
з

Он не мог все же избегнуть довольно длинных
доказательств и выкладок; часть из них набрана петитом;
мелким шрифтом набраны также и некоторые
подробности исторического характера о расходящихся рядах.
Читатель может пропускать все эти места с тем, чтобы
вернуться к ним после прочтения всей книжки.
Для дальнейшего изучения предмета можно назвать
книгу Н. К. Бари «Теория рядов» (Учпедгиз, 1938) и
более трудную, но и более богатую материалом книгу
Г. М. Фихтенгольца «Основы математического анализа»,
т. II («Наука», 1968), а также «Теорию рядов» Н. Н.
Воробьева («Наука», 1975). Наконец, читатель может
познакомиться и с произведениями классиков науки,
переведенными с латинского языка на русский: И. Ньютон,
«Математические работы» (Гостехиздат, 1937) и Л. Эйлер
«Введение в анализ бесконечно малых», т. 1 (Физматгиз,
196J).

ГЛАВА I
о функциях
Смысл, вкладываемый в слово «функция» в
математике, отличается от разговорного смысла этого слова.
Обычно говорят о функциональном расстройстве сердца,
имея в виду неправильности в сердечной деятельности;
говорят, что в функции т. Иванова входит то-то и то-то,
имея в виду обязанности т. Иванова, и т. п. Короче
говоря, обычно под словом «функция» понимают
деятельность, обязанности. И это вполне правильное
словоупотребление, связанное с корневым значением
латинского слова functio.
В математике термин «функция» прилагается к
величинам. Говорят, что площадь круга есть функция его
радиуса, давление данной массы газа при данной
температуре есть функция его объема, длина данной
металлической линейки есть функция ее температуры, число
всех возможных делителей данного целого числа есть
функция этого числа и т. д. Ясно, что при этом под
функцией разумеют не деятельность и не обязанности,
а нечто иное. Приблизительно смысл математического
понятия функции можно передать посредством слова
«зависит». Именно, каждое из перечисленных
предложений становится вполне понятным, если слова «есть
функция» заменить словами «зависит от ...». Например, тогда
получится: «длина данной металлической линейки
зависит от ее температуры».
Однако слово «зависит» не передает достаточно точно
и определенно смысла современного понятия функции.
Например, урожай ржи в центнерах в Воронежской
области, без сомнения, зависит от количества атмосферных
осадков, приходящихся за лето на 1 га (в среднем).
5

Но математик не скажет, что этот урожай есть функция
количества осадков. Вес человека зависит от его роста,
но опять-таки математик не скажет, что вес человека
есть функция его роста.
В двух последних примерах, и в каждом из примеров
первой группы, имеется по две величины, из которых
первая зависит от второй. Но в примерах первой группы
(площадь круга, давление газа, длина линейки и число
делителей) вполне достаточно указать числовое значение
второй величины (называемой в математике аргументом
функции или просто аргументом), чтобы получить
определенное соответствующее значение первой. Например,
если радиус круга равен 3 м, то его площадь равна
лЗ2 м2 = 3,14-9 м2 = 28,26 м2\ если температура
линейки (из чистой меди, имевшей при 0° длину 1 м) равна
45°, то длина ее равна 1,000765 м *).
Но в остальных примерах (урожаи, вес человека)
задание определенного значения второй величины
недостаточно для определения первой величины. Например,
узнав количество осадков, мы не можем указать
величину урожая, так как она существенно зависит от сроков
и качества обработки почвы, от качества семян, от свойств
почвы и т. д. Но даже знание этих факторов (которые
при современном уровне техники и науки не поддаются
точной числовой характеристике) не позволило бы нам
определить величину урожая по количеству осадков.
Опыт показывает, что в одних и тех же (насколько можно
судить) условиях и при одном и том же количестве
ссадков величина урожая может колебаться.
Аналогичные замечания можно высказать и по поводу
второго примера (вес и рост человека).
После этих примеров можно дать полное определение
математического понятия функции. Именно, в
современной математике одну величину (будем обозначать ее у)
называют функцией другой (обозначим ее х), если
каждому числовому значению величины х соответствует
определенное числовое значение величины у. При этом
величину х называют обычно аргументом функции у
или просто аргументом.
В этой формулировке мы уже не употребляем
недостаточно точного термина «зависит». Вся суть понятия функ-
*) Коэффициент линейного расширения меди равен 0,000017.
6

ции заключается именно в том что определенному
значению аргумента (величине X) соответствует вполне
определенное значение функции (величина у).
Желая выразить короче факт, что величина у есть
функция ху пишут: у = f (jc), где / есть начальная буква
латинского слова functio (функция).
Приведенные обозначения не являются
единственными. Можно пользоваться и другими буквами. Так,
например, площадь круга, так же как и длина окружности,
является функцией радиуса. Обозначая площадь круга
буквой S, длину окружности L, а радиус /?, мы можем
писать:
S=f(R) и L = F(R). (1)
Здесь для обозначения функций употреблены две
разные буквы / и F, потому что площадь круга и длина
окружности являются разными функциями радиуса /?. Именно,
для того чтобы вычислить площадь круга, зная длину
радиуса, нужно R возвести в квадрат и помножить на л,
а чтобы найти длину окружности, нужно R помножить
на 2я, т. е.
S = nR2 и L = 2nR. (2)
Две последние формулы имеют более богатое содержание,
чем формулы (1). Из формул (2) следует не только, что
каждому определенному численному значению R
соответствуют определенные числовые значения S и L, т. е.
что S и L суть функции от R (а это и только это выражают
формулы (1)), но также и то, каким способом можно
находить значения S и L по заданному значению R.
В элементарной математике (алгебре и
тригонометрии) мы привыкли сталкиваться с различными
комбинациями чисел, букв и математических знаков (знаков
действий, скобок и т. д.). Рассмотрим лишь те из них,
в которых отсутствуют знаки равенств или неравенств,
т. е. выражения вида:
{/2cx+d* 2sin*+lg*
Каждое из этих выражений превратится в определенное
число, если заменить входящие в него буквы
определенными числами (например, если в первое подставить I
7

вместо я, 2 вместо &, получится: I3 — 3-12-2 + 3-1 -22 —
•— 23=1 — 6+12 — 8 = —1; если подставить 0,5
вместо я, 0 вместо Ь, получится +0,125 и т. д.). Поэтому
численное значение каждого из этих выражений можно
рассматривать как функцию величин, в них входящих,
именно, первое и второе — как функции от а и Ь, третье —
как функцию от с, d и х, четвертое как функцию от х.
Это можно записать в виде формул:
а» _ 3a*b + 3ab* -b* = f (а, Ь); 4гр£- = F («. Ь*
УШ+й = <Цс,*,х); 2^+'^=Ф(х); ...
(ср и Ф — малая и большая греческие буквы,
соответствующие русской букве Ф. Эта греческая буква имеет
свое название: «фи»).
Мы имеем здесь большую группу функций,
рассматриваемых в математике. Только ими мы и будем
заниматься в этой книжке. Заметим, что в приведенных примерах
встречаются функции от двух и трех величин (от а и Ь,
от с, d и х). Мы будем заниматься в дальнейшем лишь
функциями от одной величины.
Рассмотрим подробно несколько простейших
примеров функций, заданных формулами:
l/i=l+ xz\ i/2 = sin х] у3 = lg х.
В каждом из них достаточно задать числовое значение
аргумента х, чтобы иметь возможность найти
соответствующее значение функции. Однако это нахождение
значения функции делается разными способами. Так,
в первом примере, при х = 0,5:
*/1=1+(0,5)3= 1+0,125= 1,125.
Здесь значение функции получено в результате простых
арифметических действий над значением х.
Перейдем теперь ко второму примеру и положим
здесь л: = -=- = 0,34906..., что соответствует углу в 20°.
Мы не знаем из курса элементарной тригонометрии,
какие арифметические действия нужно производить над
числом ~ = 0,34906..., чтобы найти величину sin ■—.
Однако известно, что существуют таблицы, например
8

таблицы Брадиса, по которым можно находить
значения тригонометрических функций. Пользуясь ими,
получаем:
sin -J = sin 20° = 0,342.
Но пока остается загадочным, откуда получено это
значение, иными словами, нам неизвестно, как составлялась
эта таблица.
Правда, можно обойтись и без таблицы. Для этого
достаточно было бы вспомнить, что sin 20° есть
отношение катета прямоугольника, лежащего против угла
в 20°, к гипотенузе. Откладывая угол в 20° по
транспортиру и строя прямоугольный треугольник с
гипотенузой, равной, например, 10 см, мы, измеряя катет,
лежащий против угла в 20°, получаем 3,45 см, откуда
sin 20° = ^-= 0,345.
Этот результат значительно менее точен, чем указанный
в таблице, и ясно, что при помощи чертежа нельзя вообще
получить большой точности.
В последнем примере у = lg х мы оказываемся в том
же положении, что и с синусом. Полагая, например,
х = 2, мы не знаем, какие действия нужно произвести
над 2, чтобы найти lg 2. Мы не знаем даже и графического
приема для решения этой задачи, и для нас единственное
средство получить ответ, это — воспользоваться
таблицей логарифмов, хотя бы снова таблицей Брадиса. В ней
находим:
lg 2 = 0,3010.
И снова непонятно, каким образом был получен этот
ответ составителем таблицы.
Можно было бы и здесь обойтись без таблиц, пользуясь самым
определением логарифма. Пусть нужно найти lg 2 с точностью до
0,1. Это значит, что нужно найти две дроби со знаменателями,
равными 10, между которыми заключается lg 2, причем числители дробей
отличаются друг от друга на единицу. Пусть ~г и -^-jk искомые
дроби (р — целое число). Должно выполняться двойное неравенство:
10^ig^ 10 •
9

Следовательно,
p. .£±1
Ю10^10^2^10 10 .
Но 10 g2 = 2, так как lg 2 это есть тот показатель степени, в которую
нужно возвести 10, чтобы получить 2. Поэтому:
р_ р+1
1010^2^10 10 .
Или, возвышая каждый член неравенства в 10-ю степень:
10?=^ 2™^ 10? + 1.
Итак, чтобы найти число р, а следовательно, и искомое
приближение, надо только посмотреть, между какими двумя
последовательными степенями числа 10 заключается 210 = 25-25 = 32-32 = 1024.
Очевидно, что
103 < Ю24 < 104.
Поэтому р = 3, и приближенное значение lg 2 (по недостатку) есть
-^- = -т^г- = 0,3. Однако ясно, что, желая этим же путем вычислить
lg 2 с точностью до 0,00001, пришлось бы искать число Р такое, что:
10p^2iooooo^10p + 1)
для чего пришлось бы оценить число 21о° 00° (по крайней мере число
цифр этого числа), что нелегко сделать, не зная lg 2 (ведь этот-то
логарифм мы и ищем!).
Разобранные примеры показывают, что перед нами
по крайней мере два сорта функций, задаваемых
формулами. В одних случаях для вычисления значения
функции по заданному значению аргумента достаточно
произвести над значением аргумента несколько
арифметических действий: сложений, вычитаний, умножений,
делений (и возвышений в степень с целым положительным
показателем, что сводится к нескольким
последовательным умножениям) — это так называемые рациональные
функции. В других случаях этого недостаточно, и
приходится прибегать к различным вспомогательным
средствам — графическим построениям, таблицам и т. д.
Выше мы оставили в стороне действие извлечения
корня. Когда задана функция у = Y^x, то для
вычисления значения у при заданном х, например х = 10, можно
пользоваться или хорошо известным приемом
извлечения квадратных корней, или прибегать к помощи
специальных таблиц квадратных корней из чисел. В случае
таких функций, как у = уОс, обычно пользуются либо
10

таблицами кубичных корней, либо таблицами логариф-
11
мов. Наконец, в случае функций типа у = х™= у^х11
пользуются исключительно таблицами логарифмов как
подсобным средством для вычисления значений функции.
Нужно сказать, что часто при выполнении
арифметических действий — умножения и деления — пользуются
логарифмическими таблицами или (в случаях, не
требующих большой точности) счетной линейкой. Однако,
совершенно отчетливо владея техникой арифметических
действий и понимая, как составляются таблицы
квадратов, кубов, квадратных корней и т. п., мы не имеем
часто никакого представления о том, как составляются
таблицы тригонометрических и логарифмических
функций. Эта книжка должна объяснить читателю, как это
делается. Именно, мы покажем, что значения таких
функций от х, как тригонометрическая,
логарифмическая и др., можно получить, производя над значениями к
одни лишь арифметические действия, но число этих
действий неограниченно, и чем больше их производить,
тем более точные значения функций будут получаться.
Подробные объяснения и выводы читатель будет получать
по мере чтения книжки, но, чтобы он уже сейчас
представил себе в чем дело, дадим один пример. Так, sin х
[понимая под х отвлеченную (в радианах) меру угла г)\
можно представить в виде следующего так называемого
бесконечного ряда:
• X JC3 , Хь X1 .
Х ~~1 1.2-3 + Ь2.345 ~~ 1 .23-4.5.6.7 +
+ 1.2.3.4.5.6.7.8.9 ~~
причемэту запись нужно понимать так, что за последним
написанным членом будет идти: — lt2.3.4 .5-6-7.8.9. ю-11'
X13
ДЭЛЬШе + 1.2-3.4.5.6.7.8-9.10.11-12-I3 И Т-Д'; 33
каждым членом должен идти следующий, построенный
1) Напомним читателю, что один радиан — это величина
центрального угла, соответствующего дуге, длина которой равна
радиусу круга. Один радиан содержит
180° 180° 57°17'1Г 806
^ 3,141592... -ЭТ U 44 ' 8°6-
11

по тому же закону, что и предыдущий; показатель
степени на две единицы больше, чем у предыдущего, и в
знаменателе двумя множителями больше, чем в предыдущем
знаменателе; знак каждого последующего члена
противоположен знаку предыдущего.
Если оборвать этот бесконечный ряд на каком-либо
члене, например, взять только два или три из
написанных членов, то получится многочлен:
Х_ _ X3 1_ я
1 123 ~Х 6 * •
ИЛИ
X Л? X* 1_ з_| !__ 5
1 1 . 2 • 3+1- 2-3-4- 5 ~Х ~6Г+\20Х>
значения которого будут вообще отличаться от значения
sin xy но разница будет тем меньше, чем выше степень
многочлена, т. е. чем больше членов ряда мы оставили.
Выше мы искали:
sin 20° = sin -~ = sin 0,3490658...
Если брать из ряда один, два, три члена, то получим
следующие результаты все с меньшей и меньшей
ошибкой, представляющие sin 20°:
х = 0,3490658...;
х - -|- = 0,3490658... - °>042^326- = о,3419770
Y *3 . *5 _ П <UQnMR 0,0425326 , 0,0051825 _
Х "~ ~6~ + 120" ~ U>^yubiDtt § ' 120 -
= 0,3420202...
(ошибка последнего результата не больше 0,0000002).
Итак, наш бесконечный ряд позволяет находить
приближенные выражения функции sin x в виде
рациональных функций, именно многочленов, причем мы имеем
возможность выбирать эти многочлены настолько
высокой степени, чтобы ошибка при замене sin x
многочленом была сколь угодно мала.
Цель этой книжки не ограничивается, однако, одним
объяснением принципов вычисления тригонометрических
и логарифмических функций. Задачи ее гораздо шире.
Она должна ознакомить читателя с некоторыми поня-
12

тиями высшей математики, играющими важную роль
в качестве орудий исследования в самой математике,
технике и естествознании. При этом читатель
ознакомится с математическими фактами, приемами и мыслями,
которые на протяжении столетий вырабатывались
такими выдающимися учеными, как Ньютон, Эйлер, Лаг-
ранж, Коши и др.
Наша маленькая книжка не сможет, конечно, даже
в небольшой мере исчерпать круг этих идей и фактов.
Хорошо, если она заинтересует ими читателя, вызовет
потребность к дальнейшему чтению, углубит и закрепит
то, что он узнал из курса элементарной алгебры и
тригонометрии, и заставит задуматься над вещами, которые
ему раньше казались то слишком простыми, то
непонятными или неинтересными.

ГЛАВА II
БИНОМ НЬЮТОНА
А. Толстой сказал где-то, что слово «логарифм»
ассоциируется (у широкой публики) с конкурсными
экзаменами. Пожалуй, в большей мере это относится
к «биному Ньютона». Окончивший среднюю школу
вспоминает бином Ньютона, как нечто туманное и трудное,
нужное разве для того, чтобы не провалиться при
поступлении в вуз. Между тем эта формула — одна из немногих
основных формул математики и постоянно употребляется
в разных ее отделах.
Мы начнем наше изложение, отправляясь от этой
формулы. Однако не станем предполагать, что читатель ее
помнит, а выведем заново — это займет немного места.
Мы будем пользоваться при этом только правилом
перемножения многочленов, по которому нужно образовать
всевозможные произведения членов одного многочлена
на члены другого и полученные произведения сложить
(алгебраически). При помощи этого правила можно
находить и произведения трех и большего числа
многочленов. Для этого можно, перемножив первые два и
получив в результате некоторый новый многочлен,
умножить его на третий многочлен-множитель, полученное
произведение на четвертый и так далее, пока не
исчерпаются все множители. В частности, таким путем можно
находить хорошо известные формулы для степеней
биномов (бином — двучлен), именно:
(1+х)2 = (1+*)(1+*) =
= Ы+х-1 + 1 -х + х -х =1+2*-Ь*2;
0+*)3 = (1 +*)-(1 +*).(1+х) =
= (\+2х + х*)(1+х) =
= Ы+2лг-1+а:2.1 + Ьд: + 2^.л: + х2-л: =
= 1+Зх + Зхг-\-х\
14

а также и менее известные:
(1+х)(1+*)(1+*)(1+*) =
(1+Зл: + Зх2+л:3)-(1+х) =
Ы + 3х-1 + 3х2 • 1 + x3-1 + 1 -х +
+ 3х-х + 3х2-х + х*-х =
1+4лг + 6х2 + 4л:3 + х4;
(1+*)(1+Х)(1+х)(1+*)(1+*) =
(1+4лг + 6х2 + 4лг3 + х4)(1+л:) =
1.1 +4*. 1 + 6*2-1 +4*3-1 + Х4- 1 +
+ 1 -* + 4*-х + 6х2-х + 4л;3.л: + л;4-х =
1 + 5л:+ 10jc2+ 1 Ол:3 + 5х4 + х5
и т. д.
(В каждой выкладке мы оттеняем следование
установленной выше схеме умножения нескольких многочленов —
сначала умножаются первые два многочлена, их
произведение — на третий и т. д.)
Уже эти подсчеты позволяют уловить некоторые
закономерности в получаемых результатах. Прежде всего,
получается многочлен относительно х степени, равной
показателю бинома. При этом свободный член (не
содержащий х) произведения равен единице, и коэффициент
при высшей степени х также равен единице. Все
остальные степени х, промежуточные между низшей (нулевой)
и высшей, имеют некоторые положительные
коэффициенты, так что, если расположить произведение по
возрастающим степеням буквы х (как это сделано у нас), то налицо
будут все степени без пропусков, до степени с
показателем, равным показателю бинома. Пользуясь этим
наблюдением, можно утверждать, что:
(1 + xf = 1 + агх + а2х2 + а3х3 + а4х* + аьхъ + хв\
(1+*)7 =
= 1 + Ьхх + Ь2х2 + Ь3х3 + ЪАх* + Ьъхь + ЬъХ9 + х7
и т. д.,
где аи a2t а3у а4, аь\ bly b2, Ъ3у Ь4, ЬЬУ Ьв — не известные
нам пока коэффициенты. Мы научимся их вычислять
сразу, не производя утомительного перемножения
биномов. В результате получим формулу, представляющую
любую степень бинома в виде многочлена с коэффициен-
(1+*)4
(1+*)5
15

тами, являющимися простыми функциями показателя
бинома. Эта формула и есть «бином Ньютона», точнее,
тот частный случай бинома Ньютона, который
рассматривается в элементарной алгебре.
Чтобы найти коэффициенты в правых частях
интересующих нас формул, воспользуемся приемом
умножения нескольких многочленов, отличным от того,
которым пользовались выше. Именно, вместо того, чтобы
перемножать многочлены постепенно — первый на
второй, их произведение — на третий, полученное
произведение— на четвертый и т.д., попытаемся перемножать
их одновременно, сразу, выписывая члены
окончательного произведения. Для этого придется
образовывать всевозможные произведения членов перемножаемых
многочленов, беря по одному члену из каждого
множителя.
Поясним этот прием на примере, прежде чем
воспользоваться им в общем случае. Пусть нужно перемножить
три двучлена: (5 + х), (1 + 2х), (3 + х). Для того чтобы
ввести систему в наши действия, мы расположим каждый
множитель по возрастающим степеням буквы х и члены
произведения будем отыскивать также по порядку —
сначала свободный член, далее члены с первой степенью х,
затем со второй и т. д.
Свободный член произведения получится, если
перемножить свободные члены множителей, т. е. первые
члены скобок:
5-1.3=15.
Члены с первой степенью х можно получить
несколькими способами, а именно — взять из первой скобки
член с х, а из остальных — свободные члены и
перемножить:
*.1-3 = 3*;
далее, взять член с х из второй скобки, а из первой и
третьей — свободные члены и перемножить:
5.2*.3 = 3(к;
и, наконец, взять член с х из третьей скобки, а из первой
и второй — свободные члены:
5 • 1 • X = ЪХш
16

Аналогично можно найти члены произведения,
содержащие х во второй степени. Именно, нужно взять
из первой и второй члены с ху а из третьей — свободный
член. Перемножив, получим:
х • 2х • 3 = 6л:2.
Далее, берем из первой и третьей члены с х, а из второй —
свободный член:
х-1 х = х2,
из второй и третьей члены с х, а из первой — свободный
член:
5 2х-х=\0х2.
Наконец, член, содержащий х в третьей степени,
получится в произведении только одним способом: если из
каждой скобки взять член с х:
х-2хх= 2л:3.
Произведение будет равно алгебраической сумме
полученных членов
(5 + х)(1+2л:)(3 + л;) =
= lb + 3x + 30x + 5x + 6x2 + x2+l0x2 + 2xz =
= 15 + 38л:+17х2 + 2л:3-
Читателю этот прием покажется, быть может,
громоздким. Однако после тренировки им можно
пользоваться довольно быстро и часто предпочитать его
последовательному умножению. Сейчас для нас важно то
обстоятельство, что при помощи изложенного приема
умножения мы закончим вывод бинома Ньютона.
Предположим, что нужно перемножить некоторое
число т одинаковых биномов 1 + х> иными словами,
возвысить 1 + х в степень т. Мы знаем, что в
результате получится многочлен вида:
{\+x)m=\+AlX + A2X2 + AdXZ + ...
... + Akxk + Ak+1xk+1 + ... + Am-1x'»-l + x>».
Что свободный член будет равняться единице, это
мы заметили выше. Впрочем, это ясно из того, что в
каждой из скобок
(!+*)(!+*)■■■(!+*)
т скобок
17

свободный член равен единице и, следовательно,
произведение свободных членов также равно единице.
Члены с первой степенью х будут получаться, если
из одной скобки брать член с х, а из остальных —
свободные члены, т. е. единицы, и перемножить. Таким
образом можно взять х из первой скобки, а из всех
остальных — единицы; х из второй скобки, а из остальных
единицы, и т. д., наконец, взять х из последней скобки и
единицы из остальных. Каждая комбинация дает в
произведении:
х-Ы1...1 = *,
т—\
а всего таких комбинаций получается, очевидно, столько,
сколько скобок, т. е. т. Итак, член с х в первой степени
в произведении есть тх и коэффициент этого члена,
ранее обозначенный Аъ равен, таким образом, т:
А1 = т.
Можно было бы сейчас находить постепенно Л2, Л3,
и т. д. Но лучше будет найти связь между любым
коэффициентом Ak и следующим за ним Ам. Зная эту связь,
мы из А1 выведем Л2, из А2 выведем А3 и т. д. и получим,
кроме того, общую формулу для любого коэффициента.
Желая найти член произведения, содержащий хЛ, мы, следуя
указанному выше способу, должны образовать все возможные
произведения, выбирая из каждой скобки по одному и только по одному
члену, причем из k скобок нужно выбрать члены, содержащие х
в первой степени, а из остальных т — k скобок — свободные члены.
(Если члены, содержащие х, брать из скобок, числом больше или
меньше k, то соответствующее произведение будет содержать х в
степени с показателем, большим или меньшим k> а именно равным
числу скобок.)
На рис. 1 наглядно показано, каким образом можно получить
члены (1 + х)7, содержащие х4. При этом те скобки, из которых
для образования отдельного произведения берется х, обведены
овальной рамкой.
Возвратимся к общему случаю. Каждое отдельное произведение
будет равно х*, так как члены, содержащие х, в каждой скобке
имеют коэффициенты 1 и каждый свободный член равен 1. Поэтому,
приводя подобные члены, получим один член произведения,
содержащий xfe, с коэффициентом, равным числу всех отдельных
произведений (коэффициент при хк мы обозначили выше через Аь). Легко
обнаружить связь между Ak и следующим за ним коэффициентом
Аь+г. Для этого заметим, что при вычислении Лл+1 придется
подсчитывать число отдельных произведений, дающих каждое xfe+1. А такие
в свою очередь получаются, если из k + 1 перемножаемых скобок
брать члены, содержащие х, а из остальных т — (k + 1) скобок
18

брать свободные члены. При этом можно пользоваться только что
рассмотренными комбинациями, в которых х брался из к скобок.
Достаточно к этим к скобкам присоединить еще одну, из которой
первоначально брался свободный член (т. е. единица).
О в) ®) G) (/+х> (/+х> №
О (/.х) @з) м $3)0 (м
О м м с«) ®® ®
(лдг) (Ri) (ft3) (fc3) (£3) Ы (М
Рис. 1. Каждая из строчек указывает один из способов получения
члена с х4 при возведении (1 + х) в седьмую степень. Однако на
фигуре показаны не все строчки, соответствующие всем возможным
произведениям, дающим х4, так как число их равно 35.
На рис. 2 наглядно изображено, как, отправляясь от одного
из произведений, дающих х4 при перемножении 7 биномов (1 + х),
можно получить новые произведения, дающие х6. При этом скобка,
из которой х берется вновь, обведена прямоугольной рамкой.
Очевидно, что таким путем из одной комбинации, дававшей
хк, получится несколько различных комбинаций, дающих хк+1.
(£3) (>♦*) ® м & & м
(@) [#♦£)]@) ы о@§) м
(Q м о IS] О) О ^
;/♦*» (/+х) «/♦*» (/+*) аъъ ОМ) UM
Рис. 2. В первой строчке повторена одна из комбинаций рис. 1,
соответствовавшая х4. В следующих строчках указаны новые
комбинации, соответствующие х5, в каждой из которых при
перемножении х должен браться уже из пяти скобок (заключенных в рамки).
Этих комбинаций будет столько, сколько было скобок с
неиспользованными х, т. е. т — к (на рис. 2 в первой строчке таких скобок
три; и из первой строчки получаются три новые комбинации). Итак,
каждому отдельному произведению, дававшему хк> будет
соответствовать т — к отдельных произведений, дающих хк+1. А так как
число первых есть Лд, то всего получится А^-(т — к) комбинаций,
дающих xfe+1.
Но не все новые комбинации различны. Для того чтобы в этом
убедиться, возьмем, например, комбинацию во второй строчке на
19

рис. 2. Она получится, если при умножении члены, содержащие х,
взяты из 1-й, 2-й, 3-й, 5-й и 6-й скобок. На рис. 2 указано, как
она получается из комбинации первой строчки (в которой х брался
из 1-й, 3-й, 5-й и 6-й скобок) путем присоединения х из 2-й скобки.
Однако можно было исходить из других комбинаций, дававших
х4, и, присоединяя подходящим способом еще один х, получить
комбинацию, где х берется опять-таки из 1-й, 2-й, 3-й, 5-й и 6-й
скобок. Это показано на рис. 3.
О &> @) (/+х) О ®) </+*>
(0) О ® № <S) ®(/+i)
О* 0) (В> с**) ® в с**)
О) О (0> м О) О м
& О О (/+х) & О (/«)
О (J3) & ('♦*) в 0) (/+г)
Рис. 3. В первой строчке рамками отмечены скобки, из которых
берутся члены с х для получения в произведении х6. В следующих
строчках, зачеркивая то одну, то другую из скобок, получают
комбинации, дающие х4. Присоединяя в каждой из них одну скобку
(как это делалось на рис. 2), а именно зачеркнутую, будем получать
одну и ту же первую строчку.
Таким образом, среди Ak*(m — k) вновь полученных
комбинаций одна и та же комбинация из k + 1 скобок может быть получена
путем присоединения любой из этих скобок к комбинации,
соответствующей остальным к скобкам. Поэтому каждая комбинация из
£+1 скобок встретится среди Ak*(m — k)t найденных ровно
(k + 1) раз, и различных комбинаций, дающих в произведении
xk+1t должно быть не Ak*(m — k), а в к + 1 раз меньше, т.е.
Ak.(m — k)
k + \ '
Но это число, равное коэффициенту при xft+1, обозначалось выше
через Ak+1.
Итак, мы нашли, что
Это соотношение позволяет, зная предыдущий
коэффициент AkJ найти последующий Ам. Например,
коэффициент при Xj Ах = т> поэтому
А —А -А т~{ _ А И"1) _ "Н"*-1)
20

(Здесь k = 1,а& + 1 = 2.) Теперь мы знаем Л2, а потому,
полагая в формуле (3) k = 2, можем найти Л3:
л — Л — А т~2 — А т~2 —
/*3 — ^2+1— л2 2+1 — 2 3 —
_ т(т—1) т —2 _ т(т— I) (т — 2)
2 3 2-3
Можно написать более общую формулу для любого
коэффициента Ак. Покажем, как это сделать. Мы нашли,
что
А —л т~к
Отсюда
А -А "-(*-»
Ak-Ak-f (л_1)+1 •
(Наша формула справедлива при любых натуральных
значениях букв, в нее входящих, и в частности, если
вместо k написать k — 1.) Далее:
Ль -Ль *-(*-3)
Л*_2-ЛЛ-3 (Л_3)+1 •
Ah -А» "-(*-*)
Переходя к коэффициентам с все меньшими и меньшими
значками, дойдем в конце концов до Л2:
А -А т~Х
Здесь вместо k + 1 стоит 2, вместо k стоит 1 и,
следовательно, в формуле (3) вместо т — k нужно писать т — 1
и вместо k + 1 нужно писать 2.) Перемножая почленно
равенства, написанные столбцом, найдем:
Ak' Л*-! • Ah-2 * Лд_3... Л3* Л2 =
m-(k-\) л m-(k-2)
т-(^-З) - т-2 - т-\
A/iA-3 £ — 2 •••/12 з * 2 *
21

В обеих частях равенства встречаются одинаковые
множители: Ак.ъ Л/,-2,.. .,Л2. На них можно сократить. Тогда
слева останется лишь Aky а справа, кроме произведения
дробей, еще Аъ равное, как мы знаем, т. Получается:
_ m-(k-\) m-(k-2)
Ak~ k k=\ X
m — (k — 3) m —2 m—\
X k_2 ... з -m- 2 ,
или, переписывая множители числителя и знаменателя
в ином порядке (в убывающем порядке в числителе и
в возрастающем порядке в знаменателе):
д _ т (т —1) (т-2) ... [т— (k — 3)]-[m — (fe — 2)].[m-(fe- 1)] ,дч
Пк 2-3-4 ... (k— 2).(k — l)-k ' VV
Это и есть нужная нам формула. В знаменателе стоит
произведение последовательных целых чисел: 2-3-4...
...(/г— 1)-/г. Часто в нем выписывают впереди
множитель единицу (отчего, конечно, величина произведения
не меняется.) Такое произведение
1-2-3-4...(/г-1).£
называют факториаломх), точнее, «^-факториалом», и
обозначают сокращенно следующим образом:
Ь2.3.4...(*-1).* = Л!.
Так, например:
1! = 1; 21 = 1-2 = 2; 3! = 1 23 = 6;
4! = 1.2-3.4 = 24; 5! = 1 - 2-3-4-5= 120;
6! = 1-2-3-4-5.6 = 720 и т. д.
Поэтому формулу (4) пишут часто в виде:
л __ m(m-\)(m-2)...(m-k + 2)(m-k + \) ,,,.
л/г — £] • V* )
*) От латинского слова factor, имеющего здесь смысл —
«множитель».
22

Теперь можно написать в окончательной форме бином
Ньютона:
(1+хГ =
— 1 jl т ~ » "Ч"*-1) у2 . m(m-l)(m-2) 3 ,
— а "Г"|~ *п 2! ' 3* "г* • •
t m(m—l)(m —2) .,.(m—^ + 1) у* ,
, m(m— l)(m — 2) ...(m —fe+1) (m —fe) .+ 1
"*" (k+\)\ "r••,
■ m(m-l)(m-2)...3.2 t
••'"*" (m-l)! Л "Г"
+ m(m-l)(m-2)...3-2.1 ^ g)
Выражение в правой части этой формулы (многочлен)
называется биномиальным разложением, а его
коэффициенты — биномиальными коэффициентами.
В этой формуле запись отдельных коэффициентов
может быть упрощена. Так, числитель и знаменатель
дроби, являющейся коэффициентом при хту целиком
сокращаются — остается единица (что мы и ожидали);
коэффициент при д^1-1, после сокращения числителя и
знаменателя, приводится к т и т. п.
Из формулы (5) получаются формулы для различных
значений показателя степени бинома.
Так, полагая т = 7, находим по этой формуле:
(1+*)7 =
— 1-L-— 7-6 2 7.6-5 з 7.6-5-4 4
-1+1Х+ Ь2 Х ■" 1-2-3* + 1-2-3-4* •*
1 7-6.5-4-3 . 7.6.5-4-3-2 6 7♦6♦5♦4■3-2■1 7
+ 1.2.3-4-5^+ 1-2- 3-4-5-6* + Ь2-3-4-5-6-7*'
или, сокращая дроби, являющиеся коэффициентами
при степенях х:
(\+хУ=1 + 7х + 21х* + 35х* + ЗЬ* + 2\х* + 7* + х'.
Применение бинома Ньютона [формула (5)] не
представляет никаких затруднений. Нужно только
выписывать члены один за другим, увеличивая каждый раз
на единицу показатель степени при х. Биномиальные
коэффициенты следует писать сначала в виде дробей;
23

при переходе от одного члена к следующему в числителе
и знаменателе становится одним множителем больше,
и множители в числителе постепенно (на единицу)
убывают, в знаменателе так же постепенно возрастают;
наконец, коэффициент при первой степени х имеет в
числителе показатель степени бинома, а в знаменателе единицу.
Помня этот коэффициент и правило перехода от одного
члена к следующему, можно возводить биномы в степень,
не имея перед глазами формулы (5). Пусть читатель
попробует, не глядя в книгу, написать, чему равно
(1 + лг)11, а затем сверится с тем, что написано у нас:
1Ы0.9-8 4 lb1Q.9.8.7 ,
"Г 1-2-34 л "г 1-2-3-4.5 "г
11. 10.9.8.7.6 е . 11 - 10.9-8>7-6-5 7
+ 1-2.3-4-5-6 Х+ 1-2- 34- 5-6-7 Х "*~
11.1Q.9-8-7-6-5-4 8
+ 1.2.3.4.5-6.7-8 х +
11. 10.9-8-7.6-5-4.3 9
+ 1.2-3-4.5-6-7.8-9 Х +
11- 10-9.8-7.6-5-4-3.2 10
+ 1-2-3-4-5-6-7-8-9-10 Х "+"
11- 1Q.9.8.7-6-5-4-3-2- 1 п
+ 1-2.3.4.5.6.7-8.9.10-11 Х '
Производя сокращения (конечно, лучше сначала
сократить, а затем умножить), получаем окончательно:
(1+^)Ц=1 + 11д; + 55х2+165х3 + 330^ + 462^ +

ГЛАВА III
БИНОМ НЬЮТОНА
(продолжение)
Ньютон дал формулу (5) без доказательства в 1676 г.
в первом своем письме к Ольденбургу, секретарю
Лондонского королевского общества х). Из второго письма
к Ольденбургу видно, что Ньютон нашел эту формулу
еще раньше, около 1665 г., когда ему было всего
двадцать два года. В этом втором письме Ньютон сообщал,
каким образом он пришел к биномиальной формуле.
Несколько упрощая тот окольный путь, которым шел
Ньютон, можно сказать, что он, рассматривая формулы
для степеней бинома в частных случаях:
(1+а:)2=1+2д: + л;2,
(l+x)*=l+3x + 3x2+ х\
(1+х)*=1+4* + 6х8 + 4*8 + *\
(1+л:)5 = 1+5л:+10а:2+10л:3 + 5л4 + х5,
подметил общее соотношение между коэффициентами
двух рядом стоящих членов—соотношение (3),
выведенное нами в главе II, именно:
Или, выражая это словами: коэффициент при какой-либо
степени в биномиальном разложении равен коэффициенту
1) Лондонское королевское общество — Английская академия
наук. Основано кружком ученых в 1645 г.
25

предыдущего члена, умноженному на разность между
показателем степени бинома и показателем степени
при л: в предыдущем члене и
деленному на показатель
степени при х в данном
члене. Конечно, это свойство
легко проверить на
примерах, после того как оно уже
известно, но угадать его по
отдельным примерам не так-то
просто.
Нужно сказать, что еще
задолго до Ньютона
математики интересовались видом
многочлена, который
получается при возведении бинома
И. НЬЮТОН в степень.
(1642—1727). В сочинении китайского
математика Чжу Ши-чцзе,
написанном в 1303 г., встречается следующая таблица
чисел:
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
16 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
Мы узнаем в числах этой таблицы биномиальные
коэффициенты. Первая строчка, соответствующая нулевой
степени бинома, содержит лишь 1, так как (1 + х)° = 1;
вторая строчка содержит коэффициенты первой степени
бинома (1 + х)1 = 1 + х; третья строчка—
коэффициенты второй степени бинома (1 + х)2 = 1 + 2х + х2
и т. д.; в последней строчке выписаны коэффициенты
восьмой степени бинома (1 + х)8. Дальше таблица
Чжу Ши-чцзе не идет, но, приглядевшись к самому
способу расположения чисел в ней, легко подметить простую
26

закономерность, позволяющую без труда выписывать
все новые строчки. Эта закономерность заключается
в следующем: сумма любых двух чисел, стоящих рядом
в одной и той же строчке, равна числу, стоящему в
следующей строчке между ними. Например, 1+2 = 3,
2+1=3, 1+3 = 4, 3 + 3 = 6, 3+1=4ит. д.
Пользуясь выражением (4') для биномиальных
коэффициентов, можно было бы доказать в общем виде, что
сумма коэффициентов при xk~1 и хк в разложении (1 + х)т
(эта сумма равна Ак^г + Ak) совпадает с коэффициентом
при хк в разложении (1 + x)m+l. В самом деле,
д , л _ m(m-\)...[m-(k-\) + 2][m-(k-\)+\] ,
Л*"1+Л*^ Ь2...(*-1) h
т(т— \)...(т — k + 2)(m — k + \)
+ Ь2...(Л-1)Л "
т(т—\)...(т — к + Ъ) (m—k + 2)[ + . m — k+\ \ _
1 • 2...(k-\)
т(т—\)... (m — k + S)(m — k + 2) m+\
1 • 2 ... Л— 1 k
_(m+\)m(m-\)...\(m+\)-k + 2\[(m + \)-k+\\
\-2...(k-\)k
Из формулы (4') видно, что полученный результат
совпадает с коэффициентом при хк в разложении (1 +x)m+1.
Но в эпоху Чжу Ши-чцзе формула (4') не была
известна, и закономерность, о которой идет речь,
подмечалась путем простого наблюдения над числами. Пользуясь
ею, можно всегда продолжить таблицу, если начать
новую строчку с единицы и закончить ее единицей, а в
качестве промежуточных чисел ставить суммы пар тех
чисел, которые стояли в предыдущей строчке слева и
справа от нового числа. Повторим, например, последнюю
строчку таблицы и под ней напишем новую строчку:
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
Мы получили коэффициенты разложения (1 + х)9.
Предлагаем читателю написать еще две строчки. Они дадут
биномиальные коэффициенты для (1 + х)10 и (1 + х)п.
Треугольная таблица, начальные строчки которой
были выписаны Чжу Ши-чцзе, называется
арифметическим треугольником. Арифметический треугольник и
правила перехода от чисел одной его строчки к следую-
27

щей были известны и до Чжу Ши-чцзе; индийские
математики были знакомы с ними еще за два столетия до
нашей эры. Позднее, в первой половине XV века, в
сочинении «Ключ арифметики», написанном на арабском
языке самаркандским математиком и астрономом по
имени Джемшид Гиясэддин Каши, вновь встречается
арифметический треугольник. Каши называет
биномиальные коэффициенты, исключая крайние коэффициенты,
«элементами показателя степени». Вот что Каши пишет
о них: «Знай, что элемент показателя степени квадрата
есть одно число — два, для куба это два числа — три
и три, для каждого показателя степени количество их
увеличивается на единицу в силу прибавления рядов
и соответственно увеличиваются числа на концах. Если
мы сложим любые два соседних элемента показателя
степени, мы получим среднее число следующего
показателя».
Эти правила Каши (сообщаемые им без
доказательства) дают возможность возвести бином в любую степень
с натуральным показателем. Можно считать, что это —
первая известная в истории полная словесная
формулировка теоремы о биноме Ньютона (в виде,
отличающемся от формулировки самого Ньютона).
В Европе арифметический треугольник сделался
известным из напечатанного в 1544 г. сочинения
немецкого математика Михаила Штифеля «Целостная
арифметика». В этом сочинении приводятся биномиальные
коэффициенты до 17 степени включительно.
Формула (3) предыдущей главы (стр. 20), полностью
решающая задачу о биномиальных коэффициентах, была
найдена независимо друг от друга английским
математиком Бриггом (1624 г.), французским математиком
Ферма (1636 г.) и французским же математиком и
философом Блезом Паскалем (1654 г.). Последний посвятил
арифметическому треугольнику и его свойствам
специальное сочинение «Трактат об арифметическом
треугольнике», вышедшее в свет в 1665 г., уже после смерти автора.
Благодаря этому сочинению свойства арифметического
треугольника получили наиболее широкую
известность среди математиков, почему и самый
треугольник стали часто называть треугольником Паскаля.
Название это, однако, исторически неверно, так как
арифметический треугольник, как мы видели, рассматривался
28

индийскими, китайскими и арабскими математиками
задолго до Паскаля.
Возвращаясь к Ньютону, мы должны указать теперь,
что он не сказал бы ничего нового для математиков своей
формулой, если бы ему не пришла в голову мысль
применить ее не только для целого положительного
показателя т, но и для любого показателя — положительного
или отрицательного, целого или дробного.
Гробница Ньютона в Вестминстерском аббатстве.
Мысль Ньютона имела большое значение для
развития математики. Его современники скоро осознали всю
важность этой формулы и ее многочисленных
применений. По преданию, на памятнике Ньютону, сооруженном
в Вестминстерском аббатстве вскоре после его смерти,
выгравирована биномиальная формула *).
х) Это утверждение относится к XVIII веку. Место формулы
указывалось наверху небольшого свитка, который держат перед
полулежащим Ньютоном две крылатые фигуры (см. рисунок). Однако
лица, осматривавшие памятник во второй половине XIX века,
не могли обнаружить там соответствующей надписи, потому ли, что
она стерлась со временем, или потому, что ее и вовсе не было. За-
29

Ньютон систематически стал употреблять
отрицательные и дробные показатели в алгебре.
Читатель, без сомнения, помнит, что в самом начале
курса алгебры действие возведения в степень (с целым
положительным показателем) определяется как
умножение числа самого на себя некоторое число раз. Так,
возвести а во вторую, третью и т. д. степень, это значит —
умножить а само на себя два, три и т. д. раз. При этом
результат возведения всякого числа в любую степень
с целым положительным показателем есть вполне
определенное положительное или отрицательное число.
Дальше вводится понятие возведения в степень с дробным
показателем. При этом возвысить некоторое число а
в степень -^ значит извлечь из него кубичный корень,
т. е. найти корень уравнения Xs = а. Вообще, возвести
1
число а в степень — значит найти корень уравнения
хп = а. Но здесь не всегда получается единственный и
определенный результат. Так, если единица возводится
в степень -j, то в качестве ответа годится и +1 и —1,
ибо (+1)4 = 1 и (—I)4 = 1. Всегда при п четном для
любого положительного числа а уравнение хп = а имеет
два корня (один положительный, другой отрицательный).
В дальнейшем из двух возможных результатов мы будем
брать только один — положительный или, как говорят,
«арифметическое значение корня». Итак,
1 _ L _
ц={П=19 162=1/16 = 4 и т. д.
Напротив, если —1 возводится в степень -т-» то
никакое число не годится для ответа. В самом деле, для
любого х:
Итак, в данном случае действие возведения в степень не-
возможно. Из сказанного выше следует, чтоап для п це-
метим, кстати, что биномиальная формула вовсе не является самой
крупной заслугой Ньютона перед математикой. Ньютон сделал так
много для начинавшего развиваться тогда исчисления бесконечно
малых, что его (наравне с математиком Лейбницем) считают
основателем математического анализа.
30

лого положительного определено для любого а при п
нечетном и лишь для а ^ 0 при п четном.
Возвести число а в степень с показателем — (р и q —
целые, q > 0) значит возвести а в степень р и извлечь
из результата корень с показателем q:
р. Яг—
а* =у ар.
Заметим, считая дробь — несократимой (т. е. считая, что
р и q не имеют общих множителей, а если они и были,
то на них дробь уже сокращена), что осложнения при
возведении в степень получаются тогда, когда q— четное
число. Именно, если под корнем
£ Qr—
ая =уаР
стоит отрицательное число, то действие невозможно.
Остается только напомнить, что значит возвести
некоторое число в степень с отрицательным показателем.
Когда говорят, что число а возводится в минус вторую,
минус третью и т. д. степень, то имеют в виду, что а
возводится во вторую, третью и т. д. степень и единица
делится на результат, т. е.
сг £ = — • сг 3 = —
и, вообще, если т — какое-нибудь число, целое или
дробное, то, по определению,
Относительно возможности или невозможности
возведения числа в степень с отрицательным показателем нужно
иметь в виду все сказанное выше и, кроме того, еще одно
важное замечание: если показатель степени
отрицательный, то а не должно равняться нулю (иначе действие
возведения в степень будет невозможно). В самом деле,
и а"*
и если т — положительное число (только тогда —т
может быть отрицательным) и а равно нулю, то ат также
31

равно нулю и все приводится к делению единицы на нуль
Но последнее действие не имеет смысла.
Наконец, действие возведения в степень определяется
для показателя, равного нулю. Именно, принимают
всякое не равное нулю количество в нулевой степени
равным единице:
а°=1.
Теперь выражение
ат
имеет смысл для любого т — положительного,
отрицательного или равного нулю, целого или дробного.
При этом если а положительно, то т действительно может
быть каким угодно; если а отрицательно, то т не должно
равняться несократимой дроби с четным знаменателем.
Наконец, если а = О, то т должно быть положительным.
Ньютон, получив формулу (5) для целого
положительного показателя, сразу же захотел выяснить, будет
ли верна эта формула для дробных и отрицательных
показателей. Мысль эта кажется теперь очень
естественной. Однако не следует забывать, что Ньютону первому
приходилось прокладывать пути, что современная
алгебра многим обязана самому Ньютону и, в частности,
обязана систематическим употреблением дробных и
отрицательных показателей. Странно, однако, что
школьникам, изучающим алгебру, так сказать, «на всем
готовом», знающим отрицательные и дробные показатели и
знающим, что основные свойства степеней с целыми
положительными показателями распространяются и на
все другие показатели (сложение показателей при
умножении степеней, вычитание их при делении и т. д.),
самим не приходит в голову применить бином Ньютона
к дробным или отрицательным показателям.
Как бы то ни было, приоритет (первенство) открытия
принадлежит Ньютону. Последуем за ним и начнем
с простейшего случая т = —1. Справедлива ли формула
(5), если бином возводится в степень с показателем —1?
Заметим с самого начала, что доказательство,
приведенное в главе II, не дает никаких оснований утверждать,
что формула будет справедлива. В самом деле, при
доказательстве мы существенно использовали тот факт, что
действие возведения в степень есть перемножение неко-
32

торого числа одинаковых множителей, а этот факт
относится лишь к целым положительным показателям.
Действительно, когда говорят, что 1 + х возводится в
минус первую или в половинную степень, то это никоим
образом не значит, что бином 1 + х умножается сам на
себя минус один раз (?) или полраза (?).
Сделаем еще одно важное замечание. Когда т есть
целое положительное число, то (1 + х)т есть многочлен
степени т. Вычисляя его коэффициенты по формуле (4)
Аь =
т (т—\) (т — 2)... (т — k + 2) (m— k + 1)
k~ 1.2-3. ..*
мы получаем, что Ат — коэффициент при хт — равен
т(т— 1) (т — 2) ...(m — m + 2)(т —т+1) __
1.2-3...т. ~~
_ т(т— 1) (т — 2)...2- 1 _ <
~~ 1.2-3.../я ~if
а все следующие коэффициенты
^*m + l> ^m+2» Ат + $, ..♦
равны нулю. Именно:
A/n+i=
_ m (m-1) (m-2)...[m-(m+ 1)+ 2] [m-(m+1)+1] __
~~ 1 -2-3... т (m+1) ~~
т (т^1)(т —2)... 1 -0 __ п#
~ Ь2-3...т(т + 1) ~U;
- w(m-l)(w-2)...2.bQ.H) , ft.
Лт+2— Ь2.3...т(т+1)(т + 2) "" '
- _ m(m-l)(m-2)...2-l-0-(-l)-f-2) -
/1т+3 1.2.3...т(т+1)(т + 2)(т + 3) ~~ и' в,в
(множители числителя, как мы указывали раньше,
убывают на единицу; множители знаменателя возрастают
на единицу).
Но если т не есть целое положительное число, то
(1 + х)т не может равняться никакому многочлену.
Например, если бы (1 -|-^)-1 = - равнялось какому-
нибудь многочлену степени я, то, обозначая этот
многочлен Рп (х), мы имели бы:
33

или
1=(\+Х)'Ря(х).
Однако произведение (I + х) на Рп (х) должно дать
новый многочлен степени п + 1, а никак не единицу
(многочлен нулевой степени). Итак, не существует
многочлена, который при всех значениях х равнялся бы
(1 + х)~\
В полном согласии с этим коэффициенты Aky
вычисляемые при т, не равном целому положительному числу,
не обращаются в нуль (если бы все коэффициенты,
начиная с некоторого, были равны нулю, то получился бы
многочлен). Именно, при т =—1 получаются
следующие коэффициенты:
Л1=^-=-1;
1
-i(-i-i) (-')-(-2)
= 1;
"2— 1-2 12
-1(-!-!)(-1-2) (— !).(—2)-(—3) ,.
Лз— 1-2-3 — 1-2-3 '*
-1(-1-1)(-1-2)(-1-3)
/1* — 1-2-3-4 ~~
_ (—!)■(—2)-(—3)-(—4) _ .
Аш =
1.2.3-4
_1.(_1_ 1) (— 1—2) (— 1 — 3) (-1-4)
1-2.34-5 ~~
(—1). (—2) > (—3). (—4) ■ (—5) _ ,
- 1.2.3-4.5 ~ [ И Т* Д'
Поэтому формула (5), если только она верна при т = —1,
должна иметь вид:
= (\+x)-i = \-x + x2-x3+x*-x* + xe-...t (6)
1+х
где выражение, написанное в правой части, характерно
тем, что оно не содержит последнего члена, но за каждым
членом имеется другой, содержащий хв большей степени.
Так, за +;с* следует —х7, далее +Х8, потом —х9 и т. д.
Подобного рода выражение уже нельзя назвать
многочленом, так как многочлен содержит всегда
определенное число членов, хотя бы и очень большое, и среди его
членов можно указать член, содержащий х с наивысшим
показателем.
Наше выражение можно было бы назвать «бесконечно-
членом», но в математике принят другой термин, именно
34

ряд (в данном случае степенной ряд). Не задаваясь
сейчас вопросом о том, в каком смысле ряды могут
употребляться в математике, мы начнем проверку
предполагаемого равенства, поступая с правой частью так, как если
бы это был многочлен. Такой образ действия типичен
для математиков XVII и XVIII веков. Только позднее
вырабатывается требование не употреблять в математике
ничего, что не было бы строго определено и правила
обращения с чем не были бы строго согласованы с уже
установившимися и приведенными в логически стройную
систему математическими знаниями. Это требование
вполне законно и необходимо для развития современной
науки. Однако и теперь формируются и будут
формироваться новые научные понятия. Пока они еще не
отделаны, с ними обращаются так же свободно, как это
делали наши далекие предшественники. Только теперь
такое обращение часто не выходит за стены творческой
лаборатории математика, и когда работа появляется в
печати, в ней все так отшлифовано и сглажено, что сразу
не найдешь концов — каким путем автор пришел к
новому понятию. Но вернемся к нашей теме. Для проверки
равенства (6) можно, во-первых, воспользоваться
известным правилом: делимое равно делителю, умноженному
на частное. В данном случае умножим правую часть
равенства (6) на 1 + х и посмотрим, получится ли в
произведении 1. Перемножение дает:
1-х + х2-хг + х*-х5 + х*-х7 + ...
х Н-х
1 - Х + Х2 - ЛГ3 + X4 - JC5 + *6 - X7 + XS - . . .
+ х-х2 + х3-х* + хъ-х* + х'7-х*+...
1 »»»»»» » »
Мы видим, что все члены произведения (кроме единицы)
взаимно уничтожаются. Именно, члены произведения
расположены в две строчки (между двумя
горизонтальными чертами), причем в первой из этих строчек стоят
произведения членов множимого на первый член
множителя, т. е на 1, а во второй строчке— на второй член
множителя — на х. На первый взгляд может показаться,
что не всякий член второй строчки взаимно уничтожится
с членом первой строчки. Однако это не так. Например,
над —jc8 во второй строчке произведения должен стоять
35

член, следующий за —х7, т. е. +Х8, и члены ■—Xs и +х*
снова взаимно уничтожаются. Итак, проверка оправдала
законность бинома Ньютона при т =—1. Однако
читатель может не вполне удовлетвориться одной этой
проверкой и это тем более естественно на скользком пути,
на который мы вступили, что и сам Ньютон в
аналогичных случаях (например, при т = у] прибегал к
нескольким проверкам.
Другую проверку, тесно связанную с первой, получим,
если станем делить 1 на 1 + х по тем же правилам, по
которым делят многочлен на многочлен. Тогда в частном
будем получать один за другим члены правой части
равенства (6):
1 \J±x
!+* 1— х+х2—х3 + ^—...
» — X
— х — х2
» X2
х2 + х3
ъ—х*
— Л? — л*
» X4
х*+х*
» — хь...
Сколько бы мы ни продолжали, деление никогда не
закончится, но все время в частном будут появляться
один за другим все новые и новые члены, именно — члены
интересующего нас ряда.
Так как вторая проверка может скорее вызвать
новые вопросы, чем разрешить старые (читатель видит,
например, что каждый раз получается определенный
остаток, и поэтому не верит, что ряд 1 — х + х2 — х3 +
+ х*—х6 + ... можно рассматривать как точное частное),
то мы прибегнем еще к одной проверке, чисто
арифметического характера. Именно, в изучаемой формуле
_L- = 1 —лг-1-х2 —х3 + а:4 —л^ + ...
1 -\-х
дадим х какое-нибудь определенное числовое значение,
например, * = ^-. Тогда слева получим:
36

а справа.
.-4+(i)'-a)s+(T)*-(T)s+-
Очевидно, что равенство
о.8='-4+аш+(тГ-ш!+-
следует понимать в том смысле, что, остановившись на
каком-нибудь месте в последовательном выполнении
указанных здесь арифметических действий, мы не получим
результата, равного 0,8; чтобы получить этот результат
нужно выполнить бесконечное множество вычислений.
Такое заключение может напугать кого угодно, однако
мы не испугаемся и начнем производить вычисления,
делая каждый раз передышку после нахождения
алгебраической суммы двух, трех, четырех и т. д. первых членов.
Первый член равен 1. Он значительно отличается от
числа 0,8, стоящего слева. Но сумма (алгебраическая)
1 3
первого и второго членов дает 1 — -^ = т- = 0,75 — число»
более близкое к 0,8. Далее, сумма первых трех членов
1 -1 + (х)2= 1-0,25 + 0,0625 = 0,8125;
сумма первых четырех членов
= 1 - 0,25 + 0,0625 - 0,015625 = 0,796875;
сумма первых пяти:
= 1 - 0,25 + 0,0625 - 0,015625 + 0,00390625 =
= 0,80078125
и т. д.
Как мы и ожидали, ни один из промежуточных
результатов (1; 0,75; 0,8125; 0,796875; 0,80078125; ...) не
равен 0,8; однако теперь ясно, что, вычисляя
алгебраическую сумму все большего и большего числа членов ряда
'-!+(тИ1Г+(тИтГ+(!)*-••
37

мы будем получать числа, все более и более
приближающиеся к числу
И в этом смысле равенство
(1+*)-* = 1-*+;с2-л:3 + л:*-** + *«-...
верно при х = ~4' Аналогично можно делать проверку и
для других значений х.
К сожалению, среди различных значений х встретятся
такие, которые «дискредитируют» формулу (6). Как
яркий образчик такого «несознательного» х$ мы выберем
х = —2. Слева должно бы быть
1-2 ~~ —1
между тем как справа получается:
1-(_2) + (-2)2-(-2)* + (-2)*-(-2)* + ...=
= 1+2 + 4 + 8+16 + 32 + ...
Вычисляя, как и раньше, суммы одного, двух, трех,
четырех и т. д. членов, получаем результаты:
1; 1+2 = 3; 1+2 + 4 = 7; 1+2 + 4 + 8=15;
1+2 + 4 + 8+16 = 31; ...
Эти результаты не только отличаются от —1, но и не
дают никакой надежды, что мы хоть когда-нибудь
приблизимся к ней. Поэтому мы должны иметь мужество
признать, что формула (6) не верна при х = —2.
Итак, арифметическая проверка, оказавшаяся самой
убедительной, показала, что формула бинома Ньютона
(5) при m = —1 верна для одних значений х (например,
для х = j],а для других неверна (например, для х = —2).
Для того чтобы окончательно выяснить вопрос, вернемся
ко второй проверке, при которой получались следующие
38

результаты:
1 |1+др
\+х l—x+х* — х3 + х4 —...
Первый остаток » — х
— х—х2
второй остаток » + х2
х2 + х3
третий остаток » — х3
—X3 —X4
четвертый остаток » х4
Х4+Х5
пятый остаток » — х5
Обрывая деление на каком-нибудь месте, например, на
пятом остатке, мы, согласно известному соотношению —
делимое равно делителю, помноженному на частное,
плюс остаток, — получим:
1=(1+х)(1-л: + л:2-л:3 + х4)-х5.
(Читатель может легко проверить это равенство,
перемножив многочлены в правой части и приведя подобные
члены.)
Отсюда, деля каждый член равенства на (1 + х),
найдем:
1 =\-х + х2-х3 + х* хЪ
1+х "" * Л^и' ** ^" \+х '
Последний результат ценен тем, что здесь видно,
какую ошибку мы сделаем, ограничившись при
вычислении правой части равенства (6) лишь суммой первых
пяти членов: 1 — х + х2 — х3 + х4. Ошибка эта есть,
х&
очевидно, — -рх7-
Ясно, что когда х мало по абсолютной величине, то
хъ представляет очень малую дробь, а потому и вся
ошибка—Л^ очень мала. Например, при х=-^— ошибка
iiL_..
равна: —^—^р= — -^ек = 0,00078125, что вполне сог-
ласуется с результатом вычисления на стр. 37.
Именно, сумма первых пяти членов прих=^ равнялась
39

0,80078125, а потому ошибка (разница между 0,8 и этим
числом) есть действительно —0,00078125.
Напротив, если х велико (достаточно, чтобы х по
абсолютной величине было больше единицы), то Xs
велико по абсолютной величине, а потому и ошибка
хь
. велика. Например, при х = —2 имеем:
(=V_ _ Л_ _ _ оо
1+(—2) ~~ — 1 ~~ oz»
что снова согласуется с вычислениями на стр. 38.
Легко проверить, что, вообще, п-и остаток при
делении 1 на 1 -Ь х будет равняться ±хп, причем плюс будет
стоять в тех случаях, когда п — четное, и минус, когда
п — нечетное. (В нашем примере мы останавливались
на пятом остатке; он равнялся —jc5.)
Следовательно, снова пользуясь соотношением между
делимым, делителем, частным и остатком, получаем:
l=(l+x)(l-x + x2-x3 + x*... + xn-1)±xn
или, деля каждый член равенства на 1 + х:
1 =1-х + х2-х3 + х*-... + хп~1± хп
х+х * ^-г~ - -г- к- _1+х.
Это равенство позволяет оценить в общем случае ошибку,
получающуюся, если б правой части формулы (6) брать
лишь сумму первых п членов, отбрасывая все остальные
члены. Именно, эта ошибка, равная
- (1 -х + х2-х3 + х*-... + хп-х),
\+х
есть, очевидно,
— \+х
Она вообще не равна нулю (разве лишь при х = 0).
Но если х по абсолютной величине меньше единицы,
то хп есть число, заведомо меньшее единицы. Более того,
в этом случае стоит лишь взять число п (т. е. число
членов, учитываемых в ряде 1 — х + х2 — х3 -{- х* —
— хъ + ...) достаточно большим, чтобы хп, а вместе
с ним и вся ошибка zh-т—.—, по абсолютной величине
1 -\-х '
сделалась чрезвычайно малой. Например, если х = —0,9»
40

то ошибка равна
— 1_о,9 — +0,1 — 1и V V**) •
Если я = 1, 2, 3, .., то ошибка будет
соответственно: +9; 8,1; 7,29; .., т. е. пока довольно большая.
При п = 10 получается ошибка, равная 1(Ь(0,9)10 =
= 3,48674401, при п = 20 ошибка 10- (0,9)20 =*
= 1,2157665459... — она все еще велика. Однако при
п = 200 имеем: 10- (0,9)200 = 0,000000007... Иными
словами, если, желая проверить равенство
(1+х)"1= 737= l-^+^-J^+^-^ + Jt6-...
при х = —0,9, начнем выполнять над значением х =
=—0,9 по порядку алгебраические действия, указанные
в правой части, то, взяв алгебраическую сумму первых
20 членов, получим результат, отличающийся от
значения левой части
0-0,9)-=-^ = ^-= Ю
более чем на единицу, именно, получим: 8,7842334540...
Но если подсчитаем алгебраическую сумму первых
двухсот членов правой части, т. е. сумму: 1—х+х2—*34-
+ х4 — х5 + ... + а:198 — х199, то получим число
9,999999992...,
ничтожно мало разнящееся от 10.
Итак, теперь можно утверждать, что равенство (6)
справедливо при всех х, по абсолютной величине меньших
единицы. Именно, справедливо в том смысле, что, беря
алгебраическую сумму некоторого числа идущих по
порядку членов ряда
\-х + х2-х* + х*-хъ + ...,
мы хотя и получаем результат, не равный
однако разница эта становится сколь угодно малой
если только учтено достаточно большое число членов
ряда. При этом, чем ближе х к 1 по абсолютной величине,
тем больше членов ряда приходится складывать для
41

того, чтобы получить приличное приближение. (Это ясно,
хотя бы из сравнения двух примеров: на стр. 37, где
вычисления велись при х = 0,25, и на стр. 41, где х =
= -ОД)
Что же можно сказать относительно значений лг,
равных 1 или больших ее по абсолютной величине?
При х = —1 равенство (6) нельзя и рассматривать, так
как при этом значении х теряет смысл левая часть
равенства:
1_
\+х
(знаменатель обращается в нуль). При х= 1 в левой
части формулы (6) имеем:
_[ __ J_
1 + 1 ~ 2 '
а справа:
1-1 + 1-1+1-1 + 1-1+1-...
Первый член здесь равен единице; сумма двух
первых равна нулю; сумма трех — снова равна единице,
затем опять нуль и т. д. Сколько бы членов мы ни
складывали, мы все время получаем либо единицу, либо
нуль и не только никогда не получим у, но даже и не
приблизимся к у ни в какой мере.
Поэтому при х = 1 формула (6) неверна. Выражение
ошибки
— \+х '
найденное на стр. 40, показывает, что формула (6) не
может быть верна ни при каком х, по абсолютной
величине большем 1. В самом деле, в этом случае, чем больше
мы будем учитывать членов ряда
1-лг + л;2-л;3 + л;4-л:5 + ...,
т. е. чем больше я, тем больше будет по абсолютной
величине хп и тем больше, следовательно, будет разница
между -г—— и суммой первых членов ряда, равная
1 + X
± 1 . На стр. 38 мы наглядно убедились в этом, по-
лагая х = —2.
42

В результате длинного исследования (которое, однако,
значительно сэкономит время в дальнейшем) мы пришли
к заключению, что биномиальная формула (5) верна
и при т = —1 (тогда она принимает вид (6)), но верна
не для всех х> а только для х, меньших единицы по
абсолютной величине *).
Ньютон производил проверку биномиальной формулы
1
и для других значении т, и прежде всего для т = у.
Рискуя утомить читателя, мы все же произведем
выкладки вслед за Ньютоном.
При m = Y левая часть формулы (5)
(1+*)"■ =
_ 1 _i_ т | т(т—\) 2 , т (т— 1) (т — 2) 3
— 1+ —X-h 1#2 х Н 1.2-3 Х ■"
m(m-l)(m-2)(m-3) 4
""*" 1-2-3-4 х "l"
, m(m-l)(m-2)(m-3)(m-4)^ ,
"^ 1-2.3.4-5 * "*"
m(m-l)(m-2)(m-3)(m-4)(m-5) 6
Т" 1-2-3-4-5-6 * "t"*'-
принимает вид:
(l+x)*=Vl+x,
*) Все это должно быть хорошо известно нам из курса
элементарной алгебры. Ведь ряд 1 — х + х2 — х3 + х4 — jr+ ...
представляет при | х I < 1 бесконечно убывающую геометрическую
прогрессию, со знаменателем, равным —х; поэтому сумма ее должна
равняться -j— = -г-т-— = (1 + х)~\ и никакой проверки
дальше не нужно. Если мы не ссылались на геометрическую
прогрессию, то только потому, что хотели на простейшем примере
подготовить читателя к понятию ряда.
Формула для суммы бесконечной геометрической прогрессии
появилась впервые в книге бельгийского математика Андрея Такэ
«Арифметическая теория и практика, тщательно обоснованная»
(1656 г.). Для доказательства этой формулы Такэ использовал леммы
из небольшой работы «Об измерении параболы» итальянского
математика Торричелли, напечатанной в 1644 г. Сам Ньютон
пользовался «Универсальной арифметикой» английского математика Валли-
са (1657 г.), где приводится формула суммы конечной геометрической
лрогрессии.
43

а правая:
н^-щ-ш^
1.2-34
к;-)в-»)в-')а-«)
Н~ 1•2•3-4-5 х г
"^ 1.2.3.4.5-6 *
^ 2 ' 1-2 "^ 1 -2-3 ^
, т-(-т) •(-!)• (~т),
т 1-2-3-4 * "Г
m)-(-IH-l)-K)
,ЯЧ)-КН-4):НН-!Ь,
"*" 1.2.3.4.5.6 Л "Г"
, J_ 1_ 2 ЬЗ з Ь3>5 ^4
— 1+2* 2-4 * ■" 2-4-6 * 2.4-6-8 •"
1-3.5-7 * 135.7.9 в ,
^ 2.4.6-8.10 л 2-4-6-8.10- 12
11 2 I 3 «^4 I в в I
*=1 -t-yAT — у* -Г-15"^ ~" "128 "*" 256 Х [024"^ +"<
Итак, нужно проверить справедливость равенства 1):
8 - -г 16 - 128
7_ 5 21
256 Х 1024
"" 9Rfi Х 1П94 Х "Г • • • » (')
*) Здесь непосредственно не видно, как, зная некоторый член,
написать следующий за ним. Однако это нетрудно сделать, пользуясь
формулой (3) главы II, выраженной словами следующим образом:
нужно коэффициент при данном члене помножить на разность между
показателем степени бинома (в данном случае равном -у] и показа-
44

где в правой части снова находится степенной ряд,
однако с другими, чем раньше, коэффициентами. Для
проверки возводим правую часть в квадрат. Если формула
(7) верна, то в результате возведения мы должны
получить 1 + х.
Но возвести в квадрат — это значит умножить
выражение само на себя, т. е. произвести умножение:
128" *4+156" *5 —1024" Х +"-JX
1 I 2(3 4 I
+ 256 *Ь 1024 ^+ •••]•
Сделаем это, выписывая члены произведения
строчками: в первой строчке произведение множимого на
первый член множителя, т. е. на 1, во второй — произведе-
1
ние множимого на второй член множителя, т. е. на-^-х,
1
в третьей — на — -g-*2 и т. д.:
li 2 I 3 ч>-4 I 5 -^6 I
1-hy* — у* +-fg-X "~W +>25б"Х 102?:Г+*
+ Т*~1"Т* ~1бХ ~^~32X ""256'"'" "5l2"^—'
L v2 Lv3 J L v4 L. y5 i 5 y6 _
8 x 16 * ^ 64 x 128 x ^ 1024 л
+ T6"X3+ "32"'^ 728"^+ "256"^~'
Ъ л 5 c . 5 л
128 Л 256 ^ ^ 1024 ~
7 7
""l"~256~*6+~5l2~* ""'
1024
телем степени в данном члене и разделить на показатель степени
в следующем члене. Так, за коэффициентом — ттй^г при хь идет член,
21 2 33
содержащий х1 с коэффициентом — -т^" • j— = "9048" *
45

(Мы отступаем в каждой строчке на одно место вправо,
чтобы подобные члены располагались друг под другом.)
Складывая члены в каждой колонке, убеждаемся, что
первые две колонки дают 1 + х, а каждая из остальных —
нуль.
Например, в колонке, содержащей #6, сумма
коэффициентов равна
_ 21 7 5 15 7 21 __
1024 ■" 512 + 1024 ■" 256 + 1024 ■" 512 1024 ~"
_ — 21 + 14 + 5 + 4 + 5+14-21 п
" 1024 ~~ U-
Итак, формальная проверка и здесь оправдывает
равенство (7). Однако детальный анализ показывает, что
равенство (7) справедливо не для всех значений х, а
только для значений, меньших единицы по абсолютной
величине 1). При I х I > 1 оно неверно. Вместо того,
чтобы задерживаться на исследовании этого случая, мы
ознакомимся сейчас более детально с общим понятием
ряда и его основными свойствами. После этого мы
сможем рассмотреть принадлежащее Эйлеру
доказательство биномиальной формулы (5) для любого
показателя т 2).
1) Оно верно также при х = — 1 и при х = 1.
2) Но не для любых значений х>

ГЛАВА IV
ЧТО ТАКОЕ РЯД?
Выражаясь чисто описательно, можно сказать, что
ряд есть алгебраическая сумма бесконечного числа
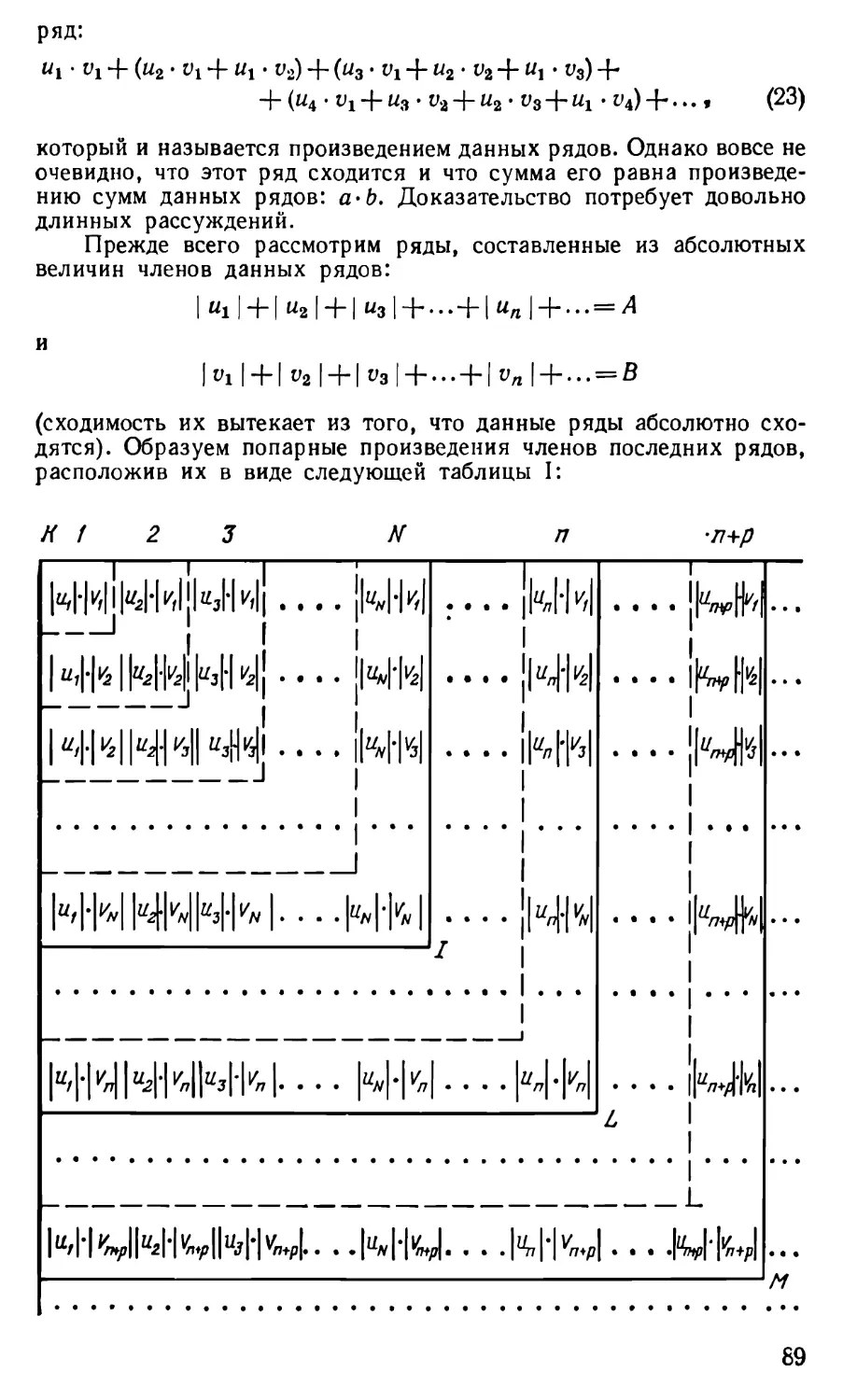
слагаемых. Всякий ряд имеет, таким образом, вид:
UX + U2 + U3 + U4 + llb + . . . + 11^! + Un + Un+1 + . . . ,
причем написанное выражение не имеет последнего члена,
но за каждым из слагаемых имеется следующее
слагаемое. Мы видели в главе III несколько примеров рядов:
1 - х+х2 - х* + х* -... qp хп~1 ± хп й= хпП ±...,
1-1 + 1-1 + 1-...+ 1±1:р1±...,
1 i 2 i 3 4 I •» Л i
1 + "2~*~ Iх +ТбХ ~~ 128* +256* —Ю24 +'••
В двух первых случаях легко указать последующий
член, зная предыдущий. Так, в первом случае за а4
должно следовать —а:6, потом х6, дальше —х1. Во втором
примере за 1 следует —1, а затем снова 1. В третьем
21
примере трудно угадать, какой член следует за — tqot*6-
Однако нам не придется ломать голову. Мы сами
получили этот ряд из биномиальной формулы при т=у.
Поэтому для получения коэффициента следующего члена
/74 21 1
(при х1) достаточно помножить — т^т на разность между ^
и 6 (показателем степени х) и разделить на 7 (показатель
степени в определяемом члене). Получаем:
21 (2"~6j_ 33
1024* 7 ~2048#
Итак, за -у^*6 следует + 2Q48*7.
47

В математике рассматриваются не только степенные
ряды (являющиеся, так сказать, «многочленами
бесконечно большой степени»), но и ряды, члены которых
являются тригонометрическими функциями —
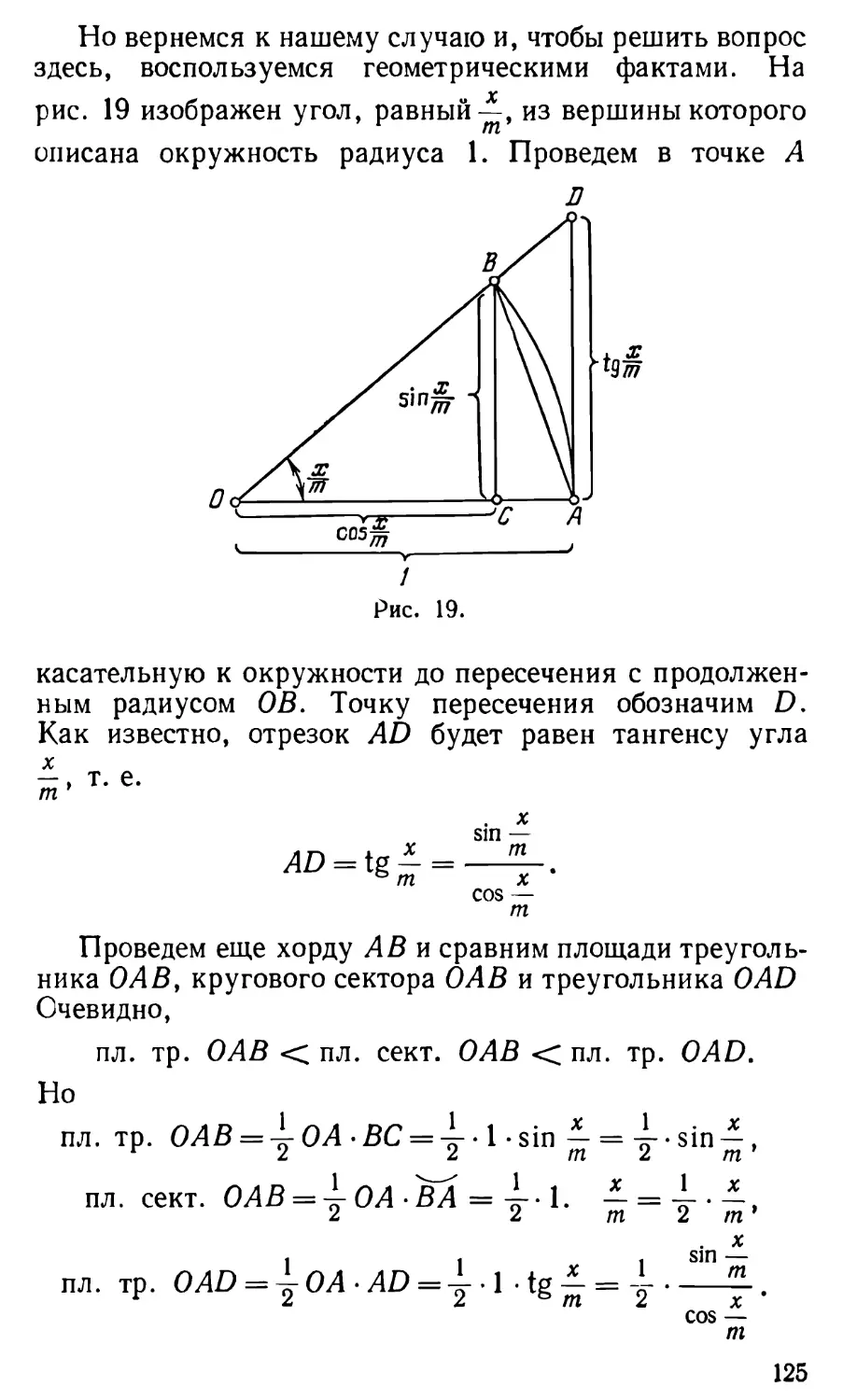
тригонометрические ряды и др. Приведем пример
тригонометрического ряда:
sin х , sin Зх , sin 5x , sin 7x , sin 9x ,
— -Ь —g— + —5— + ""т" + —9~ + • • •
В то время как сложение конечного числа слагаемых
дает всегда определенный результат, прибавление одного
за другим членов ряда может не дать никакого
результата. Этот факт, на который мы указывали в главе III,
стоит того, чтобы о нем еще поговорить.
По существу, имея дело с бесконечным количеством
действий, мы вообще не можем рассчитывать на
получение окончательного результата.
Например, в случае ряда
1+1+1+1+1+1+1+
^ 2 ^ 4 ^ 8 ^ 16 ^32^64 ^•••»
отправляясь от первого члена ряда и прибавляя один за
другим второй, третий и т. д. члены ряда, мы будем
получать каждый раз особый результат, и ни один из
результатов, по самому смыслу понятия ряда, не будет
окончательным. Именно, получатся числа:
1- 1+1--?- 1 + 1 + 1-1. 1+1+1 + 1-15.
A» lt2-2» '^ 2 ^ 4 ~ 4* Х^2^4^8~ 8'
1 + 1+1 + 1 + 1 = ^1.
l-t-2^4 + 8^16 16'
1_i_ l . i i X , 1 ,i_63
1 "•" T "*" 4 "*" 8 ■+" 16 T" 32 ~~ 32;
l + 1 + l + l + l + l + l- lJL.
1-Г 2 ^ 4 ^ 8 ^ 16 ^ 32 ^ 64 ~ 64 ' • • •
Однако, приглядываясь к этому множеству отдельных
результатов, мы видим здесь удивительную тенденцию,
которая легче всего обнаруживается, если числа
• _3_ 7_ 15 31_ 63 127
1; 2 ' 4 ; 8 ; 16' 32; 64 ' •*•
48

записать в виде
9_1- 9 L. 9 L. 9 L. 9 L.
2-1- 2-1-
* 32' 64' •"
Таким образом, находя суммы первых двух, трех,
четырех, пяти и т. д. членов ряда (эти суммы называют
иногда частичными суммами ряда), обнаруживаем, что
получаемые числа стремятся к определенному числу,
именно к 2, все меньше и меньше отличаясь от него.
Вот это число 2 и называют суммой ряда
1 + Т + Т + "8"+1б + 32^~64 + ',в
и пишут
1 + Т + Т + ^ + 7б + 32 + б4+'-' = 2#
Надлежит помнить, что, складывая некоторое число
членов ряда по порядку, начиная с первого, т. е. вычисляя
частичные суммы ряда, мы, вообще говоря, не получаем
суммы ряда, но только приближенные значения суммы.
Ошибка будет тем меньше, чем больше членов мы сложим.
Возникает вопрос — всякий ли ряд имеет
определенную сумму, иными словами, являются ли частичные
суммы всякого ряда все более и более точными
приближениями некоторого числа? Простой пример показывает,
что это не всегда так. Возьмем ряд
1-1 + 1-1 + 1-1 + 1-1+...
и станем вычислять его частичные суммы.
Мы будем получать, начиная с первого члена, который
условно можно рассматривать как первую частичную
сумму, следующие числа:
1; 1-1=0; 1-1 + 1 = 1; 1-1 + 1-1=0;
1-1 + 1-1 + 1 = 1; ...
Эти числа
1; 0; 1; 0; 1; 0; 1;
нельзя рассматривать как все более и более точные
значения некоторого числа. Ряд
1-1 + 1-1 + 1-1 + 1-1+...
суммы не имеет.
49

В математике ряды, имеющие определенную сумму,
называют сходящимися рядами, а не имеющие
определенной суммы — расходящимися рядами. Итак, ряд
1+1+1+1+1+1.±+
■^ 2 ^ 4 ^ 8 ^ 16^ 32^64 ^"'
— сходящийся, и его сумма равна 2; ряд
1-1 + 1-1 + 1-1+...
— расходящийся.
Заметим, что в XVIII веке понятие сходимости ряда не было еще
точно установлено. Математики весьма часто оперировали и
расходящимися с нашей точки зрения рядами, приписывая им
определенные суммы. Но при этом частичные суммы, конечно, уже не являлись
все более точными приближениями суммы ряда. Соображения, на
основании которых некоторым расходящимся рядам приписывались
определенные суммы, были весьма различны. Обыкновенно заранее
утверждали, что некоторый ряд имеет сумму, и затем отыскивали
ее в результате более или менее сложных выкладок. Так, например,
обозначая «сумму» ряда
1_1 + 1_1 + 1-1 + 1-1+...
буквой «S, математики XVIII века писали:
1 — 1 + 1-1 + 1 —1 + 1 —1+... = S.
Если теперь первый член ряда с обратным знаком перенести
в правую часть, то получим:
_1 + 1_1 + 1_1 + 1_1+... = S-1.
Но ряд, стоящий слева, только знаками членов отличается от ряда
1 — 1 -f-1 — 1 -f-1 — 1Н- 1 — — ,
поэтому его сумма есть —«S. Итак,
— S = 5—1, или 1=2S и 5 = у.
Рассуждали и иначе. Так, указывалось, что ряд
1-1 + 1-1 + 1-1 + 1-1+...
возникает из ряда
1_х+*2_ х* + х* — х* + л* — х7 + ...,
если в последнем положить х= 1. В свою очередь мы видели, что
ряд
имеет своей суммой функцию . (см. стр. 35 и след.):
1 -\-х
50

Таким образом, чтобы найти сумму ряда
1-1 + 1 —1 + 1-1 + 1-...
нужно в последнем равенстве положить х = 1. Тогда получим
.1_=1_1 + 1-1 + 1-1 + 1-...
Однако на это рассуждение находились возражения следующего
характера. Ряд
1-1+1-1+1-...
можно связать не только с дробью , но и с другими дробями,
1 +х
например с « , . 2 . Именно, если делить 1 на 1 + х + х2 по
тем же правилам, по которым делят многочлен на многочлен, то
будет получаться в частном ряд:
l_x_j_X3_ д4 + хв — х7 + х9 — х™ + х™ — х™ + х1Ь — х1в + ...
Вот соответствующие выкладки:
\\+х + х*
14-* + ** 1—jc-f-x3 — л«4-л:в— х7 + х» — *10-Ь..
» — х — х2
— ДГ — JT2 — JCS
» » AT»
л-э4-** + *в
» —а:4—х5
» » Ав
Ав+Х7-Ь*8
> —А*7— Xе
— X7—А"8 —X»
» » X"
jte+xio + x»
» —х10 —х11
_д:1о_Ли_
-Х«
х« ...
Пользуясь соотношениями между делимым, делителем,
частным и остатком, можно установить подобно тому, как это делалось
в главе III, что формула
1 =1— х+*з—х4 + *в —л7 + л? —лю — ...
1+х + х2 ■ ' '
будет верна при | х | < 1. Иными словами, при всяком значении х,
| х | < 1, частичные суммы ряда, стоящего справа, будут стремиться
к величине . 2 , по мере того, как мы будем брать все
больше и больше членов для вычисления сумм. Но если в последней
формуле положить х= 1, то получится -~- = 1 — 1 + 1 —
— 1 + 1 — 1+..., т.е. интересующему нас расходящемуся ряду
1 1
можно приписывать сумму, не только равную -г-, но и равную -^-.
51

Подобные противоречия нередко встречались у математиков
XVIII века, которые различными способами пытались их
разъяснить. Не останавливаясь на всех деталях длившейся около
столетия интересной дискуссии, касавшейся суммирования рядов,
которые мы теперь называем расходящимися, приведем некоторые
любопытные образчики научных мнений того времени, характер
которых не был исключительным для тогдашней науки.
Итальянец Гранди в одном из своих сочинений (1710 г.)
замечает, что если в равенстве
l_l + l_l + l_l + l_l+... = i. (8)
складывать члены попарно: первый со вторым, третий с четвертым,
пятый с шестым и т. д., получается
0 + 0 + 0 + 0 + 0 + ... = !,
или
-±.
и вместо того, чтобы подвергнуть критике рассуждения, при помощи
которых им была получена формула (8), он замечает, что его
окончательный вывод есть символ создания мира из ничего (согласно
религиозным воззрениям)!
В другом месте Гранди следующим образом пытается пояснить
равенство (8). Предположим, что отец оставил двум своим сыновьям
в наследство драгоценный камень с условием, что камень этот будет
у каждого сына попеременно, по одному году. Тогда, если
подсчитать долю каждого брата в обладании камнем, принимая год
владения за +1, а год, в течение которого камень находится у другого
брата, за —1, то получится
1-1 + 1-1 + 1-1 + 1-1 + ...
Но, с другой стороны, в условиях завещания братья поровну владеют
камнем. Следовательно, указанная доля равна -^-. Таким образом,
заключает Гранди, становится понятным, почему
1-1 + 1-1 + 1-1 + 1-... = !.
По поводу этого рассуждения знаменитый философ и математик
Лейбниц справедливо заметил, что бесконечный ряд
1-1+1-1+...
на самом деле не имеет никакого отношения к примеру Гранди. В
самом деле, если братья будут владеть камнем только два, четыре,
десять — вообще четное число лет, то и тогда они в равной мере
будут обладать камнем. Таким образом, доля каждого, если следовать
Гранди, есть -^-. Между тем сумма первых двух, четырех, десяти
и т. д. членов ряда (8) есть нуль.
52

Лейбниц иным путем пытается объяснить равенство (8), но его
объяснение, по крайней мере по форме, насквозь пропитано
метафизикой — он ссылается на чудесные свойства природы, на закон
справедливости.
Приведем еще несколько
подробностей исторического
характера относительно понятий
сходящегося и расходящегося
ряда.
Эйлер в статье «О
расходящихся рядах» (1754—1755 гг.)
называет ряд «сходящимся», если
его члены стремятся к нулю, и
«расходящимся» в противном
случае. Приписывая каждому
ряду числовое значение,
которое он называет «суммой» ряда,
Эйлер подчеркивает, что
частичные суммы далеко не всегда
являются все более и более
точными приближениями к
сумме ряда; напротив, возможны
случаи, когда частичные суммы
чем дальше, тем больше
отличаются от «суммы» ряда. По
Эйлеру, «сумма» ряда есть
числовое значение той функции, из
разложения которой ряд
получается. Так, замечая, что ряд 1
ложения функции 1 , Эйлер
-1+ ' " * 1
Л. ЭЙЛЕР
(1707—1783).
- х + х2-...
1+*'
(х = 1) «сумму»
1+1
приписывает ряду
: у; следуя Эйлеру,
— 2 + 22 — 23+ ... (х = 2) нужно приписать «сумму»
В одном письме 1745 г. (письмо к Гольдбаху)
получается из раз-
1-1+1-
1 —
_ J^
" 3
ряду
1
1+2
Эйлер рас-
и т. п.
сказывает о довольно сложных выкладках, с помощью которых он
нашел, что «сумма» ряда 1 — 1! + 2! — 3! + 4! — 5!+ ... есть
0,5963475922. К Эйлеру отчасти примыкает и Лагранж,
приписывавший (1770 г.) каждому ряду с членами, стремящимися к пулю,
т. е. «сходящемуся» в смысле Эйлера, определенную сумму.
Правда, встречались и определения сходимости, звучащие
совсем по-современному. Так, в одной работе английского математика
Варинга (1781 г.) мы читаем: «Если в а+ b -\- с + d -\- e +... суммы
а-\~ bt я + 6 + с, а + 6 + с + d, ... стремятся к конечной
величине, к которой они подходят ближе, чем любая заданная разность,
то ряд сходится». Но не эта работа определяла развитие теории
рядов. Недаром Коши спустя сорок лет, в предисловии к своему
курсу «Алгебраического анализа», приходится подчеркивать: «Я
говорю, что расходящийся ряд не имеет суммы*, а через пять лет Абель
пишет в письме к своему другу Хольмбое: «Расходящиеся ряды
в целом, дьявольское измышление, и это позор, что позволяют себе
основывать на них какое бы то ни было доказательство. Если ими
пользоваться, то можно прийти к чему угодно, и это они производят
53

столько затруднений и парадоксов. Можно ли представить себе что-
нибудь более отвратительное, чем когда говорят, что
0=1— 2* + 3'* + 4Л + ...,
где п — целое положительное число. Ну разве это не смехотворно?
Я стал обращать чрезвычайно много внимания на все это, ибо
если исключить наиболее простые случаи, вроде геометрической
прогрессии, то во всей математике
почти нет ни одного ряда, сумма
которого вполне строго определена;
другими словами, то, что в
математике наиболее важно — остается
без обоснования...».
Эти две последние выдержки
показывают, что даже в двадцатых
годах девятнадцатого века взгляды
на ряды, присущие восемнадцатому
веку, были еще настолько
распространены, что и Коши и Абелю
приходилось активно бороться с ними.
Но мы отошли в сторону от
нашего предмета. Скажем только,
что после перерыва в употреблении
расходящихся рядов, длившегося
около полстолетия (примерно
первая половина XIX века), —
перерыва, обязанного, главным
образом, критическим трудам Абеля и
Коши, давшим основы современной
теории рядов, — расходящиеся
ряды вновь появились в математике, на новых основаниях, где
отсутствует метафизическая путаница. Однако теория расходящихся
рядов, тесно связанная с различными их приложениями, представляет
особую тему, требующую для изучения более высокой математической
подготовки, чем та, которую мы можем ожидать от читателя нашей
книжки.
В дальнейшем мы будем поэтому заниматься лишь
сходящимися рядами, не приписывая расходящимся
никакой суммы.
Напомним, что мы назвали ряд
и1 + и2 + ив + и4 + ... + ип-1 + ия + ия+1 + ...
сходящимся, если его частичные суммы
Sj = «i + tt2t
53 = «1 + wa + H3f
54 = w1-f-w2 + w3 + w4,
H. АБЕЛЬ
(1802—1829).
Sn = Ui + U2+ U3 +... + Un-l + Uni
Sn+i = u± + u2 + u3 +... + un-x + un + un+l
54

являются все более и более точными приближениями
некоторого числа. И если это так, т. е. если существует
число S, для которого Sj, S2, S3,..., Sn,... являются
приближенными значениями, то S называют суммой ряда и
пишут:
Ul+U2 + U3 + tl4 + Ub + ...+ Un + Un+1+... = S.
Мы должны теперь ввести установившуюся в
математике терминологию теории пределов и в дальнейшем
ею пользоваться.
Именно, вместо громоздкого и не имеющего достаточно
резко очерченного содержания выражения «числа Sn
являются все более и более точными приближениями
числа S» будем говорить, что числа Sn стремятся к
пределу S, и записывать это следующим образом:
Sn-*S или lim Sn = S9
где lim — первые буквы латинского слова limes
(французского limite), означающего «предел». При этом
запись
Sn-+S или lim Sn = S
не будет иметь другого смысла кроме того, что разность
S—Sn (разность между величиной и ее приближенным
значением) становится и остается сколь угодно малой по
абсолютной величине, если только номер п числа Sn
(в случае частичных сумм равный числу сложенных
членов ряда) достаточно велик. Например, в случае
ряда
1 + Т + Т+8" + 1б + 32 + б4 + "-
частичными суммами являются
о 1-е ^ с ' с ^ с ^1
с _ 63 с _ 127
*Ъб-з2; *i ~ бТ""
а их предел есть число S = 2. Здесь разности:
о — Sx— 1; S — S2 = -nr; S — S3 = ~г» S — S4 = -д-;
5~Ss~l6; S"Se~32; S"S'-64; '•'
55

становятся и остаются очень малыми, начиная с
некоторого номера. Так, если заранее задаться каким-либо
очень малым числом, например 0,000001, то всегда можно
указать номер л, начиная с которого разности S—Sn
станут меньше 0,000001, и в дальнейшем будут
оставаться меньшими этого числа. Именно, как нетрудно
вычислить,
О Ooi —
1
1
«S — So.) —
1 072 576
1
22 2 145 152
<
1 000 000
1
1 000 000
и т. д.
Итак, S—Sn меньше 0,000001, если только п ^ 21.
Рассмотрим еще ряд:
-L4--L4--L4--L4--L4--L4--L4--L- +
1.2r2.3"r3.4'r4.5"r5.6'r6.7"r'7.8"r8-9 г,##
Его частичные суммы по порядку суть:
1
5i — 179 —
^2 — 1 о Г о . % ~~ 9 "Г А —
53 =
2 '
1
+ 9 . 3 "" 3 • 4 — 9 + fi +19""
12
12
°4~1.21'2.31'3.41"4.5" 2 ^ 6 "^ 12 "^ 20 —
30+10 + 5 + 3 ±
~~ 60 ~~ 5
Впрочем, в данном примере нет надобности
заниматься дальнейшими подсчетами, так как здесь очень просто
обнаруживается закон строения частичных сумм. Для
того чтобы найти его, заметим, что члены ряда мо-
1.1111
гут быть записаны в виде у-^ = ' ~~ Т» <ГГз = Т —з ;
5Т4 = т-Т'- В°°бще Л"Й членй^ = Т-^Ь"-
Поэтому частичная сумма Sn (т. е. сумма любого числа
56

п членов, начиная с первого) равна
+(±--Н+-+(Л-1)+(1-;пМ-
=1_±+±_±+±_±+±_±+ +_!__
1 2^2 3^3 4^4 5^,-,^п-1
_± + ± 1 1 !_.
п ~ п п+\ я+1
Очевидно, что при безграничном увеличении п число
—цу будет неограниченно приближаться к нулю, а
частичная сумма Sn = 1 :p-j— к 1. Иными словами,
limSn=lim(l--JT)=P).
Из этого следует, что данный ряд сходится, и его сумма
равна единице.
Возвращаясь к общему случаю, подчеркнем, что в
возможности сделать величину I S—Sn | меньшей любого
заданного положительного числа, как бы мало оно ни
было, взяв номер п достаточно большим, — и
заключается сущность стремления к пределу.
Понятие предела имеет чрезвычайную важность во
всей математике, а не только в одной теории рядов.
Читатель встречался с ним, например, в геометрии, где
длина окружности определялась как предел периметров
правильных вписанных или описанных многоугольников,
объем цилиндра и конуса — как пределы объемов
вписанных (или описанных) призм и пирамид и т. д.
Полезно при рассмотрении пределов пользоваться
геометрическим изображением чисел на числовой прямой
(рис. 4). Если на прямой, неограниченно продолженной
в обе стороны, выбрать одну из точек за начало отсчета
и считать, что она изображает 0, а затем, установив
единицу масштаба, откладывать вправо и влево от точки
О отрезки различной длины, то мы получим возможность
2) Мы пишем: п -*• оо (оо — символ бесконечности), желая
указать, что л неограниченно возрастает.
57

геометрического изображения чисел. Именно, каждому
положительному числу отнесем точку нашей прямой,
лежащую правее 0, причем расстояние между этой
точкой и точкой 0 должно равняться в установленном
масштабе данному числу. Аналогично каждому
отрицательному числу будет соответствовать определенная точка
прямой, лежащая левее точки 0.
V? /,414.:- П 3J4L.
I 1 1 1 1—о 1 f-o 1 .
-2-1 0 1 2 3 4
Рис. 4.
Итак, всякому положительному или отрицательному
числу соответствует точка прямой. Обратно, всякой точке
прямой соответствует определенное число —
положительное, если точка лежит вправо от нуля, и отрицательное,
если она лежит влево от нуля.
Будем говорить иначе, что точки прямой изображают
числа, а самую прямую называть числовой. Кроме того,
5, 52 53 S455
1 о о o-ooj—«
О 1 2
Рис. 5.
для краткости, вместо того, чтобы говорить: точка,
изображающая число +2, точка, изображающая число нуль
и т. д., будем говорить: точка два, точка нуль.
На числовой прямой может быть более или менее
наглядно представлено стремление чисел к пределу.
Так, отмечая одну за другой точки
с _ i с _ 3 о _ 7 с_15 с—51
°i— i* ^>2 — "у» °з — "4"» °4 — "з"» °5 — !£»•••>
мы ясно видим, как эти точки стремятся к точке S = 2,
сгущаются возле нее (рис. 5).
Правда, рис. 5 довольно скоро перестает служить нам,
так как точки Se, S7, ... почти сливаются с точкой S.
Вообще, факт стремления каких-нибудь чисел Su
S2, S3, S4, ..., Sn, ... к своему пределу S выражается на
58

рисунке в том, что точки Sly S2, S3, S4, ..., Sn, ...
сгущаются, начиная с некоторого номера, около точки S.
Чрезвычайно важно отметить основную черту этого
сгущения. Если мы будем стараться «отгородить» точку S
от точек Sn, стремящихся к ней, как к пределу,
посредством очень маленького интервальчика, посредине
которого лежит точка S, то нам
это не удастся.
Именно, вне
интервальчика, так сказать, «за забором»,
всегда будет оставаться лишь
вполне определенное
конечное число точек. Все же
бесчисленное множество
остальных точек будет попадать
внутрь интервала, каким бы
малым он ни был. Иными
словами, можно взять интервал
с центром в точке S
настолько малым, что вне его
очутятся сотни, тысячи,
миллионы из числа точек Sn. Но
основная их масса,
бесчисленное множество этих
точек, все же будет жаться на
тесном пространстве этого
интервала — около точки S.
Воспользуемся геометрическим представлением чисел
для того, чтобы легче усвоить основной признак
(критерий) сходимости рядов, указанный впервые Коши.
Дело в том, что когда нужно доказать, что
определенное число S является суммой ряда
Ul + U2 + U3 + U^ + Ub + ... + Un + Un+1 + ...f
то можно просто вычислять частичные суммы
Si = uu S2 = ux + u2, S3 = u1 + u2 + u3$ ...,
S* = tti + w2 + ^3 + .•• + "*, ###
и следить, будут ли они стремиться к указанному числу 5.
Иными словами, можно вычислять абсолютные величины
разностей:
IS-SJ, |S-S2|, ..., |S-S„|, IS-S.nL ...,
59
о. коши
(1789-1859).

стараясь установить, будут ли эти числа, начиная с
некоторого из них, меньше любого наперед заданного
положительного числа. Так, например, можно поступать,
желая проверить справедливость биномиальной
формулы:
при каком-нибудь значении х, скажем при х = 0,21.
Тогда слева должно быть:
(1+0,21)2=]/Щ=1,1,
и остается проследить, будут ли частичные суммы нашего
ряда стремиться к 1,1.
Однако не всегда сумма ряда S известна заранее.
Чаще требуется установить, существует ли она, т. е.
сходится ли данный ряд, и если сходится, то какова эта
сумма.
В таких случаях критерий Коши чрезвычайно важен.
Вот в чем он заключается.
Предположим сначала, что ряд сходится. Тогда его
частичные суммы
«Si, «S2, S3, o4, ..., «S/i, «S/i+ь •••
стремятся к определенному пределу S. Если на чертеже
нанести точку S и точки Sl9 S2, 53, S4, ..., S„, .♦., то
последние будут сгущаться возле S. Именно, можно взять
S
i 1 1
< ч * , '
г/2 е/2
Рис. 6.
какой угодно малый интервал с серединой в S (рис. 6)
и все же все точки, изображающие частичные суммы,
начиная с некоторой, попадут внутрь этого интервала.
Обозначим его длину буквой е («эпсилон») и
предположим, что, начиная с некоторого номера я, точка Sn и
следующие S„+1> Sn+2, Sn4.3> ..., Sn+P, S„+/H.lt ... лежат
внутри этого интервала. Как легко видеть из рисунка,
расстояние между Sn и любой из точек Sn+i, Sn+2, Sw+3» ...
60

...» Sn+P, ... меньше, чем е. Но эти расстояния, очевидно,
таковы:
|5Я —ол+1|, |оя — ол+2 |, ...
Следовательно,
\Sn — Sn+p I <8»
где е — любое малое положительное число, п —
достаточно большой номер частичной суммы, а (п + р) —
любой номер, больший чем п. Итак, в случае, когда ряд
сходится, абсолютная величина разности двух частичных
сумм делается и остается меньше любого малого наперед
заданного числа 8, если только номера сумм достаточно
велики.
Вот эта фраза и выражает собой выполнение
критерия Коши для сходящегося ряда. Грубо говоря, в
критерии Коши констатируется, что все более и более точные
приближения одной и той же величины должны сами
между собой все меньше и меньше различаться.
Из этого почти очевидного замечания вытекает
следующее, важное для теории рядов следствие: для того
чтобы ряд
сходился, необходимо, чтобы его члены стремились к
нулю, по мере удаления от начала ряда, иными словами,
чтобы ип -> 0, когда п -> оо. В самом деле, в сходящемся
ряде, согласно критерию Коши, величина I Sn+P — Sn I
стремится к нулю, когда п стремится к бесконечности.
Можно, в частности, предположить, что числа п + р
и п различаются только на единицу, т. е. что р = 1.
Тогда:
Sn+i-Sn = (u1 + u2 + u3 + ...+ un + un+1)-
-(Ui + u2 + ... + un) = un+1.
Итак, величина
•Sn+i — «Ьд = un+i
должна стремиться к нулю, когда п стремится к
бесконечности 1).
1) Очевидно, полученный результат (ип+1 -v 0 при п -*• оо)
нисколько не отличается от первоначально формулированного (ип -*-
-> 0 при п ->■ оо), так как оба означают, что величина члена
сходящегося ряда стремится к нулю, когда номер члена неограниченно растет.
61

Таким образом, относительно ряда
sin l° + sin20 + sin30 + sin40+sin50 + ... + sinAz° + ...
можно наверное утверждать, что он расходится. В самом
деле, среди его членов будут такие, как sin 90° = 1,
sin 270° = —1, sin 450° = 1, sin 630° = —1, ..., причем
эти члены, равные единице по абсолютной величине,
будут встречаться, как бы далеко мы не ушли от начала
ряда (например, на 360 000 090-м месте будет находиться
член
sin 360 000 090° = sin (1 000 000 • 360°-f 90°) = sin 90° = 1).
Таким образом, члены ряда не стремятся к нулю, а
потому ряд не может сходиться. (Если бы он сходился,
то, согласно следствию из критерия Коши, его члены
стремились бы к нулю.)
Из критерия Коши следует, что и сумма любого числа
рядом стоящих членов ряда стремится к нулю при
условии, что первый член этой суммы берется все дальше
и дальше от первого члена ряда.
В самом деле, критерий Коши утверждает, что в
сходящемся ряде Sn+P — Sn -► 0, когда п -^ оо.
Но
= («1 + "2 + «3 + -•■+"« +"я+1 + "я+2 + ... + «л+р) —
- («1 + «2 + U3 + • • • + "ft) =
= Un+l + W„+2 + Un+3 + ...-{- Un+pt
и поэтому в сходящемся ряде сумма
и л+1 + Ыя-ю+ ... + «/!+/>-> 0, когда п->со.
Поэтому, например, ряд
+ "5" + "5"+5" + У + "5" + 'б" + --"
члены которого стремятся к нулю по мере удаления от
начала ряда, все же расходится, так как сумма равных
62

между собой членов все время равна единице, т. е. не
стремится к нулю.
Рассмотрим еще ряд
^ п+1 ^ п + 2 ^ •••,
носящий название гармонического ряда. Члены его снова
стремятся к нулю. Но этот ряд, тем не менее, расходится,
1 1
так как сумма его членов от члена . до члена ^п
равна
—— + ——+ —— + +-^— >
2« + 1 i 2* + 2 ' 2Л + 3 ' *#* * 2Л+1 ^
2п членов
111 1 2" 1
^ 2«+Г i 2n+l ' 2Л+1 ' * * * * 2*+l == 2n+l == ~2
и, следовательно, к нулю не стремится.
Особое значение критерия Коши заключается в том,
что он дает не только необходимое условие для
сходимости ряда (т. е. условие, при невыполнении которого ряд
расходится), но и достаточное условие сходимости ряда.
Иными словами, если в некотором ряде
и1 + и2 + и3 + и4 + иъ + ... + ип + ип+1-\-...
разность двух частичных сумм
$п+р — Ьп,
m. е. величина
может быть сделана сколь угодно малой {по абсолютной
величине) при достаточно большом п, то ряд
и1 + и2 + и3 + и4 + иь + ... + ип + ип+1 + ...
сходится.
Чтобы убедиться в этом, станем следить, как располагаются на
числовой прямой точки, изображающие частичные суммы ряда.
Согласно предположению, можно выбрать п достаточно
большим, для того чтобы утверждать, что все частичные суммы, следую-
63

щие за Sn, будут отличаться от нее не более чем, например, на 0,1.
Отложив по обе стороны от точки Sni (пх > п) по 0,2, мы получим
интервал АХВХ (рис. 7) длины 0,4, внутрь которого попадут все
точки, изображающие Sn +1, «SWt+2, Sn +3, Sni+4,... Более того,
так как длина интервала равна 0,4, a Sn +1, Sn +2, Snj+3, ...
отличаются от Sn (соответствующей середине интервала) не более чем
на 0,1, то точки Sn +1, Sn +2, «S^+з»... не будут приближаться
к краям интервала Ах и £х ближе чем на 0,1. Возьмем теперь
частичную сумму Sn с настолько большим номером п2 (п2 > пх)у чтобы все
следующие отличались от нее менее чем на 0,01, и отложим от точки
S„2 вправо и влево по 0,02. Тогда мы получим новый интервал А2ВЪ
целиком лежащий в АХВХ. При этом все точки Sn +1, Sn +2, Sn +3» •••
будут ложиться в этот интервал, ближе к его середине, не
приближаясь к краям Л2 и В2 интервала более чем на 0,01.
|Ч \АЖ A3fjir^t В2 \в,
-о-нси-
S»2 3"Z 5"t
Рис. 7.
Далее выберем частичную сумму Sn3 с еще большим номером
пз (пз > п2 > ni) c таким расчетом, чтобы все следующие частичные
суммы Sn +l9 S„ +2> 5Я +з» ••• отличались от Snz менее чем на 0,001.
Откладывая от Sn по обе стороны расстояния 0,002, получим
очень маленький интервал A3B3t внутри которого (на расстоянии
по крайней мере 0,001 от его краев) будут лежать все точки
^"з+i» ^"з+2> S«3+3»'"» изображающие частичные суммы,
следующие за Sn .
Продолжая поступать таким же образом, т. е. отыскивая точку
Sn< (л4 > п3> п2> пх) такую, что I S„4+p — S„4 I < 0,0001,
потом S„b (пъ > пА> п3> п2> пх) такую, что I Sn^p — S„5 | <
< 0,00001, и т. д., получим множество интервалов AxBlt A2B2t
A3B3t Л4£4, ЛбВ5, Лв£б,... все меньших и меньших длин: 0,4; 0,04;
0,004; 0,0004; и т. д., вложенных один в другой, причем в каждом из
этих интервалов будут, начиная с некоторого номера, заключаться
все частичные суммы (именно, в АХВХ — все, начиная с Sn , в А2В2 —
все, начиная с Sn2, в А3В3 — начиная с S^3, и т. д.). Очевидно, что
все эти интервалы будут стягиваться к одной и той же точке S,
лежащей внутри каждого из них. Очевидно также, что именно вокруг
этой точки сгущаются точки, изображающие частичные суммы.,
Поэтому S есть предел чисел Sly S2> ...,S„lt S„1+1,..., 5Л2, ..., S„3,...,
которые в свою очередь можно рассматривать как все более и более
точные приближения «S. А раз Sn -*- S, когда п -* оо, то это
64

и значит, что ряд
"\+U2 + U3 + U* + UK + '- + tln+Un+i + ...9
из которого брались частичные суммы, сходится, и его сумма равна S.
В качестве примера непосредственного применения
критерия Коши докажем сходимость ряда
1 + 2*" + з1 + 42- + 52- + ••• + /?+ (/г+1)2 +•'"
Для этого надо рассмотреть сумму любого числа его
членов, начиная с п +1-го члена:
(П+1)2 ^(п + 2)2 ^(л + 3)» -Г'--"Г(л + р)1'
и доказать, что эта сумма может быть сделана сколь
угодно малой, при достаточно большом п (независимо от
того, чему равно р). Доказательство получается почти
тотчас, если заметить, что
' ■<: '
1 < '
(я + 2)»~^(п+1)(п + 2)'
1 <; '
(п + 3)2^(«+2)(п + 3) '
' :<; '
(п + р)*^(п + р-\)(п+р)'
(Каждая из дробей, стоящих в правых частях неравенств,
имеет меньший знаменатель, чем дробь, стоящая в левой
части, и потому больше последней.)
Далее,
1 = _1_ 1_
п(п+\) п п+\ '
1 1 1
(п+\)(п + 2) п+\ п + 2'
1 _ 1 1_
(п + 2)(п + 3) ~~ п + 2 п + 3 '
1 1 1
(п + р—\)(п + р) п + р—\ п + р
(как легко проверить простым приведением к одному
знаменателю дробей, стоящих в правых частях этих
65

равенств). Поэтому
1 + ' + * + + ' <
~ In Л. 912 ~ InЛ. 3W ~ ' ' ' ~ (п Л. п\2 ^~
(л+1)« Чл + 2)« ■ (я + 3)2 (п + р)2
< L_ + ! - - 1
л(л+1) ^(я+1)(я + 2) ^•••т-(я+р-1)(я + р)
1 1,1 1,1
п п+1 ~ n + l n+2~n + 2
Итак,
I 1 * _ 1 * ^1
ш"^ п+р—1 п+р л л+р ^ п *
(л+1)2 ~ (л + 2)2 ^(я + 3)2 ^'"^(л+р)а ^ п '
т. е. эта сумма, действительно, сколь угодно мала, если
только п достаточно велико. А отсюда, согласно
критерию Коши, следует сходимость данного ряда.

ГЛАВА V
ПРИЗНАКИ СХОДИМОСТИ
На практике, чтобы установить, сходится ли
некоторый ряд
и1 + и2 + и3+щ+и5+...+ ип + ип+1 + ...
или нет, пользуются не общим критерием Коши, а
различными специальными критериями. Из них мы
рассмотрим здесь только два критерия: критерий Лейбница для
знакопеременных рядов с убывающими членами и
критерий Даламбера для рядов с положительными членами.
Особенно простой критерий получается для так
называемых знакопеременных рядов с убывающими членами.
Знакопеременным называется ряд, члены которого
попеременно то положительны, то отрицательны. Таковы,
например, ряды
2^3 4^5 6^7 '••' [ }
1~75+7i~7i+7t~7t+7f~"'' (l0)
2 ~ 3 22 ~ 5 23 ' 7 24 ~
+ W + TT —•• <П>
sin2!» sin2 2» . sin^» sin8 4* . sin25Q ,«2\
1 22 ""■"" 32 42 "■" 52 * * * * ' '
2-1у + 1Т-1Т + 1И-1й + 1Н—• (13)
В первом, втором и последнем из этих рядов
абсолютные величины членов все время убывают, т. е.
67

абсолютная величина каждого последующего члена
меньше абсолютной величины предыдущего члена.
Так, в ряде (9):
в ряде (10)
1
в ряде (13):
1>±>±>±>±>±>
i>--> — >-L>J->-L >
2>l|>l|>li>ll>,..
Лейбницу принадлежит следующая теорема
(называемая обычно правилом Лейбница): если в знакопеременном
ряде абсолютные величины
членов все время убывают
и, кроме того у стремятся
к нулю, то ряд сходится.
На основании этого
правила ряды (9) и (10)
сходятся.
В ряде (13) члены хотя
и убывают, но не стремятся
к нулю (они, очевидно,
стремятся по абсолютной
величине к единице). А так
как во всяком сходящемся
ряде (в том числе и в
знакопеременном) члены должны
стремиться к нулю, как
мы видели на стр. 61,
то ряд (13) не может
сходиться, т. е. он
расходится. Что касается
рядов (11) и (12), то хотя в каждом из них члены и
стремятся к нулю (в ряде (12), например, 1-й член меньше
1 по абсолютной величине, 2-й меньше ^, 3-й меньше^
и т. д., вообще я-й член, по абсолютной величине равный
2"° всегда не больше
Г. ЛЕЙБНИЦ
(1646—1716).
sin2n° ^ 1
-—=—, не больше -г, так как sin*/z
единицы), но зато абсолютные величины членов этих
рядов не все время убывают. Так, в ряде (11) абсолютная
68

величина 6-го члена есть ^ = -g-, а абсолютная величина
7-го есть у > -о-- Дальше идет член, абсолютная величина
11 11
которого есть йг = yg» а за ним 1г>Тб-
В ряде (12) абсолютная величина 180-го члена равна:
S1" , =0, а абсолютная величина 181-го члена:
loir
sifi2 1Я1°
—j-gjg— >0t T- e- больше абсолютной величины
предыдущего. Точно так же в этом ряде абсолютная величина
361-го члена больше абсолютной величины 360-го, и т. д.
Поэтому правило Лейбница неприменимо к рядам (11)
и (12), и мы без специального исследования не можем
сказать, сходятся эти ряды или нет.
Но вернемся к правилу Лейбница и убедимся в том,
что оно верно. Именно, предположим, что в
знакопеременном ряде
«1 — Щ + ^3 — и4 + и5 — щ + щ —... (14)
(мы считаем здесь иъ и2, и3, м4, ... положительными
числами) абсолютные величины членов все время убывают,
т. е.
иг > и2 > и3 > и4 > иь > uQ > щ > ...
и, кроме того, стремятся к нулю: lim un = 0. Нужно
доказать, что ряд (14) сходится. При доказательстве
проще всего воспользоваться геометрическим
представлением чисел. Именно, будем отмечать на числовой оси
(рис. 8) точки Sb S2, S3, S4, S5, Se, S7, ..., изображающие
частичные суммы нашего ряда. При этом точку Sx
получим, отложив вправо отточки 0отрезок, равный их (Sx =*
= иг). Вторая частичная сумма S2 = их — и2. Поэтому
для получения точки S2 отложим от точки Si отрезок и2
влево. Так как по условию иг > и2У то точка S2 будет
лежать между 0 и Si. Третья частичная сумма равна
S3 = их — и2 + и3 = S2 + и3. Поэтому точку S3 можно
получить, отложив от точки S2 вправо отрезок длины и3.
Точка S3 должна очутиться между Sx и S2, так как и3
по условию меньше и2. Таким же образом, откладывая от
точки S3 отрезок и4 влево, получим точку S4, лежащую
между S2 и S3; затем точку S5, лежащую между S3 и S4,
и т. д. Легко видеть, что таким образом будет получаться
69

картина, отмеченная на рис. 8, т. е. точки,
изображающие частичные суммы Su S3, S5, S7, S9, ... с нечетными
номерами, будут располагаться одна за другой в
направлении справа налево; точки 52, S4, S6, S8, S10, ...,
изображающие частичные суммы с четными номерами, будут
располагаться также одна за другой, но в направлении
слева направо. При этом любая точка с четным номером
будет лежать левее любой точки с нечетным номером и,
наконец, расстояния между точками каждой пары:
Si и S2, S2 и S3, S3 и S4, 54 и о5, о5 и Se, ..., S2k-i и S2^,
S2k и S2k+U ..., становятся все меньше и меньше, стремясь
в пределе к нулю. Последнее обстоятельство следует из
I
I
I
I
ir
\s«
1
из-
-u5-
4 Ь
— u7 ^ 1
-0-9—•—([>—<J—(j>—
^ $81 $0$ |^Г7|%
i I 1 u^j 1 1
1 1
u.
1
Рис. 8.
того, что указанные расстояния равны абсолютным вели*
чинам членов ряда (14) ии и2, и3у и4, иъ, и6,..., u2ky ы2/?+ь...,
которые, по предположению, стремятся к нулю.
Из сказанного ясно, что должна существовать точка S,
отделяющая точки с нечетными номерами от точек с
четными номерами, так что первые лежат правее S, а вторые
левее (рис. 8). Ясно также, что точка такого рода может
быть только одна, так как между точками каждой пары:
oj, о2; о2, о3; *Ь3, о4; о4, о5', *Ь5, ов; ...; o2/?_i, о2^ «Ьг/?»
^2к+ъ ••• и т. д., не могут все время находиться одни и
те же две точки S и S'. Иначе расстояние точек каждой
пары не могло бы сделаться меньше, чем длина отрезка
SS' (рис. 9).
Наконец, ясно, что частичные суммы Su S2, S3, S4,
S5, Se, ..., S2fe, S2ff+U ... будут стремиться к числу S
(соответствующему точке S), как к пределу, иными словами,
расстояния от точек, изображающих частичные суммы,
70

до точки S будут стремиться к нулю. Это следует из того,
что расстояние от точки S до любой из двух точек S2k
и ^2*+1 меньше, чем расстояние от точки S2k до S2k+i
(рис. 10). Последнее равно u2k+u т. е. величине, которая,
по предположению, стремится к нулю.
р* и2* 1
I р Щ»1 *1 |
-о- 6 Ь *. »—^ i—*
^ %ю АI
u *2/г*| 1
Рис. 9.
Итак, мы доказали, что существует число S, к
которому стремятся как к пределу частичные суммы ряда (14).
А это и значит, что ряд (14) сходится, и его сумма есть S:
U1 — U2 + U3 — Ut + Ub — UQ + ...— U2k + U2k^ — .. . = S.
Из нашего рассуждения вытекает больше, чем
простая сходимость ряда (14). Именно, мы видели, что все
Рис. 10.
частичные суммы ряда с четными номерами (т. е. суммы
четного числа членов ряда) меньше, чем сумма S ряда,
т. е. представляют приближенные значения S с
недостатком, а суммы с нечетными номерами больше, чем S, т. с.
"г/г*/
Рис. 11.
представляют приближенные значения суммы ряда с
избытком. Но самое важное это то, что мы можем оценить
ошибку, с которой частичная сумма S2k или S2M
представляет сумму ряда (14). А именно, из рис. 11 следует, что
0 < S — S2k < k2*+i»
71

и из рис. 12 следует, что
Эти два результата можно сформулировать в виде
одного очень полезного правила: отбрасывая в
знакопеременном сходящемся ряде, члены которого все время
убывают (по абсолютной величине), все члены, начиная с
некоторого, мы делаем ошибку, меньшую по абсолютной
величине, чем первый отброшенный член.
S2K*2 S $2K+t
Рис. 12.
Так, например, в случае ряда:
2 "*" 3 4~r5 6 ^ 7 8 "~ 9 10"1" 11
можно утверждать, что его первые десять членов
представляют его сумму, во-первых, с недостатком (как
частичная сумма четного числа членов) и, во-вторых,
с ошибкой, меньшей уу (так как первый отбрасываемый
член есть уу). Итак, в этом примере
S10<S<S10 + 1y^S10 +0,091.
Вычисляя S10, получаем
+ 1 = 1,000 -у =-0,500
+ у = 0,333 -у= -0,250
+ у = 0,200 -у =-0,167
+ | = 0,143 -у =-0,125
+ 1 = 0,111 —^ 0,100
+ 1,787 —1,142
510 = 1,787- 1,142 = 0,645.
72

Итак
0,645 < S < 0,645 + 0,091 = 0,736.
В последней главе этой книжки мы вычислим
обходным путем сумму ряда
2^3 4^5 6^7 8^9
с большой точностью. Мы увидим, что она равна
0,69314718 ...
Рассмотрим еще пример знакопеременного ряда:
22 ^ З3 4* ~ 55 6е ^ V 88 * * *
Очевидно, что абсолютные величины его членов все
время убывают (l >^>^->^->^->ei->...) и
стремятся к нулю.
По теореме Лейбница этот ряд сходится. Найдем его
сумму с точностью до 0,00005. Для того чтобы
гарантировать такую точность, нужно, чтобы первый из
отброшенных членов был по абсолютной величине меньше, чем
0,00005 =2q-qqq, т. е. чтобы этот член представлял дробь
со знаменателем, большим 20 000. Но 22 = 4; З3 = 27;
44 = 256; 55 = 3125 и 6е = 46 656. Итак, уже шестой
член нашего ряда — -^ удовлетворяет этому требованию.
Ограничиваясь поэтому суммой первых пяти членов ряда
(которая дает приближенное значение суммы ряда S
с избытком, как частичная сумма нечетного числа членов
ряда), можем утверждать, что
S5>S>S5-^^S6-0,000021
(где — 46 656 = ~~ 6*" пеРвы" из отбрасываемых членов
ряда]. Вычисляя S5, получаем:
1= 1,000000
А-1 =0,037037 -^ = -| =-0,250000
j = sk = ^mm ^4^'2-56 = -°-003906
1,037357 —0,253906
55 = 1,037357 - 0,253906 = 0,783451.
73

Итак,
0,783451 >S> 0,783430.
Поэтому можно положить S = 0,78344 с ошибкой,
меньшей 0,000011.
После знакопеременных рядов с убывающими членами
рассмотрим знакопостоянные ряды, т. е. ряды, все члены
которых имеют один и тот же знак. Очевидно, здесь
достаточно заняться рядами с положительными членами,
так как в случае, когда все члены ряда отрицательны,
можно вынести общий знак минус за скобку и иметь дело
лишь с рядом в скобках с положительными членами.
На примере гармонического ряда
мы видели, что для рядов с положительными членами
члены могут стремиться к нулю и, однако, ряд не будет
сходиться. В этом смысле случай рядов с
положительными членами сложнее, чем случай знакопеременного
ряда с убывающими членами, так как там вопрос решался
полностью стремлением членов к нулю.
Однако и здесь можно получить очень удобный (но
годный не во всех случаях) признак, если
рассматривать поведение не только одного члена ряда, по мере
удаления от начала ряда, а поведение пары соседних членов
и именно — поведение их отношения.
Навести на эту мысль может хорошо знакомый
пример геометрической прогрессии:
где
u1 = at u2=aq, u3 = aq2, u4 = aqzt w5 = a<74, ...
..., un = aqn-1, un+1 = aqn, ...
Здесь отношение двух соседних членов —
последующего к предыдущему — остается одним и тем же для
всех членов ряда:
И мы знаем, что при q < 1 (мы считаем q положительным)
ряд (геометрическая прогрессия) сходится, и его сумма
74

равна
а в случае q ^ 1 ряд расходится.
Нечто подобное можно установить и для более общих
случаев рядов с положительными членами. Вообще
говоря, в ряде
отношение последующего члена к предыдущему не будет
оставаться одним и тем же, но будет меняться от члена
к члену.
Так, например, в случае ряда
1 + ^ + т + т + --- + т + ;г+т + ---
имеем:
ltl 112
tt2-"i = -o-: 1 =-9-; и3:и2 = '
*2*и1 — 2 — 2 ' ь*з*и2 — 3*2 — 3*
1.1 3 . _1.1_4.
«4 •' из — "J" • з ~~ Т' ^б ' ^4 ~~ "5" * Т ~~ 5 ''""'
_ 1 1 _ п
В случае ряда
^ Ь2 ^Ь2. 3^ 1-2.3.4 ^ 1.2.3.4.5^""
•'•+ 1.2-3.4-5...п+ Ь2.3-4.5...(л+1) "^,"
отношения таковы:
_ 1 - _ 1 1 . 1 _ 1 .
U2.UX — у^2 • [ — Y' ^3 * ^2 — 1.2 • 3 * 1 • 2 — 3 '
ил:и* =
1 1 1
*4-"з— Ь2.3.4'1.2.3" 4'
1 . 1 _ 1 ,
иь : "4 — i . 2 . 3 .4 • 5 : 1 • 2 • 3 • 4 5 ;
«л+1 : «/I =
1 1
л+1- "л— 1.2-3...п. (л+1) ' Ь2.3... л л+1 '
Теорема (критерий) Даламбера утверждает, что ряд
сходится, если отношение последующего члена к предыду-
75

щему не больше некоторого числа q% в свою очередь
меньшего единицы, т. е.
и„
S<7<1;
и ряд расходится, если это отношение не меньше единицы,
т. е.
"л ^ '"
Заметим, что, применяя эту теорему, мало знать, что
отношения ^^ меньше единицы. Теорема требует, чтобы
ип
эти отношения были меньше одного и того же числа q,
меньшего единицы. Так, в первом из приведенных выше
примеров (гармонический ряд) отношения по порядку
суть:
J_. A A. ±- A. A. L. . п
2 J з ; 4 ' 5 ' 6 ' 7 ' 8 ' •••' п+\ ' "•'
*) В этой общей форме теорема была сформулирована и доказана
Коши в его книге «Алгебраический анализ» (1821 г.). У самого же
Даламбера в его «Математических заметках» (Opuscules mathemati-
ques, 1768 г.) мы находим только исследование отношения
последующего члена к предыдущему в случае биномиального ряда. Если это
отношение по абсолютной величине меньше единицы, т. е.
последующий член меньше предыдущего, ряд называется «сходящимся»,
если больше единицы, то «расходящимся». С этой точки зрения гар-
моническии ряд1+-~- + -^- + -г + ...Н Ь ••• следует называть
«сходящимся», хотя он и не имеет суммы (стр. 63).
Один и тот же ряд может быть «сходящимся» в начале и
«расходящимся» в конце, и наоборот. Даламбер приводит пример
биномиального разложения (1 + х)1/2 при #=tqq. Он показывает,
что если рассматривать первые 300 членов этого разложения, то
они будут убывать, т. е. для них будет наблюдаться «сходимость»,
а начиная с 302 и далее — возрастать, т. е., как говорит Даламбер,
«ряд начнет расходиться». Другой пример — разложение (1 + х)~2
99
при д:=——; соответствующий ряд «расходится до 99-го члена»,
а дальше становится «сходящимся».
Отсюда видно, что Даламбер был далек от того, чтобы дать
признак сходимости рядов в том смысле, как это понимал Коши и
как это понимаем мы теперь. Все же признак носит имя Даламбера,
так как в этом признаке рассматривается отношение последующего
члена ряда к предыдущему, а именно Даламберу принадлежит
заслуга изучения этого отношения (хотя и в частном случае).
76

Все они меньше единицы, но они стремятся к единице
как к пределу. Поэтому не существует числа q (меньшего
единицы), которое могло
бы «отгородить» эти
отношения от единицы.
Действительно, если бы было
такое число q (q < 1)
большее, чем все отношения, то
все они отличались бы от
единицы больше, чем на
1—q> а потому не могли бы
стремиться к ней, как к
пределу. Итак, в случае
гармонического ряда
теорема Даламбера не
позволяет сделать никакого
заключения. Мы выяснили
раньше (на стр. 63), что
гармонический ряд расходится.
Во втором примере (ряд 1 +ут2"гТТ2^з_гГ. 2.3.4 ' " 7
отношения последующих членов к предыдущим по
порядку таковы:
_L. J_. _L. _L. _!. J_. i
2; з; 4; 5; 6 ; 7 ; •••; n+1 ; •••
Мы видим, что все они не больше чем q = у. Итак,
в этом случае
Ж. ДАЛАМБЕР
(1717—1783)
1
1
1
1, ^=^ О ^- Х>
и из теоремы Даламбера следует, что ряд сходится.
Возьмем, наконец, ряд
1
i i i_ _j \
32
1 + 22 + 32 + 42 + 52 "+~ * * * "^ п2 ~^ (п+ I)2
42 i 52 ' '" ' п2
Здесь отношения последующих членов к предыдущим
равны по порядку:
22 : [ — 4 • З2 : 22 "" 9 ' 42 : З2 16*
J_.J_ _ ]6ф J_. _L__ ?5.
5я" ! 42 — 25; б2 : 52 ~~ 36; *# •'
1 1 л2 я*
(п+1)2 'я2 (л+1)2 п2 + 2л+1 ' "
77

Сразу видно, что все отношения меньше единицы. Менее
очевидно, что они стремятся к единице как к пределу.
Однако это станет ясным, если переписать отношение
п2
(п + 1)-го члена к n-му, равное п2 , 2п ■ i» в ви^е
1 ,
о г (мы разделили и числитель и знаменатель
^ п ^ п2
2
дроби на я2). Если п неограниченно возрастает, то —
1 1.2,1
и ^ стремятся к нулю,1 Н \- -^ стремится к единице,
следовательно, и вся дробь ^ г стремится к еди-
1 + 7Г + ^
нице. Поэтому здесь не существует числа q, меньшего
единицы и большего всех отношений. Таким образом,
критерий Даламбера неприменим к данному ряду. На
стр. 65—66, пользуясь критерием Коши, мы доказали,
что этот ряд сходится.
После этих поясняющих теорему примеров приступим
к ее доказательству. Выпишем сначала одно за другим
неравенства:
^<я ^-<я ^-<я ^<я ^±*<я
(q < 1), существование которых предполагается в
первой части теоремы. Из них следует, что
"г «£ Щъ
и& < quit
«з
• • .
<<7"г,
, «*+i<
«4^
дип,
quz
• • •
Так как u3^qu2, a u2^qul9 то ив^ q*(qu^% т.е.
&з ^ q2Ui- Далее, «4 ^ qu3; пользуясь только что
полученным неравенством u3^q2ult находим: и4 ^ q^iq2^)
или и4 ^ ^i- Совершенно так же мы получим: иъ ^
^ <fux* Щ ^ <fux и т. д. Вообще,
un*\<zqnux (15)
при любом номере /г.
(Заметим, что если бы исходные неравенства
78

можно было заменить равенствами
иг ч> и2 ч> и3 ч> "■•• */„"•••••
т. е. если бы данный ряд представлял геометрическую
прогрессию, то доказанные нами неравенства
u2^qul9 u3^q2uu uu^q3uu ..., un+1^qnulf ...
перешли бы в хорошо известные формулы для членов
геометрической прогрессии:
u2 = quu u3 = q2uu ui = q3uu ..., un±1 = qnuu ...)
Установив это, воспользуемся критерием Коши, для
чего рассмотрим сумму любого числа членов ряда,
начиная с (п + 1)-го:
Так как
"n+i<^if tin+2^qn+1ul9
un+3^<ln+2Uu • ••» tin+p^q^P-1^,
то эта сумма меньше или равна
qnut + qa+1ux + qn+2ux +... + <f**-xux =
= Qntii^+q + q2 + ... + qP-1) = qnu^^<qnu1~.
Мы нашли, таким образом, что
.... qnUi
Un\\ -\- ип+2 + Un+З "Г • • • "Г ип+р < J^— •
Но правая часть этого неравенства представляет
произведение
Первый множитель у^— не меняется с ростом п. Что
касается второго множителя qn> то он, как п-я степень
положительного числа qt меньшего единицы, становится
тем меньше, чем больше я, и при п неограниченно
возрастающем, стремится к нулю. Но тогда и правая, а тем
более левая часть неравенства стремится к нулю, т. е.
мы доказали, что сумма
79

может быть сделана при достаточно большом п
(независимо от р) сколь угодно малой. А это и значит, по
критерию Коши, что ряд
Ы1+И2 + "з + ы4 + И5+... + Ил + «/т + .-.
сходится, что и утверждает первая часть теоремы.
Из приведенного доказательства вытекает не только
сходимость ряда, т. е. существование определенного
числа S, к которому как к пределу стремятся частичные
суммы S1$ S2t S3, S4, ..., Sni ... ряда, но и возможность
оценить ошибку, которую мы делаем, беря для
вычисления 5 частичную сумму ряда Sn = щ + и2 + us + •••
...+ ип. Действительно, эта ошибка равняется сумме
отбрасываемых членов ряда
Ып\\ -\- Urn 2 ~Г ^л+3 1 ^л+4 ~Г • • •
А так как при любом р
QnU\
Un+1 "Г ^Л+2 ~Г ^Л+3 I • • • "Г Un+p < j Q >
то и сумма ряда ип+1 + ип^ + un+z + un^ + ... будет не
больше чем т-^-, т. е.
q
Итак, ошибка в сумме ряда, вызванная отбрасыванием
всех членов, начиная с (п + 1)-го, не больше, чем
l-q-
Вернемся к примеру
II1,1, 1 1 1 ,
1Т1.2т1.2.3г1-2.3-4 ^ 1- 2-3-4- 5^*,#
Мы уже видели (стр. 77), что здесь отношения
последующих членов к предыдущим не больше чем у, и,
следовательно, этот ряд сходится. Более того, на основании
неравенства (16) можно утверждать, что ошибка, допущенная
при вычислении суммы ряда по частичной сумме его
первых 8 членов
ill,*,*, * ,
~r1.2"rL2.3't"l.2.3.4 "г" 1-2. 3-4- 5 ~г
^1.2.3-4.5-6^1-2-3.4.5-6-7^ Ь2-3-4-5-6-7-8'
80

меньше чем
p.t»»
- = Ц1 = (1)7 = ш-0^
2 2
В действительности, ошибка, равная сумме ряда
9!~ "^ ГоТ ~^~ ПТ ~^~ I2T ~^~ ГзГ "^ • *' ' '
(1.2-3-4-5-6-7-8-9 = 9!, Ь2.3-4.5-6-7.8.9-10 =
= 10! и т. д.), будет гораздо меньше, чем 0,008. В
самом деле, в ряде (17), образованном отбрасываемыми
членами, отношения последующих членов ряда к
предыдущим будут:
_!. 1 _ 1 1 . _1 _ 1 1.1 — 1
ТО!" :9!~ — 10' 11!": 10! ~~ 11 ' 12! ' 11! 12 ' —
Ни одно из них не больше уд. Поэтому для ряда (17)
можно взять «свое» q, именно, <7' = jq- Очевидно, для
членов ряда (17) будем иметь:
-1 = 1.1 1<(1]М 1<1)31
10! 10 9!' 11!^\10У 9!' 12!^\10/ 9! ' *" *
(Сравните с неравенствами (15), установленными в общем
случае.) Но отсюда следует:
1-1-1 4-JL-U-L-i- ^-1-i-i 1д-Ш2 1-L
9! ^10! "^11! "Т" 12! "^ * * * ^ 9! "^ 10 ' 9! "^ \ 10/ * 9! ""*"
+№),-i+--i['+i+(i),+(i),+-i-
= 1. —!— -1.1?- 10 - 1 -о оооооз
9! 1_ "" 9! 9 "~ 362 880 • 9 ~ 326 592 ~ и>ииииио*
10
Поэтому, пользуясь при вычислении суммы ряда
1+1+1+1+1+1+1+1+
'2! ^ 3! ^4! ^5! * 6! ^ 7! ^8! ^ '"
лишь первыми его восемью членами, мы делаем ошибку,
не большую чем 0,000003. Для того чтобы на эту малую
ошибку не повлияли еще и ошибки при обращении
членов ряда в десятичные дроби, следует брать последние
81

с точностью до половины 8-го знака после запятой.
Будем иметь:
1 = 1,00000000
1 = 0,50000000
1 = 0,16666667
1 = 0,04166667
1 = 0,00833333
1 = 0,00138889
1 = 0,00019841
1 = 0,00002480
S8= 1,71827877
(Вычисления здесь облегчаются тем обстоятельством, что
число второй строчки получается из числа первой строчки
путем деления его на 2; число третьей — из числа второй
путем деления на 3; далее переходим от строчки к
строчке, деля числа последовательно на 4, на 5, на 6, на 7 и
на 8.)
Итак, сумма ряда S равна 1,718279 с точностью до
0,000003.
Остается рассмотреть еще вторую половину теоремы,
т. е. доказать, что при ^±i^l ряд расходится. Этот ре-
зультат получается чрезвычайно просто. В самом деле,
по условию,
"2 ^ 1 "3 -^ 1 "4 ^ 1 "5 ^ 1 Un+1 ^ 1
откуда
и2^ ии и3^и2, иА^«з» tib^u49 ..., ил+1 ^ ил, ...,
т. е.
их ^ «2 ^ и3 ^ и4 < иъ <... ^ ип < и„+1...
А это значит, что члены ряда не меньше положительного
числа иъ и поэтому не могут стремиться к нулю. Но в схо-
82

дящемся ряде члены обязательно должны стремиться
к нулю. Следовательно, этот ряд не есть сходящийся,
а это и требовалось доказать.
Важно заметить, что при применении критерия Далам-
бера вовсе не нужно, чтобы неравенство
ИЛИ
выполнялось решительно для всех отношений, начиная
с первого из них. Достаточно, чтобы одно из указанных
неравенств выполнялось для всех членов, начиная с
некоторого (с третьего, с десятого, с тысячного и т. д.).
Например, в ряде
1 + ТТ + 2Г + ЗГ + 4Г + 5Г + бГ + #,#
отношения последующих членов к предыдущим суть:
1 -I J_ J_. J_ J_.
9 2 ' 3 ; 4 ' 5 ; 6 ' • • *
и нельзя сказать, что все они меньше некоторого числа q,
меньшего единицы (так как среди них есть число, равное
единице). Но, начиная с третьего, они не больше у.
Поэтому теорема Даламбера применима, и можно
утверждать, что ряд сходится. (Очевидно, этот ряд отличается
от подробно изученного нами ряда
1 + 2Г + зГ+4Г + 5Г + бГ + -'-
лишь одним добавленным членом — единицей. Поэтому
сумма нового ряда есть 1 + 1,718279 = 2,718279 с
точностью до 0,000003.)
Аналогично в ряде
lJ-A.Aj_A.A4-A1A.Aj_A1A.A4-
i_r 2 -*"" 6 "f 24^25 "»" 26^27^ 28 ^" 29 "^ 30 "■" 31 ■"'••
отношения членов суть:
А. А. А. 1А ZA !__:. !3А 1_А ?°А ?*А
2' 3; 4' 25' 52; 81 ; 112' 145' 180' 217' "в
83

Нельзя сказать, что все они больше единицы. Но
четвертое отношение и все остальные больше единицы. Отсюда
следует, что данный ряд расходится.
Общим основанием для последних утверждений
служит то обстоятельство, что первые члены ряда не могут
повлиять на самый факт его сходимости или
расходимости. Иными словами, можно приписать впереди данного
ряда сколько угодно новых членов или отбросить любое
число первых членов ряда (первые 10, 500, 1000 членов
ряда), и все-таки новый ряд будет сходиться, если
сходился первоначальный ряд (изменится только сумма на
величину добавленных и отброшенных членов), и будет
расходиться, если расходился первоначальный ряд.
Остается еще сказать несколько слов о сходимости
рядов, члены которых имеют любые знаки (т. е. не
обязательно чередующиеся или одинаковые знаки). Часто
удается свести вопрос о сходимости таких общих рядов
к вопросу о сходимости рядов с положительными
членами. Именно, вместо данного ряда
^ + U2 + U3 + U4 + U5 + UQ + . . . (18)
рассматривается ряд абсолютных величин членов ряда
\ui\ + \u2\ + \ih\ + \u4\ + \ub\ + \uB\ + ... (19)
Последний ряд есть ряд с положительными членами.
Если каким-либо образом (например, при помощи
критерия Даламбера) удастся установить, что ряд (19)
сходится, то тогда и данный ряд (18) сходится (но,
конечно, имеет вообще другую сумму, чем ряд (19)). В самом
деле, из сходимости ряда(19) следует по признаку Коши,
что сумма
I Ил+1 | + | Un+2 | + | Un+з I +• • •+ I "n+p I
может быть сделана меньше любого малого
положительного числа е, если только п достаточно велико
(независимо от того, чему равно р). Но тогда абсолютная
величина суммы соответствующих членов первого ряда (18)
I ип+1 + ип+2 + ип+3 +... + ип+р |
будет заведомо меньше е, так как всегда
I ип+1 + ип+2 +... + ип+р | ^
^|"Я+1| + |"я+2| + 1"я+в1+..-+|«11+р|.
84

(Действительно, среди чисел //Л+1, ип^ ип+3у ..., ип+р
в левой части неравенства могут быть числа разных
знаков, сложение которых равносильно вычитанию их
абсолютных величин. В правой же части неравенства
все слагаемые положительны, и поэтому при сложении
их величины фактически прибавляются одна к другой.)
Мы обнаружили, таким образом, что сумма
И/1+1 + ип+2 + ^л+з + • • • + ^л+р
может быть сделана сколь угодно малой при достаточно
большом п (и любом р). Но отсюда, опять-таки на
основании критерия Коши, следует сходимость данного ряда
uL + u2 + u3 + u4 + ... + un + un^ + .tt
Приведем примеры:
1-1- Lj-±_l±-1-1-±--!--1-JL-l.
22 За * 42 • 52 *" б2 72 82 92 102 ■"
Т- ц2 "Г 122 "Г 132 "Г 14а Т- 152 162 172 182
"ТЭ2"- 202"- 212"+ 222* + ..- (20)
Ряд абсолютных величин членов данного ряда есть
1+1+1+1+1+1+1,
х ~ 22 ' З2 ~ 42 ' 52 ' б2 ~ 72 ~ • •'
Этот ряд сходится (стр. 65—66). Следовательно, и данный
ряд сходится.
Рассмотрим ряд
2! 3! ^ 4! ^ 5! 6! 7! ^
+ 8Г + 9Г- ТО! ПТ~^,,# (21^
Ряд абсолютных величин его членов
1 + 1 + ± + ± + - + ^ + -1- +
^2! ^ 3! ^4! ^5! ^6! ^7! ^ " "
сходится. Следовательно, и данный ряд сходится.
Если для ряда (18)
их + и2 + и3 + и4 + и5 + ив + ... + ил + ип+1 + ...
сходится ряд абсолютных величин членов ряда
\и1 1+1^2 l + l "3l + KI + KI + ..'+KI + K+l| + ...,
85

то данный ряд (18) называется абсолютно сходящимся.
Таковы, например, ряды (20) и (21) в наших примерах.
Не всякий сходящийся ряд сходится абсолютно.
Действительно, ряд
2^3 4^5 6^7 8^9 10^*"
сходится (согласно правилу Лейбница), между тем как
ряд абсолютных величин его членов
1 + t + t + t + t + t + t + t + t + iS> + ---
есть расходящийся ряд.
Таким образом, ряд
I_l4.l-I4.l_l4- L_±4-±_±4-
2^3 4"t"5 6"1"? 8^9 lO"1--"
сходится не абсолютно (или, как говорят, условно
сходится).
Глубокое различие между свойствами абсолютно
сходящихся и условно сходящихся рядов проявляется
в том, что сумма условно сходящегося ряда может
измениться от одной лишь перестановки членов ряда, а сумма
абсолютно сходящегося ряда остается одной и той же
при любом порядке его членов.
Оставляя в стороне детальный анализ этих фактов,
приведем здесь пример изменения суммы условно
сходящегося ряда при перестановке его членов.
Рассмотрим условно сходящийся ряд
1_l4-l_l4-l-l4-l_l4-l-
2 "~ 3 4 "•" 5 6^7 8^9
— то + тт Т2 + тз — ••• (22)
На стр. 73 мы видели, что его сумма заключается между
0,645 и 0,736. Более точное вычисление показывает,
что эта сумма равна 0,69314718 ...
Переставим члены ряда (не меняя каждого из них
в отдельности) так, чтобы после двух положительных
членов шел один отрицательный. Получим ряд
^ 3 2 ^ 5 ^ 7 4^9^11 6 ^
86

Покажем, что сумма этого ряда не будет равна сумме
данного ряда.
Чтобы убедиться в этом, заметим, что новый ряд можно
получить из старого, если прибавить к нему ряд
1_1+1_1+1_1+1_1+
2 4^6 8 ^ 10 12^ 14 16^,#|
Действительно, выписывая эти два ряда один под
другим так, как это делаем мы:
1_± + ±_±+±_± + ±_±+±_± + ±_±4-±-±4-
2i"3 4^5 6^7 8^9 10 Ml 1243 1АТ'ш"
+ 1 _1 + 1 —L +- -1 4-1-
^2 4 ^6 8 МО 12 ^14 ""
и складывая стоящие друг под другом члены, получим
т. е.
^ 3 2 ^ 5 ^ 7 4^9^11 6 ^
4- 1 4-1 ! 4-
"•" 13+15"Т + ',#
Но сумма первого из складываемых рядов есть
0,69314718..., сумма второго, члены которого в два
раза меньше членов первого, есть у -0,69314718 =
= 0,34657359... Поэтому сумма ряда (22'), полученного
при их сложении, — ряда, отличающегося лишь
порядком членов от ряда (22), — есть 0,69314718 + 0,34657359 =:
= 1,03972077, т. е. не равна сумме ряда (22).
Этот вывод, на первый взгляд парадоксальный, учит,
что ряды, т. е. суммы неограниченно возрастающего
числа слагаемых, имеют, вообще говоря, другие
свойства, чем обычные суммы (конечного числа слагаемых).
Математики XVIII века часто упускали из виду это
обстоятельство, оперируя с рядами так же, как и с
конечными суммами, вследствие чего приходили иногда
к неверным заключениям.
В результате обстоятельных, хотя и весьма простых,
исследований первой половины XIX века (Коши, Абель,
87

Дирихле, Риман) было установлено, что лишь в
абсолютно сходящихся рядах можно произвольно менять
порядок членов и производить с этими рядами все
действия (сложение, вычитание, умножение, деление,
возведение в степень) так, как если бы это были обычные
суммы (с конечным числом слагаемых).
Что касается условно сходящихся рядов, то здесь,
переставляя члены надлежащим образом, можно добиться
того, что сумма полученного ряда будет равна какому
угодно числу, и даже добиться того, что новый ряд будет
расходиться.
Из этой особенности вытекает необходимость
всяческих предосторожностей во всех действиях над условно
сходящимися рядами. Например, умножение условно
сходящихся рядов можно производить, вообще говоря,
лишь в строго определенном порядке, затрудняющем
весьма часто приведение подобных членов результата.
Эти замечания мы будем иметь в виду в дальнейшем
и, прежде чем производить действия над рядами, будем
убеждаться, что ряды не просто сходятся, но сходятся
абсолютно.
В заключение этой главы выведем правило умножения
абсолютно сходящихся рядов.
Пусть
Ui + u2 + u3 + ... + un + ... = a
и
Vi + v2 + v3 + ... + va + ... = b
— два абсолютно сходящихся ряда. Докажем, что перемножая их
почленно и складывая произведения, получим новый сходящийся
ряд (называемый произведением данных рядов), сумма которого равна
Д'Ь. Прежде чем приступить к доказательству, поясним способ
получения произведения рядов. Помножим каждый член первого
ряда на Vi и выпишем ряд из произведений в одну строку, затем
в следующей строке, отступая на одно место вправо, выпишем ряд
из произведений членов первого ряда на и2, далее в третьей строке,
вновь отступив на одно место вправо, выпишем ряд из произведений.
тех же членов на v3, и т. д. Получим таблицу:
Ul-Vl + U2'Vi + U9-Vi + UA-Vi + ...
Ul-V2 + U2-V2 + U3-V2 + ...
u1-v3 + u2-v3+...
Если в этой таблице складывать по порядку члены, расположенные
в первой, второй, третьей и т. д. колонках, то получится новый
88

ряд:
«1 • 01 + ("2 -Vi + Uf V2) + (U3 .Vx + Ui-Vt + Ui- V3) +
+ (uA-v1 + u9-v2 + u2-v3 + u1-vA) + ...9 (23)
который и называется произведением данных рядов. Однако вовсе не
очевидно, что этот ряд сходится и что сумма его равна
произведению сумм данных рядов: а-Ь. Доказательство потребует довольно
длинных рассуждений.
Прежде всего рассмотрим ряды, составленные из абсолютных
величин членов данных рядов:
1%| + |"2| + |и3| + ...+ |^| + ...= Л
и
|fl| + |f2| + |f3|+...+ |fJ + ... = £
(сходимость их вытекает из того, что данные ряды абсолютно
сходятся). Образуем попарные произведения членов последних рядов,
расположив их в виде следующей таблицы I:
Н 1
N
•л+р
l4hll|4NJWN!...
I
4НЩ|41^!-..
4Ы1ЧНЬ№]....
кт
'.Фщ
и»№
1Ф1
Ivlk
ЧЫИЫКНЧ—Ы*К
\и>\\ЦНЫЫЫ— М*К1 — Ы*М| • • •
L
КМ^КНМКН^. • ЫЫ-.. -Kll^l • • • KI'M
м
89

В этой таблице выделена квадратная часть KL, содержащая
произведения, находящиеся на пересечении первых п строк и п
столбцов (п — какое-либо натуральное число). Составим сумму
этих произведений, обозначив ее Sn. Очевидно, что сумма
произведений, находящихся в первой строке выделенной части, равна
(l«l| + l«2l + |"8|+-..+ |tt«|)'|»l|.
во второй —
(\u1\ + \u2\ + \u3\ + ...+ \un\).\v2\t
в третьей —
(|"1| + 1"а| + |"8|+..-+|ИЯ|)'|08|.
и т. д., в п-й строке —
(\Ul\ + \u2\ + \u3\ + ... + \un\).\vn\.
Поэтому Sn равна произведению двух сумм:
Sn=(\u1\ + \u2\ + \u3\+... + \un\).(\v1\ + \v2\ + ... + \vn\).
Когда п неограниченно увеличивается, первый множитель стремится
к пределу Л, второй — к пределу В и все произведение — к
пределу А -В. Но Sn можно рассматривать как частичную сумму п
членов некоторого ряда, отдельные члены которого получаются путем
сложения произведений, находящихся в коленчатых частях нашей
таблицы, помеченных номерами 7, 2, 3, ..., л,...:
I «1 | ' | fl | + (| "2 | • I fl | + | tl2 | . | V2 \ + \ Ut | • | V2 |) +
+ (\u3\.\Vl\ + \u3\.\v2\ + \U3\.\v3\ + \u2\.\v3\+\U1\.\V3\) + ...
Следовательно, этот ряд сходится и сумма его равна А'В. В силу
критерия Коши (стр. 61) разность двух частичных сумм Sn+p — Sn
может быть сделана сколь угодно малой при достаточно большом п
и любом р. Если е — какое-либо положительное число, то можно
указать такое натуральное число N, что при п^ N будет выполняться
неравенство
$п+р — $п < ~2 •
Так как Sn есть сумма произведений, заключенных в квадрате
KL, a Sn+P — сумма произведений, заключенных в КМ, то
Sn+p — Sn есть сумма произведений, заключенных в коленчатой
фигуре LM. В силу сказанного эта сумма будет меньше чем у,
если n ^ N, а р — любое число.
Отсюда следует далее, что сумма любого количества
произведений из таблицы I, расположенных вне квадрата К7, будет также
g
меньше -у. В самом деле, всегда можно подобрать такое число п^> N
и столь большое натуральное число /?, чтобы соответствующая
коленчатая фигура LM охватила все эти произведения. Так как каждое
произведение есть число неотрицательное, то их сумма будет не
больше суммы всех произведений, заполняющих коленчатую фигуру,
т. е. будет меньше -=-.
90

Возвратимся к исходным рядам
vi + v2 + v3+... + vn + ... = b
и составим таблицу II, в которой будут стоять попарные
произведения членов этих рядов:
К 1
77 &
П+/
./ / / / /
уЩ Ъ/и* v2/ /ипЧ v2/\v\
/ / /
V
/
/ /
/
/
/
/
/
V/un+iy- • • •
/
/\^2
/
/
/ /
/ /
/ /
/ /
/ /
/ /
/
/
/
/
/
./.
/
/
/
/
/
/
/
/
/
/ /
/ /
/ /
/ /
«Wft.
/
/
/
у
Очевидно, что таблица I получается из таблицы II, если каждое
произведение из этой последней заменить его абсолютной величиной.
Поэтому абсолютная величина суммы любых произведений таблицы II
не превосходит суммы произведений, стоящих на тех же местах
в таблице I.
Сумма ап произведений таблицы II, заключенных в треугольнике
KPQ, может быть записана в виде
<уя = "1 * 01+ ("2 • »1+ "i • 0г) +
+ ("з -vl + u2.v2 + иц)3) +... + (unvx + un.xv2 +... + и&п).
Отсюда видно, что эта сумма совпадает с частичной суммой п членов
ряда (23). Чтобы доказать, что а„ -*• а-b при п -*- оо, заметим сна-
91

чала, что ап отличается от суммы $п всех произведений той же
таблицы II, заключенных в квадрате KL, на сумму произведений,
заключенных в треугольнике PLQ. Но абсолютная величина
последней суммы не больше суммы произведений таблицы I, стоящих на
соответствующих местах. Если взять п > 2Л/, то, как видно из
рис. 13, все такие места будут находиться вне квадрата /С/. Поэтому
/Г / 2 J
Рис. 13.
сумма произведений таблицы I, стоящих на этих местах, будет
меньше — и, следовательно, абсолютная величина суммы
произведений таблицы II, находящихся в треугольнике PLQ, будет также
меньше чем —. Итак,
\on-sn\<-o--
Сумму sn всех произведений таблицы II, заключенных в
квадрате KL, можно определить тем же способом, как выше подсчиты-
валась сумма 5Я. Именно, подсчитываем сначала суммы
произведений, стоящих в первой строке, затем во второй и т. д., в n-й строке,
и складываем полученные суммы. Найдем:
sn = ("i + "г + "з + .- + "/*) (Vi + v2 + v3 + *.. + vn).
Когда п неограниченно увеличивается, первый множитель здесь
стремится к пределу а, второй — к пределу 6, a sn — к пределу
а • Ь. Поэтому при достаточно большом п (п ^ Nx) будет
выполняться неравенство
92

Итак, при достаточно большом п (n4>2N и n^W,) оп отли-
е
чается от sn меньше чем на —, a sn отличается от а • Ь также
меньше чем на -~-. Но отсюда следует, что оп отличается от а*Ь
о о
меньше чем на — + -^- = е (рис. 14), т.е.
\оп — а-Ь |<е
при достаточно большом п. Так как е здесь произвольно малое
положительное число, то
lim оп = а *Ь.
п-юэ
Этим и заканчивается доказательство того, что ряд (23) сходится и
сумма его есть а-Ь.
Меньше е/2 Меньше в/2
а-Ь.
Меньше е
Рис. 14.
В виде примера рассмотрим ряды:
\+р+р2+...+рп + ... = -
1
\-р
и
l+q + q2 + ... + qn + ... = T!=j,
где \р | < 1 и I q I < 1. Мы знаем, что такие ряды (геометрические
прогрессии со знаменателями, меньшими по абсолютной величине
чем 1) абсолютно сходятся. Образуем по только что обоснованному
правилу их произведение:
l+(p + q) + (p2 + pq + q2) + (p* + P2q + pq2 + q3) + ...
Мы доказали, что этот ряд сходится и сумма его равна произведению
сумм данных рядов. Итак,
l+(p + q) + (p2+pq + q2) +
+ (P*+P*q+Pq* + q*) + -..= (l_p)\{_gy
В частности, при р = q получим:
1+2р+Зр*+4рЗ+...=- '
(\-рУ
Предлагаем читателю найти произведения рядов:
а) 1+2р + Зр*+4р» + ... и 1+р+р*+рЗ + ...;
б) 1+2/? + Зр2-(-4рЭ4-... и 1+2р + Зр2+4рЭ-
(I Р К !)•
■■;:..}

ГЛАВА VI
БИНОМ НЬЮТОНА
(окончание)
Теперь мы можем вернуться к биномиальной формуле
/1 i \m i i ^ . т (т—I) о , т(т—\)(т — 2) о ,
(I +Х)т = 1 + Тх + \<2 } х* + у Ь2М3 -х* +
т(т-1)(т-2)(т-3) 4 т^
i 1.2.3-4 * ^••' lz*'
и доказать, что она справедлива не только для m целого
положительного, но и для любого числа т. В случае,
когда т не есть целое положительное число, в правой
части равенства не будет последнего члена, как мы
указывали ранее; следовательно, будет бесконечный ряд
(степенной ряд). Первый вопрос, который должен быть
решен, — это вопрос о сходимости этого ряда. И если мы
установим, что ряд сходится, то тогда останется
убедиться, что его сумма есть (1 + х)т.
Итак, рассмотрим ряд
. , т , т(т— 1) 2 , т (т— 1) (т — 2) « .
1 + ТХ + 1-2 *+ 1-2.3 Х +
, т(т-1)(т-2)(т-3) ,
"^ 1 -2-3-4 "г" •"
и воспользуемся критерием Даламбера для того, чтобы
установить его сходимость.
Именно докажем, что этот ряд сходится, и притом
абсолютно, при условии, что абсолютная величина х
меньше единицы (| х | < 1). Если же | х | больше
единицы, то ряд расходится.
94

Для доказательства возьмем ряд, составленный из
абсолютных величин членов данного ряда
1 +
+
т(т— 1) ^2
Ь2 Х
+
т(т—\)(т — 2) 3
1.2-3 Л
+
+
m(m-l)(m-2)(m-3) 4
1.2.3-4 *
+ ...,
и образуем отношения последующих членов к
предыдущим:
т
Т
1 =
т
Т'
/w(m—1) 2
1-2 Л
w __
m-1
m(m—l)(m —2) 3
1-2-3 Л
m{m—\) (m — 2) (m —3) 4
1.2-3-4 *
mjm--n 2| |m — 2
1-2 x
m(m—\)(m — 2) 3
1.2-3 Л
m —3
-x ;
Здесь
m— 1
m
есть отношение второго члена к первому,
,т—2
— отношение третьего ко второму,
т—3
четвертого к третьему,
— пятого к четвертому
и т. д.
По аналогии легко сообразить, что отношение
тысячного члена к девятьсот девяносто девятому будет
т — 998
, миллионного к его предыдущему
т — 999 998
999 999
999
И Т. Д.
Записывая все эти величины, начиная со второй,
в виде:
|(т-т)4 1(^-1)4 1(т-т)*
I (л. _ ®®\ I I (
|\999 999^*|: ",; IV
т
999 999
999 998\
999 999 J X
замечаем, что они стремятся к числу | х | как к пределу,
по мере того как берется отношение двух членов ряда,
все более и более удаленных от начала ряда.
Действительно, первый член написанного в круглых скобках
представляет т, делящееся на все большие и большие
целые числа, а потому стремится к нулю; второй член
95

все меньше и меньше отличается от —1, стремясь к ней
как к пределу. Поэтому и вся скобка стремится к —1
как к пределу. Наконец, х, на который умножается
каждая скобка, остается одним и тем же при переходе от члена
к члену. Это значит, что отношения стремятся к | —1 -х |,
т. е. к | х |.
Предположим теперь, что х было взято меньше
единицы по абсолютной величине, и станем откладывать для
наглядности величины отношений (которые обозначим
по порядку через г1э г2, г3. г*> •••> гп> гп+и •••) на числовой
прямой. Так как эти отношения стремятся, как мы
установили, к | я |, то, начиная с некоторого из них, гп, все
точки, их изображающие, будут ложиться в сколь
угодно узкий интервальчик с серединой в точке | х |.
Выбирая интервал АВ настолько узким, чтобы он не
захватил точки +1 (рис. 15 *)), мы можем быть уверены,
А В
-о | о—о Ш Ф—о—|—о
Рис. 15.
что отношения, соответствующие точкам, попадающим
в него, не будут приближаться к единице ближе конца
(В) этого интервала, а потому и сами отношения гпу
rn+i> гп+2* ♦•• будут по абсолютной величине меньше,
чем некоторое число q, меньшее единицы (на рисунке
можно принять q = OB). Итак, в случае, когда | х | < 1,
отношения последующих членов ряда к предыдущим,
начиная с некоторого члена, будут все меньше, чем
некоторое q < 1. Поэтому ряд, образованный членами,
начиная с этого м-го, будет сходящимся (по признаку Далам-
бера). Но тогда и весь ряд будет сходиться, так как его
члены до я-го образуют собой многочлен, имеющий
определенную сумму, и, чтобы найти всю сумму ряда,
достаточно сложить сумму п — 1 его первых членов с суммой
сходящегося ряда, образованного остальными членами.
Иное получится, если абсолютная величина х больше
единицы. Как и раньше, начиная с некоторой, все точки,
изображающие отношения, будут попадать в сколь угодно
1) В случае, показанном на рисунке, I х \ = х.
96

малый интервал, с серединой в точке | х \ (рис. 16 *)),
и если интервал выбран настолько малым, что +1 лежит
вне его, то можно утверждать, что абсолютные величины
отношений больше единицы и даже все больше
некоторого числа, большего единицы. А это, в силу признака
Даламбера, означает, что ряд расходится.
Мы видим теперь, что в случае, когда т не есть целое
положительное число, нельзя утверждать, что
биномиальная формула (24) справедлива при всяком значении х>
уже по одному тому, что правая часть формулы — так
называемый биномиальный ряд—расходится при
значениях х, больших единицы по абсолютной величине,
А В
—9 Q h
Гп Гп+Ъ Х %+1Ггг+2
Рис. 16.
т. е. не имеет никакой определенной суммы. Но если
| х | < 1, то ряд будет сходиться, и можно ставить
вопрос, чему равна его сумма. Воспользуемся
рассуждениями Эйлера, чтобы обнаружить, что сумма эта есть
(1 + х)т. Для этого заметим сначала, что сумма ряда
л . т , т(т— 1) 2 i m(m—l)(m —2) 3 .
l + TX+ 1-2 * + Ь23 ■* +
, m(m-l)(m-2)(m-3) ^ ,
"*" 1.2.3-4 Х ~г"9
есть функция от т и от х, принимающая определенное
числовое значение при заданных т (каком угодно) и х
(| х | меньше единицы, иначе ряд может расходиться,
как мы только что видели). Обозначим эту сумму
F (m, х), желая подчеркнуть таким обозначением, что
она зависит как от т, так и от х. Задача заключается в том,
чтобы доказать, что
F(m, x) = (\+x)m.
Если только последнее равенство верно, то должно
быть
F(ml7 x).fK х) = (\+хГ>>(1+хГ> =
= (l+x)^+^ = F(m1 + m2, х).
*) В случае, показанном на рисунке, [ х | = х.
97

Начнем с доказательства этого соотношения, т. е. докажем, что
(при | х I < 1 )
F (mu x)-F(m2, x) = F (тх-{-т2, х)>
или
\\ _L_mi ~ . "М"*!-1) v2 , m1(m1-l)(m1-2)
|_1+Т*+—~Г2—х+ Р^ *J+
, т1(т1-\)(т1-2)(т1-3) ^ , 1
"I 1 О Q А ^ "Г"' X
L2.3-4
[l+^*-
, m2(m2—l)(m2 —2)(m2 —3) ^ , "j
+ 1.2-3-4 * + -J-
_ , , m2+m2 „ , (ли+тяН/^ + т»—1) v2 ,
— И j ХЛ jT2 x "+"
, (m1 + m2)(m1 + m2-l)(m1 + m2-2)
"^ 1-2.3 "^
1.2.3.4 ^i"'
Чтобы сделать это, будем умножать биномиальный ряд
.—l)(mt —2)
1-2-3 +
mi (mj— l)(m!—2) (/П! — 3)
1 + Т*+ р^ * + Ь2ТЗ * +
' 1-2.3.4 -*•+-
на ряд
, ,/"2 „ , m2(m2—\) ^ , m2(m2— l)(m2 — 2) ^ ,
i + TX+ Ь2 Х + Г2ТЗ * +
, m2(m2— l)(m2 — 2) (m2 — 3) ^ ,
~т~ 1.2.3-4 "i"'"
почленно, т. е. умножая каждый член первого на каждый член
второго и располагая произведения в порядке, указанном в конце
предыдущей главы (стр. 89). В данном случае это законно, так как оба
перемножаемых ряда абсолютно сходятся. Получим ряд
i+p^+^j + pi*^
, [^1(^1 — 1)^ — 2)^ , mi(wi —1)„„ m,
+ L Ь2Т3 х т Ь2 * ' 1 Х±
т, тг (т2-1) w2 (т2-1) (т2-2) ^ ,
+ 1 Х Ь2 * + ГТ^Тз *J +
т1(т1—1)(т1—2) пц
1-2-3 1 "^
. Г"*! (mi- 1) (ли-2) (От!-3) ,,„ ,
+ |_ 1-2.3-4 * +
И1 ^ щ (m2 -
l * Г
x*] + .... (25)
/ni(fflj— 1) m2(m2— 1) m! тг(т2— \)(щ—2)
Г2 * Ь2 * +Т* ГгТз * +
"*2 (ffiz— 1) (т2 —2) (от2—3)
1-2-3-4

сумма которого равна F (mx, x) F (т2, *). Очевидно, что из каждой
квадратной скобки можно вынести множителем определенную
степень х: xt x2, х3, х4, ..., после чего суммы чисел, остающихся в
скобках, дадут коэффициенты при соответствующих степенях х.
Обозначим эти коэффициенты по порядку так: Blt B2t B3t B4f ...
Теперь можно написать ряд (25) в виде
\+B1x+B2x*+B2x* + Bix* + ... = F(ml, x)-F(m2t x)>
где коэффициенты имеют значения:
В1 = т1 + т2,
р tn^jmx— 1) t mx m2 , m2(m2—1)
^2 Ь2 ~*~ 1 ' 1 ■*" 12
р m1(ml— l)(m! — 2) , тх(т1— 1) тг
Лз_ ПТТЗ + 1-2 ' 1 ■+"
. т1т2(т2—\) т2 (т2— 1) (т2 — 2)
■*■ 1 1-2 ~*~ 1.2-3
р тх(тх— 1)(т2 — 2) (т3 — 3) mt (mt— 1) (mt— 2) т^
^4~ 1-2-3.4 ~*~ 12 3 * 1 +
тх(тх— 1) т2 (т2— 1) mL m2 (т2— 1) (т2 — 2)
+ Ь2 * 1-2 "*" 1 1-2.3 +
, т2 (т2 — 1) (т2 — 2) (т2 — 3)
"*" 1.2.3-4
Нужно доказать, что эти же коэффициенты можно вычислять по
следующим формулам:
т1 + т2
*i = —j—.
(т1 + т2)(т1 + т2— 1)
Ь2 '
_ (m! + m2) (mt + ma— 1) (т! + т2 —2)
*3~ Ь2Тз •
В2 =
_(т1 + т2)(т1 + т2— \)(т1+т2 — 2)(т1 + т2 — 3)
£,4— ггогт »
1.2-3.4
Отсюда и будет следовать, что сумма ряда (25) совпадает с F (mx +
+ т2, х), т. е.
F (mv x)-F(m2, x) = F(m1+m2, х).
Формула для Бх не требует доказательства — она очевидна.
Для доказательства других формул представим их в ином виде,
заменив в левых частях коэффициенты В2, Б3, £4, — известными
выражениями и умножив обе части формулы для В2 на 1 «2, формулы
для Б3 — на 1 ♦ 2• 3, формулы для В4 — на 1.2-3-4 и т.д. Тогда
99

доказываемые формулы примут вид:
тх (тх—\)+2тхт2 + т2(т2—1) = (тх + т2) (щх-\-т2 — 1), (а)
тг (mi—1) (mi — 2) + Зтх (mi—1) т2-\-Ътхт2 (т2— 1) +
+ т2(т2—1) (т2 —2) = (т!+т2) (тх + т2 — 1) (т1+т2 — 2), (Ь)
тх (тх— 1) (тх —2) (mi — 3) + 4тх (т1— 1) (тх — 2) т2 +
+ 6т1 (тх — 1) т2 (т2— l) + 4mim2 (т2 — 1) (т2 — 2) +
+ т2 (т2— 1) (т2 — 2) (т2 —3) =
= (т1 + т2)(т1 + т2—lXmx + ma —гХтх + та —3), (с)
Эти тождества обнаруживают некоторое сходство с известными
нам тождествами:
тх • т1 + 2т1 • т2 + Щ- т2 = (тх + т2) (тх + т2),
тх- тх- тх-\- Зтх • тх- m2 + 3m i • т2 • т2 + m2 • m2- m2 =
= (mx + m2) (mi + m2) (mi + m2),
mi • mx • mx • mx + 4mxmxmxm2 + 6mxmxm2m2 + \mxm2m2m2 +
+ m2m2m2m2 = (mt + m2) (mt + m2) (mi + mz) (mi + m2),
Для доказательства формул (a), (b), (с), ... применим
искусственный прием, позволяющий вывести сначала формулу (а) из
тождества тх + т2 = тх + т2, затем формулу (Ь) из (а), затем
формулу (с) из (Ь) и т. д.
Чтобы получить правую часть (а), умножим обе части тождества
тх + т2 = тх + т2 на тх + т2 — 1. Покажем, что левую часть
после этого также можно будет преобразовать к виду левой части (а):
(тх + т2) (тх + т2— \) = тх [(тх—\) + т2] + т2 [тх + (т2— 1)] =
= тх (тх—\) + тхт2+т2т1+т2(т2—\) =
= тх (тх— l) + 2m1m2 + m2 (m2— l).
Итак, тождество (а) доказано. Чтобы получить из его правой
части правую часть (Ь), умножим (а) почленно на тх-\-т2— 2.
Покажем, что левую часть после этого также можно будет
преобразовать к виду левой части (Ь):
[тх (тх — l) + 2m1m2 + m2(m2— 1)] (тх + т2 — 2) =
= т!(т!—l)[(m! —2) + m2]+2m1m2[(mi —l) + (m2—1)] +
+ т2(т2—1)[т! + (т2 —2)] = mi(mi—1)(тх—2) +
+ тх (mi — 1) т2-\-2тх (mt— 1) т2 + 2т!т2 (т2— 1) + тхт2 (т2— 1) -f
+ т2(ш2— 1) (т2 —2) = mj (тх— 1) (т1—2) + Зтх (тх—\)т2-{-
+ 3тхт2 (т2— 1) + т2 (т2— 1) (т2 — 2).
Итак, тождество (Ь) доказано. Чтобы получить из его правой
части правую часть (с), умножим (Ь) почленно на тх~\- т2 — 3.
Покажем, что левую часть после этого также можно будет преобра-
100

зовать к виду левой части (с):
[tni(mi— 1) (ml — 2) + 3mi Hi—1) m2 + 3mim2 (m2 — 1) +
+ m2(m2—1) (m2 — 2)] (ml + m2 — 3) = ml(ml—\) (mi— 2)x
X[(m1-3) + m2) + 3ml(ml-l)m2[(m1-2) + (m2-l)]-f
+ 3/7X^2 (/722—l) [(/т^—l) + (m2 —2)] + m2(m2—1) (m2 —2)x
Х[т! + (т2 —3)] = ml(ml —l)(m! —2)(тх —Sj + m^m!—l)x
Х(тх — 2)т2 + 3т! (тг— 1) (r^ —2) m2 + 3mi (mi —1) m2(m2— 1) +
+ 3/П! (тх—l)m2(m2—l) + 3mim2(m2—1) (m2 —2) + /^/^ (m2—l)x
X(m2 —2) + m2(m2—1) (m2 —2) (m2 — 3) =
e=m! (mx—1) (mi — 2) (тх — 3) + 4тх (mi—1) (mj —2)-m2 +
+ 6тх (mx — 1) m2 (m2— lj + to^ (m2— 1) (m2 —2) +
+ m2 (m2 — 1) (m2 —2) (m2 —3).
Итак, тождество (с) доказано.
Предлагаем читателю вывести из (с) новое тождество, умножая
обе части на т1 + т2 — 4. После того как в левой части будут
выполнены соответствующие умножения, останется лишь привести
подобные члены. При этом придется складывать по два рядом
стоящих биномиальных коэффициента, соответствующих четвертой
степени: 1 + 4, 4+6, 6+4, 4+1. Естественно, что в результате
должны будут получиться в качестве коэффициентов левой части
биномиальные коэффициенты, соответствующие пятой степени. В
результате придем к новому тождеству:
mi(mi-l) (mi-2) K-3) (тх-4) +
+5тх (тх—1) (mi—2) (mi —3) т2 +
+ 10mi (тх — 1) (mi — 2) т2 (т2 — 1) +
+ 10mi (/Hi—1) т2(т2—1) (т2 —2) +
+ 5mim2 (т2— 1) (т2 —2) (т2 — 3) +
+ т2 (т2— 1) (т2 —2) (т2 —3) (т2 — 4) =
= (тх + т2) (ml + m2—\) (ml + m2 — 2).(mi-\-m2 — ?>) (т1+т2 — А)Ф
Очевидно, что умножая обе части его на ml + m2 — 5 и
преобразуя левую часть аналогично тому, как это делалось выше,
получим тождество, в левой части которого коэффициенты будут
совпадать с биномиальными коэффициентами шестой степени и т. д.
Из доказанных тождеств следует, что коэффициенты ряда (25)
(стр. 98) совпадают с соответствующими коэффициентами ряда
F (mx + т2, х).
Итак, мы доказали, что
F{mlfx)-F (m2, x) = F (тг + тъ х) (26)
при любых тх и т2 и при |х| < 1.
Но что это значит? Пока лишь то, что сумма
биномиального ряда F(m, x) обладает свойством, аналогичным
одному из свойств бинома (1 + х)т: подобно тому, как
при перемножении двух биномов (1 + х)т± и (1 + х)т*
101

показатели гп\ и m2 складываются и получается (1 -f-
+ x)mi+m2, так и при перемножении двух биномиальных
рядов F(mlt x) и F(m2i x) числа т1 и т2 складываются,
и мы получаем биномиальный ряд F(rrii + /я2, х).
Можно ли отсюда вывести, что сумма биномиального
ряда
равна (1 + х)т? Мы покажем сейчас, что можно.
Для этого заметим сначала, что
F(0, ,) = 1+^ + 217^1^ + 0(07^0з-2)^ + ... = 1
и
Р(1,х) = 1+±-х + Ц^1х* +
"l lo.^ I" • • • == * Г" X*
Далее, /г(2, х) = F(l, х) • F(l, л:) на основании равенства
(26). Следовательно,
F(2,x) = [F(l9x)]* = (l+x)*.
Точно так же на основании равенства (26)
F(3,x) = F(2, x).F(l,x) = (l+x)*.(l+x) = (l+x)*,
F(*9x)=F{39x)-F{l9x) = (l+x)*.(l+x) = (l+x)*
и т. д.
Вообще таким путем заключаем, что
F(mt x) = (l+x)m
при т целом положительном. Это результат не
представляет ничего нового, так как биномиальная формула была
уже установлена для целого положительного показателя
в главе II *).
Рассмотрим теперь случай целого отрицательного
числа — т. Из равенства (26) имеем:
F(—m, x)-F(m, x) = F(—m + m, x)=F(09 x).
*) При т целом положительном ограничение Ul < 1,
необходимое вообще для сходимости ряда, не нужно, так как здесь ряд
обращается в многочлен (все члены ряда, содержащие х в степени выше
т, имеют коэффициенты, равные нулю).
102

Но, если т есть число целое положительное, то по
доказанному:
F(mt х) = (1+х)т. (27)
Кроме того, мы видели, что
F(0,x) = l.
Поэтому
F(—m, x)-(l+x)m = l
и
F(-«i, *)=^^ = (1 +*)-* (28)
Итак, биномиальная формула верна и для отрицательных
целых показателей. Положим теперь т = —, где р —
какое-нибудь целое число и q — целое положительное
число. Тогда
'(f-*HH-'(f+f*)-'(M
-['(**Mf*)Mf*)-
_,ft.,).,(f,)_,(A+ *.,)_,(*.,),
'(H-'(f*Mf*H**)-
-'(**MH-'(S+f *)-'&*)
и т. д.
Подобным образом, помножая F (—, я) самое на себя q
раз, получим
'(*.*)•'(**)••■'(*.*)-'(?.*)-'<*.*
Но р — целое число. Следовательно,
F[p, x) = {l+xy,
103

и мы имеем:
[F(±,x)]9 = (l+xy. (29)
Отсюда выводим, что
р_
Итак, формула
F(|, x) = V{l+x)P = (l+x)^). (30)
F(m, х) = (1+*)«,
иными словами, биномиальная формула
, . т , т(т—\) , , т(т— \) (т—2) , .
1 +TX + ~l^-Lx+ 1-2-3 * +
+ m(m-l)(m-2)(ff,-3);c4+^ = (1+A:)OT
верна при всяком т, положительном или
отрицательном, целом или дробном. (Если т не есть целое
положительное число, то в этой формуле нужно брать значения
Ху не большие единицы по абсолютной величине, так как
иначе биномиальный ряд будет расходиться.)
*) Равенство (29) еще не вполне определяет сумму биномиального
ряда, так как полученное уравнение относительно F (—, х) имеет,
вообще говоря, не одно решение. Так, например, если р = 1, q = 2,
х = — 0,64, имеем:
Wi.f _0,64W+ /1-0,64 = ± }ЛШ = ± 0,6,
и не сразу ясно, чему же равна F f -^-, —0,64) (сумма биномиального
ряда): 0,6 или —0,6. Покажем, что всегда нужно брать
положительное решение уравнения (29), т. е. формула (30) справедлива (перед
корнем стоит знак «+»).
В самом деле, согласно основному свойству (26) функции F (m, х),
должно быть:
f,„.»,_f(f.»).f(f,«),[f(f.,)]'.
А так как F ( —, х ] при любом х — положительном или
отрицательном — есть вполне определенное положительное или отрицательное
число (если только ряд сходится), то F (т, х) есть число обязательно
положительное, как квадрат числа F(-^-t х),
104

Однако решение задачи еще не закончено, так как, кроме целых
и дробных чисел, существуют еще иррациональные числа, которые
не являются ни целыми, ни дробными. (Например, 1^2 не есть целое
число и в то же время не есть дробное, так как нет дроби — с целыми
числителем и знаменателем, равной |/^2.) Но прежде всего нам
нужно вспомнить, что означает степень с иррациональным
показателем. Что, например, должно означать 1,1^2?
Чтобы ответить на этот вопрос, станем отыскивать рациональные
числа, все менее и менее отличающиеся от данного иррационального
числа а (показателя). Так, в случае 1,1 у* в качестве таких чисел
можно взять 1,4 (значение "К 2 с точностью до 0,1), 1,41 (значение
V2 с точностью до 0,01), 1,414 (до 0,001), 1,4142 (до 0,0001) и т. д.
Если теперь вместо степени с иррациональным показателем
рассматривать степени с этими рациональными показателями, то каждая
из них будет иметь вполне определенный смысл с точки зрения
алгебры. В нашем примере вместо 1,1 ^2 мы рассматриваем:
1 ,iM = iVTJr*=¥U~7\
ifi,-4l = Ifv/TTIiI;
1,11,414 = 1о7йтш=Т1Тйзг;
1 11,4142-. 1000ЛЛ1 J 14142 _ 500^ J J7071
И Т. Д.
Можно доказать, что по мере того, как рациональные
показатели: ги г2> /з» U* ••• (в нашем случае гх = 1,4; г2 = 1,41; г3 = 1,414;
г4 = 1,4142; ...) приближаются к иррациональному числу а (в
нашем случае а= У"2) как к пределу, соответствующие степени аГх%
ar\ ar\ ar\ ... (в нашем примере: 1,11,4; U1'41; U1'414 ; 1,1Ь4142;...)
также стремятся к определенному пределу Л.
Вот этот-то предел и рассматривается как степень числа а
с иррациональным показателем а, т. е. аа полагают равным А.
Иными словами, под степенью какого-нибудь положительного числа
а с иррациональным показателем а понимается предел степеней а
с рациональными показателями при условии, что эти показатели
стремятся к числу а. В виде формулы это определение можно записать
так:
оа= lim а я»
гп~*а
Возвращаясь к примеру, мы должны рассматривать степени
с рациональными показателями 1,11,4, l,ll,4J, 1,1Ь414, 1,1Ь4142, ...
как приближенные значения (все более и более точные) искомого
числа 1,1^2- Чтобы действительно найти эти приближенные значе-.
ния, мы не будем извлекать корни с показателями 5, 100, 500, 5000,...
105

(мы видели выше, что 1,1 м = у^ 1,17, 1,11»4Г= |/l,li4i и т.д.) просто
потому, что мы этого не умеем делать, а обратимся к биномиальной
формуле. Ее применение вполне законно, так как для рациональных
показателей она уже проверена. Кроме того, в наших случаях:
1,11.4 = (1 + 0,1)ь*; 1,11,41 = (1 + 0,1)1*41 и т. д. (х = 0,1; \х\ < 1).
Находим:
14 1 4 (\ 4 П
l,P'4 = (l+0,I)b4=l+ill . 0Л+^^у^-^-.(0,1)2 + ...=
= 1+0,14 + 0,0028 + ...^ 1,1428;
1,11.41 = (1+0,1)Ы1 =
=1+м1.о,1+1'41(;-421-1)-(о.1)24-.=
= 1 +0,141 +0,0029 + ...^ 1,1439;
1,1ь*и = (1+0,1)Ь4М =
=1+lii-4.o,i+1'414(11:4214-1)-w+...=
= 1+0,1414 + 0,0029 + ...^ 1,1443;
1,1Ь4И2 = (1+0,1)Ь4142 =
= 1+1^.0Л + Ь4Н2 (1,4142-1) (0>1)2 +
1,4142 (1,4142-1) (1,4142-2)
"г 1-2-3 '{ ' } ■*"•• —
= 1+0,14142 + 0,00293-0,00006 + ... ^1,14429.
При последнем вычислении мы взяли не три, а четыре члена
биномиальной формулы, так как отбрасывание четвертого члена
(равного — 0,00006) привело бы к ошибке, делающей ненужной
такую большую точность в показателе степени. Последний
полученный результат дает 1,г2 с точностью до 0,00001. Если в качестве
показателя брать более точные значения ^2, то будут получаться
результаты, у которых первые шесть знаков те же, что и у
найденного числа, т. е. 1,14429.
После этого отступления можно уже без труда доказать, что
биномиальная формула верна и для иррациональных показателей.
В самом деле, пусть т — иррациональное число и |jc| < 1. Докажем,
что
. , т , т(т — 1) . , т(т— \) (т — 2)
1 + Т*+ \.2 *Ч 1>2 з -*3 + ... = (1+*)т.
Для доказательства рассмотрим последовательность
рациональных чисел rlt r2, r3, rA, ..., стремящихся к числу т как к пределу:
гп-г т.
106

Если в биномиальный ряд подставлять вместо т числа rlt r2t r3f г4> ••••
то будем получать ряды
1+^,+ M£3zdL,2+M^3-l)^-2) x3+ f
1 , U _ , Г4 (Г4- 1) Г4 (/-4-1) (/-4-2)
1 + ТЛ:+ Г2 "■ ГГ2Т3 * +•••■
члены которых стремятся к членам ряда
т m(m-l) m(m-l)(m-2)
1~h~F Н Ь2 ^ Ь2-3 *+ —
На основании одного этого, вообще говоря, нельзя еще заключить,
что и суммы наших рядов стремятся к сумме последнего ряда. Однако,
можно было бы без особого труда убедиться (мы опускаем здесь
доказательство), что в данном случае последнее обстоятельство
имеет место, т. е. что
П
, . т т (т—\) т(т—\) (т—2)
= 1 + Т *+ \.2 *2+ !,2.3 L х*+-
Сумма ряда
есть (1 + х)гп (гп — рациональное число, а для рационального
показателя биномиальная формула доказана). Поэтому имеем:
lim (\+х) п = \+ х-{ \ ; х2 +
гп-*т
1 "^ 1-2
, т(/я—1)(т-2)
и так как lim (1+х) Л равен (1 + х)т по самому определению
степени с иррациональным показателем, то получаем окончательно
,i , чт 1 i т . т(т—\) 9 . т(т—\)(т — 2)
(1+х)^=1 + Т^+ 1<2 * + 1.2.3 *? + -"
что и требовалось доказать.
107

В частности, имеем
l.lv"s_(l+0,l)1'5-
_,+^.w+m^o.№V+
Если бы мы захотели пользоваться этой формулой для
вычисления 1,1^» то пришлось бы, во-первых, ограничиться несколькими
первыми членами формулы (тремя, четырьмя, пятью), а во-вторых,
заменить ^2 каким-либо его приближенным значением (например,
1,41; 1,4141 и т. п.). Таким образом пришлось бы проделать те же
вычисления, что и выше (на стр. 106).
Мы довели до конца доказательство утверждения
Ньютона, т. е. доказали, что
при любом т и при \х\ <с 1.
Небесполезно отметить, что сам Ньютон не имел еще
доказательства и что последнее сделалось возможным
лишь в результате работ ряда выдающихся математиков
(Ньютон, Эйлер, Коши, Абель и др.) на протяжении
полутора столетий. Причина этого лежала не столько
в технических трудностях доказательства (которые, по
существу, невелики), сколько в выработке ясных и
четких понятий, относящихся к бесконечным рядам и к
действиям над ними. Это в свою очередь требовало
выработки понятия предела и изучения законов
предельного перехода.
Опираясь на понятия предела и ряда и на
биномиальную формулу, мы сможем в дальнейшем без особого труда
получить интересные и важные ряды для sin x, cos jc,
lg(l + х) и др. Но, прежде чем перейти к этому, укажем
на некоторые весьма употребительные приближенные
формулы, вытекающие из биномиальной формулы. Для
этого применим биномиальную формулу к некоторым
частным случаям.
Полагая последовательно в левой и правой ее частях
11,1 1
т = у, т = у, т = —1, т = — у, т = —у,
108

получаем:
VT+^ =
= <1+*)* = ! + ±х-±* + ^*-*&* + .
= (l+x)"3 = l+i-^-4-x2 + ^xa-^^ + ...;
1 = (1 +л:)-1= 1 — jc + .v2 —jc34-jc4 —...;
J+*
V\+>
VT+~>
0 1 \ 9 1 * I 2 1 I A.
-(i+x) 3=i—i-^+l*8--gf-^+S**--
Если Ul —малое число, то я2, х3, х4, ... являются
числами весьма малыми. Поэтому мы не сделаем большой
ошибки, отбросив в каждой из написанных формул все
члены, начиная с третьего (содержащего х2). Получатся
следующие приближенные формулы:
У1+х**1+-±х, (31)
{/T+x^l+^-x, (32)
1 1-х, (33)
\+х
■=^1-1*, (34)
У\+х 2 ' v '
1 1--х. (35)
Легко оценить величину ошибки, которую мы
допускаем, пользуясь этими формулами в том случае,
когда х > 0. Тогда получаются знакопеременные ряды,
члены которых убывают по абсолютной величине. По-
109

этому ошибка при отбрасывании членов ряда не
превосходит абсолютной величины первого из отбрасываемых
членов. Следовательно, при х > 0 ошибка первой фор-
1 2 1 а
мулы меньше -^ г2, второй — меньше -д-х2, третьей — мень-
v2 „—<* v2 •
ше дг, четвертой — меньше -g-jr < у ^ наконец, пятой —
2 1
меньше, чем у г2 <; -j- x2. Приведем примеры вычислений
с помощью этих формул.
1) |/~1,02^1,01 (по формуле (31)); ошибка меньше,
чем i-(0,02)2 = 0,00005;
0,03
2) 1/0,97 = УТ- 0,03^*1 -^-=0,985;
3) КЩ^1+^^ 1,0233 (по формуле (32));
ошибка меньше -д- (0,07)2< 0,0006;
4) V0M = Vl —0,18^ 1 -^ = 0,94;
5) -р^-^ 1-0,06 =0,94 (по формуле (33)); ошибка
меньше' (0,06)2 = 0,0036 < 0,004;
7) , я^ 1—:— = 0,98 (по формуле (34)); ошибка
меньше у (0,04)2= 0,0008<0,001;
8) -J= = ^=~l-^°^ = 1,01;
; К0,98 /1-0,02 2
9) 8-т==^1 - — = 0,98 (по формуле (35)); ошибка
у 1,06 3
меньше -i- (0,06)2 = 0,009 < 0,01;
10)iJ= = 7=L=~l-=^.= li02.
' УЪЩ ]Л-0,06 3
Во всех этих примерах ошибка невелика. Если х
в выражении (1 + х)т брать большим, т. е. порядка
десятых, а не сотых, то ошибка будет большей. Так,
например, ]/1,24 ^ 1,12 с ошибкой меньшей, чем
ПО

i- (0,24)2 = 0,007... < 0,01; VTJ2 ъ 1,21 с ошибкой
меньшей, чем у(0,42)2я^0,02. Здесь уже нельзя ручаться
за второй знак после запятой.
Если же мы захотим применить формулу (31) к
случаю "|/"1,9^ 1+-^-= 1,45, то здесь ошибка будет
порядка -g- (0,9)2^0,1. (В действительности 1/1,9 =
= 1,378 ...)
Не следует думать, что формулами (31) — (35) можно
пользоваться только при действиях с числами, мало
отличающимися от единицы (вида 1 + х, где х мало
по абсолютной величине). Покажем, например, как
можно пользоваться формулами (31) и (32) для
приближенного извлечения квадратных и кубичных корней
из любых чисел:
0,56
1Л56 = К1,56-100 = 10/1,56^ 10 (Л + 2
= 10-1,28=12,8.
Ошибка этого результата меньше, чем 10- -^-(0,56)2« 0,4.
о -. 0,4-100 Л/ „
.эта ошибка представляет —12 8 %наиденного числа,
т. е. около 3%. Это — значительная ошибка. Ее можно
уменьшить, если заметить, что 156 довольно близко
к 122 = 144. Тогда можно писать:
l/l56=Kl44+12 = |/"l44(l+-^) =
= 12|/T+I^12(l+l) = 12,5.
Здесь ошибка меньше, чем 12-g- • т^ = gg^0,01.
Найдем еще J/175. Замечая, что 175 близко к 169=
= 132, находим:
1/175=1Аб9Тб = ]/Г169(1+^) =
-13/1+ш^13(1 + 1йЬ13.231-
111

Ошибка этого результата меньше, чем 13 • -g- • (—) <
< 0,002.
Пусть, наконец, надо вычислить \/ 500. Так как 500
близко к 512 = 83, то пишем:
УШ =УЪ\2- 12 =|/ 512(1-^) =
Ошибка этого результата менее 0,002.
Вообще такой способ приближенного извлечения
корней приводит к тем более точным результатам, чем
ближе подкоренное выражение к точному квадрату или
кубу х).
1) Точнее, если А = а2 + Ьу где \Ь\ < а2, то
= а +-
2а2 / г2о
1^4 = ^ + 6 =jA2(l+J-) =
Ошибка результата при — > 0 меньше, чем
J_/_6_\2==_62_
й ' 8 U2 / &*з •
Аналогично, при Л = а3 + &, где I&I < |д31, имеем:
-•^~.('+£)-;+£-
При — > 0 ошибка этой формулы меньше, чем а • -^ [ --) = —i.
ad У \а3/ 9а5

ГЛАВА VII
РЯДЫ ДЛЯ СИНУСА И КОСИНУСА
В предшествующих главах было получено
разложение функции (1 + х)т в бесконечный ряд. Мы отмечали
уже значение подобных разложений. Теперь мы
намерены двинуться дальше и найти разложения в ряды
для тригонометрических
функций sin х и cos х.
Читатель помнит, что
sin х и cos х в
тригонометрии вводились чисто
геометрическим путем, как
функции угла х, и
допускают весьма простую
геометрическую
интерпретацию (истолкование).
Именно, если начертить
окружность радиуса 1 (рис. 17)
и, выбрав один из
радиусов, например О А, за начальный, откладывать от него
углы х, беря центр круга О за вершину углов, то
перпендикуляр ВС дает синус углах, а отрезок ОС — косинус.
При этом число х, измеряющее угол (в радианах, т. е.
численно равное длине дуги, стягиваемой сторонами
угла), может быть любым положительным или
отрицательным числом. Если оно положительно, то угол отсчи-
тывается от ОА в направлении против часовой стрелки,
если отрицательно, то — по часовой стрелке. Может
случиться, что х по абсолютной величине больше, чем
2л, т. е. больше, чем длина всей окружности. В этом
случае полезно представлять себе, что угол BOA обра-
Рис. 17.
113

зуется поворотом подвижного радиуса ОВ (стрелки)
от начального положения ОЛ. Для того чтобы получить,
например, угол, равный Зя, мы должны заставить
радиус ОВ описать против часовой стрелки всю
окружность (2я) и еще половину (я), так что окончательное его
положение будет в 0ВХ. По внешнему виду положение
будет такое же, как и при угле, равном л(180°). Однако,
имея в виду происхождение этого угла, мы все же
говорим об угле в Зя. Следует еще напомнить, что при
различных положениях подвижного радиуса ОВ линия синуса
(ВС) может располагаться то выше, то ниже
неподвижного радиуса ОЛ, а линия косинуса (ОС) —то вправо,
то влево от центра. Эти случаи различаются знаками
тригонометрических функций: именно синус считается
положительным, если линия синуса расположена выше
неподвижного диаметра, и отрицательным, когда она
расположена ниже. Аналогично косинус считается
положительным, если линия косинуса лежит вправо от центра
круга, и отрицательным, когда она лежит влево.
Повторяем, что все это предполагается известным
читателю и напоминается лишь для того, чтобы читатель
знал, на какие факты из числа ему известных мы будем
здесь опираться.
Из многочисленных формул тригонометрии
понадобятся лишь две (зато наиболее важные) — это так
называемые формулы сложения аргумента:
sin (а + Р) = sin а • cos р + sin р • cos а,
cos (а + P) = cos а • cos p — sin а • sin p.
Их-то мы и выбираем за основу при разложении
тригонометрических функций в степенные ряды. И прежде всего
выведем формулы, позволяющие находить синусы и
косинусы двойного, тройного, четверного и других
кратных углов по синусу и косинусу одинарного угла.
Известно, как из формул (36) выводится синус и
косинус двойного угла. Именно:
8in 2л: = sin (х + х) =
= sin х • cos x + sin x • cos x = 2 cos x • sin x9
cos 2# = cos (* + *) =
= cos x • cos x — sin x • sin x = cos2 x — sin2 x.
114

Теперь легко получить синус и косинус тройного угла:
sin Зх = sin (2* + *) = sin 2x • cos x + sin x • cos 2x =
= (2 cos x • sin x) • cos x + sin x (cos2 x — sin2 jc) =
= 2 cos2 л; • sin x + cos2 jc • sin # — sin3 x =
= 3 cos2 x • sin * — sin3 jc;
cos Зх = cos (2* + jc) = cos 2jc • cos x — sin 2x • sin a: =
= (cos2 x — sin2 jc) • cos x — 2 cos x • sin x • sin x =
= cos3 x — cos x • sin2 jc — 2 cos л: • sin2 x =
= cos3 x — 3 cos x • sin2 x.
Итак,
sin 3jc = 3 cos2 x • sin л: — sin3 #,
cos 3x = cos3* — 3 cos x • sin2*.
Выведем еще синус и косинус четырехкратного и
пятикратного аргументов:
sin 4 х = sin (За; + х) = sin Зх • cos jc + sin л; • cos Зх =
= (3 cos2 х • sin * — sin3 х) • cos jc +
+ sin x • (cos3 x — 3 cos x • sin2 #) =
= 3 cos3 л: • sin x — cos л; • sin3 x + cos3 x • sin * —
— 3 cos a: • sin3 * = 4 cos3 л: • sin x — 4 cos x • sin3 jc;
cos 4* = cos (3jc+jc) = cos Зх -cos * — sin 3* • sin x =
= (cos3 x — 3 cos x - sin2 x) • cos a: —
— (3 cos2 jc • sin x — sin3 jc) • sin x =
«= cos4 x — 3 cos2 jc • sin2 x — 3 cos2 x • sin2 x + sin4 * =
= cos4jc — 6 cos2 x • sin2 * + sin4 jc;
sin 5jc = sin (4* + jc) = sin \x • cos jc + cos \x • sin jc =
= (4 cos3 jc • sin x — 4 cos x • sin3 x) • cos x -f-
+ sin jc • (cos4 jc — 6 cos2 jc • sin2 jc + sin4 jc) =
= 4 cos4 jc • sin jc — 4 cos2 jc • sin3 jc + cos4 jc • sin x —
— 6 cos2 x • sin3 x + sin5 * =
= 5 cos4jc • sin jc — 10 cos2 x • sin3* + sin5 x;
cos 5jc = cos (4jc + jc) = cos 4jc • cos x — sin 4jc • sin x =
= (cos4x — 6 cos2 jc • sin2 jc + sin4 jc) • cos x —
— (4 cos3 jc • sin jc — 4 cos jc • sin3 jc) • sin jc =
= cos5x — 6 cos3 x • sin2 jc + sin4 jc • cos x —
— 4cos3 jc • sin2x + 4 cos x sin4x =
= cos6 jc — 10 cos3 x • sin2 jc + 5 cos * • sin4 x.
115

Этот материал достаточен, чтобы сделать необходимые
выводы. Желая облегчить читателю усмотрение
закономерностей в найденных формулах, выпишем результаты
в виде особой таблицы:
sin 2х =
cos2# =
sin Ъх =
cos Зх =
sin 4x =
cos 4x =
sin Ъх =
cos Ъх =
+ 2 sin х-cos*
cos2 x — sin2*
+ 3 cos2 x • sin x— sin3 x
/ \ /
cos3 x — 3 cos x • sin2 x
+ 4 cos3 x • sin x — 4 cos * • sin3 x
/ \ / \
cos4 * — 6 cos2 *. sin2 * + sin4 x
+ 5 cos4 x • sin x — 10 cos2 x • sin3 x + sin5 x
/ \ / \ /
cos a;5 — 10 cos3 x • sin3 x -f- 5 cos x • sin4 x
В этой таблице мы расположили полученные выше
формулы попарно, поместив между двумя
параллельными чертами выражения синуса и косинуса для одного
и того же угла, кратного х. Если читать в каждом
разделе таблицы коэффициенты членов один за другим
в порядке, указанном стрелками (не обращая
внимания на знаки коэффициентов), то мы узнаем в них
уже знакомые нам биномиальные коэффициенты. Так,
разделы таблицы дают следующие коэффициенты:
1-й (для sin 2д: и cos2x): 1, 2, 1;
2-й (для sin3* и cos3x): 1, 3, 3, 1;
3-й (для sin 4л: и cos Ax): 1, 4, 6, 4, 1;
4-й (для sin 5* и cos 5а:): 1, 5, 10, 10, 5, 1.
Но это как раз числа третьей, четвертой, пятой и
шестой строчек арифметического треугольника (стр. 26),
т. е. биномиальные коэффициенты для т = 2, 3, 4 и 5.
Мы близки теперь к тому, чтобы окончательно
овладеть закономерностью. При этом трудно не поддаться
116

впечатлению, что выражения для cos mx и sin mx
являются двумя половинками одной и той же формулы,
в которой фигурирует бином Ньютона. Рассмотрим,
например, cos 5* и sin 5*. Если возвести в пятую степень
бином cos х + sin *, то получится:
(cos x + sin х)ъ = | cos5x | + 5 cos4x • sin x +
+ | 10cos3*-sin2*| + 10cos2*-sin3* +
+ | 5 cos л:-sin4 л: | + sin5*.
При сравнении с таблицей становится очевидным, что
члены, обведенные рамками в последней формуле (т. е.
члены, стоящие на нечетных местах: первом, третьем,
пятом), отличаются только знаками от членов выражения
для cos 5jc. Точно так же члены, стоящие на четных местах
(втором, четвертом, шестом), только знаками отличаются
от членов формулы для sin Ъх.
Аналогичные наблюдения можно сделать и для cos 4*
и sin 4*, cos Ъх и sin Ъх и т. д. В итоге приходим к
следующему правилу: если написать выражение (cos x + sin x)m
по биномиальной формуле, то члены, стоящие на
нечетных местах, выписанные с измененными, а именно
чередующимися знаками -\ 1 Ь •••, дадут выражение
для cos mx, а члены, стоящие на четных местах,
выписанные также с чередующимися знаками, дадут выражение
для sin mx.
Применим это правило для нахождения формул для
косинуса и синуса шестикратного аргумента (cos 6x и
sin 6*). Имеем:
(cos х + sin *)6 = |cos6*| + 6 cos5 x • sin x +
+ | 15cos4*-sin2*| + 20 cos3 x • sin3* +
+ | 15cos2*-sin4*j+6cos*-sin5*+| sin6*|.
Здесь на нечетных местах (первом, третьем, пятом,
седьмом) стоят члены:
cos6*, 15 cos4*-sin2*, 15 cos2*-sin4*, sin8*.
Выписывая их с чередующимися знаками, мы, согласно
правилу, должны получить выражение для cos 6*.
Именно:
cos 6* = cos8 * — 15 cos4 * • sin2* 4-15 cos2 * • sin4 * — sin6 *.
117

Аналогично для sin 6х получится формула
sin Ъх = 6 cos6х sin x — 20 cos3 x • sin3 x + 6 cos x • sin5 x.
Если бы мы захотели проверить эти формулы, то
достаточно было бы воспользоваться формулами
сложения аргументов. Именно, заметив, что
sin 6x = sin (5л: + л:) = sin 5л: • cos x-\- cos 5х- sin x
и
cos 6# = cos (5а: + х) = cos Ьх • cos х — sin 5x sin x,
подставить сюда уже найденные выше выражения cos Ьх
и sin Ъх.
Правило, которое мы нашли путем неполной
индукции (обнаружив его справедливость на частных случаях),
можно записать математически в виде формул. Именно,
применяя это правило для получения выражений cos wx
и sin тх при каком угодно т (целом положительном),
пишем сначала:
(cos х + sin x)m = | cosm х | + -р cos"1-1 x • sin x +
I trt Im 1 \
m (m— 1) m « . о
7 cosm_zA:-sin2A:
1.2
+
m(m— l)(m — 2)
1-23
cos
m-3
#-sin3;t-f-
+
m (m—l)(m —2)(m —3)
1.2-3-4
cosm~4A:.sin4A:
+
m (m—I) (m —2) (m —3) (m—4)
" 1.2.3.4.5
COS"
'#-sin5 * + ...,
а затем, отбирая члены, стоящие на нечетных и четных
местах, и меняя у них соответствующим образом знаки,
получаем:
cos тх = cosm х — m ^7" 7 cosm-2 л: • sin2 x +
m(m-l)(m-2)(m-3) m_4
"1 1.2.3.4 СОЬ
*-sin** —..
(37)
sin тх = -у- cos
m-l.
x-sin* —
-ffl(m-;H3m-2)cos"'-3x.sin3x +
+ «(m-l)(m-^(m-3)(m-4) CQsm_5 ^ . 8in.x _ _
118
(38)

Эти формулы, в которых ранее полученные содержатся
как частный случай, были известны еще Виету г) (1590 г.).
Посредством этих формул тригонометрии, которые
обычно в средней школе не рассматриваются, мы найдем
выражения для cos х и sin х в виде степенных рядов.
Но для этого необходим еще ряд преобразований.
Прежде всего нужно применить формулы (37) и (38)
к cos х и sin х. Это можно сделать, рассматривая х
как т • —. Тогда
т
sin x = sin т (— 1, cos # = cosm(—
и формулами (37) и (38) можно пользоваться, полагая
в них — вместо х. Получим
т
т х т (т— 1) т о х . о х .
cos х = cosm \ п f cosm~2 — • sin2 —h
tn l • z m m
+ OT(m-11).(2ffl,^2l(m"3)cos-^.Sin^-,..t (39)
sin x = " cos-» ^ ■ sin £ - "<"-'> ("~2> cos— ^ x
1 m m 1 • z • о tn
з * m(m-l)(m-2)(m-3)(m-4)
X Sin HiЛ 1.2.3-4.5 X
X COSm~5 -£■ - sin5 -£- — ... (40)
Эти формулы верны для любого значения т, и, полагая
в них т = 2, 3, 4, 5 и т. д., мы получим бесчисленное
множество различных по форме выражений для cos x
и sin х. Так, например, для cos х при т = 2, 3, 4, 5
2) Франсуа Виет (1540—1603) — французский математик XVI
века. По профессии юрист, он, несмотря на обширную юридическую
практику, находил время для глубоких математических
исследований.
Его основные работы относятся к алгебре и тригонометрии, где
он сделал много открытий. Но главная его историческая заслуга
заключается в систематическом употреблении букв для обозначения
величин. До него буквами обозначались одни лишь искомые
(неизвестные) величины, т. е. по существу буквенное исчисление
отсутствовало.
119

получаем выражения:
cos x = cos2 у — sin2 у = cos3 -*- — 3 cos у • sin2 у =
= cos4 4- — 6 cos2 4 • sin2 -£- + sin4 -£ =
4 4 4 4
= cos5 4-Ю cos3 4 * sin2 4 + 5 cos 4 • sin4 4,
5 ob oo
а для sin x — выражения:
sin x = 2 cos у • sin у = 3 cos2 у • sin у — sin3 ~ =
= 4 cos3 -r • sin -:— 4 cos -r- • sin3 -r- =
4 4 4 4
= 5 cos4 у • sin у — 10 cos2 у • sin3 у + sin5 у.
По мере того, как т берется все большим и большим,
выражения становятся все более длинными. Читателю,
быть может, покажется на первый взгляд странным,
что мы, желая получить наиболее удобные выражения
для cos х и sin xy будем
увеличивать т до
бесконечности в формулах (39) и (40)
и формулам, содержащим
конечное число членов,
предпочтем бесконечно
длинные формулы — ряды.
Однако он скоро увидит,
что это действительно
выгодно.
v CQS7n , В соответствии с нашим
/ замыслом мы станем безгра-
Рио 18 нично увеличивать т в
формул ах (39) и (40). От этого
будет меняться каждый член в отдельности, а число их
будет безгранично расти. Проследим сначала за
изменением отдельных членов на примере выражения для sin x.
Первый член равен
т cos'71-1 — -sin—.
т tn
Когда т растет, то — становится все меньше и меньше,
X
приближаясь к нулю. Поэтому cos — будет приближаться
к единице, a sin — — к нулю (рис. 18).
120

Мы покажем ниже, что msin— стремится при этом
к х, a cosm_1 — — к единице. Тогда будет очевидно, что
первый член выражения для синуса
X • X т Л X • X
— • sin — = cos™-1 — т sin —
mm mm
стремится к 1 *х = х.
Второй член выражения для синуса, имеющийся
в формуле (40):
т (т—\) (т — 2) _ я х . « х
_v—^_L^ L coSm"3-- . Sin3 --
i • z • 6 m m
можно написать в виде
т-т(
■Ю-Ю
cos"1"3 — -sin3—.
1 • l • о /я /я
Теперь достаточно лишь перегруппировать
множители:
т о * -cosm"3^-.m3sin3^-=
1 • Z • О /72 /W
= l 79\ m' cos*-3-^.(msin^3;
1 -2-3 /я \ m/ '
чтобы заметить, что этот член стремится к . 3, когда
m безгранично возрастает. В самом деле, в выражении
(i_±\(i_2\
\ m/\ my m о x I . x \з
i / > L cosm~3 — • [m sin —
1-2-3 m \ my
1 2
1 >-l и 1 >\ (стрелкой мы будем для
corn т J
кращения заменять слово «стремится»), так как — и —
стремятся к нулю, когда т безгранично возрастает.
Кроме того,
cosm-3 ^ 1 и msjn >х^
что мы докажем ниже.
121

Поэтому, действительно,
cosm-3 .
(т sin —
1-2-3 m
1-2-3 W 1•2•3'
Такие же рассуждения убеждают нас, что третий
член в выражении sin x, именно
т (т- 1) (m-2) (m-3) (m-4) R х . х
1.2.3-4.5 C0S m Sin m »
стремится к
четвертый
т (т— 1) (т
стремится
член
-2)(т-
1.2-3
к
-3)(т
•4-5
1-2-34
-4)(т-
•6-7
X?
•5 '
-5)(т-
-6)
cosm-
-7 А
/я
• sin7
а:
т
1.2.3.4.5.6.7
И Т. Д.
Не производя преобразований в каждом отдельном
случае, наметим нужные этапы, например, для
четвертого члена выражения (40). Именно, сначала
переписываем этот член
т (т— 1) (т — 2) (т — 3) (т —4) (т — 5) (т —6) со$т_7 _£ . sin7 —
1.2.3«4.5.6.7 т * т
в виде
■(-ач'-х-а-кн-ач-э..
^ т j \ m t
1.2.3.4.5.6.7
XCOSm-7 —
-sierra m
(вынося т множителем за скобку в каждом из биномов:
т — 1, т — 2, т — 3, т — 4, т — 5 и т — 6).
Затем группируем множители так, чтобы все т (дающие в
122

произведении m7) стояли рядом с sin7 —:
т \ т \ mJ
зюо-аю
1-2-3-4-5-6-7
X
-('
XCOsm-7— .m7sin7 — =
т т
4)('-i)('-i)('-i)('-i)('-f
1-2.3-4.5-6-7
X
xcos»-7—.(msin—Y.
т \ т J
1,
1,
т '
т '
i-i
т
i-i
т
Наконец, замечаем, что при бесконечном возрастании т
происходит следующее:
i-i.
т
i-i.
т
cos"1-7— -> 1, msin—^х,
а потому все вышенаписанное выражение стремится к
1.2.3.4.5.6.7 W 1.2.3.4.5.6.7'
Итак, мы видим, что когда т неограниченно
возрастает, члены правой части формулы (40) становятся
все более близкими к членам степенного ряда
х3 хь х1
х —
1.2-3" 1.2-3.4.5 1.2.3.4-5.6.7"
А так как правая часть равенства (40) при любых
значениях т, как бы они ни были велики, равняется sin x,
то можно думать, что и этот ряд представляет собой
sin x, т. е.
_ х3 , хь х1 /лл.
Sin*-X-b23+1.2.3.4.5~1.2.3.4.5.6.7 + --- I41'
Подобным же образом, рассматривая один за другим
члены выражения (39) для косинуса, можно прийти
к формуле:
« X2 X4 JCe X*
С0&Х=1-»+й-61+Ш-- <42>
123

Прежде чем заниматься формулами (41) и (42),
получение которых и является целью этой главы, нужно
оправдать справедливость сделанных выше утверждений,
а именно, что msin — стремится к х, a cosw —f
CDS'"-1 —, cos"*-2 —, cosm_3 —, ... стремятся к 1, когда
m безгранично возрастает.
Мы уже видели, что sin >■ О, когда т -> оо. Отсюда,
быть может, кто-нибудь поспешит сделать заключение,
что msin >0, поскольку к нулю стремится один из
сомножителей. Но такое заключение будет неверно.
Дело в том, что величина произведения т • sin— зависит
от обоих множителей, и в то время, как второй
множитель стремится к нулю, первый (т) безгранично
возрастает. Что в таких случаях результат действия
противоположно направленных факторов (а именно бесконечного
возрастания одного сомножителя и одновременно
бесконечного убывания другого) может быть самым различным,
на это указывают простейшие примеры. Так, если взять
один множитель равным тг, второй — равным -^ и
давать т все большие и большие значения, то один из
сомножителей будет бесконечно расти, другой бесконечно
убывать, а их произведение все время будет оставаться
равным единице:
т2
Вот другой пример: пусть один сомножитель равен т2,
а второй —з. Тогда их произведение
»2.
1 т* 1
m3 m3 m
стремится к нулю, когда т безгранично растет.
Пусть, наконец, первый сомножитель равен
по-прежнему т2, а второй равен—. В этом случае произведение
равно
171 m = ~^Г = т
т т
и безгранично растет вместе с т.
124

Но вернемся к нашему случаю и, чтобы решить вопрос
здесь, воспользуемся геометрическими фактами. На
рис. 19 изображен угол, равный—, из вершины которого
описана окружность радиуса 1. Проведем в точке А
Л
Рис. 19.
касательную к окружности до пересечения с
продолженным радиусом ОВ. Точку пересечения обозначим D.
Как известно, отрезок AD будет равен тангенсу угла
х
— , т. е.
^ = tg£- =
sin -
т
х
cos —
т
Проведем еще хорду АВ и сравним площади
треугольника ОАВ, кругового сектора ОАВ и треугольника OAD
Очевидно,
пл. тр. ОАВ < пл. сект. ОАВ < пл. тр. OAD.
Но
пл. тр. ОАВ = ±гОА-ВС = ±гЛ-ъ'т ^ = l.sin-,
г 2 2 т 2 т '
пл. сект. ОАВ = ~ОАШ = ~1. - = !•-,
2 2 т 2 т *
х
1 1 ! SIM —
пл. тр. 0AD = \0A-AD = \-1 . tg £ = |.
COS —
m
125

Поэтому
. х
1 х . 1 х , I m
T'Slnm<T'm<T Г'
COS —
m
(Мы считаем здесь угол — положительным и острым.)
Последнее неравенство остается верным, если каждый
его член помножить на одно и то же положительное
число 2т. Тогда получится:
. х
т sin —
. х ^ ^ т
msin — <*< .
т ^ х
cos —
m
(Множитель 2m был подобран так, чтобы получить
соотношение, содержащее выражение msin —, которое
мы сейчас исследуем.)
Что же можно утверждать теперь относительно
msin—?Во-первых (глядя на первые два члена
неравенства), что
msin-^<Ar,
во-вторых (на основании последних двух членов
неравенства), что
. х
т sin —
Х<
х
cos —
m
или, умножая каждый член на положительное число
cos — , что
х cos — < msin —.
т т
Итак, с одной стороны, m sin — при любом т меньше,
чем х. С другой стороны, m sin — также при любом m
больше, чем х cos —. Но когда m безгранично возрастает,
126

то cos — стремится к единице, поэтому х cos — стремится
к х (оставаясь все время меньше, чем ху так как cos —-
меньше единицы, если только х не равен нулю).
Следовательно, т sin —, будучи все время меньше, чем х, и в то же
время больше, чем х cos —, — неограниченно
приближающееся к а; по мере роста т, — должно само стремиться
к х, что мы и должны были установить.
Остается доказать, что cosm —, cosm_1 — ,cosm~2 —,
cosm_3 —,... стремятся к единице, когда т безгранично
растет. На первый взгляд кажется, что здесь дело
решается проще, чем в только что рассмотренном случае.
В самом деле, раз cos — стремится к единице, то и любая
степень его также стремится к единице. Это заключение
справедливо, когда речь идет об определенной степени —
второй, третьей и т. д. Но ведь в случае, например,
cosm— и сам показатель не остается постоянным, а не-
ограниченно возрастает. Это приводит к действию двух
противоположных факторов, аналогичных тем, которые
имели место в случае msin—.
J tn
Например, если у ат фиксировать показатель степени
т и увеличивать основание а, тоат будет расти. С другой
стороны, если фиксировать а < 1 и увеличивать
показатель степени т, то в произведении
ат = а-а ... а
т раз
число сомножителей увеличивается и, следовательно
(так как каждый сомножитель а < 1), ат будет
уменьшаться.
И снова встает вопрос, к какому результату для
cosm — приводят два фактора, сопровождающие
увеличение т: с одной стороны, основание степени а = cos —
т
растет и как бы «стремится» увеличить атг с другой
127

стороны, растет показатель степени т (где а = cos — j,
«стремясь» уменьшить ат.
Для выяснения этого вопроса воспользуемся
следующими выкладками. Прежде всего,
cos — = cos [2• тг-j = cos2 £- — sin2£- =
m \ 2m] 2m 2m
= (1-sin22^)-sin22^ = 1-2sin22^:
но sin2^<2^> поэтому
sin2f5-<1—г и 2sin2^- <2--j—5- = jr-^-.
2m 4m2 2m 4m2 2m2
Заменяя в выражении для cos— вычитаемое 2sin2£-
большим числом, мы уменьшаем разность, т. е.
cos- = l-2sin2^>l-^,
m 2m 2m2'
а потому
«-■£-(i-2.i"£)->(i-£)--
1 ^2т2У+ 1.2 \2"*2/
_ m(m-l)(m-2) / *2 \з
1-2-3 \2m2j + "*
(по биномиальной формуле). Мы только уменьшим
правую часть этого неравенства, если все знаки + (кроме
знака перед первым членом) заменим на — .
Следовательно,
cos- *.>1 -HL [*-\ _ "С"-1) 1^Л2 _
СОЬ т^1 1 ^2т2У Ь2 \2m2j
^ т(т—1)(т—2) / х2 \з _^
Ь2-3 \2т2)
Далее, в каждой из дробей, которые вычитаются из 1,
увеличим числители и уменьшим знаменатели. Именно,
в числителях всюду вместо т — 1, т — 2, т — 3, ...
будем писать большее число т, а в знаменателях вместо
2, 3, 4, ... — меньшее число 1. От этого каждая
вычитаемая дробь увеличится, и вся правая часть неравенства
128

заменится еще меньшим числом. Поэтому и подавно
СОЬ т^1 1 \2m*J Ы \2tri*)
1-Ы \2m2/
, x2 о дг4 о хв
2 т2 4 т4 8тв
__ « X2 X4 X*
"" 2т " 4т2 ~~ 8т5"~~' *' ~~
-\-Х1(\л_х2 4-^-4- \
1 2т V ^ 2т ^ 4т2~г"7*
Члены в круглой скобке образуют геометрическую про-
х2
грессию со знаменателем^-. Если этот знаменатель
меньше единицы (что, наверное, будет, когда т —
достаточно большое число) и если прогрессию считать
продолженной до бесконечности (отчего неравенство только
усиливается), то, пользуясь формулой для суммы
бесконечной геометрической прогрессии, получаем:
т 2т . _а^_ 2т —х2*
~2т
Если теперь т безгранично увеличивается, то
знаменатель дроби
2т —х*
также увеличивается, а вся дробь стремится к нулю.
Следовательно, величина
1-
2т — х2
стремится к единице, и величина cos"1—, которая,
с одной стороны, меньше единицы (так как cos — < 1 ],
X2
а с другой стороны, больше, чем число 1 —2 _ 21
неограниченно приближающееся к единице, сама
стремится к единице, т. е.
cosm v 1, когда т -> оо.
т •
129

Но теперь уже само собой получается, что и cos"1 *—,
cosm-2 Л f Cosm"3 --, ... стремятся к единице. В самом
деле, имеем следующие неравенства:
cosm — < cos™-1 — < 1,
C0Sm--<C0Sm"2--<lf
COSm — < COSm"3 — < 1,
(так как чем в большую степень возводится число cos—,
меньшее единицы, тем меньший получается результат).
Поэтому cosm-x —, cosm~2 —, cosm~3—,... — числа, заклю-
ченные между единицей и cosm —, неограниченно
приближающимся, как мы доказали, к единице, — сами должны
стремиться к единице.
Мы установили в итоге, что, если в правых частях
формул (39) и (40)
cos х = cos'" - - m(tm71) cos'"-2- • sin2 - +
m 1-2 m m '
+ m(m-l)(m-2)(m-3) ± ^
1 1-2-3-4 m m '
m m л x . x
sin x = -г- cosm_1 — • sin
1 m m
m(m—l)(m —2) m « x . « x .
1.2-3 ,cos^-ffr-sin3-+...
неограниченно увеличивать m, то, во-первых, будет
неограниченно расти число членов правой части и, во-
вторых, каждый из членов будет стремиться к
соответствующим членам степенных рядов:
*з хь х1 , х» /ААЛ
130

Спрашивается, можно ли утверждать, что первый из
степенных рядов представляет собой cos х, а второй sin х?
Оказывается, что да, но этот вопрос требует особого
исследования.
В самом деле, какие у нас основания ожидать
утвердительного ответа?
Во-первых, то, что правые части формул (39) и (40)
при любом т, сколь угодно большом, дают cos x и sin x,
и, во-вторых, то, что каждый из членов этих правых
частей при больших т все меньше и меньше отличается
от членов рядов (43) и (44).
Затруднение здесь может возникнуть потому, что мы
снова встречаем два фактора, действующих в разные
стороны: с одной стороны — неограниченно
уменьшающиеся разности между членами рядов (39) и (40) и рядов
(43) и (44), а с другой — неограниченно возрастающее
число членов. Могут быть случаи, внешне похожие на те,
с которыми мы имеем дело сейчас, где быстрота
увеличения числа членов с избытком покрывает уменьшение
разности членов и в результате набегает большая разность
между суммами. Вот простейший пример такого случая.
Рассмотрим сумму т одинаковых слагаемых вида —
1+1+1+1+...+1.
т раз
Очевидно, что при любом сколь угодно большом т
эта сумма будет оставаться одной и той же, равной
единице:
т т т т т
т раз
Станем теперь неограниченно увеличивать т. От этого
число слагаемых будет неограниченно возрастать,
каждое же слагаемое будет стремиться к нулю.
Если напишем ряд:
0 + 0 + 0 + 0 + 0 + 0 + ...,
то можем утверждать, что члены нашей суммы стремятся
к членам этого ряда. Однако величина суммы равна
единице, в то время как сумма ряда равна нулю.
131

Итак, одних оснований, приведенных на стр. 130,
еще недостаточно для того, чтобы утверждать, что суммы
рядов (43) и (44) будут те же, что и для правых частей
формул (39) и (40), т. е. cos х и sinx. Однако все же можно
убедиться в том, что это верно.
Пусть, например, мы хотим доказать, что
х2 х4 х° х&
coex=l__ + _f__ + __... (42)
Заметим сначала, что ряд, стоящий справа, сходится и притом
абсолютно, при любом значении х. Чтобы доказать это, воспользуемся
признаком Даламбера. Именно, рассмотрим абсолютные величины
отношений последующих членов к предыдущим. Абсолютная вели-
х2 л
Xй
четвертого к третьему:
х2
чина отношения второго члена к первому есть | — -^-: 1
"4Г : 2!
третьего ко второму: ■ . . — . — ~ 4
Xе х4 I х2
- -ft : тг\ = ?—ё и т. д. Вообще абсолютная величина последую-
6! 4! | 5 • 6
щего члена к предыдущему имеет вид
х2
(п—\)п '
где п — 1 и п — целые числа (причем п — 1 — нечетное, an —
четное).
По мере удаления от начала ряда числа п — 1 и л неограниченно
х2
возрастают и число -. тт >-0. Поэтому, начиная с некоторого
момента, оно станет и будет оставаться меньше любого
положительного числа <7, меньшего единицы. А отсюда, по признаку Даламбера,
следует абсолютная сходимость рассматриваемого ряда.
Чтобы доказать, что сумма ряда равна cos x при любом х, нужно
убедиться, что частичные суммы ряда стремятся к cos x как к
пределу, т. е. что разность между cos x и этими частичными суммами
при достаточно большом числе слагаемых может быть сделана меньше
любого малого положительного числа е. Выберем число членов
частичной суммы
х2^ х*__х« х^
2Г + 4Т ЬТ + '"±'п\
(а это число равно — +1 = ~У ) настолько большим, чтобы сумма
абсолютных величин всех остальных членов ряда
I * \п+2 I х |л+4 | х 1*+6
(я+ 2)! +(/i + 4)! ~*~(я + 6)! + '"
g
была меньше-^-. (Это можно сделать ввиду абсолютной сходимости
ряда.)
132

Возьмем теперь в правой части формулы (39) число т ббльшим,
чем п% и рассмотрим разность
/, х2 х4 хй Xs хи .
r0S д_^, __ + __-_ +.__... + _..
Заменяя здесь cos x его выражением по формуле (39) и
группируя члены попарно — первый член выражения для cos x с первым
членом ряда, второй со вторым, третий с третьим и т. д., получим:
I т * 1 I \т(т—\) ,„ 0 х . ., х х21 ,
COS™ 1 — —FT* L COS™-2 — • SHI2 оТ +
|_ m | I 2! m m 2! J
, \m(m— \)(m — 2) (m — 3) mlx . x x4 1
+ — ^-Ц-,—— ^-cosm"4 • sm4 -,-. +- ...
1 I 4! m m 4! | ~~
\m (m— 1) ...(m — /i + I) ^ „ x . „ х хл|
... + —* —г !—~ cosm~fI - - • sin* , hp
[ я' m m n\ \
_ \m (m — \)...(m — n-\- \)(m — n)(m — n—\)
~* I 0T+2)I X
Xcos™"""2 _.. 8тл+2
m m
m (m—1)... (m —л —3) m „ . x . „.A x ,
v - * ■ cosfn_n_4 - • smn+4 1-
(л + 4)! т т
m{m— 1)... (m — n — 1) „ „ u x . m.a x
■т—гът, cos™-"-» — • sinn+e —
fn + 6)! m m
, III \ТП II ... \IU П II * . „._ Л 1
H zr-rhTi ~ cosm~n-« «• • sinn+e — — ....
В последнюю квадратную скобку заключены все члены
выражения (39) для cos х, которым не нашлось парных в частичной сумме
. х2 , х4 хп
2| -г 41 —-Я! •
(Не забудем, что мы взяли т ббльшим, чем п. Поэтому правая часть
формулы (39) содержит больше членов, чем наша частичная сумма.)
Каждая квадратная скобка (кроме последней) содержит
разность двух членов: одного из формулы (39), другого из ряда (43).
Но первые, как мы видели, стремятся ко вторым как к пределам
при неограниченном возрастании т. Поэтому величина каждой из
этих скобок может быть сделана сколь угодно малой при достаточно
большом т — настолько, что все эти скобки, вместе взятые (число
их равно числу членов частичной суммы и не зависит от т), дадут
сумму, меньшую -=- по абсолютной величине.
Что касается последней квадратной скобки, содержащей все
члены выражения (39), которым не нашлось парных в частичной
сумме, то их число будет безгранично возрастать вместе с ростом т.
Однако абсолютная величина каждого из них будет меньше, чем
соответствующий член ряда
| X |"+2 | X |*+4 | X j^b
(л+ 2)1 +(п + 4)! + (п + 6) +-1
сумма которого меньше -~- (стр. 132).
133

В самом деле, например, первый из этих членов
т (т— 1) (т — 2)... (т — п— 1) „_„ _ х . „,„ х
—i ;-±-—/ к L cos"1 п~2 — • sin/I+2 —
(/z + 2)! га m
может быть записан в виде:
m.m(l-l).«(l-
mj \ m_J_ cQsm_n_2 х_ sjnn+2 x =
(л+ 2)! m m
(,_±)(,_2\...
п+\
(л + 2)!
Ио каждое из чисел
cosm-/i-2 2L . mn\2 . S[nn 1-2 _£_
m га
i-i, .-i i- ra+1
m
m
меньше единицы. Кроме того,
и (как мы видели на стр. 126)
т sin
т
<1
<м.
Поэтому абсолютная величина рассматриваемого выражения меньше,
чем
1 * "•• V \m-n-2. 1ИЯ+2— I * I
(я+ 2)!
(л + 2)! *
Аналогично найдем, что абсолютная величина второго члена из
последней квадратной скобки (на стр. 133) меньше, чем
(я+ 4)1 '
третьего — меньше, чем
(я + 6)1 •
и т. д.
Но это значит, что абсолютная величина всей квадратной скобки
меньше суммы ряда
\х\»+* 1 X ]"+*
+
|я+6
(« + 2)1 т (я+ 4)1 Чп + 6)!
+ ...,
т. е. меньше --
134

Сопоставляя этот результат с тем, что сумма абсолютных
величин остальных скобок также меньше -^, заключаем, что все
выражение на стр. 133, равное
cos х
У 2! +41 п\)>
меньше е I при л, выбранном так, что
I х |"+* | х |«+« | х |»+» е \
(/х + 2)!+ (п+4)! "*" (n + 6)l f-^ 2Г
А так как е — любое малое положительное число, то отсюда следует,
что
n.irna)[Cosx-(l-| + J-...±5)] = 0)
или что
f X2 , X4 Xе , X* Хп+2 Хп+*
cosx=l-^- + -rr-^- + ...±-r=r:
2! ^ 4! 6! ^ л! ~^ (п + 2)\ — (п + 4)! "■""»
что и требовалось доказать.
Совершенно так же можно установить, что
X3 X5 X7 X* X11
sin *=*~зГ + 5Т~~ 7Г + 9Г~~ \й + '~
Для этого нужно доказать сначала, что ряд, стоящий в правой части,
сходится абсолютно при всяком х (по признаку Даламбера), а затем,
что сумма этого ряда равна sin x, т. е. что абсолютная величина
X** X** Х'*
разности между sin x и частичной суммой х — от + ei ...it—г
может быть сделана меньше любого малого числа е, если только п
взять достаточно большим.
Укажем важнейшие применения выведенных рядов.
Прежде всего с их помощью можно вычислять значения
cos х и sin х по заданному углу. Нужно только твердо
помнить, что в наших формулах угол х выражен в
радианах. Поэтому, если угол задан в градусной мере, следует
вычислить сначала радианную меру угла, а затем уже
пользоваться рядами. Заметим, что при вычислениях
можно с самого начала ограничиться значениями xt
положительными и не большими -j- (т. е. 45°). В самом
деле, мы знаем, что тригонометрические функции любых
аргументов всегда могут быть «приведены» к функциям
аргументов, положительных и не больших ~ = 0,785398...
135

(45°). Так, например,
cos (—0,3) = cos 0,3; sin (— 15°) = —sin 15°;
cos 10,27 = — cos (10,27 - Зл) = — cos (10,27 - 9,42) -
= — cos 0,85 = — sin (j - 0,85) = - sin 0,72
и т. д.
Но если О^х^с^-, то оба ряда
X3 X5 X7
« X2 . X4 Xе .
COsx = l —2Г + 4Г-ёГ+ ...
будут знакопеременными с убывающими членами
(действительно, знаменатели увеличиваются, а числители
уменьшаются как степени с возрастающими показателями
числа jc, меньшего единицы (х < 0,785398...)).
Следовательно, отбрасывая в каждом из рядов все члены, начиная
с некоторого, мы делаем ошибку, меньшую, чем первый
из отброшенных членов. Поэтому, если нужно вычислить
значения cos л; и sin л: с точностью до 0,0005 х), то можно
даже в самом неблагоприятном случае наибольшего к
(* = -£■ = 0,785398...) ограничиться лишь тремя
первыми членами обоих рядов:
х3 . х5
COS X ^ 1 - 2j- + 4j .
В самом деле, в первом случае отброшенный член по
абсолютной величине равен ^г = 5040 • При х = -^ =
= 0,785...
_х» (0,785...)' (0,79)' 0,192039... 0,2 _nnnnn.
5040 5040 ^ 5040 5040 ^ 5000
L) To есть до половины третьего знака после запятой; такую
точность дают трехзначные таблицы тригонометрических функций.
136

Во втором случае (для cos x) первый отброшенный член
по абсолютной величине равен ~1г =720* ^Ри Х==^С
х« _ (0.785...)» (0,79)в 0,243087... п mfm
720 ~ 720 < "У2Г < 720 < U>UUU^'
Однако такое количество членов нужно брать лишь
в случае х, близкого к ^ = 0,785398... Для меньших
аргументов та же точность может быть достигнута при
меньшем числе членов.
Рассмотрим, для каких аргументов можно брать лишь
по два первых члена из рядов для cos х и sin л:, т. е.
пользоваться приближенными формулами:
х3
sin*^*—g-, (46)
cos x ^ 1 — у (47)
(при этом мы хотим, чтобы точность оставалась той же,
т. е. до 0,0005).
х5
Так как ошибка первой формулы меньше ^ то вопрос
заключается в указании таких значений х, для которых
** < 0,0005,
или, так как
б! = 1-2-3-4-5=120
и
**< 0,0005-120 = 0,06,
K^oU? = ^.., = 0,5696...
Итак, при х < 0,5696 ..., что в градусной мере
соответствует углам, меньшим 32°38' ..., можно при вычислении
sin* с точностью до 0,0005 довольствоваться формулой
(46). Аналогично найдем, что при х < 0,3309 ..., что
соответствует углам, меньшим 18°57', можно
пользоваться формулой (47) для вычисления cos л* с точностью
до 0,0005. Наконец, можно считать, что
sin*^*,
cosjt^l,
137

с точностью до 0,0005, если в первом случае
-£< 0,0005,
откуда х < 0,1144 ..., что в градусной мере соответствует
углам, меньшим 6°33'; во втором случае для достижения
требуемой точности должно быть
у < 0,0005,
откуда х < 0,0316 ..., что в градусной мере соответствует
углам, меньшим 1°48\
Итак, при вычислении sin х, с точностью до 0,0005,
при
0,569 < х < 0,785
(0,569 соответствует 32°, а 0,785 — 45°) следует
пользоваться формулой
при
0,114 < х < 0,569
(0,114 соответствует 6°) — формулой
sin х ^ х — ~г
6
и, наконец, при
0^*^0,114
— формулой
sin*^*.
Аналогично, для вычисления cosat, с точностью до
0,0005, при
0,330 <лг^ 0,785
(0,330 соответствует 19°) нужно пользоваться формулой
(45):
« X2 , X*
при
0,031 < х < 0,330
138

(0,031 соответствует 2°) — формулой
COS X я^ 1 — у
0 <#< 0,031
cosx^l.
и, наконец, при
— формулой
Например,
sin 1° = sin 0,0175 ^ 0,0175.
Однако ошибка формулы
sinx^#
при х = 0,0175 (1°) меньше, чем
<0'0f)3=°-00006053-< 0,000001;
поэтому стоит 1° перевести в радианную меру с большей
точностью, чем это сделали мы. Замечая, что Г =
= 0,0175453 радиана, находим:
sinl° = sin0,0175453^0,017545
(ошибка здесь не больше 0,000001).
Еще пример:
cos 40° = cos (40. щ) = cos ~ jt = cos 0,6981 •
По формуле (45) имеем:
cos 40° = cos 0,6981 ~ 1 - <^ + <^ ~
^ 1 - 0,2437 + 0,0099 = 0,7662.
Этот результат, во всяком случае, верен до 0,0005. Более
того, в данном случае ошибка формулы меньше, чем
(0,6981)6 (QJ^ 0,117. Q
720 ^ 720 720 ^ u,uuuz.
а:2 л4
Так как второй и третий члены формулы, — у и 4р
мы вычисляли с точностью до 0,00005 каждый, то в
результате ошибка не может превосходить 0,0003.
Итак,
cos 40° я^ 0,7662 ±0,0003.
139

Но применения полученных рядов не ограничиваются
вычислением значений sin x и cos x для заданных числовых
значений х. С помощью этих рядов и ранее полученного
биномиального ряда можно выводить новые формулы,
точные и приближенные. В самых различных вопросах
математики, естествознания и техники ряды используются
с этой целью. Не предполагая у читателя специальных
знаний, необходимых для того, чтобы разбираться в этих
вопросах, приведем здесь примеры применения рядов
к некоторым задачам геометрических построений
(приближенных).
Рис. 20.
Именно, займемся задачей о спрямлении дуги круга,
т. е. о построении с помощью циркуля и линейки отрезка
прямой, длина которого равна длине данной дуги
окружности. Эта задача может быть решена (как доказывается
из теоретических соображений) лишь приближенно.
Однако существуют простые способы (Снеллия, Ренкина),
дающие решение с точностью, удовлетворяющей всем
требованиям практики.
Предположим, что задача заключается в построении
отрезка прямой, равного по длине дуге А В окружности
(рис. 20).
Снеллий х) следующим образом решал эту задачу.
Проведем в точке А касательную AT к окружности и
*) Виллеброрд Снеллий (1581 —1626) — профессор в
Лейдене (Голландия). Известен открытием закона преломления
световых лучей.
140

предположим, что отрезок AD дает решение, т. е. AD =
= дл. АВ. Соединяя точки D и В прямой, продолжаем
DB до пересечения в точке С с продолженным радиусом
АО. Отрезок АС мы можем найти, лишь зная отрезок
AD. Но и, обратно, зная отрезок АС, можно, продолжив
прямую ВС до пересечения с касательной Л Г, найти
отрезок AD. Итак, постараемся построить отрезок АС
и для этого найдем его длину d. Опустив из В
перпендикуляр на АО, получаем из подобия треугольников
ADC и FBC:
АС__ АР
FC ~ FB '
Но
AC = dy AD = AB = ra\
FC = OC + OF = (d-r) + rco$a, FB = rs\na.
Таким образом,
d ra а
d — r + rcosa ~~ rsina sin a '
откуда
d sin a = da — ra + ra cos a.
Следовательно,
da — d sin a = ra — ra cos a
и
, _ ra (1— cos a)
a — sin a
Весь успех способа Снеллия заключается в том, что
он нашел для d чрезвычайно простое и в то же время
достаточно хорошее приближение. Оказывается,
d^3r.
Проверим это и оценим ошибку в длине отрезка AD9
вызванную употреблением такого приближенного
равенства. Для этого воспользуемся разложениями в ряды
sin a и cos a:
1 — cosa= 1 — (1
a — sin a = a — (a
3! 5! ^ 71 9! ^ * * '
a2 , a4 ae , a8
2Г + 4f ~~ 6Г + 8f
— -L —
4! + 6! "
a» , a* __ aP_ , a» _ \
3! +5Г 7!~ + 9Г •,7 —
= 2f_ 4T +
a»
"3!
ry5 ~7
8! ^'
«9
141

Поэтому
d=-
'a[T\ ~4[ +6[ ~~ '")
l43! 5Г+ 7l "')
¥(■
a2
a4
3-4 ' 3-4-5-6
6
aa
4-5 ^4.567
=3r
a2 a4
12" + 360
l-^- + -a-4--
20 ^840
Деля числитель на знаменатель по правилам деления
многочлена на многочлен (а все действия с абсолютно
сходящимися рядами можно производить по тем же
правилам, что и действия с многочленами), получим;
12 ^ 360
1-°^ + ^-
20 ^ 840
Итак,
d = 3r(l -
1 —
— ... 1-
аа
а2
»-з6"
а2
30
а*
30
г 630
4- а4
1 600
а4 !
12600 '
а4
12600 '
...
...
■•)-'(
а*
а*
20 ' 840
а4
30 12600
...).
Приближение Снеллия (d ж Зг) получится, если в
найденном ряде отбросить все члены, начиная со второго.
Так как ряд не является знакопеременным, то мы не
можем утверждать, что ошибка будет меньше первого
отброшенного члена, т. е. ~. Однако, рассматривая
равенство
d = 3r
12 ^ 360 —
20^840
142

можно установить, что
з-'Го*<4<з
(при OsscasS 1 (57°17\..)).
Так, при a = 0,7854 ... (45°) мы получаем:
„ 2(0,7854)2 d _
6 19 <~<-6
ИЛИ
2,935r < d < Зг.
Действительно, при а = -^- имеем:
^r.|(l-cos|)=r,
л . д 0,7854 — 0,7071
--, sin -г-
4 4
При меньших углах а разница между d и Зг гораздо
меньше. Но нас интересует не ошибка в построении
Рис. 21,
отрезка Л С, а ошибка в построении AD; ее легко оценить.
В самом деле, если отрезок АСг = Зг (рис. 21), то
соответствующий отрезок AD1 определится из пропорции
АРХ _ АСХ
FB ~ FCL'
где
FB = r sin a, AC1 = 3r
и
FCX = ОСг + OF = 2r + r cos a.
143

Таким образо\т,
ADt _ Зг _ 3
г sin а 2г -|- г cos а 2 + cos а *
Подставляя сюда вместо sin а и cos а их разложения в ряд,
найдем:
AD H-V+S-) '"(■-g + g--)
' "• + (.-£+£-...) ".(.--& + £-•)"
а2 а4 а2 а4 _
ЗГ + 5Г"" "• 6 + 120 *•*
= га 5 -л = га
2! 3 ^4! 3 •" 6 ^72
Разделив числитель на знаменатель, получим:
. а2 а4 а6 I а2 а4 а0
"й т 'юл cn/m г • • • * а Г ~*7~,
6 ' 120 5040 ^'" 6 ^ 72 2160
а2 а4 а6 а4 _
72 2160 ' "• 180 1512
а4 , а8
180 ^ 3780
а4 а6
Тол "г"
180 ' 1080
1512
+ •
Итак,
Л^=га(1-^-^-...),
а надо было построить отрезок
AD = га.
Разность между искомым и найденным отрезками
составляет величину
5 гу7
аа , а
= гТяп + г
180 ^ 1512 ' •"
Чтобы оценить эту величину (ошибку построения),
вернемся к действию деления рядов, которое мы только
что производили, и остановим его на первом остатке.
144

В частном будет единица, а в остатке — щ + 37^ — •. • ;
поэтому выражение для ADX может быть записано в виде:
а2 а4 а8
1 _:L л- - - l
лп 6 ^ 120 5040^
Аих = га ■ =
1-^ + -а.
6 W2
а4 а6
"Г80~ 3780 + "
а2 , а4 ав
= га
72 2160
В числителе и знаменателе дроби, находящейся в
скобках, стоят знакопеременные ряды. Члены этих рядов
убывают по абсолютной величине, во всяком случае,
если а < 1 (что соответствует 57°17'...). Поэтому мы
увеличим эту дробь и тем самым уменьшим заключенную
в скобках разность, если в числителе поставим большую
а4 « а2 т-,
величину щ,ав знаменателе меньшую 1 — -g-. Получим
а4
ADX > га
Если а ^ 1, то
1-
180
а4 а4
а2 5 180 ^Ш а4
6-^6' а2 ^ _5_ 150
6 6
AD1>ra(l-^).
С другой стороны,
/
а4 а6
\
лгл \ л 180 3780^" \ ^
AD1 = ra[ 1 т -г i < га.
\ 6 W2 2160 ^'" I
Поэтому
ra>AD1>ra(l-"^) = га-
гось
150
0>ЛО1-га>-^.
145

Итак, мы установили, что ADX < га (га — длина дуги
АВ), но разность ADX<— га по абсолютной величине не
га5
больше, чем
150#
Что касается относительной ошибки
га6
а4
ADi — га
га
-^. При а = 0,7854... (45°)
то
от-
она меньше 1СЛ — |СЛ.
150. га 150
иосительная ошибка не превосходит, таким образом,
величины
(0,7854)* ОД
150 ^ 150 u»uuzo ■
,< 0,003.
При меньших углах она гораздо меньше. Заметим, что
относительная ошибка, будучи пропорциональной а4,
убывает в 24 = 16 раз при уменьшении дуги в 2 раза. Поэтому,
прежде чем применить этот
способ к некоторой дуге,
следует разделить ее на 2,
4 или 8 частей (если она не
слишком мала) и построить
отрезок, равный по длине
этой части дуги. Взяв его
затем 2, 4, 8 и т. д. раз,
получим окончательное
решение задачи.
Чтобы привести пример,
в котором одновременно
употребляют и
биномиальный ряд и ряды для синуса
и косинуса, рассмотрим еще
принадлежащий Ренкину
способ приближенного
спрямления дуги
окружности. Он заключается в следующем. Хорду АВ (рис. 22)
данной дуги продолжаем на половину ее длины и из
полученной точки /С, как из центра, радиусом KB засекаем
касательную Л Г. Отрезок ADX и будет равняться
(приближенно) длине дуги АВ. Чтобы оценить точность этого
построения, выразим длину ADX через г и а и сравним
полученное выражение с длиной га дуги АВ.
Из треугольника AKDl9 опуская высоту КМ на
продолжение стороны ADlf имеем:
ADX = DLM -AM= VKDi-KM2 - AM.
Рис. 22.
146

Но
KDt = KB=±AB~-2BL=3r sinf ,
2 * 2 " " 2
3 ,o 3
KM = AK sin WAI = r sin -| • sin |-
Итак,
/0M=rsin*~
и
AM = AK • cos К AM = r sin -«- • cos -— = у г sin a.
Окончательно
ADx=y (3rsiny] — (rsin2yj — yrsina =
= r(3sin-~y 1 —-g-sin2-^- —ysinaj.
Разложим теперь в ряд выражение, заключенное в
скобки. Имеем по порядку:
. a
Sin-2
У'
a \ 2 у \ 2 У a a3
~~ 2 3! + 5! " • ~~ 2" 48
1 . о a Л 1 . 2 a \L
-9"Sln y = (1--9Sln TJ2 =
= l+-2-(--9-sin2|) +
.2 \ 2 ) 1 1 . -a\« ,
^3840
! 1 . о a 1 . x a
= 1-Tssln y-wsin y----
Получился ряд, расположенный по степеням siny
f собственно, sin2yj, а не по степеням а. Чтобы получить
степенной ряд, в данном случае можно поступить двояко.
Во-первых, пользоваться приемом перемножения
рядов (по тем же правилам, по которым мы перемножали
147

многочлены в главе II) *). Тогда получим:
Sln ~2 ~~ \"2 48 + 3840 "7\2 48 + 3840 ~~ * * *J ~~
а а а а3 а3 а , а5 а , а3 а3 ,
"" 2" " 2" ~~ 2" 48 "" 48 ' 2 + 3840 ' 2 + 48 ' 48+
4- ~ а5 _ _ ?2 а4 | а0
+ 2 " 3840 ~~ "'' "" "4" "" 48 + Г440 ~~ ''' :
sin*T = (sin- 2-J =
^а2 а4 aft Wo2 а4 а«
"• ТЙО ~ " 7 \7 ~~ 48 ' 1440
4 48 ' 1440 "7 \ 4 48 ' 1440 '"] ~
_ а2 а2 а*_ а2 а2 а4 __ а4 а«
"" Т " 4" "~ 48" ' Т ~~ Т ' 48 ~~ '' * ~~ Тб "" 96
и т. д.
Впрочем, проще те же результаты можно получить
с помощью предварительных тригонометрических
преобразований:
а2 , а4 а*
-|2
Sin4 -- =
а 1—cosa * V 2! + 4! 6! +"
2 2
а2 а4 а6
У ~ 24+720 ~ '" а2 а4 , ав
2 4 48 ^ 1440 '••'
. А а / . « а \2 /1—cosa\2 1 — 2 cosa + cos2a
S,n -2=(Sln 2 J =(—2—; = 4 =
l+cos_2a
l^^cosa-h 2 ^2-4cosa + l+cos4a_
~ 4 8 ~
3 — 4 cos a + cos 2a
~" 8 ~~
3-Ч1"2Г + 4Г"вт+-; + [|""2Г + "41 бГ + '"| _
~~ 8 ""
3_4+2а2-т+ш5-...+ 1-2а. + -6---180- + ...
2 12 "*" *' * a4 ae
16 96 + '
И Т. Д.
*) To есть в данном случае, выписывая сначала произведение
всех тех членов рядов, которые дадут низшую степень a (a2), затем
всех тех, которые дадут следующую степень (а4), потом (ай) и т. д.
148

Так или иначе, находим:
/
1— -g-Sin у— 1 — y-^-j- — 28 + J440 — •
1_ /а* _ а» \ . _ а2 Па*
648 116 96 +'' 7 "" 72 •" 10368
Наконец, последний ряд, нужный для подстановки
в выражение AD1% есть ряд для sin а:
а3 . а5
8ша = а--6- + ш-...
Подставляя найденные ряды в выражение для ADl9
получаем:
лп _ U/a a3,_aj>_ \/t a2 , 11a4 \
яиг-Г^^2 - jg + 3840 "~ "'Д 72+10368 "V
LI a3 J_ a&L ^ I
" 2 Г ~~ 6 + 120 ~~ '' 7 I "
Раскрывая здесь скобки (после перемножения рядов),
находим:
^_,[s.f-i-s-S-i+3-l(-S) +
+ 3,3840,1~3,48(""72J +
. ~ _a 11a4 _ _ J_ , J_ a»
+ **' 2 ' 10368 '•• 2 a+ 2 ' "6
2 " 120 "f" —J Г\ 2 16 48 + 1280+ 1152 "^
+ 6912 "• 2 + 12 240+ " V ~"
a5
= r a
1080
_...) = ra(l_r*-_...).
Таким образом, разность между длиной дуги А В
и длиной отрезка ADX равна
дл. АВ — дл. Л£>х =
Путем простого, но кропотливого подсчета можно
установить, что, во всяком случае, при a <= 1 (57°17\..)
0<дл. ЛБ-дл. AD1<-m.
149

Насколько точен этот способ, видно из того, что при
углах, не больших 30°, абсолютная ошибка не достигает
одной двадцатипятитысячной доли радиуса, а
относительная составляет около 0,6 %о (не процента, а промилле!)
измеряемой величины.
Как видно из последнего неравенства, способ Ренкина
гарантирует точность, в 5—6 раз большую, чем способ
Снеллия. Однако при небольших углах каждый из
способов дает настолько точный результат, что ошибка
способа полностью поглощается неточностями построения
(обусловленными несовершенством линейки и циркуля,
тем, что начерченные «линии» имеют ширину и т. п.).

ГЛАВА VIII
ЛОГАРИФМЫ И ЛОГАРИФМИЧЕСКИЙ РЯД
Незаменимый инструмент для вычислений, начиная от
многозначных таблиц в руках астронома или геодезиста
и кончая счетной линейкой в руках техника или
мастера, — логарифмы насчитывают около трехсот
пятидесяти лет существования.
Мы предлагаем читателю вообразить себе, что он на
чудесной машине времени перенесен в начало XVII века,
когда идеи так называемой высшей математики
(аналитической геометрии, дифференциального и интегрального
исчисления) еще только бродили в головах немногих
выдающихся математиков. В это время ученые
располагали по существу лишь методами элементарной
математики, и в эту же пору появились первые таблицы
логарифмов (Бюрги, Бригга, Непера) *).
Мог ли читатель, окончивший среднюю школу
XX века, отлично знающий пользу и способы
употребления логарифмов, встать в ряды «открывателей» логариф-
*) Иобст Бюрги (1552—1632). Не будучи профессиональным
ученым (он был механиком и часовщиком), швейцарец Бюрги являлся
крупным математиком. Однако свои открытия он не опубликовывал
или опубликовывал с большим опозданием (так было с его
таблицами логарифмов).
Генри Б р и г г (1561—1630) — английский математик,
профессор Оксфордского университета. Составил большие
(четырнадцатизначные) таблицы логарифмов, употребляя при этом им самим
изобретенные способы вычисления.
Джон Н е п е р (1550—1617) — шотландский математик. Ему
принадлежат не только таблицы логарифмов, более совершенные,
чем таблицы Бюрги, но также и оригинальное определение
логарифмов, заключающее в себе идеи лишь зарождавшейся тогда высшей
математики. Кроме того, он известен своими формулами сферической
тригонометрии (так называемые неперовы аналогии).
151

мов и опубликовать им самим составленные таблицы
с объяснениями? Надо думать, что многие читатели
сочтут последнее столь же невозможным, как и
переселение на 300 лет назад. Дело вычисления логарифмов,
особенно с большой точностью, представляется им
туманной и сложной задачей.
Но «не боги горшки обжигают». И составление
таблицы логарифмов вполне доступно школьнику старших
классов.
Напомним сначала, что логарифмом числа N по
основанию а называется показатель степени, в которую надо
возвести а, чтобы получить N. Иными словами, мы пишем
a = \ogaN9
если
a? = N.
Так, в главе VI мы видели, что
1,1^ = 1,14429...,
поэтому
log,,, 1,14429... = /2 = 1,41421 ...
Чрезвычайно важным является то обстоятельство, что
достаточно иметь таблицы логарифмов, вычисленных по
одному какому-нибудь основанию а, чтобы с их помощью
получить, почти без всякого труда, логарифмы по
любому другому основанию Ь. Например, если каждый из
логарифмов по основанию 10 умножить на 3,3219, то
получатся логарифмы по основанию 2; если десятичные
логарифмы помножить на 24,160, то получатся логарифмы
по основанию 1,1, и т. д.
Чтобы убедиться в этом, рассмотрим вопрос о
переходе от логарифмов при одном основании к логарифмам
при другом основании в общем виде. Пусть
<x = logaN, $ = logbN.
Это значит, что
a* = N и b* = N.
Отсюда находим:
аа = Л
152

Из этого соотношения легко выразить а через р, или
Р через а. Именно, беря логарифмы по основанию а от
обеих частей равенства, будем иметь:
a loga a = p loga b,
и так как loga a = 1, то
а = р • logrt Ь.
Подставляя сюда вместо а и Р их значения (т. е.
log„ N вместо а и log^ N вместо Р), получаем:
logaJV = log*AMogeft. (48)
Итак, чтобы получить логарифм числа при «новом»
основании а, нужно умножить логарифм числа N при
«старом» основании b на логарифм «старого» основания
при «новом» основании а.
Зта формула справедлива при любом значении N.
Подставим в нее, в частности, N = а. Получим:
logaa = log*a-loga&
или
l=log,a.loga6. (49)
Из последнего равенства следует, что
1
\ogab-
' logba *
Заменив loga b через -j в правой части равенства (48),
можем записать еще:
'**-1Й7- <50>
Последняя формула дает следующее правило: чтобы
найти логарифм числа по основанию а, нужно разделить
логарифм этого числа по «старому» основанию b на
логарифм «нового» основания а по «старому» основанию.
Так, если мы хотим найти логарифмы чисел при
основании 2, отправляясь от «старого» основания 10, то,
полагая в формуле (50) а = 2, b = 10, найдем:
^"=Ш-оИш=М2т^-
153

Аналогично,
^ём™ logioirl 0,04139 ^»1DU1£'V
и т. д.
Полезно заметить следующее правило, облегчающее
запоминание формул (48), (49) и (50): если в любой из
этих формул отбросить значки логарифмов и с
оставшимися в правой части величинами производить действия
как с дробями, считая логарифмируемые количества
числителями, а основания логарифмов — знаменателями,
то в результате получится левая часть. Так, если в
формуле (48) отбросим значки логарифмов, а на оставшиеся
величины будем смотреть как на числители и
знаменатели дробей, то получим:
К = JL . А
а ~~ b ' а *
И действительно, левая часть равна произведению двух
дробей, стоящих справа.
Аналогично, отбрасывая значки логарифмов в
формуле (50), получим равенство:
IL
N _ Ь
а ~~ а '
~Ь
в котором снова левая часть равна частному двух дробей,
стоящих справа.
Но вернемся к нашей задаче составления таблицы
логарифмов.
Так как переход от таблицы логарифмов при одном
основании (Ь) к таблицам при другом основании (а)
очень легко осуществляется посредством формулы (50),
то при составлении таблицы логарифмов можно брать
основание, при котором логарифмы вычисляются проще
всего. Если окажется, что для целей использования
таблиц удобнее какое-либо другое основание, то к этому
последнему легко перейдем, помножив (или разделив)
каждый табличный логарифм на одно и то же число.
154

Итак, при каком основании проще всего составлять
таблицу логарифмов 1)? На первый взгляд может
показаться, что лучше всего для этого взять какое-либо
«круглое» число: 2, 5, 10, 12 и т. д. Но при ближайшем
рассмотрении «круглое» число в качестве основания
оказывается неудобным. В самом деле, как бы вы стали
с точностью до четвертого или пятого знака вычислять
десятичные логарифмы
lg7, lg 12 и т. д.?
С другой стороны, как бы вы стали решать обратный
вопрос: нахождение чисел по логарифмам, если,
например, lg х = 0,1; 0,27; 0,304; ... и т. д.? Очевидно, можно
было бы сказать, что
х= Ю0'1 =уЛ1"0, или x=10°'27 = ,0fT(F,
и т. п., но действительное вычисление х потребовало бы
вычисления корней различных степеней из 10, что
является опять-таки трудным делом. (Можно, конечно,
воспользоваться биномиальной формулой, но в начале
XVII века общая биномиальная формула не была
известна.)
Совсем другое дело получится, если специально
подобрать основание системы логарифмов. Именно,
построим такое число, которое легко можно было бы
возводить в степени с различными дробными показателями
(иными словами, из которого легко извлекать корни
различных степеней). Таким числом, например, является
Ъ = 210 00°.
В самом деле,
£o,oooi _ /210000)0.oooi _ 2-
£0,ооо2 __/210000)0'0002 = 22 = 4* Ь°.°003 = 23 = 8 и т. д.
Таким образом, выбирая логарифмы при основании Ь
равными 0,0001; 0,0002; 0,0003; ... и т. д., мы сейчас
же получаем числа, соответствующие этим логарифмам:
2, 4, 8, ... По существу таким путем можно построить
таблицу вида:
*) Мы пока предполагаем, что для вычисления логарифмов
у нас нет других средств, кроме средств элементарной математики.
Примерно в таком положении находились первые составители
таблиц логарифмов (Бюрги, во всяком случае).
155

lofyN
0,0000
0,0001
0,0002
0,0003
0,0004
0,0005
0,0006
0,0007
0,0008
0,0009
0,0010
N
1
1
2
4
8
16
32
64
128
256
512
1024
lo^/v
0,0011
0,0012
0,0013
0,0014
0,0015
0,0016
0,0017
0,0018
0,0019
0,0020
/V
2048
4096
8192
16384
32768
65536
131072
262144
524288
1048576
•••
Однако пользование этой таблицей чрезвычайно
неудобно, потому что числа N в правом столбце таблицы
идут со слишком большими (и притом быстро
увеличивающимися) промежутками. Если мы, например, захотим
найти число, логарифм которого при основании Ь =
= 210 00° равен 0,00156, то сможем лишь утверждать, на
основании нашей таблицы, что это число лежит между
32 768 и 65 536 — «дистанция огромного размера»!
Ошибка в логарифме на 0,0001 может вызвать ошибку
в результате на несколько сотен тысяч или миллионов.
Вся беда, повторяем, заключается в том, что дробные
степени основания Ь слишком быстро растут.
Чтобы устранить этот недостаток, будем по-прежнему
брать основание в виде степени некоторого числа с очень
большим показателем; например, возьмем Ь = Р10 00°, но
само число р подберем соответствующим образом.
Последовательные дробные степени Ь будут равняться:
£0,0001 _ /ft 10000)0,0001 = ft. £0,0002 _ R2.
£0.0003 __ ft3. £0.0004 _ ft4.
Для того чтобы соседние степени были весьма близки
между собой, необходимо, чтобы их отношение было
возможно более близко к единице. В нашем случае это
отношение есть:
^0,0002
^0.0001
= ь°-от = р,
^0,0003
сО.0002
= fco.ocoi = ^
^0.0004
^0,0003
= £0.0001 =^ §(
156

Поэтому следует выбрать р возможно более близким
к единице. Так, полагая р = 1,0001, получим в качестве
основания системы логарифмов число Ь = (1,0001)10 00°,
удовлетворяющее выдвинутым нами требованиям:
дробные степени его с показателями, идущими через 0,0001,
легко вычислять (они представляют целые степени числа
Р = 1,С001) и, кроме того, степени для двух «соседних»
(отличающихся на 0,0001) показателей мало отличаются
друг от друга (их отношение есть 1,0001, т. е. каждая
последующая степень больше предыдущей лишь на одну
десятитысячную ее величины).
Станем теперь составлять таблицу логарифмов при
основании Ь= (1,0001)10 00°. При этом будем задавать
значения логарифмов (т. е. показателей степеней, в
которые возводится Ь) и по ним будем вычислять
соответствующие числа N (степени Ь). В результате получим
таблицу, приведенную на стр. 157—158. Само составление
этой таблицы чрезвычайно облегчается тем
обстоятельством, что каждое следующее число левого столбца
таблицы получается из стоящего над ним путем
прибавления одного и того же числа 0,0001 (т. е. числа левого
столбца представляют арифметическую прогрессию с
разностью 0,0001), а каждое следующее число правого
столбца получается из предыдущего путем умножения
его на одно и то же число р = 1,0001 (т. е. числа
правого столбца представляют геометрическую прогрессию
со знаменателем 1,0001).
\ogbN
0,0000
0,0001
0,0002
0,0003
0,0004
0,0005
0,0009
0,0010
0,0011
0,0005
N
1,000000
1,000100
1,000200
1,000300
1,000400
1,000500
1,000900
1,001000
1,001101
1,005012
\ogb N
0,0101
0,0150
0,0151
0,0152
0,0153
0,0175
0,0176
0,0199
N
1,010151
1,015112
1,015214
1,015315
1,015417
1,017653
1,017755
1,020098
157

Продолжение
\ogb N
0,0051
0,0052
0,0053
0,0060
0,0090
0,0091
0,0099
0,0100
N
1,005113
1,005213
1,005314
1,006018
1,009040
1,009141
1,009949
1,010050
\ogbN
0,0200
0,0201
0,0202
0,0247
0,0248
0,0249
0,0250
0,0251
0,0252
0,0253
Л/
1,020200
1,020302
1,020404
1,025007
1,025110
1,025212
1,025314
1,025416
1,025519
1,025621
Но что значит умножить какое-нибудь число N на
1,0001? Это значит — прибавить к N одну
десятитысячную его величины:
#.1,0001 =N + 0,ОООЬ N.
Иными словами, чтобы умножить некоторое число на
1,0001, следует перенести в нем запятую на четыре цифры
влево и полученное число (0,0001 N) прибавить к
первоначальному. Вот этим-то простым правилом мы и
пользуемся при составлении таблицы. Следует заметить, что
одна из первых таблиц логарифмов, именно таблица
Бюрги, отличается от нашей таблицы только тем, что
все числа левого столбца у него увеличены в 100 000 раз,
а все числа правого столбца увеличены в 100 000 000 раз.
Благодаря этому Бюрги избегает дробей в своей таблице.
Таблицы Бюрги вышли в 1620 г. под названием
«Арифметические и геометрические таблицы прогрессий».
Однако он запоздал с опубликованием своего открытия,
к которому он пришел гораздо раньше 1620 г. Джон
Непер, совершенно независимо от Бюрги, составил и
в 1614 г. напечатал свои таблицы логарифмов под
названием «Описание удивительной таблицы логарифмов»1).
х) Само слово «логарифм» впервые употребляется Непером и
образовано им от греческих слов loioz dpiujAoO, означающих:
158

500
1000
iyoo
2 000
1|"00
$000 I з;оо
JOOOOOOOO
•••«хоооо
...«aoooi
JOO/O/ 1 J 7
• • • . I I 177
■ ■•'ля»
l ОlOO4<}66
>Jf067
J01/J i 23OI
21381
ЭМ24
idiOaooja
•10IJ4
4^417
•02Г)1314
•4/6*37
•/189.
lOj04fZ99\
• •••0/9O9I
103/6179*
••• 7214<
82 fo
••.30003
• • «40006
••4X431
••П4в7|
• '4П74
••t<4~~
•41087
П84/
• /064 1
'60646
-6H46
•7240J
8206'
• •76il6\
••i6fl)
-96839
92001
IOJ6O32H
• -6ooi/|
•'700»X
•-вОО»в
• 61 T4J
•71/991
• 8/0/б|
•0//84
•7Г691
•81799
• 711 ft
§2309
9144*
8i*f9\
•91467
"1Л76
••.9*918
0260JJ77
• • J343g
03/^7142
•'••174Г7
■ . ..t7~6A
«*J942
4466
••..90036
Г0ОЮОО4/
• • • • ЮвГГ
lOOdOl 7 73
••••II«34
■9*997
lOOOl7
• /0/">7
j002027
• 12787
• I Kl7
•11091
■11699
•33961
•4422Г
}*077\
•4839'
■т°г\
6/39
7/70
U20
Изо
[14 0
u7o~
i«o
|I7Q
1I8O
I190
boo
UtZT
1120
J» J о
|2fO
ибо
'аТо"
|2«0
I29O
JOO~
no
>ao
|ззо
340
|3/o
|з~Зо"
|3 то
|)80
. • •10066\
••«20078
• • .4"Os>I
•2189/
•3»9f2
.4-0-"*
•16239
•зб?г*
•4040Г
• -33" I
• 43274
42/2J
f*738
Г44891
•047ГГ
•7fOjI
•• djOlI
"•7S138
• • -896га
• '86,П\
96(01
IOI706871
•fOIOf
.601 20
• 70130
f2O04
•02 1/0|
•Г0Г8О
■ оа<з$б\
768 t 2
.63004
•7377c
•73109
«3386
• -8/289
•• -9ГГГ7
'"•'7«"»/J»7 7
99971
1ЯЗЧ029Г
...-ггб\б
• I 724f
17013
•37986|
•SOI П
•90171
10070010л
«2383
•9»3<"'
•8693c
•9704)
•-941061
I 7042 7f|
• • 1 4446
^2203824
. • • 14О4f
• • •242061
• • t6097
..96369
• «3064'
•J093«
41201
•Г'ГМ
4836'
•Г8734
•6pi
•ioj ic
• 2013'
• I 249'
22/02
•32634
•17289
•27411
• -24017
••34790
. «44003
•34488
•447
•Г4930|
••4091Г
• •Г719<"
• •67400
•019Ю
• 72237
8*1*64
7 4 7\
8 8бЛ
(O380I 244
•••40170
.../OJOO
••-бо-if
•4270-
•f2 7t:
6'8Г~
•470ГГ|
Т27вг
• 079"
• -1П ЗЬ\
• 0Г313
. ♦7Г49°1
•0ГГ62
•7гз«*>
•8/010
•-77742
• -88020
•98299
9289Г
ГО)30122 I
•♦ • n<t •
Ю624
•2l< 0\
З'ЗН
4J770[
•Г21Г
6-^4
•7О3П
•e<>378
0040<
•72933
• 8301•
-7809/
•88161
•9ВД91
• 8/00
••9f*46
IfiOrtO? /I
• -9Г84Г|
02300=74
♦ -l6}Q
028O8/7P
- - -18860
• ..-«9142
•2310Э
•34210
44140
too3004 3 r1
• • • . Ю40Г
. .. .20496I
IOO8O3I68
• • • f3248
••••П1Г
01308421
•18ГГ*
.28084
•|d206
•203871
•36^701
. 20/30
•«36769
• 47003
• 3942;
'• «49708
••Г9993
•••Г48#3
..-6/219
♦••7fff
•7292
8J3i
••30f28
•'40f62
..fOf96
3J4I2
43490
/3/80I
•388J7
•489ГО
•F9n8f
•40 7/4
•/0?39
•0П24
f7237|
•0 7473
•70a 79
•8Of06|
•9°8ГГ
•• -81893
•• -96232
2U*6S7I
103^04091
144в1
i< f7>
. -6063
..7О667
. .•^7"4
•6366/
•737У2
•83839|
•6922 I
•793f«
••89496
•773"
•87499
•97087
•-.87947]
•••98180
O24O8420
02901X44
•••1/434
• ••2172 Г,'
— 1091a!
••• 272Г4
3 7/96'
?f20r
- • • -4r6/^
• • • f0ОГ7
|390
MOO
Uio
... 90742
J 00400781
I082J
• -93927|
I OO904017
--141*7
• • -9903*"
0140977/I
\9°7b7 I
• • 1600.I
••2020o|
..18007)
•••28909
••39'Г2
••32О17
• -423Ю
••/•0O4
. • .•4 794Г
•"Г818Г
...0>6,.
6644
708*6
•8724J
<20
f30
4V40
•20602
.3О9О4
•40948
•24199)
.34291
•44384
•JOO/8
•4020I
•Г034Г
♦-J84/-
. «4804Г
• -T8B4 1
•49390
•f964 I
•69887
♦6290*'
•73»90
•3493
•••7897<
..893*6
...99674
•• •9 64
JO4008O4-
.... и 44
fJ-°
460
|»7Q
кво
peo
too
-.{099i
• -610371
•Г44 70|
••64/74
•♦74071
-60489
•7O630
•flO703
•.09037
••79234
••Я9»32
•80133
••poje I
О2/0ОбЗ<>1
... j>3 79.
О3ОО4О9/
- ••!4-»9/
103//0024
•• -2037/
•28*4
•39*4
♦106/
л, i)/
....91178
lOOfOf 127
....84 708
. ...94вб7|
•0Ю04966
•9093/
oi foioeol
...H230I
•9903'
02009831
200J1
•ГО88О
•a» '32
•3>3«4
••2409*
••3499.
...4Г299
•4Ю8
•/»43f
-вl 790
• 6oor
.7046
eofie
Страница из таблиц Бюрги.
Его таблица (если не говорить о множителе, равном
10 000 000, который Непер вводит, чтобы не иметь дела
с дробями) соответствует основанию Ь, равному р10 00° 00°,
где р = 1 — 0,0000001 = 0,9999999. Таким образом,
основание системы логарифмов Непера меньше единицы,
и поэтому числа, меньшие единицы, имеют положитель-
«число отношения». Последний термин, вытесненный впоследствии
термином «показатель степени», был в духе старинной
математической терминологии, принятой еще в древней Греции.
159

ные логарифмы. Этого и хотел добиться Непер, так как
его таблицы представляют, собственно, логарифмы sin к
и cos х (т. е. чисел, меньших единицы). При составлении
своих таблиц Непер по существу пользуется приемом,
поясненным нами выше, на примере логарифмов с
основанием (1,0001) 1000°.
Гораздо разнообразнее способы, примененные другом
Непера Бриггом при вычислении десятичных
логарифмов. Он издал в год смерти
Непера (1617)
четырнадцатизначные таблицы
десятичных логарифмов для
чисел первой тысячи, а
позднее (в 1624 г.) в своем
труде «Логарифмическая
арифметика» дал таблицы
(также
четырнадцатизначные) для чисел от 1 до 20000
и от 90 000 до 100 000.
Не останавливаясь на
разнообразных и
остроумных приемах Бригга,
обладавшего
исключительными талантами вычислителя,
перейдем к вычислению
логарифмов при помощи
рядов (вычислению, наиболее
простому и в то же время не известному ни Бюрги,
ни Неперу, ни Бриггу). Но предварительно более
подробно остановимся на построенных нами основаниях
типа b = Ря, где Р очень близко к единице, а п очень
велико.
В разобранном выше примере (соответствующем
таблицам Бюрги) было
/? = (1,0001)10000.
Здесь логарифмы шли, отличаясь друг от друга на
0,0001. Если бы мы захотели, поступая совершенно
так же, составить таблицу, где табличные логарифмы
(и соответствующие им числа) отличаются на меньшие
величины, то следовало бы принять за основание,
например, число
61 = (1ДЮ0001)10000000
Н. НЕПЕР
(1550—1617).
160

(или b2 = (0,9999999)10 00° 00°, что привело бы нас к
таблицам Непера). Однако, следуя этим путем, мы не смогли
бы двигаться слишком далеко. Таблица, в которой
логарифмы идут, начиная от 0, через 0,0000001, должна
содержать 10 000 000 пар чисел, для того, чтобы дойти до
логарифма, равного 1, соответствующего самому
основанию Ьг.
О величине оснований Ь и Ьх легко составить
представление при помощи биномиальной формулы.
Например,
6 = (1,0001)1О0ОО = (1+0,0001)100ОО =
= 1+jocoo 0>0001+ loooo(ioooo-i) ((Щ)01)2 +
+ ю ooQ(iQQOQ-i)(1QQQQ-2) (0,оо01)з +
ю соо (Юооо-1) (ю000-2) (ю ооо-з) 0 0001)4
10 000(10 000—1) (10 000 —2) (10 000 — 3) (10 000 —4)
+ 1-2.3-4-5 Х
Х(0,0001)6 + ...
Вычисление по этой формуле вовсе не так сложно,
как может показаться, — нужно только преобразовать
сначала каждое слагаемое. Для этого заметим, что
показатель степени числа 0,0001 равен числу множителей в
числителе соответствующего биномиального коэффициента.
Поэтому можно переписать нашу формулу, помножив
каждый множитель в числителе дроби на 0,0001. Получим:
1
, 1 • 0,9999 .
+ 1-2 +
+
+
1 • 0,9999
12
1 • 0,9999
1
1 • 0,9999
0,9998
+
3
0,9998 • 0,9997
2-3-4
+
, - „,„„ • 0,9998 . 0,9997 . 0,9996
+ 1-2-34-5 +
1 ♦ 0,9999 . 0,9998 . 0,9997 . 0,9996 . 0,9995
"+" 1.2.3-4.5.6 +
1.0,9999.0,9998.0,9997.0,9996.0,9995-0,9994
+ 1-2-3-4.5-6-7 "+"
1 . 0,9999. 0,9998 • 0,9997 - 0,9996. 0,9995 - 0,9994 . 0,9993
+ 1.2.3.4.5-6.7.8 +•••
161

Ограничиваясь написанными членами (всего членов
справа должно быть 10 001, так как показатель степени
бинома равен 10 000) и заменяя в числителе каждой
дроби множители 0,9999, 0,9998, 0,9997, ...—весьма
близкие к единице — единицами, получим следующее
приближенное значение Ь:
Ь^ 1+Т + ТГ2 + 1.2-3+ 1.2.3-4 +
+ 1.2.3-4.5+ 1.2.3-4.5.6+ 1-2.3.4.5-6.7 +
~ 1 -2-3-4-5-6-7-8'
Можно легко подсчитать, что ошибка этого
приближенного равенства не более 0,0002. Поэтому мы с его
помощью вычислим число Ь с точностью до 0,0003, если
каждую дробь обратим в десятичную с точностью до
0,000005 (до половины пятого знака после запятой).
(В самом деле, если ошибка в каждом из 9 слагаемых не
больше, чем 0,000005, то ошибка суммы не больше, чем
9.0,000005 = 0,000045. Прибавляя эту величину к ошибке
формулы, равной 0,0002, получим 0,000245 < 0,0003.)
Имеем:
1 = 1,00000
-[=1,00000
у^2 = 0,50000
1^3 = 0,16667
Т72^ = °.04167
l-2.3-4.5-0>00833
1.2.314.5-6-0>00139
1.2.3.1.5-6.7-0>00020
1.2.з.4.Уб-7.8=0>00002
2,71828 *
162

Окончательно b = 2,7183 ± 0,0003.
Точно таким же путем можно было бы вычислить и
Ъг = (1,0000001)10000 00°. Только здесь после
преобразований, подобных проделанным выше, числители дробей
еще менее отличались бы от единицы, и мы сделали бы
ошибку, гораздо меньшую, чем в предыдущем случае,
заменив их единицами. Можно утверждать, что с
точностью до 0,0000003
Ьх = 2,7182818.
Эти два результата наводят на мысль, что числа вида
1 \*
(ч4)
(из которых Ь получается при п = 10 000, а Ьх при
п = 10 000 000) при безграничном увеличении числа п
стремятся к определенному пределу, равному
приблизительно 2,71828 ... Такой предел действительно
существует. Это число, встречающееся в математике почти так
же часто, как и число л (и, кстати сказать, связанное
с числом я простым соотношением), со времен Эйлера
обозначается буквой е и называется в честь Непера
«неперовым числом».
Итак,
Л™('+^--
Легко представить число е в виде ряда, пользуясь
разложением по биномиальной формуле. Именно:
\
(,+!)■_, + •+^(±)' +
л(п—1)(л —2) М \3 П(п-\)(п-2)(п-3) /_1\4
"*" Ь2.3 \п) 1 1.2.3-4 [п] "Г"
п(п-\)(п-2)(п-3)(п-4) М \5
^ N2.3.4.5 \п) "*""•
Это выражение можно преобразовать так же, как мы
это делали выше в частном случае (при п = 10 000).
163

Получим:
i-i
1 \/. 2
^ 1-2.3-4 ^
1
+ -
1.2-3.4.5 т...
(Правая часть должна содержать п + 1 членов, как
разложение az-й степени бинома.) Если теперь мы станем
придавать п неограниченно возрастающие значения
(например, п = 10 000, п = 100 000, дг = 1 000 000, п =
= 10 000 000 и т. д.), то число членов будет
неограниченно расти, а каждый из множителей, стоящих в
числителе, будет стремиться к единице. Таким образом,
члены правой части последней формулы будут стремиться
каждый в отдельности к членам бесконечного ряда
i-J._L._l_. ! , ! .
^ 1 ^ 1-2^1.2-3^ 1.2-3-4 ^ 1.2-3.4.5 ^
+ 1.2.3.4.5.6 + ^- (51>
Мы уже встречались с этим рядом на стр. 75 и видели,
что он сходится. Можно было бы доказать (так же, как
мы это делали при выводе ряда для cos х), что сумма
всех членов правой части разложения (1 + —)\ по
биномиальной формуле, будет стремиться к сумме
бесконечного ряда (51). Иными словами, сумма ряда (51)
представляет предел (1 Н—] при п неограниченно
возрастающем *).
Пользуясь обозначением этого предела,
предложенным Эйлером, можем записать:
1,1 , J_ л_ 1,1, 1 ,
е~ х ""ту "г 1 -2 + 1-2-3 + 1.2.3.4 + 1.2.3.4.5 +
1.2-3.4.5.6
1) Такое доказательство одновременно устанавливает существо-
/ 1 \п
вание предела ( I-|— J при п -*- оо и дает его выражение в виде
ряда.
164

С помощью этого ряда е можно вычислять с любой
степенью точности. Вот его значение с 19 знаками после
запятой:
е = 2,7182818284590452353...
(чтобы получить это значение, нужно взять сумму 22
первых членов ряда, обращая каждый из них в
десятичную дробь с точностью до половины 21-го знака после
запятой).
Когда мы брали за основание системы логарифмов
и 1л х 1 V0000
число b=ll + 1QQQQ) » т0 мы тем самым брали за
основание приближенное значение числа е (выше мы
видели, что Ь = 2,7183 zt 0,0003). Поэтому и логарифмы
наши являлись приближенными выражениями
логарифмов при основании е. Последние имеют особое название и
обозначение. Называются они натуральными
логарифмами 1) и обозначаются сокращенно In N> так что
\r\N = \ogeN.
Буквы In этого обозначения — начальные буквы слов
logarithmus naturalis (т. е. натуральный логарифм). Мы
увидим сейчас, что для натуральных логарифмов можно
весьма просто вывести разложение в ряд, позволяющее
легко вычислять эти логарифмы (и, следовательно, в
соответствии со сказанным ранее, вычислять логарифмы
при любом основании).
Будем исходить из логарифмов при основании Ьу где
Ъ имеет видЬ=(1Н—) (п —какое-нибудь большое
х) Это название (натуральный — значит естественный)
противопоставляет их десятичным логарифмам, в которых за основание
принято число 10. Особая роль, которую играет последняя система
логарифмов во многих приложениях математики, объясняется тем,
что 10 есть основание десятичной системы счисления. Однако
возможны и другие системы счисления (двоичная, троичная, двенадца-
теричная и т. п.). До сего времени (в делении часа на 60 минут,
а минуты на 60 секунд и в делении градуса на 60 угловых минут
и минуты на 60 угловых секунд) сохранились следы
шестидесятиричной системы счисления, существовавшей в древнем Вавилоне.
В языках некоторых народов (например, у французов) сохранились
намеки на существование двадцатеричной системы счисления. При
другой системе счисления десятичные логарифмы не играли бы
никакой роли, между тем как натуральные, основание которых не
зависит от системы счисления, по-прежнему встречались бы в
различных теоретических вопросах.
165

число, например 10 000, 10 000 000 и т. п.). Если
logbN=y,
то это значит, что
b* = N
или
(l+if-ff. (52)
Постараемся из этого уравнения определить у и тем
самым получить возможность вычисления логарифма по
заданному числу N. (Когда выше строилась таблица
логарифмов при основании Ь, то мы, собственно, искали
числа по заданным логарифмам и притом не по любым,
, 12 3 4
а по логарифмам вида — ,—,—,—,..., т. е. в нашем
примере: 0,0001; 0,0002; 0,0003; 0,0004 и т. д.)
Извлечем сначала из обеих частей равенства (52)
корень с показателем я, а затем разложим левую часть
в ряд, по биномиальной формуле. Получим:
1
(1+!)»_^
i
, ,1 1 ■ У(у-1) 1 , У(У-1)(У-2) J, _Л/7Г
1 "♦" 1 ' п "f" 1-2 ' п2 "Т" 1-2-3 ' пз "Г"- —iv •
(53)
Мы получили уравнение относительно t/, которое,
несмотря на его сложность, нетрудно решить приближенно.
Действительно, если п — число очень большое, то--,
а тем более-у ,-^ и т. д. — числа очень малые. Поэтому,
отбрасывая в левой части уравнения (53) все члены,
начиная с третьего, мы сделаем лишь небольшую ошибку,
которая незначительно отзовется на величине у, т. е.
логарифма. Тогда получится приближенное уравнение:
1 п '
166

содержащее у лишь в первой степени. Из него находим:
Чтобы пользоваться этой формулой, т. е. по данному N
находить его логарифм г/, нужно возводить N в степень
с показателем — (например, в степень с показателем
0,0001). Последнее действие в свою очередь может быть
выполнено с помощью биномиального ряда, но лишь
в том случае, когда N имеет вид N = 1 + х, где I х I < 1
(например, N = 1,736 = 1 + 0,736; N = 0,3745 =
= 1 — 0,6255 и т. д.).
Делая это допущение (ниже мы увидим, как надо
поступать при нахождении логарифмов любых чисел N),
получим:
У'
= п
| П ■(Н(М
1 I n
1 +-,-*
.3
1 1-2
1 П \П
1
Л, |
О(т-)
1-2.3-4
1-2-3
(1-з)
X | ..
л Т
.-1
Замечая, что +1 и —1 в скобках взаимно
уничтожаются, и раскрывая квадратные скобки, найдем
следующее выражение для у:
■-I
И(1-«)
У^Т~* П2~Х ' 1 -2-3 х "*"
+ U 1.2-3.4 ^+- <54>
Но при очень больших значениях п число — чрезвычайно
мало. Отбрасывая числа — в числителях дробей в
формуле (54), мы лишь незначительно изменим каждую из
этих дробей, а вместе с тем и всю их сумму (последнее
утверждение нуждается в особом доказательстве, так
как эта сумма является бесконечным рядом, т. е.
содержит бесконечно много слагаемых). Таким образом,
167

получаем следующее приближенное выражение для
log/ + j_\„ (1+ х) = log* N =у;
i/~ 1 t^I.2^1-2-3^ I -2-3-4 A r
| -1--2--3--4
^ 1.9. 3.4. R л -|- . . .
1.2.3.4.5
__ **L 4_ X-
1 2 + "3
У i*2 *# y4 v5
... = т-т + т-т+т —• (65)
Пользуясь признаком Даламбера, можно легко
проверить, что ряд, стоящий в правой части равенства (55),
абсолютно сходится при всяком х, меньшем единицы по
абсолютной величине.
Из всего предыдущего можно ожидать, что ошибка
равенства (55) тем меньше, чем больше я, т. е. чем ближе
основание логарифмов b =( 1 -\—] к неперову числу е,
являющемуся пределом выражения fl + -J при
неограниченно возрастающем п. Докажем, что
приближенное равенство (55) становится абсолютно точным, если у
означает логарифм при основании е= lim (1 Н—) , т. е.
если у есть натуральный логарифм числа N = 1 + х.
Чтобы доказать это, т. е. доказать равенство
ln(l+x)=*-£ + f-£ + £-£ + ..., (56)
нужно только внимательно просмотреть вывод
приближенной формулы (55), а именно оценить величину
ошибки, заключающейся в этой формуле. Начнем
с оценки членов биномиального ряда в левой части
уравнения (53), которые были отброшены нами так
бесцеремонно. Для этого прибегнем к обычному приему
сравнения членов интересующего нас ряда:
у (у-О 1 у(у —О (у-2) j_
1-2 ' я2 1-2-3 * п* "1"
, У(У-1)(У-2)(у-3) J_ ,
^ 1-2.3-4 'п*1"
. У(у-\)(у-2)(у-3)(у-А) 1 ,
+ 12-3-4.5 «»+••• (5/^
168

(мы выписываем здесь члены левой части равенства (53),
начиная с третьего члена) с надлежащим образом
выбранной геометрической прогрессией. В ряде (57) отношения
последующих членов к предыдущим суть:
</(</-!) Q/-2) 1 \у(у-\) i|=^z2 1 = J L.
1-2-3 ' пз * I 1 • 2 ' л2 J 3 п п
у{у-\)(у-2){у-г) 1 . у (у-1) (у—2) j =
1.2-3-4 " л* ' 1 • 2 • 3 'я»
4 4
У(У-»)(У-2)(У-3)(У-4) 1 .ГУ(У-1)(У-2)(У-3) I
1
Я*
■I1
(У-
У-3 1
4 ' /2
-1)(у —2)(у-
1-2-3-4
у-4 1
~~ 5 ' ~п
=
-3)
=
1-2-3-4-5
Следующие за этими отношения будут:
JL _ А _£. _ *L -^ _ _ _
6 6 7 7 8 8
—=—; —=—; —=— и т. д.
£_1
5 5
Очевидно, каждое из них по абсолютной величине
меньше, чем Ш_±_. Если предположить, что п (которое
мы впоследствии будем неограниченно увеличивать)
настолько велико, что 'у ' < -0 , то отношение после-
п 2
дующего члена к предыдущему в ряде (57) будет по
абсолютной величине меньше у. А это значит, что
абсолютные величины членов этого ряда будут не больше,
чем члены геометрической прогрессии, первый член
которой равен абсолютной величине первого члена
ряда (57), а знаменатель равен-л. Эта прогрессия есть:
|0to-l)| 1 ,\y(y-D\ 1 1 ,
1-2 ' п2 "г 1-2 п2 2 "г
| </({/-1)| 1 /1\«
'г 1-2 ' л* ' \, 2 J "1"
+ 1-2 'л*'^/"1" 12 "я*'^/"1"-"
(58)
169

Но из того, что члены прогрессии (58) больше
абсолютных величин членов ряда (57), следует, что сумма
прогрессии больше абсолютной величины суммы ряда
(57). А так как сумма прогрессии равна
IУ (У-1)1 1
1-2 ' п2
■-4
|У(У-')1
J
|У(У-1)1
то
У (У-0 1 , У (У—1)(У —2) _1_ .
-2 "Г 1.2-3 ' яз ~Г
1-2
Я2
У(У-1)(У-2)(у-3) J_
1.2.3-4 ' я*
+ ■
^|У(У~1)1
^ я2
Отсюда, между прочим, следует, что сумма ряда (57)
у (У — О
составляет лишь некоторую часть величины ^-^—-,
т. е. может быть записана в виде
у (у-О 1 , у(у—1)(у—2) _1 ,
1 . 2 ' д» "Г" 1-2.3 ' п» "t"
У(У-1)(У-2)(у-3) _1_
^ 1.2.3-4 «4Г'
. = <х
у (у-О
я2 •
где а — положительное или отрицательное число,
меньшее единицы по абсолютной величине |а|<1.
Подставляя выражение а 7" в формулу (53),
получим:
откуда
JL.iV--l-a«^=^
,_n^_l)-«a*^ = n(^-l)-ai^
170

Это равенство является уже не приближенным, а
точным, но имеет тот недостаток, что в правой части
наряду с известными величинами N и п стоят также
неизвестные у и а (о последнем мы знаем лишь, что
|а|<1).
Полагая снова N = l+x и считая |х|<1, найдем,
как и выше, после применения биномиальной формулы
и простейших преобразований:
У" 1 + 1-2 * + 1-2-3 * +
(izOli-fliH).
^ 1-2-3-4 Л ^•'- а й
Это равенство отличается от (54) лишь тем, что в
правую часть введена поправка: — а у{<у~ ' , делающая его
точным.
Остается оценить, какое влияние окажет здесь
отбрасывание малых величин —, фигурирующих в числителях
дробей в правой части равенства. Для этой цели
перепишем формулу так, чтобы каждый множитель в
числителях дробей изменил знак на обратный. От этого
изменятся знаки перед теми дробями, в числителях
которых находится нечетное число множителей. Получим:
,_i (i-i)(2-i
У~Л 1-2 * "^ 1-2-3 Л ""
\ "Л "Л ~) у4 , „У (У—О /спч
1-2-3.4 X -|-...-а . (Щ
Выражения, стоящие в числителях,
Ы>. ('Ч)(*Ч); ('-i)(*-i)(3-i)i
C-i)(a-T)(»-i)(«-i);-
171

могут быть записаны следующим образом:
1-1=1-1;
п п •
(60)
\ п J \ п J п п2 п\ п у'
(i_±y2--L)(3-l) = 1-2.3-^+1-1 =
\ л / \ л У \ л У л ' л2 л3
= l.2.3-lfll-l + l);
(>ЧН2-4)(3-4)(<ЧЬ
_,.2.s.4-?+--i;_i-
-••2.3.4-1(50-?+!?-!),
В правых частях этих тождеств мы заключили в скобки
1 1 п
члены, содержащие — , вынеся за скооки —. Для наших
целей достаточно оценить сумму абсолютных величин
коэффициентов в каждой скобке. Делается это крайне
просто: достаточно в обеих частях каждого из
тождеств (60) подставить — 1 вместо п. Тогда получаем,
выписывая равенства (60), начиная со второго:
23 = Ь2 + (3 + 1);
2-3-4 = 1 -2-3 + (11+6 + 1);
2-3-4-5 = 1-2.3.4+ (50 + 35 +10+1),
т. е. суммы коэффициентов равны по порядку:
2-3-1.2, 2.3.4-1.2-3, 2-3-4-5-1-2-34, ...
Установив это, вернемся к формуле (59) и подста^
вим в нее вместо произведений
(•-■аы). («-до-ас-;).
172

их выражения, по формулам (60). Получим:
,_± 1.2-1(3—М
х я_ 2 п \ п) з
#~Т"~ Ь2 Х "• Ь2~3 Х~
1 Л. 6,1
—-.с-^к
1.2-3.4 Х "+"
я \ я ^ я2 лз J
^ 1.2-34-5 л ... а я .
Разбивая здесь каждый член (кроме первого) на
два слагаемых, одно из которых не содержит дроби —
(и ее степеней), а другое содержит, и выписывая сна-
1
чала члены, не содержащие —, а затем остальные,
получим:
х 1 о , 1 -2
У=Т-Т72Х -^
1 -23
X3-
•2-3 , , 1-2-3-4 к .11
*5-... + VT70*2-
1 -2-J-4 ' Ь2-3-4.5" '"^ п 1 -2
/Г 1-2.3Л "*" п ' 1 -2.3-4 л
_1. П П% П3 ХЬ+ -дУ(У-') /61>
я 1-2.3-4-5 Х +"• а л ' (Di'
Члены, стоящие в двух последних строчках,
образуют ряд, сумму которого легко оценить, предполагая,
что п > 1 (мы вообще рассматриваем лишь очень
большие положительные значения я). Именно, каждый из
членов этого ряда по абсолютной величине меньше
соответствующего члена геометрической прогрессии
-\х\2 + --\х\'6+ ~ |х|4 + 1|х|б + ...
Я111 Я1 ' Я ' ' 'я11
В самом деле, относительно первого члена — • -=—^ г%
это не вызывает сомнений. Абсолютная величина вто-
173

рого равна — • утуГз 1*1° Иу 0ЧевиДН0» меньше, чем
1 3+"~ i 13 ^ 1 3+! i is 1 2.3-1-2 , |3^
^ * 2 • 3 I 13 I Х I3 ЬГ
<— • | о.з' Iх! — • Итак, для второго члена ряда,
стоящего во второй строчке равенства (61), наше
утверждение также справедливо. Аналогично для абсолютной
величины третьего члена имеем:
я 1-2-3-4 |Л| ^ я
1 11 + 6+1,.>4 . ..о.-,-.-... ,„,„ ^
<-Н" 1-2.3.4'*' =^Г lo.q.a 1*14<
11
1
1
п
4
• 2.;
2
<
+
.з.
1
1
п
1
1
• 4-
.2
"I
■|*|4<
-I .2-3
.3-4
2.3-4
.2.3-4
l*l4 =
х|*
я
Для четвертого:
чп 35л.10 ' ™_i_35_i.10_i_ '
1 50~^г+^-^, ..1 50+т + ^+п? , „^
-я-' 1.2.3-4-5 l*l'<T' 1-2-3-4.5 1*1'<
1 50 + 35 + 10+1 1 2-3.4.5-1.2-3-4 ■
^ я 1.2-3-4.5 |Л|— я 1-2-3-4-5 1*1 <•
М 2-3-4.5 . .. |х|5
<-В-'1.2.3.4.5'Х1 = я >•" ИТ'Д-
Наше рассуждение годится для всех членов второй и
третьей строчек формулы (61). Но тогда сумма всех
этих членов не больше, чем сумма членов
геометрической прогрессии со знаменателем I*!1):
±\х\2 + ^\х\* + \\х\* + ^\х\ь+.*.=
п Ul2
1— >*i Л (1 — I JC l> •
*) Это — убывающая прогрессия, так как 1 х i < 1.
174

и можно утверждать, что
1 3-1 f 11—^ + 1
J_ 1 2 1_ П_ з _| L П П 4
л#Ь2* И ' ТТ2ТзХ +Т * 1-2.3.4 Х ~~
1 п+п* пз _о 1*1»
л 1-2-3-4-5 л -г...— РП(1_|Х|),
где (J — положительное или отрицательное число,
меньшее 1 по абсолютной величине (|Р|<1). Итак, из
формулы (61) вместо приближенной формулы (55) получаем
новую формулу:
</ = ^1 + ^(1+х) = у-у + Т-Т + Т- —
••• + Рп(1_|х|)-а Л • (Ь2)
Эта формула позволяет оценить ошибку, содержащуюся
в формуле (55). Именно, ошибка оказывается равной
ft 1*12 дУ^-У
Заметим, что при очень большом п эта ошибка очень
мала, если только |х| не близко к единице. Так, в слу-
д. и 1л . 1 V0000 /
чае основания логарифмов о = ( 1 + i0QQ0) (где п =
= 10 000) имеем ошибку формулы (62), меньшую, чем
|*12 , |У(У-1)|
10 000(1—1*1) 10000 •
(Напомним, что |а| и |Р| — числа, меньшие единицы.)
2
Если |х|^-«-, то \y\ = \ogb(l+x)1 во всяком случае,
меньше единицы. В самом деле, у =^1+х^1 у, и так как
6 = 2,718... (стр. 163), то
log,l|< log* 2,718... = 1
175

|logft-§-| = l1oeftl-1o?A2| = |-logfc2|<Iogft2,718...= l.
Поэтому ошибка формулы (55) меньше, чем
I
"4 ,1-2
= 0,00025.
юооо-4- 1000°
Но если х равняется, например, 0,999, то уже слагае-
мое юоооо-|*1) Равно приблизительно 10(Ю0(11_0999Г
= yg = 0,1, т. е. ошибка при пользовании формулой (55)
может получиться не малая.
Чтобы закончить вывод, перейдем к пределу в обеих
частях формулы (62) при дг->оо. Как мы знаем, по
формуле (50) этой главы
Inrf /1_Lvl lQgg(l+*) _ ln(l+X)
^+v{ + ) 4FW\~4hW\
При я->-оо величина fl-f—J стремится к е\ отсюда
следует, как мы покажем ниже,
1п[(1+4)"]-Ипе=1, (*)
поэтому
1°§(1 + 1)^1+х)->1П(11+Х) =1п(1+дг).
Что касается правой части формулы (62), то в ней
два слагаемых, р—^ и а у-^- -, при п -+со стре-
/2(1 — | X J ft
мятся к нулю, а остальные от п не зависят.
176

В итоге получаем формулу (56):
х2
X3
X*
л*
г/ = 1п(1 4-х) =-1— — + — __ + ___+...
— основную формулу этой главы.
Осталось обосновать (*), Покажем, как это можно
сделать. Заметим сначала, что
Это следует из почленного сравнения между собой
двух выражений для (1 + —) (см. стр. 164):
1 -2-3
'(■-1)(--4)-('-¥)
и для е. (там же):
е = 1 +
1-2 "i 1-2-3
•-..+
1-2-3.
1
1.2-3..
.. п
. /I
+.
Беря натуральные логарифмы от обеих частей (**),
получим:
In I
т. е.
или, наконец,
[(. + !)"]< те.
„1„(1+±)<1
W + {)<i
(#**)
In
Обратимся теперь к поставленному нами вопросу.
Нужно доказать, что
(1+^)"]->1пг, т. е. что lne-In [fl+ !)"]->().
Но разность логарифмоз можно записать в виде
логарифма частного:
ta.-ta[(l + l)"j_lnf •
1КГ
177

Так как (l -\—) ->е при /г-vco, то число т-^-,
превышающее 1, в силу неравенства (##) стремится
к 1 при п->оо.
Поэтому можно записать:
к>
*-<+»..
где ея>>0, причем еЛ-^0 при п-^оо.
Остается доказать, что
1п(1+ел)-^0 при е„->0.
Но каково бы ни было натуральное N,
положительное число е„ при достаточно больших значениях
номера п будет меньше, чем-тт. Тогда 1п(1+ел) будет
меньше lnfl^--^), что в свою очередь по неравен-
ству (***) меньше, чем -тт-. Следовательно, мы
установили, что когда п достаточно велико, то
0<1п^-1п[(1 + |)п] = 1п(1+ел)<1
для любого наперед заданного N. Отсюда и следует,
что
lne — In (Н Г ->0 при м-^оо,
т. е. выполняемый нами предельный переход обоснован.
С помощью формулы (56) можно вычислять лишь
натуральные логарифмы таких чисел N = I + х, для
которых | х I < 1, так как при этом предположении мы
выводили формулу (56). (Если бы мы взяли | х | > 1, то
не смогли бы вообще пользоваться биномиальным рядом.)
Можно показать, однако, что формула (56) остается
справедливой и при х = 1. Иными словами,
Ь2-1-! + 4—| + ТГ-! + ... (63)
178

Однако последний ряд сходится очень медленно, т. е.
нужно взять очень большое число его членов для того,
чтобы получить In 2 со сколько-нибудь значительной
точностью. Действительно, чтобы гарантировать, например,
результат вычисления с точностью до 0,001, нужно, чтобы
первый из отброшенных членов ряда был меньше 0,001.
Но таким будет член, стоящий на тысяча первом месте,
т. е. чтобы вычислить In 2 по формуле (63) с точностью
до 0,001, нужно взять сумму 1000 членов ряда. Эту
трудность легко обойти, вычисляя не In 2, a lny, п0 Ф°Р~
муле (56). Действительно,
In 2
—14—1п(1-4)__[Ы К
+t£_KLKLKLK)'
3 4 ' 5 6 ' 7
^1,1.1,1,1,1,1,
2 •" 2 • 22 "•" 3 • 23 •" 4 • 24 "•" 5 • 25 "т~ 6 • 2е ' 7 • 27 •"* "
Достаточно вычислить сумму написанных членов, чтобы
получить In 2 с точностью до 0,001:
у = 0,50000
-^ = 4" = 0,12500
1 =^- = 0,04167
3-23 24
аЛг = i = 0,01562
4 • 24 64 •
1 =tL = 0,00625
5-25 ~~ 160'
1 = _i_ = o ,00260
6 • 2в 384 "
^ = 3^ = 0,00112
0,69226
Находим: In 2 = 0,692.
179

Из формулы (56) можно получить ряды, по которым
вычисляются логарифмы любых чисел, и притом ряды,
сходящиеся гораздо быстрее ряда (56). Чтобы сделать
это, заменим сначала в формуле (56) х через —х.
Получим:
in/i и-(-х) (~*)2 , (~*)3 (~*)4 , (-*)5
или
|п(1-^)=-1-|-?-Т-|--- <64)
Вычитая почленно равенство (64) из равенства (56),
найдем:
]n(l+x)-ln(l-x) = ^ + 2f + 25-+...,
или
|пт^=2(т + у + т + у + -9-+--)
— равенство, справедливое при | х I < 1. В частности,
полагая здесь л: = 2д/4-1 » где ^ —целое
положительное число, найдем:
1
1-
1п
1 1
2N + 1
еч
14
2l_2W+l +3(2# + 1)з + 5 (2N + 1)* + " у
или, замечая, что
1
2Л/ + 1 2N + \ + l 2N+2 N + \
2N + 1
и что
1
j 1 2N+1 — 1 2N — N
1
In р— = In —^— = In (N + 1) — In N,
1_ 2N+\
получим окончательно формулу
1п(ЛГ + 1) =
= In iV + 2 [27\Г=РТ + 3(2Л/ + 03"^ 5(2iV + l)5 + ---J> (65)
180

позволяющую находить In (N 4- 1), если известен
In Л/.
Например, зная, что In 1 = 0, мы можем утверждать,
полагая в формуле (65) N = 1, что
In 2 = 2 [т+т.- + -.- + 1.-7 - + ...].
Вычисляя сумму членов, указанных в скобках (первых
четырех членов ряда), получим In 2 с точностью до
0,00002:
In 2 = 0,69313.
Сумма первых восьми членов ряда дала бы
результат
1п2 = 0,69314718
с ошибкой, меньшей 0,00000001.
Вычислим с помощью ряда (65) натуральный
логарифм 10. Так как
1п10 = 1п2 + 1п5,
то нам остается найти лишь логарифм 5. Формула (65)
позволяет найти логарифм какого-либо числа (N + 1)
лишь в том случае, когда известен логарифм числа, на
единицу меньшего (N). В данном случае, чтобы найти
In 5, надо знать In 4. Но последний равен
In 4 = 2 • In 2 = 2.0,69314718 = 1,38629436.
Полагая N = 4 в формуле (65), находим
^5 = ^4 + 2(1+^ + ^ + 7^ + ...).
или, вычисляя сумму членов, указанных в скобках, и
подставляя значение In 4, получаем:
In 5 = 1,38629436 + 2 • 0,111571775 = 1,60943791
и, следовательно,
1п10 = 1п2 + 1п5 =
= 0,69314718+1,60943791=2,30258509
— результат, верный до 0,00000003.
Теперь можно указать формулу для вычисления
десятичных логарифмов. Для этого нужно лишь вспомнить
181

формулу (50) этой главы (стр. 153), которая в данном
случае позволяет перейти от натуральных логарифмов
к десятичным. Из нее имеем:
Ъ" = К = ^зЙЙоэ = 0,43429448 • In N.
Итак, чтобы найти десятичный (обыкновенный)
логарифм числа N, зная натуральный логарифм N,
достаточно умножить натуральный логарифм N на число
0,43429448. Последнее число обычно обозначается
буквой М:
М = 0,43429448
и называется модулем (модулем системы обыкновенных
логарифмов). В случаях вычислений, не требующих
большой точности, можно пользоваться удобно
запоминаемым значением М:
М = 0,4343.
Теперь можно соответственно двум основным
известным нам формулам для вычисления натуральных
логарифмов (56) и (65) написать две формулы для
вычисления десятичных логарифмов. Именно:
lg(l+;0 = 0,43429448 (x-f + f-т + f ""•)
и
\g(N + \)=\gN +
+ 2 • 0,43429448 [2N + l + 3(2/v+l)3 + b(2N + ))* +•• -J»
или
lg (N + l) = lg N + 0,86858896 [^Y +
+ 3 (2Л/ + 1)3 + 5 (2N + 1)5 +'' "J " (66)
Укажем некоторые детали построения таблицы
логарифмов с помощью формулы (66).
Пусть нужно, например, построить пятизначные
таблицы логарифмов (где логарифмы должны даваться с
точностью до 0,000005).
Можно ограничиться при этом вычислением
логарифмов целых чисел, лежащих в промежутке от 1000 до
10 000,
182

В самом деле, имея логарифмы всех четырехзначных
чисел (1000, 1001, 1002, ..., 9999), мы сможем находить
логарифмы любых чисел, изображенных пятью
значащими цифрами (хотя бы они не лежали в промежутке
от 1000 до 10 000). Именно, целую часть десятичного
логарифма (характеристику) можно найти без таблицы
по очень простому правилу. Дробная же часть
десятичного логарифма (мантисса) не зависит от положения
запятой, а только от цифр числа и их взаимного
расположения. (Эти два обстоятельства, объясняющиеся тем, что
10 лежит в основании системы счисления, составляют
основные преимущества системы десятичных
логарифмов перед всеми другими.)
Так, например, отыскивая логарифм 11,506, можно
утверждать, что характеристика логарифма есть 1, а
мантисса такая же, как и у логарифма числа 1150,6
(заключенного между 1000 и 10 000). Но в нашей таблице будут
помещены мантиссы логарифмов чисел 1150 и 1151. Мы
найдем поправку к ним, соответствующую последней
цифре (6) числа 1150,6, посредством приема линейной
интерполяции.
Беря в формуле (66) один член в квадратных скобках,
мы можем вычислить логарифм числа N + 1 по
известному логарифму числа N при помощи формулы
lg(yV + l) = lg^ + °f^8196. (67)
Так, зная, что lg 1000 = 3, можно найти lg 1001:
lg 1001 = lg 1000 + 0,8^)81896 =
= 3 + 0,0004340769 = 3,0004340769.
Далее можно отыскать lg 1002:
lgl002 = lg1001+2^^ =
= 3,0004340769 + 0,0004336435 = 3,0008677204,
затем lg 1003, lg 1004, lg 1005, ... Чрезвычайно важно
дать себе отчет в точности употребляемой формулы (67),
Мы получили ее из формулы (66), отбросив члены
0,86858896 [з(2^+1), + 5(2л/+1)* +
183

Заменяя множитель 0,86858896 большим числом 1,
а числа 5, 7, 9, ... в знаменателях дробей — меньшим
числом 3, мы, очевидно, получим большую сумму:
3 (27V— 1)з ^ 3(2Л/+1)5^3(2# + 1)7^--- '
которая (как сумма бесконечно убывающей
геометрической прогрессии со знаменателем (од/ ■ i )•) Равна
1
3(2Л/ + 1)з
1. '
(2W-H)2
Итак, ошибка формулы (67) меньше, чем
1 1
3(2#+1)» ' 1
(2W + 1)2
а при N > 1000 меньше, чем
1 1
3-20013 { 1
< 0,00000000005,
20012
т. е. меньше, чем половина десятого знака после запятой!
Однако такая точность гарантируется лишь при условии,
что lg jV, входящий в правую часть формулы (67), дан
точно (не содержит ошибки). Конечно, этого при нашем
способе нельзя ожидать. Именно, lg 1000 точно равен 3,
и поэтому ошибка в определении lg 1001 по формуле (67)
не больше 0,00000000005. Но при вычислении lg 1002 мы
исходим уже из приближенного значения lg 1001 (с
точностью до половины десятого знака после запятой).
К этому добавится еще ошибка формулы такого же
порядка, т. е. тоже 0,00000000005. Общая ошибка при
определении lg 1002 будет порядка 2-0,00000000005 =
= 0,0000000001. Рассуждая далее, найдем, что при
определении lg 1003 ошибка может достигать 3-0,00000000005,
при определении lg 1004 ошибка может достигать 4 х
X 0,00000000005 и т. д. Таким образом, к концу таблицы
при вычислении lg 9999 ошибка может дойти до 8999 х
X 0,00000000005 « 0,0000005.
184

При этом мы не учитывали еще ошибок при обраще-
„ 0,86858896 _
нии дроби 2М4-\— в десятичную. Если вычислять эту
величину с десятью знаками после запятой (т. е. с
точностью до 0,00000000005), то ошибка формулы (даже
при точном значении lg N) будет равна 2-0,00000000005 =
= 0,0000000001, и, таким образом, к концу таблицы
ошибка будет в два раза более, чем вычисленная выше,
т. е. будет равна 0,000001. Следовательно, производя
вычисления по формуле (67) с десятью знаками после
запятой, мы в конце таблицы будем получать логарифмы
лишь с шестью верными знаками после запятой.
Этого вполне достаточно для принятой нами точности»
но слишком невыгодно производить все время
вычисления с десятью знаками, а получать верные результаты
лишь с шестью знаками. Чтобы избежать излишней
работы, предварительно вычисляют с шестью верными
знаками логарифмы чисел в пределах первой сотни (начиная
от 10): 10, И, ... , 98, 99. Это осуществляется с помощью
формулы (66), где число членов в скобке берется с таким
расчетом, чтобы логарифмы получались с точностью
до 0,000001 (сначала два члена формулы, а потом
один).
Имея эти логарифмы, мы вместе с тем будем знать
с достаточной точностью логарифмы чисел: 1000, 1100,
1200, 1300, 1400, ... , 9800, 9900, т. е. логарифмы
четырехзначных чисел через каждую сотню. Затем мы снова
пользуемся формулой (67) для вычисления логарифмов
остальных четырехзначных чисел, но здесь уже не даем
ошибке накапливаться на всем большом «перегоне» от
1000 до 10 000, а пользуемся «перекладными» через
каждую сотню единиц. Именно, отыскивая логарифмы
чисел, одного за другим: 1001, 1002 ,1003, 1004, 1005, ...
(по формуле (67)), мы, дойдя до 1099, уже не вычисляем
lg 1100 по формуле, а берем ранее вычисленное значение
этого логарифма и в дальнейшем отправляемся от него.
Теперь мы снова вычисляем по формуле (67) логарифмы
чисел: 1101, 1102, 1103, ... , причем ошибка снова
накапливается. Однако мы не даем ей делаться большой, так
как, дойдя до lg 1199, следующий за ним lg 1200 не
вычисляем по формуле, а берем заранее вычисленное
значение его.
Так же поступаем и далее, до конца таблицы.
185

Теперь ошибка накапливается уже не на протяжении
9000 операций (от 1000 до 10 000), а каждый раз на
протяжении лишь 100 операций (от 1000 до 1100, от 1100
до 1200, от 1200 до 1300 и т. д.). Поэтому, производя все
вычисления по формуле (67) с восемью знаками после
запятой (с точностью до 0,000000005), мы не накопим
нигде ошибки, большей, чем
2 • 0,000000005 • 100 = 0,000001.
Кроме того, ошибка в 0,000001 заключается в
логарифмах чисел: 1100, 1200, 1300, 1400, ... (т.е. в
логарифмах чисел, отправляясь от которых мы начинаем
каждую соседнюю операцию).
В итоге значения логарифмов будут верны с точностью
до 0,000002, т. е. с точностью, большей, чем мы хотели.

ОСНОВНЫЕ ФОРМУЛЫ
I
Бином Ньютона
(1+*)*=1 + ™х + ^^
m(m-\)...(m-k+l) k ■ . m (m-1)... 3 . 2 .1
где m — натуральное число, а х —любое число.
Биномиальный ряд
(1+х)- = 1+^ + ^^^ + ...
, m(m — \)...(m — k + \) k ,
-t- Л! x -i-...,
где m не является натуральным числом, |х|<1.
Приближенные формулы
l/l+x^l+yx, y^l+x^ 1+yx; __^l-x;
1,1 1.1
1--х, ,,_- ^1 --х,
КГ+* 2 ' ^Т+х 3
где |х|<1.
II
Косинус и синус кратных дуг
cos 2x = cos2x — sin2x; sin2x = 2 sin х-cos x;
cos 3x = cos3 x — 3 cos x • sin2 x,
sin 3x = 3 cos2x • sin x — sin3x;
187

cos 4x = cos4 x — 6 cos2 x • sin2 x + sin4 x;
sin 4x = 4 cos3 x • sin x — 4 cos x • sin3x;
cos5x = cos5x— 10 cos3x-sin2x + 5 cos x-sin4 x;
sin 5x = 5 cos4 x-sin x— 10 cos2x -sinax + sin6x;
cos mx = cosmx— m 2Г } cosm 2x-sin2x +
, m(m— \)(m — 2) (m — 3) m4 . 4
H - -^—— cosm-4 x • sin4 x —...
m nm , tnlm — \)(m — 2) m ч
sin ш^ = -р- cosm-1 x • sin x oi cosm_3x x
w „ з , rn(m— \)(m — 2)(m — 3)(m — 4) mR . .
X sin3x-| * — ^ ^ -cosm-5xsin5x—...
Замечательный предел
,. sin x «
lim —--= 1.
Разложение в ряд косинуса и синуса
COS Х= 1 - -gj- + 4Т - ёу + ... + ( -1)" L
(2k)\ ^"' 9
Х 31^5! 7! ^-"^1 1> (2Л-1)!^""
sinx
где х —любое число.
Приближенные формулы для sinx w cosx
с точностью до 0,0005
sinx^x при 0^x^0,114;
6
X3
sinx^x—g- при 0,114 <х^ 0,569;
sinx^x — ^" + "J20* ПРИ 0,569 <х^ ^ ^^0,785;
cosx^l при 0^x^:0,031;
cosx^l--^- при 0,031<х^ 0,330;
cosx^1—^- + ^: при 0,330 <х^-^-^0,785.
188

Ill
Натуральные логарифмы и логарифмический ряд.
Замечательный предел
lim (/1+1)л = г = 2,7182818 ...
Формула перехода от натуральных логарифмов
к десятичным
logex = lnx;
lg x = -^ = 0,43429448 In x.
Логарифмические ряды
ln(l+x)=x-4- + 4---;4- + ... + (-l)-15 + ---'
lg(l+x) =
=, 0,43429448^--^- +^--... + (-1Г1^ + ...),
где — 1 <x^l;
где |х|<1.
Приближенная формула
i /аг . i\ i лг i 0,86858896
lg(Af + l)^lgAf + 2yv + 1
(при AfS= 1000 ошибка этой формулы меньше 0,5-10~10).

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абель 53, 54, 87
Арифметический треугольник
(треугольник Паскаля) 27
Бином Ньютона 23, 108
Биномиальное разложение 23,
94, 108
Биномиальные коэффициенты 23,
27
Бригг 28, 160
Бюрш 151, 158
Даламбер 75—78
Даламбера критерий
сходимости ряда 75, 76
Каши Джемшид Гиясэддин 28
Коши Огюст 53, 54, 59, 76
Критерий сходимости рядов 60,
61
Лейбниц 52, 68
Лейбница правило (критерий
сходимости ряда) 68
Логарифм 152
— натуральный 165
Непер 151, 158
Неперово число 163
Ньютон 23, 25, 26, 29, 32 и др.
Паскаль 28
Произведение рядов 88—93
Разложение в ряд косинуса 123
логарифма 177
синуса 123
Ренкин 146
Ряд 35, 47, 48
— расходящийся 50
—, сумма 49, 55
—, — частичная 49
— сходящийся 50, 54, 55
абсолютно 86
условно 86
Снеллий 140—142
Спрямление дуги окружности
140
Факториал 22
Ферма 28
Функция 5—7
Чжу Ши-чцзе 26
Число г (неперово число) 163,
164
Штифель 28
Эйлер 46, 53, 97, 164

СОДЕРЖАНИЕ
К читателю 3
Глава I. О функциях 5
Глава II. Бином Ньютона 14
Глава III. Бином Ньютона (продолжение) 25
Глава IV. Что такое ряд? 47
Г л а в а V. Признаки сходимости 67
Глава VI. Бином Ньютона (окончание) 94
Глава VII. Ряды для синуса и косинуса 113
Глава VIII. Логарифмы и логарифмический ряд 151
Основные формулы 187
Алфавитный указатель 190

Алексей Иванович Маркушевич
РЯДЫ
М., 1979 г., 192 стр. с илл.
Редактор И. Е. Морозова
Техн. редактор Л. В. Лихачева
Корректоры Е. В. Сидоркина, В. П. Сорокина
И Б № 11369
Сдано в набор 20.07.78. Подписано к печати
29.12.78. Т-23095. Бумага 84х108'/з2. тип. № 3.
Литературная гарнитура. Высокая печать.
Условн. печ. л. 10,08. Уч.-изд. л. 10,04. Тираж
70 000 зкз. Заказ № 85. Цена книги 30 коп,
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции, ордена
Трудового Красного Знамени Ленинградское
производственно-техническое объединение
«Печатный Двор» имени А. М. Горького «Союз-
полиграфпрома» при Государственном
комитете СССР по делам издательств, полиграфии
и книжной торговли. 197136, Ленинград, П-136,
Гатчинская, 26.

/>?*
IS
5j