А.Г ЦЫПКИН
СПРАВОЧНИК
ПО МАТЕМАТИКЕ
ДЛЯ СРЕДНИХ
УЧЕБНЫХ
ЗАВЕДЕНИЙ
А. Г, ЦЫПКИН
СПРАВОЧНИК
ПО МАТЕМАТИКЕ
' ДЛЯ СРЕДНИХ
УЧЕБНЫХ ЗАВЕДЕНИЙ
Под редакцией С. А. СТЕПАНОВА
ИЗДАНИЕ ТРЕТЬЕ, ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1983
22.1
Ц 97
УДК 51
Справочник по математике для средних учебных заведений» Цып»
к и н А. Г./Под ред. С. А. Степанова. — 3-е изд. — М.: Наука. Глав*
ная редакция физико-математической литературы, 1983. — 480 о.
Справочник предназначен для учащихся средних школ и средник
специальных учебных заведений. Он содержит все необходимые опре*
деления, формулы, теоремы и методы решения задач. В него включенье
помимо классических разделов элементарной математики, такие разде*
лы, как элементы теории множеств, комплексные числа, основы мате*
матического анализа и векторной алгебры, метод координат и т. д.
Материал, излагаемый в справочнике, в основном носит теоретический
характер. Новое издание справочника (второе выходило в 1981 г.)
дополнено разделами, которые внедряются в школьное обучение.
К ним, в частности> относится теория вероятностей.
гт 1702010000—161
Ц 053 (02)-83 ’ 62-83
© Издательство «Наука».
Главная редакция
физико-математической
литературы, 1983
ОГЛАВЛЕНИЕ
Предисловие редактора...................................... 9
От автора. • ............................................. 11
Глава 1. ЭЛЕМЕНТЫ	ТЕОРИИ МНОЖЕСТВ................... 13
§ 1.	Множества и операции над множествами................. 13
1.1.	Множества и подмножества. 1.2. Операции над множествами,
1.3. Упорядоченные множества.
§ 2.	Соответствие между множествами и отображение множеств 17
2.1. Соответствие и отображение. 2.2. Взаимно однозначное
отображение. 2.3. Эквивалентность множеств, 2.4. Класси-
фикация множеств.
§ 3.	Множества с бинарными операциями • .................. 21
3.1.	Бинарные операции в множествах. 3.2. Изоморфизм мно-
жеств. 3.3. Группы. 3.4. Кольца. 3.5. Поля.
Г л а в а 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА......................... 26
§ 1.	Натуральные числа.................................... 27
1.1.	Множество натуральных чисел. 1.2. Аксиоматическое
построение множества натуральных чисел. 1.3. Простые числа.
Основная теорема арифметики. 1.4. Некоторые признаки дели-
мости натуральных чисел. 1.5. Наименьшее общее кратное.
Наибольший общий делитель. Алгоритм Евклида.
§ 2.	Целые числа.......................................... 35
2.1.	Множество-целых чисел. 2.2. Арифметические операции
с целыми числами. 2.3. Теория целых чисел как упорядоченных
пар натуральных чисел,
§ 3.	Рациональные числа..................................  40
3.1.	Рациональные дроби. 3.2. Рациональные числа. 3.3. Тео-
рия рациональных чисел как упорядоченных пар целых чисел,
§ 4.	Десятичные дроби..................................... 46
4.1.	Десятичная позиционная система счисления. 4.2. Понятие
десятичной дроби. 4.3. Арифметические действия о конечными
десятичными дробями. 4.4. Обращение конечной десятичной
дроби в рациональную дробь. 4.5-. Обращение бесконечной
периодической дроби в рациональную дробь. 4.6. Десятичные
представления рациональных чисел. 4.7, Непрерывные дроби,
§ 5.	Действительные числа................................  57
5.1.	Множество действительных чисел. 5.2, Аксиоматическое
построение множества действительных чисел. 5.3, Представле-
ние действительных чисел десятичными дробями. 5.4. Геоме-
трическое изображение множества действительных чисел,
5.5. Степени и корни. 5.6. Логарифмы. 5.7. Пропорции. 5.8. Де-
сятичные представления иррациональных чисел. 5.9. Некоторые
способы доказательства иррациональности чисел. 5.10. Алгеб-
раические и трансцендентные числа.
§ 6.	Приближенные вычисления.............................. 71
6,1.	Приближенное значение числа и погрешности, 6.2. Деся-
тичная запись приближенных значений числа. 6.3. Округление
чисел. 6.4. Метод касательных. 6.5. Алгоритмы извлечения
квадратного корня.
Глава 3. КОМПЛЕКСНЫЕ ЧИСЛА t.............................. 78
§ 1.	Множество комплексных чисел.......................... 79
1.1.	Аксиоматическое построение. 1.2. Теория комплексных
чисел как упорядоченных пар действительных чисел,
1*
4
ОГЛАВЛЕНИЕ
§ 2.	Геометрическое изображение и тригонометрическая форма
записи комплексных чисел........................................ 83
2.1.	Геометрическое изображение комплексного числа. 2.2. Гео-
метрическое изображение суммы и разности. 2,3. Тригономет-
рическая форма записи.
§ 3.	Степень комплексного числа................................ 86
3.1.	Натуральная степень комплексного числа. 3.2. Корень
n-й степени из комплексного числа.
Глава 4. АЛГЕБРА ............................ 88
§ 1. Многочлены одного переменного.............................. 88
1.1. Понятие многочлена. Арифметические операции над
многочленами. 1.2. Делители многочлена. 1.3. Деление много*
членов. 1.4. Алгоритм Евклида. Ц5. Корни многочлена.
1.6. Формулы сокращённого умножения. 1.7. Формулы Виета.
1.8. Основная теорема алгебры. 1.9. Разложение многочлена
на множители. 1.10. Некоторые следствия основной теоремы
алгебры.
§ 2.	Многочлены нескольких переменных......................... 98
2.1.	Одночлены и многочлены нескольких переменных. 2,2. Ле-
ксикографическое расположение членов многочлена.
§ 3.	Рациональные алгебраические дроби....................... 100
3.1.	Множество рациональных алгебраических дробей.
3.2.	Правильные алгебраические дроби. 3.3. Простейшие дроби.
§ 4.	Иррациональные алгебраические выражения.................. ЮЗ
§ 5.	Уравнения. Алгебраические уравнения..................... 108
5.1. Основные определения. 5.2. Линейное уравнение. 5.3. Квад-
ратное уравнение. 5.4. Кубичное уравнение. i5.5. Уравнения
четвертой степени. 5.6. Двучленные уравнения. 5.7. Решение
алгебраического уравнения с целыми коэффициентами. 5.8. Ра-
циональные алгебраические уравнения. 5.9. Иррациональ-
ные уравнения. 5.10. Уравнения, содержащие неизвестное под
знаком абсолютной величины. 5.11. Решение уравнений в мно-
w жестве комплексных чисел. 5.12. Диофантовы уравнения.
§ 6.	Трансцендентные уравнения............................. 124
6.1.	Показательные уравнения. 6.2. Логарифмические урав-
нения.
§ 7.	Системы уравнений..................................... 128
7.1. Основные определения. 7.2. Системы линейных урав-
нений. 7.3. Метод последовательного исключения неизве-
стных (метод Гаусса). 7.4. Некоторые способы решения систем
нелинейных алгебраических уравнений.
§ 8. Исследование систем линейных уравнений с помощью
определителей.............................................. 137
8.1.	Матрицы и операции над ними. 8.2. Определители.
8.3.	Ранг матрицы. 8.4. Исследование систем линейных урав-
нений с помощью определителей. Формулы Крамера.
§ 9.	Неравенства ............................................   151
9.1.	Определения и основные свойства неравенств. 9.2. Не-
которые важные неравенства.
§ 10.	Решение неравенств и систем неравенств.................... 154
10.1. Основные определения. 10.2. Линейные неравенства
и системы неравенств. 10.3. Квадратные „неравенства. 10.4. Ме-
тод интервалов. 10.5. Решение иррациональных неравенств.
Ю.6. Показательные неравенства. 10.7. Логарифмические не»
равенства. 10.8. Геометрическое изображение множества реше*
ний неравенства с двумя неизвестными.
ОГЛАВЛЕНИЕ
5
§11.	Приемы доказательства справедливости неравенств ...	166
11.1.	Доказательство с помощью цепочки эквивалентных не-
равенств. 11.2. Доказательство с использованием свойств
функций, входящих в неравенства. 11.3. Некоторые специаль-
ные приемы доказательства. 11.4. Некоторые способы про-
верки справедливости числовых неравенств.
Глава 5. ГЕОМЕТРИЯ ..........................................  173
§ 1.	Луч. Отрезок. . . . ;................................... 173
1.1.	Луч. 1.2. Отрезок.
§ 2.	Углы на плоскости.....................................   175
2.1.	Понятие угла. 2.2. Градусная мера измерения углов.
2.3.	Радианная мера измерения углов. 2.4. Классификация
углов. 2.5. Угол между направлениями.
§ 3.	Параллельность и перпендикулярность на плоскости . .	177
3.1.	Параллельность на плоскости. 3.2. Перпендикулярность
на плоскости. 3.3. Расстояние от точки до прямой.
§ 4.	Параллельность и перпендикулярность в пространстве . ,	179
4.1.	Параллельность прямой и плоскости. 4.2. Параллель-
ность плоскостей. 4.3. Перпендикулярность прямой и плоско-
сти. 4.4. Расстояние от точки до плоскости. 4.5. Перпенди-
кулярность плоскостей. 4.6. Наклонная. 4.7. Скрещивающиеся
прямые.
§ 5.	Проектирование на плоскость..................•	. . . .	181
5.1.	Параллельное проектирование. 5.2. Ортогональное проек-
тирование.
§ 6.	Углы в пространстве..................................... 182
6.1.	Угол между наклонной и плоскостью. 6.2. Двугранный
угол. 6.3. Угол между двумя плоскостями.
§ 7.	Ломаная. Многоугольник-................................. 183
§ 8.	Треугольники............................................ 185
8.1.	Основные свойства. 8.2. Медианы треугольника. 8.3. Высоты
треугольника, 8.4. Биссектрисы треугольника. 8.5. Средняя
линия треугольника. 8.6. Равнобедренный треугольник. 8.7. Рав-
носторонний треугольник. 8.8. Прямоугольный треугольник,
§ 9.	Четырехугольники........................................ 189
9.1.	Параллелограмм. 9.2. Ромб. 9.3. Прямоугольник, 9.4. Ква-
драт. 9.5. Трапеция.
§ 10.	Подобные многоугольники................................  191
10.1.	Признак подобия многоугольников. 10.2. Признаки
подобия треугольников.
§11.	Окружность и круг....................................... 193
11.1.	Окружность и круг. 11.2. Касательная и секущая.
11.3.	Взаимное расположение двух окружностей. 11.4. Цен-
тральные углы и дуги окружности. Ц.5. Дуги и хорды окруж-
ности. 11.6. Углы в окружности. 11.7, Длины и площади
в окружности и круге.
§ 12.	Многоугольники и окружность............................. 197
12.1.	Вписанные и описанные многоугольники. 12.2. Вписанные
треугольники. 12.3. Описанные'Треугольники. 12.4. Вневпи-
санная окружность. 12.5. Соотношения между сторонами тре-
угольников и радиусами вписанной и описанной окружностей.
•	12.6. Вписанные четырехугольники. 12.7. Описанные четы-
рехугольники.
§ 13.	Геометрические построения............................... 200
13.1.	Построение прямых, параллельных и перпендикуляр-
ных данной прямой, 13,2, Построение углов. 13,3, Построение
6
ОГЛАВЛЕНИЕ
отрезков. 13.4» Построение окружностей и дуг. 13.5. Построение
касательных к окружностям. 13.6. Построение окружности,,
описанной около многоугольника, и многоугольника, вписан-
ного в окружность. 13.7. Построение окружности, вписанной
в многоугольник, и многоугольника, описанного около окруж»
ности. 13.8. Построение треугольников.
§ 14.	Многогранный угол.................................... 213
§'15. Многогранная поверхность. Многогранник.............	215
§ 16.	Призма............................................... 216
§ 17.	Параллелепипед. Куб.................................. 217
§ 18.	Пирамида. Усеченная пирамида......................... 218
§ 19.	Правильные многогранники............................  220
§ 20.	Цилиндр ............................................. 222
§21.	Конус. Усеченный конус............................... 223
§ 22.	Сфера. Шар........................................... 225
§ 23.	Части шара..........................................  226
23.1.	Шаровой сегмент. 23.2. Шаровой сектор. 23.3, Шаровой
слой. 23.4. Шаровой пояс. 23.5. Телесный угол.
§ 24.	Преобразования плоскости и пространства.............. 228
24.1.	Отображение фигуры в фигуру и отображение фигуры'на
фигуру. 24.2. Преобразование плоскости и пространства. 24.3.
Изометрия пространства и плоскости. Равенство фигур-. 24.4. По-
ворот плоскости вокруг точки. 24.5. Центральная симметрия
и центрально-симметричные фигуры. 24.6. Осевая симметрия
плоскости. 24.7. Осевая симметрия пространства. 24.8. Сим-
метрия относительно плоскости. 24.9. Гомотетия плоскости.
24.10. Гомотетия пространства. 24.11. Преобразование подо*
бия плоскости. 24.12. Подобные фигуры.
§ 25. Система аксиом и неопределяемых понятий геометрии
(по Гильберту) . .............................г	236
Глава 6. ТРИГОНОМЕТРИЯ .......................  .	. .	240
§ 1. Тригонометрические функции. .................... 240
1.1.	Обобщение понятия угла. 1.2. Тригонометрические функ-
ции. 1.3. Квадранты единичной окружности. 1.4. Тригономе-
трические функции числового аргумента. 1.5. Обратные триго-
нометрические функции. 1.6. Значения тригонометрических
функций некоторых углов.
§ 2.	Тригонометрические формулы............................... 253
2.1.	Формулы приведения. 2.2.Связь между тригонометрическими
функциями одного аргумента. 2.3. Тригонометрические функ-
ции суммы и разности углов. 2.4. Тригонометрические функции
двойных, тройных и половинных углов. 2.5. Преобразование
суммы (разности) тригонометрических функций в произведение.
2.6.	Преобразование произведения тригонометрических функ-
ций в сумму. 2.7. Простейшие соотношения между обратными
тригонометрическими функциями.
§ 3.	Решение тригонометрических уравнений и неравенств . . .	258
3.1.	Простейшие тригонометрические уравнения. 3.2. Примеры
более сложных тригонометрических уравнений. 3.3. Решение
простейших тригонометрических неравенств. 3.4. Примеры
решения уравнений и неравенств, содержащих обратные три-
гонометрические функции.
§ 4. Соотношения между элементами треугольника............. 266
4.1. Основные формулы. 4.2. Вычисление элементов треуголь-
ника.
Глава 7. МЕТОД КООРДИНАТ.................................. 271
§ 1. Системы координат..................................... 271
1.1.	Координатная ось. 1.2. Прямоугольная декартова система
координат на плоскости. 1.3. Полярная система координат. Связь
между прямоугольными и полярными координатами. 1.4. Пря*
моугольная декартова система координат в пространстве.
ОГЛАВЛЕНИЕ
7
§ 2.	Линии на плоскости и поверхности в пространстве • • •	276
2.1.	Линии первого и второго порядка. 2.2. Прямая. 2.3. Ок-
ружность. 2.4. Эллипс. 2.5. Гипербола. 2.6. Парабола.
2.7.	Плоскость и шар.
§ 3.	Векторы..................................................... 285
3.1.	Векторы. Основные понятия. 3.2. Угол между векторами.
Скалярное произведение векторов. 3.3. Координаты вектора
на плоскости. 3.4. Координаты вектора в пространстве. 3.5. Век*
торное произведение. 3.6. Смешанное произведение векторов.
Глава 8. ТЕОРИЯ ПРЕДЕЛОВ....................................... 295
§ 1.	Числовые последовательности............................... 295
1.1.	Понятие числовой последовательности. 1.2. Некоторые
способы задания последовательностей. 1.3, Геометрическое
изображение членов последовательности. 1.4. Ограниченные
последовательности. 1.5. Монотонные последовательности.
§ 2.	Предел последовательности................................. 299
2.1.	Понятие предела последовательности. 2.2. Необходимое
условие сходимости последовательности. 2.3. Теоремы о пре-
делах последовательностей. 2.4. Достаточное условие сходи-
мости последовательности. 2.5. Необходимое и достаточное
условие сходимости последовательности.
§ 3.	Числовые ряды и бесконечные произведения.................. 311
3.1.	Понятие числового ряда. 3.2. Положительные числовые
ряды. 3.3. Признаки сходимости числовых рядов. 3.4. Понятие
бесконечного произведения. 3.5. Связь бесконечных произ-
ведений с рядами,
§ 4.	Прогрессии .••••*> * > » . • . * ........................  318
4.1.	Арифметическая прогрессия. 4.2. Геометрическая про-
грессия.
§ 5.	Числовые функции.........................................  319
5.1.	Понятие числовой функции. 5.2. Способы задания функ-
ций. 5.3. Сумма, произведение, разность и частное двух функ-
ций. 5.4. Сложная функция. 5.5. Четные и нечетные функции.
5.6.	Периодические функции. 5.7. Ограниченные функции.
5.8.	Монотонные функции. 5.9. Понятие обратной функции.	\
§ 6.	Предел функции............................................ 328
6.1.	Понятие предела функции. 6.2. Односторонние пределы.
6.3.	Теоремы о пределах функций. 6.4. Некоторые важные
пределы;	,
§ 7.	Бесконечно малые и бесконечно большие величины. . .	337
7.1.	Понятие бесконечно малой и бесконечно большой величины.
7.2.	Сравнение бесконечно малых и бесконечно больших ве-
личин.
§ 8.	Непрерывность (и разрывы) функций . , ,................... 340
8.1.	Понятие непрерывности функций. 8.2. Основные теоремы
о непрерывных функциях. Непрерывность элементарных функ-
ций. 8.3. Односторонняя непрерывность. Классификация
разрывов функций.
Глава 9. НАЧАЛА ДИФФЕРЕНЦИАЛЬНОГО И ИН-
ТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ................................... 344
§ 1.	Производная......................................... 344
1.1.	Понятие производной. 1.2. Геометрическая интерпре-
тация производной. 1.3. Кинематический смысл производной.
1.4.	Теоремы о производных. 1.5. Вычисление производных
влементарных функций. Д.6. Производные высшего порядка.
1.7.	Производные функции, заданной в параметрической форме.
8	ОГЛАВЛЕНИЕ
§ 2.	Дифференциал .......................................   355
2.1.	Понятие дифференциала. 2.2. Геометрическая интерпре-
тация дифференциала. 2.3. Инвариантность дифференциала,
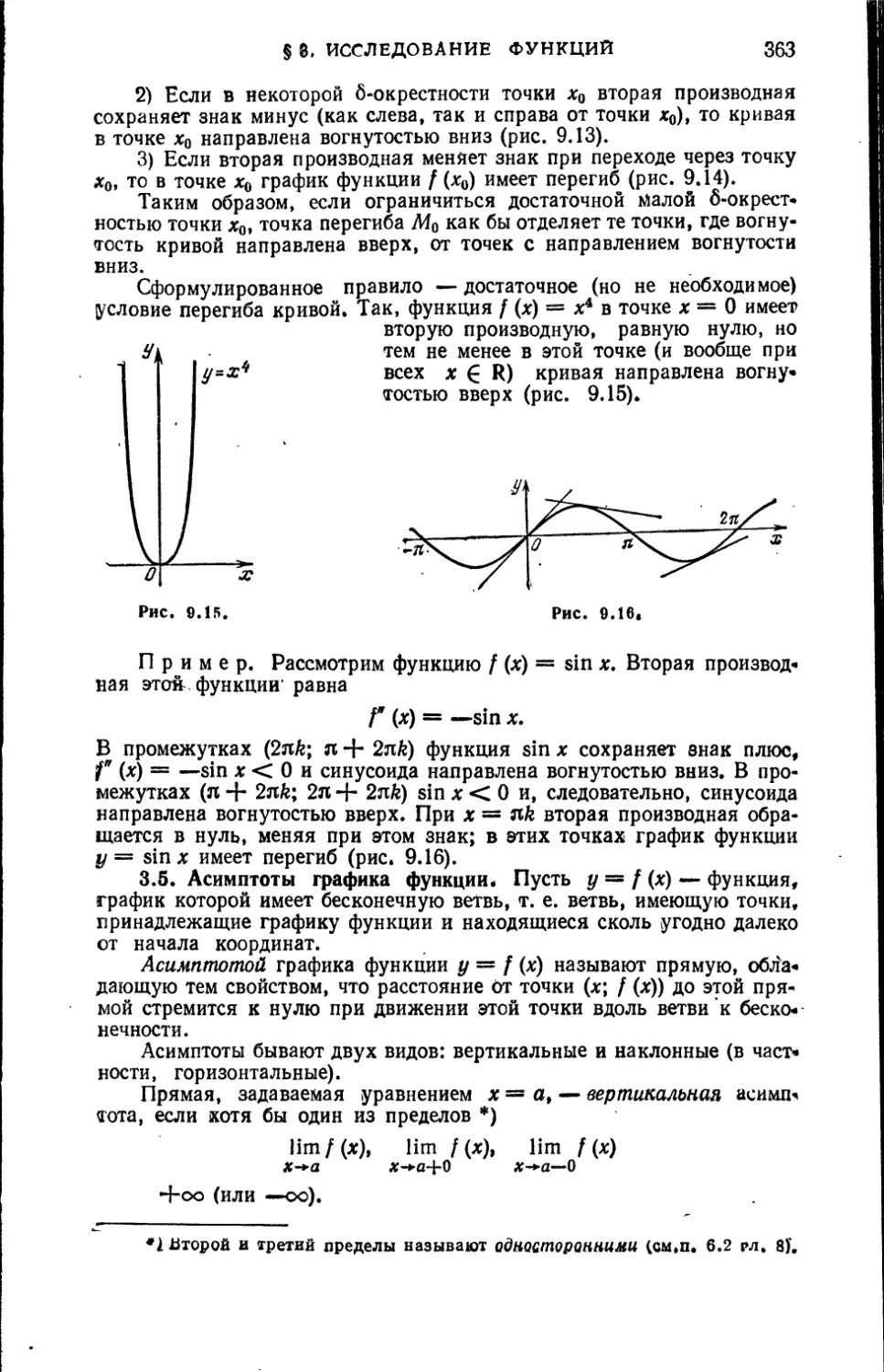
§ 3.	Исследование функций. Построение графика функции . . .	358
3.1.	Условия постоянства и монотонности функций. 3.2. Макси-
мумы и минимумы функции. 3.3. Наибольшее и наименьшее
значения функции. 3.4. Направление вогнутости кривой.
3.5.	Асимптоты. 3.6. Построение графика функции.
§ 4.	Первообразная. Неопределенный интеграл................ 367
4.1.	Понятия первообразной и неопределенного интеграла.
4.2.	Простейшие правила интегрирования. 4.3. Метод интег-
рирования по частям. 4.4. Интегрирование методом замены
переменной. 4.5. Некоторые классы интегрируемых функций.
Подстановки Эйлера.
§ 5.	Определенный интеграл................................. 380
5.1.	Задача вычисления площади плоской фигуры. 5.2. Понятие
определенного интеграла. 5.3. Определенный интеграл как
функция верхнего предела. Основная; формула интеграль-
ного исчисления. 5.4. Вычисление площадей и объемов с по-
мощью определенного интеграла.
§ 6.	Дифференциальные уравнения............................ 389
6.1.	Понятие дифференциального уравнения. 6.2. Дифферен-
. циальные уравнения первого порядка. 6.3. Некоторые дифферен-
циальные уравнения первого порядка. 6.4. Дифференциальные
уравнения порядка выше первого. Примеры дифференциальных
уравнений второго порядка. 6.5. Линейные дифференциальные
уравнения с постоянными коэффициентами.
§ 7.	Функции нескольких переменных......................... 405
7.1.	Понятие функциональной зависимости между несколь-
кими переменными. 7.2. Предел и непрерывность функций двух
независимых переменных. 7.3. Понятие частной производной.
7.4.	Экстремумы функции двух независимых переменных.
Глава 10. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ ............................................   412
§ 1.	Метод математической индукции........................  412
§ 2.	Комбинаторика ........................................ 414
2.1.	Перестановки. 2.2. Подстановки. 2.3. Размещения. 2.4. Со-
четания. 2.5. Бином Ньютона. 2.6. Перестановки с повторени-
ями. 2.7. Сочетания с повторениями.
§ 3.	Элементы теории вероятностей.......................... 423
3.1.	Испытание. Исход. Событие. 3.2. Операции над событиями.
3.3.	Понятие вероятности. 3.4. Условная вероятность. 3.5. Фор-
мула полной вероятности. 3.6. "Формула Бернулли.
ПРИЛОЖЕНИЯ ................................................ 433
1. Элементарные функции.................................... 433
II. Системы счисления ..................................... 442
Основные формулы..........................................  447
Литература................................................  461
Список основных обозначении................................ 466
Предметный указатель....................................... 469
ПРЕДИСЛОВИЕ РЕДАКТОРА
Справочник предназначен для учащихся средних школ и средних
специальных учебных заведений и в полном объеме содержит понятия,
определения, формулы, теоремы и методы решения задач, входящие
в курс математики средних учебных заведений. Кроме того, в справоч-
ник дополнительно включен ряд разделов, необходимых как для более
глубокого понимания основ математики, так и для выявления связей
между различными разделами математики. К дополнительному мате-
риалу, в частности, относятся: делимость целых чисел и многочленов,
алгоритм Евклида, комплексные числа, основная теорема алгебры,
кривые второго порядка, понятия эквивалентности и изоморфизма
множеств, элементы теории вероятностей, начала теории дифференциаль-
ных уравнений, основные сведения о матрицах и определителях и т. д.
В большинстве разделов изложение материала ведется без исполь-
зования теоретико-множественной концепции и поэтому отличается
от принятого в настоящее время в учебниках для средней школы. К та-
ким разделам относится прежде всего геометрия, построение которой
на основе теории множеств приводит к ряду как терминологических,
так и смысловых несообразностей. Поэтому геометрический материал
излагается в справочнике на основе аксиоматики Гильберта и с ис-
пользованием традиционной терминологии. Кроме того, в справочнике
иным способом определены вектор, числовая последовательность,
определенный, интеграл и некоторые другие понятия.
В справочнике дается систематическое изложение теории действи-
тельных чисел. В школьном курсе сведения о действительных числах
слишком разрозненны, чтобы можно было получить полное представле-
ние о структуре и принципах построения действительных чисел. В спра-
вочнике теория действительных чисел излагается с единой точки зрения,
а именно множества целых, рациональных и действительных чисел
последовательно вводятся как естественное расширение множества
натуральных чисел.
Несколько расширен круг вопросов, связанных с приближенными
вычислениями. Наряду с элементарными сведениями общего характера
в справочнике рассмотрены аппроксимирующие свойства непрерывных
дробей и изложен один из наиболее простых и известных методов при-
ближенного вычисления — метод касательных Ньютона.
Обозначения, принятые в справочнике, за редким исключением,
совпадают с обозначениями, принятыми в школьных учебниках. К ука-
занным исключениям относится обозначение интервала: в справочнике
интервал обозначается круглыми скобками, как это принято в боль-
шинстве учебников и книг по математике.
Материал, излагаемый в книге, в основном теоретический —
в справочнике нет таблиц, отсутствуют сведения о логарифмической
линейке и микрокомпьютерах, получивших в последнее время широкое
распространение, и сравнительно мало сказано об арифметических
операциях с десятичными дробями, Эти сведения можно найти в книгах
10	ПРЕДИСЛОВИЕ РЕДАКТОРА
М. Я. Выгодского «Справочник по элементарной математике», Д. Ю. Па*
нова «Счетная линейка» и других.
В заключение следует отметить, что справочник отличается логи*
ческим единством и достаточной степенью подробности в изложении
материала. Вводимые математические понятия и методы решения задач
проиллюстрированы многочисленными примерами. Ввиду этого справоч-
ник может быть использован в качестве пособия для повторения курса
математики средних учебных заведений,
ч
С. А. Степанов
ОТ АВТОРА
Справочник в основном предназначен для учащихся 9—10 классов
средней школы и может быть использован для получения кратких
сведений об основных понятиях, теоремах, формулах и методах решения
простейших задач, встречающихся в курсе математики средней школы.
Для получения справки о формуле удобно обращаться к сводке формул;
для получения справки о математическом термине — к предметному
указателю.
Для получения достаточно цельного представления об интересую-
щем читателя разделе математики рекомендуется полностью прочесть
соответствующий параграф (или главу).
При пользовании справочником следует иметь в виду, что он не
может полностью заменить учебник: большая часть материала дается
без доказательства. Более полное и законченное представление о соот-
ветствующих разделах математики читатель может получить в следую-
щих книгах;
Понтрягин Л. С. Знакомство с высшей математикой. Метод
координат.—М.: Наука, 1977.
Понтрягин Л. С. Математический анализ для школьников. —
М.: Наука, 1983.
Понтрягин Л. С. Знакомство с высшей математикой. Анализ
бесконечно малых. — М.: Наука, 1980.
П о г о р е л о в А. В. Элементарная геометрия. — М.: Наука,
Тихонов А. Н., Костомаров Д. П. Рассказы о приклад-
ной математике. —М.: Наука, 1979.
Маркушевич А. И. Комплексные числа и конформные ото-
бражения.— М.: Наука, 1979.
Е ж о в И. И., С к о р о х о д А. В., ЯдренкоМ. И. Эле-
менты комбинаторики. — М.: Наука, 1977.
Фомин С. В. Системы счисления. — М.: Наука, 1980.
В справочнике принята следующая рубрикация: глава, параграф,
пункт; названия всех пунктов указаны в оглавлении. Сплошная нумера-
ция рисунков ведется в пределах одной главы. При ссылке в тексте на
материал той же самой главы указывается только номер параграфа и
пункта; при ссылке на материал другой главы, кроме номера параграфа
и пункта, также указывается номер главы. В конце справочника даны
достаточно подробный предметный указатель, сводка наиболее распро-
страненных формул и список используемых обозначений. В предметном
указателе приведены страницы, на которых определяется данный тер-
мин. В списке обозначений также указаны страницы, на которых впервые
введено то или иное обозначение. В конце приводится приложение
о системах счисления.
Автор пользуется случаем выразить свою благодарность Л. Д. Куд-
рявцеву за полезные обсуждения, способствовавшие улучшению содер-
жания и структуры справочника, Е. В. Шикину за ценные советы и
12	ОТ АВТОРА
замечания относительно изложения глав «Геометрия» и «Метод коорди*
нат», В. В. Тихомирову за замечания по содержанию справочника.
В настоящем издании справочник отличается от предыдущих как
по построению, так и по содержанию. Переработана значительная часть
текста. Без существенных изменений остались только главы 2, 3 и 5—7.
Комбинаторика, бином Ньютона и метод математической индукции из
1-й главы перенесены в 10-ю, а сведения о матрицах и 'определителях —
в § 8 гл. 4. Главы 8 и 9 переработаны и расширены. Материал прежней
гл. 10 частично перенесен в гл. 8, частично — ц Приложение I. В новую
гл. 10 включен параграф «Элементы теории вероятностей».
При переработке справочника ставилась цель — расширить круг
читателей. Автор надеется, что справочник в таком виде окажется
полезным не только школьникам, но и учащимся техникумов, а может
быть, и студентам первого курса втузов (для повторения).
А. Г, Цыпкин
ГЛАВА 1
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Теория множеств — это раздел математики, изучающий общие
свойства множеств (преимущественно бесконечных). Выделение теории
множеств в самостоятельный раздел математики произошло сравни-
тельно недавно — на рубеже XIX и XX веков. Теория множеств ока-
зала очень большое влияние на развитие современной математики — она
явилась фундаментом ряда новых разделов математики, позволила
по-новому взглянуть на классические разделы математики и глубже
понять сам предмет математики.
§ h Множества и операции над множествами
1.1. Множества и подмножества. В математике некоторые понятия
являются первичными, неопределяемыми. К ним относятся понятия
~ натурального числа, точки, прямой и т. д.
Одним из таких неопределяемых понятий является понятие «мно-
жество». Этому понятию нельзя дать формального определения, которое
не сводилось бы просто к замене слова «множество» его синонимами
«совокупность», «набор элементов» и т. п. Множества можно составлять
на основе самых различных признаков из самых разнообразных объектов
(которые в дальнейшем будем называть элементами множества). Мно-
жество можно-задать, указывая,например, некоторое свойство объектов,
образующих множество, правило построения элементов множества и
' т. д. Можно говорить не только о множествах, элементами которых явля-
ются материальные объекты, но и о множествах, элементы которых —
некоторые абстрактные понятия (числа, геометрические фигуры, сим*
волы и т. п.).
Сразу оговорим, что понятие «множество» не следует понимать
буквально и тдлковать его. как совокупность, содержащую «много»
элементов. Под множеством также понимается совокупность объектов,
которая может состоять, например, из одного, двух и т. д. элементов.
Более того, оказывается удобным считать множеством даже пустое
множество, т. е. множество, не содержащее ни одного элемента. Рас-
сматривать пустое множество необходимо хотя бы только потому, что,
когда мы определяем тем или иным способом множество, мы можем и не
знать заранее, содержит ли оно хотя бы один элемент.
Множества чаще всего обозначаются прописными буквами латин-
ского алфавйта А, В, ...» X, а их элементы — малыми буквами: а,
Ъ, х. Пустое множество обозначается специальным символом 0.
Если множество А состоит из п элементов а19 а29 ап, то пишут
А = {аг\ а2\...; ап}.
Говорят: «элемент а принадлежит множеству А»—и записывают^
а £ А или А $ а (А содержит а); запись а & А или А а означает,
что элемент и не принадлежит множеству А (А не содержит а).
14
ГЛ. I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Множество В называют подмножеством множества Д, если все
элементы множества В принадлежат множеству Д, и пишут
в а а.
Например, пусть А — множество рациональных чисел, В — мно-
жество натуральных чисел. В этом случае В CZ Д.
Любое множество А имеет в качестве своих подмножеств пустое
множество и само множество Д.
Если для двух множеств А и В одновременно справедливы утверж-
дения А С В и В CZ Д, то множества А и В состоят из одних и тех же
элементов. Такие множества А и В называют равными (или совпадаю*
щими) и пишут
А ® В.
Непустое подмножество В множества А называется собственным'
если В не совпадает с Д.
1.2. Операции над множествами. Объединением двух множеств на-
зывается множество, состоящее из всех элементов, принадлежащих
хотя бы одному из этих множеств. Объединение множеств А и В обозна-
чается A (J В. Для наглядности изобразим множество в виде плоской
геометрической фигуры (на рис. 1.1 элементы множества — точки
заштрихованной части плоскости). На рис. 1.2 множество A (J В
выделено двойной штриховкой.
Пересечением двух множеств называется множество, состоящее
из всех элементов, принадлежащих одновременно обоим множествам.
Пересечение множеств Д и В обозначается А Г) В. На рис. 1.3 множество
С = А П В выделено двойной штриховкой.
Множества Д и В могут быть такими, что их пересечение будет
пустым множеством: Д П В = 0 (рис. 1.4).
Свойства операций объединения и пере-
сечения:
1)	коммутативность:
A (J В = В (J Д, А П В = В П Д*
2)	ассоциативность:
(Л U В) и А и (В U О, М Л В) Л С= А Л (В ПО;
3)	дистрибутивность!
(А и В) л С = (Л л О и (В Л О,
(А Л В) и (А и Q л (В U О-
§ I. МНОЖЕСТВА И ОПЕРАЦИИ НАД МНОЖЕСТВАМИ 15
Разностью множеств А и В называется множество, состоящее из
всех элементов Л, не принадлежащих В. При этом, вообще говоря, не
предполагается, что В С 4. Разность множеств А а В обозначается
А \ В (или А — В).
Рис. 1.8.	Рис. 1.4.
Рис. 1.5.
Если В — подмножество Л, то разность Л \ В также называют
дополнением множества В до множества Л. Если R ~ А \ В, то /? П
fl В = 0 и R (J В == Л. На рис. 1.5 дополнение Л \ В выделено
двойной штриховкой.
Поясним смысл этих определений следующим примером. Пусть Л —
множество всех натуральных чисел, кратных двум, а В — множество
всех натуральных чисел, кратных трем.
Объединением этих множеств будет множе-
ство всех натуральных чисел, кратных числу 2
или числу 3. Их пересечением будет мно-
жество всех натуральных чисел, кратных >
как числу 2, так и числу 3, т. е. кратных
числу 6.
Пусть теперь Л — множество всех на-
туральных чисел, кратных числу 2, а В —
множество всех натуральных чисел, кратных
числу 6 (т. е. кратных- как числу 2, так и
числу 3). Множество В является подмноже-
ством множества Л. Дополнением множе-
ства В до множества Л будет множество всех
натуральных чисел, кратных числу 2, но не
кратных числу 3.
Понятия объединения и пересечения, данные для случая двух
множеств, могут быть распространены и на случай любого числа мно-
жеств.
Так, объединением конечного числа множеств Л| (t« 1, 2, л)
называют множество В, состоящее из элементов, каждый из которых
принадлежит хотя бы одному из множеств Ль и пишут
В = U Аг
*==1
Пересечением конечного числа множеств At (t = 1, 2, ..., и) назы-
вают множество С, состоящее из всех элементов, принадлежащих
одновременно всем множествам Ль и пишут
с = n At.
1=1
16	ГЛ. 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Если At — бесконечная совокупность множеств (i=l, 2, ..., п, ...),
фо объединение и пересечение этих множеств обозначают с помощью
символов
U At и ПЛ/
i	i
соответственно.
Пусть At — конечная или бесконечная совокупность подмножеств
(i = 1, 2, 3, ...) множества А. Связь между подмножествами At и
множеством А устанавливается следующими равенствами, называемыми
соотн ош ен и ям и двойственност и:
Л\П Al = и (4\4i),	4\U At = п (Л\Л0.
i	i	i	i
Пусть Д и В — два произвольных множества. Пара (а, Ь) элементов
а £ В и b £ В, взятых в данном порядке, называют упорядоченной
парой. Считают, что пары (alt Ь±) и (а2> ^г) равны тогда и только^тогда,
когда Gj = а2 и = Декартовым произведением двух множеств А
и В называется множество всех упорядоченных пар (а, Ь). Декартово
произведение множеств А и В обычно обозначается А X В.
1.3. Упорядоченные множества. Вводя операции надмножествами,
мы не учитывали, что сами множества могут иметь свою внутреннюю
структуру, т. е. мы считали, что все элементы множества равноправны.
Однако в математике такие «чистые» множества представляют мало
интереса, и гораздо чаще изучаются множества, между элементами
которых существуют те или иные отношения. Одним из важнейших
отношений между элементами множества является отношение порядка.
Отношение порядка есть не что иное, как правило, устанавливаю-
щее порядок «следования» элементов - множества.
Пусть А — некоторое множество. Множество А называется у пор я*
доченным множеством, если для любых его двух элементов а, b установ-
лено одно из следующих отношений порядка'.
либо а b (а не превосходит Ь),
либо b а (Ь не превосходит а),;
обладающих следующими свойствами:
1) рефлексивность: любой элемент не превосходит самого
себя;
2)'а нтисимметричность: если а не превосходит bt а b не
превосходит а, то элементы а и b совпадают;
3) транзитивность: если а не превосходит b, а b не превос-
ходит с, то а не превосходит с.
Пустое множество условились считать упорядоченным. В сформу-
лированном выше определении упорядоченного множества, элементами
которого могут быть объекты любой природы, знак читается «не
превосходит». Привычное чтение и смысл этот знак (как знак «меньше
или равно») приобретает в случае, когда элементы множества А —
числа.
Два множества, составленные из одних и тех же элементов, но с раз-
ными отношениями порядка, считаются различными упорядоченными
множествами.
Одно и то же множество можно упорядочить различными способами,
получая тем самым различные упорядоченные множества. Например,
§ 2. СООТВЕТСТВИЕ И ОТОБРАЖЕНИЕ МНОЖЕСТВ 17
рассмотрим множество, элементами которого являются различные вы-
пуклые многоугольники: треугольник, четырехугольник, пятиугольник,
шестиугольник и т. д. Один способ образования упорядоченного мно-
жества из данного неупорядоченного множества может, например,
состоять в том, что в качестве первого элемента упорядоченного мно-
жества мы берем треугольник, в качестве второго — четырехугольник,
третьего — пятиугольник и т. д., т. е. упорядочиваем множество в по-
рядке возрастания числа внутренних углов многоугольников. Мно-
жество многоугольников может быть упорядочено и другим способом,
например перечислением многоугольников в порядке возрастания пло,-
щадей, когда в качестве первого выбирается многоугольник, имеющий
наименьшую площадь, в качестве второго — многоугольник с площадью,
не превышающей площадь всех остальных, кроме уже выбранного,
и т. д.
Упорядоченные (конечные или счетные), множества часто записы-
вают, располагая их элементы в заданном порядке в круглых скобках.
Например, записи
(1; 2; 3) и (2; 1; 3)	(1)
представляют различные конечные упорядоченные множества, которые
можно получить из одного и того же множества {1; 2; 3}, -упорядочивая
его двумя различными способами. Для записи счетного упорядоченного
множества в виде, аналогичном (1), необходимо указать первый элемент
упорядоченного множества и указать порядок (правило) расположения
последующих элементов.
§ 2.	Соответствие между множествами
и отображение множеств
2.1.	Соответствие и отображение. Понятие соответствия отно-
сится к первичным, неопределяемым понятиям математики. Говорят,
что между двумя множествами установлено соответствие, если опреде-
лено правило, по которому для каждого элемента одного множества
выбирается определенный элемент или подмножество элементов другого
множества. При этом допускается, что некоторым элементам первого
множества может соответствовать пустое подмножество.
На основе понятия соответствия между множествами вводится
понятие отображения множеств. При этом различают отображение
множества «в» множество и отображение множества «на» множество.
Соответствие, при котором каждому элементу множества А отвечает
единственный элемент множества В, называется отображением мно*
оюества А в множество В.
Соответствие, при котором каждому элементу множества А отвечает
единственный элемент множества В и, кроме того, каждому элементу
множества В отвечает хотя бы один элемент множества А, называется
отображением множества А на множество В,
Отображения множеств обычно обозначают буквами g, и
пишут
1	g	h
А-* В, А-+В, А-+В
или '
f; А В, g: Л -> В, h\ А-> В.
18	ГЛ. 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Если при отображении f элементу а £ А соответствует элемент
b £ Bt то элемент b называют образом элемента а, элемент а называют
прообразом элемента b и пишут
b e f (а).
Множество всех прообразов элемента b называют его полным прообра*
еом. В случае отображения множества А «на» множество В пишут также
В = /(Д).
Отображение f: 4 -> В называется инъективным^ если разные
элементы множества А имеют различные образы.
Равенство f = g двух отображений
Л Д->В, g: Д->В
Означает, что для любого а £ Л / (а) = (а).
2.2.	Взаимно однозначное отображение.. Отображение множества
Д на множество В, при котором разным элементам множества А соответ-
ствуют разные элементы множества В, называется взаимно однозначным
отображением множества А на множество В. Другими словами, отобра-
жение f: А -> В взаимно однозначно, если оно отображает множество А
на множество В и оно инъективно. Взаимно однозначное отображение
называют также биекцией.
Если множества Д и В совпадают и f — взаимно однозначное
отображение, т. е. f\ Д~>Д, то говорят, что множество Д взаимно
однозначно отображается на себя.
Единичным (или тождественным) отображением е множества 4
на себя:
е: Д-> А
называется отображение, переводящее любой элемент а € А в себя2
е (а) = а.
Пусть множество А взаимно однозначно отображается на множество
В (f : А -> В), т. е. каждому элементу а £ А при отображении f
соответствует единственный элемент b множества В (образ а) и каждому
элементу b £ В соответствует единственный элемент a £ А (прообраз
Ъ). Отображение, ставящее в соответствие каждому элементу b £ В его
прообраз а С Д, называют обратным отображением для отображения
/, обозначают и пишут
В-> А или	В->4.
Если f — взаимно однозначное отображение, то обратное отображение
f"1 — также взаимно однозначное отображение; обратным для отображе-
ния /'* будет исходное отображение /.
2.3.	Эквивалентность множеств. Если множество А взаимно одно-
значно отображается на множество В, то множества А и В называются
эквивалентными. Эквивалентность множеств записывается с помощью
знака
А~В
(читается: А эквивалентно В). Об эквивалентных множествах Д и В
также говорят, что между ними установлено отношение эквивалент-
ности.
Отношение эквивалентности множеств обладает следующими свой-
ствами:
1)	рефлексивность; А ~ А (любое множество эквнва*
лентно самому себе);
§ 2. СООТВЕТСТВИЕ И ОТОБРАЖЕНИЕ МНОЖЕСТВ 	19
2)	симметричность: А ~ В <=> В~А (если множество А
эквивалентно множеству В, то множество В эквивалентно множеству А,
и наоборот);
3)	транзитивность: 4 и В ~ С=>А ~ С (если мно«
вкество А эквивалентно множеству В, а множество В эквивалентно
множеству С, то и множество А эквивалентно множеству С).
2.4.	Классификация множеств. Множества делятся па конечные
и бесконечные.
Множество, эквивалентное отрезку натурального ряда *), называ-
ется конечным множеством (пустое множество также считается конеч-
ным множеством). Иными словами, конечное множество (если оно не
густо) — это множество, элементы которого можно «пересчитать» за
конечное число шагов. Если при этом каждому элементу конечного
множества А присвоить какой-нибудь номер от 1 до некоторого нату-
рального числа п таким образом, чтобы все числа от 1 до п были исполь-
вованы и различные элементы множества получили различные номера,
то число п укажет число элементов данного множества 4.
Число элементов конечного множества 4 называется мощностью
конечного множества.
Для конечных множеств справедлива следующая теорема, которая
называется основной теоремой о конечных мно-
жествах:
Любое конечное множество не эквивалентно никакому его собствен*
ному подмножеству.
Из этой теоремы, в частности, также следует, что всякое непустое
конечное множество эквивалентно одному и только одному отрезку
натурального ряда.
Множество, не являющееся конечным множеством, называется
бесконечным. В качестве «эталона» для сравнения бесконечных множеств
можно выбрать простейшее бесконечное множество — множество всех
натуральных чисел N.
Если проводить сравнение всевозможных бесконечных множеств
с множеством всех натуральных чисел N, то оказывается, что все
бесконечные множества разбиваются на два класса: на класс множеств,
эквивалентных множеству всех натуральных чисел (такие множества
называют счетными), и на класс множеств, не эквивалентных
множеству натуральных чисел (такие множества называют несчет-
ными).
Таким образом, счетное множество— это такое бесконечное мно-
жество, элементы которого можно «перенумеровать» при помощи мно-
жества натуральных чисел, т. е. можно указать такой способ нумерации
элементов множества, при котором каждый элемент множества получит
свой единственный номер. Счетными множествами будут, например,
множество всех четных натуральных чисел, множество всех рациональ-
ных чисел и т. д.
Приведенные примеры различных счетных множеств кажутся на
первый взгляд несколько необычными: очевидно, что множество всех
четных натуральных чисел является подмножеством множества всех
натуральных чисел, и в то же время множество четных чисел эквива-
лентно множеству натуральных чисел. Этот парадокс кажущийся и
связан с тем, что на практике мы обычно имеем дело с конечными мно«
*) Множество всех натуральных чисел, меньших или равных некоторому
натуральному числу nt называется отрезком натурального ряда и обозна-
чается U, л j или 1, п»
20
ГЛ. I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
жествами, т. е. с множествами, состоящими из конечного числа элемен-
тов, для которых изъятие хотя бы одного элемента приводит к уменьше-
нию их числа. В результате такого изъятия у нас получается новое
конечное множество, которое,уже не будет эквивалентно исходному, так
как конечные множества эквивалентны лишь в случае равенства числа
их элементов. Совсем по-другому обстоит дело со счетными множествами.
Изъятие из счетного множества конечного (а иногда даже бесконечного)
числа элементов по-прежнему оставляет множество счетным.
. В качестве примера покажем, что множество всех натуральных
чисел и множество всех четных натуральных чисел эквивалентны между
собой. Начертим две параллельные числовые оси Ох и О'х' (рис. 1.6)>
выбирая единичные масштабные отрезки таким образом, чтобы единич-
ный отрезок оси Ох был в два раза больше единичного отрезка оси О'х\
О f 2	Множество натуральных чи-
- - - »_____j_______।______j сел будет изображаться точ-
у у у ками числовых осей Ох и
/	/	/	. О’х'. Поставим в соответ-
/	/	/	ствие числу 2 числовой оси
/	/	/	ЧИСЛО 1 числовой оси Ох,
>--1---!-------г	> числу 4 числовой оси О'х' —
О' 1 2 3 4 3 Я 7	число 2 числовой оси Ох,
числу 6 — число 3 и т. д.
Рис» !•••	При этом окажется, что лю-
бому четному натуральному
числу соответствует единственное натуральное число и, наоборот,
любое натуральное число отвечает единственному четному натураль-
ному числу, т. е. между множеством всех четных натуральных чисел
и множеством всех натуральных чисел установлено взаимно однознач-
ное соответствие, и, значит, эти множества эквивалентны.
Приведенный пример показывает, что множество натуральных чисел
содержит собственное, эквивалентное ему подмножество (множество
четных чисел). Таким свойством — содержать собственное подмноже-
ство, которое эквивалентно самому множеству, обладают все бесконеч-
ные множества. Указанное свойство можно взять в качестве определения
бесконечного множества.
Свойства бесконечных множеств:
1)	Всякое подмножество счетного множества конечно или счетно.
2)	Сумма любого конечного или счетного множества счетных мно-
жеств есть счетное множество.
3)	Всякое бесконечное множество содержит счетное подмножество.
Последнее свойство говорит о том, что среди бесконечных множеств
счетные множества — «самые маленькие».
Существуют бесконечные множества, не являющиеся счетными; это
несчетные множества. Заметим, что такое «определение» несчетного
множества нельзя считать вполне удовлетворительным по следующей
причине: вводя понятие бесконечного множества, мы были уверены, что
хотя бы одно такое множество существует. Этим множеством является
множество натуральных чисел. При данном же «определении» несчет-
ного множества уже приходится в качестве теоремы доказывать, что
такие множества существуют. Эта теорема формулируется такз
Множество действительных чисел, заключенных между 0 и 1,
несчетно.
Мы не будем приводить доказательство этой фундаментальной
теоремы теории множеств, а лишь заметим, что оно основано на пред-
ставлении действительных чисел в виде бесконечных десятичных дробей.
§ 3. МНОЖЕСТВА С БИНАРНЫМИ ОПЕРАЦИЯМИ -	21
Суть же доказательства состоит в том, что, как бы мы ни нумеровала
числа, лежащие между нулем и единицей, используя все натуральные
числа, всегда найдется такое действительное число, большее нуля и
меньшее единицы, которое будет пропущено.
Если множество эквивалентно множеству всех действительных
чисел, больших нуля и меньших единицы, то говорят, что оно имеет
М
Ж
мощность континуума.
Примерами множеств, эквивалентных множеству действительных
чисел, заключенных между нулем и единицей, т. е. имеющих мощность
континуума, являются: множество всех точек любого отрезка прямой,
множество всех точек прямой, множество
всех прямых на плоскости и т. д.
Легко заметить, что приведенные при-
меры создают ту же «парадоксальную»
ситуацию, которая возникала и в случае
счетных множеств, а именно: множество
чисел, лежащих между числами 0 и 1,
оказывается эквивалентным множеству
всех чисел, больших нуля и меньших,
например, двух. В случае несчетных
множеств «парадокс» объясняется так
же, как и в случае счетных множеств,
поэтому не будем на нем подробно оста-
навливаться. Здесь мы лишь покажем, каким образом можно уста*
х
_z___!_

х*
Рис» 1.7.
новить взаимно однозначное соответствие между множеством чисел*
больших нуля и меньших единицы, и множеством чисел, больших
нуля и меньших двух, и тем самым доказать их эквивалентность. Нари*
суем две параллельные числовые оси Ох и О'х', выбирая на них одинако*
вые масштабные отрезки (рис. 1.7). Опишем теперь способ, позволяю*
щий установить взаимно однозначное соответствие между точками*
принадлежащими отрезку [0; 1 ] оси Ох, и точками, принадлежащими
отрезку [0; 2] оси Ох. Проведем через точки О и О' и точки 1 и 2 пря-
мые, которые пересекутся в некоторой точке М. Возьмем любую точку
хо € [0; 1 ] оси Ох и проведем прямую через точку М и точку х0. Эта
прямая пересечет ось О'х' в некоторой точке Xq, которая и будет образом
точки х0 при отображении промежутка [0; 1] оси Ох на промежуток
[0; 2] оси О'х'. Точка Xq будет единственной точкой пересечения Мх0 и
О'х', так как эти прямые не параллельны. И наоборот, взяв любую точку
€ [0; 2] оси О'х' и проведя прямую через точку М и точку x'Jt при*
надлежащую оси О'х', получим единственную точку пересечения данной
прямой с осью Ох, которую обозначим Хр Точка будет образом точки
х'1 при отображении множества [0; 2 ] оси О'х' на множество [0; 11
оси Ох. Таким образом, мы установили взаимно однозначное соответ-
ствие между нашими множествами и тем самым доказали их эквива-
лентность.
§ 3.	Множества с бинарными операциями
3.1.	Бинарные операции в множествах. Пусть А — некоторое
конечное или бесконечное множество с элементами
а, Ь, с, d,...
Бинарной операцией (или просто операцией) называют отображение
множества А в себя, которое каждой упорядоченной паре элементов
22	ГЛ. I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
(а; Ь) из множества А ставит в соответствие некоторый третий элемент
(образ пары элементов (а; Ь)) из того же множества А.	. 4
В тех случаях, когда бинарную операцию называют умножением,
образ пары элементов (о; Ь) называют их произведением и обозначают ab
или а*Ь (а X Ъ). Если при этом а*6== Ь*а, то говорят, что операция
умножения коммутативна.
В тех случаях, когда бинарную операцию называют сложением*
образ пары элементов (а; Ь) называют суммой и обозначают а+ Ь.
Если при этом а 4- b = b -j- а, то говорят, что операция сложения
коммутативна.
Пусть a, Ь, с — три различных элемента множества А, в котором
определена бинарная операция (скажем, умножение). Так как произве-
дение а*b (образ пары (д; Ь)) — элемент множества Л, то упорядоченной
паре (а*Ь\ с) будет соответствовать элемент (a*b)*c. С другой стороны,
для той же тройки элементов а, b и с можно составить и произведение
а*(Ь*с), являющееся образом пары (а; Ь-с).
Если при этом (ab) с=а (bc)t то говорят, что бинарная операция
ассоциативна.
Элемент е € А такой, что
еа == ае == а
для любого а С Л, называется единичным элементом множества А
относительно выбранной бинарной операции. (Когда бинарная опера-
ция — сложение, то единичный элемент обычно обозначают символом О,
называют нулевым элементом и пишут а-{-0==04-а=а.)
3.2.	Изоморфизм множеств. Пусть даны два множества Л и А'
и в каждом из этих множеств определено по одной (не обязательно
одноименной) бинарной операции. Множества Л и Л' называются
изоморфными, если между элементами этих множеств можно установить
взаимно однозначное отображение /, сохраняющее бинарную операцию,,
а именно:
Если элементы а' и Ь' из множества А' являются образами элементов
а и b из множества А при отображении f, то а'Ь' есть образ элемента ab.
Например, рассмотрим два подмножества множества всех натураль-
ных чисел: множество всех четных чисел и множество всех чисел, крат-
ных числу 5. В этих множествах определена бинарная операция (сложе-
ние): сумма любых двух четных чисел — четное число, а сумма любых
двух чисел, кратных 5, — число, кратное пяти. Поставим в соответствие
четному числу 2п число 5n (п £ N). Это соответствие между множеством
всех четных чисел и множеством всех чисел, кратных числу. 5, будет
взаимно однозначным отображением, обладающим перечисленными
выше свойствами, и, следовательно, данные множества изоморфны.
Изоморфные множества с бинарными операциями могут отличаться
друг от друга как природой своих элементов, так и названием бинарной
операции.
Например, рассмотрим два множества чисел: множество всех дей-
ствительных чисел R и множество всех положительных действительных
чисел R+. Поставим в соответствие положительному числу а € R+ его
натуральный логарифм In а. Множество натуральных логарифмов всех
положительных действительных чисел образует множество всех действи-
тельных чисел R. В силу свойств логарифмической функции установлен-
ное соответствие будет взаимно однозначным отображением множества
положительных действительных чисел R* на множество всех действи-
тельных чисел R,
§ 3. МНОЖЕСТВА С БИНАРНЫМИ ОПЕРАЦИЯМИ	23
Известное логарифмическое равенство
In (а> Ь) = In а + In bf
где a, b g R+, показывает, что множество положительных действитель-
ных чисел с операцией умножения изоморфно множеству всех действи-
тельных чисел с операцией сложения.
Таким образом, изоморфные множества неразличимы с точки зрения
свойств операций: все, что может быть доказано для одного множества
с некоторой бинарной операцией на основании свойств этой операции, но
без использования природы элементов множества, автоматически пере-
носится на все изоморфные множества. Вследствие этого понятие изо-
морфизма позволяет отвлечься от природы элементов множеств, обра-
щая основное внимание на изучение самих бинарных операций.
3.3.	Группы. Непустое множество G={a; b\ с\...} называется
группой, если в этом множестве определена бинарная операция (обычно
называемая умножением) так, что:
1)	бинарная операция в множестве G ассоциативна, т. е.
a (be) = (ab) с;
2)	множество G содержит такой элемент е (называемый левой едини*
цей). что для каждого элемента а £ G выполняется равенство
еа = а;
3)	для каждого элемента a £ G в множестве G существует такой
элемент bt что 4
ba = е;
элемент b называется левым обратным элементом и обозначается a“h
а-1а = е.
Операция в группе G не обязана быть коммутативной. Если же она
коммутативна, то группа G называется коммутативной (или абелевой).
Из определения группы следуют ее простейшие свойства:
1) Каждая группа G имеет единственную левую и единственную
правую единицы, и эти единицы равны:
еа = ае = а.
2) Каждый элемент группы G имеет единственный левый и един-
ственный правый обратные элементы, и эти элементы равны:
= ааг1 = е.
Из последнего свойства следуют правила, называемые законами
сокращения: для любых трех элементов а, Ь. с группы G из равенств
са = cb, ас = Ьс следует равенство а = Ь.
Если группа G состоит из конечного числа элементов, то она назы-
вается конечной группой, а число элементов в ней — порядком группы;
в противном случае группа называется бесконечной. Бесконечная группа
может быть как счетной, так и несчетной.
Если групповую бинарную операцию называют умножением (что и
было принято выше), то группа также называется мультипликативной.
Если же групповую операцию называют сложением, то группа называ-
ется Аддитивной. В этом случае вместо единицы группы говорят о нуле
группы и обозначают его символом 0; элемент, обратный элементу а,
называют противоположным и обозначают —а.
24
ГЛ, I. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Примеры. 1. Множество всех целых чисел образует группу по
операции сложения — аддитивную группу целых чисел. Эта группа
абелева в силу коммутативности операции сложения целых чисел. Роль
единичного элемента в ней играет число нуль.
Множества рациональных, действительных и комплексных чисел
по операции сложения также образуют аддитивные абелевы группы.
2. Множество всех положительных действительных чисел по умно-
жению образует абелеву группу.
3. В п. 2.2 гл. 10 введено понятие подстановок n-й степени —
отображений множества из п различных элементов на себя. Все подста-
новки л-й степени о бинарной операцией (умножением) образуют неком-
мутативную группу. Это нетрудно доказать, проверяя выполнение
свойств 1)-т-3), определяющих группу: произведение подстановок опять
будет подстановкой; роль единицы будет играть тождественная подста-
новка: для любой подстановки л-й степени существует обратная подста-
новка; операция умножения подстановок ассоциативна. Убедимся на
примере подстановок четвертой степени, что умножение подстановок
некоммутативно. Пусть а и b — две подстановки четвертой степени}
/1 2 3 4\ к /1 2 3 4\
®_\2 1 4 3?	1 2 4/*
Тогда
откуда
тивно.
подстановок некоммута<
1 2
1 3
3
4
	/1 2 3 4\
Ьа~\4 2 1 3/
видно, что аЬ Ф Ьа, т. е. умножение
Группа подстановок л-й степени называется симметрической груп*
пой степени п. Она является конечной группой порядка п\ и обознача-
ется Sn..
3.4.	Кольца. Множество R называется кольцом, если в нем опре-
делены две бинарные операции — сложение и умножение, удовлетво-
ряющие условиям:
1)	множество R — коммутативная группа по сложению,
т. е.
а + (Ь + с) = (а + Ь) + с,
а + ( — а) = 0;
а + b = b + а,
а + 0 = а,
2)	для любых а, Ь, с € R
a (be) = (ab) с;
3)	сложение и умножение связаны законами дистрибу-
тивности:
а (Ь + с) = ab + ас, (Ь + с) а = Ьа 4- са.
Множество R называется коммутативным кольцом, если к этим
условиям добавлено условие коммутативности умножения.
Кольцом с единицей называют кольцо, содержащее такой элемент е
(мультипликативную единицу), что
еа = а
для всех а £ R. Если R — кольцо с единицей, то может оказаться,
что данный элемент а кольца R может иметь мультипликативный обрат-
ный элемент а~\ а может и не иметь его,'
§,3. МНОЖЕСТВА С БИНАРНЫМИ ОПЕРАЦИЯМИ 25
Примеры. 1. Кольцами являются множество всех целых чисел,
множество всех действительных чисел, множество всех комплексных
чисел.
2.	Множество четных целых чисел будет кольцом без единицы, в то
время как множество нечетных чисел кольцом не является, так как
сумма двух нечетных чисел есть число четное (незамкнутость относи-
тельно операции сложения).
3.5.	Поля. Кольцо с единицей, которое состоит не только из одного
нуля и которое для каждого своего элемента а, отличного от нуля,
содержит также его мультипликативный обратный элемент а"1, назы-
вается полем.
Используя определения кольца и поля, нетрудно проверить, что:
Множество всех натуральных чисел с определенными в нем бинар-
ными операциями сложения и умножения не является ни кольцом,
ни полем.
Множество всех целых чисел является коммутативным кольцом
с единицей.
Множество всех рациональных чисел, полученное расширением
множества целых чисел присоединением к нему частных от деления
любых двух целых чисел друг на друга (за исключением деления на
нуль), является полем.
Множество всех действительных чисел, полученное расширением
множества рациональных чисел присоединением к нему новых элемен-
тов — иррациональных чисел, также является полем.
Множество комплексных чисел, полученное расширением множества
действительных чисел присоединением к нему нового элемента —
корня уравнения х2 + 1 = 0, является полем.
Из всех числовых полей поле рациональных чисел — «самое малень-
кое», так как не существует числовых полей, отличных от поля ра-
циональных чисел и целиком в нем содержащихся, и, кроме того, поле
рациональных чисел содержится во всяком числовом поле.
ГЛАВА 2
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Число — это важнейшее математическое понятие. Натуральные
числа, используемые для счета в практической деятельности, появились
на самых ранних этапах развития человеческой цивилизации. Перво*
начально понятие отвлеченного числа отсутствовало — число было
«привязано» к тем предметам, которые пересчитывали, и в языке перво-
бытных народов существовали различные словесные обороты для’обозна-
чения одного и того же числа разных предметов. Отвлеченное понятие
натурального числа (т. е. числа, не связанного с пересчетом конкретных
предметов) появляется и закрепляется вместе с развитием письменности
и введением для обозначения чисел определенных символов.
Появление дробных (положительных рациональных) чисел было
связано с необходимостью производить измерения, т. е. процедуру,
в которой какая-либо величина сравнивается с другой величиной того же
рода, выбираемой в качестве эталона (единицы .измерения). Но так как
единица измерения не всегда укладывалась целое число раз в измеряемой
величине, и пренебречь этим обстоятельством в ряде случаев было
нельзя, то возникла практическая потребность ввести более «мелкие»
числа, нежели натуральные. Это и было источником возникновения
наиболее «простых» дробей, таких, как половина, треть, четверть и т. д.
Дальнейшее развитие понятия числа было обусловлено уже не только
непосредственной практической деятельностью человека, но и явилось
следствием развития математики.
Введение отрицательных чисел было вызвано развитием алгебры
как науки, дающей общие способы решения арифметических задач
независимо от их конкретного содержания и исходных числовых данных.
Отрицательные числа систематически употреблялись индийскими мате-
матиками еще в VI—XI веках. В европейской науке отрицательные
числа окончательно вошли в употребление лишь после работ Р. Декарта
в XVII веке, давшего их геометрическое истолкование.
Множество рациональных чисел оказывается достаточным для
удовлетворения большинства практических потребностей — с помощью
рациональных чисел измерения можно выполнять с любой наперед
заданной степенью точности.
Дальнейшее расширение понятия числа произошло в XVII веке
в период зарождения современной математики, когда возникла необхо-х
димость ввести четкое определение понятия числа. Такое определение7
было дано одним из основоположников математического анализа
И. Ньютоном во «Всеобщей арифметике»: «Под числом мы понимаем
не столько множество единиц, сколько отвлеченное отношение какой-
нибудь величины к другой величине того же рода, принятой нами за
единицу». Эта формулировка дает единое определение действительного
числа, как рационального, так и иррационального. (О существований
несоизмеримых отрезков, отношение которых есть число иррациональ-
ное, было известно еще ученым Древней Греции.) В дальнейшем, в 70-х
годах XIX века строгая теория действительного числа была развита
в работах Р. Дедекинда, Г. Кантора и К. Вейерштрасса.
§ I, НАТУРАЛЬНЫЕ ЧИСЛА	‘ 27
§ 1$ Натуральные числа
1.1а Множество натуральных чисел» Натуральные woa—это
числа, используемые для счета:
1, 2, 3, 4...., п>...	(1)
Из любых двух соседних чисел в записи (1) число, стоящее справа,
называется последующим относительно числа, стоящего слева.
Натуральные числа (1) образуют множество, называемое множест-
вом натуральных чисел. Множество всех натуральных чисел обознача-
ется символов N;
N = {1; 2; 3; . . 4 л; . . .}.
Множество натуральных чисел является упорядоченным множеств
вом, т. е. для любых двух натуральных чисел тип имеет место одно из
следующих соотношений:
либо т = п (т равно л),
либо т < п (т меньше л),
либо п < т (п меньше т).
Наименьшим натуральным числом является 1 (единица).
В множестве натуральных чисел вводятся две основные арифмети-
ческие операции — сложение и умножение. Для обозначения этих
операций используются соответственно символы + и • (или X).
Сложение натуральных чисел. Каждой паре
натуральных чисел (л; р) ставится в соответствие натуральное число s,
называемое их суммой. Сумма s состоит из стольких единиц, сколько их
содержится в числах п и р. О числе s говорят, что оно получено в резуль-
тате сложения чисел п и р, и пишут
s = п + р.	(2)
Числа п и р в записи (2) называются слагаемыми. Операция сложения
натуральных чисел:
1) коммутативна: л + р = р + л;
2) ассоциативна: (л + р) + & = л + (р + £).
Умножение натуральных чисел. Каждой упорядо-
ченной паре натуральных чисел (л; р) ставится в соответствие натураль-
ное число т, называемое их произведением. Произведение т состоит из
стольких единиц, сколько их содержится в числе п, взятых столько раз,
сколько единиц содержится в числе р. О числе т говорят, что оно полу-
чено в результате умножения чисел п и р, и пишут
т = п-р или т = п X р.	(3)
Числа п и р в записи (3) называются сомножителями.
Операция умножения натуральных чисел:
1) коммутативна: л-р = р«л;
2) ассоциативна: (n*p)-k = n-(p-k).
Операции сложения и умножения натуральных чисел связаны
законом дистрибутивности умножецу отно-
сительно сложения:
(п + р)-& = n-k+ p-k.
Т^аким образом, сумма и произведение любых двух натуральных
Чисел опять будут натуральными числами. Поэтому говорят, что мно-
28	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
жество всех натуральных чисел замкнуто относительно операций сложе*
ния и умножения.
Вычитание натуральных чисел. Вычитание нату<
ральных чисел есть операция, обратная сложению, т. е. соответствие,
которое паре натуральных чисел (л; р) относит такое Натуральное число
г, что
п ~ р + г.
О числе г говорят, что оно получено в результате вычитания числа р
из числа п, и пишут
г = п — р.
Число г называется разностью чисел п и р\ число п называется
уменьшаемым f а число р — вычитаемым.
В множестве натуральных чисел разность двух натуральных чисел
г = п — р существует тогда и только тогда, когда п > р\ поэтому го-
ворят, что множество натуральных чисел не замкнуто относительно
вычитания.
Так, например, натуральное число 5 больше’натурального числа 3.
Их разность существует и равна натуральному числу 2:
5-3=2.
Натуральное число 6 меньше натурального числа 8. Их разность
6 — 8 уже не будет натуральным числрм.
Деление натуральных чисел. Деление натуральных
чисел есть операция, обратная умножению, т. е. соответствие, которое
упорядоченной паре натуральных чисел (п; р) относит такое натуральное
число q, что
О числе q говорят, что оно получено в результате деления числа п
на число р, и пишут
п
q = — > или q = n/pt или q = п : р.
Число q называется частным натуральных чисел п и р\ число и
называется делимым t а число р — делителем.
В множестве натуральных чисел частное определено не для любой
пары натуральных чисел (и; р), т._е. множество натуральных чисел не
замкнуто относительно операции деления. Так, например, положим
п = 7, р = 2. Для этой пары натуральных чисел нельзя подобрать такое
натуральное число q, чтобы выполнялось равенство
7 = 2^.
Натуральная степень числа. Свойство ассоциатив-
ности операции умножения натуральных чисел позволяет ввести поня-
тие натуральной степени натурального числа: n-й степенью натураль-
ного числа т называется натуральное число kf полученное в результате
умножения числа т самого на себя и раз:
k = т-т-т». . .-т.
О сомножителей
§ I. НАТУРАЛЬНЫЕ ЧИСЛА	29
Для обозначения л-й степени числа т обычно используется запись!
тп,
в которой число т называется основанием степени, а число п — показа*
телем степени.
1.2. Аксиоматическое построение множества натуральных чисел»
Выше были, приведены некоторые свойства натуральных чисел, а также
были введены операции над натуральными числами, подчиненные пра-
вилам коммутативности, ассоциативности и дистрибутивности.
Излагая сведения о натуральных числах и действиях с ними, мы
неявно обращались к интуитивному пониманию многих понятий, кото-
рыми мы ежедневно пользуемся и при этом получаем правильные резуль-
таты. Так, например, нам кажется естественным, что 3+2=2 +3, и
мы даже не задумываемся, откуда берется это свойство операции сложе-
ния натуральных чисел. В математике, естественно, возникает вопрос,
а сколько же и каких именно некоторых первичных утверждений (ак-
сиом) 6 натуральных числах необходимо выдвинуть, чтобы из этих
аксиом в виде теорем можно было получать все известные из нашего
жизненного опыта свойства натуральных чисел и операций над ними.
Оказывается, что все свойства натуральных чисел могут быть выве-
дены как теоремы из пяти аксиом и формул, определяющих операции
сложения и умножения натуральных чисел.
Аксиомы натуральных чисел (аксиомы
Пеано):
I.	1 (единица) есть натуральное число.
II.	Для каждого натурального числа п имеется точно одно натураЛЬ*
ное число, называемое его последующим и обозначаемое 5 (п).
III.	Всегда S (п) /= 1.
IV.	Из равенства S (п) = S (т) следует п = т.
V.	Принцип полной индукции. Множество натуральных чисел,
содержащее 1 и для каждого из п элементов следующий за ним элемент
S (п), содержит все натуральные числа.
Сложение й умножение натуральных чисел определяются форму-
лами
п + 1 = S (n),	т + S (п) = S (т + п);
п* 1 = п,	n-S (т) = п-т + п.
Из аксиом Пеано и определения'операций сложения и умножения
натуральных чисел как теоремы следуют законы коммутативности и
ассоциативности сложения и умножения, свойство дистрибутивности
умножения относительно сложения.
Из аксиом Пеано и определения операции сложения также следует
свойство упорядоченности множества нату-
ральных чисел: для любых двух натуральных чисел тип
либо т — п (т равно и);
либо т < п (т меньше п);
либо п < т (п меньше т).
Упорядоченность множества натуральных чисел устанавливается
следующим образом. Во-первых, в качестве теоремы доказывается, что
для любых натуральных тип имеет место один из следующих трех
случаев:
либо т = п;
либо существует единственное натуральное число удовлетворяю*
Щее условию
п — т + k}
30
ГЛ. 2» ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
либо существует единственное натуральное число р такое, что
т == п + р.
Во-вторых, вводится определение знака > (больше) и знака <
(меньше):	х
натуральное число т считают больше натурального числа п (и
пишут т > п), если существует такое натуральное число k9 что
т ® п + k;
натуральное число т считают меньше натурального числа п (и
пишут т < п), если существует такое натуральное число р, что
т + р = п.
Из данных определений и сформулированной выше теоремы следует
свойство упорядоченности множества натуральных чисел.
Так как множество натуральных чисел является упорядоченным
множеством, то для натуральных чисел оказывается справедливым еще
ряд утверждений, которые связаны с понятиями «больше» и «меньше»*
К таким утверждениям относятся, например, следующие теоремыз
1)	Из	т >	п	для	любого k	следует	m + 6 > п + k;
из	m =	п	для	любого k	следует	т + k « п + А;
из	т <	п	для	любого k	следует	т + k < п + k.
2)	Из	т>	п	для	любого k	следует	m*k> n*k\
из	т =	п	для	любого k	следует	m*k = n*k\
из m< п для любого k следует n*k.
3)	В каждом непустом множестве натуральных чисел имеется
наименьшее число.
1.3. Простые числа. Основная теорема арифметики. Если для
двух заданных натуральных чисел пир найдется натуральное число q
такое, что п = p-qt то говорят, что число п делится нацело на число р.
Число р называется делителем числа п, а о натуральном числе п говорят,
что оно кратно р. Если натуральное число р является делителем нату-
рального числа п, то и натуральное число q также является делителем
числа п.
Натуральное число, единственными делителями которого являются
только оно само и единица, называется простым числом. Все остальные
натуральные числа называются составными. Натуральное число 1
$ не считается простым числом.
Представление натурального числа п в виде произведения двух
натуральных чисел p-q называется разложением на множители. При
этом считается, что если число п простое, то оно имеет разложение на
множители, состоящее из единственного числа п. Например, простое
число 37 будет иметь разложение на множители, состоящее из единствен*
ного множителя 37 (а не разложение 1 *37).
Пусть натуральное число п составное, т. е.
п = р-<7,
где р Ф 1 и q Ф 1* При этом возможны следующие случаи:
1) Если натуральные числа р и q простые, то число п представляется
в виде произведения двух простых чисел р и q.
2) Если хотя бы одно из натуральных чисел р, q составное, то это
составное число (либо оба составных числа р и q) разлагают в произведе-
ние еще меньших натуральных чисел, для которых возможны те же слу*
чаи. Поскольку имеется лишь конечное множество натуральных чисел.
§ I, НАТУРАЛЬНЫЕ ЧИСЛА	3f
меньших п, то указанный процесс разложения закончится через конечное
число шагов. В результате получим разложение числа п на множители,
каждый из которых — простое число. Представление числа п в виде
произведения простых чисел называется разложением на простые мно*
жители.
В связи с рассмотренным разложением натурального числа на про*
стые множители возникает вопрос о том, существует ли какое-нибудь
другое, отличное от уже полученного, разложение натурального числа
на простые множители. Ответ на этот вопрос дает следующая теорема,
называемая основной теоремой арифметики:
Каждое натуральное число, отличное от 1, может быть разложено
на простые множители, и притом единственным образом (если отож-
дествлять разложения p*q и q-p, где р и q — простые числа).
Объединяя в разложении числа п одинаковые простые сомножители,
получаем так называемое каноническое разложение числа п:
где pi, pi,...» ps, ki, k2,..., ks — натуральные числа и все простые
числа ру р2, ...» ps различны.
Натуральное число называется четным, если среди его простых
множителей есть число 2, и нечетным, если среди его простых множите*
лей число 2 отсутствует.
1.4. Некоторые признаки делимости натуральных чисел*
Признак делимости на 2. Число делится на 2, если его
последняя Цифра есть число четное или нуль.
Признак делимости на 4. Число делится на 4, если две
его последние цифры — нули или образуют число, делящееся на 4.
Признак делимости на 8. Число делится на 8, если три
последние его цифры — нули или образуют число, делящееся на 8,
Признаки делимости на 3 и на 9. Число делится на 3,
если сумма цифр числа делится на 3. Число делится на 9, если сумма его
цифр делится на 9.
Признак делимости на 5. Число делится на 5, если оно
оканчивается либо на нуль, либо на 5.
Признак делимости на 25. Число делится на 25, если
его последние две цифры — нули или образуют число, делящееся на 25.
Признак делимости на 11. Число делится на 11, если
сумма цифр, стоящих на четных местах, либо равна сумме цифр, стоя-
щих на нечетных местах, либо отличается от нее на число, делящееся
на11.
1.5. Наименьшее общее кратное* Наибольший общий делитель*
Алгоритм Евклида. Общим кратным нескольких натуральных чисел
называется натуральное число, являющееся кратным для каждого из
них. Наименьшее из них называется наименьшим общим кратным
(сокращенно: НОК) *).
Для того чтобы найти наименьшее общее кратное нескольких
чисел, необходимо: ,
1)	выписать канонические разложения данных чисел}
2)	перечислить все простые множители, входящие хотя бы в одно из
канонических разложений данных чисел;
*) Наименьшее общее кратное двух чисел т В п также обозначается
© помощью фигурных скобок;
32	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
3)	возвести каждый из перечисленных простых множителей в наи-
большую степень, с которой этот простой множитель входит в канони-
ческие разложения данных чисел.
Произведение полученных степеней простых множителей и даст
число, являющееся наименьшим общим кратным данных чисел.
Пример, Найти НОК чисел 49 896 и 26 460.
1)	Пишем канонические разложения данных чисел:
49 896 = 2* 3«34»7»11 и 26 460 = 22.33-5«72;
2)	выписываем простые множители, входящие хотя бы в одно кано-.
ническое разложение:
2; 3; 5; 7; 11;
3)	наибольшая степень, о которой' множитель 2 входит в канониче-
ские разложения данных чисел, равна 3; пишем число 23.
Наибольшая степень, с которой множитель 3 входит в канонические
разложения, равна 4; пишем число З4.
Аналогично, наибольшие степени, с которыми множители 5, 7 и 11
входят в канонические разложения данных чисел, равны соответственно
1, 2 и 1; пишем числа 5* = 5, 72 и 11х = 11.
Произведение 23«34*5’72*11 = 1 746 360 является наименьшим
общим кратным данных чисел.
Общим делителем нескольких натуральных чисел называется число,
являющееся делителем каждого из данных чисел. В случае, если общих
делителей несколько, наибольший из них называется наибольшим
общим делителем (сокращенно: НОД) *).
Если наибольший общий делитель нескольких натуральных чисел
равен единице, то эти числа называются взаимно простыми.
Для нахождения наибольшего общего делителя нескольких чисел
необходимо:
1)	выписать канонические разложения данных чисел;
2)	перечислить все общие простые множители, входящие в канони-
ческие разложения каждого из данных чисел;
3)	возвести каждый из перечисленных простых множителей в наи-
меньшую степень, с которой этот простой множитель входит в канони-
ческие разложения данных чисел.
Произведение полученных степеней простых множителей и даст
число, являющееся наибольшим общим делителем данных чисел.
Пример. Найти НОД чисел 49 896 и 26 460.
1)	Пишем канонические разложения данных чисел:
49 896 = 23-34-7-11 и 26 460 = 22.33-5.72;
2)	выписываем простые множители, входящие в оба канонических
разложения:
2; 3; 7;
3)	наименьшая степень, с которой множитель 2 входит в канониче-
ские разложения данных чисел, равна 2; пишем число 22.
Наименьшая степень, с которой множитель 3 входит в канонические
разложения, равна 3; пишем число З3.
♦) Наибольший общий делитель двух чисел /п* п также обозначается
3 вомощыо круглых скобок; (т, и).
§ I. НАТУРАЛЬНЫЕ ЧИСЛА	33
Наименьшая степень, с которой число 7 входит в канонические
разложения, равна 1; пишем число 7х = 7.
Произведение 2а*33«7 = 756 является наибольшим общим делителем
двух данных натуральных чисел.
Свойство НОД. Наибольший общий делитель двух чисел
делится на любой общий делитель этих чисел.
Наибольший общий делитель (т, п) двух чисел т и п и наименьшее
общее кратное {т, п} связаны равенством
т-п- (m, п)'{т, /г}.	(4)
Алгоритм Евклида нахождения НОД. Наиболь-
ший общий делитель и наименьшее общее кратное двух натуральных
чисел могут быть найдены, если известны канонические разложения
этих чисел. Однако выписать канонические разложения достаточно боль-
ших чисел часто бывает довольно трудно. Кроме способа нахождения
НОД двух чисел, основанного на канонических разложениях этих
чисел, существует способ нахождения НОД, не требующий знания всех
простых множителей этих чисел. Этот способ называется алгоритмом
Евклида. Заметим, что, отыскав НОД двух чисел с помощью алгоритма
Евклида, с помощью формулы (4) можно найти НОК этих чисел.
Прежде чем перейти к изложению алгоритма Евклида, введем опе-
рацию деления с остатком.
Разделить натуральное число т на натуральное число р (т^ р)
с остатком — это значит найти такое натуральное число k и такое
неотрицательное целое число г< р, что
т = р- k + г.
Числа k и г называются соответственно частным и остатком oi
деления числа т на число р. В случае, если г = 0, также говорят, что
остаток от деления равен нулю или что число т делится на число р.
Перейдем теперь к изложению алгоритма Евклида. Пусть т и
р — два натуральных числа, и пусть т > р. Обозначим через т^ и f\
соответственно частное и остаток от деления т на р:
zn=p-m) + r1,	0<Г!<р.	(5)
Если оказывается, что г, > 0, то будем делить р на г,, обозначая через
т2 и г2 соответственно частное и остаток от деления:
р = ггт2 + г2,	0 < г2 < гх.	(6)
Если г2 все еще не нуль, делим гх на г2 и получаем аналогичным образом
Г1 == г2-т3 + г3,	0	г3 < г2.	(7)
Так как р, rx, г2, ... — натуральные числа и р> rx > r2> г3>
> ...» то процесс деления после конечного числа шагов должен обор-
ваться, т. е. мы должны прийги к остатку, равному нулю. Пусть таким
остатком будет rrt+x “ 0, так что
Гп-1 = гп’^п+1«	(*)
Натуральное число гп и будет наибольшим общим делителем чисел
т и р. Чтобы убедиться в этом, покажем, что т ир делятся на гпг& силу
равенства (*) делится на rrt. Тогда из равенства
,	*71-2 ==	+ ^П»
предшествующего равенству (*), следует, что и гп_2 делится на гп.
2 А. Г, Цыпкин
34	гл. г. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Продвигаясь далее по цепочке построенных равенств (снизу вверх),
убеждаемся, что на гп делятся и гп_з, гП-ь ...» га, ritt а в конечном счете
в силу равенств (6) и (5) также и числа тир. Остается лишь убедиться,
что всякий общий делитель k двух чисел тир будет и делителем числа
гп (этим, очевидно, и будет установлено, что гп—наибольший общий
делитель чисел т и р). Для этого придется снова пройти всю цепочку
равенств, но на этот раз сверху вниз. Предварительно перепишем це*
почку равенств алгоритма Евклида в виде
ft == m — рти
г2==
г3 = а — г»
Г/1 == г
Из первого равенства следует, что делится на общий делитель й
двух чисел т и р. Но из второго равенства следует, что так как гг де»
дится на k и р делится на А, то и г2 делится на А. Продолжая этот процесс
далее, получим, что и rn_2t и глл делятся на А.Но тогда в силу послед-
него равенства и гп делится на k.
Способ отыскания наибольшего общего делителя двух чисел с по-
мощью алгоритма Евклида в большинстве случаев оказывается самым
коротким и потому практически наиболее выгодным.
Заметим, что в приведенном рассуждении попутно доказано упомя-
нутое выше свойство НОД.
Пример. G помощью алгоритма Евклида найти НОД чисел
13 172 и 261.
Разделим число 13 172 на 261:
_ 13172 1261
1305 ho~
122
Делим в согласии в алгоритмом Евклида число 261 да остаток от
деления (число 122):
261 1122
*“244 |у-
17
Делим число 122 на остаток (число 17)з
122 117
”“119 (7-
3
Продолжая и далее последовательно делить каждый предыдущий
остаток на каждый последующий остаток, в результате получим остаток,
равный нулю:
17 13	3 12	111
Г ~2 Т т
2	1	О
Предпоследний остаток был равен единице. Следовательно, единица
и ecjb НОД двух данных чисел, т. е. числа 13 172 и 261 взаимно простые.
§ 5. ЦЕЛЫЕ ЧИСЛА
85
§ 2.	Целые числа
2.1.	Множество целых чисел. Множество целых чисел есть множе-
ство, полученное в результате добавления к множеству всех натураль-
ных’чисел новых объектов (которые далее также будем называть чис-
лами) — числа нуль и отрицательных целых чисел.
Число нуль, обозначаемое символом 0, и отрицательные целые
числа вводятся следующим образом.
Сумма любого натурального числа п и числа 0 есть число л;
п + 0 = л.
Любому натуральному числу п соответствует единственное отри*
нательное целое число —п такое, что сумма чисел п и —л равна нулю;
л + (—л) = 0.
Число —п называется противоположным числу л. Число, проти.
всположное числу — л, есть число п : ~(—-п) == л. Натуральные числа
в множестве целых чисел называются положительными целыми чис*
лами ♦). Множество всех целых чисел часто обозначается Z.
Множество целых чисел является упорядоченным множеством,
<г. е. для любых двух целых чисел тип справедливо одно и только
одно из следующих соотношений:
либо т ~ л, либо т < л, либо п < т.
Для положительных чисел л пишут л > 0, для отрицательных
чисел пишут л < 0. Если хотят указать, что число может быть положи-
тельным или нулем, пишут п > 0 и говорят, что оно неотрицательно^
аналогично запись л < 0 означает, что л отрицательно или равно нулю.
2.2.	Арифметические операции с целыми числами. Абсолютным
еначением (или модулем) числа л называется число, обозначаемое [л |
и вычисляемое по правилу
л,
0,
—л,
1« 1 ==
если л > 0,
если л = О,
если п <0.
Абсолютное значение числа л положительно как для положитель-
ных, так и для отрицательных л и равно нулю только при л == 0.
Пример. Найти абсолютные значения чисел 4 и —3.
Так как число 4 натуральное, то I 4| = 4, Так как —3 — отри-
цательное число, то по правилу вычисления абсолютного значения
числа | —3 | == — (—3) == 3.
Сложение целых чисел. Суммой двух целых чисел п
и Р называется целое число s, вычисляемое по правилу;
если л>0 и р>0, то s = n4-p;
если л < 0 и р < 0, то s = — ([ л | + [ р |);
если л > О, а р < О и | и |> |р|, то s — ]n| — | р |j
если л >0, а р<0 и | л | = | р|, то s = 0;
если л>0, а р<0 и | л | <| р |, то s = — (| р | — | л [)}
если л<0, р>0 и | л|>|р|, то s = — () л | — \р |);
р л * } 'Ц,алее целые числа будем обозначать малыми латинскими буквами т,
2*
36	гл. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
если п < 0, р > О и | п | = | р |, то s = О;
если п<0, р>0 и | п | < | р то s=|p| —| п |;
если п = О, то $ — р\
еСЛИ р = О, ТО S as ti.
Сумма s двух целых чисел пир записывается с помощью символа+?
s=n+p.
Таким образом, вычисление суммы двух целых чисел основано на
правиле вычисления суммы или разности двух натуральных чисел.
Пример. Вычислить сумму целых чисел 6 и —8.
Данная пара чисел удовлетворяет пятому условию правила сло-
жения двух целых чисел (6 > 0, —8 <0, 161 < | —81). Сумма этих
чисел равна
s = _((-81 - 161) = -(8 - 6) = -2.
Сложение целых чисел, так же как и сложение натуральных чисел,
коммутативно и ассоциативно.
Умножение целых чисел. Произведением двух целых
чисел пир называется целое число пг, вычисляемое по правилу:
если п> 0 и.р > 0, то т= п*р\
если п < 0 и р < 0, то т » |п [• | р |;
если п < 0, а р > О или если п > 0, а р < 0, то т = —(| п |- Г р |)$
если п = 0 или р = О, то т = 0.
Произведение двух целых чисел пир записывается с помощью
символа « или X»
т п*р (или n X р).
Вычисление произведения двух целых чисел основано на правиле
вычисления произведения двух натуральных чисел.
Пример. Вычислить произведение двух целых чисел —2 и —7.
Данная пара удовлетворяет второму условию правила умножения
двух целых чисел. Абсолютные аначения этих чисел равны 2 и 7, а их
произведение равно 14.
Умножение целых чисел, так же как и умножение натуральных
чисел, коммутативно и ассоциативно.
Кроме того, операции сложения и умножения целых чисел, как
и в случае натуральных чисел, связаны законом дистрибутивности
умножения относительно сложения.
Вычитание целых чисел. Ровностью двух целых чисел
дир называется целое число г, вычисляемое по правилу:
Г — п + (—р),	(1)
т. е. разность двух целых чисел пир есть сумма целого числа п и
числа (—р), противоположного числу р. Следовательно, разность
вычисляется по правилу вычисления суммы двух целых чисел. О числе г
говорят, что оно получено в результате вычитания числа р из числа п,
и пишут
г = п — р.	Г2>
В записи (2) число п называется уменьшаемым! а число р — вычитаемым,
§ 2. ЦЕЛЫЕ ЧИСЛА
37
Пример. Вычислить разность двух целых чисел 2 и —7.
Число, противоположное числу —7, равно 7, а потому по пра-
ри^у (9 разность этих чисел равна г= 2 + 7 — 9.
Таким образом, множество целых чисел замкнуто относительно
операций сложения, умножения и вычитания, т. е. для любых двух
данных целых чисел существует единственное третье целое число, яв-
ляющееся суммой двух заданных целых чисел; существует единственное
целое число, являющееся их разностью, и‘> наконец, единственное целое
число, являющееся их произведением.
Деление целых чисел. Частным от деления целого -
числа т на целое число п называется целое число р, которое удовлетво-
ряет равенству
т= п-р.	(3)
О числе р говорят, что оно получено в результате деления числа т
на число п, и пишут
т
р=т:п, или р = —, или р = т/п.
В множестве целых чисел, как и в множестве натуральных чисел,
операция деления не всегда выполнима — не для любой пары целых
чисел т и п существует их частное. Поэтому говорят, что множество
целых чисел не замкнуто относительно операции деления. Однако между
операциями деления в множестве натуральных чисел и в множестве
целых чисел есть одно существенное различие: если в множестве на-
туральных чисел частное двух натуральных чисел существовало, то
оно было единственным. По-другому обстоит дело в множестве целых
чисел: пусть т'— произвольное целое число, а п = 0; тогда равенство
(3) примет вид
т=0-р.	(4)
Попытаемся найти такое число р, которое удовлетворяло бы равен-
ству (4). Здесь могут быть две возможности:
если m #= 0, то не существует такого целого числа р, при котором
это равенство выполняется;	__
если т = 0, то р может быть любым целым числом.
Таким образом, частное от деления целого числа на число нуль
либо не существует, либо определяется не единственным образом,
юбы избежать такой неопределенности, необходимо запретить
деление целого числа на число нуль.
2.3.	Теория целых чисел как упорядоченных пар натуральных
чисел. Множество натуральных чисел N замкнуто относительно сло-
ги ения и умножения, но не замкнуто относительно вычитания: сумма
и произведение любых двух натуральных чисел есть число натураль-
ное, в то время как разность п — р двух натуральных чисел в мно-
жестве натуральных чисел определена только тогда, когда п > р.
Множество целых чисел Z получается как расширение множества
натуральных чисел добавлением новых числовых объектов, таких,
что в расширенном множестве Z:
1)	множество N является собственным подмножеством;
2)	сложение и умножение натуральных чисел в Z совпадает с одно-
именными операциями в N;
3)	'вычитание в множестве Z всегда возможно, т. е. разность любых
Двух элементе* .чисел) из Z является элементом (числам) из Zj
88	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
4)	расширенное множество Z минимально в том смысле, что оно
не содержит собственного подмножества, удовлетворяющего условиям
О -3).
Один из методов пополнения множества всех натуральных чисел
до множества целых чисел основан на представлении целых чисел
как упорядоченных пар натуральных чисел. Этот метод состоит в сле-
дующем:
Целыми числами называют упорядоченные пары
(т\ п)
натуральных чисел /пип, подчиненные следующим законам сравнения
и законам арифметических операций:
Пара (т\ п) считается больше (>), равной (=) или меньше (<)
пары (р\ q)> тогда и только тогда, когда
m + g> п+ р> tn+q~n-i-pt т+ q<Cn-± р
соответственно.
Как следствие определения равенства пар получаем, что всякая
пара переходит в равную ей, если к обеим ее элементам прибавить
одно и то же натуральное число:
(т + г\ п-\~ г) — (т\ п).
Суммой двух пар (/и; п) и (р; q) называется пара (т + р\ я + q).
Говорят, что пара (m+ р\ п + q) получена в результате сложения пар
(т; п) и (р; q)t и пишут
(т; п) + (р; q) = (т + р\ п+ q).
Ассоциативность и коммутативность операции сложения пар сле-
дует из определения суммы пар и ассоциативности и коммутативности
операции сложения натуральных чисел.
Разностью пар (т\ п) и (р; q), обозначаемой
(т\ n) — (р; q),
называется пара (х; у), удовлетворяющая равенству
(т; п) = (х; у) + (р; q).
По определению суммы пар и условию равенства пар последовательно
получаем
(ш; п) == (х + р; у + q), т+ у + q~ п + х+ р.
Одним из решений этого уравнения с двумя неизвестными будет пара
натуральных чисел
х = т+ q\ у—п+р.
. Пара (т + q; и + р) есть разность пар (т\ п) и (р; q)i
(пц п) — (р; q) == (т + q; п + р),
или, точнее говоря, пара (т-\- q\ ti+ р) есть одна из множества рав-
ных между собой пар, являющихся разностью пар (/п; п) и (р; q).
Пара (т + q\ п + р) может быть записана как сумма пар (т; п) ~h
+ (q'> р), т. е. разность пар (m; n) — (р; q) может быть заменена суммой
(т; п) + {q\ р).
Пару (q\ р) называют противоположной паре (р; q) и пишут
й; Р) = —(р; Й.
§ 2. ЦЕЛЫЕ ЧИСЛА
39
Из определения разности пар также следует, что
(т; n) — (m; n) = (т + п; т + п).
Пару с равными элементами называют нулем и обычно обозначают
символом 0.
Произведением двух пар (т\ п) и (р; q) называется пара
(т-р+ n-q\ tn>q+ п-р).
Об этой паре говорят, что она получена в результате умножения
пар (т\ п) и (р; <?), и пишут
(т; п)*(р\ q) — (т-р + n-q] m-q+n>p).
Ассоциативность и коммутативность операции умножения пар,
а также свойство дистрибутивности операции умножения относительно
сложения следуют из определения операции умножения и соответ-
ствующих свойств операций сложения и умножения натуральных
чисел.
Множество натуральных чисел включается в множество упорядо-
ченных пар следующим определением:
Любая пара (т\ п) при т > п считается равной натуральному
числу т — п.
Нетрудно проверить, что пара (т\ п), отождествляемая при .т > п
с натуральным числом т — п, больше нуля (нулевой пары). Нетрудно
также проверить, что при таком способе отождествления пары (т\ п)
с натуральным числом т — п результаты операций сложения и умно-
жения пар (т; п) и (р; q) при т > /г, р> q совпадут с результатами
операций сложения и умножения натуральных чисел г = т — п и
s = р — q, т. е. операции сложения и умножения натуральных чисел,
рассматриваемых как пары (гп; п), при условии т> п сохраняют тот
смысл, который они имели в множестве натуральных чисел,
Действительно, по определению суммы и произведения пар
(т; п) + (р; q) == (т + р; п + q).
(т\ п)-(р; q) = (т-р+ n-q\ m-q+ п>р).
Так как по условию т > п и р> q, то
т + Р> п+ q и тр+ nq> mq+ пр,
т. е. первые элементы пар, стоящих в правых частях равенств, больше
вторых элементов, и, следовательно, эти пары можно отождествить
с натуральными числами /п + р — п — q и mp^nq — mq — пр соот-
ветственно.
С другой стороны, складывая и перемножая натуральные числа
г = т — п и $ = р — р, мы снова получаем те же натуральные числа
/и + р — п — q и тр+ nq — mq — пр.
Таким образом, мы проверили, что результаты сложения и умно-
жения пар совпадают с результатами тех же операций с соответствуй
ющими натуральными числами.
Из определения операции вычитания пар следует, что разность
двух натуральных чисел, рассматриваемых как упорядоченные пары,
в множестве пар всегда существует, т. е. пара (х; у), полученная как
разность пар (т; п) и (р; $, при условии, что т > п и р > q, существует
как при х > у, так и при х < у.
Итак, определив соответствующим образом операции сложения,
умножения и вычитания пар и отождествив пару натуральных чисел
40	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
(т\ п) при т > п с натуральным числом т — п, мы получили, что раз-
ность двух пар, каждую из которых можно отождествить с натуральным
числом, всегда существует, но не всегда может быть отождествлена
с каким-либо натуральным числом.
Обозначая пару (х; у) при х<у так же, как и при х > у, т. е.
через х — у, и используя данные выше определения, нетрудно про-
верить, что пара (х; у) при х < у меньше нулевой пары, что в новы#
обозначениях будет записываться в виде
х — г/ < 0,
и противоположна паре (у\ х), отождествляемой с натуральным числом
г/ — х: х — у = — (у — х).
Упорядоченные пары (х; у) при х < у называют отрицательными
целыми числами.
§ 3. Рациональные числа
3.1..Рациональные дроби. Рациональные дроби появились как
форма записи чисел, более «мелких», нежели натуральные. История
введения рациональных дробей отражена и в самих обиходных назва-
ниях некоторых наиболее простых рациональных дробей. Например,
дробь 1/2 (одну вторую) называют «половиной», дробь 1/4 (одну четвер-
тую) называют «четвертью» и т. д. Иногда дают интуитивно понятное,
но математически нестрогое определение рациональной дроби как не-
которой части единицы или нескольких равных частей единицы. При
таком «определении» понятия рационального числа и рациональной
дроби оказываются отождествленными.
Рациональную дробь записывают в виде т!п ^или	це’
лоё число т называют числителем дроби, а целое число п 0 — ее
внаменателем. Сумма, произведение, разность и частное двух дробей
т/п и p/q вычисляются по правилам
5 т 1 JL — m'Q + n,P
п "* q	n-q
т р m-q— п-р
п q"	rTq
(В случае частного р ф 0.)
Дроби, стоящие в правых частях равенств (1), называются соот-
ветственно суммой, произведением, разностью и частным дробей т!п
и plq.
Более строго рациональные дроби вводятся как множество упоря-.
доченных пар целых чисел.
Рациональными дробями называют упорядоченные пары целых
чисел (т\ п), из которых второе отлично от нуля, подчиненные пере-
численным ниже законам арифметических действий и правилам
сравнения.
Первое число пары (т\ п) называют числителем дроби, а второе —
внаменателем. Дробь (т\ п) обычно записывают -^-или т/п.
п
Две пары (т\ п) и (р; q) называют эквивалентными и пишут
(т Р \
или “ ~ V / ’
если wq == п-р.
/и	р	___	т-р
п	q	~~	n-q	’
т	.	р	__	т-д
п	'	q	~~	пр	*
(1)
§ 3. РАЦИОНАЛЬНЫЕ ЧИСЛА
41
Как следствие этого определения получаем, что всякая пара (т\ п)
переходит в эквивалентную, если оба ее элемента умножить на одно
и то же отличное от нуля число, т. е.
/ m-k т \
(m-k; n-k) ~ (m; п) ^или ~	.
„	m-k	„	т
Переход от дроби - к эквивалентной дроби называют
сокращением дроби на число k. Используя правило сокращения дробей,
любую рациональную дробь можно привести к эквивалентной рацио-
нальной дроби, знаменатель которой — натуральное число. Поэтому
часто дают и такое определение рациональной дроби:
Рациональной дробью называют упорядоченную пару чисел (т; п),
обозначаемую символом m/я, где т — целое число, ап — натуральное.
Суммой двух пар (т\ п) и (р\ q) называется пара
(m-q+п-р\ n-q).
Говорят, что пара (m*q + п-р\ n-q) получена в результате сложе-
ния пар (/и; п) и (р; q), и пишут
х	( т . Р m-q + n-p\
n) + (p; q) ~(m-q + n-p\ n-q) ^или —+ “~---------nq----
Ассоциативность и коммутативность операции сложения пар
следует из определения суммы пар и ассоциативности и коммутатив«
ности операций сложения целых чисел.
Ровностью пар (т; п) и (р; q), обозначаемой
(т; п) — (р; q),
называется такая пара (х; у), что
(х; У) + (р; Ч) ~ (т; п).
Из определения суммы пар следует, что
(x-q+yp; y-q) ~(т; п)
и, следовательно, по определению эквивалентных пар
x-q*n + у-р-п — y*q*m.
Одним из решений этого уравнения с двумя неизвестными является
пара целых чисел
x—m-q — n*pt y=n-q.
Пара (m-q — п-р\ n-q) есть разность пар (ш; п) и (р; д):
, ч	imp m-q — п-рх
№n)-(p\q)~(m-q — n-p\ n-q). (или—------------ ~------------).
Точнее говоря, пара (m-q — n*q\ n-q) есть одна из множества эквива-
лентных между собой пар, являющихся разностью пар (т\ п) и (р; </).
Если из некоторой пары (т; п) вычесть эквивалентную ей пару
(k*m\ k-n)t то их разность — нулевая пара (0; п).
Произведением двух пар (т\ п) и (р; q) называется пара (ш»р;
n-q). Говорят, что пара (m-р; n-q) получена в результате умножения
ьар (т; п) и (р; q)t и пишут
,	,	/ т р т-р \
№\n)-(p\q) ~ (jn p\ n-q) \или V* V *
42
ГЛ, 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Ассоциативность и коммутативность операции умножения пар#
а также дистрибутивность умножения относительно сложения следует
из определения произведения пар и соответствующих свойств опера-
ций умножения и сложения целых чисел.
Частным двух пар (т; п) и (р; q) при р ф 0, обозначаемым
(т; п): (р; <?),
называется такая пара (х* у), что
(Р> Я)'(х; У) ~ (т-, п).
Из определения произведения пар следует, что
(рх; qy) ~ (т; п);
и по определению эквивалентных пар
р>п-х~ q*m*y,
Одним из решений этого уравнения с двумя неизвестными является
пара целых чисел
х = q*mt у == р*п.
Пара fa-т; р*п) есть частное пар (т; д) и (р\ q)t
I т р т*а \
(m; п): (р; <?) ~ (<?т; р п) ^или —: ~~“nV/ ‘
Точнее говоря, пара (q*m\ р*п) есть одна из множества эквивалент*
ных между собой пар, являющихся частным пар (т; и) и (р; q).
Из определения частного пар (т; п) и (р; q) следует, что
(т; п) : (р; q) ~р*п) ~ (т\ n)*(q't р),
т. е. деление пары (nvt п) на пару (р; q) может быть заменено умножением
на пару (q't р), которая называется обратной паре (р; д).
Пара (т\ д) считается больше пары (р; q)\
или меньше пары (р; q)*.
(т р \
~<т)
тогда и только тогда, когда
m*q> п*р и т*#< д»р
соответственно.
Пару (0; q) называют нулевой парой и обозначают символом 0.
Согласно правилам сравнения дробей пара (т; п) больше нуля
(нулевой пары (0; q))9 если т > 0, и меньше нуля (нулевой пары (0; q)),
если т<0.
Рациональную дробь m/д, где т — целое число, ад — натураль*
ное, называют положительной и пишут mln > 0, если т — положи*
тельно, и отрицательной: m/n<0t если т — отрицательно.
Отрицательную рациональную дробь mln (т — отрицательное
целое число, д — натуральное} обычно записывают в виде—1^1 #
$ 3. РАЦИОНАЛЬНЫЕ ЧИСЛА
43
Например, отрицательную рациональную дробь -у— записывают в
5
виде--у*
Положительная рациональная дробь m/п называется правильной,
если ее числитель меньше знаменателя (т < п), и неправильной, если
ее числитель больше или равен знаменателю (т > п), В случае, если
положительная рациональная дробь неправильная, ее числитель пред-
ставим в виде m = n*k 4- г, где k — натуральное число, ar — н&мрн*
нательное целое число, удовлетворяющее условию г<п. Число b
называется целой частью дроби.
Если г й 0, то неправильную дробь m/п иногда записывают
(2)
Запись (2) называют записью неправильной дроби в виде смешанной
дроби. Например, неправильная рациональная дробь 10/3 может быть
записана в виде смешанной дроби З-л
о
Дробь называется несократимой, если ее числитель и знамена-
тель — взаимно простые числа. Всякую рациональную дробь можно
привести к эквивалентной ей несократимой дроби.
Пример. Привести рациональную дробь 15/75 к эквивалент-
ной ей несократимой дроби.
Разложим числа 15 и 75 в произведение простых сомножителей:
15=3*5, 75=3*5*5.
„ л 15	‘	3-5
Дробь может быть записана в виде Сокращая одинаковые
/О	м*О*О
сомножители в числителе и знаменателе, приводим дробь 15/75 к экви-
валентной несократимой дроби 1/5.
3.2. Рациональные числа. Рациональным числом называется мно-
жество всех эквивалентных между собой рациональных дробей. В со-
гласии с определением рационального числа различные эквивалентные
между собой дроби — это лишь различные записи одного и того же
рационального числа. Так, например, три различные эквивалентные
рациональные дроби
"Г’
— это различные записи одного и того же рационального числа.
Можно дать и несколько другое определение рационального числа,
отождествляя его не с множеством всех рациональных, эквивалентных
между собой дробей, а с некоторой фиксированной дробью этого мно-
жества. Один из возможных способов выделения такой фиксирован-
ной дроби заключается в следующем.
Возьмем любую дробь т/п из множества эквивалентных между
собой дробей (здесь т — целое число, отличное от нуля, ап — нату-
ральное). Если числа | т | и п взаимно простые, то считаем, что дробь
т/п и есть нужная фиксированная дробь. Если же числа | т | и п не
являются взаимно простыми, то делим числитель и знаменатель дроби
на наибольший общий делитель чисел | т | и л. В результате деления
получаем дробь пц/пи в которой | пц | и п — взаимно простыв числа*
Найденная дробь т^пг н есть нужная фиксированная дробь»
44
ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Теперь можно дать следующее определение рационального (отличи
ного от нуля) числа:
Рациональное число — это такое число, которое может быть пред-
ставлено в виде mln, где I т | и п — взаимно простые (несократимые)
натуральные числа.
Запись рационального числа в виде т!п, где | т | и п — взаимно-
простые числа, называется записью рационального числа в виде не-
сократимой дроби. Рациональное число mln будет целым, если
знаменатель несократимой рациональной дроби равен единице.
Сравнение рациональных чисел, понятия суммы, произведения,
разности и частного двух рациональных чисел вводятся так же, как
и соответствующие понятия для рациональных дробей. Математическая
вались сравнения рациональных чисел, операций сложения, умноже-
ния, вычитания и деления двух рациональных чисел — такая же,
как и запись соответствующих операций над рациональными дробями,
лишь вместо знака эквивалентности следует ставить знак равенства.
Для вычисления суммы, разности, произведения и частного ра-
ционального числа и целого числа п достаточно записать целое число п
в виде дроби, знаменатель которой равен единице, т. е. в виде п/1,
и воспользоваться правилами вычисления суммы, разности, произве-
дения и частного двух рациональных дробей.
Примеры. L Умножить целое число 3 на рациональное число
5/7.
Запишем целое число 3 в виде дроби со знаменателем, равным
единице, и, по определению произведения дробей, получим
. 5 _ 3	5 _ 3-5 _ 15
' ‘ 7 “ 1 ‘ 7 “ Ь7 7 ‘
2. Разделить целое число 2 на рациональное число 1/3.
Записывая целое число 2 в виде дроби со знаменателем, равным
единице, и пользуясь определением частного двух дробей, получаем
о. 1 _ 2 . 1	23	6 А
2.—= — = — -6.
Свойство ассоциативности умножения рациональных чисел позво-
ляет ввести понятие натуральной степени рационального числа;
fe-й степенью рационального числа mln называется рациональное
число q, полученное в результате умножения числа т!п самого на
себя k раз:
т т т
а — — . — • • —
4 п п п
k сомножителей
Для обозначения fe-й степени числа р== mln обычно используется
запись
в которой число mln называется основанием степени, а число k — пока*
ватедем степени.
3.3.	Теория рациональных чисел как упорядоченных пар целых
чисел. Множество всех целых чисел Z замкнуто относительно операций
сложения, умножения и вычитания, но не замкнуто относительно
§ 3. РАЦИОНАЛЬНЫЕ ЧИСЛА
45
операции деления: сумма, разность и произведение двух целых чисел
есть число целое, в то время как частное mln двух целых чисел т и п
будет целым числом лишь в том случае, если число | т | кратно числу л.
Множество рациональных чисел получается как расширение множества
целых чисел добавлением новых числовых объектов, таких, чтббы:
1)	расширенное множество содержало в качестве своего собствен-
ного подмножества множество всех целых чисел;
2)	арифметические операции, определенные для Целых чисел,
были определены и для элементов' расширенного множества, причем
смысл этих операций для целых чисел, рассматриваемых как элементы
расширенного множества, должен совпадать с тем, какой они имели
в множестве целых чисел до расширения;
3)	в расширенном множестве была выполнима операция деления
(кроме деления на нуль), которая в множестве целых чисел не всегда
выполнима, — частное двух элементов из расширенного множества
должно быть элементом этого множества;
4)	расширенное множество было минимальным в том смысле, что
оно не должно содержать собственного подмножества, удовлетворя-
ющего условиям 1) — 3).
Существует единственное множество, удовлетворяющее условиям
1) — 4). Этим множеством является упорядоченное множество всех
рациональных чисел с введенными в нем арифметическими операциями.
Множество всех рациональных чисел часто обозначается Q.
В качестве метода попрлнения множества всех целых чисел до
множества всех рациональных чисел может быть выбран способ пред-
ставления рациональных чисел как упорядоченных пар целых чисел
(т. е. как рациональных дробей с определенными правилами сравнения
и правилами арифметических действий (см. п. 3.1)). При таком опреде-
лении рациональных чисел множество всех целых чисел есть подмно-
жество множества всех рациональных чисел, если считать, что любая
пара (/и; п) при т = £*л, где k — целое число, равна целому числу
k = т : л.
В частности, все нулевые пары (0; п) оказываются в силу этого
определения равными целому числу 0.
Нетрудно проверить, что при таком способе отождествления пары
(т\ п) при т == k-n (k — целое) с целым числом k результаты операций
сложения, вычитания и умножения пар (т\ п) и (р; q) при т = k*n и
р = r*q совпадают с результатами операций сложения, вычитания и
умножения целых чисел k и г, т. е. эти операции, производимые над
целыми числами как над парами, сохраняют тот же смысл, который они
имели в множестве целых чисел.
Действительно, пусть (пг, п) и (р; q) — две пары такие, что число
|/л| кратно л, а число |р| кратно q, т. е.
tn = k*n и р =
где k и I — отличные от нуля целые числа.	,
По определению суммы пар
(т; л)+ (р; q) ~ (m*q+ n-p-t n>q}.
Но так как число т = /г«л, ар = bqt то пара (m*q+ п*р\ n*q)
отождествляется с целым числом k+ I,
С другой стороны, пара (т; л) по принятому правилу отожде-
ствляется с целым числом /г, а пара (р; q) — с целым числом I, и, следо-
вгиельно, сумма этих пар, как сумма целых чисел, также равна k + U
46	гл. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Аналогично проверяется и совпадение результатов умножения
и вычитания пар с соответствующими результатами умножения и вы-
читания целых чисел.
Из определения операции деления пар следует, что частное двух
пелых чисел, из которых второе отлично от нуля, рассматриваемых
как упорядоченные пары, всегда существует в множестве пар, т. е.
пара (т\ п), полученная как частное двух целых чисел, существует
для любых целых чисел mt п(п Ф 0), а не только для т =» где
k — целое. Действительно, используя определение операций умноже-
ния и деления, для любых целых чисел т и п (п Ф 0) имеем
т : п = (т\ 1): (n; 1) == (т\ !)• (1; п) » (т\ л).
Таким образом, в тех случаях,[когда т не делится на п, пара (т; п)
представляет собой не совпадающее ни с каким целым числом рацио-
нальное число, являющееся частным от деления т на п.
§ 4. Десятичные дроби
4.1. Десятичная позиционная система счисления. Наиболее рас-
пространенный способ записи чисел — это запись чисел в десятичной
системе счисления *). Суть этого способа записи состоит в следующем:
1. Все натуральные числа от единицы до девяти обозначаются
следующими индивидуальными символами:
1, 2, 3, 4, 5, 6, 7, 8, 9.
К этим символам дополнительно присоединяется десятый символ 0,
называемый нулем. Перечисленные десять символов называются циф-
рами десятичной системы счисления.
2. Одна и та же цифра имеет разный смысл в зависимости от рас-
положения этой цифры относительно других цифр, участвующих в за-
писи числа (в этом и заключается позиционность системы счисления).
Так, например, в позиционной десятичной системе счисления комбина-
ции 4521 и 4125 четырех различных цифр 1, 2, 4, 5 дают запись двух
различных натуральных чисел.
Цифра, стоящая на первом месте справа в записи натурального
числа указывает на количество единиц, содержащихся в данном числе,
на втором — количество десятков, на третьем — количество сотен,
на четвертом — количество тысяч и т. д.
При записи натурального числа в десятичной позиционной системе
счисления о первой цифре, стоящей справа, говорят, что она стоит
в разряде единиц, о второй — что она стоит в разряде десятков,
о третьей — что она стоит в разряде сотен, и т. д.
В десятичной системе счисления запись
где nft, пал» •••> ЛП ло — цифры, есть условная запись числа
10*4*• 10й	10^**^-J-• • •	104* По. (1)
При записи натурального числа в десятичной системе счисления
также принято следующее соглашение: последней левой цифрой в за-
писи числа может быть любая из десяти цифр, кроме цифры нуль.
*) Обычно слово «позиционная» опускают и говорят просто ^десятичная
система счисления».
$ 4. ДЕСЯТИЧНЫЕ ДРОБИ
47
Так, например, принято записывать число двенадцать в виде 12, а но
в виде 012 или 0012. С помощью этого соглашения избавляются от воз-
можной неоднозначности в записи одного и того же числа.
4.2. Понятие десятичной дроби. Десятичная дробь есть форма
ваписи действительного числа в десятичной позиционной системе
счисления. Десятичная дробь
N, П}П2п$ ...	(2)
где W — целое число, а nlt	...» ль,... — цифры десятичной
системы счисления, — это условная запись действительного числа
101	10а	1(Я	ю*
Целое число ДО называется целой частью десятичной дроби (2}.
О цифре nj, стоящей^в десятичной дроби (2) на первом месте после
запятой, говорят, что она стоит в разряде десятых долей единицы;
о цифре п2, стоящей на втором месте, говорят, что она стоит в разряде
сотых долей единицы; о цифре я3 — что она стоит в разряде тысячных,
и т. д.
В соответствии с данным выше определением десятичной дроби,
в случае, если N — отрицательное целое число, знак минус ставят
не перед всей дробью, а над числом | N |. Например, десятичная дробь
2,135... есть условная запись действительного числа
-2+0,135...
Следует отметить, что при отрицательном N такая запись десятич-
ной дроби в ряде случаев (например, при выполнении арифметических
действий) весьма неудобна. Поэтому часто используют другую форму
ваписи:
Пусть а — положительное действительное число, имеющее деся-
тичное представление
а =3,521.
Число —а, противоположное числу а, в соответствии с принятым
выше обозначением будет иметь десятичное представление
—а = 4,479.
Чтобы избежать несоответствия в обозначениях действительных
чисел и их десятичных представлений, число —а записывают также
в виде
3,521 =—3 —цр
Десятичная дробь ДО, nLn2n$ ... называется бесконечной,
если для любого натурального k найдется номер I > k такой, что
ni Ф 0.
Десятичная дробь V, ... пь... называется конечной, если
найдется такое натуральное число k, что пк Ф 0 и п/ = 0 при всех
Z>fc. Цифры числа N и nt, п2, ..., пк называют значащими цифрами.
Обычно в записи конечной дроби нули, стоящие после последней
значащей цифры, опускают, т. е. дробь
... пк 00 ... О..^
48	-	гл. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
где пк 0, записывают в виде
N, niti2n3 ... пк»
Периодические десятичные дроби. Бесконеч-
ная десятичная дробь N,	••• называется периодической,
если существуют такие натуральные числа р, q, что пк+р = пк для всех
k > q. Для обозначения бесконечной десятичной периодической дроби
используется запись N, п1п2 ... nq (nq+1nq+2 ••• л^+р), где совокупность
цифр nq^nq+2 Kq+р называется периодом дроби.
Иногда периодические дроби разделяют на чисто периодические,
которые записываются в виде
N, (n,n2 ... пр),
и сметанные периодические, которые записываются в виде
;Л, П1П2 . . . пк (nh+ink^ . . . nft+p) (k > 1).
Например, дробь 2,131313 ... = 2,(13) — чисто периодическая,
а дробь 2,41313 ... = 2,4 (13) — смешанная периодическая.
Разбиение множества десятичных дробей на подмножества конеч-
ных и бесконечных десятичных дробей весьма условно, так как любая
конечная десятичная дробь (исключая число нуль) может быть записана
как бесконечная периодическая дробь. Это можно сделать совсем оче-
видным способом, представив, например, конечную десятичную дробь
0,2&как 0,25000 ... 0 ... == 0,25 (0), т. е. приписав к конечной десятич*
ной дроби бесконечное число нулей.
Бесконечные десятичные дроби, период которых состоит не только
из одной цифры 9, называются допустимыми десятичными дробями.
В множестве допустимых десятичных дробей может быть введено
отношение порядка,, т. е. множество всех допустимых десятичных
дробей является упорядоченным множеством.
Две допустимые бесконечные дроби
А/, пгп2п3 ... л^... и М, пцгщть ... тк...
считаются равными, если целая часть первой дроби равна целой части
второй дроби (N = М) и цифры, стоящие на одних и тех же местах
в записях этих дробей, одинаковы:
= ть п2 = т2, .... hk = ть, ...
Допустимая бесконечная десятичная дробь 0; ntn2n3 ... пк... счи-
тается меньше допустимой бесконечной дроби 0, тгт2т3 ... тк..Л
0, пхп2п3 ... пк... < 0, т1т2т3 ...
если найдется такой номер k, что
п2 = т2, . .	=	но пк<ть,
т. е. сравнение допустимых десятичных дробей проводится по первой
встретившейся паре неравных цифр. Например, дробь 0,72159... меньше
дроби 0,72160..., так как первые три цифры, стоящие после запятой,
у обеих дробей совпадают, а четвертая цифра первой дроби меньше
четвертой цифры второй дроби.
Допустимая десятичная дробь N, п1п2п3 ... пк... считается меньше
допустимой десятичной дроби М, mim2m3 ... если целая часть
Первой дроби меньше целой части второй дроби (N < М) либо если
§ 4. ДЕСЯТИЧНЫЕ ДРОБИ
49
целые части этих двух дробей равны (N = Л4), десятичная дробь О,
... пи... меньше десятичной дроби 0, т^тз ... тд...
Сравнение двух конечных, а также конечной и допустимой беско-
нечной десятичных дробей производится по тем же правилам, что и
сравнение двух допустимых бесконечных десятичных дробей.
4.3.	Арифметические действия с конечными десятичными дробями.
Арифметические действия с конечными десятичными дробями будем
производить, полагая, что если положительное число а может быть
записано в виде конечной десятичной дроби
No, ... Пи,
то отрицательное число —а записывается в виде конечной десятичной
дроби
—Mb П±П2 ... пи.
Например, отрицательное число —37/25 будем записывать в виде
—1,48, а не в виде 2,52.	>
Использование такой формы записи отрицательных чисел в виде
десятичных дробей позволяет производить арифметические действия
с десятичными дробями во многом аналогично арифметическим дей-
ствиям с целыми числами.
Сложение и вычитание конечных десятичных дробей выполняется
так же, как сложение и вычитание целых чисел; необходимо только
записывать каждый разряд одной дроби под разрядом того же наимено-
вания второй дроби, а на место пустующих разрядов ставить нули.
Пример 1. Сложить дроби 2,14 и 0,151.
Запишем дробь 2,14 в виде 2,140 и произведем сложение целых
чисел 2140 и 151:
2140+ 151 = 2291.
Отделив справа у целого числа 2291 то же самое число знаков, что было
отделено у дробей 2,140 и 0,151 (а именно три знака), получим
дробь 2,291, которая является суммой данных дробей.
. Умножение конечных десятичных дробей производится следующим
образом: не обращая внимания на запятые, конечные дроби перемно-
жают, как целые числа; в получившемся произведении отделяют справа
число знаков, равное сумме числа знаков после запятой у всех сомно-
жителей.
Пример 2. Найти произведение двух конечных десятичных
дробей 2,1 и 0,27,
Перемножив целые числа 21 и 27 (нуль в числе 027 можно от-
бросить), получим число 567. Отделив справа три знака, получим, что
произведение двух данных дробей равно 0,567.
Деление конечной десятичной дроби йа целое число производится
следующим образом:
1)	Если делимое меньше делителя, пишем в целой части частного
нуль и ставим после него запятую. Затем, не обращая внимания на за-
пятую в делимом, присоединяем к целой части делимого первую цифру
его дробной части; если после такого присоединения получается число,
меньшее делителя, ставим после запятой в частном нуль и присоеди-
няем к полученному ранее числу следующую цифру делимого; если
50	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
и после этого получаем число, меньшее делителя, ставим еще нуль и
Т. д., пока не получим число, превосходящее делитель. В дальнейшем
деление совершается так же, как о целыми числами, причем делимое
можно неограниченно «расширять» вправо от запятой, приписывая
в конце нули.
Пример 3. Разделить десятичную дробь 0,525 на число 2.
В согласии е приведенным правилом вычисление частного будет
Выглядеть так/
0,525 [J_______
*“5~*	0,262g1*
*“4
\2*
12
Т
~~4
10
—10
о
Может оказаться, что описанный процесе деления никогда не за*
кончится. В таком случае частное нельзя выразить конечной десятич*
ной дробью.
2)	Если делимое больше делителя, делим сначала целую часть,
записываем в частном результат деления и ставим запятую. После
этого деление продолжается, как в предыдущем случае.
Деление конечной десятичной дроби на конечную десятичную
дробь производится по следующему правилу:
Чтобы разделить десятичную дробь (или целое число) на десятич*
ную дробь, отбрасываем запятую в делителе; в делимом же переносим
запятую вправо на столько знаков, сколько их было в дробной части
делителя (в случае необходимости к делимому в конце приписываем
нули). После этого выполняем деление десятичной дроби на целое
число, как указана выше. Так, например, деление десятичной дробя
0,525 на дробь 0,2 сводится к делению десятичной дроби 5,25 на число 2.
Арифметические действия над бесконечными периодическими де-
сятичными дробями довольно сложны и громоздки, а потому гораздо
проще поступать следующим образом: перевести бесконечные периоди-
ческие десятичные дроби, над которыми требуется произвести арифме-
тические действия, в рациональные дроби; над рациональными дро-
бями произвести необходимые операции; дробь, получившуюся в ре-
зультате вычислений, если это необходимо, перевести в десятичную.
4.4.	Обращение конечной десятичной дроби в рациональную дробь.
Пусть АГ, ... ilk — конечная десятичная дробь; N — целая часть
дроби, a hi, п2, ...» лд — ее значащие цифры. По определению деся-
тичная дробь 0, пу п2... пи может быть записана в виде *)
ttjrtg . . . rtft ж
10*
К этой дроби прибавим целую часть данной десятичной дроби. В ре*
вультате получим искомую рациональную дробь.
*) В числителе дроби не умножение чисел л*.	а завись числа,
^нфрама которого являются цифры
$ 4. ДЕСЯТИЧНЫЕ ДРОБИ
Пример. Конечную десятичную дробь 2,135 можно обратить
В следующую рациональную:
2,135 = 24-0,135
135 _ 2135
103 ~ 1000 •
а конечную десятичную дробь 1,091 — в дробь
—	91	900
1,091 =-1 + 0,091 =-1+-^-=—«О*-.
4.5.	Обращение бесконечной периодической дроби в рациональную
дробь.
1)	Представляем бесконечную периодическую десятичную дробь
О, п1п2 ... fik (nk+i ... Пк+р) в виде суммы конечной десятичной дроби
и бесконечной периодической дроби:
О, П1П2 . . . Пк (пк+г . . • /Ц+р) =»
= 0,	. . . Пк + 0, 0 ... 0 (пд+1 < . • пл+р).
> -
2)	Бесконечную периодическую дробь 0, 0 ... 0 (п*+1 пь+р>
представляем в виде произведения:
О, 00 . . . Ofafett .. . Bfc+p) e“~fe,0> ("Л+1ЛЛ+2 • •. лл+р)« (3)
k
3)	Чисто [периодическую дробь 0, (пк&Пк+ъ... пл+р) валисы*
паем в Виде
П /и	_ ла+1^а+2 * • • ftfc+p т
0t	• • • ^А+р)---------—------=— 4*
4) Вычисляем
ской прогрессии,
102р
es ftfe+iftfe+a » «  nk+p Г j 1	а t 1
L юр io2p J’
сумму членов бесконечно убывающей геометриче*
стоящей в квадратных скобках. Она равна
10р
10₽—1 ’
и, следовательно, чисто периодическая дробь 0, (пк^пк^ ••• flft+p)
обращается в следующую рациональную дробь:
0» 0А+1^А+2 • • а Лй+р) —
яа+1'*а+2 . . . Пк+р . юр
1QP	* 10р — 1
. ЛА+1ЯА+2 • • » лА+р
Ж — 1
52	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Теперь с помощью равенства (3) нетрудно обратить десятичную
дробь 0, пхп2 ... «а («а+1^а+2 ... «А+р) в рациональную дробь;
О, tiin2 • . . fih (^a+i^a+s • • . fik+p) =
Л *» *» м I I Я&+1ЛА+2* • *flk+D
S= О, «1^2 ... Пк-]---J— -----------=3
10*	10₽—1
s= П1Па' ♦ -ПЬПЬ+1П}1+2- - -flk+p — П^. . .Hfe
=	. 10*(1О₽—1)
Правило перевода смешанной периодической десятичной дроби
в рациональную дробь можно сформулировать так:
Чтобы обратить смешанную периодическую десятичную дробь
в рациональную, нужно из числа, образованного цифрами, стоящими
после запятой до начала второго периода, вычесть число, образованное
из цифр, стоящих после запятой до начала первого периода; получен-
ную разность взять в качестве числителя дроби, а в знаменателе на-
писать цифру девять столько раз, сколько цифр в’Периоде, и со столь*
кими нулями, сколько цифр между запятой и началом первого периода.
Примеры. 1. Перевести чисто периодическую дробь 2,(13)
в рациональную дробь.
Представим эту дробь в виде
2,(13) = 2 + 0,(13) =
_2| 13 	>3	.	13	13	_
100 т 10000 т	102 т 104 -г
== 2'*’ 102	10*	“То4-*
В скобках стоит'сумма членов бесконечно убывающей геометрической
прогрессии с первым членом, равным 1, и знаменателем q = 1/102.
Используя формулу для суммы членов бесконечно убывающей геоме-
трической прогрессии, получаем
2>(13) = 2 + ~[оГ'• 1 _ 1/ю2 =
13	10-	-о. 13	211
102	102 -И	99 ~ 99 *
Таким образом, периодическая десятичная дробь 2,(13) может быть
обращена в рациональную дробь 211/99.
2. Перевести смешанную периодическую дробь 2,5 (13) в рацио*
нальную дробь.
Представим дробь 2,5 (13) в виде
2,5 (13) = 24-0,5 + 0,0 (13) = 2+ 0,5+ О, (13).
Далее необходимо перевести чисто периодическую дробь 0,(13)
в рациональную дробь аналогично тому, как это было сделано в при-
мере 1, и произвести сложение.
4.6, Десятичные представления рациональных чисел. Рациональ*
ное число определяется как число, которое может быть записано в виде
§ 4. ДЕСЯТИЧНЫЕ ДРОБИ	. 53
т/п, где тип — целые числа и п > 0. Рассмотрим три примера пред-
ставления различных рациональных чисел в виде десятичных дробей.
Пример 1. Записать рациональное число 1/4 в виде десятичной
дроби:
___1_ 14____
10 I 0,25
“ 8
20
20
0
Из проведенных вычислений видно, что процедура деления закан-
чивается через конечное число шагов и число 1/4 может быть записано
в виде конечной десятичной дроби 0,25.
Пример 2. Записать рациональное число 5/11 в виде десятич-
ной дроби:
___5_	(JJ_____
*	50	I 0,4545
~ 44
60
~55
:♦	50
х	“44
60
“55
♦	5
Из проведенных вычислений следует, что если мы будем продол-
жать процесс деления, то и дальше будем получать в остатке последо-
вательно числа 6 и 5, и каждый раз, получая в остатке число 5, мы на-
чинаем цикл деления заново (в разобранном примере звездочками от-
мечены начала первых трех таких циклов). В этом примере процедура
деления никогда не закончится, следовательно, рациональное число
5/11 записывается в виде бесконечной десятичной периодической дроби
0,(45).	• .
Пример 3. Записать рациональное число 131/990 в виде деся-
тичной дроби:
131	I 990
1310	I 0,132
“ 990
»	3200
2970
2300
“ 1980
*	320
В этом примере, так же как и в предыдущем, процедура деления
никогда не закончится. Однако здесь повторение цикла деления начи-
нается не с того числа, с которого мы начинали деление, а с другого
числа (здесь числа 320), которое появилось в одном из остатков. Сле-
довательно, рациональное число 131/990 записывается в виде смешан-
ной периодической десятичной дроби 0,1 (32).
Б4	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Три разобранных примера описываю! все возможные случаи, ко-
торые встречаются при записи рационального числа в виде десятичной
дроби. В самом деле, рассмотрим произвольное положительное число
/п/п, где т и п—положительные целые числа (случай отрицательного
рационального числа может быть разобран аналогично). При делении
натурального числа т на натуральное число п в остатке могут появиться
лишь следующие числа;
О, 1, 2, ...» п - 1. -
Если в процессе деления в остатке появится число 0, то процесс деления
будет закончен и, следовательно, рациональное число т/п будет пред-
ставлено в виде конечной десятичной дроби. Если же в процессе деле-
ния число нуль в остатке не появится, то по крайней мере через п — 1
шаг неизбежно возникнет повторение остатка; с этого места начинается
новый цикл. Результатом деления является бесконечная периодиче-
ская десятичная дробь (точнее говоря, допустимая периодическая де-
сятичная дробь).
Таким образом, всякое рациональное число т/п представимо либо
в виде конечной, либо в виде бесконечной периодической дроби; об-
ратно, любая конечная, а также любая бесконечная периодическая
десятичная дробь есть запись некоторого рационального числа.
Рациональное число т/п (т, п — целые, взаимно простые числа
ип> 1) может быть записано в виде конечной десятичной дррби тоьа
и только тогда, когда число п имеет своими простыми делителями лишь
числа 2 и 5. При этом число п не обязано иметь среди своих простых
делителей как число 2, так и число 5; оно может делиться лишь на одно
из них. Если n = 1, то дробь т/п также, очевидно, записывается в виде
конечной десятичной дроби. Например, рациональные числа 1/25,
1/16 и 7/1, где п равно соответственно 25, 16 и 1, представляются в виде
конечных десятичных дробей:
1	1	7
— = 0,04; — = 0,0625; 4-=7.
20	10	1
4.7.	Непрерывные дроби. Алгоритм Евклида (см. п. 1.5) нахожде-
ния наибольшего общего делителя двух натуральных чисел приводит
к одному весьма интересному способу представления рациональных
чисел.
Например, применение алгоритма Евклида к числам 840 и 611
дает следующий ряд равенств:
840= 1-611 4- 229,
611 = 2-229 + 153,
229= 1-153 + 76,
153= 2-76+ 1,
которые можно записать в виде
840	, , 229 t ,	1	229	, т 76 __ , , I
W ~ ±-бГГ ~	611 >	153	1 ‘ ~153“ “ 1 + “Т53~~9
229	76
611	153 _ I 153	,	।
'229‘“	г 229 —	'г 229	’	76	“ т	76	*
153
$ 4. ДЕСЯТИЧНЫЕ ДРОБИ	55
Комбинируя последние равенства, приходим наследующему пред-
ставлению рационального числа 840/611:
840	, .	1
Рассмотрим теперь цепочку равенств алгоритма Евклида нахо-
ждения наибольшего общего делителя двух натуральных чисел т и п\
m~n'tnt-]r fit
п = rrm2+ r2,
Г1= г2-/и3 + Пь
rk_2 = rk_i-mk+ fk,
гкл =
Перепишем эту цепочку равенств в виде
m	,	п
---------- mi Ч—— .
п----1	п	*
П	,	Г2
Г1	1	Гх	9
= т3 +	,
г2	Г2
ГЛ-2	f rk
----— т^-\---------
ГЪЛ
rkJL „
Каждое из приведенных равенств (за исключением последнего)
описывает выделение целой части неправильной дроби, т. е. пред*
сгавляет неправильную, дробь в виде суммы натурального числа и не-
которой правильной дроби. Замечая, что левая часть каждого равенства
есть величина, обратная второму слагаемому правой части предыдущего
равенства, рациональное число mln можно записать, используя лишь
числа	т3,	т^\
— =т1 +--------
/п2 4~
I
1
(4)
, 1
/72« -4----------
+ -
1

56
ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
где /Па, т3, /и4,	— натуральные числа, a mi — либо натураль-
ное число, либо нуль.
Выражение, стоящее в правой части равенства (4), называется
конечной непрерывной (или цепной) дробью.
Если рациональное число min отрицательно (т< 0, п> 0),
то при записи числа т/п в виде непрерывной дроби используют сле-
дующий прием. Отрицательное рациональное число т!п представляют
в виде
т м » k
— = м Ч-------,
п ' П 9
где М — отрицательное число, a k —
Положительную рациональную дробь
рывной дроби:
натуральное тасло, меньшее п.
k
— записывают в виде непре-
Тогда отрицательная рациональная дробь mln записывается в виде
~ = м +------------Ц—:-----.
“ h+---------------5-j-----
Непрерывную дробь, стоящую в правой части равенства (4), обо-
значают
[/пх; т2, т3,	тл+1],	(5)
где точка с запятой отделяет целую часть рационального числа от
его дробной части.
Непрерывная дробь
[шх; /Из, /и8, ms] (s<£+ 1)
называется подходящей дробью s-ro порядка для непрерывной дроби (5)
и кратко обозначается p^Qs-
Подходящая непрерывная дробь называется четной, если s четно, ~
и нечетной, есди s нечетно. Все подходящие дроби четного порядка
меньше mtn, и величина их возрастает с ростом порядка; все подходя-
щие дроби нечетного порядка больше mln, и величина их убывает
о ростом порядка:
Рз <	< Лчи
(б — четное).
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
57
Модуль разности между подходящими дробями ps/qs и ps+i/qs+i
DaBeH -!-1 а потому разность между подходящей дробью s-ro
qs'Qs+i
порядка и числом т/п можно оценить неравенством
-	|21_^l<—(6)
I П Яз I ЯзЯз+i	v '
Теория непрерывных дробей исторически возникла из потребности
замены рациональной дроби с большими числителем и знаменателем
другой рациональной дробью, у которой числитель и знаменатель
были бы значительно меньше (и меньше некоторого^ наперед заданного
числа) и такой, чтобы она по своей величине как можно меньше отли-
чалась от исходной дроби. Пусть тип — числа, равные, например,
1355 и 946 соответственно. Необходимо заменить дробь 1355/946 дробью
Ph/qh* где qh должно быть меньше 100, а также оценить погрешность,
возникающую при такой замене. Представим дробь 1355/946 в виде
непрерывной дроби и вычислим подходящие дроби. При этом окажется,
что
2L = Jg_ = ii; 2, 3, 5, 8, 3],	^-=-S-
п 946	1	яз 37 q^ 303
Нашему условию (знаменатель меньше 100) удовлетворяет дробь 57/37.
Неравенство (6) позволяет просто оценить абсолютную погреш-
ность между данной дробью и подходящей дробью третьего порядка:
I _*355_ __53_ I   1_ = _1_< о oool
| .946	37 Р <73 94	П211 <'и-иииь
В теории непрерывных дробей вводится также понятие бесконеч-
ной непрерывной 'дроби и доказывается, что любое действительное
число может быть единственным образом записано в виде непрерывной
дроби. При этом рациональные числа записываются в виде конечных,
а иррациональные — в виде бесконечных непрерывных дробей.
Заметим, что как в случае рационального, так и в случае иррацио-
нального числа подходящие непрерывные дроби обладают тем свой-
ством, что они дают «наилучшее» приближение любого действитель-
ного числа рациональным числом, а именно:
Для любой подходящей дроби k-ro порядка pk/qk нельзя подобрать
рациональную дробь со знаменателем, меньшим чем qk, такую, чтобы
она давала лучшее приближение действительного числа а, чем подхо-
дящая дробь piJqk>
§ 5. Действительные числа
5.1. Множество действительных чисел как расширение множества
рациональных чисел. В §§ 2, 3 было последовательно проведено расши-
рение множества натуральных чисел до множества целых чисел и расши-
рение множества целых чисел до множества рациональных чисел. Мно-
жество всех рациональных чисел представляет собой множество, зам-
кнутое относительно операций сложения, умножения, вычитания и
деления (кроме деления на нуль), — сумма, произведение, разность и
частное двух рациональных чисел опять будет рациональным числом.
Однако оказывается, что существуют алгебраические и геометри-
ческие задачи, которые не имеют решения в множестве рациональных
58	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
чисел. Так, задачей, часто не имеющей решения в множестве рацио*
нальных чисел, является извлечение корня из положительного целого
числа. Например, число JA2 (см. п. 5.9) не является рациональным
числом, т. е. его нельзя записать в виде т!п, где т и п — целые числа
и п ф 0. Нетрудно привести и другие примеры чисел, которые не могут
быть представлены в виде m/п, т. е. не являются рациональным^ чис-
лами.
Число, которое нельзя представить в виде т/п, где m и п — целые
числа и п Ф 0, называют иррациональным числом.
Множество всех действительных чисел также может быть получено
как естественное расширение множества всех рациональных чисел.
Однако, в отличие от довольно простых способов расширений мно-
жества натуральных чисел до множества целых чисел и множества
целых чисел до множества рациональных чисел, метод расширения
(или пополнения) множества всех рациональных чисел до множества
действительных чисел оказывается гораздо более сложным. Математи-
чески строгая теория действительных чисел была развита лишь в се-
редине прошлого века в трудах Р. Дедекинда и Г. Кантора, и при ее
создании был использован ряд весьма тонких результатов математи-
ческого анализа.
Один из методов пополнения множества рациональных чисел до
множества действительных чисел основан на понятии фундаменталь-
ной последовательности рациональных чисел. Покажем схематически,
в чем состоит суть этого метода.	~
Последовательность (хп) рациональных чисел хп называется фун-
даментальной, если для любого рационального 8> 0 существует
такое натуральное число п0, что
\хр — xq\<z
для всех р и q, больших я0. Используя определение сходящёйся после-
довательности, нетрудно доказать, что всякая сходящаяся последова-
тельность будет фундаментальной. С другой стороны, всякая фундамен-
тальная последовательность рациональных чисел будет иметь предел,
однако может оказаться, что этот предел не будет рациональным числом.
Примером такой последовательности может служить последователь-
ность положительных рациональных чисел (rrt), квадраты которых
становятся сколь угодно близкими числу 2:
И-2|<_ПГ’ 1г2~21<’Тог’ ’ • • ’ 1гп~ 2| <"10"’ * * ’'
Из способа задания последовательности (rrt) следует, что ее предел
— число, не принадлежащее множеству рациональных -чисел; это
есть иррациональное число К2.
Множество всех действительных чисел получается пополнением
множества рациональных чисел новыми числовыми объектами, назы-
ваемыми иррациональными числами, которые являются пределами все-
возможных фундаментальных последовательностей рациональных чи-
сел. Множество действительных чисел обычно обозначается буквой R.
5.2. Аксиоматическое построение множества действительных чисел.
Множество всех действительных чисел может быть описано как мно-
жество, элементы которого удовлетворяют перечисленным ниже свой-
ствам I—VI. Элементы этого множества, хотя это и не совсем корректно,
далее будем называть числами.
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
59
I.	Свойство упорядоченности.
Для любых двух чисел а и b определено отношение порядка, т.
для любых двух действительных чисел а и b
либо а = b (а равно Ь),
либо a<Z b (а меньше 6),
либо 6< а (Ь меньше а);
причем если а< b и с, то с.
II.	Свойства операции сложения.
В множестве действительных чисел определена бинарная операция
сложения, т. е. любой упорядоченной паре чисел (а; Ь) ставится в соот*'
ветствие единственное число, называемое суммой чисед^дД обозна*
чаемое а + 6; при этом:
1)	для любой тройки чисел a, b, С
(а + Ь) + с = а + (Ь + с) (ассоциативный закоц £$ожения);
2)	для любой пары чисел а и b
a-^b-br а (коммутативный.закон сложения);
3)	существует число, обозначаемое символом 0 и называемое ну*
дем, такое, что для любого числа а
а + 0 = а}
4)	для любого числа а существует число, обозначаемое —а, такое*
что
а + (—а) = 0;
число —а называется противоположным числу а;
5)	если а< д, то для любого числа с
а 4“ с < b + с.
Число а > 0 называется положительным, а число а < 0 — втрц*
цательным.
Для любой упорядоченной пары чисел (а; Ь) число
а + (— Ь)
называется разностью чисел а и b и обозначается а — bl
а — Ь = а + (—6).
III.	Свойства операции умножения.
В множестве действительных чисел определена бинарная операция,
называемая умножением, т. е. любой упорядоченной паре чисел (а; Ь}
ставится в соответствие единственное число, называемое их произведем
нием и обозначаемое а*Ь, причем:
1)	для любой тройки чисел а, Ь, с
(а-Ь)-с~ а-(Ь-с) (ассоциативность);
2)	для любой пары чисел а, b
a-b—b-a (коммутативность);
3)	существует число, обозначаемое символом 1 и называемое
единицей, такое, что для любого числа а
а-1 = а;
60
гл. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
4)	для любого числа а, отличного от нуля, существует число,
обозначаемое 1/а, такое, что
а.2_=1;
а
число 1/а называется обратным числу а;
5)	если а< b и* с> 0, то а*с< Ь-с; если а< Ь и с< 0, то
а*с> Ь'С.
Для любой упорядоченной пары чисел а и b (Ь отлично от нуля)
1	.	а
число а--г- называется частным от деления а на b и обозначается т- ?
b	Ь
IV.	Связь операций сложения и умноже-
ния.	"
Для любой тройки чисел а, b и с
(а + Ь)-с = а*с+ Ь'С
(дистрибутивность умножения относительно сложения).
V.	Свойство Архимеда.
Для любого числа а существует такое целое число п, что п > а.
Из этого свойства, в частности, следует, что для любых чисел а
и Ь при а> 0 существует натуральное число п такое, что
п«а> Ь.
VI.	Свойство непрерывности.
Перечисленные выше свойства I—V были присущи и некоторым
другим числовым множествам (например, множеству всех рациональ-
ных чисел). Множество действительных чисел, в отличие от множества
рациональных чисел, имеет еще одно, существенно новое свойство —
свойство непрерывности.
Существует несколько различных формулировок свойства непре-
рывности множества действительных чисел. Одна из них будет при-
ведена ниже и называется принципом вложенных отрезков или аксио*
мой непрерывности множества действительных чисел (по Кантору).
Если заддны два числа а и Ь, а Ь, то множество всех чисел х
таких, что а х Ь, называется числовым отрезком и обозначается
[а; 6]. Число Ь—а называется длиной числового отрезка.
Система числовых отрезков
•••>
называется системой вложенных отрезков, если
01 а* . ^ад bд I	^1 •
Относительно системы вложенных отрезков [ап\ bn], п=* 1, 2, 3, ...,
говорят, что длина этих отрезков стремится к нулю с возрастанием /г,
если для любого числа 8> 0 существует такой номер /г0, что для
всех номеров п п0 выполняется неравенство
— ап <Z 8.
Принцип вложенных отрезков. Для всякой си*
стемы вложенных отрезков существует хотя бы одно число, которое
принадлежит всем отрезкам данной системы.
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧЙёЛА	61
Из принципа вложенных отрезков, в частности, вытекает, что для
всякой системы вложенных отрезков, по длине стремящихся к нулю,
существует единственное число, принадлежащее всем отрезкам данной
системы.
5.3. Представление действительных чисел десятичными дробями.
По свойству Архимеда для любого неотрицательного числа а найдется
неотрицательное целое число W такое, что
N ^а< N+ 1.
Разобьем числовой отрезок [N; N + 1] на десять равных частей
и рассмотрим отрезки
[N\ N, И, [N, 1; N, 2], [tf, 9; W + 1].
Возможны два случая: либо а не совпадает ни с одной из точек де-
ления, либо а совпадает с одной из точек деления. В первом случае а
принадлежит только одному из перечисленных отрезков, который
обозначим If
Zi= [N, nf N, /ii+ 11,
где nt — одна из цифр 0, 1, 2, ..., 9. Если а — точка деления, то
в качестве отрезка 1± выберем тот, для которого а является левым
концом.
Разобьем отрезок на десять равных частей и выберем из полу-
ченных десяти отрезков тот, который содержит точку а и для которого а
не является правым концом. Обозначим выбранный отрезок через /2.
Продолжая этот процесс, получим систему вложенных отрезков
= nin2...nft; W, nin2... (nft+ 1)],
где ni (i = 1, 2, 3, ...» k) — одна из цифр 0, 1, 2, ...» 9. Каждый из
отрезков 1ъ содержит точку а, и ни для какого из этих отрезков
точка а не является правым концом.
Дроби
N, пхп2 ... nk и Nt nfi2 ... (пд + 1)
называют соответственно нижней и верхней подходящими десятичными
дробями порядка k и обозначают и а^. Эти дроби удовлетворяют
соотношениям
< «л,
Gk
&k > сд+1,	(1)
Последовательности (а^) и (ад), образованные соответственно
из нижних и верхних подходящих дробей, имеют пределы а и а:
lim N, П1П2.	= a- lim N, nfi2.. .(лд + 1) = а.
Л-»оо	“	&->оо
В силу последнего из соотношений (1) десятичные дроби а и а
равны, т. е. представляют собой одну и ту же десятичную дробь. С дру*
гой стороны, а — единственная точка, принадлежащая всем отрез^
кам /д с длинами, стремящимися к нулю,
62	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА /
Таким образом, числу а поставлена в соответствие десятичная
дробь N, Л1П2 ... rik ..., которую называют десятичной записью (или
десятичным представлением) числа а и пишут
а = N, пхП2 ... nk..."
Соответствие между множеством всех действительных чисел и
множеством всех десятичных дробей не является взаимно однозначным:
разным десятичным дробям может соответствовать одно число. Именно,
дробям вида
N, «1^2 ... ЛА (9) и 2V, «хПа ... (л& + 1)
соответствует одно и то же рациональное число. Так, рациональное
число 1/4 допускает запись в виде двух различных десятичных дро-
бей: 0,25 и 0,24 (9), в чем нетрудно убедиться, используя алгоритм
перевода бесконечной периодической дроби в рациональную дробь
(см. п. 4.5 настоящей главы).
Если рассматривать множество десятичных дробей, не имеющих
периода, состоящего только из цифры 9 (такие дроби называют до*
пустимыми), то между множеством всех действительных чисел и мно-
жеством всех допустимых десятичных дробей можно установить вза-
имно однозначное соответствие и отождествлять само число и его
десятичное представление.
Исходя из определений суммы, разности, произведения и частного
двух рациональных чисел, с помощью представления действительного
Числа в виде десятичной дроби можно’ввести понятие суммы, произве-
дения, разности и частного любых двух действительных чисел (кроме
деления на нуль), а также понятие абсолютной величины действи-
тельного числа.
Пусть а и два действительных числа:
а == NOt о. ...j b А40, т±т2 ... ть ...
Суммой, произведением и разностью двух действительных чисел а
h b называются соответственно числа
Нт (аъ, +bk)	а bt lim (ak-Ьь) ® a-bt lim (a&— bk) ~ a•— b*
k-rao ~	A-+00 " ~	A->oo **	**
Частным двух чисел а и b при b Ф 0 называется число
При таком определении частного двух действительных чисел может
оказаться, что при некоторых k bk~Q. Однако в силу условия
всегда найдется такой номер &о, что bk Ф 0 при k > kQt и тогда по-
следовательность ak/bk следует рассматривать не при всех k g N,
а при k == &о, &о+~1,	2, ...
Абсолютной величиной (модулем) действительного числа а назы*
вается неотрицательное число
|а| = lim | ah |.
k-+oo
5.4. Геометрическое изображение множества действительных чи-
сел. Рассмотрим прямую линию (которую будем называть осью) с вы-
бранной на ней произвольной точкой, которую обозначим буквой О
$ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА	Й
(пока именно буквой, а не числом нуль). Выберем любую другую
точку Е, лежащую на прямой справа от точки О. Точка О делит
прямую на два луча: луч, которому принадлежит точка Е и который
называют положительной полуосью^ И второй луч, который называют
отрицательной полуосью,
Рассмотрим теперь отрезок прямой с концами О и Е (рио4 £.1),
Длину отрезка ОЕ, обозначаемую | ОЕ |, примем за единицу длины
(отрезок ОЕ также называют масштабным отрезком). Установим теперь
соответствие между двумя числами 0 и 1 и точками О и Et полагая*
что точка, обозначенная буквой О, соответствует числу нуль, а точка,
обозначенная буквой Е, — числу 1 (точку О также называют нача*
лом координат). Теперь легко установить соответствие между любым
фиксированным натуральным числом и некоторой, вполне определен-
ной, точкой прямой. Например, точка, соответствующая 5,
Рцс* 2Л.
будет лежать справа от начала координат на расстоянии, равном пяти
длинам отрезка ОЕ*, отрицательному целому числу —п будем ставит^
в соответствие точку, лежащую слева от точки О на расстоянии^
равном п длинам* отрезка ОЕ*. п-|ОЕ|. Например, точка, отвечающая
числу —5, лежит слева от точки О на расстоянии, в пять раз боль-
шем единицы длины.
Далее, если взять единичный отрезок ОЕ, разделить его на п
равных частей и отложить от точки О вправо п-ю часть отрезка ОЕ,
то точка, являющаяся правым концом отложенного отрезка, считается
точкой, изображающей число 1/я. Если отложить вправо от точки О
сумму т отрезков длины | ОЕ |/п, то правый конец суммы является
точкой, изображающей положительное рациональное число т/п.
Аналогичным способом можно построить точки, соответствующие отри*
цательным рациональным числам.	1
Остается указать способ сопоставления иррациональных чисел
точкам прямой. Пусть положительное число а иррационально. По-
строим последовательности подходящих десятичных дробей для ирра-
ционального числа ан
£i; п2; ДзЬ-Л ffebq Ц #2»
Члены этих последовательностей — рациональные числа, которым
отвечают соответствующие точки прямой. Построим систему отрезков
1«1; ^11; [а2; а21; ...; Ьл; в*]; ♦..» вложенных друг в друга. Длина
этих отрезков стремится к нулю с возрастанием k. Эти отрезки имеют
только одну общую точку, а именно точку, отвечающую иррациональ*
ному числу а.
Таким образом, можно отобразить множество всех действительных
чисел R на множество точек прямой. Верно и обратное: каждой точке
прямой можно поставить в соответствие единственное действительное
число.
Между множеством действительных чисел и множеством точек
прямой существует взаимно однозначное соответствие, и часто вовсе
не различают эти &ва множеству проста Ачиодсвая прямая^
64	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
• 5.5. Степени и корни. Свойство ассоциативности операции умно-
жения^ действительных чисел позволяет ввести понятие натуральной
степени любого действительного числа:
n-й натуральной степенью действительного числа а называется
действительное число Ь, получаемое в результате умножения числа а
самого на себя п раз:
b = а-а-а* *... «а;
п сомножителей
п-ю степень числа а обозначают ап и пишут
b = ап.
Число а называется основанием степени, а число п — показателем
степени.
При а =/= 0 по определению а0 = 1; 0° не определен.
При а Ф 0 по определению а~п = 1/ап (п — натуральное число).
Корнем п-й степени (или арифметическим корнем п-й степени)
из положительного действительного числа а называется единственное
положительное решение уравнения хп ® а.
Корень п-й степени из числа а обозначается символом или
а]/п *). Корень 2-й степени (квадратный корень) обычно обозначают
просто У а.
При а=0 уЛ) = 0 (или 01/п = 0).
Если действительное число а отрицательно, то корень п-й степени
из числа а определяется лишь при нечетном п как единственное дей-
ствительное отрицательное решение уравнения хп = а.
Корень п-й степени из отрицательного действительного числа а
обозначается тем же символом у а (п— нечетное).
Рациональной степенью mln (т — целое, п — натуральное) по-
ложительного действительного числа а называется число (у^а )т»
Рациональная степень числа а также записывается в виде
(7^ Г = (а''п)т =	= 7^ = ат/п.
Из определения рациональной степени положительного числа
следуют равенства
2/V 7«
7^ = 7а.7ь, V
Степень а любым действительным показателем может быть вве-
дена, например, следующим образом. Пусть b — действительное число,
записанное в виде бесконечной десятичной дроби;
b = N, nyi2 ... n^...,
а
*1 Символ У также называют радикалом степени*
§ 5* ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА	65
и пусть (bk) — последовательность нижних подходящих десятичных
дробей fc-го порядка для числа Ь, т. е.
bi = Af, /и; b2 — N, niti2t . . bk — nin2 .. .	. ..
Для любого положительного числа а можно образовать бесконечную
последовательность
ь ь ь
(Г1, а”2;..а”^;...
Предел этой последовательности обозначается J2 и представляет собой
действительную степень числа а.
Из определения числа аь следуют равенства
а“+р=а“.Л	(а“)р = а“р, (а-6)“ =
а“/йр = а°-р,	(а/б)а=—.
6а
5.6.	Логарифмы. Пусть а — положительное действительное число,
отличное от единицы, a М — любое- положительное действительное
число. Логарифмом числа М по основанию а называется число, обо-
значаемое ' loga Al, такое, что
а а = М.
Логарифм loga М положительного числа М при положительном
и отличном от единицы основании а можно также определить как
решение уравнения
а* = А1.
Основные свойства” логарифмов)
logaa=l (а>0, а =£ 1); loga(a*) = £ (a>0, a=£l);
loga (All- Al2) = logaAli + \ogaM2 (Mi >0, M2 > 0};
loga (Mi/M2) = logaAli — logaAl2 (Alt >0, A!2 > 0))
log(I(^)=clogafc; logaC = 22gl; iogaC = __l_.
Десятичные логарифмы (логарифмы по основанию 10) Iogi0a
обычно обозначают 1g а.
Натуральные логарифмы (т. е. - логарифмы по основанию е =
— 2,718281828...) loge а обычно обозначают Ina.
Десятичные и натуральные логарифмы связаны равенствами
Ina =-1Н^-= In 10-lg а = (2,30259...) 1g a,
lg a = -Дтг = lg «• In a = (0,43429...) In a.
& In ID b	v	'
5.7.	Пропорции. Равенство вида
a с
~-~d	•	(2)
3 A. F. Цыпкин
66
ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
называют пропорцией, а9 b, с, d — членами пропорции. В пропор-
ции (2) а и d называют крайними, а b и с — средними членами про-
порции.
Из равенства (2) следует:
1) а-d = b*c\
a±b _ c±d	a-h _c-d t	та + nb _ tnc + nd
b	d ’	а д ““ сpa + qb"~ pc + qd'
(производные пропорции^
где т, п, pt q — произвольные числа (р и q не равны нулю одно-
временно).
5.8. Десятичные представления иррациональных чисел. Рацио-
нальное число определяется как число, которое может быть записано
в виде m/п, где тип — целые числа и п#=0 (см. п. 3.2). Любое
рациональное число может быть записано либо в виде конечной деся-
тичной дроби, либо в виде бесконечной периодической десятичной
дроби (см. п. 4.6). Так как любое действительное число может
быть записано в виде десятичной дроби (см. п. 5.3), то любое ирра-
циональное число может быть записано в виде бесконечной непериоди-
ческой десятичной дроби.
Это свойство иррациональных чисел иногда принимают за опре-
деление иррациональных чисел:
Иррациональным числом называется действительное число, деся-
тичная запись которого является бесконечной непериодической деся-
тичной дробью.
Свойства иррациональных чисел. В противопо-
ложность множеству рациональных чисел, которое было замкнуто
относительно операций сложения, вычитания, умножения и деления
(исключая деление на нуль), множество иррациональных чисел не обла-
дает свойством замкнутости ни для одной из перечисленных вышр
операций. Чтобы убедиться в незамкнутости множества иррациональ-
ных чисел, например относительно операции сложения, достаточно
указать лишь одну пару иррациональных чисел, сумма которых ра-
циональна. В качестве пары таких чисел могут быть взяты, например»
числа 0,1010010001...; 0,0101101110..., первое из которых образовано
последовательностью единиц, разделенных соответственно одним ну-
лем, двумя нулями, тремя нулями и т. д., второе — последователь-
ностью нулей, между которыми поставлены одна единица, две единицы*
три единицы и т. д. Каждое из этих чисел будет иррациональным
числом, в то время как их сумма будет рациональным числом, десятич-
ное представление которого имеет вид
0,111...!... = 0,(1) « 1/9.
Сумма, разность, произведение и’частное иррационального числа а
и рационального числа г — иррациональные числа.
Из этого свойства иррациональных чисел, в частности, следует,
что, имея лишь одно иррациональное число, с помощью рациональных
чисел можно построить бесконечно много иррациональных чисел.
5.9. Некоторые способы доказательства иррациональности чисел*
Доказательство иррациональности чисел,
основанное на определении рационального:
числа. Иррациональность некоторых чисел может быть доказана
с помощью, метода доказательства «от противного».
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА	67
Пусть, например, требуется доказать иррациональность числа J/^2.
Предположим, что j/*2 — рациональное число, т. е. является числом,
которое может быть представлено* в виде
У 2 = т/п,	(3)
где т и п — взаимно простые натуральные _числа. Для доказатель-
ства невозможности представления числа /2 в виде (3) мы восполь-
зуемся тем, что числа тип —взаимно простые. Говоря точнее, мы
воспользуемся тем, что числа т и п не являются оба четными —
в противном случае дробь т/п была бы сократимой. Возведя обе части
равенства (3) в квадрат, получим
/п2
2 = —7-ч=> 2-п2 =/п2.
п2
Число 2-п2 четно. Поэтому т2 и, следовательно, т также четно. По-
лагая т = 2«&, равенство 2-n2 = т2 можно записать в виде
2‘П2 = (2.k)2 о2-п2 = 4&2 -<=>п2 = 2*&2.
Из последнего равенства видно, что число п2 также оказывается
четным; следовательно, п также четно. Мы пришли к заключению,
что как т, так и п — четные числа, в ю время как дробь т/п по пред-
положению несократима. Полученное противоречие и доказывает, что
число 2 непредставимо в виде т/п и, следовательно, иррационально.
Аналогичным способом может быть доказана и иррациональность
числа J/3. Только, в отличие от предыдущего случая, здесь решающим
фактором окажется, . что числа тип делятся одновременно на 3.
Доказательство иррациональности чисел
спомощью основной теоремы арифметики. Ирра-
циональность некоторых чисел можно доказать с помощью основной
теоремы арифметики (см. п. 1.3). По основной теореме арифметики
любое натуральное число единственным образом разлагается в про-
изведение простых сомножителей.
Например, докажем, что число 1g 2 иррационально. Предполо-
жим, что это не так, т. е. имеются такие натуральные числа m ип, что
1g 2 = т/п, или 2 = 10m/rt.
Возводя обе части последнего равенства в степень п, получим
2n = IO'77 <->2п== 2ш-5т.
Согласно основной теореме арифметики равенство 2п =» 2т^т не-
возможно, так как 2п — натуральное число, ни при каких п не де-
лящееся на 5, в то время как 2w-5m делится на 5, поскольку т —
натуральное число. Следовательно, число 1g 2 иррационально..
Один общий метод доказательства ирра«
циональности ряда чисел (в томчисле иррациональности
некоторых значений тригонометрических функций). Один довольно
общий метод доказательства иррациональности чисел основан на .сле-
дующей теореме:
Если алгебраическое уравнение
nQXk 4- niXk^~t- ... 4- ПЬ-хХ 4- nk ss 0
3*
68	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
с целыми коэффициентами имеет рациональный корень mln (числа т
и п взаимно простые), то число т является делителем числа пь, а число
п — делителем числа nQ.
В частности, рациональными корнями уравнения
xk + np?“"! 4----h	= О
с целыми коэффициентами и старшим коэффициентом, равным единице,
мохут быть лишь целые числа.
Доказательство иррациональности чисел с помощью сформулиро-
ванной теоремы проводится следующим образом *):
1)	Составляют алгебраическое уравнение наименьшей натураль-
ной степени с целыми коэффициентами, одним из корней которого за-
ведомо будет число а, иррациональность которого необходимо дока-
зать.
2)	Находят все простые делители первого коэффициента п0 полу-
ченного уравнения и свободного члена пь. Из полученных целых
чисел составляют всевозможные рациональные числа с числителем,
который является делителем числа пл, и знаменателем, который яв-
ляется делителем числа п0. Тогда по сформулированной выше тео-
реме лишь эти рациональные числа могут являться рациональными
корнями данного уравнения.
3)	Подстановкой этих рациональных чисел в уравнение прове-
ряют, является ли хотя бы одно из них,корнем уравнения. Если ни
одно из построенных рациональных чисел не является корнем урав-
нения, то данное уравнение рациональных корней не имеет и, следо-
ъательно, рассматриваемое число иррациональное. Если же какое-
нибудь из построенных рациональных чисел является корнем урав-
нения, то доказывают, что рассматриваемое число не равно этому
корню и, следовательно, оно иррационально. _
Примеры: 1.-Доказать, что число —КЗ иррационально.
Положим х — 1^2— 1^3. Тогда * + КЗ = |^2. Возводя обе части
равенства в куб, после несложных преобразований получим уравнение
2==—3/3 (х2+ 1).
Возводя обе части последнего уравнения в квадрат, после приведения
подобных членов придем к уравнению
х* — 9х* — 4Хз + 27х2 — 36х — 23 = 0.
Из способа построения этого уравнения следует, что число 7/2" — j/"3 —»
его корень. С другой стороны, единственно возможными рациональ-
ными корнями этого уравнения являются целые числа — делители
числа —23, т. е. + 1, —1, +23, —23. Непосредственная подстановка
этих чисел в уравнение показывает, что эти числа не являются кор-
нями уравнения. Таким образом, рациональных1 корней наше урав-
нение не имеет, и число — КЗ иррационально.
2.	Доказать, что число cos 20° иррационально.
По формуле тройного аргумента cos 60° == 1/2 и cos 20° связаны
формулой
cos 60° = 4 cos8 20° — 3 cos 20°.
♦) Излагаемый ниже метод применим только для доказательства ирра*
цнонельиости алгебраических чисел (см» а» 5,10).
§ 5. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА	69
Обозначая cos20°=x, запишем последнее равенство в виде
8х3 — бх — 1 = 0.	(4)
Число х == cos 20° — корень этого уравнения. Применяя к этому
л равнению сформулированную выше теорему, видим, что возможными
рациональными корнями этого уравнения являются числа ±1, ±1/2,
±1/4, ±1/8. Подстановкой этих чисел в уравнение (4) можно убе-
диться, что ни одно из них не является его корнем. Следовательно,
уравнение (4) не имеет рациональных корней, и потому число cos 20°
иррационально. Следует отметить, что подобный способ непосредствен-
ного использования формулы тройного аргумента непригоден для
доказательства, например, иррациональности числа cos 10°, так как
алгебраическое уравнение третьей степени, корнем которого будет
число х = cos 10, имеет иррациональные коэффициенты. Иррацио-
нальность числа cos 10° проще доказать в два этапа: сначала доказать,
ч го число cos 20° иррационально, после чего, воспользовавшись фор-
мулой
1 + cos 20° = 2 cos2 10°, .
методом доказательства от противного показать, что число cos 10Q
не может быть рациональным числом.
Сформулируем еще одно утверждение, позволяющее доказать ирра-
циональность некоторых значений тригонометрических функций:
Если угол 0 таков, что число cos 20 иррационально, то и числа
cos 0, sin 0, tg 0 также иррациональны.
Чтобы убедиться в справедливости этого утверждения, достаточно
применить метод доказательства от противного, предварительно вос-
пользовавшись тригонометрическими формулами половинного аргу-
мента и известным тригонометрическим тождеством
,+‘г‘в—
Так, например, предположим, что sin 0 — число рациональное,
тогда 2 sin2 0 будет также рациональным числом. Так как sin2 0
и cos 20 связаны равенством
1 — cos 20 = 2 sin2 0,
из рациональности числа 2 sin2 0 будет следовать рациональность
числа cos 20. Полученное противоречие и доказывает, что число sin 0,
как и число cos 20, иррационально.
5.10. Алгебраические и трансцендентные числа. Множество дей-
ствительных чисел, помимо деления на множество рациональных и
множество иррациональных чисел, может быть разделено на два дру-
гих множества — множество алгебраических чисел и множество транс-
цендентных чисел.
Действительное число, являющееся корнем некоторого алгебраи-
ческого уравнения вида
nQxk + гцх*1"1 Н---1- nk~±x + nk = 0
с целыми коэффициентами n0, ni> •••» nk-l> nk, из которых хотя бы
один отличен от нуля, называется алгебраическим числом.
Действительное число, не являющееся корнем никакого алгебраи-
ческого уравнения с целыми коэффициентами! называется трансу
цендентным числом.	'	*
70	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Множество всех рациональных чисел является подмножеством
множества алгебраических чисел, так как любое рациональное число
т/п является корнем алгебраического уравнения первой степени
пх — т = 0.
Отсюда также следует, что всякое трансцендентное число иррацио-
нально.
Разбиение множества действительных чисел на различные под-
множества схематически можно изобразить так:
Действительные числа —
—Рациональные (все они
являются алгебраическими)
|—Алгебраические
—Иррациональные — _
’-Трансцендентные
[—Рациональные
Действительные числа -	'-Иррациональные
'—Трансцендентные (все они являются
иррациональными)
Некоторые трансцендентные числа. Ранее (см.
п. 5.9)* были приведены доказательства иррациональности некоторых
чисел, в частности иррациональности числа 1g 2. В то 'же время 1g 2
является трансцендентным числом. Впервые предположение о транс-
цендентности числа 1g 2 было высказано Л. Эйлером в XVIII веке.
Доказательство трансцендентности числа 1g 2 значительно сложнее,
чем доказательство его иррациональности, и основано на методах
гораздо более общих и глубоких, чем те, которые используются при
доказательстве его иррациональности, Трансцендентность числа 1g 2
следует из теоремы:
Число аь трансцендентно, если числа а и Ь алгебраические (слу«
чаи а = 0, а = 1 и случай рационального b исключены).
Трансцендентными числами будут и хорошо известные числа е
и л; их трансцендентность была доказана в конце девятнадцатого века.
Вопрос об алгебраичности или трансцендентности числа л связан
с решением одной геометрической задачи, сформулированной еще
за несколько веков до нашей эры. Эта задача называется задачей
о квадратуре круга и формулируется так:
Можно ли с помощью только циркуля и линейки построить ква-
драт с площадью, равной площади круга единичного радиуса?
Доказано, что с помощью циркуля и линейки можно строить лишь
такие геометрические фигуры, площадь которых выражается алгебраи-
ческим числом. Поэтому трансцендентность числа л указывает на
невозможность решения задачи о квадратуре круга.
Напротив, значения тригонометрических функций при некоторых
значениях аргумента (например, значения cos 20° и sin 10°, ирра-
циональность которых была доказана в п. 5.9) являются алгебраиче-
скими числами, что вытекает из следующей теоремы;
Для любого рационального числа г числа sin (90°-r), cos (90°*г)
и tg (90°т) являются алгебраическими (в случае tg (90°-r)f г ±1,
хЬЗ,
§ 6. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ	71
В заключение отметим, что множество всех алгебраических чисел
образует счетное множество, а множество всех трансцендентных чисел—
несчетное.
§ 6> Приближенные вычисления
6.1.	Приближенное значение числа и погрешности. Для выпол-
нения вычислений действительные числа часто бывает удобно записы-
вать в виде десятичных дробей. Однако не любое рациональное, а тем
более действительное число может быть записано в виде конечной
дроби, с которой можно проводить требуемые вычисления. Поэтому
часто бесконечную десятичную дробь, представляющую запись данного
действительного числа, приходится обрывать на некоторой цифре
после запятой и оперировать с полученной конечной десятичной дробью.
Число, представляемое конечной десятичной дробью, полученной
в результате обрывания бесконечной десятичной дроби, называется
приближенным значением данного числа. Например, различными
приближенными значениями числа от == 3,14159 ... будут числа 3,14;
3,1415 и т. д.; в качестве приближенных значений числа	2,71828..к
можно взять числа 2,7; 2,71; 2,7182 и т. д. Приближенные значения
чисел могут появиться не только в результате обрыва записи числа
в виде десятичной дроби. При решении любой практической задачи
мы используем числа, полученные в результате некоторых измерений.
Однако при всяких измерениях появляется ошибка, связанная с не-
совершенством наших измерительных инструментов, геометрической
неправильностью измеряемого предмета и т. п.
Обозначим приближенное значение числа а через а*. Абсолютную
величину разности числа а и его приближенного значения а*
|а —а*|
называют абсолютной погрешностью приближенного значения а*.
Абсолютная погрешность является одной из характеристик при-
ближенного значения числа. Часто она представляет только теоре-
тический интерес, так как в большинстве случаев числа а мы можем
и не знать. В ряде случаев можно указать границы, в которых изме-
няется абсолютная погрешность. Эти границы обычно определяются
способом получения приближенного значения числа. Например, пре- ‘
изводя измерения длины с помощью ученической линейки с метками,
расставленными на расстоянии в 1 мм, мы можем гарантировать, что
абсолютная погрешность измерений не будет превышать 1 мм.
Предельной абсолютной погрешностью приближенного значения
числа называют число А такое, что
|а — а* |< А.
По своему определению предельная абсолютная погрешность может
вводиться неоднозначно. Так, в случае рассмотренного выше примера
измерения длин линейкой предельная абсолютная погрешность может
быть взята равной 1 мм, 1,5 мм и т. д.
Заметим, что нй абсолютная погрешность, ни предельная абсо-
лютная погрешность сами по себе еще не характеризуют, с какой точ-
ностью мы заменяем число а его приближенным значением. Например,
пусть предельная абсолютная погрешность результата некоторого
измерения равна 10 км. Если измерялось расстояние между двумя
домами одного и того же города, то такая точность, вообще говоря,;
72	гл. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
неудовлетворительна. Если же измерялось расстояние между полю-
сами Земли, то указанная точность очень хороша.
Характеристиками точности результата измерения (или замены
числа а его приближенным значением), в которых, кроме погрешности,
участвует и сам результат измерений, являются величины, называемые
относительной погрешностью и предельной относительной погреш-
ностью.
Относительной погрешностью называется отношение абсолютной
погрешности к абсолютной величине приближенного значения числа:
fi |a-g*|
l«*l * .
Предельной относительной погрешностью приближенного значе-
ния числа называется отношение предельной абсолютной погрешности
к абсолютной величине приближенного значения числа:
А- А
Kl’	_
Например, число 3,14 является приближенным значением числа л.
Абсолютная погрешность этого приближенного значения равна
0,00159...; предельную абсолютную погрешность можно считать рав-
ной 0,0016, а предельную относительную погрешность
= 0,000509...
□ , 14
можно положить равной 0,00051.
6.2.	Десятичная запись приближенных значений числа. Любое
положительное действительное число а может быть записано в виде
конечной или бесконечной десятичной дроби:
a=nz.10z4-n/_i-10/-1+ ••• +	10'~ *+1 + ....
где nt — цифры числа а (щ = 0, 1, 2,	9), причем п/ =/= 0, а I —
некоторое целое число.
Приближенное значение а* числа а можно получить, обрывая
десятичную запись числа а. При этом в записи приближенного зна-
чения а* в десятичной позиционной системе счисления иногда при-
ходится вводить дополнительные нули в начале или в конце числа.
Например, в качестве приближенного значения числа
& = 2« 10~2 +4» 10“8+О* 10”4 +910“S-f« •••
можно взять числд
b* — ‘| о", О 12409,
I —— I
а в качестве приближенного значения числа
с = Ы0! +0* 104 +7« 103 +3-102+ •••
— число
с* = 107 1000!.
Значащей цифрой приближенного значения числа называется
всякая отличная от нуля цифра его десятичной записи и нуль, если
он находится между значащими цифрами или является представителем
сохраненного десятичного разряда.
§ 6. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
73
Нули, стоящие перед и после запятой в записи числа b*t и нули,
стоящие в конце записи числа c*t не считаются значащими цифрами
(в записи чисел Ь* и с* указанные нули выделены квадратиками).
Пусть, например, число 0,002080 есть приближенное значение
некоторого числа. Первые три нуля не являются значащими цифрами,
так как они служат только для указания десятичных разрядов других
цифр. Остальные два нуля являются значащими цифрами, так как
первый из них находится между значащими цифрами 2 и 8, а второй
указывает, что. приближенное значение числа получено обрыванием
десятичной записи числа с сохранением шестого разряда после запя-
той. В случае, если в приближенном значении 0,002080 последняя цифра
не является значащей, оно должно быть записано в виде 0,00208.
Таким образом, приближенные значения 0,002080 и 0,00208 не равно-
ценны, так как первое из них содержит четыре значащие цифры, а вто-
рое — три.
При записи приближенных значений целых чисел нули, стоящие
в конце десятичной записи числа, могут служить как для обозначения
значащих цифр, так и для указания разряда других цифр. Поэтому
обычная запись приближенных значений целых чисел может пони-
маться неоднозначно. Например, пусть известно, что число 134 000
есть приближенное значение некоторого числа. По виду числа 134 000
нельзя сделать вывод, сколько значащих цифр в этом числе (хотя сразу
можно сказать, что их не меньше трех). Для того чтобы избежать
такой неопределенности, целое число записывают с помощью десятич-
ных дробей и степеней числа 10. Например, если хотят указать, что
число 134 000 имеет три значащих цифры, то его записывают в виде
0,134-10е (или 1,34-105 или 13,4-104 или 134-103). Если же хотят
указать, что число 134 000 имеет пять значащих цифр, то его записы-
вают в виде 0,13400-106 (или соответственно 1,3400-10б, 13,400-104,
134,00-103).	-
. Говорят, что п первых значащих цифр приближенного значения
числа являются верными, если абсолютная погрешность приближен-
ного значения числа не превышает половины единицы разряда и-й
значащей цифры, считая разряды слева направо.
Таким образом, если для приближенного значения а* числа
а= т-101 +«/_!• ю'-14-----------+ •••
известно, что
|a—a* |C0,5-10'“ft+1,
то первые k цифр и/, п/л, ...» приближенного значения яв-
ляются верными.
Например, для числа 121,57 число 122,00 является приближенным
значением.с тремя верными цифрами, так как
1121,57 — 122 | = 0,43 <0,5-10°.
Результат арифметических действий над приближенными значе-
ниями чисел представляет собой также приближенное значение неко-
торого числа. Погрешность полученного результата оценивается с по-
мощью следующих правил:
1)	Предельная абсолютная погрешность алгебраической суммы
приближенных значений чисел не превышает сумму предельных абсо-
лютных погрешностей слагаемых.
74	ГЛ. 2, ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
2)	Относительная погрешность суммы приближенных значений
чисел заключена между наибольшей и наименьшей из относительных
погрешностей слагаемых.
В согласии со сформулированными правилами, во избежание лиш*
них вычислений, при подсчете суммы приближенных значений чисел
производят предварительное округление слагаемых (см. п. 6.3). При
этом слагаемое, имеющее наименьшее число верных знаков, оставляют
неокругленным, а в остальных слагаемых оставляют на один или два
знака больше по сравнению с неокругляемым числом.
6.3.	Округление чисел. Чтобы округлить число до п значащих
цифр, отбрасывают все его цифры,’ стоящие после n-го разряда, или,
если это нужно для сохранения разрядов, заменяют их нулями. При
этом:
1)	Если за последней сохраняемой цифрой следует цифра 0, 1,
2, 3 или 4, то при округлении сохраняются все цифры до последней
сохраняемой включительно. Такое округление называется округлением
с недостатком.
2)	Если за последней сохраняемой цифрой следует 9, 8, 7, 6
или 5, то к последней сохраняемой цифре прибавляется единица.
Такое округление называют округлением с избытком.
Примеры. 1. Округление числа 219,364 до четырех знача*
щих цифр дает число 219,4. Последняя цифра округленного числа
увеличена на единицу, так как первая отбрасываемая цифра больше
пяти.
2.	Округление числа 6,4502 до двух значащих цифр дает число 6,5.
Последняя цифра округленного числа увеличена на единицу, так кик
первая отбрасываемая цифра равна 5.
3.	Округление числа 1836 до трех значащих цифр дает число
1,84-103.
При использовании правил округления абсолютная погрешность
округления не превосходит половины единицы разряда последней
оставленной значащей цифры, т. е. все значащие цифры приближенного
значения числа, полученного с помощью правил округления, являются
верными цифрами.
6.4.	Метод касательных (метод Ньютона). Метод касательных
является одним из самых эффективных численных методов решения
уравнения.
Допустим, нам известно, что уравнение f (х) = 0 имеет корень
на промежутке [a; ft] (функция / (х) дифференцируема на [a; ft]
и ее производная не обращается на [a; ft] в нуль). Отыскать этот ко-
рень можно следующим способом. Возьмем произвольную точку
Xj € [a; ft] и напишем уравнение касательной к графику функ*
ции f (х) в точке с абсциссой *)
У = f («1) + Г (*i) (« “ Ж1).
Решая уравнение
f (*1) + Г (*1) (X — Xi) = 0,
») Необходимо# чтобы точка хх была расположена достаточно близко от
корня уравнения f (х) == 0, поэтому для выбора точки xt иногда приходится
проводить предварительное исследование функции [
§ 6. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
75
найдем точку пересечения касательной с осью Oxi
X~Xi
fM
ГМ *
Обозначим найденную точку через х2'
Напишем уравнение касательной к графику функцйч f (х) в точке
с абсциссой х2:
у — f (XS) + f (х2) (х — х2),
п найдем точку х3 переселения касательной о осью Ох:
r -х
3 ~ 2 Г (х2) ’
Продолжая этот процесс, получим последовательность (хД зада-
ваемую рекуррентной формулой
f (хп)
=	---jr~-, nGN.	(1)
Если функция f (х) удовлетворяет некоторым дополнительным
условиям (например, f (х) имеет положительную (или отрицательную)
вторую производную во всех внутренних точках [а; 6], то последова-
тельность (1) сходится к числу, являющемуся корнем уравнения
f W = 0.
Метод касательных может быть применен для решения задачи
извлечения корня из произвольного положительного числа а. Зна-
чение У а будем искать как решение уравнения
f (х) = х2 — а = 0.
Рекуррентная формула (1) в данном случае принимает вид
х„+1=4-(х„ + -£).	(2)
Здесь в качестве первого члена последовательности (xrt) можно взять
любое число Xi £ (0; +оо). Если в качестве числа xt выбрано число,
удовлетворяющее неравенству xj — а > 0, то абсолютные погрешности
приближенных значений числа а на n-м и (п+ 1)-м шагах вычис-
лений определяются равенствами
8п = хп — V"a > 0, Cn+i = xn+i — Vq > 0.
Используя рекуррентную формулу (2), установим связь между
6«+1 и бп:
$n+i = Xn+i — ]/"а = Ц- (хп +	— v~a =
= -у +	Л/--) — V а =
* '	бп+Иа /
76	ГЛ. 2. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
= 4 Sn + о/х	“ 4	= 4Г6п “	+ Г"
2(6П + у а) *	I	&п + v а J
1	г
2	. 6П 4- V а .
Так как > 0, то, отбрасывая в знаменателе последней дроби
слагаемое 6Л, мы тем самым увеличиваем ее значение, и, следовательно,
%
8n^Wa"	<3)
Полученная рекуррентная оценка абсолютной погрешности ука-
зывает на высокую скорость сходимости последовательности прибли-
женных значений хп-
Например, будем вычислять с помощью метода касательных
КЗЗ.520. В качестве х± возьмем число 200. Это значение данного корпя
с избытком. Абсолютная погрешность бг не превышает 20. Тогда
по формуле (3)
б2<4^г<,*5: 63<4iir<°>001-
Здесь для упрощения оценок Ко* в формуле (3) заменен на меньшее
число: 180.. Таким образом, при вычислении значения К33 520 уже
после третьего шага получается приближенное значение корня, отли-
чающееся от его точного значения меньше чем на 0,001.
6.5. Алгоритм извлечения квадратного корня из натурального
числа. Часто при решении квадратных уравнений требуется извлечь
квадратный корень из натурального числа. Приведем алгоритм извле-
чения квадратного корня для случая, когда число, стоящее под знаком
корня, является квадратом натурального числа. Пусть требуется
вычислить К33 489. Число 33 489 разобьем на группы цифр (по две
цифры), двигаясь справа налево:
3 34 89.
Ищем наибольшее число, квадрат которого не превосходит числа 3,
стоящего в первой группе цифр. Этим числом будет число 1. Записы-
ваем его в ответ. Возводим единицу, в квадрат и вычитаем из числа 3.
К полученной разности приписываем вторую группу цифр. Получаем
- число 234.
Удваиваем число, которое было записано в ответ (в нашем слу-
чае 1), и приписываем к полученному числу справа такую наиболь-
шую цифру, чтобы- произведение полученного двузначного числа на
эту цифру не превосходило 234. В нашем* случае этой цифрой будет
цифра 8:	\
28-8 = 224 < 234.
Пишем цифру 8 вслед за цифрой 1 в ответ. Из числа 234 вычитаем
число 224 и к полученной разности приписываем последнюю группу
цифр. Получаем число 1089.
Удваиваем число, которое было записано в ответ (в нашем слу-
чае 18), и приписываем справа к полученному числу (в нашем случае
числу 36) такую наибольшую цифру, чтобы произведение полученного
§ 6. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ	77
трехзначного числа на приписанную цифру не превосходило числа
1089. б нашем случае этой цифрой будет цифра 3:
363*3= 1089.
Записываем цифру 3 в ответ. Процедура извлечения, квадратного
корня завершена:
/33189 = 183.
Обычно описанную процедуру записывают в виде следующей
схемы:
/ 3 34 89 = 183.
~“1
х 8
224
v 363
Х____3
1089
234
~224
1089
~ 1089
0
ГЛАВА 3
КОМПЛЕКСНЫЕ ЧИСЛА
Исторически введение комплексных чисел оказалось связанным
С получением формулы вычисления корней кубичного уравнения:
х3=рх+?.	(1)
В первой трети XVI века итальянский математик Н. Тарталья
показал, что корень, этого уравнения всегда представляется выраже-
нием
х = Yu 4-	,	(2)
где и и и — решения системы уравнений
w + v = g,	(3)
Так, например, чтобы найти корень кубичного уравнения
х3=9х+28,
необходимо составить систему (3) для данного уравнения, решая кото-
рую получим: «=27, v = 1 и и = 1, v = 27.
Используя соотношение (2), находим х = 4, т. е. число 4 яв-
ляется корнем данного уравнения.
Однако оказалось, что существуют кубичные уравнения, < для
которых система (3) не имеет решений в множестве действительных
чисел, в то время как кубичное уравнение заведомо имеет действитель-
ный корень. Например, уравнение
х3 = 15х + 4
имеет действительный корень х = 4, в чем легко убедиться, подставив
в данное уравнение вместо х число 4. Если же для данного уравне-
ния написать систему (3), то окажется, что эта система не будет иметь
решений в множестве действительных чисел. Это непонятное тогда
явление впервые объяснил итальянский математик Р. Бомбелли в 1572 г.
и его объяснение, по существу, было основано на введении понятия
комплексного числа и правил действий над комплексными числами.
Однако вплоть до XIX века, несмотря на то, что аппарат комплексных
чисел позволил получить много важных фактов, относящихся также
и к действительным числам, само существование комплексных чисел
многим математикам казалось весьма сомнительным. Лишь в XIX веке
после появления работ К. Гаусса, в которых давалось наглядное гео-
метрическое изображение комплексных чисел (как точек или векто-
ров на плоскости), существование комплексных чисел стало обще-
признанным фактом.
Упомянем еще один факт, который также приводит к мысли о не-
обходимости расширения множества действительных чисел до мно-
жества комплексных чисел. Как известно, натуральная степень любого
действительного числа опять будет действительным числом. Однако
- § I. МНОЖЕСТВО КОМПЛЕКСНЫХ ЧИСЕЛ
79
операция извлечения корня (обратная операции возведения в степень)
не всегда выполнима в множестве действительных чисел: не существует
действительного числа а, четная степень которого была бы отрица-
тельным числом. Другими словами, в множестве действительных
чисел не существует числа, которое было бы корнем уравнения
где п — четное число, а b — отрицательное действительное число.
Следуя общему плану расширения числовых областей, как это
уже неоднократно делалось (например, при введении, понятий отри-
цательных чисел и рациональных чисел), множество4действительных
чисел можно расширить до множества чисел, которое будет замкнуто
относительно операции извлечения корня. Забегая вперед, заметим,
что при этом попутно получается существенно новый результат и
для тех случаев, когда операция извлечения корня выполнима в мно-
жестве действительных чисел.
Один из способов построения множества комплексных чисел за-
ключается в том, что множество действительных чисел расширяется
путем присоединения к множеству действительных чисел нового чис*
лового объекта — корня уравнения
х2+ 1	0.
Полученное «расширенное» множество называется множеством ком*
плексных чисел.
§ 1. Множество комплексных чисел
1.1. Аксиоматическое построение множества комплексных чисел*
Комплексные числа не являются числами в элементарном смысле этого
слова, применяемыми при подсчетах и измерениях, а представляют
собой математические объекты, определяемые перечисленными ниже
свойствами.
Комплексное число обозначается символом а + Ы, где а и b —
действительные числа, называемые соответственно действительной
частью и мнимой частью комплексного числа а + bi, а символ i,
определяемый условием i2 ==—1, называется мнимой единицей.
Обычно комплексное число а + Ы обозначают одной буквой (чаще
всего г):
г= а+ bl.
Действительная и мнимая части комплексного числа г = а + Ы обо-
значают Re z и Im z соответственно *):
а = Re г, b= Imz.
Два комплексных числа z± = аг + bxi и z2 = а2 + b2i считаются
равными (zi == 22), если равны их действительные и мнимые части
= bj =* Ь2). Комплексное число z = а + bi считается равным
нулю (г = 0), если его действительная и мнимая части равны нулю
(а = Ь = 0). Комплексное число г = а + Ы при b = 0 считается
совпадающим с действительным числом а (а + 0Z = а). Комплексное
число z= а + Ы при а = 0 называется чисто мнимым и обозна-
чается Ы (0 + Ы = /и)-
*) Re от слова гёе! действительный (франц.), Im от слова hnagb
Haire « мнимый (франц,).
80	ГЛ. 3. КОМПЛЕКСНЫЕ ЧИСЛА
Суммой комплексных чисел zj =	+ bri и z2 = а2 + b2i назы-
вается комплексное число z, 'действительная часть которого равна
сумме действительных частей чисел Zi и z2, а мнимая часть — сумме
мнимых частей чисел г± и z2, т. е.
z == («! + а2) + (^1 + Z.
О числе z говорят, что оно получено в результате сложения комплекс-
ных чисел Zj и z2, и пишут
Z = Z1 + z2.
Числа Zi и г2 называются слагаемыми.
Свойства операции сложения комплекс*
пых чисел:
1) ассоциативность: (zx + г2) + г?/ = гх + (z2 + z3);
2) коммутативность: Zj + г2 = z2 + zt.
Комплексное число —а — Ы называется противоположным ком-
плексному числу а + hi. Комплексное число, противоположное ком-
плексному числу г, обозначается —г. Сумма комплексных чисел 2
и —z равна нулю (z + (—г) ~ 0).
Разность комплексных чисел Zi =	+ bti и г2= а2+ b2i есть
комплексное число г, являющееся суммой числа и числа, противо-
положного z2:
г = + (--г2) =	— а2) +	— b2) it
т. е. комплексное число, действительная и мнимая части которого
равны соответственно разности действительных и мнимых частей
уменьшаемого и вычитаемого. О числе г говорят, что оно получено
в результате вычитания комплексного числа z2 из комплексною
числа zt, и пишут
2=zi~z2.
Произведением комплексных чисел zj«» ах + b^i и z2 == а2 + b2i
называется комплексное число
Z « (Я1Я2 — М2) + (°Л + «2^1)
О числе z говорят, что оно получено в результате умножения комплекс-
ного числа zj на комплексное число г2, и пишут
t
г=г^22.
Числа Zi и z2 называются сомножителями.
' Свойства операци и умножеи и я комплекс-
ных чисел:
1) ассоциативность: (zrz2)-z3 = Zi* (z2*23);
2) коммутативность: ZfZ» ® z2’2f.
Частным двух комплексных чисел Z[ и z2 (z2	0) называется
такое комплексное число z, что zt = z*z2. Частное комплексных чисел
Zi =»at + bii и	b2i вычисляется по формуле
_	01^2 -Ь bjbt .	—- Uibt
~ 4+^	4+^2
§ h МНОЖЕСТВО КОМПЛЕКСНЫХ ЧИСЕЛ	81
О числе г говорят, что оно получено в результате деления комплекс-
ного числа zi на комплексное число 22, и пишут
z = — ИЛИ г == 21/22.
Сложение и умножение комплексных чисел связаны правилом,
называемым законом дистрибутивности умножения
относительно сложения:
(zt + 22) 23 == 2Г23 + 22‘23.
Число |/*а2 + Ь2 называется модулем комплексного числа 2=
== с + Ы. Л1одуль комплексного числа обозначают |г|. Модули двух
любых комплексных чисел zt и 23 (в случае частного предполагается,
что г2 5^ 0) удовлетворяют соотношениям
I + 22 к 1 21 I + I ZS [,	| 21 — г2 | > || *1 | —’ | *2 II»
|?1?2| = к1|-|гг|,	|21/2г| = |?1|/|гг|,	|г"| = | г |п == [ 2 |п.
Комплексное число а — Ы называется комплексно сопряженным
с числом г = а + Ы и обозначается z.
Свойство комплексно сопряженных чисел:
I)	Произведение комплексного числа г ~ а + Ы и комплексно
сопряженного с ним числа z~a— bi есть действительное число!
2‘2s=a2+fr2-
2)	Если z — число, комплексно сопряженное с числом 2, тояисло2
комплексно сопряженное с числом 5, есть число г:
3)	Если 2i, Si и г2, г2 — две пары комплексно сопряженных чисел,
то сумма, произведение, разность и частное чисел Zj и z2 являются
числами, комплексно сопряженными сумме, произведению, разности
и частному чисел z± и г2 соответственно:
71 + г2 ==- (г1 + г2), Zj — г2 ~ (21 —22),
Z1.72 = (21 Га)» ?1/*2 (Zl/Za) (z2	0).
4)	Если 2 = а + Ы и 2 = а- Ы — пара комплексно сопря-
женных чисел, то
n	. г —г
о=Кег=—~, d=Ifrz = —.
2	2z
1.2. Теория комплексных чисел как упорядоченных пар действитель-
ных чисел. При аксиоматическом способе введения комплексных чисел
как абстрактных математических объектов, удовлетворяющих пере-
численным свойствам, остается неясным вопрос о том, какой смысл
в записи а + Ы приписывается знакам + и •, которые раньше исполь-
зовались для обозначения суммы и произведения действительных
чисел. Для выяснения этого вопроса проведем другое, отличное от
изложенного выше, построение множества комплексных чисел.
82
ГЛ. 3. КОМПЛЕКСНЫЕ ЧИСЛА
Рассмотрим множество упорядоченных пар (a; Ь), где а и b — дей-
ствительные числа. Две пары (а; Ь) и (с; d) считают равными, если
а~ с н b — d, и пишут
(a; b) = (с; rf).
Суммой пар (а\ Ь) и (е; d) называют пару (а + с; b + d). Говорят,
что пара (а + с; b + d) получена в результате сложения пар (а; Ь)
и (с; d) и пишут
(а; b) + (с; d) = (а + с\ b 4- d).
Произведением пар (а; Ь) и (с; d) называют пару (ас — bd, ad +
be). Говорят, что пара (ас — bd\ ad-)- be) получена в результате
умножения пар (а; Ь) и (с\ d) и пишут
(а; b)*(c\ d) = (ac — bd; ad + be).
Из определения суммы и произведения пар и свойств операции
сложения и умножения, действительных чисел следует, что операции
сложения и умножения пар ассоциативны и коммутативны, и умноже-
ние дистрибутивно относительно сложения.
Нулевой парой называют пару (х; y)t удовлетворяющую условию
(а; Ь) 4- (х; у) = (а; Ь),
где (а; Ь) — произвольная пара. Из определения операции сложения
и равенства пар следует, что пара (0; 0) — нулевая.
Единичной парой называют пару (х; у), удовлетворяющую условию
(а; Ь)*(х\ у) — (a; b)t
где (а; Ь) — произвольная пара. Из определения операции умножения
и условия равенства пар следует, что пара (1; 0) — единичная.
В множестве упорядоченных пар операции сложения и умножения
пар имеют обратные операции — вычитание и деление. Разность
и частное пар (а\ Ь) и (с\ d) вычисляются соответственно по формулам
(a; b) — (с; d) = (а — с; b — d),
/	п./’а fa-cA-b-d* Ъ*с — a>d\
(«; мл. (	+	).
(В случае частного предполагается, что пара (с; d) — не нулевая.)
Будем отождествлять пару вида (а; 0) с действительным числом а.
Нетрудно проверить, что при таком отождествлении суммой и произ*
ведением пар (а; 0) и (Ь; 0) будут пары
(а; 0) + (*; 0) == (а+ Ъ\ 0),	(а; 0). (Ъ\ 0) =* (а- Ь\ 0),
которые по принятому соглашению отождествляются с действительными
числами а+ b и а*Ь соответственно.
§ 2. ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ	83
Аналогично можно показать, что разность и частное пар (а; 0)
я (&’» 0) — пары с нулевыми вторыми элементами, т. е. действительные
числа (в случае частного предполагается, что b Ф 0).
Таким образом, множество всех действительных чисел является
подмножеством построенного множества упорядоченных пар, причем
все арифметические операции для действительных чисел, рассматри-
ваемых как пары со вторым нулевым элементом, сохраняют тот же
смысл, который они имели для действительных чисел.
Возьмем теперь пару (0; 1) и по правилу умножения пар умно-
жим ее на себя:
(0; 1)-(0; 1)= (—1; 0).	(1)
В результате умножения получилась пара (-—1; 0), которая соответ-
ствует действительному числу —1. Введя для пары (0; 1) специальное
обозначение
(0; 1) = g
равенство (1) можно записать в виде *)
i'i =—1 или i2 =—L
Простая проверка показывает, что любая пара действительных чи-
сел (а; Ь) можех быть записана в виде
(а; 6) = (а; 0)+ (d; 0)-(0; 1)
или, по принятому соглашению об отождествлении множества всех
пар (а; 0) и множества всех действительных чисел а и принятого
обозначения для пары (0; 1), в виде
а + Ъ* i или а + Ы.	(2)
При аксиоматическом способе введения комплексных чисел (см.
п. 1.1) комплексное число обозначалось единым символом а + b»i,
в котором символам арифметических операций «+» и «•» не
приписывался какой-либо конкретный смысл. Теперь, когда введены
операции сложения и умножения упорядоченных пар действительных
чисел и показано, что любое комплексное число может быть записано
в виде комбинации упорядоченных пар действительных чисел, симво-
лам этих арифметических операций в записи (2) можно придать смысл
операций сложения и умножения пар.
§ 2.	Геометрическое изображение
и тригонометрическая форма записи
комплексных чисел
2.1.	Геометрическое изображение комплексного числа. Подобно
тому как действительные числа можно изображать точками числовой
прямой, комплексные числа можно изображать точками плоскости.
Возможность такого изображения основана на отождествлении множе-
ства комплексных чисел а+ Ы и множества пар действительных чи-
сел (а; Ь), которые в прямоугольной системе координат Оху можно
трактовать как координаты точек плоскости.
По сути дела эти равенства означают, что символом I обозначается
Корень уравнения
'	Ж2 + 1 «₽ 0»
84	ГЛ. 3. КОМПЛЕКСНЫЕ ЧИСЛА
Далее, с каждой точкой А координатной плоскости Оху можно
1 — >
связать вектор ОА, выходящий из начала координат и оканчивающийся
в точке Д. Поэтому комплексные числа допускают и еще одну геометри-
ческую интерпретацию: каждое комплексное число а+ bi можно
геометрически интерпретировать как вектор ОА с координатами (а; Ь)
<рис. 3.1). Координаты вектора О А при этом будут такими же, как
и координаты точки Д, а именно (а; Ь).
2.2.	Геометрическое изображение суммы и разности комплексных
чисел. Геометрическая интерпретация комплексных чисел позволяет
наглядно истолковать сумму и разность двух комплексных чисел. Пусть
даны два комплексных числа Zi =	+ b±i и г2 = а2 + b2i. Их сум-
мой будет комплексное число + z2 = (ty + а2) + (&i + b2) i. С дру-
гой стороны, известно, что при сложении векторов их соответственные
Нис. 3,1.	Рис. 3.2.
координаты складываются. Поэтому, если вектор OAt имеет коорди-
наты (af, дх) (рис. 3.2), а вектор О А 2 — координаты (а2;#2), то их
сумма (вектор ОВ) будет иметь координаты (ах a2i Ьг + Ь2). Век-
тор О В и есть геометрическое изображение суммы комплексных чи-
сел Zi И Z2.
Так как разность двух комплексных чисел Zi = ах+ b^i и z2 ==*
= а2 + b2i есть сумма комплексного числа гх и числа, противопо-
ложного комплексному числу z2, то геометрически ее можно изобразить
как сумму вектора ОДХ с координатами (ах; Ьг) и вектора О А 2 с ко-
ординатами (—а2, —Z?2) (рис. 3.3), т. е. как вектор ОВ с координа-
тами (аг — а2\ Ьг — &2)-
2.3.	Тригонометрическая форма записи комплексного числа. На-
ряду с записью комплексного числа в виде а + Ы, которая называется
алгебраической формой записи, также употребляется и другая, назы-
ваемая тригонометрической. Пусть комплексное число z = а + bi
изображается вектором ОА с координатами (а; Ь) (рис. 3.4). Обо-
значим длину вектора ОА буквой г:
г=|ОД|,
а угол, который он образует с положительным направлением оси Ох, —
через ф (угол ф считается измеренным в радианах).
Воспользовавшись определениями функций sin ф и cos ф;
sin ф = b/rl cos ф = а/г.
§ 2. ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ
85
комплексное число z = а+ bi можно записать в виде
z = г-(cos ср + i sin <р),	(1)
где г = V а2 + Ь2 , а угол ф определяется из условий
Ь	а
/g2 + Ь2	/а2 4- Ь2	'
Записи комплексного числа в виде (1) называется тригонометрии
ческой формой записи комплексного числа. Действительное число г
называется модулем комплексного числа и обозначается |г|, а угол ср,
измеренный в радианах, — аргументом комплексного числа г. Аргу-
мент Ф комплексного числа г обозначается Arg z.
Если комплексное число не равно нулю, то модуль его положи-
телен; если же г = О, т. е. а = b = 0, то и модуль его равен нулю,
Модуль любого комплексного числа, определен однозначно.
44
Рис. 8.3.
Рис. 3.4»
а
Если комплексное число г = а + Ы не равно нулю, то его аргу-
мент определяется формулами (2) с точностью до угла, кратного 2л.
Если же 2=0, то г = 0 и аргумент комплексного числа, равного
нулю, не определен.
Обычно для того, чтобы исключить неоднозначность, возникающую
при вычислении аргумента комплексного числа, используют понятие
главного значения аргумента комплексного числа (обозначение arg z),
считая, что arg г € (—л]. Аргумент комплексного числа г связан
с главным значением' аргумента соотношением
Arg z = arg z + 2л£, k £ Z.
I lycTb zt и z2 — два отличных от нуля комплексных числа,
записанных в тригонометрической форме:	-	*
21 = Гр (cos Ф1 + i sin ф^, z2 = (cos Фз + i sin ф2).
Произведение двух комплексных чисел zi и г2 есть комплексное число,
модуль которого равен произведению модулей сомножителей, а аргу-
мент — сумме аргументов сомножителей:
zt-z2 = rvr2- [cos (Ф1 + ф2) + i sin (ф2 + ф2)].
Вектор, изображающий произведение комплексных чисел zt и z2,
получается поворотом вектора zt против часовой стрелки на угол, рав-
ный ф2, и растяжением его в |z2 | раз (для случая |z2 | > 1 см. рис. 3.5).
СЗ	ГЛ. 8. КОМПЛЕКСНЫЕ ЧИСЛА
Частное двух комплексных чисел гх и г2 представляет собой комп-
лексное число, модуль которого равен частному модулей делимого и
делителя, а аргумент частного двух не равных нулю комплексных чи-
сел равен разности аргументов делимого и делителя:
г1 г /	ч .	.	-	,
77 = — • [cos (Ф1 — <р2) + I sin (<Р1 — <р2)].
Вектор, изображающий частное двух комплексных чисел zt и г2,
получается поворотом вектора, изображающего комплексное число zlt
по часовой стрелке на угол, равный.ф2, и сжатием его в |г2| раз (для
случая | z2 I > 1 см. рис. 3.6).
§ 3* Степень комплексного числа
3.1. Натуральная степень комплексного числа. Закон ассоциатив-
ности умножения комплексных чисел позволяет ввести понятие нату-
ральной степени комплексного числа:
п-й степенью комплексного числа z называется комплексное число wt
получающееся в результате умножения числа z самого на себя п раз:
w = zz-...«z ,	(1)
«сомножителей
Обычно используется следующая, более короткая запись:
W == 2п,	(2)
в которой число z называется основанием степени, а натуральное число
п — показателем степени.
. п-я степень комплексного числа z, заданного в тригонометрической
форме
z = г (cos ф + i sin ф),
вычисляется по формуле Муавра
гп «= И1 (cos nq> + i sin пф).
3.2. Корень л-й степени из комплексного числа. Корнем п-й
степени из комплексного числа г называется такое комплексное число wt
п-я степень которого равна z:
wn = z.
§ 3. СТЕПЕНЬ КОМПЛЕКСНОГО ЧИСЛА
87
Корень п-й степени из комплексного числа г обозначается симво-
лом -/7В отличие от корня из действительного числа, корень п-й
степени из комплексного числа определяется неоднозначно. Именно,'
в множестве комплексных чисел существует ровно п корней п-й степени
из данного комплексного числа.
Все корни п-й степени из комплекс-
ного числа z, заданного в тригонометриче-
ской форме
z = г (cos <p + i sin ф),
вычисляются по формуле
______«/- I__„ ф+2л& ।
/г = /7(cos------------+
+ I Sin	.
п '	Рис. 3,7,
где k = 0, 1, 2, п — 1.
Геометрически все корни п-й степени из комплексного числа 2=*
= г (cos ф + i sin ф) изображаются точками, лежащими на окруж-
ности с центром в начале координат, радиус которой равен а
центральные углы между радиусами, проведенными в соседние точки*
равны 2 л/п.
Пример. Вычислить корни четвертой степени из числа —L
Число —1 в тригонометрической форме может быть записано так2
—1 = Ь (cos я + i sin л).
Корни четвертой степени из числа —1 — это комплексные числа
—	4г7-/ л + 2л/г ,	. л + 2л& \
7-1 = 7^ (cos -----------+ [I sin	,
где k — 02	2, 3, т. е. комплексные числа
л . п ]/~2 , 72 .
cos — +1 Sin -5- = -4-+-4- I,
Зл • , . . * Зя
cos —k t sm ——
4 1	4
5л , . . 5л
COS-T—+ I Sin—7—
4 1	4
2*2
72 , 72 .
2 + 2 ’»
72	72 .
Г1’
2 ‘
2
72
2
7л ... 7л
COS—7- + t sin ——
4	‘	4
(см. рис. 3.7).
Аналогичным образом в множестве комплексных чисел можно вы-
числить корень п-й степени из любого действительного числа. При
этом хотя бы один корень из положительного действительного числа
будет действительным.
ГЛАВА 4
АЛГЕБРА
Термин «алгебра» происходит от названия сочинения Мухаммеда
аль-Хорезми «Альджебр аль-мукабала» (IX век), содержащего общие
методы решения задач, сводящихся к уравнениям 1-й и 2-й степени.
К середине XVII века в основном сложилась современная алгебраиче-
ская символика. Вплоть до XVIII века под алгеброй понималась наука
о буквенных вычислениях — тождественные преобразования буквен-
ных формул *), решение уравнений первой — четвертой степеней, лога-
рифмы, прогрессии, комбинаторика. В настоящее время все эти разделы
алгебры принято называть элементарной алгеброй.
В XVIII—XIX веках предмет алгебры — это прежде всего изуче-
ние многочленов, теория алгебраических уравнений с одним неиз-
вестным, теория систем линейных уравнений с несколькими неизвест-
ными, а также теория матриц и определителей.
Третий (современный) этап развития алгебры как науки об алгеб-
раических операциях начался в.середине XIX века и был связан с по-
явлением разнообразных примеров алгебраических операций над объ-
ектами совсем иной природы, нежели действительные числа. Первыми
такими примерами явились умножения подстановок и операции над
комплексными числами.
§ 1.	Многочлены одного переменного
1.1.	Понятие многочлена. Арифметические операции над много-
членами. Произведение вида ахп, где а — отличный от нуля числовой
коэффициент, а п — неотрицательное целое число, называется одно-
членом относительно переменной х. Число п называют степенью одно-
члена.
Два одночлена ал/1 и bxk называются подобными, если п ~ k.
Замена суммы двух подобных одночленов ахп + на одночлен
(а + Ь) хп называется приведением подобных членов.
Многочленом (полиномом) п-й степени относительно переменной
величины х называется выражение вида
Р (х) = а^хп 4- Ci л/2 1 4“ a,zxn 2 4* • • • 4- an.jX 4"	(D
где п — неотрицательное целое число; а0,	а2, ...» a^i, ап — коэф*
фициенты многочлена, причем Oq, называемый старшим коэффициентом,
считается не равным нулю.
Многочлен первой степени также называют линейным многочленом,
многочлен второй степени — квадратным, а многочлен третьей сте-
пени — кубичным многочленом.
*> В алгебре, в отличие от арифметики, имеют дело не с числами, а с бук*
венными выражениямнв называя их алгебраическими выражениями»
§ L МНОГОЧЛЕНЫ ОДНОГО ПЕРЕМЕННОГО	89
Запись многочлена в виде (1) называется записью по убывающим
степеням х\ именно этой записью мы и будем пользоваться в дальней-
шем, если не будет оговорено противное. Каждое из слагаемых в выра-
жении (1) называется членом многочлена.
Из определения многочлена n-й степени следует, что существуют
многочлены n-й степени для любого Неотрицательного л. В частности,
любое отличное от нуля действительное число является многочленом
нулевой степени. Число нуль также считается многочленом; это един-
ственный многочлен, степень которого не определена.
Два многочлена Р (х) и Q (х) считают равными (или тождественно
равными), если равны их коэффициенты при одинаковых степенях
переменной х, и пишут
P(x)=Q(x).
Суммой многочленов .
Р 00 = Ч* Ч~ «-J* *1 * + апл* Ч"
Q (х) » box'” + bix”1’’"1 Ч~ b2xm~~2 Ч- • • • Ч- Ч~ бщ
называется многочлен 3 (х), коэффициенты которого при каждой сте-
пени х равны сумме коэффициентов при этой степени х многочленов Р (х)
и Q (х). О многочлене 3 (х) говорят, что он получен в результате сложе-
ния многочленов Р (х) и Q (х), и пишут
3(х)=Р(х)Ч-0(х).
Пример 1. Суммой многочленов Р (х) = х4 —* х3 + 3 и
Q (х) = 2х3 — х + 2 является многочлен
3 (х) = х4 + х3 — х Ч~ 5.
Произведением многочленов
Р (х) == aQxn Ч- а1хп'^1 Ч~ а2хп~2 Ч- • • • + ап-1х 4“
Q (х) == ЬоХт 4“ Ь]Хт~~1 + b2xm"~2 + • • • 4“ &т-1х + Ьт
называется многочлен М (х) степени п +.т, коэффициенты которого г0>
Q, ^2» -•••!	С/н/n вычисляются по формулам
Со = «о^о,
Г1 = а^о Ч- uoblt
Ck = akbo Ч“ ak-ibi + • • • Ч~ aibk-i + a(fih>
Cn+m — CLnbmt
т. e. коэффициент ct есть сумма произведений коэффициентов а/ и bk
многочленов Р (х) и Q (х) таких, что сумма их индексов равна i (I Ч~
Ч~ k = i). О многочлене М (х) говорят, что он получен в результате
умножения многочлена Р (х) на многочлен Q (х), и пишут
Л4(х) = P(x)-Q(x).
Пример 2. Произведением многочлена второй степени Р (х) =»
= х2 + 1 на многочлен четвертой степени Q (х) = 2х* — х + 3 яв-
ляется многочлен шестой степени
М (х)= P(x)<Q(x) = 2х6+ 2х4 —х3Ч" Зх2-х+ 3.
90
ГЛ. 4. АЛГЕБРА
Операции сложения и умножения многочленов ассоциативны, ком-
мутативны и связаны между собой законом дистрибутивности.
Противоположным для многочлена
р (х) = сохп +	4- а2^2 + • • • 4- ап^х 4 ап
называется многочлен
—ацхп —	— а2хп~2 — • • • — аплх — ап.
Многочлен, противоположный многочлену Р (х), обозначают — Р (х).
Сумма .многочлена Р (х) и противоположного ему многочлена — Р (х)
равна нулю:
Р (х) + (—Р (х)) = 0.
Разностью многочленов Р (х) и Q (х) называется многочлен L (х),
являющийся суммой многочлена Р (х) и многочлена, противополож-
ного многочлену Q (х):
L« = P(x)+(-Q(x)).
О многочлене L (х) говорят, что он получен в результате вычитания
многочлена Q (х) из многочлена Р (х), и пишут
£ (х) = Р (х) —- Q (х).
Сумма, произведение и разность любых двух многочленов — тоже
многочлены.
1.2.	Делители многочлена. Если для заданных многочленов Р (х)
н Q (х) найдется многочлен G (х) такой, что
Р(х)= Q(x).G(x),
то говорят, что многочлен Р (х) делится (или нацело делится) на много-
член Q (х); при этом многочлен Q (х) называют целым делителем (или
просто делителем) многочлена Р (х), а многочлен G (х) — частным
многочленов Р (х) и Q (х). Если многочлен Q (х) — делитель много-
члена Р (х), то и частное G (х) — делитель многочлена Р (х).
Основные свойства делителей многочлена:
1)	Если многочлен Р(х) делится на многочлен К (х), а К (х) де-
лится на многочлен Q (х), то и Р (х) делится на Q (х).
2)	Если многочлены Р (х) и К (х) делятся на многочлен Q (х),
то их сумма и разность также делятся на Q (х).
3)	Если многочлен Р (х) делится на многочлен Q (х), то произве-
дение Р (х) на любой многочлен К (х) также делится на Q (х).
4)	Всякий многочлен Р (х) делится на любой многочлен нулевой
степени (т. е. на число, отличное от нуля).
5)	А^ногочлены cP (х) и только они являются делителями много-
члена Р (х), имеющими такую же степень, что и Р (х).
6)	Многочлены Р (х) и Q (х) тогда и только тогда одновременно де-
лятся друг на друга, когда Р (х) = cQ(x) (с=^0).
Наибольший общий делитель двух много-
членов. Многочлен Р (х) называется общим делителем для много-
членов Р (х) и Q (х), если он служит делителем для каждого из этих
многочленов. Согласно свойству 4) (см. выше) общими делителями про-
извольных многочленов Р (х) и Q (х) будут все многочлены нулевой сте-
пени (т. е. все действительные числа, за исключением числа нуль).
Если других общих делителей два многочлена не имеют, то эти много*
члены называются взаимно простыми,
§ 1. МНОГОЧЛЕНЫ ОДНОГО ПЕРЕМЕННОГО	91
Наибольшим общим делителем многочленов Р (х) и Q (х) называется
такой многочлен D (х), который является их общим делителем и вместе
с тем сам делится на любой общий делитель этих многочленов.
Если D (х) является наибольшим общим делителем многочле-
нов Р (х) и Q (х>5 то наибольшим общим делителем этих многочленов
будет и многочлен cD (х), где с — произвольное число, отличное от нуля,
т. е. наибольший общий делитель двух многочленов определен лишь
с точностью до постоянного множителя. Чтобы добиться полной одно-
значности в определении наибольшего общего делителя двух много-
членов, обычно выставляют следующее условие: из всех многочле-
нов cD (х) наибольшим общим делителем называется тот, у которого
старший коэффициент равен единице.
Теперь можно сказать» что два многочлена являются взаимно
простыми, если их наибольший общий делитель равен единице.
1.3.	Деление многочленов. Схема Горнера. Теорема Безу. Пусть
Р (х) и Q (х) — заданные многочлены и степень многочлена Р (х)
больше или равна степени многочлена Q (х). Если оказывается, что
многочлен Р (х) не делится (нацело) на многочлен Q (х), т. е. не суще-
ствует многочлена G (х) такого, что
Р (х) = Q (x)-G (х),
то вводят операцию деления многочленов с остатком.
Разделить многочлен Р (х) на многочлен Q (х) с остатком — это
значит найти два многочлена G (х) и R (х) таких, что
Р(х)= Q(x).G(x)+/?(x),	(2)
причем степень многочлена R (х) меньше степени многочлена Q (х).
Многочлен Р (х) называется делимым, Q (х) — делителем, 6 (х}-~
частным, а Р (х) — остатком. При делении многочлена Р (х) на много-
член Q (х) многочлены G (х) и R (х) находятся однозначно.
Для деления многочлена на многочлен обычно применяется пра-
вило «деления углом». Для этого располагают многочлены Р (х) и Q (х)
но убывающим степеням х и находят старший член частного G (х)
из условия, что при умножении его на старший член делителя Q (х)
должен получиться старший член делимого Р (х). Найденный старший
член частного умножают затем на делитель и полученный многочлен
вычитают из делимого. В результате вычитания получается многочлен
Р] (х). Следующим членом частного будет такой одночлен, который,
будучи умноженным на старший член делителя Q (х), дает стар-
ший член многочлена Рг (х), и т. д. Процесс продолжается до тех пор,
пока степень очередной разности (т. е. степень некоторого многочлена
г\(х)) не станет меньше степени делителя. Многочлен Рь (х) и будет
остатком от деления многочлена Р (х) на многочлен Q(x).
В результате деления многочлена n-й степени Р (х) на многочлен
степени Q (х) (k п) в частном получается многочлен сте-
пени п —
Пример. Разделить многочлен Р (х) = х* + х3+ Зх2 + Зх+ 2
на многочлен Q (х) ~ х2+ х+ 1.
Старшим членом многочлена Р (х) является член х4, а старшим
членом многочлена Q (х) — член х2. Разделив х4 на х2, получим х2
Одночлен х2 — старший член частного. Умножая одночлен х2 на много-
член Q (х), получаем многочлен х4 + х3 + х2» Вычтем этот многочлен
92	ГЛ'. 4. АЛГЕБРА
из многочлена Р (х):
(х*+ х3 + Зх2 + Зх+ 2) — (х4 + х3 + х2) =
= 2х2 + Зх + 2 = Pi (х).
Так как степень многочлена Р$ (х), получившегося в результате
вычитания, не меньше степени многочлена Q (х), можно продолжить
процесс деления; делим старший член 2х2 многочлена Р^ (х) на старший
член многочлена Q (х):
х2
Многочлен нулевой степени (число 2) будет следующим членом част-
ного.
Умножаем многочлен Q (х) на число 2. В результате умножения
получается многочлен 2х2 + 2х+ 2, который мы вычитаем из много-
члена Pi (х):
Pi (х) - (2х2+ 2х+ 2) = 2х2+ Зх+ 2 —(2х2 + 2х+ 2) =
= х = Р2 М.
На этом процесс деления прекращается, так как степень много-
члена Р2 (х) меньше степени многочлена Q (х). Многочлен Р2 (х) и бу-
дет остатком от деления многочлена Р (х) на многочлен Q (х). Вся опи-
санная процедура деления многочлена Р (х) на многочлен Q (х) коротко
отражается в следующей записи:
, х4 + X3 + Зх2 + Зх + 2 I х2 + х+ 1
х4 + х3 + х2	I х2 2
2х2 + Зх + 2
~ 2х2 + 2х + 2
х
Таким образом, частное от деления многочлена
р (х) = *4+ х3 + Зх2+ Зх + 2
на многочлен Q (х) == х2 + х + 1 есть многочлен G (х) = х2 + 2,
а остаток — многочлен Р (х) == х, т. е. многочлен Р (х) может быть за-
писан в виде	j
х4^ х3 + Зх2 + Зх + 2 = (х2 + х + 1) (х2 + 2) + х.
Схема Горнера. Теорема Бе з у. Для^еления много-
члена n-й степени Р (х) = а^п + а1хп~1 +• • •+	+ ап на много-
член первой степени х — с обычно используется метод сокращенного
деления (называемый схемой Горнера). Он получается как следствие
определения операции деления многочленов, из которого следует, что
при делении многочлена n-й степени на линейный многочлен х—с
в остатке может получиться либо многочлен нулевой степени (т. е. от-
личное от нуля число), либо нуль, а степень частного равна п — L
Пусть частное многочленов Р (х) и х—с имеет вид
G (х) = аахПч₽1 -f- aixn~2 + • • • + an.2X +
§ 1. МНОГОЧЛЕНЫ ОДНОГО ПЕРЕМЕННОГО	93
а остаток R (х) равен числу ₽. Для рассматриваемого случая формула
(2) принимает вид
сохп + GjX71*"1 +	• • • + ЯдЛ* 4~ ап =*
= (х — с) (аоХ71^1 + ai%n“"2 + • • ♦ 4- ссд.гХ + ад.л) + Р* (3)
Раскрывая скобки и приводя подобные члены в правой части ра-
венства (3), на основании определения равенства многочленов полу-
чаем систему линейных уравнений для нахождения коэффициентов 04,
^1» ^2» •••» ®Я-2>	1> Р«
«0 = #0>
ai = ax 4- ca01
Ct 2 г*= ^2 4"
an_i = ^дл + саП-.2>
Р == Од 4'
Эту систему называют схемой Горнера.
Первое уравнение системы дает значение а0 = aQ, Подставляя
это значение а0 во второе уравнение системы, получаем ах = Я] ~Ь
4- caQ. Подставляя полученное значение ос-, в третье уравнение системы,
получаем значение а2, и т. д. Последним будет найдено выражение для
остатка Р:
Р = а§сп 4“ aicn~~l 4- a2cn^ 4- • • • 4“ ад-1^ 4" ап*
Это равенство известно под названием теоремы Безу:
Многочлен аохп +	+• • •+ a/z-i* + ап при делении на х—с
дает остаток, равный значению этого многочлена при х=с.
1.4. Алгоритм Евклида нахождения наибольшего общего делителя
двух многочленов. &Пусть \Р (х) и Q (х) — два произвольных много-
члена и степень многочлена Р (х) больше или равна степени много-
члена Q (х). Делим многочлен Р (х) на многочлен Q (х), т. е. нахо-
дим частное G (х) и остаток R (х) от деления этих многочленов.
Делим затем Q (х) на R (х) и получаем остаток 7?х (х); делим R (х)
на (х) и получаем остаток R2 (х); делим	(х) на R2 (х) и т. д.
Так как степени остатков все время понижаются, то в этой цепочке
последовательных делений через конечное число шагов появятся два
многочлена Rn-i (х) и Rn (х) таких, что Rn_l (х) разделится на
Rn (х) нацело. Тот остаток Rn (х), на который нацело делится
предыдущий остаток Rn~t (х), и будет наибольшим общим дели-
телем многочленов Р (х) и Q (х). Правда, следует заметить, старший
коэффициент этого наибольшего общего делителя не будет, вообще го-
воря, равен единице.
Наибольший общий делитель двух многочленов 'со старшим коэф-
фициентом, равным единице, получится, если все коэффициенты полу-
ченного общего делителя поделить на коэффициент при старшем
члене.
94
ГЛ. 4. АЛГЕБРА
Для наглядности запишем алгоритм Е в к л и д а в виде це-
почки равенств:
P(x)==Q(x).G(x) + P(x),
Q(x) = R(x)^G1(x) + Ri(x)f
R (х) == Ri (x) • G2 (x) + R2 (x),
Pi (x)==P2 (x)-G3 (x) + /?3 (*),
Rn_2 (x) = PnJ (x)*Gn (x) Rn (x)f
Pn_i (x) = Rn (x)-Gn+i (x).
Отметим еще раз, что наибольшим общим делителем многочленов Р (х)
и Q (х) будет многочлен Рл (х), поделенный на старший коэффициент.
Алгоритм Евклида нахождения наибольшего общего делителя двух
многочленов полностью аналогичен алгоритму Евклида нахождения
наибольшего общего делителя двух натуральных чисел.
Пример. Найти наибольший общий делитель многочленов
Р (х) == х5 — х4 — 2х3+ 2х2+ х — 1, Q (х) = х3 — 1.
Разделив «углом» многочлен Р (х) на многочлен Q (х):
__х® — х4 — 2х3 + 2х2 + х — 1 I х3 — 1
а?____________— х2__________ |ха — х — 2
__ —х4 ~ 2х3 + Зх2 + х
—	X4___________X
—	2х3	+ Зх2	—1
	—2х3	-f-2
Зх2 — 3
получим частное — многочлен G (х) — х2 — х — 2 и остаток — много-
член R (х) — Зх2 — 3.
Делим многочлен Q (х) на остаток Р (х):
х3 — 1	3x2 — 3
Частное обозначаем Gj (х), а остаток Rf (х). В согласии с алгорит-
мом Евклида делим остаток предыдущего деления R (х) на получив-
шийся остаток Pi (х);
Зх2 — 3 х — 1
Зх2 — Зх Зх + 3
__3х —3
Зх — 3
О*
Многочлен Р (х) = Зх2 — 3 нацело разделился на многочлен
Pi (х) = х — 1. Следовательно, многочлен х — 1 является наиболь-
шим общим делителем двух данных многочленов Р (х) и Q (х).
1.5, Корни многочлена. Пусть
Р (х) = Oqx" +	+ аа*ч'“’2+• • 	+ «л
§ I. МНОГОЧЛЕНЫ ОДНОГО ПЕРЕМЕННОГО	95
— некоторый многочлен n-й степени. Возьмем число с и подставим его
вместо переменной х в многочлен Р (х). Полученное число
И- ait/1-1 + 02е””"2 + • • •+ о>плс + ап называется значением много*
члена Р (я) при х ® с и обозначается Р (с). Число с называется корнем
многочлена Р (х), если число Р (с) — нуль.
Связь между корнем многочлена и существованием делителя много-
члена устанавливается следующей теоремой:
Если число с — корень многочлена п-м. степени Р (х), то многочлен
Р (х) делится на линейный многочлен х—с, т. е. многочлен Р (х) можно
представить в виде
где Q (х) — многочлен степени п — 1.
Может оказаться, что многочлен л-й степени Р (х) делится не
только на линейный многочлен х—с, но и на его более высокую степень,
т. е. на многочлен вида (х—c)k, где k — натуральное число, большее
единицы. Число с называется корнем кратности k многочлена Р (х)
(или k-кратным корнем), если многочлен Р (х) делится на многочлен
(х—c)k, но не делится на многочлен (х—с)^1. Если многочлен Р (х)
делится на линейный многочлен х—с, но не делится на (х—с)\ то число с
называют простым корнем многочлена Р (х).
Для того чтобы число с было ^-кратным корнем многочлена Р (х),
необходимо и достаточно, чтобы число с было (k — 1)-кратпым корнем
производной от многочлена Р (х), т. е. многочлена Р' (х).
1.6. Формулы сокращенного умножения. Так как число с является
корнем многочлена хп — d1 (п — любое), а число (— с) — корнем много*
членов хп—сп (п — четное} и хп + d1 (п — нечетное), то:
1)	многочлен х"—d1 делится на двучлен х—с при любом натураль*
НОМ п\
2)	многочлен х”—d1 делится на двучлен х + с при любом четном п;
3)	многочлен хп + сп делится на двучлен х + с при любом нечет-
ном п.
В результате деления получаются соответственно многочлены
(л — 1)-й степени:
+ хп~*с -{- jc"*3? 4-... 4- хсп-2 4- с"*1 =
n—1
«к J] х"мс* (п—любое);
£=о
— ~~	= х***4 — хп^2с + хп~~3с2 — ... 4- xd1^2 —	=
к + о	1
л—1
8= У (— 1)^ хГ1"т‘А:’~1с& (л —четное);
*=о
~+с'>  = Xя-’ - х”*2С 4-	- . .. - хс”“2 4- (Г*' =
X с
л—1
S (—(п — нечетное).
л=о
ГЛ. 4. АЛГЕБРА
96
В частности, из приведенных равенств следуют простейшие форму-
лы, называемые формулами сокращенного умножения:
(х + с) (х—с) = X2 — с2,
(х + с) (х2— хс + с2) = х3 + с3,
(х—с) (х2 + хс + С2) = х3 — с3.
1.7.	Формулы Виета. Между корнями cj, с2, ..., сп многочлена
п-й степени
Р (х) == хп + <2ixn“'1 + а2хп~2 + • •. + an_ix + aTi
со старшим коэффициентом, равным единице (каждый корень взят та-
кое число раз, какова его кратность), существуют зависимости, назы-
ваемые формулами Виета:
Ci + С2 + £з + • • • + cn-i + Сп == —fli,
С1С2 + С1С3 -[-••*+	»= a2i
С1С2Г3 4- С1Г2С4 4* • •“ + ^П-2Гп-1^П == —Оз»
С1С2Сз-.-Сп-1Сп = (—1)?ПП.
Если Р (х) — квадратный трехчлен, т. е.
Р (х) = х2 + рх + qt
а числа с± и с2 — его корни, то формулы Виета имеют вид
+ с2 = —Pt с\съ e Я-
Если Р (х) — кубичный многочлен, т. е.
Р (х) = х3 + рх2 + qx+ rt
а числа Ci, c2i с3 — его корни, то формулы Виета имеют вид
Ci + с2 + с3 = — р,	сгс2 + с2с3 + СхС3 = qt схс2с3 = —г.
1.8.	Основная теорема алгебры. Вводя - понятие корней много-
члена, мы не ставили вопроса о том, всякий ли многочлен с действитель-
ными коэффициентами имеет корни. Известно, что существуют много-
члены с действительными коэффициентами, не имеющие действитель-
ных корней (х2 + 1 — один из таких многочленов}, и именно этот факт
послужил одной из причин введения новых математических объектов —
комплексных чисел. Можно было бьь ожидать, что существуют много-
члены, не имеющие корней даже в множестве комплексных чисел, осо-
бенно если рассматривать многочлены с любыми комплексными коэф-
фициентами (частным случаем которых являются многочлены с действи-
тельными коэффициентами). Если бы это было так, то система комплекс-
ных чисел нуждалась бы в дальнейшем расширении. На самом деле,
однако, справедлива следующая основная теорема ал-
гебры:
Всякий многочлен п*й степени с комплексными коэффициентами
в множестве комплексных чисел имеет ровно п корней) если каждый
кратный корень считать такое число раз, какова его кратность.
Все доказательства этой теоремы (а их найдено весьма много)
основаны на использовании свойства непрерывности множеств действи-
§ I. МНОГОЧЛЕНЫ ОДНОГО ПЕРЕМЕННОГО
97
тельных и комплексных чисел, вследствие чего все эти доказательства
нельзя считать чисто алгебраическими.
Основная теорема алгебры справедлива и при п — 0, так как много-
член нулевой степени корней не имеет. Основная теорема алгебры не-
применима лишь к нулевому многочлену (числу нуль), степень которого
не определена.
1.9.	Разложение многочлена на множители. По основной теореме
алгебры многочлен n-й степени
Р (х) « а^хГ1 4» aix^””1 + azxn^ 4** • •+ an_ix 4- ап
с любыми комплексными (и, в частности, действительными) коэффи*
циентами имеет п корней (с учетом их кратностей) и, следовательно, де-
лится нацело на линейные многочлены
X—Clt X—С2, •••» Х—Сп,
где cit с2, ...» сп — корни многочлена; значит, многочлен Р (х) предста-
вим в виде произведения п линейных сомножителей:
Р (х) == а0 (х—сД (х—й)’ • • (х—сп).
Разложение многочлена Р (х) в произведение линейных многочле»
нов единственно р точностью до порядка следования сомножителей.
1.10.	Некоторые следствия основной теорёмы алгебры для много-
членов с действительными коэффициентами. Если комплексное (но
не действительное) число с = а 4~ & является корнем многочлена п-й
степени с действительными коэффициентами, то и число с = а — Pi,
комплексно сопряженное с числом с = а 4* Pi, будет корнем данного
многочлена.
Из свойства сопряженности комплексных корней многочлена
с действительными коэффициентами следует, что всякий многочлен
нечетной степени с действительными коэффициентами имеет по крайней
мере один действительный корень.
Пусть Р (х) — многочлен n-й степени с действительными коэффи-
циентами, а с == а + Pi — его корень. Тогда число с = а — Pi также
является корнем многочлена Р (х), и, следовательно, многочлен Р (х)
может быть представлен в виде
Р (х) — (х —с) (х—с) Q (х),
где Q (х) — многочлен (п — 2)-й степени. Так как произведение
(х—с) (х——с) — х2 — (с 4- с) х 4- сс = х2 — 2ах + а2 4“ Ра
представляет собой многочлен второй степени с действительными коэф-
фициентами, то и все коэффициенты многочлена Q (х) также будут
действительными числами.
Таким образом, всякий многочлен с действительными коэффи-
циентами представим, и притом единственным пособом (о точностью
до порядка сомножителей), в виде произведения своего старшего коэф-
фициента а0, нескольких линейных многочленов с действительными
коэффициентами вида х—с, соответствующих его действительным кор-
ням, и квадратных многочленов х2 — (с 4“ с) х 4* сс, соответствующих
парам сопряженных комплексных корней.
Заметим, что среди многочленов с действительными коэффициен-
тами и со старшим коэффициентом, равным единице, неразложимыми
на множители меныпей степени в множестве действительных чисел
4 А. Г. Цынлин
98	ГЛ. 4. АЛГЕБРА
{неприводимыми многочленами) являются лишь линейные [многочлены
х—с и квадратные многочлены вида ха — (с + с) х + сё.
Установленное свойство многочленов с действительными коэффи-
циентами аналогично свойству разложимости любого натурального
числа на простые сомножители. Для любого многочлена Р (х) п-й
степени с действительными коэффициентами и первым коэффициентом,
равным единице, можно написать разложение, аналогичное канониче-
скому разложению натуральных чисел (см. п. 1.3 гл. 2):
Р (X) = (X — С!)*1 (X — сг)*а ... (X — Clfi (Ха — (С/+1 + СМ) X 4-)
+	4- Cl+m) X +
+ ^2 + • • • + &/ + 2 (&/+i + • • • + ki+m) = П,
где ci, c2f ...» Ci — .действительные корни многочлена с кратностями ki,
k2, ...» ki, a {c/+i; c/+i}, ..., {ci+m> ci+m}— пары комплексно сопряжен-
ных корней с кратностями ki+i, ..., ki+m соответственно.
§ 2, Многочлены нескольких переменных
2.1. Одночлены и многочлены нескольких переменных. Выражение
вида
^14 ---V»
где a — отличный от нуля числовой коэффициент, a k±9 k2,..., kn —
неотрицательные целые числа, называется одночленом от п переменных
хъ x2l •••> хп» одночлена от п переменных
ах{ *х2 2... хпп и bxfx22,.. хлп
называются подобными, если	= Z2,	= Zrt.
Замена суммы двух подобных одночленов ахх Ч2 2« • *xknn + bx\*х2 а- • •
на равный им одночлен (а+ Ь) х^х^* • *х^п называется приве*
дением подобных членов.
Многочленом Р (xj, х2,хп) от п переменных х^ х2, хп
называется сумма конечного числа одночленов вида ах^х22» • •х^п
Одночлены, образующие многочлен, называются членами многочлена.
При этом предполагается, что в многочлене Р (х±, х2, х8, ..., хп)
все подобные члены уже приведены и что рассматриваются лишь члены
с отличными от нуля коэффициентами. Степенью многочлена Р (xlt
х2, х3, ...» хп) по отношению к некоторой выбранной переменной xt (i
— 1, 2, 3, ...» п) считается наивысший показатель, с которым перемен-
ная xt входит в многочлен.
Степенью одночлена
(или степенью по совокупности переменных) называют число
#1+ ^а+ &з + ’,’+ kni
/
§ 2. МНОГОЧЛЕНЫ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ Q9
т, е. сумму показателей степеней всех переменных х;, входящих в дан-
ный одночлен. Наибольшее значение суммы + k2 +	+ • • •+ kn,
встречающееся в каком-либо из членов многочлена, называется степенью
многочлена по совокупности всех переменных.
Многочлен Р (xj, х2, х3, хп) называют однородным, если степени
всех одночленов, входящих в многочлен, равны.
2.2. Лексикографическое расположение членов многочлена. В то
время как для многочленов от одной переменной существуют два есте-
ственных способа расположения членов многочлена — по убывающим
и по возрастающим степеням переменной, для многочленов от несколь-
ких переменных таких естественных способов уже не существует. Су-
ществует, однако, часто используемый способ вполне определенного
расположения членов многочлена от нескольких переменных, называе-
мый «лексикографическим». Этот способ аналогичен способу располо-
жения слов в словарях: считая буквы упорядоченными так, как это
принято в алфавите, мы определяем взаимное расположение двух слов
в словаре по их первым буквам; если же первые буквы совпадают, то
по вторым буквам, и т. д.
Пусть Р (xj, х2,	•••> хп) — многочлен от п переменных х19 x2t
х3...... и пусть
ykn и	jn
xl *2 Х3 * * *ХП И *1 Х2 Х3 ‘ * *Хп
— два различных члена данного многочлена. Следовательно, хотя бы
одна из разностей показателей степеней
k± 4» ^2	^2» •••>	“ In	(1)
__	ka
отлична от нуля. Член х/х2	• *хл * считается выше члена
х^х2/2хз3*»»хл/п, если первая отличная от нуля разность в (1) положи-
k-i ka k„
тельна. В противном случае член Xjх2 ,,,хп считается ниже члена
х^х^-’Х^. Другими словами, член х^х^х/* • *х*л выше члена
я^х^Хз3- *«х*п, если > Ц или если kx = lv то fc2> 12 и т. Д. Заме-
<гим, что из того, что член x11x24x3it-^xnn выше члена х{гх2Зх38-•
вовсе не следует, что степень члена х^х^х*3* • «х*п больше степени члена
х^х^Хз3* ••хлп. Так, например, член xfx2 считается выше члена XjX2,
хотя его степень (по совокупности переменных) меньше.
Сравнивая между собой все члены многочлена Р (xj, х2, ..., хп),
выделяем из них тот, который выше всех остальных, и записываем его
на первом месте. Сравниваем оставшиеся члены многочлена и выделяем
из них наивысший, который записываем на втором месте, и т. д. В ре-
вультате получим запись многочлена от п переменных, в которой каж-
дый член, начиная со второго, ниже предыдущего.
Эта форма записи называется лексикографическим способом записи
многочлена от нескольких переменных. Член многочлена, стоящий на
первом месте, считается высшим членом многочлена.
Пусть
Р (*р *2» *з) = *1*2*3 + *1*2*3 + *1*2*3 + *1*2*3	(2)
— многочлен трех переменных.
4*
100
ГЛ. 4. АЛГЕБРА
Запишем многочлен, располагая его члены в лексикографическом
порядке.
В записи (2) второй член выше всех остальных, так как в этом члене
переменная xj возводится в наибольшую степень по сравнению с осталь-
ными членами. Значит, член х$х%х3 будет первым в лексикографической
записи многочлена (2).
Вторым членом в лексикографической записи будет первый член
записи (2), так как в этом члене переменная х± возводится в наиболь-
шую степень среди оставшихся членов.
Из двух оставшихся членов (третьего и четвертого записи (2))
третий будет выше четвертого, так как в этих членах степени перемен-
ных xi и х2 равны, а переменная х8 в третьем члене возводится в боль-
шую степень, нежели в четвертом.
Запись многочлена Р (х±, х2, х8) с членами, расположенными в лек-
сикографическом порядке, будет следующей:
Р (Хр #2> *3) = *1*2*3 + *1*2*3 + *1*2*3 “Ь *1*2*3*
§ 31	Рациональные алгебраические дроби
3.1.	Множество рациональных алгебраических дробей» Рационалъ*
ной алгебраической дробью называют выражение вида
(или P/Q),	«	(1)
где Р и Q — многочлены одной или нескольких переменных. Мнрго*
член Р называется числителем дроби, а многочлен Q — ее знаменателем.
Рациональную алгебраическую дробь также называют рациона лъ*
ным алгебраическим выражением.
Рациональная алгебраическая дробь (1) определена при всех зна-
чениях переменной х, за исключением конечного набора значений, об-
ращающих многочлен Q (х) в нуль (корней многочлена Q (х))*). Мно-
жество значений переменной х, при которых знаменатель дроби отличен
от нуля, называют множеством допустимых значений алгебраической
дроби.
Две рациональные дроби Р (x)/Q (х) и М (x)/N (х) называются
равными:
Р(х) _ М(х)
Q (х) ~ N (х) ’
если Р (х)*М (х) ® Q (х)-Л1 (х) при всех значениях х, при которых
Q (х) Ф 0 и N (х) Ф 0.	*
Из определения равенства дробей следует, что если числитель и
знаменатель дроби умножить на один и тот же многочлен К (х), то полу-
чится дробь, равная исходной:
Р(х)	Р(х)-К(х)
Q(*)	Q(x)K(x) •
На этом свойстве основано правило сокращения рациональных
алгебраических дробей: деление числителя и знаменателя дроби на
их общий делитель, а также приведение дробей к общему знаменателю.
•) Далее, если не оговорено противное, будем рассматривать дроби>
числитель и знаменатель которых >» многочлены одной переменной»
§ 3. РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ ДРОБИ Ю1
В результате сокращения алгебраической дроби, вообще говоря, по*
лучается алгебраическая дробь с множеством допустимых значений,
не совпадающим с множеством допустимых значений исходной дроби.
Сумма, произведение, разность и частное двух дробей Р/Q и MIN
вычисляются по правилам
Р	М	__	P-N + Q-M	.	Р	М	_	Р>М
Q + N	~	Q-N	’	Q	’	N	“	Q./V	9
Р	М	_	P-N — Q-M	.	Р	.	М	Р
Q	N	~	Q-N	9	Q	:	N	~	Q-M	9
причем частное определено при всех тех допустимых значениях пере*
менной х дробей Р/Q и М/N, при которых М. (х) #= 0.
Операции сложения и умножения рациональных алгебраических
дробей ассоциативны, коммутативны и связаны законом дистрибутив*
ности умножения относительно сложения.
Более строго, множество рациональных алгебраических дробей
может быть определено следующим образом.
Рациональными алгебраическими дробями называют упорядочен*
ные пары (Р; Q) двух многочленов, определяемые перечисленными ниже
свойствами.
Две упорядоченные пары (рациональные дроби) (Р; Q) и (М; N)
называют равными и пишут
(Р; Q) == (АГ; А),
если Р • N = Q* М при всех значениях, при которых Q (д') ¥= 0 и
N (х) Ф 0.
Суммой двух пар (Р; Q) и (M; N) называется пара (P*N +
Q'N). Об этой паре говорят, что она получена в результате сложения
пар (Р; Q), (2И; N), и пишут
(Р; Q) + (М; Х) = (P-N+ Q-M-, Q-N).
Ассоциативность и коммутативность операции сложения пар еле*
дует'из определения суммы пар и соответствующих свойств операций
сложения и умножения многочленов.
В множестве упорядоченных Пар многочленов операция вычита*
ния, обратная операции сложения, всегда выполнима, т. е. для любых
двух пар (Р; Q) и (Af; N) существует пара (X; У) такая, что
(Af; N) + (X; У) = (Р; Q).
Пару (X; У) называют разностью пар (Р; Q) и (М; М), обозначают
(Р; Q) — (Af; N) и вычисляют по формуле
(Р; Q) —(2И; N) = (P-N - Q<M; Q-N).
В частности, из определения разности пар следует, что
(Р; Q) - (Р; Q) == (0; Q).
Пары вида (0; Q) называют нулевыми парами.
Произведением двух пар (Р; Q) и (Af; N) называется пара (Р-АГ;
Q-N). О паре (Р-А4; Q-N) говорят, что она получена в результате
умножения пар (Р; (?) и (А4; А), и пишут
(Р; N) = (P-Al; Q-N).
102
ГЛ. 4. АЛГЕБРА
Из определения произведения пар и свойств арифметических
операций над многочленами следует, что операция умножения пар ас-
социативна и коммутативна, и операция умножения дистрибутивна по
отношению к сложению.
В множестве упорядоченных пар многочленов обратная умноже-
нию операция деления пары (Р; Q) на ненулевую пару (Л4; /V) выпол-
нима, т. е. для любых двух таких пар существует пара (X; У) такая,
что
(М; Y) = (Р; Q).
Пару (X; У) называют частным пар (Р; Q) и (М; JV), обозначают
(Р; Q) : (М; N) и вычисляют по формуле
(Р; Q) : (Af; N)=(P-N; Q-M).
Из определения частного пар следует равенство
(Р; Q) : (М; АО == (Р;	М)9
т. е. деление на пару (Л4; N) может быть заменено умножением на обра т
ную делителю (Af; N) пару (X; М).
Пусть многочлены Р и Q в упорядоченной паре (Р; Q) таковы, что
многочлен Р представим в виде
Р« Q-R,
где R — некоторый многочлен, т. е. многочлен Р нацело делится на
многочлен Q.
Будем отождествлять пару таких многочленов (Р; Q) с многочлен
ном R.
Пусть (Р; Q) и (М; N) — такие две пары многочленов, что
Р = Q-R и М == N-S,	(2)
где R и S — многочлены.
При принятом отождествлении пар (Р; Q) и (Л4; N) с многочле-
нами R и S соответственно, сумма, разность и произведение пар
(Р; Q) и (М; N) представляют собой сумму, разность и произведение мно-
гочленов R и S.
Действительно, сумма пар (Р; Q) и (A4; N) по правилу сложения
пар представляет собой пару
(P-N+Q-M-, Q-N).
Так как многочлен Р = Q*R, а многочлен М = то получен-
ная сумма пар может быть записана в виде
(Q-R-N+Q-N'S-t Q-N).	'	(3)
Нетрудно заметить, что первый многочлен этой пары нацело де-
лится на второй многочлен пары и их частным является многочлен
(Q-R-N + Q-N-S): (Q-N) = /? + $,	(4)
т. е. пара (3) отождествляется с многочленом R + S.
Таким образом, показано, что если многочлены, образующие пары
(Р; Q) и (М; N), связаны равенствами (2), то сумма многочленов R
и S, вычисляемая как сумма пар (Р; Q) и (М; Af), представляет собой
пару, которую можно записать как сумму многочленов R + S.
Аналогично проверяется, что произведение и разность многочле-
нов R и S, рассматриваемых как пары (Р; Q) и (М; с условием (2)
$ 3. РАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ ДРОБИ
103
по правилу умножения и вычитания пар определяют пары, которые мож-
но отождествить с многочленами R*S и R—S соответственно.
Из определения операций умножения и деления пар следует, что
частное двух многочленов R и S, рассматриваемых как упорядоченные
пары (Р; Ф) и (Al; N), при условии (2) в множестве пар всегда сущест-
вует. Действительно, если многочлены Р и Q записать в виде (Р; 1)
и (ф; 1) соответственно, то из равенства
Р : Ф = (Р; 1) : (ф; 1) = (Р; 1)-(1; ф) = (Р; ф)
следует, что частное двух многочленов Риф всегда представляется
в виде пары (Р; ф), а не только в случае, когда Р = Q-R.
В тех случаях, когда многочлен Р не делится нацело на многочлен ф,
пара (Р; ф) представляет собой не совпадающее ни с каким многочленом
частное от деления многочлена Р на многочлен ф, которое называется
рациональной алгебраической дробью и обычно обозначается символом
Р/ф.
Рациональная алгебраическая дробь Р/ф называется несократимой,
если многочлены Риф взаимно простые (см. п. 1.2). Всякая рациональ-
ная алгебраическая дробь равна некоторой несократимой дроби, оп-
ределяемой однозначно с точностью до числового множителя, общего
для числителя и знаменателя. Для того чтобы представить рациональ-
ную алгебраическую дробь в виде несократимой дроби, необходимо
найти наибольший общий делитель многочленов Р и ф и произвести со-
кращение дроби.
3.2.	Правильные алгебраические дроби. Рациональная алгебраи-
л Р (х)
ческая дробь называется правильной, если степень многочлена,
стоящего в числителе дроби, меньше степени многочлена, стоящего
в ее знаменателе, и неправильной в противном случае.
Так, дробь
X2
л3+ 1
будет правильной, а дроби
х2
ха —3 и
— неправильными дробями.
X8
D	Л	-Г Р (Х)
Всякую неправильную рациональную алгебраическую дробь -
ч (х)
можно представить в виде суммы многочлена и правильной дроби.
Для этого следует найти частное G (х) и остаток R (х) от деления много-
члена Р (х) на многочлен ф (х) и записать дробь в виде
= G (х) 4- R
ф(х) °(Х;+ф(х)
(5)
R (х)	/ X
где л/“V -* правильная дробь, а и (х) - многочлен, называемый це-
ч \х)
лой частью рациональной алгебраической дроби.
р (х)
Представление неправильной дроби в виде (5) называется
выделением целой части неправильной алгебраической дробщ
!04
ГЛ. 4» АЛГЕБРА
Пример. Рациональная алгебраическая дробь
*+*
может быть записана в виде следующей суммы многочлена и правиль*
ной рациональной алгебраической дроби:
X»	211	1
х+1 ~х	1 ’
где многочлен № — х -|- 1 — целая часть неправильной алгебраической
дроби.
3.3.	Простейшие дроби. Правильная рациональная алгебраиче-
Р (х)
ская дробь 75-7-7 называется простейшей, если ее знаменатель Q (х)
ч (*)
является натуральной степенью некоторого неприводимого много*
члена q (х)*):
Q(x)x=^(x)	(й>1),
а степень числителя Р (х) меньше степени многочлена q (х). Напомним,
что среди многочленов с действительными коэффициентами и со старшим
коэффициентом, равным единице, неприводимыми являются лишь линей*
ные многочлены х—си квадратные многочлены х2 4- рх + q при усло-
вии, что коэффициенты квадратного трехчлена удовлетворяют нера-
венству р2 — 4q < 0. Вследствие этого рациональная алгебраическая
дробь может быть простейшей лишь в случаях, когда ее числитель
Р (х) — либо многочлен первой степени, либо многочлен нулевой сте-
пени (т. е. число, не равное нулю).
__j
П р и м е р ы. 1. Дробь	& — натуральное) будет про-
стейшей рациональной алгебраической дробью, так как ее знаменатель
является степенью неприводимого многочлена, а степень неприводимого
многочлена больше степени числителя.
х8 —3
2. Дробь не является простейшей, так как степень много-
члена, стоящего в числителе дроби, больше степени многочлена, стоя-
щего в знаменателе.
3. Дробь --2й—-у не является простейшей, так как ее знаменатель
можно разложить на множители, т. е. знаменатель не является непри* .
водимым многочленом.
В теории рацирнальных алгебраических дробей центральное место
занимает следующая теорема:
Всякая правильная рациональная дробь разлагается в сумму про*
стейших дробей, и это разложение единственно.
Р (х)
Точнее, если дана правильная дробь знаменатель которой
ч	ч \х)
имеет разложение на неприводимые множители:
ь. ь	ь
Q (X) = 911 (х)Ch* (X). • • qi' (х),
неприводимых многочленах см, п, 1J0.
§ 4. ИРРАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 105
причем qi (х) qj (X) при i ф j и	А/ — натуральные числа,
ю
Р (х) __ pi (х) ,	(х) ,	, Pi (х)
. ()
где все слагаемые в правой части — правильные дроби, каждая из ко-
торых может быть представлена в виде суммы простейших дробей:
г(х) _ Sk (х) Sk-1 (х)	Sa (X) Si(x)
+ qk^(x) ‘‘"Ч" q*{x) * q (x)
Степени всех числителей, стоящих в правой части разложения (7),
меньше степени многочлена q(x).
Пример. Разложить в сумму простейших дробей правильную
, Р(х>
дробь [ОТ’где
Р (х) = 2х* — Юх3 4- 7х» 4- 4х + 3,
Q (х) = х8 — 2Х3 4-2г* — Зх 4-2.
Многочлен Q (х) может быть представлен в виде произведения не*
приводимых многочленов:
— 2х84-2>^ — Зх 4* 2 = (х 4* 2) (х — 1)а (х2 4- 1).
Р (х)
В согласии с равенствами (6), (7) искомое разложение дроби : -
ч (х)
должно иметь вид
Р(х) _ А В С Dx + E
Q(x) ~ х+2 + (х — 1)а+ х — 1 + ха4-1 ’
где числа Я, Bt Ct D, Е еще должны быть найдены. Приводя правую
часть дроби к общему знаменателю, из условия равенства дробей полу-
чаем равенство многочленов
2х4 — Юх* 4- 7Х2 + 4х+ 3 == А (х — 1)а (х2+1)4-
+В(х+2)(х2+ 1) + С(х4-2)(х- 1)(х3+ 1) +
+ Dx (х+ 2) (х — 1)а 4- Е (х 4- 2) (х — 1)а.
Далее, приравнивая коэффициенты при одинаковых степенях
неизвестных в левой и правой частях последнего равенства, получим
систему пяти линейных уравнений с пятью неизвестными, которая имеет
единственное решение:
А = 3, В = 1, С = — 2, D = 1, Е = —3.
Следовательно, искомое разложение имеет вид
Р(х) _	3	1	2 х —3
Q(x) -	(х—1)а х—l^x^l *
§ 4$ Иррациональные алгебраические выражения
Алгебраическое выражение называют иррациональным, если над
переменными, входящими в алгебраическое выражение, наряду с опе-
рациями сложения, вычитания, умножения и деления производится
операция возведения в рациональную (не целую) степень.
106
ГЛ. 4. АЛГЕБРА
Примеря. 1. Алгебраическое выражение
х2 а 1^* х 4" Ь
относительно переменной х является иррациональным алгебраиче-
ским выражением, так как переменная х находится под знаком квадрат-
ного корня.
2. Алгебраическое выражение
/2 х3—I
относительно переменной х не будет иррациональным алгебраическим
выражением. Если же переменной в данном алгебраическом выражении
считать а, то оно — иррациональное. Таким образом, ответ на вопрос
об иррациональности алгебраического .выражения зависит от того,
какие величины в данном алгебраическом выражении считаются пере-
менными, а какие—коэффициентами.
Преобразования иррациональных алгебраических выражений вы-
полняются в соответствии с общими законами арифметических дейст-
вий и правилами действий над радикалами.
Исключение иррациональности из числи-
теля (знаменателя) иррациональной алгебраи-
ческой дроби. Алгебраическое выражение вида
называют дробным иррациональным выражением, если хотя бы одно
из алгебраических выражений f (х) или g (х) является иррациональным
относительно переменной х.
Пусть S (х) — некоторое иррациональное алгебраическое выраже-
ние относительно переменной х. Алгебраическое выражение S (х)#
не равное тождественно нулю, называют дополнительным множите»
лем для алгебраического выражения <S (х), если произведение
S (х) § (х) — рациональное алгебраическое выражение относительно
переменной х. Знание дополнительных множителей для алгебраиче-
ских выражений, стоящих в числителе (или знаменателе) дроби (1),
позволяет представить ее в виде дроби, у которой числитель (знамена-
тель) — рациональное алгебраическое выражение:
f ~ f-f = f-8
8 g-f 8*8 9
где f — дополнительный множитель числителя, g — дополнительный
множитель знаменателя. Такое преобразование иррационального вы-
ражения называется исключением иррациональности соответственно из
числителя или знаменателя иррационального дробного выражения.
Таким образом, процедура исключения иррациональности из
числителя или знаменателя дробного иррационального выражения
сводится к нахождению дополнительного множителя для алгебраиче-
ского выражения «S, содержащего радикалы. В общем случае трудно
указать универсальный способ нахождения дополнительного множи-
теля для произвольного иррационального выражения. Ниже приве-
дены дополнительные множители для некоторых простейших иррацио-
§ 4. ИРРАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 107
нальных выражений, зависящих от двух переменных х и у, полученные
с помощью формул сокращенного умножения.
s (X, у)	s (X, у)	S (х, у) S (х, у)
У xkxl	Пг	Г	7 1/ vn^kt.n-“l У л у	ху
Ух ± Уу	Ух =F у у	х — у
Ух ± У у		Х±у
П /	 п у	 У * — V У	И г*	г	П,	-  ]/ хп 1 + у хп 2у + • •	•4-yV-1	х — у
(п — любое) У^ + Уу	У Х*_\ _ухп-2у + ..	• + Iх Г1-1	х + у
(п — нечетное).
Если алгебраическое выражение S (х, у) — дополнительный мно-
житель для алгебраического выражения S (х, у), то и алгебраическое
выражение S (х, у) будет дополнительным множителем для алгебраи-
ческого выражения S (х, у),
В случае, когда число слагаемых в выражении, содержащем ради-
калы, больше двух, в некоторых случаях удобно исключать радикалы
из числителя (знаменателя) дроби, используя формулы сокращенного
умножения иррациональностей.
Примеры. 1. Исключить иррациональность из знаменателя
алгебраической дроби
________х______
+ Ух + 1
„Дополнительным множителем для знаменателя служит иррацио-
нальное алгебраическое выражение
n-L
Умножая числитель и знаменатель дроби на выражение у^х —
получаем алгебраическую дробь, знаменатель которой является рацио-
нальным алгебраическим выражением:
х	х(77-1) _Х(УТ—1)
^ + 77+1	(У7-1)(У^+|<х + 1)	•
2. Исключить иррациональность из знаменателя дроби
________1______ ч
/х + ИГ— /г”
Обозначая Ух	У у = t и умножая числитель и знаменатель
данной дроби на выражение t + У г , получим
Т = t + Уг =	/Г_+ У г = У^+ У У + У[_
t — Уг	& — г	г л + у — г±2Уху
108
ГЛ. 4. АЛГЕБРА
В результате проведенных преобразований исходной алгебраиче-
ской дроби мы получили алгебраическую дробь, содержащую в зна-
менателе лишь один радикал. Теперь, умножая числитель и знаменатель
дроби на выражение
(•«+«/ — г)— 2 Уху,
получим дробь, уже не содержащую иррациональности в знаменателе:
(/х + /у + КП (х + р —• ?	2 1<х7)
(х-h у-— г)2 — 4ху
§ 5.	Уравнения. Алгебраические уравнения
5.1.	Основные определения. В алгебре рассматриваются два вида
равенств — тождества и уравнения.
Тождество — это равенство, которое выполняется при всех (до-
пустимых) значениях входящих в него букв *). Для записи тождества
наряду со знаком = также используется знак = .
Уравнение — это равенство, которое выполняется лишь при не-
которых значениях входящих в него букв. Буквы, входящие в уравне-
ние, по условию задачи могут быть неравноправны: одни могут прини-
мать все свои допустимые значения (их называют коэффициентами, а
реже параметрами, уравнения и обычно обозначают первыми буквами
латинского алфавита: a, bf с,... — или теми же буквами, снабженными
индексами:	... или by bZt...); другие, значения которых тре-
буется отыскать, называют неизвестными (их обычно обозначают по-
следними буквами латинского алфавита: х, у, г,... — или теми же
буквами, снабженными индексами, например, xj, х2,...
В общем виде уравнение с п неизвестными xj, х2,..., хп может быть
записано как
F (*1, .....ХП) == О,
где F — некоторая функ1Хйя указанных аргументов.
В зависимости от числа неизвестных уравнение называют уровне*
нием с одним, двумя и т. д. неизвестными.
Областью (множеством) допустимых значений неизвестных уравне-
ния называют область определения функции F (xj, х2, ...»хп).
Значения неизвестных, обращающие уравнение в тождество, на-
зывают решениями уравнения.
Уравнение считается решенным, если найдены все его решения
или показано, что уравнение решений не имеет.
Если все решения уравнения F == 0 являются решениями уравне-
ния G = 0, то говорят, что уравнение G = 0 есть следствие уравнения
F « 0, и пишут
F =з 0 => G = 0.
♦)	Под допустимыми понимаются те численные значения букв, при ко*
торых выполз имы все операции, совершаемые над буквами, входящими в ра-
венство. Например, допустимыми значениями букв, входящих в равенство
Н-1	,--
будут следующие; а б V) U СО; х € (2; +<»)» Ь 6	-*-»)<
$ Б. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ	109
Два уравнения
F=0hG=0
называют эквивалентными, если каждое из них является следствием
другого, и пишут
F=0<=>6 = 0.
Таким образом, два уравнения считаются эквивалентными, если
множества решений этих уравнений совпадают.
Уравнение F = 0 считают эквивалентным двум (или нескольким)
уравнениям /^ = 0, F2 = 0, если множество решений уравнения F = 0
совпадает с объединением множеств решений уравнений Ft = 0, F2 = 0.
Некоторые эквивалентные уравнения:
1)	Уравнение F 4- G » О эквивалентно уравнению F = 0, рас-
сматриваемому на множестве допустимых значений исходного урав-
нения.
F
2)	Уравнение -д- = 0 эквивалентно уравнению F = 0, рассма-
триваемому на множестве допустимых значений исходного уравнения.
3)	Уравнение s= 0 эквивалентно двум уравнениям F » 0
и 6 = 0.
4)	Уравнение Fn == 0 эквивалентно уравнению F = 0.
5)	Уравнение Fn = Gn при нечетном п эквивалентно уравнению
F = G, а при четном п эквивалентно двум уравнениям F = G и F =
= —G.
Алгебраическим уравнением называется уравнение вида
Рп = 0,
где Рп — многочлен n-й степени от одной или нескольких переменных.
Алгебраическим уравнением с одним неизвестным называется урав-
нение, сводящееся к уравнению вида
Сод/1 14“	+ • • • 4" fln-ix 4“	= 0»
где п—неотрицательное целое число; коэффициенты многочлена Оо,
alt а2, •••, «пл, ап называются коэффициентами (или параметрами)
уравнения и считаются заданными; х называется неизвестным и является
искомым. Число п называется степенью уравнения.
Значения неизвестного х, обращающие алгебраическое уравнение
в тождество, называются корнями (реже решениями) алгебраического
уравнения.
h Прежде чем перейти к частным случаям алгебраического уравне-
ния с действительными коэффициентами (линейным, квадратным и дру-
гим уравнениям), заметим, что методы решений линейных и квадрат-
ных уравнений были известны очень давно, в то время как методы ре-
шения уравнений третьей и четвертой степеней были найдены лишь
в XVI веке. После этого почти три столетия продолжались безуспешные
попытки сделать* следующий шаг, т. е. найти формулы, выражающие
при помощи радикалов корни любого уравнения пятой степени через
его коэффициенты. Эти попытки прекратились лишь после того, как
Н. X. Абель в двадцатых годах прошлого века доказал, что такие фор-
мулы для уравнений л-й степени при п > 5 заведомо не могут
быть найдены.
Этот результат Абеля не исключал, однако, возможности того, что
корни некоторых конкретных многочленов с числовыми коэффициент
ПО	гл. 4. АЛГЕБРА
тами всё же каким-либо способом выражаются через коэффициенты
при помощи некоторой комбинации радикалов. Полностью вопрос об
условиях, при которых данное уравнение разрешимо в радикалах, был
исследован Э. Галуа в тридцатых годах прошлого века. В частности,
им было показано, что для всякого п 5 можно указать неразрешимые
в радикалах уравнения п-й степени, даже с целочисленными коэффи-
циентами. Таким будет, например, уравнение & — 4х — 2 = 0.
5.2.	Линейное уравнение. Линейным уравнением называется урав-
нение первой степени
сх 4*^ = 0,	(1)
где а и Ь — некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень х = — —,
который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число —Ь, получаем урав-
нение
ах = — Ь,
эквивалентное уравнению (1). Разделив обе части последнего уравне-
ния на число а =^= 0, получаем корень уравнения (1)
5.3.	Квадратное уравнение* Алгебраическое уравнение второй
степени
ах2 + Ьх -}- с = 0,	(2)
где а, Ъ, с — некоторые действительные числа, называется квадратным
уравнением. Если а = 1, то квадратное уравнение (2) называется
приведенным.
Корни квадратного уравнения вычисляются по формуле
—Ь ±
Xi'8	2а
(3)
где выражение I? — 4ас называется дискриминантом квадратного урав-
нения.
При этом:
если &2 — 4ас > 0, то уравнение имеет два различных действитель-
ных корня;
если б2 — 4ас а 0, то уравнение имеет один действительный корень
Кратности 2;
если б2 — 4ас < 0, то уравнение действительных корней не имеет,
а имеет два комплексно сопряженных корня:
b ,	b* ,	b ]f4ac—b* ,
Ki~ 2а + 2а	*8 “ 2а 2а 1‘
Формула (3) может быть получена в результате следующих преоб-
разований исходного уравнения.
Запишем квадратный трехчлен ах2 + bx с, стоящий в левой
части уравнения (2); в виде полного квадрата и проведем преобразова*
$ б. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
111
ния, в результате которых каждый раз будет получаться уравнение,
эквивалентное исходному * *):
/ , b \2 Ь2 — 4ас _	/ , b \2
Ч* + -2Г) —Та-----------°**ЧХ + -2Г) =
Ь \2 _ № — 4ас
ИГ )	4а2
f b2 — 4ас I , b | _
^2	** I х + ~2Т I —
Последнее уравнение эквивалентно двум уравнениям:
, b _ j/^2 — 4ас
*"1"2а	Щ] ’
b	У Ь2 — 4ас
Х'~2<Г~ Ца] ’
Используя определение абсолютной величины числа, легко убедиться,
что уравнения (4) и (4') эквивалентны уравнениям
Ь , /Ь2 — 4ас .. b V &—4ас
Ь2 — 4ас
4а
2
УЬ2 - 4ас
2|а|
(4)
(4')
_ , /Ь2 —4ас
Х~ 2а + 2а • Х~ 2а 2а
Объединяя эти формулы, получаем формулу для вычисления кор-
ней квадратного уравнения:
—b ± К^2 — 4ас
х1,«— 2а
Частными видами квадратного уравнения (2) являются:
1)	Приведенное квадратное уравнение (в случае, если а= 1)л
которое обычно ваписывается в виде
х2 4- рх q ss 0.
Его корни вычисляются по формуле
*1,2=— 
2)	Квадратное уравнение с четным вторым коэффициентом, которое
обычно записывается в виде
ах* 4- 2kx 4- с = 0 (k — целое число).
Корни этого квадратного уравнения удобно вычислять по формуле
—k ± Ук2 — ас
Xif з -----------------•	(6)
Формулы (5) и (6) являются частными видами формулы (3) вычис-
ления корней квадратного уравнения.
♦) Преобразование квадратного .трехчлена ахг + Ьх 4- б в виду
( b \а 4ас	а	_
* 4- -jj-i — — 4а  называется выдшнием юаням ляадрста»
112
ГЛ. 4. АЛГЕБРА
Корпи приведенного квадратного уравнения
жа 4- рх 4- q х= О
связаны е его коэффициентами формулами Виета
4- х2 =»	*1*8 ®» Q-
В случае, если приведенное квадратное уравнение имеет 'действи*
тельные корни, формулы Виета позволяют судить как о знаках, так
и Об относительной величине корней квадратного уравнения, а именно:
если q > 0, р > 0, то оба корня отрицательны;
если q > 0, р < 0, то оба корня положительны;.
если ^<0, р > 0, то уравнение имеет корни разных знаков,
причем отрицательный корень по абсолютной величине больше поло-
жительного;
если q < 0, р < 0, то уравнение имеет корни разных знаков,
причем отрицательный корень по абсолютной величине меньше поло-
жительного корня.
6.4. Кубичное уравнение. Кубичным уравнение е действительными
коэффициентами называется уравнение третьей степени
ах* 4* Ьха 4- сх + =а 0,	(7)
где а, Ь, с, d — некоторые действительные числа.
Кубичное уравнение (7) ааменой х == у-приводится к «не-
полному» кубичному уравнению относительно У'.
ya+Py+q^O,
где
1 / Ь \2 , с	_ / Ь \3 be , d
₽	3 \ а ) а *	9 =	\ За ) Заа а *
Корни yi, у2, у3 «неполного» кубичного уравнения вычисляются
по формулам Кардано
у± = А 4- В,
гл.	8--^-1-/5. о- (f )+(!)’•
причем в качестве Л и В берутся любые аначения кубичных корней
из соответствующих комплексных чисел, удовлетворяющие равенству
Л*В==—р/3.
Если коэффициенты уравнения (7) действительны, то оно имеет
или один действительный корень и два комплексно сопряженных корня»
или три действительных корня, из которых по крайней мере два равны»
или три различных действительных корня в зависимости от того, будет
ли Q соответственно положительно, равно нулю или отрицательно.
5.5. Уравнения четвертой степени. Биквадратное уравнение.
Некоторые уравнения четвертой степени, сводящиеся к квадратным.
Уравнение четвертой степени
ах* 4- Ьх 4- схг 4- dx4* k = 0
§ 8. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ	ИЗ
является последним из алгебраических уравнений (после линейных»
квадратных и кубичных), корни которого выражаются через коэффи-
циенты a, b, с, d, k в виде некоторой комбинации радикалов. Формулы
вычисления корней уравнения четвертой степени в общем случае
весьма громоздки, и мы их приводить не будем. Укажем лишь, что корни
уравнения четвертбй степени могут быть представлены в виде комбина-
ций корней некоторого кубичного уравнения, соответствующего
данному уравнению четвертой степени.
Алгебраическое уравнение четвертой степени вида
ах* + Css О,
где а9 Ь, с — некоторые действительные числа, называется биквадрат*
ным уравнением. Заменой ха = у решение биквадратного уравнения
сводится к решению квадратного уравнения ay* + 6у4-с==0 с по-
следующим решением двух двучленных уравнений х3 == pt и х2 = уа
(У1 и У % — корни соответствующего квадратного уравнения).
Если > 0 и у* > 0, то биквадратное уравнение имеет четыре
действительных корня:
Х1, 8 = ±/{/Г.	*8, 3 = ±У17-
Если > 0, у2 < 0 *), тобиквадратное уравнение имеет два дей-
ствительных корня Xjj2 = ±Кухи два чисто мнимых сопряженных
корня: -
х3> 4 = ±i
Если yi < 0 и у9 < 0, то биквадратное уравнение имеет четыре
чисто мнимых попарно сопряженных корня:
*1, г = ± «У —У1> x»,l —
Если у} и у2—комплексные корни соответствующего квадрат- .
ного уравнения, то для нахождения четырех корней биквадратного
уравнения надо извлечь квадратные корни из комплексных чисел у±
и у*. Этой, довольно громоздкой операции можно избежать следующим
образом. Запишем исходное уравнение ах4 + бх2 + с = 0 в виде
х4 4- рх2 -J- q а 0,	(8)
где р = b/a, q = da, причем коэффициенты р и q, в силу предположе-
ния о комплексности^ корней квадратного уравнения» удовлетворяют
условиям | р | < 2J/”q и q > 0.
Преобразуем левую часть уравнения (8):
я4 4- рх2 4- $ =з (х4 4- ?) 4- рх2 =»
= (ж4 + 2 х2 + q) — (2 К? — р) Xs — (*2+ К7 )2—(2 У"? — р)х2 =
= (xa + *K2yV—д+УТ)(*а-“*1/2У’7—р4-У7)"
♦) Случай у < 0» р» О аналогичен разобранному»
114	ГЛ. 4. АЛГЕБРА
Теперь решение биквадратного уравнения ах* + bx* 4- с = 0 сводится
к решению двух квадратных уравнений с действительными коэффи-
циентами:	__________
X* + xJ/2 Yq-p+Vq =0,
х2 — хИ2 — р+ V“q = 0.
Решение уравнений вида ax2k +	+ с = 0 (a	натураль-
ное число) заменой х^ = у сводится к решению квадратного уравнения
ау2 + by + с = 0 с последующим решением соответствующих дву-
членных уравнений.
Алгебраическое уравнение четвертой степени вида
ах* + Ьх* 4- сх2 4- dx 4- е » 0	(9)
при е=£ 0 называется возвратным, если коэффициенты уравнения
a, b, d, е связаны равенствами	е=Х2а (X — некоторое от-
личное от нуля число). Используя эту связь между коэффициентами,
уравнение (9) можно записать в виде
ах* 4- Ьх9 4- сх2 4- hbx 4- №а = 0.	(10)
Так как х = 0 не является корнем уравнения (9), то, разделив почленно
обе части уравнения (10) на х2 и проведя соответствующую группировку
членов левой части уравнения, получим уравнение, эквивалентное
уравнению (10):
а(х2+-^-) + *(* + 4) + Св0-
А- /	X2	\
Теперь заменой х4" — ==у (учитывая, что х24-	=* 02 — 2Х j
последнее уравнение сводится к квадратному уравнению относи-
тельно у\
ау2 + ЬУ+ с — 2ка = 0.	(11)
Решая уравнение (11), получаем, что решение возвратного урав-
нения (10) сводится к решению двух квадратных уравнений:
х2 — 0jx+ Х = 0,
х2 — у2х 4- X =s 0,
где У! и корни уравнения (11).	<
Частным случаем возвратного уравнения является симметрии
песков уравнение (соответствующее Х= 1)
ах* 4- bx* + tx3 4- bx 4- а = 0.
и кососимметрическое уравнение (соответствующее X = — 1)
ах* 4- Ьх* 4- сх2 — Ьх+ а==0.
Заменой х+~~ = 0 Для симметрического и х—-^- = 0 для косо-
симметрического уравнений эти уравнения сводятся к квадратным урав-
нениям относительно неизвестной у.
Уравнение четвертой степени вида
(х2 4. Ьх 4- с) (х2 4- Ьх 4- d) =з k9	(12)
§ 5. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ	115
где Ь, с, d, А -— некоторые действительные числа, заменой
х2 + Ьх = у
сводится к следующему квадратному уравнению относительно неиз-
вестной у\
y2+(c+d)y — k = 0.	(13)
Если уравнение (13) имеет действительные корни yt и у2, то корни
уравнения (12) отыскиваются как корни двух квадратных уравнений
с действительными коэффициентами:
ха + Ьх — У± — О»
х2 + Ьх — у2 ~ 0.
Решение уравнения вида
х (х+ а) (х-J- Ь) (х + а 4- Ь) = с,	(14)
где а, Ь, с — некоторые действительные числа, может быть сведено
к решению двух квадратных уравнений следующим образом.
Перемножая первый и четвертый, второй и третий сомножители,
получаем уравнение
[х2 + (аЬ) х] [х2 + (а 4- b) х аЬ] « с.
Которое заменой
х24- (а 4- Ь)х = у
сводится к квадратному уравнению относительно новой неизвестной у:
y^+aby^c^O.	(15)
Если уравнение (15) имеет действительные корни у± и y2t то множество
корней уравнения (14) находится как множество корней следующих
двух квадратных уравнений с действительными коэффициентами:
х2 4- (а + Ь) х — yt = 0,
х2 + (а 4* Ь) х — у2 = 0.
5.6.	Двучленные уравнения. Уравнение n-й степени
ох" ± д == 0	(16)
называется двучленным уравнением. При а>0 и &>0 заменой*)
х=уу где у —-—арифметическое значение корня, уравне-
ние (16) приводится к уравнению
уп ± 1 = 0,
которое и будет далее рассматриваться.
Двучленное уравнение t/1 — 1 = 0 при нечетном п имеет один
действительный корень у = 1. В множестве комплексных чисел од
Исли.а в 6.имеют разные знаки, то х = у у
116
ГЛ. 4. АЛГЕБРА
Я-I).	(17)
уравнение имеет п корней (из которых один действительный и п — 1
комплексных), вычисляемых по формуле
2nk , . . 2лА	л t ft
Ук s cos	* sin ~п~	= °’	2‘
Двучленное уравнение if1 — 1 = 0 при четном n в множестве дей-
ствительных чисел имеет два корня {у = 1; у = —1}, а в множестве
комплексных чисел п корней, вычисляемых по формуле (17).
Двучленное уравнение ^4-1 = 0 при нечетном п имеет один дей-
ствительный корень г/ = — 1, а в множестве комплексных чисел п .
корней, вычисляемых по формуле
2лА + п . . . 2пА4-я ' л t л	,,оч
yfe = cos-+ *sin-------------(6 = 0, 1, 2, я—I). (18)
н	п	п
Двучленное уравнение уп 4- 1 = 0 при четном п действительных
корней не имеет. В множестве комплексных чисел уравнение имеет п
корней, вычисляемых по формуле (18).
Корни двучленного уравнения для некоторых конкретных значе-
ний я следующие:
1)	у2 — 1 = 0 (я = 2). Уравнение имеет два действительных кор-
ня у1>2=±1.
2)	у3— 1 = 0 (я = 3). Уравнение имеет один действительный
.	— 1 =Ь i /3
корень У1= 1 и два комплексных корня у2>8 =-----------------•
3)	у* — 1 = 0 (я = 4). Уравнение имеет два действительных корня
2 = ± 1 и два комплексных корня = ±1.
4)	r/a + 1 = 0 (п= 2). Уравнение действительных корней не имеет.
Комплексные корни: yi>2= ±t.
5)	У3 + 1 = 0 (я = 3). Уравнение имеет один действительный ко*
1	1 ± //з
рень yt = — 1 и два комплексных корня у2>3 = -------.
6)	У*+ 1 = 0 (я = 4). Уравнение действительных корней не
имеет. Комплексные корни:
У1, 2 == О =Ь О, Уз, 4 —----------(1 ± 0«
5.7.	Решение алгебраического уравнения с целыми коэффициен-
тами. Рациональные корни алгебраического уравнения я-й степени
OqX^1 -J-	-J-	+ • • • 4 an_ix + ап = 0,	(19)
где Oq, ci, 02, апл» оп — целые числа, можно найти, используя
следующую теорему:	/
Рациональными корнями уравнения (19) могут быть лишь числа
т!р (т — целое, р — натуральное), где число \т | является делителем
числа \ап I, а число р — делителем числа | я0|.
Пример. Найти корни уравнения
4х44- 8х3 — Зх2 — 7х4- 3 = 0.	(20)
Делителями числа 3 будут числа 1, 3, а делителями числа 4 —
числа 1, 2, 4. Множеством значений т будет {1; —1; 3; —3), а мно*
жеством значений д? — {1; 2; 4). Множеством всевозможных различ<
пых рациональных чисел будет {±1; ±3; ±1/2; ±1/4; ±3/2; ±3/4}»
§ 5. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
117
Непосредственная подстановка этих чисел в уравнение (20) показывает,
что числа 1/2 и —3/2— корни данного уравнения, и, следовательно,
данный многочлен делится на линейные многочлены
(«-•})  («+!)•
а также и на их произведение
Произведя деление «углом», находим многочлен частного?
4ха + 4х — 4.
Решая квадратное уравнение
4ха + 4х — 4= 0,
получим еще два действительных корня уравнения (20)$
-1 + Г5	-1-/5
------------9 х4--------2	•
Итак, задача полностью решена — найдены все четыре корня исходного
уравнения:
_ 1	_	3
Х1 — “2” । Х% — — “2” । Х3
+ Кб ' _ -1-/5
"9-->	*4 —	9---•
(21)
5.8.	Рациональные алгебраические уравнения. Рациональным
алгебраическим уравнением называется уравнение вида
Q (х)	°’
где Р (х) и Q (х) — многочлены. Далее для определенности будем по-
лагать, что Р (х) — многочлен m-й степени, a Q (х) — многочлен п-й
степени.
Множество допустимых значений рационального алгебраического
уравнения (21) определяется условием Q (х) Ф 0, откуда следует, что
x=/=cit х ф с3, ..., х #= сп> где c±t ..., сп — корни многочлена
Q (х).
Метод решения уравнения (21) заключается в следующем. Решаем
уравнение
Р (х) - 0,
корни которого обозначим через
Xi, *2, X3t xm.
Сравниваем множества корней многочленов Р (х) и Q (х). Те корни
многочлена Р (х), которые не являются корнями многочлена Q (х),
являются корнями (решениями) рационального уравнения (21).
Пример. Найти действительные корни уравнения
Q (х) U*
где Р (х) = х* — 1, Q (х) =: х — 1.
118
ГЛ. 4. АЛГЕБРА
Многочлен Р (х) имеет два действительных корня (оба простые)!
Х1= 1, х2 = — 1.
Многочлен Q (х) имеет один корень q = 1. Следовательно, уравнение
имеет один действительный корень х=—1.
Решая то же самое уравнение в множестве комплексных чисел^
Р (х) п	„
получим, что уравнение = 0 имеет, кроме указанного действи-
ем (х)
тельного корня, два комплексно сопряженных корня:
х2 = i, х8 = — i.
5.9.	Иррациональные уравнения. Уравнение, содержащее неиз-
вестное (либо рациональное алгебраическое выражение от неизвестного)
под знаком радикала, называют иррациональным уравнением. В эле-
ментарной математике иррациональные уравнения решаются в мно-
жестве действительных чисел.
Всякое иррациональное уравнение с помощью элементарных пре-
образований (умножения, деления, возведения в целую степень обеих
частей уравнения) может быть сведено к рациональному алгебраиче-
скому уравнению. При этом следует иметь в виду, что полученное
рациональное алгебраическое уравнение может оказаться неэквива-
лентным исходному иррациональному уравнению, а именно может
содержать «лишние» корни, которые не будут корнями исходного ирра-
ционального уравнения. Поэтому, вычислив корни полученного алге-
браического уравнения, необходимо проверить, будут ли все они также
и корнями исходного иррационального уравнения.
В общем случае трудно указать какой-либо универсальный метод
решения любого иррационального уравнения, так как желательно,
чтобы в результате преобразований исходного иррационального урав-
нения получилось не просто какое-то рациональное алгебраическое
уравнение, среди корней которого будут и корни данного иррацио-
нального уравнения, а рациональное алгебраическое уравнение, об-
разованное из многочленов как можно меньшей степени. Желание полу-
чить рациональное алгебраическое уравнение, образованное из много-
членов как можно меньшей стецени, вполне естественно, так как на-
хождение всех корней рационального алгебраического уравнения само
по себе может оказаться довольно трудной задачей,' решать которую
полностью мы можем лишь в весьма ограниченном числе случаев.
Приведем некоторые стандартные методы решения иррациональных
алгебраических уравнений.
1) Одним из самых простых приемов решения иррациональных
уравнений является метод освобождения от радикалов путем последо-
вательного возведения обеих частей уравнения в соответствующую
натуральную степень. При этом, если обе части уравнения возводят-
ся в нечетную степень, то получается уравнение, эквивалентное ис-
ходному; если же обе части уравнения возводятся в четную степень,
то полученное уравнение может оказаться неэквивалентным исход-
ному уравнению. В этом легко убедиться, возведя обе части урав-
нения
= g W
в любую четную степень 2п. В результате этой операции получается
уравнение
и WJ2n= [gwft
$ Б. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ .	119
множество решений которого представляет собой объединение мно-
жеств решений двух уравнений:
f W = g W и f (х) = —g (х).
Однако, несмотря на этот недостаток, именно процедура возведения
обеих частей уравнения в некоторую (часто четную) степень является
самой распространенной процедурой сведения иррационального урав-
нения к рациональному уравнению.
Пример 1. Решить уравнение
V’Pr(x)+VQ^) = R(x),	(22)
где Р (х), Q (х), R (х) — некоторые многочлены.
В силу определения операции извлечения корня в множестве дей-
ствительных чисел допустимые значения неизвестного х определяются
условиями
P(x)>0, Q(x)>0.
Возведя обе части уравнения (22) в квадрат, получим уравнение
2 VP (х) Q (х) = Я2 (х) — Р (х) — Q (х).
После повторного возведения обеих частей уравнения в квадрат
получается рациональное алгебраическое уравнение
4Р (х) Q (х) = [/?2(х)-Р (x) — Q(x)P,	(23)
Так как обе части уравнения (22) возводились в квадрат, может
оказаться, что не все корни уравнения (23) будут являться решениями
исходного уравнения, и необходима проверка корней.
2) Другим приемом решения иррациональных уравнений является
способ введения новых неизвестных, относительно которых получа-
ется либо более простое иррациональное уравнение, либо рациональное
уравнение.
П р и м е р 2. Решить иррациональное уравнение
<з-«>
Множество допустимых значений этого уравнения]
*€ (—оо; 1) (J (1; 3) U (3; + ©о).
з/"з_х'
Положив 1/ ‘х_1’ — У> после подстановки получим уравнение
(3-х)у + ^=1 = 2
У
или эквивалентное ему уравнение
(3 — х) у* — 2у + х — 1 = О,
которое можно рассматривать как квадратное уравнение относительно у»
Решая это уравнение, получим


3-х •
х—- 1
120 *	ГЛ. 4. АЛГЕБРА
Следовательно, множество решений исходного иррационального урав-
нения представляет собой объединение множеств решений следующих
двух уравнений:
,3/ 3 —х	3 —х х-1
V х—1	у х—1 з —х •
Возведя обе части каждого из этих уравнений в куб, получим два
рациональных алгебраических уравнения:
3 — х_,	3—х /х—1\3
х—1	’ х — 1 — \ 3 — х) 9
Решая эти уравнения, находим, что данное иррациональное урав-
нение имеет единственный корень х = 2.
В заключение заметим, что при решении иррациональных уравне-
ний не следует начинать решение уравнения с возведения обеих частей
уравнений в натуральную степень, пытаясь свести решение иррацио-
нального уравнения к решению рационального алгебраического урав-
нения. Сначала необходимо посмотреть, нельзя-ли сделать какое-ни-
будь тождественное преобразование уравнения, которое может су-
щественно упростить его решение.
- ПримерЗ. Решить уравнение
° Vе I + * + ~ V1 + * = у/*х.	(24)
Множество допустимых значений уравнения: х g (0; -J-oo). Сделаем
следующие преобразования данного уравнения:
aj^l4~x-|- — jA + xey/x а 14- х 1 -J- —^ ==
7^Т(1+±)=1.
Далее, записывая уравнение в виде
«(+4Г-ь
получим, что:-
при а == 0 уравнение решений не имеет;
при а 0 уравнение может быть записано в виде
('+4ГЧ:
при а < 0 данное уравнение решений не имеет^ так как при лю-
бом х, принадлежащем множеству допустимых значений уравнения,
выражение, стоящее в левой части уравнения, положительно.
При а > 0 получаем
1
$ Б. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ	121
Принимая во внимание, что множество допустимых значений-неиз-
вестной определяется условием х > 0, из неравенства
VT75J-1 >0
находим значение параметра а, при- которых найденное значение не-
известной х является решением уравнения (24). Такими значениями
параметра а являются значения а £ (0; 1).
При всех остальных значениях а уравнение решений не имеет,
т. е. множество его решений >— пустое множество.
5.10. Уравнения, содержащие неизвестное под знаком абсолют-
ной величины. Уравнения, содержащие неизвестное под знаком абсо-
лютной величины, можно свести к уравнениям, не содержащим знака
абсолютной величины, используя ее определение. Так, например,
решение уравнения
^-5|х-А|---------*=0	(25)
сводится к решению двух уравнений с дополнительными условиями.
1) Если х — -у > 0, то уравнение (25) приводится к виду
х2 — 5х +6 = 0.	(26)
5
Решения этого уравнения: Х} = 2, х2 = 3. Условию х—g->0
удовлетворяет лишь второй корень квадратного уравнения (26), и,
следовательно, число 3 является корнем исходного уравнения (25).
2) Если х —< 0, то уравнение (25) приводится к виду
х2 + 5х — 19 = 0.
~	— 5+КТоТ
Корнями этого уравнения будут числа х± ----------и х2 ==
&
—5—/То! „ я	—5+КЙЙ
CS —  —- ГТРППМи irnnPlJU Ул —	 - .... ПР \7ПЛППРТПППпАТ
условию
уравнения
Таким образом, решениями уравнения (25) будут числа 3 и
—5- /101
2
Заметим, что коэффициенты уравнения, содержащего неизвестную
под знаком абсолютной величины, можно подобрать таким образом,
что решениями уравнения будут все значения неизвестной, принад-
лежащие некоторому промежутку числовой оси. Например, решим
уравнение
kl + |3-*[«3.	' (27)
2
5
х----х- < 0 и поэтому не является
(ЭД.
решением данного
122
ГЛ. 4. АЛГЕБРА
Отметим на числовой оси Ох точки 0 и 3 (нули функций, стоящих
под знаком абсолютной величины). Эти точки разобьют числовую ось
на три промежутка (рис. 4.1):
— оо<х<0;	0 < х С 3;	3<х< + оо.
На этих промежутках:
1) При х С (—оо; 0) уравнение (27) приводится к виду 3 — 2х = 3.
В промежутке (—-оо; 0) последнее уравнение решений не имеет. Анало-
гично, при х £ (3; 4-00) уравнение (27) приводится к виду 2х — 3=3
и в промежутке (3; 4-оо) решений не имеет.
О	3	х
Рис. 4.1.
2) При х С [0; 3] уравнение (27) приводится к виду х + (3 —х) =
е= 3, т. е. обращается в тождество. Следовательно, любое значение
х € [0; 3] является решением уравнения (27).
5.11. Решение уравнений в множестве комплексных чисел. Рас-
смотрим два примера решения уравнений в множестве комплексных
чисел.
Пример!. Найти комплексные числа г, удовлетворяющие ура-
внению *)
a|zH-oz-M = 0,	(28)
где а — некоторое положительное действительное число.
По определению* любое комплексное число z записывается в виде
z = х + iy,	(29)
где х, у — действительные числа.
По определений) модуля комплексного числа
|г| = Г*2+^а-	(зо)
Подставив в уравнение (28) вместо г и | z | их выражения через
х и у, заданные формулами (29) и (30), получим следующую запись
уравнения (28):
х Vx^ + y2 + ах 4- i[y У"хё~+& + ед + 1 ] = 0 4- Oi.	(3!)
Из определения равенства двух комплексных чисел следует, что
уравнение (31) эквивалентно системе двух уравнений
х j/\2 + + ах = О, у К«*2 + у2 + ^ + 1 = 0,	(32)
решения которой отыскивается уже в множестве действительных чисел.*
Нетрудно заметить, что множество решений первого уравнения
системы (32) может быть найдено крк объединение множеств решений
двух уравнений:	_____
х = 0 и Ух2 + у2-}-а = 0.
*) Здесь мы неизвестную величину будем обозначать не буквой xt а бук-
вой z, подчеркивая тем самым, что решения уравнений отыскиваются в мно-
жестве комплексных чисел»
§ 5. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
123
Второе уравнение решений не имеет в силу условия а>0.
Подставляя х = 0 во второе уравнение системы (32), получаем
уравнение для действительного числа у *):
У IУI + аУ + 1 = О,
множество решений которого получается как объединение множеств
решений двух систем:
y>Q’	(33)	У<°’	(34)
^+аг/+1=О;	( ’	-у* + оу + 1 = 0.	( '
Нетрудно убедиться в том, что с учетом условия а > 0 система
(33) решений не имеет, а система (34) имеет единственное решение
у— 2
Таким образом, решением уравнения (28) является чисто мнимое
число	______
. а — j/’a2 + 4
г = /-----
П р и м е р 2. Найти комплексные числа z, удовлетворяющие
уравнению
z = г"-1,	(35)
где z — комплексное число, сопряженное z, а п — натуральное.
Так как для двух комплексно сопряженных чисел гиг имеем
|г| = 1П
то из уравнения (35) следует уравнение
|z| = |*ln-1-	(36)
Уравнение (36) — алгебраическое уравнение (п — 1)-й степени
относительно переменной |z|. Множество решений этого уравнения
следующее:
1)	при п ss 1	|z| = 1;
2)	при п =£ 1 (и С N) | z | == 1 и | z | = 0.
Рассмотрим случай, когда |z| = 1. Умножая обе части уравнения
(35) на z, получаем уравнение
z" = 1,	(37)
которое будет эквивалентно уравнению (35), так как | z |	0, следо-
вательно, и г Ф 0.
Решениями уравнения (37) будут комплексные числа
2л/г , . .	2л&	л «	п
—cos —------И sm - —	(& = 0, 1, 2, . , n —1).
Итак, окончательно решения уравнения (35) имеют вид
1) г = cos —+ i sin —-— (k = 0, 1,2, • . п — 1) при лю-
бом натуральном п\
2) z — 0 при любом натуральном 1.
*) Здесь j у 4 =» обозначение абсолютной величины действительного
числа у.
124
ГЛ. 4. АЛГЕБРА
►	5.12. Диофантовы уравнения. Диофантовым уравнением называ-
ется алгебраическое уравнение с несколькими неизвестными, все коэф-
фициенты которого — целые числа, решения которого отыскиваются
в множестве целых чисел.
Диофантовы уравнения могут либо вовсе не иметь решений, либо
иметь конечное или бесконечное число решений.
Простейшее диофантово уравнение — линейное уравнение с двумя
неизвестными х, у.
ах 4- by = ci	(38)
где a, bt с — целые числа.
Полное решение этого уравнения может быть найдено с помощью
следующего следствия алгоритма Евклида (см.
п. 1.5 гл. 2):
Если число d есть наибольший общий делитель целых чисел а и Ь*
то существуют такие целые числа k и I, что d = ka +
Линейное диофантово уравнение (38) не будет иметь решений,
если числа end взаимно простые. Если же число с кратно числу d
(т. е. представимо в виде с = pd, гдер — целое число, отличное от нуля),
то одно из решений уравнения (38) будет иметь вид
х* » pkt у* = pl.
Множество всех решений диофантова уравнения (38) задается фор*
мулами
где п € Z.
§ 6.	Трансцендентные уравнения
Уравнение, не сводящееся к алгебраическому уравнению с помо-
щью алгебраических преобразований, называется трансцендентным
уравнением *).
Простейшими трансцендентными уравнениями являются показа-
тельные, логарифмические и тригонометрические уравнения.
6.1.	Показательные уравнения. Показательным уравнением на-
зывается уравнение, в котором неизвестная входит только в показатели
степеней при некоторых постоянных основаниях.
Простейшим показательным уравнением, решение которого сво-
дится к решению алгебраического уравнения, является уравнение
вида
(1)
где а и b — некоторые положительные числа (а=£ 1), a f (х) — неко-'
торое алгебраическое выражение. Показательное уравнение (1) экви-
валентно алгебраическому уравнению
f (*) = bga b.
*) Под алгебраическими. преобразованиями уравнения F==0 понимают
следующие преобразования:
1) прибавление к обеим частям уравнения одного и того же алгебраиче-
ского выражения:
2) умножение обеих частей уравнения на одно и то же алгебраическое
выражение;
3) возведение обеих частей уравнения в рациональную степень.
§ 6. ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ	125
В случае, когда / (я) == х, показательное уравнение (1) имеет ре-
шение
X SB loge b.
Множество решений показательного уравнения вида
/>(**)= 0,	(2)
где Р — некоторый многочлен, находится следующим образом.
Вводится новая переменная #== d*, и уравнение (2) решается как
алгебраическое относительно неизвестной у. После «этого решение ис-
ходного уравнения (2) сводится к решению простейших показатель-
ных уравнений вида (1).
Пример 1. Решить уравнение
9.8х— 18.4х — 2.2* + 4 «0.
Записывая уравнение в виде
9 (2*)3 — 18 (2*)2 — 2.2* + 4 = 0
и вводя новую неизвестную у = 2*, получаем кубичное уравнение
относительно неизвестной у,
9^—18уа — 2#+4 =s 0.
Нетрудно убедиться (см. п. 5.7 гл. 4), что данное кубическое урав-
нение имеет единственный рациональный корень = 2 и два ирраци-
/2	/2
овальных корня:	и у3 ----.
о	о
Таким образом, решение исходного уравнения сведено к решению
простейших показательных уравнений:
2* = 2,	2* = -^_ 2х ________—.
•	*	3 ’	3
Последнее из перечисленных уравнений решений не имеет. Решениями
первого и второго уравнений являются следующие значения х:
Х=1 и	X==10g2——.
Некоторые простейшие показательные
уравнения:
1)	Уравнение вида	х
аа2* +	+ «у == 0
заменой я*»у сводится к квадратному уравнению
ад2+ ₽*/+ 7=0.
2)	Уравнение вида
аа* + ₽а** + уг=0
заменой а* « у сводится к квадратному уравнению'
аУ2+ ^+ g = 0.
126
ГЛ. 4. АЛГЕБРА
3)	Уравнение вида
аа2* + ₽ (ab)x + yb2x » О
л / а \*
ваменой ( —) = У сводится к квадратному уравнению
«Р2 +	+ У - 0.
6.2.	Логарифмические уравнения» Логарифмическим уравнением
называется уравнение, в котором неизвестной является аргумент
логарифмической функции.
Простейшим логарифмическим уравнением, решение которого
сводится к решению алгебраического уравнения, является уравнение
JogJW»*,	(3)
где а — некоторое положительное число, отличное от единицы, b —
любое действительное число, a f (х) — некоторое алгебраическое вы-
ражение. Логарифмическое уравнение (3) эквивалентно алгебраиче-
скому уравнению
f (х) = аь.
В случае, когда f (х) а= х, логарифмическое уравнение (3) имеет
решение
х ов сА
Множество решений логарифмического уравнения вида Р (loga х) »
с= 0, где Р — некоторый многочлен, находится следующим образом.
Вводится новая неизвестная у = log* х, и уравнение решается
как алгебраическое уравнение относительно у. После этого решаются
простейшие логарифмические уравнения вида (3).
Пример 1. Решить уравнение
log2*+ log2x —2 =0.	(4)
Относительно неизвестной у =» log2 ж данное уравнение — квад-
ратное:
у2 + у — 2 s 0.
Корни этого уравнения: yi «= 1, у2 «= —2.
Решая логарифмические уравнения
log2x = 1, log2x== — 2,
получаем решения логарифмического уравнения (4): Xj = 2, х2 = 1/4.
В некоторых случаях, для того чтобы свести решение логарифми-
ческого уравнения к последовательному решению алгебраического и
простейших логарифмических уравнений, необходимо предварительно
сделать подходящие преобразования логарифмов, входящих в уравне-
ние. Такими преобразованиями могут быть преобразование суммы ло-
гарифмов двух величин в логарифм произведения этих величин, пере-
ход от логарифма с одним основанием к логарифму с другим основа-
нием и т. д.
Пример 2. Решить уравнение
2	2 logj6x — У log2 х — 6 = 0.	(5)
f б. ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
127
Для того чтобы свести решение данного уравнения к последователь-
ному решению алгебраического и простейших логарифмических урав-
нений, необходимо прежде всего привести все логарифмы к одному
основанию (здесь, например, к основанию 2). Для этого воспользуемся
формулой
iogaw=J^L,
iOgd Я
, 1	10g2 X logs* f-r
в силу которой logfe х =s «а——• Подставив в уравнение
(5) вместо logie* равную ему величину получаем уравнение
У logl х — j/log2x —6 = 0.
3 _____
Заменой yiog^x^y это уравнение сводится к квадратному
уравнению относительно неизвестной у:
у3 — у — 6 == 0.
Корни этого квадратного уравнения: у± = 3, t/2 =□ —2. Решаем урав.
нения У logs х « 3 и log2 х =з —2:
Viog2* == 3 ч=> log2 х == 27 ч=> х = 227*
Vlog2* = —2 •<=> logs х = — 8 <=> х = 2“8.
ПримерЗ. Решить уравнение
logs (2х— 1) — log8 (* — 1) == 1.
Преобразуя разность логарифмов двух величин в логарифм част-
ного этих величин:
log, (2х —1) - logs (X- О = logs
сводим данное уравнение к простейшему логарифмическому уравнению
,	2х—1	, 2х—I о _
logs “7—Г = 1^’;—т-=*3ох:=2.
Уравнение вида
logga)/ (х) = С,
где с — число, a f (х) и g (х) — некоторые функции переменной X.
эквивалентно уравнению
[g(x)f,
рассматриваемому на множестве допустимых значений исходного урав-
нения, которое определяется как множество решений системы не»
равенств
Пример 4, Решить уравнение
logxл (2х2 — 8х + 9) =« 2.	(6)
Множество допустимых значений х определяется как множество
решений системы
2х2-8х-{-9>0,
128
РЛ. 4. АЛГЕБРА
Первое неравенство системы выполняется при любых значениях х, и,
следовательно» решениями системы будут значения х € (1; 2) (J
U (2; +©о).
Логарифмическое уравнение (6) эквивалентно уравнению 2х2 —
— 8х + 9 sss (х — 1)а, КОрНЯМИ КОТОрОГО ЯВЛЯЮТСЯ Xf = 4, х2 == 2.
Множеству допустимых значений уравнения (6) принадлежит лишь
первый корень (Xf = 4), который и есть единственное решение данного
логарифмического уравнения.
§ 7, Системы уравнений
7.1.	Основные определения» Решением некоторого множества (си-
стемы) уравнений
?l хи.... хп) == 0, Fm (xi, хг, хп) = О
с неизвестными х2, ...» хп называется множество значений неиз-
вестных, обращающих одновременно все уравнения системы в тож-
дества. Система уравнений считается решенной, если найдены все та-
кие значения неизвестных или доказано, что не существует набора зна-
чений неизвестных, обращающих одновременно все уравнения системы
в тождества. В последнем случае говорят, что системане имеет решений
или что она несовместна.
Систему уравнений иногда записывают, объединяя уравнения фи-
гурной скобкой.
Две системы уравнений считают эквивалентными, если они имеют
одно и то же множество решений. (Две несовместные системы по оп-
ределению' считаются эквивалентными.)
Говорят, что система уравнений (S) эквивалентна двум системам
уравнений (Si) и (S2), если множество решений системы (S) совпадает
с объединением множеств решений систем (Si) и (S2).
Свойства систем уравнений:
1)	При замене любого уравнения системы эквивалентным уравне-
нием получается эквивалентная система.
2)	Если одно из уравнений системы (S) эквивалентно некоторым
двум уравнениям, то исходная система (S) эквивалентна двум системам
(S1) и (S2), в каждой из которых это уравнение заменено на одно из
уравнений эквивалентной совокупности, а остальные оставлены без
изменений.
Например, система
*2 + У*~Ъ
8 которой первое уравнение эквивалентно двум уравнениям: х 4- у =
0 и хг— ху 4- у2 = 3, эквивалентна двум системам:
х4-у = 0, х4 — ху 4- у2 = 3,
Xs 4- у2 = 7)	х4 4- у2 =• 7.
§ 7. СИСТЕМЫ УРАВНЕНИЙ	129
7.2.	Системы линейных уравнений. Системой s линейных алге-
браических уравнений с п неизвестными хъ х2, ...» Хп называется си-
стема вида /
011*1 + Л12*2 + • • • + а1ПхП =
а21х1 + а22*2 + • • • + ^2ПХП = ^2»	(D
aslxl + as2*2 + ’ * ’ + а8ПхП = &S-
Величины Oil, 0^2» •••» ain> #21» ^22» •••> а2п» •••> #si> as2, ..., asn на-
зываются коэффициентами данной линейной системы уравнений. Ин-
дексы у коэффициентов линейной системы означают следующее: первый
индекс указывает номер уравнения системы в записи (1), второй индекс
указывает номер неизвестной, при которой стоит данный коэффициент.
Так, например, о25 — коэффициент, стоящий во втором уравнении си-
стемы (1) при неизвестной х5.
Величины blt b2, ...» bs называются свободными членами первого,'
второго, ..., s-ro уравнений системы (1). Система уравнений (1) назы-
вается однородной, если все числа bi равны нулю (i = 1, 2, 3, ...» s),
и неоднородной, если хотя бы одно bi отлично от нуля.
Упорядоченное множество п чисел klt k2, k3, ..., kn называется
решением системы (1), если при подстановке его в систему вместо неиз-
вестных xlt х2, х3, ..., хп все уравнения системы обращаются в тожде-
ства. Система уравнений называется совместной, если она имеет хотя
бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система линейных уравнений называется определенной,
если она имеет единственное решение, т. е. существует только один
набор п чисел klt k2, kn, который обращает все уравнения системы
в тождества.
Совместная система линейных уравнений называется неопределен-
ной, если решений больше, чем одно.
Система однородных уравнений всегда имеет нулевое решение:
= Х2 = х3 = ••• = Хп == 0.
Если система однородных уравнений имеет ненулевое решение
klt k2, ..., kn (т. е. хотя бы одно из чисел k{ 1, 2.../г)) отлично
от нуля), то такая система имеет и бесчисленное множество реше-
ние: вида lkif lk2, ..., lkn, где I — любое число.
7.3.	Метод последовательного исключения неизвестных (метод
Гаусса). Одним из наиболее распространенных методов решения си-
стем линейных алгебраических?уравнений является метод последователь-
ного исключения неизвестных — метод Гаусса. Этот метод основан
на некоторых преобразованиях системы линейных уравнений, в ре-
зультате которых получается система, эквивалентная исходной системе.
Проведем эти преобразования на примере системы трех линейных
уравнений с тремя неизвестными
анх + а12у + a13z = bit
a2lx + а22у + fl23z = b2,	(2)
a31x + a32y + a33z = b3.
1) Если обе части какого-либо уравнения системы домножить
на одно и то же (не равное нулю) число, то полученная система будет
5 А. Г. Цыпкин
130
ГЛ. 4. АЛГЕБРА
эквивалентна первоначальной (т. е. они или обе несовместны, или же
обе совместны и множества их решений совпадают).
Например, система
0ц* + ai2y + a13z = bt,
Сй21Х + Сй22У +	= ct>2 (0 =/= 0),
031* + а^у + 0зз2 = ь3
эквивалентна системе (2).
2) Если обе части какого-либо уравнения системы, умноженные на
некоторое отличное от нуля число, вычесть из соответствующих частей
другого уравнения и составить систему, в которой вместо одного из
упомянутых уравнений стоит уравнение, полученное в результате вы-
читания, а остальные уравнения оставлены без изменений, то получен-
ная система будет эквивалентна исходной.
Например, каждая из систем
0Ц х-р а12 у+ ai3 z = bit
(an — ca2i) x + (ai2 — ca22) у 4- (0i3 — ca23) z=bt — cb2,
G3i	X 4“	032	У +	033	2	= ^з>
(0ii — C021)	x + (ai2 — ca22)	у + (a13 — ca23) 2 = b± — cb2,
Chi	X 4“	022	У 4-	023	2	~ ^2>	<
031	X +	032	У +	033	2	= Ь3
при с Ф 0 будет эквивалентна исходной системе (2) и обе эти системы
эквивалентны между собой.
Заметим, что если после выполнения этих преобразований в системе
появляется уравнение, у которого все коэффициенты в левой части ра-
вны нулю, а правая часть (свободный член) также равна нулю, то оче-
видно, что это уравнение обращается в тождество при любых значениях
неизвестных и после отбрасывания этого уравнения получается система
уравнений, эквивалентная исходной системе. Если же свободный член
такого уравнения не равен нулю, то это уравнение не может обратиться
в тождество ни при каком наборе значений неизвестных, и поэтому полу-
ченная система уравнений, равно как и эквивалентная ей исходная
система, будет несовместной.
Метод последовательного исключения
неизвестных. Пусть дана система s линейных уравнений с п
неизвестными
аИх1 + 012*2 4- • • • 4- ЯугХп = bi,
021*1 4“ Д22*2 + • • •• + 02П*П = ^2>	(3)
0si*i 4- as2x2 + ... 4- asnxn — bs.
Положим для определенности, что коэффициент ац не равен нулю
(хотя он может оказаться и равным нулю, и тогда необходимо начать
описанную ниже процедуру с другого уравнения системы, а именно
с уравнения, у которого коэффициент при. неизвестной х± отличен от
нуля). Преобразуем систему (3), исключая неизвестную хг из всех урав-
нений, кроме первого. Для этого обе части первого уравнения умножим
на число 021/0Ц и вычтем из соответствующих частей второго уравне-
§ 7» СИСТЕМЫ УРАВНЕНИЙ	-	131
ния, затем обе части первого уравнения, умноженные на число ая/ед,
вычтем из соответствующих частей третьего уравнения и т. д.
В результате указанных преобразований приходим к системе
ИЗ $ линейных уравнений с п неизвестными
+ 012 *2 + Я13 *з + • • • + 01» хп = bj,
’ "	«22**2 + «23**3 Н--h а2пХп =
«32**2 +«33**3 +----Ь аЗпХп == *3°.	.(4)
as2X2 + fls3* *3 + • • • + °snxn = bs'\
где ajp и ftp — новые коэффициенты при неизвестных и новые сво-
бодные члены, выражающиеся через коэффициенты и свободные члены
исходной системы (3). Система (4) эквивалентна системе (3). Преобразу-
ем теперь систему (4). При этом первое уравнение не будем трогать
совсем и будем преобразовывать- лишь часть системы (4), состоящую из
всех уравнений, кроме первого. Кроме того, мы будем считать, что среди
этих уравнений нет таких, у которых все коэффициенты левых частей
равны нулю, — такие уравнения мы отбросили бы, если бы их свобод-
ные члены были равны нулю (в противном случае мы уже доказали бы
несовместность нашей системы). Итак, среди коэффициентов име-
ются отличные от нуля; для определенности примем, что =/= 0.
Преобразуем теперь систему (4), вычитая из обеих частей третьего и
каждого из следующих уравнений обе части второго уравнения, умно-
женные соответственно на числа .
д(1)
g32	042	as2
л(1)	9	fl(D	9 * ‘ ’ 9	а(1)	*
°22	°22	а22
В результате из этих уравнений, кроме первого и второго, будет исклю-
чена неизвестная х2, и мы придем к следующей системе уравнений,
эквивалентной системе (4), а следовательно, и системе (3):
аИх1 + 012 х2 4“ 013 х3 + • • • 4- 01» Хп = ftl»
+	------Ь <414 = *1”.
«!?«,+ • + <«4-‘!я.
Система содержит теперь t уравнений, причем t s, так как некоторые
уравнения оказались, возможно, отброшенными. В дальнейшем будем
подвергать преобразованиям лишь часть полученной системы, содер-
жащую все уравнения, кроме двух первых.
В результате этого процесса последовательного исключения не-
известных может оказаться, что:
1) если мы придем к системе, в которой одно из уравнений
имеет отличный от нуля свободный член, а все коэффициенты левой ча-
сти равны нулю, то исходная система несовместна;
5*
132
ГЛ. 4. АЛГЕБРА *
ч 2) либо мы получим следующую совместную систему уравнений,
эквивалентную системе (3):
flll*l + °12 *2 + Я1Э х3 + * * * + 01П ХП = ^1»
«22 х2 i «23 *3	+ •			
«23 х3		.. 4- а(2)х а3п хп	М2).	\D)
akk _ xk П------Г akn хп — °k
Здесь пи=^0,	=/= О, =/= О, . .	а верхний ин-
декс, стоящий в скобках, указывает на номер преобразования,
после которого получены эти коэффициенты при неизвестных и но-
вые свободные члены. Отметим также, что и, очевидно, k С п.
Эта система будет определенной при k = п (число уравнений
равно числу неизвестных) и неопределенной при k <п (число урав-
нений меньше числа неизвестных). Действительно, так как при
k = п система (5) имеет вид
011*1 + 012 *2 + 013 хз + • • • + ain хп = ^1»
4’)Х.. + 4’>*з+ ••.+ а2пхп =621)»
a(-2)v ._____________La<2K	— Л<2>	()
с33 *3	“Зп	— °3 ♦
л(п—1)у _/Лп—1)
ипп лп п »
то из последнего уравнения мы получаем вполне определенное значение
для неизвестной хп. Подставляя его в предпоследнее уравнение, мы
найдем единственное значение для неизвестной xn_i.
Подставляя найденные значения хп и xn_i в третье снизу урав-
нение системы, найдем значение хп_ъ. Продолжая эту процедуру под-х
становки найденных значений неизвестных в оставшиеся уравнения,
получим, что система (6), а следовательно, и система (3) имеют един-
ственное решение, т. е. являются совместными и определенными (в этом
случае также говорят, что система (3) приводится к треугольному виду).
Если же £< п.то для «свободных» неизвестных хп+ъ ...» хп
мы возьмем произвольные числовые значения, после чего, двигаясь по
системе (5) снизу вверх, мы, как и выше, найдем для неизвестных *&,
xk-i, х2, xi вполне определенные значения. Так как значения сво-
бодных неизвестных можно выбирать бесконечным числом различных
способов, то система (5), а следовательно, и система (3) будут совмест-
ными, но неопределенными. (В этом случае говорят, что система при-
водится к трапецеидальной форме.)
Итак, метод Гаусса применим к любой системе линейных урав-
нений. При этом система будет несовместной, если в процессе преоб-
разований мы получим уравнение, в котором коэффициенты при всех
неизвестных равны нулю, а свободный член отличен от нуля; если же
такого уравнения не встретим, то система будет совместной. Совместная
система уравнений будет определенной, если она приводится к треуголь-
ному виду (6), и неопрёделенной, если приводится к трапецеидальному
виду (5) при k< п.
§ 7. СИСТЕМЫ УРАВНЕНИЙ	133
Пример. Исследовать, при каких значениях параметров а и b
система трех линейных уравнений о тремя неизвестными
х + у + z =» О,
2х+ Зу + z~ 1,	(7)
х + 2у + az == b
а) имеет единственное решение (и найти это решение), б) несовместна
и в) неопределенна.
Будем исследовать систему (7) методом Гаусса. Умножая обе части
второго уравнения системы на (—1/2), а обе части третьего уравнения
па (—1), получим системуч эквивалентную системе (7):
* + У + ? = 0,
-х-4^-Тг = ~Т’	(8)
—х — 2у — аг — —Ь.
Сложим первое уравнение системы (8) со вторым, а третье с первым;
уравнения, ролученные в результате сложения, возьмем в качестве
второго и третьего уравнений новой системы, эквивалентной системе (8):
X + у + г = 0,
— у У + у г я 2"»	(9)
—f/+(l — a)z = — b.
Теперь умножим обе части третьего уравнения на (—1/2) и сложим
второе уравнение с преобразованным третьим уравнением; полученное
уравнение возьмем в качестве третьего уравнения системы. В резуль-
тате этих преобразований система (9) примет вид
*+У+г = О,
1,1	1
"2	У +	2	2 *	2	’
1	1	А	1
2	aZ~	2	6	2	•
Умножая обе части второго уравнения на (—2), а третьего на 2,
окончательно получаем систему
х у + г = 0,
4/— 2 = 1,	(Ю)
az ~ Ъ — 1.
В зависимости от значений параметров а и b возможны следующие
случаи:	' •
1) При а =/= 0 и любом b система имеет единственное решение
2 — 2Ъ—а	о Ч- b — 1	b — 1
—-—,	, г= ——
2) При а = 0 и b 1 левая часть третьего уравнения системы (10)
обращается в нуль» а правая отлична от нуля. Следовательно» при
134	ГЛ. 4. АЛГЕБРА
этих значениях параметров а и b система оказывается несовместной.
3) При а == 0 и b == 1 система (10) принимает трапецеидальную
форму. При этих значениях параметров а и b система совместна, не-
определенна и имеет вид
х + у + z = О,
£/ — 2= 1.
Полагая z = ct где с — любое число, получаем множество решений
системы
х = —2с —J, у = с + 1, z = с.
Метод Гаусса решения систем линейных уравнений с числовыми
коэффициентами в силу простоты и однотипности выполняемых опера-
ций пригоден для счета на электронно-вычислительных машинах.
Существенным недостатком этого метода является невозможность
сформулировать условия совместности и определенности системы в за-
висимости от значений коэффициентов и свободных членов. С другой
стороны, даже в случае определенной системы этот метод не позволяет
найти общие формулы, выражающие решение системы через ее коэффи-
циенты и свободные члены, которые необходимо иметь при теоретиче-
ских исследованиях. Существуют и другие методы решения и исследо-
вания систем линейных уравнений, которые лишены отмеченных недо-
статков. Эти методы основаны на теории матриц и определителей
(см. § 8).
7.4. Некоторые способы решений систем йелинейных алгебраиче-*
ских уравнений. Для систем нелинейных алгебраических уравнений,
в отличие от систем линейных уравнений, не найдено какого-либо
универсального практически удобного метода решения, а потому при
решении каждой конкретной системы нелинейных уравнений прихо-
дится применять специальные приемы решений, основанные на исполь-
зовании особенностей алгебраических уравнений, составляющих дан-
ную систему.
Разберем на примерах два приема решения систем нелинейных ал-
гебраических уравнений.
Пример 1. Решить систему уравнений
ха — Ьху + 4#2 ® 0,	(1)
х2 — 15^2 _ х + 11^==
Замечая, что многочлен двух переменных х и у; стоящий в левой
части первого уравнения системы (1), — однородный, систему (1)
можно свести к двум следующим системам, эквивалентным системе (1)з
Xa-5X{/ + 4^ = O,	/х\2 еМХ.Д-п
У = о,	(2)	\ у )	\ у )	’	(2')
х2—15г/2 — *+ 1117 ss — 4;	х2—15р2—	= —4.
Найдем решения системы (2). Подставляя значение у == 0 в первое
и третье уравнения системы (2), получаем систему двух уравнений для
нахождения значения одного неизвестного х:
х = 0, х2 — х = —4.
Так как не существует числа х, удовлетворяющего обоим уравнениям
системы, то система (2) несовместна. Перейдем к решению системы (2'),
§ 7. СИСТЕМЫ УРАВНЕНИЙ
135
Решим первое уравнение системы (2') как квадратное относительно
переменной и = х/у. Уравнение
и2 — 5и + 4 = О
имеет корни и± = 4, и2 = 1, т. е. xly = 4, xly « 1.
Таким образом, система (2') эквивалентна двум системам:
х = 4у,	х = у,
(3)	(3')
х2 — 15г/а — х + Иг/ — —4;	х2 — 15г/а — х + Иг/ — —4.
Подставляя выражения х через у во вторые уравнения систем,
получаем соответствующие им уравнения для нахождения у\
У2 + 7у + 4 = 0,	— 14z/2 + Юг/ + 4 = 0.
Решения первого уравнения:
—7 + /33	—7 — /33
Решения второго уравнения:
Уз = 1. У* = —2/7.
Системы (3) и (3') имеют соответственно решения:
хг = 2 /33 — 14, х2 = -2/33-14, х3 = 1, х4 = —2/7,
/33 — 7	— /33 — 7
У1 =-----2----’ У* =----------2-----’ Уз = 1 ’	yi== ~2/7’
которые и будут решениями системы (1).
Симметрические системы уравнений. Си-
стема уравнений с двумя неизвестными х и у называется симметричен
ской, если она не меняется при замене неизвестной х на неизвестную г/,
а неизвестной у на неизвестную х.
Часто решение таких систем может быть найдено с помощью вве-
дения новых переменных — элементарных симметрических много-
членов Gj и а2:
Oi<= х+ yt о2 = ху.
Пример 2. Найти решения системы
х2 + ху + у2 = 4,
X + ху + у = 2.	(4)
Введем новые переменные — элементарные симметрические мно-
гочлены
х+ г/, о2= ху.
Относительно переменных <ji и о2 система (4) запишется в виде
— а2 — 4г
Oi + о2 = 2.	*
Выражая о2 из второго уравнения системы через Gji
о2 = 2 — ох	(6)
136
ГЛ. 4. АЛГЕБРА
и подставляя ст2 = 2 — oj в первое уравнение системы (5), получаем
квадратное уравнение о? + О; — 6 = 0, корни которого равны
2 и — 3.
Подставляя найденные значения Oi в равенство (6), получаем зна-
чения о2. Таким образом, множество решений системы (5) имеет вид
ох = 2, оа = 0; Gt — —3, о2 = 5.
Теперь множество решений исходной системь! (4) может быть полу-
чено как объединение множеств решений двух более простых система
х+ у ~ 2, х + у = — 3,
ху = 0;	ху = 5.
Вторая система решений не имеет. Решениями первой системы являются
пары чисел х± == 2, yt = 0 и х2 = 0, у2 == 2.
Пример 3. Решить систему уравнений
X + у = 5,
х* + у6 = 275.
Замена Oi = х-р У, <т2 = ху приводит данную систему уравнений
к виду
Qi — 5,
'	erf — 5о^о2 + 5а|а| = 275.
Подставляя значение ог = 5 во второе уравнение, получим уравнение
ДЛЯ О2:
о2 —25о2+ 114 = 0.
Корнями этого уравнения будут числа 6 и 19.
Таким образом, множество решений исходной системы находится
как объединение множеств решений двух более простых систем:
х + у = 5, х + У = 5,
ху =6; ху = 19.
Решим первую систему. Из первого уравнения имеем 5 — х.
Подставляя у = 5 — х во второе уравнение, получаем квадратное
уравнение относительно неизвестной х: х2-—5х+б = 0, корнями
которого являются Xi = 3 и х2 = 2. Из равенства у = 5 — х находим
уг = 5 — хг = 2 и у2 == 5 — х2 = 3. Итак, решения первой системы —
пары чисел xt = 3, ух = 2 и х2 = 2, у2 = 3.
Аналогичным способом можно убедиться, что вторая система не
имеет решений.
В п. 7.3 были рассмотрены системы линейных алгебраических
уравнений, в которых число уравнений было меньше числа неизвест-
ных. При этом оказывалось, что одни неизвестные выражались через
другие («свободные») неизвестные, т. е. система имела бесчисленное
множество решений. По-другому обстоит дело в случае решения систем
нелинейных алгебраических уравнений, в которых число неизвестных
больше, чем число уравнений. Может оказаться, что такая система
имеет как бесчисленное, так и конечное число решений или даже вовсе
не имеет решений. Сейчас мы рассмотрим в качестве примера систему
двух алгебраических уравнений с тремя неизвестными, которая имеет
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 137
единственное решение (т. е. множество решений представляет собой
единственную упорядоченную тройку чисел, обращающую оба урав-
нения в тождества).
Пример 4. Найти действительные решения системы
х + у = 2,	(7)
xy — z2~ 1.
Выражая у через х из первого уравнения и подставляя у = 2 — х
во второе уравнение, получаем уравнение (х — I)2 + г2 = 0, которое
эквивалентно системе
х — 1 = 0, г = 0.
Эта система имеет единственное решение, а поэтому и система (7)
двух уравнений с тремя неизвестными имеет.только одно решение
(1; I; 0).
§ 8. Исследование систем линейных уравнений
с помощью определителей
8.1. Матрицы и операции вад ними. Прямоугольная таблица
«11	012	«1з	•	• •	«in
«21	«22	«23	.	. .	О-гп
.fynl	ат2	атз	•	• •	О'гпп
составленная из т*п чисел, называется матрицей из т строк и п went)*
цов или матрицей размера mXn, а также тХ/г-матрицей.
Числа aij (1 = 1, 2, ...» m; /= 1, 2, ..., /г) называются эле*
ментами матрицы; первый индекс i элемента указывает номер строки*
в которой стоит элемент матрицы, а второй индекс / — номер столбца.
Матрица (1) может обозначаться также
||«О||, i = 1, 2, ..., т; /= 1, 2, ..., п.
Кроме того, для матриц используются
обозначения
«и	«12	«13	• • •	«1п
«21	«22	«23	. . .	«2П
ат1	«m2	«m3	• • • «тп/
~ «11	«12	'«13	• • • «1п
«21	«22	«23	• • •	«2П
_ ат1	«m2	«m3	• • • «тп _
или [«,;].
ИЛИ (Ojj)J
Если число строк матрицы равно числу ее столбцов (и равно п),
то матрица называется квадратной матрицей (порядка п).
Две матрицы ||а^-1| и называются равными, если числа их
строк и столбцов соответственно равны и равны числа, стоящие на
соответственных местах:
aij = bki при := k и / = /.
138
ГЛ. 4. АЛГЕБРА

Основными арифметическими операциями над матрицами являются
умножение матрицы на число, сложение матриц и умножение матриц.
Далее для краткости матрицы также будем обозначать буквами А, В, ...
Умножение матрицы на число. Произведением
числа Л и матрицы А = || atj || называется матрица В = || btj ||, эле-
менты которой вычисляются по правилу btj — к-ац, т. е. каждый эле-
мент матрицы btj представляет собой произведение числа к и элемента
матрицы atj.
Например,
#11	#12 I	I ^-#11	^-#12
#21	#22 I	I ^#21	^#22
Матрица, все элементы которой равны нулю, называется нулевой ма-
трицей и обычно обозначается символом 0 (или 0/7).
Свойства операции умножения матрицы
на число:
1) коммутативность:
М = Д4;
2) ассоциативность:
(а.р).Д = а. (Р.Д).
Сложение матриц. Суммой двух матриц А = ||atj|| и
имеющих соответственно равные числа строк и столбцов
(t, k = 1, 2 m и /, / = 1, 2, ..., п), называется- матрица S=
— размера /иХп с элементами, равными суммам соответственных
элементов матриц А и В: stj = а/7* + btj. Сумма матриц А и В
обозначается А + В.
Например, суммой матриц
2	1	1 I	|	—2	—2	31|
О	—1	5 I’	I	2	3	1||
Является матрица
10	—1	4	1
[2	2	6	Г
Свойства операции сложения матриц:
1) коммутативность:
А + В — В+ А;
2) ассоциативность:
(Д + В) + С = А + (В + О;
8) дистрибутивность относительно сложения матриц!
X. (Д + В) = Х.Д + Х-В;
4) дистрибутивность относительно сложения чисел!
(а+ ₽)-Д = а.Д + 0.Д.
Перечисленные свойства операций умножения матрицы на число и опе-
рации сложения матриц есть следствия определения этих операций
и свойств коммутативности и ассоциативности операций сложения и
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 139
умножения действительных чисел, а также дистрибутивности умноже-
ния относительно сложения.
Операция сложения матриц имеет обратную операцию — вычи-
тание. Разностью матриц А и В называется матрица С, составленная
из разностей соответственных элементов заданных матриц А и В.
О матрице С Говорят, что она получена в результате вычитания матрицы
В из матрицы Л, и пишут С — А —В.
Умножение матриц. Пусть Л и В — две матрицы,
причем число столбцов первой матрицы равно числу строк второй ма-
трицы, т. е. эти матрицы имеют вид
ап ап ... ain
^2t	а%2 ... а2п
amt ат2 • . . атп
&Н	Ьп	т	&ik
^2i	^22	♦ • •	&2k
^tli	Ьп2	• • •	Ь/lk
и В =
Произведением матриц Л = || аг j || и В = (| btj || называется матрица
С порядка тХ kt элементы которой вычисляются по правилу
Cij = anbij + ai2b2j + • • • + atnbnji i = 1 f 2, . . M mt
7=1, 2, . . k,
т. e. элемент, стоящий в i-й строке и /*-м столбце произведения двух
матриц, получается в результате умножения первого элемента i-й
строки матрицы Л на первый элемент /-го столбца матрицы В, второго
элемента i-й строки матрицы Л на второй элемент /-го столбца матрицы В
и т. д. и последующего сложения всех таких произведений пар элементов
матриц Л и В. Произведение матриц А и В обозначается Л «В. Сог-
ласно, данному определению произведение матриц Л’В существует,
если число строк матрицы Л равно числу столбцов матрицы В.
Операция умножения матриц, вообще говоря, некоммутативна.
Например,
т. е. произведение матриц зависит от порядка следования сомножителей.
Более того, если перемножать неквадратные матрицы, то может ока-
заться, что произведение двух матриц, перемножаемых в рдпом порядке,
существует, а в другом — нет.
s Операция умножения матриц ассоциативна;
(Л-В).С= Л-(В-С).
Основные свойства операции умножения
матриц*):
а-(Л-В) = (а-Л)-В;	Л-(а-В) = (Л-а)-В;
(Л-В)-а= Л-(В.а); (Л + В)-С = Л-С+ В-С;
С-(А + В) = С-Л + С-В.
В множестве квадратных матриц фиксированного порядка п опе-
рации сложения и умножения определены для любых двух матриц —
суммой и произведением двух квадратных матриц порядка п снова
Эти свойства справедливы, естественно, лишь в том случае, если ука-
занные действия над матрицами имеют смысл (т. е. только для тех матриц,
число строк и столбцов которых удовлетворяет соответствующйм условиям).
140
ГЛ. 4. АЛГЕБРА
будут, квадратные матрицы порядка л, т. е. множество всех квадрат-
ных матриц фиксированного порядка замкнуто относительно операций
сложения и умножения, причем операция умножения ассоциативна,
но, вообще говоря, не коммутативна.
Элементы а1ь а22, ...» аПп квадратной матрицы порядка п назы-
ваются диагональными элементами.
Квадратная матрица, все диагональные элементы которой равны 1,
а остальные — нули, называется единичной и обозначается Е (или Еп,
где п — ее порядок, или ||6ij||, где i, / = 1, 2, п. Символ $tj имеет
специальное название — «символ Кронекера»).
Для любой квадратной матрицы А порядка п справедливо ра-
венство
£п-А = А*ЕП =А.
Матрица порядка и, у которых ац = 0 для всех i ц 1. е.
матрицы вида
«И	0	0	...	0
0	«22	0	...	0
0	0	«зз	...	0
0	0	0	...	ипГ1
называются диагональными матрицами (об элементах ац, a22i ..., апп
также говорят, что они стоят на главной диагонали).
Свойство диагональных матриц. Сумма и произ-
ведение двух диагональных матриц т- также диагональные матрицы.
Транспонирование матриц. Пусть А = || ац || —•
матрица размера тХп:
«и
«21
ат1
Д—
«12	.	.	.	«1л
«22	•	•	•	«2Л
«m2	•	•	•	«тл
Матрица, получающаяся из матрицы А заменой строк столбцами,
называется транспонированной матрицей по отношению к матрице А
и обозначается Ат.
Квадратная матрица А называется симметрической, если Ат= А,
и кососимметрической, если Ат = —А.
Элементы, расположенные симметрично относительно главной
диагонали, у симметрической матрицы равны, а у кососимметрической
противоположны. Все диагональные элементы кососимметрической
матрицы равны нулю.
8.2. Определители. Существенным недостатком решения систем
линейных уравнений методом последовательного исключения неиз-
вестных (см. п. 7.3) является то, что он не позволяет сформулировать
условия совместности и определенности системы линейных уравнений
через ее коэффициенты и свободные члены, а также (в случае опреде-
ленной системы) не дает формул, выражающих решение системы через
ее коэффициенты и свободные члены, которые могут быть полезными
при теоретических исследованиях.
Понятие определителя возникло при решении задачи нахождения
общих формул для решений систем линейных уравнений через ее коэф-
фициенты и свободные члены.
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Щ
Рассмотрим систему двух линейных уравнений с двумя неизвест-
ными х и у.
,аих + а12у = Ьь	(2)
а21х + а22у — Ь2.
Матрицы
д _ || аИ fl12 I Д — I 011 ’ ai2 II
|| «21	«22 I 9	| «21	«22	Ь-2 ||
называют соответственно основной и расширенной матрицами системы (2).
Умножим первое уравнение системы на «22, второе на (—а12) и
сложим эти уравнения. В результате сложения получим уравнение
(«Ц«22 — «12«21) ’ Х = ^1«22 - ^2а12«	(3)
Аналогично, умножая обе части первого уравнения на (—а21),
второго на ап и складывая эти уравнения, получим уравнение
(«Ц«22 — «12«21)’Z/ = «11^2 - «21^1*	(3')
Коэффициент при неизвестных х-и у в левых частях уравнений (3),
(3') один и тот же и выражается через элементы матрицы А следующим
образом: он равен произведению- элементов главной диагонали минус
произведение элементов второй диагонали.
Выражение апа22 — ^i2a2i называется определителем (или детер-
минантом) матрицы А — ||<2fj|| (i, j = 1,2) и обозначается det А
(или | А |, или | atj |). Выражение апа22 — «i2«2i — определитель вто-
рого порядка, так как матрица А является матрицей второго порядка.
В правых частях равенств (3), (3') стоят выражения, имеющие
такой же вид, как и коэффициент в левой части, и также представляют
собой определители второго порядка: правая часть равенства (3) яв-
ляется определителем матрицы, полученной из матрицы А заменой
ее первого столбца на столбец свободных членов системы (2)г правая
часть равенства (3') — определитель ^матрицы, полученной из матрицы Л
заменой ее второго столбца на столбец свободных членов системы (2).
Уравнения (3), (3') теперь можно записать в виде
Д.х = Дх, к-у = Ьу,
где через А, Дх и Ду обозначены определители
| «ц «12 I
Д =	= «11«22 — «12«21,
I «21	«22 I
А	|^1	Й12|
Дх =	| — ^1«22 - ^2«12>
I «2	«22	I
.	I «И	bi	I
Д„ =	= «цОг— «21^1-
I «21	Ь2	|
Рассмотрим систему трех уравнений с тремя неизвестными х,
у и г:
оцх + а12у + а13г = bit
аг1х + а.22у.+ a2Sz = 62,	(4)
«si* +	+ аззг = Ь3.
142
ГЛ, 4. АЛГЕБРА
Матрицы
л = || аМ|| =
0ц	cig	013
02i	022	023
031	032	033
011
021
031
012	013	^1
022	023	^2
032	0зз	Ь3
д =
называются основной и расширенной матрицами системы (4).
Так же как и в случае системы двух линейных уравнений с двумя
неизвестными, для неизвестной х можно получить уравнение, коэф-
фициенты которого выражены через коэффициенты системы и ее сво-
бодные члены:
(0Ц022038 + 012023031 + 013021032 —’ 013022031	012021033
— 011023082)** = ^1022033 Н* 012028^3 Н* G 13^20.32
— 013022^3 — 012^2033 — ^1023032*	(5)
Коэффициент при х в уравнении (5) называется определителем
(или детерминантом) квадратной матрицы третьего порядка А и обоз-
начается |Д | или det ||о/у|| или |а/у|.
Таким образом, определитель матрицы третьего порядка вычис*
ляется по правилу
0Ц 012 013
021 022 023
031 032 033
= 0Ц022033 + 012023031 + 013021032 — 013022031 —
«— О12О21033 — 0Ц023032.
Правило вычисления определителя матрицы третьего порядка
графически можно изобразить следующим образом: на рис. 4.2 пря-
мыми соединены элементы матрицы третьего порядка, произведение
которых входит в определитель со знаком плюс, а рис. 4.3 прямыми
соединены элементы этой матрицы, произведение которых входит
в определитель со знаком минус.
Правая часть равенства (5) также будет определителем третьего
порядка матрицы, полученной из матрицы А заменой ее первого столбца
на столбец свободных членов системы (4). Если обозначить определи-
тель матрицы А через А, а определитель, стоящий в' правой части ра-
венства (5)f через АЛ1 то уравнение (5) примет вид
Д*х~ А*.
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 143
Аналогично из системы (4) можно получить уравнения для нахож-
дения неизвестных у и г:
д.у = Ду, Д-2 = дг,
где через и Аг соответственно обозначены определители третьего
порядка матриц, полученных из матрицы А заменой ее второго (соот-
ветственно третьего) столбца столбцом свободных членов, т. е.
	bi 012 013		0ц bi at3		011 012 bi	
Ал =	^2 022 023	* д0 =	021 *2 023		021 022 Ь^	•
	Ь$ 082 083		081 bs азз		a3i 033	
Понятие определителя вводится для любой квадратной матрицы
А « || а/; || л-го порядка.
Образуем всевозможные произведения по п элементов этой матрицы,
расположенных в разных строках и разных столбцах, т. е. произведе-
ния вида
. •аЫд,	(6)
где индексы ij, f2, in образуют некоторую перестановку из чисел 1,
2, ..., п. Число таких перестановок (а следовательно, и всевозможных
произведений вида (6)) равно п\
Определителем квадратной матрицы n-го порядка
II aii	aiz	• • •	01п
021	022	• • •	въп
Qnl ап2 • • • апп
называется алгебраическая сумма всевозможных различных произ-
ведений
£(—l)palfl.a2i2. . . . -anjn, .
где р1, если подстановка
/1	2	3
\ h	h	*з
п \
in /
нечетная, и р =» 2, если указанная подстановка четная.
Определитель квадратной матрицы n-го порядка обозначается
ли	012	...	atn
021	а22	•••	02/1
0«1	0fl2	• • •	Ann
или det || ay[|,. i, ] = 1, 2, . . n.
Основные свойства определителей:
1)	определитель транспонированной матрицы равен определителю
исходной матрицы;
2)	если одна из строк определителя состоит только из нулей, то
определитель равен нулю;
3)	при перестановке местами двух строк определителя получается
определитель противоположного знака;
144
ГЛ. 4. АЛГЕБРА
4)	определитель, имеющий две одинаковые строки, равен нулю;
5)	если все элементы некоторой строки определителя умножить
на число k, то сам определитель умножится на k't
6)	если одна из строк определителя пропорциональна другой
строке, то определитель равен нулю;
7)	если все элементы i-й строки определителя n-го порядка пред-
ставлены в виде суммы двух, слагаемых aj+ bj (j = 1, 2, ..., 0), то
определитель равен сумме двух определителей, у которых все строки,
кроме Z-й, такие же, как и в исходном определителе, а i-я строка одного
из определителей состоит из элементов ajt а другого — из элементов bj;
8)	определитель не меняется, если к элементам одной из строк
прибавляются элементы другой строки, умноженные на одно и то же
число.
Вычисление определителей порядка выше третьего может быть
основана на следующем свойстве определителей, которое называется
разложением определителя по строке.
Пусть ||atj|| — матрица м-го порядка. Определитель этой матрицы
может быть записан в виде
det |||1 ==0ц*| ^111 — 012*1 ^12 !+••• + (—О*1”*1 ffi/rMtfl|>
где через |Л^| обозначен определитель матрицы (п — 1)-го порядка,
полученной из матрицы |]а^|| вычеркиванием первой строки и /-го
столбца.
С помощью этого свойства определителей нетрудно, например,
вычисление определителя произвольной квадратной матрицы четвер-
того порядка свести к вычислению определителей третьего порядка,
если записать ее определитель в виде
0ц	012	013	014
021	022	023	024
031	032	033	034
041	042	043	044
= 011 •
024		021
034	— 012	031
044		041
023 024
022 023
032 033
042 043
033 034 +
043 044
	021'022 024		021
+ 01. •	031 032 0.34	— 014’	031
	041 042 044		041
022 023
032 033 •
042 043
8.	3. Ранг матрицы. Пусть ЛжвЦа^Ц— матрица размера тХп
(i = 1, 2, ...» т; / — I, 2, ..., п), т. е. матрица, состоящая из т строк
и п столбцов. Выберем какие-нибудь k строк и k столбцов матрицы А
(k не превосходит наименьшего из чисел т, п). Элементы матрицы Л,
находящиеся на пересечениях отмеченных строк и отмеченных столб-
цов, записанные в их естественном порядке, образуют квадратную
матрицу порядка k. Определитель этой квадратной матрицы порядка k
называют минором Z?-ro порядка матрицы А.
Рангом матрицы А называют наивысший порядок отличныл от
нуля миноров матрицы А.
Пример. Найти ранг матрицы
2
1
О
А =
—4 3
—2 I
1 О
§ 8# ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 145
На пересечении первой строки и первого столбца стоит элемент
матрицы ац =» 2. Следовательно, ранг матрицы А не меньше единицы.
Из элементов, стоящих на пересечении первых двух строк и пер-
вых двух столбцов образуем матрицу
2 —4II
1 — 2 ||’
определитель которой равен нулю. Однако в матрице А содержатся
и отличные от нуля миноры второго порядка. Таким минором, например,
будет определитель матрицы, составленной из элементов, стоящих
на пересечении первого и второго столбцов и второй и третьей строки:
Следовательно, ранг данной матрицы по крайней мере равен двум.
Минором следующего (третьего) порядка будет определитель
матрицы Д, который равен нулю.
Следовательно, ранг данной матрицы равен двум.
Ранг матрицы может быть найден и без вычисления различных
миноров этой матрицы. Этот метод вычисления ранга матрицы основан
на использовании следующих элементарных преобразований матрицы,
не меняющих ее ранга:
1)	перемена местами двух строк или двух столбцов;
2)	умножение строки или столбца на произвольное отличное от
нуля число;
3)	прибавление к одной строке (столбцу) другой строки (столбца),
умноженной на некоторое число.	- '
Для нахождения ранга матрицы размера т X п необходимо с по-
мощью указанных элементарных преобразований привести матрицу
к виду, в котором все элементы ац (i j) равны нулю. Ранг исходной
матрицы будет равен числу отличных от нуля элементов полученной
матрицы.				
Пример.	Найти ранг i		матрицы	
		0	2	—4
		—I	—4	5
	А =			
		3	1	7
		0	' 5'	— 10
Меняя местами в этой матрице первый и второй столбцы и умно-
жая новую первую строку на 1/2, получаем матрицу, у которой эле-
мент ац равен 1:
1	0	-V
—4	— 1	5
13	7*
5	0	—10
146
ГЛ. 4. АЛГЕБРА
Прибавляя к третьему столбцу удвоенный первый столбец, полу»
чаем матрицу
1	О	О
-4	—1	—з
1	3	9
5	0	0
Преобразуем строки матрицы, начиная со второй. Умножим пер-
вую строку на 4 и сложим со второй строкой; умножим первую строку
на (—1) и сложим с третьей строкой; умножим первую строку на (—5)
и сложим с четвертой строкой. В результате этих элементарных пре-
образований получится матрица
1	0	0
0	—1	— 3
0	3	9
ООО
Далее последовательно будем преобразовывать строки и столбцы
матрицы, не меняя первой строки и первого столбца:
1)	умножим вторую строку на (—1);
2)	умножим вторую строку на (—3) и сложим с третьей строкой^
3)	умножим второй столбец на (—3) и сложим с третьим столбцом.
В результате этих трех элементарных преобразований последовательно
получаются матрицы
1	0	0		1	0	0		1	0	0	
0	1	3		0	1	3		0	1	0	
0	3	9	>	0	0	0		0	0	0	•
0	0	0		0	0	0		0	0	0	
В последней матрице все элементы atj (i j) равны нулю. Из
элементов alt отличны от нуля лишь ац и а22- Ранг этой матрицы
(а следовательно, и ранг матрицы Я) равен двум.
8.4. Исследование систем линейных уравнений с помощью опре->
делителей. Формулы Крамера. Рассмотрим систему т линейных урав-
нений G и неизвестными xit х2, ...»хп:
ЛИ *1 + Хг + • • • + ain хп == Ьи
#21 Xi + 022 Х2 + • • • + 02П Хп == b2t
(7)
&mlXi 4- am2X2 + • • • + ChnnXn == ^rn-
Для записи системы уравнений (7) используется и более короткая
(матричная) форма записи. Записывая неизвестные xj, х2, ..., хп и
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
147
свободные члены b^, Ь2, bm в виде столбцов (матриц размера лХ1
и /пХ 1 соответственно) и обозначая эти столбцы через X и 5}
систему (7) можно записать
в виде
Д-Х = В.
Матрица
Л = || ^|| =
ап
#21
#12
«22
ain
&2П
ат! ат2 • • • атп
называется основной матрицей системы (7), а матрица
011	#12	• • • #ln bi
ТГ «21	«22	• • •	«2П bi
ami ат2 . . . атп bm
— расширенной матрицей этой системы, причем ранг матрицы А либо
равен рангу матрицы А, либо на единицу превышает его.
Определитель матрицы А называется определителем системы (7).
Система уравнения называется крамеровской, если число уравне-
ний совпадает с числом неизвестных и определитель системы отличен
от нуля.
Любая крамербвская система уравнений имеет единственное реше-
ние (хь х2, ...» хп), даваемое формулами
&Xi
(8)
где Дхг — определитель матрицы, полученной из матрицы А заменой
i-го столбца на столбец свободных членов системы (7). Формулы (8)
называются формулами Крамера.
Полный ответ на вопрос о существовании решения системы т
линейных уравнений с п неизвестными дает следующая теорема
Кронекер а—К а п е л л и:
Для того чтобы система уравнений (7) имела решение, необходимо
и достаточно, чтобы ранг расширенной матрицы был равен рангу
основной матрицы системы. Если ранги основной и расширенной мат-
риц совпадают с числом неизвестных, то система имеет единственное
решение. Если ранг г основной и расширенной матриц меньше числа
неизвестных (г< п), то система (7) имеет более одного решения,
В последнем случае число «свободных» неизвестных, через кото-
рые выражаются остальные неизвестные, равно п — г.
148	ГЛ. 4. АЛГЕБРА
Система двух линейных уравнений с двумя
неизвестными. Система двух линейных уравнений с двумя
неизвестными
(9)
матрицы:
012 Ь\
«22	^2
причём ранг матрицы А равен рангу матрицы А или на единицу больше
его.
Система двух линейных
быть записана в виде (см.
011* + 012*/ =
«21^ “Ь 022# = ^2
имеет следующие основную и расширенную
л = ||ап а,2||, л = ||а11
I 021 . 022 I	|| 021
уравнений с двумя неизвестными может
п. 8.2)
&1	012 I	I «11	^1
где
д _ I 011 0,2
| «21	«22 |	I &2	«22 |	7	| «21	^2 |
Для системы (9') (а следовательно, и для системы (9)) возможны
следующие случаи:
I) Если определитель этой системы
Я «и Я12
«21	«22
не равен нулю, то ранг матрицы А равен двум, ранг матрицы А также
равен двум, система (9) — крамеровская и имеет единственное реше-
ние, определяемое формулами Крамера.
2) Если определитель этой системы равен нулю (А = 0), то ранг
матрицы А равен единице (так как хотя бы одно из чисел allf «12, «21,
«22 отлично от нуля), и возможны два случая:
а)	ранг расширенной матрицы А равен двум, т. е. отличен от нуля
хотя бы один из определителей
^1	0121 . А 1«и
, I» Ду == I
«2	«22 I	I 021	«2
тогда согласно теореме Кронекера—Капелл и система (9) решений не
имеет;
б)	ранг расширенной матрицы А равен единице, т. е.
Ах = А^ = 0.
Тогда согласно теореме Кронекера—Капелли система имеет более
одного решения; число свободных неизвестных равно числу неизвест-
ных минус ранг матрицы Л, т. е. равно единице, и связь между неизве-
стными дается одним из уравнений системы.
Решения системы двух линейных уравнений с двумя неизвестными
имеют следующую геометрическую интерпретацию.
Каждое из уравнений системы (9) задает линейное соответствие
между переменными х и у. Всякое линейное соответствие между пере-
менными х и у определяет в прямоугольной системе координат Оху
Ах ==
§ 8. ИССЛЕДОВАНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 149
некоторую прямую. В случае, когда система имеет единственное ре-
шение, прямые, задаваемые первым и вторым уравнениями, пересе-
каются (рис. 4.4). Если система имеет бесчисленное множество решений,
прямые совпадают (рис. 4.5); если система несовместна) прямые па*
раллёльны (рис. 4.6).
.Система трех линейных уравнений с тремя
неизвестными. Система трех линейных* уравнений с тремя
неизвестными х, у, г
0ц* + а12у + a13z = blt
а21х + а22у + a23z == Ь2,	(10)
031* “Ь ty&y Н” «зз* = Ь3
имеет основную и расширенную матрицы								
	0и	012	' 013	,	А =	011	012	013	bi
Д =	а2т	022	а23		021	022	023	bi
	031	Й32	0зз		031	032	033	Ьз
причем ранг матрицы А равен рангу матрицы А или на единицу
больше его. Для системы (10) возможны следующие случаи:
1)	Если определитель этой системы
Д = | А | = det
ац	а12	aig
021	а22	0гз
0м	аза	азз
150
ГЛ. 4. АЛГЕБРА
не равен нулю, то система (10) — крамеровская и она имеет единствен-
ное решение, определяемое формулами Крамера:
где ]
^1
Д» =
012 013
022 <223
032 033
	0Ц	bi	013		0Ц	012	Ь1
д»=	021	^2	023	> =	021	022	bi
	031	Ьз	033		031	032	bs
Ьз
2)	Если определитель Д ==_0, т. е. ранг матрицы А меньше трех,
а ранг расширенной матрицы А больше ранга матрицы А, то система
не имеет решений (несовместна).
Рис. 4,8.
3)	Если определитель Д = 0 и ранг матрицы А равен рангу рас*
ширенной матрицы А, то система имеет более одного решения. При
этом, если ранги матриц А и А равны двум (единице), то число свобод-
ны^ неизвестных равно разности числа неизвестных и рангу матриц А
и А, т. е. равно одному (двум).
Рис. 4.9.
Рис. 4.10а
Более подробный анализ случаев 1) **- 3) приведен ниже, где ра-
зобраны все возможные различные соотношения между рангами мат-
риц А и А*).
Линейное уравнение с тремя неизвестными х, г определяет
плоскость в пространстве и соответственно три уравнения системы (10)—
три плоскости. Возможны следующие случаи взаимного расположения
этих трех плоскостей af, a2, a3, задаваемых соответственно первым,
вторым и третьим уравнениями:
♦) Здесь опущены случаи? когда ранг матрицы А равен нулю, а ранг
матрицы А равен единице или нулю. Геометрическая интерпретация $тих
случаев весьма тривиальна.
§ 9. НЕРАВЕНСТВА
151
1)	Если система имеет единственное решение (ранг матрицы равен
трем), то все три плоскости различны и пересекаются в одной точке
(рис. 4.7). Решением системы являются координаты этой точки.
2)	Если ранг матрицы А равен двум, а ранг матрицы А равен трем,
то система не имеет решения. Две плоскости пересекаются по пря-
мой /, параллельной третьей плоскости (на рис. 4.8 плоскости а3).
3)	Если ранг матрицы А равен единице, а ранг матрицы А равен
двум, то система не имеет решений. Плоскости, задаваемые уравне-
ниями системы, параллельны (рис. 4.9), причем две плоскости (на
рис. 4.10 плоскости Oj и а2) могут совпадать.
4)	Если ранги матриц А и А равны между собой и равны 2, то
система имеет бесчисленное множество решений. Все три плоскости
пересекаются по
одной прямой (рис. 4.11). При этом две плоскости
могут совпадать (рис. 4.12). Ре-
шением системы будут коорди-
наты любой точки, принадле-
жащей указанной прямой.
Рис. 4.11.
Рис, 4.13,

5) Если ранги матриц Л и Л равны между собой и равны единице,
то система имеет бесчисленное множество решений. Все три плоскости
совпадают (рис. 4.13). Решением системы будут координаты любой
точки, принадлежащей совпадающим плоскостям.
§ 9.	Неравенства
9.1.	Определения и основные свойства неравенств. Неравенства-
ми называют выражения вида
а<Ь	я>Ь (а>Ь),
где а и b могут быть числами или функциями. Символы < (^), > (>)
называются знаками неравенства и читаются соответственно: меньше
(меньше или равно), больше (больше или равно).
Неравенства, которые записываются с помощью знаков > и <,
называются строгими неравенствами, а неравенства, в записи которых
участвуют знаки > и С, — нестрогими.
Нестрогое неравенство эквивалентно строгому неравенству того же
внака и равенству.
Различают два вида неравенств: арифметические (или числовые),
в записи которых участвуют только числа, и неарифметические, в за-
писи которых наряду с числами участвуют функции одной или не-
скольких переменных.
Например, числовыми неравенствами будут
2> 1,	/2 <7.
Неарифметическими неравенствами будут, например, неравенства
а < 1, Iga х + tg х > 0, х2 + у* > /?2.
152
ГЛ. 4. АЛГЕБРА
Функции, входящие в неравенства, могут принимать различные
числовые значения в зависимости от различных значений своих аргу-
ментов. При одних значениях аргументов неравенство может быть
справедливым, при других — нет.
Основные свойства неравенств*):
1)	Если а> Ь, то &< ал z	ч
если а < Ь, то 6> а (антисимметричность).
2)	Если а > b и Ь > с, то а > с; (тоан9итивност. ч
’ если а< b и Ь< с, то а< с (транзитивность).
Арифметические действия с неравенствами.
1)	Два неравенства одинакового знака можно складывать; при
этом в результате сложения получается неравенство того же знака: -
если а > b и с > d, то а + с> b + d\
если а < b и с < dt то а + с < b+ d.
2)	Если обе части неравенства умножить (разделить) на одну и
ту же положительную величину, то получится неравенство того же
знака; если же обе части неравенства умножить (разделить) на отри-
цательную величину, то получится неравенство противоположного
знака:
если а У	> b и с *	> 0, то ас	> Ьс\
если а <	С Ь и с	> 0, то ас <	С Ьс\
если а х	> b и с <	С 0, то ас <	Z Ьс;
если а <	Z b и с <	С 0, то ас х	> Ьс\
3)	Как следствие правил сложения неравенств и умножения обеих
частей неравенств на одну и ту же величину получается правило вычи-
тания неравенств разного знака:
Из одного неравенства можно почленно (из левой части — левую,
а из правой части — правую) вычитать другое неравенство противо-
положного знака. В результате получится неравенство, имеющее знак
первого неравенства:	_	.	-
если а < b и с > dt то а — с < д — d;
если а > b и с < d, то а — с > b — d.
4)	Если к левой и правой частям неравенства прибавить одну и
ту же величину, то в результате получится неравенство того же знака:
если а > Ь, то а + с > b + с.
9.2.	Некоторые важные неравенства.
1)	Для любых действительных чисел а и b выполняется неравенство
|а+Я<|а| + |5|,
т. е. абсолютная величина суммы двух действительных чисел не пре-
восходит суммы абсолютных величин этих чисел.
Методом математической индукции можно доказать, что для любого
конечного числа слагаемых at справедливо неравенство
п
1=1
< S 1**1.
/=1
♦) Все сказанное ниже для случая строгих неравенств остается справед-
ливым и для нестрогих неравенств.
§ 9. НЕРАВЕНСТВА
153
причем равенство достигается в том и.только в том случае, когда все
слагаемые — числа одного знака.
2)	Для любых действительных чисел а и b выполняется неравен-
ство
т. е. абсолютная величина разности двух чисел не меньше абсолютной
величины разности абсолютных величин этих чисел.
3)	Для любых двух действительных чисел а и b выполняется
неравенство
а2 + ЬI 2,	2 | ab |,
причем равенство достигается в том и только том случае, когда | а | ==
== I b |.
4)	Если а и Ъ — действительные числа одного знака (ab >0), то
а I- 2
причем равенство достигается в том и только том случае, когда а == bt
5)	Неравенство Коши\ если а и Ъ — неотрицательные действи-
тельные числа, то
о -4- b 1/“~т
—у—
т. е. среднее арифметическое двух неотрицательных чисел не меньше
их среднего геометрического.
Аналогичное неравенство справедливо и для любого конечного
набора неотрицательных чисел at (i = 1, 2, 3, ...» n):
^.+ .^±°.1+_-:.±.а".>Уа1а2аз . :: ап,
т. е. среднее арифметическое п неотрицательных чисел больше или
равно их среднему геометрическому; равенство достигается, кдгда
все п чисел равны.
6)	Неравенство Коши—Буняковского\ для любых действительных
чисел fli, а2» аз>...» 0п, blt b2,..., Ьп выполняется неравенство
(я А +	+ а3д3 + •• • + arfinf (а1 + а2 + • * ’ + сп) X
X (&1 + + • • • +	.
Равенство достигается тогда и только тогда, когда числа и bi
пропорциональны, т. е. когда существуют такие числа а и Р, что а2 -р
4- Р2 0, и для всех i = 1, 2, 3,..., п выполняется равенство
аа/ + P&i = 0.
7)	Связь между средним арифметическим и средним квадратичным
нескольких чисел: абсолютная величина среднего арифметического
любого конечного числа действительных чисел не превосходив сред-
него квадратичного этих^ чисел, т. е.
I «1 + «2 + •  • + Дп |	1 а1 + °2 +-----Н
п	""у	и"	’
причем равенство достигается тогда и.только тогда, когда все п чисел
равны между собой.
154
ГЛ. 4. АЛГЕБРА
8)	Неравенство Гёлъдера (обобщение неравенства Коши—Буня-
ковского): для любых действительных чисел alt a2i ...» an, bx.bn
при любом p > 1 выполняется неравенство
I <21 bi *J- Я2&2 + • • • + O'nbn |
<(| aj Г+ 1021°+ • •• 4-1 an |p)1/₽ (| 61 |’+|62|?+---+|6n |’)l/l?.
p
где ? = 7=T-
При p = 2 неравенство Гельдера превращается в неравенство
Коши—Буняковского.
§10. Решение неравенств и систем неравенств
10.1. Основные определения. Пусть/—числовая функция одной
или нескольких переменных (аргументов). Решить неравенство
£<0	(1)
— это значит найти множество значений аргумента (аргументов) функ •
ции /, при которых неравенство (1) справедливо.
Аналогично, решить неравенство
f > 0	(2)
— это значит найти множество значений аргумента (аргументов)
функции /, при которых неравенство (2) справедливо.
Множество решений нестрогих неравенств вида / ^ 0 и / :> О
находится как объединение множеств решений уравнения / = 0 и
соответствующих строгих неравенств.
Множество значений аргументов функции /, при которых соот-
ветствующее' неравенство справедливо, называют множеством решений
неравенства или просто решением неравенства. Два неравенства счи-
таются эквивалентными, если множества их решений совпадают.
Решить систему нескольких неравенств — это значит найти все те
значения аргументов функций, входящих в неравенства, при которых
все неравенства системы одновременно справедливы.
Две системы неравенств считаются эквивалентными, если мно-
жества их решений совпадают. Система неравенств «S считается экви-
валентной двум системам неравенств и S2, если множество решений
системы S совпадает с объединением множеств решений систем и S2.
10.2. Линейные неравенства и системы линейных неравенств
с одним неизвестным. Под линейными неравенствами понимают нера-
венства вида
ахb > 0, ах-|-Ь<0, ахЦ-b^O, ах^Ь^О,
где а и b — действительные числа (а ф 0).
Линейные неравенства решают заменой исходного неравенства
ему эквивалентным. При этом используются следующие преобразова-
ния неравенств, приводящие к эквивалентным неравенствам: прибав-
ление к обеим частям неравенства одного и того же числа и умножение
(д еление) обеих частей неравенства на одно и то же число. Так, мно-
жество рршений неравенства
ах + b > 0	(3)
может быть найдено следующим образом.
§ 10. РЕШЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 155
Прибавим к обеим частям'неравенства (3) число —6, в результате
чего получим эквивалентное неравенство
ах > —д,	(4)
и разделим обе части неравенства на а. Тогда!
1) Если а > 0, то получаем неравенство
которое и дает множество решений исходного неравенства (3). Это
множество решений также можно записать в виде
2) Если а<0, то получаем неравенство
Множество действительных чисел, удовлетворяющих этому нера-
венству, и есть множество решений исходного неравенства (3):
Аналогичным образом могут быть найдены решения любых линей-
ных неравенств.
Множество решений системы двух линейных неравенств
ах-\- b > 0,
сх + d > 0
находится как пересечение множеств решений этих неравенств.
10.3» Квадратные неравенстваПод квадратным неравенством по-
нимается неравенство, которое может быть приведено к одному из
следующих неравенств:
ах2 + Ьх 4- с > 0, ах2 4- Ьх 4- с < 0,
ах2 + Ьх 4- с 0, ах2 4- Ьх 4- с 0,
где а~ Ь, с — некоторые действительные числа и а=/=0.
Простейшими квадратными неравенствами являются неравенства
х2 < т и х2 > т.
Множество решений неравенства х2 < т:
1) при т 0 х = 0 (т. е. нет решений)?
2) при т > 0 х £ (—Кт; Ут), т. е. — У1п <^х<^ Ут, или
]х| < Ут.
Множество решений неравенства х2 > т:
1) при т < 0 х С R (т. е. х-~ любое действительное число);
2) при т^ 0 х_£ (—оо; —Ут) U (Ут; 4~2?)> е« —00 <
< х < —- Ут и Ут<х<-^оо9 или
156
ГЛ. 4. АЛГЕБРА
Квадратное неравенство ах2 + bx -f- с > 0 в зависимости от зна-
чений своих коэффициентов а, Ь и с имеет множества решений:
1)	при а > О, D е Ь2 — 4ас> 0 х £ оо;	j U
2а
2)	при а > О, D < 0 х f R;
О»о +
\ 2а	2а /
4)	при а < О, D < 0 х = 0 (т. е. решений нет).
Решение неравенства ах2 4- ftx-f- с< 0 сводится к решению рас-
смотренного выше неравенства, если обе части неравенства умножить
на —1.
Множество решений нестрогих неравенств ах2 4- Ьх -|- с > 0 и
ах3+&х-|-с^0 находится как объединение множеств решений
соответствующих строгих неравенств и уравнения ах2 + Ьх 4* с — 0.
Дробно-линейными неравенствами называют неравенства, приво-
дящиеся к виду
ах-\-Ь
cx-}~d >
(5)
где a, bt c,d, k — некоторые действительные числа и с Ф 0 (если с = 0,
то дробно-линейное неравенство превращается в линейное). К дробно-
линейным неравенствам относятся и неравенства вида (5), в которых
вместо знака > стоят знаки <,
Решение дробно-линейного неравенства сводится к решению квад-
ратного неравенства. Для этого необходимо умножить обе части нера-
венства (5) на выражение (сх + d)2, которое положительно при всех
к С R и х Ф —die,
10.4. Метод интервалов. Пусть Р (х) — многочлен п-й степени
с действительными коэффициентами, cj, c2i ...» ci — все действительные
корни многочлена с кратностями kx, k2t ...» ki соответственно, причем
ci > с2 > ... > с/. Тогда многочлен Р (х) можно представить в виде
Р (х) = (X — Cl)*1 (X — е2?2 ... (X — С/)*' <2 (X),	(6)
где многочлен Q (х) действительных корней не имеет и либо положи-
телен, либо отрицателен при всех х (.R. Положим для определенности,
Нто Q (х) > 0. Тогда при х > с± все сомножители в разложении (6)
положительны и Р (х) > 0. Если q — корень нечетной кратности
(kt — нечетное), то при с2 < х < Q все сомножители в разложении (6),
еа исключением первого, положйтельны и Р (х) < 0. В этом случае
говорят, что многочлен Р (х) меняет свой знак при переходе через
корень ср Если же —корень четной кратности — четное), ю
все сомножители (в том числе и первый) при с2 < х < q положительны
и, следовательно, Р (х) > 0. В этом случае говорят, что многочлен
Р (х) не меняет своего знака при переходе через корень q.
Аналогичным способом, используя разложение (6), нетрудно убе-
диться, что при переходе через корень с2 многочлен Р (х) меняет знак,
если нечетно, и не меняет знака, если четно.
§ 10. РЕШЕНИЙ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 157
Рассмотренное свойство многочленов используется для решения
неравенств методом интервалов. Для того чтобы найти все решения
неравенства
р W > о,
достаточно знать все действительные корни многочлена Р (х), их крат-
ности и знак многочлена Р (х) в произвольно выбранной точке х0,
не совпадающей с корнем многочлена.
Пример 1. Решить неравенство
х2 (*+ 2) (х — I)3 (х2 -J- 1) > 0.	' (7)
Отметим на числовой оси Ох корни многочлена, стоящего в левой
части неравенства (рис. 4.14).,
При х > Г многочлен положителен, так как все сомножители,
стоящие в левой части равенства, положительны. Будем двигаться
по оси Ох справа налево. При переходе через точку х = 1 многочлен
меняет свой знак и становится отрицательным, так как х = 1 — корень
кратности 3; при переходе через точку х = 0 многочлен знака не ме-
няет, так как х = 0 — корень кратности 2; при переходе через точку
х == —2 многочлен опять меняет знак и становится положительным.
Промежутки знакопостоянства данного многочлена изображены
схематически на рис. 4.14. Используя этот рисунок, легко выписать
множество решений неравенства (7):
*€(-оо; —2) (J (1; +оо).
Рациональное неравенство вида
где Р (х) и Q (х) — многочлены, может быть также решено методом
интервалов. Умножая обе части неравенства (8) на многочлен [Q (х)]2,
который положителен при всех допустимых значениях неравенства (8),
получаем неравен про'
Р (х) Q (х) >0,	-	'
еквивалентнсе неравенству (8).
Пример 2. Решить рациональное неравенство
Х2(х 1)3 (х+2) < о
х — 3
, Умножив обе части неравенства на (х — З)2, получим неравенство,
еквивалентное неравенству (9):
х2 (х — I)3 (х + 2) (х — 3) < 0.
158
ГЛ. 4. АЛГЕБРА
Множество решений последнего неравенства находится методом
интервалов и будет следующим:
X е (-оо; -2) U (1; 3).
10.5. Решение иррациональных неравенств. Под иррациональным
неравенством понимается неравенство, в котором неизвестные вели-
чины (или рациональные функции неизвестных величин) находятся
год знаком радикала. Для того чтобы найти множество решений ирра-
ционального неравенства, приходится, как правило, возводить обе
части неравенства в натуральную степень. Несмотря на внешнюю
схожесть процедуры решения иррационального уравнения (см. п. 5.9)
и иррационального неравенства, между ними существует большое отли-
чие. При решении иррациональных уравнений можно не заботиться
о том, чтобы после возведения в степень получилось уравнение, экви-
валентное исходному: алгебраическое уравнение имеет конечное число
корней, из которых проверкой нетрудно отобрать решения исходного
иррационального уравнения.
Множество решений неравенства представляет собой, как правило,
бесконечное множество чисел, и поэтому непосредственная проверка
решений путем подстановки этих чисел в исходное неравенство ста-
новится принципиально невозможной. Единственный способ, гаран-
тирующий правильность ответа, заключается в том, что мы должны
следить за тем, чтобы при каждом .преобразовании неравенства у нас
получалось неравенство, эквивалентное исходному.
Решая иррациональные неравенства, следует помнить, что при
возведении обеих его частей в нечетную степень всегда получается
неравенство, эквивалентное исходному неравенству. Если, же обе
части неравенства возводить в четную степень, то будет получаться
неравенство, эквивалентное исходному и имеющее тот же знак,
лишь в случае, если обе части исходного неравенства неотрица-
тельны.
Пример. Решить неравенство
— /9^х> 1.	(10)
Множеством допустимых значений х, которое находится как ре-
шение системы
х — 5 > 0,
9 — х > 0,
является промежуток [5; 9].
Неравенство (10) эквивалентно неравенству
+ (11)
обе частя которого неотрицательны. Возводя обе части неравенства (11)
в квадрат, в результате несложных преобразований получаем нера-
венство
2х — 15>2КЭГГх>	(12)
эквивалентное неравенству (11). Далее возможные два случая:
1) Если 2х — 15 < 0, т. е. х < 15/2, левая часть неравенства
отрицательна или равна нулю, а правая неотрицательна. Поэтому
ни при каком $ 6 15; 15/2] неравенство (12) не выполняется.
§ 10. РЕШЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 159
2) Если 2х — 15 > 0, то обе части неравенства неотрицательны
и после возведения в квадрат получаем неравенство, эквивалентное
неравенству (12):
(2х — 15)2 > 4(9— х).
Таким образом, множество решений неравенства (10) получается
как множество решений системы неравенств
5 < х < 9,
2х — 15 > 0,
(2х — 15)2>4(9— x)t
- I 14 + V7 . О1
откуда получаем * € I------! 91,
10.6.	Показательные неравенства. Простейшим показательным не-
равенством является неравенство вида
ах > Ь9	(13)
где а и b — некоторые действительные числа (а > 0, а =# !)•
В зависимости от значений параметров а и b множество решений
неравенства (13) будет следующим:
1)	при а > 1, 6 > 0 х £ (loga b\ -(-оо);
2)	при 0 < а < 1, 6 > 0 х£ (—оо; loga 6);
3)	при а > 0, b < 0 х £ R .
Множество решений неравенства
а* < b	(14)
в зависимости от значений параметров а и b будет следующим!
1)	при а > 1, b > 0 х С (~°°>* loga ^);
2)	при 0 < а < 1, b > 0 х g (loga b\ 4~оо);
3)	при а > 0, b < 0 х=0 (т. е. неравенство решений не имеет).
Неравенства вида (13) и (14) могут быть обобщены на случай,
когда в показателе степени стоит некоторая функция от х. Так, напри-
мер, множество решений неравенства
2f <*> > 3	(15)
находится как множество решений неравенства
f (х) > loga 3,
эквивалентного неравенству (15).
Методы сведения более сложных показательных неравенств к не-
равенствам вида (13), (14) аналогичны методам, используемым при
решении показательных уравнений (см. п. 6.1). Так, например, реше-
ние показательного неравенства вида Р (ах) >0, где Р (х) — много-
член указанного аргумента, заменой ах = у сводится к последователь-
ному решению неравенства Р (у) > 0 и решению простейших показа-
тельных неравенств вида (13), (14) или систем простейших показатель-
ных неравенств.
160
ГЛ. 4. АЛГЕБРА
Пример. Решить неравенство
Ю ЗХ +9^0.
Решение. Обозначим 3х = у. Так как 9х = (31 2 * * *)х = (3х)2,
то 9х = у2 и данное неравенство для’неизвестной у принимает вид
у2 — \Qy -f- 9	0. Решение этого квадратного неравенства: 1 у 9.
Это двойное неравенство эквивалентно системе двух неравенств
У> 1,
*/<9,
которая для неизвестной х имеет вид
3х > I,	х> 0,
-<=>	* или 0^х<2.
3х <9	х<2
10.7.	Логарифмические неравенства. Простейшими логарифмиче-
скими неравенствами являются неравенства вида
loga х > b,
loga х < b,
(16)
• (П)
где с и b — некоторые действительные числа (а > 0, а Ф 1).
В зависимости от значений а множества решений неравенства (16)
будут следующими:
1)	при	а	>	1	х	С	(a6; +°°h
2)	при	0	<	а <	1	х	С	(0; ab)t
а неравенства (17):
1) при	а	>	1	xg	(0; аь);
2) при	0	<	а <	1	х	€	(а6; +оо).
Неравенства вида (16), (17) могут быть обобщены на случай, когда
аргументом логарифмической функции является некоторая функция
f(x). Так, например, логарифмическое неравенство вида loga f (х) > b
эквивалентно следующим системам неравенств *):
1) при а > 1
f (х) > о,
f W > а6;
Неравенство вида
мам неравенств:
1) при ' а > 1
ZW>o,
f (X) <
2) при 0 < а < 1
f (х) > 0,
f (х) < аь.
logo f М < b эквивалентно следующим систе-
2) при 0 < а < 1
/ (х) > 0,
f (X) > а6.
Более сложные логарифмические неравенства сводятся к неравен-
ствам вида (16), (17) методами, аналогичными используемым при реше-
нии логарифмических уравнений (см. и. 6.2).
♦) В .случае, если исходное неравенство нестрогое, вторые неравенства
систем также нестрогие.
9 10- РЕШЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 161
Так, например, множество решений неравенства вида
Р (logo X) > 0,
(18)
а также неравенств Р < О, Р > О, Р 0, где Р — многочлен ука-
занного аргумента, находится следующим образбм: вводится новая
неизвестная у == logfl х и неравенство (18) решается как алгебраическое
относительно неизвестной у. После этого решение исходного нера-
венства сводится к решению соответствующих простейших нера-
венств (16}, (17) или систем этих неравенств.
Пример. Решить логарифмическое неравенство
log? х — log2 х — 15 > 0.
(19)
Множество допустимых значений неизвестной данного неравен-
ства: х > 0. Приведя все логарифмы к одному основанию (скажем,
к основанию 2), получаем неравенство, эквивалентное неравенству (19):
log2 х — log2x — 15 > 0.
(20)
Решаем это неравенство как квадратное относительно новой неизвест-
ной у = log2 х- В результате получаем, что логарифмическое нера-
венство (20) эквивалентно двум простейшим неравенствам: log2 х > 10
и log2x<—-6. Объединение их множеств решений и дает множество
решений неравенства (19):
х£(0; 2~G) U (210; +оо).
В заключение отметим еще один часто встречающийся тип лога-
рифмических неравенств, в которых как основание логарифма, так и
аргумент логарифма являются функциями неизвестной х. Таким
логарифмическим неравенством будет, например, неравенство
10gg(x) f (х) >С,
(21)
где f (х) и g (х) — некоторые многочлены, ас — некоторое действи-
тельное число. Множество допустимых значений неизвестной х нахо-
дится как множество решений системы
f (X) > о,
g (X) > о,
g (х) ¥= 1.
Логарифмическое неравенство (21) эквивалентно двум системам алгеб-
раических неравенств:
I (х) > 0,
g (х) > 1,
/ (X) > lg (X) )с;
f (х) > 0,
0<g(x)< 1,
f (х) < [g (х) f.
Пример. Решить неравенство
log» (2х-	> 2.
(22)
6 А. Г. Цыпкин
162
ГЛ. 4. АЛГЕБРА
Данное логарифмическое неравенство эквивалентно двум системам
неравенств:
2х ?> О,	2х	Х> О,
х>1,	0<х<1,
2х---7- > х2;	2х---< х2.
4	4
Множество решений логарифмического неравенства (22) находим
как объединение множеств решений этих двух систем и окончательно
получаем
10.8. Геометрическое изображение множества решений неравен-
ства с двумя неизвестными. Пусть имеется некоторое неравенство
с двумя неизвестными. Множество решений такого неравенства — это
множество упорядоченных пар действительных чисел (х; у), которое
геометрически может быть изображено как множество точек коорди-
натной плоскости Оху.
Объединение множеств решений неравенств
Г (х, у) > 0, F(x,y)<0
и уравнения
F(x,y) = 0
дает множество всех точек координатной плоскости Оху, за исключе-
нием точек, в которых функция двух переменных F (х, у) не опреде-
лена. -Так, например, объединение множеств решений неравенств
и уравнения
дает множество всех точек числовой плоскости R2, за исключением
множества точек, принадлежащих оси Ох.
Уравнение F (х, у) = 0 задает множество точек «границы раздела»
(либо часть этой границы) между множествами точек, задаваемых
неравенствами F (х, у) > 0 и F (х, у) < 0.
Если уравнение F (х, у) = 0 имеет единственное решение отно-
сительно переменной у (х считается параметром), то говорят, что урав-
нение F (х, у) = 0 задает функцию
у = f W.
Если уравнение F (х, у) = 0 имеет единственное решение отно-
сительно переменной х (у считается параметром), то говорят, что урав-
нение F (х, у) = 0 задает функцию
* == g (у),
где у считается независимой переменной, ах — зависимой.
Может оказаться, что уравнение F (х, у) = 0 не имеет един-
ственного решения ни относительно переменной х, ни относительно
§ 10. РЕШЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 163
Рис, 4.15,
Рис. 4.16ф
Рис. 4.19(
£ИС. 4.2Q,
164
ГЛ. 4. АЛГЕБРА
Гис. 4.26.
^>51П.2?
?1!С. 4.2 7.
Гис. 4.2V.
§ 10. РЕШЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ 165
Рис. 4.3ft,
166
ГЛ. 4. АЛГЕБРА
переменной у: В этом случае говорят, что уравнение F(x, у)—О задает
соответствие между множествами допустимых значений перемен-
ных х и у.
На рис. 4.15—4.30 изображены некоторые фигуры, задаваемые
неравенствами вида у > f (х). Эти фигуры представляют собой часть
координатной плоскости Оху, лежащую выше линии у = f (х). Фигуры,
задаваемые неравенствами у < f (х), представляют собой часть плос-
кости, лежащую ниже линии у = f (х).
На рис. 4.31—4.33 заштрихованы фигуры, задаваемые неравен*
ствами вида х > g (у).
На рис. 4.34--4.36 изображены фигуры, задаваемые неравен-
ствами вида F (х, у) > 0, в случае, когда уравнение F (х, у) « 0 задает
соответствие между переменными х и у:
1)	неравенство х2 + У2 > R2 задает внешность круга радиуса R
с центром в начале координат (см. рис. 4.34);
2)	неравенство (х — а)2 + (у — b)2 > R2 задает внешность круга
рддиуса R с центром в точке с координатами (а; Ь) (см. рис. 4.35);
3)	неравенство вида | х | -f- | у | > а (а > 0) задает внешность
квадрата е вершинами в точках (а; 0), (0; а), (—а; 0) и (0; —а) (см.
рис. 4.36).
На рис. 4.15—4.36 изображены простейшие фигуры, задаваемые
неравенствами с двумя переменными х и у. Однако умение строить
эти простейшие фигуры позволяет строить и более сложные фигуры^
задаваемые, например, системой нескольких неравенств е двумя пере-
менными. Геометрическая фигура, задаваемая системой неравенств
с двумя переменными, представляет собой общую часть (пересечение)
всех фигур, задаваемых неравенствами системы,
§11. Приемы доказательства
справедливости неравенств
11.1.	Доказательство справедливости неравенств с помощью це-
почки эквивалентных неравенств. Один из методов доказательства
справедливости неравенств основан на построении цепочки эквива-
лентных неравенств, в конце которой получается неравенство! спра-
ведливость которого очевидна.
Пример 1. Доказать неравенство
а3+&3	/ а + b \3	л	л
——>(• J' -) , где а>0 и Ь>0.
Заменим это неравенство на эквивалентное неравенство
Раскрывая скобки и группируя слагаемые левой части неравен»
ствах получим эквивалентное неравенство
Q
-§-(*+ Ь)
Так как а > 0 и Ь > 0, то справедливость последнего неравенства
очевидна, что и доказывает справедливость эквивалентного ему исход-
ного неравенства.
§ И. ПРИЕМЫ ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ 167
Пример 2. Доказать неравенство
1 , 1 >2
log2n т log„2
На основании свойства логарифмов
Т5Е^-“ 108,11
исходное неравенство преобразуется к эквивалентному неравенству
,og2n+-iir>2-	W
Так как log2 л > О, то в левой части неравенства (1) стоит сумма
двух взаимно обратных положительных чисел, отличных от единицы.
В силу неравенства 4) п. 9.2 неравенство (1) справедливо, а следова-
тельно, справедливо и исходное неравенство.
Пример 3. Доказать, что для любых действительных х и у
выполняется неравенство
ха + 2ху 4- бу2 + 2х + бу + 3 > 0.
Преобразуем левую часть данного неравенства:
х2 4~ 2x^4	3t/2 4- 2х 4- бу 4- 3 =
= (х2 + 2ху + у2) 4- 2у2 4- 2х 4- бу 4- 3 =
== (х + У)2 + 2 (х 4- у) 4~ 2г/2 4- 4у 4- 3 =
= 1(* + У)2 4~ (х 4- у} 4- П + %У2 + 4^/ 4~ 2 =
«= [(*4-*/)+ И24-2(^2+2^+ 1)= [(х+ «/)+ 1]2+ 20/ + D2.
В результате проведенных тождественных преобразований исход-
ное неравенство приводится к эквивалентному неравенству
(х+ У+ D2+ 2 0/+ I)2 > 0,
справедливость которого очевидна.
Аналогичным образом, используя неравенства п. 9.2, можно
доказать, например, следующие неравенства:
1)	а2 4- Ь2 4- с2 4- 3 > 2 (а 4- b 4- с);
2)	+ -у-4--^’>а+6 + с (а>0, ОО, ОО);
3)	(а 4- Ь) (Ь + с) (а + с) 8abc (а > 0, b > 0, с > 0);
4)	а2 4- д2 4- с2 > ab 4- Ьс + ас (а, Ь, с — числа одного знака).
11.2. Доказательство справедливости неравенств с использованием
свойств функций, входящих в неравенства. Справедливость некоторых
неравенств может быть доказана с использованием свойств функций,
□ходящих в неравенства.
168
ГЛ. 4. АЛГЕБРА
Так, например, справедливость неравенства
tg х 4- ctg х > 2
для всех х £ (0; л/2) следует из формулы, связывающей тригономе-
трические функции tg х и ctg х:
ctg х ~	.
tg* /
Действительно, в силу этой формулы исходное неравенство запишется
в виде неравенства
которое справедливо для всех значений х £ (0; л/2), так как в этом
промежутке tg х положителен, а сумма двух любых положительных
взаимно обратных чисел больше или равна двум.
Другим примером неравенства, справедливость которого дока-
зывается на основании свойств входящих в него функций, является
неравенство
0 sin8 х + cos20 х 1.
Справедливость этого неравенства/ а также, например, нера-
венства
sin х + У cos х	1
следует из ограниченности функций у = sin г, у = cos х и соотноше-
ний п. 3.2 главы 6.
В следующем примере доказательство справедливости неравенства
основано на использовании свойства монотонности показательной
функции.
Докажем, что если а-\- b ~ с (а > 0, b > 0), то;
1) аа + Ьа > са, где а < 1;
2) а$ 4- Ь® < с^, где (3 > 1,
По условию задачи
а , b	а	Ь
— 4- — = 1 и — > 0,	--- > 0.
Если сумма двух положительных чисел равна единице, то каждое
из этих чисел меньше единицы
0<А<1>	п<4<1.
В силу свойства монотонного убывания ппиязатетчяэй
С основанием, меньшим единицы, имеем
функции
§11. ПРИЕМЫ ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ 169
где а — любое действительное число, меньшее единицы, а р — дей-
ствительное число, большее единицы. Складывая попарно неравен-
ства (2), получаем
что и требовалось доказать.
11.3. Некоторые специальные приемы доказательства справед-
ливости неравенств.
1.	Один из специальных приемов доказательства справедливости
неравенств состоит в следующем. Пусть, например, требуется дока-
зать справедливость неравенства А < В. Если удается подобрать
такую величину С, что Л < С, и доказать справедливость неравен-
ства С В, то тем самым будет доказана справедливость исходного
неравенства А < В. Именно такой прием использовался при доказа-
тельстве ограниченности последовательности (см. п. 2.4 главы 8)
2.	Справедливость некоторых неравенств, в которых левая и
правая части — функции натурального аргумента, может быть дока-
зана следующим приемом. Исходное неравенство преобразуется к эк-
вивалентйому неравенству, у которого правая часть постоянная,
а левая есть функция натурального аргумента. Тогда, рассматривая
функцию^ натурального аргумента, стоящую в левой части неравенства,
как общий член некоторой последовательности, доказательство спра-
ведливости неравенства можно свести к исследованию свойств этой
последовательности.
П р.и м е р. Доказать, что неравенство
2Л—1 С «I
справедливо при любом натуральном п. -
 Преобразуем данное неравенство к эквивалентному неравенству
с)П—1
Рассмотрим последовательность (хп), задаваемую формулой общего
члена
Нетрудно доказать, что эта последовательность — монотонно убы-
вающая и, следовательно, наибольший член данной последователь-
ности — это первый член, который равен единице. Но так как при
п = 1 неравенство (3) верно, то оно будет верно и при всех остальных
вначениях п.
3.	Справедливость некоторых неравенств может быть доказана
методом математической индукции, Именно этот метод использован
170
ГЛ. 4. АЛГЕБРА
для доказательства ограниченности последовательности (см. пример 3
п. 2.4 главы 8)
Хп = с + J/ c + • • •	•
п корней
Методом математической индукции могут быть также доказаны,
например, следующие неравенства:
2) |sinnxKn|sinx|;
3) п \ > г"*"1, если п > 2;
4)2пп!<п”, если и >2.
11.4. Некоторые способы проверки справедливости числовых
неравенств. При решении некоторых уравнений и неравенств иногда
необходимо выяснить, какое из двух (или нескольких) чисел наиболь-
шее, а какое — наименьшее. Ниже на примерах рассмотрены некото-
рые простейшие способы проверки справедливости числовых нера-
венств .
1) Для того чтобы выяснить, какое из двух рациональных чисел
т/п и plq больше, вычислим разность этих чисел:
т	р _тд — пр
п	q — nq	'
Если разность больше нуля,* то — >	; если разность меньше
т р
нуля, то — < —.
2) При сравнении двух иррациональных чисел а и b часто исполь-
зуют следующий способ: предполагают, что одно число больше другого
(скажем, а > Ь), и строят цепочку эквивалентных неравенств, приво-
дящую либо к неравенству, справедливость которого очевидна (и тогда
предположение, что а > Ь, верно), либо к неравенству, которое заве-
домо несправедливо (в этом случае сделанное предположение, что
а > bf неверно, и, следовательно, _а< Ь). Например, пусть требуется
выяснить, какое число больше: 14 — 1^3 или 2. Предположим, что
К14 — ]/"3 меньше 2:
/14 - /3 < 2.	(4)
Так как обе части неравенства (4) положительны, то их можно
возвести в квадрат и сохранить тот же знак, который был у предыду-
щего неравенства: (К 14 — У З)2 3 < 4. Раскрывая скобки, получаем
14 — 2	+ 3<4. Последнее неравенство можно переписать в виде
13 < 2 У42. Возведя обе части Неравенства в квадрат, получим нера-
венство 169 < 168. Очевидно, что последнее неравенство несправед-
ливо, следовательно, предположение о том, что число 1^14 — Уз
меньше 2, неверно. Число У14 — У 3 больше 2.
3) Разберем на двух примерах, как можно проверить справед-
ливость неравенства с помощью приближенных вычислений.
§ IT. ПРИЕМЫ ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ 171
Пример 1. Доказать, что
1//3 < sin 39°.	(5)
Попытаемся найти такое число а, чтобы а < sin 39° и l/j/T< о»
Ближайшее «табличное» значение функции sin х меньшее, чем sin 39°,—
это sin 30° = 1/2:
sin 30° < sin 39°.	(6)
Однако, выбирая а равным 1/2, мы ничего не докажем, так как
1/2 < 1/К3. Попытаемся улучшить оценку sin 39Q, Это можно сделать
двумя способами. Первый способ заключается в том$ что, последо-
вательно вычисляя с помощью формул половинного угла sin 15°, cos 15%
sin 7° 30', cos 7° 30', мы можем вычислить
sin 37° 30' = sin 30° cos 7° 30' -f* sin 7° 30' cos 30Q
и, учитывая неравенство
sin 37Q 30' < sin 39°,	(7)
взяв в качестве а число sin 37° 30', доказать, что sin 37° 30' >l/j/*3.
Однако, как будет показано ниже, нам достаточно иметь более
грубую оценку, нежели оценка (7). В главе 6 п. 1.6 вычислен sin 36° >
sa,3b.„ZEpZ.
4
Так как в первой четверти sin х — монотонно возрастающая функ*
ция, то из неравенства 36° < 39° следует неравенство sin 36° < sin 39%
т. е.
ЫП OV >>----———
4
Способом, изложенным выше в 2), докажем, что
4	/3
Справедливость последнего неравенства следует из приведенный
ниже вычислений:
(V10 —2J<5 \\ 1
\	4	) >-3»
5-Г5\ 1
8	3 ’
15 - 3 Кб > 8,
7>3J/T,
49 > 45.
Таким образом, доказано, что если положить а равным sin 36°, то
sin 39° > sin 36° и sin 36’ > 1//3.
172	ГЛ 4 АЛГЕБРА
Из этих двух неравенств следует неравенство l/j/’З < sin 39°, спра-
ведливость которого и требовалось доказать.
Пример 2. Сравнять, какое из двух чисел больше: log2 3
или logo 5.
Числа 3 и 5, логарифмы которых требуется сравнить, заключены
между следующими степенями чисел 2 и 3, являющихся соответственно
основаниями первого и второго логарифмов:
21 < 3 < 22 3, 31 < 5 < З2.	(8)
Так как функция loge х при а > 1 — монотонно возрастающая
функция, из неравенств (8) следуют неравенства
log2 (21) < log2 3 < log2 (22), logs (З1) < log3 5 < logs (З2),
1 < log2 3 < 2, 1 < log3 5 < 2;
однако на основании этих неравенств нельзя сделать вывод, какой из
логарифмов больше, так как они «зажаты» между одними и теми же
числами.
Улучшим оценки (8), оценивая числа 3 и 5 дробными степенями
чисел 2 и 3 соответственно. Сравним с числами 2	= 2 J/ 2 и 3	*
=^=3^3 числа 3 и 5 соответственно. С помощью способа, изложенною
ь 2), можно показать, что
3>2/Г и 5<3/3.
Таким образом, имеем
23/-<3<22, З1 <5 <З3/2,
откуда соответственно следует, что
y<log23<2,	J<log35<-1.	(9)
Сравнивая последние неравенства, видим, что log2 3 больше
logy 5.
Заметим, что в случае необходимости оценки (9) можно улучшать
и далее. Так, доказывая справедливость неравенств
22	4 =2-/2 .|/2 >3,	3	4 =3V3 <5,
получаем следующие оценки для log2 3 и iog3 5:
3	.7	5	, с 3
y<Jogt0<y, -4-е logs 5 < у.
ГЛАВА 5
ГЕОМЕТРИЯ
Возникновение геометрии восходит к глубокой древности и было
обусловлено практическими потребностями человеческой деятельности
(необходимостью измерения земельных участков, измерения объемов
различных тел и т. д.). Простейшие геометрические сведения и понятия
были известны еще в Древнем Египте. В этот период геометрические
утверждения формулировались в виде правил, даваемых без доказа-
тельств. С VII века до н. э. по I век н. э. геометрия как наука бурно
развивалась в Древней Греции. В этот период происходило не только
накопление различных геометрических сведений, но и отрабатывалась
методика доказательств геометрических утверждений, а также делались
первые попытки сформулировать основные первичные положения
(аксиомы) геометрии, из которых чисто логическими рассуждениями
выводится множество различных геометрических утверждений. Уровень
развития геометрии в Древней Греции отражен в сочинении Евклида
«Начала». В этой книге впервые была сделана попытка дать системати-
ческое построение планиметрии на базе основных' неопределяемых
геометрических-понятий и аксиом (постулатов). Особое место в истории
математики занимает пятый постулат Евклида (аксиома о параллельных
прямых). Долгое время математики безуспешно пытались вывести пятый
постулат из остальных постулатов Евклида и лишь в середине XIX века
благодаря исследованиям Н. И. Лобачевского, Е^Римана и Я. Бойяи
стало ясно, что пятый постулат не может быть.'выёеден из остальных,
а система аксиом, предложенная-Евклидом, не единственно возможная.
< Начала» Евклида оказали огромное влияние на развитие математики.
Эта книга на протяжении более чем двух тысяч лет была не только
учебником по геометрии, но и служила отправным пунктом для очень
многих математических исследований, в результате которых возникли
новые самостоятельные разделы математики.
Систематическое построение геометрии обычно производится по
следующему плану:
I.	Перечисляются основные геометрические\ понятия, которые
вводятся без определений.
II.	Дается формулировка аксиом геометрии.
III.	На основе аксиом и основных геометрических понятий форму-
лируются остальные- геометрические понятия и теоремы.
§ 1. Луч. Отрезок
1.1. Луч. Пусть а — некоторая прямая, а О—некоторая точка
прямой а. Точка О разбивает множество точек прямой на два множества:
множество точек, лежащих левее точки О, и множество точек, лежащих
правее точки О (рис. 5.1). Эти множества называют открытыми лучами*
исходящими из точки О (или открытыми лучами с началом в точке О).
Множество всех точек прямой а, лежащих правее (левее) точки О,
174
ГЛ. В. ГЕОМЕТРИЯ
включая точку О, называют лучом и обозначают Оа (указывая прямую и
начало луча) *). О луче Оа говорят, что он принадлежит прямой а.
Возможны следующие случаи взаимного расположения двух лучей
Ofa и O2h2.
1) Лучи Oihi и O2h2 принадлежат одной прямой. Говорят, что лучи
Oihi и O2h2 сонаправлены, если один из лучей содержится в другом
(рис. 5.2), т. в. их пересечением является
а луч, и пишут
9 А
РИС’ 6,1 •	Говорят, ЧТО лучи 0^ И О2^2~
противоположно направлены, если ни
один из них не содержится в другом (рис. 5.3), т. е. их пересечение не
является лучом, и пишут
2) Лучи OJif и лежат на параллельных прямых. Проведем
плоскость через эти параллельные прямые. Через точки Of и 02 проведем
прямую, разбивающую плоскость на две полуплоскости с границей
01Р2. Если оба луча лежат в одной из этих полуплоскостей (рис. 5.4),
то такие лучи также называют сонаправленными. Если же лучи OJii
и 0^ лежат в различных полуплоскостях, то их называют противо-
положно направленными (рис. 5.5). Лля обозначения сонаправленных и
Рис. 5.4.
Рис. 5.5.
противоположно направленных лучей в случае 2) используются те же
обозначения, что и в случае 1). Для лучей, принадлежащих непарал-
лельным прямым, понятие сонаправленности (или противоположной
направленности) не вводится.
Множество всех лучей плоскости, каждый из которых сонаправлен
с одним и тем же лучом, называется направлением на плоскости.
Множество всех лучей пространства, каждый из которых сонаправ*
лен с одним и тем же лучом, называется направлением в пространстве.
*) Луч также обозначается одной малой латинской буквой (когда точка
начала известна) или двумя заглавными буквами QAt где О & начало луча#
в 4 « произвольная точка (открытого) луча.
$ 2. УГЛЫ НА ПЛОСКОСТИ
175
1.2. Отрезок. Пусть А и В — две различные точки прямой а.
Множество, состоящее из всех точек прямой а, лежащих между точками
А и В, включая точки А, В, называется отрезком. Точки А и В называ-
ются концами отрезка, а все остальные точки — внутренними точками
отрезка. Отрезок с концами А, В обозначается АВ.
Длина отрезка АВ часто обозначается | АВ |. Отрезки считаются
равными, если равны их длины.
§ 2S Углы на плоскости
2.L Понятие угла. Пара различных лучей Оа и ОЬ, выходящих
из одной точки О, называется углом и обозначается символом л (а, д).
Точка О называется вершиной угла, а лучи ОапОЬ — сторонами угла *).
Если А и В — две точки лучей Оа и Од, то (а, Ь) обозначается также
символом АОВ (рис. 5.6).
Угол л (а, Ь) называют развернутым, если лучи Оа и Од, выходя-
щие из одной точки, лежат на одной прямой и не совпадают (т. е. проти-
воположно направлены).
Два угла считаются равными, если один угол можно наложить на
другой так, чтобы стороны углов совпадали. Биссектрисой угла называ-
ется луч с началом в вершине угла, делящий угол на два равных уГЛа.
Говорят, что луч OG, исходящий из вершины угла АОВ, лежит
между его сторонами, если он пересекает отрезок АВ (рис. 5.7). Говорят,
что точка С лежит между сторонами угла, если через эту точку можно
провести луч с началом в вершине угла, лежащий между сторонами
угла. Множество всех точек плоскости, лежащих между сторонами угла,
образует внутреннюю область угла (рис. 5.8). Множество точек пло-
скости, не принадлежащих внутренней области и сторонам угла, обра-
зует внешнюю область угла.
Угол л (а, д) считают больше угла (с, d), если угол (с, d)
можно наложить на угол л (а, д) так, что после совмещения одной пары
сторон вторая сторона угла (с, d) будет лежать между сторонами угла
(а, д). На рис. 5.9 АОВ больше АОС.
Пусть луч с лежит между сторонами угла (а, Ь) (рис. 5.10). Пары
лучей а, с и с, b образуют два угла. Об угле (а, д) говорят, что он
является суммой двух углов (а, с) и (с, д), и пишут
л (а, Ь) *= л. (а, с) +	(с, Ь).
Реже угол определяется как фигуру, образованная двумя лучамч
о общим началом и ограниченной ими частью плоскости,
176
ГЛ. В. ГЕОМЕТРИЯ
Обычно в геометрии имеют дело с углами, меньшими развернутого.
Однаков результате сложения двух углов может получиться угол,
больший развернутого. В этом случае ту часть плоскости, которая счи-
тается внутренней областью угла, отмечают дугой. На рио. 5.11 внутрен-
няя часть угла АОВ, полученного в результате сложения углов
АОС и СОВ и большего развернутого, отмечена дугой.
2.2.	Градусная мера измерения углов. При градусном измерении
углов в качестве основной единицы измерения углов (эталонного угла,
с которым сравниваются различные углы) берется угол в один градус
(обозначается 1°). Угол в один градус — это угол, равный 1/180 части
развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну
минуту (обозначается Г). Угол, равный 1/60 части угла в одну минуту,—
это угол в одну секунду (обозначается Г).
2.3.	Радианная мера измерения углов. Наряду с градусной мерой
измерения углов в геометрии и тригонометрии употребляется и другая
мера измерения углов, называемая радианной. Рассмотрим окружность
радиуса R с центром О. Проведем два радиуса О А и ОВ так, чтобы длина
дуги АВ была равна радиусу окружности (рис. 5.12). Получившийся
при этом центральный угол АОВ будет углом в один радиан. Угол
в 1 радиан принимается за единицу измерения радианной меры измере-
ния углов. При радианном измерении углов развернутый угол равен л
радиан.
Градусная и радианная единицы измерения углов связаны равен-»
ст вами:
1 радиан =	>« 57° 17' 45";
~ Тётг радиана 0,017453 радиана}
1OU
§ 3. ПАРАЛЛЕЛЬНОСТЬ И ПЕРПЕНДИКУЛЯРНОСТЬ 177
Г = - .л" ла радиана я» 0,000291 радиана;
I O\J • Ov
Г = -ТаёГ^гГал радиана « 0,000005 радиана.
loU-oU’OU
Градусную (или радианную) меру угла также называют величиной
угла. Величину угла АО В иногда обозначают АОВ.
2.4.	Классификация углов. Угол, равный 90Q, или в радианной
мере л/2, называется прямым углом; его часто обозначают буквой d.
Угол, меньший 90°, называется острым*, угол, больший 90°, но меньший
180°, называется тупым.
Два угла, имеющие одну общую сторону и в сумме составляю-
щие 180°, называются смежными углами. Два угла, имеющие одну
общую сторону и в сумме составляющие 90°, называются дополни*
тельными углами.
2.5.	Угол между направлениями. Если на плоскости выбраны
два направления, то в каждой точке О плоскости начинается один луч
ОА первого направления и один луч ОВ второго направления. Углом
между двумя направлениями на плоскости называется угол между
лучами ОА и ОВ. Угол между направлениями не зависит от выбора
начальной точки лучей.
Углом между двумя направлениями в пространстве называют угол
между двумя лучами этих направлений, имеющими общее начало.
§ 3. Параллельность и перпендикулярность
на плоскости
3.1.	Параллельность на плоскости. Две различные прямые а ид,
лежащие в одной плоскости, называются
имеют ни одной общей точки. Если пря-
мые а и b параллельны, то пишут а || Ь.
Свойства параллельных
прямых:
1)	Любая прямая считается парал-
лельной самой себе (рефлексивность).
2)	Если прямая а параллельна пря-
мой Ь, то и прямая b параллельна прямой а
^симметричность).
3)	Если прямая а параллельна пря-
мой д, а прямая b параллельна прямой с,
то и прямая а параллельна прямой с
\(транзитивность).
Множество всех прямых на плоское
'-прямой, называют пучком параллельных прямых.
В результате пересечения двух прямых третьей прямой образуется
восемь углов.(рис. 5.13). Цдрьт^ углов /,	5;	2,	6;	3,	7;
^4,	8 называют соответственными углами; парьг 3,	5; ^4,
б — внутренними накрест лежащими углами; пары	7;
^2, ^8 — внешними накрест лежащими-, пары 4,	3t
а 6 — прилежащими углами.
Признаки параллельности прямых:
1) Если при пересечении двух прямых а и b третьей прямой соответ*
ственные углы равны, то прямые а и b параллельны.
2) Если при пересечении двух прямых а и b третьей прямой внутрен*
ние (или внешние) накрест лежащие углы равны, то а, b параллельны.
параллельными, если они не
Рис. 5.13
данной
178
ГЛ. В. ГЕОМЕТРИЯ
3) Если при пересечении двух прямых а и b третьей прямой приле*
жащие углы в сумме составляют 180р, то прямые а и b параллельны.
Теоремы о равных отревках:
1) Если от точек О и Of в одном и том же направлении отложены
равные отрезки О А и OfA^ то отрезки OOf и А At равны и параллельны *)
(рис. 5.14).
2) (Т е о р е м а Фалеса). Если на одной прямой отложить
несколько равных отрезков и через их концы провести параллельные
прямые, пересекающие вторую прямую, то они отсекут на второй прямой
равные отрезки (рис. 5.15).
Отрезки называют пропорциональными* если пропорциональны их
длины.
Теоремы о пропорциональных отрезках:
1) Параллельные прямые, пересекающие стороны угла, отсекают
на них пропорциональные отрезки.
На рис. 5.16 прямые A At и ВВ^ параллельны и
]ОЛ1| _ |ОЛ |
|OBi| ~ |ОВ|
2) Если отрезки OAj и OBf пропорциональны отрезкам ОА и ОВ
и лежат соответственно на лучах 04f и ОА, то прямые АА^ и BBf па*
раллельны (рис. 5.16).
3.2, Перпендикулярность на плоскости. Две прямые, при пере*
сечении которых образуются прямые углы, называются взаимно перпен*
дикулярными. Если прямые а и b взаимно перпендикулярны, то пишут
a J. Ь.
Теоремы о перпендикулярных прямых:
1)	Если на плоскости даны точка и прямая, то существует единст-
венная прямая, проходящая через данную точку и перпендикуляр-
ная данной прямой.
2)	Если прямая перпендикулярна одной из прямых пучка парал-
лельных прямых, то она перпендикулярна любой другой прямой этого
пучка.
3.3. Расстояние от точки до прямой. Пусть точка А лежит вне
прямой а. Построим прямую р, перпендикулярную данной прямой а
♦) Параллельными отрезками называют отрезки, принадлежащие парал»
лельным-прямым.
$ 4. ПАРАЛЛЕЛЬНОСТЬ й ПЕРПЕНДИКУЛЯРНОСТЬ
179
и проходящую через точку А (рис. 5.17). Обозначим через О точку
пересечения прямых аир. Точка О называется основанием перпендику-
ляра р.
Расстоянием от точки А до прямой а называется длина отрезка 0Ак
Расстояние от точки А до любой точки прямой а, отличной от точки
О, больше расстояния от точки А до прямой а.
§ 4« Параллельность и перпендикулярность
в пространстве
4.1» Параллельность прямой и плоскости* Плоскость а и пря-
мая а, не принадлежащая плоскости а, ‘ называются парал*
дельными, если они не имеют ни одной общей точки. Любая прямая at
принадлежащая плоскости а, считается параллельной плоскости а.
Если плоскость а и прямая а параллельны, то пишут а || а или а || а.
Признак параллельности прямой и пл о»
скости:
Если прямая параллельна какой-либо прямой, лежащей в пло-
скости, то данные прямая и плоскость параллельны.
Теоремы о плоскости и прямой, параллель-
ной плоскости:
1)	Если плоскость проведена через прямую, параллельную другой
плоскости, и пересекает эту плоскость, то линия пересечения плоскостей
параллельна данной прямой.
2)	Если через каждую из двух параллельных прямых проведена
произвольная плоскость и эти плоскости пересекаются, то линия их
пересечения параллельна каждой из данных прямых.
4.2. Параллельность плоскостей. Две плоскости а и ₽ называются
параллельными, если они не имеют общей точки и не совпадают. Если
плоскости аи₽ параллельны, то пишут а || р.
Свойства параллельных плоскостей:
1)	Любая плоскость считается параллельной самой себе (рефлек-
сивность).
2)	Если плоскость а параллельна плоскости Р, то и плоскость Р
параллельна плоскости а (симметричность).
3)	Если плоскость а параллельна плоскости Р, а плоскость Р парал-
лельна плоскости 7, то плоскость а параллельна плоскости у (транзи-
тивность).
Признак параллельности двух плоскостей:
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двумя прямым другой плоскости то эти плоскости парал-
лельны^
180
ГЛ. 5. ГЕОМЕТРИЯ
Теоремы о параллельных плоскостях;
1) Если две параллельные плоскости аир пересечены фетьей
плоскостью у, то линии пересечения плоскостей а, у и р, у параллельны.
2) Через данную точку, не принадлежащую данной плоскости,
можно провести одну и только одну плоскость, параллельную данной
плоскости.
3) Если каждая из двух данных плоскостей параллельна третьей
плоскости, то данные две плоскости параллельны между собой.
4.3. Перпендикулярность прямой и плоскости. Две прямые в про-
странстве называются перпендикулярными, если угол между направле-
ниями, задаваемыми этими прямыми, равен 90е. Прямая и плоскость
называются и^имно перпендикулярными, если прямая перпендикулярна
каждой прямой, принадлежащей пло-
скости.
Если плоскость а перпендикулярна
прямой а, то пишут a J_ а или а _1_ а.
Прямую, перпендикулярную плоско-
сти, называют перпендикуляром к этой
плоскости. Через каждую данную точку
пространства можно провести одну и
только одну прямую, перпендикулярную
данной плоскости.
Признак перпендикулярности прямой и
плоскости:
Если прямая а перпендикулярна каждой из двух пересекающихся
прямых, лежащих в плоскости а, то прямая а и плоскость а взаимно
перпендикулярны.
Те о р ем ы о перпендикулярности п р я мой и
плоскости:
1)	Два различных перпендикуляра к плоскости параллельны.
2)	Если одна из двух параллельных прямых перпендикулярна
плоскости, то и другая перпендикулярна этой плоскости.
3)	Прямая, перпендикулярная одной из двух параллельных пло-
скостей, перпендикулярна и другой плоскости.
4)	Две плоскости, перпендикулярные одной и той же пр яд: ой,
параллельны.
4.4.	Расстояние от точки до плоскости. Пусть точка Ах не принад-
лежит плоскостиа. Через точку	проведем перпендикуляр к плоскости.
Точку пересечения перпендикуляра с плоскостью обозначим буквой А
(рис. 5.18). Точка А есть основание перпендикуляра, а длина отрезка
— расстояние от точки до плоскости а.
Расстояние от точки At до плоскости а меньше расстояния от точки
At до любой точки плоскости а. отличной от точки А.
4.5.	Перпендикулярность плоскостей. Две плоскости называются
взаимно перпендикулярными, если угол между ними равен 90°. Если
плоскости а и Р взаимно перпендикулярны, то пишут a J_ р.
Признак перпендикулярности плоско-
с т е й:
Если плоскость содержит перпендикуляр к другой плоскости, то она
перпендикулярна этой плоскости.
Теорема о взаимно перпендикулярных пло-
скостях.
Если две плоскости взаимно перпендикулярны, то прямая при-
надлежащая одной плоскости и перпендикулярная линии пересечения
плоскостей, перпендикулярна другой плоскости.
§ б ПРОЕКТИРОВАНИЕ НА ПЛОСКОСТЬ	181
4.6.	Наклонная. Прямую, пересекающую плоскость, но не пер-
пендикулярную ей, называют наклонной к плоскости.
Теорема о трех перпендикулярах:
Для того чтобы прямая, лежащая в плоскости, была перпендику-
лярна наклонной, необходимо и достаточно, чтобы эта прямая была
перпендикулярна проекции наклонной на эту плоскость.
4.7.	Скрещивающиеся прямые. Две прямые называются скрещи-
вающимися, если они не пересекаются и не параллельны. Для обозначе-
ния пары скрещивающихся прямых а и.Ъ используется запись а ~ Ь.
Признак скрещивающихся прямых:
Если одна из двух прямых лежит в некоторой плоскости, а другая
прямая пересекает эту плоскость в точке, не принадлежащей первой
прямой, то данные прямые скрещиваются.
Общим перпендикуляром двух скрещивающихся прямых а и b
называется отрезок, удовлетворяющий условиям:
1)	один конец отрезка принадлежит прямой а, а другой конец —
прямой Ь.
2)	прямая, содержащая отрезок, перпендикулярна как прямой а,
так и прямой Ь.
Расстоянием между двумя скрещивающимися прямыми называют
длину общего перпендикуляра двух скрещивающихся прямых.
§ 5.	Проектирование на плоскость
5.1.	Параллельное проектирование. Пусть даны плоскость а и
прямая /, пересекающая плоскость а (рис. 5.19). Возьмем произвольную
точку пространства Лj и проведем через эту точку прямую /ь параллель-
ную/. Прямая пересечет плоскость а в некоторой точке А. Полученная
таким образом точка Л называется проекцией точки Л^ на плоскость а
при проектировании параллельно прямой I. Обычно кратко говорят, что
точка Л есть параллельная проекция точки Лх.
Параллельной проекцией пространственной фигуры называется
множество Ф параллельных проекций всех точек данной фигуры.
Свойства параллельного проектировани я*):
1)	Проекция прямой есть прямая.
2)	Проекции параллельных прямых параллельны?
3)	Отношение проекций двух параллельных отрезков равно отно-
шению проектируемых отрезков.
5.2.	Ортогональное проектирование. Частным случаем параллель-
ного проектирования является ортогональное проектирование.
*) Здесь предполагается, что проектирование производится параллельно
прямой Ц не параллельной проектируемым прямым или отрезкам.
182
ГЛ. 5. ГЕОМЕТРИЯ
Пусть даны плоскость а и прямая /, перпендикулярная а. Возьмем
произвольную точку пространства А± и проведем через нее прямую
параллельную I (и, следовательно, перпендикулярную плоскости а).
Прямая It пересечет плоскость а в некоторой точке А (рис. 5.20), Полу-
ченная точка А называется ортогональной проекцией точки Aj на
плоскость а.
Ортогональной проекцией фигуры Ф* на плоскость а называется
множество Ф ортогональных проекций всех точек данной фигуры Ф1.
Как частный случай параллельного проектирования, ортогональное
проектирование обладает всеми свойствами параллельного проектиро-
вания.
Свойство ортогональной проекции плоского
многоугольника:
Площадь s ортогональной проекции плоского многоугольника на
плоскость а равна площади S проектируемого многоугольника, умно-
женной на косинус угла у между плоскостью многоугольника и плос-
костью а
$ = S • cos у,
§ 6f Углы в пространстве
6.L Угол между наклонной и плоскостью. Углом между наклон*
ной и плоскостью называется угол между наклонной и ее ортогональной
Проекцией на плоскость. Угол между наклонной а и плоскостью а часто
обозначается
(а, а),
6.2. Двугранный угол, Пара различных полуплоскостей а и 0,
имеющих общую границу — прямую а, называется двугранным углом
РИС, 5.21.
РИС. 5,22(
(рис. 5.21). Прямая а называется ребром двугранного угла, а полупло-
скости а и 0 — его гранями. Двугранный угол разбивает все простран-
ство на две части — внутреннюю и внешнюю области двугранного угла.
Грани двугранного угла считаются не принадлежащими ни той, ни дру«
гой области.
Двугранный угол обозначается символом и буквами, указываю-
щими его грани и ребро. При этом буква, обозначающая ребро, ставится
между буквами, обозначающими грани. Например, угол, изображенный
на рис. 5.21, обозначается ад0. Применяется и краткое обозначение
двугранного угла по его ребру, например; а\ АВ (рис. 5.21).
§ 7. ЛОМАНАЯ. МНОГОУГОЛЬНИК
183
Пересечение двугранного угла и плоскости, перпендикулярной его
ребру, называется линейным углом двугранного угла. На рис. 5.22
АОВ — линейный угол двугранного угла аа₽.
Двугранный угол измеряется своим линейным углом. Сколько
градусов, минут и секунд имеет линейный угол, столько же градусов,
минут и секунд имеет двугранный угол.
Двугранный угол будет прямым, острым или тупым в зависимости
от того, будет ли линейный угол двугранного угла прямым, острым или
тупым.
Два двугранных угла равны, если равны их линейные углы.
6.3. Угол между двумя плоскостями. Две пересекающиеся пло-
скости определяют в пространстве четыре двугранных угла. Эти дву-
гранные углы попарно равны, и сумма двух углов, имеющих общую
грань, равна 180°. Меньший из двух углов называют углом между этими
плоскостями. Если две плоскости параллельны, то угол между ними
считается равным 0°.
Угол между плоскостями а, ₽ обозначается (а, ₽).
§ 7ft Ломаная. Многоугольник
Ломаной линией (или просто ломаной) называется объединение
отрезков, в котором конец каждого отрезка (кроме, быть может, послед-
него) является началом следующего отрезка, причем отрезки, имеющие
общий конец, не лежат на одной прямой. Отрезки, составляющие
ломаную, называют звеньями ломаной, а отрезки, имеющие общий
конец, — смежными звеньями ломаной.
Ломаная называется замкнутой^ если конец ее последнего звена
совпадает с началом первого звена.
Рис, 5.23.
Ломаная называется простой, если каждое ее звено .имеет только
одну общую точку с другим звеном, и эта точка является концом звена.
На рис. 5.23 изображены два типа ломацых. Ломаные, изображен-
ные на рис. а) и б), — простые. Только такие ломаные и будут далее
рассматриваться.
Простая замкнутая ломаная разбивает плоскость на две области —
внутреннюю и внешнюю области относительно данной ломаной. Внешняя
область обладает тем свойством, что в ней можно провести прямую,
целиком принадлежащую области.
Простая замкнутая ломаная вместе со своей внутренней областью
называется многоугольником. При этом сама ломаная называется грани-
цей многоугольника, а ее внутренняя область — внутренней областью
многоугольника. Звенья границы многоугольника называются сторо-
нами многоугольника, а точки пересечения звеньев — вершинами
многоугольника. Число вершин многоугольника равно числу его сторон.
184
ГЛ. 5. ГЕОМЕТРИЯ
Две стороны многоугольника, имеющие общую точку (вершину много-
угольника), называются смежными^сторонами, Обычно многоугольник
обозначается перечислением его вершин. На рис. 5.24 в многоугольнике
ABCDE, АВ, ВС, CD, DE и АЕ — стороны многоугольника, А, В, С,
D, Е — вершины многоугольника.
Многоугольник называется выпуклым, если он целиком содержит
отрезок, соединяющий две любые его точки, или иначе, многоугольник
Рис. 5,25.
называется выпуклым, если при продолжении любой из его сторон весь
многоугольник лежит по одну сторону от этой прямой. На рис. 5.25, а, б
изображены выпуклые многоугольники; на рис. 5.25, в, г — невыпук-
лые. Далее мы будем рассматривать только выпуклые многоугольники.
Проведем из вершины многоугольника два луча, содержащие две
смежные стороны выпуклого многоугольника (рис. 5.26). Эти два луча
разобьют плоскость на две области. Выпуклый многоугольник будет
целико.м находиться в одной из областей. Эту область называют вн у трен-
ним углом (или просто углом) многоугольника. Внешним углом выпук-
лого многоугольника называется угол, смежный сего внутренним углом.
На рис. 5.27 штриховкой отмечен один из внешних углов шестиуголь-
ника ABCDEF.
Многоугольник именуется по числу своих углов. Так, например,
многоугольник с тремя углами называется треугольником, многоуголь-
ник с четырьмя углами — четырехугольником и т. д.
Сумма внутренних углов выпуклого n-угольника равна л (и — 2).
Сумма внешних углов выпуклого многоугольника, взятых по одному
при каждой вершине, равна 2л.
Сумма всех сторон многоугольника называется периметром много-
угольника. Периметр обычно обозначается символом Рп, где индекс п
указывает на .число сторон многоугольника.
Отрезок, соединяющий две не соседние вершины многоугольника,
называется диагональю многоугольника. На рис. 5.24 ACt ADt BDt ВЕ^
$ 8. ТРЕУГОЛЬНИКИ	183
СЕ — диагонали пятиугольника ABCDE. Число диагоналей'выпуклого
n-угольника равно п (п — 3).
Многоугольник называется правильным, если все его стороны равны
и все внутренние углы также равны между собой.
§ 8.	Треугольники
8.1. Основные свойства. Треугольником называется многоуголь-
ник с тремя углами (и с тремя сторонами).
Стороны и углы треугольника считаются основными элементами
треугольника.
Говорят, что в треугольнике АВС (рис. 5.28) сторона а лежит
против угла а и, наоборот, против стороны а лежит угол а. Аналогично^
b лежит против р, с — против у.
Треугольник полностью определяется *) любой из следующих
троек своих основных элементов: либо тремя сторонами, либо одной
стороной и двумя углами, либо двумя сто-
рожами и углом междутшми.
Для существования треугольника,
задаваемого тремя сторонами а, Ь, с, не-
обходимо и достаточно выполнение не-
равенств, называемых неравенствами
треугольника:
я + 6 > с,	6 + с > а.
Для существования треугольника,
задаваемого стороной а и углами а, р, не-
обходимо и достаточно выполнение нера-
венства
а + р < 180°,
а для существования треугольника, задаваемого сторонами Ь, с и углом
У между ними, необходимо и достаточно выполнение неравенства
у< 180°.
В качестве тройки элементов, однозначно определяющих треуголь-
ник, можно выбирать и другие наборы элементов. Некоторые из таких
наборов приведены в § 13.
Не любая тройка основных элементов треугольника однозначно ’
задает треугольник. Так, например, задавая три угла треугольника
а, Р, у (они не являются независимыми и связаны между собой равен-
ством а+Р+у— 180°), можно построить сколь угодно много не-
равных треугольников с углами а, Р, у (эти треугольники подобны).
Соотношения между сторонами и углами
треугольника:
1)	Против большей стороны лежит больший угол.
2)	Против большего угла лежит большая сторона.
*) Точнее говоря, задание перечисленных ниже троек элементов о.чро
леляет множество равных трехдольников. Равенство этих трсеч элементов
для двух треугольников также называют признаками равеа^пюи треуголь»
ПИКОВ,
186
ГЛ. Б. ГЕОМЕТРИЯ
3)	Против равных сторон лежат равные углы, и, обратно, против
равных углов лежат равные стороны.
Соотношение между внутренними и внеш-
ними углами треугольника:
Сумма двух любых внутренних углов треугольника равна внешнему
углу треугольника, смежного с третьим углом.
Стороны и углы треугольника связаны между собой также соотно-
шениями, называемыми теоремой синусов и теоремой косинусов (см.
гл. 6).
Треугольник называется тупоугольным, прямоугольным или остро-
угольным, если его наибольший внутренний угол соответственно больше,
равен или меньше 90°.
Площадь треугольника S может быть вычислена по
формулам:
S = j/p (р — а) (р — Ь) (р — с) (формула Герона)г
<$ = A- ab sin у,
с abc
6 “ТтГ’
S = рг.
Здесь а, Ь, с — стороны треугольника, ha, hb, hc — высоты, опущенные
на стороны а, b и с соответственно, р = (а + b + с) — полупери-
метр, R — радиус окружности, описанной около треугольника, г —
радиус окружности, вписанной в треугольник.
8.2.	Медианы треугольника. Медианой треугольника называется
отрезок, соединяющий вершину треугольника с серединой противо-
положной стороны (на рис. 5.29 от-
А резки AD, BE, CF — медианы тре-
угольника АВС). Медианы пересе-
\	каются в одной точке, лежащей	внутри
п/	Дл	треугольника.
Основные свойства м е-
\	диан треугольника:
у	1) Медианы треугольника точкой
В	В их пересечения делятся в отношении
2:1 (считая от вершин треугольника).
рис. 5.29.	2) Медиана делит треугольник
на два равновеликих треугольника.
(Два треугольника равновелики, если их площади равны.)
3) Три медианы треугольника делят треугольник на шесть равно-
великих треугольников (на рис. 5.29 треугольники АОЕ, EOC, COD,
DOB, BOF, FOA равновелики).
Медиана треугольника nva, проведенная к стороне at
выражается через стороны треугольника по формуле
ти = -^-К2^Ч-2са-«2*
§ 8. ТРЕУГОЛЬНИКИ
187
8.3.	Высоты треугольника. Пусть АВС — некоторый произволь-
ный треугольник. Проведем через вершину А перпендикуляр к прямой
а, содержащей сторону ВС . рис. 5.30). Обозначим основание перпенди-
куляра буквой D. Отрезок перпендикуляра AD называют высотой
треугольника АВС, опущенной из вершины А на сторону ВС. Сторону
ВС при этом называют основанием треугольника АВС.
В тупоугольном треугольнике АВС (см. рис. 5.30) две высоты
(AD и BE) пересекают продолжение сторон и лежат вне треугольника;
А
Рис. 5.30.
Рис, 5.31»
третья высота (CF) пересекает сторону треугольника. В остроугольном
треугольнике (рис. 5.31) все три высоты лежат внутри треугольника.
В прямоугольном треугольнике катеты являются также и высотами.
Три прямые, содержащие разные высоты треугольника, всегда Пересе-»
каются в одной точке, называемой ортоцентром треугольника. В тупо*
угольном треугольнике ортоцентр лежит вне треугольника; в остро*
£
Рис. Б.82,
угольном — внутри; в прямоугольном треугольнике ортоцентр совпа-
дает с вершиной прямого угла. Высоты треугольника, опущенные на
стороны треугольника а, Ь и с обозначаются ha, hb и hG соответственно.
Высота треугольника h* выражается через стороны
по формуле
h 2/р(р —а) (р—&) (р —с)
а	а
где Р = -§-(а+Ь4-с).
8.4.	Биссектрисы треугольника. Пусть
АВС — некоторый произвольный тре-
угольник. Проведем биссектрису угла
В А С, пересекающую сторону ВС в точке D
(рис. 5.32). Отрезок биссектрисы внут-
реннего угла треугольника называют бис-
сектрисой треугольника.
Три биссектрисы треугольника (AD, BE, CF на рис. 5.32) пересе-
каются в одной точке, лежащей внутри треугольника и являющейся
центром вписанной в треугольник окружности.
Свойства биссектрисы угла треугольника;
1) Биссектриса делит противоположную сторону на части, пропор-
циональные прилежащим к ней сторонам. Так, например, для треуголь*
ника ABCt изображенного на рис. 5.32,
М£| |ЛД|
|£С| ~ |ВС| ’
188
ГЛ. 5. ГЕОМЕТРИЯ
2) Биссектриса треугольника делит площадь треугольника в отно-
шении, пропорциональном прилежащим сторонам:
S&abe __ I	|
S&BCE	I	I
8.5. Средняя линия треугольника. Средней линией треугольника
называется отрезок, соединяющий середины двух сторон треугольника
(на рис. 5.33 ЬЕ> DF, FE — средние линии).
Свойства средней линии треугольника:
1) Прямая, содержащая среднюю линию треугольника, параллельна
прямой, содержащей третью сторону треугольника.
2) Средняя линия треугольника равна половине третьей стороны.
3) Средняя линия треугольника
отсекает от треугольника подобный
треугольник. Площадь отсекаемого
треугольника относится к площади
основного треугольника в отноше-
нии 1 : 4.
8.6. Равнобедренный треугольник.
Треугольник, у которого две стороны
равны, называется равнобедренным.
В равнобедренном треугольнике
обычно за основание принимают сто-
рон у, не равную никакой из осталь-
ных двух сторон.
Свойства равнобедренного треугольника:
1) В равнобедренном треугольнике углы при основании треуголь-
ника равны.
2) Высота, проведенная из вершины, является также биссектрисой
и медианой.
8.7. Равносторонний треугольник. Треугольник, все стороны
которого равны, называется равносторонним (или правильным) тре-
угольником.
Свойства равносторонне-
го треугольника:
1)	Все углы равны (каждый угол равен 60°);
2)	Каждая из трех высот является также
биссектрисой и медианой;
3)	Центр окружности, описанной около
треугольника, совпадает с центром окружности,
вписанной в него.
Кроме того, равносторонний треугольник,
как частный вид правильного многоугольника,
имеет все свойства правильного многоуголь-
ника.
* 8.8. Прямоугольный треугольник. Треугольник, один из углов
которого прямой, называется прямоугольным треугольником.
Сторона прямоугольного треугольника, лежащая против прямого
утла, называется гипотенузой, а две остальные стороны — катетами.
На рис. 5.34 изображен прямоугольный треугольник: ВАС = 90%
ВС —• гипотенуза, АВ и АС — катеты.
Прямоугольный треугольник, имеющий равные катеты, называется
равнобедренным прямоугольным треугольником. В равнобедренном
§ 9. ЧЕТЫРЕХУГОЛЬНИКИ
189
прямоугольном треугольнике острые углы равны (каждый из них
равен 45°).
Стороны всякого прямоугольного треугольника at b и с (с— гипо-
тенуза) связаны между собой соотношением, называемым теоремой
П и ф а I о р а:
с2 = а2 -ф-.Z?2,	У|\
которая читается так: квадрат гипоте- Jx J \
нузы равен сумме квадратов катетов.	s'	\
Свойства прямоуголь- S'	J \
н о г о треугольника:	----------- I *» ---—X
1)	Катет есть среднее пропорцио-	“с с ° с
нальное между гипотенузой и проекцией	рис 5 35
этого катета на гипотенузу (рис. 5.35):	’ * °*
bc : b = b : с, ас : а~ а: с, или Ь2 ~Ьсс и а2 — асс\
здесь через ас и Ь( обозначены проекции катетов а и b на гипотенузу с.
2)	Высота, проведенная из вершины прямого угла, есть среднее
пропорциональное между проекциями катетов на гипотенузу (рис. 5.35)
bc : h — h : ас или № — асЬс.
3)	Центр окружности, описанной около прямоугольного треуголь-
ника, лежит на середине гипотенузы.
Площадь прямоугольного треугольника может быть вычислена по
общим формулам вычисления площади треугольника. Кроме того,
площадь прямоугольного треугольника может быть вычислена по
формуле
S = ab.
т. е. Площадь прямоугольного треугольника равна полышье щоизвс-
дения его катетов.
§ 9.	Четырехугольники
9.	1. Параллелограмм. Четырехугольник, противоположные сто-
роны которого попарно параллельны, называется параллелограммом
(рис. 5.36).
Свойства параллело-
грамма:
1)	Середина диагонали парал-
лелограмма является его центром
симметрии.
2)	Противоположные стороны
параллелограмма равны.
3)	Противоположные углы па-
Рис. 5.36.
раллелограмма равны.
4)	Каждая диагональ параллелограмма делит его на два равных
треугольника.
5)	Диагонали параллелограмма делятся точкой пересечения по-
полам.
6)	Сумма квадратов диагоналей параллелограмма (dx и d2) р*шна
сумме квадратов всех его сторон:
dl Т а2 = 2 К + Н-
190
ГЛ. В. ГЕОМЕТРИЯ
Признаки параллелограмма!
1) Если в четырехугольнике противоположные стороны попарно
равны, то этот четырехугольник — параллелограмм.
2) Если в четырехугольнике две противоположные стороны равны и
параллельны, то этот четырехугольник — параллелограмм.
Каждый из признаков параллелограмма может быть взят в качестве
определения параллелограмма. Так, например, из первого признака
получается следующее определение параллелограмма:
Четырехугольник, у которого противоположные стороны попарно
равны, называется параллелограммом. .
Так как параллелограмм — это четырехугольник со специальными
свойствами, то он обладает всеми свойствами произвольного четырех-
угольника. В частности, сумма внутренних углов параллелограмма
равна 2л (360°).
Отрезок перпендикуляра к сторонам параллелограмма, заключен-
ный между ними, называется высотой параллелограмма.
Площадь параллелограмма:
1) Площадь параллелограмма равна произведению его основания
на высоту7 (рис. 5.36):
- S = aha.
2) Площадь параллелограмма равна произведению смежных’сторон
параллелограмма на синус угла между ними (рис. 5.36):
S == ab sin а.
9.2. Ромб4
вается ромбом
Рис. 5,37.
Параллелограмм, все стороны которого равны, назьь
(рис. 5.37). Ромб, являясь параллелограммом, имеет
все его свойства. Кроме того, ромб обладает следу-
ющими специальными свойствами:
1)	Прямая, содержащая диагональ ромба, яв-
ляется его осью симметрии.
2)	Диагонали ромба взаимно перпендикулярны.
3)	Диагонали ромба являются биссектрисами
его внутренних углов.
Кроме общих формул вычисления площади ромба
как площади параллелограмма, площадь ромба
может быть вычислена по формуле
S = -g- didz,
где и d2 — диагонали ромба.
9.3.	Прямоугольник. Параллелограмм, у которого все углы пря-
мые, называется прямоугольником (рис. 5.38).
Прямоугольник, являясь параллелограммом, имеет все его свойств^.
Кроме того, прямоугольник обладает следующими специальными
свойствами:
1)	Перпендикуляр, проходящий через сере-
дины противоположных сторон прямоугольника,
является его осью симметрии.
2)	Прямоугольник имеет две оси симметрии. а	а
3)	Диагонали прямоугольника равны.
Площадь прямоугольника вы- ____________________________
числяется по формуле
S = ab,
где а и Ъ — смежные стороны прямоугольника. рис. 5.зв.
§ 10. ПОДОБНЫЕ МНОГОУГОЛЬНИКИ	,191
9.4.	Квадрат. Прямоугольник, у которого все стороны равны,
называется квадратом.
И з определений квадрата и ромба следует, что квадрат (рис. 3.89)
является ромбом, у которого все углы прямые. Так как квадрат является
и параллелограммом, и прямоугольником, и ром-
бом, то все свойства этих фигур присущи и квад-
рату.
Площадь квадрата вычисляется по
формуле
S «= а\
где а — сторона квадрата.
9.5< Трапеция* Четырехугольник, две сто-
Рис. 5.39.
Рис. 5.40.
роны которого параллельны, а две другие не па-
раллельньц называется трапецией.
Параллельные стороны трапеции называются ее основаниями^
а не параллельные —• боковыми сторонами (на рис. 5.40 ВС и AD
основания, АВ и CD — боковые стороны).
Отрезок перпендикуляра к основаниям
трапеции, заключенный между основаниями!
называется высотой трапеции (на рис. 5.40
отрезок BQ — высота). Трапеция, боковые
стороны которой равны (| АВ | ~ \CD |)^
называется равнобочной (или равнобедренной^
В равнобочной трапеции углы при оснований
попарно равны:
BAD = ADC, ABQ «а A BCth

Отрезок, соединяющий середины боковых сторон трапеции, назы-
вается средней линией трапеции. Средняя линия трапеции параллельна
основаниям и равна полусумме оснований:
ш I = 1?СЛ+1.Л°1.,
Средняя линия трапеции делит высоту трапеции на два равных отрез'йй.
Площадь трапеции вычисляется по формуле

где а и b — основания трапеции, h — высота трапеции^
§ 10$ Подобные многоугольники
10.1	* Признак подобия многоугольников. Если стороны одного
многоугольника пропорциональны сторонам другого многоугольника и
соответственные углы (т. е. углы, лежащие между пропорциональными
сторонами) этих многоугольников равны, то такие многоугольники
подобны.
На рис. 5.41 изображен пятиугольник ABCDE, подобный пяти-
угольнику AiB^DiEi, с коэффициентом подобия k = 2
|4В| |ДС| |СР| |Д£| |ЛВ|
IЛ1В11 I BiCi I I CiDt I I DiEi I | AiEi) “ R ~
192
ГЛ. 5. ГЕОМЕТРИЯ
Два четырехугольника подобны, если у
ственных сторон пропорциональны и пары
них три пары соотвст-
соответственных углов,
Рис. 5.41.
заключенных между
|АВ| |ВС|
соответственными сторонами, равны (рис. 5.42):
I СР|
ТлТвГГ |ВхС1| ~ ICiDil ’
10.2	. Признаки подобия треугольников.
1)	Если три стороны одного треугольника пропорциональны трем
сторонам другого треугольника, то такие треугольники подобны
(рис. 5.43):
|АВ |	_ |ВС |	| АС|
| А^ | ~ |	| ~ | ЛЛ | ‘
2)	Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны (рис. 5.43):
3)	Если две стороны одного треугольника пропорциональны двум
сторонам другого треугольника и углы между этими сторонами равны,
то такие треугольники подобны (рис. 5.43):
ЧЛВ1 |ВС|	„
I АА I - I BiCi I ’ В -	В1-
Для подобия треугольников специального вида (прямоугольных,
равнобедренных, равносторонних) необходимо выполнение меньшего
числа условий, нежели для произвольных треугольников. Так, 1) пря-
моугольные треугольники подобны, если гипотенуза и катет одного
треугольника пропорциональны гипотенузе и катету другого треуголь-
ника; 2) прямоугольные треугольники подобны, если острый угол одного
треугольника равен острому углу другого.
Аналогичное утверждение верно и для четырехугольников (много-
угольников) специального вида. Так, например, любые два правильных
n-угольника всегда подобны*
$ II. ОКРУЖНОСТЬ и круг
193
Свойства подобных многоугольников}
1) Отношение периметров подобных многоугольников равно отно-
шению их соответственных сторон (коэффициенту подобия).
2) Отношение площадей подобных многоугольников равно квадрату
коэффициента подобия.
§ 11. Окружность и круг
11.1. Окружность и круг. Окружностью называется множество
всех точек плоскости, находящихся на данном положительном расстоя-
нии от некоторой данной точки плоскости, называембй ^нтрол/ окруж-
ности.
Радиусом окружности называется отрезок, соединяющий центр
окружности с любой точкой окружности (на рис. 5.44 отрезок ОА —
радиус). Радиус окружности обычно обозначается буквами г, R.
Отрезок, соединяющий две точки окружности, называется хордой
(на рис. 5.44 АВ — хорда).
Рис. 5.44.
Рис. 5.45,
Хорда, проходящая через центр окружности, называется диаме*
тром. Диаметр равен удвоенному радиусу окружности. Диаметр обычно
обозначается буквами d, D.
Свойства хорд окружности:
1)	Диаметр, делящий хорду пополам, перпендикулярен этой хорде.
2)	В окружности равные хорды равноудалены от центра окружности,
и, наоборот, равноудаленные от центра окружности хорды равны.
3)	Из двух не равных хорд окружности бблыпая хорда расположена
ближе к центру окружности, и, наоборот, из двух не равных хорд
большей будет та, которая ближе к центру.
4)	Отрезки пересекающихся хорд AM, МВ, СМ и MD (рис. 5.45)
связаны равенством
| AM | | МВ | = | СМ |.| MD\.
Кругом называется множество всех точек плоскости, расстояние
которых от некоторой данной точки плоскости (называемой центром
круга) не больше данного.
Радиус, хорда и диаметр окружности являются радиусом, хордой и
диаметром соответствующего круга.
11.2. Касательная и секущая. Прямая, принадлежащая плоскости
окружности и имеющая с окружностью только одну общую точку,
называется касательной к этой окружности.
Для того чтобы прямая была касательной к окружности, необхо-
димо и достаточно, чтобы эта прямая была перпендикулярна диаметру
окружности и проходила через его конец,
7 д. г. Цыпкин
194
ГЛ. 5. ГЕОМЕТРИЯ
Через любую точку, лежащую вне окружности и принадлежащую
плоскости окружности, можно провести две различные касательные
(рис. 5.46).
Прямая, имеющая с окружностью две общие точки, называется
секущей. На рис. 5.47 AD и ADi — секущие.
Если через точку А, лежащую вне круга, провести касательную и
секущую (см. рис. 5.47), то отрезки касательной и секущей связаны
равенством
| АВ рс= | AD |.| АС | = | ADi |. pCJ.
11.3. Взаимное расположение двух окружностей. Пусть на пло-
скости даны две несовпадающие точки Ох и О2, расстояние между кото-
рыми h s= I ОХО2 I, и две окружности с радиусами и /?2 и центрами
в точках 01 и О2 соответственно. Для определенности положим, что
/?2« При заданном расстоянии | ОГО21 == h и заданных радиусах
R1 и /?2 могут быть следующие случаи взаимного расположения окруж-
ностей:
1)	Если	— /?2> то окружности не пересекаются и круг
радиуса /?2 ноликом принадлежит кругу радиуса Rx (рис. 5.48).
2)	Если h = /?£ — R2i то круг радиуса R2 целиком принадлежит
кругу радиуса а окружности имеют одну общую точку М (рис. 5.49).
О таком расположении окружностей говорят, чего они касаются друг
друга изнутри в точке М.
3)	Если h > Ri 4- R2, то окружности не пересекаются, а круги не
имеют ни одной общей точки (рис. 5.50).
4)	Если h = /?! + R2t то окружности (и круги) имеют одну общую
точку М (рис. 5.51). О таком расположении окружностей говорят, что
они касаются друг друга снаружи в точке М.
5)	Если Rt — R2 < h < Ri -f- R2t то окружности имеют две общие
точки. В этом случае говорят, что окружности пересекаются в точках
Mi и М2 (рис. 5.52).
Отрезок OiOa называется линией центров окружностей. Прямая,
касательная к обеим окружностям и не пересекающая линии центров,
называется внешней касательной двух данных окружностей.
§ 11. ОКРУЖНОСТЬ И КРУГ
195
В перечисленных выше пяти случаях внешняя касательная к двум
окружностям может быть построена во всех случаях, кроме 1).
Прямая, касательная к обеим окружностям и пересекающая их
линию центров, называется внутренней касательной двух данных
окружностей. Внутренняя касательная может быть построена в случаях
3) и 4).
Если две окружности пересекаются (см. случай 5), рис. 5.52), то
отрезок называется общей хордой двух пересекающихся окруж-
ностей. Общая хорда двух пересекающихся окружностей взаимно пер-
пендикулярна с линией центров и точкой пересечения делится на два
равных отрезка:
I мл । = । км21.
11.4. Центральные углы и дуги окружности. Угол с вершиной
в центре окружности называется центральным углом окружности,
Два различных луча, выходящих из центра окружности, опреде-
ляют два центральных угла. Точки пересечения лучей с окружностью
(на рис. 5.53 точки Л и В) делят окруж-
ность на две части. Эти части окружности
называются дугами окружности. Чтобы вы-
делить одну из указанных дуг, на дугах
выбирают произвольные точки (на рис. 5.53
точки С и D) и говорят о дугах АС В и
ADB, Для обозначения дуг используется
символ 4J. Так, например, дуги А СВ и ADB
обозначаются:
о АСВ и ADB.
Центрами дуг называют центр окружности.
Дуги окружности измеряют в градусах, минутах и секундах.
Сколько градусов, минут и секунд имеет данный центральный угол^
столько же градусов, минут и секунд имеет и соответствующая дуга.
Угловая величина дуги АСВ (\jACB) иногда обозначается симво-
лом АСВ.
Дуга, соответствующая центральному углу в 180°, называется
пол уокр ужностъю.
Между дугами и соответствующими им центральными углами
окружности имеют место следующие отношения:
1) Две дуги, принадлежащие окружностям одного и того же ра-
диуса, равны в том и только том случае, когда их угловые величины
равны *).
♦) Угловые величины дуг окружностей разного радиуса могут быть
равны, но дуги тем не менее не будут равны,
7*
196
ГЛ* 5* ГЕОМЕТРИЯ
Рис. 5.54.
11.6. Углы
окружности, а
2) В одной и той же окружности большему центральному углу
соответствует большая дуга.
11.5. Дуги и хорды окружности. Пусть в окружности проведена
хорда АВ, не проходящая через центр окружности (рис. 5.54). О хорде
АВ говорят, что она стягивает дугу АВ (при этом
предполагается, что из двух дуг, на которые точки А
и В разбивают окружность, выбирается наименьшая
дуга, т. е. угловая величина дуги АВ заключена
в промежутке (0°, 180°)). Между хордами окруж-
. ности и стягиваемыми ими дугами имеют место
‘ следующие отношения:
1)	Равные дуги стягиваются равными хордами.
2)	Равные хорды стягивают равные дуги.
3)	Диаметр, перпендикулярный хорде, делит
стягиваемую хордой дугу пополам.
в окружности. Угол, вершина которого принадлежит
стороны пересекают окружность, называют углом,
вписанным в эту окружность (рис. 5.55). Говорят также, что угол ВАС
опирается на дугу BDC. Величина вписанного
угла равна половине угловой величины дуги,
на которую он опирается (или половине вели-
чины центрального угла, соответствующего дан-
ной дуге);	д
ВДС = -i- В DC.
Угол* образованный двумя касательными Рис» 5-55-
к окружности, проходящими через одну точку,
называется описанным углом (на рис. 5.56 С А и СВ — касательные).
Величина описанного угла равна полуразности угловых величин дуг,
заключенных между его сторонами:
лев = -L (лев — лЬв).
Величина угла, образованного двумя секущими, имеющими общую
точку, лежащую вне окружности, равна полуразности угловых величин
Рис. 5.56,	РИС. 5.57.	Рис. 5.58.
дуг, заключенных между его сторонами (рис. 5.57):
ДСХ = -1- (ADAt — BLBi).
Величина угла, образованного двумя секущими, имеющими общую
точку, лежащую внутри окружности, равна полусумме угловых величин
§ 12. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТЬ	197
дуг, заключенных между его сторонами (рис. 5.58):
BCBi = -t- (вйь + А&А1).
11.7. Длины и площади в окружности и круге. Длиной окруж-
ности называется предел последовательности периметров правильных
многоугольников, вписанных в дан-
ную окружность, при неограничен-
ном увеличении числа сторон *).
Длина окружностиL
вычисляется по формуле
L = nd,
где d — диаметр окружности, или
по формуле
L = 2лг,
где г — радиус окружности.
Длина дуги окружности с угловой величиной в а° вычисля-
ется по формуле
, яга
1 “~Т8(Г‘
Площадью круга называется предел последовательности площадей
правильных многоугольников, вписанных в данную окружность, при
неограниченном увеличении числа сторон.
Площадь круга радиуса г вычисляется по формуле
S = лг2.
Сектором называется часть круга, ограниченная двумя его ра-
диусами (рис. 5.59).
Площадь сектора с угловой величиной дуги а° вычисля-
ется по формуле
с - nf2a
г>сект— 3б0 .
Часть круга, ограниченная хордой и стягиваемой ею дугой, называ-
ется сегментом (рис. 5.60).
Площадь сегмента вычисляется как разность площади
сектора, ограниченного радиусами О А и О В и площади треугольника
АОВ /(см. рис. 5.60).
§ 12.	Многоугольники и окружность
12.1.	Вписанные и описанные многоугольники. Многоугольник^
все вершины которого принадлежат окружности, называется вписанным
в эту окружность, а окружность — описанной около многоугольника.
Многоугольник, все стороны которого касаются окружности, назы-
вается описанным около этой окружности, а окружность — вписанной
в этот многоугольник.
Около всякого правильного многоугольника можно описать окруж-
ность, и во всякий правильный многоугольник можно вписать окруж-
ность.
*) Вывод формул длины окружности и площади круга см, п. 6.4 гл. 8<
198
ГЛ. 5. ГЕОМЕТРИЯ
Центр вписанной в правильный многоугольник окружности совпа-
дает с центром описанной около правильного многоугольника окруж-
ности; эта точка называется центром правильного многоугольника.
Отрезок перпендикуляра, проведенного из центра правильного
многоугольника к его стороне, называется апофемой правильного
многоугольника.
Сторона правильного /г- угольника ап выража-
ется через радиус R описанной около него окружности и число сторон п
по формуле
180°
an = 2fl sin
Площадь правильного n-угольника равна
половине произведения его периметра на радиус вписанной окружности:
Sn ~ "2“ Рп?•
Площадь правильного n-угольника выража-
ется через радиус описанной окружности R и число сторон п по формуле
О 1	• 360°
8п=-^Р2пып—^—.
12.2.	Вписанные треугольники. Треугольник, все вершины кото-
рого принадлежат окружности, называется вписанным в эту окружность^
а окружность — описанной около этого треугольника. Около всякого
треугольника можно описать окружность, и притом только одну. Центр
описанной около треугольника окружности — точка пересечения
перпендикуляров, восставленных к сторонам этого треугольника и
проходящих через их середины; он лежит внутри треугольника, если
треугольник остроугольный; вне треугольника, если треугольник тупо-
угольный; на середине гипотенузы, если треугольник прямоугольный.
Радиус окружности, описанной около произвольного
треугольника, вычисляется по формулам
„Ч . а	- 1 • Ь - 1 . с
2 ' sin а 2 * sin (3 ~~ 2 * sin у ’
__ abc_______________abc___________,
45 Д 4 \/~р{р—а)(р—Ь)(р — с) ’
а, Ь, с — стороны треугольника, р = ~ (а + b 4- с) — полупериметр,
— площадь треугольника, а, 0, у — углы треугольника, лежащие
против сторон а, Ь, с соответственно.
12.3.	Описанные треугольники. Треугольник, все стороны кото-
рого касаются окружности, называется описанным около этой окруж-
ности, а окружность — вписанной в этот треугольник.
Во всякий треугольник можно вписать окружность, и притом только
одну. Центр О вписанной в треугольник окружности является точкой
пересечения биссектрис внутренних углов треугольника.
Радиус окружности, вписанной в произвольный тре-»
угольник, вычисляется по формуле
t = sд = 1 / (р ~д) (р ~ *) (р —
р V	р
§ 12. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТЬ
199
12.4.	Вневписанная окружность. Вневписанной окружностью назы-
вается окружность, касающаяся одной стороны треугольника и про-
должения двух других сторон.
Биссектрисы пары внешних углов треугольника, смежных с углами
Риу(рис. 5.61), пересекаются в точке Оа. Через эту же точку проходит
биссектриса внутреннего угла а. Точка Оа — центр вневписанной окруж-
ности, касающейся стороны а и продолжения сторон b и с. Аналогично
находятся точки Оь и 0с — центры
вневписанных окружностей, каса-
ющихся сторон b и с соответственно
(см. рис. 5.61).
Радиусы в н е в п и с а н•
н ы х окружностей га, rCt
касающихся сторон at b и с соответ-
ственно, вычисляются по формулам
г	2S*
а р — a Z? + с — а ’
г	2S^
b p — b a-\-c — b 9
r	-	2S*
c p — c “ a-^b — c
12.5.	Соотношения между сторонами правильного и прямоуголь-
ного треугольников и радиусами вписанной и описанной окружностей.
Сторона правильного треугольника а связана с радиусом описанной
окружности R и радиусом вписанной окружности г соотношениями
р_ aV3	аКЗ
R 3’6*
Центр вписанной в правильный треугольник окружности совпадает
с центром описанной около него окружности и называется центром
правильного треугольника.
Окружность, описанная около прямоуголь-
ного треугольника. Центр окружности, описанной вокруг
прямоугольного треугольника, лежит на се-
@ редине гипотенузы, и, следовательно, гипо-
тенуза прямоугольного треугольника является
диаметром окружности, описанной около прямо-
В угольного треугольника.
Все точки окружности с диаметром АВ (за
исключением точек А и В) являются вершинами
прямоугольных треугольников с гипотенузой
Рис. 5.62. АВ (РИС- 5-62)-
12.6. Вписанные четырехугольники. Четы-
рехугольник, все вершины которого принад-
лежат окружности, называется вписанным в эту окружность, а окруж-
ность — описанной вокруг этого четырехугольника.
Для того чтобы около выпуклого четырехугольника можно было
списать окружность, необходимо и достаточно, чтобы сумма противо-
лежащих углов этого четырехугольника была равна 180 /
В частности, из всех параллелограммов лишь около прямоуголь-
ника (квадрата) можно описать окружность.
200
ГЛ. 5» ГЕОМЕТРИЯ
Около трапеции можно описать окружность только тогда, когда она
равнобочная.
Если четырехугольник ABCD можно вписать в окружность, то
произведение диагоналей этого четырехугольника равно сумме про-
изведений противоположных
сторон (рис. 5.63):
| АС | .|BD| = | ДВ|.|СГ| +
+ | AD |.| ВС |.
12.7. Описанные четырех-
угольники. Четырехугольник,
все стороны которого касаются
окружности, называется опи-
санным около окружности, а
окружность —- вписанной в этот
четырехугольник.
Для того чтобы в выпуклый четырехугольник можно было вписать
окружность, необходимо и достаточно, чтобы суммы противолежащих
сторон этого четырехугольника были равны. На рис. 5.64
| АВ |+ 1 CD | = | ВС | + | AD [.
Из всех параллелограммов лишь в ромб (в частности, в квадрат)
можно вписать окружность. Центр вписанной окружности совпадает
с точкой пересечения диагоналей указанных четырехугольников.
§ 13.	Геометрические построения
Задачи на геометрические построения — один из традиционных
разделов геометрии. Геометрические построения выполняются с по-
мощью «односторонней» линейки и циркуля. Под «односторонней»
линейкой понимается инструмент, с помощью которого можно выпол-
нять единственную процедуру — проводить прямую (луч, отрезок)
через две данные точки. Под циркулем понимается инструмент, которым
можно строить окружности и откладывать на прямой геометрически
заданный отрезок. В приведенных ниже задачах слова «отрезок задан»
и «угол задан» означают, что нам дано геометрическое изображение
отрезка (соответственно угла), а не их численное значение. При выпол-
нении задач на построение также следует иметь в виду, что задача
построения некоторой геометрической фигуры заключается не в практи-
ческом вычерчивании фигуры с известной степенью точности, а в том,
как при помощи линейки и циркуля необходимое построение может быть
выполнено теоретически в предложении, что наши инструменты дают
абсолютную точность построения.
В заключение сформулируем три классические задачи построения
фигур, решение которых разыскивалось в течение нескольких столетий,
до тех пор, пока не было доказано, что эти задачи не могут быть решены
с помощью линейки и циркуля.
1)	Удвоение куба. Если данный куб имеет ребро, равное
единице длины, то его объем будет равен кубической единице. Построить
ребро куба, объем которого вдвое больше.
2)	Трисекция угла. Разделить произвольный угол на три
равных угла.
3)	Квадратура круга. Построить квадрат (сторону квад-
рата), площадь которого равна площади круга, радиус которого прини-
мается за единицу длины.
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ	201
13.1* Построение прямых, параллельных и перпендикулярных
данной прямой (данному отрезку).
1)	Построить прямую, параллельную данной прямой АВ а прохо-
дящую через данную точку С.
Произвольным раствором циркуля строим окружность е центром
в данной точке С так, чтобы она пересекла данную прямую Л В (рис. 5.65).
Тем же раствором циркуля от одной из точек пересечения прямой и ок-
ружности (на рис. 5.65 точки М) откладываем на прямой АВ в любую
Рис, 5.6Б.
Рис. 5.67,
Рис. 5.68,
сторону отрезок MN. Снова тем же раствором засекаем из точки Л/
точку окружности D. Через точки С и D проводим прямую. Прямая CD
и есть искомая прямая.
2)	Разделить данный отрезок пополам и построить перпендикуляр
к отрезку в его середине.
Из концов данного отрезка АВ как из центров (рис. 5.66) одним
и тем же произвольным ^большим 1 АВ радиусом строим две пере-
секающиеся дуги. Прямая, проходящая через
точки пересечения дуг С и D — середина
отрезка АВ.
3)	Построить перпендикуляр к данной
прямой MN в данной точке А (построение
прямого угла).
Возьмем произвольную точку О, не при-
надлежащую данной прямой Л4Л/ (рис. 5.67),
и построим окружность с центром в точке О
радиуса О А (А — данная точка). Через вто-
рую точку пересечения построенной окруж-
ности с прямой MN (на рис. 5.67 точку В) проводим диаметр ВС.
Прямая, проходящая через точки С и Л, и есть искомый перпендикуляр.
Угол, образованный лучами АС и АВ, — прямой.
4) Опустить перпендикуляр из данной точки С на данную пря*
мую MN.
Из данной точки С как из центра (рис. 5.68) произвольным радиусом
проводим дугу, пересекающую данную прямую MN в точках D и Е.
Из точек D и Е как из центров проводим одним и тем же произвольным
(но отличным от предыдущего) радиусом две дуги /j, /2, пересекающиеся
в точке F. Прямая, проходящая через точки С и F, и есть искомый
перпендикуляр.
13.2. Построение углов.
1) Построить угол, равный данному углу MNK (рис. 5.69, а).
Выбираем на плоскости произвольную точку О и проводим луч
ОА (рис. о.69, б). Из вершины N данного угла как из центра описываем
дугу PQ произвольного радиуса. Тем же раствором циркуля описываем
202
ГЛ, 5. ГЕОМЕТРИЯ
из центра О дугу P±Qi (точка Qj принадлежит лучу ОА, а точка
пока не фиксирована). Из точки как из центра радиусом, равным
длине хорды PQ, засекаем точку Р^ Проводя луч OPi, получаем угол
PjOQi, равный данному углу MNК.
2)	Построить углы, равные 60° и 30°.
Из концов А и В произвольного отрезка АВ как из центров радиу-
сом, равным [ АВ описываем две дуги, пересекающиеся в точках С и D
(рис. 5.70). Строим отрезки CD и АС, Обозначим точку пересечения
отрезков АВ и CD буквой О. Угол А СО равен 30°, а угол С АО равен 60°.
3)	Построить угол, равный 45°.
На сторонах прямого угла АОВ (рис. 5.71) откладываем равные
отрезки О А и ОВ. Через точки А и В проводим прямую АВ. Угол, обра-
зованный лучами ВА и ВО, равен 45°.
4)	Разделить данный угол ВАС на два равных угла (построить
биссектрису утла).
О	ia
Рис. 5.71.
Из вершины угла ВАС как из центра проводим дугу DE окруж-
ности произвольного радиуса (рис. 5.72). Из точек D и Е пересечения
этой дуги с лучами АВ и АС описываем произвольным радиусом пере-
секающиеся дуги If и 12. Через точку их пересечения F проводим луч AF.
Полученные углы BAF и FAC равны, а луч AF есть биссектриса угла
ВАС.
13.3. Построение отрезков.
1)	Разделить данный отрезок АВ на данное число равных отрезков.
Строим прямую, параллельную (но не совпадающую) прямой,
содержащей данный отрезок А В. Берем произвольную точку Ль при-
надлежащую построенной прямой (рис. 5.73). Из точки Af откладываем
столько равных отрезков Л^, CiDi, D^^ ,,, произвольной длины, на
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
203
сколько частей нужно разделить отрезок АВ. Конец последнего отрезка
сбозначаем буквой В±. Проводим прямые АА^ и ВВ^ до пересечения
в точке О. Через пары точек (Q; О), (Вх; О), (Ei\ О), ... проводим лучи?
которые пересекут прямую АВ в точках С, D, Е, ....делящих отрезок Л В
на нужное число равных отрезков.
2)	Разделить данный отрезок на отрезки, пропорциональные данным
величинам.
Рис. 5.73*
Рис. 5.74*
О
РИС. 5.75.
Задача решается так же, как и предыдущая, только от точки Л|
откладываются отрезки, пропорциональные данным величинам.
3)	Построить отрезок, средний пропорциональный (средний геоме*
трический) двум данным отрезкам *).
На произвольной прямой отложим данные отрезки так, чтобы конец
одного отрезка совпал с началом другого и эта точка была единственной
их общей точкой (на рис. 5.74 отрезки ЛВ и
ВС). Разделим отрезок АС пополам и радиу-
сом, равным половине отрезка АС, построим
окружность с центром в середине отрезка АС
(на рис. 5.74 точка О — середина отрезка
АС). Из точки В восставляем перпенди-
куляр к отрезку АС. Точку пересечения
перпендикуляра и окружности обозначим
буквой D. Отрезок BD — средний пропор-
циональный отрезкам ЛВ и ВС:
|ЛВ| \BD\
\BD\ | ВС| ’
4)	Построить четвертый пропорциональный отрезок (по данным
отрезкам а, b и с построить отрезок х такой, что а : b — с : х).
На одной стороне произвольного угла а (рис. 5.75) от его вершины
последовательно откладываем отрезки с и с, на другой — отрезок Ь.
Через точку С проводим прямую, параллельную прямой Л В. Отрезок
BD, отсекаемый на стороне угла ОВ, — искомый.
5)	Построить отрезок, соизмеримый данному.
Отрезок АВ называется соизмеримым с отрезком CD, если отноше*
ние длин этих отрезков — рациональное число:
| АВ | т t	ч
Trn I	— (/п’ п — натуральные числа).
*) Отрезок х, удовлетворяющий равенству а/х = х/b, где а и Ъ — данные
отрезки, называется отрезком, средним пропорциональным (средним геоме»
трическим) двум данным отрезкам,
204
ГЛ. б. ГЕОМЕТРИЯ
Пусть дан некоторый отрезок АВ и требуется построить отрезок,
соизмеримый данному. Разделим отрезок АВ на т равных частей.
Возьмем одну из этих равных частей и отложим ее п раз на луче СП
(рис. 5.76) так, чтобы конец предшествующего отрезка (за исключением
первого) был началом следующего. Тогда конец последнего отрезка даст
точку D — конец искомого отрезка CD,
6)	Примеры построения отрезков, несоизме-
рим ых с данным.	__
а)	По данному отрезку длиной а построить отрезок длиной a 2 •
т
--------1--1.л . . .t-:—f------1—.
С'----------------v---------------'Д
п отрезкой

Рис. 5.76.
Строим равнобедренный прямоугольный треугольник с катетами
длиной а (рис. 5.77). Гипотенузой такого треугольника будет отрезок
а/2.	_
б)	По данному отрезку а построить отрезок а КЗ.
Строим прямоугольный треугольник с катетом а и гипотенузой 2а
(рис. 5.78).
Вторым катетом построенного прямоугольного треугольника будет
отрезок а 1^3 .	_
в) По данному отрезку а построить отрезок а /Ъ •
Рис. 5.78.
Рис. 5.79.
Строим прямоугольный треугольник с катетами а и 2а (рис. 5.79).
Гипотенузой построенного треугольника и будет отрезок а]/"5.
7)	Примеры построения отрезков, задавав*
мых алгебраическими выражениями (под словами
«отрезок задается алгебраическим выражением» понимается, что иско-
мый отрезок задается как алгебраическая функция данных отрезков).
Для построения отрезков, задаваемых алгебраическими выраже-
ниями, используются следующие элементарные построения:
а)	построение отрезка, среднего пропорционального двум данным
отрезкам;
б)	построение четвертого пропорционального отрезка;
в)	построение отрезка, несоизмеримого с данным.
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
Пример 1. Построить отрезок, задаваемый выражением
/ а2 + ab + с2,
где а, Ь, с — заданные отрезки.
Записывая выражение, стоящее под знаком радикала в виде
a2 -f- ab + с2 = а (а + Ь) + с2,
нетрудно заметить, что если мы построим отрезок х такой, что х2 =з
= а (а+Ь), т. е. отрезок, средний пропорциональный отрезкам а
и а Ь, то искомый отрезок будет получаться как гипотенуза прямо-
угольного треугольника с катетами х и с. Таким образом, построение
искомого отрезка свелось к выполнению двух последовательных по-
строений — построению среднего пропорционального отрезка и построе-
нию прямоугольного треугольника по двум катетам.
Пример 2. Построить отрезок, задаваемый выражением
/ За2 + 562 ,
еде aub — заданные отрезки.
Строим отрезок а как катет прямоугольного треугольника
с заданными гипотенузой_2а и катетом а.
Строим отрезок b J/5 как гипотенузу прямоугольного треуголь-
ника с заданными катетами 2Ь и Ь.
Искомый отрезок строится как гипотенуза прямоугольного тре-
угольника с катетами а j/"3 и b /"5 .
Пример 3. Построить отрезок х, задаваемый соотношением
1	1.1
еде а и b — заданные отрезки.
Проделав очевидные преобразования данного равенства;
1	1.1	a+b	b	а+Ъ
х	а 1 b ab	х а	9
замечаем, что построение отрезка х сводится к построению четвертого
пропорционального отрезка.
13.4.	Построение окружностей и дуг окружностей.
1)	Через две данные точки провести окружность данного радиуса.
Из данных точек А и В как из центров данным радиусом г проводим
две пересекающиеся дуги 1± и /2- Точка их пересечения О (рис. 5.80) и
есть центр искомой окружности *).
2)	Через три данные точки А, В, С, не лежащие на одной прямой*
провести окружность.
Строим отрезки ВС и АС (рис. 5.81), концами которых служат
данные точки А, В и С, строим перпендикуляры к отрезкам ВС и АС^
проходящие через их середины. Точка пересечения этих перпендикуля-
ров (на рис. 5.81 точка О) и будет центром искомой окружности. Радиус
данной окружности равен расстоянию от точки О до любой из трех
равноудаленных от О точек А, В и С.
3)	Через две данные точки А и В провести окружность, касающуюся
данной прямой а, не проходящей через А и В.
*) Здесь возможны три случая: существуют две окружности, проходя*
щие через точки Л и В (если | АВ I < 2г); если | АВ I ® 2г — такая окруж*
ность одна; при I АВ | > 2г искомой окружности не существует.
206
ГЛ. 5. ГЕОМЕТРИЯ
Проводим прямую через данные точки А и В. Возможны два случая:
а) прямая АВ пересекается с данной прямой а;
б)	прямая АВ параллельна данной прямой а.
Рассмотрим первый случай. Обозначим точку пересечения
прямых АВ и а буквой С (рис. 5.82). Строим отрезок х, средний про-
порциональный отрезкам СА и СВ. Откладываем отрезок х на прямой а
от точки С (на рис. 5.82 х = CF). Точка F — точка касания искомой
окружности с данной прямой. Таким образом, решение данной задачи
сводится к задаче построения окружности, проходящей через три задан-
ные точки А, В и F, не лежащие на одной прямой. Рассматриваемая
вадача имеет и второе решение: можно построить вторую окружность,
проходящую через данные точки А и В и касающуюся данной прямой а.
Для этого отрезок х нужно отложить на прямой а по другую сторону от
точки С.
Второй случай. Если прямые АВ и а параллельны, то
проводим перпендикуляр через середину отрезка АВ до пересечения
с прямой а в точке С (рис. 5.83). Точка С — точка касания искомой
окружности и данной прямой а. Окружность, проходящая через точки
А, В и СУ — искомая.
4)	Найти центр данной дуги окружности.
На данной дуге выбираем любые три точки А , В, С и строим центр
окружности, проходящей через три заданные точки.
5)	Разделить данную дугу окружности на две равные части.
Концы данной дуги соединяем хордой. Строим перпендикуляр
к хорде, проходящий через ее середину. Точка пересечения перпенди-
куляра и дуги делит данную дугу на две равные дуги.
6)	Найти множество точек плоскости, из которых данный отрезок
АВ виден под данным углом а.
Множеством точек плоскости, из которых данный отрезок АВ
виден под данным углом а, является дуга окружности величиной
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
207
точки,

Рис. 5.84,
2л— 2а, стягиваемая хордой АВ. Центр и радиус этой окружности
находятся следующим образом. Из точек А и В (рис. 5.84) восставим
перпендикуляры к отрезку АВ. Обозначим эти перпендикуляры AD
и ВК соответственно. От луча В К отложим угол KBL = а так, чтобы
луч BL пересек луч AD в некоторой точке С. Середина О отрезка ВС —
центр искомой окружности, у |ВС| — ее радиус. Из любой
лежащей на дуге АСВ отрезок АВ виден под утлома,
так как любой угол, опирающийся на хорду АВ
с вершиной на дуге АСВ, измеряется половиной
дуги, на которую он опирается.
Задача допускает и второе решение — суще-
ствует вторая окружность такого же радиуса, что
и первая (на рис. 5.84 лежащая ниже отрезка
АВ), из которой данный отрезок АВ виден под
углом а.
13.5.	Построение касательных к окружностям.
1)	Провести через данную точку касательную
к данной окружности.
Если данная точка А принадлежит данной
окружности с центром О (рис. 5.85), то искомой
касательной будет перпендикуляр к АО, проведен-
ный через конец А отрезка АО.
Если точка А лежит вне круга (рис. 5.86), то необходимо разделить
отрезок АО пополам и из его середины В радиусом ОВ провести дугу
DOC (D и С — точки пересечения дуги и данной окружности). Через
пары точек (D; Л) и (С; Л) проводим прямые, которые будут искомыми
касательными.
2) Провести к данным двум окружностям общую внешнюю коса*
тельную.
Задача не имеет решений, если один круг целиком содержится
в другом и окружности не касаются. Если один круг целиком содержится
Рис. 5.85.
в другом и окружности касаются изнутри, то задача имеет единственное
решение (существует только одна прямая, касательная к обеим окруж-
ностям). Во всех остальных случаях взаимного расположения двух
окружностей задача имеет два решения (т. е. существуют две различные
общие внешние касательные к данным окружностям).
Рассмотрим случай внутреннего касания двух окружностей.
Проводим линию центров OOj этих окружностей (рис. 5.87). В точке
касания двух окружностей (на рис. 5.87 точка М) строим прямую,
перпендикулярную линии центров. Это и есть искомая касательная.
208
ГЛ. б. ГЕОМЕТРИЯ
Рассмотрим случай, когда задача имеет два решения.
а)	Если радиусы данных окружностей равны, то проведем через
центры окружностей О и Ох (рис. 5.88) диаметры АВ и Л^, перпенди-
кулярные линии центров ОО±.
Прямые, проходящие через пары точек (Л; A J и (В;	— искомые
касательные.
б)	Если радиусы R и Ri данных окружностей не равны (R > Rj), то
строим окружность радиуса ОС = R — Ri с центром, совпадающим
с центром большего круга (рис. 5.89). К построенной окружности
Рис* 5.88.	Рис. 5.89.
проводим касательные АС и ЛС^, проходящие через центр меньшего
круга Л. Через центр большей окружности О и точки касания С и Ct
проводим лучи ОС и OCj, которые пересекут большую окружность
в точках D и Dj. Проводим радиусы АЕ и ЛЕ^, перпендикулярные
прямым АС и ЛСх соответственно. Прямые, проходящие через пары
точек (D; Е), (Dt; Ej), — искомые касательные.
3)	Провести к двум данным окружностям общую внутреннюю
касательную.
Задача не имеет решения, если круги (окружности) пересекаются
или если один круг целиком содержится в другом. Если окружности
касаются друг друга извне, задача имеет единственное решение — через
точку касания проводится перпендикуляр к линии центров (рис. 5.90).
Если окружности не пересекаются, то задача имеет два решения
(т.е. существуют две различные прямые, каждая из которых будет
касательной как к одной, так и к другой окружности). Касательные
строятся так. Строим окружность радиусом, равным сумме радиусов
данных окружностей, и с центром, совпадающим с центром одной из
окружностей Л (рис. 5.91). Из центра В второй окружности проводим
касательные ВС и ВС± к построенной окружности. Проводим радиусы
АС и ЛС1 в точки касания. Эти радиусы пересекут данную окружность
с центром Л в точках D и Df. Через центр второй окружности В про*
водим радиусы BE и BE j, перпендикулярные прямым ВС и ВС± соответ-
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ	20Э
ственно. Прямые, проходящие через пары точек (£>; Е) и (£>ц EJ, —
искомые касательные.
13.6.	Построение окружности, описанной около многоугольника,
и многоугольника, вписанного в окружность.
1)	Описать окружность около данного треугольника.
Через вершины треугольника Л, В, С проводится окружность.
2) Описать окружность около данного прямоугольника (или квадрата).
Рис. 5.93,
Рис. 5.94.
Проводим диагонали АС и BD (рис. 5.92). Из точки О их пересече-
ния как из центра проводим окружность радиусом |0Л| . Построенная
окружность — искомая.
3)	Вписать квадрат в данный круг.
Проводим два взаимно перпендикулярных диаметра АВ и CD.
Четырехугольник с вершинами А, Bt Ct D —искомый квадрат (рис. 5.93).
4)	Вписать в данную окружность пра-
вильный шестиугольник и правильный тре-
угольник.
Выбирем произвольную точку (скажем,
точку Л), лежащую на окружности, и рас-
твором циркуля, равным радиусу окружно-
сти, делаем на окружности засечки, получая
последовательно точки В, С, D, Е, F
(рис. 5.94). Соединяя последовательно ука-
ванные точки, получаем правильный ше-
стиугольник, вписанный в данную окруж-
ность. Соединяя их через одну, получим пра-
вильный (равносторонний) треугольник, впи-
санный в данную окружность.
5)	Вписать в данную окружность правильный
Проводим два взаимно перпендикулярных диаметра АВ и CD
(рис. 5.95). Проведя биссектрисы четырех прямых углов, получим точки
пересечения биссектрис с окружностью (на рис. 5.95 точки Е, F, Af, N).
Соединяя последовательно полученные восемь точек Л, Е, С, F, Е, М,
Dt N, получаем искомый восьмиугольник.
13.7.	Построение окружности, вписанной в многоугольник, и
многоугольника, описанного около окружности.
1)	Вписать окружность в данный треугольник.
Строим биссектрисы двух внутренних углов треугольника. Из
точки О пересечения биссектрис (рис. 5.96) проводим перпендикуляр
к любой стороне треугольника (на рис. 5.96 к стороне Л В), который
пересечет сторону в точке D. Радиусом} OD|c центром в точке О описы-
ваем искомую окружность.
восьмиугольник.
210
ГЛ. 5. ГЕОМЕТРИЯ
2)	Вписать окружность в ромб (или квадрат).
Проводим диагонали ромба (на рис. 5.97 отрезки АС и BD). Через
точку О их пересечения проводим перпендикуляр к любой стороне
ромба (на рис. 5.97 к стороне ВС\ Е — точка пересечения перпендику-
ляра со стороной). Окружность с центром О и радиусом, равным
| ОЕ |, — искомая.
3)	Описать квадрат около данной окружности.
Проводим два взаимно перпендикулярных диаметра данной окруж-
ности (на рис. 5.98 АВ и CD — диаметры). Из их концов (точек А,
Рис. 5.97.
В, Ct D) как из центров описываем четыре полуокружности радиусами,
равными радиусу данной окружности. Точки пересечения полуокруж-
ностей — вершины искомого квадрата.
4)	Описать вокруг данной окружности правильный шестиугольник
и правильный восьмиугольник.
Отмечая на окружности соответственно шесть (восемь) точек так,
как это сделано в задачах 4), 5) п. 13.6, строим касательные к данной
окружности в отмеченных точках. Точки пересечения соседних каса-
тельных дадут вершины правильного шестиугольника (восьмиуголь-
ника).
13.8.	Построение треугольников.
1)	Построить треугольник по трем сторонам о, д, с.
Из концов отрезка АВ (| АВ | = а) как из центров проводим две
дуги окружностей радиусами b и с (рис. 5.99). Точка их пересечения
С — третья вершина искомого треугольника АВС. Задача имеет ре-
шение, если отрезки а, b и с удовлетворяют неравенствам треуголь-
ника.
2)	Построить треугольник по двум сторонам at b и углу у между
ними.
Строим угол, равный углу у. От вершины угла на его сторонах
откладываем отрезки СА и СВ, соответственно равные отрезкам b и а
(рис. 5.100). Соединяем точки А и В. Треугольник АВС — искомый.
3)	Построить треугольник по стороне а и прилежащим к ней
углам Р и у (Р + у < 180°).
При каждом из концов отрезка ВС (| ВС | == а) откладываем углы Р
и у (рис. 5.101). Точка А пересечения лучей В А и СА есть третья
вершина искомого треугольника АВС.
4)	Построить треугольник по основанию а, высоте ha и углу при
вершине а.
§ 13. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
211
Строим дугу окружности, из которой отрезок АВ (| АВ | » at)
виден под данным углом а (см. задачу 6) п. 13.4. Строим произвольный
перпендикуляр к отрезку АВ и откладываем на нем отрезок 42V(| AN |=
= М- Через точку /V проводим прямую NL, параллельную прямой,
проходящей через точки Д, В. Полученная точка пересечения прямой
NL с дугой окружности (точка С на рис. 5.102) — вершина искомого
треугольника АВС (задача имеет два решения).
5)	Построить треугольник по двум сторонам а, b и углу а, про*
тиволежащему стороне а.
Рис. 5.100.
Строим дугу окружности, из которой отрезок АВ (| АВ | = а)
виден под данным углом а. Из конца А отрезка АВ как из центра
радиусом, равным Ь, проводим дугу, пересекающуюся с первой дугой.
Точка пересечения этих дуг (на рис. 5.103 точки С и Сг) и будет третьей
вершиной искомого треугольника ABC (CJ. В зависимости от вели-
чин а, b и а задача имеет одно или два решения, или вовсе не имеет
решений.
6)	Построить треугольник по стороне а, углу при основании а
и сумме двух других сторон 6 + с.
От конца А отрезка АВ (| АВ | = а) откладываем угол а. На
луче AN откладываем данную сумму двух сторон искомого треуголь-
ника (на рис. 5.104 отрезок АВ± (| АВг | = & + с)). Из середины
отрезка BBt восставляем перпендикуляр до пересечения с лучом АВР
Точка пересечения луча и перпендикуляра (на рис. 5.104 точка С) —
третья вершина искомого треугольника АВС.
7)	Построить треугольник по стороне а, углу при основании а
и разности двух других сторон b — с.
От конца А отрезка АВ (| АВ | = а) откладываем угол а. На
луче AN откладываем данную разность b — с двух сторон искомого
треугольника (на рис. 5.105 отрезок АВЪ | АВг | = b — с). Из середины
212	ГЛ. б. ГЕОМЕТРИЯ
отрезка BBt восставляем перпендикуляр до пересечения с лучом ДЛ7»
Точка пересечения луча AN и перпендикуляра (на рис. 6.105 точка С)—
третья вершина искомого треугольника АВС.
8) Построить треугольник по двум данным углам а, р и пери*
метру Р.
Строим углыа/2, р/2. Строим отрезок АВ (| АВ | « Р). От кон-
цов 4 и В откладываем углы а/2 и р/2 так, чтобы лучи, являющиеся
вторыми сторонами этих углов, принадлежали одной полуплоскости
Рис. 5.104.	Рис. 5.105.
относительно прямой АВ (рис. 5.106). Из середин отрезков ЛЕ и BE
(Е — точка пересечения сторон углов) восставляем перпендикуляры
до пересечения с отрезком АВ в точках С и D. Треугольник CED
искомый.
9) Построить треугольник по высоте hat медиане та и биссек*
трисе 1а, проведенным из одной вершины.
Строим прямоугольный треугольник АВС с гипотенузой АС
(| 4С|=/по) и катетом АВ (| АВ | = fta) (рис. 5.107). Строим дугу ра-
диусом, равным 1а, и с центром
в точке 4, пересекающую катет ВС
в точке D. Строим прямую MN*
перпендикулярную прямой ВС и
проходящую через точку С. Обо-
значаем точку пересечения луча AD
и прямой MN буквой L. Восстав-
ляем перпендикуляр к отрезку AL
в его середине. Точка пересечения О
данного перпендикуляра и прямой
MN — центр окружности, опи-
треугольника. Радиусом, равным АО,
с центром в точке О проводим окружность, пересекающую
А' С\
//7
Рис. 5.106.
санной вокруг искомого
в
мую ВС в точках R и S. Треугольнике вершинами 4, R, S — ис-
комый.
10) Построить треугольник по трем медианам та, mb) тс.
2	2	2
Строим отрезки — та, ть, -у тс.
ООО
2	2
Строим треугольник APQ (рис. 5.108) со сторонами -^та, ^mbt
о	и
2	1
*х-тс. На луче АР от точки Р откладываем отрезок РМ — та.
О	О
Находим середину N отрезка PQ и на луче AN откладываем отре-
§ 14. МНОГОГРАННЫЙ УГОЛ
213
зок NC ~ AN. Строим луч СМ и откладываем на нем отрезок ВМ =
« СМ так, чтобы точка М принадлежала отрезку ВС. Точки Л, В
и С —- вершины искомого тре-
угольника.
И) Построение прямоугольных
треугольников.
Построение прямоугольного
треугольника по двум катетам про-
водится так же, как в задаче 2) на-
стоящего пункта, для случая у=90°.
Построение прямоугольного
треугольника по катету и острому
углу Р проводится так же, как
в задаче 3), если угол у положить
равным 90°.
Построение прямоугольного
треугольника по гипотенузе и
острому углу а сводится к задаче
3) для случая острых углов а и
р = 90° — а.
12) Построить параллелограмм
по данным сторонам а, b и углу
Рис. 5.107.
а между ними.
Строим угол MAN, равный данному углу а (рис. 5.109). На луче
AM откладываем отрезок АС — а, а на луче AN — отрезок АВ = Ь.
Проводим из точки В как из центра дугу радиуса АС, а из точки С —
дугу радиуса АВ. Точку пересечения этих дуг (на рис. 5.109 точку D)
соединяем с точками В и С. Четырехугольник ABDC — искомый
параллелограмм.
§ 14. Многогранный угол
Пусть даны плоский многоугольник Ф и точка S, не принадле-
жащая плоскости данного многоугольника (на рис. 5.110 многоуголь-
ник Ф — шестиугольник ABCDEF). Объединение всех лучей, име-
ющих общее начало $ и пересекающих данный многоугольник Ф
(рис. 5.110), называется многогранным углом ♦).
•) Иногда многогранным углом также называют множество всех лучей*
имеющих общее начало S и пересекающих замкнутую ломаную ABCDEF*
т. е. объединение всех граней многогранного угла#.
214
ГЛ. 5. ГЕОМЕТРИЯ
Точка S называется вершиной многогранного угла; лучи S4, SB,
SC, SD, SE, SF, содержащие вершины многоугольника, — его реб-
рами; плоскости, содержащие треугольники SAB, SBC и т. д., —
его гранями*
В зависимости от числа граней различают трехгранные, четырех-
гранные, пятигранные и т. д. углы. Многогранный угол обозначают,
отмечая сначала вершину, а затем последовательно по одной точке на
каждом из ребер. Так, например, шестигранный угол, изображенный
на рис. 5.110, обозначают
SABCDEF.
Каждые две грани многогранного угла, имеющие общее ребро, обра-
зуют двугранный угол.
Множество всех точек многогранного угла, не принадлежащих!
граням, называют его внутренней областью. Многогранный угол,
внутренняя область которого расположена по одну сторону от пло-
скости каждой из его граней, называется выпуклым многогранным
углом. В противном случае многогранный угол называется невыпуклым.
Углы ASB, BSC и т. д. называются плоскими углами многогран-
ного угла SABCDEF (см. рис. 5.110),
Свойства плоских углов многогранного
угла:
1) Каждый плоский угол многогранного угла меньше суммы
остальных его плоских углов.
2) В выпуклом многогранном угле сумма плоских углов мень-
ше 360°.
Простейшим многогранным углом является трехгранный угол.
Необходимым и достаточным условием существования трехгранного
угла с данными плоскими углами а, (3, у является выполнение не-
равенств
|3—Т|<а<₽+у, а+₽+у< 360°.
Теорема косинусов для трехгранного
угла. Косинус плоского угла трехгранпого угла равен произведе-
нию косинусов двух остальных плоских углов, сложенному с произве-
дением синусов тех же углов и косинуса двугранного угла, определяе-
мого этими плоскими углами (рис. 5.111):
cos а = cos р cos у + sin Р sin у cos а,
§ 15. МНОГОГРАННАЯ ПОВЕРХНОСТЬ
215
§ 15.	Многогранная поверхность. Многогранник
Многогранной поверхностью называют объединение конечного
числа плоских многоугольников такое, что каждая сторона любого
из многоугольников является в то же время стороной другого (но
только одного) многоугольника, называемого смежным с первым много-
угольником.
От любого из много-
угольников, составляющих
многогранную поверхность,
можно дойти до любого дру-
гого, двигаясь по смежным
многоугольникам.
Многоугольники, состав-
ляющие многогранную по-
верхность, называются ее
гранями} стороны много-
угольников называются реб-
рами, а вершины — верши-
нами многогранной поверх-
ности.
На рис. 5.112 изобра-
жены объединения много-
угольников, удовлетворя-
ющие указанным требова-
ниям и являющиеся многогранными поверхностями. На рис. 5.113
изображены фигуры, не являющиеся многогранными поверхностями.
Многогранная поверхность делит пространство на две части —
внутреннюю область многогранной поверхности и внешнюю область.
Из двух областей внешней будет та, в которой можно провести прямые,
целиком принадлежащие области.
Рис. 5.115,
Рис. 5.114.
Объединение многогранной поверхности и ее внутренней области
называют многогранником. При этом многогранную поверхность и ее
внутреннюю область называют соответственно поверхностью и внутрен-
ней областью многогранника. Грани, ребра и вершины поверхности
многогранника называют соответственно гранями, ребрами и верши-
нами многогранника.
Многогранник называется выпуклым, если он весь лежит по одну
сторону от плоскости любой его грани.
Отрезок, соединяющий две вершины многогранника, не принад-
лежащие одной грани, называется диагональю многогранника.
216
ГЛ. 5. ГЕОМЕТРИЯ
Многогранник обычно обозначается перечислением его вершин
и указанием его специальных свойств. Например, многогранник SABCD,
изображенный на рис. 5.114, — пирамида, многогранник ABCDAtBiCiDi
(рис. 5.115) — параллелепипед.
§ 16.	Призма
Многогранник, две грани которого — равные n-угольники, лежа*
щие в параллельных плоскостях, а остальные п граней — параллело-
граммы, называется n-угольной призмой.
Пару равных n-угольников называют основаниями призмы. Осталь*
ные грани призмы называют ее боковыми гранями, а их объединение —
боковой поверхностью призмы. На рис. 5.116 изображена пятиугольная
призма.
Стороны граней призмы называют ребрами, а концы ребер —
вершинами призмы. Ребра, не принадлежащие основанию призмы,
называют боковыми ребрами.
Рис. 5.117»
Призму, боковые ребра которой перпендикулярны плоскостям
оснований, называют прямой призмой. В противном случае призма
называется наклонной.
Отрезок перпендикуляра к плоскостям оснований призмы, концы
которого принадлежат этим плоскостям, называют высотой призмы.
Прямая призма, основанием которой является правильный много-
угольник, называется правильной призмой.
Площадь боковой поверхности призмы.
Пусть дана произвольная призма (на рис. 5.117 пятиугольная призма).
Через точку А, принадлежащую одному из ее боковых ребер, проведем
плоскость а, перпендикулярную этому ребру (и, следовательно, пер-
пендикулярную всем остальным боковым ребрам). Если плоскость а
пересекает все боковые ребра призмы, то многоугольник, полученный
в результате сечения всех боковых граней плоскостью а (на рис. 5.117
пятиугольник ABCDE), называется перпендикулярным сечением призмы
(если такого многоугольника не существует, то за перпендикулярное
сечение призмы принимают многоугольник с вершинами в точках
пересечения плоскости а с продолжениями боковых ребер).
Площадь боковой поверхности призмы вычис-
ляется по формуле
^бок == ^п*|	|>
где Рп — периметр перпендикулярного сечения призмы, 14i42H•
длина бокового ребра.
§ 17. ПАРАЛЛЕЛЕПИПЕД. КУБ
217
Площадь полной поверхности призмы равна
сумме площадей боковой поверхности призмы и двух ее оснований.
Объем наклонной призмы вычисляется по формуле
V = Sn|4M2|,
где Sn — площадь перпендикулярного сечения призмы, | AiA2 I —
длина бокового ребра, или по формуле
V — Sqch*
где 50сн — площадь основания призмы, Н — высота.
§ 17.	Параллелепипед. Куб
Параллелепипедом называется призма, основаниями которой слу-
жат параллелограммы. Все шесть граней параллелепипеда
(рис. 5.118) — параллелограммы. Отрезки, соединяющие вершины
параллелепипеда, не принадлежащие одной и той же грани, называются
диагоналями параллелепипеда.
Свойства параллелепипеда:
1)	Середина диагонали параллелепипеда является его центром
симметрии.
2)	Противолежащие грани параллелепипеда попарно равны и
параллельны.
3)	Все четыре диагонали параллелепипеда пересекаются в одной
точке и делятся ею пополам.
Рис. 5,118.
Рис. 5.119.
Параллелепипед, боковые ребра которого перпендикулярны пло-
скости основания параллелепипеда, называется прямым параллелепи-
педом (на рис. 5.119 A BCD А^С^ — прямой параллелепипед).
Прямой параллелепипед, основанием которого служит прямоуголь-
ник, называется прямоугольным пареллелепипедом. Все грани прямо-
угольного параллелепипеда — прямоугольники. Длины трех ребер
прямоугольного параллелепипеда, выходящих из одной вершины, на-
зываются измерениями прямоугольного параллелепипеда.
Свойства прямоугольного параллелепи-
педа:
1) Квадрат диагонали прямоугольного параллелепипеда равен
сумме квадратов трех его измерений:
J2= а2+ ^2+с2
2) Все диагонали прямоугольного параллелепипеда равны.
218
ГЛ. 5. ГЕОМЕТРИЯ
Так как параллелепипед есть частный случай призмы, то площадь
поверхности и объем параллелепипеда вычисляются по формулам для
площади поверхности и объема призмы. Кроме того, объем пря-
моугольного параллелепипеда можно вычислить
по формуле
V = abc,
где a, Ь, с—три измерения прямоугольного параллелепипеда.
Куб. Прямоугольный параллелепипед с равными измерениями
называется кубом. Все грани куба — равные квадраты.
Объем куба вычисляется по формуле
а3,
где а — измерение куба.
§ 18, Пирамида, Усеченная пирамида
Многогранник, одна из граней которого — произвольный много-
гранник, а остальные грани — треугольники, имеющие одну общую
вершину, называется пирамидой.
Многоугольник называется основанием пирамиды, а остальные
грани (треугольники) называются боковыми гранями пирамиды.
Различают треугольные, четырехугольные, пятиугольные и т. д.

Рис. 5.120.
С
пирамиды в зависимости от вида многоугольника, лежащего в основа-
нии пирамиды. Треугольную пирамиду
также называют тетраэдром. На рис.
5.120 изображена четырехугольная пира-
мида SABCD с основанием ABCD и бо-
ковыми гранями SAB, SBC, SCD, SAD.
Стороны граней пирамиды называ-
ются ребрами пирамиды. Ребра, принад-
лежащие основанию пирамиды, назы-
вают ребрами основания, а все остальные
ребра — боковыми ребрами. Общая вер-
шина всех треугольников (боковых гра-
ней) называется вершиной пирамиды (на
рис. 5.120 точка S — вершина пирамиды,
SD — боковые ребра, отрезки АВ, ВС, CDt
отрезки 5Д, SB, SC, <
AD — ребра основания).
Высотой пирамиды называется отрезок перпендикуляра, прове-
денного из вершины пирамиды S к плоскости основания (концами
этого отрезка являются вершина пирамиды и основание перпендику-
ляра). На рис. 5.120 SO — высота пирамиды.
Правильная пирамида. Пирамида называется пра*
сильной, если основанием пирамиды является правильный многоуголь-
ник, а ортогональная проекция вершины на плоскость основания сов-
падает с центром многоугольника, лежащего в основании пирамиды.
Все боковые ребра правильной пирамиды равны между собой;
все боковые грани — равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды, проведенная из
ее вершины, называется апофемой этой пирамиды. На рис. 5.121
S7V — апофема. Все апофемы правильной пирамиды равны между
собой.
Площадь боковой поверхности пирамиды равна сумме
площадей треугольников боковых граней, а площадь полной
§ 18. ПИРАМИДА. УСЕЧЕННАЯ ПИРАМИДА
219
поверхности равна сумме площади боковой поверхности и пло-
щади основания.
Площадь боковой поверхности правил ь<
ной пирамиды вычисляется по формуле
S = -у Ph‘
где Р — периметр основания пирамиды, h — апофема.
Объем пирамиды вычисляется по формуле
V = 4 5оенЯ,
О
где <S0Ch — площадь основания пирамиды, Н — высота пирамиды.
Усеченная пирамида. Возьмем произвольную пира-
миду. Через точку, принадлежащую какому-нибудь боковому ребру
Рис* 5.122*
и не совпадающую с его концами, проведем плоскость, параллельную
плоскости основания (рис. 5.122). Проведенная плоскость отсечет от
данной пирамиды SABCD (рис. 5.122) пирамиду SAxBjCjDx.
Многогранник, вершинами которого служат вершины основания
данной пирамиды и вершины основания отсекаемой пирамиды, назы-
вается усеченной пирамидой. Основания усеченной пирамиды — гомо-
тетичные многоугольники (на рис. 5.122 четырехугольники ABCD
и	— основания усеченной пирамиды). Центр гомотетии —
вершина пирамиды. Отрезок перпендикуляра к плоскостям оснований,
с концами на плоскостях оснований пирамиды, называется высотой
усеченной пирамиды. Боковые грани усеченной пирамиды — трапеции.
Усеченная пирамида называется правильной, если она является
частью правильной пирамиды. Боковые грани правильной усеченной
пирамиды — равные равнобедренные трапеции. Высота каждой из
этих трапеций называется апофемой правильной усеченной пирамиды.
Площадь боковой поверхности правильной
усеченной пирамиды вычисляется по формуле
$=4(Р+р)Л>
где Pt Р — периметры оснований пирамиды^ Л — апофема.
220
ГЛ. 5. ГЕОМЕТРИЯ
Площадь полной поверхности усеченной пира-
миды равна сумме площадей оснований и площади боковой поверхности
Пирамиды.
Объем усеченной пирамиды вычисляется по фор-
муле
v = 4-^(Si + rs!s7+s2),
О
где Н — высота усеченной пирамиды, и S2 — площади оснований
усеченной пирамиды.
§ 19. Правильные многогранники
Многогранник называется правильным, если все его грани — рав-
ные правильные многоугольники, а все многогранные углы имеют
одинаковое число граней. Все ребра правильного многогранника —
равные отрезки, все плоские углы правильного многогранника также
равны.
Рис. 5.123.
Рис. 5.124.
Рис. 5,127.
Существует пять различных правильных многогранников (вы-
пуклых): куб, правильный тетраэдр, правильный восьмигранник
(правильный октаэдр), правильный двенадцатигранник (додекаэдр),
правильный двадцатигранник (икосаэдр). На рис. 5.123—5.127 изоб-
ражены перечисленные правильные многогранники, а также развертки
их поверхностей.
Далее будем пользоваться следующими обозначениями: объем
многогранника будем обозначать V; площадь поверхности S; радиус
$ 19. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ	221
описанной сферы R; радиус вписанной сферы г; высоту (для тех много-
гранников, для которых это понятие имеет смысл) Я; каждое из равных
ребер — через а.
Куб. Все шесть граней — равные квадраты. Куб имеет восемь
вершин и двенадцать ребер.
V «= a3, S = 6а2,
П	а/З	а
R 2	’	2 "
Тетраэдр. Все четыре грани — равносторонние равные тре-
угольники. Тетраэдр имеет четыре вершины и шесть ребер.
V = fl3^, S = a2/3,
n	a J/*6	а Кб г, a Кб
4	>	12	’ Я 3	*
Октаэдр. Все восемь граней — равносторонние равные тре<
угольники. Октаэдр имеет шесть вершин и двенадцать ребер.
V =	S = 2a2/3,	=	r =
Додекаэдр. Все двенадцать граней — правильные равные
пятиугольники. Додекаэдр имеет двадцать вершин и тридцать ребер.
V =	г S = За2 (5+2/5),
n а ]/"3 (1 + /5 )	а ]/’10(25+11 /Г)
К =---------------, г =	.
Икосаэдр. Все двадцать граней — равносторонние равные
треугольники. Икосаэдр имеет двенадцать вершин и тридцать ребер.
v= ^(з+Г?),	5 = 5о!Кз,
_ а/2(5 +/5)	а /3 (3 + /5)
« =-------J------->	' =--------i2-----
Число ребер, число вершин и число граней правильных многогран*
ников связаны формулой Эйлера *)
N — L + F == 2,
где /V — число вершин, L — число ребер, F — число граней.
•) Формула Эйлера справедлива не только для правильных многогран*
пиков, но и вообще для всех выпуклых многогранников (например, призмы,
пирамиды и т« д.).
222
ГЛ. 5. ГЕОМЕТРИЯ
§ 20. Цилиндр
Прямым круговым цилиндром (или просто цилиндром) называется
фигура, полученная при вращении прямоугольника вокруг оси, про-
ходящей через одну из его сторон.
При вращении вокруг той же оси ломаной, составленной из сторон
прямоугольника, не лежащих на оси вращения, получается фи-
гура, которая называется поверхностью цилиндра
(рис.5.128).
Круги, полученные в результате вращения сто-
рон, смежных со стороной, принадлежащей оси вра-
щения, называются основаниями цилиндра (на рис. 5.128
основания цилиндра получаются в результате враще-
ния сторон прямоугольника АВ к CD вокруг оси ВС).
Радиус этих двух равных кругов называется радиусом
основания цилиндра. На рис. 5.128 отрезок АВ —
радиус основания цилиндра.
Фигура, полученная в результате вращения сто-
роны прямоугольника, противоположной стороне, при-
надлежащей оси вращения, называется боковой поверх*
ностъю цилиндра. На рис. 5.128 боковая поверхность
।
I
Рис. 5.128.
цилиндра получается в результате вращения стороны
AD вокруг оси ВС. Отрезок AD называется образующей ци-
линдра.
Перпендикуляр к плоскостям оснований цилиндра, концы кото-
рого совпадают с центрами оснований цилиндра, называется высотой
цилиндра. На рис. 5.128 отрезок ВС—высота цилиндра.
Развертка цилиндра представляет собой прямоугольник, одна сто-
рона которого равна длине окружности основания цилиндра, а дру-
гая — высоте цилиндра, и
два круга с радиусами, рав-
ными радиусу цилиндра
(рис. 5.129).
За объем цилиндра при-
нимают предел последова-
тельности объемов правиль-
ных призм, вписанных в ци-
линдр, при бесконечном уве-
личении числа сторон пра-
вильных многоугольников,
лежащих в основании
призмы *).
Объем цилиндра
вычисляется по формуле
V = л7?2//,

где R — радиус основания цилиндра, Н — высота цилиндра.
За площадь боковой поверхности цилиндра принимают предел после-
довательности площадей боковых поверхностей правильных призм,
вписанных в цилиндр, при бесконечном увеличении числа сторон
правильных многоугольников, лежащих в основании призм.
*) и выводе формул вычисления объема цилиндра и ддихцада боковой
поверхности цилиндра см, п. 6.4 гл, 8,
§ 21. КОНУС, УСЕЧЕННЫЙ КОНУС	223
Площадь боковой и полной поверхности
цилиндра вычисляется по формулам
•^бок e 2fiRH,
5дил =	+ 2л/?2,
где R — радиус основания цилиндра, Н — высота цилиндра.
§ 21в Конус, Усеченный конус
Прямым круговым конусом (или просто конусом) называется фигура,
полученная при вращении прямоугольного треугольника вокруг оси,
содержащей его катет.
Фигура, полученная при вращении вокруг той же оси ломаной,
составленной из гипотенузы и катета,не принадлежащего оси вращения,
называется поверхностью конуса. Фигура, полученная от вращения
гипотенузы, называется боковой поверхностью конуса, а фигура (круг),
полученная от вращения катета,—основанием конуса (рис. 5.130).
Радиус этого круга называется радиусом основания цилиндра (на
рис. 5.130 отрезок ОА),
Катет треугольника, принадлежащий оси, называется высотой
конуса (на рис. 5.130 отрезок SO — высота конуса). Гипотенуза прямо-
угольного треугольника называется образующей конуса (на рис. 5.130
отрезок 4S — образующая конуса).
Развертка боковой поверхности конуса является круговым секто-
ром, а полная развертка поверхности конуса представляет собой кру-
говой сектор и круг (рис. 5.131).
За объем конуса принимают предел последовательности правиль-
ных пирамид, вписанных в конус, при бесконечном увеличении числа
сторон правильного многоугольника — основания пирамиды *).
Объем конуса вычисляется по формуле
VKOH = 4-nR2//>
О
где R — радиус основания конуса, Н — высота конуса.
За площадь боковой поверхности конуса принимается предел
последовательности площадей боковых поверхностей правильных пи-
♦) О выводе формул для вычисления объема и площади боковой поверх-
ности конуса см. п» 6,4 гл. 8,
224
ГЛ. б. ГЕОМЕТРИЯ
рамид, вписанных в конус, при бесконечном увеличении числа сторон
правильного многоугольника, лежащего в основаниях пирамид.
Площадь боковой поверхности конуса вы*
числяется по формуле
$бок = я/?Ь,
где R — радиус основания конуса, L — образующая конуса (L =
= | AS | на рис. 5.130).
Площадь полной поверхности конуса вы*
числяется по формуле
SK0H e nRL + я/?2.
Усеченный конус. Часть конуса, ограниченная его осно-
ванием и сечением, параллельным плоскости основания, называется
усеченным конусом.
Основания усеченного конуса — гомотетичные круги с центром
гомотетии в вершине конуса (на рис. 5.132 в точке S).
5
Усеченный конус можно получить в результате вращения равно-
бедренной трапеции вокруг ее оси симметрии (на рис. 5.132 трапе-
ции АА1В1В). При вращении границы этой трапеции получается по-
верхность усеченного конуса.
Боковая сторона трапеции называется образующей усеченного
конуса; круги, полученные при вращении оснований трапеции, — осно-
ваниями усеченного конуса.
Развертка усеченного конуса представляет собой объединение
части кругового кольца и двух кругов (рис. 5.133).
Объем усеченного конуса равен разности объемов
полного конуса и конуса,отсекаемого плоскостью, параллельной осно-
ванию конуса. Объем усеченного конуса вычисляется по формуле
V = -l3i/f(R2 + 7?1R24-7?2),
где Н — высота усеченного конуса (на рис. 5.132 Н «= | ООГ |),
и R2 — радиусы верхнего и нижнего оснований усеченного конуса
(на рис. 5.132 /?!=|OA|, R2 = |	|).
Площадь боковой поверхности усеченного конуса равна
разности площадей боковых поверхностей полного конуса и конуса,
§ 22. СФЕРА. ШАР
225
отсекаемого плоскостью, параллельной основанию конуса.
Площадь боковой поверхности	усечен-
ного конуса вычисляется по формуле
•$бок в л (^1 + R2)
где L — образующая усеченного конуса (на рис. 5.132 L= | ААг |).
§ 22. Сфера. Шар
данной точки пространства О, назы«
пространства, находящихся от данной
Множество всех точек пространства, находящихся на данном
положительном расстоянии R от данной точки пространства О, назы-
вается сферой.
Данная точка О назы-
вается центром сферы
(рис. 5.134).
Отрезок ОМ (М — про-
извольная точка сферы) на-
зывается радиусом сферы
(|ОЛ4| = /?). Отрезок, соеди-
няющий любые две точки
сферы, называется ее хордой.
Хорда, проходящая чёрез
центр сферы, называется
диаметром сферы. Диаметр
сферы равен ее удвоенному
радиусу.
Множество всех точек t ж
точки О на расстоянии, не большем данного расстояния /?, называется
шаром.
Шар можно получить в результате вращения полукруга вокруг
оси, содержащей диаметр полукруга (см. рис. 5.134). Фигура, полу*
ченная при вращении полуокружности,
есть сфера — поверхность шара. Центр,
радиус и хорды этой сферы называются
соответственно центром, радиусом и хор-
дами шара. Все точки шара, не принадле-
жащие его поверхности, называются
внутренними точками шара.
Объем шара радиуса R вычисляется
по формуле *)
v=4
О
Площадъ сферы радиуса R
вычисляется по формуле
S == 4л£а.
Сечением сферы плоскостью является:
1) окружность, если расстояние от центра сферы до плоскости
сечения меньше радиуса сферы;
2) точка, если расстояние от центра сферы до плоскости речения
равно радиусу.
*) Вывод формул вычисления объема шара и площади сферы см. п.
гл. 9.
8 А. Г. Цыпкин
226
ГЛ. 5. ГЕОМЕТРИЯ
Сечение шара плоскостью, проходящей через центр, называется
большим кругом. Радиус большого круга равен радиусу шара. На
рис. 5.135 и La — окружности больших кругов.
Всякая пара больших кругов пересекается по диаметру шара,
служащему диаметром также и для каждого из пересекающихся кругов.
Через две точки сферы, лежащие на концах одного и того же диаметра,
можно провести бесчисленное множество больших кругов. Через две
точки, не лежащие на концах одного диаметра шара, можно провести
один и только один большой круг.
Касательной плоскостью к сфере (шару) называется плоскость,
имеющая со сферой единственную общую точку. Эту точку (точка А
на рис. 5.135) называют точкой касания сферы и плоскости. Для того
чтобы плоскость была касательной к сфере, необходимо и достаточно,
чтобы эта плоскость была перпендикулярна радиусу сферы и прохо-
дила через его конец. На рис. 5.135 касательная плоскость а перпен-
дикулярна радиусу О А.
Прямая, принадлежащая касательной плоскости к сфере и прохо-
дящая через точку касания (точку А на рис. 5.135), называется прямой,
касательной к сфере (шару). Через каждую точку, принадлежащую
сфере, можно провести сколь угодно много касательных.
§ 23, Части шара
23.1.	Шаровой сегмент. Фигура, полученная при вращении кру*
гового сегмента вокруг диаметра, перпендикулярного его хорде, назы-
вается шаровым сегментом (на рис. 5.136 АВ — хорда; CD — диаметр).
Фигура, полученная в результате вращения дуги кругового
сегмента, называется сегментной поверхностью, а фигура, полученная
в результате вращения хорды, — основанием шарового сегмента.
Отрезок диаметра, принадлежащий одновременно оси вращения и
круговому сегменту (на рис. 5.136 отрезок КС), называется высотой
шарового сегмента (а также высотой сегментной поверхности).
Объем шарового сегмента шара радиуса К и вы-
сотой Я вычисляется по формуле
V = 4- лЯ2 (3R - Н).
. и
Площадь сегментной поверхности вычисляется
по формуле
S = 2aRH.
§ 23. ЧАСТИ ШАРА
227
23.2.	Шаровой сектор. Шаровым сектором называют фигуру, по-
лученную при вращении кругового сектора вокруг оси, проходящей
через один из его радиусов (рис. 5.137). Дуга кругового сектора образует
при этом вращении сегмент-
ную поверхность.
Объем шарового
сектора вычисляется по
формуле
9
V = 4 nR2Ht
и
где R — радиус шара, Н —
высота шарового сегмента
(на рис. 5.137 Н = | КС |).
Площадь полной по-
верхности шарового секто-
Рис. 5.137.
ра равна сумме площади поверхности шарового сегмента и площади
боковой поверхности конуса, полученного при вращении прямоуголь-
ного треугольника ОКА вокруг оси СО, содержащей его катет КО
(см. рис. 5.137).
Площадь полной поверхности шарового
сектора вычисляется по формуле
*->ш. сект — $сегм Ч* ^бок. кон =	nR |/*2RH — Н2 =
= пЯ (2Н + /2ЛЯ —№).
23.3.	Шаровой слой. Фигура, полученная при вращении части
круга, ваключенной между двумя параллельными хордами, вокруг
оси, проходящей через диаметр, перпендикулярный хордам, назы-
вается шаровым слоем (рис. 5.138). Круги, полученные при вращении
Рис. S.138.
корд, называются основаниями шарового слоя. Радиусы этих кругов
(на рис. 5.138 отрезки AD и ВС) называются радиусами шарового слоя.
Отрезок диаметра, принадлежащий одновременно оси вращения и
шаровому слою (на рис. 5.138 отрезок АВ), называется высотой шаро-
вого слоя.
Объем шарового слоя вычисляется по формуле
v=4пнз+4"я и г2>н>
где q и г2 — радиусы шарового слоя (на рис. 5.138 | AD | = rif ] ВС j =
== Н — высота шарового слоя (на рис. 5.138 Н = [АВ 1).
8*
228
ГЛ. Б. ГЕОМЕТРИЯ
23.4.	Шаровой пояс. Фигура, полученная в результате вращения
дуги окружности, заключенной между двумя параллельными хордами*
вокруг оси, проходящей через диаметр, перпендикулярный хордам,
называется шаровым поясом (или шаровой зоной). На рис. 5,138 шаровой
пояс получен в результате вращения дуги DMC вокруг оси АВ.
Высота шарового слоя одновременно является и высотой соответ*
Ствующего шарового пояса.
Площадь шарового пояса представляет собой разность площадей
двух сегментных поверхностей (на рис. 5.138 разность сегментных
. поверхностей, образованных в результате враще-
s'	ния ДУГ и DiKD).
Площадь шарового пояса вы*
числяется по формуле
\ X ' J	п ~ 2 л 7?/7,
V	где Н — высота шарового пояса, R — радиуо
у, ?	Дуги, от вращения которой получен шаровой пояа
V л ?/ (радиусбм дуги называется радиус окружности, со-
держащей данную дугу),
у|у	23.5. Телесный угол. Пусть L — некоторая
W	замкнутая плоская линия, не имеющая самопе-
V	ресечений, S — некоторая точка, не принадлежа-
щая плоскости линии L (рис. 5.139). Объединение
Рис. 5.1Я9. всех лучей, имеющих общее начало S и пересека-
ющих часть плоскости, ограниченную линией
называется телесным углом. Точка S называется вершиной телесного
угла, Телесный угол измеряется площадью поверхности, вырезаемой
телесным углом на сфере радиуса R с центром в вершине телесного
угла.
Единица измерения телесного угла называется стерадианом.
Один стерадиан — это такой телесный угол, который вырежет на
поверхности сферы радиуса R фигуру с площадью, равной R2.
Многогранный угол является частным случаем телесного угла
и также измеряется в стерадианах, например трехгранный угол, обра-
зованный в результате пересечения трех координатных плоскостей
прямоугольной системы координат Охуг, равен л/2 стерадиан. Действи-
тельно, этот телесный угол высекает 1/8 часть поверхности шара ра*
диуса R с центром в начале координат и, следовательно, равен
4"4л7?2
о	Л
§ 24.	Преобразования плоскости и пространства
24.1.	Геометрические фигуры. Отображение фигуры в фигуру и
отображение фигуры на фигуру. Геометрической фигурой называется
любое множество точек пространства (плоскости). Геометрическую
фигуру называют плоской, если все ее точки принадлежат одной пло-
скости.
Пересечение двух (или нескольких) геометрических фигур — это
фигура, состоящая нз всех тех и только тех точек, которые принадле-
жат каждой из данных фигур. В теории множеств любые два множества
имеют пересечение (которое может быть и пустым множеством). В гео-
§ 24.	ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА 229
метрик обычно вместо слов «пересечение двух фигур пусто» говорят,
что фигуры не пересекаются.
Объединение двух (или нескольких) геометрических фигур есть
фигура, состоящая из всех тех и только тех точек, которые принадле-
жат хотя бы одной из данных фигур.
Пусть Ф и Фх — две геометрические фигуры. Если каждой точке М
фигуры Ф некоторым способом поставлена в соответствие единственная
точка 7И1 фигуры Фх, то такое соответствие называется отображением
фигуры Ф {в фигуру ФР При этом точка Afx называется образом
точки Л4, а точка М — прообразом точки М±. Если при выбранном ото-
бражении фигуры Ф в фигуру Фх некоторые точки фигуры Фх имеют
несколько прообразов, то множество всех прообразов точки С Фх
называется полным прообразом точки Mt.
Множество Ф' всех образов точек фигуры Ф называется образом
фигуры Ф.
Если при выбранном отображении f образ фигуры Ф совпадает
с фигурой Фх, т. е. Ф' = Фх, то говорят, что фигура Ф отображается
на фигуру Фх, и пишут
Ф-> Ф1 или /: Ф-> ф£.
Отображение фигуры Ф на фигуру Фх, при котором разным точкам
фигуры Ф соответствуют разные точки фигуры Фх, называется взаимно
однозначным отображением фигуры Ф на фигуру Фх.
Пусть f — взаимно однозначное отображение фигуры Ф на фи-
гуру Фх. Отображение, ставящее в соответствие каждой точке Mi
фигуры Фх ее прообраз М при отображении f называют обратным
отображением, обозначают символом f~l и пишут
Фх —► Ф или Фх Ф.
24.2.	Преобразование плоскости и пространства. Взаимно одно-
ен ачное отображение пространства (плоскости) на себя называется
преобразованием пространства (плоскости).	е
Простейшие преобразования простран-
ства (плоскости):
1)	Преобразования пространства (плоскости), сохраняющие рас-
стояния между любыми двумя точками пространства (плоскости).
Такие преобразования называются изометрией *).
2)	Преобразования пространства (плоскости), при котором расстоя-
ния между любыми двумя точками изменяются в одном и том же отно-
шении k > 0. Такие преобразования пространства (плоскости) назы-
ваются преобразованиями подобия.
Данное разбиение преобразований на да вида весьма условно —
изометрия является частным случаем преобразования подобия; пре-
образование подобия есть изометрия, еслй k = 1.
Пусть f — произвольное преобразование пространства (плоско-
сти). Если преобразование f отображает точку М пространства (пло-
скости) на точку Mi пространства (плоскости), то пишут
f(M) = Mt.
Точка Л1| называется образом точки М при преобразовании простран-
ства (плоскости) ft а точка М — прообразом точки Mv
*) Иногда вместо термина «изометрия» употребляется термин
«перемещение».
230
ГЛ. 5. ГНОМРТРИЯ
Преобразование пространства (плоскости) f можно представлять
как множество всех упорядоченных пар точек (А1; /Ир пространства
(плоскости), где Mi = f (Af). Множество всех упорядоченных пар то-
чек пространства (плоскости) (М& М) определяет обратное преобразо-
вание. Такое преобразование называется обратным преобразованием
по отношению к преобразованию f и обозначается символом Z'1.
Композиция преобразований. Пусть fi и —
два последовательных преобразования пространства (плоскости):
Mi « h (М) и Afa « fa (Mi).
Преобразование пространства (плоскости), отображающее точку М
пространства (плоскости) в точку М2 пространства (плоскости), назы-
вается композицией преобразований fa и fa и обозначается
fefa.
Тождественное преобразование. Преобразова-
ние пространства (плоскости), отображающее каждую точку про-
странства (плоскости) на себя, называется тождественным преобразо-
ванием пространства (плоскости). Тождественное преобразование обо-
значается буквой Е. Согласно определению тождественного преобра-'
вования пространства (плоскости)
Е (М) « М.
Преобразование Е можно рассматривать как множество (Af; М)
всех пар совпадающих точек пространства (плоскости).
24.3.	Изометрия пространства и плоскости. Равенство фигур*
Из всех преобразований пространства (плоскости) можно выделить
преобразования, при которых расстояние между двумя любыми точ-
ками пространства (плоскости) равно расстоянию между их образами,
т. е. если f (Л) = Л* и / (В) = где Л и В — любые две точки про-
странства (плоскости), то |ЛВ| = | AiBi |. О таких преобразованиях
пространства (плоскости) говорят, что они сохраняют расстояние.
Преобразование пространства (плоскости), сохраняющее расстоя-
ние, называется изометрией. Из определения изометрии следует:
1)	Тождественное преобразование есть изометрия.
2)	Преобразование, обратное изометрии, есть изометрия.
3)	Композиция двух изометрий есть изометрия.
Любая изометрия плоскости может быть представлена как после-
довательное выполнение трех преобразований: параллельного переноса,
поворота вокруг точки и осевой симметрии.
Две геометрические фигуры Ф и называют равными, если су-
ществует изометрия, отображающая фигуру Ф на фигуру *).
24.4.	Поворот плоскости вокруг точки. Поворотом плоскости во-
круг центра О называется такая изометрия плоскости, при которой:
1)	точка О отображается сама на себя;
2)	угол между любым лучом ОХ и соответствующим ему лучом OXt
(образом луча ОХ) имеет одну и ту же величину а, называемую углом
поворота.'
Если луч ОХ совмещается с лучом OXi поворотом против часовой
стрелки, то направление поворота считается положительным; если же
луч ОХ совмещается е лучом OXj поворотом по часовой стрелке, го
направление поворота считается отрицательным. Так, например, на
♦) В курсе геометрии средней школы вместо термина «равенством уио*
требляется термин «конгруэнтность».
§ 24 ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА 23!
рис. 5.140 лучи ОХ и OXf задают поворот на 60°, а на рис. 5.141 лучи
ОХ и 0X1 задают поворот на —60°.
Поворот вокруг центра О с углом поворота а обозначается
ГДе а С (—180°; 180°].
Поворот на угол 0 = а + 360°*п, где п £ Z и а £ (—180°; 180°],
отождествляется с поворотом
Так как поворот плоскости вокруг точки является частным слу-
чаем изометрии, то для него справедливы все общие свойства изометрии:
1)	Отображение, обратное повороту вокруг центра О, также яв-
ляется поворотом вокруг центра О, Так, например, для поворота
Рис. 5.140.
Рис. 5.141.
против часовой стрелки на угол а = 30° обратным является по-
ворот тоже на 30°, но по часовой стрелке.
2)	Композиция двух поворотов вокруг центра О на углы ах и аа
есть поворот на угол + а2 :	° /?®2 =	причем компо-
зиция двух поворотов обладает свойством коммутативности:
24.5.	Центральная симметрия и центрально симметричные фигуры.
Частный случай поворота плоскости вокруг центра О, а именно пово-
рот на 180°, называется центральной симметрией с центром О.
Рис. 5.142.
Центральная симметрия с центром О обозначается символом
По определению центральной симметрии
7 — ©180°
~ ^0	•
Геометрическая фигура, которая при центральной симметрии
с центром О отображается сама на себя, называется центрально симме-
тричной (говорят также, что такая фигура имеет центр симметрии О),
Несколько центрально симметричных фигур о центром симметрии О
изображено на рис. 5.142.
24.6.	Осевая симметрия плоскости. Говорят, что точки и М2
плоскости а симметричны относительно прямой /, принадлежащей
плоскости а и не содержащей точек Л12, если отрезок пер-
232
ГЛ. В. ГЕОМЕТРИЯ
пендикулярен прямой I и делится этой прямой пополам (I МУО [
= |0М2|, О—середина отрезка MiM2) (рис. 5.143).
Любая точка прямой I считается симметричной самой себе»
Изометрия плоскости, при которой каждая точка плоскости отоб-
ражается на симметричную ей (относительно данной прямой) точку,
называется осевой симметрией плоскости.
Данную прямую I называют осью симметрии, а осевую симметрию
относительно данной прямой I обозначают символом S/.
Так как осевая симметрия есть частный случай изометрии, то для
осевой симметрии справедливы все общие свойства изометрии. В част-
ности, отображение, обратное осевой симметрии, есть осевая симметрия.
Для осевой симметрии справедливо и более сильное утверждение:
Отображение, обратное осевой симметрии, есть та же самая осевая
симметрия.
Рис. 5.143.	Рис. 5.144.
Прямая I называется осью симметрии фигуры Ф, если фигура Ф
при осевой симметрии с осью I отображается сама на себя. В этом слу-
чае о фигуре Ф говорят, что она симметрична относительно оси Z.
На рис. 5.144 изображено несколько геометрических фигур, сим-
метричных относительно оси /.
24.7.	Осевая симметрия пространства. Говорят, что точки про-
странства и Af2 симметричны относительно прямой /, не содержащей
точек Л41, М2, если отрезок AfiA42 перпендикулярен I и делится этой
прямой пополам (| М^О | = |(Ш2|, где О — середина отрезка М^М2,
принадлежащая прямой /).
Любая точка прямой I считается симметричной самой себе.
Изометрия пространства, при которой каждая точка пространства
отображается на симметричную ей (относительно данной прямой /)
точку, называется осевой симметрией пространства.
Данную прямую I называют осью симметрии. Осевая симметрия
пространства (так же как й осевая симметрия плоскости) обозначается
символом S[.
Осевая симметрия пространства является частным случаем изо-
метрии пространства, поэтому для осевой симметрии пространства
справедливы все общие свойства изометрии пространства.
Если фигура Ф при осевой симметрии с осью I отображается сама
па себя, то говорят, что фигура Ф симметрична относительно оси /,
а ось I называют осью симметрии фигуры Ф.
На рис. 5.145 изображены две пространственные геометрические
фигуры с осью симметрии I.
Частным случаем фигуры Ф, симметричной относительно оси 19
являются фигуры вращения. Пусть в пространстве дана прямая I
и выбрана некоторая произвольная точка М9 не принадлежащая пря-
мой I. Построим плоскость а, перпендикулярную прямой I и содержа-
щую точку А1 (рис* 5,146). Плоскость а пересечет прямую I в некоторой
$ 24. ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА 233
точке О. Рассмотрим окружность радиуса ОМ с центром в точке О,
принадлежащую плоскости а. О такой окружности говорят, что она
получена при вращении точки М вокруг оси /.
Рис* 5.145,
Теперь рассмотрим в пространстве прямую I и некоторую фи*
гуру F, принадлежащую плоскости, проходящей через данную пря-
мую I (рис. 5.147). Каждой точке фигуры F,
не принадлежащей прямой Z, поставим в соот- / л
ветствие окружность, получающуюся в резуль-
тате вращения данной точки вокруг прямой I. А /ССХ
Объединение всех таких окружностей и то-
чек фигуры F, принадлежащих прямой Z, на- *
вывается фигурой вращения, полученной в ре- W \ \ j / /
вультате вращения фигуры F вокруг прямой Z,
которая называется осью вращения.	ч!	шу
Сечением фигуры вращения называется не-	Л
пустое пересечение фигуры вращения и пло-	I 1
скости.	I	, I
СеченКе фигуры вращения называется осе*
вым сечением, если оно представляет собой пе- Рис. 5.147,
ресечение фигуры вращения плоскостью, прохо-
дящей через ось вращения фигуры.
24.8. Симметрия относительно плоскости. Говорят, что точки про-
странства М и Mi симметричны относительно плоскости а (рис. 5.148),
если отрезок MMi перпендикулярен этой плоскости и делится ею по-
полам. Любая точка плоскости а считается симметричной самой себе.
Преобразование пространства, при котором каждая точка отобра-
жается на симметричную ей относительно данной плоскости точку,
называется симметрией относительно этой плоскости. Симметрию отно-
сительно плоскости а обозначают символом Sa.
Плоскость а называется плоскостью симметрии фигуры Ф, если
при симметрии относительно плоскости а фигура Ф отображается
сама на себя. В этом случае о фигуре Ф говорят, что она симметрична
относительно плоскости а.
234
ГЛ. 5. ГЕОМЕТРИЯ
На рис. 5.149 изображены две геометрические фигуры, симметрич-
ные относительно плоскости а.
24.9.	Гомотетия плоскости. Гомотетией плоскости с центром
О и коэффициентом k 0 называется отображение плоскости на
себя, при котором образом произвольной точки X является точка Xj
такая, что
0X1 = kOX.
Гомотетию с центром О и коэффициентом k обозначают символом Н^:
Н* (X) = Х„ если ОХ, = ЮХ.
Говоря о множестве гомотетий с каким-либо определенным цен-
тром, в обозначении гомотетии букву О опускают, т. е. вместо
пишут Hk. Гомотетии с отдельно указанными центром и коэффициентом
обозначают Н.
Основные свойства гомотетии:
1)	Центр гомотетии отображается на себя.
2)	Если коэффициент k > 0, то точки X и Xj = Н (X) лежат
на прямой ОХ по одну сторону от центра гомотетии, т. е. точка Xj
принадлежит лучу ОХ.
Если k < 0, то точки X и Xj = Н (X) лежат на прямой ОХ
по разные стороны от центра гомотетии, т. е. точка Xj принадлежит
лучу, имеющему то же самое начало О, что и луч ОХ, и противоположно
направленному с лучом ОХ.
3)	Если при гомотетии с коэффициентом k точки X и Y отобра-
жаются соответственно на точки Xj и Ylt то
Л1У1 = kXY.
4)	При гомотетии с коэффициентом 1 каждая точка переходит
сама в себя. Поэтому тождественное отображение плоскости на себя есть
гомотетия с любым центром и коэффициентом k = 1.
5)	При гомотетии с центром О и коэффициентом —1 каждая точка X
переходит в точку Xi, для которой 0Xt == —ОХ, т. е. в точку, цен-
трально симметричную точке X. Поэтому гомотетия с коэффициентом
k = —1 есть центральная симметрия:
/7 о 1 == Zo.
6)	Обратным отображением к гомотетии с коэффициентом k яв-
ляется гомотетия с тем же центром и коэффициентом k' = \/k.
7)	При гомотетии с коэффициентом k все расстояния между точ-
ками изменяются в | k | раз:
IXiKi | = \k\-\XY ],
где Xi = Hk (X), yt = Hk (У).
Две плоские фигуры Ф и Фх называются гомотетичными, если су-
ществует гомотетия, отображающая фигуру Ф на фигуру Фх.
Свойства гомотетичных фигур;
1)	Гомотетичные фигуры подобны.
§ 24. ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ И ПРОСТРАНСТВА 235
2)	При гомотетии с положительным коэффициентом каждый луч
переходит в сонаправленный с ним луч. При гомотетии с отрицатель-
ным коэффициентом каждый луч переходит в противоположно направ-
ленный луч. При гомотетии любая прямая, проходящая через центр
гомотетии, переходит сама в себя; прямая, не проходящая через центр
гомотетии (при k 1), переходит в параллельную прямую; угол пере-
ходит в равный угол и т. д.
24.10.	Гомотетия пространства. Гомотетия пространства опреде-
ляется так же, как и гомотетия плоскости.
Гомотетией пространства с центром О и коэффициентом k =£0
называется преобразование пространства, при котором образом про-
•*—>	• >
извольной точки X является такая точка Хх, что ОХ± = kOX. Гомо-
тетия пространства с центром О и коэффициентом k обозначается тем
же символом Яд, что и гомотетия плоскости.
Все свойства гомотетии плоскости справедливы и для гомотетии
пространства. Кроме того:
1)	при гомотетии пространства плоскость отображается либо на
саму себя, либо на параллельную плоскость;
2)	всякая сфера при гомотетии пространства с центром^ совпада-
ющим с центром сферы, отображается на сферу.
Гомотетия как пространства, так и плоскости задается либо цен-
тром гомотетии и упорядоченной парой соответственных точек X и
Хх 8= Н (X), либо двумя упорядоченными парами соответственных
точек (X; Xt) и (У; Ух), где Хх == Н (X) и Ух = Н (У).
Кроме перечисленных выше способов задания, гомотетия может
вадаваться, например, центром гомотетии О и коэффициентом гомоте-
тии k.
24.11.	Преобразование подобия плоскости. Отображение плоско-
сти на себя, при котором расстояния между любыми двумя точками
изменяются в одном и том же отношении k > 0, называется преобра*
вованием подобия или просто подобием. Число k называется коэф*
фициентом подобия.
Так, если f — преобразование подобия, изменяющее расстояние
в k раз, а А и В — две любые точки плоскости и / (Л) = Лх, / (В) =□
е= Bi, то |ЛхВх| « k- | АВ |.
Свойства преобразований подобия:
1)	Композиция /х°/2 ДВУХ преобразований подобия /х и
с коэффициентами подобия kx и k2 соответственно есть преобразование
подобия с коэффициентом kX'k2. В частности, композиция гомотетии
и изометрии есть преобразование подобия.
2)	Каждое преобразование подобия есть композиция гомотетии
и изометрии.
3)	Каждая гомотетия является преобразованием подобия.
4)	Каждая изометрия является преобразованием подобия с коэф-
фициентом подобия, равным единице.
24.12.	Подобные фигуры. Если фигуру Ф можно отобразить на
фигуру Qj так, что для любых точек А н В фигуры Ф отношение рас-
стояния | ЛхВх | между их образами (точками фигуры Фх) к расстоя-
нию | АВ | между самими точками равно одному и тому же числу
Л (I | = А>| АВ |), то говорят, что фигура Фх подобна фигуреФ
с коэффициентом подобия k, и пишут
'	k
Фх ~ф.
236
ГЛ. В. ГЕОМЕТРИЯ
Свойства подобных фигур!
1)	Каждая фигура подобна самой себе о коэффициентом подобия
k ю 1 (рефлексивность):
фДф.
2)	Если фигура Ф1 подобна фигуре Ф с коэффициентом то фи-
гура Ф подобна фигуреOj е коэффициентом &'== ш? (симметричность)»
k	1/А
Ф1 ~Ф-ф>Ф~Фь
Принимая во внимание свойство симметричности* обычно просто
говорят, что две фигуры Ф и Фх подобны.
3)	Если фигура Ф^ подобна фигуре Ф с коэффициентом а фи-
гура Фа подобна фигуре Фх с коэффициентом подобия k2, то фигура Фа
подобна фигуре Ф с коэффициентом k=kfk2 (транзитивность):
ь	ь	ь .ь
Ф1~ф и Ф2~Ф1=>Ф2 ~Ф.
§ 25. Система аксиом и неопределяемых понятий
геометрии (по Гильберту)
Основными (неопределяемыми) понятиями геометрии по Гильберту
являются три вида объектов:
1)	точки, которые будем обозначать Л, В, С,
2)	прямые, которые будем обозначать a, b, С; ...j
3)	плоскости, которые будем обозначать а, Р, у, ...
АКСИОМЫ ГЕОМЕТРИИ ПО ГИЛЬБЕРТУ
I.	Аксиомы принадлежности.
Аксиомы этой группы устанавливают отношения принадлежности
между основными понятиями геометрии.
1-1. Для любых двух точек Л и В существует прямая а, про-
ходящая через эти точки.
1-2. Для. любых двух различных точек Л и В существует не
более одной прямой, проходящей через эти точки.
1-3. На прямой существуют по крайней мере две точки. Суще-
ствует по крайней ме$е три точки, не лежащие на одной прямой.
1-4. Для любых трех точек Л, В и С, не лежащих на одной
и той же прямой, существует плоскость а, содержащая три данные
точки Л, В и С. Для любой плоскости всегда существует принадлежа-
щая ей точка.
1-5. Для любых трех точек Л, В и С, не лежащих на одной и
той же прямой, существует не более одной плоскости, проходящей
через эти точки. Эту плоскость часто обозначают ЛВС, т. е. перечис-
лением точек, через которые проходит плоскость.
1-6. Если две точки Л, В прямой а лежат в плоскости а, то вся-
кая точка прямой а лежит в плоскости а.
1-7. Если две плоскости аир имеют одну общую точку Л, то
они имеют по крайней мере еще одну общую точку В.
1-8. Существуют по крайней мере четыре точки, не лежащие в одной
плоскости.
Аксиомы 1-1—1-3 называют плоскостными аксиомами, а остальные
аксиомы — пространственными.
§ 25. СИСТЕМА АКСИОМ
237
II.	Аксиомы порядка.
Аксиомы этой группы определяют понятие «между», служащее для
описания отношения порядка точек на прямой, плоскости и в про-
странстве.
Точки, лежащие на прямой, находятся в определенных отноше-
ниях друг с другом. Для описания этих отношений используется слово
«между».
П-1. Если точка В лежит между точкой А и точкой С, то А,
В и С — три различные точки прямой и точка В лежит также между
С и А.
П-2. Для любых двух различных точек А и С, лежащих на
прямой АС, существует по крайней мере одна точка В такая, что
точка С лежит между А и В.
П-З. Среди любых трех различных
точек, лежащих на прямой, существует	/X.	/
не более одной точки, лежащей между /
двумя другими.	/
Кроме этих аксиом порядка на пря- /	/ X.
мой, вводится еще одна аксиома, опреде-	С*-—----------
ляющая отношение порядка на пло- /
скости. В формулировке этой аксиомы
используется понятие отрезка, которое	рис. 5.150.
вводится следующим образом:
Пусть А и В — две различные точки прямой а. Множество всех
точек прямой а, лежащих между точками А и В, включая А и В*
называется отрезком, а точки А и В — концами отрезка. Отрезок
с концами А, В обозначается АВ (или В А). Всякая точка отрезка,
лежащая между его концами, называется внутренней точкой отрезка.
П-4. Пусть А, В и С — три точки, не лежащие на одной пря-
мой, и а— прямая в плоскости АВС, не проходящая ни через одну
из точек А, В и С (рис. 5.150). Если при этом прямая а проходит
через одну из точек отрезка АВ, то она должна пройти через одну из
точек отрезка . АС или через одну из точек отрезка ВС.
Пусть на прямой а заданы четыре -различные точки А, В, А'
и О (рис. 5.151) так, что точка О лежит между А и В, но не лежит
между А и А'. В этом случае говорят, что точки А и А' прямой а
лежат по одну и iy же сторону от точки О, а точки А, В лежат
на прямой па разные стороны от точки О. Множество всех точек пря-
мой а, лежащих по одну сторону от точки О, включая точку О, на-
зывается лучом, исходящим из точки О.
III.	А к с и о м ы конгруэнтности.
Отрезки находятся в определенном отношении друг с другом?
для описания этого отношения служат понятия «конгруэнтности»
или «равенства» отрезков *).
Ш-1. Пусть А и В — две точки прямой а и А' — некоторая
точка прямой а! (которая, в частности, может совпадать с прямой а).
Тогда на прямой а' существует точка В', лежащая по заданную сто-
рону от точки А' и такая, что отрезок АВ равен отрезку А'В'
(рис. 5.152). Для обозначения равенства отрезков используется знак — •
Эта аксиома дает возможность откладывать отрезки.
И1-2.> Если отрезок А'В' и отрезок А"В" равны одному и тому же
отрезку АВ, то отрезки А'В' и А"В" равны.
♦) В аксиоматике Гильберта термины «конгруэнтность» и «равенство»
являются синонимами.
238
ГЛ. 5. ГЕОМЕТРИЯ
Из аксиомы III-2, в частности, вытекает, что любой отрезок равен
самому себе, а также что отношение равенства отрезков симметрично
и транзитивно.
II1-3. Пусть АВ и ВС — два отрезка прямой а, не имеющие ни
одной общей внутренней точки, а А*В* и В*С — два отрезка той же
или другой прямой а', также не имеющие общих внутренних точек
(см. рис. 5.152). Если при этом
АВ = А'В' в ВС = В'С',
то и АС г= А'С'.
Эта аксиома дает возможность складывать отрезки.
Аксиомы II1-1 и III-3 содержат утверждения, касающиеся лишь
равенства отрезков; их называют линейными аксиомами равенства
а	____________________
•-----1------}.----1-— j-------	А А	С
A’ A Q Я #
а-------,—,-----------_—,
A' S' С
Рис, 5.151.	Рис. 5.152.
При формулировке следующих двух аксиом равенства используется
понятие «угла». Углы находятся в определенном отношении, для обо*
еначения которого используется понятие «равенство».
Ш-4. Пусть даны угол	в плоскости а и прямая а'
в плоскости а , а также выбрана вполне определенная по отношению
к прямой а* часть плоскости а', отделяемая прямой а' от всей пло-
скости. Пусть h\ —луч прямой а*, исходящий из точки О'. Тогда
в плоскости а' существует один и только один луч h2 такой, что угол
(^1, Л2) равен углу Л2) и все внутренние точки угла h2)
находятся в плоскости а' по данную сторону от прямой а':
h2) = <^(^1, h2).
111-5. Если для двух треугольников АВС и А'В'С' имеют место
равенства
АВ » А'В', АС == А'С', ^ВАС = ^В'А'С',
то имеет место также равенство
^АВС= ^А'В'С'.
Аксиомы Ш-4 и Ш-5 называются плоскостными аксиомами ра-
венства.
IV.	Аксиома о параллельных прямых (а к с и*
ома Евклида):
Пусть а — произвольная прямая, а А — точка, не принадлежа-
щая прямой а. Тогда в плоскости, определяемой прямой а и точкой А,
существует не более одной прямой, проходящей через точку А и не
пересекающей прямую а.
Эта прямая называется прямой, параллельной а и проходящей
через точку А.
§ 25. СИСТЕМА АКСИОМ
239
Иногда при перечислении аксиом геометрии вместо аксиомы о па*
раллельных выдвигаются предложения, равносильные этой аксиоме.
Такими предложениями, например, будут следующие:
1) Если две прямые а и Ь, лежащие в одной плоскости, не пере-
секают третью прямую, лежащую в той же плоскости, то они не пере-
секаются также и между собой.
2) Если принята аксиома Архимеда (см. ниже), то аксиома о па-
раллельных может быть заменена требованием равенства суммы вну*
тренних углов треугольника двум прямым углам.
V	. Аксиомы непрерывности.
V	-1 (аксиома измерения, или аксиома Архи*
меда). Пусть АВ и CD — два произвольных отрезка. Тогда на пря-
мой АВ существует конечное число точек Ait А2, А3, ...э Ап таких*

^П~!3
Рис. 5.153,
что все отрезки AAj, А]А2, Л2Л3, ..., ЛплЛп равны отрезку CD
и точка В лежит между точками А и Ап (рис. 5,153).
V	-2 (аксиома линейной полноты). Точки прямой
образуют систему, которая (при условии принятия перечисленных
аксиом) не допускает никакого расширения, т. е. к множеству точек
прямой невозможно добавить еще некоторые объекты ?ак, чтобы:
1) все элементы полученного расширенного множества снова под-
чинялись перечисленным аксиомам;
2) все аксиомы сохраняли свой первоначальный смысл, т. е. суще-
ствовавшие до расширения отношение, порядка между точками и ра-
венство отрезков сохранились бы и в расширенном множестве.
ГЛАВА 6
ТРИГОНОМЕТРИЯ
Тригонометрия возникла как аппарат для вычисления неизвестных
параметров треугольника по з^данным'значениям других его пара-
q метров. Так, методами тригонометрии по данным сторонам треуголь-
ника можно вкГчисли^его углы, пр известной пдощади^и двум углам
"1	* вычислить стороны и т.д. Необходимость отыскивать неизвестные пара-
метры данного треугольника впервые возникла в астрономии, и в те-
чение долгого времени тригонометрия была одним из разделов астро-
номии.
Первые методы нахождения неизвестных параметров данного тре-
угольника были развиты учеными Древней Греции за несколько веков
до новой эры. Греческие астрономы не рассматривали синусов, косину-
' ' сов и тангенсов. Вместо таблиц этих’величин они составили и исполь-
ебваЛИ'З'абЛицы, позволяющие отыскивать хорду окружности по стя-
гиваемой ею дуге. Дальнейшее развитие тригонометрия получила в сред-
ние века в работах индийских и арабских ученых. Современные буквен-
ные обозначения появились в тригонометрии в середине XVIII века.
Приблизительно в то же время в тригонометрии стали рассматриваться
радианные меры углов, были введены тригонометрические и обратные
тригонометрические функции числового аргумента, после чего тригоно-
метрия приобрела свой современный вид.
§ h Тригонометрические функции
1.1.	Обобщение понятия угла. Пусть -^(а, Ъ) и ^:(с, d) — два
тупых угла, образованных парами лучей а, b и с, d. Совместим
лучи b и d так, чтобы они совпали, а лучи
\ .	о и с лежали по разные стороны от пря-
мой, содержащей лучи b и d (рис. 6.1).
\	В результате сложения этих двух углов
\	получается угол, больший развернутого.
\	Сторонами этого угла будут лучи а и с.
-----------а Для того чтобы отличать полученный угол
t----------от угла (а, с), имеющего те же самые сто-
\	роны и меньшего развернутого, отметим на
%	\	рисунке полученный угол дугой. Внутрен-
i	. ней областью отмеченного угла будет внеш-
няя область угла ^(а, с), а внешней —
Рис’	внутренняя область угла -^(а, с). Анало-
гичным способом можно получать углы,
большие двух развернутых углов (т. е. большие полного угла)
и т. д.
Для того чтобы представить себе угол, больший полного, удобно
рассматривать угол как геометрическую фигуру, полученную при
повороте луча вокруг своего начала.
$ Т. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ	241
Ро.зьмем на плоскости луч ОА и будем пово£ачивать^его_в^кпуг
точки О против часовой стрелки (рис. 6.2). При псГворотелучаОД
на четверть полного оборота вокруг точки О получается угол АОА'
(ОА'— образ луча О А при указанном повороте), равный 90° (л/2).
Далее, угол АОА’ — развернутый, если луч О А’ получен поворотом
луча ОА на половину полного оборота вокруг точки О\ полный угол
получится, когда в результате вращения луч О А’ первый раз совпа-
дет с лучом ОА. Угол АОА' считается больше полного, если луч ОА'
получается поворотом луча О А на угол, больший полного угла.
Углы, большие развернутого, часто отмечают, указывая направление
поворота стрелкой и число сделанных оборотов. Так, например,
на рис. 6.3 изображен угол в 450°.
Луч ОА можно вращать вокруг точки О в двух направлениях:
по часовой стрелке и против часовой стрелки. Направление вращения
против часовой стрелки называют положительным, по часовой
стрелке—отрицательным. Соответственно углы, полученные враще-
нием луча против часовой стрелки, называют положительными,
& по часовой стрелке — отрицательными.
1.2» Тригонометрические функции. Пусть Оху—некоторая пря-
моугольная декартова система координат; О А — луч, полученный
поворотом положительной полуоси Ох вокруг начала координат О
на угол а (рис. 6.4) (Л — произвольная точка луча). Обозначим ко-
ординаты точки А через х и у. А (х, у) — и рассмотрим вектор О А =
«= (х; у). Модуль этого вектора равен
Углом между осью Ох и вектором ОА называют угол между по*
ложительным направлением оси Ох и лучом ОА.
Отношения
координат вектора ОА к длине вектора ОА не зависят от длины век*
тора ОА (т. е. от положения точки А на луче ОА), но зависят от
его направления *).
*) Из множества всех векторов с началом в точке О можно выделить под-
множество векторов а началом в точке О и модулем, равным единице. Концы
всех таких векторов принадлежат окружности с центром в начале координат
и о радиусом, равным единице, — единичной окружности. Тригонометри-
ческие функции часто вводятся с использованием единичной окружности
(или множества векторов ОА с концами, принадлежащими единичной окруж-
ности), Так, например, если точка Л принадлежит единичной окружности,
то синусом угла а называют ординату вектора OAi образующего о осью Ох
угол а»
242
ГЛ. 6. ТРИГОНОМЕТРИЯ
Отношение ординаты вектора, образующего с осью Ох угол а»
к длине этого вектора называется синусом угла а и обозначается
sin а:
. У
sin as= —,
- . _____ г
Отношение абсциссы вектора, образующего е осью Ох угол а,
к длине этого вектора называется косинусом угла а и обозначается
cos а:
х
cos а = —.
г
Отношение синуса угла а к его косинусу называется тангенсом
угла а и обозначается tg а:
или, используя определения sin а и cos а,
и
tg а =	.
х
Отношение косинуса угла а к его синусу называется котангенсом
угла сх и обозначается ctg а:
или, используя определения sin а и cos а,
. х
ЧВа- —.
Синус и косинус однозначно определены для любого угла а, тан-
генс однозначно определен для Всех значений угла а, за исключением
а == 90°+180°-п	n£Z, а котангенс — для веса
значений а, за исключением а = 180*п (а == л/г), /г £ Z.
Синус и косинус одного и того же угла связаны равенством
sin2 а + cos2 а = 1,
тангенс и косинус одного и того же угла — равенством
1 Ч* tg2 & = 1 1 'а"~" >
1 ь cos2 а 9
котангенс и синус — равенством
1 + ctg2 а =	,
‘ ь sm2a 9
а тангенс и котангенс одного и того же угла — равенством
tg a* ctg a == 1.
Функции sin a, cos a, tg a и ctg a называют тригонометриче*
скими функциями угла а. Кроме основных тригонометрических функ-
ций sin a, cos a, tg a и ctg a, вводятся еще две тригонометрические
§ I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
243
функции угла а — секанс и косеканс, обозначаемые sec а и cosec а
соответственно. Эти функции определяются равенствами
sec а ---------
cos а
I
cosec а = —-----.
sm а
Секанс угла а определен при всех значениях а,гэа исключением
a =s 90°-|-180о‘П ^а = -5- + этл^, Z, а косеканс—при всех зна-
чениях угла а, за исключением а = 180°*л (а = этп), п £ Z.
1.3. Квадранты единичной окружности. Знаки значений тригоно-
метрических функций. Координатные оси Ох, Оу прямоугольной си-
стемы координат делят координатную плоскость на четыре части,
называемые четвертями или квадрантами (рис. 6.5). Часть плоскости,
лежащая выше оси Ох и правее оси Оу, — первая четверть; выше оси Ох
и левее оси Оу — вторая четверть; ниже оси Ох и левее оси Оу — третья;
ниже оси Ох и правее оси Оу — четвертая. Единичная окружность
(окружность единичного радиуса с центром в начале координат) осями
координат делится на четыре части, которые тоже называют четвер-
тями (или квадрантами) и нумеруют так же, как и четверти плоскости.
О точках единичной окружности, принадлежащих осям коорди-
нат, говорят, что они находятся на положительной (или на отрицатель-
ной) полуоси абсцисс или ординат.
Пусть луч О А, полученный поворотом положительной полуоси Ох
на угол а, пересекает единичную окружность в точке А (рис. 6.6).
Угол а считают принадлежащим первой, второй, третьей или четвер-
той четверти, если точка А принадлежит соответственно первой, вто-
рой, третьей или четвертой четверти единичной окружности.
Абсциссы точек, принадлежащих I и IV четвертям, положительны,
а точек, принадлежащих II и III четвертям, отрицательны. Ординаты
точек, принадлежащих I и II четвертям, положительны, а III и IV чет-
вертям — отрицательны. Знаки значений тригонометрических функций
устанавливаются на основании определения тригонометрических функ-
ций и зависят от того, какой четверти принадлежит угол а. В табл. 1
приведены знаки значений основных тригонометрических функций.
1.4. Тригонометрические функции числового аргумента. Углы
могут измеряться в градусах и радианах. Использование радианной
меры измерения углов позволяет ввести тригонометрические функции
числового аргумента. Это можно сделать следующим образом. Между
множеством всех действительных чисел и множеством всех углов (рас-
сматриваемых как поворот луча ОА вокруг точки О), измеренных
в радианах, существует взаимно однозначное соответствие, Например,
244
ГЛ. 6. ТРИГОНОМЕТРИЯ
ТАБЛИЦА I
Четверти	Функции			
	sin а	cos а	tg а	ctg а
I	+	+	+	
II	+		—•	—
ИГ	—			+
IV	—	4-		—
числу 1 соответствует поворот луча ОА вокруг своего начала на один
радиан против часовой стрелки; числу — 3/2 соответствует поворот
луча О А вокруг своего начала на 3/2 радиана по часовой стрелке и к д.
Синусом числа х называется число, равное синусу угла в х радиан.
Косинусом числа х называется число, равное косинусу угла в х радиан.
Аналогично определяются и другие тригонометрические функции чис-
лового аргумента.
Основные свойства тригонометрических
функций.
Свойства.функции sin х.
1)	Область определения — множество всех действительных чисел.
2)	Область изменения (множество значений) — промежуток [—1; 1 ].
3)	Функция sin х — нечетная: sin (—х)	—sin х.
4)	Функция sin х — периодическая. Наименьший положительный
период равен 2л:
sin (х + 2л) == sin х.
5)	Нули функции: sin х =» 0 при х == ли, п g Z.
6)	Промежутки знакопостоянства:
sinx>0 при xg(2nn; л4-2лп), ngZ,
sin ж 0 при л£(л + 2лл; 2л+ 2лп), ngZ.
7)	Функция sin# непрерывна и имеет производную при любом
значении аргумента:
(sin х)' ® cos х,
8)	Функция sinx возрастает при х g -+ 2ля; + 2лп^ ,
ng Z, и убывает при х g ^-~- + 2лп; 2лп^, ngZ.
9)-----Функция sinx имеет минимальные значения, равные —1, при
х =□	n g Z, и максимальные значения, равные 1, при
ж =» -у- + 2лп, п g Z.
Гра	фик функции у =» sin х изображен на рис. 6.7. График функ-
ции sin х называют синусоидой.
€ Т. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ	245
Свойства функции cos л.
1)	Область определения — множество всех действительных чисел.
2)	Область изменения (множество значений) — промежу*
ток 1—1; 1].
3)	Функция cos х — четная: cos (—х) == cos х.

Рис. 6.7.
4)	Функция cos х — периодическая. Наименьший положительный
период функции равен 2л:
cos (х + 2л) = cos х.
5)	Нули функции: cos х — 0 при х =	+ лл, п g Z.
6)	Промежутки зн а непостоянства:
. cosx>0 при х£^--------~+2лл; ~^--|-2лл^,
cos х < 0 при х £	+ 2лл; + 2лл^, п С Z.
7)	Функция cos х непрерывна и дифференцируема при любом
значении аргумента:
(cos х)' == —sin х.
8)	Функция cos х возрастает при х £ (—л + 2лл; 2лл), п £ Z,
и убывает при х £ (2лл; л + 2ял), л ( Z,
9)	Функция cos х имеет минимальные значения, равные —1,
при х== л + 2ял, п g Z, и максимальные значения, равные 1, при
х = 2лл, л £ Z.
График функции у = cos х изображен на рис. 6.8.
Свойства функции tgx.
1)	Область определения функции — множество всех действшгель- *
пых чисел, кроме чисел х = -2- + лл, л g Z.
2)	Область изменения (множество значений) — множество всех
действительных чисел.
3)	Функция tg х — нечетная; tg (—х) » —tg xf
246
ГЛ. в. ТРИГОНОМЕТРИЯ
4)	Функция tg х — периодическая. Наименьший положительный
период функции равен л:
tg (х + л) = tg х.
5)	Нули функции: tg х = О при х = лл, п £ Z.
6)	Промежутки знакопостоянства:
tgx>0 при х£ (лл; -у-+ лл^, n£Zt
tgx<0 при х^(-------у4-лп; лл^ , n£Z.
изменения
7)	Функция tg х непрерывна и дифференцируема при любом зна-
чении аргумента из области определе-
ния функции:
(tgx)/s=7SPT-
8)	Функция tg х возрастает в каж-
дом из промежутков
(л , л .	\
—2-4-л»; ~2-+пп)> n€z*
График функции у tg х изобра-
жен на рис. 6.9. График функции tgx
называют тангенсоидой.
Свойства функции ctgх.
1) Область определения функ-
ции — множество всех действительных
чисел, кроме чисел х » лл, n £ Z.
южество значений) — множество всех
действительных чисел.
3)	Функция ctg х — нечётная: ctg (—х) = —ctg х.
4)	Функция ctg х — периодическая. Наименьший положительный
период функции равен л:
ctg (х + л) == ctg л.
5)	Нули функции: ctg х = О при х = л/2 + лл, n g Z.
6)	Промежутки знакопостоянства:
ctgx> 0 при х£ (лл; -~~4-лл^, n£Zt
ctgx<0 при х£ (-^~ +лл; л(л+1)^, n£Z.
7)	Функция ctg х непрерывна и дифференцируема при любом
значении аргумента из области определения функции:
(ctg х)'
1
sin2x
8)	Функция ctg х убывает в каждом из промежутков (лл; л (л + 1)),
л € Z.
График функции //=etgx изображен на рис. 6.10.
§ Т. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ	247
Свойства функции sec х.
1)	Область определения функции — множество всех действитель-
ных чисел, кроме чисел вида х = л/2 + лп, п £ Z.
2)	Область изменения (множество значений):
(-оо; —1] U [И +оо).
3)	Функция sec х — четная: sec (—х) = sec х.
z 4) Функция sec х — периодическая. Наименьший положительный
период функции равен 2л: sec (х + 2л) = sec х.
5)	Функция sec х ни при каком значении аргумента не? бращается
в нуль.
6)	Промежутки знакопостоянства:
secx>0 при х£^-------у + 2л/г; -^-+2лп^, ngZ,
(л	Зл \
-у + 2лп; -g—F 2л/г), nZ.
7)	Функция sec х непрерывна и дифференцируема при любом
значении аргумента из области определения функции:
8)	Функция secx возрастает в промежутках [^2л/г;-g-4- 2л/гJ ;
^-^-4“2лп; л-|-2л/г^ , ngZ, и убывает в промежутках^ л + 2лп;
-^-+2лп^, (-у- + 2л/г; 2л(п4-1)^, n£Z.
График функции у =sec х изображен на .рис. 6.11.
Свойства функции cosec х.
1)	Область определения функции — множество всех действитель-
ных чисел, кроме чисел х — лп, п £ Z.
2)	Область изменения (множество значений) функции;
(—оо; —1] и [Ц +оо).
248
ГЛ. 6. ТРИГОНОМЕТРИЯ
3)	Функция cosec х — нечетная: coses (—х) = —cosec х.
4)	Функция cosec х — периодическая. Наименьший положитель-
ный период функции равен 2л:
cosec (х + 2л) «= cosec х..
каком значении аргумента не обра-
5) Функция cosec х ни при
щается в нуль.
6) Промежутки	зна непо-
стоянства:
cosec х > 0 при х £ (2лл; л +
+ 2ли), п £ Z,
cosec х < 0 при х £ (л + 2ли;
2л (п+ 1)), ngZ.
7) Функция cosec х непре-
рывна и дифференцируема
при любом значении • аргу-
мента из области определения
функции:
/ х/ cosх
(cosec х)
[Л	\
•—+ 2лл; л + 2лп )
/	Зл 1	/л
и ( л + 2лл; -2~ + 2лп I , n £ Z, и убывает в промежутках ( 2лп; -g- -f*
]г Зл	\
и -у-4-2лд; 2л+ 2лл), n£Z.
График функции у = cosec х изображен на рис. 6.12.
1.5.	Обратные тригонометрические функции.
Функция arcsin х. Функция у = sin х определена и непре-
рывна при любом х С R. Выделим на числовой оси Ох промежуток
[—л/2; л/2]. На этом промежутке функция у = sin х возрастает;
на левом конце промежутка (при х = —л/2) функция у = sin х дости-
гает своего наименьшего значения, равного —1, а на правом конце
(при х = л/2) — своего наибольшего значения, равного 1. Функция
у~ sinx,' рассматриваемая на промежутке [—л/2; л/2], имеет обрат-
ную функцию, которую называют арксинусом и записывают
х = arcsin у,
где у — независимая переменная, ах — зависимая. Обозначая, как
обычно, независимую переменную буквой х, а зависимую — буквой у,
будем далее писать у = arcsin х.
Свойства функции arcsin х.
1)	Область определения — промежуток [—1; 1].
2)	Область изменения (множество значений) — промежуток
{—л/2; л/2].
3)	Функция arcsin х — нечетная: arcsin (—х) == —arcsin х.
4)	Нули функции: arcsin х = О при х = 0.
5)	Промежутки знакопостоянства:
arcsin х > 0 при х £ (0; 1 ].
arcsin х < 0 при х £ 1—1; 0).
§ Т. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
249
6)	Функция arcsin х непрерывна и дифференцируема в каждой
точке промежутка (—1; 1):
(arcsin х)
1
7) Функция arcsin х возрастает на промежутке [—1; 1], прини-
левом конце проме-
мая свое наименьшее значение, равное —л/2, на
жутка и наибольшее значение, равное л/2, на
правом конце промежутка [—1; 1].
График функции у = arcsin х изображен
на рис. 6.13.
Функция arccos х. Функция у = cos х
определена и непрерывна при любом х С R.
Выделим на числовой оси Ох промежуток
(0; л]. На этом промежутке функция у = cos х
убывает; на левом конце промежутка (при х = 0)
функция у = cos х достигает своего наиболь-
шего значения, равного 1, а на правом конце
(при х == л) — своего наименьшего значения,
равного —1, Функция у = cos х, рассматри-
ваемая на промежутке [0; л], имеет обратную
называют арккосинусом и записывают
функцию, которую
х = arccos yt
где у — независимая переменная, ах — зависимая. Обозначая, как
обычно, независимую переменную буквой х, а зависимую — буквой у,
будем далее писать у = arccos х. -
Свойства функции arccosх.
1) Область определения — промежуток [—1; 1].
НУ	2) Область изменения (множество значений) —
промежуток [0; л].
3) Функция arccos х не является ни четной,
тг/2 ни нечетной.
\	4) Нули функции: arccos х = 0 при х = 1.
\	5) Промежутки знакопостоянства: afcoos х > 0
— V при х £ |—1; 1).
*7 О / гг? 6) Функция arccos х непрерывна и дифферен-
цируема в каждой точке промежутка (—1; 1);_
Рис. 6.14.	1
(arccos х) = -^==.
7) Функция arccos х убывает на промежутке [—1; 1], принимая
наибольшее значение, равное л, на левом конце промежутка и наимень-
шее значение, равное 0, на правом конце промежутка.
График функции у = arccos х изображен на рис. 6.14.
Функция arctg х. Функция у = tg х непрерывна в своей
/	л '
области определения (т. е. при всех х g R, не равных -у + ли,
п g Z). Выделим на числовой оси Ох промежуток (—л/2; л/2). На этом
промежутке функция # == tg х возрастает и принимает все свои зна-
чения. Функциям » tg х, рассматриваемая на промежутке (—л/2; л/2),
250	ГЛ. 6. ТРИГОНОМЕТРИЯ
имеет обратную функцию, которую называют арктангенсом и запи-
сывают
х = arctg у,
где у — независимая переменная, а х — зависимая. Обозначая, как
обычно, независимую переменную буквой х, а зависимую — буквой у,
будем далее писать у = arctg х.
Свойства функции arctg х.
1)	Область определения — вся числовая прямая.
2)	Область u изменения (множество значений) — промежуток
(—71/2; л/2).
3)	Функция arctg х нечетная: arctg (—х) = —arctg х.
4)	Нули функции: arctg х = 0 при х = 0.
5)	Промежутки зн а непостоянства.’
arctg х>0 при х£(0; +оо),
arctgx<OnpH х£(—оо; 0).
6)	Функция arctg х непрерывна и дифференцируема при
всех х £ R:
(arctg х)'=——j.
7)	Функция arctg х — возрастающая.
График функции у — arctg х изображен на рис. 6.15.
Функция arcctg х. Функция у = etg х непрерывна в своей
области определения (т. е. при всех х £ R, не равных Tin, п £ Z).
Выделим на числовой оси Ох промежуток (0; л). На этом промежутке
функция у =» etg х убывает и принимает все свои значения. Функция
у = etg х, рассматриваемая на промежутке (0; л), имеет обратную
функцию, которую называют арккотангенсом и записывают
х == arcctg у.
где у — независимая переменная, ах — зависимая. Обозначая, как
обычно, независимую переменную буквой х, а зависимую — буквой у,
будем далее писать у = arcctg х.
Свойства функции arcctg х.
1)	Область определения — вся числовая прямая.
2)	Область изменения (множество значений) — промежуток (0; л).
3)	Функция arcctg х не является ни четной, ни нечетной.
4)	Функция arcctg х положительна при всех х f R.
5)	Функция arcctg х непрерывна и дифференцируема при всех
х 6 R:
(arcctg х)'= —
§ !. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
251
6)	Функция arcctg х — убывающая.
График функции у = arcctg х изображен на рис. 6,16.
1.6. Значения тригонометрических функций некоторых углов.
Значения тригонометрических функций углов в 0°, 30°, 45°, 60° и 90°
можно вычислить, используя определения соответствующих тригоно-
метрических функций. Значения тригонометрических функций углов
1СО 15’	15°
в 15 , —н—» —з—> ... можно наити по известным значениям триго-
2	4
неметрических функций 30°, последовательно используя формулы
половинного угла (см. пример 1). Значения тригонометрических функ-
ций углов, кратных 18°, можно найти, зная значение хотя бы одной
тригонометрической функции 18°, например sin 18° (см. пример 2).
Некоторые значения тригонометрических функций приведены
в табл. 2.
ТАБЛИЦА 2
Аргумент	Функция			
	sin а	cos а	tga	ctg а
0° (0)	0	1	0	не определен
15»	/3 — 1	/3-4-1	2 —/3	2 4-/3
1 12 )	2 /2	2 /2		
18° (-ДЛ	/5- 1	/54-/5	/5 — 1	Ию 4- 2 /5
\ 10 /	4	2 /2	V 10 4- 2 /б	/5- 1
зо° (ЛА	1	/3	1	/3
k G )	2	2	/3	
36<> / л \	Иб- /5	/5 4- 1	V 10—2/5	/5 4- 1
\ 5 /	2 /2	4	/54-1	V 10—2/5
45° (ЛА	1	1	1	1
1 4 /	Vi	/2		
54® /Л\	/£+_]_	/б - /5	/54-1	Ию - 2 /5
	4	2 /2	/10 — 2/5	/5 4- 1
600 (4-)	/3 2	1 2	/з	1 /3
72° f	/в 4- /5	/5 — 1	Ию + 2/5	И«-1
\ 5 /	2 Vi	4	/5— 1	V 10 4-2 /5
7RO ( 5Л \	Уз+ ।	/3 - I		
75 (-)	2/2	2 /2	24-/3	2 —/3
900 (-г)	1	0	не определен	0
252
ГЛ. 6. ТРИГОНОМЕТРИЯ
Пример 1. Вычислить cos 15м.
Так как косинусы углов а и а/2 связаны равенством
то, полагая а 30®, получаем
. . £1
c0S2I5o=l±^30_°, C0sM5o = J_2_ .2+Я,
1<2-ь/з ГЗ+ 1
COS 15  -------------я----------7=—.
2	2/2
Значение sin 15° можно вычислить, используя связь между
функциями sin а и cos а:
sin2 а+ cos2 а«« 1,
из которой находим	______'Л
«п is- _ ггат-Й/ 
2	2/2
Здесь из двух возможных знаков (плюса и минуса) перед ради*
калом выбран знак плюс, так как 15° — угол,
лежащий в первой четверти, и sin 15® >0.
Пример 2. Вычислить значения триго*
неметрических функций угла 18°.
Рассмотрим равнобедренный треугольник
АВС (| АВ | = | ВС |) с углом при вершине
в 36° (рис. 6.17). Углы при основании треуголь-
ника АВС равны 72°. Проведем биссектрисы
угловВДСи АВС.Отрезки биссектрис, лежащие
внутри треугольника, обозначим соответственно
через AM и ВК.
Рассмотрим треугольник АМС. В тре*
угольнике АМС МАС равен 36°, ^АМС ==
= ^МСА. Следовательно, треугольник АМС
подобен треугольнику АВС.
Обозначая | ВС | через а, |ДС|через^
а | МС | через х, условие подобия треугольны-
можно записать в
|МС|
WT= I ДС| или
Так как биссектриса внутреннего
рону, которую она пересекает, на г—'
жащим сторонам, то для треугольника
| МВ |
6.17,
Рис,
Л b
ков ДВС
С
и АМС
|АС|
виде
b х
а ~~ b
yvna треугольника делит сто-
отрезки, пропорциональные приле*
□ника АВС имеем
|ДВ| |МВ|	а а — х
ТПГТГГ ~ ЛЛ7ГГ 9 ИЛИ	= ------
| AC I IМС | 9	b х
Рассмотрим прямоугольный треугольник В КС а углом КВС9
равным 18°:
(1)
(2)
J L_______L. — sin
| ВС | ~ 2а - Ш 1 •
§ 2. ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ	253
Таким образом, для нахождения значения sin 18е необходимо из
уравнений (1) и (2) найти величину Ь/(2а). Из уравнения (1) получаем
х = &/а. Подставив выражение для х в уравнение (2), получим
а а2,	,
~S=^“"L
Введя новую переменную z == Ыа9 последнее уравнение можно запи-
сать в виде
z2+z — 1 = 0.
Корни этого квадратного уравнения:
г. - - '
г1>2 _	2
По своему геометрическому смыслу величина Ы(2а} положительна
и равна (]/*5 — 1)/4. Это число и есть значение sin 18°:
sin 18° = -О~ L.
4
Далее, используя формулу sin2 а + cos2 а = I и определения
функции tg х, etg х, можно найти значения cos 18Q, tg 18 , etg 18°,
а по формулам двойного угла sin 36°, cos 36Q. Так, например, sin 36Q
можно вычислить следующим образом:
cos 18° = /1—sin218Q = ^10 + 2^ t
, sin 36° = 2 sin 18'cos 18° =
= 4-(K5- 1)И104-2/5 = 4-ИЮ-2 J<5.
o	4
§ 2» Тригонометрические формулы
2.1,	Формулы приведения. Вычисление значений тригонометриче-
ских функций любого угла сводится к вычислению значений тригоно-
метрических функций острого угла по следующим правилам:
1)	Если угол положительный и больший 2л, то функции синус
и косинус данного угла приводятся к функциям угла, большего 0 и
меньшего 2л, по формулам
sin (а + 2ли) = sin а;
/ 1 п \	а € (0; 2л), п € Z,
cos (а + 2лп) = cos а
в функции тангенс и котангенс данного угла — к функциям угла,
большего 0 и меньшего л, по формулам
tg (« + ли) = tg а;
7 ,Т_ \	Z.
etg (а + лп) = etg а
254
ГЛ. 6. ТРИГОНОМЕТРИЯ
2)	Если угол отрицательный, то тригонометрические функции
данного угла приводятся к тригонометрическим функциям положи-
тельного угла по формулам
sin (—а) = —sin а;	cos (—а) == cos а;
tg (—а) = — tg а;	ctg (—а) == —ctg а.
3)	Тригонометрические функции угла, большего л/2 и меньшего 2л,
приводятся к тригонометрическим функциям острого угла по формулам
приведения (см. табл. 3), которые можно сформулировать в виде сле-
дующего правила:
таблица з
Функция	Аргумент			
	13= ±а	p = л ± a	о 3л ±a	p s» 2л — a
Sin Р	cos a	4= sin a	—cos a	•—sin a
COS Р	=Fsin a	—cos a	±sin a	cos a
tg р	Tctga	±tga	=Fctga	—tg a
Ctg р	=Ftga	±ctg a	Ttga	—ctg a
Если в формуле приведения угол а вычитается из л/2 или прибав-
ляется к л/2, взятому нечетное число раз, то приводимая функция
меняется на кофункцию *); если же л/2 взято четное число раз, то
название приводимой функции сохраняется. При этом перед приве-
... денной функцией ставится тот знак, который имеет приводимая функция
в соответствующей четверти, если	^трыц»
2.2.	Связь между тригономе^^ч^оЙши"ф^^^ХшоЗного аргу-
мента. В табл. 4 приведены формулы, связывающие тригонометриче-
ские функции одного и того же аргумента. В приведенных формулах
перед знаком радикала должен быть выбран знак «плюс» или «минус»
в зависимости от того, в какой четверти находится угол а, а именно
таким образом, чтобы знак тригонометрической функции, стоящей
i в левой части, совпадал со знаком величины, стоящей в правой части
равенства.
2.3.	Тригонометрические функции суммы и разности углов.
sin (а ± ₽) = sin a cos 0 ± cos а sin 0;
cos (а ± 0) = cos а cos 0 sin a sin 0;
,	tga±tgB	ctgactg0=Fl
tg (a ± 0) — r .p tg a tg p , c g (a ± 0) — ctg p ± ctg a
Косинус является кофункцией по отношению к еинусу, и наоборот.
Др^гаа пара кофункций » тангенс и котангенс.
* 2. ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
255
ТАБЛИЦА
256
ГЛ. в. ТРИГОНОМЕТРИЯ
2.4.	Тригонометрические функции двойных, тройных и половин-
ных углов.
sin 2а = 2 sin а cos а;
cos 2а = cos1 2 а — sin2 а == 1 — 2 sin2 а = 2 cos2 а — 1;
tg2a = -2^а.
ё 1 - tg2 а ’
sin4За = 3 sin а — 4 sin3 а;
etg 2а ==
etg2 а — 1
2 etg а
cos За = 4 cos3 а — 3 cos а;
3tga — tg3a
1 — 3 tg2
etg За
_ etg3 а — 3 etg а .
3 etg2 а — 1	’
. а т Г 1 — cos а . а 7 Г1 + cos а
Sin-T = ± |/ -------2----; cos^- = ± |/	----
а _	1/ 1 — cos а sin а	__ I — cos а
* 2	г	1 + cos а 1 + cos а	“ sin а	’
, а —	1Л 1 + cos а _ sin а	__ 1 4- cos а
s 2	г	1 — cos а	“ 1 — cos а sin а	’
В формулах половинного угла знаки перед радикалами берутся
в зависимости от знака тригонометрической функции, стоящей в левой
части равенства.
2.5.	Преобразование суммы (разности) тригонометрических функ-
ций в произведение (преобразование тригонометрических выражений
к виду, удобному для логарифмирования).
.	।	j	q	n	j	a + р	а —В
sin а 4- sin р = 2 sin cos —---;
.	п	о	а4~р.	а —Р
sin а	— sin р == 2 cos —sin	—;
,	о	а4-Р	а — р
cos а 4- cos Р = 2 cos —--J- cos —;
д . а + Р а —р . а4-Р . Р —а
cos а —- cos р == —2 sin —sin —= 2 sm--^  sin ;
cos а + sin а = j/*2 cos (45° — а);
cos а — sin а = J/"2 sin (45° — а);
tga± tgp =
sin (а ± р) ,
cos a cos р ’
etg а ± etg р ==
sin (р zfc а)
sin a sin р
tga4-ctgp
_ cos (а — Р).
cos a sin р ’
tga —etg р
___ cos (а 4- р) e
cos a sin р ’
tga 4- etg а = 2 cosec 2а;
tg а — etg а = —2 etg 2а;
1 4- cos а = 2 cos2 —;
14- sin а == 2 cos2 ^45°-----;
1 — cos а = 2 sin2 —;
1 — sin а = 2 sin2 ^459--------уЛ ;
- . sin (45° ± а)
l±tg а=?------
& cos 45 cos а
j/2 sin (45° + а) .
cos а ’
§ 2. ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ
257
7 }	□ cos (а Р) •
— g	cos а cos 3 ’
f _ cos 2а
1-^а = ЖГ;
tg2 а — tg2 Р =
ctg2 а — ctg2 р =
. го 1 cos(a=FP),
ctg a ctg 3 ± 1 = ——-----:—7Г J
6 б' = sin a sin р ’
.	. _	cos 2а
I — ctg2 а ==----—>—;
s	sin2 а
sin (а + Р) sin (а — 3) .
cos2 a cos2 Р	’
sin (а + р) sin (Р — а) .
sin2 a sin2 р	’
tg2 а _ sin2 а == tg2 a sin2 a; ctg2 а — cos2 а = ctg2 a cos2 а.
2.6.	Преобразование произведения тригонометрических функций
в сумму.
sin a sin р = [cos (a — р) — cos (a + P)];
cos a cos 3 = [cos (a — P) + cos (a 4- p)];
sin a cos 3 — -y [sin (a — p) 4- sin (a 4- P)J;
sin a sin p sin у ==
= [sin (a4-P — Y) + sin(3 + y — a) +
4- sin (y 4- a — p) — sin (a + 3 4- y)];
sin a cos P cos у =
= ~ [sin (a 4- p — у) — sin (P 4- V — a) +
4- sin (у 4- a — P) + sin (a + 3 + y)]5
sin a sin p cos у =
= l-[—cos(a + P-.Y) + cos(p4-Y — a)4-
+ cos (y 4- a — P) — cos (a 4- p + y)],
cos a cos P cos у =
«= A- [cos (a4-p — y)4-cos(p+y--a)4-
4- cos (y + a — P) 4- cos (a + P 4- y)].
2.7. Простейшие соотношения между обратными тригонометри-
ческими функциями.
arcsin a = — arcsin (—a) = —---arccos a = arctg --r==-;
2	S / 1 — «2
/ x л	.	, a
arccosa = л — arccos (—a) = -5-arcsina=arcctg  -........ ;
z	V 1 —
.9 А. Г. Цыпкин
258
гл. е. тригонометрия
arctg а = — arctg (—а) = -----arcctg а == arcsin
arcctg а = л — arcctg (—а) = -----arctg а == arccos	•
Более сложные зависимости между обратными тригонометриче*
сними функциями могут быть установлены методами, используемыми
при решении уравнений, содержащих обратные тригонометрические
функции (см. п. 3.4).
Y Пример. Выразить сумму двух обратных тригонометрических
] функщйч^-^
I	arcsin х + arcsin у
через одну обратную тригонометрическую функцию (например, арк«
синус).
Обозначим приведенную выше сумму буквой г:
arcsin х + arcsin у = z.	(1)
<. Данное равенство можно рассматривать как уравнение с тремя неизве*
стными х, у и г. Уравнение (1) является следствием следующего урав«
? * нения:
sin (arcsin х + arcsin у) = sin z,
которое приводится к виду
sin (arcsin x)-cos (arcsin у) + sin (arcsin j/)-cos (arcsin x) я
== sin г <=> x /1 — у2 + у Y1 — *2 = sin г.
Теперь нужно решить уравнение относительно переменной zj
учитывая, что эта переменная принадлежит промежутку [—л; л].
Множество решений этого уравнения будет иметь вид
г = arcsin (х }f 1 — у2 + у 1 — х2)
при ху 0 или х2 + у2 1;
z = л — arcsin (х У1 — у2 + у j/1 — х2)
при х > 0, # > 0 и х2 + у2 > 1;
г == — л — arcsin (х /1 — у2 + у /1 — х2)
при х < 0, у < 0 и х2 + у2 > 1.
Полученные выражения для переменной г и дают искомое выра*
жение суммы двух обратных тригонометрических функций через одну
обратную тригонометрическую функцию.
§ 3# Решение тригонометрических уравнений
и неравенств
3.1.	Простейшие тригонометрические уравнения.
Решение уравнения sin х = а. Рассмотрим функцию
у = sin х на промежутке [—л/2; л/2]. На этом промежутке функция
у = sin х возрастает, меняясь от своего наименьшего значения, оав<
ного —1, на левом конце промежутка до своего наибольшего значения^
$ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 259
равного 1, на правом конце промежутка (риа. 6.18). В силу непрерыв-
ности функции у » sin х каждому значению у = а, удовлетворяющему
условию | а | < 1, соответствует единственное значение х^ £ I—л/2; л/2]
такое, что
sin Xq » а.
Угол *ь есть арксинус числа а (обозначается arcsi»a).
Уравнение вида sin х « а при | а | < 1 имеет множество решений
х « (—1)” arcsin а + лп, п g Z; при | а | > 1 уравнение решений
не имеет (т. е. множество решений — пустое множество).
Решение уравнения cos х = а. Рассмотрим функцию
у = cos х на промежутке [0; л]. На этом промежутке функция у =
«== cos х убывает, меняясь от своего наибольшего значения, равного 1,
на левом конце промежутка до своего наименьшего значения, равного
— 1, на правом конце промежутка (рис. 6.19). В силу непрерывности
функции у = cos х каждому значению у ~ а, удовлетворяющему
условию |а| < 1, соответствует единственное значение £ [0; л]
такое, что
cos х0 — а.
Угол Xq есть арккосинус числа а (обозначается arccos а).
Уравнение вида cos х = а при ] а |	1 имеет множество решений
х = -^агссозаЧ- 2лп, п £ Z; при |а| > 1 уравнение решений не
имеет (множество решений — пустое множество).
Решение уравнения tg х = а. Функция у = tgх на
промежутке (—л/2; л/2) возрастает и принимает все свои значения
(рис. 6.20). В силу непрерывности функции у == tg х каждому значе-
нию у = а соответствует единственное значение х0 £ (—л/2; л/2)
такое, что
tg х0 = а.
Угол xq есть арктангенс числа а (обозначается arctg а).
Уравнение вида tg х = а при любом а имеет множество решений
а =* arctg а + лп, л £ Z.
9*
260
ГЛ* 6. ТРИГОНОМЕТРИЯ
Решение уравнения etg х ® а. Функция у » etg х
на промежутке (0; л) убывает и принимает все свои значения (рио. 6.21).
В силу непрерывности функции у = etg х каждому значению у == а
соответствует единственное значение х0 £ (0; л) такое, что
etg х0 = а.
Угол Xq есть арккотангенс числа а (обозначается arcctg а).
Уравнение вида etg х = а при любом а имеет множество решений
х = arcctg а + лп, п g Z.
3.2.	Примеры более сложных тригонометрических уравнений^
I)	Тригонометрическое уравнение вида
Р (sin kx, cos пх, tg mx, etg lx) = 0,	(1)
где P — многочлен указанных аргументов (k, n, tn и I — натуральные
числа), с помощью формул для тригонометрических функций суммы
углов (в частности, формул двойного и тройного угла) можно свести
к рациональному уравнению относительно аргументов sin х, cos х,
tg х и etg х, после чего уравнение (1) может быть сведено к рациональ*
ному уравнению относительно неизвестной / = tg-g-с помощью фир^
мул универсальной подстановки
sinx =	2tg~r		l-tg24r.
	l + tg2-f ’		1 + tg24r ’
tg* =	2tg-j-	ctgx =	l-tg2-f-
	1 — ’		2tg“g“
Пример 1. Решить уравнение
sin 2х + tg х в» 2.
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 26!
Выражая sin 2х через tg х, получаем уравнение
которое приводится к кубичному уравнению относительной яеиэвест*
ной/etgx:
Г8 — 2/2+ 3/ — 2 « 0 <=> (/ — 1) (/а — /+ 2) « 0.
Легко убедиться, что данное уравнение имеет только один действие
тельный корень: t = 1.
Решая уравнение tg х » 1, находим множество решений исходного
уравнения: х =	+ nkt k g Z.
Изложенный общий метод сведения тригонометрического урав*
нения к целому уравнению не всегда удобен, так как в ряде случаев
он может свести решение тригонометрического уравнения к нахождению
корней многочлена довольно высокой степени.
2)	Уравнение вида
Р (sin х 4- cos х, sin х cos х) « 0,	(2)
где р — многочлен от указанных аргументов, может быть сведено
к уравнению относительно неизвестной t = sin х + cos х, если восполь*
зоваться тригонометрическим тождеством
(sin х + cos х)2 = sin2 х + cos2 х + 2 sin х cos х = 1 + 2 sin х cos х,
из которого следует, что
/а__1
sin х cos х = —.	(3)
Учитывая соотношение (3), уравнение (2) можно привести к виду
^)-0.
Аналогичным образом уравнение вида
Р (sin х — cos х, sin х cos х) =» 0
заменой sin х — cos х = t сводится к уравнению
Пример 2. Решить уравнение
sin х + cos х — 2 /2 sin х cos х = 0.
Обозначая sin х + cos х = t и пользуясь равенством
sin х cos х = —,
сводим уравнение к следующему квадратному уравнению относительно
неизвестной
—— /2 = 0;
262
ГЛ. 6. ТРИГОНОМЕТРИЯ
корнями этого квадратного уравнения будут числа
/1 = 1/2 и /а = — 1/К2.
Таким образом, решение исходного уравнения сводится к решению
двух более простых тригонометрических уравнений?
sin х 4- cos х = l/*2 и sin* + cosx =--------
/2
Умножая обе части полученных уравнений на 1/J/"2, сводим урав-
нения к двум более простым тригонометрическим уравнениям:
1	1	,	. л , . л	.
—sin х 4- cos х = 1 -фф sm х cos —г- + sin — cos х = 1<=>
у 2 ош л яг у 2	4	4
<=► sto (* + пр) = 1.
1 .	, 1	1	. / , л \	1
Sin X + —г COS X =-----5- ф=ф sin (х 4- -у- ) -------
J<2	J<2	2	\	4 /	2
Множества решений уравнений sin +	== 1 и sin +
1
«=-----g- будут соответственно иметь вид
х = 2L + 2л&,

х= (—I)n+!~---~ + шг, Z.
3)	Уравнение вида a sin х + b cos х —с (где at b и с — некоторые
числа) может быть решено при помощи формул универсальной под-
становки (см. 1)).
Кроме того, это уравнение может быть решено методом дополни-
тельного угла.	_______
Разделим обе части исходного уравнения на ]/~а2 + Ь2 Ф 0. (Если
d = Ь = 0, то уравнение превращается либо в тождество (при с=0),
либо не имеет решений (при с=й= 0).) В результате после деления полу-
чаем уравнение, эквивалентное исходному:
 ,    - sin х 4-cos х — ——==.	(4)
/а24-62	/аа4-62	/а24-62
Легко проверить, что коэффициенты а/|^а24-62 и 6/)/’aa-j-6а
связаны равенством
( -У I (-J— Г-.
\ /а2 + 62 /	\ /а2 +	/
а потому их можно считать значениями синуса и косинуса некоторого
&гла <р;
а	.	b
—........—	= Sin ф,	—	—- == COS ф,
/а2 4- о2	/а2 4- 62
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 2бЗ
Таким образом, уравнение (4) приводится к уравнению
cosхcos ф + sinхsinф =	<=>cos (x — ®) = _ g
*	T ]fa* + b*	/a2 +
множество решений которого при | с| < |Л12+62:
х = ф ± arccos -С '— 4- 2лл, пf Z.
Осталось найти какое-нибудь значение угла ф, являющееся рсше*
нием системы тригонометрических уравнений
а	b
SHI ф = _	.	, COS ф = ’—=7-.
/а2 + д2	/а2 + д2
Здесь возможны следующие случаи (для ф выбраны наиболее'
простые из нескольких возможных выражений). Если а > О, b > 0, то
а	b	а
Ф = arcsin —-=- — arccos —-z=- — arctg -г- >
/а2 + b*	У a*+ &>	b
если а > 0, b < 0, то ф - arccos -—====- J
/а2 + d2
если а<0, 6<0, то ф = л + arctg;
если a < 0, b > 0, то ф = arcsin —....- = arctg -4- •
/а2 + *2	b
4)	Уравнение вида
sinp х + cos* х = 1 (pt k = 3, 4, 5, ...)
может быть решено следующим способом.	|
Из определения функций sin х и cos х следует, что при всех зна*‘
чениях аргумента х У» —п € Z, справедливы неравенства
sinp х < | sin х |р < sin2 х, cos* х | cos х |* < cos2 х.
Как следствие этих неравенств получаем неравенство
sinp х + cos* х < | sin х |р + | cos х I* < 1.
Следовательно, решениями исходного уравнения могут быть лишь числа
из множества значений аргумента х = лп/2, п £ Z.
Далее процедура нахождения корней сводится к проверке — какие
из указанных значений аргумента являются корнями данного урав«
нения.	J
3.3.	Решение простейших тригонометрических неравенств. В табл. 5
приведены множества решений простейших тригонометрических нера<
венств. Более сложные тригонометрические неравенства решаются^
методами, сходными с методами решений тригонометрических урав*
нений.
264
ГЛ. 6. ТРИГОНОМЕТРИЯ
ТАБЛИЦА б
Вид неравенства	Множество решений неравенства (ngZ)
sin	х > а	(|	а	|	<	1) sin	х < а	(|	а	|	<	1) cos	х > а	(|	а	|	<	1) cos	х < а	(1	а	|	<	1) tg х > а tg х < а ctg х > а ctg х < а	х £ (arcsin а 4- 2лл; л —• arcsin а 4- 2лп) х g (-»л arcsin а 4- 2лп; arcsin а 4- 2лл) х £ («arccos а 4- 2лп; arccos а 4- 2лп) х £ (arccos а 4- 2лп; 2л я» arccos а 4- 2ли) х£ (arctg а 4-лп; -^-4-лл^ х £ (— -у + лл: arctg а 4- лп j х £ (лп; arcctg а 4- лп) я £ (arcctg а 4-лп; л 4-лп)
3.4.	Примеры решения уравнений и неравенств, содержащих
обратные тригонометрические функции. В табл. 6 приведены мно-
жества решений простейших неравенств для обратных тригономет-
рических функций.
ТАБЛИЦА 6
Вид неравенства		Множество решений неравенства
arcsin х > а	(М<1)	х g (sin а; 1]
arcsin х < а	/	.	Л \ (ик—)	sin fl)
arccos х > а	(0 < а < Л)	«£[—1: cos а)
arccos х < а	(0 < а < л)	x g (cos а; 1]
arctg х > а	('“K-J-)	#£(tgfl; 4-oo)
arctg х < а	С-х-т)	x £ (-* co; tg a)
arcctg х > а	(0 < а < Л)	xg(—oo: ctg a)
arcctg х < а	(0 < а < Л)	x£ (ctg a; 4- °°)
Рассмотрим несколько примеров решения более сложных уравне-
ний и неравенств, содержащих обратные тригонометрические
функции.
Пример 1. Решить уравнение
arcsin х + arcsin 2х = -у-	(5)
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 265
Множество допустимых значений неизвестного х — промежуток
[—1/2; 1/2]. Обозначая arcsin 2х = a, arcsin х = 0, получим
sina = 2x, ag[—л/2; л/2];
sin 0 = х,	pg [—л/6; л/6].
В новых обозначениях уравнение (6) запишется в виде
а + Р=4-«{=>« = ^--------Р-	(7)
О	о
Из условий (6) следует, что углы а и -----0 принадлежат проме-
жутку [—зт/2; л/2 ]. Следовательно, уравнение (7) эквивалентно урав-
нению
sin a = sin ^-^- — 0^ <=> 2х = sin	cos0 — sin £ cos (8)
Из равенства
sin2 0 + cos2 0=1,
с учетом условий (6) следует, что
cos 0 = У1 — х2.
Следовательно, уравнение (8) можно записать в виде
2х =	/1 — х2-----<=>4х =
= |/3 /1 — х2 — х <=> 5х = /3 /1 — х2.
Возведя обе части последнего уравнения в квадрат, находим един*
ственное решение этого иррационального уравнения:
Найденное значение х и есть решение исходного тригонометрического
уравнения (5).
Пример 2. Найти область определения функции
г, ч • z j \ •	/2 arccos х \
f (х) = arcsm (arcsin х) + arccos (2— ) ’
Область определения данной функции находится как множество
решений следующей системы неравенств:
—1 <х< 1,
—1 arcsin х < 1,
__.	2 arccos х .
"" л — 2
Решим второе неравенство системы:
—1 < arcsin х < 1.	(9)
Так как множество значений функции арксинус — промежуток [—л/2;
л/2], то все углы, фигурирующие в неравенстве (9) (—1, arcsin х и 1),
266
ГЛ. 6. ТРИГОНОМЕТРИЯ
принадлежат промежутку монотонного возрастания функции синус.
Следовательно, неравенство (9) эквивалентно неравенству
sin (—IX sin (arcsin x)<sin 1 О —sin 1 <x<sin L
Решим третье неравенство системы:
-l^larcc^x	()0)
Л — z
Умножая все три части двойного неравенства на положительную ве-
л — 2	/1Л.
личину —-—, получим неравенство, эквивалентное неравенству (10)5
л ~ 2	-л — 2
-----2— < arccos х < —.
Это двойное неравенство эквивалентно системе двух неравенств
л — 2
arccos х >----g—,
л — 2
arccos х< ——>
причем первое неравенство справедливо при всех значениях х £ [—1; 1 ],
так как множество значений функции арккосинус — промежуток
(0; л].
Решим второе неравенство системы. Так как величины, стоящие
в обеих частях неравенства, принадлежат промежутку монотонного
убывания функции cos х, то это неравенство эквивалентно неравенству
cos (arccos х) > cos ---1 = sin 1.
Таким образом, область определения данной функции находится как
множество значений х, удовлетворяющих системе
—1<х< 1,
—sin 1 х < sin 1,
х sin 1.
Эта система имеет единственное решение х == sin 1. Таким образом,
область определения данной функции f (х) состоит из одной точки
х = sin 1.
§ 4. Соотношения между элементами треугольника
4.1. Основные формулы. Обозначения: a, Ь, с—стороны тре-
угольника; а, 0, у — углы треугольника (рис. 6.22); р =	_
полупериметр; S — площадь; R — ра-
диус описанной окружности; г — радиус
вписанной окружности; h — высота; т —
медиана; I — биссектриса; индексы а, Ь, с
при ht т и I конкретизируют одну из
трех высот, медиан и биссектрис соот*
ветственно (например, та — медиана,
проведенная к стороне а); га — радиус
§ 4. СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКА 207
вневписанной окружности, касающейся стороны а и продолжения
сторон b и с.
1.	Теорема косинусов. Квадрат стороны треугольника
равен сумме квадратов двух других сторон минус удвоенное пр она-
ведение этих сторон на косинус угла междуTfflflbj
а» = ь2 + с2 — 2bc cos а;
д2 — а2 + с2 — 2ас cos ₽;
с2 ® а2 + 0й — 2ab cos у.
2.	Теорема синусов. Стороны треугольника пропор-
циональны синусам противолежащих углов:
-2— = _* = _Д_ = 22?.
sin a sin 3 sm у
3.	Теорема тангенсов:
а -4- 3	’ у
a+h tg ~  de“ . о + а
°~с
•8^
. а •— у
Ь-\-с
Ь — с
t а
Й8—

4.	Формулы вычисления площади треуголь-
вика:
S = -у- ab sin S = Vp{p — a)(p — b)(p — cj;
S = ₽2tg-^- tg-^-tg-y-;
S = р (р — a) tg = р (р — b) tg -у- = р (р — с) tg -у;
S = '47?"; S==pr> S==yrrarbr.-
4.2. Вычисление элементов треугольника. Треугольник можно
задать либо тремя сторонами, либо одной
либо двумя сторонами и углом между
ними. В качестве тройки элементов, за-
дающих треугольник, можно выбрать и
некоторые другие наборы элементов тре-
угольника. Например, треугольник можно
задать основанием а, высотой ha и углом
при основании. Имея тройку элементов,
задающих треугольник^ с помощью тео-
ремы синусов и теоремы косинусов
стороной и двумя углами,
Рис. 6.23.
можно вычислить все остальные эле-
менты треугольника.
Пример 1. Пусть треугольник АВС задается тремя сторо-
нами а, b и с (рис. 6.23). Требуется вычислить все остальные элементы
треугольника.
268
ГЛ. 6. тригонометрия
Углы аир данного треугольника могут быть найдены а помощью
теоремы косинусов:
 | - с2 — а2
а2 = Ь2 + с2 — 2bc cos а => cos а = —--------=> а =
Ь2 + с2 — а2
= arccos------Hsr-------
2bc
п2 -4- г2_h2
b2 = а2 + с2 — 2ас cos р cos р = —------------------=> р ==
2ас
а2 + с2 — Ь2
= arccos--------------
2ас
Третий угол треугольника у можно вычислить, используя равен-
ство, связывающее углы треугольника:
а 4- р 4- Y = 180° => -у = 180° — arccos —+	_
£uC
а2 + с2 — Ь2
— arccos-----.
2ас
Высота треугольника hc, опущенная на сторону с (см. рис. 6.23),
может быть найдена из прямоугольного треугольника СНВ*.
hc . о ,	. о	Г а2 -4- с2 — b21	.,
— = sin р => пс = a sin р = a sin arccos-------------- => hc =
a	I,	2ас J
д2 с2 — Ь2 \ 2
= а
2ас ) *
Для нахождения медианы тс воспользуемся тем, что точка М де-
лит сторону с пополам (| AM | = | МВ |); следовательно, в треуголь-
нике МВС оказываются известными две стороны | МВ | = с/2, | ВС | =а
и угол между ними р. Используя теорему косинусов для треугольника
МВС, получаем
/ Л \2
а2


2
а2 + Ь2	с2
2	Г *
Биссектрису 1С можно найти из треугольника LBC. В треуголь-
нике LBC нам известны сторона ВС (| ВС | = а) и угол р. Угол LCB =а
«= у/2 равен
V опа 1 ь2 + с2-а2
-Т = 90 “ — arccos-^---------
Отсюда
CLB = 180G— LCB—^ LBC =
b2 + с2 — а2
1 а2 -|- с2 — Ь2
ту- arccos----!--------
2ас
— j 90°------g- arccos 
а2 + с2 — Ь2
— arccos---------------
2ас
1 а2 + с2 — b21
—7Г7-------тг arccos----------- -
2Ьс 2	2аа j
оло г 1	Ь2-\-с2 — а2
80 4-arccos------------------
1	а2 + с2 — Ь2
— -х- arccos	----------
2	2ас
§ 4. СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ТРЕУГОЛЬНИКА 269
Воспользуемся теперь теоремой синусов для нахождения биссек-
трисы 1С:
1С __ а	о sin ft
'sin / ~ sin -d CLB *** c e sin x: CLB 9
Легко заметить, что вычисление синуса угла CLB> стоящего в зна-
менателе последней дроби, будет довольно трудоемкой задачей. Бис-
сектрису треугольника можно вычислить и другим способом. Каи
известно, биссектриса делит сторону треугольника в отношении, про-
порциональном прилежащим сторонам:
\AL\ \LB\
|ЛС| ~ \СВ| •
Обозначая | LB | = х, это равенство можно записать в виде
С—ХХ	,	/ I м
—-— = — => ас — ах =« Ьх =>ас = х (а + Ь)	х = —:.
b a	v ‘	а^о
Теперь в треугольнике LBC нам известны две стороны | ВС |
| LB | = —и уГол между ними 0. Применяя теорему косинусов,
а и
получаем
С = I вс |2+ I LB I2 - 2 I ВС |.| LB I cos  => I2 =
у , / ас \2	2а2,с о ,о
= а + ( ——г \------— cos 3 => 1С =
’ \ а + b / а + b	с
о , / ас v	а2 с2 — Ь2
=	-т+т------2S3—=
— 1/ <-2 . / ш V	а (а2 4-с2 —	.
г "1” \ a -f- b )	а-\- b
Площадь данного треугольника АВС может быть найдена, напри-
мер, по формуле Герона:
5давс = Ур(Р — а){р—Ь)(р — с),
а радиусы вписанной и описанной окружностей — с помощью формул
5давс =	=
Q
°ДАВС
Р
с	аЬс п _ ahc
^вс~ 47? =>/?= 45^-’
Пример 2. Рассмотрим теперь треугольник, у которого даны
сторона а и два угла аир (рис. 6.24).
Третий угол у можно найти из равенства, связывающего углы тре-
угольника: а + Р + Y = 180° «=> у = 180° — а — р. Стороны АВ и
АС треугольника находятся с помощью теоремы синусов:
| ЛВ| _ а _________|ЛВ|________а | АВ |	__
ыи у ~ sin a sin (180° — а — 3) “ sin а sin (а + £)
= _^_^MS| = £^L±P>,
sin а ‘	sin а ’
.ffi. = _л_вИЛС| = «!!±.
ьшр sin а	sin а
270
ГЛ. 6. ТРИГОНОМЕТРИЯ
Таким образом, в треугольнике найдены три стороны; все осталь-
ные элементы треугольника (медиану, высоту, биссектрису и т. д.)
можно найти так же, как и в предыдущей задаче. Заметим, что радиуо
описанной окружности при данном наборе элементов, определяющих
треугольник, удобно находить по формуле
-Л-= 2/?=»/?=	° .
sma	2 sin a
Пример 3. Если в треугольнике даны две стороны Ь, с и угол
между ними а (рис. 6.25), то с помощью теоремы косинусов сразу
можно найти третью сторону треугольника:
| ВС |2 ~ Ь2 + с2 — 2bc cos a,
после чего все остальные элементы треугольника (углы, высоты, ме-
дианы, биссектрисы и т. д.) находятся так же, как и в примере 1.
г Л А В A 7
МЕТОД КООРДИНАТ
Понятие прямоугольной системы координат на плоскости впервые
появилось в геометрии еще до начала нашей эры. С ее помощью мате-
матик Александрийской школы Аполлоний определял и изучал кривые
второго порядка — эллипс, гиперболу и параболу. В XVIII веке
французский философ и математик Р. Декарт (и одновременно с ним
П. Ферма) ввел правило выбора знаков в прямоугольной системе
координат и заложил основы аналитической геометрии на плоскости —
раздела математики, устанавливающего связь между алгеброй и гео-
метрией. Работы Декарта были подготовлены работами его соотече-
ственника Ф. Виета, который впервые ввел в алгебру буквенные
обозначения (как известных, так и неизвестных величин). Аналити-
ческая геометрия сыграла важную роль в развитии понятия числаэ
благодаря правилу выбора знаков координат отрицательные числа,
которые не признавало большинство математиков средневековья по-
лучили наглядное изображение и окончательно утвердились в мате-
матике. В последующем применение прямоугольной декартовой си-
стемы координат сыграло решающую роль при утверждении в мате-
матике комплексных чисел.
§ 1. Системы координат
1.1. Координатная ось. Координатной осью называется прямая,
на которой фиксированы две различные точки: точка О, называемая
началом координат, и точка Е, называемая единичной точкой (рис. 7.J).
Обычно точку Е располагают справа от точки О. Положительным
направлением оси координат считается направление луча, выходящего
I....	>---------------------**
О Е По х
Рис. 7.1/
из точки О и содержащего точку Е. Противоположное направление
считается отрицательным направлением оси координат. Отрезок ОЕ
называется масштабным или единичным отрезком. Координатную ось
обычно обозначают Ох.
Вектор ОЕ называют единичным вектором (или ортом) и обычно
обозначают буквой е.
Координатой точки Af0, лежащей на координатной оси, называется
| ОМ0 |
число х0, определяемое равенством х0 = ±	» пРичем пеРеД
дробью берется знак плюс, когда точки Е и Мо лежат по одну сторону
272
ГЛ. 7. МЕТОД КООРДИНАТ
от точки О, и знак минус, когда точки Е и Мо расположены по разные
стороны относительно точки О; если точка Мо совпадает с точкой О,
то = 0.
Расстояние d между точками и М2 с координатами xt и х2 вы-
числяется по формуле
d = | х2 — *11-
1.2. Прямоугольная декартова система координат на плоскости*
Прямоугольной декартовой системой координат на плоскости назы-
вается упорядоченная пара двух взаимно перпендикулярных коорди-
натных осей Ох и Оу, причем началом координат каждой из осей слу-
жит их общая точка О (начало прямоугольной декартовой системы
координат) (рис. 7.2). Оси Ох и Оу упорядочены
следующим образом: если ось Ох повернуть вокруг
точки О на угол л/2 против движения часовой
стрелки, то она совпадет с осью Оук При этом
масштабные отрезки ОЕ± и ОЕ2 координатных
осей Ох и Оу обычно выбираются таким образом,
чтобы их длины были равны: | ОЕГ | == | ОЕ2 |. Тогда
при повороте оси Ох на угол л/2 против движения
часовой стрелки вокруг точки О точки и £а
совместятся. Ось Ох называется осью абсцисс, а ось
Оу — осью ординат. Векторы — ОЕг и е2 — ОЕ2
называются базисными векторами прямоугольной декартовой системы
координат (или ортами) и обычно обозначаются буквами I и J-.	= Z,
j
Таким образом, можно считать, что прямоугольная декартова
система координат на плоскости задается некоторой точкой О (началом
координат) и упорядоченной парой взаимно перпендикулярных еди-
ничных векторов (Z;/).
Координатные оси Ох и Оу разбивают плоскость на четыре чет-
верти (квадранта). Часть плоскости, лежащая выше оси Ох и правее
оси Оу, считается первым квадрантом; часть плоскости, лежащая
выше оси Ох и левее оси Оу, — вторым квадрантом; часть плоскости,
лежащая ниже оси Ох и левее оси Оу,— третьим, и часть плоскости,
лежащая ниже оси Ох и правее оси Оу, — четвертым квадрантом.
Плоскость с построенной системой координат называется координат*
ной плоскостью.
При изложенном выше способе упорядоченности координатных
осей систему координат называют правой прямоугольной декартовой
системой координат в отличие от левой прямоугольной декартовой
системы координат, в которой оси упорядочены следующим образом:
первая ось (ось Ох) совмещается со второй осью (осью Оу) поворотом
на угол л/2 по движению часовой стрелки. Далее под словами «пря-
моугольная декартова система координат» будет пониматься правая
прямоугольная декартова система координат.
В физике и механике наряду с декартовыми системами координат
употребляются косоугольные (правые и левые) системы координат,
в которых совмещение осей происходит при повороте на угол, отлич-
ный от прямого, а также криволинейные системы координат (полярные,
сферические, цилиндрические и т. д.).
Координаты точки на плоскости. Пусть Оху —
прямоугольная декартова система координат на плоскости с началом О
(см. рис. 7.2), Л40 — некоторая точка плоскости. Опустим из точки АГа
§ 1. СИСТЕМЫ КООРДИНАТ
273
перпендикуляры на оси Ох и Оу, которые пересекут указанные коор-
динатные оси в точках и N2 соответственно. Обозначим координату
точки лежащей на оси Ох, через х0, а координату точки N2, лежа-
щей на оси Оу, — через yQ.
Координатами точки Л40 в прямоугольной декартовой системе
координат называется упорядоченная пара чисел (х0; #0).
Число х0 называют абсциссой, а число yQ — ординатой точки Л40
и пишут Мо (х0; Ро)-
Расстояние между точками А и В, имеющими координаты (xf, у$
и У2) соответственно, вычисляется по формуле
I АВ | = /(Л2 — Х1)г 4- (у2 — у^.
Преобразования прямоугольных координат
при параллельном переносе осей. Пусть Оху и
О'х'у' — две прямоугольные декартовы системы координат на пло-
скости с началом координат О и О' (О =/= О') соответственно, с одина-
ково направленными осями (рис. 7.3) и одинаковыми масштабными
Рис. 7.3»	Рис. 7.4.
отрезками. Пусть точка О' относительно системы координат Оху имеет
координаты (а; Ь). Число а называют величиной сдвига системы коор-
динат О'х'у' относительно системы Оху по направлению оси Ох, а число
b — величиной сдвига по направлению оси Оу.
Пусть точка Л40 имеет координаты (х0; г/0) относительно системы
Оху. Тогда ее координаты (х^; y'Q) относительно системы О'х'у1 связаны
с координатами относительно системы Оху формулами
Xq = Xq — а, Уа^Уо — Ь.
Эти формулы называют формулами преобразования прямоугольных
координат точки Мо при параллельном переносе осей.
Правило преобразования координат точки Л40 при переходе
от одной прямоугольной системы координат к другой можно сформу-
лировать так:
При параллельном переносе прямоугольной системы координат
на величину а в направлении оси Ох и на величину b в направлении
оси Оу абсциссы всех точек уменьшаются или увеличиваются в зави-
симости от знака величины а на величину а, ординаты — на вели-
чину Ь.
Формулы преобразования прямоугольных
координат при повороте осей. Пусть Оху и Ох'у' —
две прямоугольные декартовы системы координат, причем система
координат Ох'у' получена из системы Оху поворотом на угол а около
общего начала координат О (рис. 7.4). Пусть точка 2И0 имеет коорди-
274
ГЛ. 7. МЕТОД КООРДИНАТ
яаты (х0; у0) относительно системы координат Оху и координаты (x'Q\
относительно системы координат Ох'у'. Координаты точки Л40 в си-
схемах координат Оху и Ох'у1 связаны формулами
х0 = Хо cos а — y'Q sin а,
Уо = x'q sin а 4- yrQ cos а
или равносильными формулами
Xq » х0 cos а + yt) sin а,
у'о = — х0 sin а 4- yQ cos а.
Формулы преобразования прямоугольных
параллельном переносе и по-
вороте осей. Пусть Оху и О'х'у' —
две прямоугольные декартовы системы
координат, и пусть система координат
О'х у' получена из системы Оху парал-
лельным переносом с величиной сдвига
соответственно а и Ь и с последующим
поворотом вокруг точки О' (образа
точки О при сдвиге (а; Ь)) на угол а
(рис. 7.5).
Пусть MQ — точка плоскости с коор-
динатами (х0; £/0) относительно системы
координат Оху и координатами
относительно системы координат
относительно систем координат Оху и
координат при
(О
(хб; Ю
О'х у'.
О'х'у'1
(2)
(3)
Координаты точки Мо
связаны формулами
х0 = Xq cos а — sin а 4- а,
у0 = Xq sin а 4- j/q cos а + b,
выражающими координаты точки Мо относительно системы координат
Оху через координаты той же самой точки Л40 относительно систе-
мы О'х'у.
Так как точка Л40 — произвольная точка, то индекс нуль у пере-
менных хну обычно опускают и записывают формулы (2) в виде
х = х' cos а — у' sin а 4- а,
у = х' sin а 4- у' cos а + Ь.
Разрешая соотношения (2) относительно величин Xq и у^ получаем
выражения для координат точки относительно системы O'x'y'J
через координаты точки Л10 относительно системы Оху.
х'о = (х0 — a) cos а 4- (r/0 ~ b) sin а,
yfQ = — (х0 — a) sin а 4-	- b) cos а.
1.3. Полярная система координат. Связь между прямоугольными
и полярными координатами. Полярная система координат на плоско-
сти задается выбором точки О, называемой полюсом, и направленным
лучом Ох (полярной осью) с выбранной на нем единичной точкой Е.
Отрезок ОЕ называется единичным или масштабным отрезком (рис. 7.6).
Точке Мо, принадлежащей плоскости и отличной от точки О, ста-
вится в соответствие упорядоченная пара чисел (р0; Фо)» называемая
полярными координатами точки Л1о. Число р0? называемое полярным
§ I. СИСТЕМЫ КООРДИНАТ
275
радиусом точки Л10, представляет собой длину отрезка OMQ. Число <р0,
называемое полярным углом, есть радианная величина угла xOMQ
(см. рис. 7.6).
Между множеством всех точек плоскости (за исключением точки О)
и множеством упорядоченных пар чисел (р0; ф0), где (р0 €	2л),
Рис. 7.6.
существует взаимно однозначное соответствие. Для точки О (полюса)
величина полярного угла не определена.
Связь между полярными и прямоугольными
координатами. Если за полюс принять начало прямоугольной
декартовой системы координат, а за полярную ось — положительное
направление оси Ох (рис. 7.7), то полярные координаты точки Л!о
(Ро‘» Фо), не совпадающей с полюсом, и ее прямоугольные координаты
Уо) связаны равенствами
= Ро cos Фо, у$ = рф sin фв.
Эти формулы называют формулами перехода от полярных коорди-
нат точки Мо к прямоугольным координатам точки Мо.
Формулы перехода от прямоугольных координат точки Л40 (х0; уй)
к ее полярным координатам: полярный радиус р0 вычисляется по фор-
муле
р« =	+ у»;
а полярный угол ф0 вычисляется из равенств
sin ф0 « yn!V xl + yl,	cos фо = Хо//«2 4- yi
при условии, что ф0 С [0; 2л).
1.4. Прямоугольная декартова система координат в пространстве.
Пусть а — некоторая плоскость в пространстве с выбранной на ней
прямоугольной декартовой системой координат Оху. Проведем через
точку О прямую а, перпендикулярную плоскости а (рис. 7.8). Выберем
на прямой а направление и масштабный отрезок ОЕ3, равный масштаб-
ным отрезкам OEt и 0Е2 координатных осей Ох и Оу соответственно
(на рис. 7.8 положительное направление на прямой а отмечено стрел-
кой). Прямая а с выбранным направлением и масштабным отрезком—
третья координатная ось, которую обозначим Oz.
Прямоугольной декартовой системой координат в пространстве
называется упорядоченная тройка взаимно перпендикулярных коорди-
натных осей Ох, Оу и Oz. Прямоугольная декартова система коорди-
нат Oxyz называется правой (рис. 7.9), если Оху — правая прямоуголь-
ная система координат, а ось Оу совмещается С осью Oz поворотом на
угол л/2 против движения часовой стрелки. Прямоугольная декар-
това система координат Oxyz будет левой, если система координат Оху—
левая, либо, если Оху — правая, ось Оу совмещается с осью Oz пово-
ротом на угол л/2 по движению часовой стрелки.
276
ГЛ. 7. МЕТОД КООРДИНАТ
Ось Ох называется осью абсцисс, ось Оу — осью ординат, ось Oz—
осью аппликат. Плоскости, проходящие через каждые две координат*
ные оси, называют координатными плоскостями; пространство, в ко*
тором выбрана система координат, называют координатным про*
странством.
Векторы 0Е±, ОЕ2, 0Е3 называются базисными векторами пря*
моугольной декартовой системы координат (или ортами) и обычно
обозначаются соответственно to.
Координаты точки в пр остранстве. Пусть
А!о — некоторая точка пространства, a Oxyz — некоторая простран-
ственная прямоугольная декартова система координат с началом
в точке О (см. рис. 7.9). Построим плоскость, содержащую точку Мо,
параллельную координатной плоскости Oyz. Построенная плоскость
пересечет координатную ось Ох в некоторой точке Nit Координату
точки обозначим через х0. Построив плоскости, параллельные коор-
динатным плоскостям Oxz и Оху и содержащие точку УИ0, получаем
точки Л/2 и А^з — точки пересечения построенных плоскостей с осями Оу
и Ог соответственно. Координаты точек N2 и А/3, принадлежащих соот-
ветственно осям Оу и Oz, обозначим через у0 и z0.
Координатами точки Л40 относительно прямоугольной декарто-
вой системы координат Oxyz называют упорядоченную тройку чисел
(х0; у0; z0) и пишут (х0; yQ\ z0). Число х0 называется абсциссой
точки Л40, у0 — ее ординатой, г0 — аппликатой.
Расстояние между точками А (хг; уг; гг) и В (х2; Уг, zj вычисляема
по формуле
I АВ | = /(х2 — xj)® + (у, — уг)2 -|- (z2 — zx)a-
§ 2.	Линии на плоскости и поверхности
в пространстве
2.1.	Линии первого и второго порядка. Пусть Р (х\ у) — мно-
гочлен двух переменных х и у. Уравнение
P(x,y)=0	U)
в прямоугольной декартовой системе координат Оху задает множество
точек, которое будем называть линией.
§ 2. ЛИНИИ И ПОВЕРХНОСТИ
277
Если Р (х, у) — многочлен первой степени, то линия, определяе-
мая уравнением (1), называется линией первого порядка^ а уравнение (1)
может быть записано в виде
Ах + By +,С = 0.
Линия первого порядка — это прямая.
Если Р (х, у) — многочлен второй степени, то линия, определяе-
мая-уравнением (1), называется линией второго порядка, а уравнение (1)
может быть записано в виде
Ах2 + Вху + Су*+ Dx+ Ку+ L = 0.	(2)
Линия второго порядка, задаваемая уравнением (2), в зависимости
от значений коэффициентов Л, В, С, D, /С, L определяет эллипс, ги-
перболу или параболу, а при некоторых
значениях коэффициентов— точку или
две прямые (последние случаи назы-
вают вырожденными).
Преобразованием координат
х = х' cos а — у* sin а + х0,
у = х' sin а + у cos а + yQ
при соответствующем подборе а, х0, yQ
уравнение (2) в зависимости от значений
коэффициентов приводится к одному из
ключая вырожденные случаи):
следующих уравнений (ис-
—+ -^2-=1 (ЭЛЛИПС),
,2	,2
X У ,
—5-------= 1 (гипербола),
<= 2рх'
(парабола).
Более подробно об этих линиях см. пп. 2.4—2.6.
2.2.	Прямая. Каждое линейное уравнение с двумя переменными х
и у, т. е. уравнение вида
Ах + By + С = 0,	(3)
где Л и В не равны нулю одновременно, в прямоугольной декартовой
системе координат Оху задает прямую. Обратно, каждая прямая в пря-
моугольной декартовой системе координат может быть задана линей-
ным уравнением вида (3).
Уравнение вида (2) называется общим уравнением прямой.
Некоторые частные формы записи уравне-
ния прямой:
1)	Прямая, образующая угол а с положительным направлением
оси Ох и пересекающая ось Оу в точке (0; Ъ) (рис. 7.10), задается урав-
нением
у = kx + 6,
где k = tg а, а f [0; л/2) U (л/2; л). Коэффициент k называется
угловым коэффициентом прямой.
278
ГЛ. 7. МЕТОД КООРДИНАТ
Уравнение прямой, образующей угол а с положительным направ-
лением оси Ох и проходящей через точку (х0; у0), имеет вид
У —\Уо = k (х — Xq) № = tg а).
2)	Уравнение прямой в отрезках. Уравнение
прямой пересекающей ось Ох в точке (а; 0) и ось Оу в точке (0; Ь) (см.
рис. 7.10), имеет вид
-y- + -f- = i (**0,^0).
3)	Уравнение прямой, проходящей через две данные (не совпадаю-
щие) точки Afi (хх; i/x) и М2 (х2; у2) имеет вид
У — У1 x—xt
02 —в *3 —*1 ’
Взаимное расположение трех точек. Необ-
ходимым и достаточным условием принадлежности трех точек
М l (Хъ 01), М 2 (х2; 02), М3 (х3; у3) одной прямой является равенство
нулю определителя третьего порядка:
Х1
х2
хз
У1 1
02 1
09 1
= 0.
Координаты точки Л/ 0, делящей отрезок М ХМ 2 с концами
Л! 1 (*1‘, 01), М2 (х2*> 0г) в отношении А, определяются соотношениями
~ _ *1 + Хх2	___ £/1 + ^02
0 - 1 + X ’	у*~ 14-х •
Расстояние от точки до прямой. Расстояние d
от точки Мо (х0; 0О) до прямой, заданной в прямоугольной системе
координат уравнением Ах + By + С =• 0, вычисляется по формуле
Взаимное расположение двух прямых на
плоскости. Две прямые, заданные уравнениями
Лхх + В±у + Сх = 0, А2х + В2у + С2 == 0,
пересекаются тогда и только тогда, когда отличен от нуля определи-
тель второго порядка, составленный из коэффициентов при перемен-
ных х и у:
Координаты (х0; у0) точки пересечении двух данных прямых опре-
деляются по формулам, называемым формулами Крамера-.
|В1 С,
v I в2 С2
Л, в,
IА2 В2
Уо =
41
С2 А2
а7 Bi
Ла В2
§ 2. ЛИНИИ И ПОВЕРХНОСТИ	279
Для того чтобы две прямые, заданные уравнениями
Дре + Вху + Ci = 0, А2х + В2у + С2 = О,
были взаимно перпендикулярны, необходимо и достаточно, чтобы ко-
эффициенты Аь Вь Д2, В2 удовлетворяли уравнению
Д1Л2 + ^1^2 — О-
Для того чтобы две прямые, заданные уравнениями с угловыми
коэффициентами и k2:
у =	+ bb у = k2x+ b2,
были взаимно перпендикулярны, необходимо и достаточно, чтобы уг-
ловые коэффициенты и k2 были связаны между собой равенством
^1^2 “ —1-
Угол между двумя прямыми, задаваемыми уравнениями
у = ktx + Ъъ y—k2x+ b2t
определяется равенством
где —1» т. е. прямые не являются взаимно перпендикуляр-
ными. При ki — kb а = 0 и прямые параллельны.
2.3.	Окружность. Множество всех точек плоскости, находящихся
на данном расстоянии от данной точки, лежащей в этой плоскости,
называется окружностью.
Рис. 7.11.	Рис. 7.12.
Уравнение окружности радиуса R с центром в начале О прямо-
угольной декартовой системы координат Оху имеет вид
х2+*/2= /?а.
Уравнение окружности радиуса R с центром в точке с координа-
тами (а; Ь) в прямоугольной декартовой системе координат (рис. 7.11)
имеет вид
(х-а)2+(г/-*)2 = R2.
Уравнение окружности радиуса R с центром в точке (р0; Фо) в по"
лярной системе координат имеет вид (рис. 7.12а)
Р2 — 2рр0 cos (<р — <р0) + pg = R2.
Если центр окружности совпадает с полюсом (рис. 7.126), то уравне-
ние окружности радиуса R в полярной системе координат принимает
вид
Р=/?.
280
ГЛ. 7. МЕТОД КООРДИНАТ
2.4.	Эллипс. Множество точек плоскости, для которых сумма
расстояний от двух данных точек плоскости Fj и F2i называемых фо-
кусами, есть положительная постоянная величина, называется эллипсом.
Для того чтобы указанное множество точек плоскости не было
пустым множеством, необходимо, чтобы эта постоянная величина была
больше расстояния между фокусами.
Каноническое уравнение эллипса. Пусть на
плоскости выбрана прямоугольная декартова система координат Оху
(рис. 7.13), и пусть точки Fj и F2 с координатами (—с\ 0) и (с\ 0) соот-
ветственно — фокусы эллипса. Если М — произвольная точка эллипса^
координаты которой будем обозначать (х; у), то, в согласии с опреде-
лением эллипса, имеет место равенство *)
| FtM | + | F2M I = 2а.	(4)
Отрезки FrM и F2M называются фокальными радиусами эллипса;
их длины вычисляются по формулам
IF1M | = /(*+с)2 + ^.	| FtM | = К(х-с)а + ^.
Подставляя выражения для длин фокальных радиусов в равен-
ство (4), после несложных преобразований получаем следующую запись
уравнения (4):
(а2 — с2)	х2 +	а2у2 =	а2	(а2	—	с2).	(5)
Вводя новую величину д= j/"a2	—с2>	уравнение	(3) приводим к виду
х2	и2
—Г	~ 1 •	(6)
а2,	Ь*	'
Уравнение (6) называется каноническим уравнением эллипса.
Точки пересечения эллипса с его осями симметрии (в нашем слу-
чае осями симметрии являются координатные оси Ох и Оу) называются
вершинами эллипса. На рис. 7.13 вершины эллипса — точки с коор-
динатами (а; 0), (—а; 0), (0; Ъ), (0; — Ь). Отрезок ОА (| ОА | = а) на-
зывается большой полуосью эллипса, а отрезок ОВ (| ОВ | = Ь) — малой
полуосью эллипса. Точка О (в нашем случае начало системы коорди-
нат называется центром эллипса. Эллипс является центрально сим-
метричной фигурой относительно точки О.
Здесь удобно указанную постоянную величину обозначать через 2а,
§ 2. ЛИНИИ И ПОВЕРХНОСТИ	281
Эксцентриситетом эллипса называется отношение расстояния
между фокусами эллипса к длине его большой оси:
е = -£-<1, или	(7)
Эксцентриситет характеризует форму эллипса: чем ближе эксцен-
триситет к единице, тем меньше отношение blа и тем больше эллипс
вытянут; чем меньше эксцентриситет, тем ближе отношение Ыа к еди-
нице и тем больше эллипс «похож» на окружность.
Используя определение эксцентриситета эллипса (7), уравнение (6)
и равенство Ь2 = а2 — с2, можно получить выражения фокальных
радиусов эллипса через его эксцентриситет:
| FjM | = а + ех\ | F2M | = а — ех.
Директрисы эллипса, Предположим, что эллипс,
задаваемый каноническим уравнением
х2	и2
а2	Ь2	’
вытянут в направлении оси Ох, т. е. а > Ь. Две прямые, перпендику-
лярные к большой оси эллипса (в нашем случае оси Ох) и расположен-
ные на расстоянии а/е от центра эллипса (в нашем случае точки О),
называются директрисами эллипса (см. рис. 7.13). Уравнения дирек-
трис эллипса имеют вид
Так как для эллипса е <. 1, то правая директриса расположена правее
правой вершины эллипса; аналогично, левая директриса расположена
левее его левой вершины.
Свойство директрис эллипса: если г — расстоя-
ние от произвольной точки эллипса до какого-нибудь фокуса, а — рас-
стояние от той же точки до соответствующей этому фокусу директрисы,
то отношение r/d есть постоянная величина, равна эксцентриситету
эллипса:
г
Уравнение прямой, касательной к эллипсу, заданному канониче-
ским уравнением, проходящей через точку Л40 (х0; z/0), принадлежа-
щую эллипсу, имеет вид
XpX , уоу .
а2 Ь2 = ’
2.5.	Гипербола. Множество точек, для которых абсолютная вели-
чина разности расстояний от двух данных точек плоскости Ft и Fa,
называемых фокусами, есть постоянная положительная величина, на-
зывается гиперболой.
Множество точек М, образующих гиперболу, в согласии с данным
определением гиперболы, удовлетворяет уравнению *)
|| FiM | - | F2M || = 2а.
*1 Постоянную величину удобно обозначать через 2ai

282
ГЛ. 7. МЕТОД КООРДИНАТ
Отрезки FjM и называются фокальными радиусами гипер-
болы.
Каноническое уравнение гиперболы. Пусть
на плоскости выбрана прямоугольная декартова система координат Оху
(рис. 7.14), и пусть точки с координатами (—с\ 0) и (с; 0) —фокусы
гиперболы. Координаты точки М (х; y)t принадлежащей гиперболе,
удовлетворяют уравнению
I /(х+с)® + !/г -	+ | = 2а.	(8)
Избавляясь от иррациональностей, уравнение (8) можно привести
к виду	, _
(с2 — а2) х2 — а2//2 = а2 (с2 — а2).
Обозначая ]Лс2 — а2 через b (с>а), последнее уравнение можно
привести к виду
— j	(9)
а2 Ь2~~1'
Уравнение (9) называется каноническим уравнением гиперболы.
Точки пересечения гиперболы с ее осями симметрии (в нашем
случае осями симметрии являются координатные оси Ох и Оу) называ-
ются вершинами гиперболы (на рис. 7.14 точки At н А2 с координа-
тами (—а; 0) и (а; 0) соответственно). Точка О (в нашем случае начало
координат) называется центром гиперболы. Гипербола является как
центрально симметричной фигурой, так и фигурой, симметричной от-
носительно осей Ох и Оу, Ветви гиперболы, лежащие в первой и третьей
координатных четвертях (см. рис. 7.14), при |х|->оо приближаются
к прямой y=i-—x. Ветви гиперболы, лежащие во второй и четвертой
координатных четвертях, при ]х|->оо приближаются к прямой у
Прямоугольник со сторонами 2а и 2Ь, расположенный симметрич-
но относительно осей гиперболы, называется основным прямоуголь-
ником гиперболы (рис. 7.15). В математической литературе принята
также называть осями гиперболы отрезки длиной 2а и соединяющие
§ 2. ЛИНИИ И ПОВЕРХНОСТИ
283
середины противоположных сторон основного прямоугольника. В со-
ответствии с этой терминологией говорят, что уравнение
-1
а2 62
определяет гиперболу с полуосями а и Ь.
Эксцентриситетом гиперболы называется отношение расстояния
между фокусами этой гиперболы к расстоянию между ее вершинами:
« = -£-> 1, или е=	*	(Ю)
Эксцентриситет гиперболы характеризует форму ее основного
гиперболы: чем меньше
прямоугольника, а значит, и форму самой
эксцентриситет гиперболы, тем больше
вытянут ее основной прямоугольник в на-
правлении оси,
Гипербола
если стороны
равны.
Используя
гиперболы (10), уравнение гиперболы (9) и
равенство Ь2 = с2 — а2, можно получить вы-
ражения фокальных радиусов через эксцен-
триситет:
I F^M [ = | а + ех |, | F2M | = | а — ех |.
соединяющей вершины,
называется
основного
равносторонней,
прямоугольника
определение
эксцентриситета
Рис. 7.15.
Директрисы гиперболы. Две прямые, перпендику-
лярные к той оси гиперболы, которая ее пересекает, и расположенные
на расстоянии ale от центра гиперболы, называются директрисами
гиперболы.
Уравнения директрис в прямоугольной системе координат, от-
носительно которой гипербола задается каноническим уравнением
х2 __ у2 _
имеют вид х = —ale, х = ale. Так как для гиперболы е > 1, то правая
директриса расположена между центром и правой вершиной гиперболы;
аналогично,' левая директриса расположена между центром и левой
вершиной (см. рис. 7.14).
Свойство директрис гиперболы: если г — рас-
стояние от произвольной точки гиперболы до какого-нибудь фокуса,
d — расстояние от той же точки до соответствующей этому фокусу
директрисы, то отношение rid есть постоянная величина, равная экс-
центриситету гиперболы: rid = е.
Уравнение прямой, касательной к гиперболе, заданной канониче-
ским уравнением (9) и проходящей через точку А40 (х0; г/0)> принадле-
жащую гиперболе, имеет вид
W	у«у __
а2	Ь2 ~ ’
2.6.	Парабола. Множество точек плоскости, для которых рас-
стояние до некоторой данной точки Ft называемой фокусом! равно
284
ГЛ. 7. МЕТОД КООРДИНАТ
расстоянию до некоторой данной прямой, называемой директрисой,
называется параболой *).
Расстояние р от фокуса F до директрисы параболы называется
параметром параболы,
Множество точек М, образующих параболу, в согласии с данным
определением параболы, удовлетворяет уравнению
|ЛМ| = d.
Каноническое уравнение параболы. Пусть
на плоскости выбрана прямоугольная декартова система координат Оху,
и пусть точка с координатами (р/2; 0) — фокус параболы, а прямая,
задаваемая уравнением х == —р/2, — директриса параболы (рис. 7.16).
Координаты (х; у) любой точки М,
Li	принадлежащей параболе, удовлетворяют
р	уравнению
,	\</	,	+	+	(И)
('P/2iO)^\F(pl2iO)	5	F \	2 /	2
|	Избавляясь от иррациональности, уравне-
I	ние (11) можно привести к виду
'рис. 7.16.	<12>
Уравнение (12) называется каноническим
ш уравнением параболы.
Ось симметрии параболы (в нашем случае осью симметрии явля-
ется ось Ох), называется осью параболы. Точка пересечения параболы
с осью симметрии называется вершиной параболы (в нашем случае
вершина параболы совпадает с началом координат).
Заметим, что, в согласии с определением параболы и свойствами
директрис эллипса и гиперболы, можно условно полагать, что парабола
имеет эксцентриситет, равный единице.
Уравнение прямой, касательной к параболе, заданной канониче-
ским уравнением (12) и проходящей через точку Mo (х0; yQ), принад-
лежащую параболе, имеет вид
УоУ “ Р (* + х0).
2,7.	Плоскость и шар. В общем случае поверхность в пространстве
может быть задана уравнением
F (х, yt г) = 0.	(13)
В случае, когда F (х, у, г) — многочлен первой степени, урав-
нение (13) определяет плоскость. Если F (х, у, г) — многочлен второй
степени (по совокупности переменных), то уравнение (13) определяет
в зависимости от значений своих коэффициентов следующие поверх-
ности второго порядка: эллипсоид (частным случаем которого является
шар), двуполостный гиперболоид, однополостный гиперболоид, эллип-
тический гиперболоид и гиперболический параболоид, а также (в выро-
жденном случае) — конус и цилиндр.
В настоящем пункте даны сведения о двух простейших поверхностях
в пространстве — плоскости и шаре.
•j При этом предполагается, что точка Р не принадлежит директрисе*
§ 3. ВЕКТОРЫ
285
Каждое уравнение
Ах + By + Сг + D = О,
(14)
линейное относительно переменных %, у и z, определяет в простран-
ственной прямоугольной системе координат Охуг плоскость (Л, В,
С — числа, из которых хотя бы одно не равно нулю). И наоборот, вся-
кая плоскость в прямоугольной системе ко-
ординат Охуг может быть задана уравне-
нием вида (14).
Координаты всех точек пространства,
лежащих по одну сторону плоскости, зада-
ваемой уравнением (14), удовлетворяют
неравенству
Лх+ Ву + Cz+D >0,
а координаты всех точек, лежащих по дру-
гую сторону, — неравенству
Ах + By Cz + D <0.
В прямоугольной декартовой системе координат вектор я=
== (Л; В; С) перпендикулярен плоскости
Ах + By + Cz + D = 0.
Расстояние d от точки Мо (х0; у0; г0) до плоскости, задаваемой ура-
внением
Ах + By + Cz+D = 0,
вычисляется по формуле
d = । ^х°	+ ^г°	।
~ V А2 + В2 + С2
В прямоугольной пространственной системе координат Охуг урав-
нение сферы радиуса R с центром в точке S (а; b*t с) имеет вид (рис. 7.17),
(х — а)2 + (у — Ь)2 + (г — с)2=» R2.
§ 3» Векторы
3.1. Векторы. Основные понятия. Пусть Л и В — две различ-
ные точки плоскости. Отрезок Л В, у которого точку Л считают началом,
а точку В — концом, называют вектором АВ и обозначают АВ. О век-
торе АВ говорят также, что он приложен к точке Л. Направление,
определяемое лучом ЛВ, называется направлением вектора ЛВ, а длина
отрезка ЛВ называется длиной (или модулем) вектора ЛВ. Длина (мо-
дуль) вектора ЛВ обозначается | ЛВ |. На чертежах вектор ЛВ обычно
изображают прямолинейной стрелкой с началом в точке Л и концом
в точке В (рис. 7.18).
Среди всех векторов с началом в точке Л имеется один вектор,
длина которого равна нулю. Считается, что этот вектор начинается и
кончается в точке Л. Вектор, начинающийся и кончающийся в точке А,
286
ГЛ. 7. МЕТОД КООРДИНАТ
называется нулевым вектором и обозначается А А. Понятие направления
для нулевого вектора А А не вводится.
Определение пространственного вектора дословно совпадает с оп*
ределением вектора на плоскости, при этом лишь считают, что точки 4
и В — две точки пространства.
Равенв»во векторов. Пусть АВ и CD — два вектора
плоскости (или пространства). Говорят, что вектор АВ равен вектору
CD, и пишут АВ = CD, если:
1) длина отрезка АВ равна длине отрезка CD;
2) лучи АВ и CD одинаково направлены.
Рис. 7.18,
При таком определении равенства векторов множество всех векто*
..................>
ров, равных вектору А В, называют свободным вектором. Свободные
векторы обычно обозначают малыми латинскими буквами: а, Ъ, с, х,
а их длины — соответственно | а |, | b |, | с |, | х |. Нулевой вектор обы-
чно обозначают 0.
Каждый ненулевой свободный вектор а имеет бесконечно много
изображений в виде направленных отрезков, отложенных от разных
точек плоскости (пространства) Alt А2» •••» Ап, ...» таких, что длины
отрезков АгВъ А2В2, ...» АпВп> ••• равны длине вектора а, а лучи
AiBv А2В2, ..., АпВп, ... сонаправлены и их направление совпадает
с направлением вектора а (рис. 7.19). Нулевой свободный вектор 0
также имеет бесконечно много изображений в виде точек плоскости.
Свободный вектор обычно называют просто вектором. Множество
равных между собой векторов, принадлежащих одной прямой, назы-
вается скользящим вектором. Наряду со свободными и скользящими
векторами также рассматриваются связанные векторы, которые харак-
теризуются модулем, направлением и положением начальной точки,
называемой точкой приложения. Два связанных вектора считаются
равными, если они имеют не только равные модули и одинаковые
направления, но и общую начальную точку, т. е. равные связанные век-
торы — это совпадающие векторы.
Вектор на плоскости может быть введен с использованием поня-
тия изометрии или, точнее говоря, частного случая изометрии — по-
нятия параллельного переноса.
Изометрией называется отображение плоскости на себя, при ко-
тором сохраняются расстояния между точками.
Параллельным переносом называется отображение плоскости на
себя, при котором все точки плоскости перемещаются в одном и том же
направлении на одно и то же расстояние.
§ 3. ВЕКТОРЫ
287
В этих терминах вектором (параллельным переносом), определя-
емым упорядоченной парой несовпадающих точек (А; В), называ-
ется преобразование плоскости, при котором каждая точка М пло-
скости отображается на такую точку Mi этой плоскости, что луч
сонаправлен с лучом АВ и расстояние |	| равно расстоянию | АВ |t
Любая пара совпадающих точек задает тождественное преобразо-
вание (т. е. преобразование, которое любую точку плоскости отображает
на себя). Тождественное преобразование называют нулевым вектором
и обозначают символом 0.
Сложение векторов. Пусть а и b — два ненулевых
вектора. Отложим вектор а от точки О и обозначим его конец буквой А
(рис. 7.20): О А — а. Отложим от точки А вектор Ь и обозначим его ко-
нец буквой В: АВ = Вектор с началом в точке О и концом в точке В
(ОВ =» с) называют суммой векторов а и b и пишут
с = а + &.
О векторе С говорят^ что он получен в результате сложения векторов
а и
Свойства операции сложения векторов:
1) свойство нулевого вектора:
а-1-0 = а;
2) ассоциативность сложения:
(а + Ь) + с = а + (Ь + £);
3) коммутативность сложения:
a -|- b = b + а.
Сумму двух неколлинеарных векторов а и b можно построить по
правилу, называемому правилом параллелограмма. Отложим от точки А
векторы АВ = b и AD = а (рис. 7.21). Через конец вектора а про-
ведем прямую, параллельную вектору Ь, а через конец вектора b —
прямую, параллельную вектору а. Пусть С — точка пересечения по-
строенных прямых. Вектор АС = с — сумма векторов а и Ь:
с = а + Ь.
Вектором, противоположным вектору а, называют вектор, обозна-
чаемый —а, такой, что сумма вектора а и вектора —а равна нулевому
вектору;
е + (—а) = 0.
288
ГЛ, 7. МЕТОД КООРДИНАТ
Вектор, противоположный вектору АВ, обозначается также ВА:
АВ + Й = АА = 0.
Ненулевые противоположные векторы имеют равные длины
(| а | = | —а |) и противоположные направления.
Разность двух векторов а — Ь есть сумма вектора а и вектора,
противоположного вектору Ь (рис. 7.22), т. е. вектор
а + (-&).
Разность векторов а и Ь обозначают а — Ь.
Разность двух векторов а и b может быть получена с помощью
правила треугольника. Отложим от точки А вектор а (рис. 7.23): АВ==
Рис. 7.22.	Рис. 7.23.
== а; от конца вектора АВ отложим вектор ВС = —Ь\ вектор АС ~
— с — разность векторов а и Ь:
с = а — Ъ.
Умножение вектора на число. Произведением не-
нулевого вектора а на число X называют вектор, имеющий направление
вектора а, если X положительно, и противоположное направление,
если X отрицательно; длина этого вектора равна произведению длины
вектора а на абсолютное значение (модуль) числа X.
Произведение вектора а на число X обозначается через Ла.
В случае, если а = 0 или Л = 0, соответственно считают
Л-0 == 0 для любого Л,
0-а = 0 для любого а.
Свойства операции умножения вектора
на число:
1)	коммутативность:
Ла = аХ;
2)	ассоциативность:
X (ра) = (Лр) а;
3)	дистрибутивность относительно сложения векторов:
X (а + 6) == Ла 4- Л6;
4)	дистрибутивность относительно сложения чисел;
(Л + р,) а = Ла + ра.
$ 3. ВЕКТОРЫ	289
Два ненулевых вектора называют коллинеарными, если их направ-
лени я совпадают или противоположны.
Нулевой вектор по определению считается коллинеарным любому
вектору.
Необходимым и достаточным условием коллинеарности ненулевых
векторов а и b является существование числа X, удовлетворяющего
равенству Ь = Ьа.
Необходимым и достаточным условием коллинеарности векторов v
а и b на плоскости, заданных своими координатами относительно пря-
моугольной декартовой системы координат Оху:
а = to; 0i)» Ъ » (х2; 02),
является равенство нулю определителя второго порядка:
Г ** =0.
14/1 У г
Необходимым и достаточным условием коллинеарности двух век-
торов а и b в пространстве, заданных своими координатами относитель-
но прямоугольной декартовой системы координат Oxyz:
а = (х»: УГ, Z1). ь = (-ч; У», г»).
является равенство нулю всех следующих определителей второго по-
рядка:
I *1 у1 1X1*1 I yi а |
|х» У» ’	|х» 2» ’ 1л Й|
Три ненулевых вектора называются компланарными, если лучи,
задающие их направления, принадлежат прямым, параллельным не-
которой плоскости. Если среди трех векторов имеется хотя бы один
нулевой, то такие векторы также считаются компланарными.
Необходимым и достаточным условием компланарности трех век-
торов а, b ис, заданных своими координатами в прямоугольной декар-
товой системе координат Oxyz:
а == (xi; yr zi), Ь = (х2; у2\ z2), с = (х3; yr, z3)f
является равенство нулю определителя третьего порядка;
*1 01 21
Х9 Уъ Zi =0.
*з Уз ?з
Если векторы а и & не коллинеарны, то любой вектор с, компла-
нарный с векторами а и можно представить единственным образом
в виде
с — ха + yb.	(1)
(Под единственностью представления понимается, что существует един-
ственная упорядоченная пара чисел (х; у), для которой выполняется
равенство (1).)
Представление вектора с, компланарного с векторами а и Ь,
» виде суммы с « ха + yb_ называется разложением вектора с по век-
торам о и Ь.
IV А. Г, Цыпкин
290
ГЛ. 7. МЕТОД КООРДИНАТ
Правило параллелепипеда. Для нахождения век-
тора, являющегося суммой трех некомпланарных векторов а, b с,
часто используют правило, называемое правилом параллелепипеда.
От произвольной точки пространства О откладывают векторы
ОА « а, ОВ — Ъ и ОС = с. Строят параллелепипед так, чтобы от-
резки ОА, ОВ, ОС были его ребрами (рис. 7.24). Вектор OS, где OS —
диагональ параллелепипеда, — сумма трех данных векторов:
OS~a + b + c.
Разложение вектора по трем некомпла»
парным векторам. Пусть а, Ь, С — три некомпланарных
ненулевых вектора. Тогда любой про-
странственный вектор d единственным
образом может быть представлен в виде
суммы:
d s» ха + yb + ZC.	(2)
(Здесь под единственностью представления
понимается, что существует единственная
упорядоченная тройка чисел (х; у\ г), для
которой выполняется равенство (2).)
3.2.	Угол между векторами. Ска-
лярное произведение векторов. Углом
между двумя ненулевыми векторами назы-
вается угол между направлениями этих векторов. Угол между двумя
векторами а и b часто обозначается (а, Ь).
Если угол между векторами а и b равен 90°, то эти векторы назы-
вают перпендикулярными и пишут a Lb.
Скалярным произведением двух ненулевых векторов а и д, обоз-
начаемым (а, Ь) (или а-b), называется число, равное произведению
длин векторов на косинус угла между векторами:
(а> Ь) =* | а | • | b |cos ф,
где Ф = (а, Ь). Если хотя бы один из двух векторов а и b нулевой, то
скалярное произведение этих двух векторов считается равным нулю.
О скалярном произведении (а, Ь) говорят, что оно получено в резуль-
тате скалярного умножения вектора а на вектор Ь.
Свойства скалярного умножения векто*
ров:
1)	коммутативность:
(а, Ь) = (Ь, а);
2)	ассоциативность относительно умножения на число:
((ka), b)~k(a, b).
Операции сложения и скалярного умножения векторов связаны
дистрибутивным законом умножения относительно сложения:
(а, (д + с)) = (а, д) + (а, с).
Необходимым и достаточным условием перпендикулярности двух
ненулевых векторов является равенство нулю их скалярного произве*
дения.
$ 3. ВЕКТОРЫ
29!
Скалярное произведение вектора на этот же вектор равно квадрату
числового значения его длины. Произведение а-а называется скаляр*
ным квадратом вектора а и обозначается (а)я.
3.3.	Координаты вектора на плоскости. Пусть Оху — прямо-
угольная декартова система координат с базисными векторами (Z|/).
Любой вектор а, принадлежащий плоскости, может быть разложен по
векторам базиса Z, /, т. е. для любого вектора а существует, и притом
только одна, упорядоченная пара чисел (х0; уд такая, что
а = xqZ + yj.
Числа х0, £/0 называют координатами вектора а в базисе (Z; J) и пишут
а « (х0; £/0).
Если в прямоугольной системе координат точки 4 и В имеют
координаты (xt; уд и (х2; уд» то координатами вектора АВ будет упо-
рядоченная пара чисел (х2 — хх; у9 — уд* т. е.
ДВ = (ха — хх; у2 — yi)f
Правила действий над векторами, задан-
ными координатами. Пусть в базисе (Z; J) векторы а и Ъ
заданы своими координатами:
л = (хх; Z/i), b = (х2; Уд*
1)	Координаты суммы двух векторов равны сумме соответствую*
щих координат слагаемых:
а + Ь « (хх + х2; У! + уд-
2)	Координаты разности двух векторов равны разности соответ-
ствующих координат этих векторов:
а — Ь = (хх — х2; yt — уд.
3)	Координаты произведения вектора на число равны произведению
соответствующих координат данного вектора на это число:
pa = (рхх; руд.
4)	Скалярное произведение двух векторов равно сумме произве-
дений соответствующих координат этих векторов:
(a, b) « ххха + yty2.
Модуль вектора а, заданного своими координатами (хх; yj), вы-
числяется по формуле
|а| =	+
Угол <р между двумя ненулевыми векторами а и Ь, заданными
своими координатами (хх; уд и (х2; уд соответственно, вычисляется
из равенства
cos ф = cos (а, Ь) ==
*1U'f.

292
ГЛ. 7. МЕТОД КООРДИНАТ
Косинусы углов между вектором а = (хх; х2) и векторами базиса Ц
J называются направляющими косинусами вектора а и вычисляются
по формулам
cos а
COSp
х2
*1
У +
Направляющие косинусы любого вектора а связаны равенством
cos2 а + cos2 fa 1.
3.4.	Координаты вектора в пространстве. Пусть Oxyz — прямо-
угольная декартова система координат с тройкой базисных векторов
(Z; /*, Л). Любой пространственный вектор а может быть разложен по
векторам базиса Z, /, к, т. е. для любого'вектора а существует, и притом
только одна, упорядоченная тройка чисел (х0; i/0; z0) такая, что
а » xoi + yj + zok.
Числа х0, yQ, Zq называют координатами вектора а в базисе (Zj
/; k) и пишут
Л = (*0: £/(ь *о)«
Если в прямоугольной системе координат точки А и В имеют
координаты (хх; yt\ zx) и (х2; у2, z2), то координатами вектора АВ
будет упорядоченная тройка чисел (х2 — хх; у2 — у±\ z2 — zx), т. е.
АВ = (х2 — у2 — уг\ z2 — Zi).
Правила действий над векторами, задан-
ными своими координатами. Пусть в базисе (Z; /; k)
векторы а и Ъ заданы своими координатами:
а == (*Г, УГ, *i) и Ь = (х2; у2\ z2).
1)	Координаты суммы двух векторов равны сумме соответствую-
щих координат слагаемых:
а + b « Сч + х2; У1 + у2\ ц + z2).
2)	Координаты разности двух векторов равны разности соответ-
ствующих координат этих векторов:
а — b = (Xi — х2; у1 — у2;	— z2).
3)	Координаты произведения вектора на число равны произве-
дению соответствующих координат данного вектора на это число:
pa =» (рх^ pyt; pzj.
4)	Скалярное произведение двух векторов равно сумме произведений
соответствующих координат этих векторов:
(а, Ь) « ад + yty2 + zxz2.
Модуль вектора а, заданного своими координатами (хх; y^t zj
относительно некоторого прямоугольного базиса (Z; вычисляется
по формуле
|a| =	+
$ 3. ВЕКТОРЫ
293
Угол <р между двумя ненулевыми пространственными векторами
а и Ь, задаваемыми своими координатами (xt; уг\ zt) и (х2; 08;	,
вычисляется из равенства
cos ф = cos (а, Ь) =
*1*2 "Ь У1Уъ -Ь	#
Косинусы углов между вектором а ® (хх; zi) и векторами ба-
зиса I, J, к называются направляющими косинусами вектора а и вы-
числяются по формулам
— 1   cos 3«— У1 —
К^ + г/i + zf ’	rxi+yf + zi
zi
COS Y C= —	. — •
/zf+vi+zi
Направляющие косинусы любого ненулевого вектора а связаны ра-
венством
cos* а + cos2 ₽ + cos2 у = 1.
3.5.	Векторное произведение. Векторным произведением двух
векторов а и Ь, обозначаемым [а, Ы (или аХд), называется вектор,
определяемый следующими тремя условиями:
1)	модуль вектора [а, Ь ] равен | а |-1 b | sin ф, где ф — угол между
векторами а и Ь\
2)	вектор [а, Ы перпендикулярен как вектору а, так и вектору
3)	упорядоченная тройка векторов (а; д; [а, &])> отложенных
от одной точки, образует правый (в общем случае косоугольный) базис
(рис. 7.25).
Если хотя бы один изГ векторов а или b нулевой, то векторное
произведение двух векторов считается равным нулевому вектору!
(а, д) = 0.
Векторное произведение двух ненулевых векторов а и bt заданных
своими координатами: а == (хх; у$ zj и Ь = (ха; 2а), есть вектор
(a, N =
0У1	211	1*1	«11	1*1	01
02	hl’	1*8	2а I’	1*1	01
где
01
01
1*1
1*1
Z1
й
*1 011
— определители второго порядка.
*1 011
294
ГЛ. 7. МЕТОД КООРДИНАТ
Свойства векторного произведения)
[а, £] = — [&, а);
((ра), Ь\ = р[а, Ь\ (р—число);
[(а + b), d==[a. d + f*. d;
(а, (&, с]] = д(а, с) — с (а. Ь);
[[а, *1, с] = Ь(а> с) — а(Ь, с).
3.6.	Смешанное (скалярно-векторное) произведение векторов.
Пусть Охуг — прямоугольная декартова система координат с правым
базисом (Z; /; Л). Смешанным произведением трех ненулевых некомпла-
нарных векторов, заданных своими координатами относительно базиса
(/; /; *)•
а =* (х,; yi, zi), Ь — (х2; ya, z2), с = (х8; у3-, z3),
н азывается число, абсолютная величина которого равна объему парал-
лелепипеда, ребрами которого являются векторы а, Ь, с, отложенные
<а,Й,с>>0
у е{-я;0)
<аДс> <0
Рис. 7.26.
от одной точки. Это число положительно, если упорядоченная тройка
векторов (а; Ъ\ с) образует правый базис, и отрицательно, если (а; д; с)
образует левый базис *) (рис. 7.26).
Смешанное произведение векторов а; &; с часто обозначается
<а, bt с).
Если векторы а, д, с компланарны, то смешанное произведение
считается равным нулю:
(а, Ь, с)==0.
Смешанное произведение векторов а, д, с, заданных своими ко-
ординатами, вычисляется как определитель третьего порядка:
Xi yt Zi
(a, b, с) =
х$ Уз г3
Свойства смешанного произведения)
(а, Ь, с) = ([а, д], с);
(а, Ь, е) = ([&, с], а) == (с, [а, dj) == — (д, [а, с]).
*) В случае, если базио (/; У; k) левый, смешанное произведение векто-
ров a, с положительно, если тройка векторов (a; b't с) образует левый ба-
ему, и отрицательно в противном* случае.
ГЛAB A 8
ТЕОРИЯ ПРЕДЕЛОВ
Интуитивное понятие о предельном переходе использовалось еще
учеными Древней Греции при вычислении площадей и объемов раз-
личных геометрических фигур. Методы решения таких задач в основном
были развиты Архимедом. При создании дифференциального и инте-
грального исчислений математики XVII века (и, прежде всего, И. Нью-
тон) также явно или неявно использовали понятие’предельного перехода.
Впервые определение понятия предела было введено в работе Дж. Вал-
лиса «Арифметика бесконечных величин» (XVII век), однако истори-
чески это понятие не лежало в основе дифференциального и интеграль-
ного исчислений. Лишь в XIX веке в работах О. Коши теория пределов
была использована для строгого обоснования математического анализа.
Дальнейшей разработкой теории пределов занимались К. Вейерштрасс
и Б. Больцано. С помощью теории пределов во второй половине XIX
века было, в частности, обосновано использование в анализе бесконеч-
ных рядов, которые явились удобным аппаратом для построения новых
функций.
§ 1. Числовые последовательности
1.1. Понятие числовой последовательности. Рассмотрим беско-
нечное множество чисел
Будем считать, что каждое число этого множества снабжено номером*
соответствующим тому месту, которое оно занимает в записи (1).
Так, будем считать, что число 1, стоящее на первом месте, имеет но-
мер 1, число 1/2, стоящее на втором месте, — номер 2, число 1/3 —
номер 3 и т. д. И наоборот, в соответствии с этим соглашением о нуме-
рации множества чисел (1), какой бы номер мы ни указали, в множестве
чисел (1) найдется единственное число, имеющее указанный номер.
Например, номер 4 имеет число 1/4, номер 10 — число 1/10. Та-
ким образом, в приведенном множестве чисел (1) каждое число имеет
вполне определенный номер и полностью определяется им.
Множество чисел, занумерованных либо конечным отрезком нату-
рального ряда, либо всеми натуральными числами, называют числовой
последовательностью.
В первом случае последовательность называется конечной, во
втором — бесконечной.
Элементы этого числового множества называются членами после-
довательности и обычно обозначаются так: первый член аъ второй
о2, ..., n-й ап и т. д. Вся числовая последовательность обозначается
ui, аа, а3, ..., ап, ..., или (ап),
296
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Числа, образующие числовую последовательность, не обязательно
должны быть все различны. Бесконечная числовая последовательность
может быть образована и из конечного числа различных чисел (и даже
из одного числа). Например, из двух чисел — нуля и единицы — можно
образовать бесконечную числовую последовательность
О, 1, 0, 1,
располагая нули на нечетных местах, а единицы — на четных.
Понятие числовой последовательности также может быть введено
с помощью понятия отображения одного числового множества
на другое.
Пусть N — множество всех натуральных чисел, А — некоторое
конечное или счетное числовое множество. Зададим отображение /
множества всех натуральных чисел N на множество А, т. е. укажем
правило, в согласии с которым для каждого натурального числа п С N
выбирается некоторый вполне определенный элемент числового мно-
жества А, который обозначим ап (индекс п указывает на то, что число ап
соответствует п) и, наоборот, каждому элементу ап будет соответствовать
хотя бы одно натуральное число п.
Отображение множества N на некоторое конечное или счетное
числовое множество А называется бесконечной числовой последователь-
ностью] числа ап называются элементами или членами числовой
последовательности, а индекс п — номером члена последователь-
ности.
Задать бесконечную числовую последовательность — это значит
задать отображение, при котором каждому натуральному числу п со-
ответствует один и только один элемент числового множества А.
Иногда бесконечную числовую последовательность вводят, исполь-
зуя понятие функции: бесконечной числовой последовательностью на-
зывается числовая функция; определенная на множестве всех нату-
ральных чисел.
Суммой двух последовательностей (хп) и (£/п) называют последо-
вательность (sn), членами которой являются суммы членов последова*
тельностей (хп) и Q/n), имеющих одинаковые номера:
Sn==Xn + «/n> n£N.
Произведением, разностью и частным двух последовательностей
(хп) я(уп) называют соответственно последовательности (mn), (qn) и (гп)»
члены которых вычисляются по правилам:
mn = xn-0n; <7п == *п — Уп\ гп~‘ТГ'9
Уп
причем частное двух последовательностей (т. е. последовательность
(гп)) определено лишь для таких последовательностей (уп), у которых
пи один член не равен нулю.
1.2	» Некоторые способы задания последовательностей.
1)	Аналитический способ задания после*
довательности. Задать последовательность аналитически —
8то значит указать формулу, позволяющую по, номеру члена последо-
вательности однозначно определить этот член. Формула, позволяющая
вычислить любой член последовательности по его номеру, называется
формулой общего члена числовой последовательности.
$ Т. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
297
Например, формулы общего члена
задают соответственно следующие числовые последовательности:
, 11 11
’• —Г’ Т’ ~Т’
sin 1, sin 2, sin 3, sin 4,...,
о, i, о, 4-, о. 4-,...
2)	Рекуррентный способ задания после*
довательности. Рекуррентный способ состоит в том, что зада-
ется первый член (или несколько первых членов) последовательности
и указывается формула вычисления последующих членов последова-
тельности по заданному первому члену (или нескольким первым чле-
нам).
Примеры рекуррентного задания после*
довательностей:
а)	Ряд натуральных чисел может быть задан следующим рекур*
рентным способом:
^1 = 1, fln+i = an+l,
б)	Последовательность чисел Фибоначчи (см. гл. 10, § 1) задается
первыми двумя членами и формулой вычисления каждого следующего
члена, начиная с третьего:
= 0, b2 = 1, ^п+э — Ьп + ^п+1» n£N.
3)	Последовательность может быть также задана описанием спо-
соба получения ее членов. Так, например, говорят, что последователь-
ность
3,1; 3,14; 3,141; 3,1415; ...
образована из приближенных значений числа л с недостатком с точно-
стью до 0,1; 0,01; 0,001; 0,0001 и т. д. В подобных случаях, как правило»
нельзя указать ни формулы общего члена последовательности, ни ре-
куррентного способа вычисления ее членов.
1.3	. Геометрическое изображение членов последовательности. Под
геометрическим изображением членов последовательности обычно
77=/	п-3 л-5	п-4 л=2
.--1---------1—।—।-----1---1---->-
-1/3-1/5 О //* !/2
Рис. 8.1.
понимается изображение членов последовательности как точек число-
вой прямой (координатной оси). Например, первые пять членов после-
довательности, задаваемой формулой общего члена
ап = А—2-, n£N,	(2)
изображены на рис. 8.1. Реже члены последовательности, рассматри-
ваемой как функция натурального аргумента, изображаются точками
298
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
б прямоугольной декартовой системе координат Оху. На рис. 8.2
в прямоугольной декартовой системе координат изображены первые
пять членов последователь-
ности (2).
1.4.	Ограниченные после-
довательности.	Последова-
тельность (xrt) называется
ограниченной, если существу-
ют такие два числа т и М, что
для всех п £ N выполняется
неравенство
я* < хп С М. (3)
Рис. 8.2.
Последовательность хп называется ограниченной сверху, если су*
шествует такое число М, что для всех л f N выполняется неравен-
ство хп М.
Последовательность (хп) называется ограниченной снизу, если су-
ществует такое число mt что для всех п £ N выполняется неравенство
хп > т.
Для того чтобы последовательность была ограниченной, необ-
кодимо и достаточно, чтобы она была ограниченной сверху и ограни-
ченной снизу. Доказательство ограниченности последовательности сво-
дится к нахождению таких чисел т и М, для которых неравенство
(3) справедливо для всех п £ N.(
Примеры. 1. Последовательность (хп), задаваемая формулой
общего члена хп = п, ограничена снизу (например, числом 0) и не огра-
ничена сверху.
2. Последовательность (хп), задаваемая формулой общего члена
хп =® — п2/(п + 1), ограничена сверху (например^ числом —1/2) и
не ограничена снизу.
3. Последовательности, задаваемые формулами общего члена хп 883
« sin п, уп = (—1)п/п, ограничены числами —1; 1 и —1; 1/2 соответ-
ственно.
1.5. Монотонные последовательности. Последовательность (хп)
называется возрастающей, если каждый ее член, начиная со второго,
больше предыдущего, т. е. если для любого натурального п выполня-
ется неравенство > хп-
Последовательность (хп) называется убывающей, если каждый член,
начиная со второго, меньше предыдущего, т. е. если для любого нату-
рального п выполняется неравенство хп+1 < хп.
Последовательность (хп) называется неубывающей, если каждый
ее член, начиная со. второго, не меньше предыдущего, т. е. если для
любого натурального п выполняется неравенство xn+i > хп.
Последовательность (хп) называется невозрастающей, если каждый
ее член, начиная со второго, не больше предыдущего, т. е. если для лю-
бого натурального п выполняется неравенство < хп.
Возрастающие, убывающие, невозрастающие и неубывающие по-
следовательности образуют класс монотонных последовательностей *).
♦> Во многих случаях (например, при исследовании сходимости после-
довательности) важна монотонность последовательности, начиная с некото-
рого (не обязательно первого) члена. Поэтому удобным (и более общим) ока-
зывается такое определение монотонной последовательности*, последователь-
ность (хп) называется монотонно возрастающей (убывающей), если найдется
номер Nq такой, что для всех членов последовательности с номерами, боль-
шими JV0. выполняется неравенство > хп < хп). Такие после-
довательности —• монотонные, начиная с некоторого номера.
5 5. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	299
Возрастающие в убывающие последовательности называют строго
монотонными.
Доказательство монотонности последовательности состоит в до-
казательстве справедливости какого-либо из перечисленных выше не-
равенств для всех п £ N.
Примеры. 1. Доказать монотонность последовательности, за-
даваемой формулой общего члена
Зл -f- 1	-
Рассмотрим разность между (п + 1)-м и n-м членами последова-
тельности:
__ Зл + 4	Зл + 1 _	—5
«п+1 — Хп — 2п+ J	2п — 1 ~ (2п4- 1) (2п — 1) •
Числитель дроби, стоящей в правой части равенства, отрицателен,
знаменатель положителен при любом натуральном п; следовательно,
вся дробь отрицательна при любом п £ N, поэтому
Xn+i %п О *Ф=^“ Хд+1 Хп,
т. е. данная последовательность — убывающая.
2. Исследовать на монотонность последовательность, задавае-
мую формулой общего члена
хп == л2 — 9л — 100.
Вычислим разность между (л+ 1)-м и n-м членами последователь-
ности:
xn+i -хп = [(л + I)2 - 9 (п + 1) - 100] - [л2 - 9л - 100] =
= 2л - 8.
Выражение, стоящее в правой части равенства, отрицательно при
л = 1, 2, 3, равно нулю при л = 4 и положительно при остальных
значениях л £ N.
В согласии с определением монотонных последовательностей тре-
буется, чтобы сразу для всех л выполнялось одно из четырех неравенств
%п+1 > хп, xn+i > хп, xn+i < хп, xrt+i < хп, в то время как для дан-
ной последовательности ни одно из этих неравенств сразу для всех
значений л £ N не выполняется, и поэтому рассматриваемая последо-
вательность будет немонотонной. (Данная последовательность — моно-
тонно возрастающая начиная с пятого члена.)
§ 2. Предел последовательности
2.1. Понятие предела последовательности. Рассмотрим числовую
последовательность
задаваемую формулой общего члена
«п=1-----n€N.	(!)
300
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Нетрудно проверить, что данная последовательность ограничена
(снизу числом 0, а сверху числом 1) и монотонно возрастающая. Если
изображать члены последовательности точками числовой прямой, го
все эти точки будут расположены между точками 0 и 1 (рис. 8.3).
С ростом номеров точки, изображающие члены последовательности,
будут приближаться к точке числовой оси, имеющей абсциссу 1, и аб-
солютная величина разности
lxn —1| = |1—!—1| = —
1 П 1 I п I п
неограниченно уменьшается с ростом л. Например, для всех членов по-
следовательности, начиная с 11-го, абсолютная величина разности
хп— 1 меньше 0,1; для всех членов последовательности, начиная со
/?=/	л ЧТ/7-4
Рис. 8.3,
101-го, она меньше 0,0Ги т. д. Вообще, какое бы малое положительное
число в мы ни выбрали, в данной последовательности найдется такой
член (номер которого мы будем обозначать ДО0), что для всех членов по-
следовательности с номерами, большими Л/о, будет выполняться нера-
венство
l*n — 1 1<е,
т. е. для любого положительного числа в существует такой номер
(для каждого числа е, вообще говоря, свой), начиная с которого все
члены данной последовательности принадлежат промежутку (1 — в;
1 + в).
Число 1 называют пределом последовательности (хп), задаваемой
формулой общего члена (1), и пишут *)
Пусть (хп) — некоторая бесконечная числовая последовательность.
Число а называют пределом последовательности (хп) и пишут
Нт хп = о,
Л-*оо
если для любого сколь угодно малого положительного числа в суще-
ствует такой номер что все члены последовательности (хп) с номе-
рами, большими NOt удовлетворяют неравенству
I хп — а | < е.	(2)
Если число а является пределом последовательности (хп), то о по-
следовательности (хп) говорят, что она сходится к числу а или имеет
пределом число а. Последовательности, не имеющие конечного предела^
иногда называют расходящимися.
Неравенство (2) также может быть записано в виде
а — в < хп < а + 8.
•) Иш есть сокращение латинского слова ♦limes», означающего ^предел»*
$ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	301
Промежуток (а — в; а + е) называют ^окрестностью точки а. Исполь-
вуя понятие 8-окрестности точки а, можно дать и такое определение
предела последовательности:
Число а называется пределом числовой последовательности (xn)t
если для любого положительного числа е существует номер такой,
что все члены последовательности, начиная cxN +1, принадлежат 8-ок-
рестности числа а.
Формулируя понятие предела последовательности, необходимо
иметь в виду, что номер А/о зависит от выбора числа 8. Для того чтобы
это подчеркнуть, часто вместо Af0 пишут Az0 (8). При уменьшении поло-
жительного числа в соответствующий номер (е), вообще говоря,
увеличивается. Исключение представляет случай, когда все члены по-
следовательности (хп) равны:
*1 =	= ••• = хп = *п+1 — ...
Предел такой последовательности
а = lim хп
л-*оо
будет равен членам этой последовательности. В этом случае неравен-
ство (2) будет выполняться для любого в > 0 сразу при всех значениях
п С N.
Пример. Доказать, что предел числовой последовательности,
задаваемой формулой общего члена
П	z-
*п = 7+Т’ neN>
равен 1.
Покажем, что для любого в > 0 существует такой номер А/о, что
(хп — 11 < е для всех п > Nq. Так как
|хп— 11 = 1	— 11 = 1-----г-г| = —ГТ,	(3)
‘	1 I n -f-1 I I п +1 j n-j-l* v '
то неравенство 1 хп — 11 <8 можно записать в виде
Разрешая последнее неравенство относительно п, получаем
(5)
Из неравенства (5) следует, что если в качестве числа (е) выб-
рать любое натуральное число *), большее чем то из неравенств
8
В качестве натурального числа Л/о (8) при .JT8., >о можно, на»
пример, взять число Г-5-—-1	** Если < 0, то в качестве N9 можно
[1—— е 1
—-— I обозначается целая
часть числа . Целой частью действительного числа а называется целое
число р такое, что р < а. <р -j- 14
302	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
(4), (5) и равенства (3) следует, что все члены последовательности
с номерами п >	(в) будут удовлетворять неравенству
11 <е.
По определению предела это и означает, что число 1 является пределом
данной последовательности.
Говорят, что последовательность (хп) стремится к +оо (—оо), и
пишут
+оо(хп_> —оо),
если для любого сколь угодно большого положительного числа Е
существует такой номер Wo, зависящий от Е, что все члены последо-
вательности (хп) с номерами, большими (Е), удовлетворяют не-
равенству
хп>Е (хп < —Е).
Так, например, последовательности, задаваемые формулами общих
членов
хп = п8 И Хп я —п t
стремятся соответственно к4-оо и —оо.
2.2.	Необходимое условие сходимости последовательности»
, Пусть (хп) — некоторая последовательность, сходящаяся к числу а,
т. е.
lim хп » а.
п-*<х>
В согласии о определением предела, для любого е > 0 все члены
данной последовательности, кроме, быть может, конечного их числд,
попадают в е-окрестность точки а, т. е.
а —-8 <хп <а + ь.
Пусть число членов этой последовательности, которые не попали в ок-
рестность точки а, равно N9 и какие-то из этих членов лежат справа
от точки а+ е, а какие-то — слева от точки а — в.Так как членов,
лежащих правее точки а + е, конечное число, то, перебрав, их, мы
можем выбрать максимальный член, который обозначим через М.
Аналогично, минимальный из членов последовательности, лежащим
левее точки а — в, обозначим через т. Может, конечно, оказаться,
что справа от точки а + в (или слева от точки а — 8) не окажется ни
одного члена. В этом случае в качестве числа М можно взять число
а + в и соответственно в качестве числа т — число а — в.
Таким образом, если хп — сходящаяся последовательность, то
существуют два таких числа т и М, что для всех натуральных а
m < хп < Л4;
следовательно, (хп) — ограниченная последовательность.
Рассмотрим последовательность, задаваемую формулой общего
члена!
я» в I—
$ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
303
Данная последовательность ограничена (снизу числом —1, а сверху
числом 1). Используя определение предела, докажем, что эта после-
довательность не имеет предела.
Каждый член последовательности, имеющий нечетный номер, —>
точка числовой оси с абсциссой —1, а члены с четными номерами —
точка с абсциссой 1. Предположим, что предел данной последователь-
ности существует и равен а. Если а — некоторое число, отличное от 1
и —1, то всегда можно найти такую 8-окрестность точки а, в которую
не попадет ни один из членов данной последовательности. Следовательно,
если данная последовательность имеет предел, то он должен быть равен
либо —1, либо 1. Допустим, что предел равен —1. Тогда для любого
в > 0 все члены последовательности, начиная с некоторого, должны
попадать в е-окрестность точки —1. Возьмем в = 0,1. В промежуток
(—1,1; —0,9) попадают все члены последовательности, стоящие на не-
четных местах, но не попадает ни один из членов, стоящих на четных
местах, т. е. не существует такого номера No (е), начиная с которого
все члены последовательности попадают в данную е-окрестность точки
— 1, и, следовательно, число —1 не является пределом данной после-
довательности. Аналогично доказывается, что и число 1 не является
пределом последовательности. Значит, последовательность
— 1,1, —1,1, -1,1,...
предела не имеет.
Таким образом, из ограниченности последовательности, задавае-
мой формулой общего члена =(— 1)п, не следует ее сходимость.
Разобранные примеры позволяют сформулировать необходи-
мое условие сходимости бесконечной числовой
последовательности:
Для того чтобы последовательность сходилась, необходимо, чтобы
она была ограниченной.
2.3.	Теоремы о пределах последовательностей.
1)	Последовательность не может сходиться к двум различным пре-
делам (теорема о единственности предела).
2)	Предел последовательности, все члены которой равны одной
и той же величине, равен этой величине.
3)	Если последовательность (хп) сходится к числу а и а > р (а < q)9
то и все члены последовательности, начиная с некоторого, тоже будут
больше р (меньше q).
4)	Если последовательность (хп) имеет предел, то она ограничена.
5)	Если последовательности (хп) и (уп) имеют пределы (сходятся)»
то их сумма (разность) тоже имеет предел, причем предел суммы (раз-
ности) равен сумме (разности) пределов:
lim (хп ± Уп) = Em хп ± lim ул.
П-+-ОО	П-*оо	П-*оо
6)	Если последовательности (хп) и (уп) имеют пределы (сходятся)»
то их произведение также имеет предел, равный произведению пределов
сомножителей:
lim (хп • Уп) == Нт хп • lim уп.
п-*<х>	П-+СО П-^ОО
Из теорем 2) и 6) следует, что постоянный множитель можно выносить
304
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
еа знак предела:
Нт (схп) » с Нт хп.
П-*ОО	П-*<Х>
7)	Если последовательности (хп) и (уп) имеют пределы, причем
уп Ф 0 для всех п начиная с некоторого Af0, то последовательность
(хп/Уп) также имеет предел, равный отношению пределов последова-
тельностей (хп) и (уп):
lim хп
||гп21 = ^_.
rt->00 Уп Ит уп
П-+ОО
Покажем теперь, как при помощи сформулированных теорем на-
кождение предела последовательности можно свести к нахождению
пределов простейших последовательностей.
Пример. Вычислить предел последовательности (хл), задавае-
мой формулой общего члена
_	2я2
Хп п24-п+1 ’
Для вычисления предела данной последовательности воспользуемся
теоремами о пределах последовательностей. Заметим, что сразу исполь-
вовать теорему о пределе частного при вычислении предела
п-*оо я2 4~ я 4~ 1
нельзя, так как последовательности, стоящие в числителе и знамена-
теле дроби, не имеют конечных пределов. Преобразуем дробь, стоя*
щую под знаком предела, разделив числитель и знаменатель дроби ная2з
2я2	_	2
n2 + «+l ~	1	£•
п п*
Далее последовательно воспользуемся теоремами 7) и 5)з
..	2п2	1.	2
hm —------------- = lim ------------------
П-+0О Я2 4** Я 4“ 1 Л-*оо 1,1.1
lim 2
______________х>__________________
lim 1 4- lim J_ 4- lim —L
n-+ao П-*ао Я П-^ао Я2
Испольбуя определение предела, нетрудно доказать, что
lim-L = 0 и lim —L = о.
Я	п-*-<х> Я2
В результате для данной последовательности получаем
lim   2"2	______2.
П-^оо я2 4- Я 4- 1	14-04-0
Следует отметить, что при нахождении предела данной последо-
вательности мы не совсем «законно» пользовались теоремами 7), 5).
$ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	305
Например, используя теорему о пределе частного, мы поставили знак
равенства между выражениями
Иш2
2	П-*оо
lim 1	। и	/	1 I \ *
п—о 1+-L-I—L	lim ( 1 + -L- + -L-)
П П*	п-*оо \ П П* }
котя к этому моменту еще не знали, что пределы числителя и знаме-
нателя второй дроби существуют. Сходимость последовательности,
стоящей в знаменателе второй дроби, доказывается позже, после та-
кого же «незаконного» применения теоремы 5). То, что мы сразу ставим
знак равенства, в сущности означает, что сначала мы предполагаем,
что условия применяемых теорем выполнены, а затем, возвращаясь
обратно по цепочке равенств, обосновываем законность поставлен-
ного ранее знака равенства между этими выражениями.
2.4.	Достаточное условие сходимости последовательности (теорема
Вейерштрасса). Ограниченность последовательности является необ-
ходимым условием ее сходимости — из сходимости последовательности
следует ее ограниченность, однако ограниченность последовательности
не является достаточным условием ее сходимости. Монотонность по-
следовательности кажется вовсе не связанной с ее сходимостью — мо-
нотонная последовательность может быть как сходящейся, так и рас-
ходящейся. Например, последовательность, задаваемая формулой
общего члена хп = п, — монотонная и расходящаяся, а последова-
тельность хп == 1/п — монотонная и сходящаяся.
С другой стороны, немонотонные последовательности могут быть
как сходящимися, так и расходящимися. Так, последовательность
хп = (—1)п/п — сходящаяся, а последовательность хп = (—\)пп —
расходящаяся.
Однако последовательности, которые одновременно являются
монотонными и ограниченными, — обязательно сходящиеся. Это свой-
ство последовательностей, иногда называемое достаточным
условием сходимости последовательности, формулиру-
ется в виде следующей теоремы, впервые доказанной К. Вейерштрассом.
Если последовательность монотонна и ограничена, то она схо-
дится.
Теорема Вейерштрасса — это теорема о существовании предела
последовательности, и она не дает метода нахождения этого предела.
Однако в ряде случаев, зная, что предел последовательности существует,
можно указать способы его вычисления.При этом часто пользуются тем,
что для любой сходящейся (не обязательно монотонной) последова-
тельности (хп) справедливо равенство
lim xn+i = lim хп.	(6)
П-*оо	П->оо
Прежде чем перейти к примерам, заметим, что при вычислении
пределов с помощью равенства (6) удобно иметь рекуррентную, а не
аналитическую форму задания последовательности, а потому во всех
рассмотренных ниже примерах аналитически задаваемые последова-
тельности будут, по мере необходимости, записываться в рекуррентной
форме ♦).
•) Следует иметь в виду, что не любая последовательность, заданная
аналитическим способом, может быть записана в рекуррентной форме»
306	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Примеры. 1. Вычислить предел последовательности
хп e qn, 0 < q < 1.
Последовательность хп = qn — монотонно убывающая, так как
для любого п £N при 0 < q < 1 выполняется неравенство хп > xn+i,
и ограниченная, так как 0 < qn < 1. По теореме Вейерштрасса данная
последовательность имеет предел. Обозначим этот предел через а:
lim хп = я.	(7)
Л-*оо
Записывая данную последовательность в рекуррентной форме:
xn+i = qxn,	(8)
на основании равенства (6) и рекуррентной формулы (8) имеем
lim хп = lim xn+i => lim хп = lim (qxn).
n-*oo П-*ОО	n-+ao n-*oo
Так как постоянный множитель можно вынести из-под знака предела,
то, используя обозначение (7), последнее равенство можно записать
в виде
lim хп = q lim хп =>а = qa=> а (1 — q) = 0.
п-*оо	п-^<х>
Но так как q Ф 1, то из последнего равенства получим а = 0. Таким
образом, предел данной последовательности равен нулю.
2.	Вычислить предел последовательности
Зп + 1
Данная последовательность — монотонно убывающая, так как
Хп+1 — Хп
(2/iH-l) (2л— 1)
при всех я f N и, следовательно, наибольшим членом данной после-
довательности будет первый член, равный четырем. С другой стороны,
нетрудно проверить, что хп > 0 при всех п £ N. Значит, последо-
вательность ограниченная: 0 < хп < 4 при всех п £ N.
Таким образом, данная последовательность удовлетворяет условиям
теоремы Вейерштрасса и имеет предел, который обозначим через аз
lim хп — а.
п-*оо
Будем вычислять этот предел с помощью формулы (6), переходя от
аналитического способа задания последовательности к рекуррентному.
Для этого разрешим равенство
Зп+ 1
Хп=ъГ=Т
относительно пъ
хп + 1
а=я 2хп-3 9
$ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	3Q7
Подставляя полученное выражение для п в выражение для (п + 1)-го
члена
3«4-4
^п+ 1 ’
получим рекуррентную форму задания данной последовательности
Подставляя в левую часть равенства (6) вместо хп+1 его выражение
через xnt имеем
Пу ____ о
Jim	» Вт хп.	(9)
П->со	- 1 Я-МЮ
Используя теорему о пределе частного и учитывая, что предел
последовательности (хп) был обозначен через а, из равенства (9) полу-
чаем уравнение для нахождения числа а:
Единственное решение данного уравнения: а = 3/2. Таким обра-
зом, предел данной последовательности равен 3/2.
___	Зи 4” 1	л
Предел последовательности хп == можно вычислить и без
применения теоремы Вейерштрасса, используя сформулированные
з п. 2.3 теоремы о пределах последовательностей.
3.	Вычислить предел последовательности, задаваемой формулой
общего члена _____________________________
хл=У С+ |/с+ ••• 4- Кс <е>0).	(10)
п корней
Докажем, что данная последовательность имеет предел, и вычислим
©тот предел с помощью равенства (6). Данная последовательность может
быть задана следующей рекуррентной формулой:
=	(И)
Докажем, что данная последовательность монотонно возрастает,
«г. е. что xn+i > хп для всех л f N. Используя рекуррентную формулу
(10), это неравенство можно записать в виде хп > хп, что экви-
валентно (с учетом условия хп > 0) неравенству х2п — хп — с < 0.
С помощью формулы общего члена (10) последнее неравенство записы-
вается в виде
с 4- ]/ с 4*	 4-	— ]/” с4-УГс4---,+/я — с<0 <=>
п—-1 корень	п корней
<=> j/”с 4-	с 4- • - • 4- с <z + J/ с + • • ’ 4"
n—1 корень	п корней
Возведя обе части последнего неравенства п — 1 раз в квадрат, полу*
чмм неравенство 0 < /с, справедливость которого очевидна. Значит,
308	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
исходное неравенство верно при всех значениях с > 0 и данная после/
довательность — возрастающая.
^Последовательность (10) ограничена сверху, например, числом
j/’c+ 1. Действительно^	меньше этого числа. Если теперь
допустить, что хп < + 1, то и для следующего члена последова-
тельности будем иметь
*п+1 <	+ Т < /с+2/c+l = /£+ 1;
и ограниченность последовательности сверху доказана методом матема-
тической индукции. Ограниченность последовательности снизу следует
из того, что хп > 0 при всех л £ N.
Итак, данная последовательность — возрастающая и ограничен-
ная; следовательно, по теореме Вейерштрасса она имеет предел, ко-
торый обозначим через а ( lim хп = Для вычисления числа а исполь-
суем рекуррентную формулу (И), записывая ее в виде
^+1 = с+х„.
В силу сходимости последовательности имеет место равенство
lim 4+1 = lim (с + *га),
П->оо	П-Юо
из которого следует, что величина а удовлетворяет квадратному ураь-
нению
а2» с+ а.
Множество решений данного квадратного уравнения:
I + /5T+T	- 1 — /47+1 .
а=с 2	9	а~~	2	*
--	1	4С 1	-	<4. л и
Число  —!— отрицательно при любом с > 0. Но так как отрица-
тельное число не может быть пределом последовательности с положи-
тельными членами, то пределом рассматриваемой последовательности
является число
1 + У 4с + 1
2
4. Вычислить предел последовательности, задаваемой формулой
общего члена
on—1
-----—, n£N.	(12)
Данная последовательность — убывающая, начиная со второго
члена, что следует из неравенства
2п	2П“*1 ✓	2	\
ti — х» = jp — =	(n+ 1	1) =
2"-1 , 1— n 2'1**1 (1—n)
“ »l ’nfl " И+1JI
$ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ	399
Следовательно, наибольшими членами последовательности (12)
являются первый и второй члены, равные единице, и xn < 1 для всех
п £ N. Так как хп > 0 при всех п £ N, то эта последовательность
ограничена снизу числом нуль. Значит, последовательность (12) мо-
нотонна и ограничена: 0 < хп < 1. По теореме Вейерштрасса эта по-
следовательность имеет некоторый предел а( lim хп = а'). Найдем зна-
'n->oo	'
чение а. Члены последовательности (12) связаны рекуррентной формулой
2" 2n~x • 2	2Л~1	2	__	2
*л+* “ («4-1)1 = п\ (л 4* 1) ~ п!~ * «4-1 ~ *п п 4- I *
Применяя к равенству
2
Хп+1 — i Г
• П 4- 1
формулу (6), получаем уравнение для а
a —a- lim——
П~+-оо fl 4- 1
из которого следует, что предел данной последовательности палея
нулю.
5. Н е п е р о в о число е как предел бесконеч-
ной числовой последовательности*). Рассмотрим
последовательность, задаваемую формулой общего члена
М'+4)“-
Докажем монотонность этой последовательности. Раскладывая выра-
жение 04““~^ по формуле бинома Ньютона, получаем
		-1	\п 1 t	I	,«(«—!) I ,
Хп= 1	(ч	п	) =l+n- п 	।	2!	> +
п («— 1) (п —2) 1 л («-—1) (л — 2)..,(« —— л4-1) 1
**	3!	’ л8 + *г	П|
Если теперь написать аналогичное разложение для xn+i, то к разло-
жению для хп прежде всего добавится («+ 2)-й положительный член;
каждый же из написанных «4- 1 членов увеличится, так как любой
множитель в скобках вида 1-----заменится большим множителем
п
S
«4-1’
Отсюда и следует, что
Хп+1 > *п,
т. е. данная последовательность (хп) возрастающая.
*) О числе ч см. 1икже о, 1.5 гл.
310
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Докажем, что последовательность (хл) ограничена. Опустив в вы*
ражении для хп
•>"1 + ,+тг('-т)+тг(1-4)(1-4) + -
все множители, стоящие в круглых скобках, мы тем самым увеличим
правую часть равенства (так как каждый из опущенных множителей
меньше единицы) и в результате получим неравенство
'"<2+тг+тГГ+-+тГГ'	1131
Из ограниченности последовательности (12), рассмотренной в при-
мере 4, следует, что
г"-1 < «!,
т. е.
2<2t,	22<31,	23<4|,..., 2п~х <п!;
с помощью этих неравенств, записанных в виде
1^1 1^1 1^1 1^1
2^21’ 2а > 31 ’	2? > 41 ’ ” * ’ 2”’1 > nl ’
для неравенства (13) имеем
*'‘<2 + тг + зг+ТГ+‘“ + 7Г<2 +
"**"2*^"2Г”^'25"^..2п-1 •
В правой части последнего неравенства сумма всех членов, начиная
со второго» есть сумма п — 1 членов бесконечно убывающей геометри-
ческой прогрессии, которая равна 1, а потому при любом п £ N
хп < 3.
Таким образом, последовательность хп —	п € N, —.
монотонно возрастающая и ограниченная и, согласно теореме Вейер-
штрасса, имеет предел. Этот предел имеет специальное обо-
значение е:
lim (1+—V = е= 2,71828...
П->оо \ п /
2.5. Необходимое и достаточное условие сходимости последова-
тельности. Выше были рассмотрены два способа доказательства схо-
димости последовательностей. Один способ был основан на использова-
нии теорем о пределах последовательностей (см. п. 2.3), а второй —
на использовании теоремы Вейерштрасса (см. п. 2.4). Однако оба эти
способа доказательства сходимости последовательности применимы для
исследования весьма небольшого числа довольно простых последо-
вательностей.
$ 3. ЧИСЛОВЫЕ РЯДЫ И БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 311
Возникает вопрос: а как же доказывать сходимость, скажем, немоно-
тонной последовательности, которая задается не аналитическим,
а каким-либо другим способом (например, рекуррентным), или же по-
следовательности, которая задается аналитической формулой, но
предел которой невозможно вычислить, ограничиваясь теоремами о
пределах последовательностей? Ясно, что при этом мы уже не можем
пользоваться определением предела последовательности для доказа-
тельства ее сходимости, так как в этом определении уже участвует то
самое число а, существование которого мы должны доказать. Кроме
того, в ряде случаев нас может интересовать лишь вопрос о сходимости
последовательности, но не интересовать вопрос о том, к какому числу
она сходится.
Теорема, которая отвечает на вопрос о существовании предела по-
следовательности и в формулировке которой участвует только то, что
нам дано, а именно члены последовательности, была сформулирована и
доказана Б. Больцано и О. Коши.
Теорема Больцано — Коши (критерий схо-
димости):
Для того чтобы последовательность (хп) имела конечный предел,
необходимо и достаточно, чтобы для каждого положительного числа в
существовал такой номер Nq (8), чтобы неравенство
| %п — Хп+р | <1 в
выполнялось для всех п > и р > 1 (т. е. для любых натуральных чи-
сел п и р, удовлетворяющих этим неравенствам).
§ Зк Числовые ряды и бесконечные произведения
3.1. Понятие числового ряда. Пусть дана некоторая бесконечная
числовая последовательность
Xj, х2, х3, ..., хп, ...	(1)
Поставим перед собой задачу: вычислить сумму всех членов беско-
нечной последовательности (1). Вычислить сумму бесконечного числа
слагаемых так, как мы вычисляем сумму конечного числа слагаемых,
нельзя — мы никогда не сможем завершить процесс сложения. Однако
оказывается, что, используяпонятиепредела последовательности, можно
ввести понятие суммы бесконечного числа слагаемых. Для этого возьмем
первый член последовательности (хп) и обозначим его через Sf.
Si = Xi.
Сложим первый член последовательности х± со вторым членом х2 и
обозначим их сумму через S2:
S2 = xt + х2.
Сложим первые три члена последовательности (1) и обозначим их сумму
через 53;
$8 = *1 + х2 +
312	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Продолжая начатую процедуру, т. е. последовательно складывая че-
тыре, пять, шесть и т. д. первых членов последовательности (хп), обоз-
начим суммы четырех, пяти, шести и т. д. первых членов через S4, 5б,
5в>. .
$4 = *1 + *2 + Х3 + Х4,
s5 == Х1 + х2 + х3 + х4 + хб,
Se = *1 + Х2 + х3 + Х4 + Хб + Хв,
Для заданной числовой последовательности (хп) выражение
Х1 + х2 + х3 + • • • + хп +• • •	(2)
называют числовым рядом и обозначают символом
оо
У!
П=1
Слагаемое хп называется n-м членом ряда. Сумма п первых членов ряда
называется л-й частичной суммой этого ряда и обозначается че-
рез Sn:
1=3 xi + х2 + х3 + • • • + хп.
Если существует конечный предел S последовательности (Srt)
частичных сумм ряда (2), то говорят, что этот ряд сходится, а указанный
предел S называют суммой ряда (2) и пишут
S = Xi + х2 + х3 + • • • + хп 4- • • • s= J] Хп»
п=1
Если же Sn +оо, либо Sn-* —оо, либо предела по-
следовательности частичных сумм (Sn) вовсе не существует, то ряд (2)
называют расходящимся.
Остатком ряда
*1+ха + хзН------bxh+*ft+1-i-----!-*&+/ + •••	(3)
после k-ro члена называется бесконечный ряд
*fc+l + Xh+2-l------------------
получающийся из ряда (3) отбрасыванием первых k членов.
Простейшим примером бесконечного числового ряда служит сумма
всех членов геометрической прогрессии с первым членом, равным а,
и знаменателем, равным q:
a + aq+	(4)
л-я частичная сумма этого ряда есть сумма п первых членов геометри-
ческой прогрессии и вычисляется по формуле
s»=(ПРИ О-
* V
$ 3. ЧИСЛОВЫЕ РЯДЫ И БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 313
Если знаменатель прогрессии удовлетворяет неравенству [<?|< 1,
то последовательность частичных сумм (Sn) имеет предел
который называют суммой всех членов бесконечно убывающей геометри-
ческой прогрессии (т. е. суммой ряда (4)).
Если знаменатель прогрессии удовлетворяет неравенству \q\ :> 1,
то выражение (4) дает пример расходящегося ряда. При этом, если q < О,
то предела частичных сумм не существует, если же q > 0, то последо-
вательность частичных сумм стремится либо +оо, либо —оо.
Свойства бесконечных числовых рядов.
1)	Если числовой ряд сходится, то сходится и любой из его остат-
ков; обратно, из сходимости остатка ряда вытекает сходимость исход-
ного ряда.
2)	Если ряд сходится, то остаток ряда после k-ro члена стремится
к нулю при k OGj
3)	Если члены сходящегося ряда умножить на один и тот же мно-
житель с, то его сходимость не нарушится, а сумма умножится на а
оо	оо
2 схп=с 2] хп.
/1=1	П=1
4)	Два сходящихся ряда
оо
*1 + *2 + *3 + • • • +	+ * • * e Хп~ X,
П=1
оо
У1 + У 2 + Уз + • • • + Уп + • • • — 2 Уп = У
П=1
можно почленно складывать (или вычитать), и ряд
(*i ± */i) + (*з ± Уг) + (*з ± Уз) + • • • + (хп ± Уп) + • • •
также сходится, а его сумма (разность) равна X + У (соответственно
X-Y).
5)	Общий член хп сходящегося ряда стремится к нулю (необ-
ходимое условие сходимости бесконечного числового
ряда),
3.2. Положительные числовые ряды. Числовой ряд
оо
+ Х2 + Хд + • • • -j-	‘ = 2 Хп
/1=1
называют положительным, если все члены ряда—положительные числа:
Х1>0,	х2>0,	х3> 0, ..., хп > 0, ...
Последовательность частичных сумм положительного ряда — возра-
стающая последовательность. Положительный числовой ряд сходится»
если последовательность частичных сумм ряда ограничена сверху,
и расходится в противном случае (необходимое и достаточ-
ное условие сходимости положительного числового ряда).
Сходимость (или расходимость) положительного числового ряда
часто устанавливается путем сравнения данного числового ряда с дру-
314
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
гим, заведомо сходящимся (или расходящимся) числовым рядом. В ос-
нове этого сравнения лежит следующая теорема (свойство числовых
рядов). Пусть даны два положительных числовых ряда
оо
I. *1 + *а+*эЧ--------------Мп+••• = 2 *п.
со
п. У1 '^гУъ + Уз+ ••• + Ул + ••• = 2
П = 1
Если, начиная с некоторого члена, для всех n > No выполняется нера-
венство хп Уп, то из сходимости ряда (II) следует сходимость ряда (I),
а из расходимости ряда (I) следует расходимость ряда (II).
Таким образом, для доказательства расходимости ряда
оо
Х14- х2 + х3 н-----h хп + • • • = У, Хп	(5)
п=1
необходимо построить такой заведомо расходящийся ряд
оо
У1 + Уз + Уз + • • • + Уп + • • • e J} Ул»
П=1
чтобы уп < хп для всех п >
Для доказательства сходимости ряда (5) необходимо построить
такой заведомо сходящийся ряд
оо
*1 + *2 + 23 + • • • + Zn + • • • = 2 2п>
п=1
чтобы zn > хп для всех n > Wo.
В общем случае трудно дать какие-либо конкретные рекомендации/
оо	оо
как строить указанные ряды уп и У zn. Часто в качестве таких рядов
п—1	п=1
удобно брать ряды, образованные из членов геометрической прогрессии,
которые в зависимости от значения знаменателя могут быть как сходя-
щимися, так и расходящимися, или гармонические ряды.
Числовой ряд
называется гармоническим рядом. Каждый член такого ряда, начиная
со второго, представляет собой среднее гармоническое двух соседних
/ 1 1 / 1 , 1 \
членов (число с, удовлетворяющее равенству	4-—j t
называется средним гармоническим чисел а и 6).
Числовой ряд более общего вида
-L+-L+J_
2s 3s 4s

(6)
П'
f 3. ЧИСЛОВЫЕ РЯДЫ И БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 315
где s — любое действительное число, часто также называют гармониче-
ским рядом.
Гармонический ряд вида (6) расходится при s< 1 и сходится
при s> 1.
Сходимость (или расходимость) рядов может быть также установ-
лена с помощью следующих следствий сформулированной выше теоремы:
Пусть
*1 + +• • •+ +—•	(О
У1 + У 2 + * ’ ’+ Уп +•••	(И)
— два положительных ряда.
Тогда:
1)	Если существует предел
lim—— Л (А > 0),
П->оо Уп
то из сходимости ряда (II) при конечном А вытекает сходимость ряда
(I), а из расходимости ряда (I) при А > 0 вытекает расходимость ряда
(II), т. е. при конечном значении А оба ряда сходятся и расходятся
одновременно.
2)	Если, начиная с какого-то номера 2VO| для всех n> No выпол-
няется неравенство
Хп+1 < Уп+1
Хп Уп
то из сходимости ряда (II) вытекает сходимость ряда (I), а из расходи-
мости ряда (I) вытекает расходимость ряда (II).
3.3. Признаки сходимости числовых рядов. Сходимость (или рас-
ходимость) ряда
может быть установлена с помощью следующих признаков.
Признак Коши. Если предел
lim
n->oo
существует и равен К, то прид К < 1 ряд сходится, а при К > 1 расхо-
дится. Если К = 1, то ряд может быть как сходящимся, так и расходя-
щимся.
оо
Примеры. 1. Ряд 2 — — сходящийся, так как по признаку
Коши
а->оо
“ 2
316	гл. 8. ТЕОРИЯ ПРЕДЕЛОВ
Л—1
— расходящийся, так как по признаку Коши
П-*оо
.. 2п
= lim ——
п-><» п + 1
Признак Даламбера. Если предел
lim
П-*оо
*П+1
хп
существует и равен D, то при D < 1 ряд сходится, а при D > 1 расхо-
дится. При D =» 1 ряд может быть как сходящимся, так и расходя-
щимся.
оо
S2n
-jjj- сходится, так как по признаку Да*
П=1
ламбера
lim
п-*оо ХП
..	2п+' «I 2
«= Нт ——]im——. ==0<1
П^оо(л4-1)|	2° П-*оол+1
оо
2. Ряд п\	расходится, так как
л=1
Нт Хп^ lim (”+l)!-10n+1 Пп
пг™ (п+1ГН nl 10"
.. (n-l-l).io-n"
t= lim Д—!—1-----
rt^oo (n+lp-b1
Признак Раабе. Если предел
lim
П-*оо
существует и равен R, то при R > 1 ряд сходится, а при R < 1 расхо-
дится. При R =» I ряд может быть как сходящимся, так и расхо-
дящимся.
Признак Раабе значительно «сильнееж признака Даламбера —
если признак Даламбера дает ответ на вопрос о сходимости ряда, то
и признак Раабе его также дает. Если D < 1, то R = +оо, если D > 1,
то R ~ —<юа т. е, все возможные значения D описываются всего двумя
jS 3. ЧИСЛОВЫЕ РЯДЫ И БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ 317
значениями /?±оо. Все остальные значения R (кроме R = 1),
также дающие ответ на вопрос о сходимости рядад соответствуют слу-
чаям, когда D = 1, т. е. случаям, когда признак Даламбера не дает от-
вета на вопрос о сходимости ряда,
оо
Так, например, признак Даламбера для ряда не дает ответа
И=1
на вопрос о его сходимости, в то время как по признаку Раабе
Игл Гп f 1 —	= lim Гп(1------иг’)] =
п-оо L \ *п /J п+оо L \	(п+02 3 /J
Г 2л 4-1	1 v 2л2 + л
= hm л«-	а—--г- = lim --л-т-а—г—г- =»
л-*оо L л2 + 2л + 1 J л->оо П* 4- 2л 4* 1
= |1т-------к-------г— = 2,
П"*°° 1 I - —. J____
+ л + п2
т. е. данный ряд сходится.
3.4. Понятие бесконечного произведения. Рассмотрим бесконеч-
ную числовую последовательность хъ х2, х3, ..., хп, ... Образуем из
данной числовой последовательности последовательность, членами ко-
торой являются числа
= Xf,	Xf *х2,	X% e xpXg’Xg, ..., Xn e Xj^Xa’Xg*... *хл, .. •
1) Для заданной числовой последовательности (хп) выражение
Xj • Х2• Хд• ... • ХЛ • •..	(7)
называется бесконечным произведением. Бесконечное числовое произ-
ведение (7) обозначается
со
Пх„.
П=1
2) Произведение л первых членов последовательности (хп) назы-
вается частичным произведением данного бесконечного произведения;
Хп = хгх2 х8-... хп.
3) Если существует конечный и отличный от нуля предел X после-
довательности (Хп) частичных произведений, то говорят, что бесконеч-
ное произведение сходится', предел X называют значением бесконеч-
ного произведения (1) и пишут
X « Xj*X2’X8* ...*ХЛ*...
В противном случае (когда конечный предел последовательности ча-
стичных произведений не существует или равен нулю) бесконечное
произведение называют расходящимся.
3.5. Связь бесконечных произведений с рядами. Рассмотрим бес-
конечную числовую последовательность все члены которой положи-
318	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
тельны. Составим для этой последовательности бесконечное произвел
дение
xi-Xa-Xf ... -Хп-,.. =х Пхп.	(8)
П=з!
Для сходимости бесконечного произведения (8) необходимо и достаточно,
чтобы сходился бесконечный ряд
S lnxn.	(9)
Если ряд (9) сходится к числу S, то бесконечное произведение (8)
сходится к числу X«» е5.
§ 4.	Прогрессии
4.1.	Арифметическая прогрессия. Последовательность, у которой
вадан первый член alt а каждый следующий член, начиная со второго,
равен предшествующему члену, сложенному с одним и тем же числом d,
называется арифметической прогрессией. Число d называется разностью
арифметической прогрессии. Если число d > 0, то прогрессия назы-
вается возрастающей, если d < 0 — убывающей.
Для того чтобы последовательность (ап) была арифметической
прогрессией, необходимо и достаточно, чтобы для любого л> 1 выпол-
нялось равенство
л __ ап~1 + ^п+1
ап -------------.
Если заданы первый член а^ и разность арифметической прогрессии d,
то п-А член арифметической прогрессии вычисляется по формуле
а>п " at + d (п — 1).
Эта формула называется формулой общего члена арифметической про-
грессии. Члены арифметической прогрессии ап_(, ап и an+i (л> О
связаны между собой равенством
ап--------g-----•
Сумма первых л членов арифметической прогрес-
сии (ап) вычисляется по формуле
srt =-----g--п
или по формуле
2at + d (л- 1)
----------------п.
Ряд, образованный из членов арифметической прогрессии
+ «з + «з + • • • + «л + • • • У «л>
л-1
$ 5. ЧИСЛОВЫЕ ФУНКЦИИ
319
при любых ненулевых числовых значениях первого члена аг и разности d
будет расходящимся.
4.2.	Геометрическая прогрессия. Последовательность, у которой
вадан первый член wlt а каждый следующий член, начиная со второго,
получается умножением предыдущего члена на одно и то же постоянное
для данной последовательности число q, называется геометрической про*
грессией. Число q называется знаменателем геометрической прогрессии.
Для того чтобы последовательность (un) была геометрической про*
грессией, необходимо и достаточно, чтобы для любого п > 1 выполни*
лось равенство
Если заданы первый член и знаменатель геометрической про*
грессии qt то n-й член геометрической прогрессии вычисляется по фор*
муле
Эта формула называется формулой общего члена геометрической про-
грессии. Члены геометрической прогрессии ип и Un+i (п> /)
связаны между собой равенством
ип =un-run+l>
Сумма первых п членов геометрической прогрессии
вычисляется по формуле
U1 (1 -<р)
-----Г^—
Бесконечный числовой ряд, образованный из членов геометрической
прогрессии
Ui + «2 4» Из + • • • + ип + • • • ss 2] иП»	(1)
при |^| < 1 сходится, и его сумма 5 равна
(2)
при |gl > 1 ряд (1) расходится.
Формулу (2) также называют формулой суммы членов бесконечно
убывающей геометрической прогрессии. Здесь под «бесконечно убываю*
щей геометрической прогрессией» понимается прогрессия, члены ко-
торой убывают по абсолютной величине, т. е.
I«г I>Iм21> I«зI> ••• >!««!>•••
§ 5.	Числовые функции
5.1.	Понятие числовой функции. Пусть X и Y — два множества
действительных чисел. Элементы этих множеств будем обозначать бук-
вами х и у соответственно. Задать-соответствие между множеством X
и множеством Y — это значит указать правило, по которому для каж-
дого числа х из множества X выбирается одно, несколько или даже
320
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
бесконечно много чисел у из множества У. При этом может оказаться, что
некоторым числам х £ X не будет соответствовать никакое числом С
Например, если задать соответствие между множествами действ и-
тельных чисел X « R и У = R формулой
£/* = 1,
то каждому числу х из промежутка (—1; 1) будут соответствовать два
числа:	______ _____________________
у == 1 —- ха	и // = - /1 - х2.
Числам х» 1 и х=* — 1 соответствует единственное число у = 0, а всем
остальным х £ R не соответствует никакое у.
Соответствия между числовым множеством X и числовым мно-
жеством У обычно обозначают буквами латинского алфавита ft F9
g, ... и пишут
хЛг, х Дг, хЛк,...
Л Х-Г, F:	g:	...
Соответствие f, относящее каждому данному числу х из множества X
единственное число у из множества У, называют числовой функцией
аргумента х и пишут
y~f(x)>	(1)
При этом х называют независимой переменной, ay — вависимой пере*
менной. Буква f в записи (1) характеризует именно то правило, по ко-
торому получается значение у, отвечающее заданному значению х.
Множество X называют областью определения функции f (х), а множество
У1 (Ki С К), образованное из всевозможных чисел у, вычисляемых
по формуле (1),—областью изменения (или множеством значений)
функции f (х). Иногда область определения и область изменения функ-
ции у = f (х) обозначают D (/) и Е (/) соответственно.
В определении понятия функции существенно, что, задавая пра-
вило, по которому для заданного значения х получается значение у,
необходимо также указать область определения функции, т. е. мно-
жество X. (Множество —область изменения функции, обычно не
указывается, поскольку сам закон соответствия уже определяет мно-
жество значений функции.) В тех случаях, когда область определения
функции явно не указана, под областью определения функции пони-
мается множество X такое, что для каждого х £ X правило выбора
единственного значения у выполнимо.
Так, например, пусть функция задается равенством
Поскольку в множестве действительных чисел квадратные корни
можно извлекать лишь из неотрицательных чисел, то область опреде-
ления этой функции — множество всех чисел, принадлежащих проме-
жутку [0; +оо).
Или, например, пусть функция задается равенством
1
у=—.
У этой функции область определения — любое действительное число,
отличное от нуля, поскольку операция деления на нуль не определена»
.§ 5. ЧИСЛОВЫЕ ФУНКЦИИ
321
Числовая функция у = f (х) может быть определена и как множе-
ство упорядоченных пар действительных чисел (х; f (х)) таких, что для
каждого х в множестве этих пар имеется не более одной пары с данным
первым элементом х. Например, функция, задаваемая формулой у =
= х2, может быть также задана как множество всех упорядоченных
пар вида (х; х2).
Если переменные х и у рассматривать как декартовы координаты
точек на плоскости, то графиком функции y—f (х) называют множество
точек координатной плоскости Оху с координатами (х; f (х)).
5.2.	Способы задания функций. В математическом анализе функ-
ции обычно задаются так называемым аналитическим способом.
Основные формы аналитического задания
функции:
1)	Явная форма задания функции. Функция за-
дается в виде формулы, указывающей операции (и последовательность
их выполнения), которые необходимо совершить над значением неза-
висимой переменной, в результате которых получается значение зави-
симой переменной. .
Например, пусть функция у = f (х) имеет вид
у = (/Г— 1)2.
Область определения данной функции D (/) = [0; +оо). •
Возьмем некоторое значение х0 g D (/). Для получения значе-
ния 1/0=/ (х0) над величиной х0 следует произвести следующие операции,
в результате которых получится величина yQ: а) извлечь квадратный ко-
рень из числа х0; б) вычесть из полученного значения квадратного корня
единицу; в) полученную разность возвести в квадрат.
При аналитическом способе задания функции при одних значе-
ниях аргумента, х £ функция может задаваться одной формулой,
а при других значениях аргумента х С D2 — другой формулой (Dj (J
UD2=D(/) и А ПЯ2= 0).
Примером такой функции, определенной на всей числовой оси,
служит функция, определяемая следующими условиями;
f (х) = 1, если х> 0,
f W ~ —1, если х < 0,
f (0) = 0.
Эта функция имеет специальное обозначение:
sign х,
читается: «сигнум х» — и называется «знак числа х».
2)	Неявная форма задания функции. Под не-
явным заданием функции понимается задание функции в виде урав-
нения:
F (х, у) = 0.	(2)
Уравнение (2) задает функцию лишь в том случае, если множество
упорядоченных пар (х; у), являющихся решением данного уравнения,
таково, что для любого числа х имеется в этом множестве не более одной
пары (х0; у0) с первым элементом х0. Например, уравнение
ху — 1 = 0
Н А, Г. Цыпкин
322	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
задает функцию, в то время как уравнение вида
x2+i/2= 1
задает не функцию, а соответствие, так как среди множества упорядо-
ченных пар (х; (/), являющихся решением данного уравнения, найдутся,
например, две такие пары с совпадающим первым элементом:
/ /3 .	1 \	( /3 ._____1_\
\ 2 ’	2 )	“	\ 2 *	2 /•
3)	Параметрическая форма задания функ-
ции. При параметрическом задании функции соответствующие друг
другу значения переменных х и у выражаются через третью величину,
называемую параметром:
х = ф (0, у = ф (О-
В некоторых случаях функция, заданная в параметрическом виде,
может быть также записана и в явной форме. Например, функция, за-
данная в параметрической форме:
х = sin /, у = cos /, t £ [—л/2, л/2],
допускает запись в явной форме:
У = /1 — X2.
Кроме аналитического способа задания, функция может быть
также задана':
1)	таблицей своих значений или правилом вычисления таблицы;
2)	графиком;
3)	перечислением характерных свойств функции и т. д.
5.3.	Сумма, произведение, разность и частное двух функций.
Функции f (х) и g (х) называются равными на общей части их об-
ласти определения D (f) П D (g), если / (х) = g (х) при всех х Q
6 D(f) П D fe).
Суммой двух функций f (х) и g (х), определенных на множествах
значений независимой переменной D (f) и D (g) соответственно, назы-
вается функция S (х), задаваемая условиями:
1)	Область определения функций S (х) (если нет специальной ого-
ворки) есть общая часть множеств D (/) и D (g), т. е.
D (S) = D (f) П D (g).
2)	Значение функции S (х) в каждой точке х0 С D (S) вычисляется
как сумма значений функций f (х) и g (х) в точке х0:
s (х0) = f(xa) + g (х0).
Аналогично определяются разность, произведение и частное двух
функций, причем частное двух функций
Ж
определено лишь при тех значениях х £ D (f) П D (g), при которых
функция g (х) не обращается в нуль.
5.4.	Сложная функция (суперпозиция функций). Пусть g =
= / (х) — числовая функция с областью определения D (/) и областью
§ 5. ЧИСЛОВЫЕ ФУНКЦИИ
323
изменения (множеством значений) Е (f), а г — g (у) — числовая функ-
ция, заданная на множестве Е (/) или некотором его подмножестве,
с областью изменения Е (g). Соответствие, относящее каждому данному
числу х из множества D (f) единственное число у из множества Е (f)t
а числу у — единственное число г из множества Е (g), называют сложной
функцией (или суперпозицией функций у = f (х) и г = g (у)) и пишут:
г = g (f (*)).
Большинство функций, изучаемых в элементарной математике
и математическом анализе, можно рассматривать как сложные функции;
например, функция
г — х — I
может быть представлена как суперпозиция двух функций:
(/= КГ, г = у — 1.
5.5.	Четные и нечетные функции. Числовая функция у = f (х)
называется четной, если:
1)	область определения функции симметрична относительно
точки О числовой оси (т. е. если точка х0 принадлежит области опреде-
ления функции, то и точка —х0 также принадлежит области опреде-
ления функции);	х
2)	для любого значения независимой переменной, принадлежа-
щего области определения функции, выполняется равенство
f (X) = f (—х).	(3)
Числовая функция у = f (х) называется нечетной, если:
1) область определения функции симметрична относительно точки О
числовой оси (т. е. если точка х0 принадлежит области определения функ-
ции, то и точка —х0 также принадлежит области определения функции)-;
2) для любого значения независимой переменной, принадлежащего
области определения функции, выполняется равенство
‘ f М ==	(—х).	(3')
График четной функции симметричен относительно оси ординат,
а график нечетной функции симметричен относительно начала коорди-
нат, т. е. центрально симметричен.
Свойства четных и нечетных функций:
1) Сумма, разность, произведение и частное двух четных функций
— четная функция.
2) Сумма и разность нечетных функций — нечетная функция, а
произведение и частное — четная функция.
Доказательство четности (или нечетности) функции у == / (х)
проводится следующим образом. Выясняется, симметрична ли область
определения функции у = f (х) относительно точки О числовой оси.
Если, область определения функции не симметрична относительно
точки О, то функция не является ни четной, ни нечетной. Если же об-
ласть определения функции симметрична относительно точки О, то
переходят к проверке справедливости равенств (3) (или (3')).
Если выполняется равенство (3), то функция f (х) четная; если (3'),
то нечетная. Если не выполняется ни одно из приведенных равенств,
то Функция не является ни четной, ни нечетной.
11*
324
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Примеры. 1. Функция f (х) = —не является четной и ие
является нечетной, так как ее область определения не симметрична от-
носительно точки О (в точке х = 1 функция определена, а в точке х ==
= —1 не определена).
2.	Область определения функции f (х) = Х ^"--симметрична относи-
тельно точки О, но функция не является ни четной, ни нечетной, так как
X z и _ (- Х)2+(-	__ Х*-Х = _ Х^-Х
' 1	}	— V	— Г	X *
— X
— X
и следовательно,
f (-х) * f (х) и f (х) ф -f (—X).
3.	Область определения функции f (х) « симметРична отно-
сительно точки О, и, как нетрудно проверить, функция удовлетворяет
равенству (3):
/(—X) =	=Х2_ 1 =/(Х)-.
1
Следовательно, функция f (х) =	— четная функция*
5.6.	Периодические функции. Функция f (х) называется периоди-
ческой с периодом Т (Т — некоторое действительное число, отличное от
нуля), если:
1)	для любого значения аргумента х из области определения функ-
ции значения аргумента х + Т и х — Т также принадлежат области
определения функции;
2)	при любом х из области определения функции
f (х ± Т) =- f (х).
Обычно под периодом функции понимают наименьший из всех
положительных периодов (если такой существует). В этом случае все
периоды функции кратны ее наименьшему периоду:
T^kTQt
где То — наименьший положительный период функции, a k — целое
число, отличное от нуля.
Существуют периодические функции, не имеющие наименьшего
положительного периода. Примером такой функции является функция
Дирихле, обозначаемая D (х) и задаваемая условиями:
&	(0, если х рационально,
( 1, если х иррационально.
Доказательство периодичности (или непериодичности) функции
заключается в нахождении ее периода (или в доказательстве того, что
не существует числа Т, удовлетворяющего условиям 1), 2)),
§5. ЧИСЛОВЫЕ ФУНКЦИИ
325
Примеры. 1, Найти наименьший период функции f (х) ^=>
« sin (ах + Ь), где а =# 0.
Предположим, что данная функция периодическая, т. е, сущест-
вует число Т такое, что выполняется равенство
sin (ах + b) — sin [а (х4- Л + Ь].
-Проверим справедливость нашего предположения.
Решая уравнение sin (ах + b) — sin [а (х + Т) + относительно
величины Г, получим
1 = —+.2Д1 _ 2х - 2-—, & е Z; -	(4)
a	a	v
2лп
а
n£Z.
f
(5)
Величина Т, определяемая формулой (4), не удовлетворяет определению
периода, так как Т зависит от х. Формула (5) задает бесконечное
множество чисел Т =  - — (п € Z). Наименьшим положительным
числом из них является число
Т =  
И •
2л
То Г
По определению функции синус при любом х значения х +
и х—рур также принадлежат области определения функции, т. е.
условие 1) выполнено. Условие 2) выполнено в силу способа нахожде-
ния числа Т.
Таким образом, доказано, что число Т « удовлетворяет оп-
ределению периода, и наше предположение, что функция sin (ах + Ь) —
периодическая, справедливо.
2.	Доказать непериодичность функции' f (х) =* sin (х2).
Предположим, что существует число Т Ф 0 такое, что sin (х2) =я
= sin (х + Т)2 при любом х. Однако, решая это уравнение относитель-
но величины Т, нетрудно проверить, что Т зависит от х.
Это означает, что не существует положительного числа Т (одного
и того же для всех х), для которого выполнялось бы равенство
sin (х2) = sin (х + Т)2;
следовательно, данная функция непериодическая.
5.7.	Ограниченные функции. Функция f (х) называется ограничен*
ной сверху, если существует такое число М, что для всех значений аргу-
мента из области определения функции выполняется неравенство
t (х) М, и ограниченной снизу, если существует такое число т, что
для всех значений аргумента из области определения функции выпол-
няется неравенство /(х) т.
Функция, шраниченная сверху и снизу, называется ограни*
чинной.
326	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Примеры. 1. Функция х2 ограничена снизу, например, чис-
лом 0 и не ограничена сверху.
2.	Функция —х ограничена сверху, например, числом 1 и не ог-
раничена снизу.
3.	Функция sin х ограничена сверху, например, числом 1, и снизу,
например, числом —1.
Примеры неограниченных функцийз
/(х) = №.	f(x)=]gx, f(x) = -^-,
5.8.	Монотонные функции. Пусть функция f (х) определена в не-
котором промежутке (а; Ь).
Функция f (х) называется возрастающей в промежутке (о; Ъ), если
для любой пары значений xt С (а; Ь), х2 £ (а; Ь) из неравенства Xj>
> х2 следует неравенство f (xi)>/(x2), т. е. большему значению аргу-
мента соответствует большее значение функции. Если из неравенства
Xj > х2 следует неравенство f (хг) > f (х2), то функция называется
неубывающей.
Функция f (х) называется убывающей в промежутке (a; Ь), если для
любой пары значений х2 С (а; Ь), х2 С (я; Ь) из неравенства хг> х3
следует неравенство /(хх) < f (х2), т. е. большему значению аргумента
соответствует меньшее значение функции. Если из неравенства хг > ха
следует неравенство / (Xj) / (х2), то функция называется невоврастаю-
щей. Возрастающие и убывающие функции называются строго моно-
тонными функциями. Возрастающие, невозрастающие, убывающие и
неубывающие функции называются монотонными.
Пусть функция f (х) не монотонна во всей своей области определе-
ния, но область определения может быть разбита на некоторое (может
быть, и бесконечное) число непересекающихся промежутков таких, что
на каждом из этих промежутков функция монотонна (на одних, воз-
можно, возрастающая, на других убывающая). Такие промежутки на-
зывают промежутками монотонности функции.
Примеры. 1. Функция у = х2 — не монотонна на всей число-
вой оси, однако числовая ось может быть разбита на два промежутка
монотонности функции:
(—оо; 0)	и [0; +.оо),
2.	Функция у = tg х, определенная на всей числовой оси, за исклю-
чением точек х = -^-+ лЛ, £ Z не монотонна. Область определе-
ния функции может быть разбита на бесконечное число промежутков
( —-g- +л£;-g-+ л& к на каждом из которых функция г/= tg х
возрастающая.
Доказательство монотонности функции состоит в проверке спра-
ведливости какого-либо из неравенств
/ (*1) > f (х2), f (*i) > / М, f (xi) < f (х2), f (Xi) < / (x2J.
Пример. Доказать монотонность функции f (х) = /х. Об-
ласть определения функции — промежуток [0; +©о)^
Рассмотрим разность
=	(6)
§ 5. ЧИСЛОВЫЕ ФУНКЦИИ	327
где xt и х2 — значения^аргумента из области определения функции и
х± > х2. Разность jAxj — х2 можно представить в виде
рГ— _ J/-— = (/*7 — Уъ) (К*7 +	 Xt — x2 .
Ух1 + Ух^	Уъ + Уъ
Так как хх> х2 и Ух,+ j/”x2> 0, то Ух/ — Ух2> 0. Из послед*
него неравенства и равенства (6) при хх > х2 следует неравенство
/ (*i)> / (*г) и, следовательно, функция f (х) = j/x возрастающая.
Достаточное условие монотонности функ-
ции. Пусть функция f (х) определена и дифференцируема на промежут-
ке (а\ Ь). Для возрастания функции f (х) на промежутке (а\ Ь) достаточно,
чтобы производная данной функции была положительна при всех
х € (а\ Ь),г для убывания функции достаточно, чтобы производная была
отрицательна при всех х £ (а\ Ь).
Сформулированное условие монотонности не является необходи-
мым — можно привести примеры монотонных функций, производная
которых обращается в нуль в конечном (и даже бесконечном) числе
точек промежутка (а; Ь). Простейшим примером такой функции будет
функция
f (X) = X3.
Она возрастает при всех х С R и имеет производную, равную нулю,
в точке 0.
5.9.	Понятие обратной функции. Пусть	— числовая
функция с областью определения D (f) и областью .изменения (множе-
ством значений) Е (f). Далее для простоты будем полагать, что мно-
жества D (/) и Е (j) представляют собой некоторые промежутки.
Выберем какое-нибудь значение у0 из множества значений функ-
ции Е (/); тогда в множестве D (f) обязательно найдется хотя бы одно
значение х = х0 такое, что
f М = уа.
Если функция у = f (х) непрерывная и строго монотонная, то для
каждого значения yQ из множества значений функции Е (f) найдется
единственное значение х0 из области определения функции D (?) такое,
что
f W = Уо-
Соответствие, относящее каждому данному числу у0 из множества Е (f)
единственное число х0 из множества D (/), называют функцией, обрат-
ной функции /, обозначают символом и пишут
В последней записи: у — независимая переменная, ах — зави-
симая.
Функция обратная непрерывной и строго монотонной функции
также непрерывна и строго монотонна. Функции f и называют
взаимно обратными.
Если функция х =	(у) является обратной для функции у =
= f (х), то, очевидно, что графики этих функций совпадают. Можно
потребовать, чтобы и аргумент обратной функции обозначался буквой х9
328	гл. 8. ТЕОРИЯ ПРЕДЕЛОВ
а зависимая переменная — буквой у, т. е. рассматривать функцию
у = f -1 (х). Однако такое переобозначение не изменит график функции,
так как при этом мы обязаны переобозначить и координатные оси, т. е.
вертикальную ось называть осью Ох, а горизонтальную — осью Оу.
Если же дополнительно потребовать, чтобы, как обычно, новая ось Ох
была горизонтальной, а новая ось Оу — вертикальной, то мы должны
поменять эти оси местами и эта замена уже изменит график функции.
Проще всего указанную замену осей произвести с помощью осевой сим-
метрии координатной плоскости относительно биссектрисы первого и
третьего координатных углов. Как следствие этого преобразования
получаем, что если изображать графики двух взаимно обратных функ-
ций у = f (х) и //==/-1(х) в одной и той же системе координат Оху,
то эти графики будут симметричны относительно биссектрисы-первого
и третьего координатных углов.
Может оказаться, что на некотором промежутке (а; Ь) функция не-
прерывна, но не монотонна. Если промежуток (а; Ь) можно разбить на п
непересекающихся промежутков
\/ ХьХъХ3,...,Хп, Xi U*2U..-U*n=(a;*)
У ___таким образом, чтобы на каждом из этих проме-
жутков данная функция была монотонна, то на
каждом из промежутков Х2>	•••> Хп
данная функция будет иметь обратную функ-
цию. Например, функция у = f (х) « х2 с об-
ластью определения (—оо; +оо) не монотонна
и поэтому не имеет обратной функции. Если
разбить область определения на два проме-
жутка (—оо; 0) и [0;+‘оо), то на каждом из этих промежутков
функция будет непрерывна и монотонна, а потому на каждом из
указанных промежутков для данной функции будет существовать об-
ратная функция. На промежутке (—оо, 0) такой функцией будет функ-
ция х = —У у, а на промежутке [0; Ч~оо) — функция х = Уу*
(Здесь роль независимой переменной играет у, а роль зависимой пере-
менной х.) Графики прямой и обратной функций на промежутке [0;
+оо) после указанных выше переобозначений переменных изображены
на рис. 8.4.
Свойства взаимно обратных функций.
1)	Если функция f'1 является обратной для функции /, то и функ-
ция f будет обратной для функции f"1.
2)	Область определения функции f является областью изменения
функции Г1, а область изменения функции f — областью определения
функции f"1.
3)	Графики взаимно обратных функций симметричны относительно
биссектрисы первого и третьего координатных углов координатной
плоскости Оху.
§ 6.	Предел функции
6.1.	Понятие предела функции. Пусть функция f (х) определена
во всех точках промежутка (а; Ь), за исключением, быть может, неко-
торой точки х0 £ (а; Ь). Построим последовательность значений аргу-
мента функции / (х):
#1> X2t •*.) Xfit • • •> n£N (Хд Xq),	(1)
Рио. 8.4.
§ 6. ПРЕДЕЛ ФУНКЦИИ	329
такую, чтобы все члены последовательности принадлежали проме-
жутку (а; Ь) и последовательность сходилась к точке х0:
limxrt = х0.
П-*оо
Тогда значения функции f (х)
f (Xi), f (х2), f (xn)t ...	(2)
также образуют некоторую числовую последовательность.
Говорят, что число А является пределом функции f (х) при х, стре-
мящемся к х0, если для любой последовательности значений аргу-
мента (1), сходящейся к числу х0, последовательность значений функ-
ции (2) сходится к числу А, и пишут
lim f (х) = Л.
Х-^Х0	'
Это определение предела функции называют определением
предела по Гейне.
Существует и другое, эквивалентное сформулированному выше
.определение предела функции.
Говорят, что число А является пределом функции f (х) при х, стре-
мящемся к х0, если для любого положительного числа г найдется такое
положительное число 6, зависящее От е, что при всех х, С (а\ Ь), удовлет-
воряющих неравенству
О < | х — х0 | < 6,
выполняется неравенство
|/(х)^Л|<8.
Это определение предела функции называют определе-
ниемпределапоКоши.	"	_
Примеры. 1. Доказать, что предел функции f (х) ==? К*
при х, стремящемся к а (а> 0), равен а.
Доказательство будем проводить, используя определение предела
по Коши,, т. е. покажем, что для любого числа г > 0 найдется такое
число 6 > 0 (для каждого 8, возможно, свое), что для всех х, принадле-
жащих области определения функции, из неравенства 0 < | х—а | < б
следует неравенство 1/х — а | < 8,
Выражение \Ух — j/Ъ | можно записать в виде .
1КГ—Ка I =
х — а | 	| х — о |	 | аг — а | , •
Отбрасывая в знаменателе последней дроби неотрицательное слагае-
мое |/х и тем самым увеличивая дробь, получим

(3)
330
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Если взять 6 = 8 j/’a, то из неравенства 0 < | х — а | < б будет сле-
довать неравенство
|х-Д| ^6 |х —а| '
Уа Уа Уа
с учетом которого из (3) получаем | Ух — Уа | < е.
Таким образом, для любого 8 > 0 найдено такое б > 0 (а именно,
б = е У а), что для х, удовлетворяющих неравенству 0 < | х—а | < б,
будет выполнено неравенство | Ух — У а | < 8.
Однако при таком выборе б может оказаться, что среди значений х,
удовлетворяющих неравенству | х—а | < б, есть значения х (а именно,
отрицательные значения), которые не входят в область определения
функции f (х) = Ух и для которых выражение Ух не определено.
Если выбрать в качестве б минимальное из двух чисел 8 У а и а,
то все значения х, удовлетворяющие неравенству
принадлежат области определения функции /Дх) = У"х, и для них
выполнено неравенство
/а |<е,
т. е. число У а действительно является пределом функции / (х) = У~х
при х, стремящемся к а.
2. Доказать, что предел функции
ч Зх2 — 3
7+Т*
при х, стремящемся к —1, равен —6, {Область определений данной
функции: (—сю; —1) (J (—1, +оо).)
Докажем, что для любого числа 8=0 существует такое число б =
= б (е) > 0, что при всех х =/=—!, удовлетворяющих неравенству
। х + 11 < б, выполняется неравенство
12*2-3_+б|<е,
В самом деле, при х —1 имеем
I Зх2 —3 , fi|_ |3(х+1) (х— 1)
I *-Н + Г! *4-1
3(*-D J.J
----j---4-6|~
= 3|х4-1|. (4)
Если взять б равным, например, е/З, то из неравенства | х + 11 <
< б = в/3 слёдует, что 3 | х -|- 11 < 8, ив силу равенств (4) неравенство
I Зх2 — 3 , J
что и требовалось доказать,
§ 6. ПРЕДЕЛ ФУНКЦИИ
331
3. Доказать, что функция
f (X) = Sin -1-
не имеет предела при х, стремящемся к нулю.
Доказательство будем проводить, используя определение предела
по Гейне. Построим две последовательности значений аргумента:
2	2	2
5л 9 9л ’	л(1+4л) 9 ””
7л * Ня’ л(3 4-4п) ’
Обе последовательности сходятся к числу 0. Последовательности зна-
чений функции
f (х) = sin -1-,
соответствующие построенным последовательностям (5), следующие:
1, 1, 1, ..., 1, ,.
—1,	—1,	—I, .ч., —1,...
Пределами этих последовательностей будут числа 1 и —1 соответственно.
Таким образом, построены две последовательности значений аргу«
мента функции
f (х) = sin -,
сходящиеся к одному и- тому же
числу, такие, что соответствующие
последовательности значений дан-
ной функции имеют различные пре-
делы; следовательно, данная функ-
ция не имеет предела при г, стре-
мящемся к нулю. График функции
//= sin -i- изображен на рис. 8.5.
Сформулированные выше определения предела функции по Гейне
и по Коши могут быть обобщены и на случай, когда вместо числа х0
берется +оо (или —оо).
Так, например, пусть функция f (х) определена на промежутке
(а; +оо). Говорят, что число А является пределом функции f (х) при х,
стремящемся к +оо, если для любого положительного числа в найдется
такое положительное число А, что для всех значений х, удовлетворяю-
щих неравенству х> Д, выполняется неравенство
|/(х) — Л | <е;
в этом случае пишут
lim f (х) = А.
332	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Говорят, что функция f (х) стремится к +ро при стремлении х
к х0, если для любого сколь угодно большого положительного числа Е
найдется такое число 6 >0, что для всех значений х, удовлетворяющих
неравенству
0<|х— х0 |<6
и принадлежащих области определения функций, выполняется нера-
венство
f (х) > Е-,
в этом случае пишут
/(х) —> 4-оо при х-> х0, или
I im f (х) = 4- оо.
6.2. Односторонние пределы. Пусть функция f (х) определена на
промежутке (а; х0). Число А называют левым пределом функции f (х)
в точке х0 и пишут
lim / (х) == А,
х-*х0—О
если для любого числа е > 0 най-
дется положительное число 6, зави-
сящее от е, такое, что для всех
х g (а; х0), удовлетворяющих не-
равенству х0 — х<?6, выполняется
неравенство | f (х) — А | < е.
Аналогично определяется пра-
вый предел функции f (х). Для обо-
значения правого предела функции f (х) в точке х0 используется обозна-
чение
Нт / (х).
х->хо4-0
Левый и правый пределы функции называются односторонними
пределами.
Если функция f (х) определена на промежутке (а; Ь), за исключе-
нием, быть может, точки х0 £ (a; b)t то для существования предела
Ит/.(х) = Л
Х-+Хй
необходимо и достаточно, чтобы правый и левый пределы функции
- f(x) в точке х0 существовали и были равны:
lim f (х) = lim/(x) = 4.
х->хо4-О	х->х0—О
В общем случае левый и правый пределы функции f (х) в точке х0
могут существовать, но не быть равными. Так, например, пусть
f(x) = arctg
Область определения данной функции — любое действительное
число, отличное от нуля. Правый и левый пределы данной функции,
при х, стремящемся к нулю, соответственно равны
.. х 1 л	..	.	1	л
lim arctg— = -n-,	lim arctg— =-------,
x-H-o x 2	* x 2
т. e. правый и левый пределы существуют, но не равны. График этой
функции изображен на рис, 8.6.
§ 6. ПРЕДЕЛ ФУНКЦИИ
333
6.3. Теоремы о пределах функций. 1) Если функции f (х) и g (х)
имеют пределы при х, стремящемся к а, то функции f (х) ± g (х\
v fM
1	(*)» g(xj также имеют пределы при х. стремящемся к а а
lim [f (х) ± g (x)J « lim f (х) ± Игл g (г),
х-+а	х-+а	х-+а
lim[/(x)-g(x)J = lim f (x)-limg(x),
х-+а	х-+а х-+а
limf(x)
lim -Ц4 =	.
х-*аё(х)  l'mg(x)
х-+а
(В последнем случае предполагается, что функция g (х) не обра-
щается в нуль в достаточно малой окрестности точки а и lim g (х) Ф 0.)
х+а
2) Если при х, стремящемся к а, функция / (х) имеет предел, рав-
ный А, и этот предел больше числа с, то для достаточно близких к
а значений х функция f (х) удовлетворяет неравенству f (х) S> с.
Использование теорем о пределах функций в ряде случаев поз-
воляет свести вычисление предела функции к вычислению пределов
более простых функций.
Пр и м е р. Вычислить предел
lifn		(6)
*-4 Ух — 2
Непосредственное применение теоремы о пределе частного здесь невоз-
можно. так как предел выражения, стоящего в знаменателе дроби»
при х —* 4 равен нулю. Поэтому, прежде чем воспользоваться теоремой
о пределе частного необходимо так преобразовать данную дробь, чтобы
ее знаменателем оказалось выражение, имеющее отличный от нуля пре-
дел. Для этого умножим числитель и знаменатель выражения, стоящего
под знаком предела, на выражение j/" 1 4- 2х + 3:
У1 + 2х —3 (У 1 + 2х — 3) (/1 + 2х+3)
Ух — 2	(/х — 2) (/1 + 2х 4-3) =
2х—8 2 (х — 4)
' (Ух-2){УТ+1х+3)	(Ух-2)(УГ+1^ + 3)~
= 2(/Г+2)(/Г—2)	2(/?+ 2) .
(Ух — 2) (/1 + 2х + 3) “ /1 + 2х 4- 3 ’
Предел функции, стоящей в знаменателе последней дроби, при
х —> 4 существует и отличен от нуля, а предел функции, стоящей в чис-
лителе дроби, также существует. Поэтому к последнему выражению
уже применима теорема о пределе частного:	__
г----	. г— ч lim 2lAv 4- 2
л-»4 Ух — 2	х-»4 У1 + 2х + 3  lim (У 1 + 2х + 3)
334
ГЛ. 8« ТЕОРИЯ ПРЕДЕЛОВ
Используя далее теоремы о пределах суммы и произведения функ-
ций, получим
lim (2 J/T + 4)	2 Hm 1^7+ lim 4
X-*4___________________x-»4________x-»4
lim (K1 4- 2x 4- 3) Hm 1 4- 2x 4- lim.3
X-*4	x->4	x-*4
Принимая теперь во внимание, что lim j/"x = jAz (а> 0), имеем
х-ьа
2 lim K*4- Hm4 , . ,
x-»4______x-»4	_ 4 4“ 4   4
lim 14- 2x 4- Hm3	34-3	3 е
X->4	x->4
Таким образом,	_______
„тК1 + 2х-3_ 4,
x-*4 x — 2	3
Заметим, что здесь, так же как и при вычислении пределов после-
довательностей (см. п. 2.3), правомерность соединения знаком равен-
ства выражений, получаемых в результате использования теорем о пре-
делах, оказывается обоснованной лишь после того, как доказано, что
исходная функция имеет предел.
В тех случаях, когда предел функции неизвестен и не может быть
вычислен с помощью теорем о пределах, существование предела функ-
ции в ряде случаев может быть установлено с помощью необходимого
и достаточного условия существования предела (критерия*
Коши).'
Для того чтобы функция f (х) при х, стремящемся к а, имела конеч-
ный предел, необходимо и достаточно, чтобы для любого е > 0 существо-
вало положительное число 6 (вообще говоря, зависящее от е) такое, что
для всех значений аргумента х' и х", принадлежащих области опреде-
ления и удовлетворяющих неравенствам
0<|х' — а|<6, 0 < | х* - а | <6,
выполняется неравенство
I/(X') — Z (X") I <е-
6.4.	Некоторые важные пределы. В теорий пределов важное место
занимают перечисленные ниже пределы 1)—4), с помощью которых вы-
числяются многие пределы от элементарных функций:
1-	sinx t
1)	lim------- I,
x->0 x
2)	lim (1 4- x)1/z = e,
x-*o
ax — 1	e*__I
3)	hm “----L == ]n at lim ------- = 1.
x-*0 x	x-*0 x
ax ,•	l°ga(14-X)	.	1П(14-Х)	.
4)	!im  BO' - — = loga e, lim —i—-------= 1.
§ 6. ПРЕДЕЛ ФУНКЦИИ
335
С помощью предела 1) можно получить формулу для вычисления
площади круга радиуса R.
По определению за площадь круга принимается предел последова-
тельности площадей правильных многоугольников, вписанных в ок-
ружность, при условии, что число сторон правильных многоугольников
неограниченно возрастает.
Пусть А*, A2,,..,Art — вершины правильного n-угольника, вписан-
ного в окружность радиуса R с центром в точке О (на рис. 8.7 шести-
угольника Д1ДоД3Д4Д5Дв). Рассмотрим треугольник Д1Д2О. Угол
Д1ОД2 равен 2л/и, а его площадь
S — JL /?2 sin	-------
--J- к sm V
Площадь Sn правильного n-угольника, !/	\/ 'А
вписанного в окружность, равна	q
Sn = 4г R2n sin	fl
Рассмотрим последовательность пло-
щадей правильных п-угольников, вписан-	Рис.*8.7.
ных в окружность, при условии, что число
сторон неограниченно возрастает. Эта последовательность монотон-
но возрастающая и ограничена сверху (например, площадью лю-
бого правильного многоугольника, описанного вокруг окружности).
Следовательно, по теореме Вейерштрасса (см. п. 2.4) эта последо-
вательность имеет предел. Вычислим этот предел:
* lim$n = lim R2n sin —	7?2 lim fnsin— .
n-*oo X	И /	2 n-*oo \	/
Записывая последний предел в виде
. 2л	/	. 2л	\
sin----	/ sin-- \
-у Я2 lim -----Д— = -у 7?2-2л lim I —)
* П-*оо	1	П~>оо \ ZJl /
П	\ П	/
.	2л
и обозначая ~ =* х, нетрудно заметить, что вычисление исход-
ного предела свелось к вычислению предела
.. sinx
lim------------------------------------,
х-*о х
который равен единице.
Таким образом, окончательно имеем
limS„ = л/?2 lim = л/?2.
п^оо	Х-+0 X
Аналогичным образом могут быть получены формула для вычисле-
ния длины окружности, формулы для вычисления площадей боковой
поверхности цилиндра и конуса, а также формулы для вычисления
объемов этих фигур.	•
836	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Так, например, выведем формулу для вычисления площади боковой
поверхности конуса.
По определению за площадь боковой поверхности конуса прини-
мается предел последовательности площадей боковых поверхностей
правильных пирамид, вписанных в конус, при
д	условии, что число сторон правильных много-
угольников, лежащих в основании пирамид, не-
ту/ I \	ограниченно возрастает.
///г \	Обозначим высоту конуса через Я, а радиуа
/ h \ окружности, лежащей в основании конуса,
7/Jj=a^\ через /?. Пусть Af, Д2, Ап — вершины пра-
вильного n-угольника, вписанного в окруж-
А	ность основания конуса (на рис. 8.8 шести-
/s	угольника).	Рассмотрим треугольник
(0 — центр окружности). Угол
'	2л	л
Рис. 8.8. равен ---------; lAAJ = 2/? sin —.	Высота
п	п
треугольника | ОК | = R cos-—- * ^П0ФемУ пирамиды &4p42 • •• Ап
вычислим по теореме Пифагора из треугольника SO К'
| SKI =» /I SO |2 + I ок I2 = J/78 + К8 cos8 •
Периметр правильного многоугольника А±А2... Ап равен
Рп == 2Rn sin ,
а площадь боковой поверхности правильной n-угольной пирамиды равна
s„ = 4-1SK l-pn = ]/я8- К8cos8—-Rnsin —.
л	F	П	П
Вычислим предел, который принимается за площадь боковой по-
верхности конуса:
lim \ 1/ Я2 — R2 cos2 — • Rn sin — | =з
П-+<х И->оо \ г	П	П )
— lim 1/ цч — R2 cos2 2L. ит Rn sin JL
F	n	n
, Я
sin —
=/Я2-Я2.лЯНт --------— = лЯ/Я^~^2.
n-*oo и;
n
Величина J/"Я2 — R2 — образующая конуса, которую обозначим
через L. Тогда формула для вычисления площади боковой поверхности
конуса принимает вид
^бок ~ Um Sn == TrRLf
п-*<х>
§ 7. БЕСКОНЕЧНО МАЛЫЕ (БОЛЬШИЕ) ВЕЛИЧИНЫ 337
§ 7.	Бесконечно малые и бесконечно
большие величины
7.1.	Понятие бесконечно малой и бесконечно большой величины.
Числовая функция f (х) называется бесконечно малой функцией (или
бесконечно малой величиной) при х, стремящемся к а, если
lim/(x) = 0.
Иными словами, функция / (х) называется бесконечно малой при х,
стремящемся к а, если для любого числа е > 0 найдется такое положи-
тельное число 6, зависящее от е, что при всех х =/= а. принадлежащих
области определения функции и удовлетворяющих неравенству
I х — а | < б,
будет выполнено неравенство
I/(х) I <е.
Подчеркнем, что бесконечно малую величину следует понимать
как переменную величину, которая лишь в ггр оцессе своего
изменения (при стремлении х к а) делается меньше произвольного
числа в. Поэтому, например, утверждение типа «одна миллионная есть
бесконечно малая величина» неверно: о числе не имеет смысла говорить,
что оно бесконечно малое.
 Примеры бесконечно малых величин:
f (х) == х2	при	х, стремящемся	к нулю;
f(x) = cosx	при	х, стремящемся	к л/2;
f (х) = In х	при	х, стремящемся	к единице.
Функция f (х) называется	бесконечно большой величиной при х,
стремящемся к а( если для любого сколь угодно большого числа Е > О
найдется такое положительное число 6, зависящее от Е,что привсехх=£а,
принадлежащих области определения функции и удовлетворяющих
неравенству
О < | х-а | < б (£),
выполняется неравенство
|/(х)|>Я. •
Как и в случае бесконечно малых, необходимо отметить, что ни
одно отдельно взятое значение бесконечно большой величины не может
быть названо как «бесконечно большое» — бесконечно большая вели-
чина — это функция, которая лишь в процессе своего изменения может
стать больше произвольно взятого числа Е:
Примеры бесконечно больших вел'ичин
f(x) f(x)	__1_ ~ X — tgx	при x, стремящемся к нулю; * при х, стремящемся к л/2;
f(x)	= In 1 x|	при х, стремящемся к нулю;
t(x)		при х, стремящемся к единице»
338
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Если функция f (х) при х, стремящемся к а, — бесконечно боль-
шая и для всех достаточно близких к а значений х сохраняет определен-
ный знак (плюс или минус), то в соответствии со знаком* говорят, что
функция f (х) стремится к +оо (—оо), и пишут
/ (х) -> + оо при х а или lim f (х) = + оо
х-*а
(/ (х)	— оо при х -> а или J im / (х) = — оо).
х-+а
Из приведенных выше примеров
бесконечно больших:
lim In I х I = — oo, lim --= + oo.
x-0	x-1 (*—О2
Бесконечно малые и бесконечно большие величины связаны между
собой следующей зависимостью.
Если / (х) — бесконечно большая функция (величина) при х,
стремящемся к а, то ее обратная величина
— бесконечно малая функция (величина) при х, стремящемся к а.
7.2.	Сравнение бесконечно малых и бесконечно больших величин»
Приведенные примеры различных бесконечно малых наводят на мысль
о том, не будут ли одни бесконечно малые стремиться к нулю «быстрее»,
чем другие. Прежде всего, определим, что следует понимать под словом
«быстрее», т. е. как сравнивать две бесконечно малые величины.
Две бесконечно малые величины а (х) и (3 (х) при х, стремящемся
к а, сравниваются следующим образом. Рассмотрим отношение этих
величин
Р(х)
а(х)
(при этом полагается, что величина, стоящая в знаменателе дроби, от-
лична от нуля по крайней мере для значений х, достаточно близких
к числу а) и вычислим предел этого отношения при х, стремящемся к а.
1)	Если отношение имеет отличный от нуля предел при xt
а (х)
стремящемся к а, то бесконечно малые а (х) и Р (х) считаются бесконечно
малыми одного порядка.
2)	Если отношение само оказывается бесконечно малым (а
а (х)	v
а (х) л	ч
отношение -* бесконечно большим) при х, стремящемся к а, то
бесконечно малая Р (х) считается величиной высшего порядка малости
по сравнению с бесконечно малой а (х), а бесконечно малая а (х) счи-
тается величиной низшего порядка по сравнению с величиной Р (х).
§ Г. БЕСКОНЕЧНО МАЛЫЕ (БОЛЬШИЕ) ВЕЛИЧИНЫ 339
Например, при х, стремящемся к нулю, бесконечно малыми вели-
чинами одного порядка будут следующие пары функций:
а (х) = х,	0 (х) = У1 + х — 1;
а (х) = х,	0 (х) = sin х.
При х, стремящемся к нулю, бесконечно малая 0 (х) = 1 — cos х
является бесконечно малой высшего порядка по сравнению с беско-
нечно малой а (х) = х, так как
9 с1П2 —
Р(Х)	1-cosx 2Sin 2
Jim = lim----------------= hm ----------=г
a (x) х-*э x x->o x
sm2-^- sin-=-
«= ) im--------- lim---------- lim sin	® 1 « = 0?
X-+Q	x x-*0	x X-*Q
2	2
3)	Если при x, стремящемся к а, ни одно из двух отношений
а(*)	Р(х)
t> (X) ’ а (х)
предела не имеет, то бесконечно малые величины а (х) и (J (х) считаются
не сравнимыми между собой.
Например, бесконечно малые величины а (х) « х и 0 (х) =
B=xsin— при х, стремящемся к нулю, не сравнимы между собой.
Бесконечно малая величина высшего порядка по сравнению с бес-
конечно малой величиной а (х) обычно обозначается символом о (а).
Бесконечно йалую 0 (х) называют бесконечно малой k-го порядка
по сравнению с величиной а (х), если величины 0 (х) и (х) являются
величинами одного порядка.
Например, при х, стремящемся к нулю, бесконечно малая вели-
чина 0 (х) = 1 — cos х относительно бесконечно малой а (х) = х —
бесконечно малая второго порядка, так как
.. 1 — cos х	1
х+о х2	2
Если из нескольких бесконечно малых а (х), 0 (х), у (х), ... выбрана
одна бесконечно малая а (х) (основная бесконечно малая), то бесконечно
малые вида c*ak (с — постоянная) называют простейшими бесконечно
малыми.
Если бесконечно малая 0 (х) — бесконечно малая &-го порядка от-
носительно а (х), т. е.
ИтАтт=с или 11т
or (х)	car (х)
то бесконечно малые c*ak (х) и 0 (х) называют эквивалентными.
Простейшая бесконечно малая c*akt эквивалентная бесконечно
малой 0 (х), называется неглавной частью. Например, при х-> 0 про-
стейшая бесконечно малая -~-х2 является главной частью беско-
нечно малой 1 — cosx,
340	ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
Бесконечно большие величины сравниваются между собой так же,
как и бесконечно малые величины.
Пусть f (х) и g (х) при х, стремящемся к а, — две бесконечно боль-
шие величины.
О f (*) и S (*) считаются величинами одного порядка при х» стре-
мящемся rt а, если их отношение / (x)/g (х) имеет конечный и отличный от
нуля предел.
2) Если отношение / (x)/g (х) при х, стремящемся к а, само оказы-
вается бесконечно большим (а отношение g (x)lj (х) бесконечно малым},
то величина / (х) считается бесконечно большой высшего порядка по
сравнению g g (х), a g (х) — бесконечно большой низшего порядка по
сравнению с / (х).
3) Если отношение / (x)/g (х) ни к какому конечному пределу не
стремится и в то же время не является бесконечно большим, то / (х)
и g (х) считаются несравнимыми.
§ 8« Непрерывность (и разрывы) функций
8.1.	Понятие непрерывности функции. С понятием предела функ-
ции тесно связано другое важное понятие математического анализа —
понятие непрерывности функции.
Рассмотрим функцию / (х), определенную на некотором промежут-
ке. Пусть х0 — некоторая точка этого промежутка, в которой функция
имеет значение f (х0). В определении предела функции / (х) при х,
стремящемся к х0, отмечалось, что число х0 может и не принадлежать
области определения функции / (х) (см. п. 7.1), а если числох^и принад-
лежит области определения, значение функции в этой точке при изу-
чении предела нас не интересовало.
Однако большой интерес представляет именно случай/когда
lim f (х) = f (х0).	(1)
х->х0
Говорят, что функция f (х) непрерывна в точке х0, если выполняется
равенство (1); если же равенство (1) не выполняется, то говорят, что
в точке х0 функция терпит разрыв.
Таким образом, выяснение вопроса о непрерывности функции / (х)
в какой-либо точке х0, принадлежащей области определения функции,
сводится к вычислению предела функции в точке х0 и проверке справед-
ливости равенства (1).
Если функция f (х) определена на промежутке (а, Ь) и непрерывна
в каждой точке промежутка, то говоря, что функция непрерывна на
этом промежутке.
8.2.	Основные теоремы о непрерывных функциях. Непрерывность
элементарных функций;
1)	Если функции f (х) и g (х) определены на промежутке (а, Ь}
и непрерывны в точке х0 € (а, Ь), то в этой точке функции
f(x)±g(x),	f(x)g(x),
также непрерывны (последняя функция непрерывна при условии, что
g М 0).
2)	Если функция у f (х) непрерывна в точке х0, а функция g (у)
непрерывна в точке у0 == / (х0)э то и сложная функция g (J (х)) непре-
рывна в точке Хо«
§ 8. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 341
3)	Первая теорема Больцано — Коши. Если
функция / (х) задана на промежутке [а; Ь] и непрерывна в промежутке
(а; Ь) и если на концах промежутка значения функции f (а) и f (b)
имеют разные знаки, то между а и b существует (по крайней мере одно)
такое значение xQt при котором f (х) обращается в нуль:
/ (*о) = 0 (х0 € (а; Ь)).
Теорема Больцано—Коши находит весьма неожиданное примене-
ние при решении алгебраических уравнений, а именно, она позволяет
доказать, что любое алгебраическое уравнение нечетной степени с дей-
ствительными коэффициентами
+ aixrt~1. Н---р ап^х + ап = О
имеет по крайней мере один действительный корень.
Действительно, при достаточно больших по абсолютной величине
значениях х многочлен, стоящий в левой части уравнения, имеет знак
старшего члена, т. е. при- х > 0 — знак а0, а при х < 0 — противопо-
ложный знак. Так как многочлен — непрерывная функция на всем
множестве действительных чисел; то по теореме* Больцано—Коши обя-
зательно найдется такая точка х0, в которой этот многочлен обратится
в нуль, и, следовательно, алгебраическое уравнение обратится в тожде-
ство.
4)	Первая теорема Вейерштрасса. Если функция
/ (х) определена и непрерывна на промежутке (а, Ь], то она ограничена
на этом промежутке, т. е. существуют такие два числа т и М, что для
всех х G [а; 6] имеет место неравенство
m < f (х)< М,
Используя определение непрерывности функции в точке, нетрудно
доказать, что функции f (х) == с и f (х) = х непрерывны в любой точке
числовой оси. Из непрерывности этих функций по теореме 1) следует
непрерывность целой рациональной функции
f (х) = аеХп.+ aix"-1 -|--Ь а^х + ап
и непрерывность рациональной функции
,	_ авхп 4- aixn~{ + ’ • ‘ + ап-л* + Qn
+ •••+ bm-ix + bm
при всех значениях х, не обращающих знаменатель в нуль.
Используя определение (1) п. 8.1, можно доказать, что функции
sin х и cos х непрерывны в любой точке числовой оси. Из непрерывности
этих функций в силу теоремы 1) следует что функции tg х, ctg х, sec х
и cosec х Также непрерывны при всех значениях аргумента, принадле-
жащих области определения функций.
Непрерывность обратных тригонометрических функций следует
из свойств обратных функций (см. п. 5.9).
Степенная функция ха, показательная функция а* и логарифмиче-
ская функция loga х непрерывны в своей области определения.
342
ГЛ. 8. ТЕОРИЯ ПРЕДЕЛОВ
ТАБЛИЦА 7
Рис. 8.9.
Точка х0 принадлежит
области определения
функции f (х) — проме-
жутку (а: Ь):
х0 g (а; Ь)
Левый и правый предела функции f (х) в
точке х0 существуют и конечны (А и 6—числа)
1.	lim f(x)~A, lim f (х) = В,
x->x0—>	x->xo+0
A B, f (х^) — А, или f (x0) «= 5 (на рис. 8.9
f (x0) ® В). В этом случае говорят, что в точке
х функция f (х) терпит скачок, равный В—-Д.
2.	lim f(X) = At lim f(x)=5,
x->x0—»0	x->xoJ-0
A*Bt f (x0) Ф A, f (x0) #= В (рис: 8.10).
3.	Jim f(x)= lim f (x) « A,
X->X0—0	Х->Х0-М
f (x0) ф А (рис. 8.11). Функция терпит ска-
чок, равный f(Xo) — А.
О	я
а
Рис. 8.12.
В точке х0 функция
f (х) — не определена и
область определения
функции
D (f) = (а; х0) (J (х0; Ь)
Левый и правый пределы функции f (х) в
точке хо существуют и конечны.
1.	lim f (х) — Д, lim f (х) = Bt
х->х0—0	х-»хо4-0
А #= В. Функция терпит скачок, равный В«-Д
(рис. 8.12).
2.	lim f (х) = lim f (х) «= Д.
х->х0—0	х-»хо+0
В этом случае говорят, что точка х0 — точка
устранимого разрыва, так как, доопределяя
функцию f (х) в точке х0 равенством f (х0) «= Д,
получаем непрерывную функцию. - Примером
такой функции может служить функция
___
f (х) = 2 х2 , не определенная в точке х= 0
(рис. 8.13). Для этой функции в точке х«=0
имеем
Пт2^~= 11т2~"~Г=0.
х->—0	х->4-0
Доопределяя4 данную функцию равенством
f(0)==0, получаем непрерывную функцию в
точке х = 0
§ 8. НЕПРЕРЫВНОСТЬ (И РАЗРЫВЫ) ФУНКЦИЙ 343
8.3.	Односторонняя непрерывность. Классификация разрывов
функций. Пусть функция f (х) определена на промежутке (а; х0].
Говорят, что функция f (х) непрерывна в точке х0 слева, если
lim f (х) = f (х0).	(2)
х->х0'— О
Аналогично, функция f (х),
определеннай на промежутке [х0; Ь),
непрерывна в точке х0 справа,
если
Нт /(х) = /(х0).	(3)
Если равенство (2) не выпол-
няется, то говорят, что функция	рис* 8,14>
f (х) разрывна в точке х0 слева', если
не выполняется равенство (3), то функция разрывна в точке xQ справа.
Если функция / (х) определена на промежутке (а; Ь) и точка х0 С
£ (а; Ь), то для непрерывности функции f (х) в точке х0 необходимо
и достаточно, чтобы функция / (х) была непрерывна слева и справа
в точке х0.
Различают следующие виды разрывов функции в точке: разрывы
первого рода и разрывы второго рода.
Перечень разрывов первого рода приведен в табл. 7.
Если хотя бы один из односторонних пределов в точке х0 не сущест-
вует или равен +оо (—оо), то говорят, что функция / (х) имеет в точке
х0 разрыв второго рода (точка х0 может как принадлежать, так и не
принадлежать области определения функции). Примером функции,
имеющей разрыв второго рода, может служить функция
f (х) = 2,/х,
не определенная в нуле, для которой
lim 21/х = 4-оо	lim 2j/x = 0.
х-Н-0	х->—О
График этой функции изображен на рис. 8.14.
ГЛАВА <£
НАЧАЛА ДИФФЕРЕНЦИАЛЬНОГО
И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ
Математический анализ как раздел математики возник в результате
объединения *двух различных и первоначально не связанных направле-
ний математических исследований — дифференциального и интеграль-
ного исчислений.
Первоначально интуитивное представление о математическом объ-
екте, который мы сейчас называем определенным интегралом, встреча-
лось в работах ученых Древней Греции. Так, Архимед для вычисления
объемов и площадей поверхностей тел пользовался разбиением фигур на
элементы с последующим,суммированием этих элементов, предвосхищая
тем самым понятия интегральных сумм; Аналогичными задачами, раз-
вивая метод Архимеда, занимались Кеплер, Паскаль, Ферма и другие
ученые. Ферма также занимался задачами, которые мы сейчас относим
к дифференциальному исчислению, — проведением касательных к кри-
вым, нахождением наибольшего и наименьшего значений функций
и т. д., причем для решения этих задач он, по существу, пользовался
понятием приращения функции. Связь между этими различными клас-
сами задач была осознана учеными после исследований Ньютона и Лейб-
ница. Лейбницем и были введены используемые в настоящее время обо-
значения интеграла и дифференциала. Строгое обоснование большин-
ства понятий математического анализа было дано Коши в середине XIX
столетия на основе теории пределов. Дальнейшее развитие математиче-
ского анализа привело к выделению таких.самостоятельных разделов
математики, как теория обыкновенных дифференциальных у уравнений,
теория дифференциальных уравнений в частных производных, теория
интегральных уравнений, теория функций комплексной переменной,
теория функций действительной переменной, функционального анализа
и т. д.
§ 1. Производная
1.1. Понятие производной. Пусть f (х)— некоторая функция,
определенная на’ промежутке (а; Ь), и х0 — некоторая фиксированная
точка этого промежутка. Возьмем произвольное значение х из проме-
жутка (а; Ь) и составим разность
х —х0.
Разность х — х0 называют приращением независимой переменной (или
приращением аргумента) функции f (х) в точке Хо и обозначают Дх:
х —х0=Дх.	(1)
Приращением функции f (х) в точке х0 называют разность между
значением функции в точке х = х0 + Дх и значением функции в точке х0
и обозначают Д / (х0):
/(*о + Дх) — / (х0) = А/ (х0).	(2)
§ 1. ПРОИЗВОДНАЯ '	345
Так как точка х0 считается фиксированной, приращение функции
Д/ (х0) является функцией приращения аргумента Дх. Составим отноше-
ние
/ (х„ + Ах) — / (*о)  А/(х0)
Дх	Дх ’
которое также будет функцией приращения аргумента Дх и рассмотрим
предел этого выражения при Дх, стремящемся к нулю:
Hm / (х0 + Дх)/ (х0) .
Дх-М) ' &х
Если этот предел существует, то говорят, что функция / (х) имеет
производную в точке х0, и пишут
lim m+Ax)-j^oi = r(XB)	(3)
дх->0 ьх
Число /' (х0) .называется производной функции f (х) в точке х0.
Производную функции f (х) в точке х0 также обозначают
х/ / м	df (*о)
н*)|х=х, или
Если существует предел (3), т^кже говорят, что функция
f (х) дифференцируема в точке х0*). Если функция f (х) дифференцируема
в каждой точке промежутка (а; &), то говорят, что она дифференци-
руема в промежутке (а; Ь). Производная функции / (х), дифференцируе-
мой в промежутке (а; Ь), сама является функцией х.
Примеры. 1. Вычислим производную функции / (х) = х2 в про-
извольной точке х0 числовой оси.
Вычисляя приращение функции
f (Хо 4- Дх) — / (х0) = (х0 4- Дх)2 — х| = 2х0- Дх 4- (Дх)2,
по определению производной имеем
/ (Хо 4-Дх) — / (х0) 2хо • Дх 4- (Дх)2 _
Дх->0	Дх-*0
= lim (2х0 + Дх) 2х0,
Дх->0
т. е. /' (х0) = (х2)' 1*^ = 2х0 для любой точки х0.
2. Докажем, что производная функции f (х) = | х | в точке х === О
не существует.
Составим отношение
Д7(0) = 7(0+Дх)-~/(0)	|Ах|
Дх	Дх	Дх *
*) О дифференцируемости функции см. также п. 2.1
346 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИИ
По определению модуля
( Лх, если Ах>0,
( — (Дх), если Ах<0.
Вычислим правый и левый пределы отношения , учитывая, что
при вычислении правого предела Ах > О, а при вычислении леьих и
Ах < 0;
.. |Дх| .. Ах	t ,
hm -	- -= hm ~т—= hm 1 = 1
Дх-Н-0 ЬХ Дх->4-0 ЬХ Дх->+0
|Д*1
hm
Дх->-—0
- lim —= lim 1) = — I.
Дх->«»0 ЬХ Дх->—О
_	А/ (0)	ч
Так как правый предел отношения не равен левому пределу,
то обычного (двустороннего) предела данного отношения не существует,
и, следовательно, производная функции f (х) = | х | при х == 0 не суще-
ствует.
1.2. Геометрическая интерпретация производной. Пусть дана
некоторая линия L и на ней точка М (рис. 9.1). Возьмем на линии L
некоторую точку Af, не совпадающую с точкой М. Прямую MN назы-
вают секущей для линии L. Пусть теперь точка Af приближается к точке
А4, оставаясь на линии L. Тогда каждому положению точки Af будет со-
ответствовать своя секущая и все эти секущие будут проходить через
точку М.
Касательной к линии L в точке М называется предельное положе-
ние МК секущей MN при стремлении точки N к точке М.
Пусть у = f (х) -— некоторая функция, дифференцируемая в точке
х0. В декартовой прямоугольной системе координат точка А4, лежащая
на графике функции у = f (х) и имеющая абсциссу х0, имеет коорди-
наты (х0; f (х0)). Пусть точка N принадлежит графику функции (рис. 9.2)
и имеет координаты (х0 + Ах; f (х0 + Ах)). Проведем через точку М
прямую, параллельную оси Ох, и обозначим точку пересечения этой
прямой и прямой х0 + Ах через Р. Рассмотрим прямоугольный тре-
угольник MNP, Отношение
/ (хр + Ах) — / (х0)
.
§ 1. ПРОИЗВОДНАЯ
347
равно тангенсу угла наклона секущей MN к положительному направ-
лению оси Ох:
(4)
Если устремить приращение Дх к нулю, то геометрически это будет
означать, что точка W с координатами (х0 + bx, f (*о + Дх)) будет
двигаться по графику функции y—f (х), приближаясь к точке М,
а угол а будет стремиться к углу а0 — углу наклона касательной к по-
ложительному направлению оси Ох.
Так как предел левой части равенства (4) при Дх О равен /' (х0):
iim
Дх-о - Ьх
а предел правой части равен tg а0:
lim tga«=x tga0,
Дх->0
ТО
f (*b) = tg «0.	(5)
т. e. значение функции f'(x) в точке х0 равно тангенсу угла наклона
касательной.
Используя формулу (5), уравнение касательной к графику функции
у = f (х), проходящей через точку с координатами (х0;	= f (х0)),
можно записать в виде
У — Уй—f (ха)-(х — ха).
1.3.	Кинематический смысл производной. Пусть материальная
точка движется по прямой под действием некоторых сил. Выберем
какой-либо момент времени /0 и рассмотрим промежуток времени Д/ от
момента /0 до. момента t = /0 + bt. За этот промежуток времени точка
пройдет некоторый путь, который обозначим ДЗ (t0). Этот путь есть
функция bt. По известному из физики определению отношение
ДЗ (/р)
Д/
есть средняя скорость движения точки за время bt. Будем рассматри-
вать все меньшие и меньшие промежутки Д/, устремляя Д/ к нулю. Пре-
дел
lim -ЦИ»1=5'(/0) = о(/о)
Д/->0 Ь1
называется мгновенной скоростью точки в момент времени f0.
1.4.	Теорема о производных. Основные теоремы дифференциаль-
ного исчисления.
1)	Если функция f (х) имеет производную в точке х0, то и функция
с-/ (х) (с — постоянная) также имеет производную в точке х0, причем
(C-/(*))Ux0=c-/'(xo).
т, е. постоянный множитель можно выносить из-под знака производной.
348 ГЛ. 9. НАЧАЛА, ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
2)	Если функции f (х) и g (х) имеют производные в точке х0, то и
функции f (х) + g (х) и f (х) — g (х) также имеют производные в этой
точке, причем
(f (х) ± g (х))	= 7' (Хо) ± g' (Хс),
т. е. производная суммы (разности) двух функций равна сумме (раз-
ности) их производных.
3)	Если функции / (х) и g (х) имеют производные в точке х0, то
и функции f (x)«g (х) и f (x)/g (х) также имеют производные' в этой точке,
причем
.(/ (X)-g (х));=Хо = /’ (x0).g(х0) 4- f (Xo).g (х0),
{ f (х) \'	Г (ХО)-g (х0) — f (х„)(х0)
(Хо) *0)-
4)	Если функция у = f (х) имеет производную в точке х0, а функция
г = g (у) имеет производную в точке у^— f (х0), то и сложная функция
г = g (/ W)
имеет производную в точке х0, причем
(£ (f(x))Yx-x, = g'y (Уоу fx (х0),
где индексы у и х у производных указывают, по какому аргументу вы-
числяются производные.
5)	Пусть функция у =» / (х) удовлетворяет условиям существования
обратной функции и в точке х0 имеет конечную и отличную от нуля про-
изводную. Тогда обратная функция х =	(у) в соответствующей точке
Уо ==' /<х0) также имеет производную. Производные этих взаимно об-
ратных функций связаны равенством
(f	•
Основные теоремы дифференциального
исчисления:
.Теорема Ферма. Пусть функция f (х) определена в некото-
ром промежутке (а; Ь) и во внутренней точке с этого промежутка при-
нимает наибольшее {наименьшее) значение. Если в этой точке сущест-
вует конечная производная f (с), то f (с) = 0.
Теорема Ролля. Если функция f (х) определена и непре-
рывна на промежутке [а; Ь], имеет конечную производную во всех точ-
ках промежутка (а; Ь) и
f (а) = I (&),
то в промежутке (а; Ь) найдется такая точка ct что
Г (с) = 0.
Теорема Лагранжа. Если функция f (х) определена и не-
прерывна на промежутке [а; Ь] и имеет конечную производную во всех
точках промежутка (a; Ь), то найдется такая точка с £ (а; Ь), что
§ 1. ПРОИЗВОДНАЯ
349
1.5.	Вычисление производных элементарных функций. Производ-
ные элементарных функций вычисляются по определению производной
(см. формулу (3) п. 1.1), а также с помощью теорем о производных.
Производные показательной и логарифми*
ческой функций. Вычислим производную показательной функ-
ции f (х)=ах в точке х=0. Составим приращение функции в точке х=0;
1.
По определению производной
„дх 1
„ (ох1,=о = 1 im--*7— •
Дх==0
На основании формулы 3) п. 6.4, гл. 8
а^х______________________________1
lim --------= In а	(6)
Дх»о	Ьх
и, следовательно,
(«*К-о==1па.
Производная функции f (х) » ах во всех остальных точках числовой
оси вычисляется следующим образом:
(а*)' = lim.	_ Нт а*(аА*-1\
Дх->0 Дх Дх->0 Ьх
Так как множитель ах не зависит от Дх, то, вынося его из-под знака
предела, на основании формулы (6) получаем
пьх___-1
-т------= ах lim---------= a* In а
Ьх	дх->о Дх
.. ах (а^х~ 1)
lim —----------
Дх-М)
и, следовательно,
(ах) = ах In а.
Правило вычисления производной показательной функции позво-
ляет дать новое определение числа е (см. п. 2.4 гл. 8). Числом е назы-
вается основание показательной функции, производная которой равна
самой функции:
(гу-е*.
Теперь по теореме о производной обратной функции (см. теорему 5
п. 1.4) можно вычислить производную логарифмической функции / (х) =
== loga х:
(10gaX)'=-7iHZ-
Если a = е, то последняя формула принимает следующий простой
вид:
(lnx)=-L.
Производные Степенных функций. Используя
определение производной, нетрудно доказать, что производная функции
350 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
f (х) = с (с — постоянная) равна нулю, а производная функции f (х)= х
равна единице. Далее, используя теорему о производной произведения
функций, методом математической индукции можно доказать, что при
любом натуральном п
(хПУ — п-х/1“’1.
Производную степенной функции f (х) = ха (а — любое действи-
тельное число) можно вычислить как производную сложной функции,
если записать степенную функцию в виде
ха ==	= еа 1п *•
По правилу вычисления производной сложной функции
(ха) = (е® 1п *)' = еа 1П х (а 1пх)' = еа1п=
= ха-а.-— — ахг'~''.
X
В качестве более сложного примера на использование теоремы
о производной сложной функции вычислим производную «показательно-
степенной» функции f (х) = х\ Записывая функцию в виде хл =
<== е1п (х*) __ ех inx* ИМеем
(х*)' =(^ 1п7 = г1п^(х.1пх)г«
±=ех 1п* (1пх + х-~-) — ех 1п*(1пх-|- 1) = x*(lnx-j- 1).
Производные тригонометрических функ-
ций. Вычислим производную функции f (х) = sin х. Пусть х0 — про-
извольная точка числовой оси. Составим приращение функции
Д sin х0 = sin (х0 + Дх) — sin х0.
Разность, стоящую в правой части равенства, запишем в виде произве-
дения
sin (хо + Дх) — sin Хо == 2cos ^х0 + sin“T”*
По определению производной
Д Sin Хп	2 C0S (*° + sin ТГ
(Sin	ДЛ_|)	“ д ™0 '	=
,	!|"т
с= lim cos ( х04—) «Пт —--------.
Дх->0	\	2 / Дх-*0	Д^_
2
Первый предел, стоящий в правой части последнего равенина,
вычислим, используя свойство непрерывности функции cos х;
lim cos (xQ + 4?^ == cos *o>
Ax->0	\	2 /
§ 1. ПРОИЗВОДНАЯ
351
а второй — с помощью предела 1) п. 6.4 гл. 8, на основании которого
получаем	. Дх ’sin"T lim ——— = 1. IMC-O 2
Таким образом,
(sinx)^ = COSXfl.
Так как точка х0 — произвольная точка числовой оси, то
(sin х)' = cos х.	(7)
С помощью формулы (7) и теорем о производных можно вычислить
производные остальных тригонометрических функций. Например,
производная функции fjx) = cos х вычисляется следующим образом:
представляя функцию cos х в виде
cos х = sin / --х^ ,
вычислим ее производную с помощью теоремы о производной сложной
функции
(COS х)' ~
WtH'))'
== — cos	~ — sin x.
Производные функций tg x и etg x вычисляются с помощью тео-
ремы о производной частного.
Производные обратных тригонометрических функций f (х) =
= arcsin х, f (х) = arccos х, f (х) = arctg х и f (х) = arcctg х вычис-
ляются с помощью теоремы о производной обратной функции п. 1.4.
Например, производная функции f (х) = arcsin х вычисляется следую-
щим образом: обратной функцией для функции у = arcsin х является
функция х = sin у\ по теореме о производной обратной функции имеем
/	• v 1	1	1
(arcsin ху = -- Г> =--------==---------:—
1	(sin уу cos у cos (arcsin х)
Так как cos (arcsin х) — J/* 1 — х2, то
Z • Ч/	1
(arcsin х) = -	.....♦
/1—х2
Производные элементарных функций приведены в таблице 8.
1.6.	Производные высшего порядка. Пусть функция f (х) диффе-
ренцируема в промежутке (а; Ь). Производная данной функции f' (х)
представляет собой функцию аргумента х. Выберем некоторую точку
х0 С О2’» и составим приращение аргумента Дх = х — х0 и прираще-
ние функции f (х) в точке х0:
Д/'(*в) = f (х0 + Дх) -Г- /' (Х0).
352 ' ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
ТАБЛИЦА 8
Функция	Производная
f (X) = с	f' (0) =0
f (х)=ха	f W — axa—1
f (X) =- а*	f' (x) = ax Ina
f (х) =» ех	Г (x) — cx
f (х) « \ogax	
f (х) ~ In X	Г (X) = -i-
f (x) = sin x	f' (x) = cos X
f (x) = cos X	f' (x) = — sin X
f (x) = tgx	P / y \	1
	'	COS2 X
f (X) = Ctg X	ff (	—		I
	' '	sin2 X
	I
t (x) = arcsin x	-- -
	T txj	... .
	K> - X» 1
t (x) = arccos x	r (x) = --7=
	V 1 - x«
f (x) «'arctg x	t' = i + x»
f (x) = arcctg X	fr (x) = — yqpp
Рассмотрим предел
Дх
lim f + Ах) ~ f (*°)
Дх->0
Если этот предел существует, то говорят, что функция f (х) имеет произ-
водную второго порядка (или вторую производную) в точке х0. Произ-
водную второго порядка функции f (х) в точке х0 обозначают
Г (Хо) ИЛИ --^2^ ИЛИ Г (х)	.
Таким образом,
Г (Хо) = lim £'.(хо+Ах)-Г(Хо) .
ДХ-*0 .	ДХ •
Производная второго порядка, так же как и производная первого
порядка, допускает простое кинематическое истолкование.
Пусть материальная точка движется под действием сил по некото-
рой траектории (рис. 9.3), и пусть в момент времени tQ она занимаем
$ Т. ПРОИЗВОДНАЯ
353
положение Мо, а в момент времени ti = 10 + АГ — положение
Путь, пройденный точкой от положения 7И0 до положения равен
длине AS (М части траектории МоЛ^. Скорость точки в каждый момент
времени является производной пройденного пути:
направленной по касательной к траектории.
Предел
,lm .W-.ftl.,,,	+ «>-«<>>
Д/-М) АГ	А/-И)
М
АГ
_,|ш £<'•+«)
Д/-*0	АГ
называется мгновенным ускорением точки в момент времени Го и предста-
вляет собой вторую производную от пути S (Г):
а (Г) = S” (Г).
Далее, если для функции./" (х) в некоторой точке х существует
предел
..	Г(х0+Ах)-Г (х0)
Av	’
Дх-0 •	АХ
то говорят, что функция / (х) имеет
производную третьего порядка (или
третью производную) в точке х0:
Г W-lta ХЙ-.+ ^-''W .
Дх->0	АХ
Аналогичным способом определяются производные четвертого,
пятого и т^ д. порядков. Производная п-го порядка функции / (х) обычно
обозначается
(X) ИЛИ
dx"
Производные n-го порядка суммы и произведения двух функций
f (х) и g (х) вычисляются по формулам
(f±g)w~f{n>±g™,:
(f:g)W = tyW-g® + Cln- f(n-l'g' + C^<"-V + > -
••• + с;-1/Ул-1> + ^10|г1'|) = s clnf^g(‘\
i—0
В последней формуле (называемой формулой Лейбница) через /<°>
и g(0) обозначены функции / (х) и g (х) соответственно, С'п — число со-
четаний из п элементов по i элементов (биномиальные коэффициенты).
1.7.	Производная функции, заданной в параметрической форме»
Пусть функция задана в параметрическом виде
. * = Ф (0> У = Ф (0 (Г — параметр)	(8)
12 А. г. Цыпкин
354 ^ ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
и Ф (0 и ф (t) — непрерывные и дифференцируемые функции аргумента
/ С (^; Ь). Пусть в некоторой точке t g (a; b) x't = ф' (/) отлична от
нуля (скажем, положительна), то она положительна и в некоторой
окрестности точки t0 и, следовательно, в этой окрестности функция
Ф (/)' монотонно возрастающая. Непрерывная и монотонно возрастаю-
щая функция имеет обратную функцию t = t (х), ,и их производные
связаны равенством
< =	(9)
1х
Подставляя t = t (х) во второе из равенств (8), получаем явную
форму задания функции (8) на некотором промежутке значений х:
у = a W) = f (х).
Ее производная как производная сложной функции вычисляется по
формуле
Ух = ^’г*х-
С помощью формулы (9) эту производную можно записать в виде
«	%	У;	dy	dy I dx
У г = —Г = —г* или “7— = ~7Г /—гг
Ух ф,	Xt	dx	di I dt
Последняя формула очень проста для запоминания: производная
dyldx, стоящая в левой части равенства получается в результате сокра-
щения dt в правой части равенства.
Несколько сложнее вычисляется вторая производная функции
У == f W:
Ухх = {УхУх = (Ч’Г t'xYx = (4v)x • ‘х + • ОХ
Вычисляя производную по х от функции ф^ как производную сложной
функции
получаем
Ухх =	* Gx)2 +
Так как t'x = 1/х’, а
(х'И^-	(х')3
окончательно получаем
* _УцЪ — y't*tt
"" («;»’ ’
Полученное выражение для первой производной функции, задан-
ной в параметрическом виде, позволяет вычислить тангенс угла нак*
лона касательной к графику функции
У(
tga = -4->	(10)
xt
С 2. ДИФФЕРЕНЦИАЛ
355
а также написать уравнение касательной к графику функции х — ф (0,
у = ф (0.
Пример. Написать уравнение касательной к графику функции,
еаданной в параметрической форме:
x=acosG у = b sin tt t£ [0; 2л) (а>0), Ь>0)	(11)
при / = —.
Нетрудно проверить, что график данной функции представляет
собой кривую второго порядка — эллипс (рис. 9.4), так как из фор*
мул (11) следует, что	4
По условию задачи касательная проходит через точку с координа*
л a	. л Ь /2
тами х0 — a cos -г- = —, yQ — b sin -у- я» —, и, следователь*
4	2	4	2
но, уравнение касательной имеет вид
bV2 b [.	а/2"\
У 2	" а \Х—	2 Г
§ 2.	Дифференциал ,
2.1.	Понятие дифференциала. Пусть у = f (х)— некоторая
функция, определенная на промежутке (а; Ь) и непрерывная в некоторой
точке х0 этого промежутка, и пусть приращению аргумента Дх соответ*
ствует приращение функции
&У = & f (х0) = f (х0 + Дх) — f (х0),
которое является функцией аргумента Дх.
Если для приращения функции Ау существует такое число А =^= 0,
что приращение функции может быть представлено в виде
Дг/ = А» Дх+ со (Дх),
где слагаемое со (Дх) удовлетворяет равенству
.. со (Дх)
, lim —\—- = 0,
'	Дх->0 Ах
то говорят, что функция f (х) дифференцируема в точке х0<
Выражение А-Ах называется дифференциалом функции у = f (х) »
в точке Хо и обозначается
dy или df (х0).

35G ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Иногда дают следующее краткое определение дифференциала:
Дифференциал — это главная линейная часть приращения функ-
ции *).
Связь между дифференцируемостью функции и существованием
ее производной устанавливается следующей теоремой:
Для того чтобы функция у = / (х) в точке х0 была дифференци-
руема, необходимо и достаточно, чтобы она имела в этой точке конечную
производную /' (х0). При выполнении этого условия значение произ-
водной f (хо) равно числу А и дифференциал dy функции y~t(x)
всегда равен
" dy= f (х0) Ах. ‘	(1)
В равенстве (1) Ах не обязательно бесконечно малая; но если Ах —
бесконечно малая, то и dy — бесконечно малая и именно в этих случаях
dy (при условии, что /' Ф 0) является главной частью бесконечно ма-
лого приращения функции А#.
Дифференциалом независимой переменной х в точке х0 называют ее
приращение Ах, т. е.
dx = Ах.
С учетом этого соглашения формула (1) может быть переписана
в виде
dy = fx-dx,
или
F' АУ
х х dx 9
Выражение, стоящее в правой части последнего равенства, которое,
раньше (см. п. 1.1) было просто обозначением для производной, теперь
можно понимать как дробь с числителем
dy и знаменателем dx.
2.2.	Геометрическая интерпретация
дифференциала. Пусть у ® / (х) — неко-
торая функция, М — точка, принадлежа-
щая графику функции и имеющая коор-
динаты (х0; f (х0)). Проведем через точку М
(рис. 9.5) касательную к графику функ-
ции. Угловой коэффициент наклона каса-
тельной (тангенс угла наклона) равен зна-
чению производной f' (ха). Если аргу-
менту функции придать приращение Ах, то приращение функции A#
будет равно
&У= f(x0+ &x) — f (ХО).
На рис. 9.5 приращение функции Аг/ — длина отрезка МгР.
При том же самом приращении аргумента Ах приращение каса-
тельной будет равно длине отрезка NP. Вычисляя I NP | как катет
прямоугольного треугольника MNP, находим
|А/Р| = | MP |-tg <х = /' (Хо)-Ах.
*)*Определение понятия главной части бесконечно малой величины
см, п, 7.2 гл, 8;
- §2. ДИФФЕРЕНЦИАЛ	357
По определению дифференциала f' (х0) • Дх = dy, следовательно,
длина отрезка | NP | и есть дифференциал функции dy.
Таким образом, в то время как Др есть приращение ординаты гра-
<|ика функции, dy является приращением ординаты касательной.
2.3.	Инвариантность дифференциала. Пусть у = f (х) и х ==
= g (0 — некоторые функции указанных аргументов, такие, что из
них может быть образована сложная функция
{/=/(5(0).
Производная сложной функции у (t) вычисляется по формуле
(2)
где индексы указывают, по какому аргументу вычисляются произ*
водные. ‘	'
Дифференциал функции у = f (х) в предположении, что х — неза-
висимая переменная, определяется равенством
dy = fx dx.
Если рассматривать функцию у как функцию независимой перемен*
ной t, то ее дифференциал определяется равенством
dy = y't dt.
Подставляя в это равенство вместо производной у\ ее .выражение
через fx и gf, в соответствии с формулой (2) получаем
dy — dt.	(3)
Но, с другой стороны, g't di = dg = dx; следовательно, равенство
(3) записывается в виде
dy=fxdx.
Таким образом, предполагая, что у есть функция аргумента t9
мы получаем то же самое выражение для дифференциала dy, как и
в случае, когда предполагалось, что у есть функция аргумента х, т. е.
форма'дифференциала не зависит от того, является ли х независимой
переменной, или она в сврю очередь является функцией какой-либо
переменной.
Это свойство называется свойством инвариантности формы дыр*
ференциала.
Пример. Пусть у = sin х и х ~ In i — две функции, из кого*
рых можно образовать сложную функцию
'у «= sin (in 0.
Производная этой функции равна
I	cos (In 0
У£ ~ COS (In 0 • (In t) »-
а дифференциал
cos (in t)
dy ^ytdt  ------—’-dt<
358 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
С другой стороны,
dx<=d(\at) =Ц-с«,
Преобразуя с помощью этого равенства правую часть предыдущей
формулы, получаем также следующее выражение для дифференциала dy:
dy *=y'tdt — cos (In /) d (In t)t
или
dy == cos x dx.
Но точно такое же выражение для дифференциала dy получается и в том
случае, когда в первой из исходных функций (у = sin х) х считается
независимой переменной.
Правила вычисления дифференциалов суммы, произведения и част-
ного двух функций аналогичны соответствующим правилам вычисления
производных:
d (с*/ W) = с df (х) (с — постоянная);
d (/ (х) ± g (х)) = df (х) ± dg (х);
(/ (x)-g (х)) = g (х) df (х) + f (x)-dg (х);
d ( в е М df ~ f(х) dg .
U(x)/	g2(x)	/
Например, дифференциал функции d ( s-^~ ) равен
✓ х2 \ sinxdfx2) — x2dsinx ^Sxsin xdx — x2cosxdx ,
а \ sin х /	sin2 х e sin2 л *
§ 3.	Исследование функций.:
Построение графика функции
3.1.	Условия постоянства и монотонности функций. Пусть функ-
ция f (х) определена и дифференцируема в промежутке (а; Ь). Для того
чтобы функция в промежутке (а; Ь) была постоянна, необходимо и
достаточно, чтобы ее производная была равна нулю во всем промежутке
Пусть функция / (х) определена и дифференцируема в промежутке
(а; &). Для того чтобы функция была возрастающей в промежутке
(а\ Ь), достаточно, чтобы
f' (х) > 0 для всех х € (а; Ь).
Для убывания функции достаточно, чтобы
Г (х) < 0 для всех х £ (а; Ь).
Сформулированное условие не является необходимым. Например,
функция / (х) = х3 — возрастающая, однако в точке х = 0 ее произ-
водная равна нулю.
3.2.	Максимумы и минимумы функции. Говорят, что функция
/ (х) имеет в точке xq максимум (или минимум), если найдется такая
§ 3, ИССЛЕДОВАНИЕ ФУНКЦИЙ
359
б-окрестность точки х0, принадлежащая области определения функции,
что для всех х #= х0, принадлежащих промежутку (х0—б; х0+б),
выполняется неравенство
/ (х) < / (х0) (соответственно f (х) > / (х0)).
На рис. 9.6 изображена функция, определенная на промежутке
[а; 6], имеющая в точках Xj и х3 максимумы, а в точках х2 и х4 мини-
мумы.
Точки максимума и минимума называются точками экстремума
функции, а значения функции в этих точках называются экстремаль-
ными значениями функции. Для функ-
ции, график которой изображен на
рис. 9.6, точки а и b не являются точками
экстремума функции, так как в любой
сколь угодно малой окрестности этих точек
найдутся точки, не принадлежащие об-
ласти определения f (х).
Необходимое условие
существования экстремума
функции. Пусть функция f (х) диф-
ференцируема в промежутке (а; Ь). Если
в некоторой точке х0 С (а; 6) функция f (х)
точке производная равна нулю*):
Рис. 9.6.
имеет экстремум, то в этой
Г М = 0.
Обратное утверждение, вообще говоря, неверно — если в точке
производная функции f (х) равна нулю, то функция f (х) в точке
может не иметь экстремум. Так, производная функции f (х) = х^ в точ-
ке Хо = 0 равна нулю, но функция не имеет экстремума В этой точке.
Достаточное'условие существования экст-
ремума функции. Пусть функция f (х) определена и непре-
рывна в промежутке (а; б), и на всем промежутке (а; Ь) (за исключением,
быть может, конечного числа точек) дифференцируема.
Критическими точками функции в промежутке (а; Ь) называются
точки, в Которых производная функции либо равна нулю, либо не
существует.
Пусть точка х0 С (а; Ь) —- критическая точка функции f (х) и в не-
которой б-окрестности этой точки, по крайней мере для х =# х0, сущест*
вует конечная производная f' (х), которая слева.и справа от х0 сохраняет
знак (возможно, с разных сторон — разный). Тогда возможны следую*
щие три случая:
1)	f (х)> 0 при х < х0 и f (х) <0 при х > х0, т. е. производная
f (х) при переходе через точку х0 меняет знак с плюса на минус. В этом
случае в промежутке (х0 — б; х0) функция f (х) вбзрйстает, а в проме-
жутке (х0; х0 + б) убывает, так что значение f (х0) будет наибольшим в
в промежутке (х0—б; х0+б), т. е. в точке х0 функция имеет максимум.
2)	f (х) < 0 при х < хо и /=' (х) > 0 при х > х0, т. е. производная
/' (х) при переходе через точку х0 меняет знак с минуса на плюс, В этом
случае в точке х0 функция имеет минимум.
♦) Если расширить класс рассматриваемых функций^ полагая,' что в ко-
нечном числе точек промежутка (а; Ь) функция f (х) не имеет конечной
производной, то экстремум функции может приходиться на TQ4Kyj в которой
функция не имеет конечной производной.
360 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
3)	Г (х) > 0 как при х > х0, так и при х < х0 либо /' (х) < 0 и
слева и справа от х0, т. е. при переходе через точку х0 производная /' (х)
не меняет знака. Тогда функция либо возрастает, либо убывает на про-
межутке (х0 — б; х0 + 6); в любой сколь угодно малой окрестности точки
х0 с одной стороны найдутся точки х, в которых f (х) <? f (хо), а с дру-
гой — точки х, в которых f (х) > / (хо), и в точке xq экстремума нет.
Первое правило для проверки критической точки х0 на экстремум
ваключается в том, что,подставляя в производную f (х) сначала х < х0,
а затем х > х0, устанавливают знак производной в окрестности точки х0
слева и справа от нее. Если при этом производная f' (х) меняет знак
с плюса на минус, то в точке х0 — максимум, если с минуса на плюс —
то минимум; если же знак не меняется, то экстремума нет.
На рис. 9.7 производная функции Д (х) при переходе через точку
х0 меняет знак с минуса на плюс и функция Д (х) в точке х0 имеет мини-
мум, а функция /2 (х), производная которой при переходе через точку
х0 меняет знак с плюса на минус,*'— максимум.
На рис. 9.8 как функция Д (х), так и функция /2 W имеют в точке
Хо*производную, равную нулю: при переходе через точку Xq произвол-'
ные той и другой функции знака не меняют, и экстремумов у функций
Л W и /2 (х) в точке лг0 нет.
На рис. 9.9 и 9.10 изображены графики функций, которые не
имеют производных в точке х0. В согласии с правилами смены
знака производных для этих функций, они имеют соответственно
минимум, максимум и не имеют экстремума в точке хл.
Примером функции, не имеющей производной в точке и имеющей
в этой точке минимум, является функция #= |х| (см. п< 1.1).
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ	'
Еще раз подчеркнем, что сформулированное выше достаточное ус-
ловие сущёствования экстремума функции в точке хо пригодно как
в случаях, когда производная в точке Хо обращается в нуль, так и в слу-
чаях, когда^р этой точке производная не существует, и применимо
к непрерывным функциям, имеющим непрерывную производную f'(x)
в промежутке {a} b), за исключением быть может конечного
числа точек.
Сформулируем еще одно достаточное условие существования экс-
тремума функции в точке. Точку х0 называют стационарной точкой
функции f (х), если в этой точке функция f (х) дифференцируема и ее
производная равна нулю.
Пусть х0 — стационарная точка функции f (х) и в некоторой окрест-
ности точки х0, включая саму эту точку, функция f (х) имеет производ-
ную, а в точке х0 существует и вторая производная fn (х0). Если вторая
производная f в точке х0 положительна, то функция f (х) в точке х0
имеет минимум; если вторая производная f в точке*х0 отрицательна, —
то максимум.
Сформулированное правило имеет, вообще говоря, более узкий
круг применения по сравнению с первым правилом; оно, например,
явно неприменимо к точкам, в которых не существует первая производ-
ная. В тех случаях, когда вторая производная в точке х0 обращается .
в нуль, правило также ничего не дает и решение вопроса р существова-
нии в этой точке экстремума зависит от Поведения высших.производных.’
3.3.	Наибольшее и наименьшее значения функции. Пусть функ-
ция f (х) определена и непрерывна на конечном замкнутом промежутке
(а; Ь].
Для нахождения-наибольшего (наименьшего) значения функции
необходимо найти все максимальные (минимальные) значения функции
!в промежутке (а; Ь), выбрать из них наибольшее (наименьшее) и срав-.
‘нить его со значениями функции в точках а и Ь. Наибольшее (наимень-
шее) из этих чисел и будет наибольшим (наименьшим) значением функ-
ции f (х) на промежутке [а; Ь]. При нахождении наибольшего или наи-
меньшего значения функции может оказаться, что на промежутке
(а; Ь) функция не имеет критических точек. Это говорит о том,- что
в рассматриваемом промежутке функция возрастает или убывает и,
следовательно, достигает своего наибольшего и наименьшего значения
на концах промежутка^
П р и м е р ы. ’ 1. Найти наибольшее и наименьшее значения функ-
ции
4
/ (X) = X3 — 4х
о
на промежутке [0; 2].
Вычислим производную данной функции
/' (х) = 4х2 — 4.
При всех х (О’, 2) производная существует и равна нулю в точках
х = 1 и х = —1. В промежутке (0; 2) лежит лишь одна из этих точек:
х = 1. Значение функции в этой точке равно—8/3. При переходе через
точку х = 1 производная меняет знак с минуса _ на плюс, а потому
в точке х = 1 — минимум функции / (х). Значения функции на концах
промежутка: f (0) = 0, f (2) = 8/3. Следовательно, наиболь&ее значе-
ние данной функции f (х) достигается на правом конце промежутка
в ючке 2, а наименьшее — внутри промежутка в точке х = 1»
362 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ

Рис. 9.11.
2.	Из квадратного листа со стороной а, вырезая по углам равные
квадраты и сгибая края (рис. 9.11), составляют прямоугольную откры-
тую коробку. Чему должна быть равна сторона вырезаемого квадрата,
чтобы получившаяся коробка имела наиболь-
ший объем?
Обозначим сторону вырезаемого квадрата
через х. Тогда объем коробки V будет равен
х (а — 2х)^,
причем х принадлежит промежутку f [0; а/21.
Производная данной функции Vх (х) = (а —
— 2х) (а — 6х) на промежутке [0; а/2) обра-
щается в нуль в точке х = а/б. Вычислим вто-
рую производную: V" (х) = 24х — 8а. В точке
х = а/б вторая производная отрицательна, и*
следовательно, в точке х = а/б функция V (х):
имеет максимум. На концах промежутка [0; а/2]
функция V (х) обращается в нуль. Таким образом, объем коробки
при х = а/б будет наибольшим.
3.	4. Направление вогнутости кривой. Пусть функция f (х) опре-
делена и непрерывна на промежутке (а; Ь), а в точке х0 С имеет
конечную производную. Тогда к графику данной функции в точке
Мо (х0; f (х0)) можно провести касательную, уравнение которой имеет
вид
У — Уо = Г (*о) (% — *о).
Говорят, что в точке Мо кривая (график функции у — f (х)) направлена
вогнутостью в определенную сторону (вверх или вниз) от касательной,
если в достаточно малой окрестности точки Мо все точки кривой лежат
по одну сторону от касательной (рис, 9.12 и 9.13). Точку Мо называют
точкой перегиба, если в достаточно малой ее окрестности точки кривой
с абсциссами х < х0 лежат по одну сторону от касательной, а точки
с абсциссами х > х0 — по другую, т. е. в точке А40 кривая переходит
с одной стороны касательной на другую (рис. 9.14).
Направление вогнутости кривой у = f (х) в некоторой точке х0
выясняется по следующему правилу:
1)	Если в некоторой 6-окрестности точки х0 вторая производная
f (х) сохраняет знак плюс (как слева, так и справа от точки х0), то кри-
вая в точке х0 направлена вогнутостью вверх (рис, 9.12),
§ 8, ИССЛЕДОВАНИЕ ФУНКЦИЙ
363
2)	Если в некоторой 6-окрестности точки х0 вторая производная
сохраняет знак минус (как слева, так и справа от точки х0), то кривая
в точке х0 направлена вогнутостью вниз (рис. 9.13).
3)	Если вторая производная меняет знак при переходе через точку
х0, то в точке х0 график функции f (х0) имеет перегиб (рис. 9.14).
Таким образом, если ограничиться достаточной малой 6-окрест-
ностью точки х0, точка перегиба Мо как бы отделяет те точки, где вогну-
тость кривой направлена вверх, от точек с направлением вогнутости
вниз.
Сформулированное правило — достаточное (но не необходимое)
условие перегиба кривой» Так, функция f (х) = х4 в точке х = 0 имеет
вторую производную, равную нулю, но
тем не менее в этой точке (и вообще при
у=х4	всех х С R) кривая направлена вогну-
тостью вверх (рис. 9.15).
Рис. 9.15.	Рис. 9.16,
Пример. Рассмотрим функцию f (х) == sin х. Вторая производ-
ная этой-функции1 равна
Г (х) = —sin х.
В промежутках (2л&; л + 2л£) функция sin х сохраняет знак плюс,
f” (х) = —sin х < 0 и синусоида направлена вогнутостью вниз. В про-
межутках (л + 2л&; 2л + 2л&) sin х < 0 и, следовательно, синусоида
направлена вогнутостью вверх. При х = л& вторая производная обра-
щается в нуль, меняя при этом знак; в этих точках график функции
у — sinx имеет перегиб (рис. 9.16).
3.	5. Асимптоты графика функции. Пусть у = f (х) *— функция,
график которой имеет бесконечную ветвь, т. е. ветвь, имеющую точки,
принадлежащие графику функции и находящиеся сколь угодно далеко
от начала координат.
Асимптотой графика функции у = f (х) называют прямую, обла-
дающую тем свойством, что расстояние от точки (х; / (х)) до этой пря-
мой стремится к нулю при движении этой точки вдоль ветви к беско-
нечности.
Асимптоты бывают двух видов: вертикальные и наклонные (в част-
ности, горизонтальные).
Прямая, задаваемая уравнением х = а, — вертикальная асимп-
тота, если хотя бы один из пределов *)
lim/(x), lim f (х), lim f (x)
+oo (или —oo).
*1 Второй и третий пределы называют односторонними (см.п. 6.2 рл. 8)\
364 ГЛ. 9. НАЧАЛА ДИФФЕР, И ИНТЕГР. ИСЧИСЛЕНИЙ
Примеры. I. График функции у = — имеет вертикальную
асимптоту х = 0, так как
lim —= 4-оо и lim —— = — оо.
#-►4-0 х
2.	График функции у = имеет вертикальную асимптоту х = О,
так как
11m —~ = 4-оо.
#-о *2
3.	Вертикальной асимптотой для графика
функции у == tg х будет каждая из вертикаль-
ных прямых х = nk (k g Z).
Для существования наклонной асимптоты,
задаваемой уравнением у= kx-{- bt необходимо
и достаточно, чтобы существовали пределы
k = Нт-**-, b = lim [f (х) — kx\
при х, стремящемся к +оо (или к —оо).
Пример, Найти асимптоты графика
функции
</ = 2х--4,
Вертикальной асимптотой является прямая х == 0. Коэффициенты
уравнения наклонной асимптоты найдем из равенств
lim — Нт ---------------— =Нт (%---------^-\=2,
#-►4-00 X #->4-00 X #->4-00 \ X /
2x1 = Нт (--------—= 0.
J #-Н-оо \ х /
6= Нт [/(%) — &х] = lim [2х-----------------— —
#->4-oo	х->4-оо L	х
Таким образом, данная функция имеет наклонную асимптоту,
задаваемую уравнением
У = 2х.
График функции р = 2х------изображен на рис. 9.17. Пунктир*
ная прямая — наклонная асимптота.
3.7.	Построение графика функции. Исследование функции и по*
строение ее графика обычно состоит в следующем:
1)	Находят область определения функции.
2)	Выясняют, будет ли данная функция периодической.
3)	Выясняют, будет ли данная функция четной (или нечетной).
Если функция оказывается четной, то ее график симметричен относи-
тельно оси Оу прямоугольной декартовой системы координат. Если
§ 3. ИССЛЕДОВАНИЕ ФУНКЦИЙ	365
функция ,нечетная, то ее график центрально симметричен относительно
начала координат.
4)	В случае, если область определения функции представляет собой
либо всю числовую прямую, либо содержит лучи [а; + оо) или (—оо; b),
выясняют поведение функции в бесконечности, вычисляя соответст-
вующие пределы
lim/(x), lim f (х).
Х->4-оо	со
5)	Находят пересечение графика функции с осью Оу, вычисляя
7(0), и с осью Ох, решая уравнение f (х) = 0.
6)	Находят точки максимума и минимума, устанавливая проме-
жутки возрастания и убывания функции.
7)	Находят множество значений (область изменения) функции
£(/)•
8)	Находят точки перегиба функции, устанавливая промежутки,
где кривая обращена вогнутостью вверх или вниз, причем в точках пе-
региба вычисляют угол наклона касательной.
9)	Находят асимптоты функции.
При исследовании конкретных функций не обязательно придер-
живаться указанной последовательности исследования функции. Можно
даже опускать выяснение тех или иных свойств, если они достаточно
очевидны. Так, при исследовании рациональных функций обычно опу-
скают исследование их периодичности по той причине, что из всех эле-
ментарных функций лишь тригонометрические функции обладают свой-
ством периодичности.
Пример. Исследовать свойства функции
и построить ее график.
1)	Область определения функции — вся числовая прямая, за
исключением точки х = 0.
2)	Функция не является четной и не является нечетной* так как
и f (х) =£ —f (—х).
3)	Для того чтобы выяснить поведение функции при неограниченном
возрастании (и убывании) аргумента, вычислим пределы
2х3 + 3х —4 о ..	2x2-f-3x —4	'
hm -------------= 2, hm ------------------=2.
Х-*+<х>	х	х
4)	График данной функции не пересекает ось Оу. Точки пересече-
ния графика функции с осью Ох определяются как корни уравнения
2х2 + Зх — 4	_
х2 -
которые будут следующими:
X ~3+K?i г -з-ГП
366 ГЛ. 9. НАЧАЛА ДИФФЕР, И ИНТЕГР. ИСЧИСЛЕНИЙ
5)	Найдем точки максимума и минимума функции. Вычислим про-
изводную данной функции:
~Зх2 + 8х-Зх + 8
Производная обращается в нуль при х= 8/3 и не существует
в точке х == 0, но так как точка х =0 не принадлежит области опреде-
ления данной функции, то она не является критической точкой.
Решим неравенство f (х) > 0:
=^>о~6(о> 4),
т. е« функция f (х) возрастает при х g	и убывает при х ?
£ (—оо; 0) U Ч-оо^. Следовательно, точка х«=8/3 — точка
максимума функции.
6)	Область изменения функции (множество значений) найдем, ис-
пользуя результаты пп. 3) и 5). Нетрудно проверить, что при всех
х £ (v°°; 3/4) график функции / (х) лежит ниже прямой у == 2, тан
как для этих значений х выполняется неравенство
t W < 2,
а при х £	; +оо^ график функции лежит выше прямой г/=2,
Следовательно, максимальное значение функции /(—•) = являйся
\ О /	10
наибольшим во всей области определения функции.
При х, стремящемся к нулю:
..	.. 2х2 + 3х —4
lim f (х) = hm----!—-------= — оо,
х-*о х->о х
оо;
Таким' образом, множество значений функции — промежути^
41 1
16 J •
7)	Вычислим вторую производную функции!
Вторая производная в промежутке (4; +оо) положительна, и,
следовательно, в этом промежутке график функции направлен вогну-
тостью вверх. В промежутках (—оо, 0) и (0; 4) вторая производная от-
рицательна, и график функции направлен вогнутостью вниз. В тачке
х == 4 график функции имеет перегиб.
8)	Прямая, задаваемая уравнением х = 0, — вертикальная асим-
птота, так как
lim /В^+.Зх-4
£-*•0 \
3 4 \
&
§ 4. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 367
Покажем, что функция имеет и наклонную асимптоту, задаваемую
уравнением
у = kx + Ь.
Найдем коэффициенты этого уравнения k и Ь:
,	.. Г£ f \ л 1	1*	2х2 Зх— 4	.. Го ।	4 I
b = lira [f (х) — O x] = lira-----j-----= lim 2 + —-----------5- = 2.
Х->оо	Х-*оо л	Х-*оо L	л л J
Значит, данная функция имеет горизонтальную асимптоту у = 2.
На основании проведенного исследования можно нарисовать гра»
фик данной функции (рис* 9.18).
§ 4. Первообразная. Неопределенный интеграл
4.1. Понятия первообразной и неопределенного интеграла. При
решении ряда задач механики и физики необходимо восстанавливать
функцию по ее известной производной. Так, если материальная точка
движется по прямой, не меняя направления своего движения, и рас-
стояние, пройденное точкой, — известная функция времени S (О, то
мгновенная скорость точки-вычисляется как производная пройденного
пути:
v = S' (0.
Пусть теперь нам известен закон изменения скорости точки, т. е.
задана функция v (/), и требуется найти расстояние, которое прошла
материальная точка за некоторый промежуток времени Т. Для того
чтобы решить сформулированную задачу, необходимо по известной про-
изводной (в нашем случае скорости v (/)) восстановить саму функцию
(в нашем случае S (0).
Восстановление функции по известной ее производной составляет
одну из основных задач интегрального исчисления.
Эта задача является обратной основной задаче дифференциаль-
ного исчисления, которая состояла в нахождении произвол*
ной данной функции.
363 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Функция F (х) называется первообразной для функции f (х) на дан-
ном промежутке числовой оси, если для всех значений х из этого про-
межутка функция f (х) является производной функции F (х):
F'W«/(x).	(1)
Основное свойство первообразных: если функ-
ция F (х) — первообразная функции f (х), то и функция F (х) + С, где
С — Любая постоянная, также первообразная функции f (х). Обратно,
если F (х) — некоторая первообразная функции f (х), то любая перво-
образная функции f (х) может быть записана в виде
F(x)+C,
где С — некоторая постоянная.
Таким образом, для того чтобы найти все первообразные данной
функции f (х), достаточно найти лишь одну первообразную F (х); все
остальные первообразные будут получаться из найденной первообраз-
ной добавлением постоянных слагаемых.
Выражение F (х) + С, где С —- произвольная постоянная, пред-
ставляет собой общий вид функции, которая имеет производную f (х).
Это выражение называют неопределенным интегралом функции f (х) и
пишут
F (х) + С = J f (х) dx.
Произведение / (х) dx называется подынтегральным .выражением
a f (х) — подынтегральной функцией.
Нахождение множества всех первообразных функции / (х) назы-
вается интегрированием этой функции.
Используя формулу (1), из таблицы 8 п. 1.5 можно получить еле»
Дующую таблицу интегралов;
1)	J Odx = C;
2)	у l-dx = x + C)
Г „ xa+l
\xadx = —— + O (а=#-1)
j	а ф 1
4) у -i-dx = In | ж | + С;~
б) J pq^dx=arctgA:-pC}
6) С ------dx = arcsin х 4- Ci
J И - x2
71 J •--ТЙГ+c-	'
8)	J sin x dx = cos x -f- Cj
$ 4. ПЕРВООБРАЗНАЯ; НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 369
9)	J cosxdx = sinx-f- С}
10)	(•zi7<te = tgx+C:
11)	f-Л—dx = —ctgx + C.
' J sin2x	& 1
4.2.	Простейшие правила интегрирования.
1)	Пусть F'(х)— производная функции F (х). По определению
неопределенного интеграла
j F’ (х) dx = F (х) + С.
2)	Постоянный множитель можно выносить из-под знака интеграла:
J c-f (х) dx = с* j f (х) dx.
3)	Интеграл суммы двух функций равен сумме интегралов слагае-
мых:
j [/ {X) ± g (X)] dx = J f (x) dx ± J g (x^dx.
4)	Если функция F (x) является первообразной функции f (x), то
первообразной функции f(ax+b) является функция — F(ax-{-b)*),
Примеры. L Вычислить неопределенный интеграл
j (6х34~х — l)dx.
По правилам 2), 3) данный неопределенный интеграл можно пред*
ставить в виде суммы интегралов:
J (бх3 + х — 1) dx = 6 J х3 dx + J х dx — J 1 • dx.
Используя формулу 3) таблицы неопределенных интегралов, получаем
J (6x» + x-l)dx = -|-*4 + _‘-x«_x + C.'
2. Проинтегрировать функцию
ух
Представим данную функцию f (х) в виде
х— /х X	Кх	_ X	Х1/2 _ ^2/3	vl/6
3/7	“ 3/7	3/Т х>/з	х^~-
*( Правило 4) есть частный случай правила замены переменной в.неопре»
деленном интеграле (см. п. 4.1).
370 ГЛ. б. НАЧАЛА ДИФФЕР. Й ЙНТЕГР. ИСЧИСЛЕНИЙ
Используя правила 2), 3) и формулу 3) таблицы неопределенных ин-
тегралов, получаем
-Х dx з= J [х2/3 — х1/6 ] dx =»
= j Х^ dX- j Jx = A//3 6 х7/б +Ct
С помощью правил 2), 3) можно интегрировать лишь очень простые
функции. Существуют гораздо более эффективные (но и более сложные)
методы интегрирования функций. Одним из таких методов является ме-
тод интегрирования по частям.
4.3. Метод интегрирования по частям. Пусть и (х) и v (х) — две
непрерывные функции, имеющие непрерывные производные. Метод
интегрирования по частям основан на двух равенст-
вах:
(u-v)' = u'-v + u-v't J (u>vY dx = u-v 4-C,
первое из которых представляет собой правило дифференцирования
произведения двух функций, а второе — правило интегрирования 1)
п. 4.2. Из приведенных равенств следует, что *
^u-v'dx = u>v—^u'-vdx.	(2)
Пример. Вычислить интеграл •
J х cos х dx.
Вычислим данный интеграл методом интегрирования по частям.
Представивподынтегральную функцию в виде произведения двух со*
множителей — функции и (х) = х и производной некоторой функции
v (х), о которой известно, что
v' (х) » COS X.
Производная функции и (х) равна .единице!
(х) = 1,
а одна из первообразных функции v' (х) равна sin xl ’
. v (х) == J cos dx = sin х.
Подставляя ц(х), v (х) и и' (х) в правую часть равенства (2), полуШй
J х cos х dx х sin х — j* sin х dx.
Таким образом, вычисление данного интеграла сведено к вычислению
табличного интеграла
j sin х dx «= — cos х + Сj
Г" 	1 -
*) Равенство (2) также может быть записано в виде.
yudp«=a-& —у vdu
$ 4. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 371
и, следовательно,
J х cos х dx == х sin х + cos х + О*
Заметим, что в более сложных случаях разложение подынтеграль-
ной функции на сомножители может быть не единственным и его следует
выбирать таким, чтобы интегрирование функции v* (х) не представляло
трудностей и чтобы вычисление интеграла, стоящего в правой части
формулы (2), было проще, нежели вычисление интеграла, стоящего
в левой части.
Некоторые интегралы, вычисляемые мето-
дом интегрирования по частям. Интегралы вида
J х* lnwx dxt J xk sin bx dx, J xkeax dx,
где A, tn — натуральные, a a, b — любые действительные числа, вы- (
числяются с помощью интегрирования по частям.
Примеры. 1. Вычислить интеграл
J х3 In х dx.
Положим и «» In х, и' ® х3, так что и9 = о = -4- х4. Исполь-
’	х 4
вуя формулу интегрирования по частям, получим
( х3 In х dx = х4 In х — f “4” х4 •— dx «ж
J	4	J 4 x
t= -4- x4 In x — f x3 dx as — 1h * —iV *4 +
4	4 J	4	16	1
2, Вычислить интеграл
J x2sinxdx.
Положим и = x2, v9 = sin x, так что и9 = 2м = «—cos x. Ha ocho*
вании формулы интегрирования по частям имеем
j х2 sin х dx сз — х2 cos x + 2 j x cos x dx,
Применяя к интегралу, стоящему справа, еще раз формулу интегриро*
вания по частям, окончательно получаем
j х2 sin х dx = — х2 cos х + 2x sin x 2 COS x + 0,
3. Вычислить интеграл
j xe2x dx,
9	j
Положим u=x, v'— e2x. Тогда и'1,	— По формуле
(2) исходный интеграл запишется в виде
f хе2* dx = "4“ хе2* — -4“ [ $2х = "4“ &2х -г -4- е2* 4-
J	*	^4	4	-
372	’ ГЛ. 0. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Так же, последовательным применением интегрирования по ча-
стям, вычисляются интегралы
J Р (х) еах dx, J Р (х) sin bx dx, J Р (х) cos Ьх dx;
где Р (х) — многочлен.
Методом интегрирования по частям можно также вычислить ин*
тегралы
J еах sin bx dx, J еах cos bx dx.
Если к данным интегралам применить метод интегрирования по частям
^в обоих случаях взяв v' «= еах => v = еах^, то получим следующие
два равенства:
j еах cos Ьх dx = -i- еах cos Ьх + -у- J еах sin Ьх dx,	(3)
J еах sin bx dx *= -i- еах sin bx-J еах cos Ьх dx.	(4)
Умножая обе части равенства (4) на величину Ыа и складывая по*
лученное равенство с равенством (3), получим-линейное уравнение отно*
сительно интеграла J еах cos bxdx, в результате решения которого най-
дем требуемый интеграл:
J cosbxdx =	+ C.
Аналогично находим и второй интеграл:
' J е™ sinbxdx =	+ ct.
4. В качестве еще одного примера применения метода интегрирова-
ния по частям получим рекуррентную формулу для вычисления интег-
рала
/ - С dx
п J (х24-а2)п ’
Полагая
1	/	1
и —--------о = lt
(х2 + а2)п
по формуле (2) имеем
х	(* х2
= I*2 + «Т + 2/1J (Жа + а7*+* dX‘
$ 4. ПЕРВООБРАЗНАЯ- НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 373
Преобразуем последний интеграл:
Г х2 . Г (х2 + а2) — о2 .	.
1--------—гг dx = | —--------гтт—dx —
J (х2 + а2)"+ J (х2 4- а2)“+*
f dx	f dx	т ,,
J (х24-а2)"	J (х24-а2)',+1
Подставляя полученное выражение в равенство (5), получаем
1п = / 2-L г\п + 2п,п — 2па2,^1>
(х2 + а2)п
откуда
J________1_______X	2п — 1	1
л+1 2па2 (Х2	а2)« 2п ’ а2 п"	'
Рекуррентная формула (6) позволяет свести вычисление интеграла
ln+1 — J (х2_|_а2)П+1
к вычислению интеграла 1п.	~~
Вычислим интеграл /х с помощью правила 4) и табличного интег-
рала 5):
Зная интеграл Zf, по формуле (6) можно вычислить интеграл /2.
По известному интегралу /2 с помощью той же самой формулы (6) можно
вычислить интеграл /3 и т. д.
4.4. Интегрирование методом замены . переменной. Подстановки
Эйлера. Одним из самых эффективных методов интегрировдния является	/ -
метод замены переменной или метод подстановки. Пусть требуется  У
вычислить интеграл	?
j / (X) dx.
Этот метод основан на свойстве инвариантности дифференциала .
(см. п. 2.3) и заключается в том, что для подынтегрального выраже-
ния f (х) dx подбирают такую функцию у = <р (х), чтобы подынтеграль-
ное выражение могло быть записано в виде
f (х) dx « g (ф (х)) • ф' to dx,	(7)
где функция g(у) более удобна для интегрирования, нежели функция
/ (х). Используя свойство инвариантности дифференциала, равенство
(7) записывается в виде
Zto dx = g (у) dy, -	(8)
сводя тем самым вычисление данного интеграла к вычислению интег-
рала
Jg(!/)dy.
374 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Если удается вычислить этот интеграл:
J g (у) dy » G (у) 4- С,
чо, возвращаясь к исходной переменной х, получаем
j f(x) dx = О (ф (x)) + С.
Примеры. 1. Вычислить интеграл
J sin2 х cos х dx.
Так как d sin х = cos х dx, то, полагая у = sin х, подынтегральное
выражение можно преобразовать к виду
sin* х cos х dx = sin2 x d sin x = y2 dy\
следовательно,
J sin2 x cos x dx = J y2 dy = у9 + C*
Возвращаясь к переменной x, окончательно получаем
J sin2 x cos x dx ~ sin3 x + C,
2. Вычислить интеграл
j e*2 x dx.
Так как x dx =» d (x2), то, полагая у = x2, вычисление данного
интеграла сводим к вычислению интеграла
4“ J e^dy=-i-e^-t-Ci
следовательно,
j е*2 х dx =	е*2 + Ол
Вычислить интеграл
!	jtgxdx.
Подынтегральное выражение можно записать в вида
Обозначая cos х == у^ получаем
jtgx</x=J-y-=ln|yl + C=ln|tgx|4-C.
§ 4. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 375
Метод замены переменной упрощает вычисление интегралов
f	dx
вида j f (In х) —(подстановка у = In х), а также интегралов вида
j f (sin х) cos х dx, J f (cos x) sin x dx
(Подстановки у = sin x и у == cos x соответственно.)
4.5. Некоторые классы интегрируемых функций. Интегриро-
вание рациональных алгебраических дробей.
Интегрирование простейших дробей
А	А
(* = 2.3,...)	(9)
х —а (х — а)к
выполняется непосредственно с помощью табличных интегралов 4? )
и 3) п. 5.2 соответственно:
J^ydx=41n|x—а|4-С»
А	А 1	, п
------  dx = — -7-г  -----г-г- + С«
(x — a)k	k—1 (x—a)k 1
Интегрирование простейших дробей вида
Мх+^У Мх + N
'x*-\-px + q И (x2 + px + q)k
{k = 2, 3,
(Ю)
где	—-q<0, выполняется с помощью метода подстановки.
Полагая / = х + -у-, имеем
^4-px + 9=/2 + a2, Mx + N= Mt+ (м — dx = dt.
где аг. = q — (~^“)" • Выполняя указанную подстановку, получаем
для первой дроби (10):
Mx + N
x2 + px + q
dx = 4-Lln(Z2 + a2)+ -L(m
M. p\	t
-r)arcte-
c,
для второй дроби (10):
f Mx + N_________________1
J (x2 + px + q)k *—1
(ID
(Z2 + a2)*-1
J- ( N__f________——
+ V	2?J(Z2+a2y
(12)
где последний интеграл для любого конкретного значения k можно
вычислить по рекуррентной формуле (6) п. 4,3«
376 гл. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Для получения окончательного выражения для интегралов (10)
в формулы (11) и (12) следует подставить
2х + д	i/~	р2'
Так как рациональная алгебраическая дробь может быть записана
в виде суммы многочлена и правильной рациональной дроби (см. п. 3.2
гл. 4), а каждая правильная дробь единственным образом разлагается
в сумму простейших дробей вида (9), (10) (см. п. 3.3 гл. 4), то интегри-
рование любой рациональной дроби сводится к интегрированию мно-
гочлена и вычислению интегралов дробей (9), (10).
Пример. Вычислить интеграл
Г 2х*-_ 10х3 + 7х2 + 4х + 3
J хб — 2х3 + 2х2 — Зх + 2 йХ*
Подынтегральная функция может быть представлена в виде еле*
дующей суммы простейших дробей (см. п. 3.3 гл. 4):
3	1	2 х —3
х + 2 (х — I)2	х—1 + х2+ 1’
и вычисление данного интеграла сводится к вычислению следующих
интегралов;
jT^2rfx==31n|X+2l}	. .
f 1	.	1	.
I “7-«‘TVS- «* =---T" •
J. (X— I)2	X —1 ’
i — 2 In I x — 11;
J X ~~ 1
P~3dx-f xdx	af dx
Jx3+iax J^+i	+ ?++ .
Первый из интегралов, стоящих в правой части последнего ра-
венства, вычислим методом замены переменной: полагая /= х2+ 1,
получаем dt — 2х dx й
f xdx	\ С dt 1 . . ..	1 . z „ , ..
J х2 + 1	2 J -1 = 2 ln I * I — 2 In (X 4- I).
Так как второй интеграл — табличный интеграл 5), то
J dx ~ -§ *n (х2 +0 — 3 arctg X.
Окончательно получаем
[ 2х4 — 10х3 + 7х2 + 4х + 3
J х! —2х8 + 2№ —Зх+2 dX ~	’
1 О ,	, , (х + 2)3-/х2+ 1 I < rl
-j--3arctgх+In	т | 4-С»1
§ 4. ПЕРВООБРАЗНАЯ. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 377
Подстановки Эйлера. Интегралы вида
J R (х, Уах2 + bx + с) dx,
ГДе R — многочлен или рациональная алгебраическая дробь P/Q
(Р и Q — многочлены) указанных аргументов, сводятся к интегралам
от рациональных алгебраических дробей подстановками
Эйлера.
Первая подстановка применяется в случае, если
0. Тогда полагают
+ bx + c= i — ^ax.	(13)
Возводя обе части равенства в квадрат, получаем равенство
bx^c = t2 — 2 Vatx,
из которого следует
/2__________________________г
-77^77-	<“>
Далее, подставляя в правую часть равенства (13) вместо х его
выражение (14), получаем
 г ь , V"at2 + bt + c\/"a	..
V ах2 + Ьх + с = --’—-—	(15)
2/fl/+d	'
Из равенства (14) также следует
+ + di
(2|<в«+&)2
(16)
Если полученные выражения (14), (15) и (16) подставить в исходный
интеграл, то вычисление этого интеграла будет сведено к вычислению
интеграла от рациональной алгебраической дроби относительно пере*
менной /.
Пример. Вычислить интеграл
dx
Ух2 — а2
Полагая Кх2 — а2 = t — х, получаем
х2. — а2 =	— 2tx + х2; 2tx = t2 + а2;
t +а2	-----%	‘ t2 + a2 t2 — а2
2t-2t — (i2а2)-2 .. t2 — а2
dt --------4Г»-------dt =	2t2 dt'
Подставим полученные выражения для Ух2. — а2 и dx в данный ин*
теграл:	>
dx _ Г 2/
рх2— а2 ~~ J — &
t2 — а2  С dt ,1^1,
 2/2 dt = J — = 1п Н I + с-
378 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Возвращаясь к переменной х, получаем
Г-7=^= = In IX 4-|/’х5^а21 + О.
J	д2 1 Т '	11
Вторая подстановка применяется, если 0. В этом
случае полагают
У ах2 + Ьх -|- с = xt +
Если возвести обе части этого уравнения в квадрат, то
ах2 + Ьх + с = x2t2 + 2xt j/T+ ct
qhkjw находим
(a — t2)2
Подставляя полученные выражения для xt ах2 + Ьх.-\~ с> dx
в исходный интеграл, получаем, что вычисление этого интеграла сво-
дится к вычислению интеграла от рациональной алгебраической дроби
относительно переменной t.
Пример. Вычислить интеграл
Полагая Уа2. — х? = xt + Vа2, получаем
а2 — х2 = x2t2 + 2xt К а2 + а2}
^(Z2+1)=----2ta.
4 —f— 1
r^i2 = «о-*2). dx _ _2°(<2-n dt
VCl X i24-l	1	a*~	(/2_|_])2“f>
Подставим полученные выражения для j/"a2 х2 и dx в интеграл!
Возвращаясь к переменной х, окончательно получаем
dx
И»2
= — 2 arctg
Кд2 — х2 •— а
ж

£ 4. ПЕРВООБРАЗНАЯ- НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 379
Третья подстановка пригодна в том случае, когда
квадратный трехчлен ах2 + Ьх+ с имеет различные корни Xi и х2
и, следовательно, может быть записан в виде
ах2 + Ьх + с = а (х — xj (х — xj.
В этом случае полагаем
Vах2 + Ьх + с = t (х — Xi).
Возводя обе части уравнения в квадрат, находим
2a(Xi-Xi)t
(/2 _ 0)2
Таким образом, и в этом случае вычисление исходного интеграла
свелось к вычислению интеграла от рациональной алгебраической
дроби.
Интегрирование тригонометрических функ-
ций. Интегралы вида
J R (sin х, cos х) dx,
где R — многочлен или рациональная алгебраическая дробь указан-
ных переменных, могут быть сведены к интегралам от рациональных
х
алгебраических дробей подстановкой / = tg-^-, так как
1 —tg2 —
g 2	1 —/2
cos х j--------= j
l+tg2-J- 1 + <
J 2dt
dx ~ 1 4- t2 *
2tg 2	2/
sin х =-----------   ,	;
1 + Ч?4г ' + '
х и 2 arctg /;
X
Подстановка t= tg-g-, называемая универсальнойf довольно
часто приводит к сложным вычислениям. Во многих случаях интегралы
указанного выше вида могут быть вычислены с помощью более простых
подстановок.
Пример. Вычислить интеграл
| sin2 х cos3 х dx.
Универсальной подстановкой /==tg-~- данный интеграл при-
водится к интегралу
8/2 0 _ /2)3
—г, : ,9\й "
вычисление которого требует довольно громоздких вычислений*
380 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИИ
Проще данный интеграл может быть вычислен подстановкой t
t == sin х; dts cos x dxj
sin2 x cos3 x dx == Г sin2 x (1 — sin2 x) cos x dx «=
= J t2 (1 - P) dt =
j (t2—l*)dt =-1.19
--
® -4- sin3 x-------- sin^ x + C.
о	о
§ 5. Определенный интеграл
5.1. Задача вычисления площади плоской фигуры. Пусть на неко-
тором промежутке [а; Ь] задана непрерывная функция / (х), принима-
ющая лишь положительные (неотрицательные) значения. Построим
(неотрицательные) значения. Построим
график функции у» f (х) в прямо-
угольной декартовой системе коорди-
нат Оху (рис. 9.19).
Рассмотрим фигуру A BCD, огра-
ниченную графиком функции у= ) (х),
двумя прямыми, задаваемыми урав-
нениями х~ а и х~ Ь, и осью Ох.
Эту фигуру принято называть криво*
линейной трапецией.
Разделим основание трапеции АВ
на п отрезков с концами х0 = а, х1я
х%, ..., xn_lt хп~ b и через точки

/7
'27
2^
С
y-f(z)
. a xt х2 XfXi хы b х
Рис. 9.19.

Xf, х2, ..., xn_i проведем вертикальные прямые, которые разобьют
криволинейную трапецию на п полосок (рис. 9.19).
Для каждой полоски построим прямоугольник, основание кото-
рого тб же, что и у полоски, а высота совпадает с одной из боковых
сторон полоски, скажем с левой (на рис. 9.19 эти прямоугольники
заштрихованы).
Основание t-го прямоугольника (/=0, 1, 2, .,,, п — 1) равно
разности xi+1 — xi, которую обозначим Ахь а высота, согласно при-
нятому выше допущению, равна yt — t (х$).
Площадь i-го прямоугольника равна yt-Axt^ /(хе)-Аль Сумма
площадей <$л всех прямоугольников равна
п—1
Sn = t (Хо) Ахо + / (х1) ДХ1 +' • • +1 (х„_1) Дхп_1 = ^1 (Ki) Sxi.
i~0
Площадь Sn называют* приближенным значением площади криволи-
нейной трапеции A BCD.
Точное значение площади S получится как предел
S «= lim / (Xi) ДХ1 = Jim У yt Дх|	(1)
в предположении, что все длины Axi одновременно стремятся к нулю,
при неограниченном, увеличении числа точек разбиения отрезка АВ-
§ Б. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ	ggj
Для обозначения предельного значения суммы вида (1) Лейбниц
ввел символ J у dxt где у dx — вид слагаемых суммы (1), a J — сти-
лизованная буква S — начальная буква латинского слова Summa.
Заметим, что, вычисляя площадь криволинейной трапеции ABCD
как йредел сумм Sn, мы не касались вопроса о том, каждая ли геоме-
трическая фигура имеет площадь. В математическом анализе построены
примеры фигур, не имеющих площади.
5.2. Понятие определенного интеграла. Приведенный в предыду-
щем пункте способ вычисления площади криволинейной трапеции при-
годен лишь для весьма узкого класса функций (например, для непре-
рывных функций). Понятие площади криволинейной трапеции, на-
пример, для ограниченных функций, имеющих на промежутке [а; 5]
конечное число точек разрыва, вводится с помощью понятия определен-
ного интеграла.
Пусть ограниченная функция / (х) задана на некотором промежутке
[a; Разобьем этот промежуток произвольным образом на п частей,
вставив между точками а и b точки деления xj, х2, ...» хП-1, причем
а == х0 < *1 < *2 < • • • <*i < Xj+i < • • • < хп = b.
Наибольшую из разностей Дх/ == х/+1 — х/ (i «= 0, 1, 2, ...
...» п — 1) обозначим через X.
Возьмем в каждом из промежутков [х/; *м1 произвольную
точку It: xi xi+i и составим сумму, называемую интеграль-
ной суммой'.
П—1
о„=2/а1)д^.	(2)
1=0
соответствующей данному разбиению отрезка [а; 5]. Сумма (2) зависит
от выбора точек разбиения х/ отрезка [a; Z>] и от выбора точек
Говорят, что сумма оп имеет предел I при X, стремящемся к нулю,
если для любого сколь угодно малого числа 0 существует такое
•число б > 0, что неравенство
|ал—/|<е
выполняется при любом X < б независимо от выбора чисел 5/ (т. е. для
любого разбиения промежутка [а; 5] на части, меньшие чем б и при
любом выборе точек £/).
Конечный предел I суммы оп при-Х, стремящемся к нулю, назы-
вается определенным интегралом функции f (х) на промежутке от а
до b и обозначается
Ъ —
J f W dx.	(3)
а
Если такой предел / существует, то говорят, что функция f (х)
интегрируема на промежутке [а; б].
В записи (3) функция f (х) называется подынтегральной функцией*
f (х) dx — подынтегральным выражением, а числа а и b называются
соответственно нижним и верхним пределами интеграла.
Если функция f (х) положительна на промежутке [а; б], то суще-
ствование конечного предела / (определенн.ого интеграла (3)) озна-
382 ГЛ. g. КАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
чает, что площадь криволинейной трапеции, ограниченной графиком
функции у =х f (х), осью Ох и прямыми х = а и х = Ь, существует
и равна I.
Примером неинтегрируемой функции является функция Дирихле
D (х), задаваемая на всей числовой оси условиями:
{1, если х рационально,
О, если х иррационально.
Покажем, что функция D (х) не интегрируема, например, на про*
межутке [0; 1]. Разобьем этот промежуток произвольным образом
на п частей. На каждом из промежутков [хг, Xf+j] выберем рациональ-
ную точку и иррациональную точку и составим две интегральные
суммы оп и в'п, соответствующие данному разбиению:
п—1	п—1
4=0	i=Q
Для точек и по определению функции D (х) имеем D = 1
и D = 0 и, следовательно, on == 1, о'п = 0.
Аналогичные интегральные суммы о и о' можно составлять для
любого другого разбиения отрезка [0; 1], выбирая каждый раз
рациональным, иррациональным и каждой раз получая а= 1,
а' = 0.
Итак, можно построить две последовательности интегральных
сумм — одну, состоящую только из единиц, и другую, состоящую
только из нулей. Пределом первой последовательности будет единица,
а пределом второй — нуль. Но так как ‘для существования предела
интегральных сумм необходимо, чтобы последовательность интеграль-
ных сумм сходилась к числу I независимо от выбора точек
то установленное противоречие и доказывает, что функция Дирихле
не интегрируема на [0; 1 ].
Свойства определенных интегралов.
1)	Если функция f (х) интегрируема на промежутке [а; 6], то и
функция k-f (х) (k — постоянная) также интегрируема на этом про-
межу тке^ причем
ь	ь
j k*f (х) dx = k j f (x) dx,
a	a
f, e. постоянный множитель можно выносить за знак интеграла.
2)	Если функции f (х) и g (х) интегрируемы на промежутке [а; 6],
то и функции / (х) ± S (х) также интегрируемы на этом промежутке;
при этом
b	b	ь
j If W ± £ W1 dx = J f (х) dx ± J s W dx*
a	a	a
§ Б. ОПРЕДЕЛЕННЫЙ Й'НТЕГРАЛ	3&3
3)	При перестановке пределов интегрирования интеграл меняет
энак на противоположный:
Ь	а
j/(x)dx = — ( f(x)dx.
а	о
Из этого равенства, в частности, следует, что
а
j f (х) dx =» 0.
а
4)	Если функция f (х) интегрируема на промежутке (а; 6] и точка
с € (а; Ь), то функция интегрируема на промежутках [а; с] и [с; Ь],
причем
ь	с	ь
j / (х) dx = j f (х) dx + j f (x) dx.
a	a	c
5)	Если неотрицательная функция f (x) интегрируема на про*
межутке [а; Ь], то
Ь
j/(x)dx>0.
а
6)	Если функции f (х) и g (х) интегрируемы на промежутке [а;
и при всех х £ [а; Ь]
f(x)<g (*),
то
‘ [&	ь
J f (X) dx < J g (x) dx.
a	a
7)	Если функция интегрируема на промежутке [а; 6], где а < bt
и при всех х £ [а; Ь] справедливо неравенство
(х)<Л1,
то
ь
т (Ь — J f (х) dx < М (Ь — а),
а
5.3. Определенный интеграл как функция верхнего предела. Основ-
ная формула интегрального исчисления. Если функция / (/) интегри-
руема на промежутке [а; Ь], то по свойству 4) определенного интеграла
(см. п. 5.2) она интегрируема и в промежутке [а; х], где х — любое
число из промежутка Та; dj. Заменив верхний предел b определенного
интеграла переменной х, получим выражение
ф W = J / (0 dt,	(4)
а
384 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
*
которое можно рассматривать как функцию переменной х. Эта функция
обладает следующими свойствами:
1) Если функция f интегрируема в промежутке [а; ft], то функция
Ф (х) — непрерывная функция в промежутке (а; ft).
2) Если функция f непрерывна в промежутке [а; ft), то в любой
внутренней точке этого промежутка функция Ф (х) имеет производную,
равную f (х):
ф' (X) = f (X).
Последнее свойство функции Ф (х) является одним из важнейших
результатов математического анализа.
Для функции f (х), непрерывной в промежутке [a; ft], всегда суще-
ствует первообразная; этой первообразной является определенный ин-
теграл (4) с переменным верхним пределом.
Если F (х) есть некоторая первообразная непрерывной функции
t (х), то любая первообразная функции / (х) имеет вид
F (х) + С (С — произвольная постоянная).
Так как функция Ф (х), определяемая формулой (4), есть одна из
первообразных, то
Ф (х) = F (х) + С.	Х (5)
Полагая х == а, на основании свойства 3) определенного интеграла
'получаем, что Ф (а) = 0 и
F (а) + С «. О,
откуда следует, что С = —F (а), и формула (5) принимает вид
ф (х) = F (х) — F (а)9
В частности, при х== ft получаем
Ф (ft) == F (ft) — F (а),
или
ь
Ф(Ь) = J/(x)dx = F(6)-F(a).	(6)
а
Формулу (6) называют основной формулой интегрального исчис-
ления:
Значение определенного интеграла равно разности двух значений
любой первообразной функции, .вычисленных при х=Ь и при х~ а.
Разность, стоящую в правой части формулы (6), обычно обозначают
F(X,|a’
а саму формулу (6) записывают в виде
ь
j f (х) dx = F (х) I*.
X	a
’Основная формула интегрального исчисления позволяет сводить
вычисление определенного интеграла к вычислению значений перво-
образной (неопределенного .интеграла) с использованием всего раз-
витого аппарата вычислений неопределенных интегралов.
385 .
§ 5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример. Вычислить определенный интеграл
Я/2
j sinxdx.
Первообразной функции sin х будет функция —cos х, По основ*
ной формуле интегрального исчисления
л/2
j siaxdx = — cosx|^/2= — cos (—cosO) =— 0 + 1 =» !.
о
Аналогичным образом по основной формуле интегрального исчие»
ления вычисляются следующие интегралы:
рмх=4-д^=-1.-ох=4
о
5
г 1	15	1
I —dx = In х = In 5 — ln-ту- = In 10,
J x	h/2	2
1/2
1
f ex dx = ex Г = e* — e~1 = e-------—.
J	I—i	' a
—1
5.4. Вычисление площадей и объемов с помощью определенного
интеграла. Площадь криволинейной трапеции, ограниченной гра-
фиком непрерывной и неотрицательной
функции у = f (х), осью Ох и прямыми
х = а и х = b (рис. 9.20) вычисляется по
формуле
ь
s= р (*)<**•
а
Примеры.’-!, Вычислить площадь
фигуры, ограниченной графиком функции
у — е2х, осью Ох и прямыми х = 0 и х=1 (рис. 9.21). Площадь данной
фигуры равна
о
2. Вычислить площадь криволинейной трапеции, ограниченной
графиком функции у = In х, осью Ох и прямыми х = 2 и х == 4
13 А. Г. Цыпкин
386 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
(рис, 9.22). Площадь данной фигуры равна значению интеграла
4
J In х dx.
2
Найдем первообразную F (х) функции In xs
F (х) =» J In xdx.
Обозначим
In x = и, v' = 1.
Тогда
, 1
« И---- И X = 0.
X 1
По формуле интегрирования по частям (см. п. 4.3)
J и v' dx == u»v — j vu' dx
имеем
F (x) sa J In x dx = x In x — J x- dx «
= X in X — X = X (In X — 1) = x In *
По основной формуле интегрального исчисления (см. п. 6.3)
4
г	14	у 14	4	2
| In х dx = F (х) = х In — = 4 In--------2 In — =» j
j	»2	e 2	e	e
2
256	,4 t 64
“ e* П — ,n~•
3. Вычислить площадь фигуры, ограниченной графиком функ-
ции у ® tg х, осью Ох и прямой х = л/4. Площадь искомой
$ 5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
387
фигуры заштрихована на риз.
9.23 и равна значению интеграла
Л/4
| tgxdx.
о
Вычислим первообразную F (х) функции tg х методом замены перемен*
ной (см. п. 4.4):
„ % f ,	( sin х dx
Обозначим
cos Xе/.
Тогда
d/ — —sin х dx,
sin х dx
cosx
— In (COS X).
(В последнем выражении знак абсолютной ве.
личины опущен, так как cos х при 0 х
< л/4 положителен.)
Итак, F (х) « —In (cos х) и по основной формуле интегрального
исчисления имеем
Л/4
J tgxdx = —
о
1л/4
ID (COS X) «а
In (cos0) — to (cos-2-) = 0 — In In KF
Площадь поверхности, полученной в результате вращения вокруг
оси Ох криволинейной трапеции, ограниченной графиком непрерывной.
Рис.
неотрицательной функции у = f (х) и прямыми х == а и х » b (рис. 9.24)
вычисляется^ по формуле
ь
(х) К1 + (/' W)a dx,	(7)
а
13*
288 ГЛ. 9. НАЧАЛА	ДИФФЕР.	И ИНТЕГР. ИСЧИСЛЕНИЙ	Л
а объем по формуле	Т
V = nJ[/(x)Pdx.	(8) I
а	М
Пример. Вычислить объем и площадь поверхности шара ра- |
диуса /?. Шар может быть получен в результате вращения полукруга* |
вокруг оси, содержащей диаметр. Площадь его поверхности и объем 1
можно вычислить по формулам (7) и (8). Уравнение полуокружности
с центром в точке (/?;0) и диаметром, принадлежащим оси Ох (рис. 9.25),
имеет вил
у == И/?а — (х — RY<	(9)
Объем шара, полученного в результате вращения полукру!#, ограни*
ченного окружностью (9), равен
2R	2R
V = п j у2 dx « я J |Я2 —(X— /?)«) dx =
о	о
2Я	2Я	2/?
«= я j (2Rx — ха) dx =s л J 2Rx dx — я | x2 dx
0	0	0
D 2 F	Я Л F A n3	8л/?*
= nRx2----------— x* = 4л/?3------------—
|o 3 - |o	3
Площадь поверхности шара (площадь сферы) S вычислим по фор-
муле (7):
„ . .	, . .	(х — /?)
/ (х) = у (х) --------:
R
— я№».
У1 +(Г (х)р =	-у j
/>а-(х-Я)а
ы
S = 2л ( 1^/?^ (х-> ^)2— R ^^dx^
2Я
«= 2я J R dx ==
о
I2J?
2я/?Х ев 4л/?2.
§ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	389
§ 6« Дифференциальные уравнения
6.1. Понятие дифференциального уравнения* Обыкновенным диф*
ференциальным уравнением называется уравнение, в котором неиз-
вестной является функция одной независимой переменной, причем
уравнение содержит не только неизвестную функцию, но и ее произ-
водные различных порядков.,
Порядок наивысшей производной, входящей в уравнение, назы-
вают порядком дифференциального уравнения.
Обыкновенные дифференциальные уравнения имеют большое при-
кладное значение — они широко используются в механике, астрономии,
физике и других науках. Такое широкое распространение дифферен-
циальных уравнений в естествознании объясняется тем, что многие
явления и процессы, происходящие в природе, количественно опи-
сываются обыкновенными дифференциальными уравнениями. Так,
например, открытое в начале нашего века физическое свойство радио-
активного вещества — свойство распада — обычно формулируют в виде
«закона -радиоактивного рампада»:
Скорость радиоактивного распада вещества пропорциональна
количеству, этого вещества. .
Запишем «закон радиоактивного распада» в виде уравнения для
массы радиоактивного вещества. Так как, в согласии с законом радио-
активного распада, масса вещества меняется со временем, то обозначим
ее т (t) (t — время). Пусть — данный момент времени. За время Д$
масса радиоактивного вещества уменьшится на величину
Д/л — m (tQ + ДО — tn	<
Отношение
Am _ т (tQ + ДО — т (/0)
А/ ~	А/
показывает, насколько изменилась масса радиоактивного вещества
за единицу времени, и представляет собой «среднюю, скорость» изме-
нения массы.
Но так как при радиоактивном распаде масса вещества (функция
т (0) меняется со временем, то отношение kmlbi является функцией
Д/, и для точной Записи закона радиоактивного распада необходимо
взять предельное значение отношения Am/At при Д/, стремящемся
к нулю:
По определению этот’ предел есть производная функции т (0
по переменной /:
.. hm , „ .
hm — = m (/о).
д/->о
Так как закон радиоактивного распада справедлив в любой момент
времени (а не только в момент времени /0), то математически он может
быть записан в виде уравнения
/л' (0 =» —Р/и (0.	/
Здесь р — постоянный- положительный коэффициент пропорциональ-
ности, зависящий от вида радиоактивного вещества. Знак минус в по-
390 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ I
лученном уравнении указывает на то, что со временем масса радиоактив- й
ного вещества убывает, превращаясь в излучение (т* < 0 при любом 0. л
Дифференциальным уравнением может быть также описан процесс 
нагревания (охлаждения) тела.
Пусть известно, что в момент времени t0 тело имело температуру То.
Поместим тело в какую-либо среду, имеющую температуру 0 4s
Если 0 > То, то тело будет нагреваться, если же 0 < То, то охла-
ждаться. В некоторых случаях можно положить, что скорость измене-
ния температуры тела Т пропорциональна разности температур, т. е.
удовлетворяет дифференциальному уравнению
Г (k) ~ -k(T- 0),	(1)
где k — некоторая положительная постоянная. Знак минус указывает
на то, что при То > 0 тело будет охлаждаться, а при То < 0 — нагре-
ваться.
Необходимо отметить, что моделирование указанного физического
процесса уравнением (1) является довольно грубым и основано на сле-
дующих предположениях: считается, что в любой момент времени
тело нагрето равномерно по объему, хотя теплообмен происходит
через поверхность тела; считается, что температура окружающей
среды постоянна и равна начальной температуре среды, несмотря на то,
что физически очевидно, что температура среды также будет меняться*
6.2. Дифференциальные уравнения первого порядка. Дифферент
циальным уравнением первого порядка называют уравнение, в которое
входит лишь первая производная неизвестной функции. Это уравнение
может быть записано в виде
F (*, у W, у' W) « 0,	<2)
где х — независимая переменная, у (х) — неизвестная функция, a F —
Заданная функция трех переменных ♦).
Уравнение (2) связывает три переменные величины х, у и у\ В не-
которых случаях оно определяет переменную у' как функцию перемен-
ных x9yi
/ х	{/'=/ (Х.'у),	(3)
где f — известная функция, определенная в некоторой области D
координатной плоскости Оху.
Дифференциальное уравнение вида (3) называется разрешенным
относительно производной.
Решением дифференциального уравнения (3) называется такая
функция независимой переменной х:
У « Ф W»
определенная на некотором промежутке (я; ft), которая при подста-
новке в уравнение (3) обращает уравнение в тождество на всем про-
межутке (a; ft). Подстановка у = ф (х) в уравнение (3) возможна
лишь тогда, когда функция ф (х) дифференцируема на всем промежутке
(a; ft). Кроме того, также необходимо, чтобы при любом значении х0 £
£ (a; ft) точка с координатами (х0; ф (х0)) принадлежала области опре-
деления функции f (х, у).
♦1 О функциях нескольких переменных см. § 7.
§ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	39f
Решение дифференциального уравнения у ~ <р (х) геометрически
можно изобразить на координатной плоскости Оху в виде линии, за-
даваемой уравнением у = (р (х). Эта линия называется интегральной
кривой дифференциального уравнения (3).
В теории дифференциальных уравнений важйым теоретическим
вопросом является вопрос о том, как много решений имеет дифферен-
циальное уравнение.
Оказывается,'что каждое дифференциальное уравнение имеет бес-
конечное множество решений, т. е. существует бесконечно много’функ-
ций, являющихся его решениями. Например, решениями уравнения
радиоактивного распада вещества (см. ниже) будет любая из бесконеч-
ного множества функций (7), конкретизируемая заданием числа С.
В теории дифференциальных уравнений приходится ставить во-
прос не о числе решений дифференциального уравнения, а о том, кам
описать множество всех решений дифференциального уравнения,
именно:
1. Каким условиям должна удовлетворять функция f (х, у), стоя-
щая в левой части уравнения (3), чтобы это дифференциальное уравне-
ние имело решение?
2. Какие дополнительные условия необходимо наложить на функ-
цию f (х, y)t чтобы выделить одно-единственное решение из бесконеч-
ного множества решений уравнения (3)?
Ответ на эти вопросы дает теорема о существовании
и единственности:
Пусть
У9 =“ f (х, у),	(4)
где функция f определена в некоторой открытой области D координат-
ной плоскости Оху. Если функция f (х, у) непрерывна в области D и
ее частная производная df/dy также непрерывная функция в области D»
то:
I. Для любой точки (хв; yQ) € найдется решение у «« ф (х)
уравнения (4), удовлетворяющее условию
ЧМ = у9.	(5)
2. Если у «» ф (х) и у ф (х) — два решения уравнения (4),
удовлетворяющие условию
Ф (*о) « Ф (*о)>
то эти решения тождественно равны для всех тех значений переменной xt
при которых они оба определены *).
Числа х0, Уъ называются начальными значениями для решения
у = ф (х), а равенство (5) — начальным условием. Также говорят, что
решение у« ф (х) удовлетворяет начальному условию (5) или, что
решение у = ф (х) имеет начальные значения х0, yQ,
Пример. Решить уравнение, описывающее процесс радиоак-
тивного распада:
Р-т.	(6)
♦) Для существования решения уравнения (4) достаточно только непре-
рывности функции f {х. у) в области Df но при этом решение может не быть
единственным.
Теорема существования и единственности решения допускает и други®
формулировки: вместо условия непрерывности частной производной ofldy
выставляют некоторые другие ограничения на функцию [ (х, у).
302 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ Я
Переходя к/обозначениям, используемым в настоящем пункте, запи*Я
шем это уравнение в виде	Я
У9 = Чу-	(61|
Правая часть уравнения f (х, у) == —зависит лишь от перемен* 1
ной у и определена при любом значении у (т. е. йа всей координатной 1
плоскости Оху). Как сама функция f (х, у) = —$у> так и ее частная 1
производная —	» — р являются непрерывными функциями |
переменных х и у на всей координатной плоскости хОу и, следовательно,
правая часть уравнения (6') удовлетворяет условию теоремы существо-
вания и единственности решения.
. Непосредственной подстановкой в уравнение (6) можно проверить, .
что каждая функция *)
у~Се~**,	(7)
где С — произвольное действительное число, является решением
уравнения (6').
Придавая С всевозможные числовые значения, получим все реше-
ния уравнения (6'). Действительно, пусть у « <р (х) — произвольное
решение уравнения (б'). Покажем, что при подходящем выборе зна-
чения С
ф (х) =« Се~$х.
Пусть х0 — некоторая точка и г/0 — Ф (хА Положим С = у^Р**»
Тогда решения у = ф (х) и у == Се~$х = y<f—$ при х == х0 имеют
одинаковые начальные условия (Xq, уь). Но так как правая часть урав-
нения (6') удовлетворяет условию теоремы существования и единствен-
ности решения, то эти решения должны совпадать, т. е. ф (х)—
.«= У*~*	х«) при всех значениях х. Следовательно, формула (7)
задает все решения уравнения (6').
Возвращаясь к старым переменным (т и 0, получаем, что решение
уравнения радиоактивного распада вещества определяется формулой
m (/) = Се~^.
Для определения константы С достаточно указать какие-либо началь-
ные условия. Например, если известно, что в момент времени /== /в
масса вещества была равна то константа С будет равна
С =
и решение уравнения (6) с начальными условиями (/0, т0) имеет вид
m (/) =
В уравнении (6) скорость распада характеризуется величиной р.
Часто вместо величины р скорость распада характеризуют так назы-
ваемым «периодом полураспада», т. е. временем, за которое масса
радиоактивного вещества уменьшается в два раза. Обозначая период
полураспада через То, получим, что коэффициент р и период полу-
распада То связаны равенством
Т„ ₽ -1- In 2.
•) О методе нахождения этой функции см, п. $.3 «уравнения с раздела*
ющнмися переменными», пример 1»
§ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	393
6.3. Некоторые дифференциальные уравнения первого порядка.
Уравнения вида
у' = f W g (у)
называются уравнениями с разделяющимися переменными.
Для того чтобы найти решения уравнения с разделяющимися
переменными, необходимо обе части уравнения умножить (или раз-
делить) на такое выражение, чтобы в одну часть уравнения входила
только переменная х, а в другую только переменная у, а затем про-
* интегрировать обе части уравнения. Записывая данное уравнение
в виде
получаем
Решая уравнение с разделяющимися переменными, следует иметь
в виду, что при делении обеих частей уравнения на выражение, со-
держащее х и у, могут быть «потеряны» решения, обращающие это
выражение в нуль.
Примеры. 1. Найти решение уравнения радиоактивного [ай-
пада (см. уравнение (6'))
у' = —Ру.
Запишем уравнение в виде
# = -Ру.
dx v
Разделив обе части уравнения на у и умножив на dx, получаем
уравнение с разделяющимися переменными, которое можно проинте-
грировать
1п|у| = — Р*4-С».
Полагая постоянную интегрирования С9 равной In С и учитывая,
что по физическому смыслу задачи у > 0, находим
у =• Се~$*.
2. Решить уравнение
хуу' + 1 = у.
Запишем уравнение в виде
394 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Последовательно разделив обе части уравнения на х (у — 1) и умножив
на dx, получим уравнение
ydy	dx
у-l	х
Переменные разделены. Проинтегрируем обе части уравнения}
у+1п|р-1| = 1п|х| + С.
Последнее равенство, устанавливающее вид зависимости между пере*
менными х, у и представляет собой решение данного дифференциального
уравнения.	х
При делении мы предполагали, что х 0, и у Ф 1, т. е. могли
«потерять» решения х=0 и у = 1.
Подставляя - х = 0 и у ® 1 в исходное уравнение, убеждаемся>
что у == 1 является его решением, а х = 0 — нет.
Уравнения вида
у' = f (ах + by) (ан b - числа)
приводятся к уравнению с разделяющимися переменными заменой
г — ах + by,
где переменная г считается функцией г.
Пример. Решить уравнение
/ — У = 2х — 3.
Записывая уравнение в виде
/ =» у + 2х + 3
и производя замену
г ~ t/т 2х => г' = / + 2 => / = г' - 2,
получаем уравнение с разделяющимися переменными
,	, -	dz , -	dz
г' == z + 5 или	=* г + 5 или	—г—=- = dx.
dx 1	г 4- 5
Проинтегрировав, получаем
In | г + 51 =» х + С;
In | у 4* 2х + 51 == х + С.
Дифференциальные уравнения, которые могут быть записаны
в виде
называются однородными. Однородное уравнение сводится к уравнению
с разделяющимися переменными заменой
«/= ix,
где новая переменная t рассматривается как функция ха
$ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
395
Пример. Решить уравнение
2г8/ « 2х*у — у1.
Разделим обе части уравнения на Йх8:
, у I у*
Полученное уравнение — однородное. Сделаем замену
у — tx^y'= Гх + t
Теперь однородное уравнение записывается в виде
I’x + t-.t--
fx = —-i- l»J
JLX=_±/Sj
dx *	2 5
2 dt dx
/8 e ” x *
Проинтегрировав последнее уравнение, находим решение данного
дифференциального уравнения:
Г2=1п|х|4-С или (~у“) =»1п|х|4-0.
Дифференциальное уравнение
У1 + а (х) у ~ Ъ (х),
где а (х) и Ъ (х) — некоторые функции, называется линейным.
Решение линейного уравнения ищется в два этапа:
1.	Сначала решают уравнение с разделяющимися переменными
/ + а (х) у =» 0.
2.	В полученном решении этого уравнения произвольную по*
стоянную интегрирования С заменяют на неизвестную функцию С (х).
Выражение, полученное для у после такой замены, подставляют в исход*
ное уравнение и находят функцию С (х).
Пример. Решить уравнение
, , 1 1
X . х2 ‘
1, Решаем уравнение
у' + ~ У = 0;
4?	У	.
dx	х	’
dy _	dx *
~~У	х	9
Н—J4-:
1П|у|= In |-у|+In |С|.
396 гл. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
(Здесь постоянную интегрирования удобно записать как 1п|С|.)
Последнее равенство можно преобразовать к виду
In I ух I = In |С |; |ja| = |C|; |у| = |-£-
Далее знак абсолютной величины можно опустить! так как С+&
произвольная постоянная, которая может быть как положительной^
так и отрицательной.
2. Заменяя произвольную постоянную С на С (я), имеем ; %
„в С.(*) .	 С'(х).х-С(х)
Подставляя у й у' в исходное уравнение, получаем уравнение для
нахождения С (х):
С'	С	С __ I е
х.	ха	ха ха ’
С=Ип|х|+Съ
где Ci — произвольная постоянная#
Итак, окончательно решение данного уравнения имеет вид
Дифференциальное уравнение вида
у'+а (х) у =^ Ь (х)У* (л ф 1)
называется уравнением Бернулли.
Решение уравнения Бернулли сводится к решению Линейного
уравнения делением обеих его частей по уп и последующей заменой
I	1
~У'4-о(х)^гг =6 W;
так как
Z = (1— Л)—
то уравнение Бернулли сводится к линейному уравнению для неиз-
вестной функции г (х):
—!—z' + a(x)z==6(x).
6.4. Дифференциальные уравнения порядка выше первого. При-
меры дифференциальных уравнений второго порядка.
Дифференциальным уравнением п-го порядка, разрешенным от-
носительно старшей производной, называется уравнение вида.
У,	.	(8)
$ в. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
где х —* независимая переменная» у (х) — неизвестная функция, а/ —
еаданная функция указанных аргументов.
Решением дифференциального уравнения (8)- называется такая
функция независимой переменной х '
У и У (X),
определенная на некотором промежутке (а; Ь), которая при подстановке
в уравнение (8) обращает уравнение в тождество для всея значений
х € (а« ь)* Подстановка у« у (х) в уравнение (8) возможна лишь
в том случае, когда функция у (х) имеет все производные дохя-й включи-
тельно на промежутке (а; Ь). Кроме того, также необходимо, чтобы при
любом значении хь £ (а* Ь) точка е координатами (хо; у (х®); у' (xjj
(хо)) принадлежала области определения функции f.
Для дифференциального уравнения л-го порядка формулируют
теорему существования и единственности ре*
шения:
Пусть функция /(х, у, у\ у^*"^) определена в некоторой
открытой области D. Если эта функция непрерывна в области D и все
ее частные производные первого порядка по у, уе,	также
непрерывны в области D, то:
I) для любой точки (х0; у0; у^ Уо***1*)’ принадлежащей D,
найдется функция у (х), являющаяся решением дифференциального
уравнения (8) и удовлетворяющая условиям
V (хо)" у о,	У (*о) = Уо...	(*о) “	<9>
2) если у == Ф (х) и у в ф (х) — два решения уравнения (8),
удовлетворяющие условиям (9), то эти два решения тождественно .
равны при всех значениях х, при которых они оба определены.
Числа х0, у0, Уд, y(Qn~1} называются начальными значениями
для решения у (х), а равенство (9) — начальными условиями.
/Простейшим дифференциальным уравнением порядка выше пер*
вою является дифференциальное уравнение вида
/ ’= f (х, у, у'),
т. е. дифференциальное уравнение второго порядка, разрешенное от-
носительно второй производной.
Одним из примеров дифференциального уравнения второго по*
рядка является дифференциальное уравнение гармонических коле*
баний
у”+&у~0,	(10)
где со — заданная постоянная, а у считается функцией времени ti
Для уравнения гармонических колебаний выполнены условия
’теоремы существования и единственности решения. Действительно
функция f (/, у, у') «• —®2у не зависит от t и у9 и определена при лю-
бом у. Следовательно, область ее определения — все трехмерное про-
странство координат (t\ у, у'). Далее, так как
и |г = 0,
—
398 ГЛ. 9, НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ	Я
фо частные производные функции f непрерывны при любых значениях Я
У* У'*	J
Непосредственной подстановкой нетрудно проверить, что функ- |
ция ♦)	1
у = A cos (©/+ 0),	(11)
где А и 0 — произвольные постоянные, является решением диффе- ’ <
ренциального уравнения (10). Постоянную А называют амплитудой
колебания, © — частотой колебания, а 0 — начальной фазой коле- i
бания.
Формула (11) дает множество всех решений дифференциального
уравнения (10). Для выделения из бесконечного множества решений
(11) единственного решения необхо-
Ц димо задать следующие начальные •
условия:	i
|	j/(U = 0o. V'(to) = yo.
Si
т. е. задать значение функции у (/) и
Рис, 9.26,	ее производной у' (/) в некоторый мо-
мент времени /0, который называют
начальным моментом времени. Задание значений у0 и у'о позволяет
однозначно найти постоянные Л и 0, выделяя тем самым из бесконеч-
ного множества решений (11) единственное.
Примеры. 1. Рассмотрим движение материальной точки массы
т, скользящей по прямой / под действием переменной силы F, притя-
гивающей материальную точку к точке О, лежащей на той же прямой.
Пусть величина силы F пропорциональна величине отклонения ма-
териальной точки от точки О с некоторым коэффициентом пропорцио-
нальности fe. (На практике такая сила F может быть осуществлена при
помощи конструкции, состоящей из шара и двух пружин (рис. 9.26)).
Здесь за точку О (начало координат) принимается середина отрезка ВС.
Отклонение материальной точки от середины будем обозначать через
х (0, где t — время. Ускорение материальной точки и сила, действу*
ющая на точку, связаны вторым законом Ньютона:
тх*=»-—(12)
где х” — ускорение точки, (—kx) — сила, действующая со стороны
пружины на материальную точку, a k > 0 — коэффициент упругости
пружины.
Согласно формуле (11) решение уравнения (12) имеет вид
х(0 = Лсоз(уГ-^-/+ фо)»
откуда следует, что частота колебаний материальной точки
определяется лишь ее массой и упругостью пружины k. Задавая на-
чальные условия задачи, т. е. положение материальной точки в не-
который момент времени 4 и ее скорость в начальный момент времени
х(4>) И х'(*о).
О методе нахождения $той функции см, п, 6,5, пример U
$ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	399
мы можем найти значения постоянных А и G и тем самым полностью
определить закон движения материальной точки.
3) Составим и решим приближенно уравнение математического
маятника. Математический маятник представляет собой точку массы т,
которая под действием силы тяжести движется по дуге окружности К
радиуса /, лежащей в вертикальной плоскости
(рис. 9.27). Величина I называется длиной
маятника.
В плоскости окружности К введем поляр*
ную систему координат с центром в центре
окружности и полярной осью, направленной
вертикально вниз. Переменный угол, харак-
теризующий отклонение радиуса от вертикали,
обозначим через <р = <Р (0- Точка А1 находится
в поле силы тяжести Р = mg, направленной
вертикально вниз. Составляющая силы тяжести,
направленная по радиусу окружности, уравно-
вешивается реакцией связи (окружности или
нити, заставляющей точку двигаться по окруж- If
ности); составляющая, направленная по каса- Р-г™/*
тельной к окружности в точке М, равна Рис. 9.27.
mg sin <р. Из физики известно, что линейное
ускорение точки М связано с угловым ускорением у* формулой
а =» /ф".
Сила, действующая на точку, и ее ускорение связаны вторым законом
Ньютона:
т/ф* — —mg sin ф.	(13)
Предполагая, что колебания, совершаемые материальной точкой,
малы (т. е. угол отклонения ф (0 мал), приближенно можно написать
* sin ф « ф,
и дифференциальное уравнение (13) принимает вид
/ф» = —£ф.
Решением дифференциального уравнения (14) является функция
ф (0 = dcos(j/ -f-*+ Фо)*
(14)
Из этой формулы следует, что частота «малых колебаний» математи-
ческого маятника определяется только ускорением свободного паде-
ния g и длиной маятника Z:
Для вычисления постоянных А и ф0 необходимо задать положение
и скорость точки М в некоторый момент времени t0, после чего закон
движения математического маятника становится полностью опреде-
ленным.
400 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕЕР. ИСЧИСЛЕНИЙ
6.5.	Линейные дифференциальные уравнения с постоянными
коэффициентами.
Линейным дифференциальным уравнением n-го порядка с постоян-
ными коэффициентами называется уравнение вида
<ЗД/(П) + ад(',~1) + ... + ап^у' + any*=f (х),	(15)
где Оо,	ап — действительные числа. Если f (х) = 0, то
уравнение (Н>) называется однородным, если же f (х) О, то — не-
однородными.
Общим решением линейного однородного уравнения n-го порядка
называется функция
у= ф (х, Cb С2, ..., Сд),
зависящая от п произвольных постоянных С2, •••> Сп и обращающая,
уравнение в тождество при любых значениях этих постоянных.
Решения линейного однородного уравнения
ад(п) + щу{п~Х} + • • . + ап-лУ' + апу=*Ъ (16)
будем искать в виде у = еКх. Подставляя у = в уравнение (16),
получаем
(#оХп 1 -4- .. . *4~ Яп_л.Х *4“ ^n) в 0.
Поскольку е^х Ф 0, это уравнение эквивалентно алгебраическому
уравнению
GoA/1 “4“	1 "4* \	4“ &п ~ 0,	07)
которое называют характеристическим уравнением.
Любая функция у — е4*, где Xf — корень уравнения (17), яв-
ляется решением дифференциального уравнения (16).
Таким образом, чтобы найти решения линейного однородного диф-
ференциального уравнения (16), необходимо написать характеристи-
ческое уравнение (17) и найти все его корни.
Общее решение линейного однородного дифференциального урав-
нения (16) представляется как сумма следующих функций:
1)	Cie 1*, где — простой действительный корень уравнения
(17) и Ci — произвольные постоянные.
2)	(cm+i + Ст^	Cm+kf-1) ^х, где 1 — действи-
тельный корень кратности k, ..., Cm+k — произвольные по-
стоянные.
3)	С/+1еадс cos + С/+2еах sin Рх для каждой пары простых
комплексно сопряженных корней X — а ± ф уравнения (17);
и С/+а — произвольные постоянные.
4)	Pk-i (х) еах cos Р% 4- sin рх для каждой пары ком-
плексно сопряженных корней кратности k. Здесь Pk_\ (х) и Qk-i (х) —
многочлены (k — 1)-й степени с произвольными постоянными коэффи-
циентами.
Пр	имеры. 1. Найти решение уравнения гармонических коле-
баний (см. п. 6.4, уравнение (10))
у” + &у = 0.
§ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	401
Характеристическое уравнение, соответствующее уравнению гар-
монических колебаний, имеет вид
X2 +	= 0.
Уравнение имеет два комплексно сопряженных корня
= /со, ® —/со,
и, следовательно, общее решение данного дифференциального урав-
нения имеет вид 3)
р =* Ct cos (о/ + С2 sin at,
где Ci и — произвольные постоянные.
Методом дополнительного угла (см. п. 3.2 гл. 6) данную функцию
можно записать в виде
у = A sin (со/ + 0),
где А и 0 — произвольные постоянные, выражающиеся через Cj и С2.
2.	Решить уравнение
у(5) _ ЗуЫ + у- + у” + 4у = 0.
Пишем характеристическое уравнение
А& —+ Х3+ V+ 4 = 0.
Корни характеристического уравнения найдем, используя спо-
соб, изложенный в п. 5.7 гл. 4:
А,х == —1, Д2 =»	2,	= i,	— L
В соответствии с изложенными выше правилами общее решение
уравнения (16) имеет вид
у = Схе~х + (С2 + С^х) е2х + С4 cos х + С5 sin х,
где Cf, С2, С3, С4, С5 — произвольные постоянные.
Частным решением линейного неоднородного уравнения назы-
вается любая конкретная функция, являющаяся решением этого урав-
нения.
Общее решение линейного неоднородного уравнения есть сумма
общего решения линейного однородного уравнения, соответствующего
неоднородному уравнению и любого частного решения неоднородного
уравнения. Приведем несколько простейших способов нахождения ре-
шений линейных неоднородных уравнений.
1.	Если функция f (х), стоящая в правой части, уравнения, имеет
вид
f (X) = Pm (х) е7*,
где Рт (х) — многочлен m-й степени, то частное решение линейного
неоднородного уравнения ищется в виде
!/ = xsQm(x)^,	(18)
где Qm (х) — многочлен той же степени /п, что и многочлен Рт (х).
Число s равно нулю, если у не является корнем характеристического
уравнения; если же у — корень характеристического уравнения,
то s равно кратности этого корня. Чтобы найти коэффициенты много-
члена Qm (х), необходимо решение (18) подставить в дифференциальное
уравнение и приравнять коэффициенты при подобных членах в левой
и правой частях уравнения.
402 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР, ИСЧИСЛЕНИЙ
Пример. Решить уравнение
У — Ьу + 4у = 4х?е2х.	(19)
Составляем характеристическое уравнение для данного урав*
нения и находим его корни:
№ — 51+4=0;
л 5 ± /25 — 16 ,	А
ll, 21=1	2	*	11 = 4, lg = !•
Так как коэффициент, стоящий при х в показателе степени члена
е**, равен 2 и не совпадает ни с одним из корней характеристического
многочлена, то надо положить s = 0, х° = 1 и частное решение искать
в виде
у = (ах2 + Ьх + с) е2*, *	(20)
где коэффициенты а, b и с еще следует найти. Для этого подставим
функцию, стоящую в правой части равенства (20), в уравнение (19).
После приведения подобных членов в левой части уравнения получим
е2х 1—2 ах2 + (—2а — 2Ь) х + 2а — b — 2с] == 4х2е2х.
Приравнивая коэффициенты при одинаковых степенях неизвест-»
вых, получаем систему для нахождения коэффициентов а, b и с;
—2а = 4;
—2а — 2Ь = 0;
2а — b — 2с = 0,
решение которой: а = —2, b = 2, с = —3.
Следовательно, частное решение уравнения имеет вид
у = (—2Х2 + 2х — 3) е2*
и общее решение данного неоднородного уравнения следующее:
у з== Citx + Ctf4x — (2х2 — 2х + 3) в2*, '
где и Са — произвольные постоянные.
2.	Если функция, стоящая в правой части уравнения, имеет вид
еах (Р (х) cos Рх + Q (х) sin Рх),	(21)
то частное решение уравнения ищется в виде
у а xseax (Mk (х) cos Рх + Nk (х) sin Рх),
где s = 0, если а + pZ не является корнем характеристического мно-
гочлена; если же а + pZ — корень характеристического многочлена,
то s равно кратности этого корня; Mk (х) и Mk (х) — многочлены k-n
степени, равной наибольшей из степеней многочленов Р (х) и Q (х).
Чтобы найти коэффициенты многочленов Mk (х) и Mk (х), необходимо
решение (21) подставить в решаемое дифференциальное уравнение и
приравнять коэффициенты при подобных членах в левой и -правой ча<
стях уравнения.
$ 6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ	403
Пример. Решить уравнение
/ + у e'x sin х.	(22)
Составляем характеристическое уравнение и находим его корни:
12 + j = 0; ЗЦ = i, = — i.
Правая часть уравнения (22) — сокращенная запись выражения
eQ'x (0*cos х + х sin х).
Так как комплексное число 0 + t является простым корнем ха-
рактеристического уравнения, то частное решение уравнения (22)
следует искать в виде
у ® х (М (х) cos х + N (х) sin х),
где М (х) и N (х) — многочлены первой степени:
М (х) =» ах + b, N (х) == сх + d.
Подставляя функцию
х [(ах + Ь) cos х + (сх + d) sin х]
в уравнение (22) и приводя подобные члены в левой части уравнения,
получаем
(4сх + 2d + 2а) cos х + (—4ах + 2с — 2b) sin х = х sin х.
Приравнивая коэффициенты при подобных членах, стоящих в ле-
вой и правой частях последнего уравнения, получаем систему урав-
нений для нахождения коэффициентов a, b9 с, d;
4с == 0;
2d+2a=0;
—4а = 1;
2с —26=\0,
решение которой: а —----b = 0, d==	г=0.
Следовательно, частное решение неоднородного уравнения имеет
вид
I 9	, 1
у -----— х2 cos х 4- -j- xsin х,
а общее решение уравнения (22):
у = Ci sin х + С2 cos х-j- х2 cosx + х sin х.
3.	Если правая часть неоднородного уравнения равна сумме не-
скольких выражений вида (18) и (21k то частное решение линейного
уравнения с правой частью вида А + /а + • ••+ /л равно сумме частных
решений уравнений с той же левой частью и правыми частями А» 7s» •••
.... /л.
Метод вариации постоянных. Линейное неоднород-
ное уравнение с постоянными коэффициентами
ад(п> +	4- •.. 4- апу = f (х)	(23)
404 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
с произвольной правой частью может быть решено методом, называе-
мым методом вариации постоянных, который заключается в следующем:
Пусть у — СХУ\ +	+ • • •+ СпУп — общее решение линейного
однородного уравнения, левой частью которого является левая часть
уравнения (23). Тогда решение неоднородного уравнения (23) ищется
в виде
У=* Cf(x)yf+ Ci(x)p,4-»«+ Сп(х)уп,
где функции Cj (х), С, (х),	Сп ,(х) определяются из системы
С\У\ + ^2^2 + • • • + С'пуп ш О»
С\У '1 + С2У:2 + ' • • + СпУ'п •= 0:
......................• • • .................. (24)
С;ИП“2’ +	+ •. • +	= Ч>;
М"-'» +	4-... 4- Спу«-" - J-1 (х).
Пример. Решить уравнение
/ — у = 2е* — х®	(25)
методом вариации постоянных.
Составляем характеристическое уравнение и находим его корни:
X? — 1 = 0; kf= 1, Х2== — 1.
Общее решение однородного уравнения у* — у = 0 имеет вид у ®
«= САе* + С#"*, где и С2 — произвольные постоянные.
Общее решение уравнения (25) будем искать в виде
У = С1 (х) е* 4- сг (х) е~х.	(26)
Составим для этого решения систему типа (24)
Cfc* +	х *== 0;
из которой получаем
с; -1 —
С;--1-х2е*-?«.
Найдем функции (х) и Са (х):
б| «= J 0----i- dx *== х 4- -у- Л*ж 4- хе~х-$- <»"“*+ С?;
С2“ f (“Г*2**- ?*^dx = -l-x2e4’— хе*4- е---------**• Са> -
где и Q — постоянные интегрирования»
§ 7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 405
Подставляя найденные функции (х) и С9 (х) в формулу (26),
получаем общее решение уравнения (25)
У=(с?------^-)е* + ф“*+ хех'+ж?+2.
Обозначая С? — -i- = Cj и = С2) окончательно имеем
у =	*{- С$е*"“х хе* *1* + 2»
§ 7. Функции нескольких переменных
.. 7.1. Понятие функциональной зависимости между несколькими
переменными. В различных разделах математики и физики встре-
чаются соотношения, в которых участвуют несколько переменных ве-
личин. Так, например, из курса геометрии известно, что объем ци-
линдра V вычисляется по формуле
где R — радиус основания цилиндра, Я — его высота. Эта формула
дает простейший пример числовой функции двух переменных — объем
зависит как от радиуса основания цилиндра, так и от его высоты.
Из курса физики известна формула Клапейрона
pV - RT,
связывающая три физические характеристики состояния газа: давле-
ние р, удельный объем V и абсолютную температуру Т (R — универ-
сальная газовая постоянная). Задавая две из трех указанных величин,
можно получить вполне определенное значение третьей величины.
Таким образом, при использовании этой формулы мы опять встречаемся
с понятием функции нескольких независимых переменных.
Переменная г называется числовой функцией двух независимых
переменных хну, заданной на множестве упорядоченных пар чисел Mt
если каждой упорядоченной паре чисел (х; у) £ М по некоторому пра-
вилу (закону) ставится в соответствие одно определенное значение пе-
ременной z.
Множество М упорядоченных пар чисел (х; у) называется областью
определения функции г, а множество всех возможных значений пере-
менной г — множеством значений функции.
Тот факт, что переменная г является функцией двух переменных х
и у, принято записывать так:
г= f (х, у).
В то время как для числовой функции одной переменной областью
определения является множество точек числовой оси, область опреде-
ления функции двух переменных представляет собой некоторое мно-
жество точек числовой плоскости.
Подобно тому как функция у = f (х) геометрически изображалась
своим графиком в прямоугольной декартовой системе координат
Оху, функция двух переменных z = f (х, у) в прямоугольной простран-
ственной декартовой системе координат Охуг задает множество точек,
которое является своего рода пространственным графиком функции
г = / (х, у). Пространственный график функции f (х, у) обычно
406 ГЛ. в. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
называют поверхностью, а равенство г =» f (г, у) — уравнением по*
верхности.
'Простейшим примером такой поверхности является плоскость
в пространстве, которая в прямоугольной декартовой системе коорди-
нат определяется уравнением
Ах + By + Сг + D == 0.
Если С 0, то уравнение может быть записано в виде
Аналогичным образом может быть введено понятие функции трех,
четырех и т. д. переменных.
Все основные понятия теории функций одной переменной — та-
кие, как предел функции, непрерывность функции, дифференцируе-
мость и т. д, — обобщаются и на случай функций нескольких незави-
симых переменных. Далее эти понятия будут введены для функций
двух независимых переменный.
7.2. Предел и непрерывность функций двух независимых пере-
менных. В прямоугольной декартовой системе координат Оху упорядо-
ченная пара чисел (xt; у^ определяет точку. Расстояние между любыми
двумя точками (хг; */0 и М2 (ха; у2) вычисляется по формуле
Пусть (хо; yd — некоторая фиксированная тачка координатной пло-
скости.
Множество всех точек плоскости, координаты которых (х; у) удо-
влетворяют неравенству
(х - хо)2 + (У ~ Уо)2 <№	«Я2),
называют «открытым» кругом (замкнутым кругом).
Множество всех точек плоскости, координаты которых удовлет-
воряют неравенству
(х — х0)2 4- (у — у0)? < в2,
называют ^окрестностью точки Л10 (х0; г/о). Расстояние от любой
точки 8-окрестности до точки Мо (х0; t/o) меньше 8.
Пусть D — некоторое множество точек координатной плоскости
Оху. Точку Мо (хо’» !/о) называют внутренней точкой этого множества,
если она принадлежит множеству D вместе с некоторой достаточно
малой ее окрестностью.
Множество, состоящее только из внутренних точек, называют
открытой областью.
Точка Mq (хь, у$) называется точкой сгущения множества D, если
в каждой ее е-окрестности содержится хотя бы одна точка множества D,
отличная от точки Л10.
Точки сгущения открытой области, не принадлежащие ей, назы-
ваются граничными точками этой области. Множество всех граничных
точек области D образуют границу области.
Открытая область вместе со своей границей называется замкнутой
областью*
§ 7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
407
Так, например, границей открытой области (открытого круга),
задаваемой неравенством (х — х0)2 + (у — у<$ < является окруж-
ность (х — х0)2 +	— £о)2 “ Я2-
Пусть z = f (х, у) — некоторая функция двух независимых пере-
менных, определенная на открытой области D, и М (а; Ь) — точка
этой области *).
Говорят, что функция f (х, у) имеет пределом число А при стрем-
лении переменных х, у к числам а, b соответственно, если для любого
сколь угодно малого положительного числа е найдется такое число б,
что неравенство
|/(х, у) — 4|<в
выполняется для всех значений х, у, принадлежащих D и удовлетворя-
ющих неравенствам
О < | х — а | < б,	0 < | у — б | < б.
На «геометрическом» языке данное определение можно сформули-
ровать так:
Число А называют пределом функции, f (х, у) при стремлении
точки М (х; у) к точке Мо (а; Ь) и пишут
Пш^ f (х, у) » А или lim f (х, у) «ж А,
М->Мл	х->а
у-+Ь
если для любого сколь угодно малого числа в > 0 существует такое
число б > 0, что неравенство
I/ (х, у) — Л|<8
выполняется для всех точек Af £ D, удовлетворяющих неравенству
О< | MAlol <б.
Говорят, что функция f (х, у) непрерывна в точке Л10 (а; б), если
выполняется неравенство
lim f (х, у) =» / (а, б).
В противном случае говорят, что функция f (х, у) в точке Л40 имеет
разрыв.
Из непрерывности функции двух переменных f (х, у) отдельно по
каждой переменной не следует, что функция будет непрерывна ка£
функция двух переменных. Так, например, функция двух переменных
/ (х, у), определенная на всей координатной плоскости и задаваемая
условиями
f (X, у) =
ху
x24-i/2 ’
О,
если х2 +>2 =/= О,
если х2 z/2 — О,
непрерывна по каждой переменной в отдельности: при любом фиксиро-
ванном значении у функция и (х) == f (х, у) непрерывна при любом
значении х и при любом фиксированном значении х функция v (у) =
= f (х, у) непрерывна при любом значении у.
♦) Определение предела функции нескольких переменных может быть
обобщено и на случай, когда точка Мо (а; Ь) не принадлежит области D, но
удовлетворяет некоторым условиям, которые здесь не формулируются.
408 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Однако функция f (х, у) разрывна в начале координат, так кан Я
в любой сколь угодно малой в-окрестности точки (0; 0) существуют точки Я
вида (а; а), в которых значение функции равно 1/2.	Я
7.3. Понятие .частной производной. Пусть z == / (х, у) — веко* Я
торая функция двух переменных, определенная в открытой области D, |
и пусть точка М (х0; у0) £ D. Положим, что значение аргумента у 1
функции f (х, у) равно у0. Тогда функцию f (х, у0) можно рассматривать 1
. как функцию одной переменной х. Обозначим через Дх приращение
аргумента	'	1
Дх == х — х0.	J
Приращение функции f (х, у) при у в у# обозначим
Дх2 = f (-*0 + Дх, Уп) — f (Хп, Уп).
Приращение Дха называют частным приращением функции /(х, у)
по х. Составим отношение
/(Хо+Ах, Уп) — {(Хп, Уп)
&х	’
которое при фиксированных х« и yt является функцией приращения Дх.
Если существует предел
/<х0+ Дх, у0)~ f(x0, уп)
t
Дх->0
то говорят, что функция f (х, у) имеет чйстную производную по х в точке
(4; Уь), и пишут
f (хо + Д*, Уо) — f (х0, yQ)
Jim -------------------------
Дх->0 \
Частную производную f'x(xQ, yQ)
г« или ЙГ’
= >ИХ0- ч-
Дх
также
обозначают
df(x0, ув)
дх
или
можно
рассмотреть предел
Ду
Аналогично; полагая х «= х0,
..	/ (xt; Уп + Ду) — f (Хп, Уп)
Игл --------------------------
Ду-*0
Если этот предел существует, то говорят, что функция f (х, у)
имеет частную производную по у в точке (хь; у0).
Эту частную производную обозначают	1
,	\дг	df (х0, i/о) а
М*0>М ИЛИ ИЛИ	ИЛИ --------j
Говорят, что функция имеет частную- производную в открытой 1
области D, если она имеет частвуэд^ирединввдегую в каждой точие этой 1
области.	’]
Вычисление частной производной функции нескольких перемен- < ]
ных производится по тем же правилам» что и вычисление-обыкновенной J
производной,	1
$ 7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
409
Примеры. 1. Пусть г = ху (х> 0). Частная производная по х
•той функции вычисляется при у == const, т. е. представляет собой
производную степенной функции:
дг
дх
» у-ху^.
Частная производная по у вычисляется при х = const, т. е. вы-
числяется, как обыкновенная производная показательной функции:
дг „ г
—- = хИп х.
дУ
2. Частные производные функции
х^ + х+1
In у
равны
____ *	/ уЗ 4- г 4- 1F ® 2х-|- V •
дх “ 1пу ' + *+’> |Пу
Vе <*+*+ *>’(w) в
«= (X2 + X + 1) (---!-т-- 1 *(1п уУ = — --- :-s----,
'	' \ 1пау / '	у 1п2р
т. е. вычисляются, как обыкновенные производные по переменной х
(в предположений, что у ~ постоянная) и по переменной у (в предпо-
ложении, что х — постоянная).
Если функция г f (х, у) имеет во всех точках некоторой открытой
области D частную производную по одной из переменных, то эта про-
изводная, сама являясь функцией переменных х и у, может в свою
очередь в некоторой точке (хь; у$) £ D иметь частные производные по х
или по у. Для данной функции t« f (х, у) эти производные будут
частными производными второго порядка.
Так, например, рассмотрим предел
/; (х0 + лх, Уо) - гх (х0, к0)
hm..........-.... .1 —----- 1 1 "  •
Если этот предел существует, то говорят, что функция f (х, у) имеет
вторую частную производную по х (или частную производную второго
порядка) в точке (х0, р0). Эту производную обозначают f"xx (х0, у^
f'x(x0 + Дх, у0) - f'x (х0, у0)
------------------------------------- Гхх (*о> Уо).
&х
Частную производную второго порядка по х функции г = / (х, у)
также обозначают
d^f	дЧ
-^Г ИЛИ	или 4,.
Аналогично определяются производные
f*y> fyx»
410 ГЛ. 9. НАЧАЛА ДИФФЕР. И ИНТЕГР. ИСЧИСЛЕНИЙ
Производные fxy и fyX называют смешанными частными произ-
водными.
Условие равенства смешанных частных
производных. Если в некоторой точке (х0; у0) £ D смешанные
частные производные f” и fyx существуют и непрерывны как функции
переменных х, yt то они равны
fxy (*о» М fyx (хо» ^о).
7.4. Экстремумы функции двух независимых переменных. Пусть
функция z = f (х, у) определена в открытой области D и точка (х0,
принадлежит D.
Говорят, что функция / (х, у) имеет в точке (х0; у0) максимум (ми-
нимум), если существует такая 8-окрестность точки (х0; t/0), что для всех
точек этой е-окрестности выполняется неравенство
f (х, у) < f (х0, Уо) (I (х, у) > f (х0, £/0)).
Если 8-окрестность можно выбрать такой, чтобы знак равенства был
исключен, т. е. для любой точки 8-окрестности (кроме точки (х0; у$))
выполнялось бы строгое неравенство
(*о. Уо) (f (X, y)>f (r0, у0)),
то говорят, что в точке (х0; у^) функция имеет собственный максимум
(минимум).
Максимум и минимум функции называются экстремумами.
Необходимое условие существования экс*
тремума, Если в точке (х0; -у^) существуют частные производные'
функции z = f (х, у), то равенство нулю частных производных:
№• м=0' f'y(xo>yo) = Q
— является необходимым условием существования экстремума. .
Точки, в которых частные производные fx и f одновременно об-
ращаются в нуль, называют стационарными.
Так же как и в случае функции одной переменной, в стационарной
точке функция не обязательно имеет экстремум (так же, как и в слу-
чае функции одной переменной, равенство нулю частных производных
первого порядка функции двух переменных является необходимым,
но не достаточным условием существования экстремума).
Достаточное условие существования экс*
тремума функции. Пусть функция г == f (х, у) определена,
непрерывна и имеет частные производные первого и второго порядка
в окрестности точки (х0; */0)» которая является стационарной точкой,
т. е.
/Их0’f'o) == °-	Уо) = °-
Если в стационарной точке (х0; у9) выполняется неравенство
Гхх-Гуу-(Гху)>о,
то в этой точке функция имеет экстремум — максимум, если fxx < 0,
и минимум, если Гхх > 0. Если же
ГххГуу-(Гхуу<0,
то в точке (х0; yQ) функция не имеет экстремума,
$ 7. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
411
Если в стационарной точке
f'xxf'yy — {Лсу)2 в О,
то для решения вопроса о существовании экстремума необходимо
проводить дополнительное исследование функции.
Пример. Исследовать на экстремум функцию
г = /1 —х2 —у2.
Поверхность, определяемая данным уравнением, представляет
собой полусферу (рис. 9.28). Вычисляя частные производные дайной
функции:
находим, что точка (0; 0) — стационарная точка данной функции»
Вычислим частные производные второго порядка:
д2г_______у2 1	.	д22______________ху_______
дх2 ~ (1 — х2 — у2)372 ’ дхду "	(1 — х2 — yrfi*
д2г __ х2 — 1
.	. 1F ~ (1 — х2 — //2)3/2 *
В точке (0; 0)*
д2г _	д2г _ д2г _
дх2 ~	’ дхду U* ду2 ~~ 1
и
д2г д2г > / д2г \2
дх2 ’ ду2 \ дхду /== по-
следовательно, в точке (0; 0) функция имеет экстремум; этот экс*
д2г
тремум — максимум, так как = — 1 < 0,
ГЛАВА 10
КОМБИНАТОРИКА.
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Комбинаторика — раздел математики о выборе и расположении
элементов некоторого множества на основании какух-либо условий.
Комбинаторика начала выделяться в отдельный раздел математики
в работах Б. Паскаля и П. Ферма, хотя отдельные понятия и факты
комбинаторики были известны еще математикам античности и средне-
вековья. Большой вклад в развитие комбинаторики внесли Г. Лейб-
ниц, Я. Бернулли и Л. Эйлер. В их работах были даны определения
основных понятий комбинаторики, развиты первые комбинаторные
методы и указаны их применения, а также прослежена связь комбина-
торики с исчислением вероятностей. Именно комбинаторика послу*
жила фундаментальной основой началам теории вероятностей.
Теория вероятностей — раздел математики, посвященный изуче-
нию вероятности — меры возможности наступления какого-либо опре-
деленного события в тех или иных определенных условиях, которые .
могут повторяться сколь угодно большое число раз. Теория вероятно-
стей позволяет по вероятностям наступления одних случайных событий
находить вероятность наступления других случайных событий, каким*
либо образом связанных с первыми.
§ 1. Метод математической индукции
Ряд математических утверждений доказывается методом мате-
матической индукции, который основан на принципе математиче-
ской индукции:
Пусть А (п) — некоторое утверждение, имеющее смысл для на-
туральных чисел п. И пусть это утверждение истинно для п ® 1. Тогда,
если из истинности этого утверждения для п = k (k — любое натураль-
ное число, большее единицы) следует истинность утверждения для п =»
«= 6+ 1, то утверждение А (п) истинно для любого натурального
числа п.
Доказательство методом математической индукции состоит в сле-
дующем:	' х
1) проверяется, что утверждение Д (и) истинно; для п= 1,
2) предполагается, что утверждение А (п) истинно для п = kt
доказывается, что оно истинно и при п = k+ 1.
После этого на основании принципа математической индукции
делается вывод, что утверждение А (п) истинно для любого натураль-
ного п.
Пример, Доказать, что для любого натурального числа п и
любого действительного числа а > —1 справедливо неравенство,
называемое неравенством Бернулли:
(1 + а)” > I + an,	fl)
f I. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ	413
Если п = 1, то справедливость неравенства (1) очевидна:
(1 + а)1^ 1 + а.
Предположим, что неравенство (1) справедливо при й:
(1 + a)k > 1Н- ak.
Умножая обе части последнего неравенства на положительное
число 1 + а, получаем неравенство
(1 + а)*+1 > 1 + ak + а + А.	(2)
Отбрасывая последнее положительное слагаемое в правой части,
неравенства (2), мы уменьшаем правую часть этого неравенства,
а потому
о + а)*+’ > l + o(fe+ 1).
Полученный результат показывает, что из предположения о спра-
ведливости неравенства (I) при пs k следует, что неравенство (1)
справедливо и при п** k + 1.
Обе части доказательства методом математической индукции про-
ведены, и, следовательно, неравенство. (1) справедливо при любом
натуральном п.
Методом математической индукции может быть доказан также, на-
пример, ряд свойств чисел, образующих последовательность Фибо-
наччи. Последовательностью Фибоначчи называется последовательность
чисел Fe, Flt F2, ...» Frt, ...» где Fo = 0, Fx «= 1, а каждый последующий
член является суммой двух предыдущих, т. е. указанная последова-
тель ность имеет вид 0, 1, I, 2, 3, 5, 8, ...
Приведенная последовательность дает решение задачи, впервые
предложенной в 1202 г. Леонардо Фибоначчи, которая формулирова-
лась так: «Сколько пар кроликов получится от одной пары в течение
года? При этом предлагается принять, что каждая пара дает приплод —
пару кроликов — каждый месяц, каждая новая пара становится пло-
доносящей в возрасте одного месяца и, кроме того, кролики никогда
не мрут».
Докажем, что если через Ф *) обозначить число (1 +)/2, то
Fn	(3)
для всех натуральных п.
Если ne 1, то F|j » 1	Ф®, т. е. нестрогое неравенство (3) вы-
полнено.
Предположим, что для любого натурального А> 1 выполняются
неравенства
F,<®*, FsC®2.........../be®*-’.
Докажем, что тогда неравенство (3) справедливо и при п = + 1,
Действительно, F*+f = F^_f+ F& ^Ф*~2	«=Ф*~2 (1+Ф).
*) Число Ф называют отношением крайнего и среднего, так как оно опре-
деляется условием: если Ф » А : В, то A : В •» (А Ц- ВЦ : А. Известны и дру-
гие наевания этого числа: божественная пропорция, золотое сечение, Само
обозначение Ф происходит от первой буквы имени греческого скульптора
Фидия, который часто использовал золотое сечение в пропорциях своих скуль-
птур.
414 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Замечая, что 1 + Ф == Ф?, окончательно получаем
Fk+1 < Ф*~2Ф2 = Ф*.
Таким образом, из предположения о справедливости неравенства
(3) при п ~ k следует его справедливость и при п~ k + 1.
Обе части доказательства методом математической индукции про-
ведены, и, следовательно, высказанное утверждение справедливо
при любом натуральном п.
' Методом математической индукции также можно доказать спра*
ведливость для всех натуральных п следующих соотношений:
1)	Fn.!»®"-1;
2)	Fn+1.F„„1-F2n = (-l)n;
3)	Fn+m = Fm*Fn+l +	для любого натурального m.
В ряде случаев может оказаться, что рассматриваемое утвержде-
ние А (п) при некоторых натуральных значениях п < tn (т — фикси-
рованное натуральное число) ложно или не имеет смысла. С другой
стороны, в ряде случаев оказывается возможным доказать, что неко-'
торое утверждение А (п) истинно не только для натуральных значе-
ний п, но и для некоторого набора отрицательных значений л. В этих
случаях используется следующее обобщение принципа
математической индукции:
• Если утверждение А (п), в котором п — целое число, истинно при
п =» т и если из истинности этого утверждения для числа п» k,
где k — любое целое число, большее или равное т, вытекает, что оно
истинно для следующего числа п==/?+ 1, то утверждение А (п)
истинно и для любого целого числа п > т.
§ 2, Комбинаторика
2.1. Перестановки. Пусть А — некоторое конечное множество,
состоящее из п различных элементов:
Л =* {ах; а2; а»;...; ап).	(О
Будем образовывать из элементов множества А упорядоченные
множества. В качестве первого упорядоченного множества возьмем
множество, в котором элементы расположены в порядке возрастания
их номеров:
(щ; а3\ flg; Оя).
Второе упорядоченное множество можно образовать, поменяв
местами элементы аг и аа, а все остальные элементы первого множества
оставив на своих местах:
(аа; ац ав; ...; ап).
Поменяв местами элементы at и а3 и оставляя на своих местах
все остальные элементы в первом упорядоченном множестве, получаем
упорядоченное множество, отличное как от первого, так и от второго
упорядоченного множества. Аналогичным способом из элементов
множества А можно строить и другие упорядоченные множества.
Всевозможные конечные упорядоченные множества, содержащие
п различных элементов, которые мржно получить из некоторого не-
упорядоченного множества, состоящего из п различных элементов»
называются перестановками из п элементов.
$ 2. КОМБИНАТОРИКА
415
Таким образом, перестановка есть не что иное, как способ упорядо-
чивания элементов некоторого конечного множества. При этом любые
две различные перестановки представляют собой два различных^ спо-
соба образования упорядоченного множества (из данного неупорядо-
ченного множества).
Вычислим, сколько различных упорядоченных множеств можно
образовать из данного конечного множества А, содержащего п различ-
ных элементов, т. е. чему равно число перестановок из элементов мно-
жества (1).
Любое упорядоченное множество, полученное из множества Л;
можно записать в виде
(й>	*в)»	'*
где каждый из элементов ik есть один из элементов а9, аП9
причем ни один из этих элементов не встречается более одного раза.
В качестве элемента можно взять любой из элементов а2, aS9 ...,
.... ап, что дает п различных возможностей. Теперь, если ц уже выбран,
в качестве i2 можно взять любой из я — 1 оставшихся элементов мно-
жества А, т. е. число различных способов выбора упорядоченной
пары элементов (iit i2) будет равно (п — 1)л. Продолжая далее указан-
ный процесс, в результате получим, что последний оставшийся эле-
мент 1п можно выбрать лишь одним способом.
Таким образом, число перестановок из п элементов (которое обычно
обозначается Рп) равно произведению п последовательных натуральных
чисел, начиная с единицы. Это произведение имеет специальное обозна-
чение п\ (читается: п факториал):
Рп=* Ь2«3... (п — 1) и= п\
Для пустого множества принимается соглашение: пустое мно-
жество можно упорядочить только одним способом; поэтому считается,
что
О! == 1.
Если в заданной перестановке поменять местами какие-либо два
элемента, а все остальные элементы оставить на своих местах, то полу-
чится новая перестановка.
Такое преобразование перестановки называется транспозицией.
Все л! перестановок из п элементов можно расположить в таком
порядке, что каждая следующая перестановка будет получаться из
предыдущей одной транспозицией, причем в качестве исходной пере-
становки можно выбрать любую из л! перестановок. В частности,
от любой перестановки из п элементов можно перейти к любой другой
перестановке из тех же элементов при помощи нескольких транспо-
зиций.
Перестановка (4; /2;in) называется четной, если она получается
из перестановки (af, а2; ап) с помощью четного числа транспозиций,
и нечетной в противном случае.
Пример. Пусть А = (1; 2; 3; 4). Перестановка (1; 2; 3; 4) по
определению четна. Четной будет и перестановка (4; 2; 1; 3), так как
она может быть получена из перестановки (1; 2; 3; 4) при помощи чет-
ного числа транспозиций: поменяем местами в перестановке (4; 2; 1; 3)
первый и четвертый элементы:
(4; 2; 1; 3)-* (3; 2; 1; 4);
416 гл. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
в полученной перестановке меняем местами первый и третий элементы.4
(3; 2; 1; 4)-> (I; 2; 3; 4).
Таким образом, данная перестановка переходит в исходную в резуль-
тате двух транспозиций, и, следовательно, она четная. Аналогичным
образом можно убедиться, что перестановка (4; 1; 2; 3) будет нечет-
ной, — она переходит в перестановку (1; 2; 3; 4) после трех транспо-
виций:
(4;Л; 2; 3)-* (1; 4-~2 3)-> (I; 2; 4?3)-> (I; 2; 3; 4).
Всякая транспозиция меняет четность перестановки: число четных
перестановок из п элементов (п > 2) равно числу нечетны^, т. е. равно
nl/2.
' 2.2. Подстановки. Пусть А у- некоторое конечное множество,
состоящее из п различных элементов. Для простоты будем считать, что
это первые п натуральных чисел, т. е.
А « (1; 2; 3; ...; п).
Всякое взаимно однозначное отображение F множества А на себя
называется подстановкой п-н степени.
Для обозначения подстановки F используется запись
,/?=С t ??)’	<2>
' R1 К2 КЗ • • • Кп '
где (if, i2; ia; ...; Zn), (fcf, /?2; /г3; kn) — две перестановки из п эле-
ментов множества A (klt k2t k3, ...» kn — образы элементов i2, i3, ...
..., in при отображении F).
Одна и та же подстановка может быть записана многими способами.
Так, подстановка (2) также может быть записана в виде
/1’2 и 1*з ... i’n\ иЛИ /• • • h h
kl k3. . .kn'	'kn ^n_l’««^3	'
В частности, всякая подстановка п-й степени может быть записана
в виде
( 2 З...л\
Ч I, Ij.-.ln/
т. е. в порядке возрастания натуральных чисел в верхней строке.
При такой записи различные подстановки отличаются друг от друга
перестановками, стоящими в нижней строке, а потому число подста-
новок п-й степени равно числу перестановок из п элементов, т. е.
равно п\.
Тождественной подстановкой п-й степени называется подстановка
Е=(‘2 3-").
Ч 2 З...Л/
Рассмотрим теперь произвольную подстановку п-й степени
'&1 ki ks.'.kn/
' | 2. КОМБИНАТОРИКА
417
Перестановки из п элементов, образующие верхнюю я нижнюю
строки подстановки F, имеют либо одинаковые четности (т. е. они или
обе четны, или обе нечетны), либо противоположные четности (т. е.
одна четная, а другая нечетная), причем совпадение или несовпадение
четностей перестановок не зависит от различных способов записи дан-
ной подстановки.
Если четности верхней и нижней строк подстановки F совпадают»
то подстановка называется четной; если они противоположны — то
нечетной,.
Число четных подстановок л-й степени равно числу нечетных»
т. е. равно nl/2.
Умножение подстановок. По определению подста-
новка л-й степени есть взаимно однозначное отображение F конечного
множества из п различных элементов иа себя. Последовательное вы-
полнение двух подстановок n-й степени опять будет взаимно однознач-
ным отображением множества А на себя и приводит к некоторой вполне
определенной третьей подстановке n-й степени, называемой произвел
дением первой из заданных подстановок на вторую.
О произведении двух данных подстановок F и G также говорят, что
оно получено в результате умножения подстановки F на подстановку G.
Произведение подстановки F на подстановку G обозначают FG,
Например, пусть даны две подстановки четвертой степени
0_(231'4).
432 1/	4 4 3 2/
Произведением подстановок F и G является
подстановка
FG =
/1 2 3 4\
\2 4 1 3/
Действительно, при подстановке F число 1 переходит в 4, а при под-
становке G число 4 переходит в 2, поэтому при отображении FG число I
переходит в 2 и т. д.
Умножение подстановок определено лишь для подстановок оди-
наковой степени и обладает следующими свойствами:
1)	Умножение подстановок n-й степени при п > 3 некоммутативно,
т. е. подстановка FG. не всегда равна подстановке GF,
2)	Умножение подстановок ассоциативно: F (GH) =» (FG) Н\ по-
этому имеет смысл говорить о произведении любого конечного числа
подстановок л-й степени.
3)	Произведение любой подстановки F на тождественную (Год*
стаковку Е, а также произведение Е на F равно F:
EF~ ЕЕ F.
Обратной подстановкой к подстановке л-й степени F называется
такая подстановка л-й степени G, что
FG « QF = Е.
Подстановка, обратная подстановке F, обычно обозначается Е"*1;
FF~* = F~lF « Е.
14 А. Цыаква
41Я ГЛ. ТО. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Подстановка, обратная подстановке
Р ~~ {h h ИЛ
'Ai Ая Аз...Ап/
имеет вид
F-x *« А3...АП\
т. е. получается из F перестановкой строк.
2.3.	Размещения. Пусть дано некоторое конечное множество А,
состоящее из п различных элементов. Выберем некоторым образом
из этих п элементов т различных элементов и будем составлять из
этих т элементов различные упорядоченные множества.
Конечные упорядоченные подмножества, содержащие по т эле-
ментов, выбранных из п элементов основного множества, называются
размещениями из п элеметов по т элементов. Число всех возможных
размещений из п элементов по т обозначается А™
Нетрудно убедиться, что
= п,
т. е. один элемент из п можно выбрать п способами, а из одного эле-
мента можно образовать единственное упорядоченное множество.
Найдем, чему равно число размещений из п элементов по т. Чтобы
распределить т + 1 элементов, взятых из п элементов, по т + 1 ме-
стам, можно сначала выбрать т элементов и разместить их по первым т
местам. Это можно сделать А™ способами. При каждом таком выборе т
элементов из п остаются «свободными» п — т элементов, любой из
которых можно поставить на свободное (т + 1)-е место. Таким образом,
при каждом из 4JJ1 ваполнений первых т мест получим п — т воз-
можных ваполнений (т + 1)-го места. Следовательно, число разме-
щений по m+ 1 элементов, выбранных из п заданных элементов,
связано с числом размещений из п элементов по т равенством
Учитывая, что А\ = п, имеем
Аг. = я>
A2 = n(n— 1),
= л (n—1) (п —2),
•....................• i i > 4 Г
А™ «г л (л — 1) (л —2). ..(л —гс + 1).
Последнее равенство можно ваписать с использованием символа фак-
ториала.
дт_______п 1
а (п — т) Iе
$ 2. КОМБИНАТОРИКА
419
При т «в 0 получаем Д° — 1, т. е. из любого множества единственным
способом можно извлечь пустое множество, которое, по определению,
можно упорядочить единственным способом.
Число размещений и число перестановок связаны формулой
Ап = рп = л1.
2.4.	Сочетания. Конечные неупорядоченные множества, содержа-
щие т различных элементов, выбранных из п элементов заданного мно-
жества, называются сочетаниями из п элементов по т. Число сочетаний
из п элементов по т элементов обозначается С™ или
Найдем, чему равно число сочетаний из п элементов по т. В согла-
сии о данным выше определением размещений, из данного множества,
содержащего п элементов, можно образовать Д™ различных упорядо-
ченных множеств, содержащих по т различных элементов. Ив множе-
ства, содержащего т различных элементов, можно образовать Рт
различных упорядоченных множеств, а потому число различных
неупорядоченных множеств, содержащих по т различных элементов,
выбранных из п элементов, будет вычисляться по формуле
А”
Используя формулы для подсчета числа перестановок Рт и числа
размещений Д™, получим
/~>т _____2J____
п т \ (п — т)\
Идя числа сочетаний справедливы равенства
=	С-+1=С-+С-+«,	(3)
а также
с“+с’+сн--- + сг‘+^ = 2г>.
Последнее свойство иногда формулируется в виде следующей
теоремы о конечных множествах:
Число всех подмножеств множества, состоящего ив п элементов
равно 2п.
В табл. 9 даны значения С™ для п =» 10 и т < п.
Эта таблица называется треугольником Паскаля. Отметим, что
вторая из формул (3) позволяет и далее последовательно заполнять
строки треугольника Паскаля, пользуясь тем, что в начале и в конце
каждой строки стоят единицы. Вычислим, например, не приведен-
ное в таблице;
С11в <чо + Чо - *2» + 210 = 330.
14*
420 ГЛ. 10. КОМБИНАТОРИКА* ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ТАБЛИЦА 9
п	т										
	0	1	2	. 3	4	5	6	7	8	9	10
о	1										
1	1	1									
2	1	2	1								
3	1	3	3	I							
4-	1	4	6	4	1						-
5	1	Б	ю	10	5	1					
6	1	6	16	20	15	6	1				
7	1	7	21	35		21	7				
3	1	8	28	56	70	56	28	8	1		
9	1	9	36	84	126	126	84	36	9	1	
10	1	10	4Б	120	210	252	210	120	45	10	1
2.5.	Бином Ньютона. Натуральная степень суммы двух величин
вычисляется по формуле
(о + 0)" = с°пап 4- су-1* С™ап-тЬт 4- • • • + СппЬп =
п
~%C‘nan-V,
i==0
которая называется биномом Ньютона. Коэффициенты С™, равные
числу сочетаний из п элементов по т, называются биномиальными
коэффициентами.
Свойства биномиальных коэффициентов:
1)	Число биномиальных коэффициентов (а следовательно, и
число слагаемых в разложении степени бинома) равно п + 1.
2)	Коэффициенты членов» равноотстоящих от начала и от конца
бинома, равны между собой (так как
3)	Сумма всех биномиальных коэффициентов равна 2я/
4)	Сумма биномиальных коэффициентов, состоящих на нечетных
местах, равна сумме коэффициентов, стоящих на четных местах.
Натуральная степень разности двух величин вычисляется но
формуле, аналогичной биному Ньютона:
(а - *)’ » С°пап — су-1Ь 4.... 4. (-1)т С”а"-тЬт 4-....
п
... 4. (_1)" су = £ (-О' С1пап~‘ь1.
М
2.6.	Перестановки с повторениями. Пусть А — некоторая со-
вокупность, состоящая из п элементов: *
A —{at, а2, аз,..., ап}
т различных типов (т п), причем элементы одного типа неразли-
чимы Между собой. И пусть элементов принадлежат первому типу,
f 2. КОМБИНАТОРИКА	42i
ft, элементов принадлежат второму типу, Ag — третьему, Am—m-му
типу, причем Aj + Ag + k* + • • •+ km *=*
Например, если
А®{1, !, 2, 3, 1/3},	(4)
то, считая элементами первого типа единицы, элементами второго типа
двойки, а элементами третьего типа тройки, имеем kt» 3	.«= 1,
Ъ =2.
Различные конечные совокупности, содержащие п элементов, из
которых ki принадлежат первому типу, А, — второму типу . . ., km —
m-му, типу, называются перестановками с повторениями (кортежами),
имеющими состав (или спецификацию) (k±t k* k& . . м *m).
Число таких различных перестановок с повторениями обычно обо-
значается Сп (k^ Аа, . .., km) и вычисляется по формуле
/XI
Cn (kt, kt,..., fcm) -	•	(5)
Формула (5) может быть доказана следующим образом. Рассмотрим
некоторую конкретную перестановку с повторениями состава (At,
k£t . km) и заменим все одинаковые элементы разными. В резуль-
тате такой замены получим некоторую перестановку из п различных
элементов. Число способов, которыми можно заменить kt неразли-
чимых элементов первого типа разными элементами, равно Ар; число
способов, которыми можно заменить k2 неразличимых элементов вто-
рого типа разными, равно Agl и т. д. И наконец, число способов, кото-
рыми можно заменить km неразличимых элементов разными, равно AmL
Таким образом, число различных перестановок из п различных
элементов, которые могут быть получены из одной конкретной пере-
становки с повторениями состава (A*, Ag, . . Am), равно Ар «Ар •
.....Ami-
С другой стороны, число перестановок из п различных элементов
равно л!, и поэтому "число всех перестановок о повторениями состава
(А1} Ag, . . ., Am) связано с числом перестановок из п различных эле-
ментов равенством
Сп (Ai, Ag,•••» А/п)«А1ЬАз!-...-Ат! =п|(
из которого и следует формула (5).
П р и м е р. Сколько различных шестизначные чисел можно обра-
зовать из трех единиц, одной двойки и двух троек?
Число таких различных шестизначных чисел вычисляется как
число различных перестановок с повторениями состава (3, 1, 2) и равно
с-<3- '•2)—зГГИГ"60-
Число перестановок с повторениями состава (Af, А,, ..., Ат)
может быть введено как решение задачи о числе разбиений множества,
состоящего из п различных элементов, на сумму т непересекающихся
подмножеств.
Пусть А — некоторое конечное множество, состоящее из а различ*
ных элементов; 4
Л» {а,; а,; а,;...; в„}.
422 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Представим множество А в виде суммы т подмножеств Вь В* .
• • Вт, не имеющих общих элементов:
^ = B1UB2U^3U---U^.
Пусть число элементов в подмножестве В^ равно fy, число элемен-
тов в подмножестве ZL равно Ag, .. число элементов в подмножестве Вгп
равно km (At 4- Ag 4- • • •+ km = л). Подсчитаем число всех возмож-
ных разбиения множества А на сумму фиксированного числа подмно-
жеств Въ В2, . . Вт.
Все разбиения множества А на т Трупп Bit .. Вт можно
получить следующим образом:
Образуем подмножество Bi из At элементов множества А. Это
можно сделать С*1 способами. Из оставшихся л —А, элементов мно-
жества А образуем множество В2, содержащее А2 элементов. Это можно
сделать способами. Общее число способов образования двух
таких подмножеств и В2 равно
Qk _____	(и——А])!
Н •	Ai!(n —AJ! ’ А2Цл —Ai —А2)!
____________п\________
t Al I А21 {п — Ai — А2) 1 ’
Продолжая далее процедуру образования подмножеств В3, ..
Вт» в результате получим, что общее число способов выбора подмно-
жеств Blt B2t . . n Вт равно
п	• • * u*-*i--АтЛ - ~А1!.А2!....Ат!
Таким образом, число способов, которыми можно представить
множество А из п различных элементов в виде суммы tn подмножеств Вь
В2> .... Вт, число элементов которых равно Аь Ag, . , Ат соот-
ветственно (At + Аа + • • • • 4- Ат == л), равно
п\_______
At 1•AgI•... • Ат!
» является числом различных перестановок о повторениями Сп (Af,
Ag, . . ., Am).
Числа Сп (At, А2.....Am) также называют полиномиальными
коэффициентами — эти числа являются коэффициентами в формуле
вычисления п-й степени суммы т величин
(0, + 02-Ь-. +am)"= 2Cn(fel> k2......<6>
В правой части равенства (6) стоит сумма всевозможных слагае-
мых вида Cn(Alt А2, . .	. a^t ?№ целые числа Аь
А2, . . ., Ат связаны равенством Af+ •••+ Am==
Если ag ==•*•« am, то из формулы (5) следует равенство
S (^1» ^2» • • •» ^т) а тП*
При т = 2 формула (5) представляет собой формулу бинома
Ньютона, полиномиальные коэффициенты превращаются в биноми-
альные и их сумма равна 2ОТ«
§ 3. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ	433
2.7.	Сочетания с повторениями. Сочетаниями из т (различных)
элементов по п элементов с повторениями называют неупорядоченные
совокупности, состоящие из п элементов, каждый из которых при-
надлежит к одному из т типов.
Например, из трех различных элементов oi, я2, а3 можно составить
следующие сочетания по два с повторениями:
{Of. «1}. {“1! аг}, {ai; а3},
{аа; Оа), {а,; аз}> {Чз! аз}-
Число различных сочетаний из т элементов по п с повторениями
обозначается и вычисляется по формуле
Im = С/п+п—1 =
Справедливость этой формулы нетрудно установить на основании
следующих рассуждений. Каждое сочетание из т элементов по п с по-
вторениями полностью определяется, если указать, сколько элементов
каждого из т типов в него входит. Поставим в соответствие каждому
сочетанию с повторениями последовательность нулей и единиц, состав-
ленную по следующему правилу: напишем подряд столько единиц*
сколько элементов первого типа входит в сочетание (если элемент пер-
вого типа не входит в сочетание — не пишем ничего); после этого
поставим нуль, обозначая им «границу» между элементами первого и
второго типов. Напишем подряд столько единиц, сколько элементов
второго типа входит в сочетание (если элемент второго типа вообще
не входит в сочетание, то после нуля не пишем ничего); ставим нуль,
указывая, что количество элементов второго типа перечислено, и т. д.
Например, написанным выше сочетаниям из трех элементов по два
с повторениями будут соответствовать следующие последовательности
нулей и единиц:
1100,	1010,	1001, ОНО, 0101, ООП.
Таким образом, каждому сочетанию из т по п с повторениями
можно поставить в соответствие последовательность из п единиц и
т — 1 нулей (число «границ» между т типами элементов), и наоборот,
каждой такой последовательности единиц и нулей соответствует един-
ственное сочетание.
Число способов, которыми можно расставить п единиц по п 4
4- гп — 1-му местам, равно	С другой стороны, число способов,
которыми можно расставить т — 1 нулей по п + т — 1 местам, равно
По свойству (3) числа сочетаний	и фор-
мула (7) доказана.
Для числа сочетаний с повторениями справедлива следующая
рекуррентная формула:
l+Zm"1.
• т J т—1 • * т •
§ 3< Элементы теории вероятностей
3.1.	Испытание. Исход. Событие. В теории вероятностей под
испытанием (опытом) понимают комплекс определенных условий,
воспроизводимый сколь угодно большое число раз, наличие которого
приводит к какому-либо исходу. Исход случаен, если испытание, при-
водящее к какому-либо определенному исходу, имеет и другие исходы.
424 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Случайным событием (или просто событием} называется любая
совокупность случайных исходов. Событие может состоять и из одного
исхода, и поэтому сами исходы также можно именовать событиями.
Исходы называются независимыми, если они представляют собой ре-
ву льтаты отдельных испытаний.
Пример. Возьмем игральную кость (кубик, на гранях которого
отмечены от одного до шести очков) и бросим его на стол. На верхней
грани брошенного кубика выпадет какое-либо количество очков.
Совокупность указанных условий (наличие у нас кубика, стола и про-
цедура бросания кубика)— испытание. Количество очков, выпавших
на верхней грани брошенного кубика,— исход этого испытания Общее
число случайных исходов равно шести. Случайным событием в данном
примере будет, например, событие, состоящее в той, что на верхней
грани окажется четное число очков. Это событие есть совокупность
трех исходов: выпадения 2, 4 и 6 очков.
Случайные события обычно обозначают большими латинскими
буквами 4, В, С, ... или 4Ь 4а, 48, ,..
Достоверным событием называют событие, которое обязательно
произойдет при данном испытании. Невозможным событием называют
событие, которое заведомо не произойдет при данном испытании.
Так, в рассмотренном испытании с игральной костью событие, состоя-
щее в том, что в результате испытания выпало некоторое число очков,
не большее шести — достоверное, а событие, состоящее в том, что
выпало семь очков,— невозможное.
Два случайных события называются противоположными, если одно
из них происходит в том и только том случае, когда не проис-
кодит^другое. Событие, противоположное событию А, обычно обозна-
чают А.
Пример. Брошена игральная кость. Обозначим через А со-
бытие, которое состоит в том, что выпало шесть очков. Событие А —
выпадение от одного до пяти очков.
События Alt 4а, . . ., Ап называются несовместными, если на-
ступление одного из них исключает наступление других.
Пример. Пусть в урне находится три белых шара, занумерован-
ных цифрами 1, 2, 3, и два черных шара, занумерованных цифрами 4»
5. Вытаскиваем наугад один из шаров. Пусть событие А состоит.в том,
что вытащенный шар — белый, а событие В состоит в том, что выта-
щенный шар имеет четный номер. События А и В — совместные, так
как из урны может быть вынут белый шар с номером 2. Далее, пусть
событие С состоит в том, что вынут шар под номером 5. События А и С
несовместны, так как белые шары занумерованы цифрами 1, 2, 3.
Говорят, что события 4Х, 42, • • •, Ап образуют полную группу
событий, если в результате данного испытания обязательно произойдет
одно из них.
Пример. Пусть в урне находятся три белых шара, занумерован-
ные цифрами 1, 2 3, и два черных шара, занумерованных цифрами 1, 2.
Из урны наугад вынимают один шар. События:
At — появление шара с цифрой lt
Aa — появление шара о цифрой 2t
А3 — появление шара с цифрой 3
образуют полную группу событий.
$ 3. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Полная группа событий Лх, Л2, . . ., Лл называется полной груп~
пой несовместных событий, если в результате данного испытания обя*
вательно произойдет одно и только одно событие данной группы.
Пример. Брошена игральная кость. Пусть Лх, Л2, . . ., Лв —
события, состоящие в том, что на верхней грани брошенной кости
выпало 1, 2, . . ., 6 очков соответственно. События Лх, Л2, ...» А9
образуют полную группу несовместных событий.
Среди всех возможных событий, которые в данном испытании мо*
гут произойти,можно выделить множество так называемых элементар-
ных событий (или элементарных исходов), выделяемых из множества
всех событий по следующим признакам: ./
1.	Все они взаимно исключают друг, друга, и в результате испыта-
ния обязательно происходит одно из этих событий.
2.	Каково бы ни было событие Л, по наступившему элементарному
событию можно судить о том, наступило или не наступило событие Л.
Так, в примере с игральной костью множество элементарных
событий состоит из шести элементарных, событий Лх, Л2, ...» Л„,
ваключающихся в том, что на верхней грани брошенной кости выпало
J, 2, . . ., 6 очков соответственно.
3.2.	Операции над событиями. Два события Л и В называют
равными и пишут Л = 5, если наступление события Л влечет за собой
наступление события В и, наоборот, наступление события В влечет
ва собой наступление события Л.	_
Пример. Брошены две игральные кости. Пусть событие Л
состоит в том, что сумма выпавших на костях очков четная, а собы-
тие В — в том, что на брошенных костях четности очков совпадают
(т. е. либо на обеих костях выпало четное число очков, либо на обеих
нечетное). События Л и В равны.
Объединением (или суммой) событий Л и В называется событие,
состоящее в наступлении события Л или события В. Объединение
событий обозначается
ЛиВ или Л + В.	'
Аналогично определяется сумма k событий Лх, Ла, . . Лд,
которая обозначается
и л*.
k
Пересечением (или произведением) событий ЛиВ называется со-
бытие, состоящее в одновременном наступлении как события Л, так
и события В. Пересечение событий ЛиВ обозначается
Л П В или Л «В.
Аналогично определяется произведение k событий Лх, Л2, . . ., Л*,
которое обозначается
П Ah-
k
Разностью событий ЛиВ называется событие, состоящее в том,
что наступает событие Л» но не наступает событие В. Разность событий А
и В обозначается
Л \В.
Сумма, произведение и разность событий геометрически могут
быть изображены так же, как сумма, произведение и разность двух
произвольных множеств.
426 ГЛ. 16. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
3.3.	Понятие вероятности. Рассмотрим опыт по бросанию монеты.
Этот опыт имеет два взаимно исключающих друг друга исхода выпа-
дение «герба» и выпадение «решетки». Обозначим эти исходы буквами
«Л» и «В» соответственно. Проведем серию испытаний, состоящую из п
бросаний. Подсчитаем число выпадений «герба» и число выпадений
«решетки». Повторим эту серию из п испытаний несколько раз, под-
считывая каждый раз число выпадений «герба» и «решетки». Пусть
число испытаний, которые привели к выпадению «герба», равно п (Л).
Отношение числа выпадения «герба» п (Л) к числу всех испытаний п
данной серии называют частотой события 4 в данной серии опытов.
Как показывает практика, при больших п частоты п (А)/п в различных
сериях испытаний оказываются приблизительно одинаковыми и при
достаточно больших п близкими к 1/2.
Аналогичная ситуация будет и в случае бросания игральной кости5
при достаточно большом числе испытаний в серии частота выпадения,
скажем, шести очков в различных сериях испытаний будет примерно
одинакова и близка к 1/6.
Естественно, что как в примере с монетой, так и в примере с играль-
ной костью полагалось, что монета и игральная кость геометрически
правильны, сделаны из однородного материала и условия испытаний
в различных сериях одинаковы.
Число подобных примеров можно продолжить, но во многих слу-
чаях при многократном повторении одного и того же опыта в одних
и тех же условиях частота наступления некоторого события (т. е.
отношение числа опытов, в которых этот результат наблюдался, к об-
щему числу производимых испытаний) остается примерно одинаковой
и близкой к некоторому числу Р. Это число называют вероятностью
рассматриваемого события.
Таким образом, вероятность того или иного события можно при-
ближенно оценить по результатам серии опытов, состоящей из доста-
точно большого числа испытаний.
В так называемой классической модели теории
вероя 1 ностей полагается, что:
1.	Множество элементарных событий (исходов) одного испытания
в)1» й>з» • • •» конечно и образует полную группу несовместных
событий.
2.	С каждым элементарным исходом ац можно связать неотрица-
тельное число рг, называемое вероятностью этого исхода, причем
Р1+ ра + •••+ Pk == 1-
3.	Вероятность Р (4) наступления события 4, состоящего в том,
что наступило одно из событий ©/, ©у, . . ., ©s, равна сумме вероятно-
стей наступления этих событий
Р (4) «В pi + р; 4- • • • 4- Pg.
События со/, ©/,..., ©s называют благоприятствующими со*
бытию 4.
4.	В случае, когда события ©i, ©а, . . ., ©л равновероятны, т. е.
Pi ~ Pi » •••“ Ph 5=5 вероятность Р (4) вычисляется по формуле
Р (4) « rlk,	(1)
где г — число исходов, благоприятствующих событию 4, a k — число
всех равновозможных исходов. Формула (1) выражает так называемое
классическое определение вероятности.
Пример. Предположим, что брошены две игральные кости,
грани которых занумерованы цифрами от 1 до 6. Какова вероятность
$3 ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ	<27
выпадения «дубля»? Каждый всход этого опыта можно представить
как упорядоченную пару чисел (т; п), где т — число очков, выпавших
на первой кости, п — число очков на второй. Все исходы равнове-
роятны, и число всевозможных различных исходов, г. е. число таких
различных упорядоченных пар, равно 36. Событие А — выпадение
«дубля» — происходит тогда и только тогда, когда наступает один из
исходов (т\ л), при котором m = л. Таких исходов шесть. Следова-
тельно, в согласии с формулой (1) вероятность события 4: Р (А) =»
₽= 6/36 «=]/6.
Сложение вероятностей. Рассмотрим несовместные
события Ai и 42 и их объединение А ==. 4j U 42. Пусть проводится
серия испытаний, результатом каждого из которых могут быть события
4, Ai и Аа. Пусть п — число всех испытаний; л (4), п (4<) и л (42) —
число тех испытаний, которые привели к наступлению событии 4, 41 и
А2 соответственно. Если в каком-либо испытании произошло событие 4,
то это значит, что произошло или событие 4Х, или событие 4а (одно-
временно события 4j и 42 произойти не могут, так как они несовместны}.
Поэтому числа л (4), л (41) и л (42) связаны между собой равенством
л (4) = л (А]) + л (4а),
и, следовательно, частоты этих событий связаны равенством
л (4) __ л (4Q л (42)
л л "г л *
При достаточно большом числе испытаний л частоты становятся
близки к вероятностям соответствующих событий и, следовательно,
Р(4)==Р(41)+Р(4а).
Это равенство называется формулой сложения вероятностей.
Формула сложения вероятностей справедлива и в случае, когда
событие 4 есть объединение любого конечного числа несовместных
событий. Если 4 == (J 4л, то
Р (4) - Р №+Р (4а) + .♦>+ Р (А$.
Из формулы сложения вероятностей, в частности, следует, что
сумма вероятностей наступления события 4 и события, противополож-
ного 4 (т. е. 4), равна единице:
Р (4) + Р (4) « 1.
Вероятность произведения событий. Пусть 4 х
и 42 — независимые события, т. е. наступление события 4f никак на
отражается на условиях опыта, в результате которого может наступить
событие 42. Так, например, независимы события, состоящие в извле-
чении черного шара из двух различных урн, содержащих черные и
белые шары. Однако два последовательных извлечения черного шара
из одной урны (без возвращения вынутого шара обратно) не являются
независимыми событиями (поскольку первое извлечение черного шара
уменьшает число черных шаров, оставшихся в урне, и, следовательно,
отражается на условиях второго опыта).
Пусть проводятся две серии испытаний: первая серия, состоящая
из п испытаний, в результате которой п (4t) раз наступает событие 4f,
и вторая серия, состоящая из т испытаний! в результате которой т (4а)
4£8 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
раз наступает событие Ла В результате этих дву* серий испытания
событие А  At П Ла наступит п (А^ т раз» так как каждому
из п (Лх) исходов первого испытания соответствует m (Л2) исходов
второго испытания. Две проведенные серии испытаний всего могут
иметь л«м исходов, так как каждому из п испытаний первой серии мо-
жет соответствовать любое из т испытаний второй серин. Следовательно,
частота наступления события А =» Лх П Лв равна
п (Л1) # т(Л8) •
пт	п m
Так как при достаточно большом числе испытаний в каждой серии
частоты становятся близки к вероятностям наступления событий, то
вероятность наступления события Л == Л^ П Л2 равна
7	Р(Л)« Р (Л^.РИ^).
Для п независимых событий Ль Л2, .. ч Аъ вероятность их
произведения вычисляется по формуле
Р (Л1 • Ля-...• Ak)« Р (Лi).Р (Лж).....Р (Л*).
Вероятность суммы совместных событий.
Пусть Л и В — два совместных события. Проведем серию из п испыта-
ний. Пусть в этой серии испытаний событие А наступило п (Л) раз,
а событие В — п (В) раз. Допустим, что среди п (Л) + л (В) событий
содержатся л (Л-В) событий таких, при которых наступает как собы-
тие Л, так и событие В. С другой стороны, так как событие Л +*В на-
ступает в том случае, когда наступает событие Л или событие В, иля
то и другое одновременно, то при п испытаниях событие Л + В на-
ступит л (Л) 4- л (В) — п (Л .В) раз (в сумме л (Л) + « (В) имеется
п (Л»В) событий, которые засчитываются дважды). Следовательно,
частота наступления события Л + В равна
л (Л 4- В) п (Л) п (В) _______ п (А В) .
л	n ‘ п	л
Так как при достаточно большом числе испытаний частоты близки
к вероятностям, то вероятность суммы двух совместных событий Л и
В равна
Р (Л + В) - Р (Л) + Р (В) — Р (А-В).
Пример. Найти вероятность того, что при одновременном
бросании двух игральных костей хотя бы на одной кости выпадет 6 оч-
ков. Пусть Л — событие, состоящее в том, что 6 очков выпало на первой
игральной кости, В — событие, состоящее в том, что 6 очков выпало
на второй кости. Так как события А и В совместны (6 очков может
выпасть одновременно на первой и на второй кости), то вероятность
указанного события равна
Р (А + В) = Р (А) + Р (В) -Р (А В) =-L + 4-^-i-----------
о б 36	36
3.4.	Условная вероятность. Рассмотрим следующий опыт. Пусть .
в урне находятся л шаров: т черных и л — т белых. ’Пусть Л — со-
бытие,, состоящее в извлечении черного шара из урны, В — событие,
состоящее в извлечении черного шара из той же урны после того, как
из нее уже вынут один шар. Очевидно, что если событие Л наступили,
5 3. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ х <29
т. е. из урны первым был вынут черный шар, то в урне осталось m — I
Черных шаров и вероятность наступления события В равна «
m— I
« п — 1 •
Если же первым был вынут белый шар (т. е. событие А не насту-
пило), то в урне осталось т черных шаров и вероятность наступления
события В равна
т
л — 1 ’
Таким образом, вероятность наступления события В аависит от
того* наступило или не-наступило событие А.
Вероятность наступления события В при условии, что событие А
произошло, называют условной вероятностью события В при условии А
и обозначают
Р(В|Л>.
Вероятность произведения зависимых событий вычисляется по
формуле
Р (А*В) « Р (АуР (В | Л) ® Р (ВуР (А | В),	(2)
т. е. вероятность произведения двух зависимых событий А и В равна
произведению вероятности одного из этих событий на условную вероят-
ность другого, вычисленную при условии, что первое событие произо-
шло.
Пример. Пусть в ящике находятся 5 изделий первого сорта и
3 изделия второго сорта. Из ящика последовательно вынимают два
изделия. Найти вероятность того, что первое вынутое изделие первого
сорта, а второе — второго сорта.
Пусть А — событие, состоящее в том, что первое вынутое изделие
первого сорта, а В —.событие, состоящее в том, что второе вынутое
изделие — второго сорта.
Вероятность наступления события А
Р(А)*=ЫЬ.
Так как в ящике осталось 4 изделия первого сорта и 3 изделия второго
сорта, то вероятность вынуть изделие второго сорта равна
Р (Я]'Л) = 3/7.
Искомое событие представляет собой произведение событий Л«В,
в его вероятность вычисляется по формуле (2):
к Q	1R
/’(Лб) = Р(Л).Р(В|Л)=-2-.^---------g-.
3.5.	Формула полной вероятности. Для вычисления вероятности
того или иного события А часто бывает удобно использовать формулу
полной вероятности. Допустим, что имеется полная группа несовмепг-
ных событий Bt, В2, . . ., Bk, и пусть А — некоторое событие, которое
наступает при условии наступления некоторых из событий Bj, Вв, ...
. • Яд.
Так как события BitB2t . . ., Bk образуют полную групйу несовме-
стных событий, то событие А можно представить как сумму произве-
дений собью нй
-	А » A *Bi -у А В* «««-t* A *Bkt
430 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
где все слагаемые в правой части равенства являются несовместными
между собой событиями и, следовательно, вероятность наступления
события А равна сумме вероятностей событий А	. . ., A Bk>
Р (А) ~ Р (A-BJ + Р(А-В2)+ ---+Р (А-Вк).
Применив к каждому из слагаемых, состоящих в правой части по-
следнего равенства, формулу условной вероятности (2), получим фор-»
мулу полной вероятности
Р(А)~Р(А\ BJ-P (Bt) + Р(А | В2).Р(В2) + ... + Р(А | Bk)-P(Bh).
Пример. По цели произведено три последовательных выстрела.
Вероятность попадания при первом выстреле равна Pi =» 0,6, при
втором Ра = 0,7, при третьем Р3 = 0,9. Известно, что при одном (лю-
бом из трех) попаданий, вероятность поражения цели равна 0,4, при
двух (любых из трех) 0,8, при трех 1,0 (т. е. цель обязательно будет
поражена). Найти вероятность поражения цели при трех выстрелах.
Пусть А — событие, состоящее в том, что цель поражена, Blt В^
В3 — события, состоящие в том, что были одно, два и три попадания
в цель соответственно, — событие, состоящее в том, что в цель не
попали ни разу. Очевидно, что события Blt В2, B3t ВЛ образуют полную
группу несовместных событий (одно из них обязательно произойдет,
и наступление одного события исключает наступление другого).
Вероятность наступления события А вычислим по формуле полной
вероятности
Р (Л) = Р (А | В&Р (Вг) +Р(А\ В2)-Р (В2) +
+ Р М | В3).Р (В3) + Р (А | В4)-Р (В4).
По условию задачи вероятность поражения цели при одном попа-
дании Р (А | В^ = 0,4, при двух — Р(А | В2) я» 0,8, при трех —
Р (А | В3) == 1,0.
Вычислим вероятности наступления событий В^ В2 и В3,
Событие Bi может наступить в следующих трех случаях:
1.	Первый выстрел попал в цель, а второй и третий не попали.
Вероятность этого события можно вычислить как вероятность произ-
ведения указанных трех независимых событий:
Pl (1 —	(1 — Рз) « о,6»0,3.0,1 == 0,018,
где 1 — Р2 и 1 — Р9 — вероятности промахов при втором и третьем
выстрелах.
2.	Второй выстрел попал в цель, а первый и третий нет. Вероятность
этого события вычисляется аналогично предыдущей и равна
(1 — Pi)-Pi'(l — Р3) =» 0,4-0,7-0,1 - 0,028.
3.	Только третий выстрел попал в цель. Вероятность этого собы<
тия равна
(1 - р8).(1 — />2).р8 = 0,4.0,3-0,9 =» 0,108.
Таким образом, вероятность наступления события Bi равна
Р « 0,018 + 0,028 -t 0,108 » 0,154.
13. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ	431
Аналогично, вероятность наступления события Bt (двух попаданий
при трех выстрелах) равна
Р (В2) - Pt-P2-(1 - Р8) + Pf (1 - PJ-P9+ (1 - PJ-Pi'P* «
« 0,6-0,7-0,1 + 0,60,3-0,9+ 0,4-0,7-0,9 « 0,042 + 0,162 +
+ 0,252 = 0,456.
И, наконец, вероятность наступления события В3 равна
р (В9) =» РрР3-Р8 = 0,6-0,7-0,9 « 0,378.
Вероятность наступления четвертого события подсчитывать не
будем, так как очевидно, что вероятность поражения цели при трех
промахах равна нулю:
Р(А|В4) = 0.
Подставив полученные значения вероятностей в формулу полной
вероятности, находим вероятность поражения цели
Р (Д) = 0,4-0,154 + 0,8-0,456+ 1,0-0,378 = 0,8044.
3.6.	Формула Бернулли. Пусть производится п независимых
испытаний, в каждом из которых вероятность наступления события А
равна Р (а вероятность события А, противоположного событию Л.
равна 1 — Р). Требуется найти вероятность того, что при п испытаниях
событие А произойдет т раз.
Событие В, состоящее в том, что событие А наступило при каждом
из т первых испытаний и не произошло при остальных п — т испыта-
ниях, можно записать в виде произведения т событий А и п — tn
событий А:
В= ЛЛ.....ЛЛА...А,	(3)
т	п—т
Так как все п испытаний по условию независимым, то вероятность
наступления события В равна произведению вероятностей наступле-
ния событий Л и Л:
Р (В) = Рш-(1 — Р)п~т.
Событие Л может произойти т раз при п испытаниях, но при этом
может получиться последовательность чередований событий, отличная
от последовательности (3). Однако для любой такой последовательности
событий вероятность наступления события А т раз при п испытаниях
равна Рт-(1—P)n”m. Число всевозможных различных последова-
тельностей из п элементов, содержащих т элементов Л, равно числу
сочетаний С™ из п элементов по т элементов. Так как различные по-
следовательности из т элементов Лип — т элементов Л могут быть
рассмотрены как различные исходы серии из п независимых испытаний,
то все эти исходы (события) являются несовместными и искомая вероят-
432 ГЛ. 10. КОМБИНАТОРИКА. ТЕОРИИ ВЕРОЯТНОСТЕЙ
кость, обычно обозначаемая Рт> п, вычисляется кек сумма вероятно-
стей наступления различных исходов серии из п испытаний
Эта формула называется формулой Бернулли.
Пример. В урне находится 15 шаров: 10 черных я 5 белых*
Испытание состоит в следующем: вынимают один шар, фиксируют его
цвет и кладут обратно; перемешивают шары и вынимают еще один шар*
Указанную процедуру повторяют некоторое число раз. Какова вероят-
ность того, что при таком испытании из пяти вынутых шаров будет
четыре белых?
Вероятность появления белого шара при каждом испытании равна
Р =» 5/15 в 1/3, а вероятность того, что белый шар не будет вытащен,
равна 1 — Р » 2/3. По формуле Бернулли находим вероятность появ-
ления четырех белых шаров среди пяти вынутых:
- р)5-4 -су» a -f)=5 (4-)4, (4)=ж*.
.л
ПРИЛОЖЕНИЯ
1. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
К элементарным функциям относятся рациональные, степенные,
показательная и логарифмическая функции, а также тригонометриче-
ские функции. К классу элементарных функций, кроме того, относят
также сложные функции, образованные из перечисленных выше эле-
ментарных функций.
Показательная, логарифмическая функции, тригонометрические
функции, а также сложные функции, образованные с помощью этих
функций, называют элементарными трансцендентными функциями.
§ 1. График функции и простейшие преобразования
графика функции
Графиком функции у (х) в прямоугольной декартовой сиётеме
координат Оху называют множество всех упорядоченных пар точек
с координатами (х; f (х)).
Простейшими преобразованиями графика функции у~ f(x) в
прямоугольной декартовой системе координат иху являются пере-
численные ниже преобразования 1—5.
1. Перенос графика паралллельиа оси ор-
динат. График функции у == f (х) + а получается из графика функ-
ции у ад / (х) параллельным переносом г =* (0; а). Если число а поло-
жительно, то график функции у = f (х) + а получается сдвигом гра-
фика функции у == f (х) на а единиц вверх; если а отрицательно — на а
единиц вниз (рис. П.1),
2. Перенос графика параллельно оси аб-
сцисс. График функции у f (х — а) получается из графика
функции у = f (х) параллельным переносом г ж (о; 0). Если а < 0,
то график переносится влево, если а > 0 — вправо (рис. П.2).
З.Растяжения и сжатия графиков функ-
ций. Пусть дан график функции у=* f (х) и точка с координатами
(хь; уд принадлежит графику функции у » / (х).
434
Т. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Рассмотрим функцию у =» kf (х) (k — положительное число).
Точка графика функции y^kf (х) с абсциссой х0 имеет ординату ky^
При k > 1 ординаты точек графика ^функции у ® kf (х) увеличиваются
в k раз по сравнению с ординатами точек графика функции у—f (х),
имеющих ту же самую абсциссу. В этом случае говорят, что график
функции y^kf (х) получается из графика функции у = f (х) растя-
жением от оси абсцисс в k раз.
При 0 < k < 1 ординаты точек графика функции у — kf (х) умень-
шаются в \lk раз по сравнению с ординатами точек графика функции
У = /(х), имеющих ту же самую абсциссу. В этом случае говорят,
что график функции у = kf (х) получается из графика функции у =»
= f (х) сжатием к оси абсцисс в k раз.
Например, График функции у~ 2х2 получается из графика функ-
ции у = / (х) растяжением от оси абсцисс в 2 раза, а график функции
у =» х2 — сжатием к оси абсцисс в 2 раза (рис. П. 3),
Рис. П.5.	" Рис. П.6.
Рассмотрим функцию у~ f (kx) (k — положительное число).
Точка графика функции у — {(kx) с ординатой у0 имеет абсциссу xjk.
При k > 1 абсциссы всех точек графика функции у = f (kx) умень-
шаются в k раз по сравнению с абсциссами точек графика функции у =
s= f (х), имеющих ту же ординату. В этом случае говорят, что график
функции y~f (kx) получается из графика функции у ® / (х) сжатием
к оси ординат в k раз.
При 0 < k < 1 абсциссы точек графика функции у = / (kx) уве-
личиваются в \!k раз по сравнению с абсциссами точек графика функ-
ции у = / (х), имеющих ту же самую ординату. В этом случае говорят,
что график функции y~f (kx) получается из графика функции у =
= f (X) растяжением от оси ординат в \/k раз. Напрймер, график функ-
ции у = sin 2х получается из графика функции у = sin х сжатием
к оси ординат в 2 раза (рис. П. 4).
. 4. График функции у = —-f (х) получается из графика функции
у я» / (х) симметричным отражением относительно оси' Ох (рис. П. б).
$ 2. ЛИНЕЙНАЯ ФУНКЦИЯ	Д35
Б. График функции у = / (—х) получается из графика функции
у~ f (х) симметричным отражением относительно оси Оу (рис. Ц. 6).
Примеры. 1. С помощью перечисленных выше преобразова-
ний графиков функций получить из графика функции у = х2 график
функции у = 2х2 + 4х — 1.
Запишем квадратный трехчлен 2х2 + 4х — 1 в виде 2 (х + I)2 — 3,
график которого (рис. П. 7) получается из графика квадратного трех»
члена у ~ х2 в результате следующих преобразований:
а)	параллельного переноса г= (—1; 0);
б)	растяжения от оси абсцисс в 2 раза;
в)	параллельного переноса г == (0; —3).
2.	С помощью преобразований графиков функций получить из
графика функции у == sin х график функции у == 2 sin ^х +.
График этой функции (рис. П. 8) получается из графика функции
у ® sin х в результате следующих преобразований:
а)	параллельного переноса г == (—л/4; 0);
б)	растяжения от оси абсцисс в 2 раза;
в)	параллельного переноса г = ^0; —
§ 2.	Линейная функция
Линейной функцией называется функция вида
f (х) = kx + b,
где k и b — некоторые числа.
Свойства линейной функции.
1)	Область определения — множество всех действительных чи*
сел R.
2)	Область изменения (множество значений) при k 0 — мно-
жество всех действительных чисел. При k = 0 множество значений
функции состоит из одной точки Ь.
3)	При k =^= 0 и b =£= 0 функция не является ни четной, ни нечетной.
При k = 0 (Ь — любое) функция четная, при Ь = 0и0 - нечетная.
4)	Линейная функция непрерывна и дифференцируема на всей
числовой оси; ее производная в каждой точке равна k.
5)	Линейная функция не имеет экстремумов ни при каких значе-
ниях k и Ь. При =/= 0 критических точек нет. При k == 0 каждая точка
является критической точкой функции.
6)	При 0 линейная функция возрастает при всех х £ R, при
& < 0 убывает при всех х С R, при & « 0 постоянна.
4вб	Т. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
7)	График линейной функции пересекает ось Оу в точке у = 6. ,
При k */= 0 график пересекает ось Ох в точке х =» —bik, при k = 0 о»
параллелен оси Ох.
На рис. П. 9, П. 10 изображены графики линейных функций.
Линейная функция f (х) » kx + b может иметь своим графиком
любую прямую координатной плоскости Оху, за исключением верти»
кальных прямых.
^д
— ....... .
1	(**о>Ъ*П
Рис. П.9.
Прямая пропорциональность. Переменную у на-
зывают прямо пропорциональной переменной х с коэффициентом про-
порциональности /?, если эти переменные связаны соотношением у ==•
*= kx, где k — некоторое действительное число, отличное от нуля.
Если считать х независимой переменной, а у — зависимой, то урав-
нение у == kx определяет у как функцию х. Графиком этой функции
является прямая, проходящая через начало координат, с угловым коэф-
фициентом k (тангенс угла наклона прямой к оси Ох равен k). Прямо
пропорциональная зависимость является частным случаем линейной
функции.
§ 3. Обратно пропорциональная зависимость
Переменную у называют обратно пропорциональной переменной х,
если значения этих переменных связаны равенствбм у — klx, где k —
некоторое действительное число, отличное от нуля. Число k называют
коэффициентом обратной пропорцио-
нальности.
Если считать х независимой пере-
менной, а у — зависимой, то уравнение
у = klx определяет у как функцию
от х. График функции у = klx назы-
вается гиперболой.
Свойства функции/(х) =
= k/x.
1)	Область определения — мно-
жество всех действительных чисел, за
исключением числа 0.
2)	Область изменения (множество
значений) — множество всех действи-
тельных чисел, за исключением
числа 0.
3)	Функция f (х) « k/x — нечетная, и ее график симметричен
относительно начала координат, Она непрерывна и дифференцируема
во всей области определения; /' (х) = — &/x?t критических точек неимеет*
$ 4. ДРОВ НО* ЛИНЕЙНАЯ ФУНКЦИЯ
4)	Функция fXx)** k/x при Л>0 монотонно убывает, на проме-
жутках в (—оо, 0) и (0,4-оо), а при k < 0 монотонно возрастает на тех
же промежутках.
5)	График функции у « k/x при k > 0 в промежутке (0; +оо)
направлен вогнутостью вверх, а в промежутке (—<х>, 0) — вогнуто-
стью вниз* При k < 0 промежуток вогнутости вверх — (—оо; 0), а
промежуток вогнутости вниз — (0; +оо).
Графики функции k/x при fe» 1 и —2, изображены на
рис. П.Н.
§ 4, Дробно-линейная функция
Функция вида / (х)»	называется дробно-линейной функ-
цией (о, Ь, с, d — некоторые числа, с #= 0) *). Преобразуем дробно-
линейное выражение
ах + b
а 1 а	а
с ’ . . d	с
х+—
2±
График дробно-линейной
получен из графика обратно
ющими преобразованиями:
а)	параллельным переносом г
б)	хбкатием (или растяжением) к оси абсцисс
в) параллельным переносом г= (0; а/с).
b	da
с	с2	। а
ах 4* &
функции ex+~d~ может быть
пропорциональной зависимости следу-
(—d/c\ 0);
/ b da\
3 раз:-
ЖЖ—
Последовательное
в график функции у
преобразование графика функции у = —
2x4-5
*—Т“Т~ приведено на рис. П. 12—П. 15. На
Ч Если с«=0, то дробно’лннейная функция превращается в линейную
функцию*
438
Ъ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
рис. П. 12 изображен график функции у ® На рис. П. 13 изобра-
жен график функции у ® —-Д." Г» П0ЛУчающейся из графика функции
р = — параллельным переносом г® (—1; 0). На рис. П. 14 изобра-
растяжением от оси абсцисс в 3 раза. И, наконец, на рис. П. 15 изо-
бражен график дробно-линейной функции у ®
получается из графика у
« (0; 2).
3
х+1
2x4-5
Х4-1 ’
который
параллельным
переносом г ®
§ 5, Квадратичная функция
Функция f (х) ® ах2 + Ьх + с, где а, Ь, с — некоторые действи-
тельные числа (а 0), называется квадратичной функцией. Графин
квадратичной функции называется параболой.
Квадратичная функция может быть приведена к виду
/ ь \2
/(х) — (*+-2г)--------(1)
Представление квадратичной функции в виде (1) называется выделением
полного квадрата.
Свойства квадратичной функции и ее гра-
фик.
1)	Область определения — вся числовая прямая.
2)	При b 0 функция не является четной и не является нечетной,
При Ъ ® 0 квадратичная функция — четная»
§ 5. КВАДРАТИЧНАЯ ФУНКЦИЯ
439
3)	Квадратичная функция непрерывна и дифференцируема во всей
области определения.
4)	Функция имеет единственную критическую точку х =
— — 6/(2а). Если а > 0, то в точке х == —Ь/(2а) функция имеет мини-
мум. При х <. —Ь/(2а) функция монотонно убывает, при х > —Ь/(2а)
монотонно возрастает.
Если а < 0, то в точке х = —6/(2а) функция имеет максимум.
При х<—Ь/(2а) функция монотонно возрастает, при х>—Ь/(2а)
монотонно убывает.
Точка графика квадратичной функции с абсциссой х = — Ь/(2а)
________________________4ас
и ординатой у =------------- называется вершиной параболы.
5)	Область изменения функции: при а > 0 — множество значе-
[^2 — 4ас \	Л
------» +°° )» ПРИ 62 < ° — МН0‘
/	Ь2 — 4ас 1
жество значений функции — промежуток ( —оо;---------------1 .
Рис. П.18.
Рис. П.19.
6)	График квадратичной функции пересекается с осью Оу в точке
у—с. В случае» если Ь2— 4ас> 0, график квадратичной функции
пересекает ось Ох в двух точках (различные действительные корни
квадратного уравнения); если № — 4ас == 0 (квадратное уравнение
имеет один корень кратности 2), график квадратичной функции ка-
сается оси Ох в точке х = —Ь/(2а); если Ь2 — 4ас < 0, пересечения
с осью Ох нет.
Из представления квадратичной функции в виде (1) также следует,
что график функции симметричен относительно прямой х = —Ь/(2а)>
440	I. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
График функции у= ах2 + Ьх+ с, записанной в виде (1), может
быть получен из графика функции у = х2, следующими преобразова-
ниями:
а)	параллельным переносом г = (—Ь/(2а); 0);
б)	сжатием (или растяжением) к оси абсцисс в а раз;
в)	параллельным переносом г «== ( 0;--—----j .
Пример. Построить график функции
у = 2х2 + 2х+ 2,
Приведем квадратный трехчлен к виду (1):
f (х) = 2х* 4- 2х + 2 = г(х + -I-)2 +	•
График функции у = 2х2 + х + 2 может быть получен из графика
функции у = х2 следующими преобразованиями;
а)	параллельным переносом г == (—1/2; 0);
б)	растяжением от оси абсцисс в 2 раза;
в)	параллельным переносом г =. (0; 3/2).
Результаты последовательного применения указанных преобразо-
ваний изображены на рис. П. 16—П. 19.
§ 6.	Степенная функция
Степенной функцией называется функция вида f (х) = х% где
а — любое действительное число, называемое показателем степени,.
Свойства степенной функции.
1)	Область определения —: множество всех положительных чисел»
Область изменения — множество всех положительных чисел.
2)	Степенная функция непериодична, не является четной и не
является нечетной.
3)	Степенная функция непрерывна во всей области определения.
4)	Степенная функция дифференцируема во всей области опреде-
ления, и ее производная вычисляется по формуле
5)	Степенная функция ха монотонно возрастает во всей области
определения при а > 0 и монотонно убывает при а < 0.
« 8. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
- 6) При а < 0 и а > 1 график степенной функции направлен вогну-
тостью вверх, а при 0 < а < 1 — вогнутостью вниз.
Графики степенной функции при а= 1/2, а== 5/2 и а = —3/2
приведены на рис, П. 20—П.22 *).
§ 7.	Показательная функция
Показательной функцией называется функция вида f (ж) = а*,
где а — некоторое положительное действительное число, называемое
основанием степени. При а = 1 значение показательной функции при
любом значении аргумента равно единице, и случай а « 1 далее не
будет рассматриваться.
Свойства -показательной
функции.
1)	Область определения — вся число-
вая прямая.
2)	Область изменения (множество зна-
чений) — множество всех положительных
чисел.
3)	Функция непрерывна и дифференци-
руема во всей области определения, ее про-
изводная вычисляется по формуле
Ш (о*)' = a* In а.	Рис- п-23-
4)	При а > 1 функция монотонно возрастает, при а < 1 монотонно
убывает.
5)	Показательная функция имеет обратную функцию, называемую
логарифмической функцией.
6)	График любой показательной функции пересекает ось Оу
в точке у = 1.
7)	График показательной функции — кривая, направленная во-
гнутостью вверх.
Графики показательной функции при значениях а ® 2 и а = 1/4
изображены на рис. П. 23.
§ 8.	Логарифмическая функция
Функцию, обратную показательной функции у = а*, называют
логарифмической и обозначают
^=loga*.
Число а называется основанием логарифмической функции. Логарифми-
ческую функцию с основанием 10 обозначают 1g х, а логарифмичес-
кую функцию с основанием е обозначают In х.
Свойства логарифмической функции:
1)	Область определения — промежуток (0, +оо).
2)	Область изменения (множество значений).— вся числовая
прямая.
•) Здесь степенная функция определяется только на положительной
полуоси. Степенную функцию при некоторых конкретных а можно опреде-
лить на всей числовой прямой*
442	И. СИСТЕМЫ СЧИСЛЕНИЯ
3)	Логарифмическая функция непрерывна и дифференцируема
во всей области определения, ее производная вычисляется по формуле
(loga*) =----:-----
' * х In а
4)	Логарифмическая функция монотонно возрастает, если а > 1,
и монотонно убывает, если 0<д< 1.
5)	Графики всех логарифмических функций проходят через точк?
с координатами (1; 0).
6)	При а> 1 график логарифмической функции — кривая, на*
правленная вогнутостью вниз; при 0 < а < 1 — кривая, направлен*
ная вогнутостью вверх.
Графики логарифмической функции при а = 2 и а = 1/3 изобра-
жены на рис. П. 24.
II. СИСТЕМЫ СЧИСЛЕНИЯ
Наряду с широко используемой десятичной позиционной системой
счисления, при работе на электронно-вычислительных машинах обычно
используются двоичные, восьмеричные, шестнадцатеричные (а также
смешанные) системы счисления. Излагая основные сведения о восьме-
ричных и двоичных системах счисления и способах перевода чисел
из одной системы счисления в другую, вместо слов «число, записанное
в десятичной (восьмеричной, двоичной) системе счисления», будем
просто говорить «десятичное (соответственно восьмеричное, двоичное)
число».
§ 1. Восьмеричная система счисления
В восьмеричной позиционной системе счисления для записи чисел
используются восемь различных цифр: 0, 1,2, 3, 4, 5, 6, 7. Число «во-
семь» записывается как 10. В восьмеричной позиционной системе счисле-
ния запись
(1)
где Дп, ДпЛ» •*а1> ао> а-1» • •«» a-h> • • •— цифры восьмеричной
системы счисления и хотя бы одна из цифр отлична от нуля, представ-
ляет собой сокращенную запись положительного числа а:
a sa Дд.д *	4* • * •	4“ До *^’4*	4"
4“ • • • 4~	.8~* 4" * • •	(2)
$ I. ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
443
Для записи отрицательного числа —а перед последовательностью
цифр (1) ставят знак минус. Все понятия, введенные для десятичных
дробей, являющихся формой записи чисел в десятичной позиционной
системе счисления, дословно переносятся и на выражения вида (1),
которые можно назвать восьмеричными дробями.
Правила перевода десятичных чисел в
восьмеричные.
Перевод целой части числа. Разделим целую часть
десятичного числа на число 8. Цифра, полученная в остатке, есть по-
следняя цифра восьмеричной записи данного числа. Полученное част-
ное делим на число 8; цифра, являющаяся остатком,— предпоследняя
цифра восьмеричной записи числа. Продолжая процесс деления полу-
чаемых частных, последовательно выписываем цифры восьмеричной
ваписи числа. Процесс деления прекращается, когда в частном полу-
чится цифра, меньшая 8, которая будет первой цифрой восьмеричной
записи данного числа.
Пример 1* Записать десятичное число 201 в восьмеричной си-
стеме счисления:
201 I 8
16 I	251 8
41	24 j 3
40	1
1
Процесс деления частных закончен на числе 3, так как 3 < 8.
Десятичное число 201 в восьмеричной системе счисления записывается
как 311.
Перевод дробной части числа. Умножаем дробную
часть числа на 8. Целая часть произведения является первой цифрой
после запятой в восьмеричной записи дробной части числа. Умножая
дробную часть полученного произведения на 8, получаем число, целая
часть которого — вторая цифра восьмеричной записи дроби. Процесс
умножения продолжается до тех пор, пока дробная часть произведения
не будет состоять из одних нулей, либо до тех пор, пока не получим
требуемого количества цифр восьмеричной записи дробной части числа.
При этом может оказаться, что конечная десятичная дробь записывается
в виде бесконечной периодической восьмеричной дроби (см. пример 3).
Пример 2. Записать десятичное число 0,1875 в восьмеричной
системе счисления.
Процедуру умножения изобразим в виде двух столбцов чисел,
где левый столбец — целая часть числа, которая при выполнении сле-
дующего умножения заменяется на нуль;
X	0	1875 8
	1	5000
X		8
	4	0000
И. СИСТЕМЫ СЧИСЛЕНИЯ
444
Десятичное число 0,1875 записывается в виде восьмеричной
дроби 0,14.	1
Пример 3. Записать десятичную дробь 0,3 в восьмеричной |
системе счисления.
Перевод десятичной дроби 0,3 в восьмеричную систему счисления Л
будет осуществляться так же, как и в предыдущем примере;	;
2
X
• 3
X
8
2
8
6
Нетрудно заметить, что начиная с шага умножения, отмеченного
второй звездочкой, в левом столбце будет появляться комбинация
цифр 3146, представляющая собой период восьмеричной дроби. Таким
образом, десятичная дробь 0,3 в восьмеричной системе счисления запи-
сывается в виде бесконечной периодической дроби 0,2 (3146).
Перевод чисел, записанных в восьмеричной системе счисления
в десятичную систему обычно производят с помощью формулы (2).
Пример 4. Записать восьмеричное число 163,2 в десятичной
системе счисления.
В согласии с формулой (2) запись 163,2 есть сокращенная запись
числа
I-82 + 6-8* + 3-8»-f-2.8"» = 64-Ь 48-f-3 4-«
=, 64 4-48 4-3 4-0,25 — 1 !5,25.
Таким образом, восьмеричное число 163,2 в десятичной системе
счисления записывается как 115,25,
с 5. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
§ 2., Двоичная система счисления
В двоичной позиционной системе счисления для записи чисел
используются два символа (цифры) — 0 (нуль) и 1 (единица). Число
«два» в двоичной системе счисления записывается как 10. В двоичной
системе счисления запись
о-пвп-л • • •	a-i • • • a-h • • •»	(3)
где ani an_i, . . ., alt а^, a_lt ...» а_л, ... — цифры двоичной си-
стемы счисления (0 или 1) и хотя бы одна из цифр отлична от нуля,
представляет собой сокращенную запись положительного числа а:
а = an.2" + an_v2n-’ + ... + fli-21 + «0-2° + а_^-} +
+ "+в_й-2-*+...	(4)
Для записи отрицательного числа —а перед последовательностью
цифр (3) ставится знак минус. Все понятия, вводимые для десятичных
дробей, дословно переносятся на выражения вида (3).
Двоичные таблицы сложения и умножения имеют вид;
Таблица сложения Таблица умножения
0 + 0=0	ОХ 0 = 0
0+1 = 1	Ох 1 = 0
1+0=1	' ,	1X0=0
1 + 1 = 10	1x1 = 1
Правила перевода чисел десятичной системы счисления в двоичную
аналогичны правилам перевода из десятичной системы счисления
в восьмеричную.
Пример 5. Записать десятичное число 19 в двоичиои системе
счисления:
19 |	2
18 I	<Г	2~
1	8	4	I	2
\	4	I	2 12
0 2J 1
0
Таким образом, число 19 в двоичной системе счисления записы-
вается как 10011.
Перевод чисел из десятичной системы счисления в двоичную можно
произвести и другим способом. Этот способ основан на том, что между
числами 0, 1,2, 3, 4, 5, 6, 7 и двоичными числами, состоящими из трех
цифр, существует взаимно однозначное соответствие, а именно, пере-
численные числа в двоичной системе счисления записываются соот-
ветственно как
000, 001, 010, ОН, 100, 101, ПО, 111. •
Основываясь на существовании такого соответствия десятичное
число удобнее переводить в двоичную систему в два этапа: сначала
еаписать десятичное число в восьмеричной системе счисления; потом
446	П- СИСТЕМЫ СЧИСЛЕНИЯ
каждую восьмеричную цифру заменить соответствующей группой из
трех двоичных цифр.
Пример 6. Записать десятичное число 201, 1875 в двоичной
системе счисления.
Данное десятичное число в восьмеричной системе счисления за-
пишется как 311,14 (см. примеры 1, 2). Каждую цифру восьмеричного
числа 311,14 заменяем группой из трех двоичных цифр:
3-> ОН; 1	001; 4» 100.
В результате восьмеричное число 311,14 в двоичной системе счисле-
ния записывается в виде
011 001 001, 001 100.
Отбрасывая нули, стоящие в начале целой и конце дробной части
двоичного числа, окончательно получаем, что десятичное число 201,
1875 записывается в двоичной системе счисления в виде 1100,1001,
ООН.
Перевод чисел из двоичной системы счисления в десятичную удобно
производить с помощью формулы (4).
Пример 7. Записать двоичное число 10110.11 в десятичной
системе счисления.
В согласии с формулой (4) запись 10110,11 есть сокращенная запись
числа
Ь24 + 0-23+ 1-22+ 1-24-0-20+ 1.2“1+ 1-2~2«»
1 I	ч
«16 + 4 + 2 + — + —«22 + ^ = 22,75.
Итак, двоичное число 10110,11 в десятичной системе счисления
записывается как 22,75,
ОСНОВНЫЕ ФОРМУЛЫ
Действительные числа
Арифметические действия с рациональными дробями:
т	р__тд-\-пр	.
п ‘	q	nq	’
т Р — mq— пр .
~	q	—	nq	*
m	р	__	т-р	в
п	q	~	n-q	’
т	р	 mq
п	пр
. Формула обращения бесконечной периодической дроби в раци*
овальную:
О» . nk (rtfc+i .. < ПА+р) =
X— * * * nknk+l » « « ^й-4-Р —Jhn% • » • nk
= .	10*(10р—1)
Абсолютная величина (модуль) действительного числа:
|а| =
а, если а > О,
О, если fl = О,
а9 если а < О,
Степени и логарифмы
Степени:
flo = 1 (а 0):
ах

(ах)У =
(a*b)x = ax»bxi
а \* __ ах
Ь } ьх '
448	ОСНОВНЫЕ ФОРМУЛЫ
Логарифмы!
loga а да 1 (а > 0» а & 1);
logefa^^fe (о>0,
loga (AliAf») » loga Aft + loga Al2 (Aff > 0,
loga (-^) e 10&* № — toga № 0*1 > °| M* > O^-
toga (bc) да c loga b;
logfttf .	«	1
loga C =3 T~-— ; loga c =	.
logb a 60 logc a
Пропорции:
а с _	.	.
-г- = -j- <=r* ad = be;
b d
a±b	cdzd	a — b	c — d
—~— = —~~ ,	- v r e TTT (производные пропорции),
b	a	u “t” О	C -p a
Комплексные числа
Сумма, разность, произведение и частное комплексных чисел да
да ах +- bti и z2 = a, + b^i;
«1 + *2 == (Oi + Of) + (bi + bt) i;
~ 4 =* (at — a*) + (bi — b8) i;	;
Zj-Zg = (^1^2 — bibs) + (aibf + o2bi) ft
aiO2 + bib8 । Ogbi — Oib2 i
21-zi="l’-gl-+ ^+>2 •
Тригонометрическая форма записи:
i =» a + bi да r (cos <p + i sin <p),
где r = l/’a2 + b2 — модуль комплексного числа, <p — аргумент,
определяемый из условий
.	b	а
sin ф == —.., cos ф — —.................-.
/а»4-д»	т 1<а« + *а
Произведение и частное комплексных чисел	(cos q>t +
+ i sin фО и z2 = r2 (cos ф2 4- i sin ф2):
21-2» = rVft [cos (q>! 4- <Pi) + I sin (Ф1 + Фа)]?
21; 2» - -9“ (cos (Ф1 — Ф») + i sin (q>! — <p^ 1.
Формула Муавра вычисления n-й степени комплексного числа
g « г (cos ф + i sin ф):
=» rn [cos дф 4* i sin лф).
ОСНОВНЫЕ ФОРМУЛЫ
449
Алгебра
Формулы сокращенного умножения:
(х + с) (х — с) = х2 — г2;
(х + с) (ха — хс + с2) — х8 + f3;
(х — с) (х2 + хс + с2) ~ х? — с3.
Формулы Виета для корней приведенного квадратного уравнения
х2 + рх + q = 0 (р2 — 4g 0):
Xi +	== — р, xrx2 == q.
Корни квадратного уравнения ах2 + Ьх + с = 0:
Корни квадратного уравнения с четным вторым коэффициентом
ах2 + 2kx + с ~ 0:
—k ± Vk2 — ас
Xi 2 ------------------•
*	а
Корни приведенного квадратного уравнения х2 + рх + q = 0:
Формулы вычисления определителей второго и третьего порядка:
Цц 012 I
= а11'а22------------^12^2Ъ
a2i ^22 I
аИ	012	<213	
а21	022	fl23	= 011022ЛЗЗ +	2023^31 +
аз1	Д32	а33	
+ ^13^21^32 --Д13а22а31 -^12^21^33 -аИа32а2&
Решение системы двух линейных уравнений с двумя неизвестными
ЯцХ + 012р = bit
^21Х 4“ а22У == Ь%
записывается в виде (А =/= 0):
	1 bi 012 I	I ац bi	
Ах _	1 b2 022 1		 Ау 		1 Oil bi	
д —	0ц 012 I ’	А	0ц 012	•
	021 022 1	021	^22	
Решение системы трех линейных уравнений с тремя неизвестными
0цХ + а12у + a13z = bit
tyftX “Н &22У	^23^	^2»
0з1Х + а32у + 0зз? = &S
15 А. Г. Цыпкин
450
ОСНОВНЫЕ ФОРМУЛЫ
ааписывается в виде (Д 0):

г
Г =Й
	bl	012	013
		022	023
^x 		&3	082	033
A	an	012	013
	021	022	023
	031	032	0зз
	0ц	bl	013
	021	b2	023
		031	Ьз	033
A	0Ц	012	013
	021	022	023
	031	032	038
	011	012	bi
	021	022	Ьз
	031	032	Ьз
Д	011	012	013
	021	022	023
	031	032	038
Простейшие неравенства:
|0
Ч—— > 2 (д и & — числа одного знака)
b а
(а > о, 6 > 0).
Геометрия
Треугольник.
Площадь треугольника:
о 11.	1 Lt. Il
5 = —aha = -у bhb = -у chc;
S = Ир (P — 0) (P — b) (p — c)
C 1 L .
S = — ab sin y;
(формула Герона)\
основные формулы
451
„ _ abc .
S-~4R-’
S = pr.
Здесь a, bt c — стороны треугольника, hat hb, hc — высоты, p =
= _1_ (a + b + с) — полупериметр, R — радиус окружности, описан-
ной около треугольника, г — радиус окружности, вписанной в тре-
угольник, у — угол, лежащий между сторонами а и д.
Равносторонний треугольник.
Площадь треугольника:
„ аг/3
5 "	4	’
где а — сторона.
Радиус вписанной окружности:
	3	’
Радиус вписанной окружности:
аКз
Т 6 *
Прямоугольный треугольник,
Площадь треугольника:
s = 4’a6'
где a, b — катеты.
Радиус описанной окружности:
Я = -у- =
где с — гипотенуза, тс — медиана, проведенная к гипотенузе.
Теорема Пифагора:
а2 + 6? = А
Параллелограмм.
Площадь параллелограмма:
S = ab sin у,
S == aha;
где a, Ь — стороны, у — угол, ha — высота, опущенная на сторону ar
Связь между сторонами и диагоналями параллелограмма:
d% + d% ~ 2 (a? + b2) (di и - диагонали).
Ромб.
Площадь ромба:
S = a2 sin у = ah = -L-drftf
где а — сторона ромба, у — угол, h — высота, df и d2 — диагонали.
15*
452
ОСНОВНЫЕ ФОРМУЛЫ
Связь между сторонами и диагоналями:
+ dl = 4а2.
Прямоугольник и квадрат.
Площадь прямоугольника:
S = ab,
где а и b — смежные стороны прямоугольника.
Площадь квадрата:
S = a2t
где а — сторона квадрата.
Трапеция.
Площадь трапеции:
где а и Ъ — основания трапеция, h — высота трапеции.
Круг и окружность.
Площадь круга радиуса г:
S пгК
Длина окружности радиуса г:
I = 2лг.
Площадь сектора с угловой величиной дуги а°:
е	лг2а
5ceKT = "W
Многоугольник.
Площадь правильного n-угольника равна половине произведения
его периметра Рп на радиус вписанной окружности г;
Sn в Рд^.
Площадь правильного п-угольника:
с 1 п9 • 360°
S^ — R2n sin----------------------,
2	п 9
где R — радиус описанной окружности.
Призма.
Площадь боковой поверхности:
«$бок = Рп | Л^Л2 I»
где Рп — периметр перпендикулярного сечения призмы, | AtA21 —
длина бокового ребра.
Объем призмы:
5п|Л1Д2|,
где Sn — площадь перпендикулярного сечения призмы, | Л1Л21 —
длина бокового ребра,
ОСНОВНЫЕ ФОРМУЛЫ
453
ИЛИ
V= S0CnH,
где Soch — площадь основания призмы, Н — высота призмы*
Параллелепипед и куб.
Объем прямоугольного параллелепипеда;
V = abc
(а, Ь, с — измерения параллелепипеда)*
Объем куба:
а3
(а — измерение куба).
Пирамида.
Площадь боковой поверхности правильной пирамиды!
S=-Lph,
где Р — периметр основания пирамиды, h — апофема.
Объем пирамиды:
v= _L sh,
о
где S — площадь основания пирамиды, Н — высота пирамиды.
Усеченная пирамида.
Площадь боковой поверхности правильной усеченной пирамиды:
S = -L(P+p)h,
где Р, р — периметры оснований пирамиды, h — апофема.
Объем усеченной пирамиды:
V=-Lw(Si+/S^+S2),
о
где Н — высота усеченной пирамиды, Si и <$2 — площади оснований
усеченной пирамиды.
Цилиндр.
Объем цилиндра:
V = лР2Я,
где R — радиус основания цилиндра, Н — высота цилиндра.
Площадь боковой и полной поверхности цилиндра:
•$бок ~
•$цил — 2nRH + 2лР2;
где R — радиус основания цилиндра, Н — высота цилиндра*
Конус.
Объем конуса:
Vkoh= -^л/?2Я,
Где R — радиус основания конуса, Н — высота конуса*
454
ОСНОВНЫЕ ФОРМУЛЫ
Площадь боковой поверхности конуса:
•^бок = nRL,
где L — образующая конуса.
Усеченный конус.
Объем усеченного конуса:
У=-1-пЯ(*?+
где Н — высота усеченного конуса, /?х и R2 — радиусы верхнего и
нижнего оснований усеченного конуса.
Площадь боковой поверхности усеченного конуса;
<$бок = л (At + ^2) ^9
где L — образующая усеченного конуса.
Сфера и шар,
Площадь сферы радиуса R-.
S = 4nR2.
Объем шара радиуса R:
V=
о
Тригонометрия
( sin? а + cos? а =
tgactga=*l; X
S 1 + tg2 a = —; J
s * cos2 a j
1 + etg? a = —Д
& sm2a *
sin (a ± P) = sin a cos P ± cos a sin P;
cos (a ± P) = cos a cos P T sin a sin P;
g ±	1 =F tg a tg p"
> sin 2a = 2 sin a cos a;
cos 2a = cos2 a — sin2 a= 1
tg2a= 2J£^;
1 — tg2 a ’
1 + cos a = 2 cos2 —; 1
— 2 sin2 а= 2 cos2 а — 1}
~т~"
Д
_____________ л • а ОС
— cos а = 2 sin2 —;
1-tg2-^-
cos а =----------
1 + tg2-^-
2tg
sin а =-------
l+tg2-f
"-Ж-
ОСНОВНЫЕ ФОРМУЛЫ	455
sin а + sin р = 2 sin аcos - -%
•	а	п а + Р	. а —р
sm а —	sin	Р =	2 cos —sin —g-H
.	Q	о « + Р	а— р
cos а +	cos	Р =	2 cos ——-	cos —
а л • « + ₽ . а—В
cos а — cos р = —2 sin —sin —=
о . а + р . Р —а
= 2 sin sin ;
.	. Q sin (а ± Р) ,	, о sin (Р ± а) .
tg а =Ь tg Р =---—ctg а ± ctg В = . г . ~;
6 = ь	н cos	а cos Р	6	5 н	sm	а	sm	Р
sin а sin	Р =	[cos	(а	—	Р) —	cos (а +	Р) ];
cos а cos	Р = Ц-	[cos	(а	—	Р) +	cos (а +	Р) ];
sin а cos	р = -i-	[sin	(а	—	Р) +	sin (а +	Р) ].
Теорема синусов:
—= - JL- =	= 2/?.
sin а sin р sm у
Теорема косинусов:
а2 = Ь2 + <? — 2bc cos а;
Ь2 = а2 + с2- — 2ас cos Р;
с2- = Ь2 + а2 — 2ab cos у
(а, bt с — стороны треугольника, лежащие против углов а, р, у
соответственно, R — радиус описанной окружности).
Метод координат
Расстояние между точками А (х^ В (х2; ^2):
I АВ | =
Уравнения прямой:
1)	Ах+ Ву+ С= 0;
2)	у = kx + b (k — угловой коэффициент прямой);
х и
3)	+ -у- = 1 (уравнение прямой в отрезках).
456
ОСНОВНЫЕ ФОРМУЛЫ
Условие параллельности прямых у = k±x + bi и ==/?$* + b2i
ki — k2.
Условие перпендикулярности прямых:
ki*k2 ““I*
Угол между прямыми:
, I kl kz I
a=arctg|TTO7|-
Расстояние d от точки М (х0; yQ) до прямой Ах + By + С = 0:
d = । ^х°	।
/ Л2 + В2
Уравнение окружности с центром в начале координат радиуса /?:
хЗ+р2=з №.
Уравнение окружности с центром в точке Мо (а, Ь) радиуса №.
(х-а)2+(у-^)2 = №.
Каноническое уравнение эллипса:
£,£_1
а^+ b2 - '•
Каноническое уравнение гиперболы:
X2	У2 _ 1
а2	Ь2
Каноническое уравнение параболы:
У* — 2рх.
Уравнение плоскости:
Ах + By + Cz + D = 0.
Расстояние d от точки М (х0; Уо', Zq) до плоскости?
d = 1 ^х°	^z°
~	/ Л2 + ^2 Ч-С2
Уравнение сферы радиуса R с центром в точке М (а; Ь; с):
(х-а)2+ (у-Ь)2+ (z-c)2== Я?.
Векторы
Модуль вектора а = (xf, у^ zj:
la| =	+ +
ОСНОВНЫЕ ФОРМУЛЫ
457
Скалярное произведение векторов а и Ы
(а, ь) = I а I • | Ь | cos (а?6).
Скалярное произведение векторов, заданных координатами:
(a, b) =	+ yty2 + ziza.
Арифметическая прогрессия.
Формула n-го члена и сумма первых п членов:
л „ । А (п n с	(л — 0 „
fln = + «(л — О, on ------g-----Пл
Геометрическая прогрессия.
Формула n-го члена и сумма первых п членов:
и	<г - “’О—<Г)
«п = Wi? , On -----]”~q-•
Сумма членов бесконечно убывающей геометрической прогрессии;
Пределы.
.. sinx ,
hm—— = 1;
*->о х
lim (1 -|-х) х = е;
х->о
г аХ-1	1	.
lim----------- In а;
х-*о х
V logfl(l+x) .
hm — -	= loga е;
х-»0 х
.. In (14-х)	.
hm—-—!~ = 1.
Уравнение касательной к графику функции у = / (х), проходя-
щей через точку (х0; у0)> принадлежащую графику функции:
у — Уй = 1' (*о)(* — Хо).
458
ОСНОВНЫЕ ФОРМУЛЫ
Производные элементарных функций.
f (*)	f' (X)	f (X)	f' <x)
c	0	sin x	cosx
	axa“1	cosx	—sinx
nx	ax In a	tg*	1
a			COS2X
г	ex	ctgx	1
			sin2 x
logaX	1	arcsin x	1
	x In a		Kl-x2
In X	1	arccos x	1
	X		JA1 — x*
		arctg x	1
			
		arcctg x	1
			l + *a
Формула Лейбница,
а г)<п) = c®Z<n)g(0) + c^-^g1 + • • • +	+ cnnf^g^.
Достаточное условие существования экстремума функции в ста-
ционарной точке х0 (f' (х0) = 0):
1) если	f (х0) > 0,	то	в	точке	х0 — минимум;
2) если	f (х0) <0,	то	в	точке	х0 — максимум.
Неопределенные интегралы.
Jo«dx=C;	j sin х dx = —cos х	+ С;
J	1 -dx = х +	С;	J cos х dx = sin	x +	C;
C	xa+1
J^=T+r+c
—cts*+C:
ОСНОВНЫЕ ФОРМУЛЫ	459
Формула Ньютона — Лейбница:
ь
\f(x)dx=F(b)-F(a),
а
где F (х) — первообразная функции f (х).
Формула вычисления площади криволинейной трапеции, ограни-
ченной графиком неотрицательной функции / (х), осью Ох и прямыми
х = а и х — Ь:
ь
S = j / (х) dx.
а
Формула вычисления площади боковой поверхности, полученной
в результате вращения вокруг оси Ох криволинейной трапеции, огра-
ниченной графиком функции у = f (х) и прямыми х = а и х = 6;
ь
S = 2л j f (х) г 1 + (/' (х))« dx.
а
Объем той же фигуры вращения вычисляется по формуле
ь
V = л j (/(х))2 dx.
а
Достаточное условие существования экстремума функции двух не-
зависимых переменных / (х; у) в стационарной точке (х0, у^ (f'x (х0; у0)=
= 0.	у0)=-оу.
1)	если ГххГуу — (Гхи)г > о и < 0 в точке (х0; у0}, то в точке
(х0; Уд — максимум;
2)	если fxxfyy	0 и f'xx > 0 в точке (х0; yQ)t то в точке
(х0; уд — минимум.
Комбинаторика
Факториал:
п\ =
Число перестановок из п элементов:
Число размещений из п элементов по т элементов!
лт___________________________п
п ~ (п — т)! *
Число сочетаний из п элементов по т элементов:
Ст___ п ’
п т\(п — т)\ *
460
ОСНОВНЫЕ ФОРМУЛЫ
Формулы для числа сочетаний:
Ст = Qn—m.
ед = С- + С-+’;
^ + Ci + Cn+2".
Бином Ньютона:
(а + Ь)п = С°а" + С^а^Ь Ч---1- С™а.п~тЬт + • • • + СппЬ\
Число перестановок с повторениями состава (fej, ...» km):
Сп (ki’ k...km} = •
Число сочетаний из tn элементов по п с повторениями:
еп _______________рт—1 ____рп
•т	1	1*
Вероятность
Формула условной вероятности двух зависимых событий:
Р (А-В) = Р (А)-Р (В/А) = Р (В)-Р (А/В).
Формула полной вероятности:
Р (А) = Р (A/BJ Р (Вх) + Р (A/BJ-P (В2) + ... + Р (А/Вь)- Р (Bk)t
где Blf В2, ...» Bft — полная группа несовместных событий, А — со-
бытие, наступающее при условии наступления какого-либо из собы-
тий Вх, В2, ..., Bfe.
Формула Бернулли:
Pm(„ = C^Pm.(l-P)^,
I.
ЛИТЕРАТУРА
Справочные и учебные пособия
Абрамович М. И., Стародубцев М. Т. Матема-
тика (алгебра и элементарные функции). — М.: Высшая школа, 1976.
Баранов И. А,, Богатырев Г. И., БоковневО. А.
Математика для подготовительных курсов техникумов на базе 8 классов
средней школы. — М.: Наука, 1982, 1983.
Болтянский В. Г., Сидоров Ю. В., Шабу-
нин М. И. Лекции и задачи по элементарной математике. — Мл
Наука, 1974.
Выгодский М. Я. Справочник по элементарной матема-
тике. — М.: Наука, 1982.
Говоров В. М., Дыбов П. Т., Мирошин Н. В.»
Смирнова С. Ф. Сборник конкурсных задач по математике. —
М.: Наука, 1983.
Делоне Б. Н., Житомирский О. К. Задачник по
геометрии. — М.: Физматгиз, 1959.
Дорофеев Г. В., Потапов М. К., Розов Н. X.
Пособие по математике для поступающих в вузы. — М.: Наука, 1976.
Задачи по элементарной математике/Лидский В. Б., Овсянни-
ков Л. В., Тулайков А. И., Шабунин М. И. — М.: Физматгиз, 1960.
Зайцев В. В., Рыжков В. В., С канав и М. И.
Элементарная математика. Повторительный курс. — М.: Наука, 1974.
Киселев А. П. Алгебра, ч. II. — М.: Учпедгиз, 1959.
Киселев А. П. Геометрия, ч. I. — М.: Учпедгиз, 1960;
ч. II. — М.: Просвещение, 1970.
Ко ж е у р о в П. Я. Тригонометрия. — М.: Физматгиз, 1963.
Кречмар В. А. Задачник по алгебре. — М.: Физматгиз, 1961.
Ларичев П. А. Сборник задач по алгебре. — М.: Учпедгиз,
1961.
Маркушевич А. И., Сикорский К. П., Черка-
сов Р. С. Алгебра и элементарные функции. — М.: Просвеще-
ние, 1968.
Математика для тех нику мов/Под ред. Яковлева Г. Н. Алгебра
и начала анализа, ч. I. Алгебра и начала анализа, ч. II. Геометрия. —
М.: Наука, 1981.
Моденов П. С. Задачи по геометрии. — М.: Наука, 1979.
Моденов П. С. Сборник задач по математике с анализом
решений. — М., 1959.
Моденов П. С., Новоселов С. И. Пособие по матема-
тике для поступающих в вузы. — М.: Изд-во МГУ, 1966.
Нестеренко Ю. В., Олехник С. Н., Пота-
пов М. К. Задачи вступительных экзаменов по математике. — М.:
Наука, 1983.
Панов Д. Ю. Счетная линейка. — М.: Наука, 1982,
462
ЛИТЕРАТУРА
Пособие по математике для поступающих в вузы/Под ред. Яко-
влева Г. Н. — М.: Наука, 1981, 1982.
Потапов М. К., Александров В. В., Пасичен-
к о П. И. Алгебра и анализ элементарных функций. — М.: Наука,
1981.
Рыбкин Н. Сборник задач по геометрии, ч. I. — М.: Учпедгиз,
1959; ч. II. — М.: Учпедгиз, 1960.
Рывкин А. А., Рывкин А. 3., Хренов Л. С. Спра-
вочник по математике. — М.: Высшая школа, 1975.
Сборник задач по математике для поступающих в вузы/Под ред.
Прилепко А. И. — М.: Высшая школа, 1983.
Сборник задач по элементарной математике/Антонов Н. П., Вы-
годский М. Я., Никитин В. В., Санкин А. И. — М.: Наука, 1979.
Сборник конкурсных задач по математике для поступающих во
втузы/Под ред. Сканави М. И. — М.: Высшая школа, 1980.
Справочник по элементарной математике для поступающих
в вузы/Под ред. Фильчакова П. Ф. — Киев: Наукова думка, 1973.
Фетисов А. И., Никитин Н. Н. Геометрия, ч. I. — М.:
Учпедгиз, 1956,
Хохлов А. И. Математические таблицы. — М.: Наука, 1980.
X у д о б и и А. И., X у д о б и н Н. И., Ш у р ш а л о в М. Ф.
Сборник задач по алгебре и элементарным функциям. Пособие для
учителей. — М.: Просвещение, 1970.
Цыпкин А. Г., Пинский А. И. Справочное пособие по
методам решения задач по математике для средней школы. — М.:
Наука, 1983.
к Ш а х н о К. У. Справочник по математике. — М.: Учпедгиз,
1961.
Ш а х н о К. У. Сборник задач по элементарной математике
повышенной трудности. — Минск: Вышейша школа, 1969.
Ш а х н о К. У. Элементарная математика для окончивших
среднюю школу. — Л.: Изд-во ЛГУ, 1976.
Яремчук Ф. П., Рудченко П. А. Алгебра и элемен-
тарные функции. Справочник. — Киев: Наукова думка, 1976.
Книги для углубленного изучения математики
Бабинская И. Л. Задачи математических олимпиад. — М.:
Наука, 1975.
Башмаков М. И. Уравнения и неравенства. — М.: Наука,
Бермант А. Ф., Люстерник Л. А. Тригонометрия. —
М.: Наука, 1967.
Васильев Н. Б., Гутенмахер В. Л. Прямые и кри-
вые. — М.: Наука, 1978.
Гельфанд И. М., Глаголева Е. Г., Кирил-
лов А. А. Метод координат. — М.: Наука, 1973.
Гельфанд И. М., Глаголева Е. Г., Шноль Э. Э.
Функции и графики. — М.: Наука, 1974.
Гнеденко Б. В., Хинчин А. Я. Элементарное введение
в теорию вероятностей. — М.: Наука, 1982.
Заочные математические олимпиады/Васильев Н. Б., Гутен-
махер В. Л., Раббот Ж. М., Тоом А. Л. — М.: Наука, 1981.
Зельдович Я. Б., Яглом И. М. Высшая математика для
начинающих физиков и техников, — М.; Наука, 1982»
ЛИТЕРАТУРА	4^з
Ивашев-Мусатов О. С, Начала математического ана-
лиза.— М.: Наука, 1981.
Кириллов А. А. Пределы. — М.: Наука, 1973.
Колмогоров А. Н., Журбенко Н. Г., Прохо-
ров А. В. Введение в теорию вероятностей. — М.: Наука, 19813.
Лурье М. В., Александров Б. И. Задачи на соста-
вление уравнений. — М.: Наука, 1980.
Математические соревнования.—М.: Наука, 1974.
Международные математические олимпиады/Морозова Е. А., Пе-
траков И. С., Скворцов В. А. — М.: Просвещение, 1976.
Никольский С. М. Элементы математического анализа. —
М.: Наука, 1981.
Петраков И. С. Математические олимпиады школьников. —
М.: Просвещение, 1982.
Погорелов А. В. Геометрия. — М.: Наука, 1983.
Погорелов А. В. Элементарная геометрия. — М.: Наука,
1977.
Понтрягин Л. С. Анализ бесконечно малых. — М.: Наука,
1980.
Понтрягин Л. С. Математический анализ для школьни-
ков. —-М.: Наука, 1983.
Понтрягин Л. С. Метод координат. — М.: Наука, 1977.
Тихонов А. Н., Костомаров Д. П. Рассказы о при-
кладной математике. М.: Наука, 1979.
Фаддеев Д. К., Соминский И. С. Алгебра.-—М.:
Физматгиз, 1960.
Хинчин А. Я. Восемь лекций по математическому анализу. —
М.: Наука, 1977.
Дополнительная литература
Абрамов С. А. Математические построения и программиро-
вание. — М.: Наука, 1977eJ
Абрамов С. А. Элементы программирования. — М.: Наука,
Александров П. С. Введение в теорию групп. — М.:
Ндука, 1980.
Александров П. С. Что такое неевклидова геометрия. —
М.: Изд-во АН СССР, 1950.
Бе киш ев Г. А., Кратко М. И. Элементарное введение
в геометрическое программирование. — М.: Наука, 1980.
Берман Г. Н. Циклоида. — М.: Наука, 1980.
Бескин Н. М. Деление отрезка в данном отношении. —
М.: Наука, 1973.
Бескин Н. М. Изображение пространственных фигур. — М.:
Наука, 1971.
Виленкин Н. Я. Комбинаторика. — М.: Наука, 1969.
Виленкин Н. Я. Рассказы о множествах. — М.: Наука,
1969.
Воробьев Н. Н. Признаки делимости. — М.: Наука, 1980.
Гарднер М. Математические чудеса и тайны. — М.: Наука,
1982.
Гельфанд А. О. Решение уравнений в целых числах. —
М.: Наука, 1983.
Гжегорчик А. Популярная логика. — М.; Наука, 1979,
464
ЛИТЕРАТУРА
Гильберт Д., Кон-Фосоен С. Наглядная геоме-
трия. — М.: Наука, 1981.
Градштейн И. С. Прямая и обратная теоремы. — М.:
Физматгиз, 1959.
Дубнов Я. С, Ошибки в геометрических доказательствах. —
М.: Наука, 1969.
Ежов И. И., Скороход А. В., Я дрен ко М. И.
Элементы комбинаторики. — М.: Наука, 1977.
Игнатьев Е. И. В царстве смекалки. — М.: Наука,
1983.
Калужнин Л. А., Сущанокий В. И. Преобразова-
ния и перестановки. — М.: Наука, 1980.
Клейн Ф. Элементарная математика с точки зрения высшей.
Т. I: М. — Л., 1934; Т. II: М. — Л., 1935.
Коксетер F. С. М., Грейтцер С. Л. Новые встречи
с геометрией. — М.: Наука, 1978.
Коровкин П. П. Неравенства. — М.: Наука, 1983.
К о с т о в с к и й А. Н. Построения одним циркулем. — М.:
Физматгиз, 1959.
К у н ц м а н Ж. Численные методы. — М.: Наука, 1979.
К у р о ш А. Г. Алгебраические уравнения произвольных сте-
пеней. — М.: Наука, 1983.
Л и т в у д Дж. Математическая смесь. — М.: Наука, 1978.
Литцман В. Теорема Пифагора. — М.: Физматгиз, 1960.
Маркушевич А. И. Возвратные последовательности. —
М.: Наука, 1983.
Маркушевич А. И. Замечательные кривые. — М.: Наука,
1978.
Маркушевич А. И. Замечательные синусы, — М.: Наука,
1974,
Маркушевич А. И. Комплексные числа и конформные
отображения. — М.: Наука, 1979.
Маркушевич А. И. Площади и логарифмы. — М,: Наука,
1979.
Маркушевич А. И. Ряды. — М.: Наука, 1978.
Мосте л лер Ф. 50 занимательных вероятностных задач
с решениями. — М.: Наука, 1975.
О р е О. Приглашение в теорию чисел. — М.: Наука, 1980.
П о й а Д. Математика и правдоподобные рассуждения. — М.:
Наука, 1975.
П о й а Д. Математическое открытие. — М.: Наука, 1976.
Радемахер Г., Теплиц О. Числа и фигуры. — М.:
Физматгиз, 1962.
Салтыков А. И., Семашко Г. Л. Программирование
для всех. — М.: Наука, 1980.
Солодовников А. С. Системы линейных неравенств. —
М.: Наука, 1977.
Соминский И. С. Метод математической индукции. — М.:
Наука, 1974.
Успенский В. А. Треугольник Паскаля. — М.: Наука,
1979.
Фомин С. В. Системы счисления. — М.: Наука, 1980.
Хинчин А. Я. Три жемчужины теории чисел. — М.: Наука,
1979.
Хинчин А. Я» Цепные дроби. — М.: Наука, 1978.
ЛИТЕРАТУРА	465
Шарыгин И. Ф., Берштейн А. 3. Задачи по геоме-
трии (планиметрия). — М.: Наука, 1982.
Широков П. А. Краткий очерк основ геометрии Лобачев-
ского. — М.: Наука, 1983.
Шклярский Д. О., Ченцов Н. Н., Яг л ом И. М.
Избранные задачи и теоремы элементарной математики. Арифметика
и алгебра. — М.: Наука, 1976.
Ш к у р б а В. В. Задача трех станков. — М.: Наука, 1976.
Штейнгауз Г. Задачи и размышления. — М.: Мир, 1974.
Ш т е й н г а у з Г. Сто задач. — М.: Наука, 1982.
Я г л о м И. М. Комплексные числа и их применение в геоме-
трии. — М.: Физматгиз, 1963.
Я г л о м И. М., Болтянский В. Г. Выпуклые фигуры. —
М.: Гостехиздат, 1951.
Журнал «Кван!» (выходит ежемесячно с 1970 года).

СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
[а, Ь] — закрытый промежуток (отрезок): точки (числа) а и b
принадлежат промежутку
(а; Ь] и [а; Ь) — полуоткрытые промежутки: точка а не при-
надлежит промежутку; точка b принадлежит промежутку; соответст-
венно, точка а принадлежит, а b не принадлежит промежутку.
(а; Ь) — открытый промежуток (интервал): точки а и b не при-
надлежат промежутку
=> — символ, означающий «следует в одну сторону»
*Ф=> — символ, означающий «следует в обе стороны»
Э —символы принадлежности ЙЗ
— символ «не принадлежит» 13 '
0 —символ пустого множества 13
(J — символ объединения множеств 14
Г) — символ пересечения множеств 14
\ — символ разности и дополнения множеств 15
~ — знак эквивалентности 18 (в геометрии — символ подобия) 260
{af, a2; ап}—множество, образованное из элементов alt
Un 13
(ax; a2; ап) — упорядоченное множество, образованное из эле-
ментов alt a2, ...» ап 16
f и f~*t g и g~* и т. д. — обозначения взаимно обратных отображе-
ний 17
— в теории множеств символ «не превосходит» 18
а! — обозначение произведения Ь2*3«...«л (читается «эн факто-
риал») 415
Рп — число перестановок из п элементов 415
С? или (	) — число сочетаний из п элементов по т элементов 419
п \т)
А™ — число размещений из п элементов по т элементов 418
Iatj || или (atj) или [аг-у] — матрица, составленная из чисел а// 137
aij | или det || dij || — определитель квадратной матрицы || dt] || 143
N — множество всех натуральных чисел 27
Z — множество всех целых чисел 35
Q — множество всех рациональных чисел 45
R — множество всех действительных чисел 58
{/и, п} или НОК — наименьшее общее кратное чисел иг и п 31
(т, п) или НОД — наибольший общий делитель чисел т и п 32
— символы «больше», «меньше», «больше» или «равно»,
«меньше или равно» 29, 151
| а | — абсолютное значение (модуль) действительного числа 35
— корень л-й степени 64
— квадратный корень 64
loga М — логарифм числа Л1 по основанию а 65
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
467
lg Л4 — логарифм числа М по основанию 10 65
In М — логарифм числа М по основанию е 65
Nt П]П2 ... nk ... — десятичная дробь с целой частью W 47
N, ... tik (fik+i ... Uk+p) —десятичная дробь с периодом
лд+1 ... лл+р 48
z и z — комплексно сопряженные числа 81
i — мнимая единица 79
Re г — действительная часть комплексного числа г 79
Im z — мнимая часть комплексного числа z 79
| z | —• модуль комплексного числа z 85
Arg z — аргумент комплексного числа г 85
i>j — базисные векторы прямоугольной декартовой системы коор-
динат на плоскости 272
Л /» А? — базисные векторы прямоугольной декартовой системы
координат в пространстве 276
I а | — длина вектора а 286
(а, Ь) — угол между векторами а и Ь 290
(а, Ь) — скалярное произведение векторов а и b 290
— символ угла 175
° — градус 176
9 — минута 176
* —секунда 176
АВС — величина угла ^АВС 177
|| —символ параллельности 177
I —символ перпендикулярности 178
xi(a, а) — угол между прямой а и плоскостью а 182
xi(a, Р) — угол между плоскостями а и р 182
—АСВ— руга, с концами А и В 195
АСВ — угловая величина дуги АСВ 195
— поворот плоскости вокруг центра О на угол а 231
Zo — центральная симметрия плоскости с центром О 231
Si — осевая симметрия пространства (плоскости) с осью симме-
трии I 232
Sa — симметрия пространства относительно плоскости a 233
sin a — синус a 242 л
cos a — косинус a 242
tg a — тангенс a 242
etg a — котангенс a 242
sec a — секанс a 243
cosec a — косеканс a 243
arcsin a — арксинус числа a 248
arccos a — арккосинус числа a 249
arctg a — арктангенс числа a 250
arcctg a — арккотангенс числа a 250
(an) — последовательность с членами a2, ant ... 295
lim — символ предела 300, 329
Дх — приращение аргумента 344
Д/ — приращение функции 344
f (х) или ------первая производная функции f (х) 345
dnf
fn) (х) или —-----n-я производная функции / (х) 352
468	СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
d — символ дифференциала 355
fx (*о* #о) и fy (хо* #о) частные производные по х и по у от функ-
ции двух переменных соответственно в точке (хь,
I — символ неопределенного интеграла 368
4
J — символ определенного интеграла 381
а
max — максимум
min — минимум
Число а= 2,718281828 ...
Число л = 3,141592653 (л — отношение длины окружности
к диаметру)
Число М (модуль перехода) = 0,434294481	376
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная величина (модуль)
действительного числа 62
~ — целого числа 35
— погрешность 71
----- предельная 72
Абсцисса точки 273, 276
Аксиома измерения (Архи-
меда) 239
— линейной полноты 239
Аксиомы арифметики 29
— геометрии 236
— конгруэнтности 237
— непрерывности 239
— порядка 237
— принадлежности 236
Алгебраическая дробь непра-
вильная 103
----- правильная 103
-----простейшая 104
----- рациональная 100, 101
Алгебраическое выражение 88
-----иррациональное 105
----- рациональное 100
— уравнение 109
— число 69
Алгоритм jЕвклида нахождения
НОД двух многочленов 93
------------ чисел 33
Амплитуда колебания 398
Апофема правильного много-
угольника 198
— правильной пирамиды 218
-----усеченной пирамиды 219
Аппликата точки 276
Аргумент комплексного числа 85
Арифметическое действие над
конечными десятичными дро-
бями 49
Арифметические неравенства 151
Арифметический корень 64
Арккосинус 249
Арккотангенс 250
Арксинус 248
Арктангенс 250
Асимптоты 363
Базисные векторы в простран-
стве 276
---на плоскости 272
Бесконечная десятичная дробь
47
— числовая последовательность
295
Бесконечно большая величина
337
— малая величина 337
Бесконечное множество 19
— произведение 317
Биекция 18
Биквадратное уравнение 113
Бинарная операция 21
Бином Ньютона 420
Биномиальные коэффициенты 420
Биссектриса треугольника 187
— угла 175
Боковая грань призмы 216
— поверхность конуса 223
--- призмы 216
--- цилиндра 222
Боковое ребро пирамиды 218
---призмы 216
Боковые стороны трапеции 191
Вектор 285
—	нулевой 286
—	свободный 286
—	связанный 286
—	скользящий 236
Векторное произведение 293
Векторы коллинеарные 289
—	компланарные 289
Верная цифра приближенного
значения числа 73
Вероятность 426
—	произведения событий 427
—	суммы событий 428
Верхняя подходящая десятич-
ная дробь 56
Вершина многогранника 215
—	многогранного угла 214
470
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вершина многогранной поверхно-
сти 215
—	параболы 284
—	пирамиды 218
—	угла 175
Вершины гиперболы 282
—	многоугольника 183
—	призмы 216
—	эллипса 280
Взаимно обратные функции 327
—	простые многочлены 90
	--числа 32
Вневписанная окружность 199
Внешние накрест лежащие
углы 177
Внешний угол многоугольни-
ков 184
Внешняя касательная двух
окружностей 194
—	область многогранника 215
----- угла 175
Внутренние накрест лежащие
углы 177
—	точки отрезка 175
Внутренний угол многоуголь-
ника 184
Внутренняя касательная двух
окружностей 195
—	область многогранника 215
-----многогранного угла 214
----- угла 175
Вогнутость кривой 362
Возвратное уравнение 114
Возрастающая последователь-
ность 298
—	функция 326
Вписанный многоугольник 197
—	треугольник 198
—	четырехугольник 199
Выделение целой части алгебра-
ической дроби 103
Выпуклый многогранник 215
—	многогранный угол 214
—	многоугольник 184
Высота конуса 223
—	пирамиды 218
—	призмы 216
—	треугольника 187
—	усеченной пирамиды 219
Высота цилиндра 222
— шарового сегмента 226
----- сектора 227
----- слоя 227
Вычисление производных эле-
ментарных функций 349
Вычитаемое 28
Вычитание дробей 40, 41
— чисел комплексных 80
---- натуральных 28
----рациональных 44
----целых 36
Гармонический ряд 314
Геометрическое изображение
комплексных чисел 83
----множество решений не-
равенства с двумя неизвестны-
ми 162
Гипербола 281
—, директриса 283
—, каноническое уравнение 282
—	, фокус 281
—	, эксцентриситет 283
Гипотенуза 188
Гомотетия плоскости 234
—	пространства 235
Горнера схема 93
Градус 176
Граница области 406
Грань двугранного угла 182
—	многогранника 215
—	многогранного угла 214
—	многогранной поверхности 215
—	пирамиды 218
—	призмы 216
График функции 321
Группа 23
Двугранный угол 182
Двучленное уравнение 115
Действительная часть комплекс-
ного числа 79
Действительные числа 58
Деление десятичных дробей 50
—	многочленов 91
—	рациональных дробей 42
— чисел комплексных 80
----натуральных 28
----рациональных 44
----целых 37
Делимое 28
Делитель 28
Десятичная дробь 47
---- бесконечная 47
Десятичная дробь допустимая 48
---- конечная 47
---- периодическая 48
----подходящая 56, 61
— система счисления 46
ПРЕДМЕТНЫЙ
Десятичное представление дей-
ствительного числа 61
Диагональ многогранника 215
—	многоугольника 184
Диаметр окружности 193
—	сферы 225
Директриса параболы 284
Директрисы гиперболы 283
— эллипса 281
Дискриминант квадратного трех-
члена ПО
Дифференциал 355
—, геометрическая	интерпрета-
ция 356
—, инвариантность 357
Дифференциальное уравнение
Бернулли 396
---линейное 395
—------с постоянными коэффи-
циентами 399
--------------, однородное 400
--------------, частное ре-
шение 401
---, метод вариации постоян-
ных 403
---, однородное 394
---, с разделяющимися перемен-
ными 393
---, теорема существования и
единственности решения 391,397
Длина дуги окружности 197
— окружности 197
Додекаэдр 221
Дополнение множества 15
Дополнительные углы 177
Дополнительный множитель 106
Допустимые десятичные дроби 48
— значения переменной 100
Достоверное событие 424
Дроби десятичные 47
—	неправильные 43
—	непрерывные 56
—	несократимые 43
—	отрицательные 42
—	положительные 42
—	правильные 43
—	рациональные 47
—	смЛианные 43
Дробно-линейная функция 437
Дробно-линейное неравенство 156
Дуга окружности 195
Единичная окружность 241
Единичный вектор (орт) 271
УКАЗАТЕЛЬ	47|
Замкнутая ломаная 183
Замкнутый круг 406
Звенья ломаной 183
Знаки неравенства 151
Знаменатель дроби 40
Значащая цифра приближенного
значения числа 72
Значащие цифры десятичной
дроби 47
Золотое сечение 413
Извлечения квадратного корня
из действительного числа 76
Измерения параллелепипеда 217
Изометрия 230
Изоморфизм 22
Икосаэдр 221
Интеграл неопределенный 368
—	определенный 381
—	с переменным верхним преде-
лом 384
Интегральная кривая 391
—	сумма 381
Интегрирование, метод замены
переменной 373
—	, — интегрирования по ча-
стям 370
—	, подстановки Эйлера 377
Интервал 466
Иррациональное выражение 105
—	неравенство 158
—	уравнение 118
—	число 58, 66
Исключение иррациональности
из числителя (знаменателя)
дроби 106
Испытание 423
Исход 423
Каноническое разложение на-
туральных чисел 31
— уравнение гиперболы 282
--- параболы 284
--- эллипса 280
Касательная к окружности 193
Катет 188
Квадрант 243
Квадрат 191
Квадратичная функция 438
Квадратное неравенство 155
— уравнение ПО
Квадратный многочлен 88
Классификация разрывов функ-
ции 343
472
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Коллинеарные векторы 289
Кольцо 24
Компланарные векторы 289
Комплексно сопряженные числа
81
Комплексное число 79
----, аргумент 85
----, возведение в степень 86
----, геометрическое изображе-
ние 83
(----,	действительная и мнимая
части 79
----, извлечение корня 86
Комплексное число, модуль 85
----, тригонометрическая форма
85
Композиция преобразований 230
Конечная непрерывная дробь 56
Конечное множество 19
Конус 223
— усеченный 224
Координатная ось 271
— плоскость 272
Координаты вектора в простран-
стве 292
----на плоскости 291
—	точки в пространстве 276
----на плоскости 273
Корень из действительного
числа 64
—	многочлена 95
—	уравнения 109
Косеканс 243
Косинус 242
Кососимметрическое уравнение
114
Котангенс 242
Коэффициент гомотетии 234, 235
— подобия 235
Коэффициенты уравнения 108,
109
Кратный корень многочлена 95
Криволинейная трапеция 380
Критерий Коши 334
Критические точки функции 359
Круг 193
Куб 218
Кубический многочлен 88
Лексикографический способ за-
писи многочлена 99
Линейная система уравнений
129
— функция 435
Линейное уравнение ПО
Линейный многочлен 88
—	угол двугранного угла 183
Линия центров 194
Логарифм 65
—	десятичный 65
—	натуральный 65
Логарифмическая функция 441
Логарифмическое неравенство
—	уравнение 126
Ломаная 183
—	замкнутая 183
—	простая 183
Луч 173
Максимум функции 358, 410
Математической индукции ме-
тод 412
--- принцип 412
Матрица 137
Мгновенная скорость 347
Мгновенное ускорение 353
Медиана 186
Метод Гаусса 129
—	дополнительного угла 262
—	интервалов 156
—	касательных (метод Ньютона)
74
—	математической индукции 412
Минимум функции 358, 410
Минор 144
Мнимая единица 79
—	часть комплексного числа 79
Многогранная поверхность 215
Многогранник 215
—	правильный 200
Многоугольник 183
—	, вписанный в окружность 197
—	выпуклый 184
—	, описанный около окружности
197
—	правильный 185
Многочлен (полином) 88, 98
—	квадратный 88
—	кубичный 88
—	неприводимый 98
—	однородный 99
—	, разложение на множители 97
Многочлены взаимно простые 90
Множества бесконечные 19
—	конечные 19
—	несчетные 20
—	равные 14

ПРЕДМЕТНЫЙ
Множества счетные 19
—	упорядоченные 16
—	эквивалентные 18
Множество 13
— допустимых значений не-
известной 108
— значений функции 320, 405
—	пустое 13
Множитель дополнительный 106
Модуль вектора 285
—	действительного числа 62
—	комплексного числа 85
Монотонные последовательности
298
—	функции 326
Наибольшее значение функции
361
Наименьшее значение функции
361
Наклонная 181
Наклонная призма 216
Направление вектора 285
—	в пространстве 174
—	на плоскости 174
Направляющие косинусы 292,
293
Натуральные числа 27
Натуральный логарифм 65
Начало координат 271
Начальная фаза колебания 398
Невозможные события 424
Невозрастающая последователь-
ность 298
—	функция 326
Независимые события 424
Неизвестное 108
Необходимое и достаточное
условие существования пре-
дела функции 334
•--------сходимости положи-
тельного ряда 313
—	условие сходимости бесконеч-
ного числового ряда 313
------- последовательности 310
Неоднородная система уравне-
ний 129
Неопределенная система урав-
нений 129
Неопределенный интеграл 368
Неправильная алгебраическая
дробь 103
—	рациональная дробь 43
Непрерывная дробь 56
УКАЗАТЕЛЬ	473
Непрерывность функции 340,
407	•
Неравенства 151
—	арифметические 151
—	дробно-линейные 156
—	иррациональные 158
—	квадратные 155
—	линейные 154
—	логарифмические 160
—	показательные 159
—	тригонометрические 263
Неравенство Бернулли 412
—	Гёльдера 154
—	Коши 153
—	Коши — Буняковского 153
Несовместные события 424
Несократимая дробь 43
Нестрогие неравенства 151
Несчетное множество 20
Неубывающая последователь-
ность 298
—	функция 326
Нечетная перестановка 415
—	подстановка 417
—	функция 323
Нечетное число 31
Нижняя подходящая десятич-
ная дробь 56
Нулевой вектор 286
Область изменения функции 320
—	определения функции 320,
405
Образ элемента 18
Образующая конуса 223
—	усеченного конуса 224
—	цилиндра 222
Обратная подстановка 417
—	функция 327
Обратно пропорциональная за-
висимость 436
Обратное отображение 18
—	преобразование 230
—	число 60
Обратные тригонометрические
функции 248
Обращение десятичной дроби
в рациональную дробь 50
Общее кратное чисел 31
Общий делитель чисел 32
Объединение множеств 14
—	событий 425
Объем конуса 223
—	куба 218
474
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Объем параллелепипеда 218
—	пирамиды 219
—	призмы 217
—	тел вращения 287
—	усеченного конуса 224
—	усеченной пирамиды 220
—	цилиндра 222
—	шара 225
— шарового сегмента 226
--- сектора 227
--- слоя 227
Однородная система уравнений
129
Однородный многочлен 99
Односторонний предел функции
332
Одночлен 88, 98
Округление числа с избытком 74
-------недостатком 74
Окружность 193, 279
— вневписанная 199
—, вписанная в многоугольник
197
—,-----треугольник 198
—, описанная около много-
угольника 197
—	,--треугольника 198
Октаэдр 221
Описанный многоугольник 197
—	треугольник 198
—	четырехугольник 200
Определенный интеграл 381
Определитель 141, 142, 143
Ордината точки 273
Ортогональная проекция 182
Ортоцентр треугольника 187
Осевая симметрия плоскости 232
--- пространства 232
Осевое сечение 233
Основание конуса 223
—	логарифма 65
—	призмы 216
—	степени 64
—	трапеции 191
— шарового сегмента 226
--- слоя 227
Основная теорема алгебры 96
---арифметики 31
— формула интегрального ис-
числения 384
Основные свойства неравенств
152
Остаток от деления многочленов
91
------- чисел 33
Остаток ряда 312
Остроугольный треугольник 186
Острый угол 177
Ось абсцисс 272
—	аппликат 276
—	вращения 233
—	координатная 271
—	ординат 272
—	симметрии 232
Открытая область 406
Относительная погрешность 72
Отношение крайнего и сред-
него 413
— порядка в множестве действи-
тельных чисел 59
— эквивалентности (множеств)
18
Отображение взаимно однознач-
ное 18
— множества в множество 17
---на множество 17
------- себя 18
—	обратное 18
Отрезок 175
—	натурального ряда 19
Отрицательная полуось 63
Отрицательное направление вра-
щения 241
Отрицательные углы 241
—	целые числа 35
Парабола 283, 438
Параллелепипед 217
—	прямой 217
—	прямоугольный 217
Параллелограмм 189
Параллельная проекция 181
Параллельные плоскости 197
—	прямые 177
Параллельный перенос 286
Первообразная 368
Переменная зависимая 320
—	независимая 320
Перемещение (изометрия) 229
Пересечение множеств 14
—	событий 425
Перестановки 416
—	с повторениями 421
Период 324
—	десятичной дроби 48
Периодическая функция 324
Перпендикулярность прямой и
плоскости 180
ПРЕДМЕТНЫЙ
Перпендикулярные плоскости 180
—	прямые 178
Пирамида 218
—	правильная 218
— усеченная 219
Плоский угол многогранного
угла 214
Плоскостные аксиомы равен-
ства 238
Плоскость симметрии 233
Площадь боковой поверхности
конуса 224
------- пирамиды 219
-------призмы 216
------- цИЛИНдра 223
—	квадрата 191
—	криволинейной трапеции 380
—	круга 197
— параллелограмма 189
— поверхности усеченного ко-
нуса 225
---усеченной пирамиды 219
---шарового пояса 228
------- сектора 227
— правильного многоугольника
198
—	прямоугольника 190
—	прямоугольного треугольника
189
Площадь ромба 190
—	сегмента 197
—	сегментной поверхности 226
—	сектора 197
сферы 225
—	трапеции 191
—	треугольника 186
Поверхность многогранника 215
Поворот плоскости вокруг точ-
ки 230
Погрешность абсолютная 71
---предельная 71
—	относительная 72
		предельная 72
Подмножество 14
—	собственное 14
Подобие фигур 235
Подобные многоугольники 191
— одночлены 88
Подстановки 416
Подходящая дробь 56
Подынтегральная функция 368,
381
Подынтегральное выражение 368,
381
Показатель степени 64
УКАЗАТЕЛЬ	475
Показательная функция 441
Показательное неравенство 159
—	уравнение 124
Поле 25
Полиномиальные коэффициенты
Положительная полуось 63
Положительное направление вра-
щения 241
Положительные углы 241
—	целые числа 35
Положительный числовой ряд 313
Полюс 274
Полярная ось 274
—	система координат 274
Полярный угол 275
Последовательность бесконеч-
ная 295
—	возрастающая 298
—	монотонная 299
—	ограниченная 298
—	сходящаяся 300
—	убывающая 298
—	Фибоначчи 413
Построение графика функции
362
—	касательных к окружности 207
—	окружностей и дуг окружно-
стей 205
—	окружности, вписанной в мно-
гоугольник, и многоугольника,
описанноТо около окружности
209
---, описанной около много-
угольника, и многоугольника,
вписанного в окружность 209
—	отрезков 202
—	прямых, параллельных и пер-
пендикулярных данной пря-
мой 201
—	треугольников 210
—	углов 201
Правило параллелепипеда 290
—	параллелограмма 287
—	треугольника 288
Правильная алгебраическая
дробь 103
—	призма 216
—	рациональная дробь 43
Правильный многогранник 220
—	многоугольник 185
Предел последовательности 300
—	функции 329
---двух переменных 407
Пределы интегрирования 381
476
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Преобразование графика функ-
ции 433
— подобия 235
Приближенное значение числа
71
Призма 216
— правильная 216
Признак параллельности пло-
скостей 179
---прямой и плоскости 179
— перпендикулярности плоско-
стей 180
---прямой и плоскости 180
— сходимости числовых рядов
Даламбера 316
----------Коши 315
----------Раабе 316
Признаки делимости чисел 31
—	подобия многоугольников 191
---треугольников 192
Прилежащие углы 177
Принцип вложенных отрезков 60
— математической индукции 412
Приращение аргумента функ-
ции 344
—	функции 344
Прогрессия арифметическая 318
—	геометрическая 319
Проекция ортогональная 182
—	параллельная 181
Произведение бесконечное 317
—	вектора на число 288
—	матриц 139
—	многочленов 89
—	подстановок 417
—	последовательностей 296
—	рациональных дробей 40, 41
—	событий 425
—	чисел комплексных 80, 85
Произведение чисел натураль-
ных 27
		рациональных 44
		целых 36
Производная 345
—	, геодезическая интерпретация
346
—	, кинематический смысл 347
Производные высшего порядка
352
—	пропорции 66
Промежуток 466
—	монотонности функции 326
Прообраз 18
—	полный 18
Пропорциональные отрезки 178
Пропорция 66
Простая ломаная 183
Простейшая алгебраическая
дробь 104
Простейшие правила интегри-
рования 369
Простое число 30
Простой корень многочлена 95
Противоположно направленные
лучи 174
Противоположное комплексное
число 80
Противоположные векторы 287
—	события 424
Прямая призма 216
Прямая пропорциональная за-
висимость 436
Прямой круговой конус 223
--- цилиндр 222
—	параллелепипед 217
—	угол 177
Прямоугольная декартова си-
стема координат в пространстве
275
-------— на плоскости 272
Прямоугольник 190
Прямоугольный параллелепи-
пед 217
—	треугольник 188
Равнобедренная трапеция 191
Равнобедренный [треугольник 188
Равновероятные события 426
Равносторонний треугольник
188
Радиан 176
Радиус вневписанной окруж-
ности 199
—	окружности 193
---, вписанной в треугольник
198
---, описанной около треуголь-
ника 198
—	основания конуса 223
Радиус основания цилиндра 222
—	шара 225
Развернутый угол 175
Разложение вектора 289, 290
— многочлена на множители 97
— чисел на множители 30
-------простые множители 31
Размещения 418
Разность векторов 288
— дробей 40, 41
ПРЕДМЕТНЫЙ
Разность многочленов 90
—	множеств 16
—	последовательностей 296
—	событий 425
— чисел комплексных 80
---натуральных 28
---рациональных 44
---целых 36
Ранг матрицы 144
Расстояние между скрещива*
ющимися прямыми 181
— от точки до плоскости 180, 285
--------- прямой 179, 278
Расходящаяся последователь-
ность 300
Рациональная алгебраическая
дробь 100
—дробь 40, 41
— степень действительного чис-
ла 64
Рациональное алгебраическое
уравнение 117
— число 43, 44
Ребро двугранного угла 182
— многогранного угла 214
—	многогранной поверхности
215
—	пирамиды 218
Решение дифференциального
уравнения 390, 397
—	системы уравнений 129
Решения уравнения 108
Ромб 190
Ряд 311
—	гармонический 314
—	положительный 313
Свободные члены 129
Свободный вектор 286
Свойство Архимеда 60
—	непрерывности множества дей-
ствительных чисел 60
—	ортогональной проекции ^пло-
ского многоугольника 182
Сегмент 197
Секанс 243
Сектор 197
Секущая 193
Симметрическое уравнение 114
Симметрия осевая 232
—	относительно плоскости 233
—	центральная 231
Синус 242
Система вложенных отрезков 60
—	координат полярная 274
УКАЗАТЕЛЬ	477
Система координат прямоуголь-
ная в пространстве 275
-----на плоскости 272
— счисления 46
-----восьмеричная 442
----- двоичная 445
-----десятичная 46
— уравнений 128
----- линейных 129
-----неопределенная 129
----- однородная 129
----- совместная 129
Скалярное произведение векто-
ров 290
Скалярный квадрат (вектора)
Скрещивающиеся прямые 181
Сложение векторов 287
—	вероятностей 427
—	многочленов 89
—	рациональных дробей 41
— чисел комплексных 80
----натуральных 27
----рациональных 44
----целых 35
Сложная функция 322
Случайное событие 424
Смежные звенья ломаной 183
— углы 177
Смешанная дробь 43
---- периодическая десятичная
48
Смешанное произведение векто-
ров 294
Собственный максимум 410
— минимум 410
Сокращение дробей 41
Сонаправленные лучи 174
Соответственные углы 177
Соответствие 17
Составное число 30
Сочетания 419
— с повторениями 423
Среднее арифметическое 153
— гармоническое 314
— геометрическое 153
Средние члены пропорции 66
Средняя линия трапеции 191
----треугольника 188
Стационарная точка функции
361, 410
Степенная функция 440
Степень действительного числа 64
— комплексного числа 86
— многочлена 88, 98
478
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Степень одночлена 88, 98
—	уравнения 109
Стерадиан 228
Стороны многоугольника 183
—	угла 175
Строгие неравенства 151
Сумма векторов 287
—	матриц 138
—	многочленов 89
—	последовательностей 296
—	рациональных дробей 41
—	событий 425
—	чисел комплексных 80
---натуральных 27
---рациональных 40, 41
---целых 35
—	числового ряда 312
—	членов арифметической про-
грессии 318
---бесконечно убывающей гео-
метрической прогрессии 319
---геометрической прогрессии
319
Сфера 225, 285
Сходящаяся последовательность
300
Тангенс 242
Телесный угол 228
Теорема Безу 93
—	Больцано — Коши 311
—	Вейерштрасса 305
—	Лагранжа 348
—	косинусов 267
—	Кронекера — Капелл и 147
—	Пифагора 189
—	Ролля 348
—	синусов 267
—	Фалеса 178
— Ферма 348
Теоремы о параллельных пло-
скостях 180
---перпендикулярности пря-
мой и плоскости 180
— — плоскости и прямой, па-
раллельной плоскости 179
--- пределах последователь-
ностей 303
-------функций 333
---производных 347
---пропорциональных отрез-
ках 178
---равных отрезках 178
Тетраэдр 221
Тождественная подстановка 416
Тождественное преобразование
230
Тождество 108
Точка перегиба 362
— приложения вектора 286
Транспозиция перестановок 415
Трансцендентное уравнение 124
— число 69
Трапецеидальная форма системы
линейных уравнений 132
Трапеция 191
— криволинейная 380
— равнобочная 191
Треугольная форма системы
линейных уравнений 132
Треугольник 185
—, вписанный в окружность 198
—, описанный около окружно-
сти 198
—	остроугольный 186
—	Паскаля 419
—	прямоугольный 186, 188
—	равнобедренный 188
—	равносторонний 188
—	тупоугольный 186
Тригонометрическая форма за-
писи комплексного числа 85
Тригонометрические функции 242
Тупой угол 177
Угловой коэффициент прямой
277
Углы внешние накрест лежа-
щие 177
—	внутренние накрест лежащие
177
—	дополнительные 177
—	прилежащие 177
—	равные 175
—	смежные 177
—	соответственные 177
Угол 175
—	, вписанный в окружность 196
—	двугранный 182
—	линейный двугранного угла
183
— между векторами 290
---направлениями 177
---плоскостями 183
---прямой и плоскостью 182
— многогранный 213
—, описанный около окружности
196
— острый 177
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
479
Угол отрицательный 241
—	поворота 230
—	положительный 241
—	прямой 177
—	тупой 177
—	центральный 195
Уменьшаемое 28
Умножение десятичных дробей
49
—	матрицы на число 138
—	многочленов 89
—	рациональных дробей 41
—	чисел комплексных 80
	--натуральных 27
	--рациональных 44
	--целых 36
Упорядоченное множество 16
Уравнение 108
—	алгебраическое 109
—	биквадратное 113
—	возвратное 114
—	гармонических колебаний 397
—	двучленное 115
—	диофантово 124
—	дифференциальное 347
—	иррациональное 118
—	касательной 347
—	квадратное НО
—	кубичное 112
—	линейное НО
—	логарифмическое 126
—	плоскости 285
—	показательное 124
—	прямой 277
—	рациональное 117
—	тригонометрическое 258
Уравнения эквивалентные 109
Усеченная пирамида 219
Усеченный конус 224
Условие монотонности функции
358
Условная вероятность 428
Факториал 415
Фигура 228
—	вращения 233
Фигуры гомотетичные 234
—	подобные 235
Фокальные радиусы гиперболы
282
-----эллипса 280
Фокус параболы 283
Фокусы гиперболы 281
—	эллипса 280
Формула Бернулли 431
Формула Муавра 86 с
—	общего члена арифметической
прогрессии 318
-------геометрической прогрес-
сии 319
-------последовательности 296
—	полной вероятности 429
Формулы Виета 96
Крамера 147
Формулы приведения 253
Функция монотонная 326
—	нечетная 323
—	обратная 327
—	ограниченная 325
—	периодическая 324
—	четная 323
—	числовая 319
Хорда окружности 193
—	сферы 225
Целая часть алгебраической
дроби 103
---десятичной дроби 47
--- рациональной дроби 43
Центр гиперболы 282
—	гомотетии 234
—	окружности 193
—	правильного многоугольника
198
---треугольника 199
—	симметрии 231
—	шара 225
—	эллипса 280
Центральная симметрия 231
Цилиндр 222
Цифры 46
—	верные 73
—	значащие 47
Частичная сумма ряда 312
Частичное произведение 317
Частная производная 408
Частное многочленов 91
— последовательностей 296
— приращение 408
— рациональных дробей 40, 42
— чисел комплексных 80, 86
---натуральных 28
---рациональных 44
---целых 37
Частота событий 426
Четверти 243
Четная перестановка 415
— подстановка 417
480
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Четная функция 323
Четное число 31
Четырехугольники, вписанные
в окружность 199
—, описанные около окружности
200
Числа алгебраические 69
—	взаимно простые 32
—	действительные 58
—	иррациональные 58, 66
—	комплексные 79
—	мнимые 79
—	натуральные 27
—	нечетные 31
—	отрицательные 35
—	положительные 35
—	простые 30
—	противоположные 35
—	рациональные 43
—	составные 30
—	трансцендентные 69
—	целые 35, 38
—	четные 31
Числитель дроби 40
Число е 309
—	л 468
Числовая последовательность
295
Числовой ряд 312
Член последовательности 295
—	ряда 312
Шар 225
Шаровой пояс 228
—	сегмент 226
—	сектор 227
—	слой 227
Эквивалентные дроби 40
—	множества 18
—	неравенства 154
—	уравнения 1.09
Экстремум функции 359
---двух переменных 410
Эксцентриситет гиперболы 283
—	эллипса 281
Элемент матрицы 137
Элемент множества 13
Элементарные (простейшие) дро-
би 104
•—события 425
Александр Геннадиевич Цыпкин
СПРАВОЧНИК ПО МАТЕМАТИКЕ
ДЛЯ СРЕДНИХ УЧЕБНЫХ ЗАВЕДЕНИЙ
Редактор Т. И. Кузнецова
Техн, редакторы И. Ш. Аксельрод, А. П. Колесник ова
Корректоры О. А. С и г а л, Т. С. В а й с б е р г
ИБ № 12304
Сдано в набор 12.04.83. Подписано в печать 24.10.83.
Формат 84X108V32. Бумага тип. № 3. Литературная гарнитура,
Высокая печать. Условн. печ. л. 25,2. Уч.-изд. л. 32,16.
Тираж 300 000 экз. (2-й завод 150 001—300 000 экз.) Заказ № 1162.
Цена 1 р. 80 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Отпечатано в ордена Октябрьской Революции, ордена Трудового
Красного Знамени Ленинградском производственно-техническом
объединении «Печатный Двор» имени А. М. Горького Союзпо-
лиграфпрома при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли. 197136, Ленинград,
П-136, Чкаловский просп., 15 с матриц Ленинградской типогра-
фии № 6 ордена Трудового Красного Знамени Ленинградского
объединения «Техническая книга» им. Евгении Соколовой Союз-
полиграфпрома при Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли. 193144,
г. Ленинград, ул. Моисеенко, 10.
Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA