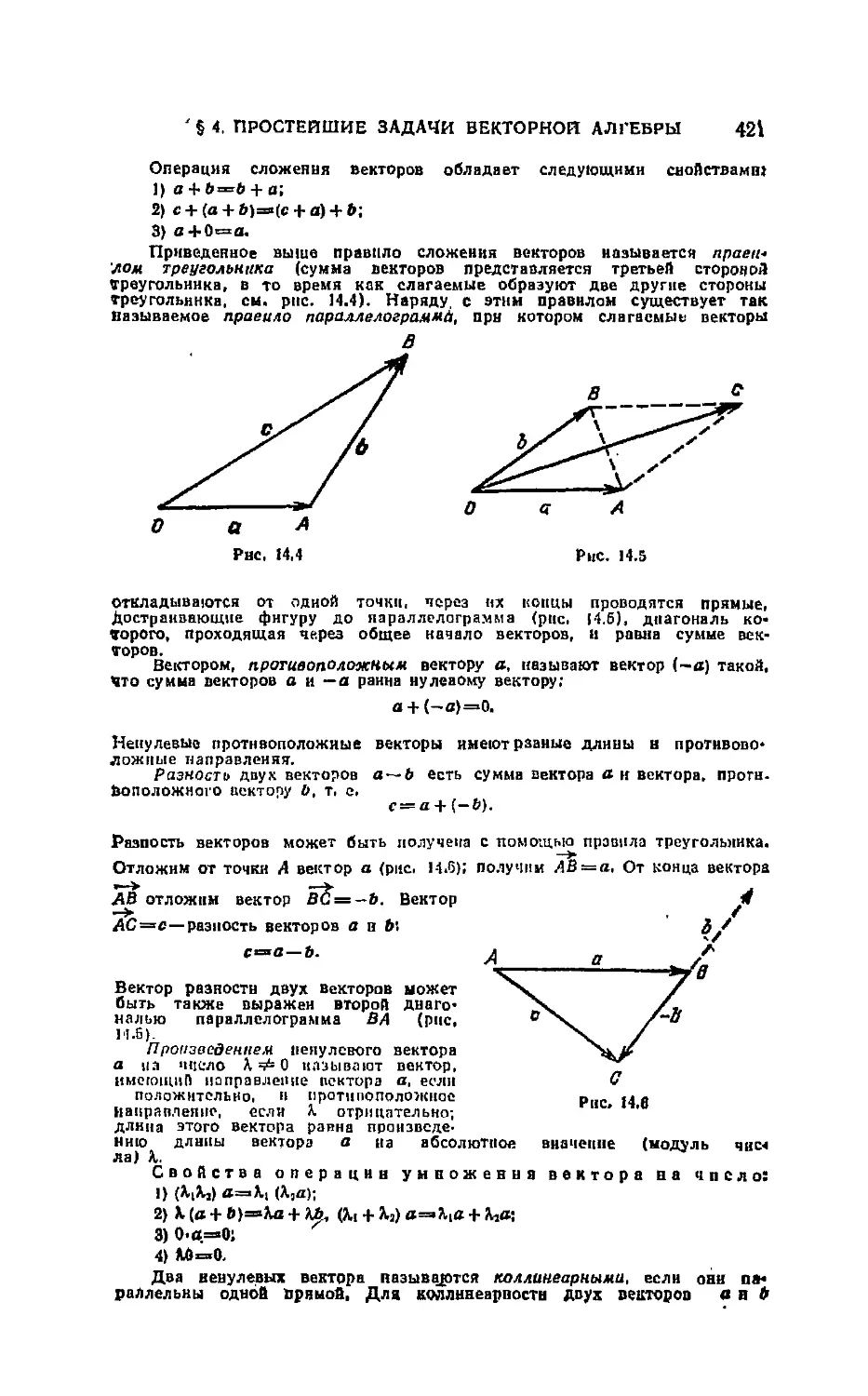
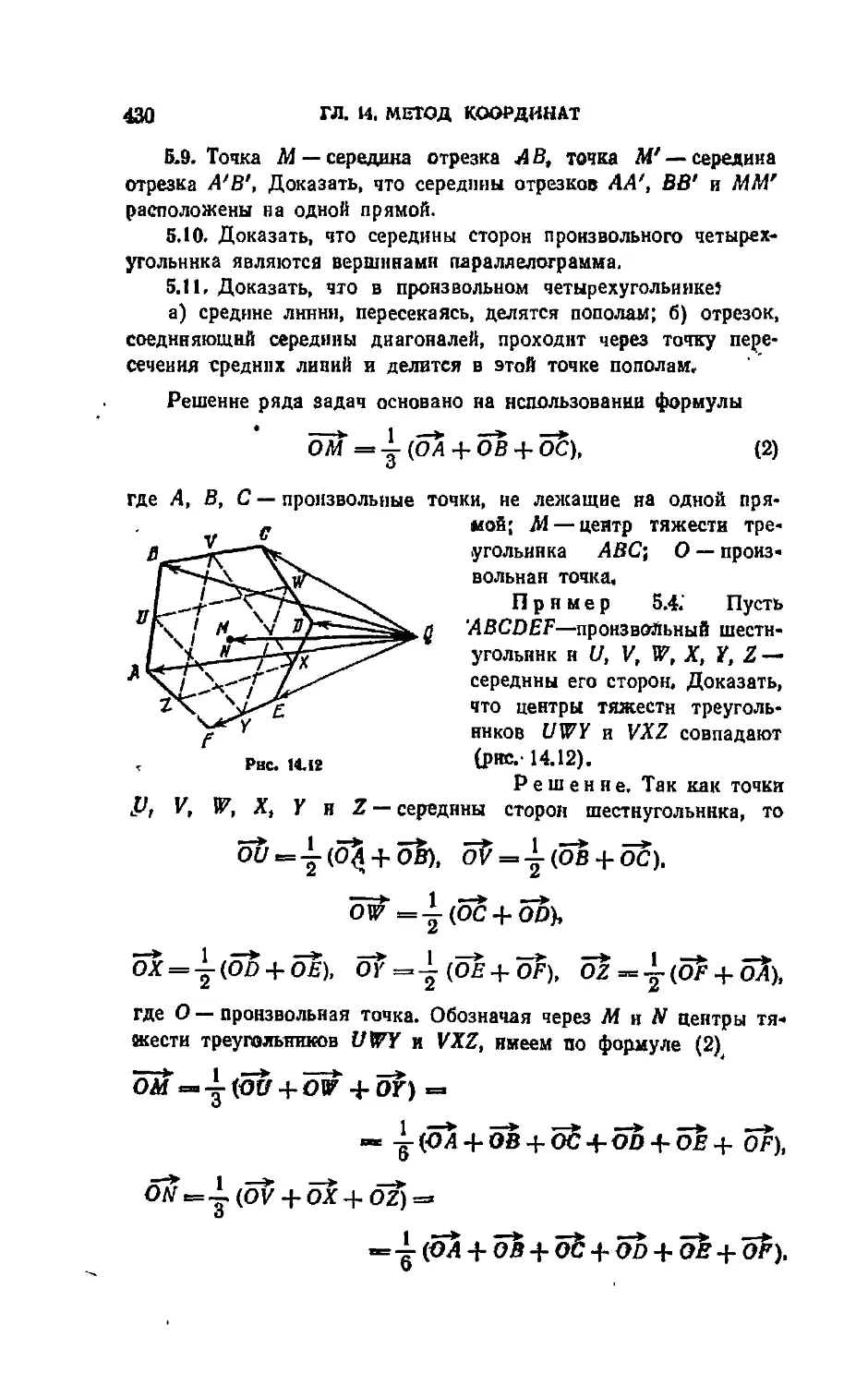
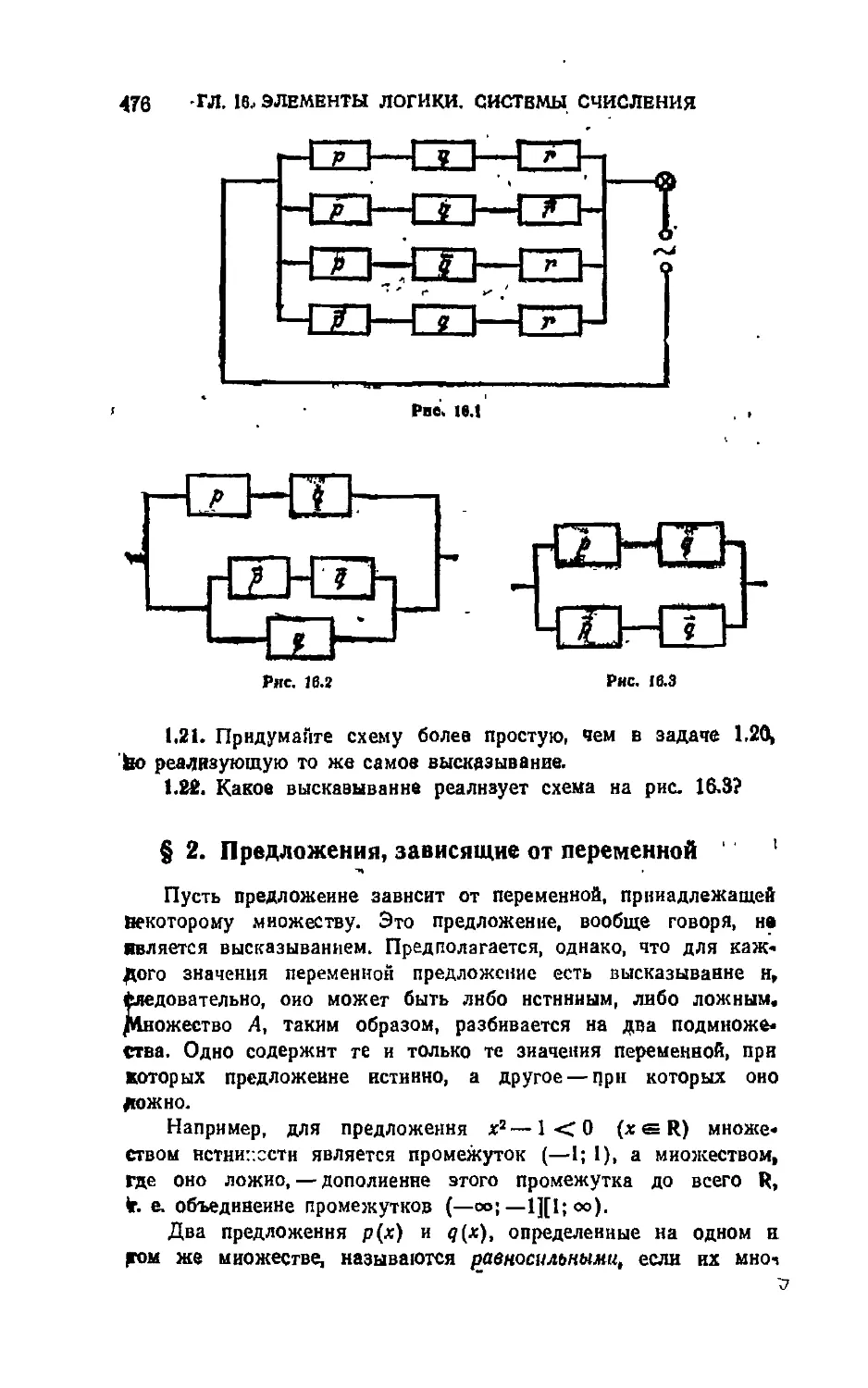
Автор: Цыпкин А.Г. Пинский А.И.
Теги: математика задачи по математике справочник физико-математическая литература издательство наука
ISBN: 5-02-013792-8
Год: 1989
Текст
А.Г ЦЫПКИН
А.И ПИНСКИЙ
СПРАВОЧНИК
пе методам
РЕШЕНИЯ ЗАДАЧ
ПО МАТЕМАТИКЕ
ДЛЯ.
СРЕДНЕЙ
ШКОЛЫ
А. Г. ЦЫПКИН, А. И. ПИНСКИЙ
СПРАВОЧНИК
; ПО МЕТОДАМ
РЕШЕНИЯ
ЗАДАЧ
,< ПО МАТЕМАТИКЕ
ДЛЯ СРЕДНЕЙ ШКОЛЫ
Издаыпе второе,
переработанное в дополненное
/^Sfc
ш
москва «наука»
главная редакция
физико-математической литературы
fee»
ББК 22.1
Ц97
УДК 51(03)
Цыпкин А. Г., Пинский А. И.
Ц97 Справочник по методам решения задач по
математике для средней школы. — 2-е изд., пе-
рераб. и доп. —М.: Наука. Гл. ред. фнз.-мат.
лит., 1989.—576 с.
ISBN 5-02-013792-8
Содержит основные методы решения задач
школьного курса математики, а также некоторые задачи, не
входящие в существующую программу средней школы.
Приводятся необходимые теоретические сведения.
Изложение метода сопровождается разбором типичных задач.
Приводятся задачи для самостоятельного решения.
Методически связан со справочником: Цыпкин А. Г.
Справочник по математике для средних учебных
заведений.
Для школьников ^гтаршнхГ классов и учащихся
техникумов. Может быть полезен для поступающих в вузы и
техникумы. '
Табл. 18. Ил. 73.
ISBN 6-02-018792-8 © Издательство «Hajia».
Главная редакция \
физико-математической
литературы, 4983; \
с изменениями, 1989 V
ОГЛАВЛЕНИЕ
От авторов 7
Глава I. Преобразование алгебраических выражений . . 9
§ 1. Упрощение иррациональных алгебраических
выражений Ю
§ 2, Преобразование алгебраических выражения, содержа*
щнх знак абсолютной величины 13
§ 3. Доказательство тождеств 19
§ 4. Условные тождества 23
§ 5. Преобразование логарифмических выражений ... 25
Глава 2. Уравненвя 31
§ 1. Нахождение корней многочленов 32
§ 2. Рациональные уравнения 38
§ 3. Уравнения, содержащие неизвестное под знаком
абсолютной величины 42
, § 4. Иррациональные уравнеяия , 43
§ 5. Показательные уравнения 48
§ 6. Логарифмические уравнения 54
§ 7. Разные задачи 59
Глава 3. Системы уравнений 61
§ 1. Системы линейных уравнений 61
§ 2. Системы нелинейных алгебраическихуравиений . . 66
fOb Системы показательных н логарифмических
уравнений . . 74
§ 4. Разные задачи 77
Глава 4. Неравенства. Уравнении и неравенства с
параметрами ......... 79
§ 1. Рациональные и иррациональные неравенства ... 79
§ 2. Показательные неравенства . ........ 86
' § 3. Логарифмические неравенства , 88
§ 4, Решение неравенств, содержащих сложные функции 93
I*
4
ОГЛАВЛЕНИЕ!
§ Б. Уравнения и неравенства с параметрами 95
§ 6. Доказательство неравенств 102
Глава 5. Тригонометрия 107
§ 1. Тождественные преобразования тригонометрических
выражений Ю8
§ 2. Вычисление значений тригонометрических функций 111
§ 3. Тригонометрические уравнения 117
§ 4. Системы тригонометрических уравнений 131
§ 5. Уравнения, содержащие обратные
тригонометрические функции . . . 134
§ 6. Тригонометрические неравенства 187
§ 7. Неравенства, содержащие обратные
тригонометрические функции 139
§ 8. Доказательство тригонометрических неравенств . . 141
Глава 6. Комплексные числа 14S
§ 1. Действия с комплексными числами 14(5
§ 2. Геометрическое изображение множества комплексных
чисел 148
§ 3. Решение уравнений в множестве комплексных чисел 160
§ 4. Применение комплексных чисел для решения
некоторых задач 153
Глава 7. Последовательности 157
§ 1. Определение и свойства последовательности . . . .157
§ 2. Предел последовательности 160
§ 3. Вычисление пределов последовательностей .... 162
§ 4. Арифметическая прогрессия 167
§ 5. Геометрическая прогрессия 171
§ 6. Смешанные задачи па прогрессии 17S
§ 7. Разные задачи 178
Глава 8. Предел функции, непрерывность фуницнн . . . 183
§ 1. Предел функции 183
§ 2. Вычисление пределов функций 185
§ 3. Непрерывность функции в точке 190
§ 4. Разные задаче 194
Глава 9. Производная и се применения 197
§ 1. Вычисление производных 197
§ 2. Промежутки монотонности и вкстремумы фувкций 202
ОГЛАВЛЕНИЕ 5
§ 3. Наибольшее и наименьшее значения функций . . > . 206
§ 4. Задачи, сводящиеся к нахождению наибольшего н
наименьшего значений н экстремумов функций . . . 209
§ 5. Текстовые задачи на нахождение наибольших и
наименьших значений функций 213
§ 6. Задачи на геометрический смысл производной . . . 223
§ 7. Приложении производной в задачах механики . . 229
Глава 10. Первообразная и интеграл . 232
§ 1. Неопределенный интеграл 232
§ 2. Задачи на свойства первообразных 236
§ 3. Определенный интеграл 238
§ 4. Интегралы с переменным верхним пределом .... 242
§ 5. Задачи иа свойства интегралов 244
§ 6. Вычисление площадей фигур 246
§ 7. Задачи иа нахождение наибольших (наименьших)
площадей фигур 250
§ 8. Вычисление объемов тел 253
§ 9. Приложения определенного интеграла в задачах
физики н механики 254
Глава 11. Задачи на составление уравнений ..... .257
§ 1. Задачи иа движение 257
§ 2, Задачи иа работу и производительность труда . . . 278
§ 3. Задачи иа процентный прирост и вычисление
«сложных процентов» 287
§ 4. Задачи с целочисленными неизвестными 291
§ 5. Задачи на концентрацию и процентное содержание 299
§ 6. Разные задачи 304
Глава 12. Планиметрия 308
§ 1. Треугольники 308
§ 2. Четырехугольники 318
§ 3. Окружность и круг 326
§ 4. Треугольники и окружности 332
§ 5. Многоугольники и окружности 345
Глава 13. Стереометрия 353
§ 1. Многогранники 354
.'• §2. Сечения многогранников •.•.'• 361
' '■ § 3. Фигуры вращения ....'.."........ 374
НЪ ф<4: КЬмбвйаЦии многограяиикбв и фигур вращения . '. 380
6 ОГЛАВЛЕНИЙ
Глава 14. Метод координат н элементы векторной алгебры 397
§ 1. Векторы в координатах 397
§ 2, Задачи на аналитическую запись линий на плоскости
и поверхностей в пространстве 405
§ 3, Решение геометрических задач с помощью метода
координат 412
§ 4. Простейшие задачи векторной алгебры 420
§ 5. Геометрические задачи, решаемые методами
векторной алгебры 426
§ 6. Скалярное произведение векторов 436
Глава 15. Комбинаторика. Элементы теории вероятностей 441
§ 1. Размещения. Сочетания. Перестановки 441
§ 2. Перестановки и сочетания с заданным числом
повторений 444
§ 3. Бином Ньютона 446
§ 4, Вычисление вероятностей событий с помощью
формул комбинаторики 461
§ 5. Задачи на вычисления вероятностей, решаемые
геометрическими методами . 455
§ 6. Вычисление вероятностей сложных событий .... 459
Глава 16. Элементы логики. Системы счисления .... 468
§ 1. Высказывания 468
§ 2. Предложения, зависящие от переменной .... 476
§ 3. Метод математической индукции 482
§ 4. Системы счисления 486
Ответы »491
Варианты экзаменационных работ письменного экзамена по
математвке в МГУ 565
ОТ АВТОРОВ
В справочнике изложены методы решения задач из курса
математики средней школы. Цель книги — помочь учащимся
систематизировать свои знания по решению задач курса средней
школы, а также ознакомиться с некоторыми методами решения
задач, которым в школе по тем или иным причинам не уделяется
достаточно внимания. Попыткой достигнуть этой цели и
определяется структура настоящего справочника: в начале каждого
параграфа кратко изложен теоретический материал
(определения, основные теоремы и формулы), знание которого
необходимо для решения задач данного раздела. Это позволяет
использовать справочник, не прибегая к учебникам. Далее указывается
метод решения задач какого-либо вида и разбирается
конкретный пример на использование метода. После этого даны условия
задач для самостоятельного решения.
Такая форма изложения, по -мнению авторов, наиболее
удобна для активного усвоения методов решения задач. В ряде
случаев при разборе конкретных примеров приводится, возможно,
не самое короткое и изящное решение задачи. Это объясняется
прежде всего тем, что при разборе примера авторы в первую
очередь стремились дать наглядное применение предложенного
метода, а вовсе не продемонстрировать примеры нестандартных
подходов к решению различных задач. Задачи для
самостоятельного решения в основном взяты из вариантов,
предлагавшихся в последние годы на вступительных экзаменах по
математике в вузы с повышенными требованиями к математической
подготовке абитуриентов.
Авторы попытались расположить задачи для
самостоятельного решения по возрастанию их сложности, сознавая при этом,
что каждый читатель, в зависимости от своих знаний и
наклонностей, возможно, изменил бы порядок следования задач. Такие
традиционные разделы школьного курса математики, как
планиметрия н стереометрия, в основном представлены задачами на
вычисление, так как именно эти задачи преобладают среди задач
этих разделов в вариантах письменных экзаменационных работ,
8
ОТ АВТОРОВ
При изложении материала, посвященного стереометрии,
авторы несколько отошли от изложенной выше структуры пара*
графов, так как в отличие от задач планиметрии, методы реше-
иия которых допускают достаточно четкую классификацию,
решение любой нетривиальной задачи по стереометрии содержит)
набор различных методов. В связи с этим примеры,
рассмотренные в главе 13, имеют довольно подробные решения, в которых
выделены основные приемы, сводящие исходную задачу к более
простым. Приведенные решения также могут- служить
иллюстрацией правильного оформления решения стереометрических задач
в письменной экзаменационной работе.
В главах 7—10 собраны и классифицированы задачи по
началам математического анализа. Заметную долю в этих глава»
представляют задачи, при решении которых следует исполъзо-
вать также сведения из традиционных разделов курса школьной
математики. Среди задач, собранных в главе 14, наряду с
обычными упражнениями присутствуют довольно трудные
геометрические задачи, решение которых значительно упрощается благодаря
применению векторов и метода координат. Следует сказать, что,
включая задачи в эти главы, авторы старались следить за тем,
чтобы решение опиралось только, на сведения, входящие в
школьную программу.
Задачи, собранные в главе 6 (комплексные числа) и главе 15
комбинаторика и элементы теории вероятностей), основаны на
материале, который сейчас не входит в программу.
Включение в справочник комбинаторики и элементов теории
вероятностей объясняется тем значительным вниманием, которое
уделяется в последнее время теории вероятностей и связанным о
ней разделам математики. Авторы учли, что для большинства
читателей этот материал — совершенно новый, и поэтому в этой
главе позволили себе несколько отойти от принятой в книге
очень сжатой формы перечисления освовиых сведений,
необходимых для решения задач.
В справочнике принята двойная нумерация задач и
примеров в каждой главе. Первое число указывает номер параграфа,
а второе — порядковый номер задачи (или примера) в этом
параграфе. Звездочка прн номере задачи указывает на более
трудную задачу, а две звездочки — иа наличие полного решения (они
приводятся в разделе «Ответы»).
Справочник в основном предназначен для учащихся старших
классов средних школ и учащихся средних специальных учебны»
заведений.
Г Л А В А 1
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ
ВЫРАЖЕНИЯ
Пря преобразованиях алгебраических выражении используются фор*
мулы сокращенного умножения:
<в + 6)<в-6)=в'-6'. (I)
(о» + а6 + 6')(в—6)=в>— 6», (2)
(в,-а6 + й')(в + 6)=в,+ 6', " (S)
(a ± 6)'=а' ±2аЬ + Ь\ (4)
(а ± 6)J=»a> ± За'б + Заб» ± 6>, (В)
и правила действия со степенями.
Если а > 0, то
emen=»am+n» (в)
(ат)п=ат-п, (7)
в"=.1, (8)
ат. дп^аш-^ (9)
/I
Уай"=.в"»/'1. п^о, <Ю)
--(т)" - w
Вели в > р. ,* >0. nsH, то
«ля
VflF"—Va" V*"t 02)
Va_Va~
V*"
п я
Г»
Vjti
(13)
.Если я < о, * < 0. я=2*. ke N, то
я я я
VaT—Vnn Vl"*T. (И)
(15)
10 ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Если я-»2*+ I, ft е N, то
п П п
Vf-^. > + *. On
■VT
Если n,«tsN,io
Чп. п
V^™-V|a|m. (18)
§ 1. Упрощение иррациональных алгебраических
выражений
Под упрощением иррационального алгебраического
выражения понимается приведение его к виду, содержащему меньшее
число алгебраических операций пад входящими в исходное
выражение переменными.
Упрощение иррационального алгебраического выражения
часто достигается разложением исходного выражения на
множители с последующим вынесением общего множителя за скобки.
д Уд + b V5" . 2 УТ ■sfab . .
(Уд + *Jb ){a — b) Уд" + л/1> а — Ь
Решение. Выделим общий множитель в числителе и
знаменателе первой дроби данного выражения. Для этого
представим числитель дроби в виде
а Уд" + Ь УГ - а3/2 + Ь3'2 - (д1'2)3 + О,"2)3.
Используя (3), получаем
(д1'2)3 + (Ь1*? - (а"2 + Ь1'2) (а - аЩЧ* + b).
Множитель д'^Ч-*"2 = Ув + УТ является общим для
числителя и знаменателя. Проведя сокращение, представим (*) в виде
д — s/ab + Ь 2 У F У<5>
а — Ь у'о + УТ а — Ь'
(**)
После приведения (**) к общему знаменателю имеем
д — л[аЬ +6 + 2 л/аЬ — 26 — Удб а — Ь
а-Ь e_fce1'
Ответ. 1.
§ I. ИРРАЦИОНАЛЬНЫЕ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 11
Упростить следующие алгебраические выражения:
х — д х — у
1.1. Vf^ ~ V^ VJ + Уу _ 2л/ху
Vx—VF , V* + vV у —х
х—у Х—У
4-1/2
1.2. ( ! f^-^ \~\
,,з,д(У«+УГу' + frfV54-Vry't
V 26 Уд / V 2а V* /
..5.((^-^Г+(^+^Г)<4#)
^--^С^ + ^У
1 =• +Ув1ГТ
,7 Уд — » . Уд- 1
1 '(д—1)УдТт—(д+ 1)Уд-г
д/д + 1 Уд — 1
(yj + yr)2-'
V1+i(Vr-v02-i(VbvO
, о (Ув + УБ")2 — 46 . д + 96 + 6 Удй V
В выражениях, содержащих произведение радикалов с
различными показателями степени, в ряде случаев удается добиться
{упрощения, приведя все радикалы к одному показателю.
Пример 1.2. Упростить выражение
12 ГЛ. 1. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Решение. Представляя выражение V2 У* — УЗх в виде
4 4
л/г У* - Уз! = V(2 УГ—Уз*)2 = У 4* - 4 Уз" х + Зх =
4
=*-\/V* — 4-\/з"*
и подставляя его в исходное выражение, получаем
4 4
У* (7 + 4 УЗ~) У2 д/7 - УзГ = У*а(7 + 4 Уз~) (7-4 Уз) =
= Уж8 (49 - 48) = У*2 = -у/Т
|](прн переходе к носледнему выражению знак абсолютной
величины может быть опущен, так как исходное выражение
определено только при х ^ 0).
Ответ. У)ё.
При преобразовании радикалов необходимо учитывать, что
но определению корень четной степени есть величина
неотрицательная, в то время как корень нечетной степени может быть
как неотрицательной, так и отрицательной величиной.
Пример 1.3. Упростить выражение
в з
У7(7 + 4 УЗ") • У УЗ* — 2 У7.
Решение. Так как Уз* — 2 УГ<ё^ 0 (в чем можно
убедиться, сравнив квадраты уменьшаемого и вычитаемого), то
перед приведением радикалов к общему показателю представим
второй сомножитель в виде
3 3 6
У Уз! — 2 У Г = — У 2 У*" — Уз! =» — У(2 Уж" — Уз!)2.
Дальнейшее упрощение проводится по схеме предыдущего
примера:
в з
У X (7 + 4 УЗ") • У Уз! - 2 У7 в
в в
=. - Уж (7 + 4 УЗ") У (Уз! - 2 Ух")2 —
в з _
= - У*2 (49 - 48) = - У*.
Ответ. — УГ.
Упростить следующие выражения:
4
§ 2. ВЫРАЖЕНИЯ. СОДЕРЖАЩИЕ МОДУЛЬ J3
О 3
1.11. У 4* (11 + 4 У(Г) • У 2 Уз1 — 4 V2x.
1.12. У(2Р + D3 + У(2р ~ О3 т *
У 4р + 2 У4ра — 1
3 в
1,10. ; j •
3
,,. У 26 - is Уз" (2 - Уз") \/
7 —4У1
1.16. \-^Уго + 14Уг • Ув-4Уг + V
+ \ У(в + з)У5"-За-1) : (2(ун" + 0 + 0 •
,,в У26-2у&2-4- „
' Уб2 - 4 - (Ь + 2)
§ 2. Преобразование алгебраических выражений,
содержащих знак абсолютной величины
Преобразование алгебраических выражений, в которых на*
ряду с арифметическими операциями присутствует знак
абсолютной величины (модуля) от некоторой функции, обычно
производится отдельно на каждом промежутке зиакопостоянства этой
функции.
Пример 2.1. Упростить выражение
^1!+*1*-н+2-4
х —. w
Решение. Преобразуем выражение, стоящее в анамена-
теле
лА-2+7
разуем вырзже
уГ^1- у2ЕЕТг_ л/1г?Е _ j-fi.
я подставим его в исходную дробь. Получим выражение
.14 . ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЙ
Разделим действительную ось на два промежутка (—оо; 1]я
.(1; оо) зиакопостояиства функции f(x) ~ х— 1 н проведем
упрощение исходного выражения на каждом из указанных
промежутков отдельно.
Так как выражение (**) определено только при х > О,
хф\, то вместо промежутка (—оо; 1] будем рассматривать
промежуток х е (0; 1). На этом промежутке по определению
модуля имеем \х — 11 = 1 — х и исходное выражение приобретает
вид
'V*0-'*)(~ + *-7) VI x»-i
^ ^ -Х£-.(ц-х»-2)= * ' .
(1-х) х У*
При хе|1; оо) по определению модуля имеем \х— 1| =
<= X— 1 И
1| ж - 1 | /JJ-UI V*
II
(,-i)V,[l-h, + |] „
х~-1 Vх
Ответ. При «е(0, +1) исходное выражение равно
7=—, а при ж s (1; оо) равно J—
л/х л/х
Упростить следующие выражения и иайти область
допустимых значений параметров, если они не указаны:
\у»-\\-\ '
2.1.
m-T^tSts-U8-81-
2.3.
2.4.
2.5.
х\х — 3|
(*2 - х - 6) | * | •
х\х — 3\ + х*-9
2х3 — Ъх* — 9х '
25
2\у + Ь\-у + -у
Ъу* + 10^-25 '
У* 12** - ж - 11
27 U-4-l*l
§ 2. ВЫРАЖЕНИЯ. СОДЕРЖАЩИЕ МОДУЛЬ 15
„ _ Уд8 - 2аЬ +~Ь* , 2а - . ^ .
2.8. \ -J =— при 0 < а < Ь.
У a* + 2ab + 6а а + fr
VI— ж + Vl — * 1 + * — VI+*/ 2
2.10. V2 (2а + У а2 — И V<* — Vaa - *2 при о > 0, 6 > О,
а> 6.
Упрощение иррациональных выражений,
содержащих полный квадрат под знаком
радикала. Для того чтобы убедиться, что под радикалом стоит
полный квадрат некоторого выражения, иногда удобво сделать
замену, рационализирующую это выражение.
Пример 2.2. Упростить выражение
л/х + 2 л/2х — 4 — V* — 2 УгТ^Т. («)
Решение. Сделаем замену
t<=ij2x — 4.
*а4-4
ToiTfa х = —^—> и выражение (*) приобретает вид
(<-2)' |< + 2| П-21
"I ""3 "Т—
-V
Дальнейшее упрощение проводится по схеме, рассмотренной
в примере 2.1. Разбиваем все множество допустимых значений t
последнего выражения на три области! (—ooj —2]; (—2j Щ\
12; то), В каждой из них получаем
— t — 2+t — 2 „ i7 _, \
т.. «, te(-«; -2},
<s(-S 2],
*е(2; оо).
Для того чтобы вернуться к исходной переменной х, необходимо
решить неравенства
2
t+2+t—2
2
t+2—t+2
2
= t
= 2
У2ж —4<—2, -2<У2ж—4<2, V2* — 4 > 2.
Их решениями будут, соответственно, следующие множества
значений!
0, 2«^*<4, *>4,
16 ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Таким образом, окончательно имеем
12, х > 4.
Ответ. При дс е [2; 4] данное выражение равно V2* — 4»
а при х г (4; оо) равно 2.
Упростить следующие выражения:
1П- VVHr+ л/йт -2-(2.+V^D.v
2,,2,f '«-; 8^±1Г.жм.^
,,,уг^ут.у
2.14. V* + 6V^=r2 + 7 + V*— бУ*~+2 + 7. ^
2.15. V* + 2 V*— 1 — V* — 2 V* — 1 • ^
2.16. У*2 - 12* + 36 - V*5- ^
2.17. (х + 2 У2ж-4)"1/2 + (* - 2 У27^"4)~1/У
Вычисление значений алгебраического
выражения с предварительным упрощением
данного выражения. В некоторых случаях для того, чтобы
вычислить алгебраическое выражение при конкретных значениях
входящих в него переменных, целесообразно его предварительно
упростить.
П р в м е р 2.3. Вычислить значение выражения
V* — 2 V2" V* + 2 л/2~
/ ,==■ / ._ — при *=.3.
У*2-4*л/2 +8 V*2 + 4xV2+8
Решение. Упрощая исходное выражение, имеем
У* — 2 V2" У* + 2 л/2~
VU-2V2")2 У(* + 2 л/2)2
| (^-2л/211/2 U + 2V2l'/2
= I * — 2 V2 I | * + 2 V2 I *
Значение х = 3 принадлежит промежутку (2 VS"'. 00) знакопо-
.стоянства функций, стоящих под зваком абсолютной величины.
На этом промежутке имеем
\х-2т/2\=>к — 2 42я\х + 2т/2\'е*х--$2.т/¥, «
в 2. ВЫРАЖЕНИЯ. СОДЕРЖАЩИЕ МОДУЛЬ 17
следовательно,
1 1 д
(*-2У2")"2~" (* + 2V2)'/2 =
^ + 2V2l'/2-U-2V2)1/i!
Подставив х = 3 в выражение (*), полупим-
(з + 2У2)'/2-(3-2У2у/2 =
(•)
•^^Ь-Ш§) ]• w
к 3 — 2 JZ
Умножим числитель в знаменатель дроби ^=- на
3 + 2 V2
3 + 2 V2~> Имеем
3 —2У2~ 3 + 2У2~ _ 9—8
3 + 2V2 ' (з+2л/¥) (3 + 2-\/2)2 (3 + 2 У2 )* '
^Теперь, с учетом равенства (l + V2) =3 + 2-\/2~, получим
, (3 + 2V2)'/2(l + V2l _g (1 + V2)(l+V2~)
3 + 2V2" (1 + V2-)2
Ответ. 2.
Вычислить значения следующих алгебраических выражений
при указанных значениях неизвестного:
2.18. _x+f _+ _x~f _, ,=2; .
V* + V * + л/з V* — V* — л/з
2<19. L±2=- ~^.' 2 = ^1. *
1 + У1+г 1 —yi-z 2
2.21. — а2—Ь% 1Я'р i Лч\ ~ — ( Д + 6 УР«Л«-РЬ ^
2 а2 + 6а
■<*■"+*«"). -(^т)2
2.22. х3 - Зх - 2 А* + В ,
Л2-В
18 ГЛ. 1, АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
2.23.
2.24.
/* 4
J «JWy — tfxy*
1 ■у/у-л/х'
x(l + 2 Д/7 + ^-) , * = 9, 0 = 0,04.
где а > 0, т > О, л > О, т> п.
Упрощение численных иррациональных
выражений. В примере 2.3 после подстановки значения х = 3
решение свелось к упрощению иррационального .числового
выражения. Приведем некоторые приемы, упрощающие решение задач
подобного типа.
Числовое иррациональное выражение удается упростить, если
под знаком квадратного радикала стоит полный квадрат
некоторого выражения. Так в случае радикала второй степени вида
■у/сР ± 26, упрощение достигается представлением
(1)
(2)
Ve2±2|61 = V(V* А л/уУ
=IV*
± л/у 1»
где х н у находятся как решение системы уравнений
х + у = а*,
ху=Ъ\
Так, в примере 2.3 упрощение
Уз + 2У2~ = (1 +
V2?
проводилось согласно (1), а система (2) при этом имела вид
х + у ш. 3,
ху = 2.
Пример 2.4. Вычислить
^т!$г<6+^-
Решение. Система (2) для выражения, стоящего в
числителе дроби, записывается в виде
х + у = Щ
ху = 216 ■
и имеет решения 412» 1а1» i18'> '2Ь
§ 3. ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ 19
Следовательно, согласно (1), получаем
У 30 — 12V6" = Vl8 — УТ2 = ЗУ2~-2Уз~.
„ , Зл/2" —2-\/з"
Домножая числитель и знаменатель дроби —Ь= h=- на
2 V3 +ЗУ2
3 У? — 2 Уз", имеем
(ЗУ2"-2УЗ~)2 ЗО-^Уб- ^.
18=15 я 6 5-2 V6.
Перемножив 5 — 2 Уб~ и 5 + 2 Уб, окончательно получаеи
(5 - 2 Уб") (б + 2 У^) =. 25 - 24 «= 1.
Ответ. 1.
Вычислить значения следующих иррациональных выражений!
2.25. У8 + 2У12-У2" _
Ув-гуТг+Уг"
».a<t 3 _ .Vg + aVf V
4 + У5 V8 — 2 У5
2.27. У6 + 2 У§" - У 6 - 2 УГ.
2.28. У2Д + 2Уа^=Р-Уа^~6
У 2а - 2 УЯ^П? + У5^^6 '
2.29. У6m + 2 У§т2 — «*' — Убт — 2 У9т2 - /»2У
§ 3. Доказательство тождеств
Доказательство тождеств
непосредственной проверкой.
Пример 3.1. Доказать, что
(а + Ь + с) (6с + са + вб) — аЬс = (6 + с) (с + а) (в + 6). (*)
Решение. Раскроем скобки в левой части выражения и
приведем подобные члены. Имеем
аЬс + Ь*с + be1 + а2с + аЬс + с'а + а!6 + аб' + аЬс — аЬс =»
= 2а6с + ЪЧ + be1 + аЧ + с*а + аъЬ + Ьга.
Раскрытие скобок в правой части выражения приводит к
такому же выражению. Действительно,
аЬс + с*а + агЬ + а*с + Ьяс + Ьсг + аЬс =
=2а6с + с*а + а26 + авс + Ь3с + Ьс*.
20 ГЛ- I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Исходное тождество доказано, так как если каждое из двух
выражений равно третьему, то эти выражения равны между
собой.
Доказать следующие тождества:
3.1. (а2 + б2) (х3 + у3) = (д* - by)1 + (Ьх + ау)\
3.2. (а2 + Ь1 + с1 + d3) (хг + у1 + z2 + t1) =
= {ах — by — С2 — dt)1 + (bx + ay — dz + ct)1 4-
+ (ex + dy + az~ Ы)1 + (dx — cy+bz + a/)*.
3.3.' .(a2 - b1)1 + (2д6)2 = (a2 + 6s)2.
3.4. (a+,6-(-c + rf)2+(e+6 — c-d)*+(a+c — 6-rf)2 +
+ (e + rf — 6 — c)2 = 4 (a2 + b1 + c* + rf2).
,, 1 ■ 1 !____=!
1 ' 1 6(a6c+a+c)
& + ■
3 6.
j_ a + T
с
д + 3 _ " д2 —5 _ 2д3 — д(1— 5д) — 1
2д — 1 4а2 — 4д + 1 8д3 — 12д2 + Оо — I ="
2а + I
(2д-1)2'
д2(с-6) 6г(Д~д) ■ с2(6-д)
3.7. —-. гт гт =; п. ;— = д+о + с.
а(с—Ь) . 6(д —с) с (6 — д)
6с дс дб
— X
3.8. .— ^^^ « *
а— х *
д + х
3.9, ■ г-г ! —. к . ^ X — \м
х + х°-ъ+1 хи5 -1
3.10.
V2fl + 4
Ve
Доказательство тождеств с помощью
условия равенства двух многочленов. Если в левой п
в правой частях тождества стоят некоторые алгебраические
выражения, которые можно рвесматрввать как два многочлена
одной н той же степени, то доказательство таких тождеств
может быть основано на следующем свойстве многочленов. Две
§ 3. ДОКАЗАТЕЛЬСТВО ТОЖДЕСТВ
21
мпогочлеиа rt-й степени одной переменной дс равны
(тождественно равны), если зиачевия этих многочленов совпадают при
х = хи х = хг, ..., х = хя, х=^хп+], где все Х\,х2, .... х„, х„+]—
произвольные, не равные между собой числа.
Пример 3.2. Доказать тождество
а» {х - Ь) (х -^ с) . Ь*(х-с)(х-а)
(а-6)(а-с) "*" (Ь-с)(Ь-а) +
, с*(х-а)(х-Ь) ,
+ (С-а)(С-6) "*'
Решение. Сравнивая значения левой и правой частей при
х = а, х = Ь, х = с, можно убедиться, что при этих значениях
переменной многочлены совпадают. Так как левая и правая
части представляют собой многочлены второй степени
относительно х, которые совпадают более чем при двух значениях
переменной, то эти многочлены тождественно равны.
Доказать следующие тождества:
a b ■
3,11.
3.12.
1*-
"Г
(х-
(а-
-а)(а
-Ь)(х
-Ь)(а
-Ь)(а
с
с)(с-
-с)
-с) '
-с)
а)(с-
(Ь-
1 (*-
-Ь) '
■ с) (х -
■«)(*-
-Ь)(6-
а)
а) >
-а)(Ь-
X
b)(x-i
~а)(х
-а) (с
-с) '
-Ь)
-Ь)
г
-с)
= 1
3.13.
b + c + d
(Ь —а) (с —a) (d-а) {х-а) г
, c + d+a
"*" (с - 6) (d — 6) (а — 6) (х— Ь) "*"
d + a + 6 .
"^ (d-c)(a-c)(& — с) (ж — с) "■"
а+ 6 + с
• + (а - d) (Ь — d) (с — d) (ж - d) e
x—a—b—c—d
3.14*.
(дс — в) [х — 6) (дс — с) (* — d)
в — Ь , Ь — с , с — а ,
а+ b b-\-c c + a
(a-b)ib-c)[c-a)
^'■(a+^ib + ^ic + a)
■ S-'IS ■■•■■■ 6~С J. С~Д 4- й~Ь =,
,'.,.(«-ft) (в-г в) + (fr-c)(fr-a) Т (c.-a)(c-fr). .
•> a ■ • 2 • 2
■ • ■** а— Ь Т.ь—с "*" с-а'
22
ГЛ. 1. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
aifi# a2-be Ь*-ае
0,,Q ' (а+Ь)(а + с) + (Ь + с)(Ь+а) "**
•afr
(с + а)(с + Ь)
К доказательству алгебраических тождеств близко
примыкают и задачи, связанные с проверкой некоторых числовых
равенств. Обычно эта проверка осуществляется теми же методами,
что и доказательство тождеств (сюда же включаются методы
упрощения алгебраических выражений, см. § 1).
Однако существуют в специальные .методы проверка
числовых равенств.
Пример 3.3. Доказать, что
1^9 + У») + ^9 — ,050 = 3.
Решен в е. Обозначим
x = $9 + s/M+'$9 — V80- (*)
Тогда, уедввяя одвв из радикалов и возводя в куб обе частв
получившегося уравнения, вмеем
(х — ^9 + Уёо)3 = 9 - V80.
х3 - Зх* ^9 + У§() + 3* (-$9 + У80)' - 9 - V80 = 9 - уёб,
х3 - 3*! -$9 + У80 + 3* ^(9 + У§0)2 = 18,
х3 — 3* ^9 + У80 (х — ^9 + Уво) => 18.
Выражение х — у 9 + У15 в силу (*) равво V9 — V80i н,
следовательно, ураввевне приводится к виду
*3-ЗхУ81-80=18ч=*-*3— Зх — 18 = 0. (♦*)
Очевидно, что ж = -у 9 + д/80 + V 9 —^§5 является корнем
уравнения (**). Кроме того, вепосредственной подстановкой
легко убедиться в том, что .х = 3 также является корнем
уравнения (**). Других действвтельных корней ураввенве (**) не
имеет, так как кубичвый мвогочлен (**) может быть записан
в виде
х3 — 3* — 18 = (х — 3) (*2 + 3х+ 6),
а дискриминант квадратного трехчлева х2 + Зле + 6 отрвцателев.
Таким образом, всходиое равевство следует вз
существования единственного действительного корня уравнения .(*),
$ 4. УСЛОВНЫЕ ТОЖДЕСТВА 23
§ 4. Условные тождества
Тождества, справедливость которых требуется установить
лишь при выполнении некоторых условий отиоснтельно входящих
в исходное тождество переменных, называют условными
тождествами.
Пример 4.1. Доказать, что если
а + Ь + с = О,
ого
а3 + 6а + с3 = ЗаЬс.
Решение. Из условия
а + 6 + с = 0
получаем
сз = _ (а + б)8.
Используя тождество (5), имеем
- с3 = — а3 - б3 — ЗаЬ (а + Ь)
или, заменяя а + Ь на —с,
а3 + Ь3 + с8 = ЗаЬс,
что и требовалось доказать.
4.1. Доказать, что если
а + Ь + с =з О,
то
а6 + б5 + с8 _ а3 + б3 + с3 аг + 6а + са
5 ~~ 3 ' 2
4.2. Показать, что из равенства
а2 + Ь2 + с1 — ab + be + ас
следует равенство а= b = с.
4.3. Доказать, что если а1'3 + 61/3 +c''3 = 0, то
(а + Ь + с)3 = 27а6с.
4.4. Доказать, что если
— + Т1 =1 и 1 ==0,
а ^ b ^ с х ^ у ^ z '
то
j£_ . г/2 . z2
4.5. Доказать, что если
24
ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
ТО
xW + yW^aW.
4.6. Доказать, что если а + 6 + с = 0, то
а) (а2 + Ьг + с2)2 = 2 (а4 + 6< + с4).
б) 2 (ае + 6s + с») = 5а6с (в2 + б2 + с2).
в) 5(в3 + Ь3 + с3)• (в2 + Ь3 + с2) =6(в5 + 6е + с5).
4.7*. Доказать, что если — ф —, то вз системы урав-
*з Уг
нений
' ctyi + $у2 = О
следует, что а2 + Р2 => 0.
4.8. Допевать, что еслв х Ф у, у ф z, z Ф х а
у — z z — x х~у
то
_* , JL
= 0.
>0.
(У-ZY Т (г_*)1Т(л-_у)1
4.9*. Доказать, что если
а? + а^ + ... + a*=V,
a,6i + ei62+ ... +ап6п = Р9.
то ai=A,6|, вг = А,б2. ...» вя = Л<6/1, где А, = —.
4.10. Доказать, что если
то
то
а Ь
а2 + 6a' a
б2 + с2 с '
4.11. Доказать, что если
ay — bx ex — az
с Ь
а ■ Ь с '
4.12. Доказать, что если
а—Ь Ь—с
х ' а+Ь ' У Ь + е1
bz— i(/
а '
с —а
"^ с + а'
то " • •'
(\ + х) (1 + у)(\ +z)~(\ - х){\ гу).{1 -г).
§ 5. ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ 25
§ 5. Преобразование логарифмических выражений
Пусть а — положительное число, отличное от единицы, а
М — любое положительное число. Логарифмом числа М по
основанию а называется такое число, обозначаемое log„ M, что
а ° = М.
Основные свойства логарифмов. Пусть а > О,
a & 1, Ь > 0, с > 0, тогда
logo (be) = ioga Ь + loga с, (I)
logo — = loSa b — logo с, (2)
log p69*=-2-log b, (3)
a pa-
log* 6 = -^, 6^1. (5)
Тождественные преобразования логарифмических выражений
проводятся с помощью формул (1)—(5) н определенвя
логарифма.
Пример 5.1. Упростить выражение
logaVa2-llogf/aVa2-l
6 •
logo' (°2 - 0 log^j Va" — I
Решение. Согласно свойству (3) имеем
(log1/a Va7^!)2- (- iogaУа^Т)2= (loga <JaT=T)\ »
в e
log^_ Vo*— 1 = ^^(^a-ja (Va2 — 0 = loga Va2 — 1 • (*♦)
loga, (a* - 1) «Iog{aJ)I/2 (a* - l)"2 - ioga V^2^!. (*♦♦)
Подставляя правые части выражений (»)—(***) в исходную
дробь, получаем
logaVaT^TJogaVaT^T
ioga Va*-U
loga Va" — 1 ioga Ve*— 1
Ответ., logaVe* — 1.
Пример 5.2. Вычислить
26 ГЛ. Т. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Решение. Согласно свойству (5) имеем
8ii/log»3_8jiog,6>
Используя свойства степеней, получим далее
Si'osjS^, /34jlogj8_,(3loe»5)',#
Согласно определенвю логарифма 3°е* =5. Таким образом*
811'10*»8 —54 = в25.
Аналогично,
34/log,9 = д4 IOB.7 — (32)2 ,0*'Т ^ (g'Off.rf „ 72 = 49,
271ок»Зб _ 27|ое>в — з3 |оВ'6 = (з'°8«6)3 = 216,
Складывая полученные значения, получаем искомое число.
Ответ. 890.
Упростить следующие выражения:
( Ion < а \
^2 ^" — в10*"*04-1*' —2aJ:(74l0ff"° —a—l).
1оц «_а
5,3. '
Б.4*. iog3 2 log« 3 log» 4 loge 6 log? 6 logs 7.
5.5. log22^+log2**,OB*<luK*X+1)-f 11ое24Л2+2-31ое1/2,08**.
( IteHi»')
loga 6 - iogaft b ' £ ioe6ioea 6 _ , •
5.7. 5,0^/8^>+ logVr__i-_-r. log,,, Ц=^.
*** V^ + л/з ^ 10 + 2V21
Связь между логарифмами составных чисел обычно удаетсн
установить, используя логарифмы нх простых сомножителей.
Пример 5.3. Найтн logao 8, если известно, Что lg 5 = о,
lg3 = 6.
Решение. Представим logao 8 в виде
lg8
logao 8 = ——
Ig30
I в. ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ iff
Разлагая чвсла 30 и 8 на иростые ывожнтелв в используя свой*
ства логарифмов, получаем
iogjo 8« 6
Ig5+lg3+lg2"
Учитывая, что
Ig2 = lg-^-=l-lg5,
я используя условвя задачи, получаем
ift<r я 3(1-д)
ъ 3(1-а)
Ответ. —I i ; .
о -\- \
5.8. Вычислить без помощи таблиц
log3135 1og3 5
logie3 Iog«is3
5.9. Зная, что lg 2 = a, logs 7=6, найти Ig 66,
5.10. Зная, что lg 3 = a, lg 2 = Ь, найти loge 6.
5.11. Известно, что Iog37 = a, log? 5»=» ft, loge 4 =» с. НайтЯ
log312.
5.12. Звая, что & = 8|'<|-|°в.а> в c = 8l/(|-loe»6), выразвтЬ
logs а через logs с.
Б.13*. Известно, что
loga* = a, log^x^p, logflx = Y. logd* = o; x Ф I.
Найти \ogabcdx.
Для доказательства тождественности двух логарифмических
выражений прв выполвевнв некоторых условий иногда удобно
сначала преобразовать дапвые условия, а затем их
прологарифмировать.
Пример 5.4. Доказать, что
если as+ 6* = 7а6, а > О, Ь > 0.
Р е ш е н в е. Преобразуем условие а* + bl «= lab, выделия
в левой части полный квадрат:
а2 + б2 + 2а6 =- 9а6,
т. е.
(а + Ь)*=-9аЬ.
■28 ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
.Логарифмируя последнее равенство по основанию 10 и приводя
подобные члены, получаем
2 lg (о + Ь) — 2 lg 3 = log a + lg Ь.
Разделив обе части равенства на 2 н используя свойство логарифм
нов (2), получаем искомое равенство.
6.14. Показать, что при условии х > 0, у > 0 из равенства
х2 + 4:у2 = \2ху следует равенство
. lg(* + 2«/)-2lg2 = l(lg*+Igj,).
6.1Б. Доказать, что
1оВа+&т + [°Ва-ь т*=21о£а+б т 1о8а_&т,
если известно, что т2 = а? — Ь2.
5.16. Доказать, что если а, 6, с — последовательные '(положи-
отельные) члены геометрической прогрессии, то
1ogfl N — logb N _ loga N
6.17. Доказать, что если
(ас) *e =c2,
то для любого положительного числа N числа logo JV, logb N,
logcN являются тремя последовательными членами
арифметической прогрессии.
При доказательстве тождеств обычно используются те же
приемы, что и при упрощении логарифмических а показатель*
ных выражений.
Пример 5.5. Доказать, что
Vvix=-«
bgp logp V v ... V!
при р > 1.
Решение. Записывая иррациональное выражение, стоящее
лод знаком второго логарнфма, в виде
Ч'<.
Ур
,w
S 5. ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ 29
н логарифмируя два раза это равенство по основанию р,
получаем
logpp'" ~-pr, Iogp-pr = -rt.
Таким образом, исходное тождество доказано.
5.18*. Доказать, что для любых допустимых положительных
чисел e»JV имеет место равенство
11 1 1 _ .
Ioga N + loga, N + loga, ЛГ + loga, ЛГ 10gJV a-
5.19*. Доказать, что
2 (VIoga V^ + Iogft <t/ab - VIoga \J± + logd д/у) X
Б.20*. Доказать, что
loga N logft ЛА + logj N logc JV + logfi ЛГ loga ЛА =
logg N log6 fl log,, Л7
l°eabcN
6.21*. Доказать тождество
loga * log6 x
'°ga'6*=log6*~loga*-
При сравнении двух логарифмических выражений удобно
пользоваться эквивалентностью следующих неравенств. Если
основания- логарифмов одинаковы, то
при а> 1:
0<b<c-**-logab<\ogac, ' v (6)
при 0< а< 1:
0< b < cs=>logab > Iogaс. (7)
Если одинаковы числа, от которых вычисляются логарифмы,
и а > 1, Ь> \ нли0<а<1 и 0< 6 < 1, то
при О 1:
loga с < Iogs с <=> а > Ь, (8)
при 0 <с< 1:
loga с < logb с «**• 6 >а. (9)
Пример 5.6. Не пользуясь таблицами, определить, что
больше;
logs 9 нлй log? 8?
fcO ГЛ. I. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Решенве. Представим исследуемые логарвфмы в виде
logs9= logs (8 + I) = 1 + log„(l +—),
log78=»tog7(7+l)=.l+logr(l+y).
В силу (8) и (6) справедливы неравенства
log*(l + y)<log7(l+y)< logT(l+T).
Таким образом,
log89<log78.
Не пользуясь таблицами, доказать неравенства]
5.22*. Iog375<log,22.
5.23*. ioga 70 < log2 20.
5.24. iogloff|2(i)>l.
Б.2Б*. Доказать, что для любого натурального N > 3
справедливо неравенство
1с%(# + i)< logw_,tf.
Г Л А В А 2
УРАВНЕНИЯ
В алгебре рассматриваются два вида равенств — тождества я урам.
пения. Тождество — 910 равенство, которое выполняется лри всех (до*
лустнмых) значениях входящих в него букв. Для записи тождества вач
ряду со знаком — также используется авак ™.
Уравнение— это равенство, которое выполняется лишь при некого*
рых значениях входящих в него бука. Буквы, входящие в уравнение^
по условию задачи могут быть неравноправными: одни могут принимать
все свои допустимые значепня и называются козффициентами (реже пал
раметрами) уравнения; Другие, значения которых требуется отыскать,
называются неизвестными (их обычно обозначают последними буквами
латинского алфавита: х, у, г, или темп же буквами, снабженпымн явм
дексамн:*,. х2 хп или yv yv .... Ук*))-
В общем виде уравнение с л нензвестныын ДСр *2. •••. *„ иоже>
быть аовнсаио в виде
P(*v*t М-0' «1
где Р (jr|t Д£г хп) — функция указанных переменных. В зависимости
от числа неизвестных уравнение называют уравнением с одним, двумя
и более неизвестными.
Знач' ня неизвестных, обращающие уравнение в тождество, вазы,
вают решениями уравнения. Уравнение считается решенным, если най-i
дены все его решения или показано, что уравнение решений не имеет.
Если все решения уравнения F — 0 являются решениями уравнения
О — 0, то говорят, что уравнение G = 0 есть следствие уравнения F — О,
и пишут
/>=о**- о=о.
Два уравнения
F=0 и 0=0
«зывают эквивалентными, если каждое из них является следствием дру«
ого, и пишут
Р=0-ФФ-О=0.
Таким образом, два уравнения считаются эквивалентными, если
множества решений этих уравнений совпадают.
Уравнение ^=0 считают эквивалентным двум (или нескольким)
уравнениям Л=0, Fj—0. если множество корней уравнения F=0 совпадает
с объединением множеств корней уравнений F,=0. Fj=0.
Неиоторыс эквивалентные уравнения:
1. Уравнение F + О - О эквивалентно уравнению F - 0, рассиатри.'
ваеному на множестве допустимых значении исходного уравнения.
р
2. Уравнение -jt-=" О эквивалентно уравнению F - 0. рассматриваем
ному на множестве допустимых значений исходного уравнения.
*) Если специально не оговорено, то считается, что нензвастпые
принимают действительные значения.
82
ГЛ. 2. УРАВНЕНИЯ
Многочленом {полиномом) л-П степени относительно переменной вел
личины х называется выражение вида
3. Уравнение Р ■ G — 0 эквивалентно двум уравнениям Р — 0 п О - О,
каждое нз которых рассматривается на множестве допустимых вначений
исходного уравнения.
4. Уравнение Fn=o эквивалентно уравнению F=0.
5. Уравнение F =0 при нечетном п эквивалентно уравнению Р — О,
В при четном л эквивалентно двум уравнениям: F - G н F - —О.
Алгебраическим уравнением с одним неизвестным называется урав«
реине. сводящееся к уравнению вида
а0*п + а|хп-1 + агх',-2+ ... +в„_1х + ап=0>
где л —неотрицательное целое число; коэффициенты многочлена
п„, а,. аг ап—\' ап называются коэффициентами (или параметрами)
дграанепня и считаются заданными; х называется неизвестным я является
искомым. Число л называется степенью уравнения.
Значений неизвестного х, обращающие алгебраическое уравнеине в
тождество, называются корнями (или решениями) алгебраического
уравнения. '
§ 1. Нахождение корней многочленов
л-П степеш
ie вида
P(x)=a0*n + eI*n-I+a2x',-2+ ... +an_tx + an,
где п—неотрицательное целое число; а0. а^ а, ап~у
"„—коэффициенты многочлена, причем коэффициент а», называемый старшин
коэффициентом, считается не равным нулю.
Многочлен первой степени называют также линейным многочленом,
многочлен второй степени — квадратным, а многочлен третьей степени —
кубичным многочленом.
Число с называется корнем многочлена, селн Р{с) — 0.
Уравнение вида
ах + Ь=-0, афО. (1)
называется линейным уравнением. Линейное уравнеине имеет
единственны ft корень х - —Ыа.
Уравнение вида
о*' + 6х + С=0, a 9s-0, (2)
называется квадратным уравнением. Выражение 6* — Aac — D называется
дискриминантом каадратиого уравнения. Если О > 0. уравнеине (2) имеет
два действительных корня:
— ь+Vo — ь—Vo"
*. Та . **= fa—
Если D — 0. то уравнение (2) имеет одни действительный корень крат»
ностн 2; х——и—. Если D < 0, то уравнение (2) действительных корней
не имеет.
Решение уравнений методом замены
неизвестного. Решение многих уравнений заключается в сведении
их к уравнениям вида (I) или (2). Одним из таких способов
является введение вспомогательного неизвестного.
Пример 1.1'. Решить уравнение
(*а - 2л)2 - (х — I)2-}- 1=0.
Решение. Обозначая у=(х—1)г, запишем исходное
уравнение в виде
(У-I)2-У+1=0- (*)
§ I. НАХОЖДЕНИЕ КОРНЕЙ МНОГОЧЛЕНОВ 33
Несложные преобразования приводят уравнение (*) к виду
у3-Зу + 2=*0. (*♦)
Решая (**), получаем, что исходное уравнение эквивалентно
двум квадратным уравнениям
(*_1)»=,1 н (*-1)2=2,
корни которых *i=>2, *г = 0 и xS|4=l±V2 являются
корнями исходного уравнения.
Ответ, х, = 2, *г = 0, х3, < = 1 ± V2 ■
Решить уравнения:
1.1. (х* + 2х)*-(х+ 1)* = 55.
1.2. (х* + х+ 1)(ха + * + 2)-12 = 0.
1.3*. (*2 - Ьх + 7)2 — (ж - 2) (х — 3) =- 0.
1.4*. (ж - 2) (* + 1) (х + 4) (х + 7) = 19.
1.5*. (2а:2 + 3* - 2) (5 — 6х — 4*2) = — 5(2*! + Зж + 2).
1.6. х* - 13*2 + 36 = 0.
• 1.7. 2х8 + *< - 15 =» 0.
1.8. (2*-1)9 + 3(2ж- 1)3 = J0.
1.9*. (1 + хУ + (1 + *2)4 = 2*«. V"
1.10. (ж — 2)9 — 19 (х — 2)" = 216.
Решение уравнений методом разложения
на множители. Один из способов решения уравнения п-й
степени (/»> 2)
Р„(*)=0
состоит в разложении многочлена Ра(х) иа множители, что
позволяет свести решение исходного уравнения к решению
нескольких уравнении более низких степеней. Этот способ основан
на следующем свойстве корней многочлена п-й степени. Если х=е
является корнем многочлена
Pn(x) = a0xn + alx"~i + ... +а„_,х + ап>
то этот многочлен можно записать в виде
Pn(x) = (x-c)Qn~, (x), (3)
где Q„_j(jc) — многочлен степени /»—1, т.е. многочлен Рп{х\
делится иа многочлен дс — с. .
Разложение многочлена на множители равносильно
нахождению корней многочлена. Нахождение корней многочлена являет-
ся. трудной задачей, и в- общем случае для многочлена я-й
степени с действительными коэффициентами нельзя указать уиивер«
сального способа нахожденвя корней.. Однако для многочленов
2 А. Г. Цыпквв, А, И, Панскиа
34
гл. а. уравнения
с целыми коэффициентами существует теорема, позволяющая
отыскивать их рациональные корни.
Рациональными корнями многочлена
а0ха + а1хп~1 + ... + я„_,лг + яд,
где во, fli Od-ii, «в — целые числа, могут быть лишь числа
вида m/p (m —целое, р— натуральное), при этом число \т\
является делителем числа |я„|, а число р—делителем числа
М-
Пример 1.2. Найти корми уравнения
З*3 — 4г" + 5ж- 18 = 0.
Решение. Делителямп числа 18 будут числа 1, 2, 3, 6, 9,
а делителями числа 3 —числа 1, 3. Множеством значений m
будет множество {—9, —6, —3, —2, —1, 1, 2, 3, 6, 9}, а
множеством значений р — множество {1, 3). Множеством всевозмож-
иых различных значений чисел вида т/р будет следующее мно-
f ■ 1 21
жество рациональных чисел:< ± i, ± 2, ±3,±6,± 9, ±-=-,±-^-Ь
Подставляя зти числа в уравнение, получаем корень уравнения —
число 2. Следовательно, многочлен, стоящий в левой части
уравнения, делится на & — 2).
Произведя деление углом, находим частное — многочлен
Зх* + 2* + 9, который действительных корней не имеет.
Следовательно, х = 2 — единственный действительный корень исходного
уравнения.
Ответ, х = .2.
Решить уравнения методом разложения на множители:
1.11. 8*4 + 6ж3 — 13*а — х + 3 = 0. V
1.12. *8+6х + 4ж2 + 3-»0.
1.13. г*4-*3 — 9*s+13,k-5 = 0.V
1.14*. (,v - I )3 + (2* + З)3 = 27а:3 + вУ
1.15. х3 - (2а + О х* + (а3 + я) х - (яа - a) = оУ
1.16. х* - 4л-3 - 19л2 + 106* - 120 = 0. V/
Некоторые уравнения специального вида.
Уравнение четвертой степени вида
(х + а) {х + Ь) (х + с) (дс + d) — т.
при условия
приводится к Евадратному уравнению относительно нензвестноЛ
у — х3 + 1х.
§ 1, НАХОЖДЕНИЕ КОРНЕЙ МНОГОЧЛЕНОВ 85
Пример 1.3. Решить уравнение
*(*+1)(*Ч-2)(* + 3) = 0,5б25. (*)
Решение. Перемножив попарно х(х + 3) и (*+ 1)(* + 2),
имеем
(Д+ Зх) (*2 + Зх + 2) = 0,5623.
Вводя вспомогательное неизвестное у = х* + 3*, после
очевидных преобразований получаем квадратное уравнение
у* + 2у — 0,6625 = 0,
корнями которого будут числа у\ = 0,25 н у% = —2,25.
Возвращаясь к исходному неизвестному, заключаем, что (*)
эквивалентно двум уравнениям:
хг + Зх — 0,25 = 0, х* + Зх + 2,25 = 0.
_ —3 + УП>
Первое уравнение имеет два различных корня: лц = ——
—3 — V10 3
н «1= 5"^ , второе — один корень дс3> 4 = — — кратности
два, _
_ З+л/Ю —3 —VT5 3
Ответ. *,= J"-51—, ж2= 2~^—, *3.4 = — ■%•
Найти корни уравнений:
1.17. (* + а) (х + 2а) (х — За) (х — 4а) = Ь*. у
1.18. (* - 4) (* - 5) (ж - 6) (ж — 7) = 1680.
1.19. (6* £ 5)2 (3* + 2) (ж + 1) = 35. V
1.20. X* — 2х3 + Х — 132 = 0.
1.21. (*-1)(х + 1)(* + 2)*="24.
1.22. (х — 4) (х + 2) (ж + 8) (х + 14) = 354. *
1.23*. (ж2 + ж + 1) (2*! + 2* + 3) = 3 (I — х — хг). :
Алгебраическое уравнение четвертой степени вида
ах* + Ьх3 + сх* + rf* + в = 0, в =5^ 0,
называется возвратным, если коэффициенты уравнения связаны
равенством d — Kb, с = Я2а (X — некоторое отлнтаое от нуля
число).
Решение возвратного уравнения может быть сведено к
решению квадратного уравнения заменой
, *■
* = * + Т'
Пример 1.4. Решить уравнение
18*' — Злг8 — 25*s + 2* + 8 = 0.
й*
36 ГЛ. 2. УРАВНЕНИЯ
Решение. Так как х = 0 не является корнем уравнения,
то, разделив обе части уравнения на л2, перейдем к эквивалент'
ному уравнению
18*» - 3* - 25 + — + Д- = 0.
1 х ' х2
Сгруппируем слагаемые в правой части этого уравнения
следующим образом:
»(-+■¥•)-.(.-■!?.)-—..
Теперь очевидно, что если в качестве новой неизвестной выбрать
2/3 ' 4/9 4
у = х —, то, так как х1 + -V-=j/2 + -r. исходное урав-
X X О
ненне приобретает вид
18^-3^-1 = 0. (**)
v 1 I
Корни этого уравнения равны -г- н —^- соответственно.
Таким образом исходное уравнение оказывается эквивалентным
следующим двум уравнениям:
2/3 1 2/3 1
X — =• — И X '-—= -.
X 3 X 6
2
Первое уравнение имеет корни *i = l и Хг = —^, а вто-
—1 ±л/97
рое — *з. ч = -
12
_ , 2 -1±V97
Ответ. Ж| = 1. «2==» —-г, *з,4=-
3' »■* 12
Решить уравнения: yj
1.24. х* + 5х3 + 2хг + 5х + 1=0. .
1.25. 2*4 + З*3 — 4*a — 3* + 2 = 0. V
1.26. 15хъ + 34*4 + 15ж3 — 15*2 — 34л — 15 =■ 0.\/
1.27. 6ж3 - х* - 20* + 12 = 0. V
1.28. Х*+ 1—2(1 + х)*. \/
Некоторые алгебраические уравнения л-й степени \п > 2)
допускают понижение порядка, если использовать формулу
бинома Ньютона (см. гл. 14, § 8).
Пример 1.5. Решить уравнение
8*s + 36r' + 54* = 98.
Решение. Воспользовавшись тем, что
(2* + З)8 = 8х3 + 36х2 + 54* + 27,
§ I. НАХОЖДЕНИЕ КОРНЕЙ МНОГОЧЛЕНОВ 37
запишем исходное уравнение в виде
{2х + З)3 = 125,
или
2х + 3 = б.
Таким образом, единственным корнем исходного уравнения будет
х= 1.
Ответ, х = 1.
Решить уравнения:
1.29. 8*3 — 36*"+ 54* = 28. ^
1.30. 16*' + 32х3 + 12*2 + 8х — 80 = 0. V
1.31. х* — 8х3 + 24ж* - 8* = 65.
Уравнение вида
а,цл + atun-lv + a3un~2t? + ... + a„tt" = 0
называется однородным уравнением л-й степени относительно
неизвестных и и о. Деление обеих частей однородного уравнения
на vn сводят его к уравнению л-й степени относительно неизвест-
и
яого «/ =—.
V
Если ап = 0, то следует отдельно рассмотреть случай, когда
о = 0.
Сводя уравнения к однородным и производя указанную
выше замену, иногда удается понизить степень исходного
уравнения.
Пример 1.6. Решить уравнение
(*« + 27)" — 5 (х1 + 27) (*2 + 3) + 6 (*г + З)2 = 0. (*)
Решение. Обозначим *а + 27 = и, хг + 3 = о. Тогда
исходное уравнение приобретает вид однородного уравнения
второй степени относительно неизвестных и и и:
u3-5uv + 6v3 — 0.
Производя замену — = у, получаем уравнение
У1- 5^ + 6 = 0,
корни которого у = 2 и у = 3.
Возвращаясь к исходным неизвестным, получаем, что урап-»
пение .(*) эквивалентно двум уравнениям
ж* + 27 = 3(** + 3), ** + 27 = 2(*» + 3),
корнями которых являются числа ±3 и ± V^I соответственно.
Ответ. xifl*+&3, *,;i-*b»it VJil- . i
38 ГЛ. 2. УРАВНЕНИЯ
Решить уравнения:
1.32. (х2 - I)2 + 5 [х* - 1) - 6 (ж2 + I)2 = 0.
1.33. (ж2 - З)2 - 7 (ж* - 9) + 6 (ж2 + З)2 = 0.
1.34. {х - 2)2 {х + I)2 - [х - 2) (ж2 - 1) - 2 (ж - 1)а = 0.W
Если уравнение может быть записано в виде fl/(Jc)] = лк то
средн корней этого уравнения содержится корень уравнения
f (дс) = х. \
Пример 1.7. Решить уравнение
{X1 - 4ж + б)2 - 4 (ж2 — 4* + 6) + 6 = *.
Решение. Найдем корни квадратного уравнения
' ж2 — 4ж + 6=ж. (*)
Его корни х = 2 н ж = 3. Следовательно, многочлен, стоящий
в левой части исходного уравнения, делится на произведение
(*-2)(*-3).
Производя деление углом, находим многочлен частного:
х*— Зж + 3.
Таким образом, исходное уравнение можно представить в
виде
{х2 — Ьх + 6) (жа — 3* + 3) = 0,
и, следовательно, оно эквивалентно двум уравнениям
х2 — бж + 6 = 0-, жж — Злг + 3 = 0. (**)
Второе из уравнений (**) действительных корней не имеет, а
действительными корнями исходного уравнения являются корня
уравнения (*).
Ответ, xi — 2, Х2 = 3.
Решить уравмевня1
1.35. (х*+ 2х — 5)2 + 2 (х*+ 2х — 5) — 5= х, V
1.36. (ж2-ж-3)*-(ж* —ж—3)—3 = ж. V
§ 2. Рациональные уравнения
Рациональным алгебраическим уравнением называется
уравнение вида
Р(ж)
<К*>
-О, <1)
где Р(х) и Q(x) —многочлены. Далее для определенности будем
полагать, что Р(ж) — многочлен nt-ft степени, a Q{x) — много-
член rt-й степени.
Множество- допустимых значений рациоиильвоп» адгебраяче-
ского уравнения (1) определяется дадвшси. QW =?(= А откуда
§ 2. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
39
следует, что хфсу, хфс3, ..,, хф с* где а, сь ..„ с„ —
корни многочлена Q(x).
Метод решения уравнения (1) заключается в следующем.
Решаем уравнение
Р{*) = 0,
корни которого обозначим через х\, х%, х3, .,., хт. Сравниваем
множества корней многочленов Р{х) и Q(x). Те корни
многочлена Р(х), которые не являются корнями многочлена Q(x),
являются корнями (решениями) рационального уравнения (1).
Пример 2.1. Решить уравнение
9 —х 5 _
X — 4 X — 4
Решение. Исходное уравнение эквивалентно уравнению
9-ж — 5 + 3(*--4)=0
прн условии х — АФО. Решая полученное уравнение, находим:
х = 4. Так как х = 4 не входит в область допустимых значений
неизвестного, то данное уравнение решений не имеет.
Пример 2.2. Решить уравнение
1 1__ J_
хХх + 2) {* + l)a===12'
Решение. Обозначая z = *2 + 2*, запишем исходное
уравнение в виде
\ 1 1 , .
Несложные преобразования сводят уравнение (*) к уравнению
z2 + z—12 л . .
12^3+1) -°' (**>
которое эквивалентно уравнению z? + z—12 = 0.
Эквивалентность этих уравнений следует из того, что корни последнего
уравнения z = —4, z = 3 принадлежат множеству допустимых
значений уравнения (**). Таким образом, исходное уравнение
эквивалентно двум квадратным уравнениям: Xя + 2х — 3 = 0 н
х1 + 2х + 4 = 0. Корни первого уравнения: Хц =. 1, хг = «—3,
Второе уравнение действительных корней не имеет.
О т в е т. xi = 1, х\ е=.--3.
40 ГЛ. 2 УРАВНЕНИЯ
Найтн корни следующих уравнений:
12*+1 9* —5 108*— 36*2-
2.1.
2.2.
2.3.
2.4.
23.
2.6.
6* - 2 3* + 1 4 (9*2 - 1) *
» 1 .,, '
2* + 3 *2- 16 ^ 2х2+ 11*+ 12
*-8
2а:3 + З*2 - 32* — 48
х2 + х + 1 7 *+ 1
*2-лг+1 "" 9 х—['
,*+! 9 1
■0.
2(х- 1) 2(* + 4) ^ *-Г "
*2 ' , * + 1 1 1
*2-4 ^ 2 (а:—2) 2-* х + 2"
4*2 + 29* + 45 - (* + 1) (2л: + 15) (х + 1) (* + 5)
(2(*- 1))2-2(* + 1)(*_2) Г (*- 1)(*-2)'
,„ (а-*)' + (*-6)* а« + й* v
"' * (а + Ъ — 2*)' (а + bf ' »
28 * I 2 6
■°" *! - 2* + 2 ^ *а — 2л- + 3 ~ х2 — 2х + 4
2-»- -5 Ц1 , ,п -*2 + 4*=6.
*2 — 4* + 10
г->°-Т^ГТ + Т5-^ = 2-
*2 + 4 ^ *2 + 5
2Л.. (£l=Mi-2- 81
,(* - З)2 (jo - З)2 "
212 __Л 15
*" *2 + 2* —8 лг2 + 2* —3
*2,+ 2* + 1 , *2 + 2* + 2 _ 7_
6'
з
2Л4' *2 + 2* + 2 + *» + 2* +
>"--(Sr)'-'(Sf),+«4sf-' Y
Уравнение вида
Ь*
с*1 + Л* + rf т с*г + г* + d
сводится к уравнению
а , Ъ
ТТЛ 7-*- = °
y + h г у + г
в 2. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ 41
введением вспомогательного неизвестного
. d
у = сх+—щ
Пример 2.3. Решить уравнение
х . 4.x
= 1.
х1 — х + 1 ' х* + х+\
Р е ш е п и е. Подстановкой проверяем, что х = 0 не является
корнем исходного уравнения. Поделив числитель н знаменатель
каждой дроби на х, получаем эквивалентное уравнение
1 • 2 — 1.
дс х г
Обозначая х-\ =>у, получаем уравнение
= 1,
у-\ ^ у+\
сводящееся к квадратному уравнению, корнями которого будут
JM = 0, у2 = 3.
Таким образом, исходное уравнение эквивалентно двум урав-.
нениям
первое нз которых ие имеет действительных корней, а корни
второго суть *«,» = (3 ± Уб")/2.
3± л/Ъ
Ответ. «1.2 = S-1—.
Решить уравнения:
2.18. — ■--> — « ^
2.19.
2.20.
2х3 — 5х + 3 + 2х* + х + 3 =6'
3* 2лс 8_
х1 + 1 — 4* х* + 1 + х = 3 *
Зх1 — 1 . 5х 119
х **" з** - х -1 в га *
42 ГЛ. 2. УРАВНЕНИЯ
§ 3. Уравнения, содержащие неизвестное
под знаком абсолютной величины
Если в уравнении некоторые выражения, содержащие
неизвестное, стоят под знаком абсолютной величины, то решение
исходного уравнения ищется отдельно иа каждом из
промежутков зпакопостоянства этих выражений.
Пример 3.1. Решить уравнение
|2х — б|=»ж-~1.
Р е ш е н* и е. Выражение 2х — 5, стоящее, под знаком
абсолютной величины} неотрицательно при х ^ 5/2 и отрицательно
при дс < 5/2. Рассмотрим исходное уравнение отдельно на
каждом из этих промежутков.
Пусть х > 5/2. Тогда по определению абсолютной величины
12лг — 51 = 2х — 5, и данное уравнение преобразуется к виду
2х — 5 = х — I.
Решая это уравнение, находим х = 4. Так как число 4
принадлежит рассматриваемому промежутку, то х = 4 является
решением исходного уравнения.
Пусть теперь х < 5/2. Тогда по определению абсолютной
величины 12дс — 51 = — {2х — 5), и данное уравнение
преобразуется к виду
- (2* - 5) = х — I.
Решая это уравнение, находим х = 2. Так как число 2
принадлежит рассматриваемому промежутку, то х = 2 является
решением исходного уравнения.
Ответ. Xt = 2, Хг = 4.
Пример 3.2. Решить уравнение
\х-\\-2\х-2\ + 3\х — 3 | = 4.
Решение. Данное уравнение эквивалентно следующим
уравнениям:
1) 1 — х + 2(х — 2) — 3(х — 3)=»4 для ж<И
2) х — 1 + 2 (х — 2) — 3 (х — 3) = 4 для 1 < х < 2[
3) х — 1 — 2 (х — 2) — 3 (ж — 3) = 4 для 2 < х < 3;
4) х — 1 — 2 (х — 2) + 3 (х — 3) =» 4 для х > 3.
Первое уравнение имеет решение х = 1; второе уравнение
обращается в тождество для всех значений х, удовлетворяющих
неравенству 1 < х ^ 2; третье не имеет решений; четвертое
имеет решение х = 5.
Ответ: хб[1; 2], х = 5,
5 4. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
43
Решить уравнения:
3.1.
3.2. |
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
*| = *
+ 2.
— Х + 2\=*2х+ 1. V/
х- 1 | + |*-2| = 1. V
*_1|+|* + 2|-|лс-3| = 4.>Г
2-| 1-|*|||-1.V-
х+\
х-\
— 1
■—— 1.
Ьх - хг — 61 = х1 - 5х + 6.
Jta — 1 | = | JC
1*»-
2 *
■2х+2
+ 1.
+ |1*»-Зл: + 4
§ 4. Иррациональные уравнения
Иррациональным уравнением называют уравнение, в
котором неизвестная величина содержится под знаком радикала.
Область допустимых значений неизвестных иррационального
уравнения состоит из тех значений неизвестного, при которых
неотрицательны все выражения, стоящие под знаками радикалов
четной степени.
Решение иррационального уравнения
возведением в степень. Один нэ способов решения
иррационального уравнения заключается в последовательном возведенин
обеих частей уравнения в степень, являющуюся наименьшим
общим кратным показателей всех радикалов, входящих в данное
уравнение. Если степень, в которую возводится уравнение, четная,
то полученное уравнение может иметь корки, не являющиеся
корнями исходного уравнения. Поэтому необходима проверка корней.
Пример 4.1. Решить уравнение
УЗ* + 4 + V* — 4 = 2 У*"- '■ (*)
Решение. Возводим обе части данного уравнения в
квадрат:
Зх + 4 + 2 У(3* + 4) (х — 4) + х — 4 = 4х. (**)
Приводя подобные члены, получаем уравнение
2У(Зл: + 4)(*-4)=0,
корни которого х = —4/3 и х = 4. Один из полученных корней,
а именно дс = —4/3, не удовлетворяет исходному уравнению, так
как не входит в область его допустимых значений. Проверкой
убеждаемся, что при х = 4 исходное уравнение обращается в
тождество.
Ответ, «я 4.
44 ГЛ. 2. УРАВНЕНИЯ
Решить уравнения:
4.1. УГП = 8- V3a-+ I.
4.2. V* + V* + 11 + V* — V* + LI = 4>
4.3. л/17 + 'Ж — У17 — Ж = 2.
4.4. V3* + 7 — V«n = 2.
4.5. V25 —JC = 2 — У§"+~*.
4.6. У*2 + 1 + V*2 — 2* + 3 = 3.
4.7. У*8 + х — б + У*2 + 8* - 4=°5.
'4.8. Уж2 + дс + 1 = У*2 — дс + I + I.
4.9. (ж2 —'4) У*+ 1 = 0.
4.10. У4ж— 3 + УбГ+1 =.уТ57+4.
4.11. УГ+5 + УГ+3 = У27+1.
4.12. У4 — х + Уб + ж = 3.
4.13. У4л; + 2 + У4дс — 2 = 4..
4.14. V* — л/х^2 + V* + У*^2 =ш 2.
4.15. УТ+1 — ж + 3 = 0.
4.16. У*+ 34 — У7^3 = 1. ^
4.17. У2* + б — УЗ* -5 = 2.
4.18. У7 + У* —16=У*^1. <
4.19. УГ+"5 + у*+~б = УгГ+ТТ. ^
4.20. УГ+1 + УзТТТ = $Т^~\. /
. 4.21. УГ+1 + УГ+2 + УГ+3 = 0. V
4.22. -1^1 + УГ + -^1 —Ух = 2. v
4.23. УбТ+7 — У5* - 12 =» 1.
4.24. ^9 —У7+1 + $7 + s/T+l ■= 4.^
4.25. ^24 + У* — -^5 + Ух = 1.1/
Некоторые специальные приемы решения
иррациональных уравнений. В некоторых случаях
Можно освободиться от нррацноыальиостн в уравнения
умножением обеих частей уравнений на некоторое не обращающееся
в нуль выражение. ■. . /
Пример 4.2. Решить уравнение »
УЗх2 + 5* + 8 — УЗ*2 + 5* + 1 = 1. (*)
Решение. Умножим обе части уравнения иа выражение
§ 4. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
43
вой части уравнения (*). После приведения подобных членов пси
лучаем уравнение
7 => Уз*2 + 5х + 8 + Уз*2 + 5*+1, (**)
которое эквивалентно исходному, так как уравнение'
Уз*а + 5* + 8 + Уз*а + 5* + 1 = О
действительных корней не имеет.
Складывая уравнения (*) н (**), получаем
УЗ*а + 5х + 8 = 4.
Возводя последнее уравнение в квадрат, получаем квадратное
уравнение
Зле» + 5ж — 8 = О,
корни которого *i = — 8/3, Xi = 1. Делая проверку,
убеждаемся, что оба корня являются корнями исходного уравнения.
Отв ет. xi = J, дс2 = —8/3.
Решить уравнения:
4.26. У3жа — 2х + 15 + Уз*2 - 2х + 8 = 7. •"
4.27. У*2+ 9 _ у*2 — 7 = 2, v-
4.28. У15-* + Уз~^£ «= 6. v
4.29. У Л** + В* + С + УЛ*2 + В* + С, = р. и
4.зо*. УД+f + VJEf ,«., м „
У21 + * — У21 — х х
Введение вспомогательных неизвестных в ряде случаев
позволяет перейти от иррационального уравнения к системе
рациональных уравнений.
Пример 4.3. Решить уравнение ■
х2 — Ах— 6=У2*2-8*+ 12. *
Решение. Обоэначая -\/2ха — 8х + 12 = у, получаем
следующую систему уравнений!
у* = 2*а-8*+12, uv
у = х1 — 4х — 6. к '
Исключая из системы (*) неизвестное х, получаем уравнение
уа — 2у — 24=0.
Корнями этого уравнения являются yi «= 6, у» = —4. Так как
через у обозначен арифметический корень, то из двух найден*
ных корней уравнения выбираем положительный. Подставляя
его во второе уравпенне сиотеиы (*), получаем уравнение
ха—4х— f2 = £
46 ГЛ. 2. УРАВНЕНИЯ
корин которого xi = —2, xt = 6. Делая проверйу, убеждаемся,
что оба корня являются корнями исходного уравнения.
Ответ. xt = 6, Xi = —2.
Пример 4.4. Решить уравнение
$х+ 1 = л/Т^Ъ. ^
Решение. Обозначим rfx+ 1 = ц, V* — 3 = v-
Исключая х из уравнений ц3 = *+ 1, о2 = ж — 3, приходим к системе
ц = о, ц3 — о2 =» 4.
Ее решение сводится к решению уравнения
1,з_о* -4 = 0,
единственный действительный корень которого 0 = 2.
Возвращаясь к исходному неизвестному, получаем линейное уравнение
4 = х — 3, корень которого является едииствеиным корнем
исходного уравнения.
Ответ, х = 7.
Решить уравнения!
5 В
4.31. V(7* — 3)3 + 8V(3 — 7*Г3 = 7. ' /
4.32*. УГ^2 _j. *JX^~x = *« — 6* + П.
4 4
4.83. V47 — 2лс + У35 + 2х = 4.
4.34. (ж + 4) (ж + 1) — 3 У** + 5ж + 2 => 6.
-л/й+л/тв1-»*
4
4.36. V*2 + 32 — 2 V*2 + 32 = 3.
4.37*. Vm+V£E±=* + v^rre-6.
2
Л/^Тз^Л/^^-2-
4.39. V х л/7 —ух Ух" =» 56.
4.40. №-*)V5=5 + (*-3)VJ^3 ,,
V5 — де + V* — З
4.4L х<$х — 4^*»+4 = 0.
4.42. *г + Зх - 18 + 4 У ха + 3* - 6 = 0.
4.43. УЗу* + 6и + 16 + л/у* + 2у = 2 Vy2 + 2j/ + 4.
S 4. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
47
аа* 3(*-2) + 4У2*'-3* + 1 ,
4'45' 2(*»-1) U
4.46. л/х — 2 + У 2* — б + У* + 2 + зУ2х—5 = 7 У2~.
4.47*. (х — З)2 + 3* — 22 = V*2 — 3* + 7 .
4-48--£—Л/т+7Л/т+^-
Решение иррациональных уравнений мето»
дом выделения полного квадрата в
подкоренных выражениях.
Пример 4.4, Решить уравнение
V* — I + 2 V* — 2 — V* — I — 2 У* — 2=1.
Решение. Обозначим V* — 2 = <; тогда исходное уравие-
пне приобретает вид »
VF+27+T — У'2 - 2< + 1 =» I. (*) !
Так как под радикалами в левой части уравнения (*) стоят
полнив квадраты, то уравнение сводится к следующему уравнению:
|/ + 1|-|*_1|в1.
Единственным корнем этого уравнения является t = 0,5. Возвра»
щаясь к исходному неизвестному, получаем уравнение
V* —2 = 0,6,
корнем которого является х = 2,25.
Ответ. *= 2,25.
Решить уравнения: I
4.49. V* + 2 + 2 УГ+7 + V* + 2 — 2 УГ+1 = 2. ^
4.50. V* + 5 - 4 У*"+7 + V* + 2 - 2 УГ+I = I-
4.51. У* + 8 + 2 У*"+7 + У* + 1 _ У*+ 7 = 4.
4.52. У!*Ч-~2~л/^==Т - V«a — 2 У*2 - 1 = 1.
4.53. У* + 2 У*^~Г — У* — 2 У* — 1 — 3.
4.54. V* + 2 Уж — I + V* — 2 УГ^1 = х - 1. v
4.56. У2х — 2 У2ж — 1 — 2 У 2* + 3 — 4 У2* — 1 +
+ 3 У 2* + 8 — 6 У2ж — 1 = 4,
4.56. У*+3 — 4Ух^П[ + Уж + 8-бУ*-{«=1.
48 ГЛ. 2 УРАВНЕНИЯ
4.58. д/"Н|- + VЛ'2 ~ 1? = А'2'
4.59. 2V6V*n + 4-V 2 V*+ I — 1 =
= V20V«T~i + 5
4.60. V2*s — 9* + 4 + 3 У2* — I = V2*2 + 2U— 11.
4.61. -s/W+W+1 - У2*2 + ж - 1 =» V*' - 1.
4.62*. У4 — ix + x1 + У 49 + 14* + x1 =
= 3+У14-5ж — л*.
4.63*. У2*2 + 8* + 6 + У*2 — 1 = 2дс + 2.
4.64. У*"^2 + У1 —"ж = 2.
4.6Б. 4 * = (УМ7* - 0 (УГ^1 + 1).
4.66.
•У* + гу* — 1 V*-2y*-i 2 *
4.67. У(в + *)2 + 4 У (а - л)2 = 5 У я2 —л2.
л п в
4.68. У(*+ I)2 + У(*-1)2 = 4 У*2—1.
У* +1 Уж + 1
4.70. (34-^)УГП-(.+ 1)Уз4^1=з0>
У34 - х — Уж + 1
4.71. У(2 — ж)» + У(7 + х)1 — У(2 - х) (7 + ж) = 3.
§ 5. Показательные уравнения
Показательными называются уравнения, в которых иевзвестг
ное входит только в показатели степеней при постоянных
основаниях. Простейшим показательным уравнением является
уравнение вида
а* = Ь. (1)
Его решением при а > 0 н 6 > 0, а Ф 1, является
х = logab.
Если вместо х в показателе степени стоит некоторая функ«
дня /(ж), т.е. уравнение нмеет вид
af(*> = 6, а>о, аф1, Ь>0, (2)
§ 6 ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 49
то, логарифмируя обе части этого уравнения, приходнм к эквнва-
лентному уравнению
f (х) = iogfl Ь.
Решение простейших показательных у р а в«
я е и н й. Некоторые показательные уравнения приводятся к виду
|1) или _(2) с помощью равенств
ах+У
{а*)У
а*
а»
(e.fr)*
=я Д* <
=>a*J
=.ах-
= а*<
■ аУ,
>
-».
-ь\
( a Y а
Пример 5.1. Решить уравнение
62*+4=3<i*.2*+8.
Решение. Перепишем данное уравнение в виде
3»*+«. 22х+* «=» З8* ■ 2*+8.
Используя свойство членов пропорции, имеем
Зг*+« 2*+8
З3* = 22*+4 '
или после упрощения З4-* = 24-*. Преобразуя данное уравнение
к виду
i«—*
"1.
(*)
получаем 4 — дс =» 0, откуда следует, что х =« 4,
Ответ. 4.
Решить уравнения:
5.1. V5* •V5S = 226.
8.2. 23*. 5* = 1600.
5.3. 93-6*.7бХ-3=1.
5.4. 88JC-|.53*+2=-|-'52*-3w.
о
5.6. 3.4х + 4-'9х+! = 6.4*+|— -£-'9*"И'
2
а**-5х—9
5А 7 2 -(V2)3'OBl7.
£.7. 4.8*+s + &-3*— 7.3*+» — 40,
БО
ГЛ, 2. УРАВНЕНИЯ
5A5(JL)9,n*X+4.6-^ = 26^etoMVr
х+& х + 17
5.9. 16 х-7 =512-64 *-3 .
5.10. 5 | •*-» | =. 253*~«. V
я 2+Ух+х
6.11. V3"-3,+VF.(-l)2(,+V5) = 8U
*-з '/' / з7=Г
блг.-в3*-7 • v v о,2б *-> = 1. V .
5.,,о,..'(^)"-'"-(^)'.
5.14. (2,4)'-8т*.[0,41(6)l^+'Z2 = (-^-)"2.
5.15. Найти решение уравнения /
0x4-4*^ 1 *
■* "25'
удовлетворяющее условию х > ~3.
Решения показательных уравнений, сводя*
шихся ааменой переменных к алгебраячееко*
му уравнению.
Если показательное уравнение имеет вид
*(«f(*>) = 0, (3)
то заменой у = а'**) оно сводится к уравнениям внда
где yi— корин уравнения g(y) = 0.
Пример 5.2. Решпть уравнение
4V^2 + х _ 5. 2Х~» + V?=* = 6.
Решение. Обозначая г"**2-2"*"* =# и производя замену
переменных, получаем квадратное уравнение
корнями которого будут yi = 4 и уг = —3/2. Таким образом, ре*
шение данного уравнения свелось к решению уравнений
2*+V^2— 4, 2* + 'v^-5'—-8/2,
5 в. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
Б1
Второе уравнение решений не имеет, так как 2*+л'х^-2>0
при всех допустимых значениях х. Из первого уравнения
получаем
* + V*2 — 2 = 2.
Уединяя радикал и возводя обе части уравнения в квадрат,
имеем
X* — 2 = 4 — 4* + х\
Приводя подобные члены, получаем единственный корень х =>
= 3/2. Проверкой убеждаемся, что этот корень удовлетворяет
исходному уравнению.
Ответ, х = 3/2.
Решить уравнения:
5.16. О*'-1 - 36. 3*'-3 + 3 = 0.
X X _
5.17. ЗУ81-10д/9 +3 = 0.
5.18. 3,_* — 31+* + 9* + 9~* = 6.
5.19. 641/х — 22+3/* +12 = 0.
6.20. 4loff »* - 6 • 21о<*» * + 210*1 й = 0.
6.21. 4^3л:'-2ж+ ' + 2 = 9 • 2Va*3-2*.
Показательные уравнения, основания степеней которых
являются последовательными членами геометрической прогрессии, а
показатели степеней одинаковы, приводятся к уравнениям вида
£3) делением на любой нз крайних членов.
Пример 5.3. Решить уравнение
6-4*— 13«6* + 6-9* = 0.
Решение. Разделим обе части уравнения На 9*. 'Имеем
;Ш*-"(!)'+в-°-
Обозначая (v) ="tf и производя замену переменных, получаем
уравнение
6у*— 13^ + 6 = 0.
корнями которого будут yt = 3/2 и уг = 2/3. Таким образом,
решение уравнения сводится к решению двух простейших
показательных уравнений
(1\* J. (LY 2
\2) "" 2' \2) = 3'
Ответ, xt =».- 1, *i == -*-1,
62
ГЛ. 2. УРАВНЕНИЯ
Решить уравнения:
5.22. 7 • 4х' — 9 • 14*" + 2 • 49*' =» 0.
5.23. 3-16*+ 36* = 2.81*.
5.24. 8х + 18х = 2 • 27*.
X _ X _ X
5.25. 6 У9 — 13 Уб + 6 У? = 0.
5.26. 16х —5-8х + 6.4* = 0.
*5.27. 2sx-e - б + 6 • 23-3* = 0.
5.28. 27Х+12Х = 2>8Х.
5.29. (4 + УТ5)* + (4 - УТб)* = 62.
5.80. (л/5 + 2 л/б" )* + (л/5-2УёГ )* = 10.V
6.31. 9"*+ 12'/*= 161/*.
5.32. б1+х'-51-х*=24.
5.33. 5х-' + б • 0,2Х~2 = 26.
5.34. 10^* + 25 "* = 4,25 • 501/х.
Уравнения вида
[a(x)]bW=*la(x)\cM
эквивалентны уравнению
а (х) = 1
н системе
b {x) = с (дс),
а (х) > 0.
Пример 5.4. Решить уравнение
|Ж_2|10*'-1=3|Ж_2|3* у
Решение. Исходное уравнение эквивалентно уравнению
|*-2| = 1
н системе
10**— 1=3*.
|х-2|*.0.
Первые два уравнения имеют корни X] — 3, *а=1, а
система —х$ = 1/2, ж, = —1/5.
Ответ. *i = 3, х3 = 1, дс3 = 1/2, *4 = ■— 1/5
Решить уравнения:
4
5.85. л/| х - 3 j*+1 - Vl x - 3 I*"2. \ /
6Ж |«-8р^-№+»—I. V
§ 5. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ
53
Б.38. (УГ)1°В,*~, = 5.
5.39. Ж1в*+Г=10(1к «+D-4
Некоторые специальные методы решения
показательных уравнений. Некоторые уравнеиня
сводятся к рассмотренным выше, если преобразовать отдельные их
элементы, используя основное логарифмическое тождество.
Пример 5.5. Решить уравнение
з^+х"*»*—lea.
Решение. Согласно сделанному замечанию преобразуем
второе слагаемое в левой части уравнения:
,to«,*_(3'°«.*)b«»*e3,0"SS. W
Подставляя полученное выражение в исходное уравнение,
получаем
о
2.з'°Вз*=162. (♦♦)
Уравнение (•*) эквивалентно уравнению log§* = 4, которое
в свою очередь эквивалентно двум уравнениям
log3 х = 2, Iog3 x = —2.
Решая последние уравнения, получаем *i = 9, *8 = —,
Ответ: Ж|=*9, *а*=7г-
Решить уравнения:
5.40. 5[«х = 50-х1*5. V
5.41. 101в'* + х,к* = 20; "f
5.42. ж" * » - 5 • 2,в'* + 6 - 0V
Некоторые уравнения, содержащие неизвестное в показателе
степени, удается решить с помощью исследования функций,
входящих в левую н правую части уравнений.
Пример 5.6. Решить уравнение
7е-* = х + 2.
Решение. Корень х = 5 может быть найден подбором.
Других решений уравнение не имеет, ,та_к как функция /(лр) =»
t«=» 7е"* монотонно убывает, a g{x\ ==#+■? монотонно возра-«
64 ГЛ, 2. УРАВНЕНИЯ
стает, и, следовательно, графики этих функций могут пересечься
ле более одного раза.
Ответ, х = 5.
Решить уравнения!
5.4з*. (Уг + л/з)* + (д/г-д/зУ = 2*.
5.44*. 3х-1 +5*-' = 34.
S.4S*. Й»*-»*'- *'+1 .
5.46*. 4х + (ж — 1) 2х = в — 2х.
5.47*. (ж + 1) 9х-3 + 4* • 3х-3 — 16 =Д
5.48* х2 - ж + 1 = 2 • 2*-' — 4х-'.
ела. 5^Г +1аУ*" — laV^".
5.50. 3*' + 4* = 5х'.
5.61. (jV=-2x2 + 6*-u.
§ в. Логарифмические уравнения
Логарифмическим называется уравнение, содержащее
неизвестную величину под знаком логарифма. Простейшее
логарифмическое уравнение
loga х-=Ь, а>0, а=И=1, (1)
с множеством допустимых значений х > 0 имеет решение х=а1'.
Логарифмическое уравнение, в котором под знаком логарнф-
ма стоит некоторая функция f(x),
logaf(x) — b, а>0, аф1, (2)
имеет множеств допустимых значений х, задаваемых
неравенством f(x) > 0, н эквивалентно уравнению
Решение логарифмических уравнений с в е •
деоиам к простейшим логарифмическим
уравнен и я и. Некоторые логарифмические уравнения решаются с
использованием основных свойств логарифмов (1)—(5) (гл. 1, § 5),
сводящих решение уравнения к решению простейшего
логарифмического уравнения.
Пример 6.1. Решить уравнение
2-* + 3logs2 = logs (3х - б2-*).
Решен, и е. Перенесем логарифм, стоящий в левой част»
уравнения, в правую часть н, воспользовавшись свойствами ло*
§ в. ЛОГАРИФМИЧЕСКИЕ РАВНЕНИЯ 65
гарифнов, аапншен уравнение в виде
Последнее уравнение эквивалентно уравнению
3х -5»-* |ДЖ_Ж
которое можно записать в виде
3* = 9-5а-х, или 3*-г = 5*-*, вли 15х"2 = 1.
Полученное показательное уравневве эквввалентно уравнению
х — 2 = 0, решевве которого х = 2.
Множество допустимых значений х данного уравнения
определяется как решение неравенства
3х _ 52_х > в.
При х = 2 данное неравенство справедливо, и, следовательно,
X = 2 является решением исходного логарифмического урав*
нения.
Ответ, х = 2.
Решить уравнения!
6.1. log5 [2 + log3 (3 + х)] = 0. Vf
6.2. lg (б - x) - -i- lg (35 - *8) = 0.
ЪЛ. kg„<3* - 8) =2 - x. V
6.4. log^ (4* - 6) - iogvr (2* - 2) = 2.
6.5. Jg (3jks + 12* + 19) - lg (3* + 4) => 1.
Логарифмическое уравнение вида
l0£a(*)fW = l°gaW£W ' .
эквивалентно уравнению
/(*) = £(*)>
рассматриваемому на множестве допустимых значений х,
задаваемом системой неравенств
fW>0. g(x)>0, а(х)>0, а(х)чЫ.
Если в данное уравнение входят логарифмы по разным
основаниям, то предварительно необходимо привести все логарифмы
к одному основанию.
Пример 6.2. Решить уравнение
igV^rT + 4-18(2*+16i=^ W
66
ГЛ. 2 УРАВНЕНИЯ
Решение. Множество допустимых значений неизвестного х
в данном уравнении находится как решение системы
х — I > 0, 2лс + 15 > О
в представляет собой промежуток (1; оо). Используя свойства
логарифмов, преобразуем данное логарифмическое уравнение в
следующему виду:
lg (V(* - 1) V2*+15) = 1.
Из последнего уравнения по определению логарифма получаем
иррациональное уравнение
>
V(*~ l)(2x+ 15) =10,
решение которого *1 = 5, Хг = —23/2. Множеству допустимых
значений х исходного уравнения припадлежит лишь корень xi =J
= 5, который и является решением исходного уравнения.
Ответ, х = 5.
Решить уравнения:
6.6 2 log3 (х ~ 2) + log3 (* — 4)! = 0.
6-8- 4" 'S <** — ,0* + 25) + '& (** — бх + 3) =
-21g(*-5)+-llg25.
6.9. -i-lg^*«-4* + 4-ilg*-lg--L- = 0.
6.10. lg (лг (Jf + 9)) -Ь lg ^±^- = 0.
6.11. logH2x» — 2) = 10g2 (5л: — 4).
б.»2. '^5-*;>=з.
lg (5 — ж)
6.13. Iogx+1 (x - 0.5) = logics (* + 1).V
6.14. log<.+2rI_a),+5 (x3 + 3x* + 2* - 1) = logM x + logto 2. V
6.15. log,+^ (2xa + 2xs — 3x + 1) « 3. "^
6.16. logx+, (x8 —9x + 8)logA:..,^+'I)=3.\'
6.17. logx+,(*' + *-6)2 = 4. ^
6.«8. log^,, (9 ~ 16*«) = 2 + loga(31_4,^)V
6.19. log3x-|-+log|x = l. ^
6.20. log.,: 16+^^64 = 3. ^
S в. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ 57
6.21 20 10g4xV7 + 7 log МжЛЕ,-31оВяр** —0. V
6.22. log, 2 - log, x + -£- = 0. ^
6.23. 2 — logu, (I + x) =з 3 log& V*- I — log&. (*' - I)2.v
6.24. 3 log, 4 + 2 log,, 4 + 3 logl(u 4 = 0. V
Решевие логарифмических ураввеннй, с во*
дящнхся заменой переменных к
алгебраическому ураввевию. Если логарифмическое уравиепие имеет
вид
f(loga*)~0,
где f—векоторая функция, то замепой у = logo x опо сводится
к уравнениям вида (1):
logo х = yi,
где yi — корпи уравнения {(у) = 0.
Пример 6.3. Решить уравнение
(loga*)2-5 (loga*)+6 = 0.
Решение. Обозначая loga х = у, получаем уравнение
у2-Ьу + 6=0,
корни которого yt = 2. у% = 3. Таким образом, исходное урав»
пение эквивалентно двум уравнениям вида (1):
loga х »=» 2, logj дс = 3,
решения которых: Х|=4 в *j = 8.
Ответ. «1=4, *2 = 8.
Решить уравнения:
6.25. lg8* — lg2* — 6lg* = 0.
6.26. 2 ^2 logfeж — ^log2 x — 6 = 0.
3 i
6JS7. — log*— * — 30 <V logf * + 36 = 0.
e-28. log1/9 (i) log1/9 [* tg» i] = 2 cos» -f-.
6.29. Vl + logx V27 logj x + 1 = 0.
6.30. 4 — lg x = 3 Vlg*.
6.31. 3yii~* + 2lgVT7* = 2.
6.32*. yig(-*) =• lg V*3.
6.33. logs (3* - 0 10gB (3*+' - 3) = 6.
в.34. 2 loga log2* + logV2 log2 (2 V2" *) = '•
58
ГЛ. !. УРАВНЕНИЯ
Решение логарифмических уравнений ме*
тодом логарифмирования. Если неизвестное входит в
.уравнение как под знаком логарифма, так и в оспеваиин
степени, то в некоторых случаях уравнения указанного типа могут
решаться логарифмированием обеих частей уравнения с
последующим использованием приведенных выше методов решения ло<
гврнфмическнх уравнений.
Пример 6.4. Решить уравнение
Решение. Прологарифмируем обе части уравнения
1од(*8+к**)-1ов,Л
используя свойства логарифмов, получаем уравнение
(2+log3A'),0g3* = 8.
Обозначая logs х — у к производя замену переменных, на'
ходим корни квадратного уравнения
у» + 2у-8 = 0,
01 =— 4, уг = 2.
Решая простейшие логарифмические уравнения, получаем
значении
log3 х = —4 «*■ х = 3~\
logj X =а 2 >*■ X «■ 3*.
Ответ, лг, = З2, ха = 3~4.
Решить уравнения:
6.35. j*»1""*-1'"1**) —Vl& ^
6Ж xl«'x+lex?+3 j - j , v
л/х+1 — 1 У*-J-1 + 1
6.37. *2|«'*=10*3.
6.38. 1б|°г»ллг1ог,9*+| = 1.
6.39. 9*lg * + 9х~ 1е *= 60.
6.40. лг 2 2 — [х + 2) (г+2^ = 3.
3 - log» дс+ =•
0.42.7.*'' a ' — 5-J-(x + 7) V« .
S 7. РАЗНЫЕ ЗАДАЧИ
S9
Решение логарифмических уравнений о
помощью свойств логарифмической функции.
Некоторые логарифмические уравнения удается решить с помощью
исследования поведения функций, входящих в левую и правую
части уравнения.
Пример 6.5. Решить уравнение
tog7(* + 2>.= 6-*.
Решение. Подстановкой проверяем, что х = 5 является
решением уравнения. Других решений уравнение не имеет, так
как функция, стоящая в левой части, возрастает, а в правой—*
убывает, и, следовательно, графики этих функций не могут иметь
более одного пересечения.
Ответ, х = б.
Решить уравнения!
6.43. {х + 1) Iog£* + 4x 1og3 х — 16 = 0. '
6.44. Зле2 — 2х* = log2 (ха + 1) — log2 х,
6.46. 3х =10 — logs ж.
6.46. logfx + (х — 1) log2 х = 6 — 2Х.
§ 7. Разные задачи
Решить уравнення1
7.1. 122*+4 = З3* • 4Х+8. ^
7.2. 2* + 4<х+1,/2 = 8 • З*'3. ^
7.3. 2*-3*/2 = 1. V
7.4. (sin l)x+ (cos 1)* = 1. V
7.5. №*2 = 2'100*. V"
' 7je.jW*-(V£V.
x+l
7.7*» 5* V§*"= ЮО.^"
7.9*. Ю^+'НЗ^+^ — г. 10<х+1)(х+2)=10|-,£-х'.
7.10. ^ = (V^)X.
7.11. 9* — 5-12* + 6.16* = 0.
7.12. log3 [(x + 2) {x - 3)] = 4 logx (2* + 1) - log^ Л
7.13. lg2*3 - 20 lg У* + 1 = 0.
7.14. | 1 - log|/e* |+ 2 = | 3 - logl/e* |.
^15. logjJ{x + \x-2\) = logJC{5x-6 + b\x-2\).
£0 ГЛ, 2, УРАВНЕНИЯ
7.16. logx+i (** + х - 6)! =» 4.
7 17 1 + 10g2 (* — 4)
Iog^(V* + 3 -V-*-3)
7.18. iog5 [(2 + V5 )* - (V5"~ 2)*] = \ - 3 log1/s 2.
7.19.б.(-^)а1П,Д,+4.5-^=2б^в1П2Х.
7^о. (VTwrr x+(V7"^4vr)co8 ■ - 4--
Г Л А В А 3
СИСТЕМЫ УРАВНЕНИЙ
Несколько урариевнВ
Л (*[• "а *п)=°< М*1' ** *п)=° pk(*V xt xn)=-°>
рассыатриввемых совместно, называют системой уравнений. Решеннеи
зтой системы называется упорядоченный набор значений неизвестных,
обращающий все уравнения системы в тождества.
Если система уравнений имеет решения, то говорят, что она сов'
местная. Если система уравнений не имеет решений, то говорят, что
она несовместная.
Линейным уравнением с п неизвестными нззывают уравнение вида
alx, + aax2 + ... +а„х„=.6.
где а,, а2, .... ап, Ь—некоторые числа.
Система уравнений называется линейной, если все уравнения
системы линейные. Совместная система называется определенной, если она
имеет единственное решение (т. е. существует единственный набор чисел
ft,, .... кп, обращающий все уравнения системы в тождества).
Совместная система уравнений называется неопределенной, еслв она
ниеет более одного решения. Две совместные системы уравнений
эквивалентны, еслп множества их решений совпадают.
При решении систем уравнений часто используются следующие
преобразования системы, приводящие к системе уравнений, эквивалентной
исходной.
1, Если обе части какого-либо уравнения системы домножнть на одно
я то же (не равное нулю) число, то полученная система будет
эквивалентна первоначальной (т. е. они или обе иесовыестны, нлн ,же обе
совместны п множества их решений совпадают).
2. Если обе части какого-либо уравненпп системы, умноженные- на
некоторое (отличное от пуля) число, вычесть яз соответствующих частей
другого уравиення и составить систему, в которой вместо одного пэ
упомянутых уравнений стоит уравиепне, полученное в результате вычитания,
а остальные уравнения оставлены без изменений, то полученная спетом а
будет эквивалентна исходной.
§ 1. Системы линейных уравнений
Решение систем линейных уравнений
методом Гаусса. При нахождении решений системы m линейных
уравнений с п неизвестными удобно использовать метод Гаусса,
состоящий в том, что систему приводят к треугольному или
трапециедальному виду. Проиллюстрируем метод Гаусса на
примере.
62 ГЛ. 3. СИСТЕМЫ УРАВНЕНИЙ
Пример 1.1. Решить систему
х + 2у + 3z = 8,
3* + у + z = 6,
2* + У + 2г = 5.
Решение. Умножая обе части первого уравнения на —3 н
складывая со вторым уравнением, получаем уравнение
—Ъу — 8z =. —18, или
5«/+8z = l8.
Умножая обе" части первого уравнения на \—2) н складывая с
третьим уравнением системы, получаем уравнение — Ъу — iz=n
-= —10, или
Zy + 4z = 10.
Следовательно, данную систему можно записать в виде
эквивалентной системы, в которой второе н третье уравнения не
содержат неизвестного х\
х + Чу + Ъг = 8,
5y + 8z=18, (♦)
3«/ + 4z=10.
Умножая обе части второго уравнения на 3, а третьего—на
(—5) и складывая эти уравнения, получаем уравнение 4г ■— 4;
таким образом, система (*) записывается в виде эквивалентной
системы
* + 2y + 3z = 8,
5i/ + 8z=l8,
z=l.
Итак, исходная система приведена к треугольному виду. Под»
ставляя z «= 1 во второе уравнение системы, находим у = 2.
Подставляя значения z = i и у = 2 в первое уравнение, вахо*
днм х = 1.
Ответ, х = 1, и = 2, z= 1.
Решить системы линейных уравнений методом Гаусса:
1.1. 2* +у+ z = 7, 1.2. Зж — 4y + 5z=18, -<
x + 2y + z = 8, 2je + Ку — Ъг = 26,
х + у + 2z = 9. ж — 6у + 8z => 0.
U. 10* — 8z=19, 1.4. * + 2y + z + 7-»0,
8х — у = 10, 2х + {Г — z — 1 = 0,
у _ 12z=10. 3*-0 + 2z-2=»O.
§ t. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
63
1.6.
X
а3
X
Ь3
X
У
У
У
~" с2
+
+
+
г
а
z
т
Z
— 1.
=-1,
= 1.
1.6. х + а*у + ЬЧ => О,
лг + ay + frz = О,
1, у x + y+z=l.
V
Решение и исследование систем двух л и <
иейных уравнений с двумя неизвестными.
Рассмотрим систему двух линейных уравнений с двумя нензвест
ними
М
при условии, что хотя бы один из коэффициентов отличен от
нуля. Пусть &, &х и Д„ — определители системы (*):
Д =
А,-
он
а2]
h
h
an
021
а,2
022
а,3
aSj
*.
62
1 вц^га — Д|ап21»
'fr|022 — ^aia,
«вц6а — oatV
При Д#0 система имеет единственное решение х~—-,
Д
д„
»--Г-
При Д = 0:
1) если хотя бы одни из определителей Д* или Ау не равен
нулю, то система (*) несовместная (т. е. не имеет решений);
2) если Ах ==» Д|/ = 0, то система (*) совместная и
Неопределенная (т.е. имеет бесконечно много решений).
Каждое из уравнений системы (*) задает линейное
соответствие между переменными хну. Всякое линейное соответствие
между переменными хну определяет в прямоугольной системе
координат некоторую прямую. Если система имеет единственное
решение, то прямые, задаваемые первым н вторым уравнениями,
пересекаются. Если система имеет бесчисленное множество реше*
ний, прямые совпадают; если система несовместна, прямые ва*
раллельны.
Пример 1.2. Решить и исследовать систему
ах + у = 2,
х + ау = 2а.
64
ГЛ 3. СИСТЕМЫ УРАВНЕНИЯ
Решение. Вычислим определители системы:
д=
д*=
Д„ =
а 1
1 а
2 1
2а а
а 2
1 2а
= аа-1,
= 2а — 2а = О,
= 2в2 — 2.
1J Пусть Д = в* — 1 ФО, т.е. аф±\. В этом случае сн->
стена имеет единственное решение)
Д*
О Д^ 2аа - 2
_ = 0, ,-_.--j-^-a.
2) Пусть Д = а*— I =0, т.е. а = ±1. В этом случае Д =
= Дл =■ Дв ■=- 0, т. е. система совместная и неопределенная.
При а в I система принимает вид
х + у=*2, х + у = 2,
в ее решениями будут все пары чисел (х, у), связанные равен*
ством дс + у •=■ 2.
При а » —-1 имеем
—х + у
х-у
■2,
■-2,'
х-у
■-2,
■-2,
сея
в ее решеннямн будут все пары чисел (х, у), связавные равен-»
ством х—у = —2.
Ответ, При а ф ± I система имеет едяиствениое решеияе
ж = 0, 0 = 2;
при а = 1 система имеет своими решениями все пары чисел
{х,у), связанные равенством х + у = 2;
при а = — 1 система нмеет своими решениями все пары чи>
(х, у), связанные равенством х— «/= —2.
Решить н исследовать системы уравнений:
1.7. * + ау — 1 =» 0, 1.8. Зх + ау=> бе»,
а* — Зау — (2а + 3) = 0. Зж — ау = а*.
1.9. (а + б) х + (2а + 3) у — (За + 2) =< О,
(За+ 10)*+(5а + 6)у-(2а + 4) = 0.
1.10. а (а — 1) х + (а + 1) ау = в3 + 2, 1.11. а* — 0 — Ь,
{а*—\)х+(а3+1)у = а, — 1. Ьх+у=а.
1.12. (в» + Ьг) х + (в2 — Ь1) у => а»,
(в + 6)дс + (о — Ь}у = а.
8 i. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ S5
1.13. Найти такие значения параметров тир, при которых
система
(Зт — бр + Ь) х + (8т — Зр — а) у ■=» 1,
(2т — Зр + Ь) х + (4т — р) у =» 2
была бы неопределенной.
1.14. Совместны ли уравнения
х + ау => 6 + с,
* + 6у = с + а,
ж + су = а + 6,
•где а2 +62 + са = 1, а, 6, с — действительные числа?
1.15. Числа а к b таковы, что система
а2* — ау = 1 — а,
Ьх + (3—2Ь)у = 3 + а
имеет единственное решение дс = 1. у •= 1. Найти числа а и В»
1.16. При каких значениях а н Ь система
а"х — Ьу = а2 — Ь,
Ьх — Ьгу=-2 + 4Ь
имеет бесконечно много решений?
1.17. При каких значениях а система
а2*+ (2 — а)'у = 4 + а3,
ах + (2а — 1) у = а? — 2
ве имеет решений?
1.18. Числа а, Ь и с таковы, что система
ах — Ьу = 2а — Ь,
(с+\)х + су=-\0-а + ЗЬ
имеет бесконечно много решеннй, причем *=1, у = Ъ— одна
&з этих решеннй. Найти а, 6 и с.
1.19. При каких значениях параметра а система уравнений
ах — 4у = а + 1,
2дс + (а + 6) у = а + 3
ие имеет решеннй?
1.20. При каких значениях параметра а система
2х + ау = а + 2,
(а + 1) ж + 2ау = 2а + 4
имеет бесконечно много решений?
3 А. Г. Цыпкнв, А, И, Ппяскна
66
ГЛ. 8. СИСТЕМЫ УРАВНЕНИИ
§ 2. Системы нелинейных уравнений
Решение систем, содержащих линейное
уравнение. Если одно нз уравнений системы двух уравнений
с двумя неизвестными линейное, а второе — нелинейное, то эта
система решается следующим способом. Из линейного уравнения
выражают одно неизвестное через другое н подставляют во вто»
рое уравнение, которое после этого превращается в
алгебраическое уравнение с одним неизвестным.
Решить системы уравнений:
2.1. \х - у) (х* - у2) _ 45, 2.2. (х + 0,2)» + (у + 0,3)» - 1,
х + у = 5. х + у = 0,9.
2.3. 4" + "Г = "Г"' 2А (*+»)*+* <*+У)*~ "7-0.
25. х* + уг = 2 {ху + 2), 2.6. хг+уг+\0х—\0у = 2*^—21,
ж + jf •= 6. #+{f = 5.
Решение систем, содержащих однородное
уравиевне. В тех случаях, когда одно из двух уравнений
нелинейной системы однородное, можно с помощью этого
уравнения линейно выразить одно неизвестное системы через другое.
Пример 2.1, Решить систему
*2-5*у + 6у! = 0,
лг* + у*=10. {*>
Решение. Разделяв первое уравнение на у1, получаем от»
носительно неизвестного t = х/у квадратное уравнение
*»_5* + 6 = 0,
корнями которого являются <i = 2, h = 3. Возвращаясь к
исходным неизвестным, получаем следующие линейные зависимости
между неизвестными, входящими в исходную систему (*):
лг — 2у, х=3у. {*♦)
Подставляя последовательно х = Зу и х = 2у во второе
уравнение данной системы, получаем отиосятельво неизвестного у
квадратные уравнения у1 = 1 и у2 = 2, корпи которых
У I, s = ± 1, уа, 4 = ± V2. Соответствующие значения *i, хг, х3, х^
находятся нз равенств (**).
Ответ. Пары чисел (3, 1), (—3,-1), (2л/2, л/Т), (— 2 У?,
-V2).
Система вида
aix2 + *iffs + c.xjr — du . л . _
5 2. СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИИ 67
сводится к системе, содержащей однородное уравнение, следую»
щим обравом: умножаем обе части первого уравнения на rfa, обе
части второго —на (—dt) и складываем первое уравнение со
вторым. В результате сложения получается однородное
уравнение. Далее исходную систему заменяем эквивалентной системой,
состоящей из полученного однородного уравнения н одного из
уравнений исходной системы.
Пример 2.2. Решить систему уравнений
х2 + ху = 2.
Решение. Умножив обе части первого уравнения на 2,
обе части второго — на (—1) и складывая полученные уравне*
пия, получаем однородное уравнение
х2 — 2уг — ху=>0.
Поделив обе части однородного уравнения на у1, получим отио-
X
сительно z == — квадратное уравнение
zs-z-2 = 0,
корни которого zi = — I, z, = 2.
Исходная система, таким образом, эквивалентна двум си-'
стемам
*»-у»-1, х*-у*=1,
i—1 И -5—2,
У У
первая из которых несовместная, а решения второй имеют вид
(1л]ъ Уз Ч ( 2 Уз" Уз~Ч
Решить системы уравнений:
2.7. *у + хV =• 12, {, 2.8. *s + у3 = 6б,\/
2.9. ^-^ = 15, \ ,
х*у — хуг = 6. V
г Решение симметрических систем. Системаypaei
нений с п неизвестными xi, дс2, ,.,, ха называется симметричен
ской, если она не меняется при перестановке неизвестных. Бела
неизвестных два [х а у), то часто решение таких систем может
быть найдено с помощью введения новых неизвестных и—х + у,
8*
68 ' гл; з. системы уравнения
v = ху. При этом удобно вспользовать следующие равенства!
хг + у» = (х + у)* — 2ху = и2 — 2о.
ж3 + У3 = (* + у)3 — 3*у (х + у) = и5 - Зио,
*< + г/« = (*2 + </2)2-2*У =
= ((* + У)г ~ 2*У)2 - 2*У =* (и2 — 2o)s — 2о\
позволяющие выразить комбинации неизвестных хг + ул, х* + у*,
*4 + У4 через неизвестные и и v.
Првмер 2.3. Решить систему уравнений
х' + у' = 2(ху+2)
х + у = 6.
Решен иЪ. Обозначим v = ху, и = ж + у. Тогда,
используя равенство
х' + у* = (* + у)2 - 2*y,
получаем относительно новых неизвестных систему
ца — 2v = 2о ■+■ 4,
и = 6,
единственным решением которой является и«6, о»=8. Воз»
вращаясь к исходным неизвестным, получаем, что решение
исходной системы сводится к решению более простой системы -
х + у = 6, ху = 8.
корни которой можно найтн, используя, например, теорему Виета,
Ответ. (2, 4); (4, 2).
Решить системы уравнений:
2.10. х"у + уЧ — 20, . , 2.11. **+у3 = а, У
ж + у 4 * *» + у* °-
2.12. ж2*/ + хуг = 6, 2.13. *« + у* = 82,
*J + * + (/ = 5, X + y^i.
2.14. ж8 + у8 = 9, 2.15. *3 + {Г3 = 2,
дсу = 2. *у (ж + у) = 2.
2.16. (*2 + у3) ху = 78, 2.17. б (х* + у*) = 41 (х*+у*)>
*< + ^ = 97. х*+у* + ху=*13.
2.18. х* + у* = 97, \/
xy = Q. V
Решить следующие системы уравнений с использованием
комбинации изложенных выше методов:
2.19*. (лс2 - х + 1) (у1 - у + 1) = 3,
(*+1) (»+!)=»в.
2.20*. £±-£- + ^^- - -£, 2.21*. 2*V - Я**2 - 36,
S !. СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИИ 60
2.22. ху — х + у *» I,
х*у — у'х — 30.
2.24, х* + ху + ж — 10.
02 + *У + 0 = 2О.
2.26*. ж2 — ху + у1— 19,
*« + *У + ^ — 931.
2.23. *ff + * — у => 3.
ж*0 — ху2 = 2.
2.26. ж* + *у + 2у2 = 37.
2** + 2*#-rV = 26.
2.27*. (*s+l)(y2 + l)-10.
(« + »)(^-D-3.
2.28*. хъ — у5 = 3093,
х-// — 3.
Симметрические системы трех уравнений с тремя неизвест-
ными х, у, г обычно решаю.ся с помощью введения новых
неизвестных
и •>» дс + у + z, v = ху + уг + xz, w = *yz.
Прн этом удобно использовать следующие равенства:
** + У* + zs = (х + у + z)s - 2 (*«, + yz + zx) = ц» - 2о.
— 3 (л; + у + z) (Jfy + yz + где) + Здсуг ■= к3 — Зко + Зш.
Пример 2.4. Решить систему уравнений
x + y + z=-l,
ху + yz + гх = —4,
*» + {Га4-г»— 1.
Решение. Система симметрическая. Вводя
вспомогательные неизвестные
* + У + z =» и, ху + yz + xz = v, xyz =» ш
в пользуясь равенством
ж» + у* + za = ц» — 3«о + Зш,
получаем систему
и -= 1, о«=—4, а3 — Зцо + Зда «= 1,
вли, возвращаясь к старым неизвестным, систему
х + у + 2=1,
xy + yz + xz=— 4, (*)
xyz = —4.
Решение системы (*) может быть найдено о помощью
теоремы Внета для кубичного многочлена: корни <ь tit h кубичного
многочлена Я + аР + Ы + с связаны равенствами
'i + h + h — —а,
tih + titt + tth^b.
70
ГЛ. 3. СИСТЕМЫ УРАВНЕНИЯ
Нетрудно заметить, что при а = —I, b •= —4, с = 4 корив
кубичного уравнении
связаны теми же равенствами, что и неизвестные х, у, z систе*
мы (*), и, следовательно, тройка значений неизвестных
* = 'i» y = h, z = h
будет решением системы (*). Кроме этой тройки значений неиз>
вестных, в силу симметричности системы решениями также будут
тройки значений неизвестных:
x = tit
X = ta,
X = iu
* — <«,
x***t3,
U = h,
y = h,
y = h.
У — 1з,
y = U,
z = ts,
z«=/,,
Z=<2>
Z = t\,
Z = tf
Таким образом, решение данной системы свелось к
нахождению корней кубичного уравнении
t3 — t2 — 4t + 4 = 0.
Ими являются числа
<1 = 2, /g«=-2, *3=1.
Следовательно, решениями исходной системы будут
следующие упорядоченные тройки чисел:
(2, -2, 1); (-2, 2, 1); (1, 2, -2); (-2, I, 2);
(I, -2, 2); (2, 1, -2).
Решить системы уравнений:
2.29. x + y + z = 0, 2.30. дс + у + z =■ 1,
*s-rV+z» = *3 + «/3 + zs, x3 + уг + z2 = },
xyz = 2. x3 + y3+zs = l.
Иногда системы трех уравнений с тремн неизвестными ре-
шаются с помощью введении вспомогательных неизвестных.
Пример 2.5. Решить систему уравнений
х + У
Решение. Данная система равносильна системе
£+й 9 х + г 2 у + г 1
ху Б ' ХЯ Т' уг 4
§ 2. СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 71
Произведя почленное деление в левых частях уравнений,
приведем ее к виду
J_ _1_ JL _Lj-_L_ A JL л. _!_ =-L
у + х** 5' * + z ~ 3 ' у + г 4 '
Обозначая — = и, — = в, —■ = т, получаем линейную
х у г
систему относительно введенных неизвестных:
3 2 1
Ее решением будет тройка чисел (-Топ". "Тго"' "ШГJ' ^ледо-
вательно, решением исходной системы будет тройка чисел
( 120 120 120 \
Ч 61 ' 11 ' 19 У
В отличие от систем линейных уравнений системы
нелинейных уравнений могут быть определенными даже в тех случаях,
когда число уравнений меньше чнсел неизвестных. Простейшим
примером такой системы является система, состоящая нз одного
уравнения
(*-!)*+(*-2)» +(z-3)»-a
единственным решением которого является * = 1, у = 2, z = 3.
Пример 2.6. Решить систему уравнений
х + у + z =■ 4,
2ху — z2 =■ 16.
Решение. Возводя обе части первого уравнения в
квадрат, имеем
х* + уг + z* + 2*jf + 2yz + 2xz = 16. (*)
Вычитая из уравнения £*) второе уравнение системы, полу
чаем уравнение
х3 + У1 + 2z2 + 2yz + 2zjc =0,
которое можно записать в виде
(* + z)a + (// + z)» = 0.
Последнее уравнение выполняется только при х = —z, у = —z,
Возвращаясь к исходной системе, получаем из первого
уравнения z = —4 и, следовательно, х = 4, у = 4.
Полученное решение |4, 4, •—4) и будет решением исходной
системы.
Ответ, £4, Л, —А),
72 ГЛ. 3. СИСТЕМЫ УРАВНЕНИИ
Решить системы уравнений:
2.31.
2.33*,
2.35.
2.37.
2.38.
у2 + ху — zl =» 4,
дс + Ьу = 8.
Q 16 К
. Зжо = —5,
J yz
3 .
UZ ~~ ' ' ^^ 1,
*2-(у-г)2 = а,
yi _ (p - дс)» = Ь,
z*-(x-y)* = c.
* + y + z=13,
*2 + y2 + z2 = 91,.
у2 = xz.
х+ «/4-z = 0,
X»+j,2 + z» = 2(j,-
*3 + уэ + z3 = 3 (ж* -
2.32.
2.34.
2.36.
-x — z)
-У2 +
*2~2«/z = — 1,
y + z — Jf = 1.
*У
x 1 - **
*H z l+*z
j 1 -^ tfZ"
y + Z l + yz
xyz
У + z *
т -».
Z+*
х + У
-2,
z2).
2.39. jt + y + z=l,
4хг + y1 + z2 —Ъх = ха + y3 + z* — 2,
*yz = 2 + yz.
2.40.
2.42.
2.44.
2.46.
2.47.
xy + yz + zx=U,
jes + «/s + z2=I4,
*yz = 6.
x(x + y + z) = a.
У С* + У + z) =» 6,
z (* + У + z) = с.
дс2у = * + У — z,
ггх = х — у + г,
угх = у — х + z.
2(x* + y*)=*xyz,
I0(«/2 + z2)~29*yz,
5 (z2 + хг) = I3*yz.
xyz1 = — у — 2х,
2x2yz = — у— z,
Zxy*z = 2* — z.
2.41. 2 (* + у) = *y,
*y + yz + где = 108,
*yz = 180.
2.43. *2 + y2 =» шгуг,
y2 + z2 =* 6*yz,
z2 + дс2 = c*yz.
2.45. 4*y + x2 + у1 = 1,
8*z + ж2 + 4z! = -2,
8«/z + ys + 4z2 = l.
2.48. дсу + дс + у = 7,
yz + у + z = — 3,
дег + де + z = —5.
Если среди уравнений системы есть иррациональные, то
ее решении обычно освобождаются от иррациональности.
5 2. СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИИ 73
этом применяются методы, используемые при решений ирра«
циоиальных уравнений.
Пример 2.7. Решить систему уравнений
VI+ 5* +V5 — У =3,
Ъх — у— 11.
4 «
Решение. Обозначая УI + 5* = и и V5 — У = °«
получаем симметрическую систему нелинейных уравнений
ц + в«=3, «« + »* —17, (*)
решения которой а = 1, к = 2 и ц = 2, о=1. Возвращаясь к
исходиым неизвестным, получаем следующие системы линейных
уравнений:
I + 5* = 16, 1 + 5* =■ I,
5-^=1, 5-у=16.
Решение первой системы х = 3, у = 4. Решение второй си*
стемы х = 0, у = — 11.
Ответ. (3, 4); (О, —II).
Решить системы уравнений:
2.49. V2* + у + I - V*T7 = I.
3* + 2«/ = 4.
2.50. $х + 2у + 4х — у + 2 = 3,
2*+ {, = 7.
2.51. V*2 - *Jf + V*Jf - </2 = 3 (.v - у),
** — у» = 41.
2.52. У> + У2 + V^ = 8 уТ,
V*+V7=4.
2ЛЗ. V*2 + 5 + VV -5=5, 2.54. V*+VF = 2.
** + «/»= 13. x —2«/ + l=0.
2.55. V7 + VF = 8.
X + У — V* + VU — 2 V*7 = 2.
2.56. *y + У* V - У4 = 8 (V*+T + т/х-у),
(x + yf2-(x-yf2 = 2e.
Используя изложенные выше методы, решить системы:
2.57. Zxs+2xy + y* — II,
*2 + 2*у + 3//» = 17.
2.58*. х* + ху + ffs = 19 (* - у)2,
Х*-ху + у*~7{х-у).
74 ГЛ. 3. СИСТЕМЫ УРАВНЕНИИ
2.БЯ1 (х— 1)»+(у+1)»-2» —(*
х — z — I =■ 0.
2.60. __ + _^— = _.,
$2х-у $2х-у = 1
у 2* 182'
2.61. ж -f У — z = 2, 2.62. х1 + ху + 02 = I,
*'+«/' + ** = 6, ^+tfz + 2» = 3,
*3 + у» —z» = 8. *s + jez+z2 — 7.
§ 3. Системы показательных н логарифмических
уравнений
Системы, содержащие показательные или логарифмические
уравнения, обычно решаются сведением показательного (или
логарифмического) уравнения к алгебраическому уравнению с
последующим решением полученной алгебраической системы.
Пример 3.1. Решить систему уравнений
8(У2Т""~0,5"-3,
logs (х - 2у) + log3 (3* + 2у) — 3.
Решение. Множество допустимых значений неизвестных х
и у определяется системой неравенств
х — 2у > 0, Зх + 2у > 0. (♦)
Из показательного уравнения исходной системы, записанного
в виде
получаем уравнение
х-у+Ъ=*6-2у;
пз логарифмического уравнения, записанного в виде
loga[(x-2y)$x + 2y)] = 3,
получаем уравнение
(х-2у)$х + 2у) = 27.
Таким образом, решение исходной системы свелось к
решению системы уравнений
х-у + 6 = 6-2у,
(х-2у)(3х + 2у) = 27, w
рассматриваемой на множестве допустимых значений неизвест*
вых, задаваемом системой (*)■ Выражен у нз первого уравнения
§ 3. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ 75
системы (**) п подставляя у = —х во второе уравнение,
получаем уравнение
3*!=27,
решения которого *t = 3, хг = —3. Из первого уравнения
системы находим yi = —3, yt = 3. Из двух найденных пар чисел
[(3, —3), (—3, 3) решений системы (*•) лишь пара (3, —3)
удовлетворяет системе неравенств (#).
Ответ. (3, —3). ^
Решить системы уравнений; —
8.1. logff х + log* у = 2, 3.2. log* x — logs у = О,
х* — у =20. ж2-2у2-8 = 0.
8.3. 4*+"-2»-» зд •-£! + !!_ 13,
4 "*» = «/*-5.
8.5. х + у = 12,
2(2\ogl/!x-logllxy) = 5.
SAK 4х - 7 о 2*-^ = г3-»,
8
— 6 = 0.
Ig(3*-y) + lg(* + y)-4lg2=»0.
8.8. 4*/"+<"*=з32,
>og. (* — «/) = I — loga (* + y).
8.9. 9^-27.3^ = 0,
8.10. 3-*.2"=П52, 3.11. 2*.3»= 6,
logyg- (* + tf) = 2. 3*.4*=I2.
8.12. (0,48x'+2)2*"<'-l,
lg (* + У) - I — Ig'6 - ig (x + 2y).
ж — 0 ■ 2.
Если основание степени в показательном уравнении сдстеиЦ
является функцией неизвестных, то систему можно с веста к *щ
«теме рациональных уранненвй, правимая в качестве одяого >4t
веизвестиых логарифм этой функции по некоторому основании
76 ГЛ. 3. СИСТЕМЫ УРАВНЕНИЯ
Пример 3.2. Решить систему уравнений
л2»'"1 = 5,
*»1+2= 125.
Решение. Логарифмируя оба уравнения системы по осно-
ранию 5, получаем систему уравнений, эквивалентную исходной
системе
(2у»-1)1ов.* —1.
(у3 + 2) loge х = 3.
Обозначая logs,* = z, получаем систему рациональных
уравнений
(2j,2-I)z=l,
(j,2 + 2)z = 3.
Выражая z нз первого уравнения системы н подставляя во вто
рое, получаем уравнение
2^-1 3'
решение которого yi =1, уг = —I. Из первого уравнения
системы находим (как при j=I, так н при у = —I), что z = 1.
Из уравнения
logs * — I
находим х = 5. Таким образом, решениями исходной системы
будут две пары чисел: (5, 1) н (б, —I).
Ответ, (б, I); (б, —I).
Решить системы уравнений:
8.14. у = I + log4 х, 3.1Б. у — logs * =» I,
:.■*=» 4». *« = 312.
3.16. (х + у) 3"-* = ~, 3.17. Xх-2» - 36,
3loge(* +«/) = *-у. 4 (ж-20) +logs ж = 9.
3.18. (х + у)-2у-1х=-6,25,
(х +«,)"<2*-") = 5.
; Некоторые системы логарифмических нлв показательных
.уравнений сводятся к системам рациональвых уравнений
непосредственной заменой входящих в них логарифмов £нлн, соответ>
хтвеино, степеней) новыми неизвестными,
■ § 4. РАЗНЫЕ ЗАДАЧИ ■ 77
Пример 3.3. Решить систему уравнений
5^.2^ = 200,
52^F + 22VF=,e89.
Решение. Обозначая z = б"** н и = 2""\ получаем
систему рациональных уравнений
zu = 200, za + u* = 689,
которая эквивалентна с учетом условий z > 0 н и > 0 системе
ги = 200,
z + ц = 33.
Решениями этой системы являются следующие пары чисел!
(25. 8); (8, 25).
Возвращаясь к исходным неизвестным, получаем следующие
системы уравнений:
5-^ = 25, 6^ = 8,
2^ = 8, 2^ = 25,
которые имеют решения * =» 8, у = 9 и * = (logs8)3! У = (log225)2.
Ответ. (8, 9); (27 logij 2, 4 logf б).
Решить системы уравнений:
3.J9*. 2л/^Г-2 + 4'^Г-1 = б>
3 (х + У) . 5 (дс - у) ^ s
ж—у *+у =
3.20». (ж2 + у) • 2"-*' = I, 3.21. I \хг — 2 • 5" = 71,
9 (*» + !,)-в*-». II2 + 2- б^"2 = 21,
И^-Ч' + Б""*—J6,
§ 4. Разные задачи
Решить системы уравнений:
4.J*. у*10*»*-**8,
logs {Г Iogj, (у — 2л;) =1.
4.2. logs л + iog4 у + Iog4 z = 2,
logs у + logs z + log9 x = 2,
log4 z + log8 ж + log,» у = 2.
4.3. 10 2 = 100УТ0\
78 ГЛ. 3. СИСТЕМЫ УРАВНЕНИИ
4.4*. *Vr+v7 = J,s^r,
4.5*. logy | logy x | = log* | log* у f,
lg2 x + lg2 tf = 8.
4.6. logia*(
log, 2 + l0g2 y) e ]0gt *'
log2 * [log3 (x + y)] = 3 log» *.
4.7. z*=>js, z» = y, д* = х.
4.8. Iogn * Ioga (xyz) = 48,
logo У logo (xyz) = 12, a > 0, a Ф I,
logo z log„ (xyz) = 84.
ГЛАВА 4
НЕРАВЕНСТВА. УРАВНЕНИЯ
И НЕРАВЕНСТВА С ПАРАМЕТРАМИ
Пусть И«) —числовая функция одного иди нескольких переменных
{аргуиевтов). Решать неравенство
fW<0 <f(*)>Q) (I)
— вто авачят найти все значения аргумента (аргументов) функции J,
при которых неравенство (1) справедливо. Множество всех звачевий
аргумента (аргументов) функции /, при которых неравевство (1) справедлива,
называется множеством решений неравенства или просто решением
неравенства.
Множество решений нестрогого неравенства
f(x)<0 <f(*)>0) (2)
представляет «обов объединение ывожества решений неравенства (1) в
Множества решений уравнения Их) — 0.
Два неравенства счвтаютсв эквивалентными, если множества их ре*
шеняй совпадают.
Под множеством допустимы» значений неизвестных, входящих в не*
равенство, понимают область определения функция fix).
Неравенства вида (I) нлн (2), составленные для различных функций
#!<*), могут быть сведены а систему неравенств. Решить систему
неравенств — это значит найти ывожество всех значений аргументов функций
и Mi прп которых справедливы все неравенства системы одновременно.
Говорят, что системы неравенств эквивалентны, если множества ох
решений совпадают.
§ 1. Рациональные н иррациональные неравенства
Алгебраические неравенства. Линейными (строгими а
нестрогими) называются неравенства вида
«х+&>0, а*-г6<0, ах+Ь>0, ах + Ь<0, а + 0, (1)
решениями которых будут)
прн а > 0
*е(-Г'00)' *е(-м- ~т) хе["Т: "У *s(_oo; -т]-
вря о<о
*s(-~. -±). *е=(--|-; „). j-s^-coj -A], *S[-±; со).
Квадратными (строгими н нестрогими) называются неравенства вида
ах*+*х+«>0, а^ + Ьх + с <0,
ох?+Ьх + с>в. a&+bx+e<0, m
где а. Ь, в—некоторые действительные числа и а •/• 0.
80
ГЛ. 4. НЕРАВЕНСТВА
Квадратно* неравенство ах' + Ьх + е > 0 в зависьиоств от вначеннй
своох коэффициентов а, Ь н с имеет решевия:
нря а> 0 и D=6'—4ос>0
,.(.-!=^и(=^-)
при а > 0 и D < 0 х— любое депстантелыюг число;
при а < 0 и £>>0
*Ч 5S : г >
при а < 0 н D < О
х=0 (т. с. решений нет).
Решение неравенства ах' + Ьх + с < Осводнтся к решению рассмотрев:'
ного неравенства, если обе части неравенства умножить на (—1).
Метод интервалов. Пусть Р„ (х) — многочлен п-й
степени с действительными коэффициентами, а с(, с2 cj — все
действительные корни многочлена с кратностями ft,, ft2, .... ft/
соответственно, причем cl>ci>- ... > ci. Многочлен ^М*);
можно представить в виде
Рп (х) - (ж - е,)*« (ж - c2)fca ... (ж - с,)*' Qm (ж), (3)
где многочлен Qm(x) действительных корней не имеет н либо
положителен, либо отрицателен при всех х е= R. Положим для
определенности, что Qm (х) > 0. Тогда при х > с4 все
сомножители в разложении (3) положительны н Рп(х) > 0. Если С\.—
корень нечетной кратности (fti — нечетное), то при х е (с»; Ci).
все сомножители в разложении (3), за исключением первого,
положительны и Рп(х) < 0. В этом случае говорят, что
многочлен Рп(х) меняет знак при переходе через корень с\. Если же
Ci — корень четной кратности (fti — четное), то все сомножители
(в том числе н первый) при х е= (a; Ci) положительны н,
следовательно, РП(х) >0 при х е (сг; Cj). В этом случае говорят,
что многочлен Рп(х) не меняет знака при переходе через
корень Ci.
Аналогичным способом, используя разложение (3), нетрудно
убедиться, что при переходе через корень сг многочлен Рп[х)
меняет знак, если kt — нечетное, и не меняет знака, если йг —
четное. Рассмотренное свойство многочленов используется для
решения неравенств методом интервалов. Для того чтобы найти
все решения неравенства
Рп М > 0, (4)
достаточно знать все действительные корни многочлена Рп(,х) их
кратности и знак многочлена Рп(х) в произвольно выбранной
точке, ве совпадающей с корнем многочлена.
§ I. РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА 81
Пример 1.1. Решить неравенство
х* + Zx3 — 4ж > 0. (*)
Решение. Разложим на множители многочлен Pt[x),
стоящий в левой части неравенства (*). Вынося множитель х за
скобку, получаем
Р4 (ж) ==■ х (х3 + Зх1 — 4).
Второй сомножитель, представляющий собой кубический
многочлен, имеет корень дс = 1. Следовательно, он может быть
представлен в виде
ж» + З*1 - 4= (х - 1) (ж2 + 4* + 4) = (х - 1) {х + 2)К
Таким образом, Р4(дс) = х(х—1)(* + 2)2 н неравенство (*)
может быть записано в виде
*(*-1)(* + 2)2>0. (♦*)
Решим неравенство (**) методом интервалов. При х > I
все сомножители, стоящие в левой части неравенства,
положительны.
Будем двигаться по оси Ох справа налево. При переходе
через точку х — I многочлен Р*.(х) меняет знак и принимает
отрицательные значения, так как х = I — простой корень
(корень кратности 1); при переходе через точку х = 0 многочлен
также меняет знак к
принимает положительные зна- -+\^" + N f + ^
чения, так как х = 0 — так- Г^ р\ — у/ х
же простой корень; при
переходе через точку дс = Рнс- *••
i= —2 многочлен знака не
меняет, так как х = —2 — корень кратности 2. Промежутки зна-
копостоянства многочлена Pt(x) схематически представлены на
рис. 4.1. Используя этот рисунок, легко выписать множество
решений исходного неравенства.
Ответ. х€=(-°о; — 2)U(—% 0)U(U °°).
Рациональные неравенства,
Решение рационального неравенства
Ш>"- (S)
где Рп(х) н Qm(x) — многочлены, сводится к решению
эквивалентного неравенства (4) следующим образом: умножив обе
части неравенства (5) на многочлен [0.м(х)]л, который
положителен при всех допустимых значениях вевзвествого х [т.е. при
82 ГЛ. 4. НЕРАВЕНСТВА
тех х, при которых Qm(x) ФО), получим неравенство
еквнвалентное неравенству (5).
Дробно-линейными называются неравенства вида
ах+Ь
cx + tt
> ft. (в)
где а, 6, о, d, к—некоторые действительные чвсла в о ■£ 0, — •& -г (если
с а
С—0. то дробво-лние&ное верааевство превращается в линейное, если —™»-т,
с а
.го неравенство (6) ве содержит аргумента), К дробво-лввейвым неравен»
стваи относятся в веравевствв вида (6). где вместо звака > стоят
ааакн <, >. ^ Решеаве дробво-лнневвого неравенства сводится к ре<
шевню квадратвого неравенства. Для этого необходимо умножить обе
части неравенства (G) ва выражение (сх + d)a, положительное прн всея
jeltuj i)b — d/a.
Пример 1,2. Решить рациональное неравенство
хг — х — 2^
Решение, Прибавляя к обеим частям неравенства 1,
получаем неравенство вида (5)
которое эквивалентно неравенству
л:2 (х* - х - 2)< 0.
Множество решений последнего неравенства находится методом
интервалов: *е (—1; 0) U (0; 2).
Отв ет. х е (—1; 0) U № 2J.
Решить неравенства:
1Л. (*+1)(3-*)(*-2)*>0. 1.4. ^g±|_>|.
1А FT8 <0' ,,в' *»-6*-7 <7^Т-
Иррациональные неравенства. Под нрраииональ*
выы неравенством понимается неравенство, в котором нензвест»
ные величины (или некоторые функции неизвестных величин), на*
§ I. РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА 83
ходятся под знаком радикала. Для того чтобы вайти множество
решений иррационального веравенства, приходится, как правило,
возводить обе части неравенства в натуральную степень. При
этом (в силу принципиальной невозможности проверки
полученных решений подстановкой) необходимо следить за тем, чтобы
при преобразовании неравенств каждый раз получалось
неравенство, эквивалентное исходному.
При решении иррациональных неравенств следует помнить,
что при возведении обеих частей неравенства в нечетную
степень всегда получается неравенство, эквивалентное исходному
неравенству. Если же обе части неравенства возводить в четную
степень, то будет получаться неравенство, эквивалентное
исходному и имеющее тот же знак лишь в случае, если обе часта
исходного неравенства неотрицательны.
Пример 1.3. Решить неравенство
У* + з < у* — | + уж —2. (*)
Решение. Множество допустимых значений неравенства
(*) представляет собой промежуток [2; оо).
Обе части неравенства (*) на промежутке [2; оо)
неотрицательны, поэтому, возведя обе части исходного неравенства в
квадрат и приведя подобные члены, получим эквивалентное
неравенство
6 — х < 2 У*2 — 3* + 2. (♦♦)
Рассмотрим теперь два возможных случая:
1) если 6 — х < 0 (т.е. х>6), то левая часть (**)
отрицательна, а правая — неотрицательна и, следовательно,
неравенство (**) справедливо при всех же (6; оо).
2) если 6 — х > 0, то для всех х е [2; 6] обе части
неравенства (**) неотрицательны. Возведя обе части неравенства (**)
в квадрат, получаем неравенство
З*2 — 28 > 0, (***)
решеннямн которого с учетом сделанного предположения будут
значения из промежутка ( л /—-; 6 I.
Объединяя множества решений, соответствующие двум
рассмотренным случаям, окончательно получаем решение исходного
неравенства — промежуток
Ответ. (л/Ц-г со).
(У?: -)■
■Мл-'- v
ГЛ. 4. НЕРАВЕНСТВА
Решить неравенства:
1.12. Vl — 3* - V5 + х > 1.
1.18. У 4 — V —* — V2 —* > 0.
1.J4. У*2 + 4* - 5 - 2* + 3 > 0.
1.18. х + 4 < У*+ 46. 1.16. У 2 — Уз~+7 < VJT+4.
U7 У24-2*-*' < к 1Л8 у£П. <,.
1.19. 4 ~ л/'* + [ < 3. 1.20. yJT^x5 - У25 — х» > х,
* 1 - У* + 3
1.21. . '' > —!—. 1.22. Ух2 —ж-2 >2х + 3.
У1 + х 2-х
1.23. Уж2 + Зх + 4 > —2.
1.24.
■^ki+y,—>
Уж —3 Уде — 3 '
1.25. УЗх2 + 5х + 7 — УЗх2 + 5х + 2 > I,
Неравенства, содержащие неизвестное под
знаком абсолютной величины. При решении
неравенств, содержащих неизвестное под знаком абсолютной
величины, используется тот же прием, что и при решении уравнений,
содержащих неизвестное под знаком абсолютной величины, а
именно: решение исходного неравенства сводится к решению
нескольких неравенств, рассматриваемых на промежутках знако-
постоянства выражений, стоящих под знаком абсолютной
величины.
Пример 1.4. Решить неравенство
| х2 - 21+ х < 0. (♦)
Решение. Рассмотрим промежутки энакопостоянства
выражения хг — 2, стоящего под знаком абсолютной величины.
1) Предположим, что
х2 — 2 5г 0,
тогда неравенство (*) принимает вид
х2 + х — 2 < 0.
Пересечение множества решений этого неравенства н неравенства
хг — 2 Js 0 представляет собой первое множество решений нс«
«одного неравенства (см. рис. 4.2): х е (—2; — У?].
2) Предположим, что х* — 2 < 0, тогда согласно
определению абсолютной величины имеем |х*~ 2| •**2~-х%, и неравен*
S I. РАЦИОНАЛЬНЫЙ И ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА 88
ство (*) приобретает внд
2 — х* + х < 0.
Пересечение множества решений этого неравенства н неравенства
лс* — 2 < 0 дает второе множество решений исходного неравен*
ства (см. рис. 4.3): хе(—V2> — 0.
Объединяя найденные множества решений, окончательно
получаем *е (—2; —1).
Ответ, хе (—2; —1).
-X
Рис. 4.2
SS
Ж
-V2r-I
\
Рис 4.S
В отличие от уравнений неравенства не допускают
непосредственной проверки. Однако в большинстве случаев можно
убедиться в правильности
полученных результатов
графическим способом.
Действительно, запишем
неравенство примера 1.4 в
виде
| х2 — 21< — х.
Построим функции у\ —
= |дс2 — 2| н t/2 =—х,
входящие в левую и правую
часть рассматриваемого
неравенства, и найдем те значения аргумента, при которых у\ < уг.
На рис. 4.4 заштрихованная область оси абсцисс содержит
искомые значения х.
Решение неравенств, содержащих знак абсолютной величины,
иногда можно значительно сократить, используя равенство
|*|2 = х\
Пример 1.5. Решить неравенство
Рис. 4.4
X— 1
х + 2
>1.
(*)
Решение Исходное неравенство при всех х ф —2
эквивалентно неравенству
1*-1|>|* + 2|. (♦*)
ее
ГЛ. 4. НЕРКВИГСТбА
Возведя обе части неравенства (**) в квадрат, после приведения
Подобных членов получаем неравенство
6* < -3,
V. е. х < —1/2.
Учитывая множество допустимых значений исходного
неравенства, определяемое условием дс ф —2, окончательно получаем,
что неравенство (*) выполняется при всех дс е (—ю; —2) U
У .<—2; -1/2). .
Ответ. (—с»; —2) U (-2; -1/2).
Рис. 4.В
На рис, 4.5 представлена графическая иллюстрация решения
приведенного неравенства.
Решить неравенства:
1.26. |я-3|>-1. 1.27.
1.28. *2+2j* + 3|-M)<u 1.2».
1.30. хг + х~ 10<2i* — 21.
1.31. х1— |3* + 2| + *>0.
| 4 — Зле К 1/2.
| х* — 11 - 2х < 0.
1.32. \хг — 3\+2х+ 1>0.
1.35. \х — 2]<|х+41.
1.36. \х*4- х + 1К2л8 -4х +7.
2х-1
*-1
>2.
§ 2. Показательные неравенства
Простейшими показательными неравенствами являются не»
равенства вида
а*>Ь, а*<Ь, (1)
где а н 6 — некоторые действительные числа (я > 0, а ^ 1)',
В зависимости от значений параметров а и b множество
решений неравенства а' > b представляется в виде:
при а > I, Ь > 0 же (Ioga b; °o);
при а < 1, b > 0 * е (~ «>; Ioga Ь);
прн 6 <0 xsR,
§ 2. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
87
Множество решений неравенства а* <. b в. зависимости от
значений а н b представляется в виде:
при а > I, b > 0 х е (— с»; log»6);
при а < I, 6 > 0 же (Ioga b; ю);
при 6 <0 Jt=0.
Множество решений нестрогих веравеяств а* р> k в а* ^ 6
находится как объединение множеств решений соответствующих
строгих неравенств и уравнения а' = 6.
Неравенства вида (1) могут быть обобщены на случай, ког«
да а ноказатеяе степени стоит некоторая функция от х. Так,
множество решений, неравенства
2^*>>3 (2)
находится как множество решений неравенства
f (jc> > log2 3.
эквивалентного неравенству (2).
Методы сведения более сложных показательных неравенств
к неравенствам вида (1), (2) аналогичны методам, используемым
при решении показательных уравнений. Так, например, решение
показательного неравенства вида
Р (а'} > О,
где Р (а*) — многочлен указанного аргумента, ааменой а1 = у
сводится к последовательному решению неравенства Р{у) > О
и решению простейших показательных неравенств вида (1) или
систем простейших показательных неравенств.
Пример 2.1. Решить неравенство
4*-2-52*-Ю*>0. (*)
Решение. Так как числа 4, 10, 25 являются яосшедова-
тельнымн членами геометрической прогрессии, то неравенство (*).
можно свести к квадратному относительно неизвестнойi/**"!?J •
Для этого разделим обе части исходного неравенства на 25* =»•
(*)"—(¥)*>'
(2 \х
-=• 1 = у, получим
у2 — у — 2 > 0. (**)
Множество решений неравенства (**) представляет собой
объединение промежутков {—«v — Ц[}{2, <»£, Исходное нера«
■ 0-
88 ГЛ. 4. НЕРАВЕНСТВА
венство, таким образом, эквивалентно дйум простейшим показа*
тельным неравенствам
X / о \Д£
(!)<-• (1) >*
Решением первого неравенства является пустое множеств, авто»
рого — промежуток (— °о; Iogj^).
Ответ. (— °о; log;^).
Решить неравенства:
2.1. 4.х + 2*+1-С<0. 2i. Г,+1'2-7-2-,-4<0,
2.3. 25-" -f 5-х+' > 50. 2.4. 4*' - 3 • 2*' + I > 0.
2.5. 2.32Л' + 4<3ДС'+2.
2.6. (l)V^>(i-)V*"iT^.
2.7. 98 - 7*'+5х-48 > 49х'+5д£-49.
2.8. 5-4* + 2.25x<7-io*.
2.9. Vl3x —б <У2.(13*+ 12) - У13* + &
2.10. 9"V^I::J + 3 < 3-\'«535-1 • 28.
2.11. 52j£-10-3'\'^-ir — 4.5,£-5<51+3'v^::J.
2.12. CjY <2z-x+25lll0«'5.
2.13. 25х —221ое,е-1 < 10.5х-1.
2.14. 52*+'+е*-Н>зо + 5*.зо*
2.15. Ve + 2^/5Г*+| - 4^?:7 + 2^3"=Г+| > б.
/ Э4*1
2.16. V**"*'1 + 17 - 5 > 2*. 2.17. Зх+' < —==г.
<у27
2.18. 4* < 3.2"^+х + 4'+^Г.
2.19. З2*-*-1 - Зх+2 + 6 > 0.
32*+2_2.3дс+2-27<0.
2.20. |з**«* — з|_** *« |^Я.
§ 3. Логарифмические неравенства
Простейшими логарифмическими неравенствами являются
неравенства вида
loga х > Ъ, (I)
ioga х < Ь, (2)
где а н 6 —некоторые действительные числа j(o>0, a_^*l|,
§ 3. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА 89.
- В зависимости от значений а множества решений
неравенства (I) будут следующими;
при а > I * е (аь; оо);
при а < 1 х е (0; аь).
В зависимости от значений а множества решений
неравенства (2) будут следующими:
прн а > I х е (С; аь);
при а < 1 * е (а*; оо).
Множества решений нестрогих неравенств logo x ^ b и
logo ж ^ Ь находятся как объединение множества решений
соответствующего строгого неравенства и уравнения
loga*=6.
Неравенство вида
logaf(*)>& (3)
эквивалентно следующим системам неравенств*):
при а > 1 f (х) > 0, ( (х) > а";
при а < I f (ж) > 0. f (х) < аь;
а неравенство вида
loga/(*)<& (4)
эквивалентно следующим системам неравенств:
прн а > 1 f (х) > 0, f (х) < аь;
прн а < 1 f (дс) > 0, f (х) > а&.
Более сложные логарифмические неравенства сводятся к
неравенствам вида (I) —(4) методами, аналогичными
используемым прн решении логарифмических уравнений. Так, например,
множество решений неравенства вида
Р (loga х) > 0, ' (б)
а также неравенств Р < 0, Р ^ 0, Р =S 0, где Р — многочлен
указанного аргумевта, находится следующим образом. Вводится
новое неизвестное у = logo x, и неравенство (5) решается как
алгебраическое относительно неизвестного у. После этого
решение исходного неравенства сводится к решению соответствующих
простейших неравенств (1), (2) нлн систем этих неравенств.
Пример 3.1. Решить неравенство
(log1/2*)s - log1/2*2 > (log1/23)» - 1. (•)
*) В случае, если неравенство (3) нестрогое, вторые веравевства этих
снстед также нестрогие.
Q0. ГЛ, 4, НЕРАВЕНСТВА
Решение. Учитывая, что множеством допустимых вначе»
пий неравенства .(*) является промежуток (0; с»), преобразуем
неравенство (•) к виду
(,0Sl/2*)2 - 2 loBi/2* > (tog,/^)2 - 1.
Обозначая # = Iogj;2*, получаем относительно у неравенство
«/*-2«/-(log1/23)2+l>0.
Множество решений последнего неравенства представляет со*
бой объединение промежутков(—с»; I + Iog^23)U(l — log^; °°),
а, следовательно, решения исходного неравенства определяются
{условиями
3
log1/2*< I + logI/2 3 <=^ л: > —,
log1/2* > 1 — log1/23 ■**■ 0 < х < -g-.
Ответ. (|;оо)и(0;1).
Решить неравенства:
8.1. logl/2 (2дс + 3) > 0. 3.2. log, -J^i < 0.
3.3. Ioew(2x*-x—|)>1.
8.4.1og1/4f^f<co3-|L.
8.5. Iog| x + log2 x — 2 < 0.
8Д 2 log* (2x* + 3)< log, (** + 6).
3.7. log2 Vr" - 2Л0К?м x + ' > °-
8.8. iog1/4 (2* + 3> > log9 27.
8.9. lg(*-4) + lg*<lg21.
3.10. logr*-log*(y)>2.
8.11. log2 [(x - 3) (* + 2)] + log1/2 (x - 3)< - logl/Vi 3.
3.12. log10a(*2) + Iog20*<2.
8.13. log3 (7 - *) < -^- log2 ^ 1 + log7_, 9.
3.14. log3x-log|*<Tlogl/(2V5)4.
3.15. log1/2 (4 - x) > log1/2 2 - log„2 (x — 1).
, 3at
sln~T 1
3.1», log, (3 — x) - log» 5-_^. > -g + log2 (* + 7).
§ 3. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА 9I
8.17. 2 log„4 (* + б) > 1 loB|/(a/V5) » + Kgj— 2.
8.18. log, (3* - 1) |og1/4 (^-) <-|.
8.19. IogI/2 ж < log1/4 дс.
3.20. log3 (34* - 3!X+1 + 3)< 2 log, 7.
3.21. log,0 12x + 3 |э + 2 Iog(2e+3), 10 < 3.
3.22. log,,,, 8 + logx/4 8 < log'°gl4.
8.23. &1о"х-2х*>х-2.
1 4л
8.24. 2 log« * — -j log*(*' — 3* + 2)< таз-у-.
8.25. log^ cos * > log^g j при * e= (—2; 3).
8.26. log1/21 x - 31 > -1.
8.27. log2 (V* + 3 — x — l) < 0.
3.28. Vhfr'-8l±j<1,
IOgi/jJC - 1
8.29. I05^/^ <1.
log1/2(* + 2) "-
8.30. logs Vs —2x • log* 3 < 1.
3.31. log, * Д/log* (^-) < 1.
о о» . /1 / 2*2 — 3* + 3 \ , , , / 2лся — Зле + 3 \
8^2. /yiog4 [^ 2 ) + ' > l0g2 {. 2 J"
l-Vl-8logb
8.33. ^- S_ < i.
2 Iogj x
8.34. loga^ < log2^1+2x
log*(l +2x) ~^ logn*
Логарифмическое неравенство ввда
logg{x)f(x)>c (в)
еквнвалеитно двум, системам неравенств:
f{x)>0, f{x)>0,
g(x)>h 0<g(x)<\, (7)
fW>te(*)n /w<ta(*)ie.
Пример З.2. Решить неравенство
loga <*?—Бх-}-в)<1. (•)
S2 ГЛ. 4. НЕРАВЕНСТВА
Р е ш е в н е. Логарифмическое веравенство эквивалентно
двум системам неравенств
О < х* — 5* + 6 < 2х, х* — 5х + 6 > 2х,
2* > I; 0 < 2х < 1,
я множество решений исходного неравенства получается кам
объединение множеств решений этих двух систем.
Ответ. *«=(0; 1/2)U(l; 2)ЩЗ; 6).
Решить неравенства:
3.35.1оЬх (V - -|г) > 4. 3.36. loga^ (x - -|) > 0.
8.37. log^4 (5дс + 20) < \oSx+l [{х + 4)»J.
8-39. log|;e+1/x)(*» + Jj--4)>l.
з.4а bg^^— (x' - з* + i)>o.
3.41. (log, x+6| 2) iog2 (*» - x - 2) > 1.
8.42. logw+e)/3 (iog2 ((* - l)/(2 + x))) > 0.
8.43. log9j(. (6 + 2x - x2) < у-
3.44. xl*x<lO-x-lex + S.
8.45. log, x, WW^TP - x - 1) > 1.
8.46. logx<Vlogx(2jcB).
8.47. logloBl ((Ш) (** - 10* + 22) > 0.
Выражевня, стоящие в левой н правой частях неравенств
6.48—3.52, положительны, поэтому для решения достаточно
прологарифмировать обе части исходного неравенства!
3.48. х,«'х-31«х+1>Ю(Ю.
3.49. *»> 2 2V2 .3 V*..
8.50. (*! - x - 1)х'~1 < 1. 3.51. | x f-*-* < 1.
3.52. xllli*-lgx< I.
Неравенства 3.53—3.58 эквивалентны системам трнгономет*
рнческих неравенств нлн системам алгебраических и трнгономет*
рнческих неравенств:
3.53. log|8ln, ,(,» - 8* + 23) > |Qga ,*„,,.
Я-54- loBeoeW) (sY~2x)< logcwv««JVх- Ч«
« 4. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ СЛОЖНЫЕ ФУНКЦИИ 93
8ЛВ. ('ogatox2)2 < l°Sainx (4 sin3 x).
8.56. Vtg*- l[locfiB x (2 + 4 с03* *) — 2] > °«
З.Б7. logs sin x > logun (3 sin x — 2).
3.58. log , л - (j£l_.5£. +з^>0.
Ba|n *+V3 coa x 4 2 2 /
Найти все целые числа, удовлетворяющие неравенствам:
-|- log» U2-3X)
3.59*. З2 — 31ог'*>83.
3.60. * - 1 < 2 iogB (* + 2).
3.61. log, „ ,(^±|^1Ъо.
§ 4. Решение неравенств, содержащих
сложные функции
Рассмотрим неравенства, в которых функция, подлежащая
сравнению, представляет собой сложную функцию, состоящую из
некоторой композиции трансцендентных н алгебраических
функций. Решение подобных неравенств сводится к
последовательному решению простейших неравенств, возникающих прн замене
аргументов сложных функций новыми переменными.
Пример 4.1. Решить неравенство
(0,5)loesloei'5<*,-4'5)< 1.
Решение. Если обозначить г = log3]ogi/6(*2 — 4/5), то
псходное неравенство сводится относительно г к простейшему
показательному неравенству
(0,5)z<(0,6)0-wz>0.
Обозначая далее у = log^ (х3 — 4/5), имеем
log3 у > 0 ■**■ у > 1.
4
Положив v = дсв—=-, получаем
log1/5 о > 1 <=> 0 < о < —.
Таким образом, мы получили неравенство, эквивалентное
исходному:
о,.„ (-„--^„(-^ ,).
94-
ГЛ..4. HEPWBBHCTBA
Г При решении неравенств, рассмотренных в примере 41, по-'
лезно проводить графическую иллюстрацию каждого отдельного
этапа решения.
Рис. 4.0
На рнс, 4.6 представлена графическая иллюстрация решении
примера 4.1.
На. каждом рисунке представлены графики функций,
поэтапно; возникающих в процессе решения. При этом на каждом
графике на вертикальной осн откладывается интересующее нао
множество значений очередной простейшей функции, а на
горизонтальной оси ищется соответствующее ему множество значений
аргументов. Найденное множество, обозначенное на рисунках
штриховкой на горизонтальной оси, на следующем рисунке
откладывается на вертикальной осн.
Решить неравенства:
4.1. ЦУ"™ > I.
4.3. (4)l0g°-25,X'+S*+8,<2,5.
4.4. ml0etl°S^X~°-b<U
4.2. 5 1о*' *' < I.
S 5. УРАВНЕНИЯ IH НЕГРАВБИСТВА (С ПАРАМЕТРАМИ Ъ&
4.6. Г-ij 1/9V 3 '<!.
Найти область определения функций:
4.7. 0=y1Og1/2-£=^-.
. п , sin x — cos x -4- 3 л/2
4.9. „-loft ^= 3L_.
4.10. 0 = yiog1/3loga|x-3|.
Решить неравенства, используя иоябинагоно рассмотренных
методов:
4.Н. Iod/v? (в*+| — Зв*) > —2.
4.12. Ioga Iogg,[6 {хл - Ах + 3)< 0.
4.13. log* [log» (4* - 6)] < I.
4.14. (-1.) 3 W < 1.
4Л6. 12* + ц/з*4 + 4л5 - 4*e • log2 *">
> 3 V9 + 4jc — 4xa + 4*3 lqg« x4.
§ 5. Уравнения н неравенства с параметрами
Уравнения и неравенства с параметрами являются наиболее
трудными задачами курса элементарной математики. Это объ<
ясняется тем, что их решения следует получать при всех допу«
«тишяс значениях входящих и них параметров.
Пример 5.1. Для всех значений .а .решить неравенство
nx>Vfx,
Р е ш е н н е. Запишем неравенство в виде
■HipL>0f
тоща «сходное "неравенство эквивалентно двум (системам нерв'
венств:
■аЯ* — Ч >-0, est* - !< 0,
Jt> 0; * < 0.
ее
ГЛ. 4. НЕРАВЕНСТВА
Рассмотрим первую систему. Первое неравенство запишем
в виде
ах2 > I.
При а > 0 оно эквивалентно неравенству х2 > 1/а, множество
решений которого * < — 1/Va н х > 1/Уа". В этом случае
решения первой системы; х е (\/-\fa; со). Прн a < 0 левая
часть неравенства ахг — I > 0 отрицательна при любом х н
неравенство решений не имеет, а следовательно, не имеет решений
В вся первая система неравенств.
Рассмотрим, вторую систему. При a > 0 решениями
неравенства ахг— 1 < 0 будут значения *е(— \/-Ja; l/Va),a
решениями системы — значения х е (— l/л/а; 0). При а <: 0 левая
часть неравенства ахг — I < 0 отрицательна при любых
значениях х, т.е. это неравенство выполняется при всех xeRh,
следовательно, решеннямв системы будут значения х s (—со; 0)\
Рис. 4.7
Ответ. Если а <: 0, то х е (—со; 0); если а>0, то
*e(-l/Va;-0) (J (1/V5"; се).
Приведем графическую нллюстрацвю решения примера 5.1.
Для этого рассмотрим отдельно два случая о>0 (см. рнс 4.7, а)
иа<0 (см. рнс. 4.7, б) и для каждого из ннх построим гра«
фики функций, стоящих в левой и правой частях исходного
неравенства. Заштрихованные промежутки оси Ох представляют со»
бой решение неравенства в рассматриваемых случаях.
Графическая иллюстрация облегчает решение уравнений и
неравенств с параметрами. Приведем пример графического
решения уравнения с параметрами.
Пример 5.2. Для каждого значения а решить уравнение
8|*| + |a|-*+L W
$ Б. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРАМИ
97
Решение. Отложим на оси абсцисс значения х, а на оси
ординат —значения а./Тогда в координатной плоскости (х, а)
геометрическое место точек, координаты которых удовлетворяют
уравнению, образуют фигуру, изображенную на рис. 4.8J Из
рисунка видно, что при \а\ > I уравнение (*) решений не
имеет. При \а\ < I каждому значению а соответствуют два
корня уравнения, а при \а\ = I—один
корень х = 0.
При 0 ^ а < I корни находятся из
следующих уравнений:
х + а = 1 и — Zx + а = 1.
Они равны х =* 1 — а и х = —s— со- -,.=
ответственно. При —I < а < 0 корни
находятся нз уравнений
х — а = I и —3* — а = 1;
онн равны х = 1 + а и * =
3
Рнс. 4.8
соответственно.
Ответ: \а\ > I =*- исходное уравнение не имеет решений;
|а| = I =*-дс = 0; 0<а < I =>* = I — а и ж=—=—; —I < а <
< 0 => * = I + а и ,v = —
а+ 1
5.1. Для каждого значения а решить уравнение
| х — а + I | + \х — 2а | = х.
5.2. Для каждого значении а решить неравенство
13* — а | + 12х + а К б.
5.3. Для каждого действительного значения а решить
уравнение
х3 + \х\ + а = 0.
5.4. Для каждого значения а определить число решений
уравнений
a) V21 х | — х1 = а; б) |*а — 2х - 3| = а.
5.5. Для каждого значения параметра а решить неравенство
2 | х — а |< lax — х2 — 2.
5.6. Для каждого значения параметра а решить неравенство
Уя + х + "Ja—'x > а.
4 А^ Г, Цыркав, А, И, Пныскнв
83
ГЛ. 4. НЕРАВЕНСТВА
5.7*. Найти все значения а, при каждом из которых пера»
венство . „
3 — | х — а | > х*
имеет хотя бы одно отрицательное решение.
5.8. Для каждого значения параметра а решить уравнение
л/а (2х — 2) + I *=• I — 2х.
5.9. Для каждого значения параметра а решить уравнение
I441 ж| — 2-121 ле,+а = 0.
5.10. Найти, при каких значениях а уравнение
logs (9* + 9а3) =■ х
имеет два решения.
5.11. Найти все значения параметра с, при которых
неравенство
1 + log» (2х* + 2* + ^) > 1о&« (сх* + с>
имеет хотя бы одно решение.
5.12. Найти все значения а, при которых неравенство
^gaia+])(\x\ + 4)>\
выполняется при любом значении х.
5.13. Найти все значения а, при которых неравенство
выполняется при любом значении х.
5.14. Найти все такие значения х, по абсолютной величине
меньшие 3, которые при всех а>5 удовлетворяют неравенству
1о&2а-х> (* — 2аХ) > L
5ЛБ. Найти все значения х > 1, которые при всех Ь,
удовлетворяющих условию 0 < b <k 2, являются решениями
неравенства
1оЩх>+х)1ъ(х + 2ь-1)< >•
5.16. Найти множество всех пар чисел (а, Ь), для каждой
пз которых при всех х справедливо равенство
а.ех + Ь=*еах+ь.
Многие задачи на решение уравнений и неравенств с
параметрами связаны с определением расположения корней
квадратного трехчлена у = ах2 -\-bx-\- с на действительной оси. При
решении этих задач следует учитывать, что если квадратный
трехчлен у »=» ах1 + Ьх +,с имеет два действительных корня Xi к
§ 5. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРАМИ 99
Xt (xi < х»), то при а > 0 у(х) принимает отрицательные
значения на промежутке (xt; x2) н положительные значения вне
промежутка [xi; xs]; при а < 0 — положительные значения в
промежутке (xi; Хз) н отрицательные значения вне промежутка
[хг, Xt]. Поэтому, для того чтобы выяснить (не находя корней
уравнения ах" + бх + с = 0), принадлежит лн произвольное
число а промежутку (xi; x2), достаточно знать знак выражения
аа? + Ьа + с н знак коэффициента а. Так, например, если а > 0
и аа2 + 6а + с > 0, то а находится вие промежутка [х\\ Хг)«
Если известно, что число а не находится между корнями xi,
х%, то для того, чтобы выяснить, по какую сторону от
промежутка (справа нлн слева) лежит число а, достаточно сравнить
его с некоторым числом, заведомо принадлежащим промежутку
{Xi; хг), например с выражением —§г, являющимся абсциссой
вершины параболы у = ах" + Ьх + с.
Пример 5.3. При каких значениях параметра а оба корня
(уравнения х- + ах — I =0 меньше чем 3?
Ответ на вопрос задачи следует дать не проводя вычислен
ння корней уравнения.
Решение. Рассмотрим квадратичную функциюу=хг-\-ах—I,'
стоящую в левой части уравнения. Так как коэффициент прн х*
равен 1, то ветви параболы направлены вверх. Для того чтобы
корни уравнения х\ а хг (*i «S Хг) были меньше чем 3,
необходимо и достаточно, чтобы число 3 лежало правее промежутка
J*t; хг). Условия, при которых будет выполняться это
требование, можно определить следующей системой неравенств:
ая + 4>0,
9 + За — 1 > 0, (*)
-£<3. ' ,
Первое неравенство (которое выполняется прн всех значениях а)
гарантирует существование действительных корней, второе и
третье обеспечивают расположение точки х = 3 вне промежутка
i(xi; Хг) справа от него.
Решая систему неравенств^), получаем ае(—с-; то),
Ответ: ае(- -я*; то).
г~ Б.17. Найти все значения параметра а, прн которых оба кор
ня квадратного трехчлена
х» — бах + (2 — 2а + 9а2)
действительны я больше чем 3.
V
100
ГЛ. 4. НЕРАВЕНСТВА
5.18. Найти все значения параметра а, при которых оба
корня квадратного уравнения
х1-ах + 2 = 0
действительны и принадлежат промежутку (0; 3).
Одно неравенство является следствием другого, если
множество решений первого неравенства целиком содержит
множество решений второго. Например, если х удовлетворяет нера»
венству \х\ < 2, то хг < 5 (т.е. неравенство х2 < 5 является
следствием-неравенства |х|<2. Действительно, множество
решений второго неравенства (—\/W; л/5) целиком содержит
множество решений (—2; 2) первого неравенства.
6.19. При каких действительных значениях m неравенство
х2 -f mx -f м2 + 6m < 0
выполняется для любых х е (I; 2)?
5.20. Найти все значения т, для которых неравенство
тх1 — Ах + Ът + I > 0
выполнено при всех х > 0.
5.21. При каких действительных т из неравенства
х1 — (Зт+ \)х + т>0
следует неравенство х > I ?
5.22. Найти все значения параметра а, при которых из
неравенства ахг — х + I — а < 0 следует неравенство 0 < х < 1.
5.23. НаЙтн все значения параметра а, при которых из
неравенства 0 <: дс ^ I следует неравенство
(а2 + а - 2) х1 - (а + 5) х - 2 <0.
5.24. Найтн все значения а, для которых справедливо
неравенство
2г» — 4а2х — os + I > 0
прн любых \х\ < I.
5.25. Найти все значения параметра а, прн которых корнн
уравнения
хг + х + а = 0
действительны н больше а.
5.26. Найтн все значения а, прн которых неравенство
*-2а~1 <о
* — а
выполняется для таких х, что 1 < х «^ 2.
1 В. УРАВНЕНИЯ И НЕРАВЕНСТВА С ПАРАМЕТРАМИ 104
Следующие логарифмические в показательные неравенства
с параметром сводятся к квадратным с помощью замены
переменной.
5.27. Найтн все решения неравенства
а2_9*+1— 8.3*.а>0.
5.28. Найтв все значения параметра а, при которых
неравенство
4*_a.2* — a+ 3<0
имеет хотя бы одно решение.
5.29. Ыайти все значения параметра а, прн которых
неравенство
a.9* + 4 (а— 1).3* + а>1
справедливо прн всех х.
При сведении тригонометрических уравнений н неравенств
к рациональным следует учесть, что замена у = sin x или у ■=
= соз д; предполагает \у\ =S I.
Решить следующие задачи.
5.30. Для каждого действительного числа а решить
уравнение
sin * + соз (а + х) + соз (а — х) = 2.
5.31. Для каждого значения параметра а решить уравнение
(Ig sin л-)2 — 2a Ig sin x — a» + 2 = 0.
5.32. Найтн все значения 6, при каждом из которых
неравенство
cos* х + 26 sin x — 26 < b3 — 4
выполняется для любого числа х.
5.33. Определить все значения а, прн каждом из которы.х
уравнение
соз« х — (а + 2) cos2 х — (а + 3) = О
имеет решения, и найти эти решения.
5.34. При каких значениях параметра а уравнение
sin2 4л- + (а2 — 3) sin 4х + а2 — 4 = О
имеет четыре корня, расположенных на отрезке [Зл/2; 2л]?
5.35. Прн каких значениях 6 уравнение
6 cos у 6 + sin х
2 cos 2х — I = (cos2 х — 3 sin2 *) tg х
имеет решения? Найтн эти решения,
102 ГЛ. 4. НЕРАВЕНСТВА
5.86. для каждого значения параметра а решить уравнение
5.37. Для каждого значения параметра а > 0 решить нера«
венство
ррн условии, что х е (0; я/2).
5.38. Найти множество всех пар чисел (а, 6), для каждой
нз которых при всех х справедливо равенство
a (cos х — I) + Ь1 = cos (ax + Ь2) — I.
5.39. Определить, при каких целых значениях k система
(arctg х)г + (arccos у)1 = n2/k,
arctg x + arccos у = я/2
имеет решения, и найти все эти решения.
5.40. Найти все значения а, при которых уравнения
а соз 2* + | а | соз Ах + cos 6х => I
и
sin х cos 2* = sin 2x cos 3* — -5- sin 5x
эквивалентны.
5.41. Определить, при каких значениях а уравнение
*-|—4|4|*|-а»|
имеет три корня. Найти эти корни.
5.42. Найти все значения а, при которых уравнение
| I - ах | =» I + (I - 2а) х + ах1
имеет одно решение.
6.43. Решить уравнение
\х + 3\ — а\х— I | = 4
Я найти, при каких значениях а оно имеет два решения.
§ 6. Доказательство неравенств
Сведение к очевидному неравенству.
Пример 6.1. Доказать, что при а ^ 0, b ^ 0, с 5» 0 спра>
ведлнво неравенство
ab + ас + be ^ а2 + Ьг + с2.
Решение. Умножим обе части неравенства на 2, Получим
Stab + 2ас + 26с < 2а2 + 26а + 2с8.
§ в. ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ ЮЗ
. Сгруппируем теперь члены аеравенства следующим образош
а2 — 2аЬ + Ь1 + Ь2 — 26с + с! + а2 — 2ас + с*:> О,
или
(а - Ь)1 + (6 - с)3 + (с - а)3 > 0.
Мы пришли к очевидному неравенству.
Доказать, что еслн а, Ь, с— положительные числа, то:
6.1. а* + Ь3 + с3 > ЪаЬс. 6.2. ^L+LEi > (.£±1 )".
6.3. а*+&* + с2 + 3>2(а + 6 + с).
6.4. Доказать, что
х3 + 4«/2 + 3z2 + 14 — 2х — 12у — 6z > 0.
6.5. Доказать, что
*2 + У% + z2 + и3 + а3 + а (х + у + г + и) > 0.
6.6. Доказать, что
х* + 2ху + Зуг + 2х + 6у + 3 > 0.
Средним арифметическим чисел ai, ..,, ал называется число
fli + я» -4- • ■ • 4- ап ^
■ ' ■ ! ■ , средним геометрическим неотрицательных
п
чисел аи аг, ,,,, а„ называется число Ya,a2 ... a„.
Решение ниже приведенных задач опирается на следующее
неравенство Коши, справедливое для любого набора неотрица-
цельных чисел аи .,., я,,:
Д1 + аг + ••• + а*
• V«i •••««• С)
Пример 6.2. Доказать, что еслн a + 6 + с = I и а, Ь, с —
положительные числа, то
1 + 1 + ±>9.
а ' Ь с —
Решение. Так как а + 6 + с = 1. то, используя (I), мож*
но утверждать, что
а + b + с . 8/-Т- I ^ о , v
—! !—^'Sjabc «лн ■ ,. >3. (*)
3 s/abc
Воспользовавшись неравенством Кошн для чисел—, -г-, —,
получаем
1+1 + 1
5 >W Ы
104' ГЛ. 4. НЕРАВЕНСТВА
Учитывая неравенство (*), окончательно убеждаемся в
справедливости исходного неравенства.
6.7. Доказать, что
(а + Ь) (Ь + с) (с + а)>8аЬс,
где а, Ь, с — неотрицательные числа.
6.8. Доказать, что при р > 0 и q > О
(p + q)(p + 2)(q + 2)>l5pq.
6.9. Доказать, что при х > О
6.10. Доказать, что
('+±)('+-Й('+т)>*
где а, Ь, с— положительные чнсла на + Ь + с=1.
6.11. Доказать, что
(I + oi)-(I+oi)' ••• •(1 + а«)>2,\
где а,, ...,а„ — положительные числа, произведение которых
равно 1.
6.12. Доказать, что
Ч] + аг+ ... +а„>п,
где at, ..., a„ — положительные числа, произведение которых
равно 1.
6.13. Доказать, что если а, Ь, с — положительные числа, то
(a+u + c)(JL + -L + -L)>9.
6.14. Доказать, что если а, Ь, с—положительные числа, то
(be + са+ аЬ)г > ЗаЬ (а + Ь + с).
6.15. Доказать, что если а,, а%, ..., ая — положительные
числа, то
(а, + а2 + ... + a») (-J- + ~Г+ • • • + ~-) > А
6.16. Доказать, что если ait .,., а„ — положительные чнсла,
то
§ в. ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ 109
6.17, Доказать, что
п1<{-2~) •
где п — натуральное число, п ^ 2.
в. 18. Доказать, что
где а, Ь — положительные числа, афЬ. i
Если требуется установить справедливость некоторого иера»
венства сразу для всех членов двух последовательностей а„ в &»,
то удобно использовать метод математической индукция.
Пример 6.3. Доказать, что
п1>2"-1, если п>2.
Решение. Используя метод математической индукции, убе»
днмся в том, что для л = 3 утверждение справедливо. Действн»
тельно, 31 > 22, так как
31=»6, 22 —4.
Далее удобно воспользоваться следующим утверждением: если
для всех k, больших некоторого N, выполняется неравенство
ak+i ^ bk+\
К
еде я* и bk — k-e члены сравниваемых последовательностей, то
ak+i > ак
bk+i Ък
По индуктивному предположению -т— > 1. Следовательно, мож>
°к
но утверждать, что а* > 6* для всех k > N, Используем этот
подход в рассматриваемом случае. Имеем
ak = k*> «*+,=»(*+1)1"*-~-*+1.
к
А+1>2, если А>2.
Таким образом, доказано, что . > I для всех k ^ 2, т. е.
(требуемое неравенство установлено.'
J06 ГЛ. А. НЕРАВЕНСТВА
В некоторых случаях метод математической нндушшн удоб«
вее применять в следующем виде: если для некоторого N
Он> Ьц н для всех k ^ N а*+1 — ак > 6*+1 — 6*, то для всех
к > N ак > bk.
Доказать следующие неравенства:
6.19. 2" > я2 + 2 (л > 5).
6.20. я" > (л + I)"-1 (rt > 2).
6.2^ 3я > пЯ (n * 3).
6.22. (w-)" > /tl (rt£»6).
6.25. 2 (лАГ+Т - I) < 1 + -L- + -L- + ...
-=- <2 Vя"»
e.2e.(i+i-)"<3. M7.|B(l+i)<i.
6.28. '•3'S.....(2b+1) 1
2«4»6. ... .(2л) """"У2п+1"
M9L («0' <[(n+1)fЛ+1)]".
6.30. rti > (±\n. asi. "+V5F" < Ц^-.
6.32. Доказать, что последовательность xn <=> [I H J
монотонно возрастает.
ГЛАВА 5
ТРИГОНОМЕТРИЯ
Основные формулы тригонометрии»
sin2 a + cos1 а => I,
. sin а . cos о
tga=,T3sT' Ctga—sln^
I I
seca = -i , cosec a = -
—i I W^CL \A — Г ■
cos a sin a
ctga 6 tga'
1 + tg2 a = sec2 a, I + ctg2 a = cosec2 a,
sin (a ± B) = sin a cos в ± cos a sin в,
cos (a ± B) = cos a cos В Т sin a sin в,
f _ f- ... ox tgctdbtgB .>,.,, ^y» _ ctgactgBTl
tg(a±B) = |4:,gatgp. ctg(a±B) = ctgMctga ,
8in 2a = 2 sin a cos a, cos 2a = cos2 a — sin2 a,
tg2a = -rrfe-.
sina = , cosa =
i+tg2f l + tgȣ
1 + cosa = 2cos2-5-, I —cosa =>2 sin2-y,
, a 1 — соз a , a sin a I — cos a
S 2 — 1+cosa* gT~ I +cosa — sin a '
, • a « • a+P a-B
sina-f sin В =2 sin —r-'-cos —-,
sin a — sin в = 2 sin —y-*- cos —-тр—f
0 _ a+B а—в
cos a + cos в = 2 cos —5-*- cos —5-*-,
о + В В -»-а
cos « — cosB = 2 sin--TK «'Д-^—»
108 ГЛ. Б. ТРИГОНОМЕТРИЯ
. _,_, . sin (а ± Р) , J , о sln (P±°)
tga±tgp = —-^ ^-, ctga ± ctgр = —йГ~-йГЕ-,
r cos a cos p sin a sin p
sin a sin р* = —• [cos (а — 0) — cos (а + ($)],
cos a cos р* = — [cos (а — Р) + cos (a + ($)],
sin a cos p* •= у [sin (a — Р) + sin (a + (J)].
Формулы приведения
Наименование
функции
зШ a
cos a
tg a
ctg a
Значение аргумента
—a
-sin о
соз a
-tg a
-ctgo
n
cos a
sin a
ctg a
tg a
y + a
cos a
—sin a
-ctgo
-tgo
n—a
sin a
—cos a
-tg a
-clga
n + a.
-sin a
—cos e
tg о
cTg о
Зл
-__a
—cos о
—зшо
ctg a
tg a
3n ,
-co» о
вш a
-ctgo
-tgo
§ 1. Тождественные преобразования
тригонометрических выражений
При доказательстве тригонометрических тождеств
используются формулы сокращенного умножения н формулы,
связывающие между собой основные тригонометрические функции.
Пример I.I. Доказать тождество
2 (sin» a + соз" a) — 3 (sin4 a + cos* a) + 1 = 0. (•)
Решение. Воспользуемся формулой сокращенного
умножения j
х3 + у*=(х + у)(х*-ху + у*),
полагая в ней * = sin'a, y=cos2a. Тогда получим
sin" a + cos" a = (sin' a + cos'a) (sin* a— sin2 a cos2 a + cos* a).
С помощью тождества
sin2 о + cos' a = I (**)
левая часть равенства (*) преобразуется к виду
2 sin4 a — 2 sin2 a cos' a + 2 cos* a — 3 sin* a — 3 cos* a + 1 = 0.
После приведения подобных членов получаем равенство
I — 2 sin' a cos' a — sin* a — cos* a = 0,
которое можно записать в виде
l = (sms* + cos**)s.
§ I. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 109
С учетом тождества .(**) получаем
1-1.
т. е. исходное тождество доказано.
Доказать тождества:
3
1.1. sin" a + cos" a = 1—— sin2 2а.
1 + sin 2а + cos 2а ,
Ь2* 1 + sin 2а - cos 2а = С g а-
1.3. (sin а + sin р)2 + (cos а + cos Р)« = 4 cos2 ■а~^.
1.4. tga + tg2a — tg3a= — tgatg2atg3a.
1 к 2 sin a — sin 2a , » ji_
2 sin a + sin 2a Г 2 *
1.6.
sin a + 2 sin 3a + sin 5a sin 3a
sin 3a + 2 sin 5a + sin 7a sin 5a *
1.7. sin2 3a — sin2 2a ==• sin 5a sin a.
я sin a — sin 3a — sin 5a + sin 7a e ^_ , ~
cos a — cos 3a + cos 5a — cos 7a 8
1.9. t-o ; j—о : =" c'g 2a-
tg3a —tga ctg3a —ctga
1.10. sin a + sin p* + sin у — sin (a -f p* + y) =
= 4sini^sInl±XsInJL±i,
1.11. sin a+ sin 3a + sin 5a + sin 7a = 4 cos a cos 2a sin 4a.
sin 3a cos3 a + cos 3a sin3 a sin 4a
1.12. ^ j .
, ,„ sin 2a — sin 3a + sin 4a . „
1.13. = =—! -.— = ts3a.
cos 2a — cos 3a + cos 4a
1.14. sin 2a (I + tg 2a tg a) + -1 "*" 8ln a —
I — sin a
■tg2a + tg2(^ + i).
, ,, . . » „a sin2 a —4
1.15. sm" ——cos"-5- = г-—-cosa.
JL a 4
i.16. cos (-~ + 4a\ + sin (Зя — 8a) — sin (4я — 12a) =
«=■ 4 cos 2a cos 4a sin 6a.
. ... 1 » 1 »Л cos2a —cos2в
l.»7.ctg'a-ctB»p= sln,g3|n>pP.
1.18. , 8'n'*. - ■'"'+■««*•, 8,п х + C09 *.
sin x — cos* tg3 * — I.
110 ГЛ. Б, ТРИГОНОМЕТРИЯ
1.19. Доказать, что если а + {$-т-у=я. т0
а В v
cos а + cos в + cos у = 1 + 4 sin -=- sin -Jp sin —.
1.20. Доказать, что если а, в, у— углы треугольнике, то
tg -§• tg -§- + 'В -§• 'в -£* + * Т * Т =» >•
1.21. Доказать, что если cos(a+p) = 0, то
sin (a + 2в) = sin a.
1.22. Доказать, что если sin2 р = 3in a cos a, то
cos 20 = 2 cos» (я/4 + a).
1.23. Доказать, что если tga и tg p — корня уравнения
Л* + рх + q = 0, то справедливо равенство
sin2 (а + Р) + р sin (а + Р) cos (а + р) + <? cos* (о + Р) => д.
1.24. Показать, что если углы аир связаны соотношением
sin р п , , , ,
ыпсга + р)--^' l«KI*b
то справедливо равенство
1+tgpytga I — tg a tg ft
in + n m — n
1.25. Известно, что a, p4 у составляют арифметическую
прогрессию. Доказать, что
sin a — sin у , „
— ■=■ ctg й.
cosy —cosa
1.26. Доказать, что если а+'р + у = я, то
ctg a ctg p + ctg p ctg v -Ь ctg у ctg а = 1.
1.27. Доказать тождество
£Ш {"I"-'0) С03 ("б""7"0) +"С03 ("f"_(X) S'n ("f""*" a) = l*
1.28. Доказать, что если stn^^^ sin a cos a, to
cos2p = 2sln2f-j- —aY
1.29. Доказать тождество
1 + sin 2a
cos (2a — 2я) tg (a j-)
- 1 sin 2a [rfg -f- + ctg [Щ- + -|)] = - sin* a.
§ 2. ВЫЧИСЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ Ш
1.30. Доказать тождество
1.31. Доказать тождество
, За
3in —
slnT
l-tes —
1 + sin 2а & 2
— ; = Sin О.
sin а + соз а 2 а
I+Ig Т
1.3Я. Доказать, что если а + р + у = я, то
sin2 а — cos2 в — coss \ = 2 cos а cos р cos у.
1.33. Упростить выражение для »е[0; 2л]:
Vl + cos и + Vt — cos a
УI + cos a — д/l — cos a
1.34. Упростить выражение
2. sin a + sin 2a t — cos a
2 cos a + sin 2a I — sfn a *
§ 2. Вычисление значений тригонометрических
функций
Задачи, связанные с вычислением значений
тригонометрических выражений без использования таблиц, обычно решаются о
помощью тождественных преобразовании, приводящих искомое
выражение к виду, содержащему только табличные значения
тригонометрических функций.
Пример 2.1. Вычислить без таблиц
tg20°tg40°tg80°.
Решение.
sin 20° sin 40° sin 80° sin 20° • 2 sin 20° cos 20° • 2 sin 40° cos 40°
cos 20° cos 40° cos 80° "^ cos 20° cos 40° cos 80° """**
_ 2 sin 20° (cos 20° — cos GQ°) _ sin 40° — sin 20° _
— cos 80° — cos 80°
2 cos 30° sin 10° 2 cos 30° cos (90° — 10°) vj-
"" SslO? ™ сБШ5 ==Vd'
Ответ. ■y/W.
Вычислить без использования таблиц!
„, sip 24°cos6° — |in6esin6g!
112
ГЛ. 5. ТРИГОНОМЕТРИЯ
2.2. sin2 70° sin2 50° sin" 10°. 2.3. sin 15°.
, Зя . я „ „ „ 4я 2я я
2.4. sin —jr- sin -гтр. 2.Б. 8 cos -3- соз -jr- соз -jr-.
2.6.
l Уз
я я
sln Iff С03 Ж
2.7. sin4 — + cos4 -g- + sin 4 -g- + cos4 -^-.
2.8*. sin 18°. 2.9*. sin 42°.
Вычисление зваченнй одной
тригонометрической функции по известному значению
другой функции.
Пример 2.2. Вычислить
2 sin 2а — 3 cos 2а
4 sin 2а + 5 cos 2а '
если tg а = 3.
Решение. Выражая sin 2а и cos 2а через tg а, получаем
2 sin 2а — 3 cos 2а _ 4 tg а — 3 + 3 tg2 а
4 sin 2а + 5 cos 2а — 8 tg а + 5 — 5 tg2 а '
Подставляя в -правую часть этого выражения tg а = 3, имееи
4.3 — 3 + 3-9 9
8-3 + 5-5-9" Т*
Ответ. —9/4.
2.10. Вычислить sin а, если sin — + соз ~~-«= 1,4.
2.11. Вычислить 1 + 5 sin 2а — 3 cos-1 2а, если tg а «= —2.
2.12. Найти значение lg4a + cfg4a, если fga + ctga = a.
2.13. Вычислить значение sin3 a — cos3 a, если sin a — cos a=n.
I_2sin!t4-
_ a 2
2.14. Зная, что tg —=m, найти
't2 ' I + sin a "
2.16. Вычислить cos (6 — q>), если cos 6 + соз q> = a, sin 6 —
— sin Ф = 6. a* + б2 Ф 0.
2.16. Сумма трех положительных чисел a, 8, у равна я/2.
Вычислить произведение ctg a ctg у, если известно, что ctg a,
ctg 6, ctg-у являются последовательными членами
арифметической прогрессии.
ft
2.17. Вычислить lg-5-+tg-|-, если
sin a + sin В « о, cos a + cos В «а 6.
§ 2. ВЫЧИСЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ ИЗ
2.18*. Найти tg(a + 2p), если
з1п (а + Р) •= 1, sin (а — Р) = 1/2,
где а, р е= [О; я/2].
2.19. Найтн отношение ctg p/ctg а, если известно, что
sin(a-T-P) p
sin (a — Р) 9 "
2.20. Найти tg—, если известно, что sin a + cos a=-=-.
2, О
»». r. i a sin 3a II
2.21. Вычислить tg-^-, если —г—- = —.
a Sin Ct aD
2.22. Составить уравнеине для нахождения cos —, если
cos a ■=» m.
2.23. Найтн tg-т-, если известно, что
cos a I — m
I + sin a I + m '
2.24. Вычислить sin2a, если tga удовлетворяет
соотношению
Ig'a — atga+ 1=0
н известно, что a>0n0<a< я/4.
Вычисление значений тригонометрических
функций от значений обратных трнгономет*
рнческнх функций.
Пример 2.3. Вычислить значение tg f — arcctg3 J.
Решение. Обозначим а = arcctg 3. Тогда clga = 3,
О < a < л/2. Вычислим теперь значения sin a н cos а. Имеем
I I 1
sin a =
cos a-
Vl+ctg2a Vl+32 V'O '
ctg a 3
Vl+ctg2a лАГО
.a sin a
Используя формулу lg-=- = , , получаем
a 1 ~4~ COS u
114
ГЛ. & ТРИГОНОМЕТРИЯ
ВЫЧИСЛЯТЬ!
2.2Б. sin [2arcco3-j-J. 2.26. cos [arcsfn F —-yYl.
2.27. sin (arcsin-=- +arcsin-тг-J. 2.28. tg Ci arcsin -g- J»
2.29*. arcsin (sin 2). 2.30. tg (arcsin — + arccos -y J.
2,31. sin (arctg 2 + arctg 3). 2.32. cos f arcsin -^ — arccos •* J.
2.33.' sin (2 arctg yY +cos (arctg 2Уз~).
Проверка справедливости равенств, с о д е р«
жащнх обратные тригонометрические
функции. Прн решении этих задач следует иметь в виду, что сумма
двух обратных тригонометрических функций, вычисленных от по-
ложительиых величин, заключена в промежутке [0; я], а
разность—в промежутке [—я/2; я/2].
Пример 2.4. Проверить справедливость равенства
. 4 , 2 .2
arcsin —к arccos—;=•=■ arcctg—.
& V5 И
Решение. Вычислим котангенс от левой и от правой
частей равенства:
ctg( arcsin—J- arccos—/=-)=■
ctg J arcsin — J ctg j arccos—■=- j — I
ctg | arcsin — ) + ctg ( агссоз ._ \
ctg (arcctg-jf)=-n-^
Итак, получаем
clg (arcsin •—\- arccos _. j = ctg (arcctg —).
4 2
Так как угол arcsin j + arccos -т=г- принадлежит промежутку
(0; я) — промежутку мопотоиностн функции котангенс — то нз
равенства значений функции котангенс следует равенство
значений аргументов, что я требовалось доказать.
Проверить справедливость равенств!
<,«., . V5" , V§" n
2.34, arceln -V-•}■ arccos-— = -%■•
S 2. ВЫЧИСЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИ 115
2.35. arctg I + arctg 2 = л — arctg 3.
Уб"+1 я
VI-
2.3J. arccos a / arccos ^ .
3 2V3 6
2.37. Доказать, что если
arclg a + arctg в + arctg у = «,
то а + В + v = a • В • v.
2.38. Доказать, что
, У 2~ + I , У? я
arctg v._ arctg-*— = —,
У2 - 1 2 4
2.39. Доказать, что
Уб
arctg 3 — arcsin -^— = -7-.
2.40. Доказать, что
. б , , 12 Я
aresm-Tg- + arcsln-j5—T.
2.41. Доказать, что
я , .77 , 8 , / 3\
-д- + arcsin -gg- = arcsin -ту + arccos I — -ё" I •
2.42**. Проверить, справедливо ли равенство
arccos х + arccos Г-^- + ~ Уз — Зх2 J = -^- для ж еI -j-, 11.
2.43**. Проверить, справедливо ли равенство
. (л/2 , У2-2*=\
я.
arcsin ж =-;-.
4
Суммирование конечного ряда трнгоиометрнческнх функций
Sn=ul + u1 + u3+ ... +ип (I)
часто удается осуществить с помощью подбора так называемой
производящей функции, т. е. функции, обладающей свойством
/ № + I) - f (A) = uk.
Если функция /(ft) иайдеиа, то сумма (I) представляется в еидй
S.-/(n+I)-/(l). (2)
Пример 2.5. Просуммировать
8п =• sin а + sin (а + Л) + sin (а + 2А) + ... + sin (а + nh),
116 ГЛ. 6. ТРИГОНОМЕТРИЯ
Решение. Воспользуемся тем, .что
соз ^а + —^— А J — cos ^а + —^— A J
—2 sin (а + ftA) з!п -|-.
[Тогда в качестве производящей функции можно взять
f(*)- Цгсоз(а+ 2fe~' й).
2sinT
Согласно (2) получаем
S„ = - ' л [соз (а + -^±1 Л) - соз (а - -£-)].
2slnT
Преобразуя выражение в квадратных скобках в произведение,
имеем
,1. («+ -!-»).in (iL±l/.)
Sn ва Т .
sinT
Найти следующие суммы:
2.44. sin a sin 2а + sin 2а sin За + з'ш За sin 4а +
... + sin ла sin (л + 1)а.
2.45. cos За + cos 5а + cos 7а + ... + cos (2гс + 1) а.
2.46. tga + ytg-^- + 4-tgiL"r- ... +4r»s|r-
„ ._ я Зя , 5я . 7я
2.47. соз -jg. + соз -д. + cos -j. + cos — +
. л9я , Пя
+ СОЗ -Г5" + СОЗ
13 т w" 13 *
2.48. cos* а + cos2 (а + —) + соз! (а + —) + ...
...+cos»(a+ (Л~1)Я).
„ .„ я . Зя . 5я . . 17я
2.49. соз — + cos —g- + соз-гг- + ... + cos
19 ^w° 19 п w* 19 ^ "• т"~ 19
„_„ ят , Зят , 5ят ,
2.50. cos h cos h cos h
n n я
i «л. (2д — 1) nm
+ COS — ■
a
2gI sin a + sin 2a + ... + sin яа
cos a + сад 2a + ... + cos m '
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 117
§ 3. Тригонометрические уравнения
Решения простейших тригонометрических
уравнений.
&\пх*=а, * = (—l)ftarcsin a + nk, |а|<1,
cos х = а, х = ± arccos а + 2я&, | а | < I,
tg х = я, * = arctg а + яб,
ctg ж = а, х = arcctg а + itk.
Уравнения вида
Р (sin *)•=(), Р(соз*)=0, P (tg де) = 0, P(clgx)=0,
где Р — многочлен указанных аргументов, решаются как
алгебраические уравнения относительно указанных аргументов с
последующим решением простейших тригонометрических уравнений.
Решить уравнения, сводя их к алгебраическим уравнениям
относительно одной тригонометрической функции:
3.1. 2 sin2 х + sin x— I =0.
3.2. tg3n + 2te2* + 3te*=o.
3.3. 4 sin4 x + cos ix = 1 + 12 cos* x.
3.4. 6 coss x + cos Зх = соз x,
З.Б*. a/ -jg- + cos4 x — -jj- cos2 x -{-
+ V"^ + cos4*-tc03S*=t-
Решение однородных уравнений. Уравнения
вида
а0 sin"х + a, sin"-1 х cosx + а2 sin"-2* cos2x + ...
... + а„ cos" j; = 0,
где ао, ai а„ — действительные числа н сумма показателей
степеней при sin x н cos x в каждом слагаемом равна п,
называются однородными относительно sin дс, cos x. Такие уравнения
при соз дс Ф 0 эквивалентны уравнениям
a0tgnx + altgn-lx+ ... +а„ = 0.
Пример 3.1. Решить уравнение
3 sin3 дс — б sin х cos x + 8 cos2 дс = 2.
Решение. Для того чтобы свести данное уравнение к
однородному, воспользуемся основным тригонометрическим
тождеством
pin2 л + cos* ж =1,
118 ГЛ. 6. ТРИГОНОМЕТРИЯ
записывая уравнение в виде
3 sins х — 5 sin x cos x + 8 cos2 x = 2 (sin* дс + cos2 x).
После приведения подобных членов получаем
sin2 x — 5 sin x cos x + 6 cos8 x = 0.
Разделив обе части уравнения на cos2*, приходим к
квадратному уравнению относительно неизвестной у = tg дс
уг-5у + 6 = 0.
Корнями t полученного квадратного уравнения будут числа
у, = 2 и y2 = Z.
Следовательно, решение исходного тригонометрического урав«
пения сведено к решению двух простейших трягонометряческня
уравнений
tgx = 2 н tgac = 3,
решения которых
х = arclg 2 4- nk,
х = arctg3 4- яд, k, nsZ.
Решить следующие уравнения сведением к Однородным:
3.6. 2 sin х cos x + 5 cos2 дс = 4.
3.7. 8 sin 2x — 3 cosa x = 4.
3.8. 4 cos» -у + -i- sin дс + 3 sin2 ^-= 3.
3.9. sin4 x — cos* дс = 1/2.
8.10. 2 sin3 * + 2 cos * sin2 дс — sin дс cos2 дс — cos3 дс = 0.
3.11. 3 —7 cos2 .«sin* —3 sin3 ж = 0.
3.12. 2 sin8 дс — sin2 x cos дс + 2 sin дс cos2 дс — cos3 дс =0.
3.13. sin* x + cos4 * = sin 2дс — 0,5.
3
8.14. sin6 2.v + cos6 2x = -j (sin4 2* + cos4 2дс) +
+ -5-(sin дс + создс).
8.18. cos" x + sin» x — cos2 2дс => 1/16.
3.16. sin6 дс + cos8 дс = cos3 2x.
3.17**. Найти решение уравнения
sin" x + cos6 дс = a (sin4 jc + cos* дс)
при всех действительных значениях а.
Метод дополнительного угла. Уравнения вида
acos*+ Ь sinje^g
5 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ П9
эквивалентны тригонометрическому уравнению
с
Bin (* + ф) >
Va*+ &«'
где ф находится из системы
Ь
Пример 3.2. Решить уравнение
3 sin дс + 4 cos х = б.
Решение. Так как V3" + 4а = б, то данное уравнение
Эквивалентно уравнению
sin (х + ф) = I,
Где ф определяется из системы уравнений
sin ф = 4/5, cos Ф = 3/5.
Так как sin ф н cos ф больше нуля, то в качестве Ф можно взять
<р = arcsin -g-, я решение данного уравнения имеет вид
4 л
х =• — arcsin — + — + 2яп.
4 л
Ответ. х=>— arcsin -г + —+ 2яп (л sZ).
Заметнм, что уравнение примера 3.2 может быть сведено к
однородному, если представить
sin х = 2 sin — cos -д-, a cos дс = cos8 -5— sin2 -^-.
Решить уравнения методом введения дополнительного угла;
3.18. sin 8* — cos 6* = V3" (sin 6jc + cos 8x).
3.19. sin 11* + ~~ sin 7x + -g cos 7* = 0.
3.20. sin 10a- + cos 10* = V2" sin 15л:.
3.21. Найти все решения уравнения
V + sin 2* — s/2 cos 3* = 0,
заключенные между л н Зя/2.
8.22. 4 cos2 д: = 2 + -|г соз 2х (-^-| I- ' ).
^2 \ cos 2х т sin 2ж /
8.23. 4 sin 3* + 3 cos 3* = 5,2.
120 ГЛ. Б. ТРИГОНОМЕТРИЯ
Решение уравнений методой уннверсаль*
ной тригонометрической подстановки.
Тригонометрическое уравнение вида
7? (sin kx, cos гаде, tgmx, ctg /де) = 0, (3)
где R — рациональная функция указанных аргументов (k, n, m
н / — натуральные числа), с помощью формул для трнгономет-
рнческнх функций суммы углов (в частности, формул двойного
и тройного углов) можно свести к рациональному уравнению
относительно аргументов sin х, cos х, tg дс и ctg дс, после чего урав-
ненне (3) может быть сведено к рациональному уравнению отно-
х
ентельно неизвестного t = tg -5- с помощью формул универсалЬ'
ной тригонометрической подстановки'.
2ti?T 1 — *g9 -f-
sin x = ; cos x = ■
tg* = —■; ctg* = -
1~&T 2tgT
Пример 3.3. Решить уравнение
(созле — sin x) ( 2 tg дс -| J 4.2 = 0.
x
Решение. Обозначая t = tg —, с помощью формул
универсальной тригонометрической подстановки запишем уравнение
в виде
$t* + б/3 + &t2 — 2t — 3
(f2+0(l-f2)
-=0;
корнями его будут t,= i/V3\ h = — l/V3. Таким образом,
решение уравнения сводится к решению двух простейших
уравнений
. х \ . х I ,.,
tgT~vT *7—vf (4)
Делая проверку, убеждаемся, что числа ял — корни уравне-
пня cos—»О— ие являются корнями данного уравнения, и,
следовательно, все решения исходного уравнения находятся как
решения уравнений (4}.
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 12Г
Ответ. ж=±-^- + 2яЛ (k е= Z).
Решить уравнения методом универсальной подстановки!
3.24. sin* + ctg-|- = 2.
8.25. ctg (^— х\ — б tg2х + 7
3.26. 3 sin 4х = (cos 2дс — 1) tg ж.
3.27. (I + соз дс) д/tg -|- — 2 + sin дс = 2 соз ж.
Уравнение вида
R (sin ж + cos х, sin ж cos дс) = 0, (5)
где Я — рациональная функция указанных в скобках аргументов*
может быть сведено к уравнению относительно неизвестного
t = sin x + cos x, если воспользоваться тригонометрическим тож«
деством
(sin х + cos х)г = sin2 х + coss х + 2 sin дс cos x = 1 + 2 sin ж cos др,
аз которого следует равенство
31П ДСС03ДС = .
Учитывая это равенство, уравнение (5) можно привести к виду
Аналогичным образом уравнение вида
R (sin дс — соз дс, sin дс cos х) = О
заменой sin дс — cos дс = t сводится к уравнению
Пример 3.4. Решить уравненне
sin дс + cos дс — 2 V2 sin дс cos дс = 0.
Р е ш е и н е. Обозначив sin дс + cos дс = t и воспользовавшись
равенством sin дссоз дс = (Р— 1)/2, сведем исходное уравненне
к уравнению относительно t:
У!" <2-г-У2"=0.
Корнями этого квадратного уравнения будут числа /i=V^i
<,=. -1/У2.
122
ГЛ. Б. ТРИГОНОМЕТРИЯ
Таким образом, решение исходного уравнения сводится к ре*
Шеншо двух тригонометрических уравнений:
sin х + cos x = yir, sin * + cos* = — l/VsT
Умножая обе части этих уравнений на число 1/д/2, сводим ия
е двум более простым урааненням:
—=■ sin х -}—j=- cos x = I <=> cos — sin x + sin — cos x =»
V? V2 4 4
=■ I <*- sin
SX+V~
Решениями уравнений sin (* + -j- J = I н sin (ж+ -7-J >
r=- sin дс -| — cos * = -ФФ- sin
5—
у будут
* = -j- + 2яй,
,-(_!)»+» «-_
51 i
4eZ,
nsZ.
Решить уравнения:
3^38. 6 (sin jc + cos x) + sin 3* — cos Zx = 2 VsT (2 + sin 2*).
3.29. sin * + cos x + sin ж cos x •=* 1.
,3.80. sin x + cos * — 2 sin * cos x =* 1.
3.31*. Найти решение уравнения
I 1 I
cos x ' sin * ' sin * cos x
при всех действительных значениях а.
Упрощение некоторых тригонометрических уравнений может
быть достигнуто с помощью понижения нх степени. Если
показатели степеней синусов н косинусов, входящих в уравнение,
четные, то понижение степени производится по формулам
половинного аргумента.
Пример 3.5. Решить уравнение
29
sin10 х + cos10 х =з —— cos4 2х.
ID
Решение. Используя формулы половинных углов, данное
уравнение можно представить в виде
( I — cos 2х \б / 1 + cos 2х V 29 , „
I 5 J + К 2 ) - IF MS 2X'
S 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 123
Обозначив cos 2х = t, представим это уравнение в виде
Раскрывая скобки н приводя подобные члены, приходим к би«
квадратному уравнению
24f* - 1<M2 —1=0,
единственный действительный корень которого Р = 1/2. Возврат
таясь к исходному неизвестному, получаем
cos22* = — -<=>• I + cos 4* =» I <* cos 4ж = 0-*=*- х =»
~Т+ 4' АеЗВ*
Ответ. х = -5- + —г* NZ).
о 4
Решить уравнения:
3.32. sin2 6* + 8 sin2 3* = 0.
3.33. sin2 x + a sin2 2* = sin -jr. Исследовать решение.
17
3.34. sin6 ж + cos" x = -£5-.
3.35. соз 2x + 4 sin4 jc==8 cose *.
3.36. cos 4* — 2 cos2 дс — 22 sin2 x + 1 = 0.
3.37. cos2 3* + cos2 4x + cos2 5* =-|-
3.38. sin2 3* + sin2 4* = sin2 5* + sin2 6*.
3.39. cos2 j + cos2 ~ x — sin2 2x — sin* 4x = 0. '
3.40. sin4 x + cos4 x =• cos2 2x + 0,26.
3.41. 2 + cos 4ж =■ 5 cos 2x + 8 sin6 дс.
5
3.42. sin4 x + cos4 ж =—-.
о
3.43. 8 sin2 x + 6 cos2 x = 13 sin 2*.
3.44. sin3 * (I + ctg x) + cos3 x (1 + tg x) = 2 УяТпТЖ]^
Решить уравнения, применяя изложенные выше методы!
3.4Б. 2 cos 2ж = л/К (соз х — sin x).
3.46. sin8 ж + cos8 x = I —5" sin 2*.
3.47. sin Зле + sin x + 2 cos x = sin 2дс + 2 cos* л
8.48. sin 5* sin 4* = -r- cos 6* COS 3*.
124
ГЛ. Б. ТРИГОНОМЕТРИЯ
8.49. tg X + sin 2x ■■
1
COS X
2 tg x + tg 2x = tg Ax.
cos 3x + sin 5x = 0.
sin x cos 5x = sin 9* cos 3x.
1 + sin x + cos x + sin 2x + cos 2x = 0.
I + sin x + cos Зле = cos x + соз 2x + sin 2*.
sin2 x (tg x + I) = 3 sin x (cos x — sin x) + 8.
sin 2x sin 6x = cos x cos 3x.
cos (x + I) sin 2 (x + 1) = cos 3 (x + I) sin 4 (x + I).
sin x sin 7x = sin 3x sin 5x.
cos x sin 7x = cos 3x sin 5x.
sin x + sin 2x + sin 3x + sin 4x = 0.
cos 2x — cos 8x + cos 6* = 1.
I
ЗЛО.
3.51.
3.52.
3.53.
3.54.
8.55.
3.56.
8.67,
8.58.
3.59.
3.60.
3.61.
3.62.
3.63.
8.64.
8.65.
8.66.
8.67.
3.68.
3.69.
8.70.
8.71.
8.72.
8.73. 2 sin 3x
sin x sin 2x sin 3x = — sin 4x.
4
3
sin8 x cos 3x + cos 3* cos3 x = -5-.
о
tg x + tg 2x = tg 3x.
(l-tgx)(l + sin2x)=l+tg*.
(I + sin 2x) (cos x — sin x) = 1 — 2sin2 x.
tg(* + tt) + tg(.«-c0=2ctg*.
sin22z + sin23z + sin24z+sin25z = 2.
sin x cos x cos 2x cos8x •=* -r- sin I2x.
4
sin 2x sin 6x — cos 2x cos 6x = л/2 sin 3x cos 8*.
tg x + ctg 2* =» 2 ctg 4x.
cos 3x — cos 2x ■*> sin 3x.
2 cos 3x +
3.74.
8.75.
3.76.
8.77.
8.78.
3.79.
8.80.
3.81.
8.82.
sin
ctg2 x — tg2 x = 32 cos3 2x.
tg 2x + ctg x = 8 cos2 x.
9
sin2 2x — tg2 x => -5- cos 2x.
sin 2x — Ig x = 2 sin 4x.
sin4x
sin (x — я/4)
cos 3x tg 5x = sin 7x
cos2 2x
cosx
V2 (sin x + cos x).
cos x + cos (я/4)
sin x ctg 3x = cos 5x.
cosx cos5x
cos 3x cos x
cos x — cos —.
4
= 8 sin x sin 3x,
§ S. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
I
cos Зх cos 4х
8.83. 5 = —2 cos 2x.
cos Зх cos х
3.84. 1-—— + ^ s- +
соз х cos 2x ' cos 2x cos Зх г
„._ sin Зх , cos Зх 2
3,Сн>* ■— ■■ - -I- — ^з — ■ - ■»
cos 2x ' sin 2х sin Зх
8.86*. cos (x-~\ + cos (х + ^Л =. -| cos2*.
3.87. 4 sin Зх + sin 5л: — 2 sin x cos 2x = 0.
3.88. sin (*+4) sin (* — 4) = sin*-
8.89. 3 cos x + 2 cos 5x + 4 cos 3x cos 4x ■» 0.
8.90. 3 sin 5x = cos 2x — cos 8x — sin I5x.
8.91. cos 2x — sin 3x — cos 8x = sin Юх — cos Sx.
3.92. sin 2x — cos 2x = tg x.
8.98. cos 3x — sin 5x — cos 7x = sin 4x — cos 2x.
3.94. sin 2x + cos 2x =» 2 tg x + 1.
3.95. 4sinsx+ 3tgzx = I.
3.96. 4 sin x sin 2x sin 3x = sin 4x.
3.97.
3.98.
sin 4x + sin 2x — 4 sin 3x + 2 cos x — 4
sin x — 1
= 0.
V i — cos 2x
sin x
3.99. cos 2x =
1 + УЗ
.У5Г (cos х- — у
(cos x + sin x).
3.100. ctgx —tgx =
cos x — sin x
■г- sin 2x
3.101. sin 7x + sin 3x + 2 sin2 x « I.
3.102. cos x — cos I7x = I + 2 sin 8x sin x — cos I6x\
3.103. sin x — cos x = 4 sin x coss x.
3.104. 2 cos 2x (ctg x — i) = I + ctg x.
3.105. tg x + 2 ctg 2x = sin x (l + tg x tg-| Y
3.106. 2 ctg 2x — ctg x = sin 2x + 3 sin x.
3.107. sin4 x — cos4 x = cos f — x ).
3.108. sin 2x + sin4 j =■ cos4 у.
3.109. cos x «= V3~ sin x + 2 cos 3x.
ЗЛЮ. !*15* = (sin x + cosx)a.
8.111. sin3x+sinx=«4 sin8x. ,
ГЛ. 5. ТРИГОНОМЕТРИЯ
3.112. tg (^ cos х J = ctg (тг*'п x J.
Решение некоторых тригонометрических уравнений
предполагает последующую проверку условий, которым должны
удовлетворять найденные корни. Если эти условия заключаются в том,
что корни уравнения должны принадлежать заданному
промежутку, то решение задачи выделения этих корней сводится к
решению некоторого неравенства в целых числах.
Пример 3.6. Найти все решения уравнения
(tg2x— I)-1.= l + cos2x, («)
удовлетворяющие неравенству 2*+' — 8 > 0.
Решение. Приведем исходное тригонометрическое
уравнение к виду
1- \ Л
(I + cos2x)(l +
2 cos 2х
Решениями этого уравнения будут следующие значения х:
х •= — у + пп, x = ± — + nk, »,JeZ,
По условию задачи средн этих значений х необходимо отобрать
те значения, которые удовлетворяют неравенствам
2*+J-8>0, cos*=?£=0.
.Такими значениями будут
х = ±-5- + ял, /teN.
Ответ, х =- ± у + яд, п е N.
3.113. Найтн асе решения уравнения
д/sin (I — х) = Vc°s х,
удовлетворяющие условию х t= [0; 2л].
3.114. Найтн все решения уравнения
cos4 х — 3 cos Зх = 3 cos x — cos3 x cos Зле,
лежащие в промежутке [—я; я/2].
З.Пб, Найтн все решения уравнения
X X
sin-=— cos — = I — sin x,
удовлетворяющие условию
1х я I Зя
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И0
3.116. Найти все решения уравнения
у (соз 5* + cos 7х) — cosa 2х + sin* Зх = О,
удовлетворяющие условию |дс| < 2.
Решить уравнения:
8.117». tg*2=-ctg5x.
3.118*. sin — = cos За;.
х
3.119*. sin x = соз л/х.
3.120**. Доказать, что уравнение
sin (соз х) = cos (sin у i
не имеет действительных корней.
3.121*. sin Г-^- cos дс 1 = соз Г —g- sin jc J.
3.122*. sin (я clg x) = cos (я tg дс).
3.123. Найти корни уравнения sin(x — 2) = sln(3x— 4),пр*>
надлежащие промежутку (—я; я).
В случаях, когда дополнительные условия представлены
неравенством, содержащим трягонометрнческие функции, выделе»
ине нужных корней производится на промежутке, равном' яан*
меньшему общему кратному периодов тригонометрических
функций, входящих в уравнения н неравенства.
Пример 3.7. Найти все решения уравнения
я 5
1 + (sin х — cosx) sin-j-=• 2 соз3-s-*, (*)
удовлетворяющие условию
sin 6* < 0. (*♦)
Решение. Упростим исходное уравнение:
It 5jt Л/2
1 + (sin х — cos д:) sin -г- •= 2 cos2 — -<*=>■ 1 + (sin д; — cos x) -Tj-=■
= i + cos 5,v -t=s- cos 5x + cos I x\+ -j 1 = 0 -*=*-
-Ф*-2cos(zx + j\ cos (zx--|Л = 0.
Таким образом, исходное уравнение (*) эквивалентно
уравнениям
cos (з* + -f) = 0, cos (2* - £) « 0>
128 ГЛ. Б. ТРИГОНОМЕТРИЯ
корни которых равны соответственно
я . ягс _
х=-8+—' Пе2,
5я , пп _
х=Тб+—' rteZ-
Наименьшее общее кратное периодов тригонометрических
'функций, входящих в уравнения (•) н неравенства (*•), равно
2я. Из найденных решений уравнения, принадлежащих
промежутку [D; 2я), неравенству (**) удовлетворяют числа бя/16 я
бя/16 + я. BCfe решения задачи получаются прибавлением к каж<
Дому полученному корню чисел, кратных 2я.
Ответ, дс = -г£- + nk (fee Z).
3.124. Найти все решения уравнения
. 5 —8cos Гж ——я J =2sln f 2ж —-д-л),
удовлетворяющие неравенству cos * > 0.
3.125. Найти все решения уравнения
Vtg дс + sin х + л/ig х — sin x = л/ЪЛ%~х
а) на промежутке [0; л]; б) на всей действительной осн.
3.126. Решить уравнение
V2 + tgje — cos" ж — Д/-д- + 'В х "= д/"о"~~ со&'х •
3.127**. Найтн все решение уравнения
sin (* ~ 1") " C0S(* + Т") " '•
2 cos 7x
удовлетворяющие неравенству ■ „ „ > 2C0S 2x.
3.128*. Найти все решения уравнения
sinf х-\ | = т= ,
V 4 / 2 д/2 cos х
удовлетворяющие неравенству logaln»3(l + соз (2л: + 4)) < соз 4*.
3.129*. Найти все решения уравнения
sin Ux + *Л + cos (\х + х) = V2,
cos 2* 8ta 4х
удовлетворяющне неравенству. 2 _ . 2' > 2 " .
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ 129
8.130*. Найтн все решения уравнения
з1п(2* — ^\=*л/2 з1п*ж,
удовлетворяющие неравенству Iogcoe.3 (I + sin (7* + б)) < sin 8x.
Некоторые тригонометрические уравнения удается решить,
используя оценку левой н правой частей уравнения.
Пример 3.8. Решить уравнение
1в(т+*)+1в(т-*)=2' <•>
Решение, Используя формулу приведения, получаем
*(т+')-Чт-т-)-*(т-)-
(Гак как
*НТ_*)= с1В(я/4-*)'
то левая часть данного уравнения представляет собой сумму
двух взаимно обратных величин. Известно, что при а > О
а+ 1/а>2.
Таким образом, равенство (*) достигается только при
'в (т+ *)-'• (">
Множество решений уравнения {**) имеет вид
х =- яп, neZ,
Ответ. а; = яя (ftsZ).
Пример 3.9. Решить уравнение
sin дс + з!п 3* = 2.
Решение. Так как |sin*| ^ I, |sin3*| < I, то исходное
уравнение эквивалентно системе уравнении
sin Jt = 1, sin3;e=l.
Множества решений каждого нз этих уравнений имеют вид
* = у + 2яй, fcesZ, (•)
«-ТГ + ИГ' neZ> (">
0 А. Г. Цыпквв, At И, ПннскнА
130
ГЛ. Б. ТРИГОНОМЕТРИЯ
соответственно. Решением системы, а следовательно н исходного
уравиеиня, являются те зиачеиня х, которые принадлежат как
первому, так и второму множеству. Для того чтобы найти эти
значения, приравняем выражения, стоящие в правых частях
равенств (*) и (**)• Если найдутся целые значения дни, при
которых эти выражения совпадают, то полученные значения х
удовлетворят обоим уравнениям системы.
Приравнивая правые части (*) и (**), нолучаем уравнение
я , а . я , 2л/»
T + 2*fc=- + —,
которое после тождественных преобразований приводится к виду
2л. — 6fe = I. (**♦)
Очевидно, что уравнение (***) не имеет решений в целых числах,
так как прн любых п н k слева стоит четное число, а справа —
нечетное. Таким образом, множества (*) и (**) ие имеют общих
точек и исходное уравнение решения не имеет.
Решить уравнения:
3.13U ski х + si» 5jc = 2. 3.132. sin x sin у = I.
3,133. 3'« '« * + 3lg elg x = 2.
3
3.134**. cos x + cos у — cos (ж + у) = —.
8.13Б. sfn дс + sin у = 2. 3.136. sin дс + sin у + sin z = —3.
3.137. iogc03 x sin x + logs,,, x cos x = 2.
3.138, cos2 дс + cos x cos у + cos2 у = 0.
3.139*. Доказать, что уравнение
(sin ж + Уз~ cos x) sin Ax = 2
не имеет решений.
• 3.140. ■\/2 — \у\ (5 sin2 ж — 6 sin * cos x — 9 соза х + 3 i^33~) =
. » , 2 Sat3
= arcsin2 ж + arccos'' x — —т—.
4
ы«-**-4(|*-тН*-т«|)-
8.142. Найти все х, удовлетворяющие уравнению
У49 — 4х Г sin их + 3 cos -5-) *> 0.
3.143. Найти все значения ж, при которых выражение
у4** - 3 - х* {I - cos [2л (2* + 21 ж2)!}
не обращается в нуль.
9 4. СИСТЕМЫ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЯ 181
§ 4. Системы тригонометрических уравнений
Системы уравнений, в которых неизвестные являются
аргументами тригонометрических функций, называются системами
тригонометрических дравяенай. При решении систем
тригонометрических уравнений используются методы решения систем
уравнений и методы решения тригонометрических уравневий.
Пример 4.1. Решить систему уравнений
sin х sin у = д/3 /4,
cos дс cos у =- Vs"/4.
Решение. Складывая уравнения системы, приходим к
(уравнению
i л/з~ , , V3"
sin х sin у + соз х соз у = * •<=>• cos (x — д) = „ .
Вычитая из второго уравнения системы первое, приходим к
уравнению
cos х cos у — sin x sin у = 0 ■**• cos (ж + у) = 0.
{Таким образом, исходная система равносильна системе
V3
cos(*-«,)=-^-,
cos (x+y) = 0,
ж — у = ± -т- -г 2ял,
* + У = "J + "*•
п, k e Z,
откуда
*■=£ + £ (2« + *). * = £ + £(*« + *).
ff-J + f(*-2n), jr—f +f (*-2n). -
Ответ. («.+ |(2n + ft). T + f(^-2")):
(f + т{2n + k)- f+f(fe"2л))' где *•nez
Решить следующие системы уравнений;
4.1. sin xcosy =»—1/2, 4.2. sin xcos у =»0,36,
cos * sin у = 1/2. cos* sin 0 = 0,175.
4.3. sin * sin у =• 3/4, 4.4. соз x cos # = -^-—,
tg*tgy«-3. ctgjectg«/ = 3+2V2~.
4.5. 8in x — sin у = 1У2,
cos * -J- cos jf« Уз/2,
132
ГЛ. Б. ТРИГОНОМЕТРИЯ
4.в. sin 2х + sin 2у = 3 (sin x + sin у),
cos 2х + cos Ч.у = cos x + cos у.
4.7. sin xcigy = Уё"/2. 4.8. Ig ж = sin //.
Ig xcos у = д/З /2. sin x = 2 ctg у.
4.9. sin// = 5 sin x,
3 cos x + cos у = 2.
4.10. 3 tg |- + 6 sin ж = 2 sin (у - ж),
tg -f — 2 s'n ж = 6 sin (y + x).
4.11. sin8.*; + cos x sin у = cos 2//,
cos 2ж + sin 1y = sin2 i/ + 3 cos i/ sin x.
4.12. 2 sin2//+ sin 2// = cos (лс-f-j/),
cos2 x + 2 sin 2y + sins у =• cos (ж — у).
4.13. s!qs (-2*) - (3 - л/2) tg by = 3л^~Т ,
tg» Ьу + (3 - V?) sin (-2*) = 3л/^~'.
4.14. sin" 3x + (4 — л/3") ctg (-7i/) = 2 V3~ — 3/4.
dff2 (-7(/) + (4 - д/З") sin 3* = 2 д/З" - 3/4.
4.15. 4s:n у — 6->/2 cos x = 5 + 4 cos2 //,
cos 2jc = 0.
4.16. I+2cos2x —0,
л/б" соз у — 4 sin x = 2 л/Т (1 + sln! y).
4.17. 2 V3~ cos * + 6 sin у = 3 + 12 sin* ж,
4 V3~ cos x + 2 sin у = 7.
4.18. л/2" «г + VT2" ctg x = 4,
2 д/2~ у — л/27" ctg л; = I.
4.19. 3 tg 3y + 2 cos x = 2 tg 60°,
5
2 tg 3y — 3 соз x ==■ — -5- cos 30°.
4.20. sin (у — Zx) => 2 sin» *,
cos (1/ — Sjf) = 2 cos8 x.
4.21. sin (x — y) = 3 sin * cos у — I,
sin (x + y) =• —2 cos * sin y.
4.22. Найти решения системы
| sin je|sin 1/=—1/4,
cos {x + jr) + cos (* — y) = 3/2,
удовлетворяющие условиям x е (О, 2я), # e.(«; 2я).
§ i. СИСТЕМЫ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИИ 133
4.23. tg2 х + ctg2 х = 2 sin3 у, 4.24. x + у «-j,
sin» y + cos2 2—1. WT"
4.25. 481n* + 3.9c03!' = 3,
4-sln* + 5.8,co3 y+lt2 = , i/2>
4.26». х + у + г*=л, 4.27*. tg*/tgy = 2,
tg x tg у = 2, tg y/tg z = 3,
lg* + tgy + tgz=6. ж+у + г=>я.
Если одно из уравнений системы рационально относительно
аргументов тригонометрических функций, то решение системы
обычно сводится к решению тригонометрического уравнения для
одного из неизвестных.
Пример 4.2. Решить систему уравнений
х + у = 2я/3,
sin у
Решение. Преобразуем второе уравнение системы к виду
sin х =» 2 sin у. (♦)
Используя первое уравнение системы, исключим из уравнения
"(*) неизвестное у:
2я
sin
де = 2 sin Г -я ж) ■*=»- sin х = V3~ cos x + sin x.
Полученное уравнение эквивалентно тригонометрическому
уравнению
соз х = 0. (**)
Подставляя корни уравнения (*») в первое уравнение систе«
мы, получим значения для неизвестного у. к
Я Я '
Ответ. х = -~- + nk, y = -7T — nk, где k e Z.
Решить системы:
4.28. х — у=*п/\8,
s'n(* + T§")sin0' + f) = T*
4.29. I ~ Iе * = tg у,
1 + tg х J
х — у = я/6.
4.30. tg x + ctg у =. 3,
U-ff| —я/3.
4.31. sin x + sin у = sin (ж + y)i
134
ГЛ. Б. ТРИГОНОМЕТРИЯ
4.32, Выяснить, при каких значениях а решения системы
8 cos х cos у cos (x — у) + I = О,
х + у = а
существуют, и найти эти решения.
§ 5. Уравнения, содержащие обратные
тригонометрические функции
Решения простейших уравнений
Уравнение
arcsin *—а
агссоз х=а
arctg ж=а
arcclg x=a
Уравнения вида
(1о1<л/2)
( | а | <Я/2)
(0<а<Я)
р (»(*»-а
Решение
х=з|п а
x=cos a
X = tg 0
x=ctga
где Р — некоторая рациональная функция, а у(х) — одна из
аркфункций, сводятся к простейшим уравнениям
У (х)=Уе
где yi — корни уравнения Р(у) = 0.
Пример 5.1. Решить уравнение
2 arcsin2 х — arcsin дс — 6 = 0.
Решение. Вводя новое неизвестное у = arcsin x, получаем
уравнение
2у2 — У — 6 = 0,
решение которого yi = 2, у° = —1,5. Следовательно, решеина
исходного уравнения сводится к решению двух простейших урав^
нений
arcsin х = 2, arcsin x = —1,5.
Так как 2 > я/2, а |—1,5| < я/2, то единственным
решением будет х = —sin 1,5.
Ответ, х = —sin 1,5.
Решить уравнения:
Б.1. arctg8 -r — 4 an
8.2. arctg* (Зх + 2) + 2 arctg (Зж + 2) = О.
X X
Б.1. arctg8 -^ — 4 arctg -5- — 5 == 0,
§ 5. УРАВНЕНИЯ, СОДЕРЖАЩИЕ ОБРАТНЫЕ ФУНКЦИИ 135
,.„ « , Я . Я*/9
5,3. 2 arcs п х »= -я- Ч .
3 ^ arcsin ж
Б.4. 3 arctg2 х — 4я arctg ж + я" «=> 0.
5.5*. Найти решения уравнения 2агссоз* = а
действительных значениях а.
Если в уравнение входят выражения, содержащие разные
аркфункцнн, или эти аркфункцни зависят от разных аргументов,
то сведение уравненяя к его алгебраическому следствию
осуществляется обычно вычислением некоторой тригонометрической
функции от обеих частей уравиевия. Получающиеся при этом
посторонние корни отделяются проверкой. Если в качестве
прямой функции выбираются тангенс или котангенс, то решения, не
входящие в область определения этих функций, могут быть
потеряны. Поэтому перед вычислением значений тангенса или
котангенса от обеих частей уравнений следует убедиться в том, что
среди точек, не входящих в область определения этих функций,
нет корней исходного уравнения.
П р в м е р 5.2. Решить уравнение
arcsin 6* + arcsin 6-y/Wx = — я/2. (♦)
Р е ш е и в е. Перенесем arcsin 6* в правую часть уравнения
и вычислим от обеих частей получившегося уравнения значения
синуса:
sin (arcsin 6*) = sin (— arcsin 6 V§" x — я/2).
Преобразуя правую часть этого уравнения по формулам
приведения, получаем следствие исходного уравнения;
6* = — Vl — Ш8ж».
Возведем обе части уравнения в квадрат. После привелення
подобных членов получаем уравнение
144** =1,
корнями которого являются числа 1/12 и —1/12.
Сделаем проверку. Подставляя в уравнение (*) значение
а <=> — I/I2, имеем
arcsin (- 4") + arcsin (- if) »_£_£--£.
Таким образом, х = — I/I2 является корнем исходного
уравнения.
Подставляя в уравнение (*) значение я =1/12, замечаем,
рто левая часть получившегося соотношения положительна, а
arccos х
а»
при
186 ГЛ. 5. ТРИГОНОМЕТРИЯ
правая — отрицательна. Таким образом, значение х = I/I2 —
посторонний корень уравнения (*).
Ответ. *== —1/12.
Пример б.З. Решить уравнение
2 arclg (2.v + i) = arccos x. (*)
Решение. Вычисляя от обеих частей уравнения значение
косинуса, получаем
cos [2 arctg (2* + I)] = х.
. Левую часть этого уравнения можво преобразовать к виду
го ♦' ,о , ,м 1 — (2лг+ 1)а 2*а + 2дс
co3[2arctg(2*+l)]^l + ^+||2= l + 2x + 2xi-
Таким образом, следствием уравнения (*) будет уравнение
2х"+2х „ . .
, , „ , „ i = х -**- 2х3 — х = О,
1 + 2х + 2дс*
корни которого равны О, д/2/2, — д/2/2. Для того чтобы
выяснить, какие из этих чисел удовлетворяют исходному
уравнению, произведем проверку. При * = 0 обе части уравнения
равны я/2. Прн х = -\/272 правая п левая части уравнения
равны соответственно я/4 и 2 arctg (д/з" + 0- Но д/2 + 1 > 1
и, следовательно, arctg (л/2 -Ь 0 > я/4. Значит, х = д/2/2 не
является корнем исходного уравнения. При * = — д/2/2 левая
часть уравиекия отрицательна, а правая — положительна.
Следовательно, х = — д/2/2 также не является корнем уравне»
ния (*).
Ответ, х = 0.
Решить уравнения:
х
6.6. агссоз "о""= 2 arctg (.v — I).
4х
5.7. агссоз х — л = arcsln -=-.
О
6.8. arctB(*+l)+.rdg(*-l)-i.
5.9. arctg 2x + arctg 3* = —.
5.10. arcsin x + arccos (ж — I) = л
5.11. 2 arccos x + arcsin ж = —7—.
о
Б.12. 2 arccos Г—|-J ™ arccos (лс + 3).
§ 6. ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА' !37
6.13. 2 arcsin * = arcsin V2 х-
X X
Б.14. arctg-5- + arctg —«- ardg x.
5.15. arccos x — arcsin *=»-=-.
О
X Я
6.16. arcsin x + arcsin
V3 2 '
5.17. arcsin 2* = 3 arcsin x.
5.18. arccos x — arcsin x = arccos V3 x.
5.19. arcsin x — arccos x = arcsin (3x — 2).
5.20. arcsin x = arccos VI — x*.
5.21. arccos дс =■ я — arcsin VI — x2.
Vi — *2
Б.22. arccos x ■=■ arctg — .
Б.23. arcsin (2x"V 1 — дс2) = arccos (2x2 — I).
5.24. 2 arccos x = arccos (2л;2 — I).
5.26. 2 arctg x =« arcsin ( i ■ хг ) ♦
6.26. 2 arctg x «a arccos f j ■ „ J.
x
Б.27. arccos ж ■= arcctg — ■ , л .
VI —x
2л:2-1
5.28. 2 arccos x = arcctg ■
2л-V -л:8 '
5.29*. Решить уравнение arcsin x = 2 arcsin а при всех
действительных значениях а.
5.30*. Решить уравнение arccos x = агсз'ш 2а при всех
действительных значениях а.
§ в. Тригонометрические неравенства
Решения простейших
тригонометрических неравенств
Вид неравенства
em x>a (
sin x<t (
созх>а (
созлс<а (
"Jg х>а
,ig x<a
eta x>a
clg х<а
а
а
а
а
<!>
<1!
<0
<1)
Множество решений неравенства
же (arcsin а+ 2яя; я—arosln а + 2ял)
ж е(-я—агез1па+2лл; arcsin а + йи)
х е (—arccos а + 2ял; arccoa а + 2яп)
< s (агссоз а + йи; 2я—агссов а + 2яп)
х в (arcta a + Лп: к/2 + яя)
ж <э(-я/2 + яп; arctga + nn)
х а (яя; erects а + пц)
х s(aructs а + лп; я+лп)
138
ГЛ. 5. ТРИГОНОМЕТРИЯ
Решить неравенства:
6.1. sin х > —1/2. 6.2. tg x> 2.
6.3. ctgx > -3. 6.4. sin (x - 1)< — УЗ~/2.
6.Б. sin х2 < 1/2. 6.6. sin x + cos x> — л/2.
6.7*. cos (sin x) < 0. 6.8. sin (cos дс) >0.
Неравенства вида i?(y)>0, i?(y) < 0, где R — некоторая
рациональная функция, а у — одна нз тригонометрических
функций (синус, косинус, тангенс нлн котангенс), решаются в дна
этапа — сначала решается рациональное неравенство
относительно неизвестного у, а потом — простейшее тригонометрическое
неравенство.
Пример 6.1. Решить неравенство
2 sin8 х — 7 sin де + 3 > 0.
Решение. Обозначая sin x = у, получаем неравенство
2«/s-7j, + 3>0,
множество решений которого у < 1/2, у > 3. Возвращаясь к
исходному неизвестному, получаем, что данное неравенство
эквивалентно двум неравенствам
sin х < 1/2, sln*>3.
Второе неравенство не имеет решений, а решение первого
*ef g-+2ttrt, -5- + 2rtrtJ, nsZ,
Ответ: *е( £~ + 2яя» -g- + 2ялJ» где «eZ.
Решить неравенства:
6.9. ctg8 х + ctg2 x — ctg x — 1 < 0.
6.10. 2 cos 2x + sin 2x > tg *.
6.11. tg x + ctg ж < —3. 6.12. sin 2x > cos x,
6.13. cos x + Уз~ cos x < 0.
6.14. УЗ — 4 cos2 jc > 2 sin * + L
6.15. УЗ sin x + 1 > 4 sin x + 1.
6.16. 2Чп'*+в1п*-1
sin * — 1
6.17. 6 + 2 cos 2* < 31 2 sin x — 1 |.
Решение неравенств разложением на мио«
жители.
Пример 6.2. Решить неравенство
cos х + cos 2x + cos 3* > 0.
§ 7. НЕРАВЕНСТВА. СОДЕРЖАЩИЕ ОВРАТНЫВ ФУНКЦИИ 139
Решение. Преобразуя сумму крайних влагаемых в произ->
селение, получаем неравенство
соз 2х + 2 cos 2х cos х > 0.
Выиося cos2;e за скобки, имеем
cos 2х (2 соз х + I) >0,
Последнее неравенство эквивалентно двум снодмвм простейших
неравенств!
cos 2x < 0, cos 2x > 0,
cos х < —1/2; cos x > —1/2.
Объединяя решение этих систем, получаем решенн? исходного
неравенства.
Ответ. (-у- + 2я/ц ^5. + 2ш|)и(-^- + 2ял; -§- +
+ 2rtttjuf— ~ + 2nn; ~ + 2nnA, гдепег.
Решить неравенства:
6.18. sin х sin 2x — cos ж cos 2x > sin 6л.
6.19. 2 sin ж sin 2* sin 3* < sin 4дс.
6.2d. sin * sin 3* > sin 5x sin 7#.
6.21. cos' x sin 3* + cos 3* sin3 i < 3/8.
6.22. sin x > cos 2x.
6.23. 2 tg 2x < 3 tg *. 6.24. sin x < | cos x |.'
§ 7. Неравенства, содержащие обратные
тригонометрические функции
Решение простейших неравенств
Вид неравенства
агс$[П х>а М а|<я/2)
arcsln X<b ( |ai<n/2)
arccoe x>a №<а<я)
arccos л:<а (0<а<Я)
arctg x>a ( 1 а 1<я/2)
arclg х<а ( ) a )<d/2)
arcctg х>а (0<а<я)
arcctg x<a (П<п<Л)
Реакция неравенства.
х s (sin а; 1]
*е -1; з|па)
хе i-i; ctSia)
>: s (cos a; ii
х е (tg а; + °°)
же (- oo; Ig а)
д; 1= (— oo; ctg а)
х е (ctg а; + со)
-*
Решить неравенства:
7.1. arcsin х < б. 7.2. arcsln x > —2.
7.3. arccos х < atccos -г-. 7.4. arccos x > я/6.
7.Б, arotg x > — я/3. 7.6. aicctg х > 2,
140
ГЛ. S. ТРИГОНОМЕТРИЯ
Неравенства вида R(y) > 0, R(y) < 0, где R — некоторая
рациональная функция, а у— одна нз обратных
тригонометрических функций (арксинус, арккосинус, арктангенс,
арккотангенс), решаются в два этапа — сначала решается неравенство
относительно неизвестного у, а потом — простейшее неравенство,
содержащее обратную тригонометрическую функцию.
Пример 7.1. Решить неравенство
arcctg2 х — б arcctg дс + 6 > 0.
Решение. Обозначая arcctg x = у, исходное веравенство
-перепишем в виде неравенства
Уа - 5«/ + 6 > 0,
решения которого у < 2 н у > 3. Возвращаясь к исходному
неизвестному, получаем, что исходное неравенство сводится к двум
простейшим неравенствам
arcctg дс < 2 и arcctg х > 3,
решения которых соответственно равны х е (ctg 2; ю) н дсе
е (—оо; ctg3). Объединяя эти решения, получаем решение
исходного неравенства.
Ответ, (ctg2; oo)U(—°o; ctg3).
Решить неравенства:
7.7. arctg2 дс — 4 arctg х + 3 > 0.
7.8. iog3 (arctg дс) > I.
7.9. 2arct« * + 2-arct* * > 2. 7.10. 4 (агееоз х)* — I > 0.
Для того чтобы решить неравенства, связывающие значения
различных обратных тригонометрических функций нлв значения
одной тригонометрической функции, вычисленные от разных
аргументов, удобно вычислить значение некоторой
тригонометрической функции от обеих частей неравенства. Следует помнить, что
получающееся при этом неравенство будет эквнвалевтно
исходному лишь в том случае, когда множество значений правой а
левой частей исходного неравенства принадлежит одному и тому
же промежутку монотонности этой тригонометрической функции.
Пример 7.2. Решить неравенство
arcsin х > агееоз х. (*)
Решение. Множество допустимых значений х, входящих в
неравенство, имеет вид дс е [— I; 1). При дс < 0 arcsin дс < 0, а
агееоз дс > 0. Следовательно, значения дс < 0 не являются
решениями неравенства. При дс -^ 0 как правая, так и левая части
неравенства имеют значения, принадлежащие промежутку
[0; л/2]. Так как на промежутке [0; я/2] функция синус моно-
§ 8 ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ
141
тоино возрастает, то прв х е [0; I] неравенство (*) эквивалентно
неравенству
sin (arcsin x) > sin (агссоз х) <=*■ х > s/\ —х\
Последнее неравенство при рассматриваемых значениях
неизвестного эквивалентно неравенству
2*3 > I. (**)
Таким образом, решениями исходного неравенства будут те
решения неравенства (»*), которые попадут в промежуток [0; 1].
Ответ: же (Y2/2; l].
Решить неравенства:
7.11. arcsin х < arccos x.
7.12. arccos x > агссоз х2.
7.13. arctg* > arcctgjf.
7.14. arcsin x < arcsin (I — x).
7.16. tg2 (arcsin x) > I.
§ 8. Доказательство тригонометрических
неравенств
Доказательство неравенств, связывающих значения
тригонометрических функций на всей числовой оси или на некотором ее
промежутке, обычно основано на исследовании свойств функций}
монотонности, ограниченности и т. д.
Пример 8.1. Доказать, что если а, В е (—я/2; л/2), то
а + В ^ соз а + соз В
cos-p> 2 -•
Решение. Для доказательства данного неравенства
достаточно представить правую часть неравенства в виде \
cos а + соз В а + В а — В
i Р^соз-р-соз-^
0 ( я я \ а —В / я я \
и учесть, что при а, В е= ^— —; -^ J ь r е= ^— -j'> -jj-J*
н следовательно, 0 < соз —^— < 1.
Доказать, что для х е [0; л/2] выполняются следующие
неравенства:
8.1. sin х соз х < 1/2. 8.2. sin x + cos x < V2 •
8.3. tg х + ctg x > 2. 8.4. tg*>sin*.
х
8.6.. sin 2x < 2 sin *. 8.6. Vc°s x < У? c°s -g-»
142 ГЛ Б. ТРИГОНОМЕТРИЯ
в.7. Доказать, что если а, В е [©; я], то
rin-^->,lng+.,inp.
Доказать, что при любом действительном х справедливы
соотношения:
8.8*. | a cos х + Ь sin х |< */а*-\- Ьг.
«;9** а + с- Уа*+&2 + с'-2ас"
< а sin2 * + Ь sin ж cos х •+■ с cos3 ж <|
^ 2
Часто при доказательстве справедливости
тригонометрических неравенств используются неравенства, устанавливающие
связь между средним геометрическим и средним арифметическим
двух нлн нескольких положительных чисел.
Пример 8.2. Доказать, что если а + В + у = я в а, В,
у > 0, то
1 1 I
— + —Ц- + —>6. (»>
sm T sin у sin X
Решение. Так как sin-д-, sin -—, sinX неотрицательны,
то, используя неравенство, связывающее сведшее арифметическое
трех чисел я лх среднее геометрическое, имеем
+ г- + > „, „ -• (**)
- о В iu 3/ а В . v
*,ПТ 8Ш2 3inT VSlnTSin 2 Sln 2
Преобразуем теперь подкоренное выражение:
„•„ а , Р , Y 1.аГ В — -у Р + V1
„и т sin f sin X = _ sin _ [cos X_X _ cos JLiXj.
Так как а + В + у = я, то
/я «\ а В — -у . ,
и, следовательно,
Наибольшее значение функция, стоящей а правой части
неравенства f (у) =■ ■к-У^1™*)^™ 3in "§")* ш а?ожжУ![ЯЛ t°l
„„„ Р + V /я к\ , а В — v
§ 8. ДОКАЗАТЕЛЬСТВО' НЕРАВЕНСТВ' 143
1] равно 1/4. Следовательно,
а В v I
sinT3in2Sin2 <T-
Из последнего неравенства получаем неравенство
3
з/ а В v
sinTSln 2 Sin 2
(*♦•)
Из неравенств (**) н (***) следует справедливость исходного
неравенства.
8.10*. Доказать, что если а + в + у = яио, в, v > 0, то
(I — cos а) (I — соз в) (I — cos у) < 1/8.
8.11*. Доказать, что если а + в + у = я н а, в, ^е(0; я/2),
то
cos а cos p cos v
8.12*. Доказать, что если а + В + у = л и а, в, у <= (0; я/2)г
то
tg^ се + tg2 Э + tga V > 9.
8.13. Доказать, что если а + в -}- у = я, то
соз
« Р V ^ 3 /г
8.14**, Доказать, что если а + В + у = л, то
,,ni|.+ Sln.i.+ sl„iX>|..
8.15. Доказать, что если а+р + у=я, то
со» а + cos Э + cos у < 3/2.
В примере 8.2 требовалось найтн наибольшее значение
функции — sin -=- ( I —sin ^ )• После замены переменной
искомое значение совпадало с наибольшим значением функции
Ну) =■*■!/ (I — и) на промежутке [0; 1]. Аналогичный прием
часто используется в тех случаях, когда требуется найтн
множества значений некоторых сложных тригонометрических
выражений.
8.16, Доказать, что
—4<cos2x-f- 3slnx<2-g-.
144 гл в. тригонометрия
8.17. Доказать, что
cos3 х + cos8 x <; 1/4.
8.18. Доказать, что если \р\ < 2, то
• з . i -^ — Р2 ~ 4q
sm2 x -f- p sin x -\- q > £-j —.
8.19. Доказать, что sin* x cos4 * ^ 1/4.
Доказательство неравенств, связывающих
тригонометрические функции и некоторые многочлены, рассмотренные на
интервалах изменения аргументов, проводится с использованием
комбинации рассмотренных выше приемов. При этом часто
используется неравенство
sin х < х < tg х, (1)
справедливое для всех х е [0; я/2].
Пример 8.3. Доказать, что на промежутке (0; я) имеет
место неравенство
х3
X J- < Sin X.
Решение. Представим функцию sin x в виде
sin* = 2tg|-cos2-|- = 2tg^-(l-sIn2^-).
Используя неравенство (1), имеем
Подставляя полученные оценки в правую часть исходного нера«
венства, убеждаемся в его справедливости.
8.20*. Доказать, что на промежутке (0; я) справедливо
неравенство
C08*<l--r+-jg-.
8.21*. Доказать, что на промежутке (0; я/2) справедливо
неравенство
Xs
X - -j- < tg X.
8.22*. Доказать, что
1 — cos х ■■
2 "
ГЛАВА 6
КОМПЛЕКСНЫЕ ЧИСЛА
Запись числа z в виде а + Ы, где а в 6 — действительные числа,
называется алгебраической формой комплексного числа. Число а
называется действительной частью комплексного числа и обозначается Re г,
число 6 — мнимой частью комплексного числа в обозначается Imz.
Символ I называется мнимой единицей.
Два комплексных числа г.—ai + bii, zi**a> + b,l равны, если а,—а, и
Комплексное число —о — 6/ называется противоположны* комплекс
вому числу а ■¥ Ы.
Правила деЛстний с комплексными числами. Пусть
г.—>ai+b,i и zi=aj + 64j —дна комплексных числа. Сумма zi + z3, разность
Я—zj. произведение 2\-Zi н частное — <г: т* 0) комплексных чисел zi и »i
Zl
вычисляются по формулам
г| + г,—(ai + a») + (fti + *») Л
г,—zj»»(ai—а,) + (*1—6:)Л (О
21-zj—'(aiaj— ЬМ + <ai&i + a26i) J.
zi д oibi + Qa&i , Qjbi —gift; .
Сложение н умножение комплексных чисел коммутативно в ассоина*
тивно, умножение дистрибутивно относительно сложения.
Комплексное число а — Ы называется комплексно сопряженным с
числом г — а + Ы и обозначается г Свойство комплекспо сопряженных
чисел: z-2—a' + 6'.
Пусть г - а + 6( — отличное от нуля (т. е. о' + Ь< ф 0) комплексное
число. Модулем комплексного числа (обозначается I z | или г) называется
величина у а? + ft' Аргументом комплексного числа z называется угол Ф.
определяемый нз условий
Ь а
sin ф -■— , cos ф= .
Va' + fr1 Va' + ft" «-
.{обозначается Arg z влн <p). Главным зна- | >ф
чением аргумента комплексного чнсла z (обо- I N.
вначается arg z) называется значенве Ф, I
принадлежащее промежутку (—я; я]. —к
Запись комплексного чнсла z - а + Ы
В виде
z=»r (соз ф+i aln ф). Рис. 6Л
где ф—аргумент иаэываетсн тригонометрической формой комплексного чнсла.
Геометрически модуль комплексного чнсла может быть изображен
как отрезок (раднус-вектор) длины г, нмеющпЯ своими концами точки
(0; 0) я (а; Ь); аргумент комплексного чнсла — как угол, который обра-
аует радиус-вектор с положительным направлением оси Ох (рис. 6.1).
Два комплексных чнсла, вапнсанные в тригонометрической форме,
gaent* тогда н только тогдв, когда равны нх модули, а аргументы
глнчаются на 2пД (fteZ),
146 ГЛ. 8. КОМПЛЕКСНЫЕ ЧИСЛА'
Провэведеннсы п частным двух отличных от нуля комплексных чисел
г, =r, (cos ф, + i sin ф|) ii Zi=r; (cos (fi + t aln ф,), записанных в тригономег*
рпческой форме, являются числа
zi • zj=» Л ■ п [соа (ф| + ф5) + / sin (ф, + фа)],
—=-9-[cos (ф, — ф,) + *51п (ф,—ф,)].
п-д степень комплексного числа г=г(соз Ф + /5ln ф) вычисляется по
формуле Муавра
Z ="Г (СОЗ Яф + / Sin Пф). (2)
Корнем п-й степени нз комплексного числа z называется комплекс
вое число го, удовлетворяющее уравнению
го" = 2.
л
Все решения этого ураввевия обозначаются VF и для числа г, запн»
сввного в трнгонометрнческоЯ форме г=г(соз ф +/ sin ф). вычисляются по
формуле
"/— П1-( Ф + 2лй . . . Ф + 2я*\ ...
Уг—V' Icos-S-^ + /3in-2^— 1 (з)
где ft=0, 1, 2,.... я—1.
§ 1. Действия с комплексными числами
Действия с комплексными числами проводятся по форму»
Лам (1). При вычислении произведения и частного комплексных)
чисел удобно использовать представления комплексных чисел в
тригонометрической форме.
Пример 1.1. Представить в тригонометрической форме
комплексное число г = —3 +1.
Решение. По определению модуля комплексного числа
имеем
|z| = V(-3)2+l =-\А0.
Обозначая аргумент комплексного числа через <р, получаем
I 3
sin ф = —=r, cos ф ==» ==-,
откуда следует, что угол <р принадлежвт второй четверти и
равен агссоз (—з/л/Ш)* Следовательно, комплексное число г *=•)
•=• —3 + I имеет тригонометрическую форму:
. = VIO [cos(агссоз (- -»-.)) + | sin (агссоз (--^))].
Предствить в тригонометрической форме комплексные числа!
1.1. 1. 1.2. -3. 1.3. I.
1.4. I + f. 1.6. -1 + /. 1.6. 1 + 1л/3~.
§ I. ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
147
1.7. 3 - 41.
ts. —з — -и.
1.9. - cos •%- +1 sin -^-. 1.10. sin о - / cos a.
О О
UI- (тЬ-)
100
Вычисление корней fe-й степени из комплексного числа
обычно производятся с помощью представления комплексных чисел в
тригонометрической форме.
Пример 1.2. Вычислить yi.
Решение. Запишем комплексное число f = 0 + Ы в
тригонометрической форме. Так как \i\ = 1, argf = я/2, то число I
имеет тригонометрическую форму
, я . . , я
I = cos -5- + i sin -5-.
to
^
Отсюда согласно (3) получаем
Ink
-4Т_,. Ф = £+ 3
\ "Г
\ dir^ff If а
Рис. 6.2
при k =0, ft = l, k = 2, и, следовательно, искомые корни
имеют внд
я , , , я л/3
COsT + ,sinT = —
■'4-
5я , , , 5я
cos -т- + i sin —r-
6 6
Зя , , . Зя
cos -j- +1 sin -jj- =
V3~
■"t-
Геометрические образы полученных корней представляют собой
точки, лежащие на единичной окружности (так как г= 1),
радиусы-векторы которых составляют углы я/6, бл/6 н Зя/2 с
положительным направлением осп Ох (рнс. 6.2).
Вычислить, используя тригонометрическую форму
комплексных чисел:
1.12. л/21.
4
1.15. У11!
7
1.18. V3 + 4/.
1.13. У-87.
4
U6. V2-2/V3".
s _
1.19. Vl«
1.14. УЗ-4/.
4
1.17. V'".
148 ГЛ. в. КОМПЛЕКСНЫЕ ЧИСЛА
§ 2. Геометрическое изображение множества
комплексных чисел
Для геометрического изображения комплексных чисел в си>
стеме координат Оху, удовлетворяющих некоторым соотиоше-
нням, обычно используется алгебраическая форма комплексного
числа.
Пример 2.1. Найтн множество точек координатной пло
скости Оху, изображающих комплексные числа г, для которых
\z + l-~2| sg2.
Решение. Запишем комплексное число г в алгебраическое
форме г = х + 1у. Тогда
г + «-2 = (*-2) + /((,+ 1).
По определению модуля комплексного числа
|z + *-2|~V(*-2)8 + ((/+l)s,
вследствие чего равенство \z-\-i — 2| ^ 2 принимает вид
VC* — 2)а Н- (у Н- 1)я < 2 •<=!- (х - 2)г + (ff + I)* < 2».
Множество точек координатной плоскости Оху, удовлетворяю'
щих последнему неравенству, представляет собой множество всех
точек, лежащих внутри окружности н на окружности радиуса 2
с центром в точке (2; —1).
Пример 2.2. Найти множество точек координатной плоско*
стн Оху, для которых действительная часть комплексного числа
(I +1)гг положительна.
Решение. Представим число г в алгебраической форме)
г = х + 1у. Тогда
(1 + 0 2* = (1 + 0 \х* -уг + 1 (2*0)1 =
= (jji _ 2ху -уг)+1 (х» + 2ху - у%
По условию задачи действительная часть комплексного числа
(1 +i)z* положительна:
х2 — 2ху — уа>0. (*)
Предполагая, что у Ф 0, и разделив обе части неравенства на у\
получаем неравенство
Решая это квадратное неравенство, получаем
х/у > 1 + л/2. х/у<1- V2". (f*l
§ 2. ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ЧИСЕЛ
149
При у > 0 неравенства (**) можно записать в виде
У<
1 + V2
~х, у<
1 —V2
г=- лг.
Множество точек плоскости Оху, удовлетворяющих этим
условиям, отмечено штриховкой иа рис. 6.3.
При у < 0 неравенства (**) записываются в виде
У>
I
1+V2
— х, у>
1
1-V2"
х,
и множество точек координатной плоскости Оху, удовлетворяю»
wax этим неравенствам, отмечено штриховкой иа рис 6.4.
У=-*-пга
1-й 1
^^0
а
я
Рис. 0.3
Рис. 6.4
Прн у = 0 нельзя делить обе части неравенства (#) на у*,
ио при у «= 0 само неравенство (*) превращается в неравенство
х1 > 0, решением которого является / „.
любое действительное число х, от- " " "
личное от нуля, т. е. решением
неравенства (*) является любая точка
оси Ох, аа исключением нуля.
Объединяя все три случая,
окончательно получаем: искомым
множеством являются углы, содержащие
ось Ох, без своих границ, стороны
1
которых — прямые у = =- х н у =
Рис. 8.5
1
1=гХ
, .. я — i=r » (рнс. 6.5).
1+V2 1-V2
Найти множество точек координатной плоскости Оху,
изображающих комплексные числа z<= x + iy, для которых:
2.1. |г| —1. 2Л. z=|z|.
2.3. arg z = я/3, 2.4. 1 < | z | < 4.
2.5. |2z-l|>2. 2.6. ||z|-H|<10.
!50
ГЛ. 8. КОМПЛЕКСНЫЕ ЧИСЛА
2.7. |z + l|-=|z-H 2.8. \г+1\*~\я + 2\.
Й.9. \г+1\>\г\. 2.10. l<|z-H|<4.
2.11. (l — i)z = (\ +l)z.
2.12. На координатной плоскости Opq изобразить множество
точек (р, q) таких, что корни уравнения
x* + px + q = 0
(возможно, комплексные) по модулю не превосходят единицы.
2.13. Указать все точки комплексной плоскости, такие, что:
1) га, 2) г + а — действительные числа (сс = а + Ь/
—заданное комплексное число).
2.14. Найти множество точек координатной плоскости Оху,
удовлетворяющих неравенству
2.15. Найти на плоскости Оху множество всех точек, коорди»
наты которых удовлетворнют следующему условию: чнсло г2 -ft
Н- z + 1 — действительное положительное число.
2.16. Изобразить на плоскости все комплексные числа г, для
которых (1 +()г действительно.
2.17. Точки Zi, гг, гв — вершины треугольника. Какое ком»
плексное число соответствует центру тяжести этого треуголь*
инка?
2.18. Точки Zi, гг, гг — три вершины параллелограмма. Найти
четвертую вершину.
2.19*. Доказать, что три различные точки Z\, za, Ze лежат
на одной прямой тогда и только тогда, когда— '—деистви«
z3 — Z\
тельиое число.
2.20. При каких Zi и гг справедливо равенство
|z, + z2| = |z, — г2| ?
2.21. Доказать, что четырехугольник, сумма квадратов длин
сторон которого равна сумме квадратов длин его диагоналей,—»
параллелограмм.
§ 3. Решение уравнений в множестве
комплексных чисел
Решение уравнений в множестве комплексных чисел сводится
к решению систем уравнений в множестве действительных чисел,
полученных в результате сравнения действительных и мнимых
частей выражений, стоящих в левой в правой частях исходного
уравнения.
§ 3. РЕШЕНИЕ УРАВНЕНИИ 151
Пример 3.1. Решить в комплексных числах уравнение
2z=-\z\ + 2i.
Решение. Запишем комплексное число г в алгебраической
форме: z = x + ly, где х, «/ — действительные числа. Тогда
\z\ = <^x*-{- у1 и данное уравнение принимает вид
2х + 21 у <=. V*2 + Уг + 2'.
Из определения равенства двух комплексных чисел получаем
систему уравиеннй для нахождения х н у.
2х — л/хг + уг^0.
2у — 2~0.
Из второго уравнения находим у = 1. Подставляя у = 1 в пер-
вое уравнение системы, получаем уравнение 2х = V*2 + 1 ■
решение которого* = —j=r. Итак, решением данного уравнения явля-
ется комплексное число 2 = —=- + I.
V3
Ответ, z = —■=- + I.
V3
Пример 3.2. Для каждого действительного числа а > О
найти все комплексные числа г, удовлетворяющие равенству
z | z | + аг + i = 0.
Решение. Запишем комплексное число z в
алгебраической форме: z = x + ig. Тогда | z | = У*г + уй и уравнение
примет вид
(* + iy) л/хг+у* + а(х+1у) + 1<=*0<*- " ,
**.{хл/х* + уг + ах) + 1(ул/х* + у1 + ау+1) = 0-± 0-1.
Из определения равенства двух комплексных чисел следует, что
последнее уравнение эквивалентно системе двух уравнений
ул/х* + у* + ау+1=0,
решения которой отыскиваются уже в множестве действнтель»
ных чисел.
Нетрудно заметить, что множество решений первого
уравнения системы (*) может быть найдено как объединение множеств
решений двух уравнений:
*=0, V** + 0J+ »=•<>.
162
ГЛ. 8. КОМПЛЕКСНЫЕ ЧИСЛА
Второе из этих уравнений решений ие имеет в силу условия
а > 0. Подставляя % = 0 во второе уравнение системы (*),
получаем уравнение для действительного числа у
у\у\ + ау+\=0,
множество решений которого получается как объединение
множеств решений двух систем:
If > 0, у < 0,
У* + ау+1=0; -у2+ау + 1*~0.
Нетрудно* убедиться в том, что с учетом условия а > 0 первая
система решенкй не имеет, а вторая имеет едииствениое решениез
а — Vo2 -f- 4
J" = д • Таким образом, решением данного уравне*
ння является чисто мнимое число
а — J а1 + 4
2=°' ^ •
Ответ: *-,£^£Е±1.
Решить уравнения:
3.1. (2 + 0 z2 - (5 - 0 г + 2 - 11 = 0.
3.2. г2 + г = 0. 3.3. | z | - iz = 1 - 2/. 3.4. г2 = (г)3.
3.5. (х + у)2 + Ь+ ix = 5 (х + у) +1 (у + !)(*, (/-действи-
тельные числа).
3.6. При каких действительных значениях х я у справедливо
равенство
*-2 + (y-3)iml_3f?
1 + i
3.7. Доказать, что уравнение z'+te— 1 = 0 не имеет
действительных решений.
3.8. Вычислить zu + 1/z", если z есть корень уравнения
г+ l/z=l.
3.10. Решить в комплексных числах системы:
г3 — г1 + г — 1 = 0.
3.10. Решить в комплексных числах системы:
a) zsai7=l, б) zl3ai,s=l,
z» — фз _, о- г5ш7 = 1э
г*+ш2 = — 2.
3.11. Какому условию должно удовлетворять комплексное
число о -f- W для того, чтобы его можно было представить в.
5 4. РЬШЕНИБ НЕКОТОРЫХ ЗАДАЧ
153
виде
где х — действительное число?
3.12. Среди комплексных чисел г найтн все те, для которых*
logu (13 + | г1 - 411) + log199 (13 + |га + 4/[)а = °-
3.13. Для каждого действительного числа а 5» 1 иайти все
комплексные числа г, удовлетворяющие уравнению
я + а\г+1\ + 1<=*0.
3.14*. При каких действительных значениях параметра а
хотя бы одно комплексное число г = х + iy, удовлетворяющее
равенству
| z + ^2 | «= о1 - За + 2,
удовлетворяет одновременно и неравенству
| z + i У2" | < а1 ?
3.15. При каких действительных значениях параметра а хотя
бы одно комплексное число г = х + iy, удовлетворяющее
равенству
| z — ai | = а + 4,
удовлетворяет одновременно и неравенству
|z-2|< 1?
3.16. Найтн минимальное по модулю комплексное число г,
удовлетворяющее условию
I z - 2 + 2/1 =- 1.
§ 4. Применение комплексных чисел
для решения некоторых задач
Использование тригонометрической формы комплексного
числа и представление этого числа точкой комплексной
плоскости допускает простое решение некоторых систем
тригонометрических уравнений.
Пример 4.1, Решить систему
V2~
sin х + sin у = -у-,
V2*
соз л; + cos у =* ——.
164
ГЛ. в. КОМПЛЕКСНЫЕ ЧИСЛА
Решение. Умножим первое уравнение системы на i и
сложим со вторым. Получаем уравнение
cos х Н- I sin х + cos у + I sin у •
V2" , . л/2
М-
г, cos у + I sin у = т. ~- + I -^- =
Обозначим cos х + / sin x
= я. Тогда получаем уравнение для комплексных чисел
z Н- w = и,
V2 . , V2~.
.где |z| яо |ш| = |«| =з 1, т.е. все три точки лежат на окруж»
ности единичного радиуса и, следовательно, четырехугольник о
вершинами г, и, w, О—ромб с диагональю Ои, длина которой
равна единице (см. рис. 6.6). Таким
образом, треугольники Оги н Ouw —
равносторонние и углы uOw и гОи
равны -яг'. Так как Arg и = — +
+ 2nk, то из рис. 6.6 видно, что
если х = Arg z и у = Arg ш, то
* 4" + 1" + 2л&, 0 = Т-Т +
7
-}- 2я«, т. е. х = ---- я Н- 2~.ft, # ■=-■
12
Рис. 6.6
.--J5-+2W».
Ответ. (-^-я + 2яА;. --jj + 2ял.); (--*-• +2яя,
Решить системы уравнений:
4,1, sin * + sin </ = sin a,
cos - + cos </ = cos а.
Уз-
1
4.3, sin х + sin у ■
coa х + соз- у =» --
4.2. 2 sin * cos у = sin а,
2 cos * cos ^ = cos а.
4*4. sin x — sin у ■=» sin a,
сое ж — cos i/ => cos a.
Для лары любых комплексных чисел 2 = a -f 6i и ш = с -f- di)
справедлива формула
|ш-г|=-|->l*lzl> (1)
которая имеет следующий вид:
(a* + 6s) (с» + d*) •=■ (ас - 6rf)J + (ad + &еД
(2)
S 4. РЕШЕНИЕ НЕКОТОРЫХ ЗАДАЧ 155
Используя формулу (1), можно находить целочисленные
решения уравнении вида
х*+у2 — п,
где п—натуральное число.
Пример 4.2. Найти хотя бы одно целочисленное решение
уравнения
*2 + у2 = 21126. (*)
Решение. Разложим 21 125 на простые множители. Имеем
21 125 = 5»-13я.
Числа 5 и 13 являются суммой двух полных квадратов целых
чисел 5 = 4+1, 13 = 9 + 4. Используя формулу (1), можно
записать, например,
| (2 + 0 (2 + 0 (2 + /) • (3 Л- 20 (3 + 2i) Is = 21 125.
Перемножая комплексные числа, стоящие под знаком
модуля, получаем
| 79/ — 122|2 = 21 125.
Таким образом, одним из решений исходного уравнения
являются числа х = 122, у = 79.
Очевидно, изменяя комплексные числа, квадраты модулей
которых равны 5 н 13, можно получать другие целочисленные
решения уравнения (*).
Найти хотя бы одно решение в натуральных числах
следующих уравнений:
4.5. *a+i/a=.32 045.
4.6. х* + у3 = 84500.
4.7. На окружности радиуса 5 л/3 найти хотя бы одну точку;
с целыми положительными координатами.
Тригонометрическая форма записи комплексного числа и
связанная с ней формула Муавра в некоторых случаях
используются для вывода различных тригонометрических формул.
Пример 4.3. Выразить sin 4x и cos Ax в виде некоторой
функции от sin* и cos*.
Решение. Воспользовавшись формулой Муавра, запишем
(cos х + t sin x)* = cos Ax +1 sin 4x (*)
Расписывая левую часть уравнения (*) по формуле бинома Нью:
тона, имеем
(cos х +1 sin х)* =»
= cos Ax + ii cos3 х sin x — 6 cos2 x sin2 x — 41 cos x sin3 л; + sin4x.
156 ГЛ. в. КОМПЛЕКСНЫЕ ЧИСЛА
Пользуясь условием равенства двух комплексных' чисел,
получаем
cos 4х = cos4 х — 6 cos2 х sin2 х + sin4 x,
sin Ax ■= 4 cos3 * sin * — 4 cos * sin3 x.
Ответ, cos 4x =■ cos4 x — 6cos2* sin2* + sin4x, sin 4x =>
= 4 cos3 * sin x — 4 cos * sin3 x.
4.8. Представить sln3* в виде функции от sin» и cos x.
4.9*. Вычислить суммы
Si = cos ф Н- cos 2ф Н- ... Н- cos шр,
S2 = sin ф + sin 2ф Н- ... Н- sin юр, л е N.
4.10. Доказать, что cos па может быть представлен как
многочлен с целыми коэффициентами от cos a.
4.11*. Доказать, что cos 31°—число иррациональное.
' 4.12. Вычислить сумму
sin х + a sin 2х + ... + ап~1 sin nx.
41.3*. Вычислить сумму
С\ sin х + С2п sin 2х + ... + С* sin/w,
где Сп — число сочетании из л по L
4.14. Выразить tg5ct через tga.
Г Л А В А 7
ПОСЛЕДОВАТЕЛЬНОСТИ
§ 1. Определение и свойства последовательности
Множество чисел, занумерованных либо конечным отрезкой
натурального ряда, либо всеми натурвльныин чнслвин, называют числовой
последовательностью.
В первом случае последовательность называется конечной, во
втором — бесконечной.
Элементы этого числового множества начинаются членами последо*
вательности и обычно обозначаются так: первый член аи второй аг, ,, ■,
в-й—ап н т. д. Вся числовая последовательность обозначается
а1- Н- аз "л- - нли (ап) *»•
Понятие последовательности может быть введено я с помощью
понятия функции: бесконечной числовой последовательностью (*„)
называется числовая функция f(n), определенная на иножестне всех
натуральных чисел. Формула, позволяющая вычислить любой член
последовательности по его номеру п, называется формулой общего члена
последовательности.
Последовательность (*п) называется ограниченной, если существуют
такие даа числа m и М, что для всех п= N выполняется двойное")
неравенство
т<*п<М. (I)
Последовательность (*„) называется ограниченной сверху (снизу),
если сущестнует такое число Л1, что для всех пеЫ выполняется
неравенство
Хп<М (хп>М). (2)
Последовательность (*„) называется монотонно
возрастающей, еелн для любого натурального п выполнено неравенство
*Л+1 > *В> (3)
и монотонно убывающей, если для любого натурального п
выполнено неравенство
*л+1 < *п- (4)
Последовательность \хп) называется неубывающей \невоз-
растающей), если неравенство (3) (соответственно (4))]
нестрогое.
*) Числовые последовательности будеи также обозначать (Уя)<
(2„). птП.
**) Слово «двойное» дла краткости далее опускаем.
158
ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
Возрастающие, убывающие, невозрастающие, неубывающие
последовательности называются монотонными
последовательностями. Можно обобщить определение монотонности и на те
последовательности, которые обладают этим свойством, лишь
начиная с некоторого члена. В этом случае соответствующее
неравенство должно выполняться для всех п > По, где по — номер
члена, начинай с которого последовательность становится
монотонной.
Пример 1.1. Доказать, что последовательность,
задаваемая формулой общего члена
Зп — 1
возрастающая.
Решение. Рассмотрим разность
_ 3(/t + Q-1 _ Зп-1
Xn+i *»= 5(д+1) + 2 5п + 2
и проверим выполнение неравенства *„-ц — х„ > 0 для всех
л е N:
3 (д + 1) - 1 Зп - 1 11 п
5(/i+l) + 2 5п + 2 >" ИЛИ (5я + 7)(5л + 2)
Так как последнее неравенство справедливо при всех л е N, то
согласно (3) данная последовательность — возрастающая.
1.1. Доказать, что последовательность
6 — п
Уп= Бв-1
является убывающей.
1.2. Является ли монотонной последовательность
2/1-3 ,
" л
1.3*. Является ли монотонной последовательность
2* ,
1.4. Найтн, при каких соотношениях между а, Ь, с, d
последовательность
an + Ь
Уп ~ cn + d
будет возрастающей.
Пример 1.2. Найти наибольший член последовательности
у„=ш — п? + Ъъ — 6.
§ !. ОПРЕДЕЛЕНИЕ И СВОЙСТВА
153
Решение. Рассмотрим функцию
у (х) = — х* + Ьх — 6.
Наибольшее значение она принимает в точке х = 2,5, причем
на промежутке (—оо; 2,5) функция у(х) возрастает, а на проме-
хсутке (2,5; оо) — убывает. Следовательно, возвращаясь к
последовательности, можно записать
УI < Уг И Уз > У*.
Таким образом, наибольшим будет либо уг, либо </з, но уг =*
= (/з = 0.
Ответ. Наибольшими являются второй и третий члены
последовательности.
Найти наибольшие и наименьшие члены последовательности:
1.5. (,„ = ла-1.
1.6. уп = 6л — л2 — 5.
1.7*. хп = 2/г + Щ--
и3
1.8. Последовательность (х„) задана формулой общего
2п-3 п
члена *п = • При каких натуральных значениях л
выполняются условия:
а) |*я-2|<0,1; б) |*„-2|<0,01?
1.9*. Сколько членов последовательности
Уп = I л2 — 5л + 61
удовлетворяет неравенству 2 < </„ < 6?
1.10*. Начиная с какого номера члены последовательности
Уп = л2 — 5л + 6
удовлетворяют неравенству *„+« > *„?
1.11*. Начиная с какого номера л последовательность,
задаваемая формулой общего члена у„ = nq", будет монотонна,
если 0 < q < 1 ?
Еслн последовательность задана формулой общего члена
х„ = f(n), то ограниченность последовательности сверху и снизу
может быть выведена из ограниченности функции /(*•) для хе
.е[1; оо).
Пример 1.3. Будет лн ограничена последовательность
Зл + 8
*» 5Г^
Решение. Рассмотрим функцию
160 ГЛ 7. ПОСЛЕДОВАТЕЛЬНОСТИ
которая при х = л определяет члены дайной последовательности.
Найдем множество значение функции на промежутке [1; сю).
Записывая функцию }(х) в виде
/(*)—3/2 + 4/*, <*)
убеждаемся, что при х ^ 1 эта функция монотонно убывает.
Следовательно, наибольшее значение функция имеет при х = 1,
н оно равно 11/2. Из записи (*) видно, что при всех *е[1; со)
f(*)>3/2.
Следовательно, f(n) s J3/2; 11/2].
Ответ. -Последовательность ограничена: все ее члены
заключены в промежутке (3/2; 11/2].
Выяснить, будут ли следующие последовательности
ограничены:
1.12. хпг=2{~1)П.'
U8-*»-T+$- »-14*.*„ = №»_21я + 3-
U5*-^-(Trw~Tr+-2jr)(ft+2)-
§ 2. Предел последовательности
Говорят, что число а является пределом бесконечной
числовой последовательности (ха), и пишут llm *„ = а, если для
любого 8 > 0 существует такой номер ло(в), что при всех п >]
>По(е) выполняется неравенство \хп — а\ < е. Если
последовательность (хп) имеет предел, то она называется сходящейся.
Необходимое условие сходимости числовой
последовательности: для того чтобы последовательность сходилась, необходимо,
Чтобы она была ограниченной.
Пример 2.1. Доказать, что
llm -£±1-1.
Решение. Для того чтобы доказать, что предел последо-
п+1
вательностн хп = —!— равен единице, достаточно указать
способ построения для любого е > 0 числа ло(е), входящего в
определение предела. Зададим е > 0 и составим неравенство
п+ 1
1 <•*, (•)
§ 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
161
которое эквивалентно неравенству I/ft < в. Следовательно, если
в качестве числа по(е) выбрать число [1/е]+1*), то для всех
п>яо(е) будет выполняться неравенство (*). Таким образом,
доказано утверждение о том, что единица является пределом
ft+1
последовательности хп=* •
п
Доказать, что:
f Зл — 2 1
2.1. lim —5-— = 1,6. 2.2. lim ,., , , =0.
5п-3 Б .4 ,. 6»'
ft + 1 я*
2.5. lim „. ■т=0> 2>e- Hm ■ i , = 1.
П-»оо
Для решения некоторых задач на доказательство сходимости
последовательности удобно пользоваться следующей
геометрической интерпретацией понятия предела последовательности.
Число а является пределом последовательности {хп), если
для любого положительного числа в существует такой номер
л = ло(е), что все члены последовательности, начиная cxrh+l>
принадлежат е-окрестности числа а, т. е. промежутку (а — в}
в+ 8).
Используя приведенную выше геометрическую интерпрета»
цию, убедиться в справедливости следующих утверждений:
2.7*. Если последовательность сходятся к некоторому числу,
то она ограничена. (Необходимое условие сходимости.)
2.8*. Известно, что lim*n = a, a < q. Доказать, что почти
П-»оо
все члены последовательности (*„) (за исключением, быть может,
конечного числа членов) меньше q.
2.9*. Известно, что lim an = p, lim bn = q, рФя. Сущест-
вует ли предел последовательности alt bi, аг, 6а, .... аП, Ьп, ...?
2.10. Используя результат предыдущей задачи, доказать, что
последовательность
*л-1+(-1)л
предела не имеет.
2.11*. Выяснить, имеет ли предел последовательность
x„ = sinn-r-.
*> Символом [г] обозначается целая часть г.
в А, Г. Цьшкнн, AL И, Пинскнй
162 ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
2.12*. Выяснеть, имеет ли предел последовательность
1 . я
2.13. Выяснить, имеют ли предел последовательности:
t п/» / / lirt\ я
a)^=l + i_ii_; 0) х„ = (^ 1 -Ь ~Г~) sin«-J-.
§ 3. Вычисление пределов последовательностей
Свойству сходящихся последовательностей.
Если две последовательности (х„) и (//„) сходятся к Hm xn а
В-»оо
Mm у„, то:
1) последовательность (хп ±(/п) сходится и
lim [xn rfc у а) = lira *а ± lim UtA Ш
2) ооследоаательвость (х„у„) сходится я
Пт хпУп = ( Пт хп) (lira упУ, (2)
3) последовательность ( —^J (если дополнительно ^#0н
lim у„ Ф 0) сходится и
Л-»оо
lim *„
Пт Js.e »±S_. (3)
n-»~ #n Um ffn
Обычно при вычисления пределов иепосредстпениовгу
применению формул (1)—(3) предшествуют некоторые тождественные
преобразования. При вычислении пределов вяла
хп
П-><М W'»
где хп и уп — неограниченно возрастающие последовательности,
таким преобразованием является деление числителя н
знаменателя дроби на одно и то же выражение.
Пример 3.1. Вычислить предел
5п+ 1
lim 7 — 9n "
Решение. Так как числитель и знаменатель представляют
собой неограниченные последовательности, то непосредственно
воспользоваться формулой {3j[ нельзя» Разделам числитель и
i 3. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ 163
знаменатель на л, К полученной дроби уже можно применить
формулу (3)i
_,.. Um(5+l/«)
Л» 7/»-9 Нт(7/л-&Г
я-»оо
Применяя далее формулу (1), получаем
lim (5+1/n) lim 5+ lim (1/л)
л-^-oo Л->-эо n->-Q0
Urn (7/n—9) lim (7/ft) — lira 9 *
Учитывая, что предел постоянной равен этой постоянной, а
lim —=~0.
Я-»оо '*
окончательно получим
5« + 1 5
Ответ. —5/9.
С помощью деления числителя и знаменателя дроби на
старшую степень п вычислить следующие пределы:
Зл2 - 7 л + 1 Уя8 + 2л — 1
зл- ^г-Бп-вп»- 3-2- J!™» «Т2 •
4 3
о, „ (я+!)'-<я-1)« „, ,. У^+~2 - Уд» +1 '
3.3. lira /„,,,<■_,„_ Uv 3.4. lim 5
\Лг + 2+У/(Ч-1
Вычисление пределов выражений, содержащих
показательные функции с натуральным аргументом, может быть ..основано
на следующем равенстве:
Ilm ?rt = 0, если \q\< 1. (4)
п-»оо
Пример 3.2. Вычислить предел ijm
п-^со
2" + З'1
Р е ш е и [I е. Разделим числитель и знаменатель дроби на
3"+«. Применяя формулу (4), получаем
rt-»oo
(2 \n+l Z' 2 \я + 1
т) +' Лт~Ы +1
I / 2 у 1 1 / 2 \п 1 1 1 "
„_ _^^ — 0+1 _._о
»т 1 • о ч„ i ; у о ч„ г"^=-; г- = *
Ответ. 3,
6*
164
ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
Вычислить пределы:
2" + 3rt
З.б, Ит пи _ on •
3.6*. Iim
rt-*o> 2"+1—5-3rt+l+6 '
При вычислении пределов иногда удобно пользоваться
следующим свойством последовательностей; если члены двух
последовательностей (а„) н (Ь„) связаны соотношением
I ап |< | Ьа |,
то из равенства нулю предела последовательности (Ьп] следует
равенство нулю предела последовательности (а„).
Пример 3.3. Вычислить предел
п1тЛ^тт)П'
Решение. Убедимся сначала в том, что для всех п е N
справедливо неравенство
<-^-.
In. + 1 2
Разделив числитель и знаменатель дроби, стоящей в левой части
неравенства, на л, получим очевидное неравенство
2 + -^ 2
п
Используя далее свойство степеней, заключаем, что для всех
л е N справедливо неравенство
U+1/л ) <\Т) *
Так как, согласно (4), llm (~£~J =0, то из приведенного
выше свойства последовательностей следует
Ответ. 0.
Вычислить пределы:
(9n+J_y
В-»оо
§ 3. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ
165
Г п1 — 1 у»
S'8\!lmooU2*H-l)(/i + 2)J *
_ -^ . л sin nt
Л->оо П ^ 1
При вычислении пределов, содержащих иррациональности,
часто используют перевод иррациональности из знаменателя в
числитель илн наоборот.
Пример 3.4. Вычислить предел
Ilm (У ft3 + 2ft — и).
п->со
Решение. Умножим и разделим выражение, стоящее под
знаком предела, на сопряженное выражение. Тогда имеем
цт (Ув3 + 2д - п) (Уд' + 2ft + ft)
"-><» ^п1 + 2п 4- ft
n2 + 2п - n2 2ft
■=" 4m —/ „ . „ -—= Urn /»;„=-; •
n-*» Уп2 +2я 4-ft n->oo Уп24-2п + ft
Разделив числитель и знаменатель на л, получим
2« 2 ,
Um /..„=-: =* 4m ' /. . „. - . . =1»
л->«> yft24-2ft +п я-*» У1 + 2/ft + I
Ответ. 1.
Вычислить пределы:
ЗЛО. iim [(УлТ2—Уп"). 3.11. lim (У ft2 — б/г + 6 - я).
Я-*оо П-*ео
8.12. lira ft(yfta4-l -ft). 3.13*. lim (ft + У1 - ft3).
я-*оо П-*оо
Для того чтобы установить сходимость монотонной
последовательности, можно использовать следующую теорему. Если
Последовательность монотонно возрастает (убывает), то для ее
сходимости достаточно, чтобы оиа была ограничена сверху
(снизу).
Если доказано, что предел последовательности существует,
то для его вычисления в ряде случаев удобно использовать
формулу
lim xn = lim xn+i. (5)
Л-*оо Я-*оо
Убедиться в существовании предела, а иногда и найти его
можио, используя следующее утверждение. Если для трех
последовательностей начиная с некоторого N справедливо неравенство
166 ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
и ilm an= lim cn, то lim bn существует н
Л.-*оо «-»» п-Юо
lim bn= lim (in- (6)
Пример 3.5. Найти предел последовательности *я = qn,
если известно, что |<?| < I.
Р е ш е п и е. Представим последовательность в рекуррентном
виде:
Так как \q\ < I, то |*,,+!| < \х„] для любого п е N, н
последовательность (|.c,i|) монотонно убывает. Так как |.«п| ^0 для
любого neN, то (|*„|) ограничена снизу. Следовательно,
последовательность (|*„|) сходится. Обозначим lim | хп \ ■= у. Тогда
Я-*оо
для вычисления у„ согласно формуле (5) получаем уравнение
У = к I У- <*)
Так как \q\ < I, то уравнеине (*) имеет единственный корень
</ = о. •
Аналогично доказывается, что lim (— \x,t |)=0. Так как
П->оо
неравенство
- I Хп I < хп < | хп |
справедливо для всех л е N, то
Гип хп — 0.
3.14**. Последовательность (х„), первый член которой
Xi — Л/2 , определяется рекуррентио по формуле
Найти предел (л„).
3.15*. Последовательности (.v*), первый член которой дп = 1,
определяется рекуррентным соотношением
*,.+. = 4 +(1-2«) *„ + «*.
Найти предел (хя).
3.1G. Последовательность задана рекуррентным соотношением
х"+*=тЦ; + Хп)'
где Xi > 0, о > 0. Найти предел (*„).
3.17. Доказать, что последовательность, первый член которой
х, = -~-, а каждый последующий удовлетворяет рекуррентному,
§ 4. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ 167
соотношению
а , *й-1
хп-
2 '
возрастает и ограничена сверху. Найти ее предел.
3.18*. Найти предел последовательности, у которой
«I— 2. *« — 2 —
кп~1
9.19. Последовательность определяется рекуррентным
соотношением
*»-',=*т(2*в+"^)'
где а>0 и х > 0. Доказать, что lim х„. = -$а~.
R->0o
3.20. Последовательность определяется рекуррентным
соотношением
хп (4 + 2а)
Хл+i = ——^ ,
2х3п +а
где а>0 п х > 0. Доказать, что lim *п = -^а.
§ 4. Арифметическая прогрессия
Последовательность, у которой задай первый член 0|, а
каждый следующий член, начиная со второго, равен
предыдущему, сложенному с одним н тем же чяслом d. называется
арифметической прогрессией:
aa+i = aa + d, »sN; (l)
где а„ — п-й член прогрессии, d — разность прогрессии. Формула
общего члена арифметической прогрессии:
«„ = й, + d (п. — 1). (2)
Сумма л членов прогрессии S„ вычисляется по формуле
0 _ ot + а„ _ _ га, + d (в — I) „
Ьп= ^ Л = g П. (3)
Свойство членов арифметической
прогрессии. Любой член арифметической прогрессии (кроме первого)
168
ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
равен полусумме равноотстоящих от него членов;
а„= s ■ к < п: (4)
при /г = I получаем
ап = 5 • W
Дд-i + й/1 + i
Арифметическая прогрессия полностью определена, если из-
вестны в| н d.
Пример 4.1. При делении девятого члена арифметической
прогрессии иа ее второй член в частном получается 5, а при
делении 13-го члена этой прогрессии на ее шестой член в
частном получается 2 и в остатке 5. Найти первый член н разность
прогрессии.
Решение. Условие задачи можно записать в виде
следующей системы уравнений:
До = aj • 5,
<Ji3 = 2ав + б.
Используя формулу общего члена арифметической прогрессии,
получаем систему
я, + 8d =■ 5 (а, + d).
о, + 12rf = 2(a, + 5rf) + 5,
в которой присутствуют только два неизвестных а, и d. Приводя
в уравнениях системы подобные члены, получаем систему
4a,=3d,
at — 2d+ 5 = 0,
решением которой являются а, = 3, d = 4,
Ответ. Д| = 3, d = 4.
4.1. Сумма первого и пятого членов арифметической
прогрессии равна 5/3, а произведение третьего п четвертого ее членов
равно 65/72. Найти сумму 17-ти первых членов прогрессии.
4.2*. Найти арифметическую прогрессию, если известно, что
Д| -\-а3 + аъ = —12, aiO2a6 = 80.
4.3*. Сумма трех чисел, являющихся последовательными
членами арифметической прогрессии, равна 2, а сумма квадратов
ьтнх чисел равна 14/9. Найти эти числа.
4.4. В арифметической прогрессии дано: а„ = q u a, = pj
найти формулу общего члена прогрессии ап {р*Фц).
4.5*. Показать, что если для положительных чисел а, Ь, о
числа а2, б2, с8 являются последовательными членами арифметн»
.§ 4. АРИФМЕТИЧЕОКАЯ ПРОГРЕССИЯ
169
1 I 1
ческой прогрессии, то числа -j—j-—, —^—. —^ц-т* тоже
являются последовательными членами арифметической прогрессии,
4.6. Сумма и разность членов арифметической прогрессии
положительна. Если увеличить разность на 2, не меняй первого
члена, то сумма прогрессии увеличится в 3 раза. Если же
разность исходной прогрессии увеличить в 4 раза, то сумма
увеличится в 5 раз. Определить разность исходной прогрессии.
4.7. Найти число членов арифметической прогрессии, у
которой отношение суммы первых 13 членов к сумме последних 13
1
равно—, а отношение суммы всех членов без первых трех к
4
сумме всех членов без последних трех равно -s-.
При решении задач, в которых используется понятие суммы
членов арифметической прогрессии, удобно применять
следующую формулу, связывающую /г-й член с суммой п членов:
ап+] — Sn+l — Sn. (6)
Пример 4.2. Известно, что при любом п сумма Sn членов
некоторой прогрессии выражается формулой
S„ = 4л2 - Зл..
Найти общий член прогрессии.
Решение. Используя (6), имеем
a„+I =S„+l - Sn = 4 (а + I)2 - 3 (rt + 1) - {An2 - 3«) =8/i + 1,
a„ = 8(rt— l)+ l=Sn — 7.
Ответ, а„ = 8n — 7.
4.8. Известно, что при любом п сумма Sn членов некоторой
последовательности S„ «= 2л2 + Зл. Найти десятый член этой
последовательности и доказать, что эта последовательность
является арифметической прогрессией,
4.9. Последовательность чнсел 1, 4, 10, 19, ... обладает тем
свойством, что разности соседних членов (последующего н
предыдущего) образуют арифметическую прогрессию 3, 6, 9, ...
Найти номер члена последовательности, равного 15 454.
Пример 4.3. Найти сумму всех четных двузначных чисел.
Решение. Первое четное двузначное число равно 10, а
последнее — 98. Используя формулу общего члена прогрессии
для d = 2, ai = 10, о, = 98, получаем
. . 98 - 10 ,к
/! =■ 1 4 s = 46.
tro
ГЛ. 7, ПОСЛЕДОВАТЕЛЬНОСТИ
Подставляя найденное значение п в формулу 5П» ■' ^ " п,
ааходпм
Sn= 98+10 . 45 = 54 ■ 45 =■ 2430.
Ответ. 2430.
4.10. Решить уравнение 2 + 6 + 8 + 1J + ..,+* = 155,
4.11. За изготовление н установку первого железобетонного
кольца было уплачено 10 руб., а за каждое следующее кольцо
■ платили на 2 руб. больше, чем за предыдущее. Кроме того, по
окончании работы было уплачено еще 40 руб. Средняя стоимость
изготовления и установки одного кольца оказалась равной
4
22-Q- руб. Сколько колец было установлено?
х-I х — 2 1
4.12. Решить уравнение ) )-•■•+ — =3.
4.13*. В арифметической прогрессии сумма т первых ее чле>
цов равна- сумме п ее первых членов (m#/i). Доказать, что
в этом случае сумма ее первых т + п. членов равна нулю,
4.14*. Найти сумму всех четных трехзначных чисел, деля-
щихся на 3.
4.15. Определить такую арифметическую прогрессию, в
которой отношение между суммой п первых членов и суммой я чле-
нов, следующих за ними, не зависит от п.
4.16*. Найти сумму 502 - 492 + 482 - 472 + ... + 22 - 1.
4.17*. Найти сумму первых 19-ти членов арифметической
прогрессии ai, аг, ,.., если известно, что
я« + us + Qia + aie = 224.
4.18. Нантн Д| + а» + оц + Дю, если известно, что <ц,
as, ... — арифметическая npoi ресеня и
а, + аА + а7 + ... + а!в = 147.
4.19*. Найти последовательность, в которой сумма любого
числа членов, начиная с первого, в четыре раза больше квадрата
числа членов.
4.20*. Доказать, что если Sn, *^2rti 5$/: — суммы л, 2л, Зя
членов арифметической прогрессия, то
5зв = 3 (S2n — Sn),
4.21*. Известно, что для некоторой арифметической
прогрессии н для некоторой пары натуральных чисел тип имеет
§ 6. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
171
место равенство —гР-1**—w~- Доказать, что
ат 2/п— 1
ап ~~ 2п — 1'
4.22*. При каких значениях параметра о найдутся такие
значения х, что числа
б'+я + б.!-* \, 25* + 2б~*
будут тремя последовательными членами арифметической
прогрессии?
4.23. При каких значения? х три числа lg2, lg (2х—1),
lf?(2* + 3) являются тремя последовательными членами
арифметической прогрессии?
4.24. Доказать, что если ц(, us, «з («i Ф "г) — члены
(необязательно последовательные) арнфметическон прогрессии, то
существует такое рациональное число %., что
«з -г «г ,
к2 —«»
4.26*. Доказать, что числа V^\ V^i Vo не могут быть
членами (необязательно соседними) арифметической прогрессии.
4.26*. Могут ли числа 2; -у/К; 4,5 быть членами
арифметической прогрессии?
4.27*. Длины сторон четырехугольника образуют
арифметическую прогрессию. Можно ли вписать в него окружность?
458. Пусть Sn — сумма п членов некоторой
последовательности и известно, что S„/Sm = ;i2/m2. Доказать, что для членов
этой последовательности справедливо отношение
ап/ат~.(2п-1)/(2т-\).
§ 5. Геометрическая прогрессия
Последовательность, у которой задан первый член Ь{ Ф О,
а каждый следующий, начиная со второго, получается
умножением предыдущего па одно и то же число q Ф 0, называется
геометрической прогрессией:
bn=bn-iq\ (1)
где Ь„ — п-й член прогрессии, q — знаменатель прогрессии.
Формула общего члена геометрической прогрессии:
bn^btf*-1.
(2)
172
ГЛ. ?. ПОСЛЕДОВАТЕЛЬНОСТИ
Сумма л членов геометрической прогрессии вычисляется по
формуле
Sn^h^f.. (3)
Если \q\ < 1, то прогрессию называют бесконечно
убывающей. Предел суммы ее членов S =» lim Sn называют суммой бес
Л-*оо
конечно убывающей геометрической прогрессии. Он вычисляется
по формуле
t
Свойство членов геометрической прогрес«
сии. Квадрат любого (кроме первого) члена геометрической
прогрессии равен произведению равноотстоящих от него членов}
*S-*n-**»+* k<n> feeN- W
Геометрическая прогрессия полностью определена, если
известны bi и ц.
Пример 6.1. Найти четыре последовательных члена
геометрической прогрессии, из которых второй член меньше первого
на 35, а третий больше четвертого на 560.
Решение. Пусть by, Ьг, bs, 6t — четыре последовательных
члена геометрической прогрессии. Условие задачи можно запи>
сать в виде следующей системы уравнений:
6| — 35 «■ &2.
6,-560 — bt.
Используй формулу общего члена, эту систему перепишем в виде
Ь\ — bjq =35,
6,(/2-6I(73 = 560.
Подставляя значение bi(l — а) во второе уравнение системы,
получаем для q уравнение qa = 16, корни которого равны 4 и
(-4).
Теперь нз первого уравнения системы по значениям q = 4
и q = —4 получаем соответственно значения &i =—35/3, Ь%=1.
Ответ.
/ 35 35-4 35-16 35-64 4 OQ
• V-T' ~з~• Г~' з~~)'• (7' ~28'
—448, —1008).
5.1. Доказать, что для любого четного числа членов геомет»
рической прогрессии Sna, —сумма членов, стоящих на, нечетных
§ 5. ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
173
местах, и S4ern — сумма членов, стоящих на четных местах,
связаны равенством qSnn «= S^™.
5.2. Найти первый и пятый члены геометрической прогрессии,
если известно, что знаменатель ее равен 3, а сумма шести ее
Первых членов равна 1820.
6.3. Найтн четыре последовательных члена геометрической
прогрессии, если известно, что сумма крайних членов равна
X—49), а сумма средних членов равна 14.
6.4. В геометрической прогрессии с положительными членами
52 = 4, Ss = 13. Найти Si.
5.5. Сумма первых трех членов геометрической прогрессии:
равна 13, а их произведение равно 27. Найти эти числа.
5.6. Сумма первых трех членов геометрической прогрессии
равна 13, а сумма квадратов тех же чисел равна 91. Найти эти
числа.
5.7. Определить три числа, являющихся тремя
последовательными членами геометрической прогрессии, если сумма нх
равна 21, а сумма обратных величин равна 7/12.
5.8. Сумма первых четырех членов геометрическом
прогрессии равна 30, а сумма их квадратов равна 340. Найти данные
числа.
5.9. Произведение первых трех членов геометрической
прогрессии равно 64, а сумма кубов этих членов равна 584. Найти
прогрессию.
5.10. Сумма первых трех'членов геометрической прогрессии
равна 31, а сумма первого и третьего равна 26. Найти
прогрессию.
Б.П. Число членов геометрической прогрессии четно. Сумма
всех ее членов в три раза больше суммы членов, стоящих на
нечетных местах. Определить знаменатель прогрессии.
5.12. Дана геометрическая прогрессия с положительными
членами. Выразпть произведение первых ее п членов через их
сумму S„ н через S„ — сумму обратных велнчни этих членов.
5.13. Сумма любых пяти последовательных членов
возрастающей геометрической прогрессии в 19 раз больше третьего
из них. Найти эту прогрессию, если известно, что ее m-Pi член
равен единице.
5.14. Вычислить сумму квадратов п членов геометрической
прогрессии, у которой первый член равен щ и знаменатель
ЯФ 1.
Б.15. Доказать, что отношение суммы квадратов нечетного
числа членов геометрической прогрессии к сумме первых
степеней тех -же членов является некоторым многочленом относи*
тельно q [q — знаменатель прогрессии).
174
ГЛ, 7, ПОСЛЕДОВАТЕЛЬНОСТИ
5.18. Доказать, что если Sn, S*,, S»„ — суммы я, 2л, Эл
первых членов геометрической прогрессии, то
5П (53п — 5гп) = (Sun — Sn)3'
5.17*. Найти сумму
(^+т)2+(*2+^-)2+- + (^+^)2- **±l-
Б.18*. Найти сумму
5.19*. Найтн сумму
Sn = х •{■ 2х3 + Zx2 + ... + пхп, хф 1.
6.20. Найти число членов геометрической прогрессии, у
которой отношение суммы последних 14-ти членов к сумме первых
14-ти равно 9, а отношение суммы всех членов без первых семи
к сумме всех членов без последних 7-ми равно 3.
Пример 5.2. Найтн отличный от нуля знаменатель
бесконечно убывающей геометрической прогрессии, у которой каждый
член в 4 раза больше суммы всех ее последующих членов.
(Считается, что Ь, Ф 0).
Решение. Составим уравнение, связывающее по условию
задачи п-й член прогрессии с суммой членов, начиная с (п-f- 1)-го
члена. Имеем
Ь„ = 4
Ьп+\
1-Я
Выражая b„, bn+\ через Ь\ и q, получаем уравнение
которое после деления правой и левой его частей на biq"~{
4а
приобретает вид l=-j-^—• Его корнем является 9=1/5,
Ответ, q = 1/5.
5.21. Сумма бесконечно убывающей геометрической прогрес-
сия равна 16, а сумма квадратов ее членов равна 153 -g-. Най-ш
четвертый член и знаменатель этой прогрессии.
5.22*. .Найтн знаменатель бесконечно убывающей
геометрической прогрессии, у которой отношение каждого члена к сумме
2
всех последующих членов равно -тг-.
§ 8. СМЕШАННЫЕ ЗАДАЧИ НА ПРОГРЕССИИ 175
5.23. В бесконечно убывающей геометрической прогрессии о
положительными членами сумма первых трех членов равна 10,5,
а сумма прогрессии равна 12. Найтн прогрессию.
5.24. Сумма бесконечно убывающей геометрической
прогрессии равна 4, а сумма кубов ее членов равна 192. Найтн первый
член и знаменатель прогрессии.
5.2R. Первый член некоторой бесконечно убывающей геомет-
рической прогрессии равен единице, а ее сумма равна S. Найти
сумму квадратов членов этой прогрессии.
5.26*. При каком значении х прогрессия
а + х а—х (а — х\Ъ „ ^ п
—!—, —:—i I —;— I » .... где а > О,
а—х' а+ х \а + х ) '
будет бесконечно убывающей? Найти сумму членов этой про-
грессни.
5.27. Сторона квадрата равна а. Середпиы сторон этого
квадрата соединили отрезками. Получился новый квадрат.
С этим квадратом поступили так же, как и с исходным, и т. д.
Найти предел Р суммы периметров и предел S суммы площадей
8тнх квадратов.
5.28. Найти условие, при котором три числа о, Ь и с были
бы соответственно k-u, р-м и m-м членами геометрической
прогрессия.
5.29. Могут ли числа II, 12, 13 быть членами (не
обязательно соседними) одной геометрической прогрессии?
5.30. Бесконечно убывающая геометрическая прогрессия,
сумма которой равна -к-, содержит член -х-. Отношение суммы
всех членов, стоящих до него, к сумме всех членов, стоящих
после него, равно 30. Определить порядковый номер этого члена.
6.31. Найти отношение первого члена бесконечно убывающей
геометрической прогрессии к сумме всех ее членов, если
отношение всех членов этой прогрессии, имеющих четные номера, к
сумме всех членов, номера которых кратны трем, равно 3.
§ 6. Смешанные задачи на прогрессии
Смешанными задачами на прогрессию принято называть
такие задачи, при решении которых используются свойства как
арифметических, так и геометрических прогрессий.
Пример 6.1. Три чнсла являются последовательными
членами геометрической прогрессии. Если от третьего отнять 4, то
эти числа будут последовательными члевами арифметической
прогрессии, Если же от второго п третьего членов полученной
176
ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
арифметической прогрессии отнять по единице, то полученные
числа снова будут последовательными членами геометрической
прогреснн. Найтн эти числа.
Решение. Обозначим искомые числа а, 6, с. Для
составления первого уравнения, связывающего а, 6 и С, используем
свойство членов геометрической прогрессии:
Ь2=*ас,
Из условия задачи и свойства членов арифметической прогрессия
получим второе уравнение
26 = а + с - 4.
И, наконец,, последнее условие задачи можно записать в виде
уравнения
(6-1)а = а(с-Б).
Для решения системы
б2 в ас,
26=»а + с — 4,
(6-1)2 = а(с-5)
вычтем из первого уравнения третье. При этом получается линей*
ное уравнение 26 — 1 = 5а, связывающее Ь и а. Выражая
теперь из системы линейных уравнений
26 — 1 = 5а;
26 = а + с — 4
неизвестные а и с через 6, имеем
26 — 1 86 + 21
а g , с 1 .
Исключим из системы неизвестные а и с, подставив их
выражения через 6 в первое уравнение системы. Тогда получим
относительно 6 квадратное уравнение
№ — 346 + 21=0,
корни которого равны 3 и 7/9. Подставлия эти значения 6 в
выражения для а и с, получаем искомые числа.
Ответ. (1, 3, 9); (1/9, 7/9, 49/9).
6.1. Найти три числа, являющихся последовательными
членами геометрической прогрессии, если известно, что увеличение
второго числа на 2 делает эти три числа членами
арифметической прогрессии, а если после этого увеличить последнее число
на 9, то вновь полученные числа снова будут членами
геометрической прогрессии
5 в. СМЕШАННЫЕ ЗАДАЧИ НА ПРОГРЕССИИ 177
6.2. Три числа, из которых третьим является 12, являются
(гремя последовательными членами геометрической прогрессии»
Если вместо 12 взять 9, то эти трн числа будут тремя
последовательными членами арифметической прогрессии. Найти эти числа.
6.3*. Даио трехзначное число, цифры которого являются
рремя последовательными членами геометрической прогрессии.
Если из этого числа вычесть 792, то получается число,
записанное теми же цифрами, ио в обратном порядке. Если из цифры
исходного числа, обозначающей число сотен, вычесть 4, а
остальные цифры оставить без изменения, то получится число, цифры
которого являются последовательными членами арифметической
прогрессии. Найти это число.
6.4. Даны четыре числа, из которых первые трн являются
(гремя последовательными членами геометрической, а последние
отри — членами арифметической прогрессии; сумма крайних чисел
равна 32, сумма средних чисел равна 24. Найти эти числа.
6.5. Первые члены арифметической и геометрической
прогрессий одинаковы и равны 2, третьи члены тоже одинаковы, а
вторые отличаются на 4. Найти эти прогрессии, если все их члены
положительны.
6.6. Первый член арифметической прогрессии равен 1, а
сумма первых девяти членов равна 369. Первый и девятый члены
геометрической прогрессии совпадают с первым и девятым
членами арифметической прогрессии. Найти седьмой член этой
геометрической прогрессии.
6.7. Среди 11 членов арифметической прогрессии первый,
пятый и одиннадцатый являются тремя последовательными
членами некоторой геометрической прогрессии. Найти формулу
общего члена этой арифметической прогрессии, если первый ее
член равен 24.
6.8. В некоторой арифметической прогрессии второй член-
является средним пропорциональным между первым и четвертым.
Показать, что четвертый, шестой н девятый члены этой
прогрессии являются последовательными членами геометрической
прогрессии. Найти знаменатель этой прогрессии.
6.9. Доказать, что если a, b и с одновременно являются 5-м,
•37-м и 37-м членами как арифметической, так н геометрической
прогрессии, то ab~cbc~°ca~b = 1.
в.10. Доказать, что если а, Ь, с — три последовательных
члена геометрической прогрессии, то
_1 1 1
iog0W' log(,W logcN
— последовательные члены арифметической прогрессии.
(Считается, что числа а, Ь, с положительны и ие равны единице.).
178
ГЛ, 7, ПОСЛЕДОВАТЕЛЬНОСТИ
€.11. Даиы две прогрессии: геометрическая с Ьп > 0 и зна*
иенателем q и возрастающая арифметическая *т с разностью </<
Найти х из условна
log* 6rt — ап — \ogx 6, — а,.
§ 7. Разные задачи
Проверять, будут ли ограничены следующие последователь»
вости:
7.Lrfe-l + (-l)"-jp
7.2. хп = п{\~{-\)п).
7з* х - Зп + 5
7.4*. Общий член послеьовательвости представлен в виде
1,1, 1
*п = ~2" ■" ~ + ■ ■ • + "2Я"-
^ * «ИЗ ,
Сколько членов последовательности будет меньше ■ -.. ?
7.6. Доказать, что последовательность
2 + 4
«i = 3, «n+i=-
2а8
является убывающей.
7^6. Доказать, что последовательность
** = I + -g" + -gr + • ■ • + "go"»
является возрастающей.
7.7*. Пусть а„ — сторона правильного 2"+1-угольника, впи-
санного в окружность раднуса 1. Доказать, что
последовательность (ап) является убывающей, а последовательность перимет*
ров (Рн) — возрастающей.
7.8. Катет равнобедренного прямоугольного треугольника
равдеяен на я равных частей, я на полученных отрезках
построены втасаниые арямоугольаекя. Найти предел
последовательности (S„) площадей, образованных из ступенчатых фигур.
7.9. Найтя площадь фигуры, ограниченной параболой у=х2,
отрезком [0; I] оси абсцисс н прямой х= I, как предел
последовательности площадей ступенчатых фигур, состоящих из
прямоугольников, построенных так же, как в предыдущей задаче.
7.10. Haflra Hm ($n? + 1 - я).
S 7. РАЗНЬШ ЗАДАЧИ
179
7.11*. Найти трехзначное число, которое делится на 45 и
цифры которого являются членами арифметической прогрессии.
7.12**. Доказать, что если в арифметической прогрессии
S„ = п*р, Si — k*p, k ф п, то S„ = р».
7.13*. Доказать, что если <ц, аг, ,,,, а„ — члены
арифметической прогрессии с разностью d, то
1 -+-=нч=+...+- '
Vo? + л/ъ V"» + V<*3 V*^T + Vort-и
Удд+1 — ^ygf
7.14. Четыре числа а, Ь, с, d являются членами
геометрической прогрессии. Доказать, что
(а - с)г +(Ь- cf + {b- d)1 = {a- d)\
7.15*. Решить систему уравнений
jc у_ 2_ _и_ _£_
* = 8u,
х + у + г + и + s + t = IS -г-.
7.16*. Доказать равенство
(66 ... 6)2 + 88 ... 8 = 44 ... 4.
л цифр я аифр 2л вдф[>
7.17*. Пусть Х\ и хг — корми уравнения хг — Зл + Л = 0, а
*а и А—корни уравнения л"г — i2,v + В = 0. Известно, что
последовательность *!, *2, *з, *4 является возрастающей
геометрической прогрессией. Найтн А и 5.
Сумма п членов произвольной последовательности в
некоторых случаях может быть найдена с помощью построения
вспомогательной последовательности {Sn}, удовлетворяющей условию
•Sfc+1 — S* = «А-
Нетрудно убедиться, что
и\ + ui + ... + ип — (S2 — St) + (S, — S2) + ...
...-г(5„+|-5„) = 5„+|-5,. (2)
Пример 7.1. Hafiin сумму
1 . . . + I
есля известно, что fli aa+i — последовательные члены
арифметической прогрессии с разностью d<£> 0, ии один из которых
пе равен нулю.
180 ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
Решение. Записывая дробь в виде
J Y_L__LV_J (_____Л__
atau \ о, а.г ) as — at \ at аа J d '
где d = аг— oi, и взяв S* равным
- 1 1
имеем
s*+I - s*- - т (— - ±.) _-!■ ( в*я+^-^*) -
1
Oft+iaft
Далее, используя (1) и (2), получаем
■ -+■ ~~~~ + .. • + = Ол_|.1 — Si =
!"ft.
d \ an+i ai ) an+iai
Ответ. .
7.18. Доказать тождество
_J_j._L_j._L_j. 4-______i !_
1.2"r2.3"1"3-4"r","rn(ftH-l) ft+1*
7.19*. Доказать тождество
i , + ___н_____н..... + . »
|.2.3T2.3.4T3.4'5T,"T/i(n + l)(n + 2)
2 V.2 {п+1)(п + 2)Г
7.20*. Доказать тождество
1 +чгг!тт + - + -
ЬЗ-б^З-5.7 1 '•' ' (2/t — 1) (2/i H- 1) (2/1 + 3)
п (я + 1)
2 (2л + I) (2л + 3) "
7.21. Пусть <ц aa — арифметическая прогрессия.
Доказать тождество
_!_ч L_+ +_! =
а,а„ п a3an-i ' ' апа{
— *-(± + ±+...+±\
7.22, Найтн сумму п чисел вида 1, И, 111, 1111, ...
% 7. РАЗНЫЕ ЗАДАЧИ 181
7.23. Определить следующие суммы:
а) 1-2+3-4+ ... + (-1);
б) i»_2a+3a-42+ ... + (-l)rt+l-n;
в) 2.1* + 3-2s+ ... + (я+ 1)я2.
При вычислении пределов последовательностей, члены
которых являются результатами суммирования, используются ела*
дующие формулы:
1+2+... + п=Ш±±, (3)
1» + »+... + ^-в<в+1>6<2в+1>, (4)
l3 + 2»+...+ft3=ft3(n4+l)3. (6)
Используя (3), (5) и формулы для сумм п членоо арнфме»
аической и геометрической прогрессий, вычислить пределы;
1 + 2 + ... + 2"
'■"•Л™- 1+6+... + 6*'
7.26. ^(vr+^ + ^+...+Д).
^ + ^+."+Ь^-+Т). ' ..
^ f 7 . 29 i i 5n + 2n\
7-2в-Лт.11о+1ог+-" + -|&-)-
7-зк Лтм (wr+~^г+• • •+ ^гг) ■
где (Оя)—арифметическая прогрессия с разностью d, члены
которой отличны от нуля.
7-32-Дгасо(^ + ^+"' + Й-
Ш ГЛ. 7. ПОСЛЕДОВАТЕЛЬНОСТИ
Найти пределы последовательностей^
2 2
7.33**. art=-^=
д/2 л/2 Ц- л/2
2
(в последнем сомножителе п.
V24-V2+ ... + V* + л/2
рвднкалов),
7.34. а„ = Л/а + V <Н- ... + л/а {п радикалов).
Л/2 — Л/2-1- 4- -\/2"
7.35*. дп =' '':- (« радикалов).
Л/ 2 - л/2 + ... + л/3"
ГЛАВА 8
ПРЕДЕЛ ФУНКЦИИ,НЕПРЕРЫВНОСТЬ
ФУНКЦИИ
§ I. Предел функции
Пусть (а; Ь) — некоторый промежуток числовой оси1 н Хц е
е (а; Ь). Будем считать, что функция у = f{x) определена во
всех точках промежутка (я; Ь) за исключением, может быть,
точки *о. Говорят, что число А—предел функции y-=f{x) в
точке. хй, я пишут Um | (*) = Д если для. любого е >- 0 суще-
Х-*Ха
ствует такое число б(е) >-0, что Для всех »e(a;i),
удовлетворяющих неравенству 0 < \х — Яц\ < 6(e), выполняется не-,
равенство \f{x) — А\ < е.
Говорят, что число А — предел функция y = f(x) при х,
стремящемся к бесконечности, и пишут lim f (x) = А, если для
Х-Юс
любого е >■ 0 существует такое число н<>{£). что для всех х >
>• Ио(е) выполняется неравенство \1(х) —Л\ < е.
Функция f{x) называется ограниченной на промежутке [а; Ь],
если существуют такие числа m и М, что для всех ie=|a; 6]
выполняется неравенство m ^f(x) ^ М.
Функция f(x) называется бесконечно малой пра х-*Хц, если
для любого е>0 существует такое Й(е), что для всех *е(а;6),
удовлетворяющих неравенству 0< |.г — *o| < 6(e), справедливо
неравенство |/(*)| < е. В этом случае пишут lim/(*) = 0.
х-*х,
Фуикаия f(x) называется бесконечно большой ври х-*Хо,
если для любого числа Е > 0 существует такое 6(E), что для
всех х е (а; Ь), удовлетворяющих веравеиству 0< \я — *0| <
< 6(Я), справедливо неравенство |/(д;)|>£. В этом случае
пишут lim f (*} = оо.
Для того чтобы доказать, что число А является пределом
функции f(x) прн х-*-ха, достаточно для любого 8 найти числа
6(e), фигурирующее в определении предела.
184 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТИ ФУНКЦИИ '
Пример 1.1. Доказать, что
lim — 9~ = 4.
х-*2 х~ L
Решение. Для того чтобы для данного е найти нужное
число б (в), составим неравенство
I хг — 4
\ х — 2
< 8. (♦)
При х ф 2 оно эквивалентно неравенству
О < | х — 2 | < е, (♦*)
из которого видно, что в качестве 6(e) можно взять 6(e) = в,
и в силу эквивалентности неравенств (*) и (+*) при всех зна*
чениях х, удовлетворяющих неравенству (**), будет выполняться
неравенство (*).
Пример 1.2. Доказать, что
11т 2"*а=оо.
*-*о
Решение. Для того чтобы для данного Е найти требуе-i
мое число S(s), составим неравенство
21'*' > £. (*)
Логарифмируя обе его части по основанию 2, получаем
эквивалентное неравенство
-j3- > log2 В. (•*)
решая которое относительно х получаем
'"<(т^гУ
Таким образом, в качестве 6(E) можно взять
Доказать, что!
1.1. Urn (*4-5)=8. 1.2. lim (*2~4) = 0.
х-*3 х-+2
1.3. lim V^"=Vo". a>0. 1.4. lim (6 — 2х) = 4.
х-*а х->1
1
1.5. lim — =0. 1.6. lim 21*-"! = со.
х-»оо ■* х-*а
1.7. lim ~т = со,
х->0 *
§ 2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ 185
При решении некоторых задач удобно использовать следую»
щее определение предела функции. Пусть функция f{x)
определена во всех точках промежутка (а; Ь), за исключением, может
быть, точки Хо е (о; Ь). Говорят, что число А — предел функции
f(x) при х, стремящемся к *о, если для любой
последовательности значений аргумента (х„), стремящейся к х0 (*„■/= *о), для
соответствующей последовательности значений функции f{xn\
I'm f(xn) = A.
/1-Х»
\х I
Пример 1.3. Доказать, что функция f {х) = ~—1при х-*-О
предела не нмеет.
Решение. Возьмем две последовательности значений аргу*
мента, сходящиеся к нулю: хЦ* = 1/«, *{,2) = —1/я. Тогда
• lim /(4")'= ,im ТИТ"** llm 1=*1'
lim f(xf)= lim 4тПГ= I™ (-l)--l.
lim ,(*<;>) ^m/(^>
Таким образом, построены две последовательности значений
аргумента, отличные от нуля, пределом которых является нуль,
такие, что соответствующие последовательностн значений
функции сходятся к разным числам (одна к 1, другая к —1). Но
так как в определении предела требуется, чтобы для каждой нз
рассмотренных последовательностей значений аргумента предел
последовательности значений функции был одним и тем же
числом, то мы тем самым доказали, что данная функция при *-+0
предела не имеет.
Доказать, что следующие функции не вмеют пределам
1.8*. f(je)=. sin (1/л:) прн х->0.
1.9. f{x) = e~l,x прн *->0.
1.1<WM=.{_!;*>2' при*^0.
1.11. f(x)<={x}, *->4, где М — дробная часть числа х>
§ 2. Вычисление пределов функций
Если существуют lim fi (х) и llm /а (х), то существуют
х-+й х-*а
пределы
lim cfi (x) = c lim f,(x), (1)
х-»а х-+а
lim [f ,-(*) ± U (*)] = "га h (х) ± Ига f2 (x), (2)
*-*а х-*а х-*а
186 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТЬ' ФУНКЦИИ
Ига If i (*) h (*)] = Ига ft {х) llm h <*). (3)
Um [/, (x)lh (x)) = lim /, (*)/ lira /a (*) (lira /, (*}■*(>). (4)
*-»a x-ya x-*a x-*a
При отыскании предела отношения двух многочленов, зави*
сящнх от х, при х -*■ оо, оба члена отношения необходимо пред*
варительно разделить ва хп, где п — наввысшая степень этих
многочленов,
1х — S) (х — 2}
Пример 2.1. Найти Um ' 2Ё*~—si'+3 '
Решена,е. Разделим числитель и знаменатель дроби ва **,
Тогда
.- (* - 3) (* - 2)
(^)(^)
2aj*-5* + 3 = Д^, 2-б/* + 3/** '
Воспользовавшись теперь формулами {4), (3), а также j[2) и П)
(прн с = — 1), получим
lim (1 — 3/ж) lim (1 —2/х)
5 3
lim 2 — llm — + lira -ту
С»)
Используя равенство lim "Т" = 0, получни
Х-*оо *
(l- llm |-Vl- Um -^
2— llm — + lim —3-
Ответ, 1/2.
Вычислить пределы:
(a-+1)2 —хг+5х — 6
8Л. lim , QT' , оч . 2.2. lim
х^со (*-3)(* + 2Г "* ^ (*-!)(*-2) (х-3)'
У* . 2х + 5
2.3. Um ■ , ==. 2.4. llm ^т^.
Если Р(дг) н Q (лг) —многочлены н Q(a) Ф 0, то предел от»
ношения
, Р М
находится непосредственно с помощью формул (1) —(4). Если
же Р{а) = 0 в Q{a) = 0, то, записывая многочлены Р^х\ н
§ 2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЯ 187
Q(x) в виде
Р (х) = (х - а)ь Я, (х), Q(x) = (x-a)nQ1{x)
\k н п. — кратности корня х = а многочленов Р(х) и Q(x)), не»
обходимо до перехода к пределу произвести сокращение числн«
теля в знаменателя дроби P(x)JQ(x) иа общий множитель,
Пример 2.2. Вычислить предел
х2 - 5х + 6
Нш
х*-9
*-*з
Решение. Записываем выражение, стоящее под знаком
предела, в виде
х1 — 5а:+6 (х — 3) (х — 2) ^_ * — 2
*2— 9 = (* — 3)(* + 3) в а: + 3'
Предел полученной дроби вычисляем с помощью формул (I)-*
(4):
х~2 _ 1
Ответ. 1/6.
Вычислить пределы:
*3 + 1 „ л . (* + О8
2.5. Ifm 'aii-- 2.6. 11m v3 , ■ .
x-»-i * t l x-*-l x -r '
8a:3-I «n . (* + ft)3-x8
2.7. lim -rTJ C..-L i • 2-8- lim fc *
2.10. Urn Г^-«^-А + 2^)С«-2аГ| +
n a:2 — ax
—I
— ai
2.11. a) lim"7M. 6) ilm "/(*).
X-» 1/2 x-*3/2
где f (at) =
l-plL + .u-H + a-l.
Va: —2+ 1/д:
2.12. a) lim / (a:), 6) lim /(at), где /(x) = ..J~_*. , ■.
x* — ,t9 — a; + 1
im »■?,*'-«to»+ 7J»-8-
Вычисление пределов от выражений, содержащих иррацно*
нальности, иногда упрощается введением новых переменных.
188 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Пример 2.3. Вычислить предел
,. ^-2^7 + 1
llttl ; 775 •
x+i (х-l)2
Решение. Обозначим $х = t. Тогда для переменного t
выражение, стоящее под знаком предела, можно записать в виде
t» — 2f + 1
(t3-l)a •
Число, к которому стремится новое переменное t при *-*■!,
находится как предел значения функцииt (х) = tfx при ж-> 1, t. е.
lim / (х) = lim tfx = I.
x-+i х-ы
Таким образом,
.. f2-2f+l „ V-l)'
Um
1 =-l
<Ti (t* + t+ l)2 9
Ответ. 1/9.
Вычислить пределы:
„.. „ "Уд: — 1 „ ,_ ., Vl + * — 1
2.14. 11m —4 . 2.15. 11m —!
*'"*' -!fx — 1 """" *"*° ^l + x ~ l '
2.,e. lim V^ + Ag^T-l
Вычисление предела от иррационального выражения иногда
можно осуществить переводом иррациональности из числителя в
знаменатель или наоборот.
Пример 2.4. Вычислить предел
lim — .
х-+0 *
Решение. Умножая числитель и знаменатель дроби,
стоящей под знаком предела, иа выражение, сопряженное
числителю, получим
lim — = lim —. , г
*-*0 х х-ю х(-\/х2 + 1 + 1)
х"
11т
хТо х(«/х*+1 + 1)
О т в е т. 0.
§ 2. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЯ 189
Вычислить пределы}
2.17. lim (л/х*ТТ-х). 2Л8. Um V/! + 4 *~2-.
х-»» х-+о V-* + 9 —3
2.19. Нт , *~3 . 2.20. Ilm -^&-
х-*з ■yjx + 1 — 2 ' ' х-*9 У* — Б — 2 '
ад,. „„, ДГ2 . 2.22. ит ^Ц"2,
2.23*. lim *(У4*2 + 7 + 4.x). 2.24. 11т ,, * ~3 .
х-*-» х-+з -ух2— 1 —2
.„ ,. 9*-У*2-4 noo ,. V^+T —4
2.25. lim - . 2.26. lim -*-г—' „ , с .
При вычислении пределов выражений, содержащих тригоно»
метрическяе функции, часто используется предел
I'm sin * i
lim • = 1.
Пример 2.5. Найти предел
I — cos 2*
lim
x-+o x
Решение. Преобразуем числитель дроби по формуле
I — cos 2* = 2 sin**.
Тогда получаем
.. 1— cos 2* „ 2 sin2* „ ,. sin x .
lim = lim = 2 lim lim sin* = 0.
x-»o x x->o x x->0 * . x-»o
О т в ет. 0.
Пример 2.6. Найти предел
,. /arcsin x
lim .
х-»о *
Р е ш е н н е. Обозначим у = arcsin я; тогда х = sin у. Так
как при х -г 0 arcsiiuc стремится к нулю, чо
arcsin х ,, н ,
lim = lim —r— =» 1.
*-+:> * j/-+o sin ^
Ответ. 1.
Вычислить пределы-
„ ~_ „ „sin пх „ м«, .. sin х — sin «
2.27. Um =-r . 2.28*. Km
ж-xjslnm* ж^а ж- а
190 ГЛ. 8, ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТЬ ФУНКЦИИ
2.29*. lim (л sin — V 2.30*. lim -^тг.
2.3,. lim si°*-c°s*, 2.32*. l,m &*-***
х-»п/4 1 — tg* х-+л/з соз(х + я/6)
2.33*. lim si,n(y-"/3). 2.34. lim ' ~sin'^2) . '
ж-*я/з 1 — 2 cos x *_>„ n — *
2.85*. lim V + sms-Vl-sin* ^
*-*0 *
§ 3. Непрерывность функции в точке
Функция f(x), определенная на промежутке (а; 6),
называется непрерывной в точке дг0 е (я; Ь), если:
1) существует предел lim f{x);
2) этот предел равен значению функции в точке ха, т.е.
lim /(*)-/(*•)•
Х-+Ха
Доказательство непрерывности функции f(x) в точке Хц
состоит в проверке справедливости раненства
lim /(х)=/(лг0). (1)
Х-*Хч
Пример 3.1, Доказать, что функция
[ (*) = 3*2 + Б
непрерывна в точке х = 2.
Решение. Используя теоремы о пределах, имеем
lim (Здга + 6) = 3 lim x1 + 5 = 17.
Х-*2 Х-+2
С другой стороны, значение функции в точке 2 тоже равно 17.
Следовательно, равенство (1) выполняется и данная функция
непрерывна в точке х = 2.
Доказать непрерывность следующих функций в указанных
точках:
3.1. f {х) = х3 — 2х + 1 в точке I.
- « с, v I + cos 2х п
3.2. / f.v) = —■ в точка х =-г.
' w cos л: 4
3.3. f (*) = ■! ~ ' *^ J' в точке л- =1
• f (*) = {'
f sin х
8.4. f (*) «= { x ' * в точке х = 0.
I 1, * = 0
i 3, НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ IfJ
3.6.;w = r ' ж,ь2' в точке х=0-
(.0, х = 0
3.6. /(*) = (<1 + *) * *^°> в точке * = 0.
I е, х = 0
( Vi + * - ^Т+7
j* л л
8.7. f(x) = i х ' 'в точке х = 0.
1/6, * = 0
При доказательстве непрерывности функции f(*), опреде*
лейкой на промежутке (о; 6), в точке *о е (а; &) в ряде слу*
чаев вместо равенства (I) удобнее проверить справедливость'
равенства
Um [f(x«+Ax)-/(«•)] — % (2)
Дх-*0
при выполнении которого функция непрерывна в точке *с
Пример 3.2. Доказать, что функция
f (х) = sin х
непрерывна для любого значения аргумента х.
Решение. Для данной функции составим разность
Пх + Ьх)-Пх):
8Ш (X + &Х) — Sin X = 2 Sin — COS I 5 1,
Воспользовавшись тем, что
sin (Д*/2) , | / . Дх Ч I _.
д'Ло-^72 ''• I «»(*+—J^1'
с помощью формул (2), (5) из § 2 получаем
lim [sin (x + Д*) — sin *] = 0.
Дх-+о
Доказать непрерывность следующих функций иа всей оЯла»
стн их определения:
3.8. }(х)<=х\ 3.9*. f(*) = cos*.
ЗЛО*. / (х) = In х. 3.11*. f (x) = е*.
При доказательстве непрерывности часто используется еле»
дующая теорема.
Если функции 1(х) и g(x) непрерывны в точке Хо, то их
сумма, разность, произведение н часгиое (если g(xo) ф 0) не-i
прерывны в точке ха.
Пример 3.3. Доказать непрерывность функции
2х2 — 2
на всей числовой рсн.
w д= "_'_ . . (ad — ЬсфО) непрерывна в своей области опре-
"г ^
192 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ, НЕПРЕРЫВНОСТЬ" ФУНКЦИИ
Решение. Так как f(x) представляет собой отношение
двух многочленов, причем знаменатель всюду положнтелен, то
непрерывность f{x) в любой точке х е R следует из
непрерывности в этой точке числителя и знаменателя.
3.12. Доказать, что дробио-рациональиая функция
аг+_Ь
сг •
деления.
3.13. Будет ли функция у ==tgx непрерывна на всей
числовой осн.?
Если lim f {x) существует, но функция не определена в
Х-*Хо
точке хо, то говорят, что хо — точка устранимого разрыва,
В этом случае можно доопределить функцию f{x) по
непрерывности, положив
f (*„)- llm f (x). (3)
X-**j
Пример 3.4. Доопределить функцию
в точке х = 2 по непрерывности.
Решение. Точка х = 2 не принадлежит области
определения данной функции, но
х3 — 4
*н>2 х—2 x-*V
tlm - £->=llm (x + 2)=4.
Доопределяя функцию f (х) в точке х = 2 значением, равный 4,
получаем функцию
х1 — 4
Г(*)=Лт=Г ПРИ хф2>
I 4 при х=2.
при *=2,
которая на всей области определения исходной функции
совпадает с исходной функцией и будет непрерывной на всей число-
soft оси.
О т в е т. 7 (2) = 4.
Доопределить по непрерывности следующие функции в ука-
ванных точках:
3.14. f(*)=-£i£iL в Т0ЧКе х=0.
ех — е~х
8.15. f (х) = в точке х = 0.
§8. НЕПРЕРЫВНОСТЬ" ФУНКЦИЙ В ТОЧКЕ J 93
.,« ... лЛ Н- х — л/l — х
3.16. f(x)<= v ^ i в точка х«=0.
X
3.17. f(х) = 8~^ в точке л = 81.
9— У*
Подобрать параметры так, чтобы f(x) стала непрерывной в ука-
занной точке ,(еслн точка не указана, то на всей числовой
прямой):
хг — 5х + 6
3.18. f(x)---' '■ -Q ' Хфг'
( хг — 5л;+ 6
>{ *-3 '
U.
3.19. f(je)«i'2~",/**' *^01
v ' I А, х = 0.
3.20. f {x) = \ sin 2*' *^и'
3.21./(*) = { _
1д
■{г
х = 3.
х*=0.
п
в точке х = 0.
1 — CQS X
sm2x в точке х = 0,
х = 0
2
-, х¥-0,
3.22. f (х) = { 1 — cos mx ' ' в точке х = 0.
х = 0
3.23*. f (ж) = { v' ~ ^ tg ~' * ^ '' в точке х — 1.
ж=.1
Пусть функция f(x) определена ira промежутке (о; хо)<
Число А называют левым пределом функции /(х) в точке хо а
пишут
Hm f(x)=A,
Х-ЬХь-0
если для любого 8 > 0 существует такое 6(8) > 0, что Для
любого х е (о; хо), удовлетворяющего неравенству Хо — 6(e) < х,
выполняется неравенство
|/(*)-Л|<е.
Функция f(x) называется непрерывной в точке хо слева,
если точка хо принадлежит области определения фупкцни и
Urn f(x)=f(x„).
Аналогично определяются правый предел функции н
непрерывность функции справа.
7 А. Г, Цыпкнв, Aj И,. Пипскпо. ..
194 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТб ФУНКЦИИ
Для непрерывности функции f{x) в точке Хо необходимо а
Достаточно, чтобы она была непрерывной слева и справа в
точке Хо.
Пример 3.5. Каким условиям должны удовлетворять
параметры а п Ь, чтобы функция
f, ч i х — 1 при *< 1,
7 **'в \ ах1 -*• Ьх нрн х> I
была непрерывной?
Решение. Вычислим левый н правый пределы данной
функции.в точке х = 1:
lim (х — 1) = 0, 11т (а*2 + &*) = а + Ь.
*-»1-о *->1+0
Так как данная функция в точке х = I непрерывна слева н
f(!) =0, то для ее непрерывности необходимо и достаточно
выполнения равенства а + b •=> 0.
Ответ. а + Ь = 0.
Подобрать параметры, входящие в определение функции,
так, чтобы функция f{x) стала непрерывной:
3-24-/(*)={sIn*H-&, x>nl2.
у ' \ax-b, х < 2.
v I ад; — 6, х>3.
,W \e*»+ftx+I. *>f.
3.29. f (*) -. ^ 1НП" +1- х><*
f —
MQL^)-{*' + X+1, *>_,S
t sir
3.31. /<*)_{* + * *<3;
sin (я (x + a)), jc < 1.
x<3;
x>3.
§ 4. Разные задачи
Вычислить пределы:
. , „ cos x sin x — tg д;
4.1. Ilm _■-, ■ ■—s—
x->o x sin x
4.2, Km *
x-*w 2 - ctg x — ctg8 x *
$ 4. РАЗНЫЕ ЗАДАЧИ 193
Проверить справедливость неравенств:
., ,, 2* + 3 ^ „ 2*а-5*-3 , ,. Sln T
4.3. iim Чр=-> Um — h lim —.
x-x»x + -x/x х-*-1/2 4a-3 — 18je —10 *-*0 *«
., .. V1 + x + x* — 1 , „. д/2~ — 2 cos * _ , „ „nr-
4.4. lim — ■ \- Mm —,— —- > Ig 0,085.
л-»0 x *t^4 sin (а:-я/4) ^ e
Вычислить пределы:
4.5. lim , , ^-. 4.6. lim ——s5;—;—;^r.
*.+ i a;2 + 5* — 6 Л^0 cos 3 (* + я/2)
X-
A - .. sin 2* . V2aH- 1 —1
4.7. lim : lim * .
x-»nl + cos3* x-*o V3* + 4 — 2
- „ ,, 1— cos* . n ,. Igx — {go
4.8. lim —г-ч • 4.9. hm — -—.
х-ю sm3* *_><, x—a
, ,Л ,. sin л; — sin a ... ,, sin x—sin я
4.10. hm . 4.11. lim ■
x^.a cos x — cos а л._>а ig.v —Iga
. In ,. sin x — cos x ... ,, sin* —cos*
4.12. hm — ■ . 4.13. lim
х+я/л lg* —ctgx " • " X+„H tg.v-1
Л1Л i- lgx — sin* ,. со$(я/4 + *)
4-14. hm — = . 4.16. hm . ' —-.
x-+0 * x-*nji 1— lg«
. .„ ., cos 2.t . ._ .. sin 2a-
4.18. lim —— 7=r-. 4.17. lim
inu —-—■ . . ■. 'ли. um -:—; : ,
х-»я/.1 cos a- — y-2/2 *->3rtn 1-)-sin *
< .„ ,. cos x „ ,„ . i-r:;
4.18. hm s—. 4.19. Iim
Л-*Я/2 Я — ^A" j;_j.O 1 — COS A-
.„„ .. sin (я/3 —*) .„. .. a-sin*
4.20. hm n x ^-. 4.21. hm - .
x-»n/3 2 cos x — 1 я^о 1 — cos *
- „„ .. sec 2* + 1 . „„ ,. 1 — cos 2*
4.22. hm . 4.23. lim
х-»я/2 cos* *_>„ tgs*
-„. ,. I + cos 2* . n_ ,. sin2л-— sin2я
4.24. hm —Ц-= . 4.25. Iim —— -—,
*-+я/2 cig11* *_>,, sm(x—a)
. „„ .. I — sin * ,. sin (я/4 — .v)
4.26. hm 5 . 4.27. Iim i-i ;-—
х-»л/2 cos2 а- *_>„,< cos2* —1/2
4Л8. Hm lgXr/inX. 4.29. hm ttf*-tg'g.
x+o sm3* x^.a tg(* —a)
. on .. cos* x — cos8 a .„, ,. tg3* — tg3 *
4.30. hm . 4.31. hm -^—- -—.
s[aLll± *^o tgx
7*
196 ГЛ. 8. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
лп* „ V X + tg х — 2
4.32. Цт - . s •»
х-ьпЦ sin х — cos х
4.33. Пт [(sin x— cos*)tg( ■?"+* П.
х-»я/4 L Ч 4 /J
4.34. lim [(I - sin x) tg2 *]. 4.36. lim \(a-x) sec-^-1
*-*Jl/2 x-»a L ^O J
«г.. пт к*-;*»!!.
x-*arctg3 tg2* — 4tg*-f-3
4.40. lim l~COs3x
x->o ж sin д; cos x
Доопределить функции по непрерывности:
х — 3
4.41. f (*)■=■ ,. - = в точке х = 3.
У*2 - I - 2
4.42. f (*) = 2~У"1+4 в точке * = 0.
sin 2x
, •.„ «/ ч cos2* — sin2* — 1 „
4.43. f (x) =» , в точке х = 0.
V*2 + 1 - 1
Выяснить, при каком выборе параметров функция f (х)
будет непрерывной:
У*2+ 7 —4
4.44. f (x) <= 4 *2 - Ьх + 6 ' * фЪъ в точке * = 3.
*=3
1.44. f {х) <= J *2 -!
U,
2*+2 - 16 ^
4.45. / {х) = ^ 4* - 2< ' * "^ ^
*=2.
ГЛАВА 9
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§ 1. Вычисление производных
Пусть функция f(x) определена на промежутке {а; Ь). Возы
Мем предел отношения приращения функции
А^ (*о) ■= / (*о + Лх) — f (*o> (1)
к приращению независимого переменного Д* (Да- = х — *о) пра
А*, стремящемся к нулю:
Urn M&L. (2)
Дх-*0 Д*
Если этот предел существует, то гопорят, что функция f{x)
имеет производную в точке ха, или что f(x) дифференцируема
в точке Хо- Производная функции f(x) в точке ха обозначается
f'[Xo). Если предел ие сущестзует, то говорят, что функция f(.-.),
не дифференцируема в точке хо.
Задача, связанная с вычислением производной, исходя нз ее
определения, заключается в непосредственном вычислении
предела (2).
Пример 1.1. Вычислить производную функции
{(х) = sin х.
'■ Решение. Составим приращение функции Д/{а'..):
Л/ (*и) = sin (*0 -|- Л*) — sin Хо.
Чтобы найти предел
„ sin (х0 4- Ах) — sin x0
lim г ,
дх-»о Ьх
воспользуемся формулой
sin (х0 + Ах) — sin хо = 2 sin -5- cos I лг0 + -W- J •
193 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
С учетом непрерывности функц'.ш cos* имеем
2 Sin —— COS I A'o -| г~ 1
111,1 л
. Л'
sm —;-
=» lim - . „у- Km cos ( xa -f -^- i = cos *o.
Дх-*0 «»*/* йл-?0 V - /
Так кап точка *о виорана произвольно, то ножно заключись,'
что
(sin x)f = cos-x.
О т ii с г. (jiit л")' -- cos х.
Исходя i!3 определи ни производит:'!, вычислить производные
следующих функций:
1.1. f {х) = [/х. 1.2. / (х) = cos х.
1.3*. [ (л) = е е. 1.4*. f (*) =■ fn дс,
1.5». / (*) = ха. 1.6. /(*)=*£.
Односторонние пределы
lim —г-— (3)
Дд:-*-0 "*
lim ^Sl (4)
ЛХ-++0 Д*
называются соответственно левой и правой производными функ-<
шш /(*) в точке д:0 в обозначаются {_ (х0) н }+ (х0). Для
существования производной 1'{хо) необходимо* и достаточно, чтобы
обе производные (левак в правая) существовала в точке Хо н
были равны:
Г+(*0) = />„). (5)
Пример 1.2. Доказав, ч;о фупкпия
,, . ( х, *> I,
'М^Ы х<\,
Пе дифференцируема в точке ж— 1.
Решение. Приращение функции в точке х = 1 равно
AHDWO + M-fOJ-^f*^,..,, £>J
или, после преобразований,
лнп=Л **• д*>0'
44 *' XZ&x + tex)*, Д*<0.
* 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ 199
Следовательно, по определению (3), (4) имеем
Г.(„-'|.т 2А* + (А*)Д~2,
ДХ-+-0 Д*
/'.(!) = lim ~=l.
+ Д*-*+0 Д*
Так KaKf+ (1) Ф f'_ (l), то производная ГМ в точке * = I не
существует.
Доказать недифференцируемость следующих функций в
указанных точках:
1.7. f (х) = | х | при х — 0.
1.8. /(*) = |*г —5* + 6| при х —2 н * = 3.
при л- = 1.
1.10*. Показать, что функция
1
f д; sin —, х ф 0,
U * = о
ие имеет в точке х = 0 ни правой, ии левой производных.
'•И. Доказать, что функция f(х) = х[х\ дифференцируема
в точке к = 0.
Производ ii ы о основных элементарных
функций:
(хаУ = аха-\ (6)
(а*)' = а* 1п о, д>0, (г*)'=ех, ' % (7)
(loge*)' = 7БТ' Л>0, а¥=1, (1п*>' = У' №)
(sfn *)' = cos х, (9)
(cos х)' — — sin *, (10)
<'«*>'-таг- <">
(arcsin *)' = (13)
Vl — *
(ardgxj'-j-ly (14)
200 ГЛ- 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
Правила дифференцирования. Пусть с —
постоянная, Да:) и g(x) —дифференцируемые функции; тогда
с' = 0, (15)
[f (*) +в (*)Г = П«)+*'(*). («)
[f М g («)]' = Г (*) в (*) + 8' (*) f (*). <17)
7(*)Г = H*)g (*)-«'<*)/(*)
g2(*)
UwJ
(18)
Теорема о дифференцировании сложной
функции. Пусть y = f(x) имеет производную в точке *о, а
функция 'g(y) имеет производиую в точке yo=*f{xo); тогда
сложная функция F(x) — g[f(x)] имеет производиую в точкехо,
равную
^'(*о) = й'ЫГЫ. (19)
Пример 1.3. Вычислить производную функции
F (х) = (х* + ж + О'00.
Решение. Полагая ff = /(*)=>** + *+I, g(y) =• Ут,
имеем
g'(</)=!00//м, Г (X) «- 2х + К
Тогда, согласно (19), получаем
F' {х) = 100{х2+х+ l)ss (2a: + 1).
Ответ. F' {х) = 100 (а:2 + ж + 1)вв (2х + 1).
Вычислить производные следующих сложных функций]
« .„ 2 +У* , ,0 I \—хг
1.12. у = ,- > 1.13. ц=Д/ . -
2-У* * V 1+*2
1.14. (/ = Vsin У*. 1.15. (/ = eVin(a*+te+e)#
• «. , 1 + * , ,, (а + Ьхп)т
1.18. у =**-rj cos3 а: (3 cos2 a: — 5).
11Q . (tg»*-l)(tg's+10tg3*+l)
1.19. у j^ .
.„. . X — 1
1.20. у = In cos .
Предварительно упростив выражения, вычислять производ-
иые следующих функций:
х л/х +х-\- -ух
§ 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ 201
_____ * ___—-—_
i.22. f W --=== .
1.25. f (X) = (л/Г=^ + l) : ( Yf=T + VT=T?").
V2~- VT vT + Vsi"
..27./(,) w* ; , vt4 '■•
(2-V7T2): (Vj+I-^)
/V*-l , V*+l , Л'д
1.29. f(x) V x+\ _/ -;
i3o f/и., ^' + V^3^" (VoT^P"-Vd -*)3)
K 2+ Vl-*2
ни. / w=fV^-fe~ + i±_V_Tf2 x
xV'+'VF + T-
Если функция f(x) определена на некотором промежутке
[а; Ь], то в качестве значений ее производных на концах этого
промежутка принимаются значения левой производной на правом
конце и правой — на левой конце ■соответственно.
Пример 1.4. Вычислить на промежутке [0; 2] производную
функции
202 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
Решение. Так как выражение под радикалом представ»
ляет собой полный квадрат, то, согласно определению модуля,
представим данную функцию в следующем виде:
ч \ i it f*— 1, хе[1; 2], , v
Дифференцируя f{x) отдельно на промежутках [0; I) и '(!; 2],
получаем
гм-{-[; Г[°;1)'
(1; 2].
Так как левая., и правая производные f(x) в точке х <= 1 не
совпадают, то в точке дг = 1 производной не существует; в ка>
честве значения f (x) на концах промежутка [0; 2] принимаем
значения левой производной функции (*) в точке 2 и правой
производной функции (») в точке 0.
<"■«'■<•»-{-!; ;:й а
Вычислить производные следующих функций:
.... ., . V* — 2Vv — I
1.32*. f (*)=•*—■- - —
1.33. / (х) =
1.34. f(x) =
(*2 + i)^
1.35*. / (jc) = л/х + 2 V2c — 4 + V* — 2л/2* — 4 .
§ 2. Промежутки монотонности и экстремумы
функций .
Говорят, что функция у => ((х) возрастает на промежутке
(а; Ь), еслн для любых xt и *», принадлежащих (а; 6), из
неравенства лп < х2 следует неравенство f (х,) < {(ха). Говорят,
что функция у = f (х) убывает на промежутке (а; 6) если для
любых xt в Х2, принадлежащих (о; 6), из неравенства xt < ж»
следует неравенство f(xi)> f(x3) Функции, возрастающие
(убывающие) ва промежутке {а; Ь\, называются монотонными на
этом промежутке.
§ 2. ПРОМЕЖУТКИ МОНОТОННОСТИ И ЭКСТРЕМУМЫ 203
Достаточные условия монотонности функ-
п и п. Пусть функция у = f{x) определена и дифференцируема
на промежутке (о; Ь). Для того чтоОы функция была
возрастающей па промежутке (о; Ь), достаточно, чтобы выполнялось
условие
У {х) > 0 прн любом х е (о; 6).
Для того чтобы функция была убывающей на промежутке (а; Ь),
достаточно, чтобы выполнялось условие
f (х) < 0 при любом х е (а; Ь).
Точки, принадлежащие промежутку {щ Ь), в которых про*
взводная равна нулю или не существует, называются
критическими точками функции f/r=f(x). Из определения критической
точки следует, что если производная функции меняет знак, то
это может произойти только при переходе через критическую
точку. Таким образом, промежутки убывямн:;, возрастания
(промежутки монотонности) функции f(x) ограничены критическими
точками. Поэтому, для того чтобы определить промежутки мо«
нотонности функции, необходимо:
1) найти критические точки f(x)\
2) определить знак производной /'(*) внутри промежутков^
ограниченных критическими точками.
Пример 2.1. Исследовать иа возрастание и убывание
функцию
f(x) = xe~3x.
Решение. Находим производную
/' (*) = е-з* _ зх-е"3* = в~3х (1 - 3*).
Производная /'(*) существует всюду и обращается в -нуль о
точке 1/3. Точка х = 1/3 делит числовую ось на два промежут*
ка: (—оо; 1/3) в (1/3; оо). Так как функция е~*х всегда. полей
жительна, то знак производной определяется вторым сомножнг*
телем. Следовательно, па промежутке (—оо; 1/3) }'(х)>0, й на
промежутке (1/3; оо) /'(.*) < 0.
Ответ. Функция f(x) nojpacTaeT ни громежутке ](—оо; 1/3J
и убывает на промежутке (1/3; ос).
Исследовать на возрастание и убывание функции:
2.3. f (*)=-|-л:-sin2*.
2.4. f (x) = 2 In {x — 2) - х3+ Ах + 1,
«>()4, гл- 9 ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
«•б. f w = {х~ 1)» - 2-в-' w=•LxL-
2.7*. Найти множество всех значений параметра о, при ко*
торых функция
/ (х) = sin 2* - 8 (а + 1) sin x + (4я2 + 8о - 14) х
является возрастающей для всех х е R и прн этом не имеет
критических точек.
2.8*. Найти все значения параметра а, -при которых функция
у (х) = Sax — о sin 6* — 7* — sin Ьх
возрастает и не имеет критических точек для всех х е R.
Говорят, что функция у = f(*) имеет в точке хо максимум
(нлн минимум), если найдется такая fi-окрестность точки х0,
принадлежащая области определения функции, что для всех
х Ф Хо, принадлежащих промежутку (*о — б; хо + Ь),
выполняется неравенство
f (*)</(*<>) (соответственно f (*) > f (*0)).
.Точки максимума и минимума называются точками экстремума,
а значения функции в этих точках называются экстремальными
значениями.
Необходимое условие существования экс<
трем ума функции. Пусть функция f{x) дифференцируема
на промежутке (а; 6). Если в некоторой точке х0 е (а; 6)
функция f{x) достигает своего экстремума, то f'{xo) = 0.
Достаточное условие существования
экстремума функции. Пусть функция определена и
непрерывна на промежутке (о; Ь) и на всем промежутке (за
исключением, быть может, конечного числа точек) дифференцируема.
Если при переходе через критическую точку производная
функции меняет знак, то такая критическая точка является точкой
экстремума функции: точкой максимума, если знак меняется с
плюса на минус, н точкой минимума, если знак меняется с
минуса на плюс.
Пример 2.2. Найти экстремум функции
f (x) = V2*2-* + 2.
Решение. Находим производную
§ 2. ПРОМЕЖУТКИ МОНОТОННОСТИ II ЭКСТРЕМУМЫ 205
Приравниваем производную f'(x) нулю:
I 4х —I
= 0.
2 У2*2-л + 2
Отсюда находим критическую точку хо = 1/4. Из выражения (*),
видно, что прн х > 1/4 /'(*) > 0, а при * < 1/4 { (х) < 0, т.е.
прн переходе через хо = 1/4 производная меняет знак с минуса
иа плюс. Следовательно, ха = 1/4 — точка минимума, причем
f (*o) ='Vl5/8. Знаменатель выражения (*) положителен для
всех «eR, Следовательно, других критических точек, кроме
х = 1/4, функция f{x) не имеет.
Ответ. minf{x)=f (1/4) = У15/8.
x<=R
Найтн экстремумы следующих функций:
■ 2.9. / (х) = (* ~ 2)а (* + 4) ^ 2.10. /(*) — *+ efci .2*.
2.11. / (х) = .ГС*-* . 2.12. f(x) =
2*
2.13, / (*) = 2х3 + Зх2 - 12* + 6. 2.14. / (х) =
2.15. [ {х) = 2х3 - 6х* - 18* + 7.
2.10. / (*) - —~ 2* + 2
л:8 + 9 *
X
1п.«
*-1 '
Методы исследования функций на экстремум позволяют
устанавливать справедливость некоторых трансцендентных
неравенств.
Пример 2.3. Доказать справедливость иеразепства
ех — х > 1 при х =Ф= 0. (*)
Решение. Рассмотрим функцию
/(х) = ех-1-х
н найдем ее экстремум, Решая уравнение /'(*) = 0, т.е. ураине-
ние е* — 1 = 0, получаем х = 0.
Прн х = 0 функция 1(х) достигает своего единственного
минимума, так как f'{x) при переходе через точку х = 0 меняет
знак с минуса на плюс. Так как f(0) =0, то для всех хф§
справедливо f(x) > 0, т.е. е* — 1 — х > 0, нла е* — х > 1, что
и требовалось доказать.
Доказать неравенства:
2.17. х — х3/6 < sin X < х прн х > 0.
2.18. cos*> 1 — ^/2 при хфО,
2.19. In (1 + х)< х прн х > 0,
206 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§ 3. Наибольшее и наименьшее значения функций
Пусть функция f(x) определена и непрерывна на конечном
промежутке [a; ft], Для нахождения наибольшего (наименьшего)
значения функции необходимо найти все максимумы (мнннмумы)']
функции на промежутке (о; ft), выбрать из mix наибольший
'(наименьший) и сравнить его со значениями функции в точках
о и 6. Наибольшее (наименьшее) из этнх чисел и будет
наибольшим {наименьшим) значением функции f(x) на промежутке
[а; &]; оно обозначается max f{x){ min (x)). При нахо-
<е]«; Ь] же .[с; Ь]
жденни наибольшего или наименьшего значения функции может
оказаться, что внутри промежутка [a; ft] производная
существует во всех точках промежутка и ни в одной точке промежут<
ка в нуль не обращается (т. е. критические точки функции от-
сутствуют). Это говорит о том, что в рассматриваемом проме«
жутке функция возрастает или убывает и, следовательно,
достигает своего наибольшего и наименьшего значения на концах
промежутка.
Прнме.р 3.1. Найти наименьшее п наибольшее значения
х 2
функции f (*) = -£--| на промежутке [1; 6].
Ре ш е и пс. Так как
то единственной критической точкой, попадающей в заданный
промежуток, будет точка х = 4. Сравнивая значения функции в
точке х = 4 со значениями функции на концах промежутка, по«
лучаем
f(4) = l, Hl)-2i-, i(e)m, i_^.,
т.е. наименьшее значение f[x) достигается в точке х = 4, а
наибольшее—на левом конце промежутка (при х = 1).
Ответ, max f(x) = f{l) = 2^-; min / (*)«=f(4)= I,
xs|I;B| 8 je<=|t;6l
Найти наибольшие и наименьшие значення функций на
указанных промежутках:
3.1. f (*) = *5 - *3 -Ь * + 2, х<= [-1; 1].
3.2. f (x) = Зх* + 4х3 + I, х (= 1-2; I].
3.3. f (х) = cos2 у sin ж, х е (О; я].
§ 3. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИЙ 207
1
3.4. f (х) г* ^ с°з 2х + sin х, * s= Го; ^-]-
х 1 I
3.5. / (дг) = у —j sin 2.v + -^ cos5 .« — соз х,
*eL-TJ tJ-
При отыскании наибольших "(наименьших) значений
некоторых функций иногда удобно использовать следующее свойство,
Если непрерывная функция F(x) па промежутке [о; Ь]
может быть представлена в вида F{x) = l[g(x)], где g(x) п f(y) —
непрерывные функция иа промежутках х t=[a; b] и у е [с; d]
соответственно, с = min g(*), <* = max g (x), то
X« |a: ft] xe[c; d\
max F(*) = max f (у) и mill F (aj) =» min f(y).
x s [a; *] j/ s ic•, d] x es [a: ft| и в [с; d\
Пример 3.2. Найти наибольшее и паимеиьшее значения
функции F (х) -,.„*"+„/4) на промежутке [о; Д.
Решение. Используя формулы
sin Г-^- + х}=д 2 (sin х + соз х),
sin 2x = (sin * + cos *)2 — 1,
представляем данную функцию в виде сложной функции
где
2 I
f (у) = -' ~— ^/2, g (дг) = sin х + соа х.
if
Найдем наибольшее и наименьшее значения g(x). Критическими
точками g(x) будут корин уравнения
cos х — sin x = 0,
пз которых в промежуток [0; я/2] поиалает только х = л/4.
Сравнивая g(0), #(л/4) и g(n/2), заключаем, что областью
изменения g(x) является промежуток [l; V^l- Нетрудно заметить,
что
PM-V? (l+-pr)>0-
на всей области определения f(y), в том чнеле и дли
i/e[l; л/2]. Следовательно, функция /(</) возрастает на
промежутке [l; V2] и достигает своего наибольшего и наименьшего
208 ГЛ. 9. ПРбЙЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
значений сответственио на празом п левом концах промежутка{
max_ f(y)=,f(-y/2)=\,
i/e[liVi]
min _ f(j/)=/(|) = o.
fie[l; V2]
Эти же значения являются наибольшими и наименьшими и для
исходной функции F(x).
Ответ, max F (х) = I, т'т F{x)=Q.
х е [0; я/21 * в [0; я/2|
Найти- наибольшие и наименьшие значения функций:
о л г/ \ • sin 2х Г ЗяП
З.в. f {х) = , , ,. ,—г, »е я; -=- .
' sin (я/4 + .v) L 2 J
3.7». /(х) = . 1 , т !—т-, *eR,
w sin х + 4 cos ж — 4
3.8. f(x)r=tgx + dgx, «е[я/6; я/3].
3.9*. Найти наименьшее значение функции
2 + cos * "\2
v ' \ sm ж /
на промежутке [0; л].
Нахождение наибольших а наименьших
значений функций, содержащих знак абсолют»
ной величины.
Пример 3.3. Найти наибольшее н наименьшее значения
функции
f{x)-\x*-bx + 6\ (*)
па промежутке [0; 2,4].
Решение. Для того чтобы раскрыть модуль в выражении
(*), найдем корни уравнения f{x)=Q. Решая уравнение
Xй—5* + 6 = 0, получаем х — 2, х = 3. Таким образом,
f f r»-5x-6 при х <= (- оо; 2) U (3; оо);
'W-|_(^_5x + 6) при л-е[2;3]. (**'
Из '(**) видно, что на исследуемом промежутке [0; 2,4]
функция f{x) допускает два представления в зависимости от зиаче*
пня аргумента:
_ (Ж« - 5* + 6), * е (2; 2,4],
хг — 5х + 6, х е [0; 2].
f (*) = {'
Вычислим производную функции 1(х):
rw={
— {2х — 5), * е (2; 2,4];
2х — 5, »е [0; 2),
§ 4. ЗАДАЧИ НА НАХОЖДЕНИЕ ЭКСТРЕМУМОВ 209
При *(='(2;2,4] f'(x)'>0, следовательно, f(x) возрастает, а
при *(=[0;2) /'(*)< 0, следовательно, f(x) убывает; точка
х = 2 — критическая точка, так как производной f'{x) в этой
точке не существует. Сравнивая значения функции на концах
промежутка [0[ 2,4] с ее зиачеинем в критической точке,
заключаем, что
max f(*) = f(0)=6, min f {x) = f (2) = 0.
X <= 10; 2,4] X e |0i 2.4]
Ответ. max f (x) = f (0) =. 6. min f (x) = f (2) = 0.
ач=10;2,'Ц *е[0;2,'!]
Найти наибольшее и наименьшее значения следующих
функций на указанных промежутках1-
1+ж
■|, *е[-2;01.
8.10. /(«)■ 1-ж
3.11. f (*)=лЛ —2* +*2 + V* + 2* + *2 •
а)*е [0; 2]; б) х е= [-2; 0].
3.12. f (л) = Vl — 2.v + л;2 — л/l +2* +л2, * е= (— оо; оо).
3.13. Н*) = |*г + 2*-3|+-||пл:, Jfs[l; 4J.
3.14. Найти точки минимума функции
f{x) — 4x*-x\x-2\, же[0;31
и ее наибольшее значение на этом промежутке.
3.1Б. Найти наибольшее и наименьшее значения функции
f(x) = V*(10-*).
3.16*. Найти наибольшее и наименьшее значения функции"
/(*) = (*-l)2V*2-2* + 3, jc<=[0;3].
3.17. Найти наибольшее и наименьшее значения функции
у^\х*+х\ + \хг + 5х + Ъ{
на отрезке
Г--- -1
L 2' 2J"
§ 4. Задачи, сводящиеся к нахождению
наибольшего и наименьшего значений
и эстремумов функций
В условиях многих задач явно ие формулируется, что
требуется иайти наибольшее н наименьшее значения п экстремумы.
К таким задачам относятся, например, задачи, связанные С
Нахождением множества значений функций.
210 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
Пример 4.1. Найти образ промежутка [—1; 3] при
отображении, заданном функцией
f (x) =* 4л-3 — 12*.
Решение. Чтобы найти образ данного промежутка, нужно
найти множество значений функции /(*) для х<=[— 1; 3],
которое в снлу непрерывности исходной функции представляет собой
промежуток Г min f(x); max /(*)"!. Таким образом, пс«
Lxe[-I; 3) *s[-I; 31 J
ходная задача сводится к задаче иа отыскание наибольшего и
наименьшего значений функции f(x) на промежутке [—1; 3].
Критические точки f(x) находятся из уравнения
12,г2 — 12=0,
корнями которого являются jet = I, Хг = —1. Сравнивая
значения функции !(х) в критических точках н на концах
промежутка, получаем
max /(x)=f(3)=72,
я<=1-1; 3|
rain /(*)=/■(!) ==-8.
xe|-l; 3|
Следовательно, образом промежутка [—1; 3] при отображеннн,
заданном исходной функцией, будет промежуток [—8; 72].
Ответ. [—8; 72].
4.1. Найтн множество, на которое отображает луч [J; °°)
производная функции f(x) = хЦах— I).
4.2. Найтн образ промежутка [0; 0,5] при отображении,
заданном производной функция f{x) = tg 3*.
4.3. Найти пересечение множеств, на которые отображается
х + 3
промежуток [0; I] производными функций tj\ = х_х> Уг^
= $6х + 5.
4.4*. В какой промежуток переводит всю действительную
прямую функция у = xi _ ~ + э ?
4.5. Найти множество значений функций:
4,6*. Доказать, что справедливо перавенство
ах1 + b 2 -y/ab
§ 4 ЗАДАЧИ НА НАХОЖДЕНИЕ ЭКСТРЕМУМбВ £Ц
4.7*. Доказать, что для функции / (х) = cos % sin 2х
справедливо неравенство
mln f (х) > —7/9.
X s 1-я; я|
4.8*. Доказать, что для функции f{x) = sin tfsln 2x выпол«
начо неравенство
max f (x) < 0,77.
uei-л; я1
4.9*. Доказать, что для х е [0; л/2] справедливо неравенство
cos x VsTnT < 2Ш • 3-3/4.
4.10. Доказать, что при хе[3/4; 2] справедливо неравенство
4.11*, Показать, что при любых действительных значениях Я
фуикипя
хг + х -|-1
У-
х2 + \
не может иметь значений, больших 3/2, п значений, меньших 1/2,
4.12*. Найти все а, при которых имеется хотя бы одна пара
.чнеел {х, у), удовлетворяющих условиям
*2+(;/+3)а<4, у = 2ах\
4.13*. Сумма третьего п девятого членов арифметической
прогрессии равна наименьшему значению квадратного трехчлена
2*2 — 4*+10. Найти сумму одиннадцати первых членов этой
Лрогрессии.
4,14*. При каком значении параметра а значения функции
у = х3 — 6х* + Эх+а
в точке х = 2 и в точках экстремума, взятые в некотором
порядке, являются членами геометрической прогрессни?
4.15. Сумма членов бесконечно убывающей геометрической
прогрессии равна наибольшему значению функции
/ (а) = х3 + 3* - 9
на промежутке [—2; 3]; разность между первым и вторым чле«
нами прогрессии равна f (0). Найти знаменатель прогрессии.
4.16. Сумма бесконечно убывающей геометрической прогресс
сии равна наименьшему значению функции
/(*)=3х»-* + -§-,
212 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ. ПРИМЕНЕНИЯ
а первый член прогрессии равен квадрату ее знаменателя. Найтн
знаменатель прогрессии.
4.17*. Найтн наименьшее значение а, при котором уравнение
4 I
—: г- ~, : =*а
sin х 1 — sin х
имеет на промежутке (0; я/2) хотя бы одно решение.
4,18*» Доказать, что функция
*-(*+1/*)'+(У+1/»)2
. Ие меньше 12,6, если х > 0, у > 0, х + у — 1.
4.19*. Показать, что функция
z = 2х2 + 2*(/ + у2 — 2* + 2у + 2
ие меньше чем (—3).
4.20*. При каком значении а сумма квадратов корней
уравнения
*» — (а — 2)х-а- 1=0
принимает наименьшее значение?
4.21*. Доказать, что при всех значениях *sR имеет место
неравенство
2 ** 1 + х2 ^ 2
4.22. Доказать, что на промежутке
[о „ . /logo 5 logi 7 "j
-f; I0"3V V25"+ V49"J
справедливо неравенство 0 ^ 2x + 3 лУ*2" ^ 1.
4.23. Доказать, что прн а е [0; я/3] справедливо
неравенство
1 _l 1 ^ 4-y/3~
sin (я/3 + a) sin (я/3 — а)
4.24, Доказать, что для всех х н i/ справедливо неравенство
4.25*, Доказать справедливость неравенства
9 —УШГ — 2* +3 9 + УШГ
2 < *2 + 6* + 10 < 2
4,26*. Доказать, что 1/4 < sin8 * + cos" x < I,
§ Б. ТЕКСТОВЫЕ ЗАДАЧИ " 213
4.27. Доказать, что при х е [0; 2/3] справедливо неравенство
5е"3 < (З*2 - 7х + 7) ех < —- №.
4.28. Сколько корней иа отрезке [0; 1] нмеет уравнение
&х {2х2 - I) (4х* - 8х2 + 1)=1?
4.29. При каких значениях р и q график кубической
параболы у = х3 + рх + q касается оси Ох}
4.30. При каком условии уравнение х3 + рх + q = 0 имеет:
1) одни действительный корень;
2) три действительных корня?
§ 5. Текстовые задачи на нахождение наибольших
и наименьших значений функций
Для решеиня текстовой задачи на наибольшее (наименьшее)
значение следует сначала, используя условия задачи, составить
функцию /(*) и определить промежуток изменения ее аргумента,
а затем отыскать наибольшее (наименьшее) значение этой
функции на найденном промежутке.
Пример 5.1. Число 26 представить в виде суммы трех
положительных слагаемых, сумма квадратов которых наименьшая,
если известно, что второе слагаемое втрое больше первого.
Решение. Обозначим неизвестные слагаемые *, у, z. По
условию задачи введенные неизвестные удовлетворяют
следующей системе уравнений:
л:+ ,/+2 = 26, ,
У=*3х. к '
Используя (*), выразим неизвестные у я г через х\
у = 3х, z = 26 — 4x. ' (**)
Составим теперь функцию, минимум которой требуется
найти:
S (х) = х*+ 9хг + (26 — 4х)2.
Промежуток изменения аргумента в данном случае определяется
из условия положительности всех слагаемых. Решая систему
неравенств
*>0,
26 - 4х > 0,
(13 Ч
0; -g-J- Таким
образом, задача свелась к отысканию минимума функции S(x)
иа промежутке (0; -5-). Единственной критической точкой
214 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
фуикини S(x) на промежутке ГО; -^-1 является точка х = 4.
При переходе через эту точку производная функции S{x) меняет
знак с минуса на плюс, следовательно, S(x) убывает на
промежутке (0; 4) и возрастает па промежутке f 4; -tj-J. Таким
образом, при х = 4 функция S(x) достигает своего минимума,
Подставляя х = 4в уравнения (**), получаем значения
остальных неизвестных.
Ответ. 26=4+ 12+ 10.
5.1. Число 18 представить в виде суммы двух
положительных слагаемых так, чтобы сумма их кнадратов была наименьшей.
5.2. Число 36 представить в виде произведения двух
сомножителей так, чтобы сумма их квадратов была наименьшей.
5.3. Число 180 представить в виде суммы трех
положительных слагаемых так, чтобы два из них относились, как 1:2, а
произведение всех трех слагаемых было наибольшим.
5.4. Данное положительное число о представить в внде
суммы двух положительных слагаемых так, чтобы их произведение
было наибольшим.
5.5*. Парабола tj = x2-]~px-\-q пересекает прямую у=2х — 3
в точке с абсциссой 1. При каких р и q расстояние от вершины
параболы до оси Ох минимально? Найти это расстояние.
5.6. Найти наименьшее из расстояний от точки М с
координатами (0, —2) до таких точек (*, у), что
5.7. В сегмент параболы у1 — 2рх, отсекаемый прямой х =
— 2а, вписать прямоугольник наибольшей площади.
Пример 5.2. Найти высоту конической воронки
наибольшего объема, если ее образующая равна I.
Решение. Объем конуса, площадь основания которого
равна S, а высота— И, вычисляется по формуле
V = ~Sff,
где S = я#а, R — радиус окружности, лежащей в основании
конуса. По теореме Пифагора R и Н связаны равенством
Воспользовавшись этим равенством, выразим V как функцию
только одного переменного Я:
V = -ijT(J*-№')/f.
5 5 ТЕКСТОВЫЕ ЗАДАЧИ
215
Решая уравнение
V (Я) •= - (Я - ЗЯг) = О,
нзходнм две критические точки функции V(H)\ Я[ ™//V3,
Иг и» — f/VS". из которых только точка Н\ принадлежит
промежутку (0; 0- При перекоде через точку Н\ функции V (Я) ==
«= -=■ {I2 — ЗЯ2) меняет знак с плюса на минус, и, следовательно,
«а промежутке (0; //V3) функция V (Я) возрастает, а на
промежутке (//Уз~, /) убывает. Таким образом, Я =■ f/V§" — высота
конуса максимального объема при заданной длине образующей I.
Пример 5.3. В трапецию ABCD, боковая сторона АВ
которой (длины 6 см) перпендикулярна основанию, вписать
прямоугольник наибольшей площади так, чтобы одна из его сторон
лежалз на большем основании трапеции. Основания трапеции
равны 6 и 10 см соответственно. Вычислить площадь этого
прямоугольника.
Решение, Рассмотрим от- в^
дельно два случаи. Первый —
оерпиша прямоугольника Р лежит
на боковой стороне трапеции
CD (см. рис 9.1). Второй —вер-
Р
S
ч
ч
^_
\
пиша Р лежит на основании а 1
трапеции ВС. ч
В первом случяе обозначим ' *•'
стороны прямоугольника Л О = х
и AM. ■» у. Составим уравнение, связывающее неизвестные х и у.
Для вгого проведем вспомогательный отрезок BL, параллельвый
стороне CD (см. рис 9.1), и рассмотрим два прямоугольных
треугольника ABL в QPD. Катеты втнх треугольников равны
соответственно АВ =* 8, AL •= 4, QD = 10 — х, PQ =» у.
Искомое уравнение получается из условия подобия треугольников
ABL в QPD)
У
10 -х
> 2, или у «= 20 — 2х.
Площадь прямоугольника AKPQ равна
S U) =- х (20 - 2х).
Интервал взмеиенвя х в первом случае находится из условия,
что точка Q — проекция точки Р, лежащей на стороне CD,
следовательно, д; 5» 6.
216 ГЛ. 9. ПРОИЗВОДНАЯ И ЕВ ПРИМЕНЕНИЯ
Таким образом, задача свелась к отысканию наименьшего
8fia4ciiHa функции S(x) на промежутке [6; 10]. Единственная
критическая точка функции S(x): x = 5 ие принадлежит
найденному промежутку. Следоиителыю, производная функция S(x).
не меняет на асом пром.якутке знак. Вычисляя производную
S{x) в произвольной точке промежутка [6; 10], убеждаемся, что
она отрицательна. Таким образом, наибольшее значение S(x)t
достигается в левом конце промежутка, т. е.
max S(x)=*S (6) =» 48 см».
5св[6; 10] ;
Площадь прямоугольников, относящихся ко второму случаю,
Не превосходит 48 см2, гак как при одинаковой боковой
стороне, равной 8 см, длины их оснований не могут быть больше
6 см.
Ответ, 48 см*.
5.8. Из всех конусов, вписанных в шар радиуса R, найти
тот, у которого площадь боковой поверхности наибольшая.
8.9. Определить размеры цилиндра, имеющего наибольший
объем, если площадь его полной поверхности раина 2я.
5.10*. Среди всех прямоугольных треугольников площади S
найти тот, для которого площадь описанного круга будет
наименьшей.
5.11*. В полукруг радиуса I вписана трапеция ABCD так,
что ле основание AD является диаметром, а вершины В и С
лежат на окружности. Какова величина угла <р при основании
трапеции ABCD, имеющей наибольший периметр?
5.12*. Из всех треугольников с одинаковым основанием я
одним н тем же углом при вершине а найти треугольник с
наибольшим периметром.
5.13. В равнобедренный треугольник ABC вписан
прямоугольник, две вершины которого леж^т на основании АС, два
другие — на сторонах АВ и ВС. Наннтн наибольшее значение
влощадн прямоугольника, если |АВ| = 12, \BD\ = 10, BD —
высота треугольника ABC.
5.14. Рассматриваются всевозможные трапенцн, обе боковые
стороны и меньшее основание которых равны а. Найти величину
большего основания трапеции, имеющей наибольшую площадь.
5.15. Длина стороны квадрата ABCD— 10 см. На его
сторонах отложены отрезки AAt, BBU CC,. DDt длины х каждый,
причем At е АВ, Si e ВС, Ci<=CD, D,s^DA. Доказать, что
четырехугольник AiBiCiDi — квадрат, и найти значеине я, при
котором площадь этого квадрата — наименьшая.
§ 5. ТЕКСТОВЫЕ ЗАДАЧИ
217
5.IG. В окружность радиуса R вписан равнобедренный
треугольник. При каком значении угла а прн вершине треугольника
высота Н, проведенная к боковой стороне, имеет наибольшую
длину? Найти эту длину.
5.17*. Каков должен быть угол а прн вершине
равнобедренного треугольника заданной площади S, чтобы радиус г
вписанного в этот треугольник круга был наибольшим?
При участии тела в двух независимых движениях его путь
"(или проекция пути на некоторое направление) является
функцией от двух или более переменных, связь между которыми,
может быть установлена из физических соображений.
5.18, Путннку требуется попасть на противоположный берег
реки. Под каким углом а ему следует направить лодку, чтобы
добнтьси наименьшего сноса, если скорость лодкн равна Vx,' a
скорость рекн — VP?
5.19. Тело бросают под углом а к горизонту со скоростью
Vo. Пря каком значении угла а тело улетит дальше всего?
5.20*. Определить наименьшую высоту ft= \ОВ\ двери
вертикальной башни ABCD, чтобы через эту дверь в башню можно
было внести жесткий стержень длины /; конец стержня скользит
вдоль горизонтальной прямой, на которой находнтся основание
башнн АВ. Ширина башнн \АВ\ — d< I.
5.21. На странице текст должен занимать 384 см2. Верхние
н нижние поля должны быть по 3 см, а правые и левые — по
2 см. Если примять во внимание только экономию бумаги, то
каковы быть должны оптимальные размеры страницы?
5.22. Из круглого бревна диаметра d требуется вырезать
балку прямоугольного сечения. Каковы должны быть ширина х
н высота у этого сечения, чтобы балка оказывала наибольшее
сопротивление: а) на сжатие; б) на изгиб?
Примечание. Сопротивление балки иа сжатие прЪпор-
ционально площади ее поперечного сечения, а на изгиб —
произведению ширины этого сечення иа квадрат его высоты.
5.23. Лампа внсит над центром круглого стола радиуса г.
Прн какой высоте h лампы над столом освещенность предмета,
лежащего на краю стола, будет наилучшей? (Освещенность
прямо пропорциональна косинусу угла падения луча света и обратно
пропорциональна квадрату расстояния от источника света.)
5.24. Требуется устроить прямоугольную площадку так, что-;
бы с трех сторон она была огорожена сеткой, а четвертой
стороной прнмыкала к длинной каменной стене. Какова
наивыгоднейшая (в смысле плошадн) форма площадки, если имеется /
погонных метров сетки?
218 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
5.25. На прямолинейном отрезке АВ длины а, соединяющем
два источника света А (снлы р) н В (силы q), найти точку М,
освещаемую слабее всего. (Освещенность обратно
пропорциональна квадрату расстояния от источника света.)
5.26*. Лодка находится на расстоянии 3 км от ближайшей
точкн А берега. Пассажир лодки желает достигнуть точкн В,
находящейся на берегу иа расстоянии 5 км от А, Лодка
движется со скоростью 4 км/час, а пассажир, выйдя из лодки,
может в час пройти 5 км. К Какому пункту берега должна
прибыть лодка, чтобы пасса жнр достиг точкн В в кратчайшее
время?
5.27*. Дождевая капля, начальная масса которой Шо, падает
под действием снлы тяжести, равномерно испаряется так, что
.убыль массы пропорциональна времени (коэффициент
пропорциональности равен k). Через сколько секунд после начала падения
кинетическая энергия капли будет наибольшей и какова она?
(Сопротивлением воздуха пренебрегаем.)
5.28*. Расходы на топку парохода пропорциональны кубу
его скорости. Известно, что при скорости 10 км/ч расходы на
топливо составляют 30 руб. в час; остальные расходы (не
зависящие от скорости) составляют 480 руб. в час. При какой
скорости парохода общая стоимость 1 км пути будет наименьшей?
Какова будет при этом общая сумма расходов в час?
5.29. Для доставки продукции завода из пункта N в город А
строится шоссе NP, соединяющее завод с железной дорогой АВ,
проходящей через город А. Стоимость перевозок по шоссе вдвое
больше, чем по железной дороге. К какому пункту Р нужно
провести шоссе, чтобы общая стоимость перевозок продукции
завода из пункта N в город А по шоссе и по железной дороге была
наименьшей? Расстояние от N до железной дороги равно 100 км,
а расстояние от города А до станции железной дороги,
находящейся па одной окружности с А и N, которые находятся в
концах диаметра этой окружности, равно а к.ч.
При решении задач о времени достижения наименьшего
расстояния между двумя объектами, двигающимися под углом друг
к другу, следует воспользоваться тем, что расстояние между
объектами, достигнутое к моменту времени /, представляет
собой одну нз сторон треугольника, двумя другими сторонами
которого являются некоторые функции расстояний, пройденных
объектами к этому моменту.
5.30. По двум улицам движутся к перекрестку две машины
с постоянными скоростями 40 н 50 км/ч. Считан, что улицы
пересекаются под прямым углом, и зная, что в некоторый мо«
§ 5. ТЕКСТОВЫЕ ЗАДАЧИ
219
мент времен» машины находятся от перекрестка на расстояниях
2 и 3 км (соответственно), определите, через какое время
расстояние между ыимн станет наименьшим,
5.31*. Три пункта А, В, С расположены так, что ZABC «
= 60°. Одновременно из точки А выходит автомобиль, а из
точки В — поезд. Автомобиль движется по направлению к В со
скоростью 80 км/ч, а поезд—к пункту С со скоростью 50 км/ч.
В какой момент времени (от начала движения) расстояние
между поездом н автомобилем будет наименьшим, если \АВ\ =
= 200 км?
5.32*. Два самолета летят горизонтально на одной сысотс
под углом 120° друг к другу с одинаковой скоростью о. В
некоторый момент одни из самолетов прилетел в точку пересечения
путей, а второй в этот момент находился в а км от нее (не
долетев до точки пересечения). Через сколько времени после этого
момента расстояние между самолетами будет наименьшим?
5.33. Определить, при каком диаметре круглого отверстия в
плотине секундный расход воды Q будет иметь наибольшее
значение, если Q = ci/ л/h — у , где h — глубина низшей точки
отверстия (считать k и коэффициент с постоянными).
5.34. Стоимость бриллианта пропорциональна квадрату его
массы. При обработке бриллиант был расколот На две части.
Каковы размеры частей, если известно, что при этом произошла
максимальная потеря стоимости?
5.35. Составляется электрическая цепь из двух параллельно
соединенных сопротивлений. При каком соотношении между
этими сопротивлениями сопротивленце цепи минимально, если при
последовательном соединении сопротивлений oiio равно ^?
5.36*. Гонцу нужно добратьсн из пункта А, находящегося на
одном берегу реки, в пункт В, находящийся па другом берегу.
Зная, что скорость движения по берегу в к раз больше
скорости двил(ення по воде, определить, под каким углом а гоиец
должен пересечь реку, для того чтобы достичь пункта В в
кратчайшее время. Ширина реки равна h, расстояние между
пунктами А и. В (вдоль берега) — d.
5.37*. Точки Л и В расположены в различных оптических
средах, отделенных одна от другой прямой линией. Скорость
распространения света в первой среде равна vi, а во второй —
t>2. Пользуясь принципом Ферма, согласно которому световой
луч распространяется вдоль той кривой АМВ, для прохождения
которой требуется минимум времени, вывести закон преломления
светового луча.
5.38*. Пользуясь принципом Ферма, вывести закон
отражении светового луча от плоскости в однородной среде,
220 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЙ ПРИМЕНЕНИЯ
5.39. Если в электрической цепи, имеющей сопротивление R,
течет ток /, то количество тепла, выделяющегося в единицу
времени, пропорционально 12R, Определять, как следует разветвить
ток / на токи /4 ц /3 при помощи двух проводов с
сопротивлениями Ri и Ri, чтобы выделение тепла было наименьшим. '
6.40. Прямоугольный участок площадью 9000 м2 необходимо
огородить забором, две противоположные стороны которого
Каменные, а другие—деревянные. Одни метр деревянного забора
стоят 10 р., а каменного — 25 р. Какое наименьшее количество
денег может быть выделено по смете на строительство этого
забора? '
5.41*. Требуется построить некоторое количество одинаковых
жилых домов с общей площадью 40 000 м2. Затраты на
постройку одного дона складываются из стоимости фундамента,
пропорциональной корню квадратному из величины жилой площади
дома, и стоимости наземной части, пропорциональной кубу корня
квадратного из величины жилой площади. Строительство дома
иа 1000 мг обходится в 184,8 тыс. р., причем в этом случае
стоимость наземной части составляет 32 % стоимости
фундамента. Определить, какое количество домов нужно построить, чтобы
стоимость затрат была наименьшей, н найти эту стоимость.
При решении некоторых задач вместо нахождения
наибольшего (наименьшего) значения величины, указанной в
формулировке задачи, удобнее искать наибольшее (наименьшее) значение
другой величины, представляющей монотонную функцию от-
первой.
5.42*. Статуя высотой 4 м стоит на колонне, высота которой
5,6 м. На каком расстоянии от колонны должен стоять человек
ростом (до уровни глаз) 1,6 м, чтобы видеть статую под ланч
большим углом?
5.43*. По прямолинейному шоссе едет экскурсионный
автобус. В стороне от шоссе расположен дворец, от парадного входа
которого идет дорога перпендикулярно шоссе. На каком
расстоянии от точки пересечения этих дорог должен остановиться
автобус, чтобы экскурсанты моглн лучше рассмотреть нз автобуса
фасад дворца, если длина» дворца — 2а, фасад расположен под
углом 60° относительно шоссе и расстояние от парадного входа
(который является центром симметрии дворца) до шоссе
равно 6?
5.44*. Груз весом Р, лежащий на горизонтальной площадке,
должен быть сдвинут с места приложенной силой. Сила трепня
пропорциональна силе, прижимающей тело к плоскости, и
направлена против двигающей силы; коэффициент
пропорциональности (коэффициент трения) равен к, Под каким углом а к го->
§ 5. ТЕКСТОВЫЕ ЗАДАЧИ
221
ризонту надо приложить силу, чтобы величина ее. оказалась
наименьшей? Определить наименьшую величину сдвигающей
силы.
6.45*. На наклонной плоскости лежит груз весом Р. На
вершине наклонной плоскости расположен блок, через который
перекинута веревка, привязанная одним концом к грузу, а
другим— к гире весом р(р<Р). Прн каком угле а груз будет
удержан иа наклонной плоскости гирей наименьшего веса, если
коэффициент треннп равен bus [arctg k; л/2]?
6.46. Рычаг второго рода имеет точку опоры в А, а в
точке В (АВ = а) подвешен груз Р. Вес единицы длины рычага
равен р. Какова должна быть длина рычага, чтобы груз Р
уравновешивался наименьшей силой? (Момент уравновешивающей
силы должен быть равен сумме моментов груза Р н рычага)
Иногда задачи, сформулированные как задачи на наибольшее
и наименьшее значения, допускают более простые решении,
основанные иа геометрических соображениях.
Пример 5.4. Русла двух рек (в пределах некоторой
области) представляют параболу у = л* и прямую % — у — 2 = 0.
Требуется соединить эти реки прямолинейным каналом
наименьшей длины. Через какие точки его провести?
Решение. Геометрическое место точек, находящихся на
расстоянии d от прямой линии, представляет собой две прямые,
параллельные данной, проведенные иа этом расстоянии по обе
стороны от нее. Точки, лежащие внутри образованной таким
образом полосы, находятся от данной прямой на расстоянии,
меньшем d, а вне полосы — на расстоянии, большем d. Если прямая
не пересекает параболу, то, увеличивая ширину полосы, мы в
конце концов коснемся параболы. Полученная точка касания
будет точкой параболы, находящейся ближе всего к прямой. Следо*
вательно, для нахождения этой точки достаточно иайти коорди*
паты точки касания той касательной, которая параллельиа дайной
прямой. Из условия параллельности (см. § 6) имеем
2х = 1 -»■ х = 1/2 и (/ = !/+.
Для того чтобы найти точку на прямой (второй конец канала),
запишем уравнение прямой, перпендикулярной прямой
х—у—2—0 и переходящей через точку (1/2, 1/4);
у — 1/4 = — (х— 1/2), или # = — * + 3/4»
Решая систему уравнений *
у = - х + 3/4,
у = х-2, ч
получаем х = 11/8, у =» —5/8.
222 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
Ответ, Координаты концов канала: (1/2, 1/4) н (11/8,
~5/В).
6,47, Прямая / проходит через точки (3, 0) и (0, 4), Точка Л
лежит на параболе у = 2х — х2. Найти расстояние р от точки А
до прямой в случае, когда А совпадает с началом координат, и
указать координаты точки А(х0, уо) на параболе, при которых
расстояние от нее до прямой будет наименьшим.
6.48*. Четыре точки А, В, С, D в указанном порядке лежат
на параболе у = ахг + Ьх + с. Координаты А, В a D известны}
А (—2, 3), В (—1, 1), D (2, 7). Определить координаты С в
случае, когда площадь четырехугольника ABGD наибольшая.
6.49. На координатной плоскости даны точки А (—2, 0) и
В (0, 4) и прямая /: у = х. Найти периметр треугольника АМВ,
где М — точка с абсциссой 3, лежащая иа прямой /, При каком
положении точки М иа прямой / периметр треугольника АМВ
наименьший?
5.50*, Дан угол ZAOB п внутри него точка М. Как следует
провести через точку М прямую, чтобы она отсекла от угла
треугольник наименьшей площади?
5.51. Дай угол ZAOB и внутри него точка М. Как построить
треугольник наименьшего периметра, чтобы одна его вершина
была в точке AJ, вторая —на стороне АО и третья —на стороне
ВО данного угла?
5.52. Рассматриваются такие всевозможные трапеции,
вписанные в окружность радиуса R, что центр окружности лежит
внутри трапеции, а одно из оснований равно R -\/3. Найтн
боковую сторону той из трапеций, которая имеет наибольшую
площадь.
5.53. Дана правильная треугольная пирамида DABC '(D —
вершина, ABC — основание). Известно, что \АВ\ = a, \AD\ = b.
Пирамиду пересекает плоскость а, параллельная ребрам AD и
ВС. На каком расстоянии от ребра AD должна быть
проведена плоскость а, чтобы площадь сечения была наибольшей?
5.54. Рассматриваются всевозможные прямоугольные
параллелепипеды, у которых основаниями являются квадраты, а
каждая из боковых граней имеет периметр 6 см. Найти среди инх
параллелепипед с наибольшим объемом и вычислить величину
этого объема.
5.55. В круговой сектор радиуса R с прямым центральным
углом вписан прямоугольник так, что одна его вершина
совпадает с центром круга, а противоположная вершина лежит на
окружности. Найтн длины сторон прямоугольника, имеющего
наибольшую площадь,
§ 6. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 223
5.66. Хорда АВ paBiia радиусу окружности. Хорда CD,
параллельная АВ, проведена так, что площадь четырехугольника
ABCD максимальна. Найти угловую величину меньшей из дуг,
стягиваемых хордой CD.
5.67*. В данный круговой сектор радиуса R вписать
прямоугольник наибольшей площадн (угол сектора равен ее),
Вычислить значение этой площадн,
§ 6. Задачи на геометрический смысл производной
Пусть функция i/of(x) дифференцируема в точке Xt в
уо =» /.(*о), Прямая, определяемая уравнением
У= Уо + f (хо) {х — х0), (1)
называется касательной к графику функции y=*f{x) в точке
М(ха, уо). Записывая уравнение (1) в виде
У — Уо = Г {ха) (х — xQ), (2)
можно заключить, что из всех прямых, проходящих через точку
'М{ха, уо), касательной к графику функции f[x) будет та
прямая, угловой коэффициент которой равен f'(xo). (угловой
коэффициент есть тангенс угла наклона прямой К положительному
направлению оси Ох).
Прямая, перпендикулярная касательной в точке касания, иа«
еывается нормалью к графику функции у = f (ж) в этой точке.
Уравнение нормали имеет вид
№-*>)/'(*о)+(*-*о)=0. (3)
Под углом между графиками функций
y=*fi(x) и y = h(x)
в их общей точке М{хо, уа) понимается угол а между касателы
ными к этим графикам в точке М(хц, уо). Тангенс угла вычис»
ляется по формуле
tga= ш-ш ш
Если выражение 1 + f[ (х0) f2 (х0) обращается в нуль, то
кривые пересекаются под прямым углом.
Для того чтобы получить уравнение касательной (нормали)
к графику функции у «= f (x) в точке, абсцисса которой известна
и равна Хо, достаточна яайтв значения /'(*о). н jef^oj, н под-
Ш ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ' ПРИМЕНЕНИЯ
ставить их в уравнение (1) (соответственно в (3)). Координаты
точки на графике функции, в которой требуется провести
касательную, определяются из условий задачи.
Условия параллельности и
перпендикулярности двух прямых. Пусть прямые заданы уравнениями
у — k\X-\-b\ и у = ktf. 4- Ьг. Для того чтобы эти прямые были
параллельны, необходимо и достаточно, чтобы k\ = кг. Для того
чтобы эти прямые были перпендикулярны, необходимо и
достаточно, чтобы kika = —1.
Пример 6.1. На кривой у = х% — 7х + 3 иайтя точку, н
которой'касательная параллельна прямой у = — 5* + 3.
Решение. Из условия параллельности двух прямых
следует, что угловой коэффициент касательной в искомой точке
должен быть равен (—5) Тогда абсциссу точки касания найдем,
используя равенство
у'(х) = 2х-7=?-$=>х = 1,
а ординату — подстановкой х = 1 в уравнение крнвой (/(!) =
== —3.
Ответ. Искомая точка имеет координаты (1, —3).
6.1. На кривой у = х3 — 3* + 2 найти точки, в которых
касательная параллельна прямой у = Ъх.
G.2. Записать уравнение горизонтальной касательной к
графику функции у = е* + е~х,
6.3. Записать уравнение касательной к графику функции
у = соз'(2* — я/3) + 2 в точке с абсциссой ха = я/2.
6.4. Какой угол образует с осью абсцисс касательная к
параболе у = х1 + 4х — \7, проведениая в точке М (5/2, —3/4)?
Записать уравнение этой касательной.
3 3
6.6*. Известно, что прямая у = —-тх—— является каса->
тельной к графику функции / (х) = •=■ х4 — х, Найти координаты
точки касания.
6.6. Показать, что координаты точки пересечения
касательных к кривой у = 1 — ха/ал, проведенных через точки с
координатами у = 0, не зависят от параметра а. Найти координаты
точки пересечения. *
6.7. Вычислить площадь треугольника, ограниченного осями
координат и касательной к графику функции у = х/{2х — 1) в
точке с абсциссой х0 = 1.
6.8. Найти уравнение общей касательной к кривым
у = х* + 4х + 8, у — х1 + 8* + 4.
§ в. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ * £25
6.9. При каком значении Хо е [0, я/2] касательные к
графику функцнн {{х) = sin X + sin 2x в точках с абсцисса мн ^и
Хо + я/2 параллельны?
в.10. Найти все значения хо, при которых касательные к
графикам функций
у {х) =» 3 cos Ъх, у {х) = 5 cos Зх + 2
в точках с абсциссой *о параллельны.
6.11. Найти координаты точек пересечения с осью Ох тех
касательных к графику функции
которые образуют с осью Ох угол Зя/4.
6.12*. На графике функцнн у(х) = х* — 3*' — 1х + 6 иайтн
все точки, в каждой из которых касательные к этому графику
отсекают от положительной полуоси Ох вдвое меньший отрезок,
чем от отрицательной полуоси Оу. Определить длины отсекаемых
отрезков.
6.13*. Хорда параболы у = —агхг-\-Ьах — 4 касается
кривой у = 1/(1 — х) в точке х = 2 и делится этой точкой пополам.
Найти а.
6.14. Записать "уравнение касательной к графику функции
f[x) .= \х3— |*|| в точке с абсциссой х = —2.
6.16. Две касательные к графику функции у=^П{х2 + 1)
пересекаются под прямым углом в некоторой точке оси Оу.
Записать уравнения касательных.
Пример 1.2. Определить, под каким углом синусоида
у = —==- sin Ъх
л/3
пересекает ось абсцисс в начале координат.
Решение, Искомый угол по определению равен углу
наклона касательной к осн абсцисс, проведеииой к сннусоиде п
начале координат. Таким образом, тангенс искомого угла
совпадает с угловым коэффициентом этой касательной и равен
значению производной функции у «= —т=- sin Ъх, вычисленному прн
V3
х = 0. Так как
. 3 я
то tg О = —=■ н, следовательно, О = -%•■
уз
Ответ, а = я/3.
8 А, Г, Цыакви, А, И, Ппнскнй
226 гл. 9. производная и ее применения
в.16. Показать, что касательные, проведеивые к графику
функции
х — 4
в точках пересечения его с осями координат, параллельны,
в. 17. В каких точках касательная к графику функции
образует с осью Ох угол 45°?
6.18. Под каким углом к осн Ох наклонена касательная,
проведенная к кривой у = 2а;3—х в точке пересечения этой кри*
вой с осью 0(/?
6.19**. Показать, что кривые, задаваемые уравнениями
ху = а», хг — у2 = Ь\
пересекаются под прямым углом.
6.20*. Показать, что семейства линий, задаваемых
уравнениями
yr=aX, у* + Х<>==(?,
при любых а и с пересекаются под прямым углом.
В случае, когда требуется найти уравнение касательной к
графику функции y = f(x), проходящей через заданную точку
M(xt, yi), не принадлежащую графику этой функции, абсциссу
Хо и ординату ув точки касания можно определить из системы
уравнений
У\ — Уа = V (*о) (*i — хо),
f (*о) = (/о-
Пример 6.3. В какой точке кривой
0 = ** —блг + б (»)
следует провести касательную для того, чтобы последняя
проходила через точку Mi(1, 1)?
Решение. Составим систему (5):
l-i/o = (2*o-5)(l-*o),
0о = *о-бдго-Ь6.
Подставляя уо из второго уравнения в первое, получаем
квадратное уравнение
Отсюда искомые точки имеют координаты (2, 0J и (0, 6J,
Ответ, (2, 0), (0, 6).
§ 5. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПР01ШОД1ТОТГ 227
С.21. В какой точке кривой
у = ах3 + bx + с
нужно провести касательную для того, чтобы касательная
проходила через начало координат? Исследовать, при каких значениях
a, b и с задача имеет решение.
0.22. В какой точке кривой
у = *г — 5х + 6
нужно провести касательную, чтобы она проходила через точку
М(а, 6)? Исследовать, при каких значениях а к b задача имеет
решение.
6.23. Записать уравнение касательной к кривой
У =■ (* + О/*.
если известно, что касательная проходит через точку М(а, Ь),
Сколько существует решений в зависимости от выбора точки?
Найти эти решения.
624*. Записать уравнение прямой, проходящей чгрез точку
с координатами (1/2, 2), касающейся графика
ff(*)---J- + *
н пересекающей в двух точках график функция
U (х) = <slT=tf,
6.26. В какой точке /ilo кривой y = *j2 х касательная
перпендикулярна прямой 4х -f Ъу -f 2 = 0?
Известно, что равенство нулю дискриминанта квадратного
уравнения означает, что соответствующая парабола касается, оси
абсцисс (прямой у — 0). Аналогичные соображения могут быть
использованы при нахождении уравнений касательных.
Пример 6.4. Найтн те касательные к окружности
х* + у* = 25,
которые параллельны прямом
2* — у + 1 = 0.
Решение. Все прямые, параллельные прямой 2« — у -\-
+ 1=0, описываются уравнением вида у = 2х + с. Условие
пересечения данной прямой и окружности состоит в совместности
следующей системы:
2* + с = у,
х* + f « 25.
8*
22й гл. 9. Производная и ее применения
Подставив у из второго уравнения в первое, нмеем -
х2 -f (2* -f с)2 = 25.
Условие существования единственного решения заключается в
том, что дискриминант последнего уравнения равен нулю. Из
этого условия получаем для с следующие возможные значения:
С) •=> 5 V^ и d = —5 V^.
Ответ. у = 2х + Ь V6". 0 = 2* — 5 Уб".
6.26*. Под каким углом видна окружность
х* 4- у2 = 16
из точки (8, 0)?
6.27. Точка М двигалась по окружности
{х-4)> + (у-&у = 20,
потом сорвалась с нее и, двигаясь по касательной к
окружности, пересекла ось Оде в точке (—2, 0). Определить точку окруж-
иости, с которой сорвалась движущаяся топка.
6.28. Найтн условие, при котором прямая у = kz -f 6 ка«
сается параболы у2 = 2рх,
6.29*. Найти геометрическое место точек, из которых пара- -
бола у =» х* видна под прямым углом.
G.30. Найти угол между касательными к графику функция
у = х*, проходящими через точку с координатами (0, —1),
6,31*. Прямой угол перемещается так, что стороны его все
х1 иг
время касаются кривой —r + 'fr^l- Найти геометрическое
место вершин угла.
G.32. Докажите, что две касательные к параболе у = Xя, про<
1
веденные нз произвольной точки прямой у = — -j-, взаимно пер-
пендикулярны.
6.33. Через произвольную точку оси абсцисс проведены две
прямые, одна из которых касается параболы у *=• хг (и не
совпадает с осью абсцисс), а другая проходит через точку (0, -j)>
Докажите, что прямые перпендикулярны.
6.34. Докажите, что любая касательная к гиперболе у = —
образует равные по величине углы с двумя прямыми «дна нз
которых прохо'днт через точку касания и точку (уй\ -^2), а
другая — через точку касания н точку (— Y2, — -у/2~\
§ 7. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ В МЕХАНИКЕ 229
6.35. Докажите, что отрезок любой касательной к гиперболе
у = —гш заключенной между осями координат, делится точкой
касания пополам.
6.36. Докажите, что площадь треугольника, ограниченного
осями координат и произвольной касательной к гиперболе
»•=—. равна 2.
6.37. Прн каком значении параметра а парабола у = ах3
касается кривой у = 1п х.
6.38. Найтн координаты точки, лежащей на графике функции
у = \ + cos х при 0 < х < п и наименее удаленной от вряуой
х^З+2у + 4 = 0.
§ 7. Приложения производной в задачах механики
Если путь, пройденный телом к моменту времени /,
определяется функцией
</=/('). С)
то скорость движения V в момент времени t равна производной
функции {{():
V-ПО. (2)
а ускорение — производной скорости:
а = 1Г (<)}'. О)
Пример 7.1. Человек приближается со скоростью Ь к
подножию башни высотой А. Какоза скорость его приближения к
вершине башни, когда он находится на расстоянии / от
основания?.
Решение. Обозначим x(t)—расстояние от человека до
подножия башпн в момент времени t. Тогда расстояние y(t) от
человека до вершины башни в момент времени t вычисляется по
формуле^ (/) = УЛа + х* (t). Дифференцируя у[!) но /, получаем
х (0 х' U)
*'(') =
V/i2 + А"2 (О
и, учитывая, что х'(1) = 6. а расстояние от человека до модно-
жия башни — I, имеем
230 ГЛ. 9. ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
Найдя закон движения, вычислить скорость движения в
следующих задачах.
7.1*. Нижний конец лестпнаы длиной 5 м скользит по полу
в направлении от степы, у которой она стоит. Какова скорость
верхнего конца лестницы в тот момент, когда нижний конец
находится на расстоянии 3 м от стены, если скорость нижнего
конца постоянна н равна 2 м/с?
7.2. Человек, приближающийся к вертикальной стене,
освещен сзади фонарем, находящимся на расстоянии / от стены.
Скорость .человека равна о. С какой скоростью увеличивается
его тень, если рост человека ft?
7.3. Точка движется по гиперболе у = Ю/.v так, что ее
абсцисса растет равномерно со скоростью единица а секунду. С
какой скоростью изменяется се ордината, когда точка проходит
положение (5, 2)?
7.4*. По оси Ох движутся две точки, имеющие законы
движения
*, = 100 + 5/, Xi = jl2, <>0.
Какова относительная скорость этих точек в момент встречи (я
дается в сантиметрах, t — в секундах)?
7.5**. Колесо радиуса R катится без скольжения по прямой.
Центр круга движется со скоростью v. В обод колеса вбит
гвоздь. Найти скорость перемещения гвоздя в момент времени к
7.6*. Точка движется с угловой скоростью ш по окружности
радиуса R с центром в начале координат. Какую скорость имеет
изменение абсциссы точки при прохождении ею оси Ох?
7.7*. Тело брошено под углом а к горизонту со скоростью v.
Какова максимальная высота подъема тела?
7.3. Угол а (в радианах), па который повернется колесо за
/ секунд, равен а = ЗР — 12^ + 33. Найти угловую скорость
колеса в момент t = 4 си момент, когда колесо остановится.
7.9*. Два тела движутся иод умом 60° друг к другу; урав-
пепие движения первого тела
S, (*) = /»-2г.
а уравнение движения второго тела
В момент времени t = 0 тела находились о одной точке. С
какой скоростью увеличивается расстояние между телами?
7.10. Лошадь бежнт но окружности со скоростью 20 км/ч.
В центре окружности стоит фонарь, по касательной к окружно-
§ 7. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ В МЕХАНИКЕ 231
cm в точке, откуда лошадь начинает свой бег, расположен за*
бор. С какой скоростью будет перемешаться тень лошадн вдоль
забора в момент, когда лошадь пробежит 1/8 окружности?
7.11**. Ракета движется прямолинейно по закону S(l) =
= IV + аР/2. Через время ti после начала движения от нее
отделяется некоторый предмет, который продолжает двигаться
по инерции. В какой момент времени i и какую новую скорость
V надо придать предмету, чтобы, двигаясь дальше равномерно,
он догнал ракету в момент U, имея при этом одинаковую с ней
скорость? Приведите геометрическую интерпретацию задачи. Ка«
ков закон движения этого предмета?
7.12*. Ракета запускается по прямой из некоторой точки.
Закон движения ракеты S ~ /2/2 (/ ^ 0). В какой момент
времени /о, считая от начала движения, следует отключить
двигатели, чтобы ракета, двигаясь дальше по инерции с набранной
скоростью, оказалась в момент U на расстоянии S\ от
первоначальной точки?
ГЛАВА 10
ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§ 1. Неопределенный! интеграл
Дифференцируемая функция F(x) называется первообразной
для функции f(x) ва данном промежутке, если для всех
значений х из этого промежутка справедливо равенство
F'(x)=f{x). (1)
Если на некотором промежутке F(x) — первообразная для f'(x),
то выражение
\f(x)dx — F(x) + C. (2)
где С —произвольная постоянная (константа питегрнрования),
называется неопределенным интегралом функции f{x) на этом
промежутке.
Основные правила интегрирования:
^ af (х) dx = a ^f (х) dx, (3)
где а — постоянная величина;
J [/. (*) ± /а Ml dx = jj /, {*) dx±^f2 (x) dx; (4)
f (ax + b) dx = — F (ax +b) + C (5)
J
(а Ф 0 и Ь — постояипые).
Таблица неопределенных интегралов;
г „n+i
J*rtd*=-^TT + C- n^-i; (6)
J "^ In | jb 1 Ч- CS (7)
§ I. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 233
\e*dx=*ex + C;
\ sin х dx =» — cos x + О,
\ cos x dx =a sin x 4- C;
(_*£_=, tg*4-C;
J cos2* 5 ^ '
dx . , _
j-t- dgx + C;
\
J^-—|*(т+т)|+«
_-_- = -arctg - 4-C,
д;2 + os a a
fC;
a^O;
o#0,
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
\ -, -=ЯГГ^П 1. С,
J Va2 — *2 о
Вычисление неопределенного интеграла (нахождение
первообразной) дайной функции осуществляется сведением с помощью
правил интегрирования неопределенного интеграла от данной
функции к табличному ннтегрвлу.
Пример 1.1. Найти все первообразные функции
\х"1 - хпУ
f(*)='
УГ
где man — Целые числа.
Решение. Преобразуем f(x) к виду
f(x)°~x2m~ll2 — 2x'n+n-lli + x2n~i<2.
Используй правила интегрирования (3), (4) я формулу (6),
получим
„m+rt+1/2 i I ,2'»+I/2 i Г =
А Т с> L I /О ~
m + n + 1/2 '2/1+1/2
"" 4m -f 1 2/п + 2п + 1 + 4п 4-1
2хшл/Т 4*",+"УГ гх^УГ -
0твеТ- 4/Л+1 2т + 2л+1+ 4«+1 +-.'
dt.
234 ГЛ, 10, ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
Применяя основные правила витегрнровання и таблицу
неопределенных интегралов, найти первообразные следующих фуик-
дни:
и.. /w = <Щ^Р=Е.я ,.2> mmmi^L.
У 4 — x* <V*
1.3*. / CO - * V^1^". 1.4*. f (*) - ~/==£.
U** f ^ " (2*-!)*' "*' ' W = f ^П^.
Упростив подынтегральное выражение, найти следующие
Неопределенные интегралы:
1.7. [ (У^+О^-У? fa
J ^У* + x + V*
W''^(VT-v-)-t(VT-v')
! 9 С A / 2* A,/l±*/£±*l*Ldx
J V (l+x)-^I -fx v д/2
J V . 2 2 У7 ./ V V^ -И л/x-lj
J a; Wl -*s +* — 1
+ •ff+* v*-
V4-* -л/\—х J
ыз. \ -^ . *' ** bL_ dJB.
J (2-*»-5Vl—x2)
l.U. Cf ^-6-64 *» 4*» (2*+1)4
' ' J (д-1/m + Зд;!/")2 _ 12х1"Ч-путя rf*'
(n , . i , 5*2 — 6* + 3 \
lie f (»-* +4"+ ,_/ ) ,
-J
§ I. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
23S
d*.
Vi - * 4* 1/Vl + *
^+2)(^-')-(^-2>(^*0
*« + 5*34- 15* -9 9
1 (О \ X , OX X
' J (*3 — 4x + 3*s -I2) /Xs aX'
tfl—x*
. «... С i * • 21
1.21*. \ 4 cos -5- cos x sin — x dx.
1.22. \ — 4 sin — sin x sin — * dx.
1.23. \ 2 д/2~ cos a sin (-^- + 2a) da.
1.24. \ 2 sin2 (Зя — 2x) cos2 (osi + 2x) dx.
1.26. V ctg Г-т-я — 2лЛ cos 4* d*.
"*$[-(тг+т)—Чтг+т)Ь
1.27. [ [cos2 (45° — x) cos* (60° + x) — соз 75° sin (75°-2.*)l d».
f sin 2x 4- sin Sx — sin Зл:
cos x 4- 1 — 2 sin2 2*
1.29. J [ ctg2 2x_!
2 ctg 2*
cos 4x 4- 1
dx.
cos 8* ctg 4л ] dx.
dx.
1.30. \ . .
J ctg x — tg x
1.31. V sin a sin (x — a) -[- sin2 (—— a J dx.
s[-
1 4- sin 2a
' cos (2a — 2it)ctg (a— — я)
1.33. ^ tg2 д; dx.
4- cosJ a
da,
1.34,
. J ctg3
*&C.
J238 ГЛ. 10. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
§ 2. Задачи на свойства первообразных
Для функции f(x) первообразной, график которой проходит
через точку М(х„, уо), будет функция
G(x) = F(x) + C, (1)
где F(x) — произвольная первообразная f(x), а постоянная С
удовлетворяет уравнению
F(x0) + C—у» (2)
Пример 2.1. Для функции f{x) =cos?x найти ту
первообразную, графнк которой проходит через точку М{п/2, я/4),
Решение. Вычислим неопределенный интеграл от функции
f £х) = cos2 x:
С я j С 1 + cos 2х . 1 . sin 2х , _
^ cosa х dx =» ^ —^ dx=*jx-\ ^— -f С.
Для того чтобы из всех найденных первообразных выбрать веко»
ыую, составим, согласно (2), уравнение
1 я . sin п , „ п
корнем которого является С = 0.
„ _, . 1 , sin 2x
Ответ. F (,х) = y х -\ т—.
2.1. Найти уравнение кривой, проходящей через точку А
(1,2), у которой тангенс угла наклона касательной в каждой
точке в трн раза больше квадрата абсциссы этой точки.
2.2. Найтн уравнение кривой, проходящей через точку Л
(1, 1), тангенс угла наклона которой в каждой точке равен
(удвоенной абсциссе этой точки.
2.3. Найти уравнение кривой, проходящей через точку А
(0, —1), если все ее касательные параллельны прямой у =*•'
«= 5х - 3,
Если графики дифференцируемых функций yt=ft\x) и
у == h{x) касаются друг друга в точке М{хо, уо), то
выполняются соотношения
Ы*о)~Ы*о), (3)
tf(*o) = fz(*o)- (4)
Пример 2.2. Найти все первообразные функции у = х + 2,
касающиеся кривой у = хг.
Ре шеи не. Так как функция у=*х + 2 является
производной любой своей первообразной, то, согласно (4), уравнение
§ 2. ЗАДАЧИ НА СВОЙСТВА ПЕРВООБРАЗНЫХ 237
для отыскания абсднссы точки касания имеет вид
2х = х + 2.
Корень этого уравнения будет х = 2. Значение функции i/ = *3
в точке * = 2 равно 4. Следовательно, из всех первообразных
функций у = * + 2, т. е. функций / (*) ==> у *я + 2* + С,
требуется найти ту, график которой проходит через точку Л4(2, 4).
Постоянную С найдем из условия / (2) = —«4 + 2 • 2 + С =4=>
=*-С=—2.
Ответ. Р{х)=^х* + 2х — 2.
2.4. Найти ту первообразную функцнн /'(*) = х, график
которой касается прямой у = х — I,
2.5. Найти все первообразные фуикцни f\(x) = х2, графики
которых касаются параболы fz{x) = *2 + 1.
2.6. Найти все первообразные функции f\x) = 3/я, графики
которых касаются кривой у = *3.
Если тело движется со скоростью, изменяющейся по закону
0-/(0. (5)
то зависимость пути, пройденного телом, от времени t
представляется в виде
SU)-F[t) + C, (6)
где F(t) — некоторая первообразная функции f{t), а константа С
находится из дополнительных условий.
Пример 2.3. Тело движется прямолинейно со скоростью,
изменяющейся по закону
о =» 21 м/с.
Найти закон движения тела, если известно, что за первые 2 с
оно прошло 15 м. •
Решение. Множество всех первообразных функции v(t)'^,
= 2t будет S{t) =■ Р+С. Согласно дополнительному условию
имеем
- S(2) = 22 + C=15,
откуда получаем С= 11, Таким образом, закон движения тела
будет
3(0-*»+И.
2.7. Материальная точка движется прямолинейно со
скоростью v(t) e-elnfcos./ м/с. Найти уравнение движения точки,
. если прн t == jt/З пройденный путь составляет 17/8 м,
238 ^Л. 10. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
2.8. Первый пешеход вышел из пуншга А со скоростью,
«изменяющейся по закону v(t) =21, а второй в тот же момент вышел
из пункта В, отстоящего от А на 4 км, вслед за первым с
постоянной скоростью Чр км/ч. При каких значениях р второй
пешеход догонит первого? Найти значение р, при котором
пешеходы поравняются только одни ,раз.
§ 3. Определенный интеграл
Определенным интегралом иа промежутке [а; Ь] от
непрерывной функции 1(х) называется приращение F{b) — F(a)
любой первообразной F этой функции иа промежутке [а; Ь] в
обозначается
Ь
\ J (x) dx='F ,(#) — F (а) (формула Ньютона — Лейбница). (1)
а
Здесь а, Ь — нижний н верхний пределы интегрирования
соответственно; ?(л?)— подынтегральная функция. Разность F(b)~ F(a),
стоящая в правой части формулы (1), иногда обозначается
F (*) t
Для того чтобы вычислить определенный интеграл от
функции f[x) на промежутке .[а; 6], необходимо найти любую
первообразную функции и вычислить разность ее значений в цравом
и левом концах промежутка .[а; Ь]. Вычисление определенного
интеграла функции f(x) на промежутке [а; Ь] называется
интегрированием данной функции.
Основные правила интегрирован и л:
ь ь ь
J [/ (*) + g (* )1 dx = J / (х) dx+^g (x) dx; (2)
a a a
b b
[ k! (x) dx = It [f (x) dx;
(3)
a
6 kb+p
J / (kx + p) dx =. JL Ц f(t)di, A^O;
W
ka+p
с
^{ (x).dx = J f (x) dx + ^ .f (x) dx, с s 4a; *.•]. <5)
5 3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 239
Пример 3.1. Вычислить определенный интеграл
Г
cos4 х dx*
Решение. Представим подынтегральную функцию в виде
cos4 х = ( {+с°* 2х V = 1 (1 -Ь 2 cos 2х + cos2 2х) =
1 (i . о „ . I + cos 4*\ 3,1 „ . 1
""TV + s ч ~2 ') =Т + Тcos + ¥cos '
Первообразной функции cos** будет функция
Р U) = 4 * + \ Sin 2* + -— sin 4г.
Вычислим определенный интеграл по формуле Ньютона —
Лейбница:
я/2
\ cos4 x dx = — х + — sin 2д; -J- — sin 4л | J'2 = — п.
a
Ответ. Зя/16.
Вычислить интегралы:
. . f 4x — 2 л/х . ч , Г ,
3.1. \ —ах, <>•*• \ coixsmxdx.
1 О
л
3.3. \ cos * sin 3* dx.
о
Пример 3.2. Вычислить пнтеграл
-18
S л/нй*
3
Решение. Перепишем интеграл в виде
-13
| (,_}.)-*
Восгкшьзовавгансь формулой (4) при- ft = —1/3, р = 2, паха*
дш* нижний и верхний предел» интегрирования' в право* части
240 ГЛ. 10. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
формулы (4):
fta-fP = —4--34-2=1
kb
+ P-(-l8)(-j) + 2 = e
соответственно. Обозначая 2 —5" =' в согласия с формулой (4),
получаем
I_36 + i-=— 33,75.
Ответ. —33,75.
Вычислить интегралы:
8 2
3.4, \ -*L=.. 3.5.* \ -^=.
Ja VS + х/2 Jt V2-AJ/2
6/3 2
3.6*. \ (х-2)д/3* — 1 d*. 3.7*. \ , d* ■■ -г
„J J V^i + Vi-M
9 7/3
3.8. WT^ldA:. 3.9. \ *+' dx.
я/4 1
3.10. \ (sln2f-cos20*#. 3.11. \ i*?Xl)t.
о о
я/2 я/*
3.12. \ sIn*cos3*d;i:. 3.13. \ (tg * + ctg х)~*с1х.
о ■ я/в
л
3..4. $[«.■(£»-£)-«■(■£* + -£)]*;
о
я/3
ЗЛб- \ ['-l-iln-(L + to/2)]rfjt'
n/S
Если, подынтегральная фуакция представляет собой выраже*
вне, содержащее переменную под знаком абсолютной, величины,
§3, ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 241
то вычисление определенного интеграла с данными пр.еделамп
ннтегрнроваиия можно свести к вычислению суммы определенных
интегралов с подынтегральными функциями, уже не
содержащими переменную под знаком абсолютной величины.
Пример 3.3. Вычислить
6
$(U-3|+|l-*|)*t.
1
Решение. Подынтегральную функцию можно представить,
в виде
{ 4-2*. *<1,
f(x) = \ 2, Кх<3,
{ 2х—4, *>3.
Воспользовавшись свойством (5) определенного интеграла,
получаем
з 5
$(|х-3|+|1-*1)** + $(|*-3|+|1-*1)«»*-
1 3
3 В
= f 2dx+^ (2*-4)d* = 2*|?-f(*,-'t*)l3 = 4+8=.12.
I 8
Ответ. 12.
Вычислить интегралы:
I 2
3.16, [ У*2 - 2х + 1 dx. 3.17. \ У*2-2*+ \dx.
-I U
я/2 я
3.18.
3. \ У1 — cos2 x dx. 3.19. \ yi —sin2x dx.
-я/4 0
Б
3.20. \ Wx + 2 УгТ^1 + У* - 2 угТ^Т) dx.
з
з
3.21. \ Г > ' ■ -!- У*2 - l.t -1- 4^ d*.
J \ Ух3 + 4* + 4 У
1/2
-1/2
ЗЯ/2 ЗЯ/2
8ЛЗ. С yi^eos2xrf*. 8.24, [ -у/1 + cos 2*dx.
242
ГЛ. ГО ПЕРВООБРАЗНАЯ Й ИНТЕГРАЛ
§ 4. Интегралы с переменным верхним пределом
Интеграл с переменным верхним пределом
Л
F(x)~\i(t)dt (1)
— ато та первообразная функции f(x) \F'{x) = f{x)), значение
которой в-точке а равно нулю.
Пример -4.1. Найти наибольшее и наименьшее значения
функции
х
О
на промежутке [2; 3].
Решен не. Найдем критические точки функции F(x), Так
как F{x) — первообразная для функции х + 1, то F'{x) = х + 1]
функция F'(x\ не обращается в пуль иа промежутке [2; 3] it
является положительной. Следовательно, наибольшего значения
функция достигает па правом конце отрезка, а наименьшего —
иа левом:
з
max
ХБ
s,'M-'(»>-jtf+i>«-(4+0t-7*
2
mln F {x)=F {2)=[v + \) dt~(-£- + t)f=>4.
xei»3i o_
Найти наибольшие н наименьшие значения функций на
урванных промежутках!
х
4.1. F {х) = \ Ыа I dt, х е= Гос ~^.
о
х
4.2. F (д-) = { (21 - 5) Л. л: е 1-1; 31.
о
4.3. F (х) — | (<а — 5/ + 6) d/, х s"{0, 4}.
§ 4. ИНТЕГРАЛЫ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ 243
4.4, Найти наибольшие и наименьшие значения фут«*и
'(*)«-$Ш«к
1
на промежутке —у» -к\-
4,5, Записать уравнения касательных к графику функции
А
F (*) =* \ (2/ - 5) dt
в точках, где он пересекает ось абсцисс.
4.6. Найтн абсциссы точек пересеченна графиков функц»
х х
F, (х) =» $ (И - 5) Ы< Рг (*) — J (й - 5) Л.
4! 3
4.7. Найтн точки пересечения графиков функций
X X
F, (а) = \(21 - 5) Л, F, (х) =Л 2/ Л,
2 О
4.8. Найтн ту первообразную от функции
f (*) = $ (2/ - 5) d/,
график которой проходпт через начало координат.
4.9. Для графика функции
*
f(*)-$2|/|*K
О
пайтн касательные, параллельные биссектрисе первого
координатного угла.
Пусть материальная точка движется прямолинейно со
скоростью v\t)', А—некоторая точка на траектории движения
материальной точки. Если в момент времени t = jfo расстояние
между движущейся точкой н точкой А равно So, то в любой
момент времени t > U расстояние от движущейся точки до
точки А вычисляется по формуле
t
S«)= ^v(x)dx + S0. (2)
244 ГЛ- 10' ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
Пример 4.2. Скорость движущейся прямолинейно тачки
меняется по закону о (t) = Л/t -\-2t (км/ч). В момент времени
t = 1 q точка находилась в 5 км от пункта А, расположениого
на траектории движения точки. На каком расстоянии от пунк-
та А окажется точка в момент t = 3 ч?
Решение. Координату точки как функцию времени
представим, согласно (1) и (2), в виде
t
Вычислим -значение S(t) при t = 3:
з
S (3) = J (Vr + 2t) dl + 5 = (-^ + /a) [ + 5 =
= 2V3" + 9-|--l+6 = I2i- + 2V3'.
Ответ. На расстоянии f 12 — + 2^3 J км от пункта А.
4.10, Скорость движения тела пропорциональна квадрату
времени. Найтн зависимость между пройденным расстоянием и
временем, если известно, что за первые 3 с тело прошло 18 см,
а движение началось в момент времени t = 0.
4.11*. Сила, действующая на материальную точку, равномерно
меняется относительно пройденного пути* В начале пути она
равнялась 100 Н, а когда'точка переместилась на 10 м, сила
возросла до 600 Н. Найти функцию, определяющую зависимость
работы от пути.
4.12. Тело движется равноускоренно, причем известно, что
скорость его к моменту t ■= 2 с достигла величины 4 м/с, а
пройденный путь стал равен 3 м. Найти закон движения тела.
4.13. При постоянном ускорении тело за первую секунду
преодолело расстояние 4 м от пункта А, а за первые 3 с
расстояние между ними возросло до 16 м. Найти зависимость
расстояния, пройденного телом, от времени, «ели известно, что при
t.ns 0 тело находилось в пункте Л.
§ 5. Задачи йа свойства интегралов
5.1. Решить неравенство
§ 5. ЗАДАЧИ НА СВОЙСТВА ИНТЕГРАЛОВ 246
5.2, Решить неравенство
х я
V5* — 6 — хл -}- —- иг > х \ sin5 x dx.
о о
Б.З. Решить неравенство
х лр
У*2 — х — 12 —\dz<x\ cos 2x dx.
о о
Б.4. Найти такие числа А и В, чтобы функции вида
f {x) = A sin nx + В
удовлетворяла условиям
ГО)-8, J/(*)«fr-4
о
Б.5. Найти все числа а (а > 0), для которых
а
^ (2 — 4* + 3*V*<a.
о
5.6. Найти вес решения уравнения
а
cos (* + а2) Лс = sin а,
о
принадлежащие промежутку [2; 3].
5.7. Две точки начинают двигаться по прямой в один н тот
же момент из одного и того же места в одном направлении,
Скоростн точек равны fi(0=3<2 м/с, кг(/) ■= 2( м/с соответ*
ственно. Через сколько секунд расстояние между ними соста*
вит 216 м?
5.3. Доказать, что любая первообразная почетной
непрерывной функции, определенной на промежутке [~-а; а], есть
функция четная.
5.9. Доказать, что четная непрерывная функции,
определенная па промежутке [—а; а], имеет иа этом промежутке по
крайней мере одну нечетную первообразную.
5.10. Справедливо ли следующее утверждение: для того
чтобы любая первообразная непрерывной функции f(x) была четиой
ца промежутке [—а; а\ необходимо и достаточно, чтобы
функция f{x) была нечетной на этом промежутке?
246
ГЛ. 10. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
6.11. Найти значения А, В, С, прн которых функция вида
f (х) = Ах1 + Вх + С
удовлетворяет условиям
ГО)-8, /(2)+/"(2) = 33, J/(x)<fc-l.
о
6.12. .Найтн все значения а нз промежутка [0; 2я],
удовлетворяющие уравнению
п
\ sin х dx = sin 2«.
П/2
5.13. Наптн положительные значения а, которые
удовлетворяют уравнению
а
[ (3*5 + Ах — 5) dx= о3 - 2.
5.14. Найти все значения а из промежутка [—я; 0],
удовлетворяющие уравнению
2а
sin а + \ cos 2* d* = 0.
§ 6. Вычисление площадей фигур
Фигура, ограниченная графиком непрерывной функции f(xy
(f(x) 5= °)> прямыми х = а, х = Ь н осью ОХ, называется
криволинейной трапецией. Ее площадь вычисляется яо формуле
Ь
S =
а
V
\f(x)dx. (1)
Если для всех х нз промежутка [а; Ь] выполняется условие
Ь'М 5»М*)Ш*)' — №0 5*0), то площадь фнгуры,
ограниченной графиками непрерывных функций y—ft(x), у — fi{x) и
прямыми х = а, х = Ь, вычисляется по формуле
ь
S-$lM*)-/i(*)]<fc. (2)
§ в. ВЫЧИСЛЕНИЕ ПЛОЩАДЕП ФИГУР 247
Если для всех у из промежутка [с; d] выполняется условие
М>гТ</) &■ tyi'lil) falsi) — tyilsi) ^ 0)> то площадь фигуры,
заключенной между прямымн у — с, у = d и графиками непрерывных
функций ж = $!.((/), ж е=з tyi\y), вычисляется по формуле
d
S-$(*.(*)-*1<»)М*. (3)
с
Пример 6.1. Найти площадь фигуры, ограниченной
линиями
ж = 0. ж» я/2, f i (ж) =» sin х, fi (ж) ■- cos ж.
Ре шеи не. Поскольку знак разности f*'(*)—М*У на
промежутке [0; я/2] не остается постоянным, то разобьем этот
промежуток на области, где эта разность сохраняет знак. Для
этого составим уравнение
Ы*)-М*) = о.
единственным корнем которого, принадлежащим промежутку
[0; л/2], является точка ж —. я/4. Так как
sin х > cos ж при ж е 1я/4; я/2],
sin ж < cos ж при ж е [0; я/4),
то, согласно (2), получаем
я/4 я/2
S=\ (cos ж — sin ж) с/ х + \ (sin ж — cos ж) </ж =
0 П/4
= (sin ж + cos ж) |"/4 + (— cos х — sin ж) |£^ =•
= (V2" - 1) + (-1 + V2) - 2 (у§Г - I).
Ответ. S = 2(V2"— 0..
Заметим, что, используя симметрию фигуры относительно
осн х = л/4, можно было бы вычислить площадь по формуле
я/4
S = 2 V (cos ж — sin ж) dx. <
в
Вычислить площади фигур, ограниченных указанными
линиями:
6.1. <, = жа + ж, у — х+1.
6.2. у = — 2ж2 + Зж + 6, (/ = ж-т-2.
6.4 (/ — О, у =• 20 — 2ж2 — 6*.
6.4. у*=хг, у = \Jx, у=0, х =» 2.
6.5. //=1(1/2)*, ж — 20 +2 = 0, ж«=»2.
248 ГЛ. 10. ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
в.6. y—ix — x1, у — х =»0.
6.7. 0 = 5/*, 0 = 6 — х.
6.8. I/ = х\ 0 = 1 /х, х = 2.
G.9. 0 = ** + 1. // =» - *2 + 3.
в. 10. у = I /cos2 х. v — 0, д; = 0, * = я/4.
6.11. 0 = 2*. 0 = 2, * = —1.
6.12. ху=*7, // = 0, *=4, л: = 12.
G.I3. 0=>(* — I)2, 0 = *+ 1.
6.14. 0=_х24-1.д;4- 1, 0 = 2"*, х-=2(*<2).
6.15. i=l, x = 2, 0=0, log2* + log20=O.
6.1G. 0 = 2.*2 +1. 0 = х + -2, 0 = 1,5.
0.17. 0 = 2V, 0 = 4*. х = 1.
G.18. 0 = ж2, 0 = 2 V^<.
6.19, 20*=~16 + л:г, 0=.б.
в.20. 0 = -1 + 8л:2 - х«, 0 «= 15, л- = I (х > I).
6.21. 0—1/(1 + *»), 0 = *V2.
G.22. 30 = — хг + 8.V — 7, 0 + 1 = 4/(* — 3).
6.23*. 0 « V*. У =■ V4 — 3*. 0 =>0.
6.24*. Найти площадь фигуры, множество точек которой
удовлетворяет системе неравс-пств
**+**«£ Л г>0,
* — 0 < 0. 0 > 0.
6.25*. Вычислить площадь плоской фигуры, ограниченной
частями линий тах(л:, 0) = 1 н *а + 0г= 1, лежащими в первом
квадранте)
. . f х, если х^ху,
max (*, 0)=< "S
■" 10, если х < 0.
6.26. Найтн площадь фигуры, ограниченной графиками фупгс-
ций у = х\ у =» 2х — ж2.
Если функция 0 = f(*) на промежутке [а; 6] строго
монотонна, то вычисление плошади, ограниченной графиком функции
па этом промежутке н осью Ох. иногда удобно свести к
вычислению площади, ограниченной графиком обратной функции х =ч
<= #(0) на промежутке [с; d] и осью Оу, где
c = mln[f(a);/(6)],
• d=max[f{a);f(b)}.
Пример 6.2. Вычислить площадь фигуры, ограниченной
графиком функции у = In x, прямой «=2в осью ОХ.
§ G. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ФИГУР 249
Р е m е и н е. Функцией, обратной к у = Ых, является
х =■ е". Из рнс. 10.1 видно, что площадь заштрихованной
фигуры Si равна разности площадей S — прямоугольника со
сторонами 2 и In 2 и S2
—криволинейной трапеции О ABC.
Согласно (3)
1п2
,!п2
Sa=J e»dy = ey\l
1.
пла-
= е'п2_е0_2 — 1
S=-2In2.
Таким образом, искомая
щадь есть
S, = S — Sj=>2!n2— I
Найтн площади фигур, ограниченных графиками функций;
6.27. у = arcsln х, х = 1, у = 0.
6.28. у = агссоз х, х = 0, у = 0.
Площади некоторых фигур легко вычисляются, если
использовать известные значения площадей частей круга радиуса R.
Пример 6.3. Вычислить площадь фигуры, ограниченной
линиями
у = л/\~х', i/ = 0.
Решение. Возводя обе части уравнения у = л/1—х3 в
квадрат, получаем уравнение окружности единичного радиуса;
уг + хг = 1. Таким образом, график функции у = Vl — *
представляет собой верхнюю полуокружность радиуса 1.
Следовательно, искомая площадь равна половине плотадн круга
единичного радиуса.
Найтн площади фигур, ограниченных линиями:
з
6.29*.
+
I.
6.30*. у* + х2 + 2х = 0.
6.31**. В декартовой системе координат Oxt/ фигура F
ограничена осью Ох, кривой у = 2Х2 и касательной к этой кривой;
абсцисса точки касания равна 2. Найтн площадь фигуры F.
0.32. Вычислить площадь фигуры, ограниченной параболой
у = х2 — 2х + 2, касательной к ней в точке М (3, 5) н осью
ординат. Сделать рисунок.
6.33. Вычислить площадь фигуры, ограниченной линиями
у ■= 1/*+ 1, х ■=» 1 и касательной, проведенной в точке (2J3/2)
к кривой у = 1/х+ 1,
250 **л- 10- ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ
6.34*. Найтн площадь фигуры, ограниченной линией у =
с= х* — 4х + 5 и прямыми, касающимися ее в точках с
абсциссами х,== 1 н хг = 4.
6.35. Из точки (3/2, 0) к параболе у = 2х* — 6х + 9
проведена касательная, образующая острый угол с положительным
направлением осп Ох. Определить площадь фигуры, заключенной
между параболой, осью Ох, осью Оу и этой касательной.
G.36**. Какую часть площади квадрата отсекает парабола,
проходящая через две соседние вершины квадрата и касающаяся
середины одной нз его сторон?
G.37*. Какую часть площади полукруга отсекает парабола,
проходящая через концы диаметра полукруга и касающаяся
окружности в точке, равноудален поп от концов диаметра?
6.38*. Найти площадь фигуры, ограниченной прямой у =>
= —8л; —46 и параболой у = 4л;2 + ах + 2, если известно, что
касательная к параболе в точке х = —5 составляет с осью Ох
угол я — arctg 20.
0.39*. При каком значении а площадь фигуры, ограниченной
4
линиями у = \jx, у = \/(2х— I), х = 2, х = а, равна 1п —=•?
<у5
6.40. При каком значении а прямая у = а делнт площадь
фигуры, ограниченной линиями у = Q. у = 2-\-х — хг, пополам?
6.41*. При каком значении параметра а>0 площадь
фигуры, ограниченной кривыми у = a -\fx, у=у2—х и осью
Отбудет равна числу 6? При каких значениях b задача имеет решение?
6.42*. Найтн, прн каком значении о площадь фигуры,
ограниченной кривой у = sin 2х, прямыми х = л/6, х = а и осью
абсцисс, равна 1/2.
6.43*. Найти все значения параметра 6 (&>0), прн которых
площадь фигуры, ограниченной кривыми у = 1—х1 п у = Ъх*-,
будет раона о. При каких значениях а задача имеет решение*
6.44*. Через точку (.v0, i/o) графика функции (/= дЛ + cos 2x
провести нормаль к этому графику, если известно, что прямая
х = ха делит площадь, ограниченную данной кривой, осью Ох и
3
.прямыми х = 0 hx = -j п, на равные части.
§ 7. Задачи па нахождение наибольших
(наименьших) площадей фигур
1£сли в задаче требуется найтн положение кривых,
зависящих от одного илн нескольких параметров, при котором площадь
фигуры, ограниченной этими кривыми, максимальна
(минимальна), то следует сначала составить функцию, выражающую завн-
§ 7. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИБОЛЬШИХ ПЛОЩАДЕП 251
снмость этой площади от параметров, а затем решать задачу
на отыскание наибольшего (наименьшего) значения этой
функции на области возможного изменения параметров.
Пример 7.1. НайтИ все значения параметра а (о > 1),
при которых площадь фигуры, ограниченной прямыми у = 1,
у = 2 и кривыми у = а&, у = — ахг, будет наибольшей.
Решение. Вычислим знамение площади при
фиксированном значении а. В данном случае удобно вычислять площадь,
считая у независимым переменным. В силу симметрии парабол
у => ах2 и у=>~ъ ах2 относительно оси Оу площадь фигуры,
лежащей в полуплоскости х > 0, равна площади фигуры,
лежащей в полуплоскости х < 0, и поэтому искомая площадь будет
равна удвоенной площади фигуры, ограниченной линиями
х = л/у/а, х = л/2у/а, у = \, (/ = 2:
»«-i(V¥-V*K
_2
у;
2 4(V2"~ \)(2л/2-\), где ве[1;«).
л/а 3
Очевидно, что функция S(a) монотонно убывает на промежутке
[I; со) и наибольшее значение принимает иа левом конце
промежутка [I; оо), т.е. прн а = 1.
От вет. а = 1.
7.1. При каком значении а площадь, ограниченная кривой
у = (fix2 + ах + 1 и прямыми у = 0, ж = 1, будет наименьшей?
7.2. Найти все значения параметра а (а > 0), при которых
, .1 (о2 — ах)
площадь фигуры, ограниченной пряыоп у =» ■ . , j - и пара-
й . (*а + 2а.* + За2) л л
болой у = г—ц-—5 , будет наибольшей.
7.3. Прн каком положительном а площадь S криволинейной
трапеции, ограниченной линиями
у=1Г + ~хг* у=,°' х°=>а, х = Ча,
принимает наименьшее значение?
252 ГЛ. 10. ПЕРВООБРАЗНАЯ К ИНТЕГРАЛ
7.4*. Обозначим через S(k) площадь, заключенную между
параболой у, = х* + 2х — 3 н прямой уг=кх + 1, Найти S(— 1)
в вычислять наименьшее значение S(k).
Пример 7.2. Касательная к параболе у = х1 проведена
так, что абсцисса х0 точки касания принадлежит промежутку
[I; 2]. Определить хо, при котором треугольник, ограниченный
касательной, осью ордннат.и прямой у^х\, имеет наибольшую
площадь.
Решение. Уравнение касательной в точке хц для функции
у = х* имеет вид у — х$ = 2х0 (х — х0). Ордината точки
пересечения касательной и оси О у равна
в площадь искомого прямоугольного треугольника вычисляется
по формуле
с. , ч *« \*0 + *о) 3
S(*b)e § =■
Потребуется найтн наибольшее значение S(*o)' на промежутке
[I; 2]. Очевидно, что функция S{xa) возрастает на этом
промежутке, п, следовательно,
max S (х„) = S (2) =» 8.
х,е[и 2|
Ответ, хо = 2.
7.6. Касательная к графику функции y^ylx* такова, что
абсцисса Ха точки касания принадлежит промежутку [1/2; 1].
При каком значении хц плошадь S(*0) треугольника,
ограниченного этой касательной, осью Ох и прямой х = 2, будет наи*
меньшей и чему равна эта наименьшая площадь?
7.G*. Криволинейная трапеция ограничена кривой у = хъ + 1
я прямыми х = 1, * = 2. В какой точке данной кривой с
абсциссой хб[1| 2] следует провести касательную, чтобы она
отсекала от криволинейной трапеции обычную трапецию
наибольшей площади?
7.7*. При каком значении параметра а площадь фигуры,
ограниченной осью абсцисс, графиком функции у = х3 + Зх2 +
Ч-х + а и прямыми, параллельными оси ординат я
пересекающими ось абсцисс в точках экстремума этой функции, будет паи*
меньшей?
7.8*. Для каких значений а из промежутка [0; 1] площадь
фнгуры, ограннченной графиком функцнн у =* f (x) н прямыми
к в 0, х = 1, у = f (а), имеет наибольшее в для каких наныень-
S 8. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ 263
шее значенне, если f (х) = ха + Зх& (а, В е R, причем а > 1. В >
> 1)?
7.9*а Для каких значений а площадь фигуры, ограниченной
Xs
графиком кривой-^ х3-\-а, прямыми - х = 0, х = 2 н осью
Ох, достигает своего минимума?
7.10*. Для каких значений а из промежутка [0; 1] площадь
фигуры, ограниченной графиком функции f(x) н прямыми х = 0,
х = 1, y = f(a), имеет наименьшее и для каких ианбольшев
значенне, если / (х) = Vl — х1?
7.11*. При каких значениях а площадь фигуры, ограниченной
прямыми x=Xi, х=хз, графиком функции </=|sin x + cos x — а\
и осью абсцисс, где хл и Хг — два последовательных экстремума
функции /(x)=»V2 sln (* + я/4). будет наименьшей?
§ 8. Вычисление объемов тел
Объем V тела, полученного в результате вращения криво-
линейной трапеции, ограниченной линиями у = f(x) (J(x) > 0),-
х = а, х = Ь \Ь> а), вокруг осн Ох, вычнсляется по формуле
6
V = n^ft(x)dx. (1)
а
Объем V тела, образованного вращением криволинейной
трапеции, ограниченной графиком функции *_=<p(i/), (<р(</) ^s 0),
прямыми у = с, у = d (rf > с) н осью Оу, вокруг осн Оу,
вычисляется по формуле
&
V = 7t\<t*(y)dy. ^ (2)
с
Пример 8.1, Вычислить объем тела, образованного враще-
иием одной аркн синусоиды (график функции у = sin x на
промежутке [0; п\) вокруг оси Ох.
Решение, По формуле (1) находим
я я
V = п \ sin2* dx = n \ g dx<=
( 1 , sin 2x \ Iя' 1 1 .
О т в е tv я2/2« ■ • •• - j . . . ,. , ., •
J54. ГЛ. Ж ПЕРВООБРАЗНАЯ И ИНТГЕГМЛ
8.1. Вычислить объем тела, образованного вращением вокруг
оси абсцисс криволинейной трапеции, ограниченной гиперболой
ху = 2, пряными х = 1, х = 2 н осью абсцисс.
8.2*. Вычислить объем тела, образованного вращением
вокруг осн абсцисс фигуры, ограниченной параболами уг = х,
у = хг.
8.3. Ценная лилия у= {е*+е-х)/2 вращается вокруг оси
абсцисс. При этом получается поверхность, называемая
катеноидом. Вычислить объем тела, образованного катеноидом в двумя
плоскостями, перпендикулярными оси абсцнсс и отстоящими от
начала координат соответственно на расстояния а и Ь.
8.4*. Вычислить объем тела, полученного от вращения
фигуры, ограниченной параболой у=2х — х* и осью абсцисс,
вокруг осн ординат.
8.6*. Найти объем тела, полученного от вращения
криволинейной трапеции, ограниченной линиями у = arcsin к, у = я/2 н
х = '0, вокруг осн Оу.
8.6*. Найти объем тела, полученного вращением фигуры,
ограниченной линиями у-=\п% у = In х, у =» 0 и х = 0.
вокруг оси Оу.
§ 9. Приложения определенного интеграла
в задачах физики и механики
Вычисление пути. Путь S тела, движущегося со
скоростью V{t), за время, прошедшее от момента tt до момента h,
вычисляется по формуле
U
S-J 7(/) Л. (1)
h
Пример 9.1, Тело движется прямолинейно со скоростью
о (/) = 2/2 - t + I (м/с).
На*тн путь, пройденный за первые 5 с.
Ретн-еои-е. Согласно (I) имеем
Б
Я3 *- . ,.5
10 '
и
S(t) = y2t*-t+\)dt i-_T + fg
5
Ответ. 75-5- м,
250 25 , е _с б
в.I. Тело движется прямолинейно со скоростью f(f)=.
2t4- а (м/с). Найти значение а, если известно, что *а проме-
? 9. ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 0
жуток времени от U = 0 до t2 =» 2 с тело прошло путь длиной
40 м.
9.2*. Тело движется прямолинейно со скоростью и =
= \2t—Р (м/с). Найти длину пути, пройденного телом от
начала движения до его остановки.
9Л. Два тела начали двигаться по прямой в один в тот же
момент из одной точки в одном направлении. Одно тело
двигалось со скоростью f) (t) = 3/г + 2г (м/с), другое — со скоростью
va(t) = 2t (м/с). Какое расстояние будет между телами через
6 с?
9.4. Точка движется прямолинейио под действием постоя»
ной силы с ускорением 2 м/с2 и с нулевой начальной скоростью.
Через 3 с после начала движения сила прекращает действовать
и точка начинает двигаться равномерно с набранной к этому
моменту скоростью. Найти закон движении точки S(t).
Если материальная точка движется вдоль оси Ох под
действием силы F(x), зависящей от координаты х, то работа силы
по перемещению материальной точки из а в b (Ь > а)
вычисляется по формуле
ь
А = \ F (х) dx. (2)
а
'' Пример 9.2, На материальную точку действует сила,
которая линейно зависит от пройденного пути. В начале движения
она составляет 100 Н, а когда точка переместилась на 10 м,
сила возросла до 600 Н. Найти работу, произведенную этой
силой иа пройденном пути.
Решение. Из условия следует, что сила F(x),
действующая иа точку, меняется по закону F(x) <■= ах + Ь, где
параметры а и Ь находятся нз условий
F (0) = 100, Ъ« 100, Ь = 100,
или или
Г(10) = 600, 100а + 100 = 600, а = 50.
Таким образом, F(x) = 50л; -{- 100 н работа силы на прой-*
деином пути, согласно (2), равна
ю
А = [ (50* + 100) dx = 25*а + 100* |0° « 25 • 100 + 100 • 10 = 3600.
о
Ответ, 3500 Дж.
ЭДф ГЛ. 10. ПЕРВООБРАЗНАЯ И ИН1ЕГРАЛ
9.5*. На материальную точку действует сила, которая
меняется обратно пропорционально квадрату расстояния до
некоторого объекта. Известно, что она составляла 1 Н в момент, когда
.расстояние до объекта было 2 м. Вычислить работу этой снлы
по переносу материальной точки из пункта, находящегося'.иа
расстоянии 10 м от объекта, до пункта, Находящегося на рас»
стоянии 3 м.
9.6*. Вычислить работу, совершаемую при сжатия пружнпы
иа 15 см, если известно, что действующая сила пропорциональна
сжатию .пружины и что для сжатия иа 1 см необходима сила
#0Н.
ГЛАВА 11
ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
§ 1. Задачи на движение
Система уравнений, которую необходимо составить на осно
ваиии условия задачи на движение, обычно содержит следующие
величины; расстояние, которое будем обозначать буквой S;
скорости движущихся тел, которые будем обозначать буквами и, о,
w, ... (нли буквами, снабженными индексами: vi, v2, ...);
время, которое будем обозначать буквами t, Т. В случае, если
движение равноускоренное (или равиозамедлеииое), ускорение
будем обозначать буквой а.
Равномерное движение по прямой. Примем
следующие допущения:
1. Движение на отдельных участках считаетси равномерным)
при этом пройденный путь определяется по формуле S = vt.
2. Повороты движущихся тел считаются мгновенными, т.е.
происходит без затрат времени; скорость при этом также
меняется мгновенно.
3. Если тело движется по течению реки, то его скорость W
(относительно берега) слагается из скорости тела в стоячей воде
и (собственной скорости тела) и скорости течения4 реки v:
w =» и + v. Если тело движется против течении рекн, то его
скорость (относительно берега) w = и — v. Если в условии задачи
речь идет о движекин плотов, то полагают, что плот движется
со скоростью течения реки.
В задачах на равномерное движение иногда встречается
условие, состоящее в том, что либо два тела движутся навстречу
друг другу, либо одно тело догоняет другое. Если прн этом
расстояние между телами равно S, а скорости тел равны fiHtii, toi
1) при движении тел навстречу друг другу время, через ко-
S
ffopoe они встретятся, равно ———;
2) прн движения тел в одну сторону (vt > »г) время, че-
S
рез которое первое тело догонит второе, равно —_ ■.
9 А. Г. ЦьШКЕЯ, А. И. Пинский
258 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЙ УРАВНЕНИИ
Пример 1.1. Из города А в город В выезжает
велосипедист, а через три часа после его выезда нз города В выезжает
навстречу ему мотоциклист, скорость которого в трн 'раза
больше скорости велосипедиста. Велосипедист и мотоциклист
встречаются посередине между А л В. Если бы мотоциклист
выехал не через три, а через два часа после велосипедиста, то
встреча произошла бы ка 15 км ближе к Л. Найти расстояние
между А в В.
Решение. Обозначим искомое расстояние между пунктами'
А и В через S км, скорости велосипедиста и мотоциклиста —
через vB км/ч в Ум км/ч соответственно. Запишем условия задачи н
уравнения, соответствующие этим условиям, в виде следующей
таблицы:
Условие задачи
Уравнение
Скорость мотоциклиста в три раза
больше скорости велосипедиста
Велосипедист я мотоциклист
встречаются посередине между А а В,
причем мотоциклист выехал нз В на 3 м
Позже, Чем велосипедист нз города А
Если бы мотоциклист выехал через
2 ч после велосипедиста, то встреча
произошла бы на 15 км ближе к А
-L=JL + 3
4-« т-+»
+ 2
Используя первое уравнение, второе и третье уравнения
можно ааписать в виде
5 S
2ов
S-30
6о
S + 30
f 3,
2uB
6wB
+ 2.
Из первого уравнения этой системы получаем v0 = S/9.
Подставляя во второе уравнение системы ив = S/9, получаем
уравнение для нахождения величины S:
В^Ж = 2^8:
180.
Ответ. Расстояние между городами А а В равно 180 км.
Пример 1.2. От пристани отправился по течению реки
плот. Через 5 ч 20 мин вслед за плотом от той же прнстанн
отправилась моторная лодка, которая догнала плот, пройдя 20 км.
Какова скорость плота, если известно, что собственная скорость
моторной лодки больше скорости плота на 9 км/ч?,
§ I. ЗАДАЧИ НА ДВИЖЕНИЕ
259
Решение. Обозначим собственную скорость лодки (т. е.
скорость в стоячей воде) через v» км/ч, а скорость течения
реки — через «р км/ч. По условню аадачн собственная скорость
моторной лодкн больше скорости плота на 9 км/ч:
ол — ор = 9.
Моторная лодка, двигаясь по течению реки, прошла 20 км за
время 20/(ол + ор); плот прошел те же 20 км за время 20/Ор.
Так как время, за которое плот проплыл 20 км, на 5 ч 20 мни
(т.е. иа 16/3 ч) больше времени, за которое то же расстояние
проплыла моторная лодка, то
20 20 16
Ор ол + v p 3
Таким образом, решение задачи сводится к решению системы
"л — "р = 9,
20 20 16
Ор "л + Ор 3
Из первого уравнения получаем ол = ор-|-9- Подставляя во
второе уравнение vx = vf 4- 9, получаем уравнение для
нахождения о„:
Решая последнее уравнение, находим «„ = 3, (Второй корень
уравнения vf = —45/8 не подходит по смыслу задачи.)
Ответ. Скорость течения реки (а также и скорость плота)
равпа 3 км/ч.
1.1. Пароход прошел 4 км против течения рекн, а затем
прошел еще 33 км по теченню, аатратив на это один час Найти
скорость парохода и стоячей воде, если скорость рекн равна
6,5 км/ч.
1.2. Катер вышел одновременно с плотом, плывшим по
течению реки, и прошел по течению реки 13 -г- нА, а затем, ие
останавливаясь, 9— км в обратном направлении, где и встретился
с плотом. Найти, во сколько раз собственная скорость катера
больше скорости течения.
1.3. Два автомобиля выехали одновременно из одного пункта
в одном направлении. Первый автомобиль едет со скоростью
40 км/ч, скорость второго составляет 125 % от скорости первого.
Через 30 мяв из того же пункта в том же направлении выехал
0*
260 ГЛ. П, ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
третий автомобиль, который сначала обогнал первый н через
1,5 ч после этого обогнал второй. Какова скорость третьего
автомобиля? '
1.4. В соревнованиях по бегу на дистанции 120 м участвуют,
три бегуна. Скорость первого из них больше скорости второго.иа
1 м/с, а скорость второго равна полусумме скоростей первого н
третьего. Определить скорость третьего бегуна, если известно,
что первый бегун пробежал дистаицню иа 3 с быстрее третьего.
1.5. Искусственный водоем имеет форму прямоугольника .о
разностью сторон в 1 км. Два рыбака, находящихся в.одной вер*,
шине этого прямоугольника, одновременно отправились в пункт,
расположенный в противоположной вершине. Прн этом один ры>
бак поплыл напрямик на лодке, а второй пошел пешком вдоль
берега. Определить размеры водоема, если каждый рыбак
передвигался со скоростью 4 км/ч и один иа ннх прибыл к месту
назначения на 30 мин раньше второго.
1.6. Два велосипедиста выехали одновременно из двух мест,
отстоящих одно от другого на 270 км, и едут навстречу друг
другу. Второй проезжает в час на 1,5 км меньше, чем первый, и
встречается с ним через столько часов, сколько километров в чао
делает первый. Определить скорость каждого велосипедиста.
1.7. Турнет проплыл по реке на лодке 90 км, а затем прошел
пешком 10 км. Прн этом на пеший путь было затрачено иа 4 ч
меньше, чем на путь по реке. Если бы турист шел пешком
столько времени, сколько он плыл по реке, а плыл по реке столько
времени, сколько шел пешком, то этн расстояния были бы равны.
Сколько времени он шел пешком н сколько плыл по реке?
1.8. Расстояние между двумя городам» равно S км. Два
автомобилиста, выехав из этих городов навстречу друг другу,
встретятся на полпути, если первый выедет на t ч раньше
второго. Еслн же онн выедут одновременно навстречу друг другу о
теми же скоростями, то встреча произойдет через 2t ч. Опреде»
лить скорость каждого автомобиля, если считать, что скорости
.постоянны на всем путн. ■
1.9. Из города А в город В, расстояние между которыми
120 км, на мопеде отправился курьер. Через час после этого из Л
на мотоцикле выехал второй курьер, кбторый, нагнав первого н
передав ему поручение, немедленно с той же скоростью двинулся
обратно и возвратился в Л в тот момент, в который первый
достиг В. Какова скорость первого курьера, если скорость второго
равна 50 км/ч?
1.10. Из порта А в порт С отправился пароход, который
должен по пути пройти мимо маяка В, причем расстояние от А до Я
равно 140 км, а расстояние от В до С равно 100 км, Через 3 ч
§ !. ЗАДАЧИ НА ДВИЖЕНИЕ
261
после выхода парохода за ним вышел из порта А быстроходный
катер, который, догнав пароход, передал приказание увеличить
скорость на 5 км/ч. Приказание было немедленно выполнено, н
в результате пароход прошел мнмо мзяка В на полчаса раньше
н прибыл в порт С иа полтора часа раньше. Найтн
первоначальную скорость парохода и скорость катера.
1.1 К Первый турист, проехав 1,5 ч на велосипеде со ско<
ростыо 16 км/ч, делает остановку на 1.5 ч, а затем продолжает
путь с первоначальной скоростью. Спустя 4 ч после отправки
в дорогу первого туриста вдогонку ему выезжает на мотоцикле
второй турнет со скоростью 56 км/ч. Какое расстоянне они
проедут, прежде чем второй турист догонит -первого?
1.12. От пристани А одновременно отходят вннз по течению
реки к пристани В две лодки. Первая лодка подходит к
пристани В на 2 ч раньше второй. Если бы лодки отошли от этих
пристаней одновременно, двигаясь навстречу друг другу (первая
от А, а вторая от В), то онн встретились бы через 3 ч.
Расстояние между пристанями равно 24 км, Скорость второй лодки в
стоячей воде в три раза больше скорости течения рекн. Найти
скорость течения рекн.
1.13. Сначала катер шел 5 км по течению реки, а затем
вдвое большее расстояние — по озеру, в которое река впадает,
Весь рейс продолжался 1 ч. Найти собственную скорость катера,
если скорость течения реки v км/ч.
1.14. В 9 ч самоходная баржа вышла из пункта А вверх по
реке и прибыла в пункт В; 2 ч спустя после прибытия в пункт В
баржа отправилась в обратный путь и прибыла в пункт А в
(|9 ч 20 мни того же дня, Предполагая, что скорость течения
рекн 3 км/ч н собственная скорость баржи постоянна,
определить, когда баржа прибыла в В, если расстояние АВ рав^ио 60 км.
1.16. Автомобиль выехал из города А в город В в через 2 ч
остановился на 45 мнн. После этого он продолжал движение
к городу В, увеличив первоначальную скорость на 20 км/ч, н
прибыл в город В. Если бы автомобиль ехал без остановки с
первоначальной скоростью, то на путь из А в В он затратил бы
столько же времени. Найтн первоначальную скорость автомобиля,
если расстояние между городами А и В равно 300 км.
1.16. Мотоциклист отправился из пункта А в пункт В,
расстояние между которым» 120 км. Обратно он выехал с той же
скоростью, но через час после выезда должен был остановиться
•иа 10 мнн. После этой остановки он продолжал путь до А,
увеличив скорость на 6 км/ч. Какова была первоначальная скорость
: мотоциклиста, если известно, что на обратный путь он затратил
. столько же времешь сколько иа путь рт j4 до б?
262 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
1.17*. Мотоциклист проезжает 1 км на 4 мип быстрее, чем
велосипедист. Сколько километров проезжает каждый нз них за
5 ч, если известно, что мотоциклист проезжает за это время иа
100 км больше велосипедиста?
1.18. По графику поезд всегда проходит перегон в 120 км
с одной и той же скоростью. Вчера поезд прошел половину
перегона с этой скоростью и вынужден был остановиться на 5 мин.
Чтобы вовремя прибыть в конечный пункт перегона, машинисту
иа второй половине перегона пришлось увеличить скорость
поезда иа 10 км/ч. Сегодня повторилась остановка поезда на
середине того же перегона, только задержка продолжалась 9 мни.
С какой скоростью машинист вел поезд сегодня на второй
половине перегона, если опять в конечный пункт этого перегона поезд
прибыл по расписанию?
1.19. Одновременно начали гопкн с одного старта в одном
направлении два мотоциклиста: один со скоростью 80 км/ч,
другой со скоростью 60 км/ч. Через полчаса с того же старта и в
том же направлении отправился третий гонщик. Найти скорость
третьего гонщика, если известно, что ои догнал первого гонщика
на 1 ч 15 мни позже, чем второго.
1.20. Два велосипедиста выехали нз пункта Л одновременно
и в одном направлении. Первый велосипедист ехал со скоростью
7 км/ч, а второй — со скоростью 10 км/ч. Через 30 мин из
пункта А в том же направлении выехал третий велосипедист,
который догнал первого велосипедиста, а через 1,5 ч после этого
догнал и второго велосипедиста. Определить скорость третьего
велоснпедиста.
1.21. От пристани А вниз по течению рекн одновременно
отплыли пароход н плот. Пароход, доплыв до пристани В,
расположенной в 324 км от пристани А, простоял там 18 ч и
отправился назад в Л. В момент, когда ои находился в 180 км
от А, второй пароход, отплывший из А на 40 ч позднее первого,
нагнал плот, успевший к этому времени проплыть 144 км.
Считая, что скорость течения реки постоянна, а скорости пароходов
в стоячей воде постоянны и равны между собой, определить
скорости пароходов и течения рекн.
1.22. Пункт А находится по реке выше пункта В. В одно и
то же время из пункта А отплыли вниз по реке плот и первая
моторная лодка, а из пункта В вверх — вторая моторная лодка.
Через некоторое время лодки встретились в пункте С, а плот за
это время проплыл третью часть пути от А до С. Если бы первая
лодка без остановки доплыла до пункта В, то плот за это время
прибыл бы в пункт С. Если бы нз пункта А в пункт В отплыла
вторая лодка, а из пункта В в пункт А — первая лодка, то они
§ 1. ЗАДАЧИ НЛ ДВИЖЕНИЕ
263
встретились бы в 40 км от пункта А. Какова скорость обеих
лодок в стоячей воде, а также расстояние между пунктами А
и В, если скорость течения реки равна 3 км/ч?
1.23. Из города А в город В одновременно выехали
автомобиль н мотоцикл, а в тот момент, когда мотоцикл преодолел
шестую часть пути, из А в том же направлении выехал
велосипедист. К моменту прнбытия- автомобиля в город В велосипедист
проехал четвертую часть пути. Скорость мотоцикла на 21 км/ч
меньше скорости автомобиля н на столько же больше скорости
велосипедиста, Найтн скорость автомобиля.
1.24. Из пункта А в пункт В, иаходящийсн в 100 км от
Пункта Л, в одно и то же время отправились велосипедист и
пешеход, Одновременно им навстречу из пункта В выехал
автомобилист. Через чао после выезда автомобилист встретил
велосипедиста, а проехав еще 240/17 км, — пешехода, посадил его в
машину, после чего они поехали вдогонку за велосипедистом и
настигли его. Вычислить скорости зелосипедпста н
автомобилиста, если известио, что скорость пешехода равна 5 км/ч.
1.26. В полдень нз пункта А в пункт В вышел пешеход и
выехал велосипедист, и в полдень же из В в Л выехал верховой.
Через 2 ч встретились велосипедист н верховой на расстоянии
3 км от середины АВ, а еще через 48 мни встретились пешеход
и верховой. Определить скорость каждого и расстояние АВ, если
известно, что пешеход движется вдвое медленнее велосипедиста.
1.28. Из пунктов А и В одновременно навстречу друг другу
выехали два велосипедиста, которые встретились в 12 км от
пункта В. Продолжая свое движение и доехав до пунктов В и
А, онн сразу же повернули обратно и снова встретились в 6 км
от пункта А, Определить скорости велосипедистов и расстояние
АВ, если известно, что второй велосипедист вернулся bv пункт В
через час после того, как первый велосипедист вернулся в
пункт А.
1.27. Расстояние между двумя городами А и В
пассажирский поезд проходит иа 4 ч быстрее товарного. Если бы каждый
из поездов шел то время, которое тратит на путь от Л до В
другой поезд, то пассажирский прошел бы на 280 км больше,
чем товарный. Если бы скорость каждого из поездов была
увеличена на 10 км/ч, то пассажирский поезд проходил бы
расстояние между Л и В на 2 ч 24 мин быстрее товарного. Найти
расстояние между городами Л и В.
1.28. На лыжных соревнованиях на дистанции 10 000 м
сначала стартовал первый лыжник, а через некоторое время после
него — второй, причем скорооть второго лыжника была на 1 м/с
больше скорости первого, В момент, когда второй лыжник до-
264 ГЛ. It. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
гнал первого, первый увеличил свою скорость на 2 м/с, з
скорость второго лыжника осталась без изменения. В результате
второй лыжник финишировал через 7 мии 8 с после первого.
Если бы длина дистанции была на 500 м больше, то. второй
лыжник финишировал бы на 7 мин 33 с позже первого. Найтн,
сколько времени прошло между выходом со старта первого и
второго лыжников.
1.29. Два велосипедиста выехали одновременно из пункта А
в пункт В. Первый остановился через 42 мни, не доехав 1 км,
а второй — через 52 мин, ие доехав 2 км до В. Если бы. первый
велосипедист проехал столько, сколько второй, а второй столько,
сколько первый, то первому потребовалось бы иа 17 мин меньше
второго, Сколько километров между пунктами А к В?
1.30. Расстояние между станцией и поселком 4 км. Мальчик
и автомобиль одновременно отправились со станции в поселон.
Через 10 мин мальчик встретил автомобиль, возвращающийся из
поселка; пройдя еще 1/14 км он снова встретил автомобиль,
который, дойдя до станции, снова поехал в поселок. Найтн
скорости Мальчика и автомобиля, если известно, что они двигались
равномерно и без остановок.
1.31. От станции железной дороги до пляжа 4,5 км. Мальчик
и рейсовый автобус одновременно отправились от станций к
пляжу. Через 15 мин мальчик встретил автобус,
возвращающийся с пляжа, и успел пройти еще 9/28 км от места первой встречи
с автобусо*, прежде чем его догнал тот же автобус, который
доехал до станции и опять отправился к пляжу. Найтн скорости
мальчика и автобуса, считая, что эти скорости постоянны и ни
мальчик, ни автобус в пути не останавливались, ио у пляжа и
на станции автобус делал остановки продолжительностью в
4 мин каждая.
1.32. Велосипедист проезжает половину расстояния от
пункта А до пункта В на 2 ч быстрее, чем пешеход проходит треть
расстояния от А до В. За время, требуемое велосипедисту на
весь путь от А до В, пешеход проходит 24 км. Если бы скорость
велосипедиста увеличилась иа 7 км/ч, то за то время, за которое
пешеход пройдет 18 км, велосипедист проехал бы весь путь от А
до В н еще 3 км. Найтн скорость пешехода.
1.33. Буксиру нужно отогнать за минимальное времн два
понтона вниз по реке иа расстояние 1 км. Было решено, что
один понтон будет отправлен по течению реки самостоятельно,
а другой будет некоторое время транспортировать буксир, после
чего он оставит его, вернется за первым и отбуксирует его до
конечного пункта. Сколько километров должен транспортировать»
ся второй понтон, чтобы оба пришли к конечному пункту одиоч
S I. ЗАДАЧИ НА ДВИЖЕНИЕ
263
временно, и сколько потребуется времени на всю перевозку, если
собственная скорость буксира о км/ч, а скорость течения рекн
и км/ч?
1.34*. Пассажир поезда знает, что на данном участке пути
скорость этого поезда равна 40 км/ч. Как только мимо окна
начал проходить встречный поезд, пассажир пустнл секундомер
н заметил, что встречный поезд прошел мимо окна за 3 с
Определить скорость встречного поезда, если известно, что его дллиа
75 м.
1.35. По прямым параллельным путям, расстояние между
Которыми равно 60 м, равномерно в противоположных
направлениях движутся два поезда. Длина каждого поезда равна 100 м.
Стрелочпнк находится на расстоянии 40 м от ближайшего к нему
пути. Первый поезд загораживает от стрелочника часть второго
поезда в течение 5 с. Скорость первого поезда равна 16 м/с,
Определить скорость второго поезда. (Шириной поездов
пренебречь.)
1.36. Два одинаковых парохода отходят одновременно от
двух пристаней: первый пароход от пристани А вниз по течению,
второй от пристани В вверх по течению. К моменту встречи
первый пароход проходит втрое больший путь, чем второй.
Каждый из пароходов, дойдя до конечного пункта, стоит там иеко*
topoe время, а затем возвращается обратно. Если стоянка первого
парохода в В на 40 мнн больше стоянки второго парохода в А,
то на обратном пути пароходы встречаются в 12 км от А. Если
же стоянка первого парохода в В на 40 мин меньше стоянки
второго парохода в А, то на обратном пути пароходы встречают*
ся в 26 км от В. Найти расстояние между Л и В и скорость
пароходов в стоячей воде.
1.37. Пристани А и В находятся иа противоположных
берегах озера. Пароход плывет из А в В н после деситнмнцутной
стоянки в В возвращается в Л, двигаясь в обоих направлениях
с постоянной скоростью 18 км/ч. В момент выхода парохода из А
навстречу ему из В в Л отправляется движущаяся с постоянной
скоростью лодка, которая встречается с пароходом в II ч Ю мнн,
В II ч 25 мин лодка находится на расстоянии 3 км от Л.
Направляясь из В в Л после стоянки, пароход догоняет лодку в
11 ч 40 мин. Определить время прибытия лодки в Л.
1.38. Колонна мотоциклистов с интервалом между соседними
машинами в 50 м движется со скоростью 15 км/ч. В
противоположном направлении вдоль колонны (от первой машины) едет
велосипедист. Поравнявшись с 45-м мотоциклистом, он
увеличивает свою скорость иа 10 км/ч, доезжает до последнего мотоцикл
листа, поворачивает и с той же (увеличенной) скоростью догол
266 ГЛ. И, ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
няет первую машину. Если бы велосипедист о самого начала дви«
гался с этой увеличенной скоростью, то он вернулся бы к голове
колонны на 15/8 мнн раньше. Найтн первоначальную скорость
велосипедиста (длинами велосипеда, мотоцикла и временем пово
рота велосипедиста пренебречь).
При решении текстовых задач прежде всего необходимо ре«
шить вопрос о том, для каких неизвестных составлять систему
[уравнений. В основу выбора неизвестных может быть положен
следующий прннциш неизвестные следует вводить так, чтобы"
с помощью уравнений наиболее просто записать имеющиеся в
'задаче условия. При этом вовсе не обязательно, чтобы величина,
которую требуется найти, содержалась среди выбранных неизвест*
йых. Как правило, при таком выборе неизвестных искомая вели-
чина будет представлять собой некую комбинацию введенных не*
известных, для нахождения которой нет необходимости опреде-
лять по отдельности все входящие в нее неизвестные.
В задачах иа движение в качестве неизвестных обычно бы-
оает удобно выбирать расстояние (если оно не задано) и
скорости движущихся объектов, фигурирующих в условии задачи.
Пример 1.3. Из пункта А в пункт В выехал автомобиль,
н одновременно нз пункта В в пункт А выехал велосипедист.
После встречи они продолжали свой путь. Автомобиль, доехав
до пункта В, повернул назад и догнал велосипедиста через 2 ч
после момента первой встречи. Сколько времени после первой
встречи ехал велосипедист до пункта А, если известно, что к
моменту второй встречи он проехал 2/5 всего пути от В до Л?
Решение. Введем следующие неизвестные: расстояние S
между пунктами А к В, скорости велосипедиста н автомобилиста
V, и V» соответственно, t—время от начала движении до пер-
. вой встречи. Выпишем условие задачи в таблицу:
Условие задачи
Уравнение
X моменту первой встречи t автомобиль
it велосипедист вместе проезжают все
расстояние между пунктами Л и В.
.Через два часа после момента первой
встречи автомобиль, доехав до пункта В
л повернув, догнал велосипедиста, т. е.
путь, пройденный автомобилем,
складывается нз удвоенного расстояния,
пройденного велосипедистом до первой
встречи, н расстояния, которое велосипедист
Тепел проехать за 2 ч.
К моменту второй встречи велосипедист
проехал 3/5 всего расстояния между
пунктами А в В
Ca+"B)-'=S
«к.-ик. + а/.
^B« + 2)=-|S
§ I. ЗАДАЧИ HA ДВИЖЕНИЕ 267
Неизвестное х, которое требуется найти по условию задачи,
представляет собой время, необходимое велосипедисту, чтобы
доехать до пункта Л, после первой встречи. Оно может быть
выражено как следующая комбинация введенных неизвестных f,
* VB *
Из системы уравнений
2Va = 2tVB + 27*
V.(* + 2)—|-S
определим t в выразим отношение скоростей VJV* через t.
Из второго уравнения системы имеем
V«/VB-*+l. (♦)
Исключая S из первого н третьего уравнения системы и учнты-
вая равенство (*), получаем для неизвестной t уравнение
<(* + 2) = (/ + 2).-|-,
корни которого /i = —2 п t* ~ 5/2.
Так как по физическому смыслу задачи t > 0, то искомое
неизвестное нмеет вид
Ответ. 8 ч 45 мнн.
1.39. Из города А в город В вышел пассажирский поезд,
В то же время нз В в А вышел товарный поезд. Скорость
каждого нз поездов на всем участке движения постоянна. Через 2 ч
после того, как поезда встретились, расстояние между ними
составило 280 км. Пассажирский поезд прибыл к месту назначения
через 9 ч, а товарный — через 1G ч после встречи, Определить,
какое время находился в пути каждый поезд.
1.40. Два поезда отправляются навстречу друг другу с
постоянными скоростями, одни из Москвы, другой из Ленинграда.
Они могут встретиться на середине пути, если поезд из Москвы
отправится на 1,5 ч раньше. Если бы оба поезда вышли
одновременно, то через 6 q расстояние между ними составляло бы
268 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЯ
десятую часть первоначального. Сколько часов каждый поезд
Тратнт на прохождение пути между Москвой и Ленинградом?
1.41. Два велосипедиста оыезжают одновременно из
пунктов А и В навстречу друг другу и, двигаясь каждый с
постоянной скоростью, встречаются через 2-=- ч. Если бы первый
велосипедист увеличил свою скорость на 50%, а второй —на 20%, то
на преодоление расстояния между пунктами А к В первому
велосипедисту понадобилось бы времени на 2/3 ч больше, чем
второму. За какое время преодолевает расстояние между пунктами
А и В каждый велосипедист, двигаясь с первоначальной
скоростью?
1.42. Из пункта А по шоссе выехали одновременно два ав«
томобиля, а через час вслед за ними выехал третий. Еще через
час расстояние между третьим и первым автомобилями
уменьшилось в полтора раза, а между третьим я вторым — в два
раза. Скорость какого автомобиля, первого или второго, больше
н во сколько раз? (Известно, что третий автомобиль не обогнал
первые два.)
1.43. Пассажирский поезд вышел нз пункта А в пункт В.
Через 3 q вслед за ним нз А вышел скорый поезд. Скорый поезд
догнал пассажирский на середине пути между пунктами А н В.
В момент прибытия скорого поезда в пункт В пассажирский
поезд прошел 13/16 расстояния от А до В. Сколько времени
потратил пассажирский поезд на весь путь от А до В, если
скорости движения пассажирского и скорого поездов постоям*
вы?
1.44. Из пункта А в пункт В выехал велосипедист. В тот
момент, йогда он проехал 1/4 часть пути между А к В, аз В в А
выехал мотоциклист, который, прибыв в Л, не задерживаясь,
повернул обратно и одновременно с велосипедистом прибыл в В.
Время движения мотоциклиста до первой встречи с
велосипедистом равно времени движения мотоциклиста из Л в fi. Считая
скорости мотоциклиста при движении изЛвЙнизВвЛ
различными, иайтя, во сколько раз скорость мотоциклиста при двн*
&енни аз А в В больше скорости велосипедиста.
1.46. Из пункта А в пункт В выезжает автобус. Достигнув
пункта В, он продолжает движение в том же направлении. В тот
момент, когда автобус достиг пункта В, из пункта А выезжает
автомобиль и движется в том же направлении, что и автобус.
Время, необходимое автомобилю на путь из А в В, на 3 ч 20 мин
меньше времени, необходимого автобусу на тот же путь. Найти
эти времена, если сумма их в 1,5 раза больше времени, за
которое автомобиль догонит автобус.
§ I. ЗАДАЧИ НА ДВИЖЕНИЕ '
269
1.4G. Два велосипедиста н пешеход одновременно
отправились из пункта А в пункт В. Более чем через 1 ч после выезда
у первого велоснпеднста сломался велосипед, и он продолжал
путь пешком, двигаясь в 4,5 раза медленнее, чем на велосипеде.
Его обгоняю™ второй велосипедист—через 5/8 ч после поломки,
а пешеход — через 10,8 ч после поломки. К моменту поломки
второй велосипедист проехал в два раза большее расстояние, чем
ТО, которое прошел пешеход к моменту, на 5/36 ч более
позднему, чем момент поломки. Через сколько часов после начала
движения сломался велосипед?
1.47. Два пешехода вышли одновременно: первый из Л в В,
второй из В в А. Когда расстояние между ними сократилось в
шесть раз, аз В в А выехал велосипедист. Первый пешеход
встретился с ним в тот момент, когда второй прошел 4/9
расстояния между В и Л. Велосипедист в пункт А и первый пешеход в
пункт В прибыли одновременно. Определить отношение скоростей
пешеходов к скорости велосипедиста.
1.48. Города А и В расположены на берегу реки, прячем
город В расположен инже по течению. В 9 ч утра из города А
в город В отправляется плот. В это же время из города В в
город А отправляется лодка, которая встречается с плотом
через 5 ч. Доплыв до города А, лодка поворачивает обратно в
приплывает в город В одновременно с плотом. Успеют лн лодка
и плот прибыть в город В к 21 ч (того же дня)?
1.49. Из пункта А в пункт В едет трактор. Радиус переднего
колеса трактора меньше радиуса заднего колеса. На пути из А
в В переднее колесо сделало на 200 оборотов больше, чем заднее.
Если бы длина окружности переднего колеса была в 5/4 раза
больше, то на пути нз Л в В оио сделало бы на 80 оборотов
больше, чем заднее колесо. Найти длины окружностей переднего
н заднего колес трактора, если длина окружности заднего
колеса иа 1 м больше длины окружности переднего колеса. 1
1.50. В авторалли одновременно стартовали 3 спортивных
автомобиля разных марок. Экипаж первого автомобиля во время
пути 3 ч устранял поломку н в результате финишировал на 1 ч
позже второго экипажа. Определить скорости автомобилей, если
известно, что скорость второго автомобиля относится к скорости
третьего как 5 :4, скорость третьего на 30 км/ч меньше скорости
первого и что между моментами финиша второго и третьего
автомобилей прошло 3 ч.
1.61. Пароход делает рейсы между двумя городами; он идет
с одной скоростью при хорошей погоде и с другой — при плохой.
В понедельник хорошая погода во время рейса стояла на 1 ч
дольше, чем плохая, Во вторник пароход шел при хорошей по-
270 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
годе столько, сколько накануне при плохой, а при плохой
погоде — на 1 ч 4 мнн дольше. В среду пароход шел прн хорошей
погоде на 2 ч 30 мни дольше, чем накануне, н плохая погода
застигла его в 9 км от места назначении. В четверг хорошая
погода длилась па 0,5 ч дольшр, чем во вторинк, а затем
произошла авария, н пароход снизил скорость на 5 км/ч, Найдите
расстояние, которое проходил пароход за день, и скорость парохода
в хорошую и в плохую погоду, если известно, что пароход шел
после аварии иа полчаса дольше, чем до нее.
1.52. Три пешехода одновременно вышли в путь, Каждый по
своему мвршруту. Через t ч второму пешеходу осталось идти в
лолтора раза больше того, что прошел первый, а первому
осталось идти втрое больше того, что прошел третий. Через 2t ч
после выхода первому осталось идти вдвое меньше того, что
лрошел второй, а третий пешеход прошел столько, сколько
осталось идти первому и второму вместе. За какое время первый н
второй пешеходы прошли своя маршруты?
Некоторые задачи содержат условия, математическая запись
которых представляет собой неравенство.
Пример 1.4. Из города А в город В, находящийся иа
расстоянии 105 км от А, с постоянной скоростью v км/ч выходнт
автобус. Через 30 ми» вслед за ним из А со скоростью 40 км/ч
•выезжает автомобиль, который, догнав в путн автобус,
поворачивает обратно и движется с прежней скоростью. Определять все
те значения v, при которых автомобиль возвращается в город А
позже, чем автобус приходит в город В.
Решение. Наряду с неизвестной скоростью автобуса о
введем также неизвестное t — время, прошедшее от момента
отправления автобуса до встречи его с автомобилем.
Первое уравнение представляет собой математическую
запись условия того, что автомобиль, вышедший на 0.5 ч позже,
догнал автобус, который к моменту его выхода отъехал от го-
ррда А на 0,5о км:
Второе условие, которое выражено в виде требования,
заключается в том, что автобус должен дойти до города В
быстрее, чем автомобиль вернется в город А. Очевидно, что для
возвращения автомобилю понадобится столько же времени, т. е. t,
а автобусу, чтобы доехать до города Й, понадобится время
105 - 40*
, Тогда требование можно записать как нера-
§ Т. ЗАДАЧИ НА ДВИЖЕНИЕ £71
веиство
Ю5740<«.. («>
Подставляя в неравенство (**) t из уравнения (*), получаем
относительно v следующее неравенство:
и2 + 250о — 210 ■ 40 > 0. (***)
Так как автомобиль должен был догнать автобус в пути, то
расстояние до встречи не должно превышать 150 км. Следовательно,
второе неравенство имеет вид
40* < 105
или
Решение системы неравенств (***), (*■***) представляет
собой интервал 30 < v sg 33,6.
Ответ. Скорость автобуса должна находиться в интервале
вначеиий 30 < v <. 33,6.
1.63. Лодка спускается по течению реки на расстояние 10 км,
а затем поднимается против течения на 6 км. Скорость течения
равна I км/ч. В каких пределах должна лежать собственная
скорость лодки, чтобы вся поездка заняла от 3 до 4 ч?
1.64. Лодка плывет по реке против течения, скорость
которого v км/ч. Через 1 км пути она попадает в озеро со стоя'чей
водой. С какой собственной скоростью должна двигаться лодка,
чтобы общее расстояние S км она прошла не более чем за t ч?
1.66. Из пунктов А н В, расстояние между которыми ,120 км,
одновременно навстречу друг другу выезжают два велосипедиста
и встречаются позже чем через 5 ч. На следующий день онн
выезжают одновременно в одну сторону из пунктов С a D,
расстояние между которыми 36 км. причем велосипедист, едущий
впереди, движется со скоростью, на 6 км/ч большей, чем
накануне, а велосипедист, едущий сзади, движется с той же
скоростью, что н накануне. Хватит ли второму велосипедисту 2 ч,
чтобы догнать первого?
1.56. От пристани А к пристани В, находящейся от Л на
расстоянии 12 км, вниз по течению реки отходит моторная
лодка, скорость которой в стоячей воде равна 6 км/ч. Одновременно
с ней нз В в А выходят катер, скорость которого в стоячей воде
равна 10 км/ч. После встречи они разворачиваются и возврвща-
272' ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
ются к своим пристаням. Определить все возможные значения
скорости течения реки и, при которых лодка прнходит в Л не
раньше чем через час после возвращения катера в В.
1.67. От пристани А вниз по реке, скорость течении которой
равна v км/ч, отходит плот. Через час вслед за ним выходит
катер, скорость которого в стоячей воде равна 10 км/ч. Догнав
глот, катер возвращается обратно. Определить все те значения о,
при которых к моменту возвращения катера в А плот проходит
более 15 км.
1.58. Деревня расположена иа берегу реки, а школа — на
шоссе, пересекающем реку под прямым углом. Зимой школьник
ходит нз деревни в школу напрямик иа лыжах н тратит иа
дорогу 40 мин. Весной, в распутицу, он идет берегом рекн до
шоссе, а дальше — по шоссе до школы и тратит иа дорогу
1 ч 10 мин. Наконец, осенью он проходит вдоль реки половину
(расстояния, отделяющего деревню от шоссе, а дальше идет
напрямик. При этом он доходит до школы быстрее чем за 57 мни.
Установить, что дальше: деревня от шоссе или школа от рекн,
если известно, что пешком школьник ходит всегда с одной и
.той же скоростью, а на лыжах—со скоростью, на 25 % большей
(реку н шоссе считать прямыми линиями).
Движение по окружности. Если два тела движутся
по окружности радиуса R с постоянными скоростями vt и t>2 в
разных направлениях, то время между их встречами вычисляется
по формуле 2nRl{vt + и2).
Если два тела движутся по окружности радиуса R с
постоянными скоростями v% и о% (vt > vi) в одном направлении,
то время между их встречами вычисляется по формуле
2яД/(01 — о2).
Пример J.5. Два тела, движущихся в разные стороны по
окружности длиной 1 м с постоянными скоростями, встречаются
каждые 6 с. При движении в одну сторону первое тело догоняет
второе каждые 48 с. Найти линейные скорости этих тел.
Решение. Обозначим скорости первого и второго тел
через vt м/с и Ог м/с соответственно. Тогда в согласии с условием
задачи получаем следующие системы уравнений:
l/(»i + о5) =■ 6, i>i + fj=l/6,
1/(о, —1)2) = 48, Vj — 02=1/48.
Решая последнюю систему, получаем гд = 3/32. t>a = 7/96.
Ответ. Скорость первого тела равна 3/32 м/с, скорость вто«
рого равна 7/96 м/с
§ I. ЗАДАЧИ ЙА ДВИЖЕНИЙ 273
1.59. Два тела движутся по окружности равномерно в одну
сторону. Первое тело проходит окружность на 2 с быстрее
второго и догоняет второе тело каждые 12 с. За какое время
каждое тело проходит окружность?
1.60. Два спортсмена бегут по одной замкнутой дорожке на
стадионе. Скорость каждого постоянна, но на пробег всей
дорожки первый тратит на 10 с меньше, чем второй. Если онн
начнут бег с общего старта в одном направлении, то еще раз
встретятся через 720 с. Какую часть длины всей дорожки
пробегает в секунду каждый?
1.61. По двум концентрическим окружпостям равномерно
вращаются две точки. Одна из них совершает полный оборот на
5 с быстрее, чем другая, и поэтому успевает сделать в 1 мнн
на два оборота больше. Сколько оборотов в мннуту совершает
каждая точка?
1.62. По окружности радиуса R равномерно в одном направ-'
ленин движутся две точки. Одна нз них делает полный круг иа
t с быстрее второй, а время между последовательными встреча»
ми равно 7". Определить скорости точек.
1.63. На беговой дорожке состязались два конькобежца иа
дистанции S км. Когда победитель подошел к финишу, другому
оставалось бежать еще целый круг. Определить длину беговой
дорожки, если победитель, проходя каждый круг на о с быстрее
побежденного, закончил дистанцию за t мин.
1.64*. Часовая п минутная стрелки совмещаются в полночь.
В какое время нового дня впервые пновь совпадут часовая и
минутная стрелки, если допустить, что стрелки часов движутся без
скачков?
1.05. Часы показывают в некоторый момент на 2 мин
меньше, чем следует, хотя онн спешат. Если бы онн показывали на
3 мин меньше, но уходнлн бы вперед в суткн на 1/2 мин больше,
чем уходят сейчас, то верное время они показали бы на суткн
раньше, чем покажут. На сколько минут в сутки спешат эти
часы?
1.68. По сигналу дресснронщика два понп одновременно
побежали равномерно вдоль внешней окружности арены цирка п
противоположных направлениях. Первый понн бежал быстрее
второго и к моменту встречи пробежал на 5 м больше, чем
второй. Продолжая бег, первый понн подбежал к дрессировщику
через 9 с после встречи со вторым понн, а второй — через 16 с
после встречи. Каков диаметр арены?
1.67. На дороге, представляющей собой окружность длиной
в 36 км, пункты Л и В являются диаметрально
противоположными точками этой окружности, Велосипедист выехал нз пунк-
274 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
та А н сделал два круга. Первый круг он прошел с некоторой
постоянной скоростью, после чего уменьшил скорость на 3 км/ч.
Известно, что время между двумя его прохождениями через
пункт В равно 5 ч. Определить скорость, с которой велосипедист
прошел первый круг.
1.68. Три гонщика — сначала А, потом В и затем С—
стартуют с интервалом в 1 мни из одной точки кольцевого шоссе н
двигаются в одном направлении с постоянными скоростями.
Каждый гонщик затрачивает на круг более 2 мин. Сделав три круга",
.гонщик А в первый раз догоняет В у точки старта, а еще через
3 мнн он вторнчпо обгоняет С. Гонщик В впервые догнал С
также у точки старта, закончив 4 круга. За сколько минут
проходит круг гонщик А?
1.69. Трн гонщика А, В к С, стартовав одновременно,
движутся с постоянными скоростями в одном направлении по
кольцевому шоссе. В момент старта гоищнк В находился перед
гонщиком А на расстоянии 1/3 длины' шоссе, а гонщик С — перед
гонщиком В иа таком же расстоянии. Гонщик А впервые догнал
В в тот момент, когда В закончил свой круг, а еще через
10 мин впервые догнал гонщика С. Гонщик В тратит на круг на
2,5 мии меньше, чем С. За сколько минут проходит круг
гонщик Л?
1.70. Из пункта А кольцевого шоссе одновременно в одном
направлении выехали автомобиль и мотоцикл, каждый с
постоянной скоростью. Автомобиль без остановок дважды проехал по
шоссе в одном направлении. В момент, когда автомобиль догнал
мотоциклиста, мотоциклист повернул обратно, увеличил скорость
на 16 км/ч и через 22,5 мин после разворота одновременно с
автомобилем прибыл в пункт А. Найти длнну всего пути
мотоцикла, если этот путь па 5,25 км короче длины шоссе.
Задачи на равноускоренное движение. При
решении этих задач используются две следующие формулы,
связывающие время t, пройденное расстояние S, начальную скорость
tfo, ускорение а и скорость и:
S = o0* + a*2/2,
а = (и — va)/t,
где а > 0, еелн движение равноускоренное, и о < 0, если
движение равнозамедленное.
Пример 1.7. Автомобиль едет от пункта А до пункта В
с постоянной скоростью 42 км/ч. В пункте В он переходит на
равиозамедлениое движение, причем за каждый час его скорость
уменьшается на а км/ч, н едет так до полной остановки. Затем
он сразу же начинает двигаться равноускоренно С ускоренней
§ I. ЗАДАЧИ НА ДВИЖЕНИИ
275
а км/ч2. Каково должно быть значение я, чтобы через 3 ч после
возобновления движения автомобиль находился ближе всего к
пункту б?
Р е ш е н н е. Обозначим расстояние от пункта В до места
остановки автомобиля через S, км, а время движения автомобиля
от момента выезда из пункта В до момента остановки — через
<i ч. Через Si км обозначим расстояние, которое проехал
автомобиль за 3 ч после возобновления движения. Условия задачи с
помощью введенных неизвестных можно записать в виде системы
уравнений, полученных из таблицы:
Услоапе задачи
Уравнение
В пункте В автомобиль, движущийся со
скоростью 42 км/ч, переходит на равно-
замедленное движение, причем sa каждый
час его скорость уменьшается на а км/ч,
и едет так до полноп остановки
Автомобиль движется равноускоренно с
ускорением а км/ч5 в течение 3 ч
Я"'
•«?
о - "У
s,—j-
Такнм образом, получена система трех уравнений
a = 42/fb
S, =» 42f, - а^/2,
S2 = 9а/2
для нахождения четырех неизвестных a, t\, S\ и S2. Однозначно
найти искомое ускорение о нз данной системы нельзя. Однако
в условия задачи содержится еще одно условие, позволяющее
найти величину а, а именно требуется найти такое значение а,
чтобы расстояние Sj + Sa было минимальным. Запишем
расстояние Si+Ss в виде функции ускорения о. Из первого уравнения
системы получаем t\ = 42/а. Подставляя вместо ti во второе
уравнение системы величину 42/а и складывая полученное
уравнение с третьим уравнением системы, получаем
Функция f(a) = Sj + S» на промежутке (0; оо) достигает
наименьшего значения пра а = 14.
Ответ, а = 14 км/ч1.
1.71. Известно, что свободно падающее тело проходит в
первую секунду 4,9 м, а в каждую следующую — на 9,8 м больше,
276 ГЛ. И. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
чем в предыдущую. Пусть два тела начали падать с одной
высоты одно за другим с интервалом 5 с Через какое время они
будут друг от друга на расстоянии 220,6 м?
1.72. Два тела начали двигаться одновременно в одном в
том же направлении нз двух точек, расстояние между которыми
20 м. Одно нз ннх, находящееся позади, движется
равноускоренно и проходит в первую секунду 25 м, а в каждую следую-:
щую — иа 1/3 м больше, чем в предыдущую; другое тело,
двигаясь равнозамедлеяио, проходит в первую секунду 30 м, а в
каждую следующую —на 1/2 м меньше, чем в предыдущую.
Через сколько секунд онн встретятся?
1.73. Две материальные частицы, находящиеся на расстоянии
295 м одна от другой, одновременно начали двигаться навстречу
друг другу. Первая частица движется равномерно со скоростью
15 м/с, а вторая в первую секунду продвинулась на 1 м, а в
каждую следующую секунду продвигается на 3 м больше, чем
в предыдущую. На какой угол переместится секундная стрелка
часов за время, прошедшее от начала движения частиц до их
встречи?
1.74. Два тела движутся навстречу друг другу из двух
точек, расстояние между которыми 390 м. Первое тело прошло в
первую секунду 6 м, а в каждую следующую проходило на 6 м
больше, чем в предыдущую. Второе тело двигалось равномерно
со скоростью 12 м/с и начало движение спустя 5 с после
первого. Через сколько секунд после того, как начало двигаться
первое тело, они встретится?
1.76. Два парохода движутся навстречу друг другу в тумане
с одинаковыми скоростями V0. На расстоянии 4 км между ними
капитаны включают иа некоторое время обратный ход с
ускорением 0,1 м/с2. Какова наибольшая скорость пароходов Vo, при
которой они не столкнутся?
I.7G. Мяч катится по футбольному полю перпендикулярно
его боковой линии. Предположим, что, двигаясь равнозамедлен-
но, мяч катился в первую секунду 4 м, а в каждую следующую
секунду — на 0,75 м меньше, чем в предыдущую. Футболист,
находящийся первоначально в 10 м от мяча, побежал в
Направлении движения мяча, чтобы догнать его. Двигаясь
равноускоренно, футболист пробежал в перную секунду 3,5 м, а в каждую
следующую секунду пробегал иа 0,5 м больше, чем в
предыдущую. За какое время футболист догонит мяч и успеет лп он
догнать мяч до выхода того за боковую л ни ню, если до лнинн
поля футболисту надо пробежать 23 м?
1.77. Автомобиль ехал в гору. В первую секунду после
достижения пункта А он проехал 30 м, а в каждую следующую
§ I. ЗАДАЧИ НА ДВИЖЕНИЕ
277
секунду он проезжал на 2 м меньше, чем в предыдущую. Через
9 с после того, как автомобиль достиг пункта Л. м.тветречу ему
выехал автобус из пункта В, находящегося на расстоянии 258 м
от пункта А. В первую секунду автобус проехал 2 м, а в
каждую следующую секунду он проезжал на 1 м больше, чем в
предыдущую. Какое расстояние проехал автобус до встречи в
автомобилем?
1.78. Мотоциклист выезжает пз пункта А и движется с
постоянным ускорением 12 км/ч2 (начальная скорость равна нулю).
Достигнув скорости о км/ч, он едет с этой скоростью 25 км, а
затем переходит на равнозамедлениое движение, причем за
каждый час его скорость уменьшается на 24 км/ч, и движется так
до полной остановки. Затем он сразу же поворачивает обратпо
н едет до пункта А с постоянной скоростью v км/ч. При какой
скорости v мотоциклист быстрее всего проделает обратный путь
от остановки до пункта А?
1.79. Два автомобиля едут по шоссе друг за другом на
расстоянии 20 м со скоростью 24 м/с. Шоферы, заметив впереди
препятствие, начинают тормозить. В результате автомобили
переходят на равнозамедлениое движение с ускорениями д. и аз
(ai < 0 и аг < 0) и движутся так до полной остановки. Шофер
переднего автомобиля начал торможение на 2 с раньше шофера
заднего автомобиля, Ускорение переднего автомобиля есть
ai = —4 м/с2. Наименьшее расстояние, на которое
сближались автомобили, равнялось 4 м. Определить, какой
автомобиль остановился раньше, и найти ускорение а2 заднего
автомобиля.
1.80. Грузовой лифт опускается в башне высотой 320 м.
Сначала он движется со скоростью 20 м/с, а потом его скорость
мгновенно переключается и становится равной 50 м/с Спустя
некоторое время после начала движения лифта с вершины башни
сбрасывают камень, который совершает свободное падение и
достигает земли одновременно с лифтом. Известно, что во время
падения Камень был все время выше лифта, причем
максимальная разность высот между ними составляла 60 м. В момент
переключения скорости лифта скорость камня превышала 25 м/с,
но была меньше 45 м/с. Определить, спустя какое время после
начала движения лифта сбросили камень. При решении задачи
ускорение свободного падения камня считать равным 10 м/с2.
1.81*. Из пунктов А и В навстречу друг другу вышли
одновременно два поезда. Каждый из них двигался сначала
равноускоренно (начальные скорости поездов равны нулю, ускорения
различны), а затем, достигнув некоторой скорости, равномерно.
Отношение скоростей при равномерном движении поездов равно
278 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЯ
4/3. В момент встречи поезда имели равные скорости, а в пункты
В и Л прибыли одновременно. Найти отношение ускорений
поездов.
1.82*. Из пунктов А и В навстречу друг другу одновременно
вышли два поезда. Каждый из них двигался сначала
равноускоренно, а затем, достигнув некоторой скорости, равномерно.
Отношение скоростей равномерного движения поездов равно 5/4.
В некоторый момент времени скорости поездов оказались
равными; один нз инх прошел к этому моменту расстояние, в
1 —г- раза большее, чем другой. В пункты В я А поезда прибыли
одновременно. Какую часть пути прошел каждый нз поездов к
тому времени, когда их скорости оказались равными?
1.83. С поезда сошли два пассажира и направились в одгш
и тот же пункт. Первый шел половину времени со скоростью
о км/ч, а вторую половину — со скоростью Ъ км/ч, а второй
первую половину пути — со скоростью Ь км/ч, а вторую половину —
со скоростью о км/ч. Который из них пришел быстрее к месту
назначения?
§ 2. Задачи на работу и производительность труда
Система уравнений, которую можно составить на основании
условий, в задачах на работу обычно содержит следующие
величины: время t, в течение которого производится работа,
производительность N — работу, произведенную в единицу времени, и
собственно работу А, произведенную за время t.
Уравнение, свнзывающее эти трн величины, имеет внд А =».
К задачам на работу можно с очевидными изменениями
отнести часто встречающиеся задачи на перекачивание жидкости
насосами. В качестве произведенной работы в этом случае
удобно рассматривать объем перекачанной воды.
Прнмер 2.1. В бассейн проведены две трубы — подающая
и отводящая, причем через первую трубу бассейн наполняется
на 2 ч дольше, чем через вторую опорожняется. Прн
заполненном на одну треть бассейне были открыты обе трубы, н бассейн
оказался пустым спустя 8 ч. За сколько часов одна первая труба
может наполнить бассейн н за сколько часов одна вторая труба
может опорожнить полный бассейн?
Решение. Пусть V м3 — объем бассейна,
производительность падающей трубы— х м3/ч, отводящей — у м3/ч. Время, не«.
обходимое подающей трубе для заполнения бассейна, — V/x ч,
время, необходимое отводящей трубе на опорожнение бассей-
§ 2. ЗАДАЧИ НА РАБОТУ И ПРОИЗВОДИТЕЛЬНОСТЬ' 279
на, — V/y ч. По условию задачи
V/x — V/y « 2.
Так как производительность отводящей трубы больше
производительности наполняющей (х < у), то при обеих включенных
трубах будет пронсходнть опорожненне бассейна и одна треть
бассейна опорожнится за время т—-—, которое по условию
задачи равно 8 ч.
Итак, условие задачи может быть записано в виде системы
двух уравнений для трех неизвестных
V/x-Vly = 2,
VI(y-x) = U.
Разделим числитель и знаменатель дроби, стоящей во
втором уравнении системы, на V. Тогда относительно непрерывных
V V
и — — и 0==—- получим следующую систему уравнении:
А у
u — v = 2,
-22 24,
и — v
которая эквивалентна системе
и — v = 2,
и - v = 48,
т. е. и = 8, и = 6.
Ответ, 8ч нбч.
Пример 2.2. Для прокладка траншей выделены два
экскаватора разных типов. Время, необходимое первому экскаватору
для самостоятельной прокладки траншеи, на 3 ч меньше временн,
необходимо второму экскаватору. Сумма этих времен' в
4"35" раза больше временн, необходимого для прокладки
траншеи при совместной работе двух экскаваторов. Определить,
сколько времени необходимо каждому экскаватору для
самостоятельной прокладки траншеи.
Решение, В качестве неизвестных введем следующие
величины: Л м3—объем вынутого грунта, Nt м3/ч и JVi м»/ч—
производительности первого и второго экскаваторов. Время,
необходимое первому экскаватору для самостоятельной прокладки
траншеи, — AJNi, а второму — A/JVa. По условию задачи эти две
величпны связаны равенством
AJNi + 3 = AlN2,
280 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
4
а их сумма A/Mi + Л/ДГ2 в 4 -^ раза больше времени,
необходимого для прокладки траншеи при совместной работе двух экс-
каваторов, т. е.
4 A _d_j_JL ,4 1 _ А А
~+ A
л л
Введем неизвестные * = -rr— и » == -тт—. Тогда исходная снстё-
ма может быть записана в виде
л 4 *U
х + У
35 х + у
х + Ъ^у.
Подставляя у из второго уравнения в первое, получаем
относительно х следующее уравнение:
4*а+ 12* — 315 = 0.
Положительный корень этого уравнении х =* 7,5 представлнет
собой время самостоятельной прокладки траншеи первым
экскаватором. Из второго уравнения системы получаем, что у = 10,5,
Ответ. 7,5 ч н 10,5 ч.
2.1. Бригада лесорубов должна была по плану за несколько
дней заготовить 216 м3 дров. Первые три дня она работала по
плану, а затем каждый день заготовляла на 8 м* дров больше,
чем предусмотрено планом; поэтому уже за день до
назначенного срока было заготовлено 232 м3 дров. Сколько кубометров
дров должна была заготавливать бригада в день по плану?
2.2. Бригада слесарей может выполнить некоторое задание
по обработке деталей на 15 ч быстрее, чем бригада учеников.
Если бригада учеников отработает 18 ч, выполняя это задание,
а потом бригада слесарей продолжит выполнение задания в
течение 6 ч, то и тогда будет выполнено только 3/5 всего
задания. Сколько времени требуется бригаде учеников для
самостоятельного выполнения данного задания?
2.3. Бак наполняется двумя кранами А и В. Наполнение
бака только через край А длится иа 22 мин дольше, чем
наполнение через кран В. Если же открыть оба крана, то бак
наполнится за 1 ч. За какое время каждый кран в отдельности может
наполнить бак?
2.4. В кинозале нмеютсн две (разные) двери. Через обе две-
pti зрители после сеанса могут покинуть зал в течение 3— мвн»
§ 2. ЗАДАЧИ НА РАБОТУ И ПРОИЗВОДИТЕЛЬНОСТЬ' 281
Если нх выпускать через одну большую дверь, то выход из зала
займет времени иа 4 мин меньше* чем в том случае, еслн нх
выпускать через меньшую дверь. Сколько времени требуется,
чтобы выпустить зрителей из зала кино через каждую дверь
в отдельности?
2.5. Три вычислительные машины разных систем выполняют
некоторую работу. Одна вторая машина затрачивает на
выполнение всей работы на 2 мин больше, чем одна первая. Одна
третья машина может выполнить всю работу вдвое медленнее,
чем одна первая. Так как части работы однотипны, то всю ра»
боту можно поделить между тремя машинами. Тогда, работая
вместе, онн закончат работу через 2 мин 40 с. За какое время
может выполнить эту работу каждая машина, работая,
самостоятельно?
2.6. А выполняет некоторую работу иа t дней дольше, чем В,
и на 7" дней дольше, чем С; А н В, работая вместе, выполняют
эту работу за столько же дней, что и С. Определить время, за
которое каждый выполняет эту работу самостоятельно. При
каком соотношении между t к Т задача имеет решение?
2.7. Каждому из трех рабочих для выполнения некоторой
работы требуется определенное время, причем третий рабочий
выполняет ее на час быстрее первого. Работая все вместе, онн
выполнят работу за 1 ч. Если же первый рабочий проработает
i ч, а затем второй рабочий проработает 4 ч, то вместе они
выполнят всю работу. За сколько времени может выполнить всю
работу каждый рабочим?
2.8. Двое рабочих получили одинаковые задания изготовить
определенное число деталей за определенный срок. Первый вьь
полнил задание в срок, а второй выполнил в срок только 90 %'
задания, не додав столько деталей, сколько первый делал за
40 мин. Еслн бы второй рабочий делал в час на три детали
больше, он выполнил бы задание на 95 %• Сколько деталей
должен был изготовить каждый рабочий?
2.9. Два рабочих выполнили всю работу за 10 дней, причем-
последние 2 дня первый нз них не работал. 3-а сколько дней
первый рабочий выполнил бы всю работу, еслн известно, что за
первые 7 дней они вместе выполнили 80 % всей работы?
2.10. Две бригады штукатуров, работая совместно, оштука»
турнлн жилой дом за 6 дней. В другой раз они штукатурили
клуб и выполнили втрое больший объем работы, чем на штука«
турке жилого дома. В клубе они работали по очереди: сначала
работала первая бригада, а затем ее сменила и довела до конца
штукатурку клуба вторая бригада, причем первая бригада вьь
полнила вдвое больший объем работы, чем вторая. Клуб был
282 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
оштукатурен за 35 дней. За сколько дней первая бригада смогла
бы оштукатурить жилой дом, если известно, что вторая бригада
потратила бы на это более 14 дней?
2.11. Бригада из трех тракторов (два трактора марки А и
один трактор марки В) вспахивает поле площадью 400 га за
10 суток при одновременной работе всех трех тракторов.
Трактор марки В вспахивает все это поле на 8 -^- суток быстрее, чем
то же поле вспахивает одни трактор марки А. Сколько гектаров
в сутки вспахивают трактор марки А и трактор марки В
каждый в отдельности?
2.12*. Каждому нз двух рабочих поручили обработать
одинаковое число деталей. Первый начал работу сразу н выполнил
ее за 8 ч. Второй же потратил сначала больше 2 ч па наладку
приспособления, а затем с его помощью закончил работу на 3 ч
раньше первого. Известно, что второй рабочий через час после
начала своей работы обработал столько же деталей, сколько
к этому моменту обработал первый. Во сколько раз
приспособление увеличивает производительность стайка (т.е. количество
обрабатываемых деталей за час работы) ?
2.13. Два трактора вспахивают поле, разделенное на две
равные части. Оба трактора начали работу одновременно, и
каждый вспахивает свою половину. Через 5 ч после того момента,
когда они совместно вспахали половину всего поля, выяснилось,
что первому трактору осталось вспахать 1/10 часть своего
участка, а второму—4/10 своего участка. Сколько времени понадо-
битсн второму трактору, чтобы одному вспахать все поле?
2.14. Бригада рабочих должна была изготовить 360 деталей.
Изготовляя ежедневно иа 4 детали больше, чем предполагалось
по плану, бригада выполнила задание на день раньше срока.
Сколько дней затратила бригада на выполнение задания?
2.16. Двум машинисткам было поручено выполнить
некоторую работу. Вторая приступила к работе на 1 ч позднее первой.
Через 3 ч после того, как первая начала работу, им осталось
выполнить 9/20 всей работы. По окончании работы оказалось,
что каждая машинистка выполнила половину всей работы. За
сколько часов каждая нз них в отдельности могла бы выполнить
всю работу?
2.16. Три бригады работают о постоянной
производительностью, прокладывая рельсовые путн. Первая и третья бригады,
работай совместно, прокладывают 15 км путей в месяц. Три
бригады вместе укладывают в месяц в два раза больше путей,
чем первая и вторая бригады при их совместной работе. Найти,
. сколько километров путей укладывает в месяц третья бригада,
§ 2. ЗАДАЧИ НА РАБОТУ И ПРОИЗВОДИТЕЛЬНОСТЬ 283
если известно, что вторая бригада совместно с третьей уложили
некоторый участок пути в четыре раза быстрее, чем его уложила
бы одна вторая бригада.
2.17. Для разгрузки парохода выделены две бригады
грузчиков. Сумма времени, необходимого первой бригаде для
самостоятельной разгрузки парохода, н времени, необходимого второй
бригаде для самостоятельной разгрузка парохода, равна 12 ч.
Найтн эти времена, если их разность составляет 45 % от
времени, необходимого бригадам для совместном разгрузки
парохода.
2.18. К резервуару объемом 24 м3 подведены две трубы. Че»
рез первую трубу вода может только выливаться со скоростью
2 м'/ч, а вторая труба может только наполнять резервуар.
Вначале, когда резервуар был пуст, одновременно открыли две
трубы. После того как резервуар оказался заполненным наполовину,
первую трубу закрыли, а вторая продолжала наполнять
резервуар. В результате резервуар был наполнен за 28 ч 48 мни.
Какое количество воды за 1 ч подает вторая труба?
2.19. Два насоса перекачали 64 м3 воды. Онн начали
работать одновременно н с одинаковой производительностью. После
того как первый нз них перекачал 9 м3 воды, его остановили иа
1 ч 20 мин. После перерыва производительность первого насоса
увеличили на I м3/ч. Определить начальную производительность
насосов, еслн первый насос перекачал 33 м3 воды и оба насоса
окончили работу одновременно.
2.20. На угольной шахте сначала работали два участка, а
через некоторое время вступил в строп третий участок, в
результате чего производительность шахты увеличилась в полтора раза.
Сколько процентов составляет производительность второго
участка от производительности первого, если известно, что-за четыре
месяца первый и третий участки выдают угля столько же/рколь-
ко второй за весь год?
2.21. Два рабочих, из которых второй начал работать на
■1,5 дня позже первого, работая независимо один от другого,
оклеили обоямн несколько комнат за 7 дней, считая с момента
выхода на работу первого рабочего. Еслн бы эта работа была
поручена каждому отдельно, то первому для ее выполнения
понадобилось бы на 3 дня больше, чем второму. За сколько дней
каждый нз них отдельно выполнил бы эту же работу?
2.22. Если две трубы открыть одновременно, то бассейн
наполнится за 2 ч 24 мин. В действительности же сначала была
открыта только первая труба на 1/4 времеип, необходимого
второй трубе длн наполнения бассейна. Затем первую трубу
закрыли и открыли, вторую трубу на 1/4 временя, необходимого пер-
284 ГЛ. If. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
вой, чтобы одной наполнить бассейн. После этого оказалось, что
остается наполнить еще 11/24 часть объема бассейна. Сколько
времени необходимо для наполнения бассейна каждой трубой в
отдельности?
2.23. Два студента одновременно начали готовиться к
экзамену, назначенному для обоих на один и тот же день. Первый
студент должен прочитать 240 страниц, а второй — 420. Каждый
читает ежедневно одно и то же целое число страниц, причем
Первый прочитывает иа 12 страниц меньше второго. После того
как каждый прочел свой материал по одному разу, у них
осталось время иа повторение: у первого — 7 дней, у второго—5 дней.
Определить, какое целое число страниц в день надо было бы
читать каждому студенту, чтобы на повторение им осталось по
8 дня.
2.24. В одном нз отсеков судна возникла течь, и отсек ока-
вался целиком заполнен водой. Длн откачки воды включены два
насоса разной производительности. Через 18 ч после этого течь
была устранена, второй насос выключен, и еще через 12 ч воды
* отсеке не осталось. Если бы течь устранить не удалось, то два
ласоса осушяли бы отсек наполовину черев 10 ч совместной
работы. За какое время второй насос осушил бы отсек
наполовину, если бы не удалось устранить течь?
2.25. Три экскаватора участвовали в рытье котлована объ-
емом 340 м3. За час первый экскаватор вынимает 40 м3 грунта,
второй — иа с м3 меньше первого, а третий — на 2с м3 больше
Первого. Сначала работали одновременно первый и второй
экскаваторы н выкопали 140 м' грунта. Затем оставшуюся часть кот»
«оваиа выкопали, работая одновременно, первый и третий
экскаваторы. Определить значение с (0 < с < 15), при котором
котлован был выкопан за 4 ч, если работа велась без перерыва.
2.20. Три экскаватора получили задание вырыть по
котловану: первый а второй — емкостью по 800 м3, а третий — емкостью
,'£00 м3. Первый и второй экскаваторы вместе вынимают за чао
^руита в 3 раза больше, чем третий; первый н третий
экскаваторы начали работу одновременно, а второй — в тот момент,
когда первый вынул уже 300 м3 грунта. Когда третий экскаватор
выполнил 2/3 своей работы, второй вынул 100 м» грунта.
Первым выполнил свое задание третий экскаватор. Сколько
кубометров грунта вынул первый экскаватор к моменту, когда
третий закончил рыть свой котлован?
2.27*. Имеется три насоса. Второй насос перекачивает за чао
iuwoe больше воды, чем первый, а третий насос перекачивает за
|iac на 8 ма больше, чем второй. Два бассейна вместимостью
(600 м» н 1680 м* начали заполнять одновременно. Бассейн вме-L
I
§ 2. ЗАДАЧИ НА РАБОТУ И ПРОИЗВОДИТЕЛЬНОСТЬ 285
стнмостью 600 м3 заполнял первый насос. В другой бассейн
сначала вторым насосом накачали 240 м3, а затем его без потери
времени заменили третьим насосом, который н заполнил
полностью этот бассейн. Больший бассейн был заполнен на 6 ч
позднее, чем меньший бассейн. Еслп бы в больший бассейн о
самого начала качал воду только третий насос, то ои был бы
заполнен на 5 ч позднее, чем первый бассейн. Сколько
кубометров воды перекачивает за час первый насос?
В некоторых задачах искомая величина является комбина- •
цией неизвестных, относительно которых удается составить
уравнения, нспользун условия задачи.
Пример 2.3. Бассейн был наполнен водой несколькими
насосами одинаковой производительности, которые включались в
работу одни за другим через равные промежутки времени.
Первый насос перекачал иа V» больше последнего. Если промежутки
времени между включениями насосов уменьшить втрое, то время
наполнения уменьшится на 10%. Какой объем воды перекачает
каждый насос при наполнении бассейна, если одновременно
включить все насосы?
Решение. Введем неизвестные, неявно фигурирующие в
условии задачи: п— число насосов, х—производительность, fi —
время работы одного насоса в первом случае, d — интервал
между включениями насосов, h — время работы одного насоса при
одновременном включении.
Так как времена работы насосов образуют арифметическую
прогрессию и последним прн этом перекачивает воды на V*
меньше первого, можно составить уравнение
*/,-*[/,-(л-l)d] = l^. (*)
В первом случае объем перекачанной воды V можно .выразить
через введенные неизвестные, нспользуя формулу суммы
арифметической прогрессии:
„ 2xt, — xln — [)d
У = —! 1 '—п.
Во втором случае промежутки между включениями сократились'
в три раза и время наполнения — на 10%, т.е. тот же объем
будет равен
2*0,9/, -х[п-\) -,-
Приравнивая эти выражении, получаем второе уравнение
tix = ~^-x(n — l]d. (♦*)
286 ГЛ. IT, ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ
Если сразу будут включены все насосы, то к моменту
наполнения бассейна каждый нз них проработает время <», а перекачает
x-ti литров. Так как насосов всего л, а вместе онн перекачают
весь объем, то можно составить следующее уравнение:
2xtt — х(п — 1) d
Или
. „ -= xi2 • и,
хН_2хи-х{н-\)*ш {щ^
Из уравнения (*) х(п— l)d = Vn, а из (**) xti=-^-V„.
Подставляя эти значения в (***), получаем
17 ./
xft—fV*
Ответ, s- V„.
6
2.28. Для уборки урожая было выделено несколько
одинаковых комбайнов, которые могли бы убрать поле за 24 ч, если
бы приступили к работе одновременно. Но случилось так, что
они приступали к работе один за другим через равные
промежутки времени, и затем каждый работал до окончания уборки.
За какое время была проведена уборка урожая, если первый
комбайн работал в 5 раз дольше, чем последний?
2.29*. Бассейн заполняется с помощью нескольких насосов
одинаковой производительности, которые включились один за
другим через равные промежутки времени. Последний насос
перекачал V л воды. Сколько воды перекачал первый насос, если
известно, что при уменьшении производительности каждого
насоса на 10% (при такнх же промежутках между включениями)
времн наполнения бассейна увеличится на 10%?
2.30. Трн насоса одновременно начали выкачивать воду,
каждый из своего резервуара. Когда третий иасос опорожнил а-ю
часть объема своего резервуара (а<1/2), второму оставалось
качать столько, сколько выкачал первый; когда третьему
оставалось опорожнить (1 — а)-ю часть объема, первому оставалось
выкачать столько, сколько выкачал второй. Первый насос
опорожняет второй резервуар за то же время, за какое второй
насос опорожняет первый резервуар. Какой из насосов работал
дольше других п во сколько раз? (Производительность каждого
насоса постоянна.) Исследовать зависимость решения от
величины ,а.
2.31*. Бассейн был заполнен с помощью нескольких насосов,
которые включались один за другим через некоторые промежут-
§ 3. ЗАДАЧИ НА ПРОЦЕНТНЫЙ ПРИРОСТ 287
ки времени. Большую часть времени иасосы работали вместе п
вторую половину бассейна наполнили за t ч быстрее первой.
Насколько быстрее будет заполнен бассейн, если промежутки
между включениями насосов уменьшить в п раз при той же
последов ательностн включения? (Производительность каждого
насоса постоянна.)
2.32. Бассейн наполнился несколькими насосами одинаковой
производительности, которые включались один за другим через
раоные промежутки времени. К моменту включения последнего
насоса была заполнена 1/6 часть бассейна. В другой раз при
наполнении этого бассейна производительность каждого насоса
была уменьшена на 10 %, а промежутки между включениями
остались прежними. Какую часть бассейна наполнят насосы в
этот раз за первую половину всего времени работы?
§ 3. Задачи на процентный прирост
и вычисление «сложных процентов»
Решение задач на процентный прирост и вычисление
«сложных процентов» основано на использования следующих понятий
и формул. Пусть некоторая переменная величина А, зависящая
от времени t, в начальный момент t = 0 имеет значение Л о, а
в некоторый момент времени /i имеет значение Ai. Абсолютным
приростом величины А за время t\ называется разность Ai—Ао,
относительным приростом величины А за время ti — отношение
Ai — Аа
2 и процентным приростом величины А за время fi —
"О
величина
Л'ТЛ° • loo %-.
Обозначая процентный прирост величины А через р %,
получаем следующую формулу, связывающую значения Ао, А\ н
процентный прирост р:
-^^•100% = ,,%.
л о
Запись последней формулы в виде
*-*(!+-&)-* + *-!&■
позволяет по известному значению Ао н заданному значению р
вычислить значение Л», т. е, значение А в момент времени ti,
288 ГЛ. If. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
Пусть теперь известно, что и далее при f> t\ величина Д
имеет процентный прирост р %. Тогда в момент времени ^=27i
значение величины Аг = A(t2) будет равно
В момент времеин h = З/i значение величины Л3 = А (12) есть
л, = ла(1 + ^)~л0(1+1у3
в момент времени nti:
л„ = Л„(ц-4-)".
Если за время tt (на «первом этапе») величина Л измени-
лась на pi%, на «втором этапе> (т.е. за время t2 — ti =• ti) —•
на рз %, на «третьем этапе» (т.е. за время h — h ■= '0 — на
Рз% и т. д., то значение величины Л в момент tn = nt^
вычисляется по формуле
^-^0+*)0+-й-)-(,+*)-
Пример 3,1. Предприятие работало три года., Выработка
продукции за второй год работы предприятия возросла на р%,
а на следующий год она возросла на 10 % больше, нем в
предыдущий. Определить, на сколько процентов увеличилась
выработка за второй год, если известно, что за два года она увеличилась
в общей сложности на 48,59 %.
Решение. Обозначим количество продукции,
произведенной за первый, второй н третий годы работы предприятия, через
Ai, Аг и Аг соответственно. По условию задачи за второй год
процентный прирост составил р %, а за третий год— (р-|- 10) %.
В соответствии с определением процентного прироста эти условия
дают два уравнения
Лз~л' -100%=p%, Лз~А* ■Ы0%-(р+10)%.
По условию задачи также известно, что за два года произвол»
ство выросло на 48,59 %, т. е. в третий год предприятие
производило на 48,59 % продукции больше, чем в первый год. Это
условие можно записать в виде уравнения
Ла~Л' -100% .= 48,59%.
§ 3. ЗАДАЧИ НА ПРОЦЕНТНЫЙ ПРИРОСТ 289
Запишем полученные уравнения в виде следующей системы;
*•-*• ('+-&■)■
*-* 0+-$?•)•
Умножая первое уравнение на второе, получаем
Из полученного уравнения и третьего уравнения системы
получаем уравнение для отыскания- неизвестной величины р:
0+-Аг)0+^)-Ч"*-^«*-—а
Корин последнего квадратного уравиення: р, = 17, рг =» 227,
По смыслу задачи подходит первый корень pi = 17,
Ответ. 17%.
8.1. Сберкасса начисляет ежегодно 3 % от суммы вклада.
.Через сколько лет внесенная сумма удвоятся?
3.2. Население города ежегодно увеличивается иа" 1/50
наличного числа жителей. Через сколько- лет население утроится?
3.3. За килограмм одного продукта и десять килограммов
другого заплачено 2 р. Если при сезонном изменении цен первый
продукт подорожает иа 15 %, а второй подешевеет иа 25 %, то
за такое же количество этих продуктов будет заплачено 1 р. 82 к.
Сколько стоит килограмм каждого продукта? % •
3.4. В начале года в сберкассу на книжку было Внесено
1640 р., а в конце года было взято обратно 882 р. Еще через
год иа книжке снова оказалось 882 р. Сколько процентов
начисляет сберкасса в год?
3.5. В букинистическом магазине антикварное собрание
сочинений стоимостью 350 р. уценивали дважды иа одно и то же
число процентов. Найти это число, если известно, что после
двойного снижения цен собрание сочинений стоит 283 р. • 50 к.
3.6. В течение года завод дважды увеличивал -выпуск
продукции иа одно и то же число процентов. Найти это число, если
известно, что в иачале года.завод выпускал ежемесячно 600
изделий, а в конце года стал выпускать ежемесячно 726 изделий,
8.5. Вкладанку. на -его сберкнижку за -год сберкасса
начислила 6 р. процентных денег, Добавив 44 р., вкладчик- оставил
10 А. Г. Цыдквв, Aj И, Поиски*
E90 ГЛ. Н. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЯ
деньги еще на год. По истечении года вновь было произведено
начисление процентов, и теперь вклад вместе с процентами
составил 257 р. 50 к. Какая сумма первоначально была положена
на сберкнижку и был лн этот вклад обыкновенным (2 %-иым)
или срочным (3%-ным)?
3.8. Магазин радиотоваров продал в первый рабочий день
месяца 105 телевизоров. В каждый следующий рабочий день
дневная продажа возросла на 10 телевизоров, и месячный
план — 4000 телевизоров — был выполнен досрочно, причем в
целое число .рабочих дней. После этого ежедневно продавалось на
13 телевизоров меньше, чем в последний день выполнения плана.
На сколько процентов был перевыполнен месячный план
продажи телевизоров, если в месяце 26 рабочих дней?
3.9. Известно, что вклад, находящийся в банке с начала
года, возрастает к концу года на определенный процент (свой
для каждого банка). В начале года 5/6 некоторого количества
денег положили в первый банк, а оставшуюся часть —во второй
банк. К концу года сумма этих вкладов стала равной 670
денежный единицам, к концу следующего года — 749 денежным
единицам. Выло подсчитано, что если бы первоначально 5/6
исходного количества денег положили во второй банк, а
оставшуюся часть — в первый банк, то по истечении одного года сумма
вкладов в эти банки стала ба равной 710 денежным единицам-.
В предположении, что исходное количество денег первоначально
целиком положено в первый банк, определить величину вклад»
не истечении двуж лет.
3.10. Производительность завода А составляет 40,96 %
производительности завода В. Годовой процент прироста
продукция на завода А па 30 % больше годового прнростн продукции
на заводе В. Каков годовой процент прироста продукции на
заводе А, если па четвертый год работы завод А даст то же
количество продукции, что н завод В?
3.11. Вклад в N рублей положен в сберегательную кассу с
р %-пым годовым приростом. В конце каждого года вкладчик ве-
рет М рублей. Через сколько лет после взятия соответствующей
суммы остаток будет втрое больше первоначального вклада?
3.12. В колбе в начальный момент имеется N бактерий.
К концу каждого часа количество бактерий увеличивается на
р % по сравнению с их количеством в иачяле этого часа; кроме
того, в конце каждого часа из колбы берется порция,
содержащая п (п <. N) бактерий. Через сколько часов количество
бактерий в колбе будет превышать (после изъятия соответствующей
порции) начальное их количество в два раза?.
§ 4. ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ НЕИЗВЕСТНЫМИ . 291
§ 4. Задачи с целочисленными неизвестными
Целочислеиность искомого неизвестного обычно является
дополнительным условием, позволяющий выбрать его однозначно
нз некоторого множества значений, удовлетворяющих остальным
условиям задачи.
Пример 4.1. Группа студентов, состоящая из 30 человек,
получила на экзамене оценки 2, 3, 4, 5. Сумма полученных
оценок равна 93, причем «троек» было больше, чем «пятерок», н
меньше, чем «четверок», Кроме того, число «четверок» делилось
на 10, а число «пятерок» было четным. Определить, сколько
каких оценок получила группа.
Решение. Обозначим количество «двоек» ■— л:, «троек» — у,
«четперок» — z, «пятерок» — и. Тогда условия задачи можно
записать в виде следующей системы .уравнений и неравенств!
х + !f + z+ и = 30,
2х + Zy + 4z + 5к = 93,
у > и,
У <г.
z=. k -10,
и = 21, I, k — целые числа.
Вычитая нз второго уравнения первое, получаем
* + 2yf3z + 4u=»63. (*)
Так как г кратно 10, то единственное возможное значенне для
k — это k = ], Действительно, при k > 1 уравнение (#) не имеет
решения в целых положительных числах. Используя то, что
г = 10, перейдем от уравнения (*) к уравнению
* + 2# + 4и = 33. <. {»,)
Возможные значения для и (оно должио быть положительным,
четным и меньшим у < 10) « = 2, 4, 6, 8. Однако при и =6
я и = 8 получаем, что 8 и > у при любом х. Следовательно,
проверке подлежат лишь значения 4 и 2.
При и — 4 неизвестные х и у можно найтн из следующей
системы уравнений;
* + 2у=17,
2х + 3у=.33,
решением которой является пара у =* 1, * =» 15, не
удовлетворяющая условию у> и. При и =» 2 система уравнений для х, у
имеет вид
х+2у •=*&>.
2х + 3^=43.
10*
292 ГЛ. 11. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
Решение этой системы ж =11, у = 7 удовлетворяет условиям
задачи.
Ответ. «Пятерок» —2, «четверок» —10, «троек»—7,
«двоек» —11.
4.1. Школьник переклеивает все свои марки в новый альбом.
Если он наклеит по 20 марок па один лист, то ему не хватит
альбома, а если по 23 марки на лист, то по крайней мере один
лист окажется пустым. Если школьнику подарить такой же аль-~
бом, на каждом лпстке которого наклеено по 21 марке, то всего
у него станет 500 марок. Сколько листов в альбоме?
4.2. В классе писали контрольную работу. Среди выставлёи-
пых за нее оценок встречаются только оценки 2, 3, 4, 5. Оценки
2, 3, 5 получило одинаковое число учеников, а оценок 4
поставлено больше, чем всех остальных вместе взятых. Оценки выше 3
получили менее 10 учеников. Сколько троек и сколько четверок
было поставлено, если писали контрольную не менее 12
учеников?
4.3. Квартал застроен пятиэтажными п девятнэтажными
домами, причем девятиэтажных домов меньше, чем пятиэтажных.
Если число девятнэтажных домов увеличить вдвое, то общее
число домов станет больше 24, а если увеличить вдвое число
пятиэтажных домов, то общее число домов станет менее 27,
Сколько построено пятиэтажных домов и сколько
девятиэтажных?
4.4. На стоянке находятся машины марок «Москвич» и
«Волга», .Общее число нх .менее 30. Если увеличить вдвое число
«Волг», а число «Москвичей» увеличить на 27, то «Волг» станет
больше; а еслр увеличить вдвое число «Москвичей», не изменяя
числа «Волг», то «Москвичей» станет больше. Сколько
«Москвичей» н сколько «Волг» находится иа стоянке?
4.5. В школьной газете сообщается, что процент учеников
некоторого класса, повысивших во втором полугодии
успеваемость, заключен в пределах от 2,9 до 3,1 %. Определить
минимально возможное число учеников в таком классе.
. .4.6*. Завод должен переслать заказчику 1100 деталей.
Детали для пересылки упаковываются в ящики. Имеются ящикн
трех типов. Ящик первогр типа .вмещает 70 деталей, ящик
второго типа —40 деталей, ящик третьего типа — 25 детален.
Стоимость пересылки ящика первого типа составляет 20 р., стоимость
пересылки ящика второго типа—10 р., стоимость пересылки
ящика третьего типа — 7 р. Какие ящики должен использовать
аавод, чтобы стоимость пересылки была наименьшей?
(Недогрузка ящиков не Допускается.)
S i. ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ НЕИЗВЕСТНЫМИ 203
4.7*. Колхоз арендовал два экскаватора. Аренда первого
экскаватора стоит 60 р. в день, производительность его в мягком
грунте —250 м3 в день, в твердом грунте—150 м3 в день-
Аренда второго экскаватора стоит 50 руб. в день, его
производительность в мягком грунте—180 м8 в день, а в твердом —
100 м3 в день. Первый экскаватор проработал несколько полных
дней и вынул 720 м3. Второй за несколько полных дней вынул
330 м3. Сколько дней работал каждый экскаватор, если колхоз
заплатил за аренду не более 300 р.?
4.8. В вазе лежат конфеты двух сортов, причем число
конфет первого сорта более чем на 20 штук превышает число
конфет второго сорта. Одна конфета первого сорта веснт 2 г, а
конфета второго сорта — 3 г. Из вазы взяли 15 конфет одного
сорта, вес которых составил пятую часть от веса всех конфет,
лежавших в вазе. Затем было взято еще 20 конфет другого сорта;
их вес оказался равным весу оставшихся в вазе конфет. Сколько
конфет каждого сорта лежало первоначально в вазе?
При решении некоторых задач с целочисленными
неизвестными область изменения искомого неизвестного удается получить
лишь вследствие определения области изменения
вспомогательного неизвестного, некоторой функцией от которого является
искомое неизвестное. Условие целочнсленностн при этом
используется лишь для получения однозначного ответа.
Пример 4.2. Из пункта А в пункт В сплавляют по реке
плоты, отправляя их через равные промежутки времени.
Скорости всех плотов относительно берега реки постоянны н равны
между собой. Пешеход, идущий из Л в В по берегу рекн,
прошел треть пути от Л до В к моменту отплытня первого плота.
Дойдя до В, пешеход сразу отправился в А н встретил первый
плот, пройдя более 3/13 пути от В до Л, а последний плот он
встретил, пройдя более 9/10 пути от В до А. Пешеход в пункт А
и седьмой плот в пункт В прибыли одновременно. Из пункта А
пешеход сразу вышел в В н прибыл- туда одновременно с
последним плотом. Скорость пешехода постоянна, участок реки
от Л до В прямолинейный. Сколько плотов отправлено нз
ЛвВ?
Решение. Составим систему уравнений н неравенств
исходя нз условий задачи. Для этого обозначим: расстояние от
Л до В через S, скорости пешехода п рекн через о„ п оР
соответственно, число плотов через в, расстояние от пункта В до встречи
пешехода о первым плотом через х, расстояние от пункта А до
встречи пешехода с последним плотом через у, Л — иитервал
времени между пусками отдельных плотов,
294 ГЛ.'П. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
Все уравнения составляются нз условия равенства
интервалов времени, прошедших для каждого нз движущихся
объектов от момента начала движения до встречи:
Условие задачи
Уравнение
Время, прошедшее до встречи
пешехода и первого плота
Время, прошедшее до встречи
пешехода и последнего плота
Пешеход пришел в пувкт А. когда
седьмой илот пришел в пункт В
Пешеход пришел в пункт В
одновременно с последним плотом
~S + X S-x
°П
jl;.
-К
°п
■f»
"р
-1)Д=-
S
ВР
S
+ 6Д
- + (п
5
3
S-
"п
пл
У
К этой системе уравпений исходя из условий задачи следует
добавить еще два неравенства:
x>las> y<los'
(♦>
Выразим х и у нз первого и второго уравпений системы,
заменив (л—1)Д на разность
8 с
н подставим эти выражения в неравенства (•). Имеем систему
неравенств
3 vn
' +^
>-ПГ5'
'р °П I
1 . 1 <То& <**>
»п
»п
В этой системе удобно ввести неизвестное z=—, тогда отио-
сительно этого неизвестного система (*«) приобретает внд
3 - 2* 3
•3(l + z) 13* 39-26z>9 + 9z, 9 6
I-z ■ ?l. "**40-10z<t + z. "**" 11 <Я< 7 m
1+й > 10 - ■ -
5 4. ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ НЕИЗВЕСТНЫМИ 295
Из двух оставшихся уравнений выразим искомое неизвестное
я через неизвестное г. Так как
Ть s
п — 1 = ■
fn vp
(*_Л s\6
\3 % vp )
■4±М
6 \ Рц Рр/'
"-l = —g-5 s—илк
п-1 —
3 «п
48*-18
бг-3
Функция / (г) = _ убывает на всей области определения,
таким образом, наибольшее значение этой функции иа отрезке
/964 9 234
ге1-тг, -yl достигается в точке -ту-и равно-js-, а иаи-
6 162
меньшее — в точке -=- и равно —„—, т. е. справедливо
неравенство
162 ^ , ^ 234
-д- < п - К -1Г.
Едннственным целым числом, удовлетворяющим указанному
неравенству, является число 19.
Ответ, я = 20.
4.9. Несколько самосвалов загружаются поочередно в
пункте А (время загрузки одно н то же для всех машнк) и отвозят
груз в пункт В; там они мгновенно разгружаются н ■
возвращаются в А. Скорости машин одинаковы, скорость груженой машины
составляет 6/7 скорости порожней. Первым выехал на Л
водитель Петров. На обратном пути он встретил водителя Иванова,
выехавшего из Л последним, н прибыл в А через 6 мии после
встречи. Здесь Петров сразу же приступил к загрузке, а по
окончании ее выехал в В и встретил Иванова во второй раз через
40 мня После первой встречи. От места второй встречи до А
Иванов ехал не менее 16 мяв, но ае более 19 мин. Определить
время вагруэкя.
4.10. Из пункта Л в пункт В сплавляют по реке плоты,
отправляя нх через равные промежутки времени. Скорости плотов
постоянны и равны между собой. Пешеход, пдущпй из Л в В,
прошел четверть пути от Л до б к моменту отплытия первого
296 ГЛ. 11. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
плота. Этот плот поравнялся с пешеходом, проплыв более 6/11
пути от А до В. Пешеход, прибыв в В одновременно с четвертым
плотом, сразу отправился в А. Пройдя более 9/14 пути от В
до А, он встретил последний плот и прибыл в А одновременно
с прибытием этого плота в В. Сколько отправлено плотов?
Еще одним типом задач на составление уравнений с
целочисленными неизвестными являются аадачи на запись чисел в
десятичной позиционной системе счисления.
Пример 4.3. Искомое трехзначное число оканчивается
Цифрой 1.*Еслн эту цифру перенести с последнего места на
первое, сохранив порядок остальных двух цифр, то вновь получеи-
ное число будет меньше искомого на 90. Найти это число.
Решение. Обозначим число сотен искомого трехзначного
числа через т, а число десятков — через п. Искомое трехзначное
число tnnl (знак умножения между т, в и 1 отсутствует, т,
п — цифры десятичной системы счисления, н m^fcO) есть сокрап
щенная запись числа tn-10a + n-10+ 1. Трехзначное число,
образованное в результате переноса 1 с последнего места на первое,
будет Ы0*-fm-90 + n. По условию задачи последнее число на
90 меньше искомого:
т • 102 + п ■ 10 + 1 = I • 102 + т • 10 + я + 90.
Таким образом, получено одно уравнение с двумя неизвестными
тип, причем мы анаем, что тип — цифры десятичной
позиционной системы счисления и m ф 0. Чнсло единиц в числе,
стоящем слева, должно совпадать с числом единиц в числе, стоящем
справа, н поэтому «=» 1. Теперь уравнение приобретает вид
т • 10s + 10 = 1 • 10» + m • 10 + 90,
откуда находим, что m = 2.
Ответ. Искомое число — 211.
Пример 4.4. Если двузначное число разделить на сумму
его цифр, то получится в частном 4, а в остатке 3. Если же это
число разделить на произведение его цифр, то получится в
частном 3, а в остатке 5. Найтн это число.
Решение. Прежде чем перейти к решению задачи,
напомним, что если чнсло ЛГ делится на чнсло р и в частном
получается число А, а в остатке чнсло г (г < р), то чнсло N пред-
ставнмо в виде
N = kp + г.
/На использовании этого равенства в основано решение задача*
§ 4. ЗАДАЧИ С ЦЕЛОЧИСЛЕННЫМИ НЕИЗВЕСТНЫМИ 297'
Запишем двузначное число в виде 10-/п-|-л. Условие задачи
приводит к системе двух уравнений:
Ют + п = 4 (т + п) + 3, 6т = Зя + 3,
10т + п = Зтп + 5 10т +п = 3/?т + 5,
я = 2от — I,
Ют + п = Ътп + б#
Подставляя л = 2т—1 во второе уравнение системы, полу»
чаем уравнение
2т? - 5т +1=0,
решения которого nti = 2, mt = 1/2. Условию задачи (т я л —
цифры) удовлетворяет только корень m = 2. Из первого урав-
нения системы находим я = 3.
Ответ. Искомое число — 23.
4.11. Какое двузначное число меньше суммы квадратов его
цифр на 11 и больше нх удвоенного произведения на 5?
4.12. Сумма цифр двузначного числа равна 12. Если к
искомому числу прибавить 36, то получим число, записанное теми же
цифрами, но в обратном порядке. Найти это число.
4.13. Сумма квадратов цифр двузначного числа равна 13.
Если от этого числа отнять 9, то получим число, записанное теми
же цифрами в обратном порядке. Найтн это число.
4.14*. Задумано целое положительное число меньше 10. К его
ааписи присоединили справа цифру 5 н нз получившегося нового
числа вычлн квадрат задуманного числа. Разность разделили на
задуманное .число, а затем вычлн задуманное число. Осталась
единица. Какое число задумано?
4.15. Ученику надо было умножить 72 на двузначное число,
в котором десятков втрое больше единиц-, по ошибке' он
переставил цифры во втором сомножителе, отчего получил
произведение на 2592 меньше истинного. Чему равно истинное
произведение?
4.16*. Запись шестизначного числа начинается цифрой 2.
Если цифру перенести с первого .места на последнее, сохранив
порядок остальных пяти цифр, то вновь полученное число будет
втрое больше первоначального. Найти первоначальное число.
4.17. Определить целое положительное число по следующим
данным: если к его цифровой записи присоединить справа
цифру 4, то получим число, делящееся без остатка на число,
большее искомого на 4, а в частном получится число, меньшее
делителя на 27.
4.18*. Сумму всех четных двузначных чисел разделили на
одно вз ннх без остатка, Получившееся частное только поряд-
298 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЯ
ком цифр отличается от делителя, а сумма его цифр равна 9.
Какое двузначное число являлось делителем?
4.19. К цифровой записи некоторого задуманного
положительного числа приписали справа еще какое-то лоложнтельное
однозначное число. Из получившегося таким образом нового
числа вычли квадрат задуманного числа. Эта разность оказалась
больше задуманного числа во столько раз, сколько составляет
дополнение приписанного числа до 11. Требуется доказать, что
ато возможно тогда и только тогда, когда прппвсаиное число
равно задуманному.
4.20. Найти два двузначных числа, обладающих следующим
свойством: если к большему искомому числу приписать справа 0
я затем меньшее число, а к меньшему приписать справа большее
число и затем 0, то из образовавшихся таким образом двух
пятизначных чисел первое, будучи разделенным на второе, дает
в частном 2 и в остатке 590. Кроме того, известно, что сумма
(удвоенного большего искомого числа и утроенного меньшего
равна 72.
4.21. При перемножении чисел, из которых одно на 10
больше другого, была допущена ошибка: цифру десятков в
произведении уменьшили на 4. При делении (для проверки ответа)
полученного произведения на меньший множитель получили в
частном 39, а в остатке 22. Найти сомножители.
4.22*. Найти два двузначных числа Л и В по следующему
условию: если цифровую запись числа А записать впереди В н
полученное число разделить на В, то в частном получится 121.
13олн же цифровую запись числа В записать впереди числа А и
полученное число разделить на Л, то в частной будет 84, а в
остатке 14. Найти А н В.
4.23*. Квадрат целого положительного простого числа ff
делится (с остатком) на 3, полученное неполное частное
делится (без остатка) на 3, частное вновь (с остатком) делится
на 3, и, наконец, полученное неполное частное опять с остатком
делится на 3 и дает в результате 16. Найти N.
4.24*. Знаменатель дроби больше квадрата ее числителя на
единицу. Если к числителю и знаменателю прибавить 2, то. дробь
будет больше 1/4; а если отнять от числителя и анаиенатедя 3,
то дробь будет меньше 1/10. Найти дробь.
4.25*. Два брата продали стадо овец, выручив за каждую
овцу столько рублей, сколько было овец в стаде. Желая
разделять выручку поровну, они поступили следующим образом:
каждый брат, начиная со старшего, брал из общей суммы по десять
рублей, После того как в очередной. раз старший брат взял де-
§ 5. ЗАДАЧИ НА КОНЦЕНТРАЦИЮ
299
сять рублей, остаток от выручки оказался меньше десяти рублей.
Желая его компенсировать, старший брат отдал младшему свой
нож. Во сколько рублей был оценен этот нож?
§ 5. Задачи на концентрацию и процентное
содержание
Решение задач па концентрацию и процентное содержание
основано на использовании следующих понятий и формул.
Пусть даны три различных вещества А, В и С с массами
Мл, Мв и Мс. Масса сиесп, составленной из этнх веществ, равна
Мл + Мв + Мс.
Массовой концентрацией вещества А в смесн называется
величина ел, вычисляемая по формуле
сл= мд + мв + мс'
Соответственно массовые концентрации веществ В и С в этой,
смеси вычисляются по формулам
мв мс
св= мА + мв + мс* ес= мА + мв + мс-
Массовые концентрации ел, св к сс связаны равенством
сА + св + сс = \.
Процентными содержаниями вещества Л, В, С в данной
смеси называются величины р» %, рв% н рс% соответственно,
вычисляемые по формулам
РА%=сА-100%, рв%=св.100%, рс%=ес-100%.
По аналогичным формулам вычисляются концентрации веществ
в смеси н для случая, когда число различных смешиваемых
веществ (компонент) равно двум, четырем, пяти и т. д.
Объемные концентрации веществ в смеси определяются
такими же формулами, как и массовые концентрации, только
вместо масс компонент Мл, Мв н Мс в этнх формулах будут стоять
объемы компонент Va, Ив и Vc- В тех случаях, когда речь вдет
об объемных концентрациях, обычно предполагается, что при
смешивании веществ объем смеси будет равен сумме объемов
компонент. Это предположение не является физическим законом,-
* представляет собой соглашение, принимаемое при решении
задач па объемную концентрацию.
Пример 5,1. В сосуд емкостью в л налито 4 л 70%-ного
раствора серной кислоты, Во второй сосуд той же емкости на-
300 ГЛ. II. ЗАДАЧЕ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
лнто 3 л 90%-ного раствора серной кислоты. Сколько литров
раствора нужно перелить из второго сосуда в первый, чтобы
в нем получился г %-ный раствор серной кислоты? Найти все
значения г, при которых задача имеет решение.
Решение. Обозначим через х л объем 90%-ного раствора
серной кислоты, который переливается из второго сосуда в пер-
9х
вый. В этом объеме содержится-jtt л чистой (100%-ной)
серной кислоты. Первоначально в первом сосуде объем чистой сер-
7
ной кислоты был равен -yjr • 4 (л). После того как в первый
сосуд долили х л 90%-ного раствора серной кислоты, в нем
7 9
будет содержаться-ГТГ-4 +-ттг-ч; л чистой серной кислоты.
Используя определение объемного процентного содержания, в
соответствии с условием задачи получаем уравнение
*^"4 + W".I00%->r%.
* + 4
Решая это уравнение, находим величину перелитого объема:
,. , 4 (г -70)
90-г '
Остается выяснить, при каких значениях г задача имеет
решение. Из условия задачи очевидно, что количество доливае-
' мого раствора не может превысить 2 л, так как объем первого
сосуда равен 6 л, т.е,0<х s£-2. Используя найденное значение
для х, получим ограничения на г.
Решая данное неравенство (с учетом того, что 70 <^ г ^90),
2
получим 70 < г < 76 -д-.
Ответ, —jnr^—— (л); задача имеет решение прн 70 ^ г ^
<76т-
6.1. Имеется кусок сплава меди с оловом общей массой 12 кг,
содержащий 45 % меди. Сколько чистого олова надо добавить
к втому куску сплава, чтобы получившийся новый, сплав
«одержал 40 % .меди?.
8 б. ЗАДАЧИ НА КОНЦЕНТРАЦИЮ
S01
5.2. Имеются два слнтка сплавов медн н олова. Первый
весит 3 кг и содержит 40 % меди, второй весит 7 кг н содержит
30 % медн. Какого веса пужио взять кускн этих слитков, чтобы
после их совместной переплавки получить 8 кг сплава,
содержащего г % медн? Найти все значения г, при которых задача
имеет решение.
5.3. Свежие фрукты содержат 72% воды, а сухие — 20%.
Сколько сухих фруктов получается нз 20 кг свежих?
5.4. Морская вода содержит (по весу) 5 % соли. Сколько
килограммов пресной воды нужно прибавить к 40 кг морской
воды, чтобы содержание соли в растворе составило 2 %?
6.6, В двух сосудах находился раствор вещества различной
концентрации, причем в первом сосуде на т литров меньше, чем
во втором. Из каждого сосуда взяли одновременно по п литров
и взятое нз первого сосуда перелили во второй, а взятое из
второго — в первый. После этого концентрации растворов в
обоих сосудах стали одинаковыми. Найти, сколько литров раствора
было в каждом сосуде.
5.6*. Из двух кусков с различным процентным содержанием
медн, весящих m кг u n кг, отрезано по одинаковому куску.
Каждый нз отрезанных кусков сплавлен с остатком- другого
куска, после чего процентное содержание медн в обоих сплавах
стало одинаковым. Сколько весил каждый нз отрезанных
кусков?
5.7. Сплавили два сорта чугуна с разным процентным
содержанием хрома. Если одного сорта взять в 5 раз больше
другого, то процеитное содержание хрома в сплаве вдвое превысит
процентное содержание хрома в меньшей нз сплавляемых частей.
Если же взять одинаковое количество обоих сортов, то сплав
будет содержать 8 % хрома. Определить процентное содержание
хрома в каждом сорте чугуна.
5.8*. Даны три различных соединения железа. В каждом
кубическом сантиметре первого соединения содержится на 3/20 г
железа меньше, чем в каждом кубическом сантиметре второго
соединения, а в каждом кубическом сантиметре третьего
соединения— в 10/9 раза больше, чем в каждом кубическом
сантиметре первого соединения. Кусок третьего соединения,
содержащий 1 г железа, имеет объем на 4/3 см3 больший, чем кусок
второго соединения, также содержащий I г железа. В каком
объеме третьего соединения содержится 1 г железа?
Указание.' Воспользоваться формулой т =* pV,
связывающей массу, плотность^и-объем вещества.
5.9. Величины процентного содержания спирта в трех
растворах образуют геометрическую прогрессию, Если смешать перл
302 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЯ
вый, второй и третий растворы в весовом отношении 2:3:4, то
получится раствор, содержащий 32 % спирта. Если же смешать
нх в отиошенни 3:2: I, то получится раствор, содержащий 22 %\
спирта. Сколько процентов спирта содержит каждый раствор?
5.10*. В лаборатории имеются растворы поваренной соли
четырех различных концентраций. Если смешать первый, второй
и третий растворы в весовом отношении 3:2:1, то получится
15 %-ный раствор. Второй, третий н четвертый растворы, взятые
в равной пропорции, дают при смешнвапнн 24 %-ный раствор,
и, наконец, раствор, составленный из равных весовых частей
первого и третьего растворов, имеет концентрацию 10 %. Какая
концентрация получится при смешении второго и четвертого рас-
творов в пропорции 2:1?
5.11. Три одинаковые пробирки наполнены до половины
растворами спирта. После того как содержимое третьей пробирки
разлили поровну в первые две, объемная концентрация спирта
в первой уменьшилась па 20 % своей величины, а во второй —
увеличилась на 10% своей величины. Во сколько раз
первоначальное количество спирта в первой пробирке превышало
первоначальное количество спирта во второй пробирке? (Изменением
объема при смешивании растворов пренебречь.)
6.12. Имеются два раствора солн в воде. Для получения
смеси; содержащей 10 г солн н 90 г воды, берут первого
раствора вдвое больше по массе, чем второго. Через неделю нэ
каждого килограима первого н второго растворов испарилось
по 200 г воды и для получения той же сиесн, что л раньше,
требуется первого раствора уже вчетверо больше по массе, чей
'второго. Сколько граммов солн содержалось первоначально в
'"100 г каждого раствора?
5.13. Имеются два водных раствора вещества А и В,
различающихся весовыми соотношениями веществ А, В и воды. В пер*
вом растворе вещества А столько же, сколько воды, а
вещества В в полтора раза больше, чем вещества А. Во втором
растворе вещества В в два раза меньше, чем вещества А, н в два
раза больше, чем воды. Сколько нужно взять каждого раствора
и сколько добавить воды, чтобы получить 37 кг нагого раствора,
в котором вещества А столько же, сколько вещества В, а воды
в два раза больше, чем вещества Л?
5.14. В пустой резервуар по двум трубам одновременно на-
■ чннают поступать чистая вода и раствор кислоты постоянной
концентрации. После наполнения резервуара в нем получился
5 %-ный раствор кислоты. Если бы в тот момент, когда
резервуар был наполнен наполовину, подачу воды прекратили; то
после наполнения резервуара получили бы 10 %-ный раствор
§ 6. ЗАДАЧИ НА КОНЦЕНТРАЦИЮ
303
кислоты. Определить, какая труба подает жидкость быстрее в
во сколько раз.
5.15. Две трубы, работая вместе, подают в бак 100 л
жидкости в минуту. Имеются два раствора кислоты — сильный и
слабый. Если смешать по 10 л каждого раствора и 20 л воды, то
получится 40 л 20 %-ного раствора. Известно также, что если
в течение часа подавать в первоначально пустой бак по первой
трубе слабый раствор, а по второй—сильный, то получится
30 %-ный раствор кислоты. Какой концентрации (в процентах)
получится раствор кислоты, если в течение часа подавать в
первоначально пустой бак по первой трубе сильный раствор, а по
второй — слабый? (Считается, что при смешивании воды и
кислоты объем не меняется.)
5.16. Имеются 3 слитка различных сплавов золота с
серебром. Известно, что количество золота в 2 г сплава из третьего
слитка то же, что во взятых вместе I г из первого и I г го
второго слитков. Вес третьего слитка равен суммарному весу
части первого слитка, содержащей 10 г золота, и части второго
слнтка, содержащей 80 г золота. Третий слиток в 4 раза
тяжелее первого н содержит 75 г золота. Сколько граммов золота
содержится в первом слнтке?
5.17. Имеются два сплава, состоящих из цинка, медв н
олова. Известно, что первый, сплав содержит 40 % олова, а
второй — 26 % меди. Процентное содержание цинка в нервом в вто«
ром сплавах одинаково. Сплавив 150 г первого сплава н 250 R
второго, получим новый сплав, в котором будет 30 % цинка. Оп*
ределпть, сколько килограммов олова содержится в новом сплаве,
5.18. Имеются три сплава. Первый сплав содержит 30 %
никеля н 70 % меди, второй — 10% меди н 90% марганца, тре»
- тнй —15% никеля, 25% медн и 60 % марганца. Из них
необходимо приготовить новый сплав, содержащий 40 % маргднца.
Какое наименьшее и какое наибольшее процентное содержание
меди может быть в этом новом сплаве?
5.19. Из бутыли, наполненной 12 %-ным (по массе)
раствором соли, отлили 1 л н налили I л воды, затем отлили еще 1 л
и опять долнлн водой. В бутыле оказался 3 %-ный (по Массе)
раствор соли. Какова вместимость бутыли?
5.20. Имеются два бака: первый бак наполнен чистым
глицерином, второй — водой. Взяли два трехлитровых ковша,
зачерпнули нервым полный ковш глицерина нз первого бака, а
вторым — полный ковш воды из второго бака, после чего первый
ковш влплн во второй бак, а второй ковш влили в первый бак.
Затем, после перемешивания, снова зачерпнули первым полный
ковш емесн из первого бака, вторым — полный ковш смеси из
304 ГЛ. II. ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
второго бака н влили первый ковш во второй бак, а второй
ковш — в первый бак. В результате половину объема первого
бака занял чистый глицерин. Найти объемы баков, если известно,
что их суммарный объем в 10 раз больше объема первого бака,
5.21. Из сосуда, наполненного 96%-пым раствором кислоты,
отлили 2,5 л н долили 2,5 л 80 %-ного раствора той же кислоты,
затем еще раз отлили 2,5 л и снова долили 2,5 л 80 %-ного
раствора кислоты. После этого в сосуде получился 89 %-ный
раствор кислоты. Определить вместимость сосуда.
5.22. В каждом из двух сосудов находится по V л чистой
кислоты.' Из первого сосуда отлили а л кислоты и долили а я
воды. Потом эту процедуру повторили еще раз. Из второго
сосуда отлили 2а л кислоты и долили 2а л воды. Потом эту про»
цвдуру повторили еще раз. Известно, что в результате
концентрация кислоты в первом сосуде оказалась в 25/16 раза больше,
чем концентрация кислоты во втором сосуде. Какую часть объ-
eua сосуда составляют а л?
5.23. Непромытый золотой песок содержит k % чистого
золота. После каждой промывки вымывается р % содержащихся
в нем примесей и теряется q % имеющегося в песке золота.
Сколько следует произвести промывок, чтобы процент содержа-
ивя чистого золота в золотом песке был не меньше г?
§ 6. Разные задачи
В задачах этого параграфа требуется определить значение
некоторой Комбинации неизвестных, представив ее в виде
функции от других Комбинаций неизвестных, числовые значения
которых определены условиями задачи.
Пример 6.1. Три экскаватора разной производительности
рыли котлован. Если бы производительность первого была в
2 раза, а третьего — в 3 раза больше, чем в действительности, то
котлован был бы вырыт за 5 дней. Если бы производительность
первого была в 3 раза, второго — в 2 раза, а третьего — в 4 раза
больше, чем в действительности, то котловап был бы вырыт за
о -г- Дня- За сколько дней котлован был вырыт в
действительности?
Решения. Обозначая объем котлована v, а действптель-
• "ные производительности первого, второго н третьего экскаваторов
■ х; у, г соответственно, составим следующие два уравнения:
5(2* + y-f 3z)=p,
3 -|- (Здр + 2у -f Щ •= v.
S 6. РАЗНЫЕ ЗАДАЧИ 305
Если искомую величину — число дней, за которое в
действительности был вырыт котлован, — обозначить I, то можно составить
третье уравнение
t{x-\-y + z)=v.
Полученную систему из 3-х уравнений обозначим (*).
Комбинацию неизвестных t = —, ;— требуется представить в видо
х т У т z
v
некоторой функции от комоипаций неизвестных „—г;—, „ Я
- - . , числовые значения которых б и 3—
соответственно определены условиями задачи.
Перепишем систему уравнений (*) в следующем виде:
2* + 2/ + 3z=.-jp
3* + 2y + 4z«-jg-f
* + </ + * = —.
Очевидно, что если найдутся такие действительные числа а и В,
при которых выполняется соотношение
a(2x + y + 3z) + $(3x + 2y + 4z)=x + y+z, . (»*)
то справедливым будет н уравнение
°(i)+4f)-f- (->
Из уравнения (***) t можно выразить в виде
15-5 15
15а + 20В = За + 4В "
Числа а н В находятся из сравнения коэффициентов при
неизвестных в левой н правой части уравнения (t*)i
2о + 38 = 1,
а+ 28=1,
За + 48 = 1.
Из первых двух уравнений получаем В = 1, а = —.1. . Третье
уравнение является следствием первых двух. Подставляя пай-
деиные а и В в (***), получаем
/=15,
Ответ, 16 дней.
806 ГЛ. П, ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИИ
6.1. Гвоздь, 3 винта н 2 шурупа весят 24 г, а 2 гвозде
5 винтов н 4 шурупа весят 44 г. Сколько весят вместе гвоздь,
4 винта и 2 шурупа.
6.2. Трое рабочих должны сделать некоторое количество
детален за определенное время. Если бы первый работал половину
отведенного времени, второй к" этого времени, а третий — -у
часть, то оин сделали бы 30 деталей. Если бы первый
работал -£- часть отведенного времени, второй —гтг, а третий —
-г=-, то они сделали бы 10 детален. Какое количество деталей
1о
сделали бы трое рабочих вместе, если бы работали все отведен*
ное время?
в.З. Школьник затратил некоторую сумму денег на покупку
портфеля, авторучки и кннгн. Если бы портфель стоил в 5 раз
дешевле, авторучка — в 2 раза дешевле, а книга — в 2,5 раза
дешевле, то та же покупка стоила бы 8 руб. Если бы по
сравнению с первоначальной стоимостью портфель стоил в 2 раза
дешевле, авторучка — в 4 раза дешевле, а книга — в 3 раза
дешевле, то за ту же покупку школьник уплатил бы 12 руб. Скольхо
стоит покупка и за что уплачено больше: за портфель нли за
авторучку?
6.4. Имеется три типа станков развой производительности.
При этом 3 станка первого типа, 4 второго и 2 третьего
справляются со всей работой за 2 ч, 2 станка первого типа, 5 второго
н 4 третьего -за 3 i .Объем работы увеличили в 3,5 раза, но
взилн 21 станок первого типа, 42 второго и 24 третьего.
Спрашивается, за какое время они выполнят этот объем работы?
Иногда искомая комбинация неизвестных представляется в
виде функции от другой комбниащгн, числовое значение которой
в условии задачи не дано, но сравнительно легко подлежит
определению.
Пример 6.2. С двух участков поля собрано 330 т
пшеницы. Если бы с каждого гектара первого участка поля было
собрано столько пшеницы, сколько ее собирали с каждого
гектара второго участка, то с обоих участков было бы собрано
405 т, а если бы с каждого гектара второго участка было
собрано столько пшеницы, сколько было собрано с каждого
гектара первого участка, то было бы собрано с обоих участков
270 т. Сколько зерна было собрано с каждого участка в
отдельности?
Решение. Обозначая размеры участков m и п, а
количество зерна, собираемого с одного гектара каждого участка, х
§ в. РАЗНЫЕ ЗАДАЧИ
307
и у соответственно, можно составить, следуя условиям задачи,
систему трех уравнений с четырьмя неизвестными:
тх + пу = 330,
ту + пу = 405, (♦)
тх + пх = 270.
Определению подлежат величины тх и пу. Если рассмотреть в
качестве неизвестных тх, ту, пх, пу, то числа уравнений все
равно не хватает для их определения.
Однако нз двух последних уравнении определяется
следующая комбинация: —. Действительно, разделив третье уравнение
ж 270 2 2
на второе, имеем — =»■■-■. =~о*> т. е. х = -^-у. Подставив
выраженное таким образом х в первое уравнение, получаем для
определения неизвестных ту, пу систему
2
-д- ту + пу — 330,
ту + пу = 405,
откуда -^-ту«=75, или ту = 225. Следовательно, пу=> 180, в
тх — 150.
Ответ. С участков было собраио 180 т н 15.0 т
соответственно.
6.5. На складе имеется некоторое число бочек двух образцов
общей емкостью 7000 л. Если бы все бочки были первого
образца, то емкость всех бочек увеличилась бы на 1000 л. Если
бы все бочки были второго образца, то емкость уменьшилась бы
на 4000 л. Вычислять емкость всех бочек каждого образца в
отдельности.
6.6. В двух кусках сплавов золота с серебром содержится
2 кг золота. Если бы в первом куске концентрация золота
совпадала с концентрацией во втором, то в обоих кусках было бы
2,5 кг золота. Если бы концентрации золота во втором куске
совпадала с концентрацией золота в первом, то в обоих кусках
было бы 1,5 кг золота, Определить, сколько золота было в каж«
дом куске.
Г Л А В А 12
ПЛАНИМЕТРИЯ
§ 1. Треугольники
Признаки равенства треугольников. Два треугольника
равны, если выполняется одно из следующих условий:
1) две стороны и угол, заключенный между ними, одного треуголь-
вика равны двуи сторонам н углу между ними другого треугольника!
2) два угла и прилежащая к нии сторона одного треугольника равны
двуи углам и прилежащей к ним стороне другого треугольника:
3) три стороны одного треугольника равны трем сторонам другого
треугольника.
Каждое нз условий 0—3) задает треугольник, т. е. по любому из
условий 1)—3) с помощью теорем синусон п косинусов можно вычислить
все остальные параметры треугольника.
Формулы вычисления площади треугольника:
5—*jp{p—a){p—b){p—c) формула Геронах
S—pr.
Стороны н углы треугольника связаны формулами:
а 2R теорема синусов:
Bin а з1п fi sin v
а»=6» + C—2bc cos а
Р>=*аг + сг—2accosf} теорема косинусов\
с,а-Ьг + а'—2аЬсозу
где а, 6. с—стороны треугольника; ha, ftj. hc—высоты треугольника,
опущенные на стороны а, Ь, о соответственно; а, р\ у—внутренние углы треугольника,
лежащие против сторон а, Ь, с, соответственно, р=-д-(о +6 +с)—полупери-
метр; /?—радиус окружности, описанной около треугольника; г—радиус
окружности, вписанной в треугольник.
Линии в треугольнике. Медианой треугольника называется
отрезок, соединяющий вершину треугольника с серединой протнвопо*
ложной стороны.
Основные свойства медиан.
1. Медиаиа треугольника есть геометрическое место точек; являю-
Г1хся серединами отрезков прямых,, заключенный внутри * треугрльвнка.
параллельны* той его стороне, к которой проведена медиана.
§ I. ТРЕУГОЛЬНИКИ
309
2. Медианы треугольника пересекаются в одной точке и делятся этой
точкой в отношении 2 : I, считая от вершины треугольника.
3. Медиана делит треугольник иа два равновеликих треугольника.
4. Пусть AM, BN, Ci—медианы треугольника ABC (рис. 12.1), О—точка
пересечения медиан. Площади треугольников ABO, ВСО и АС О равны между
собой н равны одной трети влощадн треугольника ABC.
Высотой треугольника называется отрезок перпендикуляра,
опущенного из вершины треугольника на противоположную сторону или ее
продолжение.
Биссектрисой треугольника называется отрезок биссектрисы
внутреннего угла треугольника, заключенный между вершиной треугольника и
точкой пересечения биссектрисы внутреннего угла с противоположной
стороной.
Основные своЛства биссектрисы.
1. Три биссектрисы треугольника пересекаются в одно!) точке,
лежащей внутри треугольника и являющейся центром окружности, вписанной
в треугольник.
2. Биссектриса треугольника есть геометрическое место точек,
равноудаленных от сторон угла.
3. Биссектриса угла треугольника делит сторону треугольника на
части, пропорциональные врилежащки к ией сторонам.
Некоторые свойства медиан, биссектрис и высот
В треугольниках специального вода,
1. Высота, проведенная нз вершины равнобедренного треугольника,
является также биссектрисой н медианой.
2. В равностороннем треугольнике высота, медиана и биссектриса,
проведенные из одной вершины треугольника, совпадают; центр
окружности, вписанной в равносторонний треугольник, совпадает с центром
окружности, описанной около треугольника, и эта точка называется
центром треугольника.
3. В прямоугольной треугольнике катеты а, Ь и гипотенуза с свя-
вавы равенством
а'+Ь'^с* теорема Пифагора.
4. Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и проекцией этого катета на гипотенузу (р.гс 12.2):
Ь.'.Ь=>Ь1с, а.:а=а',с.
5. Высота прямоугольного треугольника, проведенная из вершины
прямого угла, есть среднее пропорциональное между проекциями квтетов
иа гипотенузу:
1 "—'"«с-
be:h=h\a.
в. Центр окружности, описанной около прямоугольного треугольника,
лежит на середине гипотенузы; радиус описанной окружности равен
половине гипотенузы (а также равен медиане, проведенной нз вершины
прямого угла). "
При решении некоторых аадач достаточно использовать лишь
приведенные выше „основные метрические соотношения между
отдельными элементами треугольника, .
310
ГЛ. 12. ПЛАНИМЕТРИЯ
Пример 1.1. В треугольнике ABC приведены медианы AD
в СЕ. Известно, что AD = 5, бм: = я/8, АСЕ = я/4.
Определить площадь треугольника ABC.
Решение. Пусть О — точка пересечения медиан
треугольника ABC (рнс. 12.3). Для решения этой задачи используем
следующие свойства медиан:
1) медианы точкой их пересечения
делятся в отношении 2:1 (считая от
вершины);
2) площадь треугольника,
сторонами которого являются сторона данного
треугольника и отрезки медиан (т. е,
ААОС), равна 1/3 площади данного
треугольника (т.е. ААВС).
Таким образом, для того чтобы
найти площадь треугольника ABC,
достаточно иайтн площадь треугольника АОС. По условию задачи
в треугольнике АОС известны два угла, а в силу свойства 1) —
и длина стороны АО, равная 10/3. По теореме синусов для
треугольника АОС имеем
СО АО
Рис. 12.3
СО
10/3
sinD^ smXCE sinW8> sinW4>
■CO-
J!
' 3
sin (я/8)
sin (я/4) '
Так как сумма углов треугольника равна it, то АОС = 5я/8.
Используя формулу вычисления площади треугольника S =1
= -5- ab sin Y» получаем
SAAOC = ~2"A0'
CO ■ sin AOC =
3
10
sin (я/8) . 5я
sin'
50 sin (я/8)
sin
(t+t)
3 sin (я/4) 8 9 sin (я/4)
60 sin (я/8) cos (я/8) ^25 2 sin (я/8) cos (я/8) 25
9
sin (я/4)
9 sin (я/4)
Согласно свойству 2) медиан
Ответ. 25/3.
1.1. В треугольнике основание равно 12 см, один пз углов
при основании равен 120", сторона, лежащая против этого угла,
равна 28 см. Определять третью сторону».
§ I. ТРЕУГОЛЬНИКИ
311
1.2. Найти биссектрису угла ВАС треугольника ABC, если
АВ = с, АС= Ь, ВАС = ос.
1.3. В равнобедренном треугольнике ABC {АВ = ВС)
высота АЕ = 12, основание АС = 15. Найти площадь треугольника.
1.4. В остроугольном треугольнике ABC дано: АВ = с;
проведенная нз вершины В медпапа BD = т. Угол BDA острый и
равен р. Вычислить площадь треугольника ABC.
1.6. Есть ли в треугольнике со сторонами 4, б, 6 см угол,
меньший 22,5°?
1.6. В прямоугольном треугольнике ABC имеем: Л = а,
АВ = а. Из вершины прямого угла В опущена высота BE.
В треугольнике ВЕА проведена медиана ED, Найти площадь
треугольника AED.
1.7. В прямоугольном треугольнике ABC угол В прямой, Л =
= ос, АВ = с. На продолжении гипотенузы АС (в сторону
точки С) взята точка D так, что AD = г, Найтн площадь
треугольника BCD.
1.8. В прямоугольном треугольнике ABC нз вершины
прямого угла В опущена высота BE. Из точки С восставлен
перпендикуляр к АС, на котором отложен отрезок CD, равный г.
Найтн площадь треугольника CED, если Л = ос, АВ = с.
1.9. Угол or прн основании равнобедренного треугольника
больше, чем 45°, а площадь равна S. Найти площадь
треугольника, вершинами которого служат основания высот данного
треугольника.
1.10. Основание треугольника равно 20 см, медианы боковых
сторон равны 24 и 18 см. Найти площадь треугольника.
1.11. Заданы два равносторонних треугольника со сторонами
—2—, причем второй получается из первого поворотом на угол
у?
30° вокруг его пентра. Вычислить площадь общей части этпх
треугольников.
1.12. В треугольнике ABC Л=Ё==а, АВ = а, АН — высота,
BE — биссектриса (точка Я лежит на стороне ВС, точка Е — на
АС). Найти площадь треугольника СНЕ.
1.13. В треугольнике ABC проведены биссектрисы AD угла
ВАС я CF угла АСВ (точка D лежит на стороне ВС, а точка
F — на стороне АВ). Найти отношение площадей треугольников
ABC я AFD, если известно, что АВ = 21, АС = 28 и СВ = 20.
1.14. Основание равнобедренного треугольника равно Ь, угол
при основании равен ос. Прямая пересекает продолжение
основания в точке М иод углом 0 я делит пополам ближайшую & Л1
ЗГ2
ГЛ. 12. ПЛАНИМЕТРИЯ
боковую сторону треугольника. Найтн площадь четырехугольник
ка, отсекаемого прямой от данного треугольника.
1.15. В треугольнике ABC из вершимы В проведены высота
треугольника BD и биссектриса треугольника BE. Известно, что
длина стороны АО = 1, а величины углов ВЕС, ABD, ABE, ВАС
образуют арифметическую прогрессию. Найтн длину стороны ВС.
1.16. Угол при вершине равнобедренного треугольника равен
2а. Прямая, пересекающая высоту на расстоянии с от вершины,
образует с продолжением основания угол р\ Найтн площадь
треугольника, отсекаемого этой прямой от данного треугольника.
1.17*. Найтн площадь треугольника, если длины двух его
сторон соответственно равны 1 и Vl5 см, а длина медианы
третьей стороны—2 см.
1.18. В треугольнике ABC биссектриса угла при вершине А
пересекает сторону ВС в точке М, а биссектриса угла при
вершине В пересекает сторону АС в точке Р, причем AM = ВР,
Бнссектрпсы пересекаются в точке О. Известно, что треугольник
ВОМ подобен треугольнику АОР, ВО = (l-f У§") ОР, ВС = 1.
Найти площадь треугольника ABC.
В условиях задач 1.19—1.21 отсутствуют данные, имеющие
размерность длины. В этих задачах удобно ввести
вспомогательную величину а, имеющую размерность длины (например,
сторону треугольника), и решить задачу с доопределенным условием.
В выражениях для искомых величин а сократится и полученное
выражение будет зависеть только от величин, данных в условии
задачи.
1.19. Угол при основании равнобедренного треугольника
равен а. В каком отношении разделяет площадь этого
треугольника прямая, делящая его основание в отношении 2: 1 и
составляющая острый угол (? с меньшей частью основания?
1.20. В треугольнике ABC дано: ЛСВ = 60°, ХвС = 45е. На
продолжении АС за верншну С берется точка К, так что AC =i
= СК. На продолжения ВС за вершину С берется точка М так,
что треугольник с вершинами С, М и К подобен исходному,
Найтн ВС : МК, если известно, что СМ : МК < 1.
1.21. В треугольнике ABC угол В равен я/4, угол С равен
л/3. На медианах ВМ a CN как на диаметрах построены
окружности, пересекающиеся в точках Р и Q. Хорда PQ пересекает
среднюю линию MN в точке F. Найти отношение длины отрезка
NF к длине отрезка FM.
Некоторые задачи решаются методом введения
вспомогательного неизвестного, для которого по условию задачи необхо-
§ 1. ТРЕУГОЛЬНИКИ
31»
днмо составить н решить уравнение. В качестве
вспомогательного неизвестного можно брать линейный размер или угол. Это
вспомогательное неизвестное следует выбирать таким образом,
чтобы величины, данные в условии задачи, и вспомогательное не-
известное однозначно определяли треугольник.
Для составления уравнения обычно следует одни и тот же
элемент выразить двумя способами. Так, для получения
уравнения в треугольнике надо использовать четыре элемента (линей-,
пых или угловых).
Пример 1.2. В равнобедренном треугольнике ABC (АВ =
= ВС) медиана AD и биссектриса СЕ перпендикулярны.
Определить величину угла ADB,
Решение. Обозначим неизвестный угол ADB буквой ср.
Составим уравнение, где в качестве неизвестного будет
фигурировать некоторая тригонометрическая функция ср. Для этого
выразим какой-нибудь элемент треугольника ABC двумя
способами. Удобнее всего для этой цели использовать медиану AD
треугольника ABC. Для составления уравнения нам понадобятся
следующие элементы: длина боковой стороны АВ я угол при
основании треугольника ABC. Обозначим неизвестную длину
стороны АВ буквой а. Неизвестный угол ВСА удается выразить
через уже введенный угол ср. Действительно, так как СЕ и AD
перпендикулярны, то угол DOC прямой (О — точка пересечения
AD и СЕ). Угол <р—внешний угол ADOC. Следовательно,
справедливо равенство
ZDCO + ^ = <p,
т. е. ^/)СО = ф—£-, а так как СЕ — биссектриса, то угол
ВСА ранен 2ZDCO, т.е. 2ср — я. Аналогичные соображения,
Примененные к AADC, приводят к равенству Z.DAC = я — ср. Из
теоремы косинусов, примененной к AADB, имеем
я2 = -j- a2 + AD2 - я • AD • cos <p,
т. е.
я n _ a cos ф ± Уя2 cos2 ф + Зя2" ,*
Из теоремы синусов для AADC имеем
AD a
sin (2ф — я)
2 sin (я —
ЗН ГЛ. 12. ПЛАНИМЕТРИЯ
ели, используя формулы приведения,
AD a
sin 2ф 2 sin ф '
откуда,
AD = —a cos ф. (»*)
Приравнивая левые части уравнений (*) и (**), получаем
требуемое уравнение:
—2а cos ф = а cos ф ± V'а2 cos8 ф + За8. (♦**)
Приводя подобные члены и возводя в квадрат обе части
уравнения, имеем для cos ф два возможных значения
СОЗф =
Vt-
Однако положительное значение созф не удовлетворяет условию
задачи, так как в прямоугольном треугольнике DOC угол Z.ODC,
дополняющий ф до я, должен быть острым.
Таким образом,
ф => arccos|
Ответ, ф«■ arccos( — A/-g- )•
. . В задачах 1.22—1.27 удобно в качестве вспомогательного
неизвестного брать линейный размер, в задачах 1.28—1.32 —.
угол, а в задачах 1.33—1.35 — вводить две вспомогательные
неизвестные величины.
1.22. В треугольнике ABC высоты —CD = 7 н АЕ = 6.
Точка £ делит сторону ВС так, что BE: ЕС = 3 :4. Найти длину
стороны А В.
1.23. Найти площадь равнобедренного треугольника, если
высота, опущенная на основание, равна 10, а высота, опущенная
иа боковую стороиу, равна 12.
1.24. В равнобедренном прямоугольном треугольнике
медианы, проведенные к катетам, равны I. Найти площадь
треугольника.
1.26. В правильном треугольнике ABC со стороной а точки Е
в D являются серединами сторон ВС и АС соответственно.
Точка F лежит на отрезке DC, отрезки BF в DE пересекаются в
точке М. Найти длину отрезка MF, если известно, что площадь
четырехугольника ABMD составляет 5/8 площади треугольника
ABC.
§ I. ТРЕУГОЛЬНИКИ
31В
1.26. В треугольнике с углом 120° длины сторон образуют
арифметическую прогрессию. Найти длины всех сторон
треугольника, если наибольшая нз инх равна 7 си.
1.27. Длнны двух сторон равнобедренного треугольника и
длина высоты, опущенной на основание, образуют
геометрическую прогрессию. Найтн тангенс угла при основании
треугольника, если известно, что он больше двух.
1.28. В прямоугольном треугольнике отношение произведения
длин биссектрис внутренних острых углов к квадрату длины
гипотенузы равно 1/2. Найти острые углы треугольника.
1.29. В треугольнике ABC длина стороны АС равна 6, длина
стороны ВА равна с, а биссектриса внутреннего угла А
пересекается со стороной ВС в такой точке D, что DA = DB. Найти
длину стороны ВС.
1.30. Хорда ЛЯ стягивает дугу окружности, равную 120е.
Точка С лежит на этой дуге, а точка D лежит на хорде АВ. При этом
AD = 2, BD == 1, DC = л/2. Найти площадь треугольника ABC.
1.31. Дан треугольник ABC. Из вершины А проведена
медиана AM, а нз вершины В — медиана ВР. Известно, что угол
АРВ равен углу ВМА, косинус угла АСВ равен 0,8 и ВР =>
= 1 см. Найтн площадь треугольника ABC.
1.32. Два одинаковых правильных треугольника ABC и CDE
со стороной 1 расположены на плоскости так, что имеют только
одну общую точку С н BCD < л/3. Точка К — середина стороны
АС, точка L — середина отрезка СЕ, точка М — середина
отрезка BD, Площадь треугольника KLM равна У3/5. Найти длину
отрезка BD,
1.33. В прямоугольный равнобедренный треугольник ABC с
углом £=90° ипнсан прямоугольный треугольник MNC так,
что: MNC = 90", точка N лежит на гипотенузе АС, а точка4, М —
на стороне АВ. В каком отношении точка ЛГ должна делнть
гипотенузу АС, чтобы площадь треугольника MNC составляла 3/8
от площади треугольника ABC?
1.34. В равнобедренный прямоугольный треугольник Л ВО с
прямым углом при вершине В вписан прямоугольник MNKB так,
что две его стороны MB н KB лежат на катетах, а вершина ЛГ —
на гипотенузе АС. В каком отношении точка JV должна делить
гипотенузу, чтобы площадь прямоугольника составляла 18 %
площади треугольника?
1.35. Углы при вершинах А я С треугольника ABC соответ-
я я
ственно равны -т- в -jr. Найтн угол между высотой BD н
медианой BE этого треугольника.
BIS
ГЛ. 12. ПЛАНИМЕТРИЯ
При решении приведенных ннже задач используются
различные формулы для выпнслеиня площади треугольника. При этом
ипогда ' полезным оказывается следующее свойство площадейг
если отрезки А В и CD лежат на одной прямой, не проходящей
через точку М, и 5i и 5г — площади треугольников МАВ и MCD
Соответственно, то
Si_ AB
Si ="С~Ь~'
Пример 1.3. На стороне АВ треугольника ABC между
«очками А н В взята точка D так, что AD:AB = a (ос < 1);
на стороне ВС между точками В и С
взята точка Е так, что BE: ВС = р
(Р < 1). Через точку Е проведена
прямая, параллельная стороне АС н
пересекающая сторону АВ в точке Р.
Найти отношение площадей треугольников
BDE и BEF.
Решение. Пусть площадь тре-
Ряс, 12.4 угольника ABC равна S. Треугольник
BEF подобен треугольнику ABC, так
как FE\\ АС (рис, 12.4), Так как площади подобных
треугольников относятся как квадраты сходственных сторон, то
Sabbf BE2 t _ _ ,
—s—="ШГ p а ВБР p •
Площади треугольников BDE n ABC выражаются через стороны
и углы этих треугольников по формулам
sa BDE *=~2"^D'BE' sin В,
S=>-^-AB. ВС- sin В,
И8 которых следует
saBDB BD BE BD
—S Ш"Ш"ШШ"ЛВ^ .
По условию задачи AD = АВа, и так как i
BD = AB — AD = AB — АВа=>АВ{1 — a),
то
BD/AB = 1 — а.
Таким образом,
~6|££ - (1 - о) Р -► SA BDB ша S (1 - о) р.
5 I. ТРЕУГОЛЬНИКИ
317
В задаче требуется найти отношение SaBDE:SaBep.
Подставляя в это отношение SABEF = Sp8 и SA Вд£= S (1 — а)Р,
получаем
SA BDE 1 — а
•—а
Ответ. -—5—.
SA ВЕР Р
1.36. В треугольнике ЛВС из вершины Л проведена прямая,
пересекающая сторону ВС в точке D, находящейся между
точками В и С, причем CD: ВС = ос (а < 1/2). На стороне ВС
между точками В н D взята точка Е, и через нее проведена
прямая, параллельная стороне АС и пересекающая сторону АВ
в точке F. Найтн отношение площадей трапеции ACEF п
треугольника ADC, если известно, что CD = DE.
1.37. Точки Е, F, М расположены соответственно на
сторонах АВ, ВС, АС треугольника ABC. Отрезок АЕ составляет 1/3
стороны АВ, отрезок BF составляет 1/6 стороны ВС, отрезок AM
составляет 2/5 стороны АС. Найти отношение площади треуголь*
ника EFM к площади треугольника ABC.
1.38. На продолжениях медпап АК, BL и СМ треугольника
ABC взяты точкн Р, Q в R так, что KP = -jAK, LO=--^-BL
uMR—-^-CM. Найти площадь треугольника PQR, если
площадь треугольника ABC равна единице.
1.39. Дан треугольник ABC, площадь которого равна
единице. На медианах АК, BL и CN треугольника ABC взяты
соответственно точки Р, Q и R так, что
АР BQ.^-L £L— 5
Р/С e ' QL 2' RN * 4 *
Найти площадь треугольника PQR.
1.40. Треугольник ABC не имеет тупых углов. На стороне
3
АС этого треугольника взята точка D так, что *4D = — AC.
4
Найти угол ВАС, если известно, что прямая BD разбивает
треугольник ABC на два подобных треугольника.
1.41. Точкн Р и Q делят стороны ВС и СА' треугольника
ABC в отношении
Тс-* ^Т=р-
Пусть О — точка пересечения прямых АР и BQ. Найти
отношение площади четырехугольника OPCQ к площади данного тр&1
угольника.
318
ГЛ. 12. ПЛАНИМЕТРИЯ
1.42. В треугольнике ABC на стороне АС взята точка М, а
иа стороне ВС — точка ЛГ. Отрезки ВМ и AN пересекаются в
точке О. Найти площадь треугольника CMN, если площадп
треугольников АОМ, АОВ и BON равны соответственно Si, Sz, St.
1.43. В треугольнике ABC на стороне ВС выбрана точка D
так, что BD: CD =1:2. В каком отношении медиана СЕ делит
отрезок AD?
1.44. В треугольнике ЛВС через основание D высоты BD
параллельно стороне АВ проведена прямая, пересекающая ВС в
точке iC, Найти ВК.: КС, еслп 5Д DBK : SAABC — 3:16.
1.45. Все стороны треугольника меньше 1 см. Доказать, что
площадь треугольника меньше уЗ /4 см2.
1.46. На стороне АС треугольника ABC взята точка N, а
па стороне ВС — точка М так, что CN: NA — 5. Площади
многоугольников NMC a ANBM относятся как 5:6. Наятн СМ : MB,
■ 1.47. В треугольнике ABC проведены медиана AM,
биссектриса АЕ п высота AD. Площадь треугольника АЕМ равна 1/4
площади треугольника ABC, а площадь треугольника ADM
равна 7/50 площади треугольника ABC. Найти углы треугольника
ABC.
§ 2. Четырехугольники
Параллелограмм. Четырехугольник, у которого
противоположные 'стороны попарно параллельны, называется параллелограммом.
Параллелограмм обладает следующими основными свойствами:
I) противоположные стороны параллелограмма раины;
' 2) пропазоподажяыв утлы параллелограмма рачпы;
3) днагоаали параллелограмма делятся точкой пересечения полосам:
4) сумма квадратов дяагоиалей параллелограмма равна сумме
квадратов всех его сторон.
Площадь параллелограмма вычисляется по формулам
где а, 6—стороны параллелограмма. Afl—высота параллелограмма, ову«
щениая иа сторону а, а— угол параллелограмма.
Ромб. Параллелограмм, все стороны которого равны, называется
ромбом. Ромб, как параллелограмм специального вида, имеет все
свойства параллелограмма. Кроме того, ромб обладает следующими специаль»
ными свойствами:
1) диагонали ромба взаимно перпендикулярны;
3) аяапхшли ромба являются биссектрисами его внутренних углов.
Площадь ромба вычисляется по тем же формулам, что я шимцаль
параллелограмма. Кроме того, площадь ромба может быть вычислена
по формуле
S—~ d,d„
где d, и di — днагоиалн ромба.
Прямоугольник в квадрат. Параллелограмм, у которого
во» углы арямые, навивается прямоугольника*. Площадь прямоугольника
вычисляется по формуле
где «л(> смежные стороны прямоугольника.
§ 2. ЧЕТЫРЕХУГОЛЬНИКИ 319
Прямоугольник, у которого все стороны равны, называется коадра»
том. Квадрат обладает всеми свойствами параллелограмма, ромба п при»
моуголышка. Площадь квадрата вычисляется по формуле
S~a*.
где а — сторона квадрата.
Трапеция. Четырехугольник, две стороны которого параллельны,
а две другие непараллельны, назыввется трапецией. Площадь трапеции
с основаниями а а о а высотой h вычисляется по формуле
Отрезок, соединяющий середины боковых стнров трапеции, вазы*
вается средней линией трапеции. Средняя ливня трапеции обладает еле- -
дующими свойствами:
1) средня* линия трапеции параллельна основаниям в равна и
полусумме;
2) средняя лнвпя делнт высоту трапецнп на два равных отрезка.
Пример 2.1. Дана трапеция PQRN с основаниями PN а
QR, прячем PN = 8, QR = 4, PQ =• л/Ш, PJ?P =» 60". Через
точку R проходит прямая, делящая трапецию на две равновеликие
фигуры. Найти длину отрезка этой прямой, находящегося внутри
трапеции.
Решение. Для решения задачи нам потребуется найти ве-
лиянну площади трапеции PQRN. Так как длины сторон PN и
QR известны, то для определения этой величины необходимо
найти длину высоты трапеция ft. Сделаем следующее
дополнительное построение: проведем через точку R прямую,
параллельную боковой стороне трапеции QP, в рассмотрим
треугольник RPtN. Так как PPt = QR = 4, то PtN = 4, RPi = PQ =
= ■у/Ш. Обозначим длину стороны RN через х и, используя
теорему косинусов для треугольника RP\N, составим следующее
уравнение!
28 = 16 + х* - 4х. (»)
Единственным положительным корнем уравнения (») будет х=6.
Высота h находится из треугольника RP\N во формуле
А = 6- sta 60° = 6.-^- = 3 V».
Площадь трапеции PQRN вычисляется тогда следующим
образом;
SPQRH = Т (4 + 8)' 3 ^ = '8 ^'
Предположим теперь, что прямая RM пересекает основание
траиецвн. (Справедяшость этого предположения будет
установлена ниже.) Тогда площадь треугольника RNM рэваа по
условию ~2 SpQRN> т. е, 9 ■у/ъ. Высота треугольника RNM совпа-
820
ГЛ. 12. ПЛАНИМЕТРИЯ
дает с высотой трапеции PQRN, и, следовательно, длина
основания MN вычисляется по формуле
Так как PN = 8, MN = 6, то справедливость утверждения
О том, что RN пересекает основание трапеции, установлена. Если
бы MN оказалось больше PN, то это означало бы, что прямая,
проходящая через точку R, пересекает PQ — боковую сторону
трапеции. Выпислнм теперь искомую длину отрезка MR, а так
1п как AMRN равнобедренный, MN —•
= RN и угол RNM = 60°, то AMRN
равносторонний, т. е. RM = 6.
\ Заметим, что если бы прямая
\ пересекала боковую сторону трапе-
\ цин PQ в точке М' (рис. 12.5), то
,. ( \ длину отрезка M'R можно было бы
*•■ ь tn n n найтн из треугольника M'QR* Для
Рнс- 12-5 вычисления этого отрезка необходимо
было бы предварительно вычислить
угол трапеции PQR (который является также и углом
рассматриваемого треугольника M'QR), а затем по известному углу
PQR, площади треугольника SA m,q% =• -5- Sp(,^N н основанию
QR последовательно найти длину M'Q?- н по теореме косинусов —
длину M'R.
Ответ. Длина отрезка равна 6.
2.1. Иайтп диагональ и площадь равнобочной-трапеции, если
основания равны 3 н 5 см, а боковая сторона равна 7 см.
2.2. Найтн площадь равнобочной трапеции, у которой
основания равны 12 и 20 см, а диагонали взаимно перпендикулярны.
2.3. В трапеции ABCD длина основания AD равна 2 м, а
длина основания ВС равна 1 м. Длины боковых сторон АВ и
CD равны 1 м. Найтн длину диагонали трапеции.
2.4. Один пз углов трапеции равен 30°, а боковые стороны
при продолжении пересекаются под прямым углом. Найти
меньшую боковую сторону трапеции, если' ее средняя линия равна
10 см, а меньшее основание — 8 см.
2.5. В трапеции ABCD длина меньшего основания равна 3 м,
- длины боковых сторон АВ и CD равны по 3 м. Диагонали
трапеции образуют между собой угол в 60е, Найтн длину Ьсиова-
. вия АО,
§ 2. ЧЕТЫРЕХУГОЛЬНИКИ
321
2.6. В трапеции большее основание равно 5 см, одна нз
боковых сторон равна 3 см. Известно, что одна нз диагоналей
перпендикулярна заданной боковой стороне, а другая делит угол
между заданными боковой стороной и основанием пополам.
Найти площадь трапеции.
2.7. В равнобочной трапеции ABCD заданы АС = a, CAD —■'
= а. Найтн площадь трапеции.
2.8. В квадрат вписан другой квадрат, вершины которого ле«
жат на сторонах первого, а углы между сторонами квадратов
равны 60*. Какую часть площади данного квадрата составляет
площадь вписанного квадрата?
2.9. Дана равнобочная трапеция ABCD. Известно, что AD ™
■= 10, ВС = 2, АВ = CD = 5. Биссектриса угла BAD пересекает
продолжение основания ВС в точке К- Найти длину биссектрисы
угла В в треугольнике АВК.
2.10. В равнобедренной трапеции основания равны а и Ь,
а угол диагонали с основанием равен о. Найтн длину отрезка,
соединяющего точку пересечения диагоналей с серединой
боковой стороны трапеции.
2.11. В трапеции ABCD, где AD — основание трапеции, про-
ведены диагонали АС и BD, которые пересекаются в точке О.
Известно, что длина диагонали АС равна /, а величины углов
АОВ, АСВ, ACD, BDC, ADB образуют арифметическую
прогрессию (в том порядке, в котором они написаны). Найтн длину
основания AD.
2.12. В равнобочной трапеции ABCD дано: АВ = CD = 3,
AD = 7, BAD = 60*. На диагонали BD расположена точка М
так, что ВМ : MD = 3 : 5. Какую нз сторон трапеции — ВС или
CD — пересечет продолжение отрезка AM?
2.13. Вычислить площадь общей части двух ромбов, из
Которых у первого диагонали равны 2 и 3, а второй получен
поворотом первого на 90* около его центра.
2.14. В квадрате ABCD площадью 1 сторона AD
продолжена за точку D, и на продолжении взята точка О на расстоянии 3
от точки D. Из точки О проведены два луча. Первый луч
пересекает отрезок CD в точке М н отрезок АВ в точке N, причем
длина отрезка ON равна а. Второй луч пересекает отрезок CD
В точке L и отрезок ВС в точке К, причем =» а. Найтн пло-
"щадь многоугольника BKLMN.
2.15. В параллелограмме со сторонами а и b н углом а
проведены биссектрисы четырех углов. Найтн площадь
четырехугольника, ограниченного биссектрисами.
.11 А. Г, Цыпкии, А, И. Пинский
822 ГЛ. 12. ПЛАНИМЕТРИЯ
2.1 в. Длина боковой стороны АВ в параллелограмме ABCD
равна а\ длина перпендикуляра, опущенного нз точки
пересечения диагоналей на основание, равна h\ угол между большей
диагональю BD н основанием AD равен а. Найти площадь
параллелограмма.
2.17. В трапеции ABCD даны основания: AD = 16 н ВС =
= 9. На продолжении ВС выбрана такая точка М, что СМ =
1= 3,2. В каком отношении прямая AM делит площадь
трапеции ABCD1 ~~~ ' *"
Задачи 2.18—2.29 решаются методом введения
вспомогательного неизвестного (или нескольких неизвестных), для которого по
условию задачи составляется уравнение (соответственно система
уравнений). В качестве неизвестных
* 0 можно брать угол или неизвестный
/\ Г\ линейный размер.
\\ Пример 2.2. В выпуклом че-
1" хЛч тырехугольннке ABCD углы при вер-
I ' ^\\# • шниах А и В прямые, величина угла
1 ^^ч. ПРИ веРшнне D равна я/4, ВС = I,
-, , ' У/нч, длина диагонали BD равна 5. Найти
ас, Д площадь этого четырехугольника.
Рис_ I2 e Решение. Обозначим угол
BDC через а (рис. 12.6). Так как
сумма внутренних углов любого четырехугольника равна 2я,
а три угла четырехугольника ABCD известны по условию задачи,
то Со Зя/4. Рассмотрим треугольник BDC. Введем обозначение
CD ™> х, тогда, используя теорему косинусов для треугольника
BDC, получим уравнение
25«-1+**-2- 1. х-cos 135°.
Это уравнение преобразуется к виду
ха + У2**-24=0. (♦)
Единственным положительным корнем уравнения (*) является
х — Ъл/г.
Сделаем теперь следующее дополнительное построение.
Опустим нз вершины С перпендикуляр CCi на AD. Из
прямоугольного треугольника CCtD находим, что CCi = C\D. Так как
длина гипотенузы треугольника CC\D равна SV2, то нз теоремы
Пифагора следует, что СС\ = C\D = 3. Из прямоугольного
треугольника BAD и очевидного равенства ВА = CCt следует, что
АО* — Вй\-ВА*
в ft. ЧЕТЫРЕХУГОЛЬНИКИ
823
Так как по условию задачи углы А а В прямые, то AD II ВС и
четырехугольник ABCD — трапеция {AD и ВС — основания,
АВ — высота), откуда
•&тр = 1 ЛВ"«у.
Ответ, 15/2.
2.18. Даиы квадрат с вершинами А, В, С, D и точка О,
лежащая вне квадрата. Известно,что ОА = ОВ = 5 и DO = */\Ъ-
Найтн площадь квадрата.
2.19. В выпуклом четырехугольнике ABCD биссектриса угла
ABC пересекает сторону AD в точке М, а перпендикуляр,
опущенный из вершины А на сторону ВС, пересекает ВС в точке ЛГ
так, что BN = NC и AM = 2MD. Найти стороны и площадь
четырехугольника ABCD, если его периметр равен 5 + д/з". BAD =■
«90е н Хв£=60°.
2.20. В трапеции ABCD углы А н D при основании AD
соответственно равны 60е и 90е. Точка N лежит на основании ВС,
причем BN: NC = 3:2. Точка М лежит па основании AD,
прямая MN параллельна боковой стороне АВ и делит площадь
трапеции пополам. Найтн отношение АВ : ВС.
2.21. Длина средней линии трапеции равна 5 см, а длина
отрезка, соединяющего середины оснований, равна 3 см. Углы при
большем основании трапеции равны 30е и 60е. Найтн площадь
трапеции.
2.22. Сумма острых углов трапеции равна 90е, высота
равна 2 см, а основания —12 и 16 см. Найтн боковые стороны
трапеции.
2.23. В ромбе ABCD со стороной а угол при вершине А
равен я/3. Точки Е и F являются серединами сторон АВ в, CD
соответственно. Точка К лежит на стороне ВС, отрезки АК и EF
пересекаются в точке М. Найтн длину отрезка МК, если
известно, что площадь четырехугольника MKCF составляет 3/8
площади ромба ABCD.
2.24. В прямоугольной трапеции ABCD углы А н D прямые,
сторона АВ параллельна стороне CD, АВ =» 1, CD =• 4, AD = 5.
На стороне AD взята точка М так, что угол CMD вдвое больше
угла ВМА. В каком отношении точка М делит сторону AD?
2.26. Длина диагонали BD трапеции ABCD равна т, а
длина боковой стороны AD равна п. Найти длину основания CD,
если известно, что длины Основания, диагонали и боковой
стороны трапеции, выходящих из вершины С, равны между
собой.
11*
324 ГЛ. 12. ПЛАНИМЕТРИЯ
2.26. В трапеции ABCD диагонали АС в DB взаимно
перпендикулярны, ВАС = CDB. Продолжения боковых сторон АВ я
DC пересекаются в точке К, образуя угол AKD, равный 30%
Найти площадь треугольника AKD, если площадь трапецнн
равна S.
2.27. В равнобочной трапецнн с основаниями а п b (a> b)t
диагонали являются биссектрисами углов при большем
оснований. Найти площадь трапецнн.
2.28. В трапеции ABCD диагональ АС перпендикулярна
боковой стороне CD, а диагональ DB перпендикулярна боковой
стороне АВ. На продолжениях боковых сторон АВ в CD за
меньшее основание ВС отложены отрезки ВМ п CN так, что
получается новая трапеция BMNC, подобная трапецнн ABCDj
Найти площадь трапецнн ABCD, если площадь трапецнн AMND
равна S н сумма углов CAD и BDA равна 60°.
2.29. Дан параллелограмм ABCD со сторонами
АВ = 2 и ВС = 3.
Найти площадь этого параллелограмма, если известно, что
диагональ АС перпендикулярна отрезку BE, соединяющему
вершину В с серединой Е стороны AD.
При решении задач 2.30—2.36 используются специальные
свойства многоугольников и треугольников, вытекающие из
условий задач.
Пример 2.3. В трапеции с основаниями а и b через
точку пересечения диагоналей проведена прямая, параллельная
основанию. Найти длину отрезка
этой прямой, заключенной между^
боковыми сторонами трапеции.
Решение. Пусть в трапеции
ABCD основание ВС равно а,
а основание AD равно Ь
(рнс. 12.7), АС и BD —
диагонали, О—точка их пересечения, BN—
Рис* и-7 высота трапецнн, М — точка
пересечения высоты BN и искомого
отрезка KL. По условию задачи K.L II ВС, и, следовательно,
треугольник ABD подобен треугольнику КВО, а треугольник*
ABC подобен треугольнику АК.О, Так как в подобных
треугольниках высоты пропорциональны сторонам, на которые они опуч
ГЦеиы, то
КО ВМ КО МЫ
J 2. ЧЕТЫРЕХУГОЛЬНИКИ
825
.Как следствие этих равенств п условия задачи получаем
КО ,КО ВМ MN кп ( ВС+АР\
1о+~вс~="в1Г + -в1Г^К0{ Аоёс ) =
Аналогично, из подобия *)■ двух пар треугольников Д DOL со
со Д DBC, Д OCL со Д ACD, находим 0L = —г—г. н, следова-
a-jr о ■ '
тельно, 'Kb = КО + 0L = ~~.
• - ■ 2аЬ *.
Ответ. —гт-
а + о
2.30. Через середину М стороны ВС параллелограмма ABCD,
площадь которого равна 1, п вершпну А проведена прямая,
пересекающая диагональ BD в точке О. Найти площадь
четырехугольника OMCD.
2.31. На сторонах выпуклого четырехугольника ABCD,
площадь которого равна 1, взяты точки: К — на АВ, L — на ВС,
М — на CD, N—на AD. При этом
АК , BJL_ _l_ ЯМ.— \ DN - Х
KB ' LC 3 ' MD ~ ' NA 5 *
Найти площадь шестиугольника AKLCMN.
2.32. А, В, С, D — последовательные вершины
параллелограмма. Точки Е, F, Р, Н лежат соответственно на сторонах АВ,
ВС, CD и AD. Отрезок АЕ равен 1/3 стороны АВ, отрезок BF —
1/3 стороны ВС, а точки Р н Н делят пополам стороны, на
которых они лежат. Найтн отношение площади четырехугольника
ЕРРН к площади параллелограмма ABCD.
2.33. В выпуклом четырехугольнике ABCD длина отрезка,
соединяющего середины сторон АВ и CD, равна 1. Прямые ВС
и AD перпендикулярны. Найтн длину отрезка, сбеднняющего
середины диагоналей АС и BD,
2.34. Длины диагоналей ромба н длина его стороны обра-
вуют геометрическую прогрессию. Найтн синус угла между
стороной ромба н его большей диагональю, если известно, что он
больше 1/2.
2.36. В выпуклом четырехугольнике KLMN точки Е, F, G, Н
являются соответственно серединами сторон KL, LM, MN, NK.
Площадь четырехугольника EFGH равна Q, #£>"=* я/6, £?// =
= я/2. Найти длины диагоналей четырехугольника KLMN,
*) Знак оо означает подобие.
'326 'ГЛ. 12. ПЛАНИМЕТРИЯ
§ 3. Окружность и круг
Окружностью называется множество всех точек плоскости,
находящихся на данном положительном расстоянии от некоторой данной точки
(Плоскости, называемой центром окружности. Круг •) состоит из
окружности н внутренних точек.
Отрезок, соединяющий две точки окружности, называется хордой.
лорды обладают следующими свойствами:
1) диаметр, делящий хорду пополам, перпендикулярен этой хорде;
2) равные хорды окружности равноудалены от ее центра;
равноудаленные от центра окружности хорды равны;
Рис. 12.8 Рис 12.9
3) еслв через точку М. лежащую внутри окружности, проведены две
хорды АВ и CD (рис. 12.8), то произведения отрезков хорд равны:
AMMB=CMMD.
Теорема о касательной п секущей. Если нз точки М
(рис. 12.9). лежащей вие окружности, проведены касательная МС и
^екущая МА. то произведение секущей на се внешнюю часть равво
квадрату касательной:
МС'^МА-МВ.
Длины н площади.
Длина окружности радиуса Я:£*=2л/?.
Площадь круга радиуса RiS^nR?.
Длина дуги окружности радиуса R с центральным углои а,
(намеренный в радианах): I - /?<х.
Площадь сектора окружности радиуса R с центральным углом а
(измеренным в радианах): s^y/Pa.
Измерения углов в окружностях.
Центральный угол измеряется дутой, на которую on опирается.
Угол, образованный двумя пересекающимися хордами, измеряется
полусуммой дуг, на которые он опирается.
Угол, вершина которого находится на окружности, измеряется поло-
виной дугн, на которую он опирается.
Угол между касательной и хордой измеряется воловиной душ,
которую стягивает хорда.
Угол, образованный двумя пересекающимися секущими, измеряется
полуразностью дуг, на которые он опирается.
Свойства линий в касающихся в пересекающихся
окружностях.
1. Линия центров двух касающихся окружностей проходит через
точку касания.
2. Общая внутренняя касательная двух внешним образом
касающихся окружностей перпендикулярна нх линии центров.
3. Общая касательная Двух внутренним образом касающихся окруж*
ностеД перпендикулярна их линии центров.
4. Общая хорда двух пересекающихся окружностей перпендикулярна
нх лнВнн центров н делится точкой их пересечения пополам.
*) Иногда (если ие воэннк&ет путаницы) будет употребляться кап
синовии окружности. ,
§ 3. ОКРУЖНОСТЬ И КРУГ 827
Задачи 3.!—3.9 решаются непосредственными вычислениями,
основанными иа свойствах линий в окружностях.
Пример 3.1. Общая хорда двух пересекающихся
окружностей видна нз их центров под углами 90° и 60°. Найти
радиусы- окружностей, если расстояние между нх центрами равно
л/з~+1.
Решение. Пусть Oi и Ог — центры окружностей, АВ —
общая хорда, К — точка пересечения лнннн центров OiOs и
общей хорды АВ (рис. 12.10);
угол AOiB равен 60°, а
угол АОгВ равен 90°.
Рассмотрим треугольник AOtB.
Этот треугольник
равнобедренный (ЛО|=ВО| н 0,КЛ-
J-AB, т.е. OiK — высота,
медиана н биссектриса
треугольника АО\В. По
условию задачи угол АО\В
равен 60°, и, следовательно,
угол AOiK равен 30°. Аналогично для треугольника АОгВ по
лучаем, что угол АОаК равен 45°. Рассмотрим треугольник 0|Л02.
В атом треугольнике известны два угла (ЛОЛ н АОгК), рав
ные 30° и 45° соответственно, и отрезок 0|02, равный V3 + 1
Стороны треугольника 0\А и АОг являются искомыми радиусами
Так как сумма углов треугольника равна 180°, то угол
OiAOz равен 105", и по теореме синусов для треугольника О^АОг
имеем
О,-Л УЗ~-Н 02А уТ+ 1
Рис. 12.10
Sin 46°
sin 105°
sin 30°
sin 105°
(?)
Ho sin 105° = sin (90° + 15°) = cos 15°. По формуле 1 -f cds a =
30°, можно вычислить cos 15°:
■■ 2 cosa -s-, полагая a
2 cos215° ■=■ 1 -f cos 30° «*■ 2 cos2 15"
нз равенств (*) находим
_ 2+V#
• cos 15°
V2 + V3
2 :
0,A
уТ (Уз~+ 0'2 -уТ(Уз +i) V2"(y^+i)
02А
2 У 2 + V3~ V2 + V3"
(Уз~ +1) • 2 Уз"+1
V(V3+D2/2
УУ+1 у?.
2 V2 + л/3 V2 + V3 V( V3~ + 1 )2/2
Ответ. 2 и V2~«
328 гл- ,2- ПЛАНИМЕТРИЯ *
3.1. Три окружности расположены на плоскости так, что
каждая из них касается двух других виешинм образом. 'Две из
них имеют раднус 3, а третья — раднус 1. Найти площадь тре*
угольника ABC, где А, В и С — точки касания окружностей*
3.2. Даны две внешним образом касающиеся окружности paJ
диусов R н г. Найти длину отрезка внешней касательной, заклюй
ченпбго между точками касания. •
■ ' 3.3. Две окружности, радиусы которых равны 4 н 8, Пересе*'
каются под прямым углом. Определить длину' их общей' каса*'
тельной. " ^ . . . ■ -
3.4. Центры четырех кругов расположены в вершина* квад»
рата со стороной о. Радиусы всех кругов также равны а. Вы«
числить площадь части плоскости, общей для всех кругов. " "
3.5. Вне прямого угла с вершиной О на продолжении его
биссектрисы взята точка О так, что OC^^/F. Построена
окружность радиуса 2 с центром в точке О. Найти площадь фигуры,
ограниченной сторонами угла и дугой окружности, заключенной
между ними.
3.6. На прямой, проходящей через центр О окружности
радиуса 12 см, взяты точки А и В так, что ОА = 15 см н АВ =
= 5 см. Из точек А и В проведены касательные к окружности,
точки касания которых лежат по одну сторону от прямой ОАВ.
Найти площадь треугольника ABC, если С — точка пересечения
этих касательных.
3.7. Даны две непересекающиеся окружности радиусов R и
2R. К ним проведены общие касательные, которые пересекаются
в точке А отрезка, соединяющего центры окружностей.
Расстояние между центрами окружностей равно 2Ry3. Найти
площадь фигуры, ограниченной отрезками касательных,
заключенными между точками касания и ббльшнми дугами окружностей,
соединяющими точки касания.
3.8. Из точки А, лежащей на продолжении диаметра KL
окружности в сторону точки L, проведена к этой окружности
касательная АВ (В —точка касания), образующая с диаметром KU
угол а. Найти площадь фигуры, образованной сторонами угла н
дугой LB, если радиус окружности равен R.
3.9. Две окружности радиусов 5 н 3 см касаются
внутренним образом. Хорда большей окружности касается меньшей
окружности и делится точкой касания в отношении 3: 1. Найти
длину этой хорды.
Задачи 3.10—3.24 решаются методом введения
вспомогательного неизвестного, для которого по условию задачи составляется
уравиеиие.
§ а. окружность и круг
329
*. Пример 3.2. Две окружности радиусов R и г касаются
внешним образом. Определить радиус окружности, касающейся
втих окружностей н их общей внешней касательной.
Решение. Рассмотрим сначала случай, когда искомая
окружность заключена между данными окружностями, и
касательной. Тогда обозначим Oi, Oa н 03 соответственно центры окружл
ностей радиусов R, г и искомой окружности; MtMi — обща*
виещняя касательная данных окружностей (рис. 12.11).'
Обозначим через L точку касания
искомой окружности п
прямой MiMz. Через центр 08
искомой окружности
проведем прямую, параллельную
прямой М[М2 (Р н
К—точки пересечения этой
прямой и отрезков 0|Af( п
Oi/Мг). Прямая РК будет
перпендикулярна прямым
OiMi, ОгМг н 03L.
Обозначим радиус искомой
окружности через х. В прямоугольном треугольнике 0|POs длина
гипотенузы 0,0& = R + x; длина катета OiP — R — x. По теореме
Пифагора P03 = 2*JWc. Аналогично из прямоугольного
треугольника ОзКОг находим ОзК = 2угх.
Через центр меньшей из двух окружностей радиусов R и г
проведем прямую, параллельную общей внешней касательной (на
рис. 11.11 окружность с центром 0% имеет меньший радиус, чем
окружность с центром Оь н OiS — проведенная прямая). Из
прямоугольного треугольника OiSOa, У которого 0i02 = R + r,
OiS = R — r, находим OtS — 2 *jR~r. Отрезки SOz, PK, MiM»
между собой параллельны, так как каждый перпендикулярен
параллельным прямым OiMj н О^М^ в SOz = РК = MiM3.
Равенство SOx = РК — РО$ + 03К дает уравнение для
нахождения неизвестного х:
2 Y7FF + 2 -у/гх = 2 V^r =*Rx-\- 2x л/Rr + rx = Rr =>-
*>x(R+2-VR?+r) = Rr=>x^ %= . ~.Rr .-.,,.
Случай, когда искомая окружность находится со стороны
меньшей окружности, рассматривается аналогично предыдущему.
При этом может быть использован тот же чертеж, только
данными следует считать окружности с центрами, например, О» и
830
ГЛ. U. ПЛАНИМЕТРИЯ
О» я искомой — с центром Ot или Oi, О», а искомой — с
цензом. Ог.
Тогда если раднус большей яз данных окружностей равен/?,
А меньшей г, то, проводя аналогичные рассуждения, получим,
,ЧТо радиус искомой окружности будет равен . .
Ответ.
Rr
Rr
(V«-VT)2
W+W* (V«-VT)2'
Пример 3.3. АОВ — сектор круга радиуса г. Величина
угла АОВ равна а(ос<я). Найти раднус окружиостн, лежащей
внутри этого сектора н касающийся
хорды АВ, дуги АВ и биссектрисы
угла АОВ.
Решение. Пусть ОМ —
биссектриса угла АОВ, Oi—центр искомой
окружности, S — точка касания
искомой окружности н биссектрисы ОМ,
К — точка касания искомой
окружности и хорды АВ (рис 12.12),
Отрезок ОМ является биссектрисой
угла АОВ, н так как АЛОВ
равнобедренный, то ОМ является также
и высотой этого треугольника. Четырехугольник SMKO\ —
квадрат, так как SOi = КОи а углы OtSM, SMK и МКО, прямые.
По теореме о прямой, проходящей через центры двух
касающихся окружностей, центры окружностей О, 0« н точка касания L
Этих, окружностей лежат на одной прямой OL.
Обозначим раднус искомой окружности 0[/С = ж. Диагональ
MOi квадрата MSOiK равна V2*. Из треугольника ОМВ
находим в согласии с условием задачи OJVf = rcos-^-. В треугольнике
Рис. 12.12
ОМО\ имеем МО\-
■ Уг*. OM«=rcos—, |00,|
■ г — *,0M0i=»
— 136*. Теорема косинусов для треугольника OAIOi дает
уравнение для нензвестного х:
(г — х)* = 2*s + rs cos2 y - 2* У2 r cos -j cos 135°,
(r _ x)2 = 2*! + r* cos» j + 2rx cos ^ =*■
*>r
' *l,»."
! + 2r(cos-|.+ l)* + r»(cos2|--l)=0=>
2r Cos8 -rrd: 2r cos -j-,**- *i,a =» 2r cos -^ Г—cos -r ± 1 J,
§ з. окружность й круг
381
Так как величина х должна быть положительной, а на двух
найденных корней положителен только первый,
„ о. {. а \ . а. „ее
*i=2rcos—• I I — cos -jj=4rcos -j sm*-g-,
то он н дает величину радиуса искомой окружности.
Ответ. 4гcos-7-sina-=-.
4 о
3.10. Две окружности раднуса 32 с центрами Oi и 02,
пересекаясь, делят отрезок 0|0» на три равные части. Найтп радиуо
окружности, которая касается изнутри обеих данных
окружностей и отрезка Oi03.
3.11. Даиы два пересекающихся круга одного и того же
радиуса R. Расстояние между центрами »тнх кругов OtOt = I.
Найти площадь крута, касающегося внутренним образом обеих
окружностей н прямой 0|Оз.
3.12. Две окружности, радиусы которых равны Ri и /?з,
пересекаются. Расстояние между их центрами равно d. Найти
радиус окружности, касающейся данных окружностей н их общей
касательной.
3.13. Круг радиуса 6 см лежит внутри полукруга раднуса
24 см п касается середины диаметра полукруга. Найти радиус
меньшей окружности, касающейся заданных круга, полукруга я
диаметра полукруга.
3.14. Дана окружность раднуса г с центром в точке О. Из
точки А отрезка ОА, пересекающегося с окружностью в точке Af,
проведена секущая к окружности, пересекающая окружность в
точках К в Я; при этом точка К лежит между точками А и Р.
Величина угла МАК равна я/3. Длина отрезка ОА. равна а.
Найти радиус окружности, касающейся отрезков AM, -АК и
дугн МК.
3.15. К окружности раднуса 3 см с центром в точке О нз
точки М проведены секущая ОМ и касательная МС, касающаяся
окружности в точке С. Найти радиус окружности, касающейся
заданной окружности, прямых МС и ОМ и лежащей внутри
треугольника ОМС, если ОМ = 5 см.
3.16. В сегмент с дугой в 120° и высотой Л вписан
прямоугольник, у которого основание в 4 раза больше высоты.
Определить стороны прямоугольника.
3.17. В круговом секторе ОАВ, величина центрального угла
которого равна я/4, расположен прямоугольник КМРТ. Сторона
КМ прямоугольника лежит на радиусе ОА, вершина Р — на дуге
АВ, вершина Г —на радиусе ОВ, Длина стороны ЯГ на 3 см
832
ГЛ. В. ПЛАНИМЕТРИЯ
больше длины стороны КМ. Площадь прямоугольника КМРТ
равна 18 см2. Найти длину радиуса.
3.18. Из точки А, находящейся на расстоянии 5 см от
центра окружности радиуса 3 см, проведены две секущие АКС и
ALB, угол между которыми равен 30° {К, С, L и В —точки
пересечения секущих с окружностью) *, Найти площадь треугольни-.
ка AK.L, если площадь треугольника ABC равна 10 см2. ■■
• 3.19. Даны две одинаковые пересекающиеся
окружиостн.'Отношение расстояния между их Центрами к радиусу равно 2rtfc
Третья окуншость касается внешним образом обеих окружи
' иостей и нх общей касательной. Определить отношение шик
щадн общей части первых двух кругов к площади третьего'
Круга.
3.20. В круговой сектор, ограниченный радиусами ОА и ОВ-,
е центральным углом а (а < л/2) вписан квадрат так, что две
его соседние вершины лежат на радиусе ОА, третья вершина —
на радиусе ОВ, а четвертая вершина — на дуге АВ. Найти
отношение площадей квадрата и сектора.
3.21. В круге проведены две взаимно перпендикулярные
пересекающиеся хорды АВ и CD. Известно, что
AB = BC~CD.
Установить, что больше: площадь круга или площадь квадрата
со стороной АВ.
3.22. Две окружности радиусов V6 н V2* см пересекаются.
Расстояние между центрами окружностей равно 3 см. Через точ^
ку А (одну из точек пересечения) проведена прямая,
пересекающая окружности в точках В и С (В ф С) так, что А В = АС.
Найти длину отрезка АВ.
§ 4. Треугольники и окружности
Треугольник, все вершины которого лежат на окружности, называется
вписанным в окружность, а окружность называется описанной около
Треугольника. Центр окружности, обнсаиноЛ около треугольпнка. лсжвт
фа пересечении перпендикуляров к Серединам сторон треугольника.
РаДнус окружности, описанной около треугольника, вычисляется по
формуле
I а м 1 ft _^ I с
Т sin* °" 2 sin В™ 2 sin у
ели во формуле
R=*abcHiS),
5де а, Ь, с—стороны треугольника; а, 0, у—углы треугольника, лежащие
рот'йв сгорби а, о, с соответственно, S — площадь треугольника.
Окружность, касвющаяоя всех сторон треугольника, называется ели-
SaHH/ой. в треугольник. Центр окружности, вписанной в треугольник, ле*.
снт на пересечении биссектрис, ваутренвих углов треугольника,
§ 4. ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ 833
муле
где р=
Радиус окружности, вписанной в треугольник, вычисляется по фор»
г—S/p.
'Y (в + & + с)~ полу периметр треугольника.
Задачи 4.1—4.36 решаются непосредственными вычислениями
с использованием свойств треугольников, вписанных в
окружность, н окружностей, вписанных в треугольник.
Пример 4.1. На стороне АС остроугольного треугольника
ABC взята точка D так, что AD = 1, DC =2 н BD является
высотой треугольника ABC. Окружность радиуса 2, проходящая'
через точки Л и О, касается в точке D
окружности, описанной около
треугольника BDC. Найти площадь
треугольника ABC.
Решение. Пусть 0\ — центр
окружности радиуса 2, проходящей через
точки А и D, а 03 — центр окружности,
описанной около треугольника BDC
(рнс. 12.13). Так как BD — высота
треугольника ABC, то треугольник BDC
прямоугольный, и, следовательно, центр
описанной около треугольника BDC
окружности лежит на середине его
гипотенузы ВС.
Рассмотрим треугольник AO,D.
Этот треугольник равнобедренный, и по
условию задачи AD = I, AO{ = 0,D = 2.
сов найдем угол ADOt этого треугольника!
Рис. 12.13.
По теореме коенну-
ADO,
■■ arccos —г.
4
Так как по условию задачи окружности с центрами Ot н Oj
касаются в точке D, то линия центров 0|02 проходит через точку
касания н Oi02 = 04D + D02. Углы ADO\, CDO% вертикальные
и, следовательно, равные, т. е. CD02.
■■ arccos -r. Треугольник
4
DOzC равнобедренный, так как £Ю2 н 02С—радиусы окружно1
стн, н, следовательно, 02CD ■
1
arccos —r .
4
В прямоугольном треугольнике BCD известны катет DC*=>
= 2 и OjCD => arccos -7-. По этим данным находим гипотенузу ВС:
4
DC ( 1 \ DC 1 _„ „
-g£- - cos (^arccos Tj + -^r - _ + ВС = 8.
834^
ГЛ. 13. ПЛАНИМЕТРИЯ
8
Таким обрезом, в треугольнике АВО найдены тря параметч
ра, позволяющие вычислить площадь этого треугольника!
ДЛВС = y/ib-o^-sin DCB —-j-3-8sIn (arccos-j-j —
Dl2.^l„3VTo".
Ответ. зУПГ.
Пример 4.2. В прямоугольном треугольнике ABC е острым
углом 30° проведена высота CD вз вершппы прямого угла С.
Найтп расстояние между центрами
окружностей, вписанных в треугольники ACD и
BCD, если меньший катет треугольника
ABC равен 1.
Решение. Пусть О] п Ог — центры
окружностей, вписанных в прямоугольные
треугольники ACD n BCD соответственно;
угол CAB равен 30е, ВС = 1 (рпс 12.14).
Из прямоугольного треугольника ABC иа-
ходпм
ВС -^""^
-^-<-.1е30о=>ЛС = Уз", ЛВС = 60°.
Из прямоугольного треугольника ACD по известным данным
ЛС = Уз и Л = 30* находим
CD — л/з"/2, ЛО = 3/2.
Из прямоугольного треугольника CDB по известным данным
ВС = 1 и В = 60" находим
В£> = 1/2, DC = 8/2.
Вычислим площади и полупернметры треугольников ЛСО п
.СОВ:
SA4CB = -2 AD.DC~
зУз"
8 '
Уз"
8 '
Pa acd '■
Pa bcd z
3(1 4- Уз~)
4
3 + VS"
Далее по формуле S = рг вычисляем радиусы окружностей,
вписанных в треугольники ACD в CDB:
Г| = -
>AACD
Vs
г* =
Paacd
^ACDB
2(1 +-V^T)'
1
Рдсов 2(l + V3")
§ 4. ТРЕУГОЛЬНИКИ И ОКРУЖН00ТИ
335
Так как центр вписанной d треугольник окружности лежит на
пересечении биссектрис внутренних углов треугольника, то углы
CDOi и CDOt равны между собой н составляют по 45°. Отсюда
можно сделать два вывода. Во-иервых,
OtD = r, V2~ = -_/3 OaD = r3V2=
VsTO + VSV v V2"(i + V3)'
Во-вторых, угол 0|D02 треугольника 0|D02 прямой. Тогда по
теореме Пифагора находим 0,02:
(0,0j,"[v5-(i-fyS)J +LV2-(i+V3-)J
0,02 = -
(i + Va)2
ентрам
л/2 л/3" — I
Таким образом, искомое расстояние между центрами
окружностей
Ответ.
I + Уз л/2
У§"-1
V2 •
4.1. Найти длину окружности, вписанной в равнобедренный
Прямоугольный треугольник с гипотенузой, равной с.
4.2. В равнобедренном треугольнике даны длина боковой
стороны b и угол а, при основании. Найти расстояние от центра
описанной окружности до центра вписанной окружности.
4.3. Дан круговой сектор радиуса R с центральным углом о.
Найти радиус вписанного в сектор круга.
4.4. Из одной точки окружности проведены две хорды
длиной а и Ь. Найти радиус окружности, если расстояние между
серединами данных хорд равно с/2.
4.5. На основании равностороннего треугольника как на
диаметре построена полуокружность, рассекающая треугольник на
две части. Длина стороны треугольника равна а. Найти площадь
той части треугольника, которая лежит вне полукруга.
4.6. На одной нз сторон угла, равного к, даны две точки,
расстояния от которых до другой стороны равны ft и с. Найти
рздиус окружности, проходящей через эти две точки и
касающейся другой стороны угла.
4.7. Правильный треугольник ABC со стороной, равной 3,
вписан в окружность. Точка D лежит на окружности, причем
длина хорды AD равна у§". Найти длины хорд BD и CD.
4.8. В прямоугольном треугольнике ABC с катетами 3 и 4
вершина С прямого угла соединена с серединой D гипотенузы
836
ГЛ. 12. ПЛАНИМЕТРИЯ),
54В. Найти расстояние между цептрамн окружностей, вписанных
В треугольники ACD и BCD.
4.9. Окружность радиуса R проходит через вершяны А и В
треугольника ABC и касается прямой АС в точке Л. Найти
площадь треугольника ABC, зная, что ABC = р\ АСВ = а.
4.10. В прямоугольном треугольнике ЛВС угол А прямой,
величина угла В равна 30°, а радиус вписанной окружности
равен Уз~. Найти расстояние от вершины С до точки касания
вписанной окружности н катета АВ.
4.11.' Окружность касается стороны ВС п продолжений двух
других сторон треугольника ABC. Найти рзднус окружности,
если АВ «= с, ВД£ = а, АВС = р.
4.12. В треугольник ABC вписана окружность радиуса R,
касающаяся стороны АС в точке D, стороны АВ — в точке Е в
стороны ВС—.в точке -f.- Длина отрезка AD равна R, а длина
отрезка DC равна а. Найтн площадь треугольника BEF.
4.13. В правильный треугольник, сторона которого равна а,
вписан круг. Из вершины радиусом, равный половине его
стороны, проведена другая окружность. Найти площадь общей
части этих кругов.
4.14. В равнобедренный треугольник с основанием а и углом
при основании о вписана окружность. Кроме того, построена
вторая окружность, касающаяся основания, одной пз боковых
сторон треугольника н вписанной в него первой окружности.
Определить радиус второй окружности.
4.15. В треугольнике ABC со сторонами ВС =» а, АС = 2а
я углом С «= 120° вписана окружность. Через точки касания этой
окружности со сторонами АС н ВС через вершину В проведена
вторая окружность. Найтн ее радиус.
4.16. В треугольнике ABC длина стороны АВ равна 4, угол
CAB равен л/6, а радиус описанной окружности равен 3.
Доказать, что длина высоты, опущенной нз вершины С на сторону
АВ, меньше 3.
4.17. В треугольнике ABC боковые стороны АВ н ВС
равны а, а АВС «= 120°. В треугольник ABC вписана окружность,
касающаяся стороны А В в точке D. Вторая окружность нмеет
центром точку В н проходит через точку D. Найтн площадь той
•части вписанного круга, которая находится внутри второго
круга.
4.18. В остроугольный треугольник АВС вписан полукруп
так, что его диаметр лежит на стороне А В, а дуга касается сто»
рои АС н ВС. Найти радиус окружности, касающейся дуги этого
§ 4. ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ ,837
полукруга и сторон АС и ВС треугольника, если АС — 6, ВС а*
= а, АСВ «= ос.
4.19. Окружность радиуса I + л/2 описана около
равнобедренного прямоугольного треугольника. Найтн радиус
окружности, которая касается катетов этого треугольника н внутренним
образом касается описанной вокруг него окружности.
4.20. В прямоугольном треугольнике ABC с катетами АВ =
•е* 3 и ВС =■ 4 через середины сторон АВ и АС проведена
окружность, касающаяся стороны ВС. Найтн длину отрезка
гипотенузы АС, который лежит внутри этой окружности.
4.21. В треугольнике ABC даны длины сторон ЛВ = 21,
ВС = 15 н проведена биссектриса BD угла ABC. Найти раднус
окружности, вписаиной в треугольник ABD зная, что соз(ВЛС)=;
= 5/7.
4.22. В окружность радиуса R вписан равносторонний
треугольник ABC. Сторона ВС разделена на три равные части и
через точку деления, ближайшую к С, проведена прямая, прохо-
-дящая через вершину А и пересекающая окружность в точке D.
Найтн периметр треугольника ABD.
4.23. В треугольнике ABC АВ=л/Л, ВС = 2. Окружность
проходит через точку В, через середину D отрезка ВС, через
точку £ на отрезке АВ и касается стороны АС. НайтВ
отношение, в котором эта окружность делит отрезок АВ, если DE—
диаметр окружности.
4.24. Вокруг треугольника ABC с длинами сторон АВ=*
«= 10 л/2, АС = 20 и В = 45°описана окружность. Через точку С
проведена касательная к окружности, пересекающая
продолжение стороны АВ в точке D. Найтн площадь треугольника BCD.
4.25. В треугольнике ABC известны длины сторон АВ = 6,
ВС = 4, АС = 8. Биссектриса угла С пересекает сторону АВ о
точке D. Через точки A, D, С проведена окружность,
пересекающая сторону ВС в точке Е. Найтн площадь треугольника ADE.
4.26. В треугольнике ABC BAC = a, ВСА = р\ AC = b. На
стороне ВС взята точка D так, что BD = 3DC. Через точки В
и D проведена окружность, касающаяся стороны АС или ее
продолжения за точку А. Найти радиус этой окружности.
4.27. В треугольнике ABC Л =120°, АС=1, ВС = л/Т. На
продолжении стороны СА взята точка М так, что ВМ является
рысотой треугольника ABC. Найтн раднус окружности,
проходящей через точки А и М а касающейся в точке М окружности,
проходящей4 через точки М, В и С,
838 гл. м. планиметрия
' 4:28» Вокруг треугольника ABC со сторонами ЛВ = 5(1 +
►J- л/$), ВС = 5л/б, АС = 10 описана окружность. Через
точку .С проведена касательная к окружности, а через точку В —
прямая, параллельная стороне АС. Касательная н прямая
пересекаются в точке D. Определить площадь четырехугольника
ABDC.
4.29. В треугольник ABC со сторонами АВ = 10, ВС = 20
и углом С, равным 30°, вписана окружность. Через точку М
стороны АС, отстоящую на расстоянии 10 от вершины А, проведена
касательная к окружности. Пусть /(— точка пересечения
касательной с прямой, проходящей через вершину В параллельно
стороне АС. Найти площадь четырехугольника АВКМ.
4.30. В треугольнике BCD известно ВС = 4, CD = 8,
соЗ(BCD) = 3/4. Точка А выбрана на стороне CD так, что С-А ==:
= 2. Найти отношение площади круга, описанного около
треугольника BCD, к площади круга, вписанного в треугольник
ABD.
4.31. В треугольнике, один из углов которого равен
разности двух других, длина меньшей стороны равна 1, а сумма
площадей квадратов, построенных на двух других сторонах, в два
раза больше площади описанного около треугольника круга.
Найти длину большей стороны треугольника.
4.32. В треугольнике ABC длина стороны ВС равна 2 см,
длина высоты, опущенной из вершины С на сторону АВ, равна
V2 см, а радиус окружности, описанной около треугольника
ABC, равен V^" см. Найти длины сторон АВ и АС треугольника,
если известно, что угол ABC острый.
4.33. Треугольник ABC, угол В которого равен 2ос < я/3,
вписан в окружность радиуса R. Диаметр окружности делит
угол В пополам; касательная к окружности в точке А пересекает
продолжение стороны ВС в точке М. Найти площадь
треугольника АВМ.
4.34. Дан правильный треугольник ABC со стороной а.
Окружность проходит через центр треугольника и касается стороны
АВ в ее середине М. Прямая, проведенная из вершины А,
касается окружности в точке Е. Найти площадь треугольника
АЕМ.
4.35. Около треугольника ABC (Л > л/2) описана
окружность с центром О. Точка F является серединой большей из дуг,
стягиваемых хордой ВС. Обозначим точку пересечеиня стороны
ВС с продолжением радиуса АО через Е, а с хордой AF — че->
рез Р. Пусть АН — высота треугольника ABC. Найти отношение
площади четырехугольника OEPF к площади треугольника АРН,
§ 4. ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ 839
если известно, что радиус описанной окружности /?»2 V&,
Л£ = У§" и £#=.3/2.
4.36. Дай равнобедренный треугольник MNP, в котором
MN = NP = /, MNP = р. Окружность с центром иа стороне MP
касается сторон MN и NP. Касательная к этой окружности
пересекает сторону MN в точке Q, а сторону NP — в точке Я.
Известно, что MQ = п. Найти площадь треугольника QNR.
В условиях задач 4.37—4.44 отсутствуют данные, имеющие
размерность длины. Для решения этих задач необходимо ввести
вспомогательную величину о, имеющую размерность длины
{например, сторону треугольника), и решить задачу с
доопределенным условней. Выражения для искомых величин не будут
содержать а.
Пример 4.3. В прямоугольном треугольнике ABC катеты
АС и ВС равны. Найтн отношение площадей вписанного н
описанного кругов.
Решение. Обозначим катет АС треугольника ABC через а.
Так как по условию задачи катеты равны, то ВС = АС =* а и
Д = В = 45°. По теореме Пифагора находим гипотенузу:
АВ = Vor+^= о V2".
Радиус окружности, описанной около прямоугольного
треугольника равен половине гипотенузы:
R = а л/212.
Раднус окружности, вписанной в треугольник, вычислим по
формуле
S _ 1 . а + а + ал/2 a(2 + V2~)
г = —. где S = ^a\ p - _X_I^_v__ e ___ ,
а \ '
и, следовательно, г =- ,_ .
2 + V2
Вычислим отношение площадей вписанного п описанного
кругов:
U+V2 )
я«2 fV2"Y (1 + V2")2'
№)
Ответ. l/(l+ V2)2.
4.37. Около прямоугольного треугольника описана
окружность. Другая окружность того же радиуса касается катетоа
этого треугольника так, что одаов из точек. касания является
840
ГЛ. 12. ПЛАНИМЕТРИЯ
вершина треугольника. Найти отношение площади треугольника
К площади общей части двух данных кругов.
, 4.38. В треугольнике ABC даны углы В, С. Через середину О
стороны АВ п вершину А проведена окружность, касающаяся
стороны ВС. Найтн отношение радиуса этой окружности к длине
стороны ВО.
4.39. Найтн отношение радиусов вписанного и описанного
кругов для равнобедренного треугольника с углом а при
основании.
4.40. Дан-' прямоугольный треугольник с острым углом ос.
Найти отношение радиусов описанной п вписанной окружностей
и определить, при каком значении ос это отношение наименьшее.
4.41. В окружность вписан равнобедренный треугольник ABC,-
в котором АВ = ВС и ВАС = а. Из вершины С проведена
прямая, составляющая с АС угол, равный а/4, п проходящая внутри
треугольника, которая пересекает окружность в точке Е. Эта
прямая пересекается с биссектрисой угла ВАС в точке F.
Вершина А треугольника соединена отрезком прямой с точкой В.
Найтн отношение площадей треугольников AFC н ЛЕС.
4.42. Дан прямоугольный треугольник ABC с прямым углом
при вершине С. Угол CAB равен а. Биссектриса угла ABC
пересекает катет АС в точке К. На стороне ВС как на диаметре по»
строена окружность, которая пересекает гипотенузу АВ в точке М.
Найти угол АМК,.
4.43. В треугольнике ABC даны углы В и С. Биссектриса
угла ВАС пересекает сторону ВС в точке D, а окружность,
описанную около треугольника ABC, — в точке Е. Найтн отношение
АЕ: DE.
4.44. Вписанная в треугольник ABC окружность касается его
сторон АС и ВС соответственно в точках М н N н пересекает
биссектрису BD в точках Р и Q. Найтн отношение площадей
треугольников PQM н PQN, если Л = я/4, В = л./3.
Задачи 4.45—4.66 решаются методом введения
вспомогательного неизвестного (или нескольких вспомогательных
неизвестных), для которого по условию задачи составляется уравнение
(нлн соответственно система уравнений). Часто в качестве
вспомогательных неизвестных удобно выбирать величины, которые
вместе с данными из условия задачи дают набор элементов,
однозначно задающих треугольники.
Пример 4.4. Радиус окружности, вписанной в
равнобедренный треугольник, в 4 раза меньше радиуса окружности,
описанной окола этого треугольника. Найти углы треугольника.
§ 4. ТРЕУГОЛЬНИКИ И ОКРУЖНОСТИ 34}
Решение. Пусть а — длина основания АС треугольника
ABC, а —острый угол прн основании (рнс. 12.15). Используя
введенные параметры, вычислим радиусы вписанной н описанной
окружностей. Так как треугольник ABC равнобедренный, то бнст
сектрнса угла ABC (АВ == ВС) является одновременно медианой
н высотой треугольника ABC п угол ODA прямой, AD = а/2,
OAD = а/2 (О —' центр вписанной окружности, a QD — ее'
радиус); Из Треугольника AOD находим '
'OD<
а , а
'TtgT'
Раднус описанной окружности
найдем по теореме синусов
АС
sin
£вс
■2R,
где ABC =180° — 2а, АС ■
следовательно,
* 2 sin 2a '
и,
По условию задачи раднус описанной окружности в 4 раза
больше радиуса вписанной окружности}
а
2 sin 2a
а . а
Последнее равенство представляет собой тригонометрическое
уравнение для нахождения угла ос:
sin
, sin -=- 2 sin a cos а
1 ..в . о . . 1 2
1_ = 4tgT=*tgysm2a =т=*
а
cosT
1 4slnZTcos7cosa I 0 , sa
в= — =>• =. — =*■ cos a 2 sin* -s- =»
4 a 4 2
cosT
= -jr =*• cos a (1 — cos a) = -g =*• 8 cos* a — 8 cos a + 1 = 0.
Обозначая cos ос = у, получаем квадратное, уравнение для
942 ..v fjt. а. ПЛАНИМЕТРИЯ
неизвестного у\
i V2
1 V5"
соза=^ ±_4-«
Таким образом, составленное тригонометрическое уравнение
имеет два решения:
ai ■= arccos
(т+Пг)' «2 = arccos (i-^f.).
Каждому значению а соответствует свой угол при вершине
равнобедренного треугольника:
(\ , л/2Л 0 (1 л/2"^
и — 2 arccos I -5- + -^т— 1, л — 2 arccos 1-^- 4" )•
Ответ, я — 2arccosl^- + -^— J, n — 2arccos( -5- — -т-J*
Пример 4.5. В равнобедренном треугольнике ABC угол В
прямой, ЛВ = ВС =■ 2. Окружность касается обоих катетов в
их серединах н высекает иа гипотенузе хорду DE. Найти
площадь треугольника BDE.
Решение. Пусть точки М и N — точки касания
окружности с катетами треугольника ABC. По условию AN = NB и
ВМ = МС. Восставим перпендикуляры из точек М и N. Так как
»тн точки — середины катетов треугольника, то точка К —
пересечение перпендикуляров — представляет собой центр описанной
вокруг треугольника окружности и, следовательно, находится на
середине гипотенузы АС. С другой стороны, К — центр исходной
окружности по построению, Таким образом, KN и КМ — радиусы
этой окружности. Заметим теперь, что четырехугольник BNKM —
квадрат (прямоугольник с равными смежными сторонами). Так
как NB = KN, то KN «= 1. Рассмотрим треугольник EBD. Его
основание ED — диаметр исходной окружности (хорда,
проходящая через центр К). Следовательно, ED = 2. Высота
треугольника EBD (BK)—радиус описанной вокруг ДЛВС окружности,
следовательно, BK = V5*- Таким образом, искомая площадь
AEBD равна
„ BK-ED лг
S = =У2.
Ответ. V2.
4.45. Периметр прямоугольного треугольника равен 24 сщ
площадь — 24 см5, Найти площадь описанного круга.
§ 4. треугольники и 0КрЯкЯ6"стИ 818
4.46. Одни из катетоа прямоугольного треугольника равен
15 см, а проекция второго на гипотенузу —16 см. Найти радиуо
окружности, вписанной в этот треугольник.
4.47. Определить углы прямоугольного треугольника, зная,
что радиус описанной около него окружиостн относится к
радиусу вписанной окружности, как 5 : 2.
4.48. Длина основания равнобедренного треугольника раана
4 см. Длина боковой стороны делится точкой касании вписанной
в этот треугольник окружности в отпошепии 3:2, считая от
вершины. Определить периметр треугольника.
4.49. Площадь прямоугольного треугольника равна б см1, а
радиус вневписаниой окружности, касающейся одного пз
катетов, равен 3 см. Найтп стороны треугольника.
4.50. Каждая из двух окружностей с центрами на медианах
равнобедренного треугольника, проведенных к боковым сторонам,
касается боковой стороны н осповаипя. Вычислить расстояние
между центрами окружностей, если длина основания
треугольника равна 2 дм, а длины этих медиан равны V° Дм-
4.61. Площадь треугольника ABQ равна 15 V3* см2.
Величина угла ВАС равна 120°. Величина угла ЛВС больше величины
угла АСВ. Расстояние от вершины А до центра окружности,,
вписанной в треугольник ABC, равно 2 см. Найти длину медианы
треугольника ABC, проведенной из вершины В.
4.52*. На катете ВС прямоугольного треугольника ABC как
на диаметре построена окружность, пересекающая гипотенузу в
Точке D так, что AD : DB =1:4. Найти длину высоты,
опущенной нз вершины С прямого угла на гипотенузу, если известно,
что длина катета ВС равна 10.
4.53. В прямоугольный треугольник вписана окружность.
Точка касания с окружностью делит один нз катетов'
треугольника на отрезки длиной 6 н 10 см, считая от вершины прямого
угла. Найтн площадь треугольника.
4.54. В треугольнике ABC биссектриса АР угла А делится
центром О вписанной окружности в отношении АО: ОР =
= V3 :2sin-r^-. Найтн углы В и С, если известно, что угол А
равен бд/9.
4.55. В треугольнике ABC биссектриса АЕ относнтся к
радиусу вписанной окружности, как V2~ :(ViiF — l). Найти углы В
и С, если известно, что угол А равен я/3.
4.56. Из вершины В равнобедренного треугольника ABC па
его основание АО онущепа высота BD. Длина каждой нз
боковых сторон АВ и ВС треугольника ABC равна 8 см, В треуголь-
344 i ГЛ. 12. ПЛАНИМЕТРИЯ
инке BCD проведена медиана DE. В треугольник BDE вписана
окружность, касающаяся стороны BE в точке .К и стороиы DE
в точке М. Длина отрезка КМ равна 2 см. Найти величину угла
ВАС.
4.57. Точка пересечения медиан прямоугольного треугольника
лежит на окружности, вписанной в этот треугольник. Найти
острые углы треугольника.
4.68. Найти косинус угла при основании равнобедренного
треугольника, если известно, что точка' пересечения его высот
лежит па вписанной в треугольник окружности.
4.59. В треугольнике ABC биссектриса АК перпендикулярна
медиане ВМ, a ABC = 120°. Найти отношение площади
треугольника ABC к площади описанного около этого треугольника
Круга. """
4.60. Вокруг равнобедренного треугольника ABC описана
окружность. Через вершину А проведена хорда длиной т,
пересекающая основание ВС в точке D. Даны отношение BD: DC =
«= k п угол А {А < я/2). Найтн раднус окружности.
4.61. В равнобедренный треугольник ABC с основанием АС
вписана окружность, которая касается боковой стороны АВ в
точке М. Через точку М проведен перпендикуляр ML к стороне
АС треугольника ABC (точка L — основание перпендикуляра).
Найти величину угла ВСА, если известно, что площадь
треугольника ABC равна 1, а площадь четырехугольника LMBC
равна S.
4.62. Внутри острого угла а взята точка М, отстоящая от
сторон угла на расстояния а н 2а. Найти раднус окружности,
проходящей через точку»М п касающейся сторон угла.
4.63. На плоскости дан прямой угол. Окружность с центром,
расположенным внутри этого угла, касается одной стороны угла,
пересекает другую в точках А и В и пересекает биссектрису угла
в точках С и D. Длина хорды CD равна V7, длина хорды АВ
равна V& Найти радиус окружности.
4.64*. В треугольнике ABC на стороне АС взята точка D
так, что окружности, вписанные в треугольники ABD н BCD,
касаются. Известно, что AD = 2, CD = 4, BD = 5. Найти
радиусы окружностей.
4.65. Точка D лежнт на стороне АС треугольника ABC.
Окружность радиуса 2/V3", вписанная в треугольник ABD, касается
стороны АВ в точке М, а окружность радиуса V^, вписанная в
треугольник BCD, касается стороны ВС в точке N. Известно, что
ВМ _= 6, BN = 5. Найти длины сторон треугольника ABC.
§ 6. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТИ
ш
• 4.66. Точка D лежит на стороне АС треугольника АВБ.
Окружность /(, вписанная в треугольник ABD, касается отрезка
BD в точке Af; окружность 1%, вписанная в треугольник BCD,—'
в точке N. Отиошенне радиусов окружностей U и h равно 7/4;
Известно, что ВМ = 3, MN = ND ■= 1. Найтн длины дгорои
треугольника ABC. ■ • • >• •
§ 5. Многоугольники и окружности
Многоугольник, все вершины которого лежат ив окружности, иааы-
вается вписанным в окружность, а окружность — описанной около МнЫ
геугольника. Окружность, касающаяся всех сторон многоугольника; на-
вывается вписанной в многоугольник.
.Площадь правильного многоугольннна с л углами (/^угольника),
Stl, сторона л-уголъннка ап, периметр л-угольпнка Р„ в радиусы
описанной в ввнсаннон окружностей R а г связаны формулами
S —-Р г
я 2 п '•
=2R sin
180°
.. 1 „, , 360°
«„.-_#» .In-^
Теоремы о четырехугольниках и окружностях.
1. Для того чтобы в выпуклый четырехугольник можно было
вписать окружность, необходимо и достаточно, чтобы суммы
противоположных сторон четырехугольника были равны.
2. Для того чтобы около выпуклого четырехугольнику можно быдр
описать окружность, необходиио н достаточно, чтобы сумма протнво»
лежащих внутренних углов четырехугольника была равна 180°.
Искомые величины в задачах 5.1—5.13 находятся
непосредственными вычислениями с использованием свойств
многоугольника и окружностей, вписанных в
этот многоугольник или описанных
около него.
Пример 5.1. Дана трапеция
ABCD, боковая сторона АВ которой
перпендикулярна основаниям. В
трапецию вписана окружность с
центром в точке О. Через точки А, В, С
проведена окружность с центром в
точке Oi. Найтн диагональ АС, если
00\ =1 см, а меньшее основание
10 см.
Решение. Пусть MN — средняя линия данной трапеции
'(рнс. 12.16). Окружность, проходящая через точки А, В, С,—
»то окружность, описанная около прямоугольного треугольника
ABC (угол В прямой), н ее центр Oi лежит на середине
гипотенузы АС. С другой стороны, средняя линия трапецнн MN
пересекает диагональ трапеции АС в ее середине, Следовательно,
Рнс. 12.10
трапеции ВС равно
346 ' ГЛ. 12. ПЛАНИМЕТРИЯ
точка Ог — это точка пересечения диагонали трапеции АС а
средней лниии трапеции MN.
Выясним, где находится точка О — центр окружности,
вписанной в трапецию ABCD. Так как рассматриваемая окружность
касается двух параллельных прямых ВС н AD, то ее центр —
точка, равноудаленная от этих двух прямых. Множество точек,
равноудаленных от двух оснований трапеции, — ее средняя
линия, н, следовательно, центр окружности, вписанной в трапецию,
также лежит на средней линии MN. В треугольнике ABC
сторона АВ больше стороны ВС, так как АВ равна диаметру
вписанной окружности, а сторона ВС меньше диаметра. Так как в
треугольнике против большей стороны лежит бблыпий угол
{ВСА > CAB), а сумма углов ВСА и CAB равна 90°, то угол
CAB меньше 45°. Окружность с центром в точке О касается
сторон прямого угла BAD, точка О лежит на биссектрисе этого
угла, и, следовательно, ВСО = 45°.
Таким образом, два угла {ВАС и ВМ>) имеют общую
сторону и ВАС < ВАО. Отсюда можно сделать вывод, что луч AOi
лежит между сторонами угла ВАО, т.е. точка Ot лежит между
точками М и О.
Теперь можно иайтн радиус окружности, вписанной в
трапецию ABCD. Отрезок AlOi — средняя линия треугольника ABC,
и, следовательно,
Л10,=уВС = 5 см.
Длина отрезка МО (радиуса вписанной в трапецию окружности)!
МО = MOi + 0|0 = 6 см.
Так как длина боковой стороны трапеции АВ равна диаметру
окружности (АВ = 2, МО = 12), то из прямоугольного
треугольника ABC по теореме Пифагора получаем
ЛС = -\МВ!-т-£C2=VI22+10S =чУ24Т = 2УбГ.
Ответ. 2Уб1 см.
5.1. Вычислить площадь равнобедренной трапеции, если ее
высота равна ft, а боковая сторона видна из цеитра описанной
■окружности под углом 60°.
5.2. В окружность вписан прямоугольник ABCD, сторона АВ
которого равна а. Из конца К диаметра КР, параллельного
стороне АВ, сторона ВС видна под углом (J. Найти радиус окруж-
дости. .
§ 5. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТИ 847
5.3. Около окружности радиуса г описана равнобочная
трапеция ABCD, Е и К — точки касания этой окружности с
боковыми сторонами трапеции. Угол между основанием АВ и
боковой стороной AD' трапеции равен 60°. Доказать, что ЕК
параллельна АВ, и найти площадь трапеции АВЕК-
5.4. В параллелограмме ABCD с углом А, равным 60°,
проведена биссектриса угла В, пересекающая сторону CD в точке Е.
В треугольник ЕСВ вписана окружность радиуса г. Другая
окружность вписана в трапецию ABED. Найти расстояние между
центрами этих окружностей.
5.5. В параллелограмме лежат две окружности. Одна из них,
радиуса 3, вписана в параллелограмм, а вторая касается двух
сторон параллелограмма и первой окружности. Расстояние ме-
жду точками касания, лежащими на одной стороне
параллелограмма, равно 3. Найти площадь параллелограмма.
5.6. В ромбе ABCD со стороной 1 + Vo" и острым углом 60°
расположена окружность, вписанная в треугольник ABD. Из
точки С к окружности проведена касательная, пересекающая
сторону АВ в точке Е. Найти длину отрезка АЕ.
6.7. Каждая из двух окружностей с центрами па диагоналях
равнобочной трапеции касается боковой стороны и большего
основания. Вычислить расстояние между центрами окружностей,
если длины боковых сторон трапеции равны 4 см, а длины
оснований равны 6 и 3 см.
6.8. В трапеции ABCD известны основания AD = 39 см и
ВС = 26 см и боковые стороны АВ = 5 см н CD = 12 см.
Найти радиус окружности, которая проходит через точки А н В и
васается стороны CD или ее продолжения.
5.9. В трапеции ABCD с основаниями AD и ВС длина
боковой стороны АВ равна 2 см. Биссектриса угла BAD пересекает
прямую ВС в точке Е. В треугольник ABE вписана окружность,
касающаяся стороны АВ в точке М и сторойы BE в точке
N. Длина отрезка МЫ равна 1 см. Найти величину угла
BAD.
5.10. Сторона ВС четырехугольника ABCD является
диаметром окружности, описанной около этого четырехугольника.
Вычислить длину стороны АВ, если ВС = 8, BD <= 4 ч/Т,
РСА;АСВ = 2А.
6.11. В выпуклом четырехугольнике ABCD длина стороны АВ
g
равна •О-ттг, длина стороны AD равна 14, длина стороны CD
равна 10. Известно, что угол DAB острый, причем синус угла
DAB равен 3/5, косинус угла ADC равен —3/5. Окружность а
848
. ГЛ 12. ПЛАНИМЕТРИЯ
центром в точке О касается сторон AD, АВ, ВС. Найти длину
отрезка ВО.
5.12. Пятиугольник ABCDE (вершины обозначены
последовательно) вписан в окружность единичного радиуса. Известно, что
АВ=>л/2, ДВ£«=45°, £BD = 30° и BC=CD. Чему равна пло-
щадь пятиугольника?
5.13. В ромб CDEF, у которого DCF =,у, вписана окруж-1
пость радиуса г. Касательная к этой окружности пересекает
сторону CD в точке.Л,;а сторону,OF-—а точке 5. „Известно, что
AD = т. 'Найти площадь треугольника ABC.
В задачах 5.14—5.16 необходимо ввести вспомогательную ве>
лпчнну, имеющую размерность длины, и решить задачу с
доопределенным условием. В искомых величинах вспомогательный
параметр сократится, н искомые величины будут зависеть только от
заданных в условии задачи величин.
5.14. В круг вписана равнобедренная трапеция так, что
диаметр круга служит основанием трапеции. Найтн отношение
площадей круга и трапеции, если тупой угол трапеции равен а.
. - 5,15. Дана равнобедренная трапеция, в которую вписана
окружность и около которой описана окружность. Отношение
высоты трапеции к радиусу описанной окружности равно
Найти углы трапеции.
6.16. Около круга описана трапеция с углами при основании
аир. Найти отношение площади трапеции к площади круга.
Задачи 5.17—5.32 решаются методом введения
вспомогательного неизвестного (или нескольких вспомогательных неизвестных),
для которого составляется уравнение (соответственно система
уравнений), отвечающее условию задачи.
Пример 5.2. Сторона АВ квадрата ABCD равна 1 и
является хордой некоторой окружности, причем все остальные
стороны квадрата лежат вне этой окружности. Длина
касательной С/С, проведенной нз вершины С к той же окружности,
равна 2. Найти радиус окружности.
Решение. Пусть О — центр окружности, радиус которой
нужно найтн (рис. 12.17). Введем обозначения: R — радиус
искомой окружности, х — длина отрезка, OL — расстояние от центра
окружности до хорды АВ.
•Составим теперь следующие уравнения!
из прямоугольного-треугольника СОМ получим
VI-
§ S. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТИ
84*
нз прямоугольного треугольника OBL получим
из прямоугольного треугольника ОСК получим
ОСа=.#»+4.
Приравнивая правые части уравнении (#) и (***) о учетом (#*),
получаем уравнение
ха + 2* + 1 + 1- в жа + -j + 4 -**• 2* = 3.
3
Следовательно, * = —; искомое значение # получается из
уравнения (**):
«-VFT-V?-
Ответ.
л/10
Пример 5.3. Окружность касается сторон АВ и AD
прямоугольника ABCD н пересекает сторону DC в единственной
РИС 12.17
точке F, а сторону ВС — в единственной точке Е. Найти
площадь трапеции AFCB, если АВ = 32. AD — 40 и BE = 1.
Решение. Пусть О — центр окружности М и N — точки
касания окружности со сторонами АВ и AD (рис. 12.18); OL —
высота равнобедренного треугольника МЕО. В качестве иенз»
вестных введем R — радиус окружности и а = ВМЕ.
В прямоугольном треугольнике МВЕ по условию задачи
BE = 1, Выражаем стороны треугольника МВЕ через угол а и
Л1В = ctg а, Л1£ ■
1
sin а'
850 ГЛ. 12. ПЛАНИМЕТРИЯ
Четырехугольник AMON, образованный радиусами N0, МО,
проведенными в точки касания, н частями сторон
прямоугольника AM н АЫ, будет квадратом, так как
NO = MO=*R, NAM*=n/2, ЛАЮ = л/2, ХыЬ=п/2,
н, следовательно, AM = AN =■= R. Равенство AM -f MB = AB
дает первое уравнение, связывающее R н ai
R + ctg a = 32.
Рассмотрим треугольник ОМЕ. В этом треугольнике
МЕ = —±— = 2ML, MO = OE = R, ОМ£ = 4--а,
sin a 2
углы LOM н ВМЕ равны как углы с соответственно
перпендикулярными сторонами. Следовательно,—5—=» sin a н, подставляя
сюда найденное уже значение ML *= -=—: , получим уравнение
*• Sin СЕ
1
sin a.
2R sin a
Последнее равенство представляет собой второе уравнение для R
и а. Итак, окончательно система уравнений для R и а пмеет вид
« + ctga<=32. Л-Т^.
Исключая R из системы, получаем тригонометрическое
уравнение угла а)
которое с помощью равенства 1 -|- ctg2 a = —r-j— преобразуется
к виду
ctgsa + 2ctga + 1 = 64 =>• ctg a =» 7
(a — острый угол). Из первого уравнения системы получаем
Л = 25.
Опустим из точки О перпендикуляр на сторону DO н
рассмотрим прямоугольный треугольник OPF. В этом треугольнике
OF = R = 25,
OP = MP - МО = AD — R = 40 - 25 = 15.
По теореме Пифагора находим
§ Б. МНОГОУГОЛЬНИКИ И ОКРУЖНОСТИ 8Й
Так как ctg а = 7, то, следовательно, в треугольнике MBF сто»
рона MB — 7. Так как PC *. MB •= 7 н FC =» FP + PC, то
FC = 20 + 7 =• 27.
Теперь в искомой трапеции AFBC найдено основание FC =>
= 27, а второе основание АВ и высота AD известны по условию
задачи, и; следовательно, площадь трапеции AFBC раана
„ AB±FC_ 32 + 27 ,п_мяп
bAFBC = § = 2
Ответ. 1180.
5.17. Около круга радиуса г описана прямоугольная
трапеция, меньшее основание которой равно •=-г. Определить площадь
трапеции.
5.18. В полукруге расположен прямоугольник ABCD так, что
его сторона АВ лежит на днаметре, ограничивающем полукруг,
а вершины С и D— на ограничивающей полукруг дуге. Длина
радиуса полукруга равна 5 см. Найти длины сторон
прямоугольника ABCD, если его площадь равна 24 см3, а длниа дпагонали
больше 8 см.
5.19. Около окружности радиуса R описай параллелограмм.
Площадь четырехугольника с вершинами в точках касания
окружности и параллелограмма равна 5- Найти длины сторон
параллелограмма.
5.20. Длина средней линии равнобочной трапеции равна 10.
Известно, что в трапецию можно вписать окружность. Средняя
линия трапеции делит ее на две части, отношение площадей
которых равно 7/13. Найти длину высоты трапеции.
5.21. В кружность радиуса 6 см с центром в точке О вписан
четырехугольник ABCD. Его диагонали АС и BD взаимна,
перпендикулярны и пересекаются в точке К. Точки В и F являются
соответственно серединами АС и BD. Длина отрезка О К равна
5 см, а площадь четырехугольника OEKF равна 12 сма. Найти
площадь четырехугольника ABCD,
5.22. В трапецию ABCD с основанием ВС н AD и с
боковыми сторонами АВ и CD вписана окружность с центром О.
Найти площадь трапеции, если угол DAB прямой, а 00=2,
OD = 4.
5.23. Биссектриса АЕ угла А рассекает четырехугольник
ABCD па равнобедренный треугольник ABE (АВ = BE) и ромб
AECD. Радиус круга, описанного около треугольника ECD, в
1,5 раза больше радиуса круга, вписанного в треугольник АНЕ,
Найти отношение периметров этих треугольников.
352 ГЛ. 12. ПЛАНИМЕТРИЯ
6.24. В трапецию ABCD с основанием AD =» 40, углами при
вершинах А и D, равными 60°, и боковыми сторонами AB=CD =
•= 10 вписана окружность так, что она касается обоих оснований
AD и ВС н стороны АВ. Через точку М основания AD,
отстоящую на расстояние 10 см от вершины D, проведена касательная
к окружности. Эта касательная пересекает основание ВС в
точке К. Найти отношение площади трапеции АВКМ к площади
трапеции MDCK.
6.25. Окружность, построенная на основании AD трапеции
ABCD как на диаметре, проходит через середины боковых
сторон АВ 'и CD трапеции и касается основания ВС. Найти углы
трапеции.
5.26. А, В, С, D — последовательные вершины
прямоугольника. Окружность проходит через А и В и касается стороны CD
в ее середине. Через D проведена прямая, которая касается той
же окружности в точке Е, а затем пересекает продолжение
стороны АВ в точке К. Найтн площадь трапеции BODK, если
известно, что АВ = 10 и КЕ ;КА = 3:2.
5.27. В четырехугольнике ABCD сторона АВ равна стороне
ВС, диагональ АС равна стороне CD, а угол ABC равен углу
ACD. Радиусы окружностей, вписанных в треугольник ABC и
ACD, относятся, как 3 :4. Найтн отношение площадей этих
треугольников.
6.28. В ромб ABCD, у которого А В = I п вЪ = а,
вписана окружность. Касательная к этой окружности пересекает
сторону АВ в точке М, а сторону AD — в точке N. Известно, что
MN = 2а. Найти длины отрезков MB и ND.
5.29. В прямоугольнике ABCD сторона ВС вдвое короче
стороны CD. Внутри прямоугольника расположена точка £, причем
И£ —У2~, СЕ = 3, DE = 1. Вычислить косинус угла CDE н
площадь прямоугольника ABCD.
6.30. В параллелограмме ABCD известны длины стороны
и диагонали BD = 2. Окружность раднуса У? с
центром в точке В, лежащая в плоскости параллелограмма,
пересекается со второй окружностью раднуса 1, проходящей через
точки Л и С. Известно, что касательные, проходящие через одну
из точек пересечения окружностей, взаимно перпендикулярны.
Найтн длину диагонали АС. '
5.31. В равнобочную трапецию вписана окружность.
Расстояние от центра окружности до точки пересечения диагоналей
трапеции относится к радиусу, как 3:5. Найтн отношение
периметра трапеции к длине вписанной окружности.
ГЛАВА 13
СТЕРЕОМЕТРИЯ
Общие свойства прямых и плоскостей. Плоскость а
В прямая а. не принадлежащая плоскости а, называются параллельными,
если они не имеют ин одной общей точки.
Признак параллельности прямой и плоскости. Если врямая
параллельна какой-либо вряиой, лежащей в плоскостн, то данные прямая и
плоскость либо пвраллельны, либо прямая принадлежит плоскости.
Теоремы о плоскости и прямой, параллельной
Плоскости.
1. Если плоскость содержит прямую, параллельную другой плоскости,
в пересекает эту плоскость, то линия пересечения плоскостей
параллельна даииой прямой.
2. Еслн через каждую па двух параллельных прямых проведена
произвольная плоскость и эти плоскости вересекаются, то линия их
в*ресачеиия параллельна каждой из данных прямых.
3. Если две пересекающиеся плоскости пвраллельны данной прямой.
то ливня Ях пересечения также параллельна даииой пряной.
- Две плоскостн <х н (5 называются параллельными, еслн овя не
имеют общей точки.
Признак параллельности двух плоскостей. Еслн две пересекающиеся
пряные одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
Теорема о параллельных плоскостях.
Если две параллельные плоскостн пересечены третьей плоскостью,
то линии их пересечения параллельны.
Пряная н плоскость называются взаимно перпендикулярными, еслн
прямая перпендикулярна каждой прямой, принадлежащей плоскости.
Прямую, перпендикулярную плоскостн, называют перпендикуляром к этой
плоскости.
Признак перпендикулярности прямой и плоскости. Еслн прямая
перпендикулярна каждой на двух пересекающихся прямых, лежащих в
плоскости, то эти прямые и плоскость аэанмно перпендикулярны. -.
Теоремы о перпендикулярности врямой н пло<
скости.
1. Два различных перпендикуляра к плоскостн параллельны.
2. Еслн одна нз двух параллельных прямых перпендикулярна
плоскости, то и другая перпендикулярна этой плоскости.
3. Прямая, перпендикулярная одной из даух параллельных
плоскостей, перпендикулярна и другой плоскостн.
4. Две плоскости, перпендикулярные одной и той же прямой,
параллельны.
Признак перпендикулярности плоскостей. Если плоскость содержит
перпендикуляр к другой плоскости, то она перпендикулярна этой
плоскости.
Теоремы о взаимно перпендикулярных влоско-
с т я х.. ■ - .
1. Если две плоскостн взаимно перпендикулярны, то врямая,
принадлежащая одной плоскостн и перпендикулярная линии пересечения
плоскостей, перпендикулярна и другой плоскости.
'2. Если две плоскости взаимно перпендикулярны и к одной нз
плоскостей проведен перпендикуляр, проходящий через линию
пересечения этих плоскостей, то этот перпендикуляр целиком принадлежит
другой плоскости... :....,'.,■<..-
ХДрячую. пересекающую плоскость, но не перпендикулярную ев, щя
вывают наклонной к плоскобти,'"' "' >'* '''■•",
12 А. Г. Цышшн, А, И, Пинский
354
ГЛ. 13. СТЕРЕОМЕТРИЯ
Теорема о трех перпендикулярах. Для того чтобы пря*
Мая, лежащая в плоскости, была перпендикулярна наклонной, необхс»
Днно в достаточно, чтобы эта прямая была Перпендикулярна проекция,
наклонно!) на эту плоскость.
Углом между наклонной и плоскостью называется угол между на«
клонноп и еа ортогональной проекцией на плоскость. Дае насоввадающна
полуплоскости, имеющие в качестве общей границы прямую н ограничп»
вающне полуплоскости, называются двугранным углом. Прямая, являют
щаяся общей границей двух полуплоскостей, называется ребром двуграи»
ного угла. Полуплоскость, граница которой совпадает о ромбом дву*
гранного угла и делящая двугранный угол на два равных двугранных)
угла, называется биссекторпой плоскостью. Угол, полученный в резуль*
тате пересечения двугранного угла плоскостью, перпендикулярной его
ребру, называется линейны* углом двугранного угла.
§ 1. Многогранники
Многогранником называется тело, ограниченное плоскими мвогоуголь»
пиками. Общие стороны смежных многоугольников называются ребрами
многогранника. Многоугольники, которые ограничивают многогранник, па»
аываются его гранями,
П р н з м а. Многогранник, две грани которого" — равные л-уголънтш.
лежащие в параллельных плоскостях, а ребра всех остальных граней
параллельны, называется п-уеольной. призмой. Пару равных л-угальнн*
ков называют основаниями призмы. Остальпые грани прязиы называют
ее боковыми гранями, а их объединение — боковое поверхностью призмы.
Ребра, не лежащие в основаниях призмы, называются боковыми ребрами.
Все боковые ребра призмы равяы как отрезки параллельных пряных,
ааключелных иежду параллельными плоскостями.
Призма, боковые ребра которой перпендикулярны плоскостям ость
вапий. называют прямой призмой. Отрезок перпендикуляра к плоскостям
оснований прпэмы, концы которого принадлежат этим плоскостям, на'
вывают высотой призмы. Прямая призма, основанием которой являете*
правильный многоугольник, называется правильной призмой.
Площадь боковой поверхности призмы вычисляется по формуле
s6oK^PnAlAV
где Рп— периметр перпендикулярного сечення призмы, Л,/1а— длина бо*
нового ребра.
Объем наклонной прпэмы вычисляется во формуле
где S„ — площадь перпендикулярного сечення призмы, AJA2 — pnaaa бо*
нового ребра, или по формуле
где S(xlf— площадь основания прнзыы. И — высота призмы.
Параллелепипедом называется призма, основаниями которой служат
параллелограммы. Все тесть граней параллелепипеда — параллелограммы.
Свойства параллелепипеда:
1) середина диагопали параллелепипеда является его центром сим*
метрик;
2) противолежащие грани параллелепипеда попарно равны я параде
дельны;
3) все четыре диагонали параллелепипеда пересекаются и одной
точке и делятся ею пополам.
Параллелепипед, боконые ребра которого перпендикулярны плоско»
сти основания параллелепипеда, называется прямым. Прямой параллеле*
пппед, основанием которого служит прямоугольник, называется прямо*
угольным. Все грани прямоугольного параллелепипеда — прямоугольники.
Объем прямоугольпого параллелепипеда вычисляется по формуле
V=a6c.
где а, Ь. е — длины трех ребер прямоугольного параллелепипеда, выхо*
дящие из одной вершины.
Прямоугольный параллелепипед с рвввынн ребрвмя называется ку
боя. Все грани вуба — равные квадраты. Объем куба вычисляется по
§ 1. МНОГОГРАННИКИ
856
Пример 1.1. Найтн площадь боковой поверхности
правильной треугольной призмы высотой Л, волн прямая,
соединяющая центр верхнего основания с серединой стороны нижнего
основания, наклонена к плоскостн основания под углом а.
Решение. Пусть АВСА{В\С\ — правильней треугольная
призма, в основании которой лежат правильные треугольники
ABC и Л|В|С|, 00| — высота {00, = А), М — середина отрезка
В|С|, О и 0| — центры треугольников верхнего
н нижнего оснований (рнс. 13.1). Рассмотрим
треугольник 0\ОМ. По условию задачи
ОМО| = ос, угол 0О\М прямой, 00\ •= Л,
Из прямоугольного треугольника 0,ОМ
находим 0|Л* =« /г ctg а. Так как 0\ — центр
треугольника <4iB|C,, то А{М = 30|Af =*
1» 3ft ctg а. По условию задачи треугольник
А[В[С[ равносторонний н А\М — высота,
медиана и биссектриса. По высота треугольника А,М находим
сторону Аф\ ——:■ Z.& =.2Уз~ ft ctg а. Площадь боковой
поверхности правильной треугольной" призмы ABCAiB\C\ равна
произведению периметра основания на высоту прнзмьп
S = 3- Л,В,-Л=в-^3~ A* ctg о.
Ответ. eV3"ftsdga-
1.1. Дан куб /4BCD4iBiC,D( с ребром а. Найти угол между
диагональю А\С н ребром i4iZ?i.
1.2. Расстояние между непересекающимися диагоналями
двух смежных боковых граней куба равно d. Найтн его объем.'
1.3. Определить объем параллелепипеда, если все- его
грани — ромбы, длины сторон которых равны а н острые углы, рае-
иы ос.
1.4. Определить объем правильной четырехугольной призмы,
если диагональ образует е боковой гранью угол ос, а сторона
основания равна Ь.
1.5. Непересекающиеся диагонали двух смежных боковых
граней прямоугольного параллелепипеда наклонены к плоскостн его
основания под углами о и р\ Найти угол между этими
диагоналями.
1.6. В наклонной треугольной призме длины боковых ребер
равны 8 см) стороны перпендикулярного сечения относятся, как
9:10:17, а его площадь равна 144 см1, Найтн боковую
поверхность этой призмы.
1.7. В прямоугольном параллелепипеде угол между
диагональю основания н его стороной равен ос. Диагональ параллеле-
12*
856
ГЛ. 13. СТЕРЕОМЕТРИЯ
пипеда равна d н образует с плоскостью основания угол ф.
Найти боковую поверхность параллелепипеда.
1.8. В основании четырехугольной призмы лежит ромб со
стороной а и острым углом а, а боковые ребра призмы равны &
и наклонены к плоскости основания призмы под углом р. Найти
объем призмы.
1.9. Углы, образуемые диагональю прямоугольного паралле/
лепппеда с его гранями, пересекающимися в одной из его
вершин, равны ос, р, у- Доказать, что
s!n2o+ sli^P + sin'v^».
Пира и ii до. Многогранник, одна из гранен которого — произвола
ныл многоугольник, в остальные грани — треугольники, имеющие одыу|
общую вершину, называете» пирамидой. Многоугольник называется
основанием пирамиды, а остальные грани (треугольники) называются бока-
выми гранями пирамиды.
Стороны граней пирамиды называются ребрами пирамиды. Ребра,
принадлежащие основанию нкраипды, называют ребрами основания,
а все остальные ребра — боковыми ребрами. Общая вершина всех тре-
угольников (боковых гранен) иазынвется вершиной пирамиды.
высотой пирамиды называется отрезок перпендикуляра, проведен-
ного аз' вершниы пирамиды к плоскости основания (концами этого
отрезка являются вершина пнрамнды в основание первевднкуляра).
Правильная пирамида. Пирамида называется правильной^
если осповвипем пирамиды является правильный многоугольник, а орк
тогопальная проекция вершины пирамиды совпадает с центром много*
угольника, лежащего в основании пирамиды. Все боковые ребра
правильной пирамиды равны между собой; все боковые грани — равные
равнобедренные треугольники. Высота боковой грани правильной
пирамиды, проведенная из ее вершины, называется апофемой этой
пнрамнды.
Треугольная пирамида, в основании которой лежит треугольник,
называется твтравдром. Тетраэдр называется правильным, если все его
ребра равны.
Площадь боковой поверхности правильной пирамиды вычисляется
по формуле
рде Р — периметр пнрамнды, ft — апофема.
Объем пирамиды вычисляется по формуле
V-±SH,
где S — площадь основания пнрамнды, Н — высота пирамиды.
Усеченная пирамида. Многогранник, вершнпамн которого
служат вершины осноиання пярамнды и вершины ее сечеппя
'плоскостью, параллельной основанию пирамиды, называется усеченной
пирамидой. Основания усеченной пирамиды — гомотетичные многоугольники.
Центр гомотетии — вершнпа пнрамнды. Перпендикуляр к плоскости
оснований, с концами на плоскостях оснований пирамиды, называется
высотой усеченной пирамиды. Бокоаые грани усеченной пирамиды —
трапеции.
Усеченная пирамида называется правильной, если она является
частью правильной пирамиды. Боковые грани правильной усеченной
пирамиды — равные равнобедренные трапеции. Высота каждой из этия
трапеций называется апофемой правильной усеченной пирамиды.
Площадь боиовой поверхности Правильной усеченной пирамиды
вычисляется по формуле
S-=~(P + p)h.
где Р, р — периметры основание пирамиды, ft — апофема.
§ I. МНОГОГРАННИК»
337
Объем усеченное пирамиды вычисляется по формуле
где Н — высота усеченной пирамиды, S, п St — площади ее оснований.
Пример 1.2. В основании, пирамиды лежит
равнобедренный треугольник, равные стороны которого равны Ъ, а угол-
между ннмн равен а. Найти объем пирамиды, если каждое нз
боковых ребер пирамиды образует с высотой пирамиды угол <р.
Решение. Пусть SABC — данная пирамида, SO — высота
пирамиды, АВ = АС, А=>а, ASO =■ b'sO = €S0 •=»ф (рнс 13.2),
Рассмотрим треугольники ASO, BSO,
CSO, Все эти треугольники прямоуголь- £
вые [SO — высота пирамиды, перпендн- /У\Ч
кулярная плоскости треугольника ABC, /f Л \
и, следовательно,- SO перпендикулярна / i \ \
прямым АО, ВО, СО, принадлежащим / ' \ \
плоскости треугольника ABC), SO—об- / ^2н—С^-у
щая сторона этих треугольников, а Л^йзЯ* —-^f'Д /
(углы при вершине S равны ф по уело- *^-^У
вню. Следовательно, все эти треуголь-
ннкн равны между собой н против Рис' ,зл
равных углов этих треугольников
лежат равные стороны: АО = ВО = СО. Таким образом,
оказывается, что точка О — точка, равноудаленная от всех вершин
треугольника ABC, — является центром окружности, описанной
около треугольника ABC.
В равнобедренном треугольнике ABC известны боковая
сторона АВ = Ь и угол а при вершине А. Радиус окружности,
описанной около треугольника ABC, равен b/l 2 соз-^)- В"
прямоугольном треугольнике ASO теперь известны катет \АО\ =
a:b/(2cos-} H острый угол прн вершине S, равный ф. Находим
второй катет SO, который является высотой пирамиды:
S0 = А0 c'8<P = -2^Wdg<P-
Теперь найдем объем пирамиды SABC:
VSABC = J SA ABCS° = T * у b* s,n « ^оТЩ" °tg Ф ""
■-£-68ЗШ-у^ф.
1 /*
Ответ, -g-Ьгsin-£-ctgф.
658
ГЛ. 13. СТЕРЕОМЕТРИЯ
1.10. Определить объем правильной треугольной пирамиды,
боковое ребро которой равно / и наклонено к плоскости
основания под углом о.
1.11. Определить полную поверхность правильной
треугольной пирамиды, у которой плоский угол при основании боковой
грани равен ос, а радиус вписанной в основание окружности
ранен г.
1.12. Боковые грани треугольной пирамиды — прямоугольные
треугольники, а боковые ребра равны о. Найти угол между
боковым ребром и высотой. Вычислить объем пирамиды.
1.13. В основании пирамиды лежит равнобедренный
треугольник с основанием а и боковой стороной Ь. Боковые грани
образуют с основанием двугранные углы, равные о. Найти
высоту пирамиды.
1.14. В правильной треугольной пирамиде высота равна Н, а
двугранный угол прн боковом ребре равен ос. Найти объем
пирамиды.
1.15. НаПтн объем правильной треугольной пирамиды, зная
плоский угол ос прн вершине и расстояние а от боковой грани
до Противоположной вершины.
1.16. Боковое ребро правильной треугольной пирамиды
равно а, угол между боковыми гранями равен 2<р. Найти длину
стороны основания,
1.17. В основании пирамиды лежит прямоугольный
треугольник с гипотенузой с и острым углом ос. Каждая из боковых
граней пирамиды наклонена к основанию под углом р. Найти
боковую поверхность пирамиды.
1.18. Стороны основания треугольной пирамиды равны a, b
н с. Все плоские углы прп ее вершине прямые. Вычислить объем
пирамиды.
1.19. Боковые ребра треугольной пирамиды имеют одннако:
вую длину /, Из трех плоских углов, образованных при вершине
пирамиды этими ребрами, два равны ос, а третий равен р.
Найти объем пирамиды.
1.20. Двугранный угол прн основании правильной
треугольной пирамиды равен ос. Найти двугранный угол между боковыми
гранями.
Указание. В этой и следующей аадачах ввести
вспомогательный параметр а —длину ребра пирамиды.
1.21. В правильной треугольной пирамиде двугранный угол
при боковом ребре равен а. Найти плоский угол прп вершине
пирамиды.
1.22. Ребра оснований правильной усеченной треугольной
пирамиды равны соответственно а и Ь, Найти высоту пирамиды,
§ I. МНОГОГРАННИКИ
359
если все боковые грани наклонены к плоскости основания под
углом а.
1.23. В треугольной пирамиде SABC ребро SA
перпендикулярно плоскости грани АВС, двугранный угол с ребром SC равен
Я/4, SA = ВС = а и £АВС = я/2. Найти длину ребра АВ.
1.24. Все грани треугольной пирамиды — равные
равнобедренные треугольники, а высота пирамиды совпадает с высотой
одной нз ее боковых граней. Найтн объем пирамиды, если
расстояние между наибольшими противоположными ребрами равно
единице.
1.25. Найти объем тетраэдра, у которого каждая грань —
1реугольн!1к со сторонами а, 6, с, где а, Ь, с —различные числа.
Пример 1.3. В основании пирамиды лежит прямоугольник,
площадь которого равна Q. Две боковые грани пирамиды
перпендикулярны плоскости основания,
а две другие образуют с плоскостью
основания углы ос и (?. Найти объем
пирамиды.
Решение. Пусть SABCD—дан-
Пая пирамида, в основании которой
лежит прямоугольник ABCD
площадью Q (рис. 13.3). Так как все
боковые грани пирамиды имеют одиу
общую точку S (вершина пирамиды),
то перпендикулярными основанию
пирамиды могут быть лишь смежные
боковые граня (на рис 13.3 —
грани- BSC и DSC). Далее, так как грани BSC и DSG
перпендикулярны плоскости основания и имеют общую точку S, тЪ оин
пересекаются по прямой, проходящей через эту точку н
перпендикулярной плоскости основания, откуда следует, что высота
пирамиды совпадает с боковым ребром SC.
Так как основание пирамиды — прямоугольник, то прямая
AD перпендикулярна прямой DC, прямая АВ перпендикулярна
прямой ВС и обе эти прямые [AD и ВС) перпендикулярны
высоте пирамиды SC. Отрезки DC и ВО являются ортогональными
проекциями отрезков DS и BS на'плоскость основания
пирамиды, и по теореме о трех перпендикулярах ABA.BS и ADJ.DS.
Таким образом, оказывается, что ZSBC является линейным
углом двугранного угла, образованного плоскостями ABCD и ASB,
a ZSDC — линейный углом двугранного угла, образованного
плоскостями ABCD и ASD. По условию задачи один нз этих
углов (например, /1SBC) равен а, а другой (Z.SDC)'равен pi
360
ГЛ. 13. СТЕРЕОМЕТРИЯ
Пусть ВС = х, a DC = у. Из прямоугольного треугольника
BSC находим SC = xtga, а нз прямоугольного треугольника
DSC находим SC = у tg p. Отсюда следует, что
*tga = ytgp\
а в силу условия задачи ху = Q.
Из полученных уравнении находим у = VQ tgectgp, и,
следовательно,
SC = ytgP = VQtgatgp.
Нетрудно проверить, что если положить SBC = р, SDC=a,
то по-прежнему высота пирамиды SC будет определяться тем же
самым выражением. Найдем объем пирамиды Vsabcd:
^Bc0 = TS4flC0SC = TQVQtgatgp. ^
Ответ. yQVQtgatgp.
1.26. Определить объем правильной четырехугольной
пирамиды, у которой сторона основания равна а, а двугранный угол
между смежными боковыми гранями равен ос.
1.27. Определить объем правильной четырехугольной
пирамиды, боковое ребро которой равно /, а двугранный угол между
двумя смежными боковыми гранями равен р.
1.28. В осиованпн четырехугольной пирамиды лежит ромб,
большая диагональ которого равна d, а острый угол равен а.
Все боковые грани наклонены к плоскости основания под
углом р. Найти боковую поверхность пирамиды.
1.29. Плоский угол при вершине правильной
четырехугольной пирамиды равен о, а высота — It. Определить объем
пирамиды.
1.30. В правильной четырехугольной пирамиде высота равна
Я, объем равен V. Найти боковую поверхность Q.
1.31. В правильной четырехугольной пирамиде плоский угол
прн вершине равен о. Найти угол между противоположными
боковыми ребрами.
1.32. В правильной четырехугольной пирамиде двугранный
угол при боковом ребре равен 2а. Найти двугранный угол при
основании.
1.33. Основанием пирамиды служит прямоугольник, две
боковые граин ее перпендикулярны плоскости основания, две
другие боковые граин образуют с основанием углы ос в р соответ-.
§ 2. СЕЧЕНИЯ МНОГОГРАННИКОВ
3ft
ственно. Определить объем пирамиды, если длина наибольшего
нз боковых ребер равна /.
1.34. В четырехугольной пирамиде SABCD плоскости
боковых граней SAB, SBC, SCD, SAD образуют с плоскостью
основания углы, равные соответственно 60°, 90Р, 45е, 90°. Основание
ABCD — равнобочная трапеция; АВ = 2, площадь основания
равна 2. Найти площадь поверхности пирамиды.
1.35. Найти объем и боковую поверхность правильной
шестиугольное пирамиды, если даны боковое ребро / и диаметр d
круга, вписанного в основание пирамиды.
1.36. Плоский угол при вершине правильной шестиугольной
пирамиды равен углу между боковым ребром и плоскостью
основания. Найти этот угол.
1.37. Двугранный угол при боковом ребре правильной
шестиугольной пирамиды равен <р. Определить плоский угол при
вершине пирамиды.
1.38. Найти объем правильной пирамиды, в основании
которой лежит правильный пятиугольник, а боковыми гранями
являются правильные треугольники со стороной а.
1.39. В правильной л-угольной пирамиде боковые грани
наклонены к плоскости основания под углом ос. Под каким углом
наклонены к плоскости основания боковые ребра пирамиды?
1.40. Плоский угол при вершние правильной л-угольной
пирамиды равен а. Найти двугранный угол 9 между двумя
смежными боковыми гранями.
1.41. Найти объем правильной усеченной четырехугольной
пирамиды, у которой сторона меньшего основания равна Ь,
большего основания равна а, а угол наклона боковой грани к пло-,
скостп большего основания равен 60°.
§ 2. Сечения многогранников
Построить сечение многогранника плоскостью — это значит
указать точки пересечения секущей плоскости с ребрами
многогранника и соединить эти точки отрезками, принадлежащими
граням многогранника. Точки пересечения плоскости сечения с
ребрами многогранника будут вершинами, а отрезки,
принадлежащие граням, — сторонами многоугольника, получающегося в
сечении многогранника плоскостью.
Для построения сечения многогранника плоскостью нужно в
плоскости каждой пересекаемой грани многогранника указать
две точки, принадлежащие сечению, соединить их прямой и найти
точки .пересечения этой прямой с ребрами многогранника.
Плоскость сечення ыногограшшка может задаваться разными уело-
862 гл- |3- СТЕРЕОМЕТРИЯ
виями. Рассмотрим несколько простейших типичных способов
задания сечений куба,
Пример 2.1. Построить сечение куба ABCDA\B\C\Dt с
ребром а плоскостью, проходящей через середины ребер АВ, ВС
и CCi.
Решение. Две точки М и N (середины ребер А В и ВС
соответственно) (рис. 13.4), принадлежащие сечеиию, лежат иа
Рис 19.4 Рис 13.5
одной грани. Проведем прямую через точки М н N до пересечет
иия с продолжениями ребер AD и DC соответственно в точках
Р н L. Из треугольников MBN н NLC нетрудно найти, что
LC = JVC=.a/2.
Точки L и К (середина ребра CCt] лежат в плоскости грани
DDiCiC. Проводим прямую через точки L в К. Учитывая, что
СК = о/2, из треугольников LCK н KCtS находим SC^ = а/2,
т.е. точка S лежит «а середине ребра Did. Прямая L/C
пересечет продолжение ребра DD% в точке R. Аналогично предыдущему
можно показать, что DiR = а/2. Так как точки Р н /? лежат
в плоскости грани AiADD\, то прямая PR пересечет стороны
квадрата AiADDi в точках Т a Q, причем точка Г —середина
ребра AAi, а точка Q —середина ребра AiDi.
Итак, получены шесть точек (М, N, К, S, Q я Т),
принадлежащих плоскости сечения в лежащих па гранях куба. Соедйвяя
пары точек М н Т, N и К, S и Q, получаем искомый
шестиугольник сечения.
Пример 22. Построить сечеиие куба ABCDAiBxCtDi
плоскостью, проходящей через середины ребер АВ и ВС и центр
квадрата A&tdDt.
Решение. JB данной задаче две точки М и N (рис 13:5)
принадлежат верхней граии, а третья точка О принадлежат па-
S 2. СЕЧЕНИЯ МНОГОГРАННИКОВ
863
раллельной ей грани нижнего основания. Нетрудно убедиться,
что в данной задаче построение сечения методой, описанным а
предыдущей звдаче, пе приводит к цели. Так же обстоит дело
в задачах, в которых прямая, соединяющая две данные точки
сечения, оказывается параллельной ребру многогранника или все
три точки искомого сечепия принадлежат скрещивающимся
ребрам многогранника. В этих случаях при построении сечения
используются следующие теоремы.
1. Если две плоскости параллельны н пересекаются третьей
плоскостью, то лнинн пересечения параллельных плоскостей
третьей плоскостью параллельны между собой.
2. Если две пересекающиеся плоскости параллельны одной и
той же прямой, то линия их пересечения параллельна этой
прямой.
3. Если плоскость и прямая параллельны и через прямую
проведена плоскость, пересекающая данную, то линия
пересечения этих плоскостей параллельна данной прямой.
Искомая плоскость сечения проходит через точку О и
прямую MN, параллельную плоскости AiBiCyDi. По теореме 3
плоскость сечення пересечет плоскость гранп AiBiCiDi по прямой,
параллельной прямой MN. Так как прямая MN параллельна
прямой АС (как средняя линия треугольника ABC), a /4CIMiCj, те
линией пересечения плоскости сечения и плоскости грани
AiBiCiDi будет диагональ квадрата AiCt. Точки At и М
принадлежат грани А\АВВи а точки N и С\ принадлежат грани
BCCiBi, и, следовательно, в сечении куба плоскостью будет
получаться четырехугольник AtMNCi.
В двух рассмотренных выше примерах точки, задающие
сеченне, принадлежали поверхности куба. Однако существуют
задачи, в которых точки, задающие сечения, принадлежат
разным граням пли же одна из точек лежит внутри многогранника.
В этих случаях для решения задач необходимо сделать
дополнительные построения, позволяющие свести решение задачи к
описанной выше схеме построения сечения. Часто для этого строят
вспомогательную плоскость, содержащую какую-либо прямую,
принадлежащую плоскости сечення, и какую-либо прямую,
принадлежащую плоскости грани. В построенной вспомогательной
плоскости отыскивается точка пересечения этих прямых и тем
самым находится еще одна точка, лежащая уже в плоскости
боковой, грани.
Пример 2.3. Дан куб ABCDAiBiCiDt с боковыми ребрамя
AAt, BBt, CCi, DDt. Найти площадь сечения куба плоскостью Р,
проходящей через центр куба и середины ребер АВ и ВС, если
ребро куба равно единице.
864
ГЛ. 13. СТЕРЕОМЕТРИЯ
Решение. Пусть М н N — середины ребер A3 н ВС
соответственно (рнс. 13.6). Плоскость Р проходит через точки М
в N и, следовательно, пересекает грань ABCD по прямой MN.
Для того чтобы построить сеченне куба плоскостью Р, построим
вспомогательное сеченне куба диагональной плоскостью Q,
проходящей через вершины куба В,
Bf Nt Cf d, D\, B\. Диагональное сечение
куба представляет собой
прямоугольник со сторонами BBt =
= 1 и BD,= ^¥. Плоскости Р и
s Q пересекутся по прямой,
проходящей через точку L и точку О
(центр куба), которая также
принадлежит плоскости Q, причем
BL= — BD. Испольэуя равен-
Рис. is.e 4
ство треугольников LRO и L\R\0,
нетрудно доказать, что £i0i = -j-Bi^i. Таким образом,
доказано, что плоскость Р проходит через точку Ц,
принадлежащую верхнему основанию куба, н L\D\ = -j- BXD\.
Так как плоскости A BCD и AiBidDi параллельны и
плоскость Р пересекает обе эти плоскости, то линнн пересечения этих
плоскостей плоскостью Р параллельны между собой, Проводя
Прямую MiNi через точку Li параллельно диагонали AtCi,
получаем две точки (Mi н ЛГ]), принадлежащие плоскости сечения Р
ft ребрам куба, причем MtNi — средняя линяя треугольника
Л,С,£»„ MlNl=-^AlCl и £»,ЛГ1 = ЛГ,С1.
Продолжим ребро DC за точку С. Так как прямые MN a
DC принадлежат плоскости нижнего основания куба н
непараллельны, то они пересекутся в некоторой точке 5. Из равенства
треугольников MBN и NSC следует, что SC = MB. С другой
Стороны, точка S, принадлежащая плоскости Р, принадлежит
также грани куба DCCtDt. Таким образом, получены две точки
{S и Nt), принадлежащие как плоскости Р, так п плоскости
грани DCCiDi. Прямая, проходящая через точки S н ЛГ(, пересе:
чет ребро куба СС{ в точке /(. Из равенства равнобедренных
Треугольников CSK и KNtCt следует, что SC = С/( = КС, =
«■■ NiCi. Соединяя точки ЛГ и К, принадлежащие плоскости Р н
плоскости грани ВСС\В\, получаем еще одну сторону много*
угольника сечения.
§ 2. СЕЧЕНИЯ МНОГОГРАННИКОВ
395
Аналогично, продолжая ребро куба AD за точку А,
получаем точку St—точку пересечения прямых MN и AD. Далее,
соединяя точки Si и Alt, получаем точку /G—точку пересечения
плоскости Р с ребром AAi, причем AiKi = AtMt = AKi-
Итак, в сечеиии куба плоскостью Р получен шестиугольник
MNKNtMtKi. Из равенства треугольников MBN, NCK, KCtNt,
NtDiMt, MiAiKt, KtAM следует, что стороны этого
шестиугольника равны я длнпа его стороны равна у 2 /2. Так как
треугольники NCS, SCK, NCK равны (все они прямоугольные и NC =
1= CS = CN, то треугольник NSK равносторонний, SNK «=» 60°,
н, следовательно, MNK = 120°, Аналогично можно доказать, что
все .остальные углы шестиугольника MNKNiMiKi равны 120°, и,
следовательно, этот шестиугольник правильный. Площадь
правильного шестиугольника со стороной У2/2 равна Ъ^/ъ/ь.
Ответ. зУз74.
Для нахождения площади сечения многогранника в ряде
случаев также удобно использовать свойство
ортогональной проекции плоского многоугольника)
s = S cos о,
где S — площадь многоугольника, s — площадь его
ортогональной проекции на некоторую плоскость Р, а—угол между
плоскостью многоугольника н плоскостью Р.
2.1. Через середину диагонали куба перпендикулярно ей
проведена плоскость. Определить площадь фигуры, получившейся
в сечеиии куба этой плоскостью, если ребро куба равно а.
2.2. В кубе ABCDAtBtCtDt (AAi II BBt II CCi \\ DD\) через
середины ребер DDt н D,Ct и вершину А проведена плоскость.
Найти угол между этой плоскостью и гранью ABCD.
2.3. В кубе ABCDAiBiCiD, (АА{ \\ ВВ, II СС{ II DD{) плоскость
Р проходит через диагональ Л(С, и середину ребра DDi. Найти
расстояние от середины ребра CD до плоскости Р, если ребро
куба равно 4.
2.4. Дан куб ABCDAiBtCiDi \AAi II Bfl, || CCi \\ DDt). Найти
расстояние от вершины А до плоскости, проходящей через
вершины А,, В, D, если ребро куба равно а.
2.5. Дан куб ABCDAtBtC,Dl (AAt \\ BBt II CCt || DDt). На
продолжениях ребер АВ и BBt взяты точки М и N
соответственно так, что AM = В,'ЛГ = -j АВ (вм = BN>= у Ав\ Гдо
на ребре СС\ должна иаходнться точка Р для .того, ..что$ц..р, с^
388 ГЛ, 13. СТЕРЕОМЕТРИЯ
ченнн куба плоскостью, проведенной через точки М, N и Р, по-
лучился пятиугольник?
2.6. Пусть М и N — середины ребер AAt н CCt куба
ABCDAtBiCiDi, а на продолжении ребра DiD за точку D взята
такая точка Р, что DP = 1/2 м. Через М, N и Р проведена
плоскость. Найти площадь сечения, если ребро куба равно I м.
2.7. Длина ребра куба/(LAM/(,!,№,#, (KKALLiWMM^NM,)
равна 1. На ребре MMt взята точка А так, что длина отрезка
AM равна 3/5. На ребре KtNt взята точка В так, что длина
отрезка KtB равна 1/3. Через центр куба н точки А' в В проведена
плоскость а. Точка Р — проекция вершины N на плоскость а.
Найти длину отрезка ВР.
2.8. На ребре BBt куба ABCDAxBidD^ взята точка Р так,
что B|F = •=- SS|, на ребре С,£», — точка Е так, что £>i£ = -g-C|£>i.
ЛР
Какое наибольшее значение может принимать отношение ^ ,
где точка Р лежит па луче DE, а точка Q — на прямой AiFf
Пример 2.4. Высота прямой призмы равна I. В
основании лежит ромб со стороной, равной 2, н острым углом 30°.
Через сторону основания проведена
секущая плоскость с углом
наклона к плоскости основания 60°.
Найти площадь сечения.
Решение, Пусть призма
ABCDAiBidD i — данная призма
(см. рис. 13.7) н секущая плоскость
проходит через ребро основания
/4,S|, А,В, = 2, в,Л]£>1=30°, АА| = 1.В зависимости от
линейных размеров призмы плоскость сечення, проходящая через
ребро AtBi, пересекает либо боковую грань призмы DC&Di, либо
грань верхнего основания A BCD. Предположим (а потом и дока-,
жем), что плоскость сечения пересекает грань основания ABCD
по прямой MN. Прямая MN будет параллельна ребру AtBt
(плоскости ABCD и AiBtCtDi параллельны, н, следовательно, линии
пересечения этих двух плоскостей третьей — секущей
плоскостью—будут параллельны между собой), н MN = АВ =
= AiB|. Из точки Si проведем перпендикуляр BiK к прямой
Л|5,, принадлежащий плоскости AiMNBi, и перпендикуляр B\L
к прямой AtBt, принадлежащий плоскости AiBxCxDi. По
построению угол KB\L — линейный угол двугранного угла,
образованного секущей плоскостью н плоскостью основания. По условию
задачи KBtL = 60°.
§ 2. СЕЧЕНИЯ МНОГОГРАННИКОВ 867
Опустим из точки К перпендикуляр КР на плоскость
A[B[C{D\. По теореме о трех перпендикулярах точка Р будет
принадлежать прямой SiL. Рассмотрим треугольник В\КР. Этот
треугольник прямоугольный (угол Р прямой), а КР = 1 {КР —
высота прямой призмы), в KBtP = 60°. Из треугольника BtKP
находим
ВхК ■= 2/л/з", BtP = l/УЗ".
Рассмотрим четырехугольник AiMNB]. Как было показано
выше, AtBt || МЛГ н ,4iSi *=■ Л1ЛГ = 2. Четырехугольник, у
которого противоположные стороны равны н параллельны, —
параллелограмм. Отрезок BiK — высота параллелограмма AtMNBtf
так как по построению BiK-LAiBu Площадь параллелограмма!
5Л1АСЛГв1-Л,в1.В|К-4/-Д.
Теперь осталось доказать, что плоскость сечения
действительно пересекает верхнее основание призмы, а не ее боковую
грань. По условию задачи в основании призмы лежит ромб со
стороной, равной 2, и острым углом 30°. Из прямоугольного
треугольника B\C\L, у которого S|C| = 2 н B\C\L =» 30е, иаходн»
высоту ромба: BiL = 1.
Допустим, что секущая плоскость пересекает боковую грань
DCdDi по прямой MN. Построив линейный угол двугранного
угла с ребром A,Bi, получаем треугольник BiKL, причем точка К
лежит на боковой грани и отрезок KL — часть высоты призмы,
т.е. KL < 1. Однако из треугольника B\KL находим, что
K.L = *JZ > 1. Установленное противоречие доказывает, что
секущая плоскость ие может пересекаться с боковой гранью
DCCtDu
В заключение следует заметить, что величина острого"-угла
ромба понадобилась нам лишь при доказательстве, что
плоскость сечення пересекает верхнее основание призмы, а не ее
боковую грань, и никак ие была использована при нахождении
площади сечения. Можно рассмотреть более общую задачу,
полагая, что острый угол ромба равен а. В этом случае площадь
сечеиня будет равна 4/д/з" для всех углов а, удовлетворяющих
неравенству slna>l/(2V3).
Ответ. 4/У3" •
2.9. Через вершины А, С и D\ прямоугольного
параллелепипеда ABCDAlB\C\D\ проведена плоскость, образующая с
плоскостью основания угол 60°, Стороны основания параллелепипеда
равны 4 и 3, Найтн объем параллелепипеда,
•368
ГЛ. 13. СТЕРЕОМЕТРИЯ
2.10. Высота правильной треугольной призмы равна •//.
Плоскость, проведенная через среднюю лннню нижнего основания н
параллельную ей сторону верхнего основания, составляет с
плоскостью основания угол а. Найти площадь сечения.
2.11. Основанием прямой призмы служит равнобочная
трапеция с основаниями а и b \a> Ь) и острым углом а.
Плоскость, проходящая через большее основание верхней трапецнп
п меньшее основание нижней трапеции, образует с плоскостью
нижнего основания угол р\ Найтн объем призмы.
2.12. .В правильной четырехугольной призме через сторону
основания ' проведено сеченне под углом а к плоскости
основания. Найти угол между диагональю н стороной
основания.
2.13. В правильной треугольной призме через сторону
нижнего основания и'противоположную вершину верхнего основания
проведена плоскость, образующая с плоскостью основания
двугранный угол 45°. Площадь сеченпя равна 5. Найтн объем
' призмы.
2.14. Через вершину правильной четырехугольной прнзмы
проведена плоскость так, что в сеченни образовался роиб с
острым углом ос. Найти угол наклона этой плоскости к плоскости
основания призмы.
2.15. В правильной четырехугольной призме сторона
основания равна а. Через диагональ нижнего основания и вершину
верхнего основания проведена плоскость, пересекающая две
смежные боковые грани призмы по прямым, угол между
которыми равен а. Определить объем призмы.
2.16. Основанием прямой призмы служит прямоугольный
треугольник с гипотенузой с и острым углом 30°. Через
гипотенузу нижнего основания и вершину прямого угла верхнего
основания проведена плоскость, образующая с плоскостью
основания угол в 45°. Найти объем треугольной пирамиды, отсеченной
от прнзмы плоскостью.
2.17. Высота прямой призмы I м, ее основанием служит
ромб со стороной 2 м и острым углом 30°. Через сторону
'основания проведена секущая плоскость, наклоненная к плоскости
основания под углом 60°. Найтн площадь сечения.
2.18. В основании прямой треугольной призмы лежит
равнобедренный треугольник с боковой стороной а н углом при
основании ос. Через основание этого треугольника внутрн прнзмы
лод углом ф проведена плоскость. Определить площадь сеченпя,
< иная, что в сеченни получается треугольник.
' 2.19. В оснований прямой прнзмы лежит равносторонний
1 треугольник. Через .одну из сторон основания .и противо-
§ 2. СЕЧЕНИЯ МНОГОГРАННИКОВ
369
положную вершину проведена плоскость под углом ф к
плоскости основания. Площадь сечення равна 5. Найти объем
призмы.
2.20. В треугольной прпзме ABOAtBiCi боковое ребро
равно /. В основании призмы лежит правильный треугольник со
стороной 6, а прямая, проходящая через вершину Bt н центр
основания ABC, перпендикулярна основаниям. Найтн площадь
сечення, проходящего через ребро ВС и середину ребра АА{.
2.21. Каждое ребро правильной шестиугольной призмы
равно 1. Найти площадь сечення, проходящего через сторону
основания н ббльшую диагональ призмы.
2.22. Боковое ребро прямой призмы равно а. В основании ее
лежпт прямоугольный треугольник, меньший нз углов которого
равен ос. Через меньший катет основания н середину
противолежащего бокового ребра проведено сечеяне, составляющее с
плоскостью основания угол р. Найтн площадь сечения.
2.23. Сечение, проведенное через сторону а основания
правильной треугольной призмы под углом а к нему, делит боковое
ребро на части в отношении т: п, считая от верхнего основания.
Определить объемы образовавшихся частей и площадь
сечения.
2.24. Основанием прямой призмы ABCAtBtCt служит
равнобедренный прямоугольный треугольник ABC с катетами АВ =
= ВСе= 1. Через середины ребер АВ и ВС и точку Р, лежащую
на продолжении ребра ВВ\ за точку В, проведена плоскость.
Найтн площадь полученного сечення, если ВР = 1/2 и SS|=1,
2.25. Дан прямоугольный параллелепипед ABCDAiBtCiDi с
площадью основания S и высотой ft. Через вершину А% верхнего
основания A\B\C\Di проведена секущая плоскость,
пересекающая боковое ребро ВВХ в точке Bt, боковое ребро GCt в точке
Ct и боковое ребро DDt в точке Z)j. Найти объем той части
параллелепипеда, которая расположена под секущей плоскостью,
если известно, что ССг =■= с.
2.26. Даиа прямая треугольная призма ABCAiBid (AAi,
BBi, CCi —боковые ребра), у которой АС = 6, AAt = 8. Через
вершнпу А проведена плоскость, пересекающая ребра BBt и CCi
соответственно в точках М и N. Найтн, в каком отношении делит
эта плоскость объем призмы, если известно, что ВМ = MBt, a
AN является биссектрисой угла CACt.
2.27. В прямоугольном параллелепипеде ABCDAiBtCtD%
(ABCD . и -i4,S,CiD| — основания, AAt \\ ВВ{ \\ СС, \\ DD,) даны
длины ребер: А В = a, AD — b, AAi = с. Пусть О — центр
основания ABGD, Oi — центр основания AtBtCiDi, a S—точка,
делящая отрезок OOt в отношении 1:3, т, е. Oi&^SO. = 1:3.
B70
ГЛ. 13. СТЕРЕОМЕТРИЯ
Найти площадь сечения данного параллелепипеда плоскостью,
проходящей через точку 5 параллельно диагонали
параллелепипеда ACi и диагонали его основания BD.
2.2S. Основанием прямоугольного параллелепипеда
ABCDAiBiCiDi является квадрат ABOD. Найтн наибольшую воз«
ыожную величину угла между прямой BDt и плоскостью BDCh
Пример 2.5. В правильной четырехугольной пирамиде через
сторону основания а проведена секущая плоскость, делящая
пополам двугранный угол а при
основании пирамиды. Найти площадь
сечения.
Решение. Пусть SABCD —
правильная четырехугольная пирами*
да с вершиной S (рнс, 13.8), а
плоскость сечения проходит через ребро
основания АВ. По условию задачи
данная пирамида правильная, и в
основании ее лежит квадрат
{AB^DC); следовательно, сторона
основания АВ параллельна плоскости
DSC. Плоскость сечеиня ABMN,
проходящая через прямую АВ, пересекает плоскость боковой грани
DSC по прямой, параллельной прямой АВ (MN\\AB).
Следовательно, четырехугольник ANMB — трапеция.
Построим вспомогательную секущую плоскость, проходящую
через середину ребра АВ (точку К), середину ребра DC
(точку L) и вершину пирамиды S. Плоскость KSL пересечет боковые
гранн пнрамнды по апофемам, причем SK-LAB, KLJ.AB, и,
следовательно, угол SRL — линейный угол двугранного угла о
ребром АВ, равный ос. По условию задачи §KR = RKL и эти
углы равны а/2.
Рассмотрим треугольник KSL, в котором SKL = SLK=a,
KL =» о, KR — биссектриса угла SKL. По теореме синусов
найдем боковую сторону равнобедренного треугольника KSL:
KS _u KL ' о KS^r a
sin a ^ sin (180° —2а) "= 2 cos а"
Найдем отрезки, на которое точка R разбивает сторону SL.
Обозначим SR => х. Тогда
„, а
2 cos a
§ 2. СЕЧЕНИЯ МНОГОГРАННИКОВ
871
По свойству биссектрисы
а
SR RL х 2 coS a
/CS " KL14 а ие а
2 cos а
— ^ SR = х =
а
2 cos а {2 cos а + I) '
Из треугольника /(S# по теореме синусов найдем длину
биссектрисы KRi
a sin a
KR =
. За
51П-г
Так как KR-LAB, то /(# является высотой трапеция ABNM,
у которой по условию известно основание АВ, равное а. Для
нахождения второго основания {MN) рассмотрим треугольник
DSC и подобный ему треугольник MSN (MN \\ DC). Так как
пирамида SABCD правильная, то апофема боковой грани SL
является высотой треугольника DSC, а отрезок апофемы SR — вы«
сотой треугольника MSN. В подобных треугольниках стороны
пропорциональны опущенным на них высотам:
MN DC MN a
SR SL
2 cos a (2 cos a + 1) 2 cos a
=> MN (2 cos a + 1) = а=»-ЛШ *=•
2 cos a + } *
Площадь трапеции ABNM равна
SABNM ^
^
От в
AB + MN
2
KR*
4a2 cos' -у
CT- (1+2
cos a)
«*т 2
2as(cos
2 (2 cos a
3»
cos a + 1 as
2 .
sin
a + 1) sin a
'•+ 1) «n-g-
in a
3a
T
4o8
(1 +
•,
cos* —
2
2 cos a)2'
2.29. Боковое ребро правильной треугольной пирамиды
равно а и наклонено к плоскости основания под углом а. Найти
площадь сечения пирамиды плоскостью, проходящей через
вершину основания и через среднюю линию противоположной
боковой грани, ., ,
372 ГЛ. 13. СТЕРЕОМЕТРИЯ
2.30. Дана правильная треугольная пирамида SABC; АВ =»'
= а, а двугранный угол, образованный смежными боковыми
гранями, равен а. Найти площадь сечення пирамиды плоскостью,
проходящей через вершину А я биссектрису угла SBA.
2.31. Дана правильная треугольная пирамида с длиной
бокового ребра а н плоским углом а при вершине. Найти площадь
сечения, проходящего через сторону основания АВ и
перпендикулярного боковому ребру SC.
2.32. Сторона основания правильной треугольной пирамиды'
равна а, боковое ребро равно Ь. Найти площадь сечения
пирамиды плоскостью, проходящей через центр основания н
параллельной двум непересекающимся ребрам пирамиды.
2.33. Дана правильная треугольная пирамида с боковым
ребром /. Через сторону основания и середину противолежащего
бокового ребра проведена плоскость, составляющая угол ос с
плоскостью основания. Найти площадь сечення.
2.34. В правильной треугольной пирамиде, сторона основания
которой равна а, а боковое ребро — 2а, через середину бокового,
ребра перпендпкулярно ему проведена плоскость. Определить
площадь сечення.
2.36. Боковое ребро правильной усеченной четырехугольной
пирамиды равно стороне меньшего основания и равно а. Угол
между боковым ребром и стороной большего основания
равен а. Найти площадь диагонального сечення усеченной
пирамиды.
2.36. Площадь сечення правильного тетраэдра имеет форму
квадрата и равна тг. Найти поверхность тетраэдра.
2.37. Правильная треугольная пирамида рассечена
плоскостью, перпендикулярной основанию н делящей две стороны
основания пополам. Определить объем отсеченной пирамиды,
если сторона основания исходной пирамиды равна а, а
двугранный угол прн основании равен 45°.
2.38. В правильной треугольной пирамиде SABC плоскость,
проходящая через сторону АС а перпендикулярная ребру SB,
отсекает пирамиду SiABC, объем которой в полтора раза
меньше объема пирамиды SABC. Найти площадь боковой
поверхности пирамиды SABC, если АС = а.
2.39. Прямая призма имеет основанием равносторонний тре«
угольник. Плоскость, проведенная через одну нз его сторон под
углом а к основанию, отсекает от призмы треугольную пирамиду
объемом v. Найти площадь сечення.
2.40. В треугольной пирамиде SABC на стороне АС взята
точка D так, что АС= ЪВС; па стороне ВС взята" точка £чтак,
что ВС « ЗСЕ. Найти' плбщадь сечения пирамиды плоскостью,
§ 2. СЕЧВНИЯ МНОГОГРАННИКОВ
373
проходящей через точки D и Б параллельно ребру SC, если
известно, что SA = SB, SC = а, АС =. ВС = Ь, АСЙ = а.
2.41. В треугольной усеченной пирамиде через сторону
верхнего основания проведена плоскость, параллельная
противоположному боковому ребру. В каком отношении эта плоскость'
делит объем пирамиды, если соответственные стороны оснований
относятся, как 1:2?
2.42. В треугольной пирамиде SABC все ребра равны. На
ребре SA взята такая точка М, что SM = МА; на ребре SB —
такая точка ЛГ, что SN^-^ SB. Через точки М н ЛГ проведена
плоскость, параллельная медиане AD основания ABC. Найти
отношение объема пирамиды, отсекаемой от исходной проведенной
плоскостью, к объему пирамиды SABC.
2.43. В правильную треугольную пирамиду с плоским
углом а при вершине вписана правильная треугольная призма так,
что нижнее основание призмы лежит на основании пирамиды,
а верхнее основание совпадает с сечением пнрамнды плоскостью,
проходящей через верхнее основание призмы. Длина бокового
ребра призмы равна длине стороны основания призмы. Найти
отношение объемов призмы и пнрамнды.
2.44. Угол между боковым ребром и плоскостью основания
правильной треугольной пнрамнды SABC равен 60°. Через
точку А проведена плоскость, перпендикулярная биссектрисе угла S
треугольника BSC. В каком отношении линия пересечения этой
плоскости с плоскостью BSC делнт площадь грани BSC?
2.45. Дана правильная треугольная пирамида SABC. На
продолжении ребра АВ взята точка М так, что
АМ = АВ(МВ = ЫВ).
На ребре SB взята точка N так, что SN = NB. Где на апофеме
SD грани SBC должна находиться точка Р для того, чтобы в
сеченнн пнрамнды плоскостью, проведенной через точки М, N н
Р, получался треугольник?
2.48. Плоскость пересекает боковые ребра SA, SB н SC
треугольной пирамиды SABC в точках К, L. и М соответственно.
В каком отношении делнт эта плоскость объем пнрамнды, если
известно, что
SK:KA — SL:LB = 2,
а медиана SN треугольника SBC делится этой плоскостью
пополам?
2.47. В правильной четырехугольной пирамиде SABCD через
середины сторон основания АВ и AD проведена плоскость, па-
874 ГЛ. 13. СТЕРЕОМЕТРИЯ
раллельная боковому ребру SA. Найтн площадь сечения, зная
сторону основания а и боковое ребро Ь.
2.48. Дана правильная четырехугольная пирамида с боковым
ребром I. Плоскость сечения проходит через диагональ
основания н середину бокового ребра и составляет с плоскостью
основания угол а. Найти площадь сечения.
2.49. В правильной четырехугольной пирамиде SABCD
сторона основания равна 4. Через сторону CD основания проведено
сечение, которое пересекает грань SAB по средней линин
треугольника, SAB. Площадь сечения ра'вна 18. Найти объем
пирамиды SABCD.
2.50. В правильной четырехугольной пирамиде SABCD
плоскость, проведенная через сторону AD перпендикулярно грани
SBC, делит эту грань на две равновеликие части. Найти площадь
полной поверхности пирамиды, если AD = а.
2.51. Высота правильной четырехугольной пирамиды
составляет с боковой гранью угол 30°. Через сторону основания
пирамиды проведена плоскость, перпендикулярная противолежащей
грани. Найтп отношение объемов многогранников, полученных
при пересечении пирамиды этой плоскостью.
2.52. Дана правильная четырехугольная пирамида SABCD о
вершиной S. Через середины ребер АВ, AD и CS проведена
плоскость. В каком отношении эта плоскость делит объем
пирамиды?
2.63. Площадь боковой грани правильной шестиугольной
пирамиды равна S. Вычислить площадь сечения, проходящего через
середину высоты пирамиды параллельно боковой грани.
§ 8. Фигуры вращения
Ц н л и в д р. Прямым круговым цилиндром (плн просто
цилиндром) называется фигура, полученная при вращении прямоугольника
вокруг оси, проходящей через одну из его сторон. При вращении
вокруг той же осн ломапоЛ, составленной нз сторон прямоугольника,
не лежащих на осн вращения, получается фигура, которая
называется поверхностью цилиндра. Круги, полученные в результате
вращения сторон, смежных со стороной, принадлежащей осн вращения,
называются основаниями цилиндра. Рвднус этпх двух равных кругов
навивается радиусом основания цилиндра.
Фигура, полученная в результате вращения сторопьГ
прямоугольника, яе смежной со стороной, принадлежащей оси вращения,
называется боковой поверхностью цилиндра. Перпендикуляр к плоскостям
оснований цилиндра, концы которого совпадают с центрами оснований
Цилиндра, называется высотой цилиндра.
Объем цилиндра вычисляется по формуле
Площадь боковой н полной поверхности цилиндра вычисляется по
формулам
5бок=2п*Н.
где R — радиус основания, И — высота цилиндра.
§ 3. ФИГУРЫ ВРАЩЕНИЯ 375
Конус. Прямым круговым конусом (или просто конусом) назы»
пается фигура, полученная при вращении прямоугольного треугольника
вокруг оси, содержащей его катет. Фигура, полученная при вращении
вокруг той же оси ломаной, составленной из гипотенузы и катета, не
принадлежащего оси вращения, называется поверхностью конуса. Фи<
гура, полученная при вращеиин гипотенузы, называется боковой по*
верхностью конуса, а круг, полученный от вращения катета, — основа'
иием конуса. Радиус этого круга называется радиусом основания
конуса.
Катет треугольника, принадлежащий оси вращання, называется
высотой конуса, гипотенуза прямоугольного треугольника — образующей
ионусв.
Объем конуса вычисляется по формуле
Площадь боковой поверхности конуса вычисляется по формуле
^бок^"**"
где R — раднус основания, Я—высота, L — образующая конуса, "
Усеченный к о в у с. Часть конуса, ограниченная его
основанием н сечением, параллельным плоскости основания, называется усе*
ценным конусом. Основания усеченного конуса —гомотетичные круги с
центром гомотетии в вершине копусв.
Усеченный конус можно получить в результате вращения равней
бедренной трапеции апкруг ее оси симметрии.
Боковая сторона трапеции называется образующей усеченного ко-
нусо; круги, полученные при вращении оснований трапеции. —
основаниями усеченного конуса.
Объем усеченного конуса вычисляется по формуле
V~>jitH (Ri + i?,R2 + 4).
где И —высота, Ri н Яз — радиусы верхнего в нижнего оснований усе-
ченного конуса.
Площадь боковой поверхности усеченного конуса вычисляется по
формуле
S60K = It(«1 + "2)i-
где L — образующая усеченного конуса.
Шар. Множество всех точек пространства, находящихся на
Данном положительном расстоянии R от данной точки пространства О,
называется сферой, данная точка О.. называется' центром аферьь
Сферу также можно определить как фигуру, полученную н-
результате вращения полуокружности вокруг оси, содержащей диаметр
полуокружности. Отрезок ОМ (М — произвольная точка сферы)
называется радиусом сферы. Отрезок, соединяющий любые две точки сферы
а проходящий через ее цептр, называется диаметром сферы. Диаметр
сферы равен ее удвоенному радиусу.
Множество всех точек пространства, находящихся от данной точ<
Kii О на расстоянии, не большем данного расстояния R, называется
шаром. Шар также можно определить как фигуру, полученную в
результате вращения полукруга вокруг осн. содержащей диаметр
полукруга.
Объем шора радиуса R вычисляется по формуле
V=±nR>.
Площадь сферы радиуса R вычисляется по формуле
Сечевне шара плоскостью, проходящей через центр шара,
называется большим кругом. Касательной плоскостью к сфере (шару)
навивается плоскость, имеющая со сферой единственную общую точку.
Эту точку пвзывадрт точкой касания сферы н плоскости.- Для того
чтобы плоскость была касательной к сфере, необходимо в достаточно,
876
' ГЛ. 13. СТЕРЕОМЕТРИЯ
чтобы эта плоскость была перпендикулярна радиусу сферы н прохоа
днла через его конец.
Прямая, принадлежащая касательной плоскости к сфере н прохси
ДяЩан через точку квсвпня, называется прямой, касательной к сфере
(шару •)).
Пример 3.1. В цилиндре точка М, лежащая на
окружности нижнего основания, н точка N, лежащая на окружности
верхнего основания, соединены отрезком, проходящим через
середину высоты цилиндра. Найти объем цилиндра, если длина
отрезка MN равна а, а угол наклона прямой MN к плоскости-
основания цилиндра равен ос.
Решение. Пусть 00\ — высота цилиндра (рнс. 13.9), К —
точка пересечения высоты цилиндра н отрезка MN, причем по
условию задачи ОК = КОь Рассмотрим треугольники KON и
KOiM. Эти треугольники прямоугольные (КО Л- ON и KOi JL'
J-OiM), углы OKN и OtKM вертикальные, и ОК = КОс,
следовательно, эти треугольники равны (по стороне н двум углам).
Из равенства треугольников следует, что КО\ = ОК', КМ «|
= kn = \mn = ^.
Раднус MOi осиованнй цилиндра является проекцией
отрезка МК, а угол KMOi — угол между прямой MN и плоскостью
основания цилиндра — по условию задачи равен а. Из
прямоугольного треугольника MKOi находим
ЛЮ,=-2-соза, KOi=-2-slna = -°yi-.
Вычислим объем цилиндра;
Viiwi = SocHtf =*P {MOt)2 -OOi= -22- cos» a sin a.
^ яа3 , i
Ответ. —;—sin a cos* a.
4
Пример З.2. Угол при вершине осевого сечення прямого
кругового конуса равен а. Через его вершину под углом р
(Р < ос/2) к оси конуса проведена плоскость. Найти угол между
двумя образующими конуса, по которым проведенная плоскость
пересекает его поверхность.
Решение. Пусть SO — высота конуса, MSN — секущая
плоскость, образующая с высотой SO угол р, MN — хорда
окружности основания (рис. 13.10). Так как по условию задачи
угол прн вершине осевого сечення конуса равен ос, то угол
между любой образующей конуса (в частности, образующими SM
•) Ивогда (когда не возникает путаницы) будет употребляться каа
сввонвд сферыл
§ 3. ФИГУРЫ ВРАЩЕНИЯ
377
и SN) и высотой конуса равен а/2. Рассмотрим прямоугольный
треугольник MSO (угол MOS прямой). Обозначая радиус осно-.
вання конуса через г, получаем
SM = —-—, SO = rctg-£-.
Построим угол между плоскостью SMN и высотой SO. Для
втого в плоскости основания конуса из точки О на хорду MN
опустим перпендикуляр ОК. По свойству хорды МК = NK.
Прямая MN перпендикулярна высоте конуса SO и прямой ОК
н, следовательно, перпендикулярна плоскости треугольника KSO.
Рнс. 13.9
Плоскость MSN проходит через перпендикуляр MN к плоскости
KSO. Следовательно, плоскости треугольников KSN и KSO
взаимно перпендикулярны, а луч SK является ортогональной
проекцией луча SO на плоскость MSN. Так как по определению углом
между наклонной (SO) н плоскостью (MSN) называется угол
между наклонной н ее ортогональной проекцией на плоскость,
то угол KSO я есть угол, величина которого равна (?. Из
прямоугольного треугольника KSO получаем
sk so "**?
ОД = 5" е=^ 3—»
cos р cos р
Как было указано выше, KOA.MN н SOA.MN, н,
следовательно, по теореме о трех перпендикулярах SKJ-MN.
Треугольник MSN равнобедренный (MS = NS), и SK — высота,
медиана н биссектриса этого треугольника, Из прямоугольного
Рнс. 13.11)
«78
ГЛ. 13. СТЕРЕОМЕТРИЯ
треугольника MSK находим угол MSK:
а а
cos (MSK) =#=-—4 W-^
cos В r
slnT
arc cos \
MSN = 2MSK = 2 arccos
4 cos В /'
V cos В J'
(cost)
\ cos В /*
Ответ. 2 arccos '. _
—■;B
3.1. Боковая поверхность цилиндра, будучи развернута,
представляет собой прямоугольник, в котором диагональ равна d
и составляет угол а с основанием. Определить объем цилиндра.
3.2. Площадь сечения цилиндра плоскостью,
перпендикулярной образующей, равна slt а площадь осевого сечення равна зд.
Найтп площадь боковой поверхности и объем цилиндра.
3.3. Радиус основания конуса равен г, а угол при вершине
в развертке его боковой поверхности равен 90°. Найтп объем
конуса.
3.4. Боковой поверхностью конуса служит свернутая
четверть круга. Определить, полную поверхность конуса, если
площадь его осевого сечення равна S.
3.5. Площадь боковой поверхности прямого кругового ко'
иуса равна 5; расстояние от центра основания до образующей
равно г. Найтн объем конуса.
З.в. Площадь боковой поверхности конуса относится к
площади основания, как 2: 1. Площадь его осевого сечення равиа S.
Найти объем конуса.
3.7. Радиус основания конуса равен г, а площадь боковой
поверхности равна сумме площадей основания и осевого
сечення. Найти объем конуса.
3.8. Высота конуса равна диаметру его основания. Найти
отношение площади его основания к площади боковой поверхности.
3.9. Плоскость, проведенная через вершину конуса,
пересекает основание по хорде, длина которой равна радиусу основа*
вня. Найтн отношение объемов образовавшихся частей конуса:
3.10. Две перпендикулярные образующие прямого кругового
§ 3. ФИГУРЫ ВРАЩЕНИЯ 879
копуса делят окружность основания в отношении 1 :2. Найтн
объем конуса, если его высота равна Л.
3.11. Через две образующие конуса, угол между которыми
равен а, проведена плоскость. Найтн отношение площади
сечения к -полной поверхности конуса, если угол между образующей
конуса н плоскостью основания равен р\
3.12. Образующая конуса равна I и составляет угол Р с
высотой конуса. Найти площадь сечеиия этого конуса плоскостью,
проходящей через его вершину и составляющей угол а с его
высотой.
3.13. Через вершину кояуса проведены две плоскости. Одна
нз них наклонена к плоскости основания конуса под углом а и
пересекает основание по хорде длиной а, а другая наклонена
к плоскости основания под углом f) и пересекает основание по
хорде длиной Ь. Найтн объем конуса.
3.14. Площади параллельных сечений шара, расположенных
по одну сторону от центра, равны S, и Sz, а расстояние между
этими сечениями равно d. Найтн площадь сечения шара,
параллельного сечениям S, и S2 н делящего пополам расстояние
между ними.
3.15. В двугранный угол 60° вписан шар радиуса R. Найти
радиус шара, вписанного в тот же угол н касающегося данного
шара, если известно, что прямая, соединяющая центры обоих
шаров, образует с ребром двугранного угла угол 45°.
3.16. Две равные сферы радиуса г касаются друг друга и
граней двугранного угла, величина которого равна а. Найти
радиус сферы, которая касается граней двугранного угла и обеих
данных сфер.
3.17. Четыре равных шара радиуса г внешним образом
касаются друг друга так, что каждый касается трех остальных.
Найти радиус сферы, касающейся всех четырех шаров и
содержащей их внутри себя.
3.18. Два шара касаются плоскости Р в точках А и В н
расположены по разные стороны от этой плоскости. Расстояние
между центрами этих шаров равно 10. Третий шар касается
двуя данных шаров, а его центр О лежит в плоскости Р. Из-
оестно, что
АО = ОВ = 2л[Ш, АВ = 8.
Найтн радиус третьего шара.
3.19. Три шара касаются плоскости треугольника ABC в его
вершинах, и каждый шар касается двух других. Найтн радиусы
шаров, если длина стороны АВ равна с и прилежащие и ней
углы равны аир.
w
ГЛ. 13. СТЕРЕОМЕТРИЯ .
3.20. На плоскости лежат, пе пересекаясь, два шара
радиусов г и Д. Расстояние между центрами шаров равно р. Найти
Минимально возможный радиус шара, который лежал бы на этой
плоскости н касался заданных шаров.
§ 4. Комбинации многогранников
и фигур вращения
Призма и шар. Шар, касающийся всех граней призмы,
Называется вписанным в призму. Призма называется вписанной
в шар, если все вершины призмы лежат на поверхности шара.
В задачах на комбинацию призмы (в частности,
параллелепипеда н куба) и шара решение, как правило, необходимо начать
с геометрического построения, показывающего, где находится
центр шара. При нахождении центра шара, вписанного в призму,
используется теорема о том, что центр шара, вписанного в
призму, является точкой пересечения бнссекторных плоскостей
всех двугранных углов призмы, а центр шара, описанного около
д призмы, является точкой
пересечения всех плоскостей,
проходящих через середину ребер призмы
н перпендикулярных нм.
Пример 4.1. Три шара
радиуса г касаются нижнего осиог
вапня правильной треугольной
призмы,, причем каждый шар
касается двух других шаров и двух
боковых граней призмы.
Четвертый шар касается каждого из
втих трех шаров, всех боковых
граней н верхнего основания
призмы. Найти высоту призмы.
Решение. Пусть 0\, 02,
Оъ — центры шаров радиуса г,
ABC н AiBiCi — равносторонние треугольники, являющиеся
соответственно верхним н нижним основаниями призмы (рис. 13.11).
Так как призма ABCAiBiCi правильная, то ее боковые ребра
AAi, BBU CCi перпендикулярны плоскостям оснований и
плоскости боковых граней также перпендикулярны плоскостям,
оснований.
Через центр шара Oi проведем плоскость, параллельную
плоскости основания призмы. В сеченнн призмы этой плоскостью
получится ранносторонпнй треугольник MiNiPi со ,стороной,
равной стороне основания призмы,.Построенная плосддсть будет
§4. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 881
перпендикулярна плоскостям боковых граней призмы, а точкн
Ог н Оъ будут принадлежать этой плоскости.
Докажем, что точкн касания шарами плоскостей боковых
граней будут также принадлежать плоскости треугольника
MiNiPt. Из точкн Oi опустим перпендикуляр иа плоскость
AiACCi. Так как шар касается этой плоскости, то этот
перпендикуляр попадает в точку касания, и его длина равна т. С другой
стороны, так как плоскости MiNiPi n AtACCt взаимно
перпендикулярны, а точка Oi принадлежит плоскости MtNtPi, то
перпендикуляр, опущенный из точки Oi па плоскость AiACCi, будет
целиком принадлежать плоскости MiNiPi, н, следовательно,
основание перпендикуляра (на рис. 13.12 точка К) будет
принадлежать линии пересечения этих взаимно перпендикулярных
плоскостей (см. теорему о взаимно перпендикулярных
плоскостях).
Аналогично доказывается, что точка касания шара с
центром Oi и плоскости AiABBi также принадлежат плоскости
MiNiPi н точкн касания шаров с центрами Оз и Os и
плоскостей боковых граней принадлежат плоскости MtNiPi. Так как
плоскость AI|JV|Pi проходит через центры
всех трех попарно касающихся шаров,
то линии центров этих шаров
(отрезки 0|Ог, Ог03) 0,Ов) будет
принадлежать плоскости M\NiP]. Таким образом,
в сечении призмы плоскостью M[N\Pi
получится равносторонний треугольник зд*/\
'MiN{P], в который вложены три
окружности радиуса г, каждая из которых
касается двух других окружностей и рнс. I3.I2
двух сторон треугольника (рис. 13.12).
Рассмотрим треугольник MiNiPi. Проведем радиусы О,К и
OjL в точки касания окружностей со стороной MtPt. Так как
OiK±MiPu OsLJ_AliP, и OiK = 0%L = г, то четырехугольник
ОiOsKL — прямоугольник и KL = Ot03 = 2г. Так как
окружность с центром 0| касается сторон треугольника MiNt и MiPt,
то точка 0\ лежит па биссектрисе угла NiM\Pi н
В прямоугольном треугольнике М\0\К известны yroflOiAl/C = 30'>
и катет OiK = г. Находим второй катет:
М,/С=1гл/3~.
Аналогично на Д ЮЪР\ находим LPi = r*Jz. Таким образом,
сторона треугольника M\N\Pi равна 2л(1'+Уз~). ;. ■ '.:'•,
882
ГЛ. 13. СТЕРЕОМЕТРИЯ
Через центр О четвертого шара проведем плоскость,
параллельную плоскости основания призмы. В сечепвн призмы этой
плоскостью получится равносторонний треугольник MNP
(рнс. 13.13), а в сечеинн шара с центром О получится
окружность большого диаметра, вписанная в треугольник Л1ЛГР (точки
касания шара с центром О с плоскостями боковых граней
принадлежат плоскости MNP, что доказывается так же, как и в
случае построения сечения Л1|ЛГ|Р|). Так
как плоскости треугольников М|ЛГ|Р] и
MNP параллельны, то треугольники
AijJViP, и MNP равны, и,
следовательно, сторона треугольника MNP равна
2г (I-{-V3 )• Радиус окружности,
вписанной в треугольник MNP, а
следовательно, и радиус шара с центром О
равны г
(■+#)■
Искомая высота призмы складывается нз расстояния от
верхнего основания до плоскости MNP, расстояния между
плоскостями MNP и MtNiPi н расстояния от плоскости MiNiPi до
нижнего основания призмы. По условию задачи шар с центром. О
касается верхнего основания призмы, и расстояние It между
верхним основанием и плоскостью MNP, содержащей точку О,
равно радиусу шара с центром в точке О:
h-r 1 +
#)■
Также по условию задачи трн шара (с центрами Ои Оц, Qjjj
лежат на нижнем основании призмы, и расстояние 1% между
нижним основанием и плоскостью M\NiP%, содержащей точки
Oi, Ог, Оз, равно радиусам этих шаров:
Осталось найтн расстояние между плоскостями MNP и
Af,JV,P(. Рассмотрим многогранник с вершинами О, О,, О», Ог.
Этот многогранник — пирамида, в основапнп которой лежит
равносторонний треугольник OiOsO» со стороной 2г. Боковые реб^'а
00|, ООг, ООц равны между собой (так как все шары попарно
касаются) и равныг12Н —J. Проведем высоту ОК
правильной треугольной пирамиды 00{ОгОъ (рнс. 13.11). Отрезок ОК
перпендикулярен плоскости MiNiPi а параллельной ей плоскости
MNP, и, следовательно, длина этого отрезка есть расстояние
между плоскостями. Так как в правильной треугольной пирамиде
§ 4. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 883
основание высоты совпадает с центром основания, то OiK =■»
= 2г/У§*. Из прямоугольного треугольника OiOK по теореме
Пифагора находим
0«:= V(00,)2 —(0,/С)а =-д-гл/27+12Уз~.
Высота призмы:
# = /, + /2-f Otf = i-r (6-fV3"-f л/27Ч- 12 V5").
Ответ. -^-г(б + Уз~ +л/27+12Уз").
4.1. В основании правильной прпзмы лежит квадрат со
стороной а, а ее высота равна Н. Найтн радиус описанного шара,
4.2. Около шара описана правильная треугольная призма и
около нее опнсан шар. Найтн отношение поверхностей этих
Шаров.
4.3. Около шара радиуса R описана правильная
шестиугольная призма. Найти площадь ее поверхности.
4.4. Сфера касается боковых ребер правильной прямой
шестиугольной призмы, основание которой лежит вне сферы. Найтн
отношение площади боковой поверхпостп прпзмы, заключенной
внутри сферы, к площади поверхности сферы, находящейся вне
призмы.
4.5. В куб с ребром а вписан шар. Определить радиус
другого шара, касающегося трех граней куба и первого шара.
4.6. В полусферу радиуса R вписан куб так, что четыре его
вершины лежат на основании полусферы, а остальные четыре
принадлежат сферической поверхности полушара. Вычислить
объем куба.
4.7. Дан куб с основаниями ABCD и Л]В]С]£>|,\ где
AAi II ВВ1II 001. В угол А куба вписан шар радиуса R = 1/2.
Найтн раднус шара, вписанного в угол С и касающегося
данного шара, при условии, что ребро куба равно 3/2.
4.8. Дан куб с основаниями ABCD и AiBi&Di. Точка Я—■
середина ребра C\D\, точка F—середина ребра BiC,. Найтн
раднус сферы, проходящей через точки Е, F, А, С, если ребро
куба равно а.
Пирамида и шар. Шар называется вписанным в
пирамиду, если он касается всех граней пирамиды. Центр шара,
вписанного в пирамиду, является точкой пересечения бпссекторных
плоскостей всех двугранных углов пирамиды.
Шар называется описанным около пирамиды, если все
вершины пирамиды лежат на его поверхности. Если около пирами**
884
ГЛ. 13. СТЕРЕОМЕТРИЯ
ды описан шар, то его центр является точкой пересечения всех
плоскостей, проведенных через середины ребер ппрамнды
перпендикулярно этим ребрам.
В задачах на комбинацию пирамиды п шара решение, как
правило, необходимо начинать с геометрического построения, в
результате которого находится точка, являющаяся центром шара.
Кроме того, часто бывает удобно построить вспомогательное
сечение пирамиды и шара, разбивающее комбинацию ппрамнды и
шара на две симметричные части, в результате чего решение
стереометрической задачи иногда может быть сведено к решению
планиметрической задачи (такой метод использован в приме-
ре 4.3).
Пример 4.2. В основании пирамиды лежит равносторонний
треугольник со стороной а. Высота пирамиды проходит через
середину одного пз ребер основания
и равна За/2. Найти радиус шара,
описанного около пирамиды.
Решение. Пусть S — вершина
пирамиды, ABC — равносторонний
треугольник, лежащий в основании
пирамиды (рис. 13.14), SK — высота
пирамиды (а также высота
треугольника AS В) и по условию
задачи АК = КВ. Треугольники ASK и
BSK равны (оба прямоугольные,
SK — общая сторона, и АК=КВ),
и, следовательно, треугольник ASB
равнобедренный. По определению
пирамида вписана в шар,- если
все вершины пирамиды принадлежат поверхности шара н .центр
шара — точка, равноудаленная от всех вершин пирамиды.
Найдем геометрическое место точек, равноудаленных от всех вершин
пирамиды.
Геометрическое место точек, равноудаленных от трех вершин
A, В и С, — перпендикуляр OtM к плоскости разностороннего
треугольника ABC, восставленный нз его центра Ot (рнс. 13.14).
Геометрическое место точек, равноудаленных от вершин A, S,
B, — перпендикуляр OzN к плоскости равнобедренного
треугольника ASB, восставленный из точки Оз, являющейся центром
окружности, описанной около треугольника ASB.
Докажем, что два перпендикуляра OiM и OiN пересекаются
'По условию аадачн отрезок SK перпендикулярен плоскости
треугольника А В С, SKJLAB, К— середина отрезка АВ, и,
следовательно, АТС —высота,-меднаиа. н .биссектриса равностороннего
Рис. 13.14
§ i. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 385
треугольника ABC (KCJLAB). Таким образом, отрезок АВ
перпендикулярен двум различным прямым SK и КС н,
следовательно, перпендикулярен плоскости, проходящей через точки S, К
и С (см. теорему о взаимно перпендикулярных прямых п
плоскостях). Плоскости ASB и ABC перпендикулярны плоскости SKC,
так как каждая нз них содержит прямую АВ, перпендикулярную
плоскости SKC
Точка Oi принадлежит линии пересечения плоскостей АВО и
SKC, а точка О» — линии пересечения плоскостей A SB и SKC
Перпендикуляр- OtM к плоскости ABC будет целиком
принадлежать плоскости SKC, а перпендикуляр OzN к плоскости ASB
также будет принадлежать плоскости SKC (по теореме о двух
взаимно перпендикулярных плоскостях н перпендикуляре к одной
нз плоскостей, проходящем через лнннн нх пересечения).
Таким образом, доказано, что прямые OiM и OiN
принадлежат одной плоскости, пересекаются в точке О н четырехугольник
КОгООу, все вершины которого принадлежат плоскости SKC, —
прямоугольник. Точка О — точка, равноудаленная от точек А,
В, С, S, — является центром шара, описанного около пнрамндьц
Радиус окружности, описанной около треугольника ASB, равен
Ба/6, и OtK^SK-S02=~^--^-=>~. В равностороннем
.треугольнике ABC расстояние от центра Ох до вершины С равно
0,С = ^-КС = ^-^-. Так как ОгК=0{0 (/С0200, —
прямоугольник), то из прямоугольного треугольника 00\С по теореме
Пифагора находим длину отрезка ОС, которая равна искомому
радиусу шара:
Ответ. —я—,
4.9. В шар радиуса R вписан правильный тетраэдр. Найти
объем тетраэдра.
4.10. Основание пирамиды — правильный треугольник со
стороной 6 см. Одно из боковых ребер перпендикулярно плоскости
Основания и равно 4 см. Найти радиус шара, описанного вокруг
рнрамнды.
4.11. Сторона основания правильной треугольной пирамиды
равна а, плоский угол при вершине пирамиды равен а. Найти
радиус вписанного в пирамиду шара.
4.12. Боковые ребра н две стороны основания
треугольной пнрампды равны а, а .угол между равными сторонами
13 А. Г, Цыпкяя, А, Иг ПыыскпВ
386
ГЛ. 13. СТЕРЕОМЕТРИЯ
основания равен а. Найти радиус шара, описанного около
пирамиды.
4.13. Ребро правильного тетраэдра равно а. Определить
раднус шара, касающегося боковых ребер тетраэдра в вершинах
основания.
4.14. Ребро правильного тетраэдра равно а. Найти раднус
шара, касающегося боковых граней тетраэдра в точках, лежащих
па сторонах основания.
4.15. Найти раднус шара, касающегося основания п
боковых ребер правильной треугольной пирамиды, у которой сторона
основания равна а, а двугранный угол при основании равен а,
4.16. Грани правильной усеченной треугольной пирамиды
касаются шара. Найти отношение поверхности шара к полной
поверхности пирамиды, если боковые грани пирамиды наклонены
к плоскости основания под углом а.
4.17. В данную правильную усеченную треугольную
пирамиду можно поместить сферу, касающуюся всех граней, и сферу,
касающуюся всех ребер. Найтн стороны основания пирамиды,
если боковые ребра равны Ь.
4.18. Ребро правильного тетраэдра равно а. Определить
радиус шара, поверхность которого касается всех ребер тетраэдра.
4.19. Сторона основания правильной треугольной пирамиды
равна а, боковое ребро равно Ь. Найти раднус сферы,
касающейся всех ребер пирамиды.
4.20. В правильную треугольную пирамиду с плоским
углом Р при вершине вписан шар. Найтн отиошеине объемов шара
н пирамиды.
4.21. Ребро правильного тетраэдра SABC равно а. Найтн
радиус сферы, вписанной в трехгранный угол, образованный
гранями тетраэдра с вершиной в точке S, и касающейся плоскости,
проведенной через середины ребер SA, SC и АВ.
4.22. В правильную треугольную пирамиду вписан шар.
Определить угол наклона боковой грани пирамиды к плоскости
основания, зная, что отношение объема пирамиды к объему шара
равно 27 V3"/(4ji).
4.23. В правильной треугольной пирамиде угол между
боковыми ребрами н высотой, опущенной на основание, равен ос.
Найтн отношение объема пирамиды к объему описанного
шара.
4.24. В правильной треугольной пирамиде двугранный угол
между плоскостью основания и боковой гранью равен ос Найти
отиошеине объема вписанного в пирамиду шара к объему
пирамиды, :
§ 4, КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 387
4.25. В шар радиуса R вписана правильная треугольная
пирамида SABC, у которой двугранный угол при основании
равен ос. Найтн сторону основания пирамиды.
4.26. Внутри правильного тетраэдра с ребром а расположены
четыре равные сферы так, что каждая касается трех других сфер
и трех граней тетраэдра. Найти радиус этих сфер.
4.27. В тетраэдре SABC двугранные углы при ребрах АВ,
'АС н SB прямые, а величины двугранных углов при ребрах SA
и ВС равны 15°, Найтн раднус шара, вписанного в тетраэдр,
если ВС = 2.
4.28. Через сторону основания правильной треугольной
пирамиды и центр вписанного в нее шара проведена плоскость.
В каком отношении эта плоскость делит объем пирамиды, если
ее боковое ребро в 3,5 раза больше стороны основания?
4.29. В правильной треугольной пирамиде SABC сторона
основания ABC равна Ь, а высота пирамиды равна Ь л/2, Сфера,
вписанная в пирамиду, касается SBC в точке К. Найтн площадь
сечения пирамиды плоскостью, проходящей через точку К н
ребро SA.
4.30. В основании пирамиды лежит равносторонний
треугольник со стороной а. Одно из боковых ребер пирамиды также
равно а, а два других равны Ь. Найти раднус сферы, описанной
Около пирамиды.
4.31. Основанием пирамиды служит равнобедренный
треугольник, равные стороны которого имеют длину 6;
соответствующие им боковые грани перпендикулярны плоскости
основания, н угол между ними равен а. Угол между третьей боковой
гранью и плоскостью основания также равен а. Найтн радиус
шара, вписанного в пирамиду.
4.32. На основании правильной треугольной пирамиды с
высотой Н и радиусом круга, вписанного в основание, равным г,
лежит шар, касающийся основания в его центре. Найти радиус
шара, если плоскость, проведенная через вершину пирамиды и
середины двух сторон основания, касается этого шара.
4.33. В треугольной пирамиде SABC грань SAC
перпендикулярна грани ABC, SA = SC = 1, а угол нрп вершине В
треугольника ABC прямой. Шар касается плоскости основания
пирамиды в точке В, а грани SAC — в точке S. Найтн радиус
шара.
4.34. В правильную треугольную пирамиду с длиной ребра
основания а и двуграиным углом при основании, равным 60°,
вложены три одинаковых шара так, что каждый шар касается
двух других, плоскости основания и двух боковых граней, Найтн
радиусы этих шаров.
13*
868
ГЛ. 13. СТЕРЕОМЕТРИЯ
4.35. В правильную треугольную пирамиду помещен шар
радиуса 1. В точке, делящей пополам высоту пирамиды, он
касается внешним образом полушара. Полушар опирается на круг,
вписанный в основание пирамиды; шар касается боковых граней
пнрамнды. Найти площадь боковой поверхности пирамиды и
величину двугранного угла, образованного боковыми гранями
пирамиды.
4.36. Правильный треугольник со стороной а лежит в
плоскости Р. Средними линиями он разделен па 4 треугольника,,и
на трех из них, примыкающих к вершинам, построены как на
основаниях три правильные треугольные пирамиды с высотой а
(все трн — по* одну сторону плоскости Р). Найтв радиус шара,
лежащего между пирамидами и касающегося как плоскости Р,
так н всех трех пирамид.
Пример 4.3. В правильную четырехугольную пирамиду
вписан шар. Расстояние от центра шара до вершины пнрамнды
равно а, а угол наклона боковой граня к
плоскости основания равен ос. Найти
объем пирамиды.
Решение. Пусть SABCD (рис,
13.15) —правильная четырехугольная пн-
рамнда (ABCD — квадрат, SK—высота
пнрамнды, К — центр квадрата,
боковые грани — равные равнобедренные
треугольники). Найдем точку О — центр
вписанного в пирамиду шара.
Из вершины А треугольника AS В
Рис. is.15 •* проведем высоту к основанию SB. Из
вершины С треугольника BSC проведем
высоту к основанию SB. Так как треугольники ASB и BSC
равны, то основаниями высот будет одна и та же точка М и
AM = МС. Угол АМС по построению будет линейным углом
двугранного угла, образованного плоскостями боковых граней
ASB и BSC. В треугольнике АМС биссектриса угла АМС будет
медианой н высотой и пересечет основание АС в точке /(.
В нашем случае точка S принадлежит ребру двугранного
угла, а точка К — биссектрисе линейного угла и, следовательно,
высота пнрамнды SK принадлежит бнссекторной плоскости
двугранного угла с ребром SB. Построив бнссекторную плоскость
двугранного угла с ребром SC, аналогичным образом можно
доказать, что высота SK будет принадлежать и этой
бнссекторной плоскости. Так как две различные плоскости пересекаются
по одной прямой, а прямая SK принадлежит и той и другой
§ 4. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 389
плоскости, то лнння пересечения двух различных бнссекторных
плоскостей будет содержать высоту пирамиды SK. Центр шара,
вписанного в пирамиду, лежит на пересечении биссекториых
плоскостей всех двугранных углов пирамиды и, следовательно, в на-
шеМ случае (когда пирамида правильная) — на высоте
пирамиды.
Проведем плоскость через высоту пирамиды SK и середины
противоположных сторон квадрата L, Р (рнс 13.16). Так как
треугольник' DSC равнобед ениый,
то1 SP— медиана "и высота
треугольника DSC и SPJ.DC. Отрезок LP
также перпендикулярен DC, и,
следовательно, угол LPS — линейный
угол двугранного угла, образованного
боковой гранью DSC п плоскостью
основания ABCD, который по
условию равен ос. Аналогично можно
доказать, что SLP = ос. Центр шара,
вписанного в пирамиду, лежит в
бнссекторной плоскости двугранного
угла с ребром DC. Точка пересечення этой плоскости с высо«
той SK и есть центр вписанного в пирамиду шара (точка О
па рис. 13.16).
Плоскости DSC и ABCD перпендикулярны плоскости LSP,
Так как оин содержат прямую DC, перпендикулярную плоскости
I.SP. Из точки О, принадлежащей плоскости LSP, опустим
перпендикуляр на плоскость DSC. Основание этого перпендикуляра
(точка N) совпадает с точкой касания шара и плоскости DSC*
С другой стороны, по теореме о двух взаимно
перпендикулярных плоскостях (DSC и LSP) а перпендикуляре к одной из
плоскостей прямая ON будет целиком принадлежать плоскости
LSP. Таким образом, доказано, что точка касания шара с
плоскостью боковой грани DSC принадлежит плоскости LSP.
Аналогичным способом можно доказать, что точки касания
шара с плоскостями ABCD и ASB будут также принадлежать
плоскости LSP.
Рассмотрим треугольники OSN и PSK. Эти треугольники
подобны (они прямоугольные и имеют один общий угол). Из
Подобия треугольников следует, что SON = ос, а по условию
задачи SO=a. Из треугольника OSN находим ON = a cos а.
Высота треугольника будет равна SK. = SO = а(1 + cos ос). Из
треугольника SKP находим
КР = SК ctg а = а (1 + cos а) ctg а.
390 ГЛ. 13 СТЕРЕОМЕТРИЯ
В треугольнике LSP имеем LP=2KP=2a(l + cos ос) ctg ос=
= АВ. Таким образом, найдены величины, необходимые для
вычисления объема пирамиды:
Vsabcd —J" SKS^o = 1 а (1 + cos о) 4«* (I + cos а)' ctg2 а =
4
= у а3 (1 + cos а)3 ctg2 а.
4
Ответ. -~- а3 (1 + cos а)3 ctg2 а,
4.37. "Найти поверхность шара, описанного около правильной
четырехугольной пирамиды, если сторона основания пирамиды
равна а, а боковое ребро пирамиды наклонено к плоскости
основания под углом а.
4.88. В шар вписана правильная четырехугольная пирамида.
Раднус шара равен R, плоский угол при вершине равен ос.
Определить боковую поверхность пирамиды.
4.39. В шар радиуса R вписана пирамида, в основании
которой лежит квадрат. Две боковые грани перпендикулярны
основанию. Большее боковое ребро составляет с пересекающей его
стороной основания угол а. Найти боковую поверхность пнрампды.
4.40. В основании пирамиды лежит квадрат со стороной а.
Высота пирамиды проходит через середину одного нз ребер
основания н равна а Уз/2. Найти раднус шара, описанного около
пирамиды.
4.41. В шар радиуса R вписана правильная четырехугольная
пирамида. Найти объем пирамиды, если раднус окружности,
описанной около ее основания, равен г.
4.42. Шар радиуса Я-вписан в пирамиду, в основании
которой лежит ромб с острым углом ос. Боковые грани пнрампды
наклонены к плоскостп основания под углом q>. Найти объем
пирамиды.
4.43. В шар радиуса R вписана пирамида, в основании
которой лежит квадрат. Одно нз боковых ребер пирамиды
перпендикулярно плоскости основания, а большее боковое ребро образует
с основанием угол ос. Определить боковую поверхность пирамиды.
4.44. Площадь основания правильной четырехугольной
пнрампды равна Q, а двугранный угол прн основании — ос. Эта
пирамида пересечена плоскостью, проходящей через центр вписанного
шара параллельно основанию. Определить площадь сечения
пирамиды.
4.45. Дана пирамида SABCD, основанием которой служит
ромб ABCD. Сторона основания равна a, SA = SC = о, SB ==,
.=. SD, 6CD = 2а. Определить радиус вписанного шара.
§ 4. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 391
4.46. Центр сферы, описанной около правильной
четырехугольной пирамиды, находится на расстоянии а от боковой гра-
ни н на расстоянии b от бокового ребра. Найти раднус сферы.
4.47. В правильную четырехугольную пирамиду SABCD о
вершцной S и стороной основания а вписан шар, раднус
которого равен а/(2-\/3~). Плоскость Р, составляющая угол в 30° с
плоскостью основания, касается шара н пересекается с
плоскостью основания, не пересекаясь с самим основанием, по
линии, параллельной стороне основания. Найти площадь сечения
янрамнды плоскостью Р.
4.48. В шар вписана пирамида, боковые ребра которой
равны с. Основание ее — прямоугольник, стороны которого
стягивают дуги аир радиан в сеченпях шара плоскостями боковых
граней. Определить радиус описанного шара.
4.49. Боковые ребра правильной четырехугольной пирамиды
SABCD (S — вершина) равны а, а стороны ее основания равны
а/л/¥. Найти расстояние от центра шара, вписанного в
пирамиду SABCD, до плоскости, проходящей через диагональ BD
основания ABCD и середину Е ребра SA.
4.50. В правильной четырехугольной пирамиде расположен
шар радиуса 2. Этот шар касается боковых граней пирамиды и
внешним образом касается полусферы, опирающейся на круг,
списанный в основание пирамиды. Точка касания шара и
полусферы отстоит от основания пирамиды на расстояние, равное
одной трети высоты пирамиды. Найти объем пирамиды и
величину двугранного угла при боковом ребре пирамиды.
4.51. Дана правильная четырехугольная пирамида SABCD со
стороной основания а и боковым ребром Ь (Ь > 0). Сфера с
центром в точке О лежнт над плоскостью основания ABCD,
касается этой плоскости в точке А и, кроме того, касается ^боко-
оого ребра SB. Найтп объем пирамиды OABCD.
4.52. В шар радиуса R вписана правильная шестиугольная
усеченная пирамида, у которой плоскость нижнего основания
проходит через центр шара, а боковое ребро составляет с
плоскостью основания угол 60°. Найти объем пирамиды.
4.53. Около шара радиуса R описана правильная
шестиугольная пирамида, боковая грань которой составляет с плоскостью
основания угол а. Найти боковую поверхность н объем
пирамиды.
4.54. В шар вписана прямоугольная призма, в основании
которой лежнт правильный треугольник, а высота прнзмы равна
стороне основания. Найти отношение объема этой прнзмы к
объему вписанной в тот же шар правильной шестиугольной пи-
392
ГЛ. 13. СТЕРЕОМЕТРИЯ
рамяды, боковое ребро которой равно удвоенной стороне
основания.
4.55. Найти отношение объема правильной л-уголыюй
пирамиды к объему вписанного в нее шара, зная, что окружности,
описанные около основания н боковых граней пирамиды, равны.
Комбинацнв фигур вращения. Шар называется
вписанным в прямой круговой конус, если он касается основания
конуса в его центре н соприкасается с боковой поверхностью
конуса ро окружности. Прямой круговой конус называется в«й«
санным в шар, если его вершина н окружность его основания
лежат на поверхности шара.
Шар называется вписанным в прямой круговой цилиндр,
если шар касается оснований цилиндра в их центрах и сопри»
касается с боковой поверхностью цилиндра по окружности боль»
того круга шара, параллельной основаниям. Прямой круговой
цилиндр называется вписанным в шар, если окружности
оснований цилиндра лежат на поверхности шара.
Конус называется вписанным в цилиндр, если основание ко»
нуса совпадает с одним из оснований цилиндра, а вершина
конуса совпадает с центром другого основания.
Задачи на комбинации фигур вращения часто бывает удоб»
но решать построением вспомогательного сечення, разбивающего
комбинацию фигур вращения на две симметричные части.
Вспомогательное сечение, как правило, удобно строить таким обра»
зом, чтобы оно проходило (в зависимости от вида задачи) через
ось цилиндра (нлн ось конуса) и центр шара. При этом в
сечении цилиндра будет получаться прямоугольник, в сеченнн
конуса — равнобедренный треугольник, а в сечении шара — круг о
радиусом, равным радиусу шара. Так, например, если по усло-
пню задачи шар вписан в конус, то в осевом сечении конуса
будут получаться равнобедренный треугольник н вписанный в
него круг; если шар описан около цилиндра, то в сеченнн
получается прямоугольник, описанный около окружности.
Пример 4.4. Образующая конуса равна / и образует й
высотой конуса угол ос. Через две образующие конуса, угол
между которыми равен р\ проведена плоскость. Найти расстоя»
пне от этой плоскости до центра шара, вписанного в конус.
Решение. Пусть S — вершина конуса, О — основание вы»
соты конуса, SA и SB— образующие конуса, угол между
которыми равен Р (рис. 13.17), Из прямоугольного треугольника SOB
(угол SOB прямой, SB = /, BSO = а) находим радиус окруж»
ностн, лежащей в основании конуса, и высоту конуса;
ВО = I sin a, SO = I cos а.
§ 4. КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 393
Из равнобедренного треугольника AS В (ASB = fL, AS=^SB=tl)
находим длниу хорды АВ, высекаемой плоскостью ASB на
основании конуса:
АВ-
.2isln-|.
Расстояние от центра основания конуса до середины хорды АВ
(точки JV) найдем из треугольника NOB по.теореме Пифагора:
, " |JVP|=V(BO)a-(^B)3 r=l A/sin8a-sln2-|.
Через середину хорды А В (точку N) и высоту конуса SO
проведем плоскость. В сеченнн конуса плоскостью получится
равнобедренный треугольник MSMi с боковой стороной I н углои
$ а
при вершпне 2ос; в сеченнн шара, вписанного в конус, получится
круг с радиусом, равным радиусу шара, вписанного в
равнобедренный треугольник MSMt, а плоскости MSMi и ASB
пересекутся по прямой NS (рнс 13.18). *>
Докажем, что расстояние от центра окружности О] до
прямой SN (т. е. длина отрезка OtK) будет искомым расстоянием
от центра шара до плоскости ASB.
Обратимся к рнс. 13.17. Хорда АВ окружности основания
конуса перпендикулярна высоте конуса и перпендикулярна
радиусу ОМ, проходящему через середину хорды АВ (точку N).
Следовательно, хорда АВ перпендикулярна плоскости MSMi,
так как она перпендикулярна двум непараллельным прямым (SO
и ММ{), принадлежащим плоскости. Итак, имеем плоскость
MSMi и перпендикулярную ей прямую АВ. Так как плоскость
ASB проходит через прямую АВ, перпендикулярную плоскости
MSMi, то и сама плоскость ASB будет перпендикулярна
плоскости MSMU т.е. эти две плоскости взаимно перпендикулярны.
394 ГЛ. 13. СТЕРЕОМЕТРИЯ
Центр шара, вписанного в конус, принадлежит плоскости
MSMi. Если пз центра шара опустить перпендшсуляр па
плоскость ASB, то по теореме о двух взаимно перпендикулярных
плоскостях этот перпендикуляр будет целиком принадлежать
плоскости MSMi, т. е. основание перпендикуляра (точка К)
будет лежать на лннни пересечения плоскостей SN, что и нзобра»
жено на рис. 13.17.
Таким образом, нахождение расстояния от центра шара до
плоскости ASB сводится к нахождению длины отрезка KOi из
рис. 13.18.планиметрической задачи. Найдем радиус окружности,
вписанной в треугольник JVfSMi!
001-MO.tg(i-i)-HO.lB(i-|)-
-tttaatg(-5.-|).
Рассмотрим треугольники KSOt н NSO. Этн треугольники
подобны (оин прямоугольные и имеют общий угол NSO).
Вычислим гипотенузу SOi треугольника KSOi:
SO{ •= SO — ОхО = /(cos a — sin a tg(-j — -|Л\.
Гипотенузу SN треугольника SON вычислим по теореме Пифа«
гора:
SN = У(ЛЮ)* + (SO)2 = I /Wslnsa-sln8-|+cos8a=/co5-|.
Из подобия треугольников KSOi и NSO следуют равенства
JCOi SO, „п
/ (cos a - sin a tg (~ - |Л) /v/sln*a- sin* -|
P
cos2
/ д/ sin8 a — sin8 -|- f cos a — sin a tg f -j- —у J j
Ответ. о ■ •
4.66. В конус вписан шар. Найти объем шара, если
образующая конуса равна / и наклонена к плоскости основания под
углом ос.
4.67. Около шара радиуса R описан усеченный конус,
образующая которого составляет с плоскостью большего основапня
угол ос. Найтн объем и площадь боковой поверхности усеченного
конуса.
§ 4, КОМБИНАЦИИ МНОГОГРАННИКОВ И ФИГУР ВРАЩЕНИЯ 395
4.58. В конус вписан шар, поверхность которого равна
площади основания конуса. Найти угол при вершине в осевом сече»
пни конуса.
4.59. В конус вписан шар. Раднус окружности, по которой
касаются конус и шар, равен г. Найти объем конуса, если угол
между высотой н образующей конуса равен а.
4.60. В шар, площадь поверхности которого S, вписан конус.
Угол между образующей конуса и плоскостью основания
равен ос. Определить площадь полной поверхности конуса.
4.61. В конус вписан шар. Доказать, что отношение полной
поверхности конуса к поверхности шара равно отношению их
объемов.
4.62. В конус, образующие которого наклонены к плоскости
основания под углом ос, вписан шар. Найти отношение объема
шара к объему конуса.
4.63. В прямой круговой конус вписан шар. Отношение
объемов конуса и шара равно двум. Найти отношение полной
поверхности конуса к поверхности шара.
4.64. Высота цилиндра равна высоте конуса. Боковая
поверхность цилиндра относится к боковой поверхности конуса,
как 3:2. Кроме того, известно, что угол наклона образующей
конуса к плоскости основания равен ос. Найти отношение объема
цилиндра к объему конуса.
4.65. В усеченный конус с площадью боковой поверхности S
вписана сфера площадью $. Найти угол между образующей и
плоскостью основания конуса.
4.66. Угол при вершине осевого сечения прямого кругового
конуса равен ос, а раднус основания конуса равен R. Найтн
объем такой сферы с центром в вершине конуса, которая делит
объем конуса пополам.
4.67. В прямой круговой конус с углом 60° при вершине в
осевом сеченнн конуса вложены три одинаковых шара радиуса г
так, что каждый шар касается двух остальных, боковой
поверхности конуса н плоскости основания. Найти раднус основания
конуса.
4.68. На основании прямого кругового конуса лежат трн
шара радиуса г. На них лежит четвертый шар того же радиуса.
Каждый из этих четырех шаров касается боковой поверхности
конуса и трех других шаров. Найтн высоту конуса.
4.69. Определить угол при вершнне в осевом сечении конуса,
описанного около четырех равных шаров, расположенных так,
что каждый касается трех других.
4.70. В конус вписан шар радиуса г. Найти объем конуса,
если известно, что плоскость, касающаяся шара н перпендикуляр*
396 ГЛ. 13. СТЕРЕОМЕТРИЯ
пая одной из образующих конуса, отстоит от вершины конуса
на расстояние d.
4.71. В усеченный конус, у которого радиусы вижнего в
верхнего оснований равны Виг, вписан шар. Найти радиус
второго шара, который касается первого шара, боковой поверхности
усеченного конуса н верхнего основания.
4.72. Два конуса имеют высоты hi в hi в общее основание
радиуса R, а их вершины лежат по разные стороны от плоскости
основания. В поверхность, составленную из боковых
поверхностей этих >конусов, вписан шар. Найти радиус другого шара,
который касается как боковой поверхности первого конуса
(причем по целой окружности), так я первого шара.
4.73. Шар касается основания конуса в его центре.
Поверхность шара пересекает боковую поверхность конуса по двуи
окружностям, одна из которых имеет радиус, равный радиусу
шара, и лежит в плоскости, параллельной основанию конуса.
Известно, что радиус основания конуса в 4/3 раза больше радиуса
шара. Найти отношение объема шара к объему конуса.
4.74. Прямой круговой цилиндр описан около шара
радиуса R. Точка С расположена внутри цилиндра иа его оси и уда-
лена на -т R от нижнего основания. Через эту точку проведена
плоскость Р, имеющая с окружностью нижнего основания только
рдну общую точку. В шар вписан прямой круговой конус,
основание которого лежит в плоскости Р, а вершина расположена
выше этой плоскости. Найти объем этого конуса.
4.75. Прямой круговой конус имеет радиус основания г в
угол а в осевом сечении. Два одинаковых шара радиуса R
касаются друг друга боковой поверхности конуса (извне) и
плоскости основания конуса. Найти площадь треугольника,
вершинами которого служат центры шаров н центр основания конуса.
4.76. В прямой круговой цилиндр с радиусом основания
г=1 и высотой Я= 12/(3 + 2 Уз~) вписаны три одинаковых
шара так, что шары касаются верхнего основания цилиндра, его
боковой поверхности и попарно — друг друга. Найтд объем
прямого кругового конуса, основание которого совпадает с нижним
основанием цилиндра н который касается всех трех шаров.
4.77. Даны три одинаковых прямых круговых конуса с
углом а (а < 2л/3) в осевом сечении и раднусом основания г.
Основания этих конусов расположены в одной плоскости и
попарно касаются друг друга внешним образом. Найти раднус
сферы, касающейся всех трех конусов и плоскости, проходящей че*
рез их вершины.
ГЛАВА 14
МЕТОД КООРДИНАТ И ЭЛЕМЕНТЫ
ВЕКТОРНОЙ АЛГЕБРЫ
§ 1. Векторы в координатах
Координатами точки М» относительно прямоугольной системы коор*
дннат OXYZ называют упорядоченную тройку чисел {хц, у0, zc). Число xi
называют абсциссой точки М«, у„ — ординатой, го — аппликатой.
Пусть А и В — две различные точки пространства. Отрезок АВ,
у которого точку А считают началом, а точку В — концом, нваыввют
вектором АВ н обозначают АВ. Направление луча АВ определяет на'
правление вектора АВ, а длина отрезка АВ называется длиной пли
модулем вектора АВ и обозначается \АВ\. Вектор, начинающаяся н
кончающаяся в точке А, называется нулевым вектором н обознв-
чается АА. Понятие направления для него не вводится.
Если координаты начала н конца вектора АВ представлены в виде
—>•
А{Хд, U/\-ZA) u b{*B- У В' zB)> to координатами вектора АВ является
упорядоченная тропка чисел
(*В-^.ХА- УВ-УА- гВ~гл).
Два Вектора считаются равными, если одноименные координаты
совпадают. В дальнейшем наряду с обозначениями АВ для вектора
будем использовать н обозначения, не связанные с началом и концом
вектора в пространстве: а, Ь. с, ...
Нал множеством векторов, заданных своими координатами, 'можно
определить операции сложения, вычитания и умножения па число
по следующим правилам:
1) сумма (разность) векторов равна вектору, координаты которого
равяы сумме (разности) соответствующих координат слагаемых:
2) произведение вектора на число равно вектору, каждая координата
которого равна координате исходного вектора умноженной на это число.
Для удобства ссылок представим правила действий с векторами
в=(в|, ai, oj). 6 =■(&!, Ь:, &3) формулами
а ± 6=(а, ± bu a, ± b,, a, ± bj, (I)
Ка*={%аи Ка-„ Ка,). (2)
Векторы
/=•(!. О, 0), /=»(0, I. 0), *=-(0, 0, 1) (3)
лазыввются ортами. Любой вектор а (аь at, а,) представляется, и при
Втом единственным образом, в виде
a^aif + chj+atk.
.0
398 ГЛ. Т4. МЕТОД КООРДИНАТ
Пример 1.1. Заданы векторы
«•=2* + 3/, Ь = -3/ —2ft, c = *+/-ft.'
Найти координаты вектора a —-r-fr + c.
Решение. По условию задачи
а = (2, 3, 0), &=■((), -3. -2), с = (1, 1, -1).
Используя правила (1), (2), имеем
а-1б + с = (2-0 + 1, З + у+1, O+1-l).
Ответ, а — jft-с=Гз, -g-, 0J.
1.1. Даны векторы о = (—3, —1, 2), Ь =■ (4, 0, 6), с = (5,
—2, 7). Найти координаты векторов: а) 2а; б) —o-f3c.
1.2. Даны три вектора а ■= (2, 4), Ь => (—3, 1), с = (5, —2).
Найтн координаты векторов:
а) 2а + 36 — 5<г, б) а + 24& + 14с; в) 2а — ~- Ь; г) 5с.
Пример 1.2, Даны четыре вектора р{3, —2, 1}, ?{— 1, I,
—2), г{2, 1, —3} и с(11, —6, 5), Найти чнсла х, у, г, если
c-*xp + yq + zr.
Решение, Из условия равенства двух векторов имеем
11=3* — у + 2г,
—»= — 2jc + р + г,
5=>* — 2у — Зг.
Решая эту систему уравнений, получим
х = 2, (/ = —3, z=l.
Ответ, о = 2р — 3q + г.
.1.8. Заданы векторы ••
он(1, б, 8), 6=. (6, -4, -2),
с = (0, —5, 7) и d = (—20, 27, —3S),
Найтн такие числа а, р и уг что
ao + pft + vc+d = 0.
1.4. Даны три вектора р{3, —2, 1), ц = {—1, 1, —2}, г =
;= {2, 1, —3}, Найти координаты вектора с, если справедливо.
§ Г. ВЕКТОРЫ В КООРДИНАТАХ 399
представление
с=.2р — Ц + г.
1.5. Даиы четыре вектора р(0, 1, 2), q(l, 2, 3), г(—1, 1, —2),
с(0, 4, 3). Найти х, у, г в представлении
с = хр + gq + гг.
1.6. Выразить вектор с через векторы а и Ь в каждом нз
следующих случаев:
а) а -(4, -2), Ь = (3, 5), с = (1, -7);
б) а =.(5, 4), * = (-3, 0), с = (19, 8);
в) о = (-6, 2), 6 = (4, 7), с =(9, -3).
1.7. Найтн координаты вектора PQ по координатам точек Р.
и Q:
а) Р (2, -3, 0), Q (-1, 2, -3);
«>'(т.-М)«(-г*т)-
1.8. Даны четыре точки Л(0, 2), В(3, 1), С(-5, 3), £>{2, 4),
Найти координаты такой точки Q, что
qJ+qb + q?+qd = o.
1.9. От точки А отложен вектор Найтн координаты
точки В в каждом из следующих случаев:
а) Л(0, 0), а = (-2, 1);
б) А{-1, 5), а = (1, -3);
в) Л (2, 7), а = (-2, -б).
1.10. На оси абсцисс найтн точку М, расстояние от которой
до точки А(3, —3) равно 5.
1.11. На оси ординат найтн точку М, равноудаленную от то-
чек Л(1, -4, 7) н В(5, 6, -5).
1.12. Найтн координаты точки М, лежащей на оси Ох а
одинаково удаленной от точек /4(1, 2, 3) н В(—3, 3, 2).
1.13*. Наптн координаты центра тяжести треугольника ABC,
если точки А, В и С имеют следующие координаты:
а) А (0, 0), В (0, 3), С (5, 0);
б) Л(0, 0), В (2. б). С(-1, 7);
в) /1(1, 3), В(3, 6), С (-2, 5).
Два вектора а = (ait а2, аз) и 6 = (6], Ьг, Ь3) (Ь # 0) кол*
Чшнеарны, если существует такое число Я., что
й]=»Л&1, aj = Mj, аз^Я^з.
400
ГЛ. 14. МЕТОД КООРДИНАТ
1.14. В каждом из следующих случаев определить, прн
каком значении к вектор а + кЬ будет коллннеарен вектору с:
а) о = (2, 3), 6 = (3, 5), с«=(-1, 3);
б) о = (1, 0), 6 = (2, 2), с = (3, -5);
в) а = (3, ~2), 6 = (1, 1), с=(0. 5).
1.15. Воспользовавшись условием коллинеарности двух век*,
торов, выяснить, коллинеарпы лн векторы
../31 3 \ , / 2 1 1 \
->-(-***)• «-(■§•■-*-')•
1.16. При каких значениях X и Y векторы а = {X, —2, 5)^
и Ь = (1, У, —3) коллинеарпы?
1.17. Даны четыре точки А(—2, —3, 8), В(2, 1, 7), С(1,4,5)
и D(—7, —4, 7). Доказать, что векторы АВ и CD коллннеарны,
1.18. Отрезок с концами в точках А(3, —2) и В (6, 4)
разделен на три равные части. Найтн координаты точек деления.
1.19. Найтн координаты концов отрезка, который точками
С (2, 0, 2) и D(5, —2, 0) разделен на трн равные части,
1.20. Даны вершины треугольника /4(1, 0, 2), В(1, 2, 2) и
С(5, 4, 6). Точка L делит отрезок АС в отношении 1 : 3$ СБ —
меднаиа, проведенная нз вершины С, Найтн координаты точки
пересечения прямых BL и СЕ.
1.21. При каких значениях аир векторы а = — 21-f 3/ + ак
и b = pi — 6/ + 2k коллннеарны?
Трн вектора а = {а* в2, а8), Ь — (&,, b2, h), с = (сь oit c8)]
компланарны, если
.0.
1.22. Проверить, что векторы а = (1, 0, 2), Ь = (0, 1, 3)'|
с«= (1, 1, 5) компланарны.
1.23. Доказать, что если вектор с представляется в виде
с = а + М>, то трн вектора а, Ь, с будут компланарны,
1.24. Доказать, что если трн вектора а, Ь, с компланарны,
то существуют константы аир такие, что справедливо
представление
с = сш + рЬ.
1.25. Даны три вектора а = (1, —1, 0), Ь = (0, 1, —1), с=»
■=(1, 0, —1) н вектор «£ = аа + р6. Доказать, что при любых
я р векторы d, а, с компланарны.
«i
ь,
С\
«г
ь*
сг
а3
Ьг
Си
§ Т. ВЕКТОРЫ В КООРДИНАТАХ
401
Если векторы а=*(а,, аъ а-,). 6=>(6,, Ь,. Ь,) заданы своими координатами
в прямоугольной снстеие координат, то их скалярным произведением
называется число, которое находится по формуле
aft—Biii + Oabj + Oibj. (5)
Косинусом угла между ненулевыми векторами а в Ь называется число,
которое находится по формуле
соз(0, в)^-—, ■ е-—. ■ -\ =•• (о)
л/^+4+4 Vi+»l+*3
Условие перпендикулярности двух ненулевых векторов а а Ь имеет вид
aifti + ajbi + a,fta. (7)
Длнва вектора а вычисляется по формуле
Ul=/^if+af7af- №
Пример 1.3. Даны два вектора о= (5, 2), 6= (7, —3).
Найти вектор с, удовлетворяющий условиям ос = 38, 6с = 30.
Решение. Пусть с = (X, У), тогда на основании (5)
имеем
ЪХ + 2}' = 38,
7Х — ЗУ = 30.
Решив эту систему относительно X и У, получаем X = 6, У = 4.
Ответ, с = (6, 4).
1.26. Даны векторы а = (4, —2, —4) н 6 = (6, —3, 2).
Вычислить:
а) аб; б) (2а - 36) (а + 26); в) (а - б)8; г) 12а - 61.
1.27. Дан вектор а = (—6, 8). Найти координаты
единичного вектора, коллинеарного вектору а, и:
а) сонаправленного вектору а;
б) противоположно направленного вектору а.
1.28*. Из одной точки проведены векторы а = {—12, 16),
6 = (12, 5). Найти координаты вектора, который, будучи отло-
Кениым от той же точки, делит пополам угол между векторами.
1.29. Зная, что |о| = 3, |6|=1, |с| = 4 и а + Ь + с = 9,
вычислить ab + 6с + са.
1.30. Вычислить длины векторов:
a) a = i — j + k; б) 6 = 2i + /-3ft.
1.31. Длина вектора равна 3. Вычислить координаты
вектора, если известно, что все они равны.
1.32. Вычислить длину вектора 2а + 36, если
а=(1, 1, -1); 6 = (2, 0, 0).
1.33. Даны векторы а = (1, 1, —1), 6 = (5, —3, —3) и с =>
>= (3, —1, 2). Найти векторы, коллннеарные вектору с, длины
которых равны длине вектора о + 6,
402 ГЛ. 14. МЕТОД КООРДИНАТ
1Л4*. Векторы АВ=>—3I + 4J6 н
='(—'» 0, —2) являются
сторонамн треугольника ABQ. Найти длину медианы AM.
Пример 1.4, Вычислить угол между векторами о =>j
(=(-1, 2, -2) II 6 =(6, 3, -6).
Решение. По формуле (6) получаем
,-^>. (-0-6 + 2.3+(-2).(-6) _12 _4_
cos(a. »)- vr__v_____ 3.9 - 9 •
Ответ, (о, 6) = агссоз -g-.
1.35. Вычислить угол между векторами:
а) а = (6, —2, —3); & = (5, 0, 0);
б) а - (2, -4, 5); 6 = (0, 2, 0);
в) о = (-2, 6, -3); 6 = (0, 0, -3);
г) а = (-4, -6, 2); Ь = (4, 0, 0);
д) а = (3, -2, 6); & «(0, -5, 0);
е) в = (4, -5, -2); *=.(0, 0, 2).
1.3в. Какой угол образуют с вектором / следующие векторы!
а= (2, 3), 6= (-2, б), с= (-5, 1), <*=(-1, -1)?
1.37. Вычислить косинус угла между векторами а — Ь ц
а + Ь, если а= (1, 2, 1) и Ь = (2, -1, 0).
1.38*. Вычислить косинусы углов, которые образуют с век-(
торами i, I, k вектор:
a) a = l + j+k; б) 6 = —3/ — ft;
в) с = -51; г) <* = 3/ + 4й.
1.39. Вычислить координаты вектора р, коллннеариого век»
тору ц = (3, —4), если известно, что вектор р образует тупой
угол с вектором in \p\ = 10.
1.40. Вектор Ь коллннеарен вектору а = (6, 8, —15/2) и об*
разует с ортом ft острый угол. Зная, что |6| =50, найти его
координаты.
1.41. Вычислить угол между векторами а = 2/ + / н 6=4
= i — 2/ и определить длины диагоналей параллелограмма, по«
строенного на этих векторах как на сторонах.
1.42*. Векторы а, Ь н с имеют равные углы. Найти коорднч
паты вектора с, если а = 1 + / и Ь = / + ft.
1.43. Прямая составляет равные углы с ребрами прямого
трехгранного угла. Найти эти углы.
1.44. Векторы ЛВ = (3, —2, 2) и ВС = (—1, 0, —2) являются
смежными сторонами параллелограмма. Определить величину;
угла между его диагоналями.
§ Т. ВЕКТОРЫ В КООРДИНАТАХ 403
Пример 1.5. Вычислить координаты единичного вектора о,
если известно, что он перпендикулярен векторам 6= (1, 1, 0)
н с- (0. '. 1).
Решение Пусть вектор а имеет /соордниаты X, Y, Z,
Тогда по условию задачи
Xi + Yi+Zi=h (♦)
Из условия перпендикулярности вектора а с векторами Ь н
с получаем уравнения
Я + У = 0 и K + Z = 0.
Подставляя X a Z, выраженные через У, в равенство (*),
получаем У = ± 1/л/з". Следователыю, существуют два вектора,
удовлетворяющих условию задачи:
а'=(~ yf' vT' ~ VT/ tt2=vW' " 7Г л/Л'
Ответ. .,-(-^. Tf.-^r).
"■-(^"уГ yf)'
1.45. При каком эначенни Z векторы a = (в, 0, 12) и Ь ="
(= (—8, 13, Z) перпендикулярны?
1.4в. При каких X и Y вектор а = XI + Yf + 2k
перпендикулярен вектору Ъ = i — / + * и скалярное произведение векторон
а а с = I + 2/ равно 4?
1.47. Вектор с перпендикулярен векторам а= (2, 3, — 1) и
6=(1, —2, 3) н удовлетворяет условию c(2i — / + ft) = — 6,
Найти координаты с.
1.48. Вычислить координаты вектора с, перпендикулярного
векторам а = 2/ — k н Ь = — I -f Щ — 3ft и образующего тупой
угол с ортом /, если | с | = У7.
1.49*. Найти координаты вектора а= (X, У, Z),
образующего равные углы с векторами b= (Y,— 2Z, ЗХ),с= (2Z.3X,— У),
если а перпендикулярен вектору й=(1. —1, 2), | а 1 = 2 д/з и
угол между вектором а о ортом / тупой.
1.50. В параллелограмме ABCD известны координаты трех
вершин: А(3, 1, 2), В(0, —1, —1), С(—1, 1, 0). Найтн длину
диагонали BD.
1.51. Доказать, что точки А(\, —1, 1), В(1, 3, 1), С(4, 3, 1),
D(4, —1, 1) являются вершинами прямоугольника. Вычислить
длины его диагоналей в координаты их точки пересечения,
404 ГЛ. 14. МЕТОД КООРДИНАТ
1.52. Доказать, что точки /4(2, 4, —4), B(i, 1, —3),
С(—2, 0, 5), D(— 1, 3, 4) являются вершинами параллелограмма,
И вычислить величину угла между его диагоналями»
1.53. Найти косинус угла q> между диагоналями
параллелограмма АС и BD, если заданы три его вершины: Л (2, 1, 3),
В(б, 2, -1) и С(-3, 3, -3).
1.54. Треугольник задан координатами своих вершин:
Л(3, —2, 1), В(3, 1, 5), С(4, 0, 3). Вычислить длнны медиан
АА\ и ВВи расстояние от начала координат до центра тяжести
^реугольвика ЛВС, величины углов этого треугольника.
1.551 Вычислить координаты вершины С равностороннего
треугольника ABC, если даны координаты /4(1, 3), В(3, !)•
1.56. Вычислить координаты вершин С н D квадрата ABCD
если даны координаты А (2, 1), В(0, 4).
1.57. Даны точки В(1, —3), £>(0, 4), являющиеся вершинами
ромба ABCD. Вычислить координаты вершин Л и С, если
(Ш) т, 60°.
1.58. Даны вершины треугольника Л(1,—1,—3), В(2,1,—2)
и С(—5,2, —6). Вычислить длину биссектрисы его внутреннего
угла при вершине А.
1.59. Даны координаты трех точек Л(3, 3, 2), В(1, 1, 1) и
С(4, 5, 1). Определить координаты точки D, принадлежащей
биссектрисе угла ABC и удаленной от вершины В на расстояние
V870.
1.60. Вычислить работу силы F = J+2/ + ft при
перемещении материальной точки нз положения Л(—1, 2, 0) в положение
В(2, 1, 3).
1.61. Даны трн силы А* =» (3, -4, 2), N = (2, 3, 5) и Р =
= (—3, —2, 4), приложенные к одной точке. Вычислить работу,
производимую равнодействующей этих сил, когда нх точка
приложения, двигаясь прямолинейно, перемещается из Л (5, 3, —7)
.в В(4, 1, -4).
1.62. Найти длнны сторон н величины углов треугольника о
вершинами А(—1, —2, 4), В(—4, —2, 0) н С(3, —2, I).
1.63. Известны координаты вершин треугольника: Л(1, 1, 1),
В (2, 4, 2), С (8, 3, 3). Определить, является ли этот треугольник
прямоугольным или тупоугольным.
1.64. Вершины тргугольника находятся в точках Л (2, — 3,0),
В(2, —1, 1) н С(0, 1, 4). Найти величину угла ф, образованного
медианой DB и основанием АС.
1.65*. В треугольнике ABC точка Н — точка пересечения
высот. Известно, что ЛВ = (6, —2), ЛС = (3, 4). Найти координаты
вектора ~А%.
§ 2. ЗАДАЧИ НА АНАЛИТИЧЕСКУЮ ЗАПИСЬ' 405
1.66. Доказать, что треугольник ABC, вершины которого
расположены в точках Д(1, 0, 1), В(1, 1, 0), С(1, 1, 1),
прямоугольный. Найтн расстояние от начала координат до центра
окружности, описанной около этого треугольника.
1.67. Треугольная пирамида задана вершинами /1(3, 0, I),
В(— 1, 4, 1), С(5, 2, 3), 0(0, —5, 4). Вычислить длину вектора
АО, если G — точка пересечения медиан грани BCD.
1.68*. Объем прямой треугольной призмы ABCAiBiCi
равен 3. Определить координаты вершины Аи если координаты
вершни одного из осиованнй призмы известны: 4(1, 0, 1),
Й(2, 0, 0), 6(0, 1, 0).
1.69. В декартовой прямоугольной системе координат Оху
на кривой у = х* заданы такие точки А и В, что О А • I ■— 1 и
0% •t=>—2. Найти длину вектора 120А — 30%.
1.70. В декартовой прямоугольной системе координат Оху
на кривой у = хг — 2х + 3, лежащей в первой четверти, заданы
точка A(xi, yt) с абсциссой xi = 1 п точка В(*3, #г) с
ординатой уг = П. Найти скалярное произведение векторов О А, ОБ-
§ 2. Задачи на аналитическую запись линий
на плоскости и поверхностей в пространстве
Прямая на плоскости в декартовой прямоугольной системе
координат Оху может быть задана одним нз уравнений (I)—(7).
Общее уравнение прямой:
Ах + Ву + С=0. (I)
Уравнение прямой, проходящей через точку >t0 (x0, у0) перпендикулярно
вектору п=(А, В):
Л(х-*о) + Ва/-1М=»0. (2)
Уравнение прямой, проходящей через точку Мо (Хя, у-) параллельно
вектору а^Ьп. л): '
*=*!. м=т. о)
т п '
Уравнение прямой в отрезках:
а о
где а и 6 — координаты точек, отсекаемых прямой на координатных осях Ох
И Оу соответственно.
Уравнение прямой с угловым коэффициентом k:
y^-kx+b. (5)
Уравнение прямой, проходящей через данную точку M<,(xt» уь) с данным
угловым коэффициентом к:
U — yt,=*b(X—Xt). (8|
Уравнение.пряыой, проходящей через две точки М\ (Х\, у\) u !Ai(Xi, у-Л:
X—Xi — »-У| (П
Жа—*i »а—»»"
406 ГЛ. 14. МЕТОД КООРДИНАТ '
Углом между прямыми I, п /, называется наименьший из двух
смежных углов, образованных этими прямыми. Угол между прямым» U и 1г с
угловыми коэффициентами ki и к, вычисляется по формула
1е(^=1ттаг1- *1-*"ь-'- <8)
ЕСЛИ /ill;. ТО fe,.Aj=.-l. (9)
Ёслн /i 11и то &,<=£,. (10)
Расстояние от точки Мо(Хъ. Ус) ДО прямой /, задаваемой уравнением
Ах + Ву + С=а, находится по формуле
p(Moi 0_ii*+|a±£L. („)
Пример 2.1. Прямая / проходит через точку Л10(д:о, ^о)!
перпендикулярно вектору п = (Л, В), Написать уравнение
прямой /, если Ма(— I, 2), п = (2, 2).
Решение. Согласно формуле (2) имеем 2(д:+1) +
+ 2 (у — 2) .= 0. Раскрывая скобки я приводя подобные члены,
получаем уравнение х + у — 1 = 0.
Ответ, х + у — 1 => 0.
Пример 2.2. Написать уравнение прямой, проходящей
через точку Afo(—1, 2) и параллельной вектору а = (3, —1),
v A- I w — 2
Р е пье и и е. Согласно формуле (3) имеем —я— = ■ ,
или х + Зу — 5 = 0.
Ответ, л: + Зг/ — 5 = 0.
Пример 2.3. Заданы прямая /; —2х + у— I =0 и точка
Af(—1, 2). Требуется:
1) вычислить расстояние р(Л1, /) от точки М до прямой 1\
2) написать уравнение прямой /', проходящей через точку М
перпендикулярно заданной прямой /;
3) напнеать уравнение прямой /", проходящей через
точку М параллельно заданной прямой /.
Решение. 1) Согласно (11) имеем
'<*■>-"-"^-"-^
2) Применяя формулу (9) для k] = 2, получим k* = —1/2,
Согласно (6) имеем х + 2у — 3 = 0.
3) Применяя формулы (10) и (6), получаем у — 2=2(х+1),
т. е. у = 2х + 4.
Ответ. 1) -%=* 2) х + 2р-3 = 0; 3) г, = 2*+ 4.
■уз
§ 2. ЗАДАЧИ НА АНАЛИТИЧЕСКУЮ ЗАПИСЬ* 407
2.1. Прямая / проходит через точки Mi(Xi, yt) н Мг(х», уг),
Написать уравнение прямой I, если:
а) М, (1, 2), Mt (-1, 0)j
б) М,(1, 1), Mt(U -2);
в) М, (2, 2), М2 (0, 2).
2.2*. Составить уравнение прямой, которая проходит через
точку М(8, 6) н отсекает от координатного угла треугольник С
площадью, равной 12.
2.3. Написать уравнение прямой, параллельной двум задан*
вым прямым U и 1г н равноудаленной от 1\ н h, если:
a) h: Ъх-2у-\-Ъ, 1а: £^± = Л±±;
2.4. Треугольник ABC аадан координатами своих вершив
Л(1, 2), 5(2. —2), С(6, 1). Требуется:
1) написать уравнение прямой, содержащей сторону АВ;
2) иапнсать уравнение прямой, содержащей высоту CD н
вычислить длину ft = |СО|;
3) найти угол ф между высотой CD и медианой ВМ;
4) иапнсать уравнение биссектрис U н It внутреннего н
внешнего углов при вершине А.
2.5. Из точки М (5, 4) выходит луч света под углом ф «=»
= arctg 2 к оси Ох и отражается от нее. Написать уравнения
падающего и отраженного лучей (уравнения прямых,
содержащих эти лучи).
2.6. Написать уравнение, прямой, проходящей через точку
М (2, 1) под углом я/4 к прямой 2х + Ъу + 4 = 0-
2.7*. Две вершины треугольника ABC находятся в точках
А(—1, —1) и В(4, б), а третья вершина лежит на прямой
V = 5(х — 3). Площадь треугольника равна 9,5. Найти
координаты вершины С.
2.8. Даны три точки Л(2, 1), В(3, 1), С(—4, 0), являющиеся
вершинами равнобочной тралецнн ABCD. Вычислить координаты
точки О, если АВ = kCD.
i
Уравнение окружности радиуса R с центром в точке
Со(хо, уо) имеет вид
(*-*o)24-Q/-i/o)8 = «8.
Пример 2.4. Составить уравнение окружности,
проходящей через точки А (2, 0), В (5, 0) а касающейся осн О у.
Решение. Пусть неизвестный центр окружности Со имеет
координаты (х0, (/о).. Тогда из условия касания окружности оси
408 ГЛ. М. МЕТОД КООРДИНАТ
О у заключаем, что абсцисса центра ха равна радиусу R. Так
как точки А (2, 0) и В (5, 0) лежат на окружности, то нх
координаты удовлетворяют уравнению окружности. Используя
перечисленные условия, получим следующую систему уравнений;
<*0-5)2 + ^ = «2.
которая имеет два решения: xq*=*7I2, у0=>±^/10; Я =7/2.
Огвет. (x-^)2 + (ff~VT0)8 = -f- к (*-т)2 +
+ 0, + yio)2 = i?-.
2.9. Составить уравнение окружности, вписанной в
треугольник, стороны которого лежат на прямых х = 0, у = 0,
3* + 40-12=0.
2.10. Дана окружность хг + уг = 4. Составить уравнение
Прямой /, параллельной осп абсцпсс и пересекающей окружность
в таких точках М и N, что \MN\ = 1.
2.11*. В окружность х* + уг=\&9 вписан квадрат ABCD,
Найтн координаты вершин В, С и D, если Л (5, —12).
2.12**. Дана окружность х1 + У2 — 9- Составить уравнение
окружности, проходящей через начало координат, точку А(1, 0)
и касающейся данной окружности.
2.13. Составить уравнение окружности, проходящей через
точку Л {2, 1) и касающейся осей координат.
Плоскость а в прямоугольной системе координат Охуг может быть за»
дана следующими способами.
Общее уравнение пловкости:
Ах + By + Сг + D=»0.
Уравнение плоскости, проходящей через точку Мо (*о> Ус го) перпвНг
дикулярно вектору я=(/1, В, С):
А(х-х<,) + В{у-уь) + С(г—ъ,)—0. (12)
Углом между двумя плоскостями а{ и аг называют наименьший нз
двугранных углов, образованных этими плоскостями. Косинус этого угла
вычисляется по формуле
cos(a^8)-TJ^r *b + **t*EL— (13,
где n,=.(Ah В,, С,) в п2=(А,, В,, С,)—векторы, перпепднкулнрные
плоскостям Oi н а» соответственно.
Пример 2,5. Составить уравнение плоскости, если
известно, что точка W(3, 5, 2) является основанием перпендикуляра,
проведенного нз начала координат к этой плоскости, и
принадлежит плоскости.
§ 2. ЗАДАЧИ НА АНАЛИТИЧЕСКУЮ ЗАПИСИ 409.
Решение. Из условия задачи следует, что вектор ON
перпендикулярен искомой плоскости, где О — начало координат,
ЛГ— точка, принадлежащая плоскости, н ON = (3, 5, 2).
Согласно (12) уравнение плоскости, проходящей через точку ЛГ
перпендикулярно вектору ON, имеет вид
3 (* -3) + 5 (у - 5) + 2(z - 2)=. 0,
нлн
3* + 5у + 2г — 38 = 0.
Пример 2.6. Найти угол между плоскостью, проходящей
через точки М(0, 0, 0), ЛГ(1, 1, 1), /((3, 2, 1), и плоскостью,
проходящей через точки М(0, 0, 0), Лф, 1, 1), D{i, 1, 2).
Решение. Согласно формуле (13) для вычисления
косинуса угла между плоскостями, необходимо вайтн координаты
векторов, перпендикулярных этим плоскостям. Пусть вектор
»»i = (At, Bi, С,) перпендикулярен первой плоскости. Тогда
П]_1_ЛШ 11 ri] A.NK, и, следовательно, /i|»AfA/ = 0, tii' NK=*Q-
Записывая этн равенства в координатной форме, получаем
систему уравнений
Л. + В.+С^О,
ЗЛ, + 2В, + С, = 0, 1*'
решениями которой будут неизвестные координаты вектора пи
Так как система (*) состоит только нз двух уравнений, то одно
неизвестное, например Ct, можно взять в качестве свободного.
Полагая его равным 1, получим nt = (1, —2, 1). Проводя
аналогичные рассуждения, находим: вектор л2) перпендикулярный
второй плоскости, имеет координаты (—1/2, —1/2, 1).
Подставляя найденные координаты в выражение (13), получим: kochhvo
искомого угла равен
-1/2+1+1 1
cos m = , — . L— = -х-,
V6 V3/2 2
р. следовательно, угол между плоскостями равен 60°.
Ответ: 60".
Пример 2.7, Даны плоскость 7.x, + 2i/ — z + 4 = 0 н
прямая /, проходящая через точки ,4(2, 1, 1) и В(—3, 4, 0).
Вычислить координаты точки пересечения прямой / с данной
плоскостью.
Решение. Вычислим координаты вектораi
АВ = (-3-2, 4-1. 0-1) = (-5, 3, -1). »
1
410
ГЛ. М. МЕТОД КООРДИНАТ
Пусть точка М(хв, ув, г0) является точкой пересечения
данной плоскостн н прямой, проходящей через точки А и В. Это
значит, что, во-первых, координаты точки М удовлетворяют
уравнению данной плоскости, т. е. связаны равенством
2ло + 2ув — zo-f 4=0,
В, во-вторых, вектор AM коллннеареи вектору АВ:
AU^kAB*,.
откуда следуют равенства
х0 — 2 =. — 5k,
уа - 1 = 3ft,
гв — 1 = — к.
Решая систему уравнений (*), находим координаты точка
М: дго = —13, ув = 10, zo = —2.
Ответ. (—13, 10, —2).
2.14, Составить уравпеппе плоскости, если известно, что она
проходит через начало координат и перпендикулярна вектору
я =(-6, 3, 6).
2.15. Прямая / проходит через точки А н В. Составить
уравнение плоскостн, проходящей через точку А перпенднкуляр-
no прямой /, для каждого из следующих случаев:
а) А{\, 2, 3), В (4, 6, 9);
б) А (-1,2, 3), В(3, -2, 1);
в) А(\, 0, -3), В(2, -1, 1).
2.16. Найти угол между плоскостями:
а) 2х + у — г = 2, В) Зх — у — 2г «= 1,
х + 2у — z=l: 2x + 3y — z = 2;
в) х — г/+ 32 = 2,
—л: — 3</ + z = 2.
2.17*. Дана плоскость х — у + 2г— 1=0 и прямая,
проходящая через точки Л(2, 3, 0), В(0, 1, 1). Вычислить синус угла
между прямой А В и данной плоскостью.
2.18. Прямая задана точками А(\, —1, 1) \н В(—3, 2, 1).
Найтн угол между прямой АВ и плоскостью:
а) 6* -f 2i/ — 3z — 7 = 0; б) б* — г/ + 8z = 0.
2.19. Вычислить расстояние от плоскости 15х—10г/ +
Ц-6г— 190 = 0 до начала координат.
2.20. Вычислить расстояние:
а) от точки (3, 1, —1) до плоскостн 22л + Ау — 20г — 45=>j
>=0;
(•)
§ 2. ЗАДАЧИ НА АНАЛИТИЧЕСКУЮ ЗАПИСИ 41]
б) от точкн (4, 3, —2) до плоскости 3* — у + 5z + 1 =0;
в) от точки (2, 0, —1/2) до плоскости Ах—4у+2г-\-17 = 0«
2.21. Вычислить высоту (/is) пирамиды с вершинами
S(0, 6, 4), Л(3, 5, 3), В(-2, II, -5), 0(1, -1, 4).
2.22. Составить уравнение плоскости, отстоящей иа
расстояние 6 единиц от начала координат и отсекающей на осях
координат отрезки, связанные соотношением а:Ь:с= 1:3:2.
2.23. Найтн координаты точкн пересечения плоскости
2х — у -{• г = Q и примой, проходящей через данные точки
Д(-1, 0, 2) и В(3, 1, 2).
2.24. Найти точку пересечения:
а) прямой, представляющей собой линию пересечения двух
плоскостей 3* — Ау = 0 и у — 32 = 6 и плоскости 2х — Ъу —
— 2 — 2 = 0;
*ч . х — 7 и — 4 г — 5 „ .
б) прямой —z— = -=;—j— = —-г— и плоскости ах — у -+■
+ 2z — 5 = 0.
Уравнение сферы с центром в точке Со (а'о. j/o, го) п радиусом R имеет
BUS
(*-*>>' +(У-!/»)'+(г-го)>=./Р. (14)
Если центр сферы совпадает с началом координат, то уравнение приобретает
вид
*> + !/' + «*=./{'. (15)
Пример 2.8. Составить уравнение сферы, проходящей
через данную точку Л(1, —1, 4) н касающейся координатных
плоскостей.
Ре шеи не. Так как искомая сфера касается координатных
плоскостей и центр сферы находится в той части пространства,
для каждой точкн которой х >■ 0, у <. О, z > О (ибо в- этой
части расположена точка А(\, —1, 4)), то координаты центра
будут (R, —R, R). С другой стороны, так как точка А
принадлежит сфере, то ее координаты удовлетворяют уравнению (14)j
(1 -R2) + (-1 + Я)Ч- (4-R)* = R\
откуда следует, что
Я*-6Я + 9 = 0 или (tf-3)2 = 0, т. е. Я = 3.
Ответ. (х — 3)*+{у + 3у+(г — 3)2 = 9.
2.25*. Вычислить расстояние от плоскости 2х + 2у — z -f-
4- 15 = 0 до сферы х* + у1 + гг — 4 = 0.
2.26. Дана сфера x2 + yi + zi — 25 = 0 и прямая /, прохо»
дящая через точку Л (2, 1, 1) параллельно вектору о= (2, —4,
412
ГЛ. U. МЕТОД КООРДИНАТ
— I). Вычислять координаты точек пересечения прямой / со
сферой.
2.27. Найтн множество точек пространства, сумма квадратов
расстояний от каждой нз которых до данных двух точек
Л (2, 3, —1) и В(1, —1, 3) имеет одно и то же значение т8.
§ 3. Решение геометрических задач
с помощью метода координат
Геометрические задачи этого параграфа решаются введением
декартовой системы координат на плоскости илп в
пространстве. Приведённые ниже задачи могут быть решены н методами
элементарной геометрии. Однако, как правило, эти решения
требуют использования петривиаль-
Ly ных, искусственных приемов.
Пример 3.1. В
равнобедренном треугольнике ABC (|ЛВ|=;
= \ВС\ = 8) точка Е делит
боковую сторону А В в отношении
3; I (считая от вершины В),
Вычислить угол между векторами
СЕ и С%, если |СЛ |=12.
Решение, Введем систему координат Оху так, как
указано на рнс. 14.1 (по свойству высоты равнобедренного
треугольника \ОА\ = |ОС|). Из треугольника ОВС находим
|0S|=»ViSC|2-|OC|2 = 2V?".
Поскольку А~Е=*-^-Ав, то СЕ=*СА + -т'АВ п координаты
векторов С~Х и СИ равны соответственно
с а
С%= (-12, 0), А§ ~ (б, 2 У7~), СЁ = (-
2 Г
Подставляя найденные координаты в формулу скалярного
произведения векторов, получаем
(-{2). (—21/2) зУГ
cos а =
12У(21/2)2+(л/7/2)2
Ответ. Искомый угол равен arccos —-^—.
о
J&iu В равнобедренном треугольнике ABC (\AB\ = \ВС\ =*
= 15) точка Е делит сторону ВС в отношении 1 [4 (считая от
S 3. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 413
!вершнны В). Вычислить угол между векторами АЁ в АС, если
| ЛС J =. 20.
<=—ЗА-В прямоугольном треугольнике ABC угол В прямой,
\АВ\ =3, |6С| =4. Вычислить угол между медианами AM и
BD.
3.3. В прямоугольном треугольнике с катетами АВ и ВС
(|ЛВ|=»8, |ВС|=6) проведена прямая AD, делящая ВС в
отношении \BD\: \DC\ = 4:5. Вычислить угол между
векторами АВ н AD.
3.4. В прямоугольном треугольнике а катетами ВС н ВЛ
(|6С| ев 4, |ВЛ| = 3) проведена прямая AD, делящая сторону
ВС в отношении \BD\ ; |£»С| = 3:5. Вычислить угол между
векторами AD и ВС.
3.5*. Дан прямоугольный равнобедренный треугольник А ВС
с прямым углом прн вершине В; BS — его высота,' К—середина
высоты BS, a M — точка пересечения
прямой АК со стороной ВС.
Вычислить отношение, в котором точка Л1
делит отрезок ВС.
Пример 3.2. Доказать, что если
основания высот треугольника ABC
соединить прямыми, то получим
треугольник, для которого этн
высоты будут биссектрисами.
Решение. Опустим высоты
треугольника из его вершин: AAiA.BC,
ВВ{±АС и CCt±AB, точку
пересечения высот обозначим О.
Выберем систему координат так, чтобы
ее начало совпадало с точкой Cit
ось Ох прошла через вершину В (рис. 14.2). Тогда ось Оу
пройдет через вершину С. Пусть координаты вершин
треугольника таковы: Л (—а, 0), В(Ь, 0), С(0, с), Докажем, что высота
СКС — биссектриса угла /}|CtB|.
Уравнение прямой, проходящей через точки А и С, имеет
Рнс. 14.2.
вид
у=*тх + с.
(*)
Уравнение прямой, проходящей через точки В и О
перпендикулярной прямой АС, имеет вид
У
а , аЪ
■■ хА •
С ^ С
W
414 ГЛ. Т4. МЕТОД КООРДИНАТ
(при получении последнего уравнения использовано соотношение
между угловыми коэффициентами двух взаимно
перпендикулярных прямых: АгЙ2 = —1). Решая систему уравнений (*) п (»*),
находим координаты точки пересечения этих прямых (точки Si) 5
a (ab — с3) ас (а + Ь)
-f с2 ' а* + с2
Аналогично, записывая уравнения прямых, проходящих через
пары точек В, С и А, О, находим координаты точки At:
Ь {с1 - ab) be (а+Ь)
л ( °(с ~ аЬ> Ьс (а + ь> Л
Ai\ Ь* + сг ' Ь3 + с* )'
Записывая уравнения прямых, проходящих через пары точек
А\, Ct и Bi, G, находим угловые коэффициенты этих прямых}
с (а+Ь) с (а + Ь)
ВА1С,= с*-аЪ ' *fl'C.= ab — c* '
откуда следует, что £fl|Ci = — kAlC{. Так как угловой
коэффициент представляет собой тангенс угла наклона прямой к
положительному направлению оси Ох, то получаем
ВС^В1=п — BCiAu
откуда следует, что АСХВ\<^=ВСХА\. Так как прямая Cfi
перпендикулярна прямой А В, то •=»3iC]C, т. е. высота С&
треугольника АВС действительно является биссектрисой
треугольника AiBtCi.
Аналогично можно* доказать, что и другие две высоты
треугольника АВС являются биссектрисами соответствующих углов
треугольника А\В\С\.
3.6. На высоте ССХ треугольника АВС дана произвольная
точка Р, Прямые АР н ВР пересекают стороны ВС н СА
соответственно в точках Ai н Si. Доказать, что луч CiP является
биссектрисой угла AtCiBi. ..
3.7*. Дан прямоугольный треугольник АВС с катетами а
я Ь, С = 90°. Составить уравнение множества точек М, для
которых
\МА\2+\МВ\2=>2\МС\2.
3.8. В плоскости прямоугольника ABCD даиа точка М.
Доказать, что
** \MA\2+\MC\*=\MBf+\MD\\
§ 3. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 415
3.9. Окружность вписана в ромб с углом 60°. Расстояние от
центра окружности до ближайшей вершины равно 1. Доказать,
что для любой точки Р окружности имеет место равенство
| РА |2 + | РВ |2 + | PC f + | PD |2 = 11.
3.10. Доказать, что сумма квадратов расстояний от точки М,
взятой на диаметре некоторой окружности, до концов любой из
параллельных этому диаметру хорд постоянна.
3.11. Около окружности описан квадрат ABCD. Из вершин
квадрата к произвольной прямой, касающейся окружности,
проведены перпендикуляры ААХ, BBt, CCt и Z)0,. Доказать, что
| -А-Л, |- 1СЯСГ, ! — | вв. |-|Z>Z>. |.
3.12. Дай равносторонний треугольник ABC и окружность,
проходящая через вершимы А н В, центр которой D
симметричен вершине С относительно прямой АВ. Доказать, что если
М — произвольная точка этой окружности, то из отрезков МА,
MB, МС можно составить прямоугольный треугольник.
3.13. В окружность вписан прямоугольник ABCD. Из
произвольной точки Р окружности проведены перпендикуляры к
прямым АВ, ВС, CD н DA, пересекающие эти прямые
соответственно в точках К, L, М и ЛГ. Доказать, что точка N —
ортоцентр треугольника KLM.
3.14. В квадрат вписана окружность. Доказать, что сумма
квадратов расстояний от точки окружности до вершин квадрата
не зависит от выбора точки на окружности. Hafhn эту сумму.
3.15. Около квадрата описана окружность. Доказать, что
сумма квадратов расстояний от точки окружности до вершин
квадрата не зависит от выбора точки на окружности. Найтн^эту
сумму.
Если объектом задачи является куб или прямоугольный
параллелепипед, то наиболее удобной является система координат,
начало которой находится в одной пз вершин нижнего основания
этих тел, а координатные осп проходят через ребра, выходящие
из этой вершины.
Пример 3.3. Длина ребра куба ABCDAxBxCiDi равна 1.
На ребре AAt взята точка Е так, что длина-- отрезка АЕ равна
1/3. На ребре ВС взята точка F так, что длина отрезка BF
равна .1/4. Через центр куба Oi и точки Е и. F проведена
плоскость ос. Найтн расстояние J3 от вершины Si до плоскости а.
Решение. Выберем систему координат так, чтобы ее
начало совпало с точкой А, а оси Ох, Оу и Ог проходили через
416
ГЛ. 14. МЕТОД КООРДИНАТ
ребра АВ, AD н AAt соответственно. В этой системе координат
f(.,i-,o). в (о, 0.1). 0,(4-, 4-. т)'
Составим уравнение секущей плоскости а. Пусть вектор
я =■ («1, Пг, п») перпендикулярен искомой плоскости. Так как
векторы
ЕР=1Я{-1'~Т'Т)> ^Oie(—Г'Т'т]
принадлежат искомой плоскости, то, используя условие
перпендикулярности пар векторов л, EF и п, Е0\, получим
следующую систему уравнений для fli, л2, я8:
-«| 4~ + ~3 °'
2- + -Г + -2 °'
Считая п3 свободным неизвестным, получим rti= —rt3 и Пдш
«=* —— п3. Полагая п, = 9 в качестве вектора,
перпендикулярного искомой плоскости, получаем вектор л = (5, —8, 9). Урав«
неиие плоскости, проходящей через точку £(0, 0, 1/3)
перпендикулярно вектору л = (5, —8, 9), будем иметь вид
5* — 8# + 9z — 3 = 0.
Координатами точки Si в выбранной декартовой системе
координат будут (1, 0, 1), Вычислим расстояние от точки
Bi(l, 0, 1) до плоскости:
5л: — 8г/ + 9z — 3 = 0.
Пусть М(хв, уо, Но)—точка основания перпендикуляра к дай*
НОЙ плоскости, проходящего через точку Si. Вычислим
координаты точки М. Так как эта точка принадлежит* плоскости, то
координаты этой точки должны удовлетворять уравнению
плоскости:
б*о — 8^0 + 9z0 — 3 = 0. (*)
С другой стороны, вектор В\М перпендикулярен данной плоско»
стн, и, следовагельно, вектор BtM коллннеарен вектору п:
§ 3. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 417
Последнее равенство в координатной форме дает следующие три
уравнения;
Хо — 1 «= 5ft,
Уа = —8fe, (**)
20 - 1 = 9fe.
Решая систему уравнений (+), (**), находим координаты
точки М
_ 115 88 _ 71
*° 170"* Ua~ 170" Zo— 170
н длину вектора |S|M| = —т=г, которая и является искомым
У170
расстоянием от точки S| до плоскости.
Ответ. 11/-/F70.
ЗЛ6. Длина ребра куба ABCDAXBXC\D\ равна 1. На ребре
ВС взята точка Е так, что длина отрезка BE равна 1/4. На
ребре C,Dt взята точка F так, что длина отрезка FDi равна 2/5.
Через центр куба н точки Е н F проведена плоскость а. Найти
расстояние от вершины Ai до плоскости ос.
Л.НГ'Длнна ребра куба ABCDAiBiCiDi равна 1. На ребре
А В взята точка Е так, что длина отрезка BE равна 2/5. На
ребре CCi взята точка F так, что длина отрезка FC равна 2/3.
Через центр куба и точки Е п F проведена плоскость ос. Найти
расстояние от вершины А до плоскости а.
3.18. Длина ребра куба KLMNKiLiMiN\ равна 1. На ребре
MMi взята точка А так, что длина отрезка AM равна 3/5. На
ребре KiNi взята точка В так, что длина отрезка /<4В равна 1/3.
Через центр куба и точки А и В проведена плоскость ос. Точка
Р — проекция вершины ЛГ на плоскость а. Найти длину .ртрез-
ка ВР.
3.19. Длина ребра куба KLMNKiLiMiNi равна 1. На ребре
KL взята точка А так, что длина отрезка AL равна 3/4. На
ребре MMt взята точка В так, что длина отрезка MB равна 3/5.
Через центр куба н точки А и В проведена плоскость а. Найти
длину отрезка ВР, где точка Я — проекция вершины N на
плоскость а.
. 3.20. Длина ребра куба KLMNKiLiMiNi равна 1. На ребре
KL взята точка А так, что длина отрезка КА равна 1/4. На
ребре ММ, взята точка В так, что длина отрезка MiB равна 2/5,
Через центр куба и точки А и В проведена плоскость ос. Точка
Р — проекция вершины Ki на плоскость ос. Найти длину от*
резка АР.
(4 А, Г. Цыпква. А. И, Пнпс&яА
418
ГЛ. 14. МЕТОД КООРДИНАТ
3.21. Дан куб ABCDAiBtCiDi; точка /( — середина ребра
AAi, L — центр грани CCiDiD. Найтн угол между плоскостями
В/О. и ADiC
3.22*. Найтн площадь сечения куба ABCDAiBtCiDi
плоскостью, проходящей через вершину А н середины ребер BiCt и
D\C\. Ребро куба равно а.
3.23**. В кубе ABCDAiBiCiDi с ребром а точка К— середина
ребра АВ, точка L—середина ребра DDi. Найтн стороны
треугольника AiKL н определить, в каком отношении делнт объем
куба плоскость, проходящая через вершины этого треугольника,
3.24." В кубе ABCDAiBiCiDi с ребром а последовательно
соединены середины ребер AAt, AiBt, SiCi, CiC, CD, DA и AAi.
Доказать, что полученная фигура есть правильный
шестиугольник, и определить его площадь.
3.25. Длина ребра куба ABCDAiBiCiDi равна а. Точки Е н
F — середины ребер ВС н S,C| соответственно. Рассматриваются
треугольники, вершинами которых служат точки пересечения
плоскостей, параллельных основаниям куба, с прямыми AiE, DF,
ADi. Найтн:
а) площадь того треугольника, плоскость которого
проходит через середину ребра А А г,
б) наименьшее возможное значение площади
рассматриваемых треугольников.
3.26. В куб вписана сфера. Доказать, что сумма квадратов
расстояний от точки сферы до вершин куба не зависит от
выбора точки. Найти эту сумму.
Пример 3.4. Основанием пирамиды SABC является
равносторонний треугольник ABC, длина стороны которого равна
4<у2- Боковое ребро SC перпендикулярно плоскости основания
к имеет длину 2. Вычислить
величину угла треугольника н
расстояние между скрещивающимися
прямыми, одна из которых
проходит через точку S п середину
ребра ВС, а другая проходит через
точку С п середину" ребра АВ.
Решение. Введем
прямоугольную систему координат,
приняв за начало координат точку
С, за ось ординат — прямую
CD (точка D — середина АВ), за ось аппликат —прямую CS, за
ось абсинсс — прямую, принадлежащую плоскости треугольника
ABC и перпендикулярную прямой CD, а за единицу масштаба —*
отрезок, длина 'которого равна 1 (рис, 14.3). В этой системе
5-3. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ 419
координат векторы CD и SE (точка Е — середина стороны СВ)
имеют следующие координаты:
ся=(о, ^§-\св\, о)=(о. 2Уе". о),
sl^iM., 1^1 _,cs|)=.(V2, Уё, -2).
Поэтому
,Р& Z& CD-SE 12 д/2
cos (CD, SE) = —=5 =?г-= r=—7=- = -V-»
|CD|.|S£1 2V^-Vl2 2
в, следовательно, искомый угол равен 45°.
Пусть PQ — общнй перпендикуляр к прямым SE н CD
(PeSE, Q^CD). Тогда существуют такие числа а и р, что
5p=a-S£, CQ»p'CD. Ясно, что
PQ = р| + SC + CQ = -aS£ -CS+ pCD,
или, в координатном виде,
PQ = (—а д/2". -а У<Г + р • 2л/б, 2а - 2>.
Так как PQ±CD н PQXSE, то PQ • CD^O^-PQ • SE = 0.
Последние два векторных уравнения в кр^грдттЗтной форме имеют
внд _ _
(-aV6 +P»2 V6")'2V6 =0,
-a V2 • V2 + (-« V6" + Р ■ 2 V6) • д/б" 4- (2а - 2) (—2) =0.
или
а = 2(5,
-За + Зр 4-1=0.
откуда a = 2/3, р = 1/3. Таким образом,
яЗ,(_!^.о,-4). IOQI-V:
8
+ "JT = -
9^9 л/3"*
Ответ. Величина угла равна я/4, искомое расстояние
равно 2/Уз.
3.27. Основанием пирамиды SABC является равнобедренный
прямоугольный треугольник ABC, длина гипотенузы АВ
которого равна 4 У2". Боковое ребро пирамиды SC перпендикулярно
плоскости основания, и его длина равна 2. Найтн величину угла
и расстояние между скрещивающимися прямыми, одна нз кота-
рык проходят через точку S и середину ребра АС, а дрхая
проходит через точку С н середину ребра А В, ^ч
U*
420
ГЛ. И. МЕТОД КООРДИНАТ
3.28. Основанием пирамиды HPQR является равносторонний
треугольник PQR, длина стороны которого равна 2л/2. Боковое
ребро HR перпендикулярно плоскости основания в имеет длину 1.
Найти величину угла и расстояние между скрещивающимися
прямыми, одна нз которых проходит через точку Н н середину
ребра QR, а другая проходит через точку R п середину ребра PQ.
3.29. Основанием пирамиды HPQR является равнобедренный
прямоугольный треугольник PQR, длина гипотенузы PQ
которого равна 2 л/2- Боковое ребро пирамиды перпендикулярно
плоскости основания, н его длина равна 1. Найтн величину
угла и расстояние между скрещивающимися прямыми, одна из
которых проходит через точку II п середину ребра PR, а
другая проходит через точку R и середину ребра PQ.
3.30. Все ребра правильной призмы ABCAJi\Ci имеют дли-
иу а. Рассматриваются отрезки с концами на диагоналях BCj
п СА% боковых граней, параллельные плоскости ABBiAi.
а) Один из этих отрезков проведен через такую точку М
диагонали В&, что |ВЛ1| : |BCi| =1:3. Найти его длину.
б) Найти наименьшую длпну всех рассматриваемых от*
резков.
3.81. Сторона основания ABCD правильной пирамиды SABCD
имеет длину а, а боковое ребро —длину 2а. Рассматриваются
отрезки с концами на диагонали основания ВО и боковом
ребре SC, параллельные плоскости грани SAD, Найтн наименьшую
длину всех рассматриваемых отрезков.
§ 4. Простейшир задачи векторной алгебры
—> —>
Два вектора АВ п CD считаются равными, если:
—> —>-
1) длина вектора АВ равна длине вектора CD;
—> —>
2) лучи АВ н СП одинаково направлены.
При таком определении равенства векторов множества всех век*
торов, равных АВ, называют свободным вектором. Понятие свободного
вектора АВ можно сеязать также с отображением пространства на
себя, при которой все точки пространства перемешаются и одном н
том же направленна (направление А В) вв одно в то* же расстояние
(длину АВ). Так определенный свободный вектор называется также
параллельным переносом, который полностью определяется
упорядоченной парой несовпадающих точек А, В.
Любая пара совпадающих точек определяет тождественное
отображение пространства или нулевой вектор.
Линейными операциями нал векторами называются операции ело»
ження и вычитания векторов, а также умножение вектора на число.
Пусть а н 6 —два ненулевых вектора. Отложим вектор а от веко»
торой точки 0 н обозначим его конец буквой А (рнс. 14.4). Отложиы
от точки А вектор Ь и обозначим его конец буквой В. Вектор в
с началом в точке 0 п концом в топке В (el ■=«) называют суммой
векторов а а Ь:
'■ ■ . а+6=»С
' § 4. ПРОСТЕЙШИЕ ЗАДАЧИ ВЕКТОРНОЙ АЛГЕБРЫ
421
Операция сложения векторов обладает следующими свойствами]
1) а + 6=6 + в;
2) с + (а + &)=»(с + а) + Ь;
3) о+0=а.
Приведенное выше правило сложения векторов называется
правилом треугольника (сумиа векторов представляется третьей стороной
треугольника, в то вреия как слагаемые образуют Две другие стороны
треугольника, си. рис. 14.4). Наряду, с этим правилом существует так
Называемое правило параллелограмма, при котором слагаемые векторы
В
откладываются от одной точки, через их концы проводятся пряные,
достраивающие фигуру до параллелограмма (рис. И.Б), диагональ
которого, проходящая через общее начало векторов, И равна сумме
векторов.
Вектором, противоположным вектору а, называют вектор (~а) такой.
Что сумма векторов а и —а раннв нулевому вектору;
а + (-а)=0.
Ненулевые противоположные векторы имеют разные длины и
противоположные направления.
Разность двух векторов а~Ь есть сумма вектора а к вектора, прогв.
Ьоположного вектору 6, т, е.
с-а + {-Ь).
Разпость векторов может быть получена с помощью правила треугольника.
Отложим от точки А вектор а (рис. 1-1.6); получпи АВ — а, От конца вектора
АВ отложим вектор Вектор
АС=с—разность векторов а в Ь\
с=*а—Ь.
Вектор разности двух векторов пожег
быть также выражен второй
диагональю параллелограмма ВА (рис,
11.fi).
Произведением непулевого вектора
а на число X Ф О называют вектор,
имеющий поправление пекторэ а, если
положительно, и чротнпоположное
Направленно, если Я. отрицательно;
длина этого вектора равна
произведению длины вектора а на абсолютное
ла) К.
Свойства операции умножения вектора а а число:
1) (*,*,) a=Ji, (А,а);
2) К (а + В)=»\а + %А, 0ц + \,) e=»?i,i<i + Mi
3) О.а=»0;
4) М=.0.
Два ненулевых вектора называется коллинеарными, если они па*
раллельны одной прямой, Для коллинеарности двух векторов а в Ь
вначеине (модуль чисч
422 ГЛ. 14. МЕТОД КООРДИНАТ
веобходнмо и достаточно, чтобы существовало число кщЫК удовлетво»
ряющее равенству
Ь==Ло. (1)
Нулевой вектор считается коллннеарным любому вектору
Пример 4.1. В трапеции ABCD вектор BC = XAD, Дока-
вать, что вектор р = АС + BD коллинеарен AD.
Решение. Согласно
определениям суммы н разности векторов
представим векторы АС и BD в виде
(рис. 14,7)
В
АС = АВ + ВС = ЛВ+ XAD,
Р||С- ы-7 BD = AD - АВ.
Для вектора р тогда справедливо следующее представление,
р = АС^+ BD = AB+\AD + AD-~ АВ = (\+ 1) AD.
Это соотношение доказывает коллинеарность векторов р н AD.
^ГГГЧерез вершину С параллелограмма ABCD проведена
прямая, параллельная диагонали BD, которая пересекает
прямую АО в точке Е; точка Q — точка пересечения диагоналей
параллелограммами. Выразить через векторы DC и CQ сумму
векторов А В н СЕ.
$Л. Пусть ABCD — параллелограмм, причем К— середина ВС,
—* —>
L — середина AD, Обозначим АК = в, AL — b. Выразить векторы
ЙК.и ЛС через а в 6.
**§. В трапеции AHCD отношение длины основания ВС к
длине основания АО равно п. Диагонали трапеции пересекаются
в точке^О. Выразить вектор АО через векторы АВ и AD.
£А. Даны три ненулевых вектора а, Ь, с, каждые два на
которых неколлинеарны. Найти и.х сумму, если а + 6
коллинеарен вектору с, a b -f с коллинеарен вектору а.
Jb£. Точки М, N, Р и Q лежат соответствевнр на сторонах
АВ, ВС, CD, DA параллелограмма ABCD, причем j^4Af }i| AfS| =
— \BN\:\NC\ — \CP\:\PD\ — \DQ\:\QA\. Доказать, что
MNPQ — параллелограмм.
Если векторы а и 6 неколлинеарны, то из равенства
«и + РЬ = 0 следует, что а = 0 и р = 0.
Пример 4,2, Векторы а и & иеколлниеарны. Найти значен
пня А. н ц, если известно, что векторы
с =А,а-г-цЬ и «г=(ц+ 1)а+(2 — К)Ь
fjaBHbiv
§ 4. ПРОСТЕЙШИЕ ЗАДАЧИ ВЕКТОРНОЙ АЛГЕБРЫ 423
Решение, Из равенства векторов cad следует
Ха + цб = (ц + I) а + (2 - X) Ь
пли
(ц Ч-1 - X) в + (2 - X - и) 6 = 0.
Но, так как а и 6 неколлянеарны, то справедливы уравнения
ц + 1 — X = О,
2-Я, — ц. = 0.
Решая эту систему, находим X = 3/2; р. = 1/2,
Ответ: X = 3/2; ц — 1/2.
.АвГ^Зекторы а а Ь неколлпнеарны. Найти X, если векторы
(А.— 1)а + 26 и За + Хб коллинеарны.
^7ГЪекторы а и 6 неколлинеариы. Найти значение ос, при
котором векторы (X —2)а + 6 п (2Х+1)а—6 будут
коллинеарны.
aAeTTJeKTopbi а ъ b неколлинеариы, Найти значения X п ц.,
при которых справедливо равенство
v_ 2а — v = w,
если а = Хя + 2ц6, о => —2jia -f- 3X6, w = 4e — 26.
Три ненулевых вектора называются компланарными, если опн
параллельны одной н тон же плоскости. Если сред» трех векторов есть хотя
бы одни нулевой, то такие векторы также ечнтаюгея компланарными.
Если три вектора а, Ь, с некоипланарны, то из равенства
aa + fib + yc—O (2)
следует, что а=»0, (5=0. y=0. n
Если векторы а и Ь пеколлннеарны. то любо!) вектор с, компланарный
С векторами а а Ь, можно единственным образом представить в виде
Если векторы а, Ь, с некомплвнврны, то любой вектор d можно
единственным образом представить в виде
d=*aa + 0ft + ус.
Три непулевых вектора а, Ь, с компланарны тогда н только тогда, когда
существуют три числа а, р. у- не все равные нулю, такие, что
аа + 06+y<;=O- (3)
Пример 4.3. Даны три нскомпланарных вектора а, 6 в с.
Доказать, что векторы а + 26 — с, За — 6 + с, — а + 56 — Зс
компланарны.
Решение. Согласно критерию комплаиарности трех
векторов, достаточно найтн трп числа ос, (J, Yi удовлетворяющих
у с ловяям
о (л+ 26 — c)+£<3e-6 + c)+v(-« + 56-3c) = 0, (*)
о8 + Р8 + Y* > 0- <**)
424 ГЛ. М. МЕТОД КООРДИНАТ
Условие (**) эквивалентно тому, что по крайней мере одно чнс-t
ло а, р или у не равно нулю.
Преобразуем (*) к виду
(а + Зр - у) в + (2а - р + 5у) Ь + (-а + р - Зу) с = 0.
Так как а, 6, с некомпланарны, то согласно (2) а, ($, у
должны удовлетворять следующей системе уравнений;
а + Зр— у=0.
2а — Р + 5\ = 0, (***)
—а+р —3у = 0.
Однпм из ненулевых решений системы (*#*) будет тройка чисел
а 2, р= 1, V= 1.
Тем самым доказано, что а + 2Ь — с, За — Ь + с в —а -$
+ 56 — Зс компланарны.
Чж Даны три некомпланарных вектора а, b н с. Вычислить
значенне к, прп котором векторы a +b + kc, b + с +ka,
с + a + kb компланарны.
ЗХГДаны трн некомпланарных вектора а, Ь, с. Доказать,
что вектрры о + Ь, Ь + с, с — а компланарны.
<4?П. Даны три некомпланарных вектора а, Ь, с. Найтн чис*
ла р и q, прн которых векторы pa + qb + с п a + pb + qc кол-
линеарны.
^4>2. Даны четыре ненулевых вектора а, Ь, с и d, каждые
трн яз которых некомпланарны. Найтн нх сумму, если а + Ь +|
,+ с** pd н Ь + с + d = (jo.
Пример 4.4. Дай параллелепипед ЛвсЬл^С^,. Разло*
жить векторы АА\, АС и DB по векторам бЛь ОС] и Z>Blt
Решение. Введем вспомогательные некомпланарные век»
—> —> -^> —>
торы a = AAi, b = AB, c = AD: выразим через них векторы ВЛ»,
DCu DB\ и искомые векторы АА\, AC, DB.
Согласно правилам сложения н вычитания векторов имеем
5л*, = д — о, DCx = a + b, DBX «= а +"& — с, (*)
АС*=Ь + с, DB=b — c, КА*, = а. (**)
Из равенств (*) выражаем векторы о, Ь, с через DAlt DC{, 5й,,
Имеем
a^DXi — DBi + DC*,, 6 = 5Si-5li, о = -ЯВ,+5?,.
Подставляя аначення а, Ь, с в (*»), получаем искомые представ^
Ленин,
§ 4. ПРОСТЕЙШИЕ ЗАДАЧИ ВЕКТОРНОЙ АЛГЕБРЫ 425
Ответ.
АА, = D%, — DB, -f DC",,
Л? = (OS, - DA{) + (—D%x + DC,) = -DA, + DC,,
Ш =» {D§1 - DA{) - (-D%, + ОС,) = —5t, + 2DBi — ОС,.
тетраэдре 0ABC точки М и N —середины ребер ОВ
и ОС. Разложить векторы AM, ВЛГ н Л1Л^ по векторам ОА, ОВ
н ОС.
^М^Ъ треугольной призме ABCAiBtCi диагонали грани
BBiCtC пересекаются в точке М. Разложить векторы AM п А[М
по векторам В А, ВВ\, ВС.
&{(5. Дана треугольная призма ABCAiBiCf. Разложить
вектор AAi по векторам АСи ВАь СВ,.
Упорядоченная троЛка некомплвнарных векторов е., 8Ъ е3 пазы,
ввется оазисом в множестве всех векторов пространства.
Всякий вектор может быть едннствеиным образом представлен
в виде
a=Xi«i+ *,«» + *«!. (4)
Упорядоченная трояка чисел (jft. X-i, JCj) иаэынается координатами вектора а
в базисе e„ е3, е3. Запись (4) называют разложением вектора а ио базис/
ей вз. в).
Пример 4.5, Дан параллелепипед ABCDAiBfiiDi. -Йайти
координаты вектора C{D в базисе ff/ et
векторов AD, АА„ АВ (рис. 14.8). *'/**/* тг-"
Решение. Вектор C\D равен
вектору В\А (рис. 14.8), который в
свою очередь равен
Ъ~Х=* -ABi = - (АА} + АВ).
Таким образом, координаты вектора C(D имеют вид (О,
-1, -I).
Отпет. (О, —I, —I).
4.16. Задан тетраэдр ОАВС, точки D н Е — середины ребер
ОА и ВС соответственно. Найтн координаты вектора DE в базисе
0%, ОВ, о£.
4.17. В тетраэдре ОАВС F — точка пересечении медиан осно<
вания ABC. Найтн координаты вектора Of в базисе О А, ОВ, ОС.
426
ГЛ. 14. МЕТОД КООРДИНАТ
4.18. В тетраэдре О ABC медиана AL грани ABC делится точ*
кой М в отношении \АМ\ : \МЦ = 3; 7. Найти координаты век-.
тора Ъ~М в базисе ОА, ОВ, ОС.
4.19. В параллелепипеде ABCDA^BfiyDi точка М — середина
грани DDiCiC (точка пересечения диагоналей). Найти
координаты вектора AM в базисе из векторов AD, АВ, AAt.
4.20. В параллелепипеде ABCDAiBiCiDi точка М делит
ребро CCi в отношении |СЛ1|: \МС]\ = 1:2, точка ЛГ делит
ребро AxDi пополам. Найти координаты вектора ММ в базисе из
векторов AD\, AB, АА{.
§ 5. Геометрические задачи, решаемые
методами векторной алгебры
Методы векторной алгебры основаны на единственности
разложения вектора на плоскости по двум неколлннеарным
векторам и на единственности разложения вектора в пространстве по
трем некомпланарным векторам.
Приведенные ниже задачи можно условно разбить на два
типа: на «прямые» задачи н на «обратные». Прямыми задачами
будем называть задачи, в которых постулируется
принадлежность трех точек одной прямой нлн принадлежность четырех
точек одной плоскости. В этих задачах обычно требуется
установить или проверить некоторые соотношения между длинами
отрезков.
В обратных задачах требуется, как правило, установить, что
при определенных соотношениях между длинами отрезков
некоторые три точки А, В, С принадлежат одной прямой или
некоторые четыре точки А, В, С, D принадлежат одной плоскости, а
также иногда требуется доказать, что некоторые прямые
пересекаются в одной точке.
Решение прямых задач на плоскости основано иа проверке
векторной формулы
A§=*kBC, (1)
выполнение которой при некотором действительном k означает,
что три точки А, В, О лежат иа одной прямой, или иа проверке
формулы
ОС = аОЛ + (1 — а)ОВ,
где А, В, С —точки одной прямой, а О — произвольная точка.
При и ер 5.1. Дан параллелограмм ABCD. Прямая I
пересекает прямые АВ, AC a AD соответственно в точках Si, С» н 0»,
§ 8. ГЕОМЕТРИЧЕСКИЙ ЗАДАЧИ
Доказать, что если ABi •=» %\АВ, ADi = ХцАВ, А3ЛС, тс?
J _L + _L
Ло Л ] л $
(прямая задача).
Решение. Пусть АВ = а. АО =» Ь я 6 (рнс. 14:9).
Тогда AB\=.'Kia, ADi=>X2b и з (а + Ь). Так как три
точки А и б|, Ci лежат па одной
прямой I, то справедливо следующее равен- . ff
ство: fa
B^C'l = kB^Du (*) О-
н!_к -* ' А —$ *%<*
5ft — А?, - А~Й, = (Яа - А.,) а + А,26, рнс l4 e
S^), => A~D, - АВх = -Л,а + А2Ь.
Подставив разложение векторов S,C| н B,D^ по неколлннеарным
векторам а и 6 в соотношение (*), получим
(Я8 — Я|) а + кгЬ = ЛА.3Ь — feXia.
На основании единственности разложения вектора по двум
неколлннеарным векторам а и Ь получим систему
Лд — Л| ^ —&Л],
Исключив коэффициент k, найдем соотношение между Xi, Хг иЛэ:
Раэделнн последнее равенство почленно на h%i>4, имеем
-L_-L + JL,
А-з Л| Л2
что и требовалось доказать.
Рассмотрим пример обратной задачи.
Пример 5.2. На стороне ON параллелограмма AMNO и
на его диагонали ОМ взяты такие точки S н С, что
_Й-£-о*. ЪЬ—Jpfon.
Доказать, чтб точки А, В и С лежат на одной прямой.
гл. и. метод координат
fP е ш е и и е. Выразим векторы АВ и АС через векторы ON
*А (рис. 14.10):
АС «=. —\-т ОМ — 0%, AB = — ON -~ОА.
Так как ОМ = 0/4 + CW я, следовательно,
то
Сравнивая разложения векторов АВ и АС по иеколлинеарным
^ векторам ON и СМ, получаем
я + 1
АВ = МС, где Я = ■
п
.^Jy Так как векторы Ли и дс коллинеар»
ны н имеют общее начало, то три
Рис. и.ю точки Л, В, С лежат на одной пря-
[ мой.
< 5.1. На прямых ВС, СА, АВ, определяющих треугольник
ЛВС, взяты соответственно точки L, М н N, лежащие на одной
прямой. Доказать, что если
tt^aLC^ CM = $Ma, М=*у№,
то ару = — 1 (теорема Менелая).
5.2. Дай треугольник MNP. На прямых MN, NP, РМ взяты
точки А, В н С так, что MA^aAN, N% = P~BP, РС**=уСМ,
Доказать, что если а(3у = —1, то точки А, В, С лежат на одной
прямой (обратная теорема Менелая),
5.3. Прямые а и b параллельны. На примой а взяты
произвольные точки Ai, Аз, As, на прямой Ь — произвольные точки Bh
S», Вз. На отрезках AiBit Лай», AtBt взяты такие точки Су, Сз,
Cj, что
|Д|С|| =а|Л,в,|, [АгСг\ = а|Л2й2|, |Л,С,| = а|Д,В,|. •
Доказать, что точки Ci, Сг, С3 расположены на одной прямой.
8.4. Точки Ci, Сг, Сз делят отрезок АВ на четыре части;
D — произвольная точка плоскости. Выразить векторы DCX, DC^
DCa через векторы DA •=» а, DB «*» ft.
§ 5. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ 429
.^б^Даиы три точки М, А, В, а четвертая — точка С — взята
так, что Выразить вектор через векторы МА н
Жв.
JiA. На плоскости взяты трн точки А, В, М. На отрезке АВ
—^
взята такая точка С, что \АС\ : \СВ\ «= ft. Выразить вектор МС
через МА и MB.
Пример 5.3. Если точка А
пересечения диагоналей
четырехугольника MNPQ н середины В, С его
противоположных сторон MN, PQ ле- f
жат на одной прямой, то
MNPQ—трапеция или параллелограмм(рнс. 14.11).
Р е ш е и н е. Положим А~М = a, AN = Ь. Тогда АР = ка ц
AQ = lb. Так как В — середина отрезка MN, то
Аналогично
АВ=±АМ +±М1 = ±(а+Ъ).
АС = \ АР + \ AQ —1- (ko + lb).
По условию точки А, В, С лежат на одной прямой, й по»
этому существует такое число т, что АС = гпАВ, т. е.
£. (а+ *)—!<*«+ /6).
■ft , т — 1 . А
2^"^ 2
о'ткуда следует, что m = ft = /. Тогда
~MN<=b — a, PQ = /& — fea = — ft (a — 6),
т. е. PQ = kMN. Следовательно, PQ||AfJV, т. е. MNPQ—
трапеция или параллелограмм.
5.7. Точка пересечения средних линий четырехугольников сов*
падает с тонкой пересечения его диагоналей, Доказать, что
четырехугольник — параллелограмм.
5.8. Доказать, что середины оснований трапеции н точка
пересечения продолжений ее боковых сторон принадлежат одной
прямой.
430
ГЛ. И. МЕТОД КООРДИНАТ
Б.9. Точка М — середина отрезка А В, течка М'— середина
отрезка А'В', Доказать, что середины отрезков АА', ВВ' и ММ'
расположены на одной прямой.
5.10. Доказать, что середины сторон произвольного
четырехугольника являются вершинами параллелограмма.
5.11, Доказать, что в произвольном четырехугольнике)
а) средине линии, пересекаясь, делятся пополам; б) отрезок,
соединяющий середины диагоналей, проходит через точку
пересечения средних линий и делятся в этой точке пополам.
Решение ряда задач основано па использовании формулы
ОМ = -g- (ОА + ОВ + ОС),
(2)
где А, В, С-
произвольные точки, не лелсащие на одной
прямой; М — центр тяжести
треугольника ABC; О —
произвольная точка,
Пример 5.4.' Пусть
'ABCDEF—произвольный
шестиугольник н U, V, W, X, Y, Z —
середины его сторон, Доказать,
что центры тяжести
треугольников UWY и VXZ совпадают
(рис-14.12).
Решение. Так как точки
— середины сторон шестиугольника, то
2
У
Рис 14.12
Р, V, W, X, Y я Z
ОУ=4-(0$ + о!), о^ = 4-(ОВ + ОС).
OW =-^(OC + ODh
OX = ±{OD + OE), OY^l(OE+OF), 02. = 1 {OF + Ш),
где О — произвольная точка. Обозначая через М и N центры
тяжести треугольников UWY и VXZ, инеем по формуле (2)^
ОМ — -^{OU + OW +ОГ)
^{ОА + ОВ+ 05 + 00 + 0% + OF),
0~H^l.(OV + OX+6Z).
-= j {OA + OB + Of + OD + OB + Op),
§ в. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ 431
Таким образом, ОМ = ОЛГ, откуда следует, что точка М
совпадает с точкой N.
5.12. Дан треугольник ABC. Доказать, что равенство ОА +
—»• —*
+ ОВ + ОС =■ 0 нмеет место в том и только том случае, когда
О —центр тяжести треугольника ABC.
5.13. а) Пусть М в N — центры тяжести треугольников ABC
н DEF, Доказать, что
А~В + 'ВЁ + Ср'=ШЫ.
б) Пусть А, В, С, D, E, F — произвольные точки плоскости.
'Доказать, что
lB+BE-{-CF=AE+BF+CD.
5.14. Точка М— центр тяжести треугольника ABC. Доказать,
что cl+cI = 3CM.
5.15. Через центр тяжести треугольника ABC проведена
прямая I, пересекающая стороны AC a ВС соответственно в точках
Р a Q. Доказать, что
IPCI"1" \Qp\ -ь
5.16. Вершины Л|, В,, О, треугольника ABC принадлежат
соответственно сторонам А,, В| и С{ треугольника ABC, причем
центры тяжести обоих треугольников совпадают. Доказать, что
точки Ai, Bi и Ci делят стороны треугольника ABC в равных
Отношениях.
При решении задач, связанных с вычислением отношения
площадей некоторых плоских фигур, используется следующее
свойство площадей треугольников. Если площадь треугольника
ABC равна S и на сторонах АС и ВС этого треугольника'
выбраны соответственно точки М а N так, что
\CM\:\CA\=-klt \CN\:\CB\ = k„,
то площадь треугольника MCN равна kik°S.
Пример 5.5. В треугольнике ABC на стороне АВ взята
точка К так, что \ЛК\ : \ВК\ = 1:2, а на стороне ВС взята
точка L так, что \CL\ i \BL\ =2: 1. Точка Q —точка
пересечения Прямых AL н СК. Найти площадь треугольника ABC, если
известно, что площадь треугольника BQC равна 1.
Решение. Пусть АВ=а, ~$С*=Ь (рис 14.13). Так как
\BL\:\LC\= 1:2, то на основании сформулированного выше
свойства площадей получаем SBQi = 1/3, SLQc =■ 2/3,
432 ГЛ. Т4. МЕТОД КООРДИНАТ
Найдем отношение \QL\ ; \AL\, Прямая, проходящая через
точку L параллельно стороне АС, пересечет сторону АВ в тоЧ«
—* 2
Ке М, при этом AM : MB = 2:1 и AM = "3" е. Прямая,
проходящая через точку L параллельно стороне АВ, пересечет сторону,
'АС в точке N, прн этом AN 1NC =1:2 и А N = у 6. Отсюда
С —* 2 1
х/Л\\
у' уШлУД Так как векторы AQ п /1L коллннеар-
N/—yLl~\_i_Ai llbI (точки A, Q, L лежат на одной
/^^^—^-Ll \\ прямой), то
^Q = u/it=.-|-(2a+6). (*)
Аналогично для точки /< можно показать, что
3
C~K~2rCA + ±-СВ*=\(а-Щ,
CQ = ХСК = у (а - 36).
Но JQ = АС + CQ. откуда
-|(2«+6) = 6 + -|(а-36).
Из условия едннственностн разложения вектора по двум иекол-t
линеарным векторам a'*« Ъ получаем систему уравнений 2ц = Я,
ц = 3 — ЗЯ, из которой находим |i =• ЗД.
Теперь можно найти отношение \QL\ i \AL\. Имеем
\QL\ _ \AL\-\AQ\ _ \AQ\
\AL\ \AL\ ~ \AL\'
IQiI 4 sARr
и no равенству (*) , ., , = 1 — ц = —. Отсюда -■"'■ =.
IA/-I ' •* ьовс
17 о .
= -у-^— — т н так как Sqbc =в '■ т0 нскомая площадь
треугольника равна 7/4.
Ответ. 7/4.
S.17. В треугольнике ABC, площадь которого равна 6, на
стороне АВ взята точка К, делящая эту сторону в отношении
\АК\ : \ВК\ =» 2: 3, а на стороне АС —точка L, делящая АС
в отношении \AL\ ; \LC\ *=. 5; 3, Точка Q пересечения прямых
§ 6. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
433
■С/С и BL отстоит от прямой Л В на расстояние 3,5. Найти длину
•Штороны АВ. s
5.18. Дай треугольник ABC. На сторонах АВ и ВС взяты
точки М и N соответственно; \АВ\ = 5|ЛЛ1|, \ВС\ = 3|ВЛГ|.
Отрезки AN н СМ пересекаются в точке О. Найти отношение
площадей треугольников О АС и ABC.
5.19. Точка К делнт медиану AD треугольника А ВС в
отношении 3: 1, считая от вершины. В каком отношении прямая
делнт площадь треугольника ABC?
5.20. На каждой медиане треугольника взята точка,
делящая медиану в отношении 1 :3, считая от вершины. Найти
отношение площади треугольника с вершинами в этих точках к
площади исходного треугольника.
Решение некоторых задач предполагает использование
вектора с, коллннеарного биссектрисе угла между векторами а н 6.
Удобным представлением пектора с является следующее;
—г5т+-гтг _?
5.21. В треугольнике ABC даны стороны а, Ь, с. Найти АА},
где AAi — биссектриса внутреннего угла А треугольника.
5.22. В треугольнике ABC медиана BD пересекается с
биссектрисой AF в точке О. Отношение площади треугольника DOA
к площади треугольника BOF равно 3/8. Найти \АС\ : \АВ\.
5.23. В треугольнике ABC биссектриса АА\ делит сторону ВС
в отношении \BD\ : \CD\ = 2 ; 1. В каком отношении медиана
СЕ делнт эту биссектрису?
5.24. Биссектрисы AD и BE треугольника ABC пересекаются
в точке О. Найтн отношение площади треугольника ABC к
площади четырехугольника ODCE, зная, что \ВС\ = а, \АС\ = Ь,
\АВ\=с. ' v
Решение некоторых задач основано на использовании
следующего векторного соотношения. Если А, В, С, D — четыре
точки, принадлежащие одной плоскости, а О — произвольная
точка пространства, то
00 = аОЛ + 0В+(1 — а-$)ОС, (4)
где ос, р е R.
5.25. Дан параллелепипед ABCDAtBfiiDi. Плоскость пере-
секает прямые АВ, AD, ААЬ АС] соответственно в точках Вв,
DB, Ав, Св. Доказать, что если ACB — XiAC{, ABB = X2ABU ADB=
= Я3Л£»|, ЛЛ0=>Л4ЛЛ,, то
434 ГЛ. 14. МЕТОД КООРДИНАТ
5.26. Точки К, L, М, N взяты соответственно на сторона*
ОА], А\Аг, АгАъ, А30 неплоского четырехугольника OAiAjAt,
причем
ОК = аКА, ~А~Х = §LA2, A~^M=\MA3, А^ = 6ЛГ0.
Доказать, что для принадлежности четырех точек К, L, М в N
одной плоскости необходимо и достаточно выполнение равенства
аруб = 1.
5.27. Даны два треугольника AiAjAt н AiA&At, не лежащий
. в одной плоскости. Доказать, что векторы MN, PQ и RS
компланарны, если М, N, Р, Q, R и S — середины отрезков AiAz,
А^Аь, <42Лз, /Ma. A3Ai, ЛЙЛ, соответственно.
5.28. Даны два треугольника ABC н /lifliCt, не лежащие в
одной плоскости; М и N — середины сторон АС и ВС, a Mi и
Afi —середины сторон AtC, n BtCi. Доказать,что &стАВ = А\В'\,
то векторы ММХ, NNt н СС\ компланарны.
5.29. Даны две скрещивающиеся прямые m и п. На
пряной m даны точки Р, Q, R, а на прямой я — точки Pt, Qj, Rt,
причем PQ = kPR, PiQi = kPtR,. Доказать, что прямые PPt,
QQt, RRi параллельны одной плоскости.
При решении задач, связанных с отношением объемов частей
тетраэдра, образующихся при сеченпн его некоторой плоскостью,
часто используется следующее утвержде-
ние: еелн объем тетраэдра ABCD равен
V п на его ребрах DA, DB, DC взяты
соответственно точки М, N, Р так,
^что
|Z>MI = ft,IZM|, \DN\*=k2\DB\,
\DP\ = k3\DC\,
то объем тетраэдра MNPD равен
ktkikaV.
Пример 5.6. Плоскость проходит
через вершину А основания
треугольной пирамиды SABC и делнт пополам
медиану SK треугольника SAB, а
медиану SL треугольника SAC пересекает в такой точке D, что
2\$D\ «= \DL\, В каком отношении эта плоскость делнт объем
пирамиды?
Решение. Обозначим SA = a, SB = Ь, SC = с (рис 14.14).
Очевидно, что' k\
= 1. Пусть SM = ft8&, SN = k3c, где М н
5 5. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ 435
N — точки пересечения плоскоств сечения с ребрами SB в SC
соответственно. Найдем ka и fea- Для этого воспользуемся
равенствами
Обозначая SAf = fe»ft, согласно (4) вектор SM можно
представать в впде
SM = aa + -J (a + 6) + -J-(l—o~p)(a + e).
Используя едннственность разложения вектора по трем неком-
плаиарным векторам, получим систему уравнений
из которой находим кг = 1/3.
Аналогично из уравнений
SN-.
к3с, SA?=(|-a + -i. + -i-)fl + {6+b-(l-a-P)<
находим къ = 1/5.
На основании сформулированного выше утверждения полу,
чаем
VSAMN= ' "3"*"5 SABC
п, следовательно, объем оставшейся части пирамиды равен
14
7=" ^ддс* Таким образом, искомое отношение объемов равно
1 : 14.
О т в е т. 1:14,
5.30. В трехгранном угле с вершиной S проведены
параллельные сечения ABC и AiBiCi. Обозначая через V, Vi, Vi, V*
соответственно объемы тетраэдров SABC, SAiBiCu SAiBC,
SABiCi, показать, что
Vt^tfW^Vl н Vt.Vt=V-Vt.
5.31. Дана правильная четырехугольная пнрамнда SABCD.
Через середины ребер АВ, AD н CS проведена плоскость. В
каком отношении эта плоскость делит объем пирамиды?
6.32. Объем пирамиды ABCD равен 5. Через середины ребер
AD н ВС проведена плоскость, пересекающая ребро CD в
точке М, При этом отношение длины отрезка DM к длине отрезка
436 ГЛ. М. МЕТОД КООРДИНАТ
МС равно 2/3. Вычислить площадь сечения пирамиды указанной
плоскостью, если расстояние от нее до вершины А равно 1.
6.33. Плоскость пересекает боковые ребра SA, SB и SC
трехугольной пирамиды SABC в точках К, L и М соответственно,
В каком отношении делит эта плоскость объем пирамиды, если
известно, что \SK\ : \КА\ = \SL\ ; \LB\ = 2, а медиана SN
треугольника SBC делится этой плоскостью пополам?
6.34. В треугольной пирамиде SABC все ребра равны. На
ребре SA взята точка М так, что SM = МА, на ребре SB —
точка N так, что 3SN = SB. Через точки М и N проведена
плоскость, параллельная медиане AD основания ABC. Найти
отношение объема треугольной пирамиды, отсекаемой от исходной
проведенной плоскостью, к обьему пирамиды SABC.
§ 6. Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов называется
произведение длин этих векторов ва косинус угла между векторанш
a.6=|o|-|6|cos(0). (О
Необходимым и достаточным условием перпендикулярности двух
ненулевых векторов является равенство нулю их скалярного пронзвеч
дення: "' . ■ -
а- 6=0, (2)
Если <р=(о, 6), то
при 0<q><-^- e-6>0; пря-у<ф<л о-6<0. (3)
Скалярное произведение вектора на себя равно квадрату его длины)
Ч aa=>a'=|a|*. (4)
Свойстве скалярного произведения:
ab — b-a (коммутативны!! закон);
(\а).&=>Я. (aft) (ассоциативный закон);
а-(Ь + с)=*а-Ь + а-с (дистрибутивный закон),
Пример 6.J. Известно, что векторы За — ЪЬ и 2а + Ь
перпендикулярны между собой и векторы я + 46 н -^а + 6 также
взаимно перпендикулярны, Найти угол между векторами а и Ь.
Решение. По условию задачи
(За-56)-(2а+6) = О,
(о + 46).(-о + 6)=0.
Отсюда следует, что
6а2 —7а-6-5&а = О, м
— ef-3o'fc+462=«0,
§ 6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 437
т, е. получены два уравнения относительно трех неизвестных в*,
Ы и ab. Согласно (1) косинус угла между векторами а и Ь
вычисляется по формуле
№ уравнений (*) находим
Возводя обе части равенства (**) в квадрат и подставляя
значения (***), получаем
'хч- 192
cosS(fl. *) = ___,
пли
cos (<р6) = ТТгГ" С05(а^) = -7^Г-
^ I9 ( 19 ^
Ответ, arccos ;=- или arccos I ■=■ I.
5 У 43 Ч 5 V43 /
6.1. Дано; |я| = 3, [ 61 •=• 4, (в, 6) = 2я/3. Вычислить:
a) fl*; б) (а + 6) *; в) (За - 26) (о + 26).
6.2. Зная, что |а|=3, \Ь\ = 1, |е| = 4~л а + 6 + е==Д
вычислить^ • Ь + Ь -т + с ■ а.
6.3. Какому условию должны удовлетворять векторы а и Ь,
чтобы имело место равенство |я + Ь| = \а — Ь\?
6.4. Доказать, что вектор (ab)c—(ac)b перпендикулярен
вектору а.
6.6. Доказать, что если а, Ъ, с — произвольные векторы,
причем а ие перпендикулярен с, то существует такое число к, что
векторы я и b+kc перпендикулярны друг другу. Найти k.
Если векторы a, b н с являются сторонами ABC, то из
равенства а + b + с = 0 следует равенство
с* = а2 + Ьг — 2а • 6,
представляющее собой векторную запись теоремы косинусов.
Задачи б.б—6.21 решаются с использованием векторной записи
теоремы косинусов.
6.6. В треугольнике ABC проведена медиана CCi. Доказать,
что если \ВС\ > \АС\, то угол СС,В тупой.
, 6.7. Доказать, что угол С треугольника ABC будет острым,
прямым или туиым в завнсвмоста от того, ■ будет ля медиана
438 ГЛ, 14. МЕТОД КООРДИНАТ
CCi, проведенная из вершины С, больше, равна иди меньше
6.8. а) Найти длину медианы \AD\ треугольника АВСУ 8ная
длины сторон |ДС| =6, \АВ\ =с и величину угла А.
б) Найти длину биссектрисы |Л£| треугольника, зная длины
сторон \АС\ = Ь, \АВ\ = с и величину угла А.
6.9. Известны стороны треугольника ABC. Наптш
а) длину медианы |AD| = m„;
б) длину биссектрисы \АЕ\ = /„.
6.10. В треугольнике ЛВС угол В прямой, медианы \AD\ и
\ВЕ\ взаимно перпендикулярны. Найти величину угла С.
6.11. В треугольнике ABC на сторонах ВС н АС
соответственно выбраны точки D в Е так, что \BD\ = \DC\, \AE\ =
— 2|С£|. Найти |ВС|:|ЛВ|, если известно, что AD±BE и
ЛВС = 60°.
в.12. В четырехугольнике ABCD угол при вершине А равен
120°, а диагональ АС является биссектрисой этого угла.
Известно, что | НС | =— | /IB | = -— | /ID |. Найти косинус угла
между векторами ВА и CD.
6.13. Доказать, что если для треугольника ABC имеет место
равенство а2 + Ьг = 2с2, то ата + Ьть = 2шс, где та, п%ь, тс —
длины медиан треугольника, а, 6, с —длины его сторон.
6.14, В треугольнике ABC проведен отрезок А\В\, параллель"
ный'стороне АВ, где точки Л» н Bt лежат соответственно на
сторонах АС и ВС. Показать, что если |i4Bt|»= \BA{\, то
треугольник ABC равнобедренный.
6.16. В треугольнике ABC проведены медианы AAi и BBi.
Доказать, что если 6 + (ДХ В~В{) = 180°, то | С А |2 + | СВ |* =
= 2|ДВ|2.
6.16. Доказать, что если G—центр тяжести треугольника
ABC, a 0 —некоторая точка пространства, то
10 А |» + \ОВ |s + | ОС |2 = 31OG |» + | AG |2 + | BG |2 + ICG |«
(георлео Лейбница).
6.17. Доказать, что если О — центр описанной около
треугольника ABC окружности и Н — его ортоцентр, toi
1) Off = 04 +ОВ + ОС;
2) | Off р = 9Д8 - (в2 + 6а + с»);
3) 1ЛЯ|=.ЗД1совЛ|.
S 6. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 439
6.18. Доказать, что центр О описанной окружности, центр
тяжести треугольника G и ортоцентр Н произвольного
треугольника принадлежат одной прямой (прямая Эйлера), причем
\OG\ :\GH\ = 1:2.
6.19. Доказать, что расстояние от центра О окружности,
описанной около треугольника ABC, до его центра тяжести О
определяется формулой
\OG\*~R*—^(aa+b* + c*).
6.20. Доказать, что если Q — произвольная точка, Н —
ортоцентр н О —центр описанной окружности треугольника ABC, то
0.21. В окружность вписан четырехугольник A BCD.
Доказать, что если |ЛВ|г+ \CD\Z = 4/?г, где R — радиус описанной
окружности, то диагонали четырехугольника перпендикулярны.
С помощью скалярного произведения можно доказать
справедливость некоторых неравенств для тригонометрических
функций углов треугольника.
Пример 6.2. Доказать, что для всякого треугольника ABC
выполняется неравенство
cos 2Л + cos 2B + cos 2C > — 3/2.
Решение. Пусть точка О — центр описанной около
треугольника ABC окружности с радиусом, равным R. Очевидно,
что (ОА + ОВ + ОС)1 > 0. Раскрыв скобки, получим
ОА3 + 20%-ОВ + ОВ2 + 20В -ОС + 20С -ОД + ОС" 5*0.
Так как центральный угол, образованный радиусамн ОА и ОВ,
вдвое больше угла С, вписанного в окружность, то
ОА ■ ОВ = fl2 cos 2C.
Аналогично
ОС.ОА = R2cos 2B, о1-ОС'=Л2соз2А
Так как ОД* = ОВ2 = OCt='Rtl то последнее неравенство
принимает вид
2Я2 (соз 2А + cos 2В + cos 2C) + ЗЯ3 > 0,
нлн
cos 2/4 + cos 2B + cos 2C > — 3/2,
что а требовалось доказать.
440
ГЛ. 14. МЕТОД КООРДИНАТ
6.22. Доказать, что для углов всякого треугольника ABC вы*
полияется неравенство
cos A + cos В + cos С < 3/2.
6.23. Доказать, что для углов всякого треугольника ABQ
выполняется неравенство
sin2 A + sin2 В + sin2 С < 9/4.
6.24. Доказать, что для углов всякого треугольника ABG
справедливо неравенство
. cos 2/1 + cos 2B — cos 1С < 3/2.
Прн каком условии неравенство обращается в равенство?
6.25. Доказать, что для любого трехгранного угла с пло*
скимн углами а, (3, у выполняется неравенство
cos о + cos р + cos y > —3/2.
ГЛАВА 15
КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ
ВЕРОЯТНОСТЕЙ
§ 1. Размещения. Сочетания. Перестановки
Пусть дано множество, состоящее-нз л различных элементов
{at,..., Ял}. Выберем из него множество, содержащее г
элементов, т. е. сделаем выборку объема г. Выборки могут
отличаться друг от друга как составом, так и порядком
расположения элементов. Если допустить, что среди элементов выборки
есть одинаковые, то объем выборки в отдельных случаях может
превышать объем исходного множества.
Примером таких выборок служат телефонные номера. Пусть
помер состоит нз 12 цифр, а телефонный диск содержит 10 цифр;
тогда при наборе номера осуществляется выборка 12 элементов
из множества, содержащего 10 элементов. Так как диск после
набора каждой цифры возвращается в исходное положение, то
цифры телефонного номера могут повторяться. Это означает, что
выборка может содержать одинаковые элементы.
Число различных выборок объема г, элементы которых могут
повторяться, нз исходного множества, содержащего л различных
элементов, равно л'. Если элементы выборки ие повторяются, то
ее объем не может превысить объем исходного множества. Число
различных выборок объема г с неповторяющимися элементами из
исходного множества объема л равно
< = «(«-1) ... (п-г+1); (1)
Ага указывает число различных размещений нз л элементов по
г позициям. Если л = г, то различные выборки отличаются
только порядком элементов. Такие выборки называются переста*
новками из л элементов. Число различных перестановок
Р„=,п(п-1) ... 1 = л1 (2)
В некоторых задачах иорядок элементов в выборке несуще»
>етвен. Например! при выборе трех человек в президиум собранна
442 ГЛ. 15. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕН
состоящего нз 200 человек, или при покупке в магазине пяти
наименований продуктов из имеющихся там 100 наименований
продуктов. В этом случае выборки одного состава (т.е.
выборки, элементы которых совпадают) считаются неразличимыми.
Число выборок различного состава объема т нз множества
объема п равно;
Агп л(л- 1)... (n-r+1) п\
Гт = - = - - = • (Я\
°п Рг г! г!(п-г)!' w
Стя называется числом сочетаний из л элементов по г.
Пример. 1.1. Буквы азбуки Морзе образуются как
последовательность точек и тире. Сколько различных букв можно
образовать, если использовать 5 символов?
Решен и е. Исходное множество в этой задаче состоит из
двух элементов: точки и тире. Так как используется пять
символов, то выборка содержит пять элементов, которые могут поато-
ряться. Таким образом, число различных выборок, каждая нз
которых представляет какую-нибудь букву, равно 2s = 32.
Ответ. 32 буквы.
1.1*. Сколько существует различных семизначных
телефонных номеров?
1.2*. Сколько существует различных телефонных номеров,
если считать, что каждый номер содержит не более семи цифр
(телефонный номер может начинаться с нуля)?
1.3. Пусть буквы некоторой азбуки образуются как
последовательности точек, тире к пробелов. Сколько различных букв
можно образовать, если использовать 5 символов?
1.4. В некотором государстве нет двух жителей с
одинаковым набором зубов. Какова может быть наибольшая численность
населения государства (наибольшее число зубов 32)?
1.5. Пусть pt, ..., рт — различные простые числа. Сколько
делителей имеет число <7 = Р['Рг2 ••• Рт"> ГДе *р ••■ ♦ *т~~
некоторые натуральные числа (делители 1 и д включаются)?
1.6. Сколько существует различных семизначны; телефонных
номеров, если в каждом номере нет повторяющихся цифр?
1.7*. Сколько существует различных исходов эксперимента,
связанного с п бросаниями монеты? (Исходы двух
экспериментов считаются различными, если очередность выпадения гербов в
ртих экспериментах не совпадает с очередностью выпадения
Дифр.)
1.8. Сколько существует таких перестановок семи учеников,
пра которых три определенных ученика находятся рядом друг с
другом?
§ I. РАЗМЕЩЕНИЯ. СОЧЕТАНИЯ. ПЕРЕСТАНОВКИ 443
1.9. На книжной полке стоит собрание сочинений в 30 томах.
Сколькими различными способами их можно переставить, чтобы:
в) тома 1 и 2 стояли рядом;
б) тома 3 и 4 рядом не стояли?
1.10*. Сколько различных аккордов можно взять на десяти
выбранных клавишах рояля, если каждый аккорд содержит от
трех до десяти звуков?
1.11*. Собрание из 40 человек избирает председателя,
секретаря и 5 членов некоторой комиссии. Сколько различных
комиссий может быть составлено?
Если требуется определить число различных выборок,
составленных из нескольких разнородных групп элементов, то
удобно считать, что элементы каждой группы выбираются из
своего исходного множества, т. е. что число различных исходных
множеств совпадает с числом различных групп, элементы
которых представлены в выборке. Так, например, пусть требуется
составить сборную команду восьми областей, состоящую из 24
спортсменов, в которую от каждой области войдет 3 спортсмена.
Эта выборка содержит 24 элемента, которые набираются из
восьми исходных множеств, причем из каждого отдельного
множества выбирается 3 элемента.
Пример 1.2. В урне т белых н п черных шаров.
Сколькими способами можно выбрать из урны г шаров, из которых
белых будет к штук? (Считается, что шары каждого цвета
различны, например, пронумерованы.)
Решение, k белых шаров из т белых шаров можно
выбрать С„ числом способов, а оставшиеся г — k черных шаров
из группы в я штук — числом способов Сг~т. При этом
каждому способу выбора k белых шаров соответствует С£ '
различных способов выбора черных. Следовательно, общее число
различных выборок равно произведению £*,£„"*.
Ответ. СктСг-к.
1.12. Из 10 роз и 8 георгинов нужно составить букет, содер»
Ш1ЩИЙ 2 розы и 3 георгина. Сколько можно составить
различных букетов?
1.13. В колоде 36 карт, из них 4 туза. Сколькими способами
можно сделать б карт так, чтобы среди них было 2 туза?
1.14. Комплексная бригада состоит из 2-х маляров, 3-х
штукатуров и 1-го столяра. Сколько различных бригад можно
создать нз рабочего коллектива, в которой 15 маляров, 10 Штука*
туров н б столяров?
444 ГЛ. 15. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.15. В лотерее «Спортлото» разыгрываются в из 48 видов
спорта. Главный выигрыш падает на ту карточку, где угаданы
правильно все 6 номеров. (Каждый вид спорта указан под
некоторым номером.) Меньшие призы достаются тем, кто угадал 5,
4 н даже 3 номера из 6. Сколько может быть различных
карточек, где угаданы: а) 5, б) 4, в) 3 из б номеров, если на каждой
карточке произвольно зачеркиваются б номеров? (Карточки, нз
которых вычеркиваются один н те же номера, считаются
одинаковыми.)
1.19. Сколько окружностей можно провести через 10 точек,
нз которых никакие четыре ие лежат на одной окружности и
никакие три не лежат па одной прямой, если каждая окружность
проходит через три точки?
1.17*. Из колоды, содержащей 52 карты (нз них 4 туза),
вынули 10 карт. В скольких случаях среди этих карт будет хотя
бы один туз?
1.18. Сколькими способами нз колоды в 52 карты (нз них
4 туза и 4 короля) можно вынуть 6 карт, содержащих туза н
короля одной масти?
1.19. В теннисном турнире участвуют 10 мужчин и 6
женщин. Сколькими способами можно составить 4 смешанные пары?
1.20*. Сколько всевозможных четырехзначных чисел можно
составить нз цифр 0, 1, 2, 3, 4, 5, 6, 7 так, чтобы в каждом
числе содержалась одна цифра 1?
1.21. Сколько всевозможных четырехзначных чисел можно
составить из цифр 0, 1,2, 3, 4, 5, б, 7 так, чтобы в каждом числе
содержалась цифра 1? (Цифры в числе не должны повторяться.)
ч
§ 2. Перестановки и сочетания с заданным числом
повторений
Рассмотрим выборки, отдельные элементы которых
повторяются заданное число раз. Пусть выборка состоит нз т
элементов, среди которых некоторый элемент (будем для
определенности считать его первым) повторяется ni раз, другой
(второй) — я» раз и т. д., А-fi элемент повторяется л* раз. Очевидно,
что
Л| + "а + • • • + «ft = m.
Набор натуральных чисел (ni, ,.., п») будем называть
составом выборки. Состав выборки определяет, из скольких
различных групп элементов состоит выборка и сколько одинаковых
■элементов каждой группы в ней присутствует. Так, например,
выборка состава (1, 2, 4) состоит из трех групц элементов, при-
§ 2. СОЧЕТАНИЯ С ЗАДАННЫМ ЧИСЛОМ ПОВТОРЕНИЙ 445
чем из первой группы в выборке присутствует 1 элемент, нз
второй — 2, а из третьей — 4 одинаковых элемента.
Число различных выборок одного состава называется числом
перестановок из m элементов с заданным числом повторение
ni, ..., л*. Это число вычисляется по формуле
/ .ml ...
р™("1 "ft)=n1l...«fe|- <!>
Пример 2.1. Требуется составить расписание отправления
поездов на различные дни педели. При этом необходимо, чтобы!
3 дня отправлялись по 2 поезда в день, 2 дня — по I поезду в
день, 2 дни — по 3 поезда в день. Сколько можно составить
различных расписаний?
Решение. Количество поездов, отправляемых в день
(числа I, 2, 3), —это три группы одинаковых элементов, нз которых
должна быть составлена выборка. При этом в расписании на
неделю число I повторяется 2 раза, число 2 повторяется 3 раза
н число 3 повторяется 2 раза. Число различных расписании
равно
р<2'3'2)~-2Тт!пГ=210-
Число различных составов выборки объема т, образованной
из k групп одинаковых элементов, равно *)
7"" — г"» = (k + m— 1)1 .„
^k-^k+m-i^ ml (ft-1)1 ' w
Пример 2.2. R шаров следует разместить по k ящикам.
Сколькими способами это можно сделать? (Считается, что
вместимость ящика достаточна для всех шаров.)
Решение. Для удобства будем считать, что имеется k
ящиков, в каждом из которых число шаров может меняться от О
до R. Тогда, считая, что каждый ящик соответствует группе
однородных элементов, имеем k различных групп, нз которых
набирается выборка с повторением объема R. Различные способы
размещения шаров соответствуют различным составам указанной
выше выборки, т. е.
р (R + k-l)l
cR+A-l"" R\(k~l)l •
') Формулу (2) можно получить, если подсчитать число
перестановок с повтореннямп нз m + * — I элементов, где т — число элементов
исходной выборки, a ft — 1 — число граянц, отделяющих группы
одинаковых элементов.
446 ГЛ. 1Б. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
2.1. Сколько различных комбинаций букв можно получить из
букв слова «МИССИСИПИ»?
2.2*. Сколько различных наборов по 8 пирожных в каждом
1ГОЖИО составить, используя 4 сорта пирожных?
2.3*. Лифт с семью пассажирами останавливается иа 10
этажах. На каждом этаже может выйтн определенное число
пассажиров (от нуля до семи). Сколько может быть различных
способов освобождения лифта? (Способы различаются только
числом людей, вышедших иа данном этаже.)
2.4.*. При игре в бридж между четырьмя игроками
распределяется колода карт в 52 листа по 13 карт каждому игроку.
Сколько существует различных способов раздать карты?
2.5*. Сколькими способами при бросании 12 игральных
костей каждое из значений 2, 3, 4, 5, 6 выпадает дважды?
2.6*. Имеются т белых в п черных шаров, причем m > iu
Сколькими способами можно все шары разложить в ряд так,
чтобы никакие два черных шара не лежали рядом?
2.7*. При бросаинн монеты будем считать успехом
выпадение герба и неудаче» выпадение цифры. Сколько различных
испытаний могло привести к 52 успехам при 100 подбрасываниях
монеты? (Испытанием считается серия опытов из 100 бросаний;
два испытания считаются различными, если не совпадают
результаты хотя бы двух бросаний.)
2.8*. 12 ученикам выданы 2 варианта контрольной работы.
Сколькими способами можно посадить учеников в два ряда так,
чтобы у сидящих рядом ие было одинаковых вариантов, а у
сидящих друг за другом был одни н тот же вариант?
2.9*. На книжной полке стоят кинги по математике и по
логике—всего 20 книг.4 Доказать, что наибольшее количество
вариантов комплекта, содержащего 5 книг по математике н 5 книг
по логике, возможно в том случае, когда число книг на подке
по каждому предмету равно 10.
§ 3. Бином Ньютона
Натуральная степень суммы двух величин вычисляется по
формуле
(а + Ь)я ~ С»ап + Clnan~lb + С^"V + ...
... + С%ап-тЬт + ... + С%Ьп. (1)
Правая часть формулы называется разложением степени бинома.
Коэффициенты С„ = ■■.-. _ .. называются биномиальными
коэффициентами, Общий вид слагаемых в правой части формулы
§ 3. БИНОМ НЬЮТОНА 44/
[(!) обычно записывается в виде*)
Гк —С*в*-*Ь* *=0, 1, 2, .... п. ■ (2)
.Число всех слагаемых равно «+ 1.
Пример 3.1. Найтн член разложения [х-\—j-J , не со*
держащий х (т. е. содержащий х в нулевой степени).
Решение. Согласно формуле общего члена (2) имеем
rA = <V°-*(-Ly
По условию число k должно удовлетворять уравнению
10 — k — 4£=0. (»)
Единственным корнем уравнения (+) является к = 2. Таким
образом, искомым будет второй член разложения:
Т2 = Ст0д: -jj- = С10 = 45.
Ответ. 45.
Пример 3.2. Найти шестой член разложения (gU*-f-*J/S)ei
если бниомиальньш коэффициент третьего от коаца члена ра<
вен 45.
Решение. Найдем сначала степень бинома. Согласно
условию задачи число я удовлетворяет уравнению
сп а=сг»=" 2 '
корнями которого являются П\ = 10, пг = —9. Так как Пг'=—9
не является натуральным числом, то степенью бинома будет
п = 10, следовательно, шестой член разложения представляетсА
в виде
Ответ. 2!0j/2*3.
3.1*. Найти сумму биномиальных коэффициентов, если ств«
пень бинома равна 10.
3.2. Найти номер члена разложения (* + *~*)*^ не
содержащего х.
"J Используют также формулу
Th—Cfi* * ■— Jf5 : <* * *
448 ГЛ. 16. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ЬЕРОЯТНОСТЕЙ
3.3*. Найти члеи разложения бинома \л/х + ух~3) , со-
держащий *в'6, если девятый член разложения имеет наибольший
коэффициент.
3.4. Найти член разложения I (- —j- J , который
содержит х2.
З.б*. Доказать, что сумма всех коэффициентов разложения
(2у — х)к при любом натуральном k равна I.
3.6. Биномиальные коэффициенты второго в девятого членои
разложения (5*~3/z— х1/3)" равны. Найти член разложения, ив
содержащий 'х.
( I 1 \100
3.7**. Найти наибольший члеи разложения |-п~ + -<г) •
3.8. Найти номер наибольшего члена разложения
3.9*. Сумма биномиальных коэффициентов разложения
равна 1024. Найти члеи разложения ( *2 Н J , содержащий х в
11-й степени.
3.10*. Доказать, что если степень бинома л — нечетное
число, то сумма биномиальных коэффициентов членов, стоящих на
четных местах, равна сумме биномиальных коэффициентов
членов, стоящих иа нечетных местах.
3.11. В разложении бинома
определить плен, содержащий а3, если сумма биномиальных
коэффициентов членов, стоящих на нечетных местах, равна 2048.
3.12. Найтн наибольший член разложения {л/5 -f V2~)2°«
(I \m
2* -J j- I не
содержит x. При каких х это слагаемое равно вторвму слагаемому
разложения (1-f-*3)30?
3.14*. При каких положительных значениях х наибольшим
слагаемым в разложении (5 + Зж)10 является четвертое?
3.15*. Найтн *, прн котором пятидесятый члеи разложения
(х + у) '00 имеет наибольшее значение, если известно, что
(х + у) = 1, *>0, {/>0.
3.16. Найти х, при котором А-й член разложения (* + {/)"
имеет наибольшее значение, если х -f- у = 1 и х >. 0, у ;> 0,
§ 3. БИНОМ НЬЮТОНА . 449
Пример 3.3. В разложении бинома
W3+V2)8
найти члены, не содержащие иррациональности.
Решение. Воспользуемся формулой общего члена
разложения
Тк = С\ № ?~к Ш" = С* • З^й7.
-ййяученное выражение будет рациональным, если —=— н -g—■
целые числа. Очевидно, что число k следует искать среди четных
чисел, меньших 5. Непосредственной проверкой убеждаемся* что
единственное значение, которое оно может принимать, равно
двум. Следовательно, в разложении бинома есть только один
.член удовлетворяющий сформулированному условию:
Тг = С\-3-2 = 6. -^- = 60.
Ответ. 60.
В. 17. Найти члены, ие содержащие иррациональности в раз-
/5 7 \М
йожеини W3~ + V2~/ .
3.18*. Сколько рациональных членов содержится в разложе*
( _ А Y00
ппн W2 + V3"/ ?
3.19**. В разложении бинома J V* Н \— J первые трв
V 2V* /
коэффициента образуют арифметическую прогрессию. Найти все
рациональные члены разложения.
3.20*. Доказать, что
I - С", + С2„ - С*+ ...+(-!)" СЯ = 0.
3.21. Сравнивая коэффициенты при х о обеих частях
равенства
(!+x)m(!+*)" = (! + *)m+n,
доказать, что
/■*fe/*»0 _!_/■*£—1/~*1 _1_ _1_ /^0/^Й . ^>Й
Vm+bn ьт -t- ... -f с„ьт = ьт+„.
&22. Воспользовавшись результатом предыдущей задачи,
найти сумму квадратов биномиальных коэффициентов. Доказать,
что сумма квадратов биномиальных коэффициентов равна' С"^.
16 А. Г. Цыпкдн, А, И, ПивскнЯ
450 ГЛ. !Б. КОМВИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
8.23*. Доказать, что справедлив© равенство
1 - 10С\п + !02С2„ - ю'С^ + ... - Ю2""'^ + W2" - (8!)п.
Некоторые формулы комбинаторики иожио получить,
дифференцируя или интегрируя ебе части разложения для (I + *)\
которое справедливо при всех х.
Пример 3.4. Доказать, что справедливо равенство
nC°n + (n-l)Cln+ ...+Cnn-t = n-2n~t.
Решение. Дифференцируя бваомиальаое разложение для
(I + х)л, имеем
{хп + ф"-1 +.. .+<*)' «= «.."-1 + (я -1) с^-Ч.-.+сГ1.
С другой стороны, справедливо равенство
l(t-t-x)nK=-«0-r-*)n"1.
Подставляя в тождество
п (!+ х)п~] =пхп~1 + (п-1) С\хп-2+ ... +CJ-1
значение х = I, нолучаем требуемое равенство!
п-2п~1 =пС°п + (п~ 1)С1п+ ... +С%-\
3.24. Доказать, что
п(п- 1)С° + (п- !)(л — 2)С^ + ... -f 2C£~a.
8Л6*. Доказать, что "
3.26*. Доказать, что
»С»-(п-1)С^ + (п-2)С2,-(«-3)С^+...
... +(_!)»-'С""1 =0.
3.27*. Доказать, что
С
^ С2. t-i)nC* (Ь п = 2/«
я п-1+"- 2 =1 _1_, «-=21+1.
*• п +1
3.28*. Упростить выражение Pi + 2P2+ ... + пРп>
3.29*. Доказать, что
СГП I /-.771 г г /".ГЦ , /".frt+l /-»/Л-Ы
„ т-ь„_1 -г- ... ть„_ю = ь0+1 — ья_ш.
азй. Доказать неравенство С^,+хС^,_х<(Са»)а.
§ i. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ФОРМУЛ КОМБИНАТОРИКИ 461
§ 4. Вычисление вероятностей событий
с помощью формул комбинаторики
Пусть в лотерее, где разыгрывается 10 билетов, принимает
участие 'несколько человек. На каждом билете пишется имя
одного из участников, после чего все <5илеты тщательно
перемешиваются. Затем наугад выбирают один билет, и тот, чье имя
записано на билете, получает приз. Спрашивается, каковы шансы
получить тгриз некоторому участнику лотереи? Если имя этого
участника написано только на одном билете, то у него один
шанс из десяти. Если на двух, то два то десяти, я т. д.
Извлечение любого билета с именем этого участника
считается благоприятным исходом. Число таких исходов, очевидно,
совпадает с числом билетов, па которых гшглсаио «го имя.
Шансы данного участника на выигрыш будут определяться
долей благоприятных исходов среди всех равиовозможных исходов
эксперимента. Для того чтобы найти эту долю, требуется число
благоприятных исходов разделить на число всех исходов
эксперимента.
При многократном проведении эксперимента его результаты
показывают, что отношение чисел исходов, ври которых данный
участник выигрывает, к числу всех «сходов эксперимента
оказывается близким к доле тех билетов, на которых написало имя
участника, среди всех билетов, разыгрываемых в лотерее.
Поэтому вероятностью выигрыша естественно считать отношение
числа благоприятных исходов к числу всех возможных исходов
эксперимента.
Подойдем теперь к понятию вероятности более формально.
Для этого введем следующее аире деление! будем называть
элементарным событием любой из равиовозможных исходов'
эксперимента (в приведенном выше примере элементарным исходом
будет извлечение одного нз билетов). Множество всех
равиовозможных неходов назовем пространством элементарных событий,
а каждое элементарное событие — точкой этого пространства (в
приведенном выше примере пространство элементарных событий
состоит нз 10 точек).
Совожушюсть элементарных событий, объединяющая вое те
■сходы, при которых происходят событие А, называют
множеством элементарных событий, благоприятных событию В. Вероят-
шастыо события А казывают отношение числа благоприятных
ему эиеигевтаряыж событий к чвелу всех возможных
элементарных событий. Если число исходов, благоприятных событию А,
ргвне га, в число воех точек, составяжнджих пространство
элементарных событий, равно п, то вероятность Р{А) события А
15*
452 ГЛ. 18. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
выразится дробью
Р(А)=т/п. . _. ж (1)
В задачах, где чвсло всех возможных элементарных событий
конечно, число элементарных событий, благоприятных событию
А, может быть найдено непосредственно.
Пример 4.1. В классе, состоящем из 20 учеников, 15 че-
л о век занимаются а математическом кружке; Какова
вероятность, что наудачу выбранный ученик окажется членом
математического* кружка? ' ■" ':г*' "•' Пъ
Решение. Пусть событие А состоит'в том,"'что Наудачу
выбранный ученик является членом математического кружка.
Тогда число элементарных событий, благоприятных событию А,
равно 15. Число всех элементарных событий в данном случав
равно 20. Следовательно, искомая вероятность равна
Р (Л) — 15/20 = 3/4,
Ответ. 3/4.
Пример 4.2, Бросают две игральные кости. Какое событие
более вероятно: сумма очков на выпавших гранях равна 11 или
сумма очков на выпавших гранях равна 4?
Решение. Поставим в соответствие исходу эксперимента
упорядоченную пару чисел (х, у), где * означает число очков,
выпавших иа первой кости, а у — иа второй. Пространство всех
элементарных событий состоит из множества пар (х, {/), Где л
и у црнинмают значения от 1 до 6. Число таких пар равно 36,
Событию А, состоящему в том, что сумма очков, выпавших йа
двух костях, равна 11, благоприятны два элементарных события,
которым соответствуют, пары (6, 5) и (5, 6). Событию В,
состоящему в том, что сумма очков, выпавшая на двух костях,
равна 4, благоприятны три элементарных события, которым
соответствуют пары (1, 3), (3, 1), (2, 2).
Вероятности событий А н В равны соответственно
Р (А) = 2/36 =«1/18 и Р (В) ■= 3/36 =. 1/12,
н, следовательно, событие В более вероятно.
4.1. Какова вероятность того, что наудачу вырванный листок
из нового календаря соответствует первому числу месяца? (Год
считается невнсокосным.)
4.2. Какова вероятность того, что наудачу выбранное число
от одного до двенадцати окажется делителем числа двенадцать?
_ (Единица считается делителем любого числа.)
4.3*. Какова вероятность того, что наудачу выбранное двул
8начное число делится иа 3?.
§ 4. ВЫЧИСЛЕНИЙ С ПОМОЩЬЮ ФОРМУЛ КОМБИНАТОРИКИ 453
4.4. Найти вероятность того, что наудачу выбранный член
последовательности С/„ «= п.2 + 1 (л «= I, 2, .... 10) делится на б.
4.6. В урне 10 белых шаров и 3 красных. Какова
вероятность вынуть из урны красный шар?
, 4.6**. Монету бросают три раза. Какое из событий более
вероятно: событие А — все трн раза выпала цифра, или событие
В—два раза выпала цифра н один раз герб? Подсчитать вероят»
-ностн этих событий.
4.7. Брошены, две игральные костн. Какова вероятность того,
что сумма очков на выпавших гранях равна 7?
.,. 4.8. Брошены две игральные кости. Какова вероятность того,
что сумма очков иа выпавших гранях четная?
4.,9. При перевозке 100 деталей, из которых 10,были
забракованы, утеряна 1 стандартная, деталь. Найти вероятность того,
что наудачу извлеченная деталь оказалась стандартной.
4.10. В условиях предыдущей задачи найти вероятность того,
что наудачу извлеченная деталь оказалась бракованной.
4.11*. В семье трое детей. Какова вероятность, что все они
мальчики? (Предполагается, что вероятиостн рождения мальчика
и девочки одинаковы.)
В некоторых случаях для непосредственного подсчета вероят»'
ностн события А удобно использовать формулы комбинаторики.
Пример 4.3. Найти вероятность того, что все учащиеся
в группе, состоящей из 40 человек, родились в разные дин года.
Решение. Все возможные неходы эксперимента
представляются различными выборками по 40 из исходного множества
рбъема 365. Прн этом выборка может содержать одинаковые
элементы (так .как любой день может быть днем рождения
нескольких человек). Следовательно, пространство элементарных
событий содержит (40)ses различных выборок. Благоприятным
событием будут соответствовать выборки, не содержащие одинаковых
элементов. Таких выборок А®5. Таким образом, искомая
вероятность равна Р(^) = Л^в/403№.
Используя формулы числа размещений, сочетаний,
перестановок, решить следующие задачи:
4.12. В урне л белых и m красных шаров. Какова
вероятность того, что наудачу взятые два шара окажутся красными?
4.13. Набирая номер телефона, абонент забыл трн последние
цифры н, помня только, что оин различны, набрал нх наудачу^
Какова вероятность, что он набрал нужные цифры?
4.14. К концу дня в магазине осталось 60 арбузов, нз кото»
рых 50 спелых. Покупатель выбирает два арбуза, Какова
вероятность, что оба арбуза спелые?
454 ГЛ. 15. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
4.15. В урне л белых, т черных, k красных шаров. Наудачу
вынимаются три шара. Какова вероятность, что все они будут
разного цвета?
4.16. В экзаменационный билет входят 4 вопроса программы,
насчитывающей 45 вопросов. Абитуриент ие знает 15 вопросов
программы. Какова вероятность, что он вытянет билет, где все
вопросы ему известны?
4.17. На карточках написаны целые числа от 1 до 15.
Наудачу извлекаются две карточка. Какова вероятность того, что
сумма цифр, написанных иа этих карточках» будет равна 10?
Решить задачи, используя формулу числа перестановок с за-
данным числом повторений.
4.18*. Какова вероятность, что при случайной расположении
в ряд кубнков, иа которых написаны буквы а, а, а, я, в, с, полу»
чится слово «ананас»?
4.19. Иа один ряд, состоящий из 7 мест, случайным образом
садятся семь учеников. Найти вероятность того, что тря
определенных ученика окажутся рядом.
4.20. На книжной полке случайным образом расставлены
4 книги по алгебре и 3 по геометрии. Какова вероятность того,
что книги по наждому предмету стоят рядом?
4.21*. Найти вероятность того, что прн игре в бридж
(четырем игрокам из колоды карт в 52 листа раздаются по 13 карт)
каждый игрок получит по одному тузу.
4.22. Известно, что прн 10-кратном бросании монеты 5 раз
выпала гербы и 5 раз цифры. Какова вероятность того, что все
гербы выпали про первых пяти бросаниях?
Пример 4.4. Из \Ъ строительных рабочих 10—штукатуры, а
5 — маляры. Наудачу отбирается бригада из 5 рабочих. Какова
вероятность того, что среди них будет 3 маляра и 2 штукатура?
Решение. Пространство элементарных событий состоит из
всех выборок различного состава объема 5 из множества
объема 15. Число таких выборок равно С15. Благоприятным
событием соответствуют выборки, содержащие трех маляров и двух
штукатуров. Трех маляров нз пята можно выбрать С\ способам
ми, а двух штукатуров (совершенно независимо от предыдущего
выбора) С2Ю способами.
Следовательно, число выборок, соответствующих
благоприятным событиям, равно произведению Cfcfg. Таким образом,
искомая вероятность определяется выражением
Р(Л)=с|сус?5.
Ответ. С\СУС%.
S«. ЗАДАЧИ. РЕШАЕМЫЕ ГЕОМЕТРИЧЕСКИМИ МЕТОДАМИ 455
В обшем случае вероятность полупить выборку объема
k + г, где k элементов принадлежат одной группе, состоящей яз
п элементов, а т — другой, состоящей из m элементов,
определяется формулой
p{A)=crmckjc++ka. m
4.23. В ящике имеются 15 деталей, 5 из которых окрашены.
Наудачу извлекаются 5 деталей. Найти вероятность того, что 4
из них окрашены, а одна — нет.
4.24. В партии нз N деталей п стандартных. Наудачу
отбираются m деталей. Найти вероятность того, что среди
отобранных k стандартных.
4.26. Какова вероятность главного выигрыша в «Спортлото»
(угадать 6 номеров из 48)? Какова вероятность угадать 5; 4;
3 номера из 48?
4.26. Какова вероятность получения 1 туза, туза и короля
при сдаче 6 карт нз колоды в 52 листа?
4.27. Имеются 6 билетов в театр, 4 нз которых на места
первого ряда. Какова вероятность того, что нз трех наудачу
выбранных билетов 2 окажутся ва места первого ряда?
4.28. В соревнованиях по футболу участвуют 20 команд.
Случайным образом они делятся на две группы по 10 команд.
Какова вероятность того, что 2 наиболее сильные команды прн
этом окажутся в одной группе?
§ 5. Задачи на вычисления вероятностей,
решаемые геометрическими методами
Существуют задачи, в которых непосредственный ' подсчет
элементарных событий, основанный иа нх равиовозможностл н
конечности нх числа, непригоден. Рассмотрим пример. Пусть
линия электропередач, соединяющая иу«кты А и В, в результате
бура оборвалась. Какова вероятность того, что обрыв произошел
на участке, заключенном между пунктами С и D,
принадлежащими отрезку АВ? Множество элементарных событий в данном
случае бесконечно, так как обрыв равиовозможеи в любой точке
отрезка АВ. При этом естественно яредпояагать, что вероятность
обрыва иа любом участке пропорциональна длине этого участка.
(Так как вероятность обрыва на всем участке равна единице
(обрыа уже произошел), то вероятность обрыва на участке CD
выразится соотношением
P{A)=*CD/AB.
456 ГЛ. IB. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
■ Введем следующее допущение. Пусть -исходы испытания,
Число которых бесконечно, распределены равномерно в' некоторой
области S. Это значит, что вероятность события Е, состоящего
в том, что исход испытания оказался заключенным в некоторой
части области S, пропорционален величине этой части и не
зависит от ее расположения н формы.
Таким образом, ,
Р (£) = от (s)fm (S), (I)
где Р(Е) —вероятность события, заключающегося в том, что
наудачу выбранная точка нз области S окажется в области s,
m(s) и m(S) — величины соответствующих областей.
Пример 5.1. Абонент ждет телефонного вызова в течение
одного часа. Какова вероятность, что вызов произойдет в
последние 20 мниут этого часа?
Решение. Пусть событие Е состоит в том, что вызов
произошел в последние 20 минут. Изобразим пространство
элементарных событий в виде отрезка длины 60. Тогда элементарные
события, благоприятные Е, заключены в последнюю треть
отрезка. Следовательно,
Р (А) = 1/3.
5.1. Минное поле заграждения устроено так, что мнны
поставлены вдоль некоторой прямой с интервалами между минами
100 м. Какова вероятность того, что корабль шириной 20 м,
проходящий минное поле заграждения под прямым углом,
подорвется на мине?
6.2. В круге радиуса R помещен меньший круг радиуса г.
Найти вероятность того.^что наудачу брошенная в большой круг
точка попадет также и в меньший круг. (Предполагается,, .что
вероятность попадания в круг пропорциональна площади круга
и не зависит от его расположения.)
Если случайное событие, вероятность которого следует найти,
состоит в попадании точки в некоторую часть плоской фигуры
и прн этом границы фигуры и ее части являются графиками
известных функций, то вычисление площадей, входящих в
выражение (I), сводится к вычислению определенных интегралов.
Пример 5.2. Наудачу выбираются два действительных
числа х и у, причем 0 ^ х ^ 1, 0*^0^1. Найти вероятность
того, что уг ^ х.
Решение. Поставим в соответствие паре чисел х а у точ«
ку на плоскости с координатами (х, у). Пространство
элементарных событий будет в этом случае квадратом, двумя
сторонами которого являются единичные отрезки осей координат, Фн-<
9 В. ЗАДАЧИ. РЕШАЕМЫЕ ГЕОМЕТРИЧЕСКИМИ МЕТОДАМИ 457
гура, множество точек которой соответствует неходам,
благоприятным событию у1 ^ х, ограничена графиками функций у = 0,
х = 1, уг = х. Ее площадь вычисляется по формуле
о ....
Так как площадь единичного квадрата равна единице, то
. . . . Р(Д)=2/3...
Ответ. 2/3,
б;3. Два действительных числа х и? у выбираются' наудачу
так, что '|jc| ^ 3, \у\ ^ б. Канова вероятность toro, что дрйбь
х/у окажется положительной?
6.4. Два действительных числа х и у выбираются наудачу
так, что |х| ^ 1, 0 sg # < I. Какова вероятность того, что
*2<t/?
6.5. Два действительных числа х и у выбираются наудачу
так, что |*| ^ I н \у\ ^ 1, Какова вероятность того, что
б.в*. Наудачу взяты два положительных числа х н у,
каждое из которых не превышает двух. Найти вероятность того, что
ху < 1, а у)х < 2.
5.7*. Наудачу взяты два положительных числа х и у, не
превышающие единицы. Какова вероятность того, что сумма их
не превышает единицы, если сумма их квадратов больше 1/4?
6.8*. Парабола касается нижней стороны квадрата и
проходит через" верхние его вершины. Какова вероятность того, что
точка, наудачу брошенная в квадрат, попадет в область,
заключенную между верхней стороной квадрата н параболой? ч,
5.0. Парабола касается полукруга н проходит через границы
его диаметра. Какова вероятность того, что точка, наудачу
брошенная в полукруг, попадает в область, ограниченную дугой
полукруга н параболой?
5.10. Пусть на отрезке [0; 1] задана такая функция f(x), что
f'(x) >0 прн хе[0; 1], причем /(0) =0, /(I) =1. Доказать,
что при бросании точки в квадрат, стороны которого —
промежуток [0; I] оси Ох н промежуток [0; 1] оси Оу, наибольшая ве^
роятиость попасть в область, ограниченную кривыми у = {(х),
y = f(a), (/ = 0, (/=1, будет достигаться при а = 1/2.
5.11*. Область ограничена линиями х = 0, *=я/2, y=sinjc,
у = sin а. Точка бросается в прямоугольник, сторонами
которого являются промежуток [0j я/2] оси Ох и промежуток [0; 1]
458 ГЛ, IS. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕН
оси Оу. При каком значении а вероятность попадания точки в
эту область наименьшая?
Для решения ряда задач геометрическим методом удобно
Предварительно ввести декартову систему координат.
Пример 5.3. Два товарища договорились о встрече в
определенном месте между 11 н 12 часами дня. Пришедший
первым ждет второго в течение 1/4 часа, после чего уходит. Найти
вероятность того, что встреча состоится, если каждый придет в
произвольный момент между 11 и 12 часами.
Решение. Поскольку момент прихода каждого из
товарищей случаен, то выбрав отрезок единичной длины, поставим в
соответствие моменту прихода первого товарища произвольную,
случайно иыбраииую точку этого отрезка, а моменту прихода
второго товарища — случайно выбранную точку второго отрезка
единичной длины. Отложим эти отрезки на осях координат,
первый — на оси Ох, второй — на оси Оу. Тогда пространство эле-1
меитарных событий будет представлять собой квадрат единичной
площади, вписанный в первый квадрант координатной плоскости,
каждая точка с координатами {х, у) которого представляет
собой пару моментов времени прихода товарищей.
Элементарные события (х, у), благоприятные событию,
состоящему в том, что товарищи встретятся, должны
удовлетворять условию
I * - у | < 1/4. (•)
Геометрическим образом, соответствующим искомому событию,
будет пересечение полосы (*) и единичного квадрата, состоящего
из точек, координаты (*, у) которых удовлетворяют
неравенствам О =S x =£ 1 и 0<#sgl. Площадь фигуры, полученной в
результате пересечения множества (*) и квадрата, равна
искомой вероятности, так как площадь единичного квадрата равна
единице.
Ответ. 7/16.
5.12. В течение 20 минут ученик А в случайный момент
звонит по телефону ученику В и ждет 2 минуты, после чего кладет,
трубку. В течение тех же 20 мннут в случайный момент времени
ученик В приходят домой, где остается в течение 5 минут, после
чего уходит. Какова вероятность того, что разговор состоится?
6.13*. На единичный отрезок осн абсцисс наудачу бросают
две точки В и С. Найти вероятность того, что длина отрезка ВС
будет меньше, чем расстояние от начала координат до
ближайшей точки.
5.14. Некто живет в городе В, соединенном железной доро<
*ой с городами А ш С, Между городами Л и С курсируют по-
§ в. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИЯ 45U
езда, которые все останавливаются в городе В. Расписание
составлено так, что поезда каждого направления проходят через
город 8 с интервалами в 1 час Некто приходит па вокзал в
случайный момент времени и садится на первый подошедший
поезд. Как должно быть составлено расписание, чтобы
вероятность уехать в город А была в 5 раз больше, чем вероятность
уехать в город С?
5.1Б*. Плоскость разграфлена параллельными пряцымв,
отстоящими друг от друга на расстояние 1а. На плоскость наудачу
бросают иглу длиной 21 (/. < а). Найти вероятность того» что
игла пересечет какую-нибудь прямую (задача Бюффона).
§ 6. Вычисление вероятностей сложных событий
События подразделяются на достоверные, невозможные и
случайные: достоверные в результате опыта происходят всегда;
невозможные не происходят никогда; случайные могут либо
произойти, либо нет. Достоверным будет, например, событие, состоя-"
шее в том, что из урны, содержащей только белые шары,
вынимают белый шар, а невозможным будет событие, состоящее в
том, что белый шар вынимают из урны, содержащей только чер«
ные шары. Если в урне есть и белые и черные шары, то
извлечение шара какого-либо определенного цвета является случай*
ным событием.
Достоверное событие совпадает со всем пространством
элементарных событий Й, а случайное событие А является
некоторым подмножеством в этом пространстве. Невозможное событие
0 не содержит нн одного элементарного события.
Суммой двух событий А н В назовем событие С, состоящее
в том, что произошло или событие А, или событие В. С;мма
двух событий обозначается
С = Л + В. *■ (1)
Поясним понятие суммы двух событий на следующем
примере. Пусть мальчик купил бнлеты двух лотерей: «Спринт» в
«Старт». Рассмотрим случайное событие С, состоящее в том, что
мальчик выигрывает хотя бы в одной лотерее. Наступление этого
события связано с наступлением хотя бы одного из следующих
событий: событие А — среди билетов, купленных мальчиком, есть
выигрышные билеты лотереи «Спринт»; В — есть выигрышные
билеты лотереи «Старт».
Произведением двух событий А и В назовем событие С,
состоящее в том, что произошли оба эти события. Произведение
двух событий обозначается
С=-А-В. (2)
460 ГЛ..1Б, КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
События А и В называются несовместными, если их
произведение представляет собой невозможное событие:
А-В = 0.
Поясним понятие произведения двух событий на следующем
примере.
Среди машнн, потерпевших аварию, есть «Жнгули> и
«Волга», Часть машин при аварии перевернулась. Событие А,
состоящее в том, что наудачу выбранная неперевернувшаяся
автомашина «Волга», будет произведением двух событий: В —
машина ие перевернулась и С — машина является «Волгой», т. е. .4 =»
Определение вероятности сложного события А, являющегося
комбинацией более простых событий Аи .,,, Ан, вероятности ко»
торых известны, основаны на формулах сложения и умножения
Вероятностей. Поясним смысл этих формул примерами.
Проведем эксперимент, связанный с бросанием двух костей,
в вычислим вероятность события С, состоящего в том, что сумма
Очков на выпавших гранях ие превосходит числа 3.
Пространство элементарных событий, возникающих в результате этого
эксперимента, можно представить упорядоченными парами целых
чисел, изменяющихся от 1 до 6. Таких пар будет 36. Среди этих
событий благоприятными событию С будут следующие: (1, 1),
J[l, 2), (2, 1). Таким образом, согласно определению, введенному
в § 4, заключаем, что вероятность события О есть
Р (С) = 3/36 = 1/12.
Рассмотрим теперь событие С как комбинацию более
простых событий. Для этого' заметим, что событие С происходит,
если происходит событие А — сумма очков на выпавших гранях
равна 2, или событие В — сумма очков па выпавших гранях
равна 3. Таким образом, событие С есть сумма событий А и Bf
С =• А ■+■ В. Из исходного пространства элементарных событий
событию А благоприятна только пара (1, 1), а событию В —
пары (1, 2) и (2, 1). Следовательно, вероятности событий А н В
равны соответственно ••
Р (А) = 1/36, Р (В) = 1/18.
Таким образом, в данном случае справедливо равенство
Р(С) = Р(А) + Р(В).
Заметим, что события А н В в этом примере являются н^
совместными (сумма очков на выпавших гранях не может одн0<
временно быть равной 2 и 3).
$ 6. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИИ 4бГ
Вычислим Вероятность события С, состоящего в том; что нз
колоды карт в 52 листа наудачу взятая карта или является ту»
зом, или имеет червонную часть. Пространство элементарных
событий в этом примере состоит нз 52 элементов. Элементарные
события, благоприятные событию С, 'заключаются в том, что
взятая карта имеет червонную масть (в колоде 13 карт одной
масти) или является тузом (в колоде 4 туза). С учетом того,
что один из тузов червонный н, следовательно, благоприятным
оказываются 16 элементарных событий, получаем
Р (С) = 16/52= 4/13.
Представим теперь С в виде комбинации более простых со*
бытнй: события А — взятая наудачу карта оказалась червонной,
и -события В — взятая наудачу карта оказалась тузом. Тогда по
определению суммы двух событий С = А + В, Вероятности
событий Л п £ соответственно равны
Р(Д).=»1/4, Р (В) =1/13.
Нам понадобится также вероятность произведения событий А
и 8, т.е. события D = А-В, которое заключается в том, что
наудачу взятой картой оказывается червонный туз. Очевидно, что
вероятность события D равна
Р (D) = 1/52.
Нетрудно убедиться, что в данном случае справедливо равенство
р (Л + В) = Р (А) + Р (В) - Р (D).
Рассмотренные примеры обобщает следующая формула!
Р(А + В)~Р(А) + Р(В)-Р(АВ), (3)
т. е. вероятность суммы двух событий А и В равна сумме
вероятностей этих событий мниус вероятность нх произведения.
В том случае, если события Ли В несовместны, формула (3)
принимает внд
Р(А + В) = Р(А) + Р{В). (4)
Рассмотрим эксперимент, связанный с бросанием двух
костей, и вычислим вероятность события С, состоящего в том, что
число очков, вьшавшнх на первой кости, больше 3, а на
второй — больше 4. Элементарные события, благоприятные событию
С, — упорядоченные пары чисел: (4,5), (4,6), (5,5), (5,6),
Кб, 5), (в, 6). Таким образом,
Р (С) = 6/36 = 1/6.
Представим теперь событие С в виде комбинации более
простых событий: события А, состоящего в том, что на первой
462 ГЛ. !В. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
кости выпало больше трех очков, и события В — на второй
кости выпало больше четырех очкои. Тогда по определению
произведения событий событие С представляется произведением
событий А н В: С = А-В.
Вычислим вероятности событий А и В. Прежде всего
заметим, что пространства элементарных событий, возникающие прп
бросании каждой кости отдельно, состоят из шести равиовоз-
можных исходов. Элементарные события, благоприятные
событию А, состоят в выпадении иа первой кости 4, 5 или 6 очков;
Следовательно, Р(В) = 1/2.
Элементарные события, благоприятные событию В, состоят в
выпадении на второй кости б или 6 очков. Следовательно,
Р(В) = J/3. Нетрудно проверить, что в данном случае
выполняется соотношение
Р(С) = Р(А)-Р(В). (5)
События А п В, для которых выполняется (5), будем
называть независимыми. Таким образом, вероятность произведения
двух событий в том случае, если они независимы, можно
вычислить по формуле (5). Если для событий А и В условие (5) не
выполняется, то такие события называются зависимыми. В этом
случае можно говорить о так называемой условной вероятности
наступления события А при условии, что событие В произошло.
Допустим, требуется вычислить вероятность события А,
состоящего в том, что сумма очков при бросании двух костей не
превысит четырех, если известно, что иа одной кости выпала
единица (событие В). Так как событие В произошло, то, считая
его достоверным, можно рассмотреть новое пространство
элементарных событий, состоящее из 11 событий, благоприятных
событию В:
(1, 1), (!, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, I), (3, 1), (4,1), (5, 1), (6, 1).
В этом новом пространстве элементарных событий событию А
благоприятны 5 элементарных событий: (1, 1), (1, 2), (1, 3),
(2, 1), (3, 1). Таким образом, вероятность события А в этом
пространстве элементарных событий равна 5/11. Полученную
величину будем называть условной вероятностью события А при
условии, что произошло событие В, и обозначать Р(А!В),
Рассмотрим теперь исходное пространство элементарных
событий, возникающее при бросании двух костей, и вычислим
вероятность события С = А-В, состоящего в том, что сумма очков,
выпавших иа костях, не превосходит четырех н что на одной из
костей выпала еднвица. Элементарные события, благоприятные
§ 6. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИИ 463
событию С, представляются следующими парами чисел: (1, 1)г
(1. 2), (1, 3), (2, 1), (3, 1). Таким образом, Р(С) =5/36.
Одиннадцать элеменарных событий, благоприятных событию В, были
рассмотрены выше. Следовательно, Р{В) = 11/36. Нетрудно
убедиться в справедливости соотношения
Р(С) = Р(А/В)-Р(В).
Рассмотренные примеры обобщает следующая формула
умножения вероятностей:
Р (АВ) = Р(А)Р (В!А) = Р(В)Р {А/В), (6)
т. е. вероятность произведения двух событий А в В равна
произведению вероятности одного из этих событий иа условную
вероятность другого, вычисленную в предположеияя, что первое
событие произошло.
Для случая трех событий формула, обобщающая формулу
(6), имеет вид
Р {ABC) = Р {А!ВС) Р (ВС) = Р (А/ВС) Р (В/С) Р (С). (7)
Пример 6.1. Из урны, содержащей п белых и m черных
шаров, вынимаются два шара. Какова вероятность того, что они
разных цветов?
Решение. Представим событие С, состоящее в том, что
вынутые шары разных цветов, в виде С = А + В, где
событие А состоит в том, что первый шар белый, а второй, черный;
событие В — в том, что первый шаг черный, а второй белый. Так
как события А н В несовместны, то, согласно (4),
Р(С)=Р(А) + Р(В). (•)
Вероятности событий А и В вычислим, используя формулу
(6). Представим событие А в виде А = Б, Ч, где буквы Б и Ч,
записанные в данной последовательности, означают, что первым
был вьигут белый шар, а вторым — черный. Тогда
Р(Л) = Р(Б)Р(Ч/Б).
Вероятность события Б представляет собой отношение числа
белых шаров к числу всех шаров, находящихся в урие. Условная
вероятность того, что вторым вынут черный шар при условии,
что первым был вынут белый, представляет собой отношение
первоначального числа черных шаров к уменьшившемуся на
единицу числу всех шаров, оставшихся в урие. Таким образом,
« т
Р(А)--
Р(В).
n + m
Аналогично
я-f-m
п+ т —
п
я 4- tit —
1
1
464 ГЛ. 15. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Подставляя полученные выражения в формулу (•), полу»
чаем-1
2пт
Р(С)
Ответ.
(л + т.) (п + т— [)'
2пт
(л + т) (я + /п— 1) '
Используя формулы умножения и сложения вероятностей,-
решить следующие задачи.
6.1. В урне находятся п белых и т черных шаров.
Вынимаются -два шара. Какова вероятность того,' что оба шара белые;
оба шара черные?
6.2*. Решить задачу 6.1 при условии, что вынутые шары
возвращаются обратно, а их цвет записывается.
6.3. Из колоды карт в 52 листа вынимают 4 карты. Какова
вероятность того, что все они разных мастей (имеются 4 масти
по 13 карт в каждой)?
6.4. Несколько раз бросают игральную кость. Какова
вероятность того, что одно очко появится впервые при третьем
бросании?
6.6. 20 машин были доставлены на станцию технического
обслуживания. При этом 5 нз них имели иенсправности в ходовой
части, 8 имели неисправности в моторе, а 10 были полностью
исправны. Какова вероятность, что машина с неисправной
ходовой частью имеет также неисправный мотор?
6.6. Готовясь к вступительном/ экзамену по математике,
абнтурнеит должен подготовить 20 вопросов по элементам мате»
матического анализа и 26 по геометрии. Однако он успел
подготовить только 15 вопросов по элементам математического
анализа и 20 по геометрии. Билет содержит 3 вопроса, 2 нз которых
по элементам .математического анализа и 1 по геометрии. Какова
вероятность, что:
а) студент сдаст экзамен на «отлично» (отвечает иа все три
допроса); б) на «хорошо» (отвечает на любые два вопроса)?
Дополнением случайного события А (или противоположным
событием) • назовем событие С, состоящее в том, что в
результате эксперимента событие А не произошло. Дополнение к
событию А обозначается X. Вероятности событий А и X связаны
формулой
Р(А) + Р(А)=1. (8)
Если сложное событие А представляется в виде
Д-Д| + ...+4ь (В).-
§ в. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИИ 465
где At — события, вероятности-которых известны, то вычисление
вероятности Р(А) иногда удобно производить, используя
формулу
I^Ji-tfa' ... 'Ак, (10)
связывающую дополнения рассматриваемых событий. Так, в
случае, если Ai независимы, получаем
Р (А) -1 - Р (А) -1 - Р Ш ... Р (Ak) =
-1-[1-Р(Д,)]...[1-Р<Д*)1. (11)
Если все события Ai равновероятны, то формула (11) приобрел
тает более простой вид:
Р(Л) = 1-(1-р)*, (12)
где р — вероятность события At.
Пример 6.2, Для разрушения моста достаточно
попадания одной авиационной бомбы. Найти вероятность разрушения,
если на мост сбрасывают три бомбы с вероятностями
попадания 0,3; 0,4; 0,7 соответственно.
Решение. Вычислим вероятность события Л, состоящего
в том, что мост не будет разрушен. Обозначим А{, Л"ц, Л»
события, состоящие в том, что в мост ие попала соответственно
первая, вторая и третья бомбы. Тогда Я«»/?[ЛаЛ3. Так как
из независимости Ai следует независимость Кь то
р (А) = Р (А{) Р (Да) Р (Л"3) — 0,3 • 0,4 • 0,7 = 0,084.
Следовательно, вероятность разрушения моста
Р(Л)=1-Р(Л) = 0,916.
Ответ. 0,916.
6.7. В урне находятся п белых, т черных и k красных
шаров. Наудачу вынимают трн шара. Какова вероятность, что
котя бы два шара будут одного цвета?
6.8. На стеллаже 15 учебников, 5 из них в переплете.
Наудачу выбираются 3 учебника. Какова вероятность, что хотя
бы один из них будет в переплете?
6.9. В лотерее разыгрывается п билетов, из которых / вы-
?грышных. Некто покупает k билетов. Какова вероятность того,
то хотя бы одни из купленных билетов выигрывает?
6.10. При одном обзоре радиолокационной станцией объект
рбнаружнвается с вероятностью р. Обнаружение объекта в
каждом цикле происходит независимо от других циклов. Какова
рероятность того, что при п циклах объект будет обнаружен?
466 ГЛ. 15. КОМБИНАТОРИКА. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
6.11*. По некоторой цели производится я выстрелов.
Каждый выстрел поражает цель с вероятностью р. Сколько
выстрелов надо произвести, чтобы вероятность поражения цели
была не меньше Р?
Вероятность события А, которое может наступить лишь
прн появлении одного из нескольких несовместных событий
Ви Bit •••, В„, равна сумме произведений вероятностей
каждого из этих событий на условную вероятность события А
при условии, что данное событие наступило:
Р(А) = Р (В,) Р (Л/В,) + Р (Ва) Р (Л/В2) + ...
...+Р(В„)Р(А/В„>. (13)
Равенство (13) называется формулой полкой вероятности.
Пример 6.3. В первой команде б мастеров спорта в
'4 перворазрядника, а во второй — 6 перворазрядников и 4
мастера спорта. Сборная, составленная из игроков первой и
второй команд, содержат 10 человек: в человек из первой
команды и 4 — нз второй. Из сборной команды наудачу
выбирается один спортсмен. Какова вероятность того, что он
мастер спорта?
Решение. Пусть событие Bi (t = 1, 2) состонт в том,
что наудачу выбранный спортсмен—член 1-й команды. Тогда
вероятности событий Bi равны соответствеипо /'(Bi)=3/5,
Р (В2) = 2/5. Пусть событие А состонт в том, что наудачу
выбранный спортсмен — мастер спорта. Тогда условные
вероятности события А прн условии, что выполнено событие Bi
(т. е. известно, нз напой команды спортсмен), равны
соответственно P{AjB\) = 3/5, <Р(А/В2) = 2/5. Используя формулу
полной вероятности, получаем
Н (А> - 5 6 + 5 5 - 25 '
Ответ. 13/25.
6Л2. Экзамен происходит по следующей схеме* если
некоторый билет уже был вытянут, то экзаменатор'* откладывает
его, т. е. последующие экзаменующиеся не могут вытянуть этот
бнлет. Ученик выучил А билетов (А -< л). В каком случае
вероятность того, что ученик вытянет выученный билет, больше—*
когда он идет отвечать первым или последним?
6.13*. В урне лежат два шара, цвета которых неизвестны
(каждый шар может быть или белым, или черным). Положим
в урну белый шар. Какова вероятность теперь вынуть из урны
белый шар?,
§ в. ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛОЖНЫХ СОБЫТИИ 467
6.14. Из пяти винтовок, из которых 3 снайперские и
2 обычные, наудачу выбирается одна, и нз нее производится
выстрел. Найти вероятность попадания, если вероятность
попадания из снайперской вннтовкн — 0,95, а из обычной — 0,7,
6.15. Имеются две урны. В первой лежат т белых н л
черных шаров, а во второй — к белых и / черных шаров
соответственно. Из первой уриы во вторую перекладывают одни
шар. Какова вероятность после этого вынуть:
а) белый шар из первой урны;
б) белый шар нз второй урны?
6.16*. Имеются две партии однородных изделий с разным
составом стандартных и дефектных: в первой партии всего
N изделий, из них п дефектных, во второй партии М изделий,
нз них т дефектных. Из первой партии берется К изделий,
нз второй L, и образуется новая партия. Какова вероятность
того, что изделие, выбранное наудачу нз повой партии,
окажется дефектным?
6.17*. В условиях предыдущей задачи нанги вероятность
того, что хотя бы одно изделие нз трек выбранных наудачу
нз вновь образованной партии окажется дефектным?.
ГЛАВА 16
ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ
СЧИСЛЕНИЯ
§ J. Высказывания
Под высказыванием понимают утверждение, про которое
имеет смысл говорить, истинно оно или ложно.
Из заданных высказываний при помощи так называемых
логических связок, которым в обычной речи соответствуют
частица «ие», союзы «и», «или», сложноподчиненный оборот
«если..., то...», выражение «в том и только в том случае», об-
разуются новые составные высказывания. Если истинному
высказыванию поставить в соответствие 1, а ложному 0, то
логические связки можно формально определить с помощью так
называемых таблиц истинности.
1. Отрицание (читают «ие р» и пишут р). Когда р истинно,
тогда р ложно, и наоборот.
2. Конъюнкция или логическое умножение двух
высказываний (читают «р н q* и пишут p/\q). Конъюнкция истинна
только в случае, когда оба высказывания истинны.
3. Дизъюнкция или логическое сложение двух
высказываний (читают «р нли о» и пишут р\/ q). Дизъюнкция истинна
в том случае, когда истинно хотя бы одно из двух
высказываний.
4. Импликация (читают «если р, то q» и пишут р -*■?)«
Здесь два высказывания в отличие от случаев 2 и 3 ие
перестановочны: высказывание р называют условием, а
высказывание q — следствием. Импликация ложна только в том случае,
когда условие истинно, а следствие ложно.
б. Эквиваленция илн двойная импликация (читают «р
эквивалентно q» , и пишут р <-+q). Эквиваленция истинна в том
случае, когда нли оба высказывания истинны, илн оба
высказывания ложны.
S I. ВЫСКАЗЫВАНИЯ 469
Таблица истинности элементарных высказываний имеет вид
р
0
0
1
1
ч
0
1
0
1
pV<7
0
1
1
1
рЛ?
0
0
0
1
р-»-«
1
1
0
I
р
1
1
0
0
Новые высказывания образовываются с помощью
логических операций. Операции могут быть использованы
многократно. Порядок, в котором проводятся операции, указывают с
помощью скобок.
Если из р следует q н нз q следует р,: то высказывания
р н q называют равносильными. Равносильные высказывания
соединяют знаком •*>• либо знаком равенства.
Таблицы нстиниостн для равносильных высказываний
совпадают.
Пример 1.1. Доказать равносильность высказываний
р-х? и (pAq)Wp-
Решение. Таблица нстиниостн для p-*-q представлена
выше. Составим таблицу истинности для высказывания
'<p_A«7)Vp>
р
0
1
т
0
I
0
1
I
рЛ т
0
1 !
р
1
1
0
1 "
рЛ <?Vp
I
1
0
1
III
В последней строке таблицы римскими цифрами обозначены
номера шагов, которыми составляется таблица истинности. На
1 шаге заполняются столбцы истинности для высказываний р
и q. На II шаге — для высказываний p/\q и р. При этом
используется таблица нстиниостн элементарных высказываний,
приведенная выше. На III шаге, рассматривая р/\q в р как
Простейшие высказывания, заполним столбец дизъюнкции этих
высказываний (pA</)Vp- Полученный столбец истинности
совпадает со столбцом истинности высказывания p-*q.
1 Таким образом, равносильность высказываний p-*-q в
Хр Д 9)У Р. установлена,
470 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЙ
Сравнив таблицы истинности, доказать)
1.!. р V q=p A q.
1.2. р A q ■= р V q.
1.3. p-*—q = {p Aq)V (р Л <?).
1.4. {pVq)/\q = q.
1.6. pV(pAq)~p.
I.e. Высказывание р означает, что у вас есть собака, а
высказывание q означает, что у вас есть кошка,
Сформулируйте, что означают следующие составные высказывания!
1) р V q;
2) р Л <?;
3) (р Л q) V ip Л 9)1
4) р -» 9.
1.7. Пусть высказывание р|д означает, что р и q не могут
быть оба ксттгаыыя. Напишите таблицу истинности для p\q,
1.8. Напишите высказывание p\q (см. задачу 1.7),
используя логические связки конъюнкции, дизъюнкции и отрнцаиня»
1.9. Докажите равносильность высказывании (p\q) \ (p\q)
н РАЯ-
1.10. Пусть р означает «идет дождь», a q означает «дует
ветер». Запишите в символической форме высказывания!
1) если идет дождь, то дует ветер;
2) если дуст ветер, то идет дожди
3) ветер дует в том и только в том случае, когда идет
Дождь;
4) если дует ветер, то нет дождя;
5) неверно, что ветер дует тогда и только тогда, когда
нет дождя.
1.11. Запишите в символической форме сложное
высказывание, состоящее из простых высказываний р, q, г, истинное
тогда н только тогда, когда истинна только одна (безразлично
какая 1) из компонент.
1.12. По мишени произведено три выстрела. Что означает
следующее высказывание, записанное в символической формез
') Pi V pi V Рз1
2) Pi Л Рг Л рг,
3) (pi V pi) Л Рз.
где pi означает высказывание: «мишень поражена при 2-м вы-j
стреле?
$ t. ВЫСКАЗЫВАНИЯ
471
Легко проверить равносильность следующих высказываний
(здесь 1 — истина, L — ложь)!
pV<7 = <?Vp, (1)
р A q = д Л р, (2)
pV(?Vr) = (pV?)Vr, (3)
Р Л (q Л г) = (р Л Я) Л г, (4)
рЛ(<? Vr) = <pA?)V(pAr), (5)
р Л р = р, (6)
pV Р = Р, (7)
р V р — Л (8)
р /\p = L, (9)
рМ=р, <Ю)
РЧ1 = Г, (11)
PAL = L, (12)
PVL = P. (13)
Используя формулы (1) —(13), можно решать довольно
сложные логические задачи.
Пример 1.2. Виктор, Роман, Юрий и Сергей заняли па
математической олимпиаде первые четыре места. Когда их
спросили о распределении мест, оин дали три таких ответа:
1) Сергей — первый, Роман — второй;
2) Сергей — второй, Виктор—третий;
3) Юрий — второй, Виктор — четвертый.
Как распределились места, если в каждой ответе только одно
утверждение истинно?
Решение. Если в каждом ответе одно из утверждений
истинно, то и дизъюнкция этих утверждений тоже истинна.
Так, скажем, истинно высказывание: «нлн Сергей первый, или
Роман — второй». Запишем это высказывание в следующем
символическом виде: Ci V Рп- Аналогично, высказывания
остальных ответов имеют внд Си V Вш и Юн V Biv соответственно.
Конъюнкция истинных высказываний — истинна. Следовательно,
истинным будет составное высказывание
(CiVPi)A(Cn V Вш) Л (Юн VBIV). (*)
Используя свойства (1)—(13), произведем упрощение
высказывания (*). Для этого представим в виде дизъюнкции
простейших конъюнкций первую конъюнкцию:
(С, УРц)Л(Сц VBni) = l(Ci VPn)AC„l V
V [(Ct V Ри) Л Вш] = ((С, Л С1Г) V (Рп Л Сн)] V
Vl(CiABm) V(PjuABni)].
Высказывание, стоящее в первых квадратных скобках, ложно,
так как является дизъюнкцией двух ложных высказывании
472 гл. 16. элементы логики, системы счисления
С1ДС11 a Pij Д Си — первое состоит в том, что Сергеи занял
одновременно I и 11 места, а второе — в том, что второе место
одновременно заняли Роман и Сергей. Таким образом, первая
конъюнкция приобретает вид
(С] V Рц) Л (Сц V Вш)=(С, Л В,„) V (Рц Л Вш).
Рассмотрим теперь оставшуюся конъюнкцию
, , I(CiABin) V(PiiAB„,)1A.(IOiiVB,v).
Испольадо, по-прежнему, правила (I) —г (13), имеем
U(Ci X ВШ) V(Pn Л В,,,)] Л Ю„} V
V {[(Ci Л Bm) v (Рц Л ВШ)] Л BIV} =i
= (Ci Л Вш Л Юц) V (Рц Л Вш Л Ю„) V (Ci Л ВШ Л B,V)V
V (Рц Л ВШ Л B,v) = (С, Л В1П Л Юц).
Второе, третье и четвертое высказывания, участвующие в этой
дизъюнкции, ложны, так как являются конъюнкциями или одн-.
наковых букв с разными номерами, или разных букв с одн-
наковьшн номерами, чего быть ие может. Следовательно,
истинной является конъюнкция
Ci Л Вш Л Юц.
Ответ. Первое место занял Сергей, второе — Юрий,
третье — Виктор и четвертое — Роман.
1.13. По обвинению в ограблении перед судом предстали
А, В и С. Установлено следующее:
1) если А не виновен нлн В виновен, то С виновен;
2) если А не виновен; то С ие виновен.
Виновен ли Л?
1.14. Определить, кто из четырех подозреваемых участво«
вал в ограблении, если известно:
1) если А участвовал, то н В участвовал;
2) если В участвовал, то илн С участвовал, нлн А на
участвовал;
. .• 3) если. D не участвовал, то А участвовал, а С не
участвовал;
4) если D участвовал, то А участвовал.
1.15. Экзамен сдавали три студента Л, В и С. Известно,
что;
1) если А не сдал или В сдал, то С сдал;
2) если А не сдал, то С не сдал.
Можно ли на основании этих данных установить, кто сдал
экзамен?.
§ Т. ВЫСКАЗЫВАНИЯ
т
В начале параграфа было показано, как строить таблицу
истинности любого составного высказывания. Интерес
представляет и обратная задача; по заданной, таблице истинности
найтн одно или несколько высказываний, которым оно
соответствует. Оказывается, обратная задача не только имеет
решение, но его можно получить, используя лишь связки Д,
V. ~
Пример 1.3. Найтн высказывание, состоящее из двух
простейших р и д, имеющее следующую таблицу истинности»
р
0
0
I
1
9 1 РАЗ
1
0
1
0
0 ,
0
1
р
1
1
0
0
ч
0
I
I
0
?
0
0'
0
I
Решение. Единица в последнем столбце таблицы
присутствует только в последней строке. Следовательно, истинным
будет высказывание р /\д. Проверни это утверждение. Для
этого составим таблицу истинности р /\ д. Действительно,
полученная таблица совпадает с исходной. Следовательно, найденное
высказывание искомое.
1.16. Постройте три составных высказывания а, Ь, с,
имеющих следующие таблицы истинности:
р
I
I
1
1
0
0
0
0
7
1
I
0
0
1
1
0
0
г
1
0
1
0
1
0
. 1
0
а
I
Q
I
0
0
1
0
0
Ь
0
0
?
0
0
0
0
О
I
1
1
0\
I
1
0
I
1.17. Какие высказывания а, Ь, с, d имеют следующие таб.
лицы истинности:
р
1
1
0
0
<7
1
0
1
0
а
1
0
0
1
ь
1
0
0
0
с
0
0
1
0
d
0
1
0
0
474 ГЛ. 18. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
Как это следует из примера 3, а также из решения
задач 1.16 в 1.17, алгоритм построения составного высказыдання
заключается в дизъюнкции тех конъюнкций простых
высказываний, которым соответствует единица в последнем столбце
таблицы истинности. Причем в отдельную конъюнкцию входит
либо высказывание, либо его отрицание в зависимости от того,
соответствуют ли ему в таблице единица нли нуль.
Попробуем использовать этот метод в следующей
«жизненной» ситуации.
Пример 1.4. Имеются два города Л и В. В городе А
живут люди, всегда говорящие правду, а в городе В живут
лжецы, всегда говорящие неправду. Жители обоих городов
свободно ходят в гости друг к другу, поэтому в каждом
городе можно встретить жителей любого из этих городов. Какой
вопрос следует задать путешественнику первому встречному,
чтобы по единственному ответу («да» нли «нет») выяснить, в
каком городе ои находится?
Решение. Пусть р означает высказывание «вы говорите
правду», я q— высказывание «это город А». Мы хотим задать
единственный вонрос, на который ответ «да» означал бы, что q
нспгаво, а ответ «нет» — что q ложно, независимо от
правдивости первого встречного.
Если человек говорит правду, то ои скажет «да», если
наше высказывание истинно, н «нет» — если оно ложно; лжец
поступит наоборот. Таблица истинности высказывания
(ожидаемого ответа) имеет следующий вид:
р
1
1
0
о
ц %
I
0
I
0
Ожидаемый ответ
да
Нет
да
нет
1
0
0
I
Эта таблица истинности соответствует эквивалентности (т. е,
(р ■+-*• q) или высказыванию
(Р Л (?) V (Р Л ?)•
Таким образом, вопрос должен выяснять истинность
эквивалентности прописки встречного н его правдивости: «Верно ли,
что это город А и вы его житель, или это город В и вы его
житель?» Так как этот вопрос направлен на выяснение
соответствия прописки встречного человека и данного города, то
* F. ВЫСКАЗЫВАНИЯ
475
on может быть сформулировав короче; «Бы житель этого
города?»
1.18. Одни логик попал к дикарям н был заключен в
темницу, имеющую два выхода. Вождь дикарей предложил
пленнику следующий шанс на спасение: «Один выход ведет на
верную смерть, другой — на свободу. Ты можешь избрать
любой. Сделать выбор тебе помогут два моих воина. Они
останутся здесь, чтобы ответить на один твой вопрос—любой,
какой ты пожелаешь им задать. Но я предупреждаю' тебя, что
одни воин всегда говорит правду, а второй всегда лжет».
И вождь ушел. Через некоторое время логак, задав вопрос
одному из воинов, вышел иа свободу. Какой вопрос он задал?
Пример 1.5. Староста, комсорг, профорг хотят
использовать электрическую схему, регистрирующую результаты тайного
голосования большинством голосов. Как она должна выглядеть?
Решение. Пусть р — высказывание «староста голосует
за», q—высказывание «комсорг голосует за», г — высказывание
«профорг голосует за>. Составим таблицу нстншюсти
интересующего нас высказываипя:
р
1
1
I
1
0
0
0
0
4
1
I
0
0
1
1
0
0
г
I
0
1
0
1
0
1
0
Искомое высказывание
\
i
0
0
0
рЛ^Лг
РЛ <7Л?
рЛ«Лг
рА? Л'
Единицы в последнем столбце поставлены в тех,строках,
где чнело единиц больше числа пулей.
Искомое высказывание имеет вид
(р Л Я Л г) V (р Л q Л г) V (р Л Я Л г) V (р Л q Л г).
'Для его реализации в впде электрической депп достаточно до«
говориться, что истинность высказываипя соответствует тому,
что цель проводит ток (см. рис. I6.I). Лампочка загорится
в том н только в том случае, если большинство
проголосовало «за».
1.19. В условиях примера 1.5 реализовать электрическую
схему, зажигающую лампочку, если хотя, бы один участник
проголосовал «за».
1.20. Какое высказывание реализует схема иа рис, 16.22
7
476 -ГЛ. 18, ЭЛЕМЕНТЫ ЛОГИКИ. СИСТВМЫ СЧИСЛЕНИЯ
i * Рве'. 18.1
?
Рис. 16.2 Рис. 16.3
1.21. Придумайте схему более простую, чем в задаче 1.20,
fao реализующую то же самое высказывание.
1.22. Какое высказывание реализует схема на рис 16.3?
§ 2. Предложения, зависящие от переменной ' '
Пусть предложение зависит от переменной, принадлежащей
Некоторому множеству. Это предложение, вообще говоря, не
является высказыванием. Предполагается, однако, что для каж«
£ого значения переменной предложение есть высказывание н,
довательно, оно может быть либо истинным, либо ложным,
ожество А, таким образом, разбивается на два
подмножества. Одно содержит те и только те значения переменной, прн
которых предложение истинно, а другое — при которых оно
дож но.
Например, для предложения х"—1 < 0 (xeR)
множеством нстни::ссти является промежуток (—I; I), а множеством,
где оно ложно, — дополнение этого промежутка до всего R,
к. е. объединение промежутков (—ooj— 1][I; оо).
Два предложения р{х) и q(x), определенные на одном и
ром же множестве, называются равносильными, если их мнем
р
1
?
- гШ
£
еле
Мн
§ 2. ПРЕДЛОЖЕНИЯ. ЗАВИСЯЩИЕ ОТ ПЕРЕМЕННОЙ 477
зкества истинности совпадают. Например, два предложения
х*—1<0 и (х —1)(х + 1) < 0 равносильны на множестве R.
Для предложений, зависящих от переменных, так же, как
в для высказываний, можно ввести логические операции.
Так, например, если предложения р[х) в q(x) определены
ва одном множестве U, то предложение р(х) V q(x),
являющееся их дизъюнкцией, определено ва том жа множестве и я
качестве .множества истинности имеет объединение множеств
истинности р(х) и q(x).
Удобной иллюстрацией логических свизок являются так
называемые схемы Вана (см. рис. 16.4). Область определения
всех предложений, участвующих в связках, — единичный
квадрат. Множества истинности предложений заштрихованы. На
рис 16.4,0 представлено множество истиниостя дизъюнкции
p(j;)V?W; на рис 16.4, б — множество истинности
конъюнкции p{x)/\q{x); на рис 16.4, е.—множество истинности нмплн«
нации р(*)-»- q(x), на рис. 16.4, г — множество истинности от«
рицання р(х).
Пример 2.1. Пусть
А (х) =. {* + 3 < 0) н В(*) = {*-2>0) .
*— два предложения, зависящие от переменной » (ie R), *
Найти множества истинности для предложений]
а) А (х) V В {х);
б) /(х)АВ(х);
в) А (х) А В (х);
г) А (*) -► В (*);
д) А (х) -> В (х).
Решение, а) Для предложения А(х)V В{х) множеством
истинности является множество тех и только тех значений X,
для которых верно хотя бы одно из неравенств
х + 3 < 0 или х — 2 > О,
т. е, объединение промежутков {—°°1—3)1Д2; oo^.
478 пя. и. элементы логики, системы счисления
б) Для предложения Д(*)ДОД множеством истинности
является множество тех и только тех значений «, для .которых
справедливы оба этих неравенства, Другими словами, это
множество является решением системы
*+3<0. *<-3
*-2>0^*>2 ^0-
в) Для предложения А\х) /\ Б(х) множеством истинности
является множество тех и только тех значений х, для которых
справедливы два неравенства * + 3<0 н *—2 < 0, *. е. это
Множество решений системы
х -+- 3 < 0, _ х < — 3,
*-2<0 ^л<2 ^(----3).
г) Для предложения А (*)-*■ В(х) («если х+3<0, то
х — 2^0») множество исгнииости не содержит ни одного
элемента.
д) Для предложения А{к)-*-Щх) -(«если дг+3<:0, то
К — 2 < 0») множеством исгиииости является вся числовая ось.
2.1. Пусть А (х) = {х — 2 > 0}, В (х) = {х + 2 ^ 0} — два
предложения, зависящие от переменной х (.г е R), Указать
множества истинности предложений;
а) А (х) V В (х); г) В {х) -±А (к);
й) АЩЛв <*); ' я) Мк) ■ BJxy;
в) А\х) -> В (ж); «) В{х)^-А (х).
2.2. Пусть А (х) = {# + х + I > 0}, В(х-) = {я + 2 > 0} —
два предложения, зависящие от переменной х (xeR). Указать
Множества истинности предложений!
а) Д(дг) V В (.v); г) В (х) -* Л (д-);
б) Л(х)лВ{х); д) Л(а-) .Bjje);
в) А (*) -> В (*); е) В (х) -> Л (*).
2.3. Определить множество истинности предложения А =
^ \ —r~r < t(> определенного для всех nsN,
I. п -t- I 6 )
2.4. Црл каких .значениях -параметра а множество
истинности предложения
Представляет собой нрямежуток; а) f2;<»); 6) {—oo,2J?
8 г. предложения1, зависящий от переменяю» 47§
8.5. Найти множество истинности1 предложения
У2*+ 1 + V2* —5 > V5 — 2*.
2.8. Пусть А(л, #) = {(а + 1)* + % = 4а}, fffx, 17) ~»
•= (ах + (а + 3)# = За— 1} —два предложения, определенные
для всех пар действительных чисел (х, у). При каком значении
параметра а предложение A(x,yJ^B(x,g-) имеет множество
ИСПШНОСТИ'.
1) состоящее только на одного элемента (х, i/h
2\ состоящее более чем из одного элемента (х*у,У',
3.J не содержащее ни одного элемента?
2.7. Пусть А(х)= (ах— I s£ О, В(х) = {х — 4а> 0> — два
предложения, определенные при всех дейетвительныж значе-
вмях я. При каких значащих в множество нетнщюеш
предложен»» А{х)/\ В(д:) не- пусто?
С предложениями, зависящими от переменной", близко свя-
запы два часто встречающихся утверждеиия.
1. Предложение А{х) (х е Af) истинно для веек элементов
множества М.
2. Найдется хотя бы один, элемент множества At, для ко-
торого А (х) (х е Af), истинно.
Эт» утверждения- настолько часта вспречаюяся- а вгспюма*
тике, что получили специальную краткую символическую залнсы
знак общности. V и знак, существования 3. Зван. V заменяет
слова: «для всех», «всякий», «любой», «каждый». Знак 3
употребляется вместо слова «хотя бы один», «найдется»,
«существует». Утверждения I и 2 с яомощыо этих знаков имеют вид
1. (V* <= М) А {х);
2. (Зл <= Л!) А (х).
В первом случае утверждение заключается в том, что
множество исти-няоети А{х) совпадает с М. Во втором случае утвер-
ждеяие заключается в. том, что множество вегиимостм Л(.г) не
пусто. Оба утверждеиия представляют собой высказывания1 а
могут быть истинны или ложны *).
Например, предложение с переменной
Л(*}={*-3>0}, JfeR,
рассматриваемое яад множеством деЯствятельнвга чисел,
допускает два высказывания
(V*eR)A(*) в (ЗхефАСг).
Первое из ннх ложно, второе истинно.
*) Знак у называют квантором общности, а знак Н — кван.
тором существования.
,480 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
Если в качестве М взять интервал (3; оо), то оба выска-
вывания (V* е Af) А (х) и {Зх е М) А (х) истинны.
Пример 2.1. Выяснить истинность следующих высказы-
BflRdft*
(V* <= R) (Зу <= R) (х + у = 3),
(Зу <= R) (V* е«) (*+(/ = 3).
Решение. Прочитаем первое высказывание; «для любого
действительного числа х существует действительное число. у
такое, что справедливо равенство х + у = 3». Это
высказывание истинно, так как для каждого х в качестве у достаточно
взять значение 3 — х.
Прочитаем второе высказывание: «существует такое
действительное число у, что для всех действительных чисел х
справедливо равенство х + у = 3». Очевидно, что нет ни одного
такого числа у, которое сразу для всех х обеспечивало бы
равенство х + у = 3. Следовательно, второе высказывание ложно.
Сформулировать и выяснить истинность следующих
высказываний.
2.8. (3* е R), (Зу <= R) (* + у = 3).
2.9. (V* <= R), (V</ eR) (х + у = 3).
2.10. (V* <= R), (Vy e R), (х < у) =*-(Зг eR) (х < z < у)
2.11. (V*sR) (х2+\ >0).
2.12. (V*eR) ((* +I) (*-l) >()=*-(*2-1)>0).
2.13. (VjsR) (д:а — 1 > 0 =s- д: — 1 > 0).
2.14. (V*eR) (x — I > 0 =s- xa — 1 > 0).
2.15. (3* e= R) (V** < *).
2.16. (3*<=R) (VJ»>x).
2.17. (V*eR), (VjeR) (1g(*.</) = 1g* + 1g0).
Для того чтобы убедиться в ложности высказывания
(V* е М) А (х), достаточно найти хотя бы один элемент х <=М,
дли которого высказывание А(х) ложно. Таким образом,
(V* <= М) А (х) = (Зх&М) А(х), (1)
*
н наоборот, для того .чтобы убедиться в ложности высказывания
(Зх е М) А (х), необходимо проверить, что для всех хеМ.
справедливо А(х), т. е.
(3* <= М) А (х) =* {Vx e=M)A (х). (2)
Равенства (1) н (2) позволяют формально строить отрицания
для утверждений, снабженных кванторами общности и суще*
ствования*
§ 2. ПРЕДЛОЖЕНИЯ, ЗАВИСЯЩИЕ ОТ ПЕРЕМЕННОЙ 481
Пример 2.2. Сформулировать с помощью логических
символов два утверждения. Первое: число а является пределом
числовой последовательности ип. Второе; число а ие является
пределом числовой последовательности ил.
Решение. Вспомним словесную формулировку
утверждения
lim ипч^а.
В-*оо
Число а является пределом числовой последовательности, если
для любого е > 0 существует такое N, что для всех п> N
справедливо неравенство \и„ — о|<в {т. е. если n>N, то
\\и„ — а\<е). С помощью логической символики получаем
(Ve>0), (3AT<=N), (VneN) (я > N ->| ц„ - а \ < е).
Для построения утверждения
lim и п. Ф я
П-»°о
с помощью логической символики воспользуемся свойствами
операции отрицания:
(Ve>0), (3W<=N), (VneN) (я > N->\ua - a \< e) =
■=(3e>0), (V/feN), (3neN) (n > N-*\ un ~ a |< e)=>
= (3e>0), (VW<=N), (3ne=N) ((n > N) A (| un - a |>8)).
(*)
Замена квантора общности на квантор существования при
построении отрицания следует из правил (1), (2). Из этих же
правил следует знак отрицания над последним высказыванием,
означающим импликацию А-+В, где высказывания А и В суть
А = {«. > N}, а В = {| ип — а |< в}.
Но отрицание импликации А -*■ В представляет собой
конъюнкцию А /\В. Действительно,
. j+l=.(iAB) v л = (Т7ГвГл л = л vl ла=*а л в.
Словесная формулировка lim un Ф а, таким образом, имеет
П-»оо
вид: «число а ие является пределом последовательности ип,
/если существует е > 0 такое, что для любого JVeN найдется
•номер fieN такой, что истинны одновременно два
высказывания n>N и \ип — а|^>е».
: 2.18. Используя логическую символику, записать
высказывания и нх отрицания:
а) «последовательность ограничена»;
'3' б) «абсйеДовательйостБ' монотонно возрастает»* ~ ■"" ■ "■'
16 А. Г, Цшгаш, Д. И. Пинский
482 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
2.10. Используя логическую символику, сформулировать
высказывание lim f (х) = ft.
х-* а
2.20. Число М называется точной верхней гранью функции
[(х) иа отрезке [a; ft], если выполняются два условия f(x)^M
для всех х е [a; ft] н для любого г > 0 найдется х е [a; ft]
такой, что f(x) > М — е. Если М—точная верхняя грань f(x) на
отрезке [а, 6], то пишут М = sup f (x).
х<={а; Ы
а) Используя логическую символику, сформулировать
высказывание М *= sup / (*).
х е [a; 6]
б) Исполбзуи логическую символику, сформулировать об-1
ратное утверждение М ф sup f (х).
х в \а; Ь\
Дать словесную формулировку.
§ 3. Метод математической индукции
В различных разделах математики часто приходится
доказывать истинность некоторого предложеипя а(п), зависящего
от натурального п сразу для всех значений переменной я е N.
Метод основан иа следующем принципе. Если а — некоторое
утверждение, имеющее смысл для всех neN, то для того,
чтобы установить его истинность для всех neN, поступают
следующим образом) проверяют истинность а(1) и истинность
импликации a(k)-*-a{k+ 1), где k — произвольное
натуральное число.
Покажем, что если выполнены а(1) и a(k)-*-a(k ■{■ 1), то
а(3) истинно. '■» -
Действительно, так как а(1) истинно, то в силу
истинности импликации a(k)-+ a(k + I) для любого ft e N, положив
k = I, получим истинность а (2), а положив в высказывании
(a(k) -»-a(fe+ l)) ft = 2, получим истинность a(3).
На языке логической символики принцип математической
индукции может быть записан следующим образом:
(а (1) Л (a (ft) -> a (ft + 1))) -> (Vn «з Ы) (а (я))
или
(а (1) л ((VA s N) (a (ft) -> a (ft + 1))) -* (Vn s N) (а (я)).
Пример 3.1. Доказать, что при любом я выражение,
n(2/is — Зл+1)
делится на в,
S 3. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ 483
Решение. Высказывание а (л), сформулированное в
задаче, определено для любого п е N. Согласно принципу
математической индукции, проверни а(1). При я = 1 получаем
1(2-3+1) = 0,
О делится на 6, следовательно, а(1) истинно.
Предположим, что истинно высказывание а (А), т. е..
в(2в2— Зв -{- I) делится на 6. Заметим, что истинность а\к-\- I)
будет следовать из истинности a (k) и равенства
(£ + l)(2(fe + l)2-3(£ + I) + I)-£(2fe2-3fe+ I)=6/, (*)
где I — некоторое натуральное число.
Раскрывая скобки в (*) и группируя члены, имеем
2[(в + 1)* - ft»] - 3 [(в + 1)» -.*»] + (* + !-*)-
- 2 [(в + I)2 + в (* + 1) + в2] - 3 [в + I + k] + 1 =
= 6fe2 + 6fe + 2 - 66 - 3 + I = 6fe2. (**)
Таким образом, для любого натурального к импликация
a(k)-*-a(k-{■ 1) истинна. Другими словами, доказана
истинность составного высказывания
о (1) Л (Vs es N) (a (ft) -> о (в + I)),
которое является условием нстнииостн импликации
<х(1) A(VfeeN)(a(ft)^a(ft + l))^-(V«eN)(e(ft)). (***)
Так как условие истинно и истинно все составное высказывание
{***), то истинно и следствие. Утверждение доказано.
Доказать, что при любом п <s N: ,
3.1. 62n_2-r-3',+1+3n-1 делится на 11.
8.2. Il™+1 -h I22™—' делится на 133.
8.3. я5 — п кратно 5.
8.4. б•2э',-2 + Зэ'^-, кратно 19.
, З.б. п7 — п кратно 7.
3.6. 22" + 1 оканчивается цифрой 7, при п > 1.
8.7. Доказать, что если п четно, то 20" + 16" — 3я — 1
делится иа 323.
3.8. Доказать, что число
(10" + 10"-1 + ... + 0 (l0rt+l + 5) + 1
есть точный квадрат.
Пример 3.2. Доказать методом математической нндукцни
формулу
i' + y + » + w\ + .'-?<" + l)efr + l). (*>
16»
484 ГЛ. W. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
Решение, Высказывание а(л) о том, что формула М]
имеет место, определено при любом натуральном я.
Высказывание сс(1) истинно, так как
,*_, t-2.3
6 '
Предположим, что а (в) нстниио, т, е, ямеет место формула
i* + 2»+.,.+fe*=fe(fe + tH2fe + 1>,
Выясним, будет ли при этом условии истинно «(ft+l), т. ft
будет ли верна 'формула
ia + 2a+„, + (fe + l)s=-_ (*+1)(*+2)Р№+1) + 1), <„,
Прн условии истинности а (в) левую часть {«») можно
представить в виде
*(»+1НЦ+П+№ + |),. ^
Преобразуем (**»)J
(fe + 1) [fe (2fc + I) + 6 (fe + 1)1 _ (fc + 1) (2fea + 7fe + 6)
6 6
Заметим, что произведение (&+ 2)(2(fe+ 1)+I), входящее в
правую часть (»»), равно 2«2 + 7й + 6.
Таким образом, из истинности a (ft) следует истинность
«(ft+l), т. е. для любого натурального ft доказана
импликация a(ft)-+a(ft-f-1).
Заключительная часть доказательства проводится так же,
как в примере 3.1. '^
Доказать, что для любого натурального п справедливы ра«
венства:
3.9. I + 3 + 5 + ... + (2« - 1) = п\
ЗЛО. I3 + За + 52 + ... + (2ft - I)3 ~» 'l (4,t'~,'} . ,.; :
О
3.11. 1.2+2.3+... + (*-1)-«=("-')^+1).
О
3-«2. -Дт+^Т + .-.-т
|.Зт3.5т""т(2п-1)(2пт1) 2п + 1*
8.13. I3 + 23 + ... + п8.= "!>(п+1)'.
С помощью метода математической индукция, удобно до*
называть справедливость некоторых неравенств. ; <' ;
5 3. МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ 485
Пример 3.3. Доказать, что при а > — 1 справедливо
неравенство
(l+e)" >} + пх.
Решение. Проверим, что а(1) истинно.
Действительно,
1 + а «= I + а.
Предположим, что нстниио a{k), т. е.
(l + a)fc>l+kx. (*)
Докажем теперь, что истинность a(ft-f-l) следует из
истинности «(ft). Умножив обе части {*) на 1 +а, имеем
(l + a)fe+l>(l + fea)(I+fl)
или
(1 + a)ftH > 1 + (fe + 1) a + ka\
Так как fta2 ^ 0, то справедливо неравенство
(\+a)h+l>l + (k + l)a.
Таким образом, доказана импликация a(u)-»-a(& + I)'.
Заключительная часть доказательства проводится так же,
как в примере 3.1.
Доказать, что для любого neN справедливы неравенства:
3.15. Если xi > О (1 ss ' < «). то
зле.
3.17.
2
2
3
'Т
•м
5
в
<1 +
_L
••
1
т
.. . Т *п
п
2л- 1
2л
+ ...+
-<V*i
<
Уз)
1
2" -1
1*2 ••■
1
1+1
<п.
Хп
3.18. Если х{> 0(1 </<я) н *,+*2Ч + *п<1/2, то
(1-х,) (1-х,) ... (!-*„)> 1/2.
3.19. Доказать, что если х{ > 0(1 <f<n) я xt + #2 + ...'
+ *rt = а, то
Х\'Х% ... *П^1"Г" I •
3-20'7f+Vr+W+-+W>V;r
■ 486 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
3.22. Пользуясь тем, что 1д(1+х) < х, доказать
неравенство
1+т+т + --- + т>|п(л+,)-
§ 4, Системы счисления
Здесь будут рассматриваться только так называемые
позиционные системы счисления. Напомним, что целое число А
называется записанным в (позиционной) системе счисления с
основанием / (или, короче, в 1-нчнои системе счисления, где
t > 1, I e N), «если оно представлено в виде
А = antn + a^t""1 + ... + а,г + ад,
где 0 sg a, < t, i = 0, I п.
Числа flo, ai, ,,., aa называют t-ичнымц цифрами числа А,
а число t — основанием l-ичной системы счисления.
При <= 10 получаем десятичную систему счисления.
Ясно, что а0 = А — (aatn + .,. + axt) является остатком от
деления А на L Неполное частное при делении А на t имеет
вид On*"-1 + . >» + «1. Если разделить его на t, то в остатке
получим ai. Поступая далее так же, получим последовательно
все цифры числа А в f-ичиой системе. Если число А =
.= fl„/-"-{-an-i'~"1"1 + ... + flr<~1, то для получения цифр
числа А требуется умножить его последовательно иа L При
первом умножении A-t = ant-n™ +ап_1<_я+2+ ... -{-<*il й\ —
уже целое число. Чтобы найти аз, следует умножить на t
число A-t—а\\ число аз будет целой частью этого числа.
Поступая так далее, мы будем получать последовательно цифры
дробного числа А в <-нчной записи.
Пример 4.1. Записать числа 606 и 0,506 в системе
счисления с основанием 4.
Согласно изложенному выше алгоритму, имеем
506 _4_
4
2
126
2
ЗП 4
3|7U
" 3 1
Записывая подчеркнутые остатки в обратном порядке,
получаем запись числа 506 в четверичной системе счисления
(506)10 = (13322)4,
'Для получения записи дробного числа 0,506 в четверичной
системе счисления, согласно изложенному выше алгоритму, про-
5 4. СИСТЕМЫ СЧИСЛЕНИЯ
487
делаем следующие вычисления:
0,506-4 =.2,024, 0,024.4 = 0,096, 0,096-4 = 0,384,
0,384-4= М36, 0,436-4=], 744, 0,744 • 4 — 2,976
и т. д. Цифры получающегося числа — это последовательные
целые части результатов умножения, т. е«
(0,б06)10 «(0,200112 ...)«.
Пример 4.2. В классе 24 девочки и 32 мальчика, всего
100 человек. В какой системе счисления записаны числа?
Решение. Составим уравнение
2 • р1 + 4 • р° + 3 • р1 + 2. р° *= р\
где р — неизвестное основание системы счисления. Приводя
подобные члены, получим уравнение
5р + 6 = р2,
корни которого р\ = 6, pi = — 1.
Ответ. Числа записаны в шестеричной системе счисления.
Иайтн следующие числа в указанной системе счисления
|[чнсла, если это не указано, даны в десятичной системе
счисления).
4.1. Представить число 10 000 в шестеричной системе,
4.2. Найтн, чему равно число (1 14 144)в в десятичной
системе.
4.3. Найти, чему равно (101)2 в десятичной системе.
4.4. Найтн, чему равно (25) 7 в десятичной системе.
4.5. В системе счисления с основанием 5 записано число
22 001. Найтн его десятичный эквивалент. Какому числу будет
соответствовать эта же запись, если система счисления
десятичная?
Для чисел, записанных в десятичной системе, пользуются
правилами умножения и сложения «столбиком», деления
«углом». Этн же правила полностью применимы в любой
позиционной системе счисления.
Сложение столбиком, как и в десятичной системе, всегда
производится поразрядно, начиная с младшего разряда. Прн
этом если в предыдущем разряде сумма превышает основание
системы илн будет равна ему, то надо сделать перенос в
следующий разряд.
Пример 4.3. Сложить столбиком (1357)8 и (2463)8.
Решение. , (1357)8
-*~ (2463)»
(4042)8
488 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
Складывая в разряде единиц 7 н 3, получаем 10 = 8 + 2,
2 записываем и I переносим в следующий разряд. Далее,
5+1+6=12, 12 = 8 + 4, 4 записываем и I переносим в
следующий разряд; 4 + 4 = 8, 8=1-8 + 0, 0 записываем,
единицу переносим в следующий разряд.
Ответ. Ц357)в+(2463)8=(4042)8.
Для умножения следует сначала выписать таблицу умно»,
жения чисел, меньших основания системы.
Возьмем в качестве примера таблицу умножения шестернч*
ной системьи
1
2
3
4
5
1
I
2
3
4
5
2
2
4
10
12
14
Э
3
10
13
20
23
4
4
12
20
24
32
5
5
и
23
32
41
Все числа в таблице записаны в шестеричной система
счисления. На пересечении столбца и строки стоят числа,
являющиеся пронзведеиием номеров строки и столбца. Пользуясь
таблицей, легко перемножать числа столбиком.
Пример 4.4. Умножить (142)6 на (212)6,
Решение. (142)в
(212)в ч
(324)6
(142),
(324)8
(34544)в
Пример 4.5. Разделить «углом» 1(120101)9 на (102)8.
Решение. (120101)3| (102)3
(102)8 I (И01)э
(1Шз
Г(Ц»Ь
(201)з
(Ю2)з
(22)з
Таким образом, j[t20 101 )3.= (П 01ЫШ2)л +Д22}д,
4.6. Сложить {23.65L)» а.(17.643)». ,. . • . ..
§ 4. СИСТЕМЫ СЧИСЛЕНИЯ 489
4.7. Сложить (423)е> (I34I)e и (521 )8.
4.8. Умножить (352)в на (24б)6.
4.9. Составить таблицу умножения двоичной системы.
4.10. Перемножить числа (101)2 и (I00)s. Результат
представить в десятичной системе.
4.11. Доказать, что число (121)л является полным квадра-
1 том, если п > 2.
4.12. Доказать, что число (1331)л является полным кубом,
Йслн « > 3.
7> 4.13. В какой системе счисления справедливо равенство
31- 13=13?
4.14. Найтн частное от деления (llll)s иа (22)3.
4.16. В какой системе счисления справедливо равенство
101-11 = 1111?
4.16*. Доказать, что если вес тела выражается целым
числом и не превосходит 31 кг, то его можно определить о по«
мощью не более пяти гирь при условии, что гири можно
ставить только на одну чашку весов. Указать веса гирь.
4.17**. Доказать, что если вес тела выражается целым
числом и ие превосходит 40 кг, а взвешивание происходит иа
рычажных весах (т. е. гнрн могут быть установлены на любую
чашку весов), то для определения веса тела понадобится не
более четырех гирь. Определить веса этих гирь и описать алч
горнтм взвешивания.
4.18**. Пусть условия взвешивания такие же, как в за«
даче 4.17** и известно, что Mv — максимальный вес, который
удается определить с помощью р имеющихся гирь. Доказать,
что если Mp+i — максимальный вес, который удается определить
с помощью р + I гири, то
Мр+1 = ЗМр+ 1.
4.19**. Доказать, что если М„ — максимальный вес груза,
который может быть взвешен /л,, ,.., тр гирями, то
М„ = (П ... 1)з.
р
4.20**. Выяснить, какое минимальное число "гирь и какого
веса потребуется для взвешивания тела весом m (m sg: л) на
рычажных весах. Указать алгоритм взвешивания.
4.21**. Пусть г = ра, где а —осиовапне системы
счисления, р — число. lpiaj!sflOB!- Если г = 30, то в какой системе'
счисления можно представить максимальное число?
490 ГЛ. 16. ЭЛЕМЕНТЫ ЛОГИКИ. СИСТЕМЫ СЧИСЛЕНИЯ
С представлением числа в той ялн иной системе счисления
связаны признаки делимости числа, которые формулируются
на основе цифровой записи числа.
Пример 4.6. Вывести признак делимости иа три в
десятичной системе счисления.
Решение. Представим число A=(a*a„-i ... ао)ю в виде
А= ап • 10" + an-ilO"-1 + ... + а010° =
= дЛю" - I + 0 + а„_, (Ю""1 - 1 + I) + ... + а, • 10°.«
«а„(Ю',-1) + а„_[(10п-1-1)+... + а(10-1) +
. + вп + ап_1 + ... + ffi +Яо.
Рее числа 10*—I делятся на 3, следовательно, А делится иа 3
в том н только в том случае, если an + fl/t-i+ ... +"i + flo—•
сумма его цифр—делится на 3.
4.22. Доказать, что А — {а„а„-\ ,,, ао)ю делится на 9, если
At -f- a„_i + • • • + «о делится на Э.
4.23. Доказать, что А = (апа„-\ ,.. аа) ц делится па 6, если
о« делится иа в.
4.24. Доказать, что А — {а„а„-, ... ао)и делится на 8, если
(oiao)ia делится па 8.
4.25. Доказать, что А — (апап-\ ... а0)12 делится на II,
если ап + вл-i + ... +flo делится на 11.
4.26. Доказать, что А = (аяая-1 ... Оо)р делится на р—\
в том и только в том случае, если ая + о„_1 + ,.. +Оо делится
на р— I.
4.27. Известно, что чкело А = (3630)Р делится иа 7. Дока-
вать, что р кратно 7.
4.28. Известно, что число Д={1210)„ делятся иа 11.
Доказать, что р кратно П.
4.29. Доказать, что если основание системы счисления р —
дростое число, большее 3, то (100),, — I делится на (100)$—I.
ОТВЕТЫ
ГЛАВА 1
§ 1
1.1. -2у. U. 1. tJS.Zab. I.44/<V*+Vtf). 1.5. 2 (Va+V*)«
|А (J.* ±Y u-a (a + {)- 1A ^T" ,'9, "L^L-
Vam-aV
1.10. V§I 1.11. --^20*; 1.12. 4p - V4p2 - 1. 1.13. *e
e[-V2i -1)=*--V2i * s (—1; У?] =»-У§! 1.14.1. 1.16.1.
1.18. 7=L=-.
Vb+2
§2
2.1. y<=l-oo, I] =*--(o* +у $2 +УТУ, }€[1, oo)=».
c» y*. 2.2. ле(-оо;1)и(1;3)=>--(л:2+л;+1);*е(3;оо)=».
^--V2
ш>х* + х+1. 2.3. x <= (- oo; 0) U О; оо) =*- YZfi'- * e № 3> *
J^.. 2.4. *<= (-oo; --|) U(-|-: O) U(ft 3)=>
* +
3 1 I
; x e (3; оо) «Ф- —. 2.6. у <= (— oo; — 5) =». ;
X (2x + 3) * v ' ' x ' " x ' ' //
»ei(-BS ч>и(о: -|)и(|-; «)*Т^Г5Г- ". **н(а и*
■*x_|ii *g<}; °°) ■*" Я1 _ я « 2.7. гб5(-оо; 0)4 ^ ~ * ;
JG[0| 1) U (1; oo)=»-^ ■. 2.8. 1. 2.9. Vl - **• 2.10. V(e+6F-
- V(e-ft)8. 2.11. ■ 4 ' 2.12. *e{0; Э^З-гУя-
Улг»- 1
x'e (9; oo) =»■ — 3. 2.13. л; <= (— oo; 0) =»• — 1/2; x& (Or, oo)«*--~.
492 ОТВЕТЫ
8.14. *<=[II; оо) «=» 2 У;Г^2| *е[2; И)=*-6. 2.1Б. хе [I; 2)-»-
«*• 2 V*— П * е I2: °°) =*■ 2- 2.16. * е (— оо; 0) =*- 6; х е [0; в)-*-
«*• в - 2л; * е= [6; оо) =► - 6. 2.17. * <= [2; 4) *> 4_ х', «е(4; оо) <*•
*»2л/*~~2 . 2.18. V2". 2.19. ^. 2.20. а е (0; 1)г*1^Д,
ж — 4 3 V«
а е (1; оо) =*• -^==!-. 2.21. f.i+A'jTT. 2.22. 0. 2.23. 0,64.
V а \ а — 6 /
1Ь24. n4/ms. 2.26. 1. 2.26. 1. 2.27. 2. 2.28. 1. 2.29. 2^3п^Н.
§8
3.14*. Указание, Привести выражение, стоящее в левой
части тождества, к общему знаменателю и рассмотреть числи*
тель дроби как многочлен второй степени относительно а,
8.16*. Указание, См. указание к задаче 3.14*.
§4
4.7*. Указание. Найти единственное решение системц,
51.9*. Указание, Поделить каждое из тождеств условия на
правую часть.
§5
8.1. I. Б.2. аЪ (а - Ь)3. Б.З. а2 + а + I. 6.4*. у. Указание.
Использовать (4) для записи всех логарифмов по некоторому
общему основанию. Б.5. (logs* + I)3. 6.6. ,_.. 6.7.6.
Б.8. 3. 5.9. в (6 + 3). 6.10. " j* . 5.11. а-Ь-с+1. 6.12.1og8a=
•= -. 6.13*. —^ —, —,—ттт • Указание.
1 — logs с a £ + P '+Y +» 1
Перейти к логарифмам по основанию х. •
6.18*, Указание. Перейти в левой части выражения к
логарифмам по основанию N. Б.19*. Указание. При
упрощении учесть, что корень четной степени понимается в
арифметическом смысле. 5,20*. Указание. См. указание к б. 18*»
5.21*, Указание, См, указание к 5.18*,, 6.22*. Указание.
Сравнить левую и правую части ■ неравенства .,< ,с .А,
6.23*. Указание, См, указание к 5,22, 5,25*. Указание,
См, пример-516» . ' ."., , . ; ...
ОТВЕТЫ К ГЛ. 2 49а
ГЛАВА 2
§ I
1.1.2; —4. 1.2. —2; 1. 1.3*. 0. Указание. Обозначить
_5 -ь д/ШГ —5 ± л/б"
z= л2 — 5*+ 6. 1.4*. ~ v —; у-*—. Указание.
«« а > е 3 п. —3 ± V65" .,
Рбозначнть z = ** + "*■ 1.5*. —„-; 0; j-1 , Указа-
4
ни е. Обозначить г = 2хг + 3х. 1.6. ±3; ±2. 1.7. ± л/у.
1.8. у(-^2~+~[); 4-(--^5"+!)• 1.9*. Нет решений.
Указание. Поделить обе части уравнения на ж*. 1.10. 0; 5. 1.11. — -=■:
1. -1+Ув ■ -1-УВ- _ 5_ _ 2_.
Т* 2 2 - * ' 2* Ь * 3*
——; 3. Указание. Использовать формулу бниома Ньютона.
LIS. 1; а + л/И', а —л/а. 1.16. 4; 3; 2; —б.
, 17 2Д±У2ва'*2У25а< + 4&« , Jg _1; ,2 j ,g -5±^
1.20. —3; 4. 1.21. —3; 2. 1.22. —5 ± УШГ; —5 ± У3~. 1.23*. —1; 0.
-5±УгТ
Указание. Ввести обозначение у = х3-\-х. 1.24.
2
U5. -2; ±1; у. 1.26. 1; --|; -1-. 1.27. -2: ~; -|.
-4 + Уб~± Vl8-8Ve -4-Уб ± Vl8.+ 8V6"
1.28. g ; 5 ; •
1.29. 2. 1.30. 1; -2. 1.81. 5; -1. 1.32. 0. 1.33. 0. 1.34.0; ± Уз"; 3.
,,.35. -'*V£T. ^±*У11. ,.3e. _,. з: ±V3".
§2
2.1. у. 2.2. -3; 5. 2.3. 2. 2.4. 5. 2.5. — у. 2.6. i-; 5.
2a 6 as + 6s '
£7*. a + 6; €: —;—r» r~r—• Указание. Ввести вспомо-
.<? + о о -+■ о
гательное неизвестное z=»—я *. 2.8. Ь 2.9. 1; 3. 2,10.. Q.
2.11. 3±У20". 2.12. 0; -% ~2 *у^. 2.13. 2;.—. 2,14.,0;-2,
494 ОТВЕТЫ
2.16. 3; ~. 2.16. 4/5; 3. 2.17. б; 0.5. 2.18. 3/4; 2. 2.19. ~5 ^ -
2.20. 2; -1/6; -«-»А^Рб".
64
§3
3.1. -1. 3.2. -J- 3-8- 11; 2]. 3.4. -8: 2. 8.6. -4; -2; 0; 2; 4.
3.6.' 0. 3.7. (- оо; 2]U[3; оо). 3.8. 0; ± 1. 3.9. 11-; 2-i; 3j.
§4
4.1. 8. 4.2. 5. 4.3. 8. 4.4. — i; 3. 4.5. Не имеет решенн».
4.6. 7±V,I53_ AJ ^ 4Jk ^ нмеет решений. 4.9. -lj 2. 4.10. 3.
17
4.11. Не имеет решений. 4.12. —5; 4. 4.13. -г^-. 4.14. Не имеет
решений. 4.1S. 7 + Vi[ . 4.16. -«1; 30. 4.17. 2. 4.18. 8; 8±4л/з".
4.19. -6; -5; —Ц-. 4.20. -1. 4.21. -2. 4.22. 0. 4.23. 4; 3.
4.24. 0. 4.25. 9. 4.26. 1; -~. 4.27. ±4. 4.28. -I.
Указание. Освободиться от иррациональности в знаменателе.
2
4,31. •=•; 5. 4.32*. 3. Указание. Воспользоваться тем, что
л/х — 2 У* — х =Уб;г — х3 — 8. 4.33. —17; 23. 4.34. —7; 2.
4.36. -Jj-r; 2. 4.30. ± 7. 4.37*. Указан и е. Обозначить // =
511 а
д * * —g • 4.38*. 1. Указание. Использовать
неравенство [-а>2, справедливое при а > 0. 4.89. 1024,
4.40. 3; S. 4.41. ±2У2~! 4.42. -5; 2. 4.43. -2; 0. 4.44*. -^-.
У к а з а и и е. Заметить, что произведение слагаемых левой части
уравнения равно 66. 4.46. ——; 0; -г\ ~ . 4.46. 15.
4.47*. —3; 6. Указание. Ввести обозначение у = Xs — Зх + 7.
4AS. ~. 4.49. [-1.0J. 4Л0. (0-г 3J. 4.51. 2. 4.Ю. ± -^-. 4£8. Нет
ОТВЕТЫ К ГЛ. 2 495
еинй. 4.64. 5. 4^6. [I; 2,61; 13. 4.6в. [б; 10]. 4.67. 4. 4.68. ± 2.
4JfL 0. 4.60. —; б. 4.61. — 1. 4.62*. —6; 1. Указание. Ввести
вспомогательные неизвестные м=—Уж — 2, о=» л/х +7.
4.63*1 ± 1. Указание. Вынести аа скобку V* + 1 • 4.64. Нет
решений. 4.66. 0. 4.66. 1. 4.67. 0; —. 4.68. (2 + Vj[) + 1
ч 65 (2 + л/3) - 1
i ■> !г4/3*)П 4- 1
1Ь~[п ■ 4.69. 1. 4.79. 26; 7. 4.71. -6; I.
i: —ЩЗ) — 1
ВЛ.\ 5.2. 2, 6.8. -|. 5.4. -3. 5.5. - ~. 8.6. -|-; 4.
5/. 1og3l!%<6.8. 4-(2ft+I); -т- + я^, feeZ. 5.9. —5; 95/11.
V_ * 4
5.!t>. 7/6. "5.11^ 81. 5.12. 5/3. 5.13. —5/2; 3. 5.14. яя, n e Z.
5.Г>. — 2 + V4 — 2 logs 5. 5.16. ± Y?; ± I. 5.17. 2; —2.
5.18. log» (2 + V5"); lo J3 ^5 0~ ' . 5.19. 3; loge8. 5.20. 9; 81.
<p<
1.21. #—J- 5.22. 1; -1; 0. 5.23. j. 5.24. 0. 5.25. -1; 1. 5.26. 1;
log4&' 5.27. i-j -0g2^ + 3. 5.28. 0. 5.29. -2; 2. 5.30. -2; 2.
О О
£31. 1оёэ/<( 2~М- 6.32. 1. 5.33. Ц 3. 5.34. --i-. 5.35. 2;
4; 11. 5.36. 4-; 2; 4. 5.37. I; a,ftt. 5.38. 4"; 25. 5.39. 10; Ю-"*.
5.40. 100. 5.41. 10; 1/10. 5.42. 10; 10!о2-3. 6.43*. 2. Указание.
Разделить обе части уравнения [иа 2х и воспользоваться
свойством монотонности показательных функций. 6.44*. 3. У к-а за-
ние. См. указание к 5,43. 6.46*. 1. Указание. Сравнить
наибольшее аваченне функции, стоящей в левой части уравнения,
с наименьшим в правой. 5.46*. 1. Указание. Найтн у\ и
Уа —корни квадратного j уравнения относительно переменной:
у=а2*, уравнения t/i(x)«=2* и yt (x) = 2х решить, используя
свойство монотонности входящих в них функций. 5.47*. 3.
Указание. См. указание к 5.46. 5.48*. 1. Указание. Сделать
замену у = х — 1 н воспользоваться указанием к 5.46*. 6.49. 4*,
5.50. ± V2". 6.61. Нет решений.
§»
6.1. -8/3. 6.2. 3; 2. 6.3. 2. 6.4. 2. 6,5. -1; 7. 6.6. 3; 3+ V2%
в.7. 3. 6.8. 7. 6.9, 1, 3. 6.10. -10. 6.11. 2, 6,12, 2; 3. МЗ. }. «.14, 1^
496 ОТВЕТЫ
6.1В. 3. 6.16. 3. 6.17. 1. 6.18. ± 1/2. 6.19. 1; 3. 6.20. 4; tf\f%
6.21. 1; 4; 1Д4 УЗ"). 6.22. 8; l/-^4~. 6.28. b2 + 1; b > 0 н Ь ф I.
в.24. 1/2; 1/8. 6.26. 1; 1<Г3; Ю-2. 6.26. 2-в; 227. 6.27. З"^5"; 88-^;
6.28. -i; 81. 6.29. i-. 6.30. 10. 6.31. 10; 10*. 6.32*. —10; —I,
Указание. Использовать тождество лр? ■= — х, справедлив
вое при *<0. 6.33. log310; Iog328 —3. 6.34. 8. 6.3В. 10; 0,Ц
0+Уз) 1-Уз
6.36. 1; 0,1; 0,01. 6.37. Ю-1; 10 2 ; 10 2 . 6.38. -±-; -jj.
..„. MV=m, ,0-л^Ш l0V4lX ,„-V4ff
6.40. 1; 2; 2_3/4. 6.41. 3* ^; З*1^ 6.42. 2~m. 6.43. 1/81; 3,
6.44. 1. 6.46. 2. 6.46. 1/4; 2.
§7
7.1. 4. 7.2. 3. 7.3. 2. 7.4. 2. 7.5. 1 + У1 + lg 2; 1 — У1 + lg2.
7.6.0; 4. *7.7**. 2; —r—=-. Решение. Разделив обе части на
lg5
г2^2, получим 5K-a.2JC+l -=1<=>-U-21+JCJ =l*^5X
— I 2
X2*+1 =1, или* — 2 = 0-t=>* = — -j-^-, илн * = 2. 7.8. у.
7.9*.-i-^/i-lg(i + yir); -1 + д/4-lgO+Vn").
Указание. Числа Ю3*'*7*; lO*4"5*; 10_(,:+JC,) -
последовательные члены геометрической прогрессии. 7.10.1; 8.7.11. (logs3 — 2)-1j
(1 -10g3 4)-1. 7.12. (5; 0,5). 7.13. 10; 101/9. 7.14. Г-i-; ooY 7.16. 2;
7/3. 7.16. 1. 7.17. б. 7.18. 2. 7.19. (2k+l)-j; -(4ft + l)~.
7.20. ±arccos(log ,-2 + ftn). 7.21. 0.
ГЛАВА 8
§1 ...'''_
1.1. (1, 2, 3). 1.2. (8, 4, 2). 1.3. (1, -2, —1). 1.4. (I, -3, -2).
,1„S. (fibc, ab + ac + Ьс, а + Ь + с). 1.6. (-(6 _ ^ц _flv,
ОТВЕТЫ К ГЛ, S
497
$ИС"Тема определена, при а»»—3 система не определена, прн
р = 0 система несовместна. 1.8. Прн а Ф О система определена,
Ьри а = 0 система не определена. 1.9. Прн а «О система ие
определена, при а«=2 система несовместна, прн остальных а
—определена, 1.10. При а— 0, а=» I система несовместна, прн а =»—!',
aM2 система не определена, прн остальных а — определена.
Ji.il, Прн а+Ь ФО система определена, прн a + b = 0 ие
определена. 1.12. При a = 0, b Ф 0; a = 0, Ь^О; афО, b = Осистема
Ие определена, при остальных значениях пары a, b система опре-
, «о г- 36 +14а
делена. 1.13. Система ие определена прн р<= г= , т =*
"* ^^^Я- |Л4" Совместиы. 1.16. а = 1, & = -1. 1.16. (1, -I);
(1, -2); (-1, -1)1 (-1, -2). 1'17. о—1. 1.18. (о, 0, ^-);
(2, —I, I). I.19. а ==.-4. 1.20. а = 3.
§8
2.1. (1, 4); (4. 1). 2.2, (0,6; 0,3); (0,4, 0,6). 2.3. (3. 2); (2, 3).
8.4. (14, -И); (11, -14). 2.6. (4, 2); (2,4). 2.6. (1, 4); (-1, 6).
2.7. (1, 2). 2Л. (4, 1); (1, 4). 2.9. (2, 1); (-2, -1). 2.10. (4, 1); (1, 4};
/-5 ±-^41 -бтлДГЛ * к
I г-* , S"1 J, где знаки —оба верхних или оба
нижних. _^___^_____
2.ц.(± л/аЬ±л/^Ь^=1ГЬг ± л/аЬ*Л/аЧ!Г^шГ\
£.12. (1, 2); (2, 1). 2.13. (3. 1); (1, 3). 2.14. (1. 2); (2, 1). 2.16. (1, I).
8.16. (±3, ±2); (±2, ±3). 2.17. (±3, ±1); (±1, ± 3).
2.18. (±3, ±2); (±2, ±3). 2.19*. (2, 1); (1. 2). Указание.
Перейти к неизвестным и = х + \, u«=t/ + l. 2.20*. (±2, гь 1);
{±2. ±1). Указание. Первое уравнение представить £ виде
квадратного относительно переменной z = (х -{- у)1(х—у).
12.21*. (2, 3); ( —j, — 4 j. У к а з а и и е. Разделить первое
уравнение иа второе. 2.22. (5, 1); (1, 5); (3, 2); (2, 3). 2,23. (2, 1);
(-1. -2)| (I±Y2~, 1:pV2). 2.24. (-2, -4); (-§-, -у-).
2.26. (1, 4); <-б, 4); (5, -4); (-1. -4). 2.26*. (3,5); (5.3); (-3, -5);
<—5, —3). Указание. Во второе уравнение, представленное
в виде х* ,-fr у* + 2х2ул = 931 + xtyi, аодсгавить (xs + у3),
выраженное из аервого уравнения. 2.27*. (2, 1); (1, 2); (—3, 0); (0, —3);
<1, —2);,(2, -pi). У к аа анне! Представить первое уравнение
р внДе (* + у)2 + (ху - 1)" •* 10. 2.28*. (б, 2); (-2, -б). У к а«
sайне, Разложить х*--у* на миозрибли, SWjeuX^.-fl^—1)»-
498
ОТВЕТЫ
(—1, —1, 2); (—1, 2, —1). 2.30. Все перестановки нз чисел {1, 0, 0jfi
2.31. (3, 1, 0). 2.32. (I, 1. I). 2.33*. (2, -i, 4); (-2, i-, -4)1
(-V¥*V?-4VD"(V?' -V$
— -=- A/fc")' Указание. Ввести новые переменные и = xyt
v=*xz, w = yz. Из первого и второго уравнений получившейся
системы выразить и и w через о, третье уравнение после
подстановки' будет квадратным относительно о. 2.34. {0, 0, 0}.
2.35. * = ш , у ^ ' z Ш *
2.36. ± {2аЬс (ab - Ьс + са)Ц(аЬ + Ьс - са) (-ab + Ьс + са)]}1/2,
± {2аЬс (аЬ + Ьс — ас)Ц(аЬ — Ьс + са) (— ab + Ьс + са)]}1!2,
± {2а&с (— аЬ + Ьс + са)Ц(аЬ — Ьс + са) (л& + Ьс — са)]}1/а.
2.37. (I, 3, 9); (9. 3, I). 2.38. (0, 1, -1); (-1, 2, -1); (—1, I, 0).
2.39. (3, —1, —I); (0, 2, —1); (0, —I. 2). 2.40. Вс« перестановки
из {1, 2, 3). 2.41. (3, 6. 10) и (6, 3, 10).
2.42.
2.43. I ±
О
«Ja + b + c ' ~ -y/a + b + с' ~ т/а+Ь + с
2
V(— а+Ь + с)(а + Ь — с)'
2
2 2 \
* V(e- Ь + с\(-а + Ь + с) • ^/(а-Ь + с)(а + Ь-с) )
и <0, О, О). У одной на координат знак положительный, а у
остальных — одинаковый. 2.44. (0,0,0); (± 1, ± 1, ± 1); (0, ± -\Д, ± V2);
(±У2~, О, ±л/2") » (± V2*. ±V2". 0)- 2.46. (l, 0, -4);
( —1> 0, -я-J. 2.46. (±1, ±2, ± 5) — у одной нз координат знак
положительный, у остальных — одинаковый. 2.47. (О, 0, 0);
("Т1 "-*1, 2)' 2'48- (_б* ~~3, 0): (3, '« ~2)- 2"49- <2, -1)'
2.50, (2, 3); (-^, --|). 2.61. (-|-, -^). 2.52. (4,4). 2.63. (2, 3);
(-2, -3); (2, -3); {-2, 3). 2.54. (1, 1). 2.65. (26, 9); (-j-, -^-),
2,56. (В,- 4). 2.87. ( ^=т, ± -^=Л 2.68*. (О, 0); (3,2); (-2, -3).
Указание, 8*0.— х* + 0*-(*-у)*> 2.59. (3, —I, -2tf
ОТВЕТЫ К ГЛ. 4 499
2.60. (± 7, ± 13); (± 6,5, ± 14). 2.61. (± 1, :р 1, -2); (±1, 2, ± 1);
(2, it 1, ± 1). 2.62. (± -JL-, Т —рг, ± -5-\ (± 1, Т I, ± 2).
§3
8.1. (5, б). 3.2. (4. 2). 3.3. (1, -■§•)• 3.4. (6, 6). 8.6. (3, 9),
(9, 3). З.в*. (1, 4). Указание. 4х, 2{х-уШ, г3-"
—последовательные члены геометрической прогрессии. 3.7. (2, 2). 3.8. (2, 1).
8.9. (1, 9); (16, 1). 3.10. (-2, 7). 3.11. (1, 1). 3.12. (2, 4).
8.13. (1, -1); (5, 3). 3.14. (16, 3)j (-£-, -2). 3.15. (27, 4);
("вТ' -3)• ЗЛ6, (4' 1)- ЗЛТ* (6> 2)' 3"18' (9, Ш)< 3,,в** (4, 1);
(—4, —1), Указание. Первое уравнение квадратное
относительно z = 2V*i>t а второе — относительно и = — ^ .
А у
3.20*. (V3, 0. (— л/3, 0. Указание. Ввеети обозначения
г=*х2 + у, к = 2"-*2 а использовать б*'-" = 3*'-«72»-*\
ЗЛ1. (2, 2, 1).
§4
4.1.(3, 9). Указание. Прологарифмировать первое урав-
/2 27 32 \
нение по основанию х. 4.2. (у, —, — J. 4.3. (4, 2)i (—4, 2).
4.4*. (1, 1)> f-gp -g-J.y к аз ание. Логарифмированием обоих
уравнений по основанию 10 свести систему к рациональной
относительно неизвестных и = -^—, о=У* + VtfV 4.5. Г100,
^ig-). (100, 100), (-4-, 100); (-i^-, -4"). Указание.
В первом уравнении перейти к десятичным логарифмам. 4.6. (2, 6);
<6, 2). 4.7. (1, 1, 1); (4, 2, V5"). 4.8. (а«, а, а?); (-1-, а, -1-).
ГЛАВА 4
§ 1
1.1. (-оо; -2) U (2; оо). 1.2. (—£•; -г) U (3; +оо). 1.3. [-1; 3].
ЬА. (-оо; —2)U(—1; 0], I.S. (-8; 1]. 1.6. (-ooj -1)U(3; 7).
1*7. [-It 2]. 1.8. (-ooj -2)U(1; 2) U (3; оо). 1.9. (1; 2}.
1.Ю. (-ooj -i)u(|-; 4). 1.И. {-oo( l)u(-f*2)u(3; «).
БОО
ОТВЕТЫ
,Л2. [-5; ^ZV!L). U3. (^±; ,]. 1Л4. (-со; -5Ш
и[1; 1±V1). ,,5. [-46; 3). 1.16. (~1+J£; l].
1.17. [-6; 0)U(3; 4]. 1.18. [-6; —I) U (1; °°). U«. [-1; oo),
1.20. Нет решений. Ul. Г—1; 5~^13 \ (2; <»). 1.22. (— ooj
Л/5?Ь~13]. 1.23. X£R. 1.24. (6; oo). 1.2Б. (-2; ~l]u[--|; ij.
1.26. «eR. 1.27. [-g-; -|]. 1.28. [l - л/Т?; «JW- l]. 1.29. W2-U
V2+ 1). 1.30. (_3+V65, 3^ , 3I ^^ _2_ ^u[t +1
+ л/3; oo). 1.32. (-oo; -1 --y/W]\j[l --y/b; +oo). 1.33. [-1; 2)(J
U (8; б+л/Гв]. 1-84. (3/4; 1) U (I; oo), 1.35. [-1; oo). 1.36. (—oo;2)U
U(3; oo).
§2
2.1. (—oo; logs (-1 + V?")]. 2.2. (-2; oo). 2.3. (—oo; -l'j.
2.4. (_«>; ^1ол^+1] у [V».o*J^ti-; oo).
2.5. [-ViogH; ViogT4]. 2.6. [-4; -2)U(0; oo). 2.7. [-10; 5].
2.8. [0; 1]. 2.9. [log,35; 1]. 2.10. (-Yf; -л/зШл/3~; Л/Т).
2.11. [2; 18). 2.12. (- !og29; oo). 2.13. (-oo; !ogs3). 2.14. (j log» 6;
log, б). 2.15. Г-1; 3). 2.16. (2; oo). 2.17. (-oo; -1) U (|-; «•)."
2.18. [0; 4]. 2.19. (-oo; 0) U (log3 2; 1).
§3
8.1. (-у; -l). 3.2. (3; »). 3.3. [-1; —j)u(-|; l].
8.4. (-oo; _l). 3.5. [-1; 2]. 8Л (-V?; л/з"). 8Л (yl 4).'
3"8, (~т: "тЮ*8,B*(4; 7)-3*10'(1; "^3-"'(3:7)-ЗЛ2, (10_г:
10). 3.13. [-2; 6)u[-y-; 7). 3.14. (о; i]u [9; 00). 3.15. (I; 2] U
Ul3i 4). 8.16. (-7; 1). 8.17.(-6;-4)U(-3;-l). 8.18. (0; ЩДЙ <*)*
3.19. [l; 00). , 3.20. (— ooj log, 2). 3.21. (- 3/2; - 1) [J
ОТВЕТЫ К ГЛ. 4 501
8.22. (0;2)U(4; oo). 3.23. (0; 1)U(2; oo). 8.24. (о; ^17д 3].
8.25. [—J; £]. 8.26. (I; 3) U (38 5). 3.27. [л/52~3; l).
8.28. (2-16; 2-»] U [2s; oo). 3.29. (-2; —I) U [0; oo). 3.30. (0; 1) U
U(V6-1; I). 8.31. (0; Oufoa'+VI]. 832 £_,. ^
U[U j). 3.33. [2-VU5; l)u(l; -^2). 3.34. (o; ^-] U (1; oo).
B.37. (-4; —3) U [I; oo). 3.38. (I; 2). 3.39. (o; 3 ~^ ] Ц
[)[2±j/L; со) .3.40. (^Ь^; з]. 3.41. (-ос; -7)U(-5; -2Ц]
Ut4; oo). 3.42. (-6; -5)U(-3; -2). 3.43. (l-т/Т; — l)|J(—1/3; 0)U
U(0; 1/3) U (2; l + Vf). 3.45. (-V8; —l)U(»i (V^DM 3.46. (О; 1]U
U(2; oo). 3.47. (3; 5-'V3)U(7; oo). 3.48. (1000; oo). 3.49. (-Щ; lJ(J
U (9; oo). 3.50. ( g+'; 2J. 8.51. (I; 2). 3.52. (0; 1) uG; л/К>).
3.53. (3; я)и(я! ^-)и(^-'.б). 3.54. (W; -5. + 2jtft)lJ
U(2nfe+^; (2fe+l)rt), fteZ. 3.55. (i-; |-). 3.56. (nJH-J;
«fe + --], fteZ. 3.57. (2jtft + arcsin -|; 2jtft + y) U (z^fe +-j'.
(2fe+l)rt-arcsln|), ft eZ. 3.58. (-|; 2) U (-^ l] U
U(2Kfe -|-; i + 2jtfcV ft«=Z, fe-^0. 8.59*. ж—1, л: = 2.
Указание. Найтн область определения неизвестного х н для
каждого целого числа нз области определения проверить
выполнимость (или невыполнимость) данного неравенства. 3.60. х а
f= — 1, х = 0, х = 1, х =■ 2. 3.61. 6, 7, 8.
§4
4.1. (-V^ -l)U(l; л/2)- 4.2. (-I;0)U(0; 1). 4.3. [-4;-1].
4.4. (0,7; 1). '4.5. (-1; 2). 4.6. [0; 1/3} U (3v 10/3]. 4.7. (-ooj -5/3)U
U(i; 00). 4.8. [^"2VS"; о)и[1?Ь/Г1 во). 4 9. (-oo; со).
Б02 ОТВЕТЫ
4.10. [0; 2)U(4; 6]. 4.11. (-оо; 0]U[loge5; I); 4.12. (i-^/2-, l]t|
U[x; 2 + V2). 4.13. (y!og87; Ioga3). 4.14. (-1; -2/VB)[)
U(7T О' ш № t)-
§5
5.1. a< I=>0, a= I«=>* = 2, a> 1 »>.*=» a + 1; х = Ъатг\.
5.2. 2.<a<3=*»jc(=[2n—5; 1]; -2<л<2=»-хе[-1; I]; —3<
<a<— 2=ф-[— 1; 2a + 5]; |a| > 3=*v*e=0. 5.8. Прн а<0
Jfi,s = ± -n" t~l + Vl ~ 4a)- nP" a = 0 д: = 0; при a > 0
уравнение решений не имеет. 5.4. а) При а <0 решений нет; при а=0 —
три решения; прн 0 < а < 1 — четыре; прн а =» 1 — два; прн
а > I нет решений, б) При а < 0 решений нет; прн а = 0 — два
решения; при 0 < а < 4 — четыре; прп а = 4 — три; при о > 4 — два.
5.8. При | а К V2" неравенство решений ие имеет. При | а | > V2*!
аа л/а3 — 1 + 1 < * < a + Ya2 — ! — •• 5.6. При а<0 и в>4
неравенство решений не имеет; при 0 < а < 2: —a < х «^ а; пря
а = 2:-2<*<2; при 2 < а < 4: - |- д/а (4 - а) < * < -£ X
X Va (4 — а). 5.7. г- <а<3. Указание, Записав
неравенство в виде 3 — х2 > | х — а \, построить н исследовать графики
функций, стоящих в левой и правой частях неравенства. 5.8. При
0<a<I *«=logsa. Прн о<0ио>! уравнение решений не
имеет. 5.9. При а< 1 х =■ ± logu(l + V ~а)- При а > 1
решений нет. 5.10. 0<a<-J=-. 8.11. 0<с<8. 5.12. ~'~Л^ <
-^36 2
5.14. —3<*<—1. 5.15. х>3. 5.10. (1;0). 5.17. а>-^-. 5.18. 2У2~<
<a<-j-. 5.19. -7-V45 <т<_4 + 2Уз~.' 5.20. m > 1.
6.21. Ни при каких. 5.22. 4" < а<1. 5.23. —3<а<3. 5.24. ^ <
2 у2
< а < —7=-. 5.25. a < —2. 5.26. — < a < 1. 6.27. При а = 0 реше-
V2 2
вий нет; при a > 0 ж < —2 + Iog3 а; при a < 0 х < log3 (-<*)•
5.28. a>2. 5.29. a>l. 5.30. При 2nfe — -5- <a<-2. + 2яй н
ОТВЕТЫ К ГЛ. 5 503
— +2jtft<a<—+2jtft x=-arcsm . 2c0Sfl q +(-l)"X
6 6 • Vl+4cos»a
X arcsin + яп (k, n <= Z). 5.31. Прн а < —У2~ или
V1 + 4 cos2 a
a>V2" * = (-I)* arcsin I0a_ л/2(°,-1,+ яА; при -У2<а<-1
*=,(—!)* arcsin I0a±'^2(aJ~,, + rtfe; при —I < a < У? уравнение
решений не имеет. 5.32. Ь < —2 — Ув", Ь > 2. 5.33. —3< a<—2,
X = ± -jr arccos2a + б + rtft, k e Z. 5.34. а!,2 = ±2. 5.35. Прн
fr < 4" (b #-д-' 6=^0,6^-1) * = rcft + (-1)* arcsin-^-p
Ирн Ь > 1/2 уравнение решений не имеет. 5.36. При а < 0 урав-
_ д/ИШ
нение решений не имеет; при а>0 аг = я6 ± arcsin2 * *" ,
fts Z. 5.37. При а>1 0 < jc < 1; при a<stn I 0 < х < arcsina,
1 < х < л/2; при sin 1 < а < 1 0 < х < I, arcsin а < д: < я/2.
5.38. (0; 0); (I; 0). 5.39. fe=I x = tg-j(l - л/Т). j^cos^X
X(l+V7~). Б.40. а<-1. а=0. Б.41. Прн а = -1 *=={-!;
il; Щ: прн а = -1 ^{-4-; 0-,^}. 5.42. {0; 1}.
5.43. При а = 1 х>1; при а = —1 — 3<* < I; 'при | а\ > 1
x—U х — —"—г", при |а|>1 уравнение имеет,два решения.
ГЛАВА 5
§ I
1.33. Прн a s [о; у J U \J^; я]: tg (|- + -j): прн а <=
е[я;^)и(|^; 2я]: ctg(|-+i). 1.34. При аФ% + mi
2 tg3 а.
§2
2.1. -1. 2.2. 4т- 2А V«-V2 t 2А I 2^ j 2Д 4
64 4 4
М. |. 2.8*. ^=±. У к а з а н н е. Использовать равенство
cos (3 • 18") = sin (2 • 18"). 2.9*. ~ (УЗ"• VlO + 2VB~- У1Г+ О,
Указание. Использовать равенство sin 42" = sin (60° — 18").
504 ответы
2.10. 0,96. 2.П. 2. 2.12. а*-4а'+ 2. 2.13. ■ ■ " . 2.14. -{-г^*
* l + m
2Л8- "?$$• 2Л6' 3- 2Л7' J+t?+2f 2Л8* -V3". Указа-
ни е. Рассматривая условия как систему тригонометрических
уравнений, найти а в Р как корин этой системы, принадлежащие
указанным промежуткам. 2.19. ,вр= _■, 2.20. tg — = 2j
*Ву——ff* 2-21' _2; -Т>' У''2, 2'22, 4*3-3*-т = 0.
2.23.tg|-=m. 2,24. -|. 2.25. -^р. 2.26. Л_. 2^7. -Ц-.
2.28. 4-y/W. 2.29*. я —2. У к а з а и и е. sin 2= sin (я — 2) и я—2s
e/\-«. »\ 2.30. .1+2-^. 2.31. V2!. 2.32. iV!±V5'
V 2 Ч.) 2V2 —-\Лб 2 9
3 , УГЗ
2.33. у + |3 •
2.42**. Имеет. Решение. Обозначая д: = cos у, преобразуем
1 л/з*
аргумент второго слагаемого по формуле ■=-cosy + -*-$— s'nУ я
= cos I-J-— у 1. Для переменной (/ равенство приобретает вид
arccos (cosj^)+ arccos cos Г-g-—у J =— или, после упроще-
иня, у + \у—з"| Т' ^ля #s|0* -о-1 данное равенство
превращается в тождество.
2.43*. Справедливое Указание. Сы. решение задачи 2.42.
2.44. 1ГПсоза-соз"№ + 2>а1соз"Ч 2.45. «=o»t("+2)alsiniia
2 L sin a J sin a
2.46. ^-Ыг-^-г^га. 2.47. 1. 2.48. -J. 2.49.1. 2.50. 0.
2.6,. iBJ5±!>i.
§з '•
Встречающиеся в ответах буквы п, /, т, k, если ие огово-<
реио противное, принимают любые целочисленные значения.
3.1. — j + 2nn; (-!)"•£■ +ял. 3.2. яп. 3.3. ± ^ + па.
3.4, у + кщ db^- + 2fert. 3.5*. j^i+яп; i + n«]u[-g- + nnj
~Я"¥ ПП ].; У' к в за в и е. Упростить выражение, выделив поде.
ОТВЕТЫ К ГЛ. 8 805
радикалами полные квадраты. 3.6. arctg j* f- яп;
— arclg — 1-яп, 3.7. arctg-jp + kn; arctg -%■-{■ kn. 3.8. -^ +
+ 2kX n (2fc + 1). 3.9. ± j + kn. 3.10. - -j + nk', ± arctg %£- +
+ „fc 221. JL(2fe+l). 3.11. 4 + 2fcrt; (-|)"т+«4'
5 ' 11 x ~ ' ' 2 ' -"■• x "' 6
i- + fcn. 3.13. -J (4fc + 1). 3.14. Я (2ft + 1); |-
3.12. arctg i- + fcrc. 3.13. 4 (4ft + 1). 3.14. я (2ft + 1); E. (4ft - 1).'
8.15.-yj(6ft ± 1). 3.16. -^-. 3.17*. При ae[-i; ll^-El^
±-^-arcsln f 2 a / _ J, при остальных значениях а решений
нет. Указание. Значения а, при которых существуют решения
уравнения, определяются из условия sin*|^l. 3.18. — + kn;
п . kn „lo п , jtfc 7л rtfe it 2ял
|2Т 7 108 г 9 * 24 г 2 ' ' 20 5 '
Ъп , 2пп ... 21 lln .„ я . 5я , пп „.. „
'too +-2Г- 3-2,-1б,1;-8--3-22-Т2- + ,1":Ж + —- 3-аз-Нет
я 3 1
решений. 3.24. у + 2яя. 8.25. arctg у + nk; nk ~ arctg -j.
3.26. nk; ± arctg л[2 + ли; ± £■ + я/г. 3.27. ■£- (4ft + 1). 3.28.4+
i Z 4
+ 2ftrt. 3.29. 2йл; ~ + 2kn. 3.30. ^--|-ял; (-l)n-j--j + nn-
3.31*. При oe(-oo; —I) U (—I; -2 (л/2 - I» U [2 {^2.+ l); oo)
* = г*2йя±агссоз t Указание. Представить в>виде
4 aV2
уравнения относительно переменной t = sin x + cos *. Значения а,
при которых уравнение имеет решение, иайтн из условия |/|^
< V2. 3.32. ~. 3.33. При аФ 0 х = kn± |- arccos^-ii^lrl(
при а = 0 Jt = ftfl±-j. 8.34. 2-"*"*.п. З.ЗБ. i + i^L. 3.36. ял.
3.87. ~ (2ft + 1); Я (3ft ± 1). 3.88. ^-; ~~. 3.39. J (2ft + 1)1
■J (2ft + I); f- (2ft + I). 8.40. J (26 + 1). 3.41. £ + ^j", у + *»•'
3.42.ib-|<+^. M3. arctg З+яЬ; arctg-j + nft. 8.44:^-<8A+l^,
БОв ОТВЕТЫ
8.45. -j + toi; ~- + 2ктс, ~ + 2kn. 3.46. 2£я; |-{-2ft,t.3.47.| +
+ bt; - j + krc, 2kn. 3.48. -j + -^-; 4}- + <эт. 3.49. (-l)nX
Xarcsm-*—s (-я». 3.50. -к-. 8.51.-^+яя; -гт-я +-;-.
^ О 4 1о 4
&52. ~; -"-(2«+l). 3.63. -~+Ая; ±^1+2Ая. 3.54. кп;
<-I)*+1 ^ + knr, ±^ + 2кя. 3.55. -3+fen: ij+йя.
&66. JL(Bfc+I); £(2ft + I). 3.57. -~-l; -jL(2ft + l)-l.
3.58. -^-. 3.59. i|L; -J (2я + 1). 3.60. ~n,r, я (2« + I); |-X
X (2/1+1). Mi.f-(2n + I); -^-.в.62. ^-; |-(2я + 1). 3.63.™+
+ (-!)" ■—> 3.64. -*^-. 3.65. •?- (4я - 1); яп. 3.66. ~ (2я + I); 2яя;
•j(4n + I). 3.67. ~ (2n +1); яя ± | arccos (sin*а). ЗЛ8. у (2ft +1);
(-I)*-|-+reft:~(2fe+l);-iL(2fe+l).3.69.i^-. 3.70. ~-(2*+i);
<-1>Й+1Т2- + -ТГ- 3JK ±-?+яя- 3'72' -^- + я«;2я,Ц-г+
+ 2в*£(2я+1). 3.73. --J + яя. 3.74. £+^; i + iHL.
n .p. Я . , ,.- Я , ЯЛ „ _„ Я , Я/1 Я . „~»
8.75. -j + ия; (-1)" -р- + —. 3.76. — + -у-; ± у+ял. 3.77. яя;
T + iF: ±yarecos(-A)+n„. 3.78. -£ + „„■ (_i)»-g+
+ SL.8.7».Wi + -^ 3.80. ±| + 2я«; ±|-+«п.8.в1.|+
, Я , Я/1 „ „. Я , ЯП „ „„ Я , Я/1 л „. Я ,
+ яя; -rj + —. 3.82. у + ^-. 3.83. -j + —. 3.84. ± — +яя.
3.85. гЬ-^ + яп. 3.86*. ±arccosf —-^L—l + 2rtft. Указание.
Ввести переменное / = х + >—• н составить уравнение относительно
tf = sinf + cos/. 3.87. -5р. 3.88. (-I)n+1 -Jr+nn. 3.89. -J + яя.
... ЯЯ Я . __ „ п, , ..я Я ЯЯ Я , ЯЯ Я ,
"«•-Г-- -Т + 2яя.3.9«. (-1)» —+—; —+_;-_ +
А-пп. яй2 iLu-iHL чем /_n«JLxiHL. JLj. 2яя. £L-u
+ ЯЛ. 8,92. 4 + -2~. 3.93. (-!> -[2+-2-. ТТ+^Т-' Т +
ОТВЕТЫ К ГЛ. в 607
3.94. ящ — ■?■ + яп. 3.95. ± -%■ агссоз (V3* — l) + я&
2л га
3.96. -5-; -g- + —. 3.97. -j + —^—, п#3/. 8.98. — + 2пп.
3.99. — -j + jtft: — |- + 2jtft; — ^-+2rtfe. 8.100, -j + ftjt.
8.101. | + ^г (-1)^ + 4- 8'102- f-* НГ' ЗЛМ- Т +
+ J™. 3.106. -i + nfe; 4" + ^- 8.107. —|+2я*; (-1)*X
Xf + n*. 3.108. (-l^ + jift; -l + яА. 8.I09. -JL+ife;
|- + :rtft. З.П0. -i + я*; nft. 3.111. -J + yfe; П*. 8.112. jX
X(-l+(-»)")+яя: - J(1 +(-!)") +л». 3.113. i + |n.
3.114. ~|л;-£ ~J; ^ f. 3.115.-J; *; 2*;|, 3.116. ±i;
■ft*. ft = 0; ±15 ** ±3. 3.1.7*. -5^V25 + 2JC(2fe+ll k =
= —2, —I, 0, 1, 2, 3, ... Указание. Возможные значении Й
следует получать из условия существования действительных
. „|10. (4т + 1) п ± У (4т +[)2л*~ 240
корней. 3.118*. ijn ' ;
— (4«+1) л ± л/(4я+ 1)2Я2 + 240
—s !—- ^ , п —любое число, да —любое
число, кроме ±1 и 0. Указание. См. указание к задаче 3.117*,
3.119*. —— !— ^—!—s !—■—, ft — любое . целое
неотрицательное число. Указание. См. указание к задаче 3.117*.
3.120**. Решение. Исходное уравнение можно записать
в виде
(я , cos х ~Ь sin х \ (я , cos х — sin x \
"»{т + 2 )С<ЧТ + 2 J=0-
/ я , соз х + sin х \ „
Решая уравнение cos I -j-Ц = I =0 методом дополни-
тельного угла, имеем л/2 sin Г— + *j = у (4ft + 1). Оценивая
левую и правую части последнего уравнения, заключаем; что для
Б08 ОТВЕТЫ
всех k e Z оио не имеет решений. Аналогично доказывается, что
* ( п i c°s * — sin x \
lie имеет решений и уравнение cos I — Ч = 1 = 0.
л I 9
3.121*. 2kn ± ф; -jr (4ft ± 1) =F Ф*. ф = -^ arcsin -r^-; знаки оба
верхние или оба нижние. Указание. См. решение 3.120**.
8.l22*.-iarcclg(ft+-i-) + я/г, -^^-агезш •* { + «в, /=?«■—I.
/■j&O. Указание. См. решение 3.120**. 8.123. — TL+2'
v. i i. Зя . 3 я , 3 , я . 3 „ ,Л. п , Л
-n+l;^-j- + T; -T + T; I; T+T. 3.124.-^ + 2™.
8.125. а) О, i; я; б) пи; -|- + 2яп. 3.126. arclg Д/v +пп-
В.127**. -J- + 2яя. Решение. Уравнение эквивалентно уравне-
i V2" Я , „ Зя , п
нню sinjc«= —^—, корнн которого x=n-j--\-2nn и * = -т—Ь"яп",
2я — наименьшее общее кратное периодов уравнения н неравен-
п Зя „
ства, следовательно, проверке подлежат значения — н —т-.
Подле
ставляя -j в неравенство, получаем числовое неравенство
cos — - я п
4 e°s*z- cos— 7я
2co33+3in3>2 2- ^к как 2 » = 1, cosf- > 0, созЗ+
+ sin 3 = л/2 соз I -у»— 3 I < 0, то полученное числовое
неравенство несправедливо. Аналогично убеждаемся, что — удовлетворяет
Зя
неравенству. 3.128*. -g- + nk. У к аз а ни е. См. решение 3.127**.
8.129*. ££-+я&.Указание. См. указание к 3.128*. 3.130*.—5*-+-
Я '
+ 2rtft. Указание. См. указание к 3.128*. 3.131. -^ (4ft + 1).
3.182. (i(4*+I); f(4»+l)); (£(4fc-l); |-(4n^l)).
8.183. ~(4Л+ 1). 3.134**. (f(6m+ !);|-(6ft + 1)); (i(6m-l)f
■sH6fe -rl) J. .Pfine пи е. .Относительно переменных и = tgTjir'A
ОТВЕТЫ К ГЛ. 8 609
о = tg -7J- исходное уравнение приобретает вид
1-й* 1-оа (1-и»)(1— о1) . 4ио £
1 + и* 1+о* (1+и2)(1+о") "*" (1+и*)(1+о*) = 2
нли, после упрощения, и* + о' — Sua + 9ц*о* + 1 =* °t последнее
равносильно уравнению (а — о)' + (Зао — l)s = 0. Возвращаясь
к исходным неизвестным, имеем
♦ * V3
tgу -л/3"
lg 2 3 '
ta* —
tg 2 =
нлн
tg*-
в 2
V3
з ■
уз"
з '
8.135. (у (4ft + I); f (4/ + I)). 3.136. (f (4ft - 1); i (4/ - I);.
у (4m-I)). 3.137. -2.(8fe+l). 3.138. (j + mn; ~ + InV
8.139*. Указание. См. решение примера 3.9. 8.140. (—1; 2);
(-1; -2). 3.141. ~ + ял; — -"- - я«; я = 0,1,2,... 3.142. |~;
7 1 f 4- 4
-3; -I; I; 3; у}-. 3.143. *<= R\|-уз; -I; 1; л/3;
-l-^l+^ (20<n<33); -' + VT+2I7T (24<П<39)}.
§4
4.1. (^~«* ~|. ^-+«* +|). 4.2. (ш±1±1,
ш — ib \ / я <p — ф л ш4-ф\
яп ± T 2 T J; ^n/n + Y±—2~^'""+'2"± 2 J'BKaat*
дом из решений внакн нли оба верхние, илн оба нижние, <р =i
= arcsln 0,535, iji=arcsin 0,185.4.3. Ink + jw+-jt, -тр— ял+— J;
(itk+nn—r. nk— ял — y J. 4.4. f уг-Ц-яй + ЯЯ, уг+яЛ — яп J;
Г^+я^+яя, -jjj+rcft — ""J; f —Ц+яй + яп, —•24"+nfe—n»J;
С- "if+nfe ~ ""• ~ ж+**+ял)-4,5< (т+2я/' т+**р):
(- -j Ч- 2я/, ^ у + 2яр). 4.6. (2ят,' bin); (~ (3/ft ± 1),
Щш* i)Ji (ш+я±ф,я+^-±ф); (я--|±Ф, я-^*ф).»
5t0 ответы
q>=arccos-* J-* . 4.7. ^27rfe + —,-y- + -g-l; { —j + 2nk,
АШ я\ ( Зя , „ . 4я/ п\ /Зл , - . 4яУ я\
4
<§& (2я*±q>, 2nl ± ф); (2nfe + я ± ф, 2я/ + я :р t|>), ф= arctg 3L,—,
4
ф = arcsin -^-=—, н берутся или оба верхних, илн оба нижних
, о
внака. 4.9. «(2я я, 2яй + я). 4.10. (як, 2пп); ( arccos •=- + 2я6,
~-у- + 2лА Г-arccos l + 2nfe, -у- + 2яя). 4.11. ((-1)"Х
*(-|"+я*)+я*, - j + Bft); ((-1)яагс1е-|+(-1)яя«-+я«1
arctgy+rtftj. 4.12. Г-^ + яй;, я«); (-^- + 2йэт + чя. — -у+яя);
(i - arctg 2 + 2kn + пи, -arctg2 + rtnV 4.13. ^(_l)n+1-i-
nn 1 , V2 , nk\ ( к л nk ( l\v
„__ „^arctg_- + _j. 4.14^(-1)^ + _ (-yJX
X arctg ^-+^). 4.15. (±^. + аяя, (-1Г£+я«).
4.16. ^(-1)п|+яп,±|+2я/я). 4.17. ^±|+2яя.(-1)^+я/!-).
^ (£ + **. V2-), 4:19. (± J + ** ^ + V).
4J!0.(-J-(2rt+l), я(2р+1)). 4.21. (-^-arcsin-| + tdi!X
■ 4.,., ,я (~l)ft . 2 (-!)" .4... ,я\
ХагС51П^+(й+п)у, —5—arcsin——v g' arcsin-g-+(fe—»>yj.
/бя 7я\ /я_ JJitN /7я 7rt\ (JJn_ 11я\
q3S- У б • 6 ;■' 1б* e J; I, в • 6 г \ в * б ;•
4.23. (-J- (2fe + 1), i 4- /я, -5- + ия). 4.24. (ф + ял, ij-ф-яя),
где ф = arctg ~7 *J^ ■ «6.^(6й+(-1)*\Г^(« + 3±1)\
4.26*. Г— + яй, arctg2+jtf, arclg3-frtm)s fnft + arctg 2, •j + nf,
ят + aietg3 J, где fe + I + m = Q. Укаааине. Вычислив
значение тангенса от обеих частей первого уравнения, свеств систему
ответы к гл. в 511
к рациональной относительно tgjt, igy, tgz. 4.27*. f arctg2 ■\fK±nkt
arctg Уб ± Jtf, erctg-^r— ±. лт\, если знаки — верхние, то
ft + / + m = 0, nfe + l + m = 2, ее ли знаки — нижние. Указание.
См. указание к 4.26*. 4Ж (jfc + Ь*. ||-+&я); (яя-^-»
13те\ .„„/бя Ля я fere \ . ол / я , (—1)*.
яп—йг)- 4'29-Ы-—Ч4--гУ 4ЛЧ-т_+V*
,Х arcsln g-*— + —, -£- + -i-^-arcsin g-*— + —J.
OL (т> ~y): (~t« t): <u 0); (-1,0); (0»1); <G> ~l)-
4.32. a = 2nt: (±Y+kn + ln, T-f — «гя+яф a = jt(2J+l)i
/ я , я(2/+1) , . я(2/ +1) ,.„ я\ _^
у ± j + 2 + ' 2 ~knzF-fi)i о^=ят:
решении нет.
§5
5.1. —3tg 1. 5.2. --|. 5.3. --j; ^~. 5.4. л/3. 5.5*. При
а е [0; я]: cos а; при а е [—2я; 0): cos ■=- а; при а е (— оо; 2n)(J
U (я; оо) иет решений. Указание. При решении квадратного
уравнения относительно переменной z = arccos х учесть, что
0<агссо»д:<я. 5.6. V2"- 5.7. — -jr. 5.8. j. 5.9. I. 5.10. 0; 1.
5.11. Нет решений. 5.12. -2. 5.13. 0; -^-j - -^-. 6.14. 0; -1;
., е,в 1 К|й V3 к„ л 1 1 В10 1 \ 1
1. 6.15. -j. 5.16. -*£-. 6.17. 0; у; -—. 6.18. -у; 0; j.
6.19. -^; 1. 6.20. [0; 1]. 5.21. [-1; 0J. 5.22. (0; I]. 5.23. \~£-\ »].
5.24. LO, 1]. 5.25. 1-1; \\. 5.26. [0; оо). 5.27. (-1; 1). 5.28. (0; I).
6.29*. При ве - . ; -^—I х = 2ал/\ —а2, при остальных
значениях о иет решений. Указание. Область допустимых зна«
ченнй а находится нз условия |2 arcsln a| s^—. 5.30*. При
о в [О; -~\ х = л/\ — 4а*, при остальных значениях а иет
решений, Указание. См. указание к 6,25*,
812 ОТВЕТЫ
§e
6.1. Г--у + 2яп; ^- + 2яА 6.2. (arclg2+ nn;^ + nn\
9Л. (ли; arcclg(— Э) + яп). 6.4. \l — -^п + 2пп; 1 — -2- + 2я«1.
и[- д/"х*+2я*; ~V~ir+25t*]' fe=0, ь а'",р
•6.6. ( -г-; -J- + 2rt" ) ■ в>7*- Нет решений. Указание.
Использовать неравенство | sin х |< I. 6.8. I — j + 2л«; -= + 2яяI.
6.9. Г-j + «";-? + Яй) U (-J- + пи; п (и + I) J. 6.10. ( — 5+яп;
— arctg2 + rtnjuf— -т+пп; ~--\-яп\. 6.11. Г— -jarcsin-g +яп;
it«)u(| + "«;f+|arcsin-2r).e.l2.(|(12fe+I);J(l2fe + 3))u
U(f (« + 2);у(46 + 3)). 6.13. (-у- + 2я&; JJL + 2я&).
6.14. (-^ + 2я& -^р + 2я*Л. 6.15. (л + 2jtft: я + q> + 2nfe] (J
U [2nk — ф; 2nfe), ф = arcsln ~. 6.16. (^ + 2jtfe; у + 2я«Л (J
U (-J + 2nk; -|L + 2jtft). 6.17. [- ^- + 2jtfe; - £ + 2jtft] н
Пя , 2яп\ „ (ft / я , \ .. /я , 5я . \
-тг+_т-)' вж [nft; т+яп)[){т+яп'' —+я")-
6.20. ^-2- + T. T + tJuIt + T' Т + ТЛ"
ej21- (т+_2Т; т(л + 1>+-2т)-e-22- U+2it*: T+2,lfe)
я /я \ / я ■• я \
и — у + гя^ 6.23. I —-j + ял; ял1|М-т + ял; -z- + nnu-.
6.24. Г-Г + 2«n; "тт + 2lt" ) U (— я + 2ял; 2я«).
§7
7.1. {-I; 1]. 7.2. [-1; I]. 7.3. [i; l]. 7,4. [-1; ^).
7,5» (--^j-^M\ 1A* (-°°5 ote2)- 7-7« (_0°: *в ')• w» 0.
ОТВЕТЫ К ГЛ. 9 813
7.9. R. 7.10. Г-1; cos—1 7.11. (-1; ~4=Л 7.12. [-1; 0).
7.13. (I; со). 7.14. [О; 1). 7ЛБ, (-^ ljlj(-l; -&).
§8
8.8*. Ввести вспомогательный угол и использовать неравен*
ство JsinjcJ «^ 1. 8.9**. Решение. Представим выражение,
подлежащее оценке, в виде
•-«g- (1 — cos 2х) + -н- sin 2* + 4" О + cos 2*) -**•
-*> -^Цр- + ■j [{с - a) cos 2* + Ь sin 2*].
Далее следует использовать неравенство, доказанное в 8.8*.
8.10*. Указание. Представить левую часть в виде функций
половинного аргумента. 8.11*. Указание. Использовать
прием, примененный в примере 8.2. 8.12*. Указание. См.
указание к 8.11*. 8.14**. Решение. Исходное неравенство
эквивалентно неравенству
cos a + cos В + cos у ^, 3
т*—^-^т-
» _ «fl+v В—v
Так как cos В + cos -у = 2 cos cos ■ ■ , то, с учетом уело-
вин н используя формулы приведения, получаем
cos a + cos В + cos v ^ cos а + 2 sin -*-.
Так как cosa= I — 2sins-r-, то задача сводится к нахождению
. наибольшего значения функции 1—2 sins -g + 2 sin -?r; Выделяя
Полный квадрат, получаем 1 + -jr — 2 I sin -g- —=-J «^ -*■ ■ Та-
3
. |гам образом, cosa + cosB + cosy^-*-, откуда следует
справедливость исходного неравенства. 8.20*. Указание. Оценить раз-
* / х3 \
вооть cos х — I 1 г~ J j используя представление 1 — соз х =•
\*=« 2 slaJ -г. 8.21*. Указание. Использовать результат преды-
. дущей задачи и примера 8.3. 8.22*. Указание. Сы. указание
% задаче 8.20*.
J7 А, Г, Цьгакнв, А» И, ПйнеВД
514 ответы
ГЛАВА в
§ 1
1.1. cos 0 + i sin 0. 1.2. 3 (cos n + / sin я), 1.3. cos-^ +isin тт.
1.4. л/2 Г cos -j + i sin -j J. 1.5. л/1 Г cos -^- + t stn -j-J.
1.6. 2 (««.■?- + * sin-5-) . 1.7. 6 cos f—arccos—J +
+ i sin ( — arccos-jT-l I. 1.8. 51 cos f n + arccos •=- J +
,■'■(, 3 \"1 , „ 2л,,": 2n , ,. /fe, V
+ isinl jt+arccos —J I. 1.9. cos-^- + / sm —.1.10. cos (-5- + <*]+
+ isin(-|L + a). 1.11. --^-. 1.12. ±(1+0. 1.13. ±2(1-0.
,,j уе-Г f 1. , arcsin (—4/5)\ ,, . / . , arccos (—4/6)41
1.14. V5 [cos \nk-\ ^——\+i sin I л*Н 1—Jl'
k = 0, 1. 1.15, ±-Ц^-, 1.18. ± - [V3 + 1 - (V3" - 1) i] ,
л/2 2
±[V3"-l + (V3" + 0i]. 1.17. cos~ + /sin|-, cos-^- +
, , . 5jt 9я . . . 9я (Зя , . . I3n
+ i sm -g- , cos -g- + i sin -g- , cos —g- + 1 sin —g—.
.VB"|c
3 3 ■
ink + arccos -=- ink + arccos ■=■
1.18. л/Б I cos = r- f sin
1.19. cos M.+ is|n^i, fe=0, 1, 2.
. §2
2.1. Окружность единичного радиуса с центром в начале
координат. 2.2. Положительная полуось Ох, включающая
точку О. 2.3. Луч, выходящий на начала координат (без точки СЩ,
составляющий с осью Ох угол я/3. 2.4. Внутренняя часть
кольца, ограниченного концентрическими окружиостямя радиусов 1
я 4 с центром в начале координат. 2.5. Множество всех внешних
точек окружности единичного радиуса с центром в точке (1/2; 0}.
2.6. Множество всех точек, лежащих внутри окружности радиуса
л/Ш с центром в начале координат. 2.7. Ось Оу, 2.8. Прямая
у = 2х + 3/2. 2.9. Полуплоскость, лежащая выше прямой у <=»,
= —1/2. 2.10. Множество всех точек, лежащих внутри кольца,
ограниченного концентрическими окружностями радиусов I и 4
(включая окружности) с центром в точке (О, —I). 2.11.
Прямая уг^.ш-х. 2.12. Множество всех точек прямоугольника
ОТВЕТЫ К ГЛ. в 515
]q\ ^ 1, \р\ ^2. 2.13. I) Прямые, задаваемые ураваеннем
ау + Ьх = 0. 2) Прямые, задаваемые уравнением у = —Ь.
2.14. Множество всех точек, лежащих вне окружности с
центром в точке (1, 0) н радиусом 10. 2.15. Ось Ox и точки с коор-
динатамн, удовлетворяющнмн условиям * =—jp 5~ ^
. < ^-|-. 2.18. Прямая у = - *. 2.17. г = 2'+ *» + *». 2.18. г=»
= «I + Zj — z», z = zi + г3 — Zj, z = za + z» — z,. 2.19*. У к а-.
з а н н е. Использовать коллинеарность векторов z8 — г, я zj —
— Z\. 2.20. Угол гхОгг прямой.
§3
..,.,-/. ±£*. 3.2. 0, -1,1 ±^- 3.3. 2-f.
3.4. 0, cos -?2i + i sin -^- (ft = 0, 1, 2, 3, 4). 3.S. (2, I); (A, 1).
3.6. (6, 1). 3.8. -I. 3.9. z, = 1, z2 = l, z3 = -j. 3.10. a) (i, i);
(- /. - i); 6) (£, 0; (- «'. - 0- 3.11. | a + 6f | = 1, a + Ы =£ -1.
3.12. Все действительные и все чисто мнимые числа. 3.13. При
а=.1 г = — 1 — /. При Ke<V2 z=^if^ /.
При а > V^ уравнение решений не имеет. 3.14*. а > 2. У к а-
s а и н е. Исследовать взаимное расположение окружностей
|'z + V2"l = a*-3a + 2 п 1 z + i л/2'] = a2. 3.1S. -j|)<<J<-|-.
3-16. z = 2--*^- + f
vr , .(£_,).
§4
4.1. fa — -j + 2я*: a + у + 2jwi J; f a + у + 2ял; a — -g-+
+ 2jtfeV 4.2. Га + я {k + n); у + л (fe - л)); (i + я (ft - n);
a+n(k +n)\ 4.3. Ггбя; -— + 2nn\, C~ + 2m; 2kn).
4.4. fa — -j + 2fen; — a — -j + 2ялJ; fa + у + 2fcjt, у — a +
+ 2ял). 4.5. (19; 178); (179; 46). 4.6. (168; 244). 4.7. (I; 18).
sin—x-"nc
4.8. sin3 * + 3 cos2 x sin at. 4.9,*.
sin-j-cos —^—q>
sin Ф/2
17*
616
OTBETiP
sin -т|- sin ""Г ■ ф
■ 7« . Указание. Если г = cos ф + ' sin Ф, то
Sin ф/2 -г i т.»
гп =»сов Яф + I в!п яф. Воспользоваться формулой' для суммы!
членов геометрической прогрессии z-\-23-\-z3 + • • • + Л
4.11*. Указание. Использовать утверждение задачи 4.10.
а"+Ч|пя* + а"з1п(я^1)*-з1п* - 2«cos£L.sin «*.,
о2 — 2о соз д: + 1 2 2
Указание. Рассмотреть бином (I + z)n, где z = cos х + / sin x.
лы «кг, 5tgg-10tg3q + tg5a
4Л4> *йta = i-10tg*a + fctg*a ' '
ГЛАВА 7
§1
1.2. Последовательность монотонно возрастает. 1.3*. После*
довательность монотонно возрастает, начиная со второго члена.
Указание. Сравнить отношение Уп+ilUn с единицей. 1.4. с=0,
йфЪ, a/d > 0 или с ■И" 0, d/c> —1, ad > be. 1.5. t/, •= 0 —
наименьший член; наибольшего члена не существует. 1.6. уз =••
= 4 — наибольший член; наименьшего члена не существует.
1,7*. хв = 24—наименьший член; наибольшего члена не суще*
ствует. Указание. Найти экстремальные точки для функции
512
/ (*) = 2х + —-т-. 1.8. а) я>31; б) я>301. 1.9*. Ни одного.
Указание. Решить в целых положительных числах
неравенство 2 < |ха — 5* + 6| < 6. 1.10*. Начиная с я = 3.
Указание. Рассмотреть промежутки монотонности функции f(x)^.
к*!- 5*+ 6. 1.1 It, Для целых чисел из промежутка
11; I —j 1 I последовательность монотонно возрастает, для
целых чисел из промежутка I I—j 1+ 1; °° )
последовательность монотонно убывает. Еслн —I/Ln ^ — целое число, то после-
довательность монотонно убывает, начиная с члена, имеющего
номер —I/In д. Указание. Рассмотреть промежутки монотон-
ностн функции f(x)=xqx. 1.12. Будет; *„е[1/2; 2]. 1.13.
Будет; *„<=[!; 4/3]. 1.14*. Будет; *п<=[0; 1/2]. Указание. У бе-
днться в том, что /(*)= жг — 2* + 3 возрастает па промежутке
[!, оо). 1.15*. Будет; *ле[0; I]. Указание. Привести к
общему знаменателю выражение в скобках.
§2
2.7*. Указание. Окружить а некоторым интервалом н
сравнить по величине члены последовательности, не попавшие
. ОТВЕТЫ К ГЛ. 7
517
в этот интервал, н концы интервала. 2.8*. Указание.
Окружить точку а интервалом, не захватывающим <\. 2.9*. Нет. У к а'«
ванне. Окружить точки р н q непересекающимися интервалами.
2.11*. Не имеет. Указание. Рассмотреть четные н нечетные
значения л. 2.12*. lim х„ = 0. Указание. Использовать ие-«
Л-»оо
равенство |sfn*| < 1. 2ЛЗ. а) Игл хп = 1; б) последователь^
вость предела не имеет.
:: §3
3.1. —1/2. 3.2. 1. 3.3. 0. 3.4. 0. 3.5. —1. 3.6*. 7/15. У к а*
в а и и е. Разделить числитель и знаменатель на Зл+| и
воспользоваться формулой (3.4). 3.7*. 0. Указание. Убедиться в том,
что основание степени для любого п меньше 3/4. 3.8*. 0.
Указание. См. указание к 3.7*. 3.9*. 0. Указание.
Воспользоваться неравенством |sinn!| < I. 3.10. 0. 3.11. —5/2. 3.12. 1/2.
3.13*. 0. Указа и и е. Домиожнть н разделить на п1— п -tfl—n3 +
-+- -V^(I — ла)2. 3.14**. lim x„ = 2- Решение. Докажем мо-
п->оо
нотонность и ограниченность исходной последовательности.
Ограниченность последовательности докажем по индукции. Так как
Xi «=» V2"» то Х\ < 2. Предположим, что ** ^ 2, тогда из
уравнения х2к+1<=хк + 2 следует,' что at»+i < 2. Таким образом,
Хп ^ 2. Легко заметить также, что *„ > 1.'
Рассмотрим неравенство
У* < 2 + у. (*)
Если члены последовательности удовлетворяют неравенству (*),
то последовательность возрастает. Действительно, подставляя
у = х„ в (*), имеем
4<2 + *„,
но 2 + *„ = #5;+1 и, следовательно. *„^*^+1. Множество
решений неравенства (*) представляет собой промежуток (1; 2].
,Так как из доказанного выше следует, что 1 ^ х„ ^ 2 для
всех nsN.TO они удовлетворяют неравенству (*).
Таким образом, последовательность возрастает и ограничена
н, следовательно, имеет предел. Значение предела, согласно (5),
должно удовлетворять уравнению у3 — у — 2 = 0, откуда i/i=I,
уз = 2. Легко проверить, что число 1 не является пределом
последовательности. Следовательно, пределом является число 2.
3.15*. lim хп = а, У к а з а и и е. Преобразовать рекуррентное
соотношение к виду хп+1 «= хп+(х„ — а)г и воспользоваться
Б18
ОТВЕТЫ
формулой (3.5). 3.16. lim *„ = *Ja. 8.17. I + Vl — «• 3.18*.
д/l+a— 1. Указание. Рассмотреть последовательности,
состоящие из четных и нечетных членов исходной последовательности.
§4
4.1. 119/3. 4.2*. (а, = 2, d = —3), (о, = —10, d = 3)'.
1). Указание. Воспользоваться формулой (4.4). 4.4. ап =
= р -f- д — л. 4.5*. Указание. Воспользоваться тем, что если
числа и, », ш — три последовательных члена арифметической
прогрессии, то v — u = w — v. 4.6. 2/3. 4.7. 20. 4.8. 167. 4.9. 102.
4.10. 29. 4.11. 9. 4.12. 7. 4.13*. Указание. Рассмотреть сумму
членов, равноотстоящих от концов, среди а,, ..., ат+п.
4.14*. 82 350. Указание. Четное число, которое делится иа 3,
делится на 6. 4.15. d = 2а,, а, # О или d = 0, ai =И= 0. 4.16*. 1275.
Указание. Воспользоваться "формулой Xs—уг={х—у){х-{-у).
4.17*. 1064. Указание. Воспользоваться указанием к 4.13*.
4.18. 98. 4-10*. Оя = 8п — 4. Указание. Воспользоваться
формулой (4-6). 4.20*. Указание. Выразить суммы а,+<**,,
«1 + din, oi + а„ через S3n, Sjn, Sn соответственно и
воспользоваться соотношением аз„ + а„ = 2а2„. 4.21*. Указание. Из
(условия получить зависимость между а, и d и использовать
эту зависимость при доказательстве утверждения. 4.22*. При
а~2& 12. Указание. Рассмотреть множество значений функции
/(*)— 25* + 25~х + 5'+* + 5'-*. 4.23. x=logs5. 4.25*. Пока-
V5 - V3"
зать, что -^ fe=- ие является рациональным числом.
4.26*. Нет. Указание. См. указание к задаче 4.25*. 4^7*. Да.
У к а з а н и е. Если длины сторон равны соответственно а, Ь,
с, d, то необходимое и достаточное условие возможности
вписать в четырехугольник окружность заключается в том, что
в + с = Ь + d.
§ 5
БА 6,=5, 6в = 405. ЬЗ. (7. -14, 28,-56). 5А. S4 = 40.
5.5. (1, 3, 9). 5.6. (1, 3, 9). 5.7. (3, 6. 12); (|-(9 + Уб5), -6,
-|-(9-Уб5)). 5.8. (2, 4, 8, 16); (16, 8, 4, 2). 5.9. (2, 4, 8) или
(8, 4, 2). 5.10. (1, 5, 25); (25, 5, 1). 5.11. д = 2, 5.12. f^f ] .
5.13.
ОТВЕТЫ К ГЛ. 7 б,д
1 1
уп-1 ' /_ , лг\Л1—2 • /л . nr-sm—3
<2 + УзТ_1 (г + л/зГ-* (2 + V3-)"
„г (^ _ о л*и-г _ **>+* _ x*i +!
5.14. ; 6.17*. Sn + 2п.
Указание. Возвести выражение в скобках в квадрат и
сложить возникающие при этом геометрические прогрессии
I п.
БЛ8* S„ =>4 -—« . . Указа.ние. Рассмотреть
разность S„ £-. 6.19*. 5„ = "*_ — ^A;_~"f-. Указание.
Домножнть обе части равенства иа х к из Sn вычесть xSn, &20. 28.
3 1 3
€.21. &4=*-г?-; 9 = т. 5.22*. -=-. Указание. Воспользоваться
lb 4 О
методом, предложенным в примере 5.2. 5.23. I 6, 3, —, ... I,
Б.24. Гб, --1V 5.25. 2SS^_ l . 5.26*. х > О, х =£ ± а.
(а 4- с)3
S=———2—-f . Указание. Для нахождения знаменателя
4 (а — х)ах
прогрессии q разделить bi иа Ь{. Относительно х решить
неравенство вида \q(x)\<U 5.27. р = *Ц=, 5=2а2. 5.28. Усло-
2 — л/2
вне имеет вид aP-m6'"-ftcfe-'' = 1. 5J29. Числа 11, 12, 13 не
могут быть членамя одной геометрической прогрессии. 5.30. 5.
&3L 3/2.
§6
6.1. (4, 8, 16); (-А-, -i|, -g-). 6.2. (3, 6, 12); (27. 18, 12).
6.3*. 931. Указание. Воспользоваться представлением^числа
в" десятичной записи, т. е. представить искомое число в виде
в-102+ 6-10 + с, где а — число сотен, 6—десятков, с — единиц.
tf.4. (32, 16, 8, 0); (2, 6, 18, 30). 6.5. (2, 10, 18, ...); (2, 6, 18, „.).
6.6. Ь7=27. 6.7. (24, 27, 30, ..., 54) и (24, 24, 24, ,..). 6.8. q=
— 3/2, q = 1.
§7
7.1. Да; *„<s[0; 1-jjj-]. 7.2. Нет. 7.3*. Да; *„е[-8; Щ.
Указание. См. указание к задаче 1.4. 7.4*. Девять членов.
Указание. Воспользоваться формулой суммы геометрической
прогрессии. 7.7*. Указание. Воспользоваться свойством сто-
G20
ОТВЕТЬ^
роя треугольника. 7.8. Нш Sn = a*/2. 7.9. 1/3. 7.10. 0. 7.П*. 630,
л-»оо
135, 765. Указание. Пусть х — число сотен, у — десятков и
z— единиц. Тогда первое условие задачи приводит к уравнению
JC-100 + t/'IO +z — 45р, где р — целое число. Так как х, у, г—•
последовательные члены арифметической прогрессии, то 2j/ =>
= х + г. Используя условия задачи, можпо составить систему
двух уравнений с четырьмя неизвестными:
jc • 100 + J/• I0 + z=»45p, 2y=»*-fz,
которую .необходимо решить в множестве, целых иеотрицательч
иых чисел. 7.12**. Решение. Согласно формуле (4.3), всполм
зуя условия задачи, получаем
ai + V_ rtn ai+ak Ьп
о = пР> 5 = кР-
а — Оь
Исключая из системы а\, получаем —=-5——=p(n"—k). Исполь*
вуя формулу (4.2), имеем d(n—k)=2p{n—k), и, следова»
телыю, d = 2р, а.\ = р. Используя опять формулу (4.3), полу»
чаем искомое выражение:
г>р ^ р — р ,
7.13*. Указание. Домножпть и разделить каждое слагаемое
на выражение, сопряженное знаменателю. 7.15*. (8, 4, 2, I, 1/2,
1/4). Указание. Из первых пяти уравнений следует, что числа
х, у, z, s н t образуют геометрическую прогрессию. 7.16*.
Указание. Представить каждое число, входящее в доказываемое
выражение, как сумму членов соответствующей геометрической
прогрессии. 7.17*. /1 = 2, В = 32. Указание. Использовать
теорему Виета. 7.19*. Указание. —-I---- «, ±. JL _
{•-%■' . ■ о . 7.20*. Указание. См. указание
k — I ^ 2 ft + 2
к 7.19». 7.22. 4-(ю- 10 ~— — «)■ 7.23. а) --£■,'" если п чет-
ное; —н—, если п нечетное; б) —д—-, если п четное,
«(«+1) . n(n+l)(3rts + 7« + 2) ,„. n
-- ■ '—-, если п нечетное; в) ——!— ■■ .„ -~i. 7.24. 0.
7.25. 0,6. 7.26. 3V3/2. Указание. Под знаком предела стоит
сумма п членов геометрической прогрессии со знаменателем
q = 1/3. 7.27. 1,6. 7.28. 1/3. 7.29. 1,26. 7.30*. 1. У к а з а и и е. Из-
ОТВЕТЫ К ГЛ, Т 52Т
пользовать соотношение ■jfc(jfc+i) —5""Т+Т' 7'31** 1ST'-
Указание. См. указание К 7.30. 7.32. 1/4. 7.33**. у.
Решение. Заметим, что —■=■ = '■• Далее,
V2 - "
cos -г
4
2
V2+V2- V20+4-) V2(,+cost)
V4cosSt
я
cosT
аналогично1
1
V2 + V2+... V2 + V2 С03тДт
п радикалов
Таким образом, ап = — • ... • Домножнм
я я я
COS — С04 — COS .„ , , ■
4 8 2rt+1
и поделим ап на 2 sin -„-, L-. Тогда получаем
2 sin
2"
я
2п+|
я я; „ я . я
cos — • cos — ... 2 cos ■ , , , • sin
ft 2 2"+'
2 sin -£-r 2" sin -J*rr-
2'»+1 2"+'
я я я . я , я
cos — cos — ... cos -л- • sin -gz sin j
Умножим и поделим последнее выражение на -*■, тогда, нсполь-
,. sin х я
ауя равенство Inn =1 и обозначая х = —т-р, получны
х-*о х 2"+l
2rt+1 . я
sin .-«я
я 2rt+1
llm an = Hra „
822 ответы
7.34. — . 7.35*. -jj-. Указание. Воспользоваться
л/2 п Уз" п . _, „ *
тем, что -^5- = соб—•, -^—= соз-тг, и формулами 2соз*х =
= 1 + cos 2л, 2 sin2 х = 1 — cos 2л.
ГЛАВА 8
§ 1
1.8*. У к аза ни е. Рассмотреть последовательности
.1) - 2 „ГО _ 2
4'--тттг. *?-
я(1+4«) я(3+4«)
§2
2.1. 1. 2.2. 0. 2.3. 1. 2.4. 2. 2.5. 0. 2.6. 0. 2.7. & 2.8. Зх\
2.9. °°. 2.10. — при а^О, при а = 0 предела не существует.
2.11. а) - -| V?; б) -j- л/|-. 2.12. а) —1/3; б> I. 2.13*. -3/2.
Указание. Выделить в числителе и знаменателе множитель
(дт— 1)г. 2.14. 4/3. 2.15. 3/2. 2.16. V2~/2. 2.17. 0. 2.18. 3/2. 2.19. 4.
2.20. —2/3. 2.21. 1,5. 2.22. !,5. 2.23*. —1,75. Указание. Перейти
к переменному у — — х. 2.24. 2. 2.25. 8. 2.26. 3/4. 2.27. п/т.
2.28*. cos а. Указание. Использовать формулу sin х — sin a =
•=2sin—5—cos—^—. 2.29*. я. Указание. Обозначить
я/л=»х. 2.30*. я. Указание. Обозначить * + 2=f/ н нсполь-
вовать формулу tg п (г/Ч- 2) = tg лу. 2.31. — l/V2". 2.32*. —24.
Указание. Преобразовать выражение, стоящее в числителе,
tg х sin (х — я/3) sin (* + t/3)
к виду —2 *—5— „, ,„. —— и воспользоваться coot-
cos2 х cos2 (я/3)
Ношением cos Г х + -=-1 = sin (-?—*J. 2.33*. -тт—.
Указание. Преобразовать выражение, стоящее в знаменателе, к виду
4 sin П/3~ * sin "/3 + * . 2.34. 0. 2.36*. 1. Указание. В
числителе добавить и вычесть единицу.
§3
3.9*. Указание. Использовать формулу cos (x+&x)—cos x=
t= — 2 sin -pr- sin ( x + -д- 1. 3.10*. Указание.
Воспользоваться неравенством In (1 + *Х *• З.П*. Указание. Исполь-
ОТВЕТЫ К ГЛ, 9
623
вовать результат предыдущей задачи. 3.13. Функция y=*tgx
терпит разрыв в точках х = я/2 + ял, neZ. 3.14. f(0) = l.
3.15. f (0) =2. 3.16. f (0) = 1. 3.17. f (81) = 1/6. 3.18. /4 = 1.
3.19. A =• 0. 3.20. Л =. 3/2. 3.21. A = 1/2. 3.22. A =» 2/ma.
3.28*. j4 = 2/ji. Указание. При вычислении предела lim /(*)
ввести обозначение г=1— х. 3.24. 6/а = я/2. 3.25. а = 1.
3.26. 2я-6 = 0. 3.27. За —6 = 0. 3.28. а4-& + 1=0. 3.29. 6=4.
3.30. а = 3/2 + 2п. 3.31. а = 3/4.
§4
4.1.-1. 4.2.3/4. 4.3. Да. (2 >-7/22+1/4). 4.4. Да.
(1/2 + л/2 > -3 + lgS). 4.5. 3/7. 4.6.2/З.М.7. оо. 4.8. оо. 4.9. l/coss о.
4.Ю. -4rtga. 4.11. cos3 я. 4.12. л/2/4. 4.13. У2~/2. 4-. 14. 1/2.
4.15. 1/2. 4.16. 2V2". 4.17. оо. 4.18. 1/2. 4.19. оо. 4.20. л/з/З.
4.21.2. 4.22.0. 4.23.2. 4.24.2. 4.25. sin 2a. 4.26.I/2. 4.27.1.
4.28.1/2. 4.29. sin 2a/cos4 a. 4.30. —2 sin 2a, 4.31.3. 4.32. 3 л/f.
4.33. — л/2. 4.34. 0. 4.35. 2<х/я. 4.36. a/я. 4.37. 2. 4.38. 1/2. 439. a.
4.40.3/2. 4.41. f(3) = 2. 4.42. f(0) = -l/8. 4.43. J (0) = -4.
4.44. /4 = 3/4. 4.45. A =1/2.
ГЛАВА 9 /
§1
1.1. f (*) = - -~. 1.2. Г (*) = - sin x. 1.3*. /' (x) =e*,
ел* — 1
Указа яле. Использовать равенство lim : = 1.
1.4*. Z' (ж) = —. Указание. Использовать равенство
Ига 1п('+&^ =1 и* f (je) = eJ6'»-'i укаваине Вое*
д*->о Д*
пользоваться формулой бинома Ньютона. 1.6. /' (*) = 0.
2
1.1**. Указание. См. задачу 7.1j6*. 1.12. —-р=г-. ;=тг»»
_ л/х (2 - V^)
,.,3. ~2* _. 1.14 C°sV*
Vl -*4(1 + x1)' ' ' 4 V* sin л/х
ет/Шах'+Ьх+с) {2ах + Ь) ,
1.15, ,, = . l.ltt. —
2*</ln(ax2 + bx + c) (ах* + Ьх+с) 1 + х1
U7. 2a6OTn,"-4a+6,r-t ш# ^, ^,.
(a-6*n)lrt+
524 ответы
,1'19- „in*Лоз'*' 1Ж --ЗГ*^ l'2U V<*>-L
1.22.. Y (*) *=> 0. 1.23. У {х) =. -2х. 1.24. f (х) = Цр ^»-2тУ«+
+ 3 i^i xU-2n»n. 1.25. f (*) — , * 1.26. f (X) =
п V1 +"**
■в JL(8-<3)-^/2. 1.27. f (x) =—. 1.28./'(*)=.! («'-I)-*'62*.
1.29. Г (*) = - 2(ж11|)У4- »•*>• /' (*) = V2". 1-31. /' (*) =
DiA/Z f.32*. /'(*)=( _1, *Stl; ^' Указание. Для
2 Л/ д: • I I. * е= (2; оо).
упрощения вида функции / (.«) обозначить У* — I =/. 1.33. f (*)я
J* *е(0:1)' 1.84. г<*>-{ -»**-<—:Ч
\ 2/3, *e=(l! оо). I 1/2, *s(0; оо). '
( 0 X s Г2* 4)
казанке. Обозначить
^__ I 1/V* — 2 ж е (4; оо).
^2*-4 = *.
§2
2.1. Прн #е(—оо; —2) U (—1; оо) f (x) возрастает, прн
*<=(—2: -3/2) U (-3/2; —1) /(*) убывает. 2.2. При х 6= (0; 1)(J
U(I; е) Дж) убывает, прн же (в; оо) /(*) возрастает. 2.8. Прн
jteR }(х) возрастает. 2.4. При х г (2; 3) /(*) возрастает, прн
*е(3; оо) /(*) убывает. 2.6. При *«=(— оо; 0)U(i; oo) f{x)
убывает, прн х е (0; I) / (х) возрастает. 2.6, Убывает при
Jfe(-ooi 0)U(0; оо). .^2.7*. о е (-оо;-2 - V5) U (V5"; <»)•
Указание. Условие задачи эквивалентно условию f (х) > 0
для *eR. Выяснить, при каких значениях параметра а
вспомогательная функция g (/), получающаяся из /' (*) заменой t = cos ж,
Положительна па промежутке [—1; 1]. 2.8*. a s (6; оо).
Указание. Вычислив значение производной, найти область измене*
"taw а, прн котором она будет положительна. Использовать
неравенство | cos ах | ^ cos 0 для любого а. 2.9. *Ших = ~2, утах = 8;
*mln = 2, ymia = 0. 2.10. хтах =-у + Ьп, утах = у + kn + Ц^-i
*mln = —у+Ы i/raln53- y+ftrt — ^~; feeZ. 2.11. *mln= — ■£,
fmln ■** о"0 * A'max = l> #max=I. 2.12. ■*max = 3, l/max = ? >
'mln™*-3. Уш1п = —g". 2.13. xmW"= —2, j/mas = 26; XTOin = I,
ответы к гл. 9 1Й8
!/т1п = —2. 2.14. *т[п=«в, утщ^е. 2.15. Хтах = — 1, !/тах=171
•*т1пш,3, Утт^~47. 2.16. «max1™ 0, {/тах*"3-^; *тц==2,
2/тГп =» 2.
§3
3.1. max f(*) = 3; min f (x)=l. 3.2. max f(*)=17;
*el-l;ll xelUll *e|-2;U
3 л/JT
min f(*) = 0. 3.3. max f (x) =>—%—; min f(x)=0.
* = 1-2;Ц *s(0;n] » *sI0;n]
3
3.4. mln f(*)=0,6; max N*)=-r. 3.5. max f(x)=*
*sI0;n/2] Jte(0in/2] 4 *<=(-я/2; я/21
= ■?■• mln f (*) = —■?•• 3.6. max f(A)=0j
* *;el-n/2; Я/21 4 хе=1п;ЗЯ/21
min f(*)=-l. 8.7*. maxf(*)=—^-=, min/(я) «a
*е1л;Зл/2) xer 8 —V2 ^R
4
= t=-. Указание. Перейти к переменному у =■ sin X +
8 + V2
л/3"
+ cos*. 3.8. max f (x) = 4-^3—, min f(x)=2,
* <= |n/6-, я/3) ° * e [я/6; я/3]
8.8*. min f (*) = 3. Указание. Перейти к переменному
ж <з |0; п|
(/ = cos*. 3.10. max f (ж) =■/(0)=»1; min f (jc)=fl(—1)=0.
X<= [-2; 0] IE [-2: 0!
3.11. a) max / (ж) = f (2) = 4, mln f(*)=2;6) max /(*)=
*e|0;2] *f=|0;2] xe[-2;0I
*= / (—2) =4; mln f (x)=2. 3.12, max f (*)=2; min f (*)=—2.
xal-2; 01 jeR xsR
3,13. max / (*) = 21 + 3 In"2, min f (*) = 0. 3.14. xmm=-3-j
*s|l/2;*] xe=|l/2;4] 3
max / (#) = 105. 3.15. max f(x)=f (5) == 5"> min f (*) =■
*<=10; 3) xs{0il0] . xs(0; 10]ч
*=H0) =f (10) =0. 3.16*, max / (*) = f (3) =»' 4 V5
*<=I0;3I
min f(*)=f(I) = 0. Указание. Перейти к переменному
xe=io: з) _
у = (ж — 1)а и воспользоваться тем, что g.(u) ■=> Vй — монотонно
возрастающая функция. 3.17. max и = 4; min «=3/2,
Ж в 1-5/2; 1/21 xs (-5/2; 1/2]
§4
4,1. [0; оо). 4.2. [3; 3/coss 1,5]. 4.3. Пустое множество,
4.4*. [—1/3; I]. Указание. Можно найти максимальное и
минимальное значения исходной функции, но есть н другой
способ, состоящий в том, чтобы рассмотреть значения у, при
которых уравневие у(х*— 3x4-3} = х — \ относительно * имеет
ж
ОТВЕТЫ
действительные решения. 4.5. a) j/e{0; 1/2]; б) у г [—1/2; 1/2].
4jfl*- Указание. Рассмотреть неравенство, связывающее
выражения, обратные к левой н правой частям исходного
.неравенства. 4.7*. Указание. Представить f(x) в виде /(х) =
fc==2sinx—2sin3* н заменой t = sin х свести задачу к
доказательству справедливости неравенства min g (t) > —7/9,
где g(t)=2t — 2/3. 4.8*. Указание. См. указание к 4.7*.
44>*. Указание. См. указание к 4.7*. 4.11*. Указание. См.
указание к 4.4*. 4.12*. ае[-оо; —У-—J. Указание.
Используя второе равнение, получить неравенство с оараметром
относительно одного неизвестного. После этого найти
наименьшее значение функции при каждом а и указать множество всех
значении а, при которых это значение меньше 4. 4.13*. 44.
Указание. Воспользоваться тем, что ов 4- <*з = <ii + flu. 4.14*. а =
= —4/3, а = —8/3. Указание. Использовать свойство
геометрической прогрессии: о|ся„_|в„+|. 4J5. 2/3. 4.1 в. Уз — 1.
4
4.17*. а = 9. Указание. Найти min функции у=—. Ь
-{-■_. иа промежутке (0; л/2); см. также указание
к 4.7*. 4.18*. Указание. Воспользоваться соотношением меж«
ду средним арифметическим и средпнм геометрическим двух
чисел. 4.19*. Указание. Представить г в виде г= {х + у +
+ 1)3+ (* — 2)2 — 3. 4.20*. 0=1. Указание.
Воспользовавшись теоремой Виета, выразить сумму квадратов корвеЗ
уравнения как функцию а. 4.21*. Указание. Найти наибольшее и
наименьшее значения функции . $■ при jteR; см. такжеука-
i -|~ X
зание к 4.4*. 4.2S*. Указание. См. указание к задаче 4.4*.
4.26*. Указание. Использовать представление sin6 x + cos* x =
= 1 --|sins2A:. 4.28. 3 кория. 4.29. (-^У + (-|-Y = 0. 4.30, I)
ШМ|У>„ (|)Mf)
2
<о.
§5
5.1; 18 = 9+9. 5.2.36 = 6-6. 5.3.40 + 80 + 60 = 180.
6.4. •£- + -д- = а. ;5.5*. р = —2, q = 0, расстояние равно 1. Ука-
ванне. Расстояние от вершины параболы до оси Ох предста-
4
вляет собой ординату вершины. 5.6. —=-. 5.7. Координаты
уз
ОТВЕТЫ К. ГЛ, 9
Ш
вершин прямоугольника, лежащих на параболе: f -5- о, ±2 Д/тг )♦
5.8, Высота конуса, имеющего наибольшую поверхность, состав*
ляет 4/3 радиуса шара. 5,9. Диаметр основания и высота
цилиндра равны 2/ч/з\ Б-М*. Площадь круга, ошканяого вокруг
равнобедренного прямоугольного треугольника с катетами
V2S, будет наименьшей. Указание. Воспользоваться тем,
что гипотенуза прямоугольного треугольника является
диаметром описанного круга. 5.11*. ф = я/3. Указание.
Воспользовавшись тем, что треугольник ABD прямоугольный, выразить
боковую сторону и меньшее основание через диаметр описанной
окружности. 5.12*. Наибольший периметр имеет треугольник,
(У которого одни из углов при основании равен я/2 — а/2.
Указание. Использовать теорему синусов. 5.13. 30 кв. ед.
5.14. 2а. 5.15. 5. 5.16. а = 2 arctg -^L, Н =--Щ=-. 5.17*.
з зуз
а = я/3. Указание. Использовать формулу г = S/p, где
S — площадь, а р — полупериметр треугольника. 5.18. а =
V
= arccos-n£-. 5.19. а — я/4. 5.20*. h ={l2'3 — сР/3)3'г. Укач
"л
ванне. Связь между аргументами функции, наименьшее
значение которой требуется налги, устанавливается из подобия
прямоугольных треугольников, гипотенузами которых являются
внешняя и внутренняя по отношению к башне части жесткого
стержня. 5£1. Длина — 30 см, ширина — 20 см. 5.22. а) х =»
г'-fa *x=fa> »~Чт »**-:&■•
Б.24. Стерона площадки, примыкающая к стене, должна быть'
вдвое больше другой стороны. 5.25. AM = а/\р (ур~ ' + -$q) ,
Б.26*. К точка отрезка АВ, удаленной от В на 1 км. Ук'аза*
н и е. Время достижения точки В как функцию координаты точ*
ки, к которой должна пристать лодка, необходимо представить
в виде суммы двух слагаемых, одно из которых — время две*
ження по воде, а второе — по суше. 5.27*. Через время <0=«
2тд 2 mjjg2 /г*см2\
e1F(с) W ('^ = OF ~F~ V, с* У у к а 3 а " н е- Кннетнчеч
т (t\ V^ (Г\
екая энергия W в момент t равна W {() = = • гл-в
m(t)—масса капли к моменту t, a V(/) —достигнутая к
моменту / скорость. SL28*. 20 км/ч, 720 р. Указание.
Воспользоваться тем, что стоимость единицы пути складывается из двуя
628 ОТВЕТЫ .
величин, из которых первая пропорциональна кубу скорости,
а вторая обратно пропорциональна первой степени скорости,
6.2». х (р) = mln(—j=r, а\ где х(р) —расстояние от станции
23 27
нселезной дороги до пункта Р, 5.30. —лг- ч. 5.31*. 1 -jg ч.
Указание. Расстояние в момент времени t между поездом
н автомобилем представляет собой третью сторону треугольника,
двумя другими сторонами которого являются расстояние, прой-.
денное поездом, и расстояние, которое осталось пройти
автомобилю, соответственно. 6.32*. Через -=— ч. Указание. См,
» &v
2
указание к задаче 5.31*. 5.33. t/ = -=-ft. 5.34. Бриллиант был
о
расколот пополам. 5.35. Сопротивления должны быть
одинаковыми и равными -^-. 5.36*. a = max-j arccos-r-, arctg-г- >.
Указание. Время движения гонца, как функция координаты
точки причаливания, складывается из времен движения по воде
и по берегу. 6.37*. s.n n д-тг-» где а — угол падения, а В —
1 sin В V» '
(утбл преломления луча. Указание. Выразить путь луча в
каждой среде через координату точки падения на границе сред;
Найти отношение путей в каждой среде к нх проекциям иа
границу сред, при котором доотнгается минимум времени прохожу
дения всего пути между точками А и В. 5.38*. а = В, где а —>
угол падения, В — угол отражения. Указание. См. указанна
К 6.37*. 5.39. /i=„ , и-, /2— п , в ■ т- е- разветвить
К\ -ТГКз А1-Г-А2
токи следует обратно пропорционально сопротивлениям, через
которые должны быть пропущены эти токи. 5.40. 6000 р.
5.41*. л = 8. Стоимость затрат «^V? млн.р. Указание.
Если 1(х) —функция, выражающая зависимость стоимости он
построенной площади, то следует искать наименьшее значение
. „. v t/40000 \
функции F (и) = пМ I, где п — число построенных домов.
6.42*. 4 <у^2 м. Указание. Искать расстояние, с которого
тангенс угла обзора будет наибольшим (тангенс — монотонная
функция своего аргумента). 6.43*..(У4Ьа — За* — b)• З-1'2 .
Указание. Искать расстояние, при котором тангенс угла,
образованного точкой остановки автобуса и двумя противоположи
иымн сторонами фасада дворца, будет наибольшим. Выразить
этот угол в виде разности углов, под которыми видны дальний;
и ближний (по отношению к шоссе) концы фасада дворца,-
ответы к гл. о
1529
КР
tf.44*. ф = arcigК; Р = —===г. Указание. Воспользо»
ваться тем, что сумма снл в плоскости движения должна бьпъ
равна нулю. 5.45*. а = р". Указание. См. указание к
предыдущей задаче. 5.4в. л/2ар/К. 6.47. р *= 2,4(*0 =» 5/3; уй = 5/9)'.
5.48*. (I/2; 7/4). Указание. Задача сводится к нахождению
точки С параболы, максимально удаленной от прямой BD.
tf.49*. Наименьший периметр треугольника АМВ равен V^O +
+ 2 *fb + Уз4! Положение точки М, при котором достигается
наименьший периметр, —М (0; 0). Указание. Рассмотреть
точку, симметричную точке А относительно'прямой у=>х.
5.50*.Точка М должна делить пополам отрезок прямой, заключенный,
между сторонами угла. Указание. Исследовать изменение
Площади треугольника при изменении наклона прямой,
проходящей через М. 5.51. Две оставшиеся вершины получаются при
Пересечении сторон угла прямой, соединяющей точки, которые
Являются симметричными образами точки М относительно
сторон угла. 5.52. 2R sin ~. 5.63. —■ ч/ЗЬг — а\ 5.64. Длина
стороны основания — 2 см, объем — 4 см3. 5.55. Стороны
прямоугольника, имеющего наибольшую площадь, равны J?V2/2.
8.56. 5я/9. 5.57*. Smax =» R2 tg -у. Указание. Рассмотреть
два случая: первый — две вершины искомого прямоугольника
Лежат на одном нз радиусов, образующих сектор; второй —
по одной вершине на радиусах и две на дуге сектора. Во
втором случае следует разбить сектор иа два одинаковых сектора,
*огда задача сведется к первому случаю, рассмотренному для
ЬаждоА половины отдельно.
§в
6.1. (V2; 2 —УЮ и (— л/% 2+V2)- 6.2. 0 = 2.
е.з. у = -узт+ "V|+3 e4 arctg9. y=9x_23j_m
РЗ*. (1/2; —15/32). Указание. Координаты точки касания
Можно получить нз уравнения f (х) = ft, где ft — угловой
коэффициент касательной, в.6. (0; 2). 6.7. 2. 6.8. у = 8* + 4. 6.9. *0=
—+ arcsin—— + —. 6.10. я«; — + —; гае Z. 6.11. (р; 0);
4V2 4 8 4
WO; 0). 6.12*. (3; —15); 21/2; 21; (-1; 9)! 19/2. 19. Указание.
(Условие задачи дает возможность сразу определить угол,
образуемый искомой касательной с положительным направлением
йен Ох. 6.13*, о==1. Указание. Условие пересечения прямой
530
ОТВЕТЫ
и параболы .равносильно существованию двух действительных
корней соответствующего квадратного уравнения; полусумма
абсцисс этих корней ао условию задачи должна быть равной 2.
§.14. у = —3* — 4. 6.15. у = х + 4, у = —х + 4. 6.17. (2; 8/3);
(3; 7/2).. 6.18 Зя/4. в.19**. Решение. Продифференцируем
каждое уравнение, считая, что у — функция от х. Имеем у +
+ У'х = 0 и 2х — 2уу' *=> 0. Выражая у' в каждом из
уравнений, имеем у' = — у/х, #' = х/у соответственно. Следовательно,
в любой точке М(хо; у<>), являющейся точкой пересечения
кривых, произведение угловых коэффициентов касательных равно
•—1.
6.20*. Указание. Показать, что произведеиве угловых
коэффициентов в точках пересечения линий разных семейств
равно -1. 6.21. (д/£; b*J± + 2с), (- д/|; 2с-Ь д/±)
при ас > О, (0, 0) при с = 0; иет решения при ас < 0.
в.22. (о + Vo3 - (5а + 6 - 6); 2а2 + V»2 — (бе + * — 6) X
Х(2а-5) —10fl-&)( {а - У<»2 - (5а + 6 - 6); 2аа —
- Vo2 - (5о + 6 - 6) (2о - 5)-Юа-&), если аа-(5а+Ь-6)>0
(о, 2о2 — 10д — Ь), если о2 — (5а + 6 — 6) = (V, нет решения
если а2 — (5а + Ь — 6)< 0. 6.23. t/ = у д: + — + L где
2 о
«о= J~T> если а = °' Ъ "^ "« *° = "о" при а*ь0> & = '! *о
приа^О. 6-1 + 1; -1±У1 + а(1-Ц
в 1 — о
1 ■ ч - 1
6=?Ы,6 < И н при а < 0, ЬФ1, Ь > Н . В остальных
случаях (а = 0, 6=1; а > 0, 6 > 1 + 1/а; о < 0, 6 < 1 + 1/«) реще»
ния не существует. 6.24*. у => — х + 5/2. Указание. Условвд
пересечения двух липни у = f, (д:) и у = }г(х) равносильно сов»
местности системы уравнений y=f\{x), y = h(x), решения
которой являются координатами точек пересечения. 6.25. (1/8|
1/16). бЛв*. ф = я/3. Указание. Искомым является угол1
вежду касательными к окружности, проведенными через точку
(8; 0). §.27. <—0,4; 8,8), если точка М двигалась по окружности
против часовой стрелки; {6; 4), если точка М двигалась в обратной
направлении. 6.28. р = 26ft. 6,29*. Прямая у «= —1/2. Указание.
Геометрическое место точек, из которых парабола видна пож
прямым углом, представляет собой множество точек пересечения
касательных к параболе, образующих прямой угол;
§.30, arctg(-4/Э). в.31*. Окружность х* + у3 =«* + 6*. Указа-
ОТВЕТЫ К ГЛ. 9 БЭТ
и я е. См. указание к 6.29*. 6.S7. а— 1/2е. 6.38. Точка с коорди-.
ватами (0, 2).
§7
7,1*. —1,6 м/с (знак минус означает, что y{t)
уменьшается). Указание. Если y(t)—закон изменения пути верхнего
конца, а *(<} — нижнего, то следует учесть, что ха + уг = 25.
hi
7.2. V (г) = jj-1, знак минус означает, что тень уменьшается.
IX Убывает со скоростью 0,4. 7.4*. 15 см/с. Указание.
Момент встречи определяется из условия Xi(t) = Xi[t).
7.5**. 2о sfn (-^р- /J. Решение. Введем систему координат
таким образом, чтобы колесо катилось по осн Ох, а ось Оу
прн t = 0 проходила через центр колеса. Тогда на основании
закона независимости движений имеем следующие законы
изменения абсциссы и ординаты гвоздя:
* (0-»(0 - Я sin (■£•<), y(t)=R-Rcos (-J-').
Таким образом,
™-£в',и(тО-'л(тО-
Скорость гвоздя в момент времени t будет равна
7= У(*')8+(</')2 - о д/l - 2 соз (^- г) + I =
—I* (*.')!•
■ 7.6*. Скорость равна нулю. Указание. При. движении
точки по окружности абсцисса изменяется по закону х =
*= R cos и/. 7.7*. h = s • Указание. Изменение вы-
8 К?
соты подъема тела происходит по закону А (/) = V sin а/ — -^-,
вертикальная составляющая скорости в точке максимального
подъема равна нулю. 7.1L 12 рад/с. Колесо остановитси через
2 с 7.9*. »(<) = —, Указание. Выразить рас-
V'4 - 4<3 + 12<s
стояние между телами в момент t как третью сторону
треугольника, двумя другими сторонами которого являются Ss(<) и
«92
ОТВЕТЫ
Si(t). 7.10. 40 км/я. 7.11**. В момент времени < = ('i + 's)/2
предмету следует придать скорость V = Vo + ah. Закон движения
предмета имеет вид
{1У-Ьа<*/2, *</„
Vot + atJ-atyz, <1</<(<1 + <2)/2,
VJ + atJ-aQ/l, t >(ti + t2)/2.
Решение. Отделившись от ракеты в момент времени U,
предмет движется равномерно со скоростью, достигнутой
ракетой, в момент отделения предмета, В некоторый момент t пред*
мет мгновение* увеличивает свою скорость до некоторой вели*
чины V и снова движется равномерно до встречи с ракетой
в момент h, причем в момент <2 нх скорости одинаковы.
Следовательно, закон движения предмета вне ракеты представляет
собой ломаную линию, авеньямн которой являются касательные
к параболе S(i)= Vot + (at3)/2 в точках /[ н t2. Абсцисса (
точки пересечения этих касательных — искомый момент временя.
Скорость, которую имеет предмет в момент времени /,
совпадает со скоростью в момент времени t3 и может быть найдена
как производная функция S{t) в момент времени h. Так как:
S'(t)=Va+at, то касательные к параболе S{t) в точках U
и tt имеют вид
S{t)=S(t{) + {V<> + at{)(t -Л), "
8(0-S(f,) + (Ve + «'i)(f-*«).
Рассматривая (*) как систему уравнений относительно пары не-
известных (S, t), находим, что t = (<i + h)l%, и, следовательно,
закон движения предмета представляется в виде, указанном
в ответе. 7.12*. tQ = tl— <y t\ — 2S(. Указание. Закон
движения ракеты после отключения двигателей может быть записан
в виде уравнения касательной к кривой, являющейся графиком
закона движения.
ГЛАВА 10
§1
1.1*. arcsln —■—■ — In (* + V*s + 2) + с. Укавание. Раз-
делить почленно на знаменатель и воспользоваться формулами*
(16) и (17). 1.2. | *в/3 - Ц- х1'5 + с. 1.3*. - -| (1 - x)W +
+ -=-(1 — *)s'2-)-c, Укавание. Преобразовать /(*) к виду
ОТВЕТЫ К ГЛ. 10 633
f (*) «■ Vl — * — (I — Jt) Vl — *• Для представлеиня f (x) в таком
виде удобно ввести переменное t<** I — *; тогда f (*) = g (f (х)),
где g«) = (I-0Vr-=V?"-'V^ 1-4*. -8 Г1--|Л,/2 +
8 / а; \з/2
+ -Д-11 —„-1 . Указание. См. указание к 1.3*.
1.5*. - j (2х - 1)~1 + i- (2х - 1)~2 + с. У к а з а и н е. См.
указание к 1.3*. 1.6*. (1+.** (1 +ж) 1- с. У к а з а.н н е. Пред-
ставить f (х) в виде f (*) =" vv J ' —j-—. 1.7. -^
т-Ж + С. 1.8. t + ln|f|+c. 1.9. -i=| he. 1.10. -jXW +
+ 4*-"2 + c. 1.11. 2л'/2--|^2+с 1-12. -x + c. 1.13.x-
— \-+c. 1.14. * + x2 + c. 1.16. m*"m + Зп*1"1 + c. 1.16.xs —
— x + c, 1.17. — з J + c t.18. 2* -8 In |*|+ с
1.19. X + 2ln|x — 2| + c. 1.20. \j2x-\-c. 1.21*. jj cos 12* —
"--rg-cos lOx—jj-cos9x rr- cos 11* + с. Указание.
Преобразовать подынтегральное выражение к виду sin 12* + sin 10*:+
*Ь sin 9* + sin Их и воспользоваться правилом 4) и формулой (4)
тгаблицы первообразных. 1.22. —-у-соз 4х +-=■ соз 5х+-~-cos 6х—
*~ у cos 7* + с. 1.23. sin а — cos а + -.- sin За — — cos За + с.
'1.24. -~х + -gy sin 8a- + с. 1.25. - Г х + -i-cos 4* Л + с.
3|.26. — V2~ cos у + с. 1.27. — i- cos 2x + с. 1.28. — 2 cos * + с.
1.29. - — cos 8* + c. 1.30. - — cos 4* + с 1.31. -j x - ^- + c.
1.32. — sin 2a — -5- a + c. 1.88. tg * — * + c. 1.84. — ctg * — * + c.
— §2
2.1. j/ = *3 + l. 2.2. j/ = xi!. 2.3. 0 = 5*- 1. 2.4. у = -^—
,-—. 2.5. y=Jj. + L H0,=,.iL+i. 2.6. j/ = 31n* + l.
-534 ответы
2.7. S</) = 2 — 0,25 cos 2< (м). 2Л р>2, один раз пешеходы
встретятся при /> = 2.
3.1. 8. 3.2. 1/2, 3.3. 0. 3.4. 8. 3.5*. — 2 ~. Указание.
о
х 73
Сделать замену t = 2—~-. 3.6*. — I-rrg-. Указание. См.
33/2 _ 2з/2 _ i
указание к 3.5*. 3.7*. ^ • Указание. Избавиться
от рациональности в знаменателе. 3.8. —-• 3.9. -т^-. 3.10. —т~.
, 4 1» 4
3.11. 1п2 —-i-. 3.12. -у. 3.13. j. 3.14. V&
V2
3.19. 2 У£ 3.20. 2 -v/2" + 4- (З3'2 - 23*2). 3.21. 1п 2,5 + 2,5.
3
я оа о л /о" я ч
3'
§4
3.22. 41п 4> 3.23. 2 У2. 3.24. 3 V2" - L'
4.1. min F (х) = f (0) = 0, max F (*) =. F (^А = 1.
х (= 10; л/21 х т 10: Я/21 Ч 2 )
4.2. min F («) = /=• (2, 5) = — 6,25, max F (x)=F (-1)=6.
JCG[-I;3] 4!ei-J;3|
18
4.8. mm F (*)«F (0) = ®, чпах F(x)=*F (4) =-5-.
*e(0;4) *s[0;<) a
4.4. max F (*) = tf f -1Л •= -1-, min f (*) =
= f (- y) = --|. 4.5. у = 2 - г, у = x - 3. 4.6. Кривые
совпадают, «eR, 4.7. Cj, ||Л. 4.8. -j- --^—• + 6*. .
1 1 2/3
4.9. yooje--^; j/ = * + -L. 4.ГО. S(/)=^-. fll*. Л (*)-
= 25xJ + 100*. Указание. Закон изменения силы F как
функции пути х лредставяяется формулой F (х) = ах + *, где
параметры а и 6 находятся нз условий задачи. Работа переменной
силы представляет собой ту ее первообразную, которая
обращается в нуль при л = 0. 4.12. 5(0 = ^y t, 4.13. S{1) =»
-4"+f<.
ответы к гл. ю Б35
§5
5.1. (- оо; -2) U (1/2; 3). 5.2. (2; 3). 5.3. [4; оо). 5.4. Л=-2/л;
В = 2. 5.5. а = 1. 8.6. У2я; ~' + У8я+ 1 ^ 5J ^ 5J„ Да>
5.11. А = 7; В 5; С=3. 5.12. -J; -^L ^-; -^-. 5.13. 1/2;
2. 5.14. -к -j\ 0.
§ в
■ в.1. -1- •■*•«■ 6.3.^. в.4.1+1п2. 6.5.3(1-^).
6.6. 4j. 6.7. 12-5 in б. 6.8. -^| 1п 2. 6.9. -|. 6.10. 1.
в,ц. 4--Д-. 6.12. 7 in 3. 6.13.4. 6.14. б-1 3
In 2' "•"•г" ' 3 41п2*
6.15. In 2. 6.16. ~. 6.17. -1 In 2. 6.18. -|-. 6.19. 15- 161п2.
6,20. 3 4-- в.21. 4т - 4-- 6.22. 9 - 8 In 2. 6.23*. 8/9. У к а з а н и е.
15 L 6
Для вычаслення площади этой фигуры удобнее использовать
.формулу (6.3). 6.24*. ■s"TO'a. Указание. Область
интегрирования следует разбить аа две области, координаты точки деления
находятся как решение системы
, х2 + у2 = г1,
. | х-у = 0,
6.25*. 1 — я/4. Указание, max (ж, у) = 1 — точки,
составляющие две смежные сторон** единичного квадрата, вписанного
в угол первой четверти. 6.26.1/3. 6.27. я/2— 1. 6.28. 1. 6.29*. nab.
Указание. Выразить у через х прн у > 0 н * > 0, при вы-
а
яяслеиин определенного интеграла 4 \ & У1 — х2/а2 dx нсполь-
0
аовать формулу (9.3.4). 6.30*. я. Указание. Выделить полный
квадрат по переменной х. 6.31**. 4/3. Решение. Уравнение
касательной к кривой j/ = 2*2 в точке с абсциссой 2 имеет внд
у — 8 = 8 (л: — 2), так как у (2) = 8, у' (2) = 8. Точка пересечения
касательной и оси абсцисс находится нз уравнения 8х — 8 =
= 0 ■*=*- х = J. Область интегрирования разбивается на два
промежутка: (0; 1] н [1; 2}, причем на [0; 1] вычисляется площадь
фигуры, заключенной между у = 2х2 и j = 0 (осью абсцисс), а
636
ОТВЕТЫ
на [1; 2]—между у = 2хг и #=»8л:—8. Таким образом,
1 2
S = \ 2л8 dx + \ (7.x- - 8х + 8) dx =
О i
_^[+(Т_^+81)|;_|+
+(£-**-4+i-)-k
0.32.9. в.&Э. In 2 — -=-. 6.84*.- 2-^-. Указ-аниа. Следует раз»
. о *
бить фигуру на две криволинейные трапеции; абсцисса точки
45 ':
деления — абсцисса точки пересечения касательных. 6.35. -т-.
в.Зв**. Парабола рассекает квадрат на две части, площади коЦ
торых относятся, как 1:2. Решение. Выберем систему коор*
дннат таким образом, что вершина параболы совпадала с
точкой (0; 0) и ось Оу являлась осью симметрии. Тогда уравнение
параболы приобретает внд у = а*3. Параметр о выбирается
следующим образом: обозначим длину стороны квадрата, середина
основания которого совпадает с началом координат, буквой /}
тогда точка {1/2; I) — правая верхняя вершина квадрата, ле«
жащая на параболе, т. е. / = a(//2)s. Из этого уравнения получ
чаем, что а = 4//. Площадь квадрата S равна Р, а площадь,
отсекаемая параболой, определяется из формулы
№
«•-Jt
l 3 |о 3 '
Таким образом, парабола рассекает квадрат на две части, пло-
щади которых относятся, как 1:2.
о о__ __ о
6.37*. —£- =—5 , где S — площадь, отсекаемая
параболой от полукруга. Указание. Выбрать систему координат так,
чтобы вершина парабблы совпадала с началом координат, а ось
Оу была осью симметрии параболы. Тогда уравнение параболы
имеет внд у •= ах3, а уравнение окружности — вид {у — /?)' +
+ *2 = #а- Связь между а и /? устанавливается из условий
2
вадачн (см. решение 6.36**). 6.38*. -=-. У к а э а и и е. Параметр a
в уравнении параболы находится из условия f (— 5) =>
2 ——
= tg (я—arctg 20). 6.39*. а = 8; о = тг (б — V21 )• У к а 8 а н и е.
ОТВЕТЬ* К ГЛ. 10
537
Рассмотреть два случая: а > 2 я а < 2. Во втором случае учесть,
1 «
что при переходе через точку * = 1 знак разности — ■„ __ ■
меняется. 6.40. — | 1 г=Л. 6.41*. 5 = 6 при а = -\/8/36 — I;
4 V. -^4 J
вадача имеет решение при b s (0; 8/3). Указание. Для того
чтобы выразить а как функцию от Ь, следует разрешить
относительно а уравнение, правая часть которого равна Ь, а левая
представляет площадь указанной в условии фигуры. Значение Ь,
при котором задача имеет решение, находится из условия а (Ь)>0,
где а(6). — искомая функция. 6.42*.' — я/6; л/3. Указание.
Учесть, что искомое значение о может быть как больше я/6,
так и меньше (во втором случае площадь будет вычисляться
я/»
по формуле S=\ | s\n2x\dx). 6.43*. а <= Го; — J; b—Q^~1'
а
Указание. См. указание к 6.37*. 6.44*. t/ = I jc —■"
-arcsin Л - Щ] / + VH VivT^- У к а-
V 4 JJ V2 (4-V2) 4
з а н и е. При решении задачи использовать формулу
V1 + cos 2х = V2" | cos х |.
§7
4
7.1.3/4. 7.2. а = л/зТ 7.8. 0=1. 7.4*. S(—1)= I25/6,
mln S (k) = S (2) = 32/3. Указание. Пределы интегрирования
ftkR
находятся как корни x{(k) н xi(k) уравнения ж2 + 2л —3 =
•=kx+l. Следует учесть, что на промежутке [*i (k); x2 (A)]
всегда выполнено неравенство i/a(*Xi/i (*). 7.5. mJti S(!tf0)=a
xoeIl/2; i]
= sf|) = ^Aii, 7.e*. (3/2; 13/4). Указание.
Воспользоваться тем, что S = ft (~Чг—)• где А=1|в=^0(1). ^=fx,(2)t
/ж (*) — уравнение касательной к у = х3 + I в точке с абсциссой
лги е [I; 2]. 7.7*. а = — 1. Указание. Между двумя
последовательным» экстремумами функция f {х) =■ л8 + З*2 + ж + а
монотонна. Дальнейшее решение аадачн может быть основано на
следующей лемме.
Лемма. Площадь фигуры, ограниченной прямыми х = с,
х = b, b > с, графиком дифференцируемой монотонной функции
538
ОТВЕТЫ
f(x) и прямой yaMf(a), где ае{с,й], достигает своего ианмень-
шего значения в том случае, когда у =>f I—я—I.
Доказательство. Для простоты докажем этот
результат в случае, когда с = О, Ь =• 1 и f (&)=■. I. При
фиксированном значении а площадь выражается в виде следующей функцию
а 1
S0a)=J[/(a) -H*)]dx + J [/ (x)-f (a))dx~
О а
• -if(e)x-/?wiu+^wii^f(e)*ii-
-=f(a)a^F(a) + f(0) + F(I)-F(a)-f(*)+f(a)a, (*)
где F(x)—некоторая первообразная /(*). Приводя в (*)
подобные члены, получаем
S (о) = f (о) (2а - I) - 2F (о) + F (0) + F (I). (**)
Дифференцируя S(a) по о с учетом того, что F'(a) = Да),
получаем уравнение для нахождения критических точек:
S' (о) =/' (а) (2о — I) + 2/ (о) — 2f (a) = 0. (*»*)
Так как по условию Да) монотонна, то f'(a) # 0 па промежутке
[0; IJ, и, следовательно, уравнение (***) имеет единственный
корень а = 1/2. При a > 1/2 S'(a) >0 и S(a) возрастает, а при
а < 1/2 S'(o)<0 и S(a) убывает. Следовательно, при а =.
= 1/2 S(fl) достигает своего минимального значения.
7.8*. При а = I площадь принимает наибольшее, а при
а = 1/2 — наименьшее значение. Указание. Воспользоваться
леммой в указании к 7.7*. 7.9*. а = 2/3. Указание.
Использовать лемму в указании к 7.7*. 7.10*. При a = 1/2 площадь
имеет наименьшее, а при а = 0 — наибольшее значение.
Указание. См. лемму в указании к 7.7*. 7.11*. a = 0.
Указание. См. лемму в указании к 7.7*.
§8
3 ■•
8.1. 2я. 8,2*. -г^г- я. Указание. Рассмотреть разность
объемов тел, полученных при вращении кривых у=<^х~и у = х3.
8.3. ■%■[* з +- 2-L— + *(»-a)J. М*.-|я.
Указание. Перейти к функциям хх (у) = 1 + Vl — у, *а (у) = 1 —
— *J\ — y н рассмотреть объем искомого тела как разность
объемов двух тел, полученных вращением фигур, ограниченных
ОТВЕТЫ К ГЛ. (1
539
кривыми *| Q/) и хл{у) вокруг оси Од. 8.5*. я2/4. Указание.
Искомый объем будет равен объему тела, образованного вра-
Зяс
щением линий у = sin х, х=* я/2 вокруг оси Ох. 8.6*. —^-.
Указание. См. указание к 8.5*.
§9
9.1. о = 18. 9.2*. 288. Указание. В моменты начала
движения н остановки скорость тела равна нулю. 9.3, 216 м.
«ж о,.. f t*t если0<<<3, .,,,,.,„ > ,г
9.4. S(0 = J „, * Г" 9.5*. 14/15 (Дж). Указ а-
(. 6t + 9, если t > 3.
и не. F(x)=kx\ где ft определяется из условия задачи.
9.6*. 33,75 (Дж). Указание. F{x) = kx, где ft определяется
из условия задачи.
ГЛАВА 11
§ 1
1.1. 32,5 км/ч. 12. -у-. 1.3. 60 км/ч. 1.4. 8 м/с 1.5. 3 X 4 км.
1.6.12 км/ч, 10,5км/ч. 1.7. 6 ч н 2 ч. 1JB. -^- (3 - <Jb), -|- (У1Г- l)-
1.9. 30 км/ч. 1.10. 20 км/ч, 60 км/ч. 1.11. 56 км. 1.12. Vp = l км/ч.
, ,„ 3S — и + V9S3 -f 2Su + v2 , ..... . ._ ап ,
1.16. 48 км/ч. 1.17*. 50 км и 150 км. У к а з а и н е. Ввести
неизвестные fDj = 1/V, и cuj=1/W, где V] и Vt — скорости
мотоциклиста я велосипедиста соответственно. 1.18.100 км/ч. 1.19. 100 км/ч.
1.20. 9 +V" км/ч. 1.21. Скорость пароходов — 15 км/ч, скорость
течения —3 км/ч. 1.22. 6 км/ч, 21 км/ч, 4Й км. 1.23. 63 км/ч.
1.24. Скорость велосипедиста — 20 км/ч, скорость автомобиля —
80 км/ч. 1.25. Скорость пешехода, велосипедиста н верхового —
6 км/ч, 9 км/ч, 12 км/ч соответственно. Расстояние — 42 ки.
1.26. 30 км/ч, 20 км/ч, 30 км. 1.27. 480 км. 1.28. 2 мин. 1.29. 15 км.
1.30. 3 км/ч, 45 км/ч. 1.31. 3 км/ч, 45 км/ч. 1.32. 6 км/ч.
3
1.33. -s—г-—. 1Л4*. 50 км/ч. Указание. Учесть, что скорость
встречного поезда относительно наблюдателя, находящегося
в одном из них, равна сумме скоростей поездов относительно
неподвижного наблюдателя. 1.35. 108 км/ч. 1.36. 28 км, 20 км/ч.
1.37. 11 ч 55 мин. 1.38. 7 км/ч. 1.39. Пассажирский — 21 ч,
товарный—28 ч. 1.40. 15 ч и 12 ч. 1.41. 6 ч и 4 ч. 1.42. Скорость
первого автомобиля в 9/8 раза больше, чем скорость второго.
1.43. 16 ч. 1.44. Скорость мотоциклиста в 4 раза больше ско-
540
ОТВЕТЫ
рости велосипедиста. 1.45. 20/3 ч и Ю/3 ч. 1.46. Через 4 ч.
1.47. 1:2, 1:3. 1.48. Не успеют. 1.49. Длина окружности переднего
колеса —2 м, заднего — 3 м. 1.50. 90 км/ч, 75 км/ч, 60 км/ч.
1.51. 117 км, 24 км/ч, 22,5 км/ч. 1.52. -j-/, ■—•(. 1.53. 4<о<
8+V61 ,влп «. ' к S+trf+V(S—vty+Uvl
^—-~—.1.54. Со скоростью, большей чем т „, .
1.55. Хватит. 1.56. 2<о < 6. 1.57. 5 < о < 10. 1.58. Деревня от
шоссе дальше, чем школа от реки. 1.59. 4 с н 6 с. 1.60. 1/80, 1/90.
1.61.4 „6. 1.62. f (д/Г-|^±.). 1.63. =£±Vg±2lO«L.s.
1.64*. 1 —- часа ночи. Указание. Использовать то, что
ам/<0ч=12, где <йм, юч —угловые скорости движения минутной
н часовой стрелок соответственно. 1.65. На полминуты. 1.66. «11м.
1.67. 9 км/ч. 1.68. 3 мин. 1.69. 1/4 ч. 1.70. 21 км. i.71. Через 7" с
после начала падения первого тела. 1.72, 1? с. 1.73, 60°. 1.74. 10 с.
1.75. 1/0 = 20 м/с. 1.76. Через 5 с за 0,5 м до лнпин поля.
1.77. 20 м. 1.78. 20 км/ч. 1.79. Второй автомобиль остановился
раньше, аг = — 8 м/с2. 1.80. 2 с. 1.81*. а,: аг = 7/9. Указание.
Учесть, что времена ускорений обоих поездов различны.
1.82*. S, = yS, S2 = -z-S. Указание. См. указание к 1.81*.
. во гт * * 2S S а + 6 •
1.83. Первый быстрее, так как ——— < -д т—.
§2
2.1. 24 м3/День. 2.2. 45 ч. 2.3. 132 мни} 110 мнц. 2.4. в мин
13 10 мин. 2.5. 6 мин, 8 мин, 12 мин. 2.6, Т + */Т (Т — t),
T-t + */T(T-i). <y/T(T-t) (T>t). 2.7. (,«3^ /, = 6 ч.
<з = 2 ч, 2.8. 400 деталей. 2.9. За 14 дней. 2Л0. За 10 дней.
2.11. Трактор марки /4—12 га, марки В— 16 га. 2.12*. В 4 раза.
Указание. Условие в виде неравенства используется для
выбора единственного нз двух найденных значений ; искомого
неизвестного, 2.13. 50 ч. 2.14, 9 дней. 2.15. 10 ч и 8 ч. 2.16. 9 км
в месяц. 2.17. буч и 5у ч. 2.18. 5/2 м3. 2.19. 3 м3/ч. 2.20, 60 %.
2.21. За 14 и 11 дней. 2.22. 4 ч и 6 ч. 2.23. Первому— по 20 стр.
в день, второму —по 35. 2.24. 12 ч. 2.25. с = 9-^. 2.26. 600 м3.
lb
2.27*, 20 м3. Указание. Проверить полученные решения
подстановкой во все уравнения системы. 2.28*. За 40 ч. Указание,
Использовать формулу суммы арифметической прогрессии.
2.29*. (5/4) V. Указание. См. указание к 2.28*. 2.30. Пусть.
ОТВЕТЫ К ГЛ. И
641
Ti (i = I, 2, 3) — время опорожнения i-м насосом своего
резервуара. Тогда Ti>T3>Tlt причем Г, :Г»:Г2=»(1 + л/о)*Ь '
:[а(1+^].еслНо<1=^..Г1:Г1:Г1--Ь^:1:тЯ-,.'
л • w . i—ct
если ^—s^a<~. 2.31*. it . Указание. Используя
условие задачи, предварительно показать, что все трубы начали
работать до того, как бассейн был наполнен наполовину.
§з
8.1. Приблизительно через 23 года 8.2. Приблизительно через
Бб лет. 3.3. 12 к.-, 80 к. 3.4. 5 %. 3.5. 10 %. 8.6. 10 %. 3.7. 200 р.
Срочный. 8.8. 42,3%. 3.9. 726. 3.10. 50%. 3.11. Через количество
лет, большее чем lg ( ™р-10ОМ )/lg 0 + Too-)' 812* Б°Лев
чем чеРез tg Смрр-!ш)/1е (1+-&■)ч-
§4
4.1. В альбоме 12 листов. 4.2. «Троек» —2, «четверок» — 7.
4.3. Пятиэтажных—9, девятнэтажных— 8. 4.4. «Москвичей»--!
10, «Волг»—19. 4.5. 33. 4.6*. 25 второго типа н 4 —третьего.
Указание. Предварительно оценить стоимость перевозки
одной детали в ящике каждого типа. 4.7*. Первый — 3 дня,
второй—2 дня. Указание. Оценить, какое "количество дней мог
работать каждый экскаватор. 4.8. 45,20. 4.9. 13 мин. 4.10. 19
плотов. 4.11. 15 или 95. 4.12. 48. 4.13. 32. 4.14*. 5. Указание.
Приписывание к числу справа некоторой цифры означает
.переход к новому числу, в котором число единиц равно
приписываемой цифре, а число десятков — исходному числу. 4.13. 6464;
4.16*. 285 714. Указание. См. указание к 4.14*. 4.17. 32.
4.18*. 54. Указание. Для получения суммы всех четных
двузначных чисел использовать формулу суммы членов
арифметической прогрессии с разностью d •= 2 и а, = 10. 4.20. 21 и 10.
4.21. 31 и 41. 4.22*. А = 42, В = 35. У к а з а н и е. Использовать
формулу /i= m-p + k, где л — делимое, т— делитель, р — част»
иое, k — остаток. 4.23*. N = 37. Указание. См. указание
3 4 5
к 4.22*. 4.24*. -rg-, -т=г, TjTT. Указание. Задача сводится
к решению системы квадратных неравенств в множестве нату»
ральных чисел, -4.25. 4 рубля.
Б42
ОТВЕТЫ
§6
1,6 кг. 6.!
2л — т + -у/т2 + 4я,* 2п + т + л/т* + An*
6.1. 1,6 кг. 6.2. 4- г - 24; 32 - 4" г; -^- < г < -^. 6.3. 7 кг.
5 5 4 4
5.4. 60 кг. 5.5.
2 ' 2
5.6*. :—. Указание. В качестве неизвестных ивестн х —
т+ п
вес отрезанного куска; с{ я с2 — концентрации медн в первой
я втором кусках соответственно. 6.7. 5 % н 11 %. 5.8*. В объейё
4 см*. Указание. Воспользоваться формулой т =■ gV,
связывающей массу, плотность н объем. "6.9. 12%; 24%; 48%'.
6.10*. 29%. Указание. В качестве неизвестных ввести
концентрации си ci, сз, ct. Условие задачи дает систему трех
уравнений дла четырех неизвестных с,, с3, с3 н сА. При исследовании
системы необходимо учесть, что ищется комбинация неизвестных
2°г * С< . 5.11. В 13/4 раза. 5.12. б г н 20 г. 5.13. 14 кг; 7 кг;
О
16 кг. 5.14. Первая труба подает жидкость в два раза быстрее
второй. 5.15. 60%. 5.16. 12,6 г. 5.17. 170 кг. 5.18. 40%; 43-^-%'.
О
5.19. 2 л. 5.20. 10 л и 90 л. 5.21. Юл. 5.22. 1/6. 5.23. Если р = <?,
то любое число промывок сохраняет процент содержания золота;
задача в этом случае имеет решение, если г <^ ft, причем число
промывок произвольно. Если q < р, то число промывок п опре-
^, г(100-к) /, 100-<7 0
деляется неравенством ff>lg-: ^тдя— >/lg 10Q_a- Если жв
' r(100-fe) A 100 —д
p<g,TOB<lgfe(1O0_r)/lg-Mir7.
§6
6.1. 28 г. 6.2. 60 дет. 6.3. 28 р. в.4. За 1 час. 6.5. 6400 л
и 600 л. б.в. 1,26 кг и 0,75 кг.
ГЛАВА 12
2bc соз (а/2)
1.1. 20 см. 1.2. z<"7 ,(а/" . 1.3. 75. 1.4. m(mcosp±
b + c
±Yc2-/7i2s!n4fl)slnfl. 1.5. Нет. 1.8. у sin 2«. 1.7.у tga(rcosa^-e).
I
i&. ^rcr Sln a . 1.9. —2S cos2 a cos 2a. 1.10. 288 см3. I.I1. л/Ъ— 1.
2 cos a y
, to a8 sin a 1 cos 2a | . .. ,. b* sin a (5 sin fl-f 3 cos В tg a)
4 cos a (1 + 2 cos a) 16 sin (a-J-B)
ОТВЕТЫ К ГЛ. 12 54?
LIB. i-. Ш.4- ^Г^' 1.17*. ^J!.. Указа-
2 2 cos (а — р) cos (а + §) 2
и и е. Убедиться в том, что треугольник прямоугольный.
1.18. ^-. 1.19. -itgactgp+l. 1.20. ^2 + V3~V IJ}, ^
1.22. 4V3T 1.23. 75. 1.24. ^ 1г. 1.25. МГ = а^. 1.2в. 3, 5, 7.
/— я 1-1-2 V2~ я 1+2 л/2*
1.27. 1 + V2. 1.28. 4 ± arccos ^, , ~r =P Pfccos LXipLi.
4 4 4 4
1.29. ВС = Уб (6 + с). 1.30. IxL. 1.31. —см*. 1.32. 2 ~.l3 .
4 3 -у5
to* NC 3 ,.. ЛАГ 1 п , ._ , V3"- I
"ЛС'^Т' "iVC^ir или==9« |'35' arctg-i-g .
1.36. 4(1-а). 1.37. Ц. 1.38.-^-. 1.39. JL. 1.40. -§-.
141 р (1 + 2а + аР) f ^ S,S3 (S8 + S.) (S, + S8)
Ц+а)(1+в)(1+а + ав)' ' ' S^Sl-S^)
U3. 3:2. 1.44.3 или 1/3. 1.46.6:5. 1.47. Я—|-, В = arc sin (4/5),
?=arcsln(3/5).
§2
2.1. 1. s=. 16 V3l f = 8. 2.2. 256 см3. 2.З. л/з м. 2.4. 2 см.
2.5. 6 м. 2.6. 9,6 см8. 2.7. — sin 2а. 2.8. -т-=Д—^-. 2.9. -^12..
2 (V3 + I)2 2
2Л0. -|- д/аЬ +-(4с73*в ' 2Л1, '' 2Л2, СтоРонУ С£>< 2ЛЗ' ~]р
2Л4- l+(1+2?gtr)8—I-v^ns: 2лБ- 4-<e-^sina
2.16. 4AS ctg а - 2A V«* - 4A*. 2.17. j. 2.18. 2. 2.19. ЛВ =■ ВС =4
^£) = V3; Z>C=>1, S = ~V3: 2.20. -i. 2.21. i^^ciA
2.22.2 V2-CM.2.23.iMK = -^Ii. 2.24.^-^i-. 2.26.^$^.
о MD a 2
2.26. %S. 2.27. S = -^ii. V(a + 6)(36-a). 2Ж -i S. 2.29. VIS.
•544 " ответы ■
8.1. -^yjp-. 3.2. 2л/«г. 3.3. 8. 3.4. -у- (з + я - 3 Уз).
3.5. l-VT+уЯ. 3.6. ~см*. 8.7. -|/?*(2Уз + 5я).
3.8.i-^ctgo-i-R»(-|-a). 3.9.8.3.I0.7. 3.11.5=^^^.
3.12.r,d;-l^-^;3.13.8oM.8.14.a^r-V^+2arV5'.
8.16. |-(3-V5). 3.16. (|-A, ^-A). 8.17. 8VT5. 8.18.—см*.
о <n 32 / ,- s, 0.n 2 sin* a
3.19. »—-J- (arccos m — м VI — mz;. 3.20. —тт—■——-д—■—, , ..
яш44 v a (I + sin 2a + slnsa)
8.21. Площадь квадрата больше площадн круга. 3.22. АВ = —j=r«
§4
4.1. » 4.2. &'COS^3g/2)l . 4.3. г «ИН«_.
I + у2 2 sin a cos (a/2) 1 + sin (a/2)
44 abc a2 (З'УЗ"— я)
V(a+6 + c) (a-fft —с) (a + c—ft) (b+c—a)' " ' 24
4e b + c-W^cosa^ 4<7> ^ 2V5-(hjih 2V- ую<
4.8. bJL. 4.9. 2/;33'"8(g + P)3lnB. 4.10. 'Vw+ТТЯ
12 sin a vi»
4,, B-r sin (a/2) cos (B/2) „ _ 1 Д»(а + Д)8
*'K * ~ ° cos (a/2 + 6/2) ■ 4Л2, 6 " 2 (a - i?) (a» + R>) '
4.13. 5"-«V3 д.4' 4I4 a , 1 —sin (a/2) t С
72 ^ 4Л4, 2 1+sin (a/2) ^T4
4.,,ад/^. 4.17. S = I^La=(|n-V3->
\^ab^a ^_2_ 4.19./? = 2. 4.20. " 4.21. r,-
= V£(14_V70), r, = ^l(21-VT06). 4.22. *W-£+9\.
6 8 V'
4* 4:3. 4.24. 150 + -^-. 4.26.1^-. 4.26. б/4~Сб^ X
V3 2 2 sin В
ОТВЕТЫ К ГЛ. 13 545
4.30. 128(3 + 2л/2"):49. 4.31. д/4Ля'' 4'32, ЛСвл/^ АВ~
^ЗлД 4.33. 4i?8sln°CQs4g. 4.34. «!^L. 4.35. 22. 4.36. S-
Y cos 3 a 26
= 4/ (I " «) sin p (l +4-s,nPtg-|-). 4.37. -£^-.
лчя p -n slnC 3-2V2~cosB n _ sin С
4Ж R,~ sin (Я + С) ППГв' *»~ sln(B+C) *
3 + 2V2COSB a 4.40. —_i -.
'N 4 sin S 2 sin a + cos a — 1
n , .eo . ., sin (a/2) sin 2a
Отношение будет наименьшим при a= 45 .4.41. — 5-J—'
sin(3a/4)sin(7a/4)"
6 = ХвС*. 4.44. ^3 ~ ' . 4.45. 25rt. 4.46.5 см. 4.47. агссоз —,
V6 б
я 3 4 я 4
-я—arccos— нля arccos-=-, -д—arccos-^-. 4.48. 14 см. 4.49. 3,
4, б. 4.50. у дм. 4.S1. УэТ см. 4.82*. 2 Уб] Указание. Ввести
в качестве неизвестного острый угол треугольника а и составить
уравнение для нахождения а с помощью теоремы о касательнов
Н секущей. 4.53. 240 см3. 4.54. jg, ~. 4.55. -^-, ~£. 4.56. j.
437. — — агссоз (—=■ ~\, — 4- агссоз (—=- -=-1.
4 ЧУёГ V2A 4 УУб -у/1)
2 S& зУз~(УТз —l) m Vfe* + 2fe соз Л + 1
4.В8. т. 4.59. -3-- 32^ •_4Лв" 2 (ft + 1) соз (Л/2) '
4Л1. агссоз V2lT^S): 4.62. 3±Д^2(У/2)- а. 4.63. Л - У2 см.
4.64*. Д/у. Д/'о"' Указание. Ввести в качестве
неизвестного расстояние от точки D до точки касания окружности с
прямой АС. 4.65. Треугольник разносторонний, длина стороны — 8.
4.66. АВ =• 10, ВС = 6, АС=> 12.
§5
5.1. А'л/З: 5.2. /?=„, а ... 6.3. 9Л^Г' . В.4. гУт".
2|cos pI 4
8.5. Ц-. 5.6. 2. 5.7. 0,Os = -|. 5.8. 12,5 см. 5.9. -^-. 5.10. 2(Уб"—
J3 А, Г, Цыпкиа а А, Н, Пнвсша
Б46 ОТВЕТЫ
(ra v\ STB 4 sin3 a cos а л
m Б 2 / SKp я 4
О— Q
™. 5.16. 25t-'(coseca + cosecP). 5.17. у г2. 6.18.3 см, 8 см.
5.19. -^S-. 5-20. 8. 5.21. 12VI5. 5.22. 14,4. 5.23. 3. 5.24. 10:11.
9"-
5.25. Трапеция равнобедренная-, 75° н 105°. 5.26. 210. 5.27. —.
5.28. NJ) | =■ о + / sin2 -°- ± /Je!+2fl/ sin*y-i2 cos8 у sin» у.
7 44 9 К
5.29. -4=-, —. 5.30. ЛС=-^=-. 5.31. —.
V85 5 V3 »
ГЛАВА 18
§1
1.1. arccos-ir-. 1.2. 3d8 V5I 1.3. 2о8 sin у д/sln у з1п у.
b^ *v cos 2d
1.4. ^y-* . 1Л q) = arccos(sinasin8). 1.6. 576 см*.
1.7. V3ds sin 2q> cos (45°-a). 1.8. аЧ sin a sJn fl. 1.10. Щ.13 cos2as!na.
U1" cos a " Ш* »>n»e—» У Г*
^3--^(^-^- "4. -4-^(3tg/^-l). 1.15. V-
a3 coss (a/2) ctg (a/2) , /5 j-=— c8 sin а соз а
3(3-4 sin8 (a/2)) • "6. qV3-ctg8<p.l.l7. 2cosp ■
1.18. V jj д/у (a8 + b8 - c8) (a2 + c8 - b2) (6s + c8 - a2).
1.19. i-Я sin 4 ^/cos'l-cos'a. 1.20. sin-| - V' + f,^.
1.21. я - 2 arcsln l- . 1.22. b-~" tg a. U3." a VV2"— U
2 sin (a/2) 2 V3
2 1 ^__^
1.24. —• 1.25. -[^-7^ V(os + bl - c8) (o8 + e» - b2) (68 + c8 - a2).
loe V2" дз ,л /~^' W2> 127 2 cos (B/2) cos p
1.20. e a /y j _ ctgS (a/2) . i.//. 3 * sin3 №/jJ) .
US, 4|^l. Л^т 1Д Q-f X
^ 2 соз p 3 cos a a
ОТ&ЕТЫ К ГЛ. 13 547
ХлЛ#3 + 3V. 1.31.2 arcsin (V2~sin — \. 1.32. arcctg л/1?.£~1.
lt33. /3ctggctgp 6y2-_yg-+4. 1.35. И-
3[1/в1п*а + ctg2 p]W
- "' V3/6' ~ *, S6oK - VI27^^.j.. ,.зв.2 arcsin ^=-U
,Л7' 2яТ^2ШШУ и»-&*%@, 1.39.arctg(tgacos-J).
1.40. 8 = 2 arcsin (^Ш. Ml. (* - *> V*".
V. cos (a/2) J 6
§2
2.,. **4L. 2.2. arctg^f-. 2.8. Уб. 2.4. £^L. 2.5. P coa-
падает с точкой С. 2.6. ^ . 2.7. — л/-щ_. 2.8. Л/—.
2Х 1&Л, 2Л0. "'VW, 2.11. (°3-^)(«-b)t2atgp.
б sin a 8 ь bi
2.12. arcctg (cos a). 2.13.— 2 ■• 2.14. arccos (tg-|-Л.
2Л5. fVacosa, 2<16> «■ 2Л7# 4 ^in_2a
2 sin (a/2) 32 уз 2 cos ф
2.19. S sin q> Vs Уз~ cos ф. 2.20. -£- Vl5b3 + 4JZ. 2.21. 3.
a'tga (3m + 2tt)aMga . a3tga „ а'Уз ■
U/' 8sinptgP' "* 8H ' 8 • й— 4coso*
2.24.
3j\/3
8
2.25. -i- (с + A) • S. 2.26. 7:17. 2.27. -jy X
X V(o2 + b1) c1 + 4as63. 2.28. <p = arcsin -j-. 2.29. S « e'^3 X
X cos a V4 + 21 cos3 а.
os /W3sins-J- + 2sin-|-<y'4sinJ-|--l +1
2.30. У- - =- . 2.31. S =
4(.ln-S-+/\/4sln«-|— l)
= a*sins-g- A/3-4si"SV- 2-32- !■«*• 2.33. „,,. ^f,. /*.
2 V 2 9 2(4tg2a+1) cosa
2.34. 2^П a1. 2.35. 2as cos2у- V-2 cos 2a. 2.36. S = 4 V3 ws.
18*
648
ОТВЕТЫ
2<37. * 2.38. 1# Л 2-39. УЗ"-^^-. 2.40." <£ sin ■§-.
128 4 cos a 9 2
2.41. 3:4. 2.42. 4"- 2.43.
6
б5'пт('~т51п8т)
________ 244 ii
( а I 4 ГаЧ3' ЮО'
2
2.45. На расстоянии от точки S, не большем чем -^-SD. 2.46. 8:37»
2.47.
5л/1аЬ
^—-. 2.48. -у /s cos a. 2.49. 32 Уз.
» ______
2.60. а2 Г I +2 д/l+—j_-j. 2.51. -|-v 2.52. 1:1. 2.53. -Ц-S.
§3
яг3 УН-
a*3 cos8 a sin a -aVJtsT
8.1. ; . 3.2. JtSj, r .
4jt 2
3.3.
3.4.
3.9.
reSVl5
,* Sr ,fi "SA~ ,7 2 ._5_!_ ЯЯ VB"
-. o.a. -5-. 0.0. _ . 0.1. -5-'—я p. 0.0. —=—.
о ' о Jt — 1 О-.
зуз
2re — 3 Уз" „ ,„ 2я ,, „,,, sin а
iOjt + зУз"'
„ .„ 2я ,-
3.10. -j- h\
-~-h\ 3.11 J
I3 cos В j
■8'12' "c^F" ^sin (P + °)sln (P ~~ a)-
4я cos В cos2 -£-
Ч1Ч " У~~~" tt* ctg" a - a" ctg» B) 1
ЗЛЗ* 24(ctA_*tg2eP 3 ' T(2S,+2S' + I1^'
_24(ctg2a-xtg2flP
2 У2 — 1 2У_"+ 1
'+ I ' 2У2
""■ТЙТТ*-^!"*- ^'О+^т^тХ
_ у _• -,- i -••у-' I
X д/з + ^^т) 3'17-' 0 + f) 3-18- 4- 3'9' r'°^;
с sing, с sin a sin p P*—(ft — r)8
Гг°Т_йГГ' r8=C2 8in3(a + B)- d-20' 4(У^ + УГ)2"
§4
4.1. V-Ч--^ 426(L 4>3t.12/?-V3- 4,4, 2 + УГ^
4.5. _J.e(V3_ 1)1 4.6. f*» д/J. 4.7. __^__.; i±VIi.
4.8: -i. 0У4Т. 4.9. •£- «3 yjf. 4.10. /? = 4 см. 4.11, R = ^A=-X
ОТВЕТЫ К ГЛ. 13
549
V^os-f-s,n-|. _ a n^yZT)
V3cosi+sin|- 2V3- V sin(60' + A)*
а
о cos -тг «г
4.12. 2 4.13. -4- 4.14. «^.
2Vs4t+t)-(t-t) V2
4Л5. £^L(V43ti^H-2ctga). 4.,в. 3 ^el* а)'
eta J- U
m а(2Ь-а) 420 4 2 д/э g(VT-l)
4'19-2V3F^-4-20' в"^^^18'- 4V2- '
4.22. ,,-i, „-2.rctg J^ 4.23. 3^ ""^' C0S<° .
ш _tesiniaipsa_i 425> j«^lili 4.26. , д _ .
3V3(|+cosa)3 4 + tg3a 2(l + V6)
4.27. V*"+' . 4.28.4. U & UH-J-'X
2 V2 + V3 + I 36 2
X(462-a2)"2(4fl262-a*-6V'2. 4.31. ^g^ffi ■
4'82"L7Tvfe^- 4-33'^ 4'34-T- 4.35.S = 3Vi5X
X (V5 + I)2, a = 2 arcsin д/-2-.
4.36. -§-. 4.37. 2rtaS
6 ' ' slns2a *
4Л8. 4#* sin 2a. 4.39. 4/?s cos a (sin a + V- cos 2a). 4.40. ?Ф- а.
о
4.41. -i- r/? (/? ± VF=7*). 4.42. 1 «• „Л+У'!' ■ 4.43. S =
6 3 cos q> sin* ф sin a
=> 2 V2~ Rs cos a fsin a + д/sln'.a + -5- coss a J. 4.44. -^- sec4 —.
4.45. , a3'"BCQ3B . 4.46. , f 4.47. V3(2-V3)g>>
V1 + cos2 a + cos a у 2a3 — 6s 4
4.48. . C 4.49. _^Vj_ 4.50. V~
V2 (cos (a/2) + cos (&/2)) 4(l+V7)
БбО ОТВЕТЫ
4.52. «J* 4.53. S - i^pl; V = !#- tf * i^L
16 sin2 a 3 sura
/„ . , я . 1 . 2л\3
Jtn2 sin1* —
n
vysln3acos3a . __ ,, 2 _„, 4-sin8 a 0_ 4nR*
X 77—; r*. 4.57. V = -=- rtft3 r-o 1 S = ■ , ■■ 4.58. n —
^(l + cosa)s 3 sin3 a slnaa
, 1 ж„«. яг3 ctg3 (Я/4 — a/2) . c . „a
- 4 afctgT. 4.59. 3^BalnB ■ 4.60. S sin a sin 2acos^.
4.62. 4tg3-|-,ctga. 4.63.2. 4.64. [6s^2tt- 4.65. arcsln д/-|%
4.66. 4 ^3c.g|cosec>|. 4.67. Jfe, 4.68. '(» + »VS + V5),
4.69. sin T-J=- 4.70. ЩТГ7? . 4.71. у т X
x(V*+7-V«ft 4,2. *№ + Ц У?+3-«.
V^2 + Л? + Л/ Л2 + *2 V ^ + А? + «
4.78. А. 4.74. Jj-яЛ». 4.75. Л [г + Я c.g (f+ ■.)} 4.76. *».
4.77. * = _tg(T-T).
ГЛАВА 14
§ I -
1.1. a) (-6, -2, 4)7 б) (18, -5, 19). 1.2. a) (-30, 21); б) (0, 0);
в) (у, y} г) (25,-10). 1.3.а = 2,р = 3,у = 5. 1.4. а) (11,-6,5).
1.6.(1,1,1). 1.6. а)с = а-Ь; б)с=2о-Зб; в)с = --|о.
1.7. а) PQ = (-3, 5, -3); 6)PQ=(--]^. ~, Ь).
1.8. (о, -|). 1.9. а) (-2, 1); б) (0, 2); в) (0, 2). 5.10. М, (7, 0) н
ЛГа (—I, 0). 1.11. Af (0, 1, 0). 1.12. М (-1, 0, 0). 1.13*. а) (-|-, |);
^ 1"3~' V' В^ ("З-' ~яГ)" Указание- Если вершины
треугольника ЛВС заданы своими ординатами А (х{, у{, z{), В (дга, уг. *з)
и С (jc3> Уз, Zj), то координаты центра тяжести G этого треуголь*
инка находятся из равенств х ■= —- (л, + *2 ■+- *3), » = — (t/i +
3 3
ОТВЕТЫ К ГЛ. 14 651
I 9
+ уг + Уз)> z => -£- (z, + z» + z3). M4. a) fe = —-jj; б) ft =
б 3 4
■=— -jgi в) fe = —3. 1.15. а) Да, а=-^-6; б) да. B=* — —d.
1.16. *~--|-, У = -jp 1.18.(4,0), (5.2). 1.19. (-1, 2, 4).
(8, -4, -2). 1.20. Cj-, ^j-, -y-Y 1.21. а = -1, 0 =4. 1.26. а) 22;
б) -200; в) 41; г) УЩ 1.27. ei = (-■|, -J), es - (у, - -|).
, ло* ^ 21 77 \ „ , а , Ь
1-28-х = Ы'Ж)' Указа"ие- *=e' + es=-|^r + W
1.29. -13. 1.30. а) |а|=л/з"; б) |6|=VTi. 1.81. (Уз~, Уз", Уз~)
или (,-л/з~. -V3". — У3"). 1.32. 6 V2". 1.33.(6,-2,4) н
(_6, 2, -4). 1.34*. -^р-. Указание. Лм =—- (ЛВ + ЛС) =
—> 1 —*■ 6 f 4 \
= Лв + "2"5С. 1.85. a) arccos---; б) arccos I — ,- 1;
3. /2N, 2. / 2 \
в) arccos -=i г) arccos I -==. 1; д) arccos-=-; e) arccos I j=}.
1.36. arccos—=-; arccosf =rl; arccosf s=-p 135°. У
Vl3 V. V29/ V V26/
з а и н e,
ка-
1
. ид/-(М).ш.тг '*')^^.^
б) 0, т=, ==s в) —1, 0, 0; г) 0, -£-, -=-. Указание.
Vio уто
|=(1, 0. 0), / = (0, 1, 0), ft = (0. 0, 1). 1.39. р=>(-6, 8).
1.40. 6 = (-24, -32, 30). 1.41. 90°, УТб. 1.42*. е,=(1, О, 1) или
сг= Г—з", -я-, —s-J. Указание. Обозначив координаты
вектора с =» (Jf, Y, 2), составить систему уравнений са=1,
е6= I, е8 = а'= 62 = 2 н, решив ее, получять ответ. 1.43. соза =
= cosfl=cosv = -4=-. 1.44. ф = -3^-. 1.45.2 = 4. 1.46. Х = 0,
<у/з ^4
У~2. 1.47. ,= (-3, 3, 3). 1.48. с = (-^., --^, --*=■).
1.49*. а = (2, —2, —2). Указание. Используя длину вектора а
и его перпендикулярность вектору d, составить два уравиеиня
относительно X, Y, 2: X — Y + 22 =■ 0, X3 + Y3 + Z3 = 12.
Замечая, что | Ь | =з | с |, находим 2XY + YZ — XZ = 0, откуда, решая
три уравнеиня относительно X, Y, Z, получим ответ. 1.50. \BD\ =»
1.53, ffl
652 ОТВЕТЫ
= 2Ve. 1.51. \AC| = 5; f-|-. '. l\ U2. arccos .^_ .
4 2 / y6441
= :i^-. arccos -Ц-. 1.55. (2 + V3~. 2 + V^D или (2 - л/ъ.
2-Уз"). 1-56. С, (3, 6), £>i(5, 3) или С2(-3, 2), Da(-1. —1).
,57. A (I±|V£, !±4L), с (Iz^Vi, iz^).
1.58. |Ad,|»4.VH>. 1.59. D(20, 23, 6). 1.60. Л =4. 1.61. A = 7.
4
1.62. |ЛВ| = 5; |BC| = 5V2"; |ЛС| = 5; Л = 90°, B=C=45°.
1.63. Тупоугольный. 1.64. <р = 46°. 1.65*. ЛЯ = (2; 1), Указание.
Учесть, что ЛЙ = (*; К)_1_В~2 и ВН <=АН - АВ _1_ДС.
1.66. ICM^ao/v/—-. 1.67. |ЛО|=-^-. 1.68*. А\(0, -2, 0) и
Л! (2, 2, 2). Указана е. Зная объем призмы, найдеи ее высоту
Н = | АА11 = V^ "• обозначив координаты вершины Л, (xit yit zx),
свяжем координаты вектора ААх = (х — I, у, z—l) с его
длиной. Другое уравнение получим из условия ЛЛ| JL АС. 1.69. 18.
1.70. 26.
§2
2.1. а) х — #+1=0; б) х— 1 = 0; в) 0 — 2=0. 2.2*. Зх —
— Чу — 12 = 0, 3* — 8jT-Ь 24 ==> 0. Указание. Воспользоваться
уравнением прямой в отрезках (4). 2.3. а) Зх — 2у — 5 = 0;
б) *-60--7p = O. 2.4. АВ: 4*+{/-6 = 0; CD: *-4{/-2 = 0;
,19 19 х~1 у-2
п =» —!=■', cos ф = -. ; 1{: —■= j=- =■ 7= т=!
■y/Tf V17-58 V26 + 5V17 -4 V26 — УТ?
l3: (V21+5VT7) (х — I) + (—4V26 — 17)(у — 2) = 0. 2.5. у =
= 2* — 6, (/ = —2* + 6. 2.6. х — 5j/ + 3 = 0 или б* + у — 11 =» 0
2.7*. С х (б, 10) и Cs(3, 0). Указание. Площадь треугольника
ABC найтн по формуле
s-4-l«IIHVl-(T^f»r),-T^lel»*l),-(e*>'
2.8. Z) (9, 0). 2,9, (х - l)s + (0 - 1)J= I. 2.10. у = ^- я у=>
ОТВЕТЫ К ГЛ. 14
553
л/ТВ
2.11*. В (12, 5), С (-5, 12), £>(-12, -5).
Указание. Точка С симметрична точке А относительно начала
координат. 2.12**. (*_-1-)2 + (у-У2)2 = -|-; (*--1)2 +
+ (у + л/Ю2 =• -г-. Решение. Центр искомой окружности
лежит на прямой, проходящей через точку (1/2, 0) н
перпендикулярной оси Ох (рис. O.l). Диаметр искомой окружности равен
радиусу данной. Записав уравнение искомой окружности в виде
Ряс. O.l
/ 1 \% 9
(х —к-\ + (у — уо)2 = "г" и потребовав, чтобы искомая
окружность проходила через точку И (1, 0), найдем уо. 2.18. (ж— 1)2 +
+ (у-1)*=1; (я-5)* +({/-5)» = 25. 2.14. 2х - у - 2z = 0.
2.15. а) 3* + 4{/ + 6z — 29 = 0; б) 2дг — 2у — z + 9 «= 0; в) х — у +
. . , ,, „ . .„ . 5 ., 5 . ч _ „ 5
4- Az + 11 =
2.17*.
Ve
■ О. 2.16. a) arccos-p-; б) arccos-rj; в) arccos-j-j-.
Укаааине. Найти косинус угла между вектором
л плоскости и вектором АВ. Используя определения угла между
18
прямой и плоскостью, найти синус этого угла. 2.18. a) arcsln —{
б) arcsln ._. 2.19. 10. 2.20. a) 4i б) 0; в) 4. 2.21. 3.
15-ylO ^
2.22. 6* + 2J/+3z±42=.0. 2.23. (-1, 0, 2). 2.24. а) (0, 0, -,2)1
б) (2, 3, 1). 2.25*. 3. Указание. Вектор п = (2, 2, —I) парал-
7
554
ОТВЕТЫ
лелей прямой, проходящей через центр сферы перпендикулярно
данной плоскости. Расстояние от центра сферы до плоскости
равно б. 2.26. (4, -3, 0) н (-1-, ~, -Ц-). 2.27. (*--|-)2 +
33 33
при т2>~5 сфера; прн
— П* = -
+ (!/-I)2 + (z-I)
4'
33
_ точка; прн т2 < —? пустое множество.
§3
3 f 1 \ 3
3.1. arccos—==-. 3.2. п — arccos I у=-|. 3.3. arccos ,_-.
Vh ч вуТзу Vio
8.4. arccos—;=-. 3.5*. -5-. Указание. Выбрать систему коор-
-уб
дннат 0*i/ так, чтобы осн Ох и Оу проходили соответственно
через катеты ВС и ВА 3.7*. Чах + 26t/ = о' + Ь2, где о, Ь —
длины катетов. Указание. Выберем прямоугольную систему
координат так, чтобы ось Ох совпадала с катетом С А, а ось Оу —
с катетом СВ. 3.14. За8, где о —длина стороны квадрата.
с-
3.15.4а2, где о —длина стороны квадрата. 3.16. _.
У170,
8.17.
0,0 ! /421 „ .„ /551 оал 1 /1373
^к—
/к/
/*
/
и
i^i, 1
"а
с
Рис. О.З
8.21. агссоз
-. 3.22**. —^ . Решение. Вводя систему
3 ' "■"" ' 24
координат Охуг так, как показано на рнс. 0.2, находим
координаты точек: Л (о, 0, 0), Е f О, -=-, а\ F (-=-, а, а} . Уравнение
плоскости, проходящей через эти три точки, имеет внд х + у +
+-й-z-{-а = 0. Косинус угла между плоскостью нижнего
основания и данной плоскостью: cosq> =
■y/Vf'
Площадь проекции
ОТВЕТЫ К ГЛ. 14 553
пятиугольника, полученного в результате сечения куба секущей
плоскостью, на плоскость нижнего основания куба равна s •=>
, a3 7aa
•= в2 8~ = —8~' и' слеД°вательно, площадь самого пятиуголь-
ш,ка-s = 13sV- 7Л/^а8- 8-23**- МДI-1Д.!I —^-0.
\KL\ = -z~a, -jr-. Решение. Из условия задачи КГ-^-, О, О),
L(o, о, ■-) (рис. 0.3). Тогда|А1£,|2 = а2+-^-=-^-, И,£. | =.
= ^-,\AlKf=^- + aMAlK\='^-. Рассмотрим две
треугольные пирамиды*. .NAKAt н NDML. У второй пирамиды
неизвестные длины ребер ND и DM обозначим через х н у соотг
ветственно. Из подобия треугольников AAiN, DLN следует х = а,
а нз подобия AARN н ADMN следует 0=-т-'> 1Х^|2 '=3 "7" +
, о8 За2 .„.. oVS" - ,, 1 I а _
+ а2 + — = —. 1ЛС/-1-—|—. Тогда удал01,-_■•-■•_■ X
. . „ о3 .. I I а а в3 л
Xa.2a = -g-; VNDML« — .^. — . — .в—g-. Отсюда
находим объем одной из частей куба, на которые разбивает его секу-
щая плоскость: Vj =■ VNAKA> — VNDML = -|g-. Тогда объем вто-
41
рой части куба равен ^J=-jo'a3- откуда Ki: Vj=7: 41.
3.24.
48
3«8УЗ док „ч а» „.7
7*—. 3.25. а) —; б) -т-г а2. 3.26. 8os, где о — длина
, ,<>, Л ?_ ,«, и _1_ чип — —!—
стороны куба. ■">•«<• 2 ^g"- ■*"■■• "J"' л/з" 3 ' W3~ "
8.30.a)£VL: б) £^L. з.31. £^И.
§4
4.1. -(4?+2CQ). 4.2. BD=*2(b-a), ЛС=»|-(о +6)
4.3. ДО <= у-|-^(ЛВ + лЛО). 4.4. 0. 4.6. X —3i X==-,2.
4.7. Л, =• 4"- 4-8- Л.= Ю/7, |Л = 4/7. 4.9. ft=»l, ft = -2. 4.tl. p-
= -7 = Ь 4.12. 0. 4.18. Лм=-1--51-0^, 2w—-g-OG--0B'
656 ОТВЕТЫ
ШГшп1.{рС - OB). 4.14. AM^-BA + ^-BBi+^BC, А^Л =
= - ВА - -j ВВ, + у ВС. 4.15. АА{ =1у(ВИ,+СВ,+Дс,).
4,e.(-l,l,2),4.1,(j,|^).4.,8.(^A(i).
4Л9. (.,1,1). 4.20. (.4. -|).
Б.5. МС = |- МЛ + 4- MB. 5.6. МС = т-^—г МА + -7-7-т ^В.
Б.17. 1ДВ|=4. 5.18.4". 8.19. 1.6. 5.20. ~. 5.21. ЛЛ, = С* t 6<?.
11 64 о + с
где ЛС=6, ЛВ = с н \АС\ = Ь, |ЛВ| = с. 5.22. у. 5.23. у.
5.24. (' + »>(? + а)(? + » + с). "»• Hi 5.82. 3. 5.33 *
а& (о + Ь + 2с) 37
6.34. \.
§в
6.1. а) 9; б) 13; в) —61. в.2. —13. 6.3. Векторы а н Ъ должны
быть взаимно перпендикулярны, в.5. k = . 6.8. а) та =
= 1у&! + 26ссо8Л+/; б) /,- 2&ссоз(Л/2) _ вд а) ^^
,|V—'+8**+^ б) la=4bCbPlp-a). 6.10. arctg^.
в.П. 3 + ^73 . 6.12. -?=-. 6.24. Я = £=30°, 6"= 120°.
8 д/7
ГЛАВА 16
§1
1.1*. I07. Указание. Из исходного множества (0, 1, 2, ...
1,,, 9) набираются выборки с повторениями, содержащие по
1Ы Ю (10г — 1) ,,
семь элементов. 1.2*. —, Указание. Найти сумму
чисел, представляющих количество различных выборок по
одному, двум и далее до семи элементов исходного множества,
1.3, 243, 1.4, 2м, 1.5, Число делителей q равно произведению
ОТВЕТЫ К ГЛ. 15
557
(fti + I) (fea + I) •. • (km + I). 1.6. A[0. 1.7*. 2". У к а з а и и е.
Исходное множество состоит нз двух элементов (Г, Ц), а выборки
с повторениями—из п элементов. 1.8. 720. 1.9. а) 2-291; б) 28-291
1.10*. 968. Указание. Следует найти сумму чисел различных
аккордов, содержащих по три, четыре и далее до десяти звуков.
Один аккорд, состоящий из k звуков, представляет собой
выборку k элементов нз исходного множества, содержащего 10
элементов; порядок элементов в выборе несуществен. 1.11*. 40-39-С^.
Указание. Председатель и секретарь образуют выборку
без повторений, состоящую из двух элементов исходного
множества, содержащего 40 элементов. 5 членов комиссии
образуют выборку без повторений некоторого состава из исходного
множества, содержащего 38 членов. 1.12. Cg-Сц,. 1.18. С$%-@%
1.14. Cl'C%-C3lf}. 1.15. а) 42. С| различных карточек; б) С%-€\
различных карточек; в) С^-Сц различных карточек. 1.16. 120.
I.I7*. Cg° — ^48- Указание. Искомое число равно разности
общего числа способов выдуть 10 карт нз 52 и числа способов
вынуть 10 карт из 48 таким образом, чтобы среди 10 карт не
было туза. 1.18. 4 • С £,. 1.19. А\й-А\. 1.20*. 1225. Указание.
Учесть, что цифровая запись числа не может начинаться с нуля.
1.21. 750.
§2
2.1. 2520. 2.2*. 165. Указание. Выборка с заданным чнс-
лом повторений объема 8 набирается нз четырех групп
однородных элементов. 2.3*. С[6=С*6. Указание. Выборка с
заданным числом повторений объема 7 набирается нз 10 групп
одинаковых элементов. 2.4*. .Д2?> . Указание. Ищется чис-
121
ло различных выборок состава (13, 13, 13, 13). 8.5*. 'гу.
Указание. Шесть различных групп однородных элементов
должны составить выборку с заданным числом повторений,
содержащую 12 элементов, имеющую состав (2, 2, 2, 2, 2, &),
2.6*. С^+1.У к аза ние. Следует рассмотреть выборку с
заданным числом повторений, имеющую состав (m-f-I, л), где т+1—
число промежутков между т белыми шарами, а п—число
черных шаров. Число различных расстановок равно числу всевоЗ-
можных выборок состава (ет+1. п). 2.7*. -ToiFor- Указание.
Находится число различных выборок состава (лх + гъ),- где п,™
в 52 —число успехов, а щ + па =» 100. 2.8*. 2-(61)5. УкаЗ$Ч
иве, Число перестановок левых мест ряда следует умножить
558
ОТВЕТЫ
на число перестановок правых мест. Учесть возможность смены
левых мест па правые. 2.9*. Указание. Воспользоваться не»
равенством C£„+ftC£n_ft < (C^,)2. доказательство которого можно
провести непосредственно.
§3
3.1*. 1024. Указание. Разложить по формуле бинома
выражение (I + I)10. 3.2. ft —4. 3.3*. Т2=*С21а- я6-5 = 153*6'5.
Указание. Воспользоваться тем, что наибольший коэффициент
имеет средний член разложения. 3.4. 28*2a-4. 8.5*. Указана е.
ЕЛ / 1 \'<Х>
Воспользоваться указанием к 3.1*. 3.6. — 1375. 3.7**.С^о I -^-J .
Решение. Рассмотрим отношение T^+i к Г ft. Так как
T'ft+l'^ioo
fi-Y00 т -cft Г±ГЮ
Tk+i 100lfei(100-fe-fl)i _100-fe+t
Tk = (ft+ 1)1(100-ft)!-100! — ft+I
_, 100-fe+l ^ , _ ._ 100-ft + l ^,
Если /fry— > ' ft+1 "^ *' а СЛИ ft + 1 '
то 7*6+1 < Tfc. Получаем, что при k < 50 члены 74 возрастают,
"а при ft > 50 — убывают. Следовательно, наибольшим членом
чо / 1 \101)
является Гвд = C^qo ly J . ЗЛ. Наибольшим членом разложения
является десятый. 3.9*. Тя = С'вж". Указание. Степень бинома
можно получить, используя указание к 3.1*. 3.10*. Указание.
Использовать разложение, (1 — 1)". ЗЛ1*. —264о3Ь7. Указание.
Использовать результат задачи ЗЛО*. 3.12. 314925-10s.
3.13. х = 2.3.14*. 5/8 < х < 20/21. У к а з а я и е. См. решение 3.7**.
3.15*. 1/2. Указание. Используя условие задачи, представить
50-й член разложения как функцию аргумента х н решить задачу
на отыскание наибольшего значения полученной функции на
промежутке [О, 1]. 3.16. *= "~fe. 3.17. Cii'32-22. 3.18. 26.
8.19**. Рациональными будут первое, пятое и девятое
слагаемые разл
п(д-1)
мые разложения. Решение. Так как коэффициенты 1, -%■,
образуют арифметическую прогрессию, то можно
о
составить уравнение
п(п-1)
-И = л.
ОТВЕТЫ К ГЛ. 18
669
корни которого равны соответственно я = 8 и я = 1; я = 1 —■
посторонний корень. Для п => 8 общий член разложения имеет
вид
А 8-й -!Ы At!
Г,-ф»(|) х 4 «2*-8ф « .
Этот член будет рациональным, если k + 8 кратно 4, где О SZ
^ fe ^ 8. Это условие выполняется прн k = О, 4 8.
Следовательно, рациональными будут члены 7о> Ть Та. 3.20*.
Указание. Использовать биномиальное разложение для (I — I)*.
3.23*. Указание. Рассмотреть биномиальное разложение для
'(10—1)г\ 3.25*. Указание. Найти приращения*
первообразной функции (I-+■*)" на промежутке [0; I] непосредственно и
записав выражение для (I-f-x)" по формуле бинома Ньютона.
8.26*. Указание. Найти производную функции (х—I)" в
точке х = I. 3.27*. Указание. Сравнить приращения
первообразной функции (х— 1)л на промежутке [0; I], найденные
вепосредствеино и с помощью предварительного разложения
(х— I)" по формуле бинома Ньютона. 3.28*. (л+ 1)1—1.
Указание. К искомому выражению прибавить н вычесть Pi -f-'
+ Pa + • • • + Рп- 3.29*. Указание. Использовать тождество
<tf + c*-"-c*+I.
§4
4.1. 12/365. 4.2. 5/12. 4.3*. 1/3. Указание. Число всех
двузначных чисел равно 90. Число двузначных чисел,
делящихся на трн, находится нз уравнения 99= 12 + 3(я—1). 4.4. ОД,
4.6. 3/13. 4.6**. Р(А) = 1/8; Р(В)= 3/8. Решение.
Пространство элементарных событий состоит из выборок с повторениями,
составленных из букв Ц, Г. Оно содержит 23 = 8 элементов.
Событию А благоприятна только одна выборка (Ц, Ц, Ц), а
событию В —трн: (Ц, Ц, Г), (Ц, Г, Ц), (Г, Ц, Ц). Таким
образом, Р(А) = 1/8; Р(В)= 3/8.
4.7. 1/6. 4.8. 1/2. 4.9. 89/99. 4.10. 10/99. 4.11*. 1/8. Указание.
См. решение 4.6»*. 4.12. C2njc\+m. 4.13. 1/720. 4.14. 246/364.
4.16. СУС%. 4.17. 4/С?в. 4.18*. 1/60.
Указание. Пространство элементарных событий состоит нз
всех перестановок с заданным числом повторений, имеющих
состав (3, 2, I). Благоприятной будет только одиа такая
перестановка. 4.19. 5-3!4i/7i 4.20. 2-4131/71 4.21*. 24- 48! 134 /521
Указание. Пространство элемептариых событий состоит
нз всех выборок, имеющих состав (13, 13, 13, 13). Благоприят»
660
ОТВЕТЫ
пымн считаются выборки состава (12, 12, 12, 12), к каждой
5151
из которых присоединяют один нз четырех тузов. 4.22. ,
4.23. it. 4.24. СЛО=*. 4.25. ' Cfp* - «^ С»-«
WS °/V °4в ^48 ^48 °48
4.2в. £*£«., £«£l£i. 4.27.-^ = 0,6. 4.28.-^.
Co * /^6 /"»3 /MO
52 42 °6 °20
§5
5.1. 0,2. 6.2. -£-. 5.3. 1. 5.4. |-. 5.5. 1. 5.6*. ! + 3 ln 2
tf2 ' 2 "3 2 8
Указание. Рассмотреть отношение общей площади фигур,
ограниченных линиями у=—, у = 2х, # = 2, у = 0, к площади
1 л
квадрата со стороной 2. 5.7*. -т г^-. Указание. См. ука-
2
занне к 5.6*. 5.8*. -д-. Указание. Коэффициенты уравнения
параболы у = ах2 + Ьх + с найти из условия прохождения ее
через три указанные точки, выбрав соответствующую систему
координат. 5.9. . 5.11*. ■=-. Указание. Использовать
утверждение задачи 5.10. 5.12. «0,314. 5.13*. ■„- Указание.
Если обозначить расстояние от точки В до начала координат
через х, а от точки С г- через у, то пространство элементарных
событий будет представлено единичным квадратом, вписанным
в первый квадрант координатной плоскости. Элементарные
события, благоприятные событию, вероятность которого требуется
найти, представляются точками, координаты которых
удовлетворяют неравенству \у — x\^min(x,y). 5.14. Поезда
направления АС должны приходить через 10 мин после отхода поезда
4.1
направления СА. 5.15*. .Указание. Ввести систему
координат Оху, где х — угол, который образует игла с параллелями,
а у — расстояние от центра иглы до ближайшей параллели.
Э этом случае пространству элементарных событий соответствует
прямоугольник со сторонами а н л/2, а элементарным событиям,
■благоприятным условию пересечения иглою параллельных
прямых, — точки, ■ тсоордвнаты которых удовлетворяют неравенству
l&inx <у>
ОТВЕТЫ К ГЛ. 18 Б61
§6
ei в(д —1) 2пот пг
(п+т){п + т-[)' (n + m)(ft + m-l) ' '(« + «)*'
т.—-г—г,-. Указание. Если шары возвращаются обратно, то
события, связанные с цветом последовательно вынимаемых шаров,
независимы. 6.8.-^-.^-.-^-«0,1055.6.4.^-. 6.5.~. 6.6. а) ^Х
VJ5 14 42 .,81 _„ , 6nmk
Хоп'То=ог: б)7ой-в-7Л-
ч20 19 95* ' 190 (n+m+k)(n+m+k-l)(n+m+k-2)'
в.8.» б.9.1 -(<,"i)(B71!"l)w"-(r/rJnl)-«*i-
91 п(п — 1) (rt — 2) ... (п — ft + 1)
— (1 — р)п. 6.11*. п > In (1 — P)/ln (1 — p), где п — число
выстрелов. Указание. Число выстрелов находится из условия, что
в серки из я выстрелов вероятность поражения цели (хотя бы
одного попадания) не меньше Р. 6.12. Вероятность сдачи
экзамена не зависит от того, идет ученик отвечать первым или
последним. 6.13*. 2/3. Указание. Рассмотреть следующие
гипотезы: А — в урне было два белых шара; В — в урне было
два черных шара; С — в урне были разноцветные шары.
Веронтности гипотез считать одинаковыми. 6.14. 0,85.
й 1R я\ (т — 1) w + nm fi. (fe + 1) т + fen
' (;rt + n-l)(m + ft)j' ' (* + *+1)(ю + я) "
6.16*. .? . "Г. /?■, . У к а з а н и е. См. указание к 6.13*.
(ft + L) MN
6.17*. [N (N-l) (ЛГ-2) (ft -j- L) (ft + L-\) (ft + L-2) -ft (ft-l)X
X(fe - 2) (N - n) (N - n - 1) (N - n - 2) -ft (k - 1) L (N - n)X
X(JV - n- l)(M~m)-«k(L-l)(L-2){N-n)(M-m)X
X(M-m-l)-HL-l){L-2)(M-m)(M-m-l)(M-
— m-2)]/N(N-l)(N-2)(k + L)(k + L- l)(ft -fc L -2).
Указание. Рассмотреть гипотезы: Яо — все три изделия из
первой партии; Hi — 2 изделия нз первой партии и 1 из второй;
Ht — 1 изделие из первой партии и 2 нз второй; Я» — все три
изделия из второй партии.
ГЛАВА 16
1.6. 1) У меня или нет собаки или есть кошка. 2) У меня
нет ни кошки, нн собаки. 3) У менн или есть и кошка, и
собака или нет ли кошки, ни собаки. 4) Если у меня иет собаки,
то у меня есть кошка, , ,
662
ОТВЕТЫ'
1.7.
р
1
1
0
0
я
1
0
1
0
Р\Я
0
1
1
1
1.8. (р A q) V (р Л Я) V (Р A q). МО- 1) р-
q: 4) q-
q\ 2) q + pt
3) p-*-+q; 4) q->p\ 5) /J-*-* g. 1.11. p A q Af. 1.12. 1) Мншень
поражена по крайней мере прн одном нз выстрелов. 2) Мншеиь
поражена прн каждом выстреле. 3) Мяшень поражена при
третьем выстреле, а прн одном нз первых двух — нет. 1.13. Да*"
1.14. Все участвовали. 1.16. А сдал экзамен. 1.16. а) (р Л q Л г) V
У (рАЗЛО V (рАд Л г): б) (рЛ?Лг); с) (pAqAf)A
А (р A q А г). ' 1.17. а) (р Л 9) V (р Л #) = Р *-*• q\ б) р A q\
с) р Л q\ д) Р A q. I.I8. «Верно ля следующее высказывание:
или ты говоришь правду и этот выход ведет на свободу, илн
ты лжешь и этот выход ведет на смерть?» 1.19. Высказывание
имеет вид pAtfAr = />VgVr и
в виде
может быть реализовано
I—Ш—1
■Ф-
1.20. (pAq)V ((Р Л <?) V 9).
1.21.
-£S&
-CZ
1.22. р «-»• 9»
§2
2.1. а) [-2; оо); б) (2; оо); в) R; г) (- оо; -2) U (2; оо);
д) 0; е) R. 2.2. a) R; б) [-2; ее); в) [-2; оо); г) R;
д) (- оо; -2); е) R. 2.3. {3; 4}. 2.4. а) 0 < о < 2/3; б) о > 2/3.
2.5. {6/2}. 2.6. о s R \ {{3} U {!}}. 2.7. (- оо; I/2J. 2.8. Истина.
2.9. Ложь. 2.10. Истина. 2.11. Истина, 2.12. Истина. 2.13. Ложь.
2.14. Истина. 2.15. Ложь. 2.16. Истина. 2.17. Ложь.
2.18. а) (ЭМ >0)(VrieN) (| u„ |< M); (VM > 0) . (Зга <= N)
(|«„|>Л1); б) (VneN) (un+t>un); (3raeN> (»„>««+i)-
ОТВЕТЫ К ГЛ. !в
563
2.19. (Ve > 0) (36 > 0) (V*e
2.20. а) М== sup f(x)-
х е |<з, 61
Л ((Ve>0) <3*sto; b])Mf (х)>М-е)); б) М Ф
■Щ (0<|*-а|<5-
(((Уд: е [о; 61) н
■|f(*)-b|<e).
(f(*)<M)) Л
<* ((Эх е [а; Ь\) (f (*) > М)) V ((Зв > 0) (V* е [а; Ь]) (f (*) <
^ М — е); М не является точной верхней гранью функции f (x)
яа отрезке [сг, Ь], если верно одно нз двух высказываний: или
для некоторого * е [a; b\f (х) > М, или существует такое е > 0,
что для всех х е [a; b] f(x)<M — е.
§4
4.1. (114144),. 4.2. 10 000. 4.3. 9. 4.4. 19. 4.5. 4380. 4.6. (42 714)8
4.7. (3126),. 4.8. (145 244)„.
4.0.
0
1
0
0
•
'
0
•
4.10. 72. 4.13. Основание системы равно 5. 4.14. (I2)s,
4.15. В любой. 4.16*. Указание. Например, если тело имеет
вес 19 кг, то, записав число 19 в двоичной системе счисления,
имеем (19)s = (10 011)2, т. е. для его взвешивания следует
взять трн гири 2* =* 16 кг, 21 = 2 кг и 2° = 1 кг.
4.17**. Решение. Представим любое число ^40 в
троичной системе с цифрами —1, 0, 1 следующим образом: если
остаток от деления очередного неполного частного на 3 равен 2, то
пишется (—1) и получающееся частное увеличивается на
единицу.
Например, вместо 20 13 пишем 20 |_3. Таким .образом,
2|6 -1I7
в троичной записи любого числа будут 1, 0, —1. Продолжая
деление в рассмотренном выше примере, имеем
20
-1
3
7
1
3
2
-1
3
]
(20)10={1 -1 1
-»>з-
Черточка над цифрой 3 означает, что число представлено в
системе с цифрами -—1, 0, 1. Так как (40) ц =(111 1)3, то для
любого тела весом ^40 хватит четырех гирь с весами I, 3,
9, 27.
664
ОТВЕТЫ
Алгоритм взвешивания будет представлен в троичной записи
числа. Так чтобы взвесить тело в 20 кг, следует на одну чашку
весов поставить гирн 27 = З3 и 3 « 3' (эти разряды в записи
представлены единицами), а на другую — 9 = 3* и I =» 3° (эти
разряды представлены —I), 4.18**. Решение. Вес следующей
ffip+i гнрн должен быть не больше чем 2МР -\-1. Действительно,
если Я1р+| > 2МР+ I, то груз весом Мр + 1 не удастся взвесить
sa счет разности тр— Мр. Если же тр+\ < 2Мр+\, то максималы
иый вес Mf4i = Щ + ... +тр+{ будет меньше возможного.
Следовательно, mp+i можно получить из уравнения
гпр+i—Мр = Мр+1.
»
Учитывай, что Mp+i =• т.\ + ... + Щ+и получаем
Мр+1 = ЗМр+1.
4.19**. Решение. Сразу же следует из утверждения предыду*
щей задачи, так как уравнение
Mp+i=3Mp + 1
показывает, что прн делении Мр на 3 для любого р остается
остаток, равный I. 4.20**. Решение, Из результатов 4.19"
и 4,18** следует, что минимальное число гирь находится из не*
равенства
3p-'<n<3p.
Алгоритм взвешивания совпадает с тем, который представлен
В задаче 4,18** и определяется записью п в троичной системе
счисления. 4.21**. Решение. Если система счисления десятич»
иая, то максимальное (.число, которое можно представить при
г = 30, равно 999. Действительно, так как р «=■ 3, то 999 — мак>
симальное • число, которое может быть записано в десятичной
системе счисления с использованием трех разрядов.
Если о > 10, например 15, то число разрядов р равно двум
я, следовательно, максимальное число равно 16-14 + 15°-14 =*'
,= 224. Если основание равно 2, то максимальное число, за*
писываемое по 'этому/основанию, 215—1; если основание равное,
to 3^—1. Очевидно, что Зш —1 > 21S—I > 6s—L, так как
95 > 88 > 6е и, наконец, по основанию 6, 6s — 1, Следовательно,
наибольшим является З10 —1,
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
ПИСЬМЕННОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ В МГУ
Ниже приведены варианты экзаменационных работ,
предложенные абитуриентам и различные годы иа вступительных
экзаменах в МГУ.
Вариант 1 (Механико-математнческвй факультет),
1) Решить неравенство
98 — 7*, + 5ж—^ >49Х, + 5Х—4Э.
2) Найти все пары чисел (х,у), удовлетворяющие условию
Я >. О и системе уравнений
ьт[(х-<^)2 + у*] = 0,
io&v_ V*s + уг + Vaiog^V^+F «- 2.
. 3) Два равных равнобедренных треугольника ABC и DBE
\{АВ = ВС ■= BD = BE) имеют общую вершину В и лежат в
одной плоскости так, что точки А к С находятся по разные
стороны от прямой BD, а отрезки АС и DE пересекаются вточке/(.
Известно, что Z.ABC = /LDBE = а, причем а<я/2, Z.AKD=$,
причем р" < а. В каком отношении прямая ВК, делит усол ЛВС?
4) Сфера радиуса 3/в вписана в четырехугольную пирамяду
SABCD, у которой основанием служит ромб ABCD такой, что
\Z.BAD => 60°; высота пирамиды, равная I, проходит через
точку К пересечения диагоналей ромба. Доказать, что существует
едняствениая плоскость, пересекающая ребра основания АВ и AD
в некоторых точках М, N таких, что MN = */5л/з, касающаяся
сферы в точке, удаленной яа равные расстояния от точек М и
'N, и пересекающая продолжение отрезка SK за точку К в
некоторой точке Е. Найти длину отрезка SE.
5) Без помощи таблиц иайти все значения х в промежутке
*=»0,5 < х < 1,5, удовлетворяющие равенству
log» [sin Зх — cos2* — ~\ в» logs (sin 7* — cos6* — -гЛ.
566 ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
Вариант 2 (Механико-математический факультет),
1) Произведение четырех целых положительных чисел
меньше, чем их сумма, а сумма трех из этих чисел равна 28. Найтн
все такие числа.
2) Решить систему уравнений:
х1 + 2х sin у + 3 cos у = О,
sin^|- + sini/)=y-j.
3) В, четырехугольной пнрамнде OABCD плоскости боковых
граней ОАВ, ОВС, OCD, ОАО образуют с плоскостью осиоваиня
углы, равные соответственно 60°, 90°, 45°, 90°. Основание ABCD —
равнобочная трапеция, ребро АВ равно 2, площадь основания
равна 2. Найтн поверхность пирамиды.
4) Найти все значения о, при которых минимум функции
f(*) = 3|*-o| + \х* + х-2\
меньше двух.
Вариант 3 (Факультет вычислительной математики и
кибернетики).
1) Иайтн точки экстремума функции
f (х) = л3 + 6*» — 3* + 3
иа интервале (—6, 1/5).
2) Решить уравнение
б1«-в[ = 25з*-4
3) В окружность вцнсаи четырехугольник ABCD, диагонали
которого взаимно перпендикулярны и пересекаются в точке Е.
Прямая, проходящая через точку Е и перпендикулярная к АВ,
пересекает сторону CD в точке М. Доказать, что ЕМ — медиана
треугольника CED, н найти ее длину, если AD = 8 см, АВ =
.= 4 см и СОВ = а.
4) Найти все целые корни уравнения
.»
cos (^ (3* - У9*2 + 160* + 800Й = 1.
5) Найти все действительные значения параметра а, при
каждом из которых уравнение
(а - ** - cos -^) У8^="^ = 0
имеет иа отрезке [—2, 3] нечетное число различных корней.
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ 567
Вариант 4 (Физический факультет).
1) Решить уравнение
2 sin х + sin Ъх == 2 cos x — cos Зх.
2) Решить неравенство
,ogv5i+r4>2-,0^+.)-i-
3) В треугольнике ABC заданы углы А и В. Биссектриса
(угла А пересекает сторону ВС в точке D. Окружность касается
сторон угла А н отсекает на продолжении биссектрисы этого
(угла за точкой D отрезок DE, равный AD. Центр окружности
лежит на отрезке АЕ. Определить отношение площади круга к
площади треугольника ЛЕС.
4) В основании треугольной пирамиды SABC лежит
прямоугольный треугольник ABC (угол С прямой). Ребро SA
перпендикулярно плоскости основания. В пирамиду вписан шар, радиус
которого равен 4aSA. Через вершину S и точку касания шара
с основанием пирамиды проходит плоскость, параллельная
ребру ВС. Эта плоскость делит поверхность шара в отношении
1 :4. Найти угол ВАС.
5) Вода нз цилиндрического бассейна глубины Л вытекает
по двум трубам разной пропускной способности, первая из
которых расположена в дне бассейна, а вторая на боковой
стенке. Если при наполненном целиком бассейне открыть только
вторую трубу, то вода будет протекать через нее в течение
времени, которое в '/а раза меньше времени, нужного дли слива
всей воды нз бассейна только через одну первую трубу. При
действии обеих труб продолжительность слива всей воды из
бассейна, наполненного целиком, в Уз раза больше, чем
наполненного на %. Пропускная способность труб не зависит от'1 уровня
воды над трубой. На какой высоте расположена вторая труба?
Вариант 5 (Физический факультет).
1) Решить неравенство
Iog3 V5 — 2* • Iog^3 < I.
2) Решить уравнение
(1 + cos x) /v/tg — — 2 + sin x = 2 cos x.
3) Из пункта А в пункт В выехал ■ велосипедист, который
сначала двигался равноускоренно с ускорением 4 км/ч2, а после
того, как его скорость возросла от 0 до о, продолжал двигаться
равномерно со скоростью о. Расстояние между пунктами А я В
'568 ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
равно 32 км. На первую половину пути велосипедист затратил
в полтора раза больше времени, чем на вторую. Определить ско«
рость v.
4) В треугольнике ABC даиы угол С и отношение стороны
ВС к стороне АС, равное 3. Из вершины С проведены два луча,
делящие угол С на три равные части. Найти отношение отрез»
ков этих лучей, заключенных внутри треугольника ABC.
5) В трехгранном угле ОАВС (О —вершина) все внутреи»
нне двугранные углы равны а. Найтн угол между ребром ОА %
биссектрисой угла ВОС.
Вариант 6 (Химический факультет).
1) Имеются два слитка сплавов меди и серебра, Первый
весит 3 кг и содержит 10 % серебра, второй весит 2 кг и со»
держит 20 % серебра. Какого веса кусок первого слитка нужно
переплавить вместе со всем вторым слитком, чтобы получить
сплав, содержащий г % серебра? Найти все г, при которых за»
дача имеет решение.
2) Дан куб ABCDA'B'C'D' с ребром АА' = о. Точка Е' -*
середина ребра В'С. Найти радиус сферы, проходящей через
точки А', Е', С', С.
3) Найти все решения уравнения
У sin Злг + cos х — sin * =» Vc<>3 * — sin 2х.
4) Сравнить без помощи таблиц log135 675 и 1о(у<5 75,
Вариант 7 (Биологический факультет; отделение почво»
ведения).
1) Два экскаватора» разных марок (одни экскаватор марки
А и одни экскаватор марки Б), работая одновременно, выка»
пывают котлован емкостью 20000 м3 за 10 суток. Если бы ра»
ботал только экскаватор марки Б, то он выкопал бы этот кот»
лован на 8— суток скорее, чем тот же котлован выкопал бы
один экскаватор марки А. Сколько кубических метров в сутки
выкапывает каждый из экскаваторов? .,
2) Решить уравнение
j logs (*5) + '°Вз \7qjf) = 3 log27 (* + 4) - 3 log3 W-
3) Найти все решения уравнения
(УМ-2) sin*-sin 2* -3 + 2sln*.
1 — COS X
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ 569-
4) Найти все значения а, при которых неравенство
(л + 3 — 2а) (* + За — 2)<О
выполняется для всех * таких, что 2 ^ * =ё 3.
5) Дан треугольник ABC, у которого стороны АВ =л/\7,
ВС = 5, АС = 4. На стороне АС взята точка D так, что BD
является высотой треугольника ABC. Найти радиус окружности,
проходящей через точки A a D и касающейся в точке D
окружности, описанной около треугольника BCD,
Вариант 8 (Биолого-почвеиный факультет; отделение
биологии).
1) Решить уравнение
Зх х
cos х + 3sln х => I + 2 cos -5- • cos -^-.
2) Решить неравенство
3.4Va—+3<10.2V2=*
3) Даны две геометрические прогрессии аи a^ o3 и Ь\, ЬъЬ3.
Известно, что числа а{ + Ьь «г + h, o3 + Ьз снова образуют
геометрическую прогрессию.
Доказать, что 0|-63 = o3-6i.
4) На сторонах выпуклого четырехугольника ABCD,
площадь которого равна единице, взяты точки: К на ДВ, L иа
на ВС, М иа CD и JV на ЛО. При этом АК: /(В = 2, SL: LC=
= 1:3, СМ : MD = I, DN : ЛМ = I : 5.
Найти площадь шестиугольника AKLCMN.
5) При каких значениях а и Ь система
а3х — by => а1 — b
Ьх — Ь*у = 2 + 4Ь
имеет бесконечно много решений?
Вариант 9 (Географический факультет).
1) Решить уравнение
cos2 2х — 5 sins х + 1 = 0.
2) Решить неравенство
log2 (V^r47+ 3) > 1о(П ( * ) + 1.
3) На катете АС прямоугольного треугольника ABC как на
диаметре построена окружность, которая пересекает гипотенузу
Б70 ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
АВ в точке К. Найтн площадь треугольника СКВ, если длина
катета АС равна b и величина угла ABC равна р\
4) Решить систему
2| х»—2х—з |—log, з _ g—у—*
4|2/|-|!/-I| + (i/ + 3)2<8.
б) Каждое нз ребер треугольной пирамиды ABCD имеет
длину I. Точка Р иа ребре АВ, точка Q на ребре ВС н точка
R на ребре CD взяты так, что длина отрезка АР равна '/s, дли.--
на отрезка BQ равна '/з и длина отрезка CR равна 7з-
Плоскость PQR пересекает прямую AD в точке S. Найти величину
угла между прямыми SP н SQ.
Вариант 10 (Геологический факультет; отделение общей
геологии).
1) Найтн все действительные решения уравнения '
(* + 1)V*2 + *—2 = 2* + 2.
2) В треугольнике ABC угол ВАС прямой, длины сторон
АВ и ВС равны соответственно 1 и 3. Точка К делит сторону
АС в отношении 7:1, считая от точки А. Что больше: длина
АС или длина ВК1
3) Решить неравенство
log3(5*s + 6x+I)<0.
4) Найтн все пары действительных чисел хну,
удовлетворяющие системе уравнений
cos 4* + sin 2t/ = — 2,
s х — у = 2я.
б) Автобус проходит путь Л£, состоящий из участков ЛВ,
ВС, CD, DE длиной 10 км, 5 км, б км, 6 км соответственно.
При этом, согласно расписанию, выезжая нз пункта А в 9 часов,
1 3
он проходит пункт В в 9-г-часа, пункт С—в9—часа, вункт
2
D — в 9— часа. С какой постоянной скоростью о должен
двигаться автобус, чтобы сумма абсолютных величин отклонений от
расписания прохождения пунктов В, С, D и времени движения
автобуса от Л до £ при скорости о не превосходила 51,7 минут?
6) В основании пирамиды SABC лежит равнобедренный
треугольник ABC, длины сторон АВ и АС равны V^". ребро SA
перпендикулярно плоскости ABC, угол ВАС вдвое больше угла
BSC. Среди всех прямых круговых цилиндров с образующей,
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ 571
параллельной SA, находящихся внутри пирамиды,
рассматривается цилиндр с наибольшей площадью боковой поверхности.
Известно, что расстояние от центра его нижнего основания до
ребра ВС составляет -г*- длины медианы AM треугольника ABC.
Найтн объем пирамиды SABC.
Вариант И (Факультет психологии),
1) Решить уравнение
2) Решить неравенство
V51 - 2х — х3
1-х <
3) В треугольниках ABC н А'В'С' длина стороны АВ равна
длине стороны А'В', длина стороны АС равна длине
стороны А'С, величина угла ВАС равна 60° н величина угла В'А'С
равна 120°. Известно, что отношение длины В'С к длине ВС
равно д/Jf (где я — целое число). Найти отношение длины
АВ к длине АС. При каких значениях л задача имеет хотя бы
одно решение?
4) В окружность радиуса 7 вписан выпуклый
четырехугольник ABCD. Длины сторон АВ н ВС равны. Площадь
треугольника ABD относится к площади треугольника BCD как 2:1.
Величина угла ADC равна 120°. Найтн длины всех сторон
четырехугольника ABCD.
б) Найтн все значения а, при каждом из которых система
уравнений
2COSAT+ a sin у — 1, "' v
Iogz sin у — (togj a) toga (2 — 3 cos x),
(ogaz + lcga^- lj = 0
имеет хотя бы одно решение относительно х, у н г. При каждом
таком значении а найтн все решения.
Вариант 12 (Экономический факультет).
1) Найтн все корнн уравнения
2|*г+2д:-5| = *-1, V
удовлетворяющие неравенству х < ч/2.
2) В выпуклом четырехугольнике ABCD диагонали AC vt
BD взаимно перпендикулярны и пересекаются в точке О, Из-»
572 ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
вестно, что ОВ = ОС = 1, О А «= 8, OD==7, Найтн косинус
угла между векторами АВ и DC. V
8) Решить уравнение
log,, (TJ
4) Имеется трн сплава. Первый сплав содержит 60 %'
алюминия, 15% меди и 23 % магния, второй —30% меДн и 70 %'"
магния, третий — 45 % алюминия и 55 % магния. Из них
необходимо приготовить новый сплав, содержащий 20 % меди. Какое
Наименьшее и какое наибольшее процентное содержание
алюминия может быть в этом новом сплаве?
б) Найтн множество всех чисел а, при каждом из которых
функция
f (*) = 8 (2а + 1) cos х — sin 2х + (I6as + 16а — 18) х
является возрастающей на всей числовой прямой и при этом
не имеет критических точек,
' Вариант 13 (Экономический факультет).
I) Найти все действительные решения уравнения
(Уз + 2V2~)S ° + (V3 - 2V2") Х=="з"'
• 2) Дана трапеция ABCD с основаниями AD и ВС. Диаго-
иалн АС и BD пересекаются в точке О, а прямые АВ н CD —
в точке К. Прямая КО пересекает стороны ВС н AD в точках
М я N соответственно; /.BAD = 30°. Известно, что в
трапеции ABMN н NMCD можно вписать окружность. Найтн
отношение площадей треугольника ВКС и трапеции ABCD.
3) Решить неравенство
д/9-т<*-лА-т- ■•
4) Зоопарк ежедневно распределяет 111 кг мяса между
лисами, леопардами и львамн. Каждой лисе полагается 2 кг мяса,
леопарду 14 кг, льву 21 кг. Известно, что у каждого льва^
бывает ежедневно 230 посетителей, у каждого леопарда 160, у
каждой лисы 20. Сколько должно быть лис, леопардов н львов
в зоопарке, чтобы ежедневное число посетителей зоопарка было
Максимальным?
ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ 573
Вариант 14 (Экономический факультет! отделение полит*
экономии).
1) Решить уравнение
2) Найти все х, удовлетворяющие уравнению
clg3x =ct(rx.
3) Решить неравенство
У(* - 4) (5* + 41)< 2 (2х — 7).
4) Сколько точек с целочисленными координатами находится
внутри криволинейной трапеции, образованной осью абсцисс,
прямыми х = 82, х «■ 730 и графиком функции у = togj (x — 1)? t
Точки, лежащие на границе указанной криволинейной трапеции,
не учитывать.
5) В группе каждый из учащихся знает хотя бы одни ниш
странный язык (английский, французский нли немецкий) и нет
ни одного учащегося, который бы знал все три указанные языка,
13 учащихся знают лишь по одному иностранному языку. Никто
нз группы не знает одновременно французский и немецкий, нр
половина учащихся, владеющих английским, знает еще один няо»
странный язык. Девушек, знающих только английский, в 2 раза
больше, чем учащихся, знающих только немецкий, и в 4 раза
больше, чем учащихся, знающих только французский. Опреде*
лить, сколько учащихся в группе, если юношей, знающих только
английский, в п раз больше, чем учащихся, знающих только
французский, причем 3 ^ «^ 15 (л— целое число),
6) Определить, при каких значениях а уравнений
*-| = 2|2|*|-а'|
имеет ровно три корня. Найти эти корни,
Вариант 18 (Филологический факультет) отделение
структурной и прикладной лингвистики),
1) Решить уравнение
logs (х- l) = \ogs.j—.
2) Решить систему уравнений
2*+'+ у +1 = 0.
574 ВАРИАНТЫ ЭКЗАМЕНАЦИОННЫХ РАБОТ
3) Найти наибольшее н наименьшее значения функции
f (*) =- 24* — cos 12* — 3 sin 8*
[я я!
—fi"; ТГГ '
4) В трапеции ABCD сторона AD является большим оснС'
ванием. Известно, что AD = CD =4—, BAD = 90° н BCD =»'
о
= 160°. На основании AD построен треугольник AED так, что-
точки В н Е лежат по одну сторону от прямой AD, причем
АЕ = DR. Длина высоты этого треугольника, проведенной из
1 2
вершины Е, равна -г. Найти площадь общей части трапеции
ABCD и треугольника AED.
5) Найти все значения а, при которых .уравнение
11 - ах | = 1 + (1 - 2а) * + ах*
имеет ровно одно решение.
Справочное ивданне
ЦЫПКИН Александр Геннадиевич,
ПИНСКИЙ Александр Иосифов^
СПРАВОЧНИК ПО МЕТОДАМ РЕШЕНИЯ ЗАДАЧ
ПО МАТЕМАТИКЕ
ДЛЯ СРЕДНЕЙ ШКОЛЫ
Заведующий редакцией Б. Ю. Ходан
Редактор Г. В. Шароватова
Художественный редактор Г. М. Коровина
Технический редактор С. Я. Щкляр
Корректоры Т. С. Вайсберг, Л. С. Сомова
ИВ № 32295
Сдано в набор 28.06.88. Подппсано к печати 24.03.89.
Формат 84X108/32. Бумага тип. № 2.
Гарнитура литературная. Печать высокая.
Усл. печ. л. 30,24. Усл. кр.-отт. 30.45. Уч.-Н8Д. л. 35.66.
Тираж 200000 экз. (2-й Завод 100 001-200 000 экз.).
Заказ № 357. Цена 2 р.
Ордена Трудового Красного Знамени
издательство «Наука»
Главная редакция
фнзико-математнческой литературы
117071, Москва В-71. Ленинский проспект, 15
Ленинградская типография № 2 головное
предприятие ордена Трудового Красного Знамени Леппц»
градского объединеиня «Техническая книга» ни,
Евгений' Соколовой Союзполнграфирома при Госу«
дарственном комитете СССР по делам издательств,
полиграфии н книжной Торговли. 19S052 г. Леиви-
град Л-52, Измайловский проспект, 29.
SOLUTION MANUAL
FOR MATHEMATICAL PROBLEMS»
FOR COLLEGE STUDENTS
Tsypkin A. G. Pinsky A. I.
In thi3 educational aid, intended for high—school students,
an altetrip has been made to classify the problems encountered
In high—school mathematics by their solution methods.
It was rather difficult to attain the aim the authors setr'lor
themselves. On one hand, a detailed classification of problems by,
methods of solution would require the consideration of a large
number of concrete problems and, on the other hand, a schematic
classification* would not yield a useful aid for solving different
kinde of problems. Therefore, alongside a large number of wor*
ked problems, the book includes many problems (about 2500) for.
the reader to eolve.
In addition to the traditional problems from the course 08
high—school mathematics, the book includes methods for solving
simple differential and integral calculus problems as well as
problems which require the use of coordinates and vector algebra.
These sections only include problems whose solutions require
knowledge that is beyond the scope of high—school mathematics.
Some problems in the book can only be solved by a combined
application of the knowledge from the traditional and new dlvn
sions of mathematics. These include, for instance, problems con-i
nected with the calculation of limits, derivatives<-imd antiderivatn
ves of functions which must first be simplified by means of iden*
tity transformations.
The authors consider all the most frequent methods of sob
ving ргоЫетз from the high—3chooI course of mathematics. The
f acf that many problems are not followed by their solutions
makes It possible to use the book for preparing for the entrance
examinations to higher educational esttablishments.
About the Authors
TSYPKIN Aleksandr Gennadeievich, Candidate of Sciences
(Physics and Mathematics), is a eenior research worker at the
Steklov Mathematical Institute of the USSR Academy of Sciences.
He is the author of a Manual of Mathematics for High Schools
and a number of scientific papers. His most important scientific
achievements are in the field of mechanics.
PINSKY Aleksandr losifovlch, Candidate of Sciences (Phy
slcs and Mathematics), is known as an experienced specialist in
the methods of teaching mathematics at higher schools. He is a
senior lecturer of mathematics at the Moscow Electrotechnical
institute of Communications, The field of his scientific interests
is mathematical statistics.