УДК 530.1@75.8)
Л22
ББК 22.31
Ландау Л. Д., Л и ф ш и ц Е. М. Теоретическая физика:
Учеб. пособ.: Для вузов. В 10 т. Т. I. Механика. — 5-е изд., стереот. —
М.: ФИЗМАТЛИТ, 2004.-224 с.-ISBN 5-9221-0055-6 (Т. I).
Настоящим томом начинается переиздание полного курса «Теоре-
«Теоретическая физика», заслужившего широкое признание в нашей стране
и за рубежом.
Том посвящен изложению механики как части теоретической фи-
физики. Рассмотрены лагранжева и гамильтонова формулировки урав-
уравнений механики, законы сохранения в механике, теория столкновения
частиц, теория колебаний и движение твердого тела.
Для студентов старших курсов физических специальностей вузов,
а также аспирантов и научных работников, специализирующихся в об-
области теоретической физики.
Ответственный редактор курса «Теоретическая физика» академик
РАН, доктор физико-математических наук Л. П. Питаевский
ISBN 5-9221-0055-6 (Т. I)
ISBN 5-9221-0053-Х	© ФИЗМАТЛИТ, 2001, 2004

ОГЛАВЛЕНИЕ
Предисловие редактора к четвертому изданию	7
Предисловие к третьему изданию	8
Предисловие к первому изданию	8
Г л а в а I. Уравнения движения	9
§ 1. Обобщенные координаты	9
§ 2. Принцип наименьшего действия	10
§ 3. Принцип относительности Галилея	14
§ 4. Функция Лагранжа свободной материальной точки	16
§ 5. Функция Лагранжа системы материальных точек	18
Г л а в а П. Законы сохранения	24
§ 6. Энергия	24
§ 7. Импульс	26
§ 8. Центр инерции	28
§ 9. Момент импульса	31
§ 10. Механическое подобие	35
Глава III. Интегрирование уравнений движения	39
§ 11. Одномерное движение	39
§ 12. Определение потенциальной энергии по периоду колебаний... .42
§ 13. Приведенная масса	44
§ 14. Движение в центральном поле	45
§ 15. Кеплерова задача	51
Глава IV. Столкновение частиц	58
§ 16. Распад частиц	58
§ 17. Упругие столкновения частиц	62
§ 18. Рассеяние частиц	66
§ 19. Формула Резерфорда	72
§ 20. Рассеяние под малыми углами	75
Г л а в а V. Малые колебания	78
§ 21. Свободные одномерные колебания	78
§ 22. Вынужденные колебания	82
§ 23. Колебания систем со многими степенями свободы	87
§ 24. Колебания молекул	95
§ 25. Затухающие колебания	100
§ 26. Вынужденные колебания при наличии трения	104
§ 27. Параметрический резонанс	107
§ 28. Ангармонические колебания	113

6	Оглавление
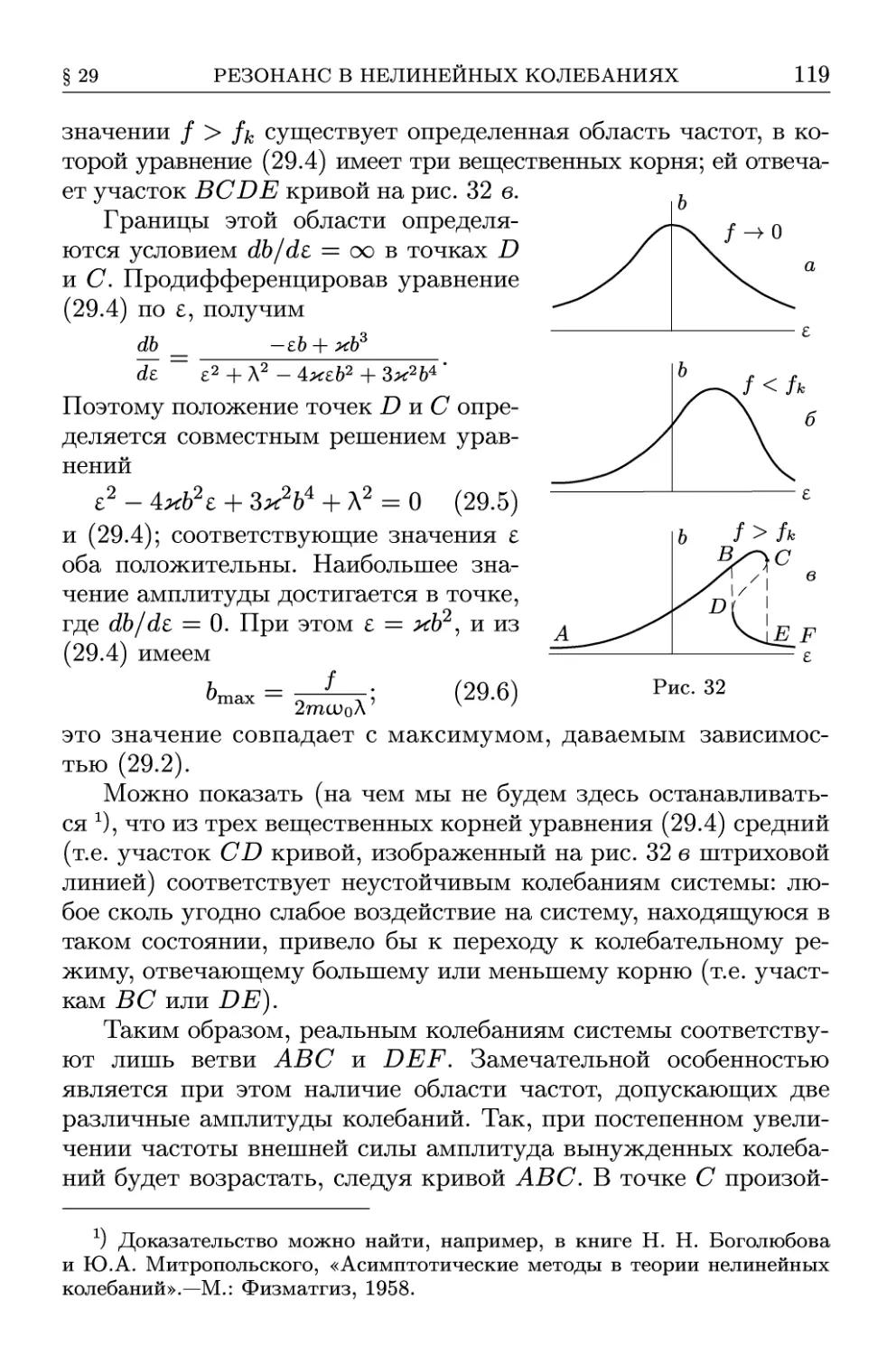
§ 29. Резонанс в нелинейных колебаниях	117
§ 30. Движение в быстро осциллирующем поле	124
Глава VI. Движение твердого тела	128
§ 31. Угловая скорость	128
§ 32. Тензор инерции	131
§ 33. Момент импульса твердого тела	140
§ 34. Уравнения движения твердого тела	142
§ 35. Эйлеровы углы	145
§ 36. Уравнения Эйлера	150
§ 37. Асимметрический волчок	153
§ 38. Соприкосновение твердых тел	161
§ 39. Движение в неинерциальной системе отсчета	166
Глава VII. Канонические уравнения	171
§ 40. Уравнения Гамильтона	171
§ 41. Функция Рауса	174
§ 42. Скобки Пуассона	176
§ 43. Действие как функция координат	180
§ 44. Принцип Мопертюи	183
§ 45. Канонические преобразования	186
§ 46. Теорема Лиувилля	191
§ 47. Уравнение Гамильтона-Якоби	193
§ 48. Разделение переменных	196
§ 49. Адиабатические инварианты	202
§ 50. Канонические переменные	205
§ 51. Точность сохранения адиабатического инварианта	208
§ 52. Условно-периодическое движение	212
Приложение
Предисловие Л.Д. Ландау к первому изданию	218
Предметный указатель	221

ПРЕДИСЛОВИЕ РЕДАКТОРА
К ЧЕТВЕРТОМУ ИЗДАНИЮ
Этим томом издательство «Наука» начинает переиздание
«Теоретической физики» Л. Д. Ландау и Е. М. Лифшица. Впер-
Впервые она выходит после смерти Е. М. Лифшица. На меня легла
печальная и ответственная обязанность готовить Курс к печати
без авторов.
В настоящем издании «Механики» исправлены опечатки, за-
замеченные с момента выхода третьего издания, и внесены неболь-
небольшие изменения, уточняющие изложение. Эти поправки были
приготовлены Е. М. Лифшицем и мною и частично учтены в
последнем английском издании книги.
Май 1987 г.	Л. П. Питаевский

ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Во втором издании эта книга почти не отличалась от пер-
первого издания. Не возникло необходимости в сколько-нибудь
значительной ее переработке и при подготовке нового изда-
издания. Поэтому большая часть книги воспроизведена стереотипно
(с исправлением лишь опечаток). Переработке и дополнению,
произведенным мной совместно с Л. П. Питаевским, подверг-
подверглись лишь последние параграфы, посвященные адиабатическим
инвариантам.
Июнь 1972 г.	Е. М. Лифшиц
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Настоящей книгой мы рассчитываем начать последователь-
последовательное переиздание всех томов нашей «Теоретической физики».
Окончательный план ее сейчас представляется в следующем
виде:
1. Механика. 2. Теория поля. 3. Квантовая механика (нереля-
(нерелятивистская теория). 4. Релятивистская квантовая теория. 5. Ста-
Статистическая физика. 6. Гидродинамика. 7. Теория упругости.
8. Электродинамика сплошных сред. 9. Физическая кинетика.
Первое издание первого тома было опубликовано в 1940 г.
Л. Ландау и Л. Пятигорским. Хотя общий план изложения
остался прежним, однако книга существенно переработана и
полностью написана заново.
Мы благодарны И. Е. Дзялошинскому и Л. П. Питаевскому
за помощь при чтении корректуры книги.
Москва, июль 1957 г.	Л. Д. Ландау, Е. М. Лифшиц

ГЛАВА I
УРАВНЕНИЯ ДВИЖЕНИЯ
§ 1. Обобщенные координаты
Одним из основных понятий механики является понятие ма-
материальной точки 1). Под материальной точкой понимают тело,
размерами которого при описании его движения можно прене-
пренебречь. Разумеется, возможность такого пренебрежения зависит
от конкретных условий той или иной задачи. Так, планеты мож-
можно считать материальными точками при изучении их движения
вокруг Солнца, но, конечно, этого делать нельзя при рассмот-
рассмотрении их суточного вращения.
Положение материальной точки в пространстве определяет-
определяется ее радиус-вектором г, компоненты которого совпадают с ее
декартовыми координатами х, у, z. Производная г по времени t
- ^L
называется скоростью, а вторая производная d2r/dt2 — ускоре-
ускорением точки. Ниже, как это принято, мы будем часто обозначать
дифференцирование по времени точкой над буквой: v = г.
Для определения положения системы из N материальных
точек в пространстве надо задать N радиус-векторов, т.е. SN
координат.
Вообще число независимых величин, задание которых необ-
необходимо для однозначного определения положения системы,
называется числом ее степеней свободы] в данном случае это
число равно 3N. Эти величины не обязательно должны быть
декартовыми координатами точек, и в зависимости от условий
задачи может оказаться более удобным выбор каких-либо дру-
других координат.
Любые s величин gi, q^ • • • •> Qs •> вполне характеризующие по-
положение системы (с s степенями свободы), называют ее обоб-
обобщенными координатами, а производные qi — ее обобщенными
скоростями.
г) Вместо термина «материальная точка» мы будем часто говорить о
«частицах».

10	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
Задание значений обобщенных координат еще не определяет,
однако, «механического состояния» системы в данный момент
времени в том смысле, что оно не позволяет предсказать поло-
положение системы в последующие моменты времени. При заданных
значениях координат система может обладать произвольными
скоростями, а в зависимости от значения последних будет раз-
различным и положение системы в следующий момент времени (т.е.
через бесконечно малый временной интервал dt).
Одновременное же задание всех координат и скоростей пол-
полностью определяет, как показывает опыт, состояние системы и
позволяет в принципе предсказать дальнейшее ее движение. С
математической точки зрения это значит, что заданием всех ко-
координат q и скоростей q в некоторый момент времени однознач-
однозначно определяется также и значение ускорений q в этот момент г).
Соотношения, связывающие ускорения с координатами и
скоростями, называются уравнениями движения. По отноше-
отношению к функциям q(t) это — дифференциальные уравнения вто-
второго порядка, интегрирование которых позволяет в принципе
определить эти функции, т.е. траектории движения механиче-
механической системы.
§ 2. Принцип наименьшего действия
Наиболее общая формулировка закона движения механиче-
механических систем дается так называемым принципом наименьшего
действия (или принципом Гамильтона). Согласно этому прин-
принципу каждая механическая система характеризуется определен-
определенной функцией
L{qi, 92, ..., Ъ, 91, 92, 9*, *)
или, в краткой записи, L(q^ q, ?), причем движение системы удо-
удовлетворяет следующему условию.
Пусть в моменты времени t = t\ и t = ?2 система занима-
занимает определенные положения, характеризуемые двумя наборами
значений координат q^ и qB\ Тогда между этими положениями
система движется таким образом, чтобы интеграл
г) Для краткости обозначений мы будем часто условно понимать под q
совокупность всех координат q\, q<i,..., qs (и под q аналогично совокупность
всех скоростей.)

§ 2	ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ	11
S = jL(q,q,t)dt	B.1)
ti
имел наименьшее возможное значение 1). Функция L называет-
называется функцией Лагранжа данной системы, а интеграл B.1) — дей-
действием.
Тот факт, что функция Лагранжа содержит только q и q, но
не более высокие производные g, 'q, ..., является выражением
указанного выше факта, что механическое состояние полностью
определяется заданием координат и скоростей.
Перейдем к выводу дифференциальных уравнений, решаю-
решающих задачу об определении максимума интеграла B.1). Для
упрощения записи формул предположим сначала, что система
обладает всего одной степенью свободы, так что должна быть
определена всего одна функция q(t).
Пусть q = q(t) есть как раз та функция, для которой S имеет
минимум. Это значит, что S возрастает при замене q(t) на любую
функцию вида	q(t) + 6q(t),	B.2)
где bq(t) — функция, малая во всем интервале времени от t\ до
?2 (ее называют вариацией функции q(t) ); поскольку при t = t\
и t = ?2 все сравниваемые функции B.2) должны принимать
одни и те же значения q^' и q^\ то должно быть:
Sq(h) = Sq(t2) = 0.	B.3)
Изменение S при замене q на q + bq дается разностью
/ L(q + bq,q + bq, t)dt— I L(q, q, t) dt.
tl	t!
Разложение этой разности по степеням bq и bq (в подынтеграль-
подынтегральном выражении) начинается с членов первого порядка. Необхо-
Необходимым условием минимальности S 2) является обращение в нуль
г) Следует, однако, указать, что в такой формулировке принцип наимень-
наименьшего действия не всегда справедлив для всей траектории движения в целом,
а лишь для каждого из достаточно малых ее участков; для всей же траек-
траектории может оказаться, что интеграл B.1) имеет лишь экстремальное, не
обязательно минимальное значение. Это обстоятельство, однако, совершен-
совершенно не существенно при выводе уравнений движения, использующем лишь
условие экстремальности.
2) Вообще — экстремальности.

12	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
совокупности этих членов; ее называют первой вариацией (или
обычно просто вариацией) интеграла. Таким образом, принцип
наименьшего действия можно записать в виде
5S = 5 Г L(q,q,t)dt = O,	B.4)
ti
или, произведя варьирование:
Замечая, что bq = -rbq, проинтегрируем второй член по частям:
¦[(--
J \dq
-bq ' ¦ ' lu±J d
dq
tl
Но в силу условий B.3) первый член в этом выражении исчезает.
Остается интеграл, который должен быть равен нулю при про-
произвольных значениях Sg. Это возможно только в том случае,
если подынтегральное выражение тождественно обращается в
нуль. Таким образом, мы получаем уравнение
^&L _ aL _ Q
dt dq dq
При наличии нескольких степеней свободы в принципе наимень-
наименьшего действия должны независимо варьироваться s различных
функций qi(t). Очевидно, что тогда мы получаем s уравнений:
Это — искомые дифференциальные уравнения; они называются
в механике уравнениями Лагранжа 1). Если функция Лагран-
жа данной механической системы известна, то уравнения B.6)
устанавливают связь между ускорениями, скоростями и коорди-
координатами, т.е. представляют собой уравнения движения системы.
С математической точки зрения уравнения B.6) составля-
составляют систему s уравнений второго порядка для s неизвестных
функций qi(t). Общее решение такой системы содержит 2s про-
г) В вариационном исчислении, рассматривающем формальную задачу
об определении экстремумов интегралов вида B.1), они называются урав-
уравнениями Эйлера.

§ 2	ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ	13
извольных постоянных. Для их определения и тем самым пол-
полного определения движения механической системы необходимо
знание начальных условий, характеризующих состояние систе-
системы в некоторый заданный момент времени, например знание
начальных значений всех координат и скоростей.
Пусть механическая система состоит из двух частей А и Д,
каждая из которых, будучи замкнутой, имела бы в качестве
функции Лагранжа соответственно функции La и Lb- Тогда в
пределе, при разведении частей настолько далеко, чтобы взаи-
взаимодействием между ними можно было пренебречь, лагранжева
функция всей системы стремится к пределу
limL = LA + LB.	B.7)
Это свойство аддитивности функции Лагранжа выражает со-
собой тот факт, что уравнения движения каждой из невзаимодей-
невзаимодействующих частей не могут содержать величины, относящиеся к
другим частям системы.
Очевидно, что умножение функции Лагранжа механической
системы на произвольную постоянную само по себе не отра-
отражается на уравнениях движения. Отсюда, казалось бы, могла
вытекать существенная неопределенность: функции Лагранжа
различных изолированных механических систем могли бы умно-
умножаться на любые различные постоянные. Свойство аддитивно-
аддитивности устраняет эту неопределенность, — оно допускает лишь
одновременное умножение лагранжевых функций всех систем
на одинаковую постоянную, что сводится просто к естествен-
естественному произволу в выборе единиц измерения этой физической
величины; мы вернемся еще к этому вопросу в § 4.
Необходимо сделать еще следующее общее замечание. Рас-
Рассмотрим две функции L\q,q,t) и L(q,q,t) , отличающиеся друг
от друга на полную производную по времени от какой-либо функ-
функции координат и времени f(q,i):
±).	B.8)
,t) +
Вычисленные с помощью этих двух функций интегралы B.1)
связаны соотношением
?2	?2	?2
S' = / !/(<?, g, i) dt = / L(q, q,t)dt+ I
ti	ti	ti

14	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
т.е. отличаются друг от друга дополнительным членом, исчезаю-
исчезающим при варьировании действия, так что условие 5Sf = 0 сов-
совпадает с условием 8S = 0, и вид уравнений движения остается
неизменным.
Таким образом, функция Лагранжа определена лишь с точ-
точностью до прибавления к ней полной производной от любой
функции координат и времени.
§ 3. Принцип относительности Галилея
Для изучения механических явлений надо выбрать ту или
иную систему отсчета. В различных системах отсчета зако-
законы движения имеют, вообще говоря, различный вид. Если взять
произвольную систему отсчета, то может оказаться, что зако-
законы даже совсем простых явлений будут выглядеть в ней весьма
сложно. Естественно, возникает задача отыскания такой систе-
системы отсчета, в которой законы механики выглядели бы наиболее
просто.
По отношению к произвольной системе отсчета пространство
является неоднородным и неизотропным. Это значит, что если
какое-либо тело не взаимодействует ни с какими другими тела-
телами, то, тем не менее, его различные положения в пространстве
и его различные ориентации в механическом отношении не эк-
эквивалентны. То же самое относится в общем случае и ко вре-
времени, которое будет неоднородным, т.е. его различные моменты
неэквивалентными. Усложнение, которое вносили бы такие свой-
свойства пространства и времени в описание механических явлений,
— очевидно. Как, например, свободное (т.е. не подвергающееся
внешним воздействиям) тело не могло бы покоиться: если ско-
скорость тела в некоторый момент времени и равна нулю, то уже
в следующий момент тело начало бы двигаться в некотором на-
направлении.
Оказывается, однако, что всегда можно найти такую систе-
систему отсчета, по отношению к которой пространство является од-
однородным и изотропным, а время — однородным. Такая си-
система называется инерциальной. В ней, в частности, свободное
тело, покоящееся в некоторый момент времени, остается в покое
неограниченно долго.
Мы можем теперь сразу сделать некоторые заключения о ви-
виде функции Лагранжа свободно движущейся материальной точ-

§ 3	ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ	15
ки в инерциальной системе отсчета. Однородность пространства
и времени означает, что эта функция не может содержать явным
образом ни радиус-вектора г точки, ни времени ?, т.е. L является
функцией лишь скорости v. В силу же изотропии пространства
функция Лагранжа не может зависеть также и от направления
вектора v, так что является функцией лишь от его абсолютной
величины, т.е. от квадрата v2 = v2:
L = L(v2).	C.1)
Ввиду независимости функции Лагранжа от г имеем
dL/dr = 0, и потому уравнения Лагранжа имеют вид х)
^&L _ п
dt dw ~ '
откуда dL/dv = const. Но поскольку dL/dv является функцией
только скорости, то отсюда следует, что и
v = const.	C.2)
Таким образом, мы приходим к выводу, что в инерциальной
системе отсчета всякое свободное движение происходит с посто-
постоянной по величине и направлению скоростью. Это утверждение
составляет содержание так называемого закона инерции.
Если наряду с имеющейся у нас инерциальной системой от-
отсчета мы введем другую систему, движущуюся относительно
первой прямолинейно и равномерно, то законы свободного дви-
движения по отношению к этой новой системе будут теми же, что
и по отношению к первоначальной: свободное движение снова
будет происходить с постоянной скоростью.
Опыт показывает, однако, что не только законы свободно-
свободного движения будут одинаковыми в этих системах, но что и во
всех других механических отношениях они будут полностью эк-
эквивалентными. Таким образом, существует не одна, а бесконеч-
бесконечное множество инерциальных систем отсчета, движущихся друг
относительно друга прямолинейно и равномерно. Во всех этих
системах свойства пространства и времени одинаковы и одина-
одинаковы все законы механики. Это утверждение составляет содер-
содержание так называемого принципа относительности Галилея —
одного из важнейших принципов механики.
г) Под производной скалярной величины по вектору подразумевается
вектор, компоненты которого равны производным от этой велечины по со-
соответствующим компонентам вектора.

16	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
Все сказанное достаточно ясно свидетельствует об исключи-
исключительности свойств инерциальных систем отсчета, в силу кото-
которых именно эти системы должны, как правило, использоваться
при изучении механических явлений. Везде в дальнейшем, где
обратное не оговорено особо, мы будем рассматривать только
инерциальные системы отсчета.
Полная механическая эквивалентность всего бесчисленного
множества таких систем показывает в то же время, что не суще-
существует никакой одной «абсолютной» системы отсчета, которую
можно было бы предпочесть другим системам.
Координаты гиг' одной и той же точки в двух различных
системах отсчета К и К1, из которых вторая движется относи-
относительно первой со скоростью V, связаны друг с другом соотно-
соотношением
г = г' + V*.	C.3)
При этом подразумевается, что ход времени одинаков в обеих
системах:
t = t'.	C.4)
Предположение об абсолютности времени лежит в самой основе
представлений классической механики х).
Формулы C.3), C.4) называют преобразованием Галилея.
Принцип относительности Галилея можно сформулировать как
требование инвариантности уравнений движения механики по
отношению к этому преобразованию.
§ 4. Функция Лагранжа свободной материальной точки
Переходя к определению вида функции Лагранжа, рассмот-
рассмотрим сначала простейший случай — свободное движение мате-
материальной точки относительно инерциальной системы отсчета.
Как мы уже видели, функция Лагранжа в этом случае может
зависеть лишь от квадрата вектора скорости. Для выяснения
вида этой зависимости воспользуемся принципом относительно-
относительности Галилея. Если инерциальная система отсчета К движется
относительно инерциальной системы отсчета К1 с бесконечно
малой скоростью е, то v' = v + e. Так как уравнения движе-
движения во всех системах отсчета должны иметь один и тот же вид,
то функция Лагранжа L(v2) должна при таком преобразовании
перейти в функцию I/, которая если и отличается от L(v2), то
г) Оно не справедливо в механике теории относительности.

§ 4 ФУНКЦИЯ ЛАГРАНЖА СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 17
лишь на полную производную от функции координат и времени
(см. конец § 2).
Имеем
L1 = L(vf2) = L(v2 + 2vi+i2).
Разлагая это выражение в ряд по степеням е и пренебрегая бес-
бесконечно малыми высших порядков, получаем
Второй член первой части этого равенства будет полной про-
производной по времени только в том случае, если он зависит от
скорости v линейно. Поэтому dL/dv2 от скорости не зависит,
т.е. функция Лагранжа в рассматриваемом случае прямо про-
пропорциональна квадрату скорости:
L777- 9	/ л -1 \
где т — постоянная.
Из того что функция Лагранжа такого вида удовлетворяет
принципу относительности Галилея в случае бесконечно малого
преобразования скорости, непосредственно следует, что функ-
функция Лагранжа удовлетворяет этому принципу и в случае конеч-
конечной скорости V системы отсчета К относительно К1. Действи-
Действительно,
J] = —yf = — (V + VJ = — v2 + 2—1
2	2	^	о
или
Второй член является полной производной и может быть опущен.
Величина т называется массой материальной точки. В силу
свойства аддитивности функции Лагранжа, для системы невза-
невзаимодействующих точек имеем г)
Следует подчеркнуть, что лишь при учете этого свойства
данное определение массы приобретает реальный смысл. Как
уже было отмечено в § 2, всегда можно умножить функцию Ла-
Лагранжа на любую постоянную; это не отражается на уравнени-
г) В качестве индекса, указывающего номер частицы, мы будем пользо-
пользоваться первыми буквами латинского алфавита, а для индексов, нумерую-
нумерующих координаты, используем буквы г, к, /,...

18	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
ях движения. Для функции D.2) такое умножение сводится к
изменению единицы измерения массы; отношения же масс раз-
различных частиц, которые только и имеют реальный физический
смысл, остаются при этом преобразовании неизменными.
Легко видеть, что масса не может быть отрицательной. В
самом деле, согласно принципу наименьшего действия для дей-
действительного движения материальной точки из точки 1 про-
пространства в точку 2 интеграл
/mv2
~2~
dt
1
имеет минимум. Если бы масса была отрицательной, то для тра-
траекторий, по которым частица сначала быстро удаляется от i, a
затем быстро приближается к #, интеграл действия принимал
бы сколь угодно большие по абсолютной величине отрицатель-
отрицательные значения, т.е. не имел бы минимума 1).
Полезно заметить, что
•"-(§)'-?•	<4-3>
Поэтому для составления функции Лагранжа достаточно най-
найти квадрат длины элемента дуги dl в соответствующей системе
координат.
В декартовых координатах, например, dl2 = dx2 + dy2 + dz2,
и, следовательно,
г — —(т2 _|_ ?/2 + f2V	(А А)
в цилиндрических dl2 = dr2 + r2dq>2 + dz2 и
в сферических dl2 = dr2 + r2dQ2 + r2 sin2 Qd(p2 и
L=^(r2 + r262 + r2 sin2 6ф2).	D.6)
§ 5. Функция Лагранжа системы материальных точек
Рассмотрим теперь систему материальных точек, взаимодей-
взаимодействующих только друг с другом, т.е. ни с какими посторонними
телами не взаимодействующих; такую систему называют зам
г) Сделанная в примечании на с. 11 оговорка не мешает этому выводу,
так как при т < 0 интеграл не мог бы иметь минимума ни для какого
малого участка траектории.

§ 5 ФУНКЦИЯ ЛАГРАНЖА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 19
кнутой. Оказывается, что взаимодействие между материаль-
материальными точками может быть описано прибавлением к функции
Лагранжа невзаимодействующих точек D.2) определенной (за-
(зависящей от характера взаимодействия) функции координат г).
Обозначив эту функцию через —С/, напишем
'2,...)	E.1)
(га — радиус-вектор а-й точки). Это есть общий вид функции
Лагранжа замкнутой системы.
Сумму
2
а
называют кинетической энергией, а функцию U — потенциаль-
потенциальной энергией системы; смысл этих названий выяснится в § 6.
Тот факт, что потенциальная энергия зависит только от рас-
расположения всех материальных точек в один и тот же момент
времени, означает, что изменение положения одной из них мгно-
мгновенно отражается на всех остальных; можно сказать, что взаи-
взаимодействия «распространяются» мгновенно. Неизбежность та-
такого характера взаимодействия в классической механике тесно
связана с основными предпосылками последней — абсолютно-
абсолютностью времени и принципом относительности Галилея. Если бы
взаимодействие распространялось не мгновенно, т.е. с конечной
скоростью, то эта скорость была бы различна в разных (движу-
(движущихся друг относительно друга) системах отсчета, так как абсо-
абсолютность времени автоматически означает применимость обыч-
обычного правила сложения скоростей ко всем явлениям. Но тогда
законы движения взаимодействующих тел были бы различны
в разных (инерциальных) системах отсчета, что противоречило
бы принципу относительности.
В § 3 мы говорили только об однородности времени. Вид
функции Лагранжа E.1) показывает, что время не только од-
однородно, но и изотропно, т.е. его свойства одинаковы по обоим
направлениям. В самом деле, замена t на — t оставляет функцию
Лагранжа, а следовательно, и уравнения движения неизменны-
неизменными. Другими словами, если в системе возможно некоторое дви-
движение, то всегда возможно и обратное движение, т.е. такое, при
) Это утверждение относится к излагаемой в настоящей книге класси-
классической — нерелятивистской — механике.

20	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
котором система проходит те же состояния в обратном порядке.
В этом смысле все движения, происходящие по законам класси-
классической механики, обратимы.
Зная функцию Лагранжа, мы можем составить уравнения
движения	j яг яг
d dL - dL
dtdwa ~ dra'
Подставив сюда E.1), получим
dwa _ _3U
Уравнения движения в этой форме называются уравнениями
Ньютона и представляют собой основу механики системы вза-
взаимодействующих частиц. Вектор
F. - "g.	E-4)
стоящий в правой части уравнений E.3), называется силой, дей-
действующей на а-ю точку. Вместе с U она зависит от координат
всех частиц, но не от их скоростей. Уравнения E.3) показывают
поэтому, что и векторы ускорения частиц являются функциями
только от координат.
Потенциальная энергия есть величина, определяемая лишь с
точностью до прибавления к ней произвольной постоянной; та-
такое прибавление не изменило бы уравнений движения (частный
случай указанной в конце § 2 неоднозначности функции Ла-
Лагранжа). Наиболее естественный и обычно принятый способ вы-
выбора этой постоянной заключается в том, чтобы потенциальная
энергия стремилась к нулю при увеличении расстояний между
частицами.
Если для описания движения используются не декартовы ко-
координаты точек, а произвольные обобщенные координаты ^, то
для получения лагранжевой функции надо произвести соответ-
соответствующее преобразование
Ха = fa(qi, 92
к
Подставляя эти выражения в функцию
L = l
получим искомую функцию Лагранжа, которая будет иметь вид
L = 2 ^2^ik(q)qiqk - u(q),	E.5)

§ 5 ФУНКЦИЯ ЛАГРАНЖА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 21
где Щк — функции только от координат. Кинетическая энергия в
обобщенных координатах по-прежнему является квадратичной
функцией скоростей, но может зависеть также и от координат.
До сих пор мы говорили только о замкнутых системах. Рас-
Рассмотрим теперь незамкнутую систему Л, взаимодействующую с
другой системой 5, совершающей заданное движение. В таком
случае говорят, что система А движется в заданном внешнем по-
поле (создаваемом системой В). Поскольку уравнения движения
получаются из принципа наименьшего действия путем незави-
независимого варьирования каждой из координат (т.е. как бы считая
остальные известными), мы можем для нахождения функции
Лагранжа LA системы А воспользоваться лагранжевой функ-
функцией L всей системы А + 5, заменив в ней координаты qB за-
заданными функциями времени.
Предполагая систему А + В замкнутой, будем иметь
L = TA(qA, qA) + TB(qB, qB) - U(qA, qB),
где первые два члена представляют собой кинетические энер-
энергии систем А и В, а третий член — их совместную потенциаль-
потенциальную энергию. Подставив вместо qB заданные функции времени
и опустив член T(c[B(t),qB(t)), зависящий только от времени (и
поэтому являющийся полной производной от некоторой другой
функции времени), получим
LA = TA(qA, qA) - U(qA, qB(t)).
Таким образом, движение системы во внешнем поле описы-
описывается функцией Лагранжа обычного типа с тем лишь отличи-
отличием, что теперь потенциальная энергия может зависеть от вре-
времени явно.
Так, для движения одной частицы во внешнем поле общий
вид функции Лагранжа
L= T?--U(r,t),	E.6)
и уравнение движения
mv = ~.	E.7)
Однородным называют поле, во всех точках которого на ча-
частицу действует одна и та же сила F. Потенциальная энергия в
таком поле, очевидно, равна
U = -Fr.	E.8)
В заключение этого параграфа сделаем еще следующее за-
замечание по поводу применения уравнений Лагранжа к различ-

22	УРАВНЕНИЯ ДВИЖЕНИЯ	ГЛ. I
ным конкретным задачам. Часто приходится иметь дело с таки-
такими механическими системами, в которых взаимодействие меж-
между телами (материальными точками) имеет, как говорят, харак-
характер связей, т.е. ограничений, налагаемых на взаимное распо-
расположение тел.
Фактически такие связи осуществляются путем скрепления
тел различными стержнями, нитями, шарнирами и т.п. Это об-
обстоятельство вносит в движение новый фактор — движение тел
сопровождается трением в местах их соприкосновения, в резуль-
результате чего задача выходит, вообще говоря, за рамки чистой ме-
механики (см. § 25).
Однако во многих случаях трение в системе оказывается на-
настолько слабым, что его влиянием на движение можно полно-
полностью пренебречь. Если к тому же можно пренебречь массами
«скрепляющих элементов» системы, то роль последних сведет-
сведется просто к уменьшению числа степеней свободы системы s (по
сравнению с числом 3N). Для определения ее движения можно
при этом снова пользоваться функцией Лагранжа вида E.5) с
числом независимых обобщенных координат, отвечающих фак-
фактическому числу степеней свободы.
Задачи
Найти функцию Лагранжа следующих систем, находящихся в од-
однородном поле тяжести (g — ускорение свободного падения).
1. Двойной плоский маятник (рис. 1).
Решение. В качестве координат берем
углы (pi и (р2, которые нити 1\ и Ь образуют с вер-
вертикалью. Тогда для точки т\ имеем
Тг = -mi/?ф?, U = -mig/icoscpi.
Чтобы найти кинетическую энергию второй точки,
выражаем ее декартовы координаты Х2, yi
(начало координат в точке подвеса, ось у — по вер-
тикали вниз) через углы (pi, (рг:
Рис. 1	Х2 = h sin (pi + I2 sin (p2, 2/2 = h cos (pi + I2 cos (p2-
После этого получаем
Ъ = ^{xl + yl) = ^[J?<Pi + /2Ф2 + 2/1/2 СО8(Ф1 - ф2)ф1ф2].
Окончательно:
ТП\ + 7712 ,2 • 2 . m2 j2 • 2 .	i i • •	/	\ ,
L =	Zicpi + — /2Ф2 +m2/i/2(pi(P2Cos((pi - ф2) +
+ (mi + m2)gh COS (pi + 17l2gl2 COS (p2-

§ 5 ФУНКЦИЯ ЛАГРАНЖА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК 23
2. Плоский маятник с массой Ш2, точка подвеса которого (с массой mi
в ней) может совершать движение по горизонталь- ¦
ной прямой (рис. 2).
Решение. Вводя координату х точки mi и
угол (р между нитью маятника и вертикалью, полу-
получаем
— ' ~	ГП2 п2 - 2
L =
-х'+'-^—A ф +2lx<jpcos (p)+m2gl cos (p.
Рис. 2
Рис. 3
3.	Плоский маятник, точка подвеса которого:
а)	равномерно движется по вертикальной окруж-
окружности с постоянной частотой у (рис. 3);
б)	совершает горизонтальные колебания по закону acosyt;
в)совершает вертикальные колебания по закону
acosyt.
Решение.
а)	Координаты точки тп:
х = acosyt + /sincp, у = — asinyt + I cos (p.
Функция Лагранжа
L = —— ф2 + mlay2 sin((p — yt) + mgl cos (p;
здесь опущены члены, зависящие только от време-
времени, и исключена полная производная по времени от
ma/y cos (cp —yt).
б)	Координаты точки т:
х = acosyt + /sin (p, y = lcos(p.
Функция Лагранж:а (после исключения полных
производных)
ml2
L= 	ф2 + mlay2 cosyt sin (p + mgl cos (p.
в)	Аналогичным образом
L = —— ф2 + mlay2 cosyt cos cp + mg/ cos (p.
4.	Система, изображенная на рис. 4; точка m2
движется по вертикальной оси, а вся система вра-
вращается с постоянной угловой скоростью Q вокруг
этой оси.
Решение. Вводим угол Э между отрез-
отрезком а и вертикалью и угол поворота (р всей системы вокруг оси вращения;
ф = Q. Для каждой из точек mi элемент перемещений
Рис. 4
ii = a2 de2
a2 sin2
Для точки 1712 расстояние от точки подвеса А равно 2а cos Э, и потому
dl2 = -2asmdde.
Функция Лагранжа
L = т1а2(в2 +Q2sin20) + 2m2a2sin2e Э2 + 2ga(rm +m2)cose.

ГЛАВА II
ЗАКОНЫ СОХРАНЕНИЯ
§ 6. Энергия
При движении механической системы 2s величин щ и сц
{% = 1,2, ..., s), определяющих ее состояние, изменяются со
временем. Существуют, однако, такие функции этих величин,
которые сохраняют при движении постоянные значения, зави-
зависящие только от начальных условий. Эти функции называют
интегралами движения.
Число независимых интегралов движения для замкнутой ме-
механической системы с s степенями свободы равно 25 — 1. Это
очевидно из следующих простых соображений. Общее решение
уравнений движения содержит 2 s произвольных постоянных
(см. с. 12). Поскольку уравнения движения замкнутой систе-
системы не содержат времени явно, то выбор начала отсчета времени
совершенно произволен, и одна из произвольных постоянных в
решении уравнений всегда может быть выбрана в виде аддитив-
аддитивной постоянной to во времени. Исключив t + to из 2s функций
Qi = Qi(t + to, С\,Съ, • • •, C^s-i),
Qi = Qi(t + to, Cl, C2, • • • , C2s-l),
мы выразим 25 — 1 произвольных постоянных Ci, С2, • • •, С25-1
в виде функций от g и д, которые и будут интегралами движения.
Однако далеко не все интегралы движения играют одина-
одинаково важную роль в механике. Среди них есть несколько, по-
постоянство которых имеет весьма глубокое происхождение, свя-
связанное с основными свойствами пространства и времени — их
однородностью и изотропией. Все эти, как говорят, сохраняю-
сохраняющиеся величины имеют важное общее свойство аддитивности —
их значение для системы, состоящей из частей, взаимодействием
которых можно пренебречь, равно сумме значений для каждой
из частей в отдельности.
Именно свойство аддитивности придает соответствующим
величинам особенно важную механическую роль. Предположим,

§ 6	ЭНЕРГИЯ	25
например, что два тела взаимодействуют в течение некоторого
времени. Поскольку как до, так и после взаимодействия каж-
каждый из аддитивных интегралов всей системы равен сумме их
значений для обоих тел в отдельности, то законы сохранения
этих величин сразу дают возможность сделать ряд заключений
о состоянии тел после взаимодействия, если их состояния до вза-
взаимодействия известны.
Начнем с закона сохранения, возникающего в связи с одно-
однородностью времени.
В силу этой однородности лагранжева функция замкнутой
системы не зависит явно от времени. Поэтому полная производ-
производная функции Лагранжа по времени может быть записана сле-
следующим образом:
dL
(если бы L зависела явно от времени, к правой части равен-
равенства добавился бы член dL/dt). Заменяя производные dL/dqi,
л	d dL
согласно уравнениям Дагранжа, на —-—, получим
dt dqi
dL _ v^ • d dL , v^ dL .. v^ d f dL ,
~dt ~
или
Отсюда видно, что величина
>g-L	F.1)
g
г
остается неизменной при движении замкнутой системы, т.е. яв-
является одним из ее интегралов движения. Эта величина называ-
называется энергией системы. Аддитивность энергии непосредственно
следует из аддитивности функции Лагранжа, через которую она
выражается, согласно F.1), линейным образом.
Закон сохранения энергии справедлив не только для замкну-
замкнутых систем, но и для систем, находящихся в постоянном (т.е. не
зависящем от времени) внешнем поле; единственное использо-
использованное в приведенном выводе свойство функции Лагранжа —
отсутствие явной зависимости от времени — имеется и в этом
случае. Механические системы, энергия которых сохраняется,
иногда называют консервативными.

26	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
Как мы видели в § 5, лагранжева функция замкнутой (или
находящейся в постоянном поле) системы имеет вид
L = T(q,q)-U(q),
где Г — квадратичная функция скоростей. Применяя к ней из-
известную теорему Эйлера об однородных функциях, получим
г	г
Подставляя это значение в F.1), найдем
E = T(q,q) + U(q);	F.2)
в декартовых координатах
2)...).	F.3)
Таким образом, энергия системы может быть представлена в
виде суммы двух существенно различных членов: кинетической
энергии, зависящей от скоростей, и потенциальной энергии, за-
зависящей только от координат частиц.
§ 7. Импульс
Другой закон сохранения возникает в связи с однородностью
пространства.
В силу этой однородности механические свойства замкнутой
системы не меняются при любом параллельном переносе систе-
системы как целого в пространстве. В соответствии с этим рассмот-
рассмотрим бесконечно малый перенос на отрезок е и потребуем, чтобы
функция Лагранжа осталась неизменной.
Параллельный перенос означает преобразование, при кото-
котором все точки системы смещаются на один и тот же постоянный
вектор е, т.е. их радиус-векторы га —> га + е. Изменение функ-
функции L в результате бесконечно малого изменения координат при
неизменных скоростях частиц есть
6т е2
а	а
а	а
где суммирование производится по всем материальным точкам
системы. Ввиду произвольности е требование ЬЬ = 0 эквива-
эквивалентно требованию
g-*	<")

§ 7	ИМПУЛЬС	27
В силу уравнений Лагранжа E.2) получаем отсюда
EI О 7" J _ _ О 7"
a OL 	 a V^ uL 	 p.
а	а
Таким образом, мы приходим к выводу, что в замкнутой ме-
механической системе векторная величина
а
остается неизменной при движении. Вектор Р называется им-
импульсом х) системы. Дифференцируя функцию Лагранжа E.1),
найдем, что импульс следующим образом выражается через ско-
скорости точек:
Р = J2ma-va.	G.3)
а
Аддитивность импульса очевидна. Более того, в отличие от
энергии импульс системы равен сумме импульсов
Ра = rnaVa
отдельных частиц вне зависимости от возможности пренебреже-
пренебрежения взаимодействием между ними.
Закон сохранения всех трех компонент вектора импульса
имеет место лишь в отсутствие внешнего поля. Однако отдель-
отдельные компоненты импульса могут сохраняться и при наличии
поля, если потенциальная энергия в нем не зависит от какой-
либо из декартовых координат. При переносе вдоль соответ-
соответствующей координатной оси механические свойства системы,
очевидно, не меняются, и тем же способом мы найдем, что про-
проекция импульса на эту ось сохраняется. Так, в однородном поле,
направленном вдоль оси z, сохраняются компоненты импульса
вдоль осей х л у.
Исходное равенство G.1) имеет простой физический смысл.
Производная дЬ/дта = —dU/dra есть сила Fa, действующая
на a-ю частицу. Таким образом, равенство G.1) означает, что
сумма сил, действующих на все частицы замкнутой системы,
равна нулю:
= 0.	G.4)
В частности, в случае системы, состоящей всего из двух мате-
материальных точек, Fi + F2 = 0: сила, действующая на первую
Устаревшее название — количество движения.

28	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
частицу со стороны второй, равна по величине, но противопо-
противоположна по направлению силе, действующей на вторую частицу
со стороны первой. Это утверждение известно под названием
закона равенства действия и противодействия.
Если движение описывается обобщенными координатами д^,
то производные лагранжевой функции по обобщенным скоро-
скоростям
Pi = Wt	G.5)
называются обобщенными импульсами, а производные
называются обобщенными силами. В этих обозначениях уравне-
уравнения Лагранжа имеют вид
Pi = Fi.	G.7)
В декартовых координатах обобщенные импульсы совпадают
с компонентами векторов ра. В общем же случае величины pi яв-
являются линейными однородными функциями обобщенных ско-
скоростей qt, отнюдь не сводящимися к произведениям массы на
скорость.
Задача
Частица с массой т, движущаяся со скоростью vi, переходит из полу-
полупространства, в котором ее потенциальная энергия постоянна и равна t/i,
в полупространство, где эта энергия тоже постоянна, но равна Ui- Опреде-
Определить изменение направления движения частицы.
Решение. Потенциальнаая энергия не зависит от координат вдоль
осей, параллельных плоскости раздела между полупространствами. Поэто-
Поэтому сохраняется проекция импульса частицы на эту плоскость. Обозначая
через 0i и 02 углы между нормалью к плоскости раздела и скоростями vi
и V2 частицы до и после перехода, получим: i>isin0i = i>2sin02. Связь же
между vi и V2 дается законом сохранения энергии, и в результате находим
§ 8. Центр инерции
Импульс замкнутой механической системы имеет различные
значения по отношению к различным (инерциальным) системам
отсчета. Если система отсчета К1 движется относительно систе-
системы отсчета К со скоростью V, то скорости v^ и va частиц по

ЦЕНТР ИНЕРЦИИ	29
отношению к этим системам связаны соотношением va = ^
Поэтому связь между значениями РиР' импульса в этих си-
системах дается формулой
ИЛИ
P = P' + V$>a.	(8.1)
а
В частности, всегда существует такая система отсчета Kf', в
которой полный импульс обращается в нуль. Положив в (8.1)
Р' = 0, найдем, что скорость этой системы отсчета равна
v = P = ?ш^	(8.2)
Если полный импульс механической системы равен нулю, то
говорят, что она покоится относительно соответствующей си-
системы отсчета. Это является вполне естественным обобщением
понятия покоя отдельной материальной точки. Соответственно
скорость V, даваемая формулой (8.2), приобретает смысл ско-
скорости «движения как целого» механической системы с отлич-
отличным от нуля импульсом. Мы видим, таким образом, что закон
сохранения импульса позволяет естественным образом сформу-
сформулировать понятия покоя и скорости механической системы как
целого.
Формула (8.2) показывает, что связь между импульсом Р и
скоростью V системы как целого такая же, какая была бы меж-
между импульсом и скоростью одной материальной точки с массой
ц = 5^7na, равной сумме масс всех частиц в системе. Это об-
обстоятельство можно сформулировать как утверждение об адди-
аддитивности массы.
Правая часть формулы (8.2) может быть представлена как
полная производная по времени от выражения
R=^^.	(8.3)
Можно сказать, что скорость системы как целого есть скорость
перемещения в пространстве точки, радиус-вектор которой да-
дается формулой (8.3). Такую точку называют центром инерции
системы.
Закон сохранения импульса замкнутой системы можно сфор-
сформулировать как утверждение о том, что ее центр инерции дви-
движется прямолинейно и равномерно. В таком виде это есть обоб-

30	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
щение закона инерции, который был выведен в § 3 для одной
свободной материальной точки, «центр инерции» которой сов-
совпадает с ней самой.
При изучении механических свойств замкнутой системы
естественно пользоваться той системой отсчета, в которой ее
центр инерции покоится. Тем самым исключается из рассмотре-
рассмотрения равномерное и прямолинейное движение системы как
целого.
Энергию покоящейся как целое механической системы обыч-
обычно называют ее внутренней энергией Евн. Она включает в себя
кинетическую энергию относительного движения частиц в си-
системе и потенциальную энергию их взаимодействия. Полная же
энергия системы, движущейся как целое со скоростью V, может
быть представлена в виде
Е = ^ + Явн.	(8.4)
Хотя эта формула довольно очевидна, дадим ее прямой вывод.
Энергии Е и Е1 механической системы в двух системах отсчета
К и К1 связаны соотношением
Е = \Y,™aV2a + U = ^5>аК + VJ + U =
или
E = E' + VP' + ^-.	(8.5)
Этой формулой определяется закон преобразования энергии при
переходе от одной системы отсчета к другой, подобно тому как
для импульса этот закон дается формулой (8.1). Если в системе
К1 центр инерции покоится, то Р1 = 0,?" = Евн, и мы возвра-
возвращаемся к формуле (8.4).
Задача
Найти закон преобразования действия при переходе от одной инерци-
альной системы отсчета к другой.
Решение. Функция Лагранжа, равная разности кинетической и по-
потенциальной энергий, очевидно, преобразуется согласно формуле, анало-
аналогичной (8.5):

§9
МОМЕНТ ИМПУЛЬСА
31
Интегрируя это равенство по времени, найдем искомый закон преобразова-
преобразования действия:
где R/ — радиус-вектор центра инерции в системе К'.
§ 9. Момент импульса
Перейдем к выводу закона сохранения, возникновение кото-
которого связано с изотропией пространства.
Эта изотропия означает, что механические свойства замкну-
замкнутой системы не меняются при любом повороте системы как це-
целого в пространстве. В соответствии с этим рассмотрим беско-
бесконечно малый поворот системы и потребуем, чтобы ее функция
Лагранжа при этом не изменилась.
Введем вектор 6ф бесконечно малого поворота, абсолютная
величина которого равна углу 6ф поворота, а направление сов-
совпадает с осью поворота (причем так, что направление поворота
отвечает правилу винта по отношению к направлению 6ф).
Найдем, прежде всего, чему равно при таком повороте при-
приращение радиус-вектора, проведенного из общего начала коор-
координат (расположенного на оси вращения) к ка-
какой-либо из материальных точек поворачива-
поворачиваемой системы. Линейное перемещение конца
радиус-вектора связано с углом соотношением
|6г| = г sin 6 • 6ф
(рис. 5). Направление же вектора перпендику-
перпендикулярно к плоскости, проходящей через г и 6ф.
Поэтому ясно, что
6г=[6<р-г].	(9.1)
При повороте системы меняется направление
не только радиус-векторов, но и скоростей всех
частиц, причем все векторы преобразуются по одинаковому за-
закону. Поэтому приращение скорости относительно неподвижной
системы координат
Sv = [бф-v].	(9.2)
Подставив эти выражения в условие неизменяемости функ-
функции Лагранжа при повороте
о
е
Рис. 5

32	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
и заменив производные dL/dva = ра, dL/dra = ра, получим
Га] + ра[6ф ' Va]) = О,
а
или, производя циклическую перестановку множителей и выно-
вынося 6ф за знак суммы, имеем
гаРа] + [vaPa]) = 6ф—
а	а
Ввиду произвольности 6ф отсюда следует, что
а
т.е. мы приходим к выводу, что при движении замкнутой систе-
системы сохраняется векторная величина
M = S>aPa],	(9.3)
а
называемая моментом импульса (или просто моментом) си-
системы х). Аддитивность этой величины очевидна, причем, как и
у импульса, она не зависит от наличия или отсутствия взаимо-
взаимодействия между частицами.
Этим исчерпываются аддитивные интегралы движения. Та-
Таким образом, всякая замкнутая система имеет всего семь таких
интегралов: энергия и по три компоненты векторов импульса и
момента.
Поскольку в определение момента входят радиус-векторы
частиц, то его значение, вообще говоря, зависит от выбора на-
начала координат. Радиус-векторы га и г^ одной и той же точки
по отношению к началам координат, смещенным на вектор а,
связаны соотношением ra = r^ + а. Поэтому имеем
? [raPa] =
а
ИЛИ
М = М' + [аР].	(9.4)
Из этой формулы видно, что только в том случае, когда система
как целое покоится (т.е. Р = 0), ее момент не зависит от выбора
начала координат. На законе сохранения момента эта неопре-
неопределенность его значения, разумеется, не сказывается, так как у
замкнутой системы импульс тоже сохраняется.
j Употребляется также названия вращательный момент или угловой
момент.

§ 9	МОМЕНТ ИМПУЛЬСА	33
Выведем также формулу, связывающую значения момента
импульса в двух различных инерциальных системах отсчета К
и К1, из которых вторая движется относительно первой со ско-
скоростью V. Будем считать, что начала координат в системах К и
К1 в данный момент времени совпадают. Тогда радиус-векторы
частиц в обеих системах одинаковы, скорости же связаны выра-
выражением va = v^ + V. Поэтому имеем
Первая сумма в правой части равенства есть момент М7 в систе-
системе К'\ введя во вторую сумму радиус-вектор центра инерции,
согласно (8.3), получаем
М = М' + ц[ВУ].	(9.5)
Эта формула определяет закон преобразования момента импульса
при переходе от одной системы отсчета к другой, подобно тому,
как для импульса и энергии аналогичные законы даются фор-
формулами (8.1) и (8.5).
Если система отсчета К1 есть та, в которой данная механичес-
механическая система покоится как целое, то V есть скорость центра инер-
инерции последней, а цУ — ее полный импульс Р (относительно К).
Тогда
М = М' + [ВР].	(9.6)
Другими словами, момент импульса М механической системы
складывается из ее «собственного момента» относительно си-
системы отсчета, в которой она покоится, и момента [RP], связан-
связанного с ее движением как целого.
Хотя закон сохранения всех трех компонент момента (отно-
(относительно произвольного начала координат) имеет место только
для замкнутой системы, в более ограниченном виде этот закон
может иметь место и для систем, находящихся во внешнем поле.
Из приведенного выше вывода очевидно, что всегда сохраняется
проекция момента на такую ось, относительно которой данное
поле симметрично, и потому механические свойства системы не
меняются при любом повороте вокруг этой оси; при этом, конеч-
конечно, момент должен быть определен относительно какой-нибудь
точки (начала координат), лежащей на этой же оси.
Наиболее важным случаем такого рода является поле с цен-
центральной симметрией, т.е. поле, в котором потенциальная энер-
энергия зависит только от расстояния до некоторой определенной

34	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
точки (центра) в пространстве. Очевидно, что при движении в
таком поле сохраняется проекция момента на любую ось, про-
проходящую через центр. Другими словами, сохраняется вектор М
момента, но определенного не относительно произвольной точки
пространства, а относительно центра поля.
Другой пример: однородное поле вдоль оси z, в котором со-
сохраняется проекция Mz момента, причем начало координат мо-
может быть выбрано произвольным образом.
Отметим, что проекция момента на какую-либо ось (назо-
(назовем ее z) может быть найдена дифференцированием функции
Лагранжа по формуле
где координата ф есть угол поворота вокруг оси z. Это ясно
уже из характера изложенного выше вывода закона сохранения
момента, но в том же можно убедиться и прямым вычислением.
В цилиндрических координатах г, ф, z имеем (подставляя ха =
= га cos фа, уа = ra sin фа):
а(хауа ~ УаХа) = ^ ГПаг1фа.	(9.8)
С другой стороны, функция Лагранжа в этих переменных имеет
вид
L = \Y,m^l + rl<pl + zl) - U
а
и ее подстановка в формулу (9.7) приводит к тому же выраже-
выражению (9.8).
Задачи
1.	Найти выражения для декартовых компонент и абсолютной величи-
величины момента импульса частицы в цилиндрических координатах г, (p,z.
Ответ:
Мх = т sin (p(rz — zr) — mrzcp cos (p,
My = m cos (p(zr — rz) — mrz<p sin (p,
Mz = mr ф,
M2 = т2г2ф2(г2 + z2) + m2(rz - zrJ.
2.	To же в сферических координатах r,Q,(p.
Ответ:
Мх = —mr2 (9 sin (p + ф sin Э cos Э cos cp),
My = mr2 (Э cos (p — ф sin Э cos Э sin (p),

§ 10	МЕХАНИЧЕСКОЕ ПОДОБИЕ	35
Mz = mr2 sin2 9 • ф,
М2 =mV(e2+sin2e-(p2).
3. Какие компоненты импульса Р и момента М сохраняются при дви-
движении в следующих полях:
а)	поле бесконечной однородной плоскости.
Ответ: Рх, Ру, Mz (бесконечная плоскость — плоскость ху).
б)	Поле бесконечного однородного цилиндра.
Ответ: Mz, Pz (ось цилиндра — ось z).
в)	Поле бесконечной однородной призмы.
Ответ: Pz (ребра призмы параллельны оси z).
г)	Поле двух точек.
Ответ: Mz (точки находятся на оси z).
д)	Поле бесконечной однородной полуплоскости.
Ответ: Ру (бесконечная полуплоскость — часть плоскости ху, огра-
ограниченная осью у).
е)	Поле однородного конуса.
Ответ: Mz (ось конуса — ось z).
ж)	Поле однородного кругового тора.
Ответ: Mz (ось тора — ось z).
з)	Поле бесконечной однородной цилиндрической винтовой линии.
Решение. Функция Лагранжа не меняется при повороте вокруг оси
винта (ось z) на угол 6(р и одновременном переносе вдоль этой оси на рас-
расстояние — 6(р ( h — шаг винта). Поэтому
откуда
Mz + — Pz = const.
Z7t
§ 10. Механическое подобие
Умножение функции Лагранжа на любой постоянный мно-
множитель очевидным образом не меняет уравнений движения. Это
обстоятельство (отмеченное уже в § 2) дает возможность в ряде
важных случаев сделать некоторые существенные заключения о
свойствах движения, не производя конкретного интегрирования
уравнений движения.
Сюда относятся случаи, когда потенциальная энергия явля-
является однородной функцией координат, т.е. функцией, удовлетво-
удовлетворяющей условию
U{ости <хг2, • • •, <*rn) = afeJ7(rb г2,..., гп),	A0.1)
где a — любая постоянная, а число к — степень однородности
функции.

36	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
Произведем преобразование, при котором наряду с измене-
изменением всех координат в а раз одновременно изменяется (в C раз)
время:
га -> ага, t -> [3?.
Все скорости va = dra/dt изменяются при этом в а/|3 раз, а
кинетическая энергия — в (Х2/[3 раз. Потенциальная же энергия
умножается на оск. Если связать а и C условием
ос2 _ к	о _ al-*/2
_ _ a , т.е. [3 - a
то в результате такого преобразования функция Лагранжа це-
целиком умножится на постоянный множитель оск, т.е. уравнения
движения останутся неизменными.
Изменение всех координат частиц в одинаковое число раз
означает переход от одних траекторий к другим, геометрически
подобным первым и отличающимся от них лишь своими линей-
линейными размерами. Таким образом, мы приходим к заключению,
что если потенциальная энергия системы является однородной
функцией к-й степени от координат (декартовых), то уравнения
движения допускают геометрически подобные траектории, при-
причем все времена движения (между соответственными точками
траекторий) относятся, как
1-к/2
A0.2)
где V/I — отношение линейных размеров двух траекторий.
Вместе с временами определенными степенями отношения /'//
являются также значения любых механических величин в со-
соответственных точках траекторий в соответственные моменты
времени. Так, для скоростей, энергии и момента имеем
k l+fc/2
И91
v1 _ A'\к/2 Е' _ A'\к М' _ (lf
7 " \Т) ' ~Ё ~ \Т) ' ~м-\Т
Приведем для иллюстрации несколько примеров.
Как мы увидим далее, в случае так называемых малых коле-
колебаний потенциальная энергия является квадратичной функцией
координат (к = 2). Из A0.2) находим, что период таких колеба-
колебаний не зависит от их амплитуды.
В однородном силовом поле потенциальная энергия — линей-
линейная функция координат (см. E.8)), т.е. к = 1. Из A0.2) имеем
t' [7
V

§ 10	МЕХАНИЧЕСКОЕ ПОДОБИЕ	37
Отсюда следует, например, что при падении в поле тяжести квад-
квадраты времен падения тел относятся, как их начальные высоты.
При ньютоновском притяжении двух масс или кулоновском
взаимодействии двух зарядов потенциальная энергия обратно
пропорциональна расстоянию между частицами, т.е. является
однородной функцией степени к = — 1. В этих случаях
t- fl-V/2
t~\l) '
и мы можем утверждать, например, что квадраты времен об-
обращения по орбитам пропорциональны кубам их размеров (так
называемый третий закон Кеплера).
Если движение системы, потенциальная энергия которой яв-
является однородной функцией координат, происходит в ограни-
ограниченной области пространства, то существует весьма простое
соотношение между средними по времени значениями кинети-
кинетической и потенциальной энергии; это соотношение известно под
названием вириальной теоремы.
Поскольку кинетическая энергия Г является квадратичной
функцией скоростей, то по теореме Эйлера об однородных функ-
функциях
дТ олт,
или, вводя импульсы дТ/dva = pa, получаем
Усредним это равенство по времени. Средним значением ка-
какой-либо функции времени /(?) называется величина
т
- [
Т J
/= lim - [ f(t)dt.
0
Легко видеть, что если /(?) является производной по времени
f(t) = dF(t)/dt от ограниченной (т.е. не принимающей бесконеч-
бесконечных значений) функции -F(t), то ее среднее значение обращается
в нуль. Действительно,
«ft = Шп ПЕЬПО) = о.
т—)-оо т

38	ЗАКОНЫ СОХРАНЕНИЯ	ГЛ. II
Предположим, что система совершает движение в конечной
области пространства и со скоростями, не обращающимися в
бесконечность. Тогда величина Y1 гаРа ограничена, и среднее
значение первого члена в правой части равенства A0.4) обра-
обращается в нуль. Во втором же заменяем ра, согласно уравнениям
Ньютона, на —dU/dra и получаем х)
Если потенциальная энергия является однородной функцией к-й
степени от всех радиус-векторов га, то, согласно теореме Эйле-
Эйлера, равенство A0.5) переходит в искомое соотношение
2Г = кп.	A0.6)
Поскольку Т + U = Е = Е, соотношение A0.6) можно пред-
представить в эквивалентных формах
U = т^—Е, Т = j^—E,	A0.7)
выражающих U и Г через полную энергию системы.
В частности, для малых колебаний (к = 2) имеем
т = п,
т.е. средние значения кинетической и потенциальной энергий
совпадают. Для ньютоновского взаимодействия (к = —1)
2Г = -U.
При этом Е = — Т в соответствии с тем, что при таком взаи-
взаимодействии движение происходит в конечной области простран-
пространства лишь при отрицательной полной энергии (см. § 15).
Задачи
1.	Как относятся времена движения по одинаковым траекториям точек
с различными массами при одинаковой потенциальной энергии?
Ответ:	.	/—-
t _ m
1 ~ \m'
2.	Как изменяются времена движения по одинаковым траекториям при
изменении потенциальной энергии на постоянный множитель?
Ответ:	Ц
j Выражение в правой части равенства A0.5) иногда называют вириа-
лом системы.

ГЛАВА III
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
§ 11. Одномерное движение
Одномерным называют движение системы с одной степенью
свободы. Наиболее общий вид лагранжевой функции такой си-
системы, находящейся в постоянных внешних условиях, есть
L=\a(q)q2-U(q),	A1.1)
где a(q) — некоторая функция обобщенной координаты q. В
частности, если q есть декартова координата (назовем ее ж), то
L=^f- U{x).	A1.2)
Соответствующие этим лагранжевым функциям уравнения
движения интегрируются в общем виде. При этом нет далее
необходимости выписывать само уравнение движения, а следует
исходить сразу из его первого интеграла — уравнения, выража-
выражающего закон сохранения энергии. Так, для функции Лагранжа
A1.2) имеем
^f + Щх) = Е.
Это есть дифференциальное уравнение первого порядка, инте-
интегрирующееся путем разделения переменных. Имеем
dx
откуда
t = А[% f dx + const.	A1.3)
Роль двух произвольных постоянных в решении уравнения
движения играют здесь полная энергия Е и постоянная инте-
интегрирования const.

40
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
ГЛ. III
Поскольку кинетическая энергия — величина существенно
положительная, то при движении полная энергия всегда больше
потенциальной, т.е. движение может происходить только в тех
областях пространства, где U(x) < Е.
Пусть, например, зависимость U(х) имеет вид, изображен-
изображенный на рис. 6. Проведя на этом же графике горизонтальную
прямую, соответствующую заданному значению полной энер-
энергии, мы сразу же выясним возможные области движения. Так
в изображенном на рис. 6 случае движение может происходить
лишь в области АВ или в области справа от С.
Точки, в которых потенциальная энергия равна полной
U(x) = Е,	A1.4)
определяют границы движения. Они являются точками оста-
остановки, поскольку в них скорость
обращается в нуль. Если область
движения ограничена двумя та-
такими точками, то движение проис-
происходит в ограниченной области
пространства; оно является, как
говорят, финитным. Если же об-
область движения не ограничена или
ограничена лишь с одной сторо-
стороны, — движение инфинитно, частица уходит на бесконечность.
Одномерное финитное движение является колебательным —
частица совершает периодически повторяющееся движение
между двумя границами (на рис. 6 в потенциальной яме АВ
между точками х\ и хъ). При этом согласно общему свойству
обратимости (с. 19) время движения от х\ до Х2 равно времени
обратного движения от Х2 до х\. Поэтому период колебания Г,
т.е. время, за которое точка пройдет от х\ до Х2 и обратно, ра-
равен удвоенному времени прохождения отрезка х\Х2 или соглас-
согласно A1.3)
U=E
Х2(Е)
Т(Е) =
f
J
A1.5)
xi(E)
причем пределы х\ и Х2 являются корнями уравнения A1.4) при
данном значении Е. Эта формула определяет период движения
в зависимости от полной энергии частицы.

§11	ОДНОМЕРНОЕ ДВИЖЕНИЕ	41
Задачи
1. Определить период колебания плоского математического маятника
(точка т на конце нити длиной / в поле тяжести) в зависимости от их
амплитуды.
Решение. Энергия маятника
Е = —	mgl cos (p = — mgl cos (po,
где (р — угол отклонения нити от вертикали; (ро — максимальный угол от-
отклонения. Вычисляя период как учетверенное время прохождения интер-
интервала углов от нуля до (ро, находим
/I/.
=24Д
Vcos <p - cos <po Vgy A/sin2(9o/2) - sin2(cp/2)
U	О
Подстановкой sin((p/2)/sin(cpo/2) = sin?, этот интеграл приводится к виду
где
— так называемый полный эллиптической интеграл первого рода. При
sin(cpo/2) « фо/2 ^С 1 (малые колебания) разложение функции if (&) дает
км = 7'
^ л/1 -
Первый член этого разлож:ения отвечает известной элементарной формуле.
2. Определить период колебаний в зависимости от энергии при движе-
движении частицы массы т в полях с потенциальной энергией:
a) U = А\х\п.
Ответ:	.
(Е/АI/71	1
dy
у/Е - Ахп	Аг/п	J у/1 -уп
о	о
Подстановкой уп = и интеграл приводится к так называемому 5-интегралу
Эйлера, который выражается через Г-функции
= 2у/2пт ГA/п) „
Л1/ГA/ + 1/2)
Зависимость Т от Е соответствует закону механического подобия A0.2),A0.3).
6)U = -Uo/ch2 осх, -U0<E < 0.
Ответ:
Т = nV2m/oiy/\E\.
в) U = U0 tg2 ocx.
Ответ:
Т =

42
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
ГЛ. III
U=E
§ 12. Определение потенциальной энергии по периоду колебаний
Рассмотрим вопрос о том, в какой степени можно восстано-
восстановить вид потенциальной энергии U(х) поля, в котором частица
совершает колебательное движение, по известной зависимости
периода этого движения Г от энергии Е. С математической точ-
точки зрения речь идет о решении интегрального уравнения A1.5),
в котором U(х) рассматривается как неизвестная, а Т(Е) — как
известная функции.
При этом мы будем заранее предполагать, что искомая функ-
функция U(х) имеет в рассматриваемой области пространства лишь
один минимум, оставляя в стороне
вопрос о возможности существова-
существования решений интегрального урав-
уравнения, не удовлетворяющих этому
условию. Для удобства выберем
начало координат в положении ми-
минимума потенциальной энергии, а
значение последней в этой точке
положим равным нулю (рис. 7).
Преобразуем интеграл A1.5), рассматривая в нем координа-
координату х как функцию U. Функция x(U) двузначна — каждое значе-
значение потенциальной энергии осуществляется при двух различных
значениях х. Соответственно этому интеграл A1.5), в котором
мы заменяем dx на -—dU, перейдет в сумму двух интегралов:
аи
от х = х\ до х = 0 и от х = 0 до х = Х2\ будем писать зависи-
зависимость х от U в этих двух областях соответственно как х = x\(U)
и х = X2(U).
Пределами интегрирования по dU будут, очевидно, ? и О,
так что получаем
Е
Рис. 7
Т(Е) =
dU
Разделим обе части этого равенства на уа — Е1, где а — па-
параметр, и проинтегрируем по Е от нуля до ос.

12	ОПРЕДЕЛЕНИЕ ЭНЕРГИИ ПО ПЕРИОДУ КОЛЕБАНИЙ	43
ос	ос Е
f Т(Е) dE _ rz— f f (dx2(U) _ dx!(U)\	dU dE
J J^E ~ V mJ J V dU	dU ) ^(ct-
0	0 0
или, меняя порядок интегрирования:
ос	ос	ос
[ T(E)dE _ пг- [ fdx2(U) dXl(U)\ „j f	dE
J 7^?~V2my \Гй dir)dUJ 7^
¦E)(E-U)
О	0	U
Интеграл по dE вычисляется элементарно и оказывается рав-
равным 7Г. После этого интегрирование по dU становится тривиаль-
тривиальным и дает
ос
T(E)dE	rz— г , ч	, чп
; ' = 7tv2m[X2{oc) — xi(oc)\
V а — Е
О
(при этом учтено, что х2@) = х±@) = 0). Заменив теперь бук-
букву а на С/, находим окончательно:
и
(X
/
0
Таким образом, по известной функции Т(Е) определяется
разность X2(U) — x\(U). Сами же функции X2(U) и x\(U) оста-
остаются неопределенными. Это значит, что существует не одна, а
бесчисленное множество кривых U = U(ж), приводящих к за-
заданной зависимости периода от энергии и отличающихся друг от
друга такими деформациями, которые не меняют разности двух
значений ж, соответствующих одному и тому же значению U.
Многозначность решения исчезает, если потребовать, чтобы
кривая U = U(x) была симметрична относительно оси ординат,
т.е. чтобы было:
В таком случае формула A2.1) дает для x(U) однозначное вы-
выражение
27tV2ra
0

44	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
§ 13. Приведенная масса
Полное решение в общем виде допускает чрезвычайно важ-
важная задача о движении системы, состоящей всего из двух взаи-
взаимодействующих частиц (задача двух тел).
В качестве предварительного шага к решению этой задачи
покажем, каким образом она может быть существенно упроще-
упрощена путем разложения движения системы на движение центра
инерции и движения точек относительно последнего.
Потенциальная энергия взаимодействия двух частиц зависит
лишь от расстояния между ними, т.е. от абсолютной величины
разности их радиус-векторов. Поэтому лагранжева функция та-
такой системы
f ^	A3.1)
Введем вектор взаимного расстояния обеих точек
г = ri - г2
и поместим начало координат в центре инерции, что дает
Ш1Г1 + 7712Г2 = 0.
Из двух последних равенств находим
г2 =	^р.	A3.2)
ТПг + 7712
П	г, г2
ТП\ + 7712	ТПг
Подставляя эти выражения в A3.1), получим
L = Щ- - U(r),	A3.3)
где введено обозначение
т = Ш1Ш2 ;	A3.4)
7711 + 7712
величина га называется приведенной массой. Функция A3.3)
формально совпадает с функцией Лагранжа одной материаль-
материальной точки с массой га, движущейся во внешнем поле С/(г), сим-
симметричном относительно неподвижного начала координат.
Таким образом, задача о движении двух взаимодействующих
материальных точек сводится к решению задачи о движении од-
одной точки в заданном внешнем поле U(r). По решению г = г(?)
этой задачи траектории ri = ri(t) и Г2 = Г2(?) каждой из ча-
частиц TTii и 7712 в отдельности (по отношению к их общему центру
инерции) получаются по формулам A3.2).

§ 14	ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ	45
Задача
Система состоит из одной частицы с массой М и п частиц с одинако-
одинаковыми массами т. Исключить движение центра инерции и свести задачу к
задаче о движении п частиц.
Решение. Пусть R — радиус-вектор частицы М, a Ra (a = 1, 2,...
..., п) — радиус-векторы частиц с массами т. Введем расстояния от части-
частицы М до частиц т
I*a = R-a — R
и поместим начало координат в центре инерции:
MR = т У^ Ra = 0.
a
Из этих равенств находим:
R=	/ ^Гд,	Rg=
a
где |х = М + пт. Подставив эти выражения в функцию Лагранжа
получим
где va = ra.
Потенциальная энергия зависит лишь от расстояний между частицами
и потому может быть представлена как функция от векторов ra.
§ 14. Движение в центральном поле
Сведя задачу о движении двух тел к задаче о движении од-
одного тела, мы пришли к вопросу об определении движения ча-
частицы во внешнем поле, в котором ее потенциальная энергия
зависит только от расстояния г до определенной неподвижной
точки; такое поле называют центральным. Сила
Or	dr г'
действующая на частицу, по абсолютной величине зависит при
этом тоже только от г и направлена в каждой точке вдоль ра-
радиус-вектора.
Как было уже показано в § 9, при движении в центральном
поле сохраняется момент системы относительно центра поля.
Для одной частицы это есть
М= [гр].
Поскольку векторы Миг взаимно перпендикулярны, посто-
постоянство М означает, что при движении частицы ее радиус-вектор

46	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
все время остается в одной плоскости — плоскости, перпендику-
перпендикулярной к М.
Таким образом, траектория движения частицы в централь-
центральном поле лежит целиком в одной плоскости. Введя в ней по-
полярные координаты г, ф, напишем функцию Лагранжа в ви-
виде (ср. D.5))
Ь=^(г2 + г2ф2)-и(г).	A4.1)
Эта функция не содержит в явном виде координату ф. Вся-
Всякую обобщенную координату ^, не входящую явным образом в
лагранжеву функцию, называют циклической. В силу уравне-
уравнения Лагранжа имеем для такой координаты:
d dL _ 8L_ _ Q
dtdqt ~ dqi ~ '
т.е. соответствующий ей обобщенный импульс щ = dL/dqi яв-
является интегралом движения. Это обстоятельство приводит к
существенному упрощению задачи интегрирования уравнений
движения при наличии циклических координат.
В данном случае обобщенный импульс
р^ = тг2ф
совпадает с моментом Mz = М (см. (9.6)), так что мы возвра-
возвращаемся к известному уже нам закону сохранения момента
М = тг2ф = const.	A4.2)
Заметим, что для плоского движе-
движения одной частицы в центральном
	^ ]Li4J i ^ч поле этот закон допускает простую
Ч геометрическую интерпретацию. Вы-
Выражение A/2)г-гс?ф представляет со-
Рис# 8	бой площадь сектора, образованного
двумя бесконечно близкими радиус-векторами и элементом ду-
дуги траектории (рис. 8). Обозначив ее как d/, напишем момент
частицы в виде
М = 2т/,	A4.3)
где производную / называют секториальной скоростью. По-
Поэтому сохранение момента означает постоянство секториальной
скорости — за равные промежутки времени радиус-вектор дви-
движущейся точки описывает равные площади (так называемый
второй закон Кеплера) 1).
г) Закон сохранения момента для частицы, движущейся в центральном
поле, иногда называют интегралом площадей.

§ 14	ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ	47
Полное решение задачи о движении частицы в центральном
поле проще всего получить, исходя из законов сохранения энер-
энергии и момента, не выписывая при этом самих уравнений движе-
движения. Выражая ф через М из A4.2) и подставляя в выражение
для энергии, получим
Е = ^(г2 + г2ф2) + U(r) = ^ + -^^ + U{r).	A4.4)
Отсюда
dr /2 rz7, TTf 4i М2
dt V rnl	v /J m2r2
= I	dr	+ const.	A4.6)
4J	/ Г t~j TTf \Л	-LVJ-
или, разделяя переменные и интегрируя
— [Е-U (г)]-
\ т	mzrz
Далее, написав A4.2) в виде
А	М А+
ац> = —2 "*?
подставив сюда dt из A4.5) и интегрируя, находим
/*	(M/r2)dr	,	,	,1у1 ,
ф = /	v 7 ;	— + const.	(ЫЛ
J ^2m[E-U(r)]-M2/r2	V
Формулы A4.6) и A4.7) решают в общем виде поставлен-
поставленную задачу. Вторая из них определяет связь между гиф, т.е.
уравнение траектории. Формула же A4.6) определяет в неявном
виде расстояние г движущейся точки от центра как функцию
времени. Отметим, что угол ф всегда меняется со временем мо-
монотонным образом — из A4.2) видно, что ф никогда не меняет
знака.
Выражение A4.4) показывает, что радиальную часть движе-
движения можно рассматривать как одномерное движение в поле с
«эффективной» потенциальной энергией
Величину М2/Bгаг2) называют центробежной энергией. Зна-
Значения г, при которых
определяют границы области движения по расстоянию от цен-
центра. При выполнении равенства A4.9) радиальная скорость г
обращается в нуль. Это не означает остановки частицы (как при

48
ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
ГЛ. III
истинном одномерном движении), так как угловая скорость ф не
обращается в нуль. Равенство г = 0 означает «точку поворота»
траектории, в которой функция r(t) переходит от увеличения к
уменьшению или наоборот.
Если область допустимого изменения г ограничена лишь од-
одним условием г ^ rmin, то движение частицы инфинитно —
ее траектория приходит из бесконечности и уходит на бес-
бесконечность.
Если область изменения г имеет две границы гш[п и rmax,
то движение является финитным и траектория целиком лежит
внутри кольца, ограниченного окружностями г = rmax и г =
= ^min- Это, однако, не означает, что траектория непременно
является замкнутой кривой. За время, в течение которого г из-
изменяется от rmax до rmin и затем до rmax, радиус-вектор повер-
повернется на угол Аф, равный, согласно A4.7),
(M/r2)dr
Аф =
y/2m(E-U) -М2/г2
A4.10)
Условие замкнутости траектории заключается в том, чтобы
этот угол был равен рациональной части от 27Г, т.е. имел вид
Лф = 27tra/n, где га, п —
целые числа. Тогда через п
повторений этого периода
времени радиус-вектор точ-
точки, сделав га полных обо-
оборотов, совпадает со своим
первоначальным значением,
т.е. траектория замкнется.
Однако такие случаи ис-
исключительны, и при произ-
произвольном виде U(г) угол Аф
не является рациональной
частью от 2тс. Поэтому в об-
общем случае траектория фи-
Рмг Q
нитного движения не замк-
замкнута. Она бесчисленное чис-
число раз проходит через минимальное и максимальное расстояние
(как, например, на рис. 9) и за бесконечное время заполняет все
кольцо между двумя граничными окружностями.

§ 14	ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ	49
Существуют лишь два типа центральных полей, в которых
все траектории финитных движений замкнуты. Это поля, в ко-
1
торых потенциальная энергия частицы пропорциональна -
или г2. Первый из этих случаев рассмотрен в следующем пара-
параграфе, а второй соответствует так называемому пространствен-
пространственному осциллятору (см. задачу 3 §23).
В точке поворота квадратный корень A4.5) (а вместе с ним
и подынтегральные выражения в A4.6) и A4.7)) меняет знак.
Если отсчитывать угол ф от направления радиус-вектора, про-
проведенного в точку поворота, то примыкающие с двух сторон к
этой точке отрезки траектории будут отличаться лишь знаком ф
при каждых одинаковых значениях г; это значит, что траекто-
траектория симметрична относительно указанного направления. Начав,
скажем, от какой-либо из точек г = rmax, мы пройдем отрезок
траектории до точки с г = rmin, затем будем иметь симмет-
симметрично расположенный такой же отрезок до следующей точки
с г = rmax и т.д., т.е. вся траектория получается повторением
в прямом и обратном направлениях одинаковых отрезков. Это
относится и к инфинитным траекториям, состоящим из двух
симметричных ветвей, простирающихся от точки поворота rmin
до бесконечности.
Наличие центробежной энергии (при движении с М ф 0),
обращающейся при г —»> 0 в бесконечность, как smallfraclr2,
приводит обычно к невозможности проникновения движущихся
частиц к центру поля, даже если последнее само по себе имеет
характер притяжения. «Падение» частицы в центр возможно
лишь, если потенциальная энергия достаточно быстро стремится
к —ос при г —»> 0. Из неравенства
или
г2С/(г) + ^ < Ег2
следует, что т может принимать стремящиеся к нулю значения
лишь при условии
т.е. U(г) должно стремиться к —ос либо как — — с ос > —, либо
4 '	г2	2т
пропорционально — — с п > 2.

50	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
Задачи
1. Проинтегрировать уравнения движения сферического маятника —
материальной точки т, движущейся по поверхности сферы радиуса / в
поле тяжести.
Решение. В сферических координатах с началом в центре сферы и
полярной осью, направленной вертикально вниз, функция Лагранжа маят-
маятника
L = ^-(ё2 + sin2 0 • ф2) + mgl cose.
Координата (р — циклическая, поэтому сохраняется обобщенный импульс
рф, совпадающий с z-компонентой момента:
ml2 sin2 Q • ф = Mz = const.	A)
Энергия
?/ = 	(9 + sin v - ф ) — mgl cos 9 =	1	. 2	77ig/ cos 9. B)
Определяя отсюда 9 и разделяя переменные, получаем
'-Л,..*	•
где введена «эффективная потенциальная энергия»
Ф = ~^= [	 ,""	D)
' ^ J sin2 Г ^ " '"ч
Для угла (р, используя A), найдем
mz r	de_
n2 ву/Е-и9ф(в)'
Интегралы C) и D) приводятся к эллиптическим интегралам соответствен-
соответственно первого и третьего рода.
Область движения по углу Э определяется условием Е > С7эф, а ее гра-
границы — уравнением Е = С/Эф- Последнее представляет собой кубическое
уравнение для cos 9, имеющее в промежутке от —1 до +1 два корня, опре-
определяющих положение двух параллельных окружностей на сфере, между
которыми заключена вся траектория.
2. Проинтегрировать уравнения движения материальной точки, дви-
движущейся по поверхности конуса (с углом 2ос при вершине), расположенном
вертикально, вершиной вниз, в поле тяжести.
Решение. В сферических координатах с началом в вершине конуса
и полярной осью, направленной вертикально вверх, функция Лагранжа
L = — (г2 + г2 sin2 а • ф2) — mgr cos а.
Координата (р — циклическая, так что снова сохраняется
Энергия
Mz = mr2 sin2 ос- ф.
z, rnr2 ,	М2
Е = —	Ь	;—г	\~ mgr cos ос.
2 2mr2 sin2 a

§ 15	КЕПЛЕРОВА ЗАДАЧА	51
Тем же способом, что и в задаче 1, находим
dr
-I
Mz	f	dr
I
тт ( ^	M*
иэф(г) =	—r^	h mgr cos oc.
2mr2sm2 a
Условие E = иэф(г) представляет собой (при Mz ф 0) кубическое урав-
уравнение для г, имеющее два положительных корня; ими определяется поло-
положение двух горизонтальных окружностей на поверхности конуса, между
которыми заключена траектория.
3. Проинтегрировать уравнения движения плоского маятника, точка
подвеса которого (с массой тп\ в ней) способна совершать движение в го-
горизонтальном направлении (см. рис. 2).
Решение. В найденной в задаче 2 § 5 функции Лагранжа коорди-
координата х — циклическая. Поэтому сохраняется обобщенный импульс Рж, сов-
совпадающий с горизонтальной компонентой полного импульса системы:
Рх = G7li + ТП2)Х + 77l2/(p COS ф = COnst .	A)
Всегда можно считать систему, как целое, покоящейся; тогда const = 0, и
интегрирование уравнения A) дает соотношение
(mi + rri2)x + 7П2/ sin (p = const,	B)
выражающее собой неподвижность центра инерции системы в горизонталь-
горизонтальном направлении. Используя A), получим энергию в виде
7712/ Ф (л ТП2	2 А	,	/оч
Е = 	 I 1	COS ф I — 77i2g/ COS (p.	C)
2 V mi + 77i2	I
Отсюда
7
2(mi + m2) J у E + 77i2g/ cos (p
U/vp.
Выразив координаты х2 = x + /sincp, 2/2 = /coscp частицы 77i2 с по-
помощью B) через (р, найдем, что траектория этой частицы представляет
собой отрезок эллипса с горизонтальной полуосью /mi/(mi + 7712) и верти-
вертикальной /. При 77ii —>¦ оо мы возвращаемся к обычному математическому
маятнику, качающемуся по дуге окружности.
§ 15. Кеплерова задача
Важнейшим случаем центральных полей являются поля, в
которых потенциальная энергия обратно пропорциональна г и
соответственно силы обратно пропорциональны г2. Сюда отно-
относятся ньютоновские поля тяготения и кулоновские электроста-

52	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
тические поля; первые, как известно, имеют характер притяже-
притяжения, а вторые могут быть как полями притяжения, так и оттал-
отталкивания.
Рассмотрим сначала поле притяжения, в котором
U = -ос/г	A5.1)
с положительной постоянной ос. График «эффективной» потен-
потенциальной энергии
су	М2
Т Т	I	/1 С^ О \
г 2mr2
имеет вид, изображенный на рис. 10. При г —> 0 она обращается
в +ос, а при г —»> ос стремится к нулю со стороны отрицательных
значений; при г = М^/ост она имеет минимум,
равный
A5.3)
Из этого графика очевидно, что при Е > 0 движе-
q \^^^—= ние частицы будет инфинитным, а при Е < 0 —
финитным.
Рис- Ю	Форма траектории получается с помощью об-
общей формулы A4.7). Подставляя в нее U = —ос/г и производя
элементарное интегрирование, получим
Mir — mot/M .	,
Ф = arccos . '	'	+ const.
Выбирая начало отсчета угла ф так, чтобы const = 0, и вводя
обозначения
М	1л , 2ЕМ	ft* л\
Р = —, е = \ И	г-,	A5.4)
mot	у	тос
перепишем формулу для траектории в виде
р/г = 1 + е cos ф.	A5.5)
Это есть уравнение конического сечения с фокусом в начале ко-
координат; р л е — так называемые параметр и эксцентриситет
орбиты. Сделанный нами выбор начала отсчета ф заключается,
как видно из A5.5), в том, что точка с ф = 0 является ближай-
ближайшей к центру (так называемый перигелий орбиты).
В эквивалентной задаче двух тел, взаимодействующих по за-
закону A5.1), орбита каждой из частиц тоже представляет собой
коническое сечение с фокусом в их общем центре инерции.
Из A5.4) видно, что при Е < 0 эксцентриситет е < 1, т.е.
орбита является эллипсом (рис. 11) и движение финитно в соот-

§15
КЕПЛЕРОВА ЗАДАЧА
53
ветствии со сказанным в начале параграфа. Согласно известным
формулам аналитической геометрии большая и малая полуоси
эллипса	п	v	M
Р
» min —
A5.6)
у/1-е2 \/2т\Е\
Наименьшее допустимое значение энергии совпадает с A5.3),
при этом е = 0, т.е. эллипс обращается в окружность. Отметим,
что большая полуось эллипса за-
зависит только от энергии (но не
от момента) частицы. Наимень-
Наименьшее и наибольшее расстояния до
центра поля (фокуса эллипса)
равны
— р — (Л — \
= ]Ц = аA+е) A5-7)
1-е
Эти выражения (с а и е из A5.6)
и A5.4)) можно было бы, конечно, получить и непосредственно
как корни уравнения С/Эф(г) = Е.
Время обращения по эллиптической орбите, т.е. период дви-
движения Г, удобно определить с помощью закона сохранения мо-
момента в форме «интеграла площадей» A4.3). Интегрируя это ра-
равенство по времени от нуля до Г, получим
2га/ = ТМ,
где / — площадь орбиты. Для эллипса / =	р\
= nab, и с помощью формул A5.6) находим
Рис. 11
A5.8)
1)
Рис. 12
Тот факт, что квадрат периода должен быть
пропорционален кубу линейных размеров
орбиты, был указан уже в § 10. Отметим также, что период за-
зависит только от энергии частицы.
При Е ^ 0 движение инфинитно. Если Е > 0, то эксцентри-
эксцентриситет е > 1, т.е. траектория является гиперболой, огибающей
центр поля (фокус), как показано на рис. 12. Расстояние пери-
перигелия от центра
Гт1п = ~^\ = а(е ~ -1-)'	A5.9)
где

54	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
	 р 	 а
п ~ е2 -1 ~~ 2Ё
— «полуось» гиперболы.
В случае же Е = 0 эксцентриситет е = 1, т.е. частица дви-
движется по параболе, с расстоянием перигелия гш[п = р/2. Этот
случай осуществляется, если частица начинает свое движение
из состояния покоя на бесконечности.
Зависимость координат частицы от времени при движении
по орбите может быть найдена с помощью общей формулы A4.6).
Она может быть представлена в удобном параметрическом виде
следующим образом.
Рассмотрим сначала эллиптические орбиты. Вводя а и е со-
согласно A5.4), A5.6), запишем интеграл A4.6), определяющий
время, в виде
V ЩЩ J
l	rdr		 /та I	rdr
J I	ос ~M^~V^J у/аЧ*-{г-а)*'
\E\ 2m\E\
С помощью естественной подстановки
г — а = —aecos?,
этот интеграл приводится к виду
гч 7г /7na3/г	- г\ ,	±.
е cos ?Ла^= \ 	(?, — е sin ?,) + const.
Выбирая начало отсчета времени так, чтобы обратить const в
нуль, получим окончательно следующее параметрическое пред-
представление зависимости г от t:
r = a(l-ecos?,), t= J^-(?, - esin?,)	A5.10)
(в момент t = 0 частица находится в перигелии). Через тот же
параметр ?, можно выразить и декартовы координаты частицы
х — г cos ф, у — г sin ф (оси х лу направлены соответственно по
большой и малой полуосям эллипса). Из A5.5) и A5.10) имеем
ех = р — г = аA — е2) — a(l — ecos?,) = ae(cos?, — e),
а у найдем, как уг^—х*. Окончательно:
х = a(cos ?, — е), у = ayl — е2 sin ?,.	A5.11)

§15
КЕПЛЕРОВА ЗАДАЧА
55
Полному обороту по эллипсу соответствует изменение парамет-
параметра ?, от нуля до 2п.
Совершенно аналогичные вычисления для гиперболических
траекторий приводят к результату
г = a(ech?, — 1), t = Wmas/oc (esh?, — ?,),
v		A5.12)
x = a(e — ch ?,),	у = a\/e2 — 1 sh ?,,
где параметр ?, пробегает значения от —ос до +ос.
Обратимся к движению в поле отталкивания, в котором
U=*	A5.13)
(а > 0). В этом случае эффективная потенциальная энергия
монотонно убывает от + ос до нуля при изменении г от нуля
до ос. Энергия частицы может быть только положительной и
движение всегда инфинитно. Все вычисления для этого случая
в точности аналогичны произведенным
выше. Траектория является гиперболой
- = — 1 + е cos ф	A5.14)
(рие определяются прежними формула-
формулами A5.4)). Она проходит мимо центра по-
поля, как показано на рис. 13. Расстояние пе-
перигелия
гШт = -^—^ = а(е + 1).	A5.15)	рис. 13
Зависимость от времени дается параметрическими уравнениями
г = а[есп с,
i=A&(esh ?,+ ?),
A5.1
х = a(ch ?, + е),	у = а\/е2 — 1 sh ?,.
В заключение параграфа укаж:ем, что при движении в по-
поле U = ос/г (с любым знаком ос) имеется интеграл движения,
специфический именно для этого поля. Легко проверить непо-
непосредственным вычислением, что величина
[vM] + — = const.	A5.17)
Действительно, ее полная производная по времени равна

56	ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ	ГЛ. III
или, подставив М = ra[rv]:
/ . \	/ . \ . av ar(vr)
rar(vv) — rav(rv) + — — —V^-;
положив здесь согласно уравнениям движения mv = ar/r3, мы
найдем, что это выражение обращается в нуль.
Сохраняющийся вектор A5.17) направлен вдоль большой оси
от фокуса к перигелию, а по величине равен осе. В этом проще
всего можно убедиться, рассмотрев его значение в перигелии.
Подчеркнем, что интеграл движения A5.17), как и интегра-
интегралы М и Е, является однозначной функцией состояния (поло-
(положения и скорости) частицы. Мы увидим в § 50, что появление
такого дополнительного однозначного интеграла связано с так
называемым вырождением движения.
Задачи
1. Найти зависимость координат частицы от времени при движении в
поле U = — ос/г с энергией Е = 0 (по параболе).
Решение. В интеграле
/г dr
/2otr М2
V т т2
делаем подстановку
и в результате получаем следующее параметрическое представление иско-
искомой зависимости:
Параметр т| пробегает значения от — оо до +оо.
2. Проинтегрировать уравнения движения материальной точки в цен-
ТТ ос
тральном поле и =	^? ос > 0.
rz
Решение. По формулам A4.6), A4.7) с соответствующим выбором
начала отсчета (р и t находим
М2	1 / 2тЕ	/ / 2mot\
а) при Е > 0, -— > а - = \ ——	 cos ср \ 1	——
'	2m	r \M2-2mot \ V	М2 I
Г
б)приЕ>0, -— <	/
'	2тп
2тп	г V 2moi - М2

§ 15	КЕПЛЕРОВА ЗАДАЧА	57
A	Z7^ n М ^	г	/ 2ш \Е\	г. /	2т0С
в) при Е < 0, -— < а - = у о	ЧЬ^ ch ' - • '
у	2т	г V 2ша - М2
Во всех трех случаях
[т
~2 V"' 2ш
В случаях б) и в) частица «падает» в центр по тректории, приближающей-
приближающейся к началу координат при (р —У оо. Падение с заданного расстояния г
происходит за конечное время, равное
3. При добавлении к потенциальной энергии U = — ос/г малой добавки
8U(r) траектории финитного движения перестают быть замкнутыми и при
каждом обороте перигелий орбиты смещается на малую угловую величину
6(р. Определить 6(р для случаев: a) 8U = C/г2, б) 8U = у/г3.
Решение. При изменении г от rmin до rmax и снова до rmin угол 6(р
меняется на величину, даваемую формулой A4.10), которую представим в
виде
Л д
(с целью избежать ниже фиктивно расходящихся интегралов). Положим
U = — ос/г + bU и разложим подынтегральное значение по степеням bU\
нулевой член разложения дает 2я, а член первого порядка — искомое сме-
смещение 6(р:
Г-max	/	П	\
д Г	2mbUdr	д I 2т
2m[E+-)
V г) г2
где от интегрирования по dr мы перешли к интегрированию по d(p вдоль
траектории «невозмущенного» движения.
В случае а) интегрирование в A) тривиально и дает
_ 271C771 _ 2Я|3
Ф ~ М2 ~ оср
(р — параметр невозмущенного эллипса из A5.4)). В случае б) r2bU = у/т,
и, взяв 1/V из A5.5), получим
_ бпосут2 _ бяу
Ф~
М4
,2 '

ГЛАВА IV
СТОЛКНОВЕНИЕ ЧАСТИЦ
§ 16. Распад частиц
Уже сами по себе законы сохранения импульса и энергии
позволяют сделать во многих случаях ряд важных заключений
о свойствах различных механических процессов. При этом осо-
особенно существенно то обстоятельство, что эти свойства совер-
совершенно не зависят от конкретного рода взаимодействия между
участвующими в процессе частицами.
Начнем с процесса, представляющего собой «самопроизволь-
«самопроизвольный» (т.е. без воздействия внешних сил) распад частицы на две
«составные части», т.е. на две другие частицы, движущиеся по-
после распада независимо друг от друга.
Наиболее просто этот процесс выглядит при рассмотрении
его в системе отсчета, в которой частица (до распада) покоилась.
В силу закона сохранения импульса сумма импульсов обеих об-
образовавшихся в результате распада частиц тоже равна нулю, т.е.
частицы разлетаются с равными и противоположно направлен-
направленными импульсами. Их общее абсолютное значение (обозначим
его ро) определяется законом сохранения энергии
где mi и 7712 — массы частиц, Е\ъш и Е^вн — их внутренние энер-
энергии, а Е"вн — внутренняя энергия первоначальной (распадаю-
(распадающейся) частицы. Обозначим буквой ? «энергию распада», т.е.
разность
? = ?вн " #1bh " #2bh	A6.1)
(очевидно, что эта величина должна быть положительной для
того, чтобы распад был вообще возможен). Тогда имеем
? = d(J_ + J-) = *i-,	A6.2)
2 Vmi ш2/ 2m'	v J
чем и определяется po (га — приведенная масса обеих частиц);
скорости же частиц г>ю = po/mi, г>20 = Ро/т2-

§ 16
РАСПАД ЧАСТИЦ
59
Перейдем теперь к системе отсчета, в которой первичная ча-
частица движется до распада со скоростью V. Эту систему отсчета
обычно называют лабораторной (или л-системой) в противопо-
противоположность «системе центра инерции» (или ц-системе), в кото-
которой полный импульс равен нулю. Рассмотрим одну из распад-
ных частиц и пусть v и vo — ее скорости соответственно в л- и
д-системах. Из очевидного равенства v = V+vo, или v—V = vo,
имеем
v2 + V2 - 2vV cos 6 = vg,	A6.3)
где 6 — угол вылета частицы по отношению к направлению ско-
скорости V. Этим уравнением определяется зависимость скорости
распадной частицы от
направления ее выле-
вылета в л-системе.
Она может быть
представлена графи-
графически с помощью диа-
диаграммы, изображен-
изображенной на рис. 14. Ско-
Скорость v дается векто-
вектором, проведенным в
какую-либо точку окружности радиуса vq х) из точки А, отсто-
отстоящей на расстояние V от центра окружности. Случаям V < vq
и V > vq отвечают соответственно рис. 14 аи б. В первом слу-
случае частица может вылететь под любым углом 6. Во втором же
случае частица может вылететь только вперед, под углом 6, не
превышающим значения 6тах, даваемого равенством
sinemax = ^	A6.4)
(направление касательной к окружности, проведенной из точ-
точки А).
Связь между углами вылета 6 и во в л- и д-системах очевид-
очевидна из той же диаграммы и дается формулой
tge= ^osin0°	A6.5)
&	v0 cos Эо + V	v J
Если решить это уравнение относительно cos6o, то после эле-
элементарных преобразований получим
б) V >v0
Рис. 14
j Точнее — любую точку сферы радиуса vo, диаметральным сечением
которой является изображенная на рис. 14 окружность.

60	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
cos е0 = -— sin2e±coseA/i - ^sin2e. A6.6)
При vq > V связь между G и Go однозначна, как это видно из
рис. 14 а. В формуле A6.6) надо при этом выбрать знак + перед
корнем (так чтобы было Go = 0 при 6 = 0). Если же г>о < V,
то связь между 6 и Go неоднозначна: каждому значению 6 от-
отвечают два значения Go, соответствующие (на рис. 14 6") векто-
векторам vo, проведенным из центра окружности в точки В или С;
им отвечают два знака перед корнем в A6.6).
В физических применениях приходится обычно иметь дело с
распадом не одной, а многих одинаковых частиц, в связи с чем
возникают вопросы о распределении распадных частиц по на-
направлениям, энергиям и т.д. При этом мы будем предполагать,
что первичные частицы ориентированы в пространстве хаоти-
хаотическим, т.е. в среднем изотропным образом.
В д-системе ответ на эти вопросы тривиален: все распадные
частицы (одинакового рода) имеют одинаковую энергию, а их
распределение по направлениям вылета изотропно. Последнее
утверждение связано со сделанным предположением о хаотично-
хаотичности ориентации первичных частиц. Оно означает, что доля числа
частиц, летящих в элементе телесного угла б?оо, пропорциональ-
пропорциональна величине этого элемента, т.е. равна doo/An. Распределение по
углам Go получим отсюда, подставив doo = 27tsinGo сЮо, т.е.
\ sinGodGo.	A6.7)
Распределения в л-системе получаются путем соответствую-
соответствующего преобразования этого выражения. Определим, например,
распределение по кинетической энергии в л-системе. Возводя в
квадрат равенство v = vo + V, находим
v2 = vl + V2 + 2г>0 V cos Go,
откуда
Вводя сюда кинетическую энергию Г = mv2 /2 (где т есть rai
или 7П2, смотря по тому, какого рода распадные частицы мы
рассматриваем) и подставляя в A6.7), получим искомое распре-
распределение
^	A6.8)
v J

§ 16	РАСПАД ЧАСТИЦ	61
Кинетическая энергия может пробегать значения от наименьше-
наименьшего Tmin = (m/2)(vQ — VJ до наибольшего Tmax = (m/2)(vo + VJ.
В этом интервале частицы распределены согласно A6.8) одно-
однородно.
При распаде частицы на более чем две части законы сохра-
сохранения импульса и энергии оставляют, естественно, значитель-
значительно больший произвол в скоростях и направлениях распадных
частиц, чем при распаде на две части. В частности, энергии раз-
разлетающихся частиц в ц- системе отнюдь не имеют одного опреде-
определенного значения. Существует, однако, верхний предел кинети-
кинетической энергии, которую может при этом унести с собой каждая
из распадных частиц.
Для определения этого предела будем рассматривать сово-
совокупность всех распадных частиц за исключением одной задан-
заданной (с массой TTii) как одну систему; ее «внутреннюю» энергию
обозначим через EfBH. Тогда кинетическая энергия частицы rai
будет, согласно A6.1), A6.2), равна
ро М — ггц / rp
(М — масса первичной частицы). Очевидно, что Гю будет иметь
наибольшее возможное значение, когда Евн минимальна. Для
этого надо, чтобы все распадные частицы за исключением ча-
частицы TTii двигались с одной и той же скоростью; тогда Евн
сводится просто к сумме их внутренних энергий, а разность
Е"вн — ?"ibh — Е'вн есть энергия распада ?. Таким образом,
^^-	A6-9)
Задачи
1. Найти связь между углами вылета 0i, 02 (в л-системе) распадных
частиц при распаде на две частицы.
Решение. В д-системе углы вылета обеих частиц связаны посред-
посредством 9ю = 7Г — 020- Обозначая 0ю просто как 0о и применяя формулу
A6.5) к каждой из двух частиц, можно записать:
V	+ v10 cos 0o = v10 sin 0o ctg 0i,
V	— 1J20 cos 0o = ^20 sin 0o ctg 02-
Из этих двух равенств надо исключить 0о- Для этого определяем сначала
из них cos 0о и sin 0o, после чего составляем сумму cos2 0o +sin2 0о = 1. Учи-
Учитывая также, что v\q/v2q = Ш2/Ш1, и используя A6.2), найдем в результате
следующее уравнение:

62	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
— sin2 02 + — sin2 0i - 2 sin 0i sin02 cos@i + 02) =
mi	m2	'
= 7	Z m/2 sin2@i+02).
(mi + m2)V2
2. Найти распределение распадных частиц по направлениям вылета в
л-системе.
Решение. При vo > V подставляем A6.6) со знаком плюс перед
корнем в A6.7) и получаем искомое распределение в виде
у	i-KvytflcoBMl
vo	/l{V2/ZJe\	У	'
При vo < V надо учитывать обе возможные связи 0о с 0. Поскольку при
увеличении 0 одно из соответствующих ему значений 0о растет, а другое
убывает, то надо взять разность (а не сумму) выражений <icos0o с двумя
знаками перед корнем в A6.6). В результате получим
3. Определить интервал значений, которые может иметь угол 0 между
направлениями вылета обеих распадных частиц в л-системе.
Решение. Угол 0 есть сумма 0i + 02 углов, определяющихся фор-
формулой A6.5) (см. задачу 1); проще всего вычисляется тангенс этого угла.
Исследование экстремумов получающегося выражения приводит к следую-
следующим интервалам возможных значений 0 в зависимости от относительной
величины V и ию, ^20 (для определенности полагаем всегда г?20 >
О < 0 < я, если г>ю < V < г>2о;
7Г — 0т < 0 < 7Г, если V < г>ю;
О < 0 < 0т, если V > V20,
причем значение 0т дается формулой
V(v10 + г>20)
sin 0m =
V2
§ 17. Упругие столкновения частиц
Столкновение двух частиц называют упругим, если оно не
сопровождается изменением их внутреннего состояния. Соответ-
Соответственно этому при применении к такому столкновению закона
сохранения энергии можно не учитывать внутренней энергии
частиц.
Проще всего столкновение выглядит в системе отсчета, в ко-
которой центр инерции обеих частиц покоится (д-система); будем
отличать, как и в предыдущем параграфе, индексом 0 значе-
значения величин в этой системе. Скорости частиц до столкновения в

§ 17	УПРУГИЕ СТОЛКНОВЕНИЯ ЧАСТИЦ	63
д-системе связаны с их скоростями vi и V2 в лабораторной си-
системе соотношениями
1712	ТП\
V10 = 	:	V, V20 =	;	V,
7711+7712	7711+7712
где v = vi — V2 (см. A3.2)).
В силу закона сохранения импульса импульсы обеих частиц
остаются после столкновения равными по величине и противо-
противоположными по направлению, а в силу закона сохранения энер-
энергии остаются неизменными и их абсолютные величины. Таким
образом, результат столкновения сводится в д-системе к поворо-
повороту скоростей обеих частиц, остающихся взаимно противополож-
противоположными и неизменными по величине. Если обозначить через по
единичный вектор в направлении скорости частицы rai после
столкновения, то скорости обеих частиц после столкновения (от-
(отличаем их штрихом) будут
/	772-2	1	ТПл	/1 гч л \
v10 =	гто, v2n = —	г>пп.	A7.1)
1и ггц + m2	U	mi+m2	v }
Чтобы возвратиться к лабораторной системе отсчета, надо
добавить к этим выражениям скорость V центра инерции. Та-
Таким образом, для скоростей частиц в л-системе после столкно-
столкновения получаем
1	1712	, TTli Vi + 7712 V2
vl — 	:	^n0 + 	;	,
7711+7712	7711+7712	(~\ 7 9)
I	ТП\	. 7711 Vl + 7712 V2	'
v2 =	¦	г>п0 +	¦	.
7711 + ТП2	7711 + ТП2
Этим исчерпываются сведения, которые можно получить о
столкновении, исходя из одних только законов сохранения им-
импульса и энергии. Что касается направления вектора по, то он
зависит от закона взаимодействия частиц и их взаимного рас-
расположения во время столкновения.
Полученные результаты можно интерпретировать геометри-
геометрически. При этом удобнее перейти от скоростей к импульсам.
Умножив равенства A7.2) соответственно на rai и Ш2, получим
pi = mviiQ + —^—(pi + р2),
771i + ТП2	(	\
(га = raira2/(rai +ГП2) — приведенная масса). Построим окруж-
окружность с радиусом mv и произведем указанное на рис. 15 построе-

64
СТОЛКНОВЕНИЕ ЧАСТИЦ
ГЛ. IV
ние. Если единичный вектор по направлен вдоль ОС, то векторы
АС и С В дают соответственно импульсы р[ и р^. При заданных
Pi и Р2 радиус окружности и положение точек Ал В неизменны,
а точка С может иметь любое положение на окружности.
Рассмотрим подробнее случай, когда одна из частиц (пусть
это будет частица гаг) до столкновения покоилась. В этом случае
длина ОВ =
+ 1712
pi = mv совпадает с радиусом, т.е. точка В
лежит на окружности. Вектор же АВ совпадает с импульсом pi
первой частицы до рассеяния. При этом точка А лежит внутри
(если TTii < ТП2) или вне (если rai > 7712) окружности. Соответ-
Соответствующие диаграммы изображены на рис. 16 а и б. Указанные
на них углы 6i и 62 представляют собой углы отклонения частиц
mi > m2
АО/OB = mi/m2
+ 7712
Рис. 15	Рис. 16
после столкновения по отношению к направлению удара (на-
(направлению pi). Центральный же угол, обозначенный на рисун-
рисунках через х (дающий направление по), представляет собой угол
поворота первой частицы в системе центра инерции. Из рисунка
очевидно, что углы 6i и 02 могут быть выражены через угол х
формулами
tg 6i =
ГП2
A7.4)
+ 1712 COS X	2
Выпишем также формулы, определяющие абсолютные величи-
величины скоростей обеих частиц после столкновения через тот же
угол х-
cosx
mi + 1TI2
sin-.
Ш1 + 7712	2
A7.5)

§ 17	УПРУГИЕ СТОЛКНОВЕНИЯ ЧАСТИЦ	65
Сумма 61 + 62 есть угол разлета частиц после столкновения.
Очевидно, что 6i + 62 > 7t/2 при rai < 7712 и 61 + 62 < 7t/2 при
7711 > ГП2.
Случаю, когда обе частицы после столкновения движутся
по одной прямой («лобовой удар»), соответствует х — тг? т-е-
положение точки С на диаметре слева от точки А (рис. ?? а;
при этом р[ и Р2 взаимно противоположны) или между А л О
(на рис. ?? 5; при этом р^ и р^ направлены в одну сторону).
Скорости частиц после столкновения в этом случае равны
I	1711—1712	I	2ТП\	/1^_^ч
Vi = —	 v, Vo =	—v.	A7.6)
mi + m2	mi + m2
Значение v^ при этом — наибольшее возможное; максимальная
энергия, которую может получить в результате столкновения
первоначально покоившаяся частица, равна, следовательно,
=
(Ш1+Ш2J
A7.7)
^^
где Е\ = —^—^ — первоначальная энергия налетающей частицы.
При TTii < ТП2 скорость первой частицы после столкновения
мож:ет иметь любое направление. Если
же TTii > Ш21 угол отклонения летящей
частицы не может превышать некото-
некоторого максимального значения, соответ-
соответствующего такому положению точки С
(рис. ??б"), при котором прямая АС
касается окружности. Очевидно, что
sin6imax = ОС/О А, или
= !!*..	A7.8)
Ш1	Рис. 17
Особенно просто выглядит столк-
столкновение частиц (из которых одна первоначально покоится) с
одинаковыми массами. В этом случае не только точка В, но и
точка А лежат на окружности (рис. 17). При этом
ei = * е2 = ^,	A7.9)
|, ^ = t;sin|.	A7.10)
Отметим, что частицы разлетаются после столкновения под пря-
прямым углом друг к другу.

66
СТОЛКНОВЕНИЕ ЧАСТИЦ
ГЛ. IV
Задача
Выразить скорости обеих частиц после столкновения движущейся ча-
частицы G7ii) с неподвижной (т2) через их углы отклонения в л-системе.
Решение. Из рис. ?? имеем р'2 = 2-OB-cosQ2 или v'2 = 2v 	 cos 02-
772-2
Для импульса же р[ = АС имеем уравнение
ОС2 = АО2 + р2 - 2АО -р[ cos9i
772-1 H~ 772-2
Отсюда
Tfl\
COS 01 ± 	 \ /772-9 — ш? sln2 01
777,1 4- 777,0 V
I?	772-1 + ГП2	ГГЦ + ГП2
(при TTii > 772-2 перед корнем допустимы оба знака, при 772-2 > тп\ — знак +).
§ 18. Рассеяние частиц
Как было уже указано в предыдущем параграфе, полное
определение результата столкновения двух частиц (определение
угла х) требует решения уравнений движения с учетом конкрет-
конкретного закона взаимодействия частиц.
В соответствии с общим правилом будем рассматривать сна-
сначала эквивалентную задачу об отклонении одной частицы с мас-
массой т в поле U(r) неподвиж-
неподвижного силового центра (распо-
(расположенного в центре инерции
частиц).
Как было указано в § 14,
траектория частицы в цент-
центральном поле симметрична по
отношению к прямой, прове-
проведенной в ближайшую к центру
точку орбиты (ОА на рис. 18).
Поэтому обе асимптоты орби-
орбиты пересекают указанную пря-
прямую под одинаковыми углами.
Если обозначить эти углы через фо, то угол х отклонения части-
частицы при ее пролетании мимо центра есть, как видно из рисунка,
Х=|тг-2фО|.	A8.1)
Рис. 18

§ 18	РАССЕЯНИЕ ЧАСТИЦ	67
Угол же фо определяется, согласно A4.7), интегралом
Фо= Г	{M/r2)dr	A8.2)
* J ^/2т[Е - U(г)] - МУг*'	V '
взятым между ближайшим к центру и бесконечно удаленным
положениями частицы. Напомним, что гт[п является корнем вы-
выражения, стоящего под знаком радикала.
При инфинитном движении, с которым мы имеем здесь дело,
удобно ввести вместо постоянных Е и М другие — скорость Vqq
частицы на бесконечности и так называемое прицельное рассто-
расстояние р. Последнее представляет собой длину перпендикуляра,
опущенного из центра на направление г^, т.е. расстояние, на
котором частица прошла бы мимо центра, если бы силовое поле
отсутствовало (рис. 18). Энергия и момент выражаются через
эти величины согласно
Е=^, M = mpVoo,	A8.3)
а формула A8.2) принимает вид
J s/l-p
Вместе с A8.1) формула A8.4) определяет зависимость х от Р-
В физических применениях приходится обычно иметь дело
не с индивидуальным отклонением частицы, а, как говорят, с
рассеянием целого пучка одинаковых частиц, падающих на рас-
рассеивающий центр с одинаковой скоростью Voo. Различные части-
частицы в пучке обладают различными прицельными расстояниями
и соответственно рассеиваются под различными углами Х- Обо-
Обозначим через dN число частиц, рассеиваемых в единицу времени
на углы, лежащие в интервале между х и х + Ф(- Само по се-
себе это число неудобно для характеристики процесса рассеяния,
так как оно зависит от плотности падающего пучка (пропорци-
(пропорционально ей). Поэтому введем отношение
da = dN/n,	A8.5)
где п — число частиц, проходящих в единицу времени через еди-
единицу площади поперечного сечения пучка (мы предполагаем,
естественно, что пучок однороден по всему своему сечению). Это

68	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
отношение имеет размерность площади и называется эффектив-
эффективным сечением рассеяния. Оно всецело определяется видом рас-
рассеивающего поля и является важнейшей характеристикой про-
процесса рассеяния.
Будем считать, что связь между х и р — взаимно однознач-
однозначна; это так, если угол рассеяния является монотонно убывающей
функцией прицельного расстояния. В таком случае рассеивают-
рассеиваются в заданный интервал углов между х и X + Ф( лишь те части-
частицы, которые летят с прицельным расстоянием в определенном
интервале между р(х) и р(х) + dp(x). Число таких частиц рав-
равно произведению п на площадь кольца между окружностями с
радиусами р и р + dp, т.е. dN = 2npdp • п. Отсюда эффективное
сечение
da = 2np dp.	A8.6)
Чтобы найти зависимость эффективного сечения от угла
рассеяния, достаточно переписать это выражение в виде
X-	A8.7)
Мы пишем здесь абсолютное значение производной dp/dx, имея
в виду, что она может быть отрицательной (как это обычно бы-
бывает) г). Часто относят da не к элементу плоского угла ф(, а
к элементу телесного угла do. Телесный угол между конусами
с углами раствора х и X + Ф( есть do = 2n sin x Ф(- Поэтому
из A8.7) имеем
dp
do.	A8.8)
sinx
Возвращаясь к фактической задаче о рассеянии пучка ча-
частиц не на неподвижном силовом центре, а на других первона-
первоначально покоившихся частицах, мы можем сказать, что формула
A8.7) определяет эффективное сечение в зависимости от угла
рассеяния в системе центра инерции. Для нахождения же эф-
эффективного сечения в зависимости от угла рассеяния 6 в лабора-
лабораторной системе надо выразить в этой формуле х через 6 соглас-
согласно формулам A7.4). При этом получаются выражения как для
сечения рассеяния падающего пучка частиц (х выражено через
6i), так и для частиц, первоначально покоившихся (х выражено
через 62).
) Если функция р(х) многозначна, то надо, очевидно, взять сумму таких
выражений по всем ветвям этой функции.

§ 18	РАССЕЯНИЕ ЧАСТИЦ	69
Задачи
1. Определить эффективное сечение рассеяния частиц от абсолютного
твердого шарика радиуса а (т.е. при законе взаимодействия U = оо при
г < а и U = 0 при г > а).
Решение. Так как вне шарика частица движется свободно, а внутрь
него проникнуть вообще не может, то траектория складывается из двух
прямых, расположенных симметрично относительно радиуса, проведенного
в точку их пересечения с шариком (рис. 19). Как видно из рисунка,
• тг-Х	X
р = a sin (ро = a sin —-— = a cos —.
А	А
Подставляя в A8.7) или A8.8), получаем
do = — sinx dx = -j- do,	A)
т.е. в д-системе рассеяние изотропно. Интегрируя da по всем углам, найдем,
что полное сечение <т = на в соот-
соответствии с тем, что прицельная пло-
площадь, в которую должна попасть час-
частица для того, чтобы вообще рассеять-
рассеяться, есть площадь сечения шарика.
Для перехода к л-системе надо
выразить х через 0i согласно A7.4).
Вычисления полностью аналогичны
произведенным в задаче 2 § 16 (ввиду
формального сходства формул A7.4) и
A6.5)). При тп\ < ГП2 [тп\ — масса ча-
частиц, 777-2 — масса шариков) получим	Рис. 19
dGl = ^ [2=i cose, + 1 + (m'/mi)cos201
4 [ m2	л/l-(ml/ml) sin2
(do\ = 27t sin9i<i9i). Если же Ш2 < mi, то
a2 1 + (ml/ml) cos 29i ,
2 ^-(mfml) sin2 9i
При 777,1 = 777,2 имеем
dGi = a | cos9i| doi,
что можно получить и прямой подстановкой х = 29i (согласно A7.9)) в A).
Для первоначально покоившихся шариков имеем всегда х = тг — 202, и
подстановка в A) дает
d(j2 = а | cos 021 do2.
2. Для того же случая выразить эффективное сечение как функцию
энергии ?, теряемой рассеиваемыми частицами.
Решение. Энергия, теряемая частицей mi, совпадает с энергией,
приобретаемой частицей Ш2. Согласно A7.5) и A7.7) имеем
/	2m1m2 2 . 2 X	• 2 X
e = E=VSm =еяп
()V~Sm 2е—яп 2'
откуда
de = - ?mrf

70
СТОЛКНОВЕНИЕ ЧАСТИЦ
ГЛ. IV
и, подставляя в формулу A) задачи 1, получаем
do = па 	.
Распределение рассеянных частиц по значениям ? оказывается однородным
во всем интервале ? от нуля до ?тах-
3.	Как зависит эффективное сечение от скорости Vqq частиц при рассе-
рассеянии в поле U со г~п?
Решение. Согласно A0.3), если потенциальная энергия есть одно-
однородная функция порядка к = — п, то для подобных траекторий р со у~2^п
или
Р = v^2/n f(x)
(углы отклонения х Для подобных траекторий одинаковы). Подставляя в
A8.6), найдем, что
do со v^4/n do.
4.	Определить эффективное сечение для «падения» частиц в центр по-
поля U = —ос/г2.
Решение. «Падают» в центр те частицы, для которых выполняется
условие 2ос > mp2v2K> (см. A4.11)), т.е. у которых прицельное расстояние
не превышает значения рт&х = л/2ос/ту2К). Поэтому искомое эффективное
сечение
_ 2 _ 27ГСХ
Pmax mvle'
5.	То же в поле U = -ос/гп (п > 2, а > 0).
Решение. Зависимость эффективной потенциальной энергии
mp2v2O0 ос
от г имеет вид, изображенный на рис. 20 с максимальным значением
-тт
«Падают» в центр поля те частицы, у которых Uq < Е. Определяя рп
условия С/о = Е, получаем
= nn(n — 2)
2-п /
2/п
6. Определить эффективное сечение для паде-
падения частиц (с массами mi) на поверхность сфериче-
сферического тела (с массой rri2 и радиусом R), к которой
они притягиваются по закону Ньютона.
Решение. Условие падения заключается в
неравенстве rmin < R, где rmin — ближайшая к цен-
центру сферы точки траектории частицы. Наибольшее
допустимое значение р определяется условием rmin = R, что сводится к
решению уравнения U3^(R) = Е или
рис 20
2R?
ос
R

§ 18	РАССЕЯНИЕ ЧАСТИЦ	71
причем а = утпхтп^ (у — гравитационная постоянная), и мы положили
m « mi, считая, что mi ^> mi. Находя отсюда /?тах5 получаем
При г>оо —> оо эффективное сечение стремится, естественно, к геометриче-
геометрической площади сечения сферы.
7. Восстановить вид рассеивающего поля U(r) по заданной зависимости
эффективного сечения от угла рассеяния при заданной энергии Е\ предпо-
предполагается, что U(r) — монотонно убывающая функция г (поле отталкива-
отталкивания), причем U@) > Е, U(oo) = О (О.Б. Фирсов, 1953).
Решение. Интегрирование d<J по углу рассеяния определяет соглас-
согласно формуле
/
A)
X
квадрат прицельного расстояния, так что функцию р(х) (а с неи и х(р))
тоже можно считать заданной.
Вводим обозначения:
Тогда формулы A8.1), A8.2) запишутся в виде
«о
2
где so (x) — корень уравнения
xw (so) — s0 = 0.
Уравнение C) — интегральное уравнение для функции w(s); его можно
решить методом, аналогичным использованному в § 12. Разделив обе ча-
части C) на у/ос — х и проинтегрировав по dx в пределах от нуля до а, найдем
а	а so(x)
/7t — х(х) dx	Г Г	ds dx
2 у/ос - х ~ J J J(xw2 -s2)(oc-x) ~
0	0 0	V V	/v	/
so (a.) ex	s0 (a)
/Г	dxds	Г ds
J J(xw2 -s2)(ot-x) ~П J ~w*
J(xw2 -s2)(
или, интегрируя по частям в левой части равенства,
so (ос)
[ ds
Пу/оС— / \/о
Полученное соотношение дифференцируем по а, после чего вместо so(cx)
2 / 2
пишем просто s, соответственно чему заменяем ос на s /w ; написав равен-
равенство в дифференциалах, получим

72	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
s2/w2
s2/w2
-ndlnw = d(^) f Щ
Это уравнение интегрируется непосредственно, причем в правой части сле-
следует изменить порядок интегрирования по dx и d(s/w). Учитывая, что при
s = О (т.е. г —»> оо) должно быть ги = 1 (т.е. U = 0), и возвращаясь к
исходным переменным г и р, получим окончательный результат (в двух
эквивалентных формах):
^d4=exp( /	} D)
dp И\	V\ П J /2	22 /	W
гги
Этой формулой определяется в неявном виде зависимость w{r) (а тем са-
самым и U(г)) при всех г > rmin, т.е. в той области значений г, которая
фактически проходится рассеиваемой частицей с заданной энергией Е.
§ 19. Формула Резерфорда
Одно из важнейших применений полученных выше фор-
формул — рассеяние заряженных частиц в кулоновском поле.
Положив в A8.4) U = ос/г и производя элементарное инте-
интегрирование, получим
фо = arccos	~
v +ti
откуда
или, вводя согласно A8.1) фо = (я —х)/2, получаем
Дифференцируя это выражение по х и подставляя в A8.7)
или в A8.8), получаем
2cos(|
ИЛИ

§ 19	ФОРМУЛА РЕЗЕРФОРДА	73
d(T=( « )*-*.	A9.3)
\2mvlb) sin4(|)
Это так называемая формула Резерфорда. Отметим, что эффек-
эффективное сечение не зависит от знака а, так что полученный ре-
результат относится в равной степени к кулоновскому полю оттал-
отталкивания и притяжения.
Формула A9.3) дает эффективное сечение в системе отсче-
отсчета, в которой покоится центр инерции сталкивающихся частиц.
Преобразование к лабораторной системе производится с по-
помощью формул A7.4). Для частиц, первоначально покоившихся,
подставляя х — тг — 202 в A9.2), получим
-d92= (^VJ -**-. A9.4)
Э2	V mvlv ) cos3 02
Для падающих же частиц преобразование приводит в общем
случае к весьма громоздкой формуле. Отметим лишь два част-
частных случая.
Если масса rri2 рассеивающей частицы велика по сравнению
с массой TTii рассеиваемой частицы, то х ~ 01? а ш ~ ШЪ так
что
("¦»)
где Е\ = miv^/2 — энергия падающей частицы.
Если массы обеих частиц одинаковы (rai = 7712, т = rai/2),
то, согласноA7.9), х — 201 и подстановка в A9.2) дает
т	о ( а A2 COS 0i 7п	( «:\2 COS 0i ,	(лс\а\
d<j\ = 27Г [ — ) —о— с?01 =т^ —а— doi.	A9.6)
КЕг) sin3 01	V^i/ sin4 0i	v J
Если не только массы обеих частиц равны, но эти частицы во-
вообще тождественны, то не имеет смысла различать после рас-
рассеяния первоначально двигавшиеся частицы от первоначально
покоившихся частиц. Общее эффективное сечение для всех ча-
частиц мы получим, складывая ddi и dd2 и заменяя 6i и 62 общим
значением 6:
dG= (^)V ^ +^_) cosGdo.	A9.7)
\Ег/ Vsm40 cos40/	V ;
Вернемся снова к общей формуле A9.2) и определим с ее по-
помощью распределение рассеянных частиц по отношению к теря-
теряемой ими в результате столкновения энергии. При произвольном

74	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
соотношении между массами рассеиваемой (mi) и рассеиваю-
рассеивающей (тг) частиц, приобретаемая последней скорость выражает-
выражается через угол рассеяния в д-системе следующим соотношением:
v2 = 	¦	Уж sin ^
(см. A7.5)). Соответственно, приобретаемая этой частицей, а тем
самым и теряемая частицей rai энергия равна
_ m2v'l _ 2m* 2 -2 X
?~ 2 " m2 Vo°Sm 2 е
Выразив отсюда sin (х/2) через ? и подставив в A9.2), получаем
^^.	A9.8)
Эта формула отвечает на поставленный вопрос, определяя эф-
эффективное сечение как функцию от потери энергии е; последняя
пробегает при этом значения от нуля до ?max = 2m2v^G/m2.
Задачи
1. Найти эффективное сечение рассеяния в поле U = ос/г2 (ос > 0).
Решение. Угол отклонения:
Эффективное сечение
2. Найти эффективное сечение рассеяния сферической «потенциальной
ямой» радиуса а и «глубины» С/о (т.е. полем С/ = 0 при г > a, С/ = —С/о при
г < а).
Решение. Прямолинейная траектория частицы «преломляется»
при входе в яму и при выходе из нее. Согласно
задаче к § 7 углы падения ос и преломления C
(рис. 21) связаны соотношением
sin а	Г~~ 2 С/о
= 71, 71=4/1+—^.
sin C
Угол отклонения х = 2(а—C). Поэтому имеем
Рис. 21	sin(a-x/2) = ^ х _ ^ х = I
sin а	2	2 п
Исключив ос из этого равенства и очевидного из рисунка соотношения
a sin ос = р,
получим связь между р и х в виде

20	РАССЕЯНИЕ ПОД МАЛЫМИ УГЛАМИ	75
Наконец, дифференцируя это равенство, получим эффективное сечение
4cos
(|)
Угол х меняется в пределах от нуля (при р = 0) до значения Хтах (ПРИ
р = а), определяемого из
2 ) п
Полное эффективное сечение, получающееся интегрированием da по
всем углам внутри конуса х < Хшахэ равно, разумеется, площади геометри-
геометрического сечения па2.
§ 20. Рассеяние под малыми углами
Вычисление эффективного сечения значительно упрощает-
упрощается, если рассматривать лишь те столкновения, которые проис-
происходят на больших прицельных расстояниях, где поле U являет-
является слабым, так что углы отклонения соответственно малы. При
этом вычисление можно производить сразу в лабораторной си-
системе отсчета, не вводя систему центра инерции.
Выберем ось х по направлению первоначального импульса
рассеиваемых частиц (частицы mi), а плоскость ху — в плоскос-
плоскости рассеяния. Обозначив через р^ импульс частицы после рас-
рассеяния, имеем очевидное равенство
Pi
Для малых отклонений можно приближенно заменить si
на 61, а в знаменателе — заменить р[ первоначальным импуль-
импульсом pi = miVoo'.
B0.1)
Далее, поскольку ру = Fy, то полное приращение импульса
вдоль оси у
оо
p'ly= I Fvdt.	B0.2)
— ОО
При этом сила

76	СТОЛКНОВЕНИЕ ЧАСТИЦ	ГЛ. IV
F _ _д? _ _d? dr _ _d?y
у	ду	dr ду	dr r
Поскольку интеграл B0.2) уже содержит малую величину С/,
то при его вычислении можно в том же приближении считать,
что частица вовсе не отклоняется от своего первоначального пу-
пути, т.е. движется прямолинейно (вдоль прямой у = р) и равно-
равномерно (со скоростью Уж). Соответственно этому полагаем в B0.2)
и получаем
F = - — Я dt= —
у	dr г'	г^оо
1 	 р I dU dx
Наконец, от интегрирования по dx перейдем к интегрирова-
интегрированию по dr. Поскольку для прямолинейного пути г2 = х2 + р2,
то при изменении х от —ос до + ос г изменяется от ос до р и
затем снова до ос. Поэтому интеграл по dx перейдет в двойной
интеграл по dr от р до ос, причем dx заменяется на
j	r dr
dx =
Окончательно получим для угла рассеяния B0.1) следующее
выражение х):
01 = -Й f ?
rmv^ j dr ^/r2 - p2
0
чем и определяется искомая зависимость 6i от р при слабом от-
отклонении. Эффективное сечение рассеяния (в л-системе) полу-
получается по такой же формуле, как A8.8) (с Q\ вместо хM причем
sin6i можно и здесь заменить на 9i:
dp
da =
B0.4)
x) Если произвести весь изложенный вывод в д-системе, то мы получим
для х такое выражение с т вместо т\ в соответствии с тем, что малые
углы 0i и х должны быть связаны, согласно A7.4), соотношением
777-1 Н~

20
РАССЕЯНИЕ ПОД МАЛЫМИ УГЛАМИ
77
Задачи
1. Получить формулу B0.3) из формулы A8.4).
Решение. С целью избежать ниже фиктивно расходящихся инте-
интегралов, представим формулу A8.4) в виде
R
Фо
д f [ р2
dp J у г2
2U
причем в качестве верхнего предела пишем большую конечную величину R,
имея в виду перейти затем к пределу R —»¦ оо. Ввиду малости U разлагаем
корень по степеням U, а 7"min заменяем приближенно на р:
pdr	д_ 7 U(r) dr
Фо =
/
Первый интеграл после перехода к пределу R —>- оо дает п/ 2. Второй же
интеграл предварительно преобразуем по частям и получаем выражение
dr
; = тг-2фо = 2 —
р	р
эквивалентное формуле B0.3).
2. Определить эффективное сечение рассеяния на малые углы в поле
U =
иФ/ Согласно B0.3) имеем:
2 рот Г
rmv2 /
dr
r-n+1
/г2 - р2
Подстановкой р2 /г2 = и интеграл приводится к В-интегралу Эйлера и
выражается через Г-функции
г B+1
V 2
Г -
Выраж:ая отсюда р через 0i и подставляя в B0.4), получим
do = —
п
¦(з)
2/п

ГЛАВА V
МАЛЫЕ КОЛЕБАНИЯ
§ 21. Свободные одномерные колебания
Очень распространенный тип движения механических си-
систем представляют собой так называемые малые колебания, ко-
которые система совершает вблизи своего положения устойчивого
равновесия. Рассмотрение этих движений мы начнем с наиболее
простого случая, когда система имеет всего одну степень свободы.
Устойчивому равновесию соответствует такое положение
системы, в котором ее потенциальная энергия U(q) имеет ми-
минимум; отклонение от такого положения приводит к возник-
возникновению силы —dU/dq, стремящейся вернуть систему обратно.
Обозначим соответствующее значение обобщенной координаты
через до- При малых отклонениях от положения равновесия в
разложении разности U(q) — U(qo) по степеням q — qo достаточно
сохранить первый неисчезающий член. В общем случае таковым
является член второго порядка
где к — положительный коэффициент (значение второй произ-
производной Uff(q) при q = qo). Будем в дальнейшем отсчитывать
потенциальную энергию от ее минимального значения (т.е. по-
положим U(qo) = 0) и введем обозначение
x = q-q0	B1.1)
для отклонения координаты от ее равновесного значения. Таким
образом,
Щх) = Щ-.	B1.2)
Кинетическая энергия системы с одной степенью свободы
имеет в общем случае вид
\a{q)f = \a{q)x\
В том же приближении достаточно заменить функцию a(q) про-

§ 21	СВОБОДНЫЕ ОДНОМЕРНЫЕ КОЛЕБАНИЯ	79
сто ее значением при q = q$. Вводя для краткости обозначение г)
a(q0) = га,
получим окончательно следующее выражение для лагранжевой
функции системы, совершающей одномерные малые колебания 2):
г _ тх2 кх2	/О1 Qx
Соответствующее этой функции уравнение движения гласит:
тх + кх = 0,	B1.4)
или
х + аJх = 0,	B1.5)
где введено обозначение
ш = у/к/т.	B1.6)
Два независимых решения линейного дифференциального урав-
уравнения B1.5): cos cut и sin cut, так что его общее решение
х — с\ cos cut + С2 sin cut.	B1-7)
Это выражение может быть написано также и в виде
х = a cos (cut + ос).	B1.8)
Поскольку cos (cut + ос) = cos cut • cos ос — sin cut • sin а, сравнение с
B1.7) показывает, что произвольные постоянные а л ос связаны
с постоянными с\ и С2 соотношениями
tg a=-c2/ci.	B1.9)
Таким образом, вблизи положения устойчивого равновесия
система совершает гармоническое колебательное движение. Ко-
Коэффициент а при периодическом множителе в B1.8) называется
амплитудой колебаний, а аргумент косинуса — их фазой] ос есть
начальное значение фазы, зависящее, очевидно, от выбора нача-
начала отсчета времени. Величина си называется циклической часто-
частотой колебаний; в теоретической физике, впрочем, ее называют
обычно просто частотой, что мы и будем делать в дальнейшем.
Частота является основной характеристикой колебаний, не
зависящей от начальных условий движения. Согласно формуле
B1.6) она всецело определяется свойствами механической систе-
системы как таковой. Подчеркнем, однако, что это свойство часто-
) Подчеркнем, однако, что величина т совпадает с массой только в
случае, если х есть декартова координата частицы!
2) Такую систему часто называют одномерным осциллятором.

80	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
ты связано с предполагаемой малостью колебаний и исчезает
при переходе к более высоким приближениям. С математиче-
математической точки зрения оно связано с квадратичной зависимостью
потенциальной энергии от координаты х).
Энергия системы, совершающей малые колебания, есть
или, подставив сюда B1.8):
Е= irawV.	B1.10)
Она пропорциональна квадрату амплитуды колебаний.
Зависимость координаты колеблющейся системы от времени
часто оказывается удобным представлять в виде вещественной
части комплексного выражения
x = Re{Aeiwt},	B1.11)
где А — комплексная постоянная; написав ее в виде
A = aeioc,	B1.12)
мы вернемся к выражению B1.8). Постоянную А называют ком-
комплексной амплитудой] ее модуль совпадает с обычной амплиту-
амплитудой, а аргумент — с начальной фазой.
Оперирование с экспоненциальными множителями в мате-
математическом отношении проще, чем с тригонометрическими, так
как дифференцирование не меняет их вида. При этом, пока мы
производим лишь линейные операции (сложение, умножение на
постоянные коэффициенты, дифференцирование, интегрирова-
интегрирование), можно вообще опускать знак взятия вещественной части,
переходя к последней лишь в окончательном результате вычис-
вычислений.
Задачи
1. Выразить амплитуду и начальную фазу колебаний через начальные
значения хо и vo координаты и скорости.
Ответ:
си2	о
2. Найти отношение частот си и си7 колебаний двух двухатомных моле-
молекул, состоящих из атомов различных изотопов; массы атомов равны соот-
соответственно 77ii, ТП2 и mi, m2-
г) Оно не имеет поэтому места, если у функции U(x) при х = 0 минимум
более высокого порядка, т.е. U ел жп, п > 2 (см. задачу 2а § 11).

§21
СВОБОДНЫЕ ОДНОМЕРНЫЕ КОЛЕБАНИЯ
81
Решение. Поскольку атомы изотопов взаимодействуют одинако-
одинаковым образом, то к = к'. Роль же коэффициентов т в кинетических энергиях
молекул играют их приведенные массы. Соглас-
Согласно B1.6) находим поэтому:
I	~ "	~~~
CU	17111712A71! + т2)
си у m'1m2(mi + т2)
3. Найти частоту колебаний точки с массой
т, способной двигаться по прямой и прикреплен-
прикрепленной к пружине, другой конец которой закреплен
в точке А (рис. 22) на расстоянии / от прямой.
Пружина, имея длину /, натянута с силой F.
Решение. Потенциальная энергия пру-
пружины (с точностью до малых величин высшего
т х
Рис. 22
порядка) равна произведению силы F на удлинение 6/ пружины. При х
Ы =
- I « х2/B1),
так что U = Fx2 /B1). Поскольку кинетическая энергия есть тх2 /2 , то
4. То же, если точка т движется по окружности радиуса г (рис. 23).
Решение. В этом случае удлинение пружины (при ф < 1)
6/ = s/r2 + (I + гJ - 2гA + г) cos <р - I
Кинетическая энергия Т = A/2)тг2ф2. Отсюда частота
5. Найти частоту колебаний изображенного на рис. 2 маятника, точ-
точка подвеса которого (с массой mi в ней) способна совершать движение
в горизонтальном направлении.
Решение. При (р < 1 из полученной в зада-
задаче 3 § 14 формулы находим
Т =
Отсюда
+m2)
Ф
си =
mi/
У//////,
Рис. 23
6. Определить форму кривой, при качании вдоль ко-
которой (в поле тяжести) частота колебаний не зависит от
амплитуды.
Решение. Поставленному условию будет удов-
удовлетворять такая кривая, при движении вдоль которой потенциальная энер-
энергия частицы будет U = ks /2, где s — длина дуги, отсчитываемая от поло-
положения равновесия; при этом кинетическая энергия Т = m's2/2 (m — масса

82	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
частицы) и частота колебаний будет си = yjk/m вне зависимости от на-
начального значения s.
Но в поле тяжести U = mgy, где у — вертикальная координата. Поэтому
имеем: ks2/2 = mgy или
си2 2
y = s
С другой стороны, ds2 = dx2 + dy2, откуда
Интегрирование удобно произвести, сделав подстановку
у= zt^1-00^)-
Тогда получим
Эти два равенства определяют в параметрическом виде уравнение искомой
кривой; она представляет собой циклоиду.
§ 22. Вынужденные колебания
Перейдем к рассмотрению колебаний в системе, на которую
действует некоторое переменное внешнее поле; такие колеба-
колебания называют вынужденными в отличие от рассмотренных в
предыдущем параграфе так называемых свободных колебаний.
Поскольку колебания предполагаются по-прежнему малыми, то
тем самым подразумевается, что внешнее поле достаточно сла-
слабо, в противном случае оно могло бы вызвать слишком большое
смещение х.
В этом случае наряду с собственной потенциальной энергией
A/2) кх2 система обладает еще потенциальной энергией Ue(x, ?),
связанной с действием внешнего поля. Разлагая этот дополни-
дополнительный член в ряд по степеням малой величины ж, получим
Ue(x,t)*Ue@,t) + x^ .
Ох х—о
Первый член является функцией только от времени и потому
может быть опущен в лагранжевой функции (как полная про-
производная по t от некоторой другой функции времени). Во втором
члене —dUe/dx есть внешняя «сила», действующая на систему
в положении равновесия и являющаяся заданной функцией вре-
времени; обозначим ее как F(t). Таким образом, в потенциальной
энергии появляется член —xF(t), так что функция Лагранжа
системы будет

§ 22	ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ	83
B2.1)
Соответствующее уравнение движения есть
тх + кх = F(t),
или
х + ш2х= —F(t),	B2.2)
777/
где мы снова ввели частоту си свободных колебаний.
Как известно, общее решение неоднородного линейного диф-
дифференциального уравнения с постоянными коэффициентами по-
получается в виде суммы двух выражений: х = х$ + х\, где хо —
общее решение однородного уравнения, а х\ — частный инте-
интеграл неоднородного уравнения. В данном случае xq представ-
представляет собой рассмотренные в предыдущем параграфе свободные
колебания.
Рассмотрим имеющий особый интерес случай, когда вынуж-
вынуждающая сила тоже является простой периодической функцией
времени с некоторой частотой у:
F(t) = /cos(yt + |3).	B2.3)
Частный интеграл уравнения B2.2) ищем в виде х\ = Ъ cos(yt +
+ C) с тем же периодическим множителем. Подстановка в урав-
уравнение дает: Ъ = //[га(си2 — у2)]; прибавляя решение однородного
уравнения, получим общий интеграл в виде
х = a cos (cut + ос) + , /—^ cos Ы + 6).	B2.4)
4	у т(ш2 -у2)
Произвольные постоянные а и ос определяются из начальных
условий.
Таким образом, под действием периодической вынуждающей
силы система совершает движение, представляющее собой сово-
совокупность двух колебаний — с собственной частотой системы со
и с частотой вынуждающей силы у.
Решение B2.4) неприменимо в случае так называемого резо-
резонанса, когда частота вынуждающей силы совпадает с собствен-
собственной частотой системы. Для нахождения общего решения урав-
уравнения движения в этом случае перепишем выражение B2.4) с
соответствующим переобозначением постоянных в виде
х = acos (cut + ос) + , ;—^t[cos (yt + C) - cos (cut + CI.
v	y m(cu2 — y2)
При у —)> cu второй член дает неопределенность вида 0/0. Рас-

84	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
крывая ее по правилу Лопиталя, получим
х = a cos (cot + ос) + -^—?sin(cu? + 6).	B2.5)
Таким образом, в случае резонанса амплитуда колебаний растет
линейно со временем (до тех пор, пока колебания не перестанут
быть малыми и вся излагаемая теория перестанет быть приме-
применимой) .
Выясним еще, как выглядят малые колебания вблизи резо-
резонанса, когда у = а) + е, где ? — малая величина. Представим
общее решение в комплексном виде, как
х = Aeia)t + Ве*(ш+?)* = (А + Веш)е*ш*.	B2.6)
Так как величина А + Beizt мало меняется в течение периода
2п/ш множителя егш*, то движение вблизи резонанса можно
рассматривать как малые колебания, но с переменной ампли-
амплитудой х).
Обозначив последнюю через С, имеем
С= \А + Веш\.
Представив Ал В соответственно в виде аегос и Ьег^, получим
С2 = а2 + Ъ2 + 2abcos (U + C - ос).	B2.7)
Таким образом, амплитуда колеблется периодически с часто-
частотой г, меняясь между двумя пределами
\а-Ъ\ ^ С ^ а + Ъ.
Это явление носит название биений.
Уравнение движения B2.2) может быть проинтегрировано и
в общем виде при произвольной вынуждающей силе F(t). Это
легко сделать, переписав его предварительно в виде
— (х + icvx) — icv(x + icvx) = — Fit)
dty	;	v	; m v ;
или
§l	B2.8)
где введена комплексная величина
l = x + iujx.	B2.9)
Уравнение B2.8) уже не второго, а первого порядка. Без правой
части его решением было бы ?, = Аегшг с постоянной А. Следуя
общему правилу, ищем решение неоднородного уравнения в виде
?, = A(t)eia)t и для функции A(t) получаем уравнение
Меняется также «постоянный» член в фазе колебаний.

§22
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
85
Интегрируя его, получим решение уравнения B2.8) в виде
t
i Г ±
о
B2.10)
где постоянная интегрирования ?,о выбрана так, чтобы представ-
представлять собой значение ?, в момент времени t = 0. Это и есть иско-
искомое общее решение; функция x(t) дается мнимой частью выра-
выражения B2.10) (деленной на си) 1).
Энергия системы, совершающей вынужденные колебания,
разумеется, не сохраняется; система приобретает энергию за
счет источника внешней силы. Определим полную энергию, пе-
передаваемую системе за все время действия силы (от — ос до + ос),
предполагая начальную энергию равной нулю. Согласно форму-
формуле B2.10) (с нижним пределом интегрирования —ос вместо нуля
и с ?, (—ос) = 0) имеем при t —»> ос:
|фо)|2 = ?
,—iuot
dt
С другой стороны, энергия системы как таковой дается выра-
выражением
Е — —(х2 + оJх2) = — l?l2	f22 111
Подставив сюда |?,(ос)|2, получим искомую передачу энергии в
виде
2
Е =
2т
^—iwt
dt
B2.12)
она определяется квадратом модуля компоненты Фурье силы
F(t) с частотой, равной собственной частоте системы.
В частности, если внешняя сила действует лишь в течение
короткого промежутка времени (малого по сравнению с 1/со),
то можно положить e~ia)t « 1. Тогда
= _W / F(t)dt) .
г) При этом, разумеется, сила F(t) должна быть написана в веществен-
вещественном виде.

86	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
Этот результат заранее очевиден: он выражает собой тот факт,
что кратковременная сила сообщает системе импульс f F dt, не
успев за это время произвести заметного смещения.
Задачи
1. Определить вынужденные колебания системы под влиянием силы
F(t), если в начальный момент t = О система покоится в положении равно-
равновесия {х = 0, х = 0), для случаев:
а)	F = const = Fq.
Fq
Ответ: х = 	-A — cos cot): действие постоянной силы приводит к
mcu2 v
смещению положения равновесия, вокруг которого происходят колебания.
б)	F = at
Ответ: х = 	т(си? — sin cut).
mcu3
b)F = F~^.
Ответ: х =
г) F = F0e
Ответ:
—-—r-^	— (e a* — cos cut H	sin cut).
m(cu2 + a2) V	cu	/
(X2	2	2\	— at r/ 2	2	2\
+ —(cu +a +C )sincut + e [(cu + a — C ) cos Ct — 2aC
cu
(при решении удобно писать силу в комплексном виде F = Foe
2. Определить конечную амплитуду колеба-
колебаний системы после действия внешней силы, меняю-
меняющейся по закону F = 0 при t < О, F = Fot/T при
О < ? < Т, F = Fq при t > Т (рис. 24); до момента
? = 0 система покоится в положении равновесия.
Решение. В интервале времени 0 < t < Т	j
колебания, удовлетворяющие начальному условию,
имеют вид
При t > Т ищем решение в виде
F
х = а cos [w(t - Т)] + с2 sin [w(t - Т)] -\	^г
mcu2
Из условий непрерывности х и х при t = Т находим
тТси3
При этом амплитуда колебаний
2F0 . cuT
mTc^Sm^"-
Отметим, что она тем меньше, чем медленнее «включается» сила Fo (т.е.
чем больше Т).

§ 23 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ 87
3. То же в случае постоянной силы i*o, действующей в течение ограни-
ограниченного времени Т (рис. 25).
Решение можно найти как и в задаче 2, но еще проще восполь-
воспользоваться формулой B2.10). При t > Т имеем свободные колебания вокруг
положения х = 0; при этом
т
ГО icvt I —icvt j,	rO /1	— icvT\ icvt
—e / e at = 	A-е )e ;
m	J	iwm
m
о
квадрат же модуля ?, дает амплитуду согласно формуле |?,|2 = а2со2. В ре-
результате находим
0
-t	0
ОТ	ОТ
Рис. 25	Рис. 26	Рис. 27
2F0 . шТ
а = 	-sin-—.
mw2	2
4. То же в случае силы, действующей в течение времени от нуля до Т
по закону F = Fot/T (рис. 26).
Решение. Тем же способом получим
гр
а	°
Tmw3
5. To же в случае силы, меняющейся в течение времени от нуля до
Т = 2л/w по закону F = Fo sin cut (рис. 27).
Решение. Подставив в B2.10)
F(t) =F0smo)t= ^(eiu)t - e~ia)t)
2г
и проинтегрировав от нуля до Т, получим
Fon
а = 	w-
§ 23. Колебания систем со многими степенями свободы
Теория свободных колебаний систем с несколькими (s) степе-
степенями свободы строится аналогично тому, как были рассмотрены
в § 21 одномерные колебания.
Пусть потенциальная энергия системы U как функция обоб-
обобщенных координат qi(i = 1, 2,..., s) имеет минимум при qi = q^.
Вводя малые смещения
Xi = qi- qi0	B3.1)

88	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
и разлагая по ним U с точностью до членов второго порядка,
получим потенциальную энергию в виде положительно опреде-
определенной квадратичной формы
YkXiXk,	B3.2)
где мы снова отсчитываем потенциальную энергию от ее мини-
минимального значения. Поскольку коэффициенты к{к и кк{ входят в
B3.2) умноженными на одну и ту же величину Х{Хк, то ясно, что
их можно всегда считать симметричными по своим индексам:
В кинетической же энергии, которая имеет в общем случае вид
2 $^ агк Ы)Ык
%,к
(см. E.5)), полагаем в коэффициентах qi = <^о и> обозначая по-
постоянные CLik{<lo) через га^, получаем ее в виде положительно
определенной квадратичной формы
B3.3)
Коэффициенты тп{к тоже мож:но всегда считать симметричными
по индексам
Таким образом, лагранжева функция системы, совершающей
свободные малые колебания, имеет вид
L = - ^2 (™>ikXiXk - kikxixk).	B3.4)
i,k
Составим теперь уравнения движения. Для определения вхо-
входящих в них производных напишем полный дифференциал функ-
функции Лагранжа
^^ (mXi dxk + mikxk dxi - kikXi dxk - kikxk dxi).
Поскольку величина суммы не зависит, разумеется, от обозначе-
обозначения индексов суммирования, меняем в первом и третьем членах
в скобках i на fc, a fc на г; учитывая при этом симметричность
коэффициентов га^ и к{к, получим
dL =

§ 23 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ 89
Отсюда видно, что
— =^mikxk, ^ =
к
Поэтому уравнения Лагранжа
к	к
Они представляют собой систему s (г = 1,2,.. . ,s) линейных
однородных дифференциальных уравнений с постоянными ко-
коэффициентами.
По общим правилам решения таких уравнений ищем s неиз-
неизвестных функций xk(t) в виде
хк = Akeiwt,	B3.6)
где А к — некоторые, пока неопределенные, постоянные. Под-
Подставляя B3.6) в систему B3.5), получаем по сокращении на ега>г
систему линейных однородных алгебраических уравнений, ко-
которым должны удовлетворять постоянные Ак:
53 (-cv2mik + kik)Ak = 0.	B3.7)
к
Для того чтобы эта система имела отличные от нуля реше-
решения, должен обращаться в нуль ее определитель
\kik - aJmik\ = 0.	B3.8)
Уравнение B3.8) — так называемое характеристическое урав-
уравнение — представляет собой уравнение степени s относитель-
относительно си2. Оно имеет в общем случае s различных вещественных
положительных корней си^., ос = 1,2,..., s (в частных случа-
случаях некоторые из этих корней могут совпадать). Определенные
таким образом величины сиа называются собственными часто-
частотами системы.
Вещественность и положительность корней уравнения B3.8)
заранее очевидны уже из физических соображений. Действи-
Действительно, наличие у си мнимой части означало бы наличие во
временной зависимости координат хк B3.6) (а с ними и ско-
скоростей хк) экспоненциально убывающего или экспоненциаль-
экспоненциально возрастающего множителя. Но наличие такого множителя
в данном случае недопустимо, так как оно привело бы к изме-
изменению со временем полной энергии Е = U + T системы в проти-
противоречии с законом ее сохранения.

90	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
В том же самом можно убедиться и чисто математическим
путем. Умножив уравнение B3.7) на А* и просуммировав затем
по г, получим
^2 (-w2mik + kik)A*Ak = 0,
i,k
откуда
2=
Квадратичные формы в числителе и знаменателе этого выра-
выражения вещественны в силу вещественности и симметричности
коэффициентов к{к и га^; действительно,
ik
— / ^kjkAjAk = у kkjAjAk = /
Они также существенно положительны, а потому положитель-
положительно х) и си2. После того как частоты сиа найдены, подставляя
каждое из них в уравнения B3.7), можно найти соответствую-
соответствующие значения коэффициентов Ак. Если все корни сиа характе-
характеристического уравнения различны, то, как известно, коэффици-
коэффициенты Ак пропорциональны минорам определителя B3.8), в ко-
котором а) заменена соответствующим значением сиа; обозначим
эти миноры через Акос. Частное решение системы дифференци-
дифференциальных уравнений B3.5) имеет, следовательно, вид
хк =
где Сое — произвольная (комплексная) постоянная.
Общее же решение дается суммой всех s частных решений.
Переходя к вещественной части, напишем его в виде
S
хк = Re {?) AfcaCaeiaJ«*} = J>fcaea,	B3.9)
(Х=1	ОС
где мы ввели обозначение
^*}.	B3.10)
г) Положительная определенность квадратичной формы, построенной
на коэффициентах kik, очевидна из их определения в B3.2) для веществен-
вещественных значений переменных. Но если написать комплексные величины Ak в
явном виде как ak -\-ibk, то мы получим (снова в силу симметричности kik):
^2kikA*Ak = ^2kik(ai - ibi)(ak + ibk) = *^2,	^
i,k	i,k	i,k
т.е. сумму двух положительно определенных форм.

§ 23 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ 91
Таким образом, изменение каждой из координат системы со
временем представляет собой наложение s простых периодиче-
периодических колебаний @i, ©2, ..., @s с произвольными амплитудами
и фазами, но имеющих вполне определенные частоты.
Естественно возникает вопрос, нельзя ли выбрать обобщен-
обобщенные координаты таким образом, чтобы каждая из них совершала
только одно простое колебание? Тамая форма общего интеграла
B3.9) указывает путь к решению этой задачи.
В самом деле, рассматривая s соотношений B3.9) как си-
систему уравнений с s неизвестными величинами ©а, мы можем,
разрешив эту систему, выразить величины ©i, ©2,..., @s через
координаты Ж1, Ж2Г .., xs. Следовательно, величины ©а можно
рассматривать как новые обобщенные координаты. Эти коорди-
координаты называют нормальными (или главными), а совершаемые
ими простые периодические колебания — нормальными колеба-
колебаниями системы.
Нормальные координаты ©а удовлетворяют, как это явству-
явствует из их определения, уравнениям
ё« + ш2явЛ = 0.	B3.11)
Это значит, что в нормальных координатах уравнения движения
распадаются на s независимых друг от друга уравнений. Ускоре-
Ускорение каждой нормальной координаты зависит только от значения
этой координаты, и для полного определения ее временной за-
зависимости надо знать начальные значения только ее же самой
и соответствующей ей скорости. Другими словами, нормальные
колебания системы полностью независимы.
Из сказанного очевидно, что функция Лагранжа, выражен-
выраженная через нормальные координаты, распадается на сумму выра-
выражений, каждое из которых соответствует одномерному колеба-
колебанию с одной из частот сиа, т.е. имеет вид
(в2а-ш2ав2а),	B3.12)
где та — положительные постоянные. С математической точ-
точки зрения это означает, что преобразованием B3.9) обе квадра-
квадратичные формы — кинетическая энергия B3.3) и потенциальная
B3.2) — одновременно приводятся к диагональному виду.
Обычно нормальные координаты выбирают таким образом,
чтобы коэффициенты при квадратах скоростей в функции Лаг-
Лагранжа были равны 1/2. Для этого достаточно определить нор-

92	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
мальные координаты (обозначим их теперь через Qa) равенствами
QOi = д/щ^ва.	B3.13)
Тогда
ос
Все изложенное мало меняется в случае, когда среди корней
характеристического уравнения имеются кратные корни. Об-
Общий вид B3.9), B3.10) интеграла уравнений движений остается
таким же (с тем же числом s членов) с той лишь разницей, что
соответствующие кратным частотам коэффициенты Д/-^ уже не
являются минорами определителя, которые, как известно, обра-
обращаются в этом случае в нуль х).
Каждой кратной (или, как говорят, вырожденной) часто-
частоте отвечает столько различных нормальных координат, како-
какова степень кратности, но выбор этих нормальных координат не
однозначен. Поскольку в кинетическую и потенциальную энер-
энергии нормальные координаты (с одинаковым ша) входят в виде
одинаково преобразующихся сумм $^ Q\ и ^2 Q^., то их можно
подвергнуть любому линейному преобразованию, оставляюще-
оставляющему инвариантной сумму квадратов.
Весьма просто нахождение нормальных координат для трех-
трехмерных колебаний одной материальной точки, находящейся в
постоянном внешнем поле. Помещая начало декартовой системы
координат в точку минимума потенциальной энергии U(x,y, z),
мы получим последнюю в виде квадратичной формы перемен-
переменных ж, у, z, а кинетическая энергия
Т =%& + ? + !?)
(га — масса частиц) не зависит от выбора направления коор-
координатных осей. Поэтому соответствующим поворотом осей надо
только привести к диагональному виду потенциальную энергию.
Тогда	.,
L = у (ж2 + у2 + z2) - \{к1Х2 + к2у2 + ksz2),	B3.14)
и колебания вдоль осей ж, у, z являются главными с частотами
CU3 =
г) Невозможность возникновения в общем интеграле членов, содержа-
содержащих наряду с экспоненциальными также и степенные временные множи-
множители, очевидна из тех же физических соображений, которые исключают
существование комплексных «частот»; наличие таких членов противоречи-
противоречило бы закону сохранения энергии.

§ 23 КОЛЕБАНИЯ СИСТЕМ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ 93
В частном случае центрально-симметричного поля {к\ = &2 =
= кз = к, U = кг2/2) эти три частоты совпадают (см. задачу 3).
Использование нормальных координат дает возможность
привести задачу о вынужденных колебаниях системы с несколь-
несколькими степенями свободы к задачам об одномерных вынужден-
вынужденных колебаниях. Функция Лагранжа системы с учетом дейст-
действующих на нее переменных внешних сил имеет вид
L = L0+^2Fk(t)xk,	B3.15)
к
где Lq — лагранжева функция свободных колебаний. Вводя вме-
вместо координат Хк нормальные координаты, получим
L = \ Е (<й - ш1<&)
ос
где введено обозначение
к
Соответственно уравнения движения
Qoc + colQoc = foc(t)	B3.17)
будут содержать лишь по одной неизвестной функции Qoc(t)-
Задачи
1. Определить колебания системы с двумя степенями свободы, если ее
функция Лагранжа
(две одинаковые одномерные системы с собственной частотой сио, связан-
связанные взаимодействием —осху).
Решение. Уравнения движения
х + colx = осу, у + ш1у = осх.
Подстановка B3.6) дает
Ах(ш1 — си2) = осАу, Ау(ш1 — си2) = осАх.	A)
Характеристическое уравнение (cuq — си2J = а2, откуда
(х>\ = си2, - а, сиз = cuq + ос.
При си = cui уравнения A) дают Ах = Ау, а при си = (х>2 Ах = — Ау.
Поэтому
* = 7i(gi + Q2)' v = ^Qi~Q^
(коэффициенты l/v2 соответствуют указанной в тексте нормировке нор-
нормальных координат).

94	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
При а <С (JOq (слабая связь) имеем
cjui « ш0 - а/Bси0), си2 ^ си0 + а/Bси0).
Изменение хну представляет собой в этом случае наложение двух колеба-
колебаний с близкими частотами, т.е. имеет характер биений с частотой си 2 — cui =
= a/cuo (см. § 22). При этом в момент, когда амплитуда координаты х про-
проходит через максимум, амплитуда у проходит через минимум и наоборот.
2. Определить малые колебания двойного плоского маятника (см. рис. 1).
Решение. Для малых колебаний (cpi^Cl, (р2 ^С 1) найденная в
задаче 1 § 5 функция Лагранжа принимает вид
Ь = 	g	 ll(Pl + ^"^Ф2 +ГП2/1/2Ф1Ф2
Уравнения движения:
(mi + m2)/i(pi + Ш2/2Ф2 + (mi + m2)gcpi = 0,
^1ф1 +Ьф2 +gф2 = 0.
После подстановки B3.6):
А1(т1 + m2)(g— /icu2) — A2cu2m2/2 = 0,
) = 0.
Корни характеристического уравнения:
2 = 9 g7 , {(mi + m2)(/i + /2) ±
/
При mi —»> сю частоты стремятся к пределам y/g/h и s/g/h, соответству-
соответствующим независимым колебаниям двух маятников.
3. Найти траекторию движения частицы в центральном поле U = кг2 /2
(так называемый пространственный осциллятор).
Решение. Как и во всяком центральном поле, движение происхо-
происходит в одной плоскости, которую выбираем в качестве плоскости ху. Изме-
Изменение каждой из координат ж, у — простое колебание с одинаковыми часто-
частотами со = у/к/т:
х = a cos (cut + а), у = bcos (cut + C)
или
х = a cos (р, у = b cos (cp + 6) = Ъ cos 6 cos (p — Ъ sin 6 sin (p,
где введены обозначения (р = cot + а, 6 = C — а. Определив отсюда cos (p и
sin (p и составив сумму их квадратов, получим уравнение траектории
х2 у2 2ху	.2
— + —	=- cos 6 = sin 6.
а2 Ъ2 аЪ
Это — эллипс с центром в начале координат х). При 6 = 0 или п траектория
вырождается в отрезки прямой.
) Тот факт, что в поле с потенциальной энергией U = кг /2 движение
происходит по замкнутой прямой, был уже упомянут в § 14.

§ 24	КОЛЕБАНИЯ МОЛЕКУЛ	95
§ 24. Колебания молекул
Если мы имеем дело с системой частиц, взаимодействующих
друг с другом, но не находящихся во внешнем поле, то не все
ее степени свободы имеют колебательный характер. Типичным
примером таких систем являются молекулы. Помимо движений,
представляющих собой колебания атомов около их положения
равновесия внутри молекулы, молекула как целое может совер-
совершать поступательное и вращательное движения.
Поступательному перемещению соответствуют три степени
свободы. Столько же имеется в общем случае вращательных
степеней свободы, так что из Зп степеней свободы п-атомной
молекулы всего Зп — 6 отвечают колебательному движению. Ис-
Исключение представляют молекулы, в которых все атомы распо-
расположены вдоль одной прямой. Поскольку говорить о вращении
вокруг этой прямой не имеет смысла, то вращательных степе-
степеней свободы в этом случае всего две, так что колебательных
имеется Зп — 5.
При решении механической задачи о колебаниях молекулы
целесообразно с самого начала исключить из рассмотрения по-
поступательные и вращательные степени свободы.
Чтобы исключить поступательное движение, надо считать
равным нулю полный импульс молекулы. Поскольку это условие
означает неподвижность центра инерции молекулы, его можно
выразить в виде постоянства трех координат последнего. Поло-
Положив га = гао + иа (где гао — радиус-вектор неподвижного по-
положения равновесия а-го атома, aufl — его отклонение от этого
положения), представим условие
в виде
$>аиа = О.	B4.1)
Чтобы исключить вращение молекулы, следует положить
равным нулю ее полный момент импульса. Так как момент не яв-
является полной производной по времени от какой-либо функции
координат, то условие его исчезновения не может быть, вообще
говоря, выражено в виде равенства нулю такой функции. Одна-
Однако случай малых колебаний как раз представляет исключение.
В самом деле, снова положив ra = rao + ua и пренебрегая малы-
малыми величинами второго порядка по смещениям ua, представим

96	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
момент импульса молекулы в виде
М = ^2ma[rava] « 5^гаа[гаОйа] = —
Условие его исчезновения в этом приближении можно, следова-
следовательно, представить в виде
О	B4.2)
(начало координат может быть при этом выбрано произвольным
образом).
Нормальные колебания молекулы могут быть классифици-
классифицированы по характеру движения атомов в них на основании сооб-
соображений, связанных с симметрией расположения атомов
(в положениях равновесия) в молекуле. Для этой цели существу-
существует общий метод, основанный на использовании теории групп; он
изложен в другом томе этого курса х). Здесь же мы рассмотрим
лишь некоторые элементарные примеры.
Если все п атомов молекулы лежат в одной плоскости, то
можно различать нормальные колебания, составляющие атомы
в этой плоскости, и нормальные колебания, при которых атомы
выводятся из плоскости. Легко определить число тех и других.
Так как всего для плоского движения имеется 2п степеней сво-
свободы, из которых две поступательные и одна вращательная, то
число нормальных колебаний, не выводящих атомы из плоско-
плоскости, равно 2п — 3. Остальные же (Зп — 6) — Bп — 3) = п — 3 коле-
колебательных степеней свободы отвечают колебаниям, выводящим
атомы из плоскости.
В случае линейной молекулы можно различать продольные
колебания, сохраняющие ее прямолинейную форму, и колеба-
колебания, выводящие атомы с прямой. Так как всего движению п
частиц по линии отвечает п степеней свободы, из которых од-
одна поступательная, то число колебаний, не выводящих атомы с
прямой, равно п—1. Поскольку же полное число колебаний сте-
степеней свободы линейной молекулы есть Зп —5, то имеется 2п — 4
колебаний, выводящих атомы с прямой. Этим колебаниям, од-
однако, отвечают всего п — 2 различные частоты, так как каждое
из таких колебаний может осуществляться двумя независимы-
независимыми способами — в двух взаимно перпендикулярных плоскостях
(проходящих через ось молекулы); из соображений симметрии
г) См. т. III, «Квантовая механика», § 100.

§ 24	КОЛЕБАНИЯ МОЛЕКУЛ	97
очевидно, что каждая такая пара нормальных колебаний имеет
одинаковые частоты.
Задачи1)
1. Определить частоты колебаний линейной трехатомной симметрич-
симметричной молекулы ABA (рис. 28). Предполагается, что потенциальная энергия
молекулы зависит только от расстояний А — В и В — Аи угла ABA.
Решение. Продольные смещения атомов Ж1,Ж2,#з связаны в силу
B4.1) соотношением
тпа(х1 + хз) + твХ2 = 0.
С его помощью исключаем Х2 из функции Лагранжа продольного движения
молекулы
т ГПА,.2 . -2\ . гпВ .2 &1 г/	\2 , /	ч2т
J-j == 	(Хл Ч~ Xi ) -Ь 	Хо — 	 (Хл — Хо ) Ч~ (Хч — Хо ) ,
2 v 1 л) 2	2 LV	Z) v	Z) J'
после чего вводим новые координаты
Qoc = Х\ + Хз, Qs = XI — Хз.
В результате получим
4тв	4	4т23	4
(|х = 27тгл + тпв — масса молекулы). Отсюда видно, что Qa и Qs являются
(с точностью до нормировки) нормальными координатами. Координата Qa
отвечает антисимметричному относитель-
относительно середины молекулы колебанию (х± = хз',	3 1 2 1 1
рис. 28 а) с частотой	•	°	•
У			А	В
kiyi
Координата Qs соответствует симметрично- "^"*	J	*~^~ б
му (х\ = — хз', рис. 28 5) колебанию с часто-	t	^	1 в
той			^^	*
wsl = АК	Рис. 28
V гал
Поперечные смещения атомов у\,у2,уъ в силу B4.1) и B4.2) связаны
соотношениями
гпа(у1 + 2/з) + msl/2 =0, 2/i = у3,
(симметричное колебание изгиба; рис. 28 в). Потенциальную энергию изги-
изгиба молекулы запишем в виде /^ 6 /2, где 6 — отклонение угла ABA от
значения я; оно выражается через смещения согласно
6= у[Ы -2/2)+ B/3-2/2)].
) Расчеты колебаний более сложных молекул можно найти в книгах:
М. В. Волькенштейн, М. А. Ельяшевич, Б. И. Степанов.
Колебания молекул.—М.: Гостехиздат, 1949; Г. Герцберг, Колебатель-
Колебательные и вращательные спектры многоатомных молекул.—М.: ИЛ, 1949.

98
МАЛЫЕ КОЛЕБАНИЯ
ГЛ. V
Выражая все смещения 2/1,2/2,2/3 через 6, получим функцию Лагранжа
поперечного колебания в виде
тв .2
2c2
б -
откуда частота
2. То же для молекулы ABA треугольной формы (рис. 29).
Решение. В силу B4.1), B4.2) составляющие смещений и атомов
по направлениям X и Y (рис. 29) связаны соотношениями
in а I /у -* | /у п I I m г> о" о ^^^ 11
' ' v J\ \ Л/ ]_ ^^ ^О/ ^^ 11 v J3 dj? 	 V/•
шлB/1 + 2/з) + гав2/2 = О,
B/1 — 2/з) sin а — (xi + жз) cos а = 0.
Изменения Ы\ и 6/2 расстояний Л — В и 5 — А получаются путем проек-
проектирования векторов ui — 112 и из — иг на направления линий АВ и В А:
Ы-i = (х\ — х2) sin a + B/1 — 2/2) cos а,
6/2 = —(жз — х2) sin а + B/3 — 2/2) cos а.
Изменение же угла ABA получается проектированием тех же векторов на
у	направления, перпендикулярное к отрезкам
АВ и В А:
6 = 1Г
-x2)cosoc- B/1 -2/2) sin a] +
+ j[-(x3 -Х2) cos а- B/з -2/2) sin а].
Функция Лагранж:а молекулы
рис 29	Вводим новые координаты
Qa = X! + Жз, 9el = X! ~ Хз, qs2 = 2/1 + УЗ-
Компоненты векторов и выражаются через них согласно
2/1 = -z{
2
Xl = ~(Qa
= ~(Qa — q8l)
X2 =	Qa,
ГПв
2/3 = x(
2
- Qa Ctg Ot), 2/2 =	~
тв
+Qa Ctga),
а для функции Лагранжа получим после вычисления:

§ 24	КОЛЕБАНИЯ МОЛЕКУЛ	99
ГПА BтПА ,	1 \Д2 , ГПА .2 , ТПАУ- .2
= ~Г~ I	Ь ~^~~2	 )Уа "^	^~^sl + 1	Qs2~
4 \шв sm2 a/	4	4тв
2кг Bта
1" .
s
Qa^1 . 2
4 V тв sm а
2	2
- — (fei sin2 а + 2&2 cos2 а) - qs2 -^-(fei cos2 a + 2&2 sin2 a)
4	4777/ d
— fci) sin a cos a.
+ #si ^S2
2ms
Отсюда видно, что координата Qa отвечает нормальному колебанию с ча-
частотой
777-А
антисимметричному относительно оси Y (х\ = хз, у\ = —уз', рис. 29 а).
Координаты же qsi, qs2 совместно соответствуют двум колебаниям
(симметричным относительно оси Y: х\ = — хз, у\ = уъ\ рис. 29 б и в),
частоты которых cusi, cuS2 определяются как корни квадратного (по си2)
характеристического уравнения
&1 /1 , 2гпа 2 \ 2/с2 /1 , 2гпа . 2 M , 2\xkik2 л
	 1 Н	cos a м	1 Н	sm a + ——^- = 0.
777,A V	ТПв	'	ГПА V	777,^	/ J ТПвТПа
2гпа 2 \ 2/с2 /1 , 2гпа . 2
	cos a м	1 Н	sm
ТПв	'	ГПА V	777,^
При 2а = я все эти частоты совпадают с найденными в задаче 1.
3. То же для линейной несимметричной молекулы ABC (рис. 30).
Решение. Продольные (х) и поперечные (у) смещения атомов свя-
связаны соотношениями	3 12 2	1\	1
•	о	о
niAXi + тпвх2 + гпсхз = 0,	С	В	А
mAyi + гпвуч + гасуз = °>	рис 30
mAhyi = тскуз-
Потенциальную энергию растяж:ения и изгиба запишем в виде
B1 = l\ + /2)- Вычисления, аналогичные произведенным в задаче 1, при-
приводят к значению
/х/2 Vttt-c тпа тпв
для частоты поперечного колебания и к квадратному (по си2) уравнению
\Шв ТП
для частот сил, tU/2 ДВУХ продольных колебаний.

100	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
§ 25. Затухающие колебания
До сих пор мы всегда подразумевали, что движение тел про-
происходит в пустоте или что влиянием среды на движение мож-
можно пренебречь. В действительности при движении тела в сре-
среде последняя оказывает сопротивление, стремящееся замедлить
движение. Энергия движущегося тела при этом в конце концов
переходит в тепло или, как говорят, диссипируется.
Процесс движения в этих условиях уже не является чисто ме-
механическим процессом, а его рассмотрение требует учета движе-
движения самой среды и внутреннего теплового состояния как среды,
так и тела. В частности, уже нельзя утверждать в общем слу-
случае, что ускорение движущегося тела является функцией лишь
от его координат и скорости в данный момент времени, т.е. не
существует уравнений движения в том смысле, какой они имеют
в механике. Таким образом, задача о движении тела в среде уже
не является задачей механики.
Существует, однако, определенная категория случаев, когда
движение в среде может быть приближенно описано с помощью
механических уравнений движения путем внедрения в них опре-
определенных дополнительных членов. Сюда относятся колебания с
частотами, малыми по сравнению с частотами, характерными
для внутренних диссипативных процессов в среде. При выпол-
выполнении этого условия можно считать, что на тело действует сила
трения, зависящая (для заданной однородной среды) только от
его скорости.
Если к тому же эта скорость достаточно мала, то можно раз-
разложить силу трения по ее степеням. Нулевой член разложения
равен нулю, поскольку на неподвижное тело не действует ника-
никакой силы трения, и первый неисчезающий член пропорционален
скорости. Таким образом, обобщенную силу трения /тр, дейст-
действующую на систему, совершающую одномерные малые колеба-
колебания с обобщенной координатой ж, можно написать в виде
/тр = OCX,
где ос — положительный коэффициент, а знак минус показывает,
что сила действует в сторону, противоположную скорости. До-
Добавляя эту силу в правую часть уравнения движения, получим
(ср. B1.4))
тх = —кх — осх.	B5.1)

§ 25	ЗАТУХАЮЩИЕ КОЛЕБАНИЯ	101
Разделим его наши введем обозначения
- = оI - = 2Л.	B5.2)
т	и т	v y
си о есть частота свободных колебаний системы в отсутствие тре-
трения. Величина Л называется коэффициентом затухания 1).
Таким образом, имеем уравнение
х + 2Хх + <?>1х = 0.	B5.3)
Следуя общим правилам решения линейных уравнений с посто-
постоянными коэффициентами, полагаем х = ert и находим для г
характеристическое уравнение
г2 + 2Лг + а>1 = 0.
Общее решение уравнения B5.3) есть
х = Clerit + с2еГ2\ п,2 = -А ± ^/л2 - си2.
Здесь следует различать два случая.
Если Л < cuo, то мы имеем два комплексно сопряженных
значения г. Общее решение уравнения движения может быть
представлено в этом случае, как
х = Re |Лехр(-Л? + г?уЧи§ - Л2) j,
где А — произвольная комплексная постоянная. Иначе можно
написать:
x = ae~Mcos(cvt + oc), ш = у си§ - Л2,	B5.4)
где а л ос — вещественные постоянные. Выражаемое этими фор-
формулами движение представляет собой так называемые зату-
затухающие колебания. Его можно рассматривать как гармониче-
гармонические колебания с экспоненциально убывающей амплитудой.
Скорость убывания амплитуды определяется показателем Л, а
«частота» со колебаний меньше частоты свободных колебаний
в отсутствие трения; при Л ^С Шо разница между си и cuo —
второго порядка малости. Уменьшение частоты при трении сле-
следовало ожидать заранее, поскольку трение вообще задерживает
движение.
Если Л ^С cuo, то за время одного периода 2п/а) амплитуда
затухающего колебания почти не меняется. В этом случае имеет
х) Безразмерное произведение ЛТ (где Т = 2я/си — период) называют
логарифмическим декрементом затухания.

102	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
смысл рассматривать средние (за период) значения квадратов
координаты и скорости, пренебрегая при усреднении изменени-
изменением множителя е~ . Эти средние квадраты, очевидно, пропорци-
пропорциональны e~^t. Поэтому и энергия системы в среднем убывает
по закону
Ё = Еое~ш,	B5.5)
где Eq — начальное значение энергии.
Пусть теперь Л > Шо- Тогда оба значения г вещественны,
причем оба отрицательны. Общий вид решения
х =
- cug)t]+c2exp[-(A+y/A2 - cug)t]. B5.6)
Мы видим, что в этом случае, возникающем при достаточно
большом трении, движение состоит в убывании |ж|, т.е. в асим-
асимптотическом (при t —>• ос) приближении к положению равнове-
равновесия. Этот тип движения называют апериодическим затуханием.
Наконец, в особом случае, когда Л = Шо, характеристическое
уравнение имеет всего один (двойной) корень г = — Л. Как из-
известно, общее решение дифференциального уравнения имеет в
этом случае вид
х = (a + c2t)e-M.	B5.7)
Это — особый случай апериодического затухания. Оно тоже не
имеет колебательного характера.
Для системы со многими степенями свободы обобщенные си-
силы трения, соответствующие координатам а^, являются линей-
линейными функциями скоростей вида
/гтр = -^2,0iikXk.	B5.8)
к
Из чисто механических соображений нельзя сделать никаких за-
заключений о свойствах симметрии коэффициентов ос^/с по индек-
индексам г л к. Методами же статистической физики можно пока-
показать х), что всегда
otik = otki.	B5.9)
Поэтому выражения B5.8) могут быть написаны в виде произ-
производных
/iTp = -g	B5.10)
См. т. V, «Статистическая физика», § 121.

§ 25	ЗАТУХАЮЩИЕ КОЛЕБАНИЯ	103
от квадратичной формы
^2	B5.11)
называемой диссипативной функцией.
Силы B5.10) должны быть добавлены к правой части урав-
уравнений Лагранжа
Диссипативная функция имеет сама по себе важный физиче-
физический смысл — ею определяется интенсивность диссипации энер-
энергии в системе. В этом легко убедиться, вычислив производную
по времени от механической энергии системы. Имеем
dt ~ dt \2^Xi дхг ) ~ 2^Xi \ dt dxi dxi) ~ 2^Xi dxi *
г	г	г
Поскольку F — квадратичная функция скоростей, то в силу тео-
теоремы Эйлера об однородных функциях сумма в правой части
равенства равна 2F. Таким образом,
-2F,	B5.13)
т.е. скорость изменения энергии системы дается удвоенной дис-
диссипативной функцией. Так как диссипативные процессы приво-
приводят к уменьшению энергии, то должно быть всегда F > 0, т.е.
квадратичная форма B5.11) существенно положительна.
Уравнения малых колебаний при наличии трения получают-
получаются добавлением сил B5.8) в правую часть уравнений B3.5):
^jrnikxk + ^2 kikxk = -^2 KikXk-	B5.14)
k	k	k
Положив в этих уравнениях
xk = Aker\
получим по сокращении на ert систему линейных алгебраиче-
алгебраических уравнений для постоянных Ак
^2 (шгкг2 + оцкг + kik)Ak = 0.	B5.15)
к
Приравняв нулю определитель этой системы, найдем характе-
характеристическое уравнение, определяющее значения г:
\mikr2 + otikr + kik\= 0.	B5.16)

104	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
Это — уравнение степени 2s относительно г. Поскольку все
его коэффициенты вещественны, то его корни либо веществен-
вещественны, либо попарно комплексно сопряжены. При этом веществен-
вещественные корни непременно отрицательны, а комплексные имеют от-
отрицательную вещественную часть. В противном случае коорди-
координаты и скорости, а с ними и энергия системы экспоненциально
возрастали бы со временем, между тем как наличие диссипатив-
ных сил должно приводить к уменьшению энергии.
§ 26. Вынужденные колебания при наличии трения
Исследование вынужденных колебаний при наличии трения
вполне аналогично произведенному в § 22 рассмотрению коле-
колебаний без трения. Мы остановимся здесь подробно на представ-
представляющем самостоятельный интерес случае периодической выну-
вынуждающей силы.
Прибавив в правой части уравнения B5.1) внешнюю силу
/cosyt и разделив на га, получим уравнение движения в виде
х + 2\х + <х>1х = ?- cosyt.	B6.1)
777/
Решение этого уравнения удобно находить в комплексной
форме, для чего пишем в правой части eiyt вместо cosyt:
х + 2Хх + cvZx = ЫУК
и	т
Частный интеграл ищем в виде х = Beiyt и находим для В:
В =	(Ж2)
Представив В в виде Ьег6, имеем для Ъ и 6:
6=		7	=, tgS^-^Ц.	B6.3)
Наконец, отделив вещественную часть от выражения ВегуЬ =
— ?ег(У*+&)? получим частный интеграл уравнения B6.1), а при-
прибавив к нему общее решение уравнения без правой части (ко-
(которое мы напишем для определенности для случая cuq > A),
получим окончательно:
х = ае~м cos (cut + ос) + bcos (yt + 6).	B6.4)
Первое слагаемое экспоненциально убывает со временем, так
что через достаточно большой промежуток времени остается
только второй член:

26 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ НАЛИЧИИ ТРЕНИЯ	105
x = bcos(yt + b).	B6.5)
Выражение B6.3) для амплитуды Ъ вынужденного колеба-
колебания хотя и возрастает при приближении частоты у к Шо, но не
обращается в бесконечность, как это было при резонансе в отсут-
отсутствие трения. При заданной амплитуде силы / амплитуда коле-
колебания максимальна при частоте у = v/cUq ~~ 2А2; при А ^С Шо это
значение отличается от си о лишь на величину второго порядка
малости.
Рассмотрим область вблизи резонанса. Положим у = Шо + ?,
где ? — малая величина; будем также считать, что Л <С too-
Тогда в B6.2) можно приближенно заменить:
у2 - ш§ = (у + сио)(у - u>o) ~ 2шО?, 2гЛу « 2гЛш0,
так что
ИЛИ
B6.7)
Отметим характерную особенность хода изменения разности
фаз 6 между колебанием и вынуждающей силой при изменении
частоты последней. Эта разность всегда отрицательна, т.е. ко-
колебание «запаздывает» относительно внешней силы. Вдали от
резонанса, со стороны у < Шо , 6 стремится к нулю, а со сто-
стороны у > Шо — к значению —п. Изменение 6 от нуля до — 7Г
происходит в узкой (ширины rsj Л) области частот, близких к
Шо; через значение — п/2 разность фаз проходит при у = со о.
Отметим в этой связи, что в отсутствие трения изменение фа-
фазы вынужденного колебания на величину п происходит скачком
при у = Шо (второй член в B2.4) меняет знак); учет трения
«размазывает» этот скачок.
При установившемся движении, когда система совершает вы-
вынужденные колебания B6.5), ее энергия остается неизменной. В
то же время система непрерывно поглощает (от источника внеш-
внешней силы) энергию, которая диссипируется благодаря наличию
трения. Обозначим через /(у) количество энергии, поглощаемой
в среднем в единицу времени, как функцию частоты внешней
силы. Согласно B5.13) имеем
= 2F,

106
МАЛЫЕ КОЛЕБАНИЯ
ГЛ. V
где F — среднее (по периоду колебания) значение диссипативной
функции. Для одномерного движения выражение B5.11) дисси-
диссипативной функции сводится к F = осх^/2 = XmiP1. Подставив
сюда B6.5), получим
F = \тЪ2у2 sin2(y? + 6).
Среднее по времени значение квадрата синуса равно 1/2, поэтому
/(у) = ЛтЬ2у2.	B6.8)
Вблизи резонанса, подставляя амплитуду колебания из B6.7),
имеем	х2
B6.9)
Am
+ Л2
Такой вид зависимости поглощения от частоты называется
дисперсионным. Полушириной резонансной кривой (рис. 31) на-
называют значение |е|, при котором величина /(е) уменьшается
вдвое по сравнению с ее макси-
максимальным значением при ? = 0.
Из формулы B6.9) видно, что в
данном случае эта ширина совпа-
совпадает с показателем затухания Л.
Высота же максимума
Рис. 31
обратно пропорциональна Л. Та-
Таким образом, при уменьшении показателя затухания резонанс-
резонансная кривая становится уже и выше, т.е. ее максимум становится
более острым. Площадь же под резонансной кривой остается при
этом неизменной.
Последняя дается интегралом
f
I(y)dy=
Поскольку 1(е) быстро убывает при увеличении |е|, так что
область больших |е| все равно не существенна, можно при инте-
интегрировании писать 7(е) в виде B6.9), а нижний предел заменить
на —ос. Тогда
dt _ nf_
?2 + Л2 ~~ 4т
B6.10)

§ 27	ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС	107
Задача
Определить вынужденные колебания при наличии трения под действи-
действием внешней силы / = /oeat cosyt.
Решение. Решаем уравнение движения в комплексном виде
т
после чего отделяем вещественную часть решения. В результате получаем
вынужденное колебание в виде
х = 6eatcos(yt + 6),
где
Ъ=	/о
тл/(ш20 + а2 - у2 + 2аЛJ + 4у2(а + ЛJ
§ 27. Параметрический резонанс
Существуют такие незамкнутые колебательные системы,
в которых внешнее воздействие сводится к изменению со вре-
временем ее параметров х).
Параметрами одномерной системы являются коэффициенты
т и к в функции Лагранжа B1.3); если они зависят от времени,
то уравнение движения гласит:
^-(тх) + кх = 0.	B7.1)
Путем введения вместо t новой независимой переменной т со-
согласно dx = dt/m(t) это уравнение приводится к виду
d2x
-— + ткх = 0.
dT2
Поэтому фактически, без всякого органичения общности, доста-
достаточно рассмотреть уравнение движения вида
g + cv2(t)x = 0,	B7.2)
которое получилось бы из B7.1) при т = const.
Вид функции cv(t) задается условиями задачи; предполо-
предположим, что эта функция периодическая с некоторой частотой у
(и периодом Г = 2п/у). Это значит, что
г) Простым примером такого рода является маятник, точка подвеса ко-
которого совершает заданное периодическое движение в вертикальном поло-
положении (см. задачу 3).

108	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
а потому и все уравнение B7.2) инвариантно по отношению к
преобразованию t —»> t + Т. Отсюда следует, что если x(t) есть
решение уравнения, то и функция x(t + T) тоже есть решение.
Другими словами, если x\{t) и X2(t) — два независимых интегра-
интеграла уравнения B7.2), то при замене t —»> t + T они преобразуются
линейным образом друг через друга. При этом можно х) выбрать
Х\ЖХ2 таким образом, чтобы их изменение при замене t на t + T
сводилось просто к умножению на постоянный множитель
Xl(t + T) = ^xi(t), x2(t + T) = \i2x2(t).
Наиболее общий вид функций, обладающих таким свойством, есть
Xl(t) = ]i/TT\!(t), x2(t) = 4/ТП2(*),	B7.3)
где TTi(t) и П2(?) — чисто периодические функции времени (с пе-
периодом Г).
Постоянные цх и ц2 в этих функциях должны быть связа-
связаны друг с другом определенным соотношением. Действительно,
умножив уравнения
Х\ + OJ(t)xi = 0, Х2 + CV2(t)x2 = 0
и вычтя их почленно одно из другого,
соответственно
получим
на
Х\Х
Х2 И,
¦2 X
XI И1
2^1 =
1 It
\2	2\	{\2	\2) = 0
или
Ж1Ж2 — xi±2 = const.	B7.4)
Но при любых функциях x\[t) и X2(t) вида B7.3) выражение в
левой части этого равенства умножается на щ Ц2 ПРИ изменении
аргумента t на t + Т. Поэтому ясно, что соблюдение равенства
B7.4) во всяком случае требует, чтобы было
цхц2 = 1.	B7.5)
Дальнейшие заключения о постоянных ць ц2 можно сде-
сделать, исходя из факта вещественности коэффициентов уравне-
уравнения B7.2). Если x[t) есть какой-либо интеграл такого уравнения,
) Этот выбор эквивалентен приведению к диагональному виду матрицы
линейных преобразований x\(t) и #2(?), что требует решения соответству-
соответствующего секулярного квадратного уравнения. Мы предполагаем, что корни
этого уравнения не совпадают.

§ 27	ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС	109
то и комплексно сопряженная функция ж* (?) должна удовлетво-
удовлетворять тому же уравнению. Отсюда следует, что пара постоянных
Ц]_, Ц2 должна совпадать с парой ц^, yi^, т.е. должно быть либо
yi^ = ц*5 либо щ и ц2 вещественны. В первом случае, учитывая
B7.5), имеем цх = 1/ц*, т.е. |Цх|2 = |Ц-2|2 — 1? постоянные цх
и ц2 по модулю равны единице.
Во втором же случае два независимых интеграла уравнения
B7.2) имеют вид
Xl(t) = ц*/тТТ1D), x2(t) = цГ*/тТТ2(*)	B7.6)
с отличным от единицы положительным или отрицательным ве-
вещественным числом ц. Одна из этих функций (первая или вто-
вторая при |ц| > 1 и |ц| < 1) экспоненциально возрастает со вре-
временем. Это значит, что состояние покоя системы (в положении
равновесия х = 0) будет неустойчивым: достаточно сколь угод-
угодно слабого отклонения от этого состояния, чтобы появившееся
смещение х стало быстро возрастать со временем. Это явление
называется параметрическим резонансом.
Обратим внимание на то, что при строго равных нулю на-
начальных значениях х и х они оставались бы равными нулю и
в дальнейшем в отличие от обычного резонанса (§ 22), в кото-
котором возрастание смещения со временем (пропорциональное t)
происходит и от равного нулю начального значения.
Выясним условия возникновения параметрического резонан-
резонанса в важном случае, когда функция ш(?) мало отличается от
некоторой постоянной величины Шо и является простой перио-
периодической функцией
ш2(?) = ш§A + h cosy*),	B7.7)
где постоянная /& «С 1 (мы будем считать h положительной, че-
чего всегда можно добиться надлежащим выбором начала отсчета
времени). Как мы увидим ниже, наиболее интенсивным обра-
образом параметрический резонанс возникает, если частота функции
cv(t) близка к удвоенной частоте Шо- Поэтому положим
у = 2ш0 + ?,
где ? < шо-
Решение уравнения движения х)
х + ш§[1 + h cos Bш0 + e)t]x = 0	B7.8)
) Уравнение такого вида (с произвольными уи/i) называется в мате-
математической физике уравнением Матьё.

110	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
будем искать в виде
х = a(t) cos(w0 + -t\t + b(i) sin(w0 + |)t,	B7.9)
где a(t) и b(t) — медленно (по сравнению со множителями cos
и sin) меняющиеся функции времени. Такой вид решения, разу-
разумеется, не является точным. В действительности функция x(t)
содержит также члены с частотами, отличающимися от a)Q + e/2
на целое кратное от 2шо + ?; эти члены, однако, высшего порядка
малости по /г, и в первом приближении ими можно пренебречь
(см. задачу 1).
Подставим B7.9) в B7.8) и произведем вычисления, сохра-
сохраняя лишь члены первого порядка по е; при этом предположим,
что a rsj ea, b ~ zb (правильность этого предположения в усло-
условиях резонанса подтвердится результатом). Произведения три-
тригонометрических множителей следует разложить в суммы
(cuo + I)t • cos Bcuo + e)t =
coso I)(o
= - cos^3cu0 + yjt + - cos^cuo + I
и т.п. и в соответствии со сказанным выше опустим члены с
частотами 3(шо + с/2). В результате получим
- Bа + Ы + ^
+ B6 - az+^a)aH cos
Выполнение этого равенства требует одновременного обращения
в нуль коэффициентов при каждом из множителей sin и cos.
Отсюда получаем систему двух линейных дифференциальных
уравнений для функций a(i) и b(t). Следуя общим правилам,
ищем решение, пропорциональное est. Тогда
2
и условие совместности эти двух алгебраических уравнений дает
B7.10)

§ 27	ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС	111
Условие возникновения параметрического резонанса заклю-
заключается в вещественности s (т.е. s2 > 0) г). Таким образом, резо-
резонанс имеет место в интервале
вокруг частоты 2 си о 2). Ширина этого интервала пропорциональ-
пропорциональна /г, и такого же порядка осуществляющиеся в нем значения
показателя усиления колебаний s.
Параметрический резонанс имеет место также при часто-
частотах у изменения параметра системы, близких к значениям вида
2а)о/п, где п — любое целое число. Однако ширина резонанс-
резонансных областей (областей неустойчивости) с увеличением п бы-
быстро уменьшается — как hn (см. задачу 2). Так же уменьшаются
и значения показателя усиления колебаний в них.
Явление параметрического резонанса существует и при на-
наличии слабого трения в системе, но область неустойчивости при
этом несколько сужается. Как мы видели в § 25, трение при-
приводит к затуханию амплитуды колебаний по закону е~м. По-
Поэтому усиление колебаний при параметрическом резонансе про-
происходит, как еE~Л)* (с положительным s, даваемым решением
задачи без трения), а граница области неустойчивости опреде-
определяется равенством s—Л = 0. Так, используя s из B7.10), получим
для резонансной области вместо B7.11) неравенства
-^/(/гшо/2J-4Л2 < е < ^/(/гшо/2J - 4Л2.	B7.12)
Обратим внимание на то, что при этом резонанс оказывается
возможным не при сколь угодно малой амплитуде /г, а лишь
начиная с определенного «порога» /г^, равного в случае B7.12)
Можно показать, что для резонансов вблизи частот 2а)о/п ве-
величина порога hk пропорциональна Л1/71, т.е. возрастает с уве-
увеличением п.
г) Постоянная |х в B7.6) связана с s соотношением |х = —eS7r/cu° (при
замене t на t + 2я/2си0 cos и sin в B7.9) меняют знак).
2) Если интересоваться лишь границами области резонанса (не интересу-
интересуясь выражением для s внутри нее), то можно упростить вычисления, заме-
заметив, что на этих границах s = 0, т.е. коэффициенты а и Ъ в B7.9) постоянны;
при этом мы сразу получим значение ? = ±Шо/2, отвечающие границам об-
области B7.11).

112	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
Задачи
1. Определить границы области неустойчивости при резонансе вблизи
у = 2сио с точностью до величин порядка h2.
Решение. Ищем решение уравнения B7.8) в виде
х = ao cos (cuo + e/2)t + 60 sin (cu0 4
+ ai cos 3(cu0 + e/2)t + &i sin 3(cu0 + e/2)t,
учитывая в нем (по сравнению с B7.9)) также и члены следующего поряд-
порядка по h. Интересуясь лишь границами области неустойчивости, предполага-
предполагаем коэффициенты ао, bo, a\, b\ постоянными (в соответствии с замечанием,
сделанным в сноске на с. 111). При подстановке в уравнение B7.8) произве-
произведения тригонометрических функций разлагаем в суммы, опуская при этом
члены с частотами 5(сио + ?/2), которые нужны были лишь в еще более
высоком приближении. Получаем
[/	?2\ ha)* , ha)* 1 / , е\ ,
-ао( сиО?+ — I + —г— а0 + —г-аЛ cos [аH + —Jt +
и (	i ?^ ^0, , ^CUq, 1 . /
—Оо сио? Н—г ]	^о Н	Oi sm
V	4/2	2	V
—^-clo — 8cuoai cos3fc
+ 	-bo — 8cuo&i sin3f cuo H— jt = 0.
В членах с частотами си о + ?/2 сохранены величины первого и второго
порядка малости, а в членах с частотами 3(сио + ?/2) — члены первого
порядка. Каждое из выражений в квадратных скобках должно обращаться
в нуль в отдельности. Из двух последних имеем
_ h	_ h
0/1 ~ 16а° 1 ~ 16 °'
после чего из двух первых находим
Решая это уравнение с точностью до членов порядка h2, получим иско-
искомые граничные значения ?:
	hivp _ h2uoo
?~ ~2	32~'
2. Определить границы области неустойчивости при резонансе вблизи
у = си0.
Решение. Написав у = сио + ?, получаем уравнение движ:ения
х + cuq[1 + hcos (cuo + e.)t]x = 0.
Имея в виду, что искомые граничные значения ? ~ h2, ищем решение в
виде
х = ао cos (cuo + ?)? + bo sin (cuo + &)t +
+ ai cos2(cuo + ?)t + bi sin2(cuo + ?)t + ci,

§ 28	АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ	113
учитывая в нем сразу члены двух первых порядков. Для определения гра-
границ неустойчивости снова предполагаем коэффициенты постоянными и по-
получаем
Н	z-^ai + hcvld cos(cjj0 + e)t +
*	J
?б + ^М sin(w + e)t + 3o)a + ^ cos2(o) +
sin 2(cuo + e)t+ Ud + ^J = 0.
Отсюда находим	h	h	h
ai = -ao, b\ = -bo, ci = ~^"ao,
и затем две границы области неустойчивости:
? = -—/12Ш0, ?= ^^2^0.
3. Найти условия параметрического резонанса для малых колебаний
плоского маятника с колеблющейся в вертикальном направлении точкой
подвеса.
Решение. По найденной в задаче 3, в § 5 функции Лагранжа най-
найдем для малых (ф ^С 1) колебаний уравнение движения
ф + Шо (l + 4у cos Bш0 + e)t) <p = О,
где (JOq = д/l. Отсюда видно, что роль введенного в тексте параметра h
играет отношение 4а/7. Условие B7.11), например, принимает вид
§ 28. Ангармонические колебания
Вся изложенная выше теория малых колебаний основана на
разложении потенциальной и кинетической энергий системы по
координатам и скоростям с оставлением лишь членов второ-
второго порядка; при этом уравнения движения линейны, в связи с
чем в этом приближении говорят о линейных колебаниях. Хотя
такое разложение вполне законно при условии достаточной ма-
малости амплитуд колебаний, однако учет следующих приближе-
приближений (так называемой ангармоничности или нелинейности ко-
колебаний) приводит к появлению некоторых хотя и слабых, но
качественно новых особенностей движения.
Произведем разложение функции Лагранжа до членов тре-
третьего порядка. В потенциальной энергии при этом появятся чле-
члены третьей степени по координатам Х{, в кинетической же энер-
энергии — члены, содержащие произведения скоростей и координат

114	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
вида Х{Хкх\\ это отличие от прежнего выражения B3.3) связано
с оставлением членов первого порядка по ж в разложении функ-
функций cbik{q). Таким образом, функция Лагранжа будет иметь вид
1	^~^,
2	/_^\ г г	г г )
i,k	1 \~^\	. .	1 \~^7	/ло ^ч
А ¦^~^"	о ¦^~^"
где щк1, Цк1 — новые постоянные коэффициенты.
Если от произвольных координат Х{ перейти к нормальным
координатам (линейного приближения) Qa, то в силу линейно-
линейности этого преобразования третья и четвертая суммы в B8.1) пе-
перейдут в аналогичные суммы, в которых вместо координат Х{ и
скоростей Х{ будут стоять Qa и Qa. Обозначив коэффициенты
в этих суммах через А^р-у и Ц(Х|Зу, получим функцию Лагранжа
в виде
- I X)
I X) fiY. B8.2)
cx,|3,y	oc,|3,y
Мы не станем выписывать полностью следующих из этой ла-
гранжевой функции уравнений движения. Существенно, что они
имеют вид
Qoc + cvlQoc = /a(Q, Q, Q),	B8.3)
где foe — однородные функции второго порядка от координат Q
и их производных по времени.
Применяя метод последовательных приближений, ищем ре-
решение этих уравнений в виде
Qa = Q$ + Q$,	B8.4)
где Qa <^i Qol, а функции Q\J удовлетворяют «невозмущен-
«невозмущенным» уравнениям
Ш + <Q$ = о,
т.е. представляют собой обычные гармонические колебания
Qa = а ос cos (со at + aa).	B8.5)
Сохраняя в следующем приближении в правой части урав-
уравнений B8.3) лишь члены второго порядка малости, получим для
величин Qol уравнения
$	{1)A){1)	B8.6)

§ 28	АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ	115
где в правую часть должны быть подставлены выражения B8.5).
В результате мы получим линейные неоднородные дифференци-
дифференциальные уравнения, правые части которых можно преобразовать
к суммам простых периодических функций. Так, например,
Qa Q® = «ос^р COS ((Vat + (Xa) COS (шр? + (Xp) =
Таким образом, в правых частях уравнений B8.6) находятся
члены, соответствующие колебаниям с частотами, равными сум-
суммам и разностям собственных частот системы. Решение уравне-
уравнений следует искать в виде, содержащем такие же периодические
множители, и мы приходим к выводу, что во втором приближе-
приближении на нормальные колебания системы с частотами cua накла-
накладываются дополнительные колебания с частотами
Wcxicup	B8.7)
(в том числе удвоенные частоты 2си(Х и частота 0, соответствую-
соответствующая постоянному смещению). Эти частоты называются комби-
комбинационными. Амплитуды комбинационных колебаний пропор-
пропорциональны произведениям а^ар (или квадратам а^.) соответ-
соответствующих нормальных колебаний.
В следующих приближениях при учете членов более высо-
высокого порядка в разложении функции Лагранжа возникают ком-
комбинационные колебания с частотами, являющимися суммами и
разностями большего числа частот ша. Кроме того, однако, воз-
возникает еще и новое явление.
Дело в том, что уже в третьем приближении среди комбина-
комбинационных частот появляются частоты, совпадающие с исходны-
исходными tvot(tvot+tvр — сир). При применении описанного выше метода
в правой части уравнений движения будут находиться, следо-
следовательно, резонансные члены, которые приведут к возникнове-
возникновению в решении членов с возрастающей со временем амплиту-
амплитудой. Между тем, физически очевидно, что в замкнутой системе
в отсутствие внешнего источника энергии не может происходить
самопроизвольное нарастание интенсивности колебаний.
В действительности в высших приближениях происходит из-
изменение основных частот cua по сравнению с их «невозмущен-
«невозмущенными» значениями си^ , фигурирующими в квадратичном вы-
выражении потенциальной энергии. Появление же возрастающих

116	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
членов в решении связано с разложением типа
cos (си|х + Дша)? и cos (а>а ?) — tAcuasin (cua't),
явно незаконным при достаточно больших t.
Поэтому при переходе к следующим приближениям метод
последовательных приближений должен быть видоизменен так,
чтобы фигурирующие в решении периодические множители с
самого начала содержали точные, а не приближенные значения
частот. Изменения же частот сами определятся в результате ре-
решения уравнений как раз из условия отсутствия резонансных
членов.
Продемонстрируем этот метод на ангармонических колеба-
колебаниях с одной степенью свободы, написав функцию Лагранжа в
L = ™?- - ^ж2 - ™х3 - ^х4.	B8.8)
A	А	о	4
Соответствующее уравнение движения
х + <х>1х = -осх2 - [Зж3.	B8.9)
Мы будем искать его решение в виде ряда последовательных
приближений
х = х^ + х™ + х&\
причем
х^ = a cos cut	B8.10)
с точным значением си, которое само будем затем искать в виде
ряда а) = Шо + си^1) + си^2) + ... (начальную фазу в х^ можно
всегда обратить в нуль надлежащим выбором начала отсчета
времени). При этом, однако, уравнение движения в виде B8.9)
не вполне удобно, так как при подстановке в него B8.10) левая
часть равенства не обратится строго в нуль. Поэтому перепишем
его предварительно в эквивалентном виде
g х + colx = -ах" - Эх8 - (l - g) x.	B8.11)
Положив здесь х = х^+х^2\ cv = cuo + cu^1^ и опустив члены
выше второго порядка малости, получим для хк > уравнение
х^ + cvlx^ = —oca2 cos2 cut
— — -7Г- — -7Г- cos Bcut) +
A	A
7Г 7Г
A	A
Условие отсутствия резонансного члена в правой части равен-
равенства дает просто си^ = 0 в соответствии с изложенным в начале
параграфа методом нахождения второго приближения. После

§ 29	РЕЗОНАНС В НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ	117
этого, решая обычным способом неоднородное линейное уравне-
уравне2	2
B)	ооа . оса	/о ,\	/оо 1 о\
ху > = ——^ + —? cos Bcut).	B8.12)
Далее, положив в B8.11) х = х^ +х^ +х^\ со =
получим уравнение для х^
или, подставив в правую часть выражения B8.10) и B8.12) после
простого преобразования:
= -а3 т + -^-2 cos (Зш*)+
cos cut.
Приравнивая нулю коэффициент при резонансном множителе
cos wt, найдем поправку к основной частоте, пропорциональную
квадрату амплитуды колебания:
шB) =
Комбинационное ж:е колебание третьего порядка
§ 29. Резонанс в нелинейных колебаниях
Учет ангармонических членов при вынужденных колебани-
колебаниях системы приводит к появлению существенно новых особен-
особенностей в резонансных явлениях.
Добавив в правой части уравнения B8.9) внешнюю периоди-
периодическую (с частотой у) силу, получим
х + 2Хх + Шдж = ?- cosyt - ах2 - (Зж3;	B9.1)
777/
здесь написана также сила трения с показателем затухания Л
(предполагаемым ниже малым). Строго говоря, при учете нели-
нелинейных членов в уравнении свободных колебаний должны учи-
учитываться также члены высших порядков в амплитуде вынуж-
вынуждающей силы, соответствующие возможной зависимости ее от
смещения х. Мы не пишем этих членов лишь с целью упроще-
упрощения формул; они не меняют качественной картины явлений.

118	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
Пусть
У = Ш0 + ?
(с малым е), т.е. мы находимся вблизи обычного резонанса. Для
выяснения характера возникающего движения можно обойтись
без непосредственного исследования уравнения B9.1), если вос-
воспользоваться следующими соображениями.
В линейном приближении зависимость амплитуды Ъ вынуж-
вынужденного колебания от амплитуды / и частоты у внешней силы
дается вблизи резонанса формулой B6.7), которую напишем в
виДе	,2
b2(?2 + A2) =	B92)
Нелинейность колебаний приводит к появлению зависимости
их собственной частоты от амплитуды; напишем ее в виде
сио + хЬ2,	B9.3)
где постоянная к выражается определенным образом через ко-
коэффициент ангармоничности (см. B8.13)). Соответственно это-
этому заменяем в формуле B9.2) (точнее в малой разности у — а>о)
Шо на Шо + кЪ2.
Сохранив обозначение ? = у — Шо, получим в результате
уравнение	2
b2[(?-xb2J + A2] = i;X_	B9.4)
ИЛИ
Л2 -л2.
Л
у 2mwobJ
Уравнение B9.4), кубическое по отношению к Ь2, и его веще-
вещественные корни определяют амплитуду вынужденных колеба-
колебаний. Рассмотрим зависимость этой амплитуды от частоты внеш-
внешней силы при заданной амплитуде силы /.
При достаточно малых значениях / амплитуда Ъ тоже ма-
мала, так что можно пренебречь в B9.4) степенями Ъ выше вто-
второй, и мы возвращаемся к зависимости Ь(е) (см. B9.2)), изобра-
изображающейся симметричной кривой с максимумом в точке ? = О
(рис. 32 а). По мере увеличения / кривая деформируется, сохра-
сохраняя сначала свой характер — с одним максимумом (рис. 32 б);
последний смещается (при и > 0) в сторону положительных е.
Из трех корней уравнения B9.4) при этом веществен лишь один.
Однако, начиная с определенного значения f = fk (которое
мы определим ниже), характер кривой меняется. При каждом

29
РЕЗОНАНС В НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
119
значении f > fk существует определенная область частот, в ко-
которой уравнение B9.4) имеет три вещественных корня; ей отвеча-
отвечает участок BCDE кривой на рис. 32 в.
Границы этой области определя-
определяются условием db/dt = ос в точках D
и С. Продифференцировав уравнение
B9.4) по ?, получим
db 		— ?б + >cb3
dt ?2 + Л2 — 4x?b2 + Зх2Ь4 '
Поэтому положение точек D ж С опре-
определяется совместным решением урав-
уравнений
?2 - 4хЬ2? + Зх2Ь4 + Л2 = 0 B9.5)
и B9.4); соответствующие значения ?
оба положительны. Наибольшее зна-
значение амплитуды достигается в точке,
где db/dt = 0. При этом ? = хЬ2, и из
B9.4) имеем
h - f . B9.6)
Рис. 32
это значение совпадает с максимумом, даваемым зависимос-
зависимостью B9.2).
Можно показать (на чем мы не будем здесь останавливать-
останавливаться х), что из трех вещественных корней уравнения B9.4) средний
(т.е. участок CD кривой, изображенный на рис. 32 в штриховой
линией) соответствует неустойчивым колебаниям системы: лю-
любое сколь угодно слабое воздействие на систему, находящуюся в
таком состоянии, привело бы к переходу к колебательному ре-
режиму, отвечающему большему или меньшему корню (т.е. участ-
участкам ВС или DE).
Таким образом, реальным колебаниям системы соответству-
соответствуют лишь ветви ABC и DEF. Замечательной особенностью
является при этом наличие области частот, допускающих две
различные амплитуды колебаний. Так, при постепенном увели-
увеличении частоты внешней силы амплитуда вынужденных колеба-
колебаний будет возрастать, следуя кривой ABC. В точке С произой-
г) Доказательство можно найти, например, в книге Н. Н. Боголюбова
и Ю.А. Митропольского, «Асимптотические методы в теории нелинейных
колебаний».—М.: Физматгиз, 1958.

120	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
дет «срыв» амплитуды, которая скачком упадет до значения,
отвечающего точке Е1, и затем (при дальнейшем увеличении
частоты) будет меняться вдоль кривой EF. Если теперь вновь
уменьшать частоту, то амплитуда вынужденных колебаний бу-
будет меняться вдоль кривой FD, в точке D скачком возрастает
до В и затем будет уменьшаться вдоль В А.
Для вычисления значения /& замечаем, что это есть то зна-
значение /, при котором оба корня квадратного (по Ь2) уравнения
B9.5) совпадают; при f = fk весь участок CD сводится к од-
одной точке перегиба. Приравняв нулю дискриминант квадратно-
квадратного уравнения B9.5), получим е2 = ЗА ; соответствующий корень
уравнения: нЪ2 = 2е/3. Подставляя эти значения Ъ и ? в B9.4),
найдем
,2 _
Jk —
Наряду с изменением характера резонансных явлений при
частотах у « Шо нелинейность колебаний приводит также к
появлению новых резонансов, в которых колебания с частотой,
близкой к Шо, возбуждаются внешней силой с частотой, суще-
существенно отличающейся от Шо-
Пусть частота внешней силы у « cuo/2, т.е.
у = сио/2 + ?.
В первом, линейном, приближении она возбуждает в системе
колебания с той же частотой и амплитудой, пропорциональной
амплитуде силы
(согласно формуле B2.4)). Но при учете нелинейных членов,
во втором приближении, эти колебания приведут к появлению
в правой части уравнения движения B9.1) члена с частотой
2у « си о- Именно, подставив х^ в уравнение
Ж() +
введя косинус удвоенного угла и сохраняя в правой части лишь
резонансный член, получим
^ cos (ш0 + 2e)t.
B9.8)
Это уравнение отличается от уравнения B9.1) лишь тем, что
вместо амплитуды силы / в нем стоит выражение, пропорцио-

§ 29	РЕЗОНАНС В НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ	121
нальное квадрату /2. Это значит, что возникает резонанс такого
же характера, как и рассмотренный выше резонанс на частотах
у ~ Шо, но с меньшей интенсивностью. Зависимость Ь(е) получа-
получается заменой / на — 8ос/2/(9та)^) (и е на 2е) в уравнении B9.4):
Ь2[B?-х62J + Л2] = ^;.	B9.9)
Пусть теперь частота внешней силы
у = 2си0 + ?.
В первом приближении имеем
При подстановке х = х^ + х^ в уравнение B9.1) мы не по-
получим членов, имеющих характер резонансной внешней силы,
как это было в предыдущем случае. Возникает, однако, резонанс
параметрического типа от члена третьего порядка, пропорцио-
пропорционального произведению х^х^2\ Если из всех нелинейных чле-
нов сохранить лишь этот, то для ху } получим уравнение
или
"~* cosBwQ + c)t\xB) = 0, B9.10)
т.е. уравнение типа B7.8) (с учетом трения), приводящее, как
мы уже знаем, к неустойчивости колебаний в определенном ин-
интервале частот.
Однако для определения результирующей амплитуды коле-
колебаний это уравнение недостаточно. Установление конечной ам-
амплитуды связано с эффектами нелинейности, для учета которых
в уравнении движения должны быть сохранены также нелиней-
нелинейные по х^ члены:
Исследование этой задачи можно очень упростить, отметив
следующее обстоятельство. Положив в правой части уравне-
уравнения B9.11)
жB) = ь cos (сио + -J ? + 6
(где Ъ — искомая амплитуда резонансных колебаний, 6 — несу-
несущественный для дальнейшего постоянный сдвиг фазы) и пред-

122
МАЛЫЕ КОЛЕБАНИЯ
ГЛ. V
ставив произведение двух периодических множителей в виде
суммы двух косинусов, получим здесь член
§)«-«]
обычного резонансного (по отношению к собственной частоте
системы Шо) характера. Поэтому задача снова сводится к рас-
рассмотренной в начале параграфа задаче об обычном резонансе в
нелинейной системе с тем лишь отличием, что роль амплитуды
внешней силы играет теперь величина сх/ЬДЗшд) (а вместо ?
стоит е/2). Произведя эту замену в уравнении B9.4), получим
Решая это уравнение относительно Ь, найдем следующие воз-
возможные значения амплитуды:
6 = 0,
B9.12)
Ш -4
На рис. 33 изображена получающаяся отсюда зависимость Ъ
от е (для к > 0; при х, < 0 кривые направлены в обратную
сторону). Точки В л С от-
вечают значениям
Слева от точки В возмож-
но лишь значение Ь = 0, т.е.
? резонанс отсутствует и ко-
колебания с частотой порядка
Шо не возбуждаются. В ин-
интервале между В ж С имеем два корня: Ъ = 0 (отрезок ВС
на рис. 33) и выражение B9.13) (ветвь BE). Наконец, справа
от точки С существуют все три корня B9.12)-B9.14). Однако
не все эти значения отвечают устойчивому колебательному ре-
Рис#

§ 29	РЕЗОНАНС В НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ	123
жиму. Значение Ъ = 0 неустойчиво на участке ВС х), и можно
показать также, что всегда неустойчив режим, соответствующий
корню B9.14) (промежуточному между двумя другими). На
рис. 33 неустойчивые значения Ъ изображены штриховой линией.
Проследим, например, за поведением первоначально «покоив-
«покоившейся» 2) системы при постепенном уменьшении частоты внеш-
внешней силы. До достижения точки С остается Ъ = 0, а затем про-
происходит «срыв» этого состояния с переходом на ветвь ЕВ. При
дальнейшем уменьшении ? амплитуда колебаний уменьшается
до нуля в точке В. При обратном же увеличении частоты ам-
амплитуда колебаний растет вдоль кривой BE 3).
Рассмотренные случаи резонансов являются основными из
возникающих в нелинейной колебательной системе. В более вы-
высоких приближениях появляются резонансы и на других часто-
частотах. Строго говоря, резонанс должен возникать на всякой ча-
частоте у, для которой пу + ma)Q = O)q (n, m — целые числа), т.е.
при всяком у = pa)o/q, где p,q — снова целые числа. Однако
с увеличением степени приближения интенсивность резонанс-
резонансных явлений (а также ширины областей частот, в которых они
должны иметь место) столь быстро убывает, что реально могут
наблюдаться лишь резонансы на частотах у « pcoo/q с неболь-
небольшими значениями р и q.
Задача
Определить зависимость Ь(е) для резонанса на частотах у « Зсио-
Решение. В первом приближении
г) Этот интеграл как раз соответствует области параметрического резо-
резонанса B7.12), причем из сравнения B9.10) с B7.8) имеем \h\ = 2a//Cma>o).
Условие же
>4Л,
при котором возможно существование рассматриваемого явления, отвечает
неравенству h > hk.
) Напомним, что мы рассматриваем здесь лишь резонансные колебания.
Их отсутствие не означает поэтому буквального покоя системы, в которой
будут происходить слабые вынужденные колебания с частотой у.
3) Следует, однако, помнить, что все выведенные формулы справедли-
справедливы лишь до тех пор, пока амплитуда Ъ (а также s) остается достаточно
малой. В действительности, кривые BE и CF в своем дальнейшем ходе
оканчиваются, соединяясь в некоторой точке; при достижении этой точки
колебательный режим «срывается» и становится 6 = 0.

124	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
Для второго приближения (х^) получаем из B9.1) уравнение
SW + 2AiB) + Ш20хB) + <ххBJ + рЖBK = -3Pa(Va)a,
где в правой части равенства написан лишь член, приводящий к рассматри-
рассматриваемому резонансу. Положив в нем х^ = Ъ cos I cuo + — )t + 6 и выделяя
из произведения трех косинусов резонансный член, получим в правой части
уравнения выражение
Отсюда видно, что зависимость Ъ от ? получится заменой в уравнении B9.4)
Ь
/ на 3(ЗЬ2//32шо) и ? на ?/3:
Корни этого уравнения
Рис.34
На рис. 34 изображен графически харак-
характер зависимости Ъ от ? (при >с > 0). Устойчивым режимам отвечают лишь
значение 6 = 0 (ось абсцисс) и ветвь АВ. Точке А соответствуют значения
_ 3Dх2Л2 - А2) 2 _ 4*г2Л2 + А2
?к~	4А ' Ьк~
4м? А ¦
Колебательный режим существует лишь при ? > ?&, причем амплитуда
Ъ > bk- Поскольку состояние 6 = 0 всегда устойчиво, то для возбуждения
колебаний необходим начальный «толчок».
Полученные формулы справедливы лишь при малых ?. Малость ? обес-
обеспечивается малостью Л, если при этом амплитуда силы удовлетворяет усло-
условию Л2/си0 <^С А/к <^С си0.
§ 30. Движение в быстро осциллирующем поле
Рассмотрим движение частицы, находящейся одновременно
под действием постоянного поля U и силы
/ = /i cos cot + /2 sin cut,	C0.1)
меняющейся со временем с большой частотой ш (/i, /2 — функ-
функции только координат). Под «большой» мы понимаем при этом
частоту, удовлетворяющую условию ш ^> 1/Г, где Г — поря-
порядок величины периода движения, которое частица совершала
бы в одном поле U. По своей величине сила / не предполага-
предполагается слабой по сравнению с силами, действующими в поле U.

§ 30	ДВИЖЕНИЕ В БЫСТРО ОСЦИЛЛИРУЮЩЕМ ПОЛЕ	125
Мы будем, однако, предполагать малым вызываемое этой силой
колебательное смещение частицы (обозначенное ниже через ?,).
Для упрощения вычислений рассмотрим сначала одномерное
движение в поле, зависящем лишь от одной пространственной
координаты х. Тогда уравнение движения частицы х)
тх = -% + /.	C0.2)
Из характера действующего на частицу поля заранее ясно,
что ее движение будет представлять собой перемещение вдоль
некоторой плавной траектории с одновременными малыми ос-
цилляциями (с частотой си) вокруг нее. Соответственно этому
представим функцию x(t) в виде суммы
ж(?) = Х(?)+ ?,(?),	C0.3)
где x(t) представляет собой указанные малые осцилляции.
Среднее значение функции x(t) за время ее периода 2п/а) об-
обращается в нуль, функция же X(t) за это время меняется очень
мало. Обозначая такое усреднение чертой над буквой, имеем:
х = X(t), т.е. функция X(t) описывает усредненное по быстрым
осцилляциям «плавное» движение частицы. Выведем уравне-
уравнение, определяющее эту функцию 2).
Подставляя C0.3) в C0.2) и разлагая по степеням ?, с точно-
точностью до членов первого порядка, получим
В этом уравнении фигурируют члены различного характера —
осциллирующие и «плавные»; они должны, очевидно, взаимно
сокращаться в каждой из этих двух групп в отдельности. Для
осциллирующих членов достаточно написать
mi = f(X,t),	C0.5)
остальные содержат малый множитель ?, и потому малы по срав-
сравнению с написанными (что касается производной ?, , то она про-
пропорциональна большой величине си2 и потому не мала). Инте-
Интегрируя уравнение C0.5) с функцией / из C0.1) (при этом вели-
величина X рассматривается как постоянная), получим
х) Координата х — не обязательно декартова, а коэффициент т соответ-
соответственно не обязательно есть масса частицы и не обязательно постоянен, как
это предположено в C0.2). Такое предположение, однако, не отражается на
окончательном результате (см. ниже).
2) Идея излагаемого ниже метода принадлежит П. Л. Капице A951).

126	МАЛЫЕ КОЛЕБАНИЯ	ГЛ. V
?,=	f—.	C0.6)
таJ	v '
Усредним теперь уравнение C0.4) по времени (в указанном
выше смысле). Поскольку средние значения первых степеней /
и ?, обращаются в нуль, получим уравнение
Ш	dX + КдХ ~ dX
dX ^8X	dX muo2j OX'
содержащее уже только функцию X(t). Перепишем его оконча-
окончательно в виде
тХ = -Щ^->	C0.7)
где «эффективная потенциальная энергия» определяется сле-
следующим образом х):
ЭСР	2таJ	4mcu2	J2J'	\ )
Сравнивая это выражение с C0.6), легко видеть, что дополни-
дополнительный (по отношению к полю U) член представляет собой не
что иное, как среднюю кинетическую энергию осцилляционного
движения:
Е/эф = Е7+у?,2.	C0.9)
Таким образом, усредненное по осцилляциям движение ча-
частицы происходит так, как если бы, помимо постоянного поля С/,
действовало еще и дополнительное постоянное поле, квадратич-
квадратично зависящее от амплитуды переменного поля.
Полученный результат может быть легко обобщен на слу-
случай системы с любым числом степеней свободы, описываемой
обобщенными координатами q{. Для эффективной потенциаль-
потенциальной энергии получается (вместо C0.8)) выражение
г, к	i,k
где величины а^,1 (вообще говоря, — функции координат) — эле-
элементы матрицы, обратной матрице коэффициентов а^ в кине-
кинетической энергии системы (см. E.5)).
г) Произведя несколько более длинные вычисления при зависящей от х
величине т, легко убедиться в том, что формулы C0.7),C0.8) остаются
справедливыми и в этом случае.

§ 30	ДВИЖЕНИЕ В БЫСТРО ОСЦИЛЛИРУЮЩЕМ ПОЛЕ	127
Задачи
1.	Определить положения устойчивого равновесия маятника, точка под-
подвеса которого совершает вертикальные колебания с большой часто-
частотой у (у > y/g/l).
Решение. Из полученной в задаче 3, в) § 5 функции Лагранжа вид-
видно, что в данном случае переменная сила
/ = — mlay2 cosyt sin (p
(в качестве величины х выбран угол (р). Поэтому «эффективная потенци-
потенциальная энергия»
B 2
— cos (р -\——— sin2 (p
4gl
Положения устойчивого равновесия отвечают минимуму этой функции. На-
Направление вертикально вниз (ф = 0) всегда устойчиво. При выполнении
условия
aV > 2gl
устойчивым является также положение вертикально вверх (ф = я).
2.	То же для маятника с горизонтально колеблющейся точкой подвеса.
Решение. По полученной в задаче 3, б) § 5 функции Лагранжа на-
находим / = mlay2 cos yt cos ф и затем
[22	~\
— cos ф -\——- cos2 ф .
4gZ	J
Если а2у2 < 2g/, то устойчиво положение ф = 0. Если же а2у2 > 2gl, то
устойчивому равновесию отвечает значение
2gl
а2у2

ГЛАВА VI
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 31. Угловая скорость
В механике твердое тело можно определить как систему ма-
материальных точек, расстояния между которыми неизменны. Ре-
Реально существующие в природе системы могут, конечно, удо-
удовлетворять этому условию лишь приближенно. Но большинство
твердых тел в обычных условиях так мало изменяет свою форму
и размеры, что при изучении законов движения твердого тела,
рассматриваемого как нечто целое, можно вполне отвлечься от
этих изменений.
В дальнейшем изложении мы будем часто рассматривать
твердое тело как дискретную совокупность материальных то-
точек, чем достигается некоторое упрощение выводов. Это, одна-
однако, ни в какой степени не противоречит тому обстоятельству,
что в действительности твердые тела можно обычно рассматри-
рассматривать в механике как сплошные, совершенно не интересуясь их
внутренней структурой. Переход от формул, содержащих сум-
суммирование по дискретным точкам, к формулам для сплошного
тела осуществляется просто заменой масс частиц на массу pdV',
заключенную в элементе объема dV (p — плотность массы), и
интегрированием по всему объему тела.
Для описания движения твердого тела введем две системы
координат: «неподвижную» , т.е. инерциальную систему XYZ,
и движущуюся систему координат Ж1 = ж, Х2 = у, х% = z, кото-
которая предполагается жестко связанной с твердым телом и участ-
участвующей во всех его движениях. Начало движущейся системы
координат удобно совместить с центром инерции тела.
Положение твердого тела относительно неподвижной систе-
системы координат вполне определяется заданием положения дви-
движущейся системы. Пусть радиус-вектор R указывает положе-
положение начала О движущейся системы (рис. 35). Ориентация же
осей этой системы относительно неподвижной определяется тре-

§31
УГЛОВАЯ СКОРОСТЬ
129
Рис. 35
мя независимыми углами, так что вместе с тремя компонентами
вектора R мы имеем всего шесть координат. Таким образом, вся-
всякое твердое тело представляет
собой механическую систему
с шестью степенями свободы.
Рассмотрим произвольное
бесконечно малое перемеще-
перемещение твердого тела. Его мож-
можно представить в виде суммы
двух частей. Одна из них есть
бесконечно малый параллель-
параллельный перенос тела, в резуль-
результате которого центр инерции
переходит из начального по-
положения в конечное при неиз-
неизменной ориентации осей подвижной системы координат. Вторая
— бесконечно малый поворот вокруг центра инерции, в резуль-
результате которого твердое тело приходит в конечное положение.
Обозначим радиус-вектор произвольной точки Р твердого
тела в подвижной системе координат через г, а радиус-вектор
той же точки в неподвижной системе — через г. Тогда бесконеч-
бесконечно малое смещение dx точки Р складывается из перемещения dR
вместе с центром инерции и перемещения [d<p-r] относительно
последнего при повороте на бесконечно малый угол dip (см. (9.1)):
dx = dR + [dip • г].
Разделив это равенство на время dt, в течение которого произо-
произошло рассматриваемое перемещение, и введя скорости
dt
dt V'
dR _ дт- dip _
~dt ~ ' ~dt ~
C1.1)
получим соотношение между ними
v = V + [ftr].	C1.2)
Вектор V есть скорость центра инерции твердого тела; ее на-
называют также скоростью его поступательного движения; век-
вектор ?1 — узловая скорость вращения твердого тела; его направ-
направление (как и направление d(X)) совпадает с направлением оси
вращения. Таким образом, скорость v любой точки тела (отно-
(относительно неподвижной системы координат) может быть выра-
выражена через поступательную скорость тела и угловую скорость
его вращения.

130	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
Следует подчеркнуть, что при выводе формулы C1.2) специ-
специфические свойства начала координат как центра инерции тела
совершенно не были использованы. Преимущества этого выбо-
выбора выяснятся лишь позже при вычислении энергии движуще-
движущегося тела.
Допустим теперь, что жестко связанная с твердым телом си-
система координат выбрана так, что ее начало находится не в цен-
центре инерции О, а в некоторой точке О1 на расстоянии а от точ-
точки О. Скорость перемещения начала О1 этой системы обозначим
через V', а угловую скорость ее вращения — через ft'.
Рассмотрим снова какую-либо точку Р твердого тела и обо-
обозначим ее радиус-вектор относительно начала О1 через г'. Тогда
г = г' + аи подстановка в C1.2) дает
v = V+[fta] + [ftr'].
С другой стороны, по определению V' и ft', должно быть v =
= V' + [ft'r']. Поэтому мы приходим к выводу, что
V' = V+[fta], п' = п.	C1.3)
Второе из этих равенств весьма существенно. Мы видим, что
угловая скорость, с которой в каждый данный момент времени
вращается жестко связанная с телом система координат, ока-
оказывается совершенно не зависящей от этой системы. Все такие
системы вращаются в заданный момент времени вокруг парал-
параллельных друг другу осей с одинаковой по абсолютной величине
скоростью ft. Это обстоятельство и дает нам право называть ft
угловой скоростью вращения твердого тела как такового. Ско-
Скорость же поступательного движения такого «абсолютного» ха-
характера отнюдь не имеет.
Из первой формулы C1.3) видно, что если V и ft (в данный
момент времени) взаимно перпендикулярны при каком-либо вы-
выборе начала координат О, то они (т.е. V' и ft') взаимно перпенди-
перпендикулярны и при определении по отношению к любому другому
началу О1. Из формулы C1.2) видно, что в этом случае ско-
скорости v всех точек тела лежат в одной и той же плоскости —
плоскости, перпендикулярной к ft. При этом всегда можно вы-
выбрать такое начало О1 х), скорость V' которого равна нулю, что
движение твердого тела (в данный момент) будет представлено
г) Оно может, конечно, находиться вне объема тела.

§ 32	ТЕНЗОР ИНЕРЦИИ	131
как чистое вращение вокруг оси, проходящей через О1. Эту ось
называют мгновенной осью вращения тела 1).
В дальнейшем мы будем всегда предполагать, что начало
движущейся системы координат выбрано в центре инерции те-
тела, так что и ось вращения тела проходит через этот центр. При
движении тела меняются, вообще говоря, как абсолютная вели-
величина ft, так и направление оси вращения.
§ 32. Тензор инерции
Для вычисления кинетической энергии твердого тела рас-
рассмотрим его как дискретную систему материальных точек:
2 '
где суммирование производится по всем точкам, составляющим
тело. Здесь и ниже мы опускаем индексы, нумерующие эти точ-
точки, с целью упрощения записи формул.
Подставив сюда C1.2), получим
= Е ?
Скорости V и Q одинаковы для всех точек твердого тела. По-
Поэтому в первом члене V2/2 выносится за знак суммы, а сумма
5^7п есть масса тела, которую мы будем обозначать буквой ц.
Второй член запишем так:
Отсюда видно, что если начало движущейся системы координат
выбрано, как условлено, в центре инерции, то этот член обра-
обращается в нуль, так как в этом случае J^rar = 0. Наконец, в
третьем члене раскрываем квадрат векторного произведения и
в результате находим
ifO2r2 — (OrY\	Dе? "Л
Таким образом, кинетическая энергия твердого тела может
быть представлена в виде суммы двух частей. Первый член в
C2.1) есть кинетическая энергия поступательного движения —
г) В общем же случае не взаимно перпендикулярных направлений V и П
начало координат можно выбрать таким образом, чтобы V и ft стали парал-
параллельными, т.е. движение (в данный момент времени) будет совокупностью
вращения вокруг некоторой оси и поступательного перемещения вдоль этой

132	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
она имеет такой вид, как если бы вся масса тела была сосре-
сосредоточена в его центре инерции. Второй член есть кинетическая
энергия вращательного движения с угловой скоростью Q вокруг
оси, проходящей через центр инерции. Подчеркнем, что возмож-
возможность такого разделения кинетической энергии на две части обу-
обусловлена выбором начала связанной с телом системы координат
именно в его центре инерции.
Перепишем кинетическую энергию вращения в тензорных
обозначениях, т.е. через компоненты Х{, ?1{ векторов г, ft г):
Здесь использовано тождество $1^ = 6^ Л&, где 6^ — единичный
тензор (компоненты которого равны единице при г = к и нулю
при г ф к). Введя тензор
1гк = Y,m (xfoik - Х{Хк),	C2.2)
получим окончательное выражение для кинетической энергии
твердого тела в виде
Т = ^ + \1гЛпк.	C2.3)
Функция Лагранжа твердого тела получается из C2.3) вы-
вычитанием потенциальной энергии
L=^ + \ЦАПк - U.	C2.4)
Потенциальная энергия является в общем случае функцией ше-
шести переменных, определяющих положение твердого тела, на-
например, трех координат X, У, Z центра инерции и трех углов,
определяющих ориентацию движущихся осей координат отно-
относительно неподвижных.
Тензор Цк называется тензором моментов инерции или
просто тензором инерции тела. Как ясно из определения C2.2),
г) В этой главе буквами г, j к обозначаются тензорные индексы, пробе-
пробегающие значения 1, 2, 3. При этом везде применяется извесное правило
суммирования, согласно которому знаки сумм опускаются, а по всем два-
дважды повторяющимся (так называемым «немым») индексам подразумевает-
подразумевается суммирование по значениям 1, 2, 3; так, А{В{ = АВ, Аг = AiAi = А и
т.д. Обозначение немых индексов можно, очевидно, менять произвольным
образом (лишь бы оно не совпало с обозначением других фигурирующих в
данном выражении тензорных индексов).

§ 32	ТЕНЗОР ИНЕРЦИИ	133
он симметричен, т.е.
hk = hi-	C2.5)
Выпишем для наглядности его компоненты в явном виде в
следующей таблице:
(
-52тух "?т(х2 + z2) -"?myz . C2.6)
-Yjnzx	~^2mzy 52m(x2 + у2))
Компоненты /жж, Iyy, Izz иногда называют моментами инерции
относительно соответствующих осей.
Тензор инерции, очевидно, аддитивен — моменты инерции
тела равны суммам моментов инерции его частей.
Если твердое тело можно рассматривать как сплошное, то
в определении C2.2) сумма заменяется интегралом по объему
тела:
Iik = [ p(xfbik ~ xiXk) dV.	C2.7)
Как и всякий симметричный тензор второго ранга, тензор
инерции может быть приведен к диагональному виду путем со-
соответствующего выбора направлений осей х\, Ж2, #з- Эти на-
направления называют главными осями инерции, а соответствую-
соответствующие значения компонент тензора — главными моментами инер-
цищ обозначим их как /i, /2, /3. При таком выборе осей
жх, #2, хз вращательная кинетическая энергия выражается осо-
особенно просто:
Гвр = \{hu\ + 12П22 + /3П§).	C2.8)
Отметим, что каждый из трех главных моментов инерции не
может быть больше суммы двух других. Так,
h + h = Е т(х\ + х22 + 2х\) > Е т{х\ + х\) = /3. C2.9)
Тело, у которого все три главных момента инерции различ-
различны, называют асимметрическим волчком.
Если два главных момента инерции равны друг другу, 1\ =
= /2^ -^3; то твердое тело называют симметрическим волчком.
В этом случае выбор направления главных осей в плоскости х±х2
произволен.
Если же все три главных момента инерции совпадают, то те-
тело называют шаровым волчком. В этом случае произволен вы-

134	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
бор всех трех главных осей инерции: в качестве их можно взять
любые три взаимно перпендикулярные оси.
Нахождение главных осей инерции очень упрощается, если
твердое тело обладает той или иной симметрией; ясно, что по-
положение центра инерции и направления главных осей инерции
должны обладать той же симметрией.
Так, если тело обладает плоскостью симметрии, то центр
инерции должен лежать в этой плоскости. В ней же лежат две
главные оси инерции, и третья — перпендикулярна к ней. Оче-
Очевидным случаем такого рода является система частиц, располо-
расположенных в одной плоскости. В этом случае существует простое
соотношение между тремя главными моментами инерции. Если
плоскость системы выбрана в качестве плоскости х±Х2, то по-
поскольку для всех частиц х% = 0, имеем
h=52mxl, l2=Y,mxb h = Y,m(x\ +ж|),
так что
h = h + h-	C2.10)
Если тело обладает осью симметрии какого-либо порядка,
то центр инерции лежит на этой оси. С ней же совпадает одна
из главных осей инерции, а две другие — перпендикулярны к
ней. При этом если порядок оси симметрии выше второго, то
тело является симметрическим волчком. Действительно, каж-
каждую главную ось (перпендикулярную к оси симметрии) можно
повернуть тогда на угол, отличный от 180°, т.е. выбор этих осей
становится неоднозначным, а это возможно лишь в случае сим-
симметрического волчка.
Особым случаем является система частиц, расположенных
вдоль одной прямой линии. Если выбрать эту прямую в качестве
оси жз, то для всех частиц х\ = Х2 = 0, и потому два главных
момента инерции совпадают, а третий равен нулю:
h = I2 = ^2mxl J3 = 0.	C2.11)
Такую систему называют ротатором. Характерной особенно-
особенностью ротатора в отличие от общего случая произвольного тела
является то, что он имеет всего две (а не три) вращательные сте-
степени свободы, соответствующие вращениям вокруг осей х\ ИЖ2;
говорить же о вращении прямой вокруг самой себя, очевидно,
не имеет смысла.
Наконец, сделаем еще одно замечание по поводу вычисления
тензора инерции. Хотя мы определили этот тензор по отноше-

§32
ТЕНЗОР ИНЕРЦИИ
135
нию к системе координат с началом в центре инерции (только
при таком определении справедлива основная формула C2.3)),
для его вычисления, однако, может иногда оказаться удобным
вычислить предварительно аналогичный тензор
определенный по отношению к другому началу О1. Если рассто-
расстояние ОО1 дается вектором а, то г = г' + а, Х{ = х^+щ] учитывая
также, что 5^ гаг = 0, по определению точки О, найдем:
4 = Iik + \i(a%k ~ <цак).	C2.12)
По этой формуле, зная Цк, легко вычислить искомый тензор Цк.
Задачи
1. Определить главные моменты инерции для молекул, рассматривае-
рассматриваемых как системы частиц, находящихся на неизменных расстояниях друг от
друга, в следующих случаях:
а) Молекула из атомов, расположенных на одной прямой.
Ответ:
т т lST /2 т п
1\ = ±2 = — 2_^ГПаТПъ*'а,Ъ, h = U,
^ афЬ
где та — массы атомов, 1аъ — расстояние между ато-
атомами а и Ь; суммирование производится по всем па-
парам атомов в молекуле (причем каждая пара значе-
значений а, Ъ входит в сумму по одному разу).
Для двухатомной молекулы сумма сводится к
одному члену, давая заранее очевидный результат — произведение приве-
приведенной массы обоих атомов на квадрат расстояния между ними:
777,1
777-1
ГП1ГП2
¦f
777-1 ~Ь ТП2
б) Трехатомная молекула в виде равнобедренного треугольника (рис. 36).
Ответ: Центр инерции лежит на высоте треу-
треугольника на расстоянии Х2 = m2h/\x от его основания.
Моменты инерции:
2m1m2 ,2
i\ = 	h ,
М-
Т ™>i 2
2 = ~Y
в) Четырехатомная молекула с атомами, располо-
расположенными в вершинах правильной трехугольной пира-
пирамиды (рис. 37).
Ответ: Центр инерции лежит на высоте пирами-
пирамиды на расстоянии
a
Рис. 37
= т2Н/\х от ее основания. Моменты инерции:
777,1
ЗГГЦГП2 ,2 ,
11 = 12 = 	h -\
h = ггца2.

136
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
При 77ii = ТП2, h = ay 2/3 мы имеем тетраэдрическую молекулу с момента-
моментами инерции
h = h = h = m^a2.
2. Определить главные моменты инерции сплошных однородных тел.
а)	Тонкий стержень длиной /.
Ответ: 11 = 12 = ц/2/12, /3 = 0 (толщиной стержня пренебрегаем).
б)	Шар радиуса R.
Ответ:
(вычислять следует сумму Д + 12 + /3 = 2p / г2с?У).
в) Круговой цилиндр радиуса .R и высотой /i.
Ответ:
h = h = i
t • /3 = fJ
(жз — ось цилиндра).
г)	Прямоугольный параллелепипед с длинами ребер а, Ь, с.
Ответ:
(оси Ж1, жг, хз параллельны ребрам а, Ь, с).
д)	Круговой конус с высотой h и радусом основания R.
f	Решение. Вычисляем сначала тензор I'ik
Жз' жз	по отношению к осям с началом в вершине кону-
конуса (рис. 38). Вычисление легко производится в
цилиндрических координатах и дает
J
Центр тяж:ести находится, как показывает про-
простое вычисление, на оси конуса на расстоянии
а = 3/i/4 от вершины. По формуле C2.12) на-
находим окончательно
Рис. 38
е) Трехосный эллипсоид с полуосями а, Ь, с.
Решение. Центр инерции совпадает с центром эллипсоида, а глав-
главные оси инерции — с его осями. Интегрирование по объему эллипсоида
может быть сведено к интегрированию по объему сферы путем преобразо-
преобразования координат х = а?,, у = br\, z = c?, превращающего уравнение поверх-
поверхности эллипсоида
х2 у2 z2
	Ь -—I	= 1
а2 Ъ2 с2
в уравнение поверхности единичной сферы

§ 32	ТЕНЗОР ИНЕРЦИИ	137
Так, для момента инерции относительно оси х получаем
h=P J J J (у2 + z2)dx dy dz =
JJJW22?f2 2
где /' — момент инерции шара единичного радиуса.
Учитывая, что объем эллипсоида равен 4яаЬс/3, получим окончательно
моменты инерции
5	2~5	3~5
3. Определить частоту малых колебаний физического маятника (твердое
тело, качающееся в поле тяжести около неподвижной горизонтальной оси).
Решение. Пусть / — расстояние от центра инерции маятника до
оси вращения, а а, C,у — углы между направлениями его главных осей
инерции и осью вращения. В качестве переменной координаты вводим угол
(р между вертикалью и перпендикуляром, опущенным из центра инерции
на ось вращения. Скорость центра инерции V = /ф, а проекции угловой
скорости на главные оси инерции: ф cos ос, фсозC, фсову. Считая угол (р
малым, находим потенциальную энергию в виде
U = ixg/(l-coscp) « -ixg/ф2.
Поэтому функция Лагранжа
/2	-|	/2
Отсюда для частоты колебаний имеем
yd2 + h cos2 a + /2 cos2 C + /3 cos2 у'
4. Найти кинетическую энергию системы, изображенной на рис. 39; О А
и А В — тонкие однородные стержни длиной /, шарнирно скрепленные в
точке А. Стержень О А вращается (в плоскости рисунка) вокруг точки О,
а конец В стержня А В скользит вдоль оси Ох. \у
Решение. Скорость центра инерции
стержня О А (находящегося на его середине)
есть /ф/2, где ф — угол АО В. Поэтому кине-
кинетическая энергия стержня О А
ц/ .2 1-2
Тл = 	ю -\- —ю	л ,
8	2	О '
(|х — масса одного стержня).
Декартовы координаты центра инерции	Рис. 39
стержня АВ : X = C1/2) cos ф Y = A/2) sin (р. Так как угловая скорость
вращения этого стержня тоже равна ф, то его кинетическая энергия
Полная кинетическая энергия системы
о
(подставлено / = ц/2/12 согласно задаче 2, а)).
Т= -^-A + 3 sin2 Ф)ф2

138
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
5. Найти кинетическую энергию цилиндра (радиуса R), катящегося по
плоскости. Масса цилиндра распределена по его объему таким образом, что
одна из главных осей инерции параллельна оси цилиндра и проходит на
расстоянии а от нее; момент инерции относительно этой главной оси есть /.
Решение. Вводим угол (р между верти-
вертикалью и перпендикуляром, опущенным из цен-
центра масс на ось цилиндра (рис. 40). Движение
цилиндра в каждый момент времени можно рас-
рассматривать как чистое вращение вокруг мгновен-
мгновенной оси, совпадающей с линией его соприкосно-
соприкосновения с неподвижной плоскостью; угловая ско-
скорость этого вращения есть ф (угловая скорость
вращения вокруг всех параллельных осей одина-
одинакова). Центр инерции находится на расстоянии
Vа2 + R2 — 2aR cos (p от мгновенной оси и пото-
му его скорость есть V = ф^а2 + R2 — 2aRcos (p.
Рис. 40
Полная кинетическая энергия
Т = ^(
+ R2 - 2aRcos ср)ф2 + ^
Найти кинетическую энергию однородного цилиндра радиуса а,
катящегося по внутренней стороне ци-
цилиндрической поверхности радиуса R
(рис. 41).
Решение. Вводим угол (р меж-
между линией, соединяющей центры обоих
цилиндров, и вертикалью. Центр инер-
инерции катящегося цилиндра находится на
оси и его скорость V = <p(R — а). Угло-
Угловую скорость вычисляем, как скорость
чистого вращения вокруг мгновенной оси, совпадающей с линией соприкос-
соприкосновения цилиндров; она равна
Рис. 41
Если
n V .R-a
Q = — = ср	.
а	а
то
C2.13)
— момент инерции относительно оси цилиндра,
T=±(R- J'2 \ /з(Д~аJ '2 =
21 п) Ф 2 а2 Ф
(Is — из задачи 2, в)).
7. Найти кинетическую энергию однородного конуса, катящегося по
плоскости.
Решение. Обозначим через 9 угол между линией О А соприкоснове-
соприкосновения конуса с плоскостью и каким-либо неподвижным направлением в этой
плоскости (рис. 42). Центр инерции находится на оси конуса и его скорость
V = a cos а • 9, где 2 а — угол раствора конуса, а а — расстояние центра
инерции от вершины. Угловую скорость вращения вычисляем, как скорость
чистого вращения вокруг мгновенной оси О А:
V
Q = —:	= Э ctg a.
asm а

§32
ТЕНЗОР ИНЕРЦИИ
139
Одна из главных осей инерции (ось хз) совпадает с осью конуса, а дру-
другую (ось Х2) выбираем перпендикулярно к оси конуса и линии О А. Тогда
проекции вектора Q (направленного параллельно О А) на главные оси инер-
инерции будут Q sin а, О, Q cos ос. В результате находим для искомой кинетиче-
кинетической энергии:
2	2	2 sin2 a
(h — высота конуса; /i, /2, a — из задачи 2 d)).
40
Рис. 42
Рис. 43
8. Найти кинетическую энергию однородного конуса, основание кото-
которого катится по плоскости, а вершина постоянно находится в точке над
плоскостью на высоте, равной радиусу основания (так что ось конуса па-
параллельна плоскости).
Решение. Вводим угол 9 между заданным направлением в плоско-
плоскости и проекцией на нее оси конуса (рис. 43). Тогда скорость центра инерции
V = ад (обозначения те же, что в задаче 7). Мгновенной осью вращения
является образующая конуса О А, проведенная в точку его соприкоснове-
соприкосновения с плоскостью. Центр инерции находится на расстоянии a sin ос от этой
оси и потому
^ 5
a sin а sin а
Проекции вектора П на главные оси инерции (ось хч выбираем перпендику-
перпендикулярной к оси конуса и линии О A): Q sin а = Э, 0, Q cos а = Э ctg а. Поэтому
кинетическая энергия
9. Найти кинетическую энергию однородного трехосного эллипсоида,
вращающегося вокруг одной из своих осей (АВ, рис. 44), причем послед-
последняя сама вращается вокруг направления CD,
перпендикулярного к ней и проходящего че-
через центр эллипсоида.
Решение. Угол поворота вокруг оси
CD обозначим через 9, а угол поворота во-
вокруг оси АВ (угол между CD и осью инер-
инерции хг, перпендикулярной к АВ) — через (р.
Тогда проекции П на оси инерции будут:
ecoscp, esincp, ф	Рис.44
(причем ось хз совпадает с АВ). Поскольку центр инерции, совпадающий

140	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
с центром эллипсоида, неподвижен, то кинетическая энергия
T=\{h cos2 cp + h sin2 <р) ё2 + i/зф2.
10. Найти кинетическую энергию однород-
однородного трехосного эллипсоида, вращающегося во-
вокруг одной из своих осей (АВ, рис. 45), причем
последняя наклонена, а эллипсоид симметричен
относительно этой оси.
Решение. Проекции Q на ось АВ и на
Рис. 45	перпендикулярные к ней две другие главные оси
инерции (которые можно выбрать произвольно):
9 cos a cos (p, Э cos а sin ф, ф + Э sin а.
Кинетическая энергия
Т= — cos2a-e2 + — (ф + esinaJ.
§ 33. Момент импульса твердого тела
Величина момента импульса системы зависит, как мы знаем,
от выбора точки, относительно которой он определен. В меха-
механике твердого тела наиболее рационален выбор в качестве этой
точки начала подвижной системы координат, т.е. центра инер-
инерции тела. Ниже мы будем понимать под М момент, определен-
определенный именно таким образом.
Согласно формуле (9.6) при выборе начала координат в
центре инерции тела его момент М совпадает с «собственным
моментом» , связанным лишь с движением точек тела отно-
относительно центра инерции. Другими словами, в определении
М = ^2m[rv] надо заменить v на [fir]:
М = ?m[r[ftr]] = ? тп{г2п - г(гП)},
или в тензорных обозначениях:
Наконец, учитывая определение C2.2) тензора инерции, полу-
получаем окончательно:
Мг = Iikuk.	C3.1)
Если оси Ж1, #2, ^3 направлены вдоль главных осей инерции
тела, то эта формула дает:
Mi=Jifib М2 = 12^2, Ms = Isns.	C3.2)
В частности, для шарового волчка, когда все три главных
момента инерции совпадают, имеем просто:

§33
МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА
141
М = /ft,	C3.3)
т.е. вектор момента пропорционален вектору угловой скорости
и имеет одинаковое с ним направление.
В общем же случае произвольного тела вектор М, вообще
говоря, не совпадает по своему направлению с вектором ft, и
лишь при вращении тела вокруг какой-либо из его главных осей
инерции М и ft имеют одинаковое направление.
Рассмотрим свободное движение твердого тела, не подвер-
подверженного действию каких-либо внешних сил. Не представляющее
интереса равномерное поступательное движение будем предпола-
предполагать исключенным, так что речь идет о свободном вращении тела.
Как и у всякой замкнутой системы, момент импульса свобод-
свободно вращающегося тела постоянен. Для шарового волчка условие
М = const приводит просто к ft = const. Это значит, что общим
случаем свободного вращения шарового волчка является просто
равномерное вращение вокруг постоянной оси.
Столь же прост случай ротатора. Здесь тоже М = /ft, при-
причем вектор ft перпендикулярен к оси ротатора. Поэтому сво-
свободное вращение ротатора есть равномерное вращение в одной
плоскости вокруг направления, перпендикулярного к этой плос-
плоскости.
Закон сохранения момента достаточен и для определения бо-
более сложного свободного вращения симметрического волчка.
Воспользовавшись произвольно-
произвольностью выбора направлений главных
осей инерции Ж1, Ж2 (перпендикуляр-
(перпендикулярных к оси симметрии волчка жз), вы- г'
берем ось Ж2 перпендикулярной к чч
плоскости, определяемой постоян-
постоянным вектором М и мгновенным по-
положением оси жз- Тогда М2 = О, а из
формул C3.2) видно, что и Г^ = 0.
Это значит, что направления М, ft и
оси волчка в каждый момент време-
времени лежат в одной плоскости (рис. 46).
Но отсюда в свою очередь следует,
что скорости v = [ftг] всех точек на
оси волчка в каждый момент времени перпендикулярны к ука-
указанной плоскости; другими словами, ось волчка равномерно (см.
Рис. 46

142	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
ниже) вращается вокруг направления М, описывая круговой
конус (так называемая регулярная прецессия волчка). Одновре-
Одновременно с прецессией сам волчок равномерно вращается вокруг
собственной оси.
Угловые скорости обоих этих вращений легко выразить че-
через заданную величину момента М и угол наклона 6 оси волчка
к направлению М. Угловая скорость вращения волчка вокруг
своей оси есть просто проекция Лз вектора Q на эту ось:
Для определения же скорости прецессии Лпр надо разложить
вектор ft по правилу параллелограмма на составляющие вдоль
х% и вдоль М. Из них первая не приводит ни к какому пере-
перемещению самой оси волчка, а потому вторая и дает искомую
угловую скорость прецессии. Из построения на рис. 46 ясно, что
Г^пр sin 6 = fix, а поскольку fix = M\jl\ = M sin 0/ii, то получаем
Оф = М/Д.	C3.5)
§ 34. Уравнения движения твердого тела
Поскольку твердое тело обладает в общем случае шестью
степенями свободы, то общая система уравнений движения дол-
должна содержать шесть независимых уравнений. Их можно пред-
представить в виде, определяющем производные по времени от двух
векторов: импульса и момента тела.
Первое из этих уравнений получается просто путем сумми-
суммирования уравнений р = f для каждой из составляющих тело
частиц, где р — импульс частицы, a f — действующая на нее
сила. Вводя полный импульс тела
и полную действующую на него силу J^f = F, получим
f = F.	C4.1)
Хотя мы определили F как сумму всех сил f, действующих
на каждую их частиц, в том числе со стороны других частиц
тела, фактически в F входят лишь силы, действующие со сто-
стороны внешних источников. Все силы взаимодействия между ча-
частицами самого тела взаимно сокращаются; действительно, при

§ 34	УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА	143
отсутствии внешних сил импульс тела, как и всякой замкнутой
системы, должен сохраняться, т.е. должно быть F = 0.
Если U — потенциальная энергия твердого тела во внешнем
поле, то сила F может быть определена путем дифференциро-
дифференцирования ее по координатам центра инерции тела:
F = -||.	C4.2)
Действительно, при поступательном перемещении тела на
6R настолько же меняются и радиус-векторы г каждой точки
тела, а потому изменение потенциальной энергии
W = Y. ?6' = 6R? 7Г = -6R? f = -F6R-
Z—f dt	z—' dt	z—'
Отметим в этой связи, что уравнение C4.1) может быть по-
получено и как уравнение Лагранжа по отношению к координатам
центра инерции
d dL _ дЬ_
dtdV ~ Ж
с функцией Лагранжа C2.4), для которой
' ж ж
Перейдем к выводу второго уравнения движения, определяю-
определяющего производную по времени от момента импульса М. Для
упрощения вывода удобно выбрать «неподвижную» (инерциаль-
ную) систему отсчета таким образом, чтобы в данный момент
времени центр инерции тела покоился относительно нее.
Имеем
В силу сделанного нами выбора системы отсчета (в котором
V = 0) значение г в данный момент времени совпадает со ско-
скоростью v = г. Поскольку же векторы v и р = rav имеют оди-
одинаковое направление, то [гр] = 0. Заменив также р на силу f,
получим окончательно:
^ = К,	C4.3)
где
].	C4.4)
Поскольку момент М определен относительно центра инер-
инерции (см. начало § 33), он не меняется при переходе от одной

144	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
инерциальной системы отсчета к другой. Это видно из фор-
формулы (9.5) с R = 0. Отсюда следует, что уравнение движения
C4.3), полученное здесь при определенном выборе системы от-
отсчета, тем самым, в силу галилеевского принципа относительно-
относительности, справедливо в любой инерциальной системе.
Вектор [rf] называется моментом силы f, так что К есть
сумма моментов всех сил, действующих на тело. Как и в пол-
полной силе F, в сумме C4.4) фактически должны учитываться
лишь внешние силы; в соответствии с законом сохранения мо-
момента импульса сумма моментов всех сил, действующих внутри
замкнутой системы, должна обращаться в нуль.
Момент силы, как и момент импульса, зависит, вообще го-
говоря, от выбора начала координат, относительно которого он
определен. В C4.3), C4.4) моменты определяются относительно
центра инерции тела.
При переносе начала координат на расстояние а новые ради-
радиус-векторы г' точек тела связаны со старыми г через г = г' + а.
Поэтому
или
K = K' + [aF].	C4.5)
Отсюда видно, в частности, что величина момента сил не
зависит от выбора начала координат, если полная сила F = 0 (в
таком случае говорят, что к телу приложена пара сил).
Уравнения C4.3) можно рассматривать как уравнение Ла-
гранжа
^&L _ dL_
dt dQ д(р
по отношению к «вращательным координатам». Действительно,
дифференцируя функцию Лагранжа C2.4) по компонентам век-
вектора ft, получим
Изменение же потенциальной энергии U при повороте тела на
бесконечно малый угол 6ф равно:
bU = -? f6t = -Е f [5<Р • г] = -бср ?[rf] = -Кбф,
откуда
K = -g,	C4.6)
так что

§ 35	ЭЙЛЕРОВЫ УГЛЫ	145
dL	8U ъг
Предположим, что векторы F и К взаимно перпендикуляр-
перпендикулярны. В этом случае всегда можно найти такой вектор а, чтобы в
формуле C4.5) К' обратилось в нуль, так что будет:
К = [aF].	C4.7)
При этом выбор а неоднозначен: прибавление к нему любого
вектора, параллельного F, не изменит равенства C4.7), так что
условие К' = 0 даст не определенную точку в подвижной си-
системе координат, а лишь определенную прямую линию. Таким
образом, при К 1 F действие всех приложенных к нему сил
может быть сведено к одной силе F, действующей вдоль опре-
определенной прямой линии.
Таков, в частности, случай однородного силового поля, в
котором действующая на материальную точку сила имеет вид
f = еЕ, где Е — постоянный вектор, характеризующий поле,
а величина е характеризует свойства частицы по отношению к
данному полю х). В этом случае имеем
F = E?e, K= [Eer E].
Предполагая, что $^е ^ О, введем радиус-вектор го, определен-
определенный согласно	^
го = §f.	C4.8)
Тогда мы получим следующее простое выражение для полного
момента сил:
K=[r0F].	C4.9)
Таким образом, при движении твердого тела в однородном
поле влияние поля сводится к действию одной силы F, «при-
«приложенной» в точке с радиус-вектором C4.8). Положение этой
точки всецело определяется свойствами самого тела; в поле тя-
тяжести, например, она совпадает с центром инерции тела.
§ 35. Эйлеровы углы
Как уже указывалось, для описания движения твердого тела
можно пользоваться тремя координатами его центра инерции и
какими-либо тремя углами, определяющими ориентацию осей
г) Так, в однородном электрическом поле Е есть напряженность поля,
а е — заряд частицы. В однородном поле тяжести Е есть ускорение свобод-
свободного падения g, а е — масса частицы т.

146
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
Рис. 47
жх, Ж2, жз движущейся системы координат относительно непо-
неподвижной системы X, У, Z. В качестве этих углов часто оказыва-
оказываются удобными так называемые
эйлеровы углы.
Так как нас сейчас интересу-
интересуют только углы между осями ко-
координат, мы выберем начала обе-
обеих систем в одной точке (рис. 47).
Подвижная плоскость жхЖ2 пере-
пересекает неподвижную XY по не-
некоторой прямой (ON на рис. 47),
которую называют линией узлов.
Эта линия, очевидно, перпендику-
перпендикулярна как к оси Z, так и к оси жз;
ее положительное направление выберем так, чтобы оно соот-
соответствовало направлению векторного произведения [гхз] (где
z, х3 — орты в направлении осей Z и жз).
В качестве величин, определяющих положение осей жх, Ж2, жз
относительно осей X, У, Z, примем следующие углы: угол 6 меж-
между осями Z и жз, угол ф между осями X и iV, угол г|; между ося-
осями N и жх. Углы ф и г|ютсчитываются в направлениях, определя-
определяемых правилом винта, соответственно вокруг осей Z и жз- Угол 9
пробегает значения от нуля до 7Г, а углы фиг|) — от нуля до 2п г).
Выразим теперь компоненты вектора угловой скорости ft по
подвижным осям жх, Ж2, жз через эйлеровы углы и их производ-
производные. Для этого надо спроецировать на эти оси угловые скорости
6, ф, г|;. Угловая скорость 6 направлена по линии узлов ON и
ее составляющие по осям жх, Ж2, жз равны:
в! = в cos-ф, 62 = -9 sin-ф, 63 = 0.
Угловая скорость ф направлена вдоль оси Z\ ее проекция на
ось жз равна фз = ф cos 6, а проекция на плоскость жхЖ2 равна
ф sin 6. Разлагая последнюю на составляющие по осям жх и Ж2,
получим
<Pi = ф sin 6 sinij>, Ф2 = ф sin 6 cosijj.
Наконец, угловая скорость л\> направлена по оси жз-
) Углы Э и (р — 71 / 2 представляют собой соответственно полярный угол
и азимут направления хз по отношению к осям X, У, Z. В то же время Э и
я/2 — *ф являются соответственно полярным углом и азимутом направления
Z по отношению к осям xi, X2, #з-

§ 35	ЭЙЛЕРОВЫ УГЛЫ	147
Собирая все эти составляющие по каждой из осей, получим
окончательно:
fil = ф sin 6 sin-ф + 6 cos-ф,
^2 = ф sin6 cost]; — 6sin\|;,	C5.1)
fi3 = ф cos 6 + ip.
Если оси xi, Ж2, х% выбраны по главным осям инерции твер-
твердого тела, то вращательную кинетическую энергию, выраженную
через эйлеровы углы, мы получим подстановкой A0) в C2.8).
Для симметрического волчка, у которого 1\ = 12 Ф /з, най-
найдем после простого приведения:
Гвр = |(ф28т2е + е2) + |(фсо8б+г1;J.	C5.2)
Заметим, что это выражение можно получить и проще, восполь-
воспользовавшись производительностью выбора направлений главных
осей инерции х\, х2 у симметрического волчка. Считая, что ось
х\ совпадает с осью узлов ON, т.е. что л\> = 0, будем иметь для
составляющих угловой скорости более простые выражения
fix = 9, ft2 = (psin9, П3 = фсо8б + -ф.	C5.3)
В качестве простого примера применения эйлеровых углов
определим с их помощью известное уже нам свободное движение
симметрического волчка.
Выберем ось Z неподвижной системы координат в направле-
направлении постоянного момента волчка М. Ось х% подвижной системы
направлена по оси волчка, а ось х\ пусть совпадает в данный
момент времени с осью узлов. Тогда для компонент вектора М
находим с помощью формул C5.3):
Mi = Jifii = Дё, М2 =
Ms = /3^3 =
С другой стороны, поскольку ось х\ (линия узлов) перпендику-
перпендикулярна к оси Z, имеем
Mi = 0, М2 = М sin 9, Ms = M cos 6.
Приравнивая друг другу эти выражения, получим следующие
уравнения:
ё = 0, Jicp = M, /3(фсо8б+-ф) = McosG.	C5.4)
Первое из этих уравнений дает 6 = const, т.е. постоянство угла
наклона оси волчка к направлению М. Второе определяет
(в согласии с C3.5)) угловую скорость прецессии ф = Mjl\,

148
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
Наконец, третье определяет угловую скорость вращения волчка
вокруг собственной оси Г^з — Mcos6//3-
Задачи
1. Привести к квадратурам задачу о движении тяжелого симметриче-
симметрического волчка с неподвижной нижней точкой (рис. 48).
Решение. Совместное начало подвижной и неподвижной систем
координат выбираем в неподвижной точке
волчка О, а ось Z направляем по вертикали
(рис. 48). Функция Лагранжа волчка в поле
тяжести
+ -у СФ + ф cos ЭJ — yigl cos 9
(|х — масса волчка, I — расстояние от нижней
Xl точки до центра инерции).
Координаты л\) и (р — циклические. По-
Поэтому имеем два интеграла движения:
дЬ
= —т- = /зСФ + Ф cos 9) = const = М3,
(i)
дь
рф = —- = (/{ sin2 Э + /3 cos2 в)ф + /з'Ф cos Э = const = Mz,
B)
где введено обозначение /{ = I\ + yil2 (величины р-ф и рф представляют
собой составляющие вращательного момента, определенного относительно
точки О, соответственно по осям жз и Z). Кроме того, сохраняется энергия
2
Из уравнений A) и B) находим
h '	2
— (гр Ч- ф cos Э) + \igl cos Э.
2
ф =
Mz — Ms cos Э
= —— — cos Э
/3
; sin2 e '
Mz — Ms cos Э
, 9
/; sin2 e
C)
D)
E)
Исключив с помощью этих равенств ф и ip из энергии C), получим
где введены обозначения
(Mz-M3cos9J
2i[ sin2 e
F)

35
ЭЙЛЕРОВЫ УГЛЫ
149
Определяя отсюда 0 и разделяя переменные, получим
G)
(интеграл — эллиптический). После этого углы Ф и *Ф выражаются как
функции от 0 в виде квадратур с помощью уравнений D), E).
Область изменения угла 0 при движении определяется условием Е' ^
^ ?/эф@)- Функция С/эф@) (при Ms ф Mz) стремится к +оо при значениях
0	= 0 и 0 = я, ав промежут-
промежутке между ними проходит че-
через минимум. Поэтому урав-
уравнение Е' = иэф @) имеет два
корня, определяющих преде-
предельные углы 0i и 02 наклона
оси волчка к вертикали.
При изменении угла 0 от
01	до 02 знак производной ф
остается неизменным или ме-
меняется, смотря по тому, оста-
остается ли неизменным или ме-
меняется в этом интервале знак разности Mz — Ms cos0. В первом случае ось
волчка прецессирует вокруг вертикали монотонно, одновременно совершая
колебания (так называемую нутацию) вверх и вниз (рис. 49 а; линия изоб-
изображает след, который ось волчка чертила бы на поверхности сферы с цен-
центром в неподвижной точке волчка). Во втором случае направление прецесии
противоположно на двух граничных окружностях, так что ось волчка пере-
перемещается вокруг вертикали, описывая петли (рис. 49 б). Наконец, если одно
из значений 0i, 02 совпадает с нулем, разности Mz — M3COS0 на соответ-
соответствующей предельной окружности ф и 0 одновременно обращаются в нуль,
так что ось волчка описывает траекторию изображенного на рис. 49 в типа.
2. Найти условие, при котором вращение волчка вокруг вертикальной
оси будет устойчивым.
Решение. При 0 = 0 оси xs и Z совпадают, так что Ms = Мг,
Е' = 0. Вращение вокруг этой оси будет устойчивым, если значение 0 = 0
отвечает минимуму функции ?/эф@). При малых 0 имеем
Го	LLp7 \ о
откуда находим условие Mf > 4I[]xgl или
Ч '
3. Определить движение волчка в случае, когда кинетическая энергия
его собственного вращения велика по сравнению с энергией в поле тяжести
(так называемый «быстрый» волчок).
Решение. В первом приближении, если пренебречь полем тяжести,
происходит свободная прецессия оси волчка вокруг направления момента М
(отвечающая в данном случае нутации волчка); она происходит согласно

150
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
C3.5) с угловой скоростью
м
A)
= к
В следующем приближении появляется медленная прецессия момента
М вокруг направления вертикали (рис. 50). Для определения скорости этой
прецессии усредним точное уравнение движения C4.3)
dM
dt
по периоду нутации. Момент сил тяжести, действующих на волчок, равен
К = jji[ri3g], где Пз — единичный вектор в направлении оси волчка. Из
соображений симметрии очевидно, что ре-
результат усреднения К по «конусу нутации»
сводится к замене вектора пз его проекцией
cos а-М/М на направление М (а — угол меж-
между М и осью волчка). Таким образом, полу-
получим уравнение
dM	yd, _ял
— = -cosa-[gM].
Оно означает, что вектор М прецессирует во-
вокруг направления g (вертикали) со средней
угловой скоростью
jj = lxlcosa
пр	М
рис 5Q	(малой по сравнению с QHyT).
В рассматриваемом приближении входя-
входящие в формулы A) и B) величины М и cos a
постоянны (хотя и не являются, строго говоря, интегралами движения).
Они связаны, с той же точностью, со строго сохраняющимися величинами
Е и Ms соотношениями
М2
Ms = M cos a, E та
§ 36. Уравнения Эйлера
Написанные в § 34 уравнения движения относятся к непо-
неподвижной системе координат: производные dP/dt и dNL/dt в
уравнениях C4.1) и C4.3) представляют собой изменения век-
векторов РиМпо отношению к этой системе. Между тем, наибо-
наиболее простая связь между компонентами вращательного момента
М твердого тела и компонентами угловой скорости имеет ме-
место в подвижной системе координат с осями, направленными по
главным осям инерции. Для того чтобы воспользоваться этой
связью, необходимо предварительно преобразовать уравнения
движения к подвижным координатам жх, Ж2, #з-

§ 36	УРАВНЕНИЯ ЭЙЛЕРА	151
Пусть dA/dt — скорость изменения какого-либо вектора А
по отношению к неподвижной системе координат. Если по от-
отношению к вращающейся системе вектор А не изменяется, то
его изменение относительно неподвижной системы обусловлено
только вращением, и тогда
(см. § 9, где было указано, что такие формулы, как (9.1), (9.2),
справедливы для любого вектора). В общем случае к правой ча-
части этого равенства надо добавить скорость изменения вектора
А по отношению к подвижной системе; обозначив эту скорость,
как dfA/dt, получим
? = ^ + [ПА].	C6.1)
С помощью этой общей формулы мы можем сразу перепи-
переписать уравнения C4.1) и C4.3) в виде
^- + [fiP] = F, ^ + [ПМ] = К.	C6.2)
Поскольку дифференцирование по времени производится здесь
в подвижной системе координат, то мы можем непосредственно
спроецировать уравнения на оси системы, написав
'd'P"
dt ' " '' V dt ) i dt ' " ''
где индексы 1, 2, 3 означают компоненты по осям жх, Ж2, жз- При
этом в первом уравнении заменяем Р на yiV и получаем
= F2,	C6.3)
Предполагая оси #i, Ж2, x% выбранными по главным осям инер-
инерции, во втором из уравнений C6.2) пишем Mi = /i^i и т.д.
h^-+ (h - hWstli = К2,	C6.4)
h^-+ (h - h^tuz = K3.
Уравнения C6.4) называются уравнениями Эйлера.

152	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
При свободном вращении К = 0 и уравнения Эйлера прини-
принимают вид
= о,
C6-5)
= 0.
В качестве примера применим эти уравнения к уже рас-
рассматривавшемуся нами свободному вращению симметрического
волчка. Положив 1\ = /2, имеем из третьего уравнения Г^з = 0,
т.е. 0% — const. После этого первые два уравнения напишем в
виде
где введена постоянная величина
a) = Os1-^-^.	C6.6)
Умножив второе уравнение на г и сложив с первым, получим
откуда
где А — постоянная; последнюю можно считать вещественной
(это сводится к надлежащему выбору начала отсчета времени),
и тогда
Oi = A cos cut, O2 = A sin cut.	C6.7)
Этот результат показывает, что проекция угловой скорости
на плоскость, перпендикулярную к оси волчка, вращается в этой
плоскости с угловой скоростью си, оставаясь постоянной по ве-
личине (л/О^ + О2 = А). Поскольку проекция 0% на ось волчка
тоже постоянна, то и весь вектор ft равномерно вращается с уг-
угловой скоростью си вокруг оси волчка, оставаясь неизменным по
величине. Ввиду связи М\ = /ifii, M2 = /2^2? -ОДз — ^3^3 меж-
между компонентами векторов ft и М такое же движение (по отно-
отношению к оси волчка) совершает, очевидно, и вектор момента М.
Полученная картина представляет собой, разумеется, лишь
другой аспект того же движения волчка, которое уже было рас-
рассмотрено в § 33 и 35 по отношению к неподвижной системе коор-
координат. В частности, угловая скорость вращения вектора М (ось
Z на рис. 48) вокруг направления х% совпадает, в терминах эй-
эйлеровых углов, с угловой скоростью — г|;. С помощью уравнений

§ 37	АСИММЕТРИЧЕСКИЙ ВОЛЧОК	153
C5.4) имеем
; Mcos9 . п Л/Г п/1 1\
гр = —	ф cos v = М cos 0 1-— —
h	\h h/
или в согласии с C6.6),
§ 37. Асимметрический волчок
Применим уравнения Эйлера к более сложной задаче о сво-
свободном вращении асимметрического волчка, у которого все три
момента инерции различны. Для определенности будем считать,
что
h>h> h.	C7.1)
Два интеграла уравнений Эйлера известны заранее. Они да-
даются законами сохранения энергии и момента и выражаются
равенствами
11П2 + 12П2 + 13П2 = 2Е,
J?fi? + l\Vi\ + 1\п\ = М2,
где энергия E и абсолютная величина момента М — заданные
постоянные. Эти же два равенства, выраженные через компо-
компоненты вектора М, имеют вид
Ml + М + М = 2Е,	C7.3)
h	h	h
Ml + Ml + M\ = M2.	C7.4)
Уже отсюда можно сделать некоторые заключения о харак-
характере движения волчка. Для этого заметим, что уравнения C7.3)
и C7.4) представляют собой, геометрически в осях Mi, M2, М3,
уравнения соответственно поверхности эллипсоида с полуосями
и сферы радиусом М. При перемещении вектора М (относи-
(относительно осей инерции волчка) его конец движется вдоль линии
пересечения указанных поверхностей (на рис. 51 изображен ряд
таких линий пересечения эллипсоида со сферами различных ра-
радиусов). Самое наличие пересечения обеспечивается очевидны-
очевидными неравенствами
М2 < 2EIS,	C7.5)

154
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
Рис. 51
геометрически означающими, что радиус сферы C7.4) лежит
между наименьшей и наибольшей из полуосей эллипсоида C7.3).
Проследим за изменением характера этих «траекторий» кон-
конца вектора М х) по мере изменения величины М (при заданной
энергии Е). Когда М2 лишь немногим превышает 2Е1\, сфера
пересекает эллипсоид по двум замкнутым маленьким кривым,
окружающим ось х\ вблизи соответствующих двух полюсов эл-
эллипсоида (при М2 —»> 2Е1\ эти кривые стягиваются в точки —
полюсы). По мере увеличения М2 кривые расширяются, а при
М2 = 2EI2 превращаются в две плоские кривые (эллипсы), пе-
пересекающиеся друг с другом в полюсах эллипсоида на оси Х2-
При дальнейшем увеличении М2 вновь возникают две раздель-
раздельные замкнутые траектории, но окружающие уже полюсы на оси
жз; при М2 —> 2Е1% они стягиваются в эти две точки.
Отметим, прежде всего, что замкнутость траекторий озна-
означает периодичность перемещения вектора М по отношению к
телу волчка; за время периода вектор М описывает некоторую
коническую поверхность, возвращаясь в прежнее положение.
Далее отметим существенно различный характер траекто-
траекторий, близких к различным полюсам эллипсоида. Вблизи осей х\
и х% траектории расположены целиком в окрестности полюсов,
) Аналогичные кривые, описываемые концом вектора О, называются
полодиями.

§ 37	АСИММЕТРИЧЕСКИЙ ВОЛЧОК	155
а траектории, проходящие вблизи полюсов на оси #2, в своем
дальнейшем ходе удаляются на большие расстояния от этих то-
точек. Такое различие соответствует разному характеру устойчи-
устойчивости вращения волчка вокруг его трех осей инерции. Вращение
вокруг осей х\ и х% (отвечающих наибольшему и наименьшему
из трех моментов инерции волчка) устойчиво в том смысле, что
при малом отклонении от этих состояний волчок будет продол-
продолжать совершать движение, близкое к первоначальному. Враще-
Вращение же вокруг оси х2 неустойчиво; достаточно малого отклоне-
отклонения, чтобы возникло движение, уводящее волчок в положения,
далекие от первоначального.
Для определения зависимости компонент ft (или пропорцио-
пропорциональных им компонент М) от времени обратимся к уравнениям
Эйлера C6.5). Выразив tti и Г^з через ft2 из двух уравнений
C7.2), C7.3)
= т(т r^	) ^ )^
Нун-Н)	C7 6)
** ~ 2Eh) - h{h /)fii}
и подставив во второе из уравнений C6.5), найдем
*ь = ^АП1п3 = —L={[BEh - м2) -
at	12	12 У1113
- h{I3 - h)u22][(M2 - 2Eh) - h{h - h)^l]}1'2. C7.7)
Разделяя в этом уравнении переменные и интегрируя, получим
функцию t(Q,2) в виде эллиптического интеграла. При приведе-
приведении его к стандартному виду будем считать для определенности,
что
М1 > 2Е12
(в обратном случае во всех следующих ниже формулах надо
переставить индексы 1 и 3). Вводим вместо t и Г^ новые пере-
переменные
и положительный параметр к < 1 согласно
к2 _ (h - h)BEI3 - М2)
Тогда получим
О
s
ds

156	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
(начало отсчета времени условно выбираем в момент, когда
Л2 = 0). При обращении этого интеграла возникает, как извест-
известно, одна из эллиптических функций Якоби
s = sn т,
чем и определяется зависимость Г^ от времени. Функции ГЬ(^)
и fts(t) выражаются алгебраически через ^(t) согласно равен-
равенствам C7.6). Учитывая определение двух других эллиптических
функций
сп т = дД — sn2 т, dn т = дД — к2 sn2 т,
получим окончательно следующие формулы:
2EI3 - M2
М2 -
C7ЛО)
Функции C7.10) — периодические, причем их период по пе-
переменной т равен, как известно, величине 4К, где if есть полный
эллиптический интеграл первого рода:
1	тг/2
К= [ , ^ == / у ^	C7.11)
о	о
Период же по времени дается, следовательно, выражением
По истечении этого времени вектор Q возвращается в свое
начальное положение относительно осей волчка. (Самый же вол-
волчок при этом отнюдь не возвращается в свое прежнее положение
относительно неподвижной системы координат — см. ниже.)
При 1\ = /2 формулы C7.10), разумеется, приводятся к фор-
формулам, полученным в предыдущем параграфе для симметриче-
симметрического волчка. Действительно, при 1\ —»> /2 параметр к2 —»> 0,
эллиптические функции вырождаются в круговые:
sn т —)> sinT, сптч cost, dn т —»> 1,
и мы возвращаемся к формулам C6.7).

§ 37	АСИММЕТРИЧЕСКИЙ ВОЛЧОК	157
При М2 = 2Е1% имеем: ?}1 = П2 = О, Г^з — const, т.е. век-
вектор ft постоянно направлен вдоль оси инерции жз; этот случай
соответствует равномерному вращению волчка вокруг оси жз-
Аналогичным образом при М2 = 2Е1\ (при этом т = 0) имеем
равномерное вращение вокруг оси х\.
Перейдем к определению абсолютного (по отношению к не-
неподвижной системе координат X, У, Z) движения волчка в про-
пространстве как функции времени. Для этого вводим эйлеровы
углы г[>, ф, 6 между осями волчка жх, x2j х% и осями X, У, Z,
выбрав при этом неподвижную ось Z вдоль направления посто-
постоянного вектора М. Поскольку полярный угол и азимут направ-
направления Z по отношению к осям жх, Ж2, жз равны соответственно
6 и 7г/2 — л\> (см. примеч. на с. 146), то, проецируя вектор М на
оси жх, Ж2, жз, получим
М sin 9 sinгр = М\ = Iiui,
М sin6 cos-ф = М2 = /2П2,	C7.13)
М cos 6 = Ms =
Отсюда
с»е = тт, *+-Ш-	C7Л4)
и, используя формулы C7.10), найдем
2Ml}dnT,
1')	C7.15)
) СПТ
чем и определяется зависимость углов 0 и \|) от времени; вме-
вместе с компонентами вектора ft они являются периодическими
функциями с периодом C7.12).
Угол ф в формулы C7.13) не входит, и для его вычисления
надо обратиться к формулам A0), выражающим компоненты ft
через производные по времени эйлеровых углов. Исключая 6 из
равенств
Vt\ = ф sin 9 sinгр + 9cosi|j,
^2 = Ф sin 9 cost]; — 9sin\|;,
получим
. 	 Qi sinip + ГЬ cos cp
ф
после чего, используя формулы C7.13), найдем

158	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
—— = JV1	—	(Л i lo)
LLli	11 *~ 2 2
Отсюда функция ф(?) определяется квадратурой, но подынте-
подынтегральное выражение содержит сложным образом эллиптические
функции. Путем ряда довольно сложных преобразований этот
интеграл может быть выражен через так называемые тэта-фун-
тэта-функции; не приводя вычислений х), укажем лишь их окончатель-
окончательный результат.
Функция ф (?) может быть представлена (с точностью до про-
произвольной аддитивной постоянной) в виде суммы двух членов
<p(t) = (pi(t) + <p2(t),	C7.17)
один из которых дается формулой
P2i<pi(t) _ floi Bt/T - га)	,	,
где -&01 ~~ тэта-функция, а ос — вещественная постоянная, опре-
определяемая равенством
(К и Г — из C7.11), C7.12)). Функция в правой части C7.18) —
периодическая с периодом Г/2, так что (pi(?) изменяется на 2п
за время Г. Второе слагаемое в C7.17) дается формулой
2nt г - М
Эта функция испытывает приращение 2п за время Т1.
Таким образом, движение по углу ф представляет собой со-
совокупность двух периодических изменений, причем один из пе-
периодов (Г) совпадает с периодом изменения углов л\> и 6, а дру-
другой (Г') — несоизмерим с первым. Последнее обстоятельство
приводит к тому, что при своем движении волчок никогда не
возвращается, строго говоря, в свое первоначальное положение.
Задачи
1. Определить свободное вращение волчка вокруг оси, близкой к оси
инерции хз (или х\).
Решение. Пусть к направлению М близка ось хз- Тогда компонен-
компоненты Mi и М.2 являются малыми величинами, а компонента Мз ~ М (с точ-
) Их можно найти в книге: Е. Т. Уиттекер. Аналитическая динами-
динамика.—М.: ОНТИ, 1937.

§ 37	АСИММЕТРИЧЕСКИЙ ВОЛЧОК	159
ностью до величин первого порядка малости). С этой же точностью первые
два из уравнений Эйлера C6.5) запишем в виде
dM1 ( h\	dM2 (h
= 1 - — Q0M2, —— = — - 1
dt \ h)	' dt \h
где мы ввели постоянную Qo = М/1$. Следуя общим правилам, ищем реше-
решение для Mi, Мч в виде, пропорциональном егш*, и для частоты си получаем
значение
Для самих же величин М\ и М2 получим
Mi = Ма\	1 cos cut, M2 = Ma\	1 sin cut,	B)
V h	V h
где а — произвольная малая постоянная. Этими формулами определяется
движение вектора М относительно волчка; в построении на рис. 51 конец
вектора М описывает (с частотой си) малый эллипс вокруг полюса на оси хз-
Для определения абсолютного движения волчка в пространстве опре-
определяем его эйлеровы углы. В данном случае угол наклона Э оси хз к оси Z
(направлению М) мал, и согласно формулам C7.14)
подставляя B), получаем
tg-ф = л/
92 = а2 [(| - Л cos2 wt+(j- l) sin2 toil .	C)
Для вычисления угла (р замечаем, что согласно третьей из формул A0)
при 0 < 1
по « из ~ 4> + Ф-
Поэтому
<р = По* - -ф	D)
(произвольную постоянную интегрирования опускаем).
Более наглядное представление о характере движения волчка полу-
получается, если проследить непосредственно за изменением направления его
трех осей инерции (единичные векторы вдоль этих осей обозначим через
ni, П2, пз). Векторы ni и пг равномерно вращаются в плоскости XY с
частотой Qo5 одновременно испытывая малые колебания с частотой си в по-
поперечном направлении; эти колебания определяются Z-компонентами ука-
указанных векторов, для которых имеем
Mi

160
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛ. VI
Для вектора пз имеем с той же точностью:
n3a;~9sm(p, пзу ~ — 9coscp, n3z ~ 1
(полярный угол и азимут направления пз по отношению к осям X, У, Z
равны 9 и (р — я/2; см. примеч. на с. 146). Далее пишем (используя при
этом формулы C7.13)):
cos-ф — 9cosn0? sin-ф =
или окончательно:
cos Qot = a\	1 sin Qot sin cot — a\/	1 cos Qot cos cut,
M	у Ii	V I2
^-1+А т--1 cos По +
Аналогичным образом
Отсюда видно, что движ:ение вектора пз представляет собой наложение
двух вращений вокруг оси Z с частотами (По =Ь си).
2. Определить свободное вращение волчка при М2 = 2EI2.
Решение. Этот случай отвечает в построении на рис. 51 перемеще-
перемещению конца вектора М по кривой, проходящей через полюс на оси х^.
Уравнение C7.7) принимает вид
— - 1 - s2
{h-h){h-h),
hh
где введено обозначение По = M/I2 = 2E/M. Интегрируя это уравнение, а
затем воспользовавшись формулами C7.6), получим
= По
ii(J8-ii)chT'
= По th т,
h{h-h)
Для описания абсолютного движения волчка вводим эйлеровы углы,
определив 9 как угол между осью Z (направлением М) и осью инерции
волчка Х2 (а не жз, как в тексте). В формулах C7.14), C7.16), связывающих
компоненты вектора П с эйлеровыми углами, надо при этом сделать цикли-
циклическую перестановку индексов 123 —>¦ 312. Подставив затем в эти формулы
выражения A), получим

38	СОПРИКОСНОВЕНИЕ ТВЕРДЫХ ТЕЛ	161
cos9 = thT, (p = Qo? + const, tg\p = W 3 2	-
Из полученных формул видно, что вектор ?1 асимптотически (при t —>¦ оо)
приближается к оси #2, которая одновременно асимптотически приближа-
приближается к неподвижной оси Z.
§ 38. Соприкосновение твердых тел
Условия равновесия твердого тела, как это видно из урав-
уравнений движения C4.1) и C4.3), можно сформулировать в виде
равенства нулю действующих на него полной силы и полного
момента сил:
F = ?f = 0, K = ? [rf] = 0.	C8.1)
Суммирование производится здесь по всем приложенным к те-
телу внешним силам, а г — радиус-векторы «точек приложения»
сил; при этом точка (начало координат), относительно кото-
которой определяются моменты, может быть выбрана произволь-
произвольным образом: при F = 0 значение К не зависит от этого вы-
выбора (см. C4.5)).
Если мы имеем дело с системой соприкасающихся друг с дру-
другом твердых тел, то в равновесии условия C8.1) должны выпол-
выполняться для каждого из тел в отдельности. При этом в число сил
должны быть включены также и силы, действующие на данное
тело со стороны остальных соприкасающихся с ним тел. Эти
силы приложены в точках соприкосновения тел и называются
силами реакции. Очевидно, что для каждых двух тел их вза-
взаимные силы реакции равны по величине и противоположны по
направлению.
В общем случае как величины, так и направления реакций
определяются в результате совместного решения системы урав-
уравнений равновесия C8.1) для всех тел. В некоторых случаях, од-
однако, направление сил реакции задается уже условиями задачи.
Так, если два тела могут свободно скользить по поверхности
друг друга, то силы реакции между ними направлены по нор-
нормали к поверхности.
Если соприкасающиеся тела движутся друг относительно
друга, то, кроме сил реакции, появляются также силы дисси-
пативного характера — силы трения.
Возможны два типа движения соприкасающихся тел —
скольжение и качение. При скольжении реакции перпендику-

162	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
лярны к соприкасающимся поверхностям, а силы трения на-
направлены по касательным к ним.
Чистое качение характеризуется тем, что в точках соприкос-
соприкосновения нет относительного движения тел; другими словами,
катящееся тело в каждый момент времени как бы закреплено
в точке соприкосновения. При этом направление силы реакции
произвольно, т.е. не обязательно нормально к соприкасающим-
соприкасающимся поверхностям. Трение же при качении проявляется в виде
дополнительного момента сил, препятствующего качению.
Если при скольжении трение настолько мало, что им мож-
можно вовсе пренебречь, то поверхности тел называются абсолют-
абсолютно гладкими. Напротив, если свойства поверхности допускают
лишь чистое качение тел без скольжения, а трением при качении
можно пренебречь, то поверхности называют абсолютно шеро-
шероховатыми.
В обоих случаях силы трения не фигурируют явным образом
в задаче о движении тел, и потому задача является чисто ме-
механической. Если же конкретные свойства трения существенны
для движения, то последнее не является уже чисто механиче-
механическим процессом (ср. § 25).
Соприкосновение тел уменьшает число их степеней свободы
по сравнению с тем, которым они обладали бы при свободном
движении. До сих пор при рассмотрении такого рода задач мы
учитывали это обстоятельство путем введения координат, непо-
непосредственно соответствующих реальному числу степеней свобо-
свободы. При качении тел, однако, такой выбор координат может ока-
оказаться невозможным.
Условие, накладываемое на движение тел при качении, за-
заключается в равенстве скоростей соприкасающихся точек (так,
при качении тела по неподвижной поверхности скорость точки
соприкосновения должна быть равна нулю). В общем случае та-
такое условие выражается уравнениями связи вида
?саг^ = 0,	C8.2)
г
где Cod — функции только координат (индекс а нумерует уравне-
уравнения связей). Если левые части равенства не являются полными
производными по времени каких-либо функций координат, то
эти уравнения не могут быть проинтегрированы. Другими сло-
словами, они не сведутся к соотношениям между одними только
координатами, которыми можно было бы воспользоваться для

§ 38	СОПРИКОСНОВЕНИЕ ТВЕРДЫХ ТЕЛ	163
того, чтобы выразить положение тел через меньшее число ко-
координат в соответствии с реальным числом степеней свободы.
Такие связи называют неголономными (в противоположность
голономным, связывающим лишь координаты системы).
Рассмотрим, например, качение шара по плоской поверх-
поверхности. Как обычно, обозначим через V скорость поступатель-
поступательного движения (скорость центра шара), а через ft — угловую
скорость вращения его. Скорость точки касания шара с плос-
плоскостью получится, если положить г = —an в общей формуле
v = V + [fir] (a — радиус шара, п — единичный вектор нормали
к плоскости качения в точке соприкосновения). Искомая связь
представляет собой условие отсутствия скольжения в точке ка-
касания, т.е. дается уравнением
V - а[пп] = 0.	C8.3)
Оно не может быть проинтегрировано: хотя скорость V пред-
представляет собой полную производную по времени от радиус-век-
радиус-вектора центра шара, но зато угловая скорость не является в общем
случае полной производной каких-либо координат. Таким обра-
образом, связь C8.3) неголономна х).
Поскольку уравнения неголономных связей нельзя исполь-
использовать для уменьшения числа координат, то при наличии таких
связей неизбежно приходится пользоваться координатами, кото-
которые не все независимы. Для составления соответствующих уравне-
уравнений Лагранжа снова вернемся к принципу наименьшего действия.
Наличие связей вида C8.2) налагает определенные ограниче-
ограничения на возможные значения вариаций координат. Именно, умно-
умножив эти уравнения на б?, мы найдем, что вариации bqi не неза-
независимы, а связаны соотношениями
= 0.	C8.4)
Это обстоятельство должно быть учтено при варьировании дей-
действия. Согласно общему методу Лагранжа для нахождения ус-
условных экстремумов, надо к подынтегральному выражению ва-
вариации действия
г) Заметим, что такая же связь для качения цилиндра была бы голо-
номной. В этом случае ось вращения сохраняет при качении постоянное
направление в пространстве, и потому Q = d(p/dt является полной произ-
производной от угла поворота (р цилиндра вокруг своей оси. Соотношение C8.3)
при этом интегрируется и дает связь между координатой центра инерции
и углом (р.

164	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
прибавить умноженные на неопределенные множители (функ-
(функции координат) Ла уравнения C8.4), после чего потребовать об-
обращения интеграла в нуль. При этом можно уже считать все
вариации bqi независимыми, и мы получим уравнения
d dL dL ^л	/qq r\
JtWrWi=^XaC™-	C8-5)
Вместе с уравнениями связей C8.2) они составляют полную си-
систему уравнений для неизвестных величин qi и Ла.
В изложенном методе силы реакции вообще не фигурируют;
соприкосновение тел целиком учитывается уравнениями связей.
Существует, однако, и другой метод составления уравнений дви-
движения соприкасающихся тел, в котором силы реакции вводятся
явным образом. Сущность этого метода (составляющего содер-
содержание так называемого принципа д'Аламбера) состоит в том,
что для каждого из соприкасающихся тел пишутся уравнения
f = Ef, ™=?[rf],	C8.6)
причем в число действующих на тело сил / включаются также
и силы реакции; эти силы заранее неизвестны и сами определя-
определяются вместе с движением тела в результате решения уравнений.
Этот метод в равной степени применим как при голономных,
так и при неголономных связях.
Задачи
1. Пользуясь принципом д'Аламбера, найти уравнения движения од-
однородного шара, катящегося по плоскости под действием приложенных к
нему внешней силы F и момента сил К.
Решение. Уравнение связи C8.3) написано уже в тексте. Вводя си-
силу реакции (обозначим ее буквой R), приложенную в точке касания шара
с плоскостью, напишем уравнения C8.6):
Hf = F + R,	A)
1^ = К - a[nR]	B)
(здесь учтено, что Р = |xV и что для шарового волчка М = ICI). Диффе-
Дифференцируя уравнение связи C8.3) по времени, получим
V = a[fln].

38
СОПРИКОСНОВЕНИЕ ТВЕРДЫХ ТЕЛ
165
Подставив в уравнение A) и исключая П с помощью B), найдем уравнение
— (F + R) = [Кп] - аК + an(nR),
связывающее силу реакции с F и К. Расписав это уравнение в компонентах
и подставив / = B/5) \ха2 (см. задачу 2 б) § 32), будем иметь
Rx = ~^~Ку — ~Fx, Ry = — z— Кх — —Fy, Rz = — Fz
(плоскость xy выбрана в плоскости качения). Наконец, подставив эти вы-
выражения в A), получим уравнения движения, содержащие уже только за-
заданные внешние силу и момент:
dVx 5
D
= KZ
Re
dt 7ixV - ' а Г dt
Компоненты Qx, Qy угловой скорости выражаются через Vx и Vy с помощью
уравнения связи C8.3), а для Qz имеем уравнение
2 2 d?lz
5	dt
(z — компонента уравнения B)).
2. Однородный стержень BD весом Р и длиной /
опирается на стену, как показано на рис. 52; его ниж-
нижний конец В удерживается нитью АВ. Определить
реакцию опор и натяжение нити.
Решение. Вес стержня представляется при-
приложенной к его середине силой Р, направленной вер-
вертикально вниз. Силы реакции Rb и Rq направлены
соответственно вертикально вверх и перпендикуляр-
перпендикулярно к стержню; натяжение нити Т направлено от В
к А. Решение уравнений равновесия дает
Р1
Re = тг sm ^a' ™в = Р — Re sin a,
Рис. 52
Т = Re cos a.
3.	Стержень А В весом Р
опирается своими концами на
горизонтальную и вертикальную
плоскости (рис. 53) и удержива-
удерживается в этом положении двумя
горизонтальными нитями AD
и ВС] нить ВС находится в од-
одной (вертикальной) плоскости
со стержнем АВ. Определить ре-
реакции опор и натяжения нитей.
Решение. Натяжения
нитей Та и Тв направлены от А	Рис. 53
к D и от В к С. Реакции Ra и Rb перпендикулярны к соответствующим
плоскостям. Решение уравнений равновесия дает
RB = P, Ts = yctga, Ra=Tb sin C, TA = TscosC.
4.	Два стержня длиной L соединены сверху шарниром, а снизу скрепле-
скреплены нитью АВ (рис. 54). К середине одного из стержней приложена сила F

166	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
(весом стержней пренебрегаем). Определить силы реакции.
Решение. Натяжение нити Т действует в
точке А от А к В, а в точке В — от В к А. Ре-
Реакции Ra и Rb в точках А и В перпендикулярны
к плоскости опоры. Посредством Re обозначим
силу реакции в шарнире, действующую на стер-
стержень АС] тогда на стержень ВС действует реак-
реакция —Re- Условие равенства нулю суммы момен-
моментов сил Rs, T и —Re, действующих на стержень
ВС, приводит к результату, что вектор Re на-
направлен вдоль ВС. Остальные условия равнове-
сия (для каждого из двух стержней) приводят к
значениям
Рис. 54
Ra = ^F, Rb = ^,Rc = -4^, T=
4	4	4 sin a
где а — угол CAB.
§ 39. Движение в неинерциальной системе отсчета
До сих пор, рассматривая движение любой механической си-
системы, мы всегда относили его к инерциальной системе отсчета.
Только в инерциальных системах отсчета функция Лагранжа,
например, одной частицы во внешнем поле имеет вид
Lo = ^ - U,	C9.1)
и соответственно уравнение движения
dt	дг
(мы будем в этом параграфе отличать индексом 0 величины,
относящиеся к инерциальной системе отсчета).
Займемся теперь вопросом о том, как выглядят уравнения
движения частицы в неинерциальной системе отсчета. Отправ-
Отправным пунктом при решении этого вопроса снова является прин-
принцип наименьшего действия, применимость которого не ограни-
ограничена никаким выбором системы отсчета; вместе с ним остаются
в силе и уравнения Лагранжа
Однако функция Лагранжа уже не имеет вида C9.1), и для ее
нахождения необходимо произвести соответствующее преобра-
преобразование функции Lq.
Это преобразование мы произведем в два приема. Рассмот-
Рассмотрим сначала систему отсчета К\ которая движется относитель-

§ 39 ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА	167
но инерциальной системы К$ поступательно со скоростью V(t).
Скорости vo и v' частицы относительно систем Ко и К1 связаны
друг с другом соотношением
vo = v' + V(t).	C9.3)
Подставив это выражение в C9.1), получим функцию Лагранжа
в системе К1
Но V2(t) есть заданная функция времени; она может быть пред-
представлена как полная производная по t от некоторой другой функ-
функции, и потому третий член в написанном выражении может быть
опущен. Далее, v' = drr/dt, где г' — радиус-вектор частицы в си-
системе координат К'\ поэтому
mV(t)v' = mV^ = UrnVY1) -тт'^.
QjXi	QjXi	QjXi
Подставив это в функцию Лагранжа и снова опустив полную
производную по времени, получим окончательно:
Li = гшР_ _ mW(ty _ ^	C9.4)
где W = dV/dt — ускорение поступательного движения систе-
системы отсчета К'.
Составляя с помощью C9.4) уравнение Лагранжа, получим
Мы видим, что в смысле своего влияния на уравнения движе-
движения частицы ускоренное поступательное движение системы от-
отсчета эквивалентно появлению однородного силового поля, при-
причем действующая в этом поле сила равна произведению массы
частицы на ускорение W и направлена в противоположную это-
этому ускорению сторону.
Введем теперь еще одну систему отсчета, К', которая имеет
общее с системой К1 начало, но вращается относительно нее с
угловой скоростью ft(t); по отношению же к инерциальной си-
системе Kq система К совершает как поступательное, так и вра-
вращательное движение.
Скорость v' частицы относительно системы К1 складывается
из ее скорости v относительно системы К и скорости [fir] ее
вращения вместе с системой К:
v' = v + [fir]

168	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
(радиус-векторы гиг' частицы в системах Кж К1 совпадают).
Подставив это выражение в функцию Лагранжа C9.4), получим
L = ^f + mv[flr] + ^[ftrf - raWr - U.	C9.6)
Это есть общий вид функции Лагранжа частицы в произ-
произвольной неинерциальной системе отсчета. Отметим, что враще-
вращение системы отсчета приводит к появлению в функции Лагранжа
члена совершенно особого вида — линейного по скорости частицы.
Для вычисления производных, входящих в уравнение Ла-
Лагранжа, запишем полный дифференциал
dL = mvdv + mdv[ftr] + rav[ft dr] + га [ft r][ft dr] -
— raW dr — —dr = rav dv + ra dv[ftr] +
+ ra dr [vft] + ra[[ftr]ft] dr - raW dr - ^ dr.
Собирая члены, содержащие dv и dr, найдем
^ = mv + m[ftr], ^ = m[vft] + m[[ftr]ft] - mW - ^.
Подставив эти выражения в C9.2), получим искомое уравнение
движения
mTt =~^~ mW + Ш^ + 2m[yfi] + тШ*Щ- C9.7)
Мы видим, что «силы инерции», обусловленные вращением
системы отсчета, слагаются из трех частей. Сила ra[rft] связа-
связана с неравномерностью вращения, а две другие присутствуют и
при равномерном вращении. Сила 2га[vft] называется силой Ко-
риолиса] в отличие от всех ранее рассматривавшихся (не дисси-
пативных) сил она зависит от скорости частицы. Сила ra[ft[rft]]
называется центробежной. Она направлена в плоскости, про-
проходящей через г и ft перпендикулярно к оси вращения (т.е. на-
направлению ft), в сторону от оси; по величине центробежная сила
равна тпрЛ2, где р — расстояние частицы от оси вращения.
Рассмотрим особо случай равномерно вращающейся системы
координат, не имеющей поступательного ускорения. Положив в
C9.6) и C9.7) ft = const, W = 0, получим функцию Лагранжа
L = Щ- + rav[ftr] + у [ftrf - U	C9.8)
и уравнение движения
^ + 2mtvft] + ™[П[гП]]	C9-9)

§ 39 ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ ОТСЧЕТА	169
Вычислим также энергию частицы в этом случае. Подставив
р = ^ = mv + m[ftr]	C9.10)
в Е = pv — L, получим
Обратим внимание на то, что в энергии линейный по скорости
член отсутствует. Влияние вращения системы отсчета сводится
к добавлению в энергии члена, зависящего только от координат
частицы и пропорционального квадрату угловой скорости. Эта
дополнительная потенциальная энергия —(га/2) [Qr]2 называет-
называется центробежной.
Скорость v частицы относительно равномерно вращающей-
вращающейся системы отсчета связана с ее же скоростью vo относительно
инерциальной системы Kq соотношением
vo = v + [ftr].	C9.12)
Поэтому импульс р (см.C9.10)) частицы в системе К совпа-
совпадает с ее же импульсом ро = ravo в системе Kq. Вместе с ними
совпадают также моменты импульсов Мо = [грр] и М = [гр].
Энергии же частицы в системах К и Kq различны. Подставив v
из C9.12) в C9.11), получим
Е = ^f - ravo[fir] + U = ^f + U - ra[rvo]fi.
Первые два члена представляют собой энергию Eq в системе Kq.
Вводя в последний член момент импульса, получим
Е = Е0-М?1.	C9.13)
Этой формулой определяется закон преобразования энергии
при переходе к равномерно вращающейся системе координат.
Хотя мы вывели его для одной частицы, но очевидно, что вывод
может быть непосредственно обобщен на случай любой системы
частиц, это приводит к той же формуле C9.13).
Задачи
1. Найти отклонение свободно падающего тела от вертикали, обуслов-
обусловленное вращением Земли. (Угловую скорость вращения считать малой.)
Решение. В поле тяжести U = — mgr, где g — вектор ускорения
свободного падения; пренебрегая в уравнении C9.9) центробежной силой,
содержащей квадрат П, получим уравнение движения в виде
v = 2[vfl] + g.	A)

170	ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА	ГЛ. VI
Решаем это уравнение последовательными приближениями. Для этого
полагаем: v = vi + V2, где vi — решение уравнения vi = g, т.е. vi = gt + vo
(vo — начальная скорость). Подставляя v = vi +V2 в A) и оставляя справа
только vi, получим уравнение для V2:
v2 = 2 [vifl] = 2t [gft] + 2 [voft].
Интегрируя, получим	2 з
^	[fi]+i2[vofi],	B)
где h — вектор начального положения частицы.
Выберем ось z по вертикали вверх, а ось х — по меридиану к полюсу; тогда
g"x=g"y = 0» ez = -&> ft* = ft cos A, fty = 0, Qz = QsinA,
где А — широта (которую для определенности предполагаем северной). По-
Положив в B) vo = 0, найдем	3
х = 0, у =	gft cos A.
о
Подставив сюда время падения t « y/2h/g, найдем окончательно:
х = 0, у = --(—) gQcosA
3 V g /
(отрицательные значения у соответствуют отклонению на восток).
2.	Определить отклонение от плоскости для тела, брошенного с поверх-
поверхности Земли с начальной скоростью vo-
Решение. Выбираем плоскость xz так, чтобы vo лежала на ней. На-
Начальная высота h = 0. Для бокового отклонения получим из B) (задача 1):
t3
У = -—gttx + t2(Qxv0z - ttzVox),
о
или, подставив время полета t « 2voz/g:
У = ~^Г [^voz^x - vOx
3.	Определить влияние, оказываемое вращением Земли на малые коле-
колебания маятника (так называемый маятник Фуко).
Решение. Пренебрегая вертикальным смещением маятника как ма-
малой величиной второго порядка, можно считать движение тела происходя-
происходящим в горизонтальной плоскости ху. Опуская члены, содержащие Q2, на-
напишем уравнения движения в виде
х + ш2х = 2Qzy, у + w2y = —2Qzx,
где си — частота колебаний маятника без учета вращения Земли. Умножив
второе уравнение на г и сложив с первым, получим одно уравнение
? + 2zQz?, + w2?, = 0
для комплексной величины ?, = х + гу. При Qz ^ со решение этого уравне-
уравнения имеет вид
?, = е-ш**(А1егш* + А2е-гш*)
или
x + iy = e li2zt(xo + iyo),
где функции xo(t), yo(i) дают траекторию маятника без учета вращения
Земли. Влияние этого вращения сводится, следовательно, к повороту тра-
траектории вокруг вертикали с угловой скоростью Qz.

ГЛАВА VII
КАНОНИЧЕСКИЕ УРАВНЕНИЯ
§ 40. Уравнения Гамильтона
Формулирование законов механики с помощью функции Ла-
гранжа (и выводимых из нее уравнений Лагранжа) предполага-
предполагает описание механического состояния системы путем задания ее
обобщенных координат и скоростей. Такое описание, однако, не
является единственно возможным. Ряд преимуществ, в особен-
особенности при исследовании различных общих вопросов механики,
представляет описание с помощью обобщенных координат и им-
импульсов системы. В связи с этим возникает вопрос о нахождении
уравнений движения, отвечающих такой формулировке механики.
Переход от одного набора независимых переменных к дру-
другому можно совершить путем преобразования, известного в ма-
математике под названием преобразования Леэюандра. В данном
случае оно сводится к следующему.
Полный дифференциал функции Лагранжа как функции ко-
координат и скорости равен
Это выражение можно написать в виде
dL = J2Pi dqi + J2Pi dqi,	I40-1)
поскольку производные dL/dqi являются, по определению, обоб-
обобщенными импульсами, a dL/dqi = pi в силу уравнений Лагранжа.
Переписав теперь второй член в D0.1) в виде
перенеся полный дифференциал d(^piqi) в левую часть равен-
равенства и изменив все знаки, получим из D0.1):
i<li ~ L) = ~Y<Pi dqi + X) Qi dpi.

172	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Величина, стоящая под знаком дифференциала, представ-
представляет собой энергию системы (см. § 6); выраженная через коор-
координаты и импульсы, она называется гамильтоновой функцией
системы
,t)=J2Piqi-L.	D0.2)
г
Из дифференциального равенства
dH = -J2Pi dqi +Y,Qi dp»	D0.3)
следуют уравнения
* = ^' » = -^г	Dа4)
Это — искомые уравнения движения в переменных ри^, так
называемые уравнения Гамильтона. Они составляют систему 25
дифференциальных уравнений первого порядка для 2s неизвест-
неизвестных функций p(t) и д(?), заменяющих собой s уравнений второго
порядка лагранжевого метода. Ввиду их формальной простоты
и симметрии эти уравнения называют также каноническими.
Полная производная от функции Гамильтона по времени
dH дН
При подстановке сюда сц и pi из уравнений D0.4) последние два
члена взаимно сокращаются, так что
В частности, если функция Гамильтона не зависит от времени
явно, то dH/dt = 0, т.е. мы снова приходим к закону сохранения
энергии.
Наряду с динамическими переменными q, q или q, p функции
Лагранжа и Гамильтона содержат различные параметры — ве-
величины, характеризующие свойства самой механической систе-
системы или действующего на нее внешнего поля. Пусть Л — такой
параметр. Рассматривая его как переменную величину, будем
иметь вместо D0.1) выражение вида
dL = Y,i>i dqi + Y,Pi dqi + ^d\
после чего вместо D0.3) получим
dH = -^2pi dqi + Y,<li dpi - -r^dX.
Отсюда находим соотношение

40	УРАВНЕНИЯ ГАМИЛЬТОНА	173
связывающее частные производные по параметру Л от функций
Лагранжа и Гамильтона; индексы у производных указывают,
что дифференцирование должно производиться в одном случае
при постоянных рид, а в другом — при постоянных q и q.
Этот результат может быть представлен и в другом аспекте.
Пусть функция Лагранжа имеет вид L = L$ + I/, где V пред-
представляет собой малую добавку к основной функции Lq. Тогда
соответствующая добавка в функции Гамильтона Н = Щ + Н1
связана с V соотношением
(H')Piq = -(L\q.	D0.7)
Заметим, что в преобразовании от D0.1) к D0.3) мы не пи-
писали члена с с??, учитывающего возможную явную зависимость
функции Лагранжа от времени, поскольку последнее играло бы
в данном аспекте лишь роль параметра, не имеющего отношения
к производимому преобразованию. Аналогично формуле D0.6)
частные производные по времени от L и от Н связаны соотно-
соотношением
Задачи
1. Найти функцию Гамильтона для одной материальной точки в декар-
декартовых, цилиндрических и сферических координатах.
Ответ: В декартовых координатах ж, у, z:
в цилиндрических координатах г, (р, z:
в сферических координатах г, Э, (р:
Н = J- U + 4 + -^
2гп \ г2 г2 siir
2. Найти функцию Гамильтона частицы в равномерно вращающейся
системе отсчета.
Решение. Из C9.11) и C9.10) получим

174	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
3. Найти функцию Гамильтона системы из одной частицы с массой
М и п частиц с массами т, с исключенным движением центра инерции
(см. задачу к § 13).
Решение. Энергия Е получается из найденной в задаче к § 13 функ-
функции Лагранжа изменением знака перед U. Обобщенные импульсы:
dL	m2 v-^
Ра = т:— = ^va	> vo.
Отсюда имеем	a
v—ч	х"	nm2 \-^	mM \-^
> pa = m > vc
1
Подставив в i?, найдем
Я=2Ь?Р°+2^й>> +С/-
§ 41. Функция Рауса
В некоторых случаях может оказаться целесообразным при
переходе к новым переменным заменить на импульсы не все
обобщенные скорости, а только некоторые из них. Соответст-
Соответствующее преобразование вполне аналогично произведенному в
предыдущем параграфе.
Для упрощения записи формул предположим сначала, что
имеются всего две координаты, которые мы обозначим, как q
и ?,, и произведем преобразование от переменных q, ?,, g, ?, к
переменным g, ?, V-, ^ гДе Р ~ обобщенный импульс, соответ-
соответствующий координате q.
Дифференциал функции Лагранжа L(q, ?,, g, ?,) равен
dL = —dq + —dq + —dl, + ^dl =
dq	dq	dl	d^	dL	dL •
= pdq + pdq+ ~^d^+ — d?,
откуда получаем
d(L -pq) =pdq- qdp+ -wrdE, -\	rd5,.
Введем функцию (так называемую функцию Рауса)
R(q,p,t,i)=pq-L,	D1.1)
в которой скорость g выражена через импульс р при помощи
равенства р = dL/dq. Дифференциал
dR=-pdq + qdp- d-^dl - ^dl.	D1.2)

§ 41	ФУНКЦИЯ РАУСА	175
Откуда следует, что
U-ft	•	U-ft	/ А -\ Г>\
*=W P = ~V	DL3)
8L _ _dR dL _ _dR	(&л .ч
Подставляя последние равенства в уравнение Лагранжа для ко-
координаты ?,, получим
±д_К = д_К	( }
dtQl дЕ,	{ }
Таким образом, функция Рауса является гамильтоновой по
отношению к координате q (уравнения D1.3)) и лагранжевой по
отношению к координате ?, (уравнение D1.5)).
Согласно общему определению энергия системы
Е = q— + ?,— - L = pq + 5,— - L.
д<1 дЕ,	дЕ,
Ее выраж:ение через функцию Рауса получается путем подста-
подстановки сюда D1.1) и D1.4)
E = R-lS^.	D1.6)
Обобщение полученных формул на случай, когда имеется по
нескольку координат q и ?,, очевидно.
Применение функции Рауса может быть целесообразным, в
частности, при наличии циклических координат. Если координа-
координаты q — циклические, то они не входят явным образом в функцию
Лагранжа, а потому и в функцию Рауса, так что последняя бу-
будет функцией только от р, ?,, ?,. Но импульсы р, соответствующие
циклическим координатам, постоянны (это следует и из второ-
второго из уравнений D1.3), которое в этом смысле не дает ничего
нового). После замены импульсов р их заданными постоянными
значениями уравнения D1.5)
=
dt д1	дЕ,
превратятся в уравнения, содержащие только координаты ?,, так
что циклические координаты тем самым исключаются полно-
полностью. Если эти уравнения решены и функции ?,(?) найдены, то,
подставив их в правую часть уравнений
dR(P,i,j)
q~ dp '
мы найдем прямым интегрированием функции q(t).

176	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Задача
Найти функцию Рауса симметрического волчка во внешнем поле
L/((p, 9), исключив циклическую координату г|:> (гр, ф, 0 — эйлеровы углы).
Решение. Функция Лагранжа
L = ^(ё2 + ф2 sin2 в) + ^-(-ф2 + ф cos ЭJ - U(<p, 9)
А	А
(ср. задачу 1 § 35). Функция Рауса
^(e + (psine)
з	2
первый член в этом выражении представляет собой постоянную, которая
может быть опущена.
§ 42. Скобки Пуассона
Пусть f(p,q,t) — некоторая функция координат, импульсов
и времени. Составим ее полную производную по времени
к
Подставив сюда вместо q^ и р^ их выражения из уравнений Га-
Гамильтона D0.4), получим
где введено обозначение
dHdf 8H8f
к
Выражение D2.2) называют скобками Пуассона для величин
Я и/.
Такие функции от динамических переменных, которые оста-
остаются постоянными при движении системы, называются, как мы
знаем, интегралами движения. Мы видим из D2.1), что условие
того, чтобы величина / была интегралом движения (df /dt = 0),
можно написать в виде
f + {Я/} = 0.	D2.3)
Если же интеграл движения не зависит от времени явно, то
{Я/} = 0,	D2.4)
т.е. его скобки Пуассона с функцией Гамильтона должны обра-
обращаться в нуль.
Для любой пары величин / и g скобки Пуассона определя-
определяются аналогично D2.2):

§ 42	СКОБКИ ПУАССОНА	177
ifg\ =
us/
к
Скобки Пуассона обладают следующими свойствами, легко вы-
выводимыми из определения.
Если переставить функции, то скобки переменят знак; если
одна из функций — постоянная (с), то скобка равна нулю:
{fg} = ~{gf},	D2.6)
{/с} = 0.	D2.7)
Далее,
{h + f2,g} = {fig} + {f2g},	D2.8)
{/1/2, g} = /i{/2g} + /2{/ig}.	D2.9)
Взяв частную производную от D2.5) по времени, получим
Если одна из функций / или g совпадает с одним из им-
импульсов или координат, то скобки Пуассона сводятся просто к
частной производной:
= ?,	D2.11)
{fPk} = -§fk-	D2.12)
Формулу D2.11), например, получим, положив в D2.5) g = q^\
вся сумма сведется при этом к одному члену, так как -^- = S&/,
д	qi
а -^ = 0. Положив в D2.11) и D2.12) функцию / равной щ и pi,
получим, в частности,
{QiQk} = 0, {piPk} = 0, {РгЧк} = Ьк.	D2.13)
Между скобками Пуассона, составленными из трех функций,
существует соотношение
{f{gh}} + {g{hf}} + {h{fg}} = 0;	D2.14)
оно называется тождеством Якоби.
Для его доказательства заметим следующее. Согласно опре-
определению D2.5) скобки Пуассона {fg} являются билинейной од-
однородной функцией производных первого порядка от величин /
и g. Поэтому, например, скобка {h{fg}} представляет собой ли-
линейную однородную функцию производных второго порядка от /
и g. Вся же левая часть равенства D2.14) в целом есть линейная
однородная функция вторых производных от всех трех функций

178	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
/, gj h. Соберем вместе члены, содержащие вторые производ-
производные от /. Первая скобка таких членов не содержит — в ней есть
только первые производные от /. Сумму же второй и третьей
скобок перепишем в символическом виде, введя линейные диф-
дифференциальные операторы D\ и D2 согласно
= {/up}.
1огда
{Hfg}} = {g{hf}} - {h{gf}} =
Легко видеть, что такая комбинация линейных дифференциаль-
дифференциальных операторов не может содержать вторых производных от /.
В самом деле, общий вид линейных дифференциальных опера-
операторов есть
к	к
где ?,&,г\к — произвольные функции переменных жх, Ж2,... Тогда
5s
/с,/	/с,/
а разность этих произведений
/с,/
есть снова оператор, содержащий только однократные диффе-
дифференцирования. Таким образом, в левой части равенства D2.14)
взаимно сокращаются все члены со вторыми производными от /,
а поскольку то же самое относится, очевидно, и к функциям g
и /г, то и все выражение тождественно обращается в нуль.
Важное свойство скобок Пуассона состоит в том, что если /
и g — два интеграла движения, то составленные из них скобки
тоже являются интегралом движения
{fg} = const	D2.15)
(так называемая теорема Пуассона).
Доказательство этой теоремы совсем просто, если / и g не
зависят от времени явно. Положив в тождестве Якоби h = Н',
получим
{H{fg}} + {f{gH}} + {g{Hf}} = 0.

§ 42	СКОБКИ ПУАССОНА	179
Отсюда видно, что если {Hg} = 0 и {Hf} = О, то и {i7{/g}} = О,
что и следовало доказать.
Если же интегралы движения / и g зависят явно от времени,
то можно записать на основании D2.1)
Воспользовавшись формулой D2.10) и заменив скобку
двумя другими при помощи тождества Якоби, получим
ИЛИ
откуда очевидно доказательство теоремы Пуассона в общем случае.
Разумеется, применяя теорему Пуассона, мы не всегда будем
получать новые интегралы движения, так как их число вообще
ограничено B5—1, где s — число степеней свободы). В некоторых
случаях мы можем получить тривиальный результат — скобки
Пуассона сведутся к постоянной. В других случаях вновь полу-
полученный интеграл может оказаться просто функцией исходных
интегралов от / и g. Если же не имеет места ни тот, ни другой
случай, то скобки Пуассона дают новый интеграл движения.
Задачи
1.	Определить скобки Пуассона, составленные из декартовых компо-
компонент импульса р и момента импульса М = [гр] материальной частицы.
Решение. С помощью формулы D2.12) находим
дмх д
{МхРу} = -— = -fyivPz - zpy) = -Pz
и аналогичным образом еще две формулы
{МхРх} = 0, {MxPz}=py.
Остальные скобки получаются отсюда циклической перестановкой индек-
индексов х, у, z.
2.	Определить скобки Пуассона, составленные из компонент М.
Решение. Прямое вычисление по формуле D2.5) дает
{MxMy} = -Mz, {MyMz} = -Mx, {MZMX} = -My.
Поскольку импульсы и координаты различных частиц являются не за-
зависимыми друг от друга переменными, то легко видеть, что полученные
в задачах 1 и 2 формулы справедливы и для полных импульса и момента
любой системы частиц.

180	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
3. Показать, что
{cpMz} = 0,
где (р — любая скалярная функция координат и импульса частицы.
Решение. Скалярная функция может зависеть от компонент век-
векторов г и р только в комбинациях г2, р2, гр. Поэтому
д(р _ д(р	д(р
~0^~ Щ* +Р
и аналогично для д(р/др. Искомое соотношение проверяется прямым вы-
вычислением по формуле D2.5) с учетом указанных правил дифференциро-
дифференцирования.
4. Показать, что
{{Mz} = {fn},
где f — векторная функция координат и импульса частицы, an — единич-
единичный вектор в направлении оси z.
Решение. Произвольный вектор f (г, р) может быть написан в ви-
виде f = rcpi + рф2 + [гр](рз, где (pi, (р2, (рз — скалярные функции. Искомое
соотношение проверяется прямым вычислением с помощью формул D2.9),
D2.11), D2.12) и формулы, указанной в задаче 3.
§ 43. Действие как функция координат
При формулировке принципа наименьшего действия мы рас-
рассматривали интеграл
t
= Г Ldt,	D3.1)
взятый по траектории между двумя заданными положениями
qi1) и qB\ которые система занимает в заданные моменты вре-
времени t\ и ^2- При варьировании же действия сравнивались зна-
значения этого интеграла для близких траекторий с одними и теми
же значениями q(t\) и q(t>2). Лишь одна из этих траекторий от-
отвечает минимальному движению — та, для которой интеграл S
минимален.
Рассмотрим теперь понятие действия в другом аспекте. Имен-
Именно, будем рассматривать S как величину, характеризующую дви-
движение по истинным траекториям, и сравним значения, которые
она имеет для траекторий, имеющих общее начало q(t{) = q^\
но проходящих в момент ?2 через различные положения. Дру-
Другими словами, будем рассматривать интеграл действия для ис-
истинных траекторий как функцию значений координат в верхнем
пределе интегрирования.
Изменение действия при переходе от одной траектории к
близкой к ней другой траектории дается (при одной степени сво-

43	ДЕЙСТВИЕ КАК ФУНКЦИЯ КООРДИНАТ	181
боды) выражением B.5)
*2
fq~Jt%)bqdt-
tl J \dq dt 8q
Поскольку траектории действительного движения удовлетворя-
удовлетворяют уравнениям Лагранжа, то стоящий здесь интеграл обраща-
обращается в нуль. В первом же члене полагаем на нижнем пределе
bq(t\) = О, а значение bqfo) обозначим просто, как bq. Заменив
также dL/dq на р, получим окончательно: bS = р bq или в общем
случае любого числа степеней свободы
bS = J2Pibqi.	D3.2)
г
Из этого соотношения следует, что частные производные от
действия по координатам равны соответствующим импульсам
Аналогичным образом действие можно понимать как явную
функцию времени, рассматривая траектории, начинающиеся в
заданный момент времени t\ в заданном положении q^\ но
заканчивающиеся в заданном положении q^ в различные мо-
моменты времени ?2 — t. Понимаемую в этом смысле частную
производную dS/dt можно найти путем соответствующего ва-
варьирования интеграла. Проще, однако, воспользоваться уже из-
известной нам формулой D3.3), поступив следующим образом.
По самому определению действия его полная производная по
времени вдоль траектории равна
f = L-	D3-4)
С другой стороны, рассматривая S как функцию координат и
времени в описанном выше смысле и используя формулу D3.3),
имеем
dS OS , \^dS . OS
+ 2 ^
i
Сравнивая оба выражения, находим
-=L->,mi
или окончательно
dS_
dt

182	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Формулы D3.3) и D3.5) вместе можно записать в виде вы-
выражения
dS = YlPidqi-Hdt	D3.6)
г
для полного дифференциала действия как функции координат
и времени в верхнем пределе интегрирования в D3.1). Предпо-
Предположим теперь, что изменяются координаты (и время) не только
конца, но и начала движения. Очевидно, что соответствующее
изменение S будет даваться разностью выражений D3.6) на обо-
обоих концах, т.е.
dS = Е P?W2) - HWdtW - Е P^dqV + HWdtV. D3.7)
Это соотношение уже само по себе показывает, что, каково
бы ни было внешнее воздействие на систему во время движения,
ее конечное состояние не может быть произвольной функцией
начального, — возможны только такие движения, при которых
выражение в правой части равенства D3.7) является полным
дифференциалом. Таким образом, уже самый факт существо-
существования принципа наименьшего действия, независимо от конкрет-
конкретного вида функции Лагранжа, накладывает на совокупность
возможных движений определенные ограничения. В частности,
оказывается возможным установить ряд общих закономерностей
(не зависящих от вида имеющихся внешних полей) для пучков
частиц, разлетающихся из заданных точек пространства. Изу-
Изучение этих закономерностей составляет предмет так называемой
геометрической оптики 1).
Интересно отметить, что уравнения Гамильтона могут быть
выведены формальным образом из условия минимальности дей-
действия, если написать последнее, на основании D3.6), в виде ин-
интеграла
S= ffepidqi-Hdt)	D3.8)
и рассматривать координаты и импульсы как независимо варьи-
варьируемые величины. Предполагая снова для краткости, что имеет-
имеется всего одна координата (и один импульс), запишем вариацию
действия в виде
bS = / \ bpdo + pd bq — -^—bqdt — -^—bpdt \ .
J I	oq	dp	)
См. «Теория поля», гл. VII.

§ 44	ПРИНЦИП МОПЕРТЮИ	183
Преобразование второго члена (интегрирование по частям) дает
SS = [ Ьр (dq - ЩйЬ) +pbq- [ Ья(ёр+Щ ей) .
На границах интегрирования мы должны положить bq = 0, так
что проинтегрированный член выпадает. Остающееся же выра-
выражение может быть равным нулю при произвольных независи-
независимых Ьр и bq лишь при условии обращения в нуль подынтеграль-
подынтегральных выражений в каждом из двух интегралов:
dq=—dt, dp=-—dt,
т.е. мы получаем после деления на dt уравнения Гамильтона.
§ 44. Принцип Мопертюи
Принципом наименьшего действия движение механической
системы определяется полностью: путем решения следующих
из этого принципа уравнений движения можно найти как фор-
форму траектории, так и зависимость положения на траектории от
времени.
Если ограничиться более узким вопросом об определении
лишь самой траектории (оставляя в стороне временную часть
задачи), то оказывается возможным установить для этой цели
упрощенную форму принципа наименьшего действия.
Предположим, что функция Лагранжа, а с нею и функция
Гамильтона не содержат времени явно, так что энергия системы
сохраняется:
H(p,q) = Е = const.
Согласно принципу наименьшего действия вариация дейст-
действия для заданных начальных и конечных значений координат
и моментов времени (скажем, to и t) равна нулю. Если же до-
допускать варьирование конечного момента времени t при фикси-
фиксированных по-прежнему начальных и конечных координатах, то
имеем (ср. D3.7)):
bS = -Hbt.	D4.1)
Будем теперь сравнивать не все виртуальные движения си-
системы, а лишь те, которые удовлетворяют закону сохранения
энергии. Для таких траекторий мы можем заменить Н в D4.1)
постоянной Е1, что дает
O.	D4.2)

184	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Написав действие в виде D3.8) и снова заменяя Н на Е, имеем
S= [ZPidQi-Eit-to).	D4.3)
J г
Первый член в этом выражении
So = [ Y,Pidqi	D4.4)
J г
иногда называют укороченным действием. Подставив D4.3) в
D4.2), найдем
SSb = 0.	D4.5)
Таким образом, укороченное действие имеет минимум по от-
отношению ко всем траекториям, удовлетворяющим закону сохра-
сохранения энергии и проходящим через конечную точку в произ-
произвольный момент времени. Для того чтобы пользоваться таким
вариационным принципом, необходимо предварительно выра-
выразить импульсы, а с ними и все подынтегральное выражение в
D4.4) через координаты диих дифференциалы dq. Для этого
надо воспользоваться равенствами
»-&*(«• 5) ¦	<446>
представляющими собой определение импульсов, и уравнением
закона сохранения энергии
Е (q, ?) = Е.	D4.7)
Выразив из последнего уравнения дифференциал dt через коор-
координаты q и их дифференциалы dq и подставив в формулы D4.6),
мы выразим импульсы через q и dq, причем энергия Е будет иг-
играть роль параметра. Получающийся таким образом вариаци-
вариационный принцип определяет траекторию системы; этот принцип
называют обычно принципом Мопертюи (хотя его точная фор-
формулировка была дана Эйлером и Лагранжем).
Произведем указанные действия в явном виде для обычной
формы функции Лагранжа E.5) как разности кинетической и
потенциальной энергий:
L = ^2,aik(q)qiqk - U(q).
i,k
При этом импульсы
dL
Pi = Wi =

§ 44	ПРИНЦИП МОПЕРТЮИ	185
а энергия
^2k + U{q).
Из последнего равенства имеем
dt = ^/Eg^	D48)
и, подставляя это выражение в
г	i,k
найдем укороченное действие в виде
So= [ V2(E-UM2aikdqidqk.	D4.9)
J	i,k
В частности, для одной материальной точки кинетическая
энергия
т_гп (<й\2
2
где m — масса частицы, a dl — элемент длины траектории, и
вариационный принцип для определения формы траектории
6 Г ^/2m(E - U) dl = 0,	D4.10)
где интеграл берется между двумя заданными точками про-
пространства. В таком виде он был представлен Якоби.
При свободном движении частицы U = 0, и D4.10) дает три-
тривиальный результат
i Г dl = 0,
т.е. частица движется по кратчайшему пути — по прямой.
Вернемся снова к выражению для действия D4.3) и произ-
произведем на этот раз его варьирование также и по параметру Е:
^ -it- to)8E - Ebt.
3S = ^
oh/
Подставив это в D4.2), находим
Для укороченного действия в форме D4.9) это равенство при-
приводит к соотношению
°<гк dqj dqk _f_f	(аал о\

186	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
которое представляет собой не что иное, как интеграл уравнения
D4.8). Вместе с уравнением траектории оно полностью опреде-
определяет движение.
Задача
Из вариационного принципа D4.10) получить дифференциальное урав-
уравнение траектории.
Решение. Производя варьирование, имеем
Во втором члене учтено, что dl2 = dr2 и потому dl dbl = dr dbr\ произведя
в этом члене интегрирование по частям и приравняв затем нулю коэффи-
коэффициент при 6г в подынтегральном выражении, получим дифференциальное
уравнение траектории
dl
Раскрыв производную в левой части равенства и вводя силу F = —dU/dr,
можно представить это уравнение в виде
d2^ _ F - (Ft)t
~dP ~ 2(E - U) '
где t = dr/dl — единичный вектор касательной к траектории. Разность
F — (Ft)t есть нормальная к траектории компонента силы Fn. Производная
же d2r/dl2 = dt/dl, как известно из дифференциальной геометрии, равна
n/R, где R — радиус кривизны траектории, an — единичный вектор глав-
главной нормали к ней. Заменив также Е — U на mv2/2, получим
mv2
n—=Fn
в соответствии с известным выражением для нормального ускорения при
движении по искривленной траектории.
§ 45. Канонические преобразования
Выбор обобщенных координат q не ограничен никакими ус-
условиями — ими могут быть любые s величин, однозначно опре-
определяющие положение системы в пространстве. Формальный вид
уравнений Лагранжа B.6) не зависит от этого выбора, и в этом
смысле можно сказать, что уравнения Лагранжа инвариантны
по отношению к преобразованию от координат ^i, ^2, • • • к лю-
любым другим независимым величинам Qi, Q25 • • • Новые коорди-
координаты Q являются функциями старых координат д, причем допу-
допустим и такой их выбор, при котором эта связь содержит в явном

§ 45	КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ	187
виде также и время, т.е. речь идет о преобразованиях вида
Qi = Qi(q,t)	D5.1)
(их называют иногда точечными преобразованиями).
Наряду с уравнениями Лагранжа при преобразовании D5.1)
сохраняют, разумеется, свою форму D0.4) и уравнения Гамиль-
Гамильтона. Последние, однако, допускают в действительности гораздо
более широкий класс преобразований. Это обстоятельство есте-
естественным образом связано с тем, что в гамильтоновом методе
импульсы р играют наряду с координатами q роль равноправных
независимых переменных. Поэтому понятие преобразования мо-
может быть расширено так, чтобы включить в себя преобразование
всех 2s независимых переменных ридк новым переменным Р
и Q по формулам
Qi = Q»(p,?,«), Pi = Pi&q,t).	D5.2)
Такое расширение класса допустимых преобразований являет-
является одним из существенных преимуществ гамильтонового метода
механики.
Однако отнюдь не при произвольных преобразованиях вида
D5.2) уравнения движения сохраняют свой канонический вид.
Выведем теперь условия, которым должно удовлетворять пре-
преобразование, для того чтобы уравнения движения в новых пе-
переменных Р, Q имели вид
«<-з?г- ъ—т	D5-3)
с некоторой новой функцией Гамильтона Н'(Р, Q). Среди таких
преобразований особенно важны так называемые канонические.
К формулам для канонических преобразований можно прий-
прийти следующим путем. В конце § 43 было показано, что уравне-
уравнения Гамильтона могут быть получены из принципа наименьшего
действия, представленного в форме
5 f&Pidqi-Hdt) = 0	D5.4)
J г
(причем варьируются независимо все координаты и импульсы).
Для того чтобы новые переменные Р и Q тоже удовлетворяли
уравнениям Гамильтона, для них тоже должен быть справедлив
принцип наименьшего действия
5 / СС Я dQi ~ H'dt) =0.	D5.5)
J i

188	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Но два принципа D5.4) и D5.5) эквивалентны друг другу только
при условии, что их подынтегральные выражения отличаются
лишь на полный дифференциал произвольной функции F ко-
координат, импульсов и времени; тогда разность между обоими
интегралами будет несущественной при варьировании постоян-
постоянной (разность значений F на пределах интегрирования). Таким
образом, положим
Y,Pi dqi-Hdt = Y, Pi dQi - H'dt + dF.
Преобразования, удовлетворяющие такому требованию, и назы-
называют каноническими 1). Всякое каноническое преобразование ха-
характеризуется своей функцией F, которую называют произво-
производящей функцией преобразования.
Переписав полученное соотношение в виде
dF = Y,Pi dqi - ? Pi dQi + (#' - H) dt,	D5.6)
мы видим, что
OF p	3F ч, TT.dF.	{A-7,
Рг = ^ Рг = ~Щ~г Я=Я + ^' D5-7)
при этом предполагается, что производящая функция задана как
функция старых и новых координат (и времени): F = F(q, Qy t).
При заданной функции F формулы D5.7) устанавливают связь
между старыми (р, q) и новыми (Р, Q) переменными, а также
дают выражение для новой гамильтоновой функции.
Может оказаться удобным выражать производящую функ-
функцию не через переменные q и Q, а через старые координаты q
и новые импульсы Р. Для вывода формул канонических преоб-
преобразований в этом случае надо произвести в соотношении D5.6)
соответствующее преобразование Лежандра. Именно, переписы-
переписываем его в виде
Выражение, стоящее под знаком дифференциала в левой части
равенства, выраженное через переменные g, P, и является новой
г) Заметим, что кроме канонических преобразований, сохраняют канони-
канонический вид уравнений движения и преобразования, при которых подынте-
подынтегральные выражения в D5.4) и D5.5) отличаются постоянным множителем.
Примером может служить преобразование вида: Pi = api, Qi = q%, H' = aH
с произвольной постоянной а.

§ 45	КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ	189
производящей функцией. Обозначив ее через Ф (g, P, t), имеем х)
п -9Ф п _ дФ „, _ гт , дФ	и. R,
Аналогичным образом можно перейти к формулам канони-
канонических преобразований, выраженных через производящие функ-
функции, зависящие от переменных р и Q или р и Р.
Отметим, что связь между новой и старой гамильтоновыми
функциями всегда выражается одинаковым образом: разность
Н1 — Н дается частной производной по времени от производящей
функции. В частности, если последняя не зависит от времени, то
Н1 = Н. Другими словами, в этом случае для получения новой
функции Гамильтона достаточно подставить в Н величины ру q,
выраженные через новые переменные Р, Q.
Широта канонических преобразований в значительной степе-
степени лишает в гамильтоновом методе понятие обобщенных коор-
координат и импульсов их первоначального смысла. Поскольку пре-
преобразования D5.2) связывают каждую из величин Р, Q как с
координатами q, так и с импульсами р, то переменные Q уже
не имеют смысла чисто пространственных координат. Различие
между обеими группами переменных становится в основном во-
вопросом номенклатурным. Это обстоятельство весьма наглядно
проявляется, например, в преобразовании Qi = pi, Pi = —qi 2),
явно не меняющем канонический вид уравнений и сводящемся
просто ко взаимному переименованию координат и импульсов.
Ввиду этой условности терминологии переменные р и q в га-
гамильтоновом методе часто называют просто канонически сопря-
сопряженными величинами.
Условие канонической сопряженности можно выразить с по-
помощью скобок Пуассона. Для этого докажем предварительно об-
общую теорему об инвариантности скобок Пуассона по отношению
к каноническим преобразованиям.
Заметим, что, взяв производящую функцию в виде
г
(где fi — произвольные функции), мы получим преобразование, при кото-
котором новые координаты Qi = fi(q,?), т.е. выражаются только через старые
координаты (но не импульсы). Это — точечные преобразования, которые
естественным образом оказываются частным случаем канонических преоб-
преобразований.
2) Ему отвечает производящая функция F = y^qiQj.

190	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Пусть {fg}p,q — скобка Пуассона величин / и g, в кото-
которой дифференцирование производится по переменным р, g, a
{f§}p,Q — скобка Пуассона тех же величин, дифференцируемых
по каноническим переменным Р, Q. Тогда
{fg}P,q = {fg}p,Q-	D5.9)
В справедливости этого соотношения можно убедиться пря-
прямым вычислением с использованием формул канонического пре-
преобразования. Можно, однако, обойтись и без вычислений с по-
помощью следующего рассуждения.
Прежде всего замечаем, что в канонических преобразовани-
преобразованиях D5.7) или D5.8) время играет роль параметра. Поэтому, если
мы докажем теорему D5.9) для величин, не зависящих явно от
времени, то она будет верна и в общем случае. Рассмотрим те-
теперь чисто формальным образом величину g как гамильтонову
функцию некоторой фиктивной системы. Тогда согласно фор-
формуле D2.1) {fg}p,q = —df/dt. Но производная df/dt есть вели-
величина, которая может зависеть лишь от свойств движения (на-
(нашей фиктивной системы) как такового, а не от того или иного
выбора переменных. Поэтому и скобка Пуассона {fg} не может
измениться при переходе от одних канонических переменных к
другим.
Из формул D2.13) и теоремы D5.9) получим
{QiQk}p,q = 0, {PiPk}p,q = 0, {PiQk}p,q = Ьк-	D5.10)
Это — записанные с помощью скобок Пуассона условия, кото-
которым должны удовлетворять новые переменные, для того чтобы
преобразование p,q —»> P,Q было каноническим.
Интересно отметить, что изменение величин р, q при самом
движении можно рассматривать как канонические преобразо-
преобразования. Смысл этого утверждения состоит в следующем. Пусть
qi,Pi — значения канонических переменных в момент времени
?, a <ft+T5 pt+т — их значения в другой момент t + т. Последние
являются некоторыми функциями от первых (и от величины
интервала т как от параметра):
%+т = q{quPut,t), Pt+ч = p{quPt,t,t)-
Если рассматривать эти формулы как преобразование от пе-
переменных qt,pt к переменным <#+т> Pt+т, то это преобразо-
преобразование будет каноническим. Это очевидно из выражения
dS = 5^(pt+T %+т - Pi dqt) ~ {Щ+i ~ Ht)dt

§ 46	ТЕОРЕМА ЛИУВИЛЛЯ	191
для дифференциала действия 5г(^+т5 Qt)t), взятого вдоль истин-
истинной траектории, проходящей через точки qt и qt+T в заданные
моменты времени t и ? + т (ср. D3.7)). Сравнение этой формулы
с D5.6) показывает, что —S есть производящая функция преоб-
преобразования.
§ 46. Теорема Лиувилля
Для геометрической интерпретации механических явлений
часто пользуются понятием о так называемом фазовом прост-
пространстве как о пространстве 2s измерений, на координатных осях
которого откладываются значения s обобщенных координат и s
импульсов данной механической системы. Каждая точка этого
пространства отвечает определенному состоянию системы. При
движении системы изображающая ее фазовая точка описывает
в фазовом пространстве соответствующую линию, называемую
фазовой траекторией. Произведение дифференциалов
dV = dqi... dqs dpi... dps
можно рассматривать как «элемент объема» фазового прост-
пространства. Рассмотрим теперь интеграл f с?Г, взятый по некото-
некоторой области фазового пространства и изображающий собой ее
объем. Покажем, что эта величина обладает свойством инвари-
инвариантности по отношению к каноническим преобразованиям: если
произвести каноническое преобразование от переменных р, q к
переменным Р, Q, то объемы соответствующих друг другу об-
областей пространств p,q и Р, Q одинаковы:
f..Idq1...dqsdp1...dps = f...fdQ1...dQsdP1...dPs. D6.1)
Как известно, преобразование переменных в кратном инте-
интеграле производится по формуле
/.. ./dQi... dQs dP1... dPs = .. jDdqi.. .dq8dp1... dp8,
где
i,... ,Qa,Pi,. ..,Pa)	/^g 2)
есть так называемый якобиан преобразования. Поэтому дока-
доказательство теоремы D6.1) сводится к доказательству того, что
якобиан всякого канонического преобразования равен единице:
D = 1.	D6.3)

192	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Воспользуемся известным свойством якобианов, которое поз-
позволяет обращаться с ними в определенном смысле, как с дробями.
«Разделив числитель и знаменатель» на d(qi,..., qSj Pi,..., Ps),
получим
...,Qa,Pi,...,Pa) I d(gu...,ga,pi,...,pa)
d(qu...,qs,Pu...,Ps) I д(д1,...,да,Р1,...,РаУ
Согласно другому известному правилу якобиан, у которого в
«числителе» и «знаменателе» фигурируют одинаковые величи-
величины, сводится к якобиану от меньшего числа переменных, причем
при всех дифференцированиях в нем выпавшие одинаковые ве-
величины должны считаться постоянными. Поэтому
1 *(*, ...,*.) /P=const / 1 9(Рг,..., P.) /g=c
Рассмотрим якобиан, стоящий в числителе этого выражения.
Согласно определению это есть определитель ранга 5, составлен-
составленный из элементов dQi/dqk (элемент на пересечении г-й строки и
к-го столбца). Представив каноническое преобразование с помо-
помощью производящей функции Ф(д, Р) в форме D5.8), получим
8qk ~
Таким же образом найдем, что г, к-й элемент определителя в
знаменателе выражения D6.5) равен	. Это значит, что
oqioPk
оба определителя отличаются только заменой строк на столб-
столбцы и обратно. Поэтому они равны друг другу, так что отноше-
отношение D6.5) равно единице, что и требовалось доказать.
Представим себе теперь, что каждая точка данного участ-
участка фазового пространства перемещается со временем согласно
уравнениям движения рассматриваемой механической системы.
Тем самым будет перемещаться и весь участок. При этом его
объем остается неизменным:
dV= const.	D6.6)
Это утверждение (так называемая теорема Лиувилля) непо-
непосредственно следует из инвариантности фазового объема при ка-
канонических преобразованиях и из того, что самое изменение р и
q при движении можно рассматривать (как было указано в кон-
конце предыдущего параграфа) как каноническое преобразование.

§ 47	УРАВНЕНИЕ ГАМИЛЬТОНА-ЯКОБИ	193
Совершенно аналогичным образом можно доказать инвари-
инвариантность интегралов
dqidpidqkdpkj
J J J J гФк
в которых интегрирование производится по заданным двух-, че-
четырех- и т.д. -мерным многообразиям в фазовом пространстве.
§ 47. Уравнение Гамильтона-Якоби
В § 43 было введено понятие о действии как функции коор-
координат и времени. Было показано, что частная производная по
времени от этой функции S(q, t) связана с функцией Гамильтона
соотношением
а ее частные производные по координатам совпадают с импуль-
импульсами. Заменив в соответствии с этим импульсы р в функции
Гамильтона производными dS/dq, мы получим уравнение
_ + Я^ь...^;—,...,_ ;tj=O,	D7.1)
которому должна удовлетворять функция S(q,t). Это уравне-
уравнение в частных производных первого порядка; оно называется
уравнением Гамильтона-Якоби.
Наряду с уравнениями Лагранжа и каноническими уравне-
уравнениями уравнение Гамильтона-Якоби также является основой не-
некоторого общего метода интегрирования уравнений движения.
Переходя к изложению этого метода, напомним предва-
предварительно, что всякое дифференциальное уравнение в частных
производных первого порядка имеет решение, зависящее от про-
произвольной функции; такое решение называют общим интегра-
интегралом уравнения. В механических применениях, однако, основную
роль играет не общий интеграл уравнения Гамильтона-Якоби,
а так называемый полный интеграл] так называется решение
дифференциального уравнения в частных производных, содер-
содержащее столько независимых произвольных постоянных, сколько
имеется независимых переменных.

194	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
В уравнении Гамильтона-Якоби независимыми переменны-
переменными являются время и координаты. Поэтому для системы с s
степенями свободы полной интеграл этого уравнения должен со-
содержать 5 + 1 произвольных постоянных. При этом, поскольку
функция S входит в уравнение только через свои производные,
то одна из произвольных постоянных содержится в полном ин-
интеграле аддитивным образом, т.е. полный интеграл уравнения
Гамильтона-Якоби имеет вид
S = /(?, gi, ...,&; ai,..., ав) + Д	D7.2)
где Oil,..., ocs и А — произвольные постоянные х).
Выясним теперь связь между полным интегралом уравне-
уравнения Гамильтона-Якоби и интересующим нас решением уравне-
уравнений движения. Для этого произведем каноническое преобразо-
преобразование от величин q,p к новым переменным, причем функцию
/(?, #, ос) выберем в качестве производящей функции, а величи-
величины (Xi, <X2j..., ocs — в качестве новых импульсов. Новые коор-
координаты обозначим через |3i,|32,...,|3s. Так как производящая
функция зависит от старых координат и новых импульсов, мы
должны пользоваться формулами D5.8):
п - Я/ а - Я/ чг _ тт+df
Но поскольку функция / удовлетворяет уравнению Гамиль-
Гамильтона-Якоби, то мы видим, что новая функция Гамильтона об-
обращается тождественно в нуль:
г) Хотя общий интеграл уравнения Гамильтона-Якоби нам не понадобит-
понадобится, но укажем, что он может быть найден, если известен полный интеграл.
Для этого будем считать величину А произвольной функцией остальных
постоянных:
S = /(*, qi, ..., Qs] ai, ..., oia) + A(ai, ...,ae).
Заменив здесь величины oti функциями координат и времени, которые на-
находим из s условий
— -О
дои ~ и'
получим общий интеграл, зависящий от вида произвольной функ-
функции A(ai, ..., 0i8). Действительно, для полученной таким способом функ-
функции S имеем
d ~ \d) +
Но величины {dS/dqi)oc удовлетворяют уравнению Гамильтона-Якоби, по-
поскольку функция S(t, q] ос) есть по предположению полный интеграл этого
уравнения. Поэтому удовлетворяют ему и производные dS/dqi.

§ 47	УРАВНЕНИЕ ГАМИЛЬТОНА-ЯКОБИ	195
Н> = Н+% = Н+^ = 0.
dt	dt
Поэтому канонические уравнения для новых переменных имеют
вид cxj = 0, (Зг = 0, откуда следует, что
оц = const, [3^ = const.	D7.3)
С другой стороны, s уравнений
дают возможность выразить s координат q через время и 25
постоянных а и C. Тем самым мы найдем общий интеграл урав-
уравнений движения.
Таким образом, решение задачи о движении механической
системы методом Гамильтона-Якоби сводится к следующим опе-
операциям.
По функции Гамильтона составляется уравнение Гамильто-
Гамильтона-Якоби и находится полный интеграл D7.2) этого уравнения.
Дифференцируя его по произвольным постоянным а и прирав-
приравнивая новым постоянным C, получаем систему s алгебраических
уравнений
решая которую, найдем координаты q как функции времени и 2 s
произвольных постоянных. Зависимость импульсов от времени
можно найти затем по уравнениям щ = dS/dqi.
Если мы имеем неполный интеграл уравнения Гамильтона-
Якоби, зависящий от меньшего чем s числа произвольных по-
постоянных, то хотя с его помощью нельзя найти общий интеграл
уравнений движения, но можно несколько упростить задачу его
нахождения. Так, если известна функция S, содержащая одну
произвольную постоянную а, то соотношение
— = const
dot
дает одно уравнение, связывающее gi,..., qs и t.
Уравнение Гамильтона-Якоби принимает несколько более
простую форму в том случае, когда функция Н не зависит от
времени явно, т.е. система консервативна. Зависимость действия
от времени сводится при этом к слагаемому —Et:
S = S0(q)-Et	D7.5)
(см. § 44), и подстановкой в D7.1) мы получаем для укорочен-

196	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
ного действия So(q) уравнение Гамильтона-Якоби в виде
=к D7-6)
§ 48. Разделение переменных
В ряде важных случаев нахождение полного интеграла урав-
уравнения Гамильтона-Якоби может быть достигнуто путем так на-
называемого разделения переменных, сущность которого состоит
в следующем.
Допустим, что какая-либо координата — обозначим ее через
q\ — и соответствующая ей производная dS/dqi входят в урав-
уравнение Гамильтона-Якоби только в виде некоторой комбинации
(p(qijdS/dqi), не содержащей никаких других координат (или
времени) и производных, т.е. уравнение имеет вид
•{••*•?•?•*«)}-•• ^
где qi обозначает совокупность всех координат за исключением q\.
Будем искать в этом случае решение в виде суммы
S = Sf(qi,t) + S1(q1).	D8.2)
Подставив это выражение в уравнение D8.1), получим
•{••'•?•? ¦»(*•?)}- °- <48-3>
Предположим, что решение D8.2) найдено. Тогда после под-
подстановки его в уравнение D8.3) последнее должно обратиться в
тождество, справедливое, в частности, при любом значении ко-
координаты q\. Но при изменении q\ может меняться только функ-
функция ф; поэтому тождественность равенства D8.3) требует, что-
чтобы и функция ф сама по себе была постоянной. Таким образом,
уравнение D8.3) распадается на два уравнения:
«1,	D8-4)
где oci — произвольная постоянная. Первое из них есть обыкно-
обыкновенное дифференциальное уравнение, из которого функция Si(qi)
может быть определена простым интегрированием. После это-
этого остается дифференциальное уравнение в частных производ-
производных D8.5), но уже с меньшим числом независимых переменных.

§ 48	РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ	197
Если таким способом можно последовательно отделить все s
координат и время, то нахождение полного интеграла уравне-
уравнения Гамильтона-Якоби целиком сводится к квадратурам. Для
консервативной системы речь фактически идет лишь о разделе-
разделении s переменных (координат) в уравнении D7.6), и при полном
разделении искомый интеграл уравнения имеет вид
S = ? Sk(qk; ocu..., ots) - Е(оси ..., аа%	D8.6)
к
где каждая из функций Sk зависит лишь от одной из координат,
а энергия Е как функция произвольных постоянных ос\,..., <xs
получается подстановкой So = ??& в уравнение D7.6).
Частным случаем разделения является случай циклической
переменной. Циклическая координата q\ вовсе не входит в явном
виде в функцию Гамильтона, а потому и в уравнение Гамиль-
Гамильтона-Якоби. Функция ф(#ь dS/dqi) сводится при этом просто к
dS/dqi, и из уравнения D8.4) имеем просто S\ = otiqi, так что
S = Sf(qht) + otiqi.	D8.7)
Постоянная оц есть при этом не что иное, как постоянное зна-
значение импульса pi = dS/dqi, отвечающего циклической коор-
координате. Отметим, что отделение времени в виде члена —Et для
консервативной системы тоже соответствует методу разделения
переменных для «циклической переменной» t.
Таким образом, все рассматривавшиеся ранее случаи упро-
упрощения интегрирования уравнений движения, основанные на ис-
использовании циклических переменных, охватываются методом
разделения переменных в уравнении Гамильтона-Якоби. К ним
добавляется еще ряд случаев, когда разделение переменных воз-
возможно, хотя координаты не являются циклическими. Все это
приводит к тому, что метод Гамильтона-Якоби является наи-
наиболее могущественным методом нахождения общего интеграла
уравнений движения.
Для разделения переменных в уравнении Гамильтона-Якоби
существен удачный выбор координат. Рассмотрим некоторые
примеры разделения переменных в различных координатах, кото-
которые могут представить физический интерес в связи с задачами
о движении материальной точки в различных внешних полях.
1. Сферические координаты. В этих координатах (г, 6, ф)
функция Гамильтона

198	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
и разделение переменных возможно, если
и = а(г) + М + ^Щ_
V >	Г2	г2 Sin2 9
где а(г), Ь@), с(ф) — произвольные функции. Последний член в
этом выражении вряд ли может представить физический инте-
интерес, и потому мы рассмотрим поле вида
U = а(г) + ^.	D8.8)
В этом случае уравнение Гамильтона-Якоби для функции So
,
2mr2 sin2 0 V d<p J
Учитывая цикличность координаты ф, ищем решение в виде
So = рфф + Si (г) + 52(9)
и для функций Si (г) и S2(9) получаем уравнения
v y 2шг2
Интегрируя их, получим окончательно:
S = -Et+P((><P + [ \/Э - 2тЬ@) -
J у
sin
a(r)]-^dr. D8.9)
Произвольными постоянными здесь являются ?>ф, C, Е1; диф-
дифференцируя по ним и приравнивая результат дифференцирова-
дифференцирования новым постоянным, найдем общее решение уравнений дви-
движения.
2. Параболические координаты. Переход к параболиче-
параболическим координатам ?,,г|, ф совершается от цилиндрических ко-
координат (которые в этом параграфе мы будем обозначать, как
р, ф, z) по формулам
\	D8.10)
Координаты ?, и г| пробегают значения от нуля до ос; поверхно-
поверхности постоянных ?, и г| представляют собой, как легко убедиться,

§ 48	РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ	199
два семейства параболоидов вращения (с осью z в качестве оси
симметрии). Связь D8.10) можно представить еще и в другой
форме, введя радиус
r = y/z* + p> = \(?J + T\).	D8.11)
Тогда
l = r + z, r\ = r-z.	D8.12)
Составим функцию Лагранжа материальной точки в коор-
координатах ?,,г|, ф. Дифференцируя выражения D8.10) по времени
и подставляя в
(функция Лагранжа в цилиндрических координатах), получим
L = ^(?, +л) (у- + —) + у?,лФ2 — U(E^r\, ф).	D8.13)
Импульсы равны
Ре, ~~ tf v^ ~1~ Л/^»? Рт\ ~~ 1
4с,	41
и функция Гамильтона
Физически интересные случаи разделения переменных в
этих координатах соответствуют потенциальной энергии вида
U = а(?) + Ъ(т\) = a(r + z) + Ъ(г - z)
? +	2	'
Имеем уравнение
2
dSo\ , л ^f 1 , _J_ №
Циклическая координата ф отделяется в виде рфф. Умножив
затем уравнение нага(?,+л) и перегруппировав члены, получим
(,)^+|| + л(^) + (л)Л + ^ = 0.
Положив
получим два уравнения
2Л

200	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
и, интегрируя их, найдем окончательно:
S = -Et -
2?, 2?, 4?,2
с произвольными постоянными Рф, C,?".
3. Эллиптические координаты. Эти координаты ?,,Л?Ф
вводятся согласно формулам
D8.17)
Постоянная а является параметром преобразования. Координа-
Координата ?, пробегает значения от единицы до ос, а координата Г| от — 1
до +1. Геометрически более наглядные соотношения получают-
получаются, если ввести расстояния г\ и т2 до точек А\ и Аъ на оси z с
координатами z = о л z = — а1):
П = y/{z- аJ + р2, г2 = ^(^ + О"J
Подставив сюда выражения D8.17), получим
Г! = а(?,-г|), г2 = а(?, + л),
Г	Г2+Г1	Г2-Г1
D8.18)
Преобразуя функцию Лагранж:а от цилиндрических коорди-
координат к эллиптическим, найдем
= 	\ч —Л
+ ^(?,2-1)A-л2)ф2-?/(?,,Л, ф)- D8.19)
Отсюда для функции Гамильтона получим
г) Линии постоянных ?, представляют собой семейство эллипсоидов
с фокусами в точках Ai и А2, а линии постоянных г| — семейство софокус-
ных с ним гиперболоидов
ст2Л2 ст2A-л2;
= 1.

§ 48	РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ	201
н= х
2шст2(?,2-л2)
). D8.20)
Физически интересные случаи разделения переменных соот-
соответствуют потенциальной энергии
U = -^1	— = -^— \а( ——— ) + Ъ ( ——— ) \, D8.21)
?,2-Г|2	ПГ2 I V 2G /	V 2G ))	V	У
где а(?,) и Ь(г|) — произвольные функции. Результат разделения
переменных в уравнении Гамильтона-Якоби гласит:
S=-i
+ J2md*E + , „Г" - j^^ A,- D8.22)
Задачи
1. Найти полный интеграл уравнения Гамильтона-Якоби для движения
частицы в поле	rv
L/ = - - Fz
г
(налож:ение кулоновского и однородного полей); найти специфическую для
такого движения сохраняющуюся функцию координат и импульсов.
Решение. Данное поле относится к типу D8.15), причем
Полный интеграл уравнения Гамильтона-Якоби дается формулой
D8.16) с этими функциями а(?,) и b(r\).
Для выяснения смысла постоянной C пишем уравнения
2
\	|| = C,
^ = -р.
Вычтя одно из этих уравнений из другого и выразив импульсы р^ =
= dS/dE, и рл = dS/дц через импульсы рр = dS/dp и pz = dS/dz в ци-
цилиндрических координатах, получим после простого приведения:
OCZ Рр ,	\ , Рф
V + ^ - №) + ^
Выраж:ение в квадратных скобках представляет собой интеграл движения,
специфический для чисто кулоновского поля (z-компонента вектора A5.17)).
2. То же в поле	^ _ ^ аз

202	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
(кулоновское поле двух неподвижных центров на расстоянии 2<т друг
от друга).
Решение. Данное поле относится к
типу D8.21), причем
О"
^
О"	О"
Действие 5(?,,г|; (р,?) получается подстанов- ос2	2<т	cxi
кой этих выражений в D8.22). Смысл посто-
постоянной C выясняется аналогично тому, как это	Ci
было сделано в задаче 1; она выражает собой в данном случае сохранение
следующей величины: 2
C = а2 (р2 + ^2.) - М2 + 2ma(oci cos 9i + а2 cos 92),
ГД6	М2 = [гр]2 = РУ + pip2 + ^ - 2грр,р„
a 0i и 02 — углы, указанные на рис. 55.
§ 49. Адиабатические инварианты
Рассмотрим механическую систему, совершающую одномер-
одномерное финитное движение и характеризующуюся некоторым пара-
параметром Л, определяющим свойства самой системы или внешнего
поля, в котором она находится х).
Предположим, что параметр Л под влиянием каких-либо
внешних причин медленно (как говорят, адиабатически) меня-
меняется со временем. Под медленным подразумевается такое изме-
изменение, при котором Л мало меняется за время периода движения
системы Г:
Г^<Л.	D9.1)
(Ль
При постоянном Л система была бы замкнутой и соверша-
совершала бы строго периодическое движение с постоянной энергией Е
и вполне определенным периодом Т(Е). При переменном пара-
параметре Л система не является замкнутой и ее энергия не сохраня-
сохраняется. Но в силу предположенной медленности изменения Л ско-
скорость Е изменения энергии будет тоже малой. Если усреднить
эту скорость по периоду Г и тем самым сгладить «быстрые»
колебания в ее величине, то получающееся таким образом зна-
значение Е определит скорость систематического медленного из-
изменения энергии системы; об этой скорости можно утверждать,
г) Для краткости записи формул мы предполагаем, что имеется всего
один такой параметр, но все результыты остаются в силе и при любом числе
параметров.

§ 49	АДИАБАТИЧЕСКИЕ ИНВАРИАНТЫ	203
что она будет пропорциональна скорости Л изменения парамет-
параметра Л. Это значит, другими словами, что понимаемая в указанном
смысле медленно меняющаяся величина Е будет вести себя как
некоторая функция от Л. Зависимость Е от Л можно предста-
представить в виде постоянства некоторой комбинации из Е и Л. Та-
Такую величину, остающуюся постоянной при движении системы
с медленно меняющимися параметрами, называют адиабатиче-
адиабатическим инвариантом.
Пусть H(q,p',X) — гамильтонова функция системы, завися-
зависящая от параметра Л. Согласно D0.5) скорость изменения энер-
энергии системы
dt dt д\ dt'	^ }
Выражение в правой части этой формулы зависит не только от
медленно меняющейся переменной Л, но и от быстро меняющих-
меняющихся переменных дир. Для выделения интересующего нас систе-
систематического хода изменения энергии надо, согласно сказанному
выше, усреднить равенство D9.2) по периоду движения. При
этом ввиду медленности изменения Л (а с ним и Л) можно вы-
вынести Л за знак усреднения:
dt ~ dt
а в усредняемой функции дН/дХ рассматривать как изменяю-
изменяющиеся величины лишь q и р, но не Л. Другими словами, усред-
усреднение производится по такому движению системы, какое имело
бы место при заданном постоянном значении Л.
Запишем усреднение в явном виде как
т
дН 1 [дН,
о
Согласно уравнению Гамильтона q = дН /dp имеем
dt- dq
С помощью этого равенства заменяем интегрирование по време-
времени на интегрирование по координате, причем и период Г запи-
записываем в виде
т

204	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
знаком § здесь обозначается интегрирование по полному изме-
изменению координаты («вперед» и «назад») за время периода1).
Таким образом, формула D9.3) принимает вид
ГдН/дЛ
~Ш _d\J дн/др q
dt ~ dt Г dq '
/ дН/др
Как уже было указано, интегрирования в этой формуле дол-
должны производиться по траектории движения при данном посто-
постоянном значении Л. Вдоль такой траектории функция Гамильто-
Гамильтона сохраняет постоянное значение Е1, а импульс является опре-
определенной функцией переменной координаты q и двух постоян-
постоянных независимых параметров ? и А. Понимая импульс имен-
именно как такую функцию p(q\E,X) и дифференцируя равенство
Н(р, д; Л) = Е по параметру Л, получим
д\ др д\	ИЛИ дН/др ~ дХ'
Подставив это в верхний интеграл в D9.5) и написав в ниж-
нижнем подынтегральную функцию в виде др/дЕ, имеем
		Гдр
dE	d\ J dAq
^ = -TJWT
или
Это равенство можно окончательно переписать в виде
где / обозначает интеграл
I=±-Spdq,	D9.7)
взятый по траектории движения при заданных Е и Л. Этот ре-
результат показывает, что величина / остается в рассматриваемом
приближении постоянной при изменении параметра Л, т.е. явля-
является адиабатическим инвариантом.
Величина / является функцией энергии системы (и парамет-
параметра Л). Ее частная производная по энергии определяет период
движения: согласно D9.4) имеем
х) Если движение системы представляет собой вращение, а координа-
координатой q является некоторый угол поворота (р, то интегрирование по d(p долж-
должно производиться по «полному обороту», т.е. от нуля до 2п.

50	КАНОНИЧЕСКИЕ ПЕРЕМЕННЫЕ	205
или	яр
Щ = ш,	D9.9)
где со = 2п/Т — частота колебаний системы.
Интегралу D9.7) может быть приписан наглядный геометри-
геометрический смысл, если воспользоваться понятием о фазовой траек-
траектории системы. В данном случае (одна степень свободы) фазо-
фазовое пространство сводится к двумерной системе координат р, д, и
фазовая траектория системы, совершающей периодическое дви-
движение, представляет собой замкнутую кривую в этой плоскости.
Интеграл D9.7), взятый вдоль этой кривой, представляет собой
заключенную внутри нее площадь. Он может быть написан и
как двумерный интеграл по площади:
2тг/
dpdq.	D9.10)
В качестве примера определим адиабатический инвариант
для одномерного осциллятора. Его функция Гамильтона
Я=^ + ^,	D9.11)
где ш — собственная частота осциллятора. Уравнение фазовой
траектории дается законом сохранения энергии
H(p,q) = E.
Это есть эллипс с полуосями \/2тЕ и ^2E/maJ и его площадь
(деленная на 2тс)
I = E/w.	D9.12)
Адиабатическая инвариантность этой величины означает, что
при медленном изменении параметров осциллятора его энергия
меняется пропорционально частоте.
§ 50. Канонические переменные
Пусть теперь параметр Л постоянен, так что рассматривае-
рассматриваемая система замкнута.
Произведем каноническое преобразование переменных д,р,
выбрав величину / в качестве нового «импульса». Роль произ-
производящей функции должно при этом играть «укороченное дей-
действие» So, выраженное в функции от q и /. Действительно, Sq

206	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
определяется как интеграл
S0(q, Е; Л) = j p(q, E; Л) dq,	E0.1)
взятый при заданном значении энергии Е (и параметра Л). Но
для замкнутой системы / является функцией одной только энер-
энергии; поэтому So можно с тем же правом выразить в виде функ-
функции /Sb(<7,/;Л), а частная производная (dSo/dq)E = Р совпадает
с производной (dSo/dq)i при постоянном /. Поэтому имеем
p=dSo{q,I;\)t	Eа2)
что соответствует первой из формул канонического преобразо-
преобразования D5.8). Вторая же формула определит новую «координа-
«координату» , которую обозначим через w:
w = 8So(^/;A).	E0.3)
Переменные law называют каноническими переменными, при-
причем / называется в этой связи переменной действия, awi — уг-
угловой переменной.
Поскольку производящая функция 5о(#, 1\ А) не зависит явно
от времени, то новая функция Гамильтона Н' совпадает со ста-
старой Н, выраженной через новые переменные. Другими словами,
Н1 есть энергия, выраженная в функции переменной действия,
ЕA). Соответственно уравнения Гамильтона для канонических
переменных имеют вид
j = 0, w = *^р-.	E0.4)
Из первого имеем, как и следовало, / = const — вместе с
энергией постоянна и величина /. Из второго же видим, что
угловая переменная является линейной функцией времени:
w = —t + const = w(I)t + const;	E0.5)
она представляет собой фазу колебаний.
Действие So(q,I) — неоднозначная функция координат. По
истечении каждого периода эта функция не возвращается к ис-
исходному значению, а получает приращение
AS0 = 2тг/,	E0.6)
как это очевидно из E0.1) и определения / согласно D9.7). За
это же время угловая переменная получает приращение
А^ = Ад50 = 2тг.	E0.7)

§ 50	КАНОНИЧЕСКИЕ ПЕРЕМЕННЫЕ	207
Обратно, если мы выразим q и р (или любую их однознач-
однозначную функцию F(q,p)) через канонические переменные, то эти
функции не будут менять свои значения при изменении w на
2тс (при заданном значении /). Другими словами, всякая одно-
однозначная функция F(q,p), будучи выражена через канонические
переменные, является периодической функцией w с периодом,
равным 2п.
Уравнения движения могут быть сформулированы в кано-
канонических переменных также и для незамкнутой системы с зави-
зависящим от времени параметром Л. Преобразование к этим пере-
переменным осуществляется по-прежнему формулами E0.2),E0.3)
с производящей функцией So, определяемой интегралом E0.1)
и выраженной через переменную /, определяемую интегралом
D9.7). Неопределенный интеграл E0.1) и определенный инте-
интеграл D9.7) вычисляются при этом так, как если бы параметр
Л(?) имел заданное постоянное значение; другими словами,
So(q, /; Л(?)) — прежняя функция, вычисленная при постоянном
Л, замененном затем заданной функцией Л(?) г).
Поскольку производящая функция оказывается теперь (вме-
(вместе с параметром Л) явной функцией времени, то новая функция
Гамильтона Н' уже не будет совпадать со старой, т.е. с энергией
Е{1). Согласно общим формулам канонического преобразования
D5.8) имеем
где введено обозначение
причем Л должна быть выражена (после осуществления диф-
дифференцирования по Л) с помощью E0.3) через / и w.
Уравнения Гамильтона принимают теперь вид
) Л,	E0.10)
где а) = (дЕ/д1)\ — частота колебаний (снова вычисленная так,
как если бы Л было постоянным).
г) Подчеркнем, однако, что определенная таким образом функция So уже
не совпадает с истинным укороченным действием для системы с зависящей
от времени гамильтоновой функцией!

208	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
Задача
Написать уравнения движения в канонических переменных для гармо-
гармонического осциллятора (функция Гамильтона D9.11)) с частотой, завися-
зависящей от времени.
Решение. Поскольку в E0.1)-E0.3) все действия совершаются при
постоянном А (роль которого играет в данном случае сама частота си), то
связь q и р с w имеет тот же вид, что и при постоянной частоте (когда
w = cot):
'	Г2/	/
_ sinw = \ 	 sin-w, p = V21шт cosw.
тш2	V гаси
So = pdq = I р\ тг~ J dw = 21 I cos2 w dw
J	J \0wJIcv	J
dS0\	fdS0\ fdw\	I .
T7— = — sin 2w.
Уравнения E0.10), E0.11) принимают теперь вид
/ = —/— cos2w, w = а) -\	s'm2w.
си	2си
§ 51. Точность сохранения адиабатического инварианта
Уравнение движения в форме E0.10) позволяет снова убе-
убедиться в адиабатической инвариантности переменной действия.
Функция So(qj /; Л) — неоднозначная функция q\ при возвра-
возвращении координаты к первоначальному значению к So прибавля-
прибавляется целое кратное от 2п1. Производная же E0.9) — однозначная
функция, так как дифференцирование производится при посто-
постоянном / и прибавляющиеся к So приращения при этом исче-
исчезают. Как и всякая однозначная функция, функция Л, будучи
выражена через угловую переменную w, будет периодической
функцией этой переменной. Среднее же (по периоду) значение
производной дЛ/dw от периодической функции обращается в
нуль. Поэтому, усредняя уравнение E0.10) и вынося при этом Л
(при медленном изменении Л) из-под знака среднего, получим
что и требовалось.
Уравнения движения E0.10), E0.11) позволяют рассмотреть
и вопрос о точности, с которой сохраняется адиабатический ин-
инвариант. Поставим этот вопрос следующим образом: пусть па-
параметр Л(?) стремится при t —»> —ос и t —»> +ос к постоянным

§ 51 ТОЧНОСТЬ СОХРАНЕНИЯ АДИАБАТИЧЕСКОГО ИНВАРИАНТА 209
пределам Л_ и Л+; задано начальное (при t = —ос) значение /_
адиабатического инварианта, и требуется найти его приращение
Д/ = /+—/_ ко времени t = +00.
Из E0.10) имеем
А/
--/?**•
E1.2)
Как уже было указано, величина Л — периодическая (с перио-
периодом 2п) функция переменной w\ разложим ее в ряд Фурье:
оо
— / ^ в А/	E1.о;
(в силу вещественности Л коэффициенты разложения связаны
при этом соотношениями Л_/ = Лг*). Отсюда для производной
dA/dw имеем
оо	оо
о д	#
^	IIP	/\ 7 	 2 Ti f ^ IIP	/\ 7	( j 1 4 I
^^^^	^^^^	v * /
/=-оо	/=1
dw
При достаточно малом Л производная w положительна (ее
знак совпадает со знаком си, см. E0.11)), т.е. w — монотонная
функция времени t. При переходе в E1.2) от интегрирования по
dt к интегрированию по dw пределы останутся поэтому преж-
прежними:
AT — - Г дА dX dt d
J dw dt dw
E1.5)
О
Подставим сюда E1.4) и преобразуем интеграл, рассматри-
рассматривая в нем формальным образом w как комплексную перемен-
переменную. Предположив, что подынтег-
подынтегральное выражение не имеет особых
точек при вещественных значениях
w, сместим путь интегрирования с
вещественной оси w в верхнюю по-
полуплоскость этой переменной. При
этом контур «зацепляется» за осо-
особые точки подынтегрального выра-
жения и, огибая их, принимает вид,
показанный схематически на рис. 56.
Пусть г^о — ближайшая к вещественной оси особая точка, т.е.
точка с наименьшей по величине (положительной) мнимой ча-
О Wq
Рис. 56

210	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
стью. Главный вклад в интеграл E1.5) возникает от окрест-
окрестности этой точки, причем каждый из членов ряда E1.4) дает
вклад, содержащий множитель ехр (—Urn wq). Сохраняя опять-
таки лишь член с наименьшим по абсолютной величине отрица-
отрицательным показателем (т.е. член с I = 1), найдем, что 1).
Д/сл exp(-Imw0).	E1.6)
Пусть to — «момент времени»(комплексное число!), отвечаю-
отвечающий особой точке г^о: w(to) = wo. По порядку величины |?о|
совпадает, вообще говоря, с характерным временем изменения
параметров системы; обозначим это время через т2). Порядок
же величины показателя степени в E1.6) будет
Imwo ~ сит ~ т/Г.	E1-7)
Поскольку, по предположению, т ^ Г, то этот показатель велик.
Таким образом, разность /+ — /_ убывает экспоненциально при
уменьшении скорости изменения параметров системы 3).
Для определения г^о в первом приближении по Г/т (т.е. с сох-
сохранением лишь члена порядка (Г/т) в показателе) можно отбро-
отбросить в уравнении E0.11) малый член, содержащий Л, т.е. писать
^ = шG,Л(*)),	E1.8)
причем аргумент / функции си(/, Л) полагается постоянным,
скажем, равным /_. Тогда
to
= Г a)(I,\(t))dt	E1.9)
(в качестве нижнего предела можно взять любое вещественное
значение ?; интересующая нас мнимая часть г^о от этого значе-
значения не зависит) 4).
г) В специальных случаях может оказаться, что разложение E1.4) не
содержит члена с / = 1 (см., например, задачу к этому параграфу); во всех
случаях надо брать член с наименьшим имеющимся в ряду значением /.
) Если медленность изменения параметра Л выражается в том, что он
зависит от t лишь в виде отношения ?, = t/т с большим т, то to = т?,0, где
?,0 — не зависящая от т особая точка функции А(?,).
3)	Отметим, что если начальное и конечное значения функции Л(?) сов-
совпадают (Л+ = А_), то экспоненциально малой будет не только разность А/,
но вместе с нею также и разность АЕ = Е+ — Е- конечной и начальной
энергии; согласно D9.9) будем иметь АЕ = сиД/.
4)	Более подробное доказательство сделаных утверждений, а также вы-
вычисление предэкспоненциального множителя в формуле E1.6), можно най-
найти в статье: Слуцкин А.А.//ЖЭТФ.—1963.—Т. 45.—С. 978.
to

§ 51 ТОЧНОСТЬ СОХРАНЕНИЯ АДИАБАТИЧЕСКОГО ИНВАРИАНТА 211
Интеграл же E1.5) с w из E1.8) (и с одним членом ряда
E1.4) в качестве дЛ/dw) принимает вид
А/ел Re
Г ieiw^-.	E1.10)
J	">(/,Л)
Отсюда видно, что в качестве конкурирующих (при отборе бли-
ближайшей к вещественной оси) особых точек фигурируют осо-
особенности (полюсы, точки ветвления) функций Л(?) и 1/си(?).
Напомним в этой связи, что заключение об экспоненциальной
малости Д/ связано с предположением, что указанные функции
не имеют вещественных особых точек.
Задачи
1.	Оценить А/ для гармонического осциллятора с частотой, медленно
меняющейся по закону	1 + аеа*
(ЛJ = CUq
от значения си_ = сио при t = — оо до си+ = л/а сио при t = оо (а > О,
а< сио) х).
Решение. Понимая под параметром Л саму частоту си, имеем
Л, _ а / а	1_
си ~ 2 \е-а* + а е-а* +
Эта функция имеет полюсы при e~cct = —1 к e~cct = —а. Вычислив интеграл
J cucfa, найдем, что наименьшее значение Im wq происходит от одного из
полюсов octo = — In (—а) и равно
Г Шоп/ос при а > 1,
Im wo = <	,_ .
^cuo7tya/a при а < 1.
Для гармонического осциллятора Л ^ sin2i(; (см. задачу к §50), так что
ряд E1.3) сводится к двум членам с (/ = ±2). Поэтому для гармонического
осциллятора
А/ со exp(-2Imw0).
2.	Частица совершает колебания в потенциальной яме. Определить за-
закон изменения ее энергии под действием силы трения /тр = —осх с малым
коэффициентом ос (х — декартова координата).
Решение. Усредним уравнение B5.13) по периоду колебаний, пре-
пренебрегая в первом приближении их затуханием. Имеем
		т
dE	~ ос Г .2,	ос Г .2,	2пос ,—.
— _ -осх - -— J х - -— j) х х - —^ К )•>
о
где 1(Е) — адиабатический вариант, т — масса частицы. Выражая период
колебаний Т через / согласно D9.8), находим
) Гармоничность осциллятора проявляется в независимости частоты ко-
колебаний от энергии.

212	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
<П_ Ш_ _ __а
dE dt ~ m
Интегрируя, получаем
Формула A) определяет в неявном виде зависимость E(t). Для гармониче-
гармонического осциллятора A) переходит в B5.5). Решение справедливо при условии
осТ/т < 1.
§ 52. Условно-периодическое движение
Рассмотрим замкнутую систему со многими степенями сво-
свободы, совершающую финитное (по всем координатам) дви-
движение. Предположим при этом, что задача допускает полное
разделение переменных в методе Гамильтона-Якоби. Это зна-
значит, что при соответствующем выборе координат укороченное
действие представляет собой сумму
5о = ?йЫ	E2.1)
г
функций, каждая из которых зависит только от одной из координат.
Поскольку обобщенные импульсы
_ dSp _ dSj
Pi ~ dqi ~ dqi'
то каждая из функций Si может быть представлена в виде
= J ju dqi.	E2.2)
Эти функции неоднозначны. В силу финитности движения
каждая из координат может пробегать значения лишь в опреде-
определенном конечном интервале. При изменении qi в этом интервале
«вперед» и «назад» действие получает приращение
E2.3)
где Ii есть интеграл
Ii = ^jpidqi,	E2.4)
взятый по указанному изменению qi 1).
) Подчеркнем, однако, что здесь идет речь о формальном изменении
координаты qi во всем допустимом интервале ее значений, а не об изме-
изменении за период реального движения (как это было в случае одномерного
движения). Реальное финитное движение системы с несколькими степеня-
степенями свободы не только является в общем случае периодическим в целом,
но даже изменение со временем каждой из ее координат в отдельности не
является периодическим (см. ниже).

§ 52	УСЛОВНО-ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ	213
Произведем теперь каноническое преобразование аналогич-
аналогично тому, как это было сделано в предыдущем параграфе для
случая одной степени свободы. Новыми переменными будут «пе-
«переменные действия» 1{ и «угловые переменные»
_ dSo(q,I) _ ^ dSk(qk,I)	,„ -ч
к
где производящей функцией снова является действие, выражен-
выраженное в функции координат и величин If, уравнения движения в
этих переменных
д=0, w, f
дают
Ii = const,	E2.6)
щ = ^lt + const.	E2.7)
Мы найдем также аналогично E0.7), что полному измене-
изменению координаты qi («вперед» и «назад» ) отвечает изменение
соответствующего wi на 2п\
Awi = 2тг.	E2.8)
Другими словами, величины Wi(q,I) являются неоднозначными
функциями координат, которые при изменении последних с воз-
возвращением к первоначальным значениям могут изменяться на
любое целое кратное от 2тс. Это свойство можно сформулиро-
сформулировать также и как свойство функции W{ (p, q) (выраженной через
координаты и импульсы) в фазовом пространстве системы. По-
Поскольку сами величины /;, если их выразить через рид, явля-
являются однозначными функциями этих переменных, то, подставив
Ii(pj q) в Wi(q, /), мы получим функцию Wi(p, q), которая при об-
обходе по любой замкнутой кривой в фазовом пространстве может
измениться на целое кратное от 2тс (либо на нуль).
Отсюда следует, что всякая однозначная функция состояния
системы F(p,q) x), будучи выражена через канонические пере-
переменные, является периодической функцией угловых перемен-
х) «Вращательные координаты» — углы (р (см. примеч. на с. 204) — неод-
неоднозначно связаны с состоянием системы, так как значения (р, отличающиеся
на целое кратное 2я, отвечают одному и тому же положению системы. По-
Поэтому, если среди координат q имеются такие углы, то они могут входит в
функцию F(q,p) лишь в виде таких выражений, как cos (p или sincp, связь
которых с состоянием системы однозначна.

214	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
ных с периодом 27Г по каждой из них. Ее можно поэтому разло-
разложить в кратный ряд Фурье вида
сю	сю
Р= ? ••• Е Allh...lsexp[i(l1w1 + --- + lsws)]
l^=—oo ls=—oo
(Zi, Z2,..., ls — целые числа). Подставив же сюда угловые пере-
переменные как функции времени, найдем, что временная зависи-
зависимость F определяется суммой вида
V2{(f	f)} E2.9)
ll=—сю ls=—сю
Каждый из членов этой суммы есть периодическая функция
времени с частотой
Ziwi + --- + Zsws,	E2.10)
представляющей собой сумму целых кратных от основных частот
о>, = f •	E2.11)
Но поскольку все частоты E2.10) не являются, вообще говоря,
целыми кратными (или рациональными частями) какой-либо
одной из них, то вся сумма в целом не является строго пери-
периодической функцией. Это относится, в частности, и к самим ко-
координатам q и импульсам р системы.
Таким образом, движение системы не является в общем слу-
случае строго периодическим ни в целом, ни по какой-либо из ко-
координат. Это значит, что если система прошла через какое-либо
состояние, то она не пройдет через него повторно ни через какое
конечное время. Можно, однако, утверждать, что по истечении
достаточно большого промежутка времени она пройдет сколь
угодно близко от этого состояния. Это свойство имеют в виду,
называя такое движение условно-периодическим.
В различных частных случаях две (или более) из основных
частот a)i могут оказаться соизмеримыми (при произвольных
значениях величин Ц). В таких случаях говорят о наличии вы-
вырождения, а если все s частот соизмеримы, то движение системы
называют полностью вырожденным. В последнем случае, оче-
очевидно, движение строго периодично и тем самым траектории
всех частиц замкнуты.
Наличие вырождения приводит, прежде всего, к уменьше-
уменьшению числа независимых величин (/;), от которых зависит энер-
энергия системы. Пусть две частоты cui и Ш2 связаны соотношением

§ 52	УСЛОВНО-ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ	215
дЕ	дЕ	,ко 1Оч
где ni и П2 — целые числа. Отсюда следует, что величины 1\ и
/2 входят в энергию лишь в виде суммы П2/1 + 774/2-
Весьма важной особенностью вырожденных движений яв-
является увеличение числа однозначных интегралов движения по
сравнению с их числом в общем случае невырожденной систе-
системы (с тем же числом степеней свободы). В последнем случае из
полного числа Bs — 1) всех интегралов движения однозначными
являются всего s функций состояния системы; их полный набор
составляют, например, s величин 1{. Остальные s — 1 интегралов
можно представить в виде разностей
Widh~WkWt-	E2ЛЗ)
Постоянство этих величин непосредственно следует из формулы
E2.7), но ввиду неоднозначности угловых переменных они не
являются однозначными функциями состояния системы.
При наличии же вырождения положение меняется. Так, вви-
ввиду связи E2.12) интеграл
w\ri2 — W2Tii	E2.14)
хотя и является неоднозначным, но его неоднозначность сводит-
сводится к прибавлению любого целого кратного 2п. Поэтому доста-
достаточно взять тригонометрическую функцию этой величины, для
того чтобы получить новый однозначный интеграл движения.
Примером вырожденного движения является движение в
поле U = —ос/г (см. задачу к этому параграфу). Именно это
обстоятельство приводит к появлению нового, специфического
однозначного интеграла движения A5.17), помимо двух (рас-
(рассматриваем движение сразу как плоское) обычных однозначных
интегралов, — момента М и энергии Е1, — свойственных движе-
движению в любом центральном поле.
Отметим также, что появление дополнительных однознач-
однозначных интегралов приводит в свою очередь еще к одному свой-
свойству вырожденных движений — они допускают полное разделе-
разделение переменных при различных, а не при одном определенном г)
выборе координат. Действительно, величины Ii в координатах,
осуществляющих разделение переменных, являются однознач-
) Мы отвлекаемся при этом от таких тривиальных изменений координат,
как преобразования вида q[ = q[(qi), q'2 = <

216	КАНОНИЧЕСКИЕ УРАВНЕНИЯ	ГЛ. VII
ными интегралами движения. Но при наличии вырождения чис-
число однозначных интегралов превышает s, и потому становится
неоднозначным выбор тех из них, которые мы хотим получить
в качестве величин 1{.
В качестве примера снова упомянем кеплерово движение, до-
допускающее разделение переменных как в сферических, так и в
параболических координатах.
В предыдущем параграфе было показано, что при одномер-
одномерном финитном движении переменная действия является адиа-
адиабатическим инвариантом. Это утверждение остается в силе и
для систем со многими степенями свободы. Оно доказывается в
общем случае прямым обобщением способа, изложенного в на-
начале § 51.
Для многомерной системы с переменным параметром Л(?)
уравнения движения в канонических переменных дают для ско-
скорости изменения каждой из переменных действия 1{ выражение,
аналогичное E0.10):	•	дА •	/гО1гч
/, = -—Л,	E2.15)
где по-прежнему Л = (dSo/dX)i. Усреднение этого равенства
надо производить по промежутку времени, большому по срав-
сравнению с основными периодами системы, но малому по сравне-
сравнению со временем изменения параметра Л(?). При этом Л снова
выносится из-под знака усреднения, а усреднение производных
дЛ/dwi производится так, как если бы движение происходило
при постоянном Л и потому было условно периодическим. То-
Тогда Л будет однозначной периодической функцией угловых пе-
переменных Wi и средние значения ее производных дЛ/dwi обра-
обращаются в нуль.
В заключение сделаем некоторые замечания по поводу
свойств финитного движения замкнутых систем со многими (s)
степенями свободы в наиболее общем случае, не предполагаю-
предполагающем разделимости переменных в соответствующем уравнении
Гамильтона-Якоби.
Основным свойством систем с разделяющимися переменны-
переменными является однозначность интегралов движения 1^ число ко-
которых равно числу степеней свободы. В общем же случае систем
с неразделяющимися переменными набор однозначных интегра-
интегралов движения ограничивается теми, постоянство которых есть
выражение свойств однородности и изотропии пространства и
времени, т.е. законами сохранения энергии, импульса и момента.

§ 52	УСЛОВНО-ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ	217
Фазовая траектория системы проходит по тем областям фа-
фазового пространства, которые определяются заданными посто-
постоянными значениями однозначных интегралов движения. Для
системы с разделяющимися переменными с ее s однозначными
интегралами этими условиями определяется 5-мерное многооб-
многообразие (гиперповерхность) в фазовом пространстве. В течение
достаточно долгого времени траектория системы покроет эту
гиперповерхность сколь угодно плотно.
У системы же с неразделяющимися переменными, с ее мень-
меньшим (при том же s) числом однозначных интегралов фазовая
траектория заполняет собой в фазовом пространстве (полно-
(полностью или частично) области (многообразия) большого числа из-
измерений.
Наконец, укажем, что если гамильтонова функция системы
отличается от функции, допускающей разделение переменных,
лишь малыми членами, то и свойства движения близки к свой-
свойствам условно-периодических движений, причем степень этой
близости гораздо выше, чем степень малости дополнительных
членов в функции Гамильтона.
Задача
Вычислить переменные действия для эллиптического движения в поле
U = -ос/г.
Решение. В полярных координатах г,фв плоскости движения имеем
2тг
•"-hi
d(p = М,
Ir=^rl y2m(E+^)-^dr=-M+ociw\-
Отсюда энергия, выраженная через переменные действия:
Е =	.
Она зависит лишь от суммы 1Г + /ф, что означает вырождение движения —
обе основные частоты (по (р и по г) совпадают.
Параметры орбиты р и е (см. A5.4)) выражаются через /гДф согласно
mot	\/<р+
В силу адиабатической инвариантности величин 1Г, /ф, при медленном из-
изменении коэффициента а или массы т эксцентриситет орбиты остается
неизменным, а ее размеры меняются обратно пропорционально т и ос.

Приложение
ПРЕДИСЛОВИЕ Л.Д. ЛАНДАУ К ПЕРВОМУ ИЗДАНИЮ
Курс теоретической физики. Механика
Физика, как известно, состоит, собственно говоря, из двух
наук: физики экспериментальной и физики теоретической. Гро-
Громадное количество известных нам физических законов может
быть выведено из очень небольшого числа весьма общих соот-
соотношений; однако такое выведение, так же как и установление
самих основных законов, требует своеобразных методов и по-
поэтому составляет задачу особой науки — теоретической физики.
Для построения своих выводов и заключений теоретическая
физика пользуется приемами и методами математики. Однако
от последней она резко отличается непосредственной связью с
результатами эксперимента. Не говоря уже о том, что установ-
установление общих законов возможно только на основе эксперимен-
экспериментальных данных, даже нахождение следствий из общих законов
нуждается в предварительном экспериментальном изучении яв-
явлений. Без такого изучения часто невозможно установить, какие
из громадного числа участвующих факторов существенны, а ка-
какими можно пренебречь. После того как получены уравнения,
учитывающие только существенные факторы, задача теорети-
теоретической физики, собственно говоря, в основном заканчивается.
Дальнейшее применение полученных уравнений к более или ме-
менее сложным конкретным случаям является уже скорее пред-
предметом математики и изучается отделом математики, носящим
название математической физики.
Теоретическая физика ставит себе целью нахождение физи-
физических законов, т.е. установление зависимости между физиче-
физическими величинами. Определение же численных значений фи-
физических величин, вообще говоря, в ее задачи не входит. Экс-
Эксперимент справляется с этим кругом вопросов относительно на-
настолько легко, что в огромном большинстве случаев отсутствует
сама необходимость подобных вычислений, которые к тому же

ПРИЛОЖЕНИЕ	219
потребовали бы громадной затраты времени и труда. Исключе-
Исключение составляют простейшие случаи, когда численные значения
величин непосредственно вытекают из теории.
Следует отметить, что поскольку задача теории состоит все-
всегда в установлении зависимостей между различными величи-
величинами, характеризующими данное явление, теория явления мо-
может быть построена только в том случае, когда в природе такая
связь действительно существует. Сплошь и рядом, однако, меж-
между представляющими интерес величинами никакой связи вовсе
не существует, т.е. эти величины могут встречаться в природе в
самых различных комбинациях. Таким образом, отсутствие те-
теории какого-либо явления не всегда означает, что оно не подда-
поддается объяснению. Отсутствие закономерности при этом так же
может вытекать из общих законов, как в других случаях сами
закономерности.
Громадную роль в теоретической физике играет приближен-
приближенное рассмотрение. Прежде всего совершенно точные законы яв-
являются приближенными, хотя в громадном большинстве случа-
случаев даваемая ими точность является весьма высокой. Более того,
требование абсолютной точности к физическим законам и не
предъявляется. Достаточно, если существует какая-то заранее
установленная область явлений, в которой точность данного за-
закона удовлетворяет поставленной задаче. Так, мы спокойно при-
применяем ньютоновскую механику к движению снаряда, хотя нам
известно не только то, что эта механика не является абсолютно
точной, но и то, что в нашем распоряжении имеется значительно
более точная релятивистская механика.
Благодаря этому в теоретической физике рядом с более точ-
точными теориями прекрасно уживаются теории, неточность ко-
которых давно установлена, — поскольку они вполне сохраняют
свою ценность для определенной области явлений (такие тео-
теории обычно называются классическими). Всякая логически за-
замкнутая теория, верность которой была с известной степенью
точности экспериментально доказана, никогда не теряет своего
значения, и всякая более точная последующая теория охватыва-
охватывает ее как приближенный результат, справедливый в некоторых
частных случаях. Это, конечно, не относится к теориям, стра-
страдающим внутренними противоречиями, которые всегда имеют
значение только одного из этапов развития теоретической фи-
физики.

220	ПРИЛОЖЕНИЕ
Таким образом, приближения играют очень важную роль в
общих физических теориях. Не менее велика, однако, их роль и
при выводе из общих теорий конкретных физических законов.
Слишком точные вычисления с учетом несущественных факто-
факторов не только бесплодны и излишне усложняют результат расче-
расчета, но могут даже привести к тому, что существующие в данном
явлении закономерности вообще выпадут из рассмотрения. Де-
Дело в том, что приближенным может оказаться не только данный
конкретный вид закона, но и само существование функциональ-
функциональной связи между характеризующими данное явление величина-
величинами, и за пределами данной точности эти величины могут встре-
встречаться в произвольных комбинациях.
Определение степени приближения, с которой данное явле-
явление должно рассматриваться, чрезвычайно существенно при его
теоретическом исследовании. Особенно грубой ошибкой являет-
является тщательное вычисление с учетом всевозможных мелких по-
поправок и применения слишком точных общих теорий в случаях,
когда одновременно с этим пренебрегают гораздо большими ве-
величинами.
1940 г.	Л.Д. Ландау

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ1)
Абсолютно гладкая поверхность
162
—	шероховатая поверхность 162
Аддитивность интегралов
движения 24
—	массы 29
Амплитуда 79
Апериодическое затухание 102
Биения 84, 94
Вариация 11
Вириальная теорема 37
Внутренняя энергия 30
Волчок асимметрический 133, 153
—	быстрый 149
—	симметрический 133, 141, 148
—	шаровой 133
Вырождение 214
Геометрическая оптика 182
Главные моменты инерции 133
—	оси инерции 133
Действие 11
—	укороченное 183
Декремент затухания 101
Дисперсионное поглощение 106
Диссипативная функция 103
Задача двух тел 44
Закон инерции 15
—	равенства действия и
противодействия 28
Законы Кеплера 37, 46
Замкнутая система 18
Замкнутые траектории 48
Изотропия пространства 15, 31
Инерциальная система отсчета 14
Интеграл движения 24
—	площадей 46
Канонические уравнения 172
Канонически-сопряженные
величины 189
Качение 161
Кинетическая энергия 19
Комбинационные частоты 115
Консервативная система 25
Линия узлов 146
Масса частицы 17
Маятник двойной 22, 94
—	плоский 22, 41, 51, 127
—	сферический 50
—	физический 137
—	Фуко 170
Мгновенная ось вращения 131
Момент силы 144
Нормальные колебания 91
Нутация 149
Обобщенная координата 9
—	сила 28
Обобщенный импульс 28
Однородное поле 21
Однородность времени 25
—	пространства 26
Осциллятор 79
—	пространственный 94
х)Этот указатель дополняет оглавление книги, не повторяя его. В ука-
указатель включены термины и понятия, непосредственно не отраженные в
оглавлении.

222
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Падение частицы в центр 49, 70
Пара сил 144
Параболические координаты 198
Переменная действия 206
Перигелия смещение 56
Полодия 154
Поступательное движение 129
Потенциальная энергия 19
—	яма 40
Преобразование Галилея 16
—	Лежандра 171
Прецессия регулярная 142
Принцип д'Аламбера 164
Производящая функция 188
Резонанс 83
Ротатор 134, 141
Связи 22
—	голономные 163
—	неголономные 163
Секториальная скорость 46
Сила 20
—	Кориолиса 168
—	реакции 161
—	трения 100, 161
—	центробежная 168
Скольжение 161
Собственная частота 89
Степени свободы 9, 95, 128
Теорема Пуассона 178
Тождество Якоби 177
Точечное преобразование 187
Точка остановки 40
"Угловая переменная 206
Уравнения Ньютона 20
Условия равновесия твердого
тела 161
Фаза 79
Фазовая траектория 191
Фазовое пространство 191
Финитное и инфинитное
движение 40
Циклическая координата 46,
175, 195
— частота 79
Эксцентриситет 52
Эллиптические координаты 200
Эффективное сечение 67, 68

Учебное издание
ЛАНДАУ Лев Давидович
ЛИФШИЦ Евгений Михайлович
МЕХАНИКА
(Серия: «Теоретическая физика», том I)
Редактор: Д. А. Миртова
Оригинал-макет: А. С. Даутов
ЛР №071930 от 06.07.99
Подписано в печать 25.05.01. Формат
Бумага офсетная №1. Печать офсетная
Усл. печ. л. 14,0. Уч.-изд. л. 13,4
Заказ №
Издательская фирма
«Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117864 Москва, Профсоюзная ул., 90
E-mail: fizmat@maik.ru, http://www.fml.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3.
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72.
E-mail: pfpv@vologda.ru http://www.vologda/~pfpv
ISBN 5-9221-0055-6
785922 100557