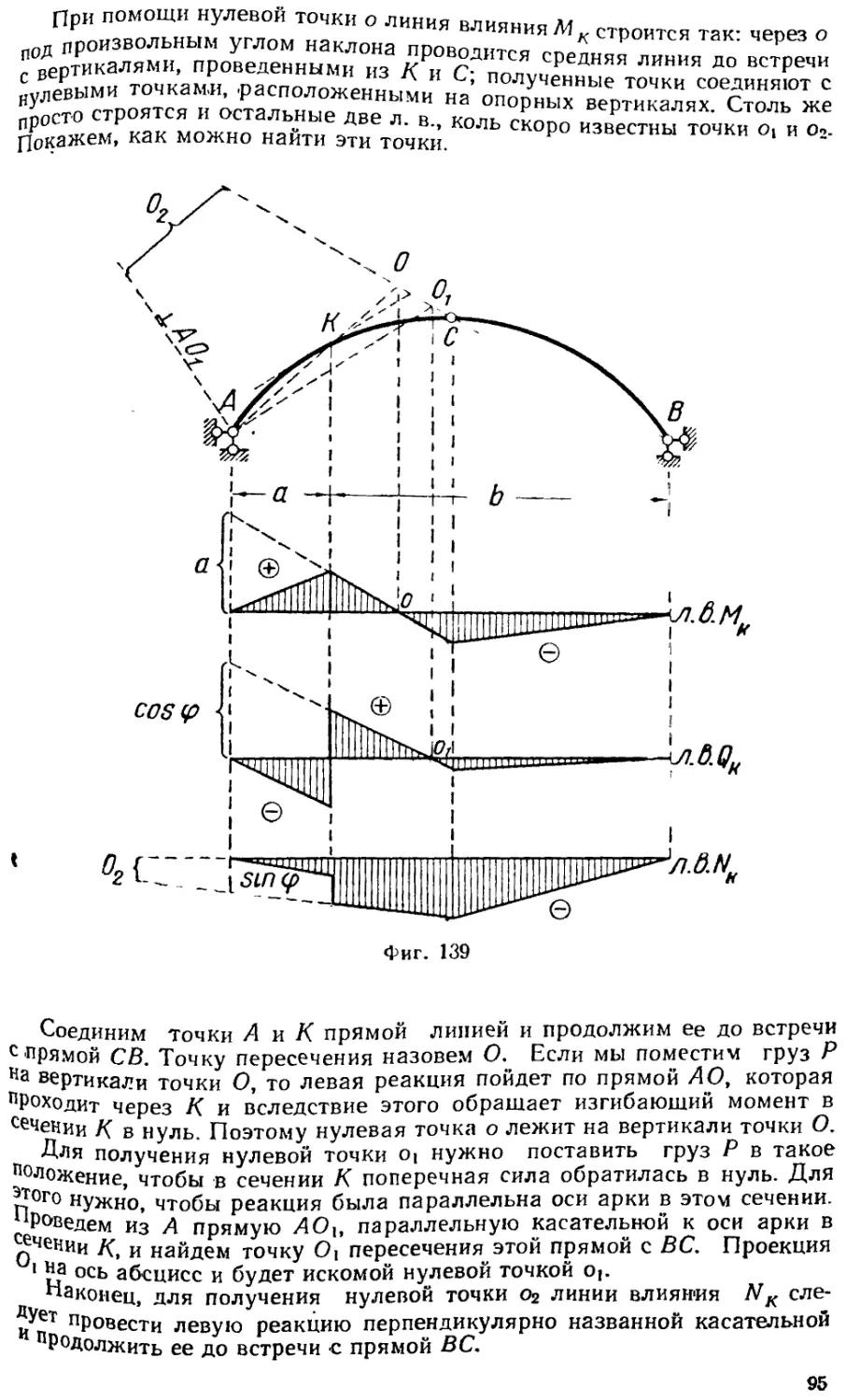
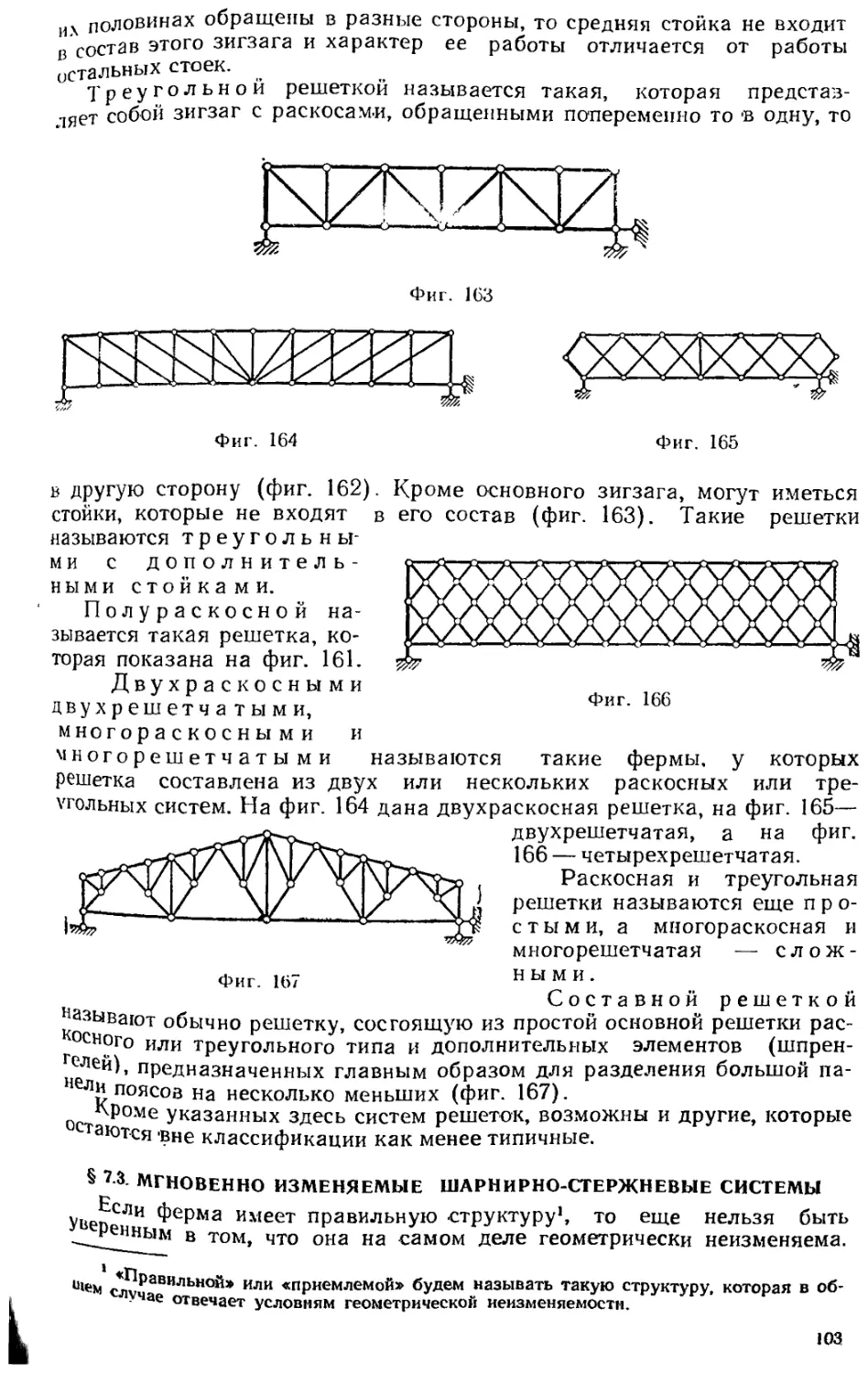
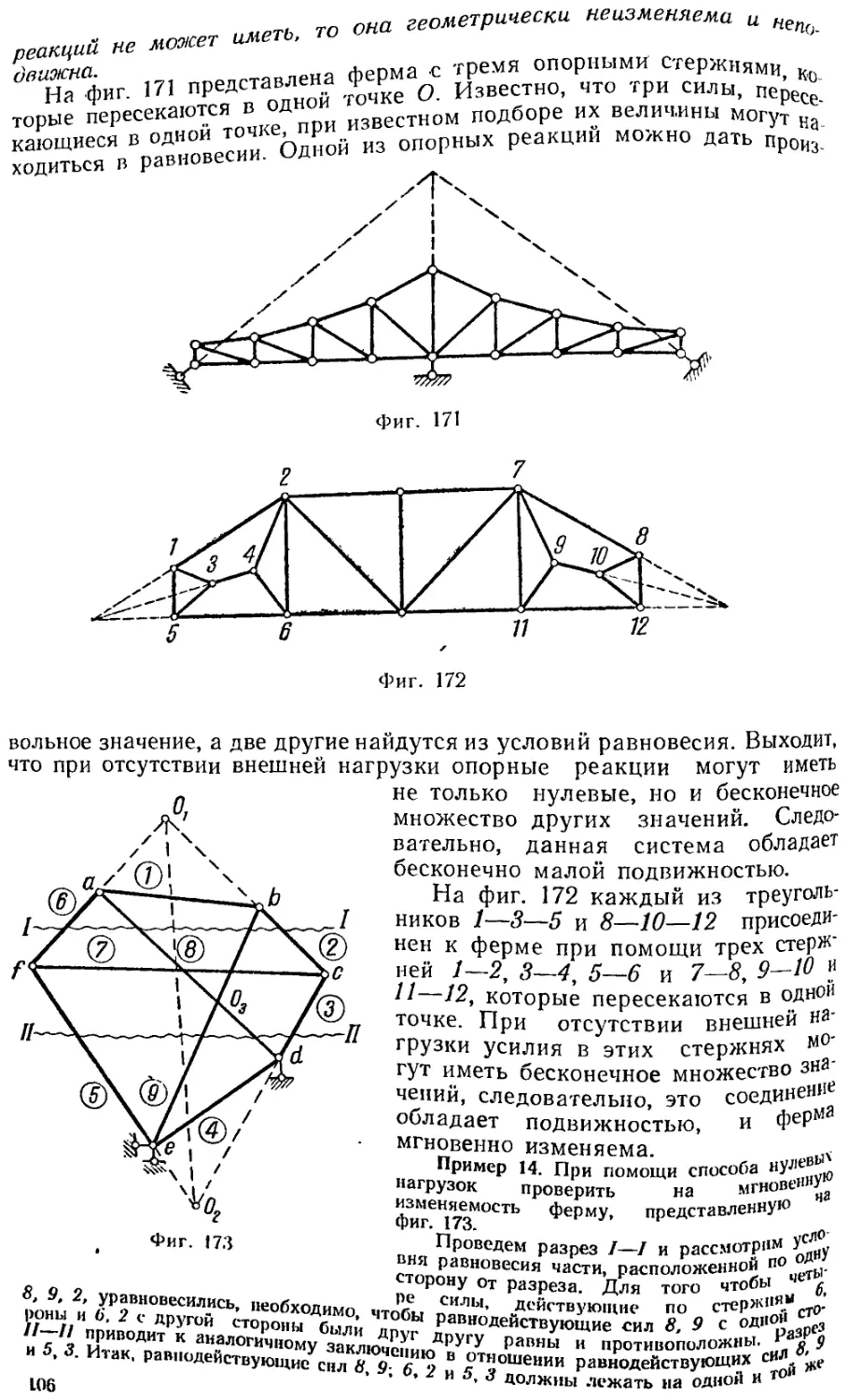
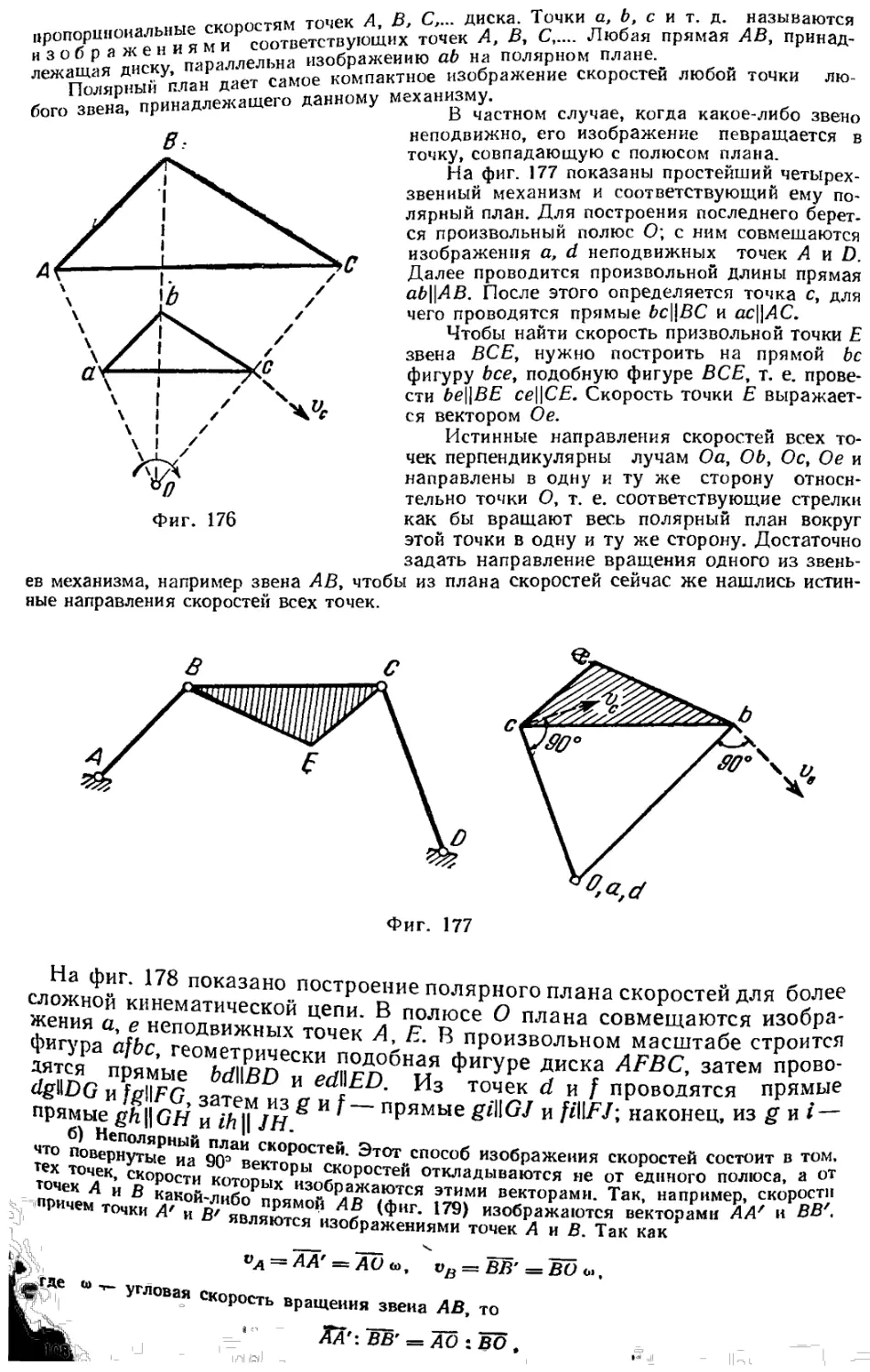
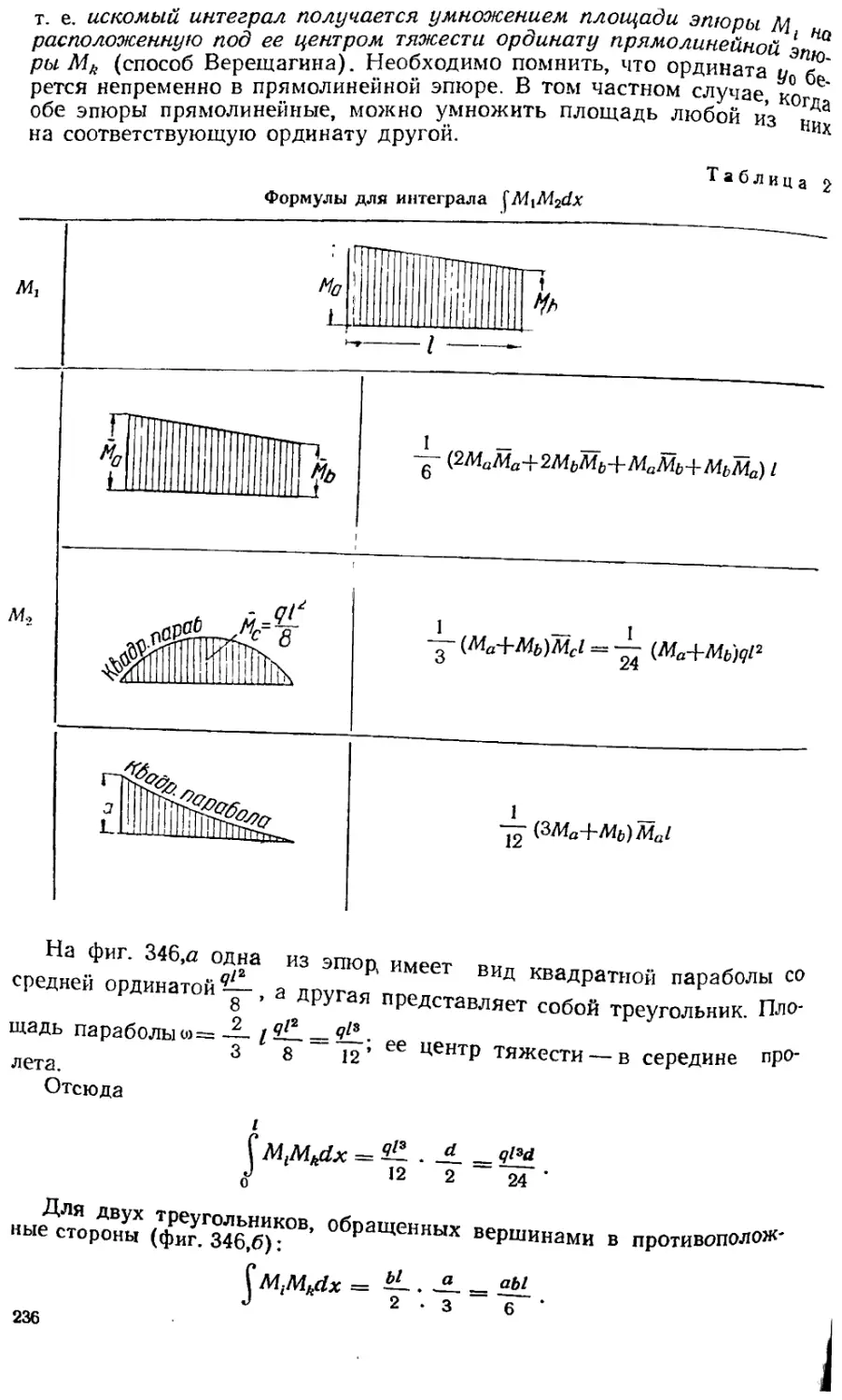
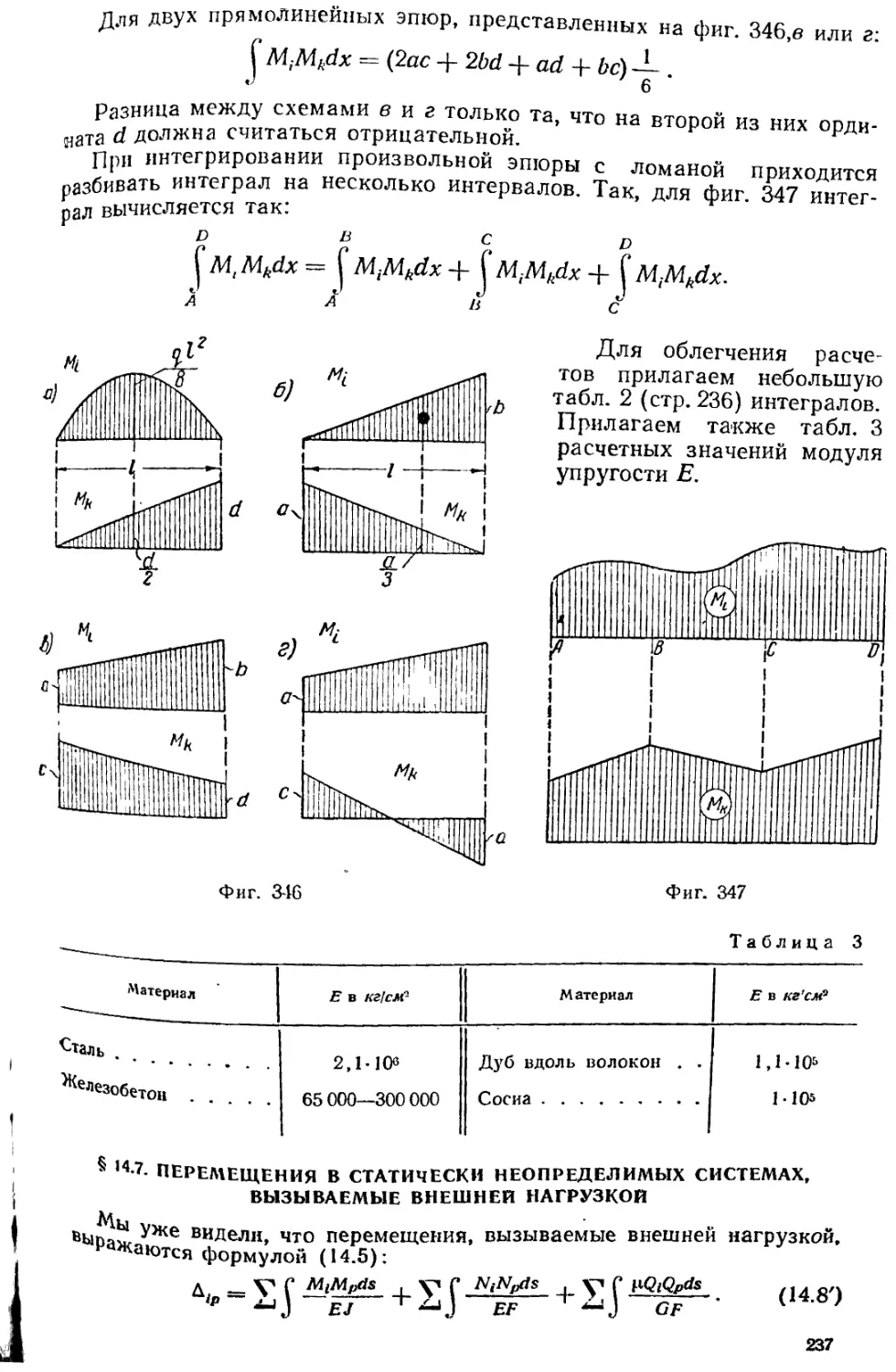
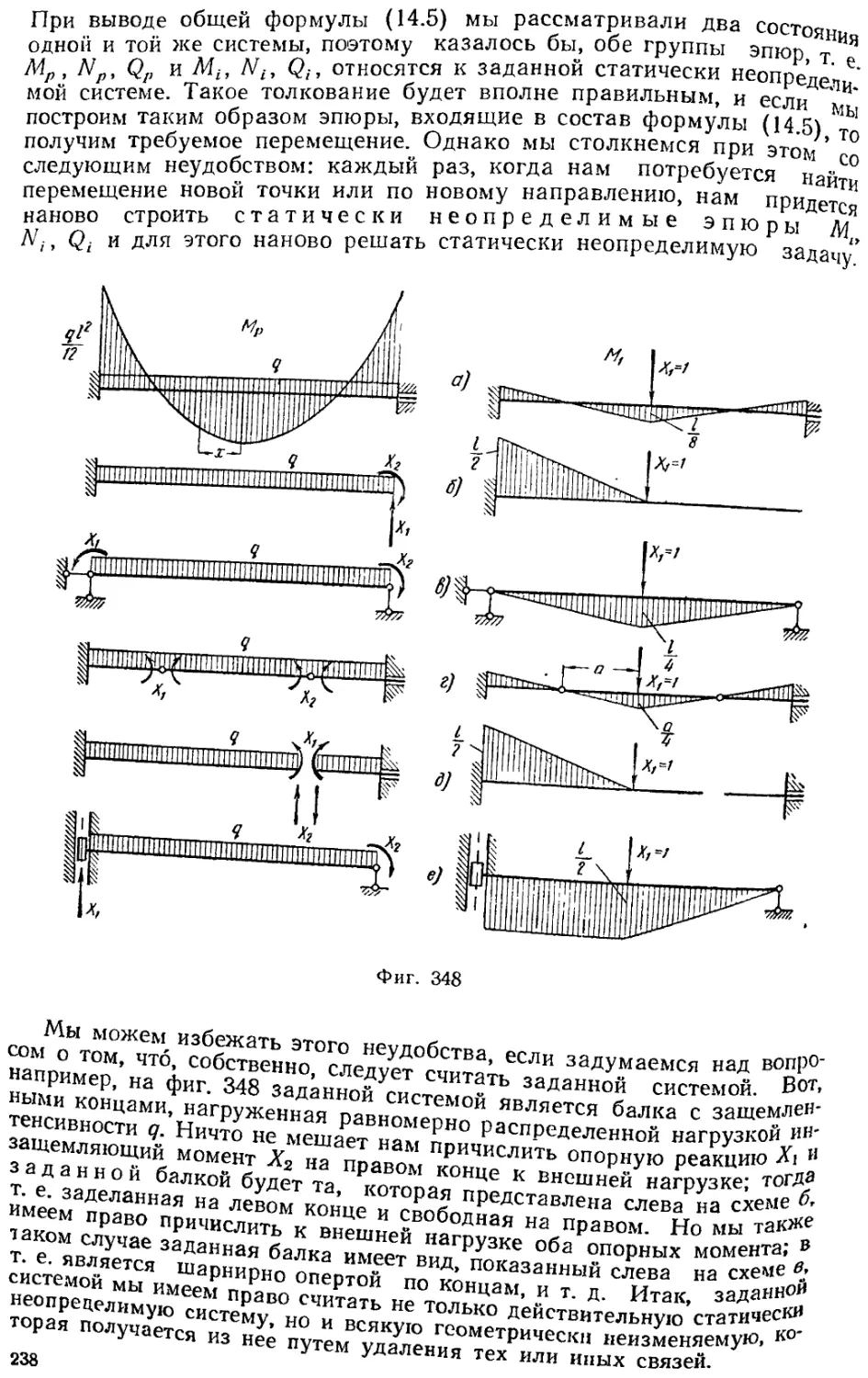
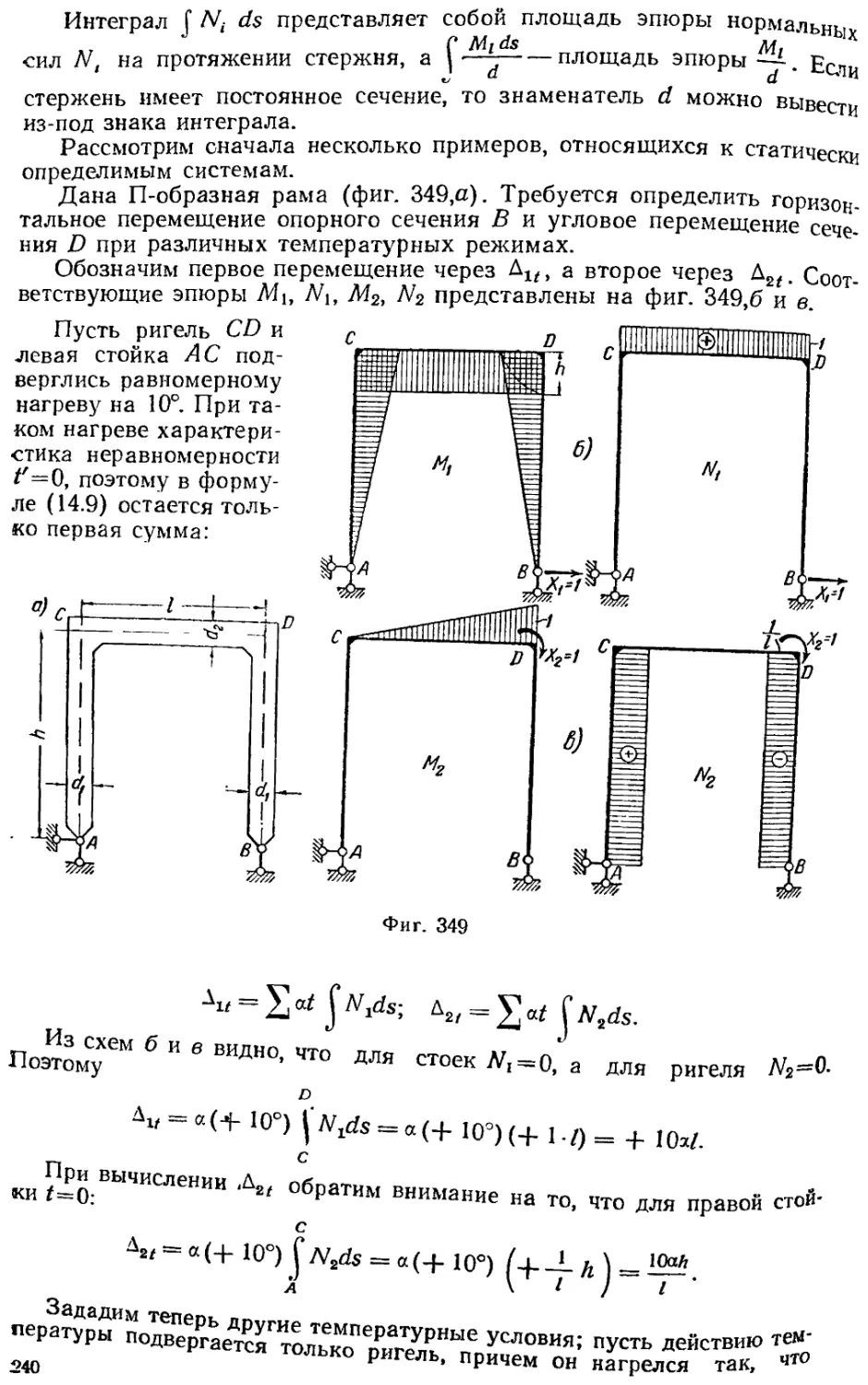
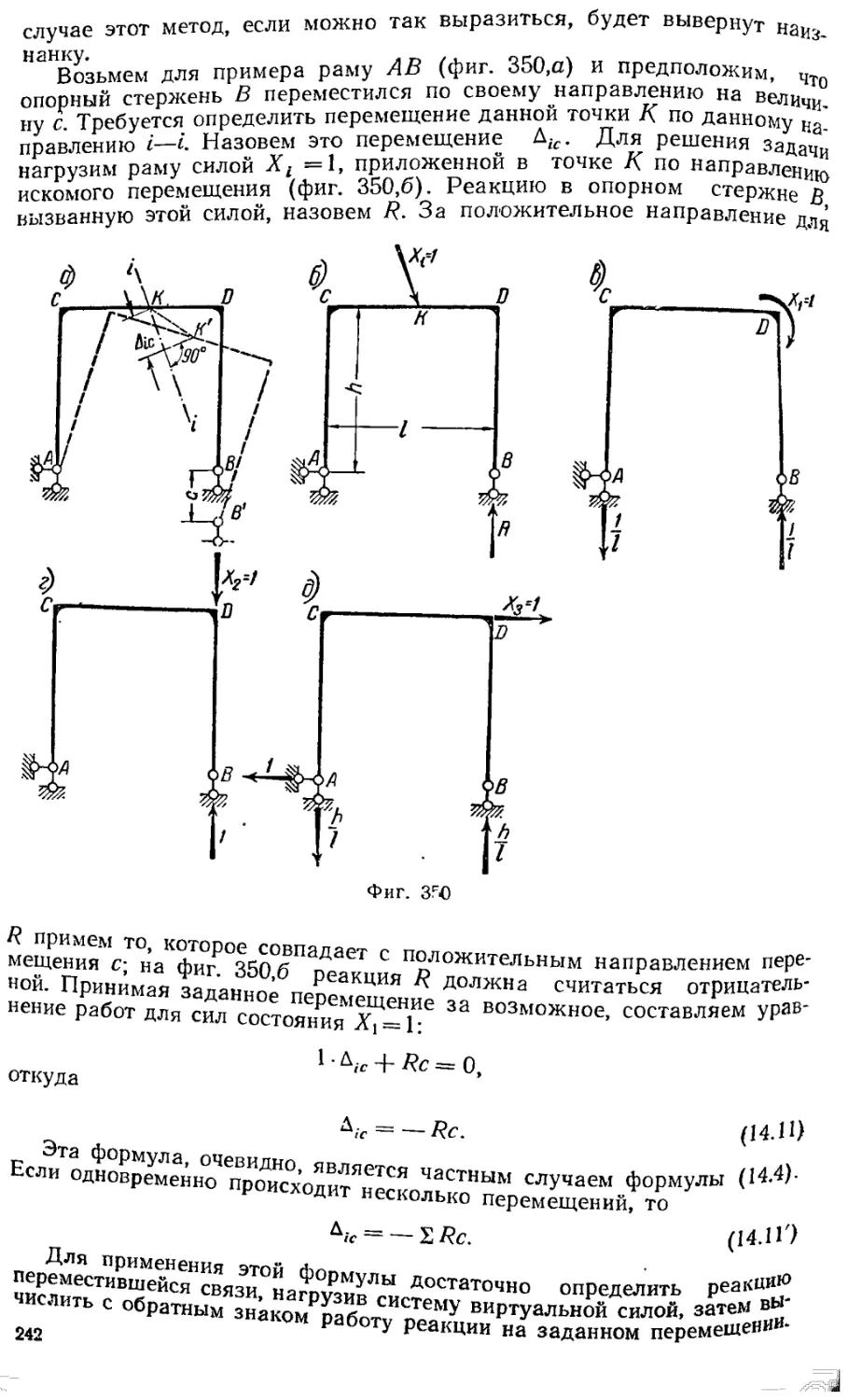
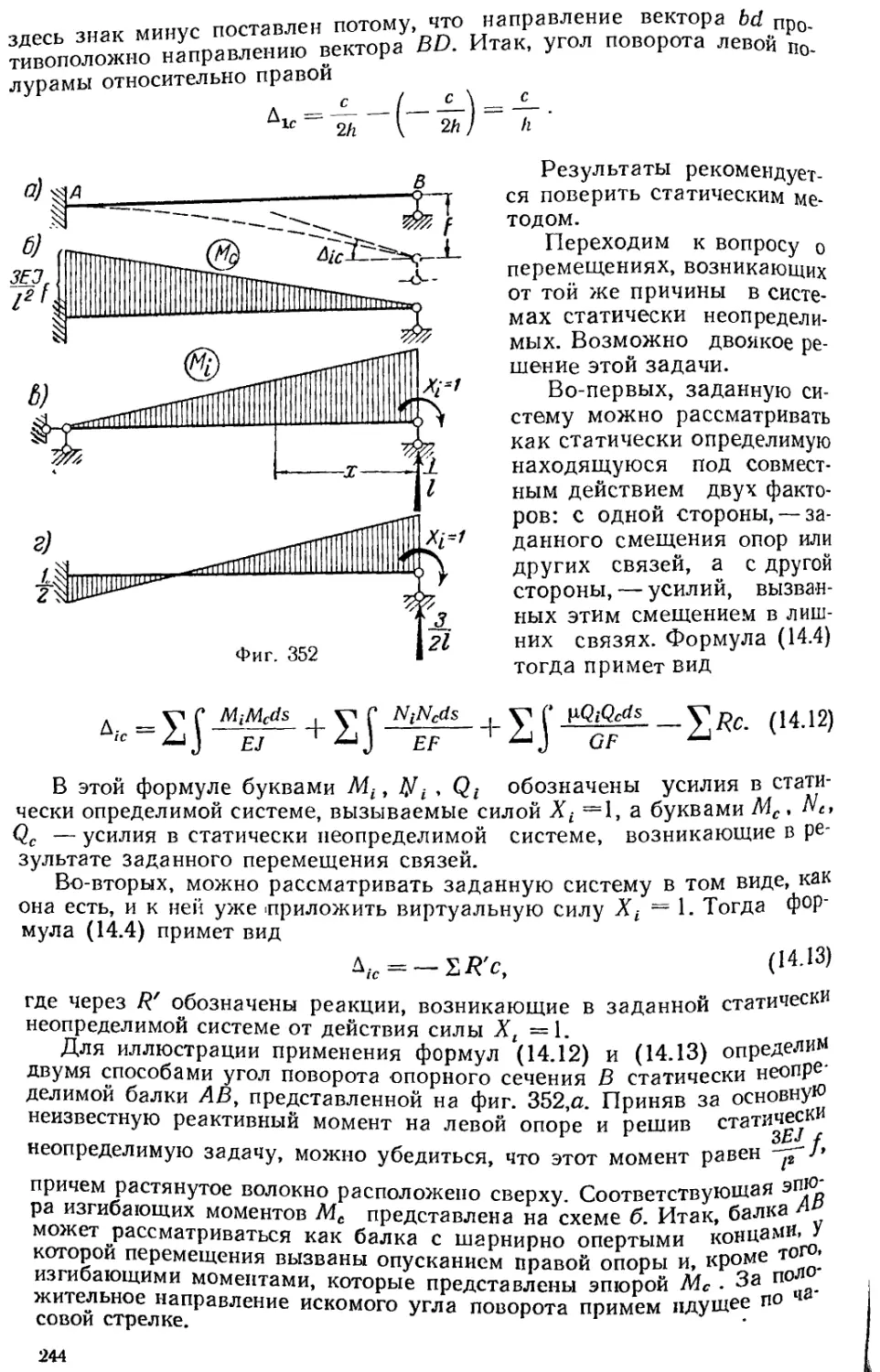
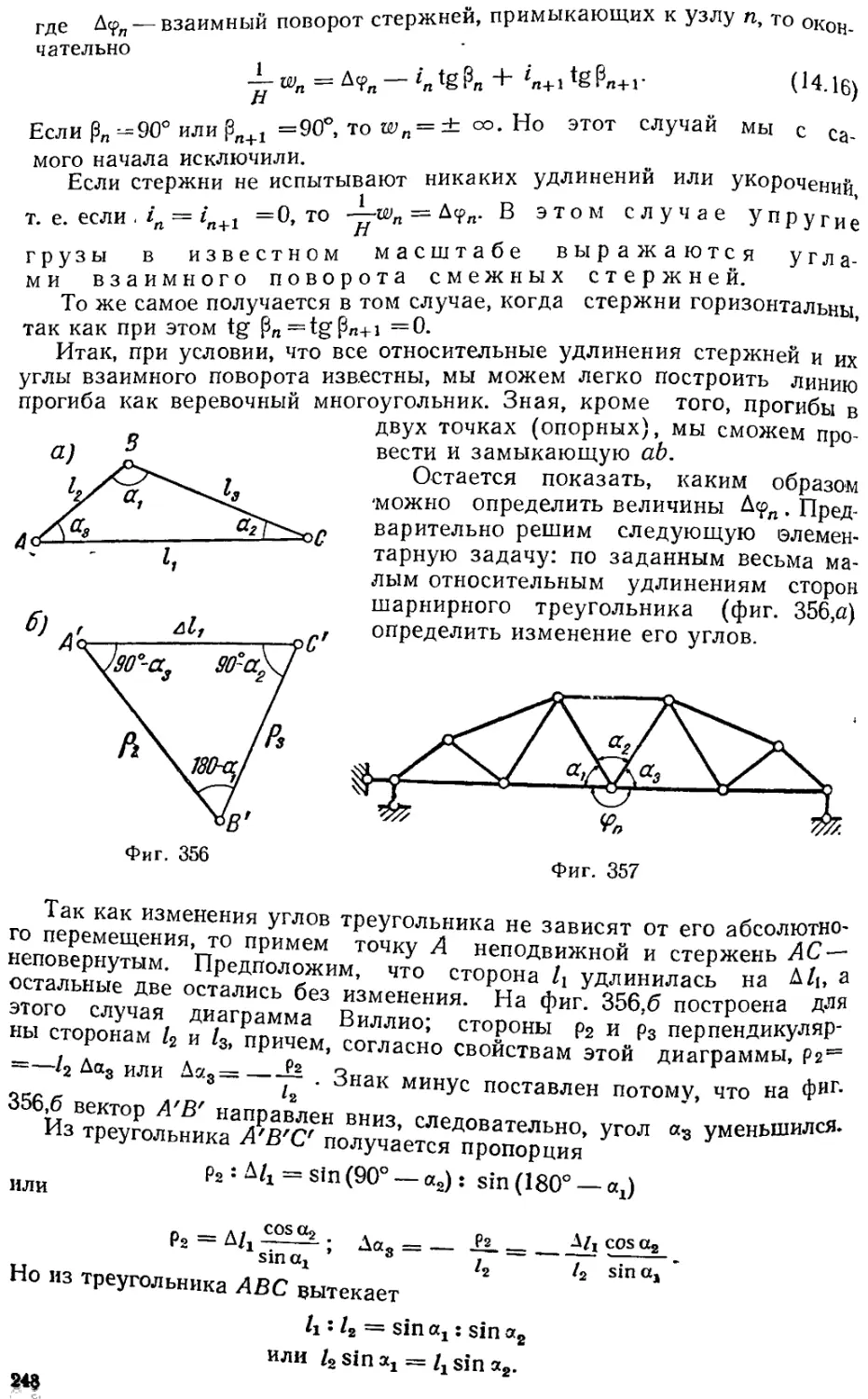
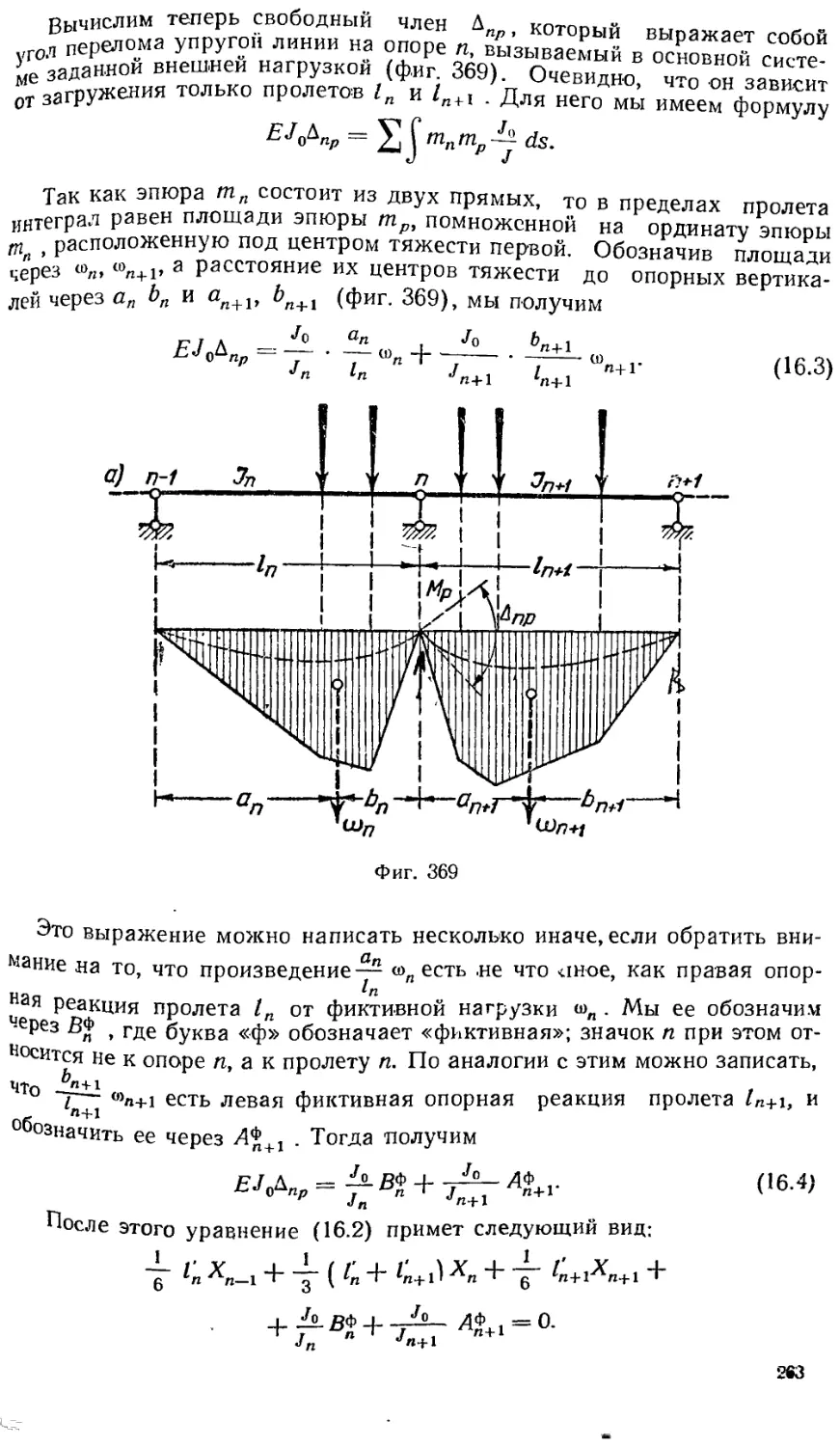
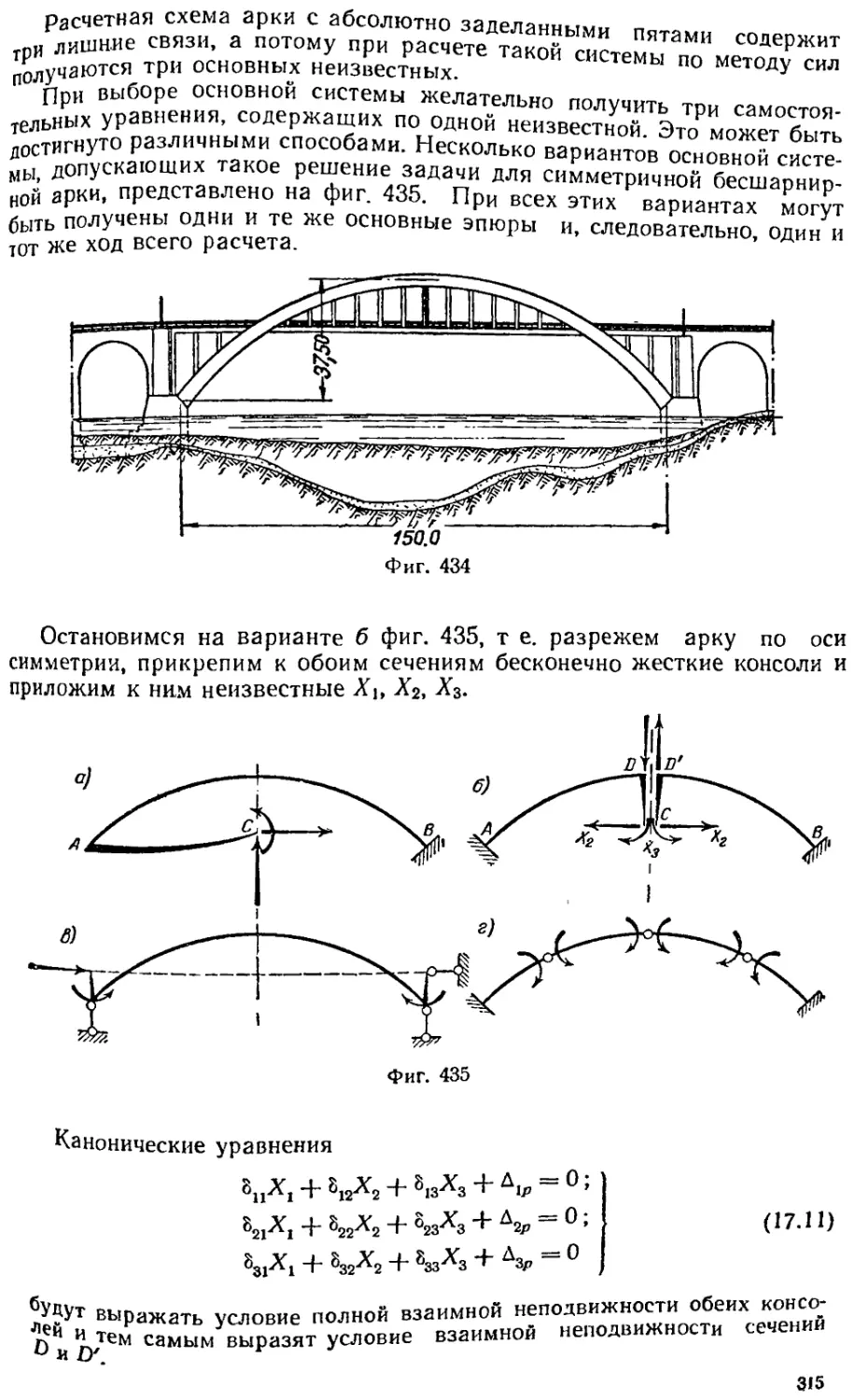
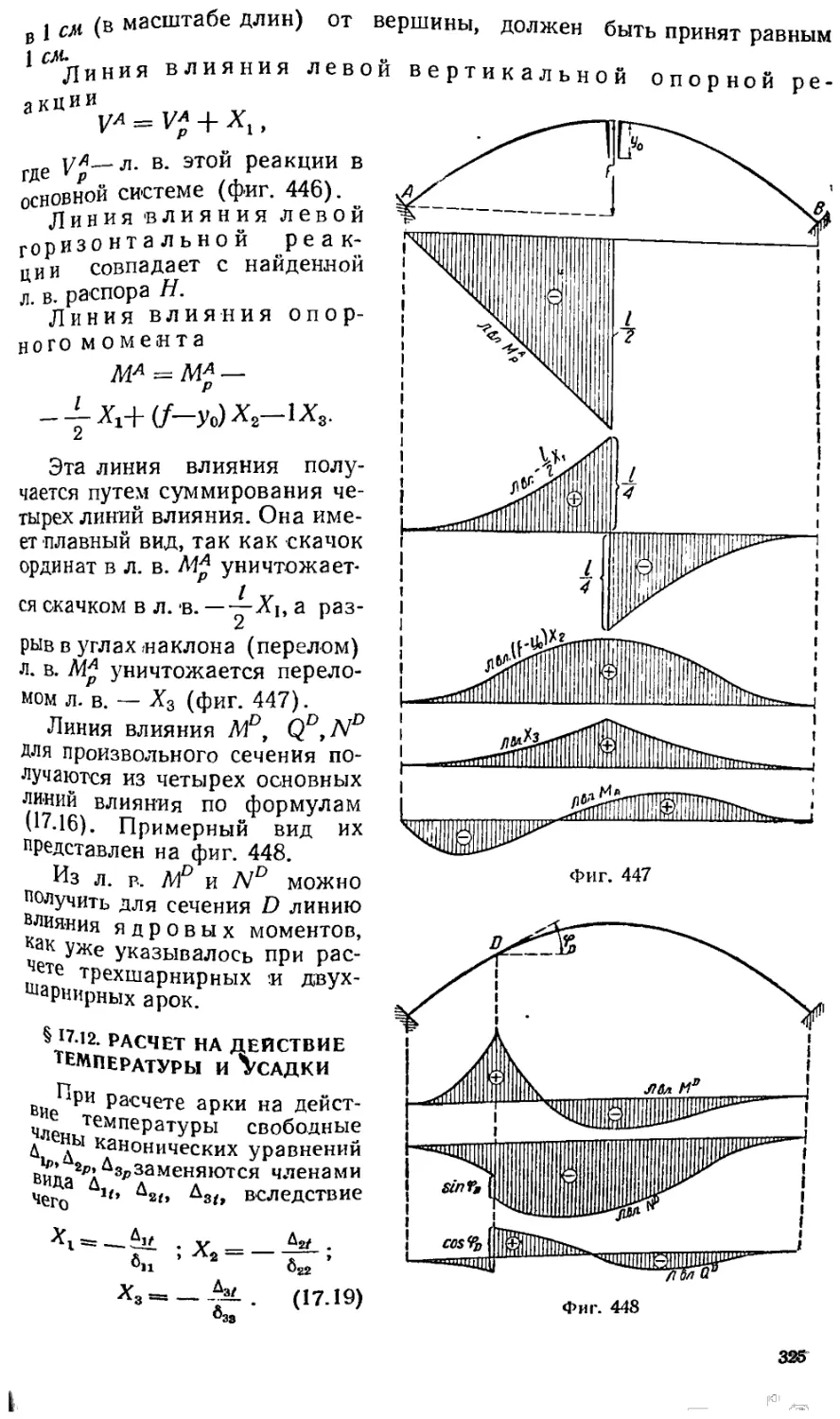
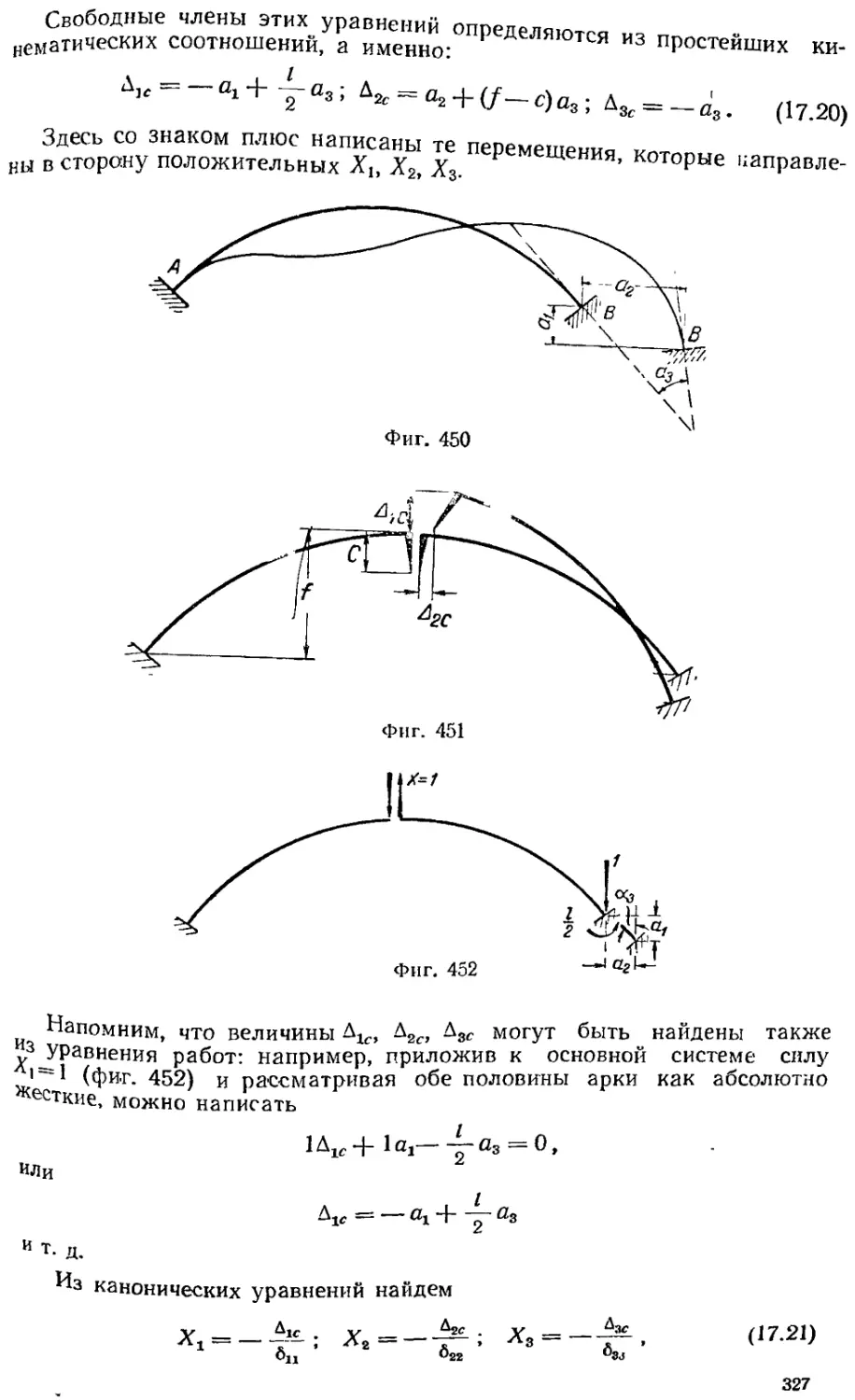
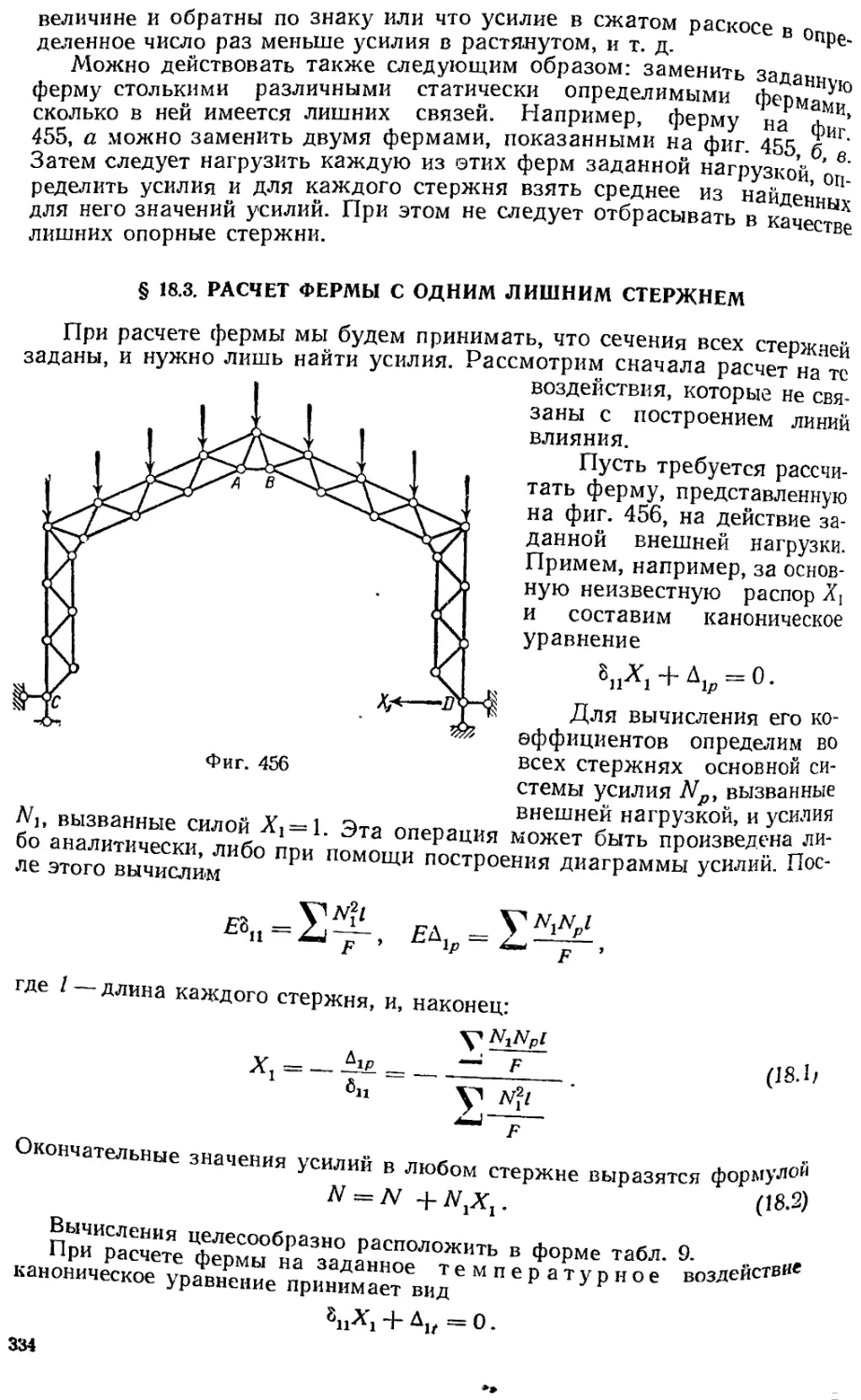
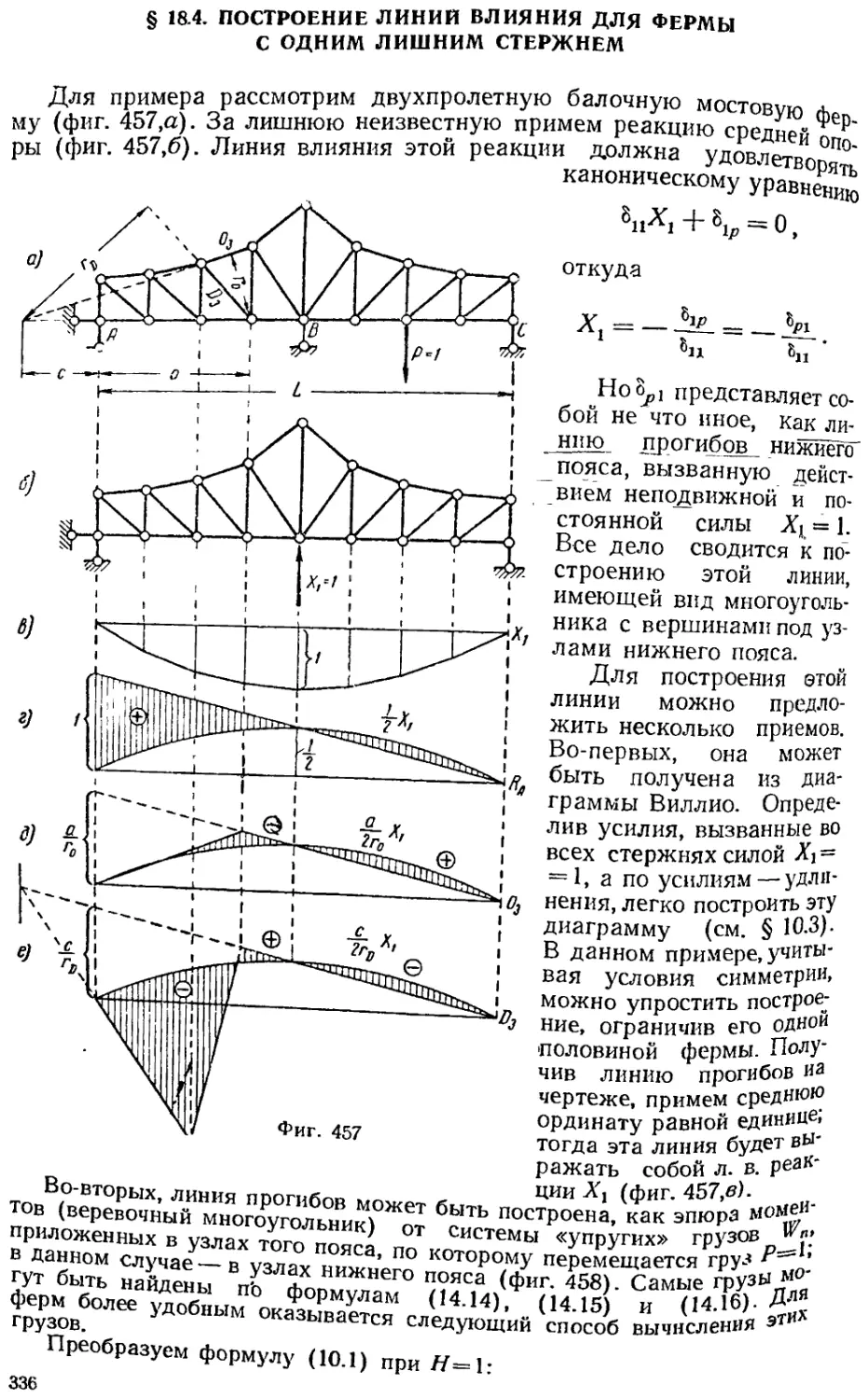
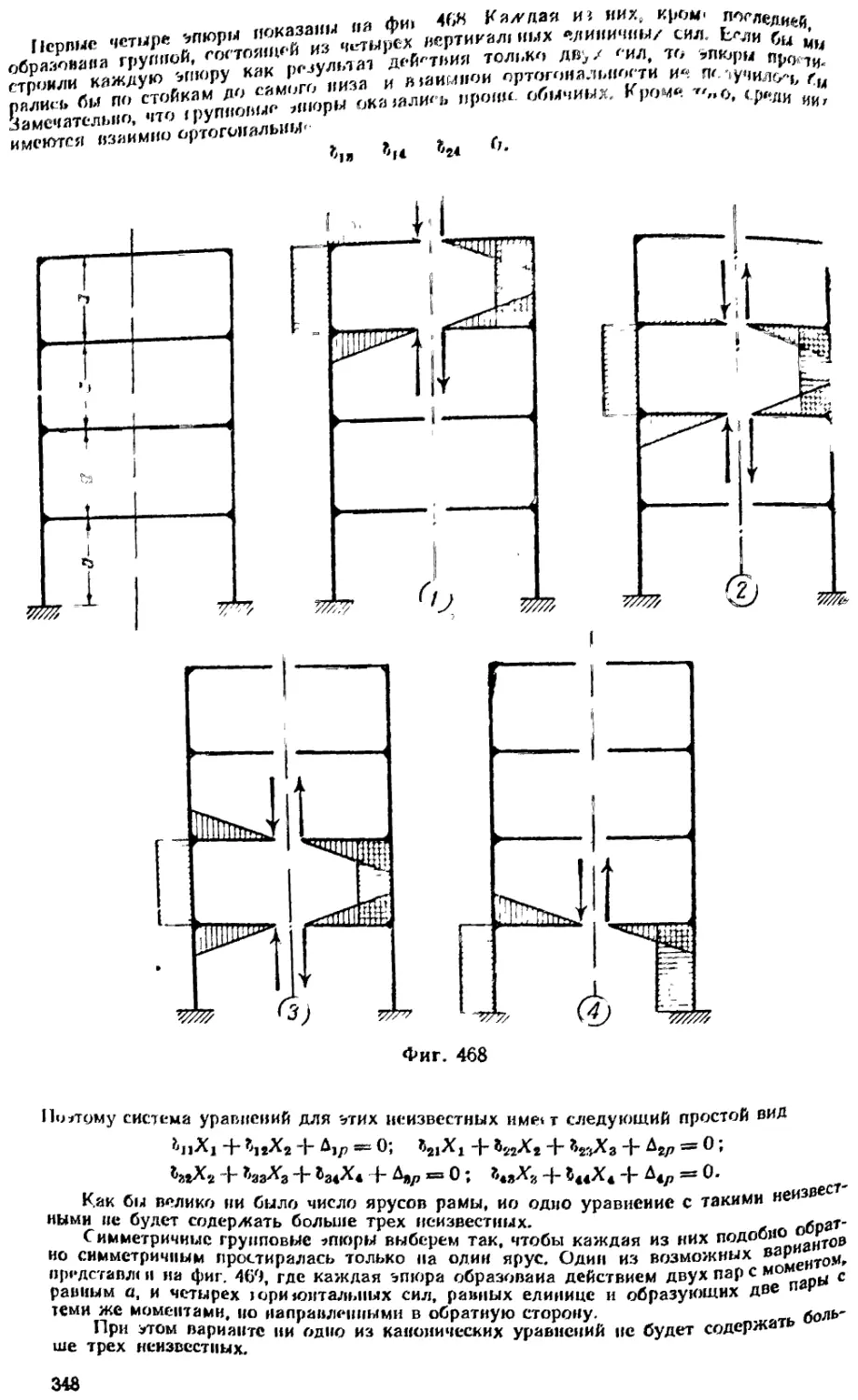
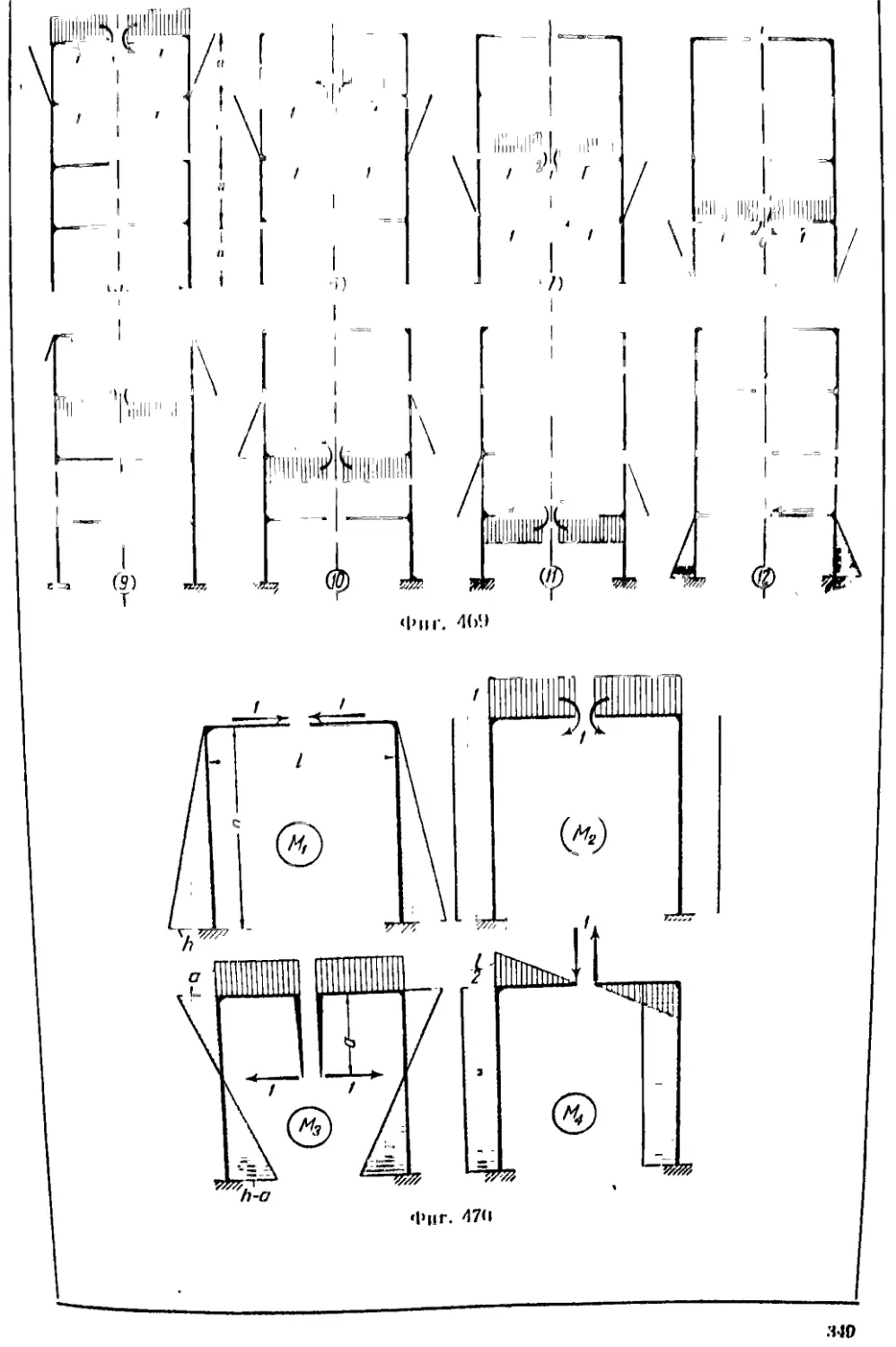
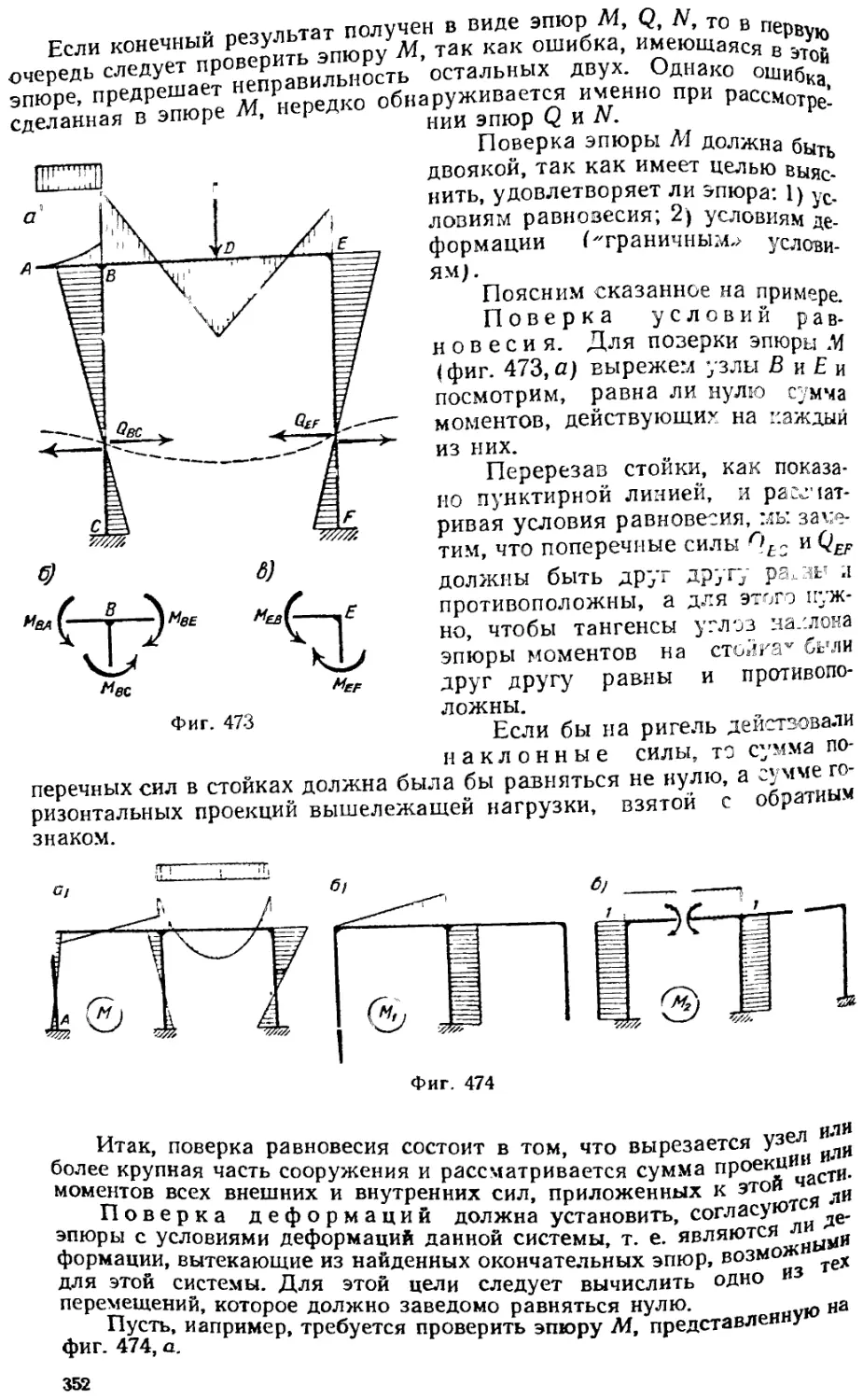
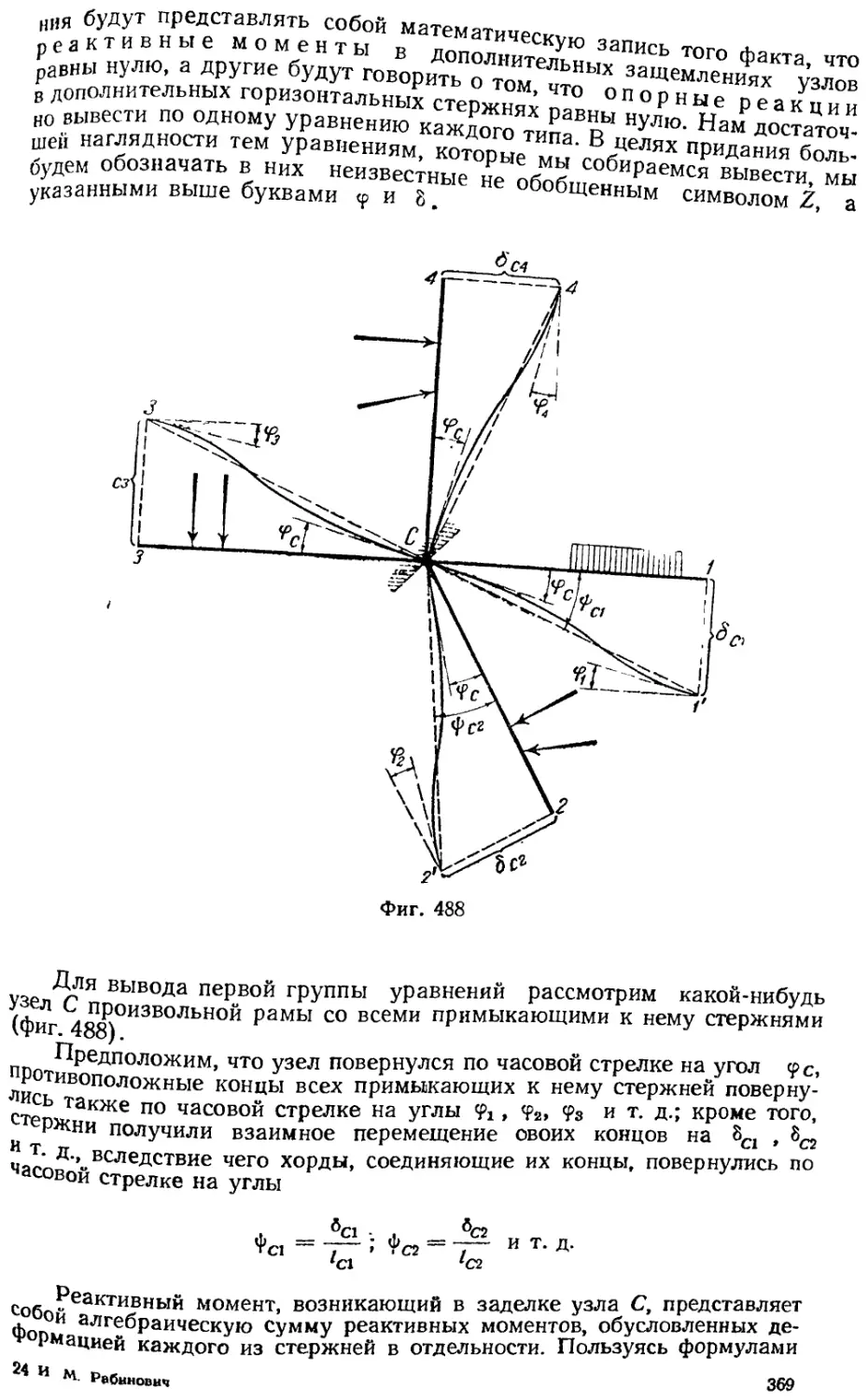
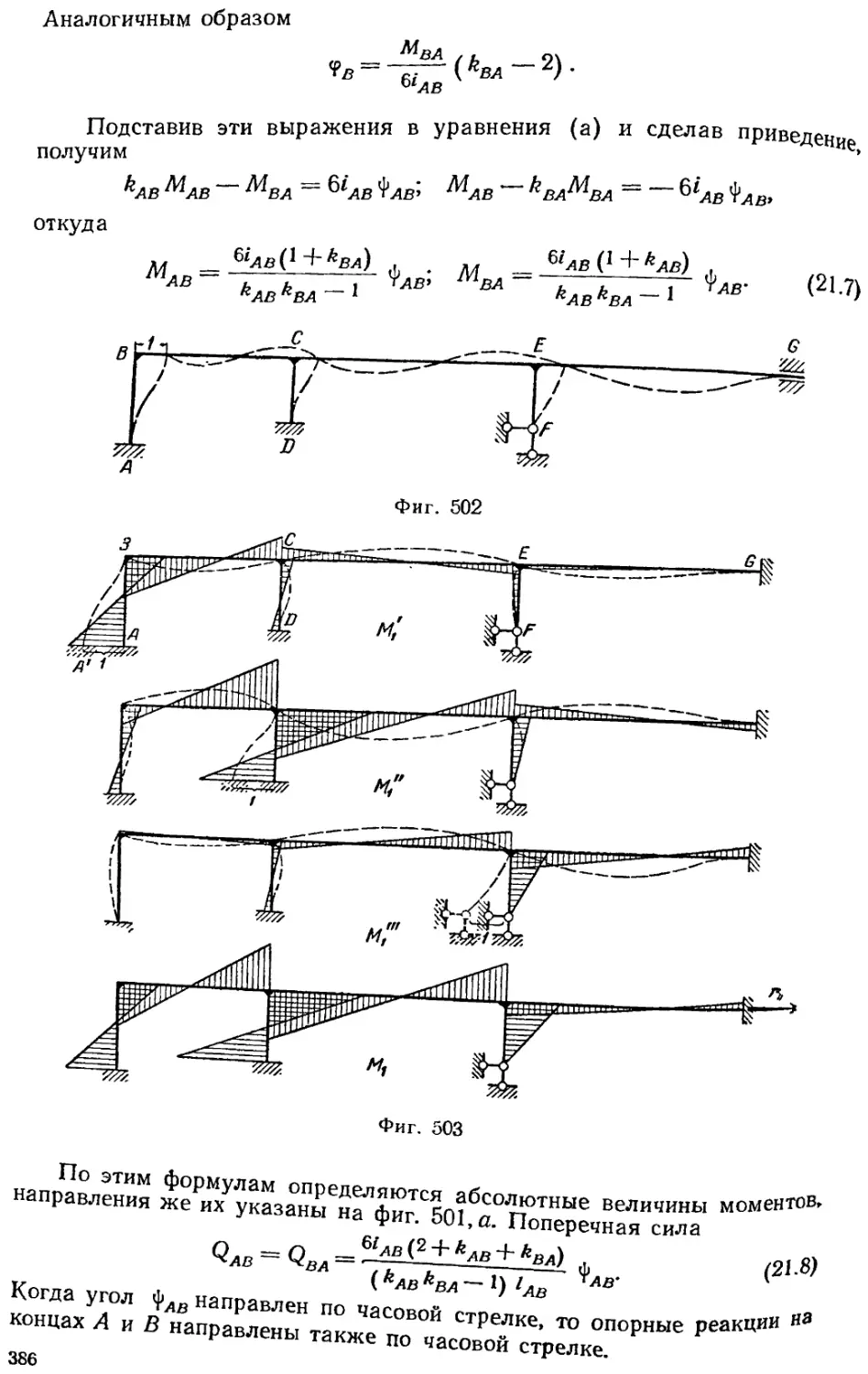
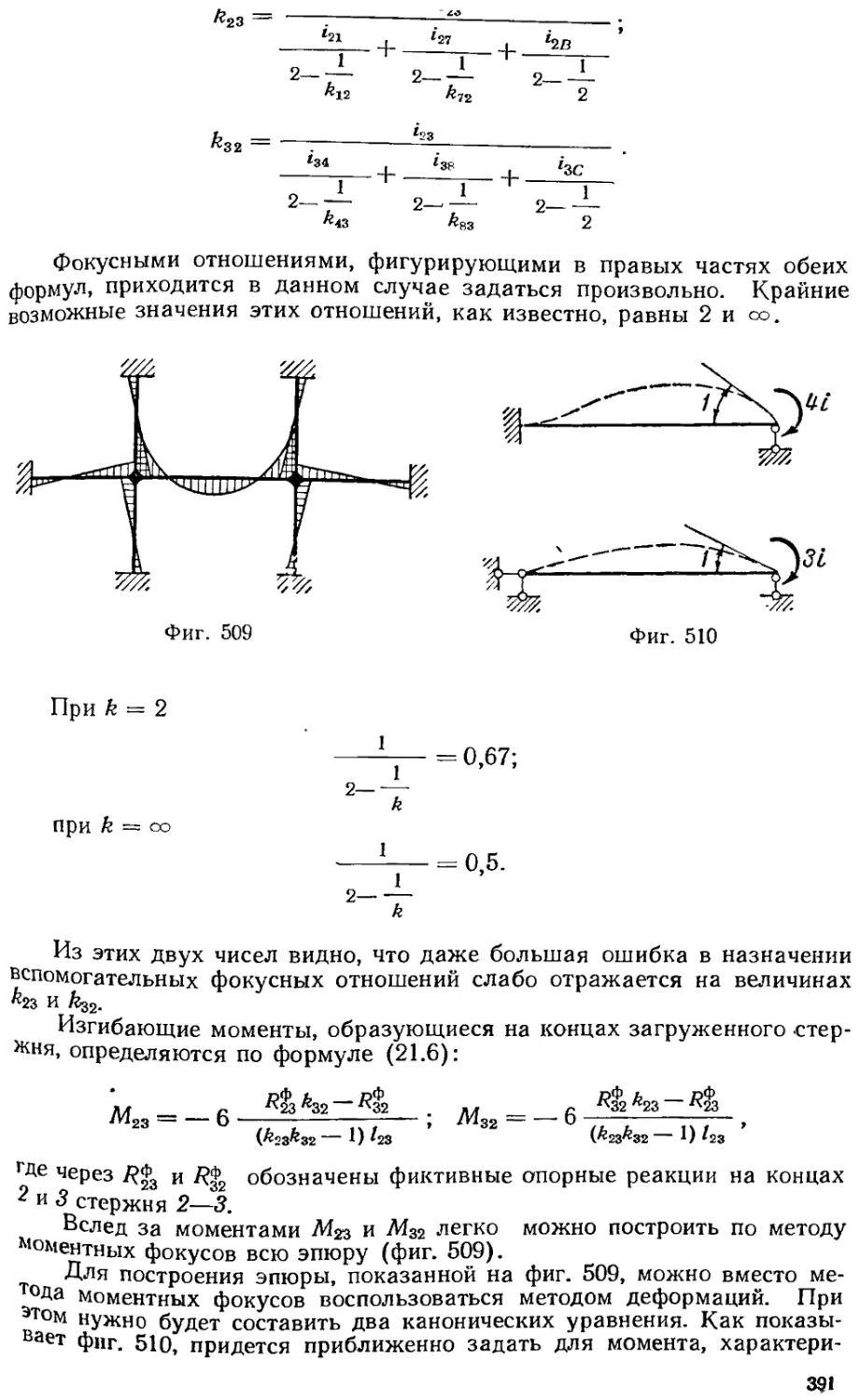
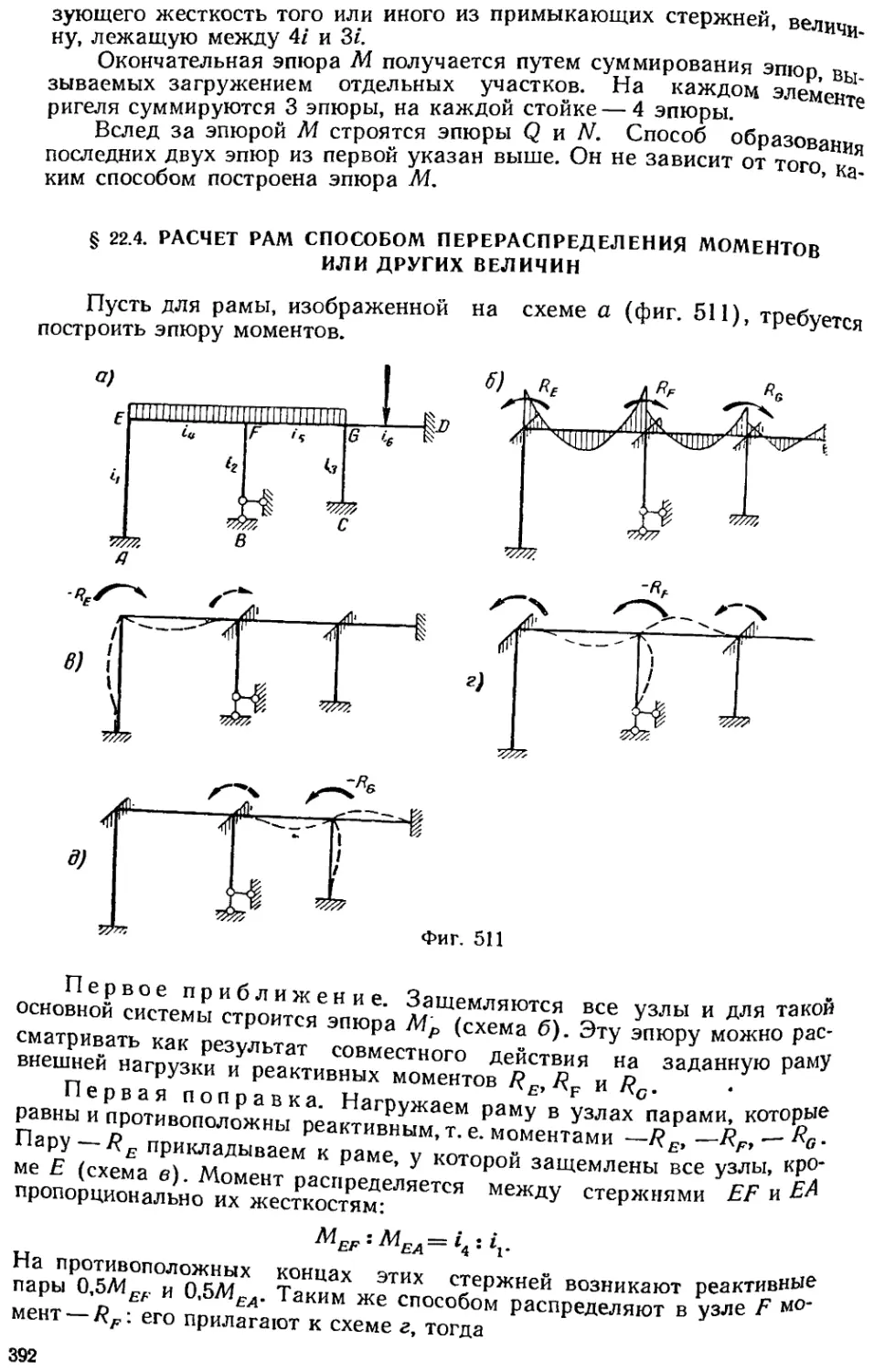
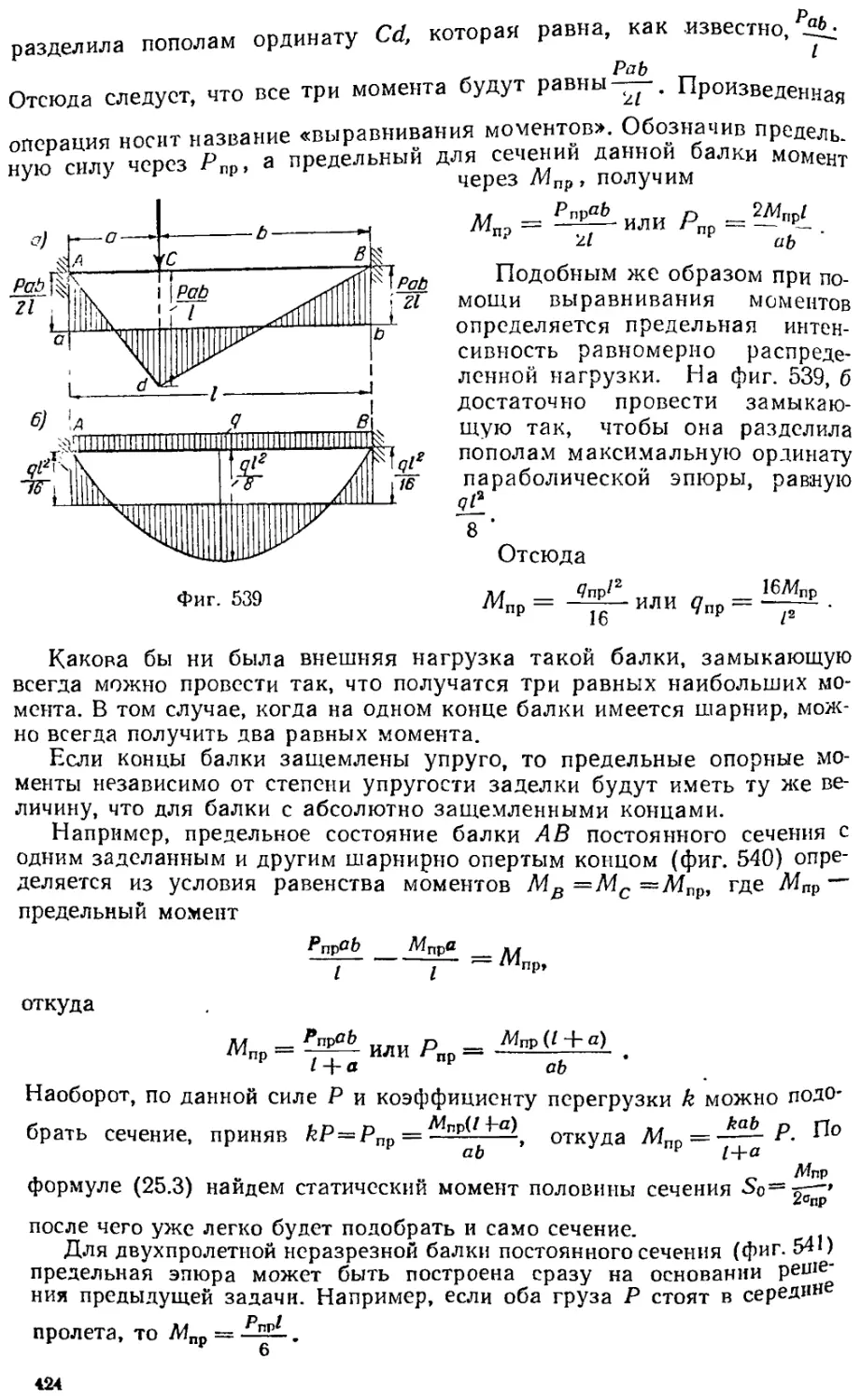
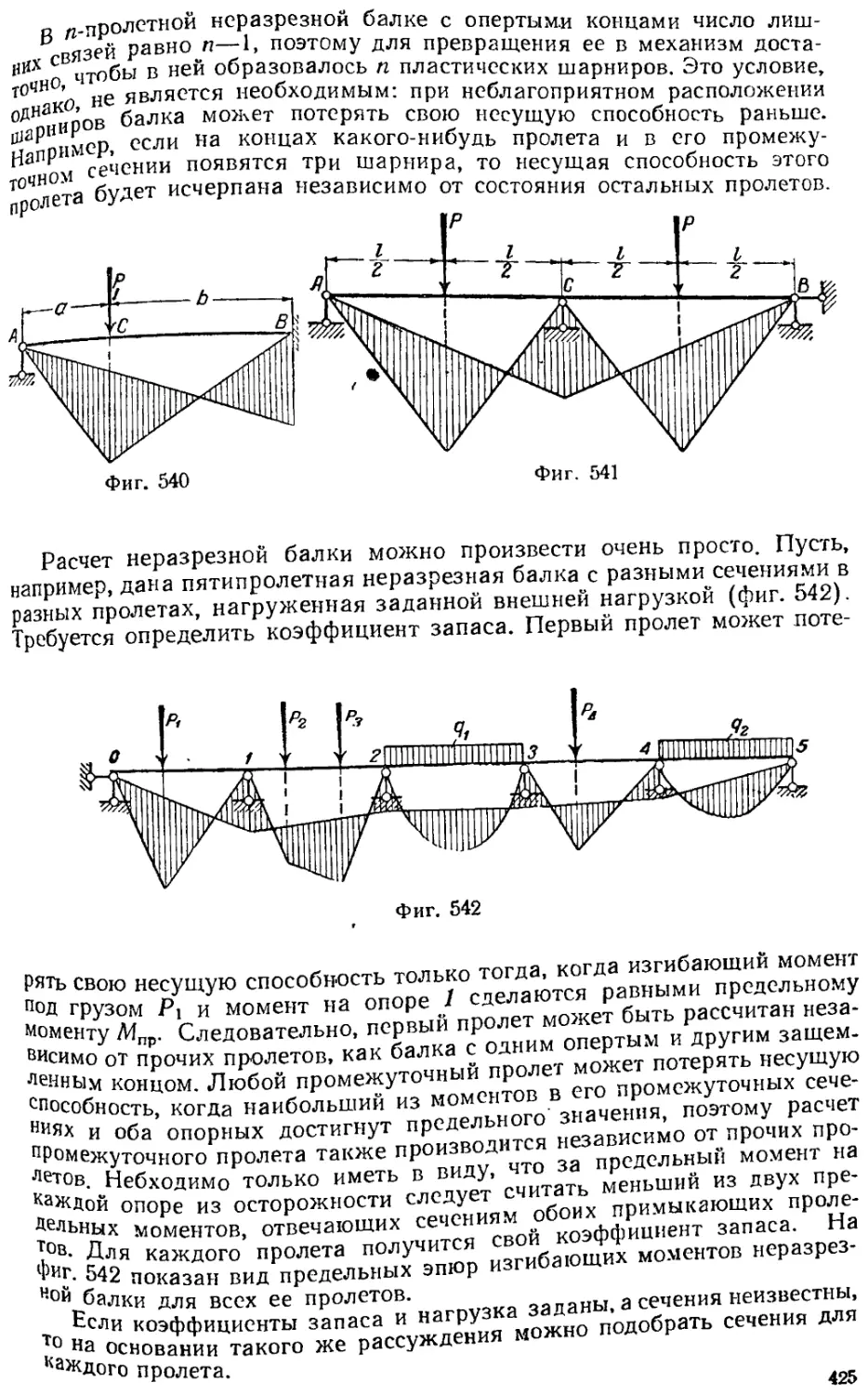
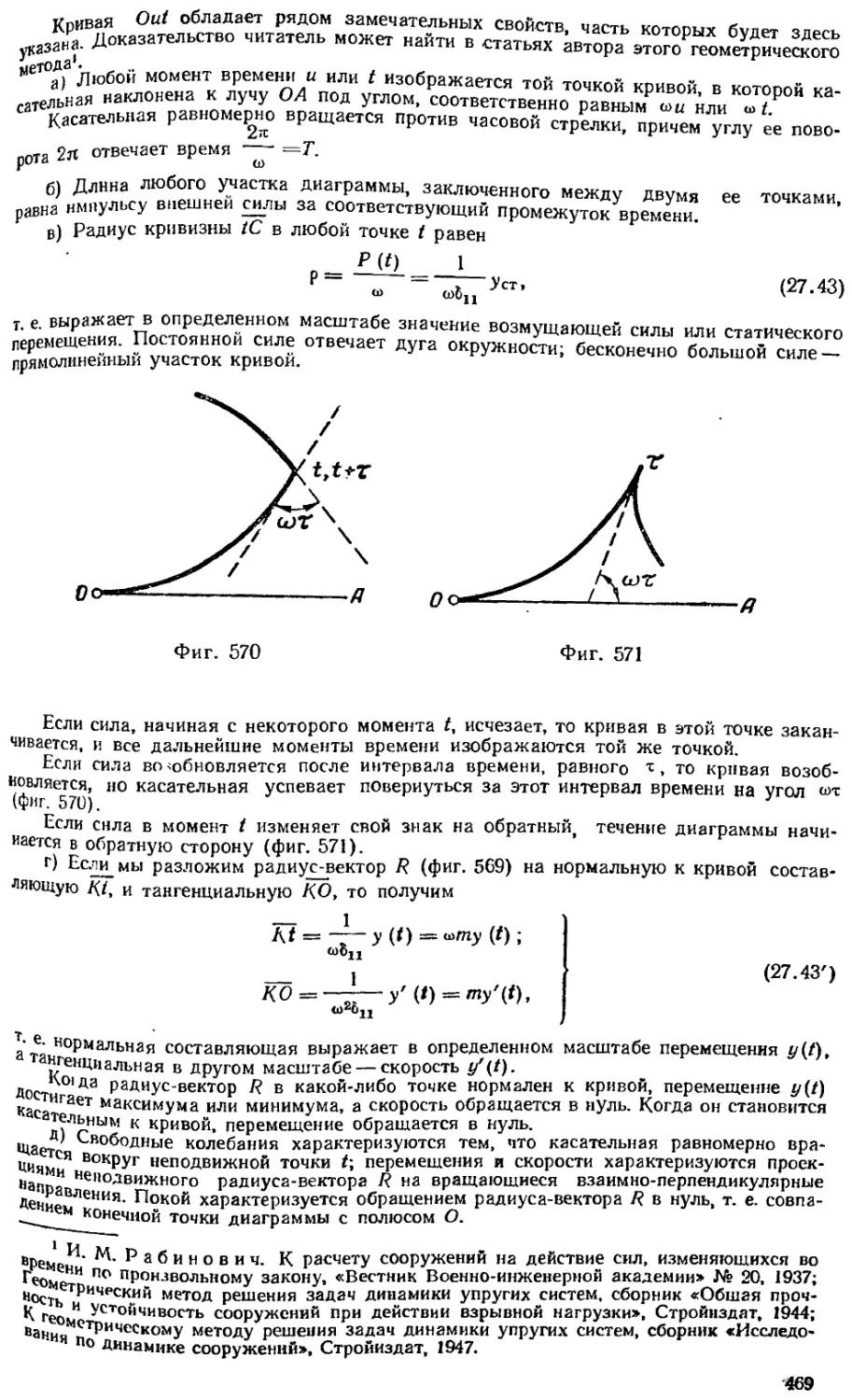
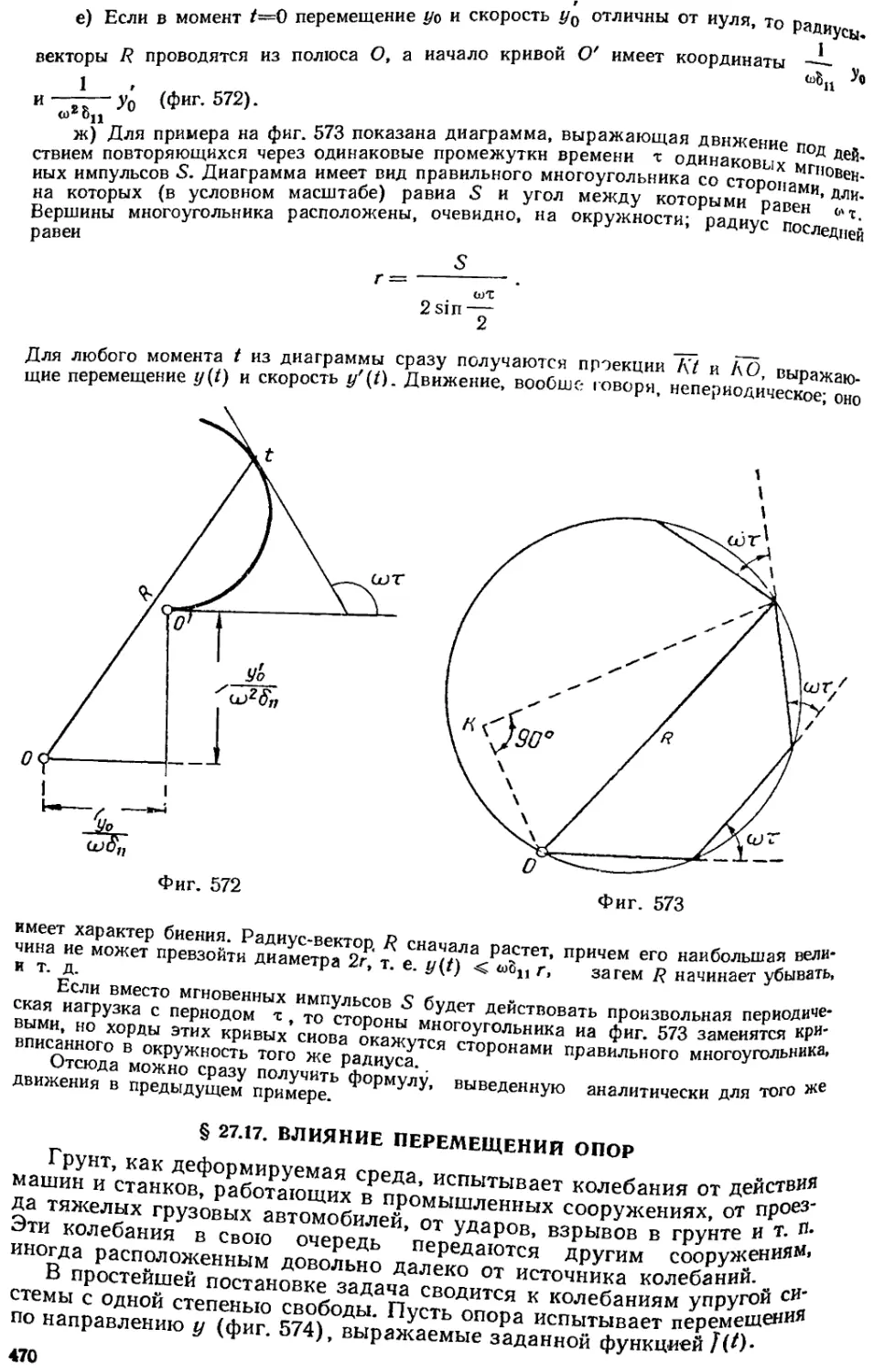
Текст
и. М. РАБИНОВИЧ,
чл-корр. Академии наук СССР, действ, член
Академии строительства и архитектуры СССР
ОСНОВЫ
СТРОИТЕЛЬНОЙ
МЕХАНИКИ
СТЕРЖНЕВЫХ
СИСТЕМ
Допущено
Министерством высшего и среднего специального
образования СССР в качестве учебника для студентов
инженерно-строительных вузов и факультетов
www.zodchii.ws
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ, АРХИТЕКТУРЕ
И СТРОИТЕЛЬНЫМ МАТЕРИАЛАМ
Москва—1960
Рецензент —кафедра строительной механики
Киевского инженерно-строительного института
Книга допущена Министерством высшего и
среднего специального образования СССР в каче-
стве учебника для студентов инженерно-строитель-
ных вузов и факультетов.
В книге излагаются 1) методы, расчета стати-
чески определимых систем, включая пространствен-
ные фермы; 2) методы расчета статически неопре-
делимых систем (неразрезных балок, рам, арок и
ферм); 3) основы расчета на устойчивость и на
динамическое действие нагрузки; 4) основы расче-
та подпорных стенок. Изложение сопровождается
примерами и задачами.
ОГЛАВЛЕНИЕ
Стр.
От автора 13
Гл а в а 1
Введение
§ 1.1. Предмет и задачи строительной механики 15
§ 1.2. Понятие о расчетной схеме сооружений 16
§ 1.3. Классификация расчетных схем сооружений . 18
§ 1.4. Классификация опор плоских стержневых систем 19
Глава 2
Кинематический анализ сооружений
§2.1. Степень свободы плоской кинематической цепи, составлеииой из дисков . 22
§ 2.2. Примеры и задачи 24
§ 2.3 Степень свободы шариирно-стержневой плоской системы . о 26
§ 2.4. Примеры и задачи —
§ 2.5. Принципы образования геометрически неизменяемых плоских систем . . 27
§ 2.6. Примеры анализа геометрической структуры 28
§ 2.7. Мгновенно-изменяемые системы 30
§ 2.8. Порядок кинематического анализа систем 32
Глава 3
Графические методы строительной механики и веревочный многоугольник
§ 3. 1. Роль графического метода в строительной механике 33
§ 3.2. Обозначения на силовом и веревочном многоугольниках 34
§ 3.3. Применение веревочного многоугольника для определения статических
моментов плоской системы сил 36
§ 3.4. Построение эпюр М ц Q при узловой передаче нагрузки 37
§ 3.5. Построение эпюр М w Q для многопролетных статически определи-
мых балок : 38
§ 3.6. Краткие исторические данные 41
Гл ав а 4
Общая теория линий влияния и примеры их применения
§ 4,1. Понятие о линии влияния 42
» 4.2. Статический способ построения линий влияния; линии влияния д^ш
простой балки , • 43
5
Стр.
п^ияния усилий многоопорных балок 48
§ 4.3. Линии «;^«^";^;^зт линий влияния 50
§ 4.4. Размерность «Р^ системы сосредоточенных сил 51
§ 4.5. Влияние "^"^^^ . сплошной нагрузки, распределенной по любому
§ 4.6. Влияние неподвижной , . , . 53
.47 о7о?номсвой;^'е прямолинейного участка линии влияния 54
§4.8; Влияние ^^^f^^^^^^^^ \ 55
§ 4. 9. KHHeMaTHjec ^^^^ ^^ построение линий влияния кинематическим методом 57
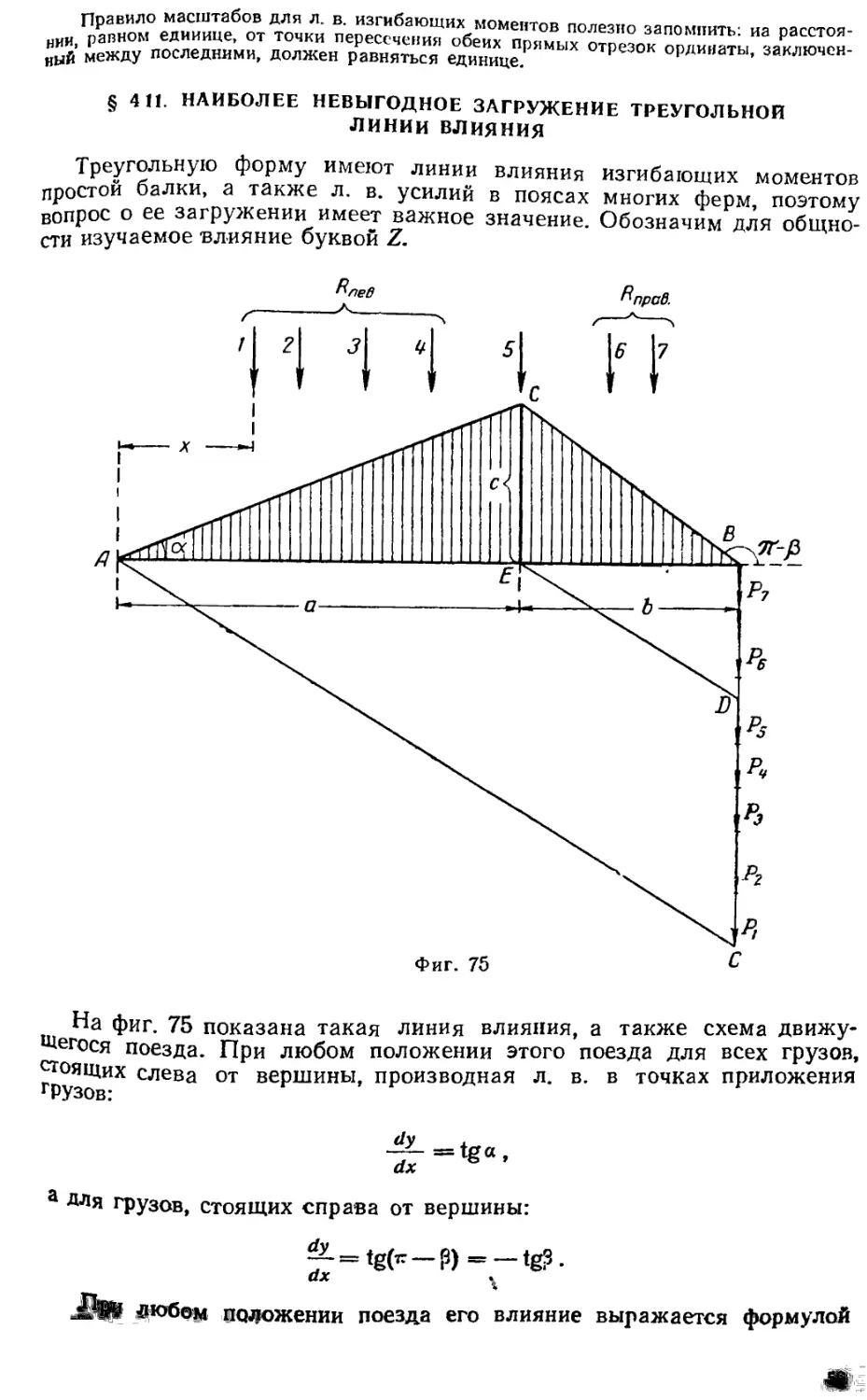
!!'п'Еоле1 выгодное загружениетреуго^^^^^ 59
HI' Наиболее невыгодное загружение поездом полигональной линии влияния 61
I 41з' Наиболее невыгодное загружение любой линии влияния равномерно
паспределенной нагрузкой 62
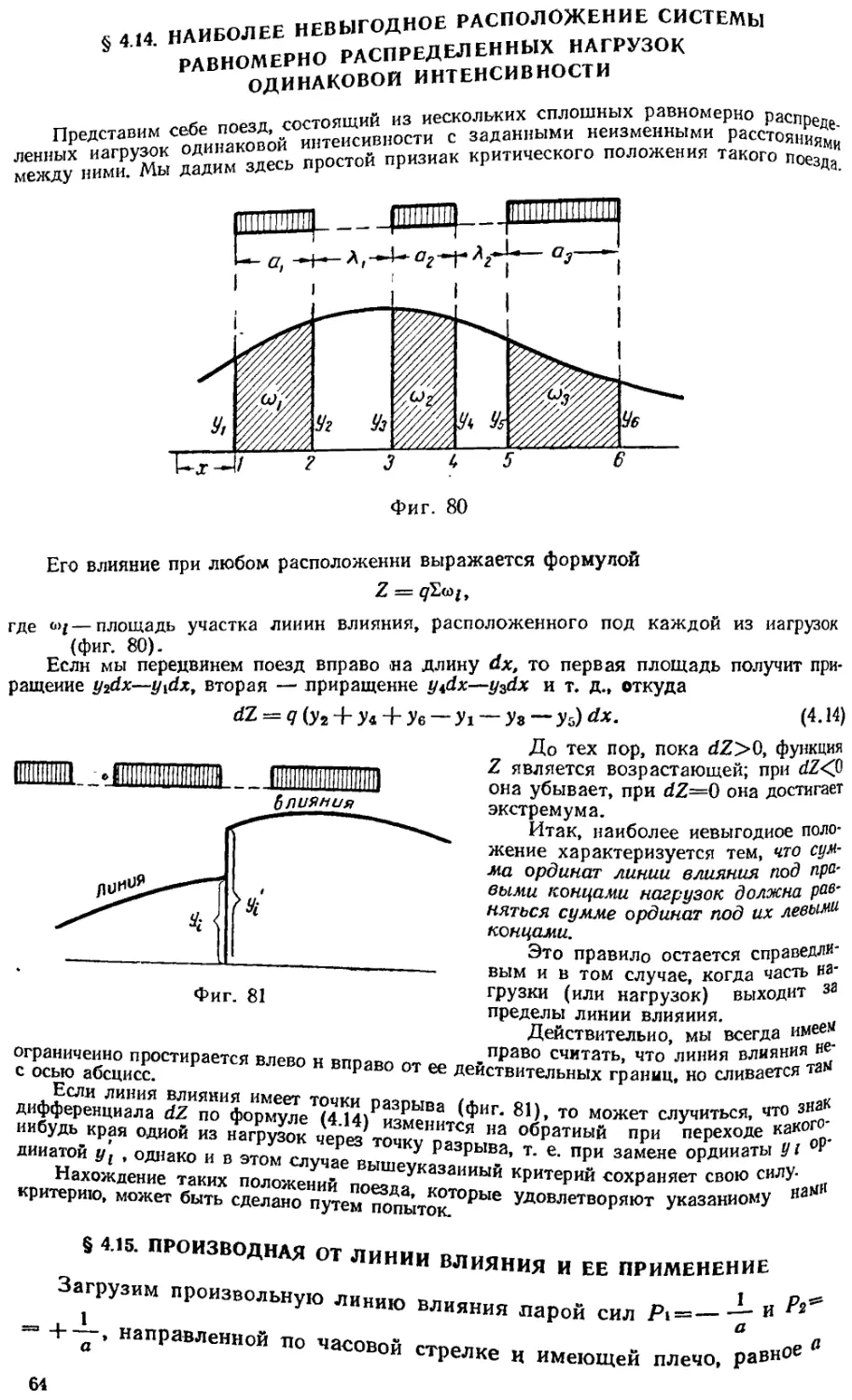
§414 Наиболее невыгодное расположение системы равномерно распределен-
ных нагрузок одинаковой интенсивности 64
§ 415 Производная от линии влияния и ее применение . .
§ 4Л6. Влияние сосредоточенной силы, вращающейся вокруг неподвижной точки
приложения (окружность влияния) 65
§ 4.17. Связь между линиями влияния для движущейся силы различных
иаправлений 67
§ 4.18. Краткие исторические данные •. . . —
Гл ав а 5
Общие свойства статически определимых систем
§ 5. 1. Что такое статически определимая стержневая система 69
§ 5. 2, Разделение неизвестных на две группы —
§ 5. 3. Связь между статической определимостью и геометрической неизменяе-
мостью системы . . 70
§ 5. 4. Статический критерий мгновенной изменяемости. Способ нулевой нагрузки —
§ 5. 5. Усилия в основной части сооружения и в элементах, прикрепленных к ней 72
§ 5. 6. Влияние уравновешенной нагрузки 73
§ 5. 7. Влияние эквивалентных преобразований нагрузки 74
§ 5. 8. Влияние изменения температуры, смещения опор и неточной разметки
длин стержней 75
Г л а в а 6
Трехшарнирные арки
§ 6. 1. Основные понятия 77
§ 6. 2. Аналитический способ определения опорных реакций .' .' 80
I 6 4 v^ ^з^ибающих моментов М . . - • • 83
' ' на?р7зкГ"'' "'''"'""' "'" трехшарнирной 'арки' для вертикаль;ой
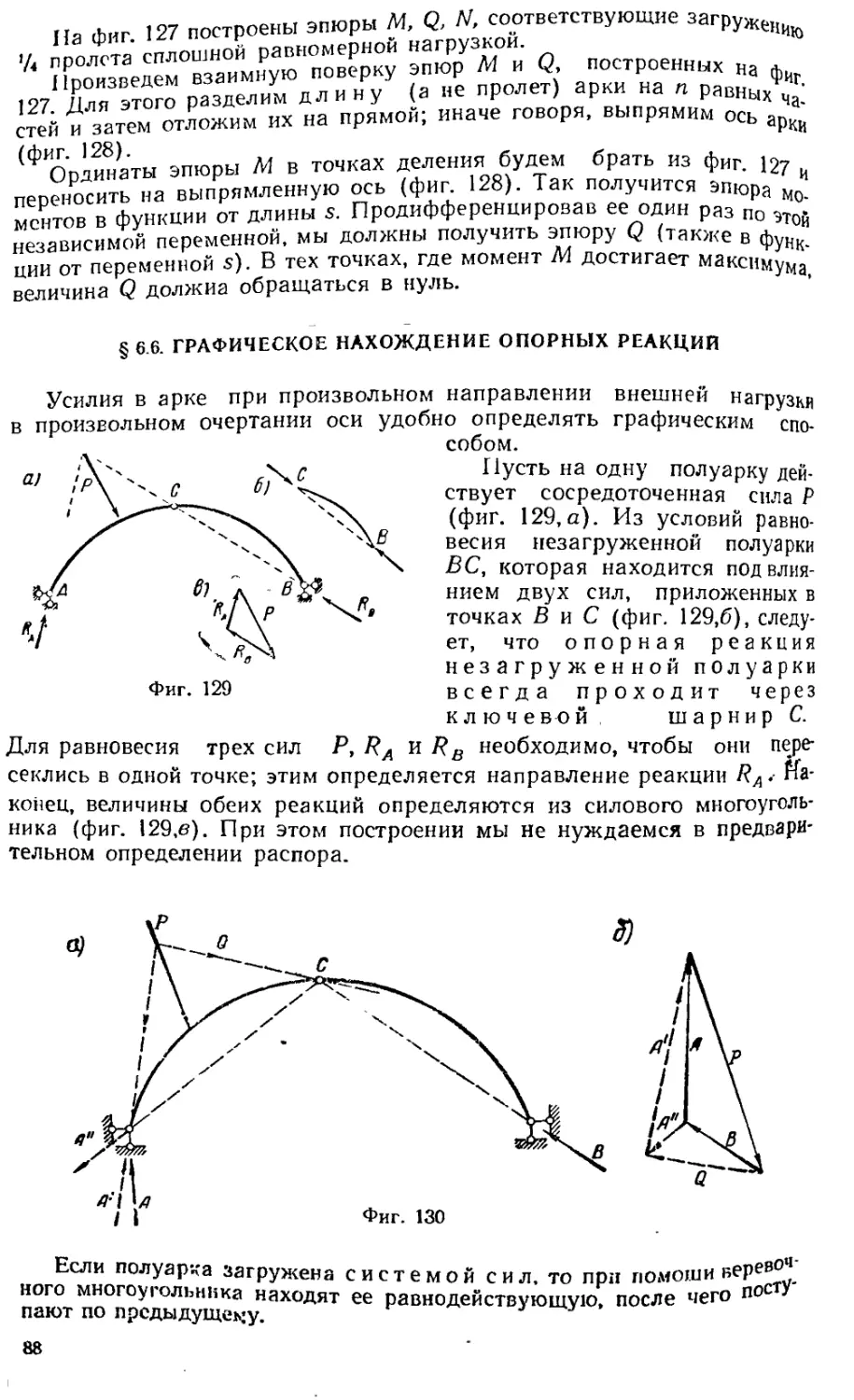
§ 6^ 6.' ГрХ^нГпжГ "Р°^°^''""х сил. вызванных вертикальной нагрузкой 86
§ 6. 7 Исполк^Г нахождение опорных реакций ... "' . 88
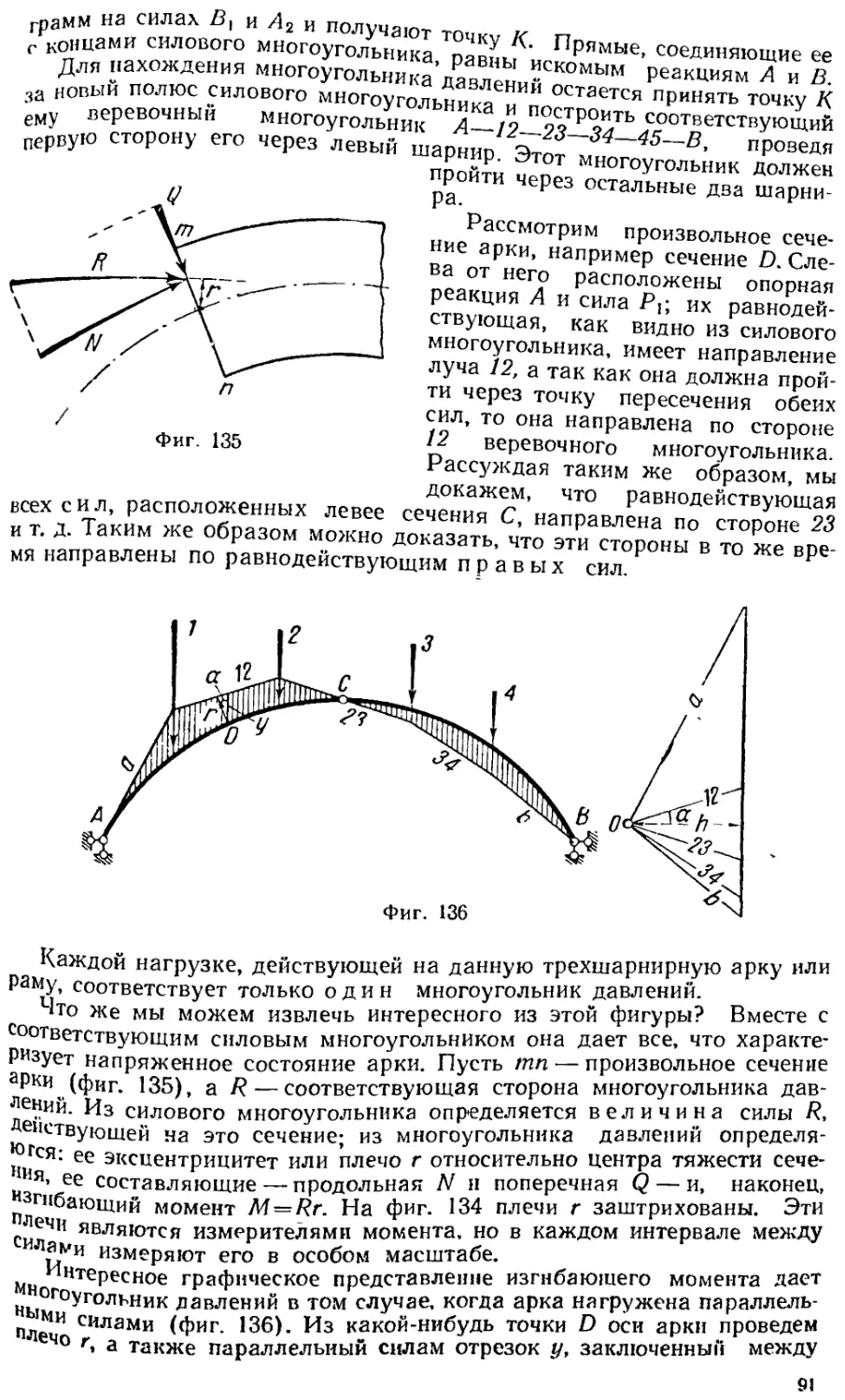
iii^?^^=^^^-.:r^.s-^.; •• •:;: 90
ЩШЗ^^ачи и прим;;^""''"^''"'»"'прапомопш нулевых точек . . — '4"
Глава 7
Расчет статически определимых плоских ферм.
Балочные и консольно-балочные фермы
§ 7. 1. Понятие о фермах 97
§ 7. 2. Классификация ферм 98
§ 7. 3. Мгновенно изменяемые шарнирно-стержневые системы 103
§ 7. 4. Статические признаки мгновенной изменяемости 105
§ 7. 5. Построение планов скоростей 107
§ 7. 6. Кинематический метод поверки мгновенной изменяемости 110
§ 7. 7. Нагрузка ферм 111
§ 7. 8. Способ вырезания узлов —
§ 7. 9. Частные случаи равновесия узлов 114
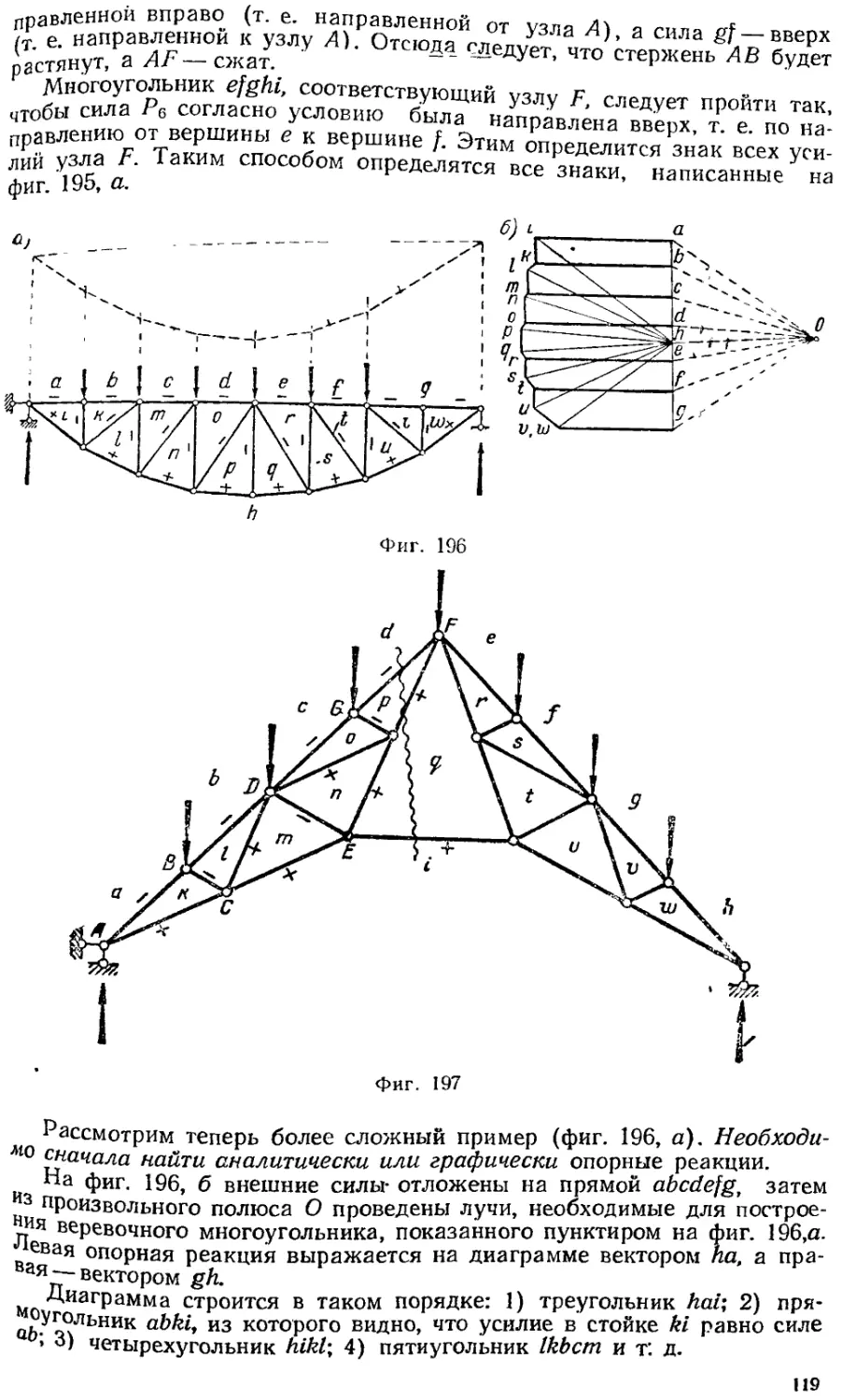
§ 7.10. Диаграммы усилий (Максвелла — Кремоны) 116
§ 7.11. Построение диаграммы при загружении узлов, лежащих внутри контура 120
§ 7.12. Построение диаграммы для ферм, содержащих пересекающиеся стержни 121
§ 7.13. Построение диаграммы при помощи разложения нагрузки —
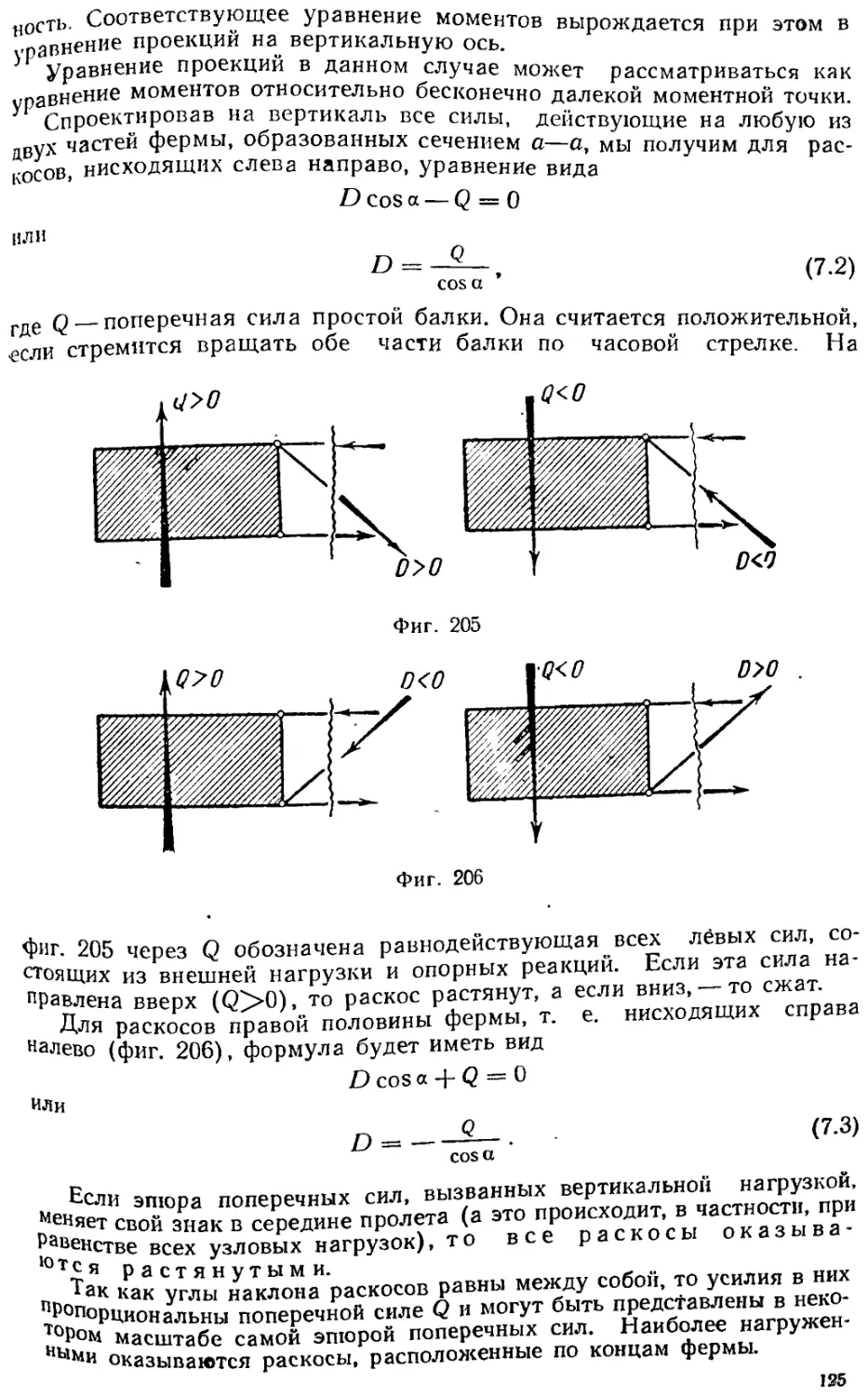
§ 7.14. Способ сеченнй 122
§ 7.15. Пример. Ферма с параллельными поясами и раскосной решеткой .... 123
§ 7.16. Пример. Ферма с непараллельными поясами и раскосной решеткой ... 127
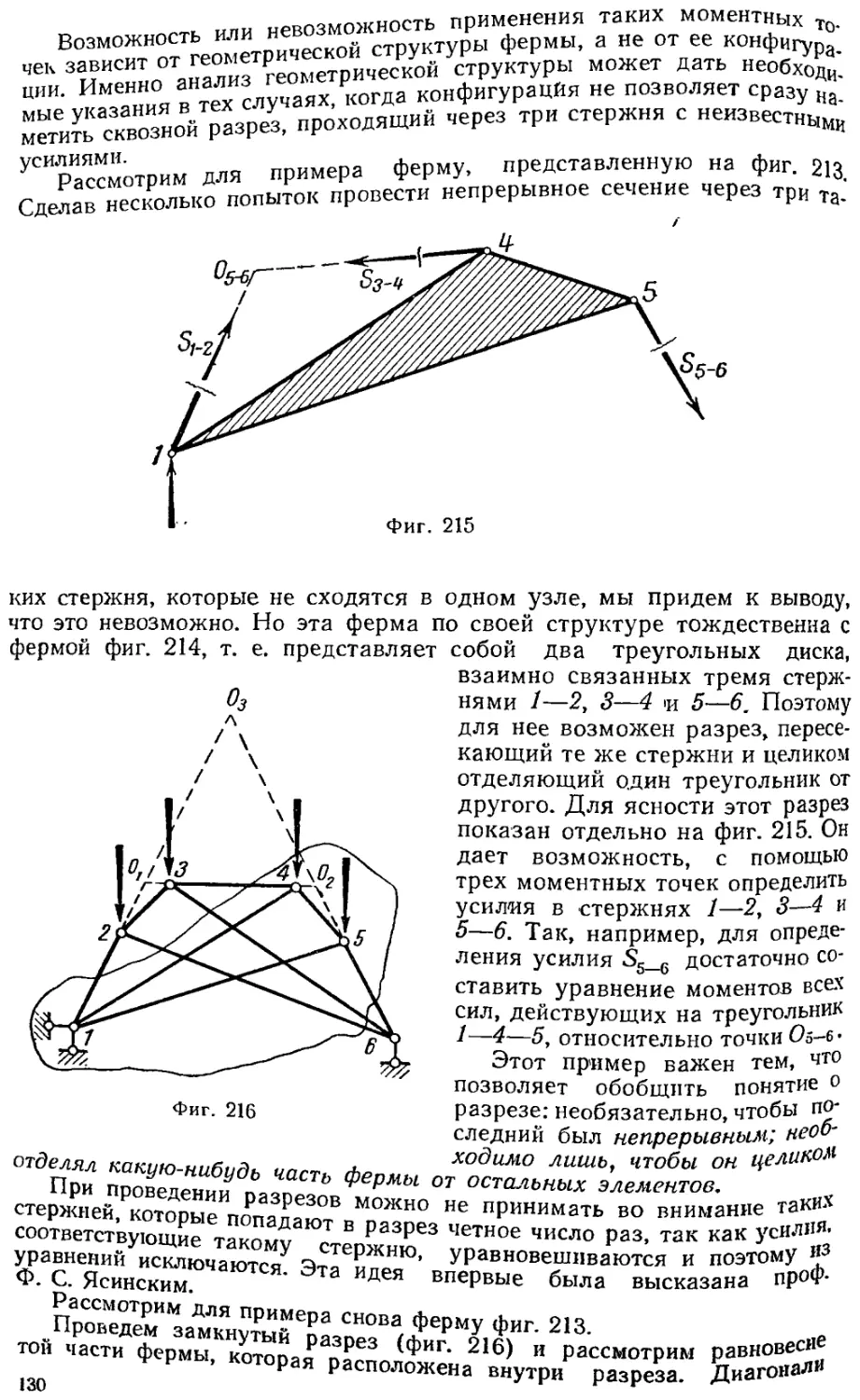
§ 7.17. Более сложные случаи применения способа сечений 129
§ 7,18. Способ равнодействующих 131
§ 7,19, Способ двух или нескольких сечений 132
§ 7,20. Способ замены стержней (способ Геннеберга) 133
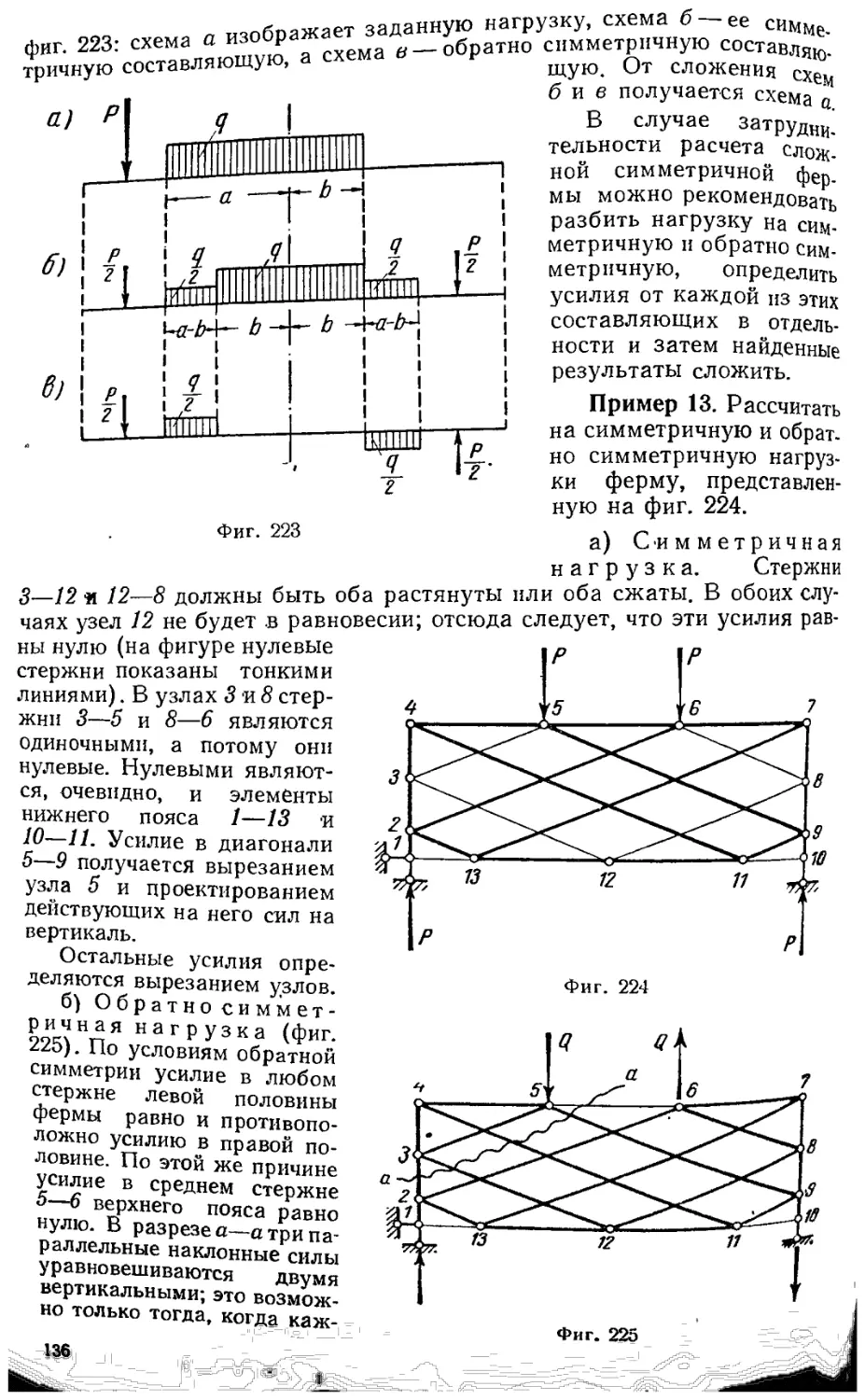
§ 7.21. Использование симметрии фермы путем разложения внешней нагрузки
на симметричную и обратно симметричную 135
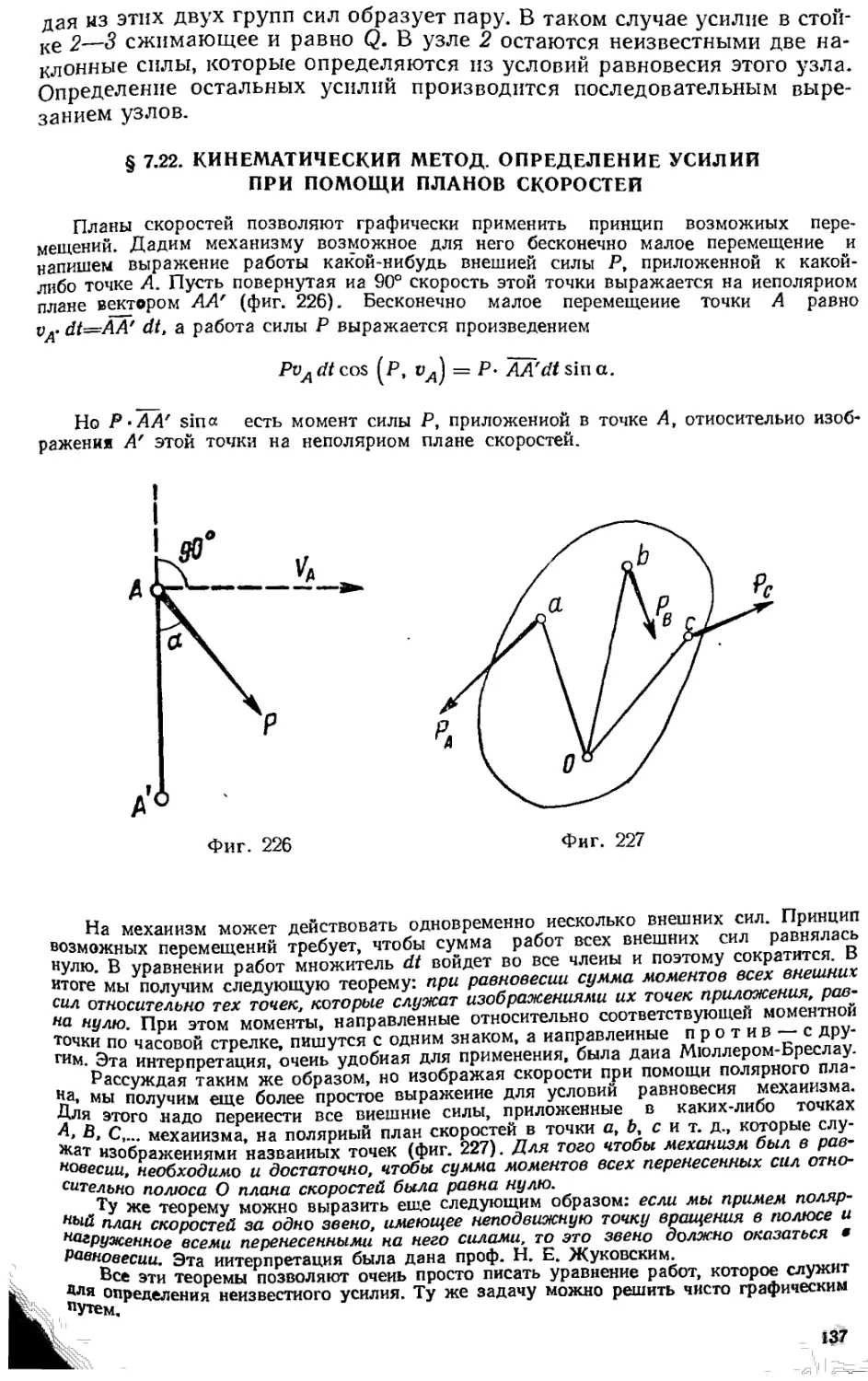
§ 7.22. Кинематический метод. Определение усилий при помощи планов скоростей 137
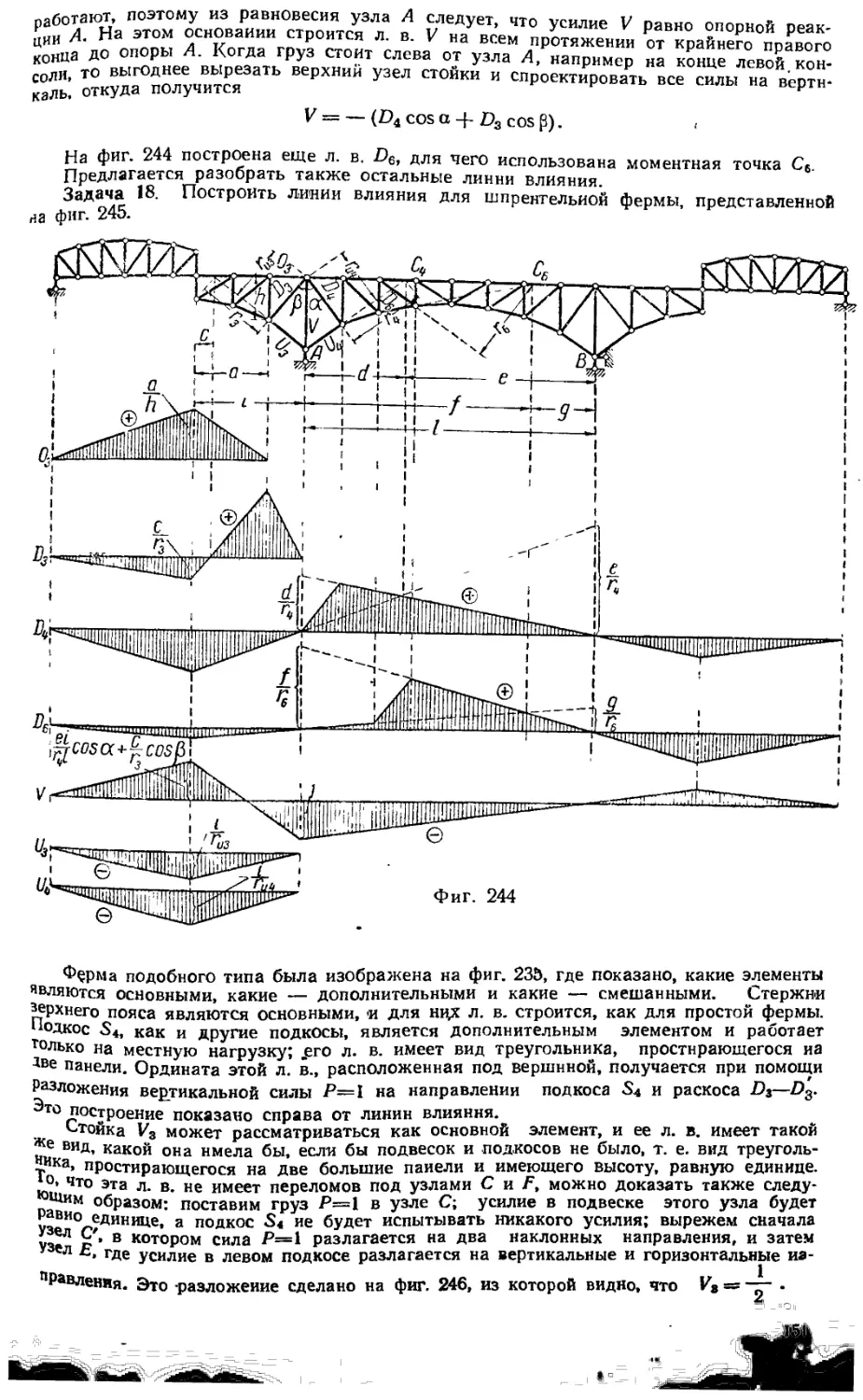
§ 7.23. Расчет ферм на внеузловую нагрузку 138
§ 7.24. Расчет составных ферм , . 139
§ 7.25. Краткие исторические данные 142
Глава 8
Линии влияния усилий в фермах балочных и консольно-балочных
§ 8. 1. Построение линий влияния при помощи сечений или вырезания узлов 144
§ 8. 2. Задачи '....: 150
§ 8. 3. Применение мгновенных центров вращения 153
§ 8. 4. Построение мгновенных центров вращения для более сложных систем 156
Глава 9
Распорные фермы и распорные комбинированные системы
§ 9. I. Трехшарнирная арочная ферма (решетчатая трехшарнирная арка) ... 158
§ 9. 2. Общие сведения о висячих системах 160
§ 9. 3. Расчет цепи, усиленной балкой жесткости 161
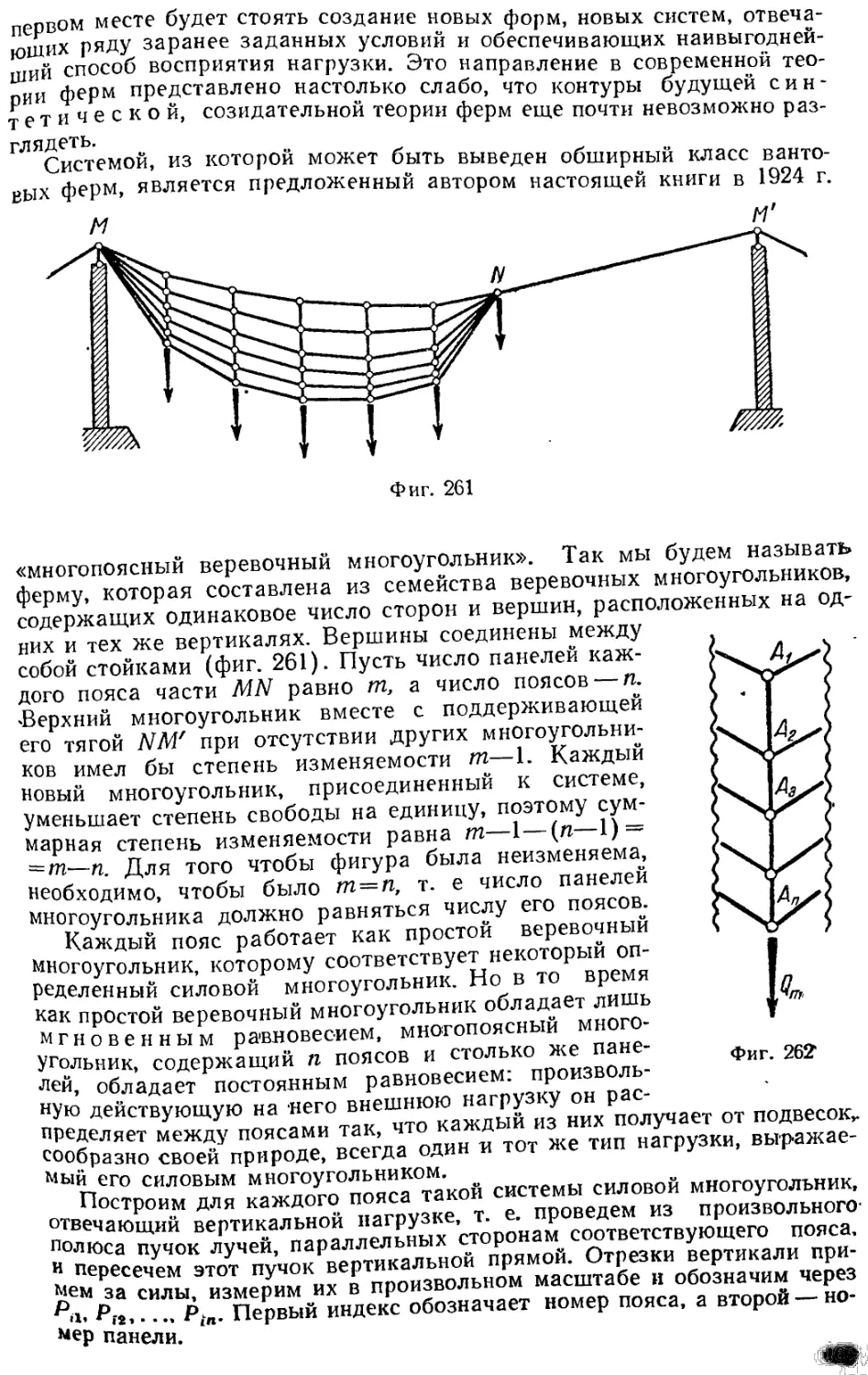
§ 9. 4. Многопоясный веревочный многоугольник и понятие об общей теории
Байтовых ферм 164
§ 9. 5. Пример расчета радиальной Байтовой фермы 167
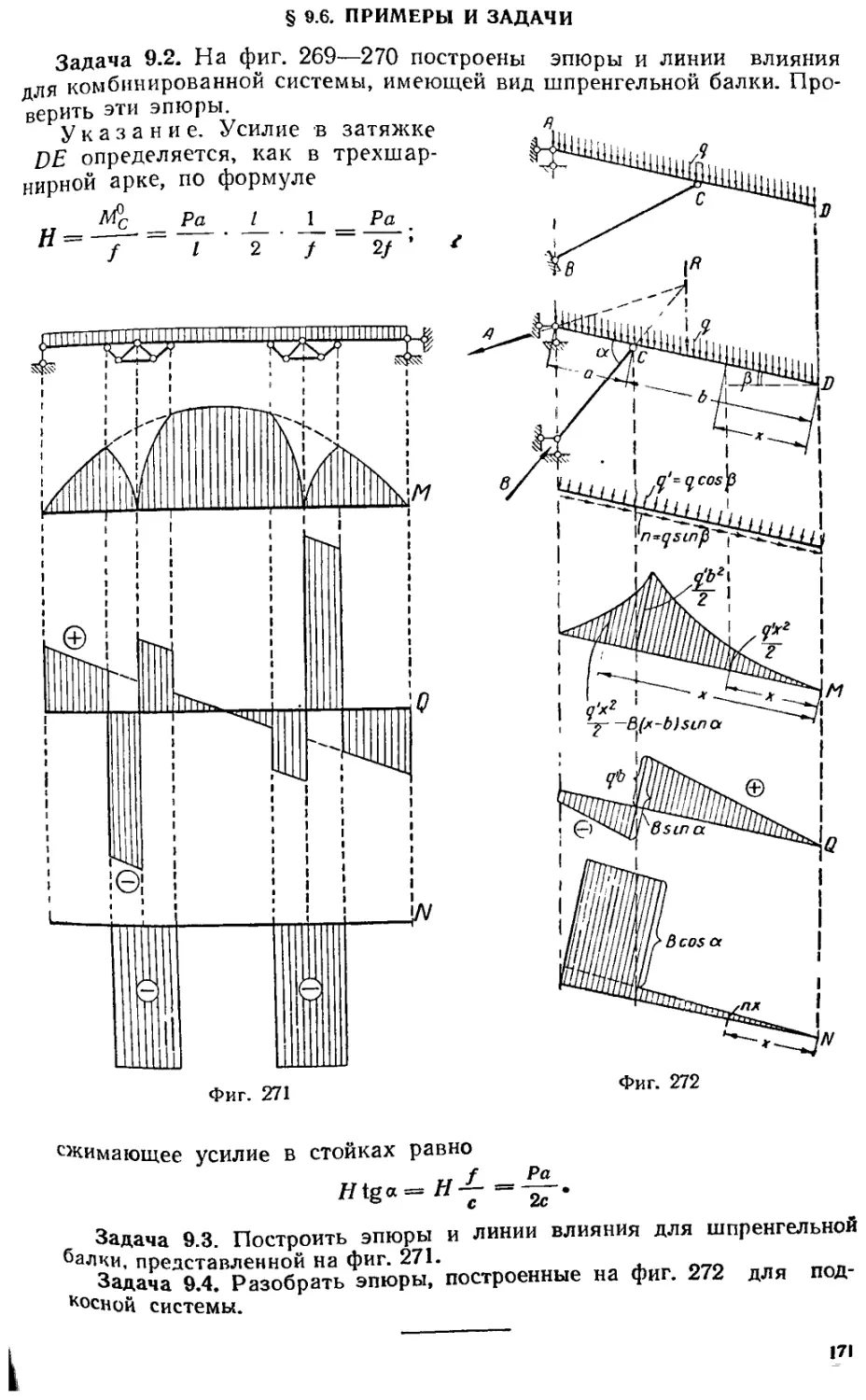
§ 9. 6. Примеры и задачи '. • . 171
Глава 10
Перемещения узлов и стержней плоских ферм
§ 10. 1. Введение 172
§ 10. 2. Понятие о диаграмме перемещений (Виллио) . 173
§ Ю. 3* Построение диаграммы перемещений в более общем случае 175
www.zodchii.ws
Стр.
Глава И
Пространственные фермы
§111 Значение расчета пространственных ферм 178
I 11*2 Сложение сил в пространстве . . .. —
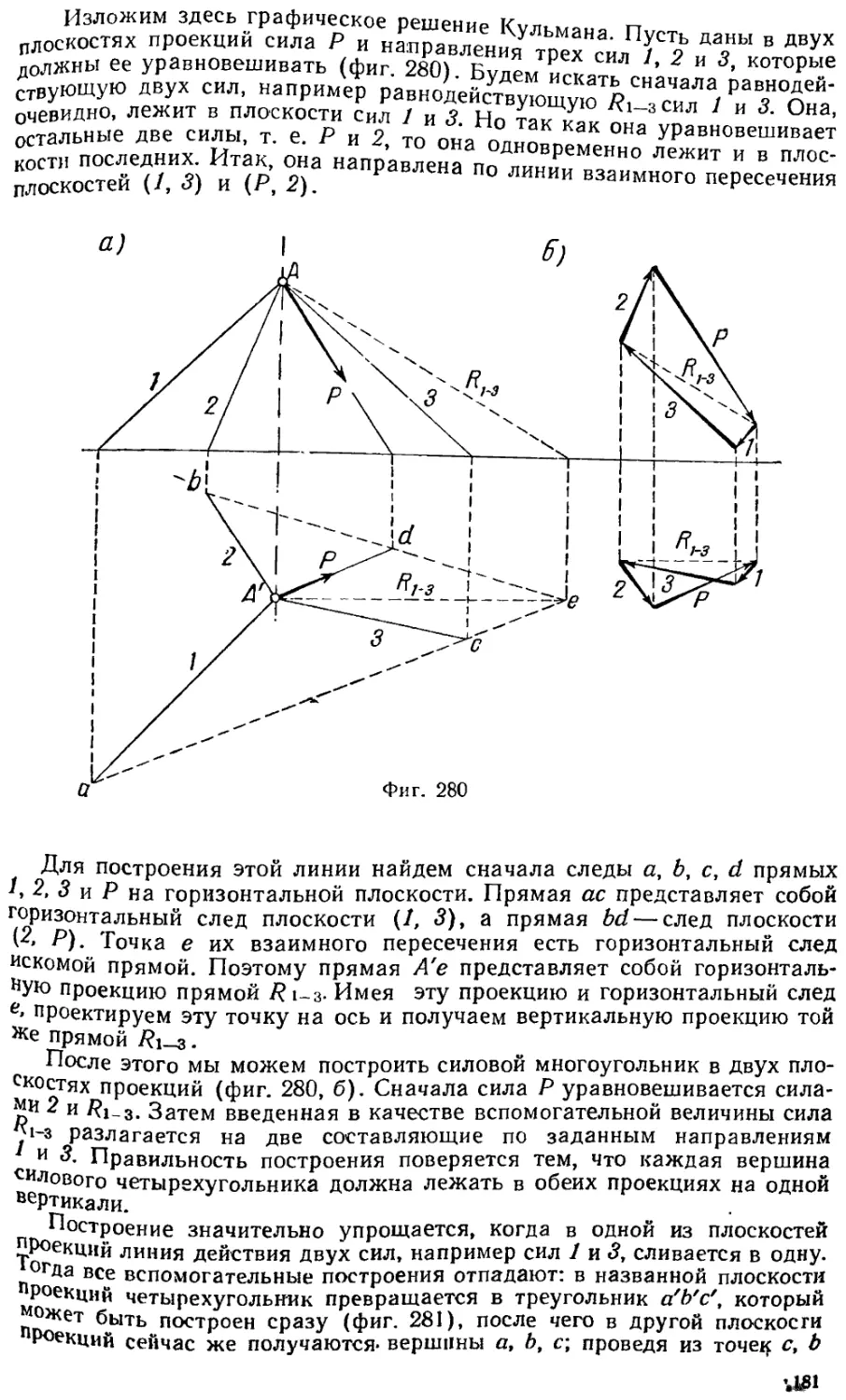
! 11 3. Разложение силы на три составляющие, пересекающиеся с ней в одной
•'*' ^ • , 180
точке „
S 11 4 случаи разложения силы на шесть направлении 182
I 11* б'Случаи неопределенности разложения силы на шесть направлений ... 183
I И 6. Признаки геометрической неизменяемости и неподвижности простран-
ственных ферм 184
§ 11. 7. Задачи и примеры 187
§ И. 8. Определение усилий в фермах способом вырезания узлов 190
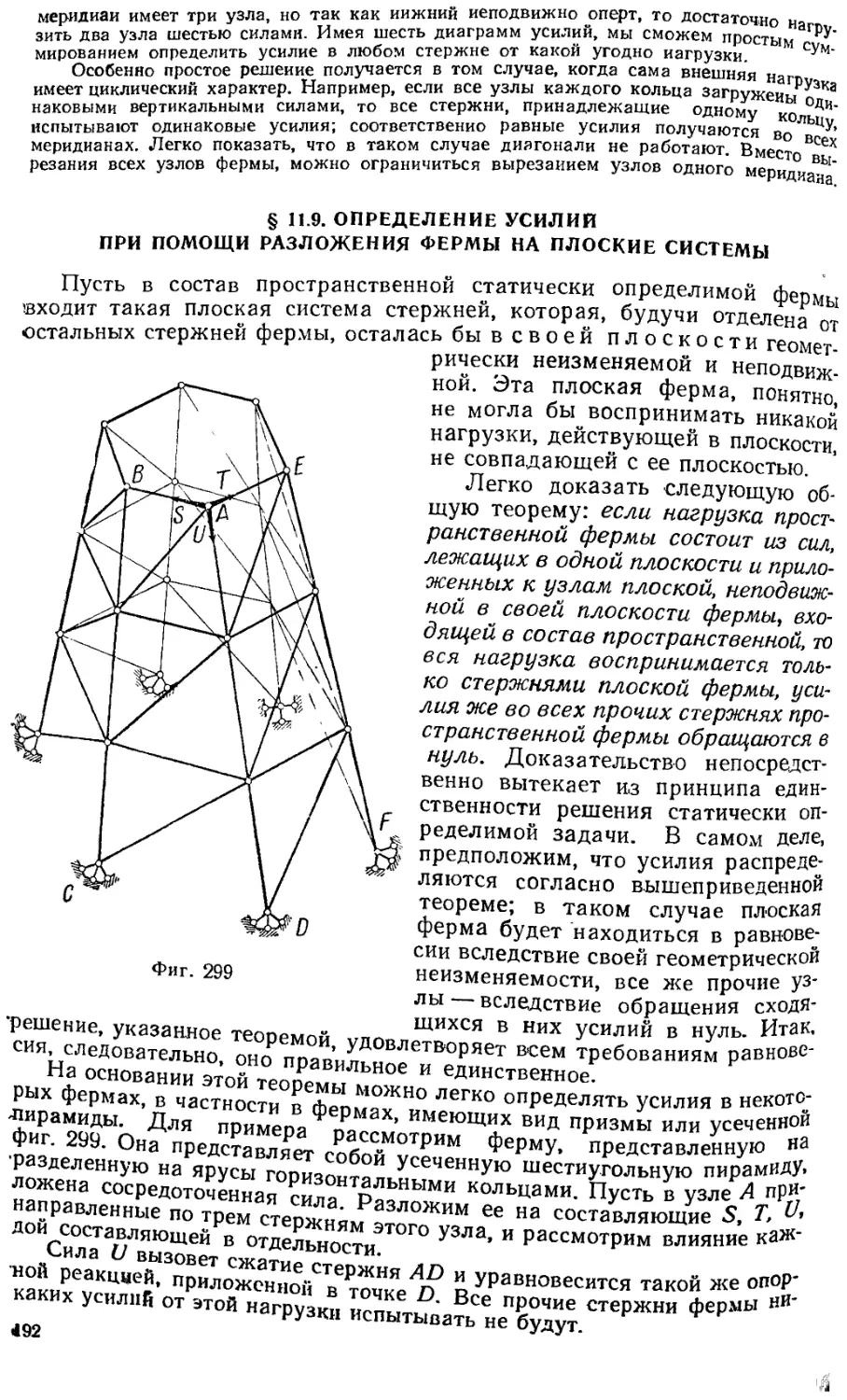
§ 11. 9. Определение усилий при помоши разложения фермы иа плоские системы 192
§ 11.10. Определение усилий способом замены стержней 193
§ 11.11. Определение усилий в элементах статически определимых «биконструкций» 194
Глава 12
Проблема расчета статически неопределимых систем
§ 12. 1. Что такое статически неопределимая стержневая система 197
§ 12. 2. Формулы для определения числа лишних связей 198
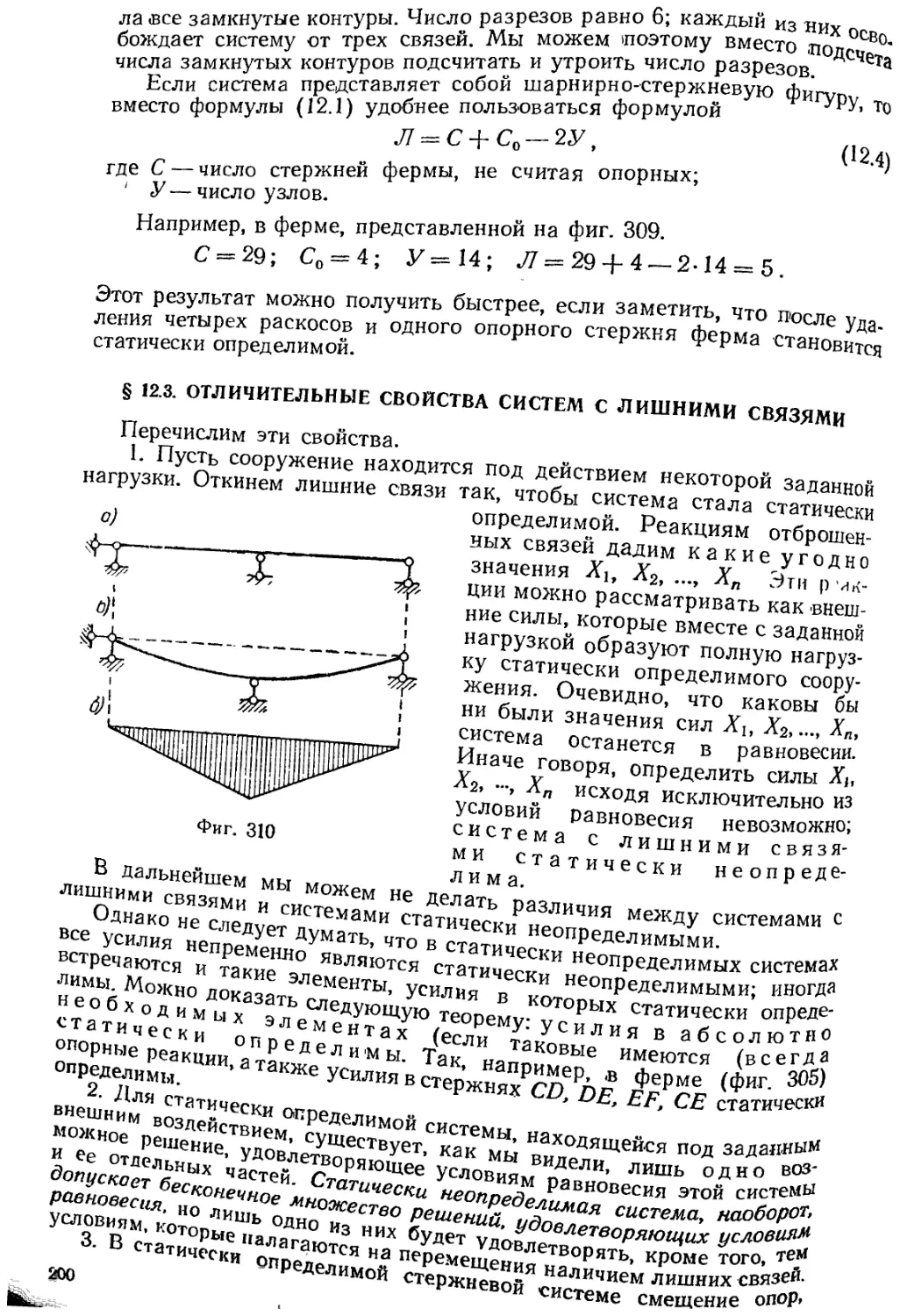
§ 12. 3. Отличительные свойства систем с лишними связями 200
§ 12. 4. Классификация методов расчета • - - 202
Глава 13
Основные теоремы об упругих системах
§ 13. 1. Основные понятия 203
§ 13. 2. Обобщенные силы и перемещения 204
§ 13. 3. Работа «статически» приложенных внец1них сил. Теорема Клапейрона 205
§ 13. 4. Примеры : 207
§ 13. 5, Работа внутренних сил плоской упругой стержневой системы —
§ 13. 6. Несколько замечаний о работе внешних и внутренних сил 210
§ 13. 7. Принцип возможных перемещений в применении к упругим системам . . 211
§ 13. 8. Приложение принципа возможных перемещений к действительным пере-
мещениям; Потенциальная энергия 212
§ 13. 9. Принцип взаимности работ 213
§ 13.10. Теорема Максвелла о взаимности перемещений 215
§ 13.11. Замечания о размерности перемещений 216
§ 13.12. Линии влияния перемещений как линии прогибов 217
§ 1313. Теорема Рэйлея о взаимности реакций 219
§ 13.14. Взаимность реакций и перемещений '. . . 220
I ]1'1а' ^^^'^^^^^ производные потенциальной энергии. Теорема Кастилнано . . 222
^ 13.16. Краткие исторические данные 223
^ Глава 14 ..^^
Определение перемещении стержневых систем
§ 14. I. Построение эпюр для статически определимых систем 225
I и t п^'^'"''!^''^^^^''''^''^' ''^''^^^''^^ • • 226
I ы А п формула для перемещений плоской стержневой системы .... 227
I 4 t ll^^'^^P''' выбора единичной силы .... 231
' 2'р^у'1коГ''" ^ ''^^^«'^^^^« определимой системе, 'вызванные внешней
^ ^^' ^' Гш|ХТя""'^«^^^""" ««^^^Р^'^ов для случая! к;г;а одна на'эпюр п^^ямо* 232
235
в
www.zodchii.ws
^ Стр
§ 14. 7. Перемещения в статически неопределимых системах, вызываемые внеш-
ней нагрузкой 237
§ 14. а Температурные перемещения в статически определимых и 'статически
неопределимых системах 239
§ 14. 9. Перемещения, вызываемые «перемещением опор или других связей ", '. *. 241
§ 14.10. Построение линии прогибов кривого или ломаного стержня при помощи
упругих грузов 245
§ 14.11. Построение лилии прогибов как веревочного многоугольника . „ . . 246
§ 14Л'2, Краткие исторические данные 249
Глава 15
Основы метода сил
§ 15. 1. Основная система и основные (лишние) неизвестные 251
§ 15. 2. Система канонических уравнений метода сил для расчета на действие
внешней нагрузки 253
§ 15. 3. Канонические уравнения для расчета на действие температуры .... 254
§ 15. 4. Канонические уравнения для случая заданного перемещения опор ... 255
§ 15. 5. Канонические уравнения для расчета на совместное действие нагрузки,
температуры и перемещения опор 256
§ 15. 6. Краткие исторические данные 257
Глава 16
Расчет неразрезных балок
§ 16. 1. Общие сведения о неразрезных балках 258
§ 16. 2, Количество лишних связей. Выбор основной системы 259
§ 16. 3. Расчет неразрезных балок на внешнюю нагрузку. Уравнения трех
моментов 260
§ 16. 4. Примеры и задачи 267
§ 16. 5. Моментные фокусные отношения и моментные фокусы 270
§ 16. 6. Применение моментных фокусных отношений к построению эпюр . . . 274
§ 16. 7. Построение линий влияния изгибающих моментов 276
§ 16, 8. Построение линий влияния поперечных сил 280
§ 16. 9. Построение линий влияния опорных реакций 281
§ ШЛО. Построение линий влияния как линий прогиба
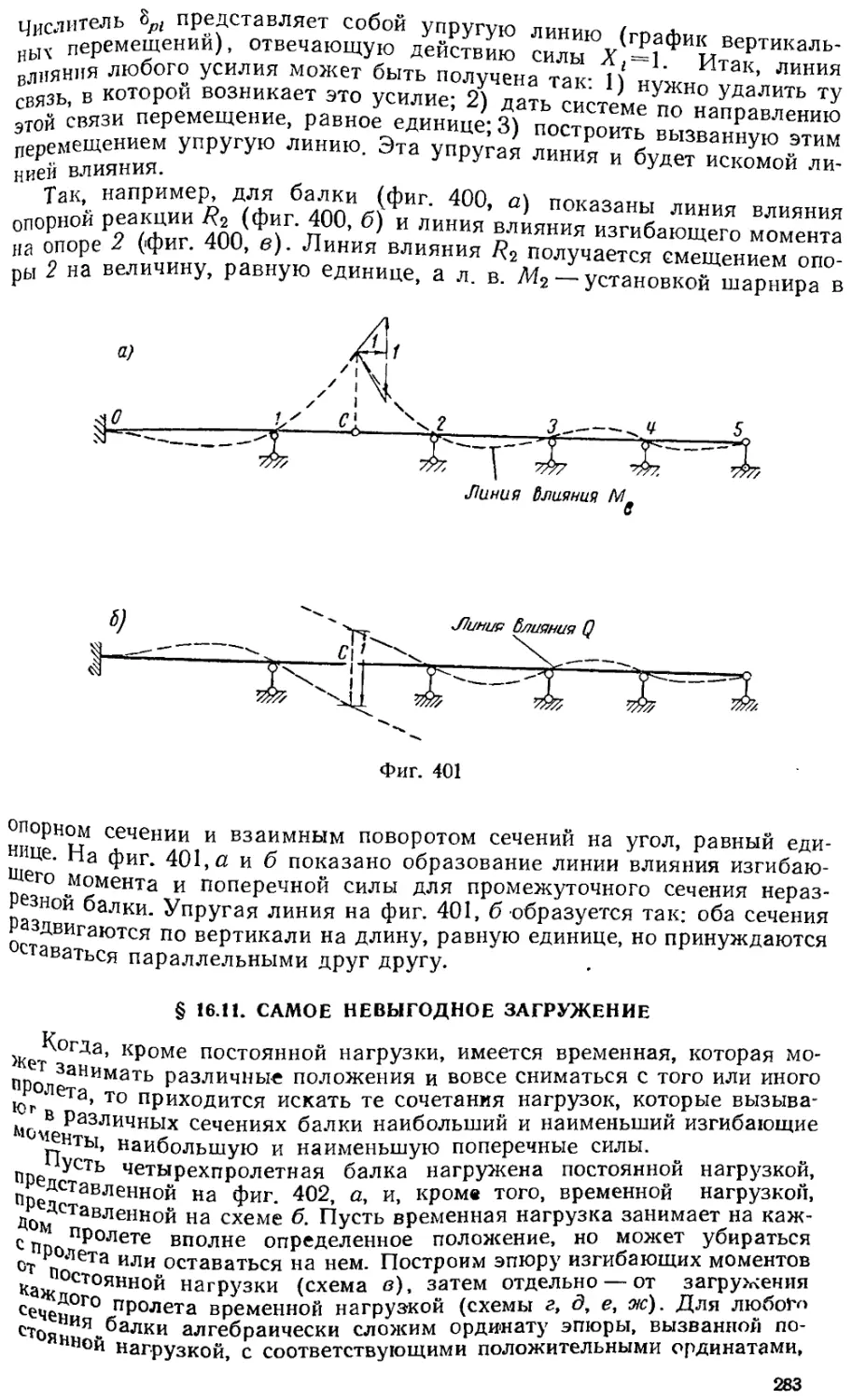
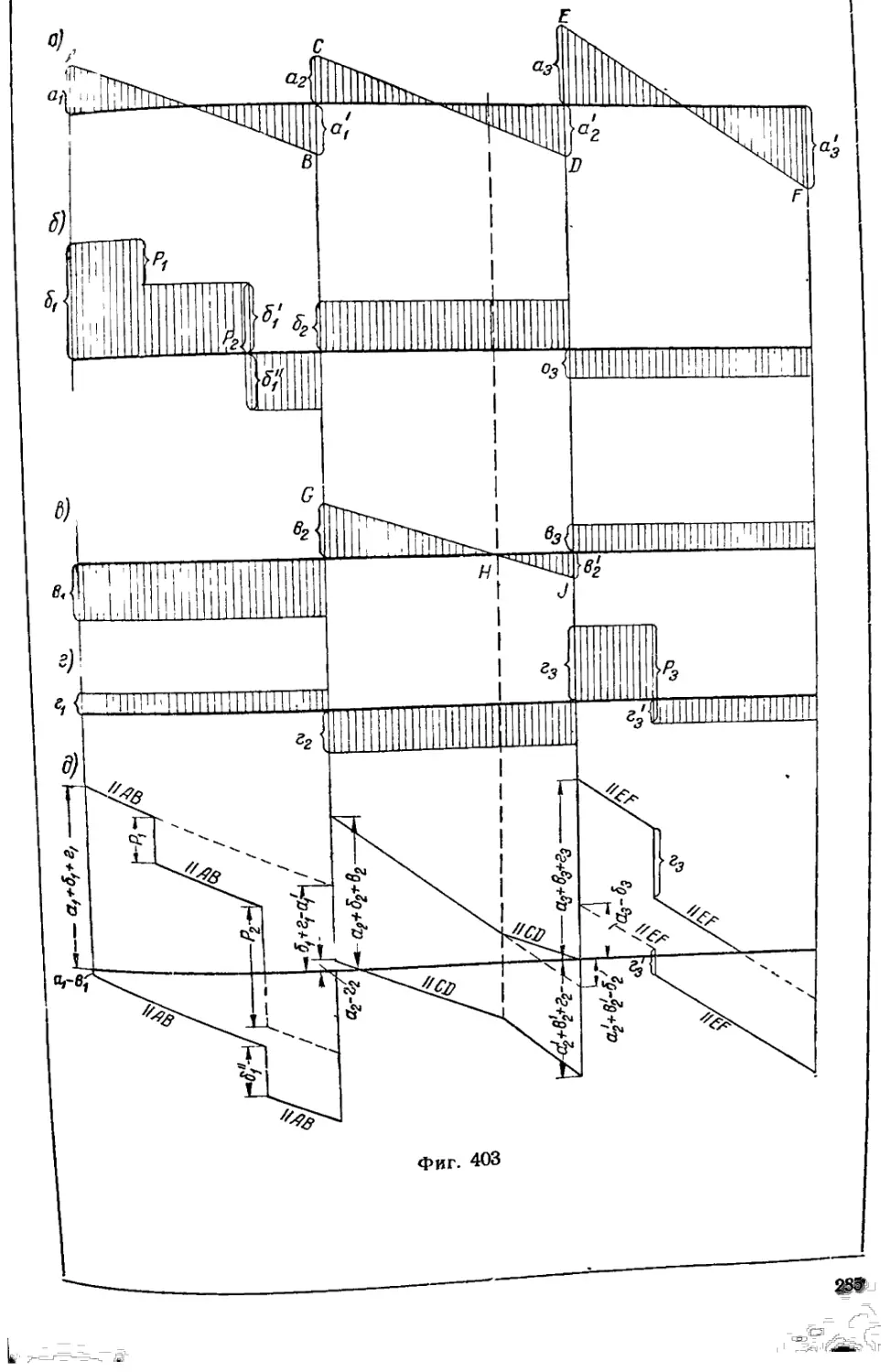
§ 16.11. Самое невыгодное загружение - 283
§ 16,12. Расчет на смещение опор 286
§ 16.13. Неразрезная балка с упруго-смещающимися опорами
§ 16.14. Понятие о расчете неразрезных балок методом заданных моментов или
напряжений
§ 16.15. Краткие исторические данные
Г л а в а 17
Расчет простых рам и статически неопределимых арок методом сил
5 17. 1. Основные понятия • 295
17. 2. Расчет рамы с одной лишней неизвестной
I 17. 3. Об упрощении канонических уравнений для ^симметричных систем. 299
Расчет рамы с тремя лишними связями *
8 17 4 Дальнейшее упрощение расчета той же рамы при помощи введения 302
жестких консолей • • - • 304
I 17. 5. Расчй" двухшарнирнои арки с затяжкой • •
« W '6. Влияние податливости затяжки. Эпюры M.Ji^^^N. Кривая давлений 311
I ^7 7. Построение линий влияния « 'J*^; * ^ . ^ . • . . * . • 313
f 17, 8. Расчет на действие темпера'^Ч з- i ..-..••••* *
9
Стр,
. ,7 9 Бесшарннрная арка. Выбор основной системы. Аналитическое и графиче-
^ ское определение коэффипиентов 314
§,7 10.Построение эпюр, кривая давлении • 320
liril Построение линий влияния • • ¦ ' ' 322
! 7 12 Расчет на действие температуры и усадки 325
I 7'п' Расчет на действие, оказываемое отеремещением опор 326
§1714. Расчет симметричной арки с упругими опорами 328
Глава 18
Расчет статически неопределимых ферм
§ 18. 1. Общие соображения о статически неопределимых фермах 332
§ la 2. О подборе сечений —
§ 18. 3. Расчет фермы с одним лишним стержнем 334
§ 18. 4. Построение линий влияния для фермы с одним лишним стержнем ... 336
§ 18. 5. Расчет фермы с несколькими лишними стержнями 338
§ 18. 6. Расчет ферм методом заданных напряжений —
Глава 19
Расчет сложных рамных систем методом сил
§ 19. 1. Общие соображения <- 341
§ 19. 2. О построении эпюр М для статически определимых основных систем и
эпюр Q, N для любой системы —
§ 19. 3. О рациональном выборе основной системы 344
§ 19. 4. Свойства групповых эпюр и групповых неизвестных 346
§ 19. 5. Пример применения способа группировки неизвестных 347
§ 19. 6. Дополнительные упрощения, вытекающие из условий симметрии . . . 350
§ 19. 7. Одновременное применение нескольких основных систем 351
§ 19, 8. Поверка эпюр и линий влияния —
§ 19, 9. Краткие исторические данные 354
Глава 20
Расчет рамных систем методом перемещений (деформаций)
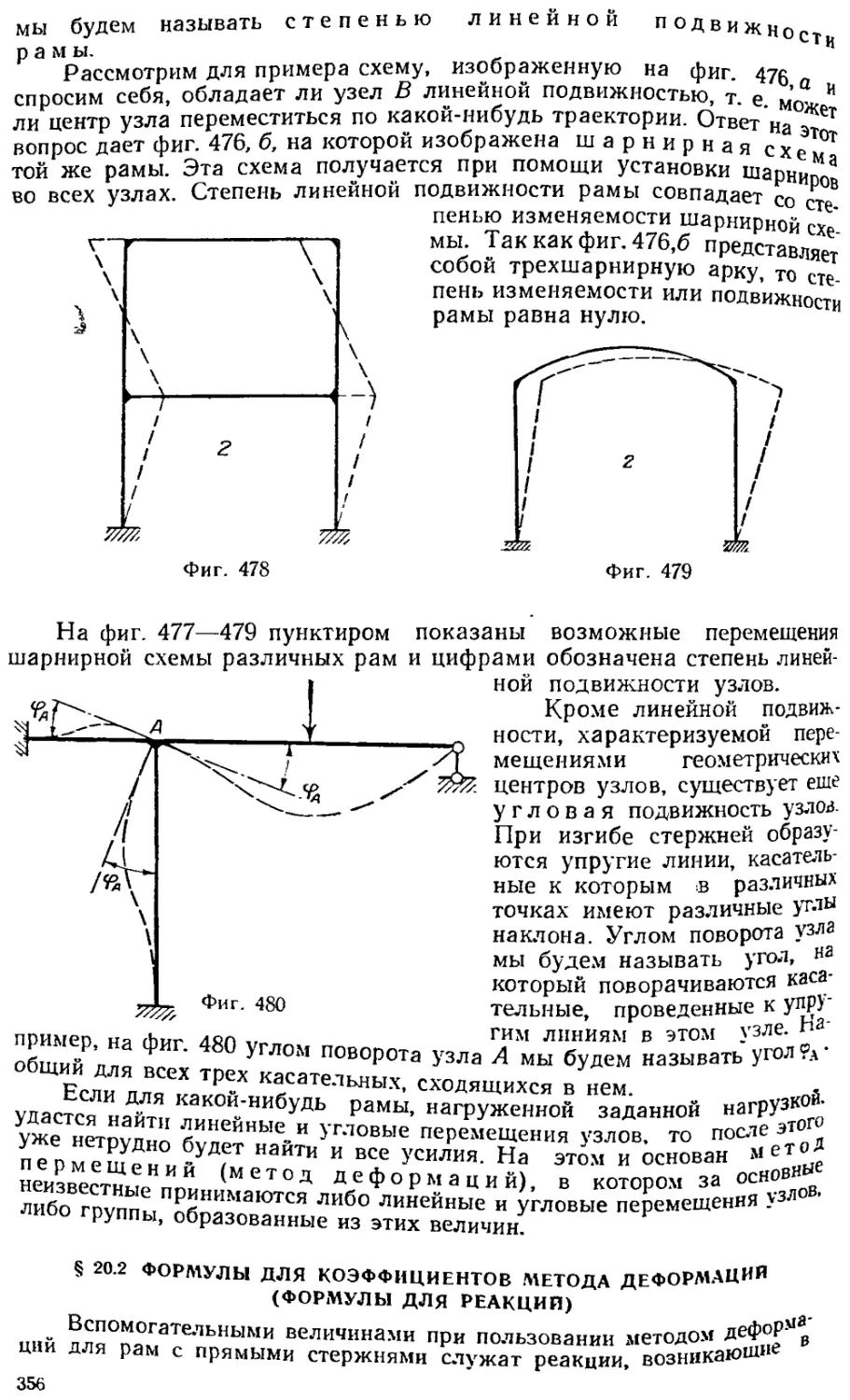
§ 20. 1. Степень упругой подвижности узлов рамной системы 355
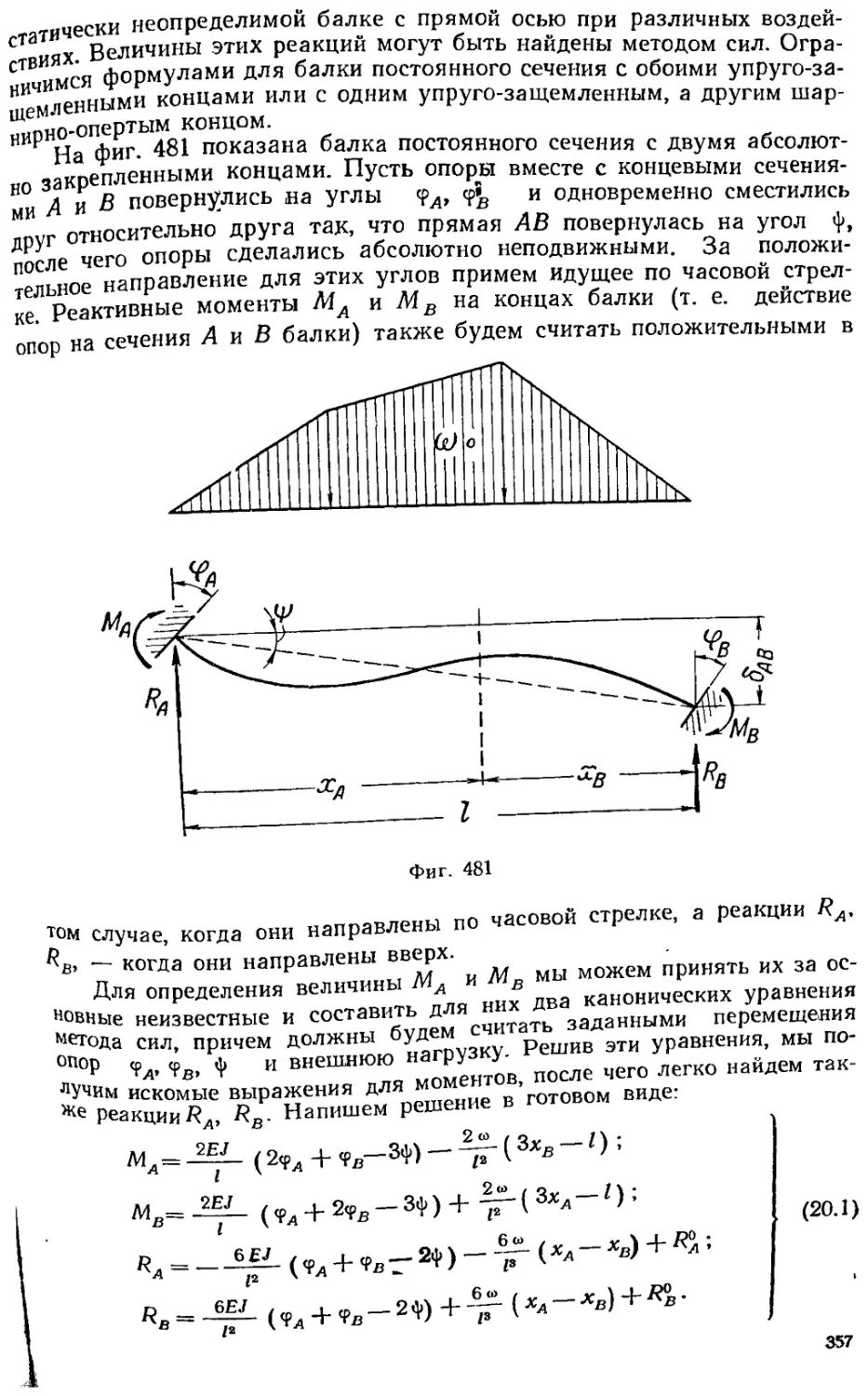
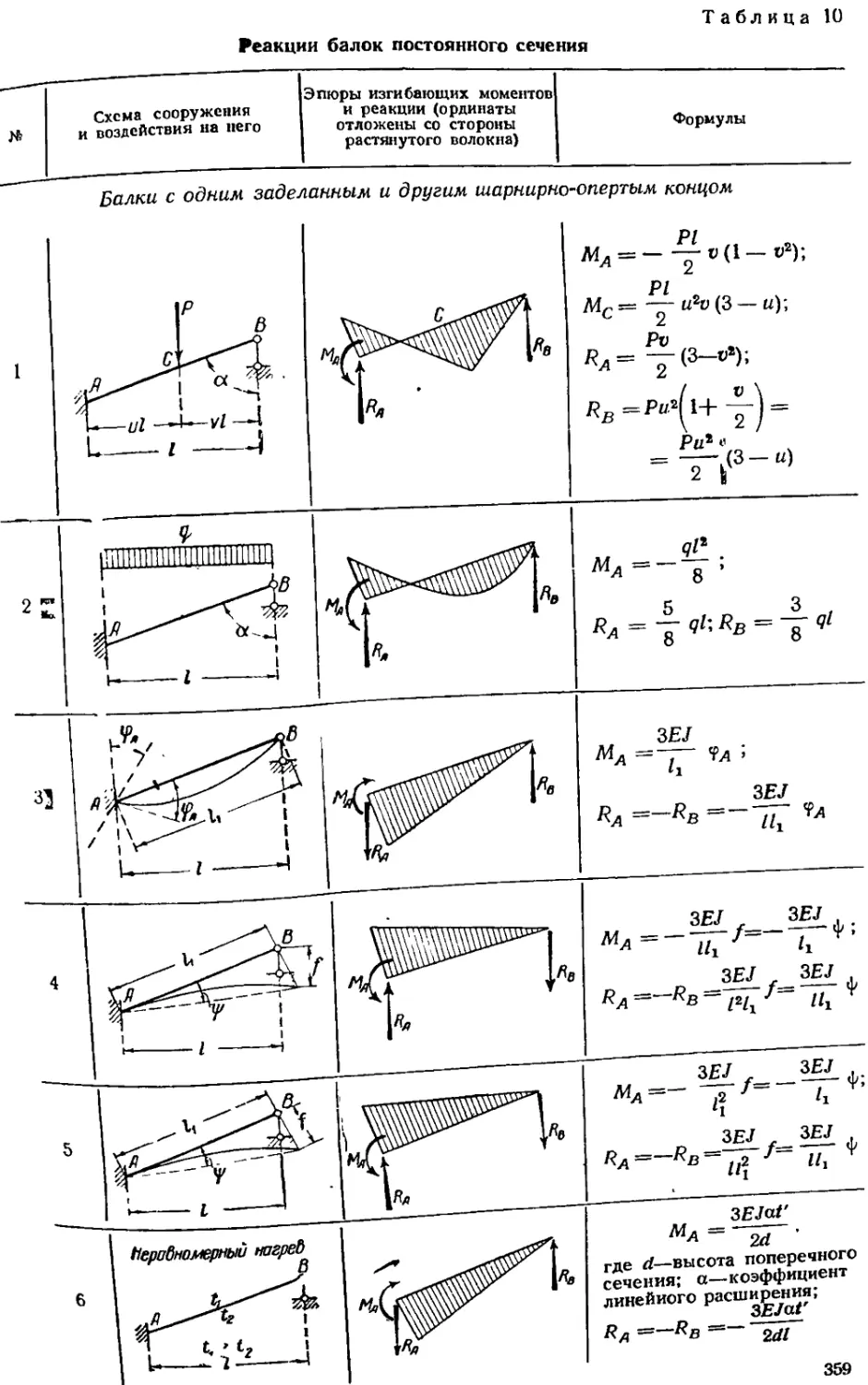
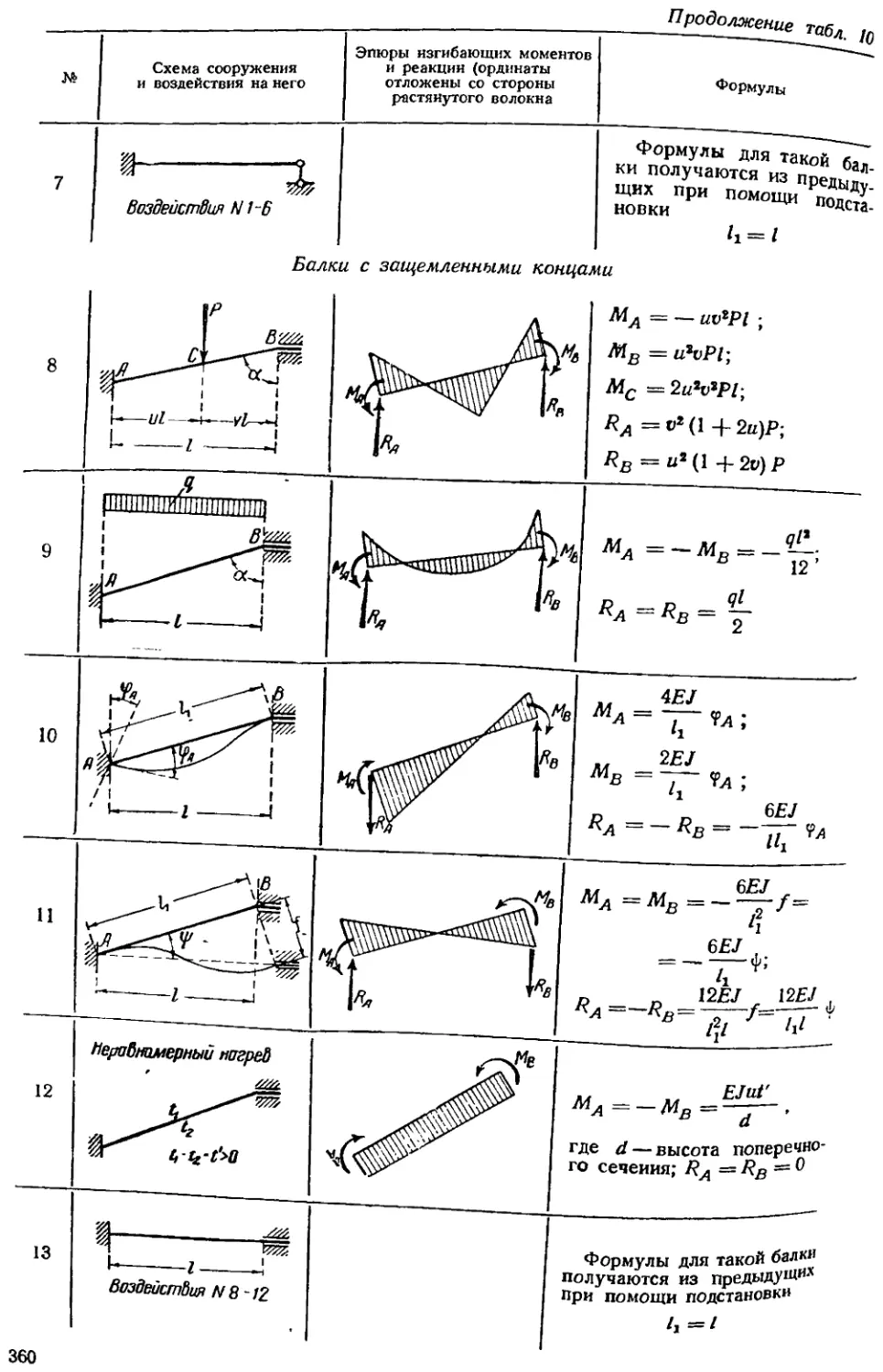
§ 20. 2. Формулы для коэффициентов метода деформаций (формулы для реакций) 356
§ 20. 3. Идея метода перемещений (деформаций) 361
§ 20. 4. Канонические уравнения метода деформаций для любой статически не-
определимой плоской стержневой системы 364
1 on" а' ^Р^^"^"^^ метода деформаций для рам с вертикальными стойками . . 367
§ 20. 6. Пример составления уравнений 373
I on* ^' ^^^^ "^ действие температуры 374
I 20. 8. Построение линий влияния 375
! 9п in ^°"^"«^Рованное решение задач методами сил и деформаций . . [ . —
S 2U.1U, Смешанный метод 376
I 9ni9 (З^^^Р''^ ^"^Р* полученных методами деформаций и смешанным . .' .* 378
S ^и.ы. Краткие исторические, данные 379
Глава 21
Расчет рам по способу моментиых фокусных отношений
I 21* 2.' Пример" .^''" "^""^""^'^ неизвестных в рамах с несмещающимися узлами 380
§ 21. 3. Расчет рам со смещающимися' узлами .'.','[[[['.[[.'. 385
Стр.
Глава 22
Приближенный расчет рам
§ 22. 1. Общие соображения 388
§ 22. 2. Приближенный расчет многопролетной многоярусной рамы на гори-
зонтальную (ветровую) нагрузку —
§ 22. 3. Приближенный расчет многопролетной многоярусной рамы на вер-
тикальную нагрузку 390
§ 22. 4. Расчет рам способом перераспределения моментов или других величин 392
§ 22. 5. Решение канонических уравнений способом последовательных при-
ближений (способом итерации) 393
§ 22. 6. О применении счетно-решающих машин в задачах расчета статически не-
определимых систем 394
Глава 23
Приведение расчета призматических рам, составленных из пластинок,
к расчету плоских стержневых рам (метод проф. В. 3. Власова)
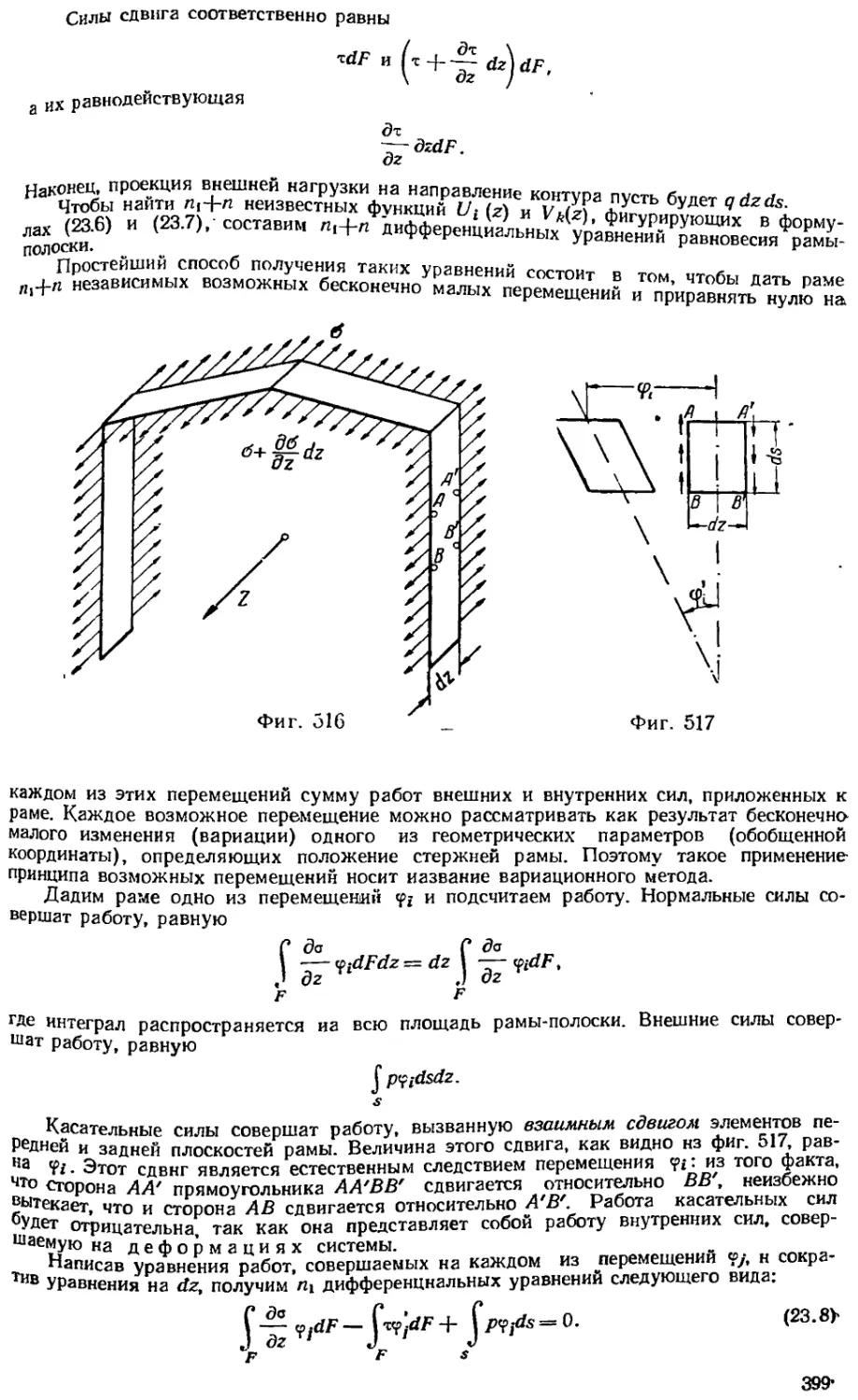
§ 23. 1. Основные гипотезы 396
§ 23. 2. Дифференциальные уравнения равновесия рамы-полоски 398
§ 23. 3. Пример ; ; : : 402
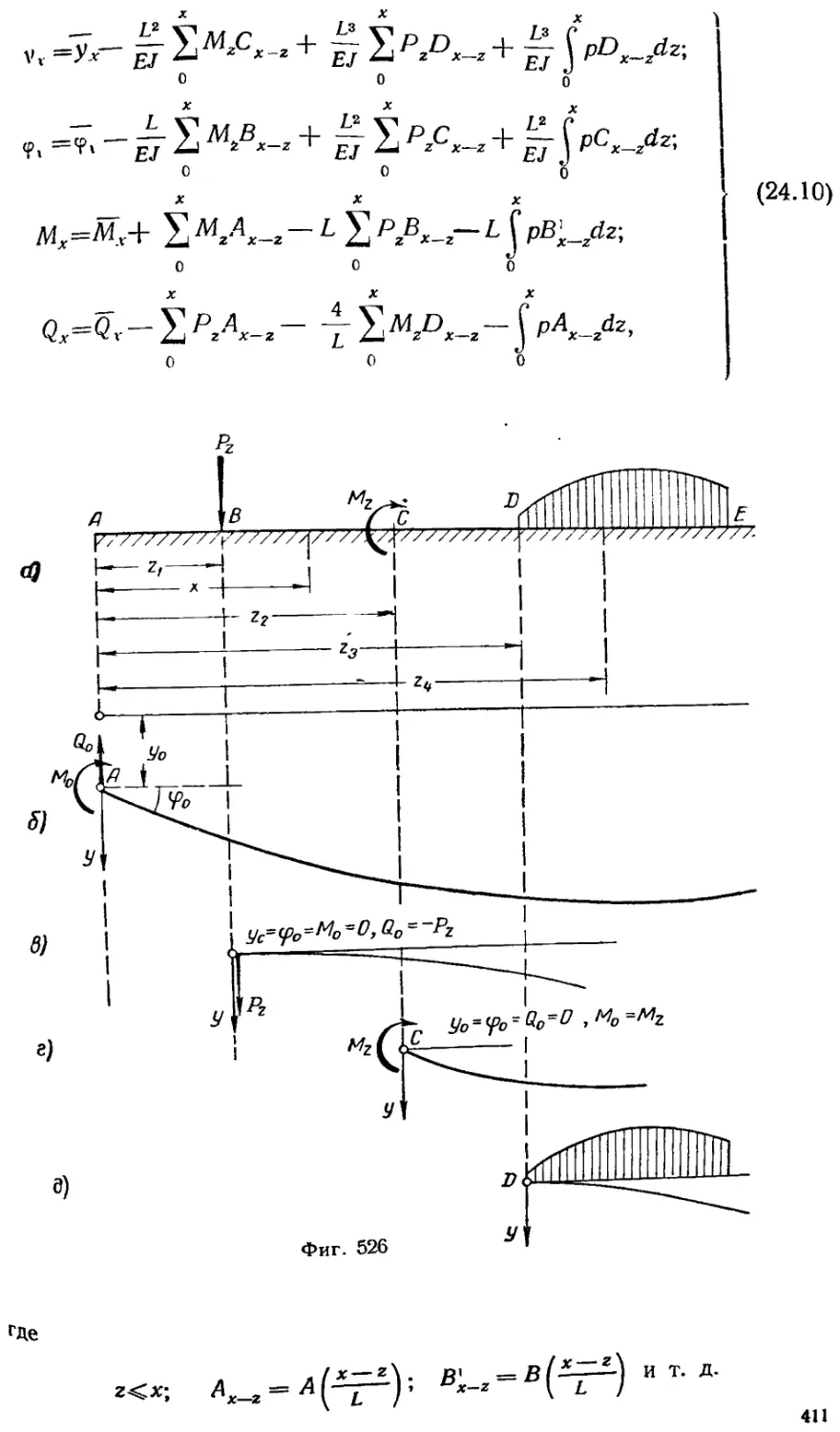
Глава 24
Расчет балки на сплошном упругом основании
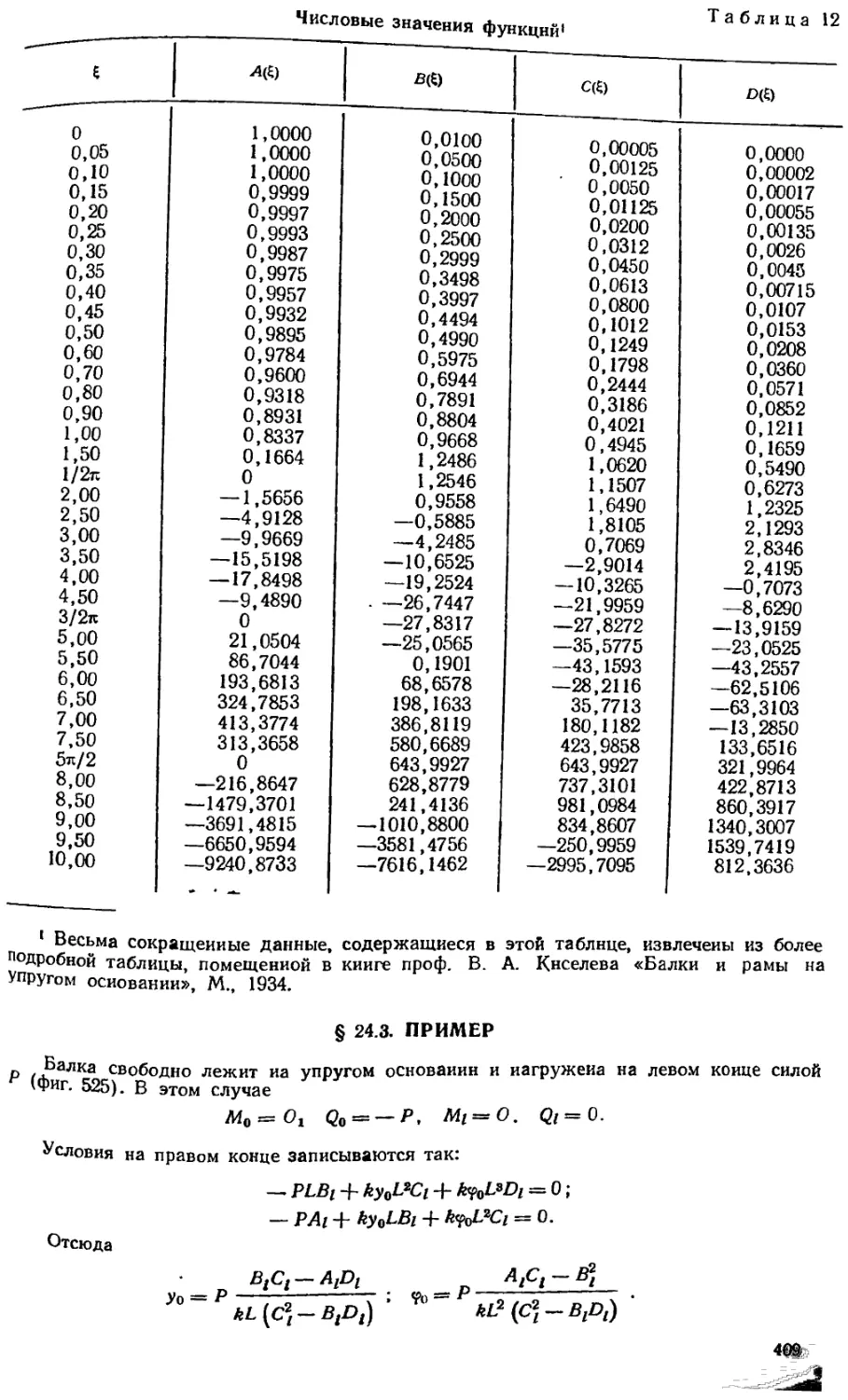
§ 24. 1. Общие соображения 406
§ 24. 2. Интеграл однородного дифференциального уравнения 407
§ 24. 3. Пример 409
§ 24. 4. Интеграл неоднородного дифференциального уравнения 410
§ 24. 5. Понятие о расчете балок на упругом изотропном основании 412
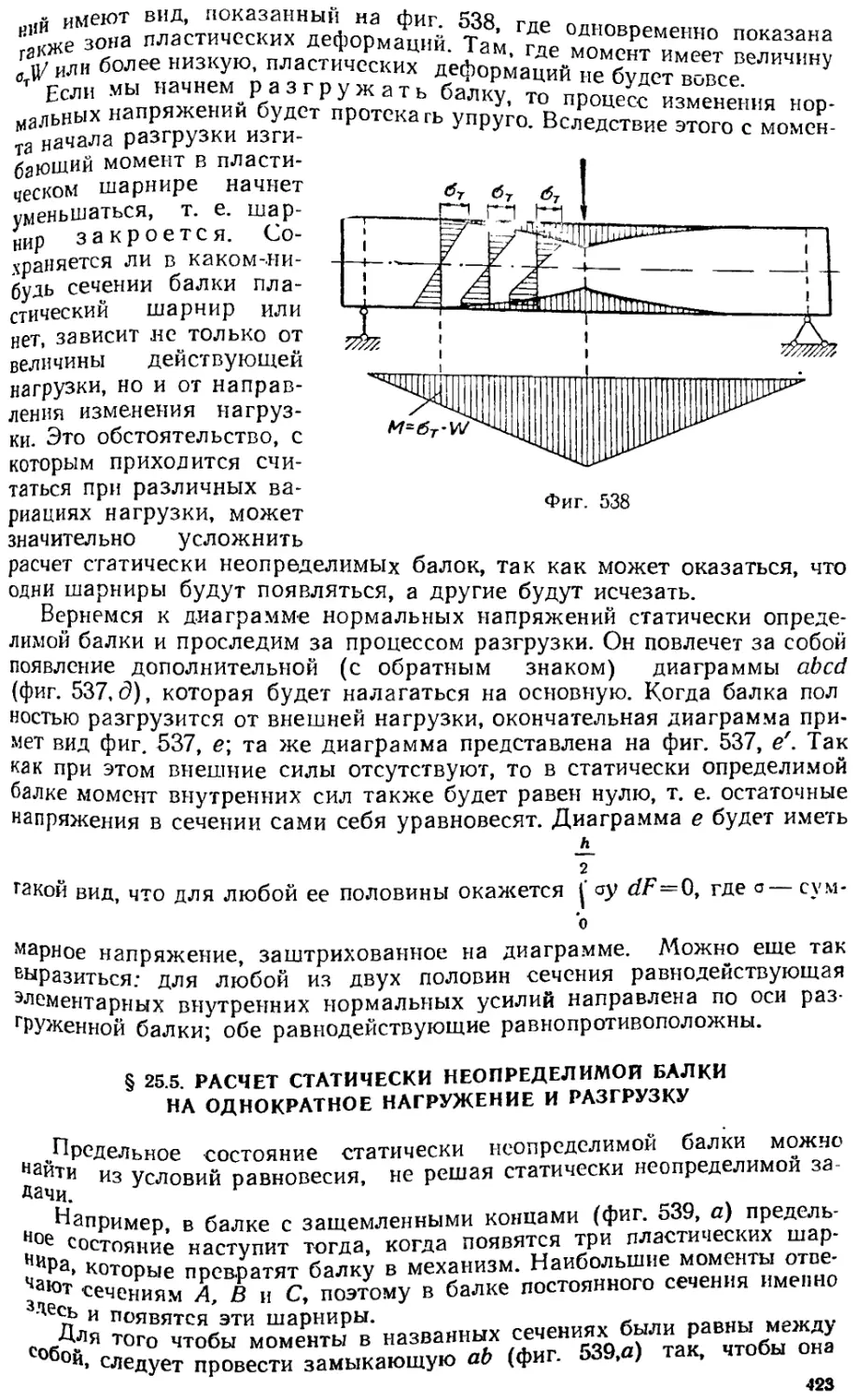
Глава 25
Напряженное состояние стержневых систем за пределом упругости
§ 25. 1.0 расчете сооружений по расчетным предельным состояниям 416
§ 25. 2. Расчетная схема идеального упруго-пластического материала .... 417
§ 25. 3. Расчет статически неопределимой фермы на постоянную нагрузку . . . 418
§ 25. 4. Расчет статически определимой балки на однократное нагружение
и разгрузку ' 421
§ 25. 5. Расчет статически неопределимой балки на однократное нагружение
и разгрузку ,,,,.,.».»» ^^'^
§ 25. 6. Пластический шарнир при совместном действии изгибающего момента
и продольной силы 427
§ 25. 7. Несколько замечаний 428
Глава 26
Расчет сооружений на устойчивость
§ 26. 1. Значение расчета на устойчивость 429
§ 26. 2. О точном и приближенном расчете 430
§ 26. 3. Определение критической нагрузки для систем с конечным и бесконечно
большим числом степеней свободы 431
§ 26. 4. Приближенные методы определения критической силы для прямого
стержня 435
§ 26. 5. Пример применения принципа возможных перемещений 438
§ 26. 6. Критическая сила для составного стержня 439
§ 26. 7, Понятие о расчете рам на устойчивость методом перемещений .... 442
§ 26. 8. Пример 445
§ 26. 9. Краткие исторические данные 446
Стр
Глава 27
Динамический расчет систем с одной степенью свободы
S 27 I Виды динамической нагрузки 448
I 97' 2" Степень свободы упругой системы ->,
I о7 з'Дифференциальное уравнение движения и его интеграл 449
§ 27 4.* Опреде!пение частоты собственных колебании системы 451
& 27. 5. Пример . - • • \ 454
§ 27. 6. Вынужденные колебания стержневой системы 455
§ 27 7 Влияние внезапного нагруження —
S 27 8. Влияние нагрузки, постепенно возрастающей или убывающей во време-
ни по линейному закону 456
§ 27. 9. Влияние кратковременного действия нагрузки 447
§ 27.10. Влияние кратковременного импульса 458
§ 27.11. Пример • 459
§ 27.12. Влияние вибрационной нагрузки 460
§ 27,13. Влияние произвольной периодической нагрузки 462
§ 27.14. Примеры ' 465
§ 27.15. Влияние периодической нагрузки большой частоты 467
§ 27.16. Геометрическое представление вынужденных и свободных перемещений 468
§ 27.17. Влияние перемещений опор 470
§ 27.18. Влияние поперечного изгибающего удара 471
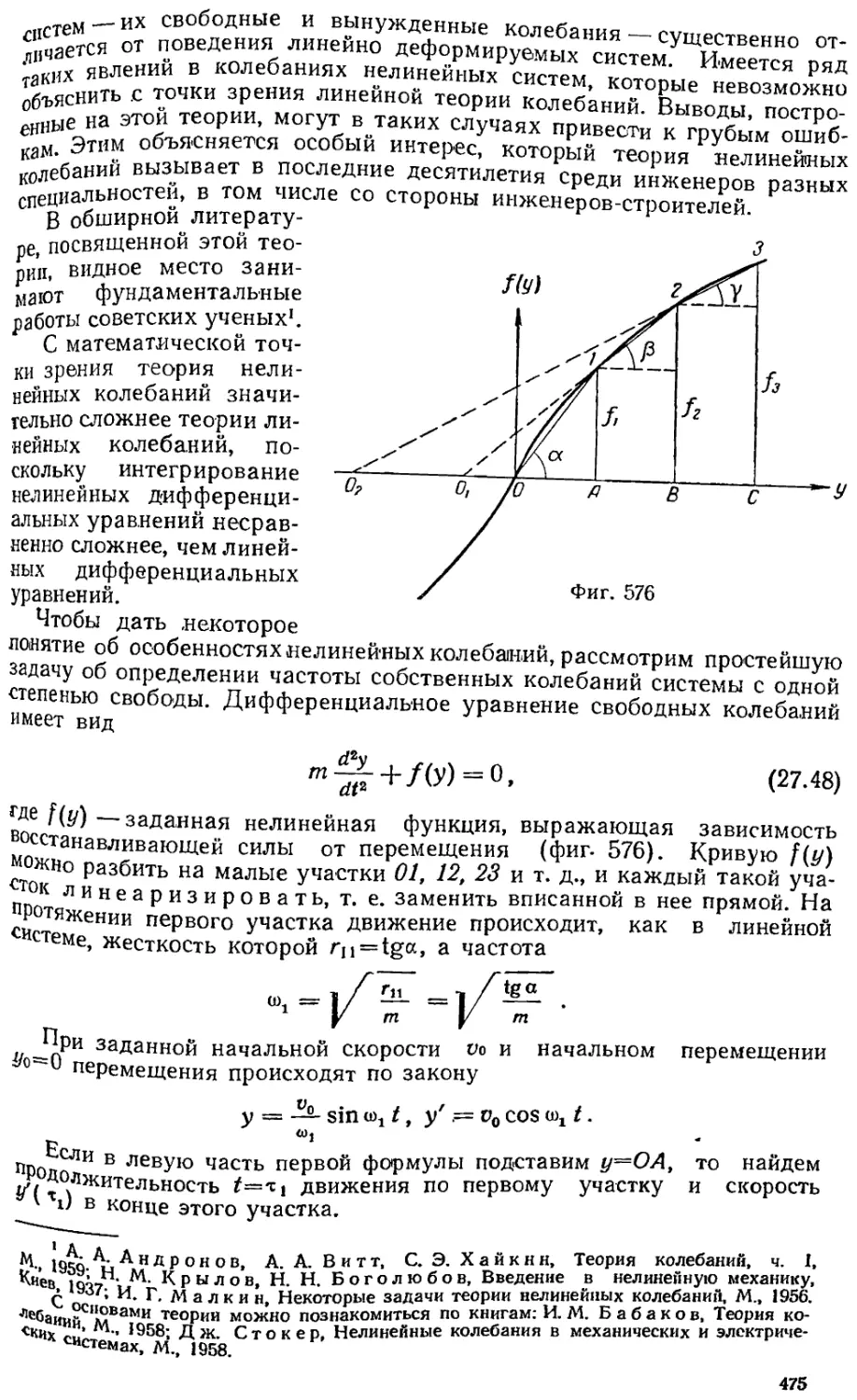
§ 27.19. О нелинейных колебаниях 474
Глава 28
Основы динамики систем с конечным или бесконечно большим числом
степеней свободы
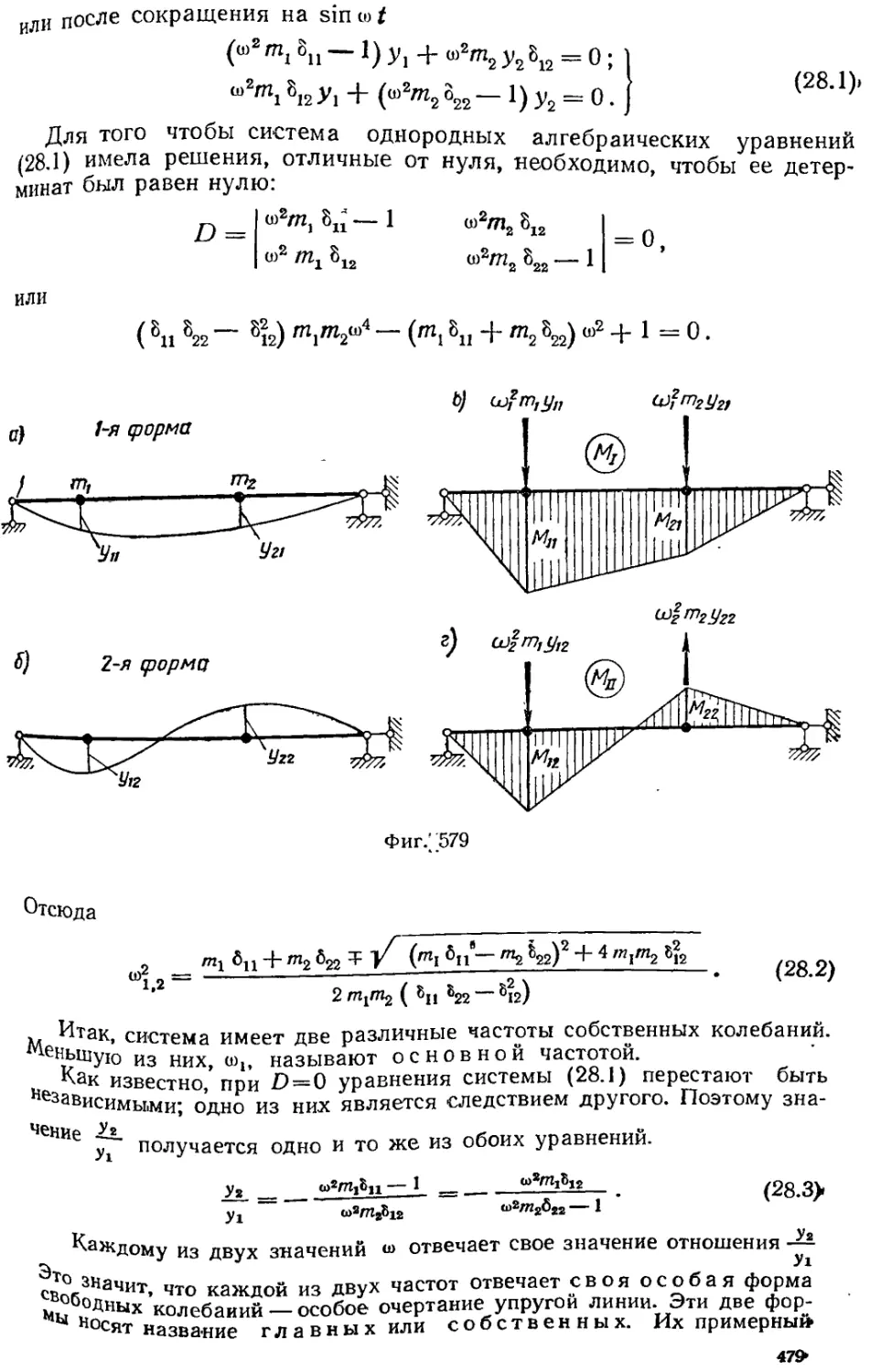
§ 28. 1. Колебания систем с несколькими степенями свободы 478
§ 28. 2. Разложение нагрузки на нормальные составляющие 481
§ 28, 3, Взаимность динамических перемещений 483
§ 28. 4. Понятие о расчете сооружений на сейсмическое воздействие .... —
§ 28. 5. Свободные колебания балки как системы с бесконечным числом степеней
свободы 486
§ 28. 6. Особые свойства нормальных (гобственных) форм колебаний .... 489
§ 28. 7. Вынужденные перемещения 490
§ 28. 8. Действие вибрационной нагрузки 492
§ 28. 9. Понятие о динамическом действии подвижной нагрузки 495
§ 28.10, Краткие исторические данные 499
Глава 29
Основы расчета подпорных стенок
§ 29. 1. Общие соображения 500
§ 29. 2. Теория Кулона - !!!!......! —
§ 29. 3. Теоремы Ребхана и графическое построение Понселе . , 503
§ 29. 4. Формулы давления земли на стенку 507
! ^^' I' -^"^гР^мма полных давлений и диаграмма интенсивности давления . . 508
§ 29. 6. Влияние временной нагрузки 510
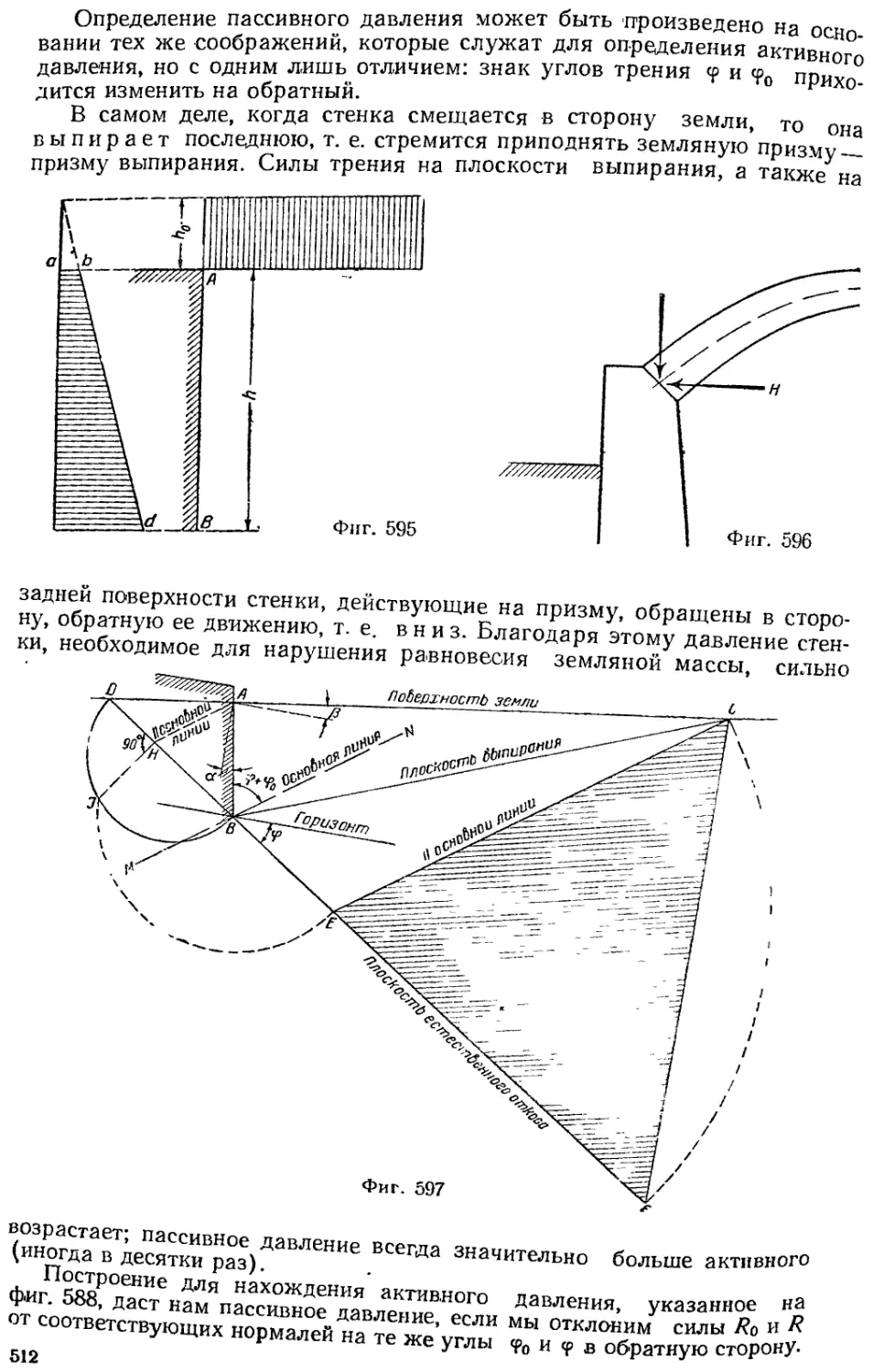
§ 29. 7. Пассивное давление (отпор) земли ,,......[,.. 511
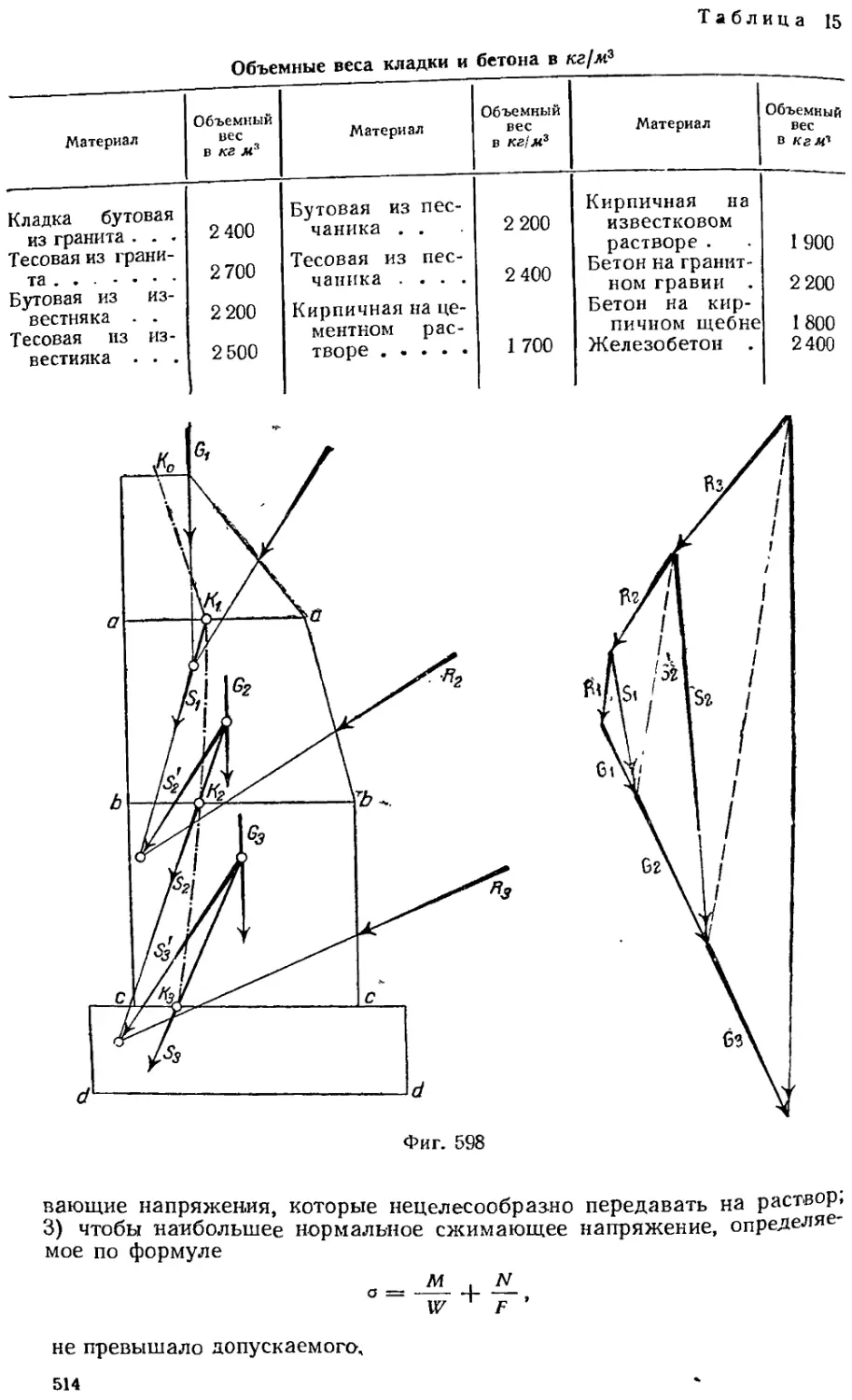
§ ^. 8. Расчет подпорной стенки на прочность . . ' 513
1 9Q'in п^''''^'' ''''^"''" "^ опрокидывание и на скольжение 516
1 9Q 11 Л''"'''''^^ ° ^^-"^^ "^о^^иой теории давления земли на подпорные стенки . . 517
S ^У 11- Краткие исторические данные 519
от АВТОРА
Настоящий учебник соответствует программе инженерно-строительных
вузов и содержит основы расчета статически определимых и статически
неопределимых стержневых систем на статическую и динамическую на-
грузки и на устойчивость, а также основы приближенного расчета под-
порных стенок. По сравнению со вторым изданием внесены небольшие
дополнения в различные параграфы, добавлена глава о расчете балки на
сплошном упругом основании и значительно расширен раздел динамики
сооружений.
Стремясь сделать учебник компактным, автор сохранил лишь тот
материал, который в основном отвечает учебным программам инженерно-
строительных вузов. В связи с этим полезно обратить внимание учащих-
ся на вышедшее в 1950 и 1954 гг. 2-е издание более полного, двухтомного,
курса того же автора. В этом издании интересующиеся найдут более
подробные исторические обзоры развития различных проблем строитель-
ной механики, а также изложение некоторых вопросов, выходящих за
пределы обязательной программы.
Выражаю свою благодарность рецензентам — кафедре Киевского
инженерно-строительного института, возглавляемой проф. Д. В. Вайн-
брергом, и профессорам Д. В. Бычкову, Г. К. Клейну и В. Г. Рекачу за
сделанные ими полезные замечания.
Глава 1
ВВЕДЕНИЕ
§ 1.1. ПРЕДМЕТ И ЗАДАЧИ СТРОИТЕЛЬНОЙ МЕХАНИКИ
Строительной механикой в широком смысле следует называть науку,
которая занимается разработкой принципов и методов расчета сооруже-
ний на прочность, устойчивость и жесткость.
Цель расчета проектируемых новых сооружений на прочностьи
устойчивость состоит в том, чтобы обеспечить достаточную, но не
излишнюю безопасность этих сооружений и таким образом сочетать их
долговечность с экономичностью. Цель р асчета на жесткость
состоит в устранении возможности появления значительных деформа-
ций сооружения (прогибов, осадок и вибраций), хотя бы и безопасных
для самого сооружения, но неприемлемых с эксплуатационной точки
зрения.
Расчетом приходится пользоваться не только при проектировании
новых сооружений, но и во всех тех случаях, когда существующее
сооружение должно подвергнуться действию новых, не предусмотренных
ранее нагрузок. Расчет должен выяснить, в какой степени эти нагрузки
допустимы, требуется ли произвести усиление сооружения и какое
именно.
Значение строительной механики в современной строительной науке
очень велико. Никакое сколько-нибудь ответственное сооружение не мо-
жет быть спроектировано надежно и экономично без помощи расчета.
Чем сложнее и крупнее сооружение, тем большее значение для сохране-
ния жизни людей и для сбережения средств и материалов имеет расчет,
производимый методами строительной механики. Расчет как бы обна-
жает перед взором проектировщика все статические и динамические си-
лы, передающиеся элементам сооружения, и позволяет подобрать такие
размеры этих элементов, при которых напряжения в материале будут
иметь продиктованные проектировщиком величины.
В СССР, где жилищное, промышленное и транспортное строительство
приняло невиданные в мире размеры и где в безопасности и экономич-
ности сооружений заинтересовано все население, строительная механика
выполняет важную и почетную задачу.
Было бы опасным заблуждением смотреть на строительную механи-
ку как на чисто математическую дисциплину. Поскольку она имеет дело
с прочностью и жесткостью реальных сооружений, сделанных из тех или
иных строительных материалов, ее выводы должны быть основаны на
изучении и познании действительных свойств этих материалов, т. е. на
соотв^;гствующим образом поставленных экспериментах.
15
, поляагы поверяться все допущения, касающиеся самих
Тем же путем ^-^^ „жительные свойства, которыми мы наделяе^
конструкции все "Р^-^^^^^твующих методов расчета,
их при выработке сои „^ опытной поверки, теория может претен-
Только пройдя чен
довать на Д0Е^Р*!1^„ика экспериментального определения усилий и де.
Современная те« ^ „^делях сооружений и в самих сооружениях
формации, ^°™усо1<ого уровня, и это является могущественным под!
достигла весьм^^^^ механики.
спорьем для строит ^^^^ относится к строительной механике в
Все, что зде'-'» и ^^^ ^^-^ ^ совокупности дисциплин, занимающихся
широком смысле ^^^;^^^„^ расчетом сооружений. Такими дисципли-
"^"'','^^ляются сопротивление материалов, теория упру.
гпЛи теория пластичности, строительная механика
« V4K0M и общеупотребительном смысле слова Первая из них занима-
Ртгя по поемуществу теорией расчета простого бруса и является дисцип-
линой одинаково важной как для строительных конструкции, так и для
машиностроения. Строительная механика в узком смысле слова в отли-
чие от сопротивления материалов занимается по преимуществу теорией
расчета системы брусьев или стержней, образующих сооружение. Обе
эти дисциплины стремятся решать свои задачи, пользуясь главным обра-
зом сравнительно простыми математическими методами. В отличие от
них теория упругости выдвигает на первый план возможно большую
строгость и точность своих выводов и поэтому вынуждена при-
бегать к значительно более сложному математическому аппарату. Сле-
дует добавить что теории упругости и пластичности занимаются задача-
ми, интересующими не только строительство, но и ряд других областей
техники.
Строительная механика в узком смысле этого слова иначе называется
еще теорией сооружений.
В дальнейшем мы для краткости будем пользоваться термином
«строительная механика» только в узком, ограниченном смысле слова,
не делая различия между ним и термином «теория сооружений».
Свою книгу мы назвали «Строительной механикой стержневых си-
стем», так как расчетом этих систем в настоящее время в основном опре-
деляется содержание курсов теории сооружений.
Та же наука в течение долгого времени называлась, а некоторыми
авторами и до сях пор называется «статикой сооружений» или
«графической статикой сооружений».
Последнее название совершенно не отвечает действительному содер-
жанию этой науки, так как аналитические методы играют в ней не
нне?.™"^"" Р°'"''' ""^"^ г-рафические. Устарелым является также назва-
mcnnnZJ'^^^'^^''''''''' ""^^ «^^' помимо статики, в современной тео-
ии сооружении видное место отводится и вопросам динамики.
§ 1.2. ПОНЯТИЕ О РАСЧЕТНОЙ СХЕМЕ СООРУЖЕНИИ
ранЙ^Ге^еГствитель^пг]?^^""'' представляет собой упрощенное изоб-
та вместо соГруж1ния ''''"РУ*^"^^' 0"а фигурирует в процессе расче-
Стремясь дать инж^илг.»..
ственно применяться ня^п1^ ™™^ решения, которые могли бы непосреД-
прибегать к упрощению ™i^™^.^' строительная механика вынуждена
ряда сравнительно мене^ря^^^""^^^^''' отказываться от учета целого
схемами вместо точного опй™я^оГр°^?к°енйй°"'Р'''°'''' ' расчетным»
Приведем пример расчетной схемы.
Стальное пролетное строение моста балочной системы состоит
обычно из двух вертикальных ферм, соединенных между собой поололь
ными н поперечными связями и проезжей частью. Последняя состоит ич
поперечных балок, приваренных своими концами к главным фепмам
продольных балок, приваренных к поперечным, и ездового полотна того
или иного устройства, опирающегося на балочную клетку проезжей части
Металлические стержни, образую-
щие каждую ферму, жестко скреп-
лены между собой своими концами.
Примерный вид такого пролетного
строения показан на фиг. 1 в пер-
спективе.
Фиг. 1
При расчете таких пролетных строений на вертикальную нагрузку
обычно отказываются от рассмотрения всей системы как пространствен-
ной, а распределяют нагрузку между обеими фермами по закону рычага
и рассматривают каждую из нпх как самостоятельную систему. Дефор-
мациями связей и проезжей части, а также некоторыми усилиями, кото-
рые эти элементы передают главным фермам, пренебрегают. Каждый
стержень фермы заменяется его геометрической осью; все эти оси счи-
таются расположенными строго в одной плоскости. Стержни, образующие
узел фермы, считаются сходящимися своими концами строго в одной
точке — в центре узла. Взаимное соединение стержней предполагается
идеально шарнирным. Внешние силы считаются приложенными строго в
плоскости полученной идеальной фигуры. Неподвижные и подвижная
опоры считаются идеально шарнирными; силы трения игнорируются.
v-овокупность Bcejc этих допущений н составляет характеристику рас-
четноивчжемын и полетного строения.
17
§ 13.
КЛАССИФИКАЦИЯ РАСЧЕТНЫХ СХЕМ СООРУЖЕНИЙ
^ ^^тткнпй механике мы будем оперировать только расчет*
^ ''Гх7м а м и сооружений, но для краткости терминологии будем
по^^Гзоваться термином <<сооружение>>, не оговаривая этого каждый раз
""^""классификация сооружений с точки зрен-ия их расчета может стро-
^Т г™о'мПТи'" ^^^^^^^ пространственной точки зре-
ния можно различать три типа сооружении:
1) сооружения, составленные из стержней, т. е. из таких элементов,
V которых один размер (длина) значительно превышает два других;
^ ^ такие сооружения мы будем называть
И стержневыми; частным случаем стерж-
I. невой системы является один стержень;
2) сооружения, составленные из та-
ких элементов, у которых размеры по
двум направлениям (длина и ширина)
^^ "* значительно превосходят размер по
третьему направлению (толщину); та-
^^^' кие элементы носят название пласти-
нок, плит и оболочек;
3) сооружения, у которых все три размера одного и того же порядка;
их можно назвать массивами, сплошными средами или
просто телами.
Классификация расчетных схем по этому признаку весьма важна,
так как указанные три типа сильно различаются между собой по харак-
теру расчета. В настоящем курсе будут рассматриваться почти исклю-
чительно стержневые системы.
Стержневые системы в свою очередь разделяются на плоские и прост-
ранственные. Плоской называется такая система, в которой оси всех
стержней (включая опорные) и линии действия внешних сил лежат в
одной плоскости; пространственной — такая, в которой это усло-
вие не соблюдено.
С кинематической точки зрения системы разбиваются на:
1) геометрически н е и 3 м е н я е м ы е и неподвижные, имеющие лишь
необходимое для обеспечения неизменяемости и неподвижности
число кинематических связей; 2) геометрически неизменяемые
и неподвижные, имеющие сверх необходимых связей то или иное
количество л и ш н и х; 3) геометрически изменяемые.
Геометрически неизменяемой называется такая система, в которой
изменение формы обусловливается лишь деформацией материала. Ина-
че говоря, геометрически неизменяемой называется такая система, кото-
и^мрЛ?^'^'' сделана из абсолютно жесткого материала, не могла бы
изменять своей формы.
coo^Z^^r^^'"''''^ признак имеет важное значение, так как в качестве
й^^яемк^Г^та "Р«^^«яться только системы первых двух типов
междГсо6пТ?п ™ "^^ ^Р^^^ ^^^ ^"^ ^РУ""Ь1 серьезно различаются
с\очТ™^Т''^ статическим свойствам и по характеру расчета-
элементен п^--'''' характера в з а и м н о го с о е д и н ения
единениями^!^^^^ сооружения: 1) с ша рнирн ы ми со-
нирован^ьте В оас^Г"^^" "^ ^ соединениями и 3) комби-
шарнир (цилиндрический tM^ схемах плоских стержневых сооружении
допускающее тoп^^^^^^^ шарнир) рассматривается как устройство,
У ющее только взаимный поворот двух стержней около осИ.
перпендикулярной их плоскости и проходящей через центр шарнира
Силы трения в шарнире считаются равными нулю. Примером стержневых
систем с жестким соединением элементов может служить рама (фиг. 2);
примером комбинированной системы —шпренгельная балка (фиг.* 3)!
Способ взаимного соединения элементов отражается на характере рабо-
ты сооружения и влияет на метод расчета.
С точки зрения направления опорных реакций
сооружения могут быть безраспорными и распорными.
^^^
Фиг. 3
К первому типу относятся такие сооружения, в которых вертикальная
нагрузка вызывает исключительно вертикальные опорные реакции, ко
второму типу относятся все остальные сооружения. Характерное для
распорных систем наличие горизонтальной составляющей опорных реак*
ций существенно влияет на работу как самих систем, так и их опор.
§ 1.4. КЛАССИФИКАЦИЯ ОПОР ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
Эти опоры допускают то или иное движение только в плоскости
системы и могут быть трех типов.
К Шарнирная подвижная опора. На фиг. 4 показан пример конструк-
ции подвижной опоры металлического пролетного строения. Пролетное
строение шарнирно свя-
зано с верхней подуш-
кой а, которая опирает-
ся на цилиндрические
катки 6; последние мо-
гут кататься в пло-
скости фермы по ниж-
ней подушке, имеющей
цилиндрическую или
плоскую поверхность,
но не могут скользить
вдоль своей образую-
щей (перпендикулярно
плоскости фермы).
Конструктивное осу-
ществление такой опо-
ры может быть весьма
разнообразным, но
расчетная схема ее все-
гда может быть изобра-
жена так, как показа-
но на фиг. 5. С кинематической точки зрения такая опора характеризу-
ется тем, что она не препятствует ни повороту системы в ее плоскости, ни
ее поступательному перемещению в направлении, параллельном прямой
MN, а устраняет лишь возможность поступательного перемещения по
нормали к этой прямой.
К тому же типу относится устройство, показанное на фиг. 6, где пад-
^^^Р^мш (щетема снабжена подушкой CD, которая может кататься и cf ""^
Фиг. 4
.ить без трения по неподвижному профилю EF, Опорная реакция всегда
прохоЙт ч^^^^ касания А и направлена по общей нормали к обеим
^^^""^^'нематические и статические свойства подвижной шарнирной опо^
п^т МОГУТ быть представлены моделью фиг. 7, а именно так называемым
рымо1у1иг,1 ^ ^ опорным стержнем АВ,
лежащим в плоскости системы и
перпендикулярным опорной пря-
мой MN (фиг. 5).
Такой стержень допускает
поворот системы вокруг шарнира
А и поступательное перемещение
по окружности, описанной из цен-
тра В радиусом ВА. Но бесконеч-
но малый элемент окружности
Фиг. 5 может рассматриваться как пря-
мая. С другой стороны, такое piso-
браженрш опоры удобно тем, что оно одновременно показывает направ-
ление и положение опорной реакции: последняя направлена по оси АВ,
Фиг. 6
Щ
F
Фиг. 7
Опорная реакция содержит лишь одну неизвестную--величину реак-
' 2. ШаршрГ»Г\°еГд!"^^'Р^"^^^^^ ^«««^ °-Р-м стерж^е'м.
вижная опора. Она допу-
скает только поворот си-
стемы около неподвижной
оси, перпендикулярной
плоскости системы. На
фиг. 8 показан пример
конструкции такой опоры
для металлической колон-
ны . Схематическое изоб-
ражение такой опоры
представлено на фиг. 9 а
^ кинематической и ста-
^;!;!^™й^^^^ек зрения она
вполне характеризуется
фиг. 9,а и б. Опорная ре
акция проходит через точ-
ку л и содержит две со-
Фиг. 8
ставляю '^ * ^^^ со-
onopHbuS"5eSS?;!!!'SocSeSr""^' что и символизируется двумя
ся в точке А. носителями этих двух реакций, пересекающими-
1952. стЙб"" ^-^^Релецкнй. Д.
20
- I еняев и др.. Стальные констрз^кции.
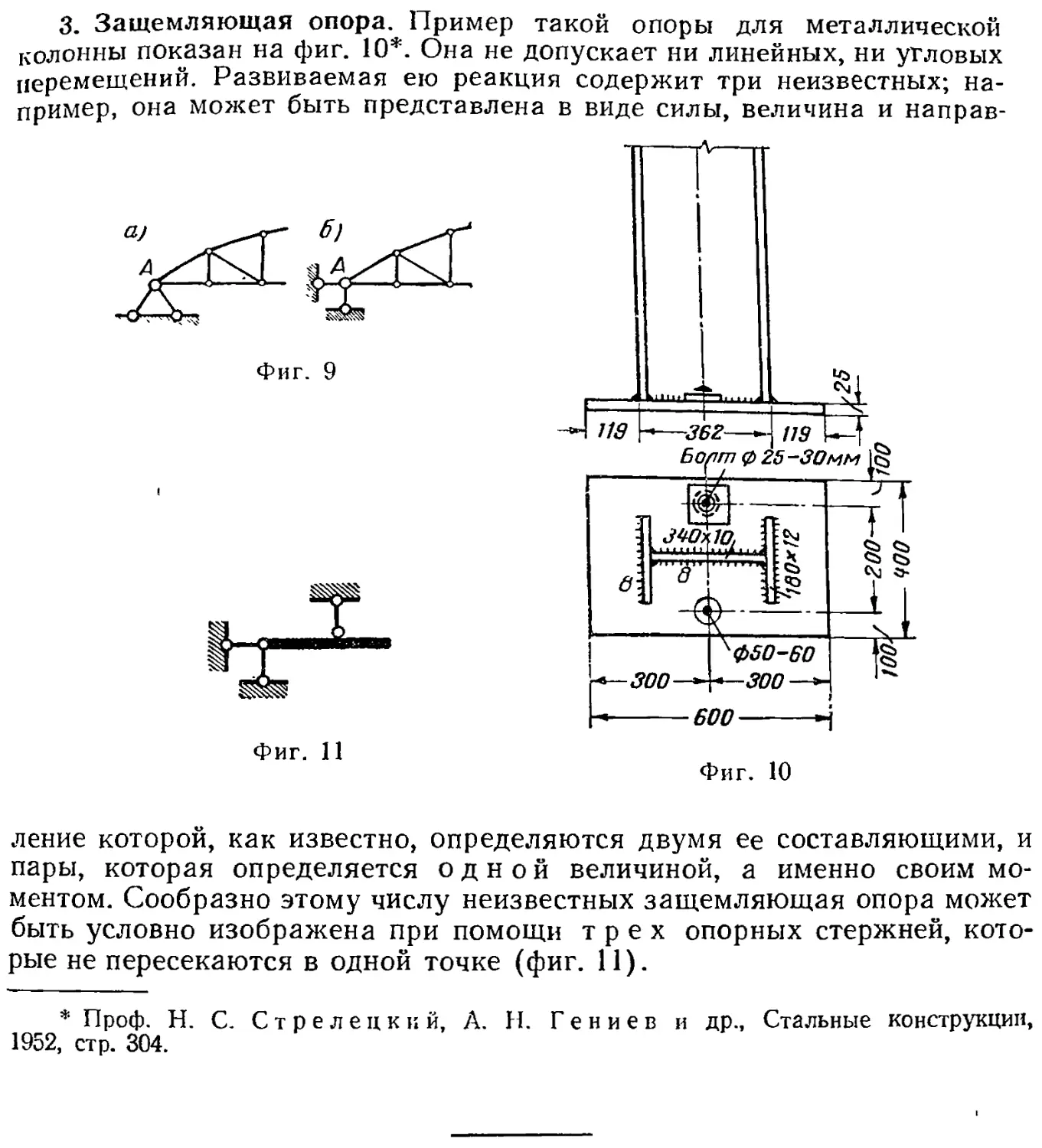
3. Защемляющая опора. Пример такой опоры для металлической
колонны показан на фиг. 10*. СЗна не допускает ни лршейных, ни угловых
перемещений. Развиваемая ею реакция содержит три неизвестных; на-
пример, она может быть представлена в вР1де силы, величина и направ-
Фиг. 9
Фиг. II
Фиг. 10
ление которой, как известно, определяются двумя ее составляющими, и
пары, которая определяется одной величиной, а именно своим мо-
ментом. Сообразно этому числу неизвестных защемляющая опора может
быть условно изображена при помощи трех опорных стержней, кото-
рые не пересекаются в одной точке (фиг. 11).
* Проф. Н. С- Стрелецкий, А. И. Гениев и др.. Стальные конструкции,
1952, стр. 304.
Глава 2
КИНЕМАТИЧЕСКИЙ АНАЛИЗ СООРУЖЕНИЙ
§ 2Л. СТЕПЕНЬ СВОБОДЫ ПЛОСКОЙ КИНЕМАТИЧЕСКОЙ ЦЕПИ,
СОСТАВЛЕННОЙ ИЗ ДИСКОВ
Степенью свободы какого-нибудь тела или системы тел называется
количество независимых геометрических параметров, определяющих
положение тела или системы.
Фиг. 12
Фиг. 13
Ограничимся здесь рассмотрением плоского движения.
Положение подвижной точки в плоскости определяется двумя ее
координатами относргтельно произвольной неподвижной системы коор-
динат в той же плоскости. Следовательно, точка обладает в плоскости
двумя степенями свободы.
Положение плоской фигуры в ее плоскости определяется тремя не-
завр1ср1мыми переменными, например: двумя координатами х, у какой-
нибудь точки А и углом наклона ср какой-либо прямой АВ (фиг. 12).
Переместившись так, что эти три независимые переменные приобре-
тут новые значения х^ Уи ?ь фигура займет снова вполне определенное
положение. Отсюда следует, что плоская фигура имеет в своей плоскости
три степени свободы.
Степень свободы фигуры может быть стеснена какими-нибудь пре-
пятствиями, которые уменьшают количество независимых параметров
движения. Всякое устройство, уничтожающее одну степень свободы,
рассматривается как одна кинематическая ев я з ь. Если какое-
jiHGo устройство уничтожает несколько степеней свободы, то оно рас-
сматривается как соответствующее количество связей.
22
Цилиндрический шарнир с неподвижной геометрической осью вокпуг
которой фигура может вращаться, эквивалентен двум связям Действи
тельно, при наличии такого шарнира точка А (фиг. 13) теряет две степени
свободы, и единственным независимым параметром движения системы
остается угол фЧ
Расчетные схемы многих сооружений имеют вид кинематических це-
пей, составленных из отдельных геометрически неизменяемых плоских
звеньев, или, как их называют, дисков (фиг. 14). Эти диски связаны
друг с другом шарнирами, а с неподвижным звеном (с землей) —опор-
Фиг. 14
ными стержнями. Степень свободы такой фигуры можно определить сле-
дующим простым способом: сначала подсчитать общее число степеней
свободы, предполагая, что никаких связей нет; затем подсчитать
число связей, налагаемое на движение системы всеми шарнирами и опор-
ными стержнями; наконец, из первого числа вычесть второе.
Пусть, например, число дисков равно Ц\ число шарниров связываю-
щих эти диски друг с другом, равно Ш, число опорных стержней —
Со (Сопор). Так как диск, ничем не стесненный в своем движении, имеет
в плоскости три степени свободы, то общее число степеней свободы при
игнорировании связей составило бы ЗД. Каждый шарнир эквивалентен
двум связям, а опорный стержень— одной связи, следовательно, полное
число связей равно 2Ш + Со, Отсюда число лишних связей системы
Л - — И^ - Со + 2ZZ/ - ЗД, (2.1)
где W — степень свободы.
Могут встретиться иногда такие цепи, в которых несколько шарни-
роц насажено на одну ось. Такой шарнир следует рассматривать как
несколько шарниров, так как он стесняет взаимное движение не-
сколькР1Х дисков. *Мы будем называть его кратным шарниром.
Так, например, шарнир А (фиг. 15), связывающий между собой три
звена, следует рассматривать как сдвоенный шарнир. Вообще шарнир,
связывающий п звеньев, играет роль п—1 простых шарниров. На фиг. 16
схема а изображает двойной шарнир, а схемы б и в —одиночные. Шар-
нир типа схемы а иногда называют пол ным, а шарниры типов ^ и ^~
неполными; в последних некоторые стержни связаны между собой
жестко. Для правильного применения формул (2.1) и (2.2) следует пони-
мать в них под величинсй Ш приведенное число шарниров, т. е.
эквивалеетное число простых шарниров.
* Предполагается, что фигура не может скользить вдоль оси шарнира перпенднй^^-
лярно плоскости чертежа; в противном случае она совершала бы пространственное дви-
жеще с /шумя степенями свободы.
1|
"^^
Фиг. 15
а)
6)
в)
Т
Фиг. 16
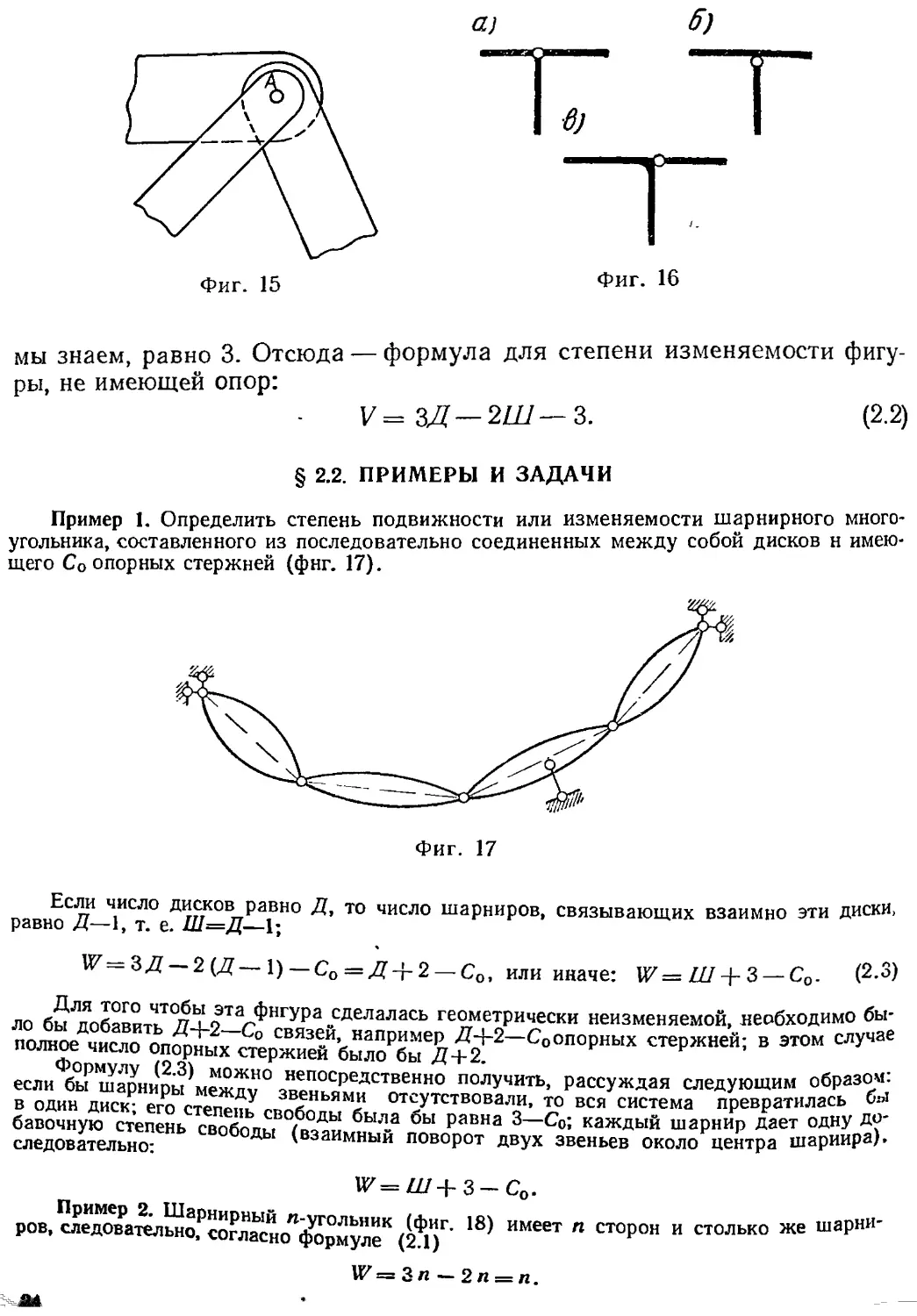
мы знаем, равно 3. Отсюда — формула для степени изменяемости фигу-
ры, не имеющей опор:
У=ЪД — 2Ш—Ъ, (2.2)
§ 2.2. ПРИМЕРЫ И ЗАДАЧИ
Пример I. Определить степень подвижности или изменяемости шарнирного много-
угольника, составленного из последовательно соединенных между собой дисков н имею-
щего Со опорных стержней (фнг. 17).
Фиг. 17
Если число дисков равно Д, то число шарниров, связывающих взаимно эти диски,
равно Л—1, т. е. Ш^Д—1;
Г=ЗД-2(Д_1)_Со=Д4-2-Со. или иначе: W=in + Z-Co. (2-3)
ло б?^по6явптГ°771Г^*"'^Р^Я^^^^''ь геометрически неизменяемой, необходимо бы-
по^^г'^ТЦ^х-5^рГи1ГбыГбТ^:?^^^^ ^-р--«=« ^-" '"^"^
если бы" шарни№?^межпг ° "1"?,?^^"°^""° "олучить, рассуждая следующим образом:
в один диск- его ст1п^"^..1«< отсутствовали, то вся система превратилась бы
следовательно: ^^°^'^' (взаимный поворот двух звеньев около центра шарнира).
W=UJ+3-Co.
poB.^S4iSfcSKo"ffy!Jr(2*r)'"' '^^ "*'^^^ " "°Р°" " "'"""'° "^^ '"^''""'
lf'=3n-2n = n.
Лпя того чтобы сделать эту фигуру .неподвижной и неизменяемой, необходимо до-
г в\1тъ п связей и в том числе — не менее трех опорных стержней, например: поместить
я каждом узле или на каждом диске по одному опорному стержню.
Степень изменяемости фиг. 18: V=n—3; для того чтобы сделать эту фигуру неиз-
меняемой, не заботясь о ее неподвижности, следует внести п—3 внутренних связей, на-
пример: из одной вершины провести все п—3 диагонали.
В
Фиг. 18
Фиг. 19
в С
D Е
-о
х^^
F
Фиг. 20
Фиг. 21
Фиг. 22
Фиг. 23
Пример 3. Трехшарнирная рама (фиг. 19) состоит из двух дисков: Д=2, Я/=1.
Со =4, поэтому
1^=3.2-2.1—4 = 0,
т. е. фигура неподвижна и неизменяема.
Пример 4. Система (фиг. 20) состоит из трех балок, соединенных двумя шарнирами,
и имеет пять опорных стержней: Д=3, Я/=2, Со =5, следовательно, по формуле (2.1)
Л=:5 + 2.2-.3.3 = 0.
25
... можно получить по формуле (2.3).
Тот же результат можно п у . о ^ О
л. . 7 Подсчитать степень подвижности систем, изображенных на
Задачи № 5—/. иод^-чид
фиг. 21—23.
ТЕПЕНЬ СВОБОДЫ ШАРНИРНО-СТЕРЖНЕВОЙ ПЛОСКОЙ СИСТЕМЫ
^ 'лд /^vnPM пассматривать здесь такие системы, у которых звенья шар-
Мы ^y^^P^f^^v собой, причем каждое звено содержит только два
нирно связаны ме д> ^ ^^^^^^у Степень свободы таких систем можно
шарнира (простыл п ^^^^^3^,^^ по формулам, которые даны выше, но
для них можно вывести и другие, более удобные
формулы.
Примем центры шарниров за отдельные точ-
ки, могущие перемещаться в плоскости. Число
таких точек, или узлов, обозначим через У
(от слова «узел»); число звеньев или стержней ~~
через С; число опорных стержней — Q.
Если бы узлы не были взаимно связаны при
помощи звеньев, то каждый из них имел бы две
степени свободы, и суммарная степень свободы
равнялась бы 2У. Каждый жесткий стержень,
соединяющий две точки А и В (рис. 24), эквива-
лентен одной связи, так как налагает на коорди-
Фиг. 24 наты этих точек единственное условие — сохра-
нение постоянного расстояния между последни-
ми. Полное число связей составляет С + Со. Следовательно, количество
избыточных, или лишних, связей сверх необходимого минимума
Л = — IF = С+ Со — 2У. (2.4)
Если система имеет лишь необходимое для обеспечения неподвиж-
ности и неизменяемости число связей, то JI=W=0.
Если мы отделим систему от ее опор, т. е. откинем все опорные стерж-
ни, то степень свободы, очевидно, увеличится на Со и будет равна
W-^-Cq, Известно, что диск имеет в своей плоскости три степени свободы.
Следовательно, в том случае, когда система, отделенная от своих опор,
представляет собой геометрически неизменяемую фигуру, мы должны
получить И^+Со = 3 или W+C^ —3 = 0.
Введем обозначение
отлр^Рт^пГ.^^'Р^'^^^^ степень геометрической изменяемости системы,
viTZ 11^^ ''"'^Р- "Р" ^^^ ™^^^^^ представляет' собой диск; при
V -1 она имеет одну степень изменяемости и т д
в сиЕГот^.Т/''''^''^^''^ неизменяемости и отсутствия.лишних связей
системе, отделенной от ее опор, имеет вид 1/-Сили
2У —С = 3. (2.5)
§ 2.4. ПРИМЕРЫ И ЗАДАЧИ
""Srr^^^^^^^^ ""^'^ ^=^^' К==2.7-^11^3=0, седо-
эта си^ем^з 1^е^Г,Г..1^^^, 'ДрЙ^' ^='^' ^^2-10-20_3=.~3. следовахельно.
Фиг. 25
Фиг. 26
§ 2.5. ПРИНЦИПЫ ОБРАЗОВАНИЯ ГЕОМЕТРИЧЕСКИ
НЕИЗМЕНЯЕМЫХ ПЛОСКИХ СИСТЕМ
Указанные выше соотношения между числом стержней и узлов или
числом дисков, шарниров и опорных стержней являются необходимыми,
но недостаточными характеристиками числа степеней свободы системы.
^5^$^
Фиг. 27
Фиг. 28
Так, Например, системы (фиг. 27 и 28) имеют одинаковое число дис-
ков, шарниров и опорных стержней: Л=2, Ш=\, Со =4, следовательно,
по формуле (2.1)
1^=3.2—2.1 — 4 = 0;
между тем сразу видно, что первая система действительно геометрически
неизменяема и неподвижна, вторая имеет в левой части лишний опорный
стержень, а в правой части — одну степень свободы. Другой пример пока-
зан на фиг. 29 и 30: обе системы имеют одинаковое количество стержней
и Шарниров, но, в то время как первая геометрически неизменяема и
неподвижна, вторая имеет в одной панели лишний стержень, а в дру-
гой — одну степень свободы.
Подсчет числа стержней, дисков, шарниров и т. д. является операцией
весьма важной, в особенности в тех случаях, когда изучаемая система
более или менее сложна. Однако| эта операция недостаточна; она должна
быть дополнена анализом геометрической структуры
сооружения. Этот анализ состоит в рассмотрении самого расположения
связей системы, в установлении порядка сочетаний элементов. Ограни-
чимся рассмотрением простейших законов образования геометрически
неизменяемых систем.
27
J. к двум дискам / и 2, связанным общим шарниром Л, присоединен
при помощи двух шарниров BvlC диск 3, причем прямая ВС не проходит
через точку Л (фиг. 31).
2. К геометрически неизменяемой системе (диску) ВС шарнирно пои
соединяется' новый узел Л при помощи двух стержней так, что три шарни-
Фиг. 29
Фиг/31
Фиг, 32
Фиг, 33
себ^ н^а пр^актшГб'^л^ьшГпп^Р™"** ^Ф'^^" ^^^^ ^^«^ способ, находящий
способа, указанного в п I "Р""^«е««^. «е отличается по существу от
пересеЙЬтТяТоХй'™^ ^Р^^^ стержнями, оси которых не
няе^ст^'шарТ^™ риТоТп^^^^^^^^ *"'^Р^' «"^'«Щей одну степень изме-
Х^~^^^^^^^^^^ ^ - иТпТин1д=т кХТи
при!::::::: ^"^^^^ -—.^«0^ с.р.кх.рь.
7аЙийГ^ ^У«"- фип?5ТаГкПяг'°';°" геометрической струк-
nOTOMvT"^ три опорных стержня нЛ?"^^^''''^^""''^'"''°^°" диск, опи-
нПвv^,a . "^"адвижна. Балка S?fnnrj'^''^''^'°"^''^'^"s одной точке, а
?тепжня Г°Р''""" стержнями в T04K?vpP^%^"^ "" неподвижному зве-
mSoLZF"^^ ^''••"•^^ CD. Ит1к ОИСГ.5 "" ^'' Р^'""^ третьего опорного
необходимый минимум связей ' ""^"^^ неподвижна и имеет лишь
^
в с
D Е
F
X
Фиг. 36
Фиг. 37
[Фиг. 38
Фиг. 39
® ®
¦>-у^'"/Г/"/7/'.^Л'/'>/'^7
Фиг, 40
Фиг Я6 представляет собой пример фермы с несложной структурой.
Чя основной простейший элемент можно принять треугольник 1-2-3.
За 0'^"°''"°^^"'' „„я двумя стержнями (диадой) точка 4. следовательно,
К нему nPf Р1"/1"5_Угеометрически неизменяема. К этой фигуре при:
креплена новая точка 5 опять диадой, затем таким же способом-точ-
""^ Ст"оуктуру этой системы можно представить себе иначе, например
гак дЕе геометрически неизменяемые части 1-2-8-7 и 9-10-17-18
^¦Жиг 37) образованные вышеуказанным способом, соединены друг с
другом тремя стержнями 8—10, 7—9 и 8—9, не пересекающимися в одной
точке
Фиг 38 имеет следующую структуру: к двум неподвижным точкам
Л и С прикреплена двумя стержнями точка В. затем к образовавшейся
неподвижной фигуре прикреплены точки D и ? —каждая при помощи
диады. Балка FH притянута вертикальными стержнями к неподвижным
точкам А В и ? и имеет сверх того три опорных стержня по концам.
Следовательно, балка FH имеет всего шесть опорных стержней; не будь
в ней среднего шарнира, число лишних опорных стержней равнялось бы
трем; благодаря этому (двойному) шарниру оно снижается до двух.
Структуру фиг. 39, имеющей большое количество стержней, можно
представить себе следующим образом (фиг. 40): заштрихованные дис-
ки 1, 2, 3 шарнирно связаны между собой и опираются на три опорных
стержня в точках Л и А Если бы других связей не было, то такая кине-
матическая цепь имела бы две степени свободы. К этой системе присое-
диняется двумя стержнями точка Е и двумя — точка F; от этого степень
свободы не изменяется. Наконец, устанавливаются опорные стержни
(стойки) ЕВ и FC, вследствие чего система теряет имевшиеся у нее две
степени свободы.
§ 2.7. МГНОВЕННО ИЗМЕНЯЕМЫЕ СИСТЕМЫ
Если мы в геометрически неизменяемой системе будем изменять дли-
ну тех или иных стержней, то получим ряд систем, имеющих одну и ту
же структуру, но отличающихся между собой длиной и наклоном стерж-
ней. Все эти системы можно
^\ рассматривать как вариации
^ ^ одной и той же системы. Вооб-
'л*^^_^ ^ 1 ^ ^^ говоря, они также будут
^У^?^ TV>^ геометрически неизменяемыми.
^^ ч ^ф Существуют, однако, такие ва-
I ^С риации, которые обладают
свойством геометрической из-
^^^' меняемости; но стоит только
___^^„^о изменить длину одного из
рып^ГЛ^^' " система снова станет геометрически неизменяемой. Такие
ctZ^u^I'^^'^^^''^''^^''''^ которых было замечено еще в 1837 г., автор на-
ва™Т1?г^поГо "Р^^-^о^ил называть «мгновенно изменяемыми». Это наз-
cnSLuT^^^^^^^ ''^''' ""^ "Р" непрерывном варьировании формы
мГпаоам^т^ппГ"Р^Р^^ изменении какогоч1ибудь из ее геометри-
о^^^=о;.Л1^^^^^^^ при каком-нибудь
опортыхТе5няЖГ4П%г^''""''"" ^^"""^ ^^' опирающейся на три
меняемая. /В том 4с?ном h?LV""^''^' «^'«««^0. неподвижная и неиз-
стержня прохоТитнР^^° случае, когда продолжение правого опорного
ржня проходит через точку А (фиг. 42), система становится мгновен- ,
В''
но изменяемой. Это доказывается следующим образом: если мы разъ-
единим стержни в точке В, то правый конец стержня АВ сможет переме-
ститься по окружности У, а левый конец стержня CD — по окружности 2
Но эти окружности на фиг. 42 имеют общую касательную, следователь-
но,—общин бесконечно малый элемент. Поэтому соединение обоих
стержней в точке В не по-
мешает бесконечно малому
перемещению общей точки j
В, Иная картина получает-
ся на фиг. 41: окружности /
и ^ не имеют общей каса-
тельной, поэтому Одновре-
менное бесконечно малое
перемещение общей точки В
по обеим окружностям не-
возможно.
По той же причине жесткий диск, опирающийся на три опорных
стержня, пересекающихся между собой в одной точке (фиг. 43), всегда
будет обладать мгновенной подвижностью. Пример такой мгновенно
изменяемой системы показан на фиг. 44, где роль наклонных опорных
Фиг. 42
Фиг. 43
Фиг. 44
стержней для среднего диска АВС играют полуарки DA и ЕС, а пря-
мые DA и ЕС пересекаются в одной точке со средним опорным
стержнем.
Диск, опирающийся на три параллельных стержня, также обладает
мгновенной подвижностью, так как эти стержни можно считать пересе-
кающимися в одной, хотя и бесконечно удаленной, точке.
Хотя мгновенно изменяемые системы, теоретически говоря, имеют
лишь бесконечно малую подвижность, фактически их перемещения, вы-
зываемые нагрузкой, оказываются настолько резко повышенными по
сравнению с перемещениями обычных геометрически неизменяемых си-
стем, что применение их в качестве строительных сооружений недопу-
стимо.
Следует избегать также систем, близких к ним («почти мгновенно
изменяемых»).
Мгновенная изменяемость такой системы, которай имеет необходимое
число связей и по своей структуре является в общем случае геометри-
чески неизменяемой, может быть обнаружена различными способами,
основанными на статических или кинематических соображениях^
Мы вернемся к этому вопросу при рассмотрении теории ферм (§ 7.4).
Здесь ограничимся следующим'указанием: мгновенно изменяемая сис-
* И. М. Рабинович, Кинематичесжий метод в строительной механике, М.. 1928^
^^- 173—226,
31
. onu пРЙствии произвольной нагрузки не находится в состоянии рав-
~;ГпСому Ура^внения статики для такой ^системы не удовлетворяв
^тсГ ИначГговоря^^ при действии произвольной конечно^г нагрузки уси^
^Ja гистемы определяемые из уравнении статики, принимают бесконечно
^1шмачения. Только при некоторых специально подобранных на-
™i^x значения усилий становятся неопределенными. Появление уси-
яий павных бесконечности или неопределенных, и служит характер.
ным признаком мгновенно изменяемой системы.
Например в системе (фиг. 41) при действии произвольной нагрузки
реакция стержня ВС будет возрастать по мере приближения направле-
ния ВС к направлению ВА и обратится в бесконечность, когда эти два
направления сольются.
§ 2.8. ПОРЯДОК КИНЕМАТИЧЕСКОГО АНАЛИЗА СИСТЕМ
При анализе схем сооружений можно рекомендовать придерживаться
следующего порядка: сначала по формулам, данным в § 2.1—2.3, подсчи-
тать степень свободы системы, затем разобраться в ее геометрической
структуре. Если окажется, что система .имеет геометрически неизменяе-
мую структуру и iHe содержит лишних связей, она в общем случае
статически определима; однако необходимо еще произвести последнюю
поверку, а именно: убедиться в том, что она не является мгновенно
изменяемой.
Если система несложна, то можно обойтись без первого этапа и пря-
мо начать с анализа ее структуры.
Глава 3
ГРАФИЧЕСКИЕ МЕТОДЫ СТРОИТЕЛЬНОЙ МЕХАНИКИ
И ВЕРЕВОЧНЫЙ МНОГОУГОЛЬНИК
§ ЗЛ. РОЛЬ ГРАФИЧЕСКОГО МЕТОДА В СТРОИТЕЛЬНОЙ МЕХАНИКЕ
При решении задач строительной механики графический метод при-
меняется либо для изображения результатов, полученных вычисли-
тельным путем, либо для нахождения этих результатов.
Уже столь скромная операция, как перевод полученной окончатель-
ной формулы на графический язык, часто имеет для инженерных расче-
тов важное значение, так как позволяет придать решению осязательную
и наглядную форму. График позволяет сразу обозреть найденный резуль-
тат, увидать скрытую в нем закономерность и обратить особое внимание
на наиболее характерные точки или участки.
График облегчает не только понимание и запоминание результатов,
ноиконтроль их, так как сомнительные места на графике несравненно
резче бросаются в глаза, чем в числовой таблице.
Во многих задачах строительной механики графический метод вычис
лений применяется не только для изображения окончательных резуль-
татов, а значительно шире и играет роль ocHvo.BHoro, т. е. он вводится
в действие не 'в конце процесса решения задачи, а значительно раньше.
Его достоинство в этом случае часто состоит не только в наглядности
получаемого решен'ия, но и в простоте самих операций, а также в
удобном и наглядном контроле, что особенно важно для пра1ктики.
Наиболее удачные графические решения некоторых задач, получившие
широкое применение в строительной механике, отличаются замечатель-
ным изящ;еством и простотой.
Суш^ествует предрассудок, будто графические построения отличаются
недостаточной точностью; в действительности же при тш;ательном вы^
полнении чертежа точность получается обычно вполне достаточной
(1-2%).
Существенным недостатком графического решен-ия по сравнению с
аналитическим является то, что оно в большинстве случаев относится
к определенному частному случаю, к определенным значениям всех па-
раметров задачи; при изменении величины какого-нибудь параметра
требуется произвести построение наново. Поэтому для получения общих
выводов, для отыскания общих законов или исследования влияния раз-
личных параметров этот метод в большинстве случаев менее пригоден,
чем аналитический.
3 и. М. Рабинович 33
в совремевной строительной механике оба метода играют крупную
роль, и вопрос о применении того или иного из них решается каждый
раз в зависимости от характера задачи.
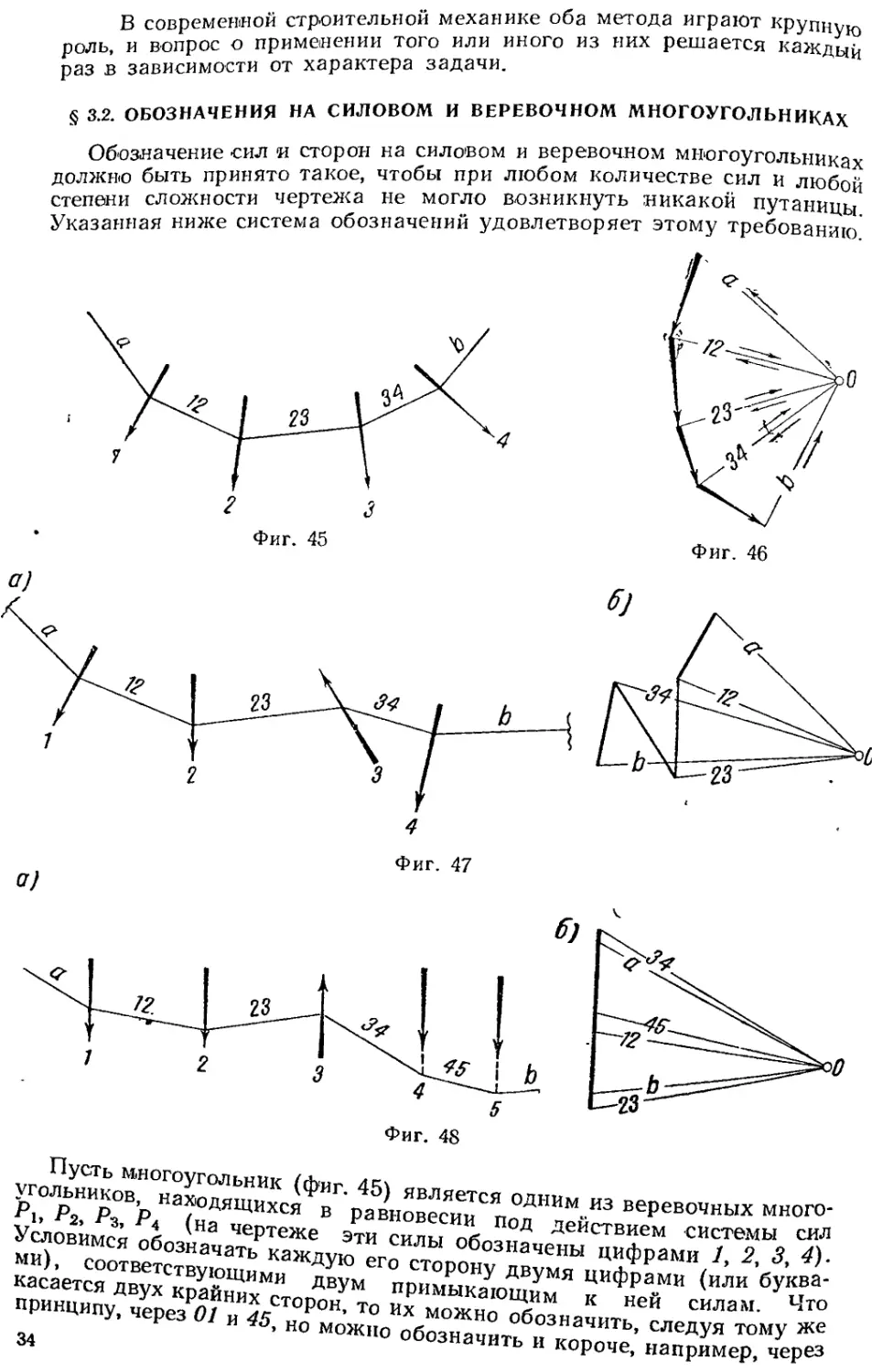
§ 3.2. ОБОЗНАЧЕНИЯ НА СИЛОВОМ И ВЕРЕВОЧНОМ МНОГОУГОЛЬНИКАХ
Обозначение сил и сторон на силовом и веревочном многоугольниках
должню быть принято такое, чтобы при любом количестве сил и любой
степени сложности чертежа не могло возникнуть никакой путаницы
Указанная ниже система обозначений удовлетворяет этому требованию
О)
Фиг. 47
уго|^оП^^^ веревочных мно^-
У^ошис/Л <«^ чертеже эти силы пй.Г'^ ^^""вием системы сил
ми) соответг'"^''^'''' •^««ДУЮ его cTODofrv"''"" ДИфрами /. 2, 3, 4).
касается пвух^^У'5>Щ«^«и Двумпп1ХУ/^У'«« Цифрами (или буква-
принц„%:ГреЖП5"°Р-- ^° «' мТжнТГозначитГ^' ^"^^" '''''
an b. Таким же образом будем обозначать усилия в соответствующих
сторонах силового многоугольника (фиг, 46).
На веревочном многоугольнике линия действия каждой силы отме-
чается цифрой (или буквой), а стороны веревочного многоугольника —
двумя цифрами (или буквами). Здесь картина получается вполне ясной.
^У
^;
Фиг. 49
Большую трудность М.ОГЛО бы представить разыскание внешних сил на
силовом многоугольнике, где картина более компактная и где парал-
лельные силы противоположных направлений покрывают друг друга.
В этом случае, стрелки
или номера, поставленные
на самих силах, мало по-
могают делу. При указан-
ной двойной нумерации
лучей первая сила на
силовом многоугольнике
оказывается расположен-
ной между лучом а и лу-
чом 12; последняя (п-я)
сила располагается меж-
ду лучом (п—\)п и лу-
чом Ь; любая промежу-
точная сила — между те-
ми двумя лучами, на
которых повторяется ее
номер. При этом сила на-
правлена от луча с мень-
шим номером к лучу с
большим номером.
На фиг. 47 и 48 по-
казаны веревочные и си-
ловые многоугольники,
снабженные такими обозначениями. Читателю нетрудно будет убедить-
ся в том, что никаких неясностей при этом способе обозначений не
возникаете
На фиг. 49 показаны силовой и веревочный многоугольники, по-
строенные для той же системы сил, что и на фиг. 48, но при измененной
нумерации сил,
* Возможны и другие способы обозначений, например обозначение каждого луча
одной цифрой или буквой; при этом каждая сила располагается между двумя луча-
ми, из которых одни содержит ее номер.
3* 35
Фиг. 50
«DUMFHEHHE ВЕРЕВОЧНОГО МНОГОУГОЛЬНИКА
ДЛЯ опрдавния сттичЕСКИх МОМЕНТОВ ПЛОСКОЙ СИСТЕМЫ сил
л.,с^г.« найти статический момент заданной системы сил
Пусть требуется найти с^^^^ ^ „^.оекости (фиг. 50).
относительно какой у^^^^^^ крайних сторон веревочного многоуголь-
ника'проведем равнодействующую R и из точки А опустим на нее пер-
ника проведем V ^^^^^ ^^ абсолютной -величине выразится формулой
пендикуляр^ .^^^^ ^ берется из силового многоугольника, а плечо
г^.ич весевочного многоугольника. При изменении положения точки А
плечо г вообще говоря, изменяется. Оно остается постоянным только
тпгпа когда точка А перемещается параллельно силе R. ^
Определение моментов по этой формуле при всей своей простоте ока-
зывается неудобным, когда требуется графически изобразить закон из-
менения момента М^ при всевозможных положениях точки А на пло-
скости. Кульман в своей «Графической статике» (1866 г.) указал более
удобный прием. Проведем через точку А параллель к вектору силы R
и отрезок ее, заключенный между сторонами а и 6 веревочного мвого-
угольника, обозначим через у. Треугольник CDE, образованный этими
сторонами и отрезком у, подобен треугольнику, заключенному на сило-
вом многоугольнике между векторами а, Ь, R. Из подобия получаем
-^ = -^ , или i?r = Ну,
г Н
откуда
М^ = Ну, (3.1)
те Н — (Полюсное расстояние вектора R,
Иначе, момент силы R относительно любой точки А плоскости равен
произведению полюсного расстояния Н на отрезок у, отсекаемый сторо-
нами а и Ъ веревочного многоугольника на прямой, параллельной R и
проходящей через точку А.
Для того чтобы получить наглядную картину зависимости статических
моментов от положения точки Л, достаточно заштриховать часть плоско-
сти, заключенную между сторонами а и 6, штрихами, параллельными R-
Так как полюсное расстояние Н остается постоянным, то моменты .про-
порциональны длинам отрезков у.
Если требуется найти статический момент не всех сил, а, например,
только сил / и 2, то вместо сторон а и b придется считать крайними
сторожами прямые а я 23, а вместо прежнего направления штриховки
придется брать новые, а именно параллельно равнодействующей сил i
и ^. ьсли речь идет о статическом моменте одной силы, например силы^,
то роль крайних сторон играют смежные с ней стороны 12 и 23, а штри-^
ховка проводится параллельно этой силе.
RPTP'l^mJf'^ статических моментов сил, расположенных слева от соот-
ветствующих моментных точек, показан на фиг 51
стоп,отТ!!.^^оГ^^^^' 'Отрезки у, расположенные «а фиг, 50 по разные
TpZhL? тГм^'"'^''^' ^ соответствующего угла (справа и слева от этой
П Гвпопк !.f *" Р^^""^'^ ^"^™' ^^«"и ^ одном из углов направление от
обратную JUX'^'no^ ''''^^ ^"'Р^' ^^ ^ ^РУ^^^ о«0' очевидно, идет в
достатовд^^ь?^^; "•^^''о^У Д'"^ получения знака статических моментов
чтоие™во S^^^ ^""^ ''''^ какого-нибудь о дн о го отрезка У^
СтатачГскм^^^^^^ мысленно через вершину С силу R.
этические моменты, выражаемые формулой
могут измеряться, как уже указывалось выше, непосредственно отрез-
ками f/. При этом получается -некоторый условный масштаб, зависящий
от того масштаба длин, который принят при вычерчивании веревочного
многоугольника, а также от масштаба сил на силовом многоугольнике
и от величины полюсного расстояния Я.
Пусть для веревочного многоугольника принят масштаб длин 1 : п.,
а для силового многоугольника — масштаб сил: 1 см = т кг; полюсное
Фиг. 51
расстояние на силовом многоугольнике выражается отрезком длиной
Н см.
При этих условиях масштаб отрезков у как измерителей статического
Момента будет:
\сл1 =^ тпН кгсм. . (3.2)
Действительно, множитель п см представляет собой натуральную
длину, соответствующую на чертеже отрезку ^==1 см, а произведение
тН кг представляет собой силу, выражаемую на силовом многоуголь-
нике отрезком Я.
При помощи формулы (3.2) можно не только определять масштаб
моментов при заданных величинах т, м, Я, но и, наоборот, подбирать
эти величины так, чтобы получать желательный масштаб.
§ 3.4. ПОСТРОЕНИЕ ЭПЮР М И Q ПРИ УЗЛОВОЙ ПЕРЕДАЧЕ НАГРУЗКИ
Схематическое изображение узловой передачи нагрузки показано
На фиг, 52. Нагрузка приложена к вспомогательным продольным балоч-
кам, опоры которых расположены в сечениях А, С, D, ?, В главной
балки Л В. Таким образом, при любом расположении нагрузки главная
балка воспринимает давления только в указанных, вполне определен-
Ш
V г точки зрения статики существо дела состоит здесь в
ных сечен11ях.> точки н^^^^^^.. ^^ продольную вспомогательную ба-
том, что любой грУ>^. А составляющие, приложенные по ее К01щам, „
лочку. Р-'^Д^.^Т.^ощие передаются на балку АВ.
уже эти сосгавляющие ^^^ ^^^^. g^^^^ „ вообще в неизменяемой фи-
-"""""".ГпmeS на три-опорных стержня, замена непосредственной
гуре. опирающейся ^^i^^^^„ ^^^^^^^^ ^^ отражается на опорных реак-
"^о''/ЛРнств.ггельно. сумма моментов или проекции двух составляющих
циях Деиствшель • J проекции самой силы.
'''°?як же ле'гко доказывается, что в узловых сечениях балки изгибаю-
Lp«TbT останутся бе зизменения. Например, при непосредственном
^аГруженГ^^но^чи^ что в сечении D (фиг. 52) изгибающий мо-
мент создается левой реакцией и силой /, а при узловой передаче-
10\\ же реакцией и двумя составляющими, на которые разложилась
сила /.
Фиг. 52
Отсюда получается простое правило построения веревочного много-
угольника и эпюры изгибающих моментов для параллельных сил:
сначала строится замк/нутый веревочный много-
угольник для нагрузки, приложенной непосредст-
венно, затем «а стороны этого многоугольника про-
ектируются узловые точки, после чего проекции
соединяются прямыми. Последняя операция основана на том,
что в промежутке между двумя силами веревочный многоугольник дол-
жен иметь вид прямой линии.
На фиг. 52 многоугольник, соответствующий узловой нагрузке, за-
штрихован. Чтобы получить давления, передающиеся на главную балку
в узловых точках, нужно провести на силовом многоугольнике дополни-
¦1ельные лучи, параллельные сторонам окончательного веревочного мно-
гоугольника. *^
§ 3.5. ПОСТРОЕНИЕ ЭПЮР М И Q ДЛЯ МНОГОПРОЛЕТНЫХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ БАЛОК
чисто nSofpTnT™''^'^'''' определимые балки могут иметь любое
ки дГжны имет!' " ^f ^° """Р""-'^ стержней равно п. где п>3. то бал-
Можно ?о бы noLc?^''"'^^™''""^ шарниров, равное п-3.
стему в однопролетныр^^Г" шарниры на опЪрах, т. е. превратить си-
V^^^^^nbLtX^^ninST^'T''^^'''''^ ^^•"™- Значительно более
нию их «аибо^ших |нп™я„й ^^'^"^"^' моментов, ведущее к сниже-
специально выбранных гГрТГж^^^ГхТечеЕ^яГ""'""''' "'''""'^' '
38
Оди<н из возможных примеров таких балок схематически изображен
на фиг. 53. Мы имеем здесь три балки, которые соединены шарнирами
в сечениях С и и п опираются на пять опорных стержней. Левая опирает-
ся на три опорных стержня, а потому неподвижна. Правая имеет два
вертикальных опорных стержня, которые устраняют возможность вер-
тикальных перемещений; роль горизонтального опорного стержня играет
балка CD. Итак, система неподвижна и не имеет лишних связей. Такая
система отличается весьма рациональным распределением изгибающих
wr I
т
-^ I
4
Ь2 1
L4U-J—\-4к-\ U,
^
^
^^
%f.
1 t
.i!k
-щш^
^пюра М
шшшщ\^т
%
дпюра О
•1Ш
lllllllllllllll
т
\Шт
Ш
1!111111111!11!;!1111
Фиг. 53
моментов и поперечных сил, а потому обладает высокой экономичностью;
она носит название балки Гербера, но правильнее будет называть ее
бал'Кой Семиколено-ва — по имени инж. Г. С. Семиколенова (19/III
1845—26/XII 1912 ст. ст.), который в 1871 г. дал полную теорию их
расчета.
Важно разобраться в том, какая часть системы является основной
и какая на нее опирается. Основными являются в данном случае две
крайние балки: если хотя бы одна из них обрушится, то обрушится и
средняя балка. Наоборот, обрушение средней балки не повлечет за собой
выхода из строя двух крайних; они смогут самостоятельно воспринимать
вертикальную нагрузку. Ниже, в главе 5, § 5.5, будет строго доказано,
что в статически определимой системе нагрузка, приложнная к основной
части, не вызывает усилий в частях, опирающихся на нее.
Мы можем подойти к системе (фиг. 53) с другой точки зрения и
доказать, что она статически определима. Для того чтобы можно было
Определить все усилия, необходимо и достаточно найти ее пять опорных
реакций. Но, кроме трех обычных уравнений равновесия всей системы
в целом, мы можем написать два дополнительных, приравняв нулю
изгибающие моменты в сечениях С и D, Таким образом мы получим
пять существенно различных (не вытекающих одно из другого) з'равне-
иий, из которых определятся все пять реакций.
39
г^пмртоической неизменяемости и статической опре-
Убедившись в геометр графическим построением реакций и эпюп
делимости »стемь, заимемо, гр Ф ^^^^^ ^^^^^^^ ^ ^ ^ ^ ^^ ^Р^
Разрежем -^ь.^^"'"^^'^"^^^^ для «агруаок. расиоложе^Гх
три оиловых и веревочных.шю^^^^ ^^ ^^ ^ ^^ расположим где угодно
"^ ^''^^т'^Г условием, чтобы все три полюсные расстояния были равнь
с тем лишь условием, соответствует веревочный мсногоугольнак
между ^_боиПервом^У^У-«^^^^^ трехьему-УоТ
75-5Р Так как опорные реакции неизвестны, то и положения замы-
кающих 11.12, 10.11 и 9.10 неизвестны.
Если бы стержни АВ, BE и EG представляли собой простые балки,
имеющие шарниры лишь на опорах А, В я Е, то замыкающие .следовало
бы провести так, чтобы в этих сечениях изгибающие моменты равня-
лись нулю: например, для пролета BE замыкающая 10.11 совпала бы с
пунктирной линией, показаннюй на фиг. 53. На самом же деле в сече-
ниях ВпЕ приложены какие-то (неизвестные моменты, которые вызывают
в пролете ВЕ дополнительную эпюру прямолинейного вида и тем
самым смещают замыкающую 10.11. Величины этих опорных моментов
должны быть подобраны так, чтобы суммарные изгибающие моменты
в сечендях С я D обратились в иуль. Их можно было бы найти, соста-
вив и решив два уравнения с двумя неизвестными.
Веревочный многоугольник позволяет обойтись без аналитического
решения уравнений. Достаточно провести замыкающую 10.11 так, как
показано иа фиг. 53 сплошной линией, т. е. так, чтобы она пересекла
веревочный многоугольник в точках, которые служат проекциями шар-
ниров С и D. Замыкающая 11.12 смыкается одним концом с 10.11, что-
бы обеспечить на опоре В найденный изгибающий момент, а на другом
конце отмечает момент, равный нулю. Сторона 9.10 своими концами
смыкается с 10.11 и 8.9. Проведением этих трех замыкающих заканчи-
вается построение эпюры моментов, причем эта операция выполйша,
несмотря на то, что ни одна из опорных реакций еще не найдена.
Для нахождения реакций достаточно провести на силовых много-
угольниках лучи, параллельные трем замыкающим. Для большей ясно-
сти эти реакции выделены стрелками. Реакция 10 состоит из двух частей:
между лучами 9.10 и 10.7 заключена та ее часть, которая возникает в
балке EG, а между лучами 6.10 и 10.11— часть, соответствующая балке
]о?. Аналогичное можно сказать о реакции И.
Эпюра Q легко получается из силовых многоугольников, где любая
ее ордината уже содержится в готовом виде.
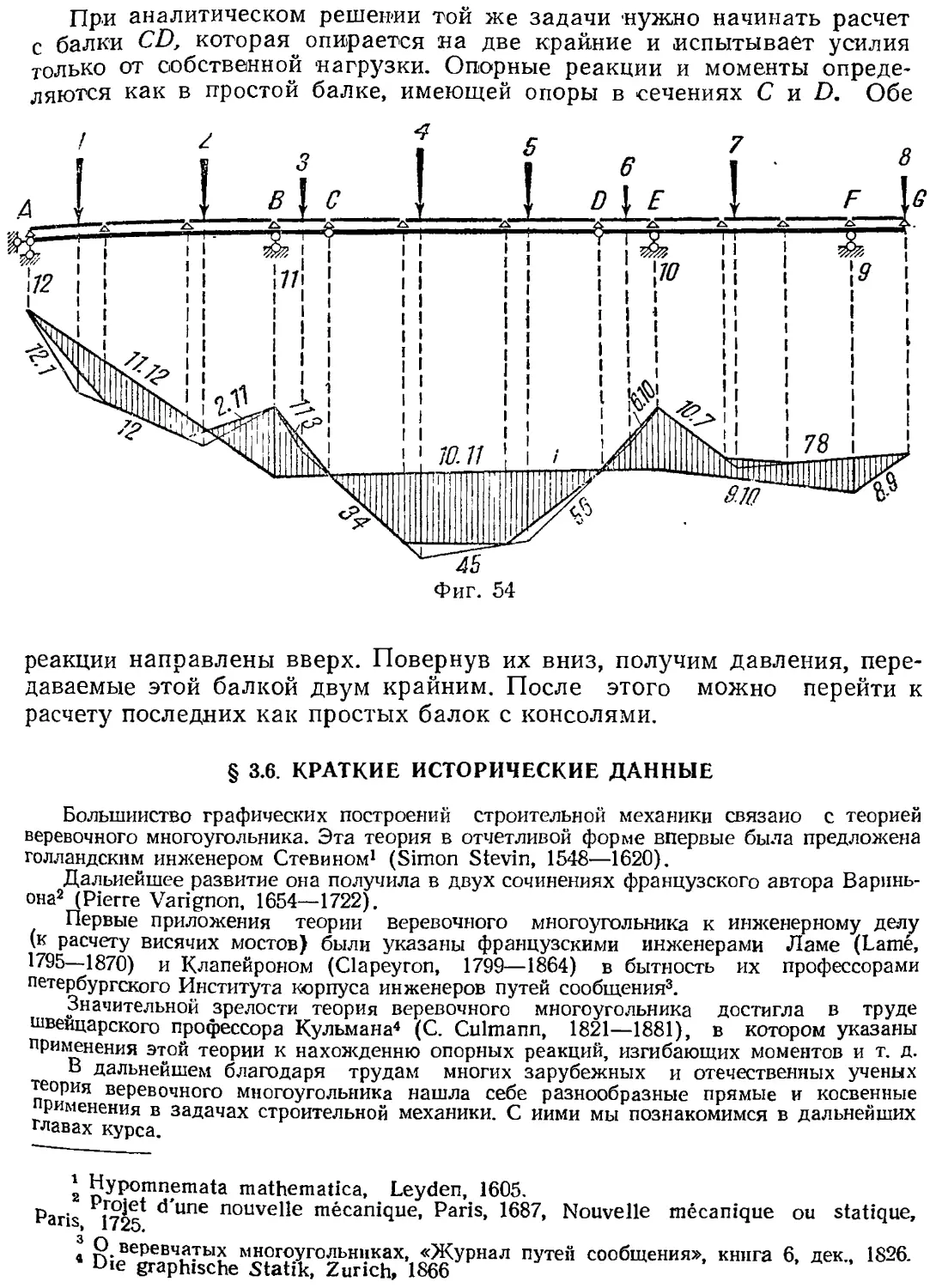
Обых^^?,^^''-''^ ^^^ ^^ ^"«'Р "Ри узловой нагрузке,
что «^? ™.*'""^ сооружений с узловой передачей нагрузки таково,
узлов Такпйп^.,''"''^''^ " каждым шарниром располагается один из
на Фиг 53 In^^r^ ™''^?^'" «^ *«''• 54. которая отличается от балки
вой.^ В этих cnvLf ^^"''" непосредственной передачи нагрузки узло-
как для ппостп7ГГ ^-"^""^ У"'"^^"" нагрузки учитывается так же,
неповд?Сной пепе • Т"'"'^" "^'^"^^ ^"«>Р^ моментов, отвечаюшая
узль,, п^леТегГогт^^^ нагрузки, а затем на эпюру проектируются
В нзло^н;^ Jt, '^'^ВДинить полученные проекции прямыми.
следу,ощ„Тпункт- поГм"Г ''P^*«'^^^«o^^ построении требует пояснения
операция оправдала tpI'''"" ""Р" Различных полюсаГо.О,, О^. Такая
•грех точек позволяет более ^кГ'**''^^''^"* «ьгбор положения э-^
и в то же время о?вает си^гт.^? ^^^^Щать эпюру мо^^ентср Ма ««ff
^Ющизс при »ров*ет*и т.^1 '"'''^'^''^^ накапливание ощЛмс. iiS»
;Кш- куядеешвд параллельных лтвйй. --л..
При аналитическом решении той же задачи нужно начинать расчет
с балки CD, которая^ опирается на две крайние и испытывает усилия
только от собственной нагрузки. Опорные реакции и моменты опреде-
ляются как в простой балке, имеющей опоры в сечениях С п D, Обе
реакции направлены вверх. Повернув их вниз, получим давления, пере-
даваемые этой балкой двум крайним. После этого можно перейти к
расчету последних как простых балок с консолями.
§ 3.6. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Большинство графических построений строительной механики связано с теорией
веревочного многоугольника. Эта теория в отчетливой форме впервые была предложена
голландским инженером Стевином^ (Simon Stevin, 1548—1620),
Дальнейшее развитие она получила в двух сочинениях французского автора Варинь-
она2 (Pierre Varignon. 1654—1722).
Первые приложения теории веревочного многоугольника к инженерному делу
(к расчету висячих мостов) были указаны французскими инженерами Ламе (Lame,
1795—1870) и Клапейроном (Clapeyron, 1799—1864) в бытность их профессорами
петербургского Института корпуса инженеров путей сообщения^.
Значительной зрелости теория веревочного многоугольника достигла в труде
швейцарского профессора Кульмана^ (С. Culmann, 1821—1881), в котором указаны
применения этой теории к нахождению опорных реакций, изгибающих моментов и т. д.
В дальнейшем благодаря трудам многих зарубежных и отечественных ученых
теория веревочного многоугольника нашла себе разнообразные прямые и косвенные
применения в задачах строительной механики. С ними мы познакомимся в дальнейших
Главах курса.
^ Hypomnemata mathematica, Leyden, 1605,
Paris i7o^* d'une nouvelle mecanique, Paris, 1687, Nouvelle mecanique ou statique,
О веревчатых многоугольниках, «Журнал путей сообщения», книга 6, дек.. 1826.
Die graphische Statik, Zurich, 1866
Глава 4
ОБЩАЯ ТЕОРИЯ ЛИНИИ ВЛИЯНИЯ
И ПРИМЕРЫ ИХ ПРИМЕНЕНИЯ
§ 4Л. ПОНЯТИЕ О ЛИНИИ ВЛИЯНИЯ
гл .W.VT.MM часто приходится иметь дело с подвижной
При расчете сооружении ^acjo пр ^ .строения железнодо^
нагрузкой Р^^-^^^»^^,^.^;'^ на .нагрузку от нро-
рожных мостов и их опоры приходится р ^^д^щ^х поездов; мосты под
обыкновенную дорогу — на
движущиеся автомобили,
тракторы, орудия, повозки,
толпу и т. д.; подкрановые
балки — на нагрузку дви-
жущимся краном и т. д. Во
всех этих случаях нагрузка
состоит из системы парал-
лельных друг другу (чаще
всего — вертикальных) гру-
зов, между которыми сохра-
няются неизменные расстоя-
ния.
Простейшей из всех воз-
можных подвижных нагру-
зок является сосредоточен-
ная сила, равная единице, точка приложения которой перемещается по
сооружению, в то время как сама сила сохраняет неизменное направлени^
График, выражающий закон изменения той или иной величины (^
пример, опорной реакции, изгибающего момента и т. д,), возникаюЩ
в определенном месте плоского сооружения, в функции от положен -^^
движущегося по сооружению сосредоточенного единичного груза, ^^^Р
няющего постоянное направление, носит название линии ^-^^^^^^J'^inyi
инфлюентной линии) соответствующей величины. Сокращенно мы буо '
писать иногда вместо «линия влияния» — «л. в,»^. ^^
Например, говорят: «линия влияния изгибающего мо-мента в данНО!
сечении, прогиба в данном сечеиии» и т. д.
Линия влияния возможна и в пространственной системе, когда точка приложен»
силы F^\ перемещается по линии.
42
Фиг. 55
Необходимо иметь отчетливое представление о том, что на этом
графике является независимой переменной и что—= функцией, что дви-
жется и что остается связанным с определенным, неподвижным местом
сооружения. Независимой переменной является координата движуще-
гося груза, функцией является изучаемая величина.
На фиг. 55 для примера показана лин-ия влияния угла -наклона уп-
ругой линии для сечен'ия С балки АВ. При движении груза Р= 1 по балке
этот угол наклона изменяется по закону, изображаемому ординатами
у этой кривой. Ординаты г/i, ^2, Уг и т. д. выражают собой угол наклона
упругой линии в одном и том же сечении С балки ЛВ^ но при раз-
личных положениях движущегося груза: ордината yi соответствует по-
ложению груза Р=1 над сечением /; ордината у2 — положению груза
над сечеН'Ием 2 и т. д.
Независимой переменной в уравнении линии вл-ияния является х —
абсцисса движущегося груза. Время t в уравнение не входит, так как
движение груза предполагается -настолько медленным, что последний в
любом своем положении может считаться неподвижным. Правильнее
было бы сказать, что линия влияния выражает собой влияние груза
не движущегося, а стоящего неподвижно, но точка прило-
жения которого может иметь любую абсциссу х.
Полез'но сравнить линии влияния с эпюрами. Под эпюрами изгибаю-
щих моментов, поперечных сил, прогибов и т. д. для какого-нибудь стерж-
ня понимаются, как известно, графики, изображающие закон изменения
соответствующих величин по всему пролету этого стержня при дей-
ствии заданной неподвижной нагрузки. Эпюра дает возможность
обозреть сразу распределение интересующей нас величины по всем
сечениям стержня, но только для одного, совершенно определенного,
положения заданной нагрузки. Как изменятся эти величины при каком-
нибудь ином расположении нагрузки, это из данной эпюры усмотреть
невозможно; для получения ответа на этот вопрос пришлось бы по-
строить новую эпюру.
Линия влия'ния, наоборот, дает возможность обозреть сразу закон
изменения какой-нибудь величины, относящейся к определенному сече-
нию стержня, при всевозможных положениях единичного груза. Однако
она ничего не говорит об изменениях аналогичной величины, относящей-
ся к другому сечению стержня.
Эпюра может быть построена при любом характере внешней нагрузки
Пр.и построении линии влияния предполагают, что имеется только груз
^=1. Мы увидим ниже, что понятие о линии влияния может быть
обобщено и на случай движущихся более сложных нагрузок, однако
основное значение имеют именно простейшие линии влияния, соответ-
ствующие силе Р= 1.
§ 4.2. СТАТИЧЕСКИЙ СПОСОБ ПОСТРОЕНИЯ ЛИНИЙ ВЛИЯНИЯ;
ЛИНИИ ВЛИЯНИЯ ДЛЯ ПРОСТОЙ БАЛКИ
Статический способ построения линии влияния состоит в том, что
тп^^. ^ ^^ устанавливается в произвольное положение, и абсцисса его
^очки приложения в произвольно выбранной системе координат обозна-
чается какой-либо буквой, например х. Считая груз неподвижным, опре-
солр^^ ^'^^^^^^У^^ величину, которая выразится некоторой формулой,
U ^^^^^^^" букву д:. Для того чтобы полученная формула превратилась
уравиенне линии влияния, необходимо только считать в ней значение
^ "ере^ейным.
? - 43
уравнение. Линия '^''"'"' Поясним сказанное примерами,
имеющих различные уравнения, иоя^^^^ ^ ^ ^ ^^^^^ ^ф^^ ^^ ^^
Линии влияния о no^PH^^^^F^ ^^ ^^^^„ ^„рри Напишем уравнение
ставим груз f—i нч F моментов всех сил сначала
т^яРтся необходимым ставить груз поочередно на не-
Иногда оказывается « ^ ^^„ каждого из них выводить особое
скольких различных у состоит из различных участков,
уравнение. Линия влияния в э^ ^j^^^^ сказанное примерами.
м уравнение
моментов всех сил сначала
относительно опоры В, а по-
том относительно опоры А,
считая, что реакции направ-
лены вверх:
А1—Р{1 — х)=^0;
В1 — Рх = 0.
Из этих уравнений най-
дем
1 — х I — X
А = Р-
I
I
В=Р—^
(4Л)
Фиг, 56
Каждое из уравнений
(4.1) содержит переменную
X в первой степени, а потому является уравнением прямой.
Для построения этих прямых достаточно найти «а каждой из hfx
по две точки. При л:=0 получается Л=1, В = 0; при х = 1 получается
Л=0, В=1. Обе прямые построены на фиг. 56. Каждая из них показы-
рг;
р»;
Р^7
L-x —L—X —4^
r~ri——^
цщцш^
--^^^^гггттгШТТТГШТ1[Ш1Т1
Фиг, 57
гтои-гГ° Р^^^'^"^' ™и ИЛИ ИНОЙ опоры paBtia единице, когда груз F=l
да rnv^ nnl^« " опорой. И уменьшается по линейному закону до нуля, ког-
да груз приближается к противоположной опоре J' « ->
иойбГлки^Гл!!/'^71''ы°\°Р"<:^'' реакций для двухконсоль-
жешя силы Д* , Л- "^ Ф""- ^^ показаны различные возможные поло-
вой onoDbi чРпГ, v "^''™ по-прежнему расстояния этой силы до ле-
прежние nni V^ ' **" получим снова формулы (4.1) и. следовательно.
оп™Ц'„'сса^х'^р; '"''^Р"" "Р^Г^"^*^" продолжать слева и справа от
V ло^цисса X слева от опоры А будет, конечно, отрицательной. Когда
44
груз будет стоять слева от этой опоры, то получится — ==/?^<0; когда
он будет стоять справа от опоры В, получится —т- =^а^^' Таким обра-
зом, |На обеих прямых появятся отрицательные участки, которым соот-
ветствуют реакции, направленные вниз.
Л и-ни и вл'иян1ия изгибающих моментов. Пусть требуется
построить л. -в. изпибающего момента в сечении С (фиг. 58). Будем счи-
тать момент положительным в том случае, когда он вызывает растяжение
в нижнем волокне,
Поставим сначала груз Р=1 слева от сечения С, т. е. примем л:< а.
Тогда изгибающий момент выразится очевидной формулой
Мс = ^вЬ-^Ь. (4.2)
Эта формула получится независимо от того, возьмем ли мы сумму
моментов всех сил, расположенных слева, или же сил, расположенных
справа от сечения С.
При переменном значении х уравневие (4.2) -выражает собой .прямую,
йоторая при л:=0 имеет ординату М^ =0, а при х = 1 — ординату М^ =6.
Можно сказать иначе: линия влияния изгибающего момента М^
представляет собой не что иное, как л. в. опорной реакции В, все ордина-
ты которой умножены на постоянное число Ь. Однако линией влияния,
построенной таким образом, мы имеем право пользоваться лишь на
участке, расположенном слева от сечения С.
Когда груз Р=\ стоит справа от сечения С, то изгибающий момент
в этом сечени-и выражается формулой
Л^с = ^л« = (^)«- (Ч)
При переменном значении х эта формула выражает прямую, а
именно л. в. опорной реакции А, все ординаты которой умножены на
постоянный множитель а. Ордината под правой опорой равна нулю, а
под левой—^.равна а. Этой прямой можно пользоваться лишь на участке,
расположенном справа от сечения С
Таким образом, линия влияния М^ состоит яз двух прямых, имею-
щих нулевые точки под опорами 'И продолжения которых отсекают на
опорных вертикалях отрезки а \\\ Ь. Ее можно построить также, поль-
зуясь .не опорными отрезками, а ординатой под сечением С, т. е. 'В вер-
шине треугольника. Эта ордината может быть вычислена как по урав-
нению (4,2), так и по уравнению (4.3) и равна '^. Формулу —
полезно запомнить.
Очертание линии влияния М^ указывает «а следующее: когда груз
^ передвигается по пролету АВ от опоры А к опоре В, то момент сна-
чала растет от нуля, достигает наибольшего значения, когда груз про-
ходит через сечение С, и затем снова уменьшается, обращаясь в нуль
при проходе груза через правую опору. При расположении груза на
консолях момент М^ имеет отрицательный з«ак и растет »по абсолют-
ной величине по мере удаления груза от опоры.
Линия влияния М^ для сечения ?>, расположенного на конооли, имеет
другой вид, а именно: вид прямой, нулевая точка которой расположена
под сечением D.
45
D
г
б*
LI
¦^—111 \j\
ГПТТТтттти^
li
i I
e
M
1 G
Г^ЩЩ
©
e
—----{IL
©
rшштmJjliFШi}Шm^mшmшm.^—_
7^
лЛМ^
\л.б.М^
лЛр,
\a6.Q,
л.бЛ
aj
Фиг. 58
I_Jl
"==d-^-^-^^^/7jt7^/?;
5
7.
к "'" 1»,
фиг. 59
46
Ли'нии в^лмяния .поперечных сил. Поперечной, или
перерезьивающей, силой, как известно, называется сумма проекций всех
сил, расположенных по одну сторону ют рассматриваемого сечения, на
нормаль к оси^ стержня в этом сечении. Будем считать поперечную силу
положительной, если обе внутренн-ие силы стремятся повернуть соответ-
ствующие части балки вокруг их концов по часовой стрелке. Например,
на фиг. 59, а внутренние поперечные силы, действующие в сечении С,
стремятся повернуть участок СА вокруг точки А и участок СВ —вокруг
точки 5 —против часовой стрелки, следовательно, Q^ <0. На фиг.
53, б направление 'враш^ения — обратное, поэтому Q >0.
Для построения л. в, Q^ (фиг. 58) расположим сначала силу Р = 1
слева от сечения С. Тогда сумма левых сил будет направлена вниз и по
абсолютной величине равна Р—Pj^ = Rj^,sl сумма правых сил будет
направлена вверх и иметь ту же величину. Согласно фиг. 59 такое на-
правление поперечных сил считается отрицательным. Итак, левый уча-
сток л. в. Qc совпадает с л. в. -опорной реакции R^, но имеет отрицатель-
ный знак. Аналогичным образом можно доказать, что правый участок
л. в. совпадает по величине и по знаку с л. в. jR^ . Обе ветви линии влия-
ния параллельны друг другу и сдвинуты одна относительно другой по
вертикади на величину, равную единице.
Под самым сечением С линия влия-ния Q^ претерпевает -разрыв, пр'И-
чем величина уступа равна единице. Нетрудно представить себе проис-
хождение этого уступа: если сила Р==1, передв/инувш-ись «на бесконечно
малую величину, перейдет с участка СА на участок СВ, то сум'ма левых
сил сразу уменьшится та величину этой силы, а сумма правых настолько
же увеличится; но каждая из этих сумм есть Q^.
Заметим, что в точке С линия влияния Q^ имеет и-менно разрыв, ио
не нулевую точку. Когда -сила Р расположена слева от сечения, хотя
и бесконечно близко к нему, величина Qc будет выражаться на фиг. 58
нижним отрезком соответствующей ординаты, а когда Р перейдет в
смежное положение на правом участке,—то верхним отрезком ординаты.
Линия влияния Q^ для сечения Z), расположенного на консоли, имеет
вид двух прямых, из 'Которых правая на всем своем протяжении сли-
вается'^ с осью абсцисс, а левая — горизонтальна и и-меет ординаты,
равные отрицательной единице.
Линия влияния О- относится к сечению, расположенному на
^лев
КОНСОЛ1И бесконечно близко к опоре Л, Она имеет такой же характер, как
литая влияния Q^.
Линия влияния О. относится к сечению, расположенному
^прав
также бесконечно близко к опоре Л, но справа от нее. Пока груз Haxoj
Дится справа от этого сечения, поперечная сила в нем равна опорной
реакции /?^ , поэтому соответствующий участок л. ib. ничем не отличает-
ся от л. в. R^. Когда же груз находится на консоли, то поперечная сила
равна и противоположна реакции R^. Итак, линия влияния состоит из
двух параллельных прямых, причем под опорой А получается уступ,
равный единице.
Ли.ния влняиня угла наклона упругой линии в
^чении А для балки постоянного сечения (фиг. 60)-
Ш
Когда груз находится в пролете между опорами, то угол наклона
выражается формулой
^л — QEJI '
следовательно, л. в. представляет собой кубическую параболу.
Когда груз находится на левой консоли, то
х'1
(4.4)
'?л=—•
3?/
а когда он стоит «а правой консоли, то
Т. е. оба консольных участка линии влияния прямолинейны.
i^^%
Фиг. 60
То, что л. в. усилий оказались ломаными, а л. в. деформаций имеет
и криволинейные участки, не является случайностью.
Ниже будет доказано, что 'В статически определимой стержневой
системе линии влияния усилий всегда состоят из прямолинейных уча-
стков.
§ 4.3. ЛИНИИ ВЛИЯНИЯ УСИЛИЙ МНОГООПОРНЫХ БАЛОК
Построим линии влияния для балочной системы, изображенной на
фиг. 61. Предварительно необходимо проанализировать систему с точки
зрения ее геометрической неизменяемости и выяснить роль отдельных
ее элементов.
В § 3.5 было указано, что для статической определимости система
балок с п опорными стержнями (где п>3) должна -иметь п—3 шарни-
ра в промежуточных сечениях. В данном случае л=5, п—3=2, а так
как в сечениях ? и / помещены два шарнира, то это требование удов-
летворено. Однако необходимо разобраться в том, как .расположены
опорные стержни -и шарниры, т. е, обеспечивают-ли они геометрическую
«еизменяемость системы.
я ип.^^^^^^ ^""^^ системы лежит опирающаяся на три опорных стержня.
Л^ЕЛТ^г^"^"^"^ Двухконсольная балка EI. Одноконсольная балка
аГеяава™^ ^/^"" ^"^Р«ый стержень, а в ?-два опорных стерЖНЯ,
пргТоГ^^^^ неподв11жна. То же самое можно сказать о
o'olZ^^^^ ясности та же схема изображена в «е-
цсм а?нГп ^"""^«"я кс . Так как балка АЕ опирается одним кон-
UOM аа неподвижную среднюю балку, она испытывает усилия только
48
? ''С D Е F G HI
пт~у—rx-T—^rr
H L
^1
\n.BR^
^ЛВН^
I
At
Цщщщы^^М^^
\лщ
\лщ
I
)<ьЧцК]1Ш1Ш-^-^^ '"^^^QFfrpaf)
Фиг. 61
А
й С
i i
i~—^,_Л-.-1
/Г Z
Фиг. 62
¦'Щкнрвнч
i
„„^ „а ней самой, поэтому л. в. Re на всем протяж^,
тогда, когда груз стоит на не j^^ участке от А до Е л. в. ми^
пштЕАоЬслтгегсясосъюМ^^ g^^^^ На фиг. 61 положител?.
Soft же вид. как для «J^JP^^,^ ^^ зсех остальных, отложены кверху
ные ординаты этой л. в., рав
от оси. р Балка EI является основной, остальные две
ЛИНИЯ.ВЛИЯНИЯ А^ . заимствуют свою неподвижноаь; „->
балки опираются «^ "^^ " ^^^ при расположении груза в любом участке
этому усилия в ней ^озника ^^ i^^ Отличается от л. в. простои двухкон-
IZTZ''Ког'.Лт с-ит на участке СЕ (фиг. 62).то реакция на
конце ? выражается формулой
Ня балку EI в сечении Е передается давление равное и противо^
положное этой реакции. От такой нагрузки на опоре F возникает реакция
При перемен-ном значении x эта формула ^^ыражает прямую, имею-
щую нулевую точку -на опоре С. Линия -влияния показана на фиг. 61.
Линия влиян:ия М^ строится, как для простой двухкансольной
балки. При движении груза по крайней левой балке давление, передаю-
щееся на конец ?, изменяется по линейному закону; можно сказать, что
балка EI нагружена неподвижной силой, приложенной в сечении
Е, но изменяющей свою величину по линейному закону. Отсюда непосред-
ственно .вытекает, что 'И момент в сечении G изменяется по линейному
закону. То же самое можно сказать о правом участке. Читателю предо-
ставляется самостоятельно построить эту линию влияния.
Линии влияния Qn, Qn* Qp и Qp показаны на фиг. 61. Они
весьма просты, что делает пояснение излишним.
§ 4.4. РАЗМЕРНОСТЬ ОРДИНАТ ЛИНИЙ ВЛИЯНИЯ
Для Получения уравнения л. -в. следует написать соответствующую
формулу, «выражающую действие груза Р, -и затем принять Р-=1- Такая
подстановка с алгебраической точки зрения эквивалентна .разделению
выражения на Р, Отсюда следует, что ординаты линии влияния для
какой-нибудь величины Z имеют размерность
ордината линии влияния = ^^^^^^^-^^^^ющая величина 2
сила
имеЙЗ;ЛГ"^?' ""¦ ^- °"°Р"'''^ Р^^^^ВДй и поперечных сил
Д»Тв «SL^''"' ''¦ '' ^"Ражаются отвлеченными числами; ор-
наты л в" проги? Тя J°"""'''" Г "'^^ размерность кгм/кг^м; орди-
BHbS. дл, лZTn."P°'^P"''' ^°™ б" "° ^'^" формулам, которые
Формально можно So^L^ '^'^'^ предыдущих параграфах. ^,
собой влияние cocSoto^.^^ сказать, что ординаты л. в выражаЮ'
кадсой-дшб№ дЖ е™ °''° "Р^^^- Р^^"^'''' не 1 г или 1 кг. иЛ»
Орд««а-ш л Гмож^ тя/"''' ^ Р*"«°'"° абстрактной едйниис
OTBeTCTBywmeii В0ЛИЧ1ШЫ к^^.^ рассматривать как отношение с»'
вызвана. Например, ^^и к^кая л'^''^ Г'^°¦'°''^""°^У '"РУ^У- '^^^"Р"" °i!
_^ F,. iJiH какая-либо ордината л. в. опорной f^as^»"
равна 0 75, то это означает, что како й угод но сосредоточенный rpv^
стоящий над этой ординатой, вызовет реакцию, величина которой'^со:
ставляет 0,75 оттогожегруза. f ^
Можно, наконец, сказать, что ордината л. в. представляет собой коэф-
фициент, стоящий при Р в соответствующей формуле Шпример шг1
бающии момент в сечении С (фиг. 58) от груза Л стоящего слева выJa-
жается формулой ' ^
М^ =
Множитель
(^)
И-х)
I
ь.
b и служит ординатой линии влияния.
§ 4.5. ВЛИЯНИЕ НЕПОДВИЖНОЙ СИСТЕМЫ СОСРЕДОТОЧЕННЫХ СИЛ
Пусть на сооружение действует нагрузка, состоящая из нескольких
параллельных сосредоточенных сил Р,, Рг,..., Р„, занимающих опреде-
ленные положения. Требуется определить влияние этой нагрузки на
Фиг. 63
некоторую (величину Z (на 'некоторое усилие или деформацию), для ко-
торой ЛИВИЯ -влияния известна.
На фиг. 63 изображена линия влияния, которая для общности пока-
зана в виде кривой. Если бы на сооружение действовала только сила
^1 и если бы последняя, кроме того, была равна единице, ее влияние
Выразилось бы ординатой r/i. Вообще же влияние силы Pi выразится
произведением Pitji. Пользуясь принципом независимости действия сил^
можно выразить влияние Z всей нагрузки однородным млогочленом
Z = Лу, + /^2^2 + • • • + РпУп - ^РУ1. (4-5)
1=1
При помощи формулы (4.5) можно быстро определять влияние систе-
мы сосредоточенных грузов, расположенных как угодно на сооружении,
^^и foлькo они имеют то направление, для которого построена линия
Итак, л, в. служит не только для -изучения влияния подвижной нагруз-»
t Но является также весьма удобным способом расчета в тех случаях.
НьГ^^ ^^^^ " '^^ ^^ сооружение приходится рассчитывать на разнообраз-
вать ^^ собой понятно, что сущность формулы (4.5) позволяет пользо-
<^ooDv^ ''^^ииями влияния только в тех случаях, когда расчетная схема
сил ^^***^^ допускает применение принципа независимости действия
Фиг. 64
,Zm/M
Фиг. 65
Фиг. 66
§ 4 6. ВЛИЯНИЕ НЕПОДВИЖНОЙ СПЛОШНОЙ НАГРУЗКИ,
РАСПРЕДЕЛЕННОЙ ПО ЛЮБОМУ ЗАКОНУ
Обозначим интенсивность нагрузки в произвольной точке через Рх
(фиг, 64). Выделим из графика интенсивностей р^, бесконечно узкую по-
ласку, площадь которой равна р^ dx, и примем ее за сосредоточенную
нагрузку. По заданной л. в. можно определить влияние этой бесконечно
малой нагрузки: оно выражается формулой р^, dx у.
Суммируя влияние всех элементарных нагрузок и переходя к пределу,
можно на основании формулы (4.5) предыдущего параграфа написать
в
Z^ {pjcydx. (4.6)
Особенно простой вид формула (4.6) принимает в том случае, когда
нагрузка равномерно распределена по длине, т. е. когда pj^==p^
^ const. Тогда
в
Z = p[ ydx =¦ ро), (4.7)
А
т. е.. влияние сплошной равномерно распределенной нагрузки равно про-
изведению площади загруженного участка линии влияния на интенсив-
ность нагрузки. Замечательно, что в этом случае форма л. в. не играет
никакой роли: важна лишь ее площадь- _
Пусть разыскиваемая величина Z имеет некоторую размерность Z;.
тогда ординаты у линии влияния имеют размерность , а площадь
сила
W —размерность ^ v длин я. Интенсивность р выражается в единицах
сила
сила
-— , следовательно:
длина
сила Z -^
/?о) = • длина = ^ •
длина сила
Найдем для примера изгибающий момент -в среднем сечении балки
АВ, загруженной по -всему пролету сплошной равномерной нагрузкой
интенсивности р=2 mJM (фиг. 65). Балка имеет длину /=3 м. Линия
влияния изгибающего момента для сечения С представляет собой тре-
угольник с высотой, равной —, следовательно:
^ А ' 2 8 8 '
Может случиться, что площадь w складывается из участков, имею-
щих разные энаки (фиг. 66); под величиной w во всех случаях пони-
мается алгебраическая сумма ее элементов.
§ 4.7. ОБ ОДНОМ СВОЙСТВЕ ПРЯМОЛИНЕЙНОГО УЧАСТКА ЛИНИИ ВЛИЯНИЯ
Если нагрузка расположена на прямолинейном участке лин^ии влия-
ия, то от замены «нагрузки ее равнодействующей суммарное влияние яе
*^змеаится.
.-Г.Я оассмотрим фиг. 67. на которой загружен прям.
Для ЯОкгзггепъсгвг?^<^си J ^^^^^^ пересечения ее с осТ«; '
линейный Участда ЛВ^1фодол^^^^^^^^ ^ ^^^^^^ ^_ ^^^^^ написать '^'^
+ Р,х, tg а + Pb'^z tg « = tg « S ^/>^г ¦
Яп тяк как сумма моментов нескольких сил относительно точки о
равнГмоменту их равнодействующей то
следовательно:
Z = tga/?Xo = ^?yo,
Фиг. 67
Фиг. 68
Итак, в рассматриваемом случае влияние нагрузки равно влиянию
ее равнодействующей.
Этот вывод, очевидно, относится не только к нагрузке, состоящей из
сосредоточенных сил, но и к нагрузке, распределенной по длине по лю-
бому закону.
Нагрузку можно заменить ;не только ее равнодействующей, но любой
другой нагрузкой того же « а пр ав л ей и я, имеющей ту
же ра'В но действующую.
^На фиг. 68 показан случай нагрузки Ри f*2, равнодействующая кото-
рой R .расположена за пределами прямолинейного участка be линии
влияния, однако в этом случае также Z^Ry^,
С другой стороны, он справедлив в общем -виде только для прямо-
линейного участка линии влияния; для участка другого вида тангенс уг-
ла а—переменный, и вынесение его за знак суммы невозможно. Следо-
вательно, от замены нагрузки ее равнодействующей влияние, вообще го-
воря, изменяется.
§ 4.8. ВЛИЯНИЕ УЗЛОВОЙ НАГРУЗКИ
v>^I^n^^LT^r^^^^ ^Р^' ^=^ перемещается по балочке ЛВ, кото-
рая передает сооружению давления при посоедстве опоп Л и 5 (фиг- 69»'
При произвольном положении груза'н'а леГуюГпр^^^^
ются давления, соответственно равные Ь^и ^ . Совместное влияние
фоТмуЗ ^"™^^«^«Ь1х, но переменных 'по в1личине сил .выразйтся
Ы
^-Ж^л+fy.,
оторая представляет собой уравнение прямой, соединяющей верхние
^онцы ординаты t/^ и у^. Влияние Z выражается ординатой у этой пря-
^^^ Итак, для получения линии -влияния, отвечающей действию узловой
узки, необходимо спроектировать узлы на линию влияния, построен-
нию для ' случая непосредственной
^Гередачи нагрузки, и проекции смеж-
ных узлов соединить прямыми ли-
ниями.
Если под какими-нибудь двумя
гмежными узлами расположен пря-
молинейный участок л. в., то проек-
тирование этих узлов, очевидно, не
изменяет характера л. в. Это вполне
согласуется с предыдущей теоре-
мой' сумма влияний обоих узловых
давлений равна влиянию их равно-
действующей.
На фиг. 70 даны примеры
линий влияния для узловой нагруз-
"1о"рГп7ина«-Т=.=о"лри ие„осред™е„„о„ дейсвии на-
Грузки.
Фиг. 69
Фиг. 70
..^^/чп ПОСТРОЕНИЯ ЛИНИЙ ВЛИЯНИЯ
§ 4.9. КИНЕМАТИЧЕСКИЙ МЕТОД ПОСТРОЕНИЯ ^^^
Кинематический метод основан на приниипе^^^^^^
НИИ. согласно которому необходимый и доста ^ ^^
55
^^^
xn.K.. сумма работ всех сил, действующих на с--
сия состоит ^^^^^^^^^™жно для нее бесконечно малом перемещении
должна быть Р^^^^^^^"!!!^- того принципа какое-либо усилие, которое.
Найдем на ™™Сдвижении груза, перпендикулярного оси АВ,
возникает в балке ^^ ^^^""^ /ф^^г 71).
например Р^^™^'^./""^^^ котором возникает .интересующая нас
Удалим o"^P«^''^;i'^^?^ которую для общности обозначим через X.
реакция, и заменим его силой, К01 ру д ^^^ только мы произвел
дем эту замену, характер
сооружения изменится: из
геометрически неизменяе-
мой и неподвижной систе-
мы оно превратится в ки-
нематическую цепь с од-
ной степенью свободы,
т. е. в механизм. Из об-
ласти статики геометриче-
ски неизменяемых систем
мы перейдем в область
статики кинематических
цепей.
При произвольном
значении силы X этот ме-
' ханизм не будет в равно-
весии, и точка А будет
двигаться вверх или вниз-
Только при одном, совер-
шенно определенном значении силы X будет существовать равновесие;
оно нарушится при малейшем отклонении значения силы в ту или иную
сторону.
Для нахождения этой силы рассмотрим бесконечно малое возмож-
ное отклонение балки как абсолютно жесткого стержня. Это отклонение
может состоять только в повороте около точки В. Предположим, что
поворот произошел против часовой стрелки; точки А и С сместились
цниз, описав дуги концентрических окружностей с центром в точке В.
11ри бесконечно малом угле поворота обе точки пройдут лишь беско-
нечно малые элементы своих дуг; поэтому можно считать, что их пере-
мещения \ и 0^ представляют собой бесконечно малые отрезки прямых,
направленных по касательным к обеим дугам и, следовательно, перпен-
дикулярных к прямой АВ. J , м ,1.
прпЗРт^."^^^^^^' "^^ ^"-"^ ^ направлена вверх. При рассматриваемом
перемещении системы сила Р совершит положительную работу РЬ^, а
павн^п.ТЛ^'''^^''?'''^"^'^ работу-;Г*,. Если мы хотим, чтобы сила X
^жны nnun''^"'''' реакции, т. е. чтобы она уравновешивала балку, мы
должны приравнять суммарную работу нулю:
Х^Р-^. (4.8)
Фиг. 71
из ня°м^^""^^ формула, несмотря на свою простоту, является одной
Fjivfin^u замечательных формул строительной механики: настолько
Хлиии,^^"^^^^^"^^^ вытекающие из нее следствия,
^ны Опи '^ ^ * бесконечно малы и, слеж)вательно, неопреде-
. дмако отноше«ие между иими является коненцым^ с^Щ)-
гпенно определенным по 'величине и по чня^^тг гчтт^ ,
Г^А расположены по одну сторону от Br7ne^2TeT,VT ^Т '"'"'''"
одинаковые знаки, а если по ра'зные стороГы,-то разные з^нГк>ГпТ
зом случае их отношение положительное, а 'во So^poM - отрицат^пХ"
?;^е'^кГили%ги"в. ^^^"^«^ ^^ ™-^' --Р«У-- - балка^пГчГоГй
Отношение между длинами отрезков % и В, не зависит от угла по-
ворота балки и, как нетрудно видеть, выражается пропорцией
к ~ АВ
Все это приводит нас к выводу, что при заданном положении точки
С правая часть формулы (4.8) не зависит от величины и направления
возможного перемещения балки АВ.
При Р=1 формула (4.8) принимает вид
Х^^
Числитель 8^, выражает собой леремещение точки приложения си-
лы Р. Если речь идет о линии влияния, то точка Сможет занимать на оси
балки АВ любое положение. Следовательно, числитель 8^, означает пере-
мещение любой точки оси балки, возникающее тогда, когда точка А пе-
ремещается на величину 8^. Итак, если мы повернем ось балки вокруг
центра В на произвольный бесконечно малый угол, то график перемеще-
ний Ьр и выразит в некотором масштабе искомую линию влияния X.
Самый масштаб определяется просто: если мы совместим точку С
С точкой л, то лолучим ^р=^х или Х= -^ = 1.
Итак, в точке А ординату графика перемещений следует принять рав-
ной единице.
Построение линии влияния как графика перемещений 8^^ и состав-
ляет сущность кинематического метода, который устанавливает анало-
гию между такими, казалось бы, чуждыми друг другу понятиями, как
закон изменения усилий X при перемещении сосредоточенного груза
^"=1 и закон распределения перемещений Ьр в том механизме, который
образуется при удалении соответствующей связи.
При выводе формулы (4.8) речь шла об опорной реакции. Но эта
формула, представляющая собой непосредственное следствие принципа
возможных перемещений, приложима в такой же степени ик любому
усилию Х — к поперечным силам, к нормальным силам, к изгибающим
Моментам и т. д.
§ 4.10. ПРИМЕРЫ И ЗАДАЧИ НА ПОСТРОЕНИЕ ЛИНИИ ВЛИЯНИЯ
КИНЕМАТИЧЕСКИМ МЕТОДОМ
Пример 10. Для балки АВ (фиг. 72) построить л. в. Qq , предполагая непосредствен-
ную нли узловую передачу нагрузки,
Откинем в сечении С одну связь, препятствующую взаимному вертикальному
"^Ремещеиию обеих частей балки. Две другие связи, из которых одна препятствует
взаимному продольному перемещению, а другая — взаимному повороту, мы должны
^^^^Ранить. Возможное перемещение полученного механизма будет состоять в повороте
^^вой части вокруг точки А и правой — вокруг точки Виа один и тот же угол,
^чевидно, что прямые АС и ВС останутся параллельными между собой. В случае непо-
Редственной передачи нагрузки нас интересуют перемещения оси самой балки, а в слу-
^ узловой — перемещения передаточных балочек. Перемещение показано йа вахней
li^Pf-; а сама линия влияния — на нижней.
за-
гпрпуюшим образом: осесть взаимное вертикаль-
пределяется с^^ду™^ с^^едовательно, отрезок ординаты
частей балкн в ^^^^""^^,^р нужно принять равным единице.
п^^ —г-V ^,p5«„v обеими прямыми ^ fj^^ aq рассматриваемого механизма, ctde^
'^"'"СТкал'ьный груз, -'^Тпо\^оЛ%еяк1 а поперечная сила, приложенная'^
„^EIoLuvTb этот участок по часовии f ^ательно, ординаты л. в. ия v„.
Масштаб ординат оп^_.,
««^г>*1м*>тение обеих частей балкн
иа уча.
HpNfV В сечении С, — •• i^
стке ЛС отрицат^ьны ^^^^ построить л. в. изгибающего момента в сечении С.
Пример U. Для "Г"*^ ^ „ D
лежащем между ^"^^Гбалки от связи, в которой возникает изгибающий момент, по-
Для ^^««^^f""r>HHD Перемещение механизма и л. в. Мс изображены на фиг. 73
ставим в сечении С шарнир, пер ^^^^ ^^ поместим на этом
механизме груз Р в каком-ни-
будь месте между опорами, точка
С опустится, и выпуклость в Этом
сечении окажется обращенной
вниз, следовательно, ординаты
л. в. в интервале Л В положитель-
ны.
Для получения масштаба ор-
динат л. в. представим себе, что
заданная балка АВ соствит из
двух жестких частей ACD и СВ
соединенных шарнирно в сечении
С и, кроме того, взаимно связан-
ных стержнем DE (фиг. 74). Оче-
видно, что такое устройство обеспечивает жесткость всей балки. Пусть С?= L В этом
случае изгибающий момент в сечении С консоли CD при любом расположении нагруз-
ки на АСВ выразится так:
"""¦ЩЩЩ^^
Фиг. 72
Мг=Х'1 = Х,
где X — усилие в стержне DE,
Фиг. 73
Фиг. 74
" ' вЕ?"Г ^^"«"ь --рГнГлТГ г ^«- Р-н усилии, в стержне DB.
Е no^^^f ^« в равном случае ппе„/ '^ построением л. в. усилия X.
^е гЖГ:^^У^-Р-ле„СвТ^„Г^^ --мное перемещение^тек D и
а величина Ь^"в^р^^"^ "^Р^мещений М^ этого'^м1Г'^^**=« ««^^в удаления стержня
(фиг. 73), мы и 1кЕ^^^«°"ь«' иПрдаТт п„1Г"^"" состоит ю двух пря^ы*
учнм требуемый масштав ""^ «®«ением Е. Приняв в* -*
Правило масштабов для л. в. изгибаюших мпмрнт^о г,^„«
НИН, рапном единице, от точки перессче.шя обе„° пГмых ZI?nt'™^ "^ Р^'""""
3 между последними, должен равняться единицГ.'^ ^^° ординаты, заключен-
§ 411. НАИБОЛЕЕ НЕВЫГОДНОЕ ЗАГРУЖЕНИЕ ТРЕУГОЛЬНОЙ
ЛИНИИ ВЛИЯНИЯ
Треугольную форму имеют линии влияния изгибающих моментов
простои балки, а также л. в. усилий в поясах многих ферм, поэтому
вопрос о ее загружении имеет важное значение. Обозначим для общно-
сти изучаемое влияние буквой Z.
Фиг. 75
На фиг. 75 показана такая линия влияния, а также схема движу-
щегося поезда. При любом положении этого поезда для всех грузов,
стоящих слева от вершины, производная л. в. в точках приложения
dx
^ ДЛЯ грузов, стоящих справа от вершины:
^=tg(7r_p)^-tg.3.
J;^ ^юб^и 10#ожении поезда его влияние выражается формулой
r.nuu rDV3 не стоит над вершиной, производ„а,
до тех пор, "°^_™з2ачения^ Например, если груз Р, стоит слева от
dz имеет определенные значс
'^¦^ D .гппава. то
"вершины, а груз Рб-^^права, ,„ , o,w гл
dx
-tgai;P,-tgPi;^,. (4.9)
HnnvPTHM что поезд передвигается слева направо, т. е. в сторону
воз^астГния'^'Лв Если^ри' каком-либо его положении получает/я
^ >0, то Z представляет собой возрастающую функцию, следователь^
н1з'; поезд еще не дошел До наиболее невыгодного .положения. Если,
наоборот — <0, то при движении поезда вправо функция Z будет
dx
убывать следовательно, самое невыгодное положение уже пройдено.,
Таким образом, искомое положение поезда характеризуется тем, что в
dZ
момент перехода через это положение производная — изменяет свой
знак на обратный.
Легко убедиться в том, что кр итич ески м может быть толь-
ко такое положение поезда, при котором один из
грузов стоит над вершиной линии влияния. Действительно,
если над вершиной или бесконечно близко к вершине нет ни одного груза,
то правая часть выражения (4.9) как не содержащая х не может изме-
нить своего знака при бесконечно малом передвижении поезда в ту или
иную сторону.
При переходе любого груза через вершину линии влияния величина
«^ ^^ . ^
производной — внезапно изменяется, так как в правой части формулы
(4.9) слагаемое, содержащее эту силу, переводится из первой суммы
во вторую, или наоборот. Как видим, эта производная не является непре-
рывной. Вот почему наибольшее значение Z не может быть найдено из
^^
условия — =0.
dx
Критический груз, т. е. тот, при расположении которого над
вершиной получается наибольшее влияние, характеризуется двумя не-
равенствами, о которых сказано было выше.
Допустим, например, что критическим является груз Ps. Тогда долж-
но оказаться следующее: когда он расположен у вершины слева от
последней, то — >0, а когда -он расположен справа, то ^<0, т. е.
dx
Подставим
tga = -?.; tgP=-?.
1^гх"З^Ти"с%Гва'и'к^^^^^^^ равнодействук.щ„е грузов, pac-
_ " « «справа от критического, содаветеп^во ч#рез Д*»
лееТбщий ХГ^^""""^ груз-через Р^,, Тогда неравенства примут бо-
^^ев ^ Якр + R^
кр -t- ^прав
(4.11)
Эти неравенства и служат аналитическим признаком критического груза.
Для лучшего запоминания этих двух неравенств можно сформули-
ровать их так: когда критический груз расположен слева от вершины,
средняя погонная нагрузка левого участка превышает правую; при
расположении его справа от вершины — наоборот.
Неравенства (4.11) выражают собой необходимый и достаточный
признак критического груза. Они дают возможность после немногих
попыток разыскать его.
Задача о нахождении критического груза весьма просто решается
сразу, без попыток, при помощи следующего графического построения^
отложим от конца В все силы Ри Рг, ->., Pj в том порядке, в каком они
встречаются, если идти от Б к Л (фиг. 75). Соединим точки Л и С и из
точки Е проведем прямую ED параллельно прямой АС, Точка D распо-
ложится как раз на критическом грузе, так как из подобия треугольни-
ков BED и ВАС нетрудно убедиться, что условия (4.11) удовлетворятся.
Если точка D совпадает с границей каких-нибудь двух сил Р^ и Pi^xy
то обе силы являются критическими. С момента, когда на вершину
вступает сила Р^, и до момента, когда это положение займет смежная
сил% Р 1^1, производная — будет равна нулю, и влияние движущегося
поезда останется постоянным. '
Решение, удовлетворяющее условиям (4.11) и найденное аналитиче-
ским или графическим путем, будет иметь реальный смысл только в
том случае, если при установке поезда в найденное критическое положе-
ние ни один из его грузов не сойдет с сооружения. Если же это произой-
дет, то анализ придется произвести снова, учитывая лишь те грузы,
которые расположены на сооружении.
При наличии такого поезда, длина которого превышает длину со-
оружения (точнее говоря, превышает длину а+Ь на фиг. 75), изло-
женное решение приводит к необходимости делать ряд попыток. При
этом возможно, что будет найден не один критический груз, а несколько,
« лоезд придется несколько раз устанавливать в различные критические
Положения, чтобы выбрать из них самое невыгодное.
Существуют общие графические приемы, которые теоретически раз-
решают задачу нахождения всех критических положений поезда при
любом очертании линии влияния^.
§ 4.12. НАИБОЛЕЕ НЕВЫГОДНОЕ ЗАГРУЖЕНИЕ ПОЕЗДОМ
ПОЛИГОНАЛЬНОЙ ЛИНИИ ВЛИЯНИЯ
Пусть л. в. имеет вид фиг. 76, и поезд весь умещается на ней. Обо-
значим для краткости суммы сил, стоящих на каждом прямолинейном
^<^ке, соответственно через Ru R2. Rz и /?4, а влияние поезда — через Z.
. С Щ. Т и м о ш е« к о. Куре статики сооружений. Л.. 1926. § 25.
^^%© строительной механики стержневых систем>, ч. I, 1^Щ>
X/ M^f. как в § 4 11, найдем, что критическим может быть
толГк'о^оГположение поезда^ при котором хотя бы один из грузов
стоит и^Д ¦J'°" J^" что "груз Р* является критическим, т. е. что поезд
оказьшаГт наибольшее действие тогда, когда этот груз стоит над верши-
Фиг. 76
НОЙ С. Если это предположение правильно, то должны удовлетвориться
два неравенства:
Ri tgc^i + /?2tga2 —/^stgag + /?4tga4 > 0 ;
Ri tg% + P2tg^-2-{P^ + ^s) tgas + /?4tga4 < 0* , (4.12)
где через a^, ag, ag, a^ обозначены абсолютные величины углов.
§ 4.13. НАИБОЛЕЕ НЕВЫГОДНОЕ ЗАГРУЖЕН НЕ ЛЮБОЙ
ЛИНИИ ВЛИЯНИЯ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКОЙ
Равномерно распределенная нагрузка весьма часто встречается, по-
этому рассмотрим отдельно вопрос о ее наиболее невыгодном распо-
Фиг. 77
предстяплар.^^^^^ считать, что эта нагрузка не имеет разрывов, т. е- .
а^ Линиа ^ сплошную полосу. Возможны три случая.
произБольноР rfp^rr!!!!'^ полностью загруженэ. Перестановка нагрузки на
______^^^ с н^^-^-тояние вправо или влево при условии, что сооружение
¦тельной ^ь^сашки^^йп^^^^^ графическое решение той же задачи см. в «Курсе строи-
сАпники стержневых систем», ч. I, 1950, стр. 116.
остается загруженным 'полностью, очевидно нр „по.,.^ « .
изменения влияния нагрузки. "'^'^видно, не влечет за собой никакого
б) Линия влияния загружена чягтиии^ „„
„о, '(ф„г. 77). Вл™„„е н'а;;руГ/в1^рГжаеГфор"м;;оГ°™ """'¦"¦
2 = 9jyc?jr = 9'''«. (4.13)
О
где со^-площадь загруженного участка линии влияния.
Когда .нагрузка покрывает участок W, ее влияние достигает макси-
мума; когда она загружает участок 02,-минимума и т. д. Д^тГточно
рассмотреть такие .положения нагрузки и сверх того - крайнее mSo^
положение, при котором загружена будет вся линия влития Из этих
величин остается выбрать абсолютно наибольшее и наименьшее
в) Нагрузка покрывает какую-то среднюю часть л. в., а крайние
участки остаются незагруженными (фиг. 78). Предложим следующее
решение этой задачи.
Спроектируем нагрузку на л. в. и проведем хорду АВ. Далее предста-
вим себе, что нагрузка передвинулась вправо на величину dx. Тогда
площадь загруженного участка, очевидно, уменьшится на ^^ dx -и уве-
личится на yjgdx, следовательно, дифференциал влияния Z будет
dZ = (yB — yA)dx.
Отсюда следует, что при У^^Уа влияние Z будет возрастающей
Функцией, при Ув'^Уа—убывающей; наконец, при Ув^Уа ^"^ будет
иметь экстремальное значение. Иначе говоря, интересующие нас свой-
^т'ва влияния Z характеризуются тем, в какую сторону наклонена хорда
' ^. Например, при ^^>0 и у^>0 хорда, восходящая от ^4 и В, свиде-
тельствует, xixo при передвижении нагрузки вправо влияние Z увеличи-
ается^ Во всех случаях критическое положение равномерно распреде-
^^««ой нагрузки характеризуется тем^ что хорда А В параллельна оси
Же ^^^^ -^«wwf/ влияния. При этом максимум .получится, если при дви-
Хол ^^^ вправо от указанного положения хорда АВ из восходящей пере-
™т в нисходящую, и минимум, — если наоборот,
р^ Р^Фическое решение задачи о нахождении критического положения
Фиг 7о^^"^ распределенной нагрузки очень просто. Оно показано на
Перо/ Достаточно передвинуть л. в. вправо на величину а, тогда точки
«kdm^^"*^"^^ К^ь /Сг обоих графиков отметят соответствующие искомые
иитические» положения нагрузки.
т
«лы1;плРЕ НЕВЫГОДНОЕ РАСПОЛОЖЕНИЕ СИСТЕМЫ
''"'' РЛВНО^^^^^^^^ "^''^'''^
'^''^ ОДИНАКОВОЙ ИНТЕНСИВНОСТИ
^. поезд состоящий из нескольких сплошных равномерно распреде.
Представим с^е поезд ^^ ^ заданными неизменными расстояниями
':^:SyZX дадГздесь простой признак критического положения такого поезде.
[ПШТПТЦ __|11
Его влияние при любом расположении выражается формулой
Z = <7^«|,
где о>^ — площадь участка лииин влияния, расположенного под каждой из нагрузок
(фиг. 80).
Если мы передвинем поезд вправо и а длину ах, то первая площадь получит при-
ращение yidx—yidx, вторая — лриращенне y^dx—y^dx и т, д., откуда
dZ^q (у2 + У4 + Уб --У! — Уз —Уб) dx. (4.14)
До тех пор, пока rfZ>0, функция
Z является возрастающей; при dZ<^
она убывает, при rfZ=0 она достигает
экстремума.
Итак, наиболее невыгодное поло-
жение характеризуется тем, что сум-
ма ординат линии влияния под при-
выми концами нагрузок должна р^^'
пяться сумме ординат под их левыми
концами.
Это правило остается справедли-
вым и в том случае, когда часть на-
грузки (или нагрузок) выходит за
пределы линии влияния.
Действительно, мы всегда имеем
Фиг. 81
Действительно, мы всегда имеем
сГГа"бГсГ ""^^"^ ^^-^ » -Р-о - ее дейсГ„^тГ„"ь^Г^ра^:ГГваГс" ^
Диф&ц'„"Г йГ„Гформуле74Т4,'':;|Р?^ ^*"'-- «')• -^^ ^оже. случиться, что зна«
иибудь края одной из нагр^ок ч^^ ¦^^VT^'^ "^ обратный при переходе какого;
яииаюй у\ . однако и в этом <^учае вьГе/.яЧ '""'^' ''¦ ^^ "Р" ^^"^«" °Р^"""" ^'
Нахождение таких положений п„Г" «критерий сохраняет свою силу-
критерию, может быть сделано п™ем^^^,^°™Р"е Удовлетворяют указанному на«я
§ 4Л5. ПРОИЗВОДНАЯ ОТ ЛИНИИ ВЛИЯНИЯ И ЕЕ ПРИМЕНЕНИЕ
Загрузим произвольную л„„„к, влияния ларой сил А=—1- и Р^^
= + „ . направленной ло часовой стрелке и имеющей плечо, равное «
64
^' ^ «*^.T^rv D rTTT<-rTlrTrv у ^Л .
Суммарное влияние Z обеих сил выражается формулой
Z= fix) + -Lf(x i- a) = A^-rci)-f{x)
=-tgcp,
(4.15)
где 9- уг'ол наклона хорды АВ к оси абсцисс линии влияния. Если момент
пары равен т, то ее .влияние равно migo.B зависимости от наклона
хорды А В одна к та же пара может дать эффект положительный или
отрицательный, или равный нулю.
Если пара сил расположена на
прямолинейном участке л. в.,
то ее эффект остается постоянным
при любом ее расположении на этом
участке.
В пределе, когда а—> О, формула
(4.15) превращается в
2=^=/;. (4.I6J
Соотношение (4.16) выражает
следующую важную теорему: произ-
водная от линии влияния какой
угодно величины по независимой пе-
ременной X (кривая тангенсов углов
наклона касательной к л. в.) представляет собой построенную в функции
от той Же переменной линию влияния, выражающую влияние движу-
щейся сосредоточенной пары с моментом, равным единице,
§4.16. ВЛИЯНИЕ СОСРЕДОТОЧЕННОЙ СИЛЫ, ВРАЩАЮЩЕЙСЯ ВОКРУГ
НЕПОДВИЖНОЙ ТОЧКИ ПРИЛОЖЕНИЯ
(ОКРУЖНОСТЬ ВЛИЯНИЯ)
Кроме смлы, сохраняюще^! постоянное направление, но меняющей свою точку при-
•поження, в расчетах сооружений иногда (хотя и значительно реже) встречаются силы,
приложенные в неподвижных точках, но изменяющие свое направление относительно
Фиг. 82
Фиг. 83
смй^51^^^«»я. Так, например, при расчете раскрывающихся мостов (фиг. 83) можно ра.-
^"атривать подвижную часть пролетного строения как неподвижную, а силы тяжести--
^^к вращающиеся. То же самое можно сказать о фермах секторных затворов плотин и
цементах некоторых кранов.
^ ^^ М. РаСинов«ч
65
л гоооужения приложена действующая в опреде,,
пусть в какой-нибудь точке^^ с Р>^ этой силы^^^^
ной плоскости иаклонная сила /^ ^^^юш^П момент н т. д.) в функции от уг,а ^'^
некоторую величину («^ "Р^н" альному направлению Оу. «а^
к.она Ф силы к неко'^^Р^^^яГмно перпендикулярные составляющие, направленные п
Оу и Ох; по своей величине ^нн уд^У ^^^^ влияние единичной силы, направленной п.
Оу через а, а единичной силы, направленной по Ох, _ Г^
пез'^ В случае действия силы Р=\ наклоненной к ot
под углом т. искомое влияние выразится очевидной фор,
мулой
Z = acos(p + 6 sin 9.
Для графического изображения искомой зависимости
сложим геометрически вертикальный вектор длины а и гори
зонтальный длины b (фиг. 85), Замыкающую ОА спроекти'
руем на ось MN, параллельную вращающейся силе Р и об.
разующую с вектором а произвольный угол <р. Так как
проекция замыкающей равна сумме проекций составляю-
щих. То
ОВ = а cos <р + 6 sin 9 = ^,
т. е. влияние силы Р выражается вектором ОВ.
Угол ОВА представляет собой прямой угол, опирающийся на неподвижный отрезок
ОА, откуда следует, что геометрическое место точек В есть окружность, описанная на
ОА, как на диаметре, а проекция ОВ есть хорда, проведенная из конца О параллельно
силе Р. *
Фиг. 84
Фиг. 85
"^'"xir'^T^^^ которые в совокупности
бой Sh4hhv^V"P^''^^««^« из точки^О nLaTnpT ^ ^^^^ вращающейся силы Р=1.
друга~о7ри^ат^1"' "^ ^^РУ^ностей cooStbv^^ ^«^^ выражает со-
Для пог?пЛ^Т '"''"'^'.''- ^y^^^w их называть Inlr?^^ положительным значениям Z, а
двух ее напоапп^^Л^ ^^и^граммы So Ih.T^^'^^''^''^^^» влияния».
чтобы хорда ОВо^рТ" ^^«'«'«а ^тттсГЦ^^ *^<^npaвmнue вращающейся силы
S*„t°""^PneS^^„*'"°' "аибольшее зиа«2^^°^~«^^в°*1^' всегда вза«л«'-
-ияш;'С.*1Г*^^бЩиг*?'^«Г''«°й- "Р°^^^^^^^^ пройденной нз О. есть
§ 4.17. СВЯЗЬ ^^>^^^^^^^^яти влияния для ДВИЖУЩЕЙСЯ силы
РАЗЛИЧНЫХ НАПРАВЛЕНИЙ
Теорема о производной от линии влияния позволяет установить за^
мечательную связь между линиями влияния, отвечающими различным
направлениям движущейся силы Р=1. Связь эта состоит в следующем:
пусть линии влияния пост- ^
роены в прямоугольных
координатах и -пусть в
точках, отвечающих одно-
му и тому же положению
груза, проведены каса*
тельные по -всем этим л. в.
Наклон этих каса-
тельных к соответ-
ствующим осям абс-
цисс есть инвари-
ант. Действительно, во
всех этих л. в. тангенс уг-
ла наклона выражает од-
но и то же: влияние со-
средоточенной пары, мо-
мент которой равен еди-
йице.
Для иллюстрации рас-
смотрим следующий при-
мер: по стержню АВ (фиг.
87) Движется один раз
вертикальная сила Р=1,
а другой раз — сила Р\ =
= 1, имеющая произволь-
ное, но постоянное на-
правление. В обоих слу-
чаях построена в прямоугольных координатах л. в. одной
величины, например л. в. acdb и щ Ci di &i — горизонтального перемеще-
ния точки В. Произвольной точке С стержня отвечают на этих л, в. точки
с и с,. Касательные, проведенные в этих точках, наклонены к соответст-
вующим осям абсцисс под одним и тем же углом '-р^
Если в какой-нибудь точке d одной из этих л. в. угол <р =0, то он ра-
вен нулю и в соответствующих точках di в остальных л. в.
Это приводит к следующей общей теореме: положение точки
^» отвечающее наибольшему влиянию движущейся
силы, не зависит от направления силы.
Фнг. 87
и той же
§ 4.18. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Могт ^^'^ рассматривать поезд как нагрузку, продвигающуюся по пролетному строению
ее л '^^^^^^•"ась в литературе еще в первой половине прошлого столетия. Мы находим
ствем И- Журавского* (1821—1891), затем у Кульмана*. Влияние такой нагрузки, есте-
нно, зависит ие^ тплккп пт пяггмятпипаемого соооужения. но и от характеристики
поезда.
зависит не только от рассматриваемого сооружения, но и от характеристики
тени ^У-яьтаты наследования системы Гау, «Журнал Главного упрарлеиия путей сооб-
"ия и публичных зданий», т. XI, 1850.
^ C>ie Graphische Statik, dritter Abschnitt. Zurich. 1866.
67
мп^« чамеиить поезд одним сосредоточенным грузом была высказа-.
Плодотворная "f^,p ^yj,-ikier 1835—1888), который применил ее к расчету стати-
яа проф, Вииклером i . Название «линия влияния» (инфлюентная линия) было
чески пеопределимои ^^-^^JJ^^ch)^
дано Веир^хом 1*- ^ у ^ния л. в. был разработан проф. Мюллером-Брес-
'^Н МшЖе^^^ и ^^РУ^"^" .вторыми.
""^^Amv^icTHKv расчета мостов линии влияния были введены в России проф.
п л Ппос^^^^^^ (1858-1926), автором крупнейших проектов мостов на русской
"^Ч „оо„му noDor конца XIX и первой четверти XX столетии, автором известного
.!пгя^\1^онт^^^^^ механики. Он первый ввел в употребление ^«таблицу моментов
ппР^па>> облсгчаюшую разыскание наиболее невыгодных положении поезда.
ПСССР теория линий влияния получила обобщение и развитие в трудах
А А Гвоздева*, И. М. Рабиновича^, Я- М. Риппенбейна^ Б. М. Иванова^, А. А. Умаи-
ского^ н др.
1 Die Lehre von der Elastizitat u. Festigkeit, 1 Theil, Prag. 1867.
2 Allgemeine Theorie u. Berechnung der kontinuierlichen u. einfachen Trager,
8 Die graphische Statik der Baukonstruktionen, Bd I, 1887.
4 Общий метод расчета сложных статичес|<и неопределимых систем, М., 1927.
5 Кинематический метод в строительной механике, М., 1928, и Курс строительной ме-
ханики стержневых систем, ч. I, М., 1938 и 1950.
6 Линии влияния в статически неопределимых системах, сборник «Исследования по
теории сооружений», М., 1936.
7 Применение фиктивных дисков для построения л. в. усилий в фермах кинематиче-
ским методом, сборник «Исследования по теории сооружений», вып. IV, 1949.
^ Специальный курс сгроительной механики, ч. I, М., 1935.
г лава 5
ОБЩИЕ СВОЙСТВА СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ
§ 5.1. ЧТО ТАКОЕ СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ СТЕРЖНЕВАЯ СИСТЕМА
Стержневая система называется статически определимой, если при
действии любой внешней нагрузки равнодействуюи^ая усилий в любом
сечении любого стержня оказывается определенной и конечной и может
быть найдена из условий равновесия системы и ее отдельных частей,
В такой системе, очевидно, опорные реакции также являются стати-
чески определимыми. Действительно, если бы оказалось, что какая-
либо реакция не может быть определена из уравнений статики, то это
означало бы, что в том сечении, к которому она приложена, и в ряде
других сечений невозможно определить и усилия.
Как видно пз данного определения, понятие о статической определи-
мости распространяется не на все величины, характеризующие напряжен-
ное состояние системы, а лишь на некоторые из них. В статически опре-
делимой системе всегда имеются и такие величины, которые не - могут
быть найдены из условий статики: напряжения в отдельных точках лю-
бого сечения, а также относительные и абсолютные удлинения, сдвиги и
углы поворота. Система может называться статически определимой лишь
в ограниченном смысле.
§ 5.2. РАЗДЕЛЕНИЕ НЕИЗВЕСТНЫХ НА ДВЕ ГРУППЫ
При расчете стержневых систем необходимо определять множества
неизвестных. Если геометрическая схема сооружения, т. е. расположе-
ние его стержней, узлов, шарниров, опор и т. д., известна, а также изве-
стна внешняя нагрузка, то в расчете фигурируют следуюш[ие неизвест-
Hbie: 1) опорные реакции; 2) нормальные силы, поперечные силы и из-
гибающие моменты в любом сечении любого стержня; 3) геометрическая
форма и размеры всех поперечных сечений всех стержней и коэффици-
енты упругости их материала; 4) нормальные и касательные напряже-
ния в любой точке любого стержня; 5) абсолютные и относительные ли-
нейные и угловые деформации и перемеш[екия во всех точках соору-
жения. Расчет состоит в задании некоторых из этих неизвестных и з со-
ставлении необходимого количества функциональных зависимостей или
уравнений для определения остальных.
Замечательной особенностью статически определимых систем яв-
-^яется то, что первые две группы неизвестных не зависят от остальных
€9
, „^ зависят от формы и размера сечений,
грипп т. е. усилия и Р^^':^^'^/'^оэффициентов упругости,
^напряжении, «^^^^^^^^Stby статически определимых сооружений,
'' BJronapnJ^J^^^yJ^^^Zlercn по сравнению с сооружениями ста-
?ич'еГки"неГределимыми.
о^ мРЖПУ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТЬЮ
^ ГгЕ^Ки^КОЙ «^^ИЗМЕНЯЕМОСТЬЮ СИСТЕМЫ
Для того чтобы установить эту^связь в общем виде, воспользуемся
принципом возможных перемещении. ^де п > 1. Нагрузим ее
"^"льноГна^р^зкой и будем'искать усилие (реакцию) R одной из
произвольной нагрузко^^^ удалим названную связь, заменив ее реакцией
Р "для полученной систшы. имеющей п+1 степеней свободы, соста-
вим равнения равновесия. Принцип возможных перемещении позво-
ляет составить п+1 таких уравнений, так как для каждого из «+I воз-
можных типов перемещений можно написать уравнение работ. Во всех
этих уравнениях будет фигурировать единственная неизвестная К, от-
куда ясно, что при действии произвольной нагрузки задача неразреши-
ма. Иначе говоря, определение усилий из условий статики невозможно.
Пусть п=0, т. е. система геометрически неизменяема и не имеет
лишних связей. Тогда принцип возможных перемещений позволит нам
написать снова п+1 уравнений, т. е. одно уравнение, и оно даст для
неизвестной/? о д н о вполне определенное и конечное значение (если
исключить случай мгновенной изменяемости).
Наконец, пусть п>0, т. е. система геометрически неизменяема и
имеет п лишних связей. Тогда удаление связи не превратит систему в
изменяемую: она останется геометрически неизменяемой, т. е. возмож-
ные перемещения всех ее точек будут равны нулю, а потому уравнение
работ удовлетворится при любом значении реакции R. Следовательно,
в этом случае уравнениям статики можно удовлетворить бесконечным
множеством способов.
Все сказанное приводит к следующим выводам: система, геометри-
чески неизменяемая и не имеюи^ая лишних связей, всегда статически
определима; наоборот, система статически определимая-т-геометриче-
ски неизменяема и не имеет лишних связей.
шп1^"^,^°^ иагруз/се системы, геометрически неизменяемой и не имею-
drUnuflU^,^ ^^^^"' (соответствует единственная система значений всех
усилии, или, короче говоря, единственное решение
^едствия последней теоремы весьма разнообразны.
eosSuno^f'' ^^^^'^ ^"^^ сформулировано следующим образом:
SStj^ ""^ стагич^с/с« определимой задачи является в то оюе
ZZ!o^^'^'^f:''''^'i¦ Э™ «У««° "онимать так: если мы 1саким бы то
кую ^^Lmv ^Г"^^"" ''''" У'^Л^^'^' ^^« элементов сооружения та-
УР?в^™я7ста™к^' тТ?'" "Р" ^^""°« «^^РУ^»^^ удовлетворяет всем
решения ив то J^T;,nm''" ''°'''^'' ^'^'''' Уверены в правильности этого
ИИ и в ТОМ, что другого не существует.
§ 5.4. СТАТИЧЕСКИЙ КРИТЕРИИ МГНОВЕННОЙ ИЗМЕНЯЕМОСТИ.
СПОСОБ НУЛЕВОЙ НАГРУЗКИ
^«St л°ишниЛ«1Л? ''^°^** структуре гео'метрически неизменяемо и
*«1Ли неизмрнв^м? • ™«°"° ^^^^"^ бь'ть либо действительно гевмет-
г. - измеряемым, либо мгновенно изменяемым. В первол, ойгчае
система уравнении статики является определенной. Это значит что при
любой нагрузке все усилия, определяемые из этой системы уравнений
будут определенными и конечными. Во втором случае система уравне^
НИИ-неопределенная; это значит, что при произвольной на?ру^^^^^
уравнениям статики ли^^ Удовлетворить \.икакими конечными
значениями усилии (все или некоторые усилия равны бесконечности),
либо можно удовлетворить бесконечным множеством значений усилий
(все или некоторые усилия равны — или бесконечности).
Фиг, 88
Фнг. 89
Отсюда следует, что любая нагрузка может быть использована
для проверки геометрической неизменяемости или мгновенной изменяе-
мости сооружений такого типа. Если при действии какой-нибудь нагруз-
ки каждое усилие в сооружении имеет только одно и притом конечное
значение, то сооружение геометрически неизменяемо. Если при какой-
нибудь нагрузке то или иное усилие оказывается неопределенным или
бесконечно большим, то сооружение мгновенно изменяемо.
Простейшей из нагрузок является отсутствие нагрузок
(нулевая нагрузка). На этом основан статический способ поверки мгно-
венной изменяемости. Очевидное возможное решение задачи при дейст-
вии нулевой нагрузки — это обращение всех усилий в нуль. Если такое
тривиальное, нулевое решение является единственно возможным, то
сооружение геометрически неизменяемо. Если, напротив, имеются еще
другие решения, то сооружение мгновенно изменяемо.
Для примера рассмотрим диск, который опирается на три опорных
стержня, не пересекающихся в одной точке (фиг. 88). Заменим эти
стержни реакциями Rj^, R^y Re и составим уравнения моментов всех сил
относительно точек Oi, О2 и Оз. Уравнение моментов относительно точ-
^и Оз при отсутствии внешней нагрузки будет иметь вид
^ так как г^ Ф О, то единственно возможным значением реакции будет
°с ^==0. Аналогичным образом доказывается, что и остальные две реак-
^1ни Могут иметь только нулевые значения. Отсюда следует, что фигура
неподвижна.
На фпг. 89 все три опорных стержня пересекаются в одной точке О,
^' ^- г^=г^=г^=0. Составив уравнения моментов относительно этой
""^очки, получим неопределенные решения:
О о.р о_о.р_о о
^.==-^ =
гв
П
пдинпГТЬ МОЖНО получить и иначе. с5аА<з/Л»т>-л и J) О И j.
Ту же H^o^SS одной из реакций, например реакции R^ . Так как
вольным зна разложить на две составляющие, пересекающиеся с
силу всегда можно р ^^^^^^^^^^ две реакции, уравновешивающие силу
р^'"' РРйияГже найдутся. Отсюда ясно, что задача имеет бесчисленное
' о пешений Все это показывает, что рассматриваемая фигура
SS мгновенной подвижностью.
,.кч УСИЛИЯ в ОСНОВНОЙ ЧАСТИ СООРУЖЕНИЯ и в ЭЛЕЛ1ЕНТАХ,
§ 5.5. УСИЛИЯ ПРИКРЕПЛЕННЫХ К НЕЙ
Анализируя схему статически определимого сооружения с геомет-
пической или кинематической точки зрения, в большинстве случаев
можно различить основную часть, которая сама по себе геометрически
/; в [ СО I е г
1
Т
Фиг. 90
неизменяема и неподвижна, и другие элементы, которые к ней прикреп-
лены и от нее заимствуют свою неподвижность и неизменяемость. Ос-
новная часть отличается от опирающихся на нее элементов следую-
щим признаком: если последние будут разрушены или удалены, то ос-
новная система все же останется неподвижной и неизменяемой; наобо-
рот, если основная часть будет разрушена, то вместе с ней рухнет и все
то, что на нее опирается.
ношеп
является
л ^..^.. л«^хо1л^ 11U ишишсиию к оалке гл\ "зсть /^ь лс^^и^
оалки является основной по отношению к ее консолям АВ и CD и т. д.
нагрузка, расположенная на основной части статически орредемшо-
рппо^^^^^^'^"^' ^^'^^^^«^^ усилия только в этой части; напротив, на-
Tiln^' Р^^'^^^^^'-^^сся на прикрепленной части, вызывает усилия как
uV '''''^ "" "" ''''^' ^^^^Р^^ служит для нее основной. ^
Р я n^J^ "^ основной части сооружения (фкг. 90) имеется нагрузка
них n^Itf^""^ "^^^^ "^ загружены. Предположим, что усилия в послед-
PaLSr^c,?:'"'^' ^^^^«^"0, что при таком предположении все условия
лиП^а^^.ш^?'' ''^^''^^ ^У^^'^ удовлетворены (система нулевых уси-
S? SSt^mIT ''У^'^^У''^ нагрузку). Откинув эти нулевые элемен-
ттт^^Ш&^^^^^ нагруженную геометрически неиз^^еняемую
-^^Р^1Ш| Сужения; как известно, мы получим для этой части
Ш ^^йМе усилия. В итоге мы п^олучим р^^^е^ уМ>^'
Фиг. 92
летвОр^'^<^^^^^ У^""^^^^^^^ равновесия всего сооружения и всех его частей.
1^0 так как двух различных решений, удовлетворяющих всем условиям
равновесия, быть не может, то справедливость теоремы доказана.
На фиг. 90 нагрузка Р вызывает отличные от нуля усилия только
R пролете 5С и в его опорах; нагрузка Q вызывает усилия на 'уча-
стке ЕВ, т. е. на протяжении двух балок, а нагрузка R — na участ*
Другой пример (фиг. 91):
нагрузка Р вызывает отлич-
ные от нуля усилия только в
части ACDE; остальная
часть фермы пе участвует в
работе.
Третий пример: если в со-
ставе геометрически неизме-
няемого и статически опре-
делимого сооружения можно
мысленно выделить такую кинематическую цепь, которая под действием
данной нагрузки находится в, состоянии мгновенного равновесия, то
можно утверждать, что она и будет воспринимать всю нагрузку, а в ос-
тальных элементах усилия будут равны нулю. Пусть, например, в трех-
шарнирной ферме (фиг, 92) внешняя нагрузка подобрана таким образол,
что нижний пояс служит для нее веревочным многоугольником. Тогда
верхний пояс и раскосы заведомо пе участвуют в работе.
§ 5.6- ВЛИЯНИЕ УРАВНОВЕШЕННОЙ НАГРУЗКИ
Если нагрузка, состоящая из уравновешенной системы сил, прило-
жена к геометрически неизменяемой части статически определимого
сооружения, то усилия во есех остальных частях сооружения равны
нулю.
2Р
./'
-а лр
Фиг. 93
^/'
Фиг. 94
Доказательство совершенно аналогично предыдущему: то, что ото»
Решение является возможным, т, е. не противоречащим уравнениям
^атики, вполне очевидно. Но возможное решение является в то же вре-
'^ действительным,
y^J^^ фиг. 93 показан пример такой нагрузки: она состоит из трех вза-
.^!^^'УРавноаешивэюшихся вертикальных сил, приложенных к геомет-
"^ **^из||.едяемой фигуре ABCD. Можно утверждать, что усилия ^
ШЩщях фермы, а также опорные реакции равны ну#ю.
прщшер: две-равно-протиБоаел@1рй^Й|^
такой
лев
ния в
O..I. стержень АВ будет испы-
^ THKw.^ нагрузки ^'^„f^n, ные э л е м е н т ы — ну-
?rr//b"ycV«e л »«„-,rj ^„г„^„е.яемой час™ соор,ж1
^^ ^ ^''^'"nv4ae играет сам стержень АВ.
3 данном СЛУ ^^^^^^^^^^^ ПРЕОБРАЗОВАНИЙ НАГРУЗКИ
g 5.7. ВЛИЯНИЕ залентными такие нагрузки которые
Будем называть ^^/^^^" ^ствующую. Эквивалентное преобразование
ямеют одну и ^У„^^^ Рз^"Тдругую, равнодействующая которой имеет
переводит одну нагрузку в a^jt ^^ ^^ величину, направление и
Р положение.
"' При всевозможных эквива-
лентных преобразованиях нагруз-
ки, приложенной к геометрически
неизменяемой части статически
определимого сооружения, усилия
в остальных частях последнего ос-
таются без изменения.
Для доказательства «возьмем
две различные эквивалентные на-
грузки, которые назовем Q\ и Q2.
Нагрузим сооружение нагрузкой,
оавной геометрической разности этих двух .нагрузок, т. е. нагрузкой
^,!!^/0ч™ что равнодействующая такой группы сил равна нулю.
Фиг. 95
Фиг. 96
т. е. совокупность сил Q\—Q2 представляет собой уравновешенную на-
грузку. На основании доказанной -в предыдущем параграфе теоремы уси-
лия в элементах сооружения, не входящих в состав нагруженной геомет-
рически неизменяемой части, равны нулю:
где Si—усилия, вызываемые нагрузкой Qf,
S2 — усилия, вызываемые нагрузкой Q2.
Отсюда следует, что
что и требовалось доказать.
Поясним сказанное несколькими примерами. В трехшарнирной арке,
^^^f«^^" "^ ^^У^ полуарок АС и СВ, соединенных шарниром (фиг. 95),
замена группы сил Pi, Р2, Р3 их равнодействующей R не изменяет ни
U «fi!!'^^ реакций в шарнирах А и В, ни взаимодействия обеих полуароК
i^ л"^^ V-" У^^^^ии в полуарке СВ.
илiГ«l?I^Jf ^*^^- ^^"^ перенос силы Р по ее направлению сверху вниз
или наоборед изшшяет усилия только в стержнях фигуры abdc.
Если силу Q. направленную вдоль стержня, перенести с одного кон-
^РП на Оригои. то исилия иЯМ^иатгс^ ^^п^,.^ ^ ^.. .,
f^^'"- TS S' '' ---:у.^ ^^ww^ty i^LCfjjtbnH, перенести с ооного кон-
его на другой, то усилия изменятся только в этом стержне, причем
перенос сверху вниз вызывает в нем дополнительное растягиваюш.ее
усилие, равное с^, а перенос в обратном направлении — такое же допол-
нительное сжатие.
Замена силы Г двумя составляющими, приложенными к панели ef,
каким бы спосооом ни была произведена эта замена, влияет только на
,г^нлия в стержне ef.
усилия В стержне ef.
§ 5-8. ВЛИЯНИЕ ИЗМЕНЕНИЯ ТЕМПЕРАТУРЫ, СМЕЩЕНИЯ ОПОР
И НЕТОЧНОЙ РАЗМЕТКИ ДЛИН СТЕРЖНЕЙ
В статически определимой стержневой системе ни один из факторов,
перечисленных в заголовке этого параграфа, не оказывает влияния на
статически определимые усилия.
Фиг. 97
Фиг. 98
Для доказательства этой теоремы достаточно сослаться на принцип
единственности решения (§ 5.3). При отсутствии внешней нагрузки ну-
левое решение удовлетворяет всем уравнениям статики; но так как
двух различных решений быть не может, то все статически определимые
усилия, вызываемые действием температуры или смещением опор или
ничтожно малой вариацией длины какого-нибудь стержня, равны нулю.
Причину отсутствия усилий легко представить себе исходя из того,
что удаление любой связи превращает статически определимое соору-
жение в механизм, т. е. в подвижную систему, которая неспособна про-
тивиться перемещениям. Пусть, например, в трехшарнирной арке ABC
(фиг. 97) левая полуарка подверглась охлаждению. Удалим ее; тогда
оставшаяся часть без всякого сопротивления может быть повернута в
%жную сторону так, чтобы длина АВ уменьшилась, после чего укоро-
ченный стержень АВ' может быть вставлен на место.
Усилия, возникающие в каком-нибудь сооружении при отсутствии
•внешней нагрузки, носят название начальных или собствен-
ных усилий. В статически определимом сооружении начальные уси-
^^я всегда равны нулю.
Это свойство статически определимых сооружений является весьма
^^^ь^м их достоинством.
Необходимо, однако, иметь в виду, что при действии температуры
статически неопределимые усилия, т. е. усилия в отдельных
^олокнах, илр напряжения, мргут оказаться отличными от нуля. Такие
спряжения,' так называемые «самонапряжения», могут возникнуть, на-
Ример, тогда, когда в стержне из однородного материала температура
{^^"Р^Делена по толщине стержня не по линейному закону или, в част-
"сти, когда температурному воздействию подвергается не все сечение.
орп г,- т п Но и в ЭТИХ случаях внутренние силы в любом
а лишь ""^'^^^^яиобгазуют уравновешенную систему, так что изг.
ZlV:'Tn.:^u;o%TZue ^поперечные силы и опорные реакц?«
^^^ТеотмТо непременном обращении в нуль относится лишь к рав-
нодействующим усилий, приложенных в любом поперечном сече-
нии стеожней, а также к опорным реакциям.
Заметим еще, что в том частном случае, когда сооружение с геомет-
рически неизменяемой структурой, не имеющее лишних стержней,
становится мгновенно изменяемым, теорема единственности решений от-
падает, вследствие чего для такого сооружения возможно бесконечное
множество систем взаимно-уравновешивающихся начальных усилий
Наоборот, если в каком-либо сооружении, которое в общем виде ста-
тически определимо, возможно равновесие отличных от нуля начальных
усилий, то оно мгновенно изменяемо.
Например, схема на фиг. 98 обладает бесконечно малой подвиж-
ностью, так как три опорные реакции, пересекающиеся в одной точке
могут при отсутствии внешней нагрузки иметь бесконечное множестве'
взаимно-уравновешивающихся значений ^ccmt
Глава 6
ТРЕХШАРНИРНЫЕ АРКИ
§ 6Л. ОСНОВНЫЕ ПОНЯТИЯ
Аркой называется распорная система, имеющая вид коивого бруса
Примерами арок могут служить схемы, показанные на фиг. 99 и 100.
Обе фигуры изображают такие кривые брусья, у которых вертикальная
Фиг. 99
Фиг. 100
нагрузка вызывает наклонные опорные реакции. Фиг. 99 статически оп-
ределимая, и наклонность ее реакций обусловлена наклонным направ-
лением правого опорного стержня; фиг. 100 — статически неопредели-
k
Фиг. 101
Фиг. 102
^ая, и наклонность ее реакций вызывается стремлением бруса А В рас-
прямиться под действием нагрузки: концы А и В стремят*^! разойтжь.
*1ему препятствуют горизонтальные слагающие опорных реакций.
77
Фиг. 103
Фиг. 105
Фиг. 106
Фиг. 107
Фиг. 108
В
Фиг. 109
Фиг. ПО
Фиг. 111
Напротив, брус на фиг. 101 не может быть причислен к аркам, так
как он является безраспорной системой. Его следует рассматривать как
криволинейную балку.
На фиг. 102 изображена система (статически неопределимая), состо-
ящая из ломаного стержня. Ее следует рассматривать как распорную-
систему рамного типа.
Наличие распора роднит между собой эти два типа систем со стати-
ческой точки зрения, поэтому арочные и распорно^рамные сооружения!
будут .рассматриваться -в настоящей главе сов-
местно.
Трехшарнирные арки (фиг. 103) или рама
(фиг. 104) представляют собой статически оп-
ределимую систему. Она coctopit из двух полу-
арок или полурам, связанных шарнирно с опо-
рам.и и между собой. Опорные шарниры назы-
ваются обычно пятовыми, а средний —-
ключевым. Статическая определимость
трехшарнирной арки может быть доказана на
основании формулы (2.1); здесь Со-=4, Ш^1,
Я = 2, откуда
Л==: 4 + 2.1 — 3-2 = 0,
Фиг. 112
т. е, число лишних связей равно нулю.
Трехшарнирная арка или рама может иметь
пятовые шарниры, расположенные либо не-
посредственно на опорах (фиг. 103 и 104), либо на консолях, заделанных
в опоры (фиг. 105). Она может быть симметричной, как на фигурах,
указанных выше, или же несимметричной (фиг. 106). Арка, у которой
опоры расположены на разных уровнях, иногда называется ползучей.
Фиг. 113
Разновидностью простой трехшарнирной арки или рамы является
^Рехшарнирная же арка или рама с затяжкой, те. с дополнитель-
ным стержнем, стягивающим обе половины (фиг. 107). Для того чтобы
такая система оставалась статически определимой, необходимо взамен
добавленной затяжки удалить один из опорных стержней. Впрочем, j^v
^амой структуры этой системы видно, что она состоит из трех т^Ш
л w^rTKHH треугольник, nuaiumj' п^ухч^<1С1СЯ
с ев АВ, образующих >'^ест1''*и ip i
;олько в трек о"°Р""^,"^^Гсположена выше уровня опор; тогда она
Затяжка может быть Р-^^^ 108—110).
.1_тг5ЯРТСЯ повышенной пт;ггТРМ MOrVT быть образованы более
;затял^^^^^ ivxv^-— ^ /сЬиг lUb—iiu;.
называется "«^^'^^""арнирных систем могут быть образованы более
Сочетанием ^pe^i^dp f арочные или рамные системы — мно-
сложные статически опреДел^^^^^^^Р^^^^ ^ф^^_ ^^2).
Фиг. 114
На фиг. 113—114 показаны примеры применения трехшарнирных
арок в мостостроении и промышленном строительстве.
§ 6.2. АНАЛИТИЧЕСКИЙ СПОСОБ ОПРЕДЕЛЕНИЯ ОПОРНЫХ РЕАКЦИЙ
Для аналитического решения задачи ограничимся случаем верти-
кальной нагрузки, приложенной к трехшарнирной арке (фиг. 115).
Соответственно числу своих опорных стержней система содер>к^^
четыре неизвестные составляющие опорных реакций. Их можно опреде-
лить, написав для всего сооружения три уравнения статики, и, кроме
того, приравняв нулю изгибающий момент в сечении С бруса АСВ.
В целях получения уравнений, содержащих лишь по одной неизвест^
ной, разложим каждую из опорных реакций на две составляющие, i
которых одна направлена по вертикали, а другая — по прямой АВ, сое^
диняющей пятовые шарниры. Такое разложение отличается от наибо^пе
часто применяемого в механике разложения сил на взаимпо-перпенди^
кулярные составляющие, но в данном случае оно является наиболе
целесообразным.
^^тР^^^^'^!^^^ Р^^^тояния каждой силы Р; от левой и правой опорЦ^^
-вертикалей соответственно через а,- и ft/ и приравняем нулю мом^)Р^
-#0
всех сил сначала относительно точки R
Моменты неизвестных сил Я, и Я' ^^' ^ "°™" относительно точки А
>. и Яз Обратятся в нуль, и мы получим:
Т .1 — > ри с\ I
' -¦'-"• "™ '•^-7-1".".^ (6.1)
Легко убедиться в том. что ппплпго»..
не отличаются от тех вертикальньТпеТ"' '"''''™ '™ ^- ^- «^^^^^
рые получились бы от рассматриваемое и""'' ''^''^^ '' '^Р^^'^^ ^™Р» ^'^'^^¦
ная арка была заменена простой балк «^^Р^^™* ^^-^^ бы трехшарнир-
наклонные составляющие опорных ог-ят?^;.'^''''^^^''" ^ '^''''^^'' Л и Б, а
рпг»1л реакции отсутствовали.
Фиг. 115
В качестве третьего уравнения составим уравнение проекиий всех
сил на горизонталь. Проекции всех сил Р,-, а также сил Т^ и Т^ обра-
тятся в нуль, и останется
//^ cos а — //^€0S а =0 , или ^^ = Я^ .
Таким образом, при действии вертикальных сил наклонные состав-
ляющие Н^ и А/^ равны между собой по абсолютной величине и направ-
•пены в противоположные стороны. Lcли силы Я/ не вертикальны, то
акого вывода сделать нельзя'. В дальнейшем мы откинем инаекс в вы-
ражениях И^ , /^л" Д-^я случая действия вертикальных сил будем пи-
сать просто Н\
Составим, наконец, выражение изгибающего момента для сечения С.
^>озьмехМ, например, момент левых сил
_^;^Р^|^едва члена выражают собой суммарный момент всех левых по
нап ^"'^^"^ о вертикали здесь является условным. В сущности все силы могз'т быть
влены как угодно, лишь бы они были взаимно-параллельны, а составляющие 7'^^,
1дие "^^"Р^*^*"^"*^ параллельно силам Я/. Наклонные параллельные силы Я; , действую-
*^РтикалГ^*^^ ^ пятами, расположенными на одном уровне, могут рассматриваться как
льные силы, действующие иа ползучую арку.
^^. М.
Рабинович
81
отношению к шарниру С вертикальных сил, т. е. изгибающ^ий
который получился бы от заданных сил Pi в сечении С просто"^^^^*^'^
Обозначим этот момент через М".. Тогда •^""™ибал,;>
Ф
или
Н' =^
f '
(6.3)
Фиг. 116
Полученная фор^,
имеет Фундаментальнп!
значение для всей теоон«
трехшарнирных систем
Она показывает, что при
любой вертикальной нагрузке наклонная составляющая Н' опорных ре-
акций, или распор;
1) при заданном расположении шарниров А. В и С не зависит от
формы оси арки;
2) при заданной нагрузке зависит исключительно от расположение
шарниров А, В и С;
3) равняется изгибающему моменту М°. простой балки, разделен-
ному на стрелу Г.
Н
Фиг. 117
Фиг. 118
изг^ба№о момшта уЙ" ''Г'' '"° Р"'"°Р ^«^Р^^^ет с увеличением
уничтожении Т. ' ' "^^«^'^^««е распора в арке состоит именно в
Из ?ого ж™ ''°'''"''' "Р^^УЩ^''° балке.
арки так, что пятовы'е 'SmAuT "^'^ ^^^'^^ ^'^"^«^^^ Ф°Р"У '''
шарнир С будет пеоепвигяти!.^ " ^ останутся на месте, а ключевой
будет изменяться обратно ппп. вертикали вверх или вниз, то распор
арка, или вообще системя "Р°"°Р«ионально стреле /'. Более пологая
ший распор, чем арка или оамГЛ'"^ значением /' будет иметь боль-
При f=0 получается Я'=^ с большим подъемом,
тически определимая по сворй г-г^^^ "^^ У^^ известно, система, ста;
нагрузки бесконечно большие%Л/^"^УР^- ""^^-^ получить от конечной
мгнозонно изменяема. Следователе!^ ^^''^'^^ ^ ^°" ^^У^ае, если она
мгно.°Р°^ все три шарнира расп^'^^; ^Р^^^^арнирная арка или рама.
мгновенно изменяема. ^ Расположены на одной прямой (фиг. Ш-
Назложимсилу Я'/Лиг JJ44
вертикальную Г и опре^л„м ^ в^ХныГ'"'""^ составляющую Я я
^ = Я'со5а = ^
cos а
pjo так как
/'
=/, то
лг
/
Вертикальная составляющая силы Я':
T'=W'sina.
(6.4)
(6.5)
Суммарные вертикальные реакции опор Л и В соответственно равны
Та + Т':
^ в ^ в— ^
(6.6)
Полная реакция левой (правой) опоры может быть получена двоя-
ким способом: либо как равнодействующая сил Т^ и Н' (Т^^ и Я'),
либо как равнодействующая сил V^ и Я (К^ и Я).
Внутренняя сила, развивающаяся в шарнире С, может быть найде-
на из условий равновесия любой полуарки (фиг. 117): горизонтальная
реакция равна и противоположна соответствующей опорной реакции
Я, а вертикальная равна и противоположна геометрической сумме сил
На практике наиболее часто встречается арка или рама с опорами,
расположенными на одном уровне. В этом случае, очевидно:
а = 0, Н'^Н, Г=:0.
Распор, вызываемый вертикальной нагрузкой, выражается формулой
Pal
(6.3). Для вертикальной сосредоточенной силы Р (фиг. 118) Я = — .
§ 6,3. ЭПЮРА ИЗГИБАЮЩИХ МОМЕНТОВ М
В произвольном сечении D арки, нагруженной вертикальными сила-
ми (фиг. 115), изгибающий момент выражается формулой
М^==М%-НУ\ (б.Г)
где MJj —изгибающий момент, который получился бы в сечении D
простой балки при отсутствии среднего шарнира.
Фиг. 119
После подстановок Я' =^^ и у' = у cos а формула переходите
cos а
Mr
NPo — Hy
(6.7)
При всевозможных положениях сечения D она выражает собой эпю-
РУ изгибающих моментов; первый член представляет собой эпюру про-
^Joft балки, опертой в точках Л и В. а второй член выражает собой кри-
вую ординат у оси арки, умноженных на постоянный множитель И.
На фиг. 119 показана эпюра моментов для арки фиг. 115. причем
• ^а ось абсцисс при построении эпюр ЛГ^, и Ну принята горизонтальная
е»
83
прямая, точки Л\ В\ С/ которой представляют собой проекции
ров А, В vi С. Эпюры М^ и Иу пересекаются между собой нал ^^^^"^и^
ром С, так кгк в этом сечении суммарная ордината изгибающих ^^^^^*
гов должна быть ргпцг нулю. ^^Ме^.
Нг фиг. \20—122 изображены эпюры изгибающих моменто
тричной трехшарнирной арки от сосредоточенной вертикально"^ ^"^^м^
"" силы Р
\Р С
Фиг. 120
Фиг. 121
нагрузки, загружающей
и от сплошной равномерно распределенной
половину пролета.
Эпюры изгибающих моментов дают яркую статическую хаоактрпи
стику трехшарнирной арки и резко подчеркивают ее отлиС от'бе^^^^^^^^
порной балки. Влияние распора ска-
зывается в резком уменьшений
^^™^^^ихт моментов: вместо орди-
нат М\ которые выражали бы мо-
мент при отсутствии распора, оста-
ются лишь разности М^~Ну. Очень
важно то. что уменьшение моментов
наиболее резко сказывается как раз
в средней части пролета, где ордина-
ты эпюры МО для балки имеют обыч-
но наибольшие значения. В этом
уменьшении влияния изгиба и состо-
ит вся особенность, все существо и
смысл применения арочных систем.
Однако не следует забывать, что
олагодаря наличию распора арка
нуждается в более массивных опо-
Рах. чем балка.
§ 6Л рациональное'04EPTAHRP ^^
Фиг. 122
.|МЯЛЬНЫМ подбором той кривой, по КОТОПпй г.тт«^,
^^%брапиую таким образом ось h^J^St7а ^То и'я п^"" "•"" Р'"""
' Пегко доказать следующую теорему Т/о Р^ ^^" ^ " а ¦" ь н о и осью,
„ой йР/с^ при действии заданной вертика^^пТ *""''^" ^ ^ре^«г«р««р.
S екг во всех сечениях был равеТнилю ZnTT'''' "f "''"'^"<""
;j?:r<^6nitt"; У^;^рь?л1". "^°"°''^««- соотв.гств,,ои,.ж о^-
Действительно, пусть в любом сечении арки </ = Шо где ;fe-неко-
торый постоянный коэффициент. Тогда в любом сечении Ь
Но так как в ключевом шарнире изгибающий момент равен пулю:
причем М°с?= О, то \~Ш—0, следовательно, и
На основании этой теоремы можно для любой заданной вертикаль-
ной нагрузки при любом расположении шарниров А, В и С без всякого
труда подобрать рациональное
очертание оси, которое обеспечит . /т ,
отсутствие изгиба. Задача имеет 'li''i!i''''''ili
бесконечное множество решений, i
т. е. удовлетворяется семейством У\ у/^
арок, оси которых имеют соот- I У^
ветственно пропорциональные ор- А\/
динаты. ^^*
Для примера рассмотрим сим- X
метричную трехшарнирную арку,
ось которой очерчена по квадрат-
ной параболе (фиг. 123). Нагру
зим ее сплошной равномерно распределенной по пролету / нагрузкой ин-
тенсивности q. Уравнение оси параболы относительно системы координат,
имеющей начало в шарнире А:
Распор:
Изгибающий момент в произвольном сечении:
„,, Очевидно, что раз момент во всех сечениях равен «У-^^^'/о ^f "^J."
иии системы ничто не изменится, если шарнир будет помешен не в се-
PffHHe пролетка в произвольном сечении Таким образом, получений
5""0Д об отсутствии изгибаюишх моментов останется в силе при про-
извольном расположении шарнира С на параболической оси.
Фиг. 123
§ 6 5. ЭПЮРЫ ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ,
ВЫЗВАННЫХ ВЕРТИКАЛЬНОЙ НАГРУЗКОЙ
Поперечной силой в каком-нибудь сечении D стержня назы
как известно, сумма проекций всех сил, расположенных по одну с^^^^^'
от сечения, на нормаль к оси стержня. Мы условились считать п ^^^^^У
ную силу положительной, если она стремится во"^^^^'
обе части стержня вокруг их противоположных кпн ^^^^
часовой стрелке (фиг. 124). Продольную fHonL"^^"^
ную к сечению стержня) силу будем считать положи^'"^'
ной в том случае, когда она растягивает стержень ^^^^
Для произвольного сечения арки, опоры котоопй
положены на одном уровне (фиг. 125): иои рас.
Фиг. 124 ^ /,г vi г^\
Q = (l^^ —1;Я.)С05С?-Я8Ш9,
где под знаком суммы стоят силы, расположенные слева от пяго.
ваемого сечения Знаки правой части получены (фиг 125 б и^?'^'^"'
составляющая F.cosc силы V, стремится\овернуть част1 лУ '^^^
точки D „о часовой стрелке, а состав„як.щая Н si/ , р.^ора ст^^
ej
н
y^cos(p \ ^
Hcosp
Фиг. 125
Е^ ~^'^"=--^^^^^^^^ первая В.З.
Введем обозначение ^' "''''' ~ "'"""'"
^-'чевидно что Оо oi,
ении опор простой балкой TvlZl '^''"^ заменена при том же
<3 = Q«cosolL •"''"°^ ^'^ью. Итак:
полЙм^-Р-в все сил. „, ,,;, Jj-J' (6.8)
¦г^ьную к оси арки в сечении д.
Из Формулы (6 8) ГГ "" ^^ ''" ^ "^ ^ ^""^ "^^ ¦ (6-9)
-e^BorSrir"^^^^^^^^^ арке не хськс
Уменьшение моментов и nL ^""Р^^и^ься "б!^^""^^- Формула {Ь.Щ по-
86 " "«перечных сил noSn«I!!^"° "°Р«ИУ '^^^^"•"
покупается ценой появления
•усилия, а именно продоль-
нового — отсутствующего ^
ного сжимающего. ростои балке -^ у1:илиа q г..
Для получения эп.оры Q „у^„, ' ™' ' ""^™° "^^^-Ь"
ЭП.ОРЫ Q0 на соотвехству,ощие'к?ждо^Г°с"чен„ °Р"""^™ «^-о™"й»
' ты L„„ " кривой вычесть ордина-
"ояГо'е^^с^л?'//^"^"""^''^ "°-
сосредоточГо^е^?ГГнГ"э;г>'
й/ \ \« т,о?^" •^"'^Ра Л' также строится
уступы равны Р sin у.
Фиг. 128
Фиг. 127
На фиг. 126 показан простейший пример построения эпюр Q и N.
Д'^я вычисления ординат этих кривых следует разделить ось арки на
несколько частей. Для каждой точки деления вычислить tg р = —» за-
тем J ""^
COS <р = —zzinnrz-. sin <р = tg 9 cos 9,
Vi + ig^9
^^^e чего можно по формулам (6.8) и (6.9) вычислить ординаты эпюр.
(Тя Лиг 127 построены эпюры М, Q. М соответствующие загруженик,
^?ей^1 затем отложим их на прямой; иначе говоря, выпрямим ось арки
^* Ординаты эпюры М в точках ДО-^^ния будем брать из фиг. 127 ,
переть на выпрямленную ось (фиг 128). Так получится эпюра мо-
ментов в функции от длины S. Продифференцировав ее один раз по этой
независимой переменной, мы должны получить эпюру Q (также в функ.
ции от переменной 5). В тех точках, где момент М достигает максимума
величина Q должна обращаться в нуль.
§ 6.6. ГРАФИЧЕСКОЕ НАХОЖДЕНИЕ ОПОРНЫХ РЕАКЦИЙ
Усилия в арке при произвольном направлении внешней нагрузки
в произвольном очертании оси удобно определять графическим спо<
собом.
Пусть на одну пол у арку дей-
ствует сосредоточенная сила Р
(фиг. 129, а). Из условий равно-
весия незагруженной полуарки
ВС, которая находится под влия-
нием двух сил, приложенных в
точках В и С (фиг. 129,6), следу-
ет, что опорная реакция
незагруженной полуарки
всегда проходит через
ключевой шарнир С.
Для равновесия трех сил Ру R^ ^ Rs необходимо, чтобы они пере-
секлись в одной точке; этим определяется направление реакции Z?^.- па-
конец, величины обеих реакций определяются из силового многоуголь-
ника (фиг. 129,в). При этом построении мы не нуждаемся в предвари-
тельном определении распора.
Фиг. 130
Если полуарка загружена системой сил, то при ло.моши веревоч
ноге многоугольника находят ее равнодействующую, после чего
пают по предыдущему. jr imj >
посту-
Если равнодействующая Р run r,r^.,»,
кается в пределах чертежа с реакцТей пп^"™^ '' полуарке, не псресе-
ке, то поступают так (фиг. 130 а б) пя.Т.гЛ'^''"""" «^^РУ^"*^ "°-''УаР-
образом на составляющие Л'и'д; ^' Р'^^^^^'^"^ ™^У ^^ произвольным
пролодящие через шарниры Л и
С; первая уравновешивается ре-
акцией левои^опоры, а вторая —
реакциями А'' и В, направленны-
ми по ЛС и ВС. Величины Л'' и В,
а также равнодействующая Л сил
А' и Л'^ находятся из силового
многоугольника (фиг. 130.6).
Если нагрузка расположена
на обеих полуарках, то, применяя
принцип независимости действия
сил, определяют отдельно реак-
ции, вызываемые загружением
одной полуарки, и отдельно — реакции, вызываемые загружением другой,
после чего полученные составляющие геометрически складывают. На
Фиг. 131
фиг. 131 сила Si вызывает реакции R^, ^i?» а сила ^2 —реакции R"^
Суммарная реакция R^ является равнодействующей сил R'^ и /?^
r;.
At
а реакция R^—равнодействующей сил /?^ и /?^ . Удобное расположе-
ние этого построения показано в § 6.7.
§ 6.7, ИСПОЛЬЗОВАНИЕ СИММЕТРИИ ПРИ ОПРЕДЕЛЕНИИ
ОПОРНЫХ РЕАКЦИЙ
Если на трехшарнирную арку или раму, имеющую ось симметрии,
дей^вует симметричная нагрузка, то опорные реакции, а также давле-
ние в среднем шарнире должны быть римметричны относительно той
же оси. Это дает возможность заменить расчет арки расчетом ее поло-
вины. Например, для определения реакции на фиг. 132 можно рассма-
тривать одну полуарку, представленную на фиг. 133, иа которой направ-
ление реакции R^^ перпендикулярно оси симметрии.
Фиг. 132
Фиг. 133
Иногда приходится встречаться с нагрузкой обратно симме-
тричной или ко с оси м метр и чн о и. Так называется нагрузка,
вторая получается из симметричной, если в одной из двух ее половин
^зменить знаки всех сил на обратные. Опорные реакции также получа-
^^ при этом обратно симметричными. Отсюда следует, что давление
„n быть направлено параллельно оси сим-
R^ В среднем "^^Р^^^Р^^'^'^акже можно ограничиться рассмотрением
метрии. Благодаря это
°""°' "Го^ольи» Рлв„од.псв.»™х „ КРОВЛЯ длв..„„„
,.8.МНОГОУ состояния арки и ДЛЯ суждения О
§6.!
Пля изучения напряженного с"^ оказывается удобным исполь-
--" dr;™"'ГЛ""р™ в н о Д е й с . в у . « -.
^гчояние м н о г о у * ^
Фиг. 1*34
Так называется веревочный многоугольник, любая сторона ^J^l^^.
направлена по соответствующей равнодействующей всех ^^вь! ^^^^^^
вых сил (эти две равнодействующие отличаются ^VY^ ^\J^^^^ много-
знаком). Для арок этот многоугольник называют ^^^^^"" _^^зкй -
угольником давлений или — в случае сплошной h<iipj
кривой давлений. Гначала Д-^^
На фиг. 134 показано построение этого многоугольника, ^и*^ ,^5Я^го*
заданной внешней нагрузки обеих полуарок строятся ^и^овь! ^^^^У^^.
угольники с произвольными полюсами 0| и Ог, а '^^J^^^^^^^t.ff Из ^^'
щие веревочные многоугольники а'—12'—6' и а"—84' 4о ^^ ^^^ц\
ловых многоугольников определяются равнодействующие oi р^делЯ'
нагрузок, а из веревочных — их положения. Опорные реакции oi.H-^ „3
реакции /^i
- 02'
,eai<-
ются по частям: от действия силы Si получаются ^ _
которых вторая проходит через средний шарнир; от действия ->2 '^^^я
ции Аг и Вг, из которых первая проходит через средний шаР ^^угоЛЬ'
направления этих реакций, находят их величину из силовых мн
НИКОВ (фиг. 134,6). j^ji этй
Для получения суммарных реакций складывают геометрич ^^^^^jq.
составляющие. Для этого на силовом многоугольнике строят пар
90
грамм на силах В, и А^ и получают той. ,г
с концами силового многоугольника пав»к^" "P"^'bie. соединяющие ее
Для нахождения многоугольии,<а'дЙ?н„""'°'""" реакциям А и В.
за новый полюс силового многоугольник . остается принять точку К
ему веревочный многоугольник Л-/9 "о^^о"/'' соответствующий
первую сторону его через левый шарнир ^rctl^^^-^' "Р^^^^дя
пройга ч.п1 ™''°У''°^''""'^ должен
пройти через остальные два шарни-
Huo^f^^^^'^P"'^ произвольное сече-
ние арки, например сечение D. Сле-
пеакУты^Т Р^'="о^о>'<ены опорная
?тву,пшя^ " '"-"^ '^'^ "'^ равнодей-
ствующая, как видно из силового
nvuI7o°''^"""^- ""^^-^ направление
луча 12. а так как она должна прой-
ти через точку пересечения обеих
сил, то она направлена по стороне
D веревочного многоугольника
Рассуждая таким же образом мы
всех сил, расположенных левее сечГнияТ'няппярпГ^""'^'""'^'''^^^
и т. д. Таким же образом можно' S:!Zl%TZ'ToponlVro'^:l^^
мя направлены по равнодействующим правых сил ^
Фиг. 135
Фиг. 136
Каждой нагрузке, действующей на данную трехшарнирную арку или
раму, соответствует только один многоугольник давлений.
'ТО Же мы можем извлечь интересного из этой фигуры? Вместе с
соответствующим силовым многоугольником она дает все, что характе-
ризует напряженное состояние арки. Пусть тп — произвольное сечение
зрки (фиг. 135), а R — соответствующая сторона многоугольника дав-
лений. Из силового многоугольника определяется величина силы R,
действующей на это сечение; из многоугольника давлений определя-
ц/^^" ^^ эксцентрицитет или плечо г относительно центра тяжести сече-
'"• ее составляющие — продольная Л^ п поперечная Q — и, наконец,
гпбающий момент M=Rr. На фиг. 134 плечи г заштрихованы. Эти
сил"^" ^'^-''я'отся измерителями момента, но в каждом интервале между
лами измеряют его в особом масштабе.
Интересное графическое представление изгибающего момента дает
„^^'^оуольник давлений в том случае, когда арка нагружена параллель-
пле ^"'"^'^и (фиг. 136). Из какой-нибудь точки D оси арки проведем
^^^ »". а также параллельный силам отрезок у, заключенный между
91
. н многоугольником давлений. Усилие действующее на сечение и
^"правл^ноТпо стороне /2, назовем /?,,. Из веревочного и силового
многоугольников видно, что ^
г =^У COS а
следовательно: „, г. /^ 1пч
R^^r^yh, или Л1 = уЛ. (6Л0>
Итак в этом случае параллельные силам отрезки у
пыоажают в о п р е д е л е нн ом и постоянном для всех
сечений арки масштабе эпюру изгибающих мо-
ментов.
Чем ближе многоугольник давлении подходит к оси арки, тем менее
эксцентрично действует сжимающая сила на сечение. При рациональ-
ном очертании'оси последняя сливается с кривой давления.
§ 6.9. ЯД?СВЫЕ МОМЕНТЫ И НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ
Нормальное напряжение при внепентренном сжатии имеет наиболь-
шее и наименьшее значения в крайних волокнах сечения. Рассмо-
трим какое-либо сечение АВ (фиг. 137). Будем считать, что оно имеет по
крайней мере одну ось симметрии и что сила N приложена в одной из
точек этой оси. Пусть точки К^ и К^^ принадлежат контуру ядра се-
чения. Как известно, продольная сила N вызывает в волокнах сече-
ния нормальные напряжения одного знака или двух знаков в зависимо-
сти от того, находится ли ее точка приложения внутри отрезка
/Cyj Яд или вне его.
Обозначим расстояния от точек
^А ^ ^в ДО центра тяжести сечения
через k^ и f'Q. Если бы нормальная
к сечению сила N была приложена
в К^ , то напряжение в волокне А
равнялось бы нулю, следовательно:
F ^
или
Фиг. 137
где F~ площадь сечения;
= 0
1^^
{6Л1)
момент сопротивления, равный — .
^«„^^^Р'^^^"^^ "Спряжение в волокне А при расположении силы iV, ука-
занном на фиг. 137. выражается формулой
(6.12)
или
м
N I
м
W
Член -у- может быть заменен через k^, следовательно:
<'^ = ~(^. + «)=-^. (6.13)
M. = N(k^ + a), (6.14)
Выражение Л1„ есть не что иное, как момент силы Л^ относительно
противоположной ядровой точки /(^, почему и называется ядровым
моментом.
Формула (6.13) показывает, что наибольшее нормальное напряже-
ние в сечении имеет такое значение, как будто никакой продольной силы
Л^ нет, а имеется лишь изгибающий момент, равный ятровому моменту
iM„ . Преимущество этой формулы перед формулой (6.12) состоит в том,
что она является одночленной и. следовательно, более просто и наглядно
выясняет закон изменения напряжений по длине арки.
§ 6.10. ЛИНИИ влияния Н, M,Q и N
Распор Н выражается формулой
откуда следует, что л. -в. распора имеет такой же вид, как л. в. М^ , и
отличается от нее лишь постоянным множителем — . Она представлена
на фиг. 138, а. Ордината под вершиной треугольника равна —- , где Л и
4^пролеты левой и правой полуарок; /=/i4-/2; / — стрела под шар-
ниром С. Если пролеты обеих полуарок равны между собой, т. е. если
^\—к= — , то это выражение переходит в — .
Остальные линии влияния построены для произвольного сечения а
(фиг. 138). Обозначим ординату этого сечения через у^^, а угол наклона
оси арки — через 9 •
При любом положении груза Р=1 изгибающий момент в сечении
^ выражается формулой
Первнй член правой части выражает собой л. в. изгибающего момен-
f2 в том же сечении простой балки пролета /. Второй член выражает л. в.
распора /У, перестроенную путем умножения всех ее ординат на постоян-
ИЬ1Й множитель у^^^ Наложив друг на друга обе эти линии влияния, как
"оказано на фиг. 138, б, получим искомую линию М^^. На фиг. 138, в орди-
наты этой льнии отложены от горизонтальной оси абсцисс.
Ордината л. в. Q^^ выражается уравнением
Qk = Q5<coS9 —/^5109,
где Qo^_ поперечная сила в сечении К простой балки с пролетом /.
Сравнение показывает, что искомая линия влияния строится путем
сложения двух: л. в. QJc ' ^^^ ординаты которой умножены на п.ктоян-
93
ros <? ил В. распора Я. все ординаты которой умножены «а
. uurlo-sin сГ. Такое построение показано на фиг. 138, г. ь
тоянное число i"' „ ^ обычным декартовым координата.
линия влияния, приведенная к показана на фиг 138 J ''
ное число
постоянное
же
ЛвН
MiJijjjH^^ S
улм.
лМ,
л.ем
Наконец, уравнение л
в. продольной силы имерт
вид ""^
Построение этой линии
влияния путем суммиро
вания двух составляю»
щих показано на фиг
138,е; та же л. в. отнесен-
ная к прямоугольной си-
стеме координат, -— на
фиг. 138,л^.
Характерные особен-
ности трехшарнирной ар-
ки, отличающие ее от
простой балки, весьма
ярко выступают в этих
линиях влияния. Напри-
мер, л. в. Mj^ имеет орди-
наты, значительно мень-
шие, чем М]^; она являег
ся двузначной и имеет \^
промежутке между опо-
рами нулевую точку. Ли-
ния влияния Qf^ также
имеет значительно умень-
шенные ординаты. Что
касается линии N^^ то ее
ординаты значительны и
в промежутке между опо-
рами при обычном очер-
тании арки имеют посто-
янный знак.
§ 6.11. ПОСТРОЕНИЕ ТЕХЖ?
ЛИНИЙ ВЛИЯНИЯ ПРИ
помощи НУЛЕВЫХ
ТОЧЕК
Фиг. 138
Как показывает Ф^^^-
138, кажлая из линии
влияния: М^, Qi^, На-
стоит из трех прямых, и
которых крайние ^^Р^^^,
рами. Для того чтп^^,.г п^. каются с осью под о
статочно ISro^K^ZT^'''''''' ""• ^' ^ произвольном масштабе, JJ
с осью абсцисс ^^^^^У ^^^Р^сечения средней прямой (или ее продолжения;
ординаты л fnfB„Vr''" ""^ ^У^^^ называть нулевыми, так как в н^
FM ты л. в. равны нулю. На фиг. 139 они обозначены через о, Ои о^
й*
при помощи нулевой точки о линия влияния М^ строится так- чепез о
под Произвольным углом наклона поовтитга .^ '^^^'^Роится так. через о
Г^рт'икалями, проведенными из' ^ГГ^ГучеСь^ГтоТГсоТли'няГ с
Сжем^'кГ^мГнТн^СэГточки "^"^^ ^'^"Р" "^-^™" --« «' " --
Фиг. 139
Соединим точки А и К прямой линией и продолжим ее до встречи
^прямой СВ. Точку пересечения назовем О. Если мы поместим груз Р
На вертикали точки О, то левая реакция пойдет по прямой АО, которая
проходит через К и вследствие этого обращает изгибающий момент в
^^чении К в нуль. Поэтому нулевая точка о лежит на вертикали точки О,
Для получения нулевой точки Oi нужно поставить груз Р в такое
положение, чтобы в сечении К поперечная сила обратилась в нуль. Для
!того нужно, чтобы реакция была параллельна оси арки в этом сечении.
проведем из Л прямую ЛО,, параллельную касательной к оси арки в
^'^^нии /С, и найдем точку Oi пересечения этой прямой с ВС. Проекция
• ^а ось абсцисс и будет искомой нулевой точкой Oi.
^^акоиец, для получения нулевой точки Ог линии влияния Л^^^ сле-
^У^т провести левую реакцию перпендикулярно названной касательной
продолжить ее до встоечи с прямой ВС,
<ить ее до встречи с прямой
95
Задача 13. Построить графически опорные реакции для Tpexmanti»
[Г. ]4г—ИЗ). -^Рнирны:
Фиг. 14?
Фиг. 143
Глава 7
РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ПЛОСКИХ ФЕРМ.
БАЛОЧНЫЕ И КОНСОЛЬНО-БАЛОЧНЫЕ ФЕРМЫ
§ 7Л. ПОНЯТИЕ О ФЕРМАХ
Фермой мы будем называть геометрически неизменяемую систему,
составленную из стержней, шарнирно связанных между собой концами!
Будем считать, что шарниры являются идеально гладкими, лишенными
трения, а оси всех стержней проходят
через геометрические центры шарниров.
Такое представление о ферме отве-
чает той расчетной схеме, которой мы
будем пользоваться на протяжении
дальнейшего расчета. Всякая расчетная
схема, как мы знаем, является упроще-
нием соответствующего ей дествительно-
го сооружения. В данном случае главное
упрощение состоит в допущении иде-
альной шарнирноЬти взаимных соедине-
ний стержней.
Ферме придают обычно такое устрой-
ство, чтобы нагрузка передавалась на
нее исключительно в узлах. Легко по-
1^азать, что при таком устройстве любая
^^агрузка будет вызывать в любом стерж-
"^ только такие усилия, которые на-
правлены по прямой, соединяющей его
^^онцы. Действительно, если какой-
"^будь стержень АВ (фиг. 144) шарнирно связан с остальными стержня-
ми только своими концами Л и В, то какие-то силы Sx и 5^ могут переда-
ваться на него только в этих двух точках. Но две силы уравновешивают-
^ только в том случае, когда они друг другу равны, противоположны и
^правлены по одной и той же прямой; следовательно, силы Si и 5^ на-
правлены по прямой АВ.
^ ^Зтсюда следует, что стержни фермы целесообразно делать прямы-
' "^^ е. с -прямой осью, проходящей через центры шарниров. В этом
Фиг. 144
случае
7 и,
каждый стержень будет испытывать исключительно про дол ь-
' ^ Рабинович
97
„^рвое растяжение или сжатие». Так,
„ ^ е иентральное осев ^^^^^^^^ стержнями схемы а
е усил-ия. т. е. ^^^ ^^^^^^ ''°^°?пвеошенно одинаковы, но в то время
например, на фип^^^^ 'f"''''^''' «озникают одновременно продольные
и поперечные усили^^^^,е или «^атие. ^^^ ^^ совместное дейст-
"»%SSN~ "Р" ЙГаЗи""ор»аль„ь,е напряжения рас„р«.
,„е йзгйба с продольными ^„о,с
Фиг. 145
ляются по сечению неравно-
мерно: наряду с сильно напря-
женными волокнами имеются
слабо напряженные. Когда
стержень работает исключи-
тельно на продольные силы,
материал может быть исполь-
зован более "ВЫГОДНО, и можно
облегчить вес конструкции.
Этим достигается двоякая эко-
номия, так как, уменьшая соб-
ственный вес конструкции при
помощи лучшего использова*
ния материала, мы тем самым
попутно уменьшаем постоян-
ную нагрузку, и, следователь-
но, дополнительно уменьшаем
поперечные сечения. Благода-
ря этому при одинаковой
нагрузке ферма получается бо-
лее легкой, чем балка сплош-
ного сечения из того же ма-
териала, имеюш.ая тот же
пролет-
Особенно резко преимуще-
ство фермы перед балкой вы-
- ^«тт,,„ оплошного
ство фермы п^у^^ сплошного
ступает при больших пролетах и тяжелой нагрузке; балки
сечения при таких условиях практически неприменимы. (ЬермаМ'^*
Такое преимуш^ество сохраняется и за^ действительными ч^^н^^^^^^
которые отличаются от принятой расчетной схемы заменой ш ^^^^^j^hx
узлов жесткими. Как показывают точные расчеты, "^*^^^^^"^ ^зую^^^""
узлов вызывает появление изгибаюш.их моментов и соответст > ^ ^^
дополнительных на-пряжений, однако последние обычно невели
имеют существенного значения.
§ 7.2. КЛАССИФИКАЦИЯ ФЕРМ
нескольким Р^з
;Лй**'
Классификация фер^м может быть проведена по
иым признакам. ^ь
1. По назначению ферм. В настоящее время фермы н^^^^^Г^еряЫ'
upfmlfo^^ " разнообразное применение в инженерном деле, что ^^J^^c^
l^^^uL^f^'"''^''''^'^'''' «^ по прюнаку назначения фермы яв^ая
Одн!м 2!^^''''''^^^^ ^^ишь кратким перечнем. ,„,ie ^^
в KaSe п п^п'^"''*'"'*''' применений ферм 5шляется нспользован'1^ ^^).
!_i^f:if^e пролетных строений мостов (мостовые Ф^Р^
аватьвыи^К®--"*™ «"««"««и."* услия надщ*
^^ )
Разнообразие мостовых ферм весьма велико.
На фиг. Иб показана схема ферм одного из мо-
стов, построенных по проекту проф. Л. Д. Прос-
курякова.
Далее идут стропильные фермы, кото-
рые насчитывают также большое количество си-
стем и форм. На фиг. 147 и 148 показаны две
схемы стропильных ферм, причем вторая имеет
надстройку, предназначенную для фонаря. На
фиг. 149 показано перекрытие, состоящее из
арочного пояса с фермой жесткости (так назы-
ваемая ферма Лангера).
Фермы применяются также в качестве карка-
сов для зданий промышленных цехов. Один из
примеров таких ферм показан на фиг. 150 (здесь
же схематически показан мостовой кран).
Большое применение фермы находят также в
подъемных кранах различного назначения, в
гидротехнических сооружениях, в мачтах для
подвески электрических кабелей, в радиомачтах,
в стрелах экскаваторов, крыльях самолета и
т. д. Примеры мостового и башенного кранов по-
казаны на схемах фиг. 151 и 152.
2. По направлению опорных реакций, вызы-
ваемых вертикальной нагрузкой. Фермы могут
быть безраспорными и распорными. Первые в
свою очередь делятся на балочные (фиг. 145),
консольные (фиг. 153) и консольно-балочные.
Вторые делятся на арочные (фиг. 154) и висячие
(фиг, 155). Суш[ествуют еще комбинирован-
ные системы, например комбинация арки с ба-
лочной фермой (фиг. 149), комбинация висячей
системы с балочной, арочной с висячей; арочной
с затяжкой (фиг. 156).
3. По очертанию поясов. Различают фермы
с поясами параллельными (фиг. 157) и полиго-
нальными (или ломаными); последние часто на-
зывают также фермами с криволинейными
поясами, имея в виду, что через узлы пояса мож-
но провести некоторую кривую. На фиг. 158 по-
казана ферма с одним ломаным поясом. Фиг. 159
изображает серповидную схему фермы, а
фиг. 160 — рыбообразную. Если узлы одного или
обоих поясов (фиг. 158) расположены на пара-
боле, то ферма называется параболической,
^сли на окружности, — то круговой и т. д.; если
узлы ломаного пояса расположены на параболе
"J^SK, как показано, на фиг. 161, то ферма в отли-
ие от изображенной на фиг. 158 называется
"О'^Упараболической.
кой ^^ си^^еме решетки. Раскосной решет-
bHHe"rtf^^^^^^^^ такая, которая в каждой поло-
зигз ^^Р^^^^ представляет собой непрерывный
сами^ ^ последовательно чередующимися раско-
и стойками (фиг. 157). Если раскосы в обе-
7*
т*..
Фиг. 147
Фиг. ЫЬ
Фиг. 149
-1M
1»^-
1 1
Фиг. 150
1 'г!е?ж
ш^
1
~^-*-**—— 4Ш/70
1 Г-35Ш-1 _
1
1
Ш^
ЦЦи!и<й|'1' ао Г
ш
ir
Фиг. 151
^^. .х^ ^^ |.
Фиг. 155
Фиг. 156
Фиг. 157
Г.
Фиг. 158
Фиг. 159
Фиг. 160
Фиг. 161
Фиг. 162
л^ половинах обращены в разные стороны, то средняя стойка не входит
13 состав этого зигзага и характер ее работы отличается от работы
остальных стоек.
Треугольной решеткой называется такая, которая предстаз-
1яет собой зигзаг с раскосам-и, обращенными попеременно то -в одну, то
Фиг. 1G3
Фиг. 164
Фиг. 165
Фиг. 166
L
В другую сторону (фиг. 162). Кроме основного зигзага, могут иметься
стойки, которые не входят в его состав (фиг. 163). Такие решетки
называются треугольны-
ми с дополнитель-
ными стойками.
Пол у р а с косн о й на-
зывается такая решетка, ко-
торая показана на фиг. 161.
Двухраскосны ми
двух решетчаты ми,
многораскосными и
многорешетчатыми называются такие фермы, у которых
решетка составлена из двух или нескольких раскосных или тре-
угольных систем. На фиг. 164 дана двухраскосная решетка, на фиг. 165—
двухрешетчатая, а на фиг,
166 — четырехрешетчатая.
Раскосная и треугольная
решетки называются еще про-
стыми, а многораскосная и
многорешетчатая — слож-
ными.
Составной решеткой
Называют обычно решетку, состоящую из простой основной решетки рас-
^осного или треугольного типа и дополнительных элементов (шпрен-
^елей), предназначенных главным образом для разделения большой па-
"^ли поясов на несколько меньших (фиг. 167).
^ ^роме указанных здесь систем решеток, возможны и другие, которые
стаются 'Вне классификации как менее типичные.
§ 73. МГНОВЕННО ИЗМЕНЯЕМЫЕ ШАРНИРНО-СТЕРЖНЕВЫЕ СИСТЕМЫ
Увеп " ^^Р^'^ имеет правильную <:тpyктypy^ то еще нельзя быть
.^^^Р^нным в том, что она на самом деле геометрически неизменяема.
uien, *ур^вильной» или «приемлемой» будем называть такую структуру, которая в об-
¦"Учае отвечает условиям геометрической неизменяемости.
103
Фиг. 167
.nvKTVPa определяет сооои целый класс фер^
п пп в том что данная стДКтУР J^^^,^ отдельного стержня могу,
^^"^.пыу длина и УГ^ь! наклонов ^ одну и ту же структуп,
в которььх длин д^^ Ф^Р^^^кно различаться между собой дЙ'
Гог^т пТвнешГму виду очень --«J> ^^^^^^^^ в этом. Если мыТу^
точно сравнить фиг. 168, а и о, изменять длины тех или инь!
^ стерма1ей, то при некотором щ
значении ферма может пре.
вратиться в мгновенно изме-
няемую.
Итак, шарнирно-стержневая
система может быть подвиж-
ной или изменяемой в следую-
щих случаях.
А. Когда- она имеет
неправильную струк-
туру. Этот случай распадает-
ся на три.
1. Система имеет недоста-
точное количество стержней.
На фиг. 169 дана модель шар-
нирной системы, которой недо-
стает одного стержня. Фиг. 170
показывает, какую форму при-
нимает эта модель после лег
кого нажатия пальцами.
2. Система имеет необходимое количество стержней, но последние
расположены так, что в одной части имеется избыточное количество пх, а
в другой — недостаточное количество.
Фиг. 169
Фиг. 170
1ПА
104
Во всех этих случаях система, вообще говоря, имеет конечную
(а не бесконечно малую) подвижность ^
Б. В некоторых случаях-даже тогда, когда она имеет пра-
вильную^ структуру. В этих случаях она называется мгновенно
изменяемой и, вообще говоря, может обладать лишь бесконечно малой
изменяемостью или подвижностью.
Для того чтобы обнаружить изменяемость в случаях «А», достаточно
рассмотреть структуру системы; для того же чтобы вскрыть случай «Б»
необходим более глубокий анализ.
Необходимо отдать себе отчет в том, что понятие о «мгновенно
изменяемой» системе является в известной степени абстракцией, подоб-
но «сосредоточенной» силе, «точечному» узлу, «идеальному» шарниру
и т. д. В реальных сооружениях не может быть такого резкого перехода
от одной категории систем к другой. Системы, близкие по своему очер-
танию к мгновенно изменяемым, хотя и не являются уже мгновенно
изменяемыми, все же обладают значительно повышенной способностью
к изменению своей формы при действии даже небольших нагрузок. Мы
будем называть их «почти изменяемыми». Класс этих систем, мало при-
годных или вовсе негодных вследствие их чрезмерной изменяемости
для практического применения, значительно шире класса систем мгно-
венно изменяемых.
§ 7Л СТАТИЧЕСКИЕ ПРИЗНАКИ МГНОВЕННОЙ ИЗМЕНЯЕМОСТИ
Если ферма мгновенно изменяема, то существует такое бесконечно
малое перемещение узлов, при котором длины всех стержней остаются
без изменения: ферма может совершить это перемещение без того, чтобы
потребовалось перерезать тот или иной стержень. При таком перемещении
всех узлов фермы работа внутренних сил Si, очевидно, окажется равной
нулю, а работа внешних сил — какой-то величине L^ , которая зависит
Не только от перемещения узлов, но и от самой внешней нагрузки. По
принципу возможных перемещений эти две работы должны быть по абсо>
лютной величине равны между собой. Могут встретиться два случая,
Если нагрузка такова, что Ь^ф О, то решение уравнений работ, которые
представляют собой не что иное, как обычные уравнения статики, ока-
жется невозможным. Если нагрузка подобрана так, что L^ =0, то урав-
нения примут вид тождеств 0 = 0, которые будут удовлетворяться при
каком угодно значении сил S/; решение уравнений сделается неопреде-
ленным. Итак, если система мгновенно изменяема, то при действии про-
извольной внешней нагрузки система уравнений статики получается либо
противоречивой, либо неопределенной.
Наоборот, если ферма с правильной структурой геометрически неиз-
меняема, то при действии любой нагрузки все усилия получают из урав-
нений статики определенные значения.
На этих соображениях основан указанный выше способ нулевой
"згрузки. Совокупность усилий, возникающих в системе при отсут-
ствии внешней нагрузки, носит название начальных усилий. К ним
относятся, между прочим, температурные усилия, которые возни-
кают в некоторых фермах при изменении температуры стержней. Теоре- ,
'^У о нулевой нагрузке можно формулировать следующим образом: если i
система, структура которой удовлетворяет требованию статической опре-
^^лимости, может находиться в равновесии при отличных от нуля на-
'вольных усилиях или реакциях, то она обладает мгновенной изменя-
емостью или подвижностью; если же она таких начальных усилий или
«.тб то она геометрически неизменяема и пещ.
реакций не Mooicer иметь,
Овижна. о н.Рпыа с тремя опорными cтepжня^
пеакции не може^^
г)п11жна. .„., (Ъеома с тремя опорными стержнями кп
"'Ш фиг. 171 представл;^ ^^^звестно, что три силы, пере?,
торые пересекаются в одной ^^^^^^^^ подборе их величины могут ка-
кающиеся в одной ^^^^'^5дн^ из опорных реакции можно дать произ^
ходиться в равиовеси .
Фиг. 172
вольное значение, а две другие найдутся из условий равновесия. Выходит.
что при отсутствии внешней нагрузки опорные реакции могут иметь
не только нулевые, но и бесконечное
множество других значений. Следо-
вательно, данная система обладает
бесконечно малой подвижностью.
На фиг. 172 каждый из треуголь-
ников 1—3—5 и 8—10—12 присоеди-
нен к ферме при помощи трех стерж-
ней 1—2, 3—4, 5—6 и 7—5, 9-10 и
11—12, которые пересекаются в одной
точке. При отсутствии внешней
грузки усилия в этих стержнях м^'
гут иметь бесконечное множество зна-
чений, следовательно, это соединение
обладает подвижностью, и фер'^^^
мгновенно изменяема. ,,,
Пример и. При помощи способа «У''^^;^^^
нагрузок проверить на мгновениУ^
фиТ^тТ"^"^*' ферму, представленную
Проведем разрез /—/ и рассмотрим V^jJ^
адя равновесия части, расположенной по оу
сторону от разреза. Для того чтобы ^^^\
ре силы. n#»ur>^«^,t^.„.w. «.ч ^^пжия** ^-.
Фиг. 173
дойствуюпи1е по стерж»*^*'
torn Л;/Ff "''''''^'^•"!*^''' необходимо чтплк, ^" м^:и.,иую1цие по civ,. .^о-
// // п^ '' ^^Р^'^'"" <-*тороиы были пп ' равнодействующие сил 8. 9 с одно? cjc'
и 7 i Т^иТ "" "«?^^^"'и«му зТключ^^^^ Р««"Ь1 „ ,фотивоположны. Pffg
и 5. 3. Итак. Равподействующие^йлTfi^ ""*^ ° отношении равнодействующих сил Л
lOfi » . . ^ и й, J должны лежать на одной и то
106
юямой. Отсюда следует, что для возможности появлеиия начальных усилий необходи-
мо чтобы точки О и Ог и Оз лежали на одной прямой. Это условие ие только иеобхо-
itrMO "О п достаточно. Действительно, мы можем задать тогда в диагоналях 8 v\ 9
1ва произвольпых усилия так. чтобы их равнодействующая пошла по линии O1O2O3
н п то же время в стержнях 6, 2 с одной стороны и 5, 3 с другой стороны задать уси-
лия, равнодействующая которых равна и противоположна первой. Тогда части, отсе-
иеиные разрезами /—/ и //—//, будут в равновесии; кроме того, все узлы будут в
равновесии. Например, из того, что силы 6, 8, 9, 2 друг друга уравновешивают, сле-
дует, что равнодействующая сила 6, 8 равна и противоположна равнодействующей силе
9 '2\ следовательно» можно подобрать такое усилие в стержне 1, которое уравновесит
как узе-п й. так и узел b и т. д. Итак, в этом случае фиг. 173 будет мгновенно изменяема.
Фиг. 174
Фиг. 175
Из наших рассуждений вытекает, что если точки Ои Oz, О3 лежат иа одной прямой
(шестиугольник Паскаля), то и точки взаимного пересечения прямых /, 5; 4^ 2 и 8^ 7
автоматически располагаются на одной прямой, а точки взаимного пересечения пря-
мых 6, 4: /, 3 и 7, 9—на другой прямой.
На фиг. 174 показана фотография модели такой мгновенно иямеияемой фермы,
а на фиг. 175 — та же система в деформированном виде; деформация достигается не-
большим нажатием пальцев. Благодаря неизбежной игре в шарнирах перемещение
оказывается не бесконечно малым, а достаточно заметным. Между тем модель фермы,
имеющей ту же структуру, но другие — произвольные — соотношения между длинами
стержней, деформировать без повреждения стержней оказывается невозможным.
§ 7.5. ПОСТРОЕНИЕ ПЛАНОВ СКОРОСТЕЙ
Существует простой, чисто кинематический, способ поверки ферм на мпювеиную
изменяемость. Для того чтобы воспользоваться им, нужно уметь строить так называе-
мые планы скоростей.
а) Полярный план скоростей. Пусть дан какой-нибудь диск, например треуголь-
ник ABC (фиг. 176). При бесконечно малом его перемещении в своей плоскости ско-
рость любой точки пропорциональна ее расстоянию до мгиовеиного центра вращения О:
tJ^ —ЛОсо; v^^BOti^; v^^COt^^
где
**>—угловая скорость диска.
Отложим величины этих скоростей от полюса О на лучах О А, ОВ^ ОС в виде отрез-
ов Оа, ОЬ, Ос, Тогда из условия пропорциональности отрезков нетрудно вывести» что
фигура аЬс подобна и параллельна основной фигуре ABC. Перенесем фигуру ОаЬс^ ие
^^няя направления ее прямых, в произвольное новое положение и назовем ее п о-
обп^ ^^^^^ плаьом повернутых или нормальных скоростей. Он
Цеп ^^^^^^* если из произвольной точки О плоскости {не обязательно из мгновенного
*^ "Тра вращения) провести лучи Оа^ ОЬ^ Ос и т. д., соответствеьшо перпендикулярные и
1Г>7
.Фопориноиальные скоростям ™.екД ^^^^^ ^^ ^^ ^__
В, с,... диска. Точки а, 6?, с и т. д. называются
¦--V' ^.^ииями cooTBt^reiuyi-uaHx точек у4, Д С,.... Любая прямая АВ, принад-
"'"".niL'ДИСКУ параллельна изображению аЬ на полярном плане
лежащая Д"^?У' ''J „„„_ самое компактное изображение скоростей любой точки лю-
"''''''^"'^^нГпле^его данному механизму.
бого звена, принадлежащего да у ^ частном случае, когда какое-либо звено
неподвижно, его изображение певращается в
точку, совпадающую с полюсом плана.
На фиг. 177 показаны простейший четырех-
звенный механизм и соответствующий ему по-
лярный план. Для построения последнего берет-
ся произвольный полюс О; с ним совмещаются
изображения а, d неподвижных точек А w D.
Далее проводится произвольной длины прямая
аЬ\\АВ. После этого определяется точка с, для
чего проводятся прямые Ьс\\ВС и ас||у4С.
Чтобы найти скорость призвольной точки ?
звена ВСЕ, нужно построить на прямой be
фигуру bee, подобную фигуре ВСЕ, т. е. прове-
сти Ье\\ВЕ се\\СЕ. Скорость точки Е выражает-
ся вектором Ое.
Истинные направления скоростей всех то-
чек перпендикулярны лучам Оа, Ob, Ос, Ое и
направлены в одну и ту же сторону относи-
тельно точки О, т. е. соответствующие стрелки
как бы вращают весь полярный план вокруг
этой точки в одну и ту же сторону. Достаточно
задать направление вращения одного из звень-
ев механизма, например звена АВ, чтобы из плана скоростей сейчас же нашлись истин-
ные направления скоростей всех точек.
',о,е/
Фиг. 177
сл"жн!Гк,!н?мяГ''^^"°«"°"Р°^Д'"^ полярного плана скоростей для более
жТиГа"/ЛГо™^Г Ге"^ Гя" "" ""^"^ совмещаются изобра-
фигура afbc гсп^^^гИ^!^ l^' ^ произвольном масштабе строится
rfg^GHfpllFG^;. F^- ^3 точек rf и / проводятся прямые
прямые gkwGH и1цт ^ "' ~ "Р^^'ые giWGJ и fiWFJ; наконец, нз g w i-
^ повернутые и " ЭО^^врктп^?^,!^?" Этот способ изображения скоростей состоит в том.
?оч.1°Т- '^«"Р""™ которь^х'^^f42?J'"^" откладываются не от единого полюса, а от
ч пп„ ^ " S какой-либо пп«мпй'^^^,^'''=" '¦^"'^и векторами. Так. например, скорости
^, причем точки .4'„Vявляйся',w <*""'• *^> изображаются векторами ХА' нВВ'.
J ивляются изображениями точек Л и В. Так как
&;
;ГАе to .
1^
\^АА'=.АОы,
= БЛ'=ВОо,.
У^^^овая скорость вращения звена АВ, то
^' ^':ВВ' = АбгВО
откуда следует, что А'В'\\АВ, те. изображение прямой, принадлежащей жестком>
днску, всегда параллельно самой прямой. ^ H^A^itr/Kdmen жестком>
Из сказанного следует,
что порядок построения не- F
-юляр юго плана для кине- а)
матической цепи ничем не
отличается от порядка пост-
роения полярного плана.
Возьмем для примера
систему, изображенную
сплошными линиями на фиг.
180. Нзбражения А\ В\ С^
неподвижных точек слива-
ются с самими этими точ-
ками.
Изображение 2' точки 2
намечаем в произвольном
месте на линии А — 2; оче-
видно, что при этом линию
А^—'2^ можно считать парал-
лельной линии А—2, так как
обе они сливаются. Далее
проводим прямую 2^—3^\\2—
—2 до встречи с прямой
В—3, затем 3'—4'\\3~4 до
встречи с прямой С—4 и
т. д.
Допустим, что точка 2
механизма переместилась
влево; для того чтобы полу-
чить действительную ско-
рость этой точки, нужно, как
показывает чертеж, повер-
нуть вектор 2—2' вокруг
точки 2 на 90^ против часо-
вой стрелки. В таком случае
действительные скорости
всех прочих точек также найдутся поворотом соответствующих векторов 3—3, 4—4
" т д. против часовой стрелки.
Фиг. 178
.^
V
/I'V—
\
\
\
в
-Г -^
IB'
\ /
I
J
Фиг. 179
109
..„ЧЕСКИИ МЕТОД ПОВЕРКИ МГНОВЕМНОП ИЗМЕНЯЕМОСТИ
g 7.6. киНЕМАТИЧЕс д изменяемостью ИЛИ подвижносгьк,,
Р.ли фигура обладает мгновенной „ ^^ наоборот, если фигура
^ян?е можно построить план скР^^^^^^„ неизменяемости стру,.*
Гблада.оЩая приемлемой ДЛя^е^^Р,, и^н полярного плана скоро.
?vS допускает построение не у подвижна,
стей то она мгновенно изменяема ^^^ фигуру, геометрическая струк-
"неполярный план представл'^ет ^ исследуемой фермы, и все прямые
хура которой совпадает со струкгур стержням фермы. Если какая
г-аГ^лТ^^^^^^ ^°°"""^''°"" """*''""•
~сЖ
Фиг. 181
Фиг. 182
то эта часть фермы движется,, как одно и^лое те представляем соб^^^
геометрически неизменяемую фигуру. Пусть, например, ферма опирается
на три опорных стержня, не пересекающихся в одной точке, отделив _.)
ферму от ее опор, мы должны получить геометрически "^'^^-'^^^^^JJ^y
фигуру, которая может двигаться в плоскости, как одно целое^ В та
случае план скоростей, построенный для нее, должен быть подооен са
ферме. Если же, кроме такого движения, фигура допускает бесконе
малое изменение своей формы, то для нее можно построить 5^°^^^1,]М
вующий план скоростей, не подобный самой фигуре. Итак, иеобходил
и достаточным признаком мгновенной изменяемости или подвижно^^^
фермы, обладающей приемлемой структурой, является возможно
построения другой фигуры, которая, не буДУ^^^ ^^
добна ей, обладает той же структурой и теми
направлениями стержней. jjji
Для симметричной фермы мы укажем здесь более простой критер
мгновенной изменяемости. ^^
Удалим один из стержней, перпендикулярных оси симметрии, и Д-
Образовавшейся кинематической цепи построим полярный план по» г
нутых скоростей. Ось симметрии плана может оказаться либо J^^%i.
лельнои, либо перпендикулярной оси симметрии кинематической ^^
Рт.!!^^''^^^ случае возможное перемещение кинематической цепи о0Р^,«е
сим.метрично, а во втором случае-симметрично. В первом слУ ^ ,
?яе^Г мгновенно изменяема, а во втором неизД^
скопп'пЛ"^^ надобности доводить п о с т р ое и и е п л ^^^^^.
метпии LI"" ДО конца. Как только выяснилось направление оси
МС1РИИ можно прекратить построение цчс-
ских^цегГей ^^Ll ^^^ "^казаны два примера сим^метричных кинемат
ских цепей, образовавшихся из ферм Справа построены планы cKOF
110
стей. На фиг. 181 ось симметрии параллельна оси/V/V; перемещение цепи
обратно симметрично. При таком перемещении расстояние между точка-
ми В и S' остается неизменным, следовательно, ликвидация разреза в
^^ержне ВВ не помешает движению; итак, ферма мгновенно изменяема.
Возможное перемещение кинематической цепи фиг. 182 —симметрично,
поэтому ликвидация разреза делает движение невозможным.
§ 7.7. НАГРУЗКА ФЕРМ
Для ферм всех видов нагрузкой служит собственный вес и так на-
зываемая полезная нагрузка, т. е. та нагрузка, для восприятия которой
ферма предназначена. Для стропильных ферм к полезной нагрузке
относятся ветровая и снеговая.
Ветровая нагрузка определяется по формуле
Рв = ^^»
где Рв-"-^^^-^^"^^ ветра в кг/м^, нормальное к воспринимающей по-
верхности;
k — аэродинамический коэффициент, зависящий от формы и поло-
жения подверженного действию ветра объекта. Аэродинами-
ческий коэффициент k для зданий с двускатными крышами
изменяется от 0,2 при угле наклона ската ср = ЗО"" до 0,8 при
9-60^.
Следует обратить внимание на то, что распределения усилий при
действии ветра слева или справа не являются симметричными отобра-
жениями друг друга; симметрия нарушается вследствие того, что гори-
зонтальный опорный стержень помещен только на одном конце фермы.
Снеговая нагрузка Рс в килограммах на 1 м^ горизонтальной проек-
ции покрытия принимается различней для разных районов в зависимо-
сти от средней максимальной толщины h снегового покрова на земле,
установленной наблюдениями за ряд лет. Для двускатных крыш в за-
висимости от района принимается рс от 50 до 200 кг/м^.
Снеговая нагрузка может располагаться на левом скате, на правом
или на обоих. Для каждого стержня принимается за расчетную наибо^
лее невыгодная комбинация ветрового и снегового давления с полезной
нагрузкой.
Для мостовых пролетных строений за полезную нагрузку прини-
мается установленный специальный нормами вес поезда, автомобилей,
Толпы и т. д.
§ 7.8. СПОСОБ ВЫРЕЗАНИЯ УЗЛОВ
Одним из простейших способов получения уравнений, содержащих
Минимальное количество неизвестных, является проведение таких раз-
Резов, из которых каждый отсекает от фермы по одному узлу. На
^^^^ 183 показан один из таких разрезов. Он рассекает ферму на две
|*асти, из которых меньшая содержит лишь узел Л. Выгоднее всего
рассматривать равновесие этой меньшей части (фиг. 184), так как она
додержит минимальное количество стержней и простейшую внешнюю
"а^Рузку.
Выделяя при помощи таких разрезов все узлы фермы (фиг. 185).
Ь1 Получим как раз такое количество уравнений, которое несбхсдим;^
ны^ ^"Р^леления усилий во всех стержнях фермы, в том числе и в опор-
^- Сравнения будут весьма простыми.
m
Итак, способ вырезания узлов является частным приложе
щего метода сечений. ^^^м щ
Его применение оказывается особенно удобным в тех
когда геометрическая структура фермы обеспечивает возмож ^'"^''^Ч
ределять неизвестные одно за другим без совместного решенысг"^^^^ ^П-
уравнений. "^ ^^ ^^стемы
На фиг. 186 показан узел Л, содержащий только два
Обозначим усилия в этих стержнях через Si и 52. Для анали ^^^^^^^я
Фиг. 183
решения задачи нужно задаться положительными направлениями уси-
лий. Предположим, что оба они направлены от узла, т. е. что оба
стержня растянуты. Спроектировав силы на. произвольные две оси,
мы получим два уравнения, в которые будут входить неизвестные 5|
Фиг. 185
^ ^2\ следовательно о"
™ мГмХТГ''''''"'"™'""""™" '>'""=''^«»™ из „«лож».*
Можно предложить '' ^ ДРУ^ую-пер-
SSSSt"^ '«'™Moc?oS„r'"'^'^ -°-б разложения
вольные точ Л „^ Г''™^ ^' и IJT*h? 1^'Г^""""«-- "^ "Р«"Ь1Х. по
относительно тоик« л/ -"^^ "^' относителк,^ ° ""^ уравнения момен-
лержать лишь адно и Р^^"^' "Улю то ,са^;°'"<и Л^ и момент силы &
Аналитическое npVf"^^^""oe. ^''^ "^ уравнений будет со-
санным На фиг 1«1«"'^""^ может быть ..
«отором направления'»°"°'0"оит в погг"^^"° графическим, пока-
Из атого построения по?'' ''"'' " «еличиня Р?""»" треугольника сил. в
•S-. 52. но и их знаки "тГ^'^^к-тся не только °Л"°й "^ «"^ (^) известны-
иаки. Таким Образом rS„^^''°-"'°^"bie величины снл
"^ • 'графическое построение силового
многоугольника заменяет собой аналитическл,^ ^
пешения системы двух уравнений с двумя hpL^ операцию совместного
Р Гтоль же простое решение пoлvuяpi.„ , "!"^^^""Ь1ми.
решения сиегсмы «вул уравнений с двум» uVu7r,^"^^'''"•^"'- --ош^^шиги
Р Столь же простое решение получается Лп"""^""
одится более двух стержней, но при том vrLll™"" ^^''°''- ^ '<«торых
(_,JU.'1U ¦'"^- ¦•! t¦^^"^^^^^^ "^'•'¦УЧаеТСЯ и Ппо о
.л-одится более двух стержней, но пои тпС .,Л ™^ У^-"""- ^ которых
-^..сялишь два усилия. всеРГ^^оч^ГуГ^иГизГе^ГьН^^
й)
/7
0^.
Фиг. 186
Определение усилий в ферме способом вырезания узлов представ-
ляет собой многократное повторение одной и той же несложной опера-
ции, состоящей в последовательном построении замкнутых силовых
г Y 1"
Фиг. 187
jjj,p^y^^'^^*HHKOB для каждого из узлов фермы. Существенную роль
ygjj f^ ^^^^^Р надлежащей последовательности перехода от узла к
Оста ^ ""^^^^ стадии расчета следует вырезать тот узел, в котором
jj^ocb лишь два неизвестных усилия,
выр^з ^^* ^^^ узлы пронумерованы в том порядке, в каком нужно их
опред^^^ Д-^я определения усилий. Рекомендуется предварительно
Узле ; ^^"^ опорные реакции из условий равновесия фермы в целом. В
Ми у "виденная левая реакция уравновешивается двумя неизвестны-
^^ИзвГс'"^^*^' После того как они будут найдены, в узле 2 останутся
^^^но ^"^^^^ усилия в верхнем поясе и в раскосе, следовательно, их
^^йдем ^'^^^ определить вырезанием этого узла. После этого мы по-
поясе 9 ^ /^"^У *^» в котором будут неизвестны усилия в стойке 3—4 и в
Ко ^ ^' ^'
*^^^^я л^^' ^^канчивая решение, мы подойдем к узлу 13, то в нем оста-
Щ Узла ^^"^ неизвестное — усилие в стойке 13—М, в то время как
^Р^внени'^л^"*^ составить два уравнения. Очевидно, что одно из этих
^ ^^ и будет контрольным. Например, спроектируем все силы в уз-
ле 13 на ось, перпендикулярную оси стоики 13—14, ъ это уравнение уг.
лне самой стойки не войдет, и мы получим контрольное равенство, g^'
зывающее внешнюю нагрузку узла и усилия Id—И и 1и~12. Т^^^.^}
ски это контрольное условие выразится в том, что равнодействующ,^
названных трех сил должна быть направлена по линии 13—14, Наконг^'^
в узле 14 мы будем иметь два уравнения или два условия и ни одн;;
неизвестной; этот узел будет целиком контрольным. Получение тпр
контрольных условий объясняется тем, что три уравнения статики v ^
были использованы ранее, когда мы определяли опорные реакции
В некоторых случаях приходится идти от концов фермы к середин
Анализ структуры ферм легко приводит к следующему заключени
для того чтобы в ферме, опирающейся на три опорных стержня, мож^
было определить все усилия последовательным вырезанием узлов (г ^^
для того чтобы существовал такой порядок обхода -
котором в каждом уравнении будут встречаться только два неизвестн
усилия), необходимо, чтобы ферма была образована из треигольиичгг ^'^
узлов, при
НЫ)
тем последовательного присоединения дв'ухстержневых i/злов'ТдиаТ
§ 7.9. ЧАСТНЫЕ СЛУЧАИ РАВНОВЕСИЯ УЗЛОВ
При вырезании узлов часто встречаются некоторые простые глуияи
решение которых может быть дано раз навсегда ьобихшш^^
А
Фиг. 188
Фиг. 189
^-^oro^l^^IZZtSTZT:^^^ 'Т ^Ф-- '88). Равновесие
татель сам найдет без тГпа^ ^ ^^"" S.^S^^O. Доказательство чи-
Условимся для краткости на^ып.^
равно нулю, нулевым МьГмп Г ^'"^Р'^^"''' ^ котором усилие
ном двухстержнев'ом уз^ТоТ'""' ""° " ненагружен-
иулевыми. " узле оба стержня являются
ней напГа2нПГодн'оТп2?^^ узел в котором оси двух стерж-
hSS°" °^^^-«ьные два стержня t ^^^• "^^^"^ стержень в узле, в
поеп!, ' ^^°Д««очного^ cSh" "i"P^«^^HH по одной прямой, носит
BviSr'^y^ соединим мысленно v^^'' "^^с"^^ '^^«^^ бы?ь сведен к
тоГько л' "^"Рзвленную по их обшр^й '''' -^i и 5^ в одну равнодейст-
в^ся?'"•""•¦ ^-^^PaBHoScSfn,,"P''''°"- Тогда в узле останутся
bSkom гТ"''" "Р" У^^овии что кя-^Г " ^^^^ "^3. Они могут уравно-
лкчине и н^^' У''"^"^ -S» и \ должн^'^^'' "' ""^ "орознь равна иул.о
ДоГны^бГь'Г^Г' " nPOT^oCSbfe'''c/'"""' "'*^У '«^°" "/^''^
"Ь1ть одинаково растянутыЧГп.^ стороны, т. е. стержни / н ^
^'«УТЬ! или одинаково сжаты. Итак:
•^1=52 и 5з = 0.
~Хг^* '"«-P.-.L il^. „а„™,„„, ^^,«.
>г^
о хрехстержневой узел с одиночным стрп*»^.
^ютеИ по направлению последнего Гбиг^опГ "ы "^грузкой, дей-
' S трехстержневой узел, в котором оги п'« ^- ^" ™^^" ^ «^У
-Сно'й прям'ой. Четыре'силы, ТавГвегЛ^сГв ^злГмГ.?
б"ыть соединены в две равнодействующие, из которых одна напра^
по прямой 1-2, а другая-по направлению оси стержня 5 Задача
приводится таким образом к случаю .Ь и можно сказать что каждая
„з'этйх двух равнодействующих равна нулю. В таком случае S=sTh
S,=^--P.r.e. оба стержня J и2 растянуть, или сжать с
одинаковой силой, а одиночный стерж ен ь и сп ытыва ет
усилие, равное Р: он будет сжат или растянут, смотря по тому
направлена ли сила Р к узлу или от узла. Что касается величины уси-
р. V'
/
Фиг. 191 Фиг. 192
ЛИЙ Si и S2, то она не может быть определена из условий равновесия
даннного узла, так как для этого потребовалось бы третье уравнение,
в то время как для узла можно составить только два уравнения. Это
усилие найдется, когда мы будем рассматривать другие узлы фермы.
4. Трехстержневой узел с одиночным стержнем при произвольном
направлении нагрузки (фиг. 191). Разложим силу Р на составляющие
^' и Р'\ из которых одна приложена к узлу параллельно оси стержней
^ и 2, а другая —параллельно оси одиночного стержня 3, Первая не
вызывает в стержне 3 никакого усилия, а вторая вызывает усилие, рав-
mt-^P'\ Что касается стержней 7 и 2, то в них от действия составля-
^оЩей Р' возникает разность усилий, равная самой силе Р', а от дейст-
вия составляющей Р'' — какие-то равные усилия. В итоге
Si=.S2-i-P' и 5з = -Я".
5. Ненагруженный четырехстержневой узел, в котором оси стержней
"вправлены по двум прямым (фиг. 192). Заменив мысленно силы I и 2
mu2"*^^ стороны и силы 5 и ^ с другой стороны их равнодействую-
^*^^и. Мы приведем задачу к случаю «1» и легко обнаружим, что
Si = 52 и 5з = S4.
в койГ**^^'^- Пользуясь приведенными выше теоремами, определим нулевые стержни
этоы^^ьной ферме (фиг 193). Узел / является ненагружеиным двухстержневым. ло-
HaxoL?^ стержни— нулевые Откинув мысленно оба стержня, мы увидим, что узел 2
?«РЖнк ^ ''^«"^ же "условиях. Так, переходя от узла к узлу, мы убедимся что все
'^^ии Р^«^п<>ложениые справа от силы Л — нулевые. Кроме того, в узлах 12, И и
5«€iCu ;^*^аде к ним сгойки и подвесш являются одиночнымя стержнями, а так как
^-^ll\"^''РУзки в этих узлах нет. то они не работают. Наконец, в узле 10 подвеска
^Иачен^Р^^^янута с силой равной Р Для большей ясности все нулевые стержни обо-
" Т0И1ед,^И линиями.
«еотйкальными силами в узлах 5, б
iQ4> «агрУ^ке»^^ „^являются одиночными стержня^
.пьная ферма (фи^; ^^^2^ 4^^' "^ Im фермы, усилие в какой-нибудь „од!
Шпренгельная Ф F^^^ ^-"i ' женных к узлаМ ^P^P^peACTBeHHO к ее нижнему концу
J 5, Я /2 и /5. ^^°^ узок, приложеии ^^^^ена иепоср а ^ ^_^,^ Ш п р енгед и
--'- из \^^^зать лишьта. ко^^^^ только/ ^^^^^ ^ соответству^о
Гом сляае из -^ .ГаГ-^^?. ^Гоа^^им один из узлов шпренгел^й
Фиг. 193
например, узел 4'. Когда подвески 4-4' не работает, то ^^^^''^^^Jzf^^^^^^^
ночным стержнем. Таким образом подвески и шпренгели «^^«^^«LoThmh в обшей ра-
элемеитами. работающими лишь на местную нагрузку и не участвующими в оиш
боте фермы.
§ 7.10 ДИАГРАММЫ УСИЛИЙ (МАКСВЕЛЛА — КРЕМОНЫ)
Каждому узлу, вырезанному из фермы, соответствует ^'^¦^^'"^л^5Я
замкнутый силовой многоугольник. Для того чтобы определить У^^ ^.
во всех стержнях, приходится построить столько силовых многоу
НИКОВ, сколько имеется узлов. Разбросанные по всему чертежу ^^""^^^j^.
многоугольники неудобны для пользования и служат источником о^^^
бок. Кроме того, каждая сила повторяется в них два раза, так
любой стержень входит в состав двух узлов. Двукратное вычерчйва
одних и тех же сил требует излишней затраты труда, а главно
влечет за собой неточность чертежа, а нередко и недоразумения.
Стремление избавиться от этих неудобств послужило толчком к
мечательному усовершенствованию метода вырезания узлов, ^^^^о-
ному на применении так называемых «взаимных диаграмм», "P^ДJ^^^
женных английским ученым Максвеллом и развитых итальянс
геометром Кремоной. Взаимные диаграммы позволяют получить ^Р^
чайно компактное, удобное и легко контролируемое графическое
строение всех усилий на одном чертеже, причем каждое усилие черт»
лишь один раз. ^
П6
Поставим себ^ задачей соединить все силовые многоугольники, ко-
пые получаются при вырезании отдельных узлов фермы, в одну фигу-
: и притом так, чтобы каждая сила встречалась на чертеже только
Р^ н рйз. Рассмотрим скачало простой пример — трехпанельную ферму
Ш1Г 195 а) у не имеющую опор и нагруженную уравновешенной систе-
1/^^ внешних сил.
Линии действия внешних сил и
опорных реакций можно рассматри-
вать как бесконечно длинные растя-
нутые или сжатые стержни. Оси всех
стержней фермы, включая и послед-
ние, разбивают плоскость чертежа
на отдельные поля, частью замкну-
тые, частью разомкнутые, которые
обозначены на чертеже буквами а,
Ь| с, d, е, f, ..., L Часть этих полей
в данном примере имеет вид тре-
угольников; вообще же они могут
иметь и другую форму. Существенно
лишь следующее обстоятельство:
если мы выдел-им часть плоскости,
заключающую данный чертеж, то в
ней каждая точка, не лежащая на
рассматриваемых прямых, принад-
•^leKHT одному и только одному по-
^^0- Если такое разделение части
плоскости на поля возможно, то и
Максвелла — Кремоны возможно.
построение требуемой диаграммы
Условимся обозначать каждую прямую двумя буквами или двумя
цифрами, обозначающими те два поля, которые разграничиваются
"^ои прямой. Прямая аЬ разделяет поля а и &, т. е. совпадает с линией
^^иствия силы Рг; прямая ag служит границей между полями а и g и
¦ -^^ Обозначение самих узлов при этом уже не играет никакой роли.
Построим силовой многоугольник для внешних сил (фиг. 195,6).
^УДем откладывать силы в той последовательности, в какой мы будем
j^g^^*^P^4aTb, если будем обходить ферму в круговом порядке, напри-
обх "^ ^^^совой стрелке. Сила Pi имеет обозначение fa: при круговом
оде мы сначала встречаем поле f. потом а, поэтому на силовом мно-
117
f начало a через a конец вектора этп-
гоугольиике обозначаем через / • ^^ „ проводится поэтому ^1
Sb.. Сила Р2 будет ?боз"ач'тку ^^ ^.оторая уже определилась „'
силовом многоугольнике через ^^дом, каждая из внешних сил рае'
предыдущего построения^ Таким t^^^^^^ ^^ фиг 195. б силовой !;„,,
положится на «™-"f .^"РеСстыми линиями. Он образует как бы кар.
гоугольник начерчен более тол _ Кремоны. '^
кас будущей f^^J^^^^^^Tусилий в стержнях фермы. Порядок пере.
Переидем к определению j^^^^_ ^^ диктуется лишь тем, что в каж.
хода от узла к узлу нам g^j^^.ne более двух неизвестных усилий
дом разбираемом У?-"е ;;°™„,, уравновеситься три Сйль^г^которе^
Начнем с узла А В «ем долж У^ ^ они должны образовать
обозначены через faag Hgh " Д н остается найти точ
Г;ТрТвоГмТаТиа%1мТе7з точкой а прямую, параллельную сте;;
S^a/фермы а из точки /-прямую, параллельную стержню fg Пере-
™че"1'^э?их прямых определит нам точку Д^ Тем самым узел А урав-
новешен; ему отвечает замкнутый треугольник }ag.
Переходим к узлу В. В нем уравновешиваются четыре силы, из ко-
торых две известны. Обходя их в круговом порядке, мы встретим силы
ga, ab, bh, hg. На диаграмме они должны образовать замкнутый че-
тырехугольник с вершинами, расположенными в том же порядке:
gabh. Нужно найти только вершину h. Для этого из точки Ь, уже имею-
щейся на диаграмме, проведем прямую bh, параллельную стержню bh,
а из g — прямую gh, параллельную одноименному стержню. Таким
образом, и здесь каждый вектор займет вполне определенное место.
Узлу F должен соответствовать на диаграмме пятиугольник e^ghi.
Нужно найти недостающую его вершину L Она получится на пересече-
нии прямых М и ei, которые следует провести из точек h я е парал-
лельно соответствующим стержням.
Узлу С соответствует многоугольник hbcki; его вершина k лежит на
пересечении прямых ik и ck, проведенных из точек /, с параллельно
стержням ik и ck.
Проделав эту часть построения, перейдем к узлу D, в котором оста-
лась одна неизвестная сила kd. На диаграмме уже имеются точки k и
й; остается их соединить прямой. Узел D уже является контрольным;
если построение произведено без ошибок, то прямая kd диаграммы
окажется параллельной линии ED.
сгг^^Л '^^°Р"*^ остался нерассмотренным, не требует никаких по-
пос?ооений Vn''^'' ^'^ ''° У"^"-""^ У^^ найдены в процессе предыдущих
диагоамГ'J?T°^'"'"^^'°"^""'^^ ^ и^'*' силы de, ei, ik, kd образуют на
диаграмме замкнутый четырехугольник deikd
ных повероГ На^римеГ п' ^'"™" Допускает множество разнообраз^
требую?!Тобы силы Spft-'*^^''"'" Р^'Р"" ^-^- Условия равновесия
обра^в^лЛамкнуты'/^^^^^У'^"^''^ "^ '^^^'^^У^о «з двух частей фермЫ.
но находим ioyroL^nL'^-i'f"^ "^ диаграмме мы действи^епь-
левой части, ub^eihTZn^t^^' ''°™Р"^ подтверждает равновес^
части. ' '^''' который имеет такое же значение для право"
В ^'обом^^^мкнУоТм^шХ^^^^ диаграммы сами собой, так ка«
ние. позволяющее обойти kdwom«! ''''"'^ образуют непрерывное те«е
правление одной стороны MHoSvmnl'' ''"''''УР- Достаточно знать «а
ния всех остальных.'^ Напр^меп^'в v^f ^ "^^бы определить напра^^^
Р.: она идет вниз. ОбЫде^ силшой 1п^ ^ извест1ю.З»яращде1Шв^Х^1
жением так. чтобы Цройти сиГ Ь Z ^'"««''НикJew Щпр^^Ш^ ^'^
— ^^^^^^^1 r^:^v I i ^'V^"
^;=?'il iliS"^ f^^
правленной вправо (т. е. направленной от узля Ал ^ г-„по .rf
;'рам.н„» от вершины Л верш„„1Тэг„"^Гре„™Г« ?„•>«• Bcex°v™'
„,й ума f. Таким способом определятся все'з„Т^ „.„ГанТе'Т,
Фиг. 196
Фиг. 197
Рассмотрим теперь более сложный пример (фиг. 196, а), Необходи-
0 с«а«^ала найти аналитически или графически опорные реакции.
На фиг. 196, б внешние силы- отложены на прямой abcdefg^ затем
^ произвольного полюса О проведены лучи, необходимые для построе-
^^ веревочного многоугольника, показанного пунктиром на фиг. 196,а.
^вая опорная реакция выражается на диаграмме вектором па, а пра-
вая^ вектором gh.
j^ -^^^^Рамма строится в таком порядке: I) треугольник hat; 2) пря-
Q. .^^^""^ьник abkly из которого видно, что усилие в стойке Ы равно силе
> ^) четырехугольник hikl\ 4) пятиугольник tkbcm и г. д.
119
в рассмотренных примерах все усилия можно было определить
ел едова тельным вырезанием узлов. На фиг. 197 показана стропильн^^
ферма Полонсо, структура которой является неподходящей для ^^
посредственного определения усилий этим методом. В то же время ch^^'
ма Полонсо, нагруженная по наружным узлам, допускает раздел ^^*
плоскости на отдельные поля, следовательно, для нее существует ^^^^
грамма Максвелла — Кремоны. Для построения этой фигуры прихо^^^'
ся комбинировать метод вырезания узлов с более общим методо ^^^
чений. В первую очередь при помощи разреза, показанного на фиг^то?
определяют аналитическим путем усилие в одном из стержней ж'
например в нижнем стержне, и наносят это усилие в соответствую^^^^'
масштабе на диаграмму. После этого построение последней может^^^^
доведено до конца без всяких затруднений. "^ь
§ 7.11. ПОСТРОЕНИЕ ДИАГРАММЫ ПРИ ЗАГРУЖЕНИИ УЗЛОВ
ЛЕЖАЩИХ ВНУТРИ КОНТУРА
^ Из фиг. 198 легко понять, какие затруднения возникают «
случае: линия действия внешней силы Рь приложенной в узле д''не
Фиг. 198
час-
в
Фиг. 199
разбивает поля а в
/V „ Р,^^» направленные гтгч ^"^'^о^ательнмо
^имои. Егп„ .., ^^Рниры. феплл. при эт^ J'''' ^' " ^^' ^ в узлах
^авались nnl^n!.^^^ статически опре-
X vr««„.4 "Р^-^оженными в узлах
бы, и вклю-
/л V '^^шения заттяим '^'^'^^ пол
/,*«;• 199). направленные пГ" "^"°
Due то пп^ ^" '^«¦"ы Я, иР^Т "Р** ^том остаетго L ^'
чет фермы (фиг ,98Л '^'^Р^^нейГэто"/ ''•^^' "^^к^е
построив. дЖг^а^м'^ fe^* ^^"^ 199? ^//J ^'^ "ра
120 -^ Максвелла - KpeioSi'' ''°''°Р°"
можно
§ 7.12. ПОСТРОЕНИЕ ДИАГРАММЫ ДЛЯ ФЕРМ,
СОДЕРЖАЩИХ ПЕРЕСЕКАЮЩИЕСЯ СТЕРЖНИ
При наличии пересекающихся стержней, не связанных между собой
в точках взаимного пересечения, поля, ограничиваемые различными
стержнями, частично перекрывают друг друга; такова, например, об-
ласть, заштрихованная на
фиг. 200.
Сравнительно простой вы-
ход из затруднения состоит
в том, что в местах попар-
ного взаимного пересечения
стержней вводится ф'иктив-
ный шарнир, который связы-
вает их между собой. Число
стержней при установке каж-
дого такого шарнира авто-
матически увеличивается на
два (вместо двух стержней
появляются четыре), но
система остается ста-
тически определимой. Усилия в ферме остаются также без изменения.
В то же время создается вполне определенное взаимное разграничение
граней, и построение диаграммы становится возможным (фиг. 201).
Приходится лишь мириться с тем, что некоторые силы фигурируют на
диаграмме по два раза: усилие в ди-
1агонали АС выражается векторами
ed п fg, а в диагонали BD
^^ >^ раыи ef и dg.
Фиг. 200
векто-
Фйг. 201
В том случае, когда в одной точке пересекаются оси трех и более
стержней, установка шарнира, связывающего все эти стержни, обраща-
ет систему в статически неопределимую. Дополнительный узел можно
помещать только в точке взаимного пересечения двух стержней.
§ 7ЛЗ. ПОСТРОЕНИЕ ДИАГРАММЫ ПРИ ПОМОЩИ РАЗЛОЖЕНИЯ НАГРУЗКИ
Скажем здесь прием, который в некоторых случаях может дать зна-
ительное упрощение. Пусть требуется построить диаграмму для фер- •
'^bi, представленной на фиг. 202, а.
I2F
o,-v на аве: пусть первая состоит из сил
Разложим внешнюю нагрузку и а Д ^^^^^^^я, что от первой на-
п р я вторая-ИЗ сил Рг. ^^- ''^тержнях простой фермы, показан-
^' "" \очнйка.от усилия только bJ^^^P^JJ^ фермы фиг. 202, е. Дейст-
'P'-'f/лиг 202. б; от второй-в стержнях ФР^^^^^.. ^^^^^^^^ ^^^^^
Гельно* каждая из --^"^„Ф^з'м^я'емаТсистема, а это в силу теоремы о
себя, как -ометрически неизменяш ^ ^^^ ^^^^^^^^,^ ,,,р^„„ „, ^^.
единственности решения д
ботают.
6)
1
!^.
1
^
—^»^-Ю* л
'' 1
:
Фиг. 202
^
;
¦^=3,
Построение диаграмм для каждой из этих двух ферм производится
без затруднений. прнпя
Этот прием, разумеется, годится и для аналитического определенн
усилий.
§ 7.14. СПОСОБ СЕЧЕНИЙ
Для определения усилий по способу вырезания узлов требуется по-
степенно переходить от узла к узлу в определенном порядке, продикт
ванном структурой фермы. В тех случаях, когда требуется определи
усилия во всех стержнях фермы, такая постепенность вполне прие
лема. С аналитической точки зрения такая операция представляет с
бой не что иное, как решение двух уравнений с двумя неизвестным »
затем подстановку найденных неизвестных в следующие два УР?^" ^,
ния, содержащие, кроме этпх неизвестных, еще два новых, и т. Д- Так ^
цепная зависимость между неизвестными отражается на точности Р
зультатов расчета.
Если мы будем применять метод сечений в более общем впде, т. '
отсекать не отдельные узлы, а более крупные части, то получим во
можность определять некоторые, а иногда и все неизвестные непоср^
ственно, т. е. каждое неизвестное—из одного уравнения, содержаше
только это неизвестное. Такой путь менее подвержен неточностям; ^Р^^^
ме того, он может иметь преимущество в том случае, когда требуете
122
опреде-п^^ь усилие только в одном стеожнр или г. . ^
Стержней, до которых при пользован^и^Гособо, -Г^ "Р^™^
шлось бы добираться издалека. способом вырезания узлов при-
Способ сечений во многих случаях дает возможность ппи аналитн
веском решении задачи получать для усилий изолированные уравнеГ^^
вместо того чтобы добиться этого результата из системы совместнь^^
уравнении путем длительных аналитических преобразований п?едс™
ляется возможным при рациональном выборе моментных точек полу-
чить его непосредственно, опираясь на наглядные указания, которью
даются структурой самой -^ ^^' '^
фермы. Этот способ со-
стоит в следующем: рас-
секают ферму на две ча-
сти, проводя разрез так,
чтобы в него попало не
^олее трех стержней с не-
известными усилиями. Ес-
ли это удается, то одну из
частей фермы удаляют, а
действие ее на оставшую-
ся заменяют усилиями,
после чего составляют три
уравнения статики, содер-
жащие три неизвестные:
5ь S2, 5з (фиг. 203). Ре-
комендуется писать уело- Ф^р 203
вия статики исключитель-
но в форме уравнений м о-
ментов причем определять моменты относительно точек Оь Ог, Оз
попарного взаимного пересечения сил Sj, 52, S^, Эти точки получили
название точек Риттера,
Нетрудно видеть, что при таком способе составления уравнений
каждое из них будет содержать только одну неизвестную. Обозначим
равнодействующую всех сил, приложенных к рассматриваемой части
фермы, кроме названных трех сил, через R. Тогда уравнение моментов
относительно точки Oi будет иметь вид
Moi(/?) + MoA) = 0
или
-Rr,+S^a, -О, {7Л)
^Де Ti, «1 — плечи сил R и Si,
Аналогичный вид будут иметь остальные два уравнения, составлен-
«1ле относительно точек Og и Оз.
Для того чтобы не ошибиться в знаках, целесообразно направлять
силы Si, Ss, S-г так чтобы онирастягив'али соответствующие стерж-
ни» а моменты писать с одним знаком (безразлично с каким), если они
вращают по часовой стрелке, и с обратным знаком,—если против.
§ 7.15. ПРИМЕР. ФЕРМА С ПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
И РАСКОСНОЙ РЕШЕТКОЙ (фиг. 204)
Для определения усилий в поясах и раскосах следует проводить
Разрезы типа а —а, г для стоек —типа b — b. Усилия в поясах и раско-
^^^ не зависят от того, как расположена вертикальная з'зловая кагруз-
-/л.
нпи по нижнему, или по обоим
гГи"^^;»-е« для -<>--;s жГ=;;г^:?,
^ в левой половине пр ^^^^^ ««««^"/узел той же панели. Таким
„ентной точкой служит __^Н^^^^„ ^^p^^^H У^^^ ^ „о абсолют-
ехержня -^^^^Х^о'^.тбуяъ стержне верхне ^^^^ ^^^^^^ ^ ^
°^?''°^ичйне равно усилию не « f" *^ей"ельно верхней по направле-
ной величине Р^ смешена относи! -^ ^.^ся также, если
смежной панели. -¦ -^^^су. В этом mv«v„^ .
м отвечают
Фиг. 204
Если эпюра М имеет наибольшую ординату в середине пролета, то
можно сказать, что любой стержень верхнего пояса сжат с силой, боль-
шей, чем та сила, с которой растянут раположенный под ним стержень
нижнего пояса. Сжатие доминирует над растяжением.
Пользуясь эпюрой моментов, изображенной на фиг. 204, б, можна
вычислить усилия в обоих поясах:
h ^
All ,. Mo
-7^ ; f/з = —^ И т.д.;
п h
h
-и.
М,
0, = _i^ = _t/,
и т. д.
h фер™ ^ "°'"^^'' оказываются обратно пропорциональными высоте
стой И^^й-Тр^л^^иГ^Р^^*" «^«о^РУО аналогию между фермой и про-
стои оалкой. увеличение высоты поперечного сечения послеяней влечет
1олокнТх.''' "''''™°' уменьшение но'рмальныГнапряже^ий в крайни^
Точка Ри-?геоа1па^яД^°''^'' определяются из сечений типа а-а-
Ючка Риттера удаляется по горизонтальному направлению в бес»®н«Ч'
191
124
дость. Соответствующее уравнение моментов вырождается при этом в
уравнение проекции на вертикальную ось Ait^icH при этом в
уравнение проекций в данном случае может рассматриваться как
уравнение моментов относительно бесконечно далекой моментной точки
Спроектировав на вертикаль все силы, действующие на любую из
двух частей фермы, образованных сечением а~а, мы получим для рас-
косов, нисходящих слева направо, уравнение вида
D Cos а — Q = О
НЛП
D =
cos а
(7.2)
где Q —поперечная сила простой балки. Она считается положительной,
если стремится вращать обе части балки по часовой стрелке. На
ij>0
Q<0
Фиг. 206
ф1г. 205 через Q обозначена равнодействующая всех левых сил, со-
стоящих из внешней нагрузки и опорных реакций. Если эта сила на-
правлена вверх (Q>0), то раскос растянут, а если вниз, —то сжат.
Для раскосов правой половины фермы, т. е. нисходящих справа
налево (фиг. 206), формула будет иметь вид
Dcosoc + Q = 0
или
D
Q
(7.3)
cos а
Если эпюра поперечных сил, вызванных вертикальной нагрузкой,
Меняет свой знак в середине пролета (а это происходит, в частности, при
Равенстве всех узловых нагрузок),то все раскосы оказыва-
^^?^ растянутыми. .
Гак как углы наклона раскосов равны между собой, то усилия в них
пропорциональны поперечной силе Q и могут быть представлены в неко-
I'^PoM масштабе самой эпюрой поперечных сил. Наиболее нагружен-
"ьши оказываются раскосы, расположенные по концам фермы.
125
Легко убедиться в том, что замена какого-либо раскоса, ни
ще'; к середине пролета, раскосом восходящим не изменяет вели^^^^
его усилия, но изменяет знак на обратный. Например, в ферме фи ^^^^
раскосы сжаты. Вообще полезно запомнить, что в раскосной X ^' ^^^
параллельными поясами при действии равномерно распределен '^^^ ^
грузки нисходящие раскосы растянуты, в о с х о д я п^^ ^^'
сжаты. Если нагрузка распределена неравномерно, то в олн '^^^
нескольких средних панелях возможно отступление от этого пп ^^ ^'^^
правила.
ill I I
Фиг. 207
Фиг. 208
Усилия V
'-M|Hr"2"08)Mb,p'a«ti\,°;"''''-"»«" ПР» помощи сече».
^= + 0
где знак минус отипги^ ~ '
схеме. Вообще если равно^т ' ^ ^"^'^ "'^«^'^ °^-
Г >^\ I /' ^о^Р^'^^ усилие Кнаправле-
няггч,. ^ ^ распределенной
Лрп;„ f сжаты, а стойки
Так ^"^- ^^'^ растянуты.
жение а гт,,й стор,. Раскосы длиннее
фиг. 204 fio„ ™^ "3 сжатие и« Dar^^' ^° «"годнее заставить
Знак усиГ ""^^««Sy ""'°6opoT.cS^^^ работать на растя-
определ'и?Г;и« в стойкГд'^^'^|" Ферма по фи? ?оТ '^'""^ ^^Р'"^'^ "^
« -^/Т4/~^ »и~- ~ «--
'^ ^- """^ знаков. Это правило
Фиг. 209
Что касается усилий в верхнем и нижнем поясах ферм (фиг. 2^4 и
907) то два стержня обоих поясов, соединенных между собой дь мя
^раллельными раскосами, имеют одинаковые усилия.
^ 7.16. ПРИМЕР. ФЕРМА С НЕПАРАЛЛЕЛЬНЫМИ ПОЯСАМИ
^ И РАСКОСНОЙ РЕШЕТКОЙ (фиг. 210)
Обозначим моменты левых сил относительно точек п—1 и п через
М __1 и iW^ , а относительно точки О^ , которая служит моментной точ-
кой Д^'^я раскоса D^ — через M'J . Усилия в верхнем и нижнем поясах и
в раскосе пусть будут 0„, t/., D^ . Из уравнений моментов относитель-
но трех точек Риттера получаются формулы
0. = -
Мп
^ п —
^'п-1
D.^
М:
Величины М^ , М„_1 , М^ могут быть взяты непосредственно из ве-
ревочного многоугольника, построенного яля заданной нагрузки. Верх-
Фиг. 210
НИИ пояс сжат, нижний растянут; это не нуждается в пояснениях. Что
Касается знака усилия Dn, то он, наоборот, требует более детального
разбора.
Графически вопрос решается так: нужно определить направление
момента М^ , т. е. момента всех сил, лежащих левее разреза, относи-
т'ельно точки О. Это направление определяется из веревочного много-
угольника. На фиг. 210 ордината М^ получилась того же знака, что и
ординаты M„_j и М„ . Но в простой балке статический момент левых
сил относительно точек п—1 и п, лежащих в пролете, направлен по ча-
совой стрелке; следовательно, статический момент М^ относительно
"^очки 0^ на фиг. 210 направлен также по часовой стрелке.
^ Можно прийти к тому же выводу и другим путем: из силового мно-
оугольника находим равнодействующую сил, расположенных по одну
^ орону от разреза. На фиг. 210 равнодействующая левых сил оказы-
^тся направленной кверху. Она приложена в точке О^ , следователь-
» ее момент относительно О^ направлен по часовой стрелке. В таком
""Учае усилие D„ должно вращать левую отрезанную часть фермы про-
.. ,,„елки т е. раскос сжат. Если бы ордината М^ оказд.
тнв часовой стрелки, т н сторону от замыкающей веревочного
лась расположенной ^^„^Р/'/ельствовало бы о том, что раскос раст'
многоугольника, то это с д раскосе зависит от соотношения ме"
нут. Следовательно знак усилР^^^^ ^^^р^^ моментов. Если „у^'
вТтГчГоГГпюры моГен^ов ле^ левее точки Риттера 0„ J^.
ответствующий раскос сжат; если правее. - то растянут. Увеличивая
иГуменьТая выпуклость верхнего пояса, можно при одной и той же
внёшГей нагрузке добиться изменения знака усилии в раскосах.
Аналитически величину и знак усилия D„ можно определить, „^
разыскивая на чертеже моментную точку и плечо г„ . с^то особенно важ-
Аналитически величину и знак усилия /J„ можно определить, „е
разыскивая на чертеже моментную точку и плечо г„ . с^то особенно важ-
но в тех случаях, когда моментная точка выходит за пределы чертежа
(фиг. 211).
г- ^,,„., все силы на горизонталь:
.. _ Мп COS а ^п—1
¦ и и -
Спроектируем
D sin р = — 0„ cos о.
Л«-1
(7.4)
Полученная формула позволяет установить следующий простой
" >1яснения вопроса о том, работают ли раскосы на растя-
жатие:
Полученная формула позвол5
критерий для выяснения вопроса и ium, puvjui^utui Jii
жение или на сжатие:
а) раскос будет растянут в том случае, когда
Мгг ^п~\ ^ ^ ^п ^ _hn_
hn
л„_
'п-\
^я-1
Фиг. 211
о или ,^ ' ^
б) он будет сжат, когда
в) наконец, он вовсе не будет рабо-
тать, когда
Мп __ hn
в последнем случае эпюра момен-
тов может быть вычерчена в таком мас-
штабе, что сольется с осью верхнего
пояса.
Отсюда можно сделать важный вы-
вод: если очертание верхнего пояса та-
ят за веревочный многоигольник дл^
отсюда можно сделать важный вы-
weo, что он может быть пппи^^^' ^^-^^ ^'^^Р'^^^^^ верхнего пояса та-
енешней нагрузки фермы rTTnZr^^'' веревочный многоугольник для
^'2 ^'^ою очередь Црас^^^^^^ выключаются из работы ^^
н^!^ЛТ' " ^^^^^'* pS^^^^^^ ""^^^Р^У влечет за собой
.пГ.Г:?..'^^^^^ усилие остп..' r'lr^ '^^^^^^ причем во всех панели
женной !"Р°''^"'«Ь1текает непХепг. .'''"'''' проекция усилий.
Если н "^^ ^ ^•^- "^"о<^Редственно из общей теоремы, изло-
\c^H^nJVafpS-f о п'^ясТ'^^.ой'-—ены' - -«^"'^
:: ''''^-' "- ^-^^^^^^^^и^^еТ^'^^опе^г длина стоек Р-
•28 ^ моментов, то раскасы. нисходя"»"^
, сереете пролета, сжаты; в противном случае они растянуты- раскосы
^е, восходящие к середине пролета, удовлетворяют обратному правду
знаков.
g 7,7. БОЛЕЕ СЛОЖНЫЕ СЛУЧАИ ПРИМЕНЕНИЯ СПОСОБА СЕЧЕНИИ
Упрощение, основанное на специальном выборе моментной точки
может быть достигнуто не только тогда, когда в разрезе встречаются
три стержня, но и в некоторых более сложных случаях
Ферма, представленная на фиг. 212, решается методом сечений в
следующем порядке. Сначала при помощи точек Риттера определяются
усилия трех стержней в сечении 1—L Далее проводится сечение 2—2
Фиг. 213
Фиг. 214
которое встречает на своем пути уже четыре стержня; однако количе-
ство неизвестных усилий в этом сечении равно трем, что и дает
возможность определить их при помощи трех моментных точек. Далее
последовательном порядке проводятся сечения 3—3, 4—4, 5—5, в
зждом из которых фигурируют по четыре стержня с тремя неизвестны-
ми усилиями, и, наконец, сечение 6—5, в которое попадают пять стерж-
^^и Опять-таки только с тремя неизвестными усилиями. Из этого при-
^^Ра видно, что необязательно проводить разрез через три стержня:
о можно проводить через любое количество стержней, лишь бы в чис-
^ их было не более трех, имеющих неизвестные усилия и не пересекав
'^'Щ^ся в одной точке.
^ о разрезе может быть и более трех стержней с неизвестными
^^силиями: если все неизвестные силы, кроме одной, пересекаются в од-
и точке, эта неизвестная может быть найдена соответствующим вы-
ъш^ ^*^ментной точки. Та же фиг. 212 может служить иллюстрацией
Мок' ^^^P^^^bi; если мы в первую очередь проведем сечение 6—6 и за
пеп'^"^**^^ точку примем узел, в котором сходятся нижний пояс и все
вест^^**^"**^^^ Ряскосы, то в уравнении моментов останется одна неиз-
4eTbi!f/* ^ именно усилие в верхнем поясе. Для определения остальных
рех ^уеилий уже невозможно ограничиться одним этим разрезом.
т
. „пи невозможность применения таких моментных то-
Возможность или нево структуры фермы, а не от ее конфигура.
чек зависит от reoMfP"^^^^^^^^^^ структуры может дать необход„,
ц„„. ^^ТУ^геГспучгях%гц,^ конфигурация не позволяет сразу на-
м^Гс'квозной разрез, проходящий через три стержня с неизвестными
^'Тасшотрим для примера ферму, представленную на фиг. 213.
Сде^аГнесколько попыток провести непрерывное сечение через три та-
Фиг. 215
КИХ стержня, которые не сходятся в одном узле, мы придем к выводу,
что это невозможно. Но эта ферма по своей структуре тождественна с
фермой фиг. 214, т. е. представляет собой два треугольных диска,
взаимно связанных тремя стерж-
нями /—2, 3—4 1и 5—6, Поэтому
для нее возможен разрез, пересе-
кающий те же стержни и целиком
отделяющий один треугольник от
другого. Для ясности этот разрез
показан отдельно на фиг. 215. Он
дает возможность, с помощью
трех моментных точек определить
усил^ия в стержнях 1—2, 3—4 и
5—6, Так, например, для опреде-
ления усилия S^_Q достаточно со-
ставить уравнение моментов всех
сил, действующих на треугольник
1—4—5, относительно точки Os-e*
Этот пример важен тем, ^^^^
позволяет обобщить понятие о
Фиг. 216 разрезе: необязательно, чтобы по-
следний был непрерывным; необ-
отделял какию-нибиа^ ип.^ й. водимо лишь, чтобы он целиком
При проведении разре^^^^^^ '^ остальных элементов.
la высказана
проф-
yiJiibHeHHH исключаются. Эта идея впервые был
Ф. С. Ясинским.
Рассмотрим для примера снова ферму фиг. 213. овесй^
Проведем замкнутый разрез (фиг. 216) и рассмотрим Р-^^^^^^лй
той части фермы, которая расположена внутри разреза. Диаг
2^6 и 5-^ попадают в разрез дважды, поэтому их усилия выключа-
^отся из любого уравнения моментов или проекций. Остаются только
пересеченные стержни 1—2 S-4 и 5-6, усилия которых найдутся при
помощи моментных точек О,, О^ и Оз. Поучительно, что этот способ ре-
шения, основанныи^на применении замкнутого разреза, проходящего
через пять стержней, тождественно совпадает с решением, показанным
на фиг. 21о и zlo.
На фиг 217 задача решается-при помощи нескольких круговых
разрезов. Круговой разрез а~а отделяет от фермы треугольник 4—5—6
Действующие на него силы направлены по трем прямым 7—8 8—9 и
9_7, которые не пересекаются в одной точке. Такие три силь1 могут
Ь
в
Фиг. 217
быть в равновесии только в том случае, если все они равны нулю. Но
если равнодействующая сил, направленных по стержням 4—7 и 4—S,
равна нулю, то это значит, что раскос 7—8 на всем своем протяжении
растянут или сжат с одинаковой силой. То же относится к стержням
8—9 и 9—7. После этого вырежем узел 4\ так как равнодействующая
Двух сил, приложенных к нему, равна нулю, то и равнодействующая
остальных двух сил, т. е. 4—5 и 4—5, также равна нулю, следова-
тельно, стержни 4—5 и 4—6 являются нулевыми. Вырезав узел 5, убеж-
даемся, что и стержень 5—6 является нулевым. Итак, при отсутствии
нагрузки в узлах треугольника 4—5—6 все его стержни являются нуле-
выми.
Усилия в сторонах треугольника /—2—5 и в примыкающих к нему
Элементах могут быть найдены следующим образом: сначала определя-
ются усилия в шести элементах, перерезанных сечениями b—b и с—с;
После этого вырезанием узла 5 определяются оставшиеся два неизвест-
ных усилия в том узле и, наконец, вырезанием узлов 1, 2 — остальные
усилия.
§ 7.18. СПОСОБ РАВНОДЕЙСТВУЮЩИХ
В тех случаях, когда невозможно иепосредственно составить такие уравнения, ко-
nnt^^^ содержали бы по одной неизвестной, иногда можно выйтн из затруднения прн
пои ^^ предварительного определения равнодействующих некоторых сил.
Риложенных к отсеченной части.
^ Для пояснения этого приема рассмотрим пример.
nnr.« У^'^ь требуется определить усилия в ферме (фиг. 218.а). В этой ферме невозможно
пеп ^" нн одного разреза, который встретил бы только три неизвестных усилия, не
ресекающихся в одной точке. Не имеется также ни одного узла, который содержал
„^ "^^-"ько два стержня Следовательно, несмотря на малое количество стержней, ферма
% сложную структуру.
,j^* проведем разрезы /—/ и //—// и рассмотрим условия равновесия той части фермы.
два?Р^я заключена между ними. Каждая из диагоналей BE и CF попадает в разрез
в огг ^^' "^^тому усилия в них сами собой уравновешиваются: следовательно, усилия
стальных четырех перерезанных стержнях также должны уравновеситься. Это ваэ-
^ 131
„. . лишь в том ^-^l' , противхположнаравиод ^^ ^^ ^ ^
далее р^'-'-'^^"/"".,' ,г1едуюш.ие uri-.«^- - - пявнод€й-Тву1«и1^« уw^..... ^ перерс-
,3 А На нее действ -т^-еДУ^^ _^., ^,,,„, 00,_, ^^Р^^^^^^^^з^^^ ,рех сил все .«,
усилий S^B и ScD • " ; ,.^ая -ерез точку О^. и.и ,
заииых диагоналях. прохс^.._ ^
должны пересекаться в одной точке. Продолжив сйлу Р до пересечения с прямой О w
найдем эту точк>^ С ^
На фиг. 218,6 построен силовой треугольник оЬс, из которого определяются ^
равнодействующие: одна сторона треугольника равна Р, две другие соответствен
параллельны прямым OOi н GO2. После этого сила Ьс разлагается на составляюаш
^АВ и S^?) , а сторона са — на составляющие S^^ и S^p •
Читателю рекоменд>ется решить задачу при условии, что нагрузка расположена
узлах А и D.
§ 7.19. СПОСОБ ДВУХ ИЛИ НЕСКОЛЬКИХ СЕЧЕНИЙ
Для определения усилий в ферме, представленной на фиг. 218. м
предварительно находили равнодействующз'Ю двух усилий, пользуяс
для этого сечениями /—/ и //—//. Это дало нам возможность решить
задачу, не составляя совместной системы уравнений.
Способ двух сечений состоит в решении той же задачи при помоШ»
составления совместной системы двух уравнений с двумя нежавестяы^
Он может быть применен в тех случаях, когда удается
разреза таким образом, что каждый из них содержит
Ш2
„ых, причем какие-либо два неизвестных усилия повторяются в обоих
разрезах.
Для фиг. 218 напишем уравнения моментов отсеченной части лежа^
шей выше сечения /-/, и той части, которая лежит шже c^itm^ И-^^
Первое уравнение составим относительно моментной точки О? а вто^
рое-относительно точки О,. Оба уравнения будут содержать одни и
те же два неизвестных усилия в пересеченных диагонали! Решив ур^в-
ненпя, найдем эти неизвестные. г-сшиь урав
^Т..?1То^ ^™^ ""^'^^ '"^ способом равнодействующих, то мож-
но сказать, что оба метода близки друг другу: один представляет собой
как бы геометрическую форму решения двух уравнений, а другой^
аналитическую. Во всяком случае можно утверждать, что все те зядачи
которые допускают решение методом двух сечений, допускают Vaкжe
решение методом равнодействующих, и наоборот
Так как решение системы двух уравнений с двумя неизвестными не
может считаться сложной или утомительной операщ1ей, то этот способ
следует признать весьма удобнь1М, если только структура фермы по-
зволяет воспользоваться им. г-^ jr ^ к
В более сложных случаях можно получить простые уравнения при
помощи трех и более специально выбранных сечений. При этом метод
все более утрачивает характер специального метода, позволяющего из-
бавиться от совместных уравнений, и приближается к общему способу
сечений. ^
§ 7.20. СПОСОБ ЗАЛ\ЕНЫ СТЕРЖНЕЙ (СПОСОБ ГЕННЕБЕРГА)
Определим этим способом усилия в ферме, представленной на
фиг. 218. Попытаемся преобразовать данную ферму, удалив один из ее
стержней и вставив вместо него другой стержень на новом месте. Эта
Фиг. 219
перацня представляет собой наиболее интересную часть расчета, так
^ак ее можно произвести разнообразными способами, среди которых
^адо выбрать достаточно удачный. Новый стержень называют «заменя-
щим стержнем»; тот, который выбрасывается, можно назвать «заме-
ияемым».
Выданном примере одним из приемлемых вариантов является следу-
JJ^**"* удалить стержень BE и вставить вместо него заменяющий CTtp-
tHb OF; на Фиг, 219 он показан двойной линией. Полученная при элал
новая ферма имеет настолько простую геометрическую структуру, что ее
геометрическая неизменяемость не может вызвать никаких сомнений.
В то же время она легко решается любым элементарным способом, на-
пример способом вырезания узлов.
Эти два свойства весьма существенны: заменяющая ферма всегда
должна выбираться так, чтобы она заведомо была геометрически неиз~
неняемой и в то же время поддавалась простому расчету.
Обозначим усилие в заменяющем стержне, вызванное данной внеш-
ней нагрузкой, через Тр ; усилие в любом из остальных стержней фер-
мы от той же нагрузки — через Sjj"^, где / — индекс стержня.
Нагрузим заменяющую ферму двумя взаимно-противоположными
силами, равными единице и приложенными по концам заменяемого
стержня BE (фиг. 220). Определим усилия во всех стержнях от этой
нагрузки. Заметим кстати, что заменяющая ферма в данном примере
представляет собой диск на трех опорных стержнях, поэтому опорные
реакции, вызванные двумя равными и прямо противоположными сила-
ми, будут равны нулю. Усилие в заменяющем стержне обозначим через
Гь'а в остальных — через S['K Величины S{^^ могут быть названы «чис-
лами влияния» сил Х=1 на стержень /.
Для того чтобы усилия во всех стержнях заменяющей фермы со-
впали с их усилиями в заданной ферме, необходимо, чтобы в узлах В и
Е были приложены силы, каждая из которых равна не единице, а дей-
ствительному усилию заменяемого стержня BE; обозначим это усилие
через X. Величина X может быть найдена из того условия, что усилие в
заменяющем стержне DF должно обратиться в нуль. Аналитически это
записывается так:
Тх Х + Т^^О,
откуда
Х- Т^.
Так как заменяющая ферма заведомо геометрически неизменяема,
то величины Тр и Ту имеют совершенно определенные, конечные значе-
ния. Если Ti ф О, то усилие X также получает совершенно определенное
значение; если же ^1 = 0, то Х= — или Х= со
О
Отсюда следует, что если заменяющая ферма геометрически неиз^
меняема, то величина усилия Т^ служит характеристикой заданной
фермы: если Ti Ф О, то заданная ферма также геометрически неизменяе-
ма, а если i 1 = 0, то она мгновенно изменяема.
Найдя значение X, можно определить все усилия уже обычным
путем, последовательно вырезая узлы или проводя сечения Можно их
также вычислить по формуле
S'^'^Sil^ + S'^X. (7.5)
Действительно, усилие в любом стержне / заданной фермы совпа-
дает с усилием того же стержня заменяющей фермы, а последний на-
ходится под совместным действием внешней нагрузк^!, вызывающей в
нем усилие Sj;) , и двух сил, равных X (где X имеет наКное выше
значение), которые вызывают в нем усилия S^o х Для того чтобы
таким способом вычислить все усилия, приходится, следовательно, два-
134
жды рассчитать заменяющую ферму и составить таблицу, в котосой
для каждого стержня должны быть выписаны значения S« и 5^°
Иногда выгодно не определять усилий 5«^ п S[" во всех стержнях
а ограничиться лишь тем минимумом стержней, который необходим для
вычисления X, остальные же суммарные усилия определить затем обыч
ным способом, не пользуясь заменой стержней
В сложных случаях приходится произвести две замены стержней
или даже более. В случае удаления двух стержней приходится опреде-
лить усилия в двух заменяющих стержнях: Т„, Т, То и U U, Uo где
Тр, Up—усилия в этих стержнях от внешней нагрузки; //и (/.-уси-
лия, вызванные действием двух единичных сил, заменяющих первый вы-
брошенный стержень; Гз и (/g — усилия от двух единичных сил, заменя-
Фиг. 221
Фиг. 222
ющих второй выброшенный стержень. Так как в обоих заменяющих
стержнях суммарные усилия должны обратиться в нуль, то, обозначив
усилия заменяемых стержней через А' и У, получим уравнения
Г,Х + Г,У+Т, = 0; j
откуда и определятся оба неизвестных.
Признаками геометрической неизменяемости заданной фермы слу-
жат определенность и конечность решения этой системы уравнений,
для чего необходимо, чтобы ее определитель был отличен от нуля:
Если Dr=o, то заданная ферма мгновенно изменяема.
На фиг. 221 приведена в качестве примера решетчатая ферма, кото-
Рая не поддается обычному простому решению. На фиг. 222 показана
заменяющая ферма, полученная путем замены трех стержней: заменяе-
мые стержни начерчены пунктиром, а заменяющие — двойными линия-
^^и. Заменяющая ферма имеет простейшую структуру: она образована
из треугольника путем последовательного добавления двухстержневых
узлов и решается при помощи вырезания узлов. Определение усилий
'^ужно начинать с правого конца фермы, постепенно передвигаясь на-
лево.
D
ФО.
§ 7.21. использование симметрии фермы путем разложения
Внешней нагрузки на симметричную и обратно симметричную
всякая нагрузка симметричного сооружения может быть представ-
лена 1$ак сумма двух нагрузок, из которых одна является симметричной,
1^Ш^о^ — обратно симметричной. Иллюстрация этой теоремы дана на
Фиг. 223
п изображает заданную нагрузку, схема б —ее сиыме-
фиг. 223: схема а изо^Р^Гс^ ^-обратно симметричную составляю-
тричную составляющую, а схема f ^^^ ^^ сложения схем
б и е получается схема а
В случае затруд^р^^
тельности расчета слож-
ной симметричной фер.
мы можно рекомендовать
разбить нагрузку на сим-
метричную и обратно сим-
метричную, определить
усилия от каждой из этих
составляющих в отдель-
ности и затем найденные
результаты сложить.
Пример 13. Рассчитать
на симметричную и обрат,
но симметричную нагруз-
ки ферму, представлен-
ную на фиг. 224.
а) С-имметричная
нагрузка. Стержни
3—12 « 12—8 должны быть оба растянуты или оба сжаты. В обоих слу-
чаях узел 12 не будет .в равновесии; отсюда следует, что эти усилия рав-
ны нулю (на фигуре нулевые
стержни показаны тонкими
линиями). В узлах 5 -и S стер-
жни 5—5 и 8—6 являются
одиночными, а потому они
нулевые. Нулевыми являют-
ся, очевидно, и элементы
нижнего пояса 1—13 -и
iO—7/. Усилие в диагонали
0—9 получается вырезанием
узла 5 и проектированием
действующих на него сил на
вертикаль.
Остальные усилия опре-
деляются вырезанием узлов,
б) Обратное и ммет-
P'l'J^^^ «^ грузка (фиг.
^^о). По условиям обратной
симметрии усилие в любом
стержне левой половины
фермы равно и противопо-
ложно усилию в правой по-
ловине. По этой же причине
усилие в среднем стержне
нулю. В разрезе а---а три па-
раллельные наклонные силы
уравновешиваются двумя
вертикальными; это возмож-
но только тогда, когда каж- ^
Фиг. 224
дая из этих двух групп сил образует пару. В таком случае усилие в стой-
ке 2—3 сжимающее и равно Q. В узле 2 остаются неизвестными две на-
клонные силы, которые определяются из условий равновесия этого узла.
Определение остальных усилий производится последовательным выре-
занием узлов.
§ 7.22. КИНЕМАТИЧЕСКИЙ МЕТОД. ОПРЕДЕЛЕНИЕ УСИЛИЙ
ПРИ ПОМОЩИ ПЛАНОВ СКОРОСТЕЙ
Планы скоростей позволяют графически применить принцип возможных пере-
мещений. Дадим механизму возможное для него бесконечно малое перемещение и
напишем выражение работы какой-нибудь внешней силы Р, приложенной к какой-
либо точке А. Пусть повернутая иа 90° скорость этой точки выражается на иеполяриом
плане вектором АА' (фиг. 226). Бесконечно малое перемещение точки А равно
v^- dt^=^AA' dt, а работа силы Р выражается произведением
Pv^dt cos (Р, v^) = Р. AA'dt sin а.
Но Р«ЛЛ' since есть момент силы Р, приложенной в точке А, относительно изоб*
ражения Л' этой точки на иеполяриом плане скоростей.
Фиг. 226
Фиг. 227
На механизм может действовать одновременно несколько внешних сил. Принцип
возможных перемещений требует, чтобы сумма работ всех внешних сил равнялась
нулю. В уравнении работ множитель dt войдет во все члены и поэтому сократится. В
итоге мы получим следующую теорему: при равновесии сумма моментов всех внешних
сил относительно тех точек, которые служат изображениями их точек приложения, рае-
«а нулю. При этом моменты, направленные относительно соответствующей моментной
точки по часовой стрелке, пишутся с одним знаком, а направленные против — с дру-
гим. Эта интерпретация, очень удобная для применения, была дана Мюллером-Бреслау.
Рассуждая таким же образом, но изображая скорости при помощи полярного пла-
на, мы получим еще более простое выражение для условий равновесия механизма.
Для этого надо перенести все внешние силы, приложенные в каких-либо точках
^> ^> С,... механизма, на полярный план скоростей в точки а, Ь, с и т. д., которые слу-
жат изображениями названных точек (фиг. 227). Для того чтобы механизм был в рае-
ковесцц, необходимо и достаточно, чтобы сумма моментов всех перенесенных сил отно-
сительно полюса О плана скоростей была равна нулю,
^Ту же теорему можно выразить еш.е следующим образом: если мы примем поляр-
«ьш fi^Qf^ скоростей за одно звено, имеющее неподвижную точку вращения в полюсе и
^^груженное всеми перенесенными на него силами, то это звено должно оказаться *
Роеновесии. Эта интерпретация была дана проф. Н. Е. Жуковским.
Все эти теоремы позволяют очень просто писать уравнение работ, которое служит
^ля определения неизвестного усилия. Ту же задачу можно решить чисто графическим
"Утем,
Определим при помощи неполярного и полярного планов скоростей усилие в диа
гонали БЕ фермы (фиг. 228) (диагональ BE заменена двумя силами).
На фиг. 228, а показан иеполярный план. Изображения F' и Е' неподвижных то
чек F и Е совпадают с самими точками. Скорость точки Л изображаем векто
ром АА\ имеющим произвольную длину и паправлеииым по линии AF; этим мы"
очевидно, удовлетворяем основному требованию: A^F^\\AF. Далее проводим A^D'\\An
и E'D'WED, причем прямая E'D\ очевидно, совпадает с прямой ED; потом HdoboL
D'aWDC и Pa\\FC; наконец аВ'\\СВ и А'В'ЦАВ. Остается вычислить момен
силы Ру^ относительно точки А\ момент Р^ относительно В^ и т. д. и, наконр
момент верхней силы X относительно В\ Что касается нижней силы Л", приложенной '
неподвижной точке ?, то ее момент относительно точки Е^ равен нулю вследгт ^
совпадения Е' с Е, То же относится к опорным реакциям. Уравнение моментов пп^^
мет вид Р""
^М^ + X'lBWsin (X, Ш') = о,
где ТМр — алгебраическая сумма моментов сил Р относительно соответствующих
то-
Фиг. 228
Отсюда
к,
^^'sin(X,^B')
Если окажется что гнпо у
На фиг 228 б покя у^ ^ ^, т. е в этом случае ферма
^l^^^^Tulol^^^-^^-^^^ ТяТо/пГаг^РИ помо.„ „„.ярного плана,
и OdllED пол^учае?Г«°" ^^^.««ь, "Р''"^'' Oa/f?V?''°^/ ™3'=''^' ^ "^«"«- ^з полюса
пересечении прямых сЬПг! = ^?,-"^Р^сеченни nmlMuv wJ^'^'^''^""" прямык adfAD
вескую сумму'^моментов^^х г''*"^* ^ ™-«а TocllJr^J^„^ " ^'^''^^ - ™''«=' '• «'
иия определить неиз^с^^^У™ '^ « ««^ X относительно .^^Р^^;?""" "У^'° ^лгебраи-
fivn^'^-™ ¦'^ из двух силП;!* стельно точки О „ из этого уравне-
^ -"И"' возникают изгибающие м^.^ «течениях, то, кроме
J38 чгащие моменты и поперечные си-
лы. Нагруженные стержни фермы работают в этом случае как балки
подвергнутые совместному действию продольных и поперечных сил
Рассмотрим влияние сосредоточенной силы Р, расположенной'меж-
ду узлами Л и ^ какой-нибудь фермы (фиг. 229). Если бы стержень АВ
представлял собой простую балку на двух опорах, то на ее концах
возникли бы опорные реакции Ra и JR^, показанные на схеме а. По-
ступим следующим образом: в узле Л фермы приложим две равные и
противоположные силы ±/?^;в узле Б —две равные и противополож-
ные силы ±Rb' От добавления такой нагрузки усилие ни в одном из
стержней фермы не изменяется. Усложнив таким образом нагрузку, т. е.
получив вместо одной силы Р пять сил, разобьем ее на две группы, из
которых одна показана на схеме фиг. 229, а, а другая — на схеме
фиг. 229,6.
Первая является уравновешенной нагрузкой; мы знаем, что такая
нагрузка статически определимой фермы заставляет работать лишь ту
геометрически неизменяемую часть последней, к которой она приложе-
на. В данном случае она вызовет усилие только в стержне АВ как в
балке.
Вторая нагрузка, показанная на схеме б, состоит из двух сил —R^
У —R^ ^ приложенных в узлах А и В, т. е. из узловой нагрузки, эквива-
лентной силе Р. Эта нагрузка вы-
зывает в стержнях фермы про-
дольные усилия, которые опреде-
лятся обычным способом.
Все сказанное относится в оди-
наковой мере ко всякой статиче-
ски определимой ферме и ко вся-
кой 'внеузловой .нагруз-ке-—без-
различно, состоит ли она из одной
силы или из нескольких.
Итак, для получения усилий,
вызываемых внеузловой нагруз-
кой во всех стержнях фермы, кро-
ме загруженного, мы имеем пра-
во заменить нагрузку двумя со-
ставляюидими, приложенными по
концам загруженного стержня. В самом же этом стержне, кроме то-
1^0, возникают еще усилия, как в простой балке.
Напряжения в загруженном стержне вычисляются по формуле
N _^ М
F ~ W '
Фиг. 229
где Л/ — продольное усилие;
f^ — площадь поперечного сечения стержня;
^^ — изгибающий момент;
*^ — момент сопротивления поперечного сечения стержня.
§ 7.24. РАСЧЕТ СОСТАВНЫХ ФЕРМ
Если мы заменим один или несколько стержней фермы более слож-
Ь1ми элементами, в свою очередь имеющими вид ферм, то получим со-
ставную, или, как ее называют еще, сложную, ферму. Первое на-
ванне более подходит к таким фермам, так как их геометрическая
РУктура может быть весьма простой.
„п^ячан на фиг. 230. Она образована и.
пример составной Ф^^^. ДО^с^зан^^ ^Ф^ ^^ ^_ CD фермами. В ^
фермы фиг. 231 "У'^^;!''^"^ащего менее трех стержней, и нельзя „ро.
нет ни одного узла, ^«f Р^^,^^^орого можно было бы сразу определить
вести ни одного ^ечен™. из кот f;^^^ ^^ менее задача решается очень
ГегГвслеГГе^Йогш^ *"' '"' " '°"^^ "Р°^^«й
фермой фиг. 231. производится совершенно таким же спосс
g„j;S<%S простой фермь? на внеузловую нагрузку. Сама идея при-
^ к
Фиг. 230
менения составных ферм основана на желании иметь большие панели,
которые часто оказываются выгодными с точки зрения уменьшения
собственного веса фермы, и в то же время избавиться от изгибающих
моментов.
Фиг. 231
Прилагаем в узлах Л и В по две равные и противоположные ^^
±/?^ и ±/?^з» где /?^ и /?^з — какие угодно две силы, уравновеш ^^^^
щие нагрузку фермочки ЛБ, как балки на двух опорах. Если ^^^^^^гь
нагрузка состоит из параллельных сил, то целесообразно ^^"^лнуЮ
силы ±Ra, ±/?? по тому же направлению. Затем рассчитываем Д ^^^^
ферму на узловую нагрузку, состоящую из сил — /?^ и — ^в* ^^,^йь
можем заменить ее фермой фиг. 231. Допустим, что при этом ^^^^д^и^
ВС окал^ется сл<атым с некоторым усилием S^^. Величина этого у^-
не зависит от формы стержня ВС; она не изменится, если мы ^Jl^,o4'
этот стержень фермочкой. Следовательно, можно сказать, что ^^^^^j^ и
ка ВС на фиг. 230 подвергается сжимающему действию Д^У^^Бт ПоС'
противоположных сил S^ , приложенных по ее концам (фиг. ^*^ '' «яс
ле этого нетрудно получить усилия от такой нагрузки во всех с
МО
нял фермочки БС. Совершенно таким же способом определяются уси-
лия в элементах фермочки CD.
Что касается стержней нижнего пояса и обоих раскосов, то для них
усилия, найденные из фиг. 231, являются окончательными.
фиг.
232
'ее
Обратимся теперь к нагруженной фермочке АВ, Нагрузка, показан-
ная на фиг. 231, вызывает в стержне АВ некоторое усилие S^^» следо-
вательно, заменяющая этот стержень фермочка АВ подвергается дей-
ствию двух равно противоположных сил S^^, приложенных по ее кон-
цам. Кроме того, фермочка АВ — одна из всей рассматриваемой фер-
I I М I I I I М 1
Фиг. 234
TTTTTTTI I I
Фиг. 233
Фиг. 235
мы — подвергается действию уравновешенной нагрузки, состоящей из
заданных сил Pi, Р2, Р3, ^4 и реактивных сил /?^, /?^. В итоге эта фер-
мочка находится под совместным действием сил, показанных на фиг.
233. Остается определить усилия от этой нагрузки.
Задача 16. Рассчитать шпренгельную ферму (фиг. 234) как состав-
ную.
Указание. Шпренгельную ферму можно представить себе как ре-
зультат замены элементов нижнего пояса простой фермы, имеющей тре-
угольную решетку, вспомогательными фермочками (фиг. 235).
Верхние пояса, а также стойки не входят в состав фермочек.
Каждая из подвесок работает только в том случае, когда нагрузка
приложена к ее нижнему концу.
Каждый подкос испытывает усилие только от груза, приложенного к
верхнему или нижнему концу примыкающей к нему подвески.
Таким образом, эти элементы воспринимают лишь местную, т. е. при-
ложенную в определенных узлах, нагрузку и не участвуют в общей щ
n-PM ,'ак прочие элементы работают при любом рас.
боте фермы, между тем как проча
положении нагрузки на «P^PJlf. ' j,a нагрузка промежуточных узлов
Усилия onPe^^„^„'^'^f,f,Jf приложенными в узлах главной фермы;
заменяется составляющими прл элементами, которые на фиг
Гр^Г?^Тф\™ r;"?;S^J.--» - »VX pea™», 3 ,™«
работе участвует лишь сама фермочка. _
Г,",Г„е"„Г""оля^^^''=оГсос«Г главной фермы, „а„р„„ер
sepxLiI пГ'верхня'^я часть раскосов и стойки; усилия в них получают^
мер подкосы н подвески; усилия в них получаются только от второй из
^^"з)"^мееть1, входящие одновременно в состав обеих ферм: нижний
пояс, нижняя часть раскосов; усилия в них получаются как алгебраиче-
ские'суммы усилий, вызываемых обеими нагрузками.
§ 7.25. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Наиболее простая геометрически неизменяемая система, способная перекрыть го-
ризонтальный пролет и воспринять вертикальную нагрузку, — это простая балка Она
является исторически предшественником фермы. Когда нужно перекрыть большой
пролет или воспринять большую нагрузку, простая балка оказывается на практике
неудобной. Необходимость заставляет сплачивать несколько балок воедино при помо-
щи раскосов и стоек, подпирать их шпренгеляМ'И, подвешивать к наклонным тягам
и т. д. Так родились те сложные стропильные и мостовые фермы, которые применялись
до начала XIX столетия.
Первые Строители крупных мостов в 30-х годах XIX в, не владели еще научным
методом расчета. Например, американский инженер Лонг (Long), автор системы
моста, носившей его имя, считал, что в ферме с параллельными поясами, нагружен-
ной равномерной нагрузкой, все раскосы испытывают одинаковые усилия. Это за-
блуждение продержалось до 1850 г., когда молодой русский инженер Д. И. Журавский
(1821—1891) дал правильное решение вопроса^ В ряде замечательных статей, объеди-
ненных впоследствии в одну книгу, Журавский вполне самостоятельно дал детальный
расчет одиопролетной и многопролегиой весьма сложных ферм. Усилия он считал
направленными вдоль стержней. Что касается статической неопределимости фермы.
то она была обойдена им при помощи некоторых допущений
M..v^f™°'' значение в создании современной теории расчета статически определи-
Гнн&Т1846^и^18^^'''^^^ ""''¦ ^^^^^^ П- w!^ Shadier. 1823-1894). опублико-
ванные им в 1Ь4Ь и 1851 гг.. и книга проф. Кульмана^,
бьш^/аГ^нТГгу^Хои^еТ"' '«^"^^""ь.й на принципе возможных перемещений,
Werk°Bert."'?930.'"^'"" " "^""^^^ •'°h«"" Wilhelm Schwedler. sein Leben u. sein
¦ Вы ^^Р'^'^^^Ье Statik. Zurich. 1866
тейсооб^^ТпублСыТздаК'^вет?™""- ^^УР"^'' Главного управления пу
^ Elementare Theorip n Rnr^^u ' * *^"**^ка 4-я.
nover. 1863. "^"^ ""¦ B-^rechnung e.serner Dach u. Bfbckenkonstruktionen, Han-
• УСТОЙЧИВОСТЬ деформаций и статика сооружений. ,903.
Теоряя взаимных фигур была дана английским физиком Максвеллом' (Clerk
Maxwell, 1831—1879) и блестяще развита в приложении к теореме ферм итальянским
геометром Кремоной^ (Luigi Cremona, 1830—1903).
Способ замены стержней был предложен проф, Геннебергом (L. Henneberg)^.
В СССР теория статически определимых ферм подвергалась дальнейшему раз-
витию. Ей посвящены работы профессоров Б. Н. Горбунова, С. А. Бернштейна,
Н. К. Сиитко, И. М. Рабиновича и др.
1 On reciprocal figures, frames and diagrams of forces, .Transactions of the Royal
Society of Edinbourgh.'' v. 26 (1869—1872).
2 Le figure reciproche nella statica grafica, Milano, 1872 (русский перевод, „Взаим-
ные фигуры в графической статике", Гл. редакция строительной литературы, 1936).
3 Die graphische Statik der starren Systeme, Darmstadt, 1886.
Глава 8
ЛИНИИ влияния УСИЛИЙ в ФЕРМАХ
БАЛОЧНЫХ И КОНСОЛЬНО-БАЛОЧНЫХ
• S81 ПОСТРОЕНИЕ ЛИНИИ ВЛИЯНИЯ ПРИ ПОМОЩИ СЕЧЕНИЙ
ИЛИ ВЫРЕЗАНИЯ УЗЛОВ
Выше мы уже познакомились с понятием о линии влияния и рас-
смотрели общие свойства, а такя^е методы построения таких линий,
В данной главе речь будет идти исключительно о линиях влияния уси-
лий в стержнях фермы, т. е. о графиках, выражающих закон изменения
усилия в рассматриваемом стержне при движении сосредоточенного
груза Р=1. При этом будем предполагать, что груз устанавливается
последовательно в узлах верхнего или нижнего пояса («езда поверху>
или «езда понизу»).
Статический метод построения л. в. состоит в том, что груз Р=1
устанавливается в произвольном узле фермы, и для искомого усилия
составляется формула, вытекающая из того или иного уравнения ста-
тики. Затем эту формулу анализируют, для того чтобы узнать характер
выражаемой ею линии влияния.
Построим линию влияния для фермы, показанной на фиг. 236.
Проведем разрез через одну из панелей, например через третью
панель.'При любом расположении груза Р=1 можно написать, что
сумма моментов всех сил, действующих на левую или правую часть
фермы, относительно любой точки равна нулю. Для определения усилия
в верхнем поясе ^Од воспользуемся моментной точкой Oq. Обозначим
сумму моментов вертикальных сил, лежащих по одну сторону от этой
точки, через Л1о; этот момент равен изгибающему моменту, который
возник бы при том же положении груза в сечении О^ простой балки АВ.
Уравнение равновесия примет вид
Л^о+ОзГоз = 0,
откуда
О = -^0
М ^Л^^^"^^^ формула показывает, что искомая л, в. отличается от л. в.
Мо (изгибающего момента в сечении О^ балки АВ) лишь знаком минус
и постоянным множителем ^, следовательно, она имеет вид треуголь-
144
'Я с вершиной, расположенной под точкой Оо, а ее прямые отсекают
НИЬ<1 V, г ah
о ппооных вертикалях отрезки, равные — и — •
Таким же способом строится л. в. усилий в нижнем поясе U. Приняв
точки Оц
за моментную, получаем формулу
где
М,
л. в. изгибающего момента в сечении 0^^ простой балки АВ.
7 а
: -" Z?
=г.л=е«—^V>
Фиг. 236
!4^
10 И. М. Рабинович
о n в раскосе следует воспользоваться
Пля получения л. в. У^«^"^ „'а пересечении стержней О, и U,.
momShS точкой Ор'-^^^"^!""\ когда груз находится в правой
моментн раскос Растянут. ^ ^^ зид
Предположим что р ^^„^^есия левой час
части фермы, то уело f ^^^^ ^ д^г^, - О,
откуда
Оз =
„ „ D., отличается от л. в. опорной реакции /^^
^ .. ппавый участок л. в. ь'з отличие
т. с. правый у _?_ Он имеет вид прямой, отсекаю-
лишь постоянным множителем - ,^" ^
«ей на левой опорной вертикали отрезок^; ее нулевая ордината рас
положена на правом конце.
Фиг. 237
Когда груз находится в левой части, то мы из рассмотрения равно-
весия правой части находим аналогичным образом
Обе прямые, выражаемые этими формулами, пересекаются между
собой, как и в двух предыдущих линиях влияния, под соответствующей
моментной точкой. Это нетрудно доказать геометрически.
Другое доказательство дано на фиг. 237. Предположим, что груз
движется по консоли, которая связана с левой или правой частью фер;
мы. В первом случае его влияние будет выражаться на л. в, левой
прямой, а во втором—правой прямой. Однако когда груз будет прохо-
дить через точку О^^, то в уравнении моментов любой из отсеченных
частей фермы он фигурировать не будет, так как его момент будет ра-
вен нулю, следовательно, различие между обоими случаями исчезнет.
Для примера составим уравнение моментов левой части фермы, пред-
полагая, что груз расположен на любой из этих двух консолей и прохо-
дит через Oj^. Уравнение имеет вид
откуда
146
^A^ + D^r^^O, ^
D,==,
^А-
Итак, под точкой О обе прямые имеют одну и ту же ординату, вы-
пяжаемую этой формулой.
^Наконец, влияние груза, расположенного между узлами на третьей
ли выражается соединительной прямой между обеими основными.
^^^йля построения л. в. усилия в стойке Vz вырежем узел с ее верх-
концом и спроектируем все силы на вертикаль (фиг. 238). Пред-
"^^'ягая, что оба верхних пояса растянуты, мы получим
%
Но так как
0з =
Мо
Гоз
и о, =
М.
''02
где Mq — момент левых или правых
вертикальных сил относительно точки
Ооу а Гоз, ''02 — плечи сил 0^ и Ог отно-
сительно этой точки, то
Фиг. 238
V, = M,
I COSQ COSP \
\ /"02 ''ОЗ /
Из ЭТОЙ формулы видно, что л. в. усилия 1^2 отличается О)
л. в. изгибающего момента простой балки лишь постоянным множите-
лем. Из чертежа ясно, что cosa;>cosP и Го2<Гоз, следовательно, V'2>0r
т. е. при движении груза понизу стойка всегда растянута.
Tllllllllliminillimmim,.. j^
^4! —"^ ©
Фиг. 239
Подвески являются в узлах лрфямолинейного нижнего пояса одиноч-
ку jj ^'^^Р^нями; поэтому они могут работать лишь на местную нагруз-
^Н^л"^' 236 построена линия влияния для усилия V^.
Поясам^"^' 239 построены линии влияния для фермы с параллельными
'^и. КОТОРУЮ можно рассматривать как частный случай предыщ-
W
которую можно рассматривать как частный случаи прадь
оси абсцисс
имеет наклон
V. ,,4я,.пв- если отрицательные ордип^Аш изложены от
^нГа шложительные'вверх, то соединительная прямая
Гпротивопол^'ожиый наклону раскоса. Для раскосов, вое,
';. ZZZZ пролета, отрицательная часть площади л. в.
T^ST\ ГрГдГГрГеТа. отрицательная часть
№S^0^.
S
Фиг. 240
превосходит положительную (от сплошной равномерно распределенной
всему пролету нагрузки раскос сжат), а для раскосов нисходя-
по
щ и X соотношение получает-
ся обратное-
Линии влияния для поя-
сов и раскосов такой фермы
остаются без изменения при
замене движения груза по-
низу движением поверху или
наоборот; изменяются толь-
ко линии влияния усилий в
подвесках.
Это объясняется исклю-
чительно характером решет-
ки, а именно наличием вер-
тикальных подвесок или
стоек (фиг. 236 и 239), Та-
кой же вывод можно сделать
для фермы с раскосной ре-
шеткой (фиг. 240).
В том случае, когда ре-
шетка состоит только из на-
клонных стержней, переход
нагрузки сверху вниз или
наоборот отражается на всех
линиях влияния. Такой при-
мер показан на фиг. 241.
Для усилия 02 при движе-
вид треугольника, при движение ^^ "^" ^РУ^^ понизу л. в. имеет
ваться ее левой пpя^юй лишГпп Т^^ "^^^Р^У ^^i можем пользо-
получается переходная прям^^.^^^^ ^' ^ правой-до узла 3, Отсюда
л.в С/зиД,,построен1шнГ1^^^^ следует разобрать также
На фиг. 242 nocTpoeibi^^^^^^^ ^^^ ^ ^^У^ вариантах
параллельными поясами Усилие Т7'''''' ^^^ полураскосной фермы с
ляется при помощи разреза al« ,f "^"^''^ °з верхнего пояса опреде;
усилия Оз имеет такой же вил "^.'^^^^^нтной точки 3\ Линия влияния
знаком^"'""" ^^^^^"- Линия влиянкЬ^-^"^"^^^^^^ момента в ce^J
^^^^^^' "" «лияния С/з отличается от Оз только своиМ
148
Усилия /)з и /^3 ^ полураскосах одной и той же панели равны друг
vrv по величине, но обратны по знаку, в чем нетрудно убедиться
^ езав тот узел, в котором они сходятся; поэтому любое из них выра
жается формулой
2 cos а
'^=^[Щ]]]]р]]Ш31ШШ=п==-
4
^3.
н
h
I 1 ®
I
^41iiiii4jjiii^^
Понизу
ш
-|СМ
\ 1 -^
л-
1
Zcoso.
Чем
^.
ПоВерхъ
Фиг. 242
'''J»^
.пике определяется при помощи выреза-
верхней полустоик^е о^ F^^^. __ ^^р^^ „омощи вырезания
р ГИЛЫ проектируются на вертикаль.
""" ""'" „^. R обоих случаях Di-e си ^ ^ случаях, когда груз
Усилие Vi в BejjAriv,». -- -^ ,
усилие К4 усилие V4
НИН верхнего Уз^^' ^_ У „„„^^^ .
не стоит е^^феТанн^м узле, усилие
МИ
cosa= —;
cos а = —
2
/
1
4 cos а
\
Фиг. 243
Acosa
Отсюда следует, что л, в. V4 при движении
груза понизу отличается лишь множителе\1
— от л. в. поперечной силы Q ]х^я простой бал-
ки, а л. в, V\ при движении грура поверху от-
личается от л. B.Q лишь множителем —.
Когда груз расположен в узле 4 (движение
поверху), то к ординате л. в. V4 добавляется —
1, следовательно, на л. в. V4 движению по-
низу в пределах двух примыкающих панелей
соответствует участок абс, а движению повер-
ху— участок adc. При помош.и такого же рас-
суждения мы найдем, что л. в. V\ движению
поверху соответствует участок efg, а движению понизу — участок ehg.
Для построения л. в. усилия Vs в средней стойке вырезаем узел 5
или 5^ Если внешняя нагрузка не приложена ни в одном из этих узлов,
то в обоих вырезанных полураскосах усилия имеют противоположные
знаки в одну и ту же величину ± ^—^^ следовательно, сумма их проек-
ций на вертикаль равна нулю, и V5=0. Когда сила Р=:1 расположена
3 узле 5', то слева от этого узла Q= — а справа Q= -1—1=—-- "^
по-
этому усилия в полураскосах, сходящихся в узле 5, имеют величину,
указанную на фиг. 243. Спроектировав их на вертикаль, найдем ^^^ ^
Если сила Р^\ приложена в узле 5, то, вырезав узел 5\ найдем таким
же способом, что Уб= . В итоге л. в. V^ имеет вид одного из ДВУ
треугольников, показанных на фиг, 242.
§ 8.2, ЗАДАЧИ
Задача 17. Построить линии влияния усилий для бал очно-консольной Ф^Р*
представленной на фиг. 244. jg
Линии влияния для элементов консоли О», Х)з, ^^з определяются из УР^Р^^аЮТ
моментов относительно соответствующих точек Риттера. Эти эле.менты Р^^° \jee
только тогда, когда груз расположен на левой консоли или на опирающейся на
фермочке.
ав™опо;1„°Г^о?/1^Л,Т„.."„°!^Т.«_Р?!Р«-. проведенного в первой_ ..^„
-ппяйя пт'ппо:1..ГТ''у7 " "*'" ""«""^" разреза, проведенного в первой пане*
то?да KornrTvA.v^'' ^^^"^ ^''^"^"^ расположен в пролете ЛБ. он работает тс
тогда, когда груз находится слева от опоры А » f
Линия влияния усилия в левой опорной стойке V стпоится тяк- пока гоУЗ нахоДИ^'
-ся в панелях, расположенных справа о? опоры Л.^ле^енГ^зи^^^^^ п°«^' "
150
конца до опоры Л. Когда груз стоит слева от узла Л, например на концГлевой кон-
каль! о?куда'5Гучи'4Т "'"""' ^''" ^'"'^^^ " спроекти'рова^^е"с\^лыТа° веГтн-
^ = -- (^4 COS а + D3 cos р).
На фиг. 244 построена еще л. в. ?>е, для чего использована моментная точка С.
Предлагается разобрать также остальные линии влияния
Задача 18. Построить линии влияния для шпрентельиой фермы, представленной
на фиг. 245.
е
Фиг. 244
Ф^рма подобного типа была изображена на фиг. 235, где показано, какие элементы
являются основными, какие — дополнительными и какие — смешанными. Стержн-и
верхнего пояса являются основными, -и для нцх л. в. строится, как для простой фермы.
1Аодкос S4, как и другие подкосы, является дополнительным элементом и работает
только на местную нагрузку; .его л. в. имеет вид треугольника, простирающегося иа
^ве панели. Ордината этой л. в., расположенная под вершиной, получается при помощи
Разложения вертикальной силы Р=1 на направлении подкоса S4 и раскоса Dz—Dq,
^•^ ^остроение показано справа от линии влияния.
Стойка Vg может рассматриваться как основной элемент, и ее л. в, имеет такой
«е вид, какой она имела бы. если бы подвесок и подкосов не было, т. е. вид треуголь-
ника, простирающегося на две большие панели и имеющего высоту, равную единице.
*о. что эта л. в. не имеет переломов под узлами С и F, можно доказать также следу-
*01Цим образом: поставим груз Р=1 в узле С; усилие в подвеске этого узла будет
^^^"о единице, а подкос S4 не будет испытывать никакого усилия; вырежем сначала
V3#^ р • ^ котором сила Р=1 разлагается на два наклонных направления, и затем
узел ?, где усилие в левом подкосе разлагается на вертикальные и горизонтальные иа-
Равлення. Это разложение сделано на фиг. 246, из которой видно, что Vs — "^ •
Стержень Ug нижнего пояса является одновременно основным и вспомогател
элементом. Пока груз находится вне большой панели ЕС, его влияние выража"^^^
линией влияния, состоящей из прямых аЬ н ее (фиг. 245), которые пересекаются л ^^
с другом под точкой Риттера н строятся, как для простой фермы. Когда груз движ ^^^
в пределах названной панели, то нижний пояс и стержни D^ и S^ получают доб ^
ные усилия как элементы фермочки, показанной на фиг. 247. На л. в. Us это ^
жается появлением дополнительного треугольника bde, вь1ра.
swfii
Фиг. 245
Фиг. 246
^я/у^^^^^ ^
Усилие в стержне EF всегда п. ^'^"^
Лииия влияния усилия LTcrTo^: ^^"^^^ ^«•
чается от нее Добавлением .п1 ^°"^^«' «ак для простой ^
Фермочке. показаииой Г фиг ^^^^^««-' "РеДставдяю;;,: ^Г ^^ ' " " ""' Т.
152 ^°^ -"• ^- усилия /?з ^
§ 8.3. ПРИМЕНЕНИЕ МГНОВЕННЫХ ЦЕНТРОВ ВРАЩЕНИЯ
Кинематическим методом построения л. в. мы пользовались уже раньше. Напом-
гим содержание этого метода. Для того чтобы плучить л. в. усилия в каком-нибудь
' ержне А^Л^ фермы, нужно его удалить и заменить двумя равными и противополож-
^^1ми силами X, приложенными в узлах М и N (фиг. 248). Полученному механизму
нужно мысленно дать бесконечно малое возможное перемещение. При этом каждое
из его звеньев повернется вокруг своего мгновенного центра вращения. Сила Р=^\ со-
вершит при этом работу, равную 1 • ^р , где ^р есть проекция перемещения точки при-
ложения этой силы на направление самой силы. Совместная работа обеих сил X выра-
зится формулой Хоху где ^х—проекция взаимного перемещения точек М v N ца
'Л
Фиг. 248
Фиг. 249
направление MN. Согласно принципу возможных перемещений, сумма работ внешних
сил должна равняться нулю:
откуда
So
Фиг. 250
В этой дроби мы имеем право считать знаменатель постоянным: действительно,
в механизме при бесконечно малых перемещениях величина ^р пропорциональна ве-
личинеЬд-. назначение дроби не зависит от абсолютной величины 5.v.
Так как точка приложения груза Р=\ может совпадать с различными точками
фермы, то под величиной Sp следует понимать перемещение любой из этих точек.
Отсюда вывод: даднм механизму бесконечно малое возможное перемещение и постро-
им график величины ор, т. е. проекций перемещений, совершаемых всевозможными
^чкамц приложения груза Р=^1, на направление груза. Этот график будет иметь ту
^ форму, что и л. в. усилия X. Отличие между ординатами обоих графиков может
"сражаться лишь некоторым коэффициентом пропорциональности.
Вместо перемещений 5р и Sv можно говорить о скоростях соответ-
твующих точек, так как эти величины соответственно пропорциональны.
1^ Аля всякого геометрически неизменяемого звена механизма (для диска) график
^ремещений Sp представляет собой прямую. Отсюда следует, что линия влияния
153
Л
Л\
>' {'^..rl^^
^^^s'Q^'jI lliiL'lIiiJlJ'JililJIilJUi^^
Фиг. 251
-ivf.
Ш
агегда содержит столько прямых, сколько различных звеньев встречает на своем пути
движущийся груз Р=1. ^ ^
Нулевая точка каждой прямой, принадлежащей линии влияния, представляет
гобой проекцию соответствующего мгновенного центра; действительно, при возможном
перемещении звена эта точка остается неподвижной, т. е. для нее ор=0. На фиг 249
показаны некоторое звено /", поворачивающееся вокруг мгновенного центра Oi, и соот-
ветствующий ему график перемещений или скоростей Ь.
Точка взаимного пересечения двух прямых, принадлежащих линии влияния, пред-
аав^гяет собой проекцию мгновенного центра взаимного вращения тех двух звеньев,
которым соответствуют эти прямые. Это вытекает из того, что взаимный мгновенный
центр представляет собой как бы мгновенный шарнир, связывающий оба звена друг
2 другом*
Эти теоремы связывают вопрос о построении линий влияния с вопросом о по-
строении мгновенных центров вращения.
Построим линии влияния для нескольких элементов фермы, показанной на
фиг. 250- Она очень проста, и дли нее все линии влияния легко получаются без помо-
щи мгновенных центров вращения, но знакомство с новым методом лучше начинать
на простом примере.
Фиг. 252
На фиг. 251 даны л. в. для четырех характерных элементов: для двух стержней
верхнего и нижнего поясов, для раскоса и для стойки.
Фиг. 25Кс дает построение для стержня DF. Механизм, который получаетси после
удаления этого стержня^, состоит из двух заштрихованных дисков, из которых левый,
обозначенный цифрой /, опирается на неподвижный шарнир Л, а правый 2—на под-
вижной опорный стержень В. Взамный мгновенный центр вращения этих звеньев со-
ападает с точкой С. Линия влияния состоит из двух прямых, пересекающихся под
точкой С и имеющих нулевые точки под опорами. Если не интересоваться масштабом,
то форма л. в. получается сразу.
Знак любой ординаты можно найти следующим образом. Возьмем произволь-
ную точку механизма, например точку С, и дадим ей мысленно перемещение по на-
правлению силы Я, т. е. вниз. При этом левый диск повернется вокруг А по часовой
стрелке, а правый — вокруг В против часовой стрелки. Угол DCF уменьшитси, следова-
тельно, точки D и f сблизятся между собой. Отсюда следует, что ордината л. в., рас-
положенная под точкой С, отрицательна. Нам достаточно найти знак одной из
ординат графика, остальные сами собой получаются из чертежа.
Для полноты исследования выясним еще вопрос о масштабе. Обозначим скорость
взаимного сближения точек D н F (фиг. 251) при возможном перемещении механизма
через bj^, а угловую скорость взаимного вращения звеньев I н 2 вокруг их взаимного
центра С — через »i2- Расстояние прямой DF до этого центра обозначим через г^
•'lerKo сообразить, что ^л-^Г;^»12. откуда
(8.1)
Представим себе, что в точке А, совпадающей с мгновенным центром вращения
^вена 7, лежат, покрывай друг друга, две точки, из которых одна принадлежит зве-
^У '. а другая скреплена со звеном 2. Скорость последней по вертикальному направ-
'Чению относительно точки А звена 1 выразится формулой
'^^^ ^^—расстояние вертикали, проходящей через точку А до центра С (в нашем
примере благодаря прямолииейиости нижнего пояса, это просто расстояние
от точки А до С). Соответствующая ордината л. в. выражается фор.мулой
Двстаточио
Ц|ад ' ^ ««wnjpuii ии миг оы ^^лилЬЗИТЬ кони
Риира; оба вйряанш показаны на фиг. 252.
цу^^'^^Ржень можно не удалять.
ШмГ^ " ^OT0|iofl ои мог бы скользить концами, или же отделить одним
.>мысленно разрезать его и тщбмШь
х,п„ пяиьше статическим путем. Если мы представим
Этот же результат мы получили рань ^^^^ звеньев, отстоящие от центра С „о
себе две совпадающие друг с ^РУЦ^ [^^ ^. то скорость их взаимного движения по
горизонтали вправо или влево на величи у соответствующий ей на л. в. отрезок
вертикальному направлению будет равна гх^^12,
ординаты будет равен ^^ ^
^лл^«1^,гп«поиять так: если на линии влияния мы возь-
Правило масштаба ^^^''^.r^^^^^/J'ff^^^^ которые были связаны межди
мем две прямые, соответствующие тем двум ^^^«^^' отступим по горизонтали на
'f.:^Llfr^^^^^^ ..е.л..\ря.ьш., . этом ме^
величину Гх» зго отрезок ^и " ' следует понимать длину перпендикуляра, onv-
Sr Г Mfnref^^^^^^^^^ -X звеньев на ось отброшенного
^^^^нГфиг 251, б построена л. в, для стержня ЕС нижнего пояса. Мгновенный центр
взаимного вращ^^ звеньев / и 2 совпадает с точкой D. Перпендикуляр г, совпадает
сГЗойБ^' длина его обозначена через г,. Отрезок ординаты, отстоящий от точ-
ки Ь на расстояние г^ и заключенный между обеими прямыми, равен единице. Линия
влияния —знакопостоянная. Чтобы получить знак какой-нибудь из ее ординат, пред-
ставим себе, что точка С передвинулась по напранлению груза Р, т. е. нниз; тогда угол
EDC увеличится, точки ? и С разойдутся, следовательно, ордината под точкой С по-
ложительна. ^ _ _.
На фиг. 251,в построена л. в. для раскоса EF. Удалив этот стержень, мы полу-
чим шестизвенный механизм, состоящий из двух заштрихованных дисков, двух соедн-
нительных стержней DF и ЕС, опорного стержня В и неподвижного звена (земли).
Диску / соответствует прямая, «имеющая нулевую точку на левой опорной вертикали^
т- е. под мгновенным центром Л. Диску 2 соответствует прямая, имеющая нулевую
точку на лравой опорной вертикали. Точка взаимного пересечения этих двух прямых
лежит под мгновенным центром 12 взаимного вращения звеньен I и 2. Нетрудно ви-
деть, что этот мгновенный центр в то же время является точкой Риттера. На чертеже
показаны также плечо и служащий для определения масштаба отрезок ординаты, рав-
ный единице.
Для определения знака какой-либо ординаты, например ординаты, расположенной
под точкой ?, дадим механизму такое перемещение, чтобы точка Е переместилась
вниз. Диск / повернется вокруг своей неподвижной точки А по часовой стрелке. Диск
2 повернется вокруг своего мгновенного центра, лежащего где-то на продолжении вер-
тикального опорного стержня В. Нам незачем разыскивать этот мгновенный центр, а
важно лишь установить, в какую сторону поворачивается диск 2,
Ответ нэ этот вопрос таков: прямые / и 2 .на линии влияния на-
клонены в одну и ту же сторону (тангенсы их углов наклона к оси
абсцисс имеют одинаковый знак), следовательно. диски / и 2 пово-
ди пе"печ~нДл^ одинаковую сторону. Такое соотношение между угловы-
и^ иеитоы Zv ,«Г '^^^'^ '^"""^^^ / и 2 мы будем иметь всегда, когда м?иовен-
Хра воащен^я ^f^^eB Расположены по одну сторону от их взаимного Мгновенного
^ч1Тр^7т^ш "^'^ Тг'У ^"^"^' ^^^ ^^^^^ '^«^^«а Е идет вниз, то
л^'^под^Ской е'положнГь^^^^ ^' увеличивается, следовательно, ордината
§ 8.4, ПОСТРОЕНИЕ МГНОВЕННЫХ ЦЕНТРОВ ВРАЩЕНИЯ
ДЛЯ БОЛЕЕ СЛОЖНЫХ СИСТЕМ
ческоГцепТ^^еТ^^^^^^^^^ вращения для сложной кинемати-
Свет,ы7пР«^Г о ^""^ ^^^"^«- включая и неподвижное.
™ых Ka^L^frj'J^^"''"^^ вращения двух звеньев, обозна-
^Мп'^ре^^^^^^^ номерами^/, k, будем называть ik или
В Se поЛ "^ «^«е«яет мгновенного центра).
трех мгновенных "S^f"'' '^^'^"^ ^^« называемая ^теорема о
обозяа^Гх «LnSr вР^'?^«ия»: три мгновенных центра,
(^апример^''^^^^^ трех букв или цафР
н, ии, ас, ОС), всегда лежат на одной прямой.
Например, в четырехзвен-
иом механизме, представленном
«je Aswwn лег» ..амт-
"^™ «исламизме, представлспич.."
на фиг, 253. мгновенные цент-
ры /2, 14, 24 лежат на одиу;*
>ГГГГ7777Г^Т777Г7777^ ' ^•:==^^ РЫ /^//О/'лёжТГна'^^- .
^ "Рямой: мгновенные центры S4^
Фиг. 253 ^^» 24 также лежат на одной
156 прямой, следовательно, точка 2^
'--Ш
лежит т псргсепеиии о^>еих прямых^ Мы это будем записывать г^имполичегки в виде
ураилгпия
21'М h 23^34 24,
tit npOHiBP/ioHHCM двух миожигслей обозпачоиа прямая, проходящая черет соответст-
fiviouiHP две точки, а суммой точка пересечения двух прямых.
J6\
/
/
/
Фиг. 254
7/
V
ГУ
С помощью таких обозначений можно записать процесс определения мгновенных
центров вращения для кинематической цепи, представленной иа фиг. 254, в виде сле-
дующей системы равенств:
Ц 8jO-WJ + 8rj*91 =^81; 2) 78'Sj0 + 7e^ej0^7J0\
3) 7J0^10J+79^91:^71\ 4) 67^71+ в,10-}0,1 ==61;
5) 34-46+ 35'Гу6 = 36\ 6) 36- 61 + 32-21 = 31;
7) 46-61 + 43-31 = 41; 8) 63^31 + 56-61 = 5L
На фиг, 254 произведены все эти построения.
Кинематическую цепь, представленную на этой фигуре, можно рассматривать как
образованную из фермы, из которой был удален один из необходимых стержней.
С помощью найденных мгновенных центров вращения сейчас же может быть постро-
ена линии влиянии усилия в этом стержне.
Глава 9
РАСПОРНЫЕ ФЕРМЫ И РАСПОРНЫЕ КОМБИНИРОВАННЫЕ
СИСТЕМЫ
§ 9 1. ТРЕХШАРНИРНАЯ АРОЧНАЯ ФЕРМА
(РЕШЕТЧАТАЯ ТРЕХШАРНИРНАЯ АРКА) (фиг. 255)
Так называется трехшарнирная арка, у которой обе полуарки пред-
ставляют собой фермы. Распор, вызываемый в такой ^системе, опреде-
ляется совершенно таким же образом, как в сплошной трехшарнирнои
арке. Он не зависит от геометрической структуры и очертания полуарок.
а зависит исключительно от расположения трех основных шарниров
(двух пятовых и одного ключевого) и, конечно, от внешней нагрузки.
В арке, у которой обе опоры расположены на одном уровне, при дейст-
вии вертикальной нагрузки распор выражается формулой:
где М^^ — изгибаюш;ий момент, который получился бы от заданной на-
грузки в сечении С простой балки АВ, совпадающем со сред-
ним шарниром.
В симметричной арке грузу Р=1, стояшему в узле С, соответству-
ет уИ^= J, поэтому ордината в вершине линии влияния распора равна
rr.J^V^^'^^ •^™™ влияния для фермы фиг. 255, определяя усилия по
с вли1н^ие7Гаспо?^ '•""'""' вертикальных опорных реакций
Начнем с усилия О в одном из стержней верхнего поягя Когла гоуз
расположен справа от «о„е„г„ой точ^ки. ypa^Se™ Гж„о ИшсгТ,
F миментную точку. Обозначим его через Мо. Тогда
^0 Го
158
Когда груз расположен слева от моментной точки, то
RBil-a) + Or,-Hf, = 0
0=-R,
l~a
Го
Го
а]
6)
в)
Ю
Фиг. 255
Но при этом снова МОЖНО написать, что/?^ (/-а) =Мо. поэтому по-
лучим прежнюю формулу ^
Мо
/о
Го ''о
Из этой формулы вытекает и построение л. в О '^^'^^ суммы лший
влияния изгибающего момента Мо. умноженного на^ постоянный мно
159
житель -—, и линий влияния распора, умноженного на посгоянное
Го
число —- .
Суммирование обеих основных линий влияния показано на фиг.
255 а где даны и величины ординат, необходимые для построения.
Для построения этой линии влияния мы могли бы воспользоваться
также нулевыми точками, подобно тому как мы это делали при расчете
сплошной трехшарнирной арки.
Линия влияния усилия и для стержня нижнего пояса фиг. 255,6
строится совершенно таким же способом, но только здесь другая мо-
ментная точка; расстояние ее до левой опорной вертикали обозначено
через с, плечо усилия t/ —через г у, плечо распора — через /^.
Тот же принцип применен для построения линии влияния усилия
раскоса D (фиг. 255,б) и усилия стойки V (фип 255,г).
Во всех четырех линиях влияния ярко отражается влияние распора:
наибольшие ординаты всех этих линий влияния оказываются сильно
сниженными по сравнению с ординатами тех же линий балочной фермы.
Одного взгляда на эти линии влияния достаточно, чтобы понять, что
распор позволяет значительно уменьшить расчетные сечения стержней,
получить экономию материала, уменьшить влияние собственного веса
как нагрузки и благодаря этому увеличить тот предельный пролет, ко-
торый может быть перекрыт данной системой.
§ 9.2. ОБЩИЕ СВЕДЕНИЯ О ВИСЯЧИХ СИСТЕМАХ
Висячей системой называется такая, у которой основная несущая
конструкция, перекрывающая пролет, работает на растяжение Простей-
шим видом висячей системы является нить (трос), которая перекинута
Фиг. 256
через перекрываемое отверстие и ирро^ г,^
конструкции, предназначенные nL подвешенные к ней элементы
висячие системы приммсь пла ^^,^"Р«^™я местной нагрузки. Такие
глубокой древности, чт™^^^^ строений мостов еще в
стью возведения. ^^^^ъясняется простотой их конструкции и легко-
Системы висячих мпгтпт. гг
им 'Т'^Р^'^^'^^ой тивмешеы1с?ъю%1-п1 ^ «^'='^^>«^ee время, облада-
им различными способами На ппи^;„™ свойство может быть придано
i^„",^y«f перевернутой трехшаснион^' '^^«^«о образовать висячею си-
Йки гп Y""^ "ио^оУ^о^ьник КопРй Г"- ^^^°" "РИ'^ер показан на
^ nJ° °Р^ ^^ ™яса работают ня^**'^^У'°"^и^ проходит внутри этой
^ Другой способ состоит о ^ растяжение. ^ *^
фермой; последние в этом случа?"oS ''""" '^ ^^^кой или балочной
160 Обычно называют балкой жесткости
или формой жегткогти. Иа фиг. 257 показан вид Крымского моста че-
ре J Москву реку; его пролетное строение состоит из цепи, сжатых пило-
П015 и балки жесткости.
Современные крупные иисячие мосты предстанляют собой выдаю-
шиеся проинк-аения инженерной науки; многие из иих поражают гран-
яиопкх 1ью np^^^'f-'^OB и ипииеггвоы fjJopMM. Тот факт, что реюрдные
Фиг. 257
объясняется главным образом тем, гто Р^^ ;' > лучшим исполь-
потери устоймииости и "О-ому могут б.^^^^
чованисм материала, а также объясняется иыси^п» j-
жеиием материала тросов па растяжение.
§ 9 3. РАСЧЕТ цепи. УСИЛСННОЙ БАЛКОЙ ЖЕСТКОСТИ
<" ...,. ,1-1 fhiii- 258 геометрнчоски мен.шепяема и
Схема, предстаилеиная на фи1. ^оо, '^^^" i , ^^^ имеющая
статически определима. Действительно, ^^^,^« ^';' ^.^.•^"^"^здала бы оаной
срсднин н,ариир С, не была ""лкренлепа ценыо ^^ «^^^^оц^и д„ух
стспспьк. свободы. К ней "P"'<P™^f,^f^ 11,еподии кно опорной точке
стержней, и. которых оя^^-^!)^--°1^^^^^^ '- изменяется
О, а другой —к балке. От этого степень «.« \ 7мг. присоединяются в по-
ДаУее таким же способом при ""^/''^'леСатХХесли бы не бы-
слсдоиательчом порядке узлы 2, 3,..., ^ {.• ^-^,,,¦^°''' „^„ь свободы. Этот
яо стержня П-12. то с"с-ма имела б- о^^^^^^^^ ;;;ектор„„ точ-
стсрже.н., если только он не "'"Ч"'"-"^; '!-'п . м псласт систему геомет-
ки //. уничтожает указанную степень свободы и дслап
рпчески неизменяемой.
161
11 И. М, Рабинопнм
....... IK III. iiixWT.iiuimM o«>0<»U тм"-"04||ыл
K.llv \ЖГ «ИМ0Ч.1.ЧО11. "'f' • 'V„,.,.,.,',„MIMO ЧОа.ШМОГ KOpillKiUll.niai.
Miioi.nuK'ibOMK, INI '^'V'1!m1 m m'ox члом.чичп uoim u » ч<.,икч1и,к .„ц
„.пижоши! II..II..V01V ^;''''" ' ,.,.оль11ИМ>м: jn-MomnM lUMiii ...„пк.,
р.|Ж.-1101Ч»1 04II1IM 011..1..1ЫМ ^"' ; M,„»|4.yiO.-ll.lllllv.l. Иогцюип к iip„
р.1Ж.-11о.ч.1 0Ч1.ПМ '¦"•"' "-^ ..„noma ми.мч.уюлышка.
''•»^'''' •''^Т\'п'ГГ' :.o. м..огоуи>лы1 мы ...м >•••
ШКОЛЬНОМ м»* nUJUl 1*»'^»
лёУ/
*^//.л/%
•1>м1. U68
а ciuw;;:;;;;\;';:p::;i;:;::;;r.:' ^'''^•'"^"^' ^'"•-'""•« ^"'^•'¦"У'•<" ^"^•''•
(^.ltt\l\l%U0'tMlt4 ¦
ClIpOOKTUpyOM
точках '" "
цени
V
точки балки Л и В ил цепь п и иолучеиим^
их 4JICTI'"
' яамтм\оЙм оит-ш ift^ "^ Дп»стт,с откинутых кр.,|1и
1«г
Равнодействующая вертикальной и горизонтальной составляющих
направлена по цепи, поэтому составляющих
K==^fig?, Ув^^^Ыъ- (9.1)
Jp^ZZlT^L^rvT-K' " '^''' ^ "^" ^•^'^'^ расположении
Составим относительно точки F уравнение моментов всей системы,
состоящей из балки АСВ и цепи EF (отрезанной в точках Е и F):
откуда
К+Ул=^1,РЛ1-^д-У^л^ (9.2)
где V^ —та вертикальная реакция, которая возникла бы на опоре Л,
если бы вся система состояла из простой балки АВ.
Г^''
Фиг. 259
Фиг. 260
Составив уравнение моментов относительно точки Е, получим
П+^>7-2^л-==П. (9-3)
где V^ —реакция, которая получилась бы на опоре В простой балки
ЛВ.
Итак, суммы вертикальных реакций на левом и правом концах не
отличаются от левой и правой реакций простой балки.
Проведем разрез через шарнир С так, чтобы пересечь цепь в точке
^ и в другой точке, бесконечно близкой к средней подвеске (фиг. 259).
Усилие в цепи на левом конце разлагается на составляющие 1/^ и Я, а
На правом — на вертикальную составляющую, проходящую через точку
^1 и горизонтальную Я. Обе горизонтальные силы образуют пару с
Плечом /, а суммарный момент внешней нагрузки, если она имеется на
участке АС, и вертикальной силы V'^ + V]^ равен изгибающему момен-
¦^ М^с простой балки АВ.
Итак:
Или
U*
Ml — Hf^O
(9.4)
r„.r;.uua Лосмуле распора для арки, имеющей
Полученная формула аналогична форму i
стрелу/ „ У" по формуле (9.1) и реакции V^. V
Зная Я. находим V^ и i^a "^^ ч i ^ в
поформулам ^ ^^,__^,g,, V,^n-Hlgcp. (9.5)
Изгибающий момент в любом сечении D балки (фиг. 258) равен
M^^Ml-Hf^- (9-6)
.г.п. П R том же сечении выражается формулой
Поперечная сила ц^?, в i^jm
(фиг. 260). .^^^
Линии влияния Я, 1/^, М^ и Q^ построены на фиг. 258 в предполо-
жрнии УЗЛОВОЙ передачи нагрузки на балку. Обращает на себя внима-
ние з^ГтеГьная разгрузка балки жесткости от изгибающих моментов
Гпопер™х сил, обусловливаемая влиянием распора Н. Линия влия-
ния V имеет отрицательный участок: нагрузка, расположенная на этом
участке, вызывает реакцию V'^. направленную вниз, причем левый ко-
нец балки стремится оторваться от опоры. Аналогичным свойством
обладает, конечно, и л. в, V^.
Балки жесткости сплошного сечения применяются преимущественно
при малых пролетах. При средних и больших пролетах они обычно за-
меняются балочлыми фермами.
§ 9.4. МНОГОПОЯСНЫй ВЕРЕВОЧНЫЙ МНОГОУГОЛЬНИК
И ПОНЯТИЕ ОБ ОБЩЕЙ ТЕОРИИ ВАНТОВЫХ ФЕРМ
Известный интерес как с практической, так и с теоретической точки
зрения представляют такие геометрически неизменяемые шарнирно-
стержневые фермы, все стержни которых от совместного действия по-
стоянной нагрузки и заданных временных испытывают исключительно
растягивающие усилия. Благодаря своей геометрической неизменяемо-
сти, такие фермы не нуждаются в балке жесткости и в то же время
сохраняют все достоинства висячих систем. Все их стержни могут быть
сделаны из гибких стальных тросов или кабелей, поэтому такие фермы
получили название в а н т о в ы х.
Отсутствие сжимающих усилий позволяет иметь в стержнях ванто-
тзых ферм высокие напряжения и приводит поэтому к значительному
уменьшению собственного веса конструкции. В то же время оно устра-
няет возможность продольного изгиба. Своеобразие расчета вантовых
ферм заключается в самой постановке задачи, т. е. необходимости по-
добрать такую систему фермы и такое расположение ее узлов, которые
обеспечили бы во всех стрежнях при всех положениях временной на-
грузки растягивающее суммарное усилие от временной и постоян-
uu'LUfJ^^^''''' Разумеется, что и при проектировании обычных фер^^
n^Zt^.!l? ^'!'"'^^" ограничиваться одной пассивной констатацией ве-
личины усилии, а должен варьировать ферму таким образом, чтооЫ
лпо^ктипп^""'"™' "'"^^.:""f экономное иЧел^ооб^ое Однако при
проектировании вантовой фермы ограничиваться определением усилии
част^ГзадачТ^''" возможности. „ синтез является sS неотъемлемой
В известной степени теория вантовых феом является одной из пер-
вых и немногих пока страниц той будущеГ?еори1 ферм. вТ^^^^ «^
первом месте будет стоять создание новых форм, новых систем, отвеча-
ющих ряду заранее заданных условий и обеспечивающих наивыгодней-
ший способ восприятия нагрузки. Это направление в современной тео-
рии ферм представлено настолько слабо, что контуры будущей син-
тетической, созидательной теории ферм еще почти невозможно раз-
глядеть.
Системой, из которой может быть выведен обширный класс Байто-
вых ферм, является предложенный автором настоящей книги в 1924 г.
Фиг. 261
«многопоясныи веревочный многоугольник». Так мы будем называть
ферму, которая составлена из семейства веревочных многоугольников,
содержащих одинаковое число сторон и вершин, расположенных на од-
них и тех же вертикалях. Вершины соединены между
собой стойками (фиг. 261). Пусть число панелей каж-
дого пояса части MN равно т, а число поясов — п.
Верхний многоугольник вместе с поддерживающей
его тягой NM^ при отсутствии других многоугольни-
ков имел бы степень изменяемости m—1. Каждый
новый многоугольник, присоединенный к системе,
уменьшает степень свободы на единицу, поэтому сум-
марная степень изменяемости равна m—1—{п—1) =
= т—п. Для того чтобы фигура была неизменяема,
необходимо, чтобы было т = п, т. е число панелей
многоугольника должно равняться числу его поясов.
Каждый пояс работает как простой веревочный
Многоугольник, которому соответствует некоторый оп-
ределенный силовой многоугольник. Но в то время
как простой веревочный многоугольник обладает лишь
Мгновенным равновесием, многопоясныи много-
угольник, содержащий п поясов и столько же пане-
•^ей, обладает постоянным равновесием: произволь-
ную действующую на него внешнюю нагрузку он рас-
пределяет между поясами так, что каждый из них получает от подвесок,,
сообразно своей природе, всегда один н тот же тип нагрузки, выражае-
мый его силовым многоугольником.
Построим для каждого пояса такой системы силовой многоугольник,
отвечающий вертикальной нагрузке, т. е. проведем из произвольного-
полюса пучок лучей, параллельных сторонам соответствующего пояса,
и пересечем этот пучок вертикальной прямой. Отрезки вертикали при-
мем за силы, измерим их в произвольном масштабе и обозначим через
.ь Pf2,..., Р.„. Первый индекс обозначает номер пояса, а второй — но-
^^р панели.
Фиг. 262
ппимрм коэффициенты пропорциональности г,, z^
За неизвестные пРИ'«^,^,„°Г!,!;ь соответствующие силовые много-
г , на которые ^^адует умнож ^^^„^^ ^^^р^У донизу и спроекти-
угольники. Вырежем "^^"^У^ -^^р 262) Номер стойки обозначим через
руем все силы на в«=Р™каль 14 ^ ^^^^^женных к сторонам верхнего по-
т. Равнодействующая двух си j^ равнодействующая двух усилий
яса. равна вертикальной силе ^^"^^^^
второго пояса равна Р.„ г, и т. д. итоод
Л.2, + Я..,г,+ Язтгз + --- + ^«-^''-^'"- (9-8)
- ..r^wHn няписать п и, решив их совместно, определить
1^'^е^Т^1ТгТГ^ь:^^::\ешеи'пе уже никаких трудностей в
^"^Если'внешняГнагрузка такова, что один из поясов фермы служит
пля нее веревочным многоугольником, то из всех поясов работает лишь
JJoT пояс у™ же в остальных обращаются в нуль. Это непосред-
SbJhho вытекает из принципа однозначности решения. Если к уже
^'
М
Фиг. 263
действующей внешней нагрузке прибавить нагрузку такого типа, усилия
изменятся только в одном этом поясе.
Если две группы нагрузок в сумме образуют систему сил, для кото-
рой один из поясов служит веревочным многоугольником, то они вызы-
вают в остальных поясах усилия, соответственно равные и противопо-
ложные. Зная эффект одной группы, мы тем самым зиаем и эффект
другой.
Если линия влияния какого-нибудь неизвестного 2, имеет слишком
большую отрицательную площадь, так что можно опасаться появления
отрицательных усилий, то нужно изменить форму многопоясного вере-
вочного многоугольника, передвинув некоторые из его узлов вверх или
вниз.
Многопоясный многоугольник принимает более простой вид, когда
некоторые пояса на протяжении того или иного числа панелей, слива-
ются между собой. На фиг. 263 показана пятипоясная ферма с частично
слившимися элементами. Пролетное строение состоит из двух таких сим-
S"''"° расположенных ферм; для сохранения статической определи-
другом °^™''' ''™^" ^ шарнире N они не были соединены ДРУГ ^
B04Horo*MHn?nvrnnTu ^^" ^"^^ ^°^^^ "Р°"ой вид четырехпоясного вере-
ГясГй Феомн с п™' "°^°Р'"" "Разводит впечатление обычной ДвуХ"
оГсостоит и, rnrvr*""™ """^ треугольной решеткой; на самом Д?ле
3) MACFN. 4) мЖТ"'' "^"Р"'' "°"^°«^ 1) Л^^^^Л^. 2) ^^^^^'
Л66
Хотя многопоясный 'Веревочный многоугольник .может принимать
весьма разнообразные формы и является родоначальником множества
Байтовых ферм, он не исчерпывает последних. Возможны и другие фер-
мы. Не существует общих правил для их нахождения, но автором ука-
заны некоторые общие геометрические свойства, обязательные для вся-
кой вантовой фермы, рассчитанной на вертикальную нагрузку. Напри-
мер, два крайних узла непременно должны быть опорными и нагружены
наклонными реакциями; все ненагруженные узлы должны лежать внутри
контура выпуклого многоугольника, описанного около фермы; система
не может быть защемленной на одном конце и свободной на другом,
и т. д.
Фиг. 264
Доказательства всех этих теорем и ряда других опубликованы были
автором в 1924 г. Здесь мы ограничиваемся краткими извлечениями
лишь для того, чтобы дать читателю понятие о своеобразии и принци-
пиальной важности поднятых там, но далеко еще не исчерпанных во-
просов.
§9.5. ПРИМЕР РАСЧЕТА РАДИАЛЬНОЙ ВАНТОВОЙ ФЕРМЫ
На фиг. 265 представлен частный случай многопоясного веревочного многоуголь-
ника, у которого оси различных поясов (многоугольников) на протя/Кенин некоторых
панелей, примыкающих к среднему шарниру, сливаются в единый многоугольник, а на
протяжении остальных панелей до пилона идут раздельно в виде прямых линий.
Фиг, 265
Стойки, очевидно, играют роль одиночных стержней; в них усилия равны нулю.
Удалив эти стойки, мы получим вантовую систему предложенную французским инже-
^•^Ром Жискляром, который назвал ее радиальной. На фиг. 266 представлена
^ема мостового прблетиого строения, которая имеет вид опрокинутой трехи»арпнрной
^Рки. составленной из двух таких радиальных вантовых ферм. Основными элеменгами
являются длинные наклонные стержни D| и D,, которые работают при любо.м распо-
DarJi^""" внешней нагрузки. Стержни D^ и U\ работают только тогда, когда нагрузка
насположеиа в левой половине фермы, стержни D^ и Ui — только тогда, когда нмеет-
"агрузка, расположенная левее точки F, и т. д.
На фиг. 266, а изображена лнння влияния D]. Когда груз находится справа
узла С, то в левой части работает только стержень Du перерезав его и соста ^'
уравнение моментов относительно опорного шарнира В, мы убедимся, что усили ^^п
изменяется по линейному закону. Ордината под узлом С проще всего определя^
так. Поставим груз Р^1 под этим узлом; тогда из всей фермы будут работать то ^^"
стержни Z), п /)j , а усилия в них определятся нз силового треугольника, предста ^^
ного на фиг. 266.а. Вторая прямая той же л. в. определяется при помощи ну ^^•'
точки, которая расположена под точкой взаимного пересечения прямых Dj и D' п ^"
'^¦Ч
л. 6л
Фнг. 266
ствительно, когда груз
""'"анТло^' и ^1. а стерж«,ь"с, 'выключается'°'"'°"' ™ °" Уравновешивается натя-
™HFE{??°""^^^^^^^^^^^^^ ~"ofl фермы. Ординаты
Фи котором получается наибольш^Р r.i"°^^^°^)' Установленной в такое
168 ^^ растягивающее усилие. ^^
суммарному растягивающему усилию н заданному напояженмтп т,. . .
и Таким способом обеспечивается необходимый запас Гочности'^^^ ''^'¦
Однако этого недостаточно. Необходимо кпомГ^^^ прочности.
„„о»...".. "Ри ко"ро« он .»ы..„ н^о7т.?Тж"ЙК'еТ:™"*' ' '""*
Фиг, 267
риваемой временной нагрузки для того, чтобы суммарное усилие в стержне обратилось
в нуль. При дальнейшем бесконечно малом увеличении временной нагрузки стержень
уже начнет сжиматься, а начало сжатия для такого стержня играет такую же ката-
строфическую роль, какую появленне .напряжения, равного пределу прочности, играет
Фиг. 268
для растянутого стержня. Коэффициент запаса, очевидно, равен отношению между
растягивающим усилием данного стержня, которое вызывается в нем постоянной на-
грузкой, и наибольшим сжимающим от временной. погттпрпрпрннпй по
Если постоянная нагрузка может быть принята равномерно распределенной по
всему';;рол^'ГГимеюще^^^^ g т!м, а временная^ радьюмернор^
ленной „а от'рицательной части л в. и имеющей^ интенивнос^ьр^^^^^^
от постоянной нагрузки будет ^(w+—о'-.)» где ш^ , _ ^«,„.,о.«.т,о^ л/гм
площадей положительной и отрицательной частей л. в., а наибольшее сжимающее уси-
лие будет pw_. Коэффициент запаса на растяжение равен
\
(9.9)
k =
g{<^^ — с^_)
ра)_
-tlr-)
i
Ро«, Л.Л. „«« жлаипгп-нибуль стержня слишком мал. то его мож-
Если коэффициент запаса для какого-нио>а1Ь lt^ Например, для того чтобы
"о увеличить путем соответствующей передвижки узлов. р поместить несколько
ГижГ""^ '/"-^ коэффициент для ^терж^^! Фи^- 26^^^^^^ ^^^^^ ,^ „^^^,,^,
no^nl'^^'^ ^'' '^^'^^^ пулевая точка ^^'^""""'"отрицат^ьного - уменьшится,
положительного участка этой ^"»^" ^^f ^^"тового^^^^^ М°ст предназначен под
V3Kn!^^ Ь^- 2^7 показана одна из '^^^^^„^^^^"^^^^ пролет его равен 156 м. ^
узкоколейную электрическую железную Доро^У- пян?овой Фермы (фиг. 268). По этой
схем^'^^''^ ^^ Построить линии »^«;;""«^%enS^^^^^
^хеме построен в 1933 г. мост пролетом 80 м через р. i i^i у н
"шоссейной дороге на Кавказе.
h*-
rf-lf^ P'^
2f 2c stnd
пен
П.бМр
-'^=^ПЗgЩ]J|J™
ЛбО^
Фиг. 269
" — :lr..^J
Фиг. 270
§ 9.6. ПРИМЕРЫ И ЗАДАЧИ
Задача 9.2. На фиг. 269—270 построены эпюры и линии влияния
для комбинированной системы, имеющей вид шпренгельной балки. Про-
верить эти эпюры
Указание. Усилие в затяжке ^
ОЕ определяется, как в трехшар-
нирной арке, по формуле
Фиг. 271
Фиг. 272
сжимающее усилие в стойках равно
4
Задача 9.3. Построить эпюры и линии влияния для шпренгельной
балки, представленной на фиг. 271. „ д, ,„ ото «п,, rтr^n
Задача 9.4. Разобрать эпюры, построенные на фиг. 272 для под-
»^осной системы.
171
I. лав а 10
ПЕРЕМЕЩЕНИЯ УЗЛОВ И СТЕРЖНЕЙ ПЛОСКИХ ФЕРМ
§ ЮЛ. ВВЕДЕНИЕ
При определении аналитическим или графическим способом усилий
в стержнях ферм мы не делали никакого различия между деформиро-
ванной и начальной системами, так как предполагали, что все деформа-
ции ничтожно малы по сравнению с основными размерами фермы — ее
пролетом, панелями, высотой и т. д. Однако существуют такие вопросы,
при решении которых мы не можем игнорировать деформации и вызы-
ваемые ими перемещения узлов. Так, например, определение усилий,
вызывамых в стержнях статически неопределимой фер-мы неподвижной
или подвижной нагрузкой, невозможно без рассмотрения деформаций;
мы в этом убедимся позже, при расчете таких ферм. С другой стороны,
жесткость фермы (статически определимой или статически неопре^
делимой) характеризуется величиной 'перемещений ее узлов. При проек-
тировании сооружений приходится уделять известное внимание вопро-
сам жесткости, т. е. заботиться о том, чтобы прогибы не были слишком
велики. Вопрос о жесткости фермы встает также при решении задачи
о действии на нее динамической нагрузки, так как частота
собственных колебаний фермы зависит в сильной степени от ее
жесткости.
В ферме с прямыми стержнями и идеальными шарнирами дефор-
мации стержней сводятся только к удлинениям или укорочениям. Если
стержень имеет по всей Длине постоянную площадь сечения и испыты-
вает усилие N, то его удлинение или укорочение, пока они не выходят
за пределы пропорциональности, выражаются формулой
д/ = ^.
EF
Концы стержня сближаются или расходятся между собой на вели-
чину д/, и это изменение расстояния между узлами влечет за собой
изменение положения последних в плоскости, а следовательно, и изл1е-
нение положения стержней.
Задача о нахождении нового положения всех узлов по заданным
удлиненштм стержней фигуры имеет чисто геометрический характер-
При графическом ее решении необходимо применять такой метод по-
172
строения, который позволил бы одновпемрмнп ггсг^г.
^кр^ом масштабе, а ферму-в ^^лТоТ^^^^^^^^
деет несколькими такими методами. Обычно^ задачГ ^ешае?ся гпа^и'
ческим или графоаналитическим путем. решается графи-
§ 10.2. ПОНЯТИЕ О ДИАГРАММЕ ПЕРЕМЕЩЕНИЙ (ВИЛЛИО)
Эта диаграмма^ дает в произвольном масштабе величш1у и направ-
ление перемещении всех узлов фермы. Все построение основано на пред-
ложенном в 1877 г. Биллио (Williot) графическом решении следующей
простой задачи: по заданным перемещениям АА' и ББ' точек Л и Б и
заданным удлинениям стержней С А и С В определить перемещение точки
С (фиг. 273, а). Это решение показано на фиг. 273, б. Из произвольного
полюса О проводится вектор А ь выражающий собой перемещение точки
Л. Из конца этого вектора проводим вектор Д/,, равный и параллельный
заданному удлинению стержня СА; если это удлинение положительное,
то точка С перемещается
вверх (удаляется от Л) и
на диаграмме Виллио век-
тор Д ^1 ведется вверх; если
же стержень С А сжат, то
точка С перемещается вниз,
следовательно, и вектор A/i
откладывается вниз. Если
бы стержень СА оставался
неповернутым, то переме-
щение точки С выразилось
бы геометрической суммой
векторов ^1 и А ^ь т. е. век-
тором OCi. На самом деле
стержень СА поворачивает-
ся вокруг точки Л на не-
известный угол, вследствие
чего точка С получает до-
полнительное перемещение
По окружности радиуса АС.
Считая перемещения нич-
тожно малыми по сравне-
нию с этим радиусом, мы
можем заменить элемент
окружности элементом прямой, перпендикулярной радиусу; поэтому к
вектору ОС, добавляем неизвестную по величине составляющую С,С
перпендикулярную А/,. Само собой понятно, что соотношения, справед-
ливые для бесконечно малых перемещений, мы имеем право изображать
на чертеже в любом, хотя бы и весьма крупном масштаОе.
Точка С принадлежит одновременно стержням СА « СБ На ^^^^^^
основании проводим из полюса О вектор Д., выражающий перемещ^^^^^^^
точки Б; к нему добавляем, заданную по величине и по H^"Pf/^«i^^
составляющую Д^, т. е. (в данном примере) У^^Р^^"f д7'Р^Генд?-
и из полученной таким способом точки С, «осставляе^м к Д/2 перт^^^
его на любую ось, например вертикальную проекцию, которая обычно
173
Фиг. 273
.гнбом Легко определяются также углы по-
неточно называется п
стеожней:
ворота Ь и фг
обоих стержней:
С, С
(10.1)
. г с направлен вправо, следовательно, стер-
На фиг. 273, б вектор i;'^; "^^о'чки И по часовой стрелке; судя по
жень СА поворачивается ^округ стержень СВ поворачивает.
гя вокруг В в ту же сторону.
На фиг 274, с для примера показаны
схема фермы и знаки усилий в ее стерж-
нях Если величина сил Р и площади
всех сечений заданы, а усилия найдены,
то удлинения всех стержней легко могут
быть вычислены.
На фиг 274, б построена диаграмма
Виллио. Построение начинается со стер-
жня АВ У которого конец А неподвижен,
я пеоемешение конца В направлено по
оси стержня. Так как стержень растянут,
то точка В перемешается вниз. Ее пере-
мещение откладывается от точки А , ко-
торая совпадает с полюсом О, в виде
вектооа А'В/ Далее находим на диаграм.
ме изображение D' точки Л: откладываем
от найденной точки В' влево в виде
вектора B'D, укорочение ^^^^^''if^^J,
от ТОЧ.КИ А' в виде вектора А D^ удлине
ние раскоса AD; на пересечении перпен-
дикуляров к этим двум векторам нахо-
дим точку D\ Аналогичным образом на
пересечении перпендикуляров к векто-
рам A'Ci и D'C2 находим точку Си на
пересечении перпендикуляров к ь ci "
D'Ei —точку Е'.
Для большей ясности построения век
торы, выражающие удлинение «-"и ук"
рочение стержней, показаны жирными
линиями. _ .„„^ /о
Перемещение узла D по величине j
выбранном масштабе) и по f правлени^
изображается вектором ои , перем
ние узла Е — вектором ОЕ' и т. Д. ^^
Перемещение точки С выражается
диаграмме вектором ОС, направленным
от О к С; перемещения точки В — ве^
ром ОВ' и т. д. . раз-
Перемещение точки В относительно точки С равно геометрическо у
ности их абсолютных перемещений, т. е.
OB' — OC' = ОВ' -f С^ = Сё'.
Следовательно, взаимное перемещение произвольных двух узл
рожается на диаграмме вектором, соединяющим их изображения, ^^^.д
В разобранном примере стержень АВ после деформации °5^дучай:
параллельным самому себе. На фиг. 275, а показан более обшии с у
174
Фиг. 274
опорный стержень на конце В не перпендикулярен оси АВ Постпоение
диаграммы для этого случая показано на фиг. 2?5. б от полюса О
проводится вектор ОБ,, параллельный стержню ЛВ и выражаюший
собой влияние удлинения; к нему восставляется перпендГГяГ^
ясаюший влияние поворота, Сум- ^ адикулир, выра
марное перемещение точки В долж-
но быть перпендикулярно опорному ^ • В
стержню, следовательно, из полюса ^-i--^^
О нужно провести прямую 0В\ вы- д ^^J^"^""^"^'^
ражаюшую это суммарное переме- Ъ-^сг"""^"^^^
щение, до встречи с прямой В^В'. ^^^
Если какая-либо часть той или '' 6) ^г
иной деформируемой фермы пере- ^^..-"-^"'''^
мешается, как одно целое, не ис- ^^„„..---•'''''''^ \
пытывая никаких деформаций, то ^с<- ^^/
ее изображение на диаграмме Вил-
лио—подобно самой части и повер- ф^^ 275
нуто относительно нее на угол 90°.
§ 10.3. ПОСТРОЕНИЕ ДИАГРАММЫ ПЕРЕМЕЩЕНИИ
В БОЛЕЕ ОБЩЕМ СЛУЧАЕ
В рассмотренном примере построение диаграммы перемещений было
облегчено тем, что с самого начала имелся один стержень, а именно
АВ, для которого были известны перемещения обоих концов. В боль-
шинстве случаев опорные узлы отделены друг от друга более чем одной
панелью (например, в фиг. 276), и тогда уже ни одного такого стержня
не имеется. Построение диаграммы перемещений, естественно, услож-
няется
Удалим сначала опорные стержни, помещенные в узлах Л и G
(фиг. 276, с), и сделаем эти узлы свободными. Вместо этого сделаем
мысленно опорными узлами концы одного (любого) стержня фермы,
например, поместим в узле D два опорных стержня, а в узле А —один.
Тогда узел D сделается неподвижным, а перемещение узла Л вполне
определится удлинением стержня DK и направлением опорного стержня,
помещенного в узле К. Проще всего направить этот стержень перпен-
дикулярно оси стержня DK; тогда последний после деформации оста-
нется неповернутым. Построенная при таких допущениях Диаграмма
перемещений показана на фиг. 276, б Ее полюс совпадает с изображе-
нием D' неподвижного узла D. Узлы А и G, естественно по-
лучились^ подвижными: их перемещения выражаются векторами
Сдел^а?н"ое построение позволяет определить ^^f твите'тьные верта-
кальные перемещения всех узлов. На фиг. 276, « "°"Р°^" ""SJ°eo-
ник вертикальных перемещений узлов нижнего "ff^-^"°^^Р°б "поек-
^^тоит в том, что изображения узлов, полученные на Фиг-Jje. б проек
тируются горизонтально на вертикали "Р0^е^^""""„,„3' ника Если
фермы. Так получаются вершины а, Ь, с я т. ^- """^^У^я " ю через
"Ь! примем за ось абсцисс последнего ''>P"^l''l^"'''^l°^;^'^^^^
вершину а многоугольника, то мы не п°^У™", "Р^,Т явХ "^ на ве^^^^^^^
так как конец G фермы окажется переместившимся вверх на вели
*^Ину PS
, Чтс-^ы исправить положение, нужно ""'Р-рт' „Хм^Ея^вК
175
""оГ?оГ>ке''ос!Га"б^сТледует измерять вертикальные перемещения
узлов верхнего пояса, которые получаются проектированием их изобра-
жений на соответствующие им вертикали.
Фиг. 276
nnJ^"^ ^^ способом получается многоугольник любых наклонных
проекции перемещений.
пео!^мрт«!^'„Г^' ^ "°^^зано построение многоугольника горизонтальных
maZZefchur^^rPT *'Р''^'- Изображения узлов, полученные на
на горизонтйи пп ^' ^^' проектируются по вертикальному направлению
на фиг 276 Л;.Г^'''^Т''."' ''^^ *е УЗ'""^- Многоугольник обозначен
жа^тся гооич/„.. "" ""' ^ • '^ " ^- ^- Горизонтальные перемещения выра-
заключает?я ?еп1оГв том" °Р^Г'"'"" многоугольника' Вся трудность
щей т е отпя!^ ''^"' ^"1°^" "Р^вильно найти положение замыкаю-
вокруг А. "''^Р^^'^^ь на фиг. 276, г тот же факт, что ферма повернулась
грамм1?^1тоЛпппГ^^''' ^^"^ """^"^ исправить первоначальную диа-
построшия допол^и?е1к^РГ' У*'''"'""" "^ °"°Р^^- Его способ требует
перечертить нТноп"Е°" Диаграммы: нужно определенным образом
F ртить наново ферму, повернув все ее стержни на 90°. после чего
176
пповести еще ряд прямых. В таком сложном випр =^тг. т..гт,.о«
?Рется до сих пор во всех курсах. На сам^Теле э^ГпЕстр^^^^^^^^^
^ьг сейчас покажем, является лишним. Можн о огТа н иТи^ься
проведением одной прямой. ихраничиться
Сравним угол gas на фиг 276, в с углом g"a^s' на фиг 281 г и
докажем, что они между собой равны: ^ ^ на фиг. zoi,a и
^gas^^g'a' S' ^а, (10.2)
Нетрудно убедиться, что измеренная в надлежащем масштабе вели-
чина ^ есть не что иное, как тот поправочный угол, на который нужно
повернуть всю ферму вокруг узла Л, чтобы посадить конец G на опору.
Следовательно, при построении многоугольника, выражающего проекции
перемещений на произвольное направление, угол между замыкающей
многоугольника и направлением проекции остается инвариантным.
Если бы мы при построении диаграммы (фиг. 276. б) приняли за непо^
вернутый стержень не стойку DK, а какой-либо другой стержень, мы по-
лучили бы, разумеется, другую величину угла а, но свойство инвариант-
ности последнего сохранилось бы.
Заметим, что для нахождения угла а нет необходимости строить
весь многоугольник вертикальных перемещений; достаточно иметь на
фиг. 276, в точки а W g. Под «вертикальным» здесь условно понимается
направление, параллельное правому опорному стержню (фиг. 276, а).
Итак, отметив угол а, который получился на фиг. 276, в, и перенеся
его на фиг. 276, г, мы получим искомую замыкающую a'g'' многоуголь-
ника горизонтальных перемещений.
Таким же способом можно построить график проекций перемеще-
ний на произвольное направление.
Инвариантность углов ос может быть использована также при по-
строении диаграммы перемещений узлов более сложных ферм, напри-
мер трехшарнирных арочных и др.^
Имея диаграмму фиг. 276, б и зная, кроме того, угол а , можно найти
угол поворота любого стержня как сумму двух углов. Например, угол
поворота стержня LM выражается на фиг. 276, б отношением отрезка
М\М' той же фигуры к длине стержня LM фермы. К этому углу нужно
добавить измеренный в надлежащем масштабе угол а.
Кроме диаграммы Виллио, существует еще один весьма распростра-
ненный способ построения перемещений узлов фермы. Он изложен ниже,
в параграфе 14.10.
,^ ^ См статью автора «Упрощение в построении диаграммы перемещений», сборник
«Исследования по теории сооружений», вып. VI, Стройиздат, 1954.
Глава 11
ПРОСТРАНСТВЕННЫЕ ФЕРМЫ
§ ПЛ. ЗНАЧЕНИЕ РАСЧЕТА ПРОСТРАНСТВЕННЫХ ФЕРМ
Плоская ферма может находиться в равновесии только в том слу-
чае когда .все действующие на нее силы расположены строго в ее плос-
кости. Так как на практике это требование невыполнимо, то -плоская
ферма неустойчива и неминуемо должна иметь закрепления, не лежащие
в ее плоскости. Так, например, плоские стропильные фермы связываются
между собой обрешеткой кровли, фермы пролетных строений мостов —
поперечными и продольными связями, а также проезжей частью и т. д.
Плоская ферма вместе с ее связями фактически является уже лростран-
ственной системой. Если мы тем не менее рассчитываем ее, как плоскую,
то мы обязаны смотреть на такой расчет как на приближенный. Имея
преимущество перед точным в отношении простоты, он менее выгоден,
так как недостаточно учитывает работу дополнительных элементов, не
лежащих в плоскости фермы.
Кроме тех ферм, которые можно с известным приближением рассмат-
ривать как плоские, существуют такие фермы, ярко выраженный прост-
ранственный характер которых не дает никакой возможности считать их
плоскими. Таковы многие системы купольных ферм, применяемых для
перекрытий гражданских и промышленных сооружений, фермы корлуса
самолета, фермы некоторых систем башен, мачт и т. д. Их необходимо
рассчитывать как пространственные системы.
Задачи и методы расчета пространственных систем принципиально те
же, что и для плоских систем, но отличаются большей сложностью, так
как приходится вести графические построения в двух плоскостях проек-
ций и удовлетворять значительно большему количеству уравнений стати-
ки, чем при решении плоских систем.
§ 11.2. СЛОЖЕНИЕ СИЛ В ПРОСТРАНСТВЕ
Сложение сил имеет целью главным образом замену одной системы
сил другой, ей эквивалентной, но более простой. Две системы сил являют-
ся эквивалентными, если их проекции на любые три оси и моменты отно-
сительно этих осей соответственно равны между собой
^.ложение сил, .пересекающихся в одной точке, может быть произве
дено при помощи силового многоугольника по правилу сложения векго-
ров. 1 азумеется, многоугольник .получается пространственным. Его замы-
178
каюшая по величине и по направлению выг>я^.,о«. л -
в V ю Щ У ю с и л у; эта равнодействуютя« 'In ^"^ ''^°" равнодейст-
пр^иложения всех заданных сил '^^°'^^'' "P°>^^ht «^ерез общую точку
Система параллельных сил приводится ли^г. „по-
ле, имеющей то же направление Е равной их гео1хп1ТГ"'^'°"^^^ Т
к паре сил. Если геометрическая cyLa" л" р\7лГьнГГиГн: ГнТнулю
то они приводятся к одной равнодействующей силе. Для нахождения по:
Фиг. 277
бледней достаточно спроектировать такую систему на две взаимно-пер-
пендикулярные плоскости и, рассматривая полученные две проекции, как
Плоские системы сил, построить для каждой из них веревочный много-
угольник и найти равнодействующую. Такое построение показано на
фиг. 277. Здесь вся система приведена к одной силе, лоложение которой в
ространстве определяется ее двумя проекциями R и R\
Если силы не пересекаются в одной точке и не параллельны между
^обой, то в общем случае они не приводятся к одной равнодействующей
иле или к паре сил. Простейшая эквивалентная им система состоят из
илы /? и пары М, причем проекция силы R на любую ось равна сумме
Роекций заданных сил; следовательно, эта сила вполне определенна по
личине и направлению. Что касается ее положения в пространстве, то
о может быть выбрано произвольно, но в зависимости от этого выбора
Удут изменяться величина момента М и плоскость действия равнодей-
^твующей пары.
T-Qj^^^*^" J^bi перенесем точку приложения силы R из А в какую-нибудь
POMAf ^*"''' ^^^^' '^^ ^ равнодействующей паре, выражаемой векто-
Л1, придется добавить пару Rd, следовательно, к вектору М геометри*
12»
179
, .гп^пный плоскости, содержащей силу
,ески прибавить вектор, перпендикулярный
^"'„проходящей через точку ^^^пендикулярные составляющие Y,
^ Разложим вектор М "2„„\^^" ^ силе i?. Всегда можно подобрать поло-
X и^ которых первая параллельна силе ^^^ ^^^^ перпендикулярна
iZr:Z« ^:;-^Тр»ГГоГС"у"и-сь И--Л,тогда .е„„р„
вектору
X и
Фиг. 278
+Х и —^ взаимно унич-
тожатся и вектор момен-
та сведется только к со-
ставляющей У, парал-
лельной силе R. В^ этом
случае линия действия
силы R называется глав-
ной осью системы, а век-
тор У — главным момен-
том. Главный момент
является минимальным
из всех возможных.
Попытки создать для
сложения сил в прост-
ранстве графическое по-
строение, которое по
своему значению было бы аналогично веревочному многоугольнику для
плоской системы, привели к теории веревочной пирамиды. Од-
нако это построение не обладает практическими достоинствами своего
прототипа и представляет главным образом теоретический интерес.
§ 11.3. РАЗЛОЖЕНИЕ СИЛЫ НА ТРИ СОСТАВЛЯЮЩИЕ,
ПЕРЕСЕКАЮЩИЕСЯ С НЕЙ В ОДНОЙ ТОЧКЕ
система сил. Силы,
Задачу о разложении всегда можно заменить задачей об уравновеши-
вании: стоит повернуть либо разлагаемую силу, либо ее составляющие^
обратную сторону, и получится уравновешенная
проходящие через одну точку, должны удов-
летворять трем условиям равновесия: ? Х = 0,
? У=0, EZ=0; поэтому задача о разложении
силы Р на три направления, пересекающиеся
с ней в одной точке, является в общем случае
определенной; разложение на большее коли-
чество направлений является неопределенным,
а на два направления — невозможным. В част-
ном случае, когда силу Р требуется разло-
жить на три направления, лежащие в одной
плоскости, задача будет неразрешимой, если
сама сила Р не лежит в той же плоскости, и
неопределенной, если она лежит в этой плоско-
сти. Определенность задачи о разложении силы
Р на три направления, не лежащие в одной
плоскости, вытекает также из геометрической неизменяемости и непо-
движности стержней системы, представленной на фиг. 279. Однако в том
случае, когда оси стержней /, 2, и 5 лежат в одной плоскости, фигура
перестает быть неподвижной: точка А, очевидно, может иметь бесконеч-
но малое перемещение, перпендикулярное этой плоскости.
^Задача о разложении силы на три направления, пересекающиеся с
ней в одной точке и не лежащие в одной плоскости, имеет важное значе-
ние для теории ферм. Для решения ее имеется много различных способов
1§0
Фиг. 279
Изложим здесь графическое решение Купкы^о о
плоскостях проекций сила Р и направления^ Ге^^^^^ ""Т' ^ ^^^"^
должны ее уравновешивать (фиг, 280) Булем иг^.. Л 2 и 5, которые
с%ющую двух сил, например равно^е&о^^^^
очевидно, лежит в плоскости сил / Л Н™ кяк S"' п*" ^ " ^' ^""^^
остальные две силы, т. е. Р и 2 то она on^nL "^ уравновешивает
кости последних. Итак, она направле^ГпГпииГ '"""^ '^''^^'' " " "^^^"
плоскостей (/, S) и (Я ^). "Р^^'""^^ "^ ™нии взаимного пересечения
Фиг. 280
Для построения этой линии найдем сначала следы а, 6, с, rf прямых
^, 2. 5 и Р на горизонтальной плоскости. Прямая ас представляет собой
горизонтальный след плоскости (/, с?), а прямая bd — след плоскости
(а Я). Точка е их взаимного пересечения есть горизонтальный след
искомой прямой. Поэтому прямая А'е представляет собой горизонталь-
ную) проекцию прямой /?1-з. Имея эту проекцию и горизонтальный след
^' проектируем эту точку на ось и получаем вертикальную проекцию той
^е прямой /?1_з.
После этого мы можем построить силовой многоугольник в двух пло-
скостях проекций (фиг. 280, б). Сначала сила Р уравновешивается сила-
п^ 2 и /?1_з. Затем введенная в качестве вспомогательной величины сила
yi-3 разлагается на две составляющие по заданным направлениям
" ^. Правильность построения поверяется тем, что каждая вершина
^илового четырехугольника должна лежать в обеих проекциях на одной
вертикали.
^ос'гроение значительно упрощается, когда в одной из плоскостей
^Роекцнй линия действия двух сил, например сил / и 5, сливается в одну.
'^'Да все вспомогательные построения отпадают: в названной плоскости
роекций четырехугольник превращается в треугольник a^h^c\ который
ПпгГ^^ бь1ть построен сразу (фиг. 281), после чего в другой плоскосги
Р^^кций сейчас же получаются- вершины а, Ь, с; проведя из точе|^ с, Ь
Ш1
прямые по направлениям 5 и /, мы на их пересечении найдем четвертую
вершину d. По ней в вертикальной плоскости проекций определится ,
вершина d\
Для дальнейших приложений важны следующие частные случаи уря
повешенной системы сил, пересекающихся в одной точке. На фиг. 282 п^'
казана система пересекающихся сил, причем все они, кроме силы S л^'
жат в одной плоскости. Спроектировав все силы на нормаль к это^"
плоскости, мы сейчас же убедимся из условий равновесия, что .S=0 "
В применении к пространственной ферме этот вывод можно сформу-
лировать так: е с л и в ненагруженном узле А имеется оди
ночный стержень S, то усилие
в нем равно нулю (одиночный
стержень узла —такой, который не
лежит в плоскости, в которой распо-
ложены все остальные стержни дан-
ного узла).
Если система состоит из трех сил
не лежащих в одной плоскости, то
Фиг. 281
Фиг. 282
каждая из них является одиночной так кят. опгл^
можно провести плоскость. ОтсГа'сл?^^. ^^^ ^^^ ^РУ"^"^ ^^^'^'
В ненагруженном пространствРяиги^^J^^^^ ' "^^^ ^^^ ^Р^ ]?гшы нулю.
ня являются нулевыми ^'''''' трехстержневом узле все три стерж^
С помощью Этих теопрм
чете пространственных ферм «^щеляются нулевые стержни при рас-
За1ГоГа1Т '''"''''""" '""" "^ "'^^^^Ь НАПРАВЛЕНИЙ
Т?^^^^^''^^^™^о1т^с?1 пТ:Г ^""авляющие. направленные
ше я^тГ'^' "'^'^ '^^^ ^ cooTBeT^BvwmMv Г" ^ °^"^"" <=-"Учае является оп-
f paCZl''"" составить, будуЖу^^по^Г™ Уравнениях статики, кото-
гЙо™"^г^Р^"'^""« этой зада^ ппе^^^'''' '""•"^^о "^^"ь неизвестных,
громоздки. Ограничимся рассмотоХ"!?"'^'^™'^^ До сих пор, достаточно
плоско^Г ""^""""^"^ссти^мыхпЛ" "^'^•^«^ьких частных случаев.
состав' ' ««^-5 и 4-в д^" „Гпп"^"Р"*'^Р ^ и ^' -"е^кат в одной
?oS двеГизвеГ" УР««"-"ия''моме2?Г"к7 ^*"'"- ^^З). то можно
прямым Для |тп!""^ '^^"««•"яющие на °п;,Л """Р"^ ^^"У" содержать
прямую ЛВ я ZT ^°статвчно вдять ^Л •"™""^"°о^^альны.мдвум
еХт5ько JsTnT-^P^^y'o^cb ^ °^"У "^ моментных осей
то проводим вторую пГсГть^; «р2 ?о\Г ^ °^«°« —ости (фиг. 254),
,82 рез точку их пересечения А и через пря-
„ую 3 и находим следы Си/) прямой 4 на обеих плоскостях Тогда одной
„3 моментных осей будет прямая AD, а другой —ппямая ВТ
Если три прямые (/, 2 и 3) лежат видной пло'скости ^фиг 285) то
„оментная ось АВ дает возможность написать уравнение содержащее
Фиг. 283
Фиг. 284
одну неизвестную силу, направленную по прямой 6\ ось ВС позволяет
определить из одного уравнения
а ось АС — силу по прямой 5.
Если три прямые пересекают-
ся в одной точке, то через нее
всегда можно провести прямую,
пересекающую две другие, и -по-
лучить одно уравнение с одной
неизвестной составляющей.
Если пять прямых лежат в па-
раллельных плоскостях, то мож-
но получить одно уравнение с
Одним неизвестным, спроектиро-
вав все силы на нормаль к этим
плоскостям.
силу, направленную по прямой 4,
Фиг. 285
§ II.5. СЛУЧАИ НЕОПРЕДЕЛЕННОСТИ РАЗЛОЖЕНИЯ СИЛЫ
НА ШЕСТЬ НАПРАВЛЕНИЙ
Для того чтобы разложение какой-нибудь силы Р на заданные шесть
направлений было возможным и определенным, необходимо, чтобы опре-
делитель шести уравнений статики был отличен от нуля. Соблюдение
этого условия совершенно не зависит от силы Р, а зависит исключитель-
но от расположения этих шести прямых.
В некоторых частных случаях мож1Но, не вычисляя определителя,
сразу сказать, что разложение неопределенно или невозможно. Таков,
Например, следующий случай: заданные шесть прямых распо-
'^ о Жены так, что их можно пересечь одной прямой.
Действительно, относительно этой секущей момент всех шести сил равен
%лю; если сила Р не пересекает той же прямой, то разложение невоз-
^^ожно; если пересекает, — то оно неопределенно.
183
То же самое получается, если более трех прямых проходит через
одну то^ку так как через нее можно провести прямую. пересекающук>
°Тот"же вьшоГсправедлив для случая, когда более трех прямых па-
рал^ьны между с5бой. так как параллельные прямые пересекаются
между собой в одной бесконечно удаленной точке.
Оода же относится тот случай, когда более трех прямых лежат в од-
ной плоскости. Например, если прямые 1,2, За 4 лежат в одной плос-
кости (Фиг 286). то прямая АВ пересекает все шесть прямых.
Если все заданные направления перпендикулярны одной и той же
прямой то проекции их на эту прямую равны нулю, следовательно, в
зависимости от направления силы Р решение будет либо невозмоя;ным,
либо неопределенным.
6
^^'
•^.
Фиг. 286
Фиг. 287
Шесть сил. которые должны уравновесить заданную систему сил,
можно рассматривать как реакции шести опорных стержней жесткого
тела. В общем случае такое количество опорных стержней уничтожает
подвижность тела; разобранные же выше частные случаи неопределен-
ности или невозможности задачи о равновесии отвечают такому распо-
ложению опорных стержней, при котором тело сохраняет бесконечно
малую подвижность.
Можно указать такое простое расположение шести опорных стерж-
ней, которое всегда гарантирует неподвижное прикрепление тела. Для
этого достаточно расположить опорные точки в вершинах произвольного
треугольника (фиг. 287), а самые стержни расположить следующим об-
nnnnt'; !^ о?^^ '^°'"'У ^ провести три стержня, не лежащих в одной
кпртк 1 п* ^ ^^^^^ """"""У ^ провести два стержня так, чтобы их плос-
жень тяк и^о^?""^ "'Р^' вершину А; 3) через С провести шестой стер-
жень так. чтобы он не пересекал прямой АВ.
^ "и JpnnSRUWMn^'"^'^''"''^^'^^" НЕИЗМЕНЯЕМОСТИ
И НЕПОДВИЖНОСТИ ПРОСТРАНСТВЕННЫХ ФЕРМ
мы?п%'опТе?еле^'Т'''.^°^ неизменяемости пространственной фер-
стержней ?Ены Хг^г аТ ' '' "^Р«<ня-^ обычно считают, что концы
торые лишенТтпени/« пп'^^'^" идеальными шаровыми шарнирами, ко-
тей через центр'^шарнирТ^''"^' вращение вокруг любой оси.'проходя-
тремя"Тор^Е''сТе?жнТи''л?йГ„ '^^^"«™чески изображаются либо
допускает вращение SeTurnl ^^У"''' ^«^^ °^""«- Первый тип опор
правлению {ъ степени свобо^Ат^'^ неподвижной точки по любому на-
ставить себе как шгр вхопяший'!^^''^ узловое соединение можно пред-
^" ^''ОДЯЩИИ в сферические углубления, устроенные в
опорной подушке и в опираемом теле (фиг. 288, а). Такую опору назы^
вают неподвижной шаровой опорой.
Второй тип, эквивалентный двум опорным стержням, допускает по-
ступательное движение тела по определенному направлению и, кроме
того, поворот вокруг трех осей (4 степени свободы) и носит название по-
движной цилиндрической отторы (фиг. 288, б). Он состоит из нижней
опорной подушки и из уложенных на нее цилиндрических катков, по ко-
торым катается верхняя опорная подушка. На последнюю при помощи
шара, лежащего в углублении, опирается тело.
Наконец, одностержневая опора может быть представлена схемой
фиг. 288,в. Она состоит из опорной подушки и шара, могущего кататься
по ее поверхности, и допускает поворот вокруг трех осей и поступатель-.
ное перемещение 'По любому направлению на поверхности (5 степеней!
свободы). Предполагается, что опираемое тело прижато к шару внешни-
ми силами и отделиться от него не может.
Обозначим число собственных стержней фермы через Сф, число опор-
ных стержней — через Со, число узлов —через У. Каждый узел или, вер-
нее, центр каждого узла можно рассматривать как точку, которая при
отсутствии каких бы то ни было связей обладала бы в пространстве^
тремя степенями свободы. Когда мы соединяем две точки стержнем, то.
уменьшаем их суммарную степень свободы на единицу, так как их шесть
координат оказываются связанными между собой зависимостью вида
(Хх- X^f + (Ух - у2? + (^1 + ^2? - d\
где d —длина стержня. Следовательно, каждый стержень эквивалентен
одной связи. Полное число связей равно
Сф + Со -
Вычтя из числа связей число степеней свободы, мы получим число-
"ЛИШНИХ связей. Обозначим его буквой Л,
Итак:
Л = Сф + Со —ЗУ.
(11Л),
Если Л < О, то система не' имеет достаточного числа стержней и по-
^JOMy является изменяемой или подвижной кинематической цепью. Если
•'^^^О, то система не имеет лишних стержней и может оказаться геомет-
рически неизменяемой и статически определимой. Если Л>0; то система
«меет лишние стержни и может оказаться геометрически неизменяемой
^ статически неопределимой. В двух последних случаях необходимо,
Конечно, не ограничиваясь -подсчетом числа стержней, рассмотреть еще
^^ расположение.
i^^^
в том случае, когда Л=0, уравнение (1) принимает вид
ЗУ=Сф + Со. (11.1')
Чтп уоавнение может служить необходимым (но недостаточным) призна-
ком статической определимости. Его можно было бы также получить,
исходя из подачета числа неизвестных сил, которое равно Сф+С„ и из
числа уравнений статики, получаемых при вырезании всех узлов, кото-
от/
''°^ели"желательно отделить вопрос о геометрической неизменяемости
(Ьермы от вопроса о ее неподвижности и выяснить, представляет ли
?обой ферма, отделенная от своих опор, одно целое, то мы должны под-
ставить в уравнение (1) Со =6, потому что геометрически неизменяемая
система для обеспечения своей неподвижности требует шесть опорных
Фиг. 289
Фиг. 290
стержней. Следовательно, число лишних стержней фермы, отделенной от
ее опор, выражается формулой
Л = Сф + 6 —ЗВ^, (И.Г)
а необходимый признак геометрической неизменяемости и статической
определимости такой фермы имеет вид
ЗУ=Сф + 6. (11.2)
Например, система (фиг. 289) содержит 8 узлов и 17 стержней, сле-
довательно:
ЗУ = 3.8 = 24; Сф+6 = 17 + 6 = 23 ; Л = -1,
т. е. недостает одного стержня. Для того чтобы эта система сделалась
неизменяемой, достаточно поставить диагональ в верхнем основании или
внутри тела.
Подсчет числа лишних или недостающих стержней сильно облегчает-
ся, если ферма имеет вид многогранника с треугольными гранями, огра-
ничивающего замкнутое пространство. Все стержни такой системы можно
рассматривать как лежащие на замкнутой наружной поверхности.
Ьслц мы обозначим число граней буквой Г. то число стержней буД^'^
равно ^
С^^
2 '
186
Сф = ЗУ —6.
Полученный вывод показывает, что стержневая система^ имеющая
вид многогранника с треугольными гранями (так называемая сетчатая
система), всегда Удовлетворяет условиям геометрической неизменяемости
и статической определимости, не нужда-
ясь ни в каких внутренних стержнях.
Эта теорема была найдена Коши
(Cauchy) в 1813 г. Она обобщается на
любые фермы, имеющие вид многогран-
ника, замыкающего односвязное прост-
ранство, при условии, что каждая его
грань представляет собой плоскую гео-
метрически неизменяемую систему без
лишних стержней.
Пользуясь этой теоремой, можно во
многих случаях быстро анализировать
геометрическую структуру ферм. Напри-
мер, для того чтобы систему по фиг. 289
люжно было считать сетчатой и, следо-
вательно, неизменяемой системой, ей не-
достает одной диагонали в верхней грани.
О системе по фиг. 290 можно, не инте-
ресуясь числом стержней и узлов, ска- Фяг^ 291
зать, что она геометрически неизменяема
и не имеет лишних стержней.
Система по фиг. 291 не является сетчатой. Чтобы стать таковой, она
должна была бы иметь диагональ «в верхнем основании, диагональ—в
нижнем и кольцо из четырех стержней в нижнем основании; но вместо
этих Недостающих шести стержней она имеет столько же дополнительных
опорных стержней (общее количество опорных стержней равно 12
вместо 6).
После того как будет выяснено, что исследуемая ферма имеет струк-
''^УРУ, приемлемую для геометрически неизменяемой и неподвижной
<^тержневой системы, необходимо выяснить, не является ли она мгновен-
но изменяемой или подвижной. Это можно сделать при помощи таких
^е методов, которые применяются для решения вопроса о мгновенной
изменяемости в теории плоских ферм; проще всего —при помощи ме-
^ода нулевой нагрузки.
§ 11.7. ЗАДАЧИ И ПРИМЕРЫ
Шиу^**^*''^ ИЛ. Определить усилия в трех опорных стержнях АВ, АС, AD, образую-
Нй * ^1Й? прямой трехгранной пирамиды с основанием в виде правильного треуголь-
KanL Ят- Ребра имеют длину /, а стороны основания — длину а. Сила Р—верти-
"*{13 (фиг. 292).
Через s^^^^"** симметрии ясно, что все три силы равны между собой. Обозначим их
^- и спроектируем на вертикаль:
Р
3Scosa=: Р; 5=^
3cosa
187
где
cos а =
Задача 11.2, То же, что в задаче 11.1, но сила Р параллельна прямой ВС (Лиг 9оо
Составим уравнение момеитов относительно оси ВС. Силы Si и Sj пересекя ^'
ся с осью, не войдут в это уравнение, и в нем останутся лишь силы 5з и Р fl^'mne.
как Р\\ВС, то момент силы Р равен нулю, следовательно, Sa=0. Силы Р s ^^^
лежат в одной плоскости, поэтому усилия S\ и S^ определяются, как в плоской Л " ^*
Фиг. 292
(фипжТ "'^^ ^° *""' "''" '"°Р«^°и"^ьной силе Р, перпендикулярной к прямой ВС
5з Ml°HrHaVTH,°TOecY3\™v B'TowK^v'b^^"^"^ ^«^" ^ Р^«^« ^'^^ Момент сил«
кальную состав";я^„ё Перв^^я neUeKaeT^^ofb ВС'Г';':^^^^ Т '•^Р''*'>«^«^ьную „ верти-
имеет_плечо, равное высот! треуголт ?сЬ f' е ^ "^ ''^^'' "'"""^'' '"'Р"'
-^l-i- А ' ' '
^ , и равна 5з sin р = Sg -^ .
Уравнение моментов имеет вид
откуда
' 2
= 0;
2/
zur-P.
параллельна мо^^с^^муголмика ВГО ff-'^^'' ''^'^ '"'^^ ^ горизонтальна, т. «
шие-параллельную и перп^енднкуляр^^? прямей'ос"п ^^""^^^ «^ Л«« составляю-
Р с!п чпо _ р""-»"" прямой i)C. Последняя составляющая
/-smso»» 2 ; ее момент равен-^ А. Отсюда
-А-5 -5-
2 -^'Т
ТАГ
= 0; 5.= ^Р.
188
Наконец, из условий симметрии следует, что S^&^
'^V~&
Ф'
'Т
г^''
.А.<Л
сГ
'Ъ
.•J
\
V
I
1
Очень просто решается задача графичес1си (л.
«поекций строим в произвольном масштабеrL^*"^ ^^5)- В вептикальнпй ..
If гак как проекция силы Р обращае^ГвтТТ^ треугольник^ со ..."^.^,."f^^
получается четырехугольник, который строится* сле'п?Г''"^^^^"^« п^-
^ выражающего собой горизонтальную проекцию силы Г ''^^^^''''¦
Рг AD
_AD_
A'D'
сторонами /', 2',
плоскости проекций
'М: длина отрезка
из пропорции
так как обе проекции этой силы пропорциональны
стержня; затем проводятся прямые / и 2 ^'^"^"^•"^"ьг
рока Ц5 принимается рав-
ной Р. Тем самым опреде-
ляется масштаб силовых
многоугольников.
Заметим, что решение
задачи 11.1—П.З дает воз-
можность определить влия-
ние любой силы, приложен-
ной в точке Л, так как силу
всегда можно разложить на
соответствующие три со-
ставляющие.
Фиг, 294
Фиг. 295
«ова ^^*'^ ^^'^- Определить опорные реакции пирамидальной фермы, имеющей в ос-
Рал ^^^ прямоугольник со сторонами л. 6 и нагруженной горизонтальной силой /\ па-
стор'^^^Л-^^ сторонам а (фиг. 296). Опорные стержни 2^4 составляют продолжение
Решши ^'''^Ржень / — продолжение стороны а\ остальные три стержня вертикальны.
ц«я положительна, если она растягивает опорный стержень.
•^5 * ^^^"ты относительно оси AD\ моменты реакций Ru R2, ^з, Ri,
i^gL.Q Р^секающлх ось AD, и силы Р, параллельной этой оси, равны нулю, поэтому
2* Момент относительно оси АВ
R^a + Ph^O, илн /?5 = -
Ph
^¦Проекции н
а вертикаль
/?3 == «^5"
Ph
"^*1роекции на направление Р
5 Проекции и на АВ
/?1-у-«2« = 0.
откуда
/?2 = — ^4=
2а
Задача П.5. Решить ту же задачу, считая, что сила Р вертикальна.
Фиг. 296
Задача 11,6. Проверить на мгновенную изменяемость ферму, представленную*
на фиг. 297.
По своей структуре эта ферма является сетчатой системой, поэтому в обш.ем слу-
чае она статически определима. Для дальнейшего анализа применим способ нулевой
нагрузки. В узле / сходятся три стержня, не лежащие в одной плоскости, следова-
тельно, при отсутствии внешней нагрузки равновесие требует, чтобы все три их уси-
лия обратились в нуль. Откинув стержни, сходящиеся в этом узле, мы замечаем, что
в узле 2 остаются только три стержня, притом не лежащие в одной плоскости; следо-
вательно, этот узел также является нулевым, .и т. д. Переходя от узла к узлу в поряд-
ке, указанном -нумерацией на чертеже, мы убедимся, что при нулевой нагрузке все
усилия равны нулю и только нулю. Следовательно, фигура неизменяема^
§ 11.8. ОПРЕДЕЛЕНИЕ УСИЛИЙ В ФЕРМАХ СПОСОБОМ ВЫРЕЗАНИЯ УЗЛОВ
Если в ферме имеется какой-нибудь трехстержневой узел, стержни
которого не лежат в одной плоскости, то решение задачи начинаем с
этого узла. Если к нему не приложена внешняя нагрузка, то во всех
трех стержнях усилия равны нулю; если же внешняя нагрузка имеется,
то усилия могут быть найдены либо графически, например способом
Кульмана, либо аналитически, если потребные для этого углы или плечи
определяются легко. После этого следует искать новый узел, хотя бы и
содержащий больше стержней, но в котором имеется только три неизве-
стных усилия, притом не лежащих в одной плоскости. Если такой уз^л
190
имеется, то вырезаем его и находим его усилия указанным выше спосо-
бом» и т. Д.
Возможность или невозможность непосредственного определения всех
усилий этим способом зависит от геометрической структуры фермы.
Задача ttJ. Определить усилия в ферме (фиг. 298) от силы Р, приложенной в
узле А
^ Ферма, которую нам нужно рассчитать, называется куполом Шведлера. На фиг
298 он состоит из двух ярусов, из которых каждый представляет собой правильную
усеченную пирамиду. Боковые гранн имеют вид плоских трапеций с одной диагональю
Если бы эта система имела ниж-
7
нее кольцо в виде шестиуголь-
ника с тремя диагоналями, а так-
же три диагонали в верхнем коль-
це, то она была бы геометрически
неизменяема, как сетчатая си-
стема. Отсутствие этих 12 стерж-
ней возмещается таким же коли-
чеством добавочных опорных
стержней. Всего имеется 18 опор-
ных стержней — по 3 в каждом
из опорных узлов.
Поместим в узле / силу Р,
имеющую произвольное направ-
ление. Прежде всего выделим ну-
левые стержни. В узле 2 стер-
жень 2^а одиночный, а так как
внешней нагрузки в этом узле нет,
то стержень 2—а является ну-
левым. После удаления этого
стержня узел а оказывается со-
стоящим из трех одиночных стер-
жней а—5, а—6, а—Ь, которые
все являются нулевыми. Вслед за-
тем отпадает узел b с оставшими-
ся в нем тремя стержнями b—5,
b—f и b—c\ затем последователь-
но отпадают узлы с и ±
В узле 6 остаются четыре
стержня, причем стержень f—6
является одиночным. Откинув его,
Получим в узле f три стержня,
не лежащих в одной плоскости,
^едовательно, этот узел отпадает.
После него, очевидно, отпадет и
узел е. Все нулевые стержни по-
казаны на фиг. 298 тонкими ли-
ниями.
а:с' Ь'
Фиг. 298
д Определение усилий во всех остальных стержнях может быть произведено после-
Уз^^^^-^ьным вырезанием узлов в порядке, указанном их нумерацией. В каждом таком
д ^ мы встретим по три неизвестных усилия, не лежащих в одной плоскости, или по
Уз^'^^^йЩих в одной плоскости. В последнюю очередь придется рассмотреть опорные
11® каждом из них неизвестными будут три опорные реакции.
y3g ^Р^Д^авим себе теперь, что сила Р переместилась из узла / в узел 2, затем в
булеы " ^' ^•' '^- ^' ^"^^ °"2 прилагается в любом узле верхнего кольца. Кроме того,
Кйм пм^л"^^'*'^» '^'^^ ^^ наклон к стержням нагруженного узла остается таким же, ка-
Усилн ¦" ® У^*"^ ^' Очевидно, что при этом благодаря полной цикличности купола
Рестярп^^ всех стержнях получаются из предыдущего решения путем циклической пе-
^иовки. Никаких новых построений или вычислений не потребуется.
HanDHiI^'^^ же первоначального решения могут быть получены и все линии влияния.
Лб 2 с ^^* усилие в стержне d—5, вызываемое вертикальным грузом, стоящим в уз-
• совпадает с усилием стержня с—е от такого же груза, стоящего в узле /, и т. д.
ся По п ^^^^^Р^^енном загружении нескольких узлов усилия в стержнях определяют-
д "Р**"*1ипу наложения, простым суммированием,
'T^yaini rJ°^° *«тобы быть в состоянии быстро определить усилия от какой угодно на-
\ ^^ любп?^'*'^^^ ^ любом узле любого яруса, достаточно сделать следующее; взяоъ уз-
I ^^мн^ *^ «меридианов» купола и нагрузить каждый нз них последовательно тремя
I "^Рпендикулярными силами, равными единице. В рассматриваемом примере
|1ь^^
^г^ипияи имеет той узла но так как нижний неподвижно оперт, то достаточно нагру-
^иПвГузла ш^^^^^^ Имея шесть диаграмм усилии, мы сможем простым сум^.
зить два Уз^ла шестью L стержне от какой угодно нагрузки.
^"'S"eH^Ho про^^^^^^^^^ - -^^ ^^У^^^' ^^^^^ ^^^^ ^"^"^"^^ «сгрузка
имеет пиклическ^^^^^ Например, если все узлы каждого кольца загружены од„
Гковь^ верти^ силами, то все стержни, принадлежащие одному коль^;,
Тсп^шают одинаковые усилия; соответственио равные усилия получаются во всех
меоид™ Легко показать, что в таком случае диагонали не работают. Вместо вы-
резания всех узлов фермы, можно ограничиться вырезанием узлов одного меридиана.
§ 11.9. ОПРЕДЕЛЕНИЕ УСИЛИЙ
ПРИ ПОМОЩИ РАЗЛОЖЕНИЯ ФЕРМЫ НА ПЛОСКИЕ СИСТЕМЫ
Пусть в состав пространственной статически определимой фермы
©ходит такая плоская система стержней, которая, будучи отделена от
остальных стержней фермы, осталась бывсвоей плоскости геомет-
рически неизменяемой и неподвиж-
ной. Эта плоская ферма, понятно,
не могла бы воспринимать никакой
нагрузки, действуюидей в плоскости,
не совпадающей с ее плоскостью.
Легко доказать следующую об-
щую теорему: если нагрузка прост-
ранственной фермы состоит из сил,
лежащих в одной плоскости и прило-
женных к узлам плоской, неподвиж-
ной в своей плоскости фермы, вхо-
дяи^ей в состав пространственной, то
вся нагрузка воспринимается толь-
ко стержнями плоской фермы, уси-
лия же во всех прочих стержнях про-
странственной фермы обращаются в
нуль. Доказательство непосредст-
венно вытекает из принципа един-
ственности решения статически оп-
ределимой задачи. В самом де-^^»
предположим, что усилия pacпpeдeJ
ляются согласно вышеприведенной
теореме; в таком случае плоская
ферма будет находиться в равнове^
сии вследствие своей геометрической
Фиг. 299 неизменяемости, все же прочие уз-
лы — вследствие обращения сходя-
•п^тт1о«т,^ щихся в них усилий в нуль. Итак,
сия rn^;^nf ^'"'^''^ теоремой, удовлетворяет всем требованиям равнове-
Ня ni ^^''^'''''' '^''^ правильное и единственное
оых |рпмГГ""" ^^'''' теоремы можно легко определять усилия в некото-
^HDaS^^^ ^ фермах, имеющих вид призмы или усеченной
Zr S Он?пп.п"Р'''^^Р^ рассмотрим ферму, представленную на
Vasne^emv^^^ '^''^^^ усеченную шестиугольную пирамйДУ.
SShTco'cp^^^^^^ --^ьцами. Ьусть в узле Л при-
направленные пптп^^^ ^^' ^^^ложим ее на составляющие 5, Т. ^'
Дой'сосТаГ"^^^^^^ узла, и рассмотрим влияние каж-
110Й^реаквдеТ'ппи^'^^^^^^^ 4^ ^ Уравновесится такой же опо^
как/. ycZS'o^r^TSaK- =,?;,^« е"?Гу? "''"" ^'""'
492
Сила S воспринимается исключительнп .„
сила Г —исключительно гранью Л?FD плоской гранью ABCD а
Совершенно таким же образом пяяпп
бом узле промежуточного кольца. •"^^"тся сила, приложенная в лю-
S ...... о„«ДЕ..„„, .е„л„„ спосовом зд„.„ь, сгеРЖ„в„
Определим усилия в стержнях KVnnn
ного в перспективе на фиг. 300 и п nn't?.^^ перекрытия, изображен-
ф„г. 301. Оно образовано из Усеченной чстГорТл;?'''^"'^'? проекциях-на
вые грани которой срезаны че- ^'^Ф^хугольнои пирамиды, боко-
гырьмя наклонными плоскостями
Верхнее основание имеет вид че^
тырехугольника, а нижнее —
-восьмиугольника. Если в ниж-
нем основании сохраняется толь-
ко четыре стержня, то число не-
достающих стержней равно 10
(диагональ верхнего основания, 5
диагоналей нижнего и 4 стороны
там же), поэтому число опорных
стержней должно быть равно
6+Ю-16. На фиг. 300 и 301 каж- Фиг. 300
дыи ИЗ восьми опорных узлов со-
дующим Образом: удалим зсе ^.rul:iSZZZ7..'SZZ^Z%^.
Фиг. 301
Фиг. 302
Ней ^^ "^известными силами Хи Х2, Хз, х^ и взамен отброшенных стерж-
гориз^^*^^^ дополнительные опорные стержни. На фиг. 302 показана
^^eD>if"^^*"**^^" проекция преобразованной фермы; заменяющие опорные
из Эти**** размещены в узлах 2, 4, 6, 8 и отмечены пунктиром. Каждый
узлов содержит ло три опорных стержня
Ферма распадается на четыре более простых. Треугольник с-~-;_„
име?т в узле 2 три опорных стержня, в узле /-два опорных стержн^
и наконец, в узле а-один опорный стержень a-S. Эти шесть опорн?,
с;ержней обеспечивают его неподвижность Совершенно в таких >^
условиях находятся треугольники b—d—4, с—о—о и G—/—в.
Решение состоит в следующем. От заданной внешней нагрузки опре
деляются усилия в заменяющей ферме. Если, например, сосредоточен
ный груз приложен в узле а, то вырезанием этого узла, в котором схо-
дятся только три стержня, определяются усилия в них; в ненагружен.
пых узлах Ь, с, d все усилия равны нулю, во всех опорных стержнях
кроме тех, которые помещены в узлах 1, 2 и 8, усилия также равны нулю'
В узлах 1. 2 и 8 опорные реакции определяются последовательным вы-
резанием.
Далее определяются усилия от двух равных и противоположных сил
Xj = I, затем Х2=\ и т. д. Благодаря простоте структуры заменяющей
фермы все эти частные задачи решаются очень легко. Можно ограни-
читься рассмотрением случая Х\ = \, влияние же остальных трех еди-
ничных нагрузок получится циклической перестановкой найденных
усилий.
Обозначим усилия в заменяющих опорных стержнях узлов 2, 4, 6 8
через 5, Т, U, V, .причем усилия, вызванные внешней нагрузкой, снаб-
дим индексом р, а усилия, вызванные состоянием Xi = 1, — индексом 1 и
т. д. Так как в действительности эти стержни отсутствуют, то
¦^1 ^1 ~Ь -^а-^г ~Ь •->з-'^з ~Ь ^4^4 -f- 6^, — (J ;
^i-"^! + ТцХ^ + TgXs -\г Т4Х4 -\- Тр = 0;
UiXi -\г U2X2 + UsXs + UiXi + f/p = О ;
УгХг + V,x^ + VsXs + V,x, + l^^, = О .
(a)
Так как при нагружении фермы силами xi = l опорный стержень
узла 6 не работает, то t/i=0. Аналогичным образом 1/2=53=^4=0.
Следовательно, в каждом из уравнений (а) будут содержаться только
три неизвестных. / -- -' f
rTeil°5fZ°''° ''^'' "^™'""'' """ ""'^ ""^ " ^^ бУДУ-г найдены, усилие N в любом
стержне фермы найдется по схеме
N = N,xi + N^x^ + /V3X3 + N^x^ -f Np ,
где Л^ь N2 и т. д. —усилия, вызванные действием х, = 1, Хг = 1 и т. Д.
сА1ичр?|!'и ^^rf^^""^ ^^"«"ИИ Ь ЭЛЕМЕНТАХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ «БИКОНСТРУКЦИИ*<
консол\н^пЙст%"н™^Тео1а"^ tfJ"^^ <^"* спереди) и в плане (вид сверху)
параллельных фер^м, сое^,е„нт по 7pnvli'°"'=°''*^''- °«^ составлена из двух плоских
одну пространственную геометпи«ег^ГРЛ"^"У "* нижнему поясам при помошл связей в
чшы сплошными лнГями а „Сние ''11Т''''''*У^ ^«'^'^^му. Верхние связи обозяа-
произвольно направленной силы Рпойо^Р^"Р°''- Требуется определить усилия ог
Для того чтобы систриа Jw„ "P™o«enHOH В узле М пеоелней Деомы
д^^агГ"^"^ ^"^« бьГим1г?'„а'51воГкон„Г,°"°''- «"^^ ^ео'метр^чГсГн^изменяе^а,
вомTt'"''^' ¦'• ^- 5 стержней Отсюда Z?,fo^^*"'^'° ""Р^иь в виде четырехугольника «
Heneot?"","- " "РУ^^« ^ п%'пе"нд™Тна' П "°''°'""^ «''«^ ^^'«"т в плоскости пе;
«-5^To-T4-o=rS^
1 ^ * ^^ ^^^^ Обозначим через S
их расчеГ™ «''—РУК«ии. предложен проф. А. А. Уманским; „„ же указан «-«^
В
ним сначала нулевые стержни. К ним относятся, во-первых, вертикальные
^^^^ педней и задней ферм, кроме стоек LD и LiDi; во-вторых, горизонтальные
СТОЙКИ "^Р рхних н нижних связей — Ли ВВи KKi LLi и т. д.. кроме краиией правой
распорки Р которая служит одновременно общим элементом обоих поясов. Нако-
распорки »^ принадлежат стержни FG и RiGi. Часть фермы, лежащая правее на-
меа» ^ "^"Т узла, не является нулевой, так как она необходима для обеспечения не-
руженного у _• „ части. Действительно, если ее отсечь, то левая часть будет закан-
» .^..СТРМОСТП i/iCOVli »,»ж г^1~, _ __ _ __^ ^^rrrtn^w.rs -ГОППИТкЯР
^5зменяемосги^^ ^^^^^^j^^^ MAli??i, не имеющим диагонали, а это, согласно теореме
чиваться пр j^ g^ejjbCTBOBaTb об изменяемости системы.
Коши. оудет
S и обозначив расстоянне между фермам ^
них связей
2
" 2
ЦТ
h
Ч^^'^ ^^"^^ ^ альиы длине самих
раскосов. По этой причине зигзаг, оор ^^^^^ым многоугольни
ь правой части системы сам служи ^^^^^^ поперечных разрезов /-^/,
ваемых ими передней или ^адиеи ф f
Усилия и пяскосах нижних связей н^^
НаскОСОВ. но этой причине •^"•^"•' * сИЛОВЫМ mnv'^-'^- •
В правой части системы, сам ^лу^и! поперечных разрезов /—/,
ваемых ими передней или ^адиеи ферме. ^^^ ,оши попер
, Усилия в раскосах иижних ^^^^f^^ направление S:
'/-// и т. д. и проектирования сил на у ^ ^^
hi w^=^—NtiA ^==^ о " h
Эти усилия также обладают указанным свойством.
Определим усилия в одной из вертикальных ферм, например в передней На
к#й для нее служат усилия, передаваемые раскосами связей. Проекции этих усил ^^^^'
направление, перпендикулярное плоскости фермы, уничтожаются в каждом уз " "^
ферму передаются только проекции этих усилий на ее пояса. В узлах ^' "^
него пояса приложены силы, равные —-• •—, а в узлах верхнего — наклонны
S b S а
риз#нтальные силы, соответственно равные-—*'— и —-¦— гпр Л--л7Б г^—
2 Л 2 Л ^—^^i^RiGi,
В книге проф. А. А. Уманского^ указан изящный графический прием пля nnn
ления моментов системы узловых сил, действующих вдоль поясов биконстоукии?. ^"
Чт1»бы найти усилие в раскосе ВК, нужно спроектировать на наппавл^о»: пг
равнодействующую правых сил. к«олсние Ijj
Для задней фермы поток нагрузок, передаваемых раскосами, имеет во «r^v „
обратное направление по сравнению с нагрузками, которые передаются переде фе^№
^ Пространственные системы, Стройиздат, 1948, стр. 15.
Глава 12
ПРОБЛЕМЫ РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
§ 12.1. ЧТО ТАКОЕ СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СТЕРЖНЕВАЯ СИСТЕМА
Статически неопределимой стержневой системой мы будем назы-
вать такую систему, у которой при действии произвольной нагрузки но
все продольные силы, поперечные силы и моменты могут быть найдены
из уравнений равновесия твердого тела или системы твердых тел
^ А В С
I)
Фиг. 304
Иначе говоря, статически неопределимой стержневой системой мы
будем называть такую геометрически неизменяемую стержневую систе-
Щ, у которой при действии произвольной нагрузки все или некоторые
из названных усилий зависят от размеров поперечных сечений стерж-
t<eu и от свойств материала.
Будем говорить, что система имеет лишние, или избыточные,
связи, если из нее можно удалить то или иное количество связей, не
нарушая этим ее свойства геометрической неизменяемости и неподвиж-
ности.
Наибольшее количество связей, которое при этом условми может быть
удалено одновременно, называется количеством лишних связей,
^ак, например, на фиг. 304 из обш^его количества пяти опорных стерж-
^^и можно одновременно удалить не более двух, так как для обеспе-
чения неподвижности балки требуется сохранить не менее трех опорных
Вместо опорных стержней можно удалить какие-либо другие связи;
апример, поместить в каких-либо сечениях балки шарниры.
Ьо всяком случае удалить можно не более двух связей, так как ила-
данная система потеряет геометрическую неизменяемость. Следова-
•"ьно, очя имерт две лишние связу.
^ 10НЯТИЮ о лишней связи можно противопоставить понятие о необ-
Димон связи. Можно различать связи условно необходимые
197
и безусловно (абсолютно) необходимые. Так, например
1 Лиг 304 любой из вертикальных опорных стержней является условно
необГодимыГ^^^ как каждый из них можно удалить при сохранен^
лв?Гдр^^^^^^ вертикальных, а также горизонтального опорного стержн?
сКдо^тельно, вертикальный стержень является необходимым или лищ
ним смотря по нашему выбору. Условно необходимый стержень можно
чяяывать также условно лишяим. На фиг. 305, где имеется одн.
лишТяя связь, лю'^ой из стержней левой панели (т. е. ^Д BQ CF^ f^'
AC viBF) является условно необходимым. Напротив, любой из стержней
правой панели {CD, DE, EF, СЕ), а также любой из трех опорных
стержней является абсолютно необходимым, так как удаление его пре-
вращает систему в геометрически изменяемую или подвижную.
Наличие или отсутствие лишних связей характеризует систему с
кинематической точки зрения. Одновременно оно характеризует ее и в
статическом отношении. Наличие лишних связей является необходимым
и достаточным признаком статической неопределимости.
Если система имеет п лишних связей, то мы можем, отбросив такое
же количество связей, -получить статически определимое сооружение.
Следовательно, наша система может рассматриваться как усложнен-
ное сооружение, которое образовалось из статически определимого путем
добавления п связей.
Статически неопределимые системы обладают некоторыми особыми,
только им присущими свойствами, которые находятся в прямой зависи-
мости от количества лишних связей. Поэтому число п является важной
и глубокой характеристикой сооружения и можег быть положено в
основу класч-^^тфикации всех статически неопределимых систем.
Количество лишних связей мы в дальнейшем будем называть сте-
пенью статической неопределимости системы.
§ 12.2. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ЧИСЛА ЛИШНИХ СВЯЗЕЙ
^Рй ^^.^^"^ ^^^^"^ вторично формулы для определения числа лишних свя-
зей, выведенные ра.гьше, и поясним их несколькими примерами.
Ш
н
ш>.
УШ
*^и''. 306
Фиг. 307
нирнГ21дин^ы Гёжлу^о^пй"^'' "^ отдельных дисков, которые шаР"
опорных стержней SnJ,? " опираются на некоторое количество
и. содержит следующее число лишних связей:
где ^-;"^° опорных стержней-
„ мездс*бой.™'""° "Р"^''''''^ шарниров, связывающих Дйскй
Д—число ,щ^^^;
Формула эта справедлива только в том cл^m.^
ков в свою очередь не представляет собой -иотрмл/'"'"'^^ "" °^"« "^ '^^'^-
Если система представляет собой многпгпп^ лишними связями.
,куточными шарнирами, то вместо формульг п 9 п ^^ "^^ ^ лроме-
также следующей: ч^^^рмулы (12.1) можно пользоваться
Действительно, при отсутствии шаониппя ™^гг^ '
^/
t
{
\ -
Г" —"—^
Е
^ . л
и
у- . ^
?й
1У
Фиг. 308
Рамная система (фиг. 306) представляет собой диск, который имеет
10 опорных стержней.
Так как для обеспечения его неподвижности достаточно иметь три
стержня, то число лишних связей равно 10—3 = 7.
То же самое мы получили бы из формулы (12.1), положив Л=1,
ш = О, Со = 10, t/7 = 10 + 2-0—3 -1 = 7; однако в таких случаях мд мо-
жем прямо считать ^ ^
Л^С,-3. (12.3)
Для комбинированной рамной системы (фиг. 307) можно написать
Д = 3; Ш = 4; С, = 6 ;
Л-6 + 2.4 —3.3-5.
Из разобранного примера видно, что с*терясень, который не имеет
промежуточных шарниров и ось которого образует замкнутый односвяз-
ный контур, заключает в се-
^^ три лишние связи. Короче —
замкнутый б е с ш а р н и р-
Ный контур содержит
"^Ри лишние связи. Каж-
^Ь1й простой шарнир, включен-
ный -в контур, снижает число
¦лишних связей на единицу.
На практике часто встреча-
^¦гся рамные конструкции, схема которых представляет собой много-
связный контур. Достаточно подсчитать число отдельных замкнутых
^онтуров, не покрывающих друг друга, и это число утроить: получен-
ный результат и будет равен числу лишних связей. Рассмотрим для при-
^^Ра фиг. 308,а.
Число различных контуров, не покрывающих друг друга, равно 6,
Поэтому Л = 3*6 = 18. На фиг. 308,6 показана та же фигура, но раз-
вязанная так, что, сохраняя геометрическую неизменяемость, она потеря-
т
Фиг. 309
ла.все замкнутые контуры. Число разрезов равно 6; каждый из них
бождает систему от трех связей. Мы можем ^поэтому вместо ,по ^^^^'
числа замкнутых контуров подсчитать и утроить число разрезов "^^^^"^^
Если система представляет собой шарнирно-стержневую фип/
вместо формулы (12.1) удобнее пользоваться формулой ^РУ, то
Л = С+Со-2У,
где С — число стержней фермы, не считая опорных; '
' У — число узлов.
Например, в ферме, представленной на фиг. 309.
С = 29; Со=:4; У=14; Л = 29 + 4-2-14 = 5 .
Этот результат можно получить быстрее, если заметить чтп п,
ления четырех раскосов и одного опорного стержня Феомя Т^^ У^^'
статически определимой. '''*'^'^'^^ Ф^рма становится
§ 12.3. ОТЛИЧИТЕЛЬНЫЕ СВОЙСТВА СИСТЕМ С ЛИШНИМИ СВЯЗЯМИ
Перечислим эти свойства
1. Пусть сооружение находится под действием некоторой заданной
нагрузки. Откинем лишние связи так, чтобы система стала статически
определимой. Реакциям отброшен-
^^ ных связей дадим кяки^ ^rr^--^--
о)
X
-5^1
1>иг. 310
»ь/х связей-^ал'имТа-ГиеТЛ"™-
значения X Хо У ^ Угодно
нГ сТлГ °к Р---Р--ь к'ак'Г^-
нагрузкой ^"п^"' """^"^ ^ зад^«™й
жениГ п ™ определимого соору-
ш были^;'''''^"°' "^^^ ^^^°^^ бы
ни оыли значения сил X, У„ у
система останетго f '' ^ "'
Иняцр Л^'-танется в равновесии,
иначе говоря, определить силы X,.
условий исходя исключительно из
сис°;^„з ^^^"овесия "^возможно;
лима "^"^^^^и неопреде-
„ ^ дальнейшем мы ., лима '""^ески неопреде-
S:.Zir.^^^^^^^^^ -жду системами с
«^е усилия неппе2„ "^^^^^ь, что в ст1?и1Г""Р^^^-^и-^ыми.
встречаются „Так "° "^^^^^гся ctS" "'''" "^""Р^^лимых системах
^имы Можно л^казать?'''"""' Усилия в к^Г°"Р-Д^лимыми; иногда
"е°бх од и/,,^/^^;ьа,едующую^^^ которых статически опреде-
onnJ"""^«" оппе„Г"^^^ (если ?а/'"""^^ « абсолютно
Zr''^P^^'<«HH.a;Pf^/-"«'Mbi. Так, напп^?Л^ имеются (всегда
So«L^''''^'^"b,x частей ??°Р««>Щее Условия.,"'^^^"' ^«^ь ?дно воз-
p2SL'"'^°«-S:\,^^^^^^^^^^ «-CSCr^^'^^^ это/системы
условиями; "° -""шь одно f ^° решений St^ "^ сйсгел«с, наоборот.
у '"ьиям. которые „а "f "О "3 «их будет Tn'J °^'^^'^^оряюших цсловиям
аоо -"Ределимой стержневой "^•"«"ием лишних связей.
°" «истеме смещение опор.
температурное воздействие и неточность сборки не вызывают усилий
В лротивоположность этому в системе с лишними связямТлюбой из
этих факторов, вообще говоря, вызывает отличные от ниля исилия На
пример, на фиг. 310 б и в показаны деформация и эпюра изгибающих
моментов неразрезнои балки (фиг. 310, а), вызванные смещением^ред^
hcii опоры.
4. Усилия, которые возникают при отсутствии внешней нагрузки, как
уже отмечалось выше, называются начальными или собственными уси-
лиями. Из сказанного в предыдущем пункте следует, что статически
неопределимые стержневые системы в отличие от статически определи-
мых могут иметь отличные от нуля начальные продольные и поперечные
усилия, а также изгибающие и крутящие моменты.
Чем бы ни было вызвано такое состояние системы, имеющей п лиш-
них связей, мы можем мысленно откинуть все эти связи и рассматривать
полученную систему как статически определимую, нагруженную п реак-
циями отброшенных связей. Каждая из этих реакций может принимать
бесконечное множество значений, поэтому можно сказать, что любое
начальное напряженное состояние системы, имеющей п лишних связей,
определяется п параметрами.
Отсюда, в частности, следует, что каждой системе с одной лишней
связью свойствен только один вид начального напряженного состоя-
ния. Будет ли это состояние результатом действия температуры, неточ-
ности сборки или перемещения опор, характер всех эпюр останется тот
же самый; изменится лишь коэффициент пропорциональности.
Существует другой вид начальных напряженных состояний — такой,
при котором в любом поперечном сечении продольные и поперечные
силы, а также моменты равны нулю. Этот вид напряженных состояний
возможен как -в статически неопределимых, так и в статически
определимых системах. Например, в однопролетной железобе-
тонной балке с шарнирно-опертыми концами такое напряженное состоя-
ние может быть вызвано предварительным натяжением арматуры или
изменением температуры.
5. Усилия в элементах рассматриваемых систем завысят от размеров
сечений стержней и. вообще говоря, также от коэффициентов упругости
материала этих стержней.
Как мы увидим ниже, в статически неопределимой системе усилия
оказываются независимыми от коэффициента упругости только в том
"lacTHOM случае, когда материал всей системы имеет один и тот же ко-
эффициент улругости, а сама система находится под действием внешней
нагрузки (но не температуры или смещения опор).
6. Система с п лишними связями после потери этих связей сохра-
няет свою геометрическую неизменяемость, в то время как для системы
статически определимой потеря даже одной связи уже является катаст-
рофической. Это различие между обеими категориями систем имеет
важное практическое значение.
Из перечня специальных свойств статически неопределимых систем
бедует, что они обладают рядом достоинств: большей монолитностью и
взаимной связанностью элементов в работе, большей живучестью, т. е.
способностью распределять нагрузку между остальными элементами в
случае повреждения пли ослабления одного из лишних элементов, мень-
шими деформациями, чем любая статически определимая система, ко-
'^<^рая может быть образована из них путем удаления тех или иных
связей.
^ С другей еторюны, они способны испытывать усилия от ряда при-
**Н|| не вызмвмшщих усилий в системах статически определимых. К то-
„ «^ рппжиее расчета систем, не имеющих
му же их расчет значительно сложнее р
лишних связей. „^х...омоются системы обоих типов. При проек»
На oipaKTHKC широко "Р^^^^ле^^^ ™й схеме, которая
тировании сооружений предпочтение следу^^^^^ рая
в данных условиях оказывается более экономичной.
§ 12-4. КЛАССИФИКАЦИЯ МЕТОДОВ РАСЧЕТА
Задача расчета статически неопределимой системы, геометрическая
схема котор^ой задана, заключается в следующем: по заданной нагрузке
SpaTb рац^ сечения всех элементовjaK, чтобы система обла.
"алГКстаТчной надежностью и достаточной жесткостью при мини-
мальной затрате материала или при минимальной стоимости. В такой
постановке, имеющей наибольшее практическое значение, задача в об-
щем виде еще не решена.
"в более узкой постановке задача расчета формулируется так: по
заданным геометрической схеме, нагрузке и сечениям всех стержней
определить усилия и деформации системы. При этом приходится зада-
ваться сечениями на основании первоначального ориентировочного рас-
чета, затем определить усилия и напряжения, после чего в случае не-
обходимости—исправить -некоторые сечения и повторить расчет снова.
Способы решения этой более узкой задачи существенно различаются
между собой выбором основных неизвестных. Основными являются
те неизвестные, которые должны быть найдены в .первую очередь и при
посредстве которых, после того как они найдены, легко определяются
все остальные неизвестные. Если основными неизвестными служат уси-
лия в лишних связях, метод решения получает название метода сил.
Если основными неизвестными служат деформации или перемещения
системы, получается так .называемый метод пер ем ещейяй (де-
формаций). Если ОСНОВНЫ'МИ неизвестными служат частью силы, а
частью — деформации, получается смешанный метод. Каждый из
этих методов в свою очередь имеет свои разновидности, число которых в
настоящее время весьма велико. Принципиально роль основных неизвест-
ных могут играть не только силы или перемещения, но также разнооб-
разные функции этих величин, имеющие статический, геометрический или
кинематический характер.
Методы расчета могут быть разделены по другому признаку на две
большие группы: расчет систем, в которых связь между нагрузкой и пере-
мещениями выражается линейными уравнениями (линейных или
линеинодеформируемых систем)_, и расчет систем, в которых эта
связь выражается более сложными уравнениями (нелинейных си-
стем). Любая линейная система при достаточном повышении нагрузки
переходит в нелинейную (например, в упруго-пластическую или пла-
в дальнейшем мы ограничимся изложением важнейших методов,
г тя,Г^°^" расчета различаются также по степени их точности: наряду
пянт-,й f.w^^^"""^" «точными» методами, которым в основном посвящен
nMfinLl^''' существуют различные упрощенные методы, которые даЮТ
ные^имТ^Р^""^""^ ^^^^''"- -^-"^ «•'^иь сложных систем приближен-
приметени" ''^^ являются единственно доступными для практического
nrHnSi'^i^r ^ теоретическими расчетами возможны экспериментальные.
™aS^KHx?"„''^"^''"" различных механических, электрических.
Хшое 6^Bvm J ^''^™'' приборов и устройств. Эти методы, имеюшие
иольшое оудущее, пока еще не получили широкого применения.
щ
Глава 13
ОСНОВНЫЕ ТЕОРЕМЫ ОБ УПРУГИХ СИСТЕМАХ
§ 13.1. ОСНОВНЫЕ ПОНЯТИЯ
Основным понятием теории статически неопределимых систем, разра-
батывавшейся в течение многих десятилетий, было и остается до на-
стоящего времени понятие об идеально упругом теле или
идеально упругой системе. Лишь значительно позднее начала
серьезно разрабатываться дополнительная теория, основанная на поня-
тии об идеальном так называемом упруго-пластическом теле.
Однако сейчас мы будем говорить исключительно о первой теории.
Мы будем рассматривать такие деформируемые системы, для кото-
рых перемещения и деформации выражаются линейными однородными
функциями внешних сил Рь Р2, -., Рп"-
Д = Я,Д, + Я,Д, + ... + ЯпДп, (13.1)
где Д — перемещение определенного типа (например, верти-
кальное, горизонтальное, угловое) в определенной
точке сооружения;
Д^, А2,..., Д„ — перемещения того же типа и в том же месте, кото-
рые вызываются соответственно одной из сил Pi = l,
Линейный закон, выражаемый формулой (13.1), носит название
обобщенного закон а Гука.
Те системы или тела, которые подчиняются формуле (13.1), мы бу-
дем для краткости называть линейно деформируемыми или,
короче, линейными.
Перемещения и деформации такой системы подчинены закону не-
зависимости действия сил, иначе называемому законом наложешя, т. е.
эффект совместного действия нескольких сил равен сумме эффектов
(действия каждой силы в отдельности.
Если при заданной внешней нагрузке линейно деформируемой систе-
^1Ь1 проекция перемещения какой-либо точки А на некоторое направле-
ние равна нулю, то она, очевидно, останется равной нулю также при
'^-кратном возрастании или убывании всей нагрузки. Отсюда следуег,
что при таком изменении нагрузки все точки упругого тела перемещают-
^^ по прямым линиям. , „ ^ „„^.
,. Для того чтобы система была линейно деформируемой, необходимо.
ч чтобы она была сделана из идеально упругого материала; 2) чтоОы
203
„n гладкие лишенные трения поверхности касания
она имела ад^^-"">°„^-1шихся элементов; 3) чтобы она имела такое ко*
всех взаимно-перемещающихся э обеспечивает ей геометриц;
личество и расположение гаязеи,»^ изменения в геометп;"
скую неизменяемость и "e"«fj«^"°" Vpe самой системы, вызываелГ""
ческих размерах, конфигурации и^арак^^^^^^^^ ^^^^^^^ _^^^^^^^„ демь^
Й7емТти"моТет".при?^^^ -ишь при напряжениях материала*^
пре'^Гающих ^;^1дел^ пропорциональности, и не может быть экстрапо-
%ТГлГейГег^сГдТя%"а\%"^^^^^ терминологии, мы будем
начыв^?ьлинЕ деформируемые системы просто упругими, но в
tS редких случаях^ ?де речь будет идти о системах упругих и в то
же в?емя нелинейно деформируемых, мы это будем особо оговаривать.
Лшейно деформируемая система может быть статически опреде-
лимой и неопределимой.
§ 13.2. ОБОБЩЕННЫЕ СИЛЫ И ПЕРЕМЕЩЕНИЯ
Для того чтобы понять дальнейшие свойства упругого тела, мы долж-
ны обратиться к рассмотрению понятия о работе сил. Когда тело
деформируется, то различные точки его и в том
числе точки приложения внешних сил перемещают-
ся. Произведение силы на путь, пройденный точкой
приложения силы по направлению последней, на-
зывается работой силы, поэтому мы можем сказать,
что при деформировании тела внешние силы со-
вершают работу.
Введем такую терминологию, которая позволит
нам высказывать все дальнейшие выводы в наибо-
лее общей и компактной форме, а именно введем
термины «обобщенная сила» и «обобщенное пере-
мещение».
Первый из этих терминов относится не только к
сосредоточенной силе, но и к любой группе сил.
Группы сил ©стречаются в строительной механике
очень часто. Простейшей группой является пара
сил. Как. известно, величина пары измеряется ее
моментом. Другим примером обобщенной силы мо-
жет служить нагрузка, равномерно распределенная
по длине стержня или по поверхности сооружения. Эта обобщенная сила
измеряется ее интенсивностью, т. е. величиной силы, приходящейся на
единицу длины или на единицу поверхности.
Для получения выражения работы .простой силы нужно, как извест-
но, перемножить две величины, а именно силу и соответствующую проек-
цию линейного перемещения. В общем случае мы будем выражать
раоогу произведением «обобщенной силы» и «обобщенного перемешс-
ruT'J^^^^^- первый множитель является измерителем данной группы
сил а второй множитель зависит от перемещений
нечшч'!!^^» обобихенной силе Р соответствует опред-еленный тип беско-
пажаетД «^ обобщенного перемещения rfcp. причем «соответствие* вы-
^^^а'соУршитГраГту"'ГаГ'"™' ^^""^^ '"' ' <>бобщенная сила Р
вопотых гГ„''!?о°^°^"^^""^^ """^^ ^^°^^тоит из двух равных и протЯ;
V. л<1А /1 И tj (|фцг 311). Пусть точка В neft8№#a в п€
Фиг. 311
1^.
u^^V
VaBHM себе, что сначала точка В перешла в В' а точка Л в i- Гр"
,очки приложения обеих сил переместились одинаково; тогда работы этих
сил будут друг другу равны и противоположны, а сумма их КнТнулю
после этого переместим точку Л^^ в положение Л- пр'и этоГв^"^"с'иТа
р произведет работу Р. А^'А ^ PdX; это и будет суммарной работой
обеих сил при заданном перемещении точек Ли Б oSTo чт?Т
есть приращение первоначальной длины отрезка АВ Итак выданном
случае обобщенной силой является Р. а обобщенным перемещением
^А—изменение длины отрезка А В. ^ ^
Если к телу приложена пара сил с моментом, равным М, то при по-
вороте тела на угол rfcp работа пары будет равна Mdc^, следовательно,
в данном случае обобщенной силой служит момент М, а соответствую-
щим обобщенным перемещением — угол d^.
Если две пары с равными и противополож-
ными моментами М приложены к двум эле-,
ментам (фиг. 312), то при взаимном пово-
роте последних на угол d^ суммарная рабо-
та обеих пар -выразится произведением Md(p.
Итак, момент любой из двух пар можно
принять за обобщенную силу, а взаимный по-
ворот обоих элементов — за соответствующее
перемещение.
В любом из получаемых выражений пер-
вый множитель можно считать обобщенной Фиг. 312
силой, а второй — соответствующим обобщен-
ным перемещением.
Из этих примеров видно, что обобщенные силы могут иметь раз-
личную размерность, например килограмм или килограммометр и т. д.;
в соответствии с этим могут быть различны и размерности соответствую-
щих перемещений, -произведение же обобщенной силы «а обобщенное
перемещение всегда имеет одну и ту же размерность — размерность
работы.
V § 13.3. РАБОТА «СТАТИЧЕСКИ» ПРИЛОЖЕННЫХ ВНЕШНИХ СИЛ.
ТЕОРЕМА КЛАПЕЙРОНА
Статическим способом приложения нагрузки мы будем называть
постепенный, плавный, спокойный процесс приложения нагрузки, при
котором тело .деформируется без заметных ускорений. Строго говоря,
статическим будет такой процесс, при котором деформация совершается
бесконечно медленно; практически же процесс можно считать статиче-
ским при условии, когда силы инерции деформируемых масс ничтожно
Малы по сравнению с прочими силами. В этом случае мы можем игно-
Р^фовать силы инерции и считать, что в любое мгновение (не только
После наступления покоя, но и во время самого процесса деформирова-
лся тела) внешние силы уравновешиваются внутренними упругими си-
лами.
^ Исходя из такой предпосылки и опираясь ъ то же время на условие
^И'Неиной зависимости между перемещениями и силами, мы неизбежно
"Ридем к выводу, что в течение того времени, когда происходит деформи-
Р^вание тела, внешняя сила не может оставаться постоянной. Нараста-
?ие деформаций свидетельствует о нарастании силы. В первоначальный
^«мент сооружению передается лишь ничтоясно малая часть нагрузки.
:го5
%
Постепенно доля нагрузки возрастает, и в прямой пропорции с ее
возрастает и деформация. Когда вся нагрузка передастся сооруж^^^^^^^
дальнейшее нарастание ее прекратится, тогда и деформация пеп^^*^^^
нарастать и наступит состояние покоя. Р^стане^
Отсюда очевидным образом вытекает следующий вывод: ее
не имеющее начальных напряжений, подвергается статическом^ ^^'^^'
енной силы Р и получает обобщенн'ое перемешены ^ ^^^^
ствию обобщенной
' - ' " ^-^^j - -J- -- "^Ремещение п^
чательная величина которого равна А , то работа, затраченная ^^^*
мирование тела, не будет равна РА , а будет меньше этого попи^^ -^^Фор.
Обозначим переменное значение внешней силы через л я ^^'^^^^^я.
ное значение соответствующего перемещения —через х' /^"^Р^^ен.
При бесконечою малом отриращ^^^
деформации работа выроится п
изведением
dW=XdX,
Но
системе \еГе^Гнг:П7о1^^^^^^^^
нально силе, т. е. график на фиГзТя
является прямолинейным. ^^'•'^''^
1г.
- -^ ^! А. А Vl
р.
¦р
Фиг. 313
^3 '4
Фиг. 314
где 8и —перемещение, вызываемое
полосТи!;"^^^^^^^^ площадь, заштрихованной
ОАВ, которая, очевидно, равна -i рд "^^^'''^ треугольника
силой Р-. ^^«^из'^ение А =. Р8, "
силой Р=1, можно написать "'
Интересно выяс ^'" ^ ^''^^P^^s Клапейрона). (13.2)
пТть\7т;!?о"1~ деформаций упруго:.
Обозначим ?конч^1^У^^ "Р°^^Ые или ofii •" "^'^" ^ обобщенных сил.
"^Ремещений через r^f ^^'^'^^^^^Zor^t'^T'''^ '^'^'^^^ ^ь Р., .... Р.
нагружена веот„1 ^' ^2'-. \ Если!ГУ''^«^ Им суммарных
через Д4-~угол пп" "°^ ^"-"ой ^ь вьТз^и ^ " "^Р^^ Л, П) через -^i
¦^«й- и т. д. ЛеТко°°Г^^ '^^ч^ния 5 вызвя^'^''^'^" внешними силами,
° показать, что ' ^^^^«««ный опять-таки всей нагруз-
(теорема Клапейрона). (13.2)
'^-ТХ'-А.
Т. е. что суммарна ^ -^^А. ^s.S)
'^?pcSyTZ7eTcJ'^^^ "^^У'Умме произведений
доказать, пpe^^cтaви« JLT^'P'^^^o nepeZll''° '"'ончательное значение
ем силы ^р,, ^/вив себе, что « npoS^^f ^- "Р^^^ всего это можно
206 •*••• f"^" .где ^ _ пра»мп!''^'^^^"ия нагрузки мы те-
правильная дробь, п^тепешо щоз-
настающая от значения {г=0 до м, =^1 Рпин
величина t^, поэтому доказательство будет SZ'-*-'"^Р^"^^"™" бУ«^^
тельства, данного выше. ^"^ точным
повторением доказа-
Ниже мы увидим, что сделанное нами n,ionr,-.„
е р е м е н « О м приложении всех сил не отра^т.я^^^ ^^ ' ^ " ^¦
результате: суммарная работа не зависит о^ппо^ ""^ окончательном
P:.L«T.a nKf^TTTPMv rwn зависит ОТ последовзтельности при-
ложения внешних сил
§ I3A ПРИМЕРЫ
Пример 13.1. Определить работу двух продольных сил Р. и
Рг, действующих на стержень так, как показано на фиг 315
Вертикальное перемещение точки Л: ^ • .
д _ (^1 + ^2)^
' EF
вертикальное перемещение точки В:
Рф .... 1
^2-=^l+"
EF ' ^== Y(^^'^^ + ^^^^)*
следовательно:
1
IP^-
{.Л^'4^+р.
?Р
[^
+jP2)j^ РйЬ
]Н
2 ЕР
[^P"^+(^ + ft)P2 + 2^^iP2]
'^^//////////А
Г
г
Фиг. 315
т
§. 13.5. РАБОТА ВНУТРЕННИХ СИЛ ПЛОСКОЙ УПРУГОЙ
СТЕРЖНЕВОЙ СИСТЕМЫ
Когда упругое тело нагружается внешней нагрузкой, то работу со-
вершают не только в'неш'ние силы, но также внутренние, которые раз-
а)
-N<
\N—
•^иваются во всех деформируемых элементах. Эту последнюю работу мы
и определим. Ограничимся выводом формулы, относящейся к плоским
^рншевым системам, притом таким, которые содержат только прямые,
ломаные или слабо искривленные стержни.
,«х.^ пягтянутого стерж'ня длиной ds (фиг. 316,п^
Рассмотрим ^^^!^^"?:,Р щен^^ к этому элементу являются силы/з!:
Внешними ^«:?^^\"^^^"ьГающ^ к нему остальных частей стержн,
меняющие A^«™/^f ™^я^^^ ^'^ Внутренними силами мы
Эти силы и вызывают растяжение ^^^^^ считать силы противо-
^^ _^ положного направления, ко-
торые по закону равенства
действия и противодействия
развиваются на границе это-
го элемента со смежными*
они показаны па фиг, 316, б!
Эти силы всегда сопротивля-
ются деформации. Если эле-
мент растянут, то внутренние
силы направлены внутрь его, а
если сжат — то наружу. Бла-
годаря этому работа внут-
ренних сил при загру-
жении тела,не имевшего
начальных напряжений,
всегда отрицательна.
Если при статическом за-
гружении элемента ds продоль-
ное усилие, равномерно рас-
пределенное по сечению, до-
стигло величины N, то удлине-
ние элемента (положительное
или от^рицательное) будет рав-
V Nds
Но , где F — площадь попе-
Фиг. 317 ^^ Tov
речного сечения стержня. 1ак
как в рассматриваемом про-
цессе сила постепенно возрастает от нуля до значения Nj то полная
работа внутренних сил в пределах элемента выразится формулой
\cfVf
\ I
2 EF
N4s
2EF
(13.4)
Если элемент ds подвергается 'изгибу (фиг. 317), то оба крайни
его сечения в результате деформации перестают быть параллельным
между собой и поворачиваются друг относительно друга на некоторы^
бесконечно малый угол df . Из курса сопротивления материалов ^^^^^[
ко, что этот угол выражается плошадью соответствующего участка эп
ры изгибающих моментов, разделенной на жесткость ?"/, т. е.
dcp =
Mas
EJ
(13.5)
Совместная работа обеих пар выражается произведением
2 2EJ '
Если элемент стержня длиной ds подвергается действию касатель-
"olL ^"^^^'^"""' возникающих при изгибе, то внутренние силы сдвига
также совершают работу. В любой полоске, которая параллельна нуле-
203
- пинии х—х (фиг. 318) и имеет площадь dF, действует при этом
вои ^^j^QCTH сечения касательное напряжение
"^ "*" QS
^ = 17'
S —статический момент вышележащей (или нижележащей) части
^^^ сечения относительно оси х^х.
Взаимный линейный сдвиг двух соответствующт^х полосок, взятых
обоих торцах (ЛВ и Л'В') элемента ds, будет ^ , где G — модуль
УГОСТИ второго рода. Отсюда следует, что полная работа сил сдвига
^" поотяясении элемента ds при постепенном возрастании этих сил вы-
¦^ 2G 2G J 20Я J х^ 2GF
^ F F
dF. (1^-7)
где
F С S^
Поперечное ce^enQS
Нетрудно видеть, что i^ ;^"\°;;;ГьГпоперТчГго^^^^^^^^^ ^висит
ад от внешней .нагрузки, ни от величин
исключительно от формы "°'^'"^'^"^„„_„., awh можно написать
Для прямоугольного сечения со стороны « « « ^ ^^
следовательно: \
-11(т-^Г* = -'^^
2
32
32 t 1 о
ДЛЯ кругового сечения ^^~^ — i,io-
и и, М. РабшюЕнч
%Ш
Для прокатных двутавровых профилей можно приближенно принять
fx^ ^, гдеГ^-площгль вертикальной стенки.
Работы, произведенные продольными силами Л^, изгибающими г^о^
ментами М и поперечными силами Q в стержне с прямой или ломаной
осью можно вычислить порознь и затем сложить.
Чтобы получить полную работу внутренних сил, нужно .просумми.
ровать элементарные работы на протяжении всей системы. Эта суммар
ная работа, взятая с обратным знаком, носит название «потенциально}
энергии» внутренних сил упругого тела. Обоснование этого трпл.,,,,.
^ ^ „ /: 1 Q Q Qn^i^L лгхга^^Р^ЬЛ ЛИТТТ1
энергии» внутренних сил упругого тела, v^uuun-unannc. этого термина
будет дано в § 13.8. Здесь укажем лишь, что это работа, которую про-
изводят внутренние силы при разгрузке упругого тела. Для плоской
стержневой системы потенциальная эн€ргия выражается следующей
формулой:
^-Е^^+'^^^^'^Ц
2GF
(13.8)
Интегралы, входящие -в состав этой формулы, являются определен-
ными, хотя и написаны здесь без указания пределов.
Совокупность интегралов, стоящих лод знаком каждой из трех сумм,
простирается на все элементы стержневой системы.
Для пространственной стержневой системы получается
аналогичная формула, но содержащая три момента (два изгибающих
и крутящий) Б д в е поперечные силы. Более сложный вид имеет форму-
ла работ внутренних сил для упругого тела любой формы.
Как видно из формулы (13.8), в которой под знаком интегралов
стоят квадраты Ж^, Л^^^ Q^^ потенциальная энергия всегда положи-
Щ'ту//////^
Щ//^///Ш
тельна:
-1
Ч^
\р
1F>0.
Фиг. 319
§ 13.6. НЕСКОЛЬКО ЗАМЕЧАНИЙ О РАБОТЕ
ВНЕШНИХ И ВНУТРЕННИХ СИЛ
В двух предыдущих параграфах были выведены
формулы для работы, производимой внешними и
внутренними силами на действительных перемеще-
ниях. Эти выражения обладают особенностью, кото-
рая заслуживает быть отмеченной.
Как видно из примеров, решенных в § 13.4, и из
формулы (13.8), работа является квадратичной
функцией внешних или внутренних сил. Умножение
нагрузки на произвольное число п влечет за собой
умножение деформаций на то же самое число п,
а потому умножение работы —на п\ работа
непропорциональна нагрузке. Отсюда
следует, что работа сил, вызывающих деформацию
тела не подчиняется принципу независимости дей-
ствия сил. Совместная работа, произве-
денная несколькими нагрузками, не
^J'J^^^ сумме тех работ, которые моглй
каждой нагрузкой в отдельности.
'%^ичи^этого%^^^^^^^^ в отТел^ност^и: " ^
легко понять из самого nnocVoro^^^^^ d^ ^^'^'"''^ представляется неожиданным,
силой Р и силой Р+0 {Ы?^^А^ ^ Рассмотрим два случая растяжения стержня:
В первом случаёработа ^*
W^
210
РЧ
2EF
Во втором случае
2EF 2EF "^ 2EF ^ EF '
Первые два члена стоящие в правой части второй формулы, представляют собой
раздельные работы оОеих сил. Что же представляет собой третий член? Каков его
физический смьхсл? Представим себе, что сначала подействовала сила Р; она совер-
шила работу ^-^ . После того как наступило равновесие, начинает действовать
сила Q. Она вызывает добавочное удлинение стержня, равное — . и совершает ра-
EF
04
боту ^— • Однако благодаря этому добавочному удлинению точка приложения си-
^ *-'•'* л#
QI
лы Р смещается на — , причем сила Р, полностью воспринятая стержнем еще до
появления силы Q, уже не изменяется. Поэтому сила Р совершает дополнитель-
ную работу, равную Р ~ , а не — • — . Таков смысл третьего члена.
Появление каждой новой нагрузки вызывает смещение точек приложения всех на-
грузок, появившихся раньше, и заставляет эти нагрузки произвести дополнитель-
ную работу.
Вот почему суммарная работа отдельной силы зависит от остальных сил.
\/ § 13.7. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
В ПРИМЕНЕНИИ К УПРУГИМ СИСТЕМАМ
Будем рассматривать упругую систему, находящуюся в состоянии
равновесия, и примем это состояние за исходное или начальное. Пред-
ставим себе какие-либо возможные бесконечно малые перемещения ее
точек. Под возможными мы подразумеваем такие -перемещения, которые
могли бы быть вызваны 'произвольными бесконечно малыми силами или
температурными изменениями, или .перемещениями опор я т. п. Совер-
шенно необязательно, чтобы возможные перемещения вызывались теми
же силами, которые отвечают рассматриваемому исходному состоянию.
Мы будем считать, что в то время, когда система совершает возмож-
ные перемещения, величина и направление действительных внешних
и внутренних сил, отвечающих ее исходному состоянию, остаются неиз^
манными. В нашем представлении все внешние и ^«У^Р^^^^^^^^^1
сохраняются такими же. как в начальном состоянии ^«^^^^
знаем, что действительный переход системы в «??^^.^^^3
состояние вызвал бы перераспределение усилии, ^f f^^^"^^^„^^^^^
внимание на это существенное различие между ^^f^^^^l^^^^ JP^^^J.
сом деформирования системы я тем условным. в<)обража^^^^^^^^ процес
сом перемещений, который рассматривается при пользовании принци
"Ом возможных .перемещений. „^.r^.n^rv прпрмршениях
Работа внешних -и внутренних сил на ««ff-^^f ^„^ы тТкак
носит ваэвание возможной или в и р ту а л ьн «и работы- 1 ак «9^
силы считаются постоянными, то при вычислении мртуальноираоот^
следует брать не половину, а полную величину произведения
каждой силы на соответствующее перемещение любой леЛор-
Принцип возможных перемещений в ^Р^^^^^^""^/,^^^1ГнЛ,-
мируемой системе .может быть сформулирован так есушш^^^^^^
^^^rcя в равновесии под действием "Р"^«^^««"^^1 "^" ^f То" е« ^ э^^
^Ри вся^м возможном бесконечно ^«^°^ "^Р^^З"%Л«еш««х и
системы (бесконечно малой деформации) сумма работ ее внешнил
^Щтренних сил равна нулю.
n^r^пягяeтcя что во время рассматриваемого переме.
При этом преД"°^;Д"^^о'^ах системы остается без изменения '
щения T^M"^P^jyPf^!,°f перемещений может быть применен к любой
Принцип возможных "ере^ "^ равновесия: к вязкому или пластиц
системе, находящейся в ^°"°™/т. д. Особенность применения его
ному телу, к ^^"^•^^"^„^в следуй Д^я ^^'^"'^ ^«"^^ ^ь, може,
к упругим системам состоит вы ДУ ^^ преодоление трения
ГаХГоГаГПьш^лг'и7\^Та. на'образование электромагнЦ?й
hL химичес^ энер?ш^ в упругом теле не происходит; в телах
"^^Й?Х^н^гоТыт^каеГ^ледующий важный .вывод: в упругой и, в
частности в линейно деформируемой системе суммарная работа внут-
оетих ciii при возможных перемещениях зависит исключительно от
исходного и конечного состояний. Она не зависит от того, каким спосо-
бом в какой последовательности, через какие промежуточные стадии
система перешла из начального состояния в конечное.
Если конечное состояние совпадает с исходным, то, каковы бы ни
были промежуточные состояния упругой системы, суммарная работа
внутренних сил равна нулю.
" § 138. ПРИЛОЖЕНИЕ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
' К ДЕЙСТВИТЕЛЬНЫМ ПЕРЕМЕЩЕНИЯМ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
На основании принципа возможных перемещений легко доказать
следующую важную теорему: когда упругая система под влиянием
какой-либо внешней нагрузки переходит из недеформированного состоя-
ния в деформированное уравновешенное состояние, то суммарная работа,
произведенная в этом процессе внешними и внутренними силами, равна
нулю.
Воспользуемся в качестве примера какой-нибудь плоской стержневой
системой. На фиг. 320 изображена упругая балка АВ. Исходное состо-
яние ее показано сплошной линией ЛСЛБ, а конечное — пунктирной
AC'D'B. Точки С и D переходят в положения С и 1У. При этом внешние
силы Р, и Ps совершают работу ^^^'"^^'^^ ., следовательно [см. форму-
лы (13.3), (13.8)]:
2 ^J 2EJ -^}4Ff 2jJ1^=0.
и r,?nT^^ следует, что действительная работа внешних сил равна
и противоположна действительной работе внутренних
мы vSoZ'T.'^tr Р'^'^У внутренних сил. взятую с обратным знаком,
Системы ипикп!^'^^^^ потенциальной энергией деформаций упругой
теп1нп ' ^ ' Р^^^~^^ потенциальной энергией Следова-
ShStpm'^^'""'"''""^ "«"Р™« ^^'^ой системы равна работе произве-
ла Гл"я1тсяТепи^Г'''^' '^^^Р"^ вызвали'ее дефСацию.'
т. е. выражает cSflTnx Работоспособности деформированного тела,
после рй™и vnnvrnT "^'^ Р^^°™^ которьТй мы можем вернуть
пружи?ГSSSJae/ nooJn*"^' "°^°^"2 ^°^У> ^^^' например, часовая
завод. ПоэтомГговопят^^^^^^^^^^^ ^^ Р^^У' ^^^^^Р^я затрачена на ее
гом теле в о б рТт и м А й Y.^°''^ внешних сил накапливается в упрУ
вается. --^'^^^"^ui^ форме. Она не пропадает И не рассеи-
начальн^15^%ТряХий'°п^Г^^''РУ*^"™У"РУ^^отела. не и-мевшег^
^^^ спряжении, действительная работа внутренних сил всегда
отрицательна. Отсюда следует, что действительная работа внешних сил
Ju потенциальная энергия внутренних сил всегда полож^телша
Для плоской стержневой системы потенциальная энТргия
жается через внутренние усилия формулой (13 8)
Проверим на примере соотношение между' действительными
тамн внешних и внутренних сил.
На фиг. 321 показана консольная балка АВ постоянного сечения,
нагруженная на конце В парой сил с моментом т. Эпюра изгибающих
моментов имеет вид .прямоугольника с высотой т. Угол поворота нл
выра-
I
рабо-
__^>Л, AjJ^_
С'
Фиг, 320
Фиг. 321
конце равен площади этой эпюры, разделенной на жесткость балки,
т. е. ^в^ VT' ^^^™^У Действительная работа внешних сил равна
тп^^ т I
~2 " 2EJ '
Работа внутренних сил, -взятая с обратным знаком, выражается инте-
гралом
J
2EJ
где М ~ изгибающий момент в сечении с абсциссой х. Но в данном слу-
чае M=m=const, следовательно:
I
тЧх тЧ
W-
\
2EJ 2EJ
Итак, обе работы по абсолютной величине равны между собой.
I § 13.9. ПРИНЦИП ВЗАИМНОСТИ РАБОТ
Пусть даны два различных состояния какой-либо линейно деформи-
РУем-ой системы, отвечающих двум различным 'нагрузкам. Обозначим
нагрузки, а также внутренние усилия и деформации, соответствующие
^тим двум состояниям, номерами 1 п 2. Будем считать, что в обоих
^^'>^Учаях система находится в равновесии, т. е. внешние силы уравнове-
^^^иваются внутре?гними.
Рассмотрим состояние системы, находящейся под совместным дей-
ствием обеих -нагрузок. Представим себе, что в первую очередь на нена-
[^ружейную систему начала постепенно действовать внешняя нагрузка L
^т этого воздействия система получила деформацию, а сама нагрузка
произвела работу, которую мы назовем Wu^ После того как этот процесс
"^1^Ружения закончился^ на систему начала постепенно передаваться
213
нагрузка 2, которая
мацию.
вызвала соответствующую дополнительную дефор,
,v4K4 назовем W22- Однако нагрузка 2, вызвав до,
Раооту ^^«""f'//';" ^^'нетелько сама совершает работу, ^
полнительную Д^Ф°Р"^^^^^'°Л "^„„ки J тем самым вовлекает ее вторичнг^
сместив точки приложения нагрузки i тем ^^^^^ ^^ РИчно
в работу. Обозначим работу произве^^^^^^^^ ^^^ Суммарная р?.
перемещениях, которые вызваны naipy ^^^ «„пазится алгебоамчйо^^...
Ф
Фиг. 322
бота внешних сил выразится алгебраической
суммой В7п+В^22+^12. Во всех трех выражениях
первый индекс указывает, какие силы соверша-
ют работу, а второй — под влиянием каких сил
происходит соответствующее перемещение.
Рассмотрим таким же образом другую воз-
можную последовательность загружения. Сум-
марная работа внешних сил выразится алгебраи--
ческой суммой 1^^22+^11+^21, где W21 —работа
внешних сил 2, совершаемая под влиянием сил 1.
Суммарная работа «внешних сил в каждом из
этих двух случаев равна работе внутренних сил,
взятой с обратным знаком, или потенциальной
энергии. Последняя, как мы знаем, не зависит от
порядка загружения упругой системы, а опреде-
ляется лишь исходным и конечным состояниями.
Но в обоих рассмотренных процессах исходное
состояние — одно н то же, а именно незагружен-
ное; конечное состояние — также одинаковое, а
именно загруженное обеими нагрузками. Следо-
вательно, работы в обоих случаях равны между собой:
Отсюда
W,,^W,,,
(13.9)
Мы получили 1простейшее доказательство так называемой теоремы
взаимности работ: в линейно деформируемом теле виртуальная работа
внешних или внутренних сил состояния 1 на перемеи^еяиях состояния 2
равна виртуальной работе внешних или внутренних сил состояния 2 на
перемещениях состояния L
Эта TejDpeMa является одной из наиболее замечательных во всей тео-
рии линейно деформируемых систем, настолько она проста по формули-
ровке, глубока по содержанию и всеобъемлюща по своим приложениям.
Какова бы ни была сама система, как бы различны ни были нагрузки и
деформации обоих состояний, внутренняя природа линейно деформируе-
мого тела такова, что .взаимность работ всегда и неизбежно должна осу-
ществляться.
Теорема взаимности работ известна в литературе под названием
теоремы Бетти (Enrico ВеШ, 1823-1892), по имени итальянского
ученого, который первым ее опубликовал,
лами р'Го^ nL^^^^"^^"^ ^^^ (*"^- 322^ « состоянии / нагружен продольными ей-
этогГ^Г^нЕг.^""^""'' си/состояния Гна'^п^шёщениях состояния 2. т
точки Л • • • -^ ; точки С • - BS^±^
EF EF
214
Отсюда
W^.^P
Ra
Я(а'\~Ь) R
EF +^^~"^F~=?F^^° + Q° + Qb)-
Для подсчета работы ^2i нужно умножать силы состояния 2 иа соответствующие
Отсюда
т.е.
W,
'ti = R[
'(P + Q)a
EF
Qb
EF
]-iF-'
^l.= ir.l.
-hQa-i-Qb),
§ 13Л0. ТЕОРЕМА МАКСВЕЛЛА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИИ
Рассмотрим два простейших нагруженных состояния упругой си-
стемы. Чтобы не сужать общности рассуждений, .ограничимся самым
схематическим чертежом, без указа-
ния вида сооружения и расположения
его опор.
На фиг. 323 одна и та же система
показана в двух состояниях^ Первая
нагрузка состоит из силы Pi = l, а вто-
рая— из силы Р2=1. Сила Pi = l на-
правлена по прямой 1—1 и приложена
в точке Л; сила Р2= 1—^по прямой 2—2
и приложена в точке В.
Под действием силы Pi=l точка В
переместилась в положение В^\ проек-
цию этого перемещения на направле-
ние силы Рг, т. е. на прямую 2—2, на-
зовем Og^. Первый индекс показывает,
в каком месте и по какому направле-
нию берется рассматриваемая проек-
ция перемещения; второй индекс по-
казывает, от какой причины происхо-
дит это перемещение.
Под действием силы Р2=1 точка А
пе1ремещается в положение А'\ Проек-
Дия этого перемещения еа направле-
ние силы Pi обозначена через 8i2
\^перемещение точки приложения силы
^1 по направлению той же силы, вы-
званное действием силы Р2===1»).
Необходимо хорошо уяснить себе и хорошо запомнить смысл таких
Обозначений, как \^^ S,i, S^ и т. д., так как без них в современной
'Глории статически неопределимых систем почти невозможно сделать
На основании теоремы взаимности работ можно приравнять вирту-
альнуш работу внешних сил 1-го состояния на перемещениях 2-го со-
^^ояния виртуальной работе сил 2-го состояния на перемещениях 1-го.
^ одном случае сила берется из верхнего чертежа, а соответствующее
Фиг. 323
перемещение — из нижнего; в другом случае — наоборот. Таким ofi
зом: Рз-
1.8,2= l-Ssi, или 8^2 = 821,
^ . „^п^мртение точки приложения первой единичной силы по ее вд,
т. е. "^/'^;««'ff "^J^'l^^^ единичной силой, равно перемещеншо
Г^ш^^лс^^Т^орТсТли по напраелени. последней. еыэе^оТу
ПГрГ^а^^С^со^яТГл^тГ лишь часхньш случаем предндуц,ей,
имеет большое значение для расчета упругих систем. Она была опубли-
кована Максвеллом в 1864 г.
0 ®
1
'ff'
.U
«^_L
._l_l4
-Г-'
"й^
П'1
Фнг. 324
С\
Ц-1
¦^4>:
4
Мо-/
С\
^^--^^'
^
"V
Uf2
Фиг. 325
Пример 13.4. Вычислить перемещения \^ и ^21 Для стержня, показанного на
фиг. 324.
Прежде всего необходимо приучить себя к обозначениям перемещений. На левом
чертеже перемещение точки В должно быть обозначено через ^2ь а на правом пере-
мещение точки А — через ^12- Кроме того, полезно заметить также перемещения,
обозначенные на чертежах через ^ц и ^22. которые понадобятся впоследствии.
Перемещения вида ^ц. ^22 и т. д., т. е. содержащие в своем обозначении два
одинаковых индекса, называются главными, а вида Ьгг, \\ и т. Д- — п о б о ч-
н ы м и.
Ответ:
=^21=
EF
Пример 13.5. На фиг. 325 требуется разобраться в обозначениях и вычис-
^13 и Bg,. Балка АВ имеет постоянное поперечное сечение. «нтаМй
Здесь первая нагрузка состоит из силы Pi==l, а вторая — из двух пар Я.*^^'^\1едует
Af2=l, т. е. обе обобщенные силы имеют различную размерность. Через ^w ^угол
обозначить прогиб в точке С, вызванный действием пар Л12= 1, а через ^%\ У
взаимного поворота концов Л и В, вызванный действием силы Pi=l.
Легко убедиться, что
В,о = bo
/2
SEJ
§ 13.11. ЗАМЕЧАНИЕ О РАЗМЕРНОСТИ ПЕРЕМЕЩЕНИЙ
Теорема о взаимности перемещений Ь.^ = Ьо. справедлива не толь-
но Гв^'т^Тл^я^^'^ ""'^^ ^ ^^=^^ ^^^^^^^^^« сос^е^?оче^ми силами^
но и в том случае, когда речь идет о каких угодно двух обобщенных
216
КО
I
1
по
во-
силах. Но различным обобщенным силяы г-^
своей размерности обобщенные перемешенна'"'7д"''^'°'' Различные ...
прос, что означает в таком случае ^венствп ?; ^°^" возникнуть во-
обе части этого равенства разнородными пртши„^ ~ Ч'* "^ являются ли
Так. например, при взгляде на фиГз25 Mnt ""
есть угол поворота, а S,^ есть вертикальнор ^^ показаться, что 8,,
Это кажущееся противоречие отпадает когпГ'"''^^"^
мание то, что каждое из этих перемещений а^п "Р"»""^^^^ во вни-
^еремещением, т. е. что оно вызыв^ S' "-•''^^''''" У^^^*'"""
произвольное, а непременно единГчно?з^Ген„еT.l' """°'^'" ""
нами мы уже встречались в теории линий влияния P^J^f"'' ^'''"™"
мещения 8,2 такова: ^ " влияния. Размерность пере-
5V обобщенное перемещенне
обобщенная сила
(а)
Числитель имеет размерность перемещения, а знаменатель-раз-
мерность той силы, которая вызвала это перемещение
Например, если обобщенная сила Р, есть сосредоточенная сила
а Рг-пара, то 8.2 есть линейное перемещение по направлению силы
Л. деленное на момент пары, т. е. Ь^^=-±-^кг~' . Перемещение 8,,
есть угловое перемещение по направлению пары Pg, деленное на силу
УГОЛ _1 -''
5. угол
т. е. ^21 = = кг
сила
Следовательно, оба перемещения имеют одинаковую размерность.
Точно так же определяется размерность перемещений вида %, ^22
и т. д. Так, например, на фиг. 325
/2
^12 = ^21 =
—1
8?/
кгм^
^11
ж
кг
^22 =
угол
= кг
{кгм)-^^,
Кроме удельных перемещений, в строительной механике приходится
рассматривать перемещения, вызванные любой (не единичной) силой
или группой сил. Эти перемещения мы будем обозначать через '^\р ,
*^2р и т. д. В отличие от удельных перемещений они имеют размерность,
вьфажающуюся числителем формулы (а).
§ 13.12. ЛИНИИ ВЛИЯНИЯ ПЕРЕМЕЩЕНИЙ КАК ЛИНИИ ПРОГИБОВ
Пусть требуется построить л. в. какого-либо перемещения S^o» т. е.
Найти закон изменения этого перемещения при условии, что сосредото--
ченная сила p2=l, сохраняющая постоянное направление, передви-
^^ается по сооружению. Например, на фиг. 326 геометрическим местом
точек приложения силы Рг
^УЖит некоторая линия
^^- Требуется найти проек-
|^ии перемещений точки А
/1. ^^JiaHHoe направление
'• Из равенства 8^2= Ь^х
вытекает, что задачу о ра-
зыскании перемещений 8^,
можно заменить задачей о
разыскании величины Ь^.
217
Фиг. 326
Эти две задачи ^.
чем ^12: во-первых, ^.ж.^^ ^^.^^
во-вторых, оно 'Вызывается
Фиг. 327
Фиг. 328
приложенной в определен
ной точке А. Заметив, что
роль точек В играют все
точки линии MN, мы полу,
чим -следующую замеча^
тельную теорему: линия
влияния перемещений Ь^^
всегда совпадает с графи-
ком^ который выражает пе-
ремещения точек 2 по на-
правлению Я2> вызываемые
силой ^1 = /, приложенной к
неподвижной точке L
В практике расчета со-
оружений приходится чаще
всего иметь дело с движу-
щейся вертикальной
силой, т. е. строить линию
влияния перемещений точ-
ки / по заданному направле-
нию /, которые вызываются
вертикальной силой Р2=Ь
Тогда график 821 будет вы-
ражать собой вертикальные
проекции перемещений то-
чек 2, /вызываемых непод-
вижной силой Pi = l, кото-
рая имеет заданное направ-
ление /.
Вертикальные перемеще-
ния обычно (хотя и неточ-
но) называют прогибами,
поэтому предыдущую теоре-
му можно короче выразить
так: линия влияния перемер
щений какой-либо заданной
точки 1 по заданному на-
правлению, вызываемых^
движущейся вертикальной
силой ^2=А есть линия про-
гибов в точках 2, отвечаю-
щая загружению системь^
неподвижной силой Ру-^-
Заметим, что в той формУ'
лировке, которая дана вы-
ше, под силой Pi можно по*
нимать не только сосредото-
ченную силу, но любую обоР
Тякпы -^'^ ^"•'IУ, НО ЛЮОуЮ uuc»v
„р '^'^ ^^"окущейся единии^^:-! ^""""^ влияния первме-
2>8 ^о'««и««ой парой Р^^1,стп&0в0
Так, например линия влияния угла поворота В.Управого конпа
балки (Ф-^327,а совпадает с линией прогибов ба;^ки,''Гз1ва™х
моментом М2=1 (фиг. 327,6). Линия влияния прогибов в точке С
^алки (фиг. 327,а) совпадает с линией прогибов, вызываемых непод-
вижно стоящим в точке С грузом Рз=1 (фиг. З27.в).
Самый процесс построения линии прогибов оказывается во многих
случаях более простым, чем процесс прямого построения л, в., поэтому
теорема о взаимности перемещений применяется не только как способ
поверки л. в., но и как способ непосредственного их построения.
§ 13.13. ТЕОРЕМА РЭЙЛЕЯ О ВЗАИМНОСТИ РЕАКЦИЙ
Рассмотрим два состояния линейно деформируемой системы. Первое
деформированное состояние вызвано тем, что некоторая связь переме-
стилась по направлению своего действия на величину, равную единице.
Такую деформацию получа-
ет, например, неразрезная
балка, когда одна из ее опор
оседает или приподнимает-
ся на величину, равную еди-
нице; при этом балка изги-
бается.
На фиг. 328, а показана
система, у которой опорный
стержень /, изображенный
сплошной линией, переме-
стился в положение, изобра-
женное пунктирной линией.
При этом точка А системы
перешла в положение А^-
Проекция АА' на ось стерж-
ня по условию равна едини-
це. Реакции, возникающие
при этом в переместившейся
овязи /ив некоторой дру-
гой связи 2, обозначим через
Гц и Г12. Буква г должна на-
поминать читателю, что речь идет о реакции (reaction. Reaction); пер
вый индекс указывает, в какой связи возникла реакция, а второй —от
какой причины' она возникла-
На фиг. 328,6 показана деформация той же системы, вызванная тем,
^^то связь 2 переместилась по направлению своего ^^^«^'^«^J^^^^^^^
ну, равную единице. Естественно, что точка В может при ^tojvi получ1т.
также некоторое перемещение в перпендикулярном направлении,
ио это перпендикулярное перемещение нас не интересует,
Фиг. 329
от
Реакции
в связях i и 2, вызванные указанным смещением, обозначены соответ-
ственно через V,2 и rj2. За положительное направление этих Реакции
принято направление, совпадающее с единичными перемещениями
На фиг. 329 показан другой пример, поясняющий эти понятия. Здесь
"¦Ji есть изгибающий момент в сечении В, вызванный единичной осадкой
опоры А, а г,,-реакция этой опоры, вызванная единичным взаимным
"°Ж«Гмся" принципом взаимности работ: напишем, что сум„а
пабоГмешнихси/первого состояния на возможном перемещении,
отвечающем BTopLy состоянию, равна сумме работ внешних сил вто!
?ого ?^:тояния на перемещении, отвечающем первому состоянию. При
Stom можно откинуть связи / и 2 и за внешние силы принять действую-
щие в них реакции. Тогда
или
Г,2=Г^1- (13.11)
Полученный вывод может быть сформулирован так: реакция, воз-
никающая в связи 1, когда связь 2 перемещается на единицу по своему
направлению, равна реакции, которая возникает в связи 2, когда связь
1 перемещается на единицу по своему направлению.
Как видно из самого доказательства, теорема о взаимности реак^
ции, доказанная в 1873 г. Рэйлеем, подобно теореме о взаимности пере^
мещений, является частным случаем теоремы о взаимности работ.
§ 13.14. ВЗАИМНОСТЬ РЕАКЦИЙ И ПЕРЕМЕЩЕНИЙ
Подобно предыдущим эта теорема также относится к любой ли-
нейно деформируемой системе. Для большей наглядности рассуждений
на фиг. 330 показан частный пример. На фиг. 330,а система нагружена
произвольной внешней нагрузкой. Реакцию в одной из связей системы,
например в верхнем горизонтальном опорном стержне, назовем г^р
или R^p.
На фиг. 330,6 пунктиром показано деформированное состояние той
же системы, вызванное единичным перемещением той же связи, в дан-
ном примере—единичным горизонтальным перемещением правого кон-
ца. Перемещения точек приложения сил Г, Q, S по направлениям этих
сил назовем соответственно Ь'^^, Ь' , Ь'^^.
Верхний ^индекс поставлен для того, чтобы оттенить характер этих
перемещений: они вызваны единичным перемещением, в то время
как через f\2. ^\\ и т. д. (без верхнего индекса) мы обозначали пере-
мегаения, вызванные единичной силой. Размерность величин вида Ьр
тачова:
перемещение, отвечающее обобщенной силе Р
перемещение, отвечающее связи /
Например, если речь идет о перемещении точки приложения сосре-
доточенной силы Р под влиянием линейного перемещения,
то получается размерность ~ = см\ Если речь идет о перемещении по
ТЛшу^^^ся''^^'^' ^^-^ Л вызванном линейным перемещением
угол _1
-— =см и т. д.
см ^
Лиг^чЖТГ^ ^^^^ состояниям системы, изображенным на
фиг. 66\i,a и б, применим к ним теорему взаимности работ. В первом
состоянии внешними силами можно считать Т, Q, s и R,p- во втором^
реакцию г,,. К внешним силам можно причислить и остальные реакции,
^0 так как в обоих состояниях^ системы соответствующие им перемеще-
ния равны нулю, то они не войдут в уравнение работ. Работа внешних
СИЛ Ьг'О состояния на перемещениях 2-го равна
Здесь положительными направлениями для величин Spi, Sqi и т. д.
считаются те, которые совпадают с направлениями сил Р, Q и т. д.
Положительным направлением для реакции R^p считается то, которое
совпадает с направлением заданного единичного перемещения связи /.
Работа внешних сил 2-го состояния
на перемещениях 1-го равна
Приравняем друг другу оба выра-
жения. Кроме того, для краткости за-
писи будем обозначать все заданные
силы Г, Q, S и т. д. буквой Р. Тогда
о)
11
А В
'IP
SP8p, + /?,p.l=0,
PI
•ЪРЬ
р\'
(13.12)
тш^
6)
^т1
ин
^^^ Фиг. 330
Фиг. 331
В том частном случае, когда имеется
Jia Р, причем Р=1, получается
R,^^-K
MP
"PI
только одна внешняя си-
(13.13)
Эта теорема была доказана Максвеллом в 1864 г. и Рэилеем в 1873
Если эта сила Р=1 перемещается по '^««РУ^^^"^'^^ Р™ влия-
«нное направление, то R,p, очевидно, представляет собой линию влия
ния реакции связи 1. Отсюда вытекает ^f ^««7" ff„°^= J "J" J
влияния реакции i?,^, , возникающей в связи 7 при
движении груза Р=1.совпадает с графиком пеое-
»*ещений 8pj, который вызывается единичны)
>pi
связи.
пер е-
м с м е-
''^бнием той же связи.
Короче, но не вполне точно этот вывод можно ^формулировать так.
что л. в. любого vcилия совпадает с линией п_Р_о/_"Л°!:..?."Л
а;
?оче. но не вполне точно этот вывод шиу^^^ ^погибов выз-
^ в. любого усилия совпадает ^= ¦"««"^" "^ „ " т/ующей
«ЭННОЙ единичным смещением соответствующе
5ЯЗИ.
221
так например, л. в. опорного момента М^ балки, представленной на
*„7чя1 Гсовпадает с линией прогибов, вызванной единичным пово-
фиг. 331,а, '^o'^"t>,a HnRPnHVR этот конец по направлению положитель-
= ^8' , то Ординаты л. в. отрицательны.
S 13 15 ЧАСТНЫЕ ПРОИЗВОДНЫЕ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ.
^ ТЕОРЕМА КАСТИЛИАНО
Потенциальная энергия упругого тела, нагруженного силами Pi,
Рг,---» ^п» выражается формулой (13.3):
V^± (Р,Д, + Р^Аг + • • • +Рп^п), (13.14)
где через Д,- обозначено суммарное перемещение точки приложения
силы Р: по направлению этой силы.
В свою очередь суммарные перемещения выражаются через «еди-
ничные» (т. е. через перемещения по тому же направлению, вызыва-
емые порознь силами Pi=l, Р2=1,..., Рп=1)э следующим образом:
д. = Р,8., + P^2 + • - + Pnhn- (13.15)
Если мы подставим эти выражения Af -^ формулу (13.14) и сделаем
приведение подобных членов, то получим
+ \гРЛ + • • • + К-ип Рп-.Рп)=Y S hn + 2 h^Pk > (13.16)
причем во второй сумме (фк.
Мы знаем, что потенциальная энергия всегда положительна. Следо-
вательно, квадратичная форма (13.16) обладает тем свойством, что ни
при каких значениях переменных Ри ^2..., Рп она не может стать
отрицательной. Такие квадратичные формы называются определен-
ными положительными.
Будем считать все силы Р^ Ps, ..., Р„ независимыми
переменными. Продифференцировав при этом условии обе
части формулы (13.1S) по одной из сил, например по Ри мы получим
|^-^-1=^х.. (13.17)
п ^Р^^^ифференцировав же после этого по той же переменной форму-
лу (iSAb) и воспользовавшись соотношением (13.17), мы найдем
= Y(Ai + Рг\г + ЯА2 + ЯЛз+ • • •+ РпЬгп) - ~ (Дх+Д1)=Д1. 0^^^^>
iX!ll^fn^n.^^^^ ''Р''''^^''^^^^ от потенциальной энергии по од^
лению nociS '^l^^^^^^^"'^ ''очки приложения этой силы по направо
я™ инженрп^^^ ^^"^"^"^ ?д^Р|^^ ^^^""^ доказана в 1875 г. италь-
янским инженером Кастилиано (А. Sastigliano, 1847—1884).
222
Если мы для данной упругой системы H^vr.
заданной нагрузки, каким-нибудь способом „оТ^^*^^*^^^ "^^ Действием
бальной энергии в функции оГвнешних сил ^^^^^^^^ 1'^''^'"
например, как интеграл работ внутренних rЛ^ '''^^'' ^'"'^'^ найдено.
Сражения сможем путем Диффере'н^р^в^ия Jl^^^^^^ ^n.n"^""'" ""^'^
направлению любой из этих сил. Следо^тель^ т^^.^Л^^^^ "^
указывает один из воз- ь^тельно, теорема Кастилиано-
можных путей для вычис-
ления перемещений в лю-
бой упругой системе от
любой нагрузки.
Проверим наши рас-
суждения на примере,
рассмотрим балку посто-
янного сечения с шарнир-
но-опертыми концами,
г
^^Av.
(М
Фиг. 332
при X < —
при X >
2
¦.-^-ЬМг-^-М,^;
Отсюда
¦=2J
2EJ ^ 96EJ
{16М\+ 16Щ + 1^Р^ —
— 16^1^2 + ЫМ^Р— ЫМ^Р).
Для определения угла поворота Дх достаточно продифференциро-
вать V по Мх\ для определения Аз — продифференцировать по Р и т. д.:
'^ = а^ = 9ткг(2.1бМ,-1бМ, + б/Я)=
^8 = -^ =
3EJ
6EJ
16 EJ
PI» . /г
(2/^Р + 6/М,-6/М,)=^ + ^
^f,.
16 ?/
М,
^'' 96 ? f
cen ^^^ силы P не было, и мы желали бы определить прогиб в
^редине пролета, то нужно было бы проделать те же вычисления и в.
^нчательную формулу для А подставить Я=О,
§ 13.16. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
«ить j}^^"^^y^^KHH ученый Пуассон* (S. D, Poisson, 1781—1840) предложил распростра-
ними сн "^*" возможных перемещений на работу, производимую внешними и виутрен-
-«..^^„.^ да ми при деформировании стержневой системы. Этим было положено основа-
'^raite de mecanique, t. 1, Paris, 1883.
,„е для вывода ряда обших теорем об упругих системах и общих методов решения
статически «^.^пределимых задач зпервые в курсе теории упругости ЛамэЧ
Теорема Клапейрона был^^^^^^ определение усилий в упругой системе на
основ^расс^реи"^ ^"^' принадлежат статьи профессоров
Н. А. Евневича^ и '^¦^^'J^^3^^^f^„ выведен в чисто математической форме француз.
Принцип взаимности Pf^l^^^^^^^^^^ а в применении к упругому Те-
ским математиком К^^^Д^^^„Г;^^ "^ м е ш е н и й -- Максвеллом^. В наиболее об-
лу-в виде ^^^^Р^^ь! вз^^^^^^^^ систем была доказана, как уже упо-
мя^^оТышГб^^^^^^^^ позже Га kCfa независимо от Бетти найдена и pasLa
^^%1з^я1—^^ фактического значения теоремы о взаимности работ для
-расч^ статически неопределимых систем много содействовала статья проф. В. Л. Кир.
пичевав дальнейшим развитием общих теорем, касающихся упругих и невполне
упругих систем, занимались П. П. Бехтерев^, профессора В. Э. Новодворскии^о, Я. Л. Ну-
дельмани, А. А. Уманский^^ Н. И. Безухов^^. И. М. Рабинович^^
» Lecons sur la theorie mathematique de I'elasticite des corps soHdes, Paris, 1852.
^ H A. Евневич, Начало наименьшей работы внутренних сил и его применение к
определению натяжений, развивающихся в частях сооружений, 1877.
3 X. С. Головин, Начало наименьшей работы в применении к расчету решетчатых
систем, 1883.
* Sur les fonctions quadratiques et homogenes de plusieurs variables, Comptes
rendus, t. XLIV, Paris, 1857. ^^ ^ ^ ^ ., , .,
5 On the calculation of the equilibrium and stiffness of frames, .Philosoph, Mags
1864 (4).
6 Teoria dell* elasticita. в журнале „И nuovo cimenlo", t. VII—VIII, 1872
7 A statical theorem. .Phil. Mag", December, 1874; March, 1875.
e B. JI. Кирпичев, Приложение теоремы лорда Рэйлея к вопросам строительной
механики, 1883.
9 Аналитическое исследование обобщенного закона Гука, ч. I, 1925.
^^ Обобщ.ение теорем строительной механики о работе деформаций для любой зави-
симости между силами и координатами, «Вестник инженеров и техников» № 8, 1931.
" Методы определения собственных частот и критических сил для стержневых
систем. М., 1949.
*^ Специальный курс строительной механики, ч. II, М., 1935.
^3 Основы теории сооружений, материал которых не следует закону Гука, Труды
-МАДИ, 1936. ^1^ у J J
*^ Курс строительной механики стержневых систем, ч. II, 1954, § 19.2.
Глава 14
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ СТЕРЖНЕВЫХ СИСТЕМ
§ 14.1. ПОСТРОЕНИЕ ЭПЮР ДЛЯ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ
Перемещения любой точки упругой стержневой системы, вызванные
теми или иными силами, очевидно, зависят от деформации системы,
т. е. от относительных удлинений или укорочений ее стержней, от их ис-
кривления и т. д. Но эти деформации в свою очередь зависят от изги-
бающих и крутящих моментов, продольных сил и поперечных сил, дей-
ствующих на сечения стержней.
Поэтому определению дефор-
маций и перемещений обычно
предшествует определение уси-
лий, построение для них эпюр.
В дальнейших главах мы
будем говорить исключительно
о плоских стержневых си-
стемах. Для них картина рас-
пределения усилий характери-
зуется тремя эпюрами: М, Q, Л^,
Q
^)
¦illllll
®
Th '^'
illlliilll
<
\
:—q
%
Фиг. 333
15 И, М. Рабинович
Фиг. 334
г „е ж-изгибающий момент, Q-поперечная или перерезывающая ^и
ла 7V-продольная или нормальная (к поперечному сечепию) сила
Мы советуем читателю посвятить 1-2 дня приобретению навыков в по.
строении этих эпюр для статически определимых систем. Такое введение
окажется очень полезным и избавит от неприятностей в дальнейшем при
пасчете более сложных статически неопределимых систем.
По понятным причинам мы не можем долго останавливаться на этом
элементарном вопросе, относящемся целиком к теории статически
определимых систем, и ограничимся несколькими примерами
Эпюры изгибающих моментов мы будем строить, принимая за ось
абсцисс ось стержня и откладывая все ординаты эпюры со стороны
растянутого волокна (можно также откладывать все ординаты со
стороны сжатого волокна). Это избавит от необходимости устанав-
ливать особые правила знаков для изгибающих моментов в случаях го-
ризонтальных, вертикальных и наклонных стержней.
Для эпюры Q такой наглядный способ затруднителен, поэтому бу-
дем откладывать ее ординаты в произвольную сторону, но ставить знаки
плюс и минус согласно фиг. 333, т. е. в зависимости от того, производят
ли силы Q вращение по часовой стрелке или против (см. также фиг. 124).
Силы Л^ будем считать положительными в случае растяжения и от-
рицательными— в случае сжатия.
На фиг. 334 построены эпюры для трехшарнирной рамы, нагружен-
ной на конце А сосредоточенной парой с моментом, равным единице.
.Построение начинается с определения опорных реакций Ra ^ ^в - ^^^
эпюры М вполне определяется тем, что эти реакции образуют пару. Ве-
личина вертикальной составляющей находится из уравнения моментов
всей рамы относительно шарнира А или В, а распор — из уравнения
моментов Одной половины рамы относительно шарнира С.
§ 14.2. ВНЕШНИЕ ВОЗДЕЙСТВИЯ: НАГРУЗКА, ПЕРЕМЕЩЕНИЕ СВЯЗЕЙ
И ТЕМПЕРАТУРА
При вычислении перемещений мы будем различать три рода внеш-
них воздействий на рассчитываемое соорул^ение, из которых каждое
является источником тех или иных перемещений.
Первое воздействие —силовое, т. е. обусловленное заданными си-
лами или нагрузками.
Второе воздействие—перемещение опор или иных
связей (фиг. 329).
Предполагается, что величина перемещения задана.
Третье воздействие — температурное, т. е. повышение или по-
нижние температуры в тех или иных частях сооружения по сравнению
с начальной температурой. Заметим раз навсегдЬ, что в дальнейшем
речь будет идти исключительно об изменениях температуры по
сравнению с некоторой начальной, и лишь для краткости мы будем за-
менять термин «изменение температуры» термином «температура». ^
для упрощения расчетов мы будем считать, что в пределах любого
сечения температура распределяется по плоскостному закону, причем по
направлению одной из главных осей сечения она постоянна, а по на-
правлению другой —имеет линейное распределение (фиг. 335). Такое
упрощение оправдывается тем, что температура, действующая па соор)
жени*-, непрерывно изменяется в течение годами в различные часы суто^^
rti^r "Р"^^лится вести весьма гадательно на какое-нибудь одпо
гипотетическое, возможное для данной местности, температурное воз
действие. ^
1Шх ^
Линейный температурный график, представленный на фиг. 335, мож-
,0 ра-^бить па два линейных графика, представленных на фиг.336,а и б.
Первый из них имеет вид прямоугольника с высотой t, которая равна
температуре по оси стержня, т. е. в центре тяжести сечения. Из фиг. 335
нетрудно выразить величину t через температуры t^ и ^2 крайних во-
нетрудно выразить
локоп
t =
a-\-b
(14.1)
h + h
г *1 + t2
Рели центр тяжести лежит в середине сечения, то получается i~~
Разумеется, что величины U и h вносятся в формулу с их знаками. Мы
сегда будем считать повышение температуры положительным.
I
Фиг. 335
Фиг. 336
График фиг. 336,6 получается как разность -^.^^^^ ^Гг ГфГ
графиком и графиком фиг. ЗЗб.а. Легко понять, что ордината ^ «а Фип
336.6 равна алгебраической разности температур в крайних ьолокнах
Вопрос о знаке, который мы должны поставить перед скобками в
(14,2), будет разобран ниже. ^. г.г.^м^хлг€лш '\"\^а вызывает
Равномерней на'грев, характеризуешь™ графиком^ ^^^ ^^^.
удлинение или укорочение стержня а l u ч у-
равномерного нагрева (с нулевой температурой по оси стержн ,
ваег искривление оси, не изменяя ее длины.
§ И.З. ОБЩАЯ *0'>^»y^^S SS'"''''
ПЛОСКОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
Желая получить формулу, одинаково пригодную мя^всех^^^^^^^^
лок. ферм. рам. арок и т. п.. мы Д»^^*^"" "^^^; „ названным системам.
который в одинаковой •"^-'^ ппиложим ко всем „
Так1
.оторый в одинаковой мере приложим -^ перемещений,
-аким законом является принцип возможныл , ^^^^^^ большую на-
Для того чтобы придать ^^•"''f "^"д//хержневого сооружения, на-
глядность, возьмем схему какого-нибудь ^^^^ действием заданной на-
пример р^мы (фиг. 337). Она «^'^°Л'"^^^зТп?реместилась в заданное
"^РУзки и температуры; кроме того, ^^"ор^ перемещения произволь-
положение В'. Требуется определить проекцию пер?
15»
^япянное направление i — i. Эту проекцию
ной точки С на произвольное заданное
назовем Д,«. ^^^, находящейся под действием ^рех поименованных
Состояние системы, находяще „дображено на фиг. 337,а Какое
факторов, назовем состоянием а- ^^^^ ^^i ни дали нашей систе-
S возможное бесконечно малое пер ^^^ ^^,^о„ния а на этом переме-
ме, сумма работ внешних » «"У^Р^^^льно, мы можем составить соответ-
щении будет равна «У-"'5;,.Гбе?конечным множеством способов. Однако
ствующее уравнение работ оеско
НИ одно из этих уравнений не приведет нас к цели, если в него не войдет
искомое перемещение А,-^ •
Мор предложил написать уравнение работ не для действительного
состояния сооружения, а для воображаемого, виртуального, специально
подобранного состояния. За такое состояние, по Мору, следует взять то,
которое показано на фиг. 337,6. Оно содержит лишь одну внешнюю hsj
грузку, а именно силу, равную единице и приложенную в той самой
точке С сооружения и по тому самому направлению, по которому тре-
буется разыскать перемещение А;^. Проще этой нагрузки невозможно
ничего придумать. Состояние сооружения, нагруженного таким обра-
зом, назовем «состоянием Ь. Будем считать, что это и есть действитель-
ное, заданное состояние сооружения.
Так как оно является уравновешенным, то сумма работ всех внеш-
них и внутренних сил этого состояния на любом возможном переме-
щении должна быть равна нулю.
Как же нам выбрать возможное перемещение? Замысел здесь таков^
за возможное надо выбрать как раз то состояние перемещений, которо
фигурирует в условии задачи, т. е. состояние а. Итак, состояние i следу-
ет трактовать как действительное, а состояние а — как виртуально •
Нужно написать выражение работ всех внешних и внутренних сил со^
стояния i на перемещениях, отвечающих состоянию а, и приравнят
его нулю.
В состоянии i имеется только одна внешняя сила Л",- =1.
228
Приняв положительное направления для Д.^совпадающим с взятым
нами направлением силы Л^ , получим ее виртуальную работу ЬА.
Внутренние силы состояния I характеризуются опорными реакци-
ями R и эпюрами, которые мы обозначим через М„ Q,-, Л^.. Реакции
можно, впрочем, причислить и к внешним силам.
Их возможная работа выразится суммой И Re, где с —заданные
в состоянии а перемещения опор по направлению реакций. Произведе-
ние вида Re считается положительным, если сила R и перемещение
с направлены в одинаковую сторону. Разумеется, что те опоры, кото-
рые остаются неподвижными, в этой сумме фигурировать не будут, так
как для них с=0.
^
^п
) (
V
/,
I
ш
^"7
/
Фиг. 338
Наконец, возможную работу внутренних сил М,-, Q,- я Ni обозначим
через А. Тогда
или
X^=^-A-^Re,
(14.3)
Остается определить выражение внутренней работы Л.
Эта работа представляет собой интеграл из бесконечно малых работ,
совершающихся в пределах каждого элемента ds каждого стержня. Мы
У^е имели случай составлять соответствующие элементарные выраже-
ния, когда вычисляли потенциальную энергию (§ 13.5).
Обозначим эпюры, отвечающие состоянию а, через М^, Qa, ^а- Вза-
имный поворот двух бесконечно близких сечений стержня, вызванный
изгибающими моментами М„, выразится по абсолютной величине
формулой
d© =
Mads
EJ
Возможная работа изгибающих моментов М-, на этом перемещении
"Ьфазится по абсолютной величине произведением M^rf?. Пусть, напри-
^^Ь ^ обоих состояниях верхнее волокно элемента ds растянуто (фиг,
"^^^А и б).
Давая этому элементу деформации а. мы тем самым увели-
^иваем деформацию, имевшуюся в состоянии /, но внутренние силы
состояния i направлены в сторону, обратную этой деформации.
т
Итак, элементарная работа моментов выразится произведением
MgMjds
" EJ
Qads
Взаимный сдвиг тех же сечений будет равен — , поэтому возмож.
ная элементарная работа сил Q, выразится формулой
~ GF '
где {х-^ коэффициент, зависящий от формы поперечного сечения [см.
формулу (13.7)]. ^ ^
Удлинение элемента ds, вызванное силами iV^, будет равно ~- ,
а возможная работа продольных сил Ni на этом перемещении выразит-
ся формулой
NgNjds
" EF
Свободное удлинение, вызванное температурой /, когда никакие свя-
зи не мешают этому удлинению, будет ос/ ds, где а — коэффициент ли-
нейного расширения; этому удлинению будет соответствовать возмож-
ная работа — N jO.ids.
Свободный взаимный поворот сечений ^9,-, вызванный неравномер-
ным нагревом (фиг. 339), очевидно, равен разности между удлинения-
ми крайних волокон (верхнего и нижнего на фиг. 339), разделенной на
расстояние между ними, т. е.
, at^ds — afg^s a(^j — tz^ ds aVds
d ~ d - d '
поэтому возможная работа моментов Mi на этом перемещении будет по
абсолютной величине равна . В том случае, когда кривизна, вы-
званная моментами М^, и кривизна, вызванная температурой, обраще-
ны в одну и ту же сторону, эта работа будет отрицательна.
При удлинении волокон, вызванном температурой никакого сдвига
сечений не получается, поэтому силы Q,- не совершают виртуальной
работы.
В итоге работа сил М,-, Q;, N. выразится суммой интегралов
.4 У Г ^i^a^^ _ у Г NjNqds у г \iQ,Qads
где суммирование интегралов распространяется на все элементы всего
сооружения.
Подставив это выражение в формулу (14.3), получим окончательно
+ 5]JN,.tds+ Y,J -^5^-Y,Rc. (И.4)
В этой формуле подинтегральное произведение М,М^ для элемен-
та as положительно, если оба момента изгибают этот элемент в однУ
сторону; произведение N^N^ положительно, если оба усилия растягива-
230
JOT
момент
или оба сжимают элемент; произведение M,t' положительно, если
,ент М, и температура f искривляют элемент в одинаковом нал-
«омми. И т. д.
оавлении, и т. д.
^ Само собой понятно, что формула (14.4) справедлива только в том
случае, когда деформации, вызываемые отдельными факторами —на-
грузкой, температурой и перемещением опор,—достаточно малы, чтобы
оправдать применение закона независимости действия сил.
Формула (14.4) дает общее решение, которое годится для всех пло-
ских упругих геометрически неизменяемых стержневых систем.
Характерно, что решение геометрического вопроса о нахожде1Ши
перемещений дано здесь в статической форме; при вычислении интегра-
лов приходится оперировать с силами того или ин
иного вида.
§ 14А ПРИМЕРЫ ВЫБОРА ЕДИНИЧНОЙ СИЛЫ
Когда эпюры М^, Qay N^, а также температура и перемещения опор-
ных или других связей заданы, то для нахождения каждого отдельного
перемещения требуется подобрать соответствующую ему единичную
силу.
б)г
Ci
Мп
Хг1
^
Ь)г
^
»¦ >
fXyl
#-'
д) с
е)
D
^5-'
-^ 9Й
/ 5«^
В,
ФИ1-. 340
Пусть, например, рамная система, представленная на фиг. 304,й на-
РУЖена заданной нагрузкой. ^...„.^„о
Если требуется найти вертикальное перемещение в точке С, которое
ЧЬ1 назовем через Д^,. то нужно приложить вертикальную силу Л, = J
в точке С (фиг 340.6). От этой силы нужно построить эпюры VW,, Уь
) и подставить их в формулу (14.4). .,^„.,„ п тп
Если требуется найти горизонтальное перемещение в точке />, то
">'^но приложить в этой точке горизонтальную силу, равную единице
231
mi й€ cnyTitfe ft
силой, обозиа^Щ
[йё обозначим через А|р
11^Ш^ сечении пару с моментом лз чч- ^^^
В, нужно прйлож
Для нахождения Bsaw
ного поворота двух пр©й^
вольных сечений С и D ну|
но «приложить в этих сеченйт^
ях две равные и взаим|фц
противоположные пары ^)
моментами Х4= 1- J
Для нахождения измене!^
ния взаимного расстояни®}
между сечениями С и
нужно приложить к ним
равные и противополозйй!
силы A^s*^!» направлеш
по линии CD (фиг. 34С
На фиг. 341, а
лена ферма, нагружёк^а|
заданной нагрузкой,
го чтобы узнать измененЩ
расстояния между узлаш ^
и Dy нужно восполшоваш^ ^
oj6o6meHHofi виртуа비"
л ой Xi^\, поКаз|1!1о%
фиг. 341,6, а дцр Ш»*;
найти угол Шво|^^
|:ледует приложить к его концам две далы JC2= ^-^4s
?Оментом, равным е^щинице (фиг. 34Э,в^ ^^^
эхих др'йм^ов виЦно, что фо
.видов
GF
(14.5'>
формула (14,5^) есть частный случай формулы (14.5). Разница
между ними состоит лишь в том, что через Мр, Np и Qp обозначены
пюры, вызванные всей совокупностью внешней нагрузки, а через Мг,
У и Qg —эпюры от единичной силы Xg^l.
^ Как показывают численные подсчеты, в балках, рамах и массивных
пках перемеш.ения, вызванные продольными деформациями стержней
^ их деформациями сдвига, обычно весьма малы по сравнению с теми
перемещениями, которые вызыва-
ются изгибом. В этих случаях
формулы (14.5) и (14.5') можно
заменить более простыми прибли-
женными ^^^^^^
(14.6)
^,-f
Фиг. 342
Фиг. 343
Пример И.1. Для балки АВ постоянного сечения (фиг. 342) определить прогиб в
точке R '^ %л ^ (^ — ^)
^ о. опюра Мр—квадратная парабола с ординатами, равными г слева
\. _^^*^^**ия С и нулю — справа от него. Эпюра М\ — прямая с ординатами, равными
Итак:
нить влияние нормальных и касательных напряжении н^ i
В данном случае »
2j —^7—= ^jl2 " 2 j 2 384 ?У
2jj Gf Gi^.r'^ 2 GF J
сил
Последний интеграл, выражающий площадь эпюры пог
НИИ половины пролета, равен разности между изгибающими моментами на концах того
же участка, т. е.
]¦
Qpdx^M -'Мо=М ^ ^
8
Приняв
получим окончательно
"1/7
\5_
384
у/4
EJ
+
1.20
3
8
_5_
384
EJ
(14-2,56^)
При—=10; 15; 20 второе слагаемое в скобках соответственно равно 0,0256; 0,0114;
0,0064; т. е. влияние поперечных сил на наибольший прогиб составляет 2,56; 1,14; 0,64%
от влияния изгибающих моментов.
1\р\\иг^ 14.3. Ферма (фиг. 344, а) нагружена тремя заданными вертикальными гру-
зами. Определить вертикальное перемещение узла 3.
Сила Хх^Х показана на фиг. 344, б.
Усилия, вызванные в любом стержне фермы силами Р, обозначим через Np, а
усилия, вызванные силой Xi — через Ni
^ip
Изгибающие моменты и поперечные силы
здесь, очевидно, равны нулю, поэтому
у С NiNpds
Для различных стержней усилия Np,
а также усилия Л''! получаются различными,
но для всех Элементов cf^ одного и то-
го же стержня они остаются постоянными,
поэтому, произведя интегрирование, получим
^ip
EF
(14.7)
Фиг. 344
где через / обозначены длины стержней.
Предположим, что панели верхнего и
нижнего поясов имеют длину cf=2,5 м\ дли-
на стойки /г=3 м\ площади сечений име-
ют размеры, указанные в табл. Z Дано
также, что Р=20 т. Усилия Ni и Л^р опреде-
или же при помоптм nuc,rt.a.,w лг ляются способом сечений и вырезания узлов
числений показТГтабл Т Кремоны - Максвелла. Порядок расположения вы-
вынос™!^ ^аменл^^^п^УГР"^^" "^^^^ переменное сечение, уже неДзя
грирование стаТот!^^^ ^"^""^ интеграла, вследствие чего инте-
разбивак^^ на к^^^^^^^ Обычно длину стержня
из ннх njHHHMarjrr ^^^''^'''' "" интегрируют на протяжении каждого
численные значениаГ''^ ""^ ^'^''"^ ^^^^^^^ постоянным. Полученные
^ tTHHbie значения интегралов затем суммируют
ги
Таблица 1
0,416
0,833
F
в кг/см
122 000
243 000
EAi^, = 2 088 300 см
§ 14.6. ПРАВИЛО ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ДЛЯ СЛУЧАЯ
КОГДА ОДНА ИЗ ЭПЮР ПРЯМОЛИНЕЙНАЯ
Очень часто одна из эпюр на том или ином участке сооружения име-
ет вид прямой линии. В этом случае интегрирование сильно упрощается
Пусть для некоторого ^ риш.с1С1^,и.
участка АВ требуется вы-
числить интеграл
\MiMkdx
J, EJ
где эпюра Mi имеет произ-
вольное очертание, а эпюра
Mf, -— прямолинейна (фиг.
345).
Сечение стержня на
участке АВ буде^м считать
постоянныхм. В этом случае
J EJ EJ J ' ^
^ А
Продолжив пряхмолиней-
ную эпюру Mf, до точки о ее
встречи с осью абсцисс,
можно написать
Фиг. 345
в
1
А
В
1
\M,M^dx = f M^ydx = f М,х tgadx = igoi Щ-xfdx.
A i "ij A
fj^ ^""У^^^нный интеграл хможно рассматривать как статический момент
Щал ^пюры Ml относительно точки О. Но статический момент пло-
в пе ^^^^" статическому мохменту ее равнодействующей, приложенной
нтре тяжести этой площади, следовательно:
в
tg а J M.xdx = tg awx^ = ioy^ ,
A
'"--площадь эпюры Mr,
»o"—расположенная под ее центром тяжести ордината эпюры Л1^.
Итак:
]M,M^dx=-v^yo,
(14.7')
* 235
т. е, искомый интеграл получается умножением площади эпюры М
расположенную под ее центром тяжести ординату прямолинейной ч ^^
ры Mfy (способ Верещагина). Необходимо помнить, что ордината и ^^^
рется непременно в прямолинейной эпюре. В том частном случае ко "
обе эпюры прямолинейные, можно умножить площадь любой из ^^^
на соответствующую ординату другой. ^^^
Таблица 2
Формулы для интеграла {MxM2dx
Y (^^аМа'Ь2МьМь+МаМь+МьМа) I
1 __
8 > другая представляет собой треугольник. Пло-
щадь параболы^у=~ l^ = s!L
лета. ^ ^ 12' ^^ ^^^"'^Р тяжести —в середине про-
лета.
Отсюда
12 2 li"
«ь.ес?ор^('УиТз46.б":°^' °^Р^"^^"«"'^ вершинами в противополож-
236
'^ 2 . 3 "^
J
Для двух прямолинейных эпюр, представленных на фиг. 346,в или г.
( M.,Mk<ix = (2ас + 2bd -\-ad^bc)~.
Разница между схемами виг только та, что на второй из них орди-
ната d должна считаться отрицательной.
При интегрировании произвольной эпюры с ломаной приходится
разбивать интеграл на несколько интервалов. Так. для фиг. 347 интег-
рал вычисляется так:
о в с о
(^ М, Mkdx = С MiM^dx + Г M^Mkdx + С MiM^dx.
А А В г
Для облегчения расче-
тов прилагаем небольшую
[^^ табл. 2 (стр. 236) интегралов.
Прилагаем также табл. 3
расчетных значений модуля
упругости Е,
Фиг. 34G
Фиг. 347
Таблица 3
Е в кг1сМ^
2,М0б
65 000—300 000
Материал
Дз^б ВДОЛЬ волокон
Сосна
Е в кг'см^
М05
J
§ «4.7. ПЕРЕЛ\ЕЩЕНИЯ В СТАТИЧЕСКИ НЕОПРЕДЕЛИЛ1ЫХ СИСТЕМАХ,
ВЫЗЫВАЕМЫЕ ВНЕШНЕЙ НАГРУЗКОЙ
вып!^ У^е видели, что перемещения, вызываемые внешней нагрузкой,
ь^ажаются формулой (14.5):
л _ V f MiMpds , V Г ^i^p^^ 4 V Г ii^^Se^
(14.89
237
При выводе общей формулы (14.5) мы рассматривали два состоя
одной и той же системы, поэтому казалось бы, обе группы эпюр т^^^
Njy, Qj, и Ml, //,-, Qy, относятся к заданной статически неопреле* ^*
Ж,
/7 »
мой системе. Такое толкование будет вполне правильным, и если
построим таким образом эпюры, входящие в состав формулы (14 5) ^^^
получим требуемое перемещение. Однако мы столкнемся при этом ^^
следующим неудобством: каждый раз, когда нам потребуется н "^^
перемещение новой точки или по новому направлению, нам прил^"^^
наново строить статически неопределимые эпюры уи^
Л^/, Q, и для этого наново решать статически неопределимую зада/
Фиг. 348
Мы можем избежят^ ^^
сом о том. что. соб?тв1нно Sefvef of • "'•"" задумаемся над вопро-
7X1?' "^ Ф"^- 348 заданной сиет.мо'''" '"^^"«°« ^""^^•«й- ^"^^
1аш?^п°"" "^^ ^"•'то не мешает на'ппг Р^^^РеДеленной нагрузкой ии-
защемляющий момент X, на правом "PfJJ"'=-""^b опорную реакцию J, "
заданной балкой буд1т та кД^'- "" внешней нагрузке; тогда
имеемТп^"""" на леюм конце и ?Й "''^'^"^"""^"^ ^-"^^а на схеме б,
1аком Л^^° "Ричислить к внешней ^Лп^"^" "^ "Р^'^ом- Но мы также
т е явлГ^^'''^'""^«ба^Гимеетв^^^^ °б^ ™орных момента; в
системой '''' шарнирно опео?ой nf ^' показанный слева на схеме в,
HeS " Г "'^'=^'^'"Раво c"iS Итак, заданной
TopaS no^v!:'^'^ ^«"^му. но и BcoKvfo гГ''" действительную статически
оран получается из нее путем удалена ''^¦'Р"^'^^'^" «еизменяемую. ко-
238 ^ "^ удаления тех или иных связей.
Предположим, что требуется определить прогиб Ai^, в какой-либо
точке балки. В зависимости от того, какую систему, образованную из
нашей балки, мы будем считать заданной, мы будем получать различ-
ный вид эпюр Ми А^ь Qb В правой части фиг. 348 показаны различные
варианты эпюр Мь окончательный результат вычислений по формуле
(14.5) должен получиться один и тот же при всех этих вариантах.
Итак, формула (14.5) обладает следующим свойством инвариантно-
сти: под эпюрами Ml, Q,-, Ni мооюно понимать эпюры, вызванные
соответствующей единичной силой Xi = l не только в действительной
статически неопределимой системе, но и в любой геометрически неиз-
меняемой системе, которая образуется из нее при помощи удаления тех
или иных связей.
Проще всего эти эпюры, конечно, получаются в статически опреде-
лимых системах. Ими и следует пользоваться. Поэтому в дальней-
шем, применяя формулы (14.4) и (14.5), мы всегда будем
понимать под Mj, TV,-, Qi эпюры, получающиеся в стати-
чески определимой системе.
§ 14.8. ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ
В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
СИСТЕМАХ
В статически определимых системах температура вызывает переме-
щения, но не вызывает ни изгибающих моментов М, ни поперечных сил
Q, ни продольных N. Стержни статически определимой системы от дей-
ствия температуры удлиняются или укорачиваются, но не
растягиваются и не сжимаются; от неравномерного нагрева или охлаж-
дения они искривляются, но не изгибаются.
При подсчете чисто температурных перемещений такой^системымь!
должны положить в формуле (14.4) M^=0, А/^-О, Qa-^. ^-^- ^
результате получаем
(14.8)
Значения коэффициентов а приведены в табл. 4.
Коэффициент линейного расширения а
Таблица 4
Материал
Материал
Стал
ь литая
• Незакаленная .
118Л0
108.10"
107-10
—7
Бетон па цементном
растворе •
Железобетон
120-10
120-10~
, Если по всей длине каждого стержня температура остается одна п
та >Kfi п>^
Же, то
^„^^at^N,cis+^<^t'^^ds.
(14.9>
i
Интеграл f ЛА/ ds представляет собой площадь эпюры норма пьнкт
сил Л/, на протяжении стержня, а ) — площадь эпюры ^. Еспи
стержень имеет постоянное сечение, то знаменатель d можно вывести
из-под знака интеграла.
Рассмотрим сначала несколько прИхмеров, относящихся к статически
определимым системахМ.
Дана П-образная рама (фиг. 349,а). Требуется определить горизон-
тальное перемещение опорного сечения В и угловое перемещение сече
ния D при различных те^мпературных режимах.
Обозначи.м первое перемещение через Ai^, а второе через Ag^. Соот-
ветствующие эпюры Ml, Nu М2у N2 представлены на фиг. 349,6 ив.
Пусть ригель CD и
левая стойка АС под-
верглись равномерному
нагреву на Ю"". При та-
ком нагреве характери-
стика неравномерности
^'=0, поэтому в форму-
ле (14.9) остается толь-
ко первая су.мма:
^Л
W^A
Ui
Фиг. 349
N2=0.
Поэ^ом?''^ ^ " « ™°. ^"о ДЛЯ стоек Л^,.о; а для ригеля N,
^^ПРИ вь„„еле„„и Л. обратим внимание на то. что для правой схой-
С
^2/ - а(+ 10-) iJN^ds = а(+ 10-) /+-1 А ) == 15?^
А \ I ) I '
Зададим тепеок пп,г^,^^
пературы подвер^гае^т?Гт^ТГГг7Г"*' У^°""«' "У"ь действию тем-
240 Р"'^^'"'' "Ричем он нагрелся так. что
температура верхнего волокна поднялась на 20° я ни^^^.^ со
тогда при^симметричном сечении ригеля получается темпера7ура' по
его оси I- — 13, а разность температур if'=± (20—6) = ±14°
Так как для остальных стержней /=f=0. то в формуле будет Лигу
рировать только стержень CD: ^ f^^y^ic иудет фигу-
D D
A,,=a(+13)U,ds±^-L4rMirfs = a.l3.1/_^4
Во втором члене поставлен знак минус, потому что температура и
момент Mi вызывают искривление ригеля в противоположные стороны
Нетрудно понять, рассматривая схему рамы и чисто геометрически что
искривление ригеля, обусловленное заданной температурой вызывает
перемещение точки В влево.
При вычислении перемещения ^^t обратим внимание на то, что для
ригеля /1^2=0, поэтому первый интеграл пропадет. Это означает, что
равномерный нагрев ригеля не вызывает поворота сечения D. Итак:
^-^1
С
Теперь обратихмся к системам статически неопределимььм. Под влия-
нием температуры возникнут усилия в лишних связях, поэтому систему
можно считать статически определихмой, но находящейся под совмест-
ным действием температуры, с одной стороны, и вызванных ею реакций
в лишних связях, с другой стороны.
От этих реакций возникнут эпюры, которые мы назовем М^ , Q^, N^
Отсюда ясно, что искомое перСхмещение хможно выразить как сумму двух
перемещений, из которых одно вызывается силами, а другое — темпера-
турой:
^^^-'L]—^J— + L}-^+L} OF "^
+ SjA^.a.rfs+2f-^^- (14.10)
Напоминаем еще раз, что М-, , Л/,^, Qi в формуле (14,10) берутся в
любой статически определимой системе, которая может быть
получена из данной при помощи удаления лишних связей, а М^ , Q^, Nj
относятся к заданной статически неопределимой системе. Само собой
понятно, что до тех пор, пока мы не решим статически неопределимую
задачу о температурных усилиях заданной системы, мы не в состоянии
^Удем найти ее перемещений.
§ 14.9, ПЕРЕМЕЩЕНИЯ, ВЫЗЫВАЕМЫЕ ПЕРЕМЕЩЕНИЕМ ОПОР
ИЛИ ДРУГИХ СВЯЗЕЙ
^ В статически определимой системе этот фактор не вызывает ника-
ких усилий, поэтому задача не связана с понятием об упругом теле и
^^ет чисто кинематический характер.
^^ Рассмотрим в первую очередь чисто статическое решение этой кине-
;^атической задачи В строительной механике, как известно, кинемати-
^^кий метод применяется для решения статических задач. В данном
^6 "^^ М. Рабииович 241
случае этот метод, если можно так выразиться, будет вывернут наиз^
нанку.
Возьмем для примера раму АВ (фиг. 350,а) и предположим
опорный стержень В переместился по своему направлению на кел ^^^
ну с. Требуется определить перемещение данной точки К по данном '^^^
правлению i—L Назовем это перемещение А^^. Для решения з ^ ^^"
нагрузим раму силой Х^ =1, приложенной в точке К по направл^^^"
искомого перемещения (фиг. 350,6). Реакцию в опорном стерж^"^
вызванную этой силой, назовем /?. За положительное направлени"^
Ф \ ф Y
^"
Фиг. 3^0
мещения с; на фиг 3506 п^^*^"^ ^ положительным направлением пере-
ной. Принимая заданное п<=п«'^'^"^ ^ Должна считаться отрицатель-
нение работ для сил состояния?Т*' ^^ возможное, составляем урав-
откуда
1.Д.^ + ^?с=0,
(14.11)
K = ~Rc.
Если^од^КеннГпроТсад^^^^^^ ^•"У''^<=^' Ф^Р^У-^^г (14.4).
идит несколько перемещений, то
(14.117
Ч = —Е/?с.
Для применения чтпй а^ч
"^f„f ^^вшейся связи нагоу^иГ."» ^«"^-^очно определить реакинК)
числить с обратным внати1Тбот^'^^^'^ виртуальной силой, затем вЫ-
242 ^^^^ реакции на заданном перемещении-
Так. например, для определения угла повооота rpup„„^ п
пар)' J^i = • (схема в) и получаем ^ сечения D прилагаем
^"-(-i)-7-
Для определения вертикального перемещения точки D прилагаем
силу ^2=1 (фиг. 350,г) и находим А^^ = — (_iw^^ ^" ^ прилагаем
Чисто кинематическое решение мы проиллюстрируем всего двумя
примерами. ^ t^j - а у.м»
Фиг. 351
Во-первых, найдем горизонтальное перемещение точки D рамьЛЛВ
(фиг. 350). Для этого удалим стержень В и заметим, что рама повора-
чивается, как один диск, вокруг точки А. Угол поворота равен —, поэто-
му горизонтальное перемещение точки D равно — h.
Во-вторых, найдем взаимный поворот полурам (фиг. 351,а), обу-
словленный горизонтальным перемещением пятового шарнира В\ назо-
вем это^ перемещение А (положительное — вправо). Удалим горизон-
тальный опорный стержень В (фиг. 351,6) и отодвинем точку В вправо
на величину Л. Построим полярный план скоростей: из произвольного
полюса О (фиг. 351,в) проведем прямую Ое^АЕ, таким способом полу-
^^им изображение точки Е, Изображение точки В найдем на пересечении
"Рямых еЪ и 0&, где еЪ\\ЕВ и Ob — вертикально.
Изображения точек С и D сливаются в одну точку с, d.
горизонтальное перемещение точки В, равное с, выражается верти-
^^альным вектором 0&, следовательно, ОЬ = с; Ос== —-. Угол поворота
*пп^^^ ролурамы равен отношению длины изображения произвольной ее
Рямой к длине самой прямой:
^АСЕ ^
^^ Поворота правой полурамы
Ос ^
АС .
BD
с
^ 2Л *
с
~ 2Л
16»
243
.„«,. MHHVc поставлен потому, что направление вектора bd про-
^Гоположно ^рав'лению вектора BD. Итак, угол поворота левой по-
лурамы относительно правой
^гс-
2/г
V 2ЛУ h '
Фиг. 352
Результаты рекомендует-
ся поверить статическим ме-
тодом.
Переходим к вопросу о
перемещениях, возникающих
от той же причины в систе-
мах статически неопредели-
мых. Возможно двоякое ре-
шение этой задачи.
Во-первых, заданную си-
стему можно рассматривать
как статически определимую
находящуюся под совмест-
ным действием двух факто-
ров: с одной стороны, — за-
данного смещения опор или
других связей, а с другой
стороны, — усилий, вызван-
ных этим смещением в лиш-
них связях. Формула (14.4)
тогда примет вид
А/с
^ у Г MjMcds , у Г NjNcds у С \xQiQcds _ у j^^
(14.12)
В этой формуле буквами М^, 1^1^ , Q^ обозначены усилия в стати-
чески определимой системе, вызываемые силой J^^ =1, а буквами М^* ^^»
Qc — усилия в статически неопределимой системе, возникающие в ре-
зультате заданного перемещения связей.
Во-вторых, можно рассматривать заданную систему в том виде, как
она есть, и к ней уже .приложить виртуальную силу J^^ = 1. Тогда фор'
мула (14.4) примет вид
где через R' обозначены реакции, возникающие в заданной статически
неопределимой системе от действия силы X, =\.
Для иллюстрации применения формул (14.12) и (14.13) определим
двумя способами угол поворота опорного сечения В статически неопре-
делимой балки АВ, представленной на фиг. 352,а. Приняв за основную
неизвестную реактивный момент на левой опоре и решив статически
неопределимую задачу, можно убедиться, что этот момент равен -^/»
причем растянутое волокно расположено сверху Соответствующая эпю-
ра изгибающих моментов М, представлена на схеме б. Итак, балка Лр
может рассматриваться как балка с шарнирно опертыми концами' >
которой перемещения вызваны опусканием правой опоры и, кроме того,
изгибающими моментами, которые представлены эпюрой Мс . За поЛО
жительное направление искомого угла поворота примем идущее по ^^
совой стрелке. * ^ -
244
очевидно, что в простой балке вертикальное перемещение правой
опоры вызывает поворот всего пролета и в том числе интересующего
j^ac сечения Б на угол-^. Но раз мы решили применить формулу
(14.12), то мы все же определим реакцию /?, вызванную парой Х^ =1.
Эта реакция равна — и направлена вверх.
Эпюра М^ представлена на схеме в. Эпюрой Q,- пренебрежем. Вы-
чпсление по формуле (14.12) дает следующий результат:
Для того чтобы воспользоваться формулой (14.13), приложим пару
Л^ =1 к заданной балке. Для этого нам придется решить статиче-
ски неопределимую задачу и построить эпюру Л1^ . Не проделывая
этого решения, приводим готовый результат в виде эпюрьь
М, на фиг. 352,г. Реакция правого опорного стержня при этом равна
—. Отсюда
2/
Д. ^^/-А\^__ 3/
\ 2/ Г 2/
Для практического применения формула (14.12) удобнее формулы
(14.13), так как не требует решения наново статически неопределимой
задачи каждый раз, когда приходится разыскивать новое перемещение.
В том случае когда заданная система статически определима, фор-
мулы (14.12) и (14.13) сливаются с (14.11).
§ 14.10. ПОСТРОЕНИЕ ЛИНИИ ПРОГИБОВ КРИВОГО
ИЛИ ЛОМАНОГО СТЕРЖНЯ ПРИ ПОМОЩИ УПРУГИХ ГРУЗОВ
Кривой стержень, не имеющий промежуточных шарниров, находя-
Ш.ИНСЯ под действием произвольной нагрузки, можно разбить на доста-
точно малые участки, которые приближенно можно считать прямолиней-
№ми; на протяжении каждого участка эпюра моментов также прини-
мается приближенно за прямолинейную. Многоугольник, образованный
вертикальными перемещениями узлов стержня, условно принимается за
веревочный, образованный вертикальными «упругими» грузами Wn
(фиг. 353).
С помощью принципа возможных перемещений можно вывести.
^ощую формулу для величин ш„ . Приводим ее без доказательства:
Е t
\^^"» ^n+i —нормальные напряжения.
*^оследние два члена правой части можно написать также в виде
где 1
п» ^ri+i — относительные удлинения.
Уд^^^^^ыкающая веревочного многоугольника проводится так, чгтобы
^лет^рорить граничным условиям.
245
1'Де
^Де/
По своей размерности величины w„ суть отвлеченные числа Р
построить из них силовой многоугольник с полюсным расстоянием '"*'
ным Я, затем построить''г'^"
ответствующий веревочный
многоугольник, то ординате,
последнего выразят прогибе
масштабе: 1 см ординаты^
-Лп см при условии, что ли
нейн_ь1е масштабы сооружГ
ния — 1 : л, а полюсное пас
стояние Н измерено в мае"
штабе, принятом на силовом
многоугольнике для сил ш
Построение веревочного
многоугольника — необяза
тельно; упругие грузы мож-
но использовать аналитиче-
ски, вычисляя прогиб в лю-
бом сечении, как умножен-
ную на Н сумму моментов
всех упругих грузов, распо-
ложенных слева или справа
От сечения.
Для цепи, образованной
прямыми стержнями, шар-
нирно-связанны1ми между со-
бой, формула (14.14) не го-
дится, так как в ней не учте-
на возможность произволь-
смежных стержней. Как вычисляются vnn,,."°^° взаимного поворота
зано в следующем параграфе. У"РУ™е грузы в этом случае, ука-
§ 14.П. ПОСТРОЕНИЕ
ЛИНИИ ПРОГИБОВ
КАК ВЕРЕВОЧНОГО
МНОГОУГОЛЬНИКА
Если нас интересуют O-A^'l
перемещения не всех уз- >Л,-^— Д
лов фермы, а лишь узлов I
верхнего или нижнего по- ! i
яса. притом не полные пе- ' '
Ремешения, а лишь проек-
ции „X на определенное
направление, то можно
обойтись без построения
диаграммы Виллиа К
этой цели разработаны не
посредственные способп
лостроения линии 'про
здесь условно понимают-
ся вертикальные пепемр
щения). переме-
246 Фиг. 354
Выделим из фермы интересующий нас пояс 0—1— ^«о-Ох..^
отдельную шарнирную цепь (фиг. 354) и будем разыскивать пппр1
ции перемещений всех узлов этой цепи на какое-ниб^Г зад1шТ^^^^
правление, например на вертикальное. Введем лишь одао ограничение-
с^еди стержней рассматриваемой цепи не должно быть ни одного н^
Давленного параллельно проекции перемещения (в данном случае ни
одного вертикального). ^ "^ ^ уна^ нп
Допустим, что линия прогибов уже
найдена. Возьмем произвольную пря-
мую аЬ и от нее отложим на вертика-
лях, проходящих через узлы, соответст-
вующие вертикальные перемещения уь ,
У2 и т. д. Примем эту линию прогибов ^jL'
за веревочный многоугольник для не-
которой фиктивной системы вертикаль- Фиг. 355
ных сосредоточенных сил Wi, Ш2,..., ко-
торые мы будем в дальнейшем называть «упругими грузами».
Запишем прежде всего связь между величинами w и у.
Ординаты у^_1, у^, у„_^1, умноженные на полюсное расстояние Я,
можно считать изгибающими моментами; величины
„ Уп—Уп^1 гг Уп-^\ —Уп
Н и п поперечными силами; разность этих по-
перечных сил — величиной сосредоточенной силы ш„ :
^sj^^^hI-^^^^^^-^^ ^"•^'~^" V (14.15)
где Я — полюсное расстояние силового многоугольника, которое мо-
жет иметь произвольную величину.
Выразим теперь разности у^ — y„_i и y^^j—у„ через удлинения
стержней и углы поворота. Рассмотрим стержень п—1,/г (фиг. 355).
Его удлинение вызывает уменьшение прогиба Уп на величину М„
sin р„, а его поворот на малую положительную величину Др„ вокруг
точки /2—1 обусловливает уменьшение прогиба на величину /^ Др„
cos р„ , следовательно:
у^ — Уп-х _ А/;, sin ^„ + in^^n cos pn
Но Х^ =/^ COS Р„; поэтому
Уп-Уп-! ^
где ^„—относительное удлинение стержня п—1,л.
Точно так же
Отсюда ^"^'
^о так как
АР„+,-ДР„=Д9„.
упругие
угла-
где Д<р„ - взаимный поворот стержней, примыкающих к узлу п, то окон-
чательно
-i- Ш„ = Д<Р„ — ^п tg ^п + Wl ^g Pn+Г (Н. 16)
Еслир„-90°илир„^1 =90° тош„ = ± «=.Но этот случай мы с са-
мого начала исключили.
Если стержни не испытывают никаких удлинении или укорочений
т. е.если./; = ^ =0, то -^ш„ - Д^п- В этом случае "
грузы в известном масштабе выражаются
ми взаимного поворота смежных стержней.
То же самое получается в том случае, когда стержни горизонтальны,
так как при этом tg pn=tgp«+i =0.
Итак, при условии, что все относительные удлинения стержней и их
углы взаимного поворота известны, мы можем легко построить линию
прогиба как веревочный многоугольник. Зная, кроме того, прогибы в
двух точках (опорных), мы сможем про-
вести и замыкающую аЬ.
Остается показать, каким образом
'МОЖНО определить величины Аср^ , Пред-
варительно решим следующую элемен-
тарную задачу: по заданным весьма ма-
лым относительным удлинениям сторон
шарнирного треугольника (фиг. 356,(2)
определить изменение его углов.
Фиг. 356
Фиг. 357
Так как изменения углов треугольника не зависят от его абсолютно-
го перемещения, то примем точку А неподвижной и стержень АС —
неповернутым. Предположим, что сторона h удлинилась на А/,, а
остальные две остались без изменения. На фиг. 356.6 построена для
V^^o^r.^!^^T''i да^^Р^^ма Виллио; стороны 92 и Рз перпендикуляр-
ны сторонам /2 и /з, причем, согласно свойствам этой диаграммы, Р2 =
=—/2 Дад или Да^^ ^
Знак минус поставлен потому, что на фиг-
^^^Hs^rnJwnf ^' "^"Р^?А^« вниз, следовательно, угол «з уменьшился.
из треугольника А'В'О получается пропорция
или
Ро = A/i = sin (90" — а,): sin (180° — aj
sina^
Но из треугольника ABC
Асс. = _ iL==_iii
вытекает
/i s/g = sinaj: sinotg
или /oSinaj^/jsinotg.
/2 sin aj
* л ^h COS «2
Подобно этому
Д«2 = —^*iCtga3,
Наконец
Д^1 == - (Д«2 + Ааз) = /Jetgag + ctgccs)- (14.17)
Влияние относительных удлинений iz и k можно найти из тех же
формул путем циклической перестановки индексов. Остается просумми-
ровать влияние всех трех удлинений, и мы получим искомый результат.
Заметив, что в случае отсутствия температурных удлинений
где через о обозначены напряжения, можно написать этот результат в
следующем виде:
Е^Н =-- (<^1 — 02) ctg «3 + {<^1 - og) ctg 0С2; ]
?Аа2 = (о2 —03)ctgai + (02—ai)ctgoc3; I (14.18)
^Лаз = (og — oi) ctg «2 + (<'з — <'2) Ctg «1. J
В этих формулах растягивающие напряжения считаются положитель-
ными, а сжимающие—отрицательными.
Обратимся теперь к ферме (фиг. 357).
Пусть требуется определить изменение угла <р„ между двумя смеж-
ными элементами нижнего пояса. Сначала определяем из отдельных
примыкающих к этому узлу треугольников величины Аа^, Aag» ^^з-
Далее, продифференцировав тождество
«1 + «2 + «3 + ?п = 27Г = const,
получим
Д?п = — (Д^з + Аа2 + Ааз).
В этом и состоит окончательное решение вопроса о нахождении ве-
личин Дср„, необходимых для вычисления упругих грузов.
§ 14.12. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Вопрос о простом и вполне общем способе определения перемещений является
центральным вопросом теории статически неопределимых систем. В течение долгого
времени, включая первую половину XIX столетия, такой формулы не было, н это в
свою очередь являлось причиной отсутствия общего метода расчета статически неоп-
ределимых систем. В 1854 г. важный шаг вперед был сделан французским ученым Брес-
сом» (А. С, Bresse, 1822—1883).
Общий путь для вывода формулы был указан в 1864 г. Максвеллом в работе, vno-
""^^Щ^йся выше: сближение двух произвольных точек А и В фермы он рассматривал
nBv ^^^^"^У ^^Ух равных и противоположных внешних сил Р=1, приложенных в этих
д ух точках. Приравняв эту работу работе внутренних продольных сил, он получил
тичр"^*? формулу. Максвеллу, следовательно, принадлежит идея использовать энерге-
Rpo "" принцип для вычисления перемещений. По этому пути пошлн в дальнейшем и
^^е другие авторы.
ISSS^Iqiox^P^^"^^^^^ систем общая формула была выведена проф. Мором^ (О. Mohr,
Бпрр„« , ,1' ^ несколько дополненном виде она была представлена проф. Мюллером-
радауз (н. Mulier-Bresiau, 1851—1925).
^^54. ^^^^^^bes analytiques sur la flexion et la resistance des pieces courbes, Paris.
^annm,t!*'^^t?. ^' Theorie der Bogenfachwerktrager, Z. der Arch. u. Ing.-Vereins zu
j^jver. 1874; Beilrag 2. Theorie des Fachwerks, там же, 1874 и 1875.
^^^ neueren Melhoden der Fesligkeilslehre, 1886.
Общая формула для любых упругих систем была дана Кастилиано^.
В СССР были разработаны практические способы вычисления интегралов, входя,
щих в формулы перемещений^; изучены некоторые общие свойства перемещений упру-
гих системе а формула перемещений стержневой системы распространена на сжато-
изогнутые стержни^.
1 Nuova teoria dell' equilibrio del sistemi elastici, Torino, 1875.
2 A. H. В ерещагин. Новые методы расчета статически неопределимых систем
«Строительная промышленность», 1925, стр. 655.
^И. М. Рабинович, О некоторых соотношениях между перемещениями точек
упругого тела. Труды Московского института инж. транспорта, вып. III, 1927.
4 Н. В. Корноухо в. Прочность и устойчивость стержневых систем, М., 1949
гл. III, § 19. ' * *
Глава 15
ОСНОВЫ МЕТОДА СИЛ
§ 15.1. ОСНОВНАЯ СИСТЕМА И ОСНОВНЫЕ (ЛИШНИЕ) НЕИЗВЕСТНЫЕ
Изложение методов расчета статически неопределимых систем мы
начнем с метода сил, который является старейшим, имеет обширную об-
ласть практического применения и является .в то же время для учащегося
в
-V-
|4i?
SJ
^ ^
е)
t*
?
Фиг. 358
превосходной подготовительной ступенью для овладения 'Всеми прочими
методами.
^ ^зрактерная особенность этого метода состоит в том, что в нем
есь ход расчета зависит от количества лишних связей заданной систе-
> или, как говорят иначе, от ее степени статической неопределимости.
Ч9и^^^^^^ лишних связей, тем легче решается задача методом сил;
м^оольше лишних связей, тем труднее.
Расчет
статически неопределимой системы по методу сил начи-
получ^ ^ '^выбора так называемой основной системы. Основная система
чео-г!^^^^ из заданной при помощи удаления того или иного коли-
^ga лишних связей.
Во (v,g^ "Р^ктике в большинстве случаев отбрасывается такое количест-
основ ^^^' которое в точности равно количеству лишних связей. Тогда
^^реде^^ ^^^^^^^ получается геометрически неизменяемой и статически
•"'имой. Необходимо обратить внимание не только на кол ичест-
251
<^)
г. „п ы на их расположение, для того чтобы
во отбрасываемых с^^^^^'^^_" обладающая в той или иной своей
случайно не получилась си^^^^^^^^
части или в целом J^^^^^PfJ;^^^^^^^ с того, что подсчитывается чис>
Выбор основной ^«^"^^^^^^^ ^.теме После этого намечают различные
ло лишних связей в зада-ннои ^^ • возможные варианты отбра-
сывания лишних связей. По-
ё)^—о ^ -—^ лученные основные системы
проверяют с точки зрения
их геометрической неизменя-
а4 I ^ ^^ ^ ш Примеры правильного и
^^ ^ "'^' ' неправильного выбора ос-
Ф^г осо ионных систем показаны на
^ • фиг. 358 и 359. Фиг. 358,а
^^w^, fhwr ЯБ8 б в г,д,е — статически опреде-
^Гяет SS дисТна трех о;горных стержнях, не пересекающихся меж^
а)
хи^.х^
S)
t Т Y
Г' гг \
^
^3
^3
А2 ^3'
Фиг. 360
ду собой в одной точке. Схема, показанная на фиг. 358Д состоит и^
диска ABC на трех опорных стержнях и прикрепленного к нсхму дву>^"
стержневого узла D, Читателю предоставляется самому рассмотреть
схему фиг. 358,е.
На фиг. 359, а, б показаны неправильные, негодные основные систе-
мы, полученные при ошибочном выборе отбрасываемых трех связей.
Статически определимая основная система, как мы уже упоминали,
применяется наиболее охотно. Однако не исключается возможность пр -
меиения основной системы статически неопределимой. Д^
получения такой системы нужно, чтобы число связей, отбрасываемь
из заданной системы, было меньше числа ее лишних связей.
Когда основная система выбрана, то усилия, которые заменяю
собой отброшенные связи, принимаются за основные неизвестные.
Так, например, 'Воэвраш.аясь к статически неопределимой ^^^'^\^
(фиг. 358,а), мы можем выбрать неизвестные так, как «показано ^
фиг. 360; на схемах б, е, г за неизвестные приняты опорные реакции,
на схеме д — изгибаюндие моменты.
Эти неизвестные являются основными по той роли, которую они
играют в расчете статически неопределилюй системы. Вся труДН<^^'^''
252
задачи заключается в том, чтобы найти эти неизвестные; коль скоро они
Отчислены, все остальные усилия определяются весьма просто. тХесли
Sbi обошачим искомый изгибающий -момент в произвольном сечении
через Ж, продольную силу - через Л^ и поперечную-через Q, то эти
величины мы сможем определить по следующим формулам-
N = N^X^ + N,X, + -^.+ N.X, + ... + N,X, + N' (15.1)
Здесь через М^, Ni, Q^ обозначены усилия, возникающие в том же
сечении основной системы при действии силы Х^ =1^ Так как
основная система —статически определимая, то и величины М-, N^, Q-
определяются из уравнений статики. ^» " t
Если речь идет о нахождении усилий М, N, Q, ^вызванных не внеш-
ней нагрузкой, а температурой или смещением опор, то в формулах
(15.1) нужно положить М^^О, N^=0, Qp=0, так как в статически
определимой основной системе ни температура, ни смещение опор не
вызывают никаких усилий.
Итак, хотя система содержит бесконечное м<ножество сечений, а сле-
довательно, общее количество неизвестных значений М, N я Q беско-
нечно велико, все они выражаются через п основных («лишних») неиз-
вестных Хь ^2, ..., Хп- Основные неизвестные — это как бы хранители
тайн статически неопределимой системы. Кто нашел значения X],
^2,..., Х^, тот разгадал и всю картину распределения усилий.
§ 15.2. СИСТЕМА КАНОНИЧЕСКИХ УРАВНЕНИЙ МЕТОДА СИЛ
ДЛЯ РАСЧЕТА НА ДЕЙСТВИЕ ВНЕШНЕЙ НАГРУЗКИ
Вообразим себе заданную статически неопределимую стержневую
систему, находящуюся под действием неподвижной внешней нагрузки.
Требуется определить усилия во всех сечениях всех стержней.
Для решения этой задачи необходимо выбрать основную систему
и основные неизвестные. Произведя эту операцию, мы тем самым как бы
заменяем заданную систему основной системой. Но в то время как задан-
ная система нагружена только заданной внешней нагрузкой, основная
система загружена сверх того всеми основными неизвестными. Таким
образом, 'ВЫХОДИТ, что мы преобразовываем одновременно как сооруже-
ние, так и его нагрузку.
Если заданная статически неопределимая система содержит п лиш-
них связей, то система п уравнений в общем виде может быть записана
Так:
\,Хг + Ь,^Х. + \,Х^ + '•' + ыХп + \р =- 0;
Кг^г + К2Х2 + KsXs + '••+ ^^ппХп + ^пР = 0.
(15.2)
,, В нашей литературе уравнения (15.2) получили название к а нон и-
l^^KHx уравне.ний метода сил. Принципиально они заклю-
ь^ в себе полное решение поставленной задачи и поэтому заслужи-
^ нашего особого внимания.
;^апись уравнений (15.2) *в буквенном виде очень проста.
Обратимся к рассмотрению их смысла. Для этого достаточно будет
"^дробно разобрать содержание какого-нибудь одного из уравнении.
253
например первого. Первый его^ле„ им^т ^-^^„^'„ь ,^^«„"«»™ь ^
есть переметение то^жиприло^^^^^^^^^^^ ^^^^^^^ ^^^^^^^^^ ^^^^ ои^Же
силы, вызванное силой л^^^ перемещение той же точки, по тому
значении ^«^^^^^/,^ Р^н^^^^^^^ Х,. Второй член, 5,, X,, выражает со^-
STp^e^SS т^^^ ™му ж'е направлению, но вызванное
си^ГиТГпоследний (свободный) член \^ выражает собой пере,
мешение-в том же месте и опять по тому же направлению но .вызванное
S швокупно^^^ -внешней .нагрузки. Пролисная буква А вместо строч-
ной 8 выбрана потому, что перемещение Д,р вызывается ие единичной
силой и имеет .поэтому другую размерность, чем о^^, Ь^^ и т. д. Вместо
Д р можно было бы написать Е Я8,р.
Вся левая часть первого уравнения выражает собой алгебраиче-
скую сумму отеремещений точки приложения силы Xi по направлению
этой силы, вызванных всеми действующими силами. Короче: левая
часть выражает собой суммарное перемещение
точки 1 по направлению 1.
Мы приравниваем это перемещение нулю согласно условию, так как
в заданной системе оно отсутствует.
Для большей ясности рассмотрим пример, представленный на
фиг. 360,6. В примонении к этой системе первое уравнение <представляет
собой математическую запись того простого факта, что вертикальное
перемещение точки D равно нулю.
Второе уравнение выражает собой то условие, что суммарное пере-
мещение точки 2 по направлению 2, .вызванное 'всеми силами, равно
нулю. Для фиг. 360, б это означает, что горизонтальное перемещение
точки D равно нулю, и т. д.
Для схемы фиг. 360,(9, где неизвестными служат моменты, первое
уравнение -выражает собой отсутствие взаимного поворота тех двух сече-
ний, к которым приложены пары Xi; -второе уравнение выражает собой
такое же условие, относящееся к парам Х2, и т. д.
Каково бы (НИ было заданное сооружение, мы всегда можем распо-
ложить неизвестные так, что .перемещения по их направлению будут
заведомо равны нулю, и тогда математическая формулировка этот
факта сейчас же приведет нас к системе канонических уравнений
нений™^ простейший, чисто геометрический смысл канонических ураз-
§ 15.3. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ РАСЧЕТА
НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ
В этом случае канонические уравнения пишутся следующим обра-
зом:
Ч..Х, + о,А ь с.Л + ... + г,„Х„ + А, = 0; [ ^,5.3>
вме^Гсвободаых''зден'^Д^ Системы (15.2) состоит только в том. «тс^
выражаюише собой '^' ^'' ' "" пр^лесъ стоят члены й,<, Дг/» ¦-'"','
системе. 'температурные перемещения i ооновнои
Геометричеокий смысл систем (15.2) и (15.3) один и тпт w^ п«^
выражают ту мысль, что суммарные перемещения по напоавленик.п?
брошенных связей равны нулю. -м ия по направлению от-
Совершенно такой же вид имеют уравнения -в том случае когда
расчет ведется на усадку бетона. В этом случае свободные члены' ^Zu
Сажают собой перемещения, воз-никающие в основной системе не от тем-
JepaTypbi, а от усадки бетона. Действительно, с геометрической тотки
зрения усадка, как фактор, вызывающий изменение размеров стесжнеТ
аналогична температуре. ^^ ^ "^ ^ержнеи.
§ 15.4. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ СЛУЧАЯ
ЗАДАННОГО ПЕРЕМЕЩЕНИЯ ОПОР
На практике смещение опор возникает как следствие подмыва грун-
та под фундаментом или оползня или просто недостаточной несущей
способности грунта. Эти смещения могут быть как линейными так и
Фиг. 361
угловыми. В статически неопределимой системе при смещении опор,
•^ак известно, появляются усилия. Для определения всех усилий не-
"оходимо предварительно найти величины основных неизвестных.
^ти неизвестные всегда можно выбрать так. что соответствующие
им перемещения будут равны нулю. Допустим для примера, что в раме
^Фиг. 361, а) опора В переместилась в положение В', т. е. передвинулась
ВДз на величину а, вправо на b и повернулась по часовой стрелке «а
1\°^ 9. В качестве основной системы .возьмем фиг. 361,6, на которой
равая стойка отделена от своей опоры. За основные неизвестные при-
сит.^ v^" взаимодействия между стойкой и опорой, т. е. две силы л,, две
пеп ^ " лве пары Хз- Очевидно, что © окончательном итоге взаимное
Ремещение конца стойки относительно опоры В равно нулю, так как
255.
члены
фактически стойка не отделена от опоры. Поэтому канонические ур^,,
нения могут быть всегда записаны так.
8,,Xi + S12X2 + 8,,Хз + " • • + hn^n + ^к - ^,
К^г + ^22^2 + ^-^^ + • • • + ^^'^^^ + ^'' ^^\ ) (5.41)
S„ А + S.2^2 + S„3^3 + ¦ • • + Кп^п + Длс = 0. ,
Здесь ^ д Д„^ — перемещения по направлению неизвестных
X. Хо j'"'вызываемые в основной системе перемещением опор.
у^и ^ъ -, у ^gj^^ ^^^ ф^^^,^ 361,6 эти свободные
имеют следующие значения:
^гс = ^; ^2с = — 6; Аз^ == — (р.
Перемещения Аг^ ^ ^зс отрицательны, так
как соответствующие взаимные перемещения
опоры В и конца стойки, как видно из чертежа,
направлены в сторону, противоположную поло-
жительным направлениям неизвестных Х2 и ^з-
Если бы мы приняли основную систему и
основные неизвестные, показанные на фиг.
361,в, то получили бы
Ai, = — а; Ag, = b\ Age = <р.
Несколько труднее строятся кинематическим способом перемещения
для основной системы фиг. 361, г. Для того чтобы найти их, лучше всего
поступить -следующим образом: построить три отдельных плана переме-
щений, учитывающих заданные перемещения опоры, и результаты сло-
жить. Не приводя самого построения, напишем здесь результат:
Фиг. 362
Ai. =
ку:
Основываясь на соотношении (14.1 Г), можно произвести подстанов-
Д,,=-
?/?с и легко найти те же самые перемещения чисто стати-
ческим путем, не пользуясь кинематикой. Рекомендуем читателю проде-
.лать это.
Уравнения (15.4) относятся не только к случаю заданного (переме-
щения опор, но также к случаю перемещения, заданного по направ-
лению любой связи. Такой вид будут иметь уравнения, например для
рамы (фиг. 362), ригель которой получил с некоторой точке С началь-
ный взаимный поворот двух бесконечно близких между собой сечений
на угол (р. ^
^ 'niJ^t!!?."**'"^^'^**^ УРАВНЕНИЯ ДЛЯ РАСЧЕТА НА СОВМЕСТНОЕ
ДЕЙСТВИЕ НАГРУЗКИ, ТЕМПЕРАТУРЫ И ПЕРЕМЕЩЕНИЯ ОПОР
спо?о^бГпяг„^™ ^^''^Р" учитываются раздельно, так как при таком
^ю"ко?бГа?и^ГсГх фГт^рГ "^^ ^^"^°^° ^^''^««^ «^«^°^^^ "^''""'"
¦сов2^)°еих™п'!^/Л'"^' ''°'^^ "° У^'^^'^и'о задачи требуется учесть
иаиГлее odiS Sf' Уравнения можно написать сразу I следуюшем.
.А, + о^Х, + о^^х, -f • ¦ • + 8,„Х„ + Лзр + Д.,, + Д^ = 0; j (15.5)
256
S„iX. Н- г,,Х, + 8„зХз +... + Й„„Х„ + Д„;+ д„" + д„^ ¦=: 0.
§ 15.6. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Метод решения статически неопределимых задач, при котором за неизвестные
„шшимаются усилия в лишних связях, зародился давно. Во всяком случае он фигури-
ппвап в невполне отчетливом виде уже в сочинении по статике Эйтельвейна^
и А Eytelvvein) в 1808 г. и в знаменитом курсе французского академика Навье^
(L М Н. Navier, 1785—1836),
" Канонические уравнения метода сил впервые в литературе были даны в 1864 г.
Максвеллом в неоднократно упоминавшейся нами работе; он рассматривал в ней ста-
тически неопределимую ферму. Распространению метода на другие статически неопре-
делимые системы содействовали своими исследованиями в конце XIX столетия Мор^ и
Мюллер-Бреслау*.
В России популяризации этого метода в первые два десятилетия XIX века содей-
ствовал своим блестящим изложением проф. В. Л. Кирпичев^ (1845—1913).
Особое внимание канонические уравнения метода сил стали привлекать к себе
тогда, когда возникла необходимость рассчитывать сложные, т. е. содержащие много
лишних неизвестных, и притом весьма разнообразные по своим формам и геометриче-
ской структуре статически неопределимые системы. Известные с середины XIX столетия
трехчленные канонические уравнения, решавшие задачу о неразрезной балке, были
недостаточными для расчета других систем.
Задача расчета статически неопределимых систем любого вида была серьезно
поставлена перед строителями только в XX столетии. Изложению этой проблемы посвя-
щены дальнейшие главы (курса.
1 Handbuch der Statik fester Когрег, zweiter Bd, BerL 1808.
2 Resume des legons donnees a Fecole des ponts et chaussees sur Tapplication de
la mecanique, t 1, 1833.
^Cm. § 14,11.
* Bedingungsgleichungen fur st. unbestimmte К'огрег, Wochenschr. f. Arch, u
Ing., 1884.
^ Лишние неизвестные в строительной механике, СПБ, 1903.
Глава 16
РАСЧЕТ НЕРАЗРЕЗНЫХ БАЛОК
§ 16.1. ОБЩИЕ СВЕДЕНИЯ О НЕРАЗРЕЗНЫХ БАЛКАХ
. ^ % тгаот.тяртгя такая балка, которая перекрывает
"г^е^аролГов Г рсхоТит через свои опоры, не прерываясь
Где шарнирамГил™ разрезами. Характерным отличием неразрезнс,
0} 11
^
Фиг. 363
балки от разрезной является то, что нагрузка, стоящая © любом ее пр
лете, изгибает балку на протяжении всех ее пролетов, создавая плавну
упругую линию. Схема неразрезной балки показана ка фиг. 363, а, схе
разрезной — на фиг. 363,6. ^j
При конструировании керазрезных балок всегда принимаются м р
к тому, чтобы дни не могли отделяться от своих опор. Свободная У^^^^у^е-
балки на опоры допускается только в тех случаях, когда имеется >
ренность, что балка, прогибаясь, будет находиться в контакте со вс
своими опорами и не будет отделяться ни от одной. ^р.
Расчетная схема неразрезной балки предполагает идеальное ^^^^^
нирное прикрепление ее ко всем промежуточным опорам. Такова с.^ _
фиг. 363,а. На крайних опорах допускается также абсолютная или У^н^^^
го-податливая заделка. Действительная конструкция прикрепления
ки к ее опорам обычно отступает от этой схемы, енйЫ^
Неразрезная балка принадлежит к числу весьма распростране
конструкций. Она -применяется в железобетонных, металлических и л
258
вянных конструкциях в качестве элемента или их основной части
На фиг. 364 показан пример моста с металлическим неразрезным пролет^
ным строением. ^ ^
Из различных статически неопределимых систем, которые будут рас-
смотрены Б настоящем курсе, мы поставили неразрезные балки на пеп-
Фиг. 364
вое место, так как они обладают простотой структуры, решаются при
помощи очень простых уравнений и являются наилучшим введением в
расчет более сложных статически неопределимых систем.
§ 16.2. КОЛИЧЕСТВО ЛИШНИХ СВЯЗЕЙ. ВЫБОР ОСНОВНОЙ СИСТЕМЫ
Для обеспечения неподвижности стержня в плоскости требуются
как известно, три опорных стержня, поэтому количество лишних связей
о)
6J
б)
Фиг. 365
!^^Разрезной балки меньше числа ее опорных стержней на три единицы.
^^. например, на фиг. 365 балка .по схеме а содержит две лишние связи.
° ^хеме б —три лишние связи; по схеме в —четыре.
Закрепление правого конца на схеме в эквивалентно двум опорные
Г^РЖням; такое устройство имеет целью устранить напряженна, которые
•^^^гли бы возникнуть от равномерного нагрева или охлаждения.
Если балка имеет т пролетов, то при шарнирном опирании обо
концов (фиг. 365, а) количество лишних связей равно т—1; при заде ^^
одного конца оно рав-но т\ при заделке обоих концов по схеме в ^^^
равно m-fl. ^^^
При выборе основной системы необходимо стремиться к тому чт
канонические уравнения получились возможно более простыми V ^^'
точки зрения весьма поучительна основная система, изображенна ^^^^
фиг. 366,6, которая получается при помощи удаления лишних опопн^^-
стержней. Такая основная система исторически была первой по впем ^^^
появления в литературе, и вряд ли можно придумать другую основн ™
Q) ^^
Фиг. 366
систему, которая была бы хуже нее Гпгт.п
мы убедимся, что в каждое м^ hLv «v канонические уравнения,
первое уравнение имеет вид: ™ "" ^^^ неизвестные. Например,
Оно вы ^"^' ^ ^""^" ^' " ¦*¦ ^^"^" + ^^^ ^ 0.
Но из фиг. 366^7 я?но''Ттп^''пРй^''™^ "^ "^Р^^й опоре равен нулю,
бон S„ Ь,^^ь,,^ s/^r "" TIT '^^^^ ^^-^ «и адин из лроги-
тельно, в первое Уравнение вой л vrnV"!'" "^ ^^^^^ 'Р^^^« «У-"ю, следова-
дет со вторым уравненирм р ; "1 Г"" "^«^вестные. То же самое произои-
При более улачип^уг и^.к ^^^^^^^ и т. д. ^
можно ДобитьсТтогоГч'то'мГожестГ^ ZT'''^^ ^^^ неразрезной балки
бол^шГ^°" «о-"ичестве пролетов ;Гn**"^^^'"™« обратится в нуль.
больше трех «еизвестных.Тэтому ре^и^ГГ'""^ "^ ^^^^^ ^°^^Р"^^^
„ _ ^ |^*;шению мы сейчас перейдем.
этому решению ..С, " "^ ^^^^^ ^°^^
^ |^*;шению мы сейчас перейдем.
§ 16.3. РАСЧЕТ НЕРАЗРРЧни.^
Вь..ерем в '"^ ^""^ -ВХ^!^о"л^^"-«> "^-ЗКУ.
"ye'i^bf'^r^-^'-^^^^^^^^^^ совокупность однспролетных
связи\Геж„ «с^Т^ "^Р^зрезной балкГппи" ""Р^Д^лимая система обра-
(Фиг. ЗбТб? '"'^«"я^и „а ка>кдой опо'^/°''°"^" устранения жесткой
Число* отбпп,,,. " замены ее шарнирной
За He„2S,e"SM.'^''' обозначим через yfe
зТаи1ГГкой';/^=^^^^^ «fitr/; j?^-T^ Действу.а,„е в опор-
и. а какоГв--- тТб^ Е~>-я^е1- в-н„:^Гз=^
?60 чть. что все они растягивают нижнее
волокно. Если на самом тле тот или иной момент направлен в обрат-
ную сторону, то это выяснится впоследствии, и мы получим для него
отрицательное значение.
Напишем какое-нибудь одно из системы канонических уравнений:
^лЛ + ^П2^2 + ^пЗ^З + h КЛ + АпЯ = 0. (16.1)
Здесь Srti^i ^^ть взаимный поворот сечений на опоре номер п, вызы-
ваемый двумя равными и противоположными парами Х^ ^х2 ^2 —взаим-
ный поворот сечений на той же опоре, вызываемый парами ^2, и т. д.
Вся левая часть уравнений выражает собой суммарный взаимный пово-
рот сечений на рассматриваемой опоре, который вызывается всеми лиш-
ними неизвестными и заданной внешней нагрузкой. Этот угол взаимно-
го поворота можно было бы назвать также «углом перелома» упругой
/¦ f 3 4 И Htf
6}
^f ^ ^ /TJ7 ^ ^ Хо
f^-^-^-^e-^-
Фиг. 367
линии на опоре п. Но так как никакого перелома не должно получиться
и упругая линия должна остаться плавной, то мы приравниваем сумму
нулю.
Насколько этот выбор основной системы является удачным, выяс-
няется сейчас же, как только мы приступаем к вычислению коэффициен-
тов. Стоит только посмотреть на фиг. 367,6, чтобы заметить следующее:
момент Хх вызывает перелом упругой линии только на опорах 1 и 2;
момент Х2 — на опорах 1, 2 и 3, момент Хз^на опорах 2, 3 и 4 п т. д.
В свою очередь перелом на опоре / зависит от моментов Xi и Х2
и от внешней нагрузки, но не зависит от остальных лишних неизвестных;
перелом на опоре 2 зависит только от Хи ^5 и ^^з и от внешней нагрузки
^ т.^д. Следовательно, в каждом из канонических уравне-
"^й, кроме первого и последнего, фигурируют толь-
ко по три неизвестных; в первом же и последнем —
'Только по два.
Эти рассуждения позволяют сразу же, без всяких вычислений, пере-
'писать уравнение (I6.I) в более простом виде:
К.п-гХп-г + КпК + Кп.гК,г + К, = 0. (16.2)
Такое уравнение называется трехчленным, так как оно содер-
^кит три неизвестных.
^ Для вычисления коэффициентов \,п-и \п> ^n.n+i нагрузим основ-
У'о систему последовательно обобщенными силами A^^^j =1, Х^ =5 1,
^+1^1. Изгибающие моменты в произвольном сечении мы будем
jj^^^"a4aTb через т в отличие от моментов на опорах, которые мы лоз-
^Удем обозначать через М.
-эпюры изгибающих моментов /n„^i, m„, m„^i представлены на
^- 368; каждая из них простирается только на два пролета и имеет вид
261
пй йпинице При интегрировании любой
треугольника с вьгсотои равн^^ получается интеграл, отличный от нуля,
такой эпюры с двумя смежными п у ^^^^^^^^^я У ^^^ общих участ-
а при и«тегрировании с прочи и ^^^j подтверждается, что перелом
ков интеграл обращается в н неизвестных.
'"ГоенебГгГя^"^ -л на деформацию, получим
для коэффициентов следующие формулы:
Ч'^Ъ] EJ '
^ ЛЛПМ.РТ иметь сечения, изменяющиеся по ее длине
"^ГоГТак'он?" тобы н усложнять расчета ограничимся рассмот-
рен ишт7коГбаЙи у которо/момент инерции / на протяжении каждо-
Фиг. 3G8
го пролета постоянен, но имеет в различных пролетах /„ различные зна-
чения /„.
Для упрощения арифметических вычислений оказывается целесо-
образным вычислять не коэффициенты S^/^, а произведения EJo^ik > ^^^
Jq — совершенно произвольный момент инерции.
Пользуясь правилом интегрирования прямолинейных эпюр, ^^^
быстро найдем
где
Jo
I' =: -^ f • /'
„ -^0
/„
•^n+l '"+!•
Величины V^, l'^^^ и т. д. носят название приведенных проле-
тов.
262
Вычислим теперь свободный член Д„^, который выпажает глблй
угол перелома упругой линии на опоре л. в^,зываеГ,ый в осшмой систе
^е заданной внеш.неи нагрузкой (фиг. 369). Очевидно! ч™ он завиги;
Г^чягоужения только пролетов /„ и / ^, Лпо ut^r~J7 , он зависит
oTsaiyy^ f i/j и i„+, . для него мы имеем формулу
Е'^о^пр
^J'""'"^"7
ds.
Так как эпюра т„ состоит из двух прямых, то в пределах пролета
интеграл равен площади эпюры т^, помноженной на ординату эпюоы
^ , расположенную под центром тяжести первой. Обозначив площади
через «„. %+1, а расстояние их центров тяжести до опорных вертика-
лей через а„ Ь„ и а^^^, 6„_^, (фиг. 369), мы получим
EJoKn =
n+l
n+r
a) nri __ ^л
¦*n
Фиг. 369
(16.3)
это выражение можно написать несколько иначе, если обратить вни-
^^ание на то, что произведение—^ «>„ есть .не что иное, как правая опор-
^^ реакция пролета /„ от фиктивной нагрузки ^^ . Мы ее обозначим
-^рез ВФ ^ рде буква «ф» обозначает «фиктивная»; значок п при этом от-
осится Не к опоре л, а к пролету п. По аналогии с этим можно записать,
1"— ^^ft+1 есть левая фиктивная опорная реакция пролета /n+i, и
обозначить ее через А^^^ . Тогда получим
EJ,^,^=^l^BФ + -J^AФ^,. (16.4)
После этого уравнение (16.2) примет следующий вид:
263
^ Г.0011Р .пплчеокнуть, что в данном случае за неизвест
„Л7„™о„1рнГмо2™'за1ен„м обозначения X X.. х^.
^значениями М.^., М.. «„, Кроме того, умножим обе час™ ура.,
веиия на 6. Тогда получим окончательно
4л*.-, + 2('» + '«.)'"»+'-'"- = -'(^^ + ^"'"')- *"''
Это и есть уравнение трех мо-
ментов.
Множитель /о входит как в ле-
вую, так и в правую часть уравне-
ния, поэтому не влияет на величину
неизвестных.
В том частном случае, когда бал-
ка имеет во всех пролетах один и
тот же момент инерции /, целесооб-
разно принять ^0=*^, и тогда уравне-
ние (5) примет более простой вид:
/>„_,+ 2 (/„ + /„^,) М„ + /„^,M„^, = - 6 (ВФ + ЛФ^,).. (16.6)
Для нагрузок, встречающихся наиболее часто, целесообразно раз
навсегда вычислить фиктивные опорные реакции, умноженные на 6.
Одной из таких нагрузок является, например, сосредоточенная сила
(фиг. 370). Обозначим расстояние от ее точки приложения до левой
опорной вертикали через ul, где и — отвлеченное число (правильная
дробь); расстояние до правой вертикали обозначим через vl, где V-
= \—и. Подсчитав площадь треугольной эпюры моментов и учтя, что
центр тяжести такого треугольника находится на расстоянии ¦ ^ "^"-от
о
левой опорной вертикали и на расстоянии ^^^ "^ ^^ от правой, найдем
6A^^Pl^uv{l + v); 6B^^PPuvil + u).
Если нагрузка состоит из нескольких сосредоточенных сил, то
фиктивные реакции равны сумме реакций, отвечающих каждой силе в
отдельности.
В табл. 5 даны величи-
ны 6Л* и 6Б* для не-
скольких различных на-
грузок. Для нагрузок, не
помещенных в этой таб-
лице, нахождение фиктив-
ных реакций также не мо-
жет вызвать никаких за-
труднений.
После того как мы
пользуясь таблицей или
сделав самостоятельное
вычисление, определим
свободные члены уравне-
^еожа™ 1^^^^^^^^ ''^^^'' '''''^"^ ^УЛ^^ написать всю ^стему уравнений,
содержащую неизвестные опорные моменты. ^ Щ
264
Фиг. 371
Таблица 5
Схема нагрузки
6Л^
ев^
Г
1/1
"[l-ujU-'VL
PV^uviX^v)
Pl^uv(\+u)
ql^
Ql^
ь»— ul
/л/{1—3«2)
упругости Е не входит ни в один из коэффициентов
rt/^—^^бОДных членов, слеповательно. в неоазоезных балках, имеюших
Посто "^^^^^ членов, следовательно, в неразрезных балках, имеющих
Него ^"^'^^ "^ всей их длине модуль упругости, опорные моменты от
кые ^-^^^и^ят. При прочих равных условиях неразрез-
Испы' сделанные из различных материалов,
Мом^^^^^^ одни и те же усилия,
^•^^нах "^^^ инерции поперечных сечений балки содержатся во всех
licex ^.^УР^Бнений (16.5) в знаменателе. Следовательно, от умножения
^^х моментов
же число величина неизвестных
зависят не от абсолютной
атолько от их соот-
одна обл"^ ^ различных пролетах. Две балки, из которых
•Задает большой жесткостью, а другая малой, будут испытывать
2т
^^ измГ инерции на одно и то же
"^^Лич ^^^"" изгибающие моменты з
Нощ"*^Ь1 моментов инерции.
одни и те же усилия, если во всех пролетах жесткость одной пропори„.
ональна ^«^"•^^'^^/йтГпостроена графически или аналитически. Гра.
Эпюра М '«о^^^,^^ ,',,„ючается в том, что для каждого пролета бал-
фическое по^ТР°^"/^_ ^на эпюру моментов простой однопролетной балки
ки на эпюруJ^P 'J„^_ я эпюра, обусловленная влиянием двух
накладывается ^рапецеад^ ^^^^ ^^^ удобства измерения орщ.
опорных моментов (фи^ противоположные знаки, откладываются по
нат flf^f^'^^.'i^H^rocH абсцисс, а эпюры с одинаковыми знаками-,
Тпячные Йороны от оси абсцисс, после чего остается измерить отрезки
^р^инат заключенные в промежутке между обеими эпюрами.
?1п
П if
*n*f
X
In —Т"» In^t
Фиг. 373
Для вывода аналитического выражения изгибающих момен-
тов предположим, что ординаты эпюры Мр и оба опорных момента
имеют одинаковые знаки (фиг. 372). В сечении с произ^льной абсцис-
сой X изгибаь щий момент выражается ординатой ad^ab + bc+cd, еле-
довательно:
JziLi. (16.7)
М
р ' ^
f+м.
Эта формула справедлива при каких угодно комбинациях знаков
величин Мр, Л1^, М^.
Формула для поперечных сил представляет собой производную от
формулы (16.7):
Q,=.Q^+iW^. (16.8)
Поперечная сила в сечении х, как уже неоднократно упоминалось,
считается положительной, если она стремится оба участка балки, разде-
ляемые этим сечением, поворачивать по часовой стрелке.
r<oori"i*P"^*' Р^^'^^^ия на любой опоре п легко получается следуют""
гтппп»?Г "^"^"^ вьфезать двумя сечениями, расположенными по обе
на «^ntuvL°"°P"^ бесконечно малый участок балки и спроектировать
?ельштми пЛ ^""^ действующие на него силы. Будем считать положи-
гилн О ^f л '^""' направленные вверх (фиг. 373). Приняв поперечное
v„ и (^„ j^j положительными, т. е. вращающими по часовой стрел-
ке, пользуясь формулой (16.8). можно написать
(16.9)
^n = Q„,i-Q„=/?o„+f!!2±LZ5.4
м„
-Х~^п
*Л+1
где через R\ обозначена та реакция опоры п. которая получается
260
на
„РЙ в основной системе от заданной внешней нагрузки, расположенной
II пролетах /„ и /„^, .
Мы вывели уравнение трех моментов, пренебрегая влиянием по-
рпечных сил на деформации. Если не делать этого упрощения то урав-
нение Бсе равно остается трехчленным, но получает, конечно, другие
коэффициенты.
§ 16.4. ПРИМЕРЫ И ЗАДАЧИ
Пример 16.1. Построить эпюры М и Q для неразрезной балки, представленной на
г. 374. _ _
Дано:
Примем:
*"'^Дано: /,=/4=3 м; /г=/з=4 м; /,=1; /2=/з=2; /4=1.5.
:мем: /o = /i = l, тогда/; = /1 = Зл; 4 = 4= —4 = 2л; 4 = —3 = 2л.
штшшш
jp-^
А
шт.
"3 Щ^ JV
L
Фиг. 374
Уравнения трех моментов имеют следующий ^ид:
, , ,, , 1 2^4 1 Я^1
" 1 Q^l
После замены буквенных коэффициентов численными эти уравнения переходят в
10Mj + 2M2 = —22,75^; 2Mi + 8M2 + 2M2 = —24^; 2М2 + 8Л1з = — 89.
Находим из первого уравнения
М2 = —5Mi —11.375^.
Подставляем это значение во второе уравнение и находим
/Из ==19 Ml+ 33,5 9.
С>ба найденных выражения подставляем в третье уравнение и получаем
Ml = —1,78^2.^.
После этого находим из предыдущих формул
Л^2 = _2,475^2'9; Мз = —0.32^2.9.
Эпюры моментов от внешней нагрузки в основной системе имеют вид трех пара-
^ ординатами в середине пролета, соответственно равными
Ql'
- = 1,125л12-.7;
2Qll
8
8
2©7
Промежуточные точки параболы могут вычисляться по уравнению папябг.
проще всего определяются по схеме, указанной на фиг. 375, где изображена ^^^* "^
на параболы, и средняя ордината принята равной единице. Таким же способо "^""^^^J-
дываются ординаты параболы в том случае, когда ее замыкающая наклонна (6 ^^^''^^'
хфиг. 3/6),
г
\-OJl-^Ojl ^Djl ^Qfl ^Djl-A
Фиг. 375
Фиг. 376
Эпюра изгибающих моментов показана на фиг. 377, а. Эпюры поперечных сил
имеют вид прямых, поэтому в данном случае достаточно определить их ординаты
для опорных сечений.
?°4s:?p??_"KSo
на опоре i
268
2 ~J^ =^ —0,907 M-q;
2 ""^==---2,093^.9;
во втором пролете—на опоре /
ч: 2 ^ 1^——2-
на опоре 2
и
=+ 3,826^.9;
-" = -4,174^.9;
в третьем пролете — на опоре 2
"^^ 2 + Т~- = 2,539и*.^:
на опоре 3
а- ^^3 ¦ -0,32 ty +2.475/7
в четвертом пролете — на опорах 3 к 4
Фиг. 379
Эптп^^ 9i ^ первом и третьем пролетах параллельны между собой.
Кажла "^^^ззаиа на фиг. 377, б.
разность мр ^"'^Р"^^ реакция, как видно из формулы (16.9), может быть найдена как
^^на: /?п==:Поп7' "°"^Р^*^"Ь1ми силами справа и слева от опоры. Реакция /?о уже най-
u,9U7 м . q. Остальные реакции имеют следующие значения:
^?1 = 3,82б9 —( —2,О93 0==5,919а1.9;
i?2 = 2,539^ — (-'4,1740 = 6,713 jw.^;
Rs^ 0,107Q-^ {— I A^l q) = г,568M-q;
П ^ " ^ia.^.r::iOA07M-q.
^^^^H hm2* *^*^* Составить для той же балки уравнения при условии, что левый
^ ^ а 3 я if2"^^Й** нагруженную заданной нагрузкой (фиг. 378).
крайней леп ** * "^зовем момент нагрузки, расположенной на консоли, относительно
^^«тов состя** ^"'^РЬ! через Mq. Этот момент известен. Первое из уравнений трех мо-
тавляется для опсГры /; оно содержит два неизвестных и имеет вид
'1Л'о + 2(/; + 4)Л1,+4Мг=-б('^В?+-^>1#). (16.10)
269
пример 16.3. Решить ту же задачу при условии, что левый конец балки заще^.
лен (фиг. 379, а). осуществить при помощи устройства дополнитель-
Заделку левого ««««^ "°:П„ имеющего на левом конце шарнирную on^v
„ого бею<оиечно малого пролет ^^^^^ ^ ^ ^д^..^^ ^^^^^ ^ .у
(фиг. 372.6). Деиствительио^^^^ благодаря бесконечиой малости пролетГТ
О и А «^^^^^P^^„^ZZ'c^opouO.TaKKBKU,pnop^ А момент _ равен hv.."
можно считать совпадающим f ^^ уравнений трех
™Го"ГЙГуТГис^атГп';рво^
ИЛИ после подстановки /о=0
пролета и
равен нулю;
W
(16.11)
Остальные уравнения не требуют пояснения.
§ 165. МОМЕНТНЫЕ ФОКУСНЫЕ ОТНОШЕНИЯ
И МОМЕНТНЫЕ ФОКУСЫ
Теория так называемых моментных фокусных отношений, имеющая
большое практическое и теоретическое значение для расчета неразрез-
ных балок и рам, естественно возникает при рассмотрении эпюры изги-
бающих моментов, отвечаюш^ей загружению одного пролета балки.
Составив для этого случая систему уравнений трех моментов и решив
Фиг. 380
ее, мы убедимся, что эпюра имеет примерно такой вид, как показано па
фиг. 380. Характерной особенностью этой эпюры является то, что на
каждом незагруженном пролете она имеет вид наклонной прямой с ну-
левой точкой в пределах пролета. Эти нулевые точки называштс:я^<мо.-
ментными фокх^ами. На фиг. 380 они обозначены буквами
-^^_^ - ^ ~ ^^^ ^^^ ^^^ ^,^ ^^^ ^^
На каждом пролете имеется два фокуса: левый и правый. Левым
(правым) моментным фокусом какого-нибудь пролета называется нуле-
вая точка эпюры моментов этого пролета при условии, что вся нагруз^^^
неразрезной балки расположена справа (слева) от него. Пци гг^р^^
расположении нагрузки фокус служит точкой перегиба упругой" лниии.
" - Необходимо усвоить, что не всякая нулевая точка какой-либо эпю*
ры моментов называется фокусом, а только га, которая получается н^
данном пролете при определенных условиях: когда на это1С "J??-"^^^
нагрузка отсутствует и вся она расподржена по одну сторону от него.
Например ка фиг. 380 нулевые точки, получившиеся на пролете 3--^'
уже не будут называться фокусами.
570
Можно без всяких вычислений доказать, что моментиые фокусы
/впадают свойством инвариантности: на заданной неразрезной балке
гР(Ьокусы занимают совершенно определенные, не зависящие от
внешней нагрузки положения.
Представим себе многопролетную неразрезную балку и вообрг
Представим »^сис мгг1^1^и^и^1С1пую иеразрезную оалку и вообразим,
что на первых нескольких пролетах, считая слева, например на первых
.^0 ---^^"^^ -^^тт^
Фиг. 381
Фиг. 382
четырех пролетах, нет никакой нагрузки (фиг. 381). Tv^ часть балки,
которая расположена справа, можно откинуть, а ее д« иствие на остав-
шуюся часть балки заменить парой т, продольно" ^^илой N и попереч-
ной Q, которые приложены
к крайнему опорному сече-
нию. Продольная сила Л^, ес-
ли она имеется, вызывает в
балке растягивающие или
сжимающие усилия, но обы-
чно принимается, что она
не влияет на эпюру изгибаю-
щих моментов. Поперечная
сила Q как приложенная на
опоре уничтожается сопро-
тивлением последней и даль-
ше не передается. Следова-
тельно, изгибающий момент возбуждается только парой jn. Она
является единственной нагрузкой рассматриваемой части балки.
Спросим себя, что же произойдет с эпюрой изгибающих моментов,
если в правой откинутой части балки произойдут какие угодно
Изменения: изменятся характер, располжение или
величина нагрузки, величина или количество про-
•^етов, способ закрепления правого конца балки,
изменяется как угодно поперечные сечения, под-
нимутся или опустятся те или иные опоры. От всех
^тих вариаций, происходящих в правой части балки, до рассматриваемо-
0 опорного сечения докатится только один отголосок: изменится вели-
ина (а может быть, и знак) момента т. Можно сказать, что этот мо-
^ент умножится на какой-то множитель. Но по закону независимости
^^иствия сил все ординаты эпюры изгибающих моментов умножатся на
лю^^ "^исло. Следовательно, в тех точках, где ординаты равнялись ну-
v^> они останутся равными нулю. Это и требовалось доказать.
^^^.^^^Умеется, то. что здесь показано для левых фокусов, в одинако-
Мере справедливо для правых фокусов.
ij-^-^^^олютная величина отношения между изгибающими моментами
ных ^^^ какого-нибудь пролета называется моментным фокус-,.
« о т н о ш е iLiie м. Различают левое и правое фокудсое отроше- ^
271
ния, смотря по тому, определяется ли оно левым или правым фокус
Например, для пролета /„ (фиг. 382) левым фокусным отношением н^'
зывается отношение ' ^'
^-- М,_, - Сп ' (16.12)
Если известно положение фокуса, то известно и фокусное отно
ние, и наоборот. ^^'
Когда нагрузка расположена где-то справа от рассматриваем
пролетов, то положение левых фокусов определяется отношениями ^^^
Мо
М2
М
n—l
Фиг. 383
Для опоры п (фиг. 383) можно составить уравнение трех моментов
откуда по разделении обеих частей на ЛГ„
/:
М.
п~1
Мп
+ 2(/: + /„,,) + /;^,
м„
= 0
или
(16.13)
пк^^1,*ТлГт^^;-^^^^^^^ .. е. позволяет переходить or
нибудь способом определить хптТби?^''''^^'' ^'^' необходимо каким-
в балке с шарнирно'-опер^ыми кп„?,^ ''^"^ "^ фокусных отношений. Но
ZT^^'' ' -"^«"м опорСм се~м"" •""''"й фокус первого пролета
расположении нагрузки с^ва от прп^ ^^'^ как момент ла конце при
справа от первого пролета равен нулю, поэтому
В таком случае
Мо —
^(^"'")=^('-^;^)-.-+|(-^)«-
272
Т> же формулы справедливы и для балки, имеющей на левом конце
КОНСОЛЬ. ^
, ^сли левый конец балки защемлен, то мы знаем (см. примео 16 3^
1,то такое закрепление эквивалентно наличию Допол-нительного н^левог^^^
пролета /о=0, имеющего шарнирно опертый левый конец К этош
пролета имеем i^o=<=^, поэтому ^' '^''^ ^^^^^
Моментов фокусное отношение для фокуса, примыкающего к за^
щемленному концу балки, всегда равно 2.
Напомним, что речь идет о балке с постоянным на протяжении про-
лета моментом инерции сечения.
Фиг. 384
Аналогичный вид имеют формулы для правых фокусных отношений
(фиг. 384).
^;=2+
-^ (2- .-L_\
4 V ^n+i/
(16.14)
вляются
ринимать всевозможные значе-
Формулы (16.13) и (16.14) показывают, что левый (правый) фокус
любого пролета зависит только от привед(енной^ длины самого пролета
йьсех лежащих слева (справа) оТ^шг-ОГно совершенно не зависит от
величин, характеризующих остальные пролеты балки
Из' этих формул видно также, что фокусные отн(
положительными числами, могущими принимать всевозможные значе
^ия от низшего предела, равного 2, до высшего, который равен беско
Зная фокусные отношения, можно графически строить эпюры мо-
'^^нтов; фокусы получатся при этом на чертеже сами собой. Можно,
днако, построить фокусы независимо от зпюры моментов, так как из
Ропорции (16.12) получается следующая простая формула для рас-
^яння левого фокуса от ближайшей левой опоры (фиг. 382):
J .==-А1. > (16.15)
Анал
логичный вид имеет формула для правого фокуса (фиг. 381):
^" ' (16.16)
dn^
l-hkn
^^^«^ расстояние фокуса до ближайшей правой опоры.
^* ^ Рабинович
273
Если левый конец балки защемлен, то фокусное отношение ^..2.
а потоку с.=^.-е. фокус, примыкающий к защемлен-
n„„v%aлки отстоит от него на расстоянии.
ному концу Ч,^-"!: ети соответствующего пролета
?,^'"°наибольшее возможное для фокусов расстояние от ближайшей
« н^имГьшГе возможное расстояние равно нулю.
§ ,6 6 ПРИМЕНЕНИЕ МОМЕНТНЫХ ФОКУСНЫХ ОТНОШЕНИЙ
^ '" • К ПОСТРОЕНИЮ ЭПЮР
Т^пгпя из всех пролетов балки загружен только один, то при помо-
щи фокусных отношений очень просто и быстро определяются все опор-
ные моменты.
nvcTb например, нагрузка расположена на пролете In (фиг, 385).
Постооение эпюры начнем с того, что определим опорные моменты на
концах загруженного пролета. Для этого составим два уравнения:
К-2 = —
м
п-1
к,1 = -
Мг
Подставив эти выражения в уравнения, мы исключим из них неиз
вестные М^_^ и M^^j и получим
2 +
*n-i
2 —
«n-i
LM„
.БФ==-6-^
L 41 \ -n+i /J
Выражения в квадратных скобках соответственно равны kn и «„ •
Сделав эту подстановку, получим весьма простую систему двух уравне-
ний:
^;л^„-1 + ^;/;м„—б^вФ.
Из нее найдем оба
неизвестных:
ж,=
^^ f^n-^t (16.17)
Моменты на концах загруженного пролета можно найти такЖе
графическим путем. Построение показано на фиг. 386.
На вертикалр:, проведенных через опоры нагруженного пролет »
6Bj бЛФ да
откладываются «перекрестные отрезки» —- — на левой и —~ -^
бл;!
in
274
fn-2 n-Z ^n-l,
Фиг. 385
Фиг. 386
Фиг. 387
18»
275
ли,-и А' и В' соединяются с В и Л. Из фоку-
правой, затем полученные^т^^^^ ^^ ^ ^, ^,^^ ^^ зстречи с этими на-
сов f „ и f „ проводятся '^ 1^ г, Искомая замыкающая эпюры мо-
клонными прямыми в точках С и.
ментов совпадает с прямой о/^. ^^^^^ доказать, что полученные
Анализируя чертеж ^'"^«^/^^^удовлетворяют формулам (16.17).
таким способом o"°f ^"1 "оение получается для сплошной равномерно
Особенно простое "^"Р^^" р!, "„агрузки (фиг. 387 , так как в этом
.ЛФ
'_?^
C.a6-^.=^6ii:=,
о
Из этих формул видно, ЧТО наклонные прямые АВ' и ЕА' пересека-
ются между собой в вершине параболы.
Найдя аналитически или графически опорные моменты ЬЛ^_^ и ЬЛп
и пользуясь фокусными отношениями, мы легко найдем все остальные
опорные моменты:
Л^П-2 =
М,
п—1
^п-г-
М
п~2
М,
п—1
^n-i
^л—2
^п-г ^п-2
Л^п-ы = -
Мп
'^п+1
м
м
п+1
Мп
п+2
^п+2
^п+1^п+2
И т. Дм
и Т. Д.
Когда нагрузка расположена одновременно на нескольких пролетах,
то сначала определяются опорные моменты, вызываемые каждой и
этих нагрузок в отдельности, затем они суммируются.
Если имеется группа пролетов, расположенных по одну сторону о
всей нагрузки, то работу суммирования моментов можно ^^^Р^^.эсй"
Так, например, при расположении нагрузки, показанном на фиг. «Зо »
можно поступить следующим образом: 1) загрузить пролет U и опред '
лить моменты Мз, М^, М^; 2) загрузить пролет /5 и определить момент^
на тех же трех опорах; 3) сложить моменты, вызванные на этих ^^^^^'^
обоими загружениями. Остальные опорные моменты определяются
суммирования, так как М2=-
без
^;М,^_^=
^2
И т. д.
§ 16.7. ПОСТР^НИЕ ЛИНИЙ ВЛИЯНИЯ ИЗГИБАЮЩИХ МОМЕНТОВ
Для построения линий влияния нужно поочередно ставить ^РУ^
Р=1 на всех пролетах балки и выражать интересующие нас величи^^^
в функции от абсциссы этого груза. Рассмотрим в первую очередь
^6
строение л. в изгибаюихего момента для какого-нибудь опорного сече-
н/я балки. Для примера возьмем пятипролетную балку и пусть ^^е-
буется построить л. в. опорного момента Afj ^ Р
,. Груз на пролете /, (фиг 389). Расстояние груза до лево-
го конца пролета обозначим через «/,, где «-отвлеченное число (пра-
вильная дробь); кроме того, обозначим l~u^v. Определяем сначала
моменты на правой опоре загруженного пролета. По табл 5 1ш-
ходим
I
I
Л затем по формулам (16.17) определяем
l^UV (\-\-U)kx— IjUV (1 + ^)
ж, = ^
k^k'l—l
-и I -
-vl,
р=1
?^7
Жо
-/.
Фиг. 389-
Из эпюры, представленной на фиг. 389, видно, что
Разделим пролет на 10 равных частей и будем ставить груз Р=1
последовательно в каждую точку деления. Им будут соответствовать
значения u\iv\
w = 0,00; 0,10; 020;-••; 1,00;
с; = 1,00; 0,90; 080;-••; 0,00.
Составим табл. 6, которая пригодится нам для вычисления ординат
любой линии влияния, относящейся к любой неразрезной балке с по-
стоянными в пределах каждого пролета сечениями.
Таблица 6
0.00
оло
0.20
0.30
0.40
0.50
..При
ПОМОЩИ этой таблицы и написанной выше формулы вычисляем
наты первого участка искомой л, в.
277
V
1.00
0,90
0.80
0,70
0.60
0.50
wt)(I+«)
0,000
0.099
0,192
0,273
0.336
0,375
wtJ(l+tJ)
!
0,000
0.171
0.288
0,357
0.384
0,375
•
и
0,60
0,70
0.80
0.90
1.00
t)
0,40
0,30
0.20
O.IO
0,00
uv{\ 4-w)
0,384
0,357
0,288
0.I7I
0,000 1
t 1
uv{\^v)
0.336
0,273
0,192
0,099
0,000
2. груз в пролете /.(фиг. 390)
По формулам (iOAi)
-vl, —1
|V--"«iiiiiillf^
Фиг. 391
^"^=^yp" >t 111X1111 '
..rr^iTTf]1%
Фиг. 392
Фиг. 393
Выражение в квадратных скобках вычисляем, пользуясь снова табл.
3. Груз в пролете h (фиг. 391)
М2 = г [^^(1 +^)^з—"^(1 + Щ-
4. Груз в пролете U (фиг. 392)
Ма^
и
k,k,~^\
\uv (1 + г^) ^4 — ^^ (1 + ^^)1 ^
«3
5. Груз в пролете h (фиг. 393)
'278
Так как ^5= "• '^^ раскрываем неопределенность и получаем
Далее
*4 ;^3 ^3^4
©
J?UHU9 влияния Mz 2
Фиг, 394
©
'14
Фиг. 395
Линия влияния опорного момента М^ для одной из пятипролетных
балок представлена на фиг. 394. Таким же способом определяются орди-
наты линии влияния всех осталь-
ных опорных моментов. ^^
Выражения uv {\ ^г v) и W^
ш) {\\-и) представляют собой ф
функции третьей степени относи- II, ,,
тельно и\ чтобы убедиться в этом,
следует только подставить вме-
сто "О выражение 1 — и.
Отсюда следует, что линия влияния опорного момента на протяже-
нии каждого пролета представляет собой кубическую параболу.
Имея линии влияния обоих опорных моментов для какого-нибудь
пролета, легко построить линию влияния изгибающих моментов пл?^
промежуточных сечений того же пролета по формуле (16,7). Например,
для какого-нибудь сечения А пролета U (фиг. 395) можно написать
Эта формула читается так: линия влияния изгибающего момента
М>, представляет собой сумму трех линий влияния, из которых первая
относится к тому же сечению в основной системе, т. е. в однопролетной
балке /4, вторая получается из л. в. Мз умножением всех ее ординат на
постоянный множитель ^* 7 ^ > наконец, третья получается из л. в. М^
и
с
на постоянный множитель — .
'4
умножением
Вид этих кривых показан на фиг. 396.
^ Если сечение А совпадает с левым (правым) фокусом (фиг, ^У/, а),
^0 1^РУз. стоящий справа (слева) от того пролета, которому это сечение
принадлежит, не вызывает в нем изгибающих моментов: следовательно,
^^ния влияния совпадает с осью абсцисс. На фиг. 397,6 представлена
'"иния влияния изгибающих моментов для правого фокуса t ^.
Если сечение А расположено на крайнем участке пролета те.
''^^ДУ фокусом и ближайшей опорой, то л. в. М^ имеет вид. представ-
•;;^«ный на фиг, 397, е. Характерное отличие от фиг. 396 состоит в том.
^^^ на фиг. 397, в линия влияния имеет в пределах того пролета, на ко-
279
тором расположено сечение Л, нулевую точку, а на остальных
тал — знаки, противоположные знакам на фиг. 396. Роле-
Ординаты линии влияния изгибающих моментов быстро убы
по мере удаления соответствующих участков («полуволн») от сеч^^'^^
^М.м,^
I
Фиг. 396
Фиг. 397
*1у
««ь еще pa, в меТующ™ ™д1:' "'°''"^''°« ('<i-8). -огору,„ пртеда»
где Q0
' I ~»
М . м Г-'истемТ'"""'^' '"" ^"^ ^'^о «е сечепня основной
""" 'ра^мГр„ТаГоГ°"'"^°^ "^ "Р-°« и левой опорах
ссматриваемого пролета неразрезной балки.
Пля того чтобы построить л. в, Q, нужно сначала построить отме-
ые три линии влияния, из которых первая является статически опре-
'^^^"мой й простирается только на один пролет, затем п^)оизвести над
^^'^\атами этих трех графиков аналитическим или графическим путем
3 /! 5
Фиг. 398
операции, указываемые формулой (16.8). Эти вспомогательные линии
влияния, а также сама л. в. Q имеют вид, показанный на фиг. 398.
§ 16.9. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ ОПОРНЫХ РЕАКЦИЙ
, Линии ВЛИЯ'НИЯ опорных реакций строятся на основании формулы
KOTopyiQ МОЖНО прочитать так: линия влияния опорной реакции пред-
Аавляет собой алгебраическую сумму л. в. реакций той же опоры в
j^HOBHoft системе и трех л. в., выраженных остальными тремя членами.
тель ^"^^ опорная реакция, направленная вверх, считается положи-
Р качестве примера на фиг. 399 представлена л. в, /?2.
ныу ^"^^ для двух бесконечно близких к опоре 2 сечений, расположен-
^ слева и справа от нее, построены линии влияния поперечных сил,
281
то г, в. R, можно построить проще. Обозначим поперечные силы для
этил'двух сечений соответственно через Ц^ и W ¦ ^огда
R^^Qlv-Щ,
т. е. линия влияния опорной реакции строится как разность двух линий
влияния.
2 J 4_ 3
^^=^2]1Щ]]1Г
Фиг. 399
§ 16.10. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ КАК ЛИНИЙ ПРОГИБА
Пусть требуется построить линию влияния какого-нибудь усилия X,-.
Отбросим ту связь, в которой возникает это усилие, и заменим ее
силой Х^.
с)
]р-'/
т
т г
'ф
ЛОИ^^ «^'^^^ /й,
/-i
^^^^^^
Ш
т
:й^ ^'
^/ Линия влияния М2 ,
3^ ^^ 4
Фиг. 400
На систему, образовавшуюся после удаления связи, действуют сила
Р-~\ и реакция X.. Так как перемещение по направлению откинутой
связи должно равняться нулю, то
(16.18)
282
^•Л + Ч-р = 0 или Х,- = -|^=-5^^
Числитель Ь I представляет собой упругую линиш / г. л,
2п перемещений), отвечающую дей°тви2 с™ы X ^f^'^M^'P™'^"^'"
влпяния любого усилия может быть получена так- l{ hv^„ '' """""''
связь, в которой возникает это усилие: 2) дать сигт/мГ^.^ УДалить ту
э'хой связи перемещение, равное единице; 3)постр™ «ыГ"^^''''™'^
;ГГ;янГ '"''-''' ^"""^- "^^ ^"Р^-^ =Тбуд™Го1Г
Так, например, для балки (фиг. 400, а\ ппкя^яттит и.....
„а опоре г (фиг. 400, е). Линия влияния R, получается смещением „по
р„ г на величину, равную единице, а л. в. /И,^уста„овкой шарнира в
а)
\,
^ ^ У г^ 47 ^
гПания блаяния М
в
Фиг. 401
порном сечении и взаимным поворотом сечений на угол, равный еди-
Це. На фиг. 401, а и б показано образование линии влияния изгибаю-
Рез^^ f^y^^^'^^ и поперечной силы для промежуточного сечения нераз-
раз"^" ¦^™* Упругая линия на фиг. 401, б образуется так; оба сечения
ocrf^^^^^^^^^ "^ вертикали на длину, равную единице, но принуждаются
1 зваться параллельными друг другу.
§ 16.11. САМОЕ НЕВЫГОДНОЕ ЗАГРУЖЕНИЕ
Жет ^'^^^ ^фоме постоянной нагрузки, имеется временная, которая мо-
г,р^^^""мать различны-е положения и вовсе сниматься с того или иного
^^ ета, то приходится искать те сочетания нагрузок, которые вызыва-
^Юм ^^^"^^^"ь^х сечениях балки наибольший и наименьший изгибающие
^нты. Наибольшую и наименьшую поперечные силы,
пре ^^^^ четырехпролетная балка нагружена постоянной нагрузкой,
Пр^^^^^^'^енной на фиг. 402, а, и, кроме того, временной нагрузкой,
д^^^^^^'^^вленной на схеме б. Пусть временная нагрузка занимает на каж-
cjij. "Р^'^ете вполне определенное положение, но может убираться
От Y'^^Ta или оставаться на нем. Построим эпюру изгибающих моментов
Ка^°^*^°^™ой нагрузки (схема в), затем отдельно — от загружения
сеце^°^° пролета временной нагрузкой (схемы г, д, е, ж). Для любо!^)
стоян ^-^^•^^^ алгебраически сложим ординату эпюры, вызванной по-
"Нои нагрузкой, с соответствующими положительными ординатами,
283
отвечающими временной нагрузке: те временные нагрузки, kotod
вают в этом сечении отрицательные моменты, считаются'otcvt'^^^^^^^'
ми. Так получается для данного сечения М^^^. Затем к ордин^^^^^^^'
эпюры, которая отвечает постоянной нагрузке, приложим алг^г^ ^^^
ски соответствующие отпи^"^^'
___„ тельные ординаты из Lln^
епюр; в итоге получится л па п.. ^^
сечения Ж„,„ .По^бсолю^но?. веп'^
''ИнеЖ.,^, разумеется, может о^'
заться большим, чем М
Проделав такую операцию л,р
достаточного количества сечений «
каждом пролете и соединив найден
ные точки, получим для изгкбаюшиу
Гфиг "402) """'я "Р'^^-^ьные кривы
^фиг. 4U2) — так называемые «объ
емлющие эпюры», из которых опня
дает для всех сечений балки величи-
ны м „ах, а другая—величины М
По этим расчетным изгибающим
моментам проверяются нормальные
напряжения. *^
На фиг. 403 построены объемлю-
щие эпюры для поперечных сил
получаются так: к ординатам эгао-
РЫ Ч^посш (фиг. 403, а) добавляются
ординаты одних положительных или
одних отрицательных участков эпюр
Ч?вре„ (фиг. 403, б, в, г).
Результатом первой операции
является объемлющая эпюра Сшах,-
40з!бГ''''^™'' второй-Q^,„ (фиг.
Для облегчения построения заме-
тим, что в рассматриваемом приме-
ре все епюры Q состоят только из
прямолинейных участков. При сло-
же1«1и нескольких прямолинейных
графиков результирующий график
получается также прямолинейным,
причем тангенс угла его наклона к
оси абсцисс равен сумме тангенсов
^^"¦"°^"зклона составляющих графи-
ков. При построеннии прямолиней-
ного участка графика отпадает не-
ооходимость разыскивать промежу-
точные тпигг». -„ .... . пве
Фиг. 402
Прп^п ^r.^r ¦'очки; достаточно иметь две
сеченир»"" ^ суммарном графике мо^Д"""^ орДинаты.
графиков '""^ "^^"^« перелом xo?ffi"°^^™^'^« то-"ько под тем
графиков. У 'ОМ хотя бы в одном из составляютих
SSl?P-^я^^ГрГиГо"^^^ «-РУЗКИ можно усга-
голько формой линии влияния °^емлющих эпюр, а руководствуясь
284
Й^^
Так, например, для пятнпролетной балки мы имеем следующие схемь
загружения (фиг, 404):
для М,шш—схему /;
для Ml шах —схему 2;
для M2min — схему 5;
для M2max—схему 4,
Вообще загружения, соответствующие минимуму и максимуму
какого-нибудь усилия, дополняют друг друга до полного загружения
всех пролетов; зная одно из двух загружении, мы тем самым знаем и
другое.
Читателю, который будет разбираться в схемах загружения, изо-
браженных на фиг. 404, мы настоятельно рекомендуем начертить или
/ ^ /( ^^ Е
ф ; 4^ ^. ^ 4^
')
^}
3)
4)
|''11!!1Ч11'':;р'М11||Г1П11||||11Н|
i;/|l|l!illi,ii!!n,illllllll!llllliilll
> 1
1 1
1 1
i' Ч111111111! I''
iliiilllllllllhii
llttllliilNIJIII'lllilNII
llllllllllllillliillllllill
1
1 t
lillllillllilllllllll!li!ll!iiiil!l!!:,Jillill
I
I
1
111 mill
iiiiiiiiiiiiiiiiii
- H
iiiiiiiiiiiiijiij;,,
1
II 1 1 M1i1i11!1111111 f
'
Фиг. 404
представить себе в уме общий характер соответствующих линий влия-
ния; ему сразу станет ясен смысл всех -этих схем, так как для получе-
ния максимума загружаются положительные участки л. в., а для мини-
мума — отрицательные участки.
§ 16.12. РАСЧЕТ НА СМЕЩЕНИЕ ОПОР
Смещение опор имеет для неразрезных конструкций серьезное зна-
чение. Если балка с прямой осью прикрепляется к плохо снивелирован-
ным опорам, то она при этом делается кривой и в ней возникает на-
пряженное состояние. То же самое происходит тогда, когда под влияни-
ем подмыва опор, плохого качества грунта, деформации самих опор
и т. п, опорные точки оказываются расположенными не на одной прямо»-
При расчете на смещение опор канонические уравнения метода сил в
общем случае имеют вид
КгХ^ + К^Х^ +.. • + bnkXr, + Д„^ = О,
г-^^^пс—то перемещение по направлению неизвестной Хп. которое в«з_
никает в основной системе под влиянием смещения опор. В применени ^
к неразрезной балке такое уравнение выражает следующую ^^^^^^
перелом упругой линии на опоре, вызываемой совместным Д^*''^*^^"ся
всех лишних неизвестных и перемещением * опор, должен равнят
286
Угол наклона пролета /„. возникающий в огнп. -
„ого смещения опор, назовем 0„ (фиг. 405), где " системе от задан-
(16.19)
П+1
и Т. Д.
п+1
Все эти З'глы мы можем считать известными п
положительными в том случае, когда они напоа^прнк,"" ^^^^ считаться
Угол перелома на п-й опоре, возникаюишй f п "° ^'^'^?''™ ^"^Р^-^'^^-
смещения опор, равен 0„^,_е„; "^""•^^•«ЩИи в основной системе от
Отсюда после умножения всех членов ня (^ft „^
уравнение трех моментов: ^ "^ ^^"^° получается следующее
In Мп^г + 2 ( /; + Ci) Я + /;, А,, + 6?/„ ( е„^, _ е„) = 0. (16.20)
-In
^ПН
Фиг. 405
Такой вид имеет любое из промежз^точных уравнений. Более про-
стой вид имеют первое и последнее уравнения. Для балок с шарнирно-
опертыми концами первое уравнение имеет вид
2 ( /; + /;) М, + 1'^М^ + 6EJ, ( ©2 - ^) = О, (16.21)
Для балки с защемленным левым корщом оно пишется так:
2/;м, + 1[М^ + 6EJq 0^ = 0. (16.22)
Коэффициенты при неизвестных iW„_i, М«, Af^^i получились, разу-
^^ется, такими же, как в случае расчета на действие внешней нагрз^зки.
^то касается свободного члена, то его принципиальное отличие от сво-
его члена А состоит прежде всего в том, что он зависит от коэф-
бодн,
фИциента упругости E, Из двух балок, имеющих совершенно одинаковые
^чения и пролеты и одинаковые перемещения опор, балка, сделанная
^3 Материала более жесткого (с большим значением коэффициента ?),
- ^^ испытывать большие усилия.
Из уравнений (16.21) следует также, что при заданном смещении
"ор изгибающие моменты пропорциональны жесткости балки,
g ^фи любом сочетании смещений опор эпюра изгибающих моментов
^УДет представлять собой ломаную линию с вершинами, расположен-
ии на опорных вертикалях.
§ 16.13. НЕРАЗРЕЗНАЯ БАЛКА С УПРУГО-СМЕЩАЮЩИМИСЯ ОПОРАМИ
Упруго-смещающейся опорой мы будем называть такую, переме-
-^^ние которой пропорционально действующему на нее давлению. При-
^Рами таких опор могут служить длинные колонны, на которых лежи г
287
лялки проезжей части металлического
„ера^резна» «--;;-,ТрГольнГнера^зрезнь,с балки; „о„то„«, ,ото-
""''"•п™"дарами "аплавного моста- шарнирно связана
""^'^.'^^дем по-прежие„у^^считать,^«о ^^^^^ ^__^^^^^, „„,, „р„,,„.
';е™Г,ГдГсг^ь^мко,.струки„ям.
т а
-^—
¦i—
Фиг. 406
Будем считать пролеты, а также сечения неразрезной ,^'"^^^р„т^Ы
вестными. Упругие характеристики опор, например их коэффии ^^^^
податливости, мы должны также
податливости мы будем называть перемещение иниуслу оих^^"--- ^pj,!,
податливости, мы должны также считать известными, КоэфФ^и^!^^^^
перемещение опоры, ^ьхзванное ^
ничной силой. Например, коэффициентом податливости такой ^^^^^^цо
которая выполнена в виде колонны длины а и сечения F, служит *
с= —, Т. е. укорочение опоры, вызванное единичной продольной
Коэффициент, относящийся к какой-нибудь опоре номер п, буд^^* i ^
значать через c^.Иногда пользуются обратным коэффициентом ^п-^сп
283
,^торЫЙ выражает собой силу, потребную для единичного перемещения
TnopbL Он носит название коэффициента жесткости или коэйвдента
упругости опоры.
^ Поведение опор целиком определяется их коэффициентами подат-
ливости ^п- Поэтому, нисколько не суживая задачи, мы можем принять
опоры за колонны, получающие от продольной силы «единицы» удли-
нение или укорочение с^.
За основную систему мы снова примем балку, разделенную шарни-
рами на ряд однопролетных балок (фиг. 406,а).
За неизвестные примем опорные изгибающие моменты. Построим
эпюры изгибающих моментов, вызванные единичными значениями этих
неизвестных, и вычислим коэффициенты канонических уравнений.
Легко заметить, что перелом упругой линии на опоре п вызывается
только моментами М^_^, ^n-v ^п, Л^^+т, М^^^ и внешней нагрузкой,
расположенной на пролетах ^^-i»'«>'п-ы>^п+2- Действительно, любой из
этих факторов вызывает в основной системе продольные усилия,
по крайней мере в одной из колонн п—1, п, /г+1, а удлинение или укоро-
чение последних, очевидно, вызывает взаимный поворот обоих сечений,
шарнирно-связанных между собой на опоре п. Моменты и внешние на-
грузки, расположенные более далеко, не вызывают в этих колоннах ни-
каких усилий.
Каноническое уравнение для п-и опоры будет иметь вид '
Оно называется уравнением пяти моментов.
При вычислении коэффициентов и свободных членов этих уравне-
ний мы будем принимать во внимание изгибающие моменты в балке и
продольные усилия в опорах. Те и другие-показаны на фиг. 406, б, в и г.
Удлинение или укорочение любой колонны равно ее продольному уси-
^1ию, помноженному на соответствующий коэффициент податливости.
Займемся перемещением 8„, „^2 • Из фиг. 406, б и г видно, что имеется
только одна опора, в которой возникают усилия как от Х^_^=-1, так и
от Х„=1: опора п—1. Эти усилия соответственно равны и
¦—р , поэтому для /г—1-й колонны получается
Г ^n-2^n^S 1_ Г/ 1\( l\ds^
] BFn-г ^^п^Л]\ ^n^^l^ '^f
^«-1
Отсюда
EF„_i /„-1 ^п ^«-1 '«
-УЛ
т^тп-^^х с„_1
IJ EJ /„_i /„
^^ Первый член равен нулю, так как эпюры т„ и /«„_, не имеют общих
- ^стков, следовательно:
^п-1
/Ф>'
Поступая таким же образом, получим
6EJ„ In \'n-l 'nj ^n V'n Wl /
i
,2
3EJ„ 3?J„+i '„ \ 'n Ы+1 I Ы-vi
Коэффициенты 8„.„+,. 8„,„+2 "впишутся no аналогии с 8„_„_„8„ „^^ .
Свободный член выражается формулой
где через Rn^v^n ^^ ^пп обозначены реакции опор п—1, п и /^+1.
вызываемые в основной системе внешней нагрузкой; через В^ и Af^J^^
обозначены по-прежнему фиктивные реакции опоры п в п-м и п+Ьм
пролетах.
Первое и последнее уравнения для многопролетной неразрезной
балки содержат по три неизвестных момента; второе и предпослед-
нее— по четыре; все остальные уравнения содержат по пяти неизвестных.
Наиболее простые уравнения пяти моментов получаются тогда, когда
балка имеет постоянное сечение и равные пролеты, а опоры — постоян-
ный коэффициент податливости с:
Введя обозначение ^|^^= «, где а имеет размерность отвлеченного
числа, и умножив обе части на ^. мы еще более упростим уравнение:
«Л1„_2+(1-4сх)М„_, + (4 + 6«)M„ + (1 - 4а)М„^.,+
го ^чеш,Г^"Д^'°"""" " ™"ере'^"ые силы для любого промежуточно;
менть по ;/м V Л °"°.Рные реакции выражаются через опорные мо
onojax '^ формулам, что н для иеразрезной балки на жесть»'
Прогиб на п-й опоре исразрезнон балкн в общем случае, когдя иР^'
290
леты и коэффициенты податливости различны, равен суммарной реак-
ции этой опоры, умноженной на коэффициент податливТтГс,: ^
+ CnRn' (16.24)
Выражение в квадратных скобках равно реакции, вызванной опор-
ными моментами, а с^н^ — прогиб в основной системе от внешней на-
грузки, стоящей на пролетах /„ и /„^j. В том случае, когда коэффициен-
ты податливости всех опор равны нулю: с„-0, балка превращается в
исразрезную балку на жестких опорах. Тогда коэффициенты 8„ „_2 «
К.п+2 становятся равными нулю и уравнения пяти моментов переходят
в уравнения трех моментов.
Построение ординат линий влияния опорных моментов производится
так: груз Р--1 ставится последовательно на каждом пролете на расстоя-
нии X от опоры, затем каждый раз решается соответствующая система
уравнений пяти моментов; в результате получаются формулы для орди-
нат л. в. опорных моментов. С помощью этих л. в. строятся линии влия-
ния моментов и поперечных сил для любого сечения; для этого служат
те же формулы, что и для балки на жестких опорах. Линии влияния про-
гибов для опорных сечений строятся по формуле (16.24).
Линии влияния для неразрезной балки на упругих опорах могут быть
построены так же, как линии прогибов (см. § 16.10).
§ 16.14. ПОНЯТИЕ О РАСЧЕТЕ НЕРАЗРЕЗНЫХ БАЛОК
МЕТОДОМ ЗАДАННЫХ МОМЕНТОВ ИЛИ НАПРЯЖЕНИЙ
Метод был предложен автором данной книги в 1936 г. Он состоит в следующем.
Зададимся эпюрой изгибающих моментов, т. е. назначим по
собственному усмотрению величины всех опорных моментов М\, М2 и т. д. Неизвест-
ными будем считать величины, зависящие от сечений балки, например приведенные
п|)олеты. Система уравнений трех моментов является однородной относительно величин
^1' h и 'т. Д.; поэтому из нее можно определить только отношение этих величин к
любой из них. Будем считать момент инерции /ь а следовательно, и приведенный
пролет /j известными. Тогда'в первом уравнении останется одна неизвестная 1^, кото-
рая и определится из него:
2 ^ 6 togbg
2М1+М2-
/2
Во втором уравнении будет содержаться только одна неизвестная /3. которая
определится таким же образом, и т. д.
*ак можно вычислить один за другим все приведенные пролеты, а следовательно,
моменты ииерцнн всех поперечных сечений.
^ Если какой-нибудь приведенный пролет, вычисленный по этим формулам, ока-
жется отрицательньтм то это будет означать, что мы задались невозможной, нелепой
^пюрой моментов Нужно «будет изменить один или несколько опорных моментов и
произвести вычисление вторично. То же самое нужно будет сделать, если один из
Риведенных пролетов получится равным нулю. ^„о„„„
Подробнее метод изложен в статье И. М. Рабиновича в сборнике «Исследования
° теории сооружений» (Госстройиздат, 1936. стр. 71).
§ 16.15. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
DaruI^^P"» неразрезной балкн имела большое значение в истории развития методов
бал^^^^ статически неопределимых систем. Важным моментом для расчета неразр^нои
"^^ки было открытие уравнения трех моментов, опубликованного французскими инже-
19* ^1
r^ , /n^rfnn и Клапейроном^. Это открытие было обусловлено развитием
нерами Берто» (^^^^^ UnnrnneHHfl широко использовавшего неразрезные пролетные
железнодорожного мостостроении, р
строения. .. ,^,прмик Бвесс сильно продвинул вперед теорию расчета неразрез-
Фрагшузскии академик ^ ^ ^^^^^ открытие существования моментных фокусовз.
ных балок, ^^^^^™^^^е влияние смещения опор, были введены в уравнение трех
момштГморомГ более общем виде это уравнение было выведено Кульманом
^ ^^Vl^^^^ui''^^^^^^ иеразрезных балок был указан французским акаде-
иком Леви (А1 1838—1910), который вывел так называемое уравнение двух
моментов^ классических работ в XIX и XX столетиях было опубликовано огром-
нпР количество исследований, посвященных методам решения системы уравнений трех
моментов а также распространению этих уравнений на более сложные случаи. Среди
этих исследований крупное место принадлежит советским авторам. По недостатку
места мы не можем здесь касаться их^.
1 Memoires et comptes rendus des travaux do la societe des ingenieurs civils, 1855.
2 Calcul d'une poutre elastique reposant librement sur des appuis inegaleraent
espaces, Coraptes rendus des saences de Tacad, des sc, 1857, p. 1076—1080.
3 Cours de mecanique appliquee, 1859, 1865.
4 Beitrag zur Theorie der Holz-u. Eisenkonstruktionen, Z. d. Arch. u. Jng.—Ver
zu Hannover, 1860, 1862.
5 La statique graphique, II partie, 1886.
6 Подробное изложение весьма поучительной истории развития этой главы строи-
тельной механики см. в книге автора: «Курс строительной механики с1ержневых си-
стем», ч. И, 1940, стр. 168—176, а также в книге проф. С. А. Бернштейна: «Очерки по
истории строительной механики», М, 1957. См. также книгу «Строительная механика в
СССР 1917—1957 гг.» под ред. проф. И. М. Рабиновича, М., 1957.
Глава 17
РАСЧЕТ ПРОСТЫХ РАМ И СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫХ АРОК МЕТОДОМ СИЛ
V
Ш7а
§ 17.1. ОСНОВНЫЕ ПОНЯТИЯ
Рамой (жесткой рамой) называется такая стержневая система, у
которой все или некоторые узловые соединения являются жесткими.
Жесткий узел в свою очередь характеризуется тем, что угол между
осями тех стержней, которые его обра-
зуют, не изменяется при действии на-
грузки. Такой пример представлен на
фиг. 407, где угол между касательными
к упругим линиям ригеля и левой стой-
ки в узле А сохраняет неизменную ве-
личину а, а угол между касательными
к упругим линиям того же ригеля и
правой стойки в узле В сохраняет не-
изменную величину р. Когда рама де-
формируется, то обе касательные, про-
веденные в узле Л, поворачиваются на
одинаковый угол.
То же самое можно сказать о касательных, проведенных в узле В^
В рамной конструкции расчетные моменты ригеля оказываются обыч-
но значительно меньшими, чем в простой балке того же пролета, сво-
бодно положенной на опоры, следовательно, сечения ригеля получаются
более экономичными С конструктивной стороны обеспечение достаточ-
ной жесткости узловых соединений является делом более простым, чем
обеспечение шарнирной подвижности. Геометрическая неизменяемость
конструкции с жесткими узлами обеспечивается при помощи гораздо
меньшего количества стержней, чем неизменяемость шарнирно-стерж-
невой системы. Так, например, фиг. 407 при условии ^^^Р^Р;
«ости узлов Л, Б, С и D нуждалась бы в дополнительной диагона
;;^и. Благодаря указанным достоинствам рамные ''''^''^^:^'1^^^
^^ирокое применение в промышленном и гражданском строительстве, а
Фиг. 407
"гакже
^е в авиастроении, судостроении и т. д.
^а фиг. 408 и 409 показаны примеры рамных
конструкций.
29^
Фиг. 408
Фиг. 409
§ 17.2. РАСЧЕТ РАМЫ С ОДНОЙ ЛИШНЕЙ НЕИЗВЕСТНОЙ
Рама, изображенная на фиг. 410, нагружена горизонтальной равно-
пно распределенной нагрузкой интенсивности q т/м и сосредоточенной
''^ тйкальной силой Р. Размеры рамы таковы: а=1,5 ж, Ь=4,2 ж, /-5 ж,
^^2 5^1- Требуется построить эпюры Ж, Q и /V.
*^^ Решение задачи начинаем с выбора основной
гтемы, т. е. с отбрасывания одной лишней свя-
и замены ее соответствующей неизвестной
гнлой.
Остановимся на варианте основной системы,
педставлениом на фиг. 411. Опорные реакции,
также самые эпюры строятся легко. Криволи-
\йная эпюра М , на протяжении стойки АВ вы-
ражается уравнением
2
Здесь за положительные изгибающие моменты приняты такие, ко-
торые вызывают растяжение в правом волокне стойки.
Вычислим коэффициенты канонического уравнения
причем пренебрежем влиянием поперечных и продольных сил на эти
коэффициенты. Для того чтобы упростить все вычисления, умножим
перемещение о^^ и ^ip на EJi.
Фиг. 410
Фиг. 411
Фиг. 412
Коэффициент EJi \i вычисляется по формуле
Так как эпюра М. состоит из двух "Р^^ь^х то штегрирование мож^
но произвести. Умножая площадь каждого W^f,"^ Результат мож-
ординату, проходящую через центр тяжести (см. § i^.o;. у
"о также взять в готовом виде из табл. 2.
Перемещение ?/i Д,р вычисляется по формуле
295
ьезультаты сложить:
^ ^/v .ья ^^^/^к ^^^(^ -^^^2' ^^'-^ь уЬ(й2_4^.)^
, Рга^г)С2/ ). ./. 1512ИГ''-^ Ь0,0133л1 'Pz{l ^ z){21 ~ А .
+ 6/ ^
Подставив эти выражения в каноническое уравнепио. получим
у ^^h^ ^ ^^'^''' ^—0,731лг-9 0.00643л/ 2/^2(/^ г){21^г)
ммр в,
0,396
\j4^2,23B
-13дЗ
\i-^UD^
{N)
Для большей определенности дальнейших вычислений примем:
(/=1,8 т/м, Р^1,5 т, 2:^ — =2,5 Л1. Тогда
Xj^ = — (0,731 -1,8 + 0,00643-1,5 «2,5-2,5.7,5) тж = — 1,769/7Ш.
Окончательная эпюра изгибающих моментов выражается формулой
для ее получения нужно умножить все ординаты эпюры Мх на найден-
ное значение Хх и к произведению алгебраически добавить эпюру ^f/;•
Эти операции можно произвести либо аналитически, либо графически.
Для стойки АВ применим аналитический способ: в сечении с произволь-
ной абсциссой у
поэтому
M,A\ = -1.769-f .
ь
М= ЖЬ^-а-")
26
^-^-1.76^
По этой формуле можно вычислить любую ординату эпюры ^¦
^mf "?Г"' "Р" ^=^ Л1=-3.794 тм. При «/= 1.59 л*. М „,ах=2,298 гпм.
Эпюра Л! показана на фиг. 413. а.
м« гп«" е Р е ч н а я сила в любом сечении может быть найдена дву-
мя способами: либо путем суммирования основных эпюр по формуле
Л1^ «"л? ^'"/""0?" поперечных сил. отвечаюни1е эпюрам момсито"
"V и Л1,. либо аналитическим--путем дифференцирования окон
290
S;r^"-b -op^rQ%f,e?rrS;LTo=^^^ -°5o-M для
Q = ^:^i2!) 9у_^7б9
26
При 1/=0 (3^ = 2.877 т. Мы могли бы получить тот же результат
фиг 411, сложив левую горизонтальную реакцию, показанную на
-TJ^-b Г-2^7ТТ^ f9'"*°?".o^" Умноженн'ойП,
Прпу-Ь 0^-2,877-1,8.4.2 = -4,683 т. На правом участее ригеля
Гг^'п'находим ''""" "^'""^ вертикальной опорной реакции; на
ИЗ
эпюре
фиг. 411 находим
Qn=—~ 4- L769-
/
Qd=—^ +1,769^==-0,396 m.
На левом участке
Q^ = P—0,396 = 1,104 кг.
Эпюра Q изображена на фиг. 413,6.
Продольная сила выражается формулой
Использовав реакции, показанные на фиг. 411, сразу найдем
Л^лв =-у-1.769^ =_ 1,104т;
Эпюра Л^ представлена на фиг. 413, е.
Поверка. Для поверки равновесия вырежем узел В и нанесем
изгибающие моменты, которые выражают действие откинутых частей на
оставшуюся, в виде стрелок, так чтобы растянутые волокна каждого
стержня оказались расположенными с той стороны, которая согласует-
ся с эпюрой.
Из фиг. 414 видно, что алгебраическая сумма моментов равна нулю.
Проверим также равенство нулю вертикальных проекций. Внешняя
згрузка дает проекцию, равную Р. Вертикальная реакция в шарнире Л,
судя по эпюре N, равна 1,104 m и направлена вверх. Вертикальная реак-
|^ия в узле jD, судя по эпюре Q, равна 0,396 т и вращает стержень BD
ротив часовой стрелки, т. е. направлена вверх. Сумма вертикальных сил
1,5—1,104 — 0,396 = 0.
Аналогичным образом можно было бы проверить сумму горизон-
тальных проекций.
тическа^^ ^"^^"^"ческой поверки, необходима еще, так сказать, кииема-
'^^Реме ^ "^^^Р^^з, т. е. необходимо убедиться в том, что деформации и
^^Разоь^^^^^^ cviCTeMH удовлетворяют условиям опорных закрепдоний и
^УЮ Р^^^^^^сти контура. Заданную раму можно рассматривать как основ-
атически определимую систему, нагруженную заданной внешней
297
L] EJ
те Л/.-эттюра моментов, вызываемая в любой из возможных основных
систем соответствующей силой Xi = l.
Воспользуемся фиг. 411: '
24
+
.№ J LJIL'. J-= 5 557 —5,313+ 0,938—
+ 1F'2,5 3 2.5
_- 1 180 = 6,495 - 6,493 = 0,002.
Л
лЛб.Х,
Фиг. 415
Разница между суммой положительных чисел и суммой отрицатель-
ных составляет в процентах по отношению к любой из этих сумм около
100-^^^ = 0,030/0. .
6,493
Такая точность более чем достаточна.
Линия влияния лишней неизвестной ^"1. В формуле,
полученной ранее для Х^ достаточно положить ^ = 0, а абсциссу z счи-
тать переменной. Уравнение л. в. получим в виде
Xi= —0,00643 л/-2.г(/ — г)(2/ —г).
Следовательно, искомая кривая представляет собой кубическую па-
раболу. Она построена на фиг. 415, а.
Линия влияния изгибающего момента в "Р^^^,^
вольном сечении ригеля. Изгибающий момент в любом сечени
ригеля или стойки выражается формулой
где М р—л. в. изгибающего момента в том же сечении основной систе
М\ — изгибающий момент там же, вызываемой силой A'l — l.
Ординаты этой линии влияния получаются путем умножения ^Р^^ре-
л. в, Хх на постоянное число Мх н добавления ординат статически
делимой л в. Мр. Так, например, для сепели,,..
J„r. 413, а) уравнение имеет вид ^^Р^дины ригеля BD (сечение ? на
Эта линия влияния изображена на фиг 4И я
^ой суммы двух линии влияния, а также в выпрямлен "^^ алгебраичес-
игЗ^Б УПРОЩЕНИИ КАНОНИЧЕСКИХ vdao„
"-даПГ СИММЕТРИЧНЫХ СИСТЕМ РАСЧЕТ PAmIV*'''
С ТРЕМЯ ЛИШНИМИ СВЯ^МИ "
Когда заданная система имеет той ип« л^п
ную систему следует выбирать так чтобы п^пл"^"^^^™"^' ^« «"'«в-
простые канонические уравнения о'собпр L», ^^'"'^'' возможно более
щать при этом на так называемые «по^ныТГ."/. "Р"''°^"^".^ °бР^-
коэффициеиты с неодинаковыми яняи!.,™'? ^°.^**"^^"^"Tb, S,,. т. е.
при C/1UM nd idK называемые «побпиимочч ,,^^л л ^ '^ "-^^ uujjd-
ициенты с неодинаковыми значкамПн Г i^^^**"^^"^bi В,„ т. е.
ми значками / и k. Чем большее количество
Фиг. 416
ЭТИХ коэффициентов обратится в нуль, тем меньше неизвестных будет
ходить в состав отдельных уравнений, тем проще, легче и точнее можно
^'^м ^^^^^^ ^^^ систему уравнений.
Мы можем получить значительное упрощение, если используем сим-
метрию рамы и постараемся ввести эту симметрию в самые эпюры,
акои вариант основной системы изображен на фиг. 415; рама разрезана
оси симметрии. Эпюры Мх и М2 — симметричны относительно этой
^^у а эпюра Мз является косо или обратно симметричной (мы будем
зывать обратно симметричной такую эпюру, у которой обе половины
личаются только знаком). Можно доказать следующее важное свой-
^Во таких эпюр: если сооружение обладает осью сим-
•^^^¦^Рии и, кроме того, одна из двух эпюрАГ^ или Af^, с и м-^
'^Рична, а другая обратно симметрична, то
«айых"™'""""°- "'"'
SJ
MgMbds _ Q
EJ
каждой из двух половин сооружения, располо-
^чевк "^ по разные стороны от оси симметрии, это выражение имеет,
Кое ?' ^-^^^У " "^У ^^^ величину, но противоположные знаки. Отмечен-
odt^^^^^^^'^J^o мы будем в дальнейшем называть свойством взаимной
ь^уогональности
^ИЧны;
эпюр.
симметричных
обратно сим мет-
299
^''«1
IIj этом основании для фиг. 416 можно написать ^^^^1 -_г,
представим себе деформацию основной системы, вызванну!^ ^^^^
МЫ предста
^1, ^2, ^3. то легко убедимся в том же, не прибегая к формуле прп^^^^^*
НИИ. Канонические уравнения ^Р^Мещ^,
^21^1 + 822-''^2+ ^2 3^3 + ^2р = О ;
Зз1^1+8з2^2+^ззА^з+Дзр=0
благодаря этому приобретают более простой вид:
8хЛ+ 8,2^2+Ахр = 0;
htX^ + b,^X^ + A^^ = 0;
8ззА:з + Аз^, = 0.
(а>
(б)
Совместная система (а) трех уравнений с тремя неизвестными
говорят, распалась на две отдельные системы, а именно: п'ня
* / Па ДВЗ
hz
h
¦ Штттп.,
Фиг. 417
оГиГнГве^тнГ""' ' ""^^"^ неизвестными, 2) „а одно уравнение с
HarpysK^'SL симметричную' '^^п °^"° У"Р0Щение. Разобьем внешнюк.
ГЬ/гт, J*^ ^^'^'^'^^тричную и обратно симметричную
и РавС;;ноГимТющТГна'лГ'"'''^'^^"^ "° Р'^^'^'^ « -^^ <^"-«"'"'"'
на правой^„';е:;гГстГ,Г(Хг''417Т'^п' ««-^н^ивность <7,+<7../
грузки эпюра Л/ пя^тто,!^^' ^' • ^''^•'^)- После преобразования на-
и Обратно Lip^rr' - ir""""™™"- »™-Р"™Г ^5
интегралов ич nnnu. ^* ^-^^^^адаря доказанному выше свойству
можно ;?верждатьчтГ"'' ^^"^^Р^^'нь.х и обратно симметричных эпюр
V Гл^и> ^ 2] Г луи> ^у л
EJ
= 0.
ама
нагружена только си"'-
метричной нагрузкой nnl,,?^''^^' '?''^^ Р^"- "-.ру^^^на .— - .
когда рама SySa ?ол?кГп^« ^^^ =^' "^'^У^^ ^'=0; в том слу-ае,
чается аналогичным образом А^^™1 симметричной нагрузкой, полу
видно, что эти вивопи? Р "^ А,р = л^р =0. откуда Xi=X2='0. Оче
^^огда на сш2,еХно ^"Р^^^'^^ ^^обой следующую общую теореМУ-
^ "л.легрич„ое сооружение действует симметричная нагрР>«^
THo симметричные неизвестные обраи^аются в нуль; наоборот,
fO ^ ^^^Цствует обратно симметричная нагрузка, то симметричные не-
^^^^^ткые обращаются в нуль.
цзоест^^ ^^ разыскиваем симметричные неизвестные, мы имеем право
^^^^ашать внимания на обратно симметричную нагрузку, а когда
^^ иваем обратно симметричные неизвестные, мы можем игнориро-
разыск ^^^^^ppJчнyю нагрузку. В большинстве случаев (хотя и не всегда)
gflTb оот пягчет
^^°попятимся теперь к заданной раме и рассчитаем ее на симметрич-
ягпузку а именно на сплошную, равномерно распределенную по
"^¦^^ "пине оигеля нагрузку с интенсивностью q. Неизвестная Хз при этом
Татится в нуль, и нам достаточно будет решить два уравнения с
°ТусТьТл™а""ригеля /=8 м; длина стоек /г=3 м; отношение момен-
в инерции — =5; интенсивность нагрузки 7=0,5 т/ж. Тогда, поль-
зуясь фиг. 416 и 417, мы найдем
EJA. ^2h+l^= 7,ем; EJA. = 2^ = 18^3-
?/Л. = 2^ = 9^'"
^, , <)Яl^^^. А =i^ - 36тл{«.
?«'i^2p = ^-^ 2 8
Уравнения напишутся так:
7,6Х,+9Х, +26.13=0;
9Хг+18Х, + 36 = 0.
Решив их, найдем
X, = - 2,623 тм; X, = - 0.689 т.
Окончательная эпюра моментов вьфажается формулой
При вычислении ординат эпюры будем писать со^^ волокне стой-
моменты. которые вызывают растяжение во j
ки или в нижнем волокне Р'^''^^^-„„„„ини причем
На стойках эпюра имеет вид трапеции, up
Л1^ = _ i^ + 2.623 + h. 0.689 = 0.690 тм ;
д, ^ + 2,623 ='-1.377 тж.
„мметоичной параболы, причем М^ =
На ригеле эпюра имеет вид симметричн
°=—1.377 тм;Мс= 2.623 тм.
Эпюра М изображена на фиг. 41»,, так же. как в предыду-
, Статическая поверка эпюры производи
''i^M примере. 3QJ
Поверка деформаций может быть произведена при помощ„ дк^бой
^^^^^^ннош^^'есГ'в" данном случае поверка при помощи первой
из этих эпюр, т. е'. при помощи эпюры М,. Так как все ординать/зД
эпюры равны единице, то
ii^^=sr
= 0,
Mds
EJ -J EJ
ИЛИ после умножения обеих частей на ?/i
Назовем для краткости график iM-^ приведенной эпюрой
изгибающих моментов. Полученное тождество выражает собой следую-
щую теорему: приведенная площадь эпюры моментов, подсчитанная для
плоского стержня, образующего замкнутый бесшарнирный контур, всег-
да равна нулю.
0,690 @
Фиг. 418
Фиг. 419
В частности, раму с защемленными концами также можно рассмат-
ривать как замкнутый стержень, имеющий бесконечно жесткий уча-
сток— фундамент (фиг. 419).
Произведем это вычисление для нашей рамы, причем эпюру, относя-
щуюся к ригелю, разложим на прямоугольник и параболу:
Y,^M^ds = 2(^
21 0,690—1,377 .g
+ — (1,377 + 2,623)8.-1
1,377-8.-f +
О
Не лелая приведения положительных членов с отрицательными, вы-
числим отдельно сумму положительных членов и отдельно отрицатель-
ных. Мы получим
y^^M^ds^ 6,337 ~ 6,334.
Разница между обоими членами составляет по отношению к люоо
му из них около 0,047о, что подтверждает правильность расчета.
§17Л^ДАЛЬНЕЙШЕЕ УПРОЩЕНИЕ РАСЧЕТА ТОЙ ЖЕ РАМЫ
---"'"^ПРИ ПОМОЩИ ВВЕДЕНИЯ ЖЕСТКИХ КОНСОЛЕЙ
и ^^^^Р^^^^ заданную раму в произвольном сечении С, С (Ф"^-Д
и прикрепим в этом месте две бесконечно жесткие консоли. Ьслн
пл^^м!"""' ^™ консоли каким-нибудь способом в одно жесткое ^^'""^^'^^s
n^S ""'' "^"^ свяжем их при помощи трех стержней, то в y^f^^^,^
раооты заданной рамы ничто не изменится. Действительно, при деи^-*
302
какой угодно внешней нагрузки смежные сечения С и С окажутся на-
глухо скрепленными друг с^другом; они не смогут друг относительно дру-
га ни повернуться на какой-нибудь угол, ни переместиться в вертикаль^
ном или в горизонтальном направлении. Поэтому все усилия во всех
элементах рамы останутся без изменения. Однако это будет справедливо
только при условии абсолютной жесткости консолей; если бы консоли
обладали податливостью, то указанное взаимное их скрепление не обес-
печило бы взаимной неподвижности сечений С
и С^
Введение таких консолей удобно главным
образом тем, что оно дает широкую возмож-
ность варьировать выбор основных неизвест-
ных. В самом jx^n^, за основные неизвестные
можно, принять усилия в соединительных
стержнях, а последние можно располагать на
плоскости как угодно, лишь бы они не пересе-
кались в одной точке.
В данном примере целесообразно взять се-
чения С и С на оси симметрии и считать, что
консоли связаны двумя горизонтальными
стержнями и одним вертикальным. Тогда
эпюры будут иметь такой вид, как на
фиг. 421. Нет надобности чертить эпюру на протяжении консолей: для
последних мы должны принять /=оо^ поэтому независимо от вида эпю-
ры все интегралы на этом участке обратятся в нуль.
ш^
Фиг. 420
Фиг. 421
Мы имеем право располагать горизонтальные силы Хх и Х2 на каком
У^'одно уровне. Используем эту возможность следующим образом: распо-
ложим силу Xi на том же уровне, на котором находится центр тяжести
¦треугольной эпюры Ms, т, е. на расстоянии —' h от ригеля. Тогда при
^Ь1Числении перемещения \^ нужно будет умножить площадь треуголь-
ной эпюры Мг на ординату эпюры Ми равную нулю, следовательно,
получится 0^2 =0 Кроме того, благодаря взаимной ортогональности
симметричных и обратно симметричных эпюр, можно написать о„=
"7 ''^-г =0. Следовательно, все три побочных коэффициента канонических
уравнений окажутся равными нулю, и система совместных уравнении
Распадется на три самостоятельных уравнения: -
ВиХ, + Д,^, =-О ; Й22Х2 + Д2р-=0; ЧъХ^ + ^^р^^.
заа
§ 17.5. РАСЧЕТ ДВУХШАРНИРНОИ АРКИ С ЗАТЯЖКОи
С повышенной 'затяжкп-
'^— содержа^;;
Расчетные схемы различных двухшарн.ирных арок с затяж '-
заны на фиг. 422. Схемы а и б изображают арку с затяжкой ^^^ ^^^^'
женной на уровне опор; схемы в и г — арку с повыше ' оят^^
и схема д—арку с ломаной затяжкой. Все эти схемы
одной лишней связи.
Арка с затяжкой при действии вертикальной нагрузки
в своих опорах только вертикальные реакции; горизонтальная с ^^^^^^^^т
щая отсутствует, поэтому, согласно установленной выше класси^гЬ^^'^^'^"
расчетных схем, она должна считаться безраспорной В то , "^^^^«
усилия, возникающие в кривом брусе, стянутом затяжкой ^и ^^^^^^
отличаются от усилий распорной системы, так как по отношени "^^^^ "^
Фиг. 422
f-J^^^^^co^mr Lm™luTrol IT ^''""Р"- ^^"""'^^^ °^ Распорной
погашается, так скя.ят. ' Л1„." ^Р»^^ ^ затяжкой распоп оооазуется
изгг^Т- ^"'^"^ устройств; позволяет '° ^°°РУ>«ения, без передачи
ZZnt "''''' моментов, свойгтвеннпр L °''"5^ь «Дновременно снижение
экономичностью опор,'cBoSSmn ?Г"°" .'"^^^^ ^ легкостью и
^(атяжка может быть спрпя^о балочной системе
мет^ь'f^''^'"" "^"Ри'ер же'^езо^е'тТ^ ^^ "^^^Риала. что „ сама арка,
Рассч;?аеГ''''^'°''^^^^У """" ^^P^^^""^" арка может
'Й"42Я°^1^'^^'"°^ну'^'с^^^^^^^^^ '""^•^«й' расположенной на
iSe S тп^^^^- "Р" «"воде SoL?nf ^Р'^У ^ разрезанной затяжкой
и noneiu J ¦"'"^¦° деформации из?51 ^^^^^ "'^^^^^а принимать во вни-
От Рдей"?'' ^"•"- ' "° " деформации от продольных
моменты М^^" "Родольной силы y._i
дующими i'l "Родольные силы Л', „"^' ^ ^Р''^ возникают изгибаюшне
"" формулами: ^ ^' " поперечные Q,, выражаемые сле-
« взатяжке-^,0 ^^=-cos<p,. Q,=.__sm<p, (i7.1)
мГ;.Тп"о;ь,„-/,ь^^^^ SnaKMHHvc указывает.
поперечные. ДействуЗе 3 "tn-''''Р^У' продольные силы с^«-
304 J' щие в левой половине, стремятся врашать
„бе части арки против часовой стрелки. На Лиг 494 г. „^
Й„ие горизонтальной силы Х,= Гна составляющие п" Г)^'''"° Р''^°-
"^ От действия внешней нагрузки получаются изгиба^^.иы'^ .
которые в функции от абсциссы х выражаются ?ак жр Jf "^менты.
Гпрямой осью. Если мы для такой балкПбУна^м' мо1еГы'и"Г
„еречные силы от тон же нагрузки через М, „ Q,, уо получим
Мр^М,; A/„ = _Q„sincp; Q^ = Q^eos<p. (17.2)
Фиг. 423
Фиг. 424
О)
^/-/
^Х^
Фиг. 425
Разложение силы Qo на составляющие показано на фиг. 425,6. Что
^[зсается затяжки, то при действии внешней нагрузки усилия в ней рав-
*^Ь1 нулю.
Основной неизвестной Xi служит усилие в затяжке или распор, ко-
Л^Рь^й мы в дальнейшем будем обозначать также буквой /Л Для того
^'^обы его найти, придется составить и решить каноническое уравнение,
**мею1дее вил
**¦ Рабинович
8,Л+^=0-
30S
о„р-ь 8 -пы.ываемое силами Х,-1 взаимное горизо.гтальное пере^.^.^
Здесь ь„ пызы ^^^^^^^^ затяжки на месте произвсдеипого разрена;
Л,р-взаимное перемещение в том же месте, вызванное внешней
Капоннчё!!Х^Ур"внепие выражает ту мысль, что ширина ще^и ,
разрезном месте'после „агруженияаркн остается равной нулю.
^ Пусть затяжка имеет постоянное сечение.
Обозначим через Fz и ?з плон1аль этого сечения и коэффициент упру,
гости затяжки; через /о-произвольный момент инерции, например „J.
мент пнорции ключевого (среднего) сечения арки. Тогда
0
+ jsin^,J^cts+^l, (17.3)
где
r^oAip = — X J y^^o^s'+ 5] J Qo sin cp cos tp ^ds-
-i;jQoSin<pcos<p^d5. (17.4)
Вычисление этих интегралов оказывается более утомительным, чем
для систем с прямолинейными стержнями. Для того чтобы произвести
эту операцию аналитически, необходимо выразить все переменные, стоя-
щие под знаками интегралов, т. е. у, sin9» cos ф, /, F, в функции от од-
ной переменной ds. В общем случае это приводит к сложным и труд-
но интегрируемым выражениям. Поэтому на практике предпочитают
заменять точное интегрирование приближенным численным, которое
всегда производится сравнительно легко, и точность которого может
быть доведена до любой степени. Для этой цели ось арки делят на доста-
точно малые участки одинаковой длины As, пронумеровывают их и Д-пя
каждого в отдельности вычисляют в среднем его сечении величины
У' "У"» sincp, coscp и т. д. Приближенность расчета состоит в том, что
все эти величины принимаются постоянными на протяжении всего эле-
мента А 5. Интегрирование заменяется суммированием конечного коли-
чества слагаемых.
Численные значения sin ср и cos ср можно определить аналитически,
если дано уравнение оси арки: y=f(x). Тогда
tg<p = ^ ; eoscp= ± ' ; sincp^tgcpcoscp-
На всем протяжении арки cos ср сохраняет один и тот же знак; sin J
в левой и в правой половинах арки имеет противоположные знаки. ^
будем считать sift ср в левой полуарке и cos 9 в обеих полуарках nOJi
жительными,
306
Если ось арки задана не своим уравненирлл о
вычисления синуса и косинуса нет надобности LU't^'"'^'''^' ^° ^^'^
^гла ?; достаточно провести в исслед^емЙ точке осГяпГ'" ^"^""""^
Ь^^Гел^н^Г^ '''''''''-^' и^горизоГа^Гй ЦТ^^^Т^^,
„ер'ГГГеТбл.''Г""^^™ ^^""^^- «^ —™ой форме, напри-
jyfe эле-
мента
Таблица 7
sin 9
cos 9
As'
cos*9——
^ F
5:,
10
sin2to--2-
Итог 8-й колонки обозначен через I^i , итог 9-й — через ^^
через ^3- Через них выражаем окончательный результат:
я.л.-х,+(2,+1;)..н-^г
и 10-й —
(17.5)
В этом выражении первый член, т. е. S^ выражает влияние изги-
бающих моментов на искомое перемещение; Sg^s —влияние продоль-
EJo
ных усилий арки; Eg^s —влияние поперечных усилий;
?з ^8
I —влия-
ние продольной деформации затяжки.
Аналогичным образом можно составить таблицу для вычисления
перемещения ?/o^ip- Входящие в формулу (17.4) три члена выражают
только влияние усилий, возникающих в самой арке; усилия в затяжке
здесь не фигурируют, так как от внешней нагрузки они равны нулю.
Распор определяется из канонического уравнения.
Xi = // = _ ^ = .
^11
?ЛД:
W _
EJo^,p
EJifbi
EJe
2+(2,+Хз)^^+-?;;7'
. (17.6)
^ По этой формуле может быть вычислено точное значение усилия
I» испытываемого затяжкой. Приближенное значение может быть по-
учено при игнорировании в числителе и знаменателе тех членов, кото-
М^ выражают влияние поперечных сил; еще более приближенное — при
^Дновремениом отбрасывании членов, выражающих влияние поперечных
"^^^'^^«"ьных усилий арки. Игнорирование этих членов значительно
сто ^^^^ вь1числение лишней неизвестной, но если сравнить полную
TDa"^^^^^^ прочного сооружения со стоимостью того труда, который за-
выч"^"^^^^^^ на вычисление нескольких колонок в таблице, то отказ от
дз^^^'^иия точного значения неизвестной Х^ вряд ли можно будет оправ-
jjy^* Если все же решено будет производить г^-^чет приближенно, то
заме^^ "^^^'гь в. виду, что влияние прол'^л^ной силы на Х^ довольно
арок ^ Д^^я весьма пологих арок значительной толщины, а также для
врй ^^^ которых совпадает с веревочной кривой, отвечающей ее вуеш-
" нагрузке.
307
Для арок подъемистых, очерченных не но веревочной кривой, влия
ние продольных сил незначительно. Вообще же сравнительное влияние
различных членов зависит не только от очертания арочной кривой и от
сечений арки, но также от самой нагрузки.
fi 176 ВЛИЯНИЕ ПОДАТЛИВОСТИ ЗАТЯЖКИ. ЭПЮРЫ М, Q, Д^.
КРИВАЯ ДАВЛЕНИЙ
Существенное влияние на величину распора Я, а следовательно, и
на все усилия в арке оказывает степень податливости затяжки, которая
характеризуется величиной - , а при заданном пролете / — величи-
ной-—— . Формулу (17.6) можно
переписать в таком виде:
А
Н
В-
Е.К1
Фиг. 426
где Л и В не зависят от жесткости
затяжки. Если мы будем постепенно
уменьшать величину E^F^ или толь-
ко величину площади F^ поперечно-
будет постепенно увеличиваться, а
го сечения затяжки, то дробь
распор Я уменьшаться. Чем тоньше, чем податливее затяжка^ тем
меньше то усилие, которое она воспринимает. Когда площадь F^ сде-
лается бесконечно малой, означенная дробь сделается бесконечно боль-
шой, и усилие Н сделается бесконечно малым. Арка, концы которой
связаны бесконечно тонкой* нитью, лишь формально будет еще стати-
чески неопределимой, фактически же будет работать как кривая
статически определимая балка. Если мы, наоборот, будем увеличи-
вать площадь Fz, то Н будет увеличиваться, однако далеко не в такой
пропорции, в какой будет увеличиваться эта площадь. При стремлении
величины F^ или E^F-^ к бесконечности распор Н будет асимптотически
стремиться к величине
т. е. к величине
Этот
1, (Х^+^з)^^
предельный распор вызовет в бесконечно жесткой затяжке удлинение,
равное нулю, следовательно, концы арки останутся неподвижными.
Итак в предельном случае арка с затяжкой превращается в арку с не-
подвижными пятовыми шарнирами — в обыкновенную двухшарнирную
арку. Графическое изображение указанной зависимости дано на
фиг. 426.
После того как распор Н будет найден, можно будет определить
усилия в любом сечении арки:
(17.7)
^х = — (QoSin ср -f W cos <р);
Qv = Q« cos cp — P sin cp ,
где Ml и Qo относятся к простой балке пролета /.
На фиг. 427 показан вид эпюр М^, Л/^, Q^.
Для двухшарнирной арки с затяжкой или без затяжки можно "
строить кривую давлений совершенно так же. как для трехшарнирн
арки. Разница состоит лишь в том, что для трехшарнирноп ар
308
^Kirnov ^ определяется из уравнений стятм1^и « ^
5"„Трной он определяет/я' „з к^нониГГого ураГеТия^^еГ/Г'
Заданные внешние силы откладываются и nno,..„7fn метода с
вертикальной прямой (фиг. ^"^ ^ произвольном масштабе
на
lOlilliUJiUJJlUIl
428); нз нее же наносим вер-
тикальные составляющие
опорных реакций V^ и V^,
которые определяются, как
цля простой балки; через
точку раздела проводится
горизонталь, и на ней откла-
дывается найденный распор
Я. Конец вектора И прини-
мается за полюс О. По этому
силовому многоугольнику
строится веревочный, кото-
рый и представляет собой
требуемый многоугольник
давлений, переходящий в
пределе, при сплошной на-
грузке, в кривую давле-
ний. Она пересекает любое
сечение арки в точке прило-
жения равнодействующей
всех внутренних сил сече-
ния. Величина равнодейст-
вующей выражается на си-
ловом многоугольнике лу-
чом Оа, параллельным каса-
тельной а—а к кривой дав-
ления. Чтобы найти нор-
мальное напряжение в ка-
ком-нибудь сечении АВ
(фиг. 429), нужно разло-
жить равнодействующую S
На нормальную силу N и по-
перечную Q и взять момент силы N относительно ядровой точки /С^ или
Фиг. 427
^в ¦ после чего можно написать
^л='
^(^ — ^в) ^в
(17.8)
В Двухшарнирной арке, как и в трехшарнирной, рассчитанной на
постоянную нагрузку, желательно, чтобы кривая давлений совпала с
осью арки, так как при этом не будет ни изгибающих моментов, ни
поперечных сил. Для того чтобы произошло такое совпадение, нобходи-
^0. чтобы ось арки была очерчена по веревочной кривой для внешней
^^'^Рузки. Действительно, для того чтобы во всех сечениях изгибающий
' омент был равен нулю, необходимо положить
М = Ml—Ну = О или у = ----; {^7.9)
И
няг "^^^^одимо, чтобы ординаты оси арки были пропорциональны орди-
**там эпюры М , которая служит веревочным многоугольником или
^^Ревочной кривой для заданной нагрузки. Но в противоположность стг-
т
н
Фиг. 428
Фиг. 429
310
гически определимой трехшарнирной апке и.
„альности педостаточно: в статачески'^неоп " ^""^ У'^-""^"^ пропорцио
кривой давлемия зависит не только пг .!!!°^Р."^^-"имой арке положен„;
оси ЯПк-ы т.^
„альности ..сди.,аточно: в статически неппп ^^"^^ ^•^•"овие пр
кривой давления зависит не только от очрпг^ '^^"""""й арке п<
плои1аяеи и моментов инерции сечение, и^'^"" ^'^и арки но
Яз. G. Только в TOV, случае, когда распоп °н ^°°™ошения вел:
нальности
кривой ИгТ:
плотадей и моментов инерции сечения""';'^от"Г °'" "Р"^""' но также"от
Яз. С. Только в том случае, когда распоп J ^"°™ошения величины ?
(17.6). удовлетворит условию % J!!^? ^' ^'^"^lI'^-^^HHb.H по ДмуГе
давления с осью арки. ^ ^«' произойдет слияние кривой
§ 17.7. ПОСТРОРНИЕ ЛИНИЙ ВЛИЯНИЯ
а) Линия влияния распора. Из формулы
следует, что л. в. распора Н ппелгтяппо^,. * -
штабе линию прогибов оси арки ^Т^^Л^шТи^^ЛП'Г'''''' ''''~
что затяжка разрезана). Эту линию пппгиЛпТм ' <"Р" Условии.
»ош„у„руп.х .рузоз. L -огоГ;<;„^Ге°„ГьТр"„°=„™;ГоГ а?!
9?t?Phu
Л.б.н
\?^оЩ
Фиг. 430
'acS Обозня^'ы?";)!'^''^^"""' "''"'^ "^ достаточно большое число равных
"естим вео?и^Г„1 ^У ''^'"'^°" '^"^^ ^'*'']^.' ^^ ^^ « ^"«3^ деления по-
отсилыЯ-1 '^ упругие грузы w^ (фиг. 430). Имея в виду, что
«^илы /V,JC^n^°"^""'^^'°^ изгнба.ющие моменты М, = ~у н продольные
-cos 9 н что
г
COS у tg у sin у
^'P^+l
^•Л
'л+1
^"0 написать на основании формулы (14.14)
р
^ "ojiio" ^""^ ^^"^ вертикальных сил построить силовой многоугольник
^''о/1Ы|и"^'''^ ^'^^^^^"""^'^' равным единице, а затем веревочный много-
^Удут п*^* ^^ ^^° ординаты, измеренные в масштабе длин чертежа арки
Уд Р?^»Ь1 искомым прогибам.
^ ^^ w^^^ откладывать на силовом многоугольнике не величины ш^,
Ecjii^ ** " произведения имеют в данном случае размерность см^.
*^а силовом многоугольнике они отложены в масштабе
311
2 „ппюсное расстояние равно 6 см и если, кроме того
, см^а см\ а "0;"'°"Г^„ ' чертеже в масштабе 1 : п. то прогибы полу!
ГсГв^^уТшГГм^асштабе^:
Тс1 ор яинаты веревочного многоугольника = -^ . т. е
г к гм1кг Для получения масштаба ординат л. в. И
Т1шо ГазлеГить масштаб построенного многоугольника на 8,. В
'^"ТГординаты линии влияния распора = -^ (отвлеченное
ло).
EJo^i
EJ^ '--ординаты
ре»
чис-
\A6.Mjf
ш'ЛЛМ^
ь---
Фиг. 431
Фиг. 432
I) у»м\тивая только влияние изгибающих моментов и разбив ось на
^ иосд)^)ение лJrlJtJИJи прогибов можно разбитъ^на два этапа:
весьма малые участки, принять у„_, = У^^, = у^, ^п+г
мула для упругих грузов примет простой вид:
'= t/^, тогда
___уД5 _
уДх
EJ EJ COS у
а линия прогибов будет служить веревочным многоугольником для это
распределенной нагрузки;
2) учитывая влияние продольных деформаций, принять упругие гру-
iu равными
ш =
sin9„
"Pn+l
EF^
ER
n+l
Оба ве-
причем ось арки может быть раз.бита на более крупные участки. ^^^ ^j^i
ревочных многоугольника нужно заменить плавными кривыми и з^
сложить
Когда продольными деформациями пренебрегают, построение, Р
моется ограничивается первым из указанных этапов. „ ^.^,от-
О) .Пиния влияния изгибающего момента, ^^^"-..^ji^i
РИМ лроичвольное сечение D. находящееся от левой опорной верти^^^
иа расстоянии а, а от правой — на расстоянии 6. причем а + ^=^-
312
Из формулы М^ ==М% _Яу^следует, что эта линия влияния пред-
ставляет собой алгебраическую сумму л. в. iWJ,, имеющей вид треуголь^
„ика с наибольшей ординатой у-. и л. в. распора//, умноженной на
постоянное число у ^ (фиг. 431).
в) Линия влияния продольной силыЛ/^. Эта л. в. строит-
ся, как сумма двух л. в., по формуле
^D-- {Ql S'H То + ^/ cos 9^,),
т. е. как сумма л. в. Q^ ^ ум-
ноженной на постоянное чис-
ло sincp^) , и л. в. Я, умножен-
ной на постоянное число
cos То . Построение показано
на фиг. 432.
Линия влияния нор-
мальных напря>1<ений
в крайних волокнах
сечения. Напряжения в
крайних волокнах сечения
выражаются через моменты,
взятые относительно соответ-
ствующих ядровых точек
этого сечения:
^Д^ i/a~ ордината ядровой
точки. Для напряжения в
верхнем волокне D^ берется
нижняя ядровая точка Ки и
наоборот. Построение линии
влияния нормальных напря-
жений в точке Di показано
«а фиг. 433,6.
Линия влияния Q^
строится, как сумма двух ли-
*^ии влияния, по формуле
Пдмбл^
тМп
^^9Vd<
<Ifi. 433
^ординатам л. в. Н нужно добавить с обратным знаком ординаты л. в
^о ctg (р^^ и полученный суммарный график умножить на sincp
(фиг. 433,в).
Ъ
§ 17.8. РАСЧЕТ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ
Распор И определяется из уравнения
нли
S„X, + A,,-0
313
Перемещение Д,^ вычисляется по формуле
где для элементов арки М=—cos ср, М,= —^, а для элементов затяжки
Примем температуру неизменной по длине арки. Югда
в
^^^ = —ai fcoscprfs + as^/ —af ] ^ ^^'
Здесь первый интеграл выражает влияние равномерног^э нагрева
арки; знак минус свидетельствует о том, что при нагреве раскрытие
mejJM в затяжке происходит в сторону, противоположную действию по-
ложительной силы Xi. Так как cos <^ds = dx, то этот интеграл равен
— at^dx = — atl.
Второй член выражает собой температурное удлинение затяжки;
ад—коэффициент линейного расширения материала затяжки, В двух-
шарнирной арке с неподвижными пятовыми шарнирами (в арке без
затяжки) следует считать «з =0. В третьем члене разность температур
крайних волокон, обозначенная через t\ считается положительной, когда
она искривляет арку выпуклостью в ту же сторону, что и положитель-
ная сила Х|, т. е, вверх.
Расчет арки обычно ведется только на равномерный нагрев, т. е. при-
нимается /^ = 0. Тогда в арке с затяжкой
^1/ = - а^/ + а^и = (аз - а) « ; Я = ^"^"^^^^ , (17.10)
а в арке без затяжки
Аи = -Ш; Я = —. (17.100
Когда ^>0, то в арке без затяжки распор направлен внутрь проле-
та, в арке же с затяжкой направление распора зависит от соотношения
между а и аз . При а > ад затяжка растянута; при а=аз она не испы-
тывает никаких усилий и при а<аз она будет сжата. Когда /<0» ^^
знаки этих неравенств изменяются на обратные. Нужно заметить, что
сжимающие усилия в затяжке нежелательны, так как она обычно весьма
гибка и при сжатии легко теряет устойчивость. Но суммарное
усилие в затяжке может оказаться сжимающим только тогда, когда
температурное сжимающее усилие превысит величину растягивающего
усилия, вызываемого постоянной нагрузкой.
В самой арке температура t вызывает следующие эпюры усилий:
ahaIJZ^ бесшарнирная арка, выбор основной системы.
АНАЛИТИЧЕСКОЕ И ГРАФИЧЕСКОЕ ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ
нии^^.^^гп^о^^^^'"^""*'''^" пятами находит себе применение в мостострое-
Р .и^п Ji^^^"^*^^'^ " промышленном строительстве, по преимушеству
чобРтп.ш^*''''""^ конструкциях. На фиг. 434 представлен пример желе
зооетонного арочного моста, ^ г
314
расчетная схема арки с абсолютно заделанными „
,пи лишнле связи, а потому при расчете такой ^и. "''^"" содержит
ручаются три основных неизвестных °" ""'""''" "° ""^'^^У ^"^
При выборе основной системы желательно получить тп.. .. .
дельных уравнения, содержащих по одной неизвестн'оГэто'можГбГ:
достигнуто различными способами. Несколько вариантов основной систе
мы, допускающих такое решение задачи для CHLeTpHMHoR бесшаонио"
ной арки, представлено на фиг. 435. При всех этих Мриантах ?огут
быть получены одни и те же основные эпюры и. следовательно один и
тот же ход всего расчета. «слсни, идин и
150.0
Фиг. 434
Остановимся на варианте б фиг. 435, т е. разрежем арку по оси
симметрии, прикрепим к обоим сечениям бесконечно жесткие консоли и
приложим к ним неизвестные A'l, Х^, Хз.
Фиг. 435
Канонические уравнения
82,^1 + 822^2 + 823^3 + ^2;, = О ; (17.11)
8зЛ + 8з2^2 + 8зз^з + ^/.=0 )
^УДУт выражать условие полной взаимной неподвижности обеих консо-
^О^й^уе^сТым^азят условие взаимной неподвижности сечении
315
Фиг. 436
/'%']
^tn%
''U>sV>
sin%
Фиг. 4J7
310
вычисления коэффициентов системы (17Л1) построим едииич-
oDbi М, Q ^ 1^' Расположим начало координат в некоторой точке С
iibie 9"' ^^^^^ppj^j^ У^ направим положи !елы1ую ось л: ов вправо, положи-
на ^^^ ^^^ (7^ов —вверх. Будем считать положительными: изгибающие
тельную ^^^^ j^,^ вызывают растяжение нижних волокон; поперечтгые
1^оменть. ^^^ стремятся повернуть обе час'1и арки по часовой стрелке;
силы. KO.I.i^,,^,, к,
оп.,пые силы, которые растягивают ось арки
"'St вызываемые силами X, ^ ^ ' "'
1; Хг' 1 и Хз 1, выражаются еле-
дуЮШИ
j^H уравнениями:
м, ~
М,-
м»-
Qг
Q-г-
Q«-
Ni -
N,-
х;
— у;
-1;
cos <р;
sin <р;
0;
sintf;
- —cos 'f:
Л/а-0.
(17.12)
Советуем читателю не при-
нимать этих формул на веру, а
тщательно разобраться в них.
При этом следует иметь в виду,
что в них sincp для сечении,
расположенных справа от оси
симметрии, принят положи-^
тельным, а слева — отрица-
тельным; C0S9, напротив, имеет
по обе стороны от оси положи-
тельный знак.
Графическое изображе-
ние эпюр представлено на
фиг. 436—438.
Мы видим, что
Фиг. 438
ч^и|. too ЧОО. ^ W
Мы видим, что все эпюры ^^^ симметрична (эпюры Qi. ^2,
принадлежат к двум типам: олн^зча
N.. М,), а другая «^асть-обратно симСТ" ^^^^^^ ортогональности
Отсюда, на основании известного свои-^т^^ касается перемещения
Таких эпюр, заключаем, что ''ц— " •
„о п наших руках имеется сред-
то оно. вообше говоря, не равно "У^'°-"«"„д'у'длину консоли f/o. кот"Р^
<=т.ю Обратить его в нуль. М»^ "'^'^^f ^ При изменении ^тои величи»^ы
«ока остается произвольной (фиг. ^f^,,бается за счет отрицательной
положи гольиая область эпюры Мг Увели
"Ли наоборот. 317
Подберем уа из условия
s.. = f'f4=o.
"""]-
Умножим обе части этого равенства на ?/о:
в в D
AAA
где ds'^ — ds. Чтобы решить это уравнение, зададимся сначала поло-
жением точки С, т. е. величиной ординаты i/o, произвольно. Тогда каж-
дой точке оси арки будет соответствовать определенное значение орди^
наты у, которое можно будет найти из уравнения оси или взять из чер.
тежа.
D
Интеграл J у ds' можно будет определить либо в общем виде, либо
А
численно, в последнем случае — путем разбивки оси арки на небольшие
отрезки As и замены интегрирования суммированием. Пусть значе-
ние этого интеграла будет К. Если мы передвинем точку С вниз на не-
которую величину а, то координата любой точки заменится величлной
y-f с, и новое значение интеграла будет
D D D D
Г(у + ci)ds' = {yds' + a\ds' =К + а Tds'.
А А А А
Приравнивая это выражение нулю, мы найдем
а = -^, (17.13)
А
те. определим то положение точки С, при котором перемещение Кз
обратится в нуль.
^ ^ыбра^нная таким образом точка С удовлетворяет трем условиям:
'''"Г'^^'з = ^23=0. Следует вдуматься в смысл этих трех равенств: от
действия двух вертикальных сил X,, приложенных к этой точке, обе
оесконечно жесткие консоли получают друг относительно друга пере-
^nu^!""^ только по вертикальному направлению; от действия двух гори-
зонтальных сил они получают горизонтальное взаимное пеоемеше-
тоцкн г^Т^^^* ^'^ действия двух пар-только взаимный повор^г вокруг
чагтп ы;*../^ ^''^''^ (вернее сказать, две точки —концы обеих консолей)
часто называют упругим центром
лого эТмРнтяУс^^п""" ^'^"''Р "^^^-^^ координат, определяют для i^^^]
сти Лятр" приведенную длину As' и ординату его центра тяже
сти у, затем вычисляют перемещения по следующим формулам:
^^o%=-^Mlds'+^2l±ds+ r|xQ2^ds-
•^ J F J ' GF
= J x4s' + j" sin^o ii ds + Г,. cos=9 ^^ds^
в в в
318
A ' A °''
EJ^b„^
¦2.14
л
EJohs = Ja^' =.Cds' - Vas'.
Вьгеисления целесообразно распаюжить в форме таблипы Fr,o
пренебречь влиянием поперечных сит т nw„»).,^ таолицы. Еслн
n?H.vepHo так. как показан? в табл 8 ^° вычисления распаюжатся
ТаблЕда 8
1
1
2
12
Us
1 ^
1 ^
/
5
1 6
X
1 7
Г
1 8
sine
|_9
cose
1 10
x^ls'
1 11
ly^Ss'
1
1 *^
F
1 ^^
' F
Вследствие симметричности арки достаточно вписать з таблицу дан-
гае, относящиеся к одной половине арки, а результаты суммирования,
заменяющего интегрирование, удвоить.
19 ^^^'^^'^У ^ ^ целесообразно принять постоянной. Тогда в графах
*^ и 13 можно не учитывать множитель Л s, но зато учесть его при под-
^Оении итога, т. е. вместо того, чтобы умножать каждое слагаемое,
J'VHoKHTb сумму.
Канонические уравнения имеют вид
откуда
^Л + ^^ = 0;г^, + Л^=.0; «зз^з + -Чр = 0,
^1 =
^1Р
Х,=
^
^,=
•^зр
(17.14)
ЧйСЛИ!
g "^''ители этих дробей, вообще говоря, не равны нулю; но на осно-
^^йи теоремы, доказанной в § 17Д можно лп-вержлать, что при леи-
^^йй симметричной нагрузки получается \р^0^ а при действии обратно
^^^метричной нагрузки ^^р^^^^р^^^- В этом можно убедиться также
л^^^Р^^ственно: при действии симметричной нагрузки получаются сим-
Как ""^^^^^ эпюры М„, Np и обратно симметричная эпюра Q^. в то время
fe.ibH ^^ Л1,, Nx обратно симметричны, а Qi — симметрична; слелова-
тится^' ^о свойству взаимно-ортогональных эпюр выражение \р обра-
•'iRBn ^ ^^^^' Аналогичное рассуждение убеждает нас также в справед-
гатк ^ остальных двух равенств. Учитывая это, целесообразно разла-
суиж.^^^'РУзку любого вида, приложенную в симметричной арке, на
ьесгй •^'1?***^тричной я обратно симметричной и при вычислении неиз-
"^** -^ь игнорировать симметричную часть внешней нагрузки, а при
319
(17.15
вычислении неизвестных ^2 и ^з —ее обратив симметричную частк
То же самое относится к действию симметричной и обратно симметриц
ной температуры и перемещения опор.
Перейдем теперь к определению числителей дробей (17.14);
Eh^,,^-Y,lyM,ds'-Y.l^osoN^^ ds+Ц^sin^q.^ds, \
Вычисление этих формул может быть произведено в табличной фор-
ме при помоши приближенной замены интегрирования численным сум-
мированием. Если знаменатели были найдены без учега влияния по-
перечных сил или без учета поперечных и продольных сил, то и числители
нет необходимости вычислять более точно.
Во избежание ошибок необходимо помнить о знаках подинтеграль-
ных величин. Например, при действии обычной вертикальной нагрузки
=^пюра Мр всюду будет отрицательной, эпюра Np — отрицательной,
эпюра Qp в левой части положительна, а в правой — отрицательна.
§ 17J0. ПОСТРОЕНИЕ ЭПЮР. КРИВАЯ ДАВЛЕНИИ
Найденные неизвестные позволяют построить окончательные эпюры.
Введя для большей наглядности новые обозначения: Xi=V, Х^=И,
Х^=М^у можно написать
-^Mp+M,V+M^H-\-M^M,=Mp-\-xV—yH—M, ;
Q=Qp+QiV-\-Q2H-\-Q^M,=Qp+V cos ^+Н sin <^;
N^Np+N^V+N^H+N^M,=Np+Vsin(^—Hcos9'f
(17.16)
Каждая из этих трех эпюр строится, как сумма соответствуюшсй
статически определимой эпюры, которая вызвана внешней нагрузкой,
с тремя единичными эпюрами, умноженными на найденные неизвестные-
На фиг. 439 представлен пример эпюр М, N и Q,
Имея эпюры изгибающих моментов, поперечных сил и продольных
сил, мы можем определить усилия М^, Q^, Л^^ и М^, Q^, jV^, действую-
щие в пятах арки.
Опорная реакция представляет собой равнодействующую поперечной
и продольной сил:
На фиг. 440 показаны левый конец арки и построена Р^^'^?^^"^-
вуюшая R^ по составляющим Л'^ и Q^. Линия действия /?>, ^"^"^ILti-
иии имеет по отношению к точке А оси арки эксцентрицитет ^/i- ^^
чина последнего определяется из уравнения
^Л^А=М^.
3%
м.
^и =
Я нашем чертеже момент М д направлен против часовой стрелки,
му сила Rji перенесена вниз; если бы при том же направлении
"^ ' силы R'j^ момент М^ был на-
правлен в обратную сторону,
;iniin!iminiiiiiiiiiimiiiiiinii ТО И эксцентрицитет е^ приш-
лось бы отложить в обратную
сторону.
laE'f^i^^
Фиг. 439
Фиг. 441
21 И. м. Рабинович
Найденная опорная реакция позволяет построить кривую давление
Гфиг 441): на силовом многоугольнике откладывается заданная нагпуч
ка- полюс О выбирается на пересечении лучей, выражающих спорны!
реакции R^ и Rb^ после чего строится веревочный многоугольник- Его
крайняя левая сторона совмещается с линией действия опорной реакции
R . Правильность построения проверяется тем, что крайняя правая сто-
рона должна совпасть с линией действия правой реакции R^.
Построение кривой давления можно начать также с середины про-
лета, так как в этом месте сторона кривой давления совпадает с рав-
нодействующей снл Хи Х2 и Хз, приложенных к консоли.
Если бы кривая давлений совпала с осью арки, то изгибающий мо-
мент во всех сечениях обратился бы в нуль. Такое совпадение весьма
желательно, однако оно нeдocтижи^vlo, так как безмоментная сжатая бес
шарнирная арка геометрически была бы возможна лишь при сближении
ее концов, а это противоречит условиям на опорах.
§ 17.11. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ
Линии влияния основных неизвестных выражаются формулами
(17.14), в которых знаменатели дробей являются величинами постоян-
ными, не зависящими от положения подвижного груза Р=1. Все дело
сводится поэтому к построению линий влияния для перемещений о^^^,
\py\pj стоящих в числителе дробей.
Пользуясь принципом взаимности перемещений, переставим индек-
сы, как уже неоднократно делалось раньше, и придем к построению
перемещений ^^ь ^^г» ^рз' т. е. к построению линий прогибов оси арки
под действием сил >^i = l, >\^2=1 и Хз=\.
Построение этих линий прогибов проще всего производится при
помощи упругих грузов, которые могут быть вычислены по формуле
(14.14) и которые имеют совершенно простой вид, когда мы принимаем
во внимание только изгибающие моменты, и несколько более сложный
вид, когда мы учитываем, кроме того, влияние продольных сил.
Обратимся прежде всего к линии прогибов ?/o^pi, которая вызы-
вается силой ^1 = 1. Разобьем ось арки на достаточно малые участки
длины As и в точках раздела участков приложим направленные вниз
вертикальные упругие грузы w^.
Упругие грузы EJqW,^ могут быть вычислены по формуле (14.14)
Нужно подставить в нее в соответствии с фиг. 442.
^п , сТ/г+1 = ^^-\ • ^as = AS
И заменить букву р буквой ср. Мы получим
EJ,w,= ^п. ^^^^^ _^ 2хп)+ ^ (2 хп + Хп^г) +
_j_--^-sin'f„tgcp„ ^Slncp„+ltgcp«+,. 0'^'
^п Рп+1
Для упрощения можно принять
*^п+1 = *^„; ^s;^i = ^s;; х„__, + х„_^^=^2х„.
322
•sin<pn+itgtp„+i,
(17.18)
n+l
g результате получится
EJo^n = ^^'^n + — sin tp„ tg (p„ —
ХД можем поставить таблицу этих величии, затем подсчитать изги-
моменты, вызванные фиктивными силами EJoW^, или построить
6а1ошп(^^^ ^^^..^*^^j^j^ силам веревочный многоугольник. Так получится
cooTBeTL^^>^ ^ ^^ ^^^ правой половине арки. На левой половине кривая
очертш ^^^^ обратно симметрично. Масштаб ординат определяется тем,
S"b середине пролета уступ равен единице (фиг. 443).
Фнг. 442
Фиг. 443
Для линии прогибов ?/о V У^РУ^"^ ^РУ^^^ "Р" полюсном расстоянии
Я=1 выражаются формулой.
Jo
EJ,W, = - у As' - cos Ъг ^ tg cpn + COS 9n-f I ^ tg cpn+1 --
Jo
Jo
8Ш9г1+Г
фиг.
'Wsr
TO упругие грузы обратятся
Если пренебречь продольными силами У н^ р^^^^ „
«T-yAs'. По свойству УпРУ^ого х^ентра сумма^^^ ^^ ^44.
^'остроеиие силового и веревочного '^"°,^™' казан в § 14.10. Для по-
'^асштаб ординат веревочного ««««•оУ-'^Хаты на SoS,.
•лучения л. в. Х2 нужно разделить все ординаты на с о -^
~~~Т~ 11 1954. стр. 224. эта формула приведена
Пол uJ* 'Курсе строительной механики», ч. • • •
°А номером (19.6) с неисправленной опиской. ^^
^„„гяя ЛИНИЯ ^3 представляет собой веревочный мнот
nSrS/yn^yrHX грузов is'Vnr. 445). На силовом многоугольн';^
угольник для упруг УУ^ обозначена через EAs .
"^^Впрочем масштаб этой линии влияния можно определить следу„,.
щим образом: так как Хв= ^^ . то линия прогибов Аз, будет прямо вы-
Фнг. 445
ражать собой л. в. Х$, если мы примем такой масштаб, при котором
Вдз = 1.Но на чертеже величина ^33 изображается углом перелома
упругой линии ъ вершине. Так как сумма двух бесконечно малых углов
может быть заменена суммой их тангенсов, то отрезок ординаты, заклю-
ченный на фиг. 446 между касательными и проходящий на расстоянии
Фиг. 446
324
1 Chi (в масштабе длин) от вершины, должен быть принят
в
1 Chi'
равным
Линия влияния левой вертикальной опорной ре-
у'/^.-^л. в. этой реакции в
основной системе (ф-иг. 446).
Линия 'ВЛИЯНИЯ левой
горизонтальной реак-
ции совпадает с найдениой
л. в, распора Я.
Линия влияния опор-
ного момента
Эта линия влияния полу-
чается путем суммирования че-
тырех линвй влияния. Она име-
ет плавный вид, так как скачок
ординат в л. в. М^ уничтожает-
ся скачком в л. Б. Х\, а раз-
рыв в углах ^наклона (перелом)
л. в. Щ уничтожается перело-
мом л. в. — Хз (фиг. 447)
Линия влияния nP,
АЛЯ произвольного сечения по-
лучаются из четырех основных
лИ'Ний влиян-ия по формулам
(17.16). Примерный вид их
представлен на фиг. 448.
Из л. R nP и 7V^ можно
получить для сечения D линию
лияния ядровых моментов,
^ак уже указывалось при рас-
ете трехшарнирных '.и двух-
шарнирных арок
§ 17.12. РАСЧЕТ НА ДЕЙСТВИЕ
ТЕМПЕРАТУРЫ И УСАДКИ
вие Р^'счете арки на дейст-
членкт^^^"^Р^'^УР^^ свободные
^1 д ^^"онических уравнений
п^* ^''•^зрЗаменяются членами
Чего ""• ^
Q^.A^^
Ji^^^^^^Mm^^.
Фиг. 447
Ыу '^zu вследствие
^,^^^
и
x,=-
^11
(17.19)
Фиг. 448
в случае равномерного нагрева всей арки на Г:
где а — коэффициент линейного расширения.
Так как эпюра распределения температуры t вдоль оси арки сим
рична, а эпюра A^i —обратно симметрична, то ^i/=0. Следовател^^^"
Xi^O. С другой стороны, Л^з=0, следовательно, Аз^=0, Х^^О. Остаег^^^
только вычислить ^^
^2/ = oi ^N^d^ = — a^Jcosods = — oi\dx = — оЦ ^
откуда
all
X,=
^22
Итак, при равномерном нагреве в основной системе возникает
только одна лишняя неизвестная ^2, приложенная в упругом центре
Она вызывает эпюры изгибающих моментов М2Х2, поперечных сил
Q2X2 и продольных сил N2X2 (эпюры Ms, N2, Q2 см. на фиг. 437).
^^^ Очевидно, что равномер-
["У^^^ч^им ^^^ усадка бетона вызывает
\ "^llllKIKIiilllil в арке такие же усилия, какие
возникли бы от равномерного
охлаждения; нужно лишь
подобрать такую температуру,
-б) ^,,!^^^Щ Р^^'"*''^^^^ЩЩ которая вызывает в основной
системе арки относительное
®^' укорочение, рйвное укорочению
От усадки бетона.
Фиг. 449 Произвольный неравно-
мерный, но симметричный от-
носительно середины пролета
нагрев или охлаждение вызывает, кроме распора Х2, еще пару ^з.
Навнодеиствующей этих двух величин является горизонтальный
распор Лг, расположенный выше или ниже упругого центра Соответст-
вующая эпюра изгибающих моментов показана на фиг 449 а. Самый
оощии вид температурной эпюры моментов, отвечающий любому несим-
Зм^^^""^ нагреву, показан на фиг. 449, б, где замыкающая ью%^'
занимать любое положение.
§ 17.13. РАСЧЕТ НА ДЕЙСТВИЕ. ОКАЗЫВАЕМОЕ ПЕРЕМЕЩЕНИЕМ ОПОР
пеошест^п^Г"^ рассмотрим следующий случай: пусть правая опора
а'^ж" и кпомГ?™''^''" ''™' «^ "' ^^' ™ горизонтали вправо--на
аз (ф1г. 450) повернулась по часовой стрелке на уго"
нию'''нГзве2ных''^"Т""х°'""''"'^ "^""^-^'^ "°"У™^ "^ "T't^
(фиг. 451) •' ^' ^ какие-то перемещения ^ic ^'-'¦'
вест^нь^х"о1«!!1Г'"'"°^"' ''"'^''^"^ перемещения по направлению этих неJ
гаемыё ппимР« "Г'°- "°^™^У' используя опять все упрощения. Д^с^"
гаемые применением упругого центра, получим
326
i
Свободные члены этих уравнений опоегтр пах^
нематических соотношений, а именно: -^^•'^"'отся из простейших ки-
2 ^^ 2-rvy с;аз, Дз^ = —?23. (17.20)
Здесь со знаком плюс написаны те пепемйто^т,
ны в сторону положительных Х,, Xg, ;^^/'''^^^^^^™я, которые цаправле-
Фиг. 450
Фнг. 452
Напомним, что величины А^^, Ag^, Дд^ могут быть найдены также
^ уравнения работ: например, приложив к основной системе силу
^1=^1 (фиг. 452) и рассматривая обе половины арки как абсолютно
Жесткие, можно написать
lAi.+ laj—-^Аз-О,
или
— ai+—as
"т.д.
^3 канонических уравнений найдем
^1 7— , ^2 — с
Оц ©22
Х^ = —
(17.21)
327
а затем построим окончательные эпюры:
м = MiXi+ М2Х2 + л^з^з; ]
N = NiXi + N2^2 + л^з^з;
Q==QiXi + Q2X2 + QsXb'
(17.22)
Каждая из эпюр М, Q. Л^ получается путем суммирования трех ос-
новных эпюр, умноженных на соответствующую основную неизвестную.
В формулах (17.21) числители не зависят от жесткости арки, а зна-
менатели уменьшаются, когда жесткость увеличивается. Отсюда следу.
ет, что при заданных перемещениях опор усилия в арке получаются тем
большими, чем она жестче.
§ 17.14. РАСЧЕТ СИММЕТРИЧНОЙ АРКИ С УПРУГИМИ ОПОРАМИ
Расчетная схема арки с абсолютно неподвижными пятами не всегда
дает удовлетворительное приближение к действительным условиям ра-
боты арки. Если опоры недостаточно массивны и притом заложены на
Фиг. 453
недостаточно жестком грунте, приходится учитывать их упругую под-
вижность.
Приложим к опоре А последовательно силы X^ = l, Х^ = 1, ^г=^
(фиг. 453) и охарактеризуем ее жесткость при помощи главных пере-
мещений о^^, о,,, Ь,^ и побочных о^^,, Ь^с, Кс- Первые три всегда по-
ложительны, вторые могут иметь любой знак.
За лишние неизвестные ^ь Х^, Х^ примем те же, что и для арки с
неподвижными опорами (фиг. 444-^446), но положение упругого центра
С теперь будет иное. Расстояние его от опорной горизонтали АВ обоз-
начим через а (фиг, 454, а), ^^ f
По условиям симметрии'^гг =S,3-0. Нужно найти точку С из усло-
вия б^з _о. Для этого примем сначала опорную горизонталь за
ось абсцисс и подсчитаем
Но
л А
Уо^а + у; Jyds' = J(y,-.a)^s'=/C —afrfs'
л А А
328
е-
329
От действия пары ^3=1. приложенной в упругом центре С, опора
А получит вертикальное перемещение 8.., горизонтальное о,, „ yj^^
ПОР S Эти перемещения опоры заставят точку С левой полуарки пе-
пеместаться в горизонтальном направлении влево на величину 5,^^
& Настапько же переместится вправо точка С правой полуарки,
Кроме того, от Х,= 1 сдеформируется сама арка.
Итак:
EJAs = 2/( - 2а j ds' + 2EJ^%c - 2EJoab,, = О
A
или
a =
A
(17.23)
После того как точка С будет найдена, система канонических урав-
нений распадется на три самостоятельных уравнения, содержащих по
одной неизвестной. Каждый коэффициент и каждый свободный член бу-
дут состоять из двух частей, из котрых одна зависит только от дефор-
маций арки, а другая — только от перемещения опор. В качестве при-
мера на фиг. 454 показаны перемещения левой опоры, вызываемые
силами X/ = 1 (при положительных значениях перемещений 8^д, \ау
^^Д Перемещения, зависящие от деформаций арки, выражаются фор-
мулами, которые приведены в § 17.9; нужно только помнить, что поло-
жение упругого центра определяется не формулой (17.13), а формулой
(17.23).
Тогда
Обозначим эти перемещения через Sji, S'
12»
ДОр и т. д.
=? Jo Чг+2EJ, (^,+lo^^+JL g; J ^^^^^^
EJ, b^, = EJ, Щ^^ + 2EJ, Ь^^ - 2EJ,ab^^ - 2EJ, ( \, - a\^) a ^
- Eh Ч. + 2? Jo ( \b ~ Ш,^ + аЧ^^) ;
Выражение \ь~2а\,-^а:^\^ всегда положительно. Нетрудно У
диться, что его минимум получается при а= ^-^и равен
бе-
Чь^сс-Щ^с
1
5<упгГгхпо''^° положительности определителей такого вида дано/
стр ПО ^^^""^ механики стержневых систем», ч. II. изд. 19S4 г..
Свободные члены выражаются формулами
330
rV,p
s V.) (
aat I
J_
ca 2
+
(17.25)
В этих формулах моменты М^,
М^
считаются положительными,
когда растянуто внутреннее волокно арки, вертикальные нагрузки по-
луарок 1^/^лев> ^^прав»—когда ОНИ направлены вниз^
* В «Курсе строительной механики стержневых систем», ч. II, § 19.6, изд. 1954 г.
в изложении расчета арки с упругими опорами вкрались ошибки в формулы для коэф-
фициентов и свободных членов канонических уравнений. Исправленные значения даны
выше в формулах (17.24) и (17.25).
Глава 18
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ
§ 18.1. ОБЩИЕ СООБРАЖЕНИЯ О СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМАХ
Те фермы, которые применяются на практике, строго говоря, никог-
да не бывают статически определимыми, потому что никогда не имеют
идеальных шарнирных соединений в узлах. В дальнейшем речь будет
идти, однако, не о той статической неопределимости, которая создается
жесткостью узлов, а исключительно о статической неопределимости
шарнирно-стержневых расчетных схем.
Статически неопределимая ферма, кад и всякая статически неопре-
делимая система, может иметь начальные усилия, обусловленные не-
точностью сборки, неточностью расположения опор и температурой. С
другой стороны, требование статической определимости конструкции
заставляет устраивать шарниры, подвижные опоры, разрезать систему
при помощи специальных швов и в итоге приводит иногда к усложне-
нию конструкции. С конструктивной точки зрения система с небольшим
количеством лишних неизвестных нередко оказывается более простой,
чем статически определимая.
Для пролетных строений железнодорожных мостов статически не-
определимая неразрезная двух- или трехпролетная балочная ферма цeJ
лесообразнее ряда разрезных ферм, так как обладает более плавной
упругой линией и поэтому не испытывает тех ударов, которые получа-
ются при переходе осей поезда с одной разрезной фермы на другу^^*
По этой же причине двухшарнирная арочная ферма целесообразнее
трехшарнирной. Как показали подсчеты, неразрезная ферма и в эконо-
мическом отношении выгоднее ряда разрезных. В то же время статиче-
ски неопределимая ферма оказывается в целом более надежной, так
как аварии отдельных ее элементов (лишних) не приводят к столь тя-
желых последствиям, как разрушение элементов статически определи-
мой фермы.
Однако вопрос о выборе той или иной схемы решается на основании
синтеза соображений о прочности, безопасности и экономичности соо-
ружения.
§ 18.2. О ПОДБОРЕ СЕЧЕНИИ
В абсолютно необходимых элементах статически
определимой
фермы усилия определяются из уравнений статики независимо от ^^ -^
чины сечений каких бы то ни было стержней, поэтому подбор сечен
332
для таких элементов по допускаемым напряжениям не встречает ника-
ких трудностей.
Во всех прочих стержнях усилия являются функциями сечений, се-
чения же в хорошо спроектированной ферме должны в свою очередь
возможно лучше отвечать усилиям.
Для первоначального назначения размеров сечений прибегают к
понблнжениому, ориентировочному определению усилий. Для этой цели
яменяют иногда статически неопределимую систему статически опре-
пелимой, т. е. выбрасывают те или иные стержни и строят линии влия-
ния для* оставшихся стержней: загрузив эти линии влияния наиболее
Фиг. 455
„г,^ «янбольшне усилия, по которым и под-
невыгодным образом, находят «f"^^^;";:'„J^ стержней, число которых
бирают сечения. Что касается «"бРошен^^ых сте^^^ стержней фермы,
обычно невелико по сравнению с о»"^™ ' „^ Однако такой способ
то их сечения берутся еще более (произвольно.
нельзя считать достаточно Paii"OHaJibHbi . ^^^^^ получить в тех слу-
Более целесообразный ""^^p се шн сопоставить со сплош-
чаях, когда данную Решетчатую систему ^^^^^^ сопоставить с не-
ным стержнем. Например, ферму )Ф"^,-^„н(,ого сечения. Найдя наи-
Разрезной балкой постоянного «-""Хлялки можно затем определить
большие изгибающие моменты такой оа^^ усилий относительно
усилия в поясах: нужно прир^'^»''''^^^ванным изгибающим моментам.
соответствующих точек Ри-^-^^Р^, "^ьш обр^^^'^' подобрать по эпюрам
Усилия в раскосах можно аналогичным up
поперечных сил неразрезной балки. ^ заменять арочные фермы
Точно так же ^ожпо для ^'>^^^^^^^^^последте. как статически иеоп-
аркамн сплошного сечения; Р^'^^^^^^зоваться найденными продольными
Ределимые системы, и затем воспол моментами. .соч
и поперечными силами и изгибающими мо^^^^^^ ^^^ далее фиг- 459)
При расчете ферм с перекрестными Р ^ ^^^^^ раскосах равны по
•«ожно принять, что в любой панели ^сил ^^
величине и обратны по знаку или что усилие в сжатом раскосе в
леленное число раз меньше усилия в растянутом, и т. д.
опре-
Ю
ленное число ра^ mchdjluc _yi^rwiriyi и ^^л^^^^^*^J'^^'^^ - *. ^-
Можно действовать также следующим образом: заменить заданную
ферму столькими различными статически определимыми фермами
сколько в ней имеется лишних связей. Например, ферму на фиг*
455, а можно заменить двумя фермами, показанными на фиг. 455, б, в
Затем следует нагрузить каждую из етих ферм заданной нагрузкой, оп-
ределить усилия и для каждого стержня взять среднее из найденных
для него значений усилий. При этом не следует отбрасывать в качестве
лишних опорные стержни.
§ 18.3. РАСЧЕТ ФЕРМЫ С ОДНИМ ЛИШНИМ СТЕРЖНЕМ
При расчете фермы мы будем принимать, что сечения всех стержней
1аны, и нужно лишь найти усилия. Рассмотрим сначала расчет на тс
воздействия, которые не свя-
заны с построением линий
влияния.
Пусть требуется рассчи-
тать ферму, представленную
на фиг. 456, на действие за-
данной внешней нагрузки.
Примем, например, за основ-
ную неизвестную распор Xi
и составим каноническое
уравнение
Для вычисления его ко-
эффициентов определим во
Фиг. 456 ^^^^ стержнях основной си-
стемы усилия Npy вызванные
внешней нагрузкой, и усилия
л/,, вызванные силой Xi = \. Эта операция может быть произведена ли-
бо аналитически, либо при помощи построения диаграммы усилий. Пос-
ле этого вычислим
^»,. = Sf, Е.,,^1!^
INPl
где / ~ длина каждого стержня, и, наконец:
X = - ii? =
V t^b
{\B.\i
Окончательные значения усилий в любом стержне выразятся формулой
N=^N +N^X^. (18.2)
Вычисления целесообразно расположить в форме табл. 9.
¦-о„о1!^^ расчете фермы на заданное температурное воздействие
каноническое уравнение принимает вид ^ у i"
334
Здесь
A« = a2;iVj«,
рде о--коэффициент линейного расширения-
/_ изменение температуры стержня по'сравнению с начальной
В том случае, когда все стержни нагреты одинаково, формула тем-
пературного перемещения переходит в H'^y^yjid тем
Найдя перемещение А-^, можно определить неизвестную:
Таблица 9
стержня
1
2
•
м
F
(отвл.)
в т
2 /
' F
ЕЬп 1
МА^я^
^^ip
А^
Температурные усилия в любом стержне / выразятся формулой
yv(o = т^)х^.
Рассмотрим еще расчет фермы, в которой один из «условно необ-
ходимых» стержней имеет длину, отличающуюся от требуемой на не-
которую величину а. Для большей наглядности рассуждений предста-
вим себе, что на фиг. 456 стержень АВ длиннее, чем это требуется по
конфигурации фермы, на величину а. Расчет фермы при етом вполне
можно уподобить расчету на действие температуры: следует принять
для стержня АВ температурное удлинение Шу^^^ =а, г лл^ всех прочих
'Стержней — удлинение ail^^O. В соответствии с этим получится ^а/=
==aiV\^^^ , где М"^^^ — усилие в стержне АВ, вызванное силой Xi = \.
Можно написать каноническое уравнение также в виде
^^^ -^1^—перемещение по направлению силы Хи вызываемое в основ-
''la-
Есл f^ ^^^ системе удлинением а,
«овт неточность монтажа выразилась в неточности р асе та-
ними^^ ^"ор С и D (фиг. 456), например в том, что расстояние между
Точка уР^^^^^^^^^т требуемое на величину а, то это означало бы, что
откуда
отошла от точки С на такое расстояние вправо. В таком случае
мели бы Aj^ =—а.
Ремещение это происходит под действием силы А,, следовательно:
Д,„=-а,
у fl-
335
§ ia4. ПОСТРОЕНИЕ ЛИНИЙ влияния для ФЕРМЫ
с одним лишним СТЕРЖНЕМ
Для примера рассмотрим двухпролетную балочную мостовую гк
му (фиг. 457,а). За лишнюю неизвестную примем реакцию средне" ^^^
ры (фиг. 457,6). Линия влияния этой реакции должна удовчетв^о^"^'
каноническому у^авне^ию
^Л + ^-0,
откуда
1 Тч -— .
«11
Но 8.
Фиг. 457
Тов
^^^1 представляет СО-
бой не что иное, как ли-
„ЛШо_ прогибов_ нижйегГ
пояса, вызванную дейст-
, _вием неподвижной и по-
стоянной силы Xi = 1.
Все дело сводится к по-
строению этой линии,
имеющей вид многоуголь-
ника с вершинами под уз-
лами нижнего пояса.
Для построения этой
линии можно предло-
жить несколько приемов.
Во-первых, она может
быть получена из диа-
граммы Виллио. Опреде-
лив усилия, вызванные во
всех стержнях силой Xi -
="1, а по ус1шиям — удли-
нения, легко построить эту
диаграмму (см. § 10.3).
В данном примере, учиты-
вая условия симметрии,
можно упростить построе-
ние, ограничив его одион
половиной фермы. Полу-
чив линию прогибов иа
чертеже, примем среднюю
ординату равной единице;
тогда эта линия будет вы-
ражать собой л. в. реак-
ции А", (фиг. 457,в).
троена, как эпюра м<^М?^"
эпюра
грз^зов
Во-вторых, линия прогибов может fi.... ^™ ^' ^Ф^'
^ (веревочный многоугольник) оЗ ^ построена, как .....р^ -
приложенных в узлах того nn^ri г? ^^^"^^^bi «упругих» груза
в данном случае^-^ в vзляv mf^t^ ^^^торому перемещается гру.^ - ^
гут быть найдены nh Го" "^'^'' ™^^^ (Фиг. 458). Самые грузы мо-
Ферм более х^,гл^ о Ф^Р^У«"ам (И.14). (14 15 и П4 6). Д-^^
грузов. ^^"^"^^^ оказывается следующий способ вычнсления этих
Преобразуем формулу (ЮЛ) при Я=1:
МО'
Уп ~Уп-
T. e. как сумму виртуальных работ упяпнппртт1о,^^т «
,нной на фиг. 458.6 на Al^Z^^nZ.^^ZT,:.^^:,^^'' .^"•"' "^«б-
Щаженной на фиг. 458.6 на Де^--.ств;гнГТеТеГи.е™яГ Г' '''Т
^„^, фермы. Эту работу мы не могли бы вычислить непосре;ст;е„но'
1К не знаем величин и-ов. но оня паро. ^„л hcai-ibchho.
I
-^n+i - ' •" ' -' ¦¦-" ¦'^- ¦"^^^^'^" иы ВЫЧИСЛИТЬ непосредственно
так как не знаем величин у-оь, но она равна работе внутренних сил
фермы, нагруженной С11стемой сил — —
на тех
т. е.
-^ +
Же перемещениях.
''п+1
n+l
w^,
л = У;Л^хЛ^х^, (18.3)
где iV, ~ усилия в стержнях
основной системы от ^i = l,
yV. -
усилия в тех же
стержнях от названной си-
стемы сил. Усг гия Л'х легко
могут быть наьаены из диа-
граммы Максвелла — Кре-
^юны или любым другим спо-
собом. Как известно (см.
§ 5.6), уравновешенная на- \
грузка вызывает усилия в
<)граниченной небольшой ча- ^^^- ^^^
стн статически опредеЛ11МОЙ
фермы, следовательно, лишь
^ HeMHoriix стержнях усилия N^ будут отличны от нуля. Для каждого
упругого груза Wn вводится наново система уравновешенных сил и про-
^^зводится наново вычисление ус11лий Л^^.
После Того как будут найдены все грузы W^, останется построить
^ызываемую ими эпюру моментов с учетом условий на опорах; это и
УДет искомая линия прогибов ^^i.
Имея линию влияния основной неизвестной Х^ нетрудно получить
• В- усилия для любого стержня; ее уравнение имеет вид:
т.е.
• е. нужно сложить статически определимую л
J^HHOH на постоянное число Ny. На фиг. 4Ь7, г.
, В. Л^^, с л. в. Х^, помно-
д, е показаны построен-
таким образом л. в. /?^, Оз, ^г- Д-^я упрошения графического по-
^троения можно поступить так: для различных линий влияния брать
К^зный масштаб так чтобы линия NiXi получилась у них одна и та же.
JihHh^ пристраивать' к этой линии л. в.; ^^ —"" -^n^o.^.. „^^^., ^ло
22
No таким образом, чтобы обе
влияния пересекались между собой под средней
^ М Рабинович
опорой, т. е.
337
„„„ятяпод ЭТОЙ опорой обратилась в нуль. Пос,
чтобы суммарная «РД "f ^а' крайней опорной ординате надписи, отн
этого остается "«'^^^^"f „"'азано на упомянутых фигурах, и масшт
сяшиеся к л. в. i^.^
сящиеся к л. в. i\p, г
получится сам собой.
отно-
•масштаб
учится сам сооои.
,85 РАСЧЕТ ФЕРМЫ С НЕСКОЛЬКИМИ ЛИШНИМИ СТЕРЖНЯМИ
^ ¦ ¦ ^^^ пппеделення неизвестных приходится решать
В этом случае Д^^ °^Р^^^ уравнений.
MV совместных '^2"°"" '^^^Р_„Я построить линии влияния ОСНОВ!
т->- ^т,1шяр когда треоуется hulih „г.^пг.'.п..,.^.,..
СИ-
МУ совместных '^2"°"")'^^!:р;„я построить линии влияния основных
в том случае, когда требуется по^^Р^ превращаются .
неизвестных Ли М. •- ^-^ииим ^. ,
в том ^.yY^•^~¦¦~ „бедные члены ^i,, -i!,. ¦-. "Н"
ГГнроп.'Зон вгзы;«„ых дейстннем сил Х,= . Л,^,,
^^
Фнг. 459
Линия влияния усилия в любом стержне фермы получается сумми-^
рованием линий вляния:
рде д^ _ л. в. в статически определимой основной системе; Nu 2 ^
т. д. служат множителями при л. в. Xi и ^2 и т. д.
На фиг. 459, а показан пример фермы, содержащей Ь •^"™^";^ ^][,
жней, а на фиг. 459, б —одна из соответствующих ей основных chl.
§ 18.6. РАСЧЕТ ФЕРМ МЕТОДОМ ЗАДАННЫХ НАПРЯЖЕНИЙ
Пусть ферма имеет п лишних стержней и должна несги только однУ.
пусть цдгрма HIVJCC1 ft лпидппл v-it|j«\ii^.ri п лл,ч7С1*1чжсд iiw^... . инЫМ СПО*
ределенную и неподвижную, н а г р у з к у. Выберем тем или и» ^^^^^^
собом лишние стержни, а остальные будем называть основными, i асчс ^ ^ ^ р я-
произвестн таким образом, что: 1)во всех основных ^"^^P^^^JJn опр^'
жения будут иметь величины, заданные заранее; 2) ^^ сов-
деления всех неизвестных не придется решать »i"^^*^''jigTC«
местных уравнеиий, а каждое неизвестное опред
самостоятельно из отдельного уравнения. разиы?^
Обозначим заданные напряжения, которые могут быть различными -^^J^j^^mU, ^
стержней, через с^ . Растягивающие напряжения будем считать положнтел ^^^дую-
сжимающие—отрицательными. Усилия в произвольном стержне к о^^^Я^^'^'^шней "^'
щим образом: через Nk —суммарное усилие, возникающее от заданной ^"^^дслпмой
грузки и лишних неизвестных; через Nkv— усилие в основной статически опр -,ствН>*
системе от действия силы A'i=l; через Nk'i — усилие в том же стержне от а
Х2==1 и т. д.; наконец, через /V*g — усилие от внешней нагрузки. «шеМ» ^^^
Напишем одно из канонических уравнений метода сил; например, "^"' ,а внв^^''
в основной системе (с перерезанными лишними стержнями), которая "^^^P^/JimeHne ^^
ней нагрузкой и усилиями Xi, Х2. ..., Xi, ..,, Х„ лишних стержней. "^Р^^ j^pHMcHfl**
направлению Х\ равно нулю. Пользуясь указанными выше обозначениями и
338
общую формулу перемещений, мы можем написать это уравнение п г,.„».
ной форме, чем обычно, а именно в следующей: л^линение в более компакт-
EFk ^' (18.4)
В состав основной системы входят все степжни Арпмы t,c^ ^
ние, с той тх>лько разницей, что последние входятТ разрезанном виде' Ко." ""'"•
основную систему действует сила Х,= 1, то в самом стержнГ/ «nZ..5 "^"^^ "*
ЛГ„= I, во всех же остальных лин.ннх стержнях получаетсяХ=0 пДп^к, « ^^™"*
написанного уравнения входит только один из лишн^ cxepi - "ер ™нь' / Выяе
лив его в формуле (^8.1) из-под знака суммы и заметив, что для него yVft=/,; Г для
остальных стержней -~=-к, где с, -заданное напряжение, получим после умно-
жения на ?
—F +-7"^=о.
Второй член всегда положителен^ так как в излагаемом ниже расчете лишние
неизвестные всегда положительны. Диалогичным образом можно написать уравнение
для всех остальных лишних стержней. Система канонических уравнений примет про-
/j 4^2^k ¦
-=0;
П8.5)
<^k^knlk+ — = 0.
Под знаком S в каждом уравнении стоят только основные стержни.
Уравнения эти замечательны тем, что каждое из них решается отдельно от других;
одна из трудных проблем расчета статически неопределимых систем — проблема рас-
членения системы канонических уравнений на отдельные, независимые уравнения —
Здесь полностью решена. В каждом из уравнений (18.5) имеется только одна неизвест-
"эя, а именно отношение — , т. е. напряжение в одном из лишних стержней. Тако?
хороший результат объясняется тем, что деформация фермы целиком определяется
заданными напряжениями всех основных стержней. Взаимное сближение или расхож
Денис концов любого лишнего стержня при этих условиях не зависит явно ни от одноп
из лишних усилий, а следовательно, и напряжение в лишнем стержне не зависим
^^ них.
^ *^з уравнений (18.5) получаются вполне определенные значения напряжений— .
т ^'
^^^ самым ещ.е раз подчеркивается, что величина этих напряжений от нас не зависи-г,
У^^^эваться ими нельзя. Но остается еше возможность выбирать по собственному
пло ^^^""^ либо усилие Xi, либо площадь/^;. Имея напряжение и усилие, мы найдек
^пь\ имея напряжение и плошадь, мы найдем усилие,
^'ассмотрим ход расчета,
•Пи ^здземся по величине и направлению растягивающими или сжимающими уся-
^ 9\ А ^^* •'•' -^п во всех лишних стержнях,
ческ ^"Ределим для всех основных стержней усилия N , возникающие в стати-
М. ^определимой основной системе от внешней нагрузки, и усилия Nkx^ Nfcz
По л °^ действия сил Х\=^\\ ^2=1; .-, X ===1; суммарные усилия N вычисляем
формуле
Nk = Nk^ + NkxX^ + NkoXi -{-'"-{- NknXn ¦ П8.6)
) Задаемся напряжениями —^ всех основных стержней. Проще всего — залать
'fakJi^"^'^^^^^""«: одно для растянутых, а другое для сжатых стержней. Не исключается
в COOT ^^^^°жиость задавать для различных сжатых стержней различные напряжения
ветствии с различной их гибкостью.
22*
339
4^ Опоедепяем из уравнений (18,5) площади сеченни всех лишних стержней.
t eTih все эт^^ площади окажется положительными, ад,„
/Л «vжнo чтобы выражения S во всех Уравненияхdgl?
^^"""^.^гГ отрицательными, то по заданным усилиям X,, К^, "^ ^1^^)
ня^йпе^нным площадям вычислим напряжения с„ с^, .... с„ во всех лишних ст*ержн"ях
найденным плщ ^^^^^^^^^ ,„^него стержня i получится отрицательной, то ^о
покажет что решение не годится, т. е что действительная деформацня стержня
ГпооТворечит тому направлению сил Xi, которым мы задались. В таком случае не
ос^я ничего другого, как изменить направление или величину усилий К, д^^
oSoro или нескольких лншних стержней определить снова знаки суммарных усиГй
Л^н определить новые значения площадей. Работа эта несложна и не требует большой
^^^^ШнакГиГнсключается и такой случай, когда после изменения направления Х-
на обратное и какого угодно изменения величины этого усилия площадь опять полу-
чится отрицательной. Это покажет, что в данной статически неопределимой ферме прн
-«ействии данной нагрузки принятое распределение напряжений в основных стержнях
неосуществимо. Приходится либо изменить основную систему, либо изменить напря-
жение в том или ином основном стержне.
Вообще можно доказать, что для заданной схемы фермы и заданной нагрузки ве-
личины лишних неизвестных Хи Х2, .-. Хп при всевозможных вариациях площадей
лежат внутри некоторой замкнутой области.
б) Если полученные из уравнений (18.5) для лишних стержней напряжения не
превышают допускаемых, то остается по заданным напряжениям <^k и полученным
усилиям Nk основных стержней вычислить площади их сечений.
Если иапряжеиня лишних стержней превышают допускаемые, то нужно произ-
вести перерасчет.
хМы изложили здесь аналитический ход расчета. Та же задача легко решается
графически. Задавшись напряжениями Of^ основных стержней, определяем их удлине-
ния нли укорочения—;—, после чего строим диаграмму Виллио без учета условий
Е
на опорах. Она дает нам непосредственно величину и знак удлинений А// лишних
стержней, откуда находятся и их напряжения — . Затем по заданным усилиям л.
и наиденным напряжениям определяются и площади Ft лишних стержней.
Как видно из всего хода расчета, в качестве лишних стержней должны выбирать-
ся такие, площадь сечения которых не зафиксирована заранее, а определяется из
соответствующего уравнения (18.5). Так как опорные стержни имеют площадь сечения
г = ос , то нх ие следует выбирать в качестве лишних.
Методом заданных напряжений можно рассчитывать статически неопределимые
фермы также на сочетание постоянной нагрузки с временными, но расчет прн этом
значительно ^сюжняется. Этот метод позволяет весьма удобно решать важную зада-
чу о таком подборе сечений, который обеспечивает минимум веса фермы. , ,
основная идея метода высказана впервые в работе немецкого автора Heimanna.
развитее метода, а также постановка и решение с его помощью ряда фундамента.ть;
KHRnf°«^iQ?^^/r''"" статически неопределимых ферм были даны автором настоящей
nZZcJnnn \^' V ""и^^^^^ того же автора, а так*е
К^ ХуСя^' tn,^^|3»^"'^- ^- ^- Протасова. А. И. Виноградова, д-ра техн. на>^
l9l7-llS!^M.!'l957t ^-^^^Р'^У^^ "^ ^ (^^^ ^Строительная механика в СССР
2 И ^ЧТ^^^^'^^^ё ^"'" Berechnung statisch unbestimmter Fachwerke. Berl l^'
1933. ^'абинович. К теории статически неопределимых ферм, ТрансжелдорнзД^т*
V
Глава 19
РАСЧЕТ СЛОЖНЫХ РАМНЫХ СИСТЕМ МЕТОДОМ СИЛ
§ 19.1. ОБЩИЕ СООБРАЖЕНИЯ
Сложные рамные конструкции встречаются в виде металлических
или железобетонных каркасов многоэтажных зданий, в виде рамных
многопролетных мостов и т. д. Как известно, большинство конструкций
имеет такие узлы, которые по характеру своей работы стоят гораздо
ближе к схеме жесткого узла, чем шарнирного, поэтому рамные конст-
рукции фактически являются весьма распространенными. Когда жест-
кость узлов вводится и в расчетную схему сооружения, т. е. когда
система рассчитывается как рамная, она получает более простую гео-
метрическ}то структуру, так как можно обходиться без решетки (рас-
косов).,В гражданских и промышленных сооружениях ра\!ный каркас
позволяет хорошо использовать пространство. Неразрезность рамных
систем, обеспечивая солидарность работы всех элементов, делает ее
экономичной. Все это обусловило широкое применение рамных конст-
рукций в разнообразных областях строительства.
При расчете рамных систем каким бы то ни было методом слож-
ность Задачи зависит главным образом от количества основных неиз-
вестных. Прн расчете по методу сил сложность зависит, следовательно,
от количества лишних связей. Чем больше таких связей, тем сложнее
расчет. Поэтому прежде всего необходимо правильно подсчитать число
лишних связей.
При большом количестве неизвестных процесс решения системы
совместных уравнений становится очень утомительным и много теряет
ь своей точности.
XJ9^0 ПОСТРОЕНИИ ЭПЮР М ДЛЯ СТАТИЧЕСКИ
^ПРЕДЕЛИМЫХТУСБОВНЫХ СИСТЕМ И ЭПЮР Q, N ДЛЯ ЛЮБОЙ СИСТЕАШ
Те основные статически определимые системы, с которыми прихо-
^тся иметь дело при расчете сложных статически неопределимых соо-
Р^'Женнй, также достаточно сложны. Опыт в построении эпюр для та-
^х систем приобретается путем решения задач. Этот опыт необходи-
*^о Довести до такого состояния, чтобы не только находить ординаты
^пюр при помощи составления соответствующих уравнений статики, но
^зучйться набрасывать общий характер эпюр на глаз, без всяких вы-
^йсленйй. Мы советуем читателю оешить самостоятельно пару десятков
примеров.
Ml
и-^гибаю-
ркомендуем чертить все эпюры .
Во избежание путаницы ре^ ^„^„рое растягивается
„,„х моментов со стороны J^^^^^^ ^^^р^^^, сжатого волокна),
моментом (или же, па
Фиг. 460
Необходимо иметь в виду
удовлетворять условиям равновесия
Фиг. 461
что эпюра изгибающих моментов должна
Если мы вырежем любой узел и
заменим действие откинутых
частей силами, то должны по-
лучить уравновешенную систе-
му. Когда разрезы сделаны
бесконечно близко к узлу, то
статические моменты продоль-
ных и поперечных сил обраща-
ются в нуль, поэтому сами со-
бой уравновешиваются. На-
пример, в узле А, состоящем
только из двух жестко связан-
ных стержней и не нагружен-^
ном сосредоточенной внешней
парой сил, моменты пар Mi и
Ms должны быть равны и про-
тивоположны друг другу- ^^^'
ры моментов вблизи такого у^
ла имеют вид, показанный н
фиг. 460, а и б: либо в обоих
стержнях растянуто «ару^*^^^
волокно, либо в обоих — ьну
реннее. Перескочить в А >'
стержневом узле из нарУ>к^
области во внутреннюю эпюр
какая-либо сосредо
к узлу приложена
то эпюра может
иметь
может только тогда, когда
точенная пара (фиг. 460, в),
Если в узле сходится больше трех стержней, ю c^m^i^d -—- уз-
разнообразный вид, но алгебраическая сумма пар, приложенных
лу, должна быть равна нулю.
Поперечная сила Q= — ; она характеризуется не величиной
^^ пментз
бающего момента в данном сечении, а законом изменения ^ ^^ю-
вдоль стержня. Так, например, четырем различным эпюрам изг ^^^^
щих моментов (фиг. 461) будет отвечать одна и та же эпюра ^' 55^ду
только наклонные прямые на всех четырех эпюрах параллельны ^^^^
собой. Основываясь на этом свойстве, можно легко находить зна
342
ры Q для любого сечения. Нужно воспользоваться нулевой точкой
эпюры Л4, которая сразу показывает направление сил Q (фиг 461 вГ
В любом сечении стержня можно искусственно получить нyлeвvю точ-
^v, передвинув эпюру М или касательную к этой эпюре без изменения
Фиг. 463
ее направления. Например, для того чтобы по эпюре М, представлен-
ной на фиг. 462, а, найти поперечную силу в сечении С нужно передви-
нуть касательную MN так, чтобы она в этом
месте пересекла ось стержня (фиг. 462, б). По
расположению растянутых волокон мы сразу
увидим, что в этом сечении Q >0.
После того, как поперечные силы найдены,
ими можно воспользоваться для определения
продольных сил N. Для этой цели можно
применить способ вырезания узлов. Напри-
мер, если для узла А (фиг. 463, а) из-
Фиг. 464
Фиг. 465
честны силы Q^^n Q^c . то силы N^^nN^^ найдутся из замкнутого си-
•"ового многоугольника, построенного на фиг. 463, б.
Вообще следует отметить, что если эпюра изгибающих моментов
"остроена, то независимо от того, является ли система статически опре-
делимой или нет эпюры QnN строятся просто. Первая получается как
производная от эпюры М, а вторая — из условий равновесия.
Задачи. Задачи № 19.1-195. Построить эпюры М. Q. н N для статически опреде-
-¦"имых систем, представленных на фиг. 464—465.
343
§ ,9.3. О РАЦИОНАЛЬНОМ ВЫБОРЕ ОСНОВНОЙ СИСТЕМЫ
'" . .^тятически неопределимая система, то нз нее можно
Когда Д^«^,^!,^зные статически определимые основные системы.
получить ^^^""^^^^^Ц'^^^птпъш образом лишние связи. Для того
выбирая и отбрасывая р действительно статически определимс"
чтобы основная "'"'^^ (-„„пала геометрической неизменяемостью. Bi
ч.^yJ^^,^ облапала reoMeiiJn-»«^'-i^^'" •—•——¦—^.^^•^^.^,^^J. оы.
Гр^^^систГГнеоб^^^^^^ в первую очередь проверить с этой точки
зрения. л^оамтла котооые предъявляются к основной системе,
Фиг. 466
му канонических уравнений, в которой возможно большее ^^'^^^^^\^^
побочных коэффициентов обратилось бы в нуль. Удачной, рациональн
и желательной будет такая основная система, которая уД^влетвор^^
этому требованию; нерациональной, неблагодарной и неприятной
кая, которая не удовлетворяет. ^ q.
Когда заданная система имеет много опорных стержней и Р^^^^л.
летов, то ее выгодно разбивать на отдельные, изолированные ^^ j,
Например, для системы (фиг. 46G, а) основная система, ^Р^-^^^^ ^^^ой
ная на фиг. 466,6, значительно выгоднее основной системы, ^^^^^^^„ло-
на фиг. 466, 8. Действительно, любая и-; 12 лишних неизвестных, "Р j^
женных к системе фиг. 466,8, вызыв-^ет перемеидения по "^!?Р^^'^емЫ
всех остальных 11 неизвестных. При таком выборе основной ^" j^g.
каждое из канонических уравнений будет содержать все неизве
344
Напротив, в основной системе фиг. 466,6, как нетрудно видеть, мно-
жество побочных коэффициентов обращается в нуль:
д Первое, второе, десятое и одиннадцатое канонические уравнения
будут содержать по шести неизвестных, третье и двенадцатое уравне-
ия—по три неизвестных, а остальные—по девяти.
«;
f—^
'^^<г^
фиг. 467
„„.мпначьной основной системы яв-
Следующим этапом в выборе рациональ ^ ^^^^^^^
^яется тщательный выбор тех 99^^^^^'J^^^ также обдумать, как наибо-
Резы или поместить шарниры. Н^°°^7онсоли.
•"ее рационально разместить «<е"'1"^„янтов основной системы для рамы
На фиг. 467 показан один «^^/„^P"^ помещены на ригелях и стоиках
с девятью лишними связями. Шарниры пом ^^^
на расстояниях, равных -^^и-^& от опор. Часть эпюр взаимно-ортого-
нальна благодаря тому, что центр тяжести плондади одной расположен
поотив нулевой ординаты другой; другая часть эпюр взаимно-ортого-
Кна по свойству прямой и обратной симметрии. Благодаря этому
много побочных перемендений обращается в нуль и уравнения прини'
мают следующий простой вид:
Ё8з^з+^з5^5+^зЛ+Дзр-0;
Всз^з+^сЛ+^^7+Ч^0;
59Л+Ч=0,
т. е. система разбивается на пять отдельных уравнений, содержащих
по одной неизвестной,' и на четыре совместных трехчленных и двучлен-
ных уравнений, содержащих остальные четыре неизвестные.
Во всех указанных выше случаях неизвестные ^ь ^2 и т. д. следует
рассматривать как множители или коэффиценты, на которые нуж-
но будет умножить соответствующие основные эпюры, чтобы получить
окончательную эпюру. Они являются коэффициентом формулы
М=М^+МгХг+М,Х^+^ ^ •+М,Хп.
^JSJ^BOnCTBA ГРУППОВЫХ ЭПЮР и ГРУППОВЫХ НЕИЗВЕСТНЫХ
Анализ различных искусственных приемов, успешно разрешающих
задачу взаимной ортогонализации эпюр, приводит к очень интересному
обобщению, а именно к применению так называемых групповых
э п ю р и соответствующих им групповых неизвестных. Эти эпюры
во многих случаях значительно упрощают весь расчет.
Пусть для данной системы с п лишними связями выбрана основная
система и основные неизвестные. Им соответствуют единичные эпюры
л^1. л^2,--, м„; A^i, л^2,--->л^п; Qi,Q2,--»Qn-
групповой эпюрой моментов мы будем называть всякую эпюру ^i'
которая образована из названных следующим образом:
где а^, р^^ ...^«С;—произвольно выбранные коэффициенты.
Некоторые из них могут, в частности, равняться нулю. Таким ^^^^^
бом можно образовать п линейно независимых групповых эпюр. ^
мощью тех же коэффициентов а^ р^, -у/, .... Ь можно образовать груп"
вые эпюры А^г. Q;. . ^^
Итак, групповой эпюрой мы будем называть такую эпюру, ^^^^^ов-
представляет собой линейную однородную функцию заданных о
ных эпюр.
346
Групповую епюру. выражаемую формулой (19 1) мпж„п о.
jHTb как результат совместного действия сил ' Рассмат-
^„ = -^.-
ривать
^1 = «г, А'а =
следовательно, групповая эпюра есть результат действия группы сил
Примеры групповых эпюр мы уже видели, хотя самое название и
не указывалось. Так, на фиг. 437 эпюра М, может рассматпиваться к.к
результат совместного действия горизонтальной силы, равК единице
приложенной в точке Д и пары сил Хг=Уо, приложенной там же От
Г=Гс"плечом ^Г'' ^°'^'''"^^« " получится горизонтальная 'сил!
J Составим каким-нибудь способом из,основных эпюр групповые уМ',,
Введем обозначение
,;. = SJ^ + SJ^ + SJ^-«i
.;, = !] fu^^-
J
Щ^
Npds у p^q: q^5
(19.2)
Выражения Sj^^, л;^, будем называть групповыми переме-
щениями.
Подобно тому как дом можно сложить из отдельных кирпичей, но
можно также сложить из блоков, предварительно образованных из тех
же кирпичей, так и окончательные эпюры М, Q, N можно сложить по
желанию либо из простейших единичных, либо из групповых. В послед-
нем случае мы получим окончательный результат в форме
(19.3)
Для нахождения неизвестных Xi, Х2, .... Хп можно составить обыч-
ым образом систему канонических уравнений вида
W + s;x, + ...-f8;„;r„ + A;p = 0(i = i.2,...,n).
'^' Поступить так же, как поступают при пользовании простыми еди-
Q^^"^^^^ "Эпюрами. Доказательство законности такой операции интере-
ующийся читатель может найти в более полном курсе того же автора
^ч-И, стр. 288 и 289, изд. 1954 г.).
Ьыгоду применения групповых эпюр покажем на примерах.
w-^ ^95. ПРИМЕР ПРИМЕНЕНИЯ СПОСОБА ГРУППИРОВКИ НЕИЗВЕСТНЫХ *
'^онечн ^^^'^^'^'^^•"ьство, что групповые эпюры можно составлять из простых эпюр бес-
оказал ^^^^"^обрззнымн способами, позволяет подобрать их таким оОразом. чтобы они
На л ^^^"""о-ортогональнымн.
^етыоех-к "*^* *^ " *^^ показано применение групповых эпюр к расчету симметричной
^^ей п РУ^"о* рамы. Основная система получена при помощи разрезания всех ри-
но симм °^" симметрии. Четыре эпюры, образованные поперечными силами, обрат-
ной альн^^*^*^"**^* остальные восемь симметричны. Благодаря свойству взаимной орто-
УРавненнп^" обоих типов эпюр, система канонических уравнений распадается на четыре
«я с четырьмя неизвестными и восемь уравнений с восемью неизвестными.
347
J 11Й Аи1 ^(i^ Кяждая иг них. «(юм. пчглеяией
ricDW^c четыре "«пюры "°'*f ^"' .'!пя»ех вертикал, шлх ч/жиичиы/ сия. Ь^т Гм »„
гтооили каждую ->п.ору ««^«'C^/f/^Va и в.аимнои ортогонял.л.огти и- m-.училгу^,, Г„
гШ'
7^
И
5^J ^^^^
^^^^.
"""^
(i.
1^ Ш^
Фиг. 468
\Ь)Пс)ыу система уравнений для этих неизвестных име*т следующий простой ВИД
Как бы велико ни было число ярусов рамы, ио одно уравнение с такими неиз
ными не будет содержать больше трех неизвестных. ^ обр^^'
Симметричные групповые ^пюрм выберем так. чтобы каждая из них "^^^^ олантов
но симметричным простиралась только на один ярус. Один из возможных ®^Р j^^oM,-
пр1»лстапл< и на фиг. 460, где каждая 'эПЮра образована действием двух пар с ^^'^^p^i с
равным о. и четырех юриюнтальных сил. равных елимице и образующих дв^
теми же моментами, но мапранленными в обратную сторону, ^ бояь-
При угом варианте ни одно из канонических уравнений не будет содерж<1Т
ше трех нсизссстных.
348
f
i
(S)
T
f ' 1
.. i^ ,
1 _ .
1
1 / 1
1
1
/,
\
— - U=-=-.
Ii""''ll'''l
/ 'П r
f * t
1
5 , /)
/ 1
\:
^!!ll .1 ll|(i^|/li(l
hl'irflni'iil!i"H
тЛщ. --^
\
1 '
f ^ * •
h-a
Mb
v6enHTbCfl. что групповые эпюры дают существенное
nnilMCDC МОЖНО У ^
На этом прп^ у ^п„мп обращать внимание иа то, чтобы вс^
У"Р°й';?„""соГав^;и групповых «^^Д чтГыZ одна нп них не была однород::^
"Р" Лезавис.мыми друг «^/Р^ это условие пе будет соблюдеио. то в системе п
они были "«ав ^.ьных. Если это yi одно из уравнении сделается
""Е*;Ггор«»,.та»™« '""•;"';Z,тогда не.ьз. голу.»» ирти,1^,ш,
:'ЛюД" какош %"\°;С того о "«™-"-" «W' '™Р" '"'¦ '"• " "'"'f
« ,.« дополнительны!! УПРОЩЕНИЯ, ВЫТЕКАЮЩИЕ
JJSi/"" „3 УСЛОВИИ СИММЕТРИИ
ПОМИМО обших упрош™ий^о<^ва„„ых „а УД..^^^^^
Rm
Е?^^
BZ]
^
^
Фиг. 471
они основаны на свойстве взаимной ортогональности эпюр симм н^^^
ных и обратно симметричных. Поэтому при расчете симметричны ^^^^^
стем в большинстве случаев следует стремиться к тому, чтобы ^^ ^|^ля
ры обладали прямой или обратной симметрией, и избегать прим
эпюр несимметричных. ^^ло
Когда сооружение имеет две оси симметрии, то получение ^^^^^з с
ортогональных эпюр значительно упрощается. На фиг. 471 дана р д^^
двумя замкнутыми контурами, содержащая шесть лишних связей. ^^
того чтобы легче разобраться в симметричных свойствах ^'^'^^^^а>К'
снабдили их символическим обозначением, которое написано ^^^^^^^ая
дой эпюре. Буквами Г и Б обозначены горизонтальная и ^^Р^**^^^^1^меТ'
симметрии, а знаками плюс и минус — прямая и обратная ^ ^ет-
оси
рия. Например, через -^В —Г обозначена такая эпюра, которая
350
оична относительно вертикальной оси и обратно симметрична относи^
гельпо горизонтальной.
Такш '^пюры обладают следующим очевидным своигтвсм: любые
две тюры, облаоающие неоаинаковыми символами, являются взаим-
^о^ортогональными, В данном случае jto приводит к тому, что сигтема
шести канонич^-ских уравнений принимает следующий простои вид:
044^-4+ 54^,4rA,^=:^ О
Мы видим, что она разби
лась на 1 + 1 .2+2 ypaBHeiiHH.
Само собой понятно, что при
наличии большего числа осей
симметрии получается еще
больше упрощений.
5 10.7. ОДНОВРЕМЕННОЕ
ПРИМЕНЕНИЕ НЕСКОЛЬКИХ
ОСНОВНЫХ СИСТЕМ
Простые взаимно-ортого-
нальные эпюры могут быгь
легко получены ттри одновре-
менном использован-ии нес-
кольких основных систем. На-
пример, групповые эпюры, .по-
казанные на фиг. 468, строятся,
как простые (негрупповые) с
помощью четырех различных
основных систем, показанных на фиг. 472. С помощью тех же четырех
основных систем могут быть построены эпюры, представленные на фиг
469. Для построения элюры Мр молено использовать еще какую-нибудь
пятую основную систему.
Фиг. 472
Поел
•.., М
е того как эпюра Л/рИ линейно независимые эпюры А1|, М2
п построены, можно вычислить коэффициенты и свободные члены
сис^^*"*^^^^^*^ уравнений, не интересуясь вопросом о том, какая основная
Но ^^^^ принята при расчете. Действительно, мы имеем право мыслен-
приписать все эти эпюры одной (любой) из основных систем.
Одновременное применение нескольких основных систем может ино-
3 'Значительно упростить решение сложной задачи.
§ 19.8. ПОВЕРКА ЭПЮР И ЛИНИИ ВЛИЯНИЯ
изво "роведении сколько-нибудь сложного расчета желательно про-
лич ^^^'^ поверку промежуточных результатов, например, численных ве-
г,р "" "^ремещений о^^^, Д^р или реакций г^,^, R^p , а также поверку
г^^'^^'^У^ти решения канонических уравнений.
Чат ^^*^ убедительной поверкой является, конечно, поверка окон-
^•"ьпых результатов.
35Ь
« ох.пктят получен в виде эпюр М, Q, Л^, то в nepBviA
Если конечный Р^^У;^^;7пюру Л1, так как ошибка, имеющаяся в это^
очередь следует проверить^^^^^^^ ^зух. Однако ошибка"
эпюре, предрешает ''^'''Р^^ обнаруживается именно при рассмотре:
сделаШ1ая в эпюре М, нередки ь^^^ ^^^р ^ ^ j^^ i
Поверка эпюры М должна быть
двоякой, так как имеет целью выяс-
нить, удовлетворяет ли эпюра: 1) ус.
ловиям равновесия; 2) условиям де-
формации Г'граничным.> услови-
ям).
Поясним сказанное на примере.
Поверка условий рав-
новесия. Для позерки эпюры М
(фиг. 473,GJ вырежем узлы В и ? и
посмотрим, равна ли нулю сумма
моментов, действующих на каждый
из них.
Перерезав стойки, как показа-
но пунктирной линией, и рассчат-
ривая условия равновесия, иь: за\;е-
ТИМ, что поперечные силы ^^^- и Q^
должны быть друг другу pa.Hi:^ л
противоположны, а для этого нуж-
но, чтобы тангенсы углоз на.:лона
эпюры моментов на стойка- были
друг другу равны и противопо-
ложны.
Если бы на ригель деистзовали
наклонные силы, то сумма по-
Фиг. 473
наклонные силы, то сумм^ и-
перечных сил в стойках должна была бы равняться не нулю, а ^?^^^^
ризонтальных проекций вышележащей нагрузки, взятой с oop^i
знаком.
т ^
Фиг. 474
Итак, поверка равновесия состоит в том, что вырезается уз^ ^^^^
более крупная часть сооружения и рассматривается сумма "Р^^^^^цастй-
моментов всех внешних и внутренних сил, приложенных к ^'^^ ^,^ ли
Поверка деформаций должна установить, ^^^'^^^^^„^ де-
эпюры с условиями деформаций данной системы, т. е. являются ^^^^^
формации, вытекаюндие из найденных окончательных эпюр, ^^^^^^ те^
для этой системы. Для этой цели следует вычислить одно
перемещений, которое должно заведомо равняться нулю. ииую ^^
Пусть, например, требуется проверить эпюру М, представлен у
фиг. 474, а.
352
Пользуясь эпюрами М^ и ЛГг (фиг. 474,6 и в), можно вычислить
умножепное на EJq вертикальное перемещение точки А по формуле
JJ угол взаимного поворота двух смелшых сечений в произвольном разре>
je по формуле
^•^o4 = II[^^^i2^dSHT. д.
При поверке нулевых перемещений нул^но поступать так: не де-
лая приведения положительных членов с отрица-
тельными, вычислить отдельно сумму положительных чисел (при-
веденную положительную площадь) и отдельно сумму отрицательных.
Если разница между обеими суммами, выраженная в процентах по от-
ношению к любой из этих сумм, невелика, то результат можно считать
удовлетворительным. Таким же способом следует проверять и другие
равные нулю перемещения.
Если коэффициенты канонических уравнений вычислялись с учетом
влияния продольных сил или продольных и поперечных сил, то, разу-
меется, и поверку эпюр нужно будет производить по точной формуле.
При поверке эпюры, вызванной действием температуры, нужно не
забывать, что любое перемещение выражается формулой
f^^^* § 14.8, формулу (14,10)].
При поверке общего вида линий влияния большую помощь оказы-
^^''^ ^принцип взаимности, согласно которому всякая л. в. представляет
^^ой линию прогибов. Если в л. в. получаются отличные от нуля орди-
^^Ь1 на неподвижных опорах или переломы в таких сечениях, где нет
^рниров и т. п.. то ошибку можно указать сразу .же, не производя
^Ь1численнй,
'^'^ " М РаС,„,от,ч 353
U\m\ im,n)JU\\\mi юпмтии пгииПмитмчч» момппн и г|иум1гм гиимщиИ
пижтмч» imiwiH ntuiynoim и мило крти»П г/ /А Ирммилыш ли уи»? Ih^j,,^'
ununo, чп» W» 1им1|типлыик
Иийипльпоо роикчтг мокй.иии» им фт* ^/Ь, 0. Иомигим и стгии,,/)
mntutnV и 11|»иложии дио пм|»ы, нужно ii|MVri;mnni. rofio литии п|иииГи,и
,си*о (чгцтии. ио К1»п»рпму диит^'и rpyi /'-I. Линии илиииии бут
ИМОГЬ МИД KpHhoft п iU
1'лмт пы игр|1И(ил1.иыП гру:* диигилги пи пижигму риггли, л. и
иио жс^ и MMiftrtHMUtMu момсмггп имг^ли с1м МИД г/ il\ (4vm Пы горииотмл!,
ИЫ(\ ГрУ » HOpOMf^niHJUMI по Л1Ми)П ГГОИКГ, л. и. ИМГЛП Пы МИД h /;, п т. д.
I \ш К1'Л1КИ1-. ис;1смм1Ч1:<:к111'/длины»
1.тм1ипльиы« MimrMiu Моими* сил, ii|MMi.iunM«MpiiiibU» дли ii|u4i.niMiPiiiiii т|)уя1им-|'гП |im
мргй сложных CKMiuMniMui tiriMipniiiviiiMMK пи')пм, lUHUUMi рщриПптыимгы'и лнтикаш
Httt^iin. 11о|»имм» ПИ111М11 рмПшймн Оыли iuii'iiptinmitii.io iimiiip mribii linpio и lO»«iiHlpniifl,
llmni tiOpmiic^Mun w нуль ((скишрых um(|ii|miMioii(im кпмтшчпгкпх упйюимшО при
ИПМИ1П11 игргиисй сил пмлп ui.ioKtn«ii«» 1И) ипдимому, Hiirjim.m KptoitiM (К, 1\И||11|И; 0шт
опич'лит» прием ииодгоии Ооскпигмии жестких кписплгП пыл иьи'Ктаи Mti[M»M% Ihuwy
приему мти'о ииимпиии уделил АЬоллер Прпслпу и иескилькпх стятьих 1ЬМ \Щ} »т,
и и споем курсе «Графический ei4iinKrUi
Идеи сруиицроики пеи.чиеетныч тикже Ичлигплись Мюллерим Ьреслиу и риле nrtif^ft
R НО X И1ДИХ ир(иилиг1) сшлетии» и и UW \\ уже Оыли и«ложеии и геи курсе. И чиш»
йиилитимеском ииде они Пыли и.гмпжеп« сиичили ироф, Л\к>ллерим^ (NleMnnnnl
A\illler) и m)f {\i йгием миимигелиии ри:шиг« и углуОлеия ироф. II. (1. Сгрелеиннм^.
Г.лелук)И1.е() гииетгельиоП и пригннилшоП риПотпП Пыл» книги ириф. Л. Л. Гип1Де1иА
U ДйльиеЛтем лигершурй, iHiemnuemimi приплеме рисчеги сложных сгитимсски
иеенределимых систем» иПпстнлиси и i\Cx\\* огромным количестиом рпПог п И1»лутиш
рмлинги^ и котором читигель может судить ovincni пи «'одсржиюио диниоП слии»и,
' ИеИшу «»И' riietMle Иег elttfeUnthen Иокеи||%ег, Z. f. linokmole, UirtO.
^^^^^ MtellcHH ». TheoddilcB l)ogenr«ehwerkce, Z. iL Arch, n JMK-Ver, 2И (Ппниоусг.
» Mn hereclnunij^ niehilitcli в(.ми1Ье»1. rrnnwerhe. /enlcnihirtll iler llnnvenv., Ii)07.
h т!!*!^'Г!'^ сложных сгйти»1ески неопределимых еистем, М,, ПШ.
tmoMin MciUH .рмеметй етитически иеоиределнмыч систем, М.. Ш27.
г лава 20
РАСЧЕТ РАМНЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
(ДЕФОРМАЦИЙ)
§ 20.1. СТЕПЕНЬ упругой ПОДВИЖНОСТИ УЗЛОВ РАМНОЙ СИСТЕМЫ
Условимся пренебрегать продольными и поперечными деформация-
ми стержней и принимать во внимание только деформации изгиба Коо-
ме того, считая деформации весьма малыми, мы не будем делать разли
I'
б)
В.^-"--^
д
Фиг. 476
С с'
1 /
/
/
/
/.
К"
\
?^
;
Фиг.
477
i
• "1
d
D Л'
Г"?
/
/
/
! /
Ч*'
/
/
/
/
^^
^^я между первоначальной длиной прямого стержня и длиной хор-
^ать^гб^^^^^^^*'^ ^^^ упругую линию; иначе говоря, будем пренебре-
солижением его концов при изгибе. Это вполне согласуется с при-
^^нным основным дифференциальным уравнением изгиба: EJ ^-^ =
"^ » Которое применяется вместо точного уравнения — = —М, где
р р
^Радиус кривизны упругой линии.
кри ^^У'^^^'гся, это не дает нам никакого права считать, что концы
Иое Ro^^^ стержня при изгибе также сохраняют свое первоначаль-
^аимное расстояние.
геоме ^^^^^ из этих двух предпосылок, очень легко разобрать, могут ли
Нагруз^*^^^^^^^^^ центры узлов рамы перемещаться под действием внешней
гео|^^ Если они могут перемещаться, то количество независимых
трических параметров, характеризующих возможные перемещения,
355
мы будем называть степенью линейной подвижност
рамы, ^
Рассмотрим для примера схему, изображенную на фиг. 476 п
спросим себя, обладает ли узел В линейной подвижностью, т. е мо^ "
ли центр узла переместиться по какой-нибудь траектории. Ответ "на зТ^
вопрос дает фиг. 476, б, на которой изображена шарнирная схем
той же рамы. Эта схема получается при помощи установки шарнипп^
во всех узлах. Степень линейной подвижности рамы совпадает со ст
пенью изменяемости шарнирной сх^*
мь1. Так как фиг. 476,6 представляет
собой трехшарнирную арку, то сте
пень изменяемости или подвижности
рамы равна нулю.
/
/
ш^
Фиг. 478
Фиг. 479
На фиг. 477—479 пунктиром показаны возможные перемещения
шарнирной схемы различных рам и цифрами обозначена степень линей-
ной подвижности узлов,
%?^- I Кроме линейной подвиж-
^^^"^"^11^ JL ^ ности, характеризуемой пере-
мещениями геометрических
центров узлов, существует еше
угловая подвижность узлоз-
При изгибе стержней образу-
ются упругие линии, касатель-
ные к которым '3 различных
точках имеют различные углы
наклона. Углом поворота узла
мы будел! называть угол, на
который поворачиваются каса-
тельные, проведенные к упр)'
примео ня гЬмг Аяп ^г^ ^^^^ линиям в этом узле. Ьа-
обшГй лп^ t ^'''''' поворота узла А мы будем называть угол?..'
оощии для всех трех касательных, сходящихся в нем
УДас?сТ^Тти""'''™'^^^ рамы, нагТуТе!.^^^^^^ нагрузкой-
уже™^^ то nocie этого
пепГешр»^^ Г"^"^*"""^"^^^ этбм и основан метоД
HenLecT^lnn^^ ^"""^^ Деформаций), в котором за осйовные
либо ™L Р^"1'^^^^^^ ^"^^ линейные и угловые перемещения узлов,
^иоо группы, образованные из этих величин:
^S^
ций
356
§ 20.2 ФОРЛ1УЛЫ ДЛЯ КОЭФФИЦИЕНТОВ .МЕТОДА ДЕФОРМАЦИЙ
(ФОРМУЛЫ ДЛЯ РЕАКЦИИ)
й ?^"^;^f'^ательными величинами при пользовании методом дефоР
и для рам с прямыми стержнями служат реакции, возникающие
0
чески неопределимой балке с прямой осью при различных воздей-
^^^^^х Величины этих реакций могут быть найдены методом сил. Огра-
ствиях. ф^ j^yjjaj^H для балки постоянного сечения с обоими упруго-за-
"^"^Тенными концами или с одним упруго-защемленным, а другим шар-
"^fi!ln-onepTbiM концом.
На фиг 481 показана балка постоянного сечения с двумя абсолют-
^якоепленными концами. Пусть опоры вместе с концевыми сечения-
^^ Ли В повернзглись на углы ср^^, ср'в » одновременно сместились
''In птносительно друга так, что прямая АВ повернулась на угол ф,
^^ пР чего опоры сделались абсолютно неподвижными. За положи-
"^тное направление для этих углов примем идущее по часовой стрел-
Ге Реактивные моменты М^ и М^ на концах балки (т. е. действие
опор на сечения А и В балки) также будем считать положительными в
Фиг. 481
„^ох^ттрмы по часовой стрелке, а реакции /?^,
том случае, когда они направлены по ч<х^
^в> - когда они направлены вверх. ^ ^^^ ^^^^^ ^р^^^^^^ ^^ ^^ ^^_
Для определения величины т^, в канонических уравнения
новные неизвестные и составить Д-"^^^^^^^^„
заданными перемещения
метода сил, причем должны будем ^^ ^^^ ^^^ уравнения, мы по-
°"0Р <Рл. <Рв. Ф и ^""^™'°'°/моментов после чего легко найдем так-
лучим искомые выражения Д-^я момент - ^^^^ зиде.
же реакции/?^, Rb- Напишем решение в
(20.1)
357
площадь эпюры моментов, которая вызывается внещ.
Здесь ш - "S нагрузкой в балке с шарнирио-опертыми конца-
Х». Xg
-расстояния центра тяжести площади ш от опорных
вертикалей;
ро ро -опорные реакции от внешней нагрузки в балке с шар.
' ^ нирно-опертыми концами.
Ппи абсолютной неподвижности концов, т. е. при <Р^ = <?^ = Ч- =0,
реактивные моменты на концах и поперечная сила в произвольном се-
чении соответственно равны
(20.1')
/
где Qo - поперечная сила в щарнирно-опертой балке. Поэтому можно
написать
Mr
2EJ .
Q = -
Z2
(20.1
Из этих общих формул получены те отдельные частные ^лучаи. ко-
торые приведены в табл. 10. Например, для балки с абсолютно защеь
ленными и неподвижными концами получается
При повороте левого конца
балки на угол 9а получаетс>1
4?У -- 2Е/^
М
Фиг. 482
¦?Л*'
М„-
/
'Ъ'^
Rb=-
eEJ
?^*
обй ре-
Полезно запомнить, что если угол <р^ положительный, то ^^
активных момента получаются положительными, причем момент
конце Л в 2 раза больше момента М^. ^^^ и
Для балки постоянного сечения с защемленным левым ^^ ^^оро^
опертым правым (фиг. 482) можно вывести формулу, приняв во
из формул (20Л) Mq =0, '
Таблица 10
Реакции балок постоянного сечения
'"Л - 2d '
где rf—высота поперечного
сечения; а-коэффициент
линейного расширения;
359
Схема сооружения
и воздействия на него
Продолжение
Эпюры изгибающих моментов
и реакции (ординаты
отложены со стороны
ристяйутого волокна
Воздейстдив N1-6
Ш
Формул
Формулы для такой л,
ки получаются из прелып'"
Щих при помовд ^под^^Г
новки "одста-
/i = /
Балки с защемленными концами
Mq = u^vPl;
М^ = 2u^V^Pl;
^A=^'4l+2u)P;
^B^^^4^+2v)P
где г/ —высота поперечно-
го сечеиия; /?^ = /?j9 = ^
Формулы для такой балки
получаются из предыдуш'*-'^
При помощи подстановки
в результате
~l^i?A-n+ -jr^B + Q"- (20.2-)
(20.2)
О = . ^^^ ' ¦- > X . 3<"
Отсюда видно, что при повороте сечения А возникает момент
ZEJ
М^= — 9л' при повороте пролета АВ на угол ф и сохранении гори-
зонтального направления касательной в сечении ^ к упругой линии по-
лучается Л^л^ 7~ Ф* ^Ри абсолютной неподвижности левого кон-
ца и отсутствии смещений правого конца М^ = ^в-
Если бы защемленный конец А был расположен справа, а шарнир-
ный В — слева, то в формулах (20.2) пришлось бы писать ш с обрат-
^>^ . пп т. ^А
ным знаком; /? =:, _Jl 4- R^- R == ^ 4- /?о
В дальнейшем для сокращения письма мы будем часто пользовать-
ся следующим обозначением:
— = /. (20.3)
Число i, имеющее размерность момента, мы будем называть «коэф-
фициентом жесткости стержня на изгиб» или короче: «коэффициентом
Жесткости» («погонндй жесткостью»).
Для стержней переменного сечения, например для стержней с ву-
тами, а также для криволинейных стержней формулы получаются,
разумеется, более сложными; для стержней с вутами имеются числен-
ные таблицы и графики.
§ 20.3. ИДЕЯ МЕТОДА ПЕРЕМЕЩЕНИЯ (ДЕФОРМАЦИЙ)
Чтобы понять идею метода деформаций, достаточно рассмотреть
простой пример, представленный на фиг. 483. Рама, изображенная на
^хеме а, имеет стержни постоянного сечения. Количество лишних связей
равно 3, степень линейной подвижности узлов равна нулю.
Подобно тому, как при расчете по методу сил выбирают основную
^истему, которая фигурирует во всех вычислениях, выберем и здесь
^-новную систему. Так же как и там, позаботимся,' чтобы основная
Во ^^^ позволяла легко строить эпюры, вызываемые всевозможными
^^здействиями. Но в отличие от метода сил образуем эту си-
^т е My не путем отбрасывания лишних связей, а
У Тем добавления новых связей.
Узр rj^^^f^oM примере достаточно будет добавить одну связь* защемить
^^ о, лишить его возможности поворачиваться. Обратим внимание на
' Что здесь речь идет не об обычной заделке, которая как известно,
361
Л^ опорным стержням, а^о такой связи, кото,
эквивалентна ^p^^i ont^ ^^ ^ ^^^^^^^^^ ^^^^^^^^^^^ движениям, в
рая препятствует ™^^Р"!^^^^^ реакция только одного вида: момент
такой связи может возни у^^^^^ ^ ^^^ считать основной системой.
Раму с заделанным УЗ^^^ усложняет задачи, а, наоборот, упроща-
Добавление этой свя ^^^^^ способом рама представляет собой
ет, так как "Р^^^Р^^^^пность двух балок с абсолютно защемленными и
не что иное, как ^овоку! ^^^^^ системы у нас уже заготовлены
несмещаюшимися концами. '^''J\
все необходимые формулы и эпюры.
Фиг. 483
Нагрузим основную систему заданной внешней нагрузкой. ^чевИД
но, что ригель ВС будет работать, как балка с защемленными ™^^^ '
а стойка ВА останется прямолинейной, следовательно, не будет ^^^^^^
нимать никаких изгибающих моментов. Она будет работать '^^^^^^^^^^^
продольную силу, но продольными деформациями мы решили пр
брегать. Э^пюра М^ представлена на схеме б, ^ jj^i
Эпюра Л1^,--^довлетворяет всем условиям деформаций, налага ^^^
на раму неразрывностью ее контура и опорными закреплениями. ^^ ^^
не удовлетворяет другим условиям задачи, так как для получения '^^^^,
эпюры необходимо приложить к узлу В тот реактивный момент, ^^^^
рый возникает в заделке. Назовем его R^p . Принимая за "^""^^^^^рой
ное направление для реактивных моментов то, которое идет по ча
стрелке, можно написать
Чр
av^PU
Если мы не приложим к узлу В этой реакции, то узел В не У ^^
в равновесии. Если мы его приложим, то впадем в противоречие с у
ВИЯМИ задачи. ^бра-
Чтобы.освободиться от противоречия, поступим следующим ^^^.
зом: представим себе, что та воображаемая опорная конструкЦия,^^^^^^1
рая защемляет узел Б, повернулась по часовой стрелке на угол, Р
362
единице, и увлекла за собой самый узел. Де(Ьоо\1я.,иа „„.
шая такому случаю, показана на фиг. 483 в р2™ J мп.' °'^^^''^«>-
вем г„. Он направлен по часовой стрелке и павен^^п °"^"'' "^^°"
Lr&T" "^^^" ^^^ ™^°' ^^'^" и?оК^\%Тй"к^-^,Г-1Т^^^
где
»,=^- i -^
Все^различне или противоречие между действительной системой и
основной сводится к тому, что в первой узел В может поворачиваться
а во второй нет. Поэтому для устранения противоречия необходимо по-
вернуть узел В основной системы на некоторый угол Z,.
Тогда окончательная эпюра примет вид
М = Л4^ + М,2,. (а)
Реактивный момент в узле Б выразится тогда формулой
Остается подобрать теперь величину Z^. Она найдется из того
условия, что в действительной системе к узлу В не приложено никакого
реактивного момента, т. е. из условия
riA + K = ^- (б)
Это уравнение можно рассматривать и как условие равновесия узла
В. Действительно, если сумма внешних моментов Гц Zii-R^p, прило-
женных к узлу, равна нулю, то отсюда следует, что в этом узле, вырезан-
ном из рамы, внутренние изгибаюихие моменты ригеля и стойки также
должны друг друга уравновесить.
При соблюдений условия (б) всякое противоречие между основной
й действительной рамой пропадет, и мы получим правильное решение
задачи.
Итак:
_^^ uvm^ M = Ai^+-^^Ai,. (в)
' ггг 4(/i+/2) ^ 4(4+4)
Окончательная эпюра моментов показана на фиг. 483,(5.
Замечательно, что вместо трех уравнений с тремя неизвестными мы
получили только одно уравнение с одним неизвестным. Это объясняется
тем, что выбранная нами основная статически неопределимая система
ближе к заданной, чем основная система метода сил. Если бы мы
отбросили лишние связи, основная система противоречила бы трем усло-
виям действительности, между тем как совокупность заделанных балок
противоречит только одному условию. „
Полученное нами решение годится также для построения линии вли-
яния. Нужно только принять величину и за независимую пере^^^^^^
Т^ак. например, изгибающий момент в сечении В ригеля ВС будет соглас-
но формуле (в):
363
^ ,.птппые изгибают его выпуклостью книзу. Полученное урав,
приняты те, которые изгио является кубической параболой ^
ириир показывает, что л. в. iyxq^
Линия влияния М,^ для верхнего конца стоики совпадает с л. в.
^^ Для произвольного сечения D ригеля (фиг. 483, а)
,^ Г 4/2 (/г — ^) 2'"2С 1 V
Р 2 0i-{-i2)
^,де м^ —л. В- изгибающего момента в том же сечении D балки ВС с
защемленными концами.
8 20 4 КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА ДЕФОРМАЦИЙ ДЛЯ ЛЮБОЙ
СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ПЛОСКОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
Во всем дальнейшем изложении мы будем пользоваться следующи-
ми, уже известными нам обозначениями: через R^p, R^p,..-, Rnp обозна-
чим реакции дополнительных связей, вызванные заданной внешней на-
грузкой; через г^^ — реакцию связи i, вызванную единичным перемеще-
нием связи k. Неизвестные величины перемещений обозначим через Zi,
Z2,..., Zn .
Представим перемещения действительной системы как сумму пере-
мещений основной системы, вызванных: 1) внешней нагрузкой; 2) ли-
нейными и угловыми перемещениями дополнительных опор. Наконец,
напишем, что в каждой из дополнительных связей суммарная реакция
равна нулю, так как фактически эти связи отсутствуют.
В результате мы получим канонические уравнения ме-
тода перемещений:
^2Л + ^2222 + ^2з2з+-' + г,„2„ + ;?2р-=0;
(20.4)
^i2i + r„,Z, + r^Z3 + -.. + r,/„+;?„^ = 0.
В левой части первого уравнения стоит суммарная реакция первой
дополнительной связи; во втором уравнении — суммарная реакция вто-
рой дополнительной связи и т. д. В случае действия температуры сво-
оодные члены заменяются выражениями /?w, /?«, .-.,/?«/ а в случае
расчета на осадку опор - выражениями r",\ /?,,..., R,"!
Коэффициенты системы (20.4) обладают, как известно, свойством
взаимности. Члены, стоящие на главной диагонали, а также детерми-
нант системы всегда положительны.
Система уравнений (20.4) о- чнаково справедлива для стержней
постоянного или переменного чения, с прямой или кривой осью, с
недеформируемыми или деф лруемыми в продольном направлении
стержнями, для плоских и просг анственных и т. д Она справедлива не
только для стержневых сооружений, но и для систем любого типа.
^ Ограничимся одним примером составления канонических .УР^^З?;
НИИ. Пусть дана рама, схематически представленная на фиг. Ш,а. ^^'
чения всех стержней — постоянные.
Для образования основной системы защемим узлы / и 2 и ДО^^^^ь
опорный стержень 5, перпендикулярный правой стойке (этот стержень»
можно направить, как угодно, но только не по направлению стойки
2В)- Полученная система, показанная на схемах 484,6, в, г ид очевид-
но, представляет собой совокупность однопролетных балок'с абсолютно
закрепленными концами, поэтому все ее реакции могут быть найдены
из табл. И.
Продольными деформациями стержней мы по-прежнему будем пре-
небрегать.
Примем положительное направление для реактивных моментов по
часовой стрелке, а для опорных реакций дополнительного стержня 3 —
вправо. Обозначим^ через Zj поворот узла Д через Zj — поворот узла 2
й через Zs — линейное перемещение опорного стержня 3 по его направ-
лению.
Рассмотрим отдельные состояния основной системы. На фиг. 484,6
изображена эпюра изгибающих моментов и соответствующие реакции
для случая действия внешней нагрузки. Реактивные моменты R^p и . R^p
находятся сразу:
Опорная реакция Rsp определяется несколько сложнее. Сначала выре-
заем мысленно узел 1; замечая, что в левой стойке поперечная
сила равна нулю, заключаем, что в ригеле продольная сила рав-
на нулю. После этого вырезаем узел 2. В нем неизвестными являются
только продольное усилие правой стойки и опорная реакция Rsp , кото-
рые уравновешиваются поперечной силой ригеля, равной — . Постро-
ив силовой треугольник для этих трех сил, найдем Rsp^^ ^-^ cos а.
На схеме 484,в показано единичное состояние основной системы,
отвечающее перемещению Z\ = \. Предполагается, что левая защемляю-
щая опора вместе с узлом / повернулась по часовой стрелке на угол
2i = l, в то время как две другие дополнительные опоры остались абсо-
лютно неподвижными. Из этой схемы, пользуясь табл. И, сразу можно
определить реактивные моменты:
Что касается реакции Гзь то ее можно определить несколькими спо-
собами. Во-первых, можно было бы вырезать узел /, определить из него
продольное усилие'в ригеле и затем перейти к рассмотрению равновесия
узла 2. Второй путь, более простой, который мы и выберем, состоит в
использовании закона взаимности: Гз1 = г,э. Он показывает, что мы moj
жем отказаться от непосредственного разыскания требуемой опорной
реакции. Вместо нее мы найдем несколько позже, когда будем рассмат-
ривать единичное растояние Zs^l, реактивный момент ris-
На схеме фиг. 484, г показана эпюра, вызванная действием переме-
щения Z2=l. Из этой схемы находим
''22=4(/,2 + Sz?)' '-12=^21-
Что касается реакции Гз2, то ее определение отложим также до рас-
смотрения эпюры Жз, так как гзг^^'гз. „ ^ ,^ о
^ Переходим к схеме фиг. 484,^, на которой изображена эта эпюра,
Она выражает собой результат единичного перемещения опорного стерж-
ня 8 по его направлению при условии, что узлы / и 2 перемещаются по-
ступательно, не поворачиваясь. Все три стержня перекашиваются, т. е.
36.^
кониы поворачиваются на некоторые -глы
хорды, соединяювде их^к^ необходимо найти эти углы. Для стойки
fe' V'которой конец 2 переместился перпендикулярно направленик>
2В. у ^°^°Р°" „невидно. Ф,в= Т^- Остальные два угла проще
стержня на единицу ^ ^^^^ ^^^^1 ,,, (ф,, 484.е). Согласно
всего определяются ил „Сворота любого стержня равен отношению
'л^1Жмо6рГе"и'яТдл„„е с'амого стержня. Огоода
—^ •„„ Г2' COS а
1'2' _
f
12
Угол 0.^ отрицателен, так как направлен против часовой стрелки.
Я1
Фиг. 484
Определив углы tb^^ ^ ф^^, Фгв » можно перейти к нахожде^^^
реакций. Реактивные моменты ris, т^г определяются сразу по форму,
взятым из табл. 12:
^13 == ^31 = — 6 ( На ^ха + ^2 Ф12) ;
^23 = ^32 == — 6 ( ^12 Ф12 + ^'2B*2b) '
Реакцию ггъ мы найдем способом вырезания узлов, ^^"^^Р^'^^^^пе-
уже неоднократно пользовались. Из эпюры Мг легко определим ^ ^^
речные силы во всех стержнях. После этого вырезаются узлы ^'^^^л^ы
другим: сначала — узел /, из которого определяются продольны ^^^^,
^\А и ^12, а затем — узел 2, из которого при помощи замкнутого ^^
вого многоугольника находим неизвестные N^^ и Гзз. Операция эт
столько проста, что не требует дальнейших пояснений.
366
Укажем другой, вполне общий путь для нахожп»«»= »„« -
am г,.. Д^я этого напишеи, что cy„lLa Раб^ ,се?в„ёшн*?" ?SS'
,равйя''рГбо?'„:"2Гь™'' """""''' "'^¦•^'"о"' — -™' >"
Приближенно
где М^, Л^^, Q^ — эпюры, возникающие от внешней нагрузки в любой
статически определимой системе, которая может быть получена из дан-
ной путем устранения тех или иных связей (см. книгу автора «Методы
расчета рам», ч. II, 1934).
Формулы эти в развернутом виде имеют особенно простой вид для
рам с прямыми стержнями, имеющими постоянное по своей длине се-
чение.
Возвращаясь к рассматриваемой раме, мы должны составить и ре-
шить три канонических уравнения, после чего останется построить окон-
чательные эпюры по формулам
^ = ^^ + '^iZ, + N,Z, + N^Z,;
Q^Q^ + Q,Z, + Q,Z, + Q,Z,.
§ 20.5. УРАВНЕНИЯ МЕТОДА ДЕФОРМАЦИЙ ДЛЯ РАМ
С ВЕРТИКАЛЬНЫМИ СТОЙКАМИ
t
Составим в развернутом виде, т. е. с окончательными формулами для
всех коэффициентов, уравнения метода деформаций для рам, применяе-
мых в качестве каркасов зданий. Эти рамы могут иметь несколько про-
•"^ов и несколько ярусов (этажей) и имеют обычно вертикальные
стойки и горизонтальные ригели. Схема такой рамы представлена на
фиг. 485.
В такой раме степень подвижности узлов равна числу ярусов. Если
какой-нибудь ригель будет ломаным, но будет иметь вершины только в
Точках примыкания стоек, то степень подвижности останется та же.
^ противном случае (фиг. 486) рама будет иметь большую степень по-
движности. Степень подвижности для схем фиг. 485 и 486 соответст-
венно равна 3 и 4 В настоящем параграфе мы будем рассматривать
только такие рамы, у которых степень подвижности равна числу ярусов.
При расчете рам по методу деформаций основными неизвестными
^УЖат две группы величин: 1) углы поворота узлов, которые мы обо-
значим через <р; 2) углы поворота стержней ф или взаимные смещения
«X концов 8 (фиг 485). Для любой стойки 8 =- ф /, где / — длина стои-
ли*, для любого ригеля 8 = О, т. е. все ригели перемещаются поступа-
Т^'^ЬНО.
367 .
Если бы стойки были непараллельны между собой или если бы
приняли во внимание их продольные деформации, то ригели также У
лучили бы некоторые угловые отклонения ф . «о-
Полное число неизвестных, отвечающих схеме фиг. 485, равн
12+3=15, и при решении той же рамы методом сил количество ней
вестных равнялось бы 27 '
Г--7
^^
V^
^^
Z^j-
Фиг. 485
?^
ш» -^
Фиг. 486
Для определения углов поворота стержней ф и взаимных горизон-
тальных перемещений о составим канонические уравнения. За основ-
ную систему примем опять раму, образуемую из заданной системы пу-
тем защемления узлов и введения дополнительных горизонтальнь^
опорных стержней. Эти закрепления превращают основную систему
совокупность однопролетных балок с несмещающимися опорами. ^^\.
схеме фиг. 487, а отвечает основная система в виде схемы 487,6. В таки
узле, в котором все стержни шарнирно связаны друг с другом, напр ^
мер в узле Л, защемление не вводится. В узле, в котором лишь *^fj.e-
стержнеи связана между собой шарнирно, например в узле В, заше^^
ние вводится. v v j ^^
Так как за неизвестные принимаются два различных вида „^^^^йХ
Щ^™и» то канонические уравнения после подстановки выражении Д-^^^^^.
коэффициентов также получатся двух различных типов. Одни УР
368
ния будут представлять собой математичрг.,
реактивные моменты к nZ^ ^^У^° запись тот а,
р^авны нулю, а другие будут'овориГоГм'Г"^ -^еГе™^^^^^^^
3 дополнительных горизонтальных стержня^ п ^ ^ " « Р н ы е р е а /ц и и
но вывести по одному уравнению kS?" ти^^^"Ь| нулю. Нам дос^аточ"
шей наглядности тем уравнениям, ад!™^- ^i^^""^^ придания боль
будем обозначать в них неизвестные не обоб. '^^^Р^^^^я^ вывести mJ
указанными выше буквами <р и 8. сообщенным символом i,
мы
а
Узел'^пп^п/Л^^!"^^"^^^ группы уравнений рассмотрим какой-нибудь
г,
предположим, что узел повернулся по часовой стрелке на угол 9 с,
узел Г гт ''''''^^'' первой группы уравнении рассмотрим какой-нибудь
(фиг A^SP^^^^^^^^^ рамы со всеми примыкающими к нему стержнями
jj^ сположные концы всех примыкающих к нему стержней поверну-
CTenJu^^^ "^ часовой стрелке на углы 9i, ?2, 9s и т. д.; кроме того,
ржни получили взаимное перемещение своих концов на 8^^ , 8^
чо^* ^''„ ^^«"ЗДствие чего хорды, соединяющие их концы, повернулись по
^^асовои стрелке на углы
ГС1
"С1 -
'с. '
i С2
"сг
и т. д.
собо" ^^^^*^^"^'*^ ^^с^^нт, возникающий в заделке узла С, представляет
Фопм ^^''^'^браическую сумму реактивных моментов, обусловленных де-
1 мацией каждого из стержней в отдельности. Пользуясь формулами
24 и м. р««...«.. 369
Рабинович
^90 П и обозначив реактивные моменты, вызванные внешней нагрузкой
ifje3 МР; ил^ через Mg , мы получим следующее уравнение:
— 6
^сг ^сг
' +
^С2 ^С2
Н ; г
/.
сг
lex 'С2
ИЛИ короче:
4TcS 'ск+25]
-ск
Тл
^ск
^СК I
ск
Ц^^с/с-О.
(20.8)
где суммирование распространяется на все стержни, жестко (не шар.
нирно) прикрепленные к узлу С.
Уравнение в таком виде пишется для рамы, у которой нет шарни-
ров. Если какой-нибудь стержень, жестко скрепленный на одном конце
с узлом С, имеет на противоположном конце k mapjHHp, то в уравнении
(20.8) происходят следующие изменения; в первой сумме слагаемое
'^^ck ^с> отвечающее этому стержню, заменяется членом 3/^^^срс
(фиг. 489); во второй сумме этот стержень совсем не участвует, так как
при повороте узла k рамы стержень не испытывает никаких усилий. На-
конец, в третьей сумме этому стержню отвечает вместо слагаемого
— ^^ck слагаемое —Зг^^ .
Для большей ясности обозначим те противоположные концы стерж-
ней, которые жестко присоединены к раме, через /г, а шарнирно
прикрепленные — через 5 и напишем вместо уравнения (20.8) более
общее:
-'И
Ck
^Ck
'-Ck
3V.^c.-^ + 2^?-o.
(20.8')
^кнЧ^с
Выведенное уравнение справедливо для любой рамы с прямыми
стержнями, имеющими постоянное по их длине сечение.
Обратимся ко второй группе урав-
нений.
Вывод их будет понятнее, если ьаь\
для иллюстрации будем пользоваться
примером (фиг. 490). Перережем ©се
стойки какого-нибудь яруса ло их даж-
нему сечению, например по линиям
Фиг. 489 N—N. К~К и т. д., и напишем, что
сумма горизонтальных проекции -b^^j^
сил, действующих на отсеченную час
выше разреза, равна нулю. При этом мы будем считать, -что суммарнь1|
усилия в дополвительных горизонтальных опорных стерлшях осповпо^
системы (эти опорные стержни, равно как и заделки узлов, на чертеж
не показаны) равны нулю, и поэтому ле будем их .вводить в расчет, i^^
самым мы получим уравнения, которые по своему смыслу эквивалента
условиям, выражающим обращение этих реакций в нуль.
370
^^
Беря по одному разрезу в каждом ярусе, мы получим для фиг. 490
_\.г)явнения — ровно столько, сколько она имеет степеней упругой
четыре^>^„^„^„^ности.
пинейной подвижности
Горизонтальные проекции сил, действующих на отсеченную часть,
дываются из горизонтальных проекций внешней нагрузки и из по-
^^^ чных сил в стойках. Посаедние в свою очередь в каждой стойке
"^^^сят от четырех факторов, представленных на фиг. 491. Поворот
^^^хнего конца по часовой стрелке на угол <Рв (« ? верхнее») вызывает
^^перечную силу, приложенную на нижнем конце слева направо и рав-
— Фв- Положительный поворот нижнего конца на угол ср„
(«Ф нижнее») вызывает направленную в ту же сторону поперечную
^j^jjy —ср„. Отклонение стержня по часовой стрелке на угол ^ вызы-
12/ I2i
вает поперечную силу обратного направления, равную — ^ = —,1^-
^offaf
1
f6
t 1 Т Т 1 Т Т 1 Т Т
7/ W Тл? \f^
\
ЬЬЩк
и
/7
1
/в
1
i
19
20
15
N' О
Фиг. 490
уХ^ Т^ 7^
-—-Л
Наконец, рассмотрем влияние внешней нагрузки. Оно выражается,
о-первых, в том, что возникают углы поворота узлов ф», (р„ и смеще-
ия 0; эти влияния ужс разобраны. При условии же, что 9^= фн =^ =
^ деформации вызываются только той горизонтальной нагрузкой, ко-
Р?я приложена непосредственно к перерезанной стойке (фиг. 491).
д^Л'^-^и^она состоит из сосредоточенной силы S и равномерно распре-
поак^^°"* имеющей интенсивность s, то вызывает поперечную силу, на-
^'«^вленную влево и равную
24»
?L4-^2(i+2c))S=-~+5w«(3 —2w).
371
Госоелоточенную и сплошную горизонтальную нагрузки, приложен-
ные непосредственно к перерезываемой стойке, обозначим через S' и «'.
Алгебраическая сумма горизонтальной внешней нагрузки, прило-
женной к стойке, и поперечной силы на ее нижнем конце равна
5' + 57 - — -5'«»(3-2«)= ^ + У (1 _ 3 к« + 2 й^) =
= i:L_)_5V(3 —2о).
Если на перерезанной стойке имеется, кроме того, крановая нагруз-
ка, дающая пару с положите.пьным моментом Рс (фиг. 491,5), то она
вызывает поперечную силу, идущую вправо и равную .
а) ^3 ^^ 3
9)
'>Ш/.
н
Фиг. 491
Из всего сказанного следует, что после сокращения на 6 уравнение
горизонтальных проекций примет такой вид:
+ ¦
+ -7^ + L—z
6
-0.
(20.9)
В уравнении (20.9) фигурируют неизвестные, от-
носящиеся исключительно к перерезанным стои-
кам. Первая и вторая суммы содержат члены, относящиеся к перере-
занным стойкам, а третья сумма содержит горизонтальную проекцию
внешней нагрузки, расположенной выше того яруса, в котором произве-
ден разрез. Что касается трех последних членов, то они относятся *
внешней нагрузке, расположенной только на перерезанных стойках.
Уравнение выведено в предположении, что ни одна из перерезанные
стоек ни на одном из своих концов не имеет шарнира. Если какая-ни-
будь из них имеет шарнир на верхнем конце, то члены уравнения (20,9;»
отвечающие этой стойке, будут иметь вид
+5:5'^^^+^(1-а-). (2o.iO)
2/ •" 2/2 ^
16
S72
Что же касается суммы 2—^,
которая относится к в ы ш е л е-
^ашим ярусам, то она, конечно, не изменится.
Если перерезанная стойка имеет шарнир на нижнем конце, то
соответствующие ей члены будут иметь вид
_5_
48
J Л-^J * x*i«V,ir) ЬИД
21 ^ 2/2 ^ 48 ^ ^ 12 ^
4/
(1^0.
(20.11)
Наконец, если стойка имеет шарниры на обоих концах, то соответ-
ствующие ей члены, выражающие влияние поворота и смещения ее
концов <Рв, ?1г и о, пропадут, а влияние внешней нагрузки, действую-
щей на нее непосредственно, выразится членами
s'l , 1 V с/ I Рс
(20.12)
В каждое из уравнений (20.9) входит только одна из величин 6,
поэтому ее легко выразить через углы 9> входящие в то же уравнение.
Подставив затем эти выражения в первую группу уравнений, мы умень-
шим общее количество неизвестных.
§ 20.6. ПРИМЕР СОСТАВЛЕНИЯ УРАВНЕНИЙ
Составим уравнения для рамы, схема которой дана на фиг. 492. Основными неиз-
вестными являются 10 углов поворота узлов и 3 горизонтальных перемещения. Для
ннх можно составить 10 уравнений реактивных моментов и 3 уравнения горизонталь*
&ЫХ проекций.
Узел /:
Уравнения реактивных моментов
+
12
12
12
= 0.
Я,
П^
Ш
и
Я$
"2
Яг
'Н
ш
i
я*
iiiiiiiiiiinfiiiiiiiiirii
р
Фнг. 492
%
</'//
378
Узел 2:
{41,, + 4/23 + 4/26 + ^hb) Ъ + 2''2i ?i + 2^23 <Рз + ^Ы
— 3f2b "
ч
^ /2
12
= 0
и т. Д. Уравненияпоперечиыхсил
Разрез в нижнем ярусе: ^ ^^^ ^ ,^^ .^^
г2
1а
2'1ь
2'L
+
Разрез в среднем ярусе:
12
= 0.
----^-fe + ^62+^73 + ^84)^n+ б '^ б "^ 12 "^
'51
(<Рб + <Р2) + "Г~ (<Р7 + <Рз) + *7^ (98 + <Р4) —
Разрез в верхнем ярусе:
*96
2/.
> +
40—7
96
2/
10-7
?1в+
'96
2/;
96
2/10-7 j
'П1
5 Рс (З — i!^)
?)
§ 20.7. РАСЧЕТ НА ДЕЙСТВИЕ ТЕМПЕРАТУРЫ
Как и раньше, будем считать, что температура, на которую ведется
расчет постоянна по длине каждого стержня и изменяется внутри сече-
ния от одной кромки до дру-
гой ло линейному закону.
Температуру по оси стержня
назовем t^ а разность тем-
ператур f.
Благодаря температур-
ному удлинению стержней
узлы займут новое положе-
ние, вследствие чего .взаим-
ные перемещения ^ концов
стержней заменятся сум-
мами Ь+Ь^, где 8'-темпе-
ратурные взаимные переме-
щения в основной систе-
ме по направлению, перпен-
дикулярному оси стержня.
Разность температур, Р^^^^
t\ не вызовет удлинении, н
моменты ^f^ указанные
МаГ
d
^
г'>0
^
Фиг. 493
в основной системе вызовет реактивные
табл. 11 под номерами 6 и 12.
Уравнение реактивных моментов примет вид
^ck-^^a
'ел
"Ck
S^c-
^Cs
k
^Ck
Cs
^CS
+ 5]m^ = o.
(20.13)
., 374
13 ураБПСИии горизонтальных проекций все члены, зависящие от
в„е.ипсй нагрузки, обратятся в пуль, а псрс-мсщсия 5 замета сум^
мой не-
что касается температурной поперечной силы Q' в стойке как в
,лемсп1е осноьнои системы, то, как видно из фиг. 493. она будет отлич-
на от пуля только при наличии заделки иа одном конце и шарнира на
другом конце. *' »"
Отсюда видно, что если ни одна из перерезанных стоек ни на одном
конце не имеет шарнира, то уравнение (20.9) заменится следующим:
J) ; (9„ f %.) - 2 ^ ;, (Н ¦ Й') О. (20.14)
Если стойки имеют на нижнем конце шарниры, а температура f
имеет знак, указанный на фиг. 493. уравнение примет вид
Если они имеют шарнир на верхнем конце, то при том же темпера-
турном воздействии нужно будет писать
Цг'>--Ц(' + ^>+1,"'^ = 0. (20.16)
Если в разрез попадут стойки различных типов, то члены пйидется
комбинировать из уравнений (20.14) — (20.16),
§ 20.8. ПОСТРОЕНИЕ ЛИНИЙ ВЛИЯНИЯ
При построении линий влияния основные уравнения имеют тот же
вид, что и при расчете на неподвижную нагрузку, но с тем отличием,
что свободные члены уже не являются постоянными, а сами представ-
ляют собой линии влияния. Например, в уравнении реактивных момен-
тов (20.8) свободный член имеет вид М^ и представляет собой л. в.
реактивного момента, возникающего в основной системе на конце С рас-
сматриваемого стержня. Ординаты этой л. в. вычисляются по формулам,
данным в табл. 11.
В уравнениях горизонтальных проекций (20.9) свободный член ра-
вен нулю, если речь идет о расчете на вертикальную нагрузку; равен
"^»«когда расчет ведется на движущуюся горизонтальную силу и по-
^едняя находится выше того яруса, в котором сделан разрез, и т. д.
В результате решения уравнений линия влияния каждой неизвестной
получится как однородная линейная функция л. в., относящихся к основ-
ной системе. Имея л. в. основных неизвестных, уже нетрудно с их по-
мощью построить л. в. любого усилия.
§ 20.9. КОМБИНИРОВАННОЕ РЕШЕНИЕ ЗАДАЧ МЕТОДАМИ СИЛ
И ДЕФОРМАЦИЙ
При решении некоторых задач оказывается выгодным комбиниро-
вать оба метода. Например, для того чтобы рассчитать раму, представ-
^<^Hiiyio на фиг. 494,а, разобьем нагрузку на симметричную и обратно
симметричную и рассчитаем раму^ на каждую из этих нагруюк в отдель-
375
" „а НИХ деформация будет симметричной,
ностй. При действии n^P^J» «^ перемещение узлов 1 и 2 будет равно
следовательно. ^°Р«^°" „а буДут взаимно равны и противоположны. Ре-
нулю, а их углы поворота оуду ^
6) ,Р , \Р ' Р\ А,| \Р
^У
t'lt*
w'
dfe
^'
Фиг. 494
"Ш
шая задачу методом деформаций (фиг, 494,6), мы будем иметь только
одну неизвестную. При действии обратно симметричной нагрузки вы-
годнее решать задачу методом сил (фиг. 494, е),
так как останется одна неизвестная поперечная си-
ла X Такой комбинированный способ решения, при-
водящий к двум самостоятельным уравнениям, вы-
годнее любого из двух основных методов.
Другой пример представлен на фиг. 495; число
неизвестных, отвечающих различным способам рас-
чета, представлено в наглядной форме в табл. 12.
Мы видим, что расчет этой рамы на симметрич-
ную нагрузку следует производить методом дефор-
маций, а на обратно симметричную — методом сил.
В итоге получается 3+3=6 уравнений вместо 9.
Таблица 12
Фиг. 495
Сравнение числа неизвестных
Метод
Сил
Деформаций . •
Комбинированный
При симметричной
нагрузке
При обратно сим-
метричной нагрузке
6
3
3
Всего
9
9
6
§ 20.10. СМЕШАННЫЙ МЕТОД
В литературе неоднократно указывались такие методы расчета,
которых одна часть неизвестных представляет собой силы, а №У^^
часть — перемещения. Многие из этих методов сведены воедино "Р^^*
А. А. Гвоздевым, который представил их в наиболее общем виде п
названием смешанного метода. ^,
Сущность смешанного метода может быть пояснена простым пр
мером. Для расчета рамы, представленной на фиг. 496,а, метод сил jp
бует составления восьми уравнений, а метод деформаций — ^l^jy
уравнений. Вместо того чтобы образовать основную систему по ^^^ ^,
из этих методов, создадим ее по смешанному принципу, а именно: ^'^ jj
временно отбросим связи в одном месте и введем дополнительные ев
в другом месте (фиг. 496, б).
376
Узел D разрежем и уничтоженные две связи заменим силами Хх
и ^2-
Узлы 3 я 4 дополнительно закрепим, а их неизвестные углы ново-
обозначим через Z^ и Z^. Запомним, что неизвестные силы у нас
Р^ YT обозначены буквами X, а перемещения — буквами Z.
На схемах в, г, д, е показаны четыре единичных состояния основной
темы. Через Ми М^у Мз, М/^ обозначены эпюры моментов, вызванные
й) «^
ж)
I—/.^{y^Ig^^
гй7
-??^
Фиг. 496
377
единичными воздействиями ;fi= 1; ^2= П ^3= 1; ^4-1. Эти эпюры строят,
ся без .всяких затруднений, равно как и эпюра М^, показанная на
фиг. 496, ж.
Канонические уравнения смешанного метода мы запишем так:
Ггг^г + 4^2 + ^зз^з + ^34^4 + ^Зр =- О
Г;Л + <2^2 + ^4з2з +^44^4 + ^4^ = 0.
(20.17)
Здесь через 8 и г, как обычно, обозначены перемещения, вызванные
единичными силами, и реакции, вызванные единичными перемещениями;
через S' и г^ — перемещения, вызванные единичными перемещениями,
и реакции, вызванные единичными силами.
Первое уравнение выражает ту мысль, что суммарное перемещение
по напра1влению A'l, вызванное всеми факторами, равно нулю. Второе
имеет аналогичный смысл, но в нем идет речь о перемещении по на-
правлению ^2- Третье уравнение представляет собой запись того усло-
вия, что реактивный момент в заделке узла 3 равен нулю, а последнее
уравнение выражает то же условле по отношению к реактивному мо-
менту в заделке узла 4.
Как видим, в смешанном методе часть уравнений выражает усло-
вия, обычные для метода сил, а другая часть—условия, характерные
для метода перемещений. В то же время в каждом из уравнений фигу-
рируют оба типа неизвестных.
Когда уравнения будут решены, то окончательную эпюру моментов
можно будет построить по формуле
М = М^ + М,Х,+ М,Х,+ M,Z,+ M,Z, .
Вычисление коэффициентов уравнений (20.17), не имеющих верх-
него значка, не требует особых пояснений, остальные же связаны сле-
дующей взаимностью:
^13 = —4» ^l4 = —^41» ^23 = —4' ^24==—^42-
Этим значительно облегчается вычисление. Из эпюр Л/, и М2 сразу
видно, что
^41 ^; ^32 = —Л; ^42== + ^-
31 о ' '41 2 * ' 32 '*'» '42
§ 20.11. ПРОВЕРКА ЭПЮР, ПОЛУЧЕННЫХ МЕТОДАМИ
ДЕФОРМАЦИЙ И СМЕШАННЫМ
о^«Л^°^^Р^^ ^"^Р' полученных этими методами, как и любыми другими т^етода^
производится по двум признакам, т. е. поверяется: 1) соблюдение условий равноведа
узлов или других элементов; 2) обращечие в нуль перемещений по направлению onov
ных или других связей. Обе поверки изложены выше в § 19.8. яет
Яля общей характеристики смешанного метода можно сказать что он облада
преимуществом перед методами сил и деформаций в тех случаях, когда одна «^с
сооружения имеет большое количество лишних связей н малую степень У"Р> ^пень
движности, а другая, наоборот, малое количество лишних связей и большую степ
упругой подвижности.
§ 20.12, КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Первые намеки на метод деформаций в неявном виде появились еще в 60-х го-
яях прошлого столетия в трудах Винклера (1862) и Бресса (1865)» ^Д« в ov; х го
В 70-х годах прошлого столетия интенсивное развитие меткллического мосто-
строения выдвинуло задачу о расчете ферм с учетом жесткости узлов. Оказалось что
эту сложную статически неопределимую задачу можно сравнительно легко решить
если принять за неизвестные не изгибающие моменты на концах стержней, а углы по^
ворота узлов. Так решили эту задачу Мандерла2 (Manderla), а затем МорЗ, тем самым
они по существу, лоложили начало методу деформаций.
' Потребовалось еще около 20 лет, для того чтобы значение этой идеи было оцене-
но по достоинству и чтобы в ней усмотрели фундаментальный и общий метод расчега
статически неопределимых систем. Для этого понадобилось, чтобы сложные статически
неопределимые рамные каркасы получили широкое распространение в строительной
практике.
Постепенное развитие метод деформаций #1олучил в трудах нескольких немецких
авторов; особенно в книге шведского профессора Остенфельда^, в которой метод впер-
вые назван «методом деформаций».
В СССР метод деформаций впервые получил широкую известность благодаря
названной выше капитальной книге проф. А. А. Гвоздева. В дальнейшей разработке
метода принимали участие многие наши ученые: профессора П. Л. Пастернак, Б. Н. Же-
мочкин, Н. И. Безухов, И., М. Рабинович и др.
Смешанный выбор неизвестных при расчете рам применялся различными авто-
рами, начиная с 1918 г. по 1925 г. Наибольшую известность получила работа Блейха
(F. Bleich), однако речь шла в ней о частном приеме. Полную общность метод полу-
чил в книге проф. А. А. Гвоздева^
1 Cours de rae'canique, applique'e troisieme partie, Paris, 1865, p. 19—20.
^ Die Berechnung der Sekundarspannungen .... Allg. Bauztg, 1880.
3 Die Berechnung der Fachwerke mit starren Knotenverbindungen, Ziviling, 1892.
* Die Deformationsmethode, Berl., 1926.
^ A. A. Гвоздев, Общий метод расчета сложных статически неопределимых
систем, М., 1927.
Глава 21
РАСЧЕТ РАМ ПО СПОСОБУ МОМЕНТНЫХ
ФОКУСНЫХ ОТНОШЕНИЙ
§ 21.1. ФОРМУЛЫ ДЛЯ ОСНОВНЫХ НЕИЗВЕСТНЫХ В РАМАХ
С НЕСМЕЩАЮЩИМИСЯ УЗЛАМИ
Теория неразрезной балки, в которой моментные фокусные отноше-
ния или моментные фокусы играют существенную роль, послужила
источником, из которого теория расчета сложных статически неопреде-
лимых систем почерпнула
г^яЕ ряд идей. Одной из простей-
^^f/» ших идей такого рода яви-
лась идея моментных фокус-
ных отношений.
-Mad
Ма1)\—
-)
\MfiB
К1/
Mac
Фиг. 498
Пусть дана такая рама, которая не имеет замкнутых контуров и
степень упругой подвижности которой равна нулю. В качестве основной
системы (выберем ее шарнирную схему, а за неизвестные примем изги-
бающие моменты, действующие на концах стержней. Решение канони-
ческих уравнений будем проводить в определенном порядке, составляю-
щем сущность способа моментных фокусных отношений.
Если рама не имеет замкнутых контуров, то любые две точки е
контура однозначно ориентированы друг относительно друга, т. е.
380
/.иной к другой можно пройти по контуру лишь одним путем. Это свойст,
Появляется для дальнейших рассуждений весьма существенным.
Выделим какой-нибудь узел А с жестко прикрепленными к нему
стержнями АБ, AQ AD, АЕ (фиг. 497).
Согласно условию задачи точки Л, Б, С D, ? неподвижны, следо-
вательно, концевые сечения стержией могут только поворачиваться.
Предположим, что нагрузка расположена справа от сечеиия В,
В таком случае для построения зпюры изгибаюплих моментов можно
заменить действие части рамы, расположенной справа от В, моментом
Примем за неизвестные две группы отношений, во-первых, отноше-
ния абсолютных величин концевых изгибающих моментов каждого
стержня (большего момента к меньшему):
^AB ^CA ^DA ^EA
эти отношения, как известно, называются фокусными (или фо-
кальны ми); во-вторых, отношения к моменту М^^ тех моментов, ко-
торые он вызывает в сечении А остальных стержней того же узла:
_ ^АС , _ ^АР ,. _ ^АЕ ,о. 0\
^АВ ^АВ ^АВ
эти вторые отношения носят название коэффициентов распре-
деления.
Расположение букв в индексе показывает, от какого стержня к
какому передается момент: первые две буквы обозначают тот стержень,
который как бы передает свой момент прочим стержням; последние две
буквы обозначают тот стержень, который воспринимает момент.
Что касается направления моментов, то при выводе формул для
названных отношений мы будем считать, что направление всех момен-
тов, уравновешивающих узел Л, противоположно направлению момента
^Ав (фиг*- 496 и 497). Если мы получим для них положительные вели-
чины, то это подтвердит правильность наших предположений.
Будем считать, что стержни имеют постоянное по их длине сечение.
Рассмотрим контур ВАС и напишем, что взаимный поворот сечений Л
стержней АВ и АС равен нулю. Поворот сечения Л в стержне АВ по
направлению часовой стрелки выражается через абсолютные величины
изгибающих моментов следующим образом:
— М J^+J^-^-^ ^ ^ВА Л 2 \
^^eEJ^^'^ k^s ^^^АВ ^'ав\ ^ав)'
Поворот того же сечения стержня АС равен
^^ЗЕ/^е ^СА ^^^АС ^'АС\ ^Са)
Приравняв друг другу оба выражения и заметив, что по абсолютной
величине
^ВА
^АС == ^АВ I'bAC =" "Т ^ВАС .
'^АВ
мы получим
•^«^с =-^^^_1),,, • (21.3)
Совершенно таким же образом можно выразить коэффициенты
распределения ^^j,^ и ^^ае- Д-"я этого достаточно заменить в формуле
(2\ 3) букву С буквой D или Е.
Формула (21.3) показывает, что все коэффициенты распределения
можно найти, когда известны соответствующие фокусные отношения.
Как мы сейчас убедимся, все фокусиые отношения имеют числен-
ное значение, большее двух, поэтому коэффициенты распределения,
вычисленные по этой формуле, всегда положитадьны.
Моменты, действующие на узел А (фиг. 498), связаны между собой
условием равновесия
Сделав на основании (21.2) подстановку
^АС-^АВ\'ВАС'^ ^Ad'=-^Ab\'bAd'^ ^АЕ =^ ^Ав\'ВАЕ
и сократив на М^^^, получим
V'bac + \'bad + ^bae'^ ^' (21.4)
Это соотношение следует запомнить: сумма коэффициентов распределе-
ния моментов в узле от одного стержня ко всем остальным равна еди-
нице.
Так как все коэффициенты распределения выражаются через фо-
кусные отношения формулами вида (21.3), то уравнение (21.4) можно
переписать в следующем виде:
(^ЛВ~^)^СЛ ^ЛС , {^АВ — '^)^РА ^АР . {^АВ—^)^ЕА ^АЕ ^ j
i^^CA-4'AB "^ {^^DA-^)^AB '^ (Ща-^)'аВ
а отсюда
*>,в = 2 + : — : = 2 + —^ . (21.5)
^АС . ^AD . ^АЕ V ^^^
I ^ 1 ^ 1 JLJ I
^СЛ ^DA ^ЕА ^ ^NA
где знак S распространяется на все стержни узла Л. кроме стержня
А
АВ, а через N обозначены для краткости противоположные концы
стержней.
Как показывает эта формула, фокусные отношения зависят не от
абсолютных, а лишь от относительных величин коэффициентов
жесткости стержней.
По формулам вида (21.5) можно определить фокусное отношение
^Ав (будем его называть прилежащим к узлу Л), если для всех
остальных стержней узла А известны противолежащие фокусные
отношения.
Если конец А стержня АВ прикреплен к узлу шарнирно, то м^-^"
считать, что он прикреплен к узлу жестко, но что все прочие стерж
бесконечно гибки и поэтому неспособны оказывать сопротивление по^
роту узла. Положив все ij^ = О, получим из формулы (21.5) к^в "
382
Если конец А стержня АВ абсолютно г,яттто1.ж«^,т
,то один или несколько из числа осталь^х ~жней °oZT° "Т^^"'
Sho большой жесткостью. Положив U"-"ГГуГимt =?' ""
Тот же результат мы получили выше, в теории неразоезной балки
Для того чтобы мы могли построить эпюру моментов от на^Р^^^и
расположенной на одном из стержней, необходимо иметь еще формулы
;„я концевых моментов загруженного стержня. Но каждый из^таких
стержней находится в таких же условиях, как какой-нибудь пролет
неразрезнои балки, т. е. имеет на концах упругую заделку. Степень
жесткости заделки вполне характеризуется соответствующими двумя
моментными фокусными отношениями. Вся сложность рамы чувствуется
в формулах для этих отношений; коль скоро они найдены, нам без-
различно, чем создана степень заделки, которая выражается этими отно-
шениями.
Сказанное позволяет нам воспользоваться теми формулами, кото-
рые были выведены в § 16.6. Мы перепишем их для произвольного
стержня АВ в следующем виде:
Для различных видов нагрузок формулы для 6Л* и 65* даны в
табл. 5.
В том случае, когда нагрузка расположена одновременно на не-
скольких пролетах, окончательная эпюра моментов получается путем
суммирования эпюр, получаемых от загружения каждого пролета в от-
дельности.
§ 21.2. ПРИМЕР
Построить эпюру М для рамы, представленной на фиг. 499. Вычислим коэффи-
циенты жесткости стержней. Приняв /у^^ —1, получим следующие относительные вели-
чины остальных коэффициентов жесткости:
^вс Ub , 3 4.5 . ^^ . . ^CD ^АВ 4.5
1 S J.^ Irn ^^^
о tyO - ^л • 1 ^^^ -"^ *_1_: 1 А\ '
4 4 .«^ 4.5 4 4,5 , _
По условиям закрепления концов известно, что
Остальные фокусные отношения вычисляются в последовательном
"орядке по формуле (21.5).
k -9. —i5^-453- k =2 + ^^^—. = 2,79:
^BA ^V-+ r~
k^E ''ВС "DC
/fe^o = 2,87; ft^ = 2,83; A^^ = 2.84;
A,, = 2,91; ftc/, = 2.76; A^ = 2,98.
383
'^^св= (2/^зс-1)'ся 8.06.1.5
1^сн;= 1-0,45 = 0,55.
Фиг. 499
Фиг. 500
Опорные моменты на концах загруженного пролета таковы (через
RcE ^ Rec^^ будем обозначать фиктивные опорные реакции на кон-
цах С и ? стержня СЕ):
^^ {f'EC^CE -\)1сЕ 2,83-2,79- I
М =(^^%с^^се-4е _ PIec^^(^ + ^)^J^-P^ec^^(^±J!} ^
^^ {^ЕС^СЕ -О ^СЕ 2,83.2,79- I
==uv{0^ll — 0,57u)Pl
ЕС
Мсв .. ^вс^
Остальные моменты
Эпюра моментов для ы=0.4. и=0,6 представлена на фиг. 500.
364
§ 21.3. РАСЧЕТ РАМ СО СМЕЩАЮЩИМИСЯ УЗЛАМИ
Для расчета таких рам вводят дополнительные связи, которые унич-
тожают подвижность узлов. Преобразованную таким способом систему
принимают за основную. Расчет распадается на две части: одна состоит
в изучении основной системы, т. е. в построении эпюр моментов вызы-
ваемых в ней внешней нагрузкой и единичными перемещениями;'другая
состоит в определении действительных перемещений из системы урав-
нений метода деформаций и в построении суммарной эпюры моментов
Первый этап решается методом сил, а второй — методом дефор-
маций.
Решим прежде всего задачу, о влиянии единичного взаимного сме-
щения концов какого-нибудь стержня АВ, считая, что оба моментных
фокусных отношения для него известны.
Фиг. 501
Допустим, что хорда стержня ВА повернулась по часовой стрелке
на некоторый угол ф^^ = Фвл == Ф,в то время как хорды всех прочих
стержней рамы сохранили свое первоначальное направление. От этого
на концах стержня АВ возникнут какие-то моменты М^^ и М^^,направ-
ленные так, как показано на фиг. 501, а, а касательные в тех же сече-
ниях к упругой линии повернутся на углы
м
Ub
3/
м
+
м
ВА
АВ
АВ
^^АВ
^ВА
+ Ф
АВ
Ы
'АВ
31
'АВ
+ <!'
АВ ¦
(а)
^ичинр^^^^^^ стороны, поворот сечений А w В стержня должен по ве-
узла А^ "вправлению совпасть с поворотами узлов Л и В. Но поворот
ем ^*^^видно, зависит только от момента Af^^g, который передается
име^7ч^^^"^^ ^^' ПР"*^""^» вызвавшая передачу такого момента, не
н:,^ значения. Поэтому мы можем определить связь между Жл« и ф
«^пример из фиг. 501,6: "^^ ^'''
^ ^' М. Рабинович
М
АВ
3/
АВ
^АВ^^АВ
м
А в
б?
АВ
^^АВ
i^AB-^h
335
Аналогичным образом
Ы
АВ
Подставив эти выражения в уравнения (а) и сделав приведен
получим ^^»
откуда
*ЛВ ^АВ - МвА = 6«^в Флв; ^АВ - '^ВаЩа = " ^^АВ I'aB'
Фиг. 502
iS3S3333!m*^>^"~^
Фиг. 503
напра^тешя же^„?^ан"ы'2ГГг'^п?^'°Г™"^ величины моментов.
^иг. oui.a. Поперечная сила
386
Из формулы (21.7) легко получить, как частные случаи, величины
опорных моментов для балки с защемленными концами, с одним опер-
тым и другим заш1емленным, наконец, с двумя опертыми концами.
Применение формул (21.7) и (21.8) к расчету рам со смещающи-
мися узлами покажем на примере рамы, рассмотренной выше, но при
условии, что правая опора скользящая (фиг. 502). Построим эпюру Мь
вызванную единичным горизонтальным перемещением ригеля. Можно
представить себе, что на конце G поставлен дополнительный горизон-
тальный опорный стержень и что последний переместился вправо на
единицу вместе с прикрепленным к нему сечением G ригеля. При этом
стойки отклоняются по часовой стрелке на углы
ЧТО В свою очередь вызывает появление трех эпюр изгибающих-моментов.
Поворот каждой стойки можно представить себе как результат того,
что нижний конец отошел влево на единицу, верхний остался на месте
(фиг. 503). Очевидно, что для построения эпюр безразлично, отошел ли
ригель вправо, а фундамент остался неподвижным или же ригель остал-
ся неподвижным, а фундамент отошел влево.
Чтобы построить эпюру М/ (фиг. 503), достаточно вычислить мо-
менты М^з и ^вА "^ формулам (21.7) и затем, воспользовавшись коэф-
фициентами распределения и фокусными отношениями, распространить
эпюру на всю раму. Аналогичным образом строятся эпюры M'^i и М"\,
после чего простым суммированием получается эпюра
Имея эпюру Ml, нетрудно определить реакцию Гц в дополнительном
горизонтальном опорном стержне узла G. В данном случае благодаря
тому, что все стойки вертикальны, эта реакция равна сумме попереч-
ных сил всех трех стоек.
Теперь нетрудно наметить весь ход расчета такойрамы, имеющей на
правом конце скользящую опору. Пусть дана какая-нибудь внешняя на-
грузка. Заменяем раму основной системой, т. е. уничтожаем смещае-
мость узлов, введя горизонтальный опорный стержень. Строим эпюру М„
для этой основной системы и находим реакцию Rip горизонтального
опорного стержня. Затем строим эпюру Mi и определяем реакцию Гц.
Чтобы найти неизвестное горизонтальное перемещение Zj узлов ригеля,
составляем и решаем уравнение
Найдя величину Z,, строим окончательную эпюру М:
M==Mp + M,Z,,
Аналогичным образом поступают в том случае, когда рама имеет
Несколько степеней упругой подвижности. В этом случае приходится
вводить несколько дополнительных стержней, давать основной системе
единичные перемещения по направлению каждого из них, строить
единичные эпюры Л/,, Мг. ... и определять неизвестные перемещения
из системы совместных уравнений.
Глава 22
ПРИБЛИЖЕННЫЙ РАСЧЕТ РАМ
§ 22.1. ОБЩИЕ СООБРАЖЕНИЯ
Разделение методов расчета на точные и приближенные является
условным, поскольку все так называемые «точные» методы также за-
ключают в себе ряд допущений (идеальная упругость и однородность
материала, идеальные шарниры, абсолютные заделки и т. п.). Однако
на практике эти две группы методов легко различаются, так как при-
ближенные методы заключают в себе ряд дополнительных допущений
и упрощений.
Потребность в приближенных методах очень велика, и она растет
тем сильнее, чем сложнее становятся те системы, которые приходится
проектировать и рассчитывать современному инженеру-строителю.
Для систем, содержащих десятки или даже сотни лишних неиз-
вестных, а также для систем, которые приходится рассчитывать на
множество различных загружений, приближенный расчет является
практически единственно возможным. К приближенным расчетам неиз-
бежно приходится также обращаться в той стадии проектирования,
когда производится предварительный подбор сечений.
Из приближенных расчетов право на существование имеют лишь те,
которые одновременно достаточно просты и достаточно'точны.
Ниже излагаются несколько приемов, дающих понятие о способах
построения таких расчетов.
§ 22.2. ПРИБЛИЖЕННЫЙ РАСЧЕТ МНОГОПРОЛЕТНОЙ МНОГОЯРУСНОЙ
РАМЫ НА ГОРИЗОНТАЛЬНУЮ (ВЕТРОВУЮ) НАГРУЗКУ (фиг. 504)
Ветровая нагрузка, распределенная непрерывно, заменяется узло-
вой (Wj, Wg, ^-з, ^4); в этом состоит первое упрощение.
Нулевые точки эпюры М принимаются на всех стойках нижнего
яруса расположенными на высоте 7зА, считая от нижнего конца стоек,
а на остальных ярусах —посредине их длины (/г—высота яруса)- При-
мерно такое расположение нулевых точек подсказывается результатами
точного расчета.
Третье допущение заключается в следующем: поперечная сила и
изгибающие моменты распределяются между всеми стойками одного и
того же яруса пропорционально соответствующим величинам — » ^^
h — длина стойки.
388
Построение эпюры М легко производится в следующем порядке.
Разрезаем стойки верхнего яруса посредине их длины. Сумма попереч-
ных сил в четырех стойках этого яруса равна W^, Распределяем ее меж-
nv стойками пропорционально соответствующим значениям — и полу-
ду h^
чаем для них таким обра-
зом эпюру М. Сумма "по-
перечных сил для стоек
третьего (считая снизу)
яруса равна ^4+\^з и
т. д. Так получается эпю-
ра М для всех стоек.
В каждом узле урав-
новешиваем сумму мо-
ментов, приложенных к
стойкам, моментами, дей-
ствующими на примыкаю-
щие два ригеля, причем
моменты распределяем
между этими ригелями
пропорционально их ко-
эффициенту жесткости t.
Так получается вся эпюра.
^ v>z
Фиг. 505
Если стойки, расположенные в разных пролетах мало отличаются
друг от друга, то можно принять, что все они имеют одинаковую упру-
гую линию В таком случае многопролетную раму можно мысленно
Расчленит^^а од^юп^^^^^ (фиг. 505). При этом у внутренних стоек
t ^яменяется величиной 0.5Л Если игнорировать обус-
момент инерции •'заменяется ^^^^^^^ между крайними рамами и
ловленное этим °^'^'^°^^^2,\.цтятъ что их деформации одинаковы
промежуточными то можно ригелях нулевые точки эпюры М рас-
(обратно симметричны; « '''Д, ^jQ^p^z достаточно произвести расчет
положены в серединах npoj. ^^^^^^ половины, какой-нибудь рамы
одной из этих рам ил" а точным способом, например мего-
(Ф"" ^"^k ?Jm nprTct' расТр"делить° заданную ветровую нагрузку
дом сил. Затем "P^f-^^"" Р^оп^орционально их жесткости. Окончатель-
между всеми полурамами "Р°"°Р^% подобны между собой и про-
ные эпюры "°"^и^°«^^,^й?Гна них нагрузке. Подобный способ был
^^r^T^cZT'^^llc:r^:.oro,'L из московских высотных
зданий.
8 223 ПРИБЛИЖЕННЫЙ РАСЧЕТ МНОГОПРОЛЕТНОЙ МНОГОЯРУСНОЙ
§ 22.3. ПРИБЛ^^;^^ ^^ ВЕРТИКАЛЬНУЮ НАГРУЗКУ (фиг. 507)
Упрощение, которое применяется при решении этой задачи, состоит:
П в игнорировании горизонтальных перемещений узлов рамы- 2) в иг-
нооиоовании работы стержней, не смежных с загруженным; 6) в при-
^ ^ ближенном задании мо-
ментных фокусных отно-
—щ
Г
1Г
\ю
I
^
-^
шении для стержней, при-
мыкающих к загружен-
ному.
Условие 2 приводит
к тому, что нагрузка, рас-
положенная на одном
стержне, например на
ютержне 2—3, вызывает
изгибающие моменты
только в простой раме, по-
казанной на фиг. 508, т. е.
вовлекает .в работу толь-
ко 3 'Стержня ригеля и
4 стержня стоек. В этом
состоит самая существенная часть упрощения условий задачи. В случае
загружения одного из крайних пролетов ригеля или одного из участков
верхнего яруса схема рамы еще
более упрощается.
Для построения з^пюры мо-
ментов, отвечающей фиг. 508, не-
обходимо знать положения «даль-
них» фокусов всех стержней, при-
мыкающих к стержню 2—8. Для ^
стоек 2—В и 8—С, имеющих
жесткое з-ащемление «концов В
и С, как известно, fe^g =^сз "^2.
Для остальных четырех стерж-
ней приходится задать фокусные Ф„^ 508
отношения приближенно. Фокус-
ные отношения для стержня 2—3 ^
выражаются через «дальние» фокусные отношения остальных стержн
по формуле (21.5):
/
Ш
Л
^
6^
ш
т
390
«23 —
1 •" ;
2-~ 2--^
«12 ^72
^2В
2—-
«32 —
^34
2— —
^43
2
«83
+ -
'ЗС
2—¦
Фокусными отношениями, фигурирующими в правых частях обеих
формул, приходится в данном случае задаться произвольно. Крайние
возможные значения этих отношений, как известно, равны 2 и оо.
4mjiiii>^
Фиг. 509
l^L
У/.
t
^0)й
^^ -7//,
Фиг. 510
При k = 2
при k ~ со
2—-—¦
k
= 0,67;
= 0,5.
Из этих двух чисел видно, что даже большая ошибка в назначении
вспомогательных фокусных отношений слабо отражается на величинах
«23 и ^32-
Изгибающие моменты, образующиеся на концах загруженного стер-
>^ня, определяются по формуле (21.6):
М23 =
^23 ^32 ~^ ^32
(^23^32 — 1) ^23
Л4з9 = — 6
¦Гччо «9Й ¦'>9Я
23
(«23^32 Ч '23
^Де через /?* и R^^ обозначены фиктивные опорные реакции на концах
2 и 5 стержня 2—8,
^след за моментами M^z и Л1з2 легко можно построить по методу
^^оментных фокусов всю эпюру (фиг. 509).
Для построения эпюры, показанной на фиг. 509, можно вместо ме-
"^^^Да моментных фокусов воспользоваться методом деформаций. При
^том нужно будет составить два канонических уравнения. Как показы-
^зет фпг. 510, придется приближенно задать для момента, характери-
3Q1
зующего жесткость того или иного из примыкающих стержней, величи-
ну, лежащую между 4/ и 31.
Окончательная эпюра М получается путем суммирования эпюр, вы-
зываемых загружением отдельных участков. На каждом элементе
ригеля суммируются 3 эпюры, на каждой стойке—4 эпюры.
Вслед за эпюрой М строятся эпюры Q и N, Способ образования
последних двух эпюр из первой указан выше. Он не зависит от того, ка-
ким способом построена эпюра М.
§ 22 4. РАСЧЕТ РАМ СПОСОБОМ ПЕРЕРАСПРЕДЕЛЕНИЯ МОМЕНТОВ
ИЛИ ДРУГИХ ВЕЛИЧИН
Пусть для рамы, изображенной на схеме а (фиг. 511), требуется
построить эпюру моментов.
^}
MMiimnmiii
/7
д) i
I
<7
—^?—/
'jfe
"yz^.
7Ш,
._ '''^
г)
¦it
'Z^
/—5^
д)
/
VTTr,
Фиг. 511
Первое приближение. Защемляются все узлы и для такой
основной системы строится эпюра Мр (схема б). Эту эпюру можно рас-
сматривать как результат совместного действия на заданную раму
внешней нагрузки и реактивных моментов /??,/?р и /?^.
Первая поправка. Нагружаем раму в узлах парами, которые
равны и противоположны реактивным, т. е. моментами —7?^, —Rp, — ^g -
Пару —/?^ прикладываем к раме, у которой защемлены все узлы, кро-
ме Е (схема е). Момент распределяется между стержнями EF и ЕА
пропорционально их жесткостям:
На противоположных концах этих стержней возникают реактивные
пары У),ЪМ^^. и О.бМ^.^. Таким же способом распределяют в узле F ^^'
меит — R^: его прилагают к схеме г, тогда
392
^FE ''М^о 'М^^^А(^гА1,ггц
jja концах En G возникают соответственно реактивные пары 0,5М^,^ и
О5Л^^.?- Момент-/?^ передается схеме д и аналогичным способом
распределяется. В результате этой операции получается первая поправ-
ка к изгибающим моментам; кроме того, образуются реактивные парц
Б заделках.
Вторая и следующие поправки. В каждом узле сум-
мируются накопившиеся в нем реактивные пары. Затем в каждом узле
принимается за внешнюю нагрузку пара, равная и противоположная
суммарной реактивной. С этими внешними парами поступают по-преды-
дущему и т. д. Так строится процесс последовательных приближений
для рамы с несмещающимися узлами. Несколько сложнее, но без прин-
ципиальных изменений строится процесс для рамы со смещающимися
узлами.
Запись получаемых результатов удобно вести в форме таблицы,
разграфленной на подобие схемы самой рамы.
Вместо моментов можно распределять углы поворота узлов или»
другие величины.
Схема расчета, изложенная в настоящем параграфе, была впервые,
предложена в 1929 г. инженером Н. М. Вернадским^; несколько позже —
в J930 и 1932 г. — аналогичный способ был опубликован в американ-
ском журнале «Transactions of the amer. soc. of civ. engrs» профессором
H. Cross, Этот способ породил за рубежом и в СССР обширную лите-
ратуру. В СССР он получил обобщение как метод перераспределения,
величин неизвестных^, распространен на задачу устойчивости рам и др.^
§22.5. РЕШЕНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ СПОСОБОМ
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ (СПОСОБОМ ИТЕРАЦИИ)
Пусть требуется решить систему уравнений:
2Ха + 15А'2 —ЗХз=10;
Хх + А2 + 6Хз = 7,5.
Представим каждое из уравнений в виде формулы, выражающей одно из неиз-
вестных через остальные:
х,==-0.2X2 + 0.15X3+1.5;
Xs = - О J33 Xi + 0.2 Хз + 0,667 '
Хз = —0.1667 Хх-^ 0.1667X2+1,25 ^
Процесс решения состоит в следующем: в качестве первого приближения для
всех неизвестных задаются произвольные значения. Подставив эти приближения в
правую часть формул (б), получим в левой части вторые приближения. Подставив в,
правую часть вторые приближения, получим третьи приближения и т. д.
Например, зададимся первыми приближениями:
Х; = 1; Х2=-1. Х;=1.
Тогда дальнейшие приближения выразятся так:
_____^ Х; = --0.2-1+0.15-1 + 1.5 =1.45;
^Т^'Н. М. Бериадский Символический расчет жестких стержневых систем.,
*РУды Среднеазиатского опытно-исследовательского института», Ташкент, 1929. ^
П. М. С о с и с Расчет рам способом перераспределения начальны:?^ значении не-.
звестных. Гостехиздат УССР, 1952.
I960 ¦ -^- Р о г и ц к и й. Новый метод расчета на прочность и устойчивость. Машгиз,
3931
(а).
(б).
>-; = -0.133.1+0.2.1+0.667 = 0.734;
X; =-0,1667.1-0.1667.1 + 1.25 = 0.917;
X,"==-0.20.734+0.15-0.917+1.5 = 1.491;
X;=-0.133 1.45+0,20.917+ 0.667 = 0.657;
X"= —0.1667.1.45 —0.1667-0.734+1,25 = 0.886 и T. д.
Для большей компактное™ целесообразно расположить вычисления в форме табл. Ц.
Таблица И
¦
>& уравнения
1 Хг
2 Х-
3 х1
1-е приближение
2-е „
3-е я
4-е
5-е
6-е
X,
1
Xj
Уравлени
—0.133
—0.1667
-0,2
-0,1667
Приближен
1
1,45
1.491
1,502
1.505
1.505
1
0.734
0,657
0,646
0.645
0.645
Хз
я
0.15
0.2
и я
1
0,917
0.886
0.892
1 0,892
0,892
Свободные члены
1,5
0.667
1,25
—
—
—
—
—
—
Как видно из таблицы, шестое приближение совпало с пятым, поэтому процесс
можно считать законченным. Вообще же процесс вычислений прерывают тогда, когда
два последовательных приближения всех неизвестных оказываются достаточно близ-
кими друг к другу.
Является ли указанный процесс сходящимся или нет, зависит от коэффициентов
при неизвестных, но не зависит от свободных членов, а также от величин произвольных
первых приближений. Неудачное задание первых приближений может иметь своям
следствием то, что увеличится количество требуемых приближений, но это не может
сделать сходящийся процесс расходящимся.
Если сумма абсолютных величин коэффициентов при неизвестных в каждой из
формул (б) меньше единицы, то процесс Заведомо будет сходящимся, В данном слу-
чае это условие соблюдается: (0,2+0.15<1; 0.133+0,2<1; 0,1667+0.1б67<1). Если хо-
тя бы одна из сумм больше единицы, то поручиться за сходимость процесса нельзя,
но сама таблица в ходе расчета обычно показывает, стремятся ли величины всех не-
известных к определенным пределам.
§ 22.6. О ПРИМЕНЕНИИ СЧЕТНО-РЕШАЮЩИХ МАШИН
В ЗАДАЧАХ РАСЧЕТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
Как известно, счетно-решающие электронные цифровые машины
получили важные применения в различных областях техники. Быстрота
и точность производимых ими вычислений, а также автоматизм работы,
который позволяет им на основе заданной программы производить
сложные последовательные вычислительные операции с выдачей оконча-
тельных результатов, делают их незаменимыми для расчета статически
неопределимых систем с большим числом лишних неизвестных.
Наиболее трудоемкая операция при расчете систем с большим
числом неизвестных состоит обычно в решении системы уравнений мето-
да сил или метода деформаций. С увеличением числа уравнснш1 за-
трата времени на их решение возрастает в устрашающей степени-
Например, чтобы решить с применением арифмометра полную систему
100 уравнений со 100 неизвестными, у которой все коэффициенты ^^^2
бодные члены даны в виде чисел, вычислитель должен затратить
394
года труда; """"^^^Т^^^^^^^^^ методами эта задача практически
^разрешима. Для сравнения можно указать на то, что быстродейству-
ющая электронная счетная машина Академии наук СССР (БСЭМ) ре-
шила систему из 800 уравнении с 800 неизвестными в течение 20 час ,
выполнив за это время 250 миллионов вычислительных операций* на
программирование было предварительно затрачено менее 20 часов
^ Опубликованные в литературе данные показывают, что для элект-
ронных цифровых машин можно составить программу таким образом,
что для данной схемы сооружения при заданных его размерах машина
автоматически составит и решит уравнения, затем вычислит изгибаю-
щие моменты и поперечные силы. При изменении нагрузки того же
сооружения, как известно, в уравнениях изменяются только свободные
члены; в этих случаях для перерасчета на машине требуется лишь
незначительное изменение программы. В итоге оказывается следующее:
чем сложнее рассчитываемая схема сооружения, тем более выгодно и
целесообразно применять счетно-решающие машины.
Кроме больших быстродействующих машин, которые стоят очень
дорого, в СССР изготовляются менее дорогие машины — «Стрела», М-2
и др., а также выпускаемая серийно сравнительно недорогая универ-
сальная машина «Урал».
Нужно различать перспективы, которые открываются перед круп-
ными и мелкими проектирующими учреждениями. Первые смогут ис-
пользовать самые сложные машины и выполнять с их помощью самые
сложные и точные расчеты уникальных и грандиозных сооружений,
которые обычными методами могли до сих пор решаться только путем
грубых приближений. Это очень повысит практическое значение
строительной механики и ее роль в прогрессе строительной техники.
Для расчета рядовых сооружений, схема которых содержит
десятки лишних неизвестных, большое применение найдут сравнитель-
но малые специализированные цифровые машины, с помощью которых
можно будет быстро производить расчеты, а также перерасчеты, свя-
занные с изменением внешней нагрузки; вычислять перераспределение
усилий, вызываемых изменением жесткости отдельных элементов; про-
изводить расчет на действие подвижной нагрузки и т. д.
^ Кроме цифровых машин, для решения различных задач строитель-
ной механики могут быть использованы различного типа интегрирую-
*^ие и моделирующие машины. В частности, для расчета стержневых
систем сравнительно легко подбираются схемы электрических цепей,
^ которых распределение тока подчиняется системе линейных уравне-
ний. Коэффициенты и свободные члены этих уравнений могут быть
подобраны так, чтобы они были пропорциональны коэффициентам за-
данной канонической системы уравнений метода сил или деформаций.
Результаты непосредственно прочитываются по показаниям амперметра
'^^ли вольтметра^
Широкое применение машин в строительной механике явится мощ-
ным средством для значительно более действенного и плодотворного
участия строительной механики в решении инженерных задач строи-
¦^ельства. Подобно математике, наука о расчете сооружений приобрета-
^¦^ в вычислительных машинах надежного и верного слугу огромной
работоспособности.
3nJ ^^* например, книгу: Ростовский инж.-строит, ин-т. Труды института, вып. ХГ.
к Л'^Рическое моделирование стержневых систем. Под ред. проф. д-ра техн. наук
* ^* Керопяна. М., 1958.
^^А -
Глава 23
ПРИВЕДЕНИЕ РАСЧЕТА ПРИЗМАТИЧЕСКИХ РАМ,
СОСТАВЛЕННЫХ ИЗ ПЛАСТИНОК,
К РАСЧЕТУ ПЛОСКИХ СТЕРЖНЕВЫХ РАМ
(метод проф. В. 3. Власова)
§ 23.1 ОСНОВНЫЕ ГИПОТЕЗЫ
В последнее время все большее применение в СССР находят весьма экономичные
тонкостенные призматические системы, составленные из пластинок. В поперечном сече-
нии они могут представлять собой рамы с замкнутыми или незамкнутыми, односвяз*
Фиг. 512
Фиг. 513
ными или многосвязными контурами. Один из примеров таких систем- "^'^^ j^a-
фиг. 512. В отличие от плоских рам такие системы испытывают простраиственн
пряженное состояние. оемени
Расчет таких систем со сложным многосвязным контуром до нелавнего ^Р^^р(,з'
представлялся настолько сложнььм, что практическое применение его ^^^-^^'''^^''дпькях
можным. Проф. В. 3. Власов* (1906—1958) предложил основанный иа «еск ^^^»^
упрощающих гипотезах приближенный расчет, когорый преодолел трудн^'^''^
сложной проблемы, сохранив при том высокую точность. числ^
Будем рассматривать призматическую оболочку, состоящую из конечно ^ ^ gge-
прямоугольных пластинок» жестко связанных между собой вдоль прямолинейны
J В. 3 Власов, Строительная механика тонкостенных простраиствеииых
гл. Ill и IV, Стройиздат, 1949.
396
систеА-
к
•П-ГнТтГмГГГиJ^^^^^^^^^^ будем определять ко-
'Cor? поперечного сечения; - - расстоя^иГ о^тсчит^^^^^^^^^ некоторого иа-
;;Тенйя оболочки до точки М от некоторой образующей "1о (фиг 51зГ^ поперечного
•^ БУД«?м рассматривать оболочку как совокупность бескпири?!^^; . '
^„о узких поперечных полосок, имеющих вид плоски. п«^ множества беско-
Тю оси Нравна dz. В плоскости поперечногГсечения система ^р п^"Л""^ "^ направле-
--^^^^^^^^ наз=~^с^ ^^'^ пГ^^аТс^Т^ГевГ^^^^^^^ ^1^о'^зт^с^^
%'Х^%^^н^У ^ '"'"'^''^ Дискретно-непрерывной («дискретио-
''''" Дальше изучается напряженное и деформированное состояние каждой оамы
полоски. Предполагается что в своей плоскости она может деформ^
^Гсвободы ^"''"' ^^Р^^^'^^""^ ^^ У'-^- в плоскости попеДГо Течения W^^
n = 2m-C->Co. (23.1)
j-де m—-число узлов (включая опорные);
С—число стержней рамы;
<Со —число опорных стержней, лежащих в ее плоскости
Рама может деформироваться также «из
плоскости», т. е. ее точки могут перемещаться па-
раллельно оси Z, Вводится гипотеза плоских се-
чений для каждой из пластинок, образующих
oбoлoчкз^ т- е. предполагается, что поперечное се-
чение (перпендикулярное оси z) каждой из них
остается плоским; поперечное сечение всей обо-
лочки, вообще говоря, не остается плоским. При
такой гипотезе выходит, что каждый стержень
рамы-полоски, перемещаясь в плоскости, парал-
лельной оси z^ не искривляется в этой плоскости,
а ведет себя, как твердое тело. Искривляться он
может только в плоскости рамы. Фиг. 514
Степень свободы узлов рамы-полоски в на-
дравлении, параллельном оси z^ равна
п^=,т~-С'^, (23.2)
тде Cq — число опорных стержней, не лежащих в плоскости рамы.
Действительно, каждый узел, ничем не стесненный, имеет в направлении оси z одну
степень свободы. Ни стержни самой рамы, ни опорные стержни, лежащие в ее плоско-
сти, не стесняют этого движения. Единственными связями, стесняющими это движение,
являются опорные стержни, не лежащие в плоскости рамы. Если таких стержней нет,
to n,=m.
Чтобы получить степень свободы депланации рамы, т. е. искажения ее
шоской формы, нужно из числа tii вычесть три степени свободы, отвечающие переме-
щению рамы из плоскости как жесткого целого (поступательное перемещение вдоль
оси Z и повороты вокруг двух осей, лежащих в плоскости рамы). Следовательно, сте-
пень свободы депланации равна
П1-3 = т —С^ —3. (23.3)
Например, в раме, показанной на фиг. 514. т=^Ъ\ С-=4; Со=4, поэтому степень
<^вободы в ее плоскости п=2; степень свободы в перпендикулярном направлении равна
«J—т—5; степень свободы депланации равна т—3=2.
Нас будут интересовать в дальнейшем: 1) движение любой точки М в направле-
нии, параллельном оси z' 2) перемещение точки М в плоскости рамы по направлению,
'^параллельному касательной к контуру в этой точке. Иначе говоря, нас будет интересе-
'Вать тангенциальная проекц11Я перемещения точки М в плоскости.
Каждое из этих перемещений рамы-полоски можно себе представить как сумму
элементарных, линейно независимых перемещений, каждое из которых отвечает одной
<^тепен11 свободы, а всего как сумму т+п элементарных перемещений. Выбор элемеи-
¦''арных перемещений простых или групповых, может быть весьма разнообразным по-
добно выбору групповых нагрузок и перемещений, с которыми мы встречались раньше.
.„ Обозначим перемещение точки М параллельное оси Jr. через и (г. 5). а переме-
*^ения в плоскости рамы —через v (z, s). Различные точки рамы, имеющие различные
•координаты 5, движутся по-разному. Рамы-полоски, расположенные в разных сечениях.
*^ Разны.мн координатами z также перемещаются неодинаково.
397
Мы можем поэтому написать
и (Z.S) = Уг (г) ^1 (5) + ^2 (2) ^2 (S) Ч h f^m (2) ^л1 («) =
= Sfy?(2)^?(s);
1
V (z,s) == Ki (;^) ^1 (s) + K2 (2) ^2 (s) Ч Ь V^« (2) ^« (s) =
1
(23.4)
(23.5)
Здесь ^i(s)y^ikis) —элементарные перемещения, выбираемые нами из числа возможных-
Ui (z), Vk (z) — неизвестные пока функции, которые должны выражать закон из-
менения перемещений по длине оболочки.
§ 23.2 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ РАМЫ-ПОЛОСКИ
На раму-полоску действуют нормальные напряжения о, параллельные оси г и
касательные 'с, параллельные сторонам контура рамы. Вследствие того что рассмат-
риваемая система тонкостенная, можно без большой погрешности считать, что оба
напряжения постоянны по толщине стенки.
Нормальные напряжения, как известно, пропорциональны относительному удлине-
нию волокон, поэтому
(23.6)
Касательные напряжения пропорциональны относительному сдвигу, т. е. величине
искажения прямого угла. Рассмотрим прямой угол, образованный в какой-нибудь точ-
ке М оболочки направлениями z и s
(фиг. 515). Если точка М получила
перемещения w, v, а смежные с ней
точки N и Р — перемещения
ди dv
и-^ ~-dz; v-^ — dz (точка N);
dz dz
ди dv ^,
и + ~- ds; v+ — (точка r),
ds ds t
TO из фиг. 509 видно, что искажение
ди dv
прямого угла равно ^т" + Т^ '
ds dz
Поэтому
\ds dz J
или
Фиг. 515
x=G sV,9;(s)+|v;4'*(s)M23.7>
На элементарную площадку dF оамы-полоски действует с одной сторон
° * dz I
(фиг. 516). Их равнодействующая равна т~" dzdF и направлена в полож
сторону оси Z. проекцию на ту же ось внешних снл, приложенных к боковой
ности рамы, обозначим через pdzds.
398
Силы сдв11га соответственно равны
•zdF
, их равнодействующая
и \^'^+~ dz]dF.
дх
dz
dz
dzdF.
я конец проекция внешней нагрузки на направление контура пусть будет qdzds.
Чтобы найти «i+rt неизвестных функций Vi (z) и Vk(z), фигурирующих в форму>
(23.6) и (23.7), составим rti-f-« дифференциальных уравнений равновесия рамы-
эски.
полоски.
Простейший способ получения таких уравнений состоит r тг... „^ л
„+. не....»™ .о.„о»»„, 6ec«,„„H„'t,„. '^SSml „"Г^Д^'^'Г»
Ji
-4>r
\S\
•fffl
\
U
Фиг. 516
Фиг. 517
каждом из этих перемещений сумму работ внешних и внутренних сил, приложенных к
раме. Каждое возможное перемещение можно рассматривать как результат бесконечна
малого изменения (вариации) одного из геометрических параметров (обобщенной
координаты), определяющих положение стержней рамы. Поэтому такое применение
принципа возможных перемещений носит название вариационного метода.
Дадим раме одно из перемещений ^i и подсчитаем работу. Нормальные силы со-
вершат работу, равную
С дс С дс
где интеграл распространяется иа всю площадь рамы-полоски. Внешние силы совер-
1^ат работу, равную
S
Касательные силы совершат работу, вызванную взаимным сдвигом элементов пе-
редней и задней плоскостей рамы. Величина этого сдвига, как видно нз фиг. 51^ рав-
«а ?i. Этот сдвнг является естественным следствием перемещения <??: из того факта,
^^то сторона Л Л' прямоугольника Л Л'ЛБ' сдвигается относит^пьно ВВ , неизбежно
вытекает, что и сторона АВ сдвигается относительно А'В\ Работа касательных сил
будет отрицательна; так как она представляет собой работу внутренних сил. совер-
Ц^аемую на деформациях системы. „ ^, ^
Написав уравнения работ, совершаемых на каждом из перемещении ?у. н сокра-
тив уравнения на dz, получим «i дифференциальных уравнении следующего вида:
(23.8>
f ^ ^.dF- Гт?;^^ + JjP?/^5- 0.
399-
л^оо^м мпжно составить уравнение работ для каждого из п во^,
.ожГхСрГтеЖГнГХ nUeme.^!;. работают только касательные ^
— darff. внешние силы q ds dz и внутренние изгибающие моменты, действующие в
плоскости рамы В действительном состоянии эти моменты выражаются суммой вида
TV'aX где Л$* отвечает перемещению^ при котором V* =1. Через Жя обозначим
"""Fir-BXreLrsrHrZeroB^^'paMi- считается освобожденной от связи с обо-
лочкоГиз которой она вырезана, а сохраняет лишь свои опорные стержни.
Уравнения работ после сокращения на dz будут иметь вид
Г| ^,,F-Y.V, J^ rfs +J,W-0. (23.9)
F \ s s
При вычислении моментов инерции / рама рассматривается как обычная плоская
•рама причем ширина всех ее стержней принимается равной dz^l.
В дифференциальные уравнения (23.8) и (23.9) нужно подставить вместо напря-
жений <J, -с и их производных соответствующие им выражения через функции
Vi {г) и Vk (2) по формулам (23,6) и (23.7). Тогда получится система обыкновенных
линейных дифференциальных уравнений второго порядка с постоянными коэффициен-
тами. Мы не выписываем этих уравнений; читатель легко может вывести их сам.
Можно показать, что теория расчета плоских рамных систем представляет собой
частный случай теории расчета тонкостенных призматических систем, а канонические
уравнения метода деформаций являются частным случаем дифференциальных уравне-
ний (23.9).
Система дифференциальных уравнений (23.8) и (23.9) известными математиче-
скими методами может быть сведена к одному дифференциальному уравнению поряд-
ка 2(п1+п). Интеграл такого уравнения содержит 2(ni+n) постоянных. Если мы за-
дадим на обоих концевых сечениях оболочки (при 2~/ и 2=0) любым способом по
ni+n кинематических или статических условий, касающихся перемещений или уси-
лий, то решение станет вполне определенным, и можно будет изучить картину рас-
пределения напряжений и перемещений во всех точках пространственного тонкостен-
ного сооружения при любых граничных условиях и любой нагрузке.
Функции Ui (z) и Vk (2) зависят от внешней нагрузки, так как она входит в ви-
де свободных членов в дифференциальные уравнения (23.8) и (23.9). После того как
^/oQA "^^"" ^У^У'^ найдены, определятся и напряжения, выражаемые формулами
\2o.bj и (23,7).
Остановимся несколько подробнее на формуле нормальных напряжений. Введем
^<^^j{s)dF = Pj, (23.10)
F
ueu?filTl^u\7f °^°^i^^»«^« с«-^а Pj численно равна работе, производимой эле-
м^шении РР rnu.t • приложенными к поперечному сечению оболочки, при пере-
мещении ее точек на величины <?j(s), г j
Подставим вместо с правую часть формулы (23.6); формула (23.10) примет вид
^/И=ЯЕб/:(г)|^Д.)^^(5)^/г.
«альны^тТиг^^!!^^"'''^ перемещения так, чтобы функции п были взаимно-ортого-
'нальны. т. е, чтобы контурные интегралы обращались в нуль при i Ф j:
f <Pi<pjdF = О при 1ф], (23. И)
F
Тогда можно будет писать
Р, (2) = EU' (г) J ^2 (s) dF = EV[ {z)«., .
где
Отсюда
400
При помоши этой подстановки уравнение (23.6) превращается в следующее:
Если мы в этой формуле даднм переменной 5 какое-нибудь произвольное, но по-
стоянное значение, то она^ будет выражать закон распределения нормальных иапряже-
йГй по длине образующей, проходящей через точки с координатой^5. Если мы дадим
^ординате z постоянное значение, а координату s будем считать переменной то фор-
м?ла (23.13) выразит эпюру нормальных напряжений. распределениьГх по соответствуй
юшему поперечному сечению оболочки. *^ ^^ "^ '^'^^
Рассмотрим несколько подробнее эпюру нормальных напряжений, получающуюся
и г=-соп51. Формула (23.13) показывает, что эпюра с (z, s) состоит из п, эпюр вн-
Ординаты каждой такой эпюры пропорциональны ординатам одной из эпюр <fi(s).
следовательно, формула (23.13) выражает собой разложение суммарной эпюры с (z. s)
на частичные эпюры по заданным формам эпюр <?|(s). Коэффициентами разложения
служат выражения — , зависящие от z, поэтому в различных поперечных сечениях
It'll
суммарная эпюра с имеет различный вид.
Особый интерес это разложение представляет тогда, когда функции <?И«) взаим-
^ ^ Pi W
но ортогональны. Тогда работа элементарных нормальных сил <fj(s) dF равна
ац
нулю иа любом из перемещений <^у (s) при 1Ф и
Если даднм раме-полоске только одно перемещение <?/ («), то в правой части
формулы (23.13) останется только один член.
Pi (2) 9/ (2)
' Работа нормальных сил на-перемещении <р| (s) выразится на основании формулы
(а) и (23.12) следующим образом:
Г а (г.5) <Pj (s) dF= ^^ Г i\ (s) dF = P/ (г). (23.14)
Это означает, что в случае разложения эпюры нормальных напряжений рамы-
Pi{z)
полоски на взаимно-ортогональные эпюры вида <pi(s) коэффициенты разлоотния
пропорциональны работе, производимой нормальными напряжениями на соответствую-
щем перемещении <pi(s).
Выберем первые три эпюры <pi (5). <?2 (5).?8(«) таким образом, чтобы они выра-
жали перемещения рамы-полоски как твердого тела. Например, пусть cpi(s) выражает
поступательное перемещение, параллельное оси z, а эпюры <?>2 (s), Ы^) — повороты
вокруг главных центральных осей д:, у площади рамы. Тогда первые три члена фор-
мулы (23.13) выразят эпюру нормальных напряжений, отвечающую гипотезе плоских
сечений всей оболочки. Например, при <?i(s)=consts=<?i имеем из формулы (23.14).
Pi (г) ^ tp J с (1.5) dF := 9iN(?h
a,, = ^<p\dF^<plF;
Pi (г) П (5) А^(г)?? N{z)
Также легко выводятся выражения второго и третьего членов.
Итак:
Л«бой из членов формулы (23Л5Ь кроме першхтр^^^^^^
^ И. м. Рабинович
„u„ статически эквивалентные иул^,
жают собой эпюры «оР"^,^«%,„^'^твечают депланацням системы, выражаемы»;
т р уравиовешенн ые. Y
^^пямн ч>л(8), 9б(«) 9ni(«)- ^^^oPTrrBvroiueH деплаиации и работает только на
^"ХжЛ-Г^^^^^ обобщенные силы"/,
„"^одГл^нТми бн моментами^ формула (23.15) представляет собой обобщу
е l^S'4^^P^^^»«o.^y^ *о^ -^ -™Р^ «^« тонкостенных призмати,,
ских стержней с односвязиым контуром.
§ 23.3. ПРИМЕР
„^„^ г. пягчете поизматических тонкостенных систем
Имея в виду дать только понятие о расчете J^^^ простейший пример из кн,.г„
|.Твл'аГва. "Soft раТобрТн ряД интересных и более сложных примеров.
Фиг. 519
®
Чг
Фиг. 520
^^...ггг^
'
Зг^ мд^
Фиг. 521
^-
Требуется выяснить состояние напряжений и перемещений призматической ^^^
мы, составленной из трех жестко связанных между собой пластинок. Ее "^"^^„лрно
сечение показано на фиг. 518. Нижний край обеих вертикальных пластинок "^^Р ^е-
оперт по всей их длине и закреплен не только от поперечных, но и от продольиы^^^^
ремещеиий. Поперечная рама-полоска имеет, следовательно, шариирио ^^^Р^"пов «^
концы. Такая рама имеет три степени свободы; перемещения двух верхних узл ^^^
плоскости (параллельно оси г) и горизонтальное перемещение верхнего ригеля п
направлению. ' пяплельна
Для упрощения примера будем рассматривать нагрузку, которая "^"f,* „чнУ*^»
ригелю рамы и приложена к ее верхнему узлу. Ее можно разложить на с^мметр ^^
которая не вызовет перемещений, и обратно симметричную, которая вызовет о у ^^^.
симметричное перемещение. Последние состоят, из деплаиации. характеризуем^
402
потом ригеля вокруг вертикальной оси симметрии ЛЛ. и из поперечных перемещений
S плоскости рамы. Всего будет две степени свободы. Обратно симметричная нагрузка
может распределяться по длине оболочки по любому закону
На фиг. 519 показана эпюра перемещений <?,. причем перемещения верхних узлов
приняты равными ±1; иа фиг. 520 показана эпюра <р[ =—^ .
фиг. 521 изображает поперечное перемещение рамы в ее плоскости. Контурные
перемещения (параллельные контуру) испытывают при этом только точки ригеля.
Эпюра контурных перемещений дана на фиг. 522.
От действия силы A'l^^l получается эпюра моментов гпи показанная на фиг. 523,
поэтому
! III!
Ч.
Hi
®
Фиг. 522
II/
Фиг. 523
Когда ригель перемещается не на b^i. а на величину Vi, эпюра моментов, очевидно,
выражается формулой
1^1
Mi =
mi.
Моменты в верхних узлах имеют величину
6EVi
^ Рассмотрим частный случай: оболочка нагружена сосредоточенной горизонталь-
ной силой Р в плоскости одной из поперечных рам; распределенных нагрузок нет.
Для нахождения неизвестных функций Ui(z) и Vi(z), которые в дальнейшем бу-
дем писать в виде U и V, подставим в дифференциальные уравнения (23,8) и (23.9)
выражения (23.6) и (23.7) для напряжений а, -^ и, кроме того, напишем p=q=0.
р
t>MecTo <ipi н 4^1 'будем писать <? и 4^. Обозначим ''-^ =7 и разделим уравнение на G:
7^/' J <f4F — и I {YfdF -V'\ <p'^dF = 0 ;
F F F
V j r^^^dF ^уЛ ^4F~ -^ J ^^
F F
В более краткой записи:
EJ
= 0.
26*
(23.8')
(23.9')
(23.16)
(23.17)
403
фнг
/9^8^ и (23 9) вычисляют по эпюрам, представленным на
Ж^П522П'акТпРи^^^^^^^^ Продифференц,
Из уравнения (23,9') исключим t/.выраз Продифференцируем уравад.
,вУ два раза по z, no^V^»" »"Р™"о%ыражения V" и t/'" В результате „с^.
""^ <^1^Тиииа'ль"ое\равнение! содержащее только функцию V и ее производные:
чится дифференциальное ур ^,^ _^^,^. _^^4 v, ^ 0. (23.,8)
. г,r.пvuяютcя В процессе указанных подстановок,
где Л, Б--постоянные, которые получаются^в IP U у^рзвненне (23.18) интересно
тем. что оно представляет собой
дифференциальные уравнения из-
гиба стержня, находящегося в
упругой среде, имеющей две ха-
рактеристики, т. е. сопротивляю-
щейся не только перемещениям V
стержня, но и его изгибу. Роль
упругой среды по отношению к
раме-полоске играет оболочка.
Аналогия эта имеет важное значе-
ние, так как позволяет воспользо-
ваться при расчете призматических
систем хорошо разработанным ап-
паратом расчета балки на упру-
гом основании, в частности, спосо-
бом начальных параметров.
Для получения интеграла уравнения (23Лв) вычисляем корин характеристического
уравнения: - *
Х^-2ЛЧ^ + 5' = 0; Xi.2=±«' 44= ±Р^
Фиг. 524
где
Общее решение однородного уравнения (23.18) можно написать в следующем виде:
Постоянные Сь Сг, Сз, Сл определяются из граничных условий.
Решим задачу для весьма длинной оболочки, которую без большой погрешности
можно принять бесконечно длинной. Начало координат расположим в том сечении, в
котором приложена сила Р. Вследствие симметрии достаточно рассмотреть половину
оболочки, лежащую по одну сторону от этого сечения:
при 2—0
при 2= OD
V = 0; Q = 0.
Из третьего и четвертого условий, вытекает, что С|=<Сз^=0:
(23.19)
(23.20)
(23.21)
У'(г) = ~аС2в-«^-рС4е-Р^ |
V (2) = а2 Сз в-^^ + fC^ е-Р^ . |
Подставим выражения V и V" в уравнение (23.17) и, проинтегрировав его, наЙД^^^
Поперечная сила Q. есть суммарная проекция всех сил. действующих в П""°?1^ву.
сечения, на направление силы Р. Она, очевидно, складывается из сил сдвига, деи*^
ющих вдоль ригеля. Согласно фиг. 520 и 522, для ригеля <р' ——. Ф—1. следовательно*
4U4
;;^ли*чниуГравную^ '''"'''"'"'"' напряжения по всей длине ригеля имеют постоянную
.= g(J-V+V').
Отсюда
Q = rb^d^ = (7(2 Ь^и + Ь^^Г). (23.23)
Используем граничные условия (23.19):
— («'г„ - 7S,,) Сг + у (pVn - 75п) Q = О ;
— OBgcfg (аСа + РС^) = -^ — .
Из этих двух уравнений определятся постоянные Cg, С4, после чего можно <5удет
написать окончательные выражения для перемещений' U(z), V{z) по формулам
(23.22) и (23.20); для напряжений о и т—по формулам (23.6) и (23.7); для изги-
бающих моментов — по формуле
М (2) = /71x^(2),
где /п: —эпюра моментов по фиг. 523, поперечную силу вычислить по формуле (23.23).
Значения всех перечисленных величии постепенно убывают по мере удаления се-
чения от нагруженного силой Р.
Эпюра продольных перемещений края горизонтальной пластинки имеет примерно
вид, показанный в перспективе на фиг. 524. Перемещения противоположного края име-
ют обратный знак.
Изложенный здесь в очень сжатом виде и проиллюстрированный простейшим при-
мером метод заслуживает исключительного внимания.
Проблема расчета призматических оболочек является частью более обширной
проблемы практического расчета тонкостенных пространственных систем типа оболо-
чек. В этой области строительной механики и теории упругости, разрабатываемой в
СССР рядом исследователей (профессорами В. 3. Власовым, А. И. Лурье. В. В. Ново-
жиловым, А. Л. Гольденвейзером, А. А. Умаиоким и др.), наша наука имеет
выдающиеся достижения.
Глава 24
РАСЧЕТ БАЛКИ НА СПЛОШНОМ УПРУГОМ ОСНОВАНИИ
§ 24.1, ОБЩИЕ СООБРАЖЕНИЯ
В практических расчетах роль упругого основания играет грунт, на
котором покоится фундамент зданий и сооружений; иногда — близко
расположенные друг к другу упругие опоры, например, поперечные бал-
ки, на которых покоятся продольные балки; иногда роль упругого ос-
нования приписывается элементам тонкостенной пространственной
конструкции, когда расчет производится путем расчленения конструк-
ции на взаимно-перпендикулярные полоски, и т. д.
При всех расчетах упругое основание заменяется той или иной рас-
четной схемой или моделью. Здесь будет дан расчет, основанный на
простейшей модели, на так называемой модели несвязного упру-
гого основания (иногда называемого Винклеровским упругим
основанием). Этому основанию приписываются следующие свойства:
1) оно имеет плоскую поверхность, 2) между перемещением у какой-
нибудь точки поверхности и давлением q, приходящимся на единицу
этой поверхности, существует зависимость вида:
Я = Ку, (24.1)
где ^0 — постоянный коэффициент, так называемый коэффициент жест-
кости основания, имеющий размерность [ — ].
Будем считать, что соотношение (24.1) сохраняется как при поло-
жительных, так и при отрицательных значениях перемещений у.
Расчет балки на упругом основании, имеющий обширную литерату-
ру в СССР и за рубежом, является прекрасным примером плодотворно-
сти метода начальных параметров, впервые предложен-
ного профессором Н. П. Пузыревским, Г Д. Дутовым и акад. А. Н.
Крыловым и затем развитого в трудах П. Л, Пастернака, Г. В. Клише-
вича, А. А. Уманского, М. М. Филоненко-Бородича, В. А. Киселева и ДР-
Здесь мы будем придерживаться изложения, данного в книге проф.
А. А. Уманского^, которое представляется нам особенно ясным по свое-
му физическому смыслу.
* А. А. Уманский. Специальный курс строительной механики, ч. I, М., 1935-
406
f д,,фференциальное уравнение изгиба балки на упругом основании
имеет вид
EJy^^ ^p-ky. (24.2)
Оно выражает ту мысль, что погонная нагрузка балки состоит из
заданной р и из реактивной, которая равна кфу=ку, где 6-ширина
основания балки. Множитель k имеет размерность [ —].
Балка на таком упругом основании представляет собой предельный
^^уцгп неразрезнои балки с бесконечно малыми пролетами, опирающей-
ся на упругие опоры. Система бесконечного множества уравнений пяти
моментов превращается в одно дифференциальное уравнение (24.2).
§ 24.2. ИНТЕГРАЛ ОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Чтобы проинтегрировать неоднородное дифференциальное уравне-
ние (24.2), займемся сначала однородным уравнением
?^У^+/гу:=0, (24.3)
которое относится к любому участку, свободному от внешней нагрузки.
Мы должны выразить прогибы у в функции от х. Введем безразмер-
ную абсциссу сечений
^ = ^ , (24.4)
L
где
Величина L зависит одновременно от жесткости балки и жесткости
основания, но не зависит от пролета /. Она имеет размерность длины.
Выразим искомый интеграл через четыре независимые линейные
комбинации из тригонометрических и гиперболических функций. Наи-
более удачными, как мы сейчас увидим, будут следующие линейные
комбинации:
Ajc = A (S) = cos % ch l\
B^^B{%) =—(sinSchS + cos^sh^);
D^^D{i) =—(sin^ch^ —cos^shS),
(24.6)
^Де ?—отвлеченный аргумент. Каждая из этих гиперболо-тригономет-
Рических функций представляет собой частный интеграл дифферен-
циального уравнения (24.3).
Замечательная особенность этих функций состоит .в том, что их
производные выражаются через те же функции. Заметим, что
dx ^ di dx L di
407
А R с . D^, убедимся, что
(24.7)
Другая, очень удобная их особенность состоит в том, что при Е =^0
они принимают следующие значения:
Л(0)=1. B(0)-C(0)-D(0)-0. (24.8)
Так как общий интеграл линейного дифференциального уравнения
представляет собой сумму его частных интегралов, то
Пусть при х=0 прогиб, угол наклона упругой линии, изгибающий мо-
мент и поперечная сила соответственно равны уо, 9о , Л^о, Qo. Из этих
четырех условий можно определить постоянные Я^ Яг, Яз, Я4, В итоге
окажется:
Q;. = QoA, + кЬуф, + *L»cpoC, —^ Mo?>^.
Написанные здесь уравнения эпюр получаются одна из другой по-
следовательно путем дифференцирования; эпюра М, кроме того, —ум-
ножением на EJ. Если мы продифференцируем последнюю строку, то
получим опять первую строку, но умноженную на —=&, что и служит
Рассматривая правые части уравнений (24,9), можно заметить, что
множители, стоящие при параметрах г/о, фо, Л^о, Qo, суть числа влия-
ния соответствующих параметров. Например, в первой строке множи-
тель LB^ есть число влияния параметра фо на f/ и т. д.
Для того, чтобы найти значение любой из функций у, ?» Л1, Q ^Р"
каком-нибудь заданном значении абсциссы х, следует сначала вычис-
лить безразмерную абсциссу ?, затем по табл. 12 найти соответ-
ствующие аргументу Е значения функций Л ( Е ), В (О, С ( О» ^ ^^^'
после чего уже можно будет вычислить требуемую величину.
Обычно два из начальных параметров г/о, сро, Мо, Qo равны нулк>>
Например, для защемленного конца ^о=0,сро =0;'для шарнирно-оперто
го ^о-=0, Mo=0 и т. д. Поэтому уравнения (24.9) для балки с заданны;
ми условиями на концах сразу же принимают более простой вид: в нид
остаются только два параметра. Последние можно найти, написав усл
ВИЯ для правого конца.
Изменение величин ?/, k, I влечет за собой изменение очертанй
всех эпюр, выражаемых уравнениями (24.9).
408
Числовые значения функций
Таблица 12
О
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,60
0,70
0,80
0,90
1,00
1,50
1/27:
2,00
2,50
3,00
3,50
4,00
4,50
3/2к
5.00
5,50
6,00
6,50
7,00
7,50
571/2
8,00
8,50
9,00
9,50
10,00
1,0000
1.0000
1,0000
0,9999
0,9997
0,9993
0,9987
0,9975
0,9957
0,9932
0,9895
0,9784
0,9600
0,9318
0,8931
0,8337
0,1664
О
— 1,5656
—4,9128
—9,9669
—15,5198
— 17,8498
—9,4890
О
21,0504
86,7044
193,6813
324,7853
413,3774
313,3658
О
—216,8647
—1479.3701
—3691,4815
—6650,9594
—9240.8733
0,0100
0,0500
0,1000
0,1500
0,2000
0,2500
0,2999
0,3498
0,3997
,4494
,4990
,5975
,6944
,7891
,8804
,9668
,2486
,2546
,9558
—0,5885
—4,2485
—10,6525
—19,2524
. —26,7447
—27,8317
—25,0565
0,1901
68,6578
198,1633
386,8119
580,6689
643,9927
628,8779
241,4136
-1010,8800
-3581,4756
-7616,1462
О,
О,
О,
О,
О,
0.
О,
1,
1.
О,
0,00005
0.00125
0,0050
0,01125
0.0200
0,0312
0,0450
0.0613
0,0800
0,1012
О,1249
0,1798
0,2444
0,3186
0,4021
0,4945
1,0620
1,1507
1,6490
1,8105
0,7069
—2,9014
— 10,3265
—21.9959
—27,8272
—35,5775
—43,1593
—28,2116
35,7713
180,1182
423,9858
643,9927
737,3101
981,0984
834,8607
—250,9959
—2995.7095
0,0000
0,00002
0,00017
0,00055
0.00135
0,0026
0.0045
0,00715
0,0107
0,0153
0,0208
0,0360
0.0571
0,0852
0,1211
0.1659
0,5490
0.6273
1.2325
2,1293
2,8346
2,4195
—0,7073
—8,6290
—13,9159
—23.0525
—43.2557
—62.5106
—63,3103
—13,2850
133,6516
321,9964
422.8713
860,3917
1340,3007
1539,7419
812,3636
Весьма сокращенные данные, содержащиеся в этой таблице, извлечены из более
подробной таблицы, помещенной в книге проф. В. А. Киселева «Балки и рамы на
упругом основании», М., 1934.
§ 24.3. ПРИМЕР
Балка свободно лежит на упругом основании и нагружена на левом конце силой
^ (Фиг. 525). В этом случае
Mo==Oi Q^=.^P, Mi = 0, Qt = 0.
Условия на правом конце записываются так:
— PLBi + kyoL^Ci + k^o^^Di = О ;
— PAi + kyoLBi + k^poL^Ci = 0.
Отсюда
Уо = Р
kL [с] — Bfii)
; 9o
==:P-
После этого можно по формулам (24.9) вычислить ^^
у - yoAjc + ^-^oBjc + ^ P^Jc.
Р 4
М = — PLBjc + kV' Уо С J, + ^<fo ^^ О^,
Пусть
у^(^ = 5 /сг/сжз ; ^ = о^о = 20 5 = 100/сг/сл2;
Е= 10^ кг/СА(2; Р=^1.
Тогда
L= |/ — =1/ =79.5 еж;
[/ ^ Г 100
J_ 300
J^^
3,773;
Фиг. 525
Уо=-
79,5
Л/= Л (3,773) = — 17.5697;
Б/= — 15,2000; С/=^ — 6,4177,
/)/== 1,1756;
15,2000»6,4177
10079.5 (41.1869 + 15.2000-1.1756)
= 10-^-2.077 СА(/кг;
<fo =
17,5697-6.4177- (15.2)^
100(79.5)2.(41,1869+15.200.1,1756)
На фиг. 525.6 и в показаны эпюры М ц у.
^_ 10-7.31,68 кг
—1
§ 24Л ИНТЕГРАЛ НЕОДНОРОДНОГО ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ
Перейдем теперь к более общему случаю — к расчету балки, у ко-
торой внешняя нагрузка расположена не только по концам, но и в про-
лете. К общему интегралу однородного уравнения нужно будет доба-
вить частный интеграл. Иначе говоря, к влиянию начальных параметров
Уо* ?о, Mq, Qo придется добавить влияние внешней нагрузки, принимая
в этой добавке ^/о= ?o=^4o=Qo = 0.
На фиг. 526 изображена балка, у которой в точке В приложена сила
Р;г. в точке С —момент М^, а на участке DE — распределенная по ка-
кому-либо закону нагрузка р. От действия параметров ^о, ?о, ^о» Go.
приложенных в сечении А (фиг. 526,6), получаются деформации и уси-
лия, выражаемые формулами (24.9). В сечении В, которое можно при^
пять за начальное для участка BD, приложен новый параметр Qo^""^^
(фиг. 526,в); дополнительное действие этого параметра на весь участок,
расположенный справа от Р, выражается теми же формулами, но с от-
счетом абсцисс от нового начала — от сечения В. В сечении С добав-
ляется новый начальный параметр Мо=М; его влияние распространяет-
ся на весь участок, расположенный справа от С. Наконец, начиная
сечения D, добавляются элементарные поперечные силы pdz. _ -
__ Обозначим для кратности правые части уравнений (24.9) через /А •
М. Q. Для любого сечения полное решение имеет следующий вид:
410
llfr
/ 7 U__^-^a t(—^)v^''~''V •^>2
s^j
925 лиф
UMPPI
(e
i«
I ^ )^H
I
(Э
(ог^-з)
'zp""-
\zv'-\i
0 0 о
X дг ДГ
'•^^^"'^^If+^~''^^c/if+-vwif-'л='^
^ ar X
I ^ Y :if
зави-
(24.11)
Если р=const, то можно этот множитель вынести из-под знака щ
теграла и^произвкти интегрирование, причем дифференциальные зав"
симости (24.7) позволяют сразу написать:
а
а
а
а
Метод начальных параметров может быть распространен на балки
со скачкообразно меняющимся на разных участках сечением.
§ 24.5. ПОНЯТИЕ О РАСЧЕТЕ БАЛОК НА УПРУГОМ ИЗОТРОПНОМ ОСНОВАНИИ
Наряду с излол<енной выше теорией расчета существует другая тео-
рия, свободная от гипотезы об отсутствии связности между частицами
грунта. Она рассматривает упругое основание балки как упругую полу-
плоскость или как упругое полупространство.
В первом случае балка лежит как бы на краю бесконечно узкой пла-
стинки, простирающейся бесконечно в двух взаимно-перпендикулярных
направлениях (фиг. 527); "во втором
случае упругое основание представ-
ляет собой среду, непрерывно запол-
няющую пространство, ограниченное
с одной стороны плоскостью (фиг.
528).
4
Фиг. 527
Фиг. 528
Возможность построить теорию расчета балок, лел<ащих на таких
основаниях, предопределяется следующим фактом: в теории упругости
еще в 1885 г. была решена задача о построении поверхностей влияния
АЛЯ перемещений упругого полупространства и в 1892 т, — о построении
л. в. перемещений упругой полуплоскости. Идея расчета здесь буД^*^
пояснена только для балки, лежащей на полуплоскости. Случай про*
^.., *w«*x-r,w м«'»л wc4.;nvi^, ^1сл\«ащ.си на полуплоскости. У^Jiy^^<^^^ '•
странственного основания несколько сложнее, но по идее оба слу*^
расчета одинаковы.
Под упругой полуплоскостью будем в дальнейшем понимать беско-
нечно простирающуюся в стороны и вниз пластинку, имеющую толш*^
ну не бесконечно малую, а равную единице.
412
икальное перемещение произвольной точки В верхнего края под
B^P^^j силы Р (фиг. 529) вырал<ается формулой.
влиянием
(24.12)
где 2 —расстояние научаемой точки В до точки Л, в которой приложе-
на сила Р;
а —расстояние произвольно взятой достаточно далекой точки С
верхнего края до той же точки Л.
Модуль упругости на .прак-
тике оказывается равным от
100 пг\т^ (для слабых грун-
тов) до 500 /с2/сж2 (для плот-
ных груйтов).
При 2;=0... ^= <^.
Вид кривой, выражаемой
формулой (24.12), показан на
фиг. 529. Нужно добавить, что
t/ есть разность между верти-
кальными перемещениями то-
чек Б и С; абсолютные переме-
щения этих точек теоретически
равны бесконечности. Фиг, 529
есть эпюра относительных вер-
тикальных перемещений верх-
него края, вызываемых силой Р.
По закону взаимности формула (24.12) выражает одновременно л. в.
относительных вертикальных перемещений точки Л, вызываемых силой
Р, приложенной в любой точке В верхнего края.
Фиг. 529
^'iTvL Yl VI
-чг^чг^.
KS'.k^^,.y\...A...h\....h\....h\"..
Фиг. 530
Фиг. 531
^ В. целях избежания значительных махемахичеаш^^^^^^^^^
Б. Н. Жемочкин! предложил заменить «^"P^Pf^"^ абсолютно жесткие
полуплоскость опиранием в отдельных т основание будут пе-
опорные стержни (фиг. 530). На балку и на УПРУ^'^^ ^ ^^е^ь только
Редаваться реакции этих стержней. ^^^^'^ будет составить кано-
конечное число лишних связен, и Д-^^ "^^„рщений или смешанного ме-
нические уравнения метода сил или перемсш,
™Д^- .,лл методом то за основную систему
Если воспользоваться смешанным "^^f^M закрепленным сечением и с
целесообразно будет принять балку с 0Д™^531). Неизвестными будут
"еререзанными опорными стержнями (фип;^^^^^^^^ перемещение у^
усилия Xi, Х2.... Х„ в опорных стержнях, в р
«,, йесконечно длинной балки на уп-
^;^^. Н. Жем очки и. плоская за^^^^^^^^^^ VThThT^h! "ta^n-
'^и^^Гй S^irTss"^! ^ L^rr^H/HaVpytoM"oio"sa«HH„ без г„по^«
^^кие методы расчета фундаментных балок и
«Синклера, Стройиздат, 1947. 413
Уравнения будут иметь вид п г _ i о
К X, +8,,Х, + - • • + 8,Л->'о-«.<Р + Д^я = О (. - 1,2.
К ним добавляются два уравнения равновесия
Х. + Х, + -- + Х„-2Я = 0; . 1
¦«)• (24.13)
(24.14)
Первое из уравнений (24.14) есть уравнение вертикальных проекций,
втооое —уравнение моментов относительно левого конца балки.
'^ Любое из перемещений 8.J или
ftji представляет собой сумму двух
I
I
] ^(>7
4
1
"ТТТТТТТТЛТТТТТТТТ?
77777777?
777ТГ777ШТ77Г/
.^1+1
Фиг. 532
слагаемых
Перемещение Vi^ обусловлено
деформацией балки и выражает-
ся формулой
Перемещение w^j^ обусловлено деформацией полуплоскости. Если
бы мы.считали, что силы Х,-и Xf^ передаются на упругое основание как
сосредоточенные, то имели бы w^f^ = оо . Поэтому будем считать каж-
дую из этих сил равномерно распределенной по обе стороны от оси
стержня на участке, полная длина которого равна расстоянияю с меж-
ду стержнями (фиг. 532).
Если Х^ =1, то интенсивность нагрузки будет равна р= — .
Влияние такой распределенной нагрузки на осадку точки А основа-
ния вычисляется по формуле (24.12) путем ее интегрирования.
1. Когда нагрузка р расположена по одну сторону от точки А {1фк):
Щк^
7t?o
— 2
-ln[(2.?-+l)(2^_l)] + 2 1п-1 + 2(1 + 1п2);
(24.15)
точки
ки!4°(?.^e"npT^''=i).'^^'^"°""°'^^"^ симметрично по обе сторойЫ от
1
X ,1+2-
-2^1п (
1—2
-ln[(l + 2^)(l_2^)]+21nf + 2(l-b,n2,
I (24.1^)
414
)
Здесь d — произвольная положительная постоянная. На свободные
члены А,рналичие упругого основания не влияет, поскольку внешняя
нагрузка приложена исключительно к балке.
Решив канонические уравнения, найдем все Х^, следовательно, смо-
жем построить все эпюры. Величина d отражается лишь на численном
значении перемещения уо, но не влияет на неизвестные Х^.
Одновременно будем знать давления, передающиеся на основание:
каждая сила Х^ передается на соответствующий участок длины с в ви-
де равномерной нагрузки интенсивности — •
Этот способ решения нашел у нас применение при проектировании
фундаментов различных ответственных сооружений как более совершен-
ный, чем способ, основанный на гипотезе Винклера.
В указанных выше книгах проф. Б. Н. Жемочкина и проф. А. П. Си-
ницына помещены вспомогательные числовые таблицы, которые значи-
тельно облегчают расчет.
Глава 25
НАПРЯЖЕННОЕ СОСТОЯНИЕ СТЕРЖНЕВЫХ СИСТЕМ
ЗА ПРЕДЕЛОМ УПРУГОСТИ
§ 25.1 О РАСЧЕТЕ СООРУЖЕНИИ ПО РАСЧЕТНЫМ
ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
Прежде чем перейти к рассмотрению тех особенностей, которые воз-
никают при работе сооружений за пределом fynpyrocTH, мы должны
вкратце остановиться на принятом в настоящее время в СССР, соглас-
но утвержденным «Строительным нормам и правилам» (СНиП), методе
расчета по так называемым «расчетным предельным состояниям». Эти
методы детально излагаются в курсах стальных, железобетонных, де-
ревянных и каменных конструкций; здесь излагается только общая
идея метода.
Расчетным предельным состоянием по прочности называется не со-
стояние разрушения сооружения, а такое состояние, которое отвечает
эксплуатационному режиму при наихудших возможных на практике
условиях. Оно является предельным не с точки зрения исчерпания
несуихей способности сооружения, а с точки зрения сгущения неблаго-
приятных предпосылок, принимаемых при расчете. Сооружение, нахо-
дящееся в предусмотренном расчетом предельном состоянии, должно
работать нормально, без перенапряжений, без дефектов, без остаточ-
ных деформаций.
В нормах предусмотрена наибольшая нагрузка, возможная при экс-
плуатации данного типа сооружений. Однако расчет ведется не на эту
«нормативную» нагрузку, а на большую, которая получается умножени-
ем на так называемый «коэффициент перегрузки». Например, для чер-
дачных перекрытий без учета специального оборудования (вентиляци-
онных камер, водяных баков, моторов и т. д.) принимается «норматив-
ная» нагрузка 75 кг1м^ и коэффициент перегрузки 1,4. Этой цифрой
обеспечивается, можно сказать, коэффициент запаса 1,4 в учете
только одного фактора — нагрузки. Для различных нагрузок
принимаются различные коэффициенты перегрузки.
Другой коэффициент запаса фигурирует в оценке «расчетного соп-
ротивления» материала. Например, «нормативный» предел текучест^
для стали марки Ст. 3 равен 2900 кг/см^; «расчетное» же сопротивление
арматуры принимается из осторожности равным 2900-0,9 кг/см^ ^^^^
О.У—так называемый «коэффициент однородности», учитывающий воз-
416
' .ожность пониженного качества материала. Кроме того, расчетное соп^
Явление снижается умножением еще на один коэффицЕ ™ ™
Йнииы, учитывающий другие неблагоприятные факторы неподд^^^^^
?ся точному учету (концентрацию напряжений^агрессивную среду
fj. п.)-Этот коэффициент носит название ^коэффициента\слЗ
оаботы».
^ Кроме расчетного предельного состояния по прочности СНиП пре-
дусматривают второе предельное состояние-по деформациям; в этом
состоянии деформации и перемещения должны еще иметь такую вели-
чину, которая не препятствует нормальной эксплуатации сооружения.
Для железобетонных соорул<ений предусматривается, кроме того, тре-
тье расчетное предельное состояние — по появлению трещин в бетоне.
Характерным для этого метода расчета является отсутствие поня-
тия о едином коэффициенте запаса. Каждый из перечисленных коэффи-
циентов обеспечивает особую величину запаса для соответствующего
параметра. Коэффициенты имеют сложную природу, так как зависят
от многих случайных или подчиненных неизвестным закономерностям
факторов. Величины их, указанные в СНиП, будут совершенствоваться
по мере накопления опытных данных и обработки последних по мето-
дам теории вероятностей и математической статистики.
При расчетном предельном состоянии сооружение обычно еще не
имеет остаточных деформаций, поэтому расчет производится, как для
упругой линейно-деформируемой системы.
Рассмотрение поведения сооружений за пределом упругости оказы-
вается необходимым, когда возникает надобность использовать сущест-
вующее сооружение в условиях повышенной нагрузки, не предусмот-
ренной первоначальным расчетом, или в тех случаях, когда при проек-
тированип сооружения ставится задача достигнуть максимального об-
легчения его веса путем максимального использования материала,
хотя бы и ценой перенапряжений и выхода в область упруго-пластиче-
ских и пластических деформаций.
При работе сооружения за пределом упругости происходит суще-
ственное перераспределение усилий между его элементами и обнаружи-
вается ряд особенностей, понимание которых важно для инженера-проек-
тировщика. Исследование области упруго-пластических и пластических
деформаций позволяет, кроме того, выяснить несущую способ-
^OQTb сооружения, т. е. ту теоретическую величину нагрузки, при кото-
рой можно было бы ожидать разрушения сооружения.
В СССР и за рубежом ведутся обширные теоретические и экспери-
'^^нтальные исследования напряженного и деформированного состояния
^ооружений за пределом ^упругости; по этим вопросам опубликована
^^ширная литература.
Некоторые основные сведения, характеризующие поведение стержне-
^^^х систем за пределом упругости, даны в следующих параграфах.
§ 25.2 РАСЧЕТНАЯ СХЕМА ИДЕАЛЬНОГО
УПРУГО-ПЛАСТИЧЕСКОГО МАТЕРИАЛА
стг.^"^ будем пользоваться расчетной схемой идеального упруго-пла-
Д^ного материала, который характеризуется диаграммой, представлен-
2 "^ фиг. 533, где на оси ординат отложены напряжения о, а на оси
деЛ''^'¦^^"^^«^^^ьные удлинения г. Предельное сопротивление (пре-
^^кучести) обозначено через о^. « ,^ ^,^ .=--^-
Ш ^^''^'^^ говоря, диаграммой с бесконечной площадкой текучест|
It ^- - -
*°-ьзо^Ться'^;оГк? вТоГ случае: когда площадка текуче.^^
nni^HV ПРИ работе сооружения не исполь-
шая разумеется, конечную длину, при р
Дуется ДО конца. ^ ^^^^^ элементах перед разрушением появля-
^В изгибаемых ^^^^-^^^^^^ет^Х бетоГа и начинается течение арматуры,
штся трещины в растянутой зоне бетона и Поэтому и для них мож-
^' ^ но считать допустимым
^ пользование той же диа-
граммой. Ею можно поль-
зоваться также для бето-
на в обойме.
§ 25.3. РАСЧЕТ СТАТИЧЕСКИ
НЕОПРЕДЕЛИМОЙ ФЕРМЫ
НА ПОСТОЯННУЮ
НАГРУЗКУ
Рассмотрим сначала
простейший пример, пред-
ставленный на фиг. 534:
абсолютно жесткая плита,
нагруженная вертикаль-
ной силой Р поддерживается тремя вертикальными стержнями. Си-
стема равно как и нагрузка, симметрична.
При обычном методе расчета, когда деформации не выходят за пре-
делы упругих, задача содержит одну лишнюю неизвестную. Решив ее.
найдем, что напряжения выражаются следующими формулами:
упруеих ^
деформации
идеально пластическая^
— областо
Фиг. 533
""ав
""EF
2bFi + aF^
Р\
CD
2bFi + aF2
-R
(25.1)
При fe<a средний стержень более напряжен, чем крайние, поэтому
при постепенном возрастании силы Р предельное напряжение появится в
первую очередь в нем.
Проследим за поведением стержней при дальнейшем возрастании на-
грузки. То обстоятельство, что мы заранее можем указать, какой стер-
жень более напряжен, позволяет нам легко разобраться во всем процес-
се. В первую очередь предельное напряжение о^ появится в стержне Си.
Усилие в нем при этом будет равно o^Fz, При дальнейшем возрастании
нагрузки этот стержень потечет, т. е., несмотря на рост деформаций, уси-
лие в нем останется постоянным. Но так как он является лишним, то эт
не опасно: рост деформаций в этом стержне будет ограниченным, так ка
весь избыток нагрузки будут брать на себя остальные два стержня, la
будет продолжаться, до тех пор, пока и в последних напряжение н
достигнет величины о^, т. е. пока нагрузка не достигнет величины
После этого несущая способность -сооружения будет исчерпана. Боль-
шей нагрузки оно уже не сможет воспринять; равновесие между внешн
ми и внутренними силами нарушится, и наступит разрушение. ^^^^
Предельная сила Рпр не зависит от соотношения между "•"^"^^^ддй
F\ и р2, а также между длинами а и 6; она зависит только от суммарн
площади всех трех стержней. ^^,
Связь между деформацией сооружения, т. е. вертикальным "^^ Ij}-
щением у плиты и переменной силой Р, может быть выражена ^Р^^,,.
ком, представленным на фиг, 535. Участок ОА отвечает упругому сое
418
...ю всех трех стержней. После того как средний степжр„ о
SCro ^гла вЕражаех собой каГ^^^ГедеГыГкг^ф^^иц^ГГ V^
^стй сооружения. Наконец, когда в обоих крайних стержнях напояже'
„е также достигнет величинное,, дальнейшая деформация будет наоа-
стать по закону горизонтальной прямой ВС. т. е. пр„ постоянной внеш
^силе Я„р, приведенный же коэффициент упругое?!! сооружения об'р^^"
тится в нуль. •' V
Фиг. 534
Фиг. 535
Если мы обозначим коэффициент перегрузки через k, а под вели-
чиной с^ будем понимать расчетное сопротивление, т. е. нормативный
предел текучести, умноженный на коэффициент однородности материа-
Jia. то получим допускаемую (эксплуатационную) нагрузку
Рп
Р — li!P
' пап
пр
k
Отличие этого расчета от того, который применяется для упругих
^"^J^M, состоит в следующем: предельная нагрузка Рпр может быть
^Шена непосредственно из условий равновесия без решения уравнении,
^^условленных статической неопределимостью сооружения, Действи-
^ад^но, в предельном состоянии усилия во всех трех стержнях равны
Редельным, откуда сразу ясно, что
(2F,+F,)o,. (25.2)
пр
Столь же просто решается обратная задача: по данной допускаемой
^грузке Р^^^ и данному коэффициенту запаса k подобрать сечения
Р*«ей; из условия (2Fi+Fi) o^=kP^„„ получается
2F, + F^-
Ох
^^^Величины F, и Fa можно выбирать произвольно, лишь бы они удо-
р,зГРЙрГн'оТГрим^рГГожно было сразу указать, какова схема
&шения'в случае' с«с?емы. содержащей много лишних неизвестныл
Pac^f. "Редельного состояния не может быть указана сразу. Приходится
Рассмо-
2Л
'¦"¦реть различные возможные схемы.
41S^
на фиг. 536 представлен пример сис^^^^^^^^^^^^
стержня Предельное со^^^^^^^^^^^^
вертикальных "сржня noiei у горизонтальный опорный стержень)
точки А невозможны (^J^^^^^ оТи тольТ во точки, лежащей на J^
поворот плиты может произойти только vy^^^^^^^ проходящей через
точку А^
Число комбинаций из
четырех стержней по три
равно четырем, следова-
тельно, существуют четы-
ре различных механизма,
в которые система может
перейти в момент ис^тер^
пания несущей способно-
сти. Они показаны пунк-
тиром на фиг. 536. Схема
б соответствует предполо-
жению, что потекли три
правых стержня: из урав-
нения моментов относи-
тельно точки прикрепле-
ния А четвертого стержня
находим
Аналогичным образом
вычисляются значения
Япр по остальным трем
схем а м. Действительной
предельной нагрузкой яв-
ляется всегда наимень-
шая из всех, найденных
таким способом, т. е. в
^оЗР
Фиг. 536
данном _ случае Рпр
Этот факт очевиден. Впрочем, невозможность остальных схем, при
которых Рпр имеет большую величину, видна из уравнений вертикаль-
ных проекций: в этих схемах четвертый стержень должен был бы иметь
усилия, соответственно равные 1,Бс, р; Зс,Р; 9а^Р, в то время как фак-
тическое усилие не может превысить величину o^F. Способ расчета, со-
стоящий в определении наихменьшей величины Рпр из рассмотрения рав-
новесия различных механизмов, проф. А. А. Гвоздев предложил назват!
кинематическим.
Кинематическая картина в данном примере настолько проста, ^iтo
некоторые комбинации знаков усилий с^Р сами собой отпали: в стер>|<
нях, лежащих по одну сторону от точки вращения диска АВ, усил1|Я
«тР не могут быть разных знаков. Если бы диск был не абсолК)Т1^
жестким, а деформирующимся, дело осложнилось бы. При расчете Ф^Р-
с лишними стержнями кинематическим методом мы и встречаемся ^^
таким осложнением: приходится рассматривать значительное количсс
во схем разрушения. j^,
Чтобы обойти это затруднение, иногда оказывается более ^^^^^^^о-
прибегнуть к «упругому» расчету. Рассматривается процесс п^^'^^^^^>,о-
го возрастания нагрузки. В первой стадии процесса сооружение, ^' ^Q
щее п лишних связей, работает упруго. Составив и решив канонич
42©
внения, "«й^^^ ™'',/;'^^P^f ^ ^^™Ро^ напряжение имеет наиболь-
^'^""'fl^ lT?"oLlZT'^^^^^^^ ™^^^^^ ^ п^Р^УК^ очередь. Во
?рой стадии этот стержень сохраняет неизменную ^елич^Т^воеТо
'силия, следовательно, его можно удалить, приложив вместо него назван-
У^е усилие как внешнюю нагрузку. Сооружение при этом имеет уже
только п-1 лишних связей и может снова рассматриваться как упругое.
Составив для него новые канонические уравнения и действуя аналогич-
ным обрязом, можно проследить за всеми стадиями постепенного сниже-
jjHH числа лишних стержней, пока мы не дойдем до последней стадии —
стятически определимой системы, в которой появление предельного
усилия в наиболее напряженном из оставшихся стержней приводит к
разрушению.
При переходе от одной стадии к другой может случиться, что какой-
нибудь стержень, находившийся в состоянии текучести, начнет разгру-
жаться. Так как разгрузка происходит по упругому закону, то усилие
в этом стержне начнет изменяться, и степень статической неопредели-
мости фермы снова повысится на единицу.
Может также случиться, что тот или иной сжатый стержень потеряет
устойчивость раньше, чем усилие в нем достигнет величины o^F.
Все это показывает, что определение несущей способности статически
неопределимой фермы представляет собой хотя и простую с теорети-
ческой точки зрения, но иногда весьма утомительную задачу.
§ 25.4. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ БАЛКИ
НА ОДНОКРАТНОЕ НАГРУЖЕНИЕ И РАЗГРУЗКУ
Рассмотрим эпюру нормальных напрял<ений в балке (фиг. 537, а),
материал которой характеризуется идеальной диаграммой, представлен-
ной на фиг. 533, Представим себе, что нагрузка постепенно возрастает,
с d
Фиг. 537
^^«^едствие чего возрастают и нормальные напряжения. Пока все на-
нГ^^""^ будут ниже предельного, эпюра будет иметь вид, показанный
3 фиг. 537, б. Такой же вид она будет иметь, когда предельное напря-
^ение о^ появится только в крайнем волокне. При нарастании нагрузки,
^^^^^"олагая справедливым закон плоских сечений, мы получим эпюру
ппр ^"^* ^^'^^ е- ^^асть волокон потечет, и в них напряжение будет равно
Уп^^^-^ьному; остальная часть сечения будет работать упруго. Высоту
i^yrofi области (упругого ядра) обозначим через 2и. При дальнеи-
нятк "врастании нагрузки пластические деформации будут распростра-
cvinn^ ^'^^ дальше вглубь сечения, однако до тех пор, пока будет
ся к.^^^'^^ть упругое ядро, момент внешних сил будет уравновешивать-
ппип^^^"^о^« внутренних. За предельное напряженное состояние сучения
снимается такое, которое представлено на фиг. 537, г, т. е. такое, при
котором все волокна испытывают предельное напряжение о^. Момент
внутренних сил достигает при этом наибольшей возможной для данного
сечения величины. При новом нарастании нагрузки он сохранит ту ^е
самую величину, следовательно, сечение уже не в состоянии будет сопро-
тивляться неограниченному нарастанию деформаций.
Сечение, находящееся в таком предельном состоянии, называют
«пластическим шарниром». Его можно рассматривать как обыкновен-
ный шарнир, к которому приложены две взаимно-противоположные пары
с постоянным моментом. Этот предельный момент внутренных сил
наповем Мпр-
Разумеется, что изгибающий момент сможет достигнуть предель-
ной величины Жлр только в том случае, если балка еще раньше не раз-
рушится от касательных напряжений.
Из предыдущего рассуждения ясно, что момент М^^ выше того мо-
мента, при котором предельное напряжение появляется только в край-
нем волокне. Расчетная нагрузка, составляющая А от предельной бул
поэтому больше той, которая составляет — от нагрузки, вызывающей
k
предельное напряжение только в крайнем волокне; мы видим, что и здесь
расчет по предельной нагрузке экономичнее расчета по допускаемым
напрял^ениям.
Момент Л^„^^ для симметричного сечения можно определить из эпюры
фиг, 537, г. Обозначим площадь сечения через F,
Тогда
2 2
Л^пр = Г yo,dF = 2а^ Г ydF = 2а^5о, (25.3)
-Л ^
2
где So —статический момент верхней или нижней половины сечения
относительно нейтральной оси.
Если принять во внимание, что при обычном расчете за предельный
момент принимается тот, при котором предельное напряжение возника-
ет лишь в крайнем волокне: М^^^ o^TF, то отношение обоих моментов
напишется так:
а = i^l^ = ^ (25А)
CrW W
Число а показывает, во сколько раз расчетная нагрузка по одном}
способу выше, чем по другому, если они исчисляются по одному и тому
же коэффициенту запаса, но отнесены к двум различным предааьным
состояниям. Например, для сплошного прямоугольного сечения, имею-
щего размеры аХй, получается
' -So- — . ^^-=-5-; « = -.
т. е. в этом случае «пластический расчет» позволяет повысить нагруз*^>
на 507о (если ее не придется несколько понизить по другим соображе-
ниям).
Распределение напряжений по длине балки будет зависеть от эпюры
изгибающих моментов. Например, для балки с опертыми концами, иагру-
женной в середине пролета сосредоточенной силой, диаграммы напряж^-
422
баюший момент в пласти-
ческом шарнире начнет
уменьшаться, т. е. шар-
нир закроется. Со-
храняется ли в каком-ни-
будь сечении балки пла-
стический шарнир или
нет, зависит ле только от
величины действующей
нагрузки, но и от направ-
ления изменения нагруз-
ки. Это обстоятельство, с
которым приходится счи-
таться при различных ва-
риациях нагрузки, может
значительно усложнить
расчет статически неопределимых балок, так как может оказаться, что
одни шарниры будут появляться, а другие будут исчезать.
Вернемся к диаграмме нормальных напряжений статически опреде-
лимой балки и проследим за процессом разгрузки. Он повлечет за собой
появление дополнительной (с обратным знаком) диаграммы abed
(фиг. 537,(3), которая будет налагаться на основную. Когда балка пол
ностью разгрузится от внешней нагрузки, окончательная диаграмма при-
мет вид фиг. 537, е; та же диаграмма представлена на фиг. 537, е\ Так
как при этом внешние силы отсутствуют, то в статически определимой
балке момент внутренних сил также будет равен нулю, т. е. остаточные
напряжения в сечении сами себя уравновесят. Диаграмма е будет иметь
h
Фиг. 538
т'акой вид, что для любой ее половины окажется ^' ау dF=0, где
CVM-
'"парное напряжение, заштрихованное на диаграмме. Можно еше так
выразиться; для любой из двух половин сечения равнодействующая
элементарных внутренних нормальных усилий направлена по оси раз-
оруженной балки; обе равнодействующие равнопротивоположны.
§ 25.5. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ
НА ОДНОКРАТНОЕ НАГРУЖЕНИЕ И РАЗГРУЗКУ
Предельное состояние статически неопределимой балки можно
"^йти из условий равновесия, не решая статически неопределимой за-
Например. в балке с защемленными концами (фиг. 539, а) предель-
но^ состояние наступит тогда, когда появятся три пластических шар-
^^^^Ра. которые превдатят балку в механизм. Наибольшие моменты отве-
^^ают сечениям Л Б Гс, поэтому в балке постоянного сечения именно
'"^^СЬ и появятся эти шарниры. ^^^^^^ ,^onмкт MPWfiv
Для того чтобы моменты в названных сечениях^ были равнь!^^^^^^
'^бой. следует провести замыкающую аЬ (фиг. 539,а) так. чтобы она
423
разделила пополам ординату Cd, которая равна, как известно/^
Раь ^
Отсюда следует, что все три момента будут равны — . Произведенная
операция носит название «выравнивания моментов». Обозначив предель
ную силу через Р^р, а предельный для сечений данной балки момент
через Мир, получим
ЛГ,
п?
• или Р,
пр
,2/Ипр/
пр J
^^ ^ аЬ
Подобным же образом при по-
мощи выравнивания моментов
определяется предельная интен-
сивность равномерно распреде-
ленной нагрузки. На фиг. 539, б
достаточно провести замыкаю-
щую так, чтобы она разделила
пополам макси.мальную ординату
параболической эпюры, равиую
Отсюда
Фиг. 539
Мпр =
_ ^пр/^
16
или <7пр =
I6M,
'пр
/2
Какова бы ни была внешняя нагрузка такой балки, замыкающую
всегда можно провести так, что получатся три равных наибольших мо-
мента. В том случае, когда на одном конце балки имеется шарнир, мож-
но всегда получить два равных момента.
Если концы балки защемлены упруго, то предельные опорные мо-
менты независимо от степени упругости заделки будут иметь ту же ве-
личину, что для балки с абсолютно защемленными концами.
Например, предельное состояние балки АВ постоянного сечения с
одним заделанным и другим шарнирно опертым концом (фиг 540) опре-
деляется из условия равенства моментов М^ =Ж^ ==ЛГ,р, где М^р -
предельный момент
РпрОЬ
М,
про
-=м,
пр.
откуда
Мпр = ^ или Я„р==.У^пр(/ + а)
1 + а
аЬ
Наоборот, по данной силе Р и коэффициенту перегрузки k можно подо-
брать сечение, приняв feP=:P„p = ^"р^^^^)^ откуда М =:J^P. По
формуле (25.3) найдем статический момент половины сечения 5о=—'
2опр
после чего уже легко будет подобрать и само сечение.
Для двухпролетной неразрезной балки постоянного сечения (фиг. 541)
предельная эпюра может быть построена сразу на основании реше-
ния предыдущей задачи. Например, если оба груза Р стоят в середине
пролета, то М„^. = fi^
*^ 6
424
ролетной неразрезной балке с опертым.и концами число лиш-
яз^й равно п—1, поэтому для превращения ее в механизм доста-
0^ ^^цтобы в ней образовалось п пластических шарниров. Это условие,
точно, ^^ является необходимым: при неблагоприятном расположении
^днако, ^gjjj^a может потерять свою несущую способность раньше.
мер ^с-^и на концах какого-нибудь пролета и в его промежу-
j^anpH' ^^[j^jj^jj появятся три шарнира, то несущая способность этого
очном^ будет исчерпана независимо от состояния остальных пролетов.
Фиг. 540
Фиг. 541
Расчет неразрезной балки можно произвести очень просто. Пусть,
например, дана пятипролетная неразрезная балка с разными сечениями в
разных пролетах, нагруженная заданной внешней нагрузкой (фиг. 542).
Требуется определить коэффициент запаса. Первый пролет может поте-
Фиг. 542
. ^г.пг.ип тогда когда изгибающий момент
рятьсвою несущую способность ™^ько тогд^^^^^ предельному
под грузом Pi и момент на «"^Р^ .^^^^^ож^^ быть рассчитан неза-
моментуМ., Следовательно первый пр^^^^^^^ /другим защем-
висимо от прочих пролетов, как балка с ^^''^ может потерять несущую
ленным концом. Любой промежуточный пролег ^жуточных сече-
способность, когда наибольший из ^^^^^"J^!lЗначения, поэтому расчет
ниях и оба опорных достигнут предельного ^ ^^^^^^^ от прочих про-
промежуточного пролета также пpoизвoдиILи ^ дельный момент на
¦^етов. Небходимо только иметь в виду. ^'"^ меньший из двух пре-
каждой опоре из осторожности ^^^^У^^^„^^ ^гюш примыкающих проле-
дельных моментов, отвечающих ^^^^^""^^^й коэффициент запаса. На
^ов. Для каждого пролета получится ^^^^g ^^^^ моментов неразрез-
фиг. 542 покя'.яи пил предельных эпюр изгиоаюш
^в. Для каждого пролета получится ^^°^ „:„;, моментов неразрез
¦иг. 542 показан вид предельных эпюр изгиоающ
«ой балки для всех ее пролетов. оопаны, а сечения неизвестны
Если коэффициенты запаса и «агрузка зад g g^b сечения для
'О на основании такого же рассуждения можно
Каждого пролета. ^9=
425
Мы говорили до сих пор только о балке постоянного сечения R
чае, когда балка имеет переменное сечение, величины предел ^^^^
случае, когда балка
моментов получаются
.-„..J для различных сечений различными, и поэ^^^^^
указать заранее те места, в которых расположатся шарниры в ппе^^^^
ном L-остоянии балки, является делом более трудным. Приходится п^^"^^'
кивать их путем по^^^к
Особенно осложняется де.*
сим<
ло при отсутствии'
метрии.
На фиг. 543 предстаи-
лен пример балки пепр
менного сечения, имею-
щей ось симметрии. Верх
няя ломаная линия прел
ставляет собой эпюру пре
дельных отрицательно
моментов, а нижняя-^
эпюру предельных поло-
жительных моментов. Ко-
гда сечения балки изве-
стны, то и обе эти эпюры
эпюра для силы Я, приложенной в середине ироТе^а!^^^^
ЗгГкГ ^ ^"^""'^ графиков в трех точках. Сила Р[, определяется и
эпюры поперечных сил (фиг. 543): рсделиется из
tl2l
¦11 Ill Hill
//21
Фиг- 543
*^щ — ^
1
в случае многопролетной неразрез-
ной балки и наличия многих грузов
или распределенной нагрузки подбор
предельной эпюры, которая касается
обоих графиков в достаточном количе-
стве точек, легче всего делается графи-
чески.
Смещение опор не влияет на пре-
дельное напряженное состояние балки,
так как в предельном состоянии пос-
ледняя превраи^ается в кинематичес-
кую цепь.
То же самое можно сказать о на-
чальных напряжениях, вызываемых
температурой, неточностью сборки и
1. п.; они не оказывают влиянм'^ »*
Фиг. 544
^. п, они^н7оказываю?'в'''° "^^Р*^" "
Перейдем теперь к вопьос^ ^1 предельное состояние системы.
Sh" п"Р'^'-""'^°й 6aS ПОЛУЧЕНО"" ^^«охРзтаой разгрузки сгаги-
гивши;. ''^''"^«°' •^™. освободившие ""^ "•"" "«ь.е остаточные дефор-
"альнм'' '""''^ « упругую системе" ,^ °1 внешней нагрузки и превра-
^льные усилия. Рассмотрим л^«' Z ^^""^ испытывать какие-то на-
Sho п?'''^'^"«''^Р^внь1ГпролетамГ'Р' Д«У>^пролетную балку по-
^ерно распределенной по всей JJJi "'"^'¦РУ>«енную сплошной, равн"-
^4. а). При постепенном возоа™„1^''РУ^''°^ интенсивности ^ (Ф«;-
^ ьозрастании нагрузки пластические дефорл'З-
,,.„ появятся в первую очередь на некотором участке, примыкающем
^средней опоре. Ьсли мы выделим ту часть эпюры, где момент превы-
шает величину ^jW, то тем самым выделим и упруго-пластический
viacTOK балки. После разгрузки этот участок балки останется искрив-
ленным, и если бы мы Убрали среднюю опору, то ось балки имела бы
д указанный на фиг. 544, б. При наличии средней опоры ось балки и
дпюра моментов будут иметь вид, представленный на фиг. 533. е. Отсю-
да ясно, что в статически неопределимых системах после разгрузки по-
п\чается более сложное напряженное состояние, чем в статически опре-
делимых: кроме тех напряжений, которые являются самоуравновешен-
ными для каждого сечения (фиг. 537,^), получаются еще напряжения
от реакций лишних связей.
Определение величины этих реакций является достаточно сложным,
так как оно требует предварительного определения величины неупругих
деформаций. Но так как на несущую способность сооружения они не
влияют, то нахождение их не является необходимым.
§ 25.6. ПЛАСТИЧЕСКИЙ ШАРНИР ПРИ СОВМЕСТНОМ ДЕЙСТВИИ
ИЗГИБАЮЩЕГО МОМЕНТА И ПРОДОЛЬНОЙ СИЛЫ
имеет вид, представленный на
Рассмотрим симметричное поперечное сечение и будем считать, что
нейтральная ось совпадает с осью симметрии. Диаграм.ма нормальных
напряжений в пластическом шарнире '" "~
фиг. 545.
Обозначим площадь сечения стерж-
ня через F, меньшую из двух площадей
(растянутой и сжатой) —через Fi. Из
фиг. 545 следует, что
N„
:a,{F-2F, ); Мпр = 2a,F, г, (25.5)
где г —расстояние центра тяжести
площади f 1 до оси симметрии. Форму-
ла (25.5) выражает величины Л^пр, ^лр
в функции от одного параметра Fi и
гем самым связывает их. При
f,=-L
при
•¦А^пр = 0. Л1„р = Л1п,ах =
Фиг. 545
=.2a^^Z=^o,W,
F, =0
•Л1пп=0. iVnp = Л^шах = <'tF.
п ^ ,.гт г- пячмевами bxh можно вывести
Для прямоугольного сечения с размерами с/^ч
формул (25.5) следующее соотношение:
из
iM,
пр
М„
I Nrnax I
(25.6)
Если
^ ^„„гг-я ИЯПОИМеП, СОЛИ А/пр =0,1 ОЛ/щах, ТО
М ¦¦ оЕ^'^м''"^'' '"-"/^ -0 2Т' ?=0.^6 >Wn,ax. в этих случаях
'"пр=0.99 М„зх; при Л^пр=0.2 ^"«••- '„"^м шаонире не зависит от про-
^«ожно считать, что момент в пластическом шарнире
Дольной силы и равен Mm» •
4?7
§ 25.7, НЕСКОЛЬКО ЗАМЕЧАНИЙ
Те расчеты, которые изложены в предыдущих параграфах данной главы
весьма неполное представление об обширном и важном разделе современной ' ^^^
тельной механики, посвященном анализу ргботы сооружений за пределом уп ^^^^^
и выяснению их несущей способности. ^^^РУгости
В теории расчета балок по их несущей способное^ приходится приник
внимание не только нормальные напряжения, но и касательные; учет послелн ^^^ ^^
вает снижение предельных изгибающих моментов^. ' Дних вызы>
В расчете рам необходимо рассматривать такие предельные состояния
которые обусловлены совместным действием изгибающего момента и пролол „ «'^^"^й,
Этому сложному способу нагружения отвечает не одно возможное пор при?" ^"•"^^•
стояние, а целая область таких состоянии, обозначаемых термином iiun^n^ ^^'
mapHifp». «:^рмином «пластический
При расчете ферм по предельному состоянию возникает осложнение о/^
ное возможностью потери устойчивости сжатых стержней, еще не ESrirruv ''^'''"-
кого состояния по прочности. достигших предель-
Многократное загружение и разгрузка статически нeoпDeпcлимктv п„.
же кХи^и^ р7^Гп=Йк I oS-r—«« =иТ?Х^„е„ие .к-
1954'г")'1о;Гс и=нte'c''к?льr=^^^^^^ стержневых сисгем. (2-е и,л
в^^о^шРрафии проф. А. А. ГвоздевУГв1н"иге проТлТ Р^аГц^^^^ "°"«^ «^"™
ного^р^внов^?С?р?й;здГ Ш^^^^^^ способное™ конструкций ло методу пр^^ель-
^ов, „зд. 2-е, м!"1пТ"' ^''-"'¦^ сооружений с учетом пластических
свойств матерна-
Глава 26
РАСЧЕТ СООРУЖЕНИЙ НА УСТОЙЧИВОСТЬ
§ 26.1. ЗНАЧЕНИЕ РАСЧЕТА НА УСТОЙЧИВОСТЬ
Известно, что равновесие может быть устойчивым и неустойчивым.
В первом случае система, отклоненная случайными причинами на малую
величину от положения равновесия, возвращается в первоначальное по-
.1ожеиие после устранения этих причин; во втором случае отклонение
может продолжать расти.
В строительной механике специальное внимание привлекает к себе
вопрос об устойчивом или неустойчивом равновесии геометриче-
ски неизменяемых систем, находящихся под действием нагрузки.
Будь они сделаны из абсолютно жесткого материала, они никогда не
могли бы потерять равновесия. Понятие о неустойчивом состоянии отно-
сится здесь к деформациям: при известной величине внешних сил
возможно такое явление, что ничтожное увеличение нагрузки будет вы-
зывать неопределенное или во всяком случае недопусти.мо большое
возрастание деформаций. Нагрузка, дающая такой эффект, носит назва-
ние к ритическо й. Во многих случаях потеря устойчивости харак-
теризуется так называемым раздвоением формы деформаций. Так, на-
npHiMep, прямолинейный центрально сжатый стержень, до того как на-
"Паузка Достигла критической величины, имеет только прямолинейную
форму равновесия, а при действии критической нагрузки может иметь
^^к прямолинейную, так и криволинейную форму; круговое кольцо,
•ужатое гидростатической нагрузкой, при критическом значении послед-
^и Может иметь как круговую, так и волнистую форму и т. д.
Tin ^^о^^^^^^о подчеркнуть, что потеря устойчивости может иногда
сж^"^^!*™ и при небольших напряжениях. Например, длинный, гибкий
^ атый стержень может выпучиться при сравнительно небольших сжи-
ппя^^^^ Напряжениях. Разумеется, после того как он потеряет свою
f^p '^^•"^^^ейную форму, напряжения могут в нем быстро возрасти, что
2.^Дет в конце концов к разрушению стержня.
1отеря устойчивости служила причиной многих крупных катастроф,
а ^^^^одивших с различными конструкциями в процессе их возведения,
-...^^^^^^ и в процессе эксплуатации'. Поэтому вопросам расчета соору-
*»а ^'^"^P^^Hbie данные об этом приведены в книге д-ра техи. наук Ф. Д. Д м н т р п-
^РУшения инженерных сооружений», М., 1953.
т
жений на устойчивость посвящена обширная теоретическая литерагур.
Г многочисленные экспериментальные исследования во всех стра^
Работа продолжается и в настоящее время; еще далеко не все доведено
до вполне удовлетворительного состояния. Однако в XIX и в особен-
ности в XX столетии теория расчета сооружении на устойчивость полу-
чила большое развитие; главным образом это относится к приближен-
ным методам расчета.
В настоящей главе мы ограничимся рассмотрением немногих приме-
ров плоских стержневых систем с прямыми стержнями, притом таких
в которых потеря устойчивости характеризуется раздвоением формы
равновесия. Те случаи, при которых стержень еще до наступления кри-
тического состояния теряет прямолинейную форму, например случаи
внеузлового загружения рам, внецентренного сжатия колонн и т. п.,
несмотря на их важность, здесь вовсе рассматриваться не будут. Точно
так же мы не будем рассматривать здесь вопроса о потере устойчи-
вости за пределом упругости, несмотря на большую практическую важ-
ность этого вопроса. Мы ограничимся изучением явлений потери устой-
чивости в упругой области.
Интересующихся вопросами устойчивости мы отсылаем к специаль-
ной литературе: А. Ф, Смирнов, Устойчивость и колебания сооружений,
М., 1958; Я. А. Пратусевич, Вариационные методы в строительной меха-
нике, М., 1948; Н. В. Корноухов, Прочность и устойчивость стержневых
систем, М,, 1949; Н. К. Снитко, Устойчивость стержневых систем, М., 1952:
С. Д. Лейтес, Устойчивость сжатых стальных стержней, М., 1954;
А Р. Ржаницын, Устойчивость равновесия упругих систем, М., 1955
С. П. Тимошенко, Устойчивость упругих систем, изд. 2-е, М.. 1955;
Н. Хофф, Продольный изгиб и устойчивость, М., 1955, и др.
§ 26.2. О ТОЧНОМ И ПРИБЛИЖЕННОМ РАСЧЕТЕ
Точный расчет сравнительно редко применяется, так как трудность
его резко возрастает с увеличением сложности сооружений. На практике
приходится пользоваться почти исключительно приближенными метода-
ми. Приближенное решение, конечно, не обладает всеми свойствами
точного решения; в той или иной степени оно от них отступает. Цля
того чтобы построить хороший приближенный метод, нужно в его осно-
ву положить свойства строгого решения, но продумать приемлемые
ul^Il^^T^^ ^1 ^™^ свойств или, лучше сказать, приемлемое смягче-
ние требований. ^
cnrln^uu^ решение всегда исходит из рассмотрения деформированного
и^-гп системы, находящейся в критическом состоянии. Составля-
оавно mfrT".!!^ Р^-'.иовесня системы. Число независимых уравнении
ь гЬппм. V? c^n^llieH свободы. Условия равновесия могут записываться
Lfx пя^^'^^"^"""и''"^"¦'°''' уравнений проекций, уравнений виртуаль-
циальнойч».п; ^- «^"° используется свойство прЬизводной от потен-
ции равновесия™ °^Р""^^'^^^« ^ "У-"ь. когда система находится в состоя-
неу^тойТомГ t°"°^"™ отвечает минимум потенциальной энерги»-
т1ЕаТьной J~''f''."""У^' безразличному-нулевое значение. Под по
генциальнои энергией понимается выражение
2 ^J Ej '^tLj -щг^
+ iSJ^-SPA-.r-VPA. „If,"
430 ' fc
'' , сУ«"аР«1" Р"!'"" внешних и внутренних сил. совеошаема» п„»
;Злг/ро"сГ ^р^Гр"^'гри^^тГи;;^.г„??оГ'''™ ^^'^=''"
5 26.3 ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ НАГРУЗКИ ДЛЯ СИСТЕМ
ОКОНЕЧНЫМ И БЕСКОНЕЧНО БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Рассмотрим систему с двумя степенями свободы, представленную на
фйГ. 546. Она состоит из трех абсолютно жестких стержней, связан-
ных между собой двумя упругими шарнирами. Реактивные моменты
возникающие в шарнирах при взаимном повороте их элементов на угол
равный единице, обозначим соответственно через г,, и Ггг. В таких усло-
виях находится, например, колонна, имеющая два упругих, недостаточно
жестких стыка.
Будем считать, что стержень получил бесконечно малую деформацию,
характеризуемую углами а,, а^, и в этом состоянии находятся в равно-
весии. Что касяется угла ад, то он определится из условия равенства
нулю горизонтальной проекции ломаной оси:
/а, -f/ig + 1ч = О, или Од = — (а, ¦+- Og).
Напишем, что моменты внутренних сил в шарнирах равны моментам
внешних относительно центров переместившихся шарниров:
Гц ih — "г) = flh и Ги («2 — яз) = Я (я, -f CTj).
После исключения угла «8 эти два однородных уравнения примут вид
(Г„ — Pi) а. — Г„а2 - 0; | ^26.2)
(г22 - Р1) °. + (2Г22 - Я) «2 = 0.
Они удовлетворяются, во-первых, при o^i—^z =0; во-вторых, при об
ращении в нуль детермината, т. е. при
/¦ц — Р1 — ''и
r^j-P/ 2/-22-Я
D
или
= 0.
/2/52 _ 21 (г„ + /-га) Р + Зг„Г22 == 0.
Последнее уравнение, квадратное относительно Р, позволяет найти
Лва значения критической силы. При обращении в нуль детерминанта
система однородных уравнений, как известно, перестает быть незави-
симой. В таком случае написанные выше два уравнения фактически
"Ревращаются в одно; из него определяется отношение -^, т. е. форма
tJOTepH устойчивости: абсолютная величина углов <'i, «2 остается неопре-
деленной. Таким образом, система имеет две критические силы и две
оответствующие им формы. j, „ „„
Мы решили задачу, составив уравнение равновесия деформирован-
ого бесконечно близкого состояния системы. ^,.^^„
-Другой путь решения состоит в том. что для бесконечно близкого
^формированного состояния системы составляется выражение потен-
•^иальной энергии? и ее частные производные по независимым парамет-
431
рам перемещения приравниваются нулю, В данном случае потенция
ная энергия упругих моментов в шарнирах равна —Гц (ог^-^-а \2
— f22 i^z — ч)^у а потенциальная энергия силы Р равна —рд
А — вертикальное перемещение точки ее приложения, т. е. разнос
между длиной стержня и длиной его вертикальной проекции: ^^
Д ^/(1 —ccscfi )+ /(1 —C0sa2)+/(1—С08аз) =
\ 2 ' 2 ' 2 )
Вследствие малости угла а можно сделать подстановку sma =
Тогда ^ ^¦'
Итак:
^ = 4- '-II («1 - ЧГ + ~ г,, (а, - a,f - -L Я j; ,2 .
Условие критического состояния
ди _
^^0; -^ = 0. (26.3)
или после исключения
(^1 + /-22 - 2Я) а, + (- г,, + 2г22 - Р1) 'J = 0;
или
(- /-11 + 2г,2 - я/) а, + (г,, + 4г,2 - 2Р1) а, = О.
Последние два уравнения не совпадают тождественно с уравненй5ьми
(26.2); они в данном случае выглядят несколько сложнее. Однако легко
убедиться, что обе системы уравнений эквивалентны, имеют одинаковый
детерминант D и приводят к одному и тому же квадратному уравнению
для критической силы Р.
Легко показать, что если бы мы, исходя из деформированного с^
стояния стержня, характеризуемого углами а^ и oig, приравняли нул
суммарную работу силы Р и упругих моментов на бесконечно ^^^ '^^
перемещении, вызываемом вариацией (приращением) оа^, затем на пер
мещении. характеризуемом вариациейoag, то получили бы те же уР^^
ния (26.3). ^ ^зр.
Если речь идет об устойчивости гибкого стержня, который "Р^'^^^^о
ляет собой систему с бесконечным числом степеней свободы, то ^^\^^q.
бесконечного множества алгебраических уравнений, отвечающих > ^^
ВИЯМ равновесия каждого элемента dx, можно написать одно ^^^J^^т-
сколько) дифференциальное уравнение. Оно будет однородным, ^-^ ^рн-
ворение граничным условиям приводит к трансцендентному хара
стическому уравнению для определения критической силы.
432
Для примера решим задачу об устойчивости прямого стержня по-
стоянного сечения нагруженного на одном конце сжимающей пХоль-
i силой Л^. Составим уравнение равновесия для деформировто
^!тояния, отвечающего действию критической силы V.^^ hCL^^^^^^
разрез в произвольном сечении, имеющем координаты х, у (фиг 547)-
бесконечно малый угол наклона оси можно принять равным его тангенсу
dy ,
^ е. величине— =у .
Поперечная сила на верхнем конце равна Ny'^^Q cos у', где Q— по-
перечная реакция на верхнем конце стержня, если таковая имеется. Мы
имеем право принять cos i/'= 1, следовательно, поперечная сила равиз
%'4-Q. На нижнем конце элемента dx поперечная силя равна
Ny' + Q + ^. (Л^у' 4- Q)dx = Л^у' + Q + Ny4x,
dx
^•^^^Довательно, погонная поперечная нагрузка на элементе dx равна
%''. Отсюда — уравнение равновесия
3 при ?/=const
EJy^ + Nf ^ 0-
Интеграл этого уравнения
у = Л^ cos ах + Az sin ах + А^х + А^,
где
Продифференцируем уравнение (26.5) последовательно по х
у' = <р = —/liasinax+ Л2ас08ал:+ Лз, 1
_ EJy" =M^EJ (Л^ «2 cos ах + Ласс^ Sfn ах), |
с /л.'// __ л —. Р7 (— А, а» sin ах 4- А^а^ COS ах). ]
— EJy
28 И. м. Рабинович
— ivi =^ i-««» v' *1 "^ V.VW —-.w , - ^
= Q =:?J(—Л, a8sinaA:4- А^о
(26.4)
(26.4'У
(26.5)
(26.5')
(26.6)
433
Отсюда при
или
х=0
= A^oi + As]
s
A,=
Mo
Qo
"^4 ""* ^0 EJa^
Лз = ?о —
?/a2 '
Подстав1им эти значения постоянных, выраженные через начальные
параметры г/о,?о, Л1о, Qo в его производные:
Qo
EJa^
{ax — sinccx);
?-=?o —
?/a
Sin ccX -
^(1 —cosa;c);
EJa^
M = Mo COS a;c + — sin ад;
Q :^ Qo COS cf.x — Mo cc sin а>:.
(26.7)
Пусть, например, стержень шарнирно оперт по концам, т. е.
Уо = У/ = 0, Мо = М^ = 0.
Из (26J) имеем
^ а
Эти два однородных уравнения могут иметь отличные от нуля значения
?о> Qo только при условиях, если их детерминант равен нулю:
I —
О
а/ — sin а/
sin а/
а
= О, или
/sin а/
= 0,
Г. е. при since
,-с, .,-ь.,/f-f.
или
N =
kht^EJ
/8 '
Зададим теперь другие условия: пусть один конец свободен, а ДРУ^
упруго защемлен. Граничные условия, отвечающие свободному kohU)'»
можно записать так: ^о==Мо=0. Для защемленного конца можно з^^
писать одно граничное условие: Mi =r(pi, где г — жесткость заде-"^*''
одно условие равновесия:
Mi= Nyi = EJa^yi.
434
На основании ^(26.7) эти два уравнения принимают вид
ИЛИ
[sin al г п
"T~+'^7^(l-COSa/)]Q,==0;
Детерминант этой системы равен
EJol sin а/ — rl cos а/.
Приравняем его нулю
Нужнонайти наименьший корень а этого трансцендентного уравнения
При абсолютно жесткой заделке г=сю, ун^ьнсния.
2 "^ 4/2 •
При отсутствии заделки
г = О, а = О, Л^ - 0.
??/JS?r^" заделке абсолютно жесткого консольного стержня
§ 26.4. ПРИБЛИЖЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ
КРИТИЧЕСКОЙ СИЛЫ ДЛЯ ПРЯМОГО СТЕРЖНЯ
Основным источником для упрощения задач об устойчивости упру-
их систем, обладающих бесконечным числом степеней свободы, являет-
я Замена их системой с конечным числом степеней свободы (иногда
даже системой с одной степенью свободы). Например, упругую линию,
^^^РУ^ принимает ось стержня при действии критической силы А^^ при-
•^иженно представляют в форме
у (х) = а^ у^ (х) + с^У2 W + Ь ^пУп W, (26.8)
гоа ^^ W» У2 (х), ..., уп(^)—заданные функции, удовлетворяющие
*р7^"^^"Ь1м условиям и отвечающие представлению о возможных формах
ни ?9^^^^^ стержня. Чем больше членов стоит в первой части уравне-
тел ^ ^'^^' "^^^ точнее получается результат, но вместе с тем значи-
ьно возрастает трудоемкость расчета,
бли ^^^^^^^^^^^ Дь «2, ..., cifi подбираются так, чтобы решение при-
зад^^^'^о удовлетворяло основному дифференциальному уравнению
Пусть это дифференциальное уравнение имеет вид
28*
435
Оно должно удовлетворяться в пределах длины стержня при любом
значении переменной х, поэтому для любой функции <?{х), имеющей
в тех же пределах конечные значения, будет тождественно удовлетво-
ряться равенство
^F{x,y,y',y",...)^{x)dx = Q.
О
(26.9)
Приближенное решение довольствуется тем, чтобы обратить уравне-
ние (26.9) в тождество не бесчисленное множество раз, а только п раз,
т, е. не для всякой функции ср(х), а лишь для п выбранных функций.
В качестве таковых выбираются те же п функций, которые выбраны
для разложения (26.8). В итоге получаются п независимых линейных
алгебраических уравнений для определения параметров aj, «2, ,.., а^:
^F(x, >;,у', ...)yjix)dx = 0{i - 1,2,... ,n). (26.10)
о
Такова идея метода Бубнова — Галеркина, который является одним
из лучших приближенных методов.
Для примера определим с его помощью критическую силу для сжато-
го прямого стержня постоянного сечения.
Функцией F Служит левая ^часть дифференциального уравнения
(26.40.
Итак:
^(EJ/'' + Ny')y,dx = 0
)
или
k=n
k=n I
EJ у ^a^yi'^y^dx + N "? U^y^^y^dx^^O;
k=l 6 k=l 0
(26.11)
оитР^^оГ система уравнений является линейной и однородной отно-
ни! Hv>KH"n ^.«"^^^P"" ''*• ^'''^ ''°^° "^^«б" получить нетривиальное реше-
ние нужно обратить определитель системы в нуль
ним KOHu^^r„f.? "Р"''^Р^ стержень с абсолютно защемленным верх-
жень ?и™пй Л Р"°^"^Р™''^' ™^™" (Ф'«г. 548, а). Заменим стер-
кривую ^ кпгпп. """"^ "епенью свободы и примем за упругую линию
пГе'р;гн'г;й'^Гг?ЙкоГ(фип мТ")Г" ''"•^" ^"•"°""°« Р—Р-«
у,=-М^
48EJ
(З/^лг —5/д^+2л*).
436
Для упрощения выкладок целесообразно принять
д = 48EJ,
Система (26.11) превращается в одно уравнение
или
EJa, f y^'y^dx + Na, f ylydx - 0
(26Л2)
Л^,
кр
7,2>35?/ _^ ?/
12/2 ^2
Этот результат превышает точный на 4,01%.
Если бы мы применили систему с дву-
мя или больше степенями свободы, то по-
лучил1И бы более точный результат.
Заметим, что, принуждая стержень
деформироваться по заданным кривым > ^
Уь У2 и т. д., мы как бы вводим дополни- ^ '
тельные связи, поэтому, естественно, при-
ходим к несколько повышенному значе-
нию критической силы.
Приближенное уравнение (26.12) мо-
жно вывести другим путем — приравняв
нулю полную потенциальную энергию
изогнутого стержня
I
U^—Ej{{ylfdx — N/!!i = О, (26.13)
yV
0
U-M
Фиг. 548
где А — вертикальное перемещение
верхнего конца.
Но работа внутренних сил балки равна работе внешних сил, т. е.
/ / I
^EJ f {y]fdx - -^^ J^y, dx==--^ EJ^y\^y,dx,
Кроме того:
Д= Uds — dx)^ rd5(l_cos/)= \dS'2s\n^^^
= f<fa-2(i)'-|-J(yT<i-
Hi ак:
0 *o
^ Произведение Л/А можно заменить работой изгибающих
^^1 на взаимных поворотах у\ dx\ тогда второй член примет bi
/
о
*^ вместо уравнения (26.14) получится (26.12).
моментов
примет вид
4^
§265. ПРИМЕР ПРИМЕНЕНИЯ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИИ
Зададимся упругой линией стержня, сжатого критической силой N
в форме
i = n
у(х)= Yi 0^/yfW-
/=i
Дадим каждому из параметров а,- поочередно приращение da,- и
приравняем нулю сумму работ внешних и внутренних сил (т. е. прира-
щение полной энергии U) на каждом таком перемещении. После сокра-
щения на da^ получим
dci dCi ^ dai ^ > > > /
Рассмотрим для примера двухпролетную неразрезную балку с проме-
жуточной упруго-смещающейся опорой, сжатую продольной силой Р
(фиг. 549). Жесткость опоры обо-
значим, через Гц. Полная потен-
циальная энергия складывается
из элергии, ютвечающей изгибу
стержня, деформации опоры, и из
работы силы Р на продольном
перемещении конца В.
~'uy%-~-f^j(yrdx,
следовательно:
VC м'""
Пусть
|^=^J^^..+,,/^^« ,.|:...о.
Тогда
^ ~ I
— = —У"= —а sin ""^ 4^ ^'^^ • 271ЛГ
EJ ^ /2 ^1 ^^п — + -_ а^ sin — ;
i
6 ^ о
t I
О о
^-°.^ 1:='^ If-»-
Аналогичный вид имеют производные по а^. Итак;
^22|г2
438
Вместо двух совместных уравнений в данном случае, как видно, по--
уцаются два самостоятельных.
Из первого уравнения при ai^ О получаем
^кр f .
/^ ' Я2
При /'ii/= — • —^^ =14,8 *-^^ значения сиды Ркр вычисленные
(а)
Для того чтобы при ЭТ0.М второе уравнение также обратилось в тож-
дество, необходимо положить а2=0. Очевидно, что эта критическая си-
ла отвечает искривлению по одной полуволне. При гц = О получается
Р —J^^
у е. в этом случае балка превращается в однопролетную. При Гц ^ О
значение Ркр растет с увеличением жесткости Гц и обращается в Ркр =
=со при Гц^оо. Следовательно, при Гц^оо потеря устойчивости с
искривлением по одной полуволне невозможна.
Из второго уравнения получается при «2^=0
Для того чтобы при этом и первое уравнение обратилось в тождест-
во, необходимо положить ai = 0. Очевидно, что это решение отвечает
обратно симметричному искривлению по двум полуволнам, при которОхМ
средняя опора остается неподвижной. Расчетной критической силой
является меньшая из двух.
ПО формулам (а) и (б), совпадают. Это значит, что при rii/>l4,8—^
первая форма потери устойчивости имеет две полуволны, как в нераз-
n^EJ
резной балке с жесткой опорой: при rii/<;i4,8—^первой формой слу-
жит одна полуволна.
Задача легко решается точным методом — путем интегрирования диф-
ференциального уравнения равновесия. При этом получается коэф-
фициент 16 вместо 14,8.
§26.6. КРИТИЧЕСКАЯ СИЛА ДЛЯ СОСТАВНОГО СТЕРЖНЯ
Рассмотрим случай продольного изгиба стержня, состоящего из
двух поясов, связанных между собой простой треугольной или раскос-
ной решеткой (фиг. 550). Концы его будем считать шарнирно опертыми.
Особенность работы такого стержня по сравнению со стержнем сплош-
ного сечения состоит в том, что в составном стержне значительную
роль играет взаимный сдвиг поясов, обусловленный деформацией
решетки.
Для упрощения расчета примем, что ось стержня изгибается по си-
нусоиде у^а sin —; более точное решение потребовало бы принятия
нескольких синусоид.
Как было показано в предыдущем параграфе, для синусоиды по-
•'^Учается
о
При вычислении работы внутренних сил на возможном перемещении
необходимо .иметь в ваду, что в стержне с прямой осью при действии
центральной продольной силы решетка не работает, она вступает в
паботу только после того, как ось примет криволинейную форму.
При возможном перемещении, отвечающем приращено^ю оа, изме-
няется кривизна оси, но не меняется ее длина, поэтому работа первона-
чальных усилий, имевшихся в поясах до выпучивания, равна нулю;
работу совершают только те поясные усилия, которые возникли благо-
даря искривлению стержня. Эти усилия найдем, разделив момент Р^^у
внешней силы Ркр на плечо /г. Но у^а sin^, откуда усилия в поясах
N =.р —sin — - Целесообразно считать, что усилие на протяжении
п кр ^ /
каждой панели пояса остается постоянным, а за х принимать абсциссу
моментной точки рассматриваемого элемента пояса. Решетка работает
dM ГУ п лх
на поперечную силу составного стержня, которая равна—=Укр^ —cos—*
Отсюда усилие в раскосах.
Л^о = Pkd^ — • — COS — ,
где за X можно принять абсциссу середины рассматриваемой панели.
Наконец, усилие в стойках Nc=Q = Pkp^ — cos —.
Уравнение виртуальных работ напишется так:
+ <.I(P.fcosf)=i-P.,^.0,
С
где первая сумма относится к поясам, вторая — к раскосам а третья —
к стойкам. Отсюда
Pj^p=: ^ . ti /о^: J 5)
" P с '
KH ^^IZ°^° '^^'^^" разобрать, какую роль играет податливость решет-
ки, заметим, что по мере уменьшения площадей F, под знаком S и 2
эти две суммы стремятся к бесконечности, а величина Р.„—к нулю.
гии°Ргк^Г;.Г^'Т^™^ ^¦"''^ площадей влечет за собой увеличение кри-
абгппЗ» v^l ""^' "°™Р'''' достигает своей наибольшей величины при
взаимш.й . п" ^^°^да"^"ии «боих поясов, устраняющем всякий
взаимный сдвиг. При этом нужно положить для элементов решетки
' ,==оо , тогда получится
р "и
"* кр— ¦ • -
или
440
;1ля того частного случая, когда оба пояса имеют по всей своей
длине постоянное сечение, это выражение совпадает с выражением
критической силы для сплошного стержня, момент инерции Зрого п^
,Р„ сумме моментов инерции обоих поясов относите^ьн^ нУральной
оси'.
Можно поставить вопрос о замене расчета составного стержня рас-
четом некоторого эквивалентного ему в смысле устойчивости сплошного
стержня. Если момент инерции последнего будет /о. то для критической
силы получится выражение: Я.р-^»; вся трудность задачи состоит.
разумеется, в нахождении величины /о. кото-
рую можно назвать «приведенным моментом
инерции» сечеаия составного стержня.
б)
-Л
1
Фиг. 551
Мы нпдели, что величина критической силы зависит от работы внут-
ренних сил системы при заданной форме упругой линии. Но работа
внутренних сил численно равна работе внешних сил. Вместо того чтобы
задать непосредственно упругую линию, мы можем задать ту попереч-
ную нагрузку, которая ее вызывает; так мы поступили, например, в
^ ^6-4. Если мы возьмем несколько балок одинакового пролета, но с раз-
ньши моментами инерции Л то для получения одной и той же упругой
инии придется брать тем большую интенсивность нагрузки, чем боль-
^^ величина /. Наоборот, при заданной нагрузке прогибы и работа
УДут обратно пропорциональны величине /.
Отсюда вытекает простой экспериментальный и теоретический прием
^^р^^-^^ния приведенного момента инерции /о и критической нагруз-
^кр.
^. У^'^ь требуется определить критическую силу Ркр (фиг. 551, а) для
noinf^"^^^ стержня. Нагрузим его поперечной нагрузкой (фиг. 551,6),
Q ^ ?-^^^^^й для ожидаемого характера деформаций, причем на схемах
Ten ^"^Рные устройства должны быть одинаковыми. Опытным или
р^^^'^'и'ческим путем определим перемещения всех узлов (в случае тео-
ф^ J^CKoro подсчета нужно рассматривать составной стержень, как
сил- После этого подсчитаем работу внешних сил или внутренних
Сил' "^^^^^м ее Wo. Одновременно подсчитаем работу тех же внешних
,.^_^^^я сплошной балки того же пролета, имеющей произвольный
**^- Ьлейх. Теория и расчет железных мостов, 1931. стр. 171.
441
г. .г. т.«^гтмп Г поперечного сечения; назовем ее W, Тогда
liT.Z: чТ^ныГГхавнГс?ержень эквивалентен в смысле жес.
кости балке сплошного сечения с моментом инерции /о. где /о=/--.
Критическая сила Р.р может быть найдена как для сплошного стержня
С моментом инерции /о.
S 26 7 ПОНЯТИЕ О РАСЧЕТЕ РАМ НА УСТОЙЧИВОСТЬ
МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Приближенные методы, изложенные в предыдущих параграфах, поз-
воляют решать такие зада^чи, которые по своей сложности недоступны
решению по точному методу. Однако приближенный метод имеет свои
недостатки главным из которых является именно его приближенность;
причем как уже указывалось, он дает преувеличенное значение крити-
411
У6
77?
Фиг. 552
Фиг. 553
ческой силы. Кроме того, он нередко оказывается довольно громоздким.
Точный метод гарантирует получение минимальной критической силы и
точной формы потери устойчивости. К сожалению, точный метод все
еще слишком громоздок, и его широкое практическое применение остает-
ся делом будущего.
Мы ограничимся поэтому самым сжатым изложением хода точного
расчета рамы с прямолинейными стержнями, нагруженной узловыми
силами. Нагрузку будем считать направленной так, что при значениях
сил, меньших критического, все стерл<ни остаются прямолинейными.
В критическом состоянии прямолинейная форма перестает быть устой-
чивой, и становится возможной искривленная форма равновесия. JX^^
определения этой формы необходимо разыскать обычные неизвестные
метода деформаций — углы поворота узлов и их линейные перемеше-
ния. При этом в целях упрощения расчета мы будем пренебрегать про-
дольными деформациями стержней^ Например, на фиг. 552 неизвестны-
ми будут шесть углов поворота узлов и два линейных смещения ярусов.
Основная система будет иметь шесть заделок в этих узлах и два опор-
ных стержня, препятствующих линейным смещениям.
Канонические уравнения составим для деформированного
состояния рамы, которое наступит при критическом значении нагрузки-
* При расчете многоэтажных (высотных) каркасов такое допущение неприемлем •
См. проф. А. И. Сегаль, Высотные сооружения» Стройиздат, 1949.
442
внешняя нагрузка, приложенная в узлах, не вызовет в названных до-
^;,„ительных закреплениях основной системы никаких реакций, поэто-
Jy уравнения получаются однородными:
''21^1 "Г ^2iA2i
+ r^rZn =- 0;
Гщ^г + Г;,222 Ч h r^^Z^ = 0.
(26.16)
Здесь Zu ^2, ..., Zn— неизвестные углы поворота и линейные сме-
шения. Смысл уравнений нам известен из предыдущего изложения ме-
тода деформаций: он состоит в том, что суммарная реакция любой до-
полнительной связи равна нулю.
Для того чтобы эта система имела решение, отличное от нуля, т. е.
для того чтобы 'рама, кроме прямолинейного, могла иметь уравнове-
шенное деф о рм и р о в а н н ое состояние, необходимо чтобы опре-
делитель системы (26.16) был равен нулю:
D =
= 0.
(26.17)
Таким образом, точ1ное решение задачи требует вычисления коэф-
фициентов г,.д, и затем решения уравнения D = 0,
Между коэффициентами г,-^ системы уравнений (26.17) и коэффи-
циентами г.д, обычных уравнений метода деформаций существует корен-
ное отличие, вытекающее из самой природы, рассматриваемой задачи.
В обычных уравнениях коэффициенты г^д, не зависят от внешней на-
грузки: нагружена ли система или нет, — для того чтобы вызвать в дан-
ном закреплении данное перемещение, всегда требуется одно и то же
усилие. В этом и состоит закон независимости действия сил. В задаче
об устойчивости мы рассуждаем иначе: мы принимаем во внимание те
изгибающие моменты, которые возникают от продольной силы после
¦того, как стержень принял криволинейную форму; поэтому для единич-
ного поворота или смещения конца стержня, нагруженного продольной
силой, требуется иное усилие г,-^ , чем лля ненагруженного. Эти коэф-
фициенты являются функциями продольных сил. Перейдем к их вычи-
слениюЧ
На фиг. 553 показан стержень, сжатый двумя равными противопо-
•"ожными силами N; на схеме а он изображен прямолинейным, а на
^>^еме б —в состоянии криволинейном. При этом искривлении сила Л^
^«жет несколько измениться, но так как мы считаем отклонение от
^^Рвоначальной формы бесконечно малым, то приращением АЛ^ по
^^Равнению с N можно пренебречь. При искривлении возникнут на кон-
"^^^ реактивные моменты М^^, М^^ и поперечные реакции (?^^, (?^^.
*^з условия равновесия ясно, что
^АВ ^ВА -' — /
*Попи? дальнейшем изложении мы будем следовать книге проф. Н. В. Корноухов
пучность и устойчивость стержневых систем». М., 1949.
Дифференциальное уравнение изгиба имеет вид
d'x^
Введем обозначение
Л72 ^ jtW
EJ ~~ Р^
t^.
(26Л8)
(26 Л 9)
Параметр t^ (отвлеченный) представляет собой увеличенное в ir^ п^.^
отношение продольной силы N к эйлеровой критической силе——
Интеграл дифференциального уравнения (26Л8) имеет вид
у = Asm-J- + В cos— ^^
А^
О-пределив постоянные Л и В из граничных условий .и сделав не-
которые преобразования, получим следующие формулы:
(26.20)
I ¦-=
Здесь
EJ ^ t
1 ' ""^ 2igt
»+р-|.^
tgt-t
2tg-f-^
^
t — sin t
2 sin ^ t
2tg-
•--t
<з
(26.21)
2tg—— <
^ 2
обь"?ого''р:счет?знач?н*ия""'"'" "РИ««^^ают следующие известные из
а =2; р = 1; а + р = 3; у = 6.
'.аех5'1^„7оГв^,е^;,7&^^^ и величина / полу-
и^ =
\N\ /2
(26.22)
где|Л/| -абсолютная величина, получим вместо формул (26.21)
и
ihtt-
- и
2 th и и
т-^ —
2sha
«3
« — Shu
2.hf-„
1
2 и
2.h--„
(26.23)
444
J
в том случае, когда стержень АВ имеет на конце В шарнир фоо-
улы (26.20) переходят в следующие: ^ t'» ^ н
гае для сжатого с^гержня
«=1^ГГГ' ^ = "-^' = 1^737' (26.25)
а для растянутого стержня
\\\и — а' i\\u~~u
(26.26)
Если продольное усилие N=0, то а=у=3.
Формулы (26.20) —(26.26) показывают, что реактивные моменты и
реактивные поперечные силы, .возникающие на концах стержня, являют-
ся трансцендентными функциями продольной силы Л^ и в то же время
линей'НЫМи функциями перемещений ср^, ?^, ^^ь-; реакция, вызываемая
каждым из этих перемещений, не зависит от остальных перемещений.
Это дает нам право писать канонические уравнения (26.16). Коэффи-
циенты r^f^ сохраняют свойство взаимности: г^^ =^л/-
§ 26.8. ПРИМЕР
Определить критическую силу Р для симметричной рамы, изображенной на
фиг 554.
Неизвестными являются углы поворота о,, og и горизонтальное перемещение
S ригеля.
Для левой стойки Л^—Я; для остальных стержней Л^=0. Поэтому
/Ph^ ^ fPh
Введем обозначение:
/2 EJ2fi
^k.
Канонические уравнения можно записать в следующем виде:
''11?! + ''i2?2 + ''13^ = О ;
Г21?1 + ''22?2 + ''23^ = о *'
'"31?! + ^"32? 2 + ''33^ = 0.
Раскрывая выражения г и, r^g и т. д., при помощи формул (26.20) получим
{2i\a + 4^2) <fi + ^h^2 - 2^'i (a + P) Y ^' ^ '
2/2?! + 4h + '2) <f2 — 3^1 — = 0 ;
"ЛИ после сокращения ^
(a + 2k) 9i + /fe'f 2 — (a + P) — -- 0;
A.(Pi + 2(*+1)92-3—«0;
-(аЧ-Р)?1 —392-1-(ТГ + 6)—=-0.
445
Приравниваем детерминант системы нулю:
I (а + 2k); « ;
?) =
(а + М
k 2(k+\); -3
-(а+р); -3; (if + 6)
0.
(26.27)
„гчп«,им усавнение второй степени относительно k.
Раскрыв этот Д^т^Р^^^и являетс^яТкГо^^^^^ входит в состав величин а. ?. ^.
Неизвестным в этом Уравнении «/•"«"^^ ;, образом: давая числу t различные значе-
Целесообразно будет "°"J^""; ^.-f^^^^^^ \ Y и по ним из уравнения (26.27) оп-
ния. вычислять '^°°"^^"'f^^.f„'"я Гпосле этого можно будет построить по точкам
КГиГзаГсимо'иТГ. ГизТого графика по заданному значению k найтн требуе-
мое значение tl
Р
Фиг. 554
Фиг. 555
Тем самым найдется и критическая сила Р:
EJi
Так как уравнение (26.27) квадратное, каждому значению t будут отвечать два
значения'^^Тполучим два графика Характер их пР^мерно показан на^^Ф^^^^
Из них ясно, что каждому значению k в свою очередь будут ^^^^^1^ два значениу^
Разумеется, мы должны считать за критическое^ значение t меньшую f J^J^
величин, т. е. ординату нижнего графика; последний получается, когда по заданн-.ы
значениям t откладывается большие значения k. о»5,иРния
Из этого же уравнения (26.27) можно было бы определить н высшие зиачеш
критической силы, так как для аргумента t тригонометрических функции а, р, 7 ^^'у
чается бесконечное множество значений; однако это не представляет практического п
тереса.
§ 26.9. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Задача 'об устойчивости упругих деформаций впервые была введена в' механику
Эйлером! в 1744 г. и с тех пор не перестает привлекать к себе внимание исследова -
лей, занимающихся расчетом сооружений и машин. Она давно вышла за пределы т
рии работы простого стержня и в настоящее время охватывает вопросы У^^^^^^^^их
сложных стержневых систем, пластинок и оболочек (простых и слоистых), ^меюш
любую форму и размеры, любые краевые условия и т. д. Литература по теории усто
чивости насчитывает огромное количество работ. „^
Первое систематическое изучение устойчивости упругих деформаций прннадлеж
Брайеиу2 (G. Н. Bryan). .^
Важным этапом в развитии теории было появление в конце XIX столетия за
чательных исследований проф. Ф. С. Ясинского^, решившего сложную задачу об уст
чивости сжатого верхнего пояса открытых мостов.
^ См. русское издание «Метод нахождения кривых линий, обладающих свойств
максимума либо минимума», Гостехиздат, 1934.
2 Ргос. Camb. Phil. Soc, VI (1888). re:
^ С работами Ясинского по устойчивости можно познакомиться по оже-
Ф. С. Ясинский. Избранные работы по устойчивости сжатых стержней, с "Р^'^д^-^^и
нием очерка проф. А. Н. Митинского о жизни и научно-иижеиерной деятельн
Ф. С. Ясинского. Гостехиздат, 1952.
446
в начале XX столетия ряд трудных задач по устойчивости н. в частности, задача
X х^гтойчивости сжатого стержня на упругих опорах была решена проф. И. Г. Бубно-
^•^1 (1872-1919), акад. А. Н. ДинникомМ1876^1950) и СаусвелломЗ (Southwell).
Энергетический метод расчета упругих систем, раскрывший возможности прибли-
ниого решения труднейших задач, не поддающихся точному решению, был значи-
ьно развит в работе проф. С. П. Тимошенко^ и в дальнейших многочисленных рабо-
тах различных авторов
Замечательный приближенный метод, не требующий вычисления потенциальной
рпгии был предложен акад. Б. Г. Галеркиным^ (1871—1945); этот метод получил
^" яльнейшем широкое распространение в СССР и за рубежом.
^ ^ В СССР вопросы устойчивости привлекают к себе глубокое внимание и подверга-
всестороннему теоретическому и экспериментальному изучению. Имеются крупные
^^^ ижения в области расчета сложных упругих стержневых систем, пластинок, оболо-
'^^к^в области изучения устойчивости за пределом упругости, динамической устойчи-
«пгти устойчивости при больших деформациях и др. Большое внимание привлекают
вопросы и за рубежом. В § 26.1 перечислено несколько книг, по которым можно
познакомиться с современным состоянием вопроса.
» Стооительная механика корабля, т. 1, 1912.
2 Список работ А, Н. Динника см. в книге: А. Н. Динник Избранные труды,
т 1 Киев 1952 См. также акад. А. Н. Динник, Продольный изгиб и кручение, М., 19о5.
'з phif Trans Roy. Soc, London, ser. A, v. 213 (1913).
4 06 устойчивости упругих систем, «Известия Киевского политехнического инсти-
^^^^5 Стержни и пластинки, «Вестник инженеров» № 19, 1915.
г лав а 21
ДИНАМИЧЕСКИЙ РАСЧЕТ СИСТЕМ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 27.1. ВИДЫ ДИНАМИЧЕСКОЙ НАГРУЗКИ
Все расчетные схемы нагрузок могут быть разбиты на две катего-
рии: статические и динамические. К первой относятся такие нагрузки,
которые вообще не сообщают массам сооружения никаких ускорений
или сообщают ускорения, настолько незначительные, что возникающи-
ми при этом силами инерции можно пренебречь по сравнению с осталь-
ными действующими силами. Ко второй категории относятся такие на-
грузки, при действии которых силы инерции играют существенную
роль; таковы нагрузки, появляющиеся или исчезающие внезапно, дей-
ствующие ударным способом; нагрузки, у которых достаточно быстро
меняются во времени величина или точка приложения или направле-
ние. Все нагрузки, которые мы рассматривали раньше, относятся к
статическим.
Основная задача динамического расчета состоит либо в определении
максимальных деформаций и напряжений, вызываемых в данном соору-
жении данной динамической нагрузкой, либо в подборе таких размеров
сооружения, которые обеспечили бы достаточно малые деформации и
напряжения. Первое имеет место при поверочных расчетах существую-
щих сооружений, а второе — при проектировании новых или реконстру-
ируемых сооружений. Промежуточное положение занимает задача
амортизации колебаний в существующих сооружениях.
§ 27.2. СТЕПЕНЬ СВОБОДЫ УПРУГОЙ СИСТЕМЫ
С понятием о степени свободы системы мы уже встречались неодно-
кратно. При анализе геометрической изменяемости или неизменяемости
стержневых систем, а также их статической определимости или неопре-
делимости мы рассматривали эти системы как составленные из беско-
нечно жестких дисков или стержней. При подсчете упругой подвижности
узлов рамы (в методе деформаций) мы интересовались только подвиж-
ностью узлов, не делая при этом различия между упругими линиями и
их хордами. В динамике упругих систем степенью свободы называют
количество независимых геометрических параметров, определяющ^^
положение всех масс при всевозможных деформациях системы^
Именно это число имеет особо важное значение для характеристики
«динамического» поведения сооружения,
448
Гйстема, представленная на фиг. 556, состоит из нескольких масс,
крепленных к абсолютно жесткому стержню, который может вра-
^Рдться вокруг неподвижной точки Л. Независимо от числа масс и пру-
йн она имеет в плоскости одну степень свободы, потому что положе-
не всех масс определяется углом поворота стержня около центра Л.
Система жестких стержней, представленная на фиг. 557, имеет три сте-
пени свободы.
Особого внимания заслуживает система, представленная на фиг. 558,
где две точечные массы помещены на упругой невесомой балке АВ;
несмотря на то, что упругая
линия балки может иметь
бесконечно разнообразные 6^- р -..^^— ^ ц^
формы, степень свободы
равна двум, потому что по--
ложение обеих масс опре-
деляется прогибами в двух Фиг. 556
точках балки. Если массы
не точечные, то положен'ие
каждой из них определяется прогибом и углом поворота, следовательно,
система имеет четыре степени свободы. Если будем считать упругую
балку весомой, т. е. введем ее массу в расчетную схему, то степень
свободы такой системы окажется равной бесконечности.
^ W ^
У/:
Фиг. 557 Фиг. 558
В настоящей главе, посвященной основам теории колебаний, уде-
лено основное внимание системам с одной степенью свободы.
Мы будем считать систему линейно деформируемой, т. е. сохраняю-
щей линейную зависимость между силами и деформациями. Как мы уже
Отмечали выше, в § 13.1 такое допущение практически приемлемо при
условии, что материал является упругим, а изучаемые деформации и
перемещения весьма малы.
§ 27.3. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ И ЕГО ИНТЕГРАЛ
Рассмотрим простейшую модель системы с одной степенью свобо-
^Ь1--массу т, подвешенную на невесомой пружине и нагруженную
^Илой P{i)^ которая представляет собой произвольную функцию от вре-
^^енй^ (фиг. 559).
Назовем жесткостью пружины ту силу, KOTopyjo нужно приложить
^ нижнему концу пружины, чтобы вызвать ее статическое перемещение,
равное единице. Разумеется, что ту же величину имеет и реакция пру-
^*^ны при единичном смещении ее нижнего конца. Обозначим эту реак-
^^ символом r,j. С другой стороны, обозначим перемещение этого кон-
^^^ вызываемое единичной силой, через Вц. Очевидно, что
«^личина S„ является мерилом податливости пружины. В дальнейшем
та пружина будет служить символом любой упругой связи.
Будем отсчитывать перемещения у от того положения массы т, в ко-
тором она находится при отсутствии внешней силы P{t). В этом'поло-
жении натяжение пружины уравновешивается собственным весом тд
массы т. Положительные перемещения у, скорости у' ускорения у'' f
также положительные силы будем считать направленными вниз.
При отклонении массы т на величину у на нее будут действовать
следующие силы: натяжение пружины ГцГ/, сила инерции — т-^ и
внешняя сила P(t)\ что касается начального натяжения пружины и ве-
са mg, то они как взаимно уравновешенные выключаются из рассмотре-
ния. Силу ГиУ называют в теории колебаний восстанавливающей силой
так как она стремится вернуть массу в начальное положение, если по-
следняя отклонена от состояния равновесия на величину у.
Приравняв нулю сумму вертикальных проекций всех
сил, получим
ИЛИ
у" +
Введем обозначение
^1
т
0)2= ^
Фиг. 559
Тогда дифференциальное уравнение примет вид
у" + о)2у—-1р(^)^0.
(27.1)
(27.2)
Интеграл этого неоднородного обыкновенного линейного дифферен-
циального уравнения второго порядка состоит из общего интеграла со-
ответствующего однородного уравнения
у" + (02у =0
(27.3)
и из частного интеграла неоднородного уравнения котопый может
"ча?тГ" ''^""" "' "^---ных'методов/н'апример'метЗ^^
Частный интеграл уравнения (27.2) имеет вид ^ ^ у ^
у = Уо COS (о/ -I 5- sin mt,
где 1/0, у^ —перемещение и скорость в момент ^=0.
Частный интеграл уравнения (27.2) имеет вид
t
у = ( P{u)s\niu{t — u)du =
о
t
= a)8ii f P{u)s\niii{t — u)du =
0
= o) f Уст (w) sin ^{t — ti) du.
(27.4)
(27.5)
450
Здесь через и во избежание путаницы обозначено время, которое из-
меняется в пределах от «=0 до u=t- через у„ (,и)^Ъ^,Р(и) обозначено
перемещение, отвечающее статическому действию силы Р(и)
Все три выражения (27.5) тождественны между собой, так как из
(27.1) следует, что — =ш8ц . В процессе интегрирования величина f счи-
тается постоянной.
Полный интеграл представляет собой сумму выражений (27 4) и
(27.5).
/
У- 1 \
У = Уо COS ш^ + — sin 0)^ + — \ Я (й) sin (О (^ — и) du. (27.6)
о
В формуле (27.6) первые два члена правой части выражают собой
свободные или собственные гармонические колебания, не зависящие от
силыР(0> последний же член выражает собой перемещения, вызывае-
мые силой P(t), Если на протяжении интервала времени от и=0 до
u—t сила P[t^) равна нулю, то остаются только свободные колебания;
если г/о=0 иг/о =0, то остаются только вынужденные перемещения.
Формулы (27.5) можно истолковать так: при уо = У'о =0 в любой
момент перемещение у равно статическому перемещению, которое полу-
t
чилось бы от силы (ОJ Р (и) sin iiy{t — u)du.
о
Продифференцировав выражение (27.6) по параметру t, найдем об-
щее выражение скорости
t
у' = — (оу^^ sin (of + Уо cos (of+(i)2S^^ j P (u) cos w{t — u) da. (27.7)
0
Выражения (27.6) и (27.7) дают полное решение задачи о движе-
нии, совершаемом упругой системой с одной степенью свободы под вли-
янием нагрузки, изменяющейся во времени по какому угодно закону.
§ 27.4. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИИ СИСТЕМЫ
Собственные колебания системы, как уже упомянуто, выражаются
так:
у =^Уо cos (ot+ —sin 0)^ (27.8)
Если мы дадим времени t приращение Т такое, что
оТ - 2ТГ, (27.9)
(Oi
¦^0 правая часть формулы (27.8) останется без изменения. Отсюда вид-
«о, что Г есть период собственных колебаний, т. е. время, в течение ко-
¦^орого система совершает одно полное колебание. Величина о) носит
название круговой, или циклической, частоты.
Для краткости будем называть ее просто частотой.
Число собственных колебаний, совершаемых в I сек., очевидно, рав-
но ~. Так как из (27.9) следует, что
со = ^. (2^10)
Т *
29* 151
то можно сказать, что круговая частота есть число полных колебаний,
совершаемых в ?т^ сек.
Одна из важнейших задач динамики состоит в определении собст-
венных частот. Для рассматриваемой модели величина (о^ выражается
формулой (27.1), Делая подстановку
а также пользуясь обозначением
где A^-m^o^j—статический прогиб пружины от действия собственного
веса массы т, можно получить следующ.ие выражения для о):
-/'t=/i=/T- <^'-")
Частота собственных колебаний растет с увеличением жесткости
пружины и с уменьшением массы т. Инженер, желающий повысить или
понизить частоту собственных колебаний проектируемого сооружения,
может добиться этого путем изменения либо жесткости конструкции,
либо ее веса, либо того и другого.
Для дальнейших приложений нам понадобится другое выражение
для (О. При свободных колебаниях условимся отсчитывать время t от
того момента, когда колеблющаяся масса проходит через свое среднее
положение.
Тогда у0=^0 и из (27.8) получается
у = — sin iot; У = у' cos Ы
или
Ушах = ^; У„ах = У;=»3'„,,,. (27.12)
Кинетическая энергия массы т непрерывно изменяется в процессе
колебаний и достигает максимума:
'^^^"^"^' = ^ о)2у2 == ^^К (27.13)
где /Стах представляет собой кинетическую энергию массы т в ее сред-
нем положении при той же амплитуде «/max. но при частоте о)=1.
Потенциальная энергия достигает максимума, когда масса т нахо-
дится в крайнем положении; кинетическая энергия в этот момент равна
нулю: она полностью перешла в потенциальную. Обозначим последнюю
через Птах- Легко видеть, что
Пп.ах=-^^1У
L>2
шах'
Приравняем друг другу оба выражения:
Птах = ^'^^^тах-
452
Отсюда
-—-¦ (27.14)
Amax
Формулой (27.14) можно воспользоваться для точного определения
частоты собственных колебаний системы с одной степенью свободы и
для приближенного определения частоты собственных колебаний упру-
гой стержневой системы, имеющей бесконечно большое число степеней
свободы. Точное решение показывает, что такая система имеет беско-
нечное множество различных частот. Свободные колебания такой систе-
мы могут быть изображены в виде геометрической суммы бесконечного
множества простых гармонических колебаний; каждому из этих гармо-
нических колебаний отвечают своя особая форма деформации стержня
и своя частота.
Как показывает опыт, свободные колебания затухают тем быстрее,
чем выше их частота. Поэтому на практике во многих случаях ограничи-
ваются определением самой низшей, так называемой «основной> часто-
ты. Ей отвечает самая простая форма деформаций.
Для определения частоты задаются приближенно формой колебаний.
Например, если речь идет о поперечных колебаниях плоской стержневой
системы с несмещающимися узлами, задаются уравнением прогибов
всех стержней в виде функции Х(х), удовлетворяющей всем условиям
закрепления концов стержней (граничным условиям). Прогиб в любой
точке, который изменяется в любой момент по закону простого гармони-
ческого колебания, выражают в форме
y(x,t)=aX{x)coSi^t, (27.15)
где G —некоторый множитель, зависящий от начальных условий.
Отсюда скорость
у' (x,t) = — ci^^X (х) sin iot
или
y:ax(^.0=-«<»^W- (27.16)
в дальнейшем для краткости будем писать X вместо Х(х).
Уравнение (27.15) является приближенным, во-первых, потому, что
заданная функция Х{х) не отвечает точному решению задачи, а во-вто-
РЬ1х, потому, что это уравнение предполагает, что в процессе колебаний
форма упругой линии остается неизменной; перемещения всех точек
предполагаются изменяющимися в одинаковой пропорции (умножаются
на COSO) t), так что соотношение между ними в любой момент остается
^63 Изменения.
В том случае, когда речь идет о колебаниях изгиба, максимальная
потенциальная энергия стержневой системы выражается так:
^ _ у г mtx^ у С EJa^ (X")g dx
Иглах- 2j J 2EJ ^J 2
dx^'
^'Максимальная кинетическая энергия при о)=-1 на основании (27.13)
равна
о
K^-Sfi^=#^-SJ^^
453
где (.-погонная масса балки и всех грузов, лежащих на ней. Отсюда
(27.17)
Задавшись формой упругой линии X, мы можем вычислить числи-
тель и знаменатель дроби (27.17) и определить таким образом ш2. ^
На практике часто бывает удобнее задаваться не упругой линией, а
статической нагрузкой (7(х), вызывающей упругую линию.
Тогда обычным путем по заданной нагрузке находят эпюру изгибающих
моментов М, а затем путем двукратного интегрирования — и упругую
линию X В этих случаях числитель может быть найден либо как удвоен-
ная потенциальная энергия деформаций, либо как удвоенная работа
статической нагрузки q{x) на вызванных ею перемещениях, т. е. можно
писать
МЧх
SJ
EJ
о
SJ
(27.17')
Х^\>Лх
ИЛИ
S J qXdX
XV^x
§ 27.5. ПРИМЕР
(27.17'0
Определить частоту собственных колебаний балки постоянного сечения с шарнир-
но опертыми концами и с равномерно распределенной по всему пролету массой f^
(фиг. 560).
Примем за функцию Х{х) упругую линию, возникающую от равномерно распре-
деленной статической нагрузки произвольной интенсивности q. Тогда
_Я
24 J
X = , J (l^x — 2/д:3 + х^). Примем ^=24. При этом получим
1 qlx qx^
EJ 2 г
г
\\2lx-^\2x'iYdx 24 /5
EJ '^ 5 ' EJ
и о
То же самое мы получили бы, если бы подсчитали удвоенную работу внешних сил:
I I
С 24 24 /5
С МЧх Г
] EJ -у
о
I получили (
I I
Далее
г Г \ 31 JLl/9
454
I отс^^^
V 5EJ "630(?/)2 ~ l^ У ~
Если бы мы задались упругой линией в форме Х= sin -^. которая также
удовлетворяет условиям на опорах и представляет собой в промежутке от х~0 по x^t
ЫПУКЛУЮ кривую, мы получили бы Fvrac«yiKe ОТ X~\J ДО Х=1
откуда
п2 , /"?/ 9.87 , /~EJ
.) tCT?^
—"^-Л?
Точное решение задачи, которое получается
из дифференциального уравнения в частных произ- Фиг. 560
водных, показывает, что самая низшая частота
03 как раз равна этой величине, - - •'^ -» /
^'-^¦i/'-
v-
§ 27.6. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕВОЙ СИСТЕМЫ
Пусть на плоскую стерл^невую систему, находившуюся в покое, в мо-
мент ^^0 начала действовать нагрузка вида q(x) • т(/), где q(x) —про-
извольная функция от X, т {t) — произвольная функция от t
Для приблил^енного решения задачи снова будем считать, что упру-
гая стерл^невая система имеет одну степень свободы. За форму колеба-
ний Х[х) примем упругую линию, отвечающую статическому действию
нагрузки q{x).
Это допустимо тогда, когда молено считать, что обе формы не сильно
отличаются друг от друга по своему общему очертанию. Решение дает-
ся формулой (27.5): в произвольный момент / прогиб в любой точке бу-
дет таков, как если бы на балку действовала статическая нагрузка, ин-
тенсивность которой равна ш ^ f т(«) sin w {t—u)du. Но от нагрузки д
о
возникает упругая линия, которую обозначили через Х{х)у следова-
тельно:
i
y{xj) = о,Х{х) ^ 'ziu)sini^(t— u)du. (27.19)
о
§ 27.7. ВЛИЯНИЕ ВНЕЗАПНОГО НАГРУЖЕНИЯ
Внезапное нагружение произвольной нагрузкой д(х), которая затем
?5.^ется постоянной, характеризуется тем, что при ^<0 т (0=0; при
40 = 1.
»Да по формуле (27.19)
у (x,t) = «>Х (х) f sin О) (^ — и) du :
о
= X (х) (1 — cos 0)0 = Уст(1 — COS шО;
y(x,t) = <iyXix)sin(ut
dt
(27.20)
455
Полученное выражение показывает, что балка совершает гармони-
ческие колебания около статической упругой линии Х{ху Перемещения
и(х t) изменяются в пределах от 2Х{х) до 0; перемены знака не проис-
ходит. При о)/=т: получается у=2Х(х), т. е. наибольший прогиб в лю-
бой точке равен удвоенному статическому прогибу.
§ 278. ВЛИЯНИЕ НАГРУЗКИ, ПОСТЕПЕННО ВОЗРАСТАЮЩЕЙ
ИЛИ УБЫВАЮЩЕЙ ВО ВРЕМЕНИ ПО ЛИНЕЙНОМУ ЗАКОНУ
Пусть нагрузка изменяется по закону, представленному на фиг. 561;
в какой-нибудь момент времени и=щ она равна Р^\ в произвольный мо-
мент и она равна
(27.21)
Такой закон изменения нагрузки встречается, например, при статиче-
ском *испытании образцов в механической лаборатории; он принимается
за модель статического прилол^ения любой нагрузки, если возрастание
последней происходит медленно. По формуле
t
у (t) = o)Ojj ( —^- usin io{t— u)du =
J ^0
= — ^11 f^ ~ sin Ы
(27.220
Ho
Фиг. 561
следовательно:
¦t = P{t); \,P{t)^y„{t),
y(t)=y,At)—^^^sin^
UQiii
(27.22)
T. e. на статическое перемещение налагается простое гармоническое ко-
лебание с частотой ш и с амплитудой ±
Ро
UQbi
Последняя прямо про-
порциональна отношению -^ , выражающему скорость возрастания на-
Uq
грузки, и обратно пропорциональна частоте о>.
Отношение
yctit)
1 —
sin <iit
(27.23)
(так называемый динамический коэффициент) является пере-
менным и с течением времени быстро стремится к единице.
Фиг. 562
Фиг. 563
456
Закон возрастания перемещений y{t) показан на фиг 562 Легко
убедиться что перемещения непрерывно возрастают; для доказатель
?тва продифференцируем выражение (27.22') по t доказатель
_ »ufi
Щ
От рассмотренного случая легко перейти к любому линейному за-
(фиг. 563). Для этого достаточно разлол<ить нагрузку на две
P{^u)==P,±J^u
и представить решение в виде суммы решений (27.22) и (27.20).
§ 27.9. ВЛИЯНИЕ КРАТКОВРЕМЕННОГО ДЕЙСТВИЯ НАГРУЗКИ
Пусть при /=0 внезапно появилась нагрузка д{х), которая затем
оставалась без изменения до момента t= т, после чего внезапно исчез-
ла. Будем считать, что продолжительность т невелика по сравнению с
периодом собственных колебаний и во всяком случае не превышает чет-
верти периода, так что ^т < — .В таком случае при t <'с получается
y{x,t)<X{x), т. е. во время действия нагрузки деформация еще не ус-
пеет достигнуть величины статической, а скорость еще остается положи-
тельной. Отсюда ясно, что деформация достигнет максимума ул<е после
исчезновения нагрузки, т. е. при Г> 'с. При этом
y(x,t) = ioX{x)[ll'Sinioit—u)du + ^'0'smi^{t — u)du] =
о "^
= X(x)[coso)(f-t)-coso)f]=2X(x)sin ^sino.^^-^). (27.24)
Из формулы (27.24) следует, что система совершает свободные гармо-
нические колебания около ненагруженного состояния с частотой «> и
амплитудой 2Х{х) sin —. Следовательно:
,;/^П , = + 2X(x)sm^. (27.25)
При статическом действии нагрузки перемещение равнялось бы Х(х),
следовательно, ^.нoжитeль 2 sinf- представляет собой дина миче-
<^кий коэффициент, т. е. орошение наибольшего перемещения к
^этическому:
ilHS-= 2 si п — = 2 sin —,
Уст 2
где Т — период собственных колебании.
п ^ г,г,т^ячывает что эффект кратковремен-
Динамический коэффициент показывает чт Ф^ J^^g з долях
иои нагрузки зависит от ее продолжительности. v
"ериода собственных колебаний. В табл. 13 дано значение 3^ при раз-
ЛИЧНЫХ значениях величины — •
^ 457
Например, при
Таблица 13
>0.50
2.00
^ =0,01 величина -^^^^=0,052, т. е. при такой продолжительности
т
у max
З'ст
0,00
0
0,01
0,052
0,02
0,126
0.05
0,313
0.10
0,618
0,167
1.000
0,20
1.175
0.30
1.617
0,40
1,902
0.50
2,00
Уст
для получения допускаемой деформации можно взять нагрузку, которая больше до-
пускаемой статической в 19 с лишним раз.
§ 27.10. ВЛИЯНИЕ КРАТКОВРЕМЕННОГО ИМПУЛЬСА
Представим себе импульс, распределенный по длине стержневой
системы по некоторому заданному закону. Интенсивность его на погон-
ную единицу обозначим через 5 (х). Мы можем воспользоваться преды-
дущим решением, если примем, что продолжительность т: действия на-
грузки q{x) бесконечно мала. Импульс элементарной нагрузки q (х) dx
{т. е. произведение нагрузки на продолжительность ее действия) равен
откуда
'zq{x)dx^s(x)dx,
q{x) = -^-^.
(27.26)
Величина q(x), очевидно, есть среднее значение интенсивности на-
грузки в точке X за время т.
Наибольшее перемещение выразится по-прежнему формулой (27.25).
Умножим и разделим правую часть ее на о)т:
sin-
= +X0)T
(27.27)
Но X сот есть упругая линия, которая возникает от статического дейст-
вия нагрузки о)^(д:) т, т. е. от нагрузки o)5(x). Отсюда непосредствен-
но вытекает, что по отношению к расчетному эффекту кратковременный
распределенный по любому закону импульс s(x) эквивалентен стати-
ческой распределенной нагрузке, имеющей в любой точке интенсивность.
от-
равную ios {х)
С1>Т
Легко убедиться, что величина 'cos(л:) имеет раз-
мерность кг/м.
Можно написать
<7экв(х)-= ±o)S(x)
(27.28)
«»х
458
Если импульс приложен в одной точке и имеет вепииыыл, с .
^экв = ± 0)5 ¦
sin-
сот
(27.29)
Полученный ^вывод дает нам возможность просто рассчитывать со-
оружения на действие импульса. Необходимо, однако, еще раз напом-
нить, что в основу этого вывода положены два допущения: 1) что коле-
бания происходят, как в системе с одной степенью свободы; 2) что
форма колебаний совпадает с упругой линией, отвечающей названной
статической нагрузке.
Известно, что для всякого угла а отношение —^^<1 и что это от-
а
ношение стремится к единице, когда а стремится к нулю. Отсюда сле-
дует, что из двух импульсов, имеющих одну и ту л^е величину, но раз-
ную продолл^ительность, более опасным будет более кратковременный.
Наиболее опасным из всех импульсов, имеющих заданную величину,
является импульс мгновенный. Для него эквивалентная статическая на-
грузка выражается так:
9экв(х)-±ш5(х), (27.280
Яэкв=±^5. (27.290
Характерным для расчета на действия нагрузки, продолжительность
^ которой ничтожна по сравнению с периодом собственных колебаний
Т системы, является следующее: закон изменения нагрузки за время 'с
не имеет существенного значения; такое значение имеет лишь инте-
гральная характеристика нагрузки, вырал^аемая ее импульсом.
§ 27.И. ПРИМЕР
Рассчитать однопролетную балку постоянного сечения с шарнирно опертыми^^^^
^шц „а действие мгновенного равномерно распределенного импульса интенсивности 5.
Для частоты cS^^ такой балки была выше получена формула
1^
Утах» min —
^max» min
Vcmax» mi г
9.88 -, A
Эквивалентная статическая нагрузка имеет интенсивность ^экв = 5а>. Отсюда
0.13S/2
EJ V EJli
in=± 2 " I V II '
(27.30)
4^9
где е —расстояние наиболее удаленного волокна до нейтральной оси;
г — радиус ннерцнн;
f/ —статический момент соответствующей части сечения.
Формулы (27.30) показывают, что увеличение жесткости EJ не вле-
чет за собой столь значительного уменьшения прогибов, какое полу-
чается при статическом действии нагрузки. Изгибающие моменты и по-
перечные силы, несмотря на статическую определимость балки, зависят
от величины EJ — растут с увеличением этого параметра. Все деформа,
ции и напряжения обратно пропорциональны корню квадратному из
погонной массы (х. Достаточно увеличить вес сооружения, чтобы тем
самым достигнуть уменьшения напряжений и деформаций. Расчетный
момент в данном примере не зависит от /, а поперечная сила даже об-
ратно пропорциональна пролету. В балках, имеющих геометрически
подобные поперечные сечения, расчетные нормальные напряжения об-
ратно пропорциональны коэффициенту подобия. Все это показывает, на-
сколько мало можно руководствоваться привычными представлениями,
взятыми из области статики сооружений, когда хотят разобраться в
явлениях динамики.
§ 27.12. ВЛИЯНИЕ ВИБРАЦИОННОЙ НАГРУЗКИ
Этот вид нагрузки встречается особенно часто в промышленных со-
оружениях и заслуживает большого внимания. Вибрационная распреде-
ленная нагрузка может быть изображена так:
q{x,t)^q{x)QosH,
где б — частота вибрации.
Нагрузка, изменяющаяся во времени по закону синуса или косинуса,
носит название гармонической.
В частном случае нагрузка q{x) может свестись к сосредоточенной
силе Q; тогда
Q(0= QcosQt.
Общее решение (27.19) принимает вид
t
у (х,0 - i^X{x) С cos б « sin ш(t—u)du ^Х(х) "^ X
X (cos6^_ cos шО= ^^f ^ (cosOt- COS ш/). (27.31;
Формула (27.31) выражает совокупность двух гармонических коле-
бании, имеющих одинаковую амплитуду -JLL!^_ „^ разные частоты
перемешениГ^! кп ''^™Р"' "''"'^^ ''""°^У '"'^ существенно влияют на
,3^;^Л ^о-"ько вначале; по прошествии времени оавного несколь-
^с^отоГоТт'якТяя^?"''"^ '-''У^^^^-' и остаются только колебания с
нуждГные к^ол\7ания) "дТ;иГ^"°^"''"'"^^^=^ "^" .стационарные. вЫ-
у(лг.О= ^^f coset. (27.32)
460
J
/г =
¦(У
7 является динамическим коэффициентом, т. е.
д1ножитель
отношением наибольшего перемещения в любой точке к тому котопор
;^гигается при статическом действии нагрузки д(х). На ф2Г^4 поГа
зана зависимость коэффициента k от отношения -1. Его абсолютная
СО
величина возрастает по мере приближения отношения ~ к единице.
При неог раниченном возрастании 6 величина k стремится к нулю.
При -^=1 (при резонансе), т. е. при совпадении частот вынужден-
ных и собственных колебаний, из формулы (27.32) получается /г-: со.
Фиг. 564
*-t
Фиг. 565
Однако в этом случае замена формулы (27.31) приближенной формулой
(27.32) становится незаконной; необходимо обратиться к более точной
формуле (27.31) и раскрыть неопределенность:
3'{^.0 =- X(х) с°^е^-;°Г' =Х(х)^ = Х(х)^ sin.t. (27.33)
-(тГ
,„ ^^^ограниченно возрастающие колебания, выражаемые формулой
1-^7.33), показаны на фиг. 565. -
Следует, впрочем, отметить, что при больших амплитудах теория
"алых колебаний неприменима, поэтому поведение сооружения при ре-
онансе является более сложным. Во всяком случае деформации мо-
Ут достигать значения, во много раз превышающего их статическую ве-
личину.
Резонанс характеризуется еще одной особенностью: вынужденные
^ремещения, выражаемые формулой (27.33), сдвинуты ло фазе на
Т * ^ относительно возмущающей силы Р cos ш/; они достигают наи-
^ольшей величины в те моменты, когда сила обращается в нуль. ^
Hv^, ^'^РаЩаясь к формуле (27.32). считаем нужным особо подчерк-
Уть. что при действии возмущающей силы, изменяющейся во времени
ь" закону cos 6 t или sin О t, резонанс возникает только при v=u>.
Кои" "^РИОД возмущающей силы, изменяющейся по гармоническому за-
""^У. является к р^?ным периода Г собственных колебании системы.
•^•еслие = 1^ где „_целое число, резонанс не возникает.
4вк
Этот вывод, как показано дальше, нельзя обоб-
щать на любую периодическую нагрузку, имеющую
частоту 6 = — О).
§ 27.13. ВЛИЯНИЕ произвольной ПЕРИОДИЧЕСКОЙ НАГРУЗКИ
Обычно ограничиваются расчетом на вибрационную нагрузку того
типа который был разобран в предыдущем параграфе. Рассмотрим те-
перь'движение, производимое нагрузкой, изменяющейся по произволь-
ному периодическому закону. Пусть P{t) —периодическая функция,
имеющая период т и соответственно частоту ^ ^ ^ •
Можно было бы разложить функцию P{t) в ряд Фурье и, следова-
тельно, представить движение в виде суммы бесконечного ряда простых
гармонических колебаний. Однако этот способ решения задачи неудо-
бен. Проще обратиться к общей формуле
у (t) = у^ COS О) ^ + — sin О)/ + 0)^11 \ Р {и) sin О) (/ — «) du .
(27.34)
Нетрудно убедиться, что в общем случае формула (27.34) выражает
непериодическое движение. Непериодичность объясняется тем, что в мо-
мент t=^ т состояние системы, вообще говоря, будет отличным от со-
стояния, которое система имела в момент /=0; поэтому второй период
начнется при других условиях, чем первый, и т. д.
Для того, чтобы движение было периодическим, необходимо так по-
добрать начальные значения величины Уо и у'^ , чтобы были выполнены
условия г/('с)=|/о и уЧ=|/'о, т. е.
Уо = Уо ^os шх -|—— sin о)т + o)S
) sin О) (t — и) du;
у^ = у^ COS (Dt — toy^oSin wT + o)*8jj J я (/г) cos ^ (x—u) du.
0
Для краткости введем обозначения:
«)SjjJP(u)sinw(T — u)du = У^;
(27,35)
о«8
и J Р(/г) cos ш (т — ti)du = У'
о
(27.36)
Величины У^ и У^ выражают перемещение и скорость, отвечаюш
моменту ^ = т при условии, что в начальный момент (при t=0) систе
находилась в покое.
Решение уравнений (27.35)
Уо = а = '
Y^ (1 -~ cos ojt) Н y'^ sin <
462
2(1 —coso)t)
(27.37)
итак, если сообщим системе в начальный момент перемещение г/о=а
.скорость У, -^ где а и 6 выражаются формулами (27.37). то движе^
„не станет периодическим, т. е. при любом целом и положительном зна-
чении можно будет писать
следовательно, достаточно будет изучить движение, происходящее во
время первого периода, в течение всех последующих периодов движение
будет точным повторен1ием первого.
Чтобы получить движение системы при заданных начальных усло-
виях ^0=0, tJQ =0, нужно вычесть из этого периодического движения то
дополнительное движение, которое мы сообщили системе в начальный*
момент, т. е. нужно сообщить движение
b .
• а cos ш sin ш^.
Итак, движение складывается из чисто вынужденных периодических
колебаний с периодом -с и из свободных с периодом Г== —. Особый
интерес представляют чисто вынужденные колебания, потому что собст-
венные благодаря внутреннему трению постепенно затухают.
Пусть дан момент t, выходящий за пределы первого периода -с, на-
пример t^k^ +^1, где ^1 < X. Окончательные формулы движения сис-
темы под действием периодической силы Р (t) имеют вид
=а)8„ \P{u)sinii^{t^ — u)du + a cos ш^^ +
+ А sin o)f - (а coso)^ + -^sin шЛ ; (27.38).
y'(f) = 3;'(Jfex + if,)=/(^) + ou)Sincof-6cosu)/ =
= _ ш«8„ J P (й) COS Ш ( /, - и) dH - oo) sin «)/, +
4- 6COS«rf, + (c u> siniot-bCOS wt). (27.39).
• Перемещение и скорость, отвечающие «^^JZ^'^Z°'lruГVшZ^oв
выражаются более простыми формулами^так как для этих
""едует подставить в формулы t=k-i •'•"'. -о, „о/ч
y(fe.) = a(l-cos«.0—fs'""»^: ^^'•^'^•
• /л-ЛП —cosort. (27.39').
Формулам (27.38) и (27.39) можно дать более компактный вид
у(,) =. У (;fe, + f,) = а„ JР(«)sinо> ( ^- «)'f«+
\ . . 14 (27.38>
I , //J-X^ (27.39>
*j ^ 463-
гае А X — некоторые постоянные, но мы не будем заниматься этим пре.
образованием, так как оно не дает особых выгод при вычислениях.
Если т =пГ, где п—целое число, т.е. если период -с является
кратным периода Т собственных колебаний системы, то
-^^==/г1г, ctg^^ = ± сх), а=± со, 6=± со;
2 2
для превращения движения в периодическое потребовалось бы сооб-
щить системе бесконечно большие начальные перемещения и скорость.
Проанализируем движение, которое будет иметь место на самом
деле.
Для примера подсчитаем перемещения, отвечающие началу какого-
нибудь периода. По формуле (27.380 и (27.37)
i— (у —о)У^ ctg -^) sin ш/ет.
НО
1 — COS ю/^т =1 — COS 2 nk^z = о ; sin ^^т = О,
y^(l_coso)/e'c) = 0; y^siniDfeT = 0; ctg-^(l —coso)fe'c) =
0)Т 1 COS Oyk'Z 0)T 0
= COS • =COS ¦ ' .
2 o)T 2 0
sin
2
Раскрыв неопределенность, найдем
COS — • ' = 2 ft sin ю/ет = 0 ;
2 o> o)T
COS —
2 2
d_ <^T . - o)T sin 0)^T
g Sin о)/ет = cos • =
^2 2 o)T
sin ¦
2
0)T CD^COSCii^T ^ , , - , _ . -,
2 <o
--- cos ox
2
Итак,
y(feT) = -i.y^Ctg-^ В1ПшЛт=^У^.
Точ)Но так же можно доказать, что У(А'с)=АУ1. Следовательно,
перемещение и скорость, отвечающие концу каждого периода, неограни-
ченно возрастают по закону геометрической прогрессии.
Можно доказать, что резонанс будет возникать также при условии
¦^^"^ ^, где m,n — целые числа. Действительно, ^ты имеем право при-
нять за период интервал времени п т = х,=тГ. Это показывает, ч^^
идеальную упругую систему можью сильно раскачать покти при ^^'
бой величине периода т, превышающего Т, если только нагрузка дейст-
вует достаточно долго.
464
Если функция P{t) такова, что У^-0 и У;=0, то У{кх)=0 и
мчк'^) ="^' ^' ^' Р^з^"^"^^ "^ будет. Следовательно, существуют такие
рпиодические функции Р(0, которые даже при условии -с =^7 неспо-
обйЫ вызвать явление резонанса. Это —те функции, для которых
jP(w) sin о)(х — u)du == О,
о
J Р(«) COS ю (т — «) й^г = о.
(27.40)
Условия (27.40) можно истолковать следующим образом. Пусть
т ;=j^r. Разложим функцию Р (/) в ряд Фурье
P{t)= S Л^sш + S Б^со8 . (27.41)
1 = 1 kT ?=1 kT
Необходимый и достаточный признак того, что условия (27.40) удовлет-
воряются, состоит в следующем: Aj^ =В^ =0. Следовательно, при
t ^кТ резонан-с не будет возникать, если в разложении Р{и) отсут-
ствуют синусоида и косинусоида с периодом Г.
§ 27Л4. ПРИМЕРЬ!
Пример 1. Вычислить перемещения y{i), вызываемые гармонической периодической
2к
нагрузкой вида P{t)~P cos 6f, 6=—' . Эта задача была решена в § 27.12, где была
получена формула
t
О) f COS Ьи sin oy{t — u)du:=
о
=z (cos 6f — COS (jyi) .
При t=-^k T +^1 можно сделать подстановку
cos Ы = cos (2 Ы + e^i) = cos e^i.
откуда
РЬ
у {kx + ti) = -~—^ (cos Of, - cos o>t).
^-(т)
Воспользуемся теперь для решения той же задачи формулами (27.38) и (27.37)
ftiZ
2eiiPsin2 —
Ъ Р 2
у ^ 11 (1 _ COS о)т) = ¦
у = • I 1 ^^^J^ ш 1,1 у г» % г» »
С1)5,,Я sin сот
V' ~
^ %-" / е \2 •
1
1 РЬш. г а)т . CUT I Р^и
^ и. м. Рабинович 465
_1_ P<»bii
-(тГ
(0)Т (ОТ \
Sin шт — 2 sin2 — ctg —j =
"li (sin o)x — sin o)t) = 0.
2 / e \2 ^
По формуле (27.38)
P5i
1
(tF
-(vf
(COS 6^1 — COS O)^).
Результаты совпали.^
Пример 2. Определить амплитуду чисто вынужденных колеОании, вызываемых мгно-
венными импульсами S, которые повторяются с периодом, равным t секунд.
Фиг. 566
Будем считать, что импульсы прилагаются в конце каждого периода (фиг. 566).
Очевидно, что на протяжении всего первого периода перемещение еще равно нулю:
Что касается скорости, то она равна нулю на протяжении всего первого периода,
за исключением последнего момента этого периода, когда она терпит разрыв:
Отсюда
o = ^SiiSctg—: 6 = —-BjjS;
у (k-z + fi) = у (<i) = -^ 6iiS f ctg Y" COS *)<! + sin o>ti) ;
(l>2 / ^^>^ \
У (kx + fj) == — b^^S (^ ctg— sin o)fi + cos cofi J .
__ Чтобы найти амплитуду чисто вынужденных колебаний, приравняем иулю скорость
— ctg •— sin to^i + COS oj^i = 0. или tg o^i = tg ,
Следовательно, наибольшие отклонения достигаются в середине интервалов межДУ
моментами появления импульсов. Далее
[у ('1)1макс = — hiS (ctg — Ctg -^ Sin ~ + sin —1 =
466
_o^^S
2 sin— 2o3msin —
2 2
Диаграммы этих перемещений и соответх:твующих скоростей представлены на
фиг. 567.
^4^ct^^^
•>t
Фиг. 567
§ 27.15. ВЛИЯНИЕ ПЕРИОДИЧЕСКОЙ НАГРУЗКИ БОЛЬШОЙ ЧАСТОТЫ
Пусть период т меньше периода Т собственных колебаний системы.
В этих случаях, очевидно:
0<
< —, или 0< —<^,
следовательно, ctg —- имеет конечное значение; поэтому величины а, Ь
^формулах (27.37) также конечны. Это показывает, что никакая пе-
Р одическая нагрузка, частота которой превы-
РТ.Т. собственную частоту о) системы, не может
''ь^звать резонанса.
Ьсли величина т не намного меньше периода 7, т. е. величина —
б ^
зка к 7г, то ctg^ имеет очень большую величину, поэтому колеба-
ия будут близки по своему характеру к резонансным.
зссмотрим следующий крайний случай:
•сияние периодической нагрузки весьма высокой частоты, т. е, такой
'^^^у при которой величина wt весьма мала, а ctg — имеет весьма
^^^ьшую величину. ^
sin ^^ "^РиОДическая нагрузка изменяется за время т по закону
^я к н ^^^ ^ ^^^ ^^' '^^ ^^ эффект, как мы видели в § 27.12, стремит-
зулкт ^^^' ^ случае периодической нагрузки произвольного вида ре-
ьтат будет другой.
^Решн '^ ^^^'^^'^^ величину wt настолько малой, что без большой по-
30» "*^сти можно писать sin ш-с = шт .
467
Р
ся
По свойству кратковременной нагрузки допустима замена перемен-
ной нагрузки Р(и) на протяжении каждого периода ее средним значе-
нием
P.,^-^^Piu)du^^,
(27.42)
где 5 — импульс силы за время т: .
При таких упрощениях, допустимых, повторяем, в тех случаях, когда
отношение ^^^^-^ близко к единице, периодическая нагрузка, имеющая
период -с, фактически превратится в постоянную нагрузку Р,р,
действующую неопределенно долго. Влияние такой нагрузки рассмотре-
но было выше в § 27.7.
Мы можем написать
Тот же результат мы получили бы, если бы обратились к формуле
(27.38) .
В том частном случае, когда нагрузка изменяется по гармониче-
скому закону, ее среднее значение за один период, очевидно, равно нулю;
этим объясняется результат, полученный в § 27J.
§ 27.16. ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВЫНУЖДЕННЫХ
И СВОБОДНЫХ ПЕРЕМЕЩЕНИИ
Интеграл (27.5), выражающий вынужденные перемещения при каком угодно виде
функции Р(0, может быть изображен геометрически в виде особой диаграммы, иагляд-
ио изображающей весь ход изменения перемещения y{t).
Фиг. 568
Фиг. 569
Пусть график Р(и) задан в прямоугольных координатах (фиг. 568). Возьмем произ-
вольную точку О (фиг. 569) и произвольную прямую О А и будем откладывать величины
P{u)du в последовательном порялке в виде бесконечно малых векторов, наклоненных
под углом <о« к лучу ОА. Cout/купность этих векторов образует непрерывную кривую^
Out, Ее уравнение в декартовых координатах (а, Р) в параметрической форме на-
пишется так:
t t
а =r f Я («) COS iiiuda ; p = j P (и) sin ь^ийи.
Обе координаты имеют размерность импульсд {кгсек).
468
1?пивая Out обладает рядом замечательных свойгтк n^o^t, .,^ ^^ ^
^..з^и"; Доказагельсгво чи^ь может „ай™ в^^ГГиТав^Гр? ^Г ?е^^?че^
»"^ а) Любой момент времени « или t изображается той точкой кривой в котопой ^я
сательная наклонена к лучу ОЛ под углом, соответственно равным со ГнлиГ?*^
Касатеяьаая равномерно вращается против часовой стрелки^причем углу ее „ово-
рота 2л отвечает время =Г.
б) Длина любого участка диаграммы, заключенного между двумя ее точками
,г импульсу внешней силы за соответствующий промежуток впемРни -^^^^^^^и.
в) Радиус кривизны
б) длина -i^x^u^iu j-^^aexiv^ /i^M^.p^iYiivibi, заключенного между двумя
равна импульсу внешней силы за соответствующий промежуток времени
в) Радиус кривизны iC в любой точке t равен
jP(0
Р =
0)дц
З'ст,
(27.43)
т. е. выражает в определенном масштабе значение возмущающей силы или статического
перемещения. Постоянной силе отвечает дуга окружности; бесконечно большой силе 1^
прямолинейный участок кривой. * v^ncwnu иильшои силе —
Фиг. 570
Фиг. 571
Если сила, начиная с некоторого момента t, исчезает, то кривая в этой точке закан-
чивается, и все дальнейшие моменты времени изображаются той же точкой.
Если сила возобновляется после интервала времени, равного т:, то кривая возоб-
новляется, но касательная успевает повернуться за этот интервал времени на угол ь>т
Если сила в момент i изменяет свой знак на обратный, течение диаграммы начи-
нается в обратную сторону (фиг, 571).
г) Если мы разложим радиус-вектор R (фиг. 569) на нормальную к кривой состав-
^^яющую /(/, и тангенциальную /(О, то получим
Д?=Т->'(0 = -^>'(0;
содц
(27.43')
g • ^^Р^альная составляющая выражает в определенном масштабе перемещения y(t),
^^^ендиальная в другом масштабе — скорость y'{t),
Дост ^'^^ радиус-вектор R в какой-либо точке нормален к кривой, перемещение y{t)
касат^^^^ максимума или минимума, а скорость обращается в нуль. Когда он становится
тельным к кривой, перемещение обращается в нуль,
^иает ^^^^^"bie колебания характери.зуются тем, что касательная равномерно вра-
^^ичми" ^^^РУ^ неподвижной точки t\ перемещения и скорости характеризуются проек-
Напоя *^^"^^^"^"ого радиуса-вектора R на вращающиеся взаимно-перпендикулярные
'^^ние^'"^"""' ^°^ой характери.зуется обращением радиуса-вектора R в нуль, т. е. совпа-
.^^^м^конечиой точки диаграммы с полюсом О.
^Ремеи " ^-^^бинович. К расчету сооружений на действие сил, и.зменяющихся во
^еоме "^ произвольному закону, «Вестник Военно-инженерной академии» № 20, 1937;
ность ^^"*^*'^'1"" метод решения задач динамики упругих систем, сборник «Обшая проч«
К гео\Г У^'*'^*"*^*1Вость сооружений при действии взрывной нагрузки», Стройиздат, 1944;
вания п ^"^^^^^'^^^У методу решения задач динамики упругих систем, сборник «Исследо-
ло динамике сооружений», Стройиздат, 1947.
е) ЕСЛИ в момент /=0 перемещение уо и скорость у', отличны от нуля, то радиуеь,.
векторы R проводятся из полюса О. а начало кривой О' имеет координаты
1
йбц У«
<1)*8|
-уо (фиг. 572).
«{*Лля примера на фиг. 573 показана диаграмма, выражающая движение под дей-
..BHeJ повторяющихся через одинаковые промежутки времени х одинаковых мгиовен-
Гыхимпульсо'^ 5. Диаграмма имеет вид правильного многоугольника со сторонами. д^,„.
^я КОТОРЫХ 7в условном масштабе) равна 5 и угол между которыми равен о г.
Вершины многоугольника расположены, очевидно, на окружности; радиус последней
равен
2sfn —
Для любого момента t из диаграммы сразу получаются проекции /\7 и Л О, выражаю-
щие перемещение ij(i) и скорость y'(t). Движение, вооСше говоря, непериодическое; оно
LOT
Фиг. 572
Фиг. 573
имеет характер биения. Радиус-вектор R сначала растет, причем его наибольшая вели-
чина ие может превзойти диаметра 2г, т. е. y(t) < coBj, г, загем R начинает убывать,
и т. д.
Если вместо мгновенных импульсов S будет действовать произвольная периодиче-
ская нагрузка с периодом -с, то стороны многоугольника иа фиг. 573 заменятся кри-
выми, но хорды этих кривых снова окажутся сторонами правильного многоугольника,
вписанного в окружность того же радиуса.
Отсюда можно сразу получить формулу, выведенную аналитически для того же
движения в предыдущем примере.
§ 27.17. ВЛИЯНИЕ ПЕРЕМЕЩЕНИИ ОПОР
Грунт, как деформируемая среда, испытывает колебания от действия
машин и станков, работающих в промышленных сооружениях, от проез-
да тяжелых грузовых автомобилей, от ударов, взрывов в грунте и т. п.
Эти колебания в свою очередь передаются другим сооружениям,
иногда расположенным довольно далеко от источника колебаний.^
В простейшей постановке задача сводится к колебаниям упругой си-
стемы с одной степенью свободы. Пусть опора испытывает nepeMcmef^n
по направлению у (фиг. 574), выражаемые заданной функцией /(О-
470
За положительные перемещения у и f{t) примем по-прежнему на-
пявленные вниз. Деформация упругой связи в любой момент выразится
пязностью </(0—/(О» поэтому дифференциальное уравнение колебаний
Р — иметь вид
будет
или
-т|^-г,[у-/(0]=0
/ + '"'У--тг-/(0 = о
(27.44)
Оно полностью совпадает с
(27.2), если
f(i)
Фиг. 574
в последнее
вместо P{t) подставить rnf(t)^^^mf{t). При такой
подстановке совпадут и интегралы обоих уравнений,
поэтому влияние перемещений опоры, вы-
ражаемых каким угодно законом )(t), на
перемещения системы с одной степенью
свободы полностью совпадает с влияни-
ем возмущающей силы riif{t)=w^tnf{i)^ дей-
ствующей на ту же систему с .неподвиж-
ной опорой.
Мгновенно возникшее и затем остающееся перемещение а эквива-
лентно внезапному приложению постоянной силы Р^Гц а.
Для определения вынужденных перемещений годятся все формулы,
выведенные выше для системы с одной степенью свободы, если в них
произвести указанную подстановку.
Если на систему одновременно с перемещением опор f{t) будет дей-
ствовать внешняя возмущающая сила, равная —ruf{t)y то совокупность
обоих воздействий будет эквивалентна тому, как будто на систему дей-
ствует сила, равная нулю, следовательно, будут происходить только сво-
бодные колебания. При начальных условиях (/о=0 и у'^ =0 система
останется в покое. Итак, влияние перемещения f{t) опор может быть
уничтожено внешней силой — rij{t) и, наоборот, влияние заданной воз-
^^УЩающей силы P{t) может быть полностью парализовано перемеще-
ниями—-Lp(^) опоры.
§ 27.18. ВЛИЯНИЕ ПОПЕРЕЧНОГО ИЗГИБАЮЩЕГО УДАРА
Пусть на стержневую систему с высоты h падает масса М. Ско-
рость этой массы в момент встречи с препятствием равна t/= К^^Л, а
количество движения равно Mv=M V2gh . По окончании процесса уда-
Р^ суммарное количество движения должно остаться таким же. Отсюда
^Ь1 Можем определить скорость движения стержневой системы, отвечаю-
^^Ую моменту окончания удара.
Предварительно, однако, нужно знать, какой характер имеет удар —
Упругий, неупругий, образуются ли на поверхности контакта обоих тел
значительные местные'деформации. Последние захватывают часть ма-
||^Риала и совершаются с известной скоростью; при этом поглощается
^асть количества движения, так что на долю общих деформаций всего
^^РУжения остается лишь часть всего количества движения. Таким
^^^Разом, местные деформации уменьшают общую деформацию сооруже-
Ограничимся рассмотрением жесткого удара, т. е. такого, при кото-
^^^ Можно пренебречь местными деформациями. В то же время будем
считать удар совершенно неупругим, т. е. т^ким, при котором по оков,
чании удара оба тела движутся совместно, не отделяясь друг от друр.
Наконец, продолжительность удара будем считать весьма малой.
При таких допущениях задача решается следующим образом. Пусть
удар произошел в некоторую точку А сооружения по направлению, сов-
падающему с ее перемещением (/^. Зададимся формой упругой линии
Х(х), Ординату этой кривой в точке А назовем Х^. Ударяющее тело
имеет массу М и скорость V,
После удара масса М и сооружение будут иметь в точке А некото-
рую скорость v^. Скорости остальных точек системы будут пропорцио-
нальны соответствующим ординатам Х(х) упругой линии, т. е. 1/'(д:) =
Ха ^
^А
Суммарное количество движения до удара и после удара должно
остаться одно и то же, следовательно:
-Ц1
Mv = Aip^ + У! С -^ v^^dx, или 1»^= —L
Л1+У ~^х
X
Для краткости введем обозначение
==SJ-:^f^^^- (27.45)
прив
Тогда
V^ = ; V .
^+'"прив
Здесь т'^^^^^ (приведенная масса) есть, очевидно, такая масса, которая,
будучи помещена в точке Л, имела бы такое же количество движения,
которое имеет вся стержневая система. В ряде других вопросов динами-
ки приведенной массой называется другая масса, а именно такая,
™РГ' ^^^^" помещена в точке Л, имела бы кинетическую энергию,
равную кинетической энергии сооружения:
откуда ^ ''
ni„^,,^YSi~-\\dx. (27А6)
Кинетическая энергия системы в момент окончания удара будет
ле ?27Л°Г ''°^"^^"""'' ''°^^^^™^ '^"'^¦'^^Ь! вь.числяется по формУ
• = /.=
1
1^11РИЛ
где Он—перемещение в точке А от силы р^} ^^ - « «той
точкепонаправлеьшюг; ' ^^* приложенной в этоя
472
' Разберем Два случая. В первом случае будем считать груз настоль-
ко незначительным, что статический прогиб, вызываемый им, можно
ПРИНЯТЬ равным нулю. Система совершает свободные колебания под
влиянием начальной скорости, следовательно, амплитуду у^ можно^
вычислить по формуле (27.4)
(Л^ + ^прив) "" ^^''^"Р"" '
В этом случае перемещение у^ пропорционально количеству движения
Afy или, иначе говоря, импульсу удара.
Второй случай: груз — большой; перемещение (/^ — вертикально. Бу-
дем отсчитывать это перемещение от начального состояния системы, де-
формированной под действием ее собственного веса.
Обозначим максимальный прогиб в точке А через у . Прогибы во
всех остальных точках будут соответственно равны —^-^ у , а потен-
циальная энергия системы в момент наибольшего прогиба будет
о о
Она Должна быть равна сумме кинетической энергии, имевшейся в
момент окончания удара, и работы, произведенной силой Mg на пути,
равном у ^ :
о
Мы можем упростить это уравнение, определив при помощи урав-
нения работ статический прогиб в точке Л, вызываемый силой Mg:
ilH^'V-
Mgyc
Подставив это выражение интеграла в предыдущее уравнение, по-
¦^Учим
или
Имея
к
ЛГёу2 -2Mgy„Уу,-(М + OT„p„„)у„t;2 = О
y^f мы тем самым получим расчетную упругую линию
473
в том частном случае, когда груз не падает с некоторой высоты, а про-
сто внезапно появляется на балке, т. е. при t; = 0, получается У^^2у^^,
Формула (27.47) показывает, что с увеличением скорости встречи
падающего с преградой (с увеличением высоты падения) прогиб резко
возрастает.
§ 27.19. О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
Под нелинейными системами в теории колебаний, так же как в ста-
тике сооружений, понимаются такие системы, в которых перемещения
не являются линейными функциями сил. В одних случаях нелинейность
вызывается свойствами материала системы, а^в других случаях —
кинематическими свойствами самой системы. Свойства материала мо-
.гут быть описаны, например, зависимостью между удлинением образца
Фиг. 575
^и растягивающей силой. Эти зависимости могут быть трех типов, кото-
рые схематически представлены на фиг. 575.
На этих схемах угол а наклона касательной имеет следующий смысл:
где г,, (у)—коэффициент жесткости системы или восстанавливающая
сила, отнесенная к единице перемещения, при данном зна-
чении переменной у. На схемах а и б мы имеем соответст-
венно
"I = -^ < О (мягкая связь),
rfy2
dy
d^P dru ^ п /
— = — > о (жесткая связь).
На схеме в связь при малых деформациях — мягкая, при больших
^деформациях — жесткая.
Примером системы с нелинейной характеристикой жесткости мо-
жет служить мачта, расчаленная тросами, которые сделаны из идеаль-
но упругого материала, но провисают под влиянием собственного веса-
Другим примером служит любая стержневая система, в состав которо*
входят сжато-изогиутые стержни. Известно, что даже при идеальной
упругости материала прогиб таких стержней является нелинейной ФУ"'
кцией продольных сил. ^
К нелинейным относятся также такие системы, у которых масса
во время движения изменяет свою величину. р
Динамика нелинейно деформируемых систем является несравяен^^
более общей проблемой, чем динамика линейно деформируемых^ ^^
стем. Ее важное значение объясняется тем, что поведение нелине1
474
систем
— их
свободные и вынужденные колебания
существенно от-
..„чается от поведения линейно деформируемых систем. Имеется ряд
таких
явлений в колебаниях нелинейных систем
которые невозможно
объяснить с точки зрения линейной теории колебаний. Выводы, постро-
енные на этой теории, могут в^аких случаях привести к грубым ошиб-
кам. Этим объясняется особый интерес, который теория нелинейных
колебаний вызывает в последние десятилетия среди инженеров разных
специальностей, в том числе со стороны инженеров-строителей
В обширной литерату-
ре, посвященной этой тео-
рии, видное место зани-
мают фундаментальные
работы советских ученыхЧ
С математической точ-
ки зрения теория нели-
нейных колебаний значи-
тельно сложнее теории ли-
нейных колебаний, по-
скольку интегрирование
нелинейных дифференци-
альных уравнений несрав-
ненно сложнее, чем линей-
ных дифференциальных
уравнений.
Чтобы дать ^некоторое
понятие об особенностях нелинейных колеба1ний, рассмотрим простейшую
задачу об определении частоты собственных колебаний системы с одной
степенью свободы. Дифференциальное уравнение свободных колебалий
имеет вид
*-!/
Фиг. 576
т^+/(У) = 0,
(27.48)
где f(y) —заданная нелинейная функция, выражаюпхая зависимость
восстанавливающей силы от перемещения (фиг- 576). Кривую f(y)
можно разбить на малые участки 01, 12, 23 и т. д., и каждый такой уча-
сток линеаризировать, т. е. заменить вписанной в нее прямой. На
протяжении первого участка движение происходит, как в линейной
системе, жесткость которой rii = tga, а частота
JlpH заданной начальной скорости vo и начальном перемещении
^0-0 перемещения происходят по закону
у'' .= Vq cos (Dj t.
Если в левую часть первой формулы подставим у=ОА, то найдем
продолжительность ^-т, движения по первому участку и скорость
' '^i) в конце этого участка.
М Inf ^- Андронов. А А. Витт. С Э. Хайкнн. Теория колебаний, ч. I.
KhJ^?^' "• ^' Крылов, Н. Н. Боголюбов, Введение в нелинейную механику,
^«ев 1937; и. Г. М а л ки н Некоторые задачи теории нелинейных колебании. М.. 1956.
^ебя« ?^"овами теории можно познакомиться по книгам: И. М. Бабаков. Теория ко-
скиу ""' М.. 1958- Дж Стокер, Нелинейные колебания в механических и элсктриче-
* системах. М., 1958.
475
у = -^ sin coi / J
Пт.ижение по участку АВ происходит, как в линейной системе,
—, начальное перемещение
//,=:0, и начальную скорость c/oCOS^Ti, и т- д.
Скооость постепенно будет уменьшаться пока на одном из участков
не обоатится в нуль. Так можно найти амплитуду колебаний и время,
в течение которого перемещение у возрастает от нуля до максимума,
^ g А-Т где Г —период собственных колебаний системы. Особенность
линейных колебаний состоит, как известно, в том, что период Т не
зависит от амплитуды. При нелинейных колебаниях свойство изохрон-
ности уже не имеет места: период Т является функцией амплитуды.
Изменяя начальную скорость с/о, мы тем самым будем изменять и пе-
риод Т, г г/ м ^
в системах, для которых кривая \у, f(t/)J обращена выпуклостью
вверх, очевидно, tga>tgP>tgT ••., т. е. с увеличением перемещения
у наклон касательной уменьшается, следовательно, средняя вели-
чина угла наклона касательных уменьшается с увеличением ампли-
туды. Отсюда можно вывести заключение, что если мы заменим пере-
менную жесткость системы некоторой средней жесткостью г, подобран-
ной так, чтобы период от этого не изменился, то при больших амплиту-
дах заменяющая система будет иметь меньшую жесткость г, следова-
тельно,— меньшую частоту собственных колебаний. Если кривая/([/)
обраохена выпуклостью вниз, то вывод получается обратный. Итак, в
системах первого рода частота с увеличением амплитуды уменьшается,
а в системах второго рода увеличивается.
Первый интеграл дифференциального уравнения (27.48) можно по-
лучить, введя подстановку
(Ру dv ^ dv dy dv
^t^'^'di'^'dy'lt'^dy '
у
У
+ J/(y)dy=^= const. (27.49)
ИЛИ
2
0
Уравнение (27.49) выражает свойство, присущее свободным колеба-
ниям ^любой идеально-упругой консервативной системы: сумма кинети-
ческой и потенциальной энергии остается постоянной.
Перепишем уравнение (27,49) в виде
^=±)/''«-^1
f(y)dy.
(27.60)
Каждому значению у отвечают два равных и противоположных значе-
ния скорости V. Будем рассматривать переменные v, у как коордиязть
некоторой точки на плоскости, которую будем называть «фязовои
плоскостью. Уравнению (27.50) отвечает некоторая кривая, называема»
«фазовой кривой» или «фазовой траекторией».
При колебаниях системы изображающая точка движется по Ф^Д^^
вой траектории. Если фазовая траектория — замкнутая, то движев
476
взятым вдоль
РЙствительной системы имеет периодический характер, а скорость и
рпемещение остаются конечными; если фазовая траектория оказыва-
тся незамкнутой, то действительные перемещения неопределенно на-
астают. Иногда фазовая траектория имеет несколько ветвей, пересе-
''-ающихся между собой; изучение точек пересечения ветвей позволяет
пелать важные заключения об устойчивости или неустойчивости движе-
ния. Вообще фазовые кривые играют важную роль в теории нелиней-
ных колебаний как средство для качественного описания движения.
Например, для системы, жесткость которой характеризуется схе-
мой б, фип 575, семейство фазовых траекторий, описываемое уравне-
нием (27.50), имеет вид, представленный на фиг. 577. Стрелки указы-
вают направление, отвечающее возрастанию времени L Каждая кривая
этого семейства изображает перио:цическое движение, отвечающее оп-
ределенной амплитуде колеба-ний. Соответствующие им периоды коле-
frfy
баний выражаются криволинейным интегралом ф—,
контура. Таким образом,
можно сказать, что нели-
нейная система имеет бес-
конечное множество соб-
ственных частот, образую-
щих непрерывный спектр.
При начальных условиях
^0=0, г/о=0 фазовая тра-
екгория сжимается в точ-
ку, совпадающую с нача-
лом координат О; эта точ- '
ка характеризует состоя-
ние покоя.
Для систем, характе-
ризуемых схемой а, фиг.
575, фазовые траектор-ии
также могут быть замкнутыми, но могут оказаться разомкнутыми; пос-
леднее будет свидетельствовать о том, что система не совершает коле-
бательного движения, а неопределенно удаляется от ^начального состоя-
ния. Примером может служить .маятник, получивший большую началь-
ную скорость.
Действие периодической нагрузки на нелинейную систему качест-
венно отличается от действия на линейную систему, так как существу-
^<>т целые области непрерывно распределенных частот возмущающей
^^^^РУзки ПРИ KOTODbi^^ возможны резонансные явления. Наличие или
-те?тетвнеТзон^^^^^^ нагрузки зависит пе
•только от еГчастоты но и от ее амплитуды. При резонансе амплитуда
поеледовательнь1х колебаний возрастает настолько -^о.ог.^к^^^^^
^ественное расхождение между частотами '^''''2 ^^^^J^^^^J^^^
етвие чего амплитуды начинают убывать пока снова не возникнет
Резонанс м т п
, в не^и^ейных системах возможно явление ^^^^l^^^Jl^^^^^l'^'J.
Резонангя ппчннкаюшего при условии, что масса или жесткость си
t)^ сумму колебаний, вызываемых каждой силой в °™^^ьности. Ло
^^^Щ нельзя разлагать нагрузку на составляющие и разыскивать
-дельно влияние каждой составляющей.
Фиг. 577
477
Глава 28
ОСНОВЫ ДИНАМИКИ СИСТЕМ С КОНЕЧНЫМ
ИЛИ БЕСКОНЕЧНО БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
§ 28.1. КОЛЕБАНИЯ СИСТЕМ С НЕСКОЛЬКИМИ СТЕПЕНЯМИ СВОБОДЫ
Теория колебаний линейных систем с п степенями свободы может
быть хорошо разъяснена на примере систем с двумя степенями
свободы. В качестве модели таких систем возьмем балку с двумя сосре-
rrfj f^2
^Ъ Уг\^
Фиг. 578
доточенными массами mi, т^ (фиг. 578); самую балку будем считать
невесомой. Во время свободных колебаний на систему действуют толь-
ко силы инерции и реакции ее связей, следовательно, ее упругую ли-
нию можно формально рассматривать как статическую, вызванную
этими силами. Амплитуды колебаний в точках приложения масс обоз-
начим через Уи У% Будем считать, что балка совершает свободные ко-
лебания, как система с одной степенью свободы, сохраняя неизменной
форму своей упругой линии. Мы сейчас увидим, что это допущение оп-
равдывается. В любой момент t перемещения при таком допущении
будут соответственно равны (/isinw/, (/2sln w/, где w —собственная
частота, t — время, отсчитываемое от момента, когда перемещения рав-
ны нулю.
Силы инерции соответственно равны
d'^ d^ • J.
— m^ —(у 1 sin tot) = w^/^j у 1 sin mt; —m^ —(Уг sin ш^ = tD^mg у2 s^" ^* •
От этих сил, как от статической нагрузки, возникают перемещения
yiSinwf = ш^т^у^ sin О)/'8jj + w^m^yg siiKD^-S^g,
У2 sin О)/ = iii^m^ у 1 sin ш^ • \i + i^^m^ y^ sin o)^ • Ь^
478
(28.1>
или после сокращения на sinwt
^'^1 ^2 У1 + {^'гп, S^^ _ 1) у^ _ О.
Для того чтобы система однородных алгебраических уравнений
(28Л) имела решения, отличные от нуля, необходимо, чтобы ее детер-
минат был равен нулю:
W^/TZj \1 — 1
0)2 т^ \^
D =
0)2/П2 Bj2
= 0,
ИЛИ
(^n^22-^12)^l'^2^'-K^I + '«2^22)^'+l=0.
S) 2-Я срорма
У22
Ь) ojfrPjyjj
U^fmzyzt
Z) U)',
й% >u
?/77,^,2
I ®
1ТПТП '
к
6u|
^гУгг
\
у
L
^^^^TITTTT.
Фиг.'579
Отсю
^ _ /П1 6,1 + /n, 6^ T / (m, 6,;.- m, \^f + 4 /Tz.m, ^?, ^^^^^
2т^щ ( ^11 ^22--~^i2)
>^ Итак, система имеет две различные частоты собственных колебаний.
^еньщу1о из них, о)„ называют основной частотой.
Как известно при 1> = 0 уравнения системы (28.1) перестают быть
«^зависимыми; одно из них является следствием другого. Поэтому зна-
чение ii
^f" получается одно и то же из обоих уравнений.
У2
У1
«D^/Wgfisa — 1
(28.3>
у J С0-/718012 " '"Х-'жл
Каждому из двух значений «> отвечает свое значение отношения -^
tw^"^™'^. что каждой из двух частот отвечает с воя особая форма
^\^бодиых колебаний —особое очертание упругой линии. Эти две фор-
«Ь! носят название главных или собственных. Их примерны»
47»
«вид для балки с двумя массами показан на фиг. 579, а и б, где переме-
щения, относящиеся к Ьй форме, обозначены через уц, у2и а относя-
щиеся'ко 2-й форме—через yi2, «/22.
Каждая из этих форм есть статическая упругая линия, для которой
нагрузкой служат соответствующие силы инерции, показанные на ф-иг.
579, в и г. На этих же схемах показан примерный вид эпюр изгибающих
моментов.
Главные формы обладают замечательными свойствами. Представим
себе, что мы сдеформировали балку, придав упругой линии очертание
;по первой форме, т. е. задав начальные прогибы
Ух = ^Уп» У2 = *У21 у
Рде /г — произвольный коэффициент. Если мы после этого предоставим
балку самой себе, то произойдет следующее: она начнет совер-
шать простое гармоническое колебание с частотой а\,
как система с одной степенью свободы, сохраняя неиз-
менно одну и ту же форму упругой линии: первую собствен-
ную форму. Аналогичное можно сказать о второй форме. Никаких дру-
гих форм упругих линий, обладающих такими свойствами, не сущест-
вует. Если мы изогнем балку по какой-либо другой кривой, то колеба-
ния будут иметь более сложный и запутанный вид, а упругая линия
будет непрерывно изменять свое очертание.
Нетрудно подобрать такие статические нагрузки, которые выгибают
балку либо по первой, либо по второй форме. Чтобы изогнуть по первой
»форме, нужно приложить к балке в точке А я В две силы, пропорцио-
нальные величинам miyn и т2У2и например,
Сравнив эти силы с силами инерции ^ ^\^ЩУ\и ^\^2У2и от которых
получаются ординаты г/ц, У2\ первой формы, и заметив, что эти две
группы сил подобны между собой, найдем, что балка изогнется по пер-
вой форме и будет иметь прогибы
^, k k
У1^ :тУпу У2^-тУ21'
Аналогичное заключение, можно сделать о статической нагрузке,
вызывающей прогибы по второй форме (фиг. 579, виг).
Собственные формы связаны между собой замечательным соотно-
шением, которое называется взаимной ортогональностью
•форм. Заметим еще раз, что первая форма есть статическая упругая
вызванная группой сил ^\т1уц, ^\т2У2и а вторая вызывается
группой сил ^1тхУ12, ^\П12У22'
Применим к этим двум статическим упругим линиям теорему Бетти:
приравняем друг другу виртуальные работы, производимые статичес-
кой нагрузкой одной из форм на перемещениях, отвечающих ДРУ^^
из них:
"^1^1 У и У12 + ^\^2 У21 У22 = ^>Х у 12 Уц + '^1Щ У22 У21 '
1ИЛИ
(«>2^0)2) {т^у^^у,2 + 'П2У21У22) = о;
так как «Чт^Шг, то
Щ Ун У12 + ^ У21 У22 = О, ^^^'
^80
^р работа внешних сил, отвечаю ittmv г.^
Генн^нх форм, на перем'ещениях "^тзечаюш^Г "'":
„%них, равна « У •" ю. Очевидно, что тем же свойст^^» -'^ ^ ^ •" °/
дадать работы внутренних сил: i«M же свойством должны об-
щ
М^М^ ds
= 0.
Р,
dt
5
Cim^y^j
Cjm^y^^
Таким же рассуждением
можно доказать, что свойство
ортогональности собственных
форм распространяется на си-
стемы с любым числом сте-
пеней свободы.
§28.2. РАЗЛОЖЕНИЕ НАГРУЗКИ
НА НОРМАЛЬНЫЕ
СОСТАВЛЯЮЩИЕ
Свойство ортогональности
позволяет легко разложить
группу сил Pi, Рг, приложен-
ных в точках Л и В, и имеющих
произвольные величины, на две
групповые составляющие, отве-
чающие собственным формам
(фиг. 580). Такие составляю-
щие называются нормаль-
ными составляющими. Неиз-
вестными в этом разложении
являются коэффициенты Су и сг.
Мы их найдем, составив выра-
^кение виртуальной работы
Wnnbi сил Рь Рг-на перемеще-
ниях, отвечающих первой соб-
ственной форме. Так как обе нормальные составляющие взаимно-ортого-
иальны, то работать на этом перемещении будет только первая состав-
•^яющая (см. фиг, б):
Сггп, у, 2
Фиг. 580
^1 7^ Уп+Р^ А У21 = ^1^1 Уп -%-Ун + ^1'"2У21 Л- У21
Или
^1 =
S Piyix
1=1.2
аналогично с^ =
S Piyi^
?=1.2
? m^yfs
(28.5)
?=1,2
^^^^Рмулы (28.5) можно упростить, основываясь на то,м, что каждая
^^ственная форма колебаний характеризуется отношением своих
РДинат; форма не нарушится, если все ее ординаты будут умножены
одно и то же произвольное число. Умножим ординаты первой формы
ц^Л^^ое tцicлo, чтобы знаменатель в выражении Сх обратился в едини-
У' аналогичным образом поступим с ординатами второй формы. Обоз-
^ чим через уц, У12, У2и У^з. ординаты таких умноженных («нормиро-
'*^Ь1х») форм. т. е. примем
М
"• М. Рабиномч
481
тогда ко,ффи««™ с, « выразятся более просто
(28.6)
..,лоп« ппияние произвольной статической нагрузки,
Мы рассмотрели «•"" Jf ^ ^ерь легко перейти к динамической зада-
составленнои из сил гь Г2- i^u ^
че о действии переменных сил
f/A-пDoизвoльнaя функция от времени. Снова разложим силы
Р.! й ^ГсостаХтТющие по формам собственных колебании, пользуясь
*°Sna" if fsyx составляющих будет изгибать балку на одной из
собственных форм и вызывать колебания, как в системе с одной сте-
пенью свободьь Результирующее перемещение будет представлять со-
S Геометрическую сумму двух простых Мы можем применить к этим
ппостым перемещениям формулу (27.19), выведенную для системы с
оЕной степе^нью свободы Для этого умножим статические перемеще-
ния, показанные на фиг. 580, б и в, на интеграл вида
О) J/(«) sin ш (/ — и) da.
В итоге
^1 J
о
t
+ — У12 (/(^^) SI" ^2 (^ — i^)du;
О
t
У2 (О = -^ У21 f/(^0 sin o)j {t — и) du +
0
+ —ya2\/(^)sinci)2(/— u)dtl.
^2 J ¦
0 /
Формулы для изгибающих моментов имеют аналогичный вид:
(28.7)
t
Mj (О = -^ Л^п (/(гг) sin ci)j (/ — гг)^гг
n
Mj2 \ f{u)sin 0)2(^ — u)du:
+
+
Cz
t
Mg (0 == *-^ Л421 \ f(u) sin («i (^ — u)du +
0
/
+ -^ M22 \ /(w) sin cDg (/ — u) du ,
J
(28.7'>
482
По этим формулам можно составить "кривые изменения изгибающих
моментов Mi{t) и МгСО во времени и найти их максимумы.
В случае систем с любым числом п степеней свободы изложенные
рассуждения остаются в силе с тем лишь отличием, что такие системы
будут иметь п собственных форм и п частот.
§ 28.3. ВЗАИМНОСТЬ ДИНАМИЧЕСКИХ ПЕРЕМЕЩЕНИЙ
Сопоставим два перемещения: 1) перемещение y{t) при условии,
^^ Р,=0, P2^0\ 2) «перемещение y^it) при условии, что Pi=0, РгФО^
Первому случаю отвечают по формуле (28.6) значения коэффициентов
d и С2:
второму случаю — значения
По формулам (28.7) имеем в первом случае
уМ) = -^^^Уп \fiti)smi>^,{f—u)du +
О
t
j^?^y^y^Jf{ti)siui^,{t-u)du. (28.8)
О
Во втором случае
,, (А = li^ii- у,, f/(и) Sin О), (/ - и) du +
t
j^?iy2^y^^f{u)sinMt — "-)d"-- ^^^-^'^
При P. = P. оба вьфажения^винмеж^^^^^^^^
ремещение массы m, в •"'« J°" "^^ «я ^ ще й свою величи-
ложенной к массе Шг ^ и л Ь1 и дкону, равно переме-
ну во времени по произвольному зако У-^Р^^^^ ^ ^^^^^
Щению, которое "мелось оы в изменяющаяся по
приложения массы ^^'^^^" ^„^'о же н а к массе т,.
такому же з а кону был а пр теорема справедлива
Из хода рассуждений нетрудно усмотреть
для системы с любым числом степеней свободы.
„^ г, рдгЧЕТЕ СООРУЖЕНИЙ
« "Г«Гм"ичвское"оздв,,сгв„в
чемлетоясения является важной
Расчет сооружений на действие ^ обширные сейсмические райо-
инженерной задачей. В СССР '"f'°^"' ,ет соружеиин на сеисмо-
ны, в особенности на юге и ^°^^°l\,'tL Эта задача исключительно
стойкость имеет практическое зиа i™ е^ся в том. что амплитуды
трудна, причем главная труД»ость з^'; которые передаются фун-
и частоты тех поверхностных ^олпв ^ У беспорядочный характер.
Даменту сооружений, имеют су10жишии^ ^^^^^^^^ обширная литера-
Анализу этих сложных колебании грун ^
СССР и за рубежом, но исчерпывающих данных и достаточной
^УР^ '.ПРЯНОСТИ в э?ом вопросе до сих пор не достигнуто. Имеется бо-
определенности в этом 1 ^ое на опыте мнение лишь по сле-
лее или "^"^„^^^^.""^Гкал^ая составляющая сейсмических колебаний
?е"елик J и Сет о^ьшно второстепенное значение; основной расчет ве-
дется на ^^^^^^^Ц^^^^ хараЙерный для данного района закон гори-
"Гкных колебаний поверхности земли и принимая приближенно,
зонтальных ''^^^^^''^'l^^^J^^ передаются фундаменту сооружения,
"'' Гп^извес™ динам^^ расчет самого сооружения, как прост-
"У'^.иКсистемьГ учитывая силы инерции всех масс и степень по-
Га^ивостГпродоТьных' и поперечных стен, перекрытии, колонн и т. д.
/77^(
П72^
Фиг. 581
Фиг. 582
При ЭТОМ следует принять во внимание затухание колебаний в грун-
те и в самом сооружении. Эта задача динамического расчета тоже до-
статочно сложна.
Не останавливаясь на детальных вопросах, которые приходится
решать инженеру-проектировщику в процессе расчета сооружения на
сейсмостойкость, разберем простейший пример, который может слу-
жить теоретическим введением в этот расчет. Пусть требуется рассчи-
тать высокое сооружение типа башни или дымовой трубы; будем рас-
сматривать его как консольную упругую балку, абсолютно защемлен-
ную на нижнем конце. Сечение балки будем считать постоянным. Зату-
ханием колебаний пренебрежем. Сейсмические перемещения фундамен-
та будем считать горизонтальными, параллельными одной из главных
плоскостей изгиба; обозначим их, как и в § 27.17, через f(t), или, коро-
че, через /.
Балку можно рассматривать либо как систему с бесконечным чис-
лом степеней свободы, либо более приближенно — как систему с конеч-
ным числом степеней свободы. Чтобы показать на примере ход расчета,
заменим массу балки четырьмя сосредоточенными массами, из ^^^^^'
рых нижняя присоединена к фундаменту и колеблется вместе с ни »
а остальные три расположены на верхнем конце и в двух промежуто^
ных сечениях (фиг. 581). Способом, изложенным в § 28.1, определи^^
собственные частоты ш^ wg, ^г этой системы, а также соответству^^^
щие им формы собственных колебаний. Эти формы вместе с обозн
нием ординат показаны на фиг. 581. л^оиячим
Перемещения масс гпи т. ^з относительно фундамента оОозн^
через Ух{Г), yzit), ys(t), или, короче, через уи У2, Уз (фиг. 582).
484
Абсолютные перемещения масс выражаются суммами f+y, f+u^
f+ys'y силы инерции равны ^ '^^^' '^^2,
где двумя значками отмечены вторые производные по времени t.
Силы инерции — m,f , —/ПзГ, -/ПзГ не зависят от изгибных переме-
щений Уи У2у Уъ, их можно поэтому рассматривать, как заданные
внешние возмущающие силы. Следовательно, задача об изгибных пе-
ремещениях ничем не отличается от задачи о колебаниях балки с не-
подвижным фундаментом при заданных внешних возмущающих
силах.
Будем для простоты записи рассматирвать силы mj'\ т^Г, т^!"
(без минуса) и разложим эту нагрузку на нормальные составляющие по
формам собственных колебаний балки подобно тому, как это было сде-
лано в § 28.1:
^1^1^11» ^\ЩУ21^ ^хЩУгЛ^"^ составляющая);
^2^1^12» ^2^2^22» ^2^зУз2(^"^ СОСТЗВЛЯЮЩая);
^3^1^13' ^3^2^23' ^з^зУзз(3-я составляющая).
Коэффициенты Си ^2, ^з определяются по формуле (27.5)
r-Y. щуп f-Y^ rniyit
/ = 1,2.3 ^ /=1.2.3
2j ^1Уа 2j /",-Уд
/ = 1.2,3 /=1,2.3
f^ • Ц miyis
Cs=-^ • (28.9)
/=1,2.3
Каждая из этих составляющих выгибает балку по одной из ее соб*
ственных форм. При любом заданном законе перемещений /(/) фунда-
мента изгибные перемещения будут представлять собой сумму переме-
рдений, происходящих в трех системах, имеющих по одной степени
свободы:
у^ (/) = ii- у„ Г/"{и) sin ш, {t-u)du +
t
+ — У,2 {f (^) Sin c«2 (t ~u)du +
С
t
+ — У1аГ/Ч^)81псоз(^- ^) ^«- (28.10)
0
Перемещения yz^t), y^{t) выражаются аналогичными формулами с
заменой индекса 1 соответственно индексами 2 и 3.
Изгибающие моменты Miit) в сечении, где расположена масса т,.
|^ожно вычислить по формуле (28.10), заменив в ней величины у,и У12,
^»з величинами Mi, М,2, Л1,з; аналогичным образом вычисляются мо-
^енты М^Ц) М^{\\
,^ Для нахождения наибольшего изгибающего момента нужно по-
^^Роить ряд эпюр, относящихся к различным моментам apei^eji^i t
Ш
Из формулы (28.10) непосредственно усматривается, что геометри-
чески подобные сооружения при одном и том же сейсмическом воздей-
ствии ведут себя неодинаково. Их упруП^е линии, а также эпюры изги-
бающих моментов не подобны друг другу; естественно, что и трещины
появляются у них не в одинаковых местах, и разрушение происходит у
них по-разному.
§ 285 СВОБОДНЫЕ КОЛЕБАНИЯ БАЛКИ КАК СИСТЕМЫ С БЕСКОНЕЧНЫМ
ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Изложенные выше теории колебаний системы с одной и с несколь-
кими степенями свободы имеют практическую ценность для приближен-
ного динамического расчета сооружений, но они дают слишком непол-
ную картину поведения сооружений, находящихся под действием дина-
мических нагрузок. Более точная теория раскрывает нам более богатую
и интересную картину и позволяет более сознательно относиться к при-
менению приближенных методов, а также судить о степени их точности.
Рассмотрим простейшую из стержневых систем — балку постоянно-
го сечения. Все характерное в поведении более сложных систем можно
усмотреть уже из этого простого примера.
Условия дина-мического равновесия элемента стержня выводятся из
условия статического равновесия
EJ^=p. (28.11)
где р — погонная нагрузка.
При свободных колебаниях погонной нагрузкой являются силы
инерции, интенсивность которых равна
где р.— погонная масса.
Тогда дифференциальное уравнение свободных колебаний переходит в
Интеграл этого однородного линейного дифференциального уравне-
ния четвертого порядка в частных производных мы будем искать в фор-
ме произведения двух функций, из которых одна зависит только от пе-
ременной X, а другая — от t:
y = X(x)T(t)=^XT, (28.13)
Производные пишутся так:
При помощи этих выражений уравнение (28Л2) принимает вид
EJTX'"^ + jxXT" = О, (28.14)
или
Ё?.^ = _.Г__^2, (28.140
Левая часть уравнения (28.14') не зависит от /, а правая — от ^»
следовательно, обе не зависят ни от той, ни от другой переменной, ^
466
^s есть постоянная. Дифференциальное уравнение (28.14) распадается
на два обыкновенных:
Г'+с.^Г=ОиХ--^^Л = 0. (28.15)
Первое из уравнений (28.15) имеет знакомый нам вид: оно совпа-
дает с уравнением (27.2) при условии, что P{t)-0, т. е, выражает собой
свободные гармонические колебания системы с одной степенью свобо-
ды, имеющей частоту о) .
Второе уравнение определяет форму X упругой линии колеблющего-
ся стержня. Эта форма такова, что
fJX^^ =^V^, (28.16)
т. е. X представляет собой статическую упругую линию, вызываемую
погонной нагрузкой o)V-^- Особенность этой упругой линии, как показы-
вает уравнение (28.16), состоит в том, что соответствующая ей нагрузка
в любом элементе dx стержня пропорциональна перемещению (проги-
бу) X того же элемента. При действии произвольной нагрузки, распре-
деленной по стержню, такое соотношение между ее интенсивностью в
любой точке и прогибом в той же точке, как известно, не имеет места.
Функции X, удовлетворяющие соотношению (28.16), носят название
«собственных функций», а по их физическому смыслу они являются
«главными» или «нормальными» формами колебаний.
Интересно отметить, что уравнение (28.16) аналогично уравнению
балки на сплошном упругом основании, но с тем отличием, что в дан-
ном случае «упругое основание» обладает отрицательным коэффициен-
том отпора, равным — соV.
Проинтегрируем уравнения (28.15), Интеграл первого из них имеет
вид
Т = л COS 0)^ + ^ sin a)/f. (28.17)
При интегрировании второго примем, что масса распределена по
длине балки равномерно, т. е. \^ =const. Тогда
X = Ст^в'ткх + Cg coskx + C^shkx + C^chkx, (28.18)
где
^^l/i'' илис„=У^^}/^. (28.19)
Постоянные А и В зависят от начальных условий движения, а по-
стоянные С, —от граничных условий.
Пусть, например, балка шарнирно оперта по концам на жесткие
^поры. Тогда
Х(0) = 0 и Х'ЧО) = 0;
^"^^Юда следует, что
С2 + С4-О и кЧ-С, + С,)=^0.
Откинув решение k=0, при котором из (28.18) получается А'^О, т. е.
^стояние покоя, мы приходим к выводу, что
Сг = Q = О, Х = Ci sinkx + Cs sh kx.
-^^«ee из граничных условий Х(/)=0, Х-(/)=0 следует:
С, sin kl + Cs sh kl-==0; | (28.20)
_Cx sinkl + Csshkl = 0. J
487
9ти два уравнения тождественно удовлетворяются при С^-Сз-О,
нп '^кое «тривиальное» решение опять выражает собой состояние покоя,
ппи котором Х=0; при отсутствии внешней нагрузки такое сосюяние,
очевидно принадлежит к числу возможных состоянии равновесия. По-
стоянные С\ и Сз могут быть отличными от нуля только при условии,
что
sin kl sh kl 1
— sin kl sh kl I
= 0.
или
2sini^/sh^/=^0.
Решение sh kt==^0 опять является тривиальным, так как приводит к
выводу k=0, A = 0. Практический интерес представляет последнее воз-
можное решение
sinW = 0.
Это так называемое характеристическое уравнение имеет бесчислен-
ное множество корней:
(28.21)
Каждому значению собственной частоты («п отвечает своя форма ко-
лебаний Хпш
Из уравнения (28.20) в связи с тем, что sin kl=0, получается Сз=0.
Итак:
X„ = C„sin^. (28.22)
Т. е. /г-я форма представляет собой кривую, содержащую п полуволн
синусоиды. Нечетным значениям п отвечает симметричная форма, а
четным — обратно симметричная форма.
Известно, что интеграл однородного линейного дифференциального
уравнения представляет собой сумму его частных интегралов, поэтому
оо со
у ix,t) = S Х„Т„ = 2 (^п S'" ^"nt+B„ COS wj) Sin ^ (28.23)
n=l n=l
(произведения постоянных СИ„ и CiB„ мы заменили обозначениями
An и Б„),
Итак, свободные колебания балки в самом общем случае представ
ляют собой сумму бесконечного множества простых гармонических ко-
лебаний, каждое из которых совершается со своей особой частотой л
и со своей особой формой изгиба Хп. ^
Нетрудно понять, что от суммирования таких вибрирующих У^РУ^„л
линий не получается постоянная форма результирующей кривой. ^^
мы будем снимать моментальную фотографию с колеблющейся ^^^^^^
то в каждое новое мгновение снимок упругой линии будет иметь -^P^^g.
очертание. Движение настолько сложно, что оно производит ^"^"^^,^^16
иие хаотичности, беспорядочности. Произведенный ^^^^''^^^^^^Jll^HTb
анализ позволяет разобраться в этом кажущемся хаосе и разл ^^^^
его в пространстве и во времени на простейшие, упорядоченные
менты. ^ лю-
Принципиально решение остается таким же самым для оалки
бым устройством опор, а также для любой стержневой системы.
488
е 28 6 ОСОБЫЕ СВОЙСТВА НОРМАЛЬНЫХ (СОБСТВЕННЫХ)
^ ' ФОРМ КОЛЕБАНИЙ
Рассмотрим любую стержневую систему с любыми граничными ус-
иями и любым законом распределения масс.
^^^а) Применим принцип взаимности работ к двум воображаемым со-
ояниям статического равновесия балки, из которых первое характе-
ризуется упругой линией Х^ и соответствующей статической нагрузкой
1чХку 3 второе —упругой линией ХпИ нагрузкой о)2(хХ^, где /е/г —про-
извольные индексы:
о о
или
Так как
то
О
I
l\iXkX^dx = 0. (28.24>
о
Соотношение (28,24) выражает собой важное свойство нормальных
форм колебаний — свойство их взаимной ортогональности.
Соотношение (28.24) справедливо не только для систем с непрерыв-
но распределенными массами, но и для систем, имеющих наряду с
непрерывно распределенными массами сосредоточенные. Сосредоточен-
ную массу nil можно рассматривать как распределенную на участке
^^ и имеюш.ую интенсивность [А^ == —- j так что для соответствующего
элемента dx получается iAcf>:=m,-, При такой расширенной трактовке
интеграла соотношение (28.24) остается без изменения. В явном виде
свойство ортогональности в рассматриваемом общем случае можно пи-
сать так:
} lxX,X,rfx + Е m,Xk {X,) Х„ (X,) - О, (28.25>
о
^Ае Под Xf^ (х.)^ Xn(Xi) следует понимать ординаты кривых А"^, Х^ в.
очке приложения массы т,-, а знак ? распространяется на все точеч-
"bie массы.
Ч Принцип взаимности, как известно, в одинаковой мере справедлив
я работы внешних и внутренних сил. В случае балочной системы, ра-
гиб^^^^^ только на изгиб, обобщенной внутренней силой является из-
^)ающий момент — EJX'\ а соответствующим обобщеннным переме-
j^"^^^ —взаимный поворот X"dx. Поэтому свойство ортогональности
РМальных форм для такой системы можно записать также в следую-
^^м Виде;
• ^\EJXlX''^dx = 0. (28.2б>
бод/ Потенциальная энергия стержневой системы, совершающей сво-
В д,^!? колебания, может быть выражена как работа внешних сил,
оое мгновение перемещение выражается формулой
4e9t
соответствующая погонная^статическая нагрузка - формулой
Потенциальная энергия
Bo второй сумме ^ ?= ^, поэтому no свойству ортогональности эта
сумма равна нулю, следовательно:
^ = Т S <П 1 ^4d^= t ^.. (28.27)
т. е. потенциальная энергия равна сумме потенциальных энергий всех
нормальных составляющих полного перемещения.
Таким же способом легко доказывается, что и кинетическая энергия
в любой момент представляет собой сумму кинетических энергий всех
нормальных составляющих. При каком-либо другом разложении пол-
ного перемещения на составляющие такой закон суммирования энергий
не будет справедлив.
Разумеется, что полная энергия, т. е. сумма потенциальной энергии
€ кинетической, во время свободных колебаний остается постоянной, что
нетрудно доказать.
§ 28.7. ВЫНУЖДЕННЫЕ ПЕРЕМЕЩЕНИЯ
Пусть на балку действует внешняя нагрузка, интенсивность которой
в любой точке выражается формулой
q{x,t) = av.XJ(t), (28.28)
где а — постоянная;
Хп—ординаты п-и нормальной формы;
fi—погонная масса;
f{t) —произвольная заданная функция от времени.
Эта нагрузка вследствие ортогональности нормальных форм совер-
шает работу только на перемещениях Х^; потенциальная энергия всех
других форм остается равной нулю, следовательно, под действием та-
кой нагрузки система будет вести себя, как система с одной степенью
свободы. Она будет колебаться по форме Х^ с частотой о)„. В любой мо-
мент перемещения будут таковы, как будто на систему действует распре-
деленная эквивалентная статическая нагрузка интенсивностью
о)„ар.Х„ If (и) sin io„ (t —и) da, (2^-29)
о
Но от нагрузки «^^р-Х^ получаются прогибы Х„, следовательно, от вы-
шеуказанной эквивалентной нагрузки получатся прогибы
у (x,t) = 5^ {f{u)sin ш„(t— u)du. (2^-^^^
490
Если на систему действует одновременно несколько нагрузок, интен-
ости которых соответственно равны
индекс п имеет несколько значений, то
У(^,0 = 11^^|/(^)5шо)„(^_гг)йгг. (28.31)
п о
Докажем теперь, что внешнюю нагрузку, распределенную по любо-
му заданному закону, можно представить в виде суммы нагрузок типа
.fl^jxXn, распространенной на всю бесконечную совокупность форм Х^.
Рассуждения здесь вполне аналогичны тем, при помощи которых выво-
дятся формулы для коэффициентов разложения произвольной заданной
функции в ряд Фурье.
Пусть дана нагрузка q{x) f{t)' Попытаемся представить функцию
q(x) в виде
д{х) = 1а,1хХ,. (28.32)
Допуская, что такое разложение нагрузки возможно, умножим обе
части этого тождества на функцию Xf^, где k — произвольный индекс, и
проинтегрируем обе части в пределах от х=0 до х^1.
lq{x)Xkdx==^a^l\^X^Xkdx.
о «=1 о
По свойству ортогональности в правой части отропадают все члены,
для которых п фк\ остается только один член, так что
I I
IqXf^dx^akWxldx.
¦Отсюда
J Q^kdx
a^^j (28.33)
о
Если в числе нагрузок имеются и сосредоточенные силы Р,- , то их
^^>кно рассматривать как распределенные на участке длины dx, при-
^^м qdx=^P^ В этом случае формула (28.33) может быть записана так:
t
а, = ^ ^ , (28.330
^liXldx
о
^^^ ^feU ;) -^ординаты кривых Х^ в точке приложения силы Р.
X ^^^ удобства вычислений целесообразно «нормировать» функции
.(28^?^o6paB для них такой масштаб, чтобы в формулах (28.33) и
•^^) знаменатель обратился в единицу:
^^\xXldx - 1 . (28.34)
491
После того как коэффициенты af, будут вычислены, перемещения
выразятся формулой
У Ш) = 11 -^ J/(^)^^^ "^^(^- «)rf«, (28.35)
а изгибающие моменты — формулой
М (x,t)=- S -^^^^ I /(«) sin О);, (f -u)du. (28.36)
28.8. ДЕЙСТВИЕ ВИБРАЦИОННОЙ НАГРУЗКИ
Пусть, например, нагрузка изменяется по простому гармоническому
закону с некоторой частотой О :
д (х,0 = д {х) COS Bt =cos O^Sa„ p- X„.
Тогда no аналогии с формулой (27.31)
оо
у (^>0 = у -4^ (cos е^ - cos V). (28.37)
п=1
Явление резонанса возникнет при б == о)„, т. е. при совпадении час-
тоты возмущающей силы с какой-нибудь из собственных частот си-
стемы.
Нужно, впрочем, заметить, что при б=«)„ явление резонанса возни-
кает только при условии, если а^фО, т. е. если нагрузка действительно
содержит составляющую, пропорциональную кривой р-А'^. Если этой
составляющей нет, резонанса не будет. Если, например, нагрузка q(x,t)
распределена по пролету симметрично, а частота 6 совпадает с частотой
^п одной из обратно симметричных собственных форм, явление резо-
нанса, теоретически говоря, не должно возникнуть. Однако на практике
мы никогда не можем гарантировать, что нагрузка абсолютно симмет-
рична или что тот или иной коэффициент а^ строго равен нулю, а не
является просто малой величиной. Это заставляет по возможности из-
бегать совпадения частот.
Собственные колебания могут иметь существенное значение лишь
во время переходного состояния; по прошествии некоторого времени
после начала действия вибрационной нагрузки сохраняется только ста-
ционарный колебательный процесс, выражаемый формулой
оо
у{x,t) = cosUY,-^^ ¦ (28-38)
Бесконечный ряд, стоящий в правой части формулы (28.38), гораздо
проще рядов (28.31) и (28.35), отвечающих любому другому закону
изменения нагрузки во времени. Действительно, по формуле (28.38) все
нормальные колебания совершаются с одинаковой частотой бив оди-
наковой фазе, т. е. система ведет себя так, как будто бы она имела
только одну степень свободы. Но для систем с одной степенью свободы
нет надобности пользоваться бесконечными рядами. Замкнутое решени
492
.ядачи указано проф.^ Н. И.^Безуховым^. Оно основано на применении в
пйнамике сооружении метода начальных параметров, оказавшегося
пезвычаино плодотворным в статике сооружений.
"^^ Поскольку речь идет только о чисто вынужденных колебаниях, сле-
дует принять
Т = cos6/ ~ ^_62
т
и дифференциальное уравнение (28.14) для участка, на котором нет
внешней нагрузки, заменить таким:
?JX^v_eVX, (28.39)
а формулу (28.19) формулой
У EJ
(28.40)
Интеграл уравнения (28.39) выразим, как это принято в методе
начальных параметров, при помощи линейных комбинаций тригономет-
рических и гиперболических функций; например, при помощи следую-
щих функций:
— (cosfejc + chfejc) = А^; -^(sin^x + sh^A:)= В^ l)
—(cos kx — ch kx)= C^; -y (sin kx — sh kx)^ D^,
(28.41)
^Де fe выражается формулой (28.40). Эти гиперболо-тригонометрические
функции удобны тем, что их производные любого порядка выражаются
через те же функции:
(28.42)
дА,
dx
ип ' ^^^ — ЬА - ^^ = kB
дх
дРг
дх
= kC.
^ также тем. что
Ло=1, ^o = Co = Z)o = 0.
(28.43
^^ Интеграл уравнения (28.39) содержит эти функции с четырьмя по-
^янными, которые мы обозначим через Ru /?2, ^з, R^-
У = 2 {R,A^ + R^C^ + R^B, + R4DJ cos Ot;
^=.2k (^-Rp^ — R^B^+R^A^ + Rf,) cosO^;
M = 2 k^EJ {R,C^ +^ A. + ^Px + ^A) cos 0^;
Q = 2k^EJ {R,B^ - R^D^ + ^3^. + ^4^.) coset.
^3 (28.43) (при jc=0) получается значение граничных параметров
**»*не iL^^* Ьезу xo в. Некоторые обобщения методов строительной механики в дин^^
и^ДагГ^^ений. сборник Гис^едования по теории сооруженииж. вып. ПЬ Госстрой-
493
nn.TOMV формулы (28.43) для аплитудных эпюр, отвечающих значению
"°''о?=1 принимают окончательно следующий вид:
COS "
-zk^
t
м
А,-
ФО^А-
k
Mo
В.+
Qo
С^ — уфВх\
EJk -^ • EJk^
9о B,+yJi'EJC^+<?JzEJD^;
k
МоЛ.+
\
]
(28.44)
Pcosdt
Фиг. 583
>'o = 0, Mo = 0, e ^
2 2
Последние два условия запишутся в виде уравнений
Пусть, например, однопролет-
ная балка с шарнирно-опертыми
концами нагружена в середине
пролета пульсирующей силой^
Р cos б/ (фиг. 583). Требуется най-
ти наибольшие значения усилий.
Наибольшие усилия и дефор-
мации образуются во всех сечени-
ях одновременно при cosOf=L
Граничные условия таковы:
==0, Q , =4-
р_
2
Решив эти два уравнения, определим параметры
PC
% =
2 ?/^2 / Л2
\)
^^~ 2 ' Л«
—С2
(28.45>
после чего сможем по формулам (28.44) построить все эпюры.
Например, эпюра изгибающих моментов выражается уравнением
M^-^B^^^JzEJD,',
(2 8-46)'
эпюра Q — уравнением
и т. д. Все эпюры — криволинейные. Ординаты кривых Л^, В^, Сг, ^^
берутся из готовых таблиц этих функций или вычисляются по обычнь-
таблицам тригонометрических и гиперболических функций.
Если мы изменим жесткость Е] или погонную массу у^-, или ^^^^^^, *
Ту пульсации G, то эпюры не останутся подобными, а примут ^У^^^^^-
венно иной характер, так как любое из указанных изменений ^^'^ ^у^
изменение параметра k, который входит ъ состав безразмерного ар у
мента функций Л^, Б^, С^., D^.
494
Для определения усилии и деформаций, характеризующих переход-
ное состояние системы, следует обратиться к формулам (28 35) и
f28.36). Без такой поверки нельзя быть уверенным в том, что наиболее
опасным является стащюнарное состояние, а не переходное.
§ 28.9. ПОНЯТИЕ О ДИНАМИЧЕСКОМ ДЕЙСТВИИ ПОДВИЖНОЙ НАГРУЗКИ
Пусть сосредоточенный груз Р перемещается с постоянной, отличной
от нуля скоростью V по прямолинейной однопролетной или многопро-
летной балке, имеющей постоянную жесткость EJ и равномерно распре-
деленную по ее длине погонную массу [х.
Абсциссы сечений балки будем обозначать через х, абсцисса же
движущейся силы Р в любой момент / равна vt (фиг. 584).
Разложим силу Р в ряд по формам соб-
ственных колебаний балки, т. е. заменим Р р
распределенными по всей длине балки на-
грузками вида a„[xX^, где через a« обозна-
чены коэффициенты, не зависящие от х. Эти
коэффициенты нужно подобрать так, чтобы
при любом положении силы Р работа пос-
ледней на любом возможном перемещении
была равна сумме работ ее составляющих.
Достаточно для этого подставить в форму-
лу (28.33') ^=0, Pi=P, Xi^vt, и мы полу-
чим формулу
% = РХЛ^); Р(1) = рТхМ))^Х,, (28.47) '^^'- ^^^
Под А'„ следует понимать «нормированную» величину ординат, т. е.
подобранную в таком масштабе, который удовлетворяет условию
(28.34).
Итак, вместо движущейся силы Р мы будем иметь ряд неподвижных,
распределенных по всей длине балки нагрузок; каждая из них, сохра-
няя Неизменной свою форму распределения по пролету, непрерывно
изменяет во времени свою интенсивность пропорционально ординате
\(^t). Последняя играет в данном случае роль функции f(t). Тем са-
мым задача сведена к решенной выше.
Перемещение любой точки оси балки выражается формулой (28.31)
П-оо t
п=1 о
Изгибающий момент в любом сечении
JCft' vt -—j
M(x,t)^ — EJpYi— f X^^«)sino)^(/ —«)rf«. (28AS'}
n=l 0
Ьсли МЫ при вычислении функций Хп, Х\ дадим абсциссе х сечения
^^кое^пибудь определенное значение и, кроме того, примем Р=1. то
J^PMyjibi (28.48) и (28.48') превратятся в уравнения соответствующих
намических линий влияния.
495
Формулы (28.48) и (28.480 справедливы только для t<^, т. е. для
того промежутка времени, в течение которого сила Р находится на дан,
шом сооружении. После схода этой силы балка продолжает колебаться;
для характеристики ее состояния при любом t> — нужно за верхний
•предел интегрирования принимать — (а не /)
у (X, О - ЯУ -^ f ХЛу^г) sina)„(/ — u)du;
n=l о
^n J
n^l 0
(28.49)
Известно, что кривая X„ состоит из п участков, знаки которых че-
редуются. Если эти участки мало отличаются друг от друга, то кривая
Х„ представляет собой почти периодическую фигуру. Время, затрачи-
ваемое силой Р на пробег одного периода кривой, т. е. двух ее участков,
2/ ^ 21 ггл 2п
т)авно —. В том частном случае, когда — = i „ = —, наступает яв-
ление резонанса, которое длится, пока сила Р не сойдет с балки; дефор-
мации и усилия, выражаемые в формулах (28.48 и 28.48') п-ым членом,
быстро нарастают. Однако «критические» скорости v, при которых на-
ступает это явление, настолько велики, что для мостов они обычно не
имеют практического значения.
Уравнения статических линий влияния в виде рядов можно по-
лучить из уравнений динамических линий влияния после того, как
будут вычислены интегралы, стоящие в правых частях формул (28.48) и
28.48'); достаточно будет подставить в них t^ = 0 и вместо vu писать Хр.
Но можно вывести уравнение статической линии «/„ (л:, О» если вспом-
нить, что от статического действия нагрузки, распределенной по закону
w^jiX^, возникают перемещения, равные Х^, следовательно, перемеще-
ние равно интенсивности нагрузки, разделенной на ^^ р. На этом осно-
вании из формулы (28.33') непосредственно выводится
М,
(28.50)
Представление статических линий влияния в форме бесконечных р^'
дов само по себе было бы бесполезным, так как имеется более простои
<:пособ построения этих линий. Формулы (28.50) интересны тем, что по-
•496
ляют выразить ординаты динамической линии влияния как сумму
^^^«ият статической линии влияния и динамической добавки; например
0рдим<2*
У (хЛ - Уст (^,0 + [у (^, 0-Уст (^,01 • (28.51)
В этом выражении первый член правой части представляет собой
яииаты статической линии влияния, которые могут быть вычислены
^бычным способом (не в виде ряда), а разность, стоящая в квадратных
^кобках, представляет собой ряд, сходящийся более быстро, чем ряд
^(28.49)/
При тех скоростях v, которые встречаются на практике при эксплуа-
ации мостов, можно для определения прогибов ограничиться одним-
^вумя членами ряда (28.49), а для вычисления изгибающих момен-
тов—одним-двумя членами ряда, выражающего динамическую
^^ Если мы в формулах (28.49) дадим переменной / какое-нибудь опре-
деленное значение, то они превратятся в уравнения эпюр прогибов, из-
гибающих моментов и т. д., отвечающих данному значению ^, если в
тех же множителях принять x-^Xp=vt, то найдем закон изменения про-
гибов, изгибающих моментов и т. д. в сечениях, постоянно совпадающих
с движущейся силой Р. ^
В частном случае однопролетной шарнирно-опертои балки мы имеем
X„=a„sin^ ; J[xX'nrfx- 1 - i^al^ ,
о
илиа^ = -.т.е.Х„ = |/ — sm —.
После подстановки выражения Х„ в формулы (28.49) найдем урав-
нения линий влияния
плх
УШ) ^,
2Р
Vsin-
\ sin—^—sinio„(r — u)du-=
I
n = l
s
rrnx
sin
— s in ¦— 7- sin co„^ I
^ 7, .^(r-^^\
2/, """^n
5^(sin^-^sino>„<)
2№ \Л I \ i ""' ^. (28.52)
BJn* 2j -(1—^^
"*' * n^jt^EJj
n= 00 iiTtx
sin -
(28.53)
32 и.
М. Рабинович
497
пх^^п. ичменение погонной массы (х, жесткости EJ, пролета I или
ско^^ти /влечет за собой изменение очертания динамических линий
влияния.
Пр,, „=о эти линии влияния переходят в статические:
/ ^x^jii^L^Tj—Sin--—Sin-—-,
/2=1
П=оо
Я2
п=1
Тот же результат можно вывести из формул (28.50).
Для поверки вычислим прогиб в середине пролета от груза Р, не-
подвижно стоящего в том же месте, т. е. при х^ Хр^- — \
v<«.')=^(' + v+^+
2Я/3 /, , 1 , 1 ^ \ __ 2Р/3 я^ _ Р1^
" 48EJ
Формула (28.52) показывает, что при движении силы Р каждое cej
чение балки совершает сложное движение, которое представляет собой
сумму бесконечного множества колебаний, налагающихся друг на дру-
га: одни из них происходят с частотами —, зависящими от скорости
движения силы Р по балке (вынужденные колебания), а другие — с час-
тотами а)„ (собственные колебания). Ряд (28.52) быстро сходится,
поэтому практически можно для расчета ограничиться первыми не-
сколькими членами; ряд, выражающий М{х, t), сходится значительна
медленнее. При малых скоростях v линия влияния мало отличается от
статической; с увеличением пролета / разница уменьшается. Даже при
скорости V порядка 100 км/час наибольший прогиб превышает стати-
ческую величину всего лишь на несколько процентов. Очень большие
скорости V дают ничтожный эффект, так как при этом продолжитель-
ность нахождения силы Р на балке мала, следовательно, импульс, пере-
дающийся балке, также мал. Легко убедиться, что при t^=co выражения
(28.52) и (28.53) обращаются в нуль.
Мы рассматривали до сих пор влияние катящегося груза Р как с и-
лы, не имеющей массы. При движении реального груза появляется сила
инерции, равная ' ^ т^ " ' следовательно, приходится иметь
дело с подвижным грузом переменной величины Pll -''-~^f~~')'
Дифференциальное уравнение в этом случае может быть проинтег-
рировано только приближенно. Как показывает исследование, влияние
инерции груза Р на деформации пролетного строения моста целесооО-
разно учитывать при пролетах примерно до 10 м\ при дальнейшем У^^'
личении пролетов оно быстро сходит на нет^
* См. Ф. Блейх. Теория и расчет железных мостов. М., 1931, стр. 63—64.
498
§ 28.10. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Первые исследования, посвященные упругим колебаниям, были опубликованы в
иях Российской Академии наук Даниилом Бернулли в 1741—1743 гг. и Эйлером
^^^?лА г В «Аналитической механике» Лагранжа*, первое издание которой вышло в
%яЯ г имеется обширный раздел «О малых колебаниях любой системы сил».
В течение XIX столетия различным задачам динамики упругих систем уделяли
мяние многие выдающиеся математики и механики: Пуассон (в 1828 и 1833 гг.).
М^В Остроградский (в 1831—1833 гг. и др.), Рэйлей2 (в 1877 г.), Сен-ВенанЗ. Особенно
^' liioe значение для развития динамики упругих систем имели работы двух послед-
'^авторов. Появление первых железных дорог поставило перед инженерами задачу
^^счета пролетных строений мостов, а также рельсов на динамическую подвижную на-
^^v3Kv и дало практическое направление разработке проблемы. Из многочисленных ра-
?пт посвященных этой проблеме, заслуживают особого упоминания работы проф.
Н П Петрова (1836-1920).
В XX столетии развитие строительства промышленных и общественных здании,
сейсмостойких сооружений, судов, самолетов, а также развитие машиностроения сде-
лали необходимой разработку простых методов определения частот собственных (сво-
бодных) колебаний сложных упругих систем, а также деформаций, отвечающих коле-
баниям. Возникла также настоятельная практическая потребность рассчитывать соору-
жения иа действие сложной ритмической нагрузки и нагрузки, быстро изменяющейся
во времени по произвольному закону, а также на действие удара и взрыва. Разработ-
ка этих проблем интенсивно продолжается в СССР и за рубежом.
Указанная здесь краткая библиография^ содержит несколько руководств по ди-
намике сооружений и теории колебаний.
* См. русское издание: Л а г р а н ж. Аналитическая механика, т. 1, Гостехиздат,
1950
2 См. русское издание его знаменитой книги «Теория звука», т. I и 11, изд. 2-е,
Гпстрхи'чпят 1 Чт^
3 Theorie de Felasticite des corps solides de Clebseh avec des notes etendues
de M. de SaintsVenant, Paris, 1883. ^^^ ^ ^^ ^^
*Cm с П Тимошенко, Колебания в инженерном деле, 1959; акад. А. Н. Кр ы-
лов. Вибрация судов, 1936 (собрание трудов, т. X. 1948); К. Гогене мзер и
B. Прагер, Динамика сооружений, 1936; А. А. Ан др о н о в, А. А Витт и
C. Э. Хайкин, Теория колебаний, 1959. ^ ,^., * т-г ^
С А. Берн штейн. Основы динамики сооружении, изд. 2-е, 1941; А. П. Ф и л и п-
лов, Колебания упругих систем, 1956. „ ..
Е. С С о р о к и н. Динамический расчет несущих конструкции здании, 1956^
К С 3 а в р и е в. Динамика сооружений, 1946. И. П П р о к о ф ь е в и А. Ф. С м и р-
«ов, Теория сооружений, ч. 111, 1948; Ф. Морз, Колебания и звук, 1949; Дж. Сто-
кер, Нелинейные колебания в механических и электрических системах, 1952; акад.
^-И. Мандельштам, Лекции по колебаниям, 1955. ^
А. Ф. С м и р и о в. Устойчивость и колебания сооружении, 1958.
Н. К. Снитко, Динамика сооружений, 1960. ^
Я. Г. Пановко, Основы прикладной теории упругих колебании, 1957
Глава 2Я
ОСНОВЫ РАСЧЕТА ПОДПОРНЫХ СТЕНОК
§ 29.1. ОБЩИЕ СООБРАЖЕНИЯ
Подпорные стенки, удерживающие землю от обрушения на выемках,
откосах, уступах и т. д., встречаются в различных областях граждан-
ского, промышленного и дорожного строительства, а также в горном
деле, в фортификации и при возведении туннелей. Задача о распределе-
нии напряжений внутри сыпучего тела и на его поверхности соприкосно-
вения с другими телами принадлежит к числу труднейших задач строи-
тельной механики.
Все теории, предложенные до настоящего времени, оперируют с
идеальным сыпучим телом, наделенным некоторыми гипотетическими
однородными свойствами. Наряду с элементарными теориями к этой
задаче прилагались и прилагаются также методы теории упругости.
Делались попытки рассматривать сыпучее тело не как непрерывную
среду, а как совокупность отдельных частиц шаровой или цилиндриче-
ской формы; пробовали применять к механике грунтов методы статисти-
ческой механики; не без некоторого успеха сделана попытка приложе-
ния теории пластичности.
Серьезным шагом на пути к общему решению задачи о равновесии
и давлении сыпучего тела явились в основном исследования проф.
В. В. Соколовского, построенные на основе общей теории предельного
напряженного состояния сыпучей среды. Результаты этих исследований
сведены им в книгуЧ Указанные в этой книге способы расчета подпор-
ных стенок и оснований сооружений значительно более обоснованы, чем
элементарные методы, составляющие содержание широко распростра-
ненной до настоящего времени теории Кулона, предложенной еще в
1776 г. Графическая трактовка идеи предельного напряженного состоя-
ния земли предложена проф. С. С. Голушкевичем^. Однако в данном
кратком курсе мы не имеем возможности изложить названные более
строгие, но и более сложные методы решения задач о давлении земли
и ограничиваемся в основном изложением теории Кулона.
§ 29.2. ТЕОРИЯ КУЛОНА (TiP^bj^ ^F^ V ' r^bv^€
Она весьма проста. Перечислим те упрощающие гипотезы, на кото-
рых она основана.
* Статика сыпучей среды, изд. 2-е, Гостехиздат, 1954. .g^j
2 С С Голушкевич, Статика предельных состояний грунтовых масс, М-
500
Во первых, сыпучее тело (земляная масса) рассматривается как од-
^^ородная сплошная среда, способная воспринимать только сжимающие
и сдвигающие усилия.
Во-вторых, принимается, что при равновесии результирующее напря-
жение на любой площадке внутри сыпучего тела может отклоняться
от нормали к площадке иа угол, не превышающий некоторой величи-
ны 9, которая зависит от физических свойств данного сыпучего тела.
Этот угол 4- носит название «угла трения». Он связан с коэффициентом
трения / такой зависимостью: /=tgcp. Почему этот угол называется
углом трения, можно понять из
фиг. 585: если на тело, могущее
скользить по плоскости, действует
сила Р, наклоненная к нормали под
углом а, то нормальная составляю-
щая имеет величину //=-P cos а, и
сила трения не может превысить ве-
личины Nf=Pf cosa, в то время
как сдвигающая сила Т^Р sin а.
До тех пор, пока T<^Nf, или иначе,
Р sine. <Р/ cosa , или tga <f, тело
будет только прижиматься к плос-
кости, но не сможет скользить. То
значение угла а , при котором нера-
венство переходит в равенство, бу-
дет предельным для состояния равновесия; при дальнейшем увеличении
этого угла начнется скольжение. Обозначив предельные значения угла
а через 9 » получ,им
^^?^:^^^5^5^^^^^^
Фиг. 585
tg?=/-
(29.1)
К сожалению, экспериментальное определение угла ^ Д-^я сыпучего
тела представляет собой трудную задачу. Приближенно принимают, что
этот угол равен «углу естественного откоса», т. е. тому углу, под которым
наклонена к горизонту образующая конуса из свободно насыпанной
(неутрамбованной) массы сыпучего тела.
На поверхности соприкосновения стенки с сыпучим телом наиболь-
шее возможное отклонение давления от нормали к поверхности прини-
мается равным 9о, причем tg <Ро=/о, где fo — коэффициент трения сы-
пучего тела о стенку.
В-третьих, предполагается, что стенка, уступая давлению сыпучего
тела, начинает отодвигаться, и разыскивается не то давление, которое
она испытывает при обычных условиях, а то предельное, которое отве-
^^ает первому мгновению процесса отодвигания стенки. Теория Кулона
поэтому известна в литературе под названием теории «предельного рав-
новесия». Она дала в руки инженерам простой и надежный, хотя, быть
^ожет, и не вполне экономный способ рассчитывать подпорные стенки.
Кулону, вероятно, представлялось очевидным, что давление на
стенку при равновесии сыпучего тела ие может превысить того, которое
отвечает моменту нарушения равновесия и началу обрушения. Однако
Такое заключение нельзя считать вполне правильным, и это является с
практической точки зрения наиболее серьезным упреком, который
можно сделать теории Кулона.
В-четвертых, принимается, что обрушение сыпучего тела, наступаю-
^^^е вслед за подвижкой подпорной стенки, происходит следующим
Образом: от сыпучего тела отделяется клин, ограниченный с одной сто-
роны поверхностью подпорной стенки, а с другой стороны — плоско-
501
л.кю ппоходящей через основание стенки. Эта плоскость называется
пло^к^стью^^ и-^^ плоскостью сползания.
^ Тя^к^ч^скГ^'ка?SS^ опыты, та поверхность, которая отде-
ляет скользящую массу от остающейся в покое, является кривой; однако
это vnS^^^ отражается существенно на окончательных выводах.
Лмый клин рассматривается при этом как абсолютно твердое тело.
R гГтых задача решается в условиях так называемой «плоской
.япячи» т е предполагается, что стенка имеет неограниченную длину,
ооп^Ртгя в плане прямолинейной и что профиль земляной массы и все
прочее условия давления остаются по длине стенки постоянными. Это
А
^с^^/1/
Фиг. 586
дает возможность провести весь расчет только для участка длиной в
I ж, ограниченного двумя перпендикулярными длине стенки вертикаль-
ными плоскостями.
Призма обрушения имеет при этом высоту, также равную I М-
Перейдем теперь к самому расчету. Рассмотрим давление, оказы-
ваемое на некоторый участок ЛБ подпорной стенки (фиг. 586). Проведем
плоскость естественного откоса BD и вообразим, что линия ВС есть
след плоскости обрушения. Угол ее наклона к горизонту обозначим
через е. Найдем вес G призмы обрушения ABC, для чего нужно опреде-
лить площадь фигуры ABC, которая служит ее основанием, и умножить
ее на объемный вес материала f:
С==7-пл. ЛБС.
Размерность G получится в кг1м.
В момент нарушения равновесия, когда клин начнет сползать вниз»
преодолевая трение, реакции /?о и /? отклонятся от нормалей вверх "^
углы, которые не превышают величии <р и<ро. Обычно принимают откло-
нение силы R равным углу естественного откоса <р. а отклонение силь
502
/?.-^ равным углу трения земли о стенку ср^. Для увеличения надежно-
сти расчета принимают часто величину сро преуменьшенной; нередко
считают, что сро=0, т. е. что стена является идеально гладкой.
Три силы — G, /?о и /? — должны уравновеситься, поэтому величина
интересующей нас силы /?о, которая противоположна давлению земли
на стенку, может быть найдена из силового треугольника, изображен-
ного справа. Это может быть сделано либо графически — из чертежа,
либо аналитически — из пропорции.
/?о : G = sin (С —9): sin [180° —(ф + 6 —ср)] ,
откуда
где
R.
Q Sin (6^ у)
sin (ф+6—9)
90° —а-
?о-
(29.2)
(29.3)
В этой формуле единственной независимой переменной является
угол б. Каждому значению этого угла отвечает новое положение пло-
скости обрушения, новое значение веса призмы G и новое значение силы
Ro. Остается лишь разыскать то значение 6, при котором величина Ro
достигает максимума. Такое значение непременно существует, так как
при совпадении линии ВС с BD^ т. е. при значении б = ср, призма обру-
шения лежит на естественном откосе и поэтому не сползает и не давит
на стенку; при совпадении же линии ВС с ВА получается G=0, а пото-
му /?о==0. Ита1^ искомая точка С лежит где-то между Л и D. Она мо-
жет быть найдена путем нескольких попыток.
В табл. 14 приведены величины т и ? лля некоторых материалов.
Таблица 14
Объемные веса и углы естественного откоса грунта
Материал
Земля разрыхленная, сухая
сырая ....
насыщенная водой
утрамбованная, сухая ...
глина разрыхленная, сухая или сырая
утрамбованная, сухая
Р » „ « сырая . . • . -
Песок сухой . .
•у- в кг'м^
1400
1600
1800
1700
1500—1550
1800
1850 1
1800
1800
2 000
9°
40
45
27—30
42
40—45
40
70
30—45
30—45
25—30
29.3. ТЕОРЕМЫ РЕБХАНА И ГРАФИЧЕСКОЕ ПОСТРОЕНИЕ ПОНСЕЛЕ
^ Удобный критерий для нахождения наиболее опасной плоскости
?брушения и для определения величины (/?о)шах был указан Ребханом.
Продифференцируем формулу (29.2) по О «.приравняем производную
нулю:
rf/?o rfO sin(e—у)^ + G — Г-iIIliizilL 1 = 0.
Отсюда после простых преобразований толучим
dG sin(6 —<у)51П(ф + 6—у)
G = —
т
51Пф
(29.4;
¦ гвс^
Но из фиг. 586 видно, что
dO нл. вес ^ _
"rfe""^'^ rfe 2
Янак минус показывает, что при возрастании угла О вес G убывает.
Кроме того, из треугольника ВСЕ легко усмотреть, что
sin (4- + о — у) ^ М.
sin ф ВС
^^^
Сделав эти подстановки в (29.4), получим
С = —-^eCBEsinCe —ср) = т-пл-АВС?.
(29.5)
Найденная Ребханом теорема гласит следующее: наиболее опасная
плоскость обрушения ВС проходит таким образом, что площадь оснс-
еания ВАС призмы обрушения равновелика площади треугольника ВСЬ.
Пользуясь этой теоремой, можно после немногих попыток найти
правильное положение точки С.
Для нахождения силы (/?о)тах сделаем еще следующее построение,
повернем отрезок СЕ вокруг точки Е до его совпадения с прямой ^с^
затем полученную точку F соединим с С. Площадь треугольника ^^ ^
можно определить .исходя из того, что он имеет общее основание Сс
треугольником ЕСВ\
sin (в -
пл. А ECF
ИЛ. л ЕСВ
FE
BE
СЕ
BE
-f)
sin(^-f в—<р)
504
Отсюда, принимая во внимание соотношения (29.5), найдем
Q sm (6 — у)
,. А ECF = т-пл. Д ЕСВ ''''(^~~f)
Полученное соотношение состаБляет содержание второй изящной
теоремы Ребхана: наибольшее давление (R,)^^^ равно площади тре^
угольника ECF («треугольника Ребхана»), помноженной на объемный
вес материала т •
Величина Ro выражается в килограммах или тоннах на погонную
единицу.
Другой граф.ический способ -основан на следующем свойстве сило-
вого треугольника аЬс (см. фиг. 586): если совместить его вершину а
с точкой В и направить сторону аЬ по линии естественного откоса BD, то
сторона ас пойдет по линии обрушения ВС, а сторона be окажется
2?
Фиг. 588
Раллельной «основной линии» MN. Это непосредствершо вытекает из
венства соответствующих углов и было замечено еще Понселе.
Шя йг^^^^^ из верши'ны В пучок воображаемых линий обруше-
пт-Г 1^^^ и т. д. (фиг. 587). Найдем Беса Gi, G2... соответствующих
ного ^^РУшения, отложим их в некотором масштабе на линии естествен-
осно ^^^Р^^ " "3 концов этих отрезков проведем прямые Ьс, параллельные
собо^"^*^ -"инии, до встречи с линией обрушения. Отрезки be выразят
с. ^ ^^ответствующие давления /?о. Геометрическое место точек Сь сг,
Нанб ^ Р^^У^т некоторую кривую, построенную впервые Кульманом.
coCoif^^'^^^ из ее ординат, параллельных основной линии, «и выразит
йой *^^^^мую максимальную -величину /?о. Соответствующая точка кри.
парап ^^ -Определяется из чертежа, как точка, -в которой касательная
Черхнт ^^"^ ЛИВИИ естественного откоса. Разумеется, что нет надобности
участкя ^^^^ кривую, можно -ограничиться построением ее среднего
33 и.
ка.
'^^ Рабивоа
505
в том случае, -когда .поверхность земли ACD представляет собой
плоскость, наибольшее возможное давление (/?о)тах определяется
сразу без попыток. Для этой цели служит построение, указанное Пон-
селе. Оно состоит в следующем (ф|иг. 588). Прямую АС продолжают до
встречи в точке D с плоскостью естественного откоса, затем на линии
SD, как на диаметре, описывают полуокружность. После этого из точки
\ проводят прямую АН, параллельную основной линии, восстанавли-
вают в точке Я перпендикуляр HJ к диаметру и поворачивают хорду
BJ вокруг точки в до совпадения с диаметром. Из полученной точки ?
проводят прямую ЕС, параллельную основной линии, до 'пересечения "с
прямой AD. Прямая СВ и является изображением искомой плоскости
обрушения.
Яи.--^ Фиг. 589
После этого строится т1реугольник СЕР Ребхана, который служит
для определения наибольшего давления.
Докажем правильность построен,ия Понселе. Согласно построению
можно написать
ВЛ^ВЕ^ - BEI'BD или BE :ВН ^ BD : BE;
кроме того, из подобия треугольников ВКН w ВСЕ следует, что
ВЕ:ВН = ВС:ВК.
(а)
(б)
Из сравнения (а) и (б) получается BD:BE^BC'BK
собой параллелог^мм, след^^^^^^^ ^^^^ представляет
^^^Т^'^'^^^^Т^^^СЛ „ ВСЕ. д.„ .^ „р„-
ЭТИМ высотам, а так как мы локяяяпГ"'' i,^ « ^^ пропорциональны
каза,но и равенство высот итак пп^^; что Л/С=?С, то тем самым до-
хана что и доказывает правилкнп?!''^'' ^^ Удовлетворяет теореме Реб-
Иногда тюверхностьчемЛ^"^ "'^ ^'^^'^° построения. ^
венного откоса. Прямые В?)" Л Г LT'^^^^o™" ^°бой плоскость естест-
между собой, точка D уходи? в fi^Lt"/' ^^ ^ ^"^"^ '^•"У-'^е параллельны
ности становится невозможным ^^^°"^™°сть, и построение пмуокруж-
возможным. В этом случае, как видно из фиг. 589,
треугольник Ребхана остается без изменения при любом наклоне плоско-
сти обрушения, поэтому построение его может быть сделано без помощи
полуокружности (точка Е берется на линии естественного откоса BE
произвольно).
Может случиться, что^поверхность земли АС (фиг. 588) совпадает
с направлением основной линии; тогда построение Понселе приводит
к неопределенности. В то же время из первой теоремы Ребхана -выте-
кает, что в этом случае след плоскости обпушения ВС совпадает с м е-
диа'ной треугольника 5Л1) (фиг. 590).
При любом из рассмотренных случаев построение Понселе можно
производить для стенок различной высоты К При этом треугольники
Wy///////A
-^^^^E?[iocn7b
Фиг. 590
Ребхана будут получаться подобными между собой и стороны их про-
порциональными! высоте Л. Следовательно, давление R^ пропорцио-
нально величине Л^.
§ 29А ФОРМУЛЫ ДАВЛЕНИЯ ЗЕМЛИ НА СТЕНКУ
ДаБление земли на стенку можно определить также аналитическим
путем. Ограничимся тем случаем, когда -поверхность земли является
плоскостью. Это даст нам возможность использовать построение
Понселе, которое .нам останется только перевести на язык анализа. Не
производя здесь вычислений, приведем готовую формулу
/?o = -i-^^'
cos2(<p—с)
W'-^
-ГЛ>Л29.6)
sin ф cos^a
sin (у 4-Уо) sin (у ^Р)
sin ф cos (g — а)
^Де |j, зависит только от углов ?, ?о, « и Р. По этой формуле можно вы-
^^ислить давление земли Л'ри любых значениях углов ?, ?о и Р (фиг. 588).
Она показывает, что при всех обстоятельствах давление земли, огра-
ниченной сверху плоской поверхностью, оказывается пропорциональным
^^емному весу земли и квадрату -высоты стенки. При больших значе-
"^^ях а (а>60'') формулой (29.6) пользоваться нельзя, так как в этих
^'"Учаях она значительно расходится с действительностью.
Наибольшей известностью пользуется формула, которая получается
"^ (29.6) в предположении, что земля ограничена горизонтальной плоско-
^тью, а стенка вертикальна и имеет идеально гладкую поверхность
^''=?=-9о= 0):
(29.7)
/?,=.^,/t4g^(45«—^).
33*
507
Еспи земля ограничена горизонтальной плоскостью, а стенка иде-
ально" гладкая, но наклонная (13=% =0, ^.ФО), то
^ 2 (cos a+sin ?)^ COS а
(29.8)
Путем несложных тригонометрических преобразований можно привести
эту формулу к другому виду:
R^^^ ТЛ^ [tg (45^- ^) +tg а J COS а. (29.9)
8 29 5 ДИАГРАММА ПОЛНЫХ ДАВЛЕНИЙ И ДИАГРАММА
ИНТЕНСИВНОСТИ ДАВЛЕНИЯ
Для (расчета прочности стенки необходимо знать полное давление
на любой ее участок, считая от поверхности земли до какого угодно
уровня. Если земля ограничена кривой или многогранной поверхностью,
то нужно определить графически по способу Кулона полное давление
Фиг. 591
Ro вз. нес1Кольких уровнях и полученные величины отложить в виде
ординат у на диаграмме (эпюре) полных давлений (фиг. 591, а). Так
как силы Ro параллельны между собой, то давление, .приходящееся на
какой-нибудь участок KKi выразится разностью ординат
Ух—У-
Так как диаграмма полных давлений не дает никаких указаний от-
носительно точки приложения давления у или yi, то наряду с
этой диаграммой полезно построить диаграмму интенсивности давления
земли на погонную единицу, взятую по направлению высоты h стенки.
Для этой цели нужно вычислить предел отношения между приращением
полного давления и приращением высоты АЛ:
V АЛ
Мы видим, что диаграмма интенсивности давления д (кг/м-) строит-
ся как производная от диаграммы пол.ных давлений. Величина Р^^^'
действующей давления, приходящегося на какой-нибудь уча.сток л Ль
равна площади соответствующего участка cdcidi диаграммы инте
508
I \hh ) dh ^
40СТИ, ^ точка прзтложения этой |равнодеиствующеи совпадает по
^-^оему уровню с центром тяжести площади cdcidi,
^^ Когда земля ограничена сверху .плоской поверхностью, то, как мы
пели полное давление пропорционально квадрату высоты стенки. По-
OMV в таких случаях диаграмма полных давлений представляет собой
^^а'дратную параболу, а диаграмма интенсивности давления — прямую
^fЛиг 592). Равнодействующая давлений на какой-нибудь участок АК
расположена на уров«е —Л от поверхности земли.
Если земля ограничена горизонтальной плоскостью, а стенка имеет
идеально гладкую вертикальную поверхность, то интенсивность давле-
ния -выражается формулой
ПоЬерхм:
осглдземли
В
Лиограмма
полиЬ/т^
доблении
диаграмма
интенсибноатш
даблеиия
Фиг. 592
эта задача ре-
;;|иг. 593).
соответству-
Интересен случай ломаной стенки. I^P"6;""''^Tr „ в в ГА
шается так- пусть стенка ограничена плоскостями ЛВ и BBi (ф
aeiLH так. пусть ^rt-Hi^d и ь- т-г „„рпе для стенки АВ; ей сошес!.....^-
^оизведем сначала "«f Р°^""; !^°^р'^мма интенсивное™ давлений аЬс.
ют треугольник Ребхана ^f/"/"^^Р „обы площадь треугольника аЬс
Величину ординаты с6 выберем так 1Тобыпощ^д ^Р^у ^^^^^ _
равнялась Умно>«^е«"ои "^^,^,е",^Гя с по'^^Р™""'^'^ """•"^^ " "Р"^''^"
Должим стенку ВВ, до пересечения с ^ BiBAi. Получив для
Дем построение Понселе для «°°бражаемои с^ i^j возможность
«его треугольник Ребхана Ci^^iV^i. J^m нулевая точка ко-
построить диаграмму интенсивности Давлении ^. ^^^^^^^ равновелика
торой будет расположена на Уровне TPT'I д" иаграммы интенсивности
умноженной на t площади ^-•^•{¦•- ^j_. ^ е cbide. Напомним, что
давления возьмем только «m^«'°'°„^^„k'o к стенке, а под углом % к
давления земли направлены не нормально к стен .
нормали. „оипрний с которыми мы познакомились.
Диаграммы интенсивности Давлен , ^^^^з стенок на прочность
имеют важное значение для приближенноги v
509
и УСТОЙЧИВОСТЬ Однако определенные с их помощью силы R и /?о, вообще
говоря, не пересекаются в одной точке с силой G и, следовательно, не
удовлетворяют условиям равновесия.
Фиг. 593
§ 29.6. ВЛИЯНИЕ ВРЕМЕННОЙ НАГРУЗКИ
Временная нагрузка, расположенная на .поверхности земли, бывает
различных ТИПОВ: сосредоточенные грузы ж виде давлений отдельных
осей паровоза и вагонов (давление земли -на мостовые устои), давлений
колес автомобиля, а также давлений, непрерывно распределенных по
какому-нибудь закону. Мы ограничимся рассмотрением простейшей
задачи: влияния напрузки, равломерно распределенной по поверхности
в пределах призмы обрушения. Нагрузка, расположен-ная за пределом
этой призмы, никакого действия на стенку не оказывает.
Пусть нагрузка имеет интенсивность д кг/м^, а объемный вес земли
составляет 7 кг/м^. Очевидно, что если мы .пожелаем заменить времен-
ную нагрузку слоем земли, оказывающим то же давление на квадрат-
ную единицу, то толщина слоя будет — ж. Приближенное решение
задачи состоит в том, что временная нагрузка заменяется таким эквива-
лентным («приведенным») слоем земли; предполагается, что интенсив-
ность давления от этого не изменяется ни в одной точке стенки.
На фиг. 594 показано построение для случая плоской поверхности
земли. Все построение производится таким образом, как будто бы по-
верхность земли совпадала с поверхностью приведенной нагрузки,
стенка продолжалась вверх до этого уровня. Найдя полное давление н^
эту воображаемую стенку и построив диаграмму интенсивности Д ^'
ления ocdy отбрасывают верхнюю часть этой диаграммы и ^^'^^^'^ ^^ы
только часть abed. При таком решении задачи площадь ^иаграм^^^
abed будет меньше умноженной на т площади треугольника Неа^^^»
она выражает собой давление, приходящееся на участок АН
510
«НИР оказываемое не всей призмой обрушения ВСА\ а лишь
'¦ ";.Гее ВСЛ'М. где ЛМ || ВС.
"^^ д литическое решение той же задачи дадим только для случая
льной, идеально гладкой стенки .и горизонтальной поверхности
вертика ^^^ '^^^^^^^ эквивалентного временной -нагрузке слоя земли
земли. ^^^ ggg^^ ^^ ^^ формуле (29.7) давление на стенку
- -{ -ihl tg^ (45°- f )• ^ ^ тЛ (Л + 2 Л„) tg^ (45°- f) ,
зеули
(29.11)
Фиг. 594
(29.12)
a интенсивность давления на уровне нижнего сечения
^ = ,(A + /to)tg^(45°'f)-
§ 29.7. ПАССИВНОЕ ДАВЛЕНИЕ (ОТПОР) ЗЕМЛИ
„ ня стенку, стремящееся опрокинуть
Давление призмы обрушения •^^^ i.^ давления земли .или
последнюю носит название активного
Р^^пора. _ „„„„ также с другим случаем, а
На практике приходится "^'^''^иться на землю и с противодавле-
именно-с тенденцией стенки «a^^Ji" удится, например, устой арочного
«исм последней. В таких условиях находи ;,„„оз%авление пяты ар«н
пролетного строения, воспринимающий ^^^^^^ ^^ стенкой называется
<Фиг. 592). Соггротивление земли №п н ^^^^^
"ассивным давлением или отп v
Опоелеление пассивного давления может быть произведено на осно-
вянии тех же соображений, которые служат для определения активного
даытения. но с одним лишь отличием: знак углов трения <р и То прихо-
•1ИТСЯ изменить на обратный.
В самом деле, когда стенка смещается в сторону земли, то она
пыпипает последнюю, т. е. стремится приподнять земляную призму-
призму выпирания. Силы трения на плоскости выпирания, а также на
Фиг. 595
задней поверхности стенки, действующие на призму, обращены в сторо-
ну, обратную ее движению, т. е. вниз. Благодаря этому давление стен-
ки, необходимое для нарушения равновесия земляной массы, сильно
Фиг. 597
возрастает; пассивное давление всегда значительно больше активного
^иногда в десятки раз).
Построение для нахождения активного давления, указанное на
Ф'Иг. 588, даст нам пассивное давление, если мы отклоним силы Ro и R
от соответствующих нормалей на те же углы <Ро и <р в обратную сторону.
512
Применяя снова теоремы Ребхана, мы аавдем ту призму, которая ока-
зывает наименьшее сопротивление выпиранию.
Построение Понселе для определения пассивного давления показано
на фиг. 597, где сохранены те же буквенные обозначения что на
фиг. 588. Вследствие изменения знаков углов ср и ср^ плоскость естествен-
ного откоса и основная линия получают новые направления. Пересе-
чение пло,скости естественного откоса с -поверхностью земли происходит
по другую сторону, чем прежде, в соответствии с чем меняется и положе-
ние полуокружности. Из чертежа видно, что площадь треугольника Реб-
хана значительно увеличилась (следует еще учесть, что фиг. 597 по-
строена в значительно меньшем масштабе, чем фиг. 588).
Аналитические выражения для пассивного давления получаются из
формул (29.6) —(29.8) путем изменения знака углов ср и сро- Например,
формула (29.7) переходит в следующую:
Ko = ~^lhHg^^45^+^y (29.13)
Пасси'вное давление земли как средство для увеличения устойчиво-
сти стенки обычно цринимается ©о /вн.имание только при расчете опор,
имеющих глубокое залол^ение.
§ 29.8. РАСЧЕТ ПОДПОРНОЙ СТЕНКИ НА ПРОЧНОСТЬ
Для расчета стен.ки на прочность разделим ее по высоте на несколько
частей при помощи горизонтальных сечений и будем определять в каж-
дом сечении -нормальные и касательные напряжения. С этой целью
постараемся определить в каждом сечении величину, направление и точ-
ку приложения равнодействующей всех сил, приложенных выше сечения.
На фиг. 598 показано это построение. На верхнюю часть стенки
действуют ее ©ее Gi .и давление /?i. Равнодействующая Si проходит через
точку взаимного пересечения обеих сил; ее величина и направление бе-
рутся из силового многоугольника, построенного справа. Так получается
точка /(i сечения а—а.
Для второго участка стенки сначала находится равнодействующая
^2 сил Si и /?2; она проходит чСгрез точки взаимного пересечения на-
званных сил, причем ее направление берется из силового многоугольника.
Силу Sg продолжают до пересечения с силой Сг и через эту точку про-
•водят равнодействующую ^2 сил S'^ , G2. Она же служит равнодействую-
щей всех сил, действующих на сечение b—b стенки. Продолжив вектор
^2 до гвстречи с прямой b—by найдем точку Kz-
Аналогичным образом получается точка /Сз сечения с—с.
Построение >веревочного многоугольника (многоугольника равно-
Действующ.их) было бы в данном случае менее удобным, так как равно-
Действующие Si So S3 и т. д. образуют друг с другом малые углы, и
"^очки их взаимного'пересечения выходят за пределы чертежа.
, Соединив точки KuKz, Кз и т. д. непрерывной линией, мы получим
Многоугольник, называемый многоугольником давлении. Для того что-
^Ь1 произвести это построение, необходимо знать.объемные веса кладки.
^Ни Даны iR тябп 1^
, Если стенка сложена из камней на растворе, то условия прочности
требуют- П чтпбм гиш« S, S, и т. д. были отклонены от нормали к сече-
•^"«м подУглоТм^ь1м Угла>ения. так как,в противном случае про-
взаимный сдвиг частей
''э! точки Д\Ь *\-^ " *• ^- -"'»•'•'* f-^-."—^
тротивном случае возникли бы растя
51^
^УДе^^ботать^а сдС- 2) чтобы точки Ки К, и т. д. были .р^положены
^«Утри ЯПГ.Я ?.u"t'^^я'Ляк в противном случае возникли бы растяги-
Материал
Кладка бутовая
из гранита . . .
Тесовая из грани-
та .• - •• •
Бутовая из из-
вестняка - .
Тесовая из из-
вестняка . . .
Таблица 15
Объемные веса кладки и бетона в кг/м^
Объемный
вес
в кг м^
2 400
2 700
2 200
2 500
Материал
Бутовая из пес-
чаника . .
Тесовая из пес-
чаника . . . .
Кирпичная на це-
ментном рас-
творе
Объемный
вес
в кг1м^
2 200
2 400
1700
Материал
Объемный
вес
в KaM"*
I
Кирпичная на
известковом
растворе .
Бетон на гранит-
ном гравии .
Бетон на кир-
пичном п^ебне
Железобетон
1900
2 200
1800
2400
вающие напряжения, которые нецелесообраано передавать на раствор,
3) чтобы наибольшее нормальное сжимающее напряжение, определяе-
мое по формуле
М , N
а = ,
W F
не превышало допускаемого,
514
Еслистенка —железобетонная, то по найденным силами <? „
„ точкам их приложения можно определить нормальные и касателы;»^;
напряжения, которые не должны превышать допускаемых ''^^^^^''^'"'^^
Что касается сжимающих напряжений ,в самом грунте ппп пп
„, т^ г.гчи «v гт/лгготт^^„ '" i^^Hie под подош-
фяжения, Kuiupoic ПС А^"'1л\иы превыша
Что касается сжимающих напряжений ,в самом грунте ппп пл,
вой стенки, то при их подсчете могут встретиться два случая '
I) Равнодействующая всех вышележащих сил пеоегАкяРт п.,
Jh внутри ядра. В таком случае гпунт пп„ »1ГР"!''^" "°^о™У
Фиг. 599
Фиг. 600
зом
Нормальное нап^ряжение в точке А выражается следующим обра-
К
W
W
(29,14)
моменты силы Л^ относительно ядровых точек /С^, /Сг,.
для прямоугольного сечения
k.=-k^^ —
Л?2
-т (' ± Ч\ <»¦"')
^^^ как по услов-ию е< — , то о^^^ <0, т. е. грунт сжат.
р 2) Точка приложения силы Л^ выходит за пределы ядра сечения.
^^ предыдущей формуле напряжение о^ получается положительным, а
J^^K Как «а самом деле грунт не в состоянии воспринимать растягиваю-
^^^ напряжений, то формула становится неприменимой; В этом случае
^^ть подошвы разгрузится совершенно, а другая часть будет иметь
Р^Молинейную диаграмму сжимающих нормальных напряжений
^Фйг. 600). Для определения ординаты о^ и расстояния а нулевой точки
д^^^Рая сечения мы располагаем двумя условиями равновесия: площадь
;|[^31^Раммы должна равняться силе М а ее центр тяжести должен ле-
^"^ь на линии действия этой силы. Иначе
д^ и —«==<?,
Q^ \йЦ<,^Т(>^^^^^-^
515
откуда ^
Если сила N приложена как .раз в ядровой точке К^.то формулы
г99 14) и (29.15) дают один и тот же результат.
Необходимые для расчета данные о допускаемых напряжениях при-
ведены ниже.
Допускаемые напряжения для кладки и грунта
При сжатии
1 Лля кладки из штучного камня получистой тески с времен-
ным сопротивлением сжатию ие менее 1 ОООнг/см^ на цемент-
ном растворе состава не ниже 1:3 80 кг/см^
2 Для кладки из грубо околотых в правильную форму камней
с временным сопротивлением сжатию не менее 600 кг/см^ на
цементном растворе состава не ниже 1:3 50
3. Для кладки из обыкновенного бутового камня с временным
сопротивлением сжатию не менее 300 кг/см^ па цементном
растворе состава не нинсе 1:4 15
4. Для кладки из обыкновенного кирпича с временным сопро-
тивлением сжатию не менее 150 кг/см^ на цементном раство-
ре состава не ниже 1:4 15
5. Для бетона с временным сопротивлением не менее 200 кг/см^ 40
6. Для грунта при глубине заложения фундамента не менее 2,5и/:
а) для мергелистого сухого грунта 5
б) „ н влажного ^ 3
в) глинистого сухого плотного „ 5
г) сухого песчаного 4—2 „
д) скалистого 30—8 ,
При растяжении Присдвиге
Для каменной кладки . . 2кг/см^ Для каменной кладки . . 2кг/см^
- бетона 5 „ „ бетона 4 ,
§ 29,9. РАСЧЕТ СТЕНКИ НА ОПРОКИДЫВАНИЕ И НА СКОЛЬЖЕНИЕ
Поверка стенки с неглубоким заложением на опрокидывание про-
изводится 'В предположении, что она может повернуться вокруг ребра.
Определяется суммарный момент сил, препятствующий опрокидыванию
стенки, и сил, стремящихся опроклнуть ее. Эти два момента сопостав-
ляются между собой. Например, на фиг. 598 устойчивость стенки вокруг
левого ребра с характеризуется суммарным моментом сил /?ь /?2, ^з,
^ь ^2, Оз, относительно этой точки. Из чертежа видно, что силы Ru ^2
являются опрокидывающими, а остальные —удерживающими. Если ,
суммарный момент первых двух сил меньше момента остальных, то
стенка устойчива
При проверке устойчивости стенки (Фиг. 598) BOKnvr левого оебра ^
опрокидывающими будут три .силы /?,. /?2, /?з
rvn.lu^'^^^ коэффициентом безопасности число, показывающее, во
сколько раз должно возрасти давление земли вместе с временной на-
иыГ.^ '^т "^ «ей для того чтобы стенка опрокинулась. Обозначим это
пппп^Л^*^^^ ''^^' «апример, на фиг. 598 коэффициент запаса на
опрокидыаание вокруг левой точки с определится »1з условия равенства
нулю суммарного момента всех сил относительно этой точки:
k [М (/?,) + М (/?,) _ м (/?з)] = М (О,) + М (G,) + М (<7з).
516
откуда
f^^ M(G^) + mG^)+M{G^) ^ (29.16)
M (Ri) + ^ (^2) — ^ (^3)
где через М {Ri),M (d) и т. д. обозначены абсолютные величины мо-
ментов.
Аналогичную сверку на опрокидывание можно произвести отно-
сительно точек fc, ( и т. д.
Поверка стенш на скольжение сводится к определению соот-
ветствующего коэ(||)ициента запаса, т. е. числа, которое показывает, во
сколько раз Д0ЛЖ10 возрасти давление земли, для того чтобы стенка
или какая-нибудь шсть ее сдвинулась. При этом сопротивлением рас-
твора сдвигу пренбрегают.
Например, для определения коэффициента запаса на сдвиг в сече-
нии b—b (фиг. 591) нужно спроектировать на -горизонтали силы
R\ и /?2, стремящие.я сдвинуть стенку; сумму их проекций назовем X.
Нормальная сила, :риложенная к тому же сечению, равна <?1 + 02+У,
где У —сумма аертзкальных проекций сил Ri и /?2. Наибольшая воз-
можная сила тренш равна / (Gi+G2+y), где / — коэффициент трения.
Исходя из данного оределения понятия о коэффициенте запаса, можно
написать
k^n9l±?A., (29.17)
(X~/F)
Многие авторы опеделяют коэффициент запаса на опрокидывание
или скольжение какэтношение суммарного момента илл .суммарной
проекции сил удерживающих к моменту или проекции сил, стремящихся
опрокинуть или сдвшуть стенку. Такая трактовка может привести к
1 совершенно неправильюму представлению о действительном коэффи-
циенте запаса так кЫ любую силу можно бесконечным множеством
способов разлагать на опрокидывающие и удерживающие составляющие.
^ R 901п ППНАТИР ОБОЛЕЕ ТОЧНОЙ ТЕОРИИ ДАВЛЕНИЯ ЗЕМЛИ
§ 29.10. ПОНЯТИЕ «^д ПОДПОРНЫЕ СТЕНКИ
йления сыпучего тела на подпорную стенку, получившая
Ьолее строгая теория ^/„дродаря работам главным образом советских ученых
«последнее время развитие»-д^^^^^^^^^ „ау^ СССР В. В. Соколовского), также осно-
'в первую очередь члена-KOjr ^^j^^^ состоянии сыпучего тела.
2На на представлении о J^P^^^^ позволяет определить только давление, отвечающее
* Подобно теории Кулона, ^ела, т. е. такому состоянию, которое непосредственно
1 JJ^^^^bHOMy состоянию сыпу^ отличие от теории Кулона предельное состояние, припи-
1 ^^Р^^^^^^твует сдвигу. Oднaкo*^^gpJ^зyeтcя не наличием одной поверхности, по которой
1 1Ьаемое сыпучему телу, ^^t^^Quneu внутри тела бесконечного множества поверхно-
I ст ?^^^^^ твердый клин, а обр^^ можно при этом указать две элементарные площадки
I ^^^ скольжения. В каждой т^рлощадок образует внутри тела два семейства поверх-
•^^льжения. Совокупность вс^^^ сетку линий скольжения. Одно семейство отвечает
^^тей, а в проекции на плoct^ ^.^ояиию, а другое — «минимальному». Тот факт, что
^*^аксимальному» предельном^ ^яиия равновесия, легко понять, если вспомнить об
-Чествует два предельных ^'^демли, с которыми оперирует теория Кулона, или если
'^тивном и пассивном давлен^ .^т^ь себе различия между касательными напряжениями
Г^^^лянуть на фиг. 585 и предс1*^0рь1Х начинается движение тела вправо нли влево.
^Поверхности контакта, при ^^^шучсго тела, находящегося в состоянии предельного
р На любой площадке внутр'^^цном состоянии соблюдается равенство
ьновесия. при плоском Hanpf^ j _ (^^ ^ щ tg р} = 0. (29. Щ
^ьное напряжения, Н — характеристика внутреннего
^J^n* °л — касательное и ноЛвная временному сопротивлению при всестороннем
**" Пения или связности грунте''
о^рном растяжении. '"
r.^u
ртворяться общне ди^еренциальные ур
/oq 18) должны УД^,^овия статики для вес, элемента и для с
Кроме уравнения (29.1»^^^^,^,„а^ т. е. ус^ов
пения равновесия люОо.о уравнении отвечакг два flencTBHTeflbf
Гейгтпуюших на |^« Т^ диФФеР^»""^^'" х а Р а к т е р л с т и к м и. _ В теории д
Этой о'^«°^«°" а" кривых, называемых х ^у^^^ урзнении характерист
paJЛИЧныx еемеиства кр ^^gg^gg^TcH о^и ^^^^ ^ ^^^^^^ точкенаклонены к осям
ференциальных УРД^„7ы" ется, что характерис ^^^^^^, сколжения, следователь
S данной задаче «Jf з^°^^„ как и соответству
активного
Фиг, 601
ЮМ говпадении основана t
характеристики тождественны с линиями скольжения. На'^^^^"^. .,ая к кривой одй
можность строить оба семейства линий. В каждой точ^^^^^^,^^^^ а касательная
(любого) семейства определяет направление площадки f^ пошадке
другой ^направление напряжения, действующего по этг^и™шний скольжеьля
На фиг. 601 показан примерный вид сетки хара.ктей'^ееохней горизоигальной
ивного давления земли на стенку пои условии что-^V t^lnn^/ и^м^^^^ оД
верхиости действует вертикальная mTiyxJ^,^!ll'^^ которой изменяется
оси у по линейному закону^ В MaccWlnvtV^^ несколько зон: в части
лиающей к ^адней\тани стенкГу^а^т^!! ^^разуе сальное предельное напР^^'^
иое состояние, а в ч^ти, иримьж^ГПеох1Лй''го1^^^^ поверхности.
Имея сетку характеристик, нетпулна «. сальную составляющую «^ _
жсння в любой то^ке педпорноГс?еГ,^ вычислить н^»,м получить более точное,
по теории Кулона, решение задачи " '^"""^^ ^^^Р' „п^пельн
Сопоставление численных результатпп К^^^"^ " "° теории пР^дел
иапряжеииого состояния показывает и?пп Р^^^^^^ по Опорных стенок а-'г"»^«ое Д^
' ^*1о А.1Я KnvriMKTv ^давления, то при
'^'3 расчета по ^порных стенок активное Д^^^
ние различается незначительно; что касае-'^ крупных ^^давления. то при больших У '
вьу1реннего трения расхождение оказыва^" "^^^"^"°/"^^^^"
» В, В Соколовский, Статика гг. - . ^- ^^^^^ *^^*Р- *^'-
»йП1ка сыпучей срсд»^
й\8
Для детального ознакомления с расчетом по теории предельно, о напряженного
^^,уояния читателю надлежит об1атить(я к упомянутой выше книге 3 В. Соколовского
]^^^ ^ специальным руководствам».
§ 29.11. КРАТКИЕ ИСТОРИЧЕСКИЕ ДАННЫЕ
Изучение законов давления земли на различные сооружения, поддерживающие
е 01 обрушения, диктовалось практическими потребностями строительного дела; в
собспности это было важно Для строителей крепостей с их высокими валами, под-
ie''*5biMH ходами и т. д. Поэтому первые теоретические исследования, начатые еще в
(VU столетии, принадлежали инжеиерам-фортнфикаторам2. Работа французского
^сеяного инженера и академика Кулона^ (Ch. А. Coulomb, 1736—1806) была опубли-
,05?на в 1776 г. Предложенный им способ расчета впоследствии С'-ыл усовершенство-
ван французским же военным инженером и академиком Понселе^ (J. V. Poncelet,
'88—1867). В развитии той же теории проф. Г. Е. Паукер (1822—.889) в 1856 г, дал
fopмyлy для определения глубины заложения фундаментов. Впосле;ствни эта формула
Ъ1ла усовершенствована проф. С. И. Белзецким^
Дальнейшим усовершенствованием теории Кулона и расширенлем круга задач,
решаемых при ее помощи, занимались лроф. И. П. Прокофьев^ и шроф. Н. И. Безухов^.
Направление, отличное от того, которое было создано Кулоном, было намечено
известным английским ученым инженером Рэнкином (W. Rankine, 1820—1872), кото-
рый разработал приближенную теорию; эта теория исходит из \с/овнй равновесия
бесконечно малого парраллелепипеда, расположенного внутри земляной массы^. Базиру-
ясь на таком рассмотрении, теорию давления земли развивал французский академик
Леви (М. Levy, 1838^-1910)9.
В XX столетии получила значительное развитие механика грунтов, основанная
на рассмотрении реальных физических свойств строительных грунтов. Наиболее зна-
чительными в этом направлении были работы Терцаги (К. Teszaghi)*^ и проф.
Н. М. Герсеванова".
Новейшее, более глубокое направление в развитии механики грунтов и других
сыпучих тел свободно от гипотез, лежащих в основе теории Кулона.
Основными в этом направлении являются работы проф. В. В. Соколовского.
* Напр. Г. К. К л ей и. Строительная механика сыпучих тел, М., 1956.
2 Bullet Traite d*architecture pratique, 1691; Couplet De la poussee de
terres i^ontre leurs revestements et la force qu'on leur doit opposer, Histoire de
I'Acad. royale des sc, 1726, 1728; Be lid or. La science des ingtnieurs . .Paris,
1729. ^
s Coulomb, Essai sur I'application des regies de maximis et minimis a
quelques problemes de statique relatifs a Г Architecture. Memoires . . . presentes a
lAc. roy. des sc, Annee 1773, Paris, 1776.
/Poncelet, Memoire sur la stabilite des revetements et de leur fondations
.Memoires de Tofficier de genie", № 13. 1840-
^ Статика сооружений, т. I; вып. 1, СПБ, '1914.
^ Давление сыпучих тел и расчет подпорных стеи, изд. 4-е, 1940.
Теория сыпучиу тел, 1934.
в Оп the stability of loose earth. Phil. Trans., London, 1857.
9 cssai sur une theorie rationelle de Tequilibre des terres . . . , Comptes rendus
de 1 Acad, des sc, Paris. 1869, 1870.
n 5'^Роит^-^ьная механика грунта иа основе его физических српйств, 1933.
Собрание сочинений, т. I и II, 1948.