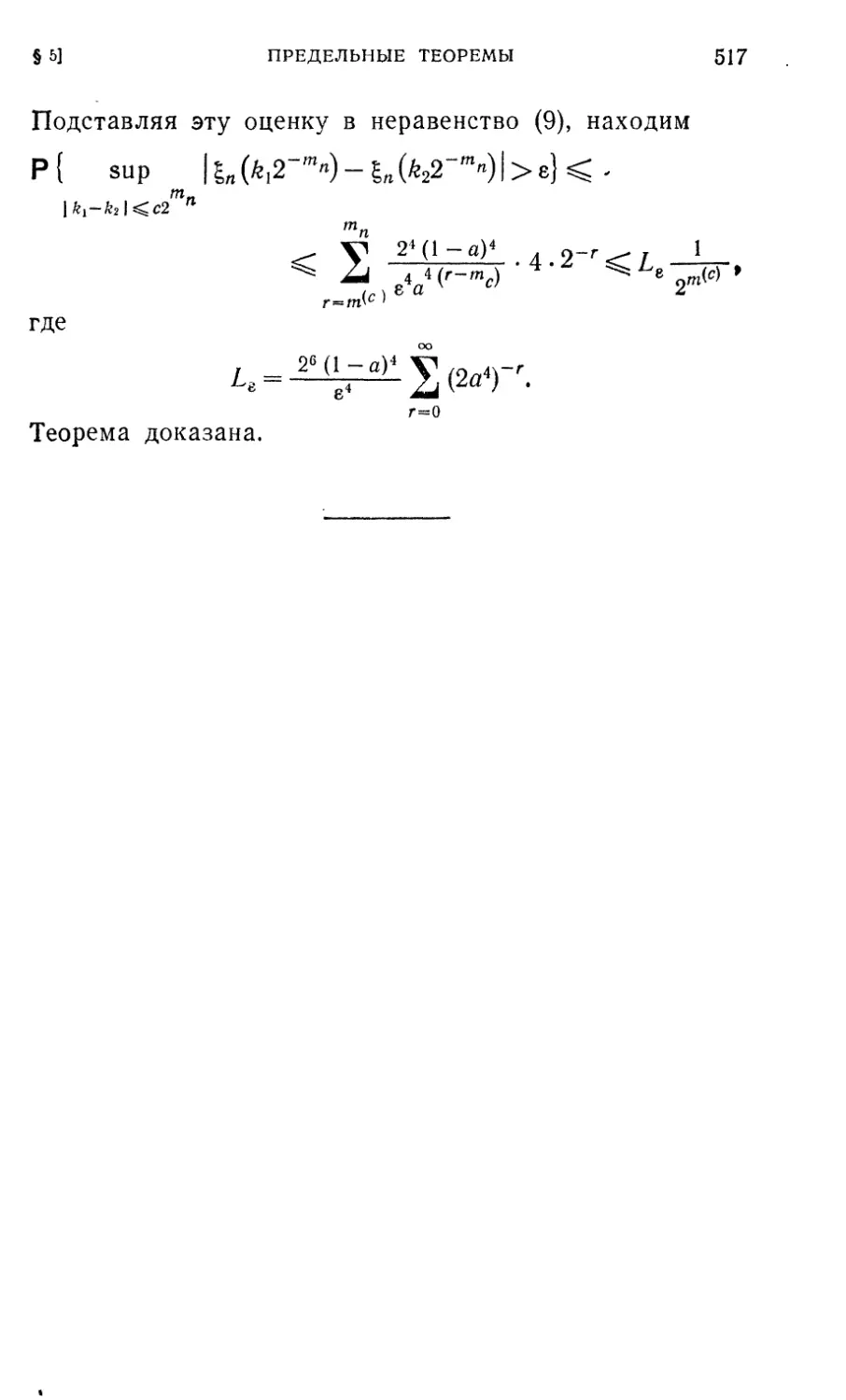
Текст
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
И. И. ГИХМАН, А. В. СКОРОХОД
ТЕОРИЯ
СЛУЧАЙНЫХ
ПРОЦЕССОВ
Том I
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 197 1
617.8
Г 51
УДК 519
Теория случайных процессов. И. И. Г и х м а н,
А. В. Скороход. Изд-во «Наука», Главная
редакция физико-математической литературы.
В книге изложены основные понятия теории
вероятностей на аксиоматической основе, общие вопросы
теории случайных функций, теория вероятностных мер в
"функциональных пространствах и общие предельные
теоремы для случайных процессов.
Библ. 117 назв.
Иосиф Ильич Гихман, Анатолий Владимирович. Скороход
ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
том I
М., 1971 г., 664 стр.
Редакторы М. Б, Невельсон, М. М. Горячая
Техн. редактор В. Н. Кондакова
Корректоры О. А. Сигал, Т. С. Вайсберг
Сдано в набор 18/Х1 1970 г. Подписано к печати 2/1Х 1971 г. Бумага 84Х1087ц
Физ. печ. л. 20,75. Условн. печ. л. 34,86 Уч.-нзд. л. 34,32. Тираж 16 000 экз.
Т-14343- Цена книги 2 р. 29 к. Заказ № 862.
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва. В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Ленинградская типография Л» 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати при Совете Министров СССР4 Измайловский проспект, 29*
2-2-3
58-7!
ОГЛАВЛЕНИЕ
Предисловие 8
Глава I
Основные понятия теории вероятностей
§ 1. Аксиомы и определения 9
События (9). Вероятность (11). Случайные вели- *
чины (12). Случайные элементы (16). Математическое
ожидание (18). Сходимость по вероятности (19).
Пространства 9?р (21). Распределения случайных
векторов (23). Характеристические функции (2бу. Случайное
время (31).
§ 2. Независимость 34
Определения (34). Независимые случайные
величины (36). Закон 0, или 1 (39).
§ 3. Условные вероятности и условные математические
ожидания 43
Определения (43). Свойства условных математических
ожиданий и условных вероятностей (46). Условное
математическое ожидание относительно случайной
величины (49). Регулярные вероятности (51). Условные
плотности (56).
§ 4. Случайные функции и случайные отображения 58
Определения (58). Построение случайной функции по ее
частным распределениям (63).
Глава II
Случайные последовательности
§ 1. Предварительные замечания 70
$2, Полумартингалы и мартингалы 73
Определения и простейшие свойства (73). Некоторые
неравенства (75). Существование предела (81).
Некоторые применения (84).
1*
4
ОГЛАВЛЕНИЕ
§ 3. Ряды 87
Некоторые' общие признаки сходимости рядов (87),
Ряды независимых случайных величин (90). Применения
к усиленному закону больших чисел (94).
§ 4. Цепи Маркова 96
Системы под случайным воздействием (96).
Стохастические ядра (99). Определение цепи Маркова (108).
§ 5. Цепи Маркова со счетным числом состояний 115
Приводимость и неприводимость (115). Возвратность (117).
Периодичность (125). Основная теорема теории
восстановления (128). Предельные теоремы для вероятностей
перехода (133). Критерии возвратности. Стационарные
распределения (136).
§ 6. Случайные блуждания на решетке 147
Неприводимость (147). Возвратные блуждания (152).
§ 7. Локальные предельные теоремы для решетчатых
блужданий 157
§ 8. Эргодические теоремы 165
Преобразования, сохраняющие меру (165). Некоторые
следствия теоремы Биркхофа — Хинчина (172).
Эргодические стационарные последовательности (174).
Глава III
Случайные функции
§ 1. Некоторые классы случайных функций 182
Гауссовские случайные функции (182). Процессы с
независимыми приращениями (188). Марковские процессы (198).
§ 2. Сепарабельные случайные функции 202
Основная теорема (202). Стохастическая
непрерывность (208).
§ 3. Измеримые случайные функции 211
§ 4. Критерий отсутствия разрывов второго рода 215
Функции без разрывов второго рода (215). Некоторые
неравенства (217). Условия отсутствия разрывов второго
рода, использующие частные распределения процесса (221).
Условия отсутствия разрывов второго рода,
использующие условные вероятности (222). Регуляризация
выборочных функций процесса без разрывов второго рода (227).
Мартингалы (228).
§ 5. Непрерывные процессы 230
Условия непрерывности процесса без разрывов второго
рода (230). Процессы с независимыми приращениями (232).
Условие Колмогорова непрерывности случайного
процесса (235). Гауссовские процессы (238).
ОГЛАВЛЕНИЕ
Глава IV
Линейная теория случайных процессов
§ 1. Корреляционные функции 240
Положительно определенные ядра (240). Процессы,
стационарные в широком смысле (245).
§ 2. Спектральные представления корреляционных функций 253
Стационарные последовательности (253). Однородные
случайные поля (256). Однородные и изотропные поля (261).
Векторные однородные поля (265).
§ 3. Элементы анализа гильбертовых случайных функций . . . 267
Интегрирование (267). Закон больших чисел (270).
Дифференцирование (273). Разложение случайного процесса
в ортогональные ряды (275).
§4. Стохастические меры и интегралы 280
§ 5. Интегральные представления случайных функций 292
§ 6. Линейные преобразования 298
§ 7. Физически осуществимые фильтры 310
§ 8. Прогноз и фильтрация стационарных процессов 325
Метод Винера (330). Метод Яглома (334).
§ 9. Общие теоремы о прогнозе стационарных процессов . . . 344
Прогноз стационарных последовательностей (344).
Прогноз процессов с непрерывным временем (358).
Глава V
Вероятностные меры в функциональных пространствах
§ 1. Меры, соответствующие случайным процессам 365
§ % Меры в метрических пространствах 372
§ 3. Меры на линейных пространствах. Характеристический
функционал 381
§ 4. Меры в пространствах 2?р 390
§ 5. Меры в гильбертовом пространстве 401
Моментные формы (404). Теорема Минлоса — Сазонова (406).
Обобщенные меры в гильбертовом пространстве (409).
§ 6. Гауссовские меры в гильбертовом пространстве 414
Линейные и квадратические функционалы (419).
Линейные и квадратические функционалы от
стационарных гауссовских процессов (424).
Глава VI
Предельные теоремы для случайных процессов
§ 1. Слабая сходимость мер в метрических пространствах . . . 429
§ 2. Условия слабой сходимости мер в гильбертов©м простран*-
стве 439
в
ОГЛАВЛЕНИЕ
§ 3. Суммирование независимых случайных величин со
значениями в гильбертовом пространстве 452
Сходимость рядов, из независимых случайных
величин (454). Безгранично делимые распределения в
гильбертовом пространстве (460). Предельная теорема для
сумм независимых случайных величин (468).
§ 4. Предельные теоремы для непрерывных случайных
процессов » , 478
Сходимость процессов, построенных по суммам
независимых случайных величин (485). Сходимость непрерывных
процессов с независимыми приращениями (492).
Сходимость непрерывных марковских процессов (494).
§ 5. Предельные теоремы для процессов без разрывов второго
рода 496
Метрика в пространстве функций без разрывов второго
рода (496). Основная предельная теорема для процессов
без разрывов второго рода (506). Предельные теоремы
для марковских процессов (508). Применение к
статистике (512).
Глава VII
Абсолютная непрерывность мер, соответствующих
случайным процессам
§ 1. Общие теоремы об абсолютной непрерывности 518
§ 2. Допустимые сдвиги мер в гильбертовом пространстве . . 528
Допустимые сдвиги взвешенных мер (539). Одно
достаточное условие допустимости сдвига (547).
§ 3. Абсолютная непрерывность мер при отображениях
пространств . . . . • 557
§ 4. Абсолютная непрерывность гауссовских мер в
гильбертовом пространстве 574
§ 5. Эквивалентность и ортогональность мер, соответствующих
стационарным гауссовским процессам 584
§ 6. Общие свойства плотностей мер, соответствующих
марковским процессам 600
Глава VIII
Измеримые функции на гильбертовых пространствах
§ 1. Измеримые линейные функционалы и операторы на
гильбертовом пространстве ..... г ... 612
Измеримые линейные операторы (618).
§ 2. Измеримые полиномиальные функции. Ортогональные
полиномы 623
Построение ортогональной системы полиномиальных
функций (626).
ОГЛАВЛЕНИЕ
?
§ 3. Измеримые отображения 634
Полиномиальные отображения (636). Разложение
измеримых отображений по ортогональным системам
полиномов (640).
§ 4. Вычисление некоторых характеристик преобразованных
мер 642
Группы преобразований (642). Преобразования, мало
отличающиеся от линейных (643). Формулы взаимности
и другие разложения по малому параметру (645),
Применение ортогональных полиномов (649).
Примечания 661
Литература 656
Указатель 662
ПРЕДИСЛОВИЕ
Авторы стремились изложить основные результаты,
методы и приложения теории случайных процессов,
но не ставили себе целью одинаково подробно охватить
различные разделы теории.
Они считают, что их труд может оказаться полезным
в первую очередь математикам, желающим изучать
теорию случайных процессов и имеющим
необходимую предварительную подготовку, примерно в объеме
трех курсов математических факультетов университетов
(включающем общий курс теории вероятностей, теорию
меры и интеграла и общий курс функционального
анализа). С другой стороны, они надеются, что книга может
представить интерес для научных работников и
аспирантов, использующих в своей работе методы теории
случайных процессов.
Первый том «Теории случайных процессов» посвящен
общим вопросам теории случайных функций и теории
меры в функциональных пространствах. В нем
использован материал из книги авторов «Введение в теорию <
случайных процессов». Главы III, IV, V и IX последней
в переработанном виде вошли соответственно в главы I,
III, IV и VI настоящей книги.
Второй том охватит следующие вопросы: теорию
марковских процессов, процессов с независимыми
приращениями, полу&арковские и ветвящиеся процессы.
Я. Я. Гихман, Л. В. Скороход
ГЛАВА I
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
§ 1. Аксиомы и определения
События. Основными понятиями теории вероятностей
являются понятия эксперимента, события, вероятности
события.
При формальном описании этих понятий принято
исходить из теоретико-множественной модели теории
вероятностей, предложенной А. Н. Колмогоровым в 1929.
Рассматриваемые в теории вероятностей
эксперименты (стохастические эксперименты) производятся при
соблюдении определенного комплекса условий У. Этот
комплекс условий* не определяет однозначно того, что
называется результатом эксперимента, его исходом или
реализацией. Последнее означает, что при повторениях
эксперимента с точным соблюдением комплекса
условий V его результаты будут, вообще говоря, различными.
' Первое фундаментальное предположение на пути
формализации теоретико-вероятностных понятий состоит
в том, что результаты рассматриваемой в определенной
ситуации совокупности экспериментов можно описать
с помощью некоторого множества О, так что каждому
событию, о котором имеет смысл говорить,
осуществлялось оно в некотором эксперименте или нет, поставлено
в соответствие определенное подмножество А из И
таким образом, что теоретико-вероятностным действиям
над событиями соответствуют теоретико-множественные
действия над соответствующими подмножествами й.
При этом точки соей играют роль атомов — всякое
событие является суммой точек, а каждая точка со
не представима в виде суммы других событий. Поэтому
точки О называют элементарными событиями.
Ю ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Сам эксперимент по отношению к О полностью
характеризуется классом тех событий (подмножеств О),
о каждом из которых можно утверждать, что оно или
осуществилось или не осуществилось в данном
эксперименте. Эти события будем называть наблюдаемыми
(в данном эксперименте).
В дальнейшем мы придерживаемся этого построения
теории вероятностей и будем отождествлять события
с соответствующими им подмножествами О. При этом
возникают двойственная терминология и словарь,
переводящий теоретико-множественные понятия в теоретико-
вероятностные. Следующая таблица является основой
этого словаря.
Теория множеств
I Пространство &
1 со — точка О,
г 0 — пустое множество
А — подмножество й, А с: &
Множество А содержится в В
(Л с: В)
С — сумма множеств А и В
(С = А[)В)
С — пересечение множеств Ли В
Л —дополнение к множеству Л
С — разность множеств А п В \
(С~А\В)
\ А и В не имеют общих точек
!• МПВ-0)
Теория вероятностей
Достоверное событие
Элементарное событие
| Невозможное событие
Событие 1
Из события А следует В 1
С — сумма событий Л и В 1
С — совмещение событий Л и В
Л — событие, противополож- |
ное Л 1
С — разность событий А п В \
События Л и В несовместимы
Отметим, что мы называем событием произвольное
подмножество й. Однако как с практической, так и
с чисто математической точки зрения не имеет смысла
считать произвольные подмножества О событиями,
представляющими интерес. Поэтому в О следует выделить
класс событий, подлежащий рассмотрению. Он должен
быть достаточно широк и содержать все те события^
которые возникают при решении разнообразных
практических задач. С другой стороны, объем этого класса
11] аксмомы и Определения П
событий ограничивается возможностью эффективного
использования математического аппарата.
Разумеется, задача выделения соответствующего
класса событий решается в каждом конкретном случае
по-своему, но в дальнейшем всегда будет
предполагаться, что он образует сг-алгебру событий.
Определение 1, Класс событий % называется
алгеброй событий, если он содержит достоверное
событие О, невозможное событие 0, вместе с произвольной
парой событий А и В из этого класса содержит их сумму,
а также и событие, противоположное Л.
Два события О и 0 образуют тривиальную алгебру.
Минимальная алгебра, содержащая_событие Л,
состоит из четырех событий: О, 0, Л и Л.
Определение 2. Алгебра событий называется
а-алгеброй, если она вместе с произвольной
последовательностью событий содержит их сумму.
Разумеется, в предыдущих определениях и свойствах
можно было говорить об алгебрах и сг-алгебрах
множеств некоторого абстрактного пространства О.
Определение 3. Пространство И вместе с
определенной на нем а-алгеброй множеств 51 называется
измеримым пространством {О, Щ, а подмножества 62
из % — %-измеримыми множествами (^-измеримыми
событиями) или, проще, измеримыми множествами
(событиями), если ясно о какой а-алгебре идет речь.
Обычно а-алгебру всех рассматриваемых в данной
ситуации событий будем обозначать буквой 5>. По
отношению к измеримому пространству {Й, ©} отдельный
стохастический эксперимент вполне характеризуется
классом событий §, наблюдаемых в этом эксперименте*
Разумеется, класс ^ должен содержаться в у и
очевидно, что класс § замкнут относительно операций
сложения, совмещения и перехода к противоположному
событию» Поэтому естественно считать, что § есть
а-алгебра событий. Таким образом, с формальной
стороны стохастический эксперимент определяется
некоторой а-алгеброй § .©-измеримых событий. Будем
называть ее а-алгеброй, соответствующей данному
эксперименту.
Вероятность. Определение 4. Тройка {С, ©, Р}4
состоящая из пространства элементарных событий О,
12 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
выделенной на нем сг-алгебры событий © и определенной
на © меры Р такой, что Р(0)=1," называется
вероятностным пространством, а мера Р — вероятностью.
Вероятностное пространство является
первоначальным объектом теории вероятностей. Это обстоятельство
не противоречит тому, что при решении многих
конкретных задач вероятностное пространство в явном виде
отсутствует.
Приведем несколько простейших хорошо известных
свойств вероятности, легко вытекающих из ее
определения (в этих свойствах 5 и 8п, д=1, 2, ...,
принадлежат @):
а)Р(0) = О;
б) если 5*П5Г=0, кфг, то Р^5Л)= 2 Р(5Л);
в) если 5!с:52, то Р(52\ 5,) = Р(52)- Р^);
Г) Р(5)=1-Р(5);
д) если 5йс5п+1, п= 1,2, ..., то р((]|5л)-НтР(5л);
е) если 5л=э5„+1,/г= 1,2, ..., то р( П5я) = Нт Р(5Й).
VI-1 I
Случайные величины. Понятию случайной величины
соответствует представление о стохастическом
эксперименте, состоящем в измерении некоторой числовой
величины |. Полагают, что для произвольной пары
чисел а, Ъ (а<Ь) событие А (а, Ъ), состоящее в том,
что 1^(а, Ь)у наблюдаемо. Соответствующей этому
стохастическому эксперименту сг-алгеброй является
минимальная (7-алгебра ^, содержащая все события
А(а, Ь), —оо<а<й<оо.
Пусть Ах (—оо<л:<оо) обозначает событие & = #.
оо
Оно измеримо. Действительно, Ах = Р) А (х —~ , х + — 1.
При этом, если ххфхъ события АХх и Ах% несовместимы
(это следует из того, что результат измерения
однозначен) и объединение всех Ах, — оо<л;<оо, даст ^,
так как результатом измерения всегда является какое-то
действительное число. Определим теперь однозначную
§1]
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
13
действительную функцию / (со), (оей, положив / (со) = х,
еслишеЛд.. Из определения вытекает, что в каждом
эксперименте 1 = 1 (со) и при этом множество {со: а < / (со) < &}==
« А (а, Ь) измеримо. Напомним, что действительная
функция/(ю), определенная на измеримом пространстве {О, ©},
называется измеримой (©-измеримой), если для
произвольных действительных а и Ь имеем {со: а</(со)<6}^©.
Таким образом, случайную величину | можно
отождествить с некоторой измеримой функцией на
вероятностном пространстве {О, ©, Р}.
Определение 5. Случайной величиной \ (на
данном вероятностном пространстве {О, ©, Р}) называется
©-измеримая действительная функция элементарного
события о.
В дальнейшем иногда будут рассматриваться
измеримые функции на {О, ©, Р}, принимающие, возможно,
значения ±оо, или функции, определенные только на
измеримом подмножестве из {О, ©, Р}. Такие функции
будем называть обобщенными случайными величинами.
В связи с определением случайной величины обратим
внимание нд, следующее обстоятельство. Принято
считать, что с эмпирической точки зрения нельзя различать
события, которые отличаются друг от друга событием
вероятности 0. Поэтому, если две случайные величины %
и т| равны с вероятностью 1, естественно было бы их
отождествить и, следовательно, понимать под случайной
величиной целый класс измеримых функций, каждая
пара которых может отличаться только на множестве
вероятности 0. Такие функции называются
эквивалентными (или Р-эквивалентными). Высказанная точка
зрения находит себе поддержку еще и в том, что
большинство вводимых понятий и получаемых соотношений
по существу относятся к классам эквивалентных
функций. Однако последовательное проведение этой точки
зрения наталкивается на некоторые сложности как
технического характера, так и по существу. Поэтому
представляется более удобным под случайной величиной
понимать индивидуальную функцию, а их
эквивалентность обозначать особо.
Определение 6. Случайные величины | и г{ будем
называть эквивалентными (Р-эквивалентными) и писать
Б = т)(тос!Р), если Р{|=^=т]}-0.
14 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Об эквивалентных случайных величинах говорят еще,
что | = т) почти наверное (п. н), или что | = г) с
вероятностью 1.
Аналогичная терминология и обозначения будут
применяться и в более общей ситуации. Так, условимся
говорить, что некоторые функции или другие объекты
обладают свойством Н почти наверное (для почти
всех со, для всех со(тос1Р)), если множество тех ш, для
которых это свойство не имеет места, имеет нулевую
вероятность. Например, если последовательность
случайных величин |д = /*(©) сходится к | = /(а>) при
каждом*), исключая некоторое множество^/, и Р{Ы) = О,
то говорят, что |л почти наверное сходится к | или что
Е»Нт6я(то<1Р).
Приведем ряд основных свойств случайных
величин, непосредственно вытекающих из соответствующих
свойств произвольных измеримых функций. При этом
предполагаем, что случайные величины заданы на
фиксированном вероятностном пространстве {О, ©, Р}*
а) Если к{1ъ 1Ъ ..., ^—-произвольная борелевская
функция п действительных переменных 1и ^ъ ..., /я,
а |1, Ь> • • •> 1«- случайные величины, то кЦи |2, ..., %п)
также является случайной величиной.
б) Если {|л; п= 1, 2, . ♦.} — последовательность
случайных величин, то зир|„, 1пГ|„, Пт|п, Нт|п также
случайные величины.
Таким образом, очень широкий класс аналитических
операций, обычно производимых над функциями,
независимо от конкретного вида а-алгебры © преобразует
случайную величину снова в случайную величину.
Нетрудно заметить, что эти операции не нарушают
соотношений эквивалентности между случайными,
величинами. Точнее, это означает следующее.
в) Если 1п и х\п эквивалентны (д= 1, 2, . . .)*
А!(/ь /2> • • •> *п) — борелевская функция /г-действительных
переменных, то А(6,, &>> • • •> Ы и к{ци т|2, ..., цп) также
эквивалентна. Более того, эквивалентными являются
следующие пары случайных величин: зир|л и бирт^,
1п[|л и т1г\п> Итп|л и Итт]л, Шп|л и Нт цп.
| 11 АКСИОМЫ И ОПРЕДЕЛЕНИЯ 15
г) Пусть |л, /г=1, 2, ..., —последовательность
случайных величин. Событие 5 = {Пт^л существует}
©-измеримо. Нетрудно видеть, что это событие может быть
представлено в следующем виде:
Важным примером случайных величин являются
индикаторы событий. Индикатором события А
называется случайная величина Хл==Хл(с°)» равная 1, если
сое Л, и 0 в противном случае. Если у!е6, то %л{(п)
©-измерима..
Отметим, что теоретико-множественным действиям
над событиями соответствуют аналогичные
алгебраические действия над индикаторами:
оо
X о. (со) = 2 1А (©), если Л* П Л- = 0 при кф г,
^л\вН = Хд(<й)-Хв(ю). если В с: А,
Хтгпл (®)-Птхд (»), ХИт>)-Нтх,(»)-
Случайная величина | называется дискретной, если
она принимает только конечное или счетное число
различных значений. Такая величина может быть записана
в виде |==2 ск%А (со), где Лл —©-измеримые множества
попарно без общих точек и и Ак=^й. В правой части
последнего равенства при каждом (о только одно
слагаемое отлично от нуля и 1 = ^, если йб4 Для
произвольной случайной величины | всегда можно
построить последовательность \п дискретных случайных
величин, имеющих только конечное множество
возможных значений и сходящихся к | при каждом ю. Для
доказательства достаточно положить
п — \ п
16 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
где
Тогда |&-&я|<^, если \$\<п.
Нетрудно заметить, что если | неотрицательна, то
можно построить монотонно возрастающую
последовательность дискретных случайных величин (счетнознач-
ных), равномерно сходящихся к |. Действительно, в этом
случае положим
оо
1п = 51^7гХл^ где Лы = {со: А^<_^1|#
Тогда || — 1п\<2"п при всех со.
Случайные элементы. Обобщением понятия
случайной величины является понятие случайного элемента
со значениями в произвольном измеримом пространстве
{36, 23}. Пусть {!Й, 6} и {36, 23}— два измеримых
пространства. Отображение §: со->л: {х^ЗВ) называется
измеримым отображением {й, ©} в {36, 23}, если ^(В)**
= {со: #(со)^Б}^© для произвольного Ве23.
Определение 7. Случайным элементом | со
значениями в измеримом пространстве {36, 23} называется
измеримое отображение {$2, ©, Р} в {36, 23}.
Если #/ — метрическое пространство, то под 23, если не
оговорено противное, всегда будем понимать сг-алгебру
борелевских множеств. Если 36—векторное пространство,
то I называется случайным вектором.
Пусть дана последовательность случайных элементов
{1к\ к = 1, 2, ..., п], заданных на фиксированном вершгт*
ностном пространстве {О, ©,. Р} со значениями в
пространстве {36к, 23^} соответственно. Эту
последовательность можно рассматривать как один случайный
элемент ?, который будем называть прямым
произведением случайных элементов |,, ..., %п со значениями
в измеримом пространстве Щ, 23}, где °Ц =* П 36к —
л
произведение пространств 36 ъ 362> ..., #/л, а 33 = Ц93^ —
произведение а-алгебр 23], 232, ..., 23л.
§1]
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
17
Последнее замечание переносится и на
произвольное множество случайных элементов |а, аеЛ, со
значениями в {8?аг 23а}, где А — некоторое множество
индексов. При этом под произведением Щ = Ц 35 а следует
понимать пространство всех отображений у = у{о)'.
а->ха) д:ае^а, аеДт, е. пространство всех функций,
определенных на Л, принимающих при каждом аеЛ
значение из ^а.
Назовем цилиндрическим множеством в Щ
множество С всех г/Е^, удовлетворяющих соотношениям
вида
у (ак) е= В^, 6 - 1, .. ., п, Вак^ 33«А.
Здесь п — любое целое число, ак — произвольные
элементы Л. Точнее, говорят, что С = Са1 >..ап(Ва1 X ... X В«п)
есть цилиндрическое множество с основанием Вщ X
X Ва2 X ... X Вап над координатами сы, а2, ..., ап.
Минимальную сг-алгебру, содержащую все
цилиндрические множества, обозначим через 23 и будем называть
произведением сг-алгебр 33а, 23 = XI ^«. Нетрудно заме-
тить, что отображение §: со->//(а), определяемое
соотношениями § (со) = § (со, а) = /а (со), где /«(со) = §а, является
измеримым отображением {О, ©} в {^, 23}. Если все <%?а
совпадают, ^а = ^, то Щ = ®6А представляет собой
пространство всех функций со значениями в 96,
определенных на Л, а отображение §('со) ставит в
соответствие каждому элементарному событию со некоторую
функцию из 98А, т. е. представляет собой случайную
функцию. Таким образом, семейство случайных величин
{|а, аеЛ} можно рассматривать как случайную
функцию.
Пусть ^ = /(со) — случайный элемент со значениями
в {«V, »}.
Определение 8. о-алгеброй, порожденной
случайным элементом |, называется а-алгебра стоили а{^},
состоящая из всех множеств вида I/"1 (В); Ве23}.
Очевидно; что класс множеств {/-1 (В); В^Щ является
а-алгеброй.
1§ ОСНОВНЫЕ ШЩЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Эквивалентной формулировкой является следующая:
ог-алгебра ст^ является минимальной ст-алгеброй в О-,
относительно которой измерим случайный элемент |.
Интуитивно представляется ясным, что измеримость
некоторой случайной величины ц относительно ст|
означает, что ц есть функция от Е,.
Лемма 1. Пусть I = /.(со) — случайный элемент на
{й, ©, Р} со значениями в {96, Щ, ц — соизмеримая
случайная величина. Тогда существует такая
^-измеримая действительная функция §{х), что т] = §($).
Доказательство. Допустим, что г\ является
дискретной случайной величиной, принимающей
значения ап, я =1,2, ... Пусть Ап=^{а>: ц=ап}. Тогда
существует Вп е © такое, что ?~1(Вп) — Ап. Положим
п-\
Вп = Вп\У} В*. Множества Вп ^ 23 не имеют общих
Я —1 /со \ оо
точек, Г1(Вп)~А„\[}Ак=Ап и /"' [Ц в'п ) = [] А„ = 0,
т. е. /(^)с:^^^б^. Положим ё(х)~ап, если х Ё 0^.
1
Тогда 4^8(1).
Перейдем к общему случаю. Существует
последовательность дискретных соизмеримых случайных величин
цп, сходящихся к т] при каждом со. Поэтрму цп ^ёп(1)*
где §п{х) 93-измерима. Множество точек 5, в которых
&п(х) сходится к некоторому пределу, 23-измеримо,
содержит /(О) и Птп^„(х) = 111X1 цп^ц при хе/(0)^
Полагая ц(х)~\\т§п(х) при х^5 и §(х)=*0 при х е 5,
получим 4 = ^(1), что и требовалось доказать.
Математическое ожидание. Математическое
ожидание случайной величины является ее важнейшей числовой
характеристикой. Оно соответствует интуитивному
представлению о среднем арифметическом значении
результатов измерения случайной величины в большой серии
идентичных стохастических экспериментов.
По определению математическое ожидание
случайной величины |=/(со) полагают равным интегралу от
^(со) по мере Р. Условимся писать
Мб- //<*)Р(«м = ]Чл».
§ п
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
19
Во многих случаях обозначение О области
интегрирования будет опускаться. Математическое ожидание
обладает свойствами, хорошо известными из теории
абстрактного интеграла.
Сходимость по вероятности. В теории вероятностей
важную роль играют различные определения
сходимости последовательности случайных величин.
Определение сходимости с вероятностью 1 (почти. наверное)
было дано ранее.
Определение 9. Если существует случайная
величина с, такая, что
Р{ил-|1>е}->0 при п->оо
для любого е>0, то говорят, что последовательность
Йп» я=1, 2, ...} сходится по вероятности к случайной
величине |,
^Р-Пт^,
В теории меры сходимости по вероятности
соответствует сходимость по мере. Из общих результатов
теории меры вытекают следующие следствия.
а) Если последовательность {|л; гс=1, 2, ...}
сходится почти наверное, то она сходится по вероятности.
Обратное, вообще говоря, неверно. Но из
последовательности случайных величин, сходящихся по вероятности,
можно выделить подпоследовательность, сходящуюся
почти наверное.
б) Необходимое и достаточное условие сходимости
по вероятности последовательности случайных величин
состоит в следующем: для любых е>0 и б>0 можно
найти такое я0 = /г,(е, 6), что при п и п'>щ
Р(|б11.-6П|>«}<4.
Это условие называют условием фундаментальности по
вероятности последовательности {|л, п=\, 2, ...}.
в) Если | = Р-Пгп|т и ц== Р-Нт^, то | = г|(тос1Р).
г) Пусть т|л = Р-Нт|Ая {к = 1, 2, ..., га) и функция
ф(/ь /2> •••» ^т) непрерывна всюду в т-мерном
евклидовом пространстве Жп, за исключением, быть может,
точек борелевского множества й {й <и $т) такого, что
20 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. [
Тогда последовательность |я = ф{|1Я, ^2п» •••» 1тп)
сходится по вероятности к х\ = 9(111, %, ..., т)т). В частности,
одновременно с последовательностями \кп сходятся по
вероятности последовательности 1\п + 12т &1л&2« и Ьп/12пу
последнее в предположении, что Р {Р-Нт ^2л = 0} = 0, и
Р-Нт (Б,й + 1Ы) = Р-Нт \Хп + Р~Пт &2||,
Р-Нт (Ъ1п • Е2л) - Р-Нт &1П Р-Нт ^
Р-Пт|^ = р"!1т^ .
12п Р-Ьт §2«
Следующее достаточное условие сходимости с
вероятностью 1 бывает полезным в конкретных задачах.
Лемма 2. Если существует такая
последовательность е„>0, что
оо оо
2 Р{1|п+1-|п1>е„}'<оо, 2е„<оо,
го |„ с вероятностью 1 сходится к некоторой случайной
величине |.. 5а/ш для любого е>0
оо
2Р{1|-1«1>е}<оо-,
го |я сходится к % с вероятностью 1.
Доказательство. Пусть Л„ обозначает событие
11ги-1~5л1>еп. Тогда
(оо оо \ то
П II А, <"п» %Р(Ап) = 0.
т-1 гс=т ' т->оо т
Поэтому члены ряда ^ + 2 (&л+1 ~&л) с вероятностью 1,
1
начиная с некоторого номера т = га(со), мажорируются
оо
членами сходящегося ряда 2 гп- Отсюда вытекает пер-
вое утверждение. Далее, пусть ВМп = || 1~1п\ >^|*
§П
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
21
Тогда
{ОО ОО ОО 'к
II л и в„п <
ОО
< Пт Пт 2 Р(Вл,„) = 0,
Л^->оо т~>оо п=т
откуда следует второе утверждение.
Пространства ^р. Под &р = &р (О, ®, Р) (р > 1)
понимают линейное нормированное пространство
случайных величин | на {О, ©, Р}, для которых М|^|р<оо.
Норма в 3!р вводится соотношением
ИБИ = {М|61р}1/р.
Сходимость последовательности \п к пределу \ в 3?р
(^р-сходимость) означает, что
М|&-&я|р-*0 при п~>оо.
Из ^р-сходимости вытекает сходимость по вероятности.
Это непосредственно следует из неравенства Чебышева
Р{!1»-Ы>в}<Ми~р^|Р-.
8
Пространство 3?р полно. Из пространств 2?р
наиболее важное значение имеют пространства <2?1=57
и 5?2- Остановимся несколько подробнее на 9?2.
Заметим, что предыдущие определения и теоремы
настоящего параграфа без всяких изменений переносятся на
комплекснозначные случайные величины.
Пространство Я?2 = <2?2(^> ©, Р) комплекснозначных
-случайных величин становится гильбертовым
пространством, если в 9?2 определить скалярное произведение
пары случайных величин ^, г|, положив его равным М2д}.
Две случайные величины % и ц ортогональны, если
Мг/п = 0. В том случае, когда 2; и т| вещественны и
М^==Мг1 = 0, ортогональность означает
некоррелированность. Сходимость последовательности^; п=1, 2,...}
в 5?2 к случайной величине 2 означает, что
IIС — С« 1Р == ЛЛ | с — С« Р —^ 0 при я-*оо.
Этот вид сходимости называют средней квадратической
сходимостью и пишут <; = 1. 1. т.?я.
22 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Р
Отметим, что скалярное произведение является
непрерывной функцией своих аргументов. В ряде случаев
удобно выразить условия сходимости в^2с помощью
ковариации семейства случайных величин.
Определение 10. Ковариацией В (/ь /2), 1{ е Г,
множества случайных величин {^; I е Г}, ^е<5?2, назы*
вается функция
В этом определении Г обозначает произвольное
множество.
Пусть на Т задана некоторая неотрицательная
функция "ф(0, принимающая сколь угодно малые значения.
Случайная величина ц (цеЗу называется пределом
семейства {^; /еГ}^ 9?2 (с к. пределом) при 'фОО-^О,
если для любого е>0 найдется такое 6>0, что
М|т]-^|2<е
для всех /, для которых 0<^(/)<6.
Лемма 3. Для того чтобы существовал предел при
ф(/)->0 некоторого множества случайных величин
{^; I е Г}, необходимо и достаточно, чтобы существовал
предел при ^ (() + ф (V) -> 0 ковариации В (^, С) = М$^«
Если это условие выполнено и г} = 1. к т. ^, го
М|цР= Игл В(/, 0.
Ф(0->о
Доказательство. Необходимость.
Необходимость вытекает из непрерывности скалярного
произведения.
Достаточность. Пусть существуетНгпВ{/4,/2)я=^
при Ф (1{) + г|) (/2) -* 0. Заметим, что В0 неотрицательна
(В0 = НтВ(/,/) при \|)(0->0). Поэтому
м^^с^^в^^^гкев^^д + в^д^о
при <ф(^) + *ф(/2)->0. Из полноты 2?2 следует, что
существует 1. 1. т.^==т] при <ф(/)->'0. Кроме того,
И1ч1Р-ЯС#1Р1<11ч-ЫИ1чВ+11ч-Ы111Ы^о при +(0-*о.
т. е. || *п |р = М Гг] I2 = Нт В (/, /) при ф (^) -► 0, что закан*
^ив^ет доказательство леммы.
$0
АКСИОМЫ II ОПРЕДЕЛЕНИЯ
23
Аналогично определяется гильбертово пространство
5^ = ЙРгЧй, ®> Р) случайных векторов со значениями
в т-мерном комплексном пространстве^™. Оно состоит
из случайных векторов 2; со значениями в Хту для
которых М|^|2<оо. При этом под скалярным
произведением двух случайных векторов ^ и ц понимают
величину М(^, г}), где (а:, у) — скалярное произведение
в %т, \х |2 = (л:, х). Лемма 3 непосредственно
переносится и на пространства 3?™\ если под В(/, V) понимать
Распределения случайных векторов. Пусть ^ —
случайный элемент со значениями в измеримого
пространстве {36, 33}. Под распределением случайного
элемента | понимают индуцируемую им в {дв, 33} меру ц
|1(В) = Р{ё<=В}, Йб8.
Значение любой статистической характеристики
случайного элемента |- можно определить с помощью ^го
распределения. Действительно,
МШ=[/(*)И^) 0)
к
для любой ЭЗ-измеримой функции }(х), для которой
одна из сторон равенства (1) имеет смысл. Формула (1)
является правилом замены переменной в абстрактных
интегралах.
Распределения в метрических пространствах-
изучаются в гл. V. В настоящем пункте рассматриваются
распределения в 01т. Под ЭЗт следует понимать а-алгебру
борелевских множеств в Ж11. Распределения в Ж11 можно
задавать с помощью функции распределения.
Условимся писать а<Ь (а^й), а = (а1, а2, ..., ат)е
еЯ"1, Ь = (Ь\ Ь\ ..., Ьгп)<=&т, если а1 <Ь1 {а1 <&')
(/=1, ..., т). Множество {х: х<а} обозначим через /а.
Функцию
Р(х) = \1(1х) = Р{1<х)
разывают функцией распределения случайного вектора $
(или функцией распределения меры \х).
Назовем множество 1{а, Ь) = {х: а^х<Ь}
интервалом в $?ш. Выразим вероятность попадания вектора §
24 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
в интервал через функцию распределения. Введем
обозначение
д[а! ь)° (*) = ° (*{> • • • > *к-[> ь> **+1> ■ • • > *т) -
-С (л:1, ..., л;*-1, а, **+|, ..., **)
для любой функции С (л:), а: е Ж11.
Величина Ака, ь)Р (х) есть вероятность события
1'<х\ ...,1к-1<хк~\ ак<&к<Ь\1к^<хк+\ ,..,1т<хт.
Нетрудно заметить, что
И (7[а, *>) = А&. 60 *Р». *2) • ■ ■ *[&. *») ^ (*)■ (2)
Наряду с интервалами /[а, 6) будем рассматривать
замкнутые интервалы /[а,- Ь] = {х: а*^х*^Ь*9 / =
= 1, 2, ..., т} и открытые интервалы /(а, &) = {*: а; <
< х^ < Ь\ I = 1, 2, ..., га}. Отметим некоторые свойства
функции распределения:
1) 0</?(х)<1; '
2) если *<*/, то ^(^Х/7^);
3) \х [а, Ь) ^ 0, где \х [а, Ь) = \х (1[а, ь)) определяется
формулой (2);
4) Р(х-0) = Р(х);
5) ^(л;)-^, если хотя бы одна из координат точки х
стремится к -~оо;
6) Р(+оо, +оо, ..., +оо)=1.
Лемма 4. Для произвольной функции Р (х) в /?"\
удовлетворяющей условиям 1) — 6), существует и притом
единственная вероятностная мера на 23т, функция
распределения которой совпадает с Р{х).
Рассмотрим класс Ш интервалов /[а, Ь) в 01т. Он
образует полукольцо. Определим на 9№ функцию
множеств Р(1[ау &)), положив ее равной выражению,
стоящему в правой части формулы (2). Функция Р(1[а9 Ь))
является аддитивной функцией на Ш.
Для того чтобы функция Р могла быть продолжена
до меры на 23т, необходимо и достаточно, чтобы она
обладала свойством полуаддитивности, т. е. чтобы
оо
^(/[%У<2н/кУ (3)
14
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
25
для любой системы интервалов 1[аку Ьк) (6=1,2, ...)
оо
таких, что {]1[аку М=>/[а0, Ь0). При этом продолжение
на 23т будет единственным. Проверим выполнимость
условия (3) в рассматриваемом случае.
Так как Р(х) непрерывна слева, то для любого
т) > О можно найти такое ек > 0, что 0 ^ Р (I [ак, — ёк, Ък)) —
-Р(1[ак, Ьк))<-^, ГАе'ёк = (е\ ..., в*) (/г = 1, 2, ...).
Открытые интервалы {ак — ёк, Ьк) покрывают замкнутый
интервал [а0, Ь0 — ё], ё > 0. В силу теоремы Гейне —
Бореля из них можно выделить конечное подпокрытие,
например {(ак — гк9 Ьк)}, к=1, 2, ..., п. Тогда
последовательность интервалов {(ак — ёку Ьк)}, к=1, 2, ..., п9
покрывает интервал [д0, Ь0 — ё). Непересекающиеся
множества
[а0> Ь0 - ё) П {[ак ~ ёь Ьк) \ {}[а1 - еь 6,)}, 6=1, ..., /г,
являются суммами непересекающихся полуинтервалов
Д/й)(/=1, 2, ..., т^). Таким образом,
п тк
К &о-8) = иУ д(Д
/г тк
Р(1[а0, &0-ё))=2 2/?(АГ)<
А-1/-1
гг оо оо
< 2 Р(11ак-ёк, М)< 2 Р(1 Ы-Ч, Ьк)) < 2 /?(/*Н л-
6=1 &=1 й=1
Переходя к пределу при е-*0, получим
оо
Р(1[ао, Ь0))^%Р(1к) + ц,
что в силу произвольности г| доказывает неравенство (3).
Лемма доказана.
Определение. 11. Последовательность конечных
мер 1хп на 23т называется слабо сходящейся к мере у,
26 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
(на Шт), если для произвольной ограниченной и
непрерывной функции / (л:)
\ I (х) Рп №) -> ] / (х) \х {(1х). щ
Семейство мер называется слабо компактным, если из
любой последовательности можно выделить слабо
сходящуюся подпоследовательность.
Имеет место следующая
Теорема 1. Для того, чтобы последовательность
мер \1п, на {&т, 23т} была слабо компактной, необходимо
и достаточно, чтобы: а) р.п(^т)^С и б) для любого
е > 0 можно найти такой интервал 1\а, Ь), что
Ш [хп(1[а, Ь))>\1п{Ят)-е. (5)
П-> оо
Доказательство этой теоремы будет дано в § 1 гл. VI.
Характеристические функции.
Характеристической функцией случайного вектора |
(или соответствующего распределения \х) в 01т
называется функция I (и), « = («|, щ, ..., ит),
/(м)« Ме'<«'*>= \е1{»> *>|х (<**)■
Характеристическая функция, очевидно, обладает
следующими свойствами:
1) /(0)-1, |/(а)|<1;
2) /(и) равномерно непрерывна, и <= Йт;
3) для любого д, любых комплексных г; и любых
«уеГ (/=1, ..., п)
п
21 / (и/ — иь) гак ^ 0.
Обратно, если функция обладает свойствами 1) — 3), то
она является характеристической функцией некоторого
распределения. Доказательство этого факта приводится
в § 2 гл. IV.
Возможность задания распределений в $,т с помощью
характеристической функции связана с тем, что
последняя однозначно определяет распределение. Например,
$ I] АКСИОМЫ И ОПРЕДЕЛЕНИЯ 27
для распределения, обладающего плотностью {(х),
характеристическая функция
"(м)« | *'<"■*>/(*) Ас
является преобразованием Фурье функции /(х), и если
/ (х) удовлетворяет некоторым дополнительным
условиям, подробно рассматриваемым в теории интеграла
Фурье, то 1(х) можно восстановить, зная /(и), по
формуле
ТМ~ЩГ \^^*4{и)йи.
Аналогичную формулу обращения можно написать для
функции распределения Р{х) в общем случае. Но мы
приведем теорему об однозначной определяемости
функции распределения по ее характеристической функций,
не используя формулы обращения.
Теорема 2. Если
| е* ("> х) \1{ {их) » | е1 <»• х) (12 (их), и €= Жт,
где \х1 — меры на {31т, 83т}, то \х{ = |12.
Доказательство. Обозначим через К класс комп-
лекснозначных ограниченных борелевских функций, для
которых
] / (х) |хх {(1х) - ] / (х) н>2 №).. (6)
Докажем, что /С содержит все ограниченные борелев-
ские функции. Очевидно, К является линейным классом.
Так как он содержит функции е1 ("» х\ то он содержит
и всевозможные линейные комбинации этих функций
Р(х)~2АСке1(ак'х\ Поскольку К замкнут относительно
операции предельного перехода по последовательностям
равномерно ограниченных функций, всюду сходящихся
к некоторому пределу, а в силу теоремы Вейерштрасса
произвольная ограниченная непрерывная функция ({х)
может быть аппроксимирована равномерно ограниченной
28 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ.. I
последовательностью Рп(х), сходящейся к }(х) для
любого х е Ж11, то К содержит все непрерывные
функции. Из замкнутости К относительно предельного
перехода теперь вытекает, что К содержит все
ограниченные борелевские функции. Полагая в (6) !(х) = %в(х),
Ве$Зт, получим \1{(В) = \12(В), что и требовалось
доказать.
Установим связь между слабой сходимостью
распределения \хп и сходимостью их характеристических
функций. Пусть 1(и) и ]п{и) обозначают характеристические
функции распределений" \х и \хп. Из слабой сходимости
\хп к \х по определению вытекает, что 1п(и)->1 (и).
Более глубокий факт содержится в следующей
теореме.
Теорема 3. Если ]п(и) при каждом и сходятся
к некоторой функции ср(и) и ср(и) непрерывна при и = 0,
то распределения \хп слабо сходятся к некоторому
распределению \х и ф (и) — характеристическая функция
распределения \х.
Доказательство. Покажем, что \хп слабо
компактная последовательность мер. Пусть Л = (а, ..., а).
Имеем
(2а)
т
^ (1-/Я(и))йи=
[-А А]
(2а)т
[-А А) я
| | (!-*-'<". *>)|ля (<**)<*" =
>1 { 1хп(ах)=^1хп([-Аи Д]),
[-Ль Л,]
(22 2 \
—, —,...,— . Перейдем
и и и /
в полученном неравенстве к пределу при я->оо.
Воспользовавшись теоремой Лебега о мажорируемой
сходимости, получим
§1]
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
29
Правая часть последнего неравенства стремится к нулю
при а~>0 в силу непрерывности ср(и) при и = 0. Из
теоремы 1 следует, что последовательность \хп слабо
компактна. Докажем, что \хп слабо сходится к некоторому
пределу. Действительно, существует
подпоследовательность \хП}, слабо сходящаяся к некоторому
распределению |Хо. Если бы \1п не сходилась слабо к ^0, то
нашлась бы другая подпоследовательность \льр слабо
сходящаяся к некоторому пределу |Ио, отличному от ц,0. Но
из ранее сделанного замечания вытекает, что
характеристическая функция как распределения \10, так и
распределения |Иэ имеет своей характеристической
функцией ф(м). С другой стороны, характеристическая
функция однозначно определяет распределение, так что
!10==Фо. Полученное противоречие показывает, что \хп
слабо сходится к \х0. Теорема доказана.
Отметим еще некоторые часто используемые свойства
характеристических функций.
Если %1 и |2~ независимые случайные векторы в 91т,
|3==^_1_|2 и /{-(и) ~ характеристическая функция \%
(/=1, 2, 3), то
■Ми) = 1Ли)12(и). (7)
Далее, пусть |/ (/=1, 2) —случайные векторы со
значениями в $2т', а ^з — Йь Ы~~ составной вектор со
значеними в $?т' X У1т\ Для того чтобы \х и |2 были
независимы, необходимо и достаточно, чтобы
/з(и» ъ)--^1х{и)12{о), (8)
где /3(и, V) = Ме^[(и^^+(V>Ш^ 1г(и) = 13(и, 0), /2(о)=>
= /з(0, V).
Необходимость очевидна.
Достаточность вытекает из единственности функции
распределения, имеющей данную характеристическую
функцию.
Определение. 12. Моментом ш\ /о... / 8-мерного
вектора ^ = (ёЛ %2, ..., |5) называется величина
т/1/,.../,-М(бУ'(12)/8...(^)Ч
30 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
если математическое ожидание в правой части равенства
конечно. Величина ц = \х + /2 + ... 4- ]8 называется
порядком момента.
Легко заметить, что если М 11к \р < со, к = 1, 2, ..., 5,
то произвольные моменты порядка <7<р конечны.
Действительно, из неравенства ме^кду средним
арифметическим и средним геометрическим следует (д = ]\ + ]2+ • ••
...+/.)
П|Б*|/*-П,^^^<2т|Б*,д'
к~\ *»1 /г-1
откуда
5
Я
к*»\ к~\ к«=\
^\{\%к\!"<^1А\\н\ч<^{т1к\р?>
Моменты гп}х... у5 с целыми индексами можно вычислить
зная характеристическую функцию, с помощью
дифференцирования. Действительно,
у 1Ч<7 дУ(и)
I 2 5
//-О
(9)
при д^р, если М Цк \р < оо. Доказательство этой
формулы вытекает из возможности дифференцирования под
знаком математического ожидания формулы
/ (а) = Ме'<«•*>.
В ряде случаев приходится пользоваться обратным
утверждением. Но последнее имеет место только для
моментов с четными индексами. Пусть Д* — операция
вычисления симметрической конечной разности по
переменной ик, а Д{ — ее /-я степень:
Да/(«1, ..., щ)*=1(ии ..., ик + 1гк, ..., и3) —
-/ {иь ..., ик-кк, ..., ня),
&к1{ии ..., ив)«
/
- 2 (~ 1)ГСГУ / (а,, ..., и* + (/ - 2г)Нк> иш, ..., **}•
Г-0
■*о
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
31
Тогда
А?/. Д*>* .
.. Д2'*/(иь ..., и3)\и_0=*
з 2}к
к—\
_ ТТ а»/* /ОЛ2* М ТТ /»1пй>6*\а/* Гб*
или
тт I"
11 (2А,)2'*
Лс«-1
Л«1
■(-О*
А-1
мп(4#Г|й*.
л=0
Л-1
*к6*
откуда, воспользовавшись леммой Фату, получаем
(-1)'П^»/
Пт
Л—I. 2, ...,5
А-1
>мПиТ*-
Л-1
ц-0
Выражение, стоящее в левой части полученного
неравенства, с точностью до знака совпадает с производной
д2я1.[ди2/1 ...ди2з!з в точке ц = 0, если I
дифференцируема 2# раз.
-Таким образом, мы имеем следующую теорему.
Теорема 4. Если характеристическая функция
1 {п\, ..., и$) р раз дифференцируема (р четное) в точке
и «0, го существуют моменты порядка ц ^ р и они
могут быть вычислены по формуле (9).
Случайное время. Представим себе, что непрерывно
во времени производятся стохастические эксперименты
и рассматривается некоторое событие Л, об
осуществлении которого можно узнать, наблюдая результаты
экспериментов до какого-то случайного момента
времени. Подобный момент времени будем называть
случайным временем. Иногда его называют случайной
32 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [Ш1. I
величиной, не зависящей от будущего, марковским
моментом или моментом остановки.
Формальное определение состоит в следующем.
Пусть Т — множество действительных чисел — моментов
времени проведения стохастических экспериментов.
Определение. 13. Монотонно неубывающее
семейство ст-алгебр {$,; I е Г}>& е ©> Ъи ^ <5/2, если ^x < /2,
данного вероятностного пространства {й, ©, Р} будем
называть потоком а-алгебр {потоком экспериментов).
При этом 3, интерпретируется как класс всех
наблюдаемых событий в экспериментах, проводимых до
момента времени / включительно.
Определение 14. Случайным временем на потоке
в-алгебр {$,, (еГ) называется функция т ==/(©) со
значениями в Г, определенная на некотором подмножестве Ог
пространства й, такая, что {т</}е ^ при любом 1^Т.
Условие {т<;^}е§, означает следующее: о том, что
случайный момент времени т наступил до момента
времени I, можно судить, наблюдая результаты
эксперимента в моменты времени 5, 5еГ, 5^^. Множество 0^
соответствует событию: т наступило в- течение периода
наблюдения Г. Разумеется, оно ©-измеримо. Если в Т
есть максимальное значение ^таx, то й^ = {т ^ ^таx}^<?5^таx^
Если же в Т нет максимального значения и^ | зир{^, /^Г},
тоОт = У{т<и.
к
Заметим, что условие {т</}е^ равносильно
требованию {т>0^5/ или в случае, когда Т счетно,
{т = /} е 5/ Для любого ^еГ.
Со случайным временем т можно связать
минимальную а-алгебру событий, о реализации которых можно
судить, наблюдая результаты экспериментов до
момента времени т включительно. Обозначим через 8*
класс тех событий В(Ве6), для которых ЯЛ{т^'}е9*
при любом /еГ, Нетрудно заметить, что §т является
а-алгеброй. Условимся называть §т ст-алгеброй,
порожденной случайным временем т.
Очевидно, что случайная величина % ^-измерима.
В качестве примера положим т = /0> 1о^Т. Тогда
{т<0 равно либо 0, либо О, так что т = /0 является
частным случаем случайного времени. Далее, ВП{т*01
равно либо 0, либо 5, так что *$тв8*д> т. е. введенное
§п
АКСИОМЫ И ОПРЕДЕЛЕНИЯ
33
обозначение для ст-алгебры, порожденной случайным
временем, в частном случае т==^0 согласуется с
предыдущими обозначениями.
Приведем несколько свойств случайного времени х
на фиксированном потоке ст-алгебр {$у, /еГ},
а) Если К — борелевское множество на оси
действительных чисел и {§ир|л:: ^е](}<^ то событие {теК)
§гизмеримо.
б) Если 8 (*)'— действительная борелевская функция,
в(-) отображает Г в Г и ^(^)^^ (^еГ), то 8 (^ —
случайное время.
Это свойство вытекает из предыдущего.
в) Если %1 — случайное время (/== 1, 2), то тт(ть т2)
и тах(ть т2) также случайное время. В частности,
одновременно с т случайным временем является величина
ппп(т, г0)> к^Т-
Доказательство этого утверждения вытекает из
того, что
{тах (ть т2) < 1} = {х{ < /} П {т2 < О
и
{тт (т], т2) < 0 = {т! < 1} [) {т2 < /};
г) Если %1~ случайное время и Т!^т2, то ?$т, сг§Т2.
Действительно, пусть Ле'^ч. Так как (т! ^ /}:э{то<^},
то ЛП{^<0 = ЛП{т1<0П{т9<0==ВП{то</}е^> так
как Б-ЛП{Т1<0^^ и {т2<0^^.
Пусть Г —конечное или счетное множество, {§^; /еГ}~
поток с-алгебр, т —случайное время на {§*; ^еГ},
ЙТ = Й. Рассмотрим множество случайных величин
{|^; /еГ} таких, что |* — ^-измеримо при каждом /еГ.
Положим \% = \и если т==^. Величина \х определена
для всех со ей.
Лемма 5. Величина 1Х ^-измерима.
Действительно, пусть ск, к= 1, 2, ... — возможные
значения т. Тогда
{ш: %%<х}(}{(*: т</}= [] ({со: |т<х}П{со: т = ^}) =
= У ((<*: Ъ(ск)<х}{){®: т = сл})е=&,
ск<*
так как каждое событие в последней сумме
принадлежит $, <=$,.
2 Г! И. Гиумзн, А. Б. Скороход
34 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Г
§ 2. Независимость
Определения. Пусть {О, ©, Р} — фиксированное
вероятностное пространство. Под событиями в настоящем
параграфе постоянно понимаются, если не оговорено
противоположное, ©-измеримые подмножества.Й.
Два события А я В называются независимыми, если
Р(А(]В) = Р(А)Р(В). Из определения непосредственно
следует:
а) О и Л, где А — произвольное событие, независимы;
б) если ^(ЛО — О, Л— любое, то N и Л независимы;
в) если Л и В; (/=1,2) независимы, ВцэВ2, то
Л и б!\В2 независимы» В частности, Л и В{
независимы.
г) если Л и В1 независимы (/=1, 2, ..., п), причем
п
В\, В2, ..., Вп попарно несовместимы, то Л и ув^
также независимы.
Заметим, что без оговорки о попарной
несовместимости событий Вь последнее утверждение, вообще
говоря, не имеет места.
д) Л не зависит от Л тогда и только тогда, когда
Р(Л) = 0 или Р(Л)-1.
Пусть / — некоторое множество, {Шь /е/}
—множество классов событий, перенумерованных с помощью
индекса /, принимающего значения из /.
Определение 1. Классы событий {Ш^ 1^1}
называются независимыми (или независимыми в
совокупности), если для произвольных попарно неравных
'ь 4, •••> 4 Ук^П и произвольных А1к, Л^еЗИ^
& = 1, 2, ..., п,
Р(^ПЛ/2П ... ПА<1-Р(А<1)Р(А4...Р(А^
Заметим, что для бесконечного множества классов
событий определение независимости эквивалентно
требованию, чтобы произвольное конечное подмножество
классов событий состояло из независимых классов со^
бытии.
В дальнейшем а{Ш} обозначает минимальную а-ал-
гебру, содержащую 2#.
зш
НЕЗАВИСИМОСТЬ
35
Назовем класс событий 51 я-классом, если он
замкнут относительно операции совмещения событий (из
•/Це51, &=1, 2, следует А\$\А%&Щ и назовем его
к-классом если:
а) из Ак*=%, к = 1, 2, ..., и Ак(]Аг = 0 при 6=^г
оо
•следует У Лй е= %\
б)Ое=51 и из В2=>ВЬ В*<=$, Л=1, 2, следует
В2\В{<=Ш.
Очевидно, что если 51 одновременно я-класс и Х-класс,
то он является а-алгеброй.
Лемма 1. Если К-класс 51 содержит п-класс Ш, то%
содержит в{Ш}.
Доказательство. Обозначим через %
минимальный Л-класс, содержащий ЗЯ (51, есть пересечение всех
^-классов, содержащих ЗК). Покажем, что ЭД1 = а{2К},
Пусть 91(13) обозначает класс всех событий А из Яь
для которых А[)Вт%.
Легко проверить, "что Ш(В) является зх-классом. Если
ВаШ, то 5ЦВ)=э9й (так как 3№-я-класс). Поэтому
51 (В) = 51! (Ве=Ж). Но это означает, что %{А)^Ш при
любом Ле 51ьт. е. 51 (А) = 211# Таким образом, 5^ является
я-классом. В.силу предшествующего замечания 511 = а{ЗИ}.
Теорема 1. Пусть {Ш^ I е /} — совокупность
независимых п-классое. Тогда минимальные о-алгебры оЩ^,
/е /, независимы.
Доказательство. Можно ограничиться конечным
числом классов 9№ь ...,. Т1п, Достаточно показать, что
если один из классов, например Ши заменить на о{Ш{},
то новая последовательность классов событий также
независима.
Обозначим через 51 класс всех событий, каждое из
которых не зависит от Ш2, ..., Шп. По определению
9И,с:51 и 51 обладает свойствами: он замкнут
относительно суммирования непересекающихся событий и
образования разности /?2\#1 при условии, что В2^эВ{.
Таким образом, 51 является Я-классом, и на основании
предыдущей леммы 51:эсг{ЭЖ1}. Теорема доказана.
Теорема 2. Пусть {Ш^ 1^1} —множество
независимых классов событий, каждый из которых замкнут
относительно операции пересечения, / = /] II 12{1{ П /г — 0)«
2*
36 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Г
Обозначим через 23/ (/ == 1, 2) минимальную о-алгебру, са?о
держащую все Ш{у *е//. Тогда %\ и 332 независимы.
В силу предыдущей теоремы можно ограничиться
случаем, когда 9йг — а-алгебрьь Рассмотрим классы
Щ/(/=1, 2), состоящие из всевозможных событий вида
А1х(\Ак(\ ...ГМ*Я, А1ке=т1к, /г-любое, ^е/,. Они
замкнуты относительно пересечений, 91/ содержит все
9№г, /е// и %х и %2 независимы. В силу предыдущей
теоремы ог{911} =« а{Э№/, 1^1\} и о{%} = а{Ш1, 1^1^
независимы.
Следствие. Если I разбить на произвольную
совокупность подмножеств, /=^1//, попарно без общих то-
чек, то в-алгебры {^/ = а(9№/, /е/Д /еМ} независимы
в совокупности.
Независимые случайные величины. Определение 2.
Случайные величины {^-, /<=/} называются
независимыми (независимыми в совокупности), если независимы
классы событий Ш{9 /е/, где Ш^ состоит из всех
событий вида
(со: ?/<а}, -оо<а<оо.
Определение ' независимости множества случайных
величин эквивалентно следующему: случайные
величины ^(/е/) независимы, если для любого п и любых
4е/, 6=1, ..., д совместная функция распределения
величин %; , ^ , ..., ^ равна произведению функций
распределения величин ^,- :
Аналогично формулируется определение независимости
множества классов случайных величин.
Рассмотрим множество случайных величин {^, ^^}»
где ^ — фиксированный индекс, а / пробегает
множество /й, зависящее от индекса \х. Для удобства назовем
это множество классом и рассмотрим множество таких
классов, перечисленных с помощью индекса \х, пробег
гающего множество М.
Определение 3. Классы случайных величин
{^.^^Н^^) называются (взаимно) независимыми,
§.2]
НЕЗАВИСИМОСТЬ
37.
если взаимно независимы множества событий Э)^([хе М),
где Шр состоит из всех событий вида
{со: ^<ар ..., Щп<ап}> (1)
п= 1, 2, ..., гк^1^ - оо<ак<оо.
: Определение 4. а-алгебра событий а{^, *^/},
порожденная, событиями вида
(со: ^Каи ..., &п<ап}9
п== 1, 2, ..., /&€=/, -оо<ай<°°,
называется а-алгеброй, порожденной классом случайных
величин {^-, ^е/}. Пополнение а-алгебры а{^-, /е/}
обозначим .через а{^, *'<=/}.
Иначе говоря, а{^-, *'е/} есть минимальная а-алгебра
событий, относительно которой все ^ являются
случайными величинами (т. е. минимальная а-алгебра множеств,
относительно которой все функции ^ = Мю) измеримы).
Отметим, в частности, что а-алгебра событий,
порождаемая одной случайной величиной ^, является
минимальной а-алгеброй, содержащей события вида {со: ^<а}
(— оо <а< оо).
Теорема 3. Если классы случайных величин [1%, 1^1^},
[1еМ, независимы, то множества а-алгебр о {^, /е/^},
[1ЕМ, г/ их пополнений о {^, *^/„) также независимы.
Доказательство вытекает из того, что классы Ш^,
введенные в определении 3, замкнуты относительно
пересечений событий внутри класса и из теоремы 1.
Следствие. Пусть §^ {1{ ,12, ..., 18) (\х^М) —
множество конечных борелевских функций от в
действительных переменных. Если последовательности случайных
величин {(^, Щ, ..., Щ, \х еМ) независимы в
совокупности, то случайные величины | = ё^ДСр ?$> • • • > %%)> М»е ^>
также независимы.
' Понятие независимости случайных величин и
доказанная теорема легко обобщаются на случайные
элементы в произвольнОхМ измеримом пространстве {$?, 23}.
Пусть ^ = /; (со), г е /, — некоторое множество
случайных элементов в {дви 23^}. Элементы {^-, /е/} называются
независимыми (или независимыми в совокупности),
38 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Г
если для произвольного пу п~ 1, 2, ..., и произвольных
Р(Л{^^^})==ПР{^^^). (2)
Аналогично определение множества независимых
классов случайных элементов.
Произвольная совокупность случайных элементов
порождает минимальную сг~алгебру множеств в 2,
относительно которой каждый случайный элемент измерим.
Из независимости некоторого множества классов
случайных элементов вытекает независимость минимальных
а-алгебр (и их пополнений), порождаемых
соответствующими классами случайных элементов. Доказательство
этого утверждения такое же, как и для случайных
величин.
Пусть дана последовательность случайных
элементов |й = Мю) в {Я?ь ^}, к= 1, 2, ..., п. Ее можно
рассматривать как случайный элемент со значениями
п
в П <%к- Действительно, обозначим через 23(/|) произве-
дение а-алгебр 2ЭЬ # ь., Ъп. Если С = А{Х А2Х ... X Ап,
Л,е^, /= 1, 2 ..., /г, то
{со: (/, (со), ..., иш))бС}«П{ш:'М©)Е4
т. е. прообраз С ©-измерим. Отсюда следует, что
прообраз любого множества из минимальной а-алгебры,
содержащей все С, т. е. прообраз любого множества
из ЭЗЫ, ©-измерим. Обозначим меру в | Ц <^ь 23(л)|>
индуцируемую последовательностью (|ь ..., |я), через
/»1.2 п,
/*!. 2 я(С)«Р{<&1, .... УеС}.
Допустим, что элементы |я, к = 1, .♦., п, независимы.
Формула (2) показывает тогда, что
/Я|,2 п(А[(]А2(] ...(\Ап) = т1(А1)т2{А2) ...тп{Ап),
$2]
НЕЗАВИСИМОСТЬ
39
еде тк{Ак) = РЦк^ Ак}. В силу единственности
продолжения меры с полукольца множеств на минимальную
а-алгебру мера /тц.2 п является произведением мер
Ши ть -"Утп- Обратное тривиально: если мера /щ, 2,..., п
совпадает с произведением мер ть тъ ..., тп, то
случайные элементы %и' \ъ ..., '\п независимы. Отсюда
следует
Теорема 4. Случайные элементы |ь |2> - - *>1п
независимы тогда и только тогда, когда мера тт,2 п, ин~
дуцируемая последовательностью (|ь &2> • • •> ?я) на о-ал-
еебре 23(п), является произведением мер гпк {к = 1, ..., я),
индуцируемых элементами %к на 33*.
Теорема 5. Пусть ё(хи дг2) —Й(2)-измеримая
конечная функция, ^1 ^1,2 — независимые случайные элементы и
1%(&„У<оо.
Гог<5а ф^) — М^(л:ь %2) является $$гизмеримой функцией
от хх и
или
Щ(1и У = [ т, (^ЛГ1)| ё(х{9 х2) т2{4х2).,
Та же самая формула остается в силе для
произвольной Й(2) измеримой функции, где значок~
означает, пополнение 0-алгебры (меры), если меры тх и т2
считаются полными. Теорема является
непосредственным следствием теоремы о замене переменных для
абстрактных интегралов, в силу которой
^ё(1и У= | Я(*1>*2)Л1Ь2(<*(*1> Х2))9
&х х а?2
и теоремы Фубини.
Следствие. Если \х и Ь,2~~независимые случайные
величины с- конечными математическими ожиданиями,
го
Закон 0 или 1. Пусть Ап, /1=1,2, ..., — некоторая
последовательность событий.
40 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ТЛ, Г
Теорема 6. Если 2Р(Ля)<оо, то событие Нт Ап
п— 1
имеет вероятность 0.
Доказательство вытекает из формулы Нт Ап =■
оо сю
«=РУ4, в силу которой
п—\к—п
I оо \ оо
Р(ЙтУ1я) = ИтР [}Ак ) < Нт 2 Р (Л») =• 0.
п -> оо \ д, в /г / гс->оо й«/1
Для последовательности независимых событии эта
теорема может быть усилена следующим образом.
Теорема 7 (теорема Б ор е л я- Конхе л л и).
Яслгг сдбытия{Ап, лг = 1, 2, ...} независимы, то
вероятность события Нт Ап равна 0 или 1 в зависимости от того,
оо
сходится ли ряд 2 Р (Ап) или расходится.
оо
Доказать нужно только, что если 2Р(4)Я°°» то
Р(ПтЛя)=1. Если Л* = НтЛя, то
оо оо
п=\к^п
И
Р(0\Л*) = Нтр(П(Й\Л,)) = НтПР(а\^)==
П->оо \двЯ / П->оок**П
-НтП0-РМ»)) = 0
/г->оо &»/г
оо
в силу расходимости ряда 2Р(4&)-
& = 1
Рассмотрим теперь произвольную последовательность
независимых а-алгебр ©я, /г= 1, 2, .... В силу теоремы
Бореля-Контелли событие Л = Нт Л„, где Ап —
произвольная последовательность такая, что Ляе©я имеет веро~,
ятность 0 или 1. Этот результат может быть обобщен
на произвольные события, порождаемые совокупностью
всех а-алгебр ©д, п= 1, 2, ,.., и не зависящие от
произвольной конечной последовательности 0-алгебр ©Ь
§21'
НЕЗАВИСИМОСТЬ
41
©«» •••> ©л- Уточним это утверждение. Пусть <т{@.,
@*+ь •••»®п» •••} = ЭЗ^—а-алгебра, порожденная
последовательностью ©л, п~к, к+1, ...; 33л образуют
монотонно убывающую последовательность сг-алгебр. И к
пересечение 33 = Р) ЯЗЛ есть снова ст-алгебра. Положим
6 = 1
по определению
оо
Очевидно, что сг-алгебра Нт®и не изменится при
замене любого конечного числа сг-алгебр ©ь .. .,©л другими.
Теорема 8 (общий закон 0 или 1 Колмогорова).
Если ©л, я = 1, 2, ..., — взаимно независимые в-алгебры,
то всякое'событие из Нт@л имеет вероятность О г/ли 1.
Действительно, пусть ЛбЙт©й. Тогда ЛеЗЗ^, при
любом А, следовательно, Л и а{©ь ...,©/г_!}
независимы. Поэтому независимы Л и а{©!, ..., ©д, ...}. Так
как Леа{ёь ..., ©„, ...}, то Л не зависит от Л. Это
возможно только тогда, когда Р(Л) = 0 или Р(Л)=1.
Следствие. Пусть {|„, га = 1, 2, . ..}
последовательность независимых случайных элементов в
фиксированном метрическом пространстве {$ву Щу @п = а {%п} — о-ал-
гебра, порожденная |„, 23„ = а{®„, ©л+ь ...}. Тогда
а) предел последовательности {|п, га= 1, 2, ...}
существует с вероятностью О или с вероятностью 1;
б) если дд сепарабельно и полно, то предел
последовательности {|п, га= 1, 2, ...}, если он существует
с вероятностью 1, постоянен (тойР).
в) если г = ^ (хь л?2, ...,*„, ...) — функция
бесконечного числа аргументов хп е $?, га = 1, 2, ... и $ (|ь %2> • • •
• ••»|л» •••) ^пгизмерима, каково бы ни было га, го ояа
с вероятностью 1 постоянна.
Доказательство, а) Если р(х, у) — расстояние
в'1/,' То множество точек, в которых %п сходится,
можно записать в виде
' оо оо
°= Г) [] П {®:Р(&«',Ы<4-}-
42 ОСНОВНЫЕ ПОНЯТМЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Так как события Ап = |~) | р (|д/, ^„//) < у г
монооо
тонно возрастают, то \^Ап&$^^ при любом г, так что
я=-1
и Ое8г при любом г и можно применить общий
закон 0 и 1.
б) Пусть Р — замкнутое множество, Р аЗ?у через Рк
обозначим открытое множество Рк~1х: р(х, Р)<-^>.
Тогда событие А = И П {Ит |п е Т7} можно представить
в виде
[оо оо "1
П II П {|»е^}
д«1 п»1 п/>п ^
откуда Л е 23г,
г=1, 2, ..., в силу тех же соображений, что и при
доказательстве а). Таким образом, Р {Ит 1п <= Р) = О
или 1 для любого замкнутого У7. Но класс множеств,
для которых аналогичное заключение имеет место,
является а-алгеброй, поэтому Р{Нт^ле5} = 0 или 1 для
любого В е 23. В случае сепарабельного и полного
пространства 36 отсюда нетрудно получить, что мера т,
индуцируемая на 33 случайным элементом Нт|л,
сосредоточена на одном атоме. Действительно, так как
т(й?)=1, то найдется сфера 5, радиуса 1 такая, что
т(51)=1. Если бы такой сферы не нашлось, то все
сферы в 36 радиуса 1 имели бы меру 0, что
невозможно, так как 36 покрывается счетным числом таких
сфер. Аналогично найдется сфера 52 радиуса -ги52с 5,
и т(52)=1. Продолжая это рассуждение, получим
последовательность вложенных друг в друга сфер 8п,
радиусы которых стремятся к нул!ю и мера которых
равна единице. Эти сферы имеют только одну общую
точку х и т{х}= 1\тт(8п) = 1, что и требовалось
доказать.
в) События Л = {ю: /Ч|ь ..., 1п, .. .)<а}е= Э3„ по
условию, и поэтому А е Нт ®п, так что А имеет
вероятность 0 или 1. Таким образом, функция
распределения случайной величины $ = /(|ь . ..,|я, ...)
принимает только значения 0 и 1 и величина ^ с
вероятностью 1 постоянна.
§зь
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
43
§. 3, Условные вероятности
и условные математические ожидания
Определения. Напомним прежде всего определение
условной вероятности и условного математического
ожидания в элементарном случае. Условная вероятность
Р{А\В) любого события Л при гипотизе В, если
Р(В)Ф0У определяется соотношением
Р(Л|В)=-^1М-.
При фиксированном В условная вероятность Р(Л|В)
является нормированной мерой, заданной на той же
а-алгебре множеств, что и «безусловная» вероятность
Р(Л). В соответствии с этим условное математическое
ожидание некоторой случайной величины |,==/((о) при
гипотезе В определяется формулой
а
Принимая во внимание определение условной
вероятности, это соотношение можно переписать следующим
образом:
Р(В)М{б|б}= | &р. (1)
В
Для того чтобы иметь возможность определить
условные математические ожидания и условные вероятности
относительно событий, имеющих вероятность 0,
необходимо несколько переосмыслить эти понятия. Отметим
прежде всего, что если | есть индикатор события Л,
то М{^|В} = Р(Л|В). Таким образом, условные
вероятности являются частным случаем условных
математических ожиданий, и мы можем пока ограничиться
последними. Пусть 2К —некоторый счетный класс
песо
совместных событий {В*; 1=1,2, ..., В* <= ©} и [} В1 = й.
1 = 1
Определим случайную величину МЙ|2№}, полагая ее
равной М{||В;}, если соеВ*, и назовем ее условным
математическим ожиданием случайной величины |
относительно заданного класса множеств 9№. Она
определена только для тех значений со, которые попадают
44 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
в такие Вь что Р (В^ Ф О, т. е. случайная величина!
М{^|3№,} определена с вероятностью 1. На множестве
В(^Ш, для которого Р(Вг)=7^=0, эта величина
постоянна и равна условному математическому ожиданию |
при гипотезе Вь. Заметим, что, зная функцию Мй|3#}>
можно определить не только М{^|В^}, когда В^Ш,
Р(В1)Ф0, но и условное математическое ожидание
случайной величины относительно любого В, Р(В)=^=0,
оо
принадлежащего а{3№}. Действительно, если В= II В;.,
то
оо
Р(В)М{Ъ\В}= 2 Р(В,к)ЩЪ\В,к}. (2)
Эта формула показывает, как, зная условные
математические ожидания при заданных Вг(/= 1, 2, ...),
можно вычислить условные математические ожидания
при заданных счетных суммах этих множеств, а
следовательно, условную вероятность относительно
любого* множества из наименьшей а-алгебры, содержащей
все В{. Заметим, что соотношение^) может быть
записано следующим образом:
/ \йР= / Мда}Р№о),
в в
причем оно имеет место для произвольного В из
а-алгебры, порождаемой^, и случайная величина ц= М{1\Ш]
измерима относительно этой а-алгебры.
Нетрудно заметить, что эти свойства однозначно
(той Р) определяют условное математическое ожидание.
Действительно, если существуют две ^-измеримые
случайные величины т)Д/=1,2), для которых
/ *)1^Р= / %^Р
в в
при любом В <= § (5 — некоторая а-алгебра), то цх и щ
Р-почти всюду совпадают.
Последнее обстоятельство может быть использовано
для определения условного математического ожиданмя
в общем случае. Пусть произведен некоторый
эксперимент, описываемый а-алгеброй событий $В. Мы же-
§3] УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ 45
лаем определить условное математическое ожидание
некоторой случайной величины | в предположении, что
известен результат эксперимента. Это условное
математическое ожидание рассматривается как функция от
результата эксперимента, т. е. как 23-измеримая
случайная величина, удовлетворяющая только что полу*
ченному соотношению.
Определение 1. Пусть 23 — произвольная ст-ал-
гебра событий, содержащаяся в ©, -| — произвольная
случайная величина, математическое ожидание которой
существует. Условным математическим ожиданием
случайной величины с, относительно о-алгебры Ъ называется
случайная величина М {|| 23}, измеримая относительно Ъ
и удовлетворяющая при произвольном В е 23 равенству
[ М{||ЗЗЫР=| 1</Р. (3)
В В
Существование и единственность (с точностью до
эквивалентности) случайной Величины М {%\23}
непосредственно вытекает из теоремы Радона — Никодима.
Действительно, правая часть формулы (3) является сг-ко-
нечной счетно-аддитийной функцией множеств на Й,
абсолютно непрерывной относительно меры Р. Поэтому
существует 23-измеримая функция ^(со) такая, что
| ЫР=/*ЫР(Жо).
в в
Функция §(со) при этом единственна (с точностью до
эквивалентности). Она и есть, по определению,
условное математическое ожидание величины ^ относительно
а-алгебры 5).
Замечание. Пусть й — пополнение 23
относительно вероятности Р. Легко убедиться, что
Мй|93}=Мй|8}(то(1Р).
Так как класс ^-измеримых функций шире класса 23-из-
меримых функций, иногда бывает целесообразно
рассматривать условное математическое ожидание
относительно пополненных ог-алгебр.
Условные вероятности Р{Л|23} относительно сг-ал-
гебры 23 определим как частный случай условных
Математических ожиданий, полагая ^ — Хл!0*).
46 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ . [ГЛ; I
Определение 2. При фиксированном Л условная
вероятность Р{Л|23} есть ^-измеримая случайная
величина, удовлетворяющая при любом В е 23 уравнению
/ Р{А\ЩаР = Р(АПВ). (4)
в
Свойства условных математических ожиданий и
условных вероятностей. В настоящем пункте постоянно
предполагается, что рассматриваемые случайные
величины обладают конечным или бесконечным
математическим ожиданием, а формулируемые и доказываемые
утверждения имеют место с вероятностью 1.
а) Если I ф О, то М{||33}>0.
б) Если % — Ъ-измеримая случайная величина, то
В частности, если событие В ^-измеримо, то
в) ММ{||33}=М|.
г) Если М^=^=оо, /=1,2, то
М {об, + Ь12\Щ = аМ & [23} + ЬМ {|2|ЭЗ}.
Для доказательства этого соотношения достаточно
проверить, что его правая часть удовлетворяет
определению условного математического ожидания случайной
величины а%\ + Ь%2-
Полагая 11 = щ, В{(]В2= 0, в частности, получаем
аддитивность условной вероятности
Р{В1[)В2\Щ = Р{В1\Щ + Р{В2\Щ.
д) Если Цп, #=1,2, ...} — монотонно неубывающая
последовательность неотрицательных случайных
величин, то
ПтМ{Ы23}=М{Пту5В}.
Доказательство немедленно получается, если
применить теорему Лебега о почленном переходе к
пределу под знаком интеграла в равенстве
/ М(Ы«ЫР= \%пйР.
в в
Для условных вероятностей доказанное свойство дает:
■М
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
47
если {Вп> п = 1, 2, ...} — монотонно возрастающая
последовательность событий, то
НтР{Вя|8} = Р(иВя18;
если АПУ п= 1, 2, ..., попарно без общих точек, то
\ °° 1
2 Р{Ап\Щ~Р\\3 АпЩ. (5)
Замечание. Последнее свойство условных
вероятностей вовсе не означает, что их'можно рассматривать
при фиксированном со как счетно-аддитивные функции
множества. Для данной последовательности Ап
равенство (5) может не иметь места только с
вероятностью 0, но соответствующее исключительное событие
зависит от выбора этой последовательности. Поэтому,
вообще говоря, возможно, что нет ни одного со, при
котором (5) было бы верным для всех
последовательностей Ап из ©.
е) Если случайная величина | и а-алгебра 93
независимы, то
МК1»} = М&. (6)
Независимость случайной величины | от а-алгебры 93
означает по определению, что независимы а-алгебры
о[^} и 93. Поэтому для любого бе93
| 6*Р = М&ХВ«М&Р(В),
в
так что равенство (3) будет удовлетворено, если
положить М{^|93} = М^.
Из доказанного свойства вытекает, что если событие
А не зависит от а-алгебры 93, то
Р{Л|93}-Р(Л). (7)
ж) Если ц — ^-измеримая случайная величина, то
МЫЩ = ф{Ъ\Щ> (8)
При доказательстве этого свойства достаточно
ограничиться предположением, что ц неотрицательна.
48 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Если г] = Хв1, 5^8, то
/ т|М&|»}<*Р- / М{1\Щс1Р^ / ^Р=/г^Р,
В В[\Вх ВПВ, В ,
так что равенство (8) выполняется. Так как класс
случайных величин, для которых (8) имеет место, линеен
и замкнут относительно предельного перехода по
монотонным неотрицательным последовательностям, то он
содержит произвольные ^-измеримые неотрицательные
случайные величины.
Поскольку условное математическое ожидание М {%\Щ
является случайной величиной, можно рассматривать
условное математическое ожидание этой величины
относительно некоторой другой а-алгебры 231# Так
приходят к итерированному условному математическому
ожиданию М {М {^|^8}| ЗЗ1}. Установим важное свойство
этой операции. Заметим, что если Ж и З^ — две
а-алгебры и 23! с: 23, то из определения условного
математического ожидания следует М {М Й|ЗЭ1}|33} = М Ш23,}.
Более глубоким является следующее свойство:
з) Пусть 8с8,, Тогда
М{МЙ|»1}|»}«МЙ|2Э}.
Действительно, если В е 23, то Ве81} следовательно,
/ М{М{||Э1}|®}^Р=/М{||81}йР =
в в
В В
Сопоставляя крайние части этой цепочки равенств,
получаем
М{Мй|аз,}|аз}=м{Ц8}.
Из доказанного вытекает: если 23(^:23! и т]
—^-измеримая случайная величина, то
Мйл1»НМ{лМ«| Я,}|»}. (9)
Следующее утверждение, обобщающее ж), бывает
часто полезным. Пусть ^~/г(й)), г] = $(©) — два
измеримых отображения {(3, ©} в {&, Щ и {X, &} соответ-
■#3]
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
49
ственно. Пусть § (л:, г) — числовая функция,
определенная на Й/Х^, измеримая относительно а {51ХЙ}
и математическое ожидание §{%, г\) конечно,
и) Если ц Ъ-измерймо (23 с: ©), то
М{ё&ч)\Щ=М{ё&г)\Щ\г^.
Для доказательства заметим, что в силу ж)
последняя формула справедлива для функций §(х, у),
п
имеющих вид: §(х, г) = 2 8к (х) "°к (г). Для произволь-
к=[
ных функций §{х, г), для которых М|#(2, л)1 <°°»
утверждение вытекает из существования
последовательности функций /гп{х, г) предыдущего вида и таких,
что /гп{Ъ, ц) сходится к §(^9 г\) с вероятностью 1 и в^.
Условное математическое ожидание относительно
случайной величины. Пусть 2; —случайная величина,
принимающая значения ги г2> ..., г„, ...,РЙ = 2„)>
>0, Вп обозначает событие {^ = гп} и
Р <л\= р(АПВп)
— условная вероятность А при гипотезе %*=2п.
Условное математическое ожидание величины ^ при
гипотезе {> = гп определяется формулой
Рассматривая эту последовательность чисел как
функцию от исхода эксперимента, состоящего в
определении значения ^, приходим к понятию условного
математического ожидания | относительно случайной
величины ^. Так называют случайную величину М {^|^},
принимающую значения М{||2; = 2П}, если Е = г„. Это
определение совпадает с данным ранее определением
условного математического ожидания относительно
счетного разложения Ж пространства Й. Роль Ш
играют события {Ёп; м=1,2, ...}. Последнее замечание
указывает путь к общему определению.
Рассмотрим измеримое отображение 1 — §{(о)
пространства {О, ©} в некоторое измеримое пространство
{$?, 23}. Таким образом, ^—случайный элемент со
50 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ {ГЛ. Г
значениями в дв. Пусть ?^ —а-алгебра, порожденная
отображением \\ ^={3; 3-е-1 (В), В€еЗЗ}.
Определение 3. Условным математическим
ожиданием М{^|^} случайной величины % относительно
случайного элемента ^ называется случайная величина
мша.
Это определение эквивалентно следующему: для
любого В е= 23
| М{Ш<*Р~ | 1ЛР. (Ю)
в""1 (В) е"1(В)
Аналогично определение условной вероятности
относительно $:
Р{А|»-РМШ.
Теорема 1. Условное математическое ожидание
относительно случайного элемента ^ является
^измеримой функцией от ^:
где 8 (х) ■— ^-измеримая функция.
Доказательство. Пусть | неотрицательна.
Имеем
| М(Ш<*Р- I ЪЛР~я№. (П)
*~"!(В) 8~1(В)
Очевидно, что ц{В) является с-конечной мерой на 23.
Кроме того, ц (В) = 0, если Р {§~1 (В)} = 0, т. е. ц
абсолютно непрерывна относительно меры Рё, где Рё(А) =
= Р{§~1(А)}. На основании теоремы Радона — Никодима
существует 23-измеримая неотрицательная функция $(х)
такая, что
я(В)~$8(х)1>ж{ах).
в
Используя правило замены переменной, хющчши
?(б) = - / в(«г(*))Р(Л>).
Сравнивая с (11), приходим к равенству
что и требовалось доказать.
§31
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
51
Доказанная теорема показывает, что условное
математическое ожидание относительно случайного
элемента Е можно рассматривать как функцию
независимой переменной х в пространстве с мерой {36, Й, Р^>
в то время как в исходном определении условное
математическое ожидание есть функция элементарного
события ш. Функция з(х) однозначно 'определяется
соотношением
| &</Р= ^ 8{х)Р,{йх\ (12)
имеющем место для произвольного В е 35.
Приведем теперь несколько предложений,
непосредственно вытекающих из ранее полученных свойств
условных математических ожиданий.
а) Пусть I и ^ независимы. Тогда М{^}=М^.
б) Если I — ^-измеримая случайная величина, то
в) Если х\1 = §1 (со) — из чгримые отображения {О, Щ
в {#,,8,} (* =1,2), то
М{Мй|(т,1,%)}|л.} = Мйк},
где {х\и %) обозначает отображение со -> (#, (со), §2 (со))
пространства {&, 6} в произведение пространств фх X д6ъ
а{Й,Х«2}}.
Регулярные вероятности. Ранее уже упоминалось,
что условные вероятности, вообще говоря, нельзя
рассматривать как меры, зависящие от элементарного
события. Все же в ряде случаев этого можно добиться.
Уточним постановку вопроса.
Условная вероятность Р {Л | 8} = к (©, А) есть
функция от соей и'/1е6, определенная при каждом
фиксированном А только с точностью до события
вероятности 0. Спрашивается, можно ли найти такую
функцию р(со, А) (соей, Ле6), что:
а) при фиксированном © функция р (со, А) является
вероятностью на сг-алгебре ©;
б) к (со, А) = р (со, А) почти наверное при любом
фиксированном А.
Определение 4. Если существует функция
|?(ш, Л), удовлетворяющая требованиям а) и б), то
52 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
семейство условных вероятностей Р{Л|93} называется
регулярным. В этом случае отождествляют Р {Л 193}
с р(со, А).
В регулярном случае условные математические
ожидания, как и следовало ожидать, выражаются
интегралами с условными вероятностями в качестве мер.
Теорема 2. Если Р {А | 93} — регулярная условная
вероятность, | = / (со), то
М й I 33} = 11 (со) Р (Ао | 93) (тех! Р). (13)
Доказательство этого утверждения не представляет
трудностей. Во-первых, по определению оно верно
в том случае, когда | есть индикатор некоторого
события Л^©. Из линейности обеих частей равенства
(13) как функционалов от [ следует, что оно имеет
место для простых функций. Предельный переход по
монотонно возрастающим последовательностям простых
функций доказывает (13) для любой неотрицательной
случайной величины |. Повторное использование
линейности правой и левой частей равенства (13)
заканчивает доказательство.
В некоторых'случаях нам необходимо подчеркнуть,
что условная вероятность есть функция элементарного
события. В этом случае будем писать Р {А | 93} = Р8(со, А)
или просто Р(со, Л), если а-алгебра 93 фиксирована.
Аналогично Р^ (со, А) — иное обозначение для Р{Л|^}.
Так как свойство регулярности условных
вероятностей не всегда имеет место, представляется
целесообразным несколько расширить его.
Пусть {$?, 93} — измеримое пространство,
^-случайный элемент в {$?, й}, § — некоторая а-алгебра,
§с©.
Определение 5. Функцию 0(со, В),
определенную на 0x93, называют регулярным условным
распределением случайного элемента 2; относительно о-ал-
гебры §, если:
а) при фиксированном В^93 0 (со, В) ^-измерима,
б) с вероятностью 1 при фиксированном со 0(со, В)
является вероятностной мерой на й,
в) при каждом В(=93 <2(со, В)-Р{($е=В)|$}(то(1Р).
§3]
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
53
Последнее требование эквивалентно следующему:
для произвольного Р&%
0((о,В)Р№) = Р{ЙЕЙ)ПП (14)
р
Теорема 3 Пусть 3? — полное сепарабельное
метрическое пространство, Ъ — в-алгебра борелевских
множеств $в, ? — случайный элемент в {36, 23}, § ~
произвольная в-алгебра, 5^®- Тогда существует регулярное
условное распределение случайного элемента ?
относительно а-алгебры §.
Доказательство. Положим ц (В) = Р ({? е В}),
#еЗЗ. В силу одной теоремы из теории меры, каково
бы ни было п, можно найти такой компакт Кп в $?>
что д{§5\Кп)<\1п (см. гл. V, § 2, замечание 1 к
теореме 1).
Через ^(й?), где й/ — некоторое метрическое
пространство, обозначим пространство непрерывных и
ограниченных на дб действительных функций с расстоянием
Р (/, Я) = I! / (^) - ^ (-^) II = {зир | / (х) - йг (х) |, л: е ^}.
Пространство *& {Кп) является сепарабельным. Пусть
Ипк (*)» ^ = 1» 2, . ..}— счетная всюду плотная сеть
в ^(Кп)- Продолжим !пь{х) на все дд так, чтобы
{&ир\1пь(х) |, хеЕШ} = {тах\1пк(х)1 хе](й}. Положим
%п = %п (?)> гДе %п {х) — индикатор компакта Кп- Из свойств
условных математических ожиданий вытекает, что
существует такое 230е©, что Р(Д) = 0 и при соеО0
имеют место следующие соотношения:
если /„,(*)> 0, то- М{Ы018»0;
если | /„,(х) -/я/ (х) |<г, то М {11пк(?) -/я/(?) |§}< г;
М{г/яя(018}-гМ{/яя(018}1
М{^(?) ± /я/ (?) 1§}=М 0ЯЯ(?) 18} ± М{/я/(?) 18),
Ит М«1-Хт)/п*(О18>в0
для всех Пу ку ] и рациональных г. С другой стороны,
для произвольного -Ре§
) (М{/(0 18}- М{/„,(О |ф) Л>|.<./ )/(*)-/„»(х)\д{ах).
я' ' I р
(15)
§4 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИЙ ВЕРОЯТНОСТЕЙ [ГЛ. Г
> Поэтому, если выбрать произвольную
последовательность !пкп(х\ так, чтобы \\%п§(х)-!пкп(х)\\-*®
(очевидно, для любой / ^^(95) такую последовательность
йыбрать можно), то окажется, что }Пкп(х) равномерно
ограничены,
1\!(х)-!пьп{х)Ъ(<1х)-+09
к
и в силу (15)
М {ШI 5} = Нт М Цпкп (О IИ (то<1 Р),
причем предел справа не зависит от выбора
аппроксимирующей последовательности (а> е= О0)- Так как
условные математические ожидания определены только
по (тос1Р), то положим, что для произвольной / е^(^)
М{/(С)1§} определяется последним соотношением.
При таком определении условного математического
ожидания оно обладает следующими свойствами (для
всех со е= /)0):
М{/(015}>0. если />0,
М Ы{ (0 + а2/2 (О|Ш = а,М {!х (?) |8> + а2М {[2 Ш>,
М0(»(1-ХивШ-*О при п->со.
Таким образом, Ь^Ф = М{/(?)!§} представляет собой
некоторый положительный линейный функционал на
%? ($/), и в силу одной теоремы о представлении
линейных функционалов (см. гл. V, § 2, теорема I) на
{<%> 23} существует мера д(д(В) такая, что
Нетрудно проверить, что мы можем считать эту
формулу определением условного математического
ожидания для произвольной й-измеримой неотрицательной
(или ^-интегрируемой) функции. Положив / {х) = %в (л;),
получим: Р{Я|§}=<7«(В) при со€=Я0 и Р{Я|8} = <7(Я)
при ©ей0< Отсюда вытекает требуемое.
Рассмотрим случайные элементы ^ и ?2 в {Щь 33г}
и {^2> ЗЗг) соответственно* где °Ц{ — полное метрическое
«31
УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
т
сепарабельное пространство, 23; — 0-алгебра борелевских
множеств °ЦI (/=1,2). Положим
Щ^2)~ЩХ X Щъ 23(1'2) = а{^, * = 1, 2}. (16)
Последовательность ^(1,2) = (^ь $2) можно рассматривать
как случайный элемент в {<^/(1,2), 23(,,2)}, а ^(1,2) —как
полное метрическое сепарабельное пространство.
Пусть с]1 обозначает распределение^- (I = 1, 2), #(1,2) —
распределение $(,,2), а </2,1) — регулярное условное
распределение ^2 относительно а-алгебры ^> ,
порожденной случайным элементом ^. Так как д{ 1 } является
^-измеримой функцией, то
где 52е232 и функция д(В2,у) 23,-измерима. Из
определения условных вероятностей следует, что
| </(Я2,$|)<*Р = <7<1>2)(Я,ХВ2),
е, \в
(В.)
где Вх — произвольное множество из 23, и ?1 = б"| (ю)-
В соответствии с правилом замены переменной это
равенство можно записать в виде
Ч«^(ВХХВ2)= \д(В2 ,ух)йЧх
Вх
ИЛИ
д"'2) (В{ X В2) « | х2! Ы ( [ х§> (у2) ц (йуъ у А йЧи
Ух \Уг I
где %а) — индикаторы множеств в пространстве Щ\. Из
последней формулы вытекает, что **
\ Пуи й)^(1,2)= ]* ( | /0/ь й)?(^2, У1))аЯ1 (17)
у(1.2) 5/, \У,
для любых 33(1,2)-измеримых неотрицательных функций.
Действительно, класс функций /, для которых формула
(17) верна, линеен и замкнут относительно предельного
56 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ.' Г
перехода по монотонным последовательностям. Так как
он содержит функции вида %(1)Х(2\ то он содержит
и их линейные комбинации. С другой стороны,
произвольную 93(1,2)-измеримую функцию можно
аппроксимировать монотонно возрастающими
последовательностями линейных комбинаций функций вида х(1)Х(2)-
'Заметим, что формула (17) верна и для
знакопеременных функций /, если только одна из сторон
равенства (17) имеет смысл. Из формулы (17) вытекает
равенство
М {/Кь &)!&,} = / !&и У2)Я(ЛУ* Ьх). (18)
Полученным результатам можно придать
следующую более общую форму. Пусть ^ ~ случайные
элементы в {<Уь ®&}> Щк — полное сепарабельное метри-
ческое пространство. Положим <3/п'5) = Д Щк, <В(1,5> =
= <т{«ь /г=1, ...,5}, г],-(^, ^2, ..., ^5),
^-распределение элемента Ьк в {Щк, 23й}, ц^ = ц^ (Взу ^, ..., Ъ-х) -
регулярное условное распределение элемента ^5
относительно а-алгебры §Л5-1 = §(^ ^б?__1). Из формулы
М {^(«сЛ - М«... {М {/1®п»-.}1»Чж-,} - • - 1®пЛ-.
повторно применяя соотношение (18), получим
М{/(С, ...,&,)!&,}= /•■• / (\1(1иУ2 Уп)Х
ХУ^> (йуп, С|, у2,..., Уп-х)) <7("",) ЫУп-и Ъь Уъ ■ ■ -,У«-2> X
■•• Х<7<2»(^2,а (19)
М {/(&„'...,&„)} = /•••//(*/< Уп)д{П)(4уп,Уи...,Уп-1)Х
X ?(,,-1) (Луп-и Уи ■■-, Уп-2) X ... X я(2) (йуг, у1)я1 «</,).
(20)
Условные плотности. Пусть {<%, 91, т) — некоторое
пространство с мерой, $ = §(©)— измеримое отображение
{42, Щ в {Я?, 91}.
§3] УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ
Говорят, что случайный элемент имеет плотность
распределения р(лг) (по мере га), если для произвольною
Л е= 91
Р(5еЛ)- $р{х)т{ах).
А
В силу теоремы Радона — Никодима случайный
элемент ^ обладает плотностью распределения тогда и только
тогда, когда мера Рч абсолютно непрерывна
относительно т.
.Пусть {^, 23, д} — некоторое другое измеримое
пространство и ц = к (со) — случайный элемент в {^, 35].
Пару (^, г|) можно рассматривать как некоторое
измеримое отображение {О, ©} в произведение пространст I
{9В X Щ, а {51 X й}}. Действительно, если множество С
из а{21х»} имеет вид С=АХВ, Л е= 21, Ве8, то
события {(^, т))еС} = {5е^}П{116В}е (2, поэтому
©-измеримым является любое событие из минимальной
0-алгебры, содержащей события вида {(%, т]) <= Л X В}9
т. е. произвольные события вида {(^, т|)бС},Сба {21x93}.
Допустим, что пара (^, г|) имеет плотность
распределения р(л:, у) по мере т X д. Тогда для любых ЛеЯ,
Вей
Р К е= Л, т| е= В} = | | р (х, у) т (</х) ц (йу).
А В
Функцию р(х, у) называют совместной плотностью
распределения случайных элементов ^ и т). Из того, ч о
существует совместная плотность распределения,
вытекает, что каждый из случайных элементов ^ и ц
обладает плотностью по соответствующей мере.
Действительно,
Р(?ееЛ)= | [ р(лг, у)т{йх)ц{(1у)= | р^(х)т(йх\
А У А
где
Рс(*) = / р(*, У)Ц{Лу).
У
Аналогично
Р(т]ЕеВ)= $ ^(у)я{Лу),
в
58 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ.-1
где
Рц(#)= | Р(*> У)т(йх).
х
Покажем теперь, как можно вычислять условное
математическое ожидание М{/(т])|^}, если (2;, тО
обладает плотностью распределения р (л:, у). Исходя из
определения условного математического ожидания,
получим
1(А) е"1(Л)
~ 1 \1(у)ъа (*) р (х> у) т (ах) я Ш =
1(А)
где
Таким образом,
М{Ш1СН (т(у)Щ&-чШ-
Величина-2-^—-—== р(//|л:) называется условной
плотностью распределения случайного элементы ц при
гипотезе 1> = х. С ее помощью условное математическое
ожидание относительно % вычисляется по формуле
М0(л)Ю- \Пу)рШя№-
У
§ 4. Случайные функции и случайные отображения
Определения. Пусть {О, @, Р} —заданное
вероятностное пространство. Если реализации некоторого
эксперимента описываются с помощью функции 1{х)
определенного аргумента х, х& Х> то говорят, что на {О, ©, Р}
задана случайная функция. Таким образом, случайная
§ 4] СЛУЧАЙНЫЕ ФУНКЦИИ И СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 59^
функция есть отображение: со -> / (х) = / {ху со), соей.
Дополнительно требуется, чтобы при фиксированном х,
}(х, со) было случайной величиной (или случайным
элементом).
Общее определение таково. Пусть X — некоторое
множество, {^/, 23} — измеримое пространство.
Определение 1. Случайным отображением %(х)
множества X в измеримое пространство {Щ, Щ
называется отображение X X й в Щ, являющееся при
произвольном фиксированном х измеримым отображением
{й, ©} в {^, 23}, т. е. такое, что для любого В е 93
{со: $(х)е=В}еЕ<5.
Вместо «случайное отображение» в дальнейшем будет
употребляться также термин «случайная функция со
значениями в Щ»\ при этом х называют аргументОхМ
случайной функции. В том случае, когда X — вещественная
прямая или отрезок прямой, а аргумент случайной
функции интерпретируется как время, вместо X и х будем
писать Ги/и называть случайную функцию случайным
процессом. Если аргумент случайной функции принимает
целые неотрицательные значения (X = Т+ = {0, 1, 2, ...
..., п, . . .}) или произвольные целые значения (X = Г =
= {..., — л, — п+ 1, ..., —1,0, 1, 2, ..., л, ...}),
случайную функцию называют случайным процессом с
дискретным временем. Если X — конечномерное евклидово
пространство Ж*\ или область в 5?т, то %(х) иногда
называют случайным полем.
Представляет интерес следующий частный случай
общего определения. Предположим, что й является
функциональным проетранством, со = со (л:), хе1, а-алгебра ©
содержит все множества пространства Й вида
{со: со(л;0)е=Б},
каково бы ни было х0^Х и В е 23, Р — произвольная
вероятностная мера на ©. Естественно сопоставить
с таким вероятностным пространством случайную
функцию §(х, со) = со (х). В некоторых задачах удобно
отождествлять случайную функцию § (л;, со) = со {х) с
вероятностным пространством {й, ©, Р} описанного типа.
Легко заметить, что общее определение случайной
функции можно свести к только что описанному частному
60 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Т
случаю. Действительно, если случайная функция 2(*)д
задана как функция двух переменных, 2; (х) = §(х, со), то^
положив и=\§(х, со), где со фиксировано, соей, и
обозначив через V множество всех функций {и: и-и(Л(х) =
1=8 # (*><*>)» сое О}, получим некоторое отображение 5
множества О на (У. При этом а-алгебра © множеств (1
отображается в некоторую сг-алгебру ©' множеств (У,
а вероятностная мера Р на 6 отображается в
вероятностную меру Р' на ©'. Для любого фиксированного х
множество^: и(х) ^ В}, В ^ 23, принадлежит 6', так как
5"1 {и: и {х) е В} =* {со: § (х, со) е В} е 6.
Таким образом, получено вероятностное пространство
{(У, ©', Р'}, где (/ — некоторое множество функций
и = и(х)у причем для любых п, хи х2, - -., хп (хк е X,
й= 1, ..., я) распределение последовательности
случайных элементов на {й, 6, Р}
#(*ь ©), ё(х2, <*>), •••> г(^я» ©)
совпадает с распределением последовательности
" (х\1 и (х2)9 ..., и (хп).
Следовательно, случайная функция в определенном
смысле эквивалентна некоторому функциональному
пространству с вероятностной мерой, т. е. вероятностному
пространству, в котором пространством элементарных
событий служит некоторое множество функций.
Пусть ?;(л:), хе X, —случайная функция со
значениями в {Щ, 23}, п — любое целое число, хк(к= 1, 2, ..., п) —
произвольные точки в X. Рассмотрим случайный элемент
в {<уп, 23"}, определяемый последовательностью
К(*1), Е(*2), .■■, ЕЫ- (1)
Ему соответствует мера Рх х ...х (В) на 93я:
Р*л...хя(В)-Р{*>: «(*,), ?(*2) С(х„))еВ}, Вб$л.
(2)
Меры (2) будем называть частными распределениями
случайной функций %{х). Семейство частных распреде-
§4] СЛУЧАЙНЫЕ ФУНКЦИИ II СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 61
лений случайной функции обладает двумя очевидными
свойствами:
!• рх1х9...хп+п(ВХ^т)^Рх1хш...хп(В)9 (3)
где В е= 93".
2. Пусть 8 — точечное преобразование в Хп,
действующее по правилу: 8 (хи х2> ..., хп) = (л:^, х^, ... , х1п), где
(/ь/2» •••» 1п) —некоторая перестановка индексов {1,2, ...,/г),
а 5 — соответствующее преобразование множеств в ^*.
Тогда
^(*1.*г....*я)(5В)«ЯхЛ...Яй(В) (4)
для любых В я п.
Свойства (3) и (4) называют условиями
согласованности семейства частных распределений.
Возвратимся к общему определению случайной
функции. Высказанные ранее соображения о практической
неразличимости эквивалентных случайных величин и для
случайных функций играет важную роль. Принято
считать, что с практической точки зрения эксперимент
позволяет различать только гипотезы, относящиеся
к частным распределениям случайной функции.
Таким образом, с помощью опытных данных нельзя
отличить две случайные функции, частные
распределения которых совпадают при любых п и хйе! В
соответствии с этим примем следующее
Определение 2. Две случайные функции 1>{х)
и %'{х), хе! со значениями в Щ, заданные,
возможно, на разных вероятностных пространствах {й, ©, Р}
и {О,', ©', Р'}, называются стохастически эквивалентными
в широком смысле, если для любого целого п ^ 1 и
любых хк е X, 6= 1, 2, ..., п их частные распределения
совпадают:
Р{<*>: (&(*,), Ь(х2), ..., 5(хд))бВ} =
^Р'{со':(П*1), .... ?{хя))&В).
В дальнейшем часто применяется понятие
стохастической эквивалентности случайных функций в более
узком смысле.
Определение 3. Две случайные функции д{{х, со),
ё2{х, со) (^е^, (о ей), заданные на одном и том же
62 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ {ГЛ. I
вероятностном пространстве {О, ©, Р}, называются стощ?
стически эквивалентными, если для любого х е X
Очевидно, что если #, (л:, со) и §2 (*> ю) стохастически
эквивалентны, то они стохастически эквивалентны в
широком смысле.
Как же задаются случайные функции в конкретных
задачах? Во-первых, случайную функцию можно
задавать, исходя из общего определения, явно указывая
вероятностное пространство (О, ©, Р},.стараясь выбрать
его и функцию $ (л;) = § (х, со) как можно более
простыми. Другой метод состоит в задании меры на
некотором функциональном пространстве (7, элементы
которого и = и(х) являются функциями на X, и рассмотрении
функции &{и) — и(х) на 0. Этот способ задания и
изучения случайной функции рассматривается в главе V.
Трудность его применения обуслозлена сложностью
конкретного описания меры в функциональном пространстве.
Эту трудность иногда можно облегчить, рассматривая
данную случайную функцию $(«)= и(х) как результат
некоторого преобразования 5, определенного в более или
менее простом функциональном пространстве Т со
сравнительно простой мерой \х: и(х) = 5 [у], уеУ, {Ту ©, |и} —
некоторое пространство с мерой.
Такой подход рассматривается в гл. IV и VIII,
посвященных соответственно линейным и нелинейным
преобразованиям случайных функций.
Третий, пожалуй наиболее распространенный, метод
задания случайной функции основан на описании
семейства ее частных распределений. Это связано с тем, что,
во-первых, во многих практических задачах случайные
функции характеризуются своими частными
распределениями, а соответствующее вероятностное пространство
при этом вообще не задается. Во-вторых, задавать
частные распределения во многих случаях бывает проще,
чем соответствующие вероятностные пространства и
функции §(ху со). Далее, оказывается, что для решения
многих важных вопросов достаточно знать только частные
распределения случайной функции. С другой стороны, как
вскоре будет доказано, при весьма широких предполо-
§ 4] СЛУЧАЙНЫЕ ФУНКЦИИ И СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 63
жениях для произвольного семейства распределений
Рх{х2...хп{В), определенных для любых целых п, и хк^Х,
заданных на {Щп, 23"}, можно построить
вероятностное пространство (О, ©, Р} и случайную функцию
5(*) = §•(*, ео), частные распределения которой совпадают
с заданным семейством.
Определение 4. Согласованный набор
распределений {РХхХ2...Хп(В\п=\$ 2, ...,**€=*, Впе=%п}у где
93 — а-алгебра множеств пространства Щ, Ъп — ее д-я
степень, называется случайной функцией в широком смысле
со значениями в Щ.
Для случайной функции в широком смысле будем
применять обычные обозначения |(лг), ц(х), ...,
называть х — ее аргументом, а распределение
последовательности {1(х{), ..., 1(хп)} отождествлять с РХ{Х2... хп(Вп).
Из сказанного ранее вытекает, что каждую случайную
функцию в широком смысле {Щ — полное сепарабельное
метрическое пространство, X — произвольно) можно
рассматривать и как случайную функцию в смысле
основного определения 1 (см. теорему 2 этого параграфа).
С другой стороны, случайную функцию в широком
смысле можно отождествить с классом всех
стохастически эквивалентных (в широком смысле) случайных
функций, имеющих заданные частные распределения.
Построение случайной функции по ее частным
распределениям. В соответствии с определением
стохастически эквивалентных в широком смысле случайных
функций наиболее характерными для случайной
функции является не вероятностное пространство и вид
функции §(х, со)==^(х), а семейство ее частных
распределений. Это означает, что мы можем менять
вероятностное пространство и вид функции §(х, со), лишь бы
при этом семейство конечномерных распределений
оставалось неизменным. Это весьма важное обстоятельство
широко используется для получения возможно более
простого и удобного для исследования представления
случайной функции. В связи с этим прежде всего
возникает следующий вопрос: пусть дано некоторое семей-
ство распределений
[Р*Л...хп{В); д-1, 2, ..., хк*=Х, Ве=93«}, (5)
64 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
где X — произвольное множество, {^/, 93} — некоторое
измеримое пространство. Существует ли случайная
функция, для которой данное семейство распределений
является семейством ее частных распределений?
Очевидно, что семейство распределений (5) не может
быть совершенно произвольным. Оно должно, во всяком
случае, удовлетворять условиям согласованности (3)и(4).
Определение 5. Если существует вероятностное
пространство {О, ©, Р} и функция двух переменных
§(х, со) со значениями в Щ, определенная на X X О,
©-измеримая при каждом фиксированном ^е!и такая,
что частные распределения случайной функции §(х, <&)
совпадают с заданным семейством (5), т. е. для каждого
В{п) е= 93*
Р{со: (§{хи со), Я(*2э со), ..., е(*п> ©)) €= В{п)} =
-^...^(5(п)), (6)
то вероятностное пространство {О, @, Р} и функция
§(ху со) называются представлением семейства
распределений (5).
Будет доказано, что при достаточно широких
предположениях согласованное семейство распределений (5)
допускает некоторое представление. Роль пространства й
при этом играет пространство всех функций, заданных
на X со значениями в Щ, элементарными событиями
являются функции от х, со = со(лг), и §(х, со) = со(л;).
Определение 6. Пусть й — пространство всех
функций со = со (л:), заданных на множестве X со
значениями в некотором измеримом пространстве {<У 9 93} и
В{п)^Ъп, Множество функций со (л;) ей, для которых
точка {®(х{)9 ..., со(.*:„)} из Щп принадлежит В{п\ т. е.
множество
^...^(5^) = ^: (©(*,), со(*2), ..., иУбВ^)}
называется цилиндрическим множеством в О, с основа-
нием В над координатами хи х2, ... , хп или, короче,
цилиндрическим множеством.
Сделаем несколько замечаний по поводу
цилиндрических множеств и действий над ними. Если п и точки
хь х2, ..., хп фиксированы, то между цилиндрическими
§ 4] СЛУЧАЙНЫЕ ФУНКЦИИ И СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 65
множествами над координатами хи х2> ■••> хп и
множествами из 33" существует изоморфизм: каждое
множество В(/г)е23" определяет цилиндрическое множество
Схх... хп(В{п)), для которого оно служит основанием;
разным основаниям соответствуют разные
цилиндрические множества; сумме, разности или пересечению
оснований соответствует сумма, разность или пересечение
цилиндрических множеств. Это непосредственно
вытекает из определения цилиндрического множества.
Рассматривая действия над цилиндрическими
множествами в общем случае, нужно иметь в виду, что
одно и то же цилиндрическое множество может
задаваться над разными наборами координат. Так, очевидно,
что
сХ1... ^(в<«>) _ сХ1 ... ,„,„,,... Хп+т(вм х у«).
Легко видеть, что любые два цилиндрических
множества С = С'Х1...Хп(ВМ) и С' = С , х, (ВМ) всегда
1 /л
можно рассматривать как цилиндрические множества
над одной и той же последовательностью координат
х", ..., х'р, содержащей как х{, х2, . .. , хп, так и
х'и *2, •••> х'т» Отсюда следует, что, рассматривая
алгебраические действия над конечным числом
цилиндрических множеств, можно считать, ято они заданы
над фиксированной последовательностью координат.
Поэтому справедлива
Теорема 1. Класс © всех цилиндрических множеств
образует алгебру множеств.
К этому следует добавить, что если X содержит
бесконечно много точек, а Щ — по крайней мере две
точки, то 6 не является 0-алгеброй. Действительно,
множество
оо
гДе {Ук)> й = 1, 2, ...,*- последовательность точек Щ,
не есть цилиндрическое множество.
Докажем теперь следующую теорему.
Теорема2 (теорема Колмогорова). Пусть
°У — полное метрическое сепарабельное пространство.
3 И. И. Гихман, А. В. Скороход
66 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. I
Семейство распределений (5), удовлетворяющее условиям
согласованности (3) и (4), допускает некоторое
представление.
Прежде всего определим на алгебре цилиндрических
множеств й пространства Й функцию множеств Р'(С),
Себ, положив
Р'(С) = />,,...,„ (В""),
если С является цилиндрическим множеством с
основанием В{п) над координатами хи хъ ..., хп. Условия
согласованности обеспечивают однозначность
определения функции Р'{С). Пусть Сь 6=1, 2, ..., п —
последовательность цилиндрических множеств. Не
уменьшая общности, можно считать, что они заданы
основаниями ВТ над одной и той же последовательностью
коэрдинат хь хъ ..., хр. Алгебраическим операциям
над множествами Ск соответствуют в точности те же
действия над основаниями В^\ Так как мера РХ{ ...Х[}(В{р))
счетно-аддитивна в <Щр, то отсюда следует, что
функция множеств Р'(С) конечно-аддитивна на К. Остается
теперь продолжить функцию Р'(С) с алгебры 6 до
меры Р на некоторой а-алгебре К. Для того чтобы это
можно было сделать, в силу известной теоремы о
продолжении мер достаточно проверить, что для любого
СеЦ и любого покрытия {СД 6=1, 2,..., /г,'...,
со
Сйе& множества С, С ст \^ Ск, выполняется нера-
венство
оо
Р'(сх2Р(д. (7)
к=\
Докажем, что если
оо
1)Ск = С (Сб6,Скб(Е, 6=1,2,...)
и СЙЛС,= 0, {кфг), то
оо
Р'(С)= %Р'(Ск). (8)
§ 4} СЛУЧАЙНЫЕ ФУНКЦИИ И СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 67
Отсюда будет следовать (7) для произвольного покрытия
цилиндрического множества С множествами из (I*
Положим
Множества Вп образуют монотонно убывающую
последовательность цилиндрических множеств с пустым
пересечением
оо со
Г\Оп=С\{)Ск=0. (9)
я = 1 /г=1
Из аддитивности Р' следует равенство Р'(С) =
п
*= ^ РЧС^ + Р'Фя). Для доказательства (8) достаточно
показать, что
Нт Р'(Д„) = 0.
Допустим противное, т. е.
Пт р/фя) = ^>0. (10)
Обозначим через Вп основание цилиндрического
множества Бп, и пусть Ип расположено над координатами
хь х2, ..., х,Пп. При этом предполагается, что при
увеличении п набор соответствующих точек хи х2у ..., хГП{1
не убывает. Это предположение, как было показано
ранее, не ограничивает общности.
Для каждого Вп найдется такое компактное
множество Кп, Кп <= Вп, что
. ^....^(^Х^Х-^, «=1,2,...
Пусть С}п — цилиндрическое множество над коорди-
п
натами хъ х2\ ..., хт с основанием Кп> бп^ПЯг
г-1
и Мп — основание множества Сп. Очевидно,
множество Мп есть компакт, так как оно является
пересечением замкнутых множеств, среди которых по крайней
мере одно, а именно Кпг компактно.
3*
68 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ [ГЛ. Г
Так как множества Сп монотонно убывают, то из
соотношения со(л:)е Оп+р (р>0) следует, что со(х)е вп.
Поэтому, если
[Уи У* --•> Уп, •• •> Утп+р) е Мп+Р, (р>0),
то
[Уи Уъ ...,Утп}*=Мп.
Множества Сп, очевидно, непустые. Более того, так как
Оп \ Оа = У ф„ \ Я,) С (] (Яг\<?г),
ТО
р/Ф»\ов)<2р/Фг\Сг)-2я*1...*т (ялдг)<-§,
откуда следует, что
Ит Р' (С„) = 11т Р' (Я„) - 11т Р' (Д, \ Сп) > -§" •
Из каждого множества Мп выберем какую-либо точку
к*. ••-<}•
В силу предыдущего при любом 6 последовательность
точек {у^}* #=1, 2,..., принадлежит компактному
множеству в ^, а последовательность
{У\П+ГК ..., &«+% г = О, 1, 2, ...
лежит в .М„. С помощью диагонального процесса найдем
последовательность индексов П] таких, что при каждом к
последовательность у{п}) сходится к некоторому
пределу у^\ Из замкнутости множества Мп следует, что
при любом п
{уМ,...,у<у<=Мп.
Определим функцию со (л:), положив © (х^ = у%\ к ==
= 1, 2, ..., #, ..., и доопределив ее в остальных
точках произвольным образом. Тогда при любом п
§ 4] СЛУЧАЙНЫЕ ФУНКЦИИ И СЛУЧАЙНЫЕ ОТОБРАЖЕНИЯ 69
имеем со(х)е 0паОп. Следовательно, ^\ йп не пусто,
что противоречит (9). Таким образом, неравенство (10)
невозможно и
НтР'фяИО.
П->оо
Значит, функция Р' удовлетворяет неравенству
(7) и допускает продолжение до полной меры
(К, Р), К =э 6. Определим функцию §{х, со), со ей, х е^
равенством §(х, со) = со(х). Для произвольного борелев-
ского множества В{п в Щп и любых пу хи ..., хп имеем
Р{(2(*1, со), §{х2, со), ..., д{хП9 й))ей("') =
ЯР(((»(4 <*(х2), ..., ®{ха))&В№} = РХ1ашшХп(ВЫ)я
Таким образом, для семейства распределений (5)
построено указанное в теореме представление. Теорема
доказана.
ГЛАВА II
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
§ 1. Предварительные замечания
Последовательности случайных величин |ь ^2» •••
..., |я, ... можно рассматривать как случайный
процесс с дискретным временем. Для общей теории
случайные последовательности играют важную роль.
Во-первых, имеется много теоретико-вероятностных
задач, в которых время по существу входит дискретно.
Во-вторых, изучение процессов с дискретным
временем в некоторых отношениях требует более простых
средств и вместе с тем в ряде случаев такими
процессами можно аппроксимировать или с их помощью
можно изучать произвольные процессы с непрерывным
временем.
Основные вопросы, рассматриваемые в настоящей
главе, связаны с изучением асимптотического поведения
случайной последовательности при неограниченном
возрастании времени. Это вопросы о существовании
предела последовательности, о сходимости рядов со
случайными членами, о поведении среднего арифметического,
об асимптотическом характере распределения членов
расходящейся последовательности и т. п. Весь этот цикл
вопросов тесно связывает классические разделы теории
вероятностей (закон больших чисел, предельные теоремы
для сумм случайных слагаемых) с общей теорией
случайных процессов.
Разумеется, для того чтобы получать существенные
результаты, отличающиеся от общих критериев
сходимости, нужно наложить на рассматриваемые
случайные последовательности специфические
теоретико-вероятностные ограничения. В соответствии с этим вводятся и
§П
ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
71
изучаются некоторые важные классы случайных
последовательностей, для которых получены нетривиальные
результаты по интересующим нас вопросам.
Пусть {О, ®, Р} —фиксированное вероятностное
пространство, [36, Щ — некоторое измеримое пространство.
В настоящей главе Т обозначает, если не оговорено
противное, либо последовательность целых
неотрицательных чисел Г+ = {0, 1, 2, ..., /г, ...}, либо
упорядоченное множество всех целых чисел Г = {..., ■—/*,...
..., -1, .. ., О, 1, .. ., п, ...}.
Функция {с, ( .) = I (/) = | (*, со), I е 7\ о е 0} со
значениями в 36 называется случайной последовательностью
или случайным процессом с дискретным временем, если
для любого Вей и /еГ {со: ^(/,©)бВ}Е ©.
Иногда значения |(/) мы будем называть
положениями или состояниями некоторой стохастической
системы 2, а.пространство 36 — фазовым пространством
системы 2.
В том случае, когда $? —метрическое пространство,
23 постоянно обозначает а-алгебру боролевских
множеств 36,
Пусть {35\ ЗЗ6} —5-я степень измеримого
пространства {36, Щ. Для любого набора целых чисел пь п2, ..., гг,
О <! щ < п2 < ... < п3 < оо, случайная
последовательность {!(/), /еГ) определяет в {363,Ъ3} вероятностную
меру РП1п2...п3(-):
/),Л...«5(В(5)) = Р(Шя1Ц(4 ...91{п8))^В{%
где В{8) — некоторое множество из 235. Эти меры
называют частными распределениями случайной
последовательности.
В определенном смысле конечномерные
распределения полностью определяют случайную
последовательность. Точный смысл этого предложения состоит в
следующем.
Рассмотрим пространство 36т всевозможных
последовательностей х = {хи I е Г}. Через К0 обозначим алгебру
цилиндрических множеств С пространства 36т\
&о=1с = СМ2...,8(В(5)); /*еГ, В,5)е=«5}, 5=1,2, ...
С^...,а(В(в,Ы*: (*, *,„, .... х^евВ^].
72 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Отображение (о->х, определяемое случайной
последовательностью &(<), 1^Т): х={хи /е=Г} = {|(^, ю), /еГ},
индуцирует преобразование вероятностной меры Р в
вероятностную меру Р', заданную на некоторой ст-алгеб-
ре (&' пространства #?г, содержащей все цилиндрические
множества.
На цилиндрических множествах мера Р' совпадает
с частными распределениями случайной
последовательности:
и, следовательно, конечномерные распределения
однозначно определяют меру Р' на минимальной а-алебре
6(6с &'), содержащей алгебру цилиндрических
множеств.
Для решения задач, возникающих в теории
случайных последовательностей, бывает достаточным знать
вероятности событий из й. Поэтому нет оснований
по существу различать случайные последовательности
(!/(/), ^П) /=1,2, с одним и тем же фазовым
пространством {«8/, 33}, но заданные на различных
вероятностных пространствах {13/, ©*, Р,}, если индуцируемые
этими последовательностями вероятности Р; совпадают
на цилиндрических множествах пространства <%т. В
соответствии с этим условимся называть естественным
представлением случайной последовательности {!(*); 1^Т}
случайную последовательность {^(/); /еГ},
стохастически эквивалентную {!(/); / е Г}, определенную на
[Ш\ 6, Р'} и такую, что !(/) = &(*, *)-**.
Целесообразность выделения 'естественных
представлений случайной последовательности связана с тем,
что во многих задачах тем или иным способом задаются
частные распределения. С другой стороны, если задано
произвольное семейство частных распределений, дв —
полное и сепарабельное метрическое пространство,
то всегда можно построить случайную
последовательность в ее естественном представлении, частные
распределения которой совпадают с заданными. Это
непосредственное следствие теоремы Колмогорова (гл. I, § 4,
теорема 2).
$21
ПОЛУМАРТИНГАЛЫ И МАРТИНГАЛЫ
73
§ 2. Полумартингалы и мартингалы
Определения и простейшие свойства. Важный класс
случайных последовательностей, имеющий
многочисленные применения, образуют мартингалы и
полумартингалы.
Чтобы избежать в дальнейшем повторений, приведем
определения, относящиеся не только к
последовательностям.
Пусть Г— произвольное упорядоченное множество
и {§,, /еГ}- поток а-алгебр, 8* <= ©.
Введем следующие обозначения:
а+ = тах(а, 0), а~ = тах( — а, 0).
Определение 1. Семейство Ц(0, §*; Ь^Т), в
котором случайные величины I (I) при каждом /еГ §гизме~
римы, называется мартингалом, если
М|6(01<оо, (1)
ма(018Л«кд *<*> мег. (2)
Оно называется субмартингалом, если
М^+ (0 < оо, М {| (0 | ЗЛ > I ($) * < *, 5, * €= Г, (3)
и супермартингалом, если
МГ(0<°°. М{|(018Л<6М, в<*. $,*е=7\ (4)
Супер- и субмартингалы называют также полу
мартингалами.
В некоторых случаях, когда семейство а-алгебр
{§;, {^Т} фиксировано и не может возникнуть
недоразумений, соответствующим термином будем называть
само семейство случайных величин {% (*), I е Г}.
Из определения следует, что §/ всегда содержит
су-алгебру, порожденную случайными величинами {&($),
з^*}. Иногда ее принимают в качестве ^ в
определении мартингала (полумартингала).
Приведем ряд свойств мартингалов и
субмартингалов. Так как при замене \{1) на —\{1) субмартингал
переходит в супермартингал, то свойства
субмартингалов легко переформулировать для супермартингалов.
74 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
а) Соотношения (2) и (3) эквивалентны соответственно
следующим ($ < /; $,1 е Г):
11(5) Р (</©)« /Б (О Р (<*«), (5)
/Е(*)Р(*о)<[б(0Р(Ло), (6)
где Б5 — произвольное ^3-измеримое множество.
Действительно, (5) и (6) получаются, если
проинтегрировать соотношения (2) и (3). Нетрудно заметить
и обратное: из (5) и (6) вытекают соответственно (2) и (3).
б) Если {&(/), ^е Т}— суб мартингал, то М$(1) —
монотонно неубывающая функция 1\ если {^(/), ^^ Т}
—мартингал, то М^ (0 = сопз!.
в) Если {1(1), §ь 1^Т} —субмартингал, / (х) —
непрерывная и монотонно неубывающая выпуклая на
действительной оси функция и М/(|(0)<°° при /еГ, то
{/(%(0)> &, ^<= П также субмартингал.
Это утверждение следует из определения
субмартингала и неравенства Иенсена. Действительно,
М {/ (I (0) I &} >ПМ{1 (О I &}) >! (I (*)). (7)
В частности,
г) Если {I(1), Зь /еГ}- субмартингал, то {(| (1) — а)+>
5Ь / е Т} также субмартингал.
д) Если {%(!), %ь 1^Т} —мартингал, а Цх)
—непрерывная выпуклая функция и М 1/(^(0) I < °°, то {/(6(0),
§/? ^еГ}- субмартингал.
Для доказательства достаточно заметить, что цепочка
неравенств (7) в рассматриваемом случае сохраняется
с тем отличием, что второй знак ^ должен быть
заменен знаком равенства и монотонность функции /(ж)
при этом не используется.
Из б) и д) следует
е) Если \(1) — мартингал, то М \1(1)\ —монотонно не
убывает на Т.
Лемма Х.ЕслиТ имеет максимальный элемент /тах,
{&(0> §ь /еГ}-субмартингал, то семейство случайных
величин (|+ (/), /ег) равномерно интегрируемо.
§21
ПОЛУМАРТИНГАЛЫ И МАРТИНГАЛЫ
75
Доказательство. Из неравенств
#Р(^(0>Аг)</ШР№о)<
< / 6 (*ш«) Р (Ао) < / I"' (/шах) Р (А»),
где Вг = {со: | (/) > ./V}, следует, что Р {Вг) -> 0 при N-> оо
равномерно относительно *. Поэтому при любом е > О
найдется такое М0, не зависящее от I, что
0</&'+(*тах)Р(Ж0)<в
В1
при Ы>Ы0. В силу неравенств предыдущей цепочки
мх(б(о>лоио<в
для всех N > #0, а это означает равномерную
интегрируемость семейства {^+(0> *^Г}.
Некоторые неравенства. В настоящем пункте
предполагается, что Г = {0, 1, 2, ..., /г}, {3&; ^^ Г}
—монотонно неубывающая последовательность сг-алгебр,
§ле ©, |й (/г е Г) — ©^-измеримая случайная величина,
М^<оо. Пусть %1(1= 1, 2)— случайное время на {5Ь /е^Г}
(тг принимают значения из Т) ит!<т2с вероятностью 1.
Положим
причем, если т^ = 0, то и % = 0.
Пусть §* обозначает сг-алгебру событий,
индуцированную случайным временем %ь. Напомним (гл. I, § 1),
что §^ состоит из тех множеств ^е6, для которых
ДП{т,<*}е=&, к = 0, 1, .... п. (8)
Лемма 2. Пусть
МЙ*|&-.,}>0, /г=1, 2 я, (9)
и Ле§;. Гогда
/^Р^оХ/гьР^со). (10)
А А
76
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
1гл. п
Если же
ТО
\чхР(й<й) = \т{2Р{йш). (11)
А А
Доказательство. Заметим прежде всего, что
$*с=§* (гл. I, § 1). Для доказательства неравенства (10)
достаточно ограничиться тем случаем, когда х{ постоянно
п
на А, ибо в общем случае Л=(^Л/, где Л/ = ЛП
/-0
Л{т1=/}е8|.- Пусть т, ==/ на Л. Тогда Ле§/ и т2>/
на Л. Имеем
/г12Р(^со)=/т11Р(й?со)+ | . 2 Б*Р(Л>Н
Л , Л АП{Ъ>П Й-/+1
Л Л\{т2</}
+ / ^/+2Р(^)+ ... + " / ЕпР(^ф)-
Л \ {%2 < /+ 1} Л \ {Т2 < л- 1}
Так как А \ {т2 < к) е 8* (А > /), то
| Б*+1Р(Ло)- / МЙй+| 18*) Р (</©)> 0,
Л\{т2</г) Л\{т2<#
откуда следует (10).
Приведенные рассуждения показывают также, что
если неравенство (9) заменено равенством (11), то имеет
место соотношение (12).
Лемму 2 можно сформулировать еще так: если
К*» 8а, ^Г}-субмартингал, т/ — случайное время на
{8л» & е Г} и Т! ^т2, то для любого А е §|
/^Р(^(о)</иР(^со), Ле?;. (12)
л
Следствие 1. Если т,, т2, ..., %в
—последовательность случайных времен на {8ь А = 0, 1, ..., я} и Т1 ^
<т2< ... <т5, то [г\к, §*, А= 1, ..., 5), лл = Ц» об^а~
$21
ПОЛУМЛРТИНГАЛЫ И МАРТИНГАЛЫ
77
зует субмартингал. Если же {^, §ь к е Т) — мартингал,
го {г^, §&> й=1, 2, ..., 5} является мартингалом.
Таким образом, мартингалы {полумартингалы),
наблюдаемые в случайные моменты времени, также
являются мартингалами {полумартингалами).
Следствие 2. Если в условиях леммы 2 условие (9)
отбросить, заменив его предположением М^ь < оо, где
*л = М{5л|§лм}, го
^ п \
1К - 2 ♦; р №) < / тьр (*»). (13)
Л V А=1 / А
Действительно, (13) следует из (10), если заменить \к
на |л-ф*.
Лемма 3. Предположим, что случайные величины
1к}$ь~измеримы, М^<оо, {%к9 &еГ}- поток о-алгебр,
С>0. Положим
и
Со «О, С* ~2*#. Л- 1, 2, ..., л.
Тогда
Р{тах^>С}<-1-М(С + Р.), (14)
где рд=2'ФГ. ^слы, кроме того, при некотором р>\
м(С+ря)р<°°.
го
м 1йа<хЯ'< (т^тГ м &»+р-)" • (15)
Доказательство. Пусть ^ — наименьший
индекс /г, при котором 5й^С (6= 1, 2, ..., п), и т1 = «,
если такой индекс не существует, т2 = л и Л —событие
{г)>С}, где т]== тах 5*.
Тогда Т! и т2- случайные времена на %к, А —
^-измеримо, Т!^Т2. Используя (13), получим
ср (Л) < | иР у©) < {(ь,+Рл) р (с/со) < м (с+ + рл),
А А
78 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. 1Г
что и доказывает неравенство (14). Далее, если %(С)
обозначает индикатор события А, то
оо
г\р=р\%(С)Св-1ас.
О
Как только что было показано,
МСх(С)<Мх(С)(^-ЬР/г),
поэтому
оо
Мг," < Рм | (5+ + Р„) % (С) с'-*ас=-^ м (с + Рп) цр~\
О
Воспользовавшись неравенством Гельдера, получим
откуда следует (15).
Следствие. Если {%к, к~\, ..., п} —
субмартингал, то
Р{тахС+>С}<^М^, (16)
1 ^ «^ п
если, сверх того, М(^)р< °° при некотором р>1, то
м^йЯр<(^гГм^+)р- (17)
Если к тому же {г\к, к^Т}~ мартингал, то
Р{тах|^|>С}<^М|?„|р. (18)
Назовем числом пересечений \\а, Ъ) полуинтервала
[а, Ъ) сверху вниз семейством случайных величин {^-(0,
/еГ} (Г —упорядоченное множество), точную верхнюю
границу чисел 5 таких, что существует
последовательность {/ь /=1, 2, ..., 25}, ^^<^^+и *1^Т, для которой
Ш>Ь, Ш<а, Ш>Ь, ..., 1(128)<а.
Оценим математическое ожидание числа
пересечений сверху вниз полуинтервала [а, Ь)
последовательностью {^, & = 1, 2, ..., п}у определенной в лемме 3.
§2]
ПОЛУМАРТИНГАЛЫ И МАРТИНГАЛЫ
79
Введем последовательность случайных
целочисленных величин /ь /2, ..., ]\, ..., которые, возможно, не
всегда существуют. Пусть Ак обозначает событие:
число \к существует. При этом ]х есть наименьшее
целое, такое, что ^^6, /г<! я, /2--наименьшее целое
число, большее /, и такое, что /2^гс, ?/, < о, и т. д.,
кт-\ ~~ наименьшее целое число, большее /2т-2> такое,
что ']2т-\^п и ^/9т_1^Ь, /2т —наименьшее целое число,
большее /2т-.ь такое, что Б/2т<я» ЬпО-
Числа /!, /2, ..., /ь ... образуют монотонно
неубывающую* последовательность случайных времен, /&<>*.
Доопределим ]к на все Й, положив ]к = п, если <о\ЛЛл.
Из определения /й и неравенства (13) имеем
°< I &„>->-*)?№)< 1 (С/1/я-*)Р(^) +
^2/72-1 А21П—\
*>' Вт,к
г>1 В
т, &
где Вт, к = А2т-1(]Ц2т- 1'2т-1> к), откуда вытекает, что
(Ь - а) Р (Аш) <
< | «„ - 6) Р (<*со) + 2 / ^т_1 + *Р ^ю) <
Л2ш-ЛЛ2/и к>1 Вт,к
< I (сл-*)+р(^)+2 / %т^т.
Суммируя эти неравенства по всем га>1, получим
(Ь-а)%Р(А,т)<М[&п-Ь)+ + 9п1 рл=2ф;.
Заметим, что V [а, Ь)= 2х(Л2т)> гДе хИ) обозначает
индикатор события Л. Поэтому
Ш[а, Ь) = 2Р(Л2т).
Таким образом доказана
80 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Лемма 4. Если последовательность {1к, %к; к = 1,
2, ..., п} удовлетворяет условиям леммы 3, то
Мч[а, 6)<1!(к^М, (19)
Для субмартингалов последнее неравенство принимает
вид
Му[а, 6)<М(^_""/)+ . (20)
Полученные неравенства легко обобщаются на тот
случай, когда Г —счетная последовательность. Так, если
Г = {1, 2, ..., п, ...}, а Г = {..., -я, -я+1, ..., -1},
неравенство (14) дает
Р{зир^>С}<^зирМ(^ + рл) (21)
лег С пеГ ч л "у
И
Р{зирС„>С)<-1м(С11 + р/), (22)
оо
где р' = 23*|Гл-
Доказательство этих соотношений вытекает из
того, что 5ир^ = Нт тах 1к, и поэтому
Р (зир 1п > С) = Нт Р { тах ^ > С}.
Аналогично, если V00[а, 6) и ^[а, й) обозначают
соответственно число пересечений сверху вниз
полуинтервала [а, й) последовательностями {г;яэ «еГ}и {^л, /ге=Г/},
а ^[а, й) и Уп[а, Ь) — урезанными последовательностями
{?ь к = 1, ••-, ^} и {^_ь к=1, ..., /г} соответственно,
то из того, что Vл[а, 6), VЦа, Ь) образуют монотонно
неубывающие последовательности, гто [а, Ь) = Пт Vл [а, й),
г^о[а, й) = Пп^Да, Ь), и из е) следуют неравенства
(й - а) Мч„ [а, 6) < зир М [(^ - Й)+ + р„], (23)
(Й - а) МV/оо[а, 6) < М[Й-! - й)+ + р']. (24)
В случае субмартингала те же рассуждения
применимы к тому случаю, когда Г—произвольное счетное
множество действительных чис!ел. Следует ввести моно-
§2]
ПОЛУМЛРТПНГАЛЫ И МАРТИНГАЛЫ
81
тонко возрастающую последовательность множеств Гл,
состоящих из конечного числа точек, применить к
последовательностям {2(0> 8ь 1^Тп} полученные
неравенства и перейти к пределу при п->оо.
Тогда мы получаем, что
Р {зир ^ (0 > С} < -^ , (25)
М [вир ^ (1)У < (-/у)" зир М К+ (*)]", (26)
5ирМ(Н0-6)+
МV[а, Ь)^*^т ь_а . (27)
При этом, если множество Т обладает максимальным
элементом ^тах, то точные верхние границы в правой
части неравенств достигаются при * = /тах-
Существование предела. Рассмотрим
последовательность {^, Ъп\ пе=Т}9 где Т = {...,- п, - п +1, ..., -1,
О, 1, ..., п~ 1, п, ...}, ^ — монотонно неубывающее
семейство а-алгебр, %п ^-измеримы, и пусть М^<оо,
Теорема 1. а) Если
п
зир М (С„+ + рп) < оо, р„ = 2 ^-,
гг> I /г=1
го с вероятностью 1 существует конечный предел 2оо —
/г
= Нт^, б) вела зирМр«<оо, где р^^'ФГд,, го с ее-
роятностью 1 существует конечный предел ^-оо^ Пт С^.
/г->оо
Доказательство. Из неравенства Фату
М Нгп &+ < Шп М?+ < оо
/г->+оо «->+оо
вытекает, что соотношение Ит 1п = + °° может вы-
полняться только с вероятностью 0. С другой стороны,
из неравенства (23) следует, что
Ит 1^[а, 6)==М Нт \[а, &) = 0,
82 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
где V [а, Ь) — число пересечений сверху вниз
полуинтервала [а, Ь) последовательностью {^п; п^1}. Поэтому,
если ^ > — оо, то с вероятностью 1 существует такое
а = а(со), что %п>а для всех п^\. Таким образом,
почти наверное \\тЪ>п> — оо.
Предположим теперь, что с положительной
вероятностью не существует конечный предел Пт %п. Тогда
неравенство Пт %п< Пт ^п также имеет положитель-
Я -» + оо Я -> + оо
ную вероятность. Поэтому найдется пара чисел а и 6,
а<Ь, такая, что с положительной вероятностью будем
иметь
Ит $п<а<Ь< Пт 1п.
Но тогда с не меньшей вероятностью число
пересечений у[ау Ь) полуинтервала [а, Ъ) сверху вниз
последовательностью {%п, п^\} равно оо. Это противоречит
неравенству (23). Таким образом, с вероятностью 1
Ит 2я= Нт 2П.
Доказательство утверждения б) теоремы аналогично
предыдущему. "Заметим только, что, полагая в
формуле (24) &->+ оо, мы получим, что Пт V/[п;, Ь) = О
с вероятностью 1, где V/[а, Ь) число пересечений сверху
вниз последовательностью {1>пу п^—1} полуинтервала
[а, Ъ). Отсюда вытекает, что Пт^л<+ оо с
вероятностью 1. Остальные рассуждения, приведенные при
доказательстве утверждения а) теоремы 1, сохраняются
при очевидных изменениях, и роль $я теперь играет ^-1.
В применении к полумартингалам доказанная
теорема дает
Следствие. Если {1>к, §ь к = ... — /г, — п + 1, ...
..., — 1} — субмартингал, то предел Пт 5я = ?-оо суще-
П->-оо
ствует с вероятностью 1. Если {^, §&, /г=1, 2, ...
..., /г, ...} — субмартингал и зир М^+ < оо, то предел
Нт 2л = ?+0О также существует с вероятностью 1.
«-> + оо
Определение 2. Случайная величина |(|)
называется замыканием субмартингала {|(*), §/, /еГ} справа
§2]
ПОЛУМАРТИНГАЛЫ И МАРТИНГАЛЫ
83
(слева), если М|ь < оо (М|+<оо), | измерима
относительно ^ =а{5/, I ^ Т} (|_ измерима относительно
§= (")5*) и для всех /еГ
1(0<М{Ц&}, (|<М{&(/)|й>).
Теорема 2. Субмартингал {^п, *5„, /г=1, 2, ...}
имеет замыкание справа тогда и только тогда, когда
последовательность {^, /г=1, 2, ...} равномерно
интегрируема.
Доказательство. Если субмартингал {1пу §«,
п=1, 2, ...} имеет замыкание справа |, то, положив
Г = {1, 2,...., п, ...}1Доо}? 8оо = аШя, л=1, 2,...},
500 = ?» получим, что {Сь Зь 1<^Т} образует
полумартингал, и множество Т имеет максимальный элемент оо.
Поэтому (лемма 1) семейство {?„, /г=1, 2, ...}
равномерно интегрируемо. Допустим теперь, что семейство
\1п, д=1, 2, ...} равномерно интегрируемо. Так как
зирМ^Т<оо, то с вероятностью 1 существует предел
5 = Птг;л. Пусть |;У = тах{^,—.V}, Л;>0. При любом N
последовательность |$^, п=\, 2, ...] является
субмартингалом, так что
для любого ЛеЗ„, /л>0 в силу определения
субмартингала. Переходя в правой части неравенства к
пределу при т->оо и учитывая, что последовательность
{!„> л=1, 2, ...] равномерно интегрируема (так как
она является суммой двух последовательностей, из
которых одна ?д равномерно интегрируема по условию,
а вторая ограничена по абсолютной величине
константой N и, следовательно, также равномерно
интегрируема), получим
щ%%(А)<тч(А).
Переход к пределу при М->оо приводит к
неравенству
М&,хИ)<М&сИ),
84 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
причем М^+^Шт1 М^л ^°°, так что I является
замыканием мартингала.
Теорема 3. Пусть {^л, §л; п = 1, 2, ...} — мартингал.
Следующие условия эквивалентны:
а) семейство {?л, я=1, 2, ...} равномерно
интегрируемо)
б) мартингал {^л, ?сп, п=1, 2, ...} имеет замыкание
справа;
в) М|Ся-{п,|-*0 "Р" п\ п-»оо.
Яслг/ од/*о из этих условий выполнено, то Нт?л = 5
существует с вероятностью 1 и в смысле сходимости
в 3?х и является замыканием мартингала справа.
Если при некотором р>1, М\^п\р ^.С, то а), б), в)
имеют место и ^ = Нт^ в смысле сходимости в 3?р.
Доказательство. Эквивалентность а) и б)
вытекает из предыдущей теоремы. Эквивалентность
равномерной интегрируемости и сходимости в 5?х есть общий
результат теории меры. Если выполнено утверждение
второй части теоремы, то последовательность %п
равномерно интегрируема. В силу (^'последовательность \{,п\р
имеет интегрируемую мажоранту зир|^|р, и,
следовательно, последовательности \%п\р и | % — %п \р, где
С = Пт^л равномерно" интегрируемы, откуда вытекает,
что М|^п — ^\р->0 при п->оо.
Некоторые применения. Пусть ^с^с.с^с...
и *5 = сг{^л> Д = 1, 2, ...}, ^ — некоторая случайная
величина, М|^|<оо. Положим
Теорема 4. Последовательность {1п, %п, п = 1, 2, ..,}
является мартингалом и с вероятностью 1
Доказательство. Имеем (гл. I, § 3)
м &,+, I Ъп)=м{М{ц з„+1} I «л= м ш„}=и,
и при этом |„ ^„-измеримо, так что последовательность
Ип, Ъп> п=1, 2, ...} является мартингалом. Кроме того,
М {М {|| 8}| ад =М&| §„) = !„.
%2]
ПОЛУМАРТИНГАЛЫ И МАРТИНГАЛЫ
85
Последнее означает, что М{||$} является замыканием
этого мартингала. Утверждение теоремы теперь
вытекает из теоремы 3.
Следствие 1. Если Ле^, то 11т Р{А\%п} = %(А*
Я->оо
с вероятностью 1.
Пусть {<Й?, 23}—измеримое пространство.
Последовательность разбиений {Апк, 6=1, 2, ...}, я=1, 2, ...,
пространства <9? назовем исчерпывающей, если:
сю
а) ЛяЛе=93, Апк()Апг=0 при 6 ^ г, ЦЛпк = %,
л= 1, 2, ...; а-1
б) /г + 1-е разбиение является подразбиением /г-го,
т. е. при любом / Ап+цС2Апк при некотором 6 = 6(/);
в) минимальная сг-алгебра, содержащая все Лл&,
6=1,2,..., п = 1, 2, ..., совпадает с 33.
Следствие 2. Пусть {Апк, 6=1, 2, ..., я, ...},
п=1, 2, ..., — исчерпывающая последовательность раз-
биений {36, Щ и т — мера на 23, т ($/)=!. Обозначим
через Ап(х) то множество Апк, которое содержит точку х.
Тогда для любой ^-измеримой и ^-интегрируемой
функции !(х) т-почти для всех х
1{и)пг(с!и)
Нт п% , Л , ,,— = /(*).
„^оо т(Ап(х)) ' к '
Последнее утверждение можно рассматривать как
аналог основной теоремы интегрального исчисления для
абстрактного интеграла. Справедливость этого
утверждения вытекает из того, что если под Щп понимать
сгалгебру, порожденную конечным или счетным числом
множеств {Апк, 6=1, 2, ...}, то в{Ъп> я= 1, 2, .. .} = &
|/(и)т(Ж0
и М{/Ш- Апк т(Лпк) , если хе=Апк (гл. I, § 3). При
этом, правая часть последнего соотношения не
определена, если т(Апк) = 0. Но т-7 мера множества тех х,
для которых последнее обстоятельство имеет место
хотя бы для одного п, равна нулю.
Из подобных рассуждений можно получить в
некотором смысле «прямое» доказательство теоремы Радона
об абсолютной непрерывности мер.
86
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. П
Лемма 5. Пусть {96, 93} — измеримое пространство
и а-алгебра 93 порождается счетной последовательностью
множеств, 23 = 0(5!, В2, .. ♦, Вп, ...}. Тогда, в {96, 93}
существует исчерпывающая последовательность разбиений.
Доказательство. Пусть последовательность
{А{к, /г = 1, 2, ...} состоит из двух множеств В{
и В{. Если {Апк, к = \, 2, ...} уже построена, то
последовательность {Ап+1к, к = 1, 2, ...} определяется как
совокупность всех различных множеств вида Апк П Вп+{
и ЛяЛП5я+1 (*=1, 2, ...).
Теорема 5. Пусть {96, 93, т} — вероятностное
пространство, д (•) — же/ш яа {«^, й}, (7 (^) < °°> лера <7
абсолютно непрерывна относительно пг и {Апк, к = 1, 2,...},
п=1, 2, . .., — произвольная исчерпывающая
последовательность разбиений 96. Положим
а (у\- Я(Ап\(х))
Вп {Х) ~ т (Апк (х))
при т (Апк (х)) > О, еде Апк (х) есть то множество
последовательности {Апк, к = 1, 2, ...}, которое содержит
точку х. Если же пг (Апк (х)) = О, то положим §п (х) = 0.
Тогда:
а) последовательность {§п, §я, п= 1, 2, ...}, где 8« =
= а{Ля1, Ля2, ...}, образует мартингал)
б) существует предел §{х)= Нт §п (х) (той пг), не за-
/г->оо
висящий (шоАт) от выбора исчерпывающей
последовательности {Апк, к = 1, 2, ...}, п = 1, 2, ... ;
в) для произвольного 5^93
?(в)=/в(*)т(**). (28)
в
Доказательство. Функция §п(х) ^„-измерима и
принимает не более счетного множества значений.
Поэтому
М/ »ск 1 ... V Я(Ап+ц) гп{Ап+1][\А„ь{х)) _
М (5/1+1 \Ъп)-24т (Ап+1 у) т (Ля* (*))
У
Я(Ап+Ц') >П(АП+1Г) ЧАпк^Х)) а , х
,, т (Лл+1 ,,) т (Л„, (*» « (Л„, (х)) ~ *» ^
2
§3]
РЯДЫ
87
что и доказывает а). Далее,
\\8п(х)\т{(1х)= \ Вп(х)т{<1х) = Ч(%)«*>
и
\ Ип(х)т(с1х) = У^ | еЛх)т(йх) = ^ц(Апк[\А) = д{А).
А к ЛПЛпк к
Так как ц абсолютно непрерывна относительно меры ш,
то для любого е>0 найдется б>0 такое, что из
т(Л)<5 вытекает д{А)<г. Отсюда следует, что
последовательность §п(х) равномерно интегрируема
(относительно меры т). Поэтому т-почти для всех х существует
предел Нт §п (х) = § (х) и §{х) является замыканием
мартингала. Следовательно, для каждого Лде8й
( § (х) т {их) = Нт ( §к (х) т {их) = ц (Ап).
Так как класс множеств А, для которых формула (28)
верна, является монотонным и содержит алгебру ^]?*Л,
п
то формула (28) верна и для о{Ъп, я=1, 2, .. .}, т. е.
для любого Ве^. Наконец, независимость функции @{х)
от выбора исчерпывающей последовательности вытекает
из утверждения в).* Если существует две функции §' и §",
для которых в) имеет место, то Г [§'(х) — §"(х)]т{йх) = О
/5
для любого ВеЭЗ, что возможно только тогда, когда
8'{х)==ё"(х)(то&т).
§ 3. Ряды
Некоторые общие признаки сходимости рядов.
В настоящем параграфе рассматриваются условия
сходимости с вероятностью 1 рядов со случайными членами.
Пусть дан ряд
1! + |2+ ... +1п+ ... (1)
88 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Теорема 1. Если существует последовательность
чисел ел>0, л=1, 2, ..., такая, что
оо оо
2е„<оо, 2Р{1Ы>е„}<оо, (2)
Л=1 « = 1
то ряд (I) с вероятностью 1 сходится абсолютно.
Доказательство. Пусть Ап = {||я |>е„}. Из
сходимости второго ряда в (2) и теоремы 6 § 2 гл. I
следует, что Р(ПтЛ„)==0, т. е. с вероятностью 1 наступает
только конечное число событий Ап. Таким образом,
существует такое Л^ = Л^(со), что при я>Л^(со), ||п|<ел
и ряд (1) сходится.
Для случайных величин |п, обладающих конечными
моментами, можно сформулировать следующее
достаточное условие сходимости ряда (1).
Теорема 2. Если
оо
2м|е„|<оо, (3)
я = 1
то ряд (1) абсолютно сходится с вероятностью 1.
Доказательство вытекает из теоремы Лебега, в силу
которой
со оо оо оо*
11 11
и, следовательно, с вероятностью 1 сходится ряд
оо оо
1 1
Следствие. Если существует такая
последовательность сп > 0, я=1, 2, ..., и р > 1, что ряды
оо оо
л = 1 «=1
сходятся, то ряд (1) сходится с вероятностью 1 и в 3?р.
§31
РЯДЫ
89
Для доказательства заметим, что в силу неравенств
Гельдера и- Иенсена имеем
т+п т+п
2м|б4|=2^'МС|к|Е4|<
т +1 т + \
/т+п \ 1/<7 /т + п \{/Р
<(&''") (2,Ч(М|У)') <
/т + п Х1'^ /т + п \1&
откуда, принимая во внимание условия следствия,
вытекает сходимость ряда (3).
Более сильные результаты имеют место для
полумартингалов. Положим
С« = Е1+б2+ — +1п> Со = 0.
Теорема 3. Пусть Ь,п% „-измеримы, {§„, п = 0, 1,...} —
поток о-алгебр. Тогда:
а) Если М{|л | «$*-!} ^ О и зирМ^<оо, то ряд (1)
сходится с вероятностью 1;
б) Если М{^л|§„-_!} = 0 и при некотором р^\
$ирМ|гп|р<оо,
п
то ряд (1) сходится с вероятностью 1 и в 3?р.
Условие а) равносильно предположению, что {^п, %п,
/г=1, 2, ...} субмартингал. Соответствующее
утверждение является поэтому следствием теоремы о
сходимости субмартингала. Условие б) означает, что {$„, §„,
я=1, 2, ...} —мартингал и утверждение этой части
теоремы вытекает из теоремы 3 § 2.
Следствие 1. Если М{|Я|5П^.1} = 0 и
оо
2М|*<оо,
го ряд (1) сходится с вероятностью 1 и в 9?2*
90 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Доказательство вытекает из того, что при к ф п
м|*бя = ме»мй„| §„_,}}=о,
Щ = м (± ъУ - 2 мц + 2 2 2 Щ&, = 2 мц,
и=1 / к=1 / = 2 к<\ ' /г=1
и из утверждения б) теоремы.
Для рядов с независимыми членами последний
результат известен как теорема Колмогорова.
Следствие 2 (теорема Колмогорова). Если
{6я> п=\, 2, ...} — независимые случайные величины,
оо
М^ = 0 и ряд 2 0^<оо, то ряд (1) сходится с ее-
роятностью 1.
Это утверждение вытекает из следствия 1, если под
§п понимать а-алгебру, порожденную случайными
величинами !-,, |2> •••> ^л> и принять во внимание, что
в силу независимости случайных величин %п
мйй|5я.,} = Мёя = о.
Ряды независимых случайных величин. Остановимся
подробнее на сходимости рядов с независимыми
слагаемыми. Как известно из предыдущего, такие ряды
сходятся или с вероятностью 0 или с вероятностью 1
(теорема 8 § 2 гл. I).
В дальнейшем понадобится одна оценка для
распределения максимума сумм независимых слагаемых.
Теорема 4. Если {%к, й=1, 2, ..., п} независимы,
М^к = 0 и \1к\<с с вероятностью 1, где с — некоторая
постоянная, то
Р{тахий|</}<(с + /)2/1Х> (4)
где о\ = Щ\ = Ъ1*.
Обозначим через Еп события { тах |?^|^0> л==1>
2, ... Они образуют монотонно убывающую
последовательность. Имеем
мх (Еп) ц = 2 м {х (Ек) й - х (*»_,) ?!-,} =
- 2 МХ(/?,_,) (Й - Й_.) - 2 М (Х{Ек_х \ Ек) & (5)
§3]
РЯДЫ
91
Далее,
Мх(Ек_1\ЕкЩ = МХ(Ек_1\Ек)(^_1 + 1ку^
^(( + сУМ%(Ек.1\Ек),
2 Мх(Ек_, \ Ек)« < (/ + с? 2 Мх(^_! \ Еь) =
л = 1 #=1
= (* +с)* [1-Р (*„)]. (6)
Кроме того,
Мх(^_1)(Ц-^_1) = Мх(^_,)(2^-,^ + Ш =
= 2МХ(^_,)^_1М^+ Мх(Ек_])Щ1 = ^кМх(Е^1). (7)
Соотношения (5), (6) и (7) дают
^(Еп)>Мх(ЕпЦ1>^а1Мх(Ек_1)-а + сГ(1-Р(Еп))>
>р(Еп){^1о1+а+с)^-а+су
или
(* + с)2>Р (Еп){^о\ + с" + 2^},
откуда следует (4).
В общем случае рядов с независимыми слагаемыми
вопрос о сходимости ряда (1) полностью решается
следующей теоремой.
Теорема 5 (теорема Колмогорова о трех рядах).
Для того чтобы ряд (1) независимых случайных величин
сходился с вероятностью 1, необходимо, чтобы для
каждого с>0, и достаточно, чтобы для некоторого с>0
сходились ряды
оо
2Р{1|„!>с}, (8)
ОО
2 Щ'п, (9)
оо
2 0Гп, (Ю)
еде Ъ'п = %п ПРи \%п\<С и ^ = ° ПРи 1М>С«
92
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
Доказательство. Достаточность. В силу
теоремы 3, следствие 2 с вероятностью 1 сходится ряд
со
2 (6„ — Щ'п)> откуда вытекает, принимая во внимание схо-
72=1
оо
димость ряда (9), что сходится ряд 2 \'п* Из условия (8)
п = 1
и теоремы Бореля — Кантелли следует, что только ко-
оо
нечное число членов ряда 2 (I — %'Л отлично от нуля.
Поэтому ряд (1) сходится с вероятностью 1.
Необходимость. Пусть ряд (1) сходится с
вероятностью 1. Тогда его общий член с вероятностью 1
стремится к нулю, так что лишь конечное число членов
ряда превосходит по абсолютной величине с (с>0). По-
оо
этому с вероятностью 1 сходится ряд 2 1п- Обозначим
Я = 1
через {г)я}, п= 1, 2, ..., последовательность независимых
случайных величин, не зависящих от
последовательности {5'Л, п=1, 2, ..., и имеющих такие же
распределения, как и %'п. Положим сп^^п — Цп. Тогда ряд
оо
21п сходится с вероятностью 1, М1„ = 0, ||л|^2с,
м = 1
оо
0|«==20^. Из сходимости ряда 2 1« следует, что
{ I я I ]
Р вир 21* <оо}=1.
11<п<оо|/г=1 I )
Поэтому при некотором /
р вир 21* <4 = а>°-
и<л<оо|й=1 | )
Из неравенства (4) следует при любом п
2 2°^=2 о1*
<
(2с + /)2
А=1
что доказывает сходимость ряда (10). Из теоремы 3,
следствие 2, вытекает тогда, что с вероятностью 1 схо-
§3]
РЯДЫ
93
дится ряд 2 (^ — М^). Отсюда в свою очередь следует
сходимость ряда (9). Сходимость ряда (8) вытекает из
теоремы Бореля — Кантелли, так как если ряд (1)
сходится, то с вероятностью 1 найдется только конечное
число членов ряда (1) таких, что ||я|>с. Теорема
доказана.
Следствие. Для сходимости ряда (1) независимых
неотрицательных случайных величин необходимо, чтобы
для любого с>0, и достаточно, чтобы для некоторого
с>0 сходились ряды
оо оо
2рй„>с}, 2 м&
Действительно, для неотрицательных величин \п
имеем М|^2^сМ|^, так что из сходимости ряда (9)
вытекает сходимость ряда (10).
Леви принадлежит интересный результат, в силу
которого ряд независимых случайных величин,
сходящийся по вероятности, сходится с вероятностью 1.
Для доказательства этого утверждения понадобится
одно неравенство, аналогичное неравенствам, ранее
полученным для субмартингалов, но уже не использующее
существования каких-либо математических ожиданий.
Теорема 6. Пусть {1п, п=1, 2, ...} — независимые
случайные величины, ?;л = ||+^2 + ••• +%п> ^о^О. Если
Р{1Ся-ЬьК'}>а, *=1, ..., п, то
Р(тах |Ел|>2/}<1^. (11)
Доказательство. Введем события ЛА = {|2;1|^
= 1, .. ., п. Тогда
{1Ся1>'}=>й(Л*ПВ*),
к = \
причем события Ак, к = 1, . . ., п, попарно несовместимы
и события АкУ Вк (к фиксировано, к=19 ..., п)
94 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ, II
независимы. Поэтому
1-а>Р{|С»1>0>Р{йм*ЛВА)}-
- 2 Р(Ак)Р(Вк)^а 2 Р(ЛА) = аР ( тах 1Ы>2Д ,
что и приводит к (11).
Теорема 7. /?сли /?я<Э (1), где {^ПУ п= 1, 2, ...} вза-
«лмо независимы, сходится по вероятности, то он
сходится и с вероятностью 1.
Пусть Л„ ^ обозначает событие { вир [2;, — 2; „|>тг|.
оо оо
Ряд (1) расходится на множестве Б = ^ []ЛПму. Оце-
ним вероятность /). Пусть е и т) произвольные
положительные числа. Из сходимости ряда (1) по
вероятности следует, что существует такое /?0 = я0(е, г|), для
которого
Р{|Ь»'-ЬИ>в}<т| при л', /г">я0.
Применим теорему 6 к величинам ^ = ^~^0, к>п0\
Р{ тах#|й|>2в|-Р( тах ^-^^е^-^,
причем здесь я7— любое целое число, большее п0.
Поэтому
р{»г1ь-Ь.1>*)«:т^.
где г) сколь угодно мало. Отсюда следует, что
Р(Л«,лг)<т^ и Р(П^.^ = 0.
для любого N. Поэтому Рф) = 0. Теорема доказана.
Применения к усиленному закону больших чисел.
Из теоремы о сходимости рядов с вероятностью 1 при
помощи простого преобразования можно получить
теоремы типа усиленного закона больших чисел, т. е.
теоремы о сходимости с вероятностью 1 некоторых средних
от случайных величин.
§3]
РЯДЫ
95
Лемма 1. Если ряд 2 %п сходится и ап — моно-
тонно возрастающая последовательность, ап>0, ап->оо7
то
п
Доказательство. Пусть
5„ = 22,(50 = 0)и|5„|<С)
где с — некоторая постоянная. Положим ак — ак-{ = Д&,
/г = 1, 2, .. ., аэ = 0. Тогда
п п п
21 ал2А=21 (Л1 + Д2+ ... +Лл)гл=2Лй(5я-5л-1).
Поэтому
п
1 у*
0/1
я***
/е=1
<
А-1
Л=»1
+ зир ! 5Я-5ЙМ|<
<2С-^ + зир |5„-5А_1|<е
для любого е>0, если п и д0 выбраны достаточно
большими.
Из доказанной леммы и теорем предыдущего
пункта вытекают следующие утверждения.
Теорема 8. а) Если ЦПУ #=1, 2, ..^ —
произвольная последовательность случайных величин с конечными
моментами 1-го порядка и
оо
^ \ М \\п - ап |<оо, ап = М|я,
го с вероятностью 1
Нт-^2(5й-ак) = 0.
96
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
б) Если (!„, п = 1, 2, ...} — такая последовательность,
что частные суммы Кя = ^ +12 + • • • + 1п\ образуют
мартингал и при некотором р ^ 1
зир М
Ь~к^
<оо,
то
*=1
с вероятностью 1.
в) Если {1п, п= 1, 2, ...} независимы и
2трОб»<«>.
Л = 1
го с вероятностью 1
Для одинаково распределенных случайных величин %п
более сильные результаты будут получены в
дальнейшем как следствия общих эргодических теорем.
§ 4. Цепи Маркова
Обобщая понятие случайного блуждания, можно
прийти к значительно более широкому понятию цепи
Маркова (марковского процесса), играющему важную
роль в теории случайных процессов. Прежде, чем дать
формальное определение, остановимся на одной
простой, .но весьма общей модели, приводящей к цепи
Маркова.
Системы под случайным воздействием. Предположим,
что* рассматривается стохастическая система 2,
состояниями которой являются точки некоторого измеримого
пространства {дВ, 23}. Допустим, что переход системы
из состояния \(1), которое система имела в момент
времени /, в новое состояние в момент времени / + 1
целиком определяется значением /, состоянием \{1) и
§4]
ЦЕПИ МАРКОВА
97
некоторым случайным фактором аи не зависящим от
состояния системы Е до момента времени I
включительно, и образующим во времени процесс с
независимыми значениями. Таким образом,
6(*+1)«/(/, Ш, а,), (1)
где /(/, х, а) — некоторая функция аргументов ^еГ,
хеЖ, оеЛ, Л —некоторое измеримое пространство.
Формула (1) позволяет выразить состояние системы 2
в любой момент времени 5, отправляясь от состояния
6 (0 (««):
Б («) = &,« (5(0. <*/> <**+1» ..., а5-!). (2)
Если в начальный момент времени /==0 |(0) не
зависит от последовательности {а,, /еГ}, то !•(*) не
зависит от последовательности {аь а^+1, ..., аЛ, ...}.
Пусть {й, ©, Р} — вероятностное пространство, на
котором определены случайные элементы щ.
Предположим, что при любых фиксированных I и $($>*)
функция ёи8(х, аь аш, ..., а5_,) 8 X ©-измерима. Тогда,
если движение системы 2 начинается с момента
времени I и известно состояние \{1)=*х, то формула (2)
позволяет определить вероятность попадания 2 в
произвольное множество /1еЭ в момент времени $>^. Эту
вероятность назовем вероятностью перехода и
обозначим через Р{1, х, 5, А]. Если %А(х) обозначает
индикатор множества Л, то
Р{/, х, 5, Л} =Мхд {&,*(*. аи ..., а3-{)}.
Пусть 1<и<ь. Из формулы (2) и независимости
случайных величин аи ..., аХ)^[ следуют равенства
Р{/, х, у, Л} =МхА[#в, *(!(")> <*«> ...» «,-!)] =
что можно записать следующим образом:
Р(*, х, у, Л) = Г Р(и, у, о, А)Р(/, х, и, йу)7 1<и<ь. .
(3)
4 И И. Гихман, А. В. Скороход
98 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Соотношение (3) называют уравнением Чепмена —
Колмогорова. Оно выражает важное свойство
рассматриваемых систем— отсутствие последействия: если известно
состояние системы в некоторый момент времени и, то
вероятности перехода из этого состояния не зависят
от движения системы в моменты времени,
предшествующие и. Системы, обладающие этим свойством,
называются марковскими. Они часто встречаются в
различных вопросах естествознания и техники. Из определения
вероятности перехода следует, что для любой
неотрицательной й-измеримой функции }(х) имеем
МНвиЛх, ))=1Ну)Р{*,х,8,ау).
Учитывая независимость ^(0 от аи щ+и ..., а5_1 (гл. I,
§ 3), отсюда получаем
т&.лт, а*..... «,-,))= ьл1пу)ра,№,8,аУ).
Последняя формула легко обобщается на произвольные
©"'-измеримые неотрицательные функции [{х1у х>, ...
..., хп), хк<=<%. Пусть 1{<и< ... <(т. Тогда
М[(Ш, Ш, .-■, 6 ('«)) =
-М/(ОД, .... *&„-■). ^..«^('л.-.)» %_,)) =
= М | /(§(/,) %((„ ,), ут) />(*,„_„ 1У,п-д, (т, АуД =
= М /|/(|(0, •••> ё(',«-2). Ут-и Ут)Х
X Р(/т_1, Ут-Ь 1т, С1ут) Р(1т-2г К^т-г). ^и-1. Аут~1)= . . .
Таким образом,
шш), ш, • • •, &(*«» = м | р(/ь к/,), *2, ^2)х
Ут-Ь *т> 4Ут) X
Х?{ии),У2, •..> Ут)- (4)
Если считать, что начальное положение системы
неслучайно, | (0) = х, и применить формулу (4) к
последовательности |(1), |(2), ..., |(/г)ик функции /(*,, х2, ♦ .,, хп) =>
§4]
ЦЕПИ МАРКОВА
№
= %в(п), где В<п) — произвольное множество из 23", то
получим семейство конечномерных распределений
{Ри\,...,п( ■ )> гс=1,2, ...}, определяемое формулой
Р\,2,...,п{н ;=»
- | ... | Л (*, йу\) Р2(Уь ЛУъ) •. • Рп(Уп-и 4уп), (5)
где Рь{х, А) = Р{к~~ 1, х, к, А) есть вероятность перс-
хода за один шаг. В том случае, когда начальное
состояние системы |(0) имеет произвольное
распределение т (т — вероятностная мера на 23), вместо формулы{5)
из (4) получаем систему конечномерных распределений
рГ\...,п(в{п+1)) =
= | ... | т{йх)Рх{х, йу{)Р2(ух, Лу2)... Рп(уп-1, йуп),
(6)
зависящих от т как от параметра. При этом
Р$\ Лв(,1+1)) = />{(!(()), 1(1) Е(л))бВ'"+|)].
Формулу (6) можно положить в основу общего
определения цепи Маркова. Но прежде чем это сделать,
следует разобраться в том, какой смысл имеют
интегралы вида (6), когда семейства мер Рк(х, А) задаются
самостоятельно, вне связи с вспомогательными
величинами щ и функциями /(/, х, а).
Стохастические ядра. Пусть даны два измеримых
пространства {^, 51} и {Щ, 93}.
Определение 1. Стохастическим ядром на {<%, 23}
называется функция Р(х, В) (л: е $6 В е 23),
удовлетворяющая следующим условиям:
а) при фиксированном х функция Р(ху • ) является
вероятностной мерой на 23;
б) при фиксированном В функция Р(-, В) 51-изме-
рима.
. Если Р(х, *) является мерой и Р{х, ^)^1, то
Р {х, В) называют полустохастическим ядром,
4*
100 случайные 'последовательности [гл. и
Лемма 1. Пусть } (х, у) — неотрицательная а {21 X $}-
измеримая функция и Р(-, -) —стохастическое (полу-
стохастическое) ядро на {<%, Щ. Тогда функция
§(х)^= |/(лг, у)Р(х, йу)
%-измерима.
Доказательство. При фиксированном х
функция /(л:, •) 23-измерима, так что интеграл в правой
части равенства имеет смысл. Класс неотрицательных
функций /(л:, •), для которых лемма верна, является
конусом и, в силу теоремы Лебега, монотонным. Так
как он содержит индикаторы множеств вида А X В,
где А е 21, Ве$, то он содержит все
неотрицательные сг{21 X 23}-измеримые функции.
Следующие предложения можно рассматривать
как обобщение известной теоремы Фубини.
Теорема 1. Пусть {Я?, 21), {Щ, »}, {Ж,
Щ-измеримые пространства, (^^х, В), (?2(#, С) — стохастические
(или полустохастические) ядра на {36, 23}, Щ, Щ
соответственно. Существует и притом единственное
стохастическое (полустохастическое) ядро (33 (х} О) на
{36, а{23 X Щ} такое, что
<Эз (х, ВХС)=1<Э1 (х, йу) <?2 (у, С). (7)
в
При этом для произвольной неотрицательной а{23хК}~
измеримой функции }(у, г) имеем
{ Ну, г)<Эз(*> ЛуХ йг)=*
' 5/Х2
= \(\Пу. г)<Э2(у,с1г))(11(х,с1у). (8)
У \* /
Для доказательства первой части теоремы
достаточно показать, что формула (7) определяет
элементарную меру на полукольце прямоугольников
пространства ^Х2. Пусть Ох = В{ X Си а> = В2 X С2 и В2 с:^.
Тогда В2аВь С2С2СХ и В{ = В2Ь О' 1)0", где В' =
=В2 X (С, \ С2), Д"= (В1 \ В2) X С{.
§4]
ЦЕПИ МАРКОВА
101
Множества Оъ />', О" попарно без общих точек.
Если применить формулу (7) последовательно к
множествам Въ В' и ^", то получим
<2з (х, В2) + (Э3 {х, &) + ^3 (*, Я") =
= | (*х (х, йу) <Эо (у, С2) + | (?, (х, йу) <Э2 (уи Сх \ С2) +
+ | (?, (х, йу) С}2 (у, С) = [ (}1 (х, йу) <32 (у, С) = С}3 (х, Д).
-©| \3г Ву
Таким образом, функция (23(х, В) аддитивна на
рассматриваемых специальных разбиениях множества В3.
В частности, если В3 = Вх [} Въ где Вг —
прямоугольники и я, п02 = 0, то ^лx, ^^)^^лx, ^2)-^Лx, й{),
и С?з(*> ^Х^)=1. (Если 0! и (?2*—
полустохастические ядра, то (?з(х, ^ Х^)< 1). Аддитивность функции
С}3(х, •) на полукольце всех прямоугольников в общем
случае нетрудно получить по индукции.
п
Пусть В =^ Вку где 7)& — прямоугольники попарно
п—I
без общих точек. Тогда 7) \ Вп = О' У О" - у 0Л, где О'
/2=1
и О" определяются только что использованными
формулами. Как уже доказано,
<Эз (*, В) = Рз (^, Аг) + <?з (х, Я') + ^з (х, О").
Используя предположение индукции, получаем
<Эз (х, до=<г3 и в> п (у д *)) === 2* & и, д' п />*)
и аналогичное выражение для СЫ*» /)")• Таким
образом,
03(х,О) = Яз(х, Яя)+2 Шх,0'ПОк) + аЛх,0"Пйь)].
Так как В/ и Л" — прямоугольники без общих точек,
в сумме покрывающие ВкУ то В' (]Ок и В'г{\Вк также
прямоугольники и (В'{\Вк)\](В" {\Вк) = Вк. Поэтому
№
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. 1Г
<Эз(*, 0'()Ок) + <ЭАх, 0"ГЮк) = д3(х,Оь) и,
следовательно,
0з(^Я)=2 0з(*эЯ*).
Таким образом, аддитивность С}3(х, •) доказана. Докажем
теперь свойство счетной полуаддитивности для ()}{х9 -.).
ОО
Пусть й0с=[)Ок9 Ок = ВкХСк9 к = 09 I,... Тогда
1
оо
%о (У, г)< 2 %0. (У. г).
Так как %Вк (у, г) = %Вк (у) гс^ (г), то
оо
ХВоШс0(г)<1>%Вк(у)ХСк(г)-
Интегрируя обе части этого неравенства по мере (22(у, •)
по пространству %9 получим
оо
%в0 (У) <Э2 {У> Я < 2 хВк (у) <Э2 (у, Ск).
Еще раз интегрируя полученное соотношение по мере
С}1(х9 •) и пространству Щ9 придем к неравенству
оо
(Зз(х,Оо)<1><Эз(х, Ок)9
к=\
доказывающему, что <Э3(#, Ок) счетно-полуаддитивна.
Отсюда вытекает, что (23(#, В X С) допускает
единственное продолжение на ст{23Х&}. Чтобы доказать
формулу (8), заметим прежде всего, что в силу предыдущей
леммы внутренний интеграл в правой части равенства (8)
является ^-измеримой функцией, так что двукратный
интеграл в правой части формулы (8) имеет смысл.
Далее, класс функций / (/^0), для которых формула (8)
верна, является конусом и монотонным классом. Кроме
того, в силу формулы (7) он содержит индикаторы
прямоугольников. Поэтому он содержит все <т{3} X
Соизмеримые неотрицательные функции. Теорема доказана.
14
ЦЕНИ МАРКОВА
Ш
Точно так же доказывается следующая
Теорема 2. Пусть {^, Щ, {^,,23,}, .... {<^, 93,} ~
измеримые пространства и {^ (*> #(1))> С}2(уь,В№)у ...
• • •> ()з(Уз-и В^3)) ~~ стохастические {полустохастические)
ядра, ук<^Щь #(й) е »Л (Л = 1, ..., 5). Существует
единственное стохастическое ядро <2(1'5)(*> -О) ## {^» Ф}
где 2) = сг^ X 932 X ... X 935} та/сое, <*го
фв){х, В(1)Х... ХВ(5)) =
= | ЯЛ*, йУ\) \ <2ъ{Уи 4У2) -.
В<#1) В<2>
... | (&(&-!, ^(5))Р5-1 (&-2, ^-1). О)
В(5~1)
При этом для произвольной неотрицательной Ъ-измери-
мой функции Цу1у у2, ..., у3)
/ }(Уь •..> У3)<Э°'8)(х, йу{ X ... Хйу$) =
у,х ... ху8
= [ОЛ*, ^) ... |/(0ь ..., Уз)<Эз(У,~и йУз). (Ю)
Замечание. Формулы (8) и (10) доказаны для
неотрицательных функций. Но они, разумеется, зерны
для произвольных /, если только одна из функций /*"
или /~ интегрируема. Аналогичное обстоятельство будет
иметь место и в других теоремах, в которых, ради
краткости, упоминаются только неотрицательные функции.
Ядро (?(1, 8) называют прямым произведением ядер
Яи Яъ • • •, 0, и пишут (}{х-5) = (?, X <22 X . .. X 05.
Если в (9) положить В{1)' = <уь ..., В(5~1) = ^5_1, то
получаем новое вероятностное ядро в {36, 235}:
дИ.,,)(Х)В(5)) = до,,)(Г) ^1х^2Х...Х^5-1ХВ(8)). (11)
Его называют сверткой ядер С^, (}■>, ..., (}$ и пишут
т
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. И
Применим формулу (10) к функции !(у1у у2у ..., у5) =
^ I {у^) =^ %в{8) {у{8)) и сопоставим ее с (11). Получим
| / (Уз) <Э°' 8\х, йу{Хйу2Х ... X йу8) =
^, х 2/2х ... ху5
= //Ы0*(,'в)(*,^). (12)
Так как класс неотрицательных функций, для которых
формула (12) имеет место, является конусом и
монотонен, то (12) имеет место для произвольной
неотрицательной 335-измеримой функции. Отсюда в свою очередь
вытекает, что для произвольной неотрицательной
а {23Ш1 X 33Ш2 X ... X 23т>г X »8}-измеримой функции г+ 1
переменной вида
1\Ут{у Ут2у •••» Утгу Уз)*
(Ут ^ V™ 0 < ш1 < т2 < ... <тг<8)
имеем
| !(Ут1. Ут2> .->, Утг, Уз) X
ЧКЧХ",ХЧХУ5
х о0* 8)(х, аущ х ^та х ... х аУз) =
... //(*«,. .... #тг, ^'^'''Ч^г' ^)" <13>
Частным случаем формулы (13) является соотношение
д* П. *> = д* (». «,) * д»(«| + Ь ™2) * . _ * <2* (тг + 1« 5),
означающее, что операций свертки ядер является
ассоциативной.
Рассмотрим бесконечные произведения
стохастических ядер. Пусть {двп, 23„}, я = 0, 1, 2, .... —
бесконечная последовательность измеримых пространств
и*Рл(., •), я=1, 2, ...,— последовательность
стохастических ядер, определенных на- {8&п-и ®«Ь В соответ-
§ <1
ЦЕПИ МАРКОВА
105
ствии с теоремой 2 построим прямые произведения ядер
Р{ип) = Р{ ХР2Х ... ХРп,
Р{ип) = Р{1'п)(х0,О), х0<==%0, Ое(Еп,
где &л — минимальная сг-алгебра, содержащая
прямоугольники Вх X В2 X ... X Вп {Вк<== »*), &„ -
«0{»1Х»2Х ... Х»я}.
оо
Введем пространство $/°° = Ц Я?л, элементами кото-
рого служат бесконечные последовательности со =
== {хь хъ ..., хПУ ...), хп^<Я?п. Через 6° обозначим
алгебру цилиндрических множеств Зу°° и определим на
&° семейство функций множеств Р(*о), зависящих от
параметра х0 {х0^%/0) следующим образом: если С
—цилиндрическое множество,
С = {со: (*0. хи ..., хп)е= /)}, Ое ®л>
то полагаем
Рио)(С) = Р(иг)(^о, О).
Это определение однозначно. Действительно, если
С = {со: (*0, хи ..., хЛ) е= О7}, Вг е= бй*
и, например, п'->п, то О' = О X 35пл-\ X ... X Я?й' и
Р(1'"'> (*0, Я') = / ... /Л (*о. <**,) Р2 (*ь Ас2) ...
где Хо7(^ь •••» хп') ~ индикатор /У. Учитывая, что
Хо'(*1. ■ • •> *п') = %о{х{, • •.. *л) и > что Рл(х, Я?А)= 1,
из последнего выражения получаем
Р{ип1(х01 О') = Р{1п)(х0уО).
Аддитивность функции Ры на 60 очевидна.
Теорема 3. На {ЗВ°°, К}, где (И — о-алгебра,
порождаемая цилиндрическими множествами простран-
106
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
АХь)
ства $?°°, существует единственное семейство мер Р
такое, что
Ры{оу. хк*=Вк9 *=1, ..., д} =
= | Рх (х0у йхх) | Р2 {х{, йх2) ...
••• ] Рп-\\хп-21 дХп-Х)Рп(хп-Х, Вп).
Доказательство. Достаточно показать, что
введенная на (Е0 мера Ры удовлетворяет условию
непрерывности: для любой монотонно убывающей
последовательности цилиндрических множеств Сп, для которой
ПСп=0, имеем Рш(Сп)-> 0. Допустим обратное:
Рш(Сп)^е при некотором х0\ основания
цилиндрических множеств Сп обозначим через Вп, индикатор Оп —
через %(йп\ хи х2, ..., **,„) = X (^п)» и пусть Оп
расположено над координатами (1, 2, ..., тп). Определим
последовательность множеств из 23
#я)=={*1: | %(ЯЛ; х19 х2, ...,хтп)Х
ХР(2,^(хь 4х2Х ...Х^дая)>|},
где <^(5, т) обозначает произведение пространств
%з х а?5+1 х ... х авт.
Из того, что Сп убывают, следует, что В{п также
монотонно убывают. Далее, если %{В{п) — индикатор В(п
*х№=1-%№), то
в<р(-»(с„)= / / (хад + х(в'"))х
Хх(0,)/)1(% </лг,)р(2-т»*>(*„ ах2Х ...йдгИя)<
< Я] (*о, ВЙ>) + | / зс И Я, (.го, <**,) < Л (хо, М0) + ±.
§4]
ЦЕПИ МАРКОВА
107
Поэтому Р\ (лго, В{п) > у. Так как Л(*о> *) является
о©
мерой, то отсюда следует, что |~| В{п Ф 0. Пусть
хх^В{п\ п=1, 2, ... Тогда
{ Х{Оп\ *1, *2, -., *тп)Х
X Р(2, т*> (хь йх2 X ... X ^тг1) > |-.
Приведенные только что рассуждения можно применить
к ядру Р^,т^[хи йхъ X ... X с1хШп) и мере Р2{хь Лх2).
Тогда будет доказано существование такой точки х2у
что для любого Оп
{ %(Оп\ *1, *ь *з> •••> хтп)Х
ХР^т"\хъ ^зХ ... Х4хтп)>^.
Таким образом, строим последовательность (хи хъ ...
..., хПУ ...), в которой хпе^„ и при любых 5, йп
] %(&п> %\у *2> •••» %з> хз+\> •••> #тл) X
х р(5+1' т*> (*„ <**я+1 х ... х </*дад) > |-.
Возьмем произвольное множество Ск. Допустим,
что его основание Ок расположено над координатами
(1, 2, ..., 5). Последнее неравенство показывает, что
(х[9 хъ ..., х3) е Ок (в противном случае было бы
%{Вп, хь х2, ..., х5, х8+1,..., хтп)^0 при всех
(дс5+1, ..., хт)). Поэтому (хь хъ ..., х5, ,.,)бСк,
каково бы ни было Ск и, значит, [}СкФ0у что противо-
речит первоначальному допущению. Теорема доказана.
Следствие. Пусть дана счетная последовательность
вероятностных пространств {$?„, 23Л, ^п}, п = 1, 2, .. •
108
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
Пусть 36°° — пространство всех последовательностей со ==
= (*1, *ъ . •., хп> • • •)» хп е ^л» и К — а-алгебра,
порождаемая цилиндрическими множествами §6°°. На
{36°°, 6} существует единственная вероятностная мера О,
такая, что
п
СЦсо: хке=Вк9 к-I, 2,..., л}=П^(вД вле»л.
/2=1
Иными словами, если задана некоторая
последовательность вероятностных пространств {36п, 9?л, ^«}, # =
= 1, 2* ..., то всегда существует вероятностное
пространство {й, 6, О} и последовательность
отображений \п пространства й в д6п таких, что случайные
элементы \п^\п(^) имеют заданные распределения цп
на Ьп и {|л, /г=1, 2, ...} независимы в совокупности.
Замечание. Доказанная теорема, в отличие от
теоремы Колмогорова (гл. I, § 4, теорема 2), не
использует каких-либо топологических предположений о
природе пространств $Вп. С другой стороны, она является
менее общей, чем теорема Колмогорова, так как
относится только к специальной конструкции мер в
произведении пространств.
Определение цепи Маркова. Определение 2.
Цепью Маркова с фазовым пространством {36, Щ
называется семейство случайных процессов с дискретным
временем /еГ+, зависящих от произвольной меры пг
на {<%, 23} как от параметра, конечномерные
распределения которых определяются формулой
Р|м,Й(*)еВА, А = р, 1, ..., п} =
= / т (их) | Л (х, аух)... / Рп (уп-и Вп), (14)
в0 вх вп_1
где {Р^{x, В), /=1, 2, ...}—некоторая система
стохастических ядер на {36, 23}.
Стохастические ядра Рг(х, В) называются
вероятностями перехода за один шаг, а мера т —начальным
распределением цепи. Фиксируя меру т, получим
случайную последовательность со значениями в 36 >
которую будем называть марковским процессом,
соответствующим начальному распределению /п.
§4]
ЦЕПИ МАРКОВА
109
Конечномерные распределения этого процесса будем
обозначать через Р(^*2,.... 1п> а операцию вычисления
математического ожидания некоторой функции от
процесса по вероятностной мере Р обозначим
символом Мт.
Если мера т сосредоточена в фиксированной точке х
фазового пространства, то х будем называть начальным
состоянием процесса, а конечномерные распределения,
меру в {д6Т, 6} и математическое ожидание некоторой
функции от процесса по соответствующей мере будем
обозначать через Р**; * *д, Р{х) и Мх соответственно.
Положим
Р(к, х, г, В) = | Рк+1{х, йук+1) | Рк+2(Ук+и Лук+2) X ...
ж эе
... X /Р,-,(у,-2, ауг-1)Рг(Уг-и 5).
С аналитической точки зрения Р(к, •, г, •) —
стохастическое ядро, являющееся сверткой вероятностей
перехода Рк+1 * Р&+2* • • • * Л- Оно также называется
вероятностью перехода. Точнее, Р{к,х,г,В) есть
вероятность перехода из состояния х за промежуток
времени {к, г) в множество В. Из ассоциативности свертки
ядер вытекает равенство
Р{к9х,з,В)=$ Р{к>х9гуйу)Р{г,уу8уВ)у к<г<8, (15)
т. е. уравнение Чепмена — Колмогорова, а формула (13)
дает
МЛШ, 602). .... К'.))-
= | ет (<**) ]* Р(0, *, /„ йух) $ Р{1Ь уи 1Ъ йу2) X ...
... X | !{уи Уъ • •., Уа)Р{*а-и Уа-ь *а> Лу8). (16)
'Таким образом, получены те же формулы, что и
раньше (см. (3) и (4)), но теперь они следуют из общего
определения марковской цепи. С другой стороны,
рассуждения, приведенные ранее, показывают, что
ПО СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
случайная последовательность (6(0, / <= Г+}, получаемая
с помощью рекуррентного соотношения
6(/+1) = /(/, 6(0, *д, '«0, 1, 2, ...,
где
1(0), а,, а2, ..., <х„, ...
— независимые в совокупности величины и 6(0) имеет
произвольное распределение т на 23 при минимальных
предположениях об измеримости функций /(/, •, •)»
образует цепь Маркова.
Формула (16) позволяет уточнить
теоретико-вероятностный смысл вероятностей перехода. Для этого
вычислим условное математическое ожидание
неотрицательной фуНКЦИИ / (6 ($), |(5+1),..., 1(8 + п))(! (Уо, Уи...,Уп) —
борелевская функция п+1 переменной) относительно
а-алгебры Зю./](^>5), порожденной величинами |(0),
|(1), ...,6(0- Соответствующее условное математическое
ожидание обозначим через У. По определению ^ есть
единственная 5>[о, ^-измеримая случайная величина такая,
что для любой неотрицательной функции §(х0, хи ..., х^
выполняется равенство
МтеЙ(0), 6(1), ..., 6(0)/(6(*), 1(5+1), ..., Е(* + *)Н
= Мт5г(6(0), 6(1), ..., 6(0)^.
С другой стороны, из (16) следует, что
Мт#(Ш> Б(1), ■ ■■, Б(0)/(6(*)э &(«+!), ...,Б(*+*))~
= Мтёг(1(0), 6(1), ..., 6(0)?,
где
7=7(Е(0)=/я(/, 6(0, 5, Л/0) /Р.+1.(#>, ^1)х ...
• ■ • X / /(^0, УЬ • • > Уд) ^+«(#/1-1» ^«).
Таким образом, Ч7 = /.
Полученная формула приводит к следующим выводам,
Теорема 4. Условное математическое ожидание
произвольной неотрицательной функции /(6 ($), 6(5+ 1), •••
..., 6 (5 + п)) относительно §[о, я С < 5) не зависит от
начального распределения пг, от вероятностей перехода,
§4]
ЦЕПИ МАРКОВА
Ш
предшествующих моменту времени (> и от значений
|(0), 60)> ..., ^(*—1). Оно дается выражением
М„{/Й(5), &(*+1), ..., 6 (* + "№,*]} =
= / р(*> КО. 5, ау0) I р5+1 (и,, ^) х ...
#1» • • • > Уп) "з+п (Уп-\, ЛУп)- (17)
Условное распределение величин 6($)> |($+1), ...
..., 1(8+ п) в {$?п+1, 23Л+1} относительно §[0, я совпадает
с прямым произведением ядер
Р(', 6(0, 5,-), Р5+1(%-), ..., Рв+Я(", •)•
В частности, вероятность перехода Р(*, 6(0> 5, В)
совпадает с условной вероятностью попасть системе в
момент времени 5 в множество В, если известны
состояния 6(0), |(1), .,., 6(0- Эта вероятность зависит только
от состояния 6(0 в последний известный момент времени
и не зависит ни от значений 6(0)» 6(1)» •••> 6(^ — 0»
ни от т, ни от вероятностей перехода Рх (•,•)> Р2 (•,•)>•• •
..., Р^{^> •)• Последнее свойство марковской цепи, как
упоминалось ранее, называют отсутствием последействия
и оно является основной качественной характеристикой
марковской цепи.
Замечание. Пусть дано измеримое пространство
{<%, Щ и на нем система стохастических ядер Рп{х, В),
/г=1, 2, ... Тогда существует марковская цепь, для
которой Рп(ху В) являются вероятностями перехода за
один шаг. Доказательство этого утверждения и
конструкция соответствующего вероятностного пространства
дается теоремой 3.
Марковская цепь называется однородной, если
вероятности перехода за один шаг -не зависят от времени:
Р*{х, В)^Р(х, В).
В этом "случае вероятности перехода за промежуток
времени (/, $) зависят только от длины этого промежутка:
Р(*. х, з} В) = | Р(х, аУ[) / Р(у[9 йу2) X ...
112
случайные последовательности
[ГЛ. II
Для однородной цепи уравнение Чепмена — Колмогорова
принимает следующий вид:
/><5+т)(*. й)= \ Р{*\х,йу)Р{т)(у, В).
Пусть марковская цепь однородна. Формула (16)
показывает, что
Мда(/(Е($+1), Б(* + 2), ..., К* + п)) =
-Мта!(ШШ •••> *(*)), (18)
где
тДВ) = | Р(0Г х, 5, В)т(йх)= \ Р{з)(х, В)т(йх).
Если величина (18) не зависит от 5, какова бы ни была
функция /(•), то однородный марковский процесс,
соответствующий заданному начальному распределению т,
называется стационарным. Для стационарности процесса
необходимо и достаточно, чтобы мера га удовлетворяла
условию
гп{В) = | Р{8){х, В)т(йх). (19)
Это условие эквивалентно более простому
т(В)= | Р(х, В)т{йх). (20)
Действительно, (20) является частным случаем (19).
Если же (20) выполнено, то
т{В)= | Р(х, В)$Р(у, йх)т{йу) =
= / Р{2) (г/, В) т (йу) =... = / Р{5) (У„ В) т (йу8).
Вероятностные меры ш, удовлетворяющие уравнению (19),
называются инвариантными или, подробнее,
инвариантными мерами, соответствующими данному
стохастическому ядру.
Таким образом, если для данного стохастического
ядра существует инвариантная вероятностная мера, то
существует такое начальное распределение для
однородной цепи Маркова, которому соответствует стационар-
§4]
ЦЕПИ МАРКОВА
113
ный марковский процесс. Вероятностью перехода за
один шаг этого процесса служит данное ядро.
Если инвариантная мера единственна, то для
данной цепи существует единственный стационарный
процесс.
Пусть 5* обозначает минимальную ст-алгебру,
относительно которой измеримы |(0), Ц1), ..., ^(0(* = 0,
1, 2, ...), т — случайное время на Ш*,/ = 0, 1, ...} и
йт —область определения т. Рассмотрим следующий
вопрос. Пусть |(0 — однородная марковская цепь. Как
ведет себя процесс 1х(^) = 1^ + г) на йт? Естественно
ожидать, что при гипотезе 1(х) = х случайный процесс
%х{1) ведет себя точно так же, как марковский процесс
%({) при гипотезе ^(0) = лг. Уточним и докажем это
утверждение. Выраженное им свойство называется
строгой марковостью.
Очевидно, |(* + т) определено на й%у и из леммы 5
§ 1 гл. I следует, что ^(/ + т)(/^0) ©-измеримо.
Положим Р(т) (*, А) = Р(х) [й/)(1 (т)б= А)}. Тогда Я(т>(х, А)
является полустохастическим ядром на {$?, 93}.
Действительно,
Р{Х)(Х, Л)=ЕРМ{[т = 5]П[|(5)еЛ]}.
5=1
Отсюда сразу вытекает, что Р {х, А) является мерой
на 93 и
Р{х)(х, %) = Р{хУ{й%}^1.
С другой стороны, существует такое множество В(5)еЗЗ*5),
что событие {т = 5} эквивалентно событию {| (0), | (1), ...
. •> &(5)}^5(5). Следовательно,
Ры{1т = 5]П1^йеЛ]} =
= Р{х) {(I (0), Е(1), ..., Ь (5)) е= В{8) п А{5)],
где Л(5) = $?Х^Х ... Х#?ХЛ ($-1 сомножитель равен Я?)
и из свойств полустохастических ядер вытекает, что эта
вероятность, а также и Р{х){х, А) являются 93-измери-
мыми функциями.
Обозначим а-алгебру, индуцируемую случайным
временем т, через Зх-
П4 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Теорема 5. Если Ве§т и О с: 12т, то
р(,) {/>п(п [&('*+^)^Лк])} ==»"
I РЧЛ [&('*) еЛ^Р^Ос, Я, <&), (21)
где Р(т) (л;, О, Л) = Р(л;) (О П [\ (т) е= Л]).
Доказательство. Так как Оси,, то
ри){дп(п(1('*+т)елА])}=
= 2Р(х1{^.п(Л[|(^ + т)еЛ,])
где /)в = О П [т = «]. Пусть %(/)5) ~ индикатор события Д,..
Имеем, учитывая свойства условных вероятностей для
марковской цепи (теорема 4):
РМ{/),п(Л[|(^ + т)еЛ,]]} =
= Мж{хФ,)Ри,(Л[|(^ + 5)еЛ,]|^)| =
= Мж{хФ,)Р(1(в))(Л[|«* + 5)еЛк])}.
В силу однородности цепи правая часть последнего
равенства равна
гр«<'>>{пи(**)елк)Ьрм-
= |" Р(й){ Л К (<*) 6 4])? (5, х, О, </0), (22)
где Р(«, х, I), •) есть мера, определяемая на {Я?, 53}
соотношением
Р(«, *, О, Л) = Рщ{О0(т = 5]ПЁ(«)еЛ]},
§ 5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ | 15
Если еще ввести меру
Р™{х, Д Л) = Р(х)РП11(т)еЛ]}=2Р(5, х, Д А)
5=1
и просуммировать равенства (22) по 5, то получим
требуемое.
§ 5. Цепи Маркова со счетным числом состояний
Приводимость и неприводимость. Пусть Х — счетное
или конечное множество. Под а-алгеброй измеримых
множеств X в этом случае условимся постоянно
понимать совокупность всех подмножеств X. При этом
измеримыми оказываются произвольные функции на X.
Точки пространства X будем обозначать буквами
I, /, ... Рассмотрим однородную марковскую цепь-со
значениями в X. Она задается вероятностями перехода
за один шаг р(/, /), *', |'е1в одноточечные множества /'.
Вероятность перехода за один шаг в произвольное
множество В выражается через р(19 }) очевидной формулой
Р{1,В)= 2 р(/, /),
/ев
а интегрирование по мере, соответствующей
стохастическому ядру Р(19 В), превращается в суммирование
X . /с=Х
Выражение для вероятности перехода за п — шагов
в одноточечное множество / принимает вид
Р{п) (/, 1) = 2 Р (/, /,) Р Ни к) .. • Р (1п-и /). (1)
Если ввести матрицу Р{п) (с конечным или бесконечным
числом строк), элементами которой служат вероятности
перехода за п шагов, Р<п} = {р{п) (/, /)Ь>/€=;р то из
формулы (1) следует, что
р{п) = рп
Иб СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
где Рп — п~я степень матрицы Р = Р(1) — матрицы
вероятностей перехода за один шаг. Матрица Р = {р(/, /)}
обладает свойствами:
а) р(*,/)>0, б) 2 р(/,/)=1. (2)
Матрица Р со свойствами а) и б) называется
стохастической. Из равенства рп+т^рпрт следует, что
/><«+»>(*, /)= 2 ^е\ *)р(/я)(а,/)• (3)
С другой стороны, формула (3) является записью
уравнения Чепмена — Колмогорова ((15), § 4) в
рассматриваемом случае.
Определение 1. Состояние /е! достижимо из
состояния /, если вероятность перехода из I в / за
некоторое число шагов положительна. Если / достижимо
из /, а I достижимо из /, то состояния / и / называют
сообщающимися. По определению состояние / всегда
сообщается с I.
Тот факт, что / и / — сообщающиеся состояния,
условимся записывать символом /«->/. Если / достижимо
из /, а к из /, то к достижимо из /. Это вытекает из
неравенства р<л+ш>(*, 6)>р<т>(г, /)/?(т)0\ &)•
Соотношение «-> является соотношением
эквивалентности:
а) 1<г-+1\
б) если I <->/, то / <-> /;
в) из /<->/ и }<-+к следует 1+->к.
Действительно, а) следует из того, что р(0) (/, /)=1»
б), вытекает из симметрии г и / в определении
сообщающихся состояний и, наконец, в) вытекает из того,
что
* р1п+т)(1, Й)>р<я)(*\ })р{т){и Ь)>09
р(я1+«»>(/5,1)>рм{ку !)р{тЧи 0>о,
если р<я>(/, /)>0, р1т*Щ, /)>0; р<т>(/, /г)>0, р<я»>(/г, /)>0.
Произвольная цепь Маркова может быть разложена
на непересекающиеся классы Ха сообщающихся
состояний. Это разложение можно осуществить следующим
образом. Выбираем произвольное состояние 1{ и
обозначаем через X/, совокупность всех состояний, сооб-
§5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ Ц7
щающихся с 1{. Из свойства в) соотношения «-*->»
вытекает, что любая пара состояний из Хьх сообщаются
между собой. Если Хи не исчерпывает Ху выбираем
состояние 12 €= Х(х и аналогично предыдущему строим
класс Хи. Так как 1г и 12 не сообщаются, то классы Х{г
и Хи не имеют общих элементов. Продолжаем
построение множеств Х(к до тех пор, пока не будет исчерпано
все X. Построенные классы Ха обладают следующими
свойствами:
1) число классов Ха не более чем счетно,
2) каждый элемент X попадает в один и только
один класс Хау
3) любая пара состояний из Ха сообщаются между
собой,
4) любая пара состояний из разных классов между
собой не сообщаются.
Последние два свойства могут быть сформулированы
еще так: из любого состояния / данного класса Ха
можно за некоторое число шагов с положительной
вероятностью попасть в любое другое состояние этого же
класса. Не исключена возможность того, что система,
находясь в данном классе, выйдет из него когда-либо,
но вероятность того, что она, покинув данный класс,
вернется в него когда-нибудь, равна нулю.
Определение 2. Марковская цепь называется
неприводимой, если она состоит из одного класса
сообщающихся состояний. Если любое состояние /,
достижимое цз I, сообщается с /, то состояние I называется
существенным. В противном случае оно называется
несущественным.
Нетрудно заметить, что из существенного состояния
достижимы только существенные состояния.
Действительно, пусть / — существенно и \ достижимо из /. Если к
достижимо из /, то к достижимо из / и, в силу
существенности состояния /, I достижимо из к. Но тогда
и / достижимо из к, т. е. / существенно.
Отсюда вытекает следствие: в классе сообщающихся
состояний или все состояния существенны, или все они
несущественны.
Возвратность. Пусть %(п) — состояние марковской
системы в момент времени /г. Обозначим через т;- = т/{/г)
число шагов, которые затрачивает марковская система,
118
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
начиная с момента времени пу чтобы впервые попасть
в состояние /. Таким образом, т/(я) определяется
цепочкой соотношений
Введем семейство сг-алгебр {§[*, я, / = 0, 1,...}, где
§[П, *] — минимальная а-алгебра, относительно которой
измеримы |(я), |(я+1), ..., |(я + 0-
Величина т/(«) является случайным временем на
этом семействе. Положим
/(5)(/, /) = Р(т,(л) = в|Е(/1) = 0. 5 = 1/2, ...
/(0) (/,/) = о.
При этом
Из однородности цепи следует, что вероятности /(5) (/, /)
не зависят от п. При / ф / они называются
вероятностями первого попадания в состояние /, а при / = / —
вероятностями первого возвращения в состояние /.
Сумма
оо
есть вероятность того, что система, выйдя из 1-го
состояния, раньше или позже попадает в /-е состояние.
Аналогично Р (I, /) есть вероятность того, что система,
выйдя из 1-го состояния, за конечное число шагов
возвратится в 1-е состояние. При Р(1У /)<1 случайная
величина ту является несобственной.
Определение 3. Состояние / называется возврат-
ним, если /7(/, 0=1» и невозвратным, если Р{1, /)<1.
Нетрудно установить связь между вероятностями
перехода и вероятностями первого попадания. Она
дается соотношением
Р(п)(*, /) = 2 /(5>(/, /)Р{п~8)(/, /), п>1, (4)
5=1
где р(0)(*\ /) = 6;у. Действительно, пус^ь т/ —время
первого попадания в /, отсчитываемое от начального мо-
§5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ Ш
мента времени. Тогда
Рм (I, /) = Р(,) | Ц Ь: = *] Л [I (п) - Л } =.
5=1
=2р<1'){т/=5}р(0{|(")-/К/ = *}= 2/(5,(^ /)р("^(Л /).
5=1
Формула (4) доказана. Отметим ее частный случай:
Р<">(<\ 0=2/(5)(^ 0р(»-5)('\ 0, (5)
что можно также перепиеать в виде
5 = 1
Последнее соотношение позволяет последовательно
вычислить вероятность возвращения, если известны
вероятности перехода. Заметим, что для вычисления
вероятностей возвращения в 1-е состояние достаточно знать
только вероятности перехода в то же состояние.
Введем производящие функции Рц{г), Рц{г)
последовательностей {р(п)(/, /), п = 0, 1, 2, ...}, {/(я)('» /)»
л = 0, 1, 2, ...}:
оо оо
Л/ (г) = 2 Р(л> (/, /) г", Л/ (^) = 2 /<"> (г, /) 2".
Из формулы (5) следует, что
оо П
Ри (г) = Р(0) (I, 0+22 }(к) (I, 0 ^р("-« (^ I) г"-* =-
««1 & = 1
оо оо
= 1 + 22 Р (г, I) гЬр^-Ъ (г, г) г»"* =
/г = 1 я=/г
оо
-1 + 2РЧ*. 0г*Л/(г)
/г=1
или
Р„(г) = Г+Р„(г)Р„(г).
120 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
Изменение порядка суммирования в проведенной
выкладке законно, так как рассматриваемые ряды
сходятся абсолютно при | г |^ 1. Последняя формула может
быть записана также в виде
Аналогично из (4) вытекает равенство
Рц(г) = Рп(г)Рц(г)> 1Ф1 (7)
Пусть теперь х — действительное число и г\ 1. Функции
Рц{г) и Рц{г) представляют собой монотонно
возрастающие функции, причем в силу теоремы Абеля
\\тРи(г) существует и \\трн(г) = РН{\)=^Р{1, /). ПоЛО-
жим 1\тРи(г)= 0(19 1) = Рц(1)- Из соотношения (6) сле-
дует
Теорема 1. Состояние г возвратно, если 0(1, I) =
оо
= 2 Р{п)(!> 0 — °°» и невозврат но у если 0(1, /) =
оо
= ^р{п)(1, /)<°°- В невозвратном случае
4 ' ' 1 — Р (г, I)
Теорема 2. Если состояния I и ) сообщаются, то
они возвратны или-невозвратны одновременно.
Доказательство. Так как I «-> /, то найдутся гщ
и га2 такие, что /^т>>(/, /)>0, р{т2)(], 1)>0. Так как
р(т.+т,+Л)(д ])^рШ(]9 1)рМ(1, /) р(т'> (/, /),
ТО
сх> сю
2 рм (/, л > р™ у, о />""•' а,!) 2 р(п) а, /).
П — Шх+Шг «==0
и ряд С(/, /) расходится, если расходится ряд О (г, /).
Меняя роль / и /, получим, что С(/, /) и 0(1, I) конечны
или бесконечны одновременно.
Таким образом, свойство возвратности для
марковской цепи является не столько свойством состояния,
сколько характеристикой класса сообщающихся
состояний.
§ 5] ЦЕПИ -МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 121
Интуитивные соображения подсказывают, что
возвращения в течение неограниченного промежутка времени
в возвратное состояние происходят бесконечно много
раз, а в невозвратное состояние только конечное число
раз. Это нетрудно доказать.
Пусть <3/(га) — событие: система попадает в /-е со-
стЬяние по меньшей мере т раз, а т;- — число шагов до
первого попадания в состояние /. Тогда
оо
Пусть ^7х/ (/^) — вероятность события (д^т), если
|(0) = /. Имеем
оо
Яц (т)=2Р «?/ (го) П [т/ = п) \% (0) = 0, =
« = 1
оо
= 2 Р(')(С/(т)|т/ = «)Р("(т/ = п|6(0) = 0 =
оо
Нетрудно проверить, что
Таким образом,
Яц(т) = Р{1, ])яп{т-1). (8)
Пусть ц{1 = цц (оо) — вероятность того, что система,
выйдя из /-го состояния, попадает в /-е состояние
бесконечно много раз. Так как Цц = Нт Цц{т), то из (8) СЛе-
дует
Чи = РЦ, /)<///• (9)
Теорема 3. /Гели / — возвратное состояние, то
Цц = /7(/, /) и, в частности, Цц = 1; если же / невозвратно,
то яц = 0 для любого /.
Доказательство. Если РЦ, /)<1, то,
положив в (9) / = у, получим ^//^О и из того же равенства
имеем: ^/ = 0. Если ^(у, /)=1, то из (8) вытекает
122
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. 1Г
Чи(т)*=[Р(1, ])]т = 1, откуда <7//=1- Из (9) тогда
следует, что ди = Р{1, /).
Пусть Р{1, /)=1. Из свойства строгой марковости
(см. § 4, теорема 5) получаем
р(,) [в л (Л{| (Т/+н)=/а}) )=р('} (В) ^(А{| {'к)=к)
для любого В^г5ч.. Из этого соотношения вытекает
Теорема 4. /Гслм Р{1,})=1, го случайный процесс
V (0 = I С*/ + О Й (0) = 0 стохастически эквивалентен
процессу I (*) с начальным состоянием I (0) = } и не зависит
от в-алгебры §т..
Следствие. Пусть %(0) = /, / — возвратное
состояние, \х — число шагов до первого возвращения в I, |2 —
число шагов между первым и вторым возвращением
в I и т. д.
Случайные величины 1и ^2> •••> 1п одинаково
распределены и независимы.
Теорема 5. Если состояние I возвратно и Р (/, /) > 0,
то система, выйдя из состояния I, посетит / бесконечно
много раз (<7х/= 1) и Р(], 0>0- В частности, Р(1, /)= 1.
Из теоремы 3 следует, что число возвращений в
состояние / бесконечно. Пусть Ск обозначает событие:
между к — 1-м и к-ы посещениями состояния г система
зайдет в состояние /. В силу строгой марковости
процесса события Ск независимы между собой и имеют
одну и ту же вероятность. Так как Р( ^/ Ск) есть
вероятность того, что система вообще когда-либо посетит /, то
оо
Р(Ск)>0 и ^Р{Ск)=оо. Из теоремы Бореля —Кан-
к = \
телли следует, что с вероятностью 1 осуществляется
бесконечно много Ск. Более того, система, попав в /-е
состояние, бесконечно много раз посетит 1-е состояние.
Следствие 1. Из возвратного состояния
достижимы только возвратные состояния. Возвратные
состояния существенны.
Это следствие уточняет теорему 2, полученную ранее
с применением производящих функций.
§5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЯ 123
Следствие2. В классе сообщающихся состояний,
содержащем возвратное состояние, все остальные
состояния также возвратны, и точка, находящаяся в этом
классе, с течением времени с вероятностью 1 попадает
во все остальные состояния класса, и притом бесконечно
много раз.
Класс возвратных сообщающихся состояний будем
называть возвратным классом.
Положим
оо
0(1, /)=2р(ге)(/, !).
Смысл этого ряда был выяснен для случая г' = /.
Установим следующее соотношение:
2 Р{п)и, I)
Нт-^ —=Р(1,1). (Ю)
""*" 2 Л,;)
Доказательство основано на формуле (4). Полагая в (4)
п= 1, 2, ..., N и суммируя полученные равенства, будем
иметь
2р,я)<*, л-2 2>-й(*. 1)рмц, /) =
-2* 2 1(п~5)а, /)р(5>(/, /н 21р(в,а /)^-3,
5 = 0 П = 5+1 5=0
где 7^-* = 2 /(п)0\ /) и РМ->Р{1, I) при #->оо. Таким
/1=1
образом,
N
«=1 -V* Р(3> (Л /)
N ~~~ 4шА Г^-5 #
2^(и*) *-0 2р<я)(лй
и=0 м=0
Справедливость формулы (10) теперь вытекает из
следующей леммы.
124 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. П
Лемма 1. Если {ЬПУ п = 0, 1, ..., Л^} — последовз-
тельность неотрицательных чисел и -^ >0, то для
2 ь*
5=0
произвольной сходящейся последовательности {сПУ п =
= 1, 2, ...} имеем
.V
2 ьисы-к
ИШ д? = 11Ш Сп.
Доказательство. Если с = \\тсПУ то
N
2 ьксы-к
к=*0
N
* = 0
С =
2^Ку-а-с) 2 ** 2 ^лг-
%
2*, 2*» 2»*
А;=0 &=0 Ь=0
Если номер п выбран так, что при п'^п имеем
\с — сп'\<еу где е>0 произвольно, то первое слагаемое
в правой части равенства (11) меньше е. При
фиксированном п второе и третье слагаемые также стремятся
к 0 при Л/г~-^оо, так как сп ограничены. Это доказывает
лемму и вместе с тем равенство (10), так как условия
леммы всегда применимы к рассматриваемому случаю,
ибо р(я)(/\ 0 ограничены.
Из формулы (10) вытекает
Теорема 6. Внутри возвратного класса О (/,/) = + оо,
если же / невозвратно, то 0(1, /)<°° при всех ь.
Действительно, если / — невозвратное состояние, то
знаменатель в левой части соотношения (10) стремится
к конечному пределу, а поэтому и предел числителя
конечен. Если же / возвратно, то предел знаменателя
равен оо, если Е(1, /)>0, то и предел числителя также
равен оо.
§-51 ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 125.
Периодичность. Заметим, что если р(/г)(*\ /)>0, то
также р{кп)(1, /)>0. Действительно, р{кг})(1,1)^
>р(п)('*> 0Р(Я)(*\ 0---Р(п)('\ 0- Обозначим через й(Ь)
наибольший общий делитель всех тех п> для которых
р{п){ь, /)>0. Если р(п)(/, /) = 0 для всех п>1, то будем
считать й(/) = оо.
Теорема 7. ^о/ш /<->/, то с1(1) = (1(}).
Доказательство. Во-первых, если /-*->/, то с1(1)
и й(/) конечны. Пусть р(5)(*\ /)>0. Найдутся некоторые
п>0 и т>0 такие, что р{п)(1, /)>0 и р(т)(/, 0>0.
Следовательно, р(«+^>5> (/, /)>р(т> (/, г) р(*> (*, /) р<*> (/, /) > 0.
Аналогично р(л+п»+**)(/, /)>0. Поэтому й(/) делит
(п + гп + 2$) — (п + пг + $) = 8. Отсюда вытекает, что с1 (/) ^
<й(/). Но из симметрии роли / и / также имеем:
й(0<<*(/), т.е. а(1) = <1(]).
Следствие. В каждом классе сообщающихся
состояний величина й{{) постоянна,
В частности, для неприводимой цепи Маркова
величина й = А(1) не зависит от состояния.
Определение 4. Если в неприводимой цепи й= 1,
то цепь Маркова называется апериодичной, если й>1,
цепь называется периодической, а число й ее периодом.
Следующая лемма носит теоретико-числовой х фактер.
Лемма 2. Пусть й — наибольший общий делитель
последовательности положительных целых чисел пь
я2, ..., п3. Существует такое число т0>0, что для всех
целых т^ш0 неопределенное уравнение
8
тй = 2 С]П1
имеет решение в целых неотрицательных числах с\.
Доказательство. Пусть Л —множество всех
чисел, представимых в виде # = 2а/Я/, где а/— целые
(положительные, отрицательные или 0). Каждое х
делится на й. Пусть й0— наименьшее положительное число
из Л. Так как х — Ы0^ А при любом целом 6, то,
каково бы ни было х, найдется такое к, что х = к(10
(в противном случае нашлось бы такое кь что х{ = х—к{й0
удовлетворял бы неравенствам 0<л:1<й0, что
противоречит определению й0). Итак, с(0 есть наибольший общий
126 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
делитель чисел из А. Пусть теперь В = | х: х = 2 ^\п\ \*
где й/ — целые неотрицательные числа, и ^1 = 2 п}-.
Число б?о можно представить в виде й0 = Ых — Ы2, где
Л[(бВ, Пусть с —наибольший из целочисленных
коэффициентов при Яу, входящих в #2. Для любого целого
га>0 положим т = Ы{ + ти где О^га^^,. Тогда
/пй0 = Ы0б?1 + т1^ое ^> если ^о > т1с> ЧТ0 наверное
будет выполнено, если к>—г-> или когда т>-г + й\.
Лемма доказана.
Теорема 8. ^ЕЪш й(г)<оо, го найдется такое п0,
что при п>п0
рШи))(1у /)>0.
Доказательство. Пусть /гл (А = 1, 2, ..., 5) —
последовательность чисел таких, что р(*)(/,/)>0, и
наибольший общий делитель чисел пь п2> ..., п3 равен й{1).
В силу предыдущей леммы найдется такое щу что
при п^Пц будем иметь пс1(1)= 2 скпк. Следовательно,
Ршта,1)>[Р^а,Ф[рыа,Ф... [/»<"•>(/, о]в*>о.
Следствие. Если р(пг)(/, ь)>0, то для всех
достаточно больших п
р{пг+пашЦ,1)>0.
Действительно,
р1™1"1™ (],!)> рм Ц, 1)р1п*1,)) (1,0.
При изучении цепей Маркова во многих случаях
удобнее сначала рассматривать апериодические цепи,
а затем обобщать полученные результаты на
периодические.
Покажем еще, что период состояния может быть
вычислен по вероятности первого возвращения.
Лемма 3. Период 1-го состояния совпадает с
наибольшим общим делителем тех п, для которых }{п) (г, /) > 0*
$5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ [27
Доказательство. Пусть ^и й- множества
тех п, п^Ы, для которых р{п)(/,/)>0 и
соответственно /(п) (/,/)> О, а йц и йы — их наибольшие общие
делители. Очевидно, 2м а2м и, следовательно, йм^йы.
При этом Й! — ^. Пусть существует N такое, что
а'а = ап при /г<#, а й'н+х>йы+х. Тогда /(ЛГ+1) (/,/)-О,
а р("+1)(М)>0. Из равенства р^1^/,/) = /(ЛГ+1)(^ 0 +
+ 2 /(й)(*\ 1)р{Ы+1"к) (I, I) вытекает при некотором 5,
0<$<М, соотношение /(5)(/, 1)р{М+{~8) {ь, /)>0, т. е. 5
и N + 1 — 5 делятся на йы> и, следовательно, N + 1
делится на йм, что противоречит соотношениям й^+{ <
<йлг+1=*^лг. Лемма доказана.
Теорема 9. Каждый класс К сообщающихся
состояний периода й{й < оо) можно разбить на й
подмножеств /Со, /Сь ..., /Сс/~1 попарно без общих элементов
так, чтобы за один шаг из К 8 (&<(!-- 1) можно было
перейти только в К8+и а из Ка-\ только в Ко-, при
этому если г ^ Кг> / ^= К3> т0 найдется такое N = N (/, /),
что рпа+3~г(I, ])>0 при п>Ы.
Доказательство. Пусть /С0 — множество всех
состояний /, для которых хотя бы при одном
положительном целом к имеем р(Ы) (г, /)>0, где / — произвольно
выбранное состояние из /С. Тогда 1^Ко- Так как / и /
сообщаются, то найдется такое т, что р{т) (/, /) > 0.
Число т кратно й. Действительно, рт+т)(1, ь)^
^ р(Ы) (/, /) р{т) (/, I) > 0, и, следовательно, Ы + /л
делится на й. Так как т делится на с/, то если вместо
состояния I в определении /Со взять любое /, для
которого р{Ы](I, /)>0 при некотором /г, то Ко не
изменится. Теперь определим К\ как множество тех /, / е /С,
для которых 2 р(/,/)>0, /С2 как множество всех
тех /, для которых 2 р (*', /) > 0, / е /С, и т. д. Из оп-
ределения множеств /С5 вытекает: Кга+з с: /С5 при
любых г и 5. С другой стороны, ,если / е /С5, то найдутся
такие /о, /ь ..., /,«/, что /ге=Хг, г<$, и р(/г-1, /г)>0,
т. е. р(* г) (;г, />> 0. Верно и обратное, если р(5 г) (/„ /) > 0,
128 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
]'г^Кп 1^К, ТО 1<=К3 (ИЗ /г->/г + 1, /г + 1-^/ И /г«->/
следует /г+1-«->/г.) Теперь убедимся, что классы Кг
и К8, 0<><$<й, не имеют общих элементов.
Действительно, пусть / е Кг, /^ К5. Тогда найдутся такие /,
и /2^4 Д^я которых р{г)(1и})>0 и /?(5)(/2, /)>0. Так
как /2 и / сообщаются, то /?(т)(/, /2)>0 Для некоторого /и.
Следовательно, /?т+5 (/2, /г) > /?(5) («2» /) /?(т) (/» У > 0,
поэтому т Н- 5 делится на й, т. е. т = Ы — $, где 5 —
некоторое целое число. Но тогда
Ъ<р(г\1иЯр(т){ик)<Р(Ы-8+Т)Ии12\
а это, как было показано выше, невозможно, так как
переходы из 1Х в /2, /,, /2е/(0, возможны только за
число шагов, кратное й. Далее, пусть 1^КГ и ]^К8-
Найдется такое т, что р{пг) (г, /)>0. Тогда т имеет
вид т = /г(4 + (^ — г). С другой стороны, в силу
теоремы 8 рШ) (/,/)> 0 для всех гс^/г0(/). Следовательно,
р (',/)>/? (*, I) р {ь,])>0 при всех
я >%(/).
Теорема доказана.
Услозимся множества /С0, /Сь ..., /С^_ 1 называть
подклассами периодического класса сообщающихся
состояний.
Основная теорема теории восстановления. Для того
чтобы рассмотреть асимптотическое поведение
вероятностей перехода р{пЩ, I) при п—>оо, понадобится одна
теорема, которую часто называют основной теоремой
теории восстановления. Ограничимся тем ее не самым
общим вариантом, который нужен для дальнейшего.
Чтобы объяснить терминологию, представим себе, что
рассматривается работа некоторого прибора, который
время от времени выходит из строя (отказывает). В
момент отказа прибор немедленно заменяется новым
экземпляром. Продолжительность исправной работы хп
п-го экземпляра прибора является случайной
величиной, принимающей значения 1, 2, ..., причем
величины тл (я = 0, 1, ...) взаимно независимы и одинаково
распределены. Положим
оо
р* = Р{т„ = А}, А=1, 2, ..., 2р*=1.
$ 5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 129
Сумму То + ^Н- ... + тп-\ назовем моментом п-го
восстановления, а величину %п — длительностью п-го
восстановления. Обозначим через 0(п) вероятность того,
что п есть момент восстановления. События
{*о = п}, {т0 + Т! = п}, ..., {т0 + %х + •.. + %к-х = д}, ...
попарно несовместимы, поэтому
С(п) = Р{т0 = л} + Р{т0 + т1=/г}+ ...
... +Р{т0 + т1+ ... +тл_,«л}+ ...
и С(д)<1 при п^\. Положим С(0)=1. Функция О {п)
называется функцией восстановления.
Основной теоремой теории восстановления называют
теорему, характеризующую асимптотическое
поведение С (я) при /г—>оо.
Обозначим через й наибольший общий делитель
тех /г, для которых рп>0. Если й=1, будем называть
процесс восстановления апериодическим, при */>1 —
периодическим, а й — периодом восстановления.
Нетрудно заметить, что в случае апериодического
восстановления О{п)>0 для всех пу начиная с некоторого п0,
п^п0. Если же */>1, то при всех достаточно
больших ку к^к0, О(М)>0. Эти утверждения вытекают
из арифметической леммы 2. Оказывается, что если
восстановление апериодично, то 00О=НтС(/г) = —,
где т=Мтй (при Мтй=оо, 0^ = 0).
Докажем сначала существование предела 0^, а
потом найдем его значение.
Лемма 4. Пусть % —случайная величина,
принимающая значение п ,(/г = 0, ±1, ±2, ...) с
вероятностью рп, I (и) — характеристическая функция
величины т. Если й=1, то }{и)Ф\ при \и\<2п, и=^0.
Доказательство. Имеем
со
/(м) = Ме1их= 2 рпеш-
— оо
?Иусть /(и0) == 1, \щ\<2п, и0Ф0. Имеем
оо
О = 1 — Ке / (щ) = 2 (1 ~ соз пщ) рп.
5 И. И, Гихман, А. В, Скороход
130
€ЖЧ№тЯЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
Поэтому со5шго=1 для всех тех пу для которых рл>0,
или пщ — 2як. Выберем последовательность целых
чисел п{, п2, ..., п8У для которых рп >0 и наибольшей
общий делитель которых равен единице. Тогда пги0 =
~ 2пкг (г = 1, 2, .*., 5). С другой стороны, уравнение
^агпг=1 имеет решение в целых числах аг. Следо-
Г=*1
вательно,
Щ = 2 агпгщ = 2я 2 а>гкг = 2кк0,
где к0 — целое число, что противоречит условию \и0\<2п.
Лемма 5. Если восстановление апериодично, то
предел 0^ = Пт О (п) существует.
Л->оо
Доказательство. Положим
оо
С (г, п) = 2 2>„(5), /г > 0, 0 <2 < 1,
5 = 0
где рп(я) = Р{т]5 = /г}, <П5 = т0 + т1+ ... + т5-!. Из
теоремы Абеля о степенных рядах следует, что
О (п) = Нт О (г, п).
Так как характеристическая функция случайной
величины % равна [/(и)]5,
где /(а) — характеристическая функция случайной
величины т0, то
я
-я
Поэтому
я
^, ч 1 Г е~1пи аи ^л
§61 ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 131
При /г<0 интеграл в правой части последней формулы
равен нулю. Следовательно,
~ , ч 1 Г соз па йи
Положим к (г, и) =— Ке(1 — г!(и)) \ Так как 0(г9п) —
вещественная функция, то
я
О (г, п)= к (г, и)соъпийи.
—я
Ядро к (г, и) (ге[0, 1], 0<|*/|<2я) положительно и
непрерывно в силу апериодичности восстановления и
леммы 4. Поэтому при любом е>0
е
0(п) = Пт к (г, и)со$пис1и+ \ к{\} и) сов пи Ли.
г А 1 *> . ^
-е е<|и|<я /|2\
Полагая здесь /г = 0, видим; что существует предел
е
/г8 = Пт Г к (г, и)йи
и /г8<О(0). Так как кг убывает при е | 0, то предел
\\ткг = к0 также существует. Следовательно, существует
е-»о
е
Нт Пт | к {г, и) соз пи йи = к.
е-»0 г ^ 1 ^
Возвращаясь к формуле (12), видим, что А(1, и) является
интегрируемой (в смысле Коши) функцией на отрезке
(— зх, л) и л
С(п) = к+ к{\, и) соз пи Ли.
-я
Так как А(1, и) интегрируема, то по теореме Римана -•
Лебега я
Пт й(1, и) соз пи йи = 0.
Таким образом, доказано, что Пт 0(п) = к существует.
5*
132 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Теорема 10. Если восстановление апериодично, то
Нт 0(п) = — } т=Мтк,
причем, если Мтй = оо, то Пт С(п) = 0.
П->оо
Доказательство. Так как предел Нт 0(п) = Н
П->оо
существует в силу предыдущей леммы, то, используя
теорему Абеля о степенных рядах, получим
А = НтМ + %гп[С{п)-С(п- 1)]) =
оо -
= Нт 2 2в(1-2)С(/1) = Пт(1-г)Ф(г),
г^ 1 п=0 г+ I
оо
где Ф (г) = 2 гпС{п)-~ производящая функция последо-
л = 0
вательности {О (я), лг == 0, 1, ...}. Из независимости и
равнораспределенности величин хк следует, что 0(я)_
удовлетворяет уравнению
О (//) = б (/г) + 2 0(п-к)ркУ п>0 (13).
(6(я) = 0 при /г>0^ 6(0)= 1). Умножая это соотношение
на гп и суммируя по всем /г^О, получим
Ф(г)=1+/Чг)Ф(г), 1г|<1.
оо
где Р(г)=^рпгп. Таким образом,
« = 1
Ф(г) = [1-Р(г)Г1
и
Если т~оо, то для любого #>0
Ьт ^ > 1|т 2^ Ря т^Г = 24 Р"п>
* 5) ^ ЦЕПИ МАРКОВА СО СНЕТНЬЩ ЧИСЛОМ СОСТОЯНИЙ 133
откуда следует, что Л = 0. Если же /л<оо, то, учиты-
I 1 — гп |
вая неравенство \ х_х \<п при |г|<1, получим
оо оо
Теорема доказана.
• \ Следствие. Если восстановление имеет период й,
то
Нт С'(/м/) = — , т = Мтл. (14)
Я->оо
Действительно, если данное восстановление
периодично и й — его период, то новое восстановление, в
котором длительность восстановления т'п = ~, является
апериодичным. Если 0(п)~- его функция восстановления,
то О (я) = О (ли). С другой стороны, Мт^*=---^==-у.
Из доказанной теоремы теперь следует (14).
Предельные теоремы для вероятностей перехода.
Теорема 11. Пусть р{п){1, ^ — вероятности перехода
неприводимой возвратной апериодической цепи
Маркова. Обозначим через пг1 среднее число шагов до
первого возвращения в 1-е состояние,
Л=1
Тогда для любого /
Нтр<«>(/,0 = -^-. (15)
1Щ
Доказательство. Пусть т0 — число шагов до
первого возвращения в 1-е состояние, х{ — число шагов
между вторым и первым возвращением в это состояние
ит.д. В силу следствия теоремы 4 величины т0, т,, ...
..., т„, ... взаимно независимы, одинаково
распределены и принимают целые значения, не меньшие единицы,
причем
Р{ч = лн/<«>(/, о, 2Р(», 0-1.
|34 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. П
Математическое ожидание величин тп равно т{.
Рассмотрим процесс восстановления, в котором хп является
длительностью п-го восстановления. Роль величин рп
и С(п) теперь играют 1{-п){1, I) и р{п)(1, ь) соответственно.
Так как цепь апериодическая, то в силу леммы 3
восстановление также апериодично.
Из теоремы 10 следует равенство
Пт/?<«>(/, /) = ~-,
что является частным случаем (15) при / = Л Нетрудно
перейти к общему случаю. Воспользовавшись
формулой (4), получим
п
Замечая, что /=<л) (/, 0 —> 0, 2 /(А) (/, 0 —> 1 при п->оо
(в силу неприводимости и возвратности цепи), и
применяя лемму 1, получим равенство (15) в общем случае.
Доказанную теорему часто называют эргодической
теоремой для цепей Маркова. По поводу эргодических
теорем см. § 8.
Теорема 12. Если неприводимая возвратная цепь
Маркова периодична с периодом й, то
Итр№(1,1)=-±.. (16)
Если К8 — подклассы, введенные в теореме 9 и 1^Кп
/е=Д'5, то
I —, / = 5 — г(тойё),
Нт /><"*+'>(/, /) = 1 "V 1 (17)
п-*°° [ 0, 1Фз-г {той 4).
Доказательство. Из леммы 3 следует, что
период неприводимой цепи Маркова совпадает с
периодом процесса восстановления, введенного при
доказательстве предыдущей теоремы. Поэтому равенство (16)
непосредственно вытекает из следствия теоремы 10.
Из теоремы 9 имеем; р{па+1)(1, /) = 0 при 1^Кп ]'^К3
§5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 135
и, 1Фз — г (той с1). Следовательно, если, например,
Г<8, ТО
Доказательство формулы (17) завершается ссылкой
на лемму 1, точно так же как доказательство
теоремы 11.
Определение 5. Возвратное состояние /
называется нулевым, если Птр(^(/, /) = 0, и
положительным, если Птр^^С/, /)>0.
В возвратном классе состояний все состояния
одновременно либо положительны, либо нулевые.
Действительно, если /«->/, то из неравенства
р(-+-у+')(/, ц>рмИ, 1)Р{паНи /)/'(/, О,
где /я и 5 таковы, что р(т)(/, у)>0, р(5)(/> /)>0,
следует
Пт р{п^ (I, 0 > Нт р<^> (/, /), й = а1 = йу.
Меняя роль *" и /, получим доказательство утверждения.
Полученные результаты можно подытожить
следующим образом.
Теорема 13. к) Чтобы состояние ] было невозврат-
оо
ным, необходимо и достаточно, чтобы 0/;= ^ р(л)(/\ /)<°°-
Яра этом для всех I
оо
Оц = 2 Р(п> («', /') < <?„ < оо, Нт р™ (I, }) = 0.
б) Пусть ] — возвратное состояние с периодом й и
средним временем возвращения Ш;. Если I достижимо
из ], тогда г также возвратное состояние с тем же
периодом й, нулевое или положительное одновременно с /,
и существует такое к, 0^к<3, зависящее только от г
и и что
I при г = к,
Нт/><**+'>(/, }) = { т1 (18)
[ 0 при гщ^к(то&(1).
138
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
в) Если г, ] принадлежат одному и тому же
возвратному классу, то
Последнее утверждение является непосредственным
следствием б). С другой стороны, в отличие от
утверждения б), формула (19) не отражает различия между
апериодическим и периодическим классами состояний.
Условимся называть неприводимую возвратную цепь
Маркова положительной {нулевой), если ее состояния
положительны (нулевые).
Критерии возвратности. Стационарные
распределения. Свойство цепи Маркова быть возвратной
(положительной или нулевой) тесно связано с
нетривиальными решениями линейной однородной системы
2 /?(/, О */ = **. 1^1> (20)
и ей транспонированной
2 р(1, /)*/ = *,, /ее/. (21)
Если система (20) обладает неотрицательным и
суммируемым решением, т. е. х^О, 2**<°°> т0 можно
считать, что 2*1 = 1, и такое решение можно
интерпретировать как инвариантное начальное
распределение, х{ = Р {I (0) = /} = Р {| (1) = /} = ..., порождающее
стационарный марковский процесс. С другой стороны,
существование стационарного марковского процесса
с заданными вероятностями перехода эквивалентно
существованию неотрицательного суммируемого решения
системы (20).
Что же касается транспонированной системы (21),
то существование нетривиального решения х( = с
очевидно. Для возвратной цепи Маркова характерно, что
(21) не имеет других нетривиальных неотрицательных
решений. Более того, имеет место следующая теорема.
Теорема 14. Неприводимия цепь Маркова возвратна
тогда и только тогда, когда система неравенств
2 Р('\ /)*/<**, *'€=/, (22)
§ 5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ {37
не имеет неотрицательных решений, отличных от
решений вида л*; = с, / е /.
Доказательство. Допустим, что цепь возвратна,
^>0 и х1(1^1) образуют решение системы (22).
Выберем произвольное л^>0 (если такого нет, то все ^=0).
Из (22) следует
хь > 2 Р (/, /) 2 р (/, к) хк = 2 Р{2) (*, к) хк,
и по индукции
*/> 2 Р(п)У, к)хк.
к<^1
Для каждого / найдется такое п, что р{п){1, /)>0,
следовательно, ^ > /?(/г) (/, /) л'/ > 0. Итак, х1 > 0 для всех / е /.
X.
Положим У1 = -Л-, где / — произвольно выбранное со-
стояние. Имеем у,->2 р('\ ])У\>Р^, 0+2 р (/, /)///.
Применяя это неравенство к величинам *//, стоящим
в его правой части, получим
&>Р(*\0+2 р(и)р(/,/)+2 2 р('\ /)р(/\ &)</* =
где /р(2) (/, &) = 2 р(/> /)/?(Л ^) есть вероятность, выйдя
}Ф1
из /-го состояния, на втором шаге попасть в к-е
состояние, не заходя при этом в 1-е состояние. Итерируя этот
прием, приходим к неравенству
^>2Т(«, 0+ 2 Л\ к)Ук,
я=1 кф1
где /р(У) (/, &) — вероятность перехода за N шагов из /-го
состояния в &~е, не заходя при этом в 1-е состояние.
•Полагая в последнем неравенстве Л^-хх», получим
т. е. х{ ^ Х(.
Так как / и / — любые, то х1 = Х/ = сопз*, т. е.
система неравенств (22) не имеет неотрицательных
138 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
решений, отличных от х-г — с, /е/, для которых во
всех соотношениях (22) имеет место знак равенства.
Пусть теперь цепь имеет хотя бы одно невозвратное
состояние (сейчас неприводимость цепи не используется).
Положим XI = 1, х1 = Р (I, /) при I ф /, где / — любое
невозвратное состояние. Заметим, что не для всех /,
/ ф /, р(1у /)= 1. Действительно, в противном случа-е
имелибыР(1,1)= 2 р{1, к)Р{к, /) + р(/, /)=Цр(/, к)=\,
кФ1 к&1
что противоречит невозвратности состояния /. Таким
образом, определенные выше неотрицательные числа хь не
все равны между собой. Имеем при / Ф1
Х1 = Р(1, 1)== 2 р(1, к)Р(к, 1)±р(1, /)= 2 Р{1, к)хк
кФ1 /ге=/
И
х1=1>Р(1, 1)= 2р(/, к)хк9
ке=1
т. е. {л;/, 1^1} образуют неотрицательное и отличное
от постоянной решение системы (22). Теорема доказана.
Перейдем к вопросу о связи между существованием
инвариантных начальных распределений и свойствами
возвратности марковской цепи, т. е. к вопросу о
разрешимости системы (20) для возвратной цепи.
Теорема 15. Пусть цепь Маркова неприводима и
возвратна. Система уравнений (20) не может иметь
больше одного решения, удовлетворяющего условиям
2и,|<оо, 2*1 = 1. (23)
Если цепь возвратна и положительна, то решение
системы (20), удовлетворяющее соотношениям (23), имеет
вид
N
x^ = V^= Нт ^ 2 р<п) (/,/). (24)
п = 1
Если же цепь возвратна и нулевая, то единственное
абсолютно суммируемое решение системы (20) тривиально
(*< = 0).
Доказательство. Сначала докажем
единственность решения системы (20) при условиях (23). Пусть
$ 6] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 139
такое решение существует. Умножая (20) на р(1, к) и
суммируя по всем I, получим
** = 2 х(р{19 к) = 2 2 */р(/. 1)р(1, к) =
= 2 */ 2 р(]\ /)р(|, &) = 2 */Р(2)(/\ *).
/е/ /е/ /е/
Перестановка порядка суммирования возможна в силу
абсолютной сходимости соответствующего двойного ряда.
Аналогично получаем
хк= 2^(|, *). (25)
Положим
тогда
хк = 2 .*:/% (/, л).
/е/
Принимая во внимание, что %(/, к)~>т-1 и
абсолютную сходимость ряда 2 */> переходя к пределу в по-
/е/
следнем равенстве, получим
*а= 2//^ = ™-*, (26)
что и доказывает единственность решения системы
(20), (23). Отсюда же вытекает, что если цепь возвратна
и нулевая, то хк = 0 для всех Ае/.
Докажем теперь, что для положительной возвратной
цепи величины (24) образуют требуемое решение
системы (20). Пусть /' — произвольное конечное
подмножество /. Из неравенства р{п+1Цк9 1)^ 2 р{п){к> /)р(/\ 0
получаем
откуда после перехода к пределу при Л/^оо вытекает,
что
я/>2 ^/р(/, *').
/е-/'
140 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Полагая теперь /'->/, получим ю^ 2 V^р(^} 0- Умно-
/е=/
жая последнее неравенство на р(/, к) и суммируя по &,
придём к неравенствам ^^2 ^1р(1у к)^ 2 ^1р{2)(1у к)
и, продолжая этот процесс, к неравенствам х>к ^
^ 2 V^р^п)(^, ^) ПРИ любом п^\. Если бы в послед-
нем соотношении хотя бы при одном к имел место знак
строго неравенства, то мы бы имели:
2 ^>2 V, 2 р{п)(1, *) = 2 ^,
что невозможно. Поэтому
**= 2 я,Р(й,С, А), *б=/, /г =1,2, ... (27)
В частности, величины ю1 образуют решение системы
(20). Из (27) получаем
ък = 2 ^$/У (/, А). (28)
Заметим, что из неравенства 2 Р(п)(*\ &)^1 вытекают
соотношения 2 <% (/, к) ^ 1 и 2 ^к ^ 1 ПРИ любом
конечном /'с:/. Отсюда 2 0*^1. Поэтому в (28)
можно перейти к пределу при АГ->оо, после чего
получим ^=2 ярк* откуда 2 VI =1. Таким образом, ре-
шение VI системы (20) удовлетворяет условиям (23).
Теорема доказана.
Замечание. Если цепь Маркова произвольна,
{хи 1^. /} — абсолютно суммируемое решение системы (20),
к — невозвратное состояние, то хк = 0.
Это утверждение следует из возможности перехода
к пределу при п->оо в. равенстве (25) и из
соотношения Пт р{п)(]\ к) = 0, имеющего место для произвольного
га->оо
невозвратного к.
С л едств и я.
1. Для того чтобы неприводимая цепь Маркова была
положительной возвратной, необходимо и достаточно,
§ 5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЯ {41
чтобы система (20) обладала нетривиальным абсолютно
суммируемым решением {х1у I е /}. При этом х^си^
где с — постоянная, юь > 0.
2. Неприводимая цепь Маркова имеет инвариантное
начальное распределение тогда и только тогда, когда
она положительная возвратная.
3. Если цепь неприводима, положительна и аперио-
дична^то единственное решение системы (20),
удовлетворяющее (23), имеет вид
*, = <^ = Нт р<*>(/, /). (29)
Последнее утверждение вытекает из того, что для
положительной апериодической цепи пределы Пт р{п) (/,«)
существуют, так что (29) следует из (24).
Из предыдущей теоремы-вытекает, что для нулевой
возвратной цепи система, (20) не может иметь
нетривиального абсолютно суммируемого решения. Однако»
она обладает важным неотрицательным несуммируемым
решением. Чтобы получить это решение, введем
вероятности перехода с запрещениями или табу-вероятности.
х Это понятие является обобщением понятия вероятности
первого попадания. Оно уже встречалось при
доказательстве теоремы 14. Табу-вероятность 1Р{п)(1, /) есть
вероятность попасть на п-м шаге в состояние / из
начального состояния I, не посещая при этом в моменты
времени 1, 2, ..., /г—1 состояния /. Таким образом,
/Р(я) (*»/) = 2 . р(1,п)ри1,12)-Р(1п-и1)> п>1-
/р /2« •••• /Я—1,
1г + 1, г=1,..., п-1 ..
Очевидно,
Л\/)=р и, я, ,Р{п\1,})=1{п)а,1).
Положим еще
,/>«»(/,/)=6 (и).
Аналогично вводятся табу-вероятности нр{1' !\ когда
запрещенным является некоторое множество
состояний #. Если запрещены два состояния /, /, то табу-
вероятность {/ /}р(/г)(*\ /) логично обозначить через /(/1)(/,/).
Это есть вероятность, выходя из начального состояния *,
142
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
впервые попасть в состояние / на п-м шаге, не заходя
до этого в состояние /.
Отметим следующие два равенства:
гРМ(*,Л- 2 /" (1,1)**-»(/,/). (30)
,рм (/,})=2 я™ (л о{!-, г)Р(п-к) а, у). (31)
Каждое слагаемое в правой части формулы (30) дает
вероятность попасть из начального состояния / на п-м
шаге в состояние / и впервые в состояние / на к-м
шаге (&^/г), не заходя до п-то шага в состояние /.
Сумма по к этих вероятностей дает левую часть
равенства (30). Слагаемые в правой части (31) имеют
следующий смысл. Они равны вероятности, выйдя из
начального состояния /, не заходя в 1-е состояние до
момента времени п, попасть на п-м шаге в состояние /,
побывав перед этим в последний раз в состоянии / на
к-м шаге (&<]/г). В частности, из формулы (31) следует
(при / = /) „
Г(/, ])=%1Р{к)&1)/п-к)а, 1). (32)
Введем производящие функции
Л/(г) = 2 ФМа,1)гп,
1рц (г) =2 ,!{п)а,1)гп, ,Г (*,/) = о.
л = 0
Правые части равенств (30) и (32) представляют собоц
свертки двух последовательностей, поэтому
1Ри{г) = 1Ри{г)1Ри{х), Ри (г) = /Р„(г)^1/ (*)• (33)
Заметим, что ряды 1рц(г) сходятся при г=1, причем,
если состояния г и / сообщаются, то 1Рц(\)>0. При
этом предположении второе из равенств (33)
показывает, что существует конечный предел ^Рц{2) при г-> 1
и, следовательно, /Р«0)<°°« Положим
оо
,0 (*,/) = 2 ,РМ (/,/). (34)
м=0
$5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 143
Таким образом, если состояния / и / сообщаются, то
'•0(1''/)=-Йлту<0°- (35)
С другой стороны, первое из соотношений (33) дает
10(^/) = Л/(1)^(/\Д
откуда
|С(/, Л<*е(/,/)<оо. (36)
Возвращаясь к решению системы (20), докажем4
следующую теорему.
Теорема 16. Пусть I — произвольное состояние
неприводимой возвратной цепи Маркова. Система (20)
имеет неотрицательное решение
*г=1, х1^1С{1, 0 (гф1) 1е=1.
Доказательство. Положим
«/=1, Щ = ,С(/, О (1,ф1). (37)
Имеем при / ф I
/ е / / Ф I
оо
= р(',0 + 2 2 ,/><">(',/)/>(/, 0 =
•=р{1, о+2 ^"с о=1С(/, /)=«(.
л-1
если же 1 = 1, то
оо оо
2 и,р (/, 0 = р (I, /)+2 /("+0 (/, 0=2 [{п) (I, I) = 1 = и,.
Теорема доказана.
Рассмотрим вопрос о единственности решения
системы уравнений (20), удовлетворяющего условиям
Ы/=1, «^0. С этой целью применим прием,
связанный с введением обращенной цепи Маркова.
Предположим сначала, что цепь положительно
возвратна, и пусть {о/, /ее /}— инвариантное начальное
распределение.
Рассмотрим стационарный марковский процесс,
соответствующий начальному распределению {о/, /е/}.
144 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Вероятностную меру, соответствующую этому
процессу, обозначим через Р*г). Введем условные
вероятности
-Р(в,й(<-1) = Ь1('-2) = Ь ■-., 6(/-/г) = /п1б(0 = Оэ
где 1>п\ имеем
. . ч *1пР 0п> /л-0 Р (/п-1'- /в-2) ' ■ ■ Р (Ь 0 _
<7* VI» /2> • • •» /га) — ~
= 9('> ЛЖ/ь /г).- чИп-и М*
где <?('> /) = /?(/, О-—"-
Таким образом, в стационарной положительно воз*
вратной цепи Маркова условные вероятности перехода,
получаемые при -изменении направления отсчета
времени (от настоящего к прошедшему), также
соответствуют некоторой цепи Маркова. При этом следует
заметить, что все V^>^, и поэтому
Я(*> /)>0, У) ?(/, /) = — Л ъ^Ц, /)с=^-=1.
Аналогичное построение можно осуществить не только
для положительной, но и для произвольной (т. е. и для
нулевой) возвратной цепи. С этой целью возьмем
произвольное положительное решение {х^ /е /} системы (20)
(ниже будет показано, что такое решение существует)
-и положим
яи,!) = р(1, 0--?-. (38)
Так же как и выше,
Цепь Маркова с переходными вероятностями (38)
будем называть обращением исходной цепи {обратной
цепью).
§ 5] ЦЕПИ МАРКОВА СО СЧЕТНЫМ ЧИСЛОМ СОСТОЯНИЙ 145
Отметим формулы для вероятностей перехода-за п
шагов в обращенной цепи. Имеем
Фп) (*\ /) = 2 я (и п) я 0*1, /2) • • • я (и-и /) =
]\, 12, •••» !п_1
= 'Л РЦи 0 Р (/2» 1\) • • • Р (/> /й-1> ~ >
/,. /2, • ••, /„_,
т. е.
Фп)а, /)=-^р(я)(/, о- <зэ)
Отсюда вытекает следующее следствие.
.ЕЪш исходная цепь неприводима, возвратна,
положительная или нулевая, то такой же будет обращенная
цепь.
Из предельной теоремы для отношений в случав
возвратной цепи имеем
2 9(й)<и)
Нт-^ =1.
""*" 2*(й)</.л
Воспользовавшись формулами (39), получим
2 Р(п)(и о
Нга^ = ^- (40)
Следствие из полученного соотношения сформулируем
в виде следующей теоремы.
Теорема 17. Для возвратной цепи неотрицательное
решение системы (20) такое, что хг = 1, единственно. При
этом х{ = х(} (/, 0 и
Нт -^ = 10(1,1). (41)
"*" 2 Л, Л
146
случадньш последовательности [гл. а^
Формула (41) следует из единственности решения
системы (20) и теоремы 16, а единственность — из
формулы (40) в предположении, что л:/>0 для всех /.
Таким образом, в силу теоремы 16 достаточно
показать, что если {х^ / е /} — неотрицательное нетривиаль^
ное решение системы (20), то #;->0. Последнее можно1
получить следующим образом. Для неотрицательного
решения системы (20) имеем
XI = 2 Х1Р (/, 0 = 22 чр (л, /) р (/, /) =
= 2^2р(^ /)р0\ 0 = 2чр{2)(К%
к I к
По индукции легко получить, что х1= 2*/гр(л)(&, 0-
кт
Пусть #/>0, для любого I найдется п такое, что
р{п){1, 0>0, поэтому Х1^Х1р{п)(1, /)>0. Построив для
данного решения системы (20) обращенную цепь и
положив */«=1, из (40) получим единственность х{, /е/.
В силу теоремы 16 л^ = ;(?(/, /).
Замечание. Формула (40) является обобщением
N
соотношения Нт Л/""1 2 Р(п)(/> 0 = у*» гДе {^} —инва-
риантное начальное распределение, имеющего место
для положительной возвратной цепи.
Теорема 17 может» быть усилена.
Теорема 18. Для неприводимой возвратной цепи
Маркова система неравенств
*1> 2 */Р(/\ «), ^>0, *,= 1. (42)
/е=/
ил/еег единственное решение и при этом ** = 2*/р(/\ 0»
В силу теоремы 16 достаточно доказать
единственность решения системы (42). Введем обращенную
марковскую цепь с вероятностями перехода Ц^,])^
^РО'эО > гДе Щ~~ положительное решение системы
и1
(20). Она будет неприводимой и возвратной. Имеем
'С! Х{ \^ X; X: X,
I * I * * '
-^ = 1.
$$ СЛУЧАЙНЫЕ БЛУЖДАНИЯ НА РЕШЕТКЕ 147
Но в силу теоремы 14 система неравенств
имеет единственное неотрицательное решение #,- = 1.
Следовательно, хь = и{ для всех /е /. Теорема доказана,
§ 6. Случайные блуждания на решетке
Неприводимость. Определение 1. Множество 2
5
векторов 2 = 2а^, где еь (/=1, ..., 5) —линейно не-
1 = 1
зависимые векторы из Мт, аь — целые числа (а,==0
±1, ±2, ...) называется решеткой.
Очевидно, что 2 есть минимальная аддитивная группа,
содержащая векторы еь е2, ..., е8. Число 5 будем
называть размерностью решетки, а векторы еи еъ ..., е3
ее базисом. Если 8<ш, решетка называется
вырожденной, при 5 = ш — невырожденной.
Случайное блуждание {^(/г), /г = 0, 1, 2, ...} на
решетке 2 определяется формулой I (п) = х + ^ -I- ... + 1п,
п^1, ?(0) = х9 где л: — неслучайный вектор — начальное
положение случайного блуждания, хе2, а |ь |2, .. •
.. • > ^п> • • • ~ одинаково распределенные независимые
случайные векторы со значениями из 2. Положим р{х) =»
= РИь — *}» х^ 2. Если ^62 (/г == 0, 1, ..., я), то по
определению случайного блуждания
Р{С(0) = *о, ?(1) = *ь ..., С(яН**Н
Таким образом, случайное блуждание на решетке
является частным случаем однородной цепи Маркова
со счетным числом состояний, с вероятностями
перехода за один шаг р(х, у) = р(у~ х). Основная
специфическая особенность случайных блужданий,
выделяющая их из общих цепей Маркова со счетным числом
состояний, состоит в пространственной однородности
вероятностей перехода:
Р {х + г, у + г) = р (х, у) = р (у - х).
148 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Это свойство является лишь иным выражением
независимости вектора смещения блуждания |я+1 =
= ^{п+ 1) — &{п) от положения блуждания в данный
момент. Разумеется, пространственная однородность
имеет место и для вероятностей перехода за п шагов:
рЫ (х + г, у + г) = Р {I (п) = у + г \ I (0) - х + г) =
-РК(л)-С(0) = ^-^1С(0) = д:} = рГлЧу-х),
где р{п) (х) = Р {^ + 12 + ••• ~Ь 1п = х) ~" вероятность того,
что сумма ах независимых одинаково распределенных
случайных векторов примет значение х.
Из пространственной однородности блуждания
вытекает, что множество Кх всех точек 2; достижимых
из данной точки х9 можно представить, в виде Ко + х,
где /Со — множество точек, достижимых из 0 (0е/С0).
Чтобы описать множество /С0, введем множество О
всех тех х е 2, для которых р (х) > 0. Множество й
называют носителем распределения случайных
векторов !•*. За один шаг из нуля достижимы только точки
из О. За два шага из нуля достижимы те и только те
точки,2, которые могут быть записаны в виде х = Х1 + х29
где х^й. Пусть Я+ обозначет совокупность всех
точек Жт вида х = п1х1 + .. . + п8х8, где $ ^ 0 и /г*
(к = 1, ..., 5) — произвольные положительные целые
числа и л'& ей. Очевидно, что
т. е. Я+ есть множество всех точек, достижимых из нуля.
Две точки х и у из 2 называются сообщающимися,
если х~у^Н+ и у — х^ Н+. Положим
я. = я+П{-#+}.
Описанное в § 5 разложение на классы сообщающихся
состояний в данном случае состоит в следующем: Я* —это
к.1асс состояний, содержащий точку нуль, все
остальные классы сообщающихся состояний имеют вид Нк =*
= хк + Я,, где хЛ — произвольная последовательность
из 2 такая, что хк — Х/ёЯ, {к Ф ]).
Из пространственной однородности случайного
блуждания вытекает, что различные классы сообщающихся
состояний существенны или несущественны
одновременно, так что свойство существенности или несуще-
§6] СЛУЧАЙНЫЕ БЛУЖДАНИЯ НА РЕЩЕТКЕ 149
ственности относится ко всему случайному блужданию
в целом.
Условие существенности эквивалентно требованию
#+ = { — Я+}, но это означает, что Н+ является группой.
Таким образом, чтобы состояния случайного
блуждания были существенными, необходимо и достаточно/
чтобы подмножество Я+ точек 2 было группой.
Следует отметить, что для изучения случайных
блужданий разбиение на классы сообщающихся состояний
и изучение поведения блуждания внутри этого класса
не является характерным.
Введем множество Я точек 2, представимых в виде
2 = х — уу где ху у<^Н+. Оно является .минимальной
группой, содержащей тачки 2Е2, достижимые из нуля.
Будет показано, -что Я есть решетка в Ж*1 (возможно,
меньшей размерности). Отсюда вытекает, что при
изучении случайных блужданий можно ограничиться
предположением, что Я совпадает с решеткой 2 всех
векторов с целочисленными координатами пространства Ж\
Обозначим решетку всех целочисленных векторов
пространства Жт через 2,т.
Теорема, о которой идет речь, носит чисто
алгебраический характер и может быть сформулирована
следующим образом.
Теорема 1. г-мерная аддитивная группа Я (Я с: 2т)
векторов линейного пространства Ж71 является г-мерной
решеткой.
Доказательство. Пусть г — максимальное число
линейно независимых векторов в Я. Докажем, что
существует г линейно независимых векторов хк е Я таких,
что Я совпадает с множеством векторов вида аххх -г
+ а2х2+ ... Л-атхт, где ак — произвольные целые числа
(ал*=0, ±1, ±2, ...,/г= 1, 2, ..., г). Пусть**, **, ...,*;.-
произвольная максимальная система линейно
независимых векторов из Я. Тогда каждый вектор х^Н
представим в виде г
где ^ — действительные числа. С другой стороны,
х\ = 21 сщер где ск} — целые и ранг матрицы \ск^ равен г.
|5Э СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Представление (1) эквивалентно системе линейных урав-
г
нений 2 Ьксм = а/, / = 1, 2, ..., т, где аь — целочис-
ленные координаты х в базисе {еку к=1, ..., т}.
Отсюда вытекает, что при 0^&й< 1 может существо?
вать только конечное число векторов вида (1), причем
числа Ък рациональны. Поэтому, если В — наименьший
общий знаменатель всех Ь'к, то представление (1) может
быть записано в виде
-2
скУк> Ук~~^
к~\
где ск — целые. Рассмотрим теперь произвольное линей-
г
ное преобразование 2*=2#л/#/ (к = \у ••-, г) с цело-
/ = 1
численными координатами и определитель
У{ги г2, ..., гг) =
П21
П2г
П
(2)
состоящий из координат векторов ги ..., гг в базисе
{#/» У— 1> • • •» г)- Он принимает целочисленные значения
и отличен от нуля тогда и только тогда, когда система
векторов ги ..., гг линейно независима. Выберем
систему векторов ги
гг так, чтобы гк е Я и
определитель (2) принял наименьшее положительное значение.
Такая система существует. Соответствующие векторы
обозначим через 1Ь ..., /г. Если бы при некотором х е Я
г
в разложении х = 2 Лк1к не все числа ^ были целыми,
то существовал бы вектор ГеЯ такой, что ^ = 2^#
0^й^<1 и б^. >0 при некотором /. При этом
г (/(, . . . , //-1, / , У/ + 1, . ♦ . , 1Г) ~
-у(/„..../,_,.^,,//+....../г)-
что противоречит минимальности определителя V {1и..., /г).
$6] СЛУЧАЙНЫЕ БЛУЖДАНИЯ НА РЕШЕТКЕ [51
Таким образом, решетка, для которой система
векторов {/ь ..., /г} является базисом, совпадает с Я.
Теорема доказана.
Определение 2. Случайное блуждание, заданное
на целочисленной решетке 2т, называется
неприводимым, если Н = 2т, и приводимым, если Н ф2т.
Следует обратить внимание на то, что введенное
понятие неприводимости случайного блуждания не
связано с определением неприводимости марковской цепи.
Предыдущая теорема показывает, что с помощью
аффинного преобразования пространства всегда можно
добиться, чтобы /п-мерное случайное блуждание
оказалось т-мерным неприводимым.
С помощью характеристических функций можно дать
следующий критерий неприводимости случайного
блуждания. Пусть
/ (и) = Ме'<«• Ь> = 2 р(х)е1&>* (3)
— характеристическая функция вектора ^ = ^ (1) — 2;
(Сводного шага случайного блуждания.
Теорема 2. Для неприводимости случайного
блуждания не'обходимо и достаточно, чтобы ] (и) ф 1 при
и ф 2лх, х е 2т.
Доказательство. Достаточность. Пусть
блуждание приводимо. Если размерность Я меньше ш,
то существует вектор е, ортогональный Я, так что
(се, 1{) = 0 с вероятностью 1 при любом с и условце
теоремы не выполнено. Допустим теперь, что
размерность Я равна т. Выберем в Я базис 1и ..., /т, и пусть
Г —линейное преобразование, переводящее базис {ек9
к = 1, ..., т) в {1к, к = 1, ..., ш}, 1к = Тек. Матрица
преобразования Т в базисе {ек, /г=1, ..., пг} состоит из
координат векторов 1к и является поэтому
целочисленной. Ее определитель, однако, отличен от ±1.
Действительно, в противном случае обратное
преобразование Т~1 тоже было бы целочисленным и каждая точка
из 2т была бы точкой из Я, что противоречит
приводимости блуждания. Рассмотрим множество 2' всех
векторов V е Жт таких, что Т*ю е 2т, где Г* —
преобразование, сопряженное с Г. Очевидно, что 2' —
аддитивная группа и 2тс:2'. С другой стороны, 1' Ф2т, так
132 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ Ч[ГЛ, II
как в противном случае целочисленное
преобразование V имело бы целочисленное обратное, что
противоречит соотношениям
1 = ОеЦгУ-"1) = Ре! (Г) Ое1(Г*~')>
так как Ое1 (Т)ф ± 1. Поэтому существует такой вектор о,
что об2', неЛ ГоеГ. Следовательно, число
(V, ек) = (V, Тек) = (Г*а, <?&) — целое при любом к и
поэтому (а, |0 с вероятностью 1 целое, так что 7(2яу) =
*= Мехр{2ш(а, |1)}= I при юШ1т. Достаточность
условия теоремы доказана.
Необходимость. Пусть блуждание неприводимо
и / (2яа) = 1. Тогда М [1 — ехр {2т (а, ^)}] = 0, что
возможно только тогда, когда (о, ^) с вероятностью
1— целое число. Из неприводимости блуждания сле-
дует? что (о, ек) будет целым (6=1, 2, ..., т), т. е.
V е 2т. Теорема доказана.
Возвратные блуждания. Пусть /(5 (л:, у) — вероятность
того, что случайное блуждание с начальным
состоянием х впервые окажется в состоянии у в момент
времени 5 и Р(х, #)=-2/(5)(*, У)-
5=1
Из соотношения (4) § 5
/<"> (х, у) = Р(п) (х, у) - ^ Р> (х, у) /><«-*> {у, у)
5=1
и пространственной однородности случайного блуждания
вытекает, что
р {Ху у) = /01) (0, у-Х) = р»(у-х),
а предыдущее равенство может быть переписано в виде
/1-1
/<«) (х) = р(»> (х) - 2 /(5) (*) р(*~5) (0).
5=1
'Функция Р{х, у) также зависит только от разности у — х,
и можно положить Р (у, у + х) = Р (х). В частности,
Р(х, х) = Р(0, 0), так что все состояния случайного блу-
•■ждания одновременно либо возвратны, либо
невозвратны. Поэтому в дальнейшем мы будем говорить
о возвратном или невозвратном случайном блуждании.
§6]
СЛУЧАЙНЫЕ БЛУЖДАНИЯ ПА РЕШЕТКЕ
153
Пусть
оо оо
Рх (г) = 2 /<га) (х) г\ Рх (г) = 2 />"•> (х) г".
Функции -Рх (г) и Р*(г) связаны между собою
соотношениями (см. § 5, (6))
Ро(г) = (1-Р0{г)Г1, Рх{г) = Ро(г)Рх(г), (хФО),
откуда вытекает утверждение:
для возвратности случайного блуждания необходимо
оо
и достаточно, чтобы О(0)= 2 р{п)(0) = оо.
/1 = 0
Напомним, что в- силу результатов § 5, если
блуждание возвратно, то возвращение в начальное состояние
в течение неограниченного промежутка времени с
вероятностью 1 происходит бесконечно много раз.
Соотношение (10) § 5 принимает вид
2 р(п)м
Р{х)= Пт *=± . (4)
/1*0
Поэтому, если состояние х достижимо из нуля .и
блуждание возвратно, то О(х)==ооу где
оо
л=0
Если же блуждание невозвратно, то
С(*)<С(0)< оо.
.Функция О (х) имеет следующий
теоретико-вероятностный смысл. Она равна среднему значению
(математическому ожиданию) числа посещений состояния х за
промежуток времени (0, оо) блужданием, начавшемся
в точке 0. Для возвратного блуждания С (х) равна или 0
или оо. В невозвратном случае О(х) называют функцией
Грина случайного блуждания.
Из усиленного закона больших чисел (§ 3) весьма
Просто вытекает следующий признак невозвратности
случайного блуждания:
Ш4
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[гл. и
Пусть математическое ожидание одного шага
случайного блуждания конечно и отлично от нуля. Тогда
блуждание невозвратно.
Действительно, с вероятностью 1
П->оо П
Поэтому почти для всех со найдется такое п0 = п0(а>)^
что 11(п) |>-™^-/г при п^пд, так что, начиная с момента
времени /г0 возвращение в точку 0 невозможно.
Ряд других критериев возвратности и невозвратности
можно получить, используя характеристическую
функцию ]{и) одного шага случайного блуждания. Нетрудно
видеть, что
О (0) ^ Пт^ ] Яе(I ~ и (и)Г]с1и9 (5)
где т — размерность решетки, С —куб в Жт, С =
= {и: | и1 |<я, *= 1, ..., п}, 0<1<1. Действительно,
во-первых,
оо
С(0) = Нт 2 Рп(0)е.
С другой стороны, выражение (3) для
характеристической функции случайного блуждания показывает,
что р(х) являются коэффициентами Фурье разложения
} (и) в ряд Фурье. Поэтому
с
и
р(п) <*> = Т2^г !]п {и) е~1 ("'х) йи' (6)
с
так что при 0</< 1
с
Поскольку Я0(/) вещественна, можно заменить
подынтегральное выражение в последнем интеграле его
вещественной частью. Предельный переход при /~>1
§6] СЛУЧАЙНЫЕ БЛУЖДАНИЯ НА РЕШЕТКЕ 1&5
приводит к формуле (5). Если положить ]с (и) = Ке / (и),
то формулу (5) можно записать в виде
Используя эту формулу, можно получить ряд частных
критериев возвратности. Докажем, что одномерное
случайное блуждание, для которого т = М|1 = 0, возвратно.
Действительно,
1 - / (и) п п
> /п == 0 при и —>0.
Поэтому, каково бы ни былое>0, найдется такое б>0,
что | 1 — /{и) Кги при | и |<6. Следовательно,
б
0 (°> > |^ Ь ) 2 [(1-<)» + | 1-1 (и) \Ц Ли >
б
откуда О(0)=оо, что и требовалось доказать.
Чтобы получить аналогичные результаты для
многомерных блужданий, понадобятся некоторые оценки для
характеристических функций.
Лемма 1. Для неприводимого случайного
блуждания размерности тп^2 существует такая постоянная к,
что
1-1с(и)>к\и\2
для и^С, где С —куб, С = {и: тах |м*|^я}.
Доказательство. Так как
\ — 1с{и) = 2 [1—соз(^, х)]р(х)
и
1-соз(и, х) = 2зт2^^>2^--Ш-) =* •&•{**, х)2
при | {и, я) |< я, то
1~1с{и)>~ 2' (и, *)2 Р (*) •
156 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
где 2'означает суммирование по л;<=2т,
удовлетворяющим условию | (и, л;)|^я. Так как блуждание
неприводимо, то в множестве {х: р(х)>0} можно выбрать
базис в &Г\ Пусть {еи ..., ет} — векторы этого базиса.
и УУ = тах{| ек |, к = 1, 2, ..., га}. Пусть далее |и|*^
^яЛГ*1; тогда
т
1 - ]с (и) > -^2 (//, ек)2 р {ек).
Квадратическая форма, стоящая в правой части
неравенства, положительно определенная. Поэтому суще-
га
ствует константа кх такая, что ^ (и, ек)2р{ек)^ кх\ и\2.
Таким образом,
1-1с(и)>^к1\и? при иКяЛГ1.
В силу теоремы 2 § 1 в области С{ = С\ {и: \ и \<лN~>}
] (и) отлично от единицы, и поэтому пип [1 — 1с(и)] =*
= к2> 0. Но тогда 1 — 1с(и)^ &2(]/гая) | и р при | и | ^
^яЛ/""1, и^С. Утверждение доказано.
Возвратимся к вопросу о возвратности случайных
блужданий. Предположим, что двумерное случайное
блуждание неприводимо, М^ = 0 и М | ^х [2 < оо. В силу
леммы Фату
,. Г \ — Ис(и) , ^. Г 1 — 1С (и) < /Г7Х
щ ,) \1-11{и)\2 ^ ^ | 1 -/(н)|2
Из леммы 1 следует, что 1 — ]с{и)^ к\ и |2, и^С.
С другой стороны, так как ^ обладает конечными
моментами второго порядка,
Ш=1-|М(^, и)2 + о(\и\2).
Следовательно, в некоторой окрестности точки и — О
| I — I (и)\^кх\и\2. Поэтому подынтегральное выражение
в правой части неравенства (7) не меньше , , ',4 ~ . .2'
в некоторой окрестности точки м = 0 и соответствующий.
%П
ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
157
интеграл расходится. Таким образом, рассматриваемое
блуждание возвратно. Что касается случайного
блуждания размерности ^3, то оно всегда невозвратно.
Действительно, так как
г .. Г \—Ис(и)л^\* Г Ли ^ Г йи
/= 1ГП т-; гД \ ,2 Ш/< 1ГП п ГТ-Г-Г^ 11 Г~ГТ >
то, воспользовавшись леммой 1, получим
7^ \ Т|7р
с
причем последний интеграл сходится, если размерность
пространства т^З. Полученные результаты можно
подытожить Следующим образом.
Теорема 3. Случайное блуждание размерности т^З
всегда невозвратно. Оно невозвратно также, если
существует М^ и М^ Ф 0. Если \А\Х = 0, то в одномерном
случае, а при дополнительном предположении, что
М|^ |2<оо, и в двумерном случае случайное блуждание
возвратно.
§ 7. Локальные предельные теоремы для решетчатых
блужданий
В настоящем параграфе рассматривается
асимптотическое поведение при п->оо вероятности р{п)(х)
попадания случайного блуждания в точку решетки х за п
шагов. С аналитической точки зрения задача состоит
в изучении - асимптотического поведения интеграла
(см. § 6, (6))
Р(пЧх)--~уп \[1(и)]пе-^"-^с1и (Г);
С
при п->оо. Рассматриваются только неприводимые
блуждания. Более того, предполагается, что блуждание
обладает свойством, которое назовем полной
неприводимостью.
Определение 1. Неприводимое блуждание
называется вполне неприводимым, если для любой точки х^О
случайное блуждание, у которого один шаг блуждания
;%^=^1 — х0у также неприводимо.
158
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
С помощью теоремы 2 § 6 легко дать критерий
полной неприводимости случайного блуждания.
Теорема 1. Для того чтобы блуждание было вполне
неприводимым, необходимо и достаточно, чтобы
\1{и)\Ф 1, если и ф 2лх, х е 2т.
Доказательство. Пусть блуждание вполне непри-
водимо и / (и) = еи, I — действительное число. Из равенств
2 еЧ*-и)р(х) = е", 2 Р(х)=1
х^гт х^гт
следует, что (х> и) = 1 + 2яп, п = п(х) для каждого х,
для которого р(х)>0 (хей), Пусть х0е^О; тогда
1 = 2 р{х) е1 <*-*•■ м>«
*е=2"
- 2 р{х + Хо)еЧ*-и)= 2 д(х)е1<х'и\
где ^(х) — распределение случайного вектора г\{ = ^ — х0.
Из неприводимости блуждания с шагом г^ и теоремы 2 § 6
следует, что последнее соотношение возможно только
тогда, когда и = 2пх, х е 2т. С другой стороны, пусть
1(щ) = еи при щ Ф 2пх (л;<=.2т). Из сказанного выше
вытекает, что блуждание с распределением первого
шага д(х) будет приводимым. Теорема доказана.
Перейдем к оценке интеграла (1). Прежде всего
преобразуем его, положив
х = па + Уп хп> а = М|ь х е 2т.
Тогда
р<п) (х) =
1
(2я)тпт/2
Уп С
1\'Ш-"Ш
хп)Ли, (2)
где У я С обозначает куб {«: \и3' \< Упл, /=1,2, ,.., т}.
Предположим, что |, обладает конечным моментом
порядка г+ 2, г>0. Разлагая е1{ц*х) по формуле
Тейлора, получим для ] {и) следующее соотношение:
1(и)^1 + 1А1(и) + РА2(и)+...+1г+2Аг+2(и) + о{\^\г+2), (3>
§п
ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
159
где Ак (&) — однородная форма от и степени к, причем
А1(и) = М(иЛ1), А2(и) = ±М(щ^.
Отсюда следует, что в некоторой окрестности точки и = О
можно определить однозначную непрерывную
функцию \п!(и) и
1п / (и) = 13х (и) + /252 (и) + ... + 1г+2Зг+2 (и) + о(\и |г+2).
Здесь 5& (и) — также однородные формы от и степени к,
5, (и) = А{ (и) = М (и, Ьх) = (и, а),
32(и) = ^0(и911)=^(Ви9и)9
В —дисперсионная матрица вектора ^.
Таким образом, положив 1Х (и) = 1{и)е~1 ("» а), получим
где
Так как
/-о
и /п+1 = 0( "—1) в области \и\^к\пп, то
\ У пг+1 )
У «Г Упг+Ч \Упг+Ч
где ($пг (и) — некоторый многочлен от и фиксированной
степени, коэффициенты которого остаются
ограниченными при /г->оо, /у(и) — многочлены от и степени 3/.
Обозначим через й) операцию ^-кратного частного
дифференцирования по и!. Заметим, что соотношение (3)
160
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ |ГЛ. И
можно дифференцировать не менее г + 2 раз, в том
смысле, что
= вЧрЪ ... ^ (2/Л («)) + о (| и Г2""),
где р^ кх-\- к2-\- ... 4-&5. Отсюда вытекает, что
аналогичное утверждение имеет место и для \х\]{и). Исходя
из этого, можно убедиться, что и соотношение (4)
допускает почленное дифференцирование по и, так что
1 , 0*(и)\ /1пЭг+3п\
... +——1г(и)+ "111+0- , (5)
Упг Упг+Ч V У1^Ч Х '
где
г><р) = д*;г>*22 .../)*;, *, + кг + ... + к, < г + 2.
Дерейдем к оценке интеграла
Уп С
.в».т-(|+^г,,(11)+...+7!:,«,(«))
*/и.
Чтобы ее получить, понадобятся некоторые неравенства
для функции 1(и). Из неприводимости блуждания и
конечности моментов второго порядка следует (см. §^ 6),
что существует такое 6>0, что при \и\<6
\1(и)\<1-\(Ви, и),
а так как распределение ^ невырождено, то I/(«)[<
< 1 — с\ и \2<е~с {и]2 при |«|<в,, где с — некоторая
постоянная. С другой стороны, из полной
неприводимости блуждания следует, что | I(и) 1^1— р,при \и\^Ь9
и&С, где 0<р<1. Эти две оценки для ](и) можн®
объединить в одну:
| / (и) | < ре~с I«I2 + 1 - р, «ЕС, <6)
Та же самая оценка применима и к 1Х (и).
$7}
ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
№
Возвратимся к величине /. Имеем
/</,+/2 + /з,
/, „ / I о"";? (-^) - №-? * "2 »-•»/, („)
Й?Н,
Й?Ы,
|(р)л-1(Вя. и) \Л
ГГ'е
%п~к\(и)
Вп={и: \и\^Ук\пп}{]{УпС),
В*п = [и: | и \ > У к 1п п} Л (Ул С).
Из (5) следует, что
/.<
м^шмт^-
Учитывая равномерную ограниченность коэффициентов
многочлена ()пг(х) как функций от п и сходимость
интегралов
Г г» / —п(Ви, и) '
\ Р{и) е 1 аи для любого многочлена Р{и),
&п
получим
Далее,
^ са(|«1>К^)
Выражение /)(р)/?(и) представляет собой некоторый
многочлен от /, (и) и частных производных /2 (//), при-
6 И И. Гихман, А. В, Скороход
162
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. П
чем 1{(и) входит в этот многочлен в степенях не ниже
п — ру частные производные от 1{ (и) имеют порядок не
более р^г + 2 и встречаются в степенях не выше р,
наконец, коэффициенты этого многочлена имеют
порядок пр. Поэтому
\0{Р)Я(и)\<Ап°\11(и)Гр,
где А не зависит от п. Следовательно из (6) вытекает
т I I ск 1п п \\П~Р Г
/2< V 2 и+ри п - ч) ^ ^<
С
:(2л)т/2Ап
(ск 1п п \
рск-р——
Поэтому независимо от п можно выбрать такое к, что
Остается оценить величину /3. Имеем
13= ^е~^{Ва'и)\ЯпгР(и)\аи<
— 4- ск 1п г
П \е-*с^1'\С1пгр(и)\аи,
где ()пгр — некоторый многочлен, степень которого
зависит только от г и р, а коэффициенты еще и от я, но
остаются ограниченными при #->оо. Из сходимости
интеграла в правой части последнего неравенства снова
следует, что можно подобрать к так, чтобы
/з=о(^г).
Итак, доказано, что при подходящем выборе к
/ =
-оЩ. (7)
§71
ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
163
Рассмотрим теперь интеграл
1 г
I = | е-1 <«. х)0(р)е~(в"' и) 2 п-№1к до ^
При г = 0, р = 0 этот интеграл представляет собой пре*
образование Фурье характеристической функции т-мер-
ного нормального распределения. Таким образом,
е
1 , . т 1
ът
1
где | В | — определитель матрицы В, В" —ее обратная
матрица. В этой формуле возможно неограниченное
дифференцирование по х, причем в левой части равенства
это дифференцирование можно производить под знаком
интеграла. Поэтому для произвольного многочлена Р{и)
/ Р(и)е~Ни'Х)^т' и) аи^2пГ2У11Ге^{В^ %х)9
где 0,{х) — многочлен от х той же степени, что и много*
член Р. Далее с помощью интегрирования по частям
получаем
/ в-«**> /)<» И (Ва'и)р(«))^=
если /)(р) = г г г—. Таким образом,
40»-'*.^.
I = (ис1р (1х2р ... (1хт)к>* (2я)2 V | В Г1 в"2 *' X
А-0
где (2Й (х) — многочлены той же степени, что и /^(и),
т. е. степени Ък и Со(#) = 1.
164
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
Теперь осталось совсем немного, чтобы получить
следующую теорему.
Теорема 2. Пусть %(п) — вполне неприводимое
блуждание, ^(п) = !■, +^2+ ••• + !«> где |^ — взаимно
независимые и одинаково распределенные векторы со
значениями в 2,т, с конечными моментами порядка г + 2,
г^О. Тогда
п 2 Р'{$ (/г) = па + V/г *л}
где равномерно по хп
в„ =
(1+|^Г2)°(^2)'
а — вектор среднего значения одного шага случайного
блуждания, В — его корреляционная матрица.
Действительно, имеем
(2я /лГ)т (/х1)*1 (*х2)*2 ... (1хт)ктр<п> (х) -
УгГс
= [ в-' («• -.)^>[в-7 <*«• ■> ^ -^-1 л+/4+/„
где
7, _ { .- С «.)„« [Л Ш - .-Т* - 2 <$>-1 „и.
Но из неравенства (7) следует, что
§8!
ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
1«*
Кроме того,
|/51< /
&т \ УпС
<е 4 ^ е 4 Н{и)йиу
где К(и) — некоторый многочлен, поэтому | /51 = 0(рЛ) =
= о(я~А) \р«= е *) при любом к. Таким образом, для
любого многочлена Р(х) степени не выше г + 2
(2п1М> (*„)/,<">(*„) =
Разумеется, второе слагаемое в правой части
последней формулы зависит от выбора Р(х). Положим Р(х)=*
т
= 1 + ттП 2 I х* Г+2. Учитывая, что Р(х) можно заме-
нить функцией, принимающей меньшие значения, и что
ш
шгП 2 I х* (+2^\ * Г+2, получим доказываемое.
§ 8. Эргодические теоремы
Преобразования, сохраняющие меру.
Определение 1. Случайный процесс {|(0, ^ЕП со значениями
в измеримом пространстве {$?, 23} называется
стационарным, если для любых я, ^, /2> • • •> ^« и * таких, что
^к + ^^Т (&= 1, ..., /г), совместное распределение
в {$/", 93"} последовательности
6(^1 + 0, 102 + 0, •••> 1('я + 0
не зависит от I.
Определение стационарного процесса эквивалентно
следующему: для произвольной ограниченной
^-измеримой функции }(хь х2, ...У хп), хк$=:с%?,
математическое ожидание
М/(б(/, + 0, 6(<2 + 0, •••> Е('» + 0)
п
(р)
~ (Ви, и)
2
* = 0
Зи<;
166
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. И
не зависит от I при любых п, /},..., /„, (4 + /6Г).
Отсюда вытекает, что если к(х{, ..., хп) — измеримое
отображение {^а, »Я}-*{<У, 6}, то т|(*) = й(&01 + О, •••
• ••> 5(^л + 0) является стационарным процессом на
множестве значений I, на котором ч\{1) определено.
В настоящем параграфе рассматриваются
стационарные последовательности, т. е. стационарные
процессы, определенные на множестве Г = {^: ^ = 0, ± 1,
±2, ...} со значениями в {<й/, Щ.
Пусть $вт обозначает пространство всех
последовательностей и = {..., х..ПУ *_„+,, ..., х0, хи ..., хП9 ...},
6 — минимальная ст-алгебра, содержащая все
цилиндрические множества $вт, Р| — мера, индуцируемая на К
последовательностью {|(0, 1^Т). Таким образом,
вероятностное пространство {35т, 6, Р|} является
естественным представлением процесса {^(0, 1^Т). Через
{й/г, 6, Р|} обозначим пространство с пополненной ме^
рой. В 36т введем операцию сдвига времени 5: и' = Зи,
если х'п = Хп+\, пе^Т, где и = {хп, /ге^ Г}, и' = {Хп\ п^Т}.
Операция 5 имеет обратную 5"1, причем если и" = 8~хи>
то ы" = {.*:«, «еГ}, л^«,гп-1. Условие стационарности
последовательности |(/) означает, что для
произвольного цилиндрического множества С
Рб(С) = Рб(5С)- (1)
Поскольку мера на цилиндрических множествах
однозначно определяет меру на 6 и на ее пополнении й,
то равенство (1) сохраняется для произвольного Ле1,
РбИ) = Р*(5Л), Ле1 (2)
Определение 2. Пусть {'З/, §, |я} — некоторое
пространство с мерой, 5 —измеримое отображение {41, 3}
в [41, §}• Преобразование 5 называется сохраняющим
меру, если для любого ЛеЗ
где 5~ Л — полный прообраз множества Л.
Преобразование 5 называется обратимым, если
существует такое измеримое преобразование 5""1, что
§8] ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ 167
55" = 5~5 = /, / — тождественное преобразование.
В этом случае преобразование 5"1 называется
обратным к 5. Определение стационарной
последовательности эквивалентно следующему: последовательность
{1У), /еГ} стационарна, если оператор сдвига
времени 5 в <^г сохраняет меру Р^.
Таким образом, задача изучения стационарных
последовательностей является частным случаем задачи
изучения сохраняющих меру обратимых
преобразований (автоморфизмов) некоторого пространства с мерой.
Рассмотрим вопрос об асимптотическом поведении
среднего
п~\
±^1(3*11), П-^ОО, (3)
& = 0
где 8к — к-я степень преобразования 5, /(и)
—произвольная ^-измеримая функция, {ф/, §, ^—некоторое
пространство с мерой \х и {а(^/)^оо. Чтобы понять
смысл этой задачи, рассмотрим тот случай, когда
Щ, 8» и) совпадает с {$т, б, Р^}, а 5 — оператор сдвига
времени. Пусть |й = |(&, и) = хк, }{и) = %в(хо), где %в(х)-
индикатор множества В е 23. Тогда
[(8ки) = %в(8ки) = хв(Ш)
и
^'«5»«)-^, (4)
где уп{В, и) есть число членов последовательности %(0),
|(1), ..., ^(/г — 1), значения которых попадают в
множество В, т. е. Vп(Ву и) есть частота попадания в
множество В первых п членов последовательности 1(1)
(/ = 0, 1, ..., /г— 1). Таким образом, поставленный
вопрос, в частности, является вопросом о поведении
частоты попадания значения случайной величины |(/)
..В произвольное множество В. Докажем прежде всего,
что предел при п-»оо средней (3) существует с
вероятностью 1. Это предложение составляет содержание
известной теоремы Биркхофа —Хинчина.
168
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ, II
Лемма 1. Если 8 сохраняет меру \ху Ое5 н
/ {и) — Ъ-измеримая неотрицательная {^-интегрируемая)
функция, то
\ !(3и))х(аи)= \ !(и)\к(йи). (5)
Если положить [(и) = %Л(и), то формула (5) перейдет
в равенство м- (5""1 (Л П О)) = ^(А П Щ> что верно для
любых Ли Ь е §. Отсюда следует, что формула (5)
верна для произвольных ^-измеримых неотрицательных
и ^-интегрируемых функций.
Следующая лемма носит элементарный
арифметический характер. Пусть аь а2, ..., ап —
последовательность действительных чисел, р~- целое число. Назовем
член последовательности ак р-отмечеиным, если в
последовательности сумм
ак> ак + ак + Ъ ?••> ак + <*к + \ + ••• +ак+р-1
по крайней мере одна неотрицательна (ак 1-отмечен
тогда и только тогда, когда он неотрицателен).
Лемма 2. Сумма всех р-отмеченных элементов
неотрицательна.
Пусть ■ щх — р-отмеченный элемент последователь*
ности с наименьшим номером и а^ + а^+1 + ... + а*,+г
(г ^ р — 1) — неотрицательная сумма с наименьшим
числом слагаемых. При Н<г а^ +а^,-и + .• • • +#&1+&<0,
следовательно, ак{+н+1 + • •• + #й,+г^0, т. е. все члены
последовательности а*„ а*, + 1, ..., а&1+г р-отмечены и их
сумма неотрицательна. Можно продолжить это
рассуждение, рассматривая последовательность, начиная
с члена аьх+г+\. Таким образом, вся последовательность
разбивается на части, каждая из которых кончается
группой р-отмеченных членов, и сумма р-отмеченных
элементов каждой части неотрицательна. Множество
р-отмеченных элементов всей последовательности
совпадает с суммой множеств р-отмеченных элементов
таких ее частей, что и доказывает лемму.
Следующая лемма является основным этапом в
доказательстве теоремы Биркхофа — Хинчина.
§8]
ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
169
, Л е м м а 3. Пусть ? (и) — ^-интегрируемая функция,
8 — измеримое, сохраняющее меру \х отображение {Ф/, §}
Е~\}\и: ±Т(8к-1и)>о\.
Тогда
|/(м)ц(^)>0. (6)
Е
Доказательство. Рассмотрим
последовательность 1(и), /(5м), ..., 1(8Ы+Р~1и) и обозначим через $(и)
сумму всех р-отмеченных элементов этой последователь^
ности. В силу леммы 2 $(и)^0. Пусть йк = {и: !(8ки)
есть р-отмеченный элемент}, %ь(и) — индикатор
множества Ок. Заметим, что
Д,=(и:зир Ъ1{Зк~1 (и))^(А и Ок = 3~1Ок-{ при к^Ы,
откуда Ок = 8~кО0 (к < Ы). Отсюда
N + р-~\
0< $8Ш(аи)= | 2 /(5*и)Х*(«МА*Н
Ы + р-1
= Ц |/(5йы)ц(й«).
В силу леммы 1
$ }(8ки) & {ёи)= | /(5*и)и(А*) =
= |/(и)|х(Л*), Й<ДГ.
я*
Следовательно,
N / I (и) р (Ли) + ^ { / (5ки) р {йи) > 0. (7)
О0 к = Ы + \ 6к
Так как
\ 1(8ки)11(с1и){^ |Ч 1(8ки) \р(йи) « / | /(и) ||1(А*)< оо,
170
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
то, разделив неравенство (7) на N и устремив N к оо,
получим
| / (и) \х (йи) > 0.
Множества О0 = О0(р) (р = I, 2, ...) образуют монотонно
возрастающую последовательность и
оо
Нт Д>(Р)= 1)Оо(р) = Е.
Переходя в (8) к пределу при р->оо, получим (6).
Лемма 4 (Максимальная эргодическая теорема.)
Если 1(и) ^-интегрируема, Я — действительное число и
Ях-й{«:42'(5'~1и)>*}' то
\ 1(и)1х((1и)^к1х(Е^ (9)
Ч
Доказательство'получим, если к функции ?(и) — Ахдх(м)
применим лемму 3.
Теорема 1 (теорема Биркхофа — Хинчина). Пусть
{°и, §, \х} — пространство с мерой, 8 — измеримое
отображение {°иу §}, в {Ш, §}, сохраняющее меру \х, и
I (и) —произвольная \х-интегрируемая функция. Тогда
[1-почти всюду в °и существует предел
Пт±У{(8ки) = Г(и)(то<11х), (10)
функция /* (и) 8-инвариантна, т. е.
Г (8и) = Г (и) (той 1х), (11)
интегрируема и, если |л(Ф/)<оо, то
\Г(и)р№= 1[(и)1х(с1и). (12)
Доказательство. Не уменьшая общности, можно
считать, что функция 1(и) конечна и неотрицательна.
§8]
ЭРГОДИЧЕСЩ1Е ТЕОРЕМЫ
171
Положим
8* (и) = ТЕ -^ ^ / (5*и), • Я. (") = Нт \ 2 / (5*и).
Нужно установить, что #*(м) = ^(ы)(тос1|х). Пусть
/Ц = {и: Я*(и)>Р, гЛ"Х«}э 0<а<р.
Достаточно показать, что ц(#ар) = 0- (Действительно,
{^: §*(и)>8*(и)} = ^| /(«р, где /? — множество неотри-
а, |Зе=Д
дательных рациональных чисел). Заметим, что
и аналогично §Л§и) = &Ли)- Это означает, в частности,
что 5~1/Сар==^а|з- Поэтому можно применить лемму 4
к пространству с мерой {Ка$, ЗПД'ар, !*}• Отсюда
следует, что
\ !(и)]1((1и)>ЫКа^ (13)
Применяя лемму 4 к функции —/(а), получим
//(и)|г(^)<а|г(^аэ). (14)
Так как р>0, то из (13) следует, что \х{Ка$)< °°> но
тогда (14) возможно лишь, когда ^(^аз) = 0. Итак,
существование (той (х) предела (10) доказано. Положим
/*(«) = &*(«)• Тогда выполняется (10) и функцця /*(н)
5-инвариантна всюду в °11.
Для доказательства формулы (12) положим
Аы^Ы^г<,Г{и)<Ц^\. Имеем <и = {} Акп,
8~[Акп = < и: -2Д < Г (5м) < 2и 1 = Акп. Применим к
множеству Акп лемму 4. Для любого е>0 получим, что
172 СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ {ГЛ. II
] }(и)\х(аи) >(-§т- в)р{Акп), откуда при е-» О ПОЛу-
чаем неравенство /(«) \л{йи)^-ш \*{Акп). Аналогично
Чп
] / (и) \х {йи) < ~г- И {Акп), откуда следует
Акп
) 1(и)\1 (йи) - ] Г (и) й (</и) < -^г М- Им).
I ^Лл л*л I
Суммируя эти неравенства по всем к, получим
I }(и\\1(с1и)— Г(и)\х(ёи)
<4г|х(^).
Принимая во внимание произвольность п в случае, когда
ц(Ф/)<°о, получим формулу (12). Теорема доказана.
Некоторые следствия теоремы Биркхофа — Хинчина.
Следствие 1. Пусть |л(<2/)<оо, /(*/) е ^р{<2/, §, \х}.
Тогда
\х(с1и)->0 при п->оо. (15)
Для доказательства возьмем какую-либо
ограниченную функцию /0 (и), и пусть || !(и) - /0 (и) \\р = б, где || / ||р-
норма элемента / в ^Р{Щ, §, \х). Тогда
й-1
л=о
+
п-1
^ 2 / (5*«) - Г (и) < Т 2 I/ (5ки) - /о (Зки)}
А=0
+
12/о(5А»)-/о(«)
*=о
+ 1Ш- Г (»)||р.
§8]
ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
173
В силу неравенства Иенсена и леммы 1
Л-1
Г п~1 Т
-|-5;(/(5А«)-/о(5*«)) Ши
У- к=*о ^
I г п"х
[ <2/ &=о
^■2 ]|/(м)-/о(и)Г|*(^)
Используя лемму Фату, получим
|| №-/»«„ =
I П~1
1/Р
\х(с1и)
Чр
<
<Нт
я-1
^и(8ки)-!0(Зки)]\ <б.
Л=0
Далее, так как функция 10(и) ограничена, то и все ее
средние ограничены одной и той же константой. Поэтому
в выражении
Л-1
т2м5*")-ж«)
к=0
л-1
1^1 *=о
[л (*/ц)
!/Р
можно переходить к пределу при п->оо под знаком
интеграла в силу теоремы Лебега. Следовательно, оно
стремится к нулю и при достаточно больших п
становится меньше 6. Таким образом,
я-1
1%[(8ки)-Г(и)
/г=0
< 36, п^п0~ п0 (6),
174
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
причем число б может быть выбрано сколь угодно
малым (6>0). Таким образом, (15) доказано.
Определение 3. Множество 5еЗ называется
^-инвариантным, если ^((5""1Л)АЛ) = 0, где А — символ
симметрической разности множеств.
Легко проверить, что класс всех 5-инвариантных
множеств образует ст-алгебру ^-измеримых множеств.
Далее, если §(и) — 5-инвариантная функция, то
множества {и: §(и)^с}, {и: §(и) = с} 5-инвариантны. С
другой стороны, если Е 5-инвариантно, то %Е(и)~~
5-инвариантная функция. Обозначим ст-алгебру ^-инвариант-
ных множеств через /. Пусть \х((И)=1. Будем считать
{Ш, 8» I*} вероятностным пространством и символом М
обозначать интегрирование по мере \х (математическое
ожидание).
Следствие 2. Г (и) = М{!(и)\1} (той (л).
Очевидно, что М{1(и)\1} является 5-инвариантной
функцией. Поэтому для доказательства следствия 2
достаточно проверить, что для произвольной
ограниченной 5-инвариантной функции §(и)
М§(и)(Г(и)-М{Ни)\1}) = 0
или что М(§(и)1*(и) —§(и)1(и)) = 0, но последнее
вытекает из (12), так как
(В МI (и) Г = Нт -^ 2 * (5^) I (^ = 8 (") Г (и) (той \х).
Эргодические стационарные последовательности.
Возвратимся к стационарным последовательностям.
Пусть {^ (*), I е Г} —стационарная последовательность
и {95т, К, Р} —ее естественное представление.
Следствие 3. Если /— измеримая функция в {95т, 23т}
и М/(^(0), |(1), ..., Цт— 1)) Ф оо, то с вероятностью 1
«-1
прип->оо -^2/(&(*), Б(*+1), •••> Ъ(Ь + т-\))->
к = 0
->М{/(&(0), 6(1), ..., Ъ(т-1)Ш еде I - о-алгебра
событий из §, инвариантных относительно сдвига времени.
Рассмотрим произвольное событие Лей и последов
вательность событий, получаемых из А «сдвигом вре-
«81
ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
175
мени»: Л, 5"*" Л, 5+2Л Если %п — индикатор события
8пА, то %п (п = 0, ±1,...) образуют стационарную
последовательность случайных величин и — \%& есть
/2=0
частота наступления события Л, вычисленная по одной
реализации последовательности {1(1), ^ = 0, 1, 2,...}
я при п— 1 последовательных сдвигах начала отсчета
времени,
п-\
1 V Уп(А)
п 1± %к - п •
/2=1
В силу теоремы Биркхофа — Хинчина с вероятностью 1
существует предел
Пт^^==я(Л)==М{хл|/} и Мя(Л) = Р(Л).
Величину я (Л) можно назвать эмпирической
вероятностью события Л. Она является случайной величиной и
определяется по одной реализации бесконечной
последовательности Ш0» ^ = 0, 1, 2, ...}. Естественно
возникает вопрос: когда эмпирическая вероятность я (Л) не
зависит от случая и совпадает с вероятностью Р(Л)?
Стационарные последовательности, обладающие этим
свойством, называются эргодическими.
Более общим является следующее определение.
Определение 4. Пусть (4/, §, |и}—вероятностное
пространство, 5-сохраняющее меру преобразование °11
в себя, VЛ(Л)==V„(Л, и) — число членов
последовательности {и, 8и, ..., 5"" и), попадающих в множество Л.
Преобразование 5 называют эргодическим, если для
любого Ле§
Ит Хп(Аи) =1х(Л)(тоМ.
Я->оо П
Преобразование 5 называют метрически транзитивным,
если любое 5-инвариантное множество имеет меру 1
или 0.
Т е о р е м а 2. Чтобы преобразование 8 в
вероятностном пространстве {°и, §, \х} было эргодическим,
необходимо и достаточно, чтобы выполнялось одно из двух
условий:
т
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
[ГЛ. II
а) 5 метрически транзитивно;
б) для любой %-измеримой \х-интегрируемой функции
1(и) функция
п-\
Г(и) = Пт±%Г(8ки)
с вероятностью 1 постоянна.
Доказательство. Пусть А — 5-инвариантное
множество, 0 < ц(Л) < 1. Множества Л, 8 А, 82А, ...
отличаются друг от друга на множества меры 0 и V,, (А) =
V (А)
= п%А(и)(то&\х). Следовательно, Пт не может
П->оо П
быть постоянной (тос!|х) величиной. Таким образом, из
эргодичности следует метрическая транзитивность. Пусть
теперь 5 метрически транзитивно. Так как функция /*(«)
5-инвариантна, то симметрическая разность множеств
8~х{и: Г(и)<х} = {и: ?*(8и)<х} и {и: Г(и)<х]
имеет ц-меру 0. Отсюда вытекает, что \х{и: }*(и)<х} = 0
или 1 для любого действительного х, т. е. Г [и) = сопз!
(тос!ц). Таким образом, из а) вытекает б). Наконец,
условие эргодичности является частным случаем
условия б), а именно, когда Ци) есть индикатор некоторого
события.
Приведем несколько следствий из эргодичности.
Пусть {35Т, (5, Р}—естественное представление
стационарной последовательности \{п), 8 — преобразование
сдвига времени в 351\ 2'2 = 2'2{ХТ, 6, Р).
Из следствия 1 теоремы 1 вытекает, что для
произвольных функций 1(и) и §(и) из 3?2
,,т \^Н5ки)8(и)Р{аи)= \г{и)8(и)Р(аи). (16)
п">°°^г *=о %,т
Будем говорить, что последовательность {1(п), п =
= 0, ±1, ...} эргодична, если эргодическим является
преобразование 5. Положим § (и) = % / (8ки) = 5йи
предположим, что исходная стационарная
последовательность (Цп), п = 0, ±1, ...} эргодична. Соотношение (16)
§8]
ЗРГОДИЧЕСКИЕ ТЕОРЕМЫ
177
принимает вид
Птп Мт11^=М^Мг1. (17)
Пусть ё(и) = %в(и)> 1{и) = хА(и), ^ и Ве1, Из (17)
следует, что
Ит1ИР(5~^ПВ) = Р(Л)Р(В) (18)
или (если Р(В)фО)
п— 1
гдб Р(5~*Л |В) —условная вероятность события 5_/гЛ
относительно В.
Лемма 5. Равенство (18) («лм (19)) для любых
А, В е 6 эквивалентно эргодичности.
Достаточно пс^казать, что из (18) следует
эргодичность. Пусть С —любое 5-инвариантное событие.
Положим в (18) А = В = С. Тогда оно переходит в
следующее: Р(С) = Р2(С), откуда Р(С) = 0 или 1, и лемхма
следует из теоремы 2:
Равенство (19) имеет следующий
теоретико-вероятностный смысл. Пусть А и б— два события из С Если
событие А неограниченно сдвигать ёо времени, то в сред-
нехМ события 8"пА и В становятся независимыми,
каково бы ни было событие В. Условие (19) можно
заменить более жестким требованием:
1мп Р(3~пА\В) = Р(А)1 (20)
П->оо
которое называется условием перемешивания.
Условие (20) является частным случаем равенства
Игл ГЙСят|=МЬ>Мть (21)
где %п = 1(8пи), г| = ^(«), [(и) и ^(и) — произвольные
функции из «2^2. С другой стороны, из (20) следует (21)
для простых функций [и §, Аппроксимируя
произвольные /(и) и § (и) из 3?2 последовательностями простых
\7В СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
функций !п(и) и ёп{и), сходящихся в 9!2 к !{и) и§(4
соответственно, нетрудно убедиться, что условие
перемешивания эквивалентно условию (21) (1{и), §{и) —
произвольные функции из &2). С другой стороны,
условие (21) достаточно проверять для некоторого
множества функций, линейная оболочка которых всюду плотна
в 3?2. В качестве таковой удобно принимать
индикаторы цилиндрических множеств.
Рассмотрим последовательность {|„, п = 0, ±1, ...}
независимых одинаково распределенных случайных
величин, М||л|<оо. Она является стационарной
последовательностью. В силу теоремы Биркхофа — Хинчина
л-1
Пт-[У|, = Г(то(1Р), М|* = 1^.
Случайная величина !•*, очевидно, не зависит от любого
конечного числа величипн |0> 61» •••» 6р- Поэтому I*
измеримо относительно Нта(У и на основании закона О
или 1 постоянна, I* = с(тойР), причем с = М^. Таким
образом, мы получаем следующую теорему.
Теорема 3. (Усиленный закон больших чисел).
Если {1П, /г = 0, ±1, ...} — последовательность
независимых одинаково распределенных случайных величин и
М\1п\<°о, то с вероятностью 1
л-1
}%и=М1о. (22)
/г=0
Доказанная теорема является следствием
эргодичности последовательности независимых одинаково
распределенных случайных величин. Но можно доказать
больше, а именно что оператор сдвига времени в 96х
является перемешиванием относительно меры,
индуцируемой в §вт, последовательностью независимых
случайных величин. Это вытекает в свою очередь из
более общего утверждения. Пусть {!■„, п = О, ±1, ±2, .. .} —
стационарная последовательность случайных элементов
в {<%, Щ, %п — (7-алгебра, порождаемая случайными
элементами 1п9 |л+ь ..., §00 = П^л==1!т^л' БУДем говорить,
п
что к последовательности ЦП9 и = 0, ±1, ...} применим
11ГП
§8]
ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
179
закон 0 или 1, если ст-алгебра *$«> содержит только
события вероятности 0 или 1.
Теорема 4. Если последовательность {1п, п =
= 0,±1, ...} удовлетворяет закону О или I, то прео&+
разование сдвига времени является перемешиванием.
Положим ?;_„ = Р{В|§„}. Последовательность {%ПУ §„,
п = ... — к, — к + 1. ..., 0}, }$-п = $П9 является
мартингалом (ср. теорему 4, гл. II, § 2) и Р{#|Зоо} является
его замыканием слева. Так как ст-алгебра ^-тривиальна,
то Р {В|8оо) = сопз! = Р (В) (той Р). В силу теоремы о
сходимости мартингалов (теорема 1, следствие, § 2 гл. II)
1\тР{В\^п} = Р (В) с вероятностью 1. Пусть А —
цилиндрическое множество над координатами м = 0, 1,2, ...
Тогда 3~~пА^%п. Поэтому при м->оо
Р(ВП5"М)= \ Р{В\Ъп}Р (йи)->Р (В)Р(5-М) =
8~Па =Р(В)Р(А).
Очевидно, что это соотношение имеет место и для
любого цилиндрического Л. Отсюда вытекает, как было
замечено ранее, соотношение (21). Теорема доказана.
Другим примером процесса, удовлетворяющего
условию перемешивания, может служить стационарная
гауссова последовательность, коэффициент корреляции
которой стремится к нулю. Пусть {1ПУ м=0, ±1, ±2, .. .} —
стационарная гауссова последовательность, М|л = т,
М(^-т)(^0-т) = ^, !(и) = !(х0, хи...9хр), §(и)=*
= §(х09 хи ..., Хр) — ограниченные достаточно гладкие
функции р + 1 переменных, имеющие абсолютно интег*
рируемые преобразования Фурье/*(Я0, ..., Яр), §* (Я0, .. ♦
. .., Яр). Тогда
•= М \ ... ] в и=° к=0 I X
— оо — оо
X Г (Я0, . .., Хр)§* (ц0, . ♦., |хр) йЛо •. • йЯрф0 ... й\Лр «
— оо —оо
X Г (Ао> ♦ ♦ * у &р) &* (ц0, . *,, цр) ЙЯ0 . « ♦ */А>р ф0 ... фр.
180
СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ.-1Т
Если Нт Кп = 0, то, переходя в написанном СООТНОЩе-
нни к пределу при д->оо, получим
= М/(6о,&1, -.., Ы^о, II, ••♦, Ы- (23)
Так как класс функций / и §", для которых доказано
последнее соотношение, всюду плотен в 3?2, то
соотношение (23) имеет место для произвольных / и §
из 3*
Таким образом, доказан следующий результат.
Теорема 5. Стационарная гауссова
последовательность, коэффициент корреляции которой Нп-+0 при
/г->оо, удовлетворяет условию перемешивания.
Приведем некоторые следствия и замечания,
относящиеся к эргодическим свойствам цепей Маркова.
Общая *эргодическая теория цепей Маркова будет
рассмотрена во втором томе.
Рассмотрим неприводимую цепь Маркова со счетным
числом состояний. Она обладает инвариантным
начальным распределением тогда и только тогда, когда она
возвратна и положительна (следствие 2 теоремы 15 § 5).
Для этого, в свою очередь, необходимо и достаточно,
чтобы система уравнений
к
обладала нетривиальным абсолютно суммируемым
решением. Решение этой системы, удовлетворяющее
условию ^хк=1у когда оно существует, имеет вид
к
N
хк = ьк= Нт ±УрЫи,к). (24)
Если к тому же цепь апериодична, то
** = »* = Нт/?<«>(/, к)
(§ 5, теорема 15). Предположим, что цепь неприводима,
возвратна и положительна. Инвариантное
начальное распределение для этой цепи единственно, и
ему соответствует стационарный марковский процесс
§8]
ЗРГОДИЧЕСКИЕ ТЕОРЕМЫ
Ш
{!■(*),/ — О, ±1, ...}. Условие эргодичности этого
процесса можно представить в виде
N
Нт 2Ргё(1) = /ь 6(2) = /2. ••- &(*) = '*,
|(п+1) = /„ ..., ^(» + г) = /г} =
= Р{|(1) = /„ ... 1(5) = иР{|(1) = /, 6(г)-/,}. (25)
Действительно, с одной стороны, это условие является
частным случаем условия (18), а с другой, нетрудно
убедиться, что из (25) следует (18) для любых
цилиндрических множеств А и В из 96 . Далее, условие (25)
эквивалентно равенствам
N
Ит ^тгЦ Ры (*\ У) == ^у/,
/1 = 1
т. е. равенствам (24).
Итак, имеет место
Теорема 6. Стационарный процесс,
соответствующий инвариантному начальному распределению
неприводимой возвратной положительной цепи Маркова, эр~
годичен.
Замечание. Аналогично можно увидеть, что
условие перемешивания стационарного процесса
Маркова сводится к требованию Нт р{п)(], к) = юк. Таким
/1->оо
образом, стационарный процесс, соответствующий
возвратной положительной и апериодической цепи Маркова,
обладает свойством перемешивания.
ГЛАВА III
СЛУЧАЙНЫЕ ФУНКЦИИ
§ 1. Некоторые классы случайных функций
Гауссовские случайные функции. Определение 1.
Действительная случайная функция %(х), х^Х,
называется гауссовскойу если для любого целого п^1 и
любых хк, к = 1, 2, ..., /г, х^е!, последовательность
{1(х\)> 1(х2)> •••> %(хп)} имеет совместное нормальное
распределение.
Из определения вытекает, что характеристическая
функция: этого распределения имеет вид
* \ХЬ Х2> • • • > хп> и у • • • у и) ^
{П П х
1^икак~^ 2 ЬкГикиГ 1, (1)
причем
я* = М|(*л), ^г = М(6(^)~^)(|(хг)-аг). (2)
Таким образом, все частные распределения гауссовской
случайной функции определяются двумя
действительными функциями — средним значением а {х) и
корреляционной функцией Ъ (хи х2)
а (х) = М^ {х)9 Ъ (хи х2) = М (\ (х{) - а (х{)) Ц (х2) - а (х2)).
Корреляционная функция Ь(х, у) обладает следующими
свойствами:
1) Ь(ху у) = Ь(у, х),
2) для любых п, действительных чисел ик и точек
хк^Х
п
2 Ь (хк, хг) икиг > 0.
к, г=1
§ 1] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 183
Действительные функции, обладающие этими
свойствами, называются положительно определенными
ядрами на X2.
Это определение эквивалентно требованию, чтобы
для любых хг и хк^Х матрица \\Ь{хк, хг)\\ (к, г=1,
2, ..., п) была действительной симметрической и
неотрицательно определенной.
Заметим теперь, что для произвольного множества X,
действительной функции а(х), хе1, и неотрицательно
определенного действительного ядра Ь(хь х2) на X2,
существует гауссовская случайная функция, для которой
а(л;) —ее среднее значение, а Ъ{хи х2) — ее
корреляционная функция. Для доказательства рассмотрим семейстЕО
распределений [рх х (•), я= 1, 2, ..., хк е X},
характеристические функции которых задаются соотношениями
(1). Нетрудно проверить, что оно удовлетворяет
условиям согласованности. Остается сослаться на теорему
Колмогорова (теорема 2 § 4 гл. I).
Аналогично определение векторного гауссовского
. процесса с действительными компонентами. Пусть | (х)7
х^ X — случайная функция со значениями в т-мерном
пространстве 52т. Она называется гауссовской, если
совместное распределение всех компонент
последовательности {Цх^, |(дг2)| •••> 1(хп)} ПРИ любом п^\ и
любых хк^Х является нормальным. Соответствующая
характеристическая функция имеет вид
Их х и^{) и,({) и^п) и{п)) =
{т п п т
г=1 &=1 к, /=1 г, 5=1
Это выражение записывается проще, если ввести
векторы и<*> = (и<*>, и2к\ ..., и№), а (х) = (а1 (х), ..., ат (х))
со значениями в Жт и матрицу Ь{хь х2) с элементами
ЬГ8{хи х2), г, 5=1, 2, ..., га. Тогда предыдущее
выражение принимает вид
1(хь ..., хп, и{1\ ..., м<я))=-
{п п
*2(и(й), а(**))-у Ц Ф(хк, х,)и{1), «<*>)
к-1 к.1-1
т
СЛУЧАЙНЫЕ ФУНКЦИИ
{ГЛ. ИГ
При этом векторная функция а(х) может быть
произвольной, а действительная матричная функция Ь (хи х2)
должна быть симметричной и удовлетворять условию:
при любом целом п^1у любых хк^Х и й^еЙ™
2 (Ь(хк, хг)и«\ ^*>)>0. (3)
к, /=1
Очевидно и обратное: произвольной функции а(х)
со значениями в Жп и матричной функции Ь(х[9 х2),
удовлетворяющей условию (3), соответствует гауссов-
екая случайная функция |(х) = (I1 (х)> ..., |т(#)), для
которой
а<*>(*) = МБ*(*), -
*" (*и *2) « М & (хг) - аг (хг)) (Г (х2) - а* (х2)).
В некоторых вопросах представляют интерес моменты
гауссовской случайной функции. Они могут быть
получены из разложения характеристической функции в ряд.
Ограничимся рассмотрением центральных моментов
скалярной случайной функции. Положим
а(х) = 0, и = (и{1\ и{2\ ..., и(я>),
В = \Ь(хк, хг)\, к, г= 1, ..., п.
Тогда
1(хи хъ ..., хп, 1и) = е 2 "' " =
*= 1 - у (В"> и) + -21^" (5"» ")2 + ' " '
••• +(-1)"-^(Я". ")"+ ....
откуда вытекает, что
М (Д «<*> & (х,))2" = (2л - 1)!! (Ви, и)" (4)
и
м (2 «<*>*(**)) =о.
Введем ^-точечные моментные функции
»Ч/2.../> ** ^) = м[1Ы]/,[Ц-2)]/2 ••• [БЫ!7*-
§ 1] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 185
Величина /1+./2+ . •• +]п называется рорядком мо-
ментной функций. Моментные функции нечетного
порядка равны нулю:
п
т., . (х х2, ..., х) = 0 при 2/* = 25-1.
Формуле (4) можно придать вид
д2п 1
т1 / / 0*1*2 •■• ' Хп) = 7 7 Г —~(В^ "Г- (5)
Моментные функции второго порядка совпадают с
корреляционной функцией
тп {хи х2) = Ь (х{9 х2); т2 {х) = тп {х, х) = й (х, х).
Для моментных функций четвертого порядка имеем
следующие формулы:
т4 (х) = Зй2 (х, я), га22(*1, х2) ==262(л:ь лг2),
^31 (*Ь Х2) = ЗЙ (*,, Х^ Й (*„ Х2),
т2ц(^1, *2» *з) = &(*1, ^1)6(^2, *3) + 2&(*И Х2) Ь (*,, *3),
^1111(^1» *2> -^3» х4)=х
= Ь (*1, *2) Ь (*3, *4) + 6 (*Ь *з) & (*2> -*ч) + Ь (*\> Х<д Ь(Х2, ХА).
В общем случае имеет место соотношение
Ш/,/2 - /»(*!' *2' ■ • • ' *п) =" 2 П & (*р> *,), (6)
структура которого может быть описана следующим
образом: записываем точки \и ..., хп в
последовательность, причем хк пишем подряд ]к раз. Написанную
последовательность разбиваем на произвольные пары.
Тогда произведение в правой части формулы (6) берется
по всем парам этого разбиения, а сумма берется по
всем разбиениям (пары, отличающиеся перестановкой
элементов, считаются за одну). Это утверждение
непосредственно вытекает из формулы (5).
В ряде вопросов рассматриваются комплекснознач-
ные гауссовские случайные функции. В определении
последних имеется одно обстоятельство, отличающее
цх от общих векторных гауссовских функций с
действительными компонентами. Ограничимся функциями
186
СЛУЧАЙНЫЕ ФУНКЦИЙ
(ГЛ. III
{^(х), х^Х} со значениями в 3&. Положим %(х) =*
= |(х) + щ(х), где Цх) и ц(х) вещественны.
Определение 2. Случайная функция {^(х), х^Х}
называется комплексной еауссовской случайной
функцией, если действительная векторная функция {{%(х),
ч)(х)), хб!} является гауссовской и ЬЛ{%(х) —а(х))Х
X &(у) — а(у)) = 09 а{х) = Щ{х), для любых х,у<=Х.
Без умаления общности можно положить а(х) = 0.
Нетрудно заметить, что условие М%(х){,(у) = 0
эквивалентно условиям
М^ (х) I (у) = Мц (х) ц (*/), М^ (х) ц(у)=-Щ(у)г\ (х). (7)
С другой стороны, если равенства (7) выполняются, то
Ь(х, {/) = МЕМШ = 2(й„(^ у)-1Ь12(х,'у)), (8),
где Ьп(ху #) = М|(д:)|(#), Ь12{х, у) = Щ{х)г\(у). Из
условий (7) вытекает, в частности, что Ь12{ху *) = М^(х) !)(*) = О,
а так как (^(х), ^(х)) имеют совместное гауссовское
распределение, то %(х) и ц(х) независимы. Из этого
следует, как нетрудно проверить, что если положить
^(х) = р(х)'е^{х\ то величины р(х) и ф(х) будут
независимыми, ф(х) имеет равномерное распределение на
(—я, я), а р(х) — плотность распределения, равную
-±^е~^), и>0, 6*{х) = 0Ъ(х) = Ь{1{х, х).
В соотношении (8) Ьп(х, у) является неотрицательно
определенным ядром, а Ь12(х, у) обладает Свойством
Ь\2{х, у)-= —ЬХ2{у, х). Используя это, нетрудно
проверить, что функция Ь (х, у), определяемая формулой (8),
в которой Ьп(х, у) и Ь12(ху ^ — произвольные функции,
обладающие указанными свойствами, удовлетворяет
соотношению
п
2 Ь (хь хг) гкгг > О
к, г=1
для любых Пу хк^Х и комплексных чисел гк. Функции,
обладающие этим свойством, называются положительно
определенными ядрами на X2.
Теорема 1. Каково бы ни было положительно
определенное ядро Ъ (х9 у) (х, у е X), существует ком-
§ 1] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 187
плексная гауссо&ская случайная функция 2; (л;), для
которой М^ (х) = 0мМ5 (*) ?,(у) = Ь (х у).
Для доказательства введем действительную
матричную функцию второго порядка В(х9 у) = \\Ъ1к(х, у)\\
(/, &= 1, 2), положив
Ьц {*, У) = Ь22 (х9 у) = ±ЛЬЛ %
Ь12(*, У)=- Ь2\ {х, У)=--^Ь"(х9 у),
где Ъ' {х9 у) = Ке Ь (х, у), Ь"(х9 у) = 1тЬ(х, у). Так как
•6 (х9 у) — положительно определенное ядро, то Ь (х, у) =
*=Ъ(у, х), откуда следует, что Ьп{х, у) = Ьп(у, х),
Ь\2{х, у)= —Ьп{у, х). Построим двумерную гауссовскую
случайную функцию (1(х)9 ц{х)) с корреляционной
матрицей В(х, у), В силу предыдущих замечаний Е(*) =
= Цх)-\- щ(х) будет комплексной гауссовской случайной
функцией и
Щ(х)Ш = 2(Ь1\{х9 у)-1Ь12(х, у)) =
= Ь' (х9 у) + 1Ъ" (х9 у) = Ь {х9 у).
То обстоятельство, что гауссовы случайные функции
играют важную роль в практических задачах, часто
можно объяснить следующим образом. При широких
условиях сумма большого числа независимых и малых
по величине случайных функций приближенно является
гауссовской случайной функцией независимо от
теоретико-вероятностной природы отдельных слагаемых. Это
так называемая теорема о нормальной корреляции,
являющаяся многомерным обобщением центральной
предельной теоремы. Приведем одну из ее формулировок.
Пусть дана последовательность серий случайных
функций {апк{х)9 хе!}, к = 1, 2, ..., тП9 п=1, 2, ...
Положим
тп
Чп (х) = 21 апк (х).
Рассмотрим «урезанные» величины апк(х) и их моменты
«** (*) =* Хе К, (х)) апк (х) а\к (х) = Щгк (х)9
Ь\ъ (х1> х2) = М К. (*0 ~ <* (*0] [<4 {х2) - <, (*2)],
где е>0, ХеМ — индикатор интервала (—е, е).
188
.СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
Теорема 2. Пусть при каждом п функции апХ (х),
а„2 (^), ..., апт (х) взаимно независимы и удовлетворяют
условиям:
1) при любом е>0
2 Р{|апл(*)1>е}->0 /гри я->оо;
2) для некоторого г = е0 = е0 (л:) > 0, при п -> оо
2 а?А (л:) -> а (х)9 2 Ь«л (л:,, х2) -> 6 (а:,, *2). (9)
Тогда частные распределения случайной функции г\п (х)
при п->оо слабо сходятся к соответствующим частным
распределениям гауссовской случайной функции с
математическим ожиданием а(х) и корреляционной
функцией Ь (хи х2).
Процессы с независимыми приращениями. Пусть
7"—конечный или бесконечный замкнутый слева
промежуток, а = гшпГ>—оо.
Определение 3. Случайный процесс {|(0> ^ ^ Т}
со значениями в Жт называется процессом с
независимыми приращениями, если для любых п, 1к е Г,
*,</2< • • • <Лг» случайные векторы |(а), 1Ц{)-Ъ>(а)9 .. .
• •, 1(*п) — 1(1п-\) взаимно независимы. Вектор Ца)
называется начальным состоянием (значением) процесса,
а его распределение — начальным распределением
процесса. Чтобы задать процесс с независимыми
приращениями в широком смысле, достаточно задать начальное
распределение Р0(В) и набор распределений Р(/, А, В)
(/>0, А>0, В<= 23ш), где йш —а-алгебра борелевских
множеств ЗИт и Р(/, А, в) есть распределение вектора
I (/ + А) — I (/). Действительно, если эти распределения
даны, то любые совместные распределения векторов
МЛ)» М'г), • • •» МЛг) однозначно определяются формулой
р(Пй('*)е5*>)=
$ РЦа-и*п-*п-ийУп). (Щ
$-П НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ [$$
Здесь В —г обозначает множество {х: х = у~гу у^В].
Что касается начального распределения Р0(В), то оно
может быть произвольным. С другой стороны, нельзя
гарантировать, что произвольно заданному семейству
распределений Р(/, /?, В) соответствует некоторый
процесс с независимыми приращениями.
Чтобы последнее имело место, необходимо и
достаточно, чтобы Р(/, к, В) обладало следующим свойством:
при любом п и любых а = 1ц<1х< .... <1п = 1 + к,
Р(/, /г, В) является распределением суммы независимых
случайных векторов |ь ^2> •••> 1п> ГДе %к имеет
распределение Р(1к-и 1к-1к-ъ В).
Действительно, если это условие выполнено, то
семейство распределений (10) удовлетворяет условиям
согласованности. Поэтому применима теорема
Колмогорова и существует случайный процесс с
конечномерными распределениями (10). Из вида этих
распределений вытекает, что этот процесс имеет независимые
приращения.
Процессы с независимыми приращениями удобно
изучать с помощью характеристических функций.
Положим
/(/, к, и)= | е^"<ЧР(/, /г, ах).
Функцию /(/, /г, и) будем называть характеристической
функцией процесса с независимыми приращениями.
Она полностью определяет совместное распределение
разностей
6 (О-6 (я), КУ-бв), ..-, 1С,.)- 6 (',1-1). (И)
Действительно, совместное распределение
последовательности векторов (11) имеет характеристическую
функцию ]{1и 1Ъ .. ., 1пч и1, и2, ..., ип), равную
п
/(^2> ■ ..,'«, и\ и2, ..., ип) = 1[1((к-и Мк1 ик),
Ь=1
Мк ^^к~~ 1к-и {о —а.
Таким образом, чтобы задать процесс с
независимыми приращениями в широком смысле, кроме Р0(В)9
достаточно задать /(/, Л, и). Сформулированное выше
190
СЛУЧАЙНЫЕ ФУНКЦИЙ
[ГЛ. III
необходимое и достаточное условие, которому должно
удовлетворять распределение Р(1, к, В), означает, что
характеристическая функция 1(1, к, и), рассматриваемая
как функция интервала [/, 1 + к) должна быть мульти-^
пликативной:
/(/, /г, -Ь /г2, и) = 1(1, ки и)1(1 + ки к2, и).
В свою очередь это условие необходимо и достаточно
для того, чтобы / (1, к, и) была характеристической
функцией процесса с независимыми приращениями.
Определение 4. Процесс с независимыми
приращениями называется однородным, если разности
1(1 +к) —1(1) имеют распределение, не зависящее от /,
т. е. Р(1, к, В) = Р(к, В). Однородный процесс назы^
вается стохастически непрерывным, если
ПшР(к, 58) = 0
для любой сферы Зе = {х: |л:|<е}, е>0.
По поводу условия стохастической непрерывности
и его значении см. § 2. Если однородный процесс
стохастически непрерывен, то при любом I разность
%(1+К) — 1(1) сходится по вероятности к нулю и,
следовательно, распределение | (1 + к) — | (1) слабо сходится
к нулю (к \ 0). Из непрерывности соответствия между
распределениями и их характеристическими функциями
вытекает, что стохастическая непрерывность
эквивалентна следующему свойству: при к 10, 1(к, и)->1
равномерно в любой ограниченной области |и|^//.
Отметим несколько свойств характеристической
функции однородного стохастически непрерывного процесса
с независимыми приращениями.
а) Характеристическая функция однородного
процесса с независимыми приращениями удовлетворяет
уравнению
1(к1 + к2, и) = 1(ки и)1(к2, и). (12)
В частности, при любом целом п
/ (пк, и) = [I (к, и)]п.
б) Характеристическая функция I (к, и) однородного
стохастически непрерывного процесса нигде не обра*
щается в нуль,
.§■■11 НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 191
Действительно, для любого и найдется такое /0, что
| / (Л, и) |^ у при 0<Н ^.^^. Если I — любое и (=*{0(п + д),
где 0<9<1, то /(*, и) = /(/(/*, и)/(*0в, и) = [/(*0, и)]п X
X / (*0в> и), откуда | / (*, и) | > (у I . Так как / (Л, и) -> 1
при Н\0 равномерно в произвольной сфере |м|^Л/,
то можно однозначно определить функцию §{ (1У и) =*
*=1п/(^,и) в области ^«=[0, А], |и|</У, Л = Л(Л0,
причем функция ^ (^, и) непрерывна по совокупности
переменных в рассматриваемой области. Из (12)
следует, что §1 (1У и) удовлетворяет уравнению
ё\ (А + *2, и) = §{ (*,, и) + §2 (/2, и), и|<Л^,
Поэтому §1ЦУ и) = {§(и) и 1{(у и) = е^^и\ Легко увидеть,
что последнее равенство должно иметь место при всех /
и и. Действительно, если это равенство имеет место
при данном и для всех I <; Н0у ^>0, то при любом I
е^ё{и)\ = **<«> при п>±.
Итак,
/(*, и) = №и\ (13)
где § (и) — однозначная и непрерывная функция.
Этот простой результат полностью характеризует
зависимость характеристической функции ]{1У и) от /.
Очевидно, что характеристическая функция, имеющая
вид (13), удовлетворяет условию (12). Остается выяснить
структуру функции § (и). Из предыдущего следует, что
она может быть произвольной функцией, лишь бы е^{и)
при любом / являлось характеристической функцией
некоторого распределения. Из (13) следует
Я(и) = 11т-^ , (И)
причем сходимость равномерна в каждой ограниченной
сфере | и |<Л/, 0<Ы< оо.
Теорема 3. Пусть ]{1У и)у ^>0, и е 52т, —
семейство характеристических функций такое, что предел (14)
существует равномерно в произвольной сфере \и\^Ы,
192
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
N>0. Тогда в {5?ш, 23т} существуют конечная мера П (б),
неотрицательно определенный в Ж4 оператор Ь и
вектор а такие, что
#(и) = /(а, /./) —у(Ы и) +
+ /[«■"--'-тЙтН-Ч^*'* <15>
Доказательство. Пусть {<?, (•), ЗЭт} —
распределение, соответствующее характеристической функции
/(/, и). Положим
В "
Ниже будет показано, что семейство мер {![/(•), />0}
слабо компактно. Выберем последовательность ^п \0
такую, что И, слабо сходятся к некоторой мере П'
на Жш. Далее "
= 4(^-1^^)+ (/(и, г)П,(Лг), (16)
где
Л(и) = /ттГ !*,<</*), *'Мв /тПТР"11^^
П"' ' \ ' 1+|г|2 ^ 2 1+М2] |2|* '
Если считать, что /(и, 0) = 0, то $(и, г) будет
непрерывной и ограниченной функцией. Поэтому
Нт //(и, г)П,я(Лг) = //(и, г)П'(йг).
Так как существует предел в левой части равенств#.(16)
при / = /„, п->оо, то существуют пределы
Нт И/д (и) = а (и), Нт Д,я (и) - В (и),
| 1] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЯ 193
причем а (и) является линейной функцией, а В (и) поло*
зрительно определенной квадратической формой, т. е.
а (и) = (а, и) и В (и) = {Ь'и, и), где Ь' — положительно
определенный симметрический оператор. Переходя в
соотношении (16) к пределу по последовательности 1т получим
8(и) = 1(а, и)-~(Ь% и) + |/(и, г)П'(с1г). (17)
Пусть П(Л) = И'(А~{0}) ({0}— множество, состоящее
из одной точки 0). В интеграле в правой части
равенства (17) меру П'(-) можно заменить мерой П(-).
С другой стороны, интеграл
существует и представляет собой некоторую квадрата-
ческую положительно определенную форму (Ь"и, и).
Нетрудно заметить, что (Ь'и, и)^(Ь"и, и). Поэтому
Ъ^Ь'—Ь" — положительно определенный симметрический
оператор. Таким образом,
ц (и) = I (а, и) - у (Ьи, и)+ ] (/ (и, г) - у ^^г) П, .(<**).
что и доказывает (15).
Перейдем к доказательству слабой компактности
семейства {Пи />0}. Нужно показать, что
а) П,(^т)<С, б) Нт НтПЛ5у} = 0,
где ^={2: и |>М.
Пусть и|<Л?,, Л^ произвольно. Из условий теоремы
и (16) следует, что для любого ф>0 найдется такое
<о = 4>(#1. 6), что
а при с > 1
-Ке#(и) + 6> |[1~соз(и, г)1П, (<**), *</„. (19)
7 И. И. Гихман, А. В. Скороход
Ш ВйУЧАГОШЕ ФУНКЦИИ [ГЛ, III
Так как 1 — соз х^-т>г — -щ- при всех х, то из (18) следует:
Чтобы получить нужные оценки, нам понадобятся
значения интегралов
/ (р) = / е{ <"• г> </и, /й (р) = | (ы, г)* йи, к = 2, 4.
Они равны:
5р 5р
/(р) = (-|^-)И/2/т/2(р|2|),
Ш-^, /4(р) = ^^^
2Г
(21)
Проинтегрируем неравенства (18) и (19) по «е5р и раз-
/ пт(2 \
делим на объем 5р, получим ( 5р = йтрт, О,
V г(т+1)/
5р "' (22)
5р
^Я1-1^* 1)(т^|-)т/2/т/2(р|г()]п,(^). (23)
Выбирая в (22) р из условия р2 = 2(т + 4) и считая,
что ^ > р, получим
пи^хгГб-^/кег^)^!.
§Щ НЕКОТОРЫЕ --КЯХОЗВГ СЛУЧАЙНЫХ ФУНКЦИЙ Ш
Замечая теперь, что функция 1тц{х) ограничена, можно
при лю&ом с > 0 выбрать р *= р{ из условия
{91с)тп ^ 2т+2/2Г (Я + 1) ,цр I /м (ж) |, (24)
и тогда получим
ПД^)<2Гб--^/кея(^)^1,
откуда следует, что П^ (^2т) < /С» Наконец, замечая, что
при р->0 имеем
*~ 0~^ \ Ке$(и)А*-*«г(0)«О,
выберем сначала р = р2 настолько малым, чтобы левая
часть неравенства (23) не превосходила 26, а затем
выберем такое с = N =» ЛГб, чтобы выполнялось (24). Тогда
получим
П,(Йв)<4*.
причем все эти неравенства установлены независимо
от ^&[0, ^0)у ^ов=^^(N^9 б). Теорема доказана.
Из полученных результатов вытекает следующая
Теорема 4. Если | (О, I ^ 0, — однородный
стохастически непрерывный процесс со значениями в Ж*1, то
характеристическая функция I(I, и) разности К5 + I) — \{$)
имеет вид
/(/, и) = *'*<«>, (25)
где § (и) дается формулой (15).
Рассмотрим некоторые частные случаи формулы (25).
а) 6=0, П(В)еО.
В "этом случае 1{1, и)=*ец(а>и\ что соответствует
характеристической функции вырожденного
распределения, сосредоточенного в точке 1а е $т. Таким
образом, с вероятностью 1 КО = I(0) + а^ и точка |(0
находится в равномерном движении со скоростью а.
б) ЩЯ)е8еО.
В этом случае приращения К' + 5)""К5) имеют
нормальное распределение со средним а и корреляционной
матрицей Ы} так что, если, например, ^ (0) = 0, то про*
7*
196 СЛУЧАЙНЫЕ ФУНКЦИИ {ГЛ, III
цесс Щ) является га^ссовским. В § 5 настоящей главы
будет показано, что в этом и только в этом случае
процесс с независимыми приращениями -стохастически
эквивалентен процессу, выборочные функции которого
с вероятностью 1 непрерывны. Рассматриваемый
процесс называют процессом броуновского движения.
Как известно, если наблюдать в микроскоп с очень
сильным увеличением маленькую крупинку коллоидного
размера, погруженную в жидкость, то оказывается, что
такая частица находится в постоянном движении и ее
путь представляет собой очень сложную ломаную линию
со стохастически направленными звеньями. Это явление
объясняется столкновением молекул жидкости с
коллоидной частицей. Коллоидная частица имеет
относительно большие размеры по сравнению с молекулами
жидкости и испытывает в одну секунду огромное число
соударений с ними. Результат каждого столкновения
частицы с молекулами проследить невозможно. Видимое
движение частицы называется броуновским движением.
В первом приближении можно считать, что смещения
частицы под влиянием столкновения с молекулами среды
.независимы между собой, и рассматривать броуновское
движение как непрерывный процесс с независимыми
приращениями. В силу вышесказанного он является
гауссовским процессом. Если |(/) — одномерный
процесс, 6 = 1, а = О, то процесс броуновского движения
называют винеровским процессом.
-в) а = 0, 6 = 0, мера II представляет собой
сосредоточенную в точке г0 массу величины ц.
Характеристическая функция (25) в этом случае
имеет вид
'«• •>-«р{ "(\У*п (•'"•"'-' -тй*)}' (26>
Легко убедиться, что приращение |(0""|(0) можно
представить в виде
где г(/) — пауссоновский процесс со средним значением
§ Г] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИИ 197
г) Пусть Ь = 0, а мера П обладает тем свойством, что
\г
I
ЩЬ- < оо. (27)
В этом случае выражение для §(и) можно
представить в виде
8(и) = Цй, и) + д [ (е1 <»■*>- 1)П0(^), (28)
где <7>0, а П0—вероятностная мера на {Лт9 ЯЗ**}.
Нетрудно истолковать полученное выражение. Имеем
оо
что представляет собой характеристическую
функцию суммы -,,•*.*, , *
где |ь ^2> •••> 1т ••• —независимые и одинаково
распределенные случайные векторы со значениями в Ят
и с распределением П0, а — постоянный вектор, V (^) — не
зависящая от совокупности ЦкУ 6=1, 2 ...}
целочисленная случайная величина, имеющая пуассоновское
распределение с параметром ц1\
п\ '
Этот процесс будем называть обобщенным пуассо-
новским процессом в 01т.
Заметим, что, . какова бы ни была функция е(и)9
определяемая формулой (15), можно построить
сходящуюся к ней последовательность функций # {и),
имеющих вид (28). Так как последние действительно
определяют характеристические функции некоторых
распределений, то е'яМ, где §(и) — произвольная функция,
имеющая вид (15), является характеристической
функцией некоторого распределения. Отсюда вытекает
Теорема 5. Для того чтобы процесс 1(1) был
однородным стохастически непрерывным процессом с
независимыми приращениями,' необходимо и достаточно,
чтобы его характеристическая функция была представима
формулами (25) и (15), где а— произвольный вектор,
ша
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш
Ь — произвольный положительно определенный оператор,
П(/?) — произвольная конечная мера на {Жт, Ът) и
Щг = 0} = 0.
Марковские процессы. Марковские процессы играют
важнейшую роль в современной теории вероятностей
и ее приложениях. Во втором томе они будут подробно
изучены. Здесь же будет приведено простейшее
определение этого классе процессов. Понятие марковского
процесса с дискретным временем было введено и
обсуждено в § 4 гл. II. В основе понятия марковского
процесса (марковской системы) лежит представление о
системе, эволюция которой в будущем зависит только
от состояния системы в данный момент времени (т. е. не
зависит от поведения системы в прошлом). Пусть %{1)у
/еГ, Г —конечный или бесконечный промежуток
времени, случайный процесс со значениями в полном
метрическом пространстве °У> 23 —а-алгебра борелевских
множеств Щ.
Пространство Щ будем называть фазовым
пространством сиетемы, а ^(0~ ее состоянием в момент
времени /. Гипотезу о «независимости будущего от
прошлого» или «об отсутствии последействия» проще всего
записать с помощью условных вероятностей
следующим образом:
РЙ(*)еВ|Б(*,), 1{к\ ..., &(*«)}«
■=Р{&(0€=Д|Б(а (тоёР) (29)
для любых Ве 23 и 1Х<12< ... <1п<1. Так как
условную вероятность относительно случайной величины можно
рассматривать как функцию от этой величины, то
положим
Р {I (0 €= А | Б (5)} « Р (5, | (5), {, А) (8 < I).
Из формулы (19) § 3 гл. I следует, что при 1Х </2< ••• <'я
для произвольной ограниченной борелевской функции
е(Х\, х2, ..., хп) (хк^ Щ, к= 1, 2, ..., п) имеет место
равенство
м&(&('|), ш..... ш)\ии))=
-[РЦ\. 1(*х), *2, «Ы / Р(/2, У2, 'а, ЛУз) ■ • •
... $ Р((п.и уа.ь 1п, Луп)§Ы1), Уь ..:,Уп\ (той Р). (30)
$1} НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 199
В частности, если положить # = %д(*з)» где %в(у) —
индикатор множества В е 33, то из (30) имеем с
вероятностью 1
Р:(*и бМ, 'з. В)**$Р{{2, уъ *3, В)Р(1и *(/,), к, й\)г\ (31)
Полученное равенство уже фигурировало в § 4 гл. II
под названием уравнения Чепмена — Колмогорова.
Определение 5. Случайный процесс \{1){1^Т)
со значениями в Щ называется марковским, если
а) для любых <1<^2<-.-<^п<^ /АбГ(Ы,..,й),
/еГ, выполняется (29);
б) существует функция Р(з, у7 I, В), ©-измерима по у
при фиксированных 5, I, В, при фиксированных 5, уу 1%
являющаяся вероятностной мерой на 33,
удовлетворяющая уравнению Чепмена — Колмогорова.
Р{1ь У, <з, 5}= | Р(/2> уъ *3, В)РЦи у, *2, йу2) (32)
и с вероятностью 1, совпадающая с условными
вероятностями .
Р(8, |(5), I, А) = Р{Щ)*=А\№}.
Функции Р(1, у, 5, В) называют вероятностями
перехода марковского процесса.
Таким образом, по определению семейство условных
вероятностей (29) регулярно и процесс |(/) не зависит
от «прошлого». Свойство процесса, выражаемое
равенством (29), будем называть марковским свойством или
отсутствием последействия.
Покажем, что из марковского свойства вытекают
более сильные утверждения. Применяя снова
формулу (19) § 3 гл. I и равенство (30), получим при ^^<^2<
... <1т< ... </„+т> 4ЕГ(Ы,...,П + Ш)
М &(*(*„+,), &('т+2), ..., Б ('«+*.) )1Б('1). Ш, -.6 ('«)Ь
= / Р(*т> &('«), '«+1, <*|М •••
••• ] Р Уп+т-\1 Уп-Ь ^п+т* ЗУп) &(Уь *••> #>г) =*
- М&(|(*т+1), ,.., %(/„+т)) ||(/„)} (той Р)>
200
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш *
Если положить §• (у{9 ..., уп) = %в{п) (ур ..., уп), где В{п) -
борелевское множество из Щп, то отсюда, в частности,
вытекает равенство, обобщающее марковское свойство
процесса:
Р {[&(*„,+,), .... I (*„+„)] еЯ(п>| &(*,), .... &(*„)}=.
= Р{[|(^+1). ..-, 6('т+»)1еВ<п)|б(и} (тойР)
ДЛЯ ЛЮбЫХ ^<^2< ••• <^а+т(€= ^)» п и т- Обозначим
через ^ а-алгебру событий, порожденную случайными
величинами |($), 5 еЕ Г, $<]/, а через §, ст-алгебру,
порожденную величинами |($), ^еГ, $>/. Тогда для
любого цилиндрического множества С€=§^ имеем при
*!<*2<... <^</
Р {С 11 (<!>, ...,1 (а = Р {С | Б (*„)} (той Р). (33)
Пусть Л — класс событий, для которых (33) имеет место.
В силу свойств условных вероятностей (§ 3 гл. I)
Л является алгеброй и монотонным классом событий.-
Поэтому Л :э %*. С другой стороны, пусть 9( — класс
событий гМ9 для которых при любом 5е§|
|Р(5|&)й!Р=|Р(5|Ш)йк (34)
N N
В силу (33) в 91 входят все цилиндрические множества
из %. Так как правая и левая части равенства (34)
являются счетно-аддитивными функциями на §ь то из того,
что они совпадают на цилиндрических множествах из ^,
следует, что они тождественны на §*. Итак, имеет место
Теорема 6. Для произвольного 5е^|
Р(5|8/) = Р(5|Б(0)(тос1Р). (35)
Соотношение (35) показывает, что условная вероят-'
ность любого события 5, определяемого поведением
марковского процесса в «будущем» при заданном
полностью «прошедшем», зависит только от «настоящего».
Марковским процессом в широком смысле,
определенным на Т = [0, Ъ) или Т = [0, оо), будем называть
семейство, состоящее из вероятностной меры м-о на {^> ^}
и вероятностей перехода Р((, у, 5, В) (/<$, /, $еГ/
Вей),, удовлетворяющих условиям б) определения 5.
§ 1] НЕКОТОРЫЕ КЛАССЫ СЛУЧАЙНЫХ ФУНКЦИЙ 201
Мера Цо называется начальным . распределением
системы.
Для произвольной ограниченной борелевской
функции ({уи у2, ..., Уп) п переменных ук^ Щ и для любых
4еГ"(/г=1, ..., п, 0<^^< ... <1п) положим
%2...и/]= |^№/о)| Я(0, уо, *1, йу{)Х ...
г/г. ••-, Уп)Р((п-ъ Уп~ь *п, ЛУп) (36)
где хА(П) — индикатор множества Л(п)е23л, а 23" — а-ал-
гебра борелевских множеств в ^^ Заметим, что для
произвольной борелевской функции / (уь у2, ..., уп)
функция
1ЛУи Уъ .-., Уп-\) =
= \ !(Уи Уь ..., Уп)Р(и Уп-и 5> ^«) ('<*)
также является борелевской, так как интеграл
представляет собой предел интегралов от простых функций,
а последние являются борелевскими функциями
переменных уи у2у ..., Уп~1- В силу свойств интеграла
Рг ... * {В{п)) есть мера на 33". Очевидно, что семейства
мер Р^... *Г1(В{п)) удовлетворяет условиям
согласованности и в силу теоремы Колмогорова (теорема 2 § 4
гл. I), если Щ — полное метрическое сепарабельное
пространство, допускает некоторое представление {й, ©, Р},
где О—пространство всех функций со(0, 1 е Г, со
значениями в Щ. Пусть ^ (Л —любой процесс, стохастически
эквивалентный {О, ©, Р}. Проверим, что
?Ш)^т(Ч\Ш, ...ЛЮ}=Р(*п,Ш,1>В)(тойР),
т. е. \{1) является марковским процессом с заданными
вероятностями перехода. Для этого достаточно
проверить равенство
\ Р^п, Уп, *> В)Р^л..9^п(ауи йуъ ..., йуп) =
-л,*, /й.Дв(й,хв)
262 СЛУЧАЙНЫЕ 4»УНКЩШ [ГЛ. III
для любых В(л)€=гЗЗ, ВенЭЗ и /1</2</3< ... </«<?.
Но оно непосредственно вытекает из формул (36), (37)
и теоремы 2 § 4 гл. II.
Таким образом, если Щ — полное метрическое сепа-
рабельное пространство, то для произвольного
марковского процесса в широком смысле существует некоторое
представление.
§ 2. Сепарабельные случайные функции
Основная теорема. Пусть на вероятностном
пространстве {О, ©, Р} задана случайная функция ^(х) =
= #(лс, со), леей? со значениями в некотором измеримом
пространстве Щ, 33}. Будем считать, что {Й, ©, Р}—-
полное вероятностное пространство.
Во многих вопросах важную роль играют события
вида
{со: ^(х)^Р для всех хбС}, (1)
К сожалению, когда О несчетно, вообще говоря, нельзя
утверждать, что событие (1) ©-измеримо. Тем не менее
имеется настоятельная потребность рассматривать
случайные функции, для которых это событие было бы
©-измеримо для достаточно широкого класса множеств
р и е.
Возможность преодоления затруднений, связанных
с несчетностью множества О основывается на
следующем замечании. Допустим, что в 36 существует счетное
множество точек/ и такое со-множество N. что Р{Л/} = 0
и симметрическая разность множества (1) н множества
{со: 1{х)^Р для всех хеС(1/}= П (со: 2"(*)е ^ (2)
содержится в N для всех Се® и Ре^. Тогда
множество (1) измеримо. Случайные функции,
удовлетворяющие только что сформулированному
предположению, называются сепарабельными (относительно классов
множеств © и §). Интуитивно представляется ясныш}
что для сепарабельности случайной функции множества
из © должны быть в каком-то смысле массивными и
содержать достаточно много -точек из / так, чтобы'
||2] СЕПАРАБЕЛЬНЫВ'"СЛУЧАЙНЫЕ ФУНКЦИИ 203
имелись основания считать множества (I) и (2)
несущественно отличающимися друг от друга.
Например, если 96 и Щ — метрические пространства,
36 — сепарабельное пространство, © — класс открытых
множеств, 3 — класс замкнутых множеств в Щ, а функ-
щщХ>(х)~ё(х, (о) почти для всех со непрерывна, то она
будет сепарабельной, если в качестве / взять
произвольное счетное всюду плотное множество в 96. При
этом множества (1) и (2) совпадают при каждом со, при
котором (;(*) непрерывна.
В настоящем параграфе постоянно предполагается,
что 96 и «^ — метрические пространства с расстояниями
г(хь х2) и р(уи у2) соответственно, ^ — сепарабельное
пространство, а Свойство сепарабельности случайной
функции понимается по отношению к классам © и §
открытых множеств в 96 и замкнутых множеств в Щ.
Определение 1. Случайная функция &(*)в#(х, (о)
называется сепарабельной, если существуют в 96 всюду
плотное счетное хмножество / точек {*/}, / = 1, 2, .,. и
в й множество N вероятности 0 такие, что для любого
открытого множества О а 96 к любого замкнутого
множества Р а Щ два множества
{со: §(х, (о)^Р для всех х е О},
{со: §(х, со) е Р для всех х^ 0(]1}
отличаются друг от друга только на подмножество N.
Счетное множество / точек л;/, фигурирующее в этом
определении, называется множеством сепарабельности
случайной функции. Оказывается, что свойство
сепарабельности не является жестким ограничением на
случайную функцию. При достаточно широких
предположениях, относящихся только к природе области
определения 96 и области значений Щ случайной функции,
существует сепарабельная случайная функция,
стохастически эквивалентная данной. Следует, однако,
заметить, что при построении эквивалентной сепарабельной
случайной функции иногда приходится расширять
область значений функции, превращая ее в компактное
множество. ,
Приведем сначала один критерий сепарабельности
случайной функции. Пусть Щ компактно, $(х, ©) —
204
СЛУЧАЙНЫЕ ФУНКЦИИ
[гл. шг
сепарабельная случайная функция со значениями в <2/,
/ — множество сепарабельности, N — соответствующее
исключительное множество точек со.
Обозначим через V класс всех открытых сфер
пространства 36 с рациональными радиусами и с центром
в точках фиксированного счетного всюду плотного
множества в 36. Класс V счетен. С другой стороны,
произвольное открытое множество О из 36 может быть
представлено как сумма (счетного числа) сфер из V'.
Пусть Л (О, со) — замыкание множества значений
функции §(х, со), когда х пробегает множество 1()6, а
А (х, со) - П Л (8, со)
есть пересечение всех А (5, со), когда 5 пробегает
совокупность сфер из V', содержащих точку х в качестве
своего элемента. Семейство замкнутых множеств А (5, со)
(*е5) является центрированным, т. е. любое конечное
число множеств этого семейства имеет общие точки, и
в силу компактности Щ их пересечение А (х, со) не пусто.
Из сепарабельности функции §(х, со) следует, что
ё(х, ©)€=Л(*, со). (3)
Обратно, если (3) выполняется для всякого со ё Лг,
Р{Л/} = 0, то §(х, со) — сепарабельная случайная
функция. Действительно, если § (х, со) е Р для всех х^ I []8,
где Р — некоторое замкнутое множество в ^ и 5ЕК,
то А (х, со) е А (5, со) для всякого хее8 и,
следовательно, §(х, (о)е/7 для всех х из «5.
Пусть О — произвольное открытое множество в 36 %
Представим его в виде суммы С = \^8к множеств из V.
к
На основании только что сказанного из "соотношения
§ (ху со) е р для всех х^ I (] Оу со е= N
имеем
§ (х, со) е Р для любого х е О.
Сформулируем полученный результат в виде следующей
леммы.
Лемма 1. Для того чтобы случайная функция
$(х, со) со значениями в компактном пространстве (Ц
была сепарабельной, необходимо и достаточно, чтобы
$ 2] СЕПАРАБЕЛЬНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ 205
существовало множество А/, Р{Лг}==0, такое, чтобы при
®Ш N выполнялось (3).
Таким образом, чтобы построить для §(х% со) сепара-
бельную стохастически эквивалентную функцию,
достаточно найти функцию §(х, со), удовлетворяющую (3) и
совпадающую с вероятностью, равной единице, с
функцией §(х, со):
РШ*, <»)Ф8(х, со)} = 0.
Лемма 2. Пусть В — произвольное борелевское
множество в Щ, Щ компактно. Существует конечная или
счетная последовательность точек хи хъ ... такая, что
множество
N (ху В) = {со: § (хк9 со) ее В, /г - 1, 2, ..., # (х, со) ^ й}
имеет вероятность 0 /г/ж любом х е Я?.
Доказательство. Пусть ^ — любое. Если х,,
я2, • ••> *л построены, то полагаем
шк = 5ирР{я(хь о)еВ, ..., е(хк, со)<е=В, 5Г(л;, со)§3}.
Если пгк = 0, то соответствующая последовательность
построена. Если т*>0, то пусть хк+х — такая точка,
что
'Я,
Р{г(^1, ©)^5, ..., §(хь со)е=В, г(*Л+1, со)^5}>^-.
Так как множества
1* = {со: §{хи й)е8,/=1,2 *, 2 {**+!> со) е В}
не имеют общих точек, то
оо оо
Следовательно, тА->0 дри 6->оо. Таким образом, при
любом .V
Р{#(*ь со)^В, й- 1, 2, ..., #(*, ©)еВ}<Нтт/к = 0.
что и доказывает лемму 2.
Из доказанного нетрудно вывести следующее
утверждение.
Лемма 3. Пусть 9К0 — счетный класс множеств,
а Ш — класс, состоящий из пересечений всевозможных
206
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш
поеледшат ель тетей множеств т 5Ш0. Существует кщ
печная или счетная последовательность точек хи х2, ...
• • • > %> • • • # для каждого х такое множество N (х), что
Р{М(х)} = 0
и
{со: §(хп, й)еВ, п = 1, 2, ..., §(х, со) Ш В} с: Л/(л)
5лл любого В ^9Я.
Для доказательства поступим следующим образом.
Пусть / — счетное множество точек из *$?, являющееся
суммой последовательностей {.*:„, /1=1,2, .,.},
построенных для каждого Яе10 в соответствии с леммой 2 и
Л/(*)= У Л/(х, В). Если В'е=Ж и ЯгэВ', Ве10, то
в &т*
{со: #(*„, со)€= В', хпее /, #(л:, й)еВ}с
с: {со: # (*Л, ©) ^ В, хп ее /, ^ (*, ©) е В} с= /V (х, В)аЫ (х).
оо
Кроме того, если В' = ^ В& е 9№0> Т(>
/2=1
{со: # (дгя, со) е В', хп е= /, я (*, ©) € В'} с:
оо
с= у {со: § (хпу со) е Б7, хп ее /, # (х, со) е В*} с:
Л-1
оо
что и доказывает лемму.
Теперь нетрудно доказать следующую теорему.
Теорема 1 (Дж. Л. Дуб). Пусть $6 и Щ —
метрические пространства, $в сепарабельно, Щ компактно.
Произвольная случайная функция § (х, со), х<^<%,
со значениями в Щ стохастически эквивалентна
некоторой сепарабельной случайной функции.
Доказательство. Фиксируем некоторое счетное
всюду плотное множество точек Ь в Щ, и пусть 9№0 —
кЛасс множеств, являющихся дополнениями к сферам
рационального радиуса с центрами в точках I. Тогда
3№ —класс пересечений множеств из Ш0 содержит все
замкнутые множества пространства Щ. Далее, рля
каждого 5еУ рассматриваем случайную функции)
§31 СЕПАРАБЕЛЫ1ЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ Щ
•%{х9 со) как заданную только для хе 5 и строим
последовательность / === / (5) # множества М(х)^Ы8 (#)
в соответствии с леммой 3. Пусть
/= и /(5), л,- и м3(х).
Положим
§(Х, ®)=:§(Х, СО),
если х е / или со е= уу*, если же со <= А^, л: Ш /, то
определим §(х, со) любым способом, так, чтобы §(#, оо)е
е Л (л:, со). Так как для точек х^1 значения функций
&(х, ®) и §(х, со) совпадают, то множества А(х, со),
построенные для функций §(л:, со) и #(л;, со), также
совпадают. Из определения @{х, со) следует, что
§{ху со)е= А(х, со)
для любого л: и со. Так как {со: §(х, (й)Ф§(х, а>)}с:ЫХ9
то Р{§(х, «>) = ^(х, со)}~1, что и заканчивает
доказательство теоремы.
Теорема 1 непосредственно обобщается и на
случайные функции со значениями в сепарабельных
локально компактных пространствах.
Теорема 2. Пусть Щ — сепарабельное локально
компактное пространство и Вв ~ произвольное метриче^
ское сепарабельное пространство. Для любой случайной
функции @(х> со), заданной на 36 со значениями в ®/,
существует стохастически эквивалентная сепарабельная
случайная функция @(х, со), принимающая значения
в некотором компактном расширении Щ
пространства щ, ^ => <у.
Доказательство вытекает из того факта, что всякое
локально компактное сепарабельное пространство Щ
можно рассматривать как подмножество некоторого
компакта Щ. Например, если §(х, со) — случайная
функция со значениями в конечномерном пространстве Щу
то, дополняя О/ одной «бесконечно удаленной»
точкой оо, легко получить компактное пространство Щ =
= ^11{00} с новой метрикой, такой, что каждое
замкнутое множество ^с^ (в топологии пространства Щ)
является также замкнутым в Щ (по отношению к
новой метрике). При построении сепарабельной реализа-
208
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
ции случайной функции ей, возможно, придется
приписывать дополнительное значение «оо», но, очевидно,
при фиксированном х вероятность этого равна нулю.
Стохастическая непрерывность. Во многих вопросах
важно знать, какое множество / может играть рояь
множества сепарабельности. Прежде чем дать ответ
на этот вопрос, введем одно важное понятие и
приведем простые теоремы, с ним связанные.
Определение 2. Случайная функция §(х, со)
со значениями в Щ называется стохастически
непрерывной в точке л?0, х0^<%?, если для любого е>0
Р{р(я(*о, со), е(х, со))>е}->0 при г{х9 л:0)->0. (4)
Если д{х, со) стохастически непрерывна в каждой точке
некоторого множества Вс^, то она называется
стохастически непрерывной на В.
Заметим, что условие стохастической непрерывности
есть условие, накладываемое на «двумерные»
распределения случайной функции, т. е. на совместное
распределение случайных элементов §(хи со) и §{х2, со),
хъ х2^<$. В частности, это понятие применимо и
к случайным функциям в широком смысле.
Требование стохастической непрерывности в точке х0
означает, что 1>(х) = §{ху со) сходится по вероятности
к Б(*0) при х->хъ.
Определение 3. Если существует точка уе <Ц
такая, что при /(->оо
аир Р{р&(*,©), у]Ж}->0, (5)
то случайная функция §(х, со) называется стохастически
ограниченной на множестве В.
Теорема 3. Случайная функция § (х, со),
стохастически непрерывная на компактном <$, стохастически
ограничена на дЗ.
Доказательство. Пусть е>0 — произвольное
наперед заданное число. Для каждой точки х построим
сферу 5Л с центром в точке х такую, что
Р{р(*(*.<*). *(*', со))>1}<|-
§ 2] СЕПАРАБЕЛЬНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ 209
для любой точки х' е 5д.. Из множества сфер 5Л
выберем последовательность 5Х1, 5^, ..., 8Хп, образующую
конечное покрытие 36. Тогда при любом у
р{ё{*> ©), */}<р(# {хи со), у) +
+ шах р{в(х{9 со), д(х1у ©))+"р(#(х/, со), §(х, со)),
г =2, .... п
где х\ обозначает центр одной из тех сфер 3Х/г (к =
= 1, ..., п), внутрь которой попала точка х. Слагаемые
в правой части неравенства являются конечными
случайными величинами. Поэтому при достаточно
большом N
Р 1р(я(*ь ю), У)+ тах р(§(хи со), д{х19 ©))>#\ <-§--•
| 1=2, .... П ) 1
Если считать, что Ы>1, то для любого х^ЗВ
Р{р(#(*, ©), ^/)>2//}<Р{р(§(^, ©), е{х> ©))>0 +
+ Р \р(8(*и ©)> у)+ тах р ($(*!, со), #(*,, со))>М <е,
I 1=2,..., п I
откуда вытекает, что
§ирР{р(§(х, со), у)>2Ю<е,
что и требовалось доказать.
Определение 4. Случайная функция §(х, со)
называется равномерно стохастически непрерывной на..$?,
если для произвольных сколь угодно малых
положительных е и г{ можно найти такое б>0, что
Р{р(г(*> ®),г(^, со))>е}<еь (6)
как только г (х, л;') < 6.
Теорема 4. ^сш §*(ху со) стохастически
непрерывна на компактном дв, то & (х9 со) равномерно
стохастически непрерывна.
Действительно, если бы это было не так, то нашлась
бы пара положительных чисел е и в{ и для любого
6Д>0 пара точек хп и х'П9 для которых г{хпу х'п)<6п и
Р{р(е(*п, со), е{х'П9 со))>е}>е1.
210
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
Можно предположить, что 6л-*0 и %->л:0, тогда
х'п -* х0 и
е!<Р{р(#(*«, <*>)> §(х'п, со))>е}<
<Р{р(^(**, о), #(*о, со))>|} +
+ р{р(#(*о> «>), §{х'п, со))>|-}.
Это неравенство противоречит условию стохастической
непрерывности.
Теорема 5. Пусть 96 — сепарабельное
пространство, Щ — произвольное метрическое пространство
и § {х, со) — сепарабельная стохастически непрерывная
случайная функция со значениями в Щ. Тогда
множеством сепарабельности случайной функции §(х, со)
может служить любое счетное всюду плотное
множество точек из 96.
Доказательство. Пусть У = {5} — счетное
множество сфер в 96 введенное ранее, 1 = {хк, &=1,
2, ..., /г, ...} — множество сепарабельности случайной
функции §(х, со), N — исключительное множество
значений ш, фигурирующее в определении
сепарабельности, и / — произвольное всюду плотное множество
точек в 96. Пусть В (5, со) обозначает замыкание
множества значений §(хк, (о), когда точка х'ь пробегает / П 5,
а N(5, й)— событие, состоящее в том, что §(хк, ®)Щ
е= В (5, (о), если хк е 5. События N (5, к) имеют
вероятность 0. Действительно, пусть х'Гу г = 1, 2, ..., п, ... —
произвольная последовательность точек из /П-5,
сходящаяся к хк. Тогда
< Нт Р\ Ит р(е(хк9 ©), 'ц{хп <&))>-;]<
< Нт Ит Р\р{ё{хь со), е(х'п (>>))>~г} = 0.
Пусть #'=У УЩ4), тогда Р{ЛГ} = 0. Если
со е Л^ II ^ и 1^,4^^ дая всех х е /П С, где О —
§3]
ИЗМЕРИМЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
211
некоторое открытое множество, а Рс^ замкнуто, то
для всякого ^бО и 5 такого, что ^е5сС, имеем
д(хъ ©)еВ(5, со) с: Л
Из определения множества {х&} отсюда вытекает, что
@(х, со)^/7 для всех х^О и ©>ё=Л/"'М$/. Итак,
множество / удовлетворяет условию, входящему в
определение множества сепарабельности случайной функции.
§ 3. Измеримые случайные функции
Пусть $в и Щ — по-прежнему обозначают
метрические пространства с расстояниями г (хи х2), р(#1, у2)
соответственно, § (дг, со) — случайная функция со
значениями в Щ и с областью определения $?, со
—элементарное событие вероятностного пространства {Й, @, Р}.
Допустим, что на дв определена ст-алгебра
множеств %, содержащая борелевекше множества, и на 91 —
некоторая полная мера \х. Через а{%хЩ обозначим
наименьшую ст-алгебру, порожденную в ^ХО
произведением сг-алгебр 21 и ©, а через ст{?1х®}- ее
пополнение относительно меры {х X Р.
Определение 1. Случайная функция § (лс, со)
называется измеримой, если она измерима относительно
д{% X ©}.
Обозначим через В ог-алгебру борелевских множеств
пространства Щ. Напомним, что в общем случае из
определения случайной функции следует, что для
любого В е 23 и фиксированного х
{со: § (х, со) е В) е©.
Если же случайная функция @(х, со) измерима, то
{(*, со): ц(х, со)нее В}е= сг{91 X ©}.
Отсюда и из теоремы Фубини вытекает, что §(ху со)
как функция от х ^(-измерима с вероятностью 1.
Рассмотрим вопрос о существовании для данной
случайной функции стохастически эквивалентной
измеримой и сепарабельной функции.
Теорема 1. Пусть дБ — полное сепарабель ное
метрическое проетрансгво, °$—хепарабельно и локально
212
СЛУЧАЙНЫЕ•ФУНКЦИИ
[ГЛ. Ш
компактно, мера \х а-конечна. Если для \х^почти всех х
случайная функция @(х, со) стохастически непрерывна,
то существует измеримая сепарабельная функция §* (ху ю),
стохастически эквивалентная функции § (л:, со).
Доказательство. Допустим сначала, что <$
и Щ компактны и \х(Зу)<оо. Из теоремы 1 § 2
следует, что существует сепарабельная случайная
функция §(ху со), стохастически эквивалентная функции
§(х, со). Пусть / — множество сепарабельности функции
§{х,(й). Будем считать, что / всюду плотно в 3?.
Расположим точки / в некоторую последовательность
{Хи Х2у . . . , ХП9 . . .} И ПОЛОЖИМ Гп = ПИП {Г (Хк, Х6),
к, 8= 1, ..., п).
Для каждого п построим конечное покрытие
множества 96 сферами 5(л), ..., 8{тп, радиус которых
равен гп/2 с центрами в точках х^ е /. При этом
предполагается, что Х/'г) = х\ при / = 1, 2, . .., п, а остальные
точки х/л)(/«=я+1, ..., тп) выбраны из /
произвольным образом, лишь бы сферы 5/я) (/ = п + 1, ..., тп)
образовывали покрытие множества <8?. Положим §п(х, со) =
= ^(Л'/е, СО) При X е 5/г1), &=1, 2, ..., Д (ЭТИ СфврЫ
не пересекаются, так что это определение
корректно) и §п (х, со) = г (х?\ со), если х е= 5$я) \ () 5?\
/ = л+1, ..., /ял, где х]п) — центр сферы 5/л).
Заметим, что #л+т(л:, со) = § (х, со), #„ (х, ю) — боре-
левские функции аргумента х при фиксированном со,
о{% X ©} — измеримые как функции пары (х, со). Кроме
того, гп->0 и
р [?«(*» ®)> #(*> ®)] = р[г№ <°)' «(*■ ®)]
при г{*«\х) <!$-'. (1)
Если положить
Опт(х) = Р{<»' р[8п(х, СО), &,+,„(*, ©)] > «К
то в силу условия теоремы [г-почти для всех х Опт(дс)-> оо
§3]
ИЗМЕРИМЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
213
при п->оо. Поэтому
(|гХР){(лг, со): р[#п(*, со), ёп+т(х, со)]>е} =
= | Сят(*)|1 («/*)-► О
при /г->оо, т. е. последовательность §п(х, со)
фундаментальна по мере \х X Р. Из нее можно выделить
подпоследовательность §Пк(х, <д), СХОДЯЩУЮСЯ \1 X Р-ПОЧТИ
всюду к некоторой а{51х©Ьизмеримой функции §(х, со).
Множество точек (х, со), где эта сходимость не имеет
места, обозначим через /С. Так как К имеет меру 0, то
[х-почти все ее сечения имеют Р-меру 0. Через Хх
обозначим множество тех х, для которых эта мера >0.
В силу предыдущего построения можно считать, что
Х\[\1~& и &{хю со) = §(хп, со). Пусть Х2 обозначает
то множество х, в котором нет стохастической
непрерывности. Из (1) следует, что
р {§ (*» ©) ф й (*» ®)) = о» если х е х{ и х2.
Положим теперь ^* (х, со) = § (х, со), когда (х, со) <== К и
хе!^^ и §*(х9 со) = ^(х, со), если (х, со)е/( или
л:е ^IIХ2. Тогда Р{^(а% со)^=^(х, со)} = 0ужедля всех л:,
так что §*(х, со) стохастически эквивалентна §(х, со).
Функция §* (х, со) сг{91 X ©}-измерима, так как она
отличается от от {91 X ©}-измеримой функции на множестве
р, X Р-меры 0. Остается заметить, что #* (х, со) сепара-
бельна. Пусть Л (О, со) обозначает (как и в § 2)
замыкание множества значений §(х, со), получаемых, когда х
пробегает множество 0(]19 а Л(х, со) — пересечение
множеств А (5, со), где 5 — произвольная сфера с центром
в точке х. Сепарабельность функции §(х, со)
эквивалентна условию §(х, ю)^А(х, со). Так как §*(х, со) =
= §(х, со) при хе/, то множество А(х, со), построенное
для §*{х, со), совпадает с А(х9 со). Далее, из
определения 8п (х, со) следует, что §* (х, со) = § (х, со) =Л\т §п (х, со)сее
е Л (я% со) при любом х ^Х{[}Х2 и (я, со) е К = #* (#, со);
= ^ (х, со) е Л (л;, со) при хе!^^ или (х, со)<=/(
по определению. Таким образом, §* (х, со) — сепарабель-
ная случайная функция, и теорема доказана в
рассматриваемом частном случае. Нетрудно получить ее теперь
в общем случае. Требование компактности простран-
ш
слшшдаш функции
[гл. т
ства Щ может быть заменено требованием локальной
компактности и сепарабельности. Действительно,
компактность пространства нужна была только для
возможности сослаться на теорему 1 § 2. Теперь же можно
ссылаться на теорему 2 § 2. При этом сепарабельное
и измеримое представление §*(ху со) функции §(х> ,#)
принимает, вообще говоря, значения из некоторого комг
пактного топологического расширения пространства Щ±
Далее, если 36 полное сепарабельное пространство,
а мера р сг-конечна, то 36 можно представить в виде
суммы счетного числа компактов {К,и л=1, 2, ...}
конечной меры и множества N р~меры 0. Последнее
вытекает из того, что в полном сеоарабельном
метрическом пространстве каждое измеримое множество А
конечной меры можно сколь угодно точно
аппроксимировать по мере компактом К с: А. К каждому
компакту Кп применимы предыдущие рассуждения. Отсюда
легко вытекает общее утверждение теоремы.
Замечание 1. Теорема 1, в частности, имеет место
для евклидовых пространств 36 и Щ, если мера р является
лебеговой мерой в 36.,
Замечание 2. Доказательство теоремы 1
упростилось бы, если не требовать сепарабельности измеримого
представления заданной случайной функции.
Множество / при атом не привлекалось бы к рассмотрению,
а точки х%] выбирались бы произвольным образом из
соответствующих множеств. Из свойств пространства Щ
использовалась бы только полнота пространства.
Следовательно, если ^ — полное, а 36— полное и
сепарабельное метрические пространства, р — сг-конечная мера,
то случайная функция §(х, а>) со значениями в Щ>
хб1, ©ей, стохастически непрерывная р-почти для
всех х, стохастически эквивалентна измеримой
случайной функции.
Следующий результат, имеющий важное значение,
непосредственно вытекает из теоремы Фубини.
Теор ем а 2. Пусть §(ж).= §{х, со) — измеримая
случайная функция, принимающая действительные или ком*
плексные значения. Если
|М||(л:)||1(^)<оо,
№
$**1 критерий отсутствия *>аз№вов второго ряда ай
т для любого множества А^%
1мих)\1(с1х) = Щ^1{х)11(с1х).
Л А
Йкюледнее равенство означает перестановочность
операции вычисления математического ожидания случайной
величины и операции интегрирования по параметру х.
§ 4. Критерий отсутствия разрывов
второго рода
Функции без разрывов второго рода. Пусть |(/),
/е[а, Ь] — случайный процесс со значениями в полном
метрическом пространстве Щ.
Определение 1. Если с вероятностью 1
выборочные функции процесса для каждого I е (а, Ь) имеют
пределы слева и справа, а в точке а(Ъ) предел справа
(слева), то говорят, что процесс не имеет разрывов
второго рода на отрезке (а, Ь).
В настоящем параграфе постоянно предполагается,
что процесс 5(0 сепарабелен. Множество
сепарабельности процесса обозначим через /.
Определение 2. Функция у = 1(1), уе^, имеет
на отрезке [а, Ь] не менее т г-колебаний (е>0), если
существуют точки /0, ..., (т, а^^0<^^< ... < 1т<Ь,
такие, что
Р (/(**-.!), /&)■)>*, * = 1, 2 т.
Лемма 1. Для того чтобы функция у = /(/) не
имела на отрезке [а, Ь] разрывов второго рода,
необходимо и достаточно, чтобы для любого е>0 у нее было
только конечное число г-колебаний на [а, Ь].
Доказательство. Н е о б х о д и м о с т ь. Пусть
число е-колебаний неограниченно. Тогда найдется такая
последовательность /0, /?,..., 1п,..., что 1п \ 1§ или 1п \^
и:р(/(Ц /(^+0)>0. Но это означает, что /(/0~0).
или /(^о + 0) не существует.
Достаточность. Пусть в некоторой точке /0 не
существует одностороннего предела (например, предела
слева). Тогда найдется последовательность 1п \ 1§ такая,
216
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Щ
что для любого п зир р(/(*т)> /(^))>е, т. е. число
т > п
е-колеба-ний неограниченно.
Заметим, что определение 2 тривиально переносится
на случайные функции, рассматриваемые на
произвольном множестве действительных значений /.
В дальнейшем, рассматривая функции без разрывов
второго рода, мы не будем различать две функции,
имеющие в каждой точке ,*е [а, Ь] одинаковые пределы
слева и справа. Поэтому естественно принять какое-либо^
стандартное соглашение о значениях этих функций
в точке разрыва. Обозначим через Л [а, Ь] = 0 [а, Ь\ Щ\
пространство функций, заданных на [а, Ь] со значениями
в Щу не имеющих разрывов второго рода, и в каждой
точке *е=[а, Ь] односторонне непрерывных. Положим
АДП== зир {гшп[р (/(/'), /(0), Р (/('"), МО)];
/-с <*'</</"<* +с, /', /, /"€=[а, Ь]} +
+ зир {р (/(/), !(а)); а<1<а + с} +
+ зир {р (/(*), !Ш Ъ-с<КЬ). (1)
Лемма 2. Для того чтобы функция у = /{I) не
имела разрывов второго рода, необходимо и достаточно,
чтобы
НтМ/) = 0. (2)
с->0
Доказательство. Необходимость. То, что
два последних слагаемых в правой части (1) стремятся
к нулю при с->0 для каждой функции [ей[а, Ь]у
вытекает из определения.
Пусть условие 2 не выполнено. Тогда найдутся такие
последовательности С, 1п, С, что &<(п<С ** — *«-*()
и р(/ЧО> /Сл))>е, р (/(*«)» /(^))>е для некоторого
е>0. Можно считать, что 1п сходится к некоторому /0
(если это не так, то можно заменить
последовательность (п некоторой сходящейся подпоследовательностью).
Из трех последовательностей [С], {^}, {*п} по крайней
мере две имеют бесконечно много точек, лежащих по
одну сторону от /о. Если, например, {/п} и {/„} лежат
слева от /0, то /(**)-* Д* —0), I {О->!((-0)г что
противоречит условию р(/ {С), [(*„)) > е. Аналогичен случай,.
§Ц КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЫВОВ ВТОРОГО РЯДА 217;
когда {^} и {{'п] имеют бесконечно много значений,
лежащих правее *0. Остальные случаи сводятся к этим
двум.
Достаточность. Из условия (2) следует, что /"(*)
непрерывна справа в точке а и слева в точке Ь. Если бы
пр# некотором 10Е(а, Ь) не. существовало Д*0 + 0), то
нашлась бы последовательность 1пЦ и е>0, для
которых р(/(^г), /(/„+1))>е, что противоречит (2). Таким
образом, существует /(/0 + 0) при любом /0е [а, Ь).
Аналогично существует /(/0 — 0): Из соотношения (2) следует
также, что либо / (*0) = / (*о — 0)> либо Д*0) = Н'о + 0)-
Лемма доказана.
Некоторые неравенства. Лемма 3. Пусть $ ОО,
/^ [0, Т] — сепарабельный стохастический непрерывный
процесс со значениями в Щ и существует такая
неотрицательная монотонно возрастающая функция §(1г) и
функция ц (С, Л)^0, Л^О, что
Р{[р(&(О.&0-Л))>Ся(Л)]П
Л [р И (/ + Щ (0) > С5 (Л)]} < Я (С, А) (3)
оо оо
0=2^(7'2-'1)<оо) р(С)=22>(С, Г2-")<оо. (4)
П=0 /1=1
Тогда
Р{ вир р(Ъ(ПЛ(П)>К}<
1>\ V е= [0, Г)
<р{р(1(0), кг))>^-}-ьд(-4-).
Доказательство. Положим
^={р(|(^-г)^(Аг))<СИ7-2-")},
6 = 0, 1,2, ..., 2я-1, п = 0, 1, 2, ...
ос 2™-1
/)0 = Л00П/)1.
В силу стохастической непрерывности можно считать
(см. теорему 5 § 2), что множеством сепарабельности /
процесса \{1) является множество чисел вида ЫТ>
218
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. ИГ
6=0, 1, 2 /1 — 0, 1, 2, Имеем,
Р {АЛ< 2 2 Р{«< 2 2тд(С, Т2~т) = Я(п, С),
оо
где<2(«,С) = 2 2^(0, Т2~т).
Из Д) вытекает, что р(1(Т), 1(0))^С§(Т), и
выполнено одно из событий: или р(^(Г/2), ^(0))^С§'(Г2"~1)
или же р(|(Г), |(Г/2))<Сг(7,2"1)- в об°их случаях
р(|(0), 6(Г/2))<С8 (Т) + Сё(Г2-1),
р (| (Г/2), 6 (Г)) < С§ (Т) + Сё (Т2~1).
Воспользуемся теперь методом индукции. Допустим, что
неравенство
т
9(1(-фгТ),1(-фгТ))<С§(Т) + 2сУ^ё(^г) (5)
5=1
доказано для т = п и для к, / = 0, 1, ..., 2п при
предположении, что Д) имеет место. Докажем, что
аналогичное неравенство имеет место и для т = п-{- 1. Пусть
к и / — нечетные числа & = 2&1 + 1, / = 2/2 — 1. Так как
из Оп+\ следует, что по крайней мере одно из
неравенств
выполняется, то
где к' равно или кх или кх + \. Аналогично найдется
целое /' такое, что
р(б(1АгГ),б(^7'))<Сг(7'2-^>).
§Щ КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЬШШ ВТОРОГО РЯДА 219
Учдаьшая теперь предположение индукции, получим
5 = 1
Аналогично рассматривается случай, когда к или /
могут быть четными. Таким образом, неравенство (5)
доказана для всех т^1. Из сепарабельности процесса
тогда следует, что если событие й0 происходит, то
вир{р(Б{0, 6 (*")). *'> <"€=[<), ПХ2СО
с вероятностью I. Отсюда следует, что
Р{ *ир р(Ъ(ПЛ(П)>Ю^
*\ V е= Ю, Т]
<р(-йг) + р{р(6(0).б(Г))>-ё-}.
Лемма доказана.
Лемма 4 Пусть выполнены условия предыдущей
леммы. Тогда
Р{^(1)>С0([\ё2^})}^([\^], С), (6)
где
оо оо
О («)- 2 8{Т2~т),. Я(п, С)= 2 2тд(С, Т2~т).
Доказательство. Продолжим ход рассуждений
предыдущей леммы. Пусть событие Вп имеет место.
Воспользовавшись индукцией, докажем, что для любых/?
и т найдется такое целое \пт (0</пт<2'п+1), что
п+т
<с2г(Г2-), (7)
п+т
<С^§(Т2~% (8)
$«Я
220
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш'
причем, как функция от т (п и к фиксированы),
величина }пт2
-(п+т)
монотонно не убывает. При т = 0
в качестве /яЭ следует выбрать нуль, если р(Ц^),
%(^))<с8{Т2-п), и единицу, если р(|(^1),
2«) )^С^(Г2~/2). При предположении Оп одно из
этих двух неравенств обязательно имеет место. Пусть /лт
уже выбрано. В качестве ]пт\\ следует взять 2]пт, если
р({([^+|й^]г).|(
2"
- + •
-]'))
<
и 2}пт+ 1, если
р(!([^+^),!(
<С§(Г2~(*+т+1)),
6-1
2/,
2*
<
<С§(Г2~(^т+1)).
Такой выбор возможен, так как одно из этих неравенств,
если происходит 1)п, обязательно имеет место; если же
выполнены оба неравенства, то выбор между
указанными значениями /ят+1 произволен.
Переходя в соотношениях (7) и (8) к пределу при
т—>оо, получим, что для каждой выборочной функции,
для которой Оп имеет место, найдется такое т = т((о),
0<т<7,2Ня"1), что
о<
й"р М^-т + А, %1Ц^т))^со{п).
<<<Г2-("-1). к " 1 \ * !)
1^в^
Пусть ее[2~("+1,Г, 2~пт] и 0</"-*'< е. Найдется
такое А, что (/г- 1)2_,гГ<^<Г<(к + 1) 2""Г. Если
*«=[*'. Г], то либо (/', 0^[(*-1)2""Г,(й-1)2""Г + т1.
либо (/, Г)с:[(Лг-1)2~пГ + т, (й + 1)2""Г]. Если при
этом /', /, и /" взяты из /, то выполняется по крайней
$4] КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЫВОВ ВТОРОГО РЯДА 221
мере однЪ из неравенств
Р(6(0, Б(0)<2СС(я), 9(№>Ь(П)<2СО(п).
Цз сепарабельности процесса вытекает, что одно из
этих неравенств будет иметь место с вероятностью 1 для
всякой выборочной функции процесса. Поэтому из Оп
вытекает, что с вероятностью 1
Де(&)<2СС(/1).
В силу неравенства (5)
Р{Ав(Б)>2СО(л)}<Р(5я)<С(л| С),
или, учитывая, что е^2~{п+1)Т и монотонность
функций ц{Н) и <7 (Л), окончательно получаем
Р{Авй)>Сс([|в2^-])}<(г([1в1^-],с).
Лемма доказана.
Условия отсутствия разрывов второго рода,
использующие частные распределения процесса. Из
последней'леммы сразу вытекает следующая
Теорема 1. Если | (*), I е [0,*Г], сепарабельный
стохастически непрерывный процесс со значениями в °1/,
удовлетворяющий условиям
РЩ>(Ш, 1И-Н))>Сё{Щ П [р(б(/ + Л>, Ш)>
>Ог (/*)]}<</(С, А), (9)
где
2 г {Т2~п)< оо, 2 2"<7 (С, Т2~п) < оо, (10)
го |(/) с вероятностью 1 не имеет разрывов второго рода.
Если, кроме того,
Я(п, С)« 2 2т(7(С, 7,2"м)-^0 (11)
П/?^ некотором п и С->оо, го с вероятностью 1 для
каждой выборочной функции процесса найдется такая
постоянная а, #го
Де(|ХаО([|82-^]) при 0<е<е0,
222
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
где
оо
Доказательство. Положив в неравенстве (6)
С=1, увидим, что в условиях теоремы Де(|)->0 по
вероятности при е-»0. Но Де(|) как функция от е
монотонно убывает при е 10. Поэтому НтДе(^) при е->0
существует с вероятностью 1 и равен нулю. Это
представляет собой первое утверждение теоремы. Второе
утверждение также просто вытекает из условия (11) и
неравенства (6).
В качестве частного случая теоремы 1 рассмотрим
сепарабельный стохастически непрерывный случайный
процесс, удовлетворяющий условию
Щр(1« + к), Ш)Р(К0, Н* - Ь))]Р <Кк1+г, (12)
где р>0, г>0. Если положить §(Н) = Нг'2р и
воспользоваться неравенством Чебышева, то увидим, что
соотношения (9), (10) и (11) удовлетворяются при д(С, Н) =
= —2^-/г1+г~г и 0<г'<г. Отсюда вытекает
Следствие 1. Если сепарабельный стохастически
непрерывный случайный процесс удовлетворяет уело*
вию (12), то его выборочные функции с вероятностью 1
удовлетворяют соотношению
Де(|)<аег'/2р,
где а = а (со) — некоторая постоянная, г' — произвольное
число из (0, г).
Укажем еще на следующее следствие теоремы 1.
Следствие 2. Пусть на [0, Т] задан стохастически
непрерывный случайный процесс в широком смысле со
значениями в полном сепарабельном локально
компактном пространстве Щ, «трехмерные» частные
распределения которого удовлетворяют условиям (9) и (10). Тогда
существует некоторое представление этого процесса, не
имеющее разрывов второго рода.
Условия отсутствия разрывов второго рода,
использующие условные вероятности. В предыдущей теореме
условие отсутствия разрывов второго рода выражалось
через свойства частных («трехмерных») распределений
§,4 КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЫВОВ ВТОРОГО РЯДА 223=
случайного процесса. Приведем результаты несколько
иного характера. Они используют предположения,
относящиеся к условным вероятностям и применимы тогда,
когда имеется важная информация о свойствах
условных распределений процесса.
Пусть {$,, / е [0, 71]}—некоторый поток а-алгебр.
Условимся говорить, что процесс !(/) подчинен потоку а-алгебр
{§*, /е [О, Г]}, если при каждом /€[0; Т] случайный
элемент |(/) ^-измерим.
Введем величину
а (е, 6) - 1п1 зир [Р {р (| (*), *(*))> в | &};
0<5<*<5 + 6<7\ ОЕй'], (13)
где 1п{ берется по всем подмножествам О' (О'е©),
имеющим вероятность 1. Нетрудно заметить, что
существует такое 0°, Р.(й0)=1, 0°е©, на котором
рассматриваемая точная нижняя граница достигается так, что
а(е, б) = зир{Р{р(|(5), |(/)»е |§Л;
0<5<*<5 + 6<7\ (ОЕЙ0}.
Покажем, что условие а(е, 6)->0 при 6->0 и любом е>0
обеспечивает отсутствие разрывов второго рода у сепа-
рабельных процессов. Пусть [с, й] —фиксированный
отрезок, [с, й]с:[0, Т] и / — произвольная конечная
последовательность моментов времени /*,/г» •••>'л» $^<?^
</! </2< *.. < 1»^4~ Через А (е, 2) обозначим событие:
выборочная функция случайного процесса | (0 на [с> й\ П1
имеет по крайней мере одно е-колебание.
Лемма 5. С вероятностью 1
Р{Л(е, /Ш<2а(-^, й-с). (14)
Доказательство. Заметим прежде всего, что так
как при $<1 8, с: 8/, то в силу свойств условных
математических ожиданий при $</<&
р{р(ио, ъ(ц))>*т-
= М{Р{Р(|(0, 6(«))>е|Щ«К *& *-& (15)
224
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш
Введем теперь события:
1=1,2, ...,к-\, р(|(с), Ц1к))>±.},
С*={р(1(У, Ш)>±}, Ок = Вк(]Ск, й=1, 2, ...,я,
С0 = {р(Ш, |(й))>т}'
п
События В& несовместимы, и если положить О = \^ Оку
то А(г, 1)аС0[}В. Действительно, если А{г, I) имеет
место, то при некотором к впервые выполняется
неравенство р(5(с), Е(4))^-|-> т. е. осуществляется одно
из событий Вк(к=1, ..., п). Если при этом В не имеет
места, т. е. если р(!(/*), 1(<0)<Т' то Р&^> Ш))>
>р(|(с), 6(/а))-р(|(/а), &(<*))>7» т. е. имеет место
событие С0. Таким образом, Л (е, /) с: С01) Д. Имеем теперь
с вероятностью 1
Р{ВкШ=М{х0к\Ъя} = М{М{хВкхск\Ък}\Ъ*) =
= М (хВ/Р {С, | Ък} | 3,} < « (|, й - с) М {хв, | &}.
где %4, как обычно, обозначает индикатор события Л.
Отсюда следует
^ а (-|- ,* й — с| (той Р).
В силу (15), Р{С0|<\Л<а(-|-, <1 — с]. Таким образом,
Р(Же, /)!бЛ<Р{О|^} + Р{С0|бЛ<2а(^, й-с) (тоёР),
что и доказывает лемму.
§ 4] КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЫВОВ ВТОРОГО РЯДА 225
Лемма 6. Пусть Ак(г, I) обозначает событие:
\{1) имеет на I по крайней мере к г-колебаний. Тогда
Р М* (е, /) 13Л < [2а (|, а - с)]" (той Р).
Доказательство. Пусть Вг (е, I) обозначает
событие: на множестве (/ь .,., 1Т) выборочная функция
процесса |(0 имеет не менее к—1 е-колебаний, но на
(/,, ..., 1Г~\) число е-колебаний менее к—1. События
п
Вг(е, /) (г=1, ..., п) несовместимы и № Вг(е, I) =
*=Ак~1(е, /)=эЛ*(е, /). С другой стороны, из Ак (е, /)Г)
ПВг(е, /) следует, что на множестве (/г, /г+ь ..., 1п)
имеется по крайней мере одно е-колебание.
Следовательно,
Ак(в, /)с=й(Вг(е, /)ПС,(е,/)),
г = 1
ще Сг(е, /) означает, что |(0 на (/г, /г+ь ..., /„) имеет
по крайней мере одно е-колебание. Поэтому
Р{Я*{е, /Ш<ЕР{Яг(е, /)ПСг(в, /)Ш (тоаР). (16)
Используя свойства условных математических
ожиданий, получим
Р {ВгЦв, I) Л С, (е, /)|§,} = М {М [%Вг <„ /)ХСг (е, /> 1&,}'| 3,} <
<М{хв,(../)р{^(в,-/)|^г}|8,}<
< 2о (^-, <* - с) Р {Вг (в, 7)|&) (той Р).
Из полученного неравенства и (16) следует, что
п
Р {Л* (е, /Ш < 2о (-5-,' <* - с) 2 Р {Вг (г, /Ш -
= 2а (^ , й - с) Р {Л'"1 (е, Щ] (той Р),
откуда и вытекает доказываемое.
$ И. И. Гихман, А. В. Скороход
&26
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
Теорема 2. Если I (() — сепарабельный процесс а
при любом е>0
Нта(е, б) = 0, (17)
6-»0
то процесс %(/) не имеет разрывов второго рода.
Достаточно доказать, что с вероятностью 1 каждая
выборочная функция %(() имеет только конечное число
е-колебаний. Пусть / — множество сепарабельности про-
сю
цесса %(()> Представим его в виде / = ^1п, где /п —моно-
/2=1
тонно возрастающая последовательность множеств,
состоящих из конечного числа элементов. Пусть дано е>0.
Разобьем [0, Т] на ш отрезков Дг, г == 1, ..., т,
одинаковой длины так, чтобы 2а (^-, —) = р<1. Тогда
Р {Л°° (е, / П Дг) 13-Л < Р {Ак (е, / П Аг) | &} =
= Нт Р{Д*(е,/вПД,Ш<Р*,
/1->оо
откудаР{Лоо(8,/ПДг)13Л = 0(тос1Р)иР{Лоо(8,/П\)} = 0.
Следовательно, Р{Л°°(е, /)} = 0. Теорема доказана.
Приведем некоторые важные следствия из
доказанной теоремы.
Теорема 3. Сепарабельный стохастически
непрерывный процесс Ь>(^)^ЕБ[0у Т] с независимыми
приращениями и со значениями в линейном нормированном
пространстве Щ не имеет разрывов второго рода.
Действительно, из определения процессов с
независимыми приращениями имеем
Р{Ш-Ш1>еШ = Р{Ю-Ш|>е} (тек! Р).
С другой стороны, из свойства равномерной
стохастической непрерывности (см. теорему 4§ 2) вытекает, что
а(е, 6) = зир[РШ(я)-Ч(/)|>е}; 0<$</<$ + 6<Г]
стремится к нулю при 6->0 и любом е>0. Таким
образом, условия теоремы 2 выполняются.
Теорема 2 дает сильные результаты и для
марковских процессов.
Теорема 4. Если Щ), ^[0, Т\ —сепарабельный
марковский процесс со значениями в метрическом про-
$4} КРИТЕРИЙ ОТСУТСТВИЯ РАЗРЫВ0В1 ВТОРОГО РЯДА ДО
атранстве Щ и переходной функцией Р($, ж, $, Л&
удовлетворяющей условию
а (е, 6) = зир [Р {5, у, /, 58 (у)};
у*=%, 0<&</<$Ч-б<Г}-->0
прид->0, где 8е (у) — сфера радиуса е с центрам в тдчке у,
8& (у) — ее дополнение, то процесс I (О не имеет разрывов
второго рода.
Последнее утверждение непосредственно вытекает,
из теоремы 2 и определения марковского процесса.
Регуляризация выборочных функций процесса без
разрывов второго рода. Ранее уже отмечалось, что,
рассматривая функции бе,з разрывов второго рода,
отождествляют функции, имеющие в каждой точке
одинаковые пределы справа и слева.
Напомним, что если процесс сепарабелен, то значения
выборочных функций \(1) с вероятностью 1 являются
предельными значениями последовательностей |(^) при ^^->^
и 1Ь из множества сепарабельности. Если при этом
процесс не имеет разрывов второго рода, то с
вероятностью 1 |(0 при каждом I равно |(< — 0) или |(* + 0).
Теорема 5. Если 1(1) — стохастически непрерывный
процесс без разрывов второго рода со значениями в
метрическом пространстве Щ, то существует эквивалентный
ему процесс |'(0> выборочные функции которого
непрерывны справа (шо<1 Р).
Доказательство. Событие А: предел.Ига| п + — )
существует для каждого I еЕ [0, Т) — имеет вероятность 1.
Положим |'(0 = Нт|(*+4) в случае Ли |'(0 = 6(0
в случае А. Имеем
оо
РГ(0^1(0}=/11гПоР{[р(|(0) 6'(*))>-й-]п4
8*
228
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш
С другой стороны,
Р{|>(1(0.6'10»-^-} =
-р{йп{р(б(«.|('+^)>^}}-
<]|т)Р{р(|(,),|(< + 1))>^.
Таким образом, Р Ц' (()Ф1(1)} = 0. Остается заметить»
что на множестве А функция |'(*) непрерывна справа.
Теорема доказана.
Аналогично доказывается существование
стохастически эквивалентного непрерывного слева процесса.
Мартингалы, Рассмотрим свойства выборочных
функций сепарабельного полумартингала {|(0> Ъь *^[0, Г]}.
Общее определение полумартингалов и мартингала было
дано ранее (гл. И, § 2). Там же были получены важные
свойства полумартингалов от дискретного аргумента.
Отметим, что полученные в § 2 гл. II неравенства легко
переносятся на сепарабельные субмартингалы. Так, для
сепарабельного процесса событие зир{^(0, *^[0, Т]} Ф
Фзир {|(0, ^/}, где / — множество сепарабельности
процессов |(/), имеет вероятность 0. Поэтому
соответствующие случайные величины имеют одинаковое
распределение. Далее, если выборочная функция процесса |(/)
имеет на [0, Т] п пересечений полуинтервала [а, Ь) сверху
вниз и ^( • )ШЫ, где N — то исключительное множество,
которое фигурирует в определении сепарабельности, то ^(Л,
рассматриваемое только на /, тоже п раз пересекает [а, Ь)
сверху вниз. Это означает, что распределение величин
^'[о, л [я, Ь) и V/ [а, Ь) совпадают (индекс внизу у, знака V
обозначает множество, н^ котором . рассматривается
процесс).
Теорема 6. Сепарабельный полу мартингал на [0, Т]
не имеет разрывов второго рода.
Для доказательства можно повторить в основном
рассуждения из доказательства теоремы 1 § 2 гл. II.
Из неравенства Р {зир {|+ (/), I <= [0, Т]} > С) < С~Щ+\Т)
§ 4] КРИТЕРИИ ОТСУТСТВИЯ РАЗРЫВОВ ВТОРОГО РЯДА 229
вытекает, что вир{|(0, /^[0, Г]}<оо с вероятностью 1.
Аналогично из неравенства МЬ[а, 6)<[Ь — а)""1 М (^(Г) —
— Ь)+ при а->— со следует, что с вероятностью 1
ш!{!(/), ^е [0, Г]}> — со. Далее, так как V[а, Ь)
интегрируемо, то существует такое множество Ых е ©,
Р{^г1} = 0, что при оеА^|,5(0 пересекает любой
полуинтервал [а, 6) только конечное число раз и, следовательно,
^(0 не имеет разрывов второго рода. В качестве Лг,
можно взять сумму всех М(а,Ь), где N (а, Ъ) есть то
множество, на котором ч[а, Ь)= ооу когда а и Ь
пробегают все рациональные числа и а<6. Теорема
доказана.
Пусть $г_0 обозначает минимальную ог~алгебру,
содержащую §5 при $</, а 3/+о — пересечение всех §5
при $>*. Очевидно, что З^с^сЗ^ и |(/-0)
является ^_0, а |(/ + 0) — ^+0-измеримой случайной
величиной.
Теорема 7. Пусть {I(/), 8/, '^ [0, Г]} — сепарабель-
ный субмартингал. Тогда {|(^ + 0), §/+0, ^[0, Г1}(|{Г+0) =
= |(Г)) также является су б мартингалом, выборочные
функции которого с вероятностью 1 непрерывны справа.
При этом Р {| (/) = | (* + 0)} = 1 в каждой точке, в
которой М|(0 непрерывно и 3* = ($*+<у
Доказательство. Заметим, что шах{1,(1), а)
является субмартингалом (гл. II, § 2) и притом
равномерно интегрируемым семейством случайных величин
(гл. II, § 2). Поэтому при $</
С тах {% ($), а) йР < Ига Г тах (| (/'), а) йР -
= | тах(|(^ + 0), а)йР
А
для любого Ле35. Полагая здесь а->— со, получим
||(5)^Р<||(/ + 0)Г/Р,
А А
т. е.
Ш<М{|(* + 0)Ш при 5</,
откуда
6(^ + 0)<МЙ(/ + 0)|8,+о), в</.
230
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. III
Это доказывает первую часть теоремы. Нетрудно
заметить, что из предыдущих рассуждений вытекают
также неравенства
Б(0<Мй(/ + 0)|^}<М{|(/0 Ш (тос1Р) при Г>/,
откуда следует, что в точке I, в которой §* = <$*+о>
имеем
Б(0<Б(' + 0)<М{|(О1^}(тос1Р).
Если теперь М&(*')-*М|(0, то &(/ + 0) = 5(/) (той Р).
Нетрудно еще убедиться, что функции &(Л-0)
непрерывны справа. Теорема доказана.
§ 5. Непрерывные процессы
Условия непрерывности процесса без разрывов
второго рода. Как и в предыдущем параграфе,
предположим, что <2/— полное метрическое пространство, ^(0,
/^[0, Т], случайный процесс со значениями в Щ.
Определение 1. Процесс %(/), /^[0, Т]
называется непрерывным, если почти все его выборочные
функции непрерывны на [0, Т].
Для процессов, не им.еющих разрывов второго рода,
можно указать довольно простое достаточное условие
непрерывности.
Теорема 1. Пусть {1пк, к = 0, 1, ..., тл}, /г=1,
2, ..., — некоторая последовательность разбиений отрезка
[0, Г], 0 = *я0</я1< ... </ятя = Г и Ля = тах (*яй-
— (пк-.г)->0 при п-> оо. Если сепарабельный процесс ^(0
не имеет разрывов второго рода, то условие
тп
2Р{рЙ(УЛ('пы)]>е}->0 при /г->оо (1)
к = 1
для любого е>0, достаточно для непрерывности этого
процесса.
Доказательство. Обозначим через Vе (0 ^ Vе ^ оо)
число тех значений /, для которых р [I {I + 0), I {I — 0)] > 2е,
а через V*** обозначим число таких индексов к, что
§5]
НЕПРЕРЫВНЫЕ ПРОЦЕССЫ
231
рйУпк)> Б('я*г1)1>в« Очевидно, что у8<Пту^>. С дру-
/1->оо
гой стороны,
тп
Му<«)= 2 Р{р [!('«*), 6 (*,»-.)]> в}.
к—\
В силу леммы Фату Муй ^ М Пт у<"> ^ Нт Му^, Итак,
Л->оо Л-»оо
Муе = 0, т. е. у8 = 0 с вероятностью I при любом е>0.
Следовательно, с вероятностью 1 | {I — 0) = § (1 + 0) при
любом/. В силу сепарабельности процесса |(0 = |(/ —0) =
= 5(^ + 0), т. е. процесс, непрерывен.
Следствие. 2?слгг {^ (/), §ь 1 ^ [0, Г]} — сепарабель-
ный полумартингал и
2Р{1?(и-?(^ы)1>е}->0 при Я„->0,
к=\
го %>(() —непрерывный процесс.
Это следствие вытекает из того, что сепарабельный
полумартингал не имеет разрывов второго рода.
Применим теорему 1 к процессам, удовлетворяющим
условиям теоремы 2 § 4. Пусть а(е, 6) определяется
соотношением (13) § 4.
Теорема 2. Если процесс |(0 сепарабелен и
Ит^-О (2)
при любом 8>0, то процесс \($) непрерывен.
Так как при выполнении условия (2) процесс 1({)
не имеет разрывов второго рода, то достаточно
проверить соотношение (1). Учитывая, что Р{р [&(*»*)»
&('л*-1)]>в}<а(в, Д/лА), где ЫПк = *пк-*пк-1, находим
2Р{риСяД Е('я*-1)]>е}<(6-а) тах *&$й->0
при Лл->0. Теорема доказана.
Применяя теорему 2 к марковским процессам,
получаем следующее условие непрерывности марковского
процесса.
232
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. Ш
Теорема 3. Если %{г) — сепарабельный марковский
процесс и
{■Р($,у,{,8е(у))-+0
при 6 -> 0 и любом фиксированном е > О равномерно
по у, $, /, Л)<;/ —$<!6, то процесс $(1) непрерывен.
Здесь 5е (л:)— дополнение к сфере 8е(х) с центром
в точке х и радиуса е.
Процессы с независимыми приращениями.
Доказанная теорема дает только достаточные условия
непрерывности случайного процесса. Оказывается, что для
частного случая процессов с 'независимыми
приращениями условия теоремы 1 являются также и
необходимыми.
Теорема 4. Если процесс I (/) с независимыми
приращениями непрерывен, то условие (1) выполняется
для произвольной последовательности {тпк, к = 0, ..., пгп],
и=1, 2, ... разбиений отрезка [О, Г], для которой
Яя= тах (/„*-/„*-!)-► 0.
Доказательство. Положим Дл = вир р[%(1\)9
1((2)]- В силу непрерывности процесса ^(/), АА~>0 при
к->0 с вероятностью 1. Поэтому ПтР{Ал>е} = 0.
С другой стороны, если Хп<Ну то
Р{Дл>8}>Р{5ирр[|(^),ё(^-1)]>е} =
= Р{ри('«1)^(и]>е} +
+р (р и Сш), 5 (и] < в} р {Р [| (<я2), & (/,и)] > в} +...
тя-1
..•+ ПР{ри(и.Б('я*-1)Ке}Р{р[1(^я), ь{*птп-х)]>*}>
>Р{Д.<е}ЩР{р[|(^)Д(^-1)]>в},
/с = I
тп
откуда %Р{р[|(Ы, 1(^-1)] > в} < р|^'| ->0 при
й->0 и любом е>0. Теорема доказана.
Нетрудно теперь дать полное описание непрерывных
процессов с независимыми приращениями и значениями
в конечномерном пространстве.
§5] НЕПРЕРЫВНЫЕ. теОЦЕССЫ 2Ш
Теорема 5. Случайный процесс ? (/), ^ ^ 0, ^ (0) = 0,
со значениями в Жп и с независимыми приращениями
непрерывен тогда и только тогда, когда 1({) является
еауссовским процессом с непрерывным средним а{1) и
непрерывной матричной корреляционной функцией
Н (/, 5) = а2 (ппп (/, 5)), где а2 (/) — матричная функция,
а2(0) = 0 и а2(/) — о2(з) при з<1 неотрицательно
определенная матрица.
Доказательство. Пусть |(/) — непрерывный
процесс с независимыми приращениями. Докажем, что
5(0"~^(5) ($<*) имеет нормальное распределение.
Возьмем произвольный вектор г, ге $,т. Скалярный
процесс ц(1) = {г> |(/)) также является непрерывным
процессом с независимыми приращениями. Если доказать,
что г)(/) — т)($) имеет нормальное распределение, то
отсюда будет вытекать, что 1У)-~1{з) имеет /п-мерное
нормальное распределение. Пусть 1пк, к= I, ..., тп, —
разбиение отрезка (5,1) на отрезки равной длины, для
которого (см. теорему 4)
2Р{!ч(и-л(^-1)1>|}<^- (3)
Положим т^-т!^)-л ('„%-,) = ДЛ„*. если \^{*ак)-
-т|('„*_|)|<7 и.т|^ = 0 в противном случае, т]; = 2Л'п4-
Из неравенства (3) следует, что Р {г)'пфг)(()-цЩ <7Г»
откуда Р-Нт ц'п = т) (0 - л («). Пусть а'пЧ = Мт^, о\к =
= ®Кк' ап = 2<6, сг2 = 2<т^. Рассмотрим два случая:
к к
1)Нта2<оо, 2) Нта~ = оо. В первом случае
существует подпоследовательность пг такая, что Итсг^ =
== а2< оо. Так как
то к сумме в правой части последнего равенства
применима центральная предельная теорема и
распределение ц'п слабо сходится к нормальному распределению
с параметрами (0, а2). Так как ц'п сходится по вероятности
234
СЛУЧАЙНЫЕ ФУНКЦИИ
[ГЛ. 111
к пределу, то агп также должно сходиться к некоторому
пределу а. Итак, л (0-" Ч ($) = я + Л, гДе т) — гауссовская
случайная величина.
Во втором случае, какое бы ни было с>0, можно
йайти такое цги что ^о^у-ьс. Это вытекает из равно-
й = 1
мерной малости величин а\к (а^<-"^~)* ^ сумме
Ч
2(Лд^ — аПк) снова можно применить центральную пре-
1
дельную теорему. Но тогда из равенства
к = \
вытекает, что
Нш | Ме™* | < Нт П Меи^а^
1 Ас= I
==е
2
*МТЬ,
где с —любое. Поэтому Нт Мб /г = 0, что противоречит
сходимости г\'п к т)(/) —т)($). Таким образом, второй
случай невозможен. Итак, доказано, что %(/) —1($) имеет
нормальное распределение. Пусть а^) = М1({), а2(/) =
= М (| (/) — а (/)) (| (/) — а (/))*. Если />$, то для
матричной корреляционной функции имеем
Я (*, 5) = М (6 (0 - а (0) (| (5) - а (з)У = а2 (5).
Из непрерывности |(/) вытекает, что
характеристическая функция
] (и, /)== М^,(|,'«(*)) = е 2
является непрерывной функцией от /. Это возможно
тогда и только тогда, когда а{1) и а2 (/) — непрерывные
функции аргумента *, а а2(/) удовлетворяет условиям
теоремы. Первая часть теоремы доказана.
Пусть теперь |(/)~~ гауссовский процесс со средним
а(1) и матричной корреляцией У?(/, $) = а2(тт(*, 5)), где
а(1) и а2(/) непрерывны. Положим %' (/) = Ъ>(1) — а (0.
*■*
НЕПРЕРЫВНЫЕ ПРОЦЕССЫ
235
Тогда, если 1\<12<4<и> то
т1'(и)-*ЦШ№-1'{*х)У =
9
т. е. процесс ^(/) имеет независимые приращения. Далее
М (Г (У - Г Л» (Г &) - Г и))* = *2 (« - *2 в),
и из известного выражения для моментов гауссовского
распределения имеем
М11' (/2) - V &) I4 = 3 [Зр {а2 (/2) - а3 (*,)}Р.
Воспользовавшись неравенством Чебышева, получаем
г*.
2
Р {I Б'('«*)-Г ('«*-!) 1> в} <
Л-1
^у 3[5р{аЧ^)~а2(^-1)}]2 ^
^ 3 тах 5р {а2 (1Пк) - о2 (^-О) 5оа2(Т)-»0
при тах(<ял —/яй_!)->0. В силу теоремы 1 процесс \' (О,
а с ним и процесс |(0, непрерывен. Теорема доказана.
Условие Колмогорова непрерывности случайного
процесса. Докажем одно удобное прямое, т. е. не
использующее предположение об отсутствии разрывов
второго рода, достаточное условие непрерывности
случайного процесса. Оно основывается на упрощенном
варианте лемм 3 и 4 § 4.
Лемма 1. Пусть I (/), I ^ [О, Г], — сепарабельный
процесс, удовлетворяющий условию: существуют
неотрицательная монотонно не убывающая функция §(Н) и
функция #(с, й), Л^О, такие, что
Р (Р (I (* + А), | (0) > С § (Н)} < ? (С, Н) (4)
0=2^(2-"Г)<оо, д(С)=22'г(7(С(2-'1Г)<оо. (5)
р{ 8ир рй(п,1Г))>ла«гЫй-) (6)
236
СЛУЧАЙНЫЕ ФУНКЦИИ
[гл. и! '
и
Р{,Л^еР(1Ю'1(/"))>СС(11ё2Й)}<
<Я([^Цс)/ (7)
где
ОО ОО
С (т) = 2 § (2-"7), <Э(т, С) = 2 2"<? (С, г^Г). (8)
п=т л = /л
Для доказательства этой леммы достаточно
повторить в упрощенном виде рассуждения из доказательств
лемм 3 и 4 § 4. Ограничимся самыми краткими
указаниями. Вводим события
Апк={р(1(Ц^т)л0гТ))^С^2-пТ)}>
А = 0, 1, .... 2я-1, п = 0, 1, 2, ...
оо 2 — 1
и полагаем Оп= (*\ (") Апк. Тогда
р{д.)«г(л,с).
Из /)„ вытекает, что для любых /' и /" из /
Р(Ъ(ПЛ(П)<2С6,
если же, кроме Оп, выполнены неравенства 0 ^/" —
- /' < 2~п, то р (I (/'), I (/")) <2СС (п). Рассуждая так же,
как и при окончании доказательства упомянутых л:*емм § 4,
получим требуемое. При этом следует иметь в виду,
что из условий (4) и (5) вытекает стохастическая
непрерывность процесса ^(/).
Теорема 6. Пусть выполнены условия леммы 1.
Тогда процесс^)непрерывен.Если, сверх того, (${т>С) -> О
при некотором т и С-> оо, то процесс %{1) обладает
следующим свойством: с вероятностью 1 существует
такая постоянная у = у(<й), что
$ир р(1(ПиП)<уО(\\ё2^-])(то4Р). (9)
Теорема легко вытекает из леммы 1.
14
НЕПРЕРЫВНЫЕ ПРОЦЕССЫ
237
В качестве частного случая, когда условия (4) и (5)
оказываются выполненными, рассмотрим процесс,
удовлетворяющий условию
мрпипкпкщ" -п1+г, т
где р>0, г>0. Положим #(А) = АГ'/Р, где 0<г'<г.
Тогда О ([182-й"]) <^е^, * р( [^г^] , с) <С"рУС2в(г"г0.
где /(} и /С2 — некоторые постоянные. Из теоремы 6 вы-
текает
Следствие 1. Если сепарабельный случайный
процесс \(1) удовлетворяет условию (10), то его выборочные
функции с вероятностью 1 удовлетворяют условию
Липшица р [|(*'), I (*")] < VI *" - *' Г7р, гдеу = у (со)—
постоянная, а в качестве г' можно взять любое число из (0, г).
Следствие 2. Рассмотрим процесс Винера-, для
которого М [| (* + Л) - & (/)] = 0, М К (* + Л) - I («И = А.
Га/с как М |-|(* + А) - I(0 |2т - (2т - 1)!! | Л \щ для любого
целого т, то выборочные функции сепарабельного вине-
ровского процесса с вероятностью А удовлетворяют
условию Липшица с показателем у — е, где е —
произвольное положительное число.
Следствие 3. Если сепарабельный процесс
удовлетворяет условиям (4), (5) и дтО(т)^Кдля всех т
при некотором д> 1, то выборочные функции процесса
с вероятностью 1 удовлетворяет условию Липшица
Р(1(ПКП)<У]*"-*'№«. •
Рассмотрим еще одно условие, обеспечивающее
выполнение предположений (4), (5), более общее, чем (10),
Пусть
мР^[^(о,I(^ + Л)]<тт^ТГм?^э Р<Г- (11)
Если положить § (А) = 11^2 |А|ГГ/Р, где р<г'<г, то
Ей*
2-Я -г. I \~Г'/Р ..
Т\\ <оо,
<Э (С) < — 2- — < оо,
2СИЫ2-»г||1+г~"г'
Л*0
238 СЛУЧАЙНЫЕ ФУНКЦИЙ [ГЛ. Щ
Следствие 4. Если сепарабельный процесс |(()
удовлетворяет соотношению (11), то он непрерывен,
Гауссовские процессы. Применим предыдущие
результаты к одномерному сепарабельному вещественному
гауссовскому процессу |(*), /е[0, Т] с корреляционной
функцией Н({, з) и средним значением 0. Разность
%{1 + Н) — 1 (0 имеет дисперсию
Поэтому
а
где а = С^(А)а~1(/, А). Воспользовавшись неравенством
оа
е-тсН^±е-а1'\ (12)
которое нетрудно получить интегрированием по частям,
находим .
2 а(1 Н). _ су<»
Р{1б(' + А)-|(')»>.Сг(Л»<тр=-^-е 2<я«-й). (13)
^(^Х,,,,^,,, /»3, (14)
Теорема 7. /Гели гауссовский процесс
удовлетворяет условию
11п17| |
го оя непрерывен.
Доказательство. Положим #(А)=| 1п| А \\"р\
где /?' — любое число, удовлетворяющее неравенству
\<р' <р~~2 . Тогда можно принять
и ряды (5) будут сходиться. Отсюда вытекает
утверждение теоремы. Более того, из второй части теоремы 6
вытекает, что с вероятностью 1 для каждой выборочной
§5]
НЕПРЕРЫВНЫЕ ПРОЦЕССЫ
239
функции процесса найдется постоянная -у = ,у(со) такая,
что
&(* + й)-К01<у[1п-1!Т]'"Р'.
Если предположить, что корреляционная функция
процесса %Ц) обладает большей гладкостью, то и
выборочные функции процесса будут более гладкими.
Предположим, что
а2(*,й)<К|й|р. р>0. (15)
Из (13) следует, что в качестве #(С, к) можно взять
функцию
Положим ёг(/г) = |ЛГ/2|1п|Л||1+е, где е>0. Тогда
оо
0(т, С)- У — Цтгв
—^г\п-1пТ\2+2е+п1п2
стремится к нулю при С->оо. Далее имеем
С(т)</С3т1+е2-тр/2.
Теорема 8, Если корреляционная функция гауссов-
ского процесса удовлетворяет условию (15), то его
выборочные функции с вероятностью 1 удовлетворяют
неравенству
1!(/ + Л)-Ш1<у1йГПп|/нГ8,
где г —произвольное положительное число, у
—некоторая постоянная.
В частности, выборочные функции сепарабельного
винеровского процесса при любом е>0 с
вероятностью 1 удовлетворяют неравенству
1Б(' + л)-б(01<уУГАТ-Цп|А|Гв, *, ^ + н^[о> г].
Последний результат представляет собой уточнение
следствия 2 теоремы 6.
ГЛАВА IV
ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
§ 1. Корреляционные функции
Положительно определенные ядра. Можно считать
замечательным и нетривиальным то обстоятельство,
что существует важный и достаточно широкий круг
задач, для решения которых достаточно знать только
весьма общие свойства случайной функции и ее
моменты первого и второго порядков. Значительная часть
теории линейных преобразований случайных функций
посвящена таким задачам и они составляют главное
содержание этой главы. Поэтому в настоящей главе
рассматриваются случайные функции со значениями
в линейном пространстве и с конечными моментами
второго порядка, если только противоположное
специально не оговорено.
Пусть I (х), хе^,- комплекснозначная случайная
функция с конечными моментами второго порядка.
Такие случайные функции условимся называть
гильбертовыми. Гильбертову случайную функцию можно
рассматривать как заданную на X функцию со значениями
в гильбертовом пространстве случайных величин 3?2'>
х->${х) = }{х, ®)*=2?2.
В частности, если X — промежуток действительных
чисел (а, Ь), 1>{х) представляет собой некоторую кривую
в 3!<1, то запись 1 = ^(х), хе(а, Ь), является
параметрическим уравнением этой кривой. В настоящей главе
рассматриваются главным образом гильбертовы
случайные функции, поэтому слово «гильбертовы» часто
§ П
КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
241
будет опускаться. Положим
а (х) = Щ (х),
Я(х, у) = М (С(х) - а (х))(С(у) -а(у)). (1)
Функция а(х) называется средним значением 2>(х),
а /?(*, у) — ее корреляционной функцией. Если
положить а: = г/, то /? (а:, а:) = М | $ (х) — а (х) р = о2 (х) дает
дисперсию • комплексной случайной величины 5 (*)•
Корреляционная функция совпадает с ранее
введенной ковариациеи множества случайных величин
1(х)-а(х).
Использование корреляционной функции вместо кова-
риации иногда бывает предпочтительнее, так как
корреляционная функция имеет важную
теоретико-вероятностную интерпретацию, а именно, она характеризует
степень линейной связи между значениями случайной
функции в двух точках.
С другой стороны, отличие между корреляционной
функцией и ковариациеи несущественно. Наряду с тем,
что корреляционная функция является ковариациеи
случайной функции 1(х) — а (х), ковариацию в свою
очередь можно рассматривать как корреляционную
функцию для 1(х)е1(р, где ф — случайная величина,
равномерно распределенная на (—я, п) и не зависящая от
{^(х), х^Х}. Это означает, что классы
корреляционных и ковариационных функций совпадают. В
дальнейшем рассматриваются как корреляционные, так и
ковариационные функции.
Ковариация В(хи х2) = М$(лгО?(дгз) случайной
функции ^(х) обладает одним характерным свойством,
которое называется положительной определенностью. Пусть
X — произвольное множество.
Определение 1. Комплекснозначная функция
С(хь х2), (х{, х2)^Х2, называется положительно
определенным ядром на X2, если для любых п(п=1, 2, ...),
хк^Х и комплексных чисел 2А(6=1, 2, ...)
2 С(хк9 хг)2кгг>0. (2)
к, г=Ч
242 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Ковариация В(хи х2) является положительно
определенным ядром на X*. Действительно,
п
2 В{хкУ хг)гкгг = М
к,г~\
2е(**)
1
*к
2
>0.
Из определения легко вытекают следующие свойства
положительно определенного ядра
1) С(х, *)>0, (3)
2) С{хи х2) = С(х2, х{), (4)
3) \С(х{9 х2)?^С(хи ху)С(хъ х2), (5)
4) \С(хи х3)-С(х2, *3)|2<
<С(дг3, х3)[С(хи х1) + С(х29 х2)-2КеС(х{, х2)]. (6)
Для ковариации эти свойства нетрудно проверить
непосредственно. Чтобы получить неравенства (3) —(6)
в общем случае, полагаем сначала в (2) /г=1.
Получаем С(хи *1)|г1р^0, что дает (3). Затем полагаем
п = 2. Сначала заметим, что С(хь х2)г1г2 + С(х2у хх)гхг2
вещественно, откуда следует (4). Неравенство (5) есть
условие положительной определенности эрмитовой квад-
ратической формы
2
2 С(хк, хг)гкгг.
к, г = 1
Чтобы получить (6), положим в (2) п = 3, гх = г,
г2 = — г. Тогда
[С(хх, хх) + С(хъ *2)-2КеС(*ь х2)]\г? +
+ 2Ке[С(*ь х3)-С{хъ х3^)]гг3+С(х3> х3)\г3\2^0,
откуда и следует (6).
Если даны две случайные функции ^х(х) и %2(х)
с конечными моментами, то как характеристику
степени линейной сзязи между ними вводят -взаимную
корреляционную функцию.
14
КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
243
Определение 2. Пусть &.(*)». &(*)■"" гильбертовы
случайные функции, М^ (х) = я^ (х). Тогда
#и2 (*, У) = М К1 (х) - а{ (х)] [&> (у) - а2 (у)]
называется взаимной корреляционной функцией ^ (лс)
и &(*)•
Чтобы описать класс возможных взаимных
корреляционных функций и для решения многих других
вопросов, удобно рассматривать некоторую
последовательность гильбертовых случайных функций ^(1) (х), ^(2) (х), ...
.,., 2(т) (х), хб1, как компоненты одной случайной
векторной функции %,(х) со значениями в 35т, При этом,
как и ранее, % (х) обозначает вектор-столбец, а ^ (х) —
вектор-строку с компонентами ?&(*) = 1{к) (*)» к=19
2, ..., т. Положим
а(х) = Шх) = {Щ<1)(х), ЩЮ(х\..., М#т>(х)},
Я(х, у) = \*Цх, у)\ = тЬ{х)-а(х))Ш-а№.
Векторную функцию а(х) = (а(1) (х), .,., а{т) (х))
называют средним значением, а Я(х, у) матричной
корреляционной функцией 1,{х).
Отметим, что
Я1 (х, у)=М (е (х) - а(1) (х)) (е} (У) - а(к) (у)),
Определение 3. Матричная функция С(х, у) =
*=||с1(х, у)\\> /, й=1, •.., га называется матричным
положительно определенным ядром на X2, если для
произвольного п, произвольной последовательности
комплекснозначных векторов гк (гк е 32"1) и
произвольных точек хк(хк^Х) имеем
}±г;С(хг хк)гк>0. (7)
244. ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛг IV
Корреляционная матричная функция является
матричным положительно определенным ядром.
Действительно,
п
%(ич)~а(хк)Угк
I А-1
-м
>0.
Отметим несколько свойств матричных положительйо
определенных ядер С (а:, */).
1. Матрица С(х, х) положительно определена, т. е.
г С (х, х)г~ 2 С[ {х, х) г}'гк > 0, (8)
2. С*(*, #) = С(г/, *). (9)
3. \сЦх, у)\<С*1(х, х)Скк(У> у). (Ю)
Свойство (8) совпадает с (7) при /г=1. Равенство (9)
вытекает „из того, что матрица х\С(х, у)г2 + г*2С {у, х)гу
вещественна при любых комплекснозначных векторах
гх и х2 {гк<^Хт). Заметим еще, что неравенство (7)
эквивалентно требованию, чтобы при любом п и любых
хи х2) ... блочная матрица
С (Хи Х\) С (Хи Х2) ... С (х{, Хп)
С (Х2г X)) С (Х2, #2/ • • • Ь (#2» хп)
^ \хпу Х\) ^ \^пу Х2/ • • • ^ ("^т *л)
была положительно определенной. Используя это
замечание, при п = 2 получим неравенство (10).
Условие положительной определенности является
характерным для корреляционной (матричной) функции.
Теорема 1. Для того чтобы функция /? {х{> х2),
х^Х была корреляционной функцией, необходимо и
достаточно, чтобы она была положительно
определенным ядром.
Необходимость вытекает из предыдущего.
Достаточность следует из того, что по произвольному поло-
§ И
КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
245
жительно определенному ядру /? 'хк, х2) можно построить
комплексную гауссовскую случайную функцию ^ (л:), для
которой Н(хи х2) будет корреляционной функцией.
Замечание. Аналогично можно доказать, что
теорема 1 имеет место и для корреляционных матричных
функций: для того чтобы матричная функция Я(хи х2)
была корреляционной функцией вектора (;(*), х&Х,
необходимо и достаточно, чтобы она была положительно
определенным матричным ядром.
Пусть X = Ш — метрическое пространство с
метрикой р.
Определение 4. Гильбертова случайная функция
{^(х), хе!) называется непрерывной в точке хъ в
среднем квадратическом (коротко, с. /с. непрерывной), если
М\Ш-Ъ(Хо)\2~>0 при р(х, *0)-*0.
Из леммы 3 (§ 1 гл. I) вытекает
Теорема 2. Для с. /с. непрерывности % (х) в точке х0
необходима и достаточна непрерывность ковариации
В(хи *2) = Щ(хЛМ в точке (х0, х0).
Замечание 1. Из с. к. непрерывности 2; (х) в точке х0
вытекает стохастическая непрерывность %(х) в той же
точке. Действительно, в силу неравенства Чебышева
ршх)-Шо)\>г}<т-их\:ихоП2.
Замечание 2. Если Цх) с. к. непрерывна на $в
(т. е. в каждой точке х), то это не означает, что
выборочные функции с вероятностью 1 непрерывны на Я?.
Действительно, для процесса Пуассона имеем М|^(/ + А) —
~ 5 (О I2 = ^А + (ЯЛ)2, но выборочные функции ?;(/) с
положительной вероятностью разрывны.
Процессы, стационарные в широком смысле. Если
предположить, что случайные функции %(х) по
отношению к переменной х обладают некоторым свойством
инвариантности, то класс соответствующих
корреляционных функций также будет обладать определенной
инвариантностью, и появляется возможность более
детального описания этого класса. В этом пункте
рассматриваются ограничения подобного рода, а в следующем
дается описание соответствующего класса
корреляционных функций.
24$ ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Начнем с одного важного обобщения понятия
стационарности случайного процесса.
Пусть С(0 = К1(0. е2(0> •••. С™ (О), *е(-оо, оо), -
стационарный процесс со значениями в %т. Тогда
величины
а(/)=М&(0, Л('о + ^ *о) =
не зависят от *,
а(*) = а = сопз1, #(*ь *2)вД(*1-'2. 0) = /?(/1-^). (11)
Функцию /?(/) = /?(' + *о> 'о) также называют (матричной)
корреляционной функцией стационарного процесса.
Разумеется, если для некоторого случайного
процесса выполнены равенства (II), то отсюда еще не
следует, что процесс стационарен. Однако для тех задач,
решение которых зависит только от значений моментов
первых двух порядков случайного процесса, условие
стационарности используется только в той мере, в
которой оно выражено в соотношениях (И). Поэтому
естественно ввести следующий важный класс процессов,
впервые рассмотренный А. Я. Хинчиным.
Определение 5. Гильбертов с. к. непрерывный
случайный процесс 5(0» —«>■</<оо, со значениями
в 32" называется стационарным в широком смысле (или
процессом Хинчина), если
М^ (0 = а = сопз*, М Й &) - а) Й (*2) - я)* = /? в - *2).
Пусть $(0 — одномерный стационарный в широком
смысле процесс. Так как корреляционная функция
Ж'1""'г) является положительно определенным ядром,
то
2 Ж'/-'*)*/**>о
/, /5 = 1
для любых /г, 1{ <= ( —оо, оо) и комплексных 2/(/ = 1, .. . ,п).
Положительно определенные ядра на линейном
пространстве $?, зависящие от разности аргументов, играют
весьма важную роль во многих вопросах анализа. Их
называют положительно определенными функциями
на X.
§ 1| КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ 247
Определение 6. Пусть <Ю — линейное
пространство. Комплекснозначная функция 1(х), л;е^,
называется положительно определенной, если для любых п,
х^Зв и комплексных чисел X} (/==1, 2, ...)
п
2 /Ч*/-*л)5/гл>0.
Положительно определенная функция обладает
следующими свойствами (см. (3) —(6)):
1) /(0)>0, (12)
2) П3 =/(-*), (13)
3) |/(*)|</(0), (14)
4) \1(х1)-Г(х2)\<121(0)[1(0)-ЪеПх2-х1)]. (15)
В частности, положительно определенная функция
ограничена в 36. Далее, если она непрерывна в точке
х = 0, то она равномерно непрерывна во всем
пространстве 36.
Возвратимся к стационарном в широком смысле
процессам со значениями в %т. Каждая компонента
такого процесса является одномерным стационарным
в широком смысле процессом, а взаимная
корреляционная функция двух компонент ^ (I) и 1^(1) процесса
зависит только от разности аргументов:
*с>с* и. У=м (с7 с.) - «О (с* (у-«*)=** (/, - д.
Определение 7. Если $(/) и г\{I) — стационарные
в широком смысле случайные процессы и составной
процесс |(*) = К(0| Л(0) также стационарен в широком
смысле, то процессы 1>{1) и т](/) называются
стационарно связанными {в широком смысле).
Из определения вытекает, что любая группа
компонент стационарного в широком смысле процесса,
рассматриваемая как самостоятельный случайный процесс,
стационарно связана с любой другой группой компонент
этого процесса.
Определение 8. Пусть й? —линейное
пространство. Матричная функция С(х) = ||С{ (х)||, хе^,
/, к= 1, ..., т, называется положительно определенной,
2^8 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV1
если для любых п, х^ г1у где х}> <^$6, г; — комплексные
векторы в Хт,
п
% г]С(х -хк)гк>0.
1, к~ I
Так как С(х{ — х2) является матричным положительно
определенным ядром, то С(х) обладает следующими
свойствами (см. (8)— (10)):
1) С (0) — положительно определенная матрица, (16)
2) С(х) = С(-х), (17)
3) \С)(х)\2<С\ (0)^(0). (18)
Из определения 5 вытекает, что матричная
корреляционная функция стационарного в широком смысле
процесса является положительно определенной
матричной функцией. В частности, она обладает свойствами
(16)-(18).
Определение стационарного в широком смысле
процесса непосредственно переносится на случайные
последовательности {1>(п), /г = 0, ±1, ±2, ...}. Для них
М^ (п) = а = соп51, М Ц (к + п) - а) Й (к) - а)' = Я (я).
Матричная корреляционная функция в этом случае
является последовательностью матриц.
Рассмотрим ряд примеров корреляционных функций
стационарных в широком смысле последовательностей.
Пример 1. Стандартной некоррелированной
последовательностью случайных векторов Й(д), д = 0, ± 1,
±2У ...} будем называть последовательность,
удовлетворяющую условиям
а = Щ(п) = 0, Я(0) = /, Я (л) «0 при пфО,
где /— единичная матрица.
Пример 2. Марковская стационарная гауссовская
последовательность.
Ограничимся рассмотрением векторной
последовательности с действительными компонентами, нулевым
средним и невырожденной матрицей Я(0) = М^{п)^*(п).
Из последнего следует, что распределение ^(п) не
сосредоточено в правильном подпространстве
пространства значений $(/г).
§ II КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ ■ 24.9
ТаккакМ($(«+ 1)-ч4С(л))С*(л) = 0, если Л = /?(1) X
X /?~~ (0), то из гауссовости процесса следует, что ^{п)
и ц(п) = ^(п+ 1)— А^(п) независимы. Поэтому
МЙ(л+1)1С(л»=М{ЛС(/|) + л(л)12(л)}-ЛС(я).
Пусть «^ — ст-алгебра, порождаемая случайными
величинами !;($), з^гс. В силу марковости процесса
М К (5 + п) | &Л = М Й (5 + л) | Б (^)}. Поэтому
Мй(5 + л)|с(5)}-М{Мй(в + /|)|35+я-,}1С(«)}-
-М{МЙ(5 + л)|С(5 + д-1)}|С(5)}«
= М{Л?(5 + м-1)|?(5)} = Л^(5).
Наконец, при п>0
Итак, корреляционная функция стационарной
марковской гауссовской последовательности имеет вид
Я(л) = ЛяЯ(0), (п>0). (19)
Например, в одномерном случае при |а|^1
К(п) = о2ап (л>0). (20)
Пример 3. Процесс скользящего суммирования.
Пусть {|(гс), я = 0, ±1, ...} —стандартная
некоррелированная последовательность случайных векторов со
значениями в 35т. Положим
оо
С(п)=2Д*|(я-6), (21)
/е=0
где Л&, & = 0, 1, 2, ..., —некоторая последовательность
матриц (операторов), отображающих Хт в себя. Ряд
в правой части последнего равенства представляет
собой сумму ортогональных векторов в З^Г^О, 6, Р}.
Для его сходимости достаточно, чтобы
оо оо > оо
2 \Ак% (п - *) р < 2 | Ак I2 И (п - к) р = 2 \Ак Р < оо.
Здесь | Л | обозначает норму матрицы Л,
|Л|==У>Р04Л*) =]/ З^а^р.
250 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Для матричной корреляционной функции имеем при
п^О выражение
Я(п)=%Ап+кА1 (22)
Пример 4. Процесс авторегрессии.
Пусть %(п) — одномерная стандартная
некоррелированная последовательность. Рассмотрим уравнение
в конечных разностях для определения
последовательности ^(п):
Ъ(п) + Ь&(п-1)+->-+ЬЛ(п-з)=*
= а&(п) + ахЬ(п-1)+ ... + а&(п-з). (23)
К уравнению вида (23) приводят многие прикладные
задачи, и оно получило название уравнения
авторегрессии. Ясно, что если задать $(0), ^(1), ..., ?(5—1), то
из уравнения (23) можно последовательно выразить
^(5), 2(5+1), ... через «начальные значения» ^(0), ...
..., ^ (5 — 1) и значения | (0), ^ (1), Рассмотрим воп*
рос о существовании стационарного решения
уравнения (23), в котором %(п) выражаются через значения
|(т), т^.п. С этой целью будем искать решение
уравнения (23) в виде процесса скользящего суммирования
оо
С (л)= 2**6 (*-*). (24)
Уравнение (23) при этом сведется к системе
с0 = а0, сх + Ь{с0 = аи ..., 1
^ + 6^-!+ ... +Ь8с0 = а8, 1 (25)
Ср + Ъ1ср-1+ ... +Ь8ср-3 = 0 при р>з. )
Введем производящие функции А (г), В (г), С (г)
последовательностей {ап}, {Ьп}у {сп}
Л(г)=2а/, В(г)=%Ьпгп, С(г)=Ъспгп,
Л = 0 /1 = 0 /1 = 0
где Ь0=1. Умножая равенства (25) ни 1, 2, г2, ... и
суммируя их, получим С (г) В(г) = А (г), или
п( \ ^(^) _ , гАг (г)
^\г> = -вЩ-а^ в (г) >
§ 13 КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ 251
где А! (г) — многочлен степени не выше 5 — 1. Допустим,
что все корни многочлена В (г) простые. Тогда
существует разложение на простые дроби вида
Ах (г) _ Ах А2 { А3
В (г) хх — г г2 — г * * *, г8 — г '
откуда
оо
И
' сп=% А^Г, п>1. (26)
При этом, если корни многочлена В (г) лежат вне
круга |г|^1, то ряд (24) будет с. к. сходиться. Не-
трудно видеть, что этот результат сохраняется и тогда,
когда В (г) имеет кратные корни. Итак, доказана
Теорема 3. Уравнение авторегрессии (23) имеет
стационарное решение (24), (26), если все корни
многочлена В (г) лежат вне круга |2|^1. Корреляционная
функция У? (п) этого процесса удовлетворяет разностному
уравнению
К{п) + Ъ{К{п-\)+ ... + М (/* - $) = 0, п>8,
К{п) + Ь1К(п-1)+ ... +Ь3К(п-8) =
= а„ё0 + а„„1ё1 + ... +а8с8„п при 0<м<$.
Приведем нескблько примеров корреляционных
функций стационарных в широком смысле процессов с
непрерывным временем.
Представляется заманчивым в качестве простейшего
примера рассмотреть процесс 5(0» Для которого
М&(0 = 0, М|?(012= 1, Ш*)Ш = 0 при 1фз.
Корреляционная функция этого процесса разрывна, так
что он- не является с. к. непрерывным и не
принадлежит к классу изучаемых здесь процессов. Можно
показать, что этот процесс не эквивалентен (стохастически)
процессу с измеримыми выборочными функциями. С
другой стороны, процессы, близкие к этому примеру и об-
252 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
ладающие ещ-е более нерегулярным поведением,
изучаются в теории обобщенных случайных процессов*
Пример 5. Случайные колебания.
Во многих физических и технических задачах
рассматривают колебательные процессы, которые в
комплексной форме описываются функцией вида
№~2уке'и*'. (27)
к
Каждая составляющая этой суммы"" характеризует
простое гармоническое колебание с частотой ик/2л и
с энергией | ук р. Совокупность величин [ик] называют
спектром (или спектром настот) процесса 5(0-
Допустим, что ук — случайные величины, "ортогональные
между собой:
МуА = 0, М|у*Р = ^, Му^у^О при кФ}.
Тогда корреляционная функция процесса 5(0 равна
/?(/„ /2)= МШ)Ш = М 2у*У/е'("*''*"^> =
«=2с2е'"*('«-'»),
к
т. е. 5(0 является стационарным процессом в широком
смысле. Его корреляционная функция полностью
определяется спектром частот и средними значениями мер
(математическими ожиданиями) энергии,
соответствующей каждому простому гармоническому колебанию,
входящему в процесс 5(0- В связи с этими
энергетическими представлениями введем важную
характеристику стационарного процесса, называемую
спектральной функцией.
Спектральная функция Р{и) процесса (27)
определяется соотношением
к, ик<и
Это означает, что Р (и) равна средней энергии,
переносимой гармоническими составляющими процесса 5(0»
частоты которых менее заданного значения и. Функция
Р(и) ^полностью характеризует как среднюю энергию
каждой гармонической составляющей процесса 5(0» так
1*1
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
253
и суммарную среднюю энергию гармонических
составляющих процесса, частоты которых лежат в любом
заданном интервале. Действительно,
сI = Р {ни + О)- Р (и*), 2 с\ = Р {и<>) - Р{и).
С помощью спектральной функции корреляционная
функция процесса Ъ,{1) может быть записана в виде
оо
#(0= \е11иаР(и). (28)
С математической точки зрения спектральная
функция является неотрицательной неубывающей
непрерывной слева функцией^ постоянной всюду, кроме
конечного числа точек, в которых она имеет скачки
величиною ер Оказывается, что понятие спектральной функции
может быть введено для произвольных стационарных
в широком смысле процессов. Этот вопрос, так же как
и вопрос об обобщении представления (28) на
произвольные стационарные процессы, рассматривается в
следующих параграфах.
§ 2. Спектральные представления
корреляционных функций
Стационарные последовательности. Рассмотрим
сначала стационарную в широком смысле
последовательность комплекснозначных случайных величин {^(п)у п=*
= ...,. —1, 0, 1, ...}, для которой
МС(л)-0, Щ(к + п)Щ = Я(п).
Последовательность чисел 7? (п) является
положительно определенной, т. е. для любого п и любых
комплексных гк, 6 = 0, 1, 2, ..., /г,
/,&=о
Теорема 1. Функция {К(п)у п = 0, ±1, ±2,..,}
тагда и только тогда является корреляционной
функцией стационарной в широком смысле последователь-
29# ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. №
ности случайных величин, когда она может быть преЩ
ставлена в виде
Я (п) = | е1пиР (Ли),
(1)
где Р{•) — некоторая конечная мера на [ — тс, я]. На бо-
релевских множествах отрезка [ — я, я] мера Р
определяется единственным образом.
Доказательство. Достаточность. После-
довательность (1) положительно определена, так как
У, /г=0 -л \/=0 / и-0 /
я 1 п 12
-л | /=0
Р{Ли)^0.
Поэтому она является корреляционной функцией
некоторой стационарной в широком смысле
последовательности.
Необходимое т,ь. Пусть Я (и) — корреляционная
функция некоторой стационарной в широком смысле
последовательности. Положим
со со
!(и, р)=2 2 е-^п~т)иЯ(п-т)(>п+т, 0<р<1. (2)
Ряд в правой части равенства (2) абсолютно сходится*
так как
N N
N
2 2 \е-1{а-^иЯ(п-т)рп+т\^Я(0)Щ р"
«=0т=0
\п=о
<
(1-Р)2*
Из положительной определенности Я(п) следует, что
1(и, р)>0. Изменяя в (2) порядок суммирования,
получим
/(«,р)= 2 в-'*«/?(А)2р'*,+2/-Ет^-/г <*)«"""•
&= — со
/=0
§ 21 СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 255
Полученное соотношение показывает, что величины
п|&|
-пт-т/?( — *) являются коэффициентами Фурье
положительной функции ${и, р). Следовательно,
Я
-Я
или
я
р|«1Д(я)= ^'«"/^(А/), (3)
— Я
где
л
причем /7р[ —я, л] = /?(0)<оо. Семейство мер/7р(-) на
[~я, я] слабо компактно. Поэтому можно найти такую
последовательность р*|1, что Ррк{%) слабо сходятся
к некоторой мере Р(>). Переходя в (3) к пределу при
р = рй->1, получим формулу (1).
Докажем единственность меры Р. Допустим, что
существуют меры Р{ и Р2у определенные на борелевских
множествах отрезка [ — я, я], с помощью которых Я{п)
может быть представлена по формуле (1). Обозначим
через К класс борелевских функций / (и) на [ — я, я], для
которых
я я
\Пи)РЛаи)= \{{и)Р2{аи).
— Я -Я
Класс К линеен, замкнут относительно операции
равномерного предельного перехода и предельного перехода
по ограниченным монотонным последовательностям
функций. Так как он содержит функции вида е1пи(п =
= О, ±1, ...), то в силу теоремы Вейерштрасса об
аппроксимации непрерывных функций он содержит все
непрерывные, а следовательно, и все ограниченные бо-
релевские функции. Полагая /(и) = %л(^)> где А
—произвольное борелевское множество на [ — я, я], получим
Р{ (А) = Р2(А). Теорема доказана.
256 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Мера Р называется спектральной .мерой стационарной
последовательности, а соответствующая функция
распределения Р(и) = Р( — оо, и) — спектральной функцией. Если
р{йи) = $(и)(1и, т. е. если мера Р абсолютно непрерывна
относительно лебеговой меры, то / (и) называется спект*
ральной плотностью последовательности ^(п).
Заметим, что условие
оо
21 я (л) к оо
— оо
обеспечивает существование спектральной плотности.
Действительно,, в этом случае ряд Фурье
оо
2я/(и)=» -2 Я{п)е-Ыи (4)
Я=-оо
сходится равномерно и абсолютно. Поэтому
Я(п) = ^е1пи\(ь1)йы.
-31.
Однородные случайные поля. Обобщим теорему 1
на стационарные поля в широком смысле с непрерывным
аргументом.
Определение 1. Случайная функция {?;(*), х^Ж*1}
называется однородным полем в Ж11, если
М^ (х) = а = сопз*,
/?(*,, х2) = Щ$(х1)-а][Ь(х2)-а] = Я(х1-х2).
Таким образом, корреляционная функция однородного
случайного поля /?(#ь х2) зависит только от вектора,
соединяющего точки хх и х2. Функцию Н(х) в правой
части равенства (5) также называют корреляционной
функцией однородного поля. Условие
положительной определенности корреляционной функции имеет вид
п
2 Я(х]-хк)г1гк^О.
Из соотношения
М|$(* + Л)-С(*)Р = 2[*(»)-Ке/г(А)]
(5)
§2]
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
257
вытекает, что если функция /?(*) непрерывна в точке
х=0, то поле ^(х) непрерывно в среднем квадрати-
ческом в каждой точке лее &т.
Теорема 2. Для того чтобы функция /?(дг), (*<=
е Ж11), была корреляционной функцией однородного с. к.
непрерывного случайного поля {^(х), х^#т}, необходимо
и достаточно, чтобы она допускала представление вида
К(х)= $ е*<*>и>Р(аи), (6)
где Р — некоторая конечная мера на борелевских
множествах в $,т. При этом мера Р на ЭЗт определяется
единственным образом.
Достаточность. Функция К{х), определяемая
формулой (6), непрерывна и положительно определена:
2 /?(*,- хк) г,гк = / ( 2 еЧ*Г** %гк) Р (ей) =
и а-1 *я\/,ы /
/. А-1
I 12
= 1
Я"
Е*"'(**,В)г*
6=1
Р{йи)>0.
Поэтому она является корреляционной функцией
некоторого с. к. непрерывного комплексного гауссовского поля
(см/ § 1 гл. III). Впрочем, можно построить весьма
простой пример однородного поля, корреляционная функция
которого дается формулой (6). С этой целью введем
случайный вектор $ в &т с распределением
РЙ<=Л}=-^(Л), Р0 = Р№т)
* б
для произвольного борелевского множества А с: #м.
Положим &(х)= ур0е*№* *)+ф], где ф —случайная
величина, равномерно распределенная на ( — я, я), ф и |
взаимно независимы. Тогда
М1 (х) = О, Я (*, у) = М? (*) Ш = /?0Ме'«. *-*> =
« [ е*<*-У>и)Р((1и).
9 И. И* Гихман. А. В. Скороход
258 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Необходимость. Докажем,что произвольная
непрерывная положительно определенная функция
допускает представление (6). Из условия положительной
определенности вытекает, что для произвольной
интегрируемой в 01т функции §{х) имеет место неравенство
Положим здесь §(х) = ехр| —-^р + *(*> г)|, где Ы>
> 0, г^Жт. Тогда
\ //?(*-у) ехр{- ]х?^у? -Цх-у, г)}с(хс1у>0.
Произведя в пространстве Жт X &т ортогональное
преобразование координат
х-у = У2иу х + у= 1/2~о,
получим
0< | ]*Д(ц)ехр{- |Ц|22^|Р|2 -ф, г)}йи& =
= (2яЛ^)т/2 | * (и) ехр { - -^ - / (и, г)} йи.
Таким образом, функция
неотрицательна. Кроме того, она является
преобразованием Фурье интегрируемой непрерывной функции
#(и)е~ы{2/2М и дифференцируема. Покажем, что &м(г)
интегрируема. Так как %м(г) и е~812,2/2, е > 0, являются
преобразованиями Фурье соответственно функций
§2]
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
259
то в силу равенства Парсеваля
8
\и\
*(°) \-ЯГ*~* ^ = (2я)2 /? (0).
Пусть е->0, Воспользовавшись леммой Фату, получим
т
Из интегрируемости 7?^ (г) следует, что к ней применима
формула обращения .для преобразования Фурье
** { '
■= /е««.^ (<**), (7)
я"'
где
Таким образом, функция в{т в~ {ц}2/2;У является
характеристической функцией некоторого распределения
в 5У71 и при N--^00 она сходится к непрерывной
функции. Поэтому (гл. I, § I, теорема 3) /?(и)//?(0)
также является характеристической функцией. Един-
ственность меры Р в представлении (6) вытекает из
теоремы о единственности распределения, имеющего задан*
ную характеристическую функцию (гл. I, § 1, теорема 2).
Теорема доказана.
Как и в случае последовательностей, мера Р(-)
в представлении (6) называется спектральной мерой,
а соответствующая функция распределения Р(и) — Р{1и),
где 1и = {х: х< и, х е 5?т}, — спектральной функцией.
Если спектральная мера абсолютно непрерывна!
Р(А)=1Ци)4и9
А
9*
260 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
то Ци) называют спектральной плотностью случайного
поля. Если спектральная плотность существует, то
спектральное представление корреляционной функции
принимает вид
/?(*)= | е*ь-*!(и)аи.
Отметим следующий признак существования
спектральной плотности: если Н(х) абсолютно интегрируемая
функция {х <= Жп)> то спектральная плотность
существует.
Чтобы увидеть это, воспользуемся обозначениями и
соотношениями, полученными при доказательстве
предыдущей теоремы. Из равенства Парсеваля для
интеграла Фурье имеем
] Ям(г)с1г= ] Ны(г)%к{г)йг=-
Г -ШИ ! -п- е1{х*ЛгНк)иН_е1(хк-Кк)ик
где К = {г: хк — Нк < г" < хк + Нк). Отсюда вытекает, что
где V (К) — объем параллелепипеда /С. Следовательно,
мера Р{-) абсолютно непрерывна относительно
лебеговой меры.
Следствие 1. Функция /?(/), *<=(— оо, оо), тогда
и только тогда является корреляционной функцией
стационарного процесса в широком смысле, когда
/?(*)= | е"иР(йи)у
где Р(-) — конечная мера на ЗЗ1.
Следствие 2. Функция 1(и), «6Й"1, /(0)=1
в том и только в том случае является
характеристической функцией некоторого распределения в Жту если она
непрерывна и положительно определена.
§ 2]
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
261
Однородные и изотропные поля. Можно получить
дальнейшую специализацию формулы (6), предполагая,
что случайное поле обладает дополнительными
свойствами. Важным и вместе с тем довольно общим
свойством является изотропность случайного поля.
Случайное поле называется изотропным, если корреляционная
функция #(хи х2) зависит только от х2 и от расстояния
между точками хх и л:2. Если оно еще и однородно, то
Н{хи х2) = /?(р),
где р —расстояние между хх и х2, Р=1/ 2(*{~ *^)2.
Найдем представление корреляционной функции с. к.
непрерывного однородного и изотропного случайного
поля. Поскольку оно однородно, его корреляционная
функция должна иметь вид (6). Проинтегрировав обе
части этой формулы по поверхности сферы 5Р радиуса р,
получим
*(р) = 1^5^ /{ ри'и)^)}^").
^т 15р )
где 8 {их) во внутреннем интеграле обозначает
интегрирование по поверхности сферы 5р. Заметим, что если Vр
обозначает шар радиуса р с центром в начале
координат, то
//(х)5(^)=-^- \т*х.
С другой стороны,
\ е'^"Ых = {^)т121тП{9\и\),
где /у(дг) — Бесселева функция первого рода. Отсюда
вытекает, что
/ е1 <*• *>5 {их) = (-у^-р! и 11(т-т (р I и |). (8)
8р
262 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. Ш
Введем на полупрямой [0, оо) меру §, положив
8{[а, Ь)) = Р{УЬ\ Уа}, 0<а<&, понимая под Кр
открытый шар радиуса р. Тогда
т^~^тЩ^^ёШ (9)
причем §([0, оо)) = Р(&т) = К(0).
Таким образом, доказана следующая теорема.
Теорема 3. Для того чтобы /? (р) (0 ^ р < оо)
была корреляционной функцией однородного и
изотропного с. к. непрерывного ш-мерного случайного поля,
необходимо и достаточно, чтобы она допускала
представление (9), где § — конечная мера на [0, оо).
При п = 2 формула (9) принимает следующий вид:
оо
Д(р)=/ /„ Й>) $(<&), (Ю)
0
а при п = 3
оо
*(р)-2/-^*(Л). (П)
0
Те же соображения показывают, что с. к.
непрерывное случайное поле |(/, х), — оо < I < оо, х е 31т, будет
однородным по переменным {I, х) и изотропным по
«пространственным» переменным х, т.. е. имеет
корреляционную функцию, зависящую только от I и р:
М1У + з,х)1&Гу) = *(*, Р),
где р —расстояние между х и г/, тогда и только тогда,
когда его корреляционная функция имеет вид
оо оо
/?('. р) = | <[в"'0Я1(рЯ.)2(Л'Х</Я.), (12)
-оо 0
где
/оч(/71-2)/2 / ч
°»(*)в(т) Г(т)Л--2)/2(*) (13)
и § —мера в полуплоскости (X, а), Я^[0, оо), V^
е (— оо, оо).
$2}
ШЕЮТАЛЬНБШ ПРЕДСТАВЛЕНИЯ
263
Найдем общий вид корреляционной функции с. к.
непрерывного однородного изотропного поля в
гильбертовом пространстве. ^Если /?(р) —такая корреляционная
т
функция, то при любом т функция /?(р), Р2=2(^)2»
является корреляционной функцией с. к. непрерывного
щ
однородного поля в Мщ. Заметим, что функция е 2
при любом X обладает этим свойством. Действительно,
при любом т
(*1+"+*т)*2
е 2
оо ™ 1_ ^п 2
=Тртг1—1е1 е ' ** — ****
— оо
Ягр2 т
т.е. функция е 2 , р2=2*| является преобразова-
нием Фурье положительной функции и поэтому
положительно определена. Отсюда следует, что и функция
*<р)«/
а,2Рг
' 2 г(^) (И)
является положительно определенной, какова бы ни была
конечная мера § на [0, оо) и при любом т, если
т
р2=2-*:2?- Докажем, что формула (14) исчерпывает все
положительно определенные непрерывные функции в
гильбертовом пространстве, зависящие только от р.
Теорема 4. Для того чтобы функция /?(р) была
корреляционной функцией с. к. непрерывного
однородного и изотропного случайного поля в гильбертовом
пространстве, необходимо и достаточно, чтобы она имела
вид (14).
Достаточность вытекает из ранее сказанного. Для
доказательства необходимости заметим, что в
соответствии с вышесказанным и теоремой 3 при каждом пг
264 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. №
имеем
л (рН / о* (*р) ёт (л), §т [о, оо) = /г (о),
о
йт(х-) = г(^)(4)^/_1(л;) =
2т + 2-4-т(т + 2) 2- 4 . 6т (т 4-2) (т + 4)
Кроме того, йт(хУ7п)-->ё~хг12 при т~>оо равномерно
на каждом конечном отрезке |#|^#. Поэтому
достаточно доказать равномерную ограниченность семейства
функций йт(х) при лее[0, со) и слабую компактность
семейства функций распределений 8т(Ут и)- С эт0**
целью заметим, что из (8) следует равенство
$ е1{и'г)8{с1и)
^т+2 (Р) = у (5р) э
где 5Р —сфера |и| = р пространства Жт, V (5р) —
площадь ее поверхности и |г|=*1. Поэтому
|От(л;)|<1.
Для доказательства слабой компактности
последовательности функций распределения %т{ц) = ёт{Ут и)
умножим соотношение
сю
Я (0) - Я (р) = / (1 - От(ри У~^)) йт №) >
О
оо
> | (1 - 0^ (ри У/тГ) ) #ш {Ли)
2/а
на р и проинтегрируем в пределах от 0 до а. Получим
^г|[#(0)-Я(р)]рФ
>
00 / а \
2/а V 0 /
§21
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
2(35
Из формулы
-д^От(г)= -—гОт+2(г)
следует (т>3, и> — ], что
а
-|-1 Мри У^Орф = ^=^ [1 - &т-Лаи Ущ)]<^,
О
откуда
а
о
Так как левая часть последнего неравенства стремится
к нулю при а~>оо, то отсюда следует компактность
меР ёт (гл. I, § 1, теорема 1). Теорема доказана.
Векторные однородные поля. Пусть {?(*); х^Ят} —
векторное случайное поле со значениями в 2&8. Оно
называется однородным, если М^ (х) = а = сопз! (условимся
в дальнейшем считать а = 0) и
Я (хх, х2) - М* (*,) 5 (х2У = /?(*,- *2).
Матричную счетно-аддитивную функцию множеств
/7(Л) = {/7Л/(Л)}, А, /=1, ..., 5, /1Е8т, будем называть
положительно определенной, если матрица /^(Л)
положительно определена при любом Ле 53т, т. е. если для
любого се^ функция множества \1С(А) = с*Р(А)с
является конечной мерой на 33"\ Используя теорему 2,
можно получить следующий результат.
Теорема 5. Для того чтобы /?(х) была матричной
корреляционной функцией с. /с. непрерывного
однородного векторного поля С(лг), необходимо и достаточно,
чтобы
Я(х)=* \ е*<*-и)Р(аи), (15)
где Р — положительно определенная матричная счетно-
аддитивная функция множеств на {31т, Ът}\
Доказательство. Пусть /?(х) — матричная
корреляционная функция с. к. непрерывного однородного
поля ^(х). Для любого се2,? введем скалярное поле
266 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ.. ЬУ
%с (х) = (2; (лс), с). Оно, очевидно, с. к. непрерывно и
однородно,
МЪС (х) = 0, Яс (х) = М^ (х + *0) 1С (х0) - с*Я (х) с. (16)
В силу теоремы 2 корреляционная функция Яс(х) может
быть представлена в виде
*«(*)- /^«^(АО, (17)
где Рс - конечная мера в [&Г, 23т}. Пусть в^ е= X*\ е{ = б|,
«М = {«1М}, А, /=1, ..., 5. Тогда Хек(х) = Хкк(х).
Положим ек! = ек + еь ек} = гек + еу. Нетрудно получить, что
2#{ (х) - [/?е^ (х) - /?*, (д:) - /?,. (*)} -
~/[/?%.(х)-/?^(^)-^у(^)].
Если положить
Ркк (Л) - ^ (Л), ^ (Л) = [Рек. (А) - ^ (Л) - Ри (А)} -
то из (16) будем иметь
Я1(х)= \е1{х>и)Р{{(1и\
причем Рк(А) предсталяют собой счетно-аддитивные
(комплексно-значные) конечные функции множеств на
{$ш, 23т}. Положительная определенность матрицы Р (Л) =
«= {р{(А)}, к, /«= 1, ..., 5, вытекает из того, что в силу
единственности представления (17) с*Р(А)с = Рс(А).
Необходимость доказана.
Для доказательства достаточности следует показать,
что функция Я(х), определяемая формулой (15), где Р
удовлетворяет условиям теоремы, является
непрерывной положительно определенной матричной функцией.
Непрерывность ее очевидна. Далее, для любых гр е %$
п
2 хрН (хр - хя)гя = \ м*Р (Ли) ш = Рт {ЗГ) > О,
п
где хю = ^^^'"Ья. Теорема доказана.
§31
ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ
267
Аналогично обобщается теорема 1,
Теорема 6. Последовательность матриц /? (п) =
= {%ь(п)}, /г = 0, ±1, ±2, ..., является матричной
корреляционной функцией стационарной в широком смысле
векторной последовательности {^(п), /1 = 0, ±1, ±2, ...}
тогда и только тогда, когда она представима в виде
я
# (п) = | е1пиР (йи),
—л
гдеР(А) — матричная положительно определенная счетно-
аддитивная функция множеству определенная на боре-
левских множествах отрезка [—я, я].
§ 3. Элементы анализа гильбертовых случайных
функций
Исследование гильбертовых случайных функций
с общей точки зрения является задачей исследования
функций в обычном смысле со значениями в
гильбертовом пространстве. Использование ковариации,
рассмотрение различных типов сходимости, применение
специфических теоретико-вероятностных понятий
придает задачам анализа случайных функций некоторые
особенности.
Интегрирование. Пусть {$?, %, т} — полное сепара-
бельное метрическое пространство с ог-конечцрй полной
мерой, {1,(х); х<= <%}— гильбертова случайная функция.
Предположим, что ^(х) = ^(х, со) —измеримая и сепара-
бельная случайная функция. Как известно из
предыдущего (гл. III, § 2), если ковариация В(х, у)
непрерывна в точке (х, х) т-почти для всех х, то для
любой 1,(х) существует стохастически эквивалентная
измеримая и сепарабельная случайная функция. Это
замечание показывает, насколько ограничительно
принятое выше допущение. Из теоремы 4 (гл. III, § 2)
непосредственно вытекает следствие.
Теорема 1. Если
I В (х} х) т {их) < оо, (1)
ж
203 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
то с вероятностью 1
\\ЬШт(йх)«х>
и
М \ | Б (х) I2 т (с!х) = | В (*, *) т [их). (2)
а? а?
Следствие. Пусть [г(х), / = 1, 2 — функции из
3?2(<%'> ^> т) и выполнено условие (1). Тогда с
вероятностью 1 существуют интегралы
я?
причем в силу теоремы Фубини
М1ЦЧ2 - м / / А (*) Ш ^ (*) Ш /п (</*) т ш =
- / | Л (*) 5 (*, у) Му) т (их) т (йу)п
'$5%
Сделаем несколько замечаний по поводу определения
интегралов от случайных функций.
Замечание 1. Пусть выполнено условие (1) и
т (§6) < оо. Тогда интеграл
^1{х)т{йх) (3)
лля измеримой случайной функции %(х) определен и
конечен с вероятностью 1 для каждой реализации %(х).
Но при определении интеграла (3) можно поступить
несколько иначе. Во-первых, интеграл (3) можно
определить как с. к. предел лебеговых интегральных сумм
для 1(х). Нетрудно убедиться, что это определение
совпадает с обычным. Для доказательства достаточно
ограничиться неотрицательными случайными
величинами. По определению интеграл (3) есть предел при п-^оо
\Ъп{х)т{йх),
§ 31 ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ 2Ф
где ^ (л:) —монотонно неубывающая последовательность
случайных функций, принимающих конечное число
значений и таких, что 1\т^п(х) = ^(х) с вероятностью 1.
Так как | %(х) — 1п{х) |<| Цх)\, то по Теореме Лебега
М
/ С(*) т{ах)~ / ^(ах)т(Ох)?^
<М /|С(*)-Ь|(*)Рт(^)т(Я?)-^0
а?
при п-> оо, так что
1%>(х)т{их) = 1л.т. Г $п(х)т{Ах).
Замечание 2. Рассмотрим случайный процесс
К (/), /е[а, 6]}. Интеграл
ь
/с (О л
а
часто определяют как с. к. предел интегральных сумм
ЕС(ЫА'Я*,
Для существования с. к. предела этих сумм в силу
леммы 3 (гл. I, § 1) необходимо и достаточно
существование предела
п т п т
м 2 е (/„*) д*яЛ 2 с ('«*) а^ = 22^ (*яЛ, *тг) д/яА д*тг
при п, га->оо, т. е. интегрируемость по Риману функции
В{1, $) (а^/, 5^6). Таким образом, данное
определение интеграла является более узким по сравнению
с первоначальным, но зато оно не связано с понятием
измеримости процесса. Легко убедиться, что когда
применимо последнее определение интеграла, оно
приводит (той Р) к тому же результату, что и исходное.
270 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Действительно,
М
/с юл-2 :(*„*) а*.
пк
пк
=22 / / 1ву,з)-в«,и-в(1пк,$)+
*-' Г=1 '«4-1 '»М
п п
+ В (/„», /пг)] Л й« < 2 ^ 2 0„,г -> 0,
где Ояйг — колебание функции В (/, 5) в прямоугольнике
Замечание 3. Под несобственным с. к. интегралом
оо / оо \
|С(0Л или \№йА (4)
— со \ а '
условимся понимать пределы
1л.т. Г 5(0 Л (1Л.т. |Ч(')Л •
Для существования этих интегралов в силу леммы 3
(гл. I, § 1) необходимо и достаточно существование
пределов
N № / N № \
Нт [ \вЦ,8)(Иа8 Ит { { ВЦ, з) (Паз).
*.*'->«, _^_^, \*. *'->«> ; ^ ;
Это определение несобственных интегралов в некоторых
случаях оказывается более широким, чем понимание
интегралов (4) как интегралов Лебега от функций ^(0
при фиксированном со.
Закон больших чисел. Пусть {^(0, ^^0}~ измеримый
гильбертовый процесс с интегрируемой ковариациеи
на каждом конечном промежутке. Будем говорить, что
{?(*)> ^2^0} удовлетворяет закону больших чисел, если
в определенном смысле
т
у- ^ 1{1)сН->с при Т -* оо #
§ 3] . ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ 271
Из леммы 3 (гл. I, § 1) вытекает, что для
существования среднего т
1Л.Ш.4- Г С (О Л
необходимо и достаточно существование предела
т г
Пт -=г В(1, 8) (11 Яз.
Г, Г'-»оо
Г Г'
г-2"-*00 о о
Далее, для равенства
( т т 1
Г-»оо | Г
о о )
необходимо и достаточно, чтобы выполнялось
соотношение
т г
Нт ~ Г [/?(*, з)<И(18 = 09 (5)
где /? (7, 5) — корреляционная функция процесса.
Нетрудно заметить, что
Т Г 12 Г Г Г' Г'
0 0 I 0 0 0 0
Поэтому равенство (5) имеет место тогда и только
тогда, когда
т т
Пт 4- Л /?(*, !)ЛЛ = 0. (6)
г->0 о о
Для стационарного процесса в широком смысле К(1, $)■
= /?(/- 5). Так как
г г г
о о ~г
то получаем следующий результат.
272 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Теорема 2. Если (;(/) — стационарный в широком
смысле процесс, то для равенства
т
Нт-]г Гс(0<й«МЕ(0 (7)
необходимо и достаточно, чтобы
т
Нт у- //?(0(1 ~ЩМ = 0. (8)
00 -г
В частности, условие теоремы выполняется, если
среднее значение' корреляционной функции равно нулю:
г
Нт-^г \Н (8)48 = 0.
Выразим условие (8) через спектральную функцию
процесса. Имеем
Т оо Т
-Т -оо -Г
откуда
т /л(о(1-^-)л- /'(1-~г,,)/>№«)-
-Г -оо
оо
-'«Р» + ]"1И^М/><&,),
— оо
где Р (Л) = Р (А \ {0}), {0} — множество, состоящее из
одной точки н = 0. Нетрудно видеть, что при Г->оо
последний интеграл стремится к нулю. Поэтому
т
11^-1 | Я (/)(! - Ш) Л - /? ({О}). (9)
Т->оо ^
Таким образом, имеет место
Теорема 3. Для стациЬнарного в широком смысле
процесса равенство (7) имеет место тогда и только
§31
ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ
273
тогда, когда его спектральная функция непрерывна
в точке и = 0.
Дифференцирование. Пусть {2;(0, *<=(я, Ъ)}, — оо ^
<] а <Ь ^ + оо,— гильбертов случайный процесс.
Определение 1. Случайный процесс 5 (0. ' е (а> ^)
с. /с. дифференцируем в точке /0 (дифференцируем
в среднем квадратическом), если существует
П'оНи-т. е(^. + *)-еЩ> , /0 + Ае(а,Я.
Случайная величина %' (10) называется с. к. (среднеквад-
ратической) производной случайного процесса в точке *0.
Легко найти необходимые и достаточные условия с. к.
дифференцируемости случайного процесса. Так как
м С(/0 + Л)-С(*о) С('о + Л1)-С(*о) =
-В(*0 + Мо) + Я('о,'о)}, (Ю)
то в силу леммы 3 (гл. I, § 1) для с. к.
дифференцируемости процесса !;(*) в точке /0 необходимо и
достаточно, чтобы существовала обобщенная смешанная
производная
д2В (/, Г) 1
МдГ !,.,_,,-
^ \\ш вУо + Ь> ;о + /*1)-В(/о, /р + Лж)-Д(*о + Л, /о) + В(/0, /0).
л, л,->о АА»
Из с. к. дифференцируемости процесса в точке I и
неравенства
|м(у(/)-С(^-С(0)|<{[м|у(0-С(<+*1-е(0Г}'&
следует, что
МСЧ')—й-МС«), (11)
причем производная справа существует.
Если процесс (;(/) с. к. дифференцируем в каждой
точке интервала (а, Ъ), то производная $'(/) образует
гильбертов случайный процесс на (а, 6),
274 ШНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Теорема 4. Пусть &(/), Iе (а, Ь)} — гильбертов
случайный процесс и обобщенная производная
д2В (/, П
д1д1'
ЫГ
существует при каждом значении I <= (а, Ь). Тогда про-
цесс 5(0 с. /с. дифференцируем на (а, 6) и
ЪгЬП-^Щ&Р-. (12)
Вгс<и')~-^§А (13)
где В^;/ (?, /') = М^ (/) I' {I) — ковариация процесса %' (*),
а В$х (*, V) = М$' (0 ^(/') — взаимная ковариация
процессов Ъ'Щ и 5(/).
В доказательстве нуждаются лишь формулы (12)
и (13). Имеем
ва(ио=м?1т'(о=
Следовательно, производная —^—- существует, и
взаимная ковариация процессов $'(*) и 5(0 дается
формулой (13). Далее
" л.л'-*> л Л
= ,. в (* + /*, г + ло-ж/, г + а;) - в (/ + л, о.+ ^ СЛ
Л, Л'->оо
/г/г'
Отсюда вытекает существование обобщенной второй
производной
д2В (/, П
д1дГ
(в условии теоремы предполагалось только, что эта
производная существует при * = *') и формула (12).
Если процесс 5(0 стационарен в широком смысле,
то В(1,У)=*В(1 — 1') и из теоремы 4 вытекает
Следствие 1. Для с. /с. дифференцируемости
стационарного в широком смысле процесса 2(<)(/е Т) необ-
| Щ ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ 2 75
ходимо и достаточно существование обобщенной второй
производной корреляционной функции /?(0 при / = 0.
Если это условие выполнено, то существует обобщенная
производная —-ф-1- и
Я;т('оЛ + 0=-
йЩ (О
сН2
Яп (*0 + '> 'о) = /?а(0 =
<*/?(*)
л
Аналогичные результаты имеют место и для с. к.
производных высших порядков.
Следствие 2. Если 5(0 — процесс стационарный
в широком смысле, /е^(— оо, оо), н
| и2Р (Ли) <оо,
еде Р — спектральная мера процесса, то процесс 5 (/) с. /с.
дифференцируем, процесс (5'(0,^(0) стационарен в
широком смысле и его матричная корреляционная
функция /?(0 имеет вид
| еЦии2Р(йи) | ешшР (йи)
— со —оо
ОО ОО
- | ёшшР{йи) | е1шР(йи)
Разложение случайного процесса в ортогональные
ряды. Пусть {^(0, /е [а, 6]}— измеримый с. к.
непрерывный гильбертов процесс. Его ковариация В{1и12)
является непрерывным неотрицательно определенным
ядром в квадрате [а, Ь] X [а, Ь]. Согласно теории
интегральных уравнений ядро В (1и /2) может быть разложено
в равномерно сходящийся ряд по своим собственным
функциям ч^(0:
Л~1
276 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. ГУ
где
ь ь
ЯдФп (0 = / В (*, т) <ря (т) ах, | Фп (/) ^(7) Л = блт,
причем собственные числа Ал положительны.
Положим
,ь
а
Этот интеграл существует (теорема 1) и в силу
следствия из теоремы 1
ь ъ
М|я|„ = / \ВЦ,%) фЛО Фт (*) Л Лх = АА«»
а а
т. е. последовательность случайных величин \п (п=1,
2, ...) является ортогональной. Далее
ь
Щ (0 1п-\в(/, т)Фп(т)Лт = АпФ„(/).
а
Отсюда следует, что
г(0-2ЬкФ*(0
м
Л-
= я(и)-2л4|ф*(ОР->о
при /г~>оо равномерно по / в силу теоремы Дини.
Теорема 5. Измеримый с. /с. непрерывный
гильбертов процесс 5 (0, * е [а, 6], может быть разложен в ряд
гю-ЗзЬкФЛО. (14)
сходящийся в 3?2 при каждом I е [а, 6]. В эгол* раз-
ложении \к — ортогональная последовательность
случайных величин, М | ^ |2 = А&, А* — собственные числа, ф# (/) —
собственные функции ковариации процесса.
§3]
ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ
277
Замечание 1. Если процесс ^ (/) гауссов, то его с. к.
ь
производная и интегралы вида I Ц^)%(1)й1 являются
а
гауссовыми случайными величинами. Поэтому, если
^(^ — вещественный гауссов процесс и М^) = 0, то
коэффициенты \к ряда (14) являются независимыми
гауссовыми величинами и ряд (14) сходится с
вероятностью 1 при каждом I.
Действительно, независимость величин ^ вытекает
из их ортогональности и гауссовости. Для сходимости
ряда (14) с вероятностью 1 достаточно, чтобы сходился
оо оо %
ряд 2 М(^<рй(0)2== 2 ^!|ф*(0|2« Но уже упоминалось,
к=\ к=1
что этот ряд сходится (и его сумма равна В(1,1)).
Теорема 6. Если
М|Ш-^ + Л)Р<—Т7ТЖГ> г>°. «<*<&. (15)
Пе1Л1Г+
то для любого е>0
Г
Р\ вир
1 а<*<6
с(0-2б*<м<)
1
1
>е}->0 при д->оо.
Доказательство основано на лемме 1 § 5 гл. III.
Положим
Тогда
Р^>еКР{|?„(0)1>-|}+Р{а8иРь|С(0-^(0)|>|-}<
^4Ми„(0)|г
где СЦп, С) и О имеют значения, указанные в
упомянутой лемме. Имеем
278 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, IV
где
<(<,А)=А1|С;(< + А)-С;(0|2в
I оо |2
= М 2 и<р*(' + л)-Ф*(')]
I /е=гс-И
оо
= 2 ^!ф,(/ + /0-ф,(012.
Учитывая (15), видим, что функции | 1§| к | |3+г ст^, Л) X
Х{Ц И \)~х (0<г'<г) непрерывны по г^[а, &] Ае[0, А0],
монотонно убывают при возрастании п и стремятся
к нулю при я->оо. В силу теоремы Дини эта
сходимость является равномерной. Следовательно,
{ |1&|^||3+г,а^(/,/г) р 1
шах | Т\1Г\ ; *^1а> ь1> ЛеЕ1°> ^о]| = 6Л —>О
При П—>оо.
Положив (см. гл. III, § 5) #(А) = | 1е| /г I Г(14Л 0<г^<— ,
получим, что
е<оо, о^сх-^,
где К — некоторая постоянная, не зависящая от п.
Таким образом, С}{п, -т^-)->0 при п~>оо. Кроме того,
и М|2„(0) |2->0. Теорема доказана.
В качестве примера рассмотрим разложение в
ортогональный ряд процесса броуновского движения на
отрезке [0,1]. При этом ^(0) = 0, М?(0 = 0, ^^}(^) = ^,
В {I, я) = М^ (/)2 М = гп1п (*, 5). Собственные числа и
функции ядра В(1,$) легко находятся. Из уравнения
КЧп С) = | П11П (*, 5) фп (5) <& = | 5ф„ ($) ^5 + | ^фп (5) й?5
о о г
имеем, во-первых, ф„(0) = 0. Дифференцируя по I, полу-
1
чим \ф^(0= ( Фл(5)^5, откуда ф„(1) = 0. Повторно диф-
§ 31 ГИЛЬБЕРТОВЫ СЛУЧАЙНЫЕ ФУНКЦИИ 279
ференцируя, придем к уравнению Ялф^' (О = — % (/).
Нормированные решения последнего уравнения, удовле*
творяющие граничным условиям Фл(0) = 0, ф^(1)=*0,
имеют вид
фя(0 = У^ып^п+^л!, Ад1 = (л+у) я2, п = 0, 1, ...
Таким образом,
/ 1 \
81П 1 П + -г- \П1
г (/)
я+т)я
(16)
где 5а — последовательность независимых гауссовских
случайных величин с параметрами (0, 1). При
фиксированном / этот ряд сходится с вероятностью 1. Так как
5(0 — гауссовский процесс и М | ^(/ +Л) — ^(/) |2==й, то
1
511р
№
81П I к + — I Ш
(*Ч)я
о
по вероятности.
Другое разложение процесса броуновского движения
может быть получено следующим образом. Положим
!(*) = 5(0"-'50)« Тогда ^(0~ гауссов процесс скова-
риацией В{ (/, 5) == тт (I, 5)~^и М\ (0 = 0. Собственные
числа и функции ядра В{ (I, $) находятся так же, как
и в предыдущем случае. Мы приходим снова к
уравнению ЯЛфд (0 = — фЛ (0 с граничными условиями фЛ(0) =
"^ Фя 0) = 0> решения которое имеют вид
Ф« (0 = У% 81П яя/, Яя * = п2п2, п = 1, 2,
Таким образом,
К0 = Ш-^(1)="1/2^„
81П ПП1
11%
и=1
где |я (/г = 1, 2, ♦♦.) — нормированная последовательность
независимых гауссовых случайных величин, причем
1
1п = ]/ 2 | | (/) 3111 ПП1 СИ.
280 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Так как М^(1)= 1, М?2(1)-1,
1
МШ1)=У^/Мв(/)-*Е(1))Е(1)з1пля*Л = 0,
о
то, положив 6о = 2(0» получим
С(/)-/6о+У'2 2ь.-^. (17)
где |о> €ь •••! ёш ••• независимы и имеют нормальное
распределение с параметрами (0, 1). Характер
сходимости ряда (17) таков же, как и у ряда (16).
§ 4. Стохастические меры и интегралы
В ряде вопросов важную роль играют интегралы,
записываемые в виде
ь
//(')<*Ш, (1)
а
где /(/)— заданная (неслучайная) функция, а
^(0~-случайный процесс. Реализации процесса 2;(*), вообще
говоря, являются фупкцияхми неограниченной вариации,
и интеграл (1) нельзя понимать как интеграл Стилтьеса
или Лебега — Стилтьеса, существующий почти для всех
реализаций 2(/), Все же и в этом случае интеграл (1)
можно определить таким образом, чтобы он обладал
свойствами, присущими обычному интегралу.
В настоящем параграфе дается определение и
рассматриваются свойства интеграла, соответствующего
интегрированию по случайной мере. Такие интегралы
называются стохастическими.
Пусть {О, ©, Р} —вероятностное пространство, 9?2 ^
= 3?2(&> ©> Р)> Е — некоторое множество и Ш —
полукольцо подмножеств Е. Предположим, что каждому
Ае Зй поставлена в соответствие комплекснозначная
§ 4] СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ 281
случайная величина 2; (А), удовлетворяющая следующим
условиям:
1) С(Л)еЕ<?2 Е(0)»О:
2) I (А, \] А2) = С (АО +1 (А2) (той Р), если ^ П А2 - 0;
3) МиА^^Ш-тС^ПА^,
где т (А) — некоторая функция множества на Ш.
Определение 1. Семейство случайных величин
К (А), А^ЗИ}, удовлетворяющее условиям 1) — 3), будем
н а з ыв ать элементарной ортогональной стохастической
мерой, а пг (А) — ее структурной функцией.
Свойство ортогональности стохастической меры
выражается условием 3): если Д1ПА2=0, то величины
Ь>{&{) и 2(А2) ортогональны.
Из определения т(А) следует, что она
неотрицательна:
т(Д) = М|&(Д)р>0, т(0) = О,
и аддитивна: если Д,ПД2=:0, то
т(А1иА2)-Ми(А]) + С(А2)|2 =
« т (АО + т (А2) + 2т (А! П А2) = т (А^ + т (А2).
Таким образом, т(А) является элементарной мерой*)
на 3».
Обозначим через 3?0{Щ класс всех простых
функций /(лг):
/(*)=2сЛхдЛ*), ДЛ€=Я1, Л-1, 2 я, (2)
где гс —любое число и %л (#) — индикатор множества Л.
Определим стохастический интеграл от функции
/ (х) е .2?0 {ЯИ} по элементарной стохастической мере 2
формулой
л-//(*)№) = 2с*Б(Д*)- (3>
Л«1
*) Элементарной мерой будем называть неотрицательную
аддитивную функцию множеств, определенную на полукольце множеств.
282 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 1У
Так как Эй — полукольцо, то любую пару функций
из 3?0{Ш} можно представить как линейные комбинации
индикаторов одних и тех же множеств из 3№. Поэтому,
если /, §^5?ъ{Ш), то положим, что ?(х) дается фор-
га
мулой (2) и г(*)=2 ак%А (х), причем ДлПДг=0 при
кфг.
Из ортогональности 2 следует, что
п
М (//(*) $ (их) / *(*)№)) = 2 сй4т(Д6). (4)
/2 = 1
Предположим, что элементарная мера т
удовлетворяет условию полу аддитивности и поэтому может быть
продолжена до полной меры {Е, 2, т}. Тогда 5?ъ{Ш)
является линейным подмножеством гильбертова
пространства 3?2{т} = 3?2{Е, 2, т), а 2"2{Щ — замыканием
3?ъ{Ш) в топологии, порождаемой скалярным
произведением
</, ё)=\1{х)ё~&)т{йх). (5)
При этом соотношение (4) может быть переписано
в следующем виде:
М / /(*)&(</*) / 8(*П(4х)= / !(х)ё(дт((1х) (6)
для любой пары функций }(х), д(х) из 3?2{т}.
. Введем теперь линейную оболочку ^0{?} семейства
случайных величин {С (А), А^ЗТО}, т. е. множество
случайных величин, представимых в виде (3), и
пространство «2*2Ш, являющееся замыканием 2?0Ш в
гильбертовом пространстве случайных величин 2?2{&, ©, Р}.
Заметим, что соотношение (3) устанавливает
изометрическое соответствие г} = я|)(/) между 3?^Щ) и 2?0Ё}« Это
соответствие может быть продолжено до
изометрического соответствия г|) между 3?2{Щ и 3?г{Оь> Если
г1 = 'Ф(/!), /^^2{3^}» то полагаем по определению
г\ = *(Г)=\Пх)Шх) (7)
и называем случайную величину т| стохастическим
интегралом функции }(х) по мере ^. Отсюда следует
$41 СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ 283
Теорема 1. а) Для простой функции (2) значение
стохастического интеграла дается формулой (3);
б) для любых Цх) и §{х) из 2?2{Е, #> пг) имеет
место равенство (6);
в) \ Ы(х) + №(хШ*х) = а$ /(*)№)+ Р/ 8(х)Шх)\
г) для произвольной последовательности функций
1{п)(х)<=2?2{Е, 8, т} такой, что
| I / (*) - !{П) (х) |2 пг {с1х) -> 0, п -> оо, (8)
выполняется соотношение
$ Г(х)Шх) = 1Л.т. $ Р*(х)Шх)-
Замечание. В частности, если /*я)(х) — простые
функции,
1{п) (х) = 2 <\(я> (*), А^^ЗТО, /1=1,2,...,
и (8) выполнено, то
тп
Существование последовательности простых
функций, аппроксимирующих произвольную функцию /(л;)е
е^?2{^» 2, т}, вытекает из общих теорем теории меры.
Таким образом, стохастический интеграл можно
рассматривать как с. к. предел надлежащих интегральных
сумм.
Обозначим через Ь0 класс всех множеств Ле2,
для которых т(Л)<оо# Определим случайную функцию
множеств 1(А):
Ш)=$ха(х)Шх)=1Шх). (9)
л
Она обладает следующими свойствами:
а) 1(А) определена на классе множеств Ь0;
284 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
б) если Л„<=10; л = 0, 1,2,..., А0=[]Ап, Ак()Аг = 0
при кфг, к>0, г>0, то С(Л0) = 2 С(А*) в смысле
с. к. сходимости;
в) м1(А)1(В) = т(А()В)9 А, Ве!0;
г) |(Д) = Е(Д) при Де=3№.
Определение 2. Случайная функция множеств I,
удовлетворяющая условиям а), б), в) называется
стохастической ортогональной мерой.
Свойство г) означает, что \ является продолжением
элементарной стохастической меры %. Таким образом,
мы имеем следующую теорему.
Теорема 2. Если структурная функция
элементарной стохастической меры % полуаддитивна, то % может
быть продолжена до стохастической меры ?.
Замечание. Так как 3?2 {$ = 3?2Ш> то
11(х)1№=\1(х)1(йх).
В соответствии с этим равенством условимся в
дальнейшем отождествлять стохастический интеграл по
элементарной ортогональной мере ^ структурная функция
которого полуаддитивна, со стохастическим интегралом
по стохастической мере ?> определенной
соотношением (9).
Сделаем несколько замечаний по поводу определения
стохастического интеграла на отрезке прямой. Пусть
5(0 (а <!/<6)-~ процесс с ортогональными
приращениями, т. е.
М(|(/2)-к/1))(ЖнШТ=о
для любых /(г[а, Ь), ^^<^2<^з<и> с-к- непрерывный
слева:
М|6(0-&(*)Р-*0 при «|/.
Положим
§ 4] СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ 285
Из ортогональности приращений процесса 5(0
следует, что при 12 > 1{
^"(^) = М| 6(/2) — Б(/1> + Б('1> — &(«) Р =
= Р(1Х)+1А\Ш-Ш?>
откуда Р(^^Р(и) и Р(() = 1\тР(з). Таким образом,
Р {I) — монотонно неубывающая непрерывная слева
функция. Пусть 9№ — класс всех полуинтервалов А =
= Р{1<^ — Р (1{). Тогда Ш — полукольцо множеств,
МаА1)"йД21 = т(А1ПА2),
2 (А) — элементарная ортогональная стохастическая мера,
структурная функция которой допускает продолжение
до меры. Таким образом, можно определить стохасти*
ческий интеграл Стилтьеса с помощью равенства
ь ь
а а
в котором ^ (0 — процесс с ортогональными
приращениями. Этот интеграл существует для произвольной
борелевской функции /(0, 1^[а, &), для которой
ь
\\1(*)?Р№<оо,
а
где Р (Л) — мера, соответствующая монотонной
функции Р{1). Аналогично определение стохастического
интеграла по всей прямой (— оо, оо).
Докажем несколько предложений о стохастических
интегралах.
Пусть 2; —ортогональная стохастическая мера со
структурной функцией т, являющейся полной мерой
на {Я, 2} и §(х)^2,2{т}\ Положим
МЛН/хл (*>*(*)№), А ей.
Тогда
М1(А)ЦВ)== \ хА(х)ХвМ\§(х)\2т(с1х)^
286 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Если на 2 ввести новую меру
/И)=/|*(*)Р/*(**),
А
то мы видим, что к (А) будет ортогональной
стохастической мерой со структурной функцией /(Л), Ле?,
Лемма 1. Если /(х)е 3?2{О, го /(х) § (х) е 5?2\т} и
1Цх)Цах) = 11(х)8(х)Шх)-
Доказательство. Утверждение леммы очевидно
для простых функций !(х), {(х) = %ск%Л.(х), Л* ее 2.
к *
Далее, если 1к{х)—фундаментальная последовательность
простых функций в 5?2{1}> т0
111п (х) Я (ах) - / 1п+т (х) к {их) |2 =
= \\Ш-итШ\8(х)?т{(1х)9
т. е. !п(х)§{х) является фундаментальной в 3?2{т)ь
Переходя в равенстве
\ ШЩх)= \ Шемш
к пределу при /г~>оо, получим утверждение леммы
в общем случае.
Лемма 2. Если Л^10, то
Заметим прежде всего, что §(х) = 0 на множестве
/-меры 0; таким образом, —т-г ф оо (той/). Далее
Г % (х) Г I
1-41
СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ
287^
Следовательно, можно воспользоваться леммой 1:
Лемма доказана.
Пусть Г —конечный или бесконечный отрезок на
прямой линии, 23 —сг-алгебра подмножеств Г, измеримых
по Лебегу, / — мера Лебега.
Допустим, что §■(/, х) 23 X 8-измерима, @({, х)^
^3?2{1 X т} и §у9 х)^3?2{т} при произвольном ^еГ.
Рассмотрим стохастический интеграл
ЪЦ)=\еИ>х)Шх). (10)
При каждом I он определен с вероятностью 1.
Лемма 3. Стохастический интеграл (10) можно
определить как функцию от I таким образом, чтобы
процесс |(0 был измерим. _
Доказательство. Если
8 С х) = 2 ск%вк (*) %Ак (х), (11)
В* е= 23, Л* е= 2, то 1У)=%ск%вк(*)Ь(Ак) является
23 X ©-измеримой функцией переменных (*, со), /еГ,
со ей. В общем случае можно построить
последовательность простых функций 8пЦ, х) вида (11) и таких,
что
| \ I б" ('» х) — §п Ц, х) |2 т (Лс) Л -> 0 при /г -> оо.
Пусть 1п (0 — последовательность процессов,
построенных по формуле (10) при @ = 8п. Тогда существует
процесс |(^) такой, что
/м|1(0-&я(*)|2<й->0 при п-»оо
и 1(0 является 23 X ©-измеримой функцией от (^, со).
С другой стороны,
I ми(0- 1п(012л = ||Iг(*,*)-*»С.*)I2т(</*)л-*о,
~288 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
откуда следует, что М 11 (*) — I {I) |2 = 0 почти для всех I.
Положим
I Ш, если Р {^ (0 ^ I (/)} > 0.
Процесс |'(0 измерим (так как |'(/) отличается от
93 X ©-измеримой функции §(/) на множестве меры 0)
и стохастически эквивалентен \(1). Лемма доказана.
В дальнейшем, рассматривая процессы, определяемые
стохастическими интегралами вида (10),
удовлетворяющие ранее перечисленным условиям, будем предполагать
их измеримыми.
Лемма 4. Если & (1Г з) и Н (/) — борелевские функцииу
Ь оо Ъ'
| ||$(*. в) Р<йт(<*«)<«>, ||А(/)рЛ<оо,. (12)
а —оо а
% —ортогональная стохастическая мера на {У?1, 251}, то
Ь оо оо
/МО /г(',*)С(<**)л= |ы*)№). (13)
а —оо —оо
где
Ь
а
Доказательство. Математическое ожидание
квадрата модуля интеграла в левой части равенства (13)
равно
Ь Ь / ОО ч
т {из) ^
оо Ь
а —оо а
Для математического ожидания квадрата модуля
интеграла в правой части равенства (13) имеем нера-
оо
I
ь
\кц)ец,$)м\
—оо | а \
Ь
§4] СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ 289
венство, указанное во второй строчке последнего
соотношения. Следовательно, правая и левая части
равенства (13) непрерывны относительно предельного перехода
по последовательностям §п((, з), сходящимся в «^{Ф)»
где Ф — прямое произведение лебеговой меры на меру т
в полосе [а, &] X (—со, сю). Далее, множество функций
§Ц, $), для которых (13) верно, линейно и содержит
все функции вида 2 ск%Ак(*)%вк (т). Следовательно, оно
содержит все функции из 3?2{ФЬ
Замечание. Если условия леммы 4 выполнены
для каждого конечного отрезка (а, Ъ) и существует
интеграл
оо Ь
( ИУ)§У, 8)сН= Игл \ к{1)${1, $)М
в смысле сходимости в 5?2{т}> то
оо оо оо
\к{1) \ё{1,з)ис1*)сИ= |М«)№), (И)
— оо —оо —оо
где
оо
и («) = |л(0г(/, *)л.
— оо
Доказательство непосредственно вытекает из того,
что левая часть равенства (14) являе/гся с. к. пределом
левой части равенства (13) и из возможности перехода
к пределу под знаком стохастического интеграла в
правой части формулы (13).
Рассмотрим теперь обобщение предыдущих
результатов на векторные стохастические меры. При этом
мы ограничимся простейшим случаем интегрирования
скалярных функций, мало чем отличающимся от
интегрирования по числовым стохастическим мерам.
Пусть %р обозначает некоторое комплексное
векторное пространство размерности р. Для простоты будем
считать, что некоторый базис в этом пространстве
фиксирован. Допустим, что каждому А^3№ поставлена
в соответствие векторная случайная величина 2; (А) со
Ю И. И. Гихман, А. В. Скороход
290 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ГГЛ. IV
значениями в ЗС", Б(А) = {Iх(А),С2(А), ..., БР(Д)}. Через
|^(А)| обозначим норму вектора ?(А),
и(д)р=2и*(Д)Р.
Предположим, что
1) Ми(А)|2<оо, Е(0) = О;
2) е(А, Ц Д2) = 5(Ьх) + С(А2)(гпос!Р), если Д1ПА2=0;
3) М^А^Д^-т^ПА^ Д,€=Эв, /=1, 2;
Л, /= 1, ..., р.
Семейство случайных векторов {^(А), А е 9№} будем
называть элементарной векторной стохастической
(ортогональной) мерой, а матрицу т(А) = (т^(А)} =
= М^ (А) $* (А) — структурной матрицей.
Отметим, что как функция от А{ и А2 матрица
пг (А! П А2) обладает свойствами корреляционной матрицы
векторной случайной функции (см. § 1). Кроме того,
если А! П А2 = 0, то
пг (&! [) А2) = пг (А^ + пг (А2).
Отсюда следует, что диагональные элементы матрицы
т(Д) являются элементарными мерами. Кроме того, из
неравенства
| пг) (А) | < Ут^(Д)т{.(А) (15)
следует, что
2 | '«ИЛг)1<{ 2 тЦ\) 2 ™КЛг)}'\ (16)
и, значит, функции множеств т) (к, /= 1, ..., р) имеют
ограниченную вариацию на А.
р
Положим т0(Д) = 5рт(Д) = 2 т*(Д). Из (16) еле-
дует также, что если 2т0(Д^)->0 при М-^оо, то и
2 | я** (А^) |-> 0. Отсюда вытекает, что функции т^(Д)
могут быть продолжены до счетно-аддитивных функций
множеств на Й> если функция т0(Д) полуаддитивна на Ш.
§ А] СТОХАСТИЧЕСКИЕ МЕРЫ И ИНТЕГРАЛЫ 291
В дальнейшем матричные функции, полученные путем
такого продолжения из структурной функции элемент
тарной ортогональной стохастической меры, будем
называть положительно определенными матричными
мерами.
Выше 2? обозначало пополнение а{Ш} относительно
продолженной элементарной меры т0(А). Простоты ради
для продолжений функций ткр т0 и матрицы т на 23
сохраним первоначальные обозначения, причем в
дальнейшем будем считать, что ш0(Л) полуаддитивна на Ж,
Определим на 2?${Ш) стохастический интеграл с
помощью формулы
п
П=//(^)С(^)-2с*С(Аа)> (17)
п
если / (х) = 2 едсдь (*)> &ь ^ 9Я (к = 1, ..., /г). Значением
6 = 1 *
этого интеграла является случайный вектор (столбец)
со значениями в 35РЛ Через 3?о{$ обозначим
совокупность всех случайных векторов ц вида (17). Если §(х)=*
п
«= 2 4к%Ак(х), ТО
М ({ / (х) С (их) (/ § (дг) I (их))) = 2 ^т (Л*),
что можно записать в виде
М(/ 1(х)Шх){\ ё(х)Ш*))*) = / 1(х)^Щт(йх). (18)
Отсюда следует равенство
М11 / (х) I {их) |2 = \ | / (*) |2 т (</*). (19)
Введем в 5?0{3#} скалярное произведение
(А Я) = //М^)^о(^).
Формула (17) устанавливает изометрическое
отображение т] —^(/) пространства 3?о{ЯЯ} на 3?оШ> если в З'оЙ)
скалярное произведение элементов г\{ и % определяется
10*
292 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
как Мт)*т)г Замыкание пространства случайных величин
3?о{$ обозначим через 5^2 ЙЬ а пополнение ^0{2№}
через &2(Щ.
Аналогично неравенству (16) выводится неравенство
||/(х)||т^|(^)<{/|/(х)|ш^(^)||/(х)|т/(^)}1/2,
(20)
где | ткЛ (А) — абсолютная вариация функции ткг
сначала для простых и с помощью предельного перехода
для произвольных 95-измеримых функций. Из
неравенства (20) вытекает существование и непрерывность
интеграла
//(*)ГОт?(</*)
как функционала от / и § в 2?2{т0}.
Исходя из этого, изометрическое соответствие т] = 'ф(/)
пространства 3?о(Ш) на 3?о(5) может быть продолжено
до изометрического соответствия 2*2{2И} на 5?2(&. При
этом случайный вектор г| называют стохастическим
интегралом и пишут-
где !(х)€Е2>2(т0).
Аналогично понятию стохастической меры в
скалярном случае может быть определена векторная
стохастическая мера 5 (А).
§ 5. Интегральные представления случайных функций
Используя результаты предыдущего параграфа
можно получать различные представления случайных
функций с помощью стохастических интегралов.
Предположим сначала, что р-мерная векторная
случайная функция %(х), х^%?, может быть представлена
в виде
Ш=\е(х, и)1(йй), (1)
где 5 — стохастическая мера на измеримом
пространстве {°и, Щ со значениями в Хр и структурной матри-
§5]
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
293
цей т(А) (мы используем здесь обозначения
предыдущего параграфа), @(х, и) — скалярная функция и при
каждом х е 9В
Я (*, и) е= &2 {тд} = $2{<?/, 23, т0}, тэ (А) = 8р т (Л).
В силу формулы (18) § 4 ковариационная матрица
случайной функции К*) имеет вид
В(хь х2) = Щ(х1)1т(х2)= \ 8(хи и)в(*2, и)т(йи\ (2)
а из (19) § 4 следует, что
М|* (х2) I(х{) = | §• (хь и) гС^Г") т0(</и). (3)
Напомним, что {<?/, 93, т0}—пространство с полной
мерой, 9?2{т^ — гильбертово пространство 23-измеримых
комплекснозначных функций с ш0-интегрируемым
квадратом.
Через 3?2{§} обозначим замыкание в 9?2{т^
линейной оболочки, порожденной системой функций {§(х, и),
х<^%?}. Тогда 3?2{§] есть линейное замкнутое
подпространство 2?2{т0}. Если 9?2{§} = 3?2{тд)> то система
функций {§(х, и), и ^.$6} называется полной в 3?2{т^.
Пусть {|(#), х<е= 36} — гильбертова случайная
функция со значениями в $&р\ 3?0{Ь}~ множество всех
случайных векторов
п
Ч=2*А|(*Й), «=1, 2, ..., хк^36, (4)
где ^ — произвольные комплексные «числа, и З^Ш —за-
мыкание 5?0Ш в смысле средней квадратической
сходимости случайных векторов.
Определение 1. Семейство случайных векторов
{г|а, аеУ1}, %\а^ 9?2{&, ©, Р}, называется подчиненным
случайной функции {| (х), х <=е $?}, если т)а е З^ Ш»
аеА
Теорема 1. Пусть ковариационная матрица
случайной функции {1(х)9 х^Щ допускает
представление (2), где ш — положительно определенная матричная
мера на Щ, 23}, @(х, и)е^гЫ хе1, и семейство
{§(х, и), х^. 96} полно в 3?2{°11, 25, т0}. ТогдаЦх) пред-
ставима по формуле (1), где-ЩВ), В е 33} — некоторая
294 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ IV
стохастическая ортогональная векторная мера, подчи*
ненная случайной функции 1(х) со структурной
функцией т( •) и равенство (1) выполняется с вероятностью 1
при каждом х.
Доказательство. Каждой линейной комбинации
п
I (и) = 2 ск§ (хк, и), хк е= Я?, (5)
к — \
поставим в соответствие случайный вектор т), г| = г^> (/)
с помощью соотношения (4). Через 2?0{§} обозначим
множество функций (5). Определим в 3?ц{ц} скалярное
произведение с помощью соотношения
(1и Т2)=\ШШп1о№- (6)
Соответствие 'П=='Ф(/) является изометрическим
отображением 3^о{§} на 5?о{с}. Следовательно, оно может быть
продолжено до изометрического отображения 3?2{ё)
на 3?2{ЪЪ Если В<е=%, то %в (х) <е= 3?2 {т0} = 3?2 {§} в силу
полноты семейства функций {§(х, и), х^Щ. Положим
^(Л) = ,ф(Хл). Тогда 2; (Л) является векторной
стохастической мерой и ее структурная функция совпадает с пи
Щ (Ах) Г (Л>) = | %А1 (х) %Ш т (г1х) = т (А{ Л Л2).
Определим теперь случайную функцию |(х) с помошыо
стохастического интеграла
!(*) = $ е(*> и)Ши\
Так как
Щ(х)?(А)= $ в(х, и)%А(и)т(с1и),
то из изометричности соответствия т] = 'ф(/!) следует
равенство
М^(х) Г(х)= $ §(х> и) §(х, и)т(йи).
Отсюда получаем
м||м-1(*)Г-
= МЕ* (х) I (х) - МГ (х) | (х) - МГ (х) I (х) + Щ* (х) I (х) = О,
что и доказывает теорему*
§3
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
295
Приведем ряд примеров на применение доказанной
теоремы. Ради краткости условимся до конца настоящего
параграфа писать «стационарный процесс» вместо
«стационарный в широком смысле».
В силу теоремы 2 § 2 гл. IV корреляционная
матрица стационарного и с. к. непрерывного процесса может
быть представлена в виде
оо
Я (*„ *2) = Я & - к) = | *'" <'>-« Р (Ли), (7)
— сю
где Р(*) — неотрицательно определенная матричная мера
(спектральная матрица процесса). Выражение (7) является
частным случаем (2), в котором функции @(х, и)
соответствуют еш, х*~>/, причем совокупность функций
[еш^ —оо<«<оо} является полной в 3?2{т^, где
т0—'любая ограниченная мера на прямой. Таким
образом, применима теорема 1, и мы получаем следующий
результат.
Теорема 2. Векторный стационарный с. к.
непрерывный случайный процесс | (I) (— оо < I < оо), М'§ (() = О,
допускает представление
оо
Ш = _[е"« С (<*"), (8)
— оо
где ^ (А) — векторная ортогональная стохастическая мера
на 93, подчиненная %(1). Между 2>2{1) и 2?2{Ро}> где
^о(') = 5р/7(«), существует изометрическое соответствие,
при котором
а) &(*)«-**"«, СИ)^Ха(м);
б) если г\1*->(11{и) (/= 1, 2), го
и
М^т)*^ | 8{(и)ё2(и)Р(с1и).
Формула 8 носит название спектрального
разложения стационарного процесса, & мера ?(Л) — стохасти-
296 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
ческой спектральной меры процесса. Из теоремы 2
следует, что
МС(А)Св(^)= / Р(йи)^Р(А1{\А2), (9)
АХ$]А2
т, е. Р(-) является структурной функцией векторной
стохастической меры ?;(•)•
Замечание 1. Для любого т] е 2?2 Ш имеем Мт] = 0.
В частности, для любого Лей будет М^(Л) = 0.
Замечание 2. Если М|(*) = 0=^=0, то
предыдущую теорему можно применить к процессу |(/) —а.
С другой стороны, представление (8) можно сохранить
и в общем случае, если к 2; (Л) добавить меру,
сосредоточенную в точке и = 0, по величине равную а.
В качестве примера применения теоремы 2 выведем
формулу Котельникова — Шеннона для одномерного
случайного процесса, спектральная мера которого
сосредоточена на конечном интервале [ — В, В]. Разложим
функцию еш на интервале [— б, В] в ряд Фурье. Имеем
00 ЯП
ш V 8'п(В/-яд) * -д-«
Ряд в правой части последней формулы сходится
равномерно по и во всяком отрезке [—В', В'], В'<В, и
имеет ограниченные частные суммы, а потому сходится
и в 2,2{т0}, В силу изоморфизма пространств 3?2{щ]
и ^ Ш имеем (в смысле с. к. сходимости)
оо
*м- 1 в/-™ Ц-в-)' (10)
Таким образом, значение случайной функции |(/) в
любой момент времени / однозначно восстанавливается
по ее значениям в равноотстоящие моменты времени
пп/В, п = 0, ±1, ±2, ...
Для стационарных векторных последовательностей
1пу я — О, ±1, ±2, ..., можно сформулировать теорему,
полностью аналогичную теореме 2. Отличие состоит
в том, что спектральная мера последовательности
сосредоточена на полуинтервале [ — я, я)> а не на всей
§5]
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
297
вещественной прямой, как в случае процесса с
непрерывным временем (см. теорему 1 § 2).
Из теорем 1 и 2 § 2 вытекает следующее
обобщение теоремы 2 о спектральном разложении однородного
с. к. непрерывного поля.
Теорема 3. Векторное однородное с. /с.
непрерывное поле I (х)7 х е 91ту может быть представлено в виде
I (х) = а + ^ е1 <*• «>I{йи\ а^Щ(д),
где 5 — векторная ортогональная мера на 23™,
подчиненная полю I (х). Между 2?2 {|} и 9?2 {Р0}9 Р0 (•) = 5 р Е (•)
существует изометрическое соответствие, при котором
а) ^(л;)«->е< <*.«);
б) если щ <-> дг (и), % е 3?2 Ш, §( (и) е= 22 {?оЪ * = 1 > 2,
го
Мл,1Ь= | ё\{и)ё2{и)Р{(1и)>
Следствие. /:сли однородное поле Цх) (М^ (л*) = 0)
(скалярное) имеет ограниченный спектр, г. в,
го эго яоле однозначно определяется по своим значениям
в точках решетки < хп = I-^-, ~^~-, ..., -^—I, л = О,
± 1, ±2, ... > по формуле
т и и
-., ,__ VI ТТ 81П {ВкХГ - ППк) ^ /ПП1 ЯП2 Т1Пт\
л=(л!, .... пт) л==1
(И)
в которой суммирование производится по всевозможным
целочисленным векторам п и ряд в правой части
формулы при каждом х сходится в среднем квадратическом.
298 'ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Рассмотрим еще спектральное разложение с. к.
непрерывного изотропного двумерного случайного поля.
На* основании формулы (10) § 2 корреляционная
функция поля имеет вид
оо
Я(хи *2) = Я(р)= | /0(ир)2(</и), (12)
о
где х{ и х2 — точки плоскости, р —расстояние между
ними. Если (г{, 6;) — полярные координаты точки х{{г = 1,2),
то
р = ^ + г2-2г1г2со5(е1-е2).
Используя формулу сложения для функции /0,
со
/о("Р)= 2 /к(^1)/*(ш-2)е'*(в'-Ч.
перепишем формулу (12) в виде
со со
/г (р) = / | /V («г.) ^еЛ ("/-2) е'^г (<*«) е (л),
0 -оо
где 8(Л) —мера, сосредоточенная в точках к = 0, ± 1,
±2, ..., причем е({6})=1. В силу теоремы 1-плоское
изотропное однородное и с. /г. непрерывное поле %{х),
х = ге1в, (М1(х)==0) допускает представление вида
со оо
|(*)= 2 е^\1к(иг)1к{йи), (13)
&=-со 0
где ^ — последовательность ортогональных между
собой стохастических мер на прямой [0, оо).
§ 6. Линейные преобразования
Представим себе некоторую систему 2 (прибор или
устройство), предназначенную для преобразования
сигналов (функций) х(1), зависящих от времени /.
Функция, которая должна быть преобразована, называется
функцией на входе системы, преобразованная
функция — функцией на выходе или реакцией на входную
функцию. Математически всякая система задается клас-
§<я
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
299
сом Б «допустимых» функций на входе и
соотношением вида
г(1) = Т(х\1),
где *==*($) (— оо <5< оо) — функция на входе, х(з)<^0,
а г(1) — значение функции на выходе в момент
времени I.
Система 2 называется линейной, если: а) класс
допустимых функций Л линеен, б) оператор Т
удовлетворяет принципу суперпозиции
Т (ах{ + $х2 Ю = аТ (хх \{) + $Т (х21*)•
Введем операцию сдвига времени 5Т (— оо<т<оо)
с помощью соотношения
хх (/) = 5Т (х | 0 = х {I + т).
Она определена на множестве всех функций
переменной I (— оо</<оо) и линейна. Система 2
называется однородной во времени (или просто однородной),
если класс допустимых функций О инвариантен
относительно операции: сдвига 5Т, 5ТЙ=Л и
Т(хх\1) = Т(х\1 + %) или Т(Зхх\1) = 8хТ (х |/),
т. е. если преобразование Т перестановочно с
операцией сдвига времени 5Т (~оо<т<оо).
Простейшим примером линейного преобразования
может служить преобразование вида
оо
2(0= / Н({,з)х(з)аз, (1)
— оо
для которого класс допустимых функций О зависит от
свойств функции Л (/,$). Пусть на вход системы
поступает функция 6Х_5, где б* —функция Дирака. Тогда
г{1) — к{1, $) при />$ и г(0 = 0 при /<я. Таким
образом, функцию Н{1У 8) 'следует интерпретировать как
реакцию системы на б-функцию в момент времени 5.
В соответствии с этим Н((, з) называется импульсной
переходной функцией системы. Если система 2 однородна
во времени, то формально
А0, а - с) = Т{Ьа„с Ю « Т(8сЬа \{) = 8сТ(6а \1) = А (< + с, а),
300 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
или, заменив а на с и I на 1-е,
Щ-с,0) = кЦ,с).
Функция А (<) = Н (/ + с, с) называется импульсной
переходной функцией однородной системы.
Таким образом, для однородной системы
уравнение (1) принимает вид
оо
2(0= § Н{(-8)Х(8)(13. (2)
— оо
Операция в правой части соотношения (2) называется
сверткой функций Н{1) и х{1).
Если функция на входе системы отличается от
функции на выходе только скалярным множителем
(преобразование Т не меняет формы сигнала)
Т{1\1) = Х1{1) (-оо</<оо),
то /(/) называется собственной функцией, а X —
собственным значением преобразования Г. Для однородных во
времени систем с интегрируемой импульсной
переходной функцией функции е1Ш (и — любое действительное
число) являются собственными. Действительно, все
ограниченные измеримые функции являются допустимыми и
оо оо
| Н {I - $) еш'а$ = | Н (5) еш <*-°Ы$ = Н (ш) еш\
— оо —оо
где
оо
Н(ш)= $ к(з)е-1$иаз (3)
— оо
— преобразование Фурье импульсной переходной
функции, является собственным значением преобразования..
Таким образом, отношение реакции системы на
простую гармоническую функцию еш к этой функции,
Н (ш) = — . / •
к ' еш1
не зависит от времени. Функция Н (ш) называется
частотной характеристикой системы или коэффициентом
передачи.
§61
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
301
Можно несколько иначе интерпретировать частотную
характеристику системы (2), рассматривая иной класс
допустимых функций. Пусть х{1) интегрируема. В силу
теоремы Фубини
оо оо оо
||г(01^< | \\Н{1-8)\\х{з)\й8й1 =
— оо — оо —оо
оо оо
= \\х{з)\йз ^\Н{1)\йК<х>,
— оо —оо
т. е. функция х{1) также интегрируема. Рассмотрим
преобразование Фурье функции г (/). Применяя теорему
Фубини, получим
оо
2(н)= | еНиг{1)(И =
— оо
оо оо
= || е-'» <'-5>/г {{- з) е~шх (з) аз А1 = Н (ш) х (и),
—-оо —оо
оо
*(«) = | е~1и8х(8)(18.
— оо
Следовательно, отношение преобразования Фурье
функции на выходе к преобразованию Фурье функции
на входе не зависит от функции на входе системы
и равно ее частотной характеристике
г (и)
#(ш) =
х(и) '
В формуле (1) реакция системы в момент времени I
зависит от значений функции на входе как в моменты
времени з<(, так и в моменты времени $>^. В
физических устройствах, однако, нет возможности
предвосхитить будущее. Поэтому для них
Н (*,$)=» 0 при К 5. (4)
Соотношение (4) называется условием физической
осуществимости системы. Для систем, удовлетворяющих
302 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
условию (4), формула (1) принимает вид
2(/)= |Л(/, 8)х{8)й8, (5)
а если система однородна, то
^ оо
2(/)= |й(*-5)х(в)</« = | к(8)х(1-8)й8. (6)
~оо О
Если на вход системы подается функция, начиная с
момента времени 0 (х(5) = 0 при $<0), то
г(/)= | к (1-8)х(8) из. (7)
о
Изучая такие системы, вместо преобразования Фурье
удобно пользоваться преобразованием Лапласа
оо
5(р)= | е-Р*гЦ)йи (8)
о
Из формулы (7) следует, что
оо
г(р) = Н(р)х(р), х(р)= $ е-'*х(()(И (9)
О
при Ке/?:>а, если функции е~а*к(1) и е~а*х{{)
абсолютно интегрируемы.
Перейдем к основной теме настоящего параграфа —
к линейным преобразованиям случайных процессов.
В основном рассматриваются однородные во времени
преобразования стационарных процессов. По поводу
более общего случая мы ограничимся, простыми
замечаниями.
Пусть %(() есть измеримый гильбертов процесс
($* оо < / < оо) с ковариацией В (^, $), причем В{1, /)
интегрируема по I в каждом конечном интервале,
так же как и функция |й"(/, 5) [2 при фиксированном ^.
|.61
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
303
Тогда с вероятностью 1 существует при любых а и Ь
интеграл
ь
Ш= /ас, «)1(5) аз.
а
Определим несобственный интеграл от — оо до оо как
с. к. предел интегралов по конечным промежуткам
интегрирования:
оо Ь
Г к (I, 8) \ ($) йв = 1л.т. Г к {I, в) I («) й&.
^ д-> —оо ^
-°° &->+оо О.
Для существования этого предела необходимо и
достаточно, чтобы интеграл
оо оо
| | к (*, зх) В ($ь 82) к {I, з2) Лз{ йз2
— оо —оо
существовал как несобственный интеграл Коши на
плоскости. Если он существует для /еГ, то ?;(*) является
гильбертовым случайным процессом на Г с ковариацией
я&(*1,/о)= / | л у1,8{)в(з1,з2)ТЩ^)а81а$2. (Ю)
— оо — оо
Предположим теперь, что |(0 — стационарный
процесс в широком смысле со спектральной мерой Р(йи)
и М|(0 = 0. Это предположение будет сохранено до
конца настоящего параграфа. Интеграл
оо
Л(0= \к{1-5)1{8)й8 (11)
—-оо
существует (в ранее определенном смысле) тогда и
только тогда, когда существует интеграл
оо оо
| ]" Й (* - $1) /? (51 - 52) к {I - 52) ^1 <*52 =
— оо —оо
оо оо
« | | А (5^ # (52 - 50 А (52) йз{ й$ъ
— оо — оо
804 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV»
где /?(0~ корреляционная.функция процесса. Для этого,
в свою очередь, достаточно, чтобы функция Н{1) была
абсолютно интегрируемой на (— оо, оо). В этом случае,
воспользовавшись спектральным представлением
корреляционной функции /?(<), получим следующее
выражение для корреляционной функции Я^\, ^) процесса г)(/):
ОО ОО
Ят) ^\ >*2)= \ / Л (/, - «!> /? (51 - 82) к {12 - $2) (1зх й$2 =
— ОО —'ОО
оо оо оо
= \ \ Iн & ~8^еГи {*'~*г)н ^ ~5г) а^й$2 Р ^м)=
— оо —оо —оо
оо
= \е1«--« • | Н (ш) |2 /? (<*и) = Лч (/, - /г).
— оо
Таким образом, процесс х\{1) также является
стационарным в широком смысле.
Определение 1. Для процесса |(/) преобразование Т
называется допустимым фильтром (или, проще,
фильтром), если оно задается формулой {11), где Л(/) —
абсолютно интегрируемая функция на ( — оо, оо) и
интегрируема в квадрате на любом конечном интервале, или
является с. к. пределом последовательности таких
преобразований (в ^гШ)-
Условие сходимости последовательности
преобразований (11) г\п^)==Тп(1\1) с импульсными переходными
функциями Нп{1) и частотными характеристиками Нп(1и)
состоит в следующем:
оо
МI л» (/) - цт (*) р = \\Нп (ш) - Нт (ш) р Р {йи) - 0 (12)
— оо
при п, т-~> оо.
Это означает, что последовательность Нп(ш)
фундаментальна в 2?2{Р}. Но тогда существует предел Н(ш) =
= \Л.т.Нп(ш) (в 2?2{Р}), который называется частотной
характеристикой предельного фильтра, и если г}(/) =
= 1л.т.ть(/), то
оо
Д„(0- \е11»\Н{1и)\*Р{йи). (13)
§ 6] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 305
Обратно, какова бы ни была функция Я (ш) е 3!2{Р},
ее можно аппроксимировать в смысле сходимости в 3?2{Р}
функциями, являющимися преобразованиями Фурье
абсолютно интегрируемых функций. Таким образом,
фильтры удобно задавать частотными характеристиками.
Теорема 1. Для того чтобы функция Н (ш) была
частотной характеристикой допустимого фильтра для
процесса ^(/) со спектральной мерой Р, необходимо и
достаточно, чтобы Н(ш)^3?2{Р}- Корреляционная
функция процесса на выходе фильтра с частотной
характеристикой Н (ш) дается формулой (13).
Если вспомнить энергетическую интерпретацию
спектральной функции, то из формулы (13) следует, что
|#(ш)|2 показывает, во сколько раз увеличивается
энергия простых гармонических составляющих процесса
с частотами в интервале {и, и + йи) при прохождении
через фильтр.
Теорема 2. Если процесс \ (/) на входе фильтра
с частотной характеристикой Н (ш) имеет спектральное
представление
оо
!(/)= \е'"%(<1и), (14)
— со
то процесс ц{1) на выходе фильтра имеет вид
оо
г,(0= \ешН{ш)Ъ(йи). (15)
— оо
Действительно, если фильтр имеет абсолютно
интегрируемую импульсную переходную функцию, то
оо сю
т)(0= | Н {1-8) 1(5)^5= \ешН{ш)1{йи).
— оо —оо
Доказательство в общем случае получается с
помощью предельного перехода по последовательностям
Нп(1и), сходящимся к Н(ш) в 3?2{Р}.
Пусть т)й(/) — процесс на выходе фильтра с
частотной характеристикой #&(ш), Мт]6(/) = 0 (&= 1, 2). Найдем
взаимную корреляционную функцию процессов г]} (/) и
306 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. Г^
г|2(^). Из изоморфизма пространств 3?2{& и 3?2{Р}
непосредственно следует, что
оо
/?12(<) = Л1т]1(^ + 5)т1^)= ^ешНх(1и)ЩЩ Р(йи). (16)
— ОО
Приведем несколько примеров фильтров и их
частотных характеристик.
1. Полосовой фильтр пропускает (не изменяя их)
только гармонические составляющие процесса с
частотами в заданном интервале (а, Ъ), Частотная
характеристика фильтра равна #(ш) = х<а, *) (ц)> и фильтр
является допустимым для произвольного процесса.
Импульсная переходная функция находится по формуле
Фурье
ь
Ни
к (0 = ^-1 е"*йи
2л 1 2щ7
а
2. Фильтр высоких частот подавляет низкие частоты
не изменяя высоких. Его частотная характеристика
Н(ш) = Х{|и|>а}(^)> а импульсная переходная функция
не существует.
3. Рассмотрим операцию с. к. дифференцирования
стационарного в широком смысле процесса. Для
существования с. к. производной процесса ^(1) достаточно
существование /?"(0) (§ 3, следствие 1). Это условие
эквивалентно требованию (теорема 4 § 1 гл. I)
сю
|и2У?(</и)<оо. (17)
— оо
С другой стороны, если это условие выполнено, то при
и в соотношении
§6]
ЛИНЕЙЙЫЕ ПРЁ0БРА30ВАНШ
307
можно перейти к пределу при Н~>0 под знаком
стохастического интеграла. Следовательно,
оо
1'{1)= 1еНашШи). (18)
■—оо
Таким образом, операции дифференцирования
соответствует фильтр с частотной характеристикой ш, который
является допустимым для всех стационарных
процессов, удовлетворяющих условию (17). Импульсная
переходная функция.не существует, но фильтр можно
рассматривать как предельный (е~->0) для фильтров с
импульсными переходными функциями Не(0 = 0 при \^ \^г
и ^е(0— — §^" при |/К е, которым соответствуют ча-
Л • 9 11г
4 51ГГ ——
стотные характеристики -
4. Операция сдвига времени. Так как
!(/ + «)= \ еше!11%{йи),
то операции сдвига времени Г5, Т8(11/) = Т {I + 5),
соответствует частотная характеристика Н (ш) = е1аз.
Импульсная переходная функция не существует.
5. Дифференциальные уравнения. Рассмотрим
фильтр, определяемый линейным дифференциальным
уравнением с постоянными коэффициентами
Ьц = М1, (19)
где
Уравнение (19) имеет смысл только тогда, когда
процесс |(0 т раз с. к. дифференцируем. Тогда мы ищем
п раз с. к, дифференцируемый стационарный процесс т)(*)',
удовлетворяющий (19). Предположим, что (19) имеет
308 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
стационарное решение. Его можно представить в виде
оо
г,(0= \ешН(ш)Ши).
— оо
Применяя к процессам \{1) и х\(1) операции М и Ь
(соответственно), получим
оо оо
| еш1 (ш) Я (/«) % {йи) = § ешМ (ш) $ (йы),
где /. (ш) = 2 ак (ш)" \ М (ш) = 2 Ьк (ш)т *, откуда,
если /,(ш) не имеет вещественных корней,
Обратно, если процесс |(/) т раз с. к. дифференцируем,
М (ш) е «^2 {^}> ^ (*«) ^=° (—оо<ц<сх)), то процесс
л(0 = /
п раз с. к. дифференцируем и удовлетворяет
уравнению (19). Таким образом, при условии М (ш) е З^{^},
Ь(ш)ф0, существует единственный фильтр,
соответствующий дифференциальному уравнению (19).
Заметим, однако, что можно определить решение
уравнения (19) и в более общих случаях. Допустим, что
многочлен Ь(ш) не имеет вещественных корней. Фильтр
с частотной характеристикой М(ш)/Ь(ш) существует и
без требования М(ш)^ 3?{Р}> достаточно требовать
только, чтобы . ,. * ^ ^2{^}- Последнее выполняется
всегда, когда степень п многочлена Ь не меньше га.
Таким образом, при п^т фильтр с частотной
характеристикой (20), знаменатель которого не обращается
в нуль при действительных и, является допустимым для
произвольного процесса на входе, и процесс на выходе
фильтра мы отождествляем со стационарным решением
уравнения (19). Ограничиваясь по-прежнему
дифференциальными уравнениями, для которых многочлен Ь (х)
*6!
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
309
не имеет чисто мнимых корней, выделим из дробно-
рациональной функции М(х)/Ь(х) целую часть Р(х)(она
отлична от нуля, если т^п) и остаток разложим на
простые дроби. Тогда
п I. п и
к / к гг
1 ('«> Д ЛП (1В - "*) й Их (|И - "*)
т-п
где Р (/а) = 2 а* (ш)* (т > /г) и Р (т) = 0 (т < /г),
Ке/^<0 и Кер^>0, р'к и р^ являются корнями
многочлена Ь (х) = 0. Так как
оо оо
г15~х С Г *8~1
^ о о
*• ** I - «# 111+11 I *■ «^ ;.,* 11
(ш-р)3 (5-1)! йр*"1 Л ^ (*-0
(Кер<0)
1
(/« - рУ
то процесс г}(/) на выходе фильтра можно представить
в виде
л(/) =
т—п оо оо
-Еа**(*)Ю+1&('-Т)С1 (Т)<*Т+ /&(' + *) <?2(-т)</т,
/г=0 О О
где
6 = 1 \5=1
* „" ^
ад-ИИйг" ««»•
(5-1)!
/г=1 \5==1
Заметим, что если многочлен Ь(х) имеет корни с
положительной действительной частью, то соответствующий
фильтр физически не осуществим-*
310 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV.
§ 7. Физически осуществимые фильтры
В настоящем параграфе рассматривается следующий
вопрос: какие спектральные функции могут быть
получены на выходе физически осуществимого фильтра. При
этом на входе фильтра рассматривается в некотором
смысле простейший случайный процесс.
Процессы, рассматриваемые в настоящем параграфе,
неизменно предполагаются одномерными и
стационарными в широком смысле. Поэтому слово
«стационарный» иногда, а слова «в широком смысле» постоянно
будут опускаться.
Начнем с рассмотрения стационарных
последовательностей. Мы не будем переносить на
последовательности всех определений и эвристических соображений,
приведенных для процессов с непрерывным временем,
хотя будем пользоваться соответствующей
терминологией. Представим себе систему, у которой состояние
на входе и выходе регистрируется только в
целочисленные моменты времени ^ = 0, ±1, ±2, ...
Пусть на вход системы в момент времени 0
поступил единичный импульс. Реакцию системы на этот
импульс в момент времени I обозначим через аи Если
система не предвосхищает будущего, то 0^ = 0 при ^<0.
Если система однородна во времени, то реакция
системы на единичный импульс, приложенный к системе
в момент времени 5, равна а^3. Реакция линейной,
однородной и физически осуществимой системы в
момент времени I на последовательность импульсов ^(/г)
(—оо</г<оо) будет
I оо
4(0= 2 а,_я| (п) = 2 ап& (*-«), (1)
т. е. является процессом скользящего суммирования.
Предположим, что \{п) — стандартная
некоррелированная последовательность
МБ (л)-0, МЪ(п)1(т) = дпт
(— оо </г, т< оо).
Она имеет постоянную спектральную плотность.
§7] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 311
Чтобы ряд (1) с. к. сходился, необходимо и
достаточно, чтобы
5|аяР<°о. (2)
Если это условие выполнено, то процесс т](/) также
стационарен в широком смысле и
оо
Мл (0 = 0, ЯЛ1)=Цап+1ап. (3)
7
Какие же последовательности могут быть таким
образом получены?
Лемма 1. Для того чтобы стационарная
последовательность ц(п) была реакцией физически осуществимого
фильтра на некоррелированную последовательность,
необходимо и достаточно, чтобы последовательность ц(п)
имела абсолютно непрерывную спектральную меру и ее
спектральная плотность ((и) допускала представление
оо оо
/(«)Нг(е'")р, г(«*) = 2>Д 21М2<оо. (4)
/2 = 0 Ц = 0
Доказательство. Необходимость. Пусть
последовательность представима в виде (1), Положим
оо
в^-ткХ5»6"1"- (5)
Тогда по формуле Парсеваля
оо Л
ад-^Х+Д,- 1еии\ё(е1а)\Чи,
П = 0 ~Л
т.. е. последовательность ц(п) имеет абсолютно
непрерывный спектр с плотностью /(и) = | §(еш) |2.
Достаточность. Пусть г|(п) — последовательность
с корреляционной функцией
л
-Я
312 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
и /(и) = 1 §{еш) |2, где §(еш) определяется
соотношениями (4). Последовательность т](п) имеет спектральное
представление
я
-Л
На сг-алгебре борелевских множеств отрезка [—я, п)
построим стохастическую меру
я
|(Л)= ( 1 %А(и)Ши).
Тогда
Щ{А)йВ)= \%АШв{и) 1м,2/(»)^» = т- СЛ'>
-Ь 2я [ # (е*и) |2 2я Л(^в
т. е. |(Л) является ортогональной мерой со
структурной функцией 1{А{]В)У где / — мера Лебега. Используя
леммы 2 и 1 § 4, получим
я я
Ч(«)= |еП(<*") = |е",1,Уг2^(е")|(Л0 =
— Л - -Я
оо Я оо
= V у%1 5к \ е' (»-« «| (<*«) = ^ а„| (* - я),
&=0 -я я = 0
Я
где йп=1/2^бП1 |(я) = \еШпЪ{йи) и М^(п)|7^) =
-Я
Я
~ Т~ е1{п~т)ийи*=Ьпт. Таким образом, |(/г) является
-я
стандартной некоррелированной последовательностью;
Доказанная лемма дает простой ответ на
поставленный вопрос. Но этот ответ в общем случае
недостаточно эффективен, так как остается неясным, когда
спектральная плотность может быть представлена
формулой (4).
Найдем условия, при которых 1(и) допускает
представление (4). Обозначим через Я2 множество всех
§71
ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ
313
функций /(г), аналитических в круге 0 = {г: | г |< 1} и
таких, что
л
||/(г)|р = 1нп [|/(ге'е)Р^9<оо.
ОО СХ)
Если / (г) = Ц алгя, то / (ге*'е) - 2 апгпе(пВ, т. е. а„г*
П=0 л=0
являются коэффициентами Фурье функции 1(гею). В силу
равенства Парсеваля
Я оо
-Я Л = 0
Отсюда видно, что !(г)^ Н2 тогда и только тогда, когда
2КР<оо.
Следовательно, для каждой функции [(г)^Н2 можно
оо
определить ряд !(ею)= ^ апе(п07 сходящийся в 9?2{1)>
«-о
где / — лебегова мера на [ — я, я). Функция /(г) (| г |< 1)
восстанавливается через функцию 1(ет) по формуле
Пуассона
я
/(">">) = ^- //(е»)Р(г, 8, и) Ли, (6)
-Я
где
оо
Р(г> 9, ц)« . 0 1Т/2 ^ о - У г1п|е/Л(е-и)#
х ' ' ' 1 — 2г соз (8 — и) + г2 АЛ
П~—оо
Доказательство этого утверждения непосредственно
вытекает из равенства Парсеваля.
В теории функций доказывается (см. Привалов [46]),
что если в формуле (6) функция I (е(д) интегрируема по
Лебегу, то почти для всех 8 существует
Пт1(ге**) = !{е%
Функцию !(ет) называют граничным значением
функции Цг) (|г|<1).
314 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ГГЛ. IV
Теорема 1. Пусть I (и) — неотрицательная и
интегрируемая по Лебегу функция на [ — я, я). Для того
чтобы существовала функция § {г) е Н2 такая, что
Пи) = \е(еш)?, (7)
необходимо и достаточно, чтобы
я
||1п/(и)|^и<оо. (8)
~Л
Доказательство. Необходимость. Пусть
оо
§" (г) = 2 апгП е Н2 и (7) имеет место. Можно считать,
что ё"(0)=И=0 в противном случае вместо $ (г) можно
рассмотреть г~тё(г), где т — кратность нуля 2 = 0
функции § (г) и положить §•(())= 1. Пусть 0<г<1 и
А = {и: \е(г4*)\<1}, В={и: \ §(геш) \> I}. Тогда
я
\\\п\д(геш)\\аи= | 1п | д (геш) \йи -
-л В
я
- | 1п | § (геш) | йи - 2 | 1п | $ {ге,а) \йи- \\п\д (геш) | йи.
А В -л
Из формулы Иенсена вытекает, что
я п
~Ш /1п|/(ге<-»)№ = 1пП7^>0,
-л 6 = 1 ' й|
где 2& — нули функции }{г) внутри круга |г|<г.
Следовательно,
/| 1п\е (геш) I \йи<2 11п| г (ге1'11) |<*« < 11 я (геш) |2 <*«
-л В В
Я оо
«=о
$7] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 315
Применяя лемму Фату» получим
я я
]"| 1п\§(еш)\\с(и= |_Пт11п |§ (геш)11йи<
-Я -Я г*!
Я оо
<Ит /|1п|<д(ге,и)||й?ы<2я5] |а„|2,
Г>М -я «=0
что и доказывает необходимость условия (8).
Достаточность. Пусть условие (8) выполнено.
Функция
я
и(г, в)=2^ §1п[(и)Р(г, 9, и)йи
— Я
является гармонической в круге 0 = {г: \ г |< 1}.
Заметим, что из неравенства Иенсена следует
^в)<1п -~- $!(и)Р{г9Ъ,и)(1и\.
Обозначим через ф (-г) аналитическую функцию в й
с действительной частью и (гу 8). Положим
Тогда
| е {геш) |2 - е^ ф (г) = ^ (г, е) ^ „1_ ^ до р ^ ^ ^ ^
-я
И
я я
||я(ге'в)р^9< ||/(и)|йа<оо.
— Я —Я
Нт « (г, 0)
Таким образом, §(г)& Н2 и Пт| §{гет) \2 = ег+{ =/(Э)
почти всюду. Теорема доказана.
Замечание 1. Как вытекает из доказательства
теоремы, функция §(г) может быть выбрана так, чтобы
при г = О она была положительной и не имела нулей в О.
Замечание 2. Функция § (г), существование
которой установлено теоремой 1, определяется не единст-
316 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ Ц\71. IV
венным образом. Но если §(г) удовлетворяет условиям
а) &(г)ФЬ, ^О, б) #(0)>0,
то она единственна и, следовательно, совпадает с
найденной нами.
Действительно, если §{{г) (/=1, 2) —две такие
функции, то -ф (г) = ё1 )2[ аналитична в Л, не обращается
в нуль и на границе В по модулю равна единице.
Функция 1п,ф(2) является аналитической в В и на
границе О ее действительная часть равна нулю.
Следовательно, \п^(г) = Иг) где к вещественно. Так как 1пф(0)
вещественно, то 1пф(г) = 0.
Сопоставляя лемму 1 и теорему 1, получим
следующее утверждение.
Теорема 2. Для того чтобы последовательность ц(/)
могла быть представлена в виде
оо оо
Л (0 =2 ял! С-л). 2 \ап\2<оо,
где | (п) — некоррелированная последовательность,
необходимо и достаточно, чтобы г\{1) имела абсолютно
непрерывную спектральную меру, а ее спектральная
плотность 1(и) удовлетворяла требованию
л
§ 1п}{и)> -оо.
-я
Пусть ^\(х), 2;2(*)> х<^к$в — две гильбертовы случайные
функции. Через ^ЙЛ обозначим замкнутую линейную
оболочку системы случайных величин {^(х), хе^}в 9?2и
Определение 1. Если^^О ^ 3?2 (?г)> то случайная
функция &{(х) называется подчиненной ^ОО- Если же
З^КО —-2?2(&г)» то ^х(х) и ^2(х) называются
эквивалентными.
Замечание 1. Как вытекает из доказательства
леммы 1, последовательности |(/г) и ц(п) эквивалентны.
Покажем, как можно выразить коэффициенты ап
в операции скользящего суммирования через
спектральную плотность }{и) последовательности т)(/)..
Ц] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 317
Введенная при доказательстве теоремы 1 функция у (г)
является аналитической функцией в I), действительная
часть которой имеет граничные значения 1п/(и).
Следовательно,
я
Ф(2)-^г \\пт^^аи. (9)
— Я
Разлагая функцию §(г) = ехр <-^ Ф (г)> в степенной ряд
сю
ё(г) ^ 2 ^«г", получим следующие значения для коэф-
«=0
фициентов ап
ап = У2пВп.
С другой стороны, выражение для #(г) можно
преобразовать следующим образом. Так как
сю
еш + г , , 2ге-*" , , «V -.* — /*„
#"(2) = ехр -~- ] 1п / 00 Ж/+-^т 2 4^ 1.
V -Я &=1 '
Я
4= |е'**1п/(и)</и.
-Я
Полагая
я
Я (г) = Р 2 с*г"
получим
оо
'к?
Таким образом,
ап=У2лРсп. (10)
Перейдем к процессам с непрерывным временем.
Обобщением операции скользящего суммирования на
818 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ (ГЛ. Т7
случайные процессы с непрерывным временем может
служить операция, ставящая в соответствие случайному
процессу 1^) процесс т)(*), *<=( — оо, оо) по формуле
ОО
Ч(0=/а(8)^(/-5). (11)
О
Будем называть процесс с ортогональными
приращениями 1(1) стандартным, если
МШ = 0, М|Б(* + А)-Б(0Р = й.
В соответствии с тем, что было сказано в § 4 о
стохастическом интеграле Стильтьеса процессу \ {I)
соответствует некоторая стохастическая ортогональная мера %(А)
ра а-алгебре множеств, измеримых по Лебегу. Эту меру
также будем называть стандартной стохастической
мерой. Для существования интеграла (11) необходимо и
достаточно, чтобы а {I) была измерима по Лебегу и
со
| \а{1)\2й1<оо.
о
Заметим, что стандартный процесс Ц() не с. к.
дифференцируем. Однако отношения
при всех 1к и сколь угодно малых А ортогональны.
Таким образом, фиктивную производную \' (/) следом
вало бы рассматривать как процесс, значения которого
в любые два момента времени ортогональны, а их
дисперсия бесконечна. Этот фиктивный процесс часто
вводят в рассуждения и называют белым шумом.
Точное определение белого шума дается в рамках теории
обобщенных случайных процессов (Гельфанд и Вилен-
кин [10]). Символически формулу (11) можно записать
в виде
г
г,(0= $аЦ-8)1'{8)48,
— оо
и интерпретировать г|(/) как реакцию физически
осуществимого фильтра на белый шум» Импульсная переходная
§7] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 319
функция этого фильтра равна нулю при /<0 и а(1)
при ^>0. Отметим, что все допустимые для процесса ^'(0
физически осуществимые фильтры исчерпываются
формулой (11). Действительно, всякий допустимый
физически осуществимый фильтр по определению или имеет
вид (11), или является предельным для фильтров такого
вида. Условие с. к. сходимости фильтров вида (11)
с импульсными переходными функциями ап{1) состоит
в следующем:
оо
\ I ап (з) — ап, (з) |2 из -> 0, при п, п! -> оо.
о
Но если это условие выполнено, то существует.
1Л.т. а^) = аУ) (относительно лебеговой меры на (0, оо)) и
оо оо
1л.т. % (0 = 1.1.т. Г а„ ($) ^ (/~-$) = I" а ($)*/|(/ — $).
о о
Таким образом, предельный переход в фильтрах вида (11)
не расширяет класса фильтров.
Формулу (11) можно переписать следующим образом:
оо
т)(0= | а(*-5)4(5), а(/)=-0 при *<0.
— оо
Следовательно, корреляционная функция процесса т](/)
равна
Я (0 = I а {I + 5 — и) а (з — и) йи
— оо
или
оо
#(0=/ а({ + з)а^)а8. (12)
о
Лемма 2. Для того чтобы стационарный (в широком
смысле) процесс т)(/) являлся реакцией физически
осуществимого фильтра на подчиненный процессу белый
шум, необходимо и достаточно, чтобы процесс т](/)
обладал абсолютно непрерывной спектральной мерой и
320 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
его спектральная плотность / (и) допускала представление
Пи) = \к(1и)?9 (13)
где
оо оо
А (ш) - | 6 (5) <г''и* Л, | | 6 (5) |2 Л < оо. (14)
о о
Доказательство. Необходимость. Пусть
процесс у\(() допускает представление (11). Положим
со
Н{ш)*=-уг=г а(8)е~18ииз. В силу равенства Парсеваля
со со
/?(0=| а(1 + 8)а(з)й8= ^ еш\к(ш)\2(1и,
0 —оо
т. е. спектр процесса абсолютно непрерывен и
спектральная плотность имеет вид (13), (14).
Достаточность. Пусть выполнены условия
леммы. Рассмотрим спектральное представление
процесса т)(^):
со
4(0= { ешШи),
— со
и стохастическую меру
оо
^>= \Ш^йи)- (15)
— со
Стохастический интеграл (15) имеет смысл для
произвольного ограниченного борелевского множества А, так
как Л. , ^ 2Б2{Р}, где Р — спектральная мера процесса,
Р(А) = \\Н{ш)\Чи.
А
Легко заметить, что \х{А) является ортогональной
мерой, причем
М |* (Л)1Г(В) =» | йи.
А{]В
§7] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 321
Положим
00
т-ш-угп\е _,; *«*• об)
— оо
Очевидно, что стохастический интеграл (16) существует.
Случайная функция интервала ^ (Л) == | (^2) — I (^1), А =
= $1» *г)> является элементарной мерой, соответствующей
стандартному процессу. Действительно, М|(А) = 0.
Далее, используя равенство Парсеваля для интегралов
Фурье, получим
сю
м,/ач7ТГТ 1 Г е~ш*-е-ш* е1ии - еш* А
V 2я *) ~ш ш
— оо
оо
- /хд,(ОХл,(ОЛ-/(А,П\).
— оо
где А1 = [*1, Ъ), А2 = [/3> ^)> / — лебегова мера на прямой.
На основании леммы 1 § 4 и формулы (15) получаем
оо
л(/)= | ешН(шЩйи). (17)
— оо
Заметим, теперь, что если
оо оо
к(ш) = ~ [ а(з)ешй8ш где § |а(я)|2^<оо,
то
[ к(ш)$(с1и)= \ а(-8)Ь(48). (18)
Действительно, так как пространства 3?2{\1} и 2}2Ц}
изоморфны пространству 3?2{1}, где / — лебегова мера
на прямой ( — оо, оо), и преобразование Фурье не
меняет скалярного произведения в 2?2{1}, то формулу (18)
достаточно проверить для простых функций. Пусть
|1 И. И. Гихман, А. В. Скороход
322 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ {ГЛ. IV
я (0 ^ 2 <^ ЭСд О» гАе А/г""" интервал (или полуинтервал)
К М- Тогда
что является частным случаем (18). Итак, формула (18)
установлена. Из (18) вытекает, что
00 СО
| ешН(ш)\х((1и)= | а («) <*| (* - в), (19)
— оо —со
так как умножение меры | на ешЬ в силу формулы (16)
приводит к сдвигу аргумента функции | на I. Из (17)
и (19) получим
ОО ОО
Ч (/) = ]* а (5) 4 (* - 5), где а (0 = -~ | Л (ги) е~шйи.
О -оо
Лемма доказана.
Пусть задана спектральная плотность ((и) процесса
т}(/). Возникают следующие вопросы. Когда спектральная
плотность допускает представление (13), (14) (или, как
говорят, факторизацию)? Как найти по функции /(«)
функцию Н(ш) (а следовательно, и функцию а(0)?
Ответы на эти теоретико-функциональные вопросы можно
получить, сведя их к уже решенным вопросам для
случая факторизации функций на окружности. Введем пре-
образование до ^-г—^отображающее круг й = {г: \ г |<1}
в правую полуплоскость Я+={ш: Кеш>0}. На границе
соответствующих областей (т = ш, г = е1д) это преобра-
зование имеет вид и = о\%-^. Пусть }(и) допускает
факторизацию (13), (14). Положим
яю-и + ^АИ-т^-Й), |
?0) = /(«)(!+и2). 1
§ 7] ФИЗИЧЕСКИЕ ОСУЩЕСТВИМЫЕ ФИЛЬТРЫ 32?
Функция /(8) допускает факторизацию I /^(©) I = \§(е(в)\*)
где д (г) аналитична в Ъ и интегрируема на (—я, я)#
Я оо
|/(9)^9 = 2 | 1(и)йи<оо}
— Я —оо
т. е. §(г)&Н2. В силу теоремы 1
-оо< /1п/(9)^9= \МШ^±^.йи,
— Я —оо
откуда
оо
— ОО
Допустим теперь обратное. Пусть 1(и) неотрицательна,
интегрируема и удовлетворяет соотношению (21). Опре*
делим /(9) с помощью (20). Тогда /(9) интегрируема й
я
|1п/'(9)^0>-оо.
— Я
Из теоремы 1 следует, что / (8) допускает факторизацию
оо оо
/>) = I § (е<в) Р, § (г) = 2 апгп, 2 I ап |2 < оо.
Положим
йН = ТТйг2а«(тТ^Г'
Тогда функция К (до) аналитична в правой полуплоскости
и /(и) = | Н(ш) |2,
оо
И (ш) = Уа„ 0"/11)!1 • (22)
, (1+/и)п+1
Учитывая, что функции —?= еш образуют полную ортсн
нормированную последовательность в 3^2{~%^ л)> не^
1 ([-ш)п
трудно увидеть, что последовательность -7=™ —гт*
у 2л (1 +шг+*
11*
324 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
является полной ортонормированнои
последовательностью на 572(~~00» °°) относительно лебеговой меры.
Поэтому ранее написанный ряд для к(ш) сходится
в среднем квадратическом. Заметим теперь, что
Л+1 П-И
([-ш)п V Ак V Ак С м . ч «.
(1 +/«)л+1 ^ (1+ш)к~ ^ к\ ) е 1 а1
&=1 &=1 О
-/
так что
А (ш) = | в"'11' 6 (0 йи где & (0 = ^ апВй (*).
О я»0
При этом надо иметь в виду, что частные суммы ряда (22)
представляют собой преобразование Фурье (с точностью
N
до множителя) функций, равных ^апВп{1) при /^0 и
1
равных нулю при /<0. Так как преобразование Фурье
не меняет нормы функции в 5?2( —оо, оо), то из с. к.
сходимости ряда (22) следует с. к. сходимость ряда
для Ь(1) и
\ \ьа)Ы(<оо.
о
По поводу единственности полученной факторизации
функции }(и) можно сделать замечания, аналогичные
тем, которые были сделаны о факторизации функций
на окружности. Выражение для Н{хю) можно получить
из формулы (9) заменив г на хю и произведя
соответственную замену переменных под знаком интеграла:
*<.>-«р{^г \^шА- <2з>
Теорема 3. Для того чтобы неотрицательная
интегрируемая функция Ци) ( — оо<^<оо) допускала фак-
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 323
торизацию (13), (14), необходимо и достаточно, чтобы
Яг$-<*•>-«•■ (И)
При дополнительных условиях Л(ш)^0 (Ке#>>0).
Л(1)>0, функция к(ы)) единственна и определяется
формулой (23).
Теорема 4. Для того чтобы стационарный процесс
г}(/) (~оо<^<оо) допускал представление (11),
необходимо и достаточно, чтобы он имел абсолютно непре+
рывный спектр и его спектральная плотность удовлетво*
ряла условию (24).
§ 8. Прогноз и фильтрация стационарных процессов
Одна из важных задач теории случайных процессов,
имеющая многочисленные практические применения, за*
ключается в следующем: требуется наилучшим образом
оценить значение случайной величины $, наблюдая
некоторое множество случайных величин {^а, а е= А]. Таким
образом, нужно найти функцию /(|а|а е Л) от множества
переменных ^а,абД с наименьшей ошибкой,
удовлетворяющей приближенному равенству
С«ё = /(г«1<хеЛ). (1)
Примером "такой задачи является прогноз (экстра?
поляция) случайного процесса. 6 этом случае требуетсй
оценить значение случайного процесса в момент
времени Г по его значениям на некотором множестве момен*
тов времени, предшествовавших Г,
Другим примером является задача фильтрации
случайного процесса. Она состоит в следующем: в моменты
времени /'еГсГ наблюдается процесс \{1)~ц(1) + Ъ> (О,
представляющий собой сумму «полезного» сигнала %({)
и «шума» т](/). Требуется отделить шум от сигнала,
т. е. для некоторого Г а.Т нужно найти наилучшее прц4
ближение 1(1) вида
1(П~1 = !(1(П\*'^Т').
326 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Постановка задачи пока еще не закончена, так как не
указано, что означает «наилучшее приближение».
Разумеется, критерий оптимальности зависит от
практического характера рассматриваемой задачи. Что же
касается математической теории, то в ней преимущественно
развиты методы решения поставленной задачи,
основанные на среднем квадратическом уклонении как на мере
точности приближенного равенства (1).
Величина
Ь = {Мк-~1(1а\а€ЕА)]У> (2)
называется средней квадратической погрешностью
приближенной формулы (1). Задача состоит в определении
функции / такой, что (2) принимает минимальное
значение. В том случае, когда А — конечное множество,
под !(1а\а^А) мы понимаем измеримую по Борелю
функцию аргументов са, а<^ А. Если же А бесконечно,
то этот символ обозначает случайную величину,
измеримую относительно а-алгебры § = сг{|а, а е Л},
порожденной множеством случайных величин {^а, аеЛ}.
В дальнейшем предполагается, что и ^ и /(|а|ае А)
обладают моментами второго порядка.
Положим
т = мда. (3)
Тогда
&=М&-!(1а\а^А)У =
= М&-уУ + 2М&-у)(у-}(1а\ае=А))+М(у-1(1а\ае=А)Г.
Так как у — }(%а\ а(= А) ^-измерима, то
МЙ-у)(у-/Й«|аеА)) =
= ММ{(С-у)(у-/Йа|ае=Л))|5} =
-М(у-?Й«|аеЛ))М{(С-7)1© = 0.
Таким образом,
откуда следует
Теорема 1. Приближение случайной величины $,
имеющей конечный момент второго порядка, с
минимальной средней квадратической погрешностью при по-
§ 8] ПРОГНОЗ СТАДИОН АРНЫХ ПРОЦЕССОВ 327
мощи 5==:сг{^а» а^ А}-измеримой случайной величины
единственно (той Р) и дается формулой
Замечание. Оценка ^ = у случайной величины $
является несмещенной, т. ё.
му = ммшнмг
и величины ? — V и ^а ПРИ любом асЛ не коррелиро-
ваны:
М(С-у)1а = ММ{(С-у)Е«13} = М|вМ{К-у)18} = 0.
К сожалению, практическое применение теоремы 1
для получения эффективных формул приближения
бывает весьма трудным. В случае гауссовских случайных
величин, однако, можно пойти дальше. Заметим прежде
всего, что более простой постановкой задачи,
приводящей в ряде случаев к законченным и аналитически
доступным решениям, является задача отыскания
оптимального приближения не в классе всех измеримых
функций от заданных случайных величин, а в более
узком классе линейных функций. Более точно это
означает следующее. Пусть {Й, ©, Р} —основное
вероятностное пространство. Предположим, что величины ^а и $
имеют конечные моменты второго порядка. Введем
подпространство .З^Йа» аеЕ А} гильбертова пространства
5?2 {й> ^> Р}> являющееся замкнутой линейной оболочкой
величин^, аЕД и константы. Можно рассматривать
подпространство З^^а» а6^) как множество всех
линейных (неоднородных) функций от ^а с конечными
дисперсиями. Наилучшим линейным приближением 2; к
случайной величине ^ является тот элемент 32{^а> а€Е^}»
который находится от ^ на кратчайшем расстоянии, т. е.
62==М|С-?|2<М|^-и2
для любого Е'^З^Йсп а^ Л}. Из теории гильбертовых
пространств известно, что задача отыскания элемента
I из подпространства Я0, который находится на
кратчайшем, расстоянии от заданного элемента 2;, всегда
имеет единственное решение. А именно, I является
проекцией 2; на Я0. Элемент I всегда может быть определен
328 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
и притом единственным образом из системы
уравнений {1-1, С") «О для любого ^" се 3?2{1а, аЕ А}, В
нашем случае эта система уравнений сводится к
уравнениям
М(йа)=М(Йа), (4)
и поскольку в ^2{|а, аЕ^} включена единица
так что оптимальные линейные оценки \ обязательно
не смещены. Можно считать, что М|а = 0 для любого а.
Поэтому в дальнейшем мы ограничимся рассмотрением
подпространства случайных величии из ^{Й, ®, Р} с
математическим ожиданием 0.
Разумеется, не всегда есть основания считать, что
линейная оценка величины ^ является приемлемой.
Например, если %(п) — е1(У,п+(*\ где у равномерно
распределена на ( — п, л), то М {| (я) |(ш)} = 0 (п=^т) и наи"
лучшая линейная оценка величины %(т) по значениям
всех Цп) {пфт) имеет вид |(т) = 0, т. е. не
использует значений величин |(я), в то время как достаточно
произвольной пары наблюдений \(к) и ^(6-Ы), чтобы
определить всю последовательность Цп) точно, а именно
Допустим теперь, что все конечномерные
распределения системы {$, са, а^А} нормальны и М%а = 0,
М^==0. В этом случае из некоррелированности величин
й~1 и 1а следует, что они независимы. Поэтому (; —?
не зависит от а-алгебры б и
Т-еорема 2. Для системы гауссовых случайных
величин {I, 1а, а е А} наилучшая (в смысле среднего
квадратического отклонения) оценка величины ^ с
помощью о{Ъа, ае АУизмеримой функции совпадает с
наилучшей линейной оценкой в «^{^а» ъ^-А}.
В дальнейшем рассматривается ряд частных задач
на построение оптимальных линейных оценок.
А) Число случайных величин^ конечно (а=1, 2, ...,я).
Задача имеет простое решение, хорошо известное из
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 329
линейной алгебры. Предполагая, что ^а линейно
независимы, можно представить проекцию \ величины ^ на
конечномерное пространство Я0, натянутое на величины
|а (а == 1, ..., п), с помощью формулы
5 —
где Г = Г(^, %2,
векторов |!, ^2»
(Ъп, 1х) ... (|я, Шп
(Е, &,) ... (С, I») О
, ЕЛ) —определитель Грама системы
(1и Ь) ...'(Бь Ь.)
1 (II» ?2> •..» 1/г) :
и (|, л) = М(^г|). Средняя квадратичная погрешность 6
приближенного равенства 1^1 равна длине
перпендикуляра, опущенного из конца вектора | на
пространство #0 и дается формулой
б2
ПБь
92^
е/2
, С)
Г(1ь 12, ..., 1п) '
Б) Рассмотрим задачу об оценке случайной
величины 2; по результатам наблюдения с. к. непрерывного
случайного процесса %(() на конечном промежутке
времени Т = [а, Ь]. Пусть /?(/, 8) — корреляционная
функция процесса |(*). В силу теоремы 5 § 3 процесс |(0
может быть разложен в ряд
оо
где Ф&(0~~ ортономированная последовательность
собственных функций, кк — собственные значения
корреляционной функции на (а, Ь):
ь
А*Ф*(') = / *(*, *) Фа ($)<&.
а
^ — нормированная некоррелированная
последовательность,
330 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, IV
Очевидно, что{^}, к= 1, 2, ..., образуют базис в ^2 (К0>
/ <= (а, 6)}. Поэтому
оо
I = 2 ся1„,
Ь
где &,= | 6(0Ф„(0Л, я- 1, 2, ...
Ь
с„ = Щ\л = | /?«(0 ф„ (0 л, /?«(0 = Ш (0.
а
Средняя квадратическая погрешность б оценки может
быть найдена по формуле
оо I Ъ
в* = М|С I2-М|5 Р= М|&Р-2| *«(/)фЛ')<«
га=0 I а
Практическое применение этого метода затруднено
сложностью вычисления собственных функций и
собственных значений ядра /?(/, 5).
Метод Винера. Пусть КО и КО, *е7\ — две
гильбертовы случайные функции. Допустим, что процесс
|(0 наблюдается на некотором множестве V значений
аргумента I. Ставится задача об определении
оптимальной оценки значения К^0)> ^о^Т, по наблюденным
значениям КО» ^Г. Если предположить, что
искомая оценка имеет вид
Ш=\ с(8)Шт№),
(5)
где т — некоторая мера на Г*, и выполнены условия,
при которых этот интеграл имеет смысл, то уравнение
(4) принимает вид
/ с (8) /?«(5, 0 т (аз) = /?й Со, 0, * €= Г, (6)
Т*
где /?^~ корреляционная функция КО, а /?^ —
взаимная корреляционная функция КО и КО- Уравнение (6)
является интегральным уравнением Фредгольма
первого рода с симметричным (эрмитовым) ядром. Далеко
§8]
ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ
33?
не всегда оно имеет решение. Однако если
/М|Ш12т(й/)<оо,
т
то интегральное уравнение (6) имеет решение с (я) е^2 {пг)
тогда и только тогда, когда оптимальная линейная
оценка 1((0) величины 5(0 имеет вид (5).
Пусть Т — ось действительных чисел, Т* = {а, Ь),
процессы'^/) и 5(0 стационарны и стационарно связаны
(в широком смысле) и в качестве меры пг взята
лебегова мера. Тогда уравнение (6) принимает вид
ъ
\ с (5) Л« (5 - 0 из = Яв (к - 0, ' е (а, 6). (7)
а
Если 5(0 = ^(0 ( —оо</<оо) и /0>6, т. е. если
задача состоит в оценке величины |(/0) по значениям %(1)
в прошлом, то,задачу будем называть задачей чистого
прогноза.
Остановимся подробнее на задаче прогноза
величины 5(^ + ?) по результатам наблюдения процесса |($)
до момента времени /, 1^8. При этом будем
предполагать, что процессы |(0 и 5(0 стационарный
стационарно связаны (в широком смысле). Прогнозирующую
величину 5(0 будем рассматривать как функцию от I
при фиксированном д. Легко заметить, что величина
1(0, определяемая уравнением (7), является
стационарным процессом. Действительно, уравнение (7) имеет
вид
г
— оо
Замена переменных / — и = я, / — $ = т, преобразует
последнее уравнение в следующее:
оо
о
Отсюда мы видим, что функция с*(/ —т) не зависит от
/. Положим с (т) = сД* — т). Уравнение (8) запишется
332 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
теперь так:
оо
| с(5)/Ы'-*)^ = #а(? + 0, ^>0, (9)
о
а формула (5) для прогнозирующей функции- имеет вид
г оо
Ш= \сЦ-&Щ$)й&=\ с{?Ш1-*)й*. (Ю)
-оо 0
Таким образом, процесс |(*) = ^(0 стационарен. Из
формулы, (10) следует, что с(1) является импульсной
переходной функцией физически осуществимогофильтра,
преобразующего наблюдаемый процесс в оптимальную
оценку величины (; {I + #).
Легко указать выражение для средней квадрата-
ческой погрешности 6 прогнозирующей функции \{1).
Так как б2 есть квадрат длины перпендикуляра,
опущенного из конца вектора ^(1 + я) на ^ {&($)> $^0> то
оо оо
«*««>)-| \7ЩКпа-5)с(8)й8. (11)
о о
Полагая /?~(0) = о^ и переходя к спектральному
представлению корреляционной функции Яц (*), получим
оо
Ь"- = а1~ | \с(ш)\ЧРЪ1(и), (12)
— оо
где Т7^ (и) — спектральная функция процесса ^(/) и
оо
с(ш)= | сЦ)е~ш аи
о
Изложим кратко метод решения уравнения (9),
предложенный Н. Винером. Допустим, что спектр процесса
!(/) абсолютно непрерывен и спектральная плотность
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 333
1ц{и) допускает факторизацию (см. теорему 3 § 7)
оо
Ы (и) = I к (ш) Р, к (г) = -~=^ \ а (1) е~г1 а(, Ке г > 0.
Из равенства Парсеваля для преобразования Фурье
следует, что
со со
-'оо 6
Предположим еще, что взаимная спектральная
функция процессов 5 (0 и I (0 абсолютно непрерывна и ее
плотность }ц.(и) удовлетворяет условию
1иЫ
Тогда
= *("*)€= #2. (13)
%(*) = |е"7к(и)4и = / е"ик(ш)к(ш)с1и =
—'ОО —СХ>
оо
= | 6 (* + в) аф) <&,
6(0 =-т^ Г к{ш)еи"йи.
у 2л ^
где
С помощью полученных выражений уравнение (9)
может быть переписано следующим образом:
оо оо
| [Ь{д + Ц-з)- § с(т)а(* - т + в) <*т]а(5)«к => 0,. *>0.
о о
(Н)
Чтобы (14) имело место, достаточно, чтобы функция
с(1) удовлетворяла уравнению
оо
Ь(д + х)= Г с(х)а(х — х)с1хг х>0, (15)
334 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Уравнение (15) того же типа, что и уравнение (9), с тем
лишь существенным различием, что функция а(1)
обращается в нуль для отрицательных значений I, Записав
(15) в виде
Ь (# + а:)== | с{х)а{х — х)йху *>0, (16)
о
мы можем непосредственно решить это уравнение с
помощью преобразования Лапласа. Умножая равенство
(16) на е~гх и интегрируя от 0 до оо, получим
где
В,(г) = С(г)к(г),
оо
О
1
с<2)в75Г/ 'О*"*'««•
Таким образом,
оо
ЬК-г) А (г) » ^ У2п _^ * (««) * '
причем выражение для Вч(г), Не(2)>0, может быть
записано в виде
Д,(2)- » (е-»Ш-^-. (18)
я V ' Т^2я _^ А(/«) г-ш
Формулировка предположений, при которых выведены
формулы (17), (18), весьма громоздкая. Проще при
решении конкретных задач непосредственно проверять
законность предлагаемых преобразований, приводящих
к решению задачи.
Метод Яглома. В методе Яглома, в отличии от
метода Винера, отыскивается не импульсная переходная
функция оптимального фильтра, которая может и не
существовать, а частотная характеристика. Не даются
общие формулы решения задачи, а предлагается только
метод подбора искомой функции, исходя из тех
требований, которым она должна удовлетворять. Во многих
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 335
важных случаях этот подбор довольно просто
осуществим.
Пусть двумерный стационарный процесс (^(/), ?,({))
допускает спектральное представление
оо сю
— ОО —ОО
с матрицей спектральной плотности
къ(и) Нь(и)\
По-прежнему рассматривается задача оптимальной
оценки величины ^ (* + я) по значениям процесса ^(з),
5<^. Прогнозирующий процесс 1>{1) подчинен 1(().
Поэтому
оо оо
&(/) = | ешс(ш)^(с(и), $ \с(1и)?Ы(и)4и<<х>. (19)
— оо —со
Уравнение
МС(/ + Г)|(Г) = МС(0Ш, «<Л
определяющее процесс $(/), принимает вид
оо
| в'»* {*'»« /й (Ы) - с (ш) /15 (и)} йи = 0, 5 > 0. (20)
— оо
Кроме условий (19) и (20), мы имеем еще требование,
чтобы с(ш) была частотной характеристикой физически
осуществимого фильтра. Эти условия будут выполнены,
если:
а) функция /|$(н) ограничена;
б) с(ш) является граничным значением функции
в) я|з(ш) = еиц1ц{и) — с(ш)/$|(н) является граничным
значением функции ^(г) из Ж^,
Здесь <^? (^2~) обозначает пространство функций
Л (г), аналитических в правой (левой) полуплоскости,
336 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
для которых интеграл
оо
) \Н(х + ш) |2 йи
— оо
равномерно ограничен при л->0 (х<0).
оо
Действительно, из б) следует, что \с(ш)\2с(и<оо9
— зо
а это вместе с а) обеспечивает выполнение условия (19).
Кроме того, из б) следует, что с(ш) есть частотная
характеристика физически осуществимого фильтра. Из
условия в) следует, что ешя(ц (и) — с (ш) 1ц (и) является
преобразованием Фурье функции, равной нулю при
положительных значениях аргумента в силу
соотношения (20).
Заметим, что, ограничив себя условием б), мы
отбрасываем фильтры, частотные характеристики которых
на бесконечности могут возрастать. Такие частотные
характеристики соответствуют операциям, связанным
с дифференцированием процесса |(*), и часто
встречаются при построении оптимальных фильтров. Поэтому
условие б) желательно заменить менее ограничительным.
Предположим, что с (г) — функция, аналитическая в
правой полуплоскости, и |с(г)|->оо при |г|->оо не
быстрее, чем некоторая степень х (например, г-я). Функция
/ ч с (г) +
Так как | сп(г)\ <|с (г)|, то
оо
Нт Г \сп(ш) — с(ш)\21ц{и)с1и = 0,
П > оо «'
— оо
если условие (19) выполнено. Таким образом, с(ш)
является пределом в 3?2{р1ь} частотных характеристик
допустимых физически осуществимых фильтров, а
поэтому с (ш) — также частотная характеристика такого
фильтра. Мы получили следующий результат.
§ 8)
ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ
337
Теорема 3. Если спектральная плотность . /^ (и)
процесса |(/) ограничена, то условия
оо
а) ] \с{ш)\21ц{и)йи<оо,
— оо
б) с (ш) является граничным значением функции с (г),
аналитической в правой полуплоскости и возрастающей
при | г | -> оо не быстрее некоторой степени \ г |,
в) ф (ш) = е1ис,^ц (и) — с {(и) /ц (и) является граничным
значением функции ^(г) из Ж2
однозначно определяют частотную характеристику с(1и)
оптимального фильтра, оценивающего величину && + (}).
Средняя квадратическая погрешность 6 оптимальной
оценки равна
6 = {М|?(/ + (7)Р-МЦ(0|2}'/2 =
{•\Чг
а\- \ |с(ш)Р/к(«)лЛ . (21)
Пример 1. Рассмотрим задачу чистого прогноза
процесса I (/) (I (/) = ^ (()) с корреляционной функцией
ЯУ) = а2е~а п(а>0). Спектральная плотность легко
находится: !ц(и) = 2 2 . Аналитическое
продолжение функции -ф(ш) имеет вид
, , ч с (г) - е2«
(г + а) (г-а) '
Функция ^(г) имеет единственный полюс в левой
полуплоскости 2= —а. Для того чтобы его нейтрализовать
с помощью функции с (г), аналитической в правой
полуплоскости, достаточно положить с (г) = сопз! = е ~ад»
При этом условие а) теоремы 3 выполняется. Итак,
со
с{ш) = е-а\ |(0= [ еше~а<!у (аи),
— оо
т. е. наилучшей формулой оптимального прогноза
величины 1(1+ д) является следующая формула:
338 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
зависящая только от значения !■(*) в последний
наблюденный момент времени. Средняя квадратическая
ошибка экстраполирования равна
Пример 2. Снова рассматривается задача чистого
прогноза процесса ^(0, т. е. оценки ^(* + <7) по
наблюденным величинам ^($), 8<(. Если спектр процесса 1(1)
абсолютно непрерывен и выполнено условие (24) § 7,т
то спектральная плотность процесса допускает
факторизацию: /ц {и) = | к (ш)|2, где Н{г)^Ж2 и не имеет
нулей в правой полуплоскости.
Рассмотрим тот важный для практики случай, когда
И (г) является дробно-рациональной функцией:
ПКг) Я (г)9
где Р (г) — многочлен степени т, 0 (г) — многочлен
степени п (т<п). Допустим еще, что спектральная
плотность !ц{и) ограничена и не обращается в нуль. Тогда
нули многочленов. Р(г) и СЦг) лежат в левой
полуплоскости. Пусть
Р (г) = А Д {г - г/)»/, (}{г) = В$[(г- 5,)*/,
2 а, = /п, 2 Р/ = п-
Положим
^^«(-О^ЛЙ^ + г^ (}[(г)-(-1У 811(2 + 1^1.
Аналитическое продолжение функции 'ф(ш) имеет вид
Функция с (г) должна быть аналитической в правой
полуплоскости, а г|>(2:) —в левой. Поэтому с (г) должна
быть аналитической во всей плоскости комплексной
переменной и может иметь полюсы в нулях многочлена
Р(г), причем порядок полюса не должен превосходить
порядка соответствующего нуля Р(г). Поэтому
с \г) р () ,
§8]
ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ
339
где М {г) — аналитическая функция в плоскости г, не
имеющая особенностей при конечных г. Так как с {г)
имеет не выше чем степенной порядок роста, М(г)
является многочленом. Ввиду интегрируемости квадрата
модуля функции
с[ш) Р(ш) Р(ш)
степень т1 многочлена М (ш) не выше п— 1, т{ ^п — 1.
С другой стороны, указанный выбор функции с {г)
обеспечивает выполнение условий а) и б) теоремы 3.
Остается подобрать многочлен М (г) так, чтобы функция
,ЬЛЛ- 1е*"Р(г)-М(г)] />,(*)
У[2) Я (г) Яг (г) >
или, что то же самое, функция
не имела полюсов в левой полуплоскости. Для этого
необходимо и достаточно, чтобы выполнялись равенства
й]М{г
___ й] (е^Р (г))
/ = 0, 1, ..., рЛ— 1, *=1,
(22)
Задача построения многочлена М(г), удовлетворяющего
условиям (22), является обычной задачей теории
интерполяции и всегда имеет единственное решение в классе
многочленов степени п— 1. Найдя многочлен М(г), мы
тем самым найдем частотную характеристику
оптимального прогнозирующего фильтра
Можно предложить еще следующую методику
определения функции с (г). Разложим функции Р(г)(}~1(2)
и М\г)0г1(г) на элементарные дроби. Пусть
Р(г) __ у< у< ск! М(г) __ ^п у у&/
Я{2) - 2а2а , - ./ ' д(г) -~2^(2-г у #
*^' А="1/«1 (2~2Л) Ч1; Л-1/=1К *'
Зй* ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Для того чтобы функция ${ (г) не имела полюсов в
точках гк, 6=1, ...,г, необходимо и достаточно, чтобы
-^(г-гк)ЧЛг)\г-гк=0, / = 0, 1, ...,Р*-1,
причем
Простой подсчет показывает, что
с*/+7гсл/+1+-2гсА/+2+ --- + (р -у Ц^в* >
й= 1, ..., г.
Зная коэффициенты у*/> мы можем написать
выражение для с(ш):
V V Ук*
/. ч _| У V У*/ „ к-\ /-1 V ^
Пример 3. Предположим, что наблюдается процесс
?(я)($<^)> н0 результаты измерений величины 2;($)
искажаются различными помехами, так что наблюденные
значения дают некоторую функцию |($), 5^*>
отличную от !;($). Примем, что величина помехи (или, как
говорят, шум) г\{1) = 1(1) — &(/) является стационарным
процессом со средним значением 0. Желательно по
результатам наблюдения процесса 5($) = ^($) + л($), 5^^>
оценить значение $(* + <7).
Такие задачи называются задачами фильтрации или
сглаживания (говорят, что от процесса Щ) нужно
отфильтровать шум т](/), или что процесс, 5(0 нужно
«сгладить», т. е. вычесть из него нерегулярный шум).
При этом для д>0 мы имеем задачу фильтрации с
прогнозом, а при <у<0 — задачу фильтрации с
запаздыванием.
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 341
Предположим, что шум т](/) и процесс 5(0 не кор*
ре'лированы и имеют спектральные плотности [ц(и) Ж
1^(и). Тогда
Я|* (0 = /?т,-п (0 + *й (0, Ы (и) = /гл (и) + Ь (и).
Так как /?й(0 = Лк(0» Т0 существует взаимная
спектральная плотность процессов ^(/), I {{) и 1ц (и) = [ц (и).
Пусть /к(ц)= ц2^а2 , ^0*) = Ц2 + Р2 ■ ТогДа
Для функции 1)5(2) мы получаем выражение
.и /~ч _ -*!«*' (*2 - Е2) + *з<? (г) (г2 - у»)
ЧНг;- (г2 - а2) (г2 - р2)
Пусть 4>0. Функция а|з(г) должна быть аналитической
в левой полуплоскости и принадлежать Жъ'. Для этого
нужно, чтобы числитель обращался в нуль в точках
г=—а и 2=—р. Это приводит к равенствам
с(-Р) = 0, с(-а) = -^-—а2„у2 -. (23)
Кроме того, с (г) должна быть аналитической в левой
полуплоскости (и по условию б) в правой), за
исключением точки 2=**—у, где она может иметь простой
полюс. Таким образом,
4 ' 2 + у *
где ф (г) — целая функция. Из условия конечности
интеграла
/ \с(ш)\2}ц{и)с1и
следует* что ер (г) — линейная функция, <р(г) = Аг + В.
Из (23) получаем
4 ; г + у ' съ у + а
342 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV.
Поэтому формула оптимального сглаживания с
прогнозом имеет вид
оо
Вспоминая, что (ш + у)"1 является частотной
характеристикой физически осуществимого фильтра с
импульсной переходной функцией е~у\ получаем
Ш-^^ге-аТ{1Ц)-ф-у) / е-'"-»&(*)*>. (24)
— оо
При <7<0 формула (23) неверна. Формально это связано
с тем, что функция ^(г) в этом случае не ограничена
в левой полуплоскости. Функция ^(г) при #<0 может
быть определена из следующих соображений. Пусть
$! (г) = — схегя (г2 — р2) + с3с (г) (г2 — V2)- Тогда с (г) должна
быть аналитической в левой полуплоскости, кроме точки
2=— у и яМ—оь) = 'фх (—Р) = 0. Так как
^ ' с3(г2-у2)
и с (г) аналитична в правой полуплоскости, то ^\(г) —
целая функция и
Ф.^)=-с1^(у2-Р2). (25)
Положим
1М2) = Л(2)(2 + а)(2 + Р).
Функция А (г) должна быть целой. Из условия а)
теоремы 3 следует, что А (г) = сопз1: = Л. Значение А
определяется из уравнения (25)
А = с{е*
„уд ~У + Р
Отсюда
ил _ с±_ (а + у) (и2 + р2) е1и* - е*< (-у + Р) (ш + а) (ш + р)
С1Ш; с, (а + у)(«2 + У2)
(26)
Для прогноза и фильтрации стационарных
последовательностей применимы методы, аналогичные тем, ко-
§ 8] ПРОГНОЗ СТАЦИОНАРНЫХ ПРОЦЕССОВ 343
торые были изложены для процессов с непрерывным
временем. Общее решение задачи прогноза стационарных
последовательностей дается в следующем параграфе.
Здесь мы ограничимся одним примером.
Пример 4. Рассмотрим стационарную
последовательность ^(/), удовлетворяющую простейшему уравне-?
нию авторегрессии
а0Ш + ах1 (I - 1) + ... + ар1 Ц - р) = ц (*), (27)
где ц (I) — стандартная некоррелированная
последовательность и 1,(1) подчинено ц(1). Пусть
Л(*)= \етй№
— спектральное представление последовательности ц(1),
I (и) — процесс с некоррелированными приращениями и
структурной функцией "^-ЦА Л В), где / — мера Лебега.
Спектральное представление последовательности I (I)
должно иметь вид
I (0 ==. ]" е""Ф (и) 4 (")> где | | <р (и) \Чи < оо. (28)
— Л —Л
Подставляя (28) в (27), получим
|^"Р(^)ф(^)^(«)= /Лб(и),
-л -л
где Я (г) = 2^ акгк. Отсюда следует, что
&=о
Ф (") = -==" (то(1/) •
Р(еш)
Предположим, что функция Р (г) не имеет нулей в
замкнутом круге |г|^1. Тогда р ,. ^ Н2. Если
■ = 2**2* (Ь0 = -
Р(г) - Аки*й Г°~ а0)>
/5 = 0
344 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
ТО
оо
&(о=2м('-*).
и мы получили представление последовательности %(1)
в виде реакции физически осуществимого фильтра на
некоррелированную последовательность г\(1). Так как
Ш=~Ы(*--1)+.--+<*А(*-р) + 1\(*)1 (29)
то оптимальный прогноз |(/) по данным 1({ — л)(/г=1, 2, ...)
имеет вид
Ш=~1а1и1-1) + <*21(*-2)+-'-+арЬ(1-р)].
Минимальная средняя квадратическая погрешность
прогноза равна
Повторное использование формулы (29) позволяет
получить оптимальный прогноз на несколько шагов вперед.
§ 9. Общие теоремы о прогнозе
стационарных процессов
В настоящем параграфе рассматриваются некоторые
общие теоремы о прогнозе стационарных
последовательностей и процессов по бесконечному прошлому.
По-прежнему под стационарным процессом понимается
процесс, стационарный в широком смысле с
математическим ожиданием 0.
Прогноз стационарных последовательностей. Пусть
{&(^)> ^ = 0, ± 1, ±2, ...} —стационарная
последовательность. Через Ж\ обозначим замкнутую линейную
оболочку в 5?2, порожденную всеми величинами §(/), а
через Ж\(1) — замкнутую линейную оболочку,
порожденную величинами ^(/г),/г</. Очевидно, что <Ж|(/)с:^(/4-1)
оо
и Ж\ есть замыкание ^ Ж\{$). Рассмотрим в Ш\
§91
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
345
операцию 5 сдвига времени. Для элементов Зё^тща.
Ц = 2^/гъ Ук) она определяется равенством
54 = 2^(^+1).
Операция 5 обладает обратной 5""1;
5-^2^(4-1)
и сохраняет скалярное произведение:
М (5(2 ск1 (4))5(Е^У) =•
к г
«=22 скйМ (| (/Л)| (тг)) = М (2 ск1 (*») 2 <*г| (т,)).
В силу этого 5 может быть по непрерывности
продолжена на Ж\. При этом она становится унитарной
операцией в Ж\.
Введем спектральное представление
последовательности !(/)
где V — спектральная стохастическая мера со
структурной функцией Р. В дальнейшем мы не будем различать
меру Р(А) и порождающую ее спектральную функцию
последовательности Р (и) **Р[ —я, и):
Напомним, что случайная величина т) принадлежит
Ж\ тогда и только тогда, когда
п
г]- ] ц>(и)у{с1и), где фе^ДР}.
—л
Рассмотрим последовательность случайных величин
Т1(0 = 5'т1 (/ = 0, ± 1, ±2, ...).
Лемма 1. Последовательность ц Ц) стационарна а
имеет спектральное представление
л
Ч(0= Гв""<р (и) V (</«). (1)
346 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Стационарность вытекает из унитарности 5:
МП(/ + 5)Л(5) = (Т|(* + Я), 1)(5)) =
= (5<+Ч 5*11) = (54 л) = М л (/) л (0).
Наконец, спектральное представление (1) легко
проверяется для элементов ц вида т) = 2о>ь\ (4)(ф (и) = 2акеги*к),
а для произвольных ц получается с помощью
предельного перехода.
Отметим еще следующие свойства оператора 5:
а) 550* (*) = 506 С+1)Г
б) если |(р)(0~ проекция ^(0 на 5#&(* —р), то
56(1)(<Н6(1)(' + 1), П^'Н*^ (< + ?).
Так как
М11{р) Ц + я) I2 = М15*|(р) (0 р = М ||"» (0 р,
то величина М|^р)(012 не зависит от /. Поэтому не за^
висит от I и величина
в?(р) = М||(0-|°')(0Р = М||(012-Ми<р)(0Р.
равная квадрату минимальной средней квадратическои
погрешности прогноза величины \(1) с помощью
величины 1(п), п^( — р. Очевидно, что
62(1)<62(2)<... <а2 = М|Ш12.
Равенство а2(/г) = а? означает, что !■(?) ПРИ любом /
не коррелирована со всехми величинами 1(к), к^.1 — п,
так что знание этих членов ничего не дает для
прогноза величины 1^). Если 6(1) ==0, то 1({) е Ж\ {I — 1),
откуда Щ(1-\) = Ш\{$) и вообще ^(«)=^(0 Для
любых I к п<1. Положим 5^| = П^(0- В рассматри-
ваемом случае Ж\^Ж>1. Это означает, что если нам
известна последовательность значений процесса 1(п),
п^.(, то все последующие члены последовательности
могут быть точно (с вероятностью 1) линейно выражены
через наблюденные. В известном* смысле
противоположным является случай, когда Ж1 = 0 (через 0
обозначено тривиальное подпространство Ж%, состоящее из
одного элемента 0). В этом случае знание членов по-
§93
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
347
следовательности Цп) (п <!$) мало дает для прогноза
величины |(5 + 0 при большом /, так как Пт М||(/) (я) | = 0
и Пт62(0-сг2.
Определение 1. Если Ж\ = Ж\, то процесс |(*)
называется сингулярным (или детерминированным), если
6(1)>0, то процесс \({) называется
недетерминированным', если же Ж\ = 0, то процесс называется регулярным
(или вполне недетерминированным),
- Определение 2. Пусть |г(I), /=1,2 — гильбертовы
случайные процессы, ^еГ, Г —произвольное множество
действительных чисел, 5#&(0 = 5?2 0;($)"> 5^^ 5е7}.
Будем говорить, что \х {I) вполне подчинен процессу Е-2(0»
если ^1 (0 ^ Щ* (0 Для всех * е г-
Теорема 1. Произвольная стационарная
последовательность допускает представление вида
1<0~БЛ') + ч(4 (2)
где \5 (I) и т| (^) — некоррелированные между собой
последовательности, вполне подчиненные \{1), ^5(0
сингулярна, а т)(0 регулярна. Представление (2) единственно#
Доказательство. Очевидно, что 55^| = 5^|. Так
как 5 унитарен, то Ж\ приводит 5, т. е. 5 взаимно
однозначно отображает подпространство Ж\=-Ж\&Ж\
на себя; {Ж\ состоит из всех векторов Ж\,
ортогональных каждому вектору из 58? |).
Пусть5в(0) —проекции|(0)на Ж\, т)(0) — проекция ^(0)
на Ж\ и |Л0 = 5^(О), Л(0 = 5'т|(0), * = 0, ±1, ±2,...
Так как & (0) = ЦО) + г) (0), то Е(0 = 5^(0) = Е8(0 + л(0,
причем последовательности ц{{), ^(0 стационарны, не
коррелированы между собой и подчинены 1^) (лемма 1).
Далее, так1 как в соотношении (2) \5{1)^Ж\ и
х\(1)<^Ж\, то 30* (0 Л ^|с= *&,(')• Поэтому Ж\<=.Ж\^
С другой стороны, из того, что 18{()^Ж1, имеем:
Яв\ (1)а2%1. Таким образом, при любом / Ж\ {I) =
= Ж\*=Ж\ , т. е. последовательность |5(0 сингулярна.
Далее из равенства Ч (/) = | (*) —18 (/) слеДУет» что
348 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
ч(/)е5»|(0. Поэтому Ж% =; Г1 ^л (О <= 50|. С другой
стороны, по определению Жх\(() ортогонально 5#|. Таким
образом, Жц = 0, т. е. процесс т|(/) регулярен.
Единственность представления (2) вытекает из того,
что в условиях теоремы проекция т|(/) на Ж\ равна
нулю, Ж\ = Ж\$ «=» Ж\з и, следовательно, \5{1) есть
проекция &(/) на Ж{. Теорема доказана.
Последовательности ц(1), |50&)'называются
соответственно регулярной и сингулярной составляющей процесса
ко.
Теорема 2. Регулярная составляющая ц{()
стационарной последовательности может быть представлена
в виде
оо
Ч(0-2а(«)Е('-»), (3)
г5е ^(/) (/ = 0, ± 1, ...) — стандартная некоррелирован-
оо
ная последовательность, Ж% (О *» Жц (/) и 2 |^(^)|2<°°.
Доказательство. Введем подпространство О (/) =
=»Ж|(0©^т1(* — 1). Оно одномерно (если бы оно было
нулевым, то в?1 (1) = 0 и т](0 была бы сингулярной
последовательностью). Выберем в О(0) единичный вектор
I(О). Тогда последовательность ^(/) = 5^(0) ортонорми-
рована &(*)€= Жу](1)(ЭЖц(1-1)9 поэтому 2(0
ортогонально Жх\{1— 1), причем 5(А) е Жц{1 — 1) при &</),
Щ (0 с: 50ч (О, Г1Щ (0 с: П ^л (О - 0.
Это означает, что последовательность 5(0 образует
базис в Ж-^ Разлагая г|(0) по элементам этого базиса,
получаем
оо оо
Ч(0)-2<Ф)С(-л), где 2|а(«)|2=М|г!(0)Р<<х).
Применяя к написанному разложению величины т}(0)
оператор 5', придем к равенству (3). Соотношение
Ж^{1)(^.Ж\(1) непосредственно вытекает из (3), а
обратное включение —из определения $(0. Теор.ема доказана.
§9]
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
349
Замечание 1. Не нарушая общности, можно
считать, что а(0) положительно.
Лемма 2. Пусть спектральная функция Р(и)
стационарного процесса Щ) равна Р{ (и) + Р2(и), где Р1(и)-~
неотрицательные монотонно неубывающие функции и
меры ^((А), соответствующие функциям /^(и),
сингулярны. Тогда существует разложение ё С)= &1 (0 + 1г (')•
где процессы ^ (7) подчинены I (/), ортогональны и имеют
спектральные функции Р((и) (/=1, 2).
Для доказательства представим отрезок [— я, я]
как сумму непересекающихся множеств Рх и Р2 таких,
что Р2{Р\) = Р\ (^2) = 0» Положим
я я
6,(0= /е'%(м)г(^), |2(0= \еиХМ)ч{йи),
где V — стохастическая спектральная мера процесса § (/),
ЗС/>; (г/) ~ индикатор множества Р^ Тогда
я
61(0 + 12(0= \е1(\{йи) = \{1),
— Я
Я
МШШ = |е'(',-',,вх|»1(")хл(«)^(«)=о,
—я
я
м&/ в) МЭ = 1 «' ('-'"'г)" ^ (") ^ («) =
—я
я
= |е'0>-'">М/!,/(и)>/=>1,2,
— Я
что и доказывает лемму.
Теорема 3. Для того чтобы последовательность $ (/)
6&/ла недетерминированной, необходимо и достаточно
условие
я
[ 1п!{и)с1и>-оо, (4)
—я
где / (и) — производная абсолютно непрерывной
компоненты Р (А) (относительно лебеговой меры).
350 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ 1ГЛ. IV
Доказательство. Необходимость. Пусть
Рг (и), Р3 (и) — спектральные функции
последовательностей т)(/), §5(0- Из некоррелированности ц(() и ^5(7)
следует, что
Р(и) = Рг(и) + Р8(и).
Согласно теореме 2 и теореме 2 § 7 Рг(и) абсолютно
непрерывна и для !г{и) = Рг(и) выполняется условие
я
Г \п!г(и)с1и> — оо. Разлагая меры Р{А), Р5{А) на абсо-
—я
лютно непрерывную и сингулярную компоненты
относительно лебеговой меры, получим
Р(А)= \[(и)Ли + Р*(А), Р3(А) = / }3{и)йи + К (А),
л л
Отсюда
и
оо оо
Г 1п/(^)^^ I \п?г(и) йи> — оо.
— оо —оо
Таким образом, если процесс не детерминирован, то (4)
имеет место.
Достаточность. Предположим, что процесс 1{1)
сингулярен. Тогда разложению/7(А) = Р3(А) = I 13(и)с1и +
А
+ Р*8(А) соответствует разложение |(^) на
некоррелированные компоненты %х(() и ^(О* подчиненные |(*)
(лемма 2). Пусть Г \п1{и)(1и = \ \п}3(и)(1и> — оо. Тогда
оо
в силу теоремы 2 § 7 ^ (/) = 2 а' (п) |' {I — /г), где |' —
некоррелированная последовательность. Так как
Щ (0 <= 5»б1 (0 0 Жь (/) и П ^ (0 = 0,
то {^\Ж1{1)с1^\Ж12(1)с1Ж12, что противоречит соотно-
шенмю Ж\ =Ш\у®Ж\ш> так что процесс \{1) не может
§9]
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
351
быть сингулярным. Поэтому
я
Г \п{{и)с1и = — оо.
-я
Теорема доказана.
Рассмотрим задачу о прогнозе недетерминированных
процессов. Воспользовавшись теоремами 1 и 2, запишем
Так как ^5(^) по прошлому восстанавливается точно,
то достаточно рассмотреть прогноз регулярной
составляющей т)(0 процесса |(^). Из теоремы 2 следует, что
проекция т)(7) на Жч(1 — д) совпадает с проекцией на
<%Ъ С "" ?)• Следовательно,
Ц^И)=Ъап1Ц-п). (5)
Величина средней квадратической погрешности
определяется из равенств
б2(?)= 2 К р. (6)
Получим формулу для оптимального прогноза, не
содержащую последовательности 2(я). Так как $(0)е5#,„
то
я я
5(0)= |<р («)*(</«), ||ф(и)р^г(и)<оо,
-Я —Я
где V — спектральная стохастическая мера процесса т|(/)
со
и К(и) = \8(еш)?, е(еш) = г^-^ааеш (лемма 1 §7).
Следовательно (лемма 1),
я
Ш = &Ш = [еии<${и)у{йи).
-Я
352 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Чтобы найти функцию ц>(и), воспользуемся формулой (3),
Имеем
оо IX сю
Л (0 = 5 аяЪ (/ - л) = \ е"\ (и) ^ аяе-"*в* (</и).
л=0 -я п=0
Сравнивая это равенство с равенством
Г)(/)= [Л(<*н),
-Я
получим
»М = (^а«в~1яи) =(ул2^7йг)Г1.
Теперь имеем
Я / ©о \
Ч^Ч'Н [I ^апе-*пиЫ(и)еииЪ(с1и),
Я
откуда
я
Ни
-я
где
9-1
V (*/и), (7)
^И0==Т7=2^г^". (8)
оо
Укажем способ определения функции §(г)=^Ьпгп,
6„ *=-уг=-ап. Тем самым мы получим как общее решение
задачи о прогнозе стационарной последовательности,
так и формулу для вычисления средней квадратической
ошибки прогноза. Функция §(г)^Н2, § (0) = 7— в е-
щественна (см. замечание к теореме 2), и с помощью §(г)
факторизуется спектральная плотность
последовательности г)(/), а именно }г(и) = \ §{е1и)\2. На основании
замечания 2 к теореме 1 § 7, если §(г) не имеет нулей
в круге | г |< 1 и §"(0)>0, то она определяется по />(н)
единственным образом. Поэтому, если построенная в со-
§9]
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
353
ответствии с теоремой 1 § 7 функция §(г) не
обращается в нуль при |г|<1, то она идентична с
функцией §{г), полученной при доказательстве теоремы 1 § 7.
Л е м м а 3. Функция § (г) отлична от нуля при \ г |< 1.
Доказательство. Заметим прежде всего, что
оо оо
если /„(«)== |/г (е'»)|2, А(г)=2с„гя, 2|с„р<оо, то
б2 (1) ^ 2я | с012. Действительно,
М
Л(0)-2^Ч(-А)|2 =
/г=1
-I
1 - Е «.'-"■ Е
сле
— гки
йи ^ 2л | с012.
/?~1 / \* = 0
Так как это верно при любых йк й #, то
. 62(1)>2як0|2. (9)
Допустим теперь, что §(г0)==0, |г0|<1. Функция
оо
дх (г) = —7== 2^ апгП обращается в нуль в точке <г0. По-
л=0
оо
лож им д{ (г) = (г - г0) У\ Ьгп гп, где К == — лГ~ . - Тогда
п=0
1я(*/в)1 =
оо
▼ ______ /У 1
1 1-е-'" г.
1 е-'"-г,
,-/пи
= 1Я1(е-'")1 =
|е-'и-20|
=
оо
п«0
• оо
2 Ке-Ш
л«0
1
2^ &«<
/1 = 0
где Ьо = 66 = -
Из (9) следует
62(1)>2я|5о,|2 = |
что при | г01< 1 невозможно в силу (6). Лемма доказана.
12 И. И ГИХМ..Н, Л. В Скороход
354 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Следствие. В формуле оптимального прогноза (7)
функция ц (г) е Н2 определяется единственным образом
{при условии, что §(0) положительно) и совпадает
с функцией, полученной в теореме 1 § 7.
Мы решили задачу о прогнозе для регулярной части
недетерминированной последовательности. Теперь нужно
выяснить следующие вопросы: как выразить
спектральную плотность последовательности ц(1) через
спектральную функцию процесса ^(/)? Какой вид имеет
формула прогноза для последовательности |(/), выраженная
через характеристики |(/)?
Лемма 4. Пусть недетерминированный процесс |(0
представлен в виде I(() = 11(0 +ЕЛО* где ц{1) и 18{1) не
коррелированы, |Л0 — сингулярный процесс, т) (/) —
регулярный, Р(и), Рг(и), Р8 (и) — спектральные функции
последовательностей ?■(/), 4(0» 1Л0- Тогда равенство
Р(и) = Рг(и) + Р3(и) (10)
является разложением функции Р(и) на абсолютно
непрерывную Рг(и) и сингулярную Р5(и) составляющие
относительно лебеговой меры.
Доказательство. Формула (10) следует из
некоррелированности последовательностей т)(/) и |Л0«
Введем спектральное представление некоррелированной
последовательности $(/), фигурирующей в
представлении (3),
я
С(')= /*"«№). (И)
-я
где 5 (Л) —стохастическая мера со структурной функцией
-^/(Л), / — лебегова мера. Подставляя (11) в (3), получим
я
ц (/) = | еии У2п §{е1и) I (с!и).
-я
Пусть
я
5Л0= /ЛЛ<*") (12)
§ 9] ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ 35#
будет спектральным представлением последователь*
ности 13({). Тогда
л я
$(/)=, | ешу (Ли) = ]* е<7" []/2я § (е1и) $ (аи) + V5 (аи)].
—я —я
Из последнего равенства вытекает, что
Я 31
|ф(иМА*)= / Ф («) [ /2я Я (в'»); (с?«) + V, (йи)] (13)
-я —я
для любой функции ФЙе^й.
Для ЕЛО можно написать еще и иное спект*
ральное представление. Так как |5(0)€^, то
я
6.(0)= /фЛ"МА*),
-л
откуда
я
1.(0 = 5*6,(0)- /е»"фЛ»Ь (<*«).
-Я
Учитывая (13), получаем
6,(0= /е«7"ФЛ»)[^§1^№)4^ЛЛ4 (14)
-Я
Сравнивая (14) с (12), видим, что
я я
- | е"« (ф, (и) - 1) V, (Ли) = | е"«ф, (и) УЪя §(е1и) & (</«).
— Я —Я
В разных частях полученного равенства стоят элементы
из ортогональных друг другу подпространств. Поэтому
они равны нулю. Следовательно,
Ф, (и) = 1 (той Р8), ф, (и) § (е{и) = 0 (той /).
Так как §(е(и) может равняться нулю только на мно-*
жестве /-меры 0, то у6{и) почти всюду равна нулю*
12*
856
ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Пусть 5 — множество, на котором (р6(и)=\. Тогда
/(5) = 0. Таким образом,
Р*(А) = 1\9Ли)?ЛР(и)^Р(А(]5)9
А
РГ(А)= 12п\е(е*«)?аи.
А
Лемма доказана.
Лемма 5. Пусть ф1(«)> Фг(и), Фз(и) таковы, что
я я я
| ф! (и) V (ЙК), [ ф2 (и) V (Йй), | фз (И) V* (<*И)'
являются проекциями величин 1(1), т](/), §Л0 ^#
<%ь{1 — ф, <№т\Ц — д), <%\М — Ц) соответственно. Тогда
Ф1 (и) = Ф2 (и) = Фз (и) = *"" ( 1 - =2-1 (той Р).
Ввиду формулы (7) достаточно доказать, что у{(и)~
= уг(и) = (р3(и). Из равенства
К')- /фЛ«М*/и) =
-4(0- /фЛ"ЖА0 +к(0- /фЛиК(*0
Ь —л ^ I.- —л ^
(15)
и ортогональности слагаемых в скобках правой части
соотношения (15) имеем
*1(?) = М|т)(')- /ф,(«)^(^«)Р +
+ М
!* (0 - С Ф1 (") V, (йи)
>&ш
§ 9
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
357
причем знак равенства возможен только тогда, когда
Ф1 И = Ф2 (и) (тоё Рг\ фь(и) = ф3 {и) (той Р3),
тс
1.(0= | Ч>1 («К (<*")•
С другой стороны, б| (</) = 6^(<7).в силу определения |5(/)#
Лемма доказана.
Полученные результаты могут быть сформулированы
следующим образом.
Теорема 4.Если|{^ — недетерминированная стацией
парная последовательность, то оптимальный прогноз
|(<?)(/) величины •!•(/) /го результатам наблюдения |($),
5 ^ / — д, дается формулой
Ь'(0 = /*"й
1_.^(^и)
*(*'"П
V (*/и),
где V — спектральная стохастическая мера последовав
тельности ^(/),
га=0 м=0
функция #(<г)^Я2 н<? имеет нулей в круге |г|<1, #(0)
положительно и \ § (еш) |2 = / (и), / (и) — производная абсо*
лютно непрерывной компоненты спектральной функции
последовательности \ (I). Квадрат средней квадратической
погрешности прогноза равен
-~ ] \п I (и) йи я
-я ^
п
причем сп определяется из соотношения
62(д) = 2ле -* 2 \с
2
п=0
{оо Я Ч оо
^Е2" \еыа\п1{и)йи\^спг\
м=1 -Я > П=0
Я
25Г />»И«)Л (16)
П=1 -Я ' П=0
В частности,
&(\) = 2пе
355 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
Теорема непосредственно вытекает из лемм 4 и 5,
формулы (7) настоящего параграфа, теоремы 1 и
замечания 2 § 7.
Прогноз процессов с непрерывным временем. Пусть
1(() ( —оо </< оо) — стационарный процесс.
оо
— оо
где V — ортогональная мера на прямой ( —оо<и<оо),
о»
—оо
Введем гильбертово пространство
и его подпространства 5#& (/) =* 5$ {& ($)» ~ оо<$</}.
В Ж\ определим группу операторов сдвига времени
8к( — оо <Н< оо), полагая
и продолжим определение 5/г на все Ш\ по
непрерывности. Тогда 5Л образуют группу унитарных
преобразований Ш\. Она обладает теми же свойствами с
очевидными изменениями, что и группа преобразований 5*
в случае дискретного времени. Задача оптимального
линейного прогноза для процессов %{1) состоит в отыскании
такой случайной величины \т {I) е Ж\ {I — Г), что
М|6(0-Бг(012<М|б(0-ч12
для любого элемента т)е Ш\{1 — Г). Эта задача имеет
единственное решение: величина \т($) является
проекцией %($) на Ж\{1 — Т). Положим
6^ (Г) = 6(Г) - УЩ№-Ы*)\2-
Величина 6 (Г) — средняя квадратическая погрешность
прогноза — является монотонно невозрастающей
функцией от Г и О<§(Г)<0, Если Птб(Г) = а, то процесс
называется регулярным (вполне недетерминированным).
§6]
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
359
Если 6(Г0) = 0 при некотором Г0, то <5М0с:^(/-Г0)
при любом I. Следовательно,
ЖъЮаПЖьЦ-кТо)
при любом / и 6(Г) = 0 при всех Г>0. В этом случае
процесс называется сингулярным (детерминированным).
Несингулярные процессы мы будем называть
недетерминированными.
Доказательство теоремы 1 непосредственно
переносится на процессы с непрерывным временем:
произвольный стационарный процесс допускает разложение
Ш = л(0 + Ы0>
где г] (0 — регулярный, ^5(^) — сингулярный стационарный
процесс, г\У) и 15(() некоррелированы и подчинены 1(().
Аналогом теоремы 2 является следующая
Теорема 5. Для того чтобы стационарный
процесс г) (0 был регулярным, 'необходимо и достаточно^
чтобы он мог быть представлен в виде
г
т|(/)= \а{1-в)Ъ(й8\ (17)
— оо
где 5 ($) — стандартный процесс с ортогональными
приращениями и
оо
— оо
В силу теоремы 4 § 7 эта теорема эквивалентна
следующей.
Теорема 6. Стационарный процесс регулярен тогда
и только тогда, когда он обладает спектральной
плотностью }(и) и
1±Ж-с1и>-оо. (18)
— оо
Докажем сначала, что процесс, допускающий
представление (17), регулярен. С этой целью введем
проекцию г)г(^) случайной величины ц{1) на Ж^^ — Т).
360 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ (ГЛ, IV
Поскольку Жг\ {1 — Т) = Жоъ {I — Т), случайная величина
%(/) может быть записана в виде
%(') = | Ф («)№).
— оо
С другой стороны, т] (/) —%(*) должно быть
ортогонально любой величине феЖ^(/-Г) и, в частности,
величине -ф^ (А), где А любое измеримое множество,
лежащее в (— оо, I — Г). Так как
М (Ч (0 - % (0)Ш) = | а (* - 5) хд («) ^ -
— оо
- / ф («) %а (5) №0 = | И'- *) - ф (*)1 <*«;-
— оо Л
то ф($) = а(* — 5), $<^ —7\ Итак,
%(0= / а(<-«){(Л)
— оо
И
1-Т оо
1!Лг(01Р = М|г!г(/)|2= / |а(/-8)|2Л-| |а(в)Р</«.
— зо Г
Таким образом, ||%(011~>0 при Г->оо, что и
означает регулярность процесса г)(^).
Более глубоким является обратное утверждение:
каждый регулярный процесс может быть представлен
по формуле (17), или, что то же самое, обладает
спектральной плотностью Ци), удовлетворяющей условию (18).
Для доказательства воспользуемся аналогичными
результатами, полученными для процессов с дискретным
временем.
Пусть 1(() — произвольный стационарный процесс и
оо
!(/)= | сииу{йи)
§ $3 ОБЩИЕ. ТЕОРЕМЫ О ПРОГНОЗЕ 361
— его спектральное представление. Перенесем меру у
с действительной оси ( — оо, оо) на интервал ( — я, л)'
с помощью формулы и = {§гу и обозначим
преобразованную меру через . V. Процессу ^(0 поставим в
соответствие стационарную последовательность 1(*) = К{%),
где
|(/г)= ]"<?"** (<Ю).
Воспользуемся теперь следующим фактом, который
будет доказан ниже: процесс \(1) регулярен тогда и
только тогда, когда регулярен процесс \{п) (лемма 7).
Таким образом, если ц{1) — регулярный процесс, то
г] (•) = /С (^1) — регулярная последовательность. Если $($) —
ее спектральная- плотность, то в силу теоремы 2 § 7
я
] 1п7(в)йв>-оо. (19)
Но тогда процесс ц{1) также обладает спектральной
плотностью !{и) и (1 + и2)!{и) = 27(0), Э=2агс1д«.
Поэтому из (19) следует (20). Теорема доказана.
Докажем теперь утверждение, использованное в
доказательстве теоремы.
Пусть ^(^ — произвольный стационарный процесс и
|(/г) определено с помощью соответствия К так, как
было указано выше.
Лемма 6. Имеет место равенство Ш^ (0) == Ж^ (0).
Доказательство. Покажем, что |( — п) е Жъ (0),
п>0 (при п = 0 это очевидно). Заметим, что е'е -----
Поэтому
Я ОО
1-й*
С другой стороны,
1 — Ш _ __
1 + ш ~~ ' 1 + ш
1_'И 1 + тАг=- 1 + 2 |<"^^5,
362 ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
откуда следует, что функцию ( ~ш ] можно
аппроксимировать ограниченной последовательностью функций
вида ^акеги8к, 8к<0, равномерно сходящихся на лю-
к
бом конечном промежутке ( — А, А). Отсюда вытекает,
что 1(-л)€= 5^(0). Покажем теперь, что 1(1)<Е1Жъ(0)
при ^<0. Имеем
ОО Я у ч
— оо —Я * '
так как при 0<р<1 и ^<0 подынтегральное
выражение в последнем интеграле остается равномерно
ограниченным.
С другой стороны, из равенства
-*е °°
'~ре-ге=(1-ре-ге)1] (-1)"РП е-м
следует, что упомянутое подынтегральное выражение
может быть равномерно аппроксимировано (р-фиксиро-
вано) функциями вида 2 ске~т. Поэтому 1(1)^ Ж% (0)
/г=0
при ^<0. Лемма доказана.
Лемма 7. Если % {I) = ^5 (I) + ц (^) есть разложение
процесса % (^) на сингулярную и регулярную компоненты,
то равенство 1(-) = К (%8) + К (ц) является разложением
\(п) на такие же компоненты.
Доказательство. Заметим, что Ж\х($) ^ Ж\2($),
I ее ( — оо, оо) тогда и только тогда, когда Ж^ (п) а Ж^ (п),
п = 0, ± 1, ... Действительно, еслиЖ^ (0) с= Ж\г (0), то
^1(0) = ^(0)с=^2(0) = ^Г2(0), откуда Ж%х {1) = 3'Жф)с^
с: 8*Ж^ (0) = Ж^2 (^), причем в этих соотношениях можно
поме&ять роли процессов (^ (*), ^> (0) и (^1 (п)> 1> (п))- О^
метим еще, что так как мера V подчинена процессу
§9]
ОБЩИЕ ТЕОРЕМЫ О ПРОГНОЗЕ
3$3
(К*), -оо<г<оо}, то Ж%^Ж%. Далее, пусть Щ)-
сингулярный процесс. Тогда Ж% = Ж^ = Ж^(0) = Ж^ (0).
Это означает сингулярность процесса %{п). Аналогично
получаем, что сингулярность %{п) влечет сингулярность
1((). Пусть 1(() регулярен. Если бы %{п) не был
регулярным, то имело бы место равенство %{п) = %{(п) + ц{ (п),
где последовательность 1\ (п) сингулярна и вполне
подчинена!^). Этому разложению соответствовало бы
разложение ^ (/) = |, (/) + г\х {I), где ^ (I) — по доказанному
сингулярный процесс, вполне подчиненный | (^). Но тогда
Р) Щ (0=>^1 (0 = 3$\х (0) ^ 0, что противоречит регу-
г
лярности процесса |(/). Итак, если Щ) регулярен, то %(п)
также регулярен. Аналогично доказывается обратное.
Отсюда вытекает утверждение леммы.
Результаты, полученные для прогноза стационарных
последовательностей, теперь можно с некоторыми
изменениями в формулировках и доказательствах перенести
на процессы с непрерывным временем. При этом нужно
пользоваться спектральным представлением
стационарных процессов с непрерывным временем и ссылаться
на результаты леммы 2 и теорем 3 и 4 § 7.
Например, формулировка леммы 4 дословно
переносится на процессы с непрерывным временем, а
доказательство нуждается только в тривиальных изменениях.
Из этого аналога леммы 4 вытекает следующая
Теорема 7. Для того, чтобы процесс \{I) был
недетерминированным, необходимо и достаточно, чтобы
оо
— ОО
где I (и) — производная абсолютно непрерывной
компоненты спектральной меры Р процесса ^(0*
Если & (0 = Л (0 + 1Л0 является разложением
процесса %(() на регулярную и сингулярную составляющие
и в соответствии с теоремой 5
Т1(0- \а{1-8)1{й8),
364
ЛИНЕЙНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. IV
ТО
*-т
— оо
а оптимальная средняя квадратическая погрешность
прогноза определяется из соотношения
т
62 (Г) = | | а (5) |2 Й5.
о
Другое выражение для оптимального прогноза имеет вид
Нт (ш)
Ы0 = |
Ли/
1
Н (ш)
V (Й«),
где V — стохастическая спектральная мера процесса I (/),
со Т
Н (ш) = —5=- | а (5) <?-'«* </$, Нт (ш) = -—=- Г а {$) е"1и8й$.
Функция Н(ш) определяется по спектральной
плотности 1{и) по формуле (23) § 7.
ГЛАВА V
ВЕРОЯТНОСТНЫЕ МЕРЫ В ФУНКЦИОНАЛЬНЫХ
ПРОСТРАНСТВАХ
§ 1. Меры, соответствующие случайным процессам
Теорема Колмогорова о построении вероятностного
пространства по конечномерным распределениям
случайного процесса со значениями в метрическом
пространстве Я?, в частности, указывает, как на измеримом
пространстве (5Г, 33), где ^ — пространство всех функций
со значениями в Я/, а 23 — минимальная а-алгебра,
содержащая все цилиндрические множества из #",
построить такую меру [л, чтобы для всякого
цилиндрического множества С величина \х(С) совпадала с
вероятностью того, что выборочная функция случайного
процесса принадлежит С. Эта мера \х называется мерой,
соответствующей случайному процессу ^(0> и ее всегда
можно построить, на каком бы вероятностном
пространстве ни был определен процесс 1(1). Если процесс %(^, со)
определен на вероятностном пространстве {Й, ©, Р},
Т — отображение О в ЗГ, определяемое соотношением
<°—>&(,,со), а ©0 —подалгебра ©, состоящая из
множеств вида Т~ С, где Се 53, тогда мера \1 является
образом меры Р, являющейся сужением меры Р на ©0>
при отображении Г, т. е.
ц(0«Р(Г-!С). (1)
Измеримое пространство (#", 23) и меру \1 на нем удобно
использовать при рассмотрении случайных процессов,
у которых заданы лишь конечномерные распределения.
С помошью этих характеристик можно исследовать
существование процессов с заданными конечномерными
366 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
распределениями, выборочные функции которых
обладают определенными условиями регулярности, различные
функционалы от выборочных функций процесса,
преобразования случайных процессов и т. п.
Рассмотрим измеримые функционалы от выборочных
функций случайного процесса. Назовем функционалом
от случайного процесса %(() всякую случайную величину,
определенную на вероятностном пространстве {ЗГ, 23, |х}.
Иногда удобнее рассматривать несколько более широкий
класс_ случайных величин: случайные величины на
{вГ9 Д р,}, где {33, \х} — пополнение меры {23, ^}. Поскольку
для всякой величины |, определенной на {&*, 23, р,},
найдется такая величина ^ на {#~, 23,. ц,}, что | = |(тос[ Д),
то это различие не принципиально. Однако при
построении различных конкретных функционалов у нас могут
получиться и 23-измеримые функционалы. Конечно, этого
можно избежать уело кнением построения, но мы этого
делать не будем.
Каждый функционал от выборочной функции
процесса должен определяться значениями процесса.
Покажем, что это справедливо для введенного класса
функционалов. Назовем функционал /(.*;(•))
цилиндрическим, если существует такая борелевская функция
1т{хь ..., хт) в дВт и точки 1Х, ..., 1т, для которых
/(*(-)) = /т(*(*!), •••> хЦт)). Если $т непрерывна, то
цилиндрическую функцию будем тоже называть
непрерывной. Очевидно, всякий цилиндрический функционал
23-измерим и, значит, определяет случайную величину
на {вГ9 23, |х}. Кроме того, значение функционала
определяется выборочной функцией процесса:
Распределение величины /т(|(^), ..., 1Ут))
совпадает с распределением величины /(*(•)) на &> ^3, \х}.
Естественно считать функционалом от выборочной
функции процесса ^(0 такую случайную величину цг для
которой найдется последовательность цилиндрических
функционалов 1{т)(х(-)) таких, что /(т)(| (• ))->Ч по
вероятности при т->оо. Покажем, что в этом случае
последовательность функционалов 1(т)(х(-)) сходится
по мере |х к некоторому ©-измеримому функционалу.
§ 1] МЕРЫ, СООТВЕТСТВУЮЩИЕ СЛУЧАЙНЫМ ПРОЦЕССАМ 367
Это вытекает из соотношения
= Р{|/(т,(1(-))-/(п)(|(-))1>е}.
(это равенство является частным случаем равенства (1))
и сходимости /(ШЧ|(')) по вероятности. Покажем теперь,
что для всякого 25-измеримого функционала / существует
последовательность цилиндрических функционалов /<*',
сходящаяся к нему по мере Д. Для этого достаточно
показать, что, каково бы ни было ^-измеримое
множество Л, существует последовательность цилиндрических
множеств Сп такая, что Хсп(х) — >Ха(х)- Если
930—совокупность указанных множеств, то: 1) 230— алгебра,
2) она является монотонным классом, 3) она содержит
все цилиндрические множества, значит она а-алгебра
и совпадает с 33.
Заметим, что если процесс |(^) определен на
вероятностном пространстве {О, ©, Р}, а ©0 —а-алгебра,
введенная выше, то функционалами от 1(-) являются все
@0-измеримые случайные величины. Если т] (со) —
©^измеримая величина, то г)(со) ^/(Г"1©), / — некоторый
ЭЗ-измеримый функционал. Мы будем писать г)(со) =
= /(!( ■,«>)).
Из формулы о замене меры в интегралах вытекает
соотношение
М/(|(.->о>)Н//(*)|1(Л0 (2)
для всякого функционала /, для которого интеграл справа
имеет смысл.
Рассмотрим теперь вопрос о возможности
построения меры на функциональном пространстве более узком,
чем пространство всех функций. Конечно, можно взять
любое 23-измеримое множество &~0, для которого \х (^0) = 1 >
и рассматривать меру на 5Г0. Но все интересные
множества функций не являются 23-измеримыми, поскольку
всякое ^-измеримое множество функций определяется
поведением функций в не более чем счетном числе
точек, а это не определяет таких свойств как
непрерывность, дифференцируемость, отсутствие разрывов
второго рода, измеримость и т. п.
368 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Поэтому естественно подойти к построению меры на
некотором функциональном пространстве ^0
следующим образом. Предположим, что пространство 8Г0 таково,
что, каково бы ни. было цилиндрическое множество С
из #", С()@~0 не пусто. Тогда можно рассмотреть в @~0
минимальную сг-алгебру 230, содержащую все множества
вида С(]ИГ0 (будем их называть цилиндрическими
множествами в Ф*^ш На цилиндрических множествах С0 в ^Г>
определим аддитивную функцию множества ^(^о) = М- {С\
если С0 = СП^го- Заметим, что это определение
однозначно: если бы С0 = С(1^"о и С0 = С, П-^"о, то тогда
пересечение [(С —&,)и(С! —С)]П^о было бы пусто, что
невозможно при СФС{. Очевидно, что 1д,э — аддитивная
неотрицательная функция множества. Необходимым и
достаточным условием для того, чтобы цэ могла быть
продолжена до меры на 330» является условие: для
всякой последовательности С% цилиндрических в ^0
множеств, для которой [}Сц=@~^ должно выполняться
п
неравенство 2 Но(^о) ^ М'О (^~о) = 1 • Это условие эквива-
п
лентно следующему: ^]х(Сп)^ 1 для всякой последова-
п
тельности цилиндрических множеств Сп^&~, для которой
п
Определим по мере \1 внешнюю меру \х*: для всякого
множества А
^(Л) = 1п1(2^(Ся); [}Сп=>А\.
Тогда возможность построения меры \х0 на 330 имеет вид:
М*(#о)—1- Сама мера |л0 при этом имеет вид \х0(А) =
= \х* (А) для всех А е 230. Покажем это. Заметим, что
|1(5) = 0 для всякого ЭЗ-измеримого множества 5, для
которого 5 (]ЗГ0--= 0. Действительно, в противном
случае $Г — 5 :э &~0 и, следовательно,
Очевидно, ст-алгебра 230 состоит из множеств вида А П ^~о>
где А — 93-измеримое множество.
Пусть А0 е= Э30, и Л0 = Л П #~0- Положим До (Л0) = \л (А):
Это определение однозначно, так как, если А3 = А Г) ^~о ^
§ Ц МЕРЫ, СООТВЕТСТВУЮЩИЕ СЛУЧАЙНЫМ ПРОЦЕССАМ 369
= ,4'П^"о, то (А-~А')1](А'-А)^ЗГ-$~0 и, значит,
1и (А) = \1 (А'). Заметим, что Д0 —счетно-аддитивная мера
на 230: если А1 попарно не пересекаются и Ло = Ак{)&~{Ь
то А* () А1 с: 9Г — &~0 при кф] и \1{Ак (] А1) = 0, а значит,
к к
Кроме того, для всякого цилиндрического множества С9
До (С0) = ^0 (С0)- Значит, Д0 = щ>' С другой стороны,
]1*(А0) = тЦ\1(А'), Л'еЗЗ, Л'гэ Л0} = ^ (Д),
если ^0 = ^4 0^0-
Таким образом, меру, соответствующую случайному
процессу, можно рассматривать на всяком множестве
функций #"0, имеющем внешнюю меру 1, при.этом мера
на этом множестве будет совпадать с внешней мерой.
Каковы же будут измеримые функционалы на
пространстве {ЗГ^ 230> Но)? Покажем, что для всякого 230-из-
меримого функционала /0(л:) существует такой 39-изме-
римый функционал Цх), что / (дс) ==/0 (х) при х е У0.
Пусть Ео,п — множество из Э50, определяемое
соотношением
Е"оп = \х: ~г<Ш<Ар-}> п>0, к = 0, ±1, ±2,...
Обозначим через Ек>п такое 23-измеримое множество,
что Ед'п = Ек'п (}@~о- Можно всегда выбрать
множества Ек* п так, чтобы выполнялись условия:
\) Екп при фиксированном п попарно не
пересекаются (в противном случае можно вместо Ек>п
рассмотреть множества
ЁКп = Ек'п- [} Еиа\
/=-оо /
2) Дк, п = Д2к, л + 1 Ц #>Л+1, п + 19 (ИШЧе МОЖНО ПОЛОЖИТЬ
делим теперь функцию 1(п)(х) равной к/2п на
множестве Ек*п и равной, например, + оо, если х^\^Ек*п*
к
370 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Тогда /<*> (х) < /<л+1> (х) < /<я> (х) + 1/272 и, следовательно,
}{п)(х) равномерно сходится к некоторой функции 1(х),
являющейся измеримой. Кроме того, | /(л)(*) — /о(*) К1/2",
если х^@~0. Поэтому 1{п) (х) -> /0 (х) при ^еУ0.
Значит, !о(х) = $(х) при х^!!Г0. Пусть существует еще одна
35-измеримая функция }'(х)у совпадающая с }0(х) на #"0.
Тогда УЗ-измеримое множество {х: /(х) Ф /' (х)} не
пересекается с ^~0 и, значит, имеет |х-меру 0. Таким
образом, каждая ©0-измеримая функция может быть
единственным образом (той |х) продолжена до ©-измеримой
функции.
Последнее соображение показывает, что для
изучения функционалов от случайного процесса перенос меры
на более узкое пространство ЗГ0 не играет существенной
роли. Однако функционалы, определенные на ^0, часто
имеют более ясный смысл. Например, если #~0 —
пространство непрерывных функций, то в #~0 будет
измеримым функционал
/0(л;) = 8ирл;(0.
Этот функционал можно продолжить на 5Г формулой
где Ы — некоторое счетное всюду плотное множество
значений аргумента. Конечно, первый функционал имеет
более естественный вид.
Очень существенным при изучении меры и
возможности ее перенесения на #~0 является следующее
обстоятельство: во многих случаях можно указать такое
счетное множество значений аргумента Ыу что
пополнение сг-алгебры 53^, минимальной а-алгебры,
порожденной цилиндрическими множествами, определяемыми
значениями х(1) при *е#, совпадает с 33. Так, если
процесс стохастически непрерывен, то в качестве N
можно взять любое всюду плотное множество значений
аргумента. То же самое будет в том случае, когда
процесс односторонне стохастически непрерывен. ,Можно
привести простое необходимое и достаточное условие
существования такого множества.
Лемма.. Для того чтобы существовало такое
множество Ы, что 33^ = 33, необходимо и достаточно, чтобы
§ II МЕРЫ, СООТВЕТСТВУЮЩИЕ СЛУЧАЙНЫМ ПРОЦЕССАМ 371
гильбертово пространство 3?2(\х) ^-измеримых функций,
интегрируемых с квадратом по мере |а, было сепарабелъным.
Доказательство. Если такое N существует, то
сепарабельность 3?2{\ь) вытекает из совпадения 3?2{\*)
с 3?2{\х,м), где М-^ — сужение меры \х, на 23^.
(Сепарабельность 3?2{\1М) вытекает из того, что в нем плотны
ограниченные цилиндрические функции, в которых в свою
очередь плотны непрерывные цилиндрические функции.)
Пусть теперь 3?2(\1) сепарабельно и [и /2> • •. — базис
в 9?2 (II). Для каждой 23-измеримой функции /й
существует такое счетное множество Мк, что /й измеримо
относительно 23^. Это вытекает из возможности
аппроксимации 1к цилиндрическими функциями. Тогда в
качестве N можно взять ^Л^.
Заметим, что существование такого Л/', что 93^ = 25,
не нужно путать с существованием такого Ыу что у
процесса есть Л^-сепарабельный эквивалент.
Построение сепарабельного эквивалента соответствует
переносу меры \х на множество ^0 всех Л^-сепарабельных
функций.
Однако для проверки непрерывности процесса
достаточно рассматривать значения процесса на множестве Л?
как в том случ_ае, когда процесс УУ-сепарабелен, так и
в том, когда 23^ = 23. Первый случай рассматривался
в гл. III, § 5. А во втором следует заметить, что для
вычисления внешней меры множества #~0 достаточно
использовать цилиндрические множества из 23^.
В заключение этого параграфа сформулируем общие
условия, обеспечивающие построение меры на
множествах <& аЯГ и @)^@~, где ^ — множество
непрерывных функций, а ^ — функций без разрывов второго
рода. Очевидно, в первом случае процесс должен быть
стохастически непрерывен, а во втором иметь не более
счетного числа стохастических разрывов. В обоих
случаях легко указать такое Лг, 'что 23^ = 23 (Л/' — счетное
всюду плотное множество значений аргумента). Сам
процесс будем считать определенным на некотором
компакте К Ь^К) в первом случае и на замкнутом
отрезке во втором. Подсчет внешней меры
соответствующих множеств облегчается тем, ' что можно указать
372 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V,
минимальное ^-измеримое множество, содержащее
множества ^ и 2).
Условия существования меры на (й?. Для
того чтобы меру \х можно было перенести на %?у
необходимо и достаточно, чтобы выполнялось соотношение
(оо оо ■ \
ПУЛ П {*(•): |*(*)-*.(5)|<-Ц|=1.
5^ )
Легко убедиться, что указанное под знаком меры \ь
множество является минимальным ЗЗ^-измеримым,
содержащим 9? (для этого достаточно рассмотреть функции
х(-) лишь на Л'т).
Условия существования меры на 3). Для
того чтобы меру \х можно было перенести на &,
необходимо и достаточно, чтобы
Пи П {х(-):\х(()-х(з)\<1}и
з<Ки<8 + \/1
и{х{-): \х{и)-х(1)\<Щ=1.
То, что множество, стоящее под знаком р,,
минимальное ЗЗ^-измеримое, содержащее 2), вытекает из
условий отсутствия у функций х(() разрывов второго
рода (см. гл. III, § 4).
§ 2. Меры в метрических пространствах
В предыдущем параграфе указывалось на
возможность переноса меры р,, соответствующей случайному
процессу с пространства всех функций У на некоторое
более узкое функциональное пространство 5Г0. В этом
параграфе нас будет интересовать тот случай, когда
пространство ^~0 является сепарабельным метрическим
пространством, а сг-алгебра 230 совпадает с сг-алгеброй
всех борелевских множеств из &~0. Чтобы было ясно,
что интерес к этому случаю не лишен смысла,
рассмотрим тот случай, когда @~0 совпадает с пространством
§2] МЕРЫ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ 373
№ вещественных непрерывных функций. Очевидно, № —
метрическое пространство с метрикой р(х, ^/)==зир|д:(/) —
— уЩ. Если рассматривать процессы, определенные на
компакте, то № будет сепарабельным. Покажем, что 230
совпадает с сг-алгеброй борелевских множеств. Заметим
сначала, что цилиндрическое множество {х( •): л;(/)е^}Ц
П №у где А — борелевское множество, является боре-
левским множеством в №. ПоэтОхМу все множества из
230 являются борелевскими в №. Чтобы убедиться в
принадлежности всех борелевских множеств из № сг-ал-
гебре 3?0, достаточно показать, что 330 принадлежит
любая замкнутая сфера из №.
Пусть
5=ф(-): 8ир|*(/)-у(/)|<р}
—•сфера с центром в у(-)^№ радиуса р. Тогда
5 = «'Л[Л {*(•): |*(*)-0(*)1<Р)1
где N — любое счетное всюду плотное в области
определения множество значений аргумента.
Как мы увидим далее, в пространстве функций без
разрывов второго рода 0 также можно ввести метрику
так, чтобы 230 совпадало с сг-алгеброй борелевских
множеств из 3). Для дальнейшего конкретный вид
пространства не играет роли. Мы будем рассматривать
некоторое абстрактное сепарабельное метрическое
пространство 35 с элементами х, у, ... , метрикой р(л;, у).
Через 23 будем обозначать сг-алгебру борелевских
множеств из 35, на 23 будет задана мера \х. Если К —
некоторое подмножество 35, то будем через №к
обозначать пространство всех непрерывных ограниченных
функций, определенных на КУ вместо №$е будем писать просто
№. В №к естественно ввести метрику
Рк(!> г) = зир \!(х)-§(х)\.
Непрерывные функции на 36 образуют более простой
и в то же время достаточно богатый класс функций;
из этих функций с памощью операции предельного
перехода можно получить все ©-измеримые функции.
374 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Поэтому мера \х полностью определяется
значениями интегралов | / (х) \х {их) при/^^: взяв
последовательность !п^сё> так, чтобы /„-^->Хл> где %А —
индикатор множества А из 23, можно найти \х(А). Во
многих случаях мера \х не задана и неизвестно
существует ли она. Заданы лишь предполагаемые значения
интегралов /,(/)= \ 1(х) \1{с1х). Возникает вопрос, при
каких условиях функционал />(/), определенный на $\
допускает представление в виде интеграла по некоторой
конечной мере? Ответ на этот вопрос для полного
метрического пространства дает
Теорема 1. Для того чтобы функционал Ь{!)у
определенный на пространстве <& непрерывных
ограниченных функций, заданных на полном метрическом се-
парабельном пространстве 8в> допускал представление
М/)=//(*М<**), (1)
где [I — конечная мера на 23, необходимо и достаточно
чтобы выполнялись условия:
1) М/)>0 для всех />0;
2) Ь^и + с^^сМЫ + с^М;
3) для любого е>0 существует такой компакт КгУ
что для всякой функции } (х), для которой / (х) = 0 при
х е /Се, выполняется условие
Щ/)1<е11Л1,
где||/|| = 8ир|/(*)|.
х
Доказательство. Необходимость.
Необходимость условий 1) и '2) очевидна. Так как для /\
удовлетворяющей условию 3)
|//(*)|1(А*)|Ч / ^и)|х(^)|<||/||ц(Я?-^е),
то для доказательства необходимости условия 3)
покажем, что для всякого е>0 существует такой компакт
Ке, что 11(3/— /Се)^е. Пусть {хкУ 6 = 1,2, ...} —всюду
плотная в #? последовательность, а 8г{х) — замкнутая
§ 2] МЕРЫ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ 375
сфера с центром в х радиуса г. Для каждого г можно
указать такое Ып что
Положим
|А(Я?) — |х ( 0 Зг(хк))<ге.
оо 1^2"П
*е= Л Г) 52-л(*д),
тогда /Се — замкнутое множество и при каждом п имеет
конечную 2~"~сеть. Значит, Кг — компакт. Далее
п = \ \ к=\ / я=1
Необходимость условий теоремы доказана.
Достаточность. Пусть Р — некоторое множество*
Положим Д (Р) = 1п! Ь (/), где 1пГ берется по всем /^0,
для которых \{х)^\ при хе/7. Отнесем Т7 к классу
230, если ДС^О^О, где Р'— граница Р. Покажем, что
©о образует алгебру множеств и Д является
аддитивной функцией на 230. Для этого заметим, что
Д (А II В) < Д (А) + Д (В) и Д (А) < Д (Б) при Л сгВ,
как легко следует из определения Д. Далее Д((#/— /7)/)==
=д (/"), а д ((/?, и р2у) < д (/>; и П)< д (^)+а (^). »
значит, множества Р, для которых |х(/7/) = 0, образуют
алгебру. Докажем аддитивность Д на 930. Пусть Р{ и Р2—
два непересекающихся множества из ЯВ0. Покажем, что
й^У^^йИ + йй).
Взяв произвольное е> 0,, можем найти такие функции
/иФ, />0, 1>Ф>0, что1(Ф)<е, !(/)< Д (/^ 1^+8,
Ф (а:) = 1 при х ей [7^] П [/У. а / (л:) > 1 при х е= У7! II /^
Положим далее
М ' 1ф(дг), *е[^2]
и продолжим !\(х) по непрерывности на все 36 так,
чтобы 0 ^/! (х) ^ / (#) + ср(х) (если ^(х) —любое не-
прерывное неотрицательное продолжение, то 1\{х)=*
■=тт[§(х),1(х) + ч>{х)]).
376 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V -
Пусть 12 (х) = I (х)„+ Ф (х) — [{(х). Очевидно, /2 —
неотрицательная непрерывная функция и \2(х) = }(х)=*\ при
х^ Р2. Поэтому
и в силу произвольности е
Из этого соотношения и полуаддитивности [I и вытекает
аддитивность [л на 930.
Заметим, что в том случае, когда [Р{] П [Р2\ — 0»
функцию ф можно выбрать равной нулю, и поэтому
для таких множеств, даже не принадлежащих 230,
выполняется соотношение
А (Л ^Н №) + №)•
Покажем теперь, что \х может быть продолжено как
мера на а(230). Для этого достаточно доказать, что для
всякой последовательности ^п убывающих множеств из
930, для которой (}&п= 0, р, (!?„)-> О при п->оо.
Предположим, что это не так и можно указать такую
последовательность множеств $п из 930, для которой
\х(9п)>6>09 а П^гг=0- Заметим, что для всякого
&7<ее330 и е>0 существует такое замкнутое множество
Р €= 230, ЧТО Р С2 % И р, (#)< р, (Р) + 8.
Действительно, пусть [(х) — непрерывная функция
и Рс = {х: }(х) = с}. Тогда для всех с, за исключением,
быть может, счетного числа, р, (Рс) = О, так как при
различных с{, ...УС1 множества РС{, ...,РС1 замкнуты
и попарно не пересекаются, и значит, ^^(/^^шУ/^Л^
<Д(Я?).
Обозначим через /(х) такую функцию, что ^(л:)=1
при х<=[%-$], !(х)<1 при хШ[%-9] и д(Я?-#)>
Пусть К <1— такое число, что \Х(Рк) = 0. Обозначим
через 5 множество {х: }{х)>к}. Тогда
$ 21 МЕРЫ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ 37Г
Так как 5е=330, то Ж — 5 = {х: !{х)^к} — замкнутое
множество из ®0 и
Остается подобрать X настолько близким к единице,
1 — X е
чтобы —г-— \х ($в — *§) + тгу- было меньше е.
Пусть теперь /^ — замкнутые множества из 930, для
которых Рка^к и И^)^Й(^)+ ^+1 - Положим
^ = П 'V Тог*а
&=1
й(/7п)>й(^)-21д(^-^)>б-5]д^тг>т-
6=1 6-1
Таким образом, мы построили убывающую
последовательность Рп замкнутых множеств из 330, для которых
\х(Рп)>у, а Р)/7«=0. Выберем теперь, воспользо-
вавшись условием 3), такой компакт К, чтобы для
всех }(х), для которых 1(х) = 0 при х е /С, ^(/)^т11Л1-
Покажем, что для всех /г множество /^ имеет непустое
пересечение с К. Действительно, если рп(]К=0, то
можно построить непрерывную функцию &(х), для
которой 0<?М<1, 8(х)=1 ПРИ х^Рп, &(*) = 0 при
*<=/С. Тогда й(/7Гг)</Ля)<11я!1 Т^Т» что ПР0ТИВ0~
речит построению Т^. Значит, последовательность
непустых компактных множеств Кп — Рп^К
удовлетворяет условиям Кп^>Кп+1 и Г)Дл==0> что невозможно.
Из полученного противоречия вытекает счетная
аддитивность \х на 930 и возможность продолжить ее на а(530).
Обозначим полученную меру на сг(230) через |х.
Заметим теперь, что, как уже указывалось, почти для всех с
множество {х: I (х) < с} <ее 330, какова бы ни была
непрерывная функция /. Поэтому {х:[(л;)<с}Еа(80) для
всех с, если только /е^. Отсюда вытекает, что а(3?0)
378 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V"
содержит 23. Покажем, наконец, что выполняется
равенство (1). Пусть 0<[(х)<1 и с0<0<с1 < ... <сп-х <
< 1 <сп таковы, что множества {х: / (х) = с$ е 230. Тогда
для всякого е>0 можно указать такие непрерывные
функции Фа-(а:)^0 и ук{х)=\ при х е Ек = {х: ск <
</(*)<<?*+,}, к = 0, ..., /г- 1, что I (срл)< ц (Дл) + ~ .
Поэтому
/п—Л \ п — \
1(})<ь(^ск+т\<^ск+111(Ек) + г^
< Г / (а:) \1 {ах) + г + тах (ск+1 - ск).
•> к
Так как е + тах{ск+1 — ск) можно сделать сколь
к
угодно малыми, то 1(/Х ( / (х) \х {их).
Точно так же
Поскольку Ь{1) = \1{%?)у то —/,(/)< — Г }{х)\х,{йх).
Значит, равенство. (1), а с ним и теорема, доказаны.
Замечание 1. Как вытекает из условия 3)
теоремы, для всякой конечной меры |х на 23 и всякого
е>0 можно указать такой компакт /С, что \х,{3в — /С)<е.
Замечание 2. Легко видеть, что при
доказательстве достаточности условий теоремы полнота никак не
использовалась. В то же время она существенна при
доказательстве необходимости. Условия теоремы будут
также необходимы, если пространство 36 является боре-
левским множеством в своем пополнении '36. Тогда для
всякого е>0 можно построить такой компакт К в 36,
чтобы Зб^К и \1{%?-К)<г.
С другой стороны, если ^ — неполное пространство,
предложенное доказательство необходимости условия 3)
теоремы даст существование компактного в 36 или
вполне ограниченного в 36 множества КУ
удовлетворяющего условию \х{36 — К)<г. Рассматривая функционал
Ь{у) лишь на тех функциях ф, которые могут быть
§ 2] МЕРЫ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ 379
продолжены по непрерывности на все 36 (это функции
равномерно непрерывные на каждом вполне ограниче-
ном множестве /С__из 36), мы можем построить меру Д
на (36, й), где Й — а-алгебра борелевских множеств
пространства й/\_ Если при этом окажется, что 36 как
подмножество 36 имеет_внешнюю меру, совпадающую
с мерой пространства 36 (т. е. с Ь(1))> то меру р, можно
перенести на 36, как это указывалось в предыдущем
параграфе. Для того чтобы внешняя мера
пространства 36 оказалась равной /,(1), достаточно, чтобы для
всякой последовательности неотрицательных непрерыв-
оо
ных функций ф„, для которой 2 Фгг (*)^1> ПРИ каждом х
оо
выполнялось неравенство ]& Ь(цп)^Ь(1). Последнее
1
вытекает из того, что внешняя мера любого
множества А из 36 может быть определена как т! 2 Ь (фД
п
где т! берется по всем последовательностям
неотрицательных непрерывных на 36 функций, для которых
2фя(*)>1, х<^А.
Сформулированное условие эквивалентно следующему-
для всякой монотонной последовательности
неотрицательных непрерывных функций уп из Ф9 для которой
срп(х) |0 при п->оо для всех х, Пт /,(фл) = 0. Из тео-
«-»оо
ремы Лебега о предельном переходе под знаком
интеграла вытекает, что это условие и необходимо. Таким
образом, в случае неполного пространства имеет место
Теорема 2. Для того чтобы функционал Ь((),
определенный на пространстве Ч? непрерывных
ограниченных функций, заданных на метрическом сепарабельном
пространстве 36, допускал представление (1), где \1 —
конечная мера на 36, необходимо и достаточно, чтобы
выполнялись условия:
1) Ь([)>0 для всех />0;
2) Ь (с^ + С2/2) = сгЬ (!\) + с2Ь (/2) для всех
вещественных с{ и с2 и Д, /2 из Ф;
380 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
3) для всякой убывающей последовательности
неотрицательных функций фя'е*??, для которой уп(х)->0
для всех х, Ь (фи) -> 0,
4) для всякого е>0 можно указать такое вполне
ограниченное множество /С, что |/, (/) |<^е||/|| для всех
I ее %?, для которых / {х) = 0 при х е /С.
В заключение этого параграфа рассмотрим вопро'с
об определении интегралов от непрерывных функций
в том случае, когда ^ — пространство непрерывных на
[а, Ь] функций 6 метрикой р(х, у) = $ир| х{1) — у{1) |,
а мера \х— мера, соответствующая некоторому
случайному процессу. Будем предполагать, что известны
частные распределения этого случайного процесса:
^/...../л(^*1> •••> &хк) ~~ совместное распределение
значений процесса в точках 1Ь ..., 1к. Обозначим через а
некоторое разбиение [а = 1оа}< 1\а)< . .. <^п} = Ь} отрезка
\аг *], |а| =тах|/Г|, - 4а)|. Пусть ,г(.)бй?. Положим
к
х» (/) - * №+-^4- [х (/&) - * 0П]
при
Очевидно, хаЦ) — кусочно-линейная функция,
совпадающая с х(1) в точках разбиения а. Если х(*)^36у то
р(лг(-)| л'а(*))—>0 ПРИ |а|~>0. Пусть теперь / —
некоторый непрерывный функционал. Тогда для всех х е 36
/(ж)=Нт/(.г0).
|а|-»0
Обозначим !(ха) = 1а(х). Функционал 1а(х) является
непрерывным цилиндрическим функционалом. Если
||/||<оо, то II/аII^11/II и на основании теоремы Лебега
[Цх)М(1х)=\\т Па(х)11(ах). (2)
* |О|->0 •>
Функционал /а (х) имеет вид фа (х (/оа)), ..., х (/«а))).
Поэтому интеграл в правой части (2) может быть вычи-
§3}
МЕРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ
381
слен с помощью конечномерных распределений:
Г /0 (X) \1 (их) = Г фа (х0у . . ., Хп) Р (а) ,(«) (А*<ц • • •, ^п)-
(3)
Формулы (2) и (3) дают возможность определять
интегралы от непрерывных функционалов.
§ 3. Меры на линейных пространствах.
Характеристический функционал
Пусть ^ — действительная прямая. Тогда
пространство & всех функций х(1), определенных на некотором
множестве Т и принимающих значения из 36, является
линейным вещественным пространством. Обозначим
через 3? пространство всех линейных функционалов I
на ЗГ следующего вида:
Цх)=%скх{*к), (1)
где /г —произвольное натуральное число, {1Ь ..., 1п}—
некоторый набор точек из области определения
процесса, <^ — некоторые вещественные числа, а-алгебра 33,
определенная в § 1, совпадает с минимальной а-алгеб-
рой, относительно которой измеримы все функционалы
из 2?. Мера |х на 33 полностью определяется значениями
ее на множествах вида {х: 1(х)<а} для всевозможных/.
Это вытекает из того, что, зная значения меры \х на
указанных множествах, мы можем вычислить интеграл
| е" <*> *х {их) = М ехр < I ^ ск\ {1к) |, (2)
где \{1) — тот случайный процесс, которому
соответствует мера |х, а значит, и совместную
характеристическую функцию величин |(^), ..., ^(/я), которая
позволит найти совместное распределение ^(/,), ..., \{1^
для любого набора значений аргумента. Таким
образом, зная интеграл (2), можно определить частные
распределения процесса |(/), они же полностью
определяют меру |х.
382 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
В том случае, когда мера \х переносится с У на
более узкое пространство &~0, это пространство @~0 часто
также оказывается линейным пространством. На этом
пространстве будут по крайней мере определены
линейные функционалы вида (1) и <т-алгебра ®0-измеримых
в @~0 множеств также будет совпадать с минимальной
а-алгеброй, относительно которой измеримы все
линейные функционалы вида (1). Из сказанного выше
вытекает, что для задания меры ц, в этом случае достаточно
знать распределения всех линейных функционалов на ^Г0.
При рассмотрении мер на различных линейных
функциональных пространствах конкретный вид
пространства часто оказывается несущественным. Поэтому
удобно исходить из следующей общей схемы. Пусть
^ — произвольное линейное пространство (над полем
вещественных чисел), 3? — некоторое линейное
множество линейных функционалов /(х), определенных на 36.
Обозначим через ® минимальную а-алгебру,
относительно которой измеримы все функционалы 1(х) из 36.
Будем рассматривать вероятностные меры \х на 36.
Мера \1 полностью определяется своим
характеристическим функционалом
Х(/)=]><*>|1 (</*). О)
Покажем это. Будем называть цилиндрическим
множеством из $Г всякое множество вида {х: 1{(х)^Аь ...
. .., 1п(х) е= Ап}, где п — некоторое натуральное число,
/], ..., 1п — функционалы из 36, а Аь ..., Ап — борелев-
ские множества на прямой. Пусть ©0 —алгебра всех
цилиндрических множеств. Очевидно, всякий
функционал 1^36 измерим относительно ©0, так что а(©0) = 23.
Поэтому достаточно определить меру \х на ©0. Если
функционал ф(х), определенный на 36, имеет вид ф(х) =
^ ё(1\(х)^ •••> 1п(х))> гДе п~" некоторое натуральное
число, 1и ..., 1п^36, а §"(5!, ..., зп) — борелевская
функция переменных, то будем называть ф
цилиндрической функцией и непрерывной цилиндрической, если
Ф — непрерывная функция. Чтобы задать меру \х на ©0,
достаточно знать интегралы \ (^{х)\1{йх) для
непрерывных ограниченных цилиндрических функций <р, а такие
§ 33 МЕРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ 383
функции являются пределами всюду сходящейся
последовательности, в совокупности ограниченной,
тригонометрических многочленов вида
N Г N }
Т(х)=%скехр\1 2 **/'/(*)• (4)
Остается заметить, что формула (3) определяет
значения интегралов от функции Т (х) вида (4)
п , п ^
Посмотрим, насколько произвольным может быть
характеристический функционал %(/).
1) Он обязан быть положительно определенным:
каковы бы ни были 1Ь ..., 1п из 3? и комплексные
числа аи ..., ап
^(/г'/)«Л>0, (5)
к, /
так как
к, / = 1 |а; = 1
|х {их) (
2) Кроме того, функционал %(1) непрерывен в
следующем смысле: будем считать, что /„->/, если 1п(х)->
->1(х) для всех х^36\ тогда %(/„)-»%(/) при /„-*/.
Пусть теперь на 35 задан функционал %(/),
являющийся положительно определенным и непрерывным
в указанном смысле. Достаточно ли этих свойств для
существования такой меры \х, чтобы выполнялась
формула (3)? Заметим, что каковы бы ни были 1и ..., 1п^2?,
функция ф^, ..., 5п) = х 2^4 является
характеристической функцией аргументов $ь ..., 8п. Поэтому
существует распределение в я-мерном пространстве
^/г .... 1п№щ, ..., йип) такое, что
ф(«1, • • •. *») = ) е1 '*"*Л, 1п{*Щ, .... йип).
384 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Определим функцию множества соотношением
)х({х: Цх)*=А19 ..., /я(*)€= Ля}) =
• А1 АП
Нетрудно убедиться, что в том случае, когда одно и
то же цилиндрическое множество может быть
выражено несколькими способами, будут получаться одни
и те же выражения для функции ^г. Функция р, будет
аддитивна на ©0 и может быть продолжена до счетно-
аддитивной на каждой а-алгебре ©^'"'^« —
минимальной сг-алгебре, относительно которой измеримы
функционалы /,, ..., 1п. Поэтому для всякой ограниченной
борелевской функции §(ии ..., ип) и любых 1Х; ..., 1а
можно определить интеграл
/#(М*)> •••> 1п{х)\1(йх).
В частности,
Таким образом, всегда по %(1) можно построить
конечно-аддитивную функцию множества \х, являющуюся
счетно-аддитивной на каждой а-алгебре ©^ '«так,
чтобы выполнялось равенство (3). Существуют простые
примеры (некоторые из них будут приведены в § 6),
показывающие, что не всегда у, будет
счетно-аддитивной на ©о и> значит, не всегда ее можно продолжить
до меры, заданной на 93. Но оказывается всегда
можно построить некоторое расширение §5
пространства Я/, в котором существует такая мера ц; при этом
§В будет также линейным и функционалы из 9? можно
продолжить на все $В так, чтобы они были линейными
на 9. Покажем, как это можно сделать.
Пусть 9"$ обозначает пространство всех числовых
функций ф(/), определенных на 3! (эти функции могут
принимать и бесконечные значения, но определенного
знака). Определим вещественную случайную функцию
1(1) на 9 так, чтобы для всякого набора 1и ..., 1п из 3?
*31
МЕРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ
385
совместное распределение величин ^(/г), ..., 1(1п)
задавалось следующей характеристической функцией:
Мехр{/21^6(/л)} = х(|11Мл].
Легко проверяется согласованность соответствующих
распределений, так что существование случайной
функции 1(1) вытекает из теоремы 2 § 4 гл. I. Пусть
р, — мера на 9"%, соответствующая \ (/). Перенесем
меру р, на более узкое пространство.
Обозначим через А# множество всех линейных
функций Я(/) на 3?, для которых
Я (сх1х + с212) = с {К (/]) + с2Х (1г)
при всех /ь 12^ 3? и вещественных сь с2.
Покажем, что внешняя мера множества А# равна
единице.
Пусть 5Д — любая последовательность цилиндриче-
оо
ских множеств в #~^, для которой |~) 5„ П Ау пусто. Не
/1=1
ограничивая общности, можно считать, что множества 5„
определяются значениями функции ф в точках 1и . . ., /д,
где {1к, к = 1, 2, ...} — некоторая последовательность
функционалов. Выпишем по порядку все линейные
соотношения, которым удовлетворяют функционалы:
п
2 спк1к = О
&=1
(если /„ линейно не зависит от 1и ..., /п_ь то
коэффициент спп = О, в противном случае с„га ^= 0).
Пусть йп = (ф: 2 спйф(/*) = О}. Тогда
оо оо
(\8п{\А?= П(5„ПЙ,П ... ПА,).
гг=1 /1=1
Так как 5П П А П .. • П &п — убывающая
последовательность цилиндрических множеств, то из соотношения
оо
0 = ГН5«по1п ••• пд„]
п = 1
13 И. И. Гихман, А. В. Скороход
886 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
вытекает: 5„ПАП ••• П^л-^0 пРи я-*оо. Заметим,
наконец, что & {йп) = 1 для всех /г, поэтому {х (5„ П А П
П ... [)Оп) = Д (5„) и, следовательно, [х(5л)->0. Это и
означает равенство единице внешней меры А#. Значит,
меру \х можно перенести на А#. Пусть далее Х0 —
линейное многообразие в 36, для которого / (л:) = 0 при
всех х^ Х0, 1^3?, а X1 — фактор-группа 36 по Х0.
Каждый элемент х1 е X1 можно рассматривать как
линейный функционал на 36 \ х1 (/) = / {х)у где а: —любой
представитель класса смежности х1 по той Х0.
Обозначим теперь через 36 множество пар х = (х; Я), где хе!0,
ЯеЛ^. Пусть Р —некоторый линейный оператор,
переводящий 36 в Х0, для которого Рх = х для всех х^Х0
а хг(х) обозначает тот класс смежности из X1,
которому принадлежит х. Тогда существует естественное
вложение 36 в 36\
х->(Рх, х1(х)).
Определим теперь на 36 а-алгебру Й множеств вида
§ = {х = (х; Я): Яе=^},
где ^ —любое подмножество из 91 — а-алгебры
подмножеств в А#, на которой определена мера \х. Положим
далее [*,(§) = \И!§) и покажем, что это и будет искомая
мера. Заметим, что функционалы / можно определить
на 36 по формуле
Цх) = Ц(х; Я)) = Я(/).
Этот функционал является линейным, причем он
совпадает с 1(х) на 36, рассматриваемом в качестве
подмножества 36\ 1(х) = 1((Рх; х1(х))), поскольку ^(л^как
элемент А# определяется формулой х1 (х) (/) = / (х).
Рассмотрим, наконец, интеграл (3). Как вытекает1 из
построения меры |1, на цилиндрических множествах
| е» <*>|1 ух) = | е* ®& (йК) - Ме*{1) = х (О-
Таким образом, [х и будет искомой мерой.
Особенно просто построить 36 в том случае, когда Х$
состоит из одного элемента 0. Это будет в том случае,
когда множество функционалов 36 настолько богато$
§ 3] МЕРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ 387
что для всякой пары хх ф х2 из 36 найдется такой
функционал /, что 1{хх) Ф 1(х2). Тогда в качестве §В можно
взять само пространство А&, причем каждый элемент
хе^Зб определяет элемент из А% по формуле
х(1) = 1(х).
Очевидно, всякая мера на 36 определяет
характеристический функционал %(1) на 36, однако он не
обязательно будет непрерывным в смысле, указанном в
условии 2). Чтобы условия 2) выполнялись, необходимо и
достаточно, чтобы мера Д обладала следующим
свойством: для всякой последовательности 1п, для которой
1п(х)"^0 для всех хе^, /«(^)->0 по мере \х. Заметим
еще, что если. 96 и 36 выбраны так, что пространство А%
совпадает с 36, построенная нами мера будет мерой на 36.
Пусть теперь «^ — линейное нормированное полное
сепарабельное пространство. Тогда в качестве 36
естественно взять пространство всех непрерывных линейных
функционалов 36* (его элементы будем обозначать х*).
Минимальная а-алгебра, относительно которой измеримы
все функционалы х* (х), совпадает с а-алгеброй 33 всех
борелевских множеств из 36. Всякая вероятностная
мера \х на 23 определяется своим характеристическим
функционалом
Х(**)= ^е1**ЬЩйх).
Этот характеристический функционал будет
положительно определенным и слабо непрерывным на 36*. Если
задан функционал % (л;*), обладающий этими свойствами,
то можно построить конечно-аддитивную меру \к на
алгебре @0 всех цилиндрических множеств. Для того
случая, когда 36* сепарабельно, найдем необходимое и
достаточное условие, чтобы эта мера могла быть
продолжена как счетно-аддитивная на 23. Для этого нужно,
чтобы \х(8п)->0 для всякой последовательности 5„
цилиндрических множеств, удовлетворяющих условию
Р)5„ = 0 и 5я:э5я+1. Пусть множество 5„ имеет вид
{х: (1Х (х), ..., 1п (х)) е Лп}, где Ап — борелевское
множество из Ж1. Назовем 5Д замкнутым, если Ап замкнуто
шг&п. Оказывается, что достаточно проверить непре-
13*
3§3 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
рывность лишь на замкнутых 5„, так как для всякого
е/г>0 можно указать такое замкнутое Рп а Ап, что
»{Зп)-ц({х: (/,(*), .... 1п(х))еРп})<*п-
Используя это соображение, найдем условие
существования меры р. на 33 с данным характеристическим
функционалом.
Пусть {**(*), к=1, 2, ...] —всюду плотное
множество на единичной сферр пространства §в\ Так как
| х | = 8ир х*к (х), то в случае счетной аддитивности меры \1
к
выполняется соотношение
0= Пт \1{{х: \х\>Щ=* Пт Пт [х({х: зирх\(х)>М).
Таким образом, для счетной аддитивности меры \х
необходимо выполнение условия
Пт Пт |х({дг: тр х!(х)> Щ) = 0. (6)
Покажем достаточность этого условия. Пустых — конечно-
аддитивная мера на цилиндрических множествах,
построенная по %. Из (6) вытекает, что для всякого е>0
можно указать такое М, что для всех п
и[\х: х\(х)<Л[, 6=1, ..., /г]) > 1 — е.
Предположим, что для некоторой последовательности
замкнутых цилиндрических множеств 8п=[х: (х*{(х), ...
..., «Г(х))е рп\ 5н=)5п+1, выполнено соотношение
И.(5я)^2е. Покажем, что тогда П ^п не пусто. Пусть
К„ = {х: и|<;У}, Кп„={х: хк(х)<:Ы, Л— 1, ..., п].
Пересечение 5Л и Км не пусто. Действительно, если
Зп(]Км пусто, то й= 1п! \х\>Ы (так, как этот т{
достигается). Положим
8(Щ, ..., ил) = т!{|л;|: х\(х) = и{, ..., ** (*) = «„}•
Тогда множество 5Л входит в множество {л;: §(х](х),...
...,^(х))>^|. Множество {(и,, ..., ип):М<ц(и{,..., «„)<<*}
в Мп открыто и является разностью двух односвязных
§ 3]
МЕРЫ НА ЛИНЕЙНЫХ ПРОСТРАНСТВАХ
389
областей. Поэтому можно указать такой многогранник
с гранями вида \(ии ..., ип): 2иТцЩ = Ъ} \, /= 1,..., т,
чтобы множество {(ии ..., мл): §"(*/!,..., *О^М лежало
целиком внутри него, а множество {(ии ...,ип): §(иь ...,ип)^с1}
вне этого многогранника. Тогда множество 8п лежит
полностью в сумме множеств
и каждое из слагаемых имеет пустое пересечение с /С,у.
п
Обозначим у* (х) = ^ гцх\ (л*).
Множество \х\ у*(х)^Ь.\ имеет с Км пустое
пересечение тогда и только тогда, когда ^/>||#)|^-
Пусть т4т = 2/. Тогда 5Л целиком лежит в мно-
. ЬА
т
жестве И [х: г) (х) > N + 6}, где 6 = Ы т-^тЬ1 - Л' > 0.
Из непрерывности /(V) вытекаег, что почти для
всех аь .. ., аш
1\пц1([х: г] к(х)<а[У ..., г^к(х)<ат}) =
«ц^ОкХа,,..., <,(*)< ат}).
если только II2* — г!|->0. Выберем последователь-
кость х* к, /= 1, ..., т из множества {л:^, А= 1, 2, ...}
так, чтобы || ж*. к — 2*|->0. Тогда
= 1 - ц ({*•' зир г) (х) < N + 6}) <
/</П
< 1 — ПтцПдс: зир х) . (х) <№)<е.
Это противоречит неравенству ^(5„)^2е. Итак, 5;гГ)/С,у
непусто. Таким образом, последовательность вложенных
МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
слабо замкнутых множеств 8п(]Км принадлежит
слабо компактному множеству Кы, и поэтому (]{8п[)Км}
п
не пусто, а, значит, П^« не ПУСТ0- Следовательно,
п
если 5„ — убывающая последовательность
цилиндрических множеств, для которой (}5п=0, то Пт |а(5л) = 0,
П П->оо
т. е. (1 счетно-аддитивна. Итак, доказана
Теорема. Для того чтобы непрерывный
положительно определенный функционал %(х*) был
характеристическим функционалом меры на (<9/, 53), где 36 —
банахово пространство, для которого 36* сепарабельно,
необходимо и достаточно, чтобы конечно-аддитивная
мера (я, порождаемая функционалом % {х*)7 удовлетворяла
условию (6) для некоторого множества [х*к, 6=1, ..., л},
всюду плотного на единичной сфере пространства 36*.
Замечание. Условие (6) можно заменить
следующим: пусть кп{х) — последовательность непрерывных
цилиндрических функций, для которой Пт Нп{х) = | х |.
П->оо
Тогда
Ит Пт \1{{х: кп(х)>Ы}) = 0. (7)
Условие (7) превращается в (6), если Н (х) = §ирх*к(х).
Кроме того, (6) можно выразить через %{х*),
воспользовавшись формулой обращения.
§ 4. Меры в пространствах 2РР
Очень важным классом линейных нормированных
пространств являются пространства 3?р [а, Ь] для
вещественных измеримых функций х (/), определенных на [а, Ь]9
для которых
ь
\\х{1)\рй1<оо.
а
Мы будем рассматривать лишь тот случай, когда р^1.
Пусть фиксировано некоторое вероятностное
пространство {О, ©, Р}. Исследуем условия, при которых
данному числовому процессу | (/, со), определенному на [а, Ъ\,
§4]
МЕРЫ В ПРОСТРАНСТВАХ 2
391
соответствует мера в 3? р. Предположим, что |(/, ш)
является измеримым процессом. Тогда по теореме
Фубини 1((, со) как функция I является с вероятностью 1
измеримой. Поэтому с вероятностью 1 определен интеграл
ъ
\ш<*)\"си
а
(он может принимать и бесконечные значения),
являющийся измеримой, функцией от со.
Предположим, что
Р /|&(*. ©)ГЛ<оо} = 1. (1)
Покажем, что при этом условии в пространстве 3!р
можно построить меру \х, отвечающую процессу ^(/, ю),
т. е. такую меру \х, что для каждого борелевского
множества В пространства 3?р
ц(ву=Р({со:|(.,со)еВ}). (2)
Соотношение (2) можно принять за определение меры щ
если только доказать, что {со: К • , со)еВ}^© при В<=33.
Чтобы убедиться в этом, рассмотрим класс Ь
функционалов, определенных на 5РР, вида
а
где /(/) —ограниченная измеримая функция.
Функционалы из Ь определены на 9?р при любом р^1, и Ь
плотно в пространстве линейных непрерывных
функционалов, каково бы ни было р. Обозначим через 2%
совокупность тех В из 93, для которых {со: ^(-, со)^ В}<= ©.
Очевидно, что ®0 является а-алгеброй. Поскольку
Щ{ ' » со)) измеримо относительно © при любом / из Ь,
то для всякого непрерывного линейного функционала /
на 5?р величина /(| (•,©)) ©-измерима. Поэтому 930
совпадает с минимальной а-алгеброй, относительно
которой измеримы все непрерывные линейные
функционалы 1(х) на 3?р, а эта а-алгебра совпадает с 93. Таким
392 меры в-функциональных пространствах- [гл. V
образом, соотношение (2) действительно определяет
некоторую меру \1. Поскольку для любого непрерывного
функционала / на 3?р величина 1Ц{ • )) измерима
относительно ©, то меру \1 можно задавать с помощью
характеристического функционала
1(1)= $ еН&р^^МеНЫ-'*". (3)
Этот характеристический функционал однозначно
определяет меру \1.
Возникает вопрос, как связана построенная мера \х
с частными распределениями процесса ^(/, со). Можно ли
по частным распределениям построить меру \х и по мере
\к — частные распределения? Покажем, что для
стохастически непрерывных процессов ответ на этот вопрос
положителен.
Пусть 1(1, со) — стохастически непрерывный измеримый
процесс (из теоремы 1 § 3 гл. III вытекает, что для
стохастически непрерывного процесса всегда существует
эквивалентный измеримый).
Положим
Тогда
ь ь
|1М', со)|^->|и(^, ©)|л
при N—> оо почти для всех 0. Процесс 1М((, со) также
является стохастически непрерывным.
Покажем, что
[Ы*, ®)Л = Ит УЫ4, ©)Д>*, (4)
« *-° /Го
где а = /а<^< ... </л = Ь, А/л = /й+1-/*, А, = тахД/4,
к
а предел понимается в смысле сходимости по вероят-
§ 4} МЕРЫ В ПРОСТРАНСТВАХ 2 393
ности. Имеем
[ 1М (/, со) (И - 2 ^ (*л, со) А/л I <
<2 Г мни*, ©)-!„(/*,«) |л<
/е-0 ^
гг —1 ^ + 1
<е(&-а)+У^ [ р{1Ь(^, ©)-6лг(^ ©).|>в}Л<
<е(6-а) + 2^(й-а)8ир[Р{|и(;, со)-^у(5, ©)|>е};
каково бы ни было е>0. Переходя к пределу при л->0
и учитывая стохастическую непрерывность \ы (/) (а
значит, и равномерную стохастическую непрерывность),
а также произвольность е>0, убеждаемся в
справедливости равенства (4). Точно так же
Ь п-\
Г | Б (*, со) Г Л = Нт Нт ^ I ^ ('ь со) \р Мк (5)
« ^^ ^ *-«
и, следовательно, выполнение условия (1) может быть
проверено с помощью частных распределений процесса
%Ц, со). Если условие (1) выполнено, то, используя
равенство
Ь п-\
Г / (*) 1С,-<о) Л = Нт Нт У/(*Л)ё.у('ь со)Д*Л, (6)
•> N-+00 А,-* О *■
а - /г==0
справедливое для всякой непрерывной на \а, Ь]
функции /(*), можем определить
7(0= 11т НтМехр]*2/(*к)|д,(*й, ю)ДЧ (7)
М->оо Л->0 I & = 0 |
для непрерывных /(/). В силу непрерывности %(1) (7)
определяет значение %(1) на замыкании множества Ь
всех функционалов
/(*)= С 1(1)х(1)А1
394 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
с непрерывными /(/). А так как Ь всюду плотно в про-'
странстве всех непрерывных функционалов на 5?р, то,
значит, %(/) определено соотношением (7) полностью.
Предположим теперь, что для измеримого
стохастически непрерывного процесса ^(7, со) на [а, Ь] выполнено
условие (1) и задана мера |х на 5?р, или, что то же
самое, определен характеристический, функционал %(/).
Пусть /(^ — некоторая непрерывная функция, М>6,
п — натуральное число.
у
Положим /п& = а Н (Ь — а),
/г=0
1пк
Почти для всех со
ъ
Пт/„,„(/) = \1Ц)Ыи со)Л.
Поэтому для характеристического функционала %м (/)
процесса ^(^, со), рассматриваемого в 3?р, справедливо
для всякой непрерывной функции /(/) соотношение
^(/)=Мехр{/ Г/МЫЛ со)л}= Нт \еи"*»{1*х) »(йх\
где
А __ п I Г
П-\ / 'ЛЛ + 1
*~° ^ '«А
непрерывный, а значит, 23-измеримый функционал в 3!р.
По непрерывности функционал %лг (/) можно продолжить
на все Ь. Покажем теперь, что
Ъ$ ЪЫЦ;®)(И-+ЫУ,<1>) (8)
§4]
МЕРЫ В ПРОСТРАНСТВАХ^
395
по вероятности при й->0. Действительно,
М
1+К
\\ (Ы$. С0)~^(/, ©))Л
<
<8 + 2Л^зир[Р{|^(5, ©)-Ы'. со) | > е}; /<*<* + й].
Последнее выражение можно сделать сколь угодно
малым выбором е>0, Л>0.
Обозначим через //а,л(л;) функционал на .2^,
определяемый равенством
Тогда из (8) вытекает, что для всех вещественных ик
и точек ({< ... <1п из [а, &)
М ехр / 2 ^ (*Л, со) [ = Пт %„ ( 2 аЛ/, Л (^ (•))) . (9)
I к=1 ) Л-»0 и = 1 *' и V
Соотношение (9) определяет частные распределения
процесса \ы{1> со). Предельный переход при Лг->оо
позволяет найти частные распределения процесса \{1, со).
Неудобство формул (5) и (7) заключается в том, что
приходится использовать вместо исходного процесса \{1, со)
урезанный процесс &дг(^, со). Кроме того, желательно
было бы получить условие, обеспечивающее выполнение
соотношения (1) в терминах не предела самих
случайных величин, а их вероятностных характеристик. Для
получения более простых формулировок
интегрируемости процесса в степени р нам понадобится
Лемма. Пусть I (^ — измеримый стохастически
непрерывный неотрицательный процесс, определенный на [а, Ь].
Для любой последовательности разбиений отрезка [а, Ь]
я = *лэ< ... < *ЛЯ = Ь, для которой Ая = тах(*яЛ+1-*яА)->0,
к »
и любых независимых от |(?) случайных величин хпк,
равномерно распределенных на промежутках [1пк, 1пь+\]
соответственно, & = 0, 1, ..., п—1, выполняется
соотношение
/1-1
Е *(*»*) А'»*-*/б (О Л
А=0
396 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
по вероятности при п —> оо (интеграл справа может
равняться + оо).
Доказательство. Поскольку процесс ^(О можно
рассматривать отдельно на каждом из множеств
со: ||(/)й/<оо и со: /ШЛ= + оо[,
то достаточно рассмотреть лишь два случая, когда
выполнено одно из этих условий с вероятностью 1.
Пусть сначала
Р $ Ъ(1)(И = + оо =1.
Тогда, как было установлено ранее
я-1
по вероятности, и значит, для всякого с>0
выполняется соотношение
> Ит Р \%1»(гпь)Ыпь> С\>Р\\ Ъ(*)М>с\.
П-»оо [к==0 ) \а )
Переходя к пределу при Л/->оо, убеждаемся, что
п~\
^1{тпк)Мпк сходятся по вероятности к +оо.
Пусть теперь
Положим
ъ
Г (/) = 6(/)э а</<&, если /|(0Л<т,
а
Ь
Г (0 = 0, а</<6, если ||(0Л>ш.
§4]
МЕРЫ В ПРОСТРАНСТВАХ X
397
Процесс ^т(/) неотрицателен, стохастически непрерывен
и измерим.
Поскольку
ъ
| 1т (О Л < т,
а
то в силу теоремы Фубини существует М|т(/) почти
ь
для всех / и [ М^т (0 Л<т. Положим %" (/) - ^ (^/п ({)).
а
Процесс Щ{1) стохастически непрерывен и ограничен
величиной N. Значит, для всякого е>0 можно указать
такое к > 0, что
М|да-^(*)|<е
ПрИ |^-5|<Л.
Используя это обстоятельство, находим'
Пт М
л-о г„ь 1
<
га_1 */г* + 1 ^гб + 1
Ч!Е?/ I м|Г(о-г(в)1^-<
М |^(0-^(5)| +
лг^ /гб
+ 2М|6«(0-6'Л(0|]Л^<
< Йт зир М I ^ (0 - |« (5) | (Ь - а) +
П->оо | 1 — з\ < Я^
Ь Ъ
+ 2\ М|5«(0-5м(01Л = 2|м|5Л(0-1м(«|Л.
Последнее выражение стремится к нулю приЛ'->оо.
398 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Наконец,
Г ""' I 1
] и*)<Н -^Игпк)Ыпь\>е\<
а /г=0
Ь
° я-1
[а ) \а к=0
Переходя к пределу при п~>оо, а затем при т->оо,
получаем доказательство леммы.
Следствие. В условиях леммы существуют неслу-
я-1
чайные точки 8пк<=[1пку /яй+1], для которых ^ |(5яЛ)Л/яЛ->
&=о
I 1(()сИ по вероятности при п->оо.
Замечание. Если для некоторой
последовательности разбиений отрезка [а, Ь] вида, указанного в лемме,
и некоторого выбора точек $яйе [*яй, *яй+1], не завися-
л-1
щих от 1((), величина 2?(5лл)А'лл (л->°°) ограничена
по
р(
вероятности,
1
то Р
Действительно, для
Ъ л
\1м{1)й1>с\
Следовательно, и
( ь
А-0
г.
/ко^<
а
всякого е
1 П— V
< Нт Р<
Л-»°о
Г я-
]
; оо |
•>о
V \8п
л-1
|2
= 1.
и с>0
й) Мпк > с
1 (Зпк) Мпк
-1
>с
<
— е
р{/шл>Л<т^
Приведем теперь условие конечности Г \1(1) |а сН для
а
а е= (0,2], выражающееся через характеристический
§4]
МЕРЫ,В ПРОСТРАНСТВАХ^
399
функционал процесса. Поскольку пока нам неизвестно,
в каком пространстве можно рассматривать процесс,
будем использовать характеристический функционал
%о{§), определенный соотношением
Хо(*НМехр{/ /б(0^(0|
для всякой ступенчатой функции §"(^), заданной на [а, Ь].
Очевидно, задание Хо(§) эквивалентно заданию частных
распределений процесса.
Построим случайную функцию ^(0> определенную
на [а, Ь] следующим образом. Пусть (пь = я-\—Ф—а),
к = 0, ..., п, %, %, ..., у)п, ...—случайные величины,
не зависящие от %((), каждая из которых равномерно
распределена на [0, 1] (совместное распределение т\к
в остальном может быть произвольным). Наконец,
величины 2о1 &1> • • • не зависят ни от Ц(), ни от %, ць ...,
независимы между собой и одинаково распределены,
причем
Ме{3^ = е~\3\а,
т. е. %к имеют симметричное устойчивое распределение
с показателем а. Положим ч*(а) = 0, V" (0 постоянно
при (*-а)я€= [(/ + %)(& — а)Г (/ + 1 +^+1)(Ь -а)] и
^(а+^(&-Ь) + о)^«(а^
Эти условия однозначно определяют ч^Ц) (за
исключением точек разрыва). При этом ^{1) является с
вероятностью 1 ступенчатой функцией, так что выражение
%о(^) определено с вероятностью 1.
Теорема. Для того чтобы для стохастически
непрерывного измеримого процесса Ц() с вероятностью 1
ь
был конечен интеграл Г | \{1) \асН при некотором ае(0, 2],
а
необходимо и достаточно, чтобы для положительных Л
существовал предел
ф(Л)=НтМх0(Л^),
4(Х) МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ, V
удовлетворяющий условию \|)(0+)=1. При этом
*(Л)=Мехр --^ /|1(0|"Л .
\ а '
Доказательство. Обозначим через $1 а-алгебру,
порожденную величинами Ц()у 1^[а, Ъ] и г\к, 6 = 0,
По условию теоремы %к не зависят от этой ст-алгебры.
Поэтому
Н(Х»М|*)-
-м(ар(^(а+^(»-«))
I
Из леммы вытекает, что - У
&=о
21
( п-\
I % Г V
1 л=о
я-1
а +
к+ х\
к = 0
тч>-4
16(01°^ П0 вероятности. Поэтому и
ир - V.! ча + --
д
(6-а))
1
^{-4^/16(0 Г л
по вероятности (мы считаем, что е~°° = 0). Так как
рассматриваемые величины не превосходят единицы,
то и
ПтМехр(-^У||(а + -^Ч&-а)
*=0
Мехр{—1^-/||(01п^}.
§5}
МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
401
А так как
п~\
л=о
= Нш М(х(А^)|Я) = Пт Мх(Ал$,
ТО
*(А)=Мехр --^1/|И01вЛ •
'а '
Очевидно, что
Ф(0+) = Р
/|Ш1"Л
< ОО
Из последнего соотношения вытекает доказательство
теоремы.
§ 5. Меры в гильбертовом пространстве
Среди пространств 36 р, рассмотренных в предыдущем
параграфе, наибольший интерес представляет
пространство «2*2• Это сепарабельное гильбертово пространство.
Поскольку все сепарабельные гильбертовы пространства
изометричны одно другому, то более удобно
рассматривать абстрактное сепарабельное гильбертово
пространство 86, Результаты, полученные для такого
пространства легко могут быть переформулированы для
различных конкретных гильбертовых пространств,
например для пространства измеримых функций на
произвольном измеримом пространстве с мерой,
принимающих значения из сепарабельного банахова
пространства и интегрируемых по норме с квадратом.
Обозначим через 23 а-алгебру борелевских
множеств 86. Пару (86, 23) будем называть измеримым
гильбертовым пространством. Основным объектом изучения
в этом параграфе будут меры ц, заданные на
измеримом гильбертовом пространстве (86, 23). Как и ранее,
нас интересуют вероятностные меры, но так как
результаты в этом параграфе справедливы для любых
конечных мер, условие \ь(86)=\ не будет накладываться.
402 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Скалярное произведение в 36 будем обозначать (х, у),
а через | х | — норму х: \х\=у{х,х). Как и во всяком
линейном пространстве, меру на (36, 23) можно
задавать с помощью характеристического функционала.
Всякий непрерывный линейный функционал 1(х),
определенный на 36, имеет вид / (х) = (х, г), где г может
быть любым элементом 36. Характеристическим
функционалом меры \х на {36, 23) будем называть функцию ф (г),
определенную равенством
ф(г)= |е'<*.*>|х(Лс) (1)
для всех г ^36.
Пусть 36 — некоторое конечномерное
подпространство пространства 36, 23^ — сг-алгебра борелевских
подмножеств 36. Множество вида
Р1еХА<е = {х\ Р<?х^А<?},
где Л^е23^, Рх — оператор проектирования на 36,
называется цилиндрическим множеством с основанием
в 36. Совокупность 23* всех цилиндрических множеств
с основаниями в 36 также является сг-алгеброй.
Множества, принадлежащие 83* при некотором 36, называются
цилиндрическими, а функции, измеримые относительно 33*
при некотором 36, называются цилиндрическими
функциями.
С каждой мерой \х на (36, 23) можно связать
множество ее конечномерных проекций (конечномерных
распределений) {м^}, определяемых равенством
1Хх(А<?) = \х{Р#1А<?) для А<е<=Ъ<е.
Меры |х^ достаточны для вычисления интегралов от
цилиндрических функций: для всякой 23^-измеримой
ограниченной функции Н(х)
| Н (х) ^ (с1х) = / А (Р^х) IX (ах). (2)
Заметим, что любая цилиндрическая функция при
некотором 36 имеет вид Н(Р#х), где Л 23^-измерима.
§ 5] МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ 403
Меры |л при различных 3? согласованы между собой
следующим образом: если ^?с:^?,, то
Это соотношение вытекает из (2) и возможности
представить функцию к(Р#х)в виде к'(Р%>х)у где к'
©^'-измерима. Условие (3) в дальнейшем будет называться
условием согласования, а семейство мер {[х^},
определенных для всех конечномерных подпространств 2 и
удовлетворяющих условию (3), будет называться
согласованным семейством конечномерных распределений.
Для определения меры |х достаточно знать лишь ге
одномерные проекции. Это вытекает из формулы
где 9?г — одномерное подпространство, порожденное
вектором г. Наоборот, зная характеристический
функционал ф(-г), можем легко определить и все меры \х^
по их характеристическим функционалам: при геЗ'
Оказывается, существование функции <р(,г),
удовлетворяющей равенству
ф(г) = | е1 {г>х)\л^{йх)у ге^
для любого конечномерного подпространства 3?, является
необходимым и достаточным условием согласованности
семейства конечномерных распределений {м^}. Убедимся
в этом. Пусть семейство {[х^} удовлетворяет (3).
Положим
Ф^ (г) =» | е* <*> *>ц* {йх)9 ге^,
Если 2?а&' и г е= ^, то
ф^ (^ = | *'(г' V- (**) = / *' (Р**' *Ч- (**)в
= | *' <* я**)н^, {их) =\е{ (2' % {йх) = ^ (г)
404 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ (ГЛ. V
в силу условия (3). Положим ф(г) = Ф^ (г), где 3?г —
одномерное подпространство, порожденное вектором г.
Поскольку при 2Е^ и 2?гс13?у то ср^,{г) = ф^ (г) = ф(г).
Наоборот, если ф(г) — функция, для которой ф(г) = <р^(.г).-
при гЕЙ', то для 3? с: 3?' и ге^ имеем соотношение
из которого вытекает совпадение мер \х^((1х) и
[^(Р"1 их) (в силу совпадения их характеристических
функционалов). Значит, условие (3) выполнено.
Моментные формы. Важными характеристиками
меры |х на (§6, Ь) являются моментные формы этой
меры. Моментная форма порядка к меры ^определяется
соотношением
пгк(*!, ..., гк)= $ {х,г{) ... (х, гк)\1 {их)
при условии, что интеграл справа определен (и конечен)
для всех наборов г{, ..., гк из й?. Очевидно, для
существования моментной формы порядка к необходимо и
достаточно, чтобы для всех г выполнялось соотношение
/ |(^2)|*»1 (**)<«>. (4)
Функция шк(гь ..., гк) является симметричной
функцией своих аргументов и, кроме того, она непрерывна
и однородна по каждому из них. Покажем, что
моментная форма порядка к (при условии, что она
определена) является непрерывной симметричной 6-линейной
формой. Чтобы убедиться в этом, достаточно показать,
что
зир Г |(2, х)\к\1((1х)<<х>, (5)
Введем функции
тп(г) = Г пН*\г\{* |1 (их). т(г) = Г | (х, г) |V{их).
* п + \х\я «/
§.5] МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ 405.
Функции тп(г) являются слабо непрерывными по г и1
тп(г)\ т(г) для всех 2 при /г->оо. Положим
*„,, = {*: тп(2)>1}{\{2: |г|<1}.
Множество Кпа слабо замкнуто и слабо компактно
(так как оно ограничено). Для доказательства (5)
достаточно показать, что К1 = (]Кп,1 пусто при некото-
ром / (тогда зир т (2)^.1). Множества К также слабо
|г|<1
замкнуты и слабо компактны. Если бы все' К были не
пусты, то [*\К1 было бы также непустым. Но тп(г)-+ оо
I
для 2^[}К1, что невозможно. Наше утверждение до-
казано.
Чаще всего используются две первые моментные
формы. Если форма тх (г) определена, то она является
непрерывным линейным функционалом относительно г.
Следовательно, существует такой вектор а в $?, что
Г (х, г) \х (их) = тх (2) = (а, 2).
Этот вектор а называется средним значением меры р.
Если определена форма щ(гь г2) (тогда определена и
тх(г))у то выражение
т2(2и22)-т{(2х)т{{22)
будет непрерывным симметричным билинейным
функционалом. Следовательно, существует такой симметричный
ограниченный линейный оператор В, что
Щ (21, 22) - т{ (гх) т{ (г2) = (Вги г2).
Этот оператор называется корреляционным оператором
меры [г. Из соотношения
О < Г (х — а, 2)2 у, (их) = | (,г, г)2 ^ (их) — (а, г)2 =
= т2 (2, 2) - (/и, (г) )2 = (Вг, г)
вытекает, что В неотрицательный оператор.
Отметим одно важное свойство корреляционного
оператора. Напомним, что симметричный неотрицательный
МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
оператор В называется ядерныму если он вполне
непрерывен и сходится ряд 2 Л* из его собственных
значений (каждое значение входит в сумму столько раз,
какова его кратность). Симметричный неотрицательный
оператор В будет ядерным, если в некотором
ортонормированием базисе {ек} пространства 9В сходится ряд
2(#еь ек). Тогда этот ряд сходится при любом выборе
базиса и его сумма не зависит от выбора базиса. Эта
сумма называется следом оператора и обозначается 5р В.
Лемма. Корреляционный оператор В меры \л
является ядерным тогда и только тогда, когда
выполнено условие
Г | х |2\х {их) < оо.
При этом
8рВ= $\х\2\1(ах)-\а\2}
где а — среднее значение |х.
Доказательство вытекает из равенства
п п п
5] (Век, ек) = | 2) (х, ек)2\1{йх) - ^ (а, ек)\
справедливого для любого выбора еи ..., еп. Беря
векторы из ортонормированного базиса и переходя
к пределу при п->оо (возможность перехода к пределу
под знаком интеграла вытекает из монотонности после-
п
довательности 2 С*» ^к)2 по п)у получаем утверждение
леммы.
Теорема Минлоса — Сазонова. Выше отмечалось,
что мера |х на измеримом гильбертовом пространстве
(Я?, 23) может задаваться либо своими конечномерными
проекциями, либо характеристическим функционалом.
При этом оказалось, что эти два способа отличаются
один от другого несущественно.
Пусть имеется согласованное семейство
конечномерных распределений {\1#}. При каких условиях
существует мера \х на (й/, 23), для которой {\1#} являются
проекциями? Поскольку \х# позволяют построить функ^
ционал ф{г), совпадающий при гЕ^с характеристик
§5]
МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
407
ческим функционалом меры \х#, то предыдущий вопрос
сводится к следующему: при каких условиях <р(г)
является характеристическим функционалом некоторой
меры |х на (Я?, 23). Ответ на последний вопрос и дает
теорема Минлоса —Сазонова.
Теорема 1. Для того чтобы комплекснозначная
непрерывная положительно определенная функция ф(<г),
заданная при гб|, являлась характеристическим
функционалом некоторой меры \1 на ($?, Ж), необходимо
и достаточно, чтобы для всякого г > 0 можно было
указать такой ядерный оператор Ле, что Не(ф(0) — ф(,г))<е
как только {Агг, г)^\.
Доказательство. Необходимость. Пусть
Ф (г) — характеристический оператор меры ц. Тогда
Ке(ф (0) - <р (2)) = ]" (1 - соз(г, х))\1{йх) <
\х \<с \х\> с
<у ]* (х, г)21х(ах) + 2ц({х: \х\>с}).
\х\<с
Выражение (х, г)2\1{йх) является при каждом с
икс
квадратическим функционалом относительно г и
представим© в виде (Всг, г), где Вс — ядерный оператор
в силу доказанной леммы, поскольку
| \х\2\1{йх)^\1(%)с2.
\х\<с
Выберем с так, чтобы выполнялось неравенство
\х({х: | х |>с})<е/4. Тогда, взяв Ае = — Вс, будем иметь
при (Аег, г) < 1
Ке'(ф(0)-ф(2))<| + 1(^,г)==| + у(Л^ 2)<е.
Необходимость условия теоремы доказана.
Достаточность. Пусть {\1У} — согласованное
семейство конечномерных распределений, построенное
по ф(^). Из теоремы § 3 и замечания к этой теореме
вытекает, что достаточно доказать существование для
468 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
всякого е>0 такого Му что для всех конечномерных
подпространств 3? выполняется неравенство
!!*({*: \х\>Щ)<е. (6)
Действительно, тогда в качестве функций кп(х),
фигурирующих в замечании § 3, можно взять функции |Р^ял:|,
где 3?п — возрастающая последовательность
конечномерных подпространств, для которой \}2?п плотно в §в>
Р#п — оператор проектирования на 3?п.
Для доказательства формулы (6) воспользуемся
неравенством Чебышева, в силу которого
( км2\~1 _тл. !_| |2
где т^((1г) — лебегова мера на 5?у /> — размерность 5?.
Меняя порядок интегрирования, находим
<(2яЛ) а С(ф(0)-ф(г))в ^|21ш^(^2).
Выберем далее ядерный оператор А так, что
Ке(ц(0)-ф(2))<-|- при (Аг, г)<1. Тогда .
\Ие"Ч|М{*: |*|>Л'})<
<-|- + (2яЯ,) 2 ] 2е * 'тИ^Х
(Лг, г) > I
§ 51 МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ 409
так как
(2лЛ) 2 ) (Аг, г)е **■ т* (</*) =
= 5] (2лЛ) 2 ^М, е/)(г, в<)(2, е,)\[е 2* т*(а?г) =
= ^ <^, е,) -р^=- | АГ"^ Л - Я. 2 (Де„ *,) < * 5р А.
Таким образом,
Ы*: |х|>^}<(| + 2Х5рЛ)(1-е~ М . (7)
Очевидно, можно так подобрать К и /V, чтобы правая
часть (7) стала меньше е. Теорема доказана.
Обобщенные меры в гильбертовом пространстве.
В § 3 была указана процедура, позволяющая для
каждой положительно определенной функции ц>(х*),
заданной на 36* (пространстве, сопряженном линейному
пространству 36), построить такое расширение 36
пространства 36 и меру \1 в 36, для которой <р(#*) было бы
характеристическим функционалом. Пусть ф(г) —
некоторая положительно определенная функция, заданная
на гильбертовом пространстве 36, Применяя упомянутый
результат, можно построить расширение пространства 36
и меру на этом расширении такую, чтобы ф(,г) было
характеристическим функционалом этой меры. Однако
процедура, указанная в § 3, приводит к слишком
широкому пространству 36. В том случае, когда 36 —
гильбертово, можно и 36 построить, как некоторое
гильбертово пространство, полученное пополнением 36 в
некотором скалярном произведении, зависящем от свойств
непрерывности у (г). Рассмотрим это построение,
принадлежащее Ю. Л. Далецкому.
Пусть б —некоторый ограниченный симметричный
положительный линейный оператор. Введем в 36 новое
скалярное произведение:
(х,у)_ = (Вх,у), \х\1 = (В,х,х). (8)
410 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Пространство 36 будет, вообще говоря, неполно в
метрике, порожденной этим скалярным произведением.
Обозначим пополнение 36 в норме | • |_ через 36^ (его
можно рассматривать как расширение 96), 96 будет
всюду плотным множеством в Зв^\ 96в_ и 96 будут
совпадать, если В""1— ограниченный оператор.
Обозначим через 96% гильбертово пространство, полученное из
области определения оператора В~1г (она плотна в 36)
введением скалярного произведения
(х, У)+ = (В~1/% В~Ушу) = (В-Хх, у). (9)
Второе равенство в формуле (9) нуждается в некоторых
пояснениях. Заметим, что для всякого х е 96^
скалярное произведение (х, г), определенное по г на 36,
может быть продолжено по непрерывности в метрике 36е.
на все 961. Действительно, пусть х = В1/2х0, х0 е 36. Тогда
| (х, гп - гт) |- | {В1/2х0, гп-гт)\ = \(х0, В42 (гп - гт)) | <
< | *о1 (В,/2 (гп - гт\ В'12 (гп - гт))ъ = \х*\\гп - гт\_.
Поэтому линейный функционал (х, г) на 36 непрерывен
в метрике й?! и, значит, его можно продолжить по
непрерывности (по г) на 96-. В дальнейшем под (х, г),
когда х^96%, г ^36^ мы будем понимать именно это
продолжение. Оператор В также можно по
непрерывности продолжить на <8?-, так как
|В*|_= У(Вх, Вх)_ - У(В2х, Вх) =
= У(в*в1,% в1/2х) <У\в2Квч% вЧ) <цдц|*ь
Будем считать в дальнейшем В продолженным на 36в_т
При этом выполняются соотношения
В1/29?1 = 9?у ВЧг96 = 96%, В9б1=36%.
Третье из них является следствием первых двух, второе
вытекает из определения 36%. Докажем первое. Пусть
г — произвольный элемент из 363., гп^36 и | гп — г |_ ->0.
Это означает, что
{В (гп - гт), 2п - гт) = | Въгп - ВЧггт |2 -> 0, п, т -> оо;
§5] МЕРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ 411
Но Вх,2гп е 36, поэтому и ВУ2г е Я?. Вернемся к
равенству (9). По данному выше, В~ х определено при
х^.36% и принадлежит $?*; так как у ^.36%, то
определено и (В""1*, */).
Пусть теперь на $?- рпределена некоторая мера р..
Тогда по этой мере можно построить
характеристический 'функционал <р_(г)= Г е1 {х' 2)~ \х{их),
определенный при г^Зб!. Поскольку (х, г)~ = (Вг, х) и В2ЕЖ+,
то меру \л на 36^. можно задавать и с помощью
характеристического функционала у(г) = е{ (2< х)\л {их), где
ге^, Заметим, что
Ф.(г) = Ф(Вг)> ф(2?) = ф_(В",2г).
Из теоремы 1 вытекает, что ф(г) является
характеристическим функционалом меры на 36в~ тогда и только
тогда, когда для каждого е>0 существует такой
ядерный оператор 5 на $?_, что Ке(<р_ (0) — ф_ (г)) < е,
если только (8г, г)-^1. Используем этот результат
для построения такого расширения 36, чтобы
заданный положительно определенный функционал ф (г)
был характеристическим функционалом в этом
расширении.
Теорема 2. Пусть ф(г) — непрерывный
положительно определенный функционал, заданный на 36. Тогда,
каков бы ни был ядерный оператор В, ф(г) является
характеристической функцией некоторой меры на 36В-.
Доказательство. Из непрерывности ф (г)
вытекает, что для каждого е>0 можно указать такое 6>0,
что Ке(ф(0) — ф(г)Xе, если {г, г)^Ь. Тогда Ке(ф(0) —
— ф(Вг))<1е для 2бЖ!, если (Вг, Вг)^6, т. е,
Ке (ф_ (0) - ф_ (г)) < е, если Ц-Вг, г) <1.
Покажем, что операторов, определенный на 36В->
является ядерным. Для этого достаточно показать, что
412 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
таким будет оператор В. Но:
1) (Вх, у)_ = (В2х, у) = [Вх, Ву) = {х, Ву)_\
2) (Вх, х)_ = (Вх, Вх) > 0.
Покажем, наконец, что
оо
3) Зр_В=2 (Век, ^)_<оо,
где {^ — некоторый ортонормироранный в Я?? базис.
Действительно, положим ек = }к1Ухк, где {/&} — базис из
собственных векторов оператора й в1, Лл = (В/л, /л),
(/*Л*)=1. Тогда
оо оо оо
5р_ (В) = ^№*• е*>= Е ( я' = 2 Я* = 8Р В-
Теорема доказана.
Замечание 1. Пусть положительно определенная
функция ф(г) удовлетворяет условию: для всякого е>0
существует такое 6>0, что Ке(ф(0) — ф(г))<е, если
только (Уг, г)<6, где V — ограниченный симметричный
положительный оператор. Рассмотрим пространство %?-,
где 5 — некоторый симметричный, коммутирующий с У
положительный оператор. Найдем условия, которые
нужно наложить на 5, чтобы в 8Р1 существовала мера
с характеристическим функционалом ф(-г). Поскольку
Ке (Ф_ (0) - Ф_ (г)) = Ке (Ф (0) - Ф (5г))
при(К5г, Зг) = (У8г, 2)_<6и 5р_К5 = 5рУ5, то такая
мера существует, если 8рК5<оо. Это утверждение
справедливо и в том случае, когда ф(2) определено на
линейном многообразии, плотном в Ж, а У
—неограниченный оператор.
Меры, определенные на #?1 при некотором 5,
характеристические функционалы которых в скалярном
произведении 36 определены на всюду плотном в
^множестве, будем называть обобщенными мерами на $6.
Теорема 2 показывает, что обобщенная мера строится
по своему характеристическому функционалу,
определенному в <9/, неоднозначно. Пусть $6' и 36" — два
расширения пространства 96, в которых определены
§5} МЕРЫ ^ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ Щ
меры \к' и -р", соответствующие одному и тому же
характеристическому функционалу ф(г). Тогда можно
указать такое расширение 36'", которое входит в
каждое из расширений 36' и З6'\ причем ц' (36' - 36'") = О,
|г"(Я?'-#?") = 0 и м/ совпадает с \х" на Я?'". Это
расширение 36'" легко строится: если
зе' = зб% зб" = збЪ; то я?"'= а?5+&.
Таким образом, обобщенная мера строится в
определенном смысле однозначно. ±
Пространства $?- позволяют в более удобном виде
сформулировать условие теоремы 1.
Замечание 2. Для выполнения условия теоремы 1
необходимо и достаточно, чтобы существовал такой
ядерный оператор В, что у (г) было бы непрерывным
в метрике 36В- и, следовательно, могло быть продолжено
на $?_. Действительно, если ф(,г) непрерывно в
метрике $?*, то для всякого е>0 найдется такое 6>0,
что Ке(ф(0) — ф(г)) ^е, если только |;г|_^д, т. е.
-^Вг, 2)^1, у В — ядерный оператор.
Наоборот, покажем, что из условия теоремы 1
вытекает существование оператора В. Выберем
последовательность еп I О, и пусть операторы Ап удовлетворяют
условию теоремы 1 для е = ел. Пусть сп — такая
последовательность (сп I 0), что
оо
2 сп5рАп<оо.
ОО
Тогда оператор Я = 2 спАп будет искомым ядерным
оператором. Действительно, для всякого е>0 можно
найти такое а, что е,г<е. Тогда при (Яг, 2)<сп имеем:
(Ап2, 2)< 1 и, значит,
Ке(ф(0)-ф(г))<е^<е.
Далее
\ц>{21) - ф (г2) | < | \е1 <*■• х) - е1 <*. х) | ц (ах) <
414 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Из этого неравенства и вытекает, что I фС^) — ф(22)| ->0
при
(В (г{ - г2), г{ - г2) -> 0.
Из последнего замечания следует, в частности, что
функция е~\г1\ являющаяся непрерывной и положи-
тельчо определенной, не будет характеристическим
функционалом меры на 36, так как она не
продолжается по непрерывности на 35^. с ядерным
оператором В.
§ 6. Гауссовские меры в гильбертовом пространстве
Пусть \1 — вероятностная мера на измеримом
гильбертовом пространстве (36, 23). Тогда (35, 23, |х) является
вероятностным пространством и любая 23-измеримая
функция §(х) является случайной величиной на этом
пространстве. Мера |х называется гауссовской, если
всякий непрерывный линейный функционал 1г(х) = (г, х)
является нормально распределенной случайной
величиной. Пусть
аг=М(г, х)=$ (г, х)\к(йх),
Рг = М (г, Х)> - <х| = | (г, х)2 II (АХ) - а\.
В силу нормальности распределения (г, х) эти величины
определены при каждом г, следовательно, как было
установлено при изучении полилинейных моментных
форм в § 5, существует вектор а и ограниченный
симметричный неотрицательный линейный оператор В такие,
что
аг = (а, г), $г = (Вг, г).
Поскольку (г, х) имеет нормальное распределение, то
Ме'<*•*>= |^^(^Нехр{/(а, г)-^(Вг, г)\.
Таким образом, для всякой гауссовой меры существует
среднее значение а й корреляционный оператор В,
причем характеристический функционал этой меры имеет
вид
Ф (г) = ехр {/ (а, г) - ~- (Вг, г)}. (1)
§6]
ГАУССОВСКИЕ МЕРЫ
4Ш
Наоборот, если характеристический функционал меры ц
имеет вид (1), то
Г еи <*• *> \х (их) - ф (**) = ехр { И (а, г) - -^ (Яг, 2)}
и, следовательно, величина (г, х) имеет нормальное
распределение со средним (а, г) и дисперсией (В,г, 2).
Значит, необходимым и достаточным условием, для
того чтобы мера [х была гауссовской, является
представление (1) для характеристического функционала
этой меры.
Из формулы (1) вытекает, что каков бы ни был
конечный набор векторов ги . .., гп, совместное
распределение величин (гь х), ..., (гП9 х) является также гаус-
совским. Действительно,
М ехр{/2/*(**> *)} = Ф (2'***) =
«= ехР {* 2 '* ^ г*> ~~ Т 2 '*'' (Вгк> *')}'
Насколько произвольны величины а и В в формуле (1)?
Если В — положительно определенный оператор, то
функция ф(2), определяемая (1), положительно
определена. Остальные ограничения на а' и В накладывает
теорема Минлоса — Сазонова. Пусть для данного е>0
Л —такой ядерный оператор, что
Ке(1-ф(г))<е при (Аг, г)<1.
Тогда при (Аг, г)<1 имеют место неравенства
\(Вху г)<ехр^~(Вгу г)}-К
<[1-ехр{--1(В2| 2)}][1-(1-ехр{-|(В2, г) })]"'<
<[1 -ехр|-у(В2, 2)|со5 (а, г)! X
х[1--(1-ехр{-|(йг, 2)}соз(а, г))]"^-^
(если е<1, то соз(а, ,г)>0). Поэтому
(Вг, гХу^Лг, г)
416 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
И
8рВ<т^_5р.4.
Следовательно, условие 5рВ<оо является
необходимым, для того чтобы формула (1) определяла
характеристический функционал меры на (Я?, 23). Покажем, что
это условие является и достаточным. Поскольку
|1-ф(2)|<у(В2>2:) + |(а>2г)|>
то | 1 — ф (г) | < е, если только — (Яг, г) + —^ (а, г)2 <\.
Полагая,
Ле = — В + -^г Л*> где Раг = (а, г) а,
убеждаемся, что выполняются условия теоремы Мин-
лоса — Сазонова, так как
5рЛе = |5рВ + ^|а|2<оо.
Таким образом, получен следующий результат.
Теорема 1. Мера \1 является гауссовской мерой
на {36, 33) тогда и только тогда, когда ее
характеристический функционал ф(,г) представим формулой (1),
в которой а — произвольный вектор из 36, а В —
ядерный оператор. При этом а является средним значением
меры ц, а В — ее корреляционным оператором.
Как вытекает из леммы § 5, для всякой гауссовской
меры |1
\\х\2\1(с1х)<оо.
Пусть еь е2, ... — ортонормированный базис
собственных векторов оператора В, его существование
вытекает из того, *1то В вполне * непрерывен. Если
Хк — собственное значение В, отвечающее ек, то
{Ве19 *?7) = ЛА/.
Поэтому случайные величины (х, ек), к = 1, . .., п имеют
такую совместную характеристическую функцию
Ме{ 2 '* <*•«*> = ехр {1% 1к (а, ек) - \ ^ Ы\ }.
§«]
ГАУССОВСКИЕ МЕРЫ
4\г
Последняя формула показывает, что величины (х, е^)г
к=\, ..., п, независимы в совокупности. Если Хк ф О,
(х — а, еЛ
то величина Г— = 1к нормально распределена со
У кь
средним 0 и дисперсией 1. Рассматривая х как
случайный элемент на вероятностном пространстве {36, 23, ^),
можно записать
х==а+2 Укь1кек9 (2)
где |й — независимые одинаково распределенные гауссов-
ские случайные величины на ($?, 33, \х), определенные
для всех к, для которых Хк>0, М^==0, 0%к = 1.
Представление (2) можно использовать при различных
вычислениях. Рассмотрим один пример применения
формулы (2). Вычислим преобразование Лапласа величины
| х р. Так как
| х |2 = 2 Ы1 + 22 УЬна&к +1 а I2» гДе ак = (а, ек),
то
I
е" ^э *г (Л*) = е8 ]а1'\[ М ехр (зЯ^ + 25 \ кк ак\к) =
*г = 1
.^.еД^еТ^^^.^.
/г=1
/2я
= е
«л
ее 1^4
ПСХР 1 1 - 2Я..9 1
^1-2^
*-1
Последнее бесконечное. произведение сходится при
Кея< 2ТЖ» что вытекает из сходимости ряда^ Лл = 3р В.
Полученное бесконечное произведение может быть про-*
сто выражено через оператор
ЯЛВ) = (1-8ВГ\ (3)
легко выражаемый через резольвенту оператора В.
\4 II И Гнчмгл, А. В. Скороход
418 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Действительно,
ОО ( 00
^ О Л = 1 ' ^ О '
Таким образом, для всех $< 2|:д-ц-. справедлива
формула
= ехр | 2а2(ВЯЛЯ)а, а) + / 8рВЪ(В)сИ + з\ а |2 ) . (4)
Эту формулу можно использовать и для
определения преобразования Лапласа величины (Ух, х) на
вероятностном пространстве (36, 93, \\), если только V —
неотрицательный симметричный оператор. Пусть V = С/2,
где У — также неотрицательный оператор. Тогда (Ух, х) =
= \1/х\2, Их является случайным элементом со
значениями в 36 на вероятностном пространстве (36, 93, |а).
Характеристический функционал величины Vх имеет вид
| е1 &*> *> \х (их) = | е1 <*• "*> |1 (Же) =
= ехр{/(С/а, г)-у(С/ВС/г, г)},
Следовательно, I)х будет иметь гауссовское
распределение со средним Ца и корреляционным оператором IIВ[/.
Значит, в силу формулы (4)
| е* 1Ух, х) ^ ух) = ехр 12$2 (ЦВ1/К8 (ЦВЦ) Оа, Ца)
5
+ | 5р 1?В1;К( ([/ВЦ) Л + в | г/а р
+
(5)
§6]
ГАУССОВСКИЕ МЕРЫ
419
Линейные и квадратические функционалы. Пусть
ц — гауссовская мера на (82, Щ. Будем называть
измеримым линейным функционалом относительно меры ц
всякую измеримую функцию §(х), представимую как
предел по мере \х последовательности непрерывных
линейных функционалов:
В (х) = Нт (х, гп)
по мере |а. Поскольку величины (х, гп), /1=1, 2, ...,
имеют совместное гауссовское распределение, то из схо
димости (х, гп) по мере \х к § (х) вытекает, что ^с (х)
также будет иметь нормальное распределение и что
(х,гп) сходится к §(х) в среднем квадратическом. Значит,
Нт Г [(*, 'гп) - (х, 2т)]2 \х {их) «
л, т->°о •»
■= Нт [(а, гп-гтУ + (В(гп-гт), гп-гт)\.
п, т->оо
Положим А = В + Ра> где Рах = {а, г) а. Тогда А — ядер*
ный оператор. Введем скалярное произведение (х, у)-***
= (Ах, У)-
Пусть Я?1— пополнение 9В в этом скалярном
произведении. Если
/К**, х)-(гт, х)]2ъ1(с1х)->0, то (гп-гт, г„-2т)_-*0,
т. е. последовательность хп фундаментальна в $?!.
Естественно поставить в соответствие функции §(х), к
которой сходится по мере \х последовательность (х, гп), тот
элемент из #?1, к которому сходится гп. Если Ит г„ = г*,
то будем обозначать §(х) = (х, г*). Легко видеть, что
установленное соответствие между измеримыми
линейными функционалами и «9/1 взаимно однозначно. В
дальнейшем пространство линейных функционалов и 36^
будут отождествляться. Пространство измеримых
линейных функционалов является гильбертовым
пространством со скалярным произведением (х, у)-. Для любого
набора г], ..., г\ из Я?! функционалы (х, г[), ..., (х, г*п)
14*
420 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
имеют совместное нормальное распределение, причем
Мехр|/ V/. ^ ^^
= ехр { / 2 ^ (**' а) ~ \ 2 V/ (Вг1> */)) »
где (г*, а) определяется как предел Пт (гП9 а), 2пе^,
гп->г* в Я?1, а (Вг*, г*) определяется как предел
11гп (в^г, г1!), 2%-+2*к9 г*}-~> г] в Я?». Существование
обоих пределов вытекает из неравенств
\2п 2т, (I) ^ (2п 2ту 2п 2т)—9
Поскольку всякий элемент 2*е8?1 представим в виде
#~*'/22, 2^^, то вместо (2% х) можно еще писать (г, В~~%х)}
где уже ге^.
Найдем представление измеримых линейных
функционалов, использующее разложение (2). Для всякого г
(2, х) = (2, а) + 2 6а V** (еь> г),
где |л — последовательность независимых одинаково
распределенных случайных величин М|й = 0, 0^=1.
Если (2Я, х)-* (г*, #) в среднем квадратическом, то
("гп," а)->(г*, а), и для тех 6, для которых Хл>0, будет
существовать предел (гя, е&), который естественно
обозначать (г*, ел). Тогда
(г*, х) = (г\ а)+Ц^^(^4 (6)
Наоборот, для всякой последовательности чисел (г*, е&),
для которой сходятся ряды
2 К (г\ екТ % и 2 (2*, ек) (а, ^) = (2*, а),
формула (6) определяет измеримый линейный
функционал.
Изучим измеримые квадратйческие функционалы для
мер (х, имеющих среднее значение нуль. Будем
различать измеримые квадратйческие функционалы и
измеримые квадратйческие центрированные функционалы.
§6]
ГАУССОВСКИЕ МЕРЫ
421
Случайная величина д(х) на вероятностном
пространстве ($?, 35, ц) называется измеримым квадратическим
функционалом, если существует такая
последовательность симметричных линейных ограниченных
операторов ЛЛ, для которой
${х)= Нгп (Апх, х)
по мере \х. Случайная величина §(х) называется иэме~
римым центрированным квадратическим функционалом,
если существует последовательность симметричных
линейных ограниченных операторов Ап и постоянные сП9
для которых
8{х)= Нш [{Апх, х) + сп]
по мере |х.
Предположим, что оператор В невырожден (в
противном случае можно было бы рассматривать меру на
замыкании области значений оператора В). Пусть далее
ап1к = {Апеь ек), где ек — собственные векторы
оператора В. Воспользовавшись разложением (2), можем
записать
(Апх, *)=2 1^ЛаЬ!&.
I, к
Поскольку У ЯД* сцк = {В^2АпВЧгеи ек)9 то формально
возможно представить {Апх, х) в виде
(Апх, х) = (Вч'АаВ\у),
где у = 21кек — некоторый обобщенный случайный
элемент в $/, т. е. случайный элемент, распределение
которого является обобщенной мерой в дБ (см. § 5).
Заметим, что для всякого г<^дВ скалярное произведение
(г, у) = 2 1к {г, ек)
определено, так как 1к независимы, М^ = О,
О (г, ек) 1к = (г, ек)\ 2 О (г, ек) Ък=\г |2. '
•А=1
422 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Значит, если V — обобщенная мера, являющаяся
распределением элемента г/, то ее характеристический
функционал ^(г) равен
ФЛг) = е 2
Пусть /ь 12> • • • —ортонормированный базис собственных
векторов оператора Вх,2АпВ42 (он вполне непрерывен).
Тогда можно положить
</=2%/ь
где цк = (у, 1к) = 2 (*/, /л) &/ - последовательность
случайных величин на вероятностном пространстве (<%?, 33, ^).
Из соотношения
е~Хг{ =Мехр{/2т|л(2> /й)} = ехр|-у5](2:, /*)2}
вытекает, что х\к — также независимые гауссовские
случайные величины, для которых М% = 0, Р%=1. Пусть
с\ — собственные числа оператора ВУ2АпВ1/\
отвечающие [к. Тогда
{Апх, *)=2«
Лемма. Пусть при каждом п задана
последовательность т]/г/г независимых гауссовских величин, для
которых ЪАцпк = 0, Оцпк = 1. Если существуют
постоянные йп, для которых при /г-> оо 2 ср&ь + ^п'*® по веР°~
к
ятности, то 2 с^ + (1„->0 и ^(с2)2—>0.
и к п к х *'
Доказательство. Заметим сначала, что в
предположениях леммы зир|^| —>0, так как для всякого к
к
и, значит, для всякого е>0
™рК1<1в(р{|?^/+*«|<в}Г.
1
<8 <
§ 6] ГАУССОВСКИЕ МЕРЫ 423
Если бы теперь выполнялось неравенство 2(^)2>й
к
для некоторой последовательности номеров п, то
величина 2 с^пь была бы в силу центральной предельной
к
теоремы асимптотически нормальной, и тогда бы для
всякого е>0
Наконец, используя соотношение
и то обстоятельство, что
м(2с?к/-1))2 = 22(с?)2->о,
убеждаемся, что 2^/ + ^->0« Лемма доказана.
Из леммы вытекает, что сходимость (Апх, х) + йп по
мере к некоторому пределу влечет сходимость (Апх, х) + йп
к тому же пределу в среднем квадратическом. Легко
подсчитать, что
/ [(Апх, х) + апт \х (ах) = 2 ^ (с-у + (2 <7 + а У =
= 2 5р (ВЧ'АПВАПВ1/*) + (Зр (В1/2Л„В1/2) + ^)2 =
= 2 5р(Л„В)2 + (5рЛ„В + 4)2. (7)
Поэтому справедливо
Следствие. Для того чтобы при некотором
выборе йп существовал предел по мере \х выражений
(Апх, х) + йп, необходимо и достаточно, чтобы
выполнялось равенство
Пт 8р([Ап-Ат]В)2 = 0;
при этом йп можно выбирать равными —$рАпВ. Если
существует Нт 5рЛдВ, то йп можно взять равными
нулю.
424 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
Используем эти соображения для нахождения общего
вида квадратического функционала. Поскольку
(Апх, х) = 2 У К К; У^,(1Л, ~\,) + ? *• А
к, ] к.
5р {[Ап - Ат] в)2 = 2 (У К ^ \% ~ УК*?, У^)2>
к, I
то в случае существования предела Пт (Апху х) + йп
по мере \1 существуют пределы
Нт \% а», УХ, = Р4/, 2 {УК К, Ук, ~ У* - 0.
п-+оо к, I
При этом
нт 2 У К К-, УТУ &|/ - «*,) = 2 Э4, (6*6, - *4/).
/?->оо к, / к, /
В дальнейшем центрированным квадратическим
функционалом будем называть функционалы, являющиеся
пределами выражений
Пт[(Апх, х)-$рАпВ].
Общий вид центрированного функционала дается
формулой
к, I
где р6/ — произвольный набор чисел, для которого
2р!/<°°- Если к центрированному функционалу при-
бавить произвольную постоянную, то получим общий,
вид измеримого квадратического функционала.
Центрированный функционал получается из любого
вычитанием математического ожидания.
Линейные и квадратические функционалы от
стационарных гауссовских процессов. Пусть 6(0 —
вещественный стационарный гауссовский процесс со
средним 0, корреляционной функцией /? (I) и спектральной
функцией Р (I):
Я (/) = | еи\ аР (к),
§61
ГАУССОВСКИЕ МЕРЫ
425
Пусть, далее у (Я) — комплекснозначный гауссовский
процесс с ортогональными приращениями, для которого
Ъа)=\е**ау(к).
Будем рассматривать Ц1) на промежутке [—Г, Т].
Тогда ему соответствует вероятностная мера на
гильбертовом пространстве 3?2[—Г, Т] вещественных
функций, интегрируемых с квадратом на [— Г, Г]. Используем
предыдущие результаты для нахождения линейных и
квадратических функционалов от процесса ^(/).
Линейным функционалом от процесса §(/) назовем
всякую случайную величину т), представимую как средне-
квадратический предел величин
ть= $№хп({)(и,
где хп(1) — последовательность непрерывных функций,
определенных на [—Г, Г]. Найдем общий вид
линейного функционала от процесса \(1). Поскольку
[ | еш йу (А,) хп (/) Л = И | еш*Л (/) Л
-г
то
где
—т
аущ,
Мг& = 1\%(к)\*ар(к)9
т
(9)
Обозначим через ЖТ{Р) гильбертово пространство
функций, содержащее все функции вида (9) и пополненное
в скалярном произведении
(фь Ф2)= /«МЛОфйМ^М-
Тогда из сходимости цп к некоторому пределу
вытекает, что функции фЛ(Я), определенные равенством (9),
426 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ [ГЛ. V
сходятся к некоторому пределу ф, принадлежащему
ЖТ(Р\ причем
т1=/ф(Я)^(Я). (10)
Очевидно, формула (10) дает при у^Жт(Р) общий вид
функционала от процесса Ц() на [ — Г, Т].
Под центрированным квадратическим функционалом
от процесса %({) будем понимать всякую случайную
величину 2;, являющуюся среднеквадратическим
пределом величин •
т т
Ь, = { | §п И, 5) [| (0 1(5) -/?(/- 8)1 й1 (18,
-Г -Г
где &п{и з) — последовательность непрерывных
вещественных симметричных функций, определенных при /,
5е[-Г, Г]. Легко подсчитать, что
М1еяР =
т т т т
= М 1 \ ! 1ёп{и8)ёп{и,ъ)1{1)1{з)ии)Шй1й8йийь =
-т -т -г -г
т т т т
= | | | \ ёп{*1$)ёп{и,ъ)К{1--8)К(и--ъ)а1а8аиаъ =
-г -т -т -т
= 2 | ||Фля, II)?ар(х)ар(II),
где
т т
ф» (к V)- \ | вп с, *) **'-** л аз. (11)
-г -г
Обозначим через Ж\[Р) гильбертово пространство
функций, содержащее все функции вида (11) и пополненное
в скалярном произведении
(<Р1> Ф2) = \\ Ф1 (К и) фЖТ) АР М АР О*)-
Тогда, если величины %п сходятся к некоторому
пределу, то ф„ сходятся к некоторой функции ф из Ж\(Р).
$61
ГАУССОВСКИЕ МЕРЫ
427
Чтобы выразить величину ^ через <р, введем
двукратный стохастический интеграл
Л Ф(Л, \1)йу{Х)1^). (12)
Определим этот интеграл как интеграл по случайной
мере с ортогональными значениями (см. гл. IV, § 4).
Пусть мера V на ЗР определена на прямоугольниках
соотношением
V([Я^, Я2]Х[Щ, *12]) =
= У(\К К\)У{[^ 1Ъ])-Р(1К Ь2]()[\1и Ц2])> (13)
где
У(\К Х2]) = у{12)-у{кх), Р([ХЬ 12]) = Р&2)-Р(КУ
Мера V — мера с ортогональными значениями, для
которой
М\у([Хь Я2]Х[щ, \12])\2 = Р([К Я2])/^([^1, ^]).
Поэтому интеграл
Л ф(я, 11)ау(х)ау{\1)= Л ф(я, ^(<ахф)
определен для всех ф, для которых
//|ф(*. \1)\2ар(х)ар(1х)<оо
и, в частности, для ср^Жт(Р). Убедимся, что
интеграл (12) при у^Жт(Р) дает общий вид
центрированного квадратического функционала. Для этого
достаточно проверить, что
т т
-г -г
= // фЛЯ, \й4у(К)йу(]йш (14)
где фя связано с §•„ формулой (11). Пусть §п{1, $) =
т т
-5 (0 * (в), 2(А.)= /в'"г(0Л, Й(А.) = /«'»*(<) Л.
-г -г
428 МЕРЫ В ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ II Л. V
Тогда
т т
/ /я(/)*(5)[Ш&(*)-*('-*)]л^ =
-г -т
= | ё(*)4у(Ь) | й(ц)^((г)- | #(Я)Щ^(Я)=>
(последнее равенство вытекает из формулы (13) для сту-
ненчатых функций, поэтому оно справедливо для всех
непрерывных функций). Значит, (14) справедливо и для
линейных комбинаций вида
2*/(ОМ*),
а, значит, и для всех ^„(/, 5).
Из доказанного вытекает следующая формула: если
<Р (К ^) = 2 СкЦ)к (Я) ф* (\1), ТО
к
Л ф(Я, |1)<*0 (А) </# ([!)=■
в2с* (II Ф*(*)^^)Г -11 «мл) 12^м) • (15>
к
Эта формула будет использоваться впоследствии.
ГЛАВА VI
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
§ 1. Слабая сходимость мер в метрических
пространствах
Пусть 93 — метрическое пространство с метрикой
Р (х, у), ® — сг-алгебра его борелевских подмножеств,
^ — пространство всех ограниченных непрерывных
функций, определенных на 93 с нормой ||Ли = 5ир| !(х) |.
зе
Последовательность мер ц„, определенных на 25,
называется слабо сходящейся к мере р,, если для всякой
функции / из ^ выполняется соотношение
Пт Г / (х) |ай (их) = Г I (х) \1 (с1х).
Множество М мер (р), определенных на 23, называется
слабокомпактным, если из всякой последовательности
мер \1п из М можно выбрать слабо сходящуюся
подпоследовательность
Теорема 1. Пусть 93 — полное сепарабельное
пространство. Для того чтобы мнооюество М мер,
определенных на Ж, было слабокомпактным, необходимо и
достаточно, чтобы выполнялись условия
а) зир{р,(<^); [х^Л1}<оо;
б) для всякого г > О существует такой компакт К,
что
8ир{ц(Я?\/С); ре=Л1}<е.
430 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Доказательство. Необходимость. Из
компактности множества М вытекает компактность
числового множества
||/(*)|1(Жк); цееЛг}
для всякой непрерывной ограниченной функции /, а
значит, и его ограниченность. Взяв /=1, получаем
необходимость условия а). Докажем необходимость
условия б). Обозначим через Кь множество тех х9 для
которых р(х, Ю<6, где р(х, /С)= т? р(х, у). Покажем, что
для всякого е>0 и 6>0 можно найти такой компакт К,
для которого \х(!%?\Кб)^:г для всех [хеЛ1.
Предположим противное, т. е. что такого компакта
для данных е>0 и 6>0 не существует. Возьмем
произвольную меру \х{ ^ М, и пусть К{1) — такой компакт, что
р1(а?\К{1))<г- Поскольку $ир\1(а?\К$))>е, то най-
дется такая мера \х2^ М, что \12(<%?\К{8))>г. Значит,
найдется компакт /С(2)с= #/\/С{^, для которого \х2 (К{2)) > е.
В силу сделанного предположения
зир IX[т\ К{6]\ К{б!) = зир (^ \ [к{1) V К%)> г.
м- м-
Поэтому найдется такая мера \х3^М, что |х3(^\^1)\
\М2))>в и такой компакт К{3) с: а?\К$)\К№> что
М-з (^С(3)) >е- Продолжая этот процесс, построим
последовательность мер \хп и компактов К}п\ для которых
1хп(К{п))>е, К{п)а%\К{б)\ .... \/С?"°. Пусть
Х,(*Н1-4р(*, К{1))
при х^К$2, %1{х) = 0 при хШЩ]г Поскольку
расстояние между каждыми двумя компактами К{п) и К
оо
больше б, то Хп (х) %т {х) = 0. Поэтому ряд ^р О) = 2 ХМ
сходится при каждом хе^ и функция §р(х)
непрерывна и ограничена единицей. Так как из
последовательности \хп можно выбрать слабо сходящуюся
подпоследовательность, не ограничивая общности, можно
§ Ц СЛАБАЯ СХОДИМОСТЬ МЕР 431
считать, что она сама слабо сходится к некоторой
мере \х. Тогда
Игл Г ёр (х) \>>п ((*х) = Г 8Р (х) \х (с1х).
Так как | §р (х) \хп (ах) > § %п (х) \хп (ах) > е при п > р, то
для всех р выполняется неравенство цр (х) |х (их) ^ е.
Последнее же невозможно, так как §р(х)->0 для всех х
при р->оо, 0^^р(л;)^1, так что в силу теоремы
Лебега Нт \ ёр(х)уь(йх)=1Ъ. Существование для всякого
е>0 и 6>0 такого компакта /С, что ц($?\/(б)^е для
всех |х^М доказано. Взяв фиксированное е>0,
построим компакт К{г) такой, чтобы
8ир1г(а?\0)<-^.
Тогда ^С = П^1/2Г будет компактом и
г=1
оо оо
|г(^-/С)<2|г(^\/С(1г>)<2е2- =8.
Необходимость условия б) доказана.
Достаточность. Пусть выполнены условия
теоремы. Из условия б).вытекает, что можно построить
последовательность компактов Кп> для которой
Гсг+1, II (II г) = 1
для всех |1еМ и ц,(Я?\/Ся)<ея, ея | 0.
Пусть Р — такое счетное множество функций /я из %?,
что для всех т функции {/„}, рассматриваемые лишь
на Кт, всюду плотны в Фкт. Существование такого
счетного множества вытекает из сепарабельности
пространств 9!?кт и возможности продолжить любую
функцию из <&кт до функции из 9Ж. Пусть ^ —
произвольная последовательность мер из М. Выберем такую
432 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
подпоследовательность пк, чтобы для всех / е Р
существовал предел
Нт \!ШпШх) = Щ).
Покажем, что тогда этот предел будет существовать для
всех фЕ^а?. Действительно, каково бы ни было ф,
||ф||^<1, и е>0, 6>0, можно указать такую функцию
/<=>, что 8ир{|/(*)-ср(*)|; хеГ}<6, ц(Я?\/Сто)<в
и ||/|К 1. Поэтому
| $ / (х) \1Ч (ах) - | ф (х) цял (их) | < 6 вир IX {96) + 2е,
и, значит,
.Нт I ф(х)\1п (ах)— Нт у(х)цп (ах) <4е + 2б5ирр,($?);
Из произвольности е>0 и 6>0 вытекает, чтб
У™ [ Ф (*) IV (<*х) = Ит I Ф (*) (V (***) =
= Нт Г у(х)\х 1йх).
Значит, для всех фЕ?^ существует Нт I у(х)\1 (ах).
к->оо «> к
Будем обозначать этот предел также через Ь(у).
Очевидно, что I (ф) удовлетворяет условиям 1) и 2)
теоремы 1 § 2 гл. V. Далее, если ф = 0 при х^Кт, то
Мф)1
Нт Ы(х)\1 (ах)
к->оо «> пк
<11ф
\% ^п1'
Поэтому выполняется и условие 3) этой теоремы.
Значит, существует такая мера ц, что Ь{ц)) = I (р(х)\х(ах).
Достаточность условий теоремы доказана..
Замечание. При доказательстве достаточности,
как и в теореме 1 § 2 гл. V (см. замечание к этой теот
реме), полнота пространства 36 не использовалась.
Следствие. Цели 36, — полное метрическое сепара-
бельное пространство и последовательность мер \хп
*п
СЛАБАЯ СХОДИМОСТЬ МЕР
433
такое», что для всех <р е ^ существует предел
1(ф)= Нт I 4>(х)\1п((1х),
то тогда существует такая мера ц,, что
Ь (ф) = Г ф (х) \х (йх\
т. е. последовательность мер \1п является обязательно
слабо сходящейся.
Доказательство. Покажем сначала, что
множество {\хп} является слабо компактным. Условие а)
теоремы 1 для этого множества выполнено. Предположим,
что условие б) не выполняется. Тогда точно так, как
при доказательстве необходимости условия б) теоремы 1,
можем построить для некоторого е>0
подпоследовательность ц, и компакты К^\ лежащие друг от друга
на расстоянии не меньшем б, такие, что \хп (К{ ])^г.
Пусть функции Х((х) определены, как в доказательстве
теоремы 1. Обозначим для каждого простого числа р
сю
^Р (х) = 2 V М-
Функции фр (х) удовлетворяют соотношениям: 0 ^г^ (лс)<Л
и г|)р(х)г|у(х) = 0 при рфр'\ ^р^^ве и, значит,
существует
ь{%)= Ит I %(х)РпА<1х).
Заметим, что при к = рт
1 % (*) Кк Vх) > | ХА (*) \^ч ^х).
Поэтому
т -> оо ^ р
Значит, для всякого N
Ш^ьфх%^>№
434 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
(здесь /?!, ..., /^ — различные простые числа), так как
1(фХЬ(/) при ф</\ Это противоречит конечности Ь(\).
Значит, условие б) теоремы выполнено. Пусть \хп —
слабо сходящаяся подпоследовательность и \х — ее
предел; тогда
ь (ф) = нш Г ф {х) а (ах) = Г ф (х) \х (ах).
к-уоо •> Ь ^
Утверждение следствия доказано.
Рассмотрим связь между слабой сходимостью мер
и сходимостью значений мер на отдельных множествах.
Определение. Пусть {д, —конечная мера на 5В.
Множество Л е 23 называется множеством
непрерывности меры \ху если ц,(Л') = 0, где Л'— граница
множества Л. В дальнейшем будем также пользоваться
обозначениями [Л] для замыкания Л, 1п1Л — для
множества внутренних точек Л.
Теорема 2. Для того чтобы последовательность
мер \1п слабо сходилась к мере \х, необходимо и
достаточно, чтобы для каждого множества Л, являющегося
множеством непрерывности для меры |а, выполнялось
соотношение (хп (Л)-> ц (Л) при д->оо.
Доказательство. Установим сначала
необходимость. Пусть \1п слабо сходится к \х, и Л — произвольное
множество из 23. Положим
вГт(*)=ехр{-/пр(х, Л)},
где р(х, Л) —расстояние точки х до множества Л. По
скольку §т(х)= 1 при х е [Л], §т(х)->0 при х ё= [Л], то
и значит, для всякого е>0 можно найти такое т, что
\ 8т(х)ч(4х)^р{[А]) + в.
Поэтому
и(И])> 1'вт(х)» (ах)-* =
= Нт Г §т (х) цп (Ох) - е > Йт |хя<Л) - е,
П-»оо •» П-»оо
*п
СЛАБАЯ СХОДИМОСТЬ МЕР
435
откуда в силу произвольности е>0
гг->оо
Значит,
|х([а?\л])> Шп |хя(я?\л) =
дг->оо
= Игл ^я (Щ ~ Игл цл (Л) = \х {36) — Нт \хп (А).
Учитывая, что \х{ [95 \ А]) = {*>(<%) — |х(1п1:Л), получаем
^(1пЫ)< Ит »1Я(Л)< Пт МЛ)<^([Л]). (1)
Поскольку м,(1п{ А) = м>(И]) для множества
непрерывности меры |а, то из (1) вытекает необходимость
условия теоремы.
Для доказательства достаточности возьмем
произвольную функцию / из ^. Границей множества
{х: а^.1(х)<Ь} является множество {х: ?(х)=*а}[}
[){х: ?(х) = Ь}. Множества Ас=*{х: /(*)■=<?} при разных
с не пересекаются. Поэтому существует не более чем
счетное множество таких с, что \х (Ас) > 0. Выберем
последовательность чисел ак, &=1, ..., N так, чтобы
|х(ЛвА) = 0, ак<ак+1<ак + г, а{< —Ц /II» я*>ИЛ|.
Обозначим Ек = {х: ак^1(х)<ак+{}. Множества Ек
будут множествами непрерывности меры \х,. Поэтому
11п(Ек)->\х(Ек). Значит,
Пт Г / (х) \хп {их) — \ !{х)\х {их) <
<Нт
ГС->оо
&~1
+
#-1
] / (*) \х {ах) - 2 ад (Ен)
к~\
N-1
<2е 2 |х(Ял) = 2в|1(Я?).
&=1
Из произвольности е>0 и вытекает доказательство
достаточности. Теорема доказана.
Приведем теперь теоремы о слабой сходимости мер,
использующие условия слабой компактности. Во всех
436 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ *ГЛ/ \П
этих теоремах используется один и тот же факт: слабо
компактная последовательность, имеющая единственную
предельную точку, является слабо сходящейся.
Будем говорить, что последовательность [пе ^
слабо сходится к /, если функции [п ограничены
в совокупности и !п(х) стремится к }{х) для всех х^З?.
Используя это понятие, естественным образом
определяем слабо замкнутое множество функций и слабое
замыкание множества функций.
Теорема 3. Для того чтобы последовательность \ап
слабо сходилась к некоторой мере \х, необходимо и
достаточно, чтобы она была слабо компактна и для
некоторого множества функций Р^аЧТя, слабое
замыкание которого совпадает с <&&, для всех {^Р0
выполнялось соотношение
Нт Г / (х) [1п {их) = Г / (х) IX {их).
Доказательство. Покажем, что все слабо
сходящиеся подпоследовательности последовательности у,п
сходятся к мере |х. Действительно, если для всех /е Ф&
Нт Г ^ {х) \1п {их) = Г / (х) II {их)
к->оо •> я *
то для \ е Р0 выполняется равенство
$ 1(х)\х(<1х)= ]* !(х)\л((1х).
Однако из теоремы Лебега о предельном переходе под
знаком интеграла вытекает, что множество тех ^ из 9^,
для которых
| / (%) Д (б?х) = $ !(х)\1((1х),
слабо замкнуто. Значит, это соотношение справедливо
для всех I из слабого замыкания Р0, т. е. для всех:
[е^. Достаточность условий теоремы установлена,
а необходимость очевидна.
В том случае, когда меры соответствуют случайным
процессам, то удобно применять теоремы, в которых
постулируется сходимость частных распределений.
Установим одну общую теорему, из которой можно,
извлекать следствия подобного рода.
*П
СЛАБАЯ СХОДИМОСТЬ, МЕР
437
„ Теорема 4. Пусть \хп — слабо компактная
последовательность, \х некоторая мера, \ — некоторый класс
открытых множеств, содержащий с каждыми двумя
множествами их сумму и пересечение и удовлетворяющий
условиям: 1) о-замыкание Па содержит все открытые
множества, 2) все множества из 210 являются
множествами непрерывности меры ц,. Если 1ип \хп (А) = \х (А)
П->оо
для всех Ле510, то \хп слабо сходится к ц.
Доказательство. Пусть \хПк — некоторая
последовательность, слабо сходящаяся к мере Д. Из (1)
вытекает, что для всех А е ?10 выполняются соотношения
Д {А) = Д (ША) < Ит \хПк (А) = \1 (Л).
Таким образом, для всех А е %0 имеет место
неравенство )ь1(Л)^ц(Л). Очевидно, это соотношение
выполняется на монотонном классе множеств и этот класс
содержит все множества из 210. Поэтому оно
выполняется и для'каждого открытого множества. А так как
каждое замкнутое множество является пересечением
убывающей последовательности открытых множеств, то
Д (Р) ^ \х (Р) и для всякого замкнутого множества Р.
Поэтому для всех множеств Ле910имеем: ^(Л7)^
<[х(Л/)=-0. Но тогда р, (Л) = 1\т\1п. (Л) = ц(Л). Из сой-
падения мер \1 и ц на % вытекает и их совпадение на 33.
Значит, все предельные точки последовательности \хп
совпадают с |и. Теорема доказана.
Замечание. В случае мер на различных
функциональных пространствах в качестве класса Ш0 обычно
рассматривается класс всех открытых цилиндрических
множеств непрерывности меры \х.
При слабой сходимости мер можно установить
сходимость интегралов и для некоторых разрывных
функций. При этом мы будем использовать то обстоятельство,
что множество точек рдзрыва 23-измеримой функции
является также 23-измеримым множеством.
Лемма. Если \лп слабо сходится к \х, то
Нт Г /(*)|ай (<**) = \!(х)р(йх)
438 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
для всякой ^-измеримой \х-почти всюду непрерывной и
ограниченной функции 1(х).
Доказательство. Пусть Л — множество точек
разрыва функции /(х). Положим ^а = {л;: }(х)<а},
пусть ^ц — граница множества ^а. При а<р множество
^а Л ^р содержится в пересечении множеств [^а] П [X \ ^],
и поэтому для х^-9'а[)8'р выполняются неравенства
Нтт[/(г/)<а, Птзир/(г/)>р. Значит, &'а(]9'с:А и
множества <&'а\А не пересекаются при разных а.
Таким образом, существует не более чем счетное число
таких а, что 11(С'а) = ц(Сд\Л)> 0, т. е. множества *§а
все, за исключением, быть может,- счетного числа
таких множеств, являются множествами непрерывности
меры \1. Поэтому для всех а, за исключением, быть
может, счетного числа
Нт \1п({х: !(х)<о)) = 1л({х: Цх)<а}). (2)
Из формулы замены переменных в интегралах
вытекает, что
\ / (х) \1п №) = \ ааа\1п ({х: I (х) < а}), (3)
//(*)!*(Ах) = \ шд* ({*: /(х) <а}). (4)
Из равенств (2), (3) и (4) вытекает утверждение леммы.
Рассмотрим, наконец, условия слабой сходимости
мер в линейных нормированных пространствах. Пусть
96 — сепарабельное банахово пространство, Ь —
линейное множество линейных функционалов на 96 такое,
что минимальная а-алгебра, относительно которой
измеримы все функционалы / из Ь, совпадает с а-алгеб-
рой всех борелевских множеств 23 пространства 96.
Будем через %„(/) и %(1) обозначать соответственно
характеристические функционалы мер \1п и ц:
Хп (I) = / е« Ю|1„ (их), х (/) = | е^*Ъ (их).
Теорема 5. Для того чтобы последовательность
мер \хп слабо сходилась к мере \х, необходимо и доста-
$2]
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
439
точно, чтобы последовательность \хп была слабо компактна
и для всех 1^Ь выполнялось равенство
Птх„(0 = х(0- (5)
Я->оо
Доказательство. Необходимость условий
теоремы очевидна. Для доказательства достаточности
опять покажем, что всякая предельная точка
последовательности \хп совпадает с \х. Пусть \х — такая
предельная точка; тогда для всех 1^Ь
Х(0 = х(')=/*"и,№)-
Из совпадения характеристических функционалов
вытекает совпадение мер, м- = Д. Теорема доказана.
§ 2. Условия слабой сходимости мер
в гильбертовом пространстве
В этом параграфе 36 — сепарабельное гильбертово
пространство, 23 — сг-алгебра борелевских множеств из 36.
Рассматриваются меры на 23 и изучаются условия
слабой компактности и слабой сходимости этих мер. Как
видно из результатов предыдущего параграфа,
основная трудность заключается в нахождении условий
слабой компактности семейства мер. Оказывается, что для
гильбертова пространства можно указать необходимые
и достаточные условия слабой компактности семейства
мер в терминах характеристических функционалов.
В дальнейшем будут использоваться следующие
обозначения для некоторых совокупностей линейных
операторов в 36 \ Тс — множество всех симметричных
неотрицательных вполне непрерывных операторов, 5 —
множество всех ядерных операторов, 8а —
подмножество 5, состоящее из операторов, след которых не
превосходит а.
Установим сначала один удобный для дальнейшего
применения критерий компактности множества в 36.
Лемма 1. Для всякого А^ТС множество {х: \ А~1х |^
^ 1} компактно. Для всякого компакта К с: 36 найдется
такой оператор А^ТС, что К^{х: \А~1х\^.1).
440 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Доказательство. Множество [х: \А~]х\^\}
является образом единичной сферы при отображении А
и компактно в силу вполне непрерывности оператора А.
Пусть /( — некоторый компакт, а {ек} — произвольный
ортонормированный базис в 36. Положим хк = (х, ек).
Из компактности К вытекает, что существует такая
последовательность сп \ 0, что ^(хк)2^сп для всех
х^К. Выберем теперь числа (1п[0 так, чтобы
выполнялись соотношения 2^п==а+00> 2^я<°°« Тогда
п п
2 (**)2 2 <// = I 4 2 (дгО2 < 2 йкск < оо.
к-1- /-1 й-1 /Хе * = 1
Определим оператор А, для которого ей являются
собственными векторами и
2 «>ч
2'/
Тогда
/-1
для всех х^К- То, что А — вполне непрерывный
оператор, вытекает из условия
Нт ^ й^1 ( 2 б?/ ] =0.
&г>оо /=1 \/ = 1 /
Лемма доказана.
Теорема 1. Пусть М — некоторое семейство мер,
%^(г), гЕ^,- характеристический функционал меры
[х е М. Для слабой компактности множества М необ-.
ходимо и достаточно, чтобы: а) %а(0) бб^ла ограничены
при |хеМ; б) Зля всякого е >0 можно было указать
оператор Ву В^ТС, и для каждого \1 е М — оператор
■.-у
§2}
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
441
Лцл е 51 такие, что Ке [%^ (0) — %^ (г)] < е, если только
(ВЛ,Вг,г)<1.
Доказательство. Необходимость условия а)
вытекает из того, что для слабо компактного множества М
выполняется условие а) теоремы I § 1. Установим
необходимость условия б). Не ограничивая общности,
можно считать, что %ц(0)=1. В силу теоремы 1 § I
для слабо компактного множества М можно указать
такой компакт К&ИР, для которого при всех \1& М
выполняется неравенство \х{9В — К)<у. Тогда
Яе[х*(0)-%*(г)] =
= /[1-соз(^г)]|1(^)<| + 4-/(г, х?ц((1х). (1)
а:
Пусть В —такой оператор из Тс, что К а [х: \в~[х\^
<^]/е}. Он существует в силу леммы 1. Пусть А^ —
неотрицательный симметричный оператор, для которого
(ВЛ^Вг, г) = | | (х, г)2» (их). (2)
\в~1х |</Г
Тогда
(Лйг, г)-~ / (х, В"1^ (</*) =
\в~[х\<УГ
и
ЗрЛвЕ(^^ ^) = ~ | \В^х\211(ёх)<и
к |в-ч<кг
т. е. Л^е^. Из (1) и (2) вытекает неравенство
Ке[у^(0)-^(г)]^ + ^(ВЛ1,Вг} г). (3)
Необходимость условия б) доказана.
.Установим достаточность условий теоремы. Из
условия а) следует ограниченность ц(<8?). Из теоремы 1 § I
442 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
вытекает, что достаточно показать существование для
каждого е>0 такого компакта /С, что \1 (ЗВ — К)<^е для
всехр,^М. Пусть В^ТС — такой оператор, что для
всех \1^М выполняется неравенство Ке[х^(0) — %^(г)] ^
<-|- при (ВА^Вг, 2)^1, где Л^е^. Тогда
Ке [%[1 (0) - %[1 {г)] < 1 + 2 (ВА^Вг, г). (4)
Оценим при Я>0 интеграл
| [!_ ехр { - А(В~*х, х)}] |х ((1х).
Пусть еь еъ ...—полная ортонормированная
последовательность собственных векторов оператора В, а % —
соответствующее ек собственное значение. Тогда
(В-%х) = %^,
где хк = (х,ек). Заметим, что
ехр
Й-1
-Л п
= (2яЯ) тПРк/ ••' 1ехр|г'2]
хкгк
X
где г1, ..., гп — вещественные переменные. Поэтому
/[1-ехр{-А(Б-^,х)}]^(^) =
= Нгп ) (2яЛ) 2 Др^ ... ] 1-е *-• X
X ехр 1 - ±- 2 р! (г6)2! йг1 ... йгпц (их) =
= Игп (2яА)"^ Д р* | ... | Ке Г1 - %11 № гО! X
§21
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
443
Хехр^^^р^И2}^1...^:
<Нт (2яЯ)"Пр* Г ... Г
к—\
+ 2^ВА„В^ек,^гкек
Хехр {-^2 рНаМ &'...«&"-
П
^| + 2АПгп 2 (V*' ек) = Т + 2ЯЗр А„<|- + 2А,.
Значит,
(В""2*, х)>С
< / [1-ехр{-!(В-2л-, х)}]|х(^)<у + 2Л.
(Б-2х,лг)>С
Выберем А>0 и С>0 так, что —?—тттт<е.
{-Щ
2 - 2ехр
Тогда для всех \1 е Л/ выполняется неравенство
р, ({х: | В~гх | > С}) < е и, следовательно, К = {х:\ В~1х | <
<Х} будет искомый компакт. Теорема доказана.
Замечание 1. Простой пример Ю. В. Прохорова
и В. В. Сазонова показывает, что для слабо
компактного семейства мер не всегда можно указать для
всякого е>0 такой оператор А из 5 (общий для всех мер
р.€= М), что Ке(хд(0)- Хц(*)Xв при (Аг, г)< 1. Пусть
К -компакт вида К = {х: | В~1х |< 1}, где В^ТС и
8рВ2=+оо. Определим меры [л,х равенствами \х{{х}) =
= 1*({-*}) = 4". р(%\{х}\{-х}) = 0 (здесь
{^-множество, состоящее из одной точки х). Рассмотрим
семейство мер М = {[хх, х е= К]. Так как |х (^\ /С) = 0 для
444 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
всех цеЛ1 то М — слабо компактное множество.
Далее имеем
Ке (зы, (0) - ъх (г)) = 1 - соз (х, г) = 2 зш2 -^ ,
вирКе(Х (0)-ь,(^))= зир 2зш2 (Д~';-Д*} -
Ы<1 2 |251П2^, \Вг\<л.
Пусть Л —такой оператор, что Ке(х^(0) — %^{г)) ^ 1 при
(Аг, г)^1. Тогда |В,г|<я при (Аг, <г)<!1. Значит,
|ВЛ~,/22|<я при | г |<! 1, т. е. ВА~!г — ограниченный
оператор. Поэтому В = СЛ,/2, где С — ограниченный оператор.
Так как В = В* = АЧ>С*, то В2 = А^ССА1/* и для орто-
нормированной последовательности {ек} собственных
векторов оператора А получим
2 (В%, ек) = 2 (ССА^еку №ек) < || СС || 2 < Леъ ек).
к к. к
Значит, обязательно Зр Л= + оо.
Условие б) теоремы выглядит несколько громоздко.
Приведем некоторые модификации этого условия.
Лемма 2. Для того чтобы семейство операторов С^
из 8 было представимо в виде Сй == ВА^В, где В е ТСЛ
Лц^5,, необходимо, чтобы в каждом ортонормирован-
ном базисе {ек} ряд
оо
ЗрС^=2(С^, ек) (5)
сходился равномерно по \х, и достаточно, чтобы этот ряд
сходился равномерно хотя бы в одном базисе.
Доказательство. Достаточность. Пусть
{ек} — ортонормированный базис, в котором ряд (5)
сходится равномерно. Положим
оо
р„ = вир 2 (С„ел, ек)
§2]
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
445
и выберем так последовательность а„>0, чтобы
2«/1== + 00> и 2а„р„<оо. Тогда
оо И .оо оо оо
2 2^ (С^еПУ еп) = 2 ак 2 {Су1епу еп) < 21 ^кРк-
п=1 к=[ к = \ п — к к=\
Пусть, далее, В — симметричный оператор, для которого
/ * I к у/,
Век = Хкекг где Ал= 2 апр*/2 О ; 5е1Г„ так как
Я&->0. Положим А^ = В~~1С^В~~{. Тогда
5р Лй - ^ (В-^/ГЧ, ^*) - 2 тг«V*, ек) =
оо й / оо
Достаточность условия леммы доказана.
Необходимость. Пусть С{1 = ВА^В, В^ТС,
Л^е 51э а (Ы — любой ортонормированный базис. Обо-
значим через Ры -оператор проектирования на линейное
подпространство, натянутое на векторы /#, /дг+1, ...,
и пусть Вм = ВРМ, Тогда
оо
1>(ВА,кв!к,!к) =
к~Ы
= 2 {РывА^вры1к, !к) _ 5 р (в; л ду) -
= зр«^)<|в;2|5рл(1<|в;|2,
* = 1
так как 5рЛВ = 5рВ*Л* и 5р АВ < 5р ВЦ Л ||, если
Ве5.
Для завершения доказательства заметим, что|в#Ц—*0
при #->оо. Действительно, поскольку множество К
векторов вида Вх при |л;|^1 компактно, а функции
\РмУ\ непрерывны и монотонно убывают к нулю, то и
8ир{| Рыу\, #<=/0^рприЛ'-*оо.Нозир{| Рыу\,у*=К}=*
= вир | РыВх | = ||В;у|. Лемма доказана.
446 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Обозначим через 5* множество операторов /), для
которых сумма 2.1 фекУ ек) | конечна и ограничена по
к
всем ортогональным базисам {ек}. Точную верхнюю грань
этой суммы будем обозначать Зр|/)|. Через 5е будем
обозначать совокупность операторов из 5*, для которых
5р|Я|<е.
Следствие. Пусть семейство операторов С^ для
всякого е>0 представимо в виде С^ = В{&)А$]В{г) + Д(8),
где В(е)е Тс, А%] 'е 5Ь й{г 'е 5е. Тогда существует такой
оператор В<==ТС, что С^ = ВА^В и Л^е5ь
Действительно, как вытекает из леммы 2, достаточно
показать, что для некоторого ортонормированного
базиса {ек} ряд 2(С„^Ь ек) сходится равномерно относи-
к
тельно \х. Но для всякого е>0
2 «V*. еА)< 2 (В«УА№%, ек) + г
к>Ы к>Ы
и, как вытекает из леммы 2, выбором достаточно
большого N сумму
2 (в(8Ч8)я(Ч, ек)
к>Ы
можно сделать меньше е одновременно для всех N.
Обозначим через Ж$е гильбертово пространство
линейных операторов Гильберта — Шмидта, определенных
на 36 (т. е. таких операторов С, для которых 5р СС*< оо)
со скалярным произведением
(Л, В) = 5рЛВ*.
Лемма 3. 1) Если В^ТС, А„,<е=Тс и Л*е= 5Ь то
множество операторов ВА^ компактно в Ж&.
2) Для всякого компактного в Ш$е множества операто-
— 1 2 — 1
ров См найдется такой оператор В<=ТСУчтоВ~1С»В-1е=8и
Доказательство. 1) Пусть {ек} — базис
собственных векторов оператора В, а Рм — оператор
проектирования на подпространство, натянутое на векторы
еи ..., ем. Тогда
(РНВА^-ВА^ РиВА^-ВА^** 2 (ВА1Век, ел)->0
§•2]
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
447*
при N -> оо равномерно относительно \х-. Далее РМВА^ =
«= ВРМА11 и компактность множества {РМВА^}У а значит
и множества {ВАу}, будет вытекать из компактности
множества {Р#ЛЙ}.'Обозначим через Рк оператор
проектирования на подпространство, натянутое на к
собственных векторов оператора А^ соответствующих
наибольшим собственным значениям. Заметим, что к+1-е по
величине собственное значение оператора А^ (в силу
условия 5рД1<Л) не превосходит , Поэтому
У к+ 1
ДЛг-РЙЛрЦ^; у^7Г1 И> значит>
5р Рм (А» - Р%А») {А» - РМ Рм < тт= -
Таким образом, достаточно показать компактность
множества операторов {р#Р!Мц}. Заметим, что Р«Лц
является линейной комбинацией к проектирующих
операторов с коэффициентами, не превосходящими единицы.
Поэтому компактность множества {Р#Р/Мц} будет
вытекать из компактности семейства операторов {РмР(г)9
I 2 | ^ 1}, где Р(г) — оператор проектирования на вектор г.
N
Так как Р^— 2 Р(^)> то достаточно показать компакт-
ность множества операторов [Р(ек)Р(г), | г |<Л}. Но
5р Р (ек) [Р (г{) - Р (е2)] [Р (гг) - Р (е2)] Р (*,) =
= \(Р(г1)-Р{гй))ек? = {г1-г2,екУ*.
Таким образом, операторы вида
Р(ек)Р(1гек+УТ^№ек+1), 1П<|>
образуют конечную е-сеть в множестве {Р(ек)Р(г)>
|г|^1}. Утверждение 1 леммы доказано.
2) Пусть Си С2, ..., См — е-сеть в множестве {С^}.
Обозначим через С^ оператор Ск с наименьшим
индексом к, для которого Зр^ — Ск)(С^ — Сй)<е2. Тогда
С1 = С» + И^ где
448 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Легко видеть, что Д^еХ* и
5р | Од | < 2 Узр С;2 5р (Сд - С,!)2 4- е2 = О (е).
Заметим теперь, что С^ принимает лишь конечное число
значений при разных \х и при каждом \х ряд 2(^1^, в^)
к
сходится для всякого ортонормированного базиса {ек}у
поэтому эта сходимость равномерна относительно \х.
Остается воспользоваться следствием из леммы 2. Лемма
доказана.
Доказанные леммы дают возможность найти более
эффективное (по сравнению с теоремой 1) условие
компактности мер.
Теорема 2. Пусть М = {ц} — семейство конечных
мер на $1 Для слабой компактности множества М
необходимо и достаточно чтобы:
1) для всякого е>0 существовало такое с, что
\х{х: |л'|>^}<8 для всех \л*=М;
2) для всякого с семейство операторов В^, опреде-»
ляемых соотношениями
\ {г,х?-\в1г\\
являлось компактным множеством в Ж&. Условие 2)
можно заменить следующим:
2') в каком-либо базисе (а значит, и во всяком базисе)
ряд
оо
сходится равномерно по \х при всяком с>0.
Доказательство. Не ограничивая общности,
будем считать \х($&)= 1. Достаточность вытекает из тео~
ремы 1, так как Ке(1 — Хц(г))^у (х> 2У М- №х) +
4- \1({х: | х | > с} )< -^ | В^г |2 4- -—, если с достаточно
большое, а в силу утверждения 2 леммы 3 (В^)2 = &А^В,
где В<=ТС, 5рЛ^<1. Докажем необходимость
§2]
УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР
449
условий теоремы. Пусть М компактно и К — такой
компакт, что \к{8в — /С)<8 для всех \х^М. Если с таково,
что |лгК> при х^К, то \х({х: \ х\>с})<г.
Необходимость условия 1 доказана. Далее, полагая Vс =» {х: \ х \^с},
находим:
| В& |2 = | (г, х)2 II (с1х) + | (г, х)2 II (с1х).
кг\ус ус\к
Пусть К={х: \В~1х\^1}у где В*=ТС. Тогда
§ (г, х)2 II (ах) < | (В~[х, Вг)2 |х (Лс) -1 А^Вг |2,
«ПК, \в-*х\<\
где оператор Л^ определяется соотношением
|в~Ч<1
Поэтому
|в~!х|<1
Таким образом,
/ (2,*)2^*)<|Л^г|2,
/спк,
где Л^е5ь а Ве Гс.
С другой стороны, если О определено равенством
[ (г, *)2 Ц (<**) = (#2, ^),
то
Эта величина может быть сделана сколь угодно
малой одновременно для всех \х выбором компакта К.
Поэтому в силу следствия из леммы 2 и утверждения 1
деммы 3 совокупность операторов {в^} компактна в Ж&.
Необходимость условия 2) доказана. Необходимость
условия 2') вытекает из леммы 2). Теорема доказана.
1& & И. Гихман, А, В, Скороход
450 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Следствие 1. Пусть для мер цеМ существуют
корреляционные операторы
(А^г, г)- | (г, х)2\\,{(1х)
и А^ е Ж%. Тогда для компактности семейства мер И
достаточно, чтобы множество операторов {А$} было
компактно в Ж&. Если можно указать такое с>0, что
\х({х: | х | > с}) = 0 для всех }аеМ, то это условие
является и необходимым.
Следствие 2. Пусть оператор А^ определяется
равенством
(4г>*)= |тТ17ТГ^*)- (6)
Тогда для. компактности семейства мер М необходимо
и достаточно, чтобы:
1) множество операторов {А^2} было компактно в Ж%>г
2) Нщ зир \х({х: \х\>с}) — 0.
Сформулируем одно удобное условие слабой
сходимости мер.
Теорема 3. Для того чтобы последовательность
мер \1п слабо сходилась к мере \х, необходимо и
достаточно, чтобы:
1) характеристические функционалы %п(г) мер \хп для
всех 2еЖ. сходились к характеристическому
функционалу %(г) меры \х,
2) семейство операторов {Л^2}, определяемых
равенством (6), былю компактным в (Ш%>,
Доказательство. Необходимость условий
теоремы вытекает из следствия 2. Для доказательства
достаточности в силу следствия 2 и теоремы 5 § 1 остается
лишь показать, что
-Пгп \[ш1хп({х: 1*|>с}) = 0. (7)
С->оо п->оо
Пусть
§2] УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ МЕР 451
Поскольку
\ (г, х)2 гя (их) - ] /^ *]', \хп {их) = (Лц2, г),
то семейство мер Vп компактно. Соотношение (7)
эквивалентно следующему:
Нт Шхп({х: | х |> 1 - е}) - 0. (8)
8->0 л->оо
Предположим, что (8) не выполняется. Тогда найдется
такая слабо сходящаяся подпоследовательность \Пк, предел
которой V будет удовлетворять условию V ({х: \ х | = 1}) > 0.
Следовательно, при некотором г, |г|==1 и 6>0 будем
иметь
у({х: 1*1=1, |(*, 2)|>6})>6.
Тогда для всех е>0 при достаточно больших пк
Vял({*: | л: I> 1 — е; | {х, г) |>б} )>б,
а значит,
'•.((^7т7г>'-^>»))>1
Таким образом, для всякого е>0
1|гп|хял({^:|(^2)|>^})>в.
С другой стороны, для всякого г
Нгп \\т \хп ({х: | (х, г) | > с)) ^
<Пт Нт^у 1 ^ МЛО-
= ИГТ1 ПЙГ я ^. Г (1-х,('*))<«-
-я/с
я/б'
-Дт.^Т /(1-х(^))Л-0.
-Я/С
Полученное противоречие доказывает теорему.
15*
452 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Замечание. Если последовательность мер \хп слабо
сходится к мере ц> то %п (г) -> % (г) равномерно при
|г|^с, каково бы ни было с>0. Пусть В —такой
оператор из Тп что можно указать операторы Ап е 5Ь для
которых Ке(1 — %п(г))<г2/8 при {ВАпВг, г)<1. Если
|Вг|<1, то тем более (АпВг, Вг)<\. Поэтому
I Хп (гх) - Хп (г2) I2 < { I 1 - *' <™ *> I2 |гд (их) =
Г е2
= 2 | (1 - со5 {г{ - г2, х)) ця [их) = 2 Ке (1 - %п [г)) < -^ ,
если только | Вгх — Вг21< 1. Поскольку множество
{Вг: | г \^с} является компактом, то существует конечный
набор точек г{, ..., гт1 для которого \хЛ\ Вг — Вгк\<\
к
для всех г, | г | ^ с. Тогда
Пт 5ир 1х„(2)-х(2)|<Нт зир | хЛ^) - %{гк) I +
+ 2 Пт 5ир5ир{|Хп(^)~Хм(^)1; I В(г-2Л)К 1}<е.
п->оо /г
Наше утверждение доказано.
§ 3. Суммирование независимых случайных
величин со значениями в гильбертовом
пространстве
В этом параграфе мы будем рассматривать не только
вероятностные меры на гильбертовом пространстве, но
и случайные величины со значениями из гильбертова
пространства, распределениями которых служат эти
меры. Пусть* {У, 51, Р} —некоторое вероятностное
пространство, {36, Щ — гильбертово пространство с сг-алгеб-
рой борелевских множеств. Случайная величина со
значениями в $6 — это функция ^(со), определенная на й и
принимающая значения из <й?, для которой {ш: ^(оэ)^В}<=91
для все* ВеЗЗ. В дальнейшем вместо %(оэ) будем писать
просто |. Распределение величины | — это мера
МВ) = Р{|еЯ} = Р{©: !(«>)€= Я}.
С каждой случайной величиной \ свяжем подалгебру Щ
алгебры 91 событий вида {<*>; ^(оэ)^В}, где В —любое
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 453
множество из 93. Случайные величины %и Ъ2> • • •> 1п>
называются независимыми, если независимы а-алгебры
событий Щх, Щ2, ..., Щп, ..., т. е. для любых событий
р{Л^}=Прш.
Рассмотрим, как выражаются характеристики суммы
независимых случайных величин через характеристики
слагаемых. Характеристическим функционалом
случайной величины | называют функцию
X* (г) = ЬАе* {2> *> = | е1 ^ *>щ {их),
т. е. характеристический функционал распределения
величины |.
Если |ь ..., 1п независимы и %к(г) —
характеристический функционал величины |ъ то
Мехр{/(2, 2|*)) = Пх»(2). (О
Таким образом, при сложении независимых случайных
величин характеристические функционалы
перемножаются. Чтобы найти выражение для распределения
суммы независимых случайных величин, рассмотрим
случай двух слагаемых. Пусть ^ = ^ + ^2 и \х^ \х^у \хь
распределения величин |, 1{, |2- Тогда
|х6(В) = Р{61 + 52еВ} = МР{61 + 62еВ1«е1} =
где В — х — множество тех уу для которых х + у^ В.
Заметим, что \хь(В — х) является 23-йзмеримой
функцией. Поэтому
МЦ2 (в - 1г) = | |хь (в - х) \х1{ (ах).
Итак, имеем формулу
454 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
т. е. распределение суммы двух независимых случайных
величин является сверткой распределений слагаемых.
Сходимость рядов из независимых случайных
величин. Приведем некоторые неравенства,
распространяющие неравенство А. Н. Колмогорова и различные
его обобщения на величины со значениями из
гильбертова пространства.
Лемма 1. Пусть 1и ^2> •••> &* — независимые
случайные величины, для которых М^ = 0, М | %к |2 < оо и
к
С* = 2 I*. Тогда
Р{зир|Ы>е}<-р-М|и2- (3)
Доказательство вытекает из того, что | ^ I2
образует полумартингал и неравенства (16) § 2 гл. II.
Лемма 2. Если %и . .., сп независимы и | Ы ^ с,
то для всякого натурального I и положительного а
Р{зир|^|>/а + (/-1)с}<(р{5ир|^|>|}У.
Доказательство. Пусть %ь=1, если |^|>
>(/— 1)а + (/ —2)с, а при *'<МЫ<(/-1)а + (/-2)с.
Хь = 0 в остальных случаях. Тогда
Р{зир|гл|>/а + (/-1)с} =
= 2Р{5ир|й|>/а + (/-1)С|Х;=1}Р{Хг=1}<
I — 1 к < «
<2Р{ зир |^~^|>а}Р{Х,= 1}<
х = 1 /<&<л
< зир Р{ зир |?Й-Ы>а}2Р{х,= 1}<
ККл «'<&<« 1 = 1
<Р{ зир 1Сл-гЛ>а}Р{ зир |^ |>(/ - 1)а + (/ -2)с}.
Остается заметить, что
Р{ зир 1СА-СП>а}<Р{зир|Сл|>-|}.
Лемма доказана.
Величина \ называется симметричной, если | и — |
имеют одинаковые распределения.
$ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 455
Лемма 3. Вели |ь ..., 1п — симметричные
независимые случайные величины, то
Р{зир|Ы>е}<2Р{|и>е}.
Доказательство. Пусть хл=1, если |^|>е,
а 15/1^8 при К к, Хь^О в остальных случаях. Тогда
Поэтому
Р{|Е»1>в}«2Р{|Е»1>в, ъ-1»
>Ц]Мх, = }Р{зири.1>вЬ
Лемма доказана.
Лемма 4. Пусть %{, ..., 1п — независимые
случайные величины такие, что для всех к^п
21/
>с
}<а.
Тогда
Р{8ир|С*1>а + с}<т4гР{|С„|>а}. (4)
Доказательство этого утверждения аналогично
доказательству теоремы 6 § 3 гл. II.
Используя эти леммы докажем теперь теорему
о трех рядах А. Н. Колмогорова для гильбертова
пространства.
Теорема 1. Если |1э ..., §п,
...—последовательность независимых случайных величин со значениями*
оо
из 36, то для сходимости ряда 2 ^ необходимо, чтобы
1 = 1
для всякого с^О сходились ряды
оо
1)2а" а<= I хНг^х),
1-1 \х\<(
456 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, VI
2) 2 I \х-аг\2^(ах),
; = 1 икс
оо
3) 2Р{1|г1>с},
* = 1
и достаточно, чтобы эти ряды сходились хотя бы при
одном с>0.
Достаточность условий теоремы доказывается точно
так, как и в одномерном случае (см. теорему 5 § 3 гл. II).
Необходимость условия 3) вытекает из того, что для
всякого с > 0 происходит лишь конечное число событий
{\1г\>с} и теоремы Бореля — Кантелли. Докажем лишь
необходимость условий 1) и 2). Пусть ^ = 1к при||й|^с
и ^ = 0 при |^|>с. Так как из условия 3) вытекает,
что среди величин 1к — ^ лишь конечное число отлич-
оо
ных от нуля, то ряд 2 % сходится вместе с рядом
6=1
2 1к- Поэтому величина зир
6=1
п,р
п + р
2 К
к—п
конечна. В силу
леммы 2 для всех натуральных /
зир
п
2 К,
&=1
>1(с + а) К(Р | зир
п, Р
п+р
к=п
>-,
Выберем такое а, для которого
I п + р
Р < зир
п,р
2«
к=п
>$\<е-К
Тогда для всех п
I
П
2 б;
>0<Ке
'I
-и.
ГДе х = —;—, К = ес+а. Из этого неравенства вытекает,
с +• а,
что М
с +
п
21;
А-1
равномерно ограничены при всех $ и, знаг
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 457
чит, в силу теоремы о предельном переходе под знаком
интеграла существует предел
Нт М
Я->оо
п
2 б;
к=\
5
= М
2 К •
А=1
В частности, при $ = 2 существует предел
Пт М
/1->оо
п
2«,
*-1 |
гс->оо \&=1
= Нт 2М|й-алр +
2 ял
*=1 *
Следовательно, ряд 2 М|^ —а^р СХ®ДИТСЯ* Но тогда
из достаточности условий теоремы вытекает сходимость
оо со
ряда 2 (^~~аА:)> а так как Ряд 2 ^ также сходится,
оо
то будет сходиться и ряд 2 а,. Теорема доказана.
оо
Следствие. Для сходимости ряда 2 1к из незави-
к=\
самых случайных величин достаточно, чтобы сходились
ОО •" ОО
ряды 2 Щи и 2 М\и-Щь?> где М|л= Г хц* (<**)-
такой вектор из $?, что для всех ге!' (М|*, г) =
- / (*> г) |и^ (с/л:).
Условия сходимости ряда из независимых случайных
величин можно выразить и в терминах
характеристических функционалов.
Теорема 2. Пусть 1Ь ..., |я, ...—независимые
случайные величины и %п (г) — их характеристические
функционалы. Для сходимости ряда 2 \н необходимо
к=\
оо
и достаточно, чтобы произведение \\ %&(%) сходилось
~к=*\
к некоторому характеристическому функционалу %{г)
равномерно в каждой области {г: \г\^с}.
453 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Доказательство. Необходимость. Пусть
п
{я= 2 ?*, 5= Пт Ъп. Тогда для каждого 6>0
к=\ п-*оо
1[%ь(г)-Цхь(г)
к = \
/г = 1
= |Мв'*°-Мв'(г-с»>|<
<М|е'(с-:»1г)-1|<2Р{|С-Сп|>4}+в|г|.
Необходимость условий теоремы доказана, так как
Пт Р{|?-^|>6}-*0.
П-»оо
Достаточность. Введем независимые между
собой и независимые от %к величины ^, имеющие такие же
распределения, как %к. Положим \=*1к — 1'ь- Докажем
сначала сходимость ряда из величин цк. Очевидно,
Из неравенства
1-П|хй(г)12<1-П1х*(г)12=1-|х(г)Р
и того, что \%{г)\2 является характеристическим
функционалом некоторой меры вытекает, что распределения
п
величин 2. Лл образуют компактное семейство мер.
Поэтому
II
Нт вир Р .
С->оо п \
Но тогда в силу леммы 3
п + р,
2%
л*
Нт Р \ зир
С-»оо I «, р
к=п
>с }< НтР
с} = 0.
зир У
<2 Нт зирР
С-»оо п
Л»
%
>
>
<
= 0.
Таким образом, величина зир
п, р
п+р
к=п
к=1
конечна. В
частности, конечна величина зир|т|л|. Поскольку для доста-
к
$ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 459
точно больших с
оо
0<Р{зирЫ<с}=П(1-Р{Ы>с})<
/е-1
<ехр(-2Р{Ы>с}
оо
то сходится ряд 2Р{|%|>^}* Пусть Г1'к = \ при
&=1
\%\^су К = О ПРИ |%|>с- Тогда величина
зир
п, р
п + р
к = п
также конечна, так как ц^ц^ за исключением
конечного числа индексов к. Из конечности этой величины
точно так, как и в теореме 1, вытекает сходимость ряда
оо
2 М | т]' Г2 (поскольку Мг(к = 0). Значит, в силу теоремы 1
к—1
сходится с вероятностью 1 ряд
оо оо
2п* = 2&-|;).
/г-1
Поэтому можно указать такую последовательность
векторов а'ь ..., хп, ... из 8В (возможные значения ^),
оо
что будет сходиться с вероятностью 1 ряд ^ Ик"~ **)•
/е = 1
оо
Остается доказать, что сходится ряд 2 *&• В силу до-
казанной необходимости условий теоремы сходится
равномерно при |г|<х бесконечное произведение
Так как можно указать такое б, что \%(г)\>-^ при
|г|^6, то при |г|^д будет существовать равномерный
предел
11т ТТ в"'(*•**>= Пт 'ТТ *-<<*.**) Хй (2).
„^оо-1-Х. д-»оо А\^ -*-1-
460 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Поэтому будет существовать предел Нт [х, 2 */?) равно-
/г->оо \ & = 1 /
мерно по г при |г|^б, а значит, и равномерно по г
при |г|^с, каково б*>1 ни было с>0. Отсюда вытекает,
п
что 2 хк имеет, во-первых, слабый предел х:
к=\
и что
Нт (г, 2 хк) = {г, х)
в совокупности ограничены. Из равномер-
\к=*\
ной сходимости вытекает, что
п
Нт 2 хк, 2 хк = Нт 2 хк, х] = (х, х).
п->оо \& = 1 к = \ I п->оо \к=\
Таким образом, 2 хк слабо сходится к хи
п
Значит, 21 л:^ —> х. Теорема доказана.
2л хк
►и!
к=\
Следствие. Если ряд 2 &й сходится по ее роят-
ности, то он сходится и с вероятностью 1. Действительно,
при доказательстве необходимости условий теоремы 2
использовалась лишь сходимость ряда по вероятности.
Безгранично делимые распределения в гильбертовом
пространстве. Распределение (мера) \1 называется
безгранично делимым, если его характеристический
функционал %(г) удовлетворяет условию: для всякого
натурального п существует характеристический функционал
некоторого распределения %п(г) такой, что %(г) = {%п(г))пв
Найдем общий вид характеристического функционала
безгранично делимого распределения.
Пусть ^ — случайная величина со значениями из $?,
для которой МеЦг> ^ =%{г), а |я1, ..., ^„ — независимые
одинаково распределенные величины, для которых
Ме ' *пк) = хп{г) и ^ = 2 1пк- Покажем, что для всякого
§31 СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИИ 461
е>0 можно указать такое с, что для всех к^п
(
V 6
>с><е.
(5)
Пусть 5 —такой ядерный оператор, что
Л:
1-Кех(г)<|- (е<|) при (5г, г)<1.
Тогда
Поэтому
|1тХ(г)|<К1-(Кех(2))2<УГе.
I аге X (-г) I < агс1е -—*— < ^>
1 - Ке(х« (г) )я"* = 1 - [ Х(2г) | »' со5[-^Аагех(^)]<
< 1 - | х (г) I созагв X (г) <-|
Используя неравенство (7) § 5 гл. V, находим
2л ^«/
/=*
>с |< -т + 2Ь5р5и-е '
^2Х~1
Из этого неравенства и вытекает возможность так
выбрать А, и су чтобы выполнялось (5). Из леммы 4 теперь
получаем
Р зир
2и ^п}'
>2с <
/-1
И, наконец,
Р{8ир|и1>4с}<р|зир
2 е.,
/-1
>с
е _
(6)
21./
Значит,
ПР{|^!<4г}
/=|
>1 -
>2с
1-е
1-е
А-1
462 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
ехр(-2Р{|?пй!>4Л>ДР{Ц„й|<4с}>
п
%Р{\1пь\>4с}^1ог^
1-2е
1-8 >
— в
•2е
й*=1
Из последнего неравенства вытекает
Лемма 5. Для всех достаточно больших с
ы$пР{\1п1\>с)<оо (7)
Нт зирдР{|Еп1|>с}-0. (8)
С-> °° ГС
Обозначим ^. - |ш. при 11„,|< с, ^ - 0 при | |„. \ > с,
где с такое, что
Тогда
8иряР{||п4|>с}<т.
Р{ вир 12^, >сг|<р| вир \Ъ1щ
><х| +
+ пР{\1п1\>с)
Из (6) и выбора с вытекает, что для достаточно
больших а
к
Р зир
2и^п!
/ = 1
>«К|
для всех /г. Поэтому в силу леммы 2 будут равномерно
/-1
по /г ограничены М
Отсюда, .в частности, вытекает, что
м.2|
у-1
, м
2
/-1
Зл/
(9)
§ 31 СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 463
Обозначим через цп меру, являющуюся распределением
величины %п1, а через пп — меру, определенную
соотношением
Г Ы2
Ял(Д) = /1 ) 1 + |х|2 М<**)«
Меры пп (А) равномерно ограничены;
яя(я?км
/е.*«'
+яр{|бл/|>с}.
Как вытекает из (8), для мер яп выполняется свойство
Пт зирпп({х: \ х\>с})~0. (10)
Покажем, что меры пп компактны. Для этого
достаточно показать, что для всякого е>0 существует такой
ядерный оператор 5, для которого
пп {Ж) ~ Ке | е1 "• х)лп {их) < е,
как только (8г, г)^.1. Но
яя(^)-Ке | е1{г'х)кпШ) =
= п ^ (1 -соз(г, х)) 1|^2|2-^(^)</г[1 - Ке х« (*)] =
-/?[1~|Х(г)|1Мсо5(^агёх(^))]<^[1-~|х(г)Г] +
Ч~д|х(^)11/"(1~со8[|агёх(^)])<
<-1^#^ + 4т[агКх(г)р.
I х (?) I
2/1
Предположим, что 1— КехОгХ-у (е< 1); тогда 11т хО) |<
< 1^е. Значит, во всякой связной области, для которой
это предположение выполняется
|агёх(^)1<агс^-^<^, 1-1х(г)К|.
{~"2
464 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, VI
Если 5 такой ядерный оператор, что 1 — Кех(2)^-|«
при (5г, г)< 1, то #при этих г
яя(Я?)-Ке | е{^х\г{йх)
< е'2
1 — -2. ^п
2
КГ
При я>1 и достаточно малых е правая часть меньше е.
Компактность мер пп доказана.
Пусть ап определяется из соотношения
Из (9) вытекает, что ап ограничены в совокупности.
Наконец, определим симметричные линейные
операторы V'п равенством
(Уп2, г) = п) у+]Тр" V" ^*)-
Заметим, что
5р Уп = п ] т^|^ |х« (их) = яп (Я?)
и, следовательно, ЗрУ^ равномерно ограничены.
Выберем такую подпоследовательность /г', чтобы:
1) пп' слабо сходилось к я/, 2) ап> слабо сходилось
к некоторому вектору а и 3) для всех г существовал
предел
11т (Уп.г,г) = (Уг,г). (11)
п'->оо
Последнее возможно, так как в силу равномерной
ограниченности (|| Уп||< 8р Уп) достаточно, чтобы (11)
выполнялось на некотором счетном всюду плотном в 36
множестве. Очевидно, V будет также ядерным
оператором, так как
,8рК< Ит 8рИп%
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 465
Положим далее л (А) = п' (Л), если ОшА, л ({0}) = 0.
Тогда
Х(2) = [ЗЬ,'(2)]"'= Нт [1 + МЦап>, г)-±{Уп,г, г) +
+ /(-"--'-т+ТТ^г)1^1!^)}Г-
= ехр | г (а, г) - у (Уг, г) +
^ ^ \е ' 1 + | х |2 ^ 2 1 + | х IV к I2 ^ ' 1 *
Функция (е^^)-1-т^ + ТТТТГ[г)-1^- при
х = 0 доопределяется по непрерывности, равной нулю.
Значит,
% (г)-ехр {/(а, г)-~(Вг, г) +
+ К^""-'-т^)-т^1»№)}. <>2>
где
(Дг,2)'=(Кг,2)-- |К^я (<**).
Поскольку
и для почти всех е > 0 (для тех 8, для которых
л ({х: | х | - е}) - 0)
г Г (2> *)2 /л \ Г (г, х)2 (* ч
I а- | > е | х | > р
Г (2 *)2
а .' /2 л (их) может быть сделан сколь угодно
1*1<в
малым выбором е>0, то (Вху г)^0 для всех г. Таким
образом, для всякого безгранично делимого
распределения найдутся такие векторы йё1, ядерный оператор В
и конечная мера я, для которой я({0}) = 0, что
характеристический функционал %(г) этого распределения имеет
вид (12).
466 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ; VI
Покажем (обратное), что формула (12) определяет
характеристический функционал некоторого
распределения. Положительная определенность %(г) вытекает из
того, что %{Рг)> где Р — проектирующий на
конечномерное подпространство 2 оператор, при 2, меняющемся
в этом подпространстве, будет характеристическим
функционалом некоторого безгранично делимого
распределения в 5?.
Далее, используя соотношения
1 -1 %{г) К ~ (Вг, г) + | (1 - соз (г, х))л {их) +
, 1 Г (-г, х)2 , , ч
агех(^) = (а, г) + | 81п(г, *)я(Лл) + / 5|"(г' *^~(г' х) л (ах),
|81п*-/|<-у, 51П2^<4(1-СО5 0,
убеждаемся, что при некотором С
1-Кех(2)<1-|5С(2)| + |(агёх(2))2<
< С [(а, г)2 + (Вг, г) + | (1 - соз (г, х)) я (Лс) +
Для меры п для каждого е>0 можно указать ядерный
оператор 5' такой, что
(1 — соз (г, х))п(йх)<~~г при (5'2,г)<1.
Полагая
где ядерный оператор V определяется равенством
((/г, г) - (а, гУ + '{ Ц^- п {йх\ 5р V = | а р + я (Ж),
будем иметь: 1 —Кех(г)<е при (5г, г)<1. Значит,
ЭС(г) — характеристический оператор. Таким образом,
доказана
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 407
Теорема 3. Для того чтобы функционал %(г) был
характеристическим функционалом некоторого
безгранично делимого распределения, необходимо и достаточно,
чтобы существовали такие векторы ае!', ядерный
оператор В и конечная мера п на "1\ для которой я({0}) = 0,
что %(г) представлялся бы по формуле (12).
Замечание. Представление (12) для %{х)
единственно. Действительно,
(Вг, г)= - 2 Пт ±1п%{(г).
Поэтому можем считать, что в дальнейшем В = 0.
Пусть {^ — некоторый базис и числа ск>0 таковы, что
2 I ск |<оо. Тогда ряд
к
2^ск\} 2 \ = ]ас^1 ~С08^> х))
сходится монотонно к ограниченной функции и, значит,
сходится ряд
2фхи-'"'('+'^'п'1('-''')Ь
оо
= ^е«*-*^ск[\-<:Ш(ек,х)]Ц№-п(ах). (13)
Таким образом, зная %(г), можно определить выраже-
Г ■ , V* / 5ш6(еь> х)\ 1 +\х\2
*~1
ние
&-=1
которое получается, если правую часть (13)
проинтегрировать по I от — б до б, а затем разделить на 26.
Значит, однозначно определяется мера
Г хч / 51П б (е„ х)\ 1 + и I2
А А-1 Ч \ Л / /
463 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ {ГЛ. VI
поскольку (14) является характеристическим
функционалом этой меры. Мера я полностью определяется
условиями:
1) я({0}) = 0,
2) если ОеЛ, то
^~' 1*1* -1А \
^.-, ,, Т+Т71Г»(^)-
А 1к = \
Г Гчп I 8*п 6 (еи% х) \
Значит, мера я определяется значениями х(^)- Поэтому
и а однозначно определено значениями %(г).
Предельная теорема для сумм независимых
случайных величин. Пусть |я1, ..., %пк — последователь-
ность серий независимых случайных величин, ?„= 2 1пь-
/г=1
Величины \пк будут предполагаться бесконечно малыми,
т. е. Нт зир Р{| %пк |>е} = 0 для всякого е>0. Будут
/г->оо к
найдены условия, при которых распределение %п при
п—>оо сходится к некоторому предельному распределен
нию. Обозначим распределение величины %пк через \хпЬ
а 1п через V,,. Пусть, далее, апк е X определяются из
равенства
(аак,г) = \ 1 + 11^!,^^)
для всех ге1. Существование таких апк и
единственность а„ъ удовлетворяющих неравенству | апк |<б < 1 для
достаточно больших п, вытекает из соотношений
1^К | х+\Хх1а\2»пЛ<1хХ* + \а\\1пк{{х< \х\>ъ}),
{Та,г)=\ 1+{*-хг\]2\1пкШ),
\Та-ТЬ\<\а-Ь\ Г (2М + | а1 + 1&Р 1*1 „ ь(йх)<.
<|а-6 \[2е2 + 26е + Ь\1пк({х: \х\>е})],
/--.щГ (2Ы + |а| + 1Н)М . ■ ,<л |-|-<д „е1<
^о (1+6)г
^^ (1-д)»'
где
§ 31 СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 469
Из этих неравенств вытекает, что оператор Т в области
|а|<6<1 будет сжимающим и будет переводить эту
область в себя. Поэтому апк существуют и единственны.
Положим , .
яя = 2 апк9 (Упг, г) = 2 (Упк** г)>
к = \ /г=1
и пусть мера \хп определяется равенством
\
Ат= 1
Теорема 4. Для тога чтобы последовательность
мер Vл яра п~>оо слабо сходилась к некоторой мере V,
необходимо и достаточно, чтобы выполнялись условия:
1) \хп слабо сходится к некоторой мере п'\
2) существует предел а= Пт ап\
П->оо
3) последовательность операторов Vп такова, что
оо
2 {Упек, ек) сходится равномерно относительно /г, и для
каоюдого г существует Пт (Клг, г) = (Кг, г), г<9^ I7 — ядер-
Я->оо
ный оператор. При этом характеристический функционал
предельного распределения задается формулой (12),
б которой
я(Л) = я'(Л) при ОеЛ я({0}) = 0.
Доказательство. Достаточность. Имеем
кп ,
Ме' (*• *«> = Ме( <*' йп)\\\ е1 ^ *-"«*) цлй (**) =
* = 1
кп
- Ме' <* вп) Д { (1 _ | (у,^, г) + ] [е1 <* *-««*> - 1 -
1(г,х-аПк) | 1 (А--а„ь2)2 1 .. /ЛуЛ
470 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Заметим, что
1-|(^^)+1[-'(-'-д-')-'-;;г,:::)|.+
< I ] [соз (г, х - апк) -\]\1пк(их) +
+//[зш(,,х-^)- 1?|^:дд;)Р]^^)18а
- О ((КяЛ2г, г) + (1 +1 г |) |лял({^: и |> 1»).
Из последнего неравенства вытекает, что
!п Ме1 (*• ^) = / (г, ая) - 1 (У„2, г) +
4-^ | [У^, *-а„,) 1 Кг.х-а,*) .
/г«1
1 (г, лс-а,^)2
2 1 + |л:-алй12
] Ця* (<**)
+
+ О [зир (1/пЛг, 2) + (1 + \г |) зир цлЛ {*: | * | > Щ].
/с - /г
Легко видеть, что
Пт зир|адй| = 0.
Я-»оо к
Кроме того,
5р^6= |1|];^2|2^(^)<262 + 1 апк р + Р{| §пЬ |>6},
и, значит,
Пт зир 5рУ^ = 0.
я-»оо /г
Поэтому для всех г в силу условий теоремы
Нт 1п Ме1 ^ ;«) = I (г, а) - 1 (^ *) +
Я-»оо *
& = 1
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 471
Заметим, что
,; п
Нт У Г \е <*'* ~а^ - 1 -
Я = 1
Цг, х-а^)
т
1 +\х-апь |2
= нт
Л"'
(г, л) _ 1
/ (г, х)
(г, х)2 \ 1 + ! *
\ 1 +1 х\2 , , ,
^1 (г, х) |
1 4-1 х р » 2 1 + ! л; |2 ,' | * |5
1+|х|* ^2 1>|хр) |*|2 Я 1а^"*
1 + I * I2
|+и|2;
так как, если доопределить функцию \е1^х) ~- 1 —
/ (г, л-) , 1 (г, л-)2 \ 1 + | х |2 ., а
—^— ' -■ . |2 равной нулю при я = 9,
1 + I х |
2 1 + дг|
то она будет непрерывна.
Значит,
Пт тМе'^^-Дг, а)~\(Вгу г) +
»->оо ^
+/1<!„,.,1__1_Т^)л^л„№).
Для доказательства слабой сходимости мер уп
достаточно показать их слабую компактность. Но
1- \ еиг-х)уа(ах)\ =
"п . I
(^,г)|+2|1 -/^(г,ж"вял)^*(^)
Ч Г
<
<1
<
А-1
472 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Используем оценки
\(ап, г)Кв + ^(ая, г)2,
[ (1 - С05 (г, х - алк)) \хпк (ах) <
< { (х-аПк> г)2 &пк (Лх) + 2 | [хпк {ах),
апк\
х"апк | > с
^ б ] 1^1Папч\2 ^пк ^ + Т ] 8|П2 ^' Х ~ ^ |Ц* ^ ^
<б
»1яЛ (<**) +
] (г, х - аггА;)2 \хпк (ах) + -у ] ^ (Л*),
*~ал*|<с
*-а„ь1>с
| (г, х - апк)2 \1пк (ах) < (1 + с2) (Упкг, г).
х~апк I <с
Из этих оценок вытекает неравенство
+ 6(М#)+ 1) + (2+~) [1п({х: | х |>с -зир| апк I».
Поскольку выбором бис выражение
6\1п т + 6 + [2+±)[1п({х:\х\>с-&ир\апк\})
можно сделать сколь угодно малым, то для
доказательства компактности уп достаточно доказать., что для
оператора 5Я, определяемого соотношением
(5Я2, г) = (Упгу г) + (аП9 г)2,
ряд
со оо оо
2 (8пек, ек) - 2 (Упек, ек) + 2 {ап, ек)2
сходится равномерно относительно п в любом орто-
нормированном базисе {ек}. Равномерная сходимость
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 473
2 ^Упеъ ек) относительно п вытекает из условия 3), а
и^\
разномерная, сходимость ряда 2 (яя> ек)1 вытекает
из того, что в силу условия (2)
Пт 2 [(ап, ек)-{а, <?А)]2 = 0.
п -> оо /а = I
Достаточность условий теоремы доказана.
Необходимость. Пусть Ё' . . ., \' — случайные
величины, принимающие значения из Ш, независимые
между собой и не зависящие от спЬ ..., Ъ>пк и |п1
и ^, имеют одинаковые распределения. Поскольку
\
Р{
\
1 I
2(бяй-Е^|>г^}<2Р{
)
>с
и величины сл.с —1'1& симметричны, то в силу леммы 3
Р{ вир
1/<*„
2 (1«* ~ &«&)
*=1
1 '
> 2с <4Р{
21,
><ч,
а значит,
Р{ вир ||„, -|,'г,| > 4с} < 4Р 2 Ы > с |.
*<*,
Если с настолько велико, что 4Р {
I
то в силу неравенства л:<! — 1п(1 —л-),
У
•пк
>с\<[,
2Р{и„,-^|>4с}<-21пР{||,!,-^|<4с} =
к^\
к = \
1пР18"р|^-^*1<4с}<
к ^ к„
<-1п 1 ~4Р{
I
ёгс&
>с •
474 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, VI
Следовательно, можно указать такие векторы Ьпк, что
21Р{|Ея*-6«*1>4с}<-1п(1-4р||21Ел*|>«|)
Поскольку зи р Р {11пк | > г} ~> 0 для всякого е > О, то
к
\Ьпк\*^ с -Ье, если только
2и|>^)]<1~5ирР{|^|>8}.
1п 1 — 4Р
*-1
Взяв е = с, получим
2Р{16»*1>9с}<-1п(1-4р{
*=1
й-1
>с| . (13)
Пусть $с(х) = 1 при |х |< с, \|)г(л:) = 0 при \х\>с.
Тогда
зир
^:2Р^
Х^^-б;,)^,-^)
/==1
> а}<
I
<2Р^
<2Р<
** I ]
2 &,-&/)> "
> а}<
/=1
/-1
а| + 2Р{8ир|^-ЕяУ|>^}
. - Е' Л
<4Р|
1 ^ (
>а[+4Р<
1 "п
1/-!
;=1
>у[ + 8Р|
]
1
~?п,)\
кп
/-1
>у|
N
<
к
Для достаточно больших а и с правая часть этого
неравенства может быть сделана сколь угодно малой,
поэтому в силу леммы 2
м|2Ш,-^Ж/-^)Г
I 1а*1 1
§ ^1 СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 475
равномерно относительно п ограничены (для всех
достаточно больших с). Но для всех 6>0
>р{|К,1 <*},*& / \х-аГцп1(<1х).
1 "^ \х\<С-б
Обозначим то а, для которого достигается Ш через ап!,
Для достаточно больших п
йя/= | хрп]{с1х).
\х\<с — б
Поскольку
«пгР{&/|<*} = |у<Р{М<*}->»
при п ~> оо, то
8иР^ / и-ЗяйрцлЛ(йГл:)<оо.
" к~\ \х\<с-Ь
Последнее неравенство созместно с (13) приводит к
следующему:
к
вир
Х/тТТ^г^^Х00' <15>
Но
I х - апк |2 - \х - апк |2 + 2 (* - апк, апк - апк) +1 Й^ - аяЛ |2.
Поскольку же
ТО
Отсюда вытекает, что
476 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Очевидно также соотношение
Поэтому, используя неравенство
<
т-'1"-*-*-(Ш&]<>*ю
убеждаемся, что
1п %п (г) = 1п Мег <*• г"> = / (о„, г) +
6=1
+ (У„г, 2)[0( зир(^е, г)) + о(1)] + о(1).
Из компактности мер V,г вытекает, что для всякого &>0
можно указать такой оператор В е Гс и операторы
4е5)5 что 1-КехЛ^Хе при (ВАпВг, г)<1. Тогда
— 1п| %/2 (аг) |<2е для достаточно малых е при (ВАпВгу г)^1,
а значит, ^ | (1—соз(2, х — апк))\1пк{(1х)<2г. Но тогда
^ (1 ~соз(г, х))\хп(<1х) =
:^] (1-соз(г, х-аяЛ))»1яА(йх)<2е.
/г = 1
Ь-1
§ 3] СУММИРОВАНИЕ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 477
Отсюда вытекает компактность мер [\п. Значит, в силу
следствия 2 теоремы 2 § 2 У)" будут компактны в Ж%,
и поэтому ряд 22 07Л, ?*) будет сходиться равномерно
в каждом базисе {ек} на основании леммы 2 § 2,
Очевидно, что
Итх„(г)= Птехр(/(а,г, г)--^(Упг, г) +
Выберем подпоследовательность /г' так, чтобы меры \хпг
сходились к некоторой мере я/ и {Уп,г, г)~->{Уг, г).
Тогда будет существовать и предел (а„/, г), равный (а, г).
Таким образом,
1мп х../(2) = ехр| /(а, г) - -^(Уг, г) +
■ .' и 1 1 + |.чз 1 2 I -гИ2/ и|2 1 'Г
Из единственности представления характеристической
функции вытекает слабая сходимость \1п к л/ и
сходимость (КЛг, г) к {У2\ 2). Кроме того, отсюда вытекает,
что ап слабо сходится к а. Чтобы убедиться в сильной
сходимости ап к а, заметим, что %п(г) равномерно
сходится к %(г) при | 2 К с (см. замечание к теореме 3 § 2),
{Упг, 2)~>(Уг, г) также равномерно при | г К с (это
вытекает из условия 3) теоремы) и, наконец, точно
так как в замечании к теореме 3 § 2, можно доказать,
что
&}\С { 1 + ! х - апк |2 + 2 1+| х - дя4 |* 1^аЛ>
также будет равномерно сходиться к
,) [е 1 1 + | л:|2 л 2 \-\-\х\ЧП {аХ)*
Поэтому и (аПУ г) будет сходиться равномерно к (а, г)
при | 2 |<:с. Отсюда, точно так как в теореме 2, можно
вывести сходимость ап к а. Теорема доказана.
478 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Замечание. Если определить апк с помощью
соотношения
(аЯА>г)= | (х,г)\1пк{ах),
|х|<<?
а величины ця> Упк, Уп, точно так же как в теореме 4, то
при выполнении условия теоремы 4 распределение
величины 2Я будет слабо сходиться к безгранично
делимому распределению с характеристической функцией
% [г) = ехр | / (а, г) - ~ (Вг, г) +
икс
\х\>с )
если только с выбрано таким образом, что
п({х: |х| = с}) = 0. Доказательство необходимости и
достаточности условий проводится точно так, как и в
теореме 4.
§ 4. Предельные теоремы для непрерывных
случайных процессов
В этом параграфе общие теоремы о слабой
сходимости мер в метрических пространствах, приведенные
в § 1, применяются для вывода предельных теорем
для случайных процессов, непрерывных с вероятностью 1.
Пусть 1п (I) — последовательность случайных
процессов, определенных на отрезке [а, 6], принимающих
значения из некоторого сепарабельного полного
метрического пространства 36 и непрерывных на [а, Ь] с
вероятностью 1. Обозначим через Ф\а,ь\{36) множество
непрерывных функций х((), определенных на [а, Ь] и
принимающих значения из 36.
Введем в Щащ Ь] (36) метрику
/*(*(•), »(•))= &ир р (*(*), УШ
где р— расстояние в 36. С этой метрикой Я!?\ащъ\{Щ
превращается в полное метрическое сепарабельное прост-
§ 4} ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 419
ранство. Обозначим через 93[Д, и(Я?) ст-алгебру всех бо-
релевских множеств Я!?\а,ъ\(Щ- Эта а-алгебра совпадает
с минимальной о-алгеброй, содержащей все
цилиндрические множества из ^[а,ь\(35) (см. § 2 тл. V, там это
доказано для того случая, когда 35 линейно,
доказательство в нашем случае ничем не отличается).
Поэтому с каждым процессом %п(1) можно связать меру \хп
на 33[Д,ъ\(Щ, значения которой на цилиндрических
множествах совпадают с конечномерными распределениями
процесса 1п(1).
Какой смысл для случайных процессов \п(1) имеет
слабая сходимость мер цп?
Пусть \1п слабо сходятся к мере \х, соответствующей
процессу |(/). Тогда для всякого ^х-почти всюду
непрерывного ограниченного Ща§ ь] (^-измеримого
функционала ф(х), определенного на Ф[а,ь](%?)> имеем
Ит Г Ф (х) цп (ах) = Ы(х)\х (с1х)
(см. лемму § 1 гл. V). Поэтому для всякого ^г-почти
всюду непрерывного ЭЗ[Д ь] (#?)-измеримого функционала
Нт \е1иырп(йх)= [ е™Ыр(йх)
для всех веществецных Я.
Заметим теперь, что
\ е*№рп(Лх)*=МеЩ{<1*{ш)\
^ е*№)хЦ1х)=ЬАеЩЪ^\
(1(1п(')) и КК •)),являются случайными величинами
для всякого 93[в, ъ) («^-измеримого функционала I,
последние формулы являются следствием формулы (2)
§ 1 гл. V). Из сходимости характеристической функции
величины 1(1п(-)) к характеристической функции
величины /(!(•)) .вытекает сходимость распределения
величины !(1п( •)) к распределению [(%(•)). Таким образом,
слабая сходимость мер \хп к \х влечет сходимость
распределений величин /(!„(•)) к распределению 1(1(-))
для всякого [х-почти всюду непрерывного Ща,ь]
(^-измеримого функционала }(х). Наоборот, если распределение
480 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ5 VI
}(1п{ш)) сходится к распределению /(?;(•)) для всякого
|х-почти всюду непрерывного 23[а> ь] (^-измеримого
функционала, то Мер (!л (•))-* Мф (К ■)) для всякого
ограниченного ц-почти всюду непрерывного 23[а, ь\
(^-измеримого функционала ф, т. е.
Пт | ф(л:)ця(й*)= ( у (х) & (Лх).
Таким образом, слабая сходимость мер \хп к \х
эквивалентна сходимости распределения /(!„(■)) к
распределению /(?;(•)) Для всякого ^г-почти всюду непрерывного
33[а. ь] (^-измеримого функционала /.
Обычно при рассмотрении предельных теорем для
случайных процессов предполагается слабая сходимость
частных распределений, т. е. сходимость меры \1п(А)
к \х(А) для всех цилиндрических множеств Л,
являющихся множествами непрерывности меры р. Поскольку
для всякой открытой сферы из 9$\а% ь\ (0) вида
{*(•): р (*(*), *(/))< е, а<*<6},
-где х(1) — заданная функция из Я2\а% ъ] {35), имеет место
соотношение
{*(.): р(*(*), *(*))< е, а<^<6} =
ОО ОО
= 11 П{х(-): 9(х((к), хЦк))<в-±-, й=1, .... М'
т=\ N = 11 т }
где {1Ь 1Ь ...} —всюду плотная на [а, Ь]
последовательность, то алгебра % открытых цилиндрических
множеств, являющихся множествами непрерывности
меры ц, удовлетворяет условиям теоремы 4 § 1.
Для применения теоремы 4 § 1 нужно найти общий
вид компакта в пространстве ^.^(Я/). В том случае,
когда 36 — конечномерное евклидово пространство, общий
вид компакта в ^[а,ь]{36) дается известной теоремой
Арцела.
В нашем 'случае имеет место аналогичный результат,
который мы сформулируем в виде следующей леммы.
Пусть Яб~- положительная монотонная непрерывная
функция, определенная при 6>0 и удовлетворяющая
условию Яб I 0 при 6 | 0, а Х{ — некоторый компакт в 36.
Обозначим через /С(Х1э Яб) множество функций х{1) из
§]4]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
481
<&&, ь\ (8?), удовлетворяющих условиям: а) х (/) е Х{,
а</<6; б) р (*(*;), х(/2КЯб при |/1-/2К*.
Лемма 1. Множество К (Хь Яб) компактно в 9[а, ь\ (3?).
Для всякого компакта К\ в 9?[а, ь] {86) можно указать
такой компакт Х{ в 96 и функцию Я0 положительную,
возрастающую, непрерывную и удовлетворяющую уело*
вию Я+о = 0> что К\ аК{Хи Я$).
Доказательстве. Для доказательства
компактности множества К(Хи Я6) рассмотрим произвольную
последовательность хп(-) из этого множества и
покажем, что из нее можно выбрать сходящуюся
подпоследовательность. Используя компактность множества
значений хп(1) при каждом I, можем диагональным
методом выбрать такую подпоследовательность хПк (/),
чтобы Хпк (0 сходилась к некоторому пределу для всех
рациональных/ из [а, Ь]. Обозначим хПк{1) через ук{{) и
покажем, что последовательность ук{1) сходится. Пусть
а</1<...<^^6 — рациональные точки, для которых
длина каждого из интервалов [а, ^], [/,, (2], ••,- » [^» Щ
не превосходит б. Тогда
зир р(укУ), уЛ*)Х зир р(#А(/,), угЦ{)) +
+ зир {(р (ук (/,), ук (0) + р (у1 (*,), у г (*)));
1*-*,|<6, 1=1, ..., Ы).
Поэтому
Ий г{ук(:\ ^(-))<2Лб.
Из произвольности 6>0 вытекает, что ук{-} —
фундаментальная последовательность и, значит, она имеет
предел. Для доказательства второго утверждения
теоремы обозначим через Хь множество значений х{1)9
когда х( • )&К\. 'Покажем, что Хх=*\^Хи 1^[а, Ь],
компактно. Пусть хп е Х{. Тогда хп = у (/„), где уп( •) е /С^
Выбирая, подпоследрвательность ял так, чтобы ^пк-~>^^^
г{Упк{-\ У(-))-+& убеждаемся, что ^->у(/0)б^
Положим, далее Яб (х (.?)) г? зцр {р (л: (/0, л: (/2)); I *1 — /г -К *}■
Легко видеть, что Яа(л:(-)) непрерывна по совокупности
15 И. И. Гихман, А. В. Скороход
482 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI*
переменных 6>0 и х{-). Поэтому из компактности /С,
вытекает непрерывность по б функции зир {Х^(х( •));
х( • )е К[} = Я6. Монотонность Лб следует из соотношения
Яб, (х (• ))<Ь2(л:( • )) при б! <62. Поскольку Яб(*( •))
стремится монотонно- к нулю при 6 | О, то в силу тес*-
ремы Динни эта сходимость равномерна на каждом
компакте. Поэтому
ПтЯб = Птзир{А,б(л-( •)); х( • )е /С1} = 0.
Значит, К\^К{Х1у Л$). Лемма доказана.
Теорема 1. Пусть частные распределения процессов
|л(0 сходятся к частным распределениям процесса %(/).
Для того чтобы для всех функционалов ^, непрерывных
на Ща, ь] (96), распределение /(!„(•)) сходилось к
распределению !(%(-)), необходимо и достаточно, чтобы
для всякого р>0 выполнялось соотношение
НтзирР{ зир р№Л(^), |л(/2))>р} = 0. (1)
А->0 п 1ИКА
Доказательство. Необходимость. Если
выполнено утверждение теоремы, то последовательность
мер> \хПУ соответствующих процессам ^„(0> слабо
компактна, так что выполнено условие б) теоремы 1 § 1.
Поэтому для всякого е>0 найдется такой компакт
К(Х1у Я6), для которого
ЫрРп(<&[а,Ь]№-К(Х1,къ))<В.
п
Тогда
Р{ ^р р(|я(^1п('2))>ЛА}<8.
Если Н достаточно мало, то Ял<р и
Пт Р { зир р Цп (*,), Ъп С2)) > р} < е.
Ввиду произвольности е>0 отсюда получаем (1).
Достаточность. Принимая во внимание
сходимость мер ц„ к \х на цилиндрических открытых
множествах непрерывности меры ц, которая вытекает из
сходимости частных распределений 1п (I) к частным
распределениям %(/), а также теорему 4 § 1, убеждаемся,
что достаточно установить компактность мер \хп. Обо-
§4]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
тз
значим через \^ меру на <$е, являющуюся
распределением 1п(1), и покажем, что множество мер {чпЬ я=1,
2, ..., 1^[а, Ь]} компактно. Действительно, если \п1п —
некоторая последовательность мер, то, выбирая атакую
подпоследовательность пк} чтобы /,гл->/о> легко
установить, что для всякой ограниченной непрерывной
функции ф(х), определенной на Шу
Игл |ф(*^/я (</*)= Нт Щ(1пк((пк))-
= Игп Мф (1„к (/0)) + Игп М [ф.(|„А (/Я4)) - Ф(1Ч (*„))] -
= Мф(и/0)),
так как для всякого компакта Хг и 6>0
ЙтМ|ф(|„А(/Пй))-ф(^))|<
<2 зир | ф (х) | Нт [Р (| (/0) € Щ +
+ Р {Р (6», (Ч),Ь.л («)>»}]+
+ зир {| ф (*) - ф {у) МЕ^р (х, */) < 6},
и правую часть можно сделать сколь угодно малой
в силу непрерывности ф(х), компактности V,, , и
условия (1).
Выберем последовательность Нк из условия
зирР { зир р(|„{Г), 1п(П)>2-"} <2~\
п \1'-1»\<Нк
Пусть Х{к) ~ такой компакт, что чп{{%~ Х{к))<,2~к-^
для всех п, I ^ [а, й]. Обозначим через А^* множество
тех х, для которых р(х, <У(Й))^2~\ Тогда
мр рал(/,), |„й))<2"Ч.
16*
484 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Поэтому
< 2 Р{1п(а + 1Нк)ШХЩ +
+ Р { вир рЦпМ, 5»(<2))>2"л} <2 • 2"
Заметим, что (*\ Х(® является компактом в 95. По-
строим теперь для е>0 такой компакт К(ХЬ Я6), что
иЛ^к,&](^)"~^С(^1» ^б))<8 Для всех я. Для этого выбе-
рем такое ш, что 2^2""^<|~ и положим Х{ = ^] Х^.
Возьмем последовательность Яг 10. Для каждого г
найдем Нг такое, чтобы /гг</?г_1 и
зир Р { зир р (%п (/0, %п {12)) > лг} < ~т.
|<1~<2|<АГ 2
Пусть Я6—неотрицательная непрерывная невозра-
стающая функция, для которой )ч, =кг-.{. Очевидно,
чго Я6 | 0 при 6 I 0. Кроме того,
Р{1п(')ШК(Хи1ь)}^\~Р{1п(()^Х^ а</<6} +
оо оо
-г У Р { зир р (1„ (*,), |„ (/2)) > Яг} < | + У -^ = е.
Теорема доказана.
Замечание 1. Вместо условия (1) можно
требовать выполнения условия
ИтПтР{ зир р(Ы'.). !«&))> в} = 0, (2)
которое часто удобнее проверять. Действительно, из (2)
вытекает, что для всякого т]>0 существует такоеб>()
и М9 что при п>Ы, Н<6
Р{ зир р(5я('1). 1|.(<2))>е}<4- (3)
*"4]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
485
Из непрерывности процессов |„(/) вытекает их
равномерная непрерывность, так что при каждом п
НтР{ зир Рая01), ^(/2))>8} = 0.
Поэтому можно подобрать такое б, чтобы при Н<д
соотношение (3) выполнялось для всех п.
Следующая теорема может оказаться более удобной
для применений.
Теорема 2. Пусть частные распределения
процессов 1пЦ) сходятся к конечномерным распределениям
процесса 1(1) и существуют такие а>0, р>0 и #>0,
что для всех 1Ь /2^[а» Ъ] и всех п
АЛРЙЛ*!), ?Я('2))]а<//|'1-'2ГЭ- (4)
Тогда для всех непрерывных на Щ^ь]^)
функционалов I распределение ?(1п(-)) будет сходиться к
распределению /(%(•))•
Доказательство. Используем лемму 1 § 5
гл. III. Условие (4) этой леммы для процесса ^л(/)
выполняется, если положить §(Н) = НУ, где 0<,у<Р/а,
#(С, к) = НС~аН1+6, где 6 = р — <ху. При этом функции
О(т) и (3(т, С), определяемые равенством (8) § 5 гл. III,
будут равны
с)—ту ■> с>—тЬ
Т = Ь-а.
Следовательно, в силу соотношения (7) § 5 гл. III
выполняется неравенство
Р { зир р (Ьп (*,),. Ьп (/2)) > 8} < 1е~а/Л
#де Ь — некоторая постоянная. Дальнейшее
доказательство1 вытекает из теоремы 1.
Сходимость процессов, построенных по суммам
независимых случайных величин. Пусть |п1, .. ., ^^ —
последовательность серий независимых в каждой серии
4Ш ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
числовых случайных величин, удовлетворяющих
условиям:
1) Щщ = 0, *= 1, .. ., кп;
2) 01ш = Ьп1, 2бл<= 1.
Построим случайную функцию &Л(/), /е[0, 1],
следующим образом: положим
к к
$пк ~ 2л %п1у ^пк ~ 2и ЬП1,
1 = 1 * = 1
при 1&[1Пк>*пк+\]1 5л0 = 0, *л0 = 0. Тогда ^п(/) является
случайной ломаной, соединяющей точки плоскости (/; %),
имеющие координаты (/пй; 5лй), /г = 0, 1, ..., кп.
Изучим условия, при которых частные
распределения процессов 1пУ) и распределения функционалов
от этих процессов сходятся к частным распределениям
и распределениям соответствующих функционалов
процесса броуновского движения ш{1).
Теорема 3. Пусть случайные величины Ъ>п1
удовлетворяют условиям 1) и 2) и условию Линдеберга: если
Р,п{х) —функция распределения величины %пЬ то для
всякого е>0
К
Нт У Г и2арп1{и) = 0. (5)
П-*°°1-1 |п|>8
Тогда конечномерные распределения процессов %п (/)
сходятся к конечномерным распределениям процесса ш (0
и распределение / (|Л ( •)) сходится к распределению
1(гю(')) для всякого непрерывного на Ф\о, п
функционала /.
Доказательство. Сходимость конечномерных
распределений процессов %п(1) к конечномерным
распределениям ш(1) вытекает из центральной предельной
теоремы. Для доказательства сходимости
распределений /(!„(•)) к распределениям /(«;(•)) Для всех не~
прерывных на ^[о, ц функционалов / проверим, что при
§4] ;
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
4%7
произвольном е>0 выполняемся условие
11т Ш Р { вир \ 1п (*,) - 1п (/2) 1 > е} = 0, (6)
и воспользуемся замечанием к теореме 1. Так как
вир 1.1п(Л)-^(^)К2зир зир I &,(')-Б„(*А) К
<4зир зир I ?я (0 - ёя (*Л) |,
то
Р{ зир иЛ^)-^(^)1>8}<
^ Р{ зир 1Ы0-&я(*А)1>т}-
Л/К1
Заметим, что
. зир \Ьп(1)-Ьп(ЬЬ)\<2 зир
**</<<*+Г) л 1п,к<г<1П, к + 1
2 &я/
где /„, а — максимальный из индексов /, для которых /л/
не превосходит 6й. Так как.при ]п,к<$<!п, к+\
(
Нт зирР |
П->оо 5 (
^/1. & + 1
Х| ?я/
/ = •5
. е I 256 ,
то при достаточно малых к в силу теоремы 6 § 3 гл. II
п-*оо { кк< *<(Л+1)Л * -»
"" е2
Из сходимости конечномерных распределений %п (/)
к конечномерным распределениям т{1) вытекает, что
^р{|^(^,+1)-^(Ч,,)1>1^}==
—4= Г
У2п 1
е 2 йи*
\и\>Ы\ъУн
488 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Следовательно,
ШР{ зир ия(/,)-Е«(4)1>в}=-
\*Л< 1 |„ |>е/1б//1 / \ |а!>е/1б/Л /
Так как
1 Г -—
то отсюда вытекает (6). Теорема доказана.
Из теоремы 3 немедленно вытекает
Теорема 4. Пусть 1{, |2> • • • > &«, • • • ~
последовательность независимых одинаково распределенных
случайных величин, для которых Л1^ = О, 0^=1.
Обозначим через %п{() случайную ломаную с вершинами (—,
\п
~-г=:5& |, где 50 = 0, 8к = 1{ + ... + %к. Тогда для любого
функционала [у определенного и непрерывного на ' ^[0,1]
почти всюду по мере \лп„ соответствующей процессу ю (I),
распределение /{%п(•)) будет сходиться к
распределению ((ш ( • )).
С л е д с т в и е. Если выполнены условия теоремы 4, то
Пш Р ( тах \8к\<а\/п} = Р{ зир |ш(/)|<а}
п -»оо 1 < /г < » 0 < * < 1
для почти всех а.
Это вытекает из непрерывности функционала ?(х( • )) =
- зир |х(0|.
Теорема 5. Пусть функция у{х) определена при
хей1, интегрируема по Риману на каждом конечном
отрезке, а величины |А. удовлетворяют условиям
теоремы 4.
Тогда
Пт
р(||1^(7^5й)<:а] = р{/ф(ш(0)Л<а
§41
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
469
для всех а, для которых
Р| / Ф(И0)Л = а| = 0.
Доказательство. Покажем, что функционал
I
?(*(.)) = /Ф(*(*))Л
О
почти всюду непрерывен по мере \1т в метрике ^[о, п-
Пусть *„ (^)-> л; (О равномерно на [0, 1]. Тогда Ф (*„ (/))-■*•
->Ф (*(/)) для всех значений /, для которых х(/)ё=Лф,
где Лф —множество точек разрыва функции ф.
Обозначим через Хф(*) индикатор множества Лф. Тогда
функционал /(*(•)) будет непрерывным в точке я( • )^[о, п»
если *(/)е=Лф почти для всех /, т. е. .если
1
/ Хф(^ (5)) Л? = О,
- о
так как в этом случае Ф (*л (0)-"* Ф (* (0) почти для
Ьсех I и ф(#д(0) ограничены одной и той же
постоянной, поскольку зир| *„(/)! конечен, а ф(х) ограничена
п, Ь
на каждом конечном промежутке. Остается заметить,
что
1
М
/эе,М0)Л =/мхф(«»(0)<й =
О
1
=Пв~х*
%Гс
0 ЛФ
-ах(Н = о,
так как Л имеет лебегову меру 0 ввиду интегрируе-
мости функции ф по Риману. Величина Г %ц{,ш{1))М
о
неотрицательна, поэтому
490 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Если обозначить через А а ^[0| 1] множество точек
разрыва функционала /, то
А
*(*): /Хф^(«))^>о[
и, значит,
1*.И)<Р*/хф(ю(0)Л^оио.
Ь )
Если |л(0~ процесс, введенный в теореме 4, то на
основании теоремы 4
Ит Р
Я-»оо
I/ф(6»(0)Л<о|-РП ф(
,(0)Л<о}-Р] ] ф(а»(/))Л<о|,
> I о I
если только
1
Гф(в>(/))Л = а } =
о
Пусть ф+ (х), ф- (ж) — две непрерывные функции,
удовлетворяющие соотношениям ф~ (х) < ф (х) < ф+ (х) и
оо
| [Ф+(х)-ФГ(*)] <**<«•
— оо
Для всякой непрерывной функции ф(х)
/ф(1.(0)Л-^2ф(7^54)
<
Л<
где
<2 Лф(1Л0)-ф(|п(|))
/е=1 6-1
п
<зир{|ф(х)~ф(^)|; и-^/кл,,, и к и,
1
- -= вир | 6* I,
§4]
ГШЩШШНШЕ ТЕОРЕМЫ
491
Поэтому
1
>е
<
|0 П к~1 'П I
<Р{чя>б} + РЙл>с},
если только бис выбраны так, что при | л; — #|^С6,
|х|^с, | ф(х) — <р(у) |<е. Но г)л —>0 по вероятности,
величина Р{^п>с) может быть сделана сколь угодно
малой выбором достаточно большого с для всех п.
Значит,
Гф(Еп(*))Л--2ф(!7^$й)
■О
по вероятности, так что
»— I"*-, ^ ; ) К
I
)Л<а},
если только
Так как
( / I
и )
<р{12ч>."(т^5»)<а},
то, переходя в этом соотношении к пределу при п->оо9
получим* что для всякого Л>0
Л=»1 )
Р\ \ ф+(в>(/))Л<о-Л|< Шп Р
< НтР]
1«Г. ^ ; I
<
<р
I/ф,-(ю(0)Л<а + А|.
492 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ГГЛ. VI
Но
1
\ Ф+(а»(/))Л-|Ф(а)(0)Л
О
Г I
<
<м
1
/ф,+ (о;(/))Л-/фе-(а»(/))Л <
■о о ^
1 оо 2
О —оо
1
Значит, распределение Г ф+(ш(0)^ сходится к распре-
1
делению | <р(ш(0)<Н при е->0. Аналогичное утвержде-
о
ние справедливо и для ф~. Переходя к пределу при
е—>0, убеждаемся, что для всех Л>0
р{ ГФ(а;(0)Л<а + Л <Шп Р |2ф(гт^5,)<а <
< Шл Р ^ф(-^5^<а|<рЦф(^(0)^<а + Л .
Переходя к пределу при Л—>0 и учитывая, что функция
Р| | у(ш(1))<11<г \ непрерывна при г— а, если только
р| I ф(ш {1))й1 = а | = 0, получаем доказательство
теоремы.
Сходимость непрерывных процессов с независимыми
приращениями. Рассмотрим непрерывные процессы с
независимыми приращениями и значениями из некоторого
банахова пространства ЗВ. Если |(^), а<!/<.&, такой
процесс, то для всех е > О
Нт 2 Р11!(**-и)-6('*)!>«>-0; (7)
Л-»0 /г=0
§4]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
493
где а = /()</!< ... <1п = Ь, Л = тах(*л+,— (к) (см. тео^
к
ремы 1,4 § 5 гл. III).
Теорема 6. Пусть \\п{1)% п = 0у 1, ... —
последовательность непрерывных процессов с независимыми
приращениями, определенных на [а, Ь] и принимающих
значения из $?. Для того чтобы для всякой функции ср(х),
непрерывной на 9!?[а, щ (Щ, ^распределение величины ф(1п (•))
сходилось к распределению величины ф (|0 (• )),
необходимо и достаточно выполнения условий:
1) частные распределения процессов Ъ>п{1) сходятся
к частным распределениям |0(0;
2) для всякого е>0
Нт П^ зир Р{\Ьпа2)-1п(11)\>г}=*0.
Доказательство. Необходимость условия 1)
вытекает из сходимости распределения цЦпЦ^, ..., |я(^))
к распределению ^(|0(^)*'- • •> ^о(4)) Для всякой
ограниченной непрерывной функции ё\хь •••> *&)>
определенной на ЗВк (функционал ф(х( • )) = §(х((1), ..., х(1к))
непрерывен на ^[а, ъ]{<%))- Необходимость условия 2)
вытекает из замечания к теореме 1, так как
вир Р{1иО-!я('2)1>е}<
\и-и\<н
<Р{ зир |^(У-|л(М1>в}.
\1х-и\<н
Для доказательства достаточности условий теоремы
нужно в силу замечания к теореме 1 лишь показать,
что условие 2) влечет для всех е>0 равенство
Нт ШР{ зир ил('1)-и'2)1>е} = 0. (8)
Точно так же как и в замечании к теореме 1
устанавливаем, что условие 2) влечет для всякого е>0
равенство
Пт зир зир Р{\\п(и)-1п(12) I > е} = 0. (9)
Выберем для данного е>0 настолько малое А, что
зир зир Р{|6я(<1)-Ы'2)1>т}<|-
494 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Тогда, используя непрерывность !;„(/) и лемму 4 § 3,
находим
р{ 8ир и„(/)-ыя)|>!}<
<2Р{ия(я + 2А)-|я(5)|>-|-}.
Поэтому
Р{ зир иЛ0-ёп(«)1>е}<
|<-«|<Л
<Р{8ир[||„-(0-|»(а + йА)|;
АА</-а«А + 2)А, 0</г<-~-]>|-1<
< Ц р{3ир[||„(0-|п(а + *Л)|;
кН < 6~а
АА</-а<(А + 2)А]>|-1<
<2 ^ Р{и„(а + АА + 2А)-|в(а + йА)|>-|-},
при 1>Ъ считаем §п(0 = |л(6)- В силу условия "1)
теоремы
ШЙР{ 8ир \Ыи)~-1«{*2)\>ъ}<
<2 2 Р{|1в(а + (А + 2)А)-|0(а + *А)|>!}<
<4 2- Р{\Ь>(а + (к+1)Н)-Ыа + Щ >|}.
То, что последняя сумма стремится к нулю при й->0,
вытекает из условия (7). Теорема доказана.
Сходимость непрерывных марковских процессов.
Рассмотрим последовательность непрерывных
марковских процессов 1п({), я = 0, 1, ..., определенных на
промежутке [а, Ь] и принимающих значения из полного
метрического пространства (Вв, р). Обозначим через
РпЦ, х, з, А) вероятность перехода для процесса !„(/).
Пусть Уг (х) = {у: р (х, у) > е},
ап (к, е) - зир {Рп (/„ х, 1Ъ V, (х)); * е #, ^ - *21 < А}.
§41
ПРЕДЕЛЬНЫЕ ТШРЕМЫ
т
Теорема 7. Пусть частные распределения
процессов 1п (0 сходятся к частным распределениям процесса &>(?),
а также выполняются условия: '
1) для всякого е>0 Нт зирал(/г, е) = 0;
л-»о п
2) если а = ^<^{< ... <1п = Ь, Я== тах(/А+1 — 4)> то
к
для всякого е>0
Нт 2 Р{р(1о(4).?о(4+.))>е} = 0.
Тогда для всякой функции ф из ^[а, ъ\ {<%) распределение
ф(5п( • )) б#дег сходиться к распределению <р(|о( • ))•
Докажем предварительно следующую лемму.
Лемма 2. Если для сепарабельного марковского
процесса % (?) величина а (к, е/2), определяемая точно
так же, как ап(к, е/2) <?ля ^„(0> меньше единицы, то
Р{8ир[р(|(0, |(5));5е[/,< + А]]>е}<
р|р(6(О.Е(^ + А))>-5-}
< 1-аМ2) ' (Ш)
Доказательство. Учитывая сепарабельность
процесса, достаточно доказать. (10), когда верхняя грань
под знаком вероятности берется по любому конечному
подмножеству / отрезка [1,1 +к]. Пусть / = # = *о> .. .
..., ^п = ^ + к}.^ Обозначим через Вк событие {р(|(^о)>
Б ('*)>«), СА«{р(6(/А)>Б('я))>|}. Тогда
Поэтому
Р{С0}>
>2р{С/|в,п ... лв^пв^в.л ... лв/_,пв/} =
2 (1 -Р{С;|В, П • •. П Внх Л В]})Р{В1 Л .. .В/_, Л В/}>
/=1
> (1,- а (А, е/2)) 2 Р {В, П ... Л б/-1 Л Ву}.
496 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Остается заметить, что
ЗР^П ... ПВ/_1ПВ/} = Р{зир[Ра(0, &(*)), *е/]>в>.
Лемма доказана.
Доказательство теоремы 7. Выберем к
настолько малым, что зирал(2/г, е/8)< 1/2. Тогда из леммы 2
вытекает неравенство
Р{ зир [р Цп (0, 6п (5)); ^ е [*, I + 2А] > ~ } <
<2Р{р(Ш,Е(* + 2Й))>±},
Из этого неравенства, так же как и в предыдущей
теореме, находим, что
П^Р{ 811 р Р(§л(*1), |л(*2))>в}<
<4 У] Р{р(6о(а + (*+1)Л),1о(о + *А))>|}
(при 1>Ь считаем 1(1) = 1(Ь)). Из этого неравенства и
условия 2) вытекает доказательство теоремы.
§ 5. Предельные теоремы для процессов
без разрывов второго рода
Метрика в пространстве функций без разрывов
второго рода. Чтобы результаты § 1 можно было применить
к процессам без разрывов второго рода, нужно
предварительно ввести в пространство функций без разрывов
второго рода подходящую метрику. Обозначим через
Ф[а, ъ] (9В) множество функций х (0, определенных на [а, Ь],
принимающих значения из полного метрического
пространства 36 и имеющих предельные значения #(/ + 0)
для а<Ц<Ъ и хЦ — 0) для а<^^Ь. Поскольку любой
отрезок [а, Ь] можно непрерывно и взаимно однозначно
отобразить в отрезок [0, 1], то в дальнейшем будем
рассматривать пространство <2)[о, ц ($?). Функции,
совпадающие во всех точках непрерывности, будут считаться
неразличными, поэтому естественно принять какое-то
стандартное определение значений функций х(1) в точках
§51
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
497
разрыва. В дальнейшем будем предполагать, что для
всех функций из 2)[о, ц (36) выполняются соотношения
х(/) = х(1 + 0), х(0) = х( + 0), х(1) = х(1 - 0). (1)
Величину р(х(/ —0), х(1)) назовем величиной скачка х{1)
в точке /. Нужно ввести в <2)ю, ц (36) метрику, в которой
й>[о, и (36) превратилось бы в сепарабельное метрическое
пространство, обладающее тем свойством, что
минимальная а-алгебра, содержащая все цилиндрические
множества, совпадает с <т-алгеброй борелевских
множеств этого пространства. Желательно при этом, чтобы
метрика была достаточно «сильной» (т. е. чтобы было
возможно меньше сходящихся последовательностей и,
значит, больше непрерывных в этой метрике
функционалов). Равномерная метрика
Р«И О, </(•)) = вир р (*(/), у (/))
для этих целей не годится, так как в этой метрике 2)[о, ц (36)
не будет сепарабельным пространством (множество
функций
[ хХу I <$,
*Л0= у ,^с Р(*1, *2Н6>0, 0<5<1,
{ Х2у I ^ 5,
имеет мощность континуума, но расстояние между
каждыми двумя элементами этого множества равно б).
Введем в пространство 3)[^{](36) метрику, являющуюся
несколько ослабленной по сравнению с равномерной.
Обозначим через Л совокупность всех непрерывных
монотонно возрастающих на [0, 1] числовых функций Л(/),
для которых Л(0) = 0, Л(1)=1 (т.е. Х(1) отображает
непрерывно и взаимно однозначно [0, 1] на самого себя).
Отметим, что для всех ^еЛ существуют обратные
функции Л""1, также принадлежащие Л. Если \х и Я2е Л,
то и. сложная функция Хг (Л2) будет принадлежать Л.
Определим теперь для каждой пары х(1) и у(1) из
й>[о, \\(36) величину
гл(х,у) = М{ 8ир р(х(1\у(Х(1))) +
+ 'вир |<-Л(01; ЯеЛ}. (2)
498 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Покажем, что г3 рпределяет метрику в 3)[0 Л<$).
Для этого нужно проверить, что функция г^
удовлетворяет трем метрическим аксиомам: а) гв{х, у)^0 и
равно нулю тогда и только тогда, когда х = у\ б) г^(х, г/) =
= гв (у, х)\ в) г3 (х, г) < г3 {х, у) + гт {у, г) для всех х (•),
у(-), г(.) из ^[ап(Я?).
Условие а) очевидно. Условие б) вытекает из
соотношения
г#(у, а-)- 1п1 { зир р{уЦ),х(Щ)))+ зир |/ — Л.(О 1} =
= 1п{{ зир рО/ОГ1^), *(*)) +
+ зир (ат1^)-'!; 1еЛ)=^(,г,^
0</<1
Остановимся на условии в) — неравенстве
треугольника. Пусть х(-), у(-) и г(•) — некоторые функции
из й)[о, 1](^)- Для всякого е>0 можно указать
функции А,! (О и Я2(0, для которых выполнялись бы
соотношения
г&{х,у)> зир р(х(0,»(М0)) +
+ зир |^ - А,! (/)
0<*<1
г3{у>г)> зир р(у(*), г(М*))) +
0<*<1
+ зир и-л2(01
(3)
Тогда
гв(х,г)< 8ир р(*(*), г(ММ/)))) +
0<*<1
+ зир |*-ММ0)К зир р(*(0, 0(МО)) +
+ зир |/-л,(01+ зир рЫМО), 2(ММ0))) +
+ зир I Я, (0 - Я2 (Я.! (0)1 =
«= зир р(*(*), #(М0)+ зчр 1'-М01 +
+ зир р(»(/), г(М*)))+ зиР 1'-М<)1.
§5]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
499
так как, если I пробегает [0, 1], то К^Ц) будет также
пробегать отрезок [0, 1]. Учитывая соотношения (3),
получаем
г а (х, г) < г & (х, у) + гв (у, г) + 2е,
откуда в силу произвольности е и вытекает в).
Таким образом, г3 можно принять за расстояние
В 0[О, 1] №.
Для дальнейшего изучения свойств метрики г3 нам
понадобятся некоторые вспомогательные утверждения.
Положим для всякой функции *(•) из 2)[0г \\фб)
А, (х) = зир {тш [р (х (П х (0); р (х (О, х (*"))];
+ зир р(х(0), хУ)) + вир{(>(х(1),х(1)); 1-с</<1}. (4)
Тогда в силу леммы 1 § 4 гл. III \\т&с(х)~0.
с-»о •
Лемма 1. Пусть *(•)"" функция из &№, ц (9В) и
[а, р] с: [О, 1]. Если х(-) не имеет скачков,
превосходящих 8 на [а, р], то при \1' — V | < с, /', /" е [а, р]
Р(*(/0,*(Г))<2ДД*) + в.
Доказательство. Выберем произвольное 6е(0, е)
И точку т в промежутке [V, /"], обладающую свойством:
при / е [Г, т)
р (*(*'),* (0 )<М*) + в. а р(х(П,*(т))>ДД*) + 6_
Если такой точки нет, то тогда р (*(/'), я(^"))<ДД*0 + 6
и, значит, утверждение леммы выполнено. Если точка т
существует, то поскольку
пип [р(*(/'), х(х)); р(х(т), х(П)]<ЬЛх),
а р (х (/')> х (т)) > Д, (я) + б, имеем р (х (т), х (/")) < А, (*).
Таким образом,
р(*(*0, х(П)<Р(х(Пх(%-0)) +
+ р(* (т - 0), х{х)) + р(х (т), х (Г))< ДДх) + б + е + А,(х).
Переходя к пределу при б | 0, получаем доказательство
леммы.
500 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ VI
Обозначим через Ут счетное множество точек утк^%?
таких, что [)^\/т{Утк) = ^> где ^а^ обозначает от-
к
крытую сферу радиуса а с центром в х. Через Нт,п
будем обозначать совокупность функцийх(•)е 2)[о \\(3в),
\ к к+\\
постоянных на каждом из интервалов —, 1 и
принимающих значения из Ут.
Лемма 2. Для каждой функции х (• ) из 2)[о, \] {Щ
существует функция х* (• ) из Ят> п такая, что
Гд>(х, х*) <- + —+ 4Д2/„(*).
Доказательство. В каждом из отрезков —,
найдется не более одной точки, скачок в которой
превосходит 2&2/п(х). Действительно, если т — одна такая
точка, то тогда
р(дф),*(т-0)) =
= пип [р (х ($),■ х (т — 0)); р (а: (т — 0), х (т))] <
< \]/п (X) При 5Е -, т) ,
р {X (з), X (т) ) < Д^ (X) При 5 ЕЕ (т, -^±±]
и, значит,
р (X ($ — 0), X ($) ) < 2Л1/и (х) < 2Л2/Л (х)у 8 ф Т.
гт Г к к + 1 1
Пусть 1к — точка отрезка —, , в которой
р (х (тЛ - 0), х (тА)) > 2Л2/„ (х),
если такая точка в этом отрезке существует.
Обозначим через 1(() функцию из Л, для которой л(——) = хк
и ( ^Я(/)<^ (такой будет, например,
кусочно-линейная функция, определяемая равенствами А(0) = 0,
1(~^~!г~)^Хк> ^ОНО- Положим хЦ) = х(кУ)).
Функция х(0 будет иметь разрывы, превосходящие 2&2/п(х)9
лишь в точках вида к/п и
/*(*»*)< зир р{хЦ), х(ХЦ)))+ вир |*_а,(/)|<±.
§5]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
501
Пусть далее х* Ц) — функция, равная х(к/п) при
Тогда
гл{х9х*)^ вир р(х(0, **('))<
<виР8ир[р(*(0. *(■!■)); |<*<41]-
Так как скачки х (/), превосходящие 2Д2м (л:), происходят
лишь в точках вида к\п, то в полуинтервале —, [
таких скачков нет, и, значит, по лемме 1
р (% (|), *</)) < 2А№ (*) + 2Д2/„ (х) при / е [|, *±1).
Оценим Ы1п{х):
А „„(*) = 8ир {гшп [р(*(О. *(0); Р (* (0> х Ц")Ъ
+ зир{р(х(0),х(0); °<'<^}+
+ 8ир{р(ж('). *0)); 1--^</<1} =
~8»р{р(*(0), *(М0)); 0</<|}+
+ 8ир{р(х(М')). *(1)); 1-|<^<1}+
+ 8ир { пип.[р (х (к (V)), х (к (/))); р (х (к (/)), х (к (П))];
Я ^ ^ ^ ^ П )
Заметим, что /,- — <: Я (/,) < Я (*2) < 12 < ^ + — при *, <
< ^ < /| + -4-., так что 0 < Я (/2) -? к (О < |" • Поэтому
АшД) < Аг/П (*)• Значит, /-д, (я, **) < 4А2/п (л).
Наконец, положим х*{1) = утк, где & т- наименьший
индекс, для которого р (х\ утк) < Цт.
502 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. V*
Так как р(Г(/),х*(/))<1/т, то г3{х*, **)< 1/т,
га (х, х*) < гв (х, х) + г3 (х} х) + гв (Г, х*) <
Лемма доказана.
Следствие. Пространство Ф^ \\{80) с метрикой г0
сепарабельно.
Это вытекает из того, что счетное множество (^ Ят> „
всюду плотно в Ф\ъ%\\{<%) по лемме 2.
Пусть ^! — некоторый компакт в 96, а Я§
—возрастающая непрерывная функция, определенная при 6>0
и удовлетворяющая условию Я+0 = 0. Обозначим через
Кз>{Х\,\ь) множество функций из Ф^>Х]{96), для
которых ^(0еАГ| при /<=[0, 1] и ДсМ<Ас при всех с>0.
Теорема 1. 1) Множество Кз> (Х\, Яб) является
компактом в <2)[\ \\{96)\ 2) для всякого компакта К\ можно
указать такой компакт Хх с: 96 и возрастающую
непрерывную функцию Х6, для которой А+0=0, что К\ с:
с: Кз){Хь Яб).
Доказательство. 1) Покажем, что К&{Х\, Хь)
для каждого е>0 имеет конечную е-сеть. Для этого
заметим, что для каждого пг существует такое кт, что
IIV (?«*)=*.
Выберем так т и п9 чтобы —1 |-4А#п<8. Тогда
множество функций Нт>п(]Р[утЬ ..., уткт\, где
Р\Уь ••■» ^ — множество функций, принимающих лишь
значения уь ..., #5, является конечной е-сетью в
множестве Кв{Хи к6). Действительно, Нтп является
(—+ —+ 4Я2/п)-сетью в Кз(Х, Х6) в силу леммы 2,
причем такую сеть будут образовывать функции со зна*
чениями из множества [утЬ ..., Уткт}- Множество
Ка>{Х\,Хь) замкнуто. Легко проверите соотношение
Ас (х) < 4с+г и у) (у) + Ъгв (х, у).
§5).
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
503
Поэтому, если га(хл, х)->0, то для всякого а>0
Д,(*Х 11т Д«.+а(*«ХА„+а.
Значит, ввиду непрерывности Я, &с(х)^1кс. Очевидно
также, что Нт ^(/)е!,, если хп(/)е1, для всех п.
Следовательно, предел последовательности,
принадлежащей К®{Х\, Ы» будет также принадлежать
/Сй>№, М« Остается показать, что всякая
фундаментальная последовательность *„(•), принадлежащая
/С<2>№, Яб), будет сходящейся. Пусть хп{ •) —последовав
тельность функций из К®{Х\> Яа), для которой
г«К»*т)->0 ПРИ ^->°° и ™-*°° (т. е.
-«„(•)-Фундаментальная последовательность). Достаточно показать,
что некоторая подпоследовательность хПк(>) имеет
предел х(-). Поэтому можно считать, что
последовательность хп( • ) такова, что г^
(хп'хп+\)<2 " '• ТогДа
существует последовательность функций Яп из Л такая, что
зир р(хпЦ), ^л+1(Ал+1(0))<-^гг.
Положим |А! (0 = А,! (0» ^д(0 = Лл(цп«, (*)). Так как
зир ||*„(/)-[хя.,(/)|< зир |ЯЛ0~'1<4г,
то щ(0 сходится к'некоторой неубывающей
непрерывной функции |ы. (/), удовлетворяющей условиям |и (0) = 0,
|л(1)= 1. Далее
8ир р(хп (МО), -«л-1 (1А/.-1 (0 ) ) =
= зир р (*„ (Яя (/)), хя-1(/))<-2я.
Поэтому яя(цл(0) равномерно сходится к некоторой
функции х*^) из 12)[о, ц ($?). Рассмотрим связь между
функциями х*(1) и |и(/). Пусть |и(/) постоянна на
некотором промежутке [а, р]. Если х* (а) = х* (Р), то **(/)
также постоянна на [а, р], если же х*(а)фх*($)у то
существует такое у е [а, р], что х* (/) = х* (а) при ^[а, V),
504 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
л** (/) = х*(Р), ^^["у, Р]. Действительно, в противном
случае нашлись бы такие точки /'</"</'",
принадлежащие [а, р], что х*(1')фх*(Г% х{1")Фх*{Г"\ и тогда
Нт тт[р(*п(М''')). хя(М'"')));
р(*п(М'")), Хп{»п(П))] =
= тт[р (*•('"), хт(Г')), р(**('"), **0'))]>О.
хотя ^(П<йЛИ<[хЛП и \1п(П Цп(П, М'"')
стремятся к \1(а). Это противоречило бы тому, что
последовательность хп(') принадлежит К'&(Х],Хь).
Обозначим через х() функцию из <2>р. и (Я?),
определенную соотношением
х(*) = *'М')), (5)
выполняющимся во всех точках /, в которых ^(5)>|и(/)
для всех 5е(/, 1]. Соотношение (5) определяет
единственную фуНКЦИЮ Х(1) ИЗ й)[0, |](#/).
Покажем, что эта функция *(•) будет пределом
последовательности *„(•)• Для этого построим
вспомогательные функции ср„ из А. Пусть хи ..., т^ — все точки
[0, 1], в которых х( • ) имеет скачки, превосходящие 1//г.
Обозначим через [а*, р^] максимальный промежуток, на
котором ц(*) принимает значение тг (этот промежуток
может содержать и одну точку).
Пусть у* — такая точка промежутка [а,, р,], что хт(() =
= х(т,- —0) при 1^[аь у{) и х*(0-*(^) при /г^, Р{].
В частности, если а; = 'Уг> то **(0 на [«*> М принимает
единственное значение лг(тг). Выберем е„, не
превосходящее 1/я, так, чтобы Де (х)< — . Пусть ср„ (/) ~ функ-
ция, удовлетворяющая соотношениям: фл (V*)= т;>
|Фя(0-»*(01<ел.
Оценим зир{р(дс*(/), *(фя(0)'> 0<^< 1}. Если * не
принадлежит ни одному из промежутков [с^, Р^], то
Р (*' (0, х (Фя (0)) = р (х (|х (0), * (Фя (<)))< 2Деп («) +1
на основании леммы 1, так как х(1) между \х{() и Ф„(/) не
имеет скачков, превосходящих 1//г. Если /е[аг-, V*), то
Р (*'(')> *(ф*(0))<
< зир {р (х (т, - 0}, х ($)'); я <= [т^ ~ гт т«)} < Де/|'(х),
§5]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
.505
поскольку р(л;(т; — 0), х (т*)) > — > Д8л (х). Аналогично
устанавливаем, что при 1^[у{, &] р(**(0, #(фя(0))^
^Де (#). Следовательно,
8ир р(**(0, *(Ф„(')))<{ + 2Ле„(*)<Т-
Оценим теперь г^ (хп, х). Имеем
гяК.*)<^К(*)> *>«'(• ))) +
< вир р(хЛ(ця(0), **(')) + *иР Р(**(0> *(<Р„('))) +
+ зир и-ФЙ(^~1(0)|<5^+4+ зир 1Мо-флок
Таким образом, га(хп, х)->0, т. е.
последовательность хп(') сходится к функции х(-). Утверждение 1)
доказано.
2) Обозначим через Х1 множество значений х(1) и
х(1 — 0) при х(-)^К\. То, что ^Х1 является компак-
I
том, доказывается точно так же, как в лемме 1 § 4.
Положим Дс = зир{Ас(х); л;(«)е/С,}. Очевидно, Дс —
монотонно возрастающая функция с. Покажем, что
НтД<. = 0. Предположим противное. Тогда можно ука-
зать последовательность функций хп(-)е=К1 и
последовательность сп->0 такие, что Д^(*„)!>6 при
некотором 6>0. Ввиду компактности К\ можно предполагать,
что хп(-)->х0(-). Но при /^(х, #)<е
ДД*)<Д,+е(*/) + Зе,
Поэтому для всякого с> 0
^ Ы > Д<-^ (,л, ,о) (*„) - Згя (*л, *0) > б - Згя (*„, *0),
как только сп<с-'Г0(хп, х'оУ Значит, ДДлг0)>6 Для
всех с>0, а это противоречит условию ПтДД#0) = 0.
с->0
Таким образом, НтДв = 0. Очевидно, можно построить
с*о
506 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
непрерывную монотонную функцию кс,
удовлетворяющую условию кс<Хс, Л+0 = 0. Тогда К\ с: К(Хи Ай).
Теорема доказана.
Основная предельная теорема для процессов без
разрывов второго рода.
Теорема 2. Пусть !„(*)» 0<^<1, /г —0, 1, ...,—
последовательность процессов без разрывов второго рода
со значениями в 36, причем частные распределения \п(1)
сходятся к частным распределениям ^0(0» Для того чтобы
для всякого функционала /, определенного на &\ъу \\ (Зв)
и непрерывного в метрике г^, распределение /(|л(-))
сходилось к распределению I (|0 (• )), необходимо и
достаточно выполнения для всех е>0 условия
Нт 1БР{Дс(Ы-))>е} = 0.' (6)
Доказательство. Из равенства (6) вытекает для
всех е>0 соотношение
ПтзирР{ДЛи-))>в} = 0.
с->0 п
Отсюда, точно так как в теореме 1 § 4, находим, что
существует такая непрерывная монотонная функция Хь,
для которой Я+о = 0 и
8ирР{Д,Йп( •))<**, 0<с<1}>1 —|. (7)
Опять, как и в теореме 1 § 4, используя сходимость
частных распределений процессов %п((), можем показать,
что семейство мер {чпи /2=1, 2, ...; 0^^^1}, где
%1* (Л) = Р {§„ (0 е ^} является компактным, значит, для
каждого к можно указать такой компакт Х{к\ что
чпЛх{к))> 1 ~2"2/г~ для всех п, /. Обозначим через Ьь
множество тех у, для которых р(у9 Х{к))^.к2-ь- Тогда
Х\ = [У\Х{к) является компактом. Поскольку из соотно-
к
шений х(^)е№, х(^)е№, Д2-л(*)< V* выте'
гя
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Ж
кает, что х(1)^Х{к) при -у <^<—у-, то
Р6«(-)е/Сд|№>^)}<1-Р{АЛЕ||(-))<^0<с<1} +
оо 2 оо 2
+22р{^)«*,}<}+22*-"|<*
й=1 /«О Л-1 /-0
Итак, для всякого е>0 построен такой компакт К@(ХР А6),
что для всех мер ця, соответствующих случайным
процессам |л(-) на <2)[ог \\($), выполняется неравенство
Остается воспользовать'ся теоремой 1 § 1 (как вытекает
из замечания к теореме 1 § 1, условия теоремы
достаточны и в неполном пространстве). Достаточность
условий теоремы доказана/
Для доказательства необходимости условия (6) введем
функционал
Га(х(.)) = *ир9(х(0),хУ))е-а1 + тр9(х(1),х(!))е-а{1-<) +
+ зир{тт[р (*(*), х(з))е~а{'~8); р{х({), х(и))е'а{и'%
0<$</<и<1}.
Легко проверить, что Ра{х(-)) является непрерывным
функционалом на Ф^% п (Я?). Поэтому, если распр*еде-
ление /(!„(•)) сходится к распределению /(&)(•)) Для
всех непрерывных функционалов Д то для всякого е> О
ШР{Ра(1п( •))>г]<Р{РаЫ ■))>*}.
П->оо
Заметим теперь, что
&с(х(-))<е°*Ра(х('))9
М*(О)<М*(О) + 5е-^зирр(*(0), х{1)).
Поэтому
'11йГР{АЛБя(-))>в}<Ш5Р{^с(Ей(.))>в-1е}<
П->оо П->оо
<Р(Рис(&>(■))>е-Ц<р{д/г&(•))> 1 е-'е}+
+ Р{ "зир р(5о(0), ?о(^))>4-е~,Ч"^=}.
508 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. ^1
Правая часть этого неравенства стремится к нулю
при с->0 в силу леммы 1 § 4 гл. III, конечности
5ирр(лг(0), х(1)) для всех х(• ) е ^)[0,1] {<$) и того, что
10 (•) е 0[о, 1] (36) с вероятностью 1. Теорема доказана.
Теорема 3. Пусть %п(1), я = 0,1, .. .. —
последовательность случайных процессов, с вероятностью 1
принадлежащих ^)[о, 1] (<^), для которых частные
распределения 1п{() сходятся к частным распределениям ^0(0
и существуют такие а>0, Р>0 и #>0, что при м^О,
1Х < 12 < ^з выполнено неравенство
М[р(1«(/,), 1„(^))Р(1П('2), |п(^))]р<Я(^-^)1+а.
Тогда для всякого. непрерывного функционала / на
&[о, п {35) распределение величины !(1п(- )) сходится
к распределению величины / (%0 (• )).
Доказательство. Используем лемму 4 § 4 гл. III.
Если положить § (/г) =/г\ где 0<^<р/а, <7(/г) = 21+а#/гб,
где б = р — а\\ то для всех процессов 1п (^) будут
выполняться условия этой леммы с
е(/п) = -^-^) д(т,с) = с-рЯ2,+а^-2-^.
Следовательно, при некотором Ь
Р{ДЛ^(.))>е}<1е-РЛ
Остается воспользоваться теоремой 2.
Предельные теоремы для марковских процессов.
Пусть 1п{1) — последовательность марковских процессов,
определенных на [0, 1], выборочные функции которых
с вероятностью 1 принадлежат Ж)^\\{9в). Обозначим
через Рп{1, х> $, А) вероятность перехода для процесса
1п((). Пусть далее Уе{х) = {у: р{хуу)>е}.
Теорема 4. Если частные распределения
процессов 1п{1) сходятся к частным распределениям |0(/) и
для каоюдого е>0
Пт Нт зир{Рп(*, х, 8, Уе(х)); х е %?', 0<5 — I <Н) = 0,
то для всякого непрерывного на 3)$, ц {Щ функционала }
распределение / {%п (•)) будет сходиться к
распределению /(&(•))•
§51
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
509
Доказательство этой теоремы опирается на
следующую лемму.
Лемма 3. Пусть %{у ^2> • • •» 1п~ Чепъ Маркова, для
которой при всех к < /
Р{р«*>Ь)>в|&л}<а<1
с вероятностью 1. Тогда
Р{5ир{тт[р(|/,5/); р(&7, Ш\ 1</</</<я}>4е} <
<7Г^р{Р^> %п)>е].
Доказательство. Событие
{зир {пип [р (|„ |у); р (|,, &)]; 1 < г < / < / <п} > 4е}
влечет одно из событий Аг П 5Г, где
Л = {р(б1, и<2е, /=1, ..., г-1; р(|„ Ы>2е},
ёг={зирр(||.,|4)>2в|.
Поэтому
Р{зир{тт[р(1;,?/); р (&,, |,)]; 1 < г </</<«}>4е} <
л п
В силу леммы 2 § 4
Р{вг|У<т^-
а
п
^ Р {ЛЛ = Р (зир р (1„ 1к) > 2е) < -^ Р {р (|1( |„) > в}.
Из этих двух неравенств вытекает требуемое. Лемма
доказана.
Следствие. Если |(^) — сепарабельный
марковский процесс, для которого вероятность перехода
Р (/, ху 5, А) удовлетворяет при 1Х ^ I < 5 ^ 12 неравенству
Р (/, х, 5, Ке (л;) )< а < 1, то
Р{вир{т1п[Р(1(пМП); р(Е(П. ЕС"))]; *1<**<*"<
< *'" < Ы > 4е} < ~^ Р {р (| &), | (/2)) > е}.
510 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ 1ГЛ. VI
Приступим теперь к доказательству теоремы 4.
Достаточно показать, что для всякого е>0
Нт Ш Р{АЛЕ«(-))>в} = 0.
Оценим эту вероятность. Пусть с настолько мало, что
для всех достаточно больших п
$ир{РпУ,х,8, Уе/8(х))\ хе^, 0<$-*<Зс}<~.
Тогда
МЫОХзир р(и0), 1п(*))+ ^р р(Б»0), &*(')) +
+ вир {тш'[р (%п (0,1п (П); р (1„ (0, %я (П )1; *с<*' < « г <
Поэтому
Р{ЛЛ1„(-))>е}<р(зир р(1„(0), 1„(/))>!] +
+ Р{ зир р(|я(1), Еп(0)>т} +
+ 2 Р{зир{тт[р (|„(/'), !„(')); Р &,(*), Ы'"))];
*<7
йс < /'< ;<*"<(& + 3) с} >-|} <
<Т^ + (Т^2 Р{Р(Е.(М. Ы** + Зс))>±},
А<-^
где
а„ = зир {Р„ (^, л:, 5, Ке/8 (л:)); х^В5, 0 < 5 — I < Зс}.
Поскольку
р{р(ЫМ. 1»(*с + Зс))>|}<
<Р{р(1»(Ас),К*с + с))>^-} +
+ Р{р(Ы*с + с), |„(^ + 2с))>^-} +
+ р{р(|„(А:с + 2с), Ы*с+3с))>-^},
$5]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Ш
-г-!—<2, то
Р{ДЛ1*'))>е}<
4а„ [1.+ 3-2 Р{И!„№, 1п(кс + с)» ^-}1
I Н- ]
Поэтому в силу условия теоремы и равенства
= Ц Р{р(Ь>(*<0. Ъ>(Ьс + с)>±\,
к<\1с
справедливого почти для всех е > 0, достаточно показать,
что сумма в правой части последнего равенства
ограничена при с->0. Выберем к таким, что
1 е
Р0({,Х} 5, КеДлОХ-^ ПрИ $-/</*, Ъ{ =-^г.
Достаточно показать ограниченность суммы
2 Р(р(1о(М, Ь>(*с + с))>4в,}
для всякого ? при данном И.
Пусть щ = 1, если р (&, (Ас), |0 (Ас + с)) > 4в!, х\к - О
в противоположном случае.
Нужно показать, что 2 Мт)л ограничена равно-
мерно по ? и с.
Оценим
Р{ 2 Чи>1\
Будем рассматривать лишь г\к с индексом А, для
которого 1^кс<1 + Н.
Пусть Аг — событие
|со: 2%=^; Лг=^.
512 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. VI
Тогда
р{2ч*>/} = 2р{лп{»:11 %>о}} =
= 2 / Р (2 1* > °1Ь> (гс + с)\ Р (</ш) <
< У Г Р /81ф Р (10 (Ас), |0 (ГС + С) )>2в, 110 (ГС + С)} Р (йГсо) <
^ 1/3
'"з
Поэтому для всех I и с
оо
2 м*<2«(^-4
4
Теорема доказана.
Процессы с независимыми приращениями в полном
линейном нормированном пространстве X являются
частичным случаем марковских процессов. Из теоремы 4
вытекает такая теорема для процессов с независимыми
приращениями.
Теорема 5. Пусть 1п(I), п = О, 1, ... —
последовательность процессов с независимыми приращениями,
определенных на [0, 1], со значениями в дв и с
вероятностью 1 принадлежащих <Ю[о, \\{8В). Если частные
распределения процесса \п(1) сходятся к частным
распределениям процесса 10(() и для всякого е>0
Нт Нт вир Р{||я(') - ^(*)| >е} = О,
то для всякого функционала /, непрерывного на <Ю[о, \\{®в)
распределение !{1,г{*))сходится к распределению !{10(ф))-
Замечание. В теоремах 2 — 5* достаточно требовать,
чтобы функционал / был измерим и ^0-почти всюду
непрерывен, где ц0 — мера, соответствующая предельному
процессу на Ф^% ц {ЗБ).
Применение к статистике. Применим предельные
теоремы для изучения асимптотического поведения
эмпирической функции распределения, используемой
в математической статистике.
§ 5} ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ 513
Пусть результаты некоторого эксперимента
представляют собой случайную величину с неизвестной
непрерывной функцией распределения Р(х). Как оценить
функцию Р(х), если известны п результатов
независимых осуществлений эксперимента: ^, ..., ^п?
В математической статистике для этой цели
используется эмпирическая функция распределения Рп(х),
определенная соотношением
где V/г(x) — число величин 1кУ попавших в интервал
( — оо, д:). Из теоремы Бернулли вытекает, что Рп(х)
сходится по вероятности к Р{х). Таким образом,
функцию Р*п (х) можно взять в качестве оценки Р (х).
Естественно, нас интересует возникающая при этом ошибка.
С другой стороны, часто удобно иметь для
приближения Р(х) аналитическое представление. Тогда нужно
решать вопрос: может ли данная функция Ф(х) служить
приближением Р(х), если известны результаты
эксперимента ^, ..., %п. И в том и в другом случае важно
знать поведение разности между эмпирической
функцией распределения и теоретической функцией
распределения Р(х).
Для изучения этой разности введем процесс
Чп(1)=У^Ш*)-?(*))•
Лемма 4. Частные распределения процессов х\п {I)
сходятся к частным распределениям гауссовского
процесса ц (^), для которого М т] (^) = 0 и при I < т
МцЩц(т)^Р^)[1-Р(х)].
Доказательство. Заметим, что
п
где е(0 = 0 при /<0 и е(/)=1 при ^>0. Так как
Мв(1к-1)в{Ьк-т) = РЦ) при 1<х,
17 И. И. Гихман, А. В. Скороход
5|4 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. УГ
и процессы г(1к — 1) — Р(1) независимы при различных кк
то дальнейшее доказательство вытекает из теоремы I
§ 1 гл. III.
Следствие. Пусть Р~ (1) — функция, обратная к
Р(1). Положим
Тогда частные распределения процессов 1п(1) сходятся
к частным распределениям гауссовского процесса 1(1)>
определенного при /е[0, 1], для которого
Щ (I) =, о, М\ (1) § (5) = I(1 - 5) при О < I < 5 < 1.
Замечание 1. Процесс \п(1) представим в виде
п .
} п "
где \\к = Р~1 Цк) — независимые равномерно
распределенные на [0, 1] случайные величины.
Замечание 2. Конечномерные распределения
процесса 1(1) совпадают с условными конечномерными
распределениями процесса броуновского движения до (1), 0^
^/<Л, при гипотезе до(1) = 0. Так как условные
распределения процесса х$)(1) при гипотезе до(1) = 0 будут
гауссовыми, то достаточно показать, что
М(ш(01ш(1))а1((1=0 = 0,
М (ха (() ш (б') | V (1) )„,(„.„ = / (1 - А'), 0 < / < 5 < 1.
Величина !(/) = да (/) —/ш(1) не коррелирована с ш(1).
Так как |(/) и ©(1) имеют совместные гауссовы
распределения, то процесс 1(1) не зависит от да(1). Поэтому
М(1(0|а»(1))=М1(0 = 0,
М(|(01(8)|ш(1))=М1(01(5).
Используя соотношение !(/) = да {() — Ш(1) и
предыдущие формулы, находим
М(ю (/)/«> (1)) = М1),
М(©(0м;(5)/ш(1))=М1(/)|(5) + ^(ш(1))2 =
= ГП1П[/; 5] —^5 + ^[ш(1)]2.
«4
ИРЕ ДЕЛЬНЫЕ ТЕОРЕМЫ
515
Полагая ш(1) = 0, убеждаемся в справедливости
сказанного в начале замечания 2.
Теорема 6. Для всякого функционала /,
непрерывного на 2)^\}(^})} распределение 1(1п(-)) сходится
к распределению ?(1( • )).
Доказательство. Заметим сначала, что сепара-
бельный процесс 1(1) будет непрерывным, так *1то 1(1)
& вероятностью 1 принадлежит 0р, п С^1). Действительно,
|!^ + Л)~ 1(1) имеет гауссов'ское распределение, причем
М Й (* + А) ~ 6 (*) )4 = 3 (М Й (( + Н)- % (/)]2)2 - О (Л2).
Поэтому процесс 1(1) непрерывен на основании
теоремы 7 § 5 гл. III. Сходимость частных распределений
процессов |„(/) к частным распределениям 1(1)
установлена.
В силу теоремы 2 остается показать, что выполняется
соотношение (6). Поскольку
Л, (*) < зир {| х (Г) - х (П |; | V - Г К с],
теорема будет доказана, если для всех е>0 будет
установлено соотношение
ИшШР{ зир 11п (Г) - \п (П | > 8} = 0. (8)
Процесс \п(1)Л-Уп1 монотонно возрастает, значит, при
~ УП(1А - *,) < Ьп (<з) ~ 6я &) < Бя (/4) ~ 1п (/!> + 1^4-'О-
Поэтому
зир Ц„(П-ЫПК
|<'-<"|<с _
А.
С;ГП
Пусть тп выбраны так, что -гг--*0 при п~>оо
2 я
и'/г2~т»>1.
Для доказательства (8) достаточно показать, что для
всякого е>0
Пт Ш Р{ ' зир 1бЙ(А,2"да||)-Ь1(*22"т,1)1>в)*0.
I *,-*.)<<* Л
17*
516 ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ, VI
Заметим, что
вир кп(Ьё~т")-1п(Ь22~тп)\<
\кх-к2\<с2 п
<
*2'»р|ь(т)-«.(^)|.
г-тМ
где т{с) — наименьшее целое число, удовлетворяющее
соотношению с2т{с)^\ (по поводу последнего
неравенства см. доказательство леммы 3 § 4 гл. II).
Выберем а<\ так, чтобы 2а4>1. Тогда
Р { вир | \п {кх2~т*) - \п (к22'тп)| > г} <
т
тп ' ,
1 гЫЦЩ-Ф)
<
™п 2Т~\
>
е а'
Лс)
2 1 -а
<
: 2 М\1.т-Ф)\>ж^-}<
'с) 1~0 '
,««?) *-о V еа '
(9)
Пусть \хп — число величин ц^ попавших в отрезок
[/, / + А]. Тогда
>&,&,
РК==*} = СЖ(1-ЛГ
и
Б(/ + л)-Б(/)-1/л(-!?--а).
Можно подсчитать (см. Б. В. Гнеденко [17], стр. 214),
что
М(МИ-Л)-!п(0)4<3/г2 + 4<3/*2 + /г2-т".
Значит, при /г ^ 2~"'п имеем
М(|1>(' + Л)-6»(0)4<4А«.
§5]
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
517
Подставляя эту оценку в неравенство (9), находим
Р{ зир \1п{к,2-тп)-1п{к22-тп)\>г}^.
\к1-к2\<с2 п
тп
где
оо
Теорема доказана.
ГЛАВА VII
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР,
СООТВЕТСТВУЮЩИХ СЛУЧАЙНЫМ ПРОЦЕССАМ
§ 1. Общие теоремы об абсолютной непрерывности
Напомним сначала некоторые определения из теории
меры.
Пусть на измеримом пространстве {36, 23) заданы
две меры III! и р2- Мера ц2 называется абсолютно
непрерывной относительно меры \лх (пишут \х2 <С \х{), если
\1<2 (А) = 0 для всех А из 23, для которых ц, (А) = 0. Если
\х{ <С \х2 и ^2 <С м-1» то пишут ^1 — \х2 и называют эти
меры эквивалентными. Меры р{ и ^ взаимно
сингулярны, если существует такое множество Л, что Мч {А) = 0,
\ь2{36 — /1) = 0. Взаимно сингулярные меры называются
еще ортогональными (пишут ц, _1_ ц2). Если меры р,} и \х2
конечны, то \л2 ~ VI + ^2, где V] -С [хь а \21. щ. Это
представление единственно. Меры V! и у2 называются
соответственно абсолютно непрерывной и сингулярной
составляющими меры р,2 относительно меры \х{.
Для конечных мер справедлива теорема
Радона — Н и к о д и м а: \х2 <С \1\ тогда и только тогда, если
существует такая ^-измеримая функция р(х), что для
всех А е 23 выполняется равенство
№ {А) = ] р (дг) (х, (</*).
А
Функция р(х), определяемая с точностью до
эквивалентности по мере ц,, называется плотностью или
производной-меры \х2 относительно 11{ и обозначается так:
§ 1] ОБЩИЕ ТЕОРЕМЫ ОБ АБСОЛЮТНОЙ НЕПРЕРЫВНОСТИ _ 519
Если \х2 не абсолютно непрерывна относительно [хи
то под -~^- понимают производную абсолютно
непрерывной компоненты меры \х2 относительно \х{. В
частности, если \х{ _1_ р.?, то -7^ = 0.
Всюду на протяжении этой главы мы будем
рассматривать тот случай, когда меры III! и ^2 являются
вероятностными, т. е. ц^ ($?)=!. Если ^—некоторое
функциональное пространство, то под 23 будет
пониматься о-алгебра, порождаемая цилиндрическими
множествами, так что меру \х^ можно трактовать как меру,
соответствующую некоторому случайному процессу.
Изучению условий абсолютной непрерывности,
эквивалентности, сингулярности для таких мер, а также
вычислению плотности одной меры относительно другой
и посвящена эта глава.
При доказательстве теорем об абсолютной
непрерывности для вероятностных мер на измеримом
пространстве {36, 23) • чаще всего используется следующая
схема. Пусть 23„ — возрастающая последовательность
а-алгебр такая, что о {\^]^п} =23, а ц" — сужение меры \х(
на 23„. Предполагается, что 0~алгебры 23„ таковы, что
проверить абсолютную непрерывность меры \хпу
относительно \хп{ не представляет затруднений. Если $6 —
функциональное пространство, то под Ъп понимают обычно
а-алгебры, порожденные цилиндрическими множествами
с основаниями из фиксированного конечномерного
подпространства 36. Пусть \х/] < \лп{ и
?п(х)^~{х).
Величины рп{х) на вероятностном пространстве {36,23, ц,)
образуют мартингал. Действительно, для всякой 23л-из-
меримой функции }{х)
//(*)рй+1ММ**Н I Пх)ря+гШ»+Ч<1х) =
= | }{х)^(йх)=11{х)\$(ах)=\ !{х)9п{х)^{{йх)^
520 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Отсюда в силу определения условного математического
ожидания на вероятностном пространстве (<^, 23, \х{)
имеем
М(ря+1(*)|»я) = Рй(*).
Но величина рп(х) является 23,гизмеримой, значит,
рп(х) — мартингал. Поскольку рп(х)^0 и \рп(х)\ь{(<1х)=*
= \х%(9в) = 1, то в силу теоремы о пределе для
мартингалов (см. теорему 1 § 2 гл. II) почти всюду по.мере \1{
существует предел
Нт рп(х) = р(х). (1)
Теорема 1. Функция р (х), определенная
соотношением (1), является плотностью абсолютно
непрерывной компоненты меры \х2 относительно \хь т. е.
Доказательство., Пусть \х2 = а\х' + Ь\х", где
а 4~ 6 = 1, ^ < |11, \х"±\хь так что ц' и ^" —
вероятностные меры. Обозначим через \1'п и \\,"п сужения этих
мер на 23/г Тогда
РлМ = аРлМ + *Ря(*),
где
Для доказательства теоремы достаточно доказать, что
р^(л')—>0 и р'п{х)^-^-(х) почти всюду по мере \х{. Для
всякой 23„-измеримой ограниченной функции ((х)
выполнено равенство
1^ ^- (а'} ^ (**= I; {х) ^{йх)=1!{х) »'п {йх).=
= | I (х) р; (х) (х, (их).
Поэтому
$ 11 ОБЩИЕ ТЕОРЕМЫ ОБ АБСОЛЮТНОЙ НЕПРЕРЫВНОСТИ 52!
где условное математическое ожидание берется на
вероятностном пространстве (36, 23, р^. В силу теоремы 4
§ 2 гл. II для всякой монотонно возрастающей
последовательности 0-алгебр З3„ с вероятностью 1
Нт М(&|©я)=М(Ца{и©я}).
П-»оо п
Значит,
Нт р' (Х) в М № (х) 1») = ^~ (х).
Докажем теперь, что р^(х)—>0 почти всюду по мере р,.
Пусть Нт р^(#) = р"(л;) (существование предела выте-
кает из того, что р"(х) — мартингал). Для всякой
^-измеримой неотрицательной функции ?(х) на основании
теоремы Фату будем иметь
/ / (Х) V" (их) = | / (^ р*п (ах) = / / (х) Р- (*) ^ (</*) =
= нт [ / (х) Р;; и) 1х{ (ах) > [/ (*) Р" и) ^ (</*),
(считаем п>т). Отсюда для Ле53 ( р'^лОр! (*/*) ^
л
< р" (Л). Пусть А таково, что р" (Л) = 0, \л{ (А) = 1. Тогда
Г р'/(д:)р)1 (с?л:)== 0. Значит, р"(л;) = 0 почти всюду по
А
мере \х{ на множестве Л, а так как \х1(А)=и то
р"(д;) = 0 почти всюду по мере р{. Теорема доказана.
Следствие 1. Если р(х), определяемое
соотношением (1), положительно почти всюду по мере \хи то
Р} < р2 и
1 *€=5,
4±(х) = 1 РМ'
0, А'бХ,
еде 8 <= 33 таково, что \х" (8) = 0, р,1 (5) = 1.
Действительно, для всякой 23-измеримой
неотрицательной функции ?(х) справедливо равенство
522 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ТЛ. VII
Взяв в качестве }(х) функцию §(х)/р(х), получим
откуда и вытекает наше утверждение.
Следствие 2. Для того чтобы мера \х2 была
абсолютно непрерывна относительно \ли необходимо и
достаточно , чтобы функция р(х), определяемая
соотношением (1), удовлетворяла условию
|р(*)М<**)'=1. (2)
Поскольку
/ря(*)М«**Н1, (3)
то для выполнения (2) необходимо и достаточно, чтобы
в (3) можно было осуществить предельный переход под
знаком интеграла, т. е. чтобы функции рп{х) были
равномерно относительно п интегрируемы по мере \х{.
Иногда вместо мер ^, являющихся сужением мер \11
на 5УЯ, удобно рассматривать аппроксимацию мер \х( не-
которыми мерами ц" для которых вычисление —~-
более просто. Здесь имеет место ситуация, аналогичная
до некоторой степени рассмотренной в теореме 1 и
следствиях из этой теоремы.
Теорема 2. Пусть на (35\ 23) заданы две
последовательности вероятностных мер \ххп и ^,
удовлетворяющих условиям:
а) на некоторой алгебре 930, о-замыкание которой
совпадает с 23, \х1п сходится к ^: Нт [х1п (А) = р10 (А) для
П->оо
б) меры \х2п абсолютно непрерывны относительно ^
при п^ 1;
в) функции рп(х) =—^(х) равномерно интегрируемы
относительно \ххп, т. е. для всякого е>0 можно указать
§ I] ОБЩИЕ ТЕОРЕМЫ ОБ АБСОЛЮТНОЙ НЕПРЕРЫВНОСТИ 523
такое Ы, что для всех п
\ Рп (*ЬС(лг. со (ря (*)) \11п (</*) < е,
где %[Ы то)(0 — индикатор интервала [ЛГ, оо).
Тогда ^0 < ^.
Доказательство. Для любого Ле^0 имеем
VI (А)« Нт ^ (А) = Нт Г Р|| (*) ^(йх) < ;У Нт ^ (А) +
А
+ ШН Г р„ (ж) х(]У „, (р„ (*)) ^ (</*) < ЛСД (А) + е,
А
если N и г выбраны так, что выполняется неравенство
в условии в). Класс множеств Л, для которых
|1§(Л)<Л^(Л) + в (4)
будет монотонным классом, содержащим алгебру 230»
следовательно (4) выполняется для всех А из 23. Из (4)
вытекает, что ^(Л) = 0, если только ^(Л) = 0, так как
е>0 можно взять сколь угодно малым.
Замечание. Для выполнения условия в) теоремы 2
достаточно выполнения одного из следующих условий:
1) при некотором а>1
8иР /[Ря(*)]а^(<**)<°°>
2) существует положительная непрерывная
функция ф(/), для которой
Кт -^щ- = О и зир ] ф (ря (х)) ця {их) < оо,
3) зир (\оё9п(х)^(с1х)~
= зир Г ря(х) 1овря(х)ц1п(ах)< оо,
4) меры \х]п также абсолютно непрерывны
относительно \х2п и для всякого е>0 можно указать такое N.
что
Нт^я *:^(*)<- <е. (5)
524 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Действительно, 1) и 3) являются частными
случаями 2), если взять ф(7) = /а и ф(/) = Лод Л-1.
Достаточность условия 2) вытекает из неравенства
] Рп (*) %, со (ря (*)) К №) <ыр-~ / Ф (ря С*)) Ия ^х).
Для доказательства достаточности условия 4)
заметим, что
.1 р« М %,., (р„ М) ^ (*0 - ^ ({*: || <*> < 7}) •
Для всех достаточно больших п это выражение можно
сделать сколь угодно малым посредством выбора
достаточно большого N в силу (5). Кроме того, поскольку
\/рп(х) почти всюду положительно по мере \\гп в силу
того, что и \\гп <С \11п, то для всех п
1!га^((,:^(,)<1))-0.
Отсюда и (5) вытекает условие в).
Теорема 2 не дает возможности вычислить —у- (х).
Поскольку функции рп(х) определены каждая по своей
мере, то невозможно говорить о пределе рп (х) при п—> оо.
В частном случае, когда все меры \х1 совпадают с ^,
то можно рассматривать предел р (х) по мере \х]о. Если
он существует, то при _ выполнении условий теоремы 2
этот предел будет совпадать с —т~(х)- Мы докажем
сейчас некоторую более общую теорему о значении
плотности —г- (х).
Теорема 3. Пусть на вероятностном пространстве
{О, ©, Р} заданы случайные величины 11п, /=1, 2,
я = 0, 1, ..., со значениями из измеримого
пространства (Зу, 53) и существует алгебра 530, а-замыкание кото-
§ II ОБЩИЕ ТЕОРЕМЫ ОБ АБСОЛЮТНОЙ НЕПРЕРЫВНОСТИ 525
рой совпадает с 23, такая, что для всех А ё 230
мо вероятности Р. Яс^ш л/ер&* ц^ {А) = Р {^ е Л} яа (^, 25)
удовлетворяют условиям б) и в) теоремы 2 и сущест-*
вует
П->оо
в смысле сходимости по вероятности, то р = —?- (ЗД.
ОД ч °'
Доказательство. Для всех А из 230 существует
предел по вероятности
"тр„(г')хл&) = РХл®)-
п-»оо
В силу условия в) теоремы 2 выражения Рд(^)хл(^)
будут равномерно интегрируемы по мере \х[п, и поэтому
возможен предельный переход под знаком
математического ожидания:
РЗМ)- Нт Мхд(ф- Нт МХд (Ц) р„ (Ц) -
л
Эти соотношения очевидным образом распространяются
на все А. Теорема доказана.
Замечание 1. Если величины —т(11) сходятся по
вероятности к некоторому пределу р>0, то условие в)
теоремы 2 автоматически выполняется, так как тогда
имеет место условие 4) замечания к теореме 2.
Замечание 2. Если не требовать выполнения
условия в) теоремы 2, но предположить, что Мр=1, то
утверждение теоремы 3 остается справедливым.
Действительно, из теоремы Фату вытекает соотношение
Мрхд$)< Нт Мр„(^)Хл(^)= Нт |^(Л) = ^(Л)
для всех А е 230. Кроме того, совокупность множеств Д,
для которых выполняется соотношение
Мрхл(^)<КИ) ^
526 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. \'1Г
образует монотонный класс. Поэтому (6) выполняется
для всех ЛеЗЗ. Если для некоторого Л будет иметь
место неравенство
Мрхл(^)<^(Л),
то
Мр - МРХл ®) + Мрз^, (Й) < \4 М) + иЗ(Я?-Л)=1,
что противоречит предположению Мр == 1. Значит,
М|>хл(!>) = ^(Л) для всех Ле» или р = ^.(^). Осо-
бый интерес представляет тот случай, когда
вероятностное пространство совпадает с {35, 93, \х) и случайные
величины задаются как измеримые отображения 36 в 35.
Из теоремы 3 вытекает
Следствие 1. Пусть: 1) заданы две
последовательности измеримых отображений Тп(х) и Т~п(х) 35 в 86,
а меры у}п определены равенствами \х(п{А) = \х (Т1п~1 (Л)),
где Тсп~1 (А) ~-полный прообраз А при отображении Т1п,
2) 2^ (*)-* Т'о (*) по<ш' для всех а: /го лере ц, 3) М-я —!*«
и существуют почти для всех х по- мере ц
неотрицательные пределы
Тогда
иА
~^02
Нт
П->оо
Нт
и
(П(*))-
=р,<
■(Г»<*))=
■(1
А
(х)) =
= р, (*).
= р2 (*).
(Ц С*))
р2(х).
Действительно, здесь выполнены условия теоремы 3
и замечания 1, если в качестве алгебры 230 взять
множества непрерывности для меры ^ + |х§ (меры \1*п слабо
сходятся к мере ^).
Следствие 2. Пусть выполнены условия I) и 2)
следствия 1 и, кроме того, 3) Цо^^о^^ 4) |^ <С ц,
$ I] ОБЩИЕ ТЕОРЕМЫ ОБ- АБСОЛЮТНОЙ НЕПРЕРЫВНОСТИ §2^
[х <С II1 и существуют отличные от нуля пределы по
мере ц
Ит
(х) = р1 (х), Пт —у- (7^ (*)) = р2 (х),
5) почти для всех х по мере р, выполняется равенство
Р,(^(*))р2 (*)=!.
Тогда \х~у и рЛх)^^(х)9 р2(х) = ^(Т10(х)).
Действительно, то, что ^^~V, вытекает из теоремы 3
и замечания 1. Далее, как было установлено в
замечании 2,
Значит,
рЛхХт&Ы» р2(х)<^-(П(х)).
1 = р, (Г« (*)) р2 (х) < -Ц- (Г« (*)) % (Ц (х)) = 1,
откуда вытекает, что 92(х) ^ ~т^ (^о (х)} почти всюду по
мере [I и рЛ(Т10 М) ^ ~^~-(Ц (х)) почти всюду по мере \х.
Но тогда р1 (^)==-—(х) почти всюду по мере V, а так
как V~р,, то почти всюду по мере р. Наше
утверждение доказано.
Рассмотрим абсолютную непрерывность мер при
отображении пространств. Пусть (й^, 3^) и {Шъ 232) — два
измеримых пространства. Отображение ф ЗВХ в $?2 будем
называть измеримым, если ф*"1(Л)^й1 для всех Ле332.
Предположим, что на 3^ заданы две меры р,ь V!, а меры
[А2, V* определены на 232 равенствами: р.2(Л)~ \х} (ф-1 (А)),
Теорема 4. Ясла V! <С щ, то и у2 "С Р>2> причем
&*-«>-"(&
8.
где Й, — о-алгебра множеств вида ф"""1 (А), А е 232, а
условное математическое ожидание берется в вероятностном
пространстве {<%и 23,, 1^).
Доказательство. Всякая 332-измеримая
функция 1{х) представима в виде §{<$(х)), где ^ ^-измерима.
628
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Поэтому
] / (х) V2 (ах) = ] § (ф (х)) V2 (ах) = ] е (*) V1 (ах) =
\ёМ^Ы»Лах)=$ёМм(^(х)
%\)\1Лах).
Пусть М (-г^- (х) ®1) = р (х). Так как р(лг) ^-измерима,
то р(ф(#)) 232~измеРима- Значит,
/ в (*)Р(*)И1 (<**)= |#(ф(*))Р(ф(*))М^) =
= //(*)р(ф(*))М<**)-
Из этого соотношения и вытекает доказательство теоремы.
§ 2. Допустимые сдвиги мер в гильбертовом
пространстве
При изучении абсолютной непрерывности мер при
различных преобразованиях важную роль играют, как
мы увидим в следующем параграфе, абсолютная
непрерывность и плотность меры при простейших
преобразованиях меры— преобразованиях переноса. Пусть
р,--некоторая мера на ($?, 8), где 36 — гильбертово
пространство, а 23 — а-алгебра борелевских множеств на этом
пространстве. Введем оператор переноса: 8ах = х + а.
Через \ха обозначим меру, определенную соотношением
\*>а(А) = р,(5_аЛ). Заметим, что если \х является
распределением случайного элемента | со значениями из $?, то
1ха — распределение случайного элемента 1 + а. Мера \ха
однозначно определяется соотношением
| / (х) \ха (ах) = | / (х + а) \х (ах),
справедливым для всех измеримых функций, для
которых интеграл справа существует.
Будем говорить, что а является допустимым сдвигом
меры \х, если \ха «С \х. Множество допустимых сдвигов
меры будем обозначать через М^ или просто М, если
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
529
ясно о какой мере идет речь. Если а е Ми, то положим
р(я> *) = Рц(я> *Н-^г(*)-
В этом параграфе изучаются структура
множества М^ и свойства плотности р^(а, х). Всюду в
дальнейшем рассматриваются вероятностные меры на 86.
Теорема 1. Множество М^ является полугруппой
по сложению, т.е. а + Ь е М^, если а е= Мй и Ь & М^\
при этом
р(а + 6, #) = р(а, х)р(6, х — а).
Доказательство. . Имеем
/ / (х) [ха+ь {&х) = | / (х + а + Ь) \х [их) =»
= //(* + а) р (6, аг) м- (<**) == | / (х) р (6, х - а) \ха [их) =
— [/Мр(й,^-а)р (а, я) М» №х).
Из этих равенств и вытекает доказательство теоремы,
так как они справедливы для всякой ограниченной
измеримой функции /(*).
Следующая теорема показывает, что допустимых'
сдвигов не так уж и много. В частности,, из нее
вытекает, что М^ является множеством первой категории
в любом бесконечномерном подпространстве 86.
Теорема 2. Пусть ф(г) — характеристический
функционал меры \х и вполне непрерывный неотрицательный
симметричный оператор В таковы, что <р (г) -> 1 при
(Вг, г) -> 0. Тогда для всякого а е М^ существует такое
Ъ^86, что а = ВЧ, т. е. М^аВШ.
Доказательство. Пусть а <= М^ и р (а, х) =*
= -т^"(х). Тогда характеристический функционал меры \ха
можно представить так:
Фа (г) = | е1 <*• 2) \ха [их) = | е< (*+а> г) м- (Лс) = е1 {а' г) Ф (г).
Кроме того,
Фа (г) = | в'<*• *> р (а, х) \1 (ах).
530
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР {ГЛ. VII
Значит,
Фа(*)-1« /(^(г-я)-1)р(а^)|1(^).
Покажем, что Фа(г)->1 при (Вг, г)~>0. Так как для
всякого характеристического функционала \|?(г)
справедливо неравенство
|1-*(г)Р<2Ке(1-♦(*)),
то достаточно показать, что
Не | (1 - в1 <*. *>)р (а, х)\1(ах)-+0
при' (Вг, г)~>0. Положим р^(х) = р(а, х) при р{а, х)^ хУ,
р/У(х)==0 при р(а, х)>Ы. Тогда
Ке | (1 -е' <*• х))р(а, х)р(йх)= [(1-со5(г, х))рм{х)\л{(1х) +
+ | (1 - соз (г, *)) [р (а, л:) - рм {х)\ \х (их) <
< Л^ Ке (1 - ф (г)) + 2 [ [р (а, х) - р.у (*)] ^ {Ах).
Второе слагаемое можно сделать сколь угодно малым
при всех г выбором достаточно большого Л/*, а первое
стремится к нулю при (Вг, г)->0, каково бы ни было N.
Итак, мы доказали, что ф (г) е1 (а> г) ~> 1 при (Вг, г)->0.
Значит, ^<а»г>->1 при (Вг, г)~>0, поэтому (а, г)->0 при
(Вг, г)->0. Пусть \(а, г)|<е, если только (Вг, г)<6.
Тогда для всех г выполняется неравенство
\(а,г)?<$-{Вг,г).
Заметим, что а принадлежит замыканию области
значений оператора В, так как для всех у, для которых
В у = 0, будет и (а, у) = 0. Пусть Кк — собственные
значения, ек — соответствующие им собственные векторы
оператора В. Полагая С = -~-, г = 2^ \ ек будем
иметь
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
531
2(а> еЛ2
к < С. Переходя к пределу при /г->оо,
со
убеждаемся в существовании вектора Ь = ^ -,/- ек>
который и будет удовлетворять соотношению В^Ь = а.
Теорема доказана.
Исследуем преобразования множества М^ и функции
р(а, х) при простейших преобразованиях меры \х.
Теорема 3. 1). Если V = \хс, то, каково бы ни было
Рч(а, х) = р11(а, х-с).
2) Если V <С [л, /(х) = ~-т— (х) и ае М^ то йе Л^
тогда и только тогда, когда выражение
Рг (а, *) = /(/(7)Д) Р^<а> *) (О
определено почти всюду по мере \х9 т. е. если
IX ({*: /(*) = 0} - {*: / (.V - а) р^ (а, х) = 0}) = 0
(лш считаем -тг=0). Яри зтсш ру(а, л) определяется
формулой (I).
3) /?*ш/ V(Л) = Н'(^""1^1)» г<3е Ь —обратимый линейный
оператор, то
М^ = АА^, рV (а, *) = р^ (Ь~1а, Ь~1х).
Доказательство. 1) вытекает из равенства
/ 8 (х) ^а (<*х) = / 8 (х + « + с) М- (***) =
= / 8 (х + с) Рц (а> *) М- (<**) = \ 8 М 9ц (а, х ~ с) \хс {их) =
= / й" М Рц (я> * -- с) V (</*)-
2) Пусть #-(#) — ограниченная измеримая функция.
Тогда, если //и Рц(а> *) почти всюду определено по
532 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
мере [х, то
\ В(х)\а(йх) = ^ §{х + а)у{с1х)^ | §(х + а)!(х)\х(с1х) -
= / 8(х)1(х-а)\1а(ах)= ]* в(х)Рц{а, х)1(х-а)[1(ах) =
= / § (х) ! (*^х)а) Р^ (а, х) V {ах):
Если жеае Му, то для всякой ограниченной измеримой
функции §{х) имеет место соотношение
| § (х) р„ {а, х)! {х) \1 {их) = ] §{х) рм (а, х)1(х-а)\1 {их).
Отсюда вытекает, что р^а, х)}{х) = р^(а, л:)/(л: — а)
почти всюду по мере ^. Наше утверждение доказано.
3) Имеем для ограниченной измеримой функции §{х)
и для а = 16, где 4еА1и,
/ 4У (а:) V,, (йа:) = | ^ (х + а) V (</*) - ] § {1х + а) ц (</*) =
= | Я (^ (* + &)) |х (их) = | # (1х) р^ (6, х) р (<**) =
= /г(*)рц(6' ^~~xx)V{(^x).
Отсюда вытекает, что Л^гэ ЬМ^ и р^а, я^р^б, 1~1л:)
при а^ЬМц. Используя обратимость оператора Ь,
находим, что Л^с: ЬМ^. Значит, М^ = ЬМ^. Теорема
доказана.
Замечания. 1) Из 1) вытекает, что если V —
распределение величины | + г), где | и г) — ^зависимые
случайные величины со значениями в #/, а ^ —
распределение величины |, то Л^гэМ^ и при а е Мц имеет
место равенство
ру(а, *) = М (рд (а, |)/| + т|)б+т,-х.
Последнее равенство вытекает из соотношения
| # (*) V,, (их) =| § (х + а) V (их) =
= // Я (* + У) Рц («• X) \1 {(IX) Р {Т| €= </*/} -
« М$ (| + т|) Р^ (а, |) = М# (| + п) М (р (а, &)/& + г|)-ц
§2]
ДОПУСТИМЫЕ СДВИГИ ^МЕР
533
2) Если в условиях 3) Ь — необратимый оператор,
то Му гэ ЬМ^ и
р„ {а, х) = М (р^ (6, ЪУЬ&ъ-х,
где Ь — любой вектор, удовлетворяющий соотношению
16 = а. Эта формула вытекает из теоремы 4 § 1.
Пусть | а | = 1. Изучим условия, при которых Ха е Л1й
для всех Я > 0. Пусть Р(/) = р, ({*: (а, х) < /}); /? (*) является
функцией распределения случайной величины (а, д;) на
вероятностном пространстве (36, 23, р,). Для всех А>0
функция распределения Р(1 — Х) величины (а, х) + А=
= (а, х + Ха) на том же вероятностном пространстве
абсолютно непрерывна относительно распределения (а, х).
Какой вывод в этих условиях можно сделать о
функции Р(1), показывает следующая лемма.
Лемма. Если мера Vx(Е), определенная на борелев-
ских множествах прямой &1 соотношением
Ъ{Е)= \йР{1-к),
Е
абсолютно непрерывна относительно меры V.)(^:) для
всех А>0, го Р(1) абсолютно непрерывна и ее произ-
йР
водная р (/) = — (/) такова, что для некоторого -1Х
{возможно, равного — оо) р (I) = 0 почти для всех К1Х и
р{1) > О почти для всех ^>^^.
Доказательство. Представим Р{1) в виде Р({) =
= Р{ {1) + Р2(1), гДе Р\ (0 абсолютно непрерывная,а Ро^) —
сингулярная составляющая Р. Пусть
Е
Поскольку у'1 <С V(^ + V*, V^ ± ^, то V^ <С Гд. Поэтому мера
оо
о
534
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
будет абсолютно непрерывна относительно меры V*,
С другой стороны,
оо
*(Е)= \ | с1Е((-к)е-хак~ || аР2{и)еи-Ш^те$Е,
О /ей ы~-/<0
где тез Е — мера Лебега множества Е. Поскольку V
сингулярна относительно меры Лебега, то V = 0 и,
значит, ^ (0 = 0.
оо
Пусть теперь Р{1)=\ Р {( - к) е^ йк и V (Е) = | ЛР (0-
0 Е
оо
Легко видеть, что -р-(<) = —-г- р(* — к)е~К<1к, причем
о
числитель этой дроби должен обращаться почти для
всех I в нуль на множестве тех 5, для которых р($) = 0.
Если множество {/: р(/) = 0} имеет положительную
лебегову меру, то можно указать такое 5, что лебегова
мера множества {1\ р(1) — Ъ}{\{8 — &> 8} положительна
при всех 6 > 0. Тогда функция
оо
| рЦ-к)е~Чк
о
обращается в нуль при некоторых ^е ($ — б, 5) каково бы
ни было 6 > 0, а так как эта функция непрерывна, то
оо
\ р(з — к)е~Кс1к = 0 и, значит, /?(2) = 0 почти для всех
о
/ < 5. Если р{1) не равно нулю тождественно, то
найдется максимальное 5, обладающее указанным
свойством. Тогда р(/) = 0 почти для всех К 8 и р(0>0
почти для всех 1>8. Лемма доказана.
Пусть 1\ обозначает гиперплоскость {а, ас) = /.
Определим меры р/ на борелевских множествах Г, с
помощью равенств
^(А) = 11<(А()Г,), ,1 (Л)- / »'(А)ёР(/).
Таким образом, р* (А) является условным
распределением х при условии (а, *)==/ на вероятностном прост-
$2} ДОПУСТИМЫЕ СДВИГИ МЕР 535
ранстве (<8?, 93, \х). Введем, условные распределения
проекции х на Г0 при условии (а, *) = /: V* {А) — {х'(5,аЛ).
Наконец, пусть V — безусловное распределение
проекции х на Г0:
Введем меры а* с помощью равенства
ц*(Л)=]\(5_,йИЛГ,])р(/)Л. (2)
Заметим, что [х* является распределением случайной
величины I, у которой величины (а, |) и проекция | на Г0
независимы, а их распределения совпадают с распреде-
ленияхми величины (а, х) и проекции х на Г0 на
вероятностном пространстве {дБ, 23, \х). Покажем, что мера ц
абсолютно непрерывна относительно ц*. Заметим, что
их. (А) « |х (5-Яв Л) = / V' (5-,« [5_ХлЛ П Г,] р (О Л -
= /^(5-(/+х)аИПГт])р(0Л-
==/^-М5-в,ИПГ|])р«-Л)Л. (3)
Следовательно, для любой ограниченной интегрируемой
функции к (А) справедливо представление
Из определения меры ц* вытекает равенство
Если ^*(Л) = 0, то ^(З-^^ПГ^^О почти для всех
по мере Лебега ^>^{ и 8>1Х (где /1 такое, как указано
в лемме). Не ограничивая общности, можно считать,
что ^(Л) = 0 при /<*!. Кроме того, естественно
рассматривать лишь множества Л, принадлежащие при
некотором 6>0 множеству {х: (а, д:)>/1 + б}, так как
цф ({х: (а, х) < /,}) « *х({х: (а, *) < /,}) = 0.
536 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР {ГЛ. VII
При указанных предположениях условие |а*(Л) = 0
влечет равенство
о о
/ иЛа (А) ах = | ах [ Р а - я) у<-Н8^а И п г,]) м = о,
а, значит, [хКа(А) = 0 почти для всех Х^[ — б, 0]. Наше
утверждение доказано, так как \х <С \х>а и, значит,
нИНО.
Заметим, что \ь*ка <С р* для всех А,>0. Действительно,
в силу определения
Р1а(А) = | Р С " *) V (5_<в [Д П Г,]) Л =
= р!^*(5_,ллпг,])/>(0<«.
Значит,
<^1а/ __ Р ((а, а:) - Я)
^1* ^)_" р((а, *)) #
Поэтому, используя теорему 3, 2) убеждаемся, что
справедлива
Теорема 4. Для того чтобы Ха е М^ для всех X > 0,
необходимо и достаточно, чтобы выполнялись условия:
1) функция Р (1) = \1({х: (а, х)-<1}) абсолютно
непрерывна, а для ее производной р(0 существует 1{
(возможно, равное — оо) такое, что /?(/) = 0 почти для всех
К1Х и р(/)>0 почти для всех 1>1Х.
2) мера \х абсолютно непрерывна относительно
меры р,*, определяемой равенством
[1*({х: а<(а, х)<®(){х: Рхе=А}) =
= \х{{х: а<(а, *)<р})|х{{*: Рхе=А}),
где Р — оператор проектирования на подпространство Г0,
и ее плотность р(я') = ~^т{х) такова, что выражение
о (X а х)= рИ0'*)-1) о(х-и) и)
Рц1Л,а, х) рца,х)) р (х) ™
определено почти всюду по мере \х*, если считать его
равным нулю всегда, когда числитель дроби равен нулю.
§2[
ДОПУСТИМЫЕ СДВИГИ МЕР
537
Замечание. Если Ха е М^ при всех
вещественных А,, то р (/) > 0 почти для всех / и меры \х и ^*
эквивалентны. Действительно, \х* будет эквивалентна
мере Г к(Х)\хКас1к, если к (А)— положительная
интегрируемая функция, а мера I к(1)\хыс1к абсолютно
непрерывна относительно \х.
Следствие. Если а1э ..., ап (| а А| = 1) — взаимно
ортогональные; векторы такие, что %ак е М^ (Зля всея
вещественных А, и к= 1, ..., п, то: 1) функции Рк{1) =
= ^ ({х: (аь л:)</)} абсолютно непрерывны и их
производные рк (/) = -77- /^ (0 почти для всех I положительны-,
2) «мера ц эквивалентна мере Д, определяемой
соотношением
6=1
л:.* ал<(аъ *)<Р*}
П{*: Р,шС} =
= |х ({*: />лх е= С}) Ц \х ({х: ак < (ал, *) <рА}),
где ак, р&, &=1,..., п — произвольные вещественные
числа, Рп — оператор проектирования на подпространство
ЗБп = {х: {ху ак) = 0, 6 = 1, ..., п}, а С — произвольное
борелевское множество из этого подпространства.
Доказательство этого утверждения вытекает из того,
что всякий допустимый сдвиг меры \х\ построенной
в доказательстве теоремы 4, ортогональный а, будет
допустимым сдвигом меры V, определенной в том же
доказательстве. Заметим, что мера Д, определенная
выше, является распределением величины
п
6=1
где т),, ..., ^ — независимые случайные величины со
значениями из Я1 и плотностями рЛ(/), а %п — не
зависящая от них величина со значениями в <%п и
распределенная, как проекция х на ЗВп на вероятностном
пространстве (8ву 23, у).
Предположим, что можно указать такую ортонор-
мированную последовательность векторов ак, что М
538 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
содержит линейную оболочку этих векторов. Можно ли
по аналогии с только что сформулированным следствием
утверждать, что тогда мера \х будет эквивалентна мере,
являющейся распределением случайной величины
с»
Б=2л*д*. (5)
где цк — последовательность независимых числовых
случайных величин, имеющих положительные плотности?
Чтобы ответить на этот вопрос, рассмотрим допустимые
сдвиги меры Д. Обозначим множество мер, являющихся
распределением величины | вида (5) через П°°.
Теорема 5. Если цк — независимые случайные
величины с положительными плотностями рк{1) и
\\,—распределение величины с-, определяемой равенством (5), то
Дя <С Д тогда и только тогда, когда с вероятностью 1
сходится ряд
оо *
2 Под рк (г)к - ак) - 1ог Рк (%)]> (6)
где ак = (а, ак). Если этот ряд расходится, то \ха 1. Д.
Доказательство. Пусть Дл и \лпа обозначают
проекцию мер Д~и Да на подпространство 36п, натянутое
на ах, ..., ап. Тогда
аК г л ТТ Рк((х'ак)~ак)
^*>-п
Если Д.а не ортогонально Д, то почти всюду по мере Д
существует предел
Нт Д
П->оо
Рк((х>ак)~ак)
Рк((х'ак))
и этот предел не равен тождественно нулю. Значит,
ряд (6) из независимых случайных величин
(последовательность {х, ак) распределена на вероятностном
пространстве (36, %, |а) так же, как последовательность \\к)
сходится с положительной вероятностью, поэтому он
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
539
сходится с вероятностью 1. Значит, если ра <С Д, ряд (6)
сходится и поэтому
^ (г) - ехо I У 1ое "* «*'"*> ~ а*> 1
„. (л)-ехр|ДЮв м(х,вл)) )
всюду положительно, так что ДЛ ~ Д. Обратно, из
сходимости ряда (6) вытекает существование отличного от
нуля предела
Ьт -ахп(х),
поэтому в силу следствия 1 из теоремы 1 § 1 Д <С Да
и, значит, по доказанному Д ~ Дй. Теорема доказана.
Следствие, Если р ~ Д, где Де П°°, го ра // р
либо эквивалентны либо ортогональны.
Таким образом, построив меру р, для которой
7мк^М1Х при всех Я, но существует такое а, что р и ря
не эквивалентны и не ортогональны, мы построим меру,
для которой не существует эквивалентной меры Д из П°°.
Далее в этом параграфе будет построен пример такой
меры.
Допустимые сдвиги взвешенных мер. Рассмотрим
сначала допустимые сдвиги линейных комбинаций мер.
Если р ~ {I1 -|- р~, то естественно рассматривать лишь
случай, когда р1 и р2 ортогональны, так как при
условии р- «р1 меры р и р1 эквивалентны и, значит, их
допустимые сдвиги совпадают, если же р2 имеет
абсолютно непрерывную относительно р1 компоненту, то ее
можно присоединить к р1 и свести рассмотрение к
случаю сингулярных мер. Далее будем предполагать, что
р'а ± р2 при всех а. Заметим, что без этого
предположения связь между допустимыми сдвигами мер р,1 и р2
установить вряд ли возможно. На это указывает при-
мер мер
»* (А) - / /А (х) р №, А = 1, 2, /, (х) + !2(х)=1,
ШШ = 0,
из которого следует, что р1 и р2 могут вообще не иметь
допустимых сдвигов, в то время как р может их иметь.
540 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Если выполнено это предположение, то тогда М^ =»
= М^ П Му?. Действительно, из соотношений \хха <С \хх и
^<[х2 вытекает, что \ха = \хха + \$а < ц-1 + \х2 = \\.
Наоборот, пусть Вв = Ех\)Е.2\\ \х1 (Я2) = 0, \х\(Е2) = 0, ^(Е{) = 0,
11^(2^) = 0 для некоторого а. Тогда, если аеМ^, то из
условия \х1(Л) = 0 вытекает, что [л (Л П -^1) = 0 и, значит,
6 = ^1а(ЛП51) = ^(^Г1^1)- Таким образом, ц^<^- Точно
так же и/; <С [х2. Значит, А1„ = А1, П ЛГ,. Посмотрим
теперь, как р^(а, .г) выражается через р*(#» *)==—^-(л-)
, 9
и р2(а, х)==-~г(х). Если множества Я! и Е2 такие, как
указывалось выше, то
- | р>(а, .XV (<**)+ ]" Р2(«, *)и2 (<**) =
= ] |р'(а. -V) хя, (-V) + р2 (а, л-)-/Е2(л-)]ц№),
л
гДе Хяй ~ индикатор множества Ек. Таким образом,
о
рм(я, *) = 2 рЧ#, *)&?,(*)•
Полученный результат легко обобщается на случай
счетного числа мер.
Теорема 6. Пусть [х1, \х29 ...—последовательность
попарно ортогональных мер, для которых \х1_1_ \хча при
1фк< каково бы ни было а^ёб. Если ц = 2рлИ-Л» где
Р/г>0 и 2рй=1, то АГ, = П ЛТ,,« /г можно указать по-
/г й = 1
парно непересекающиеся множества ЕкУ для которых
Ри (я> л0 = 2 р* (а, -V) х^ (*)» (7)
6=1
где р*(а, л;) = -^(*).
§2]
допустимые сдвиги мер
54 1
Доказательство. Включение Л1^ :э [^ Л/ % вы-
текает из того, что 21 рк\хиа <С У± рк\1к, если ^ < \1к для
всех 6. С другой стороны, из того, что для двух
сингулярных мер \хк и 2 р(\х1 выполняется условие
1Фк
йл-'- 2 №'> вытекает, что сдвиг допустим для их
1фк
суммы, если он допустим для каждого слагаемого.
Значит, М^аМ^ъ и А/м = ^| М}1ь Пусть множество <51
таково, что \х1{%^\, ^(^)=1, 2 /у1*(#,) = 0. Суще-
ствованис такого множества вытекает из- сингулярности
1*'+Х « 2 рк[1к.
кф1
Положим теперь /Г/ = ^/ \ (^/^. Очевидно, р/с(#/) = б^
кФ1
и Я/ попарно не пересекаются. Далее
Л к
= ^Рк ( Р*(Я, А-)|АЛ(^Л-) =
к АГ\Ек
- 2 / 9к (а, х) 2] /V (их) = Л ] 5СяЛ (*) Р* («, а;) (I (их).
к А(]Ек I к А
Отсюда вытекает формула (7). Теорема доказана.
Рассмотрим теперь сдвиги мер, представимых не
суммами, а интегралами от семейства мер, зависящего
от непрерывно меняющегося параметра. Пусть в
—некоторое полное метрическое пространство, 5 —сг-алгебра
его борелевских подмножеств. Будем рассматривать
семейство мер р,9 па {36, 23), 0е0, удовлетворяющее
условию: для всякой непрерывной ограниченной
функции } (х), определенной на $?, функция | /(х)[х®{их)
непрерывна по 0, Отсюда следует, что \1в{А) для всех
Ле23 является ©-измеримой функцией 0. Пусть а (г/6) —
542 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
некоторая (также вероятностная) мера на ©. Рассмотрим
меру
ц(Л)= | |хЧ4)<г(<*6), Ле=*. (8)
Теорема 7. Пусть Л1° — множество допустимых
сдвигов меры уР; тогда Мц:эр)Л1е. ^с.?^, кроме того,
е
жерь* це взаимно ортогональны и существует ^-измеримая
функция В(х) со значениями в 6, для которой
\ьЧ{х: в (дг) = в}) = 1,
то можно построить функцию ре(а, х), а^{}М®,
измеримую по 9, х относительно @ X 33 м такую, что
ре(а, лг)=»—^-(х) (той |ые) /?/?// всгл' 9е0, с/
Р>1(«, *) = р«">(а, х). (9)
Доказательство. Если а е Р) Л/е, то \х®а <С ^в
е
для всех 9, Пусть |л(Л)=*0, тогда |ле (Л) = 0 почти для
всех 9 по мере а. Но тогда \хва(А)^0 почти для всех 9
по мере а. Значит, \1а(А) = 0 и м-а <С ^.
Пусть ^—возрастающая последовательность
конечномерных подпространств 30, \х*а{п, •) и \^(п, •) —
проекции мер \$а и |ле на эти подпространства,
с1[1ва(п, •)
а р!?(а, л-) = —дт гО1")- Заметим, что функции
[ е-П*-*!^^ их),
| р»(а, х)е~'"*~*"|л9(я, Ле) = | <»-/|*+а-и |л°(/г, с?х)
непрерывны по совокупности 9 и х, поэтому такой будет
и функция
= [| е-'и-Ицв^ их)] ' [ р®(о, х)е-/,*-<',|*вК <**)•
Последняя функция при /—>оо сходится почти всюду
по мере |Ае(/г, их) к р^(а, г/). Следовательно, функция
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
543
р0(а, л')==Пт^(0, х) там, где этот предел существует,
измерима относительно @Х23 и при каждом 9
совпадает с р^(#, х) почти всюду по мере \$(п, •). Положим
р^(а, х)= Нт р®г(а> х) там, где этот предал существует,
это и будет искомая функция. Для вывода формулы (9)
запишем, используя то, что ре<*>(я, х) = ре(а, х) почти
для всех х по мере [Xе,
/ / (х) \1а {их) = | / (* + а) \к (ах) «
- \1{х + а) \\1*(йх)оШ)^
- / [/ /Мр0и)(с, *)|хв(Лг)] а (г/9) « | /(*)рв"Чя, хЫ*х).
Теорема доказана.
Замечание. Легко написать выражение для рм (а, х)
при условии, что все ^е абсолютно непрерывны
относительно некоторой меры V и функция
измерима по совокупности переменных 9, л*. Тогда
] / (х) ца {их) = \ / (л- + а) [I (ах) = / ] / (х + а) и.9 (их) а №) =»
= / / / (х) ре (а, х) § (в, х) у (4х) а (йЪ) =
г Грв(а,х-)§(е, х)о№)
ё (в', х) а (йв')
ц (</*),
поскольку для всякой ограниченной измеримой функ
ци и ф(л-)
| Ф (ж) и. (их) = / / Ф(х) § (в', л-) V (ах) а И').
Таким образом, при нашем предположении
[ рй (а, х) § (в, *) а (ЛЬ)
Рм(«. *) = - ;■ ———.
^ § (9, х) о (<Ю)
544 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР |ГЖ VII
Указанный результат можно обобщить следующим
образом.
Пусть семейство мер [ха' е зависит от двух
параметров, меняющихся соответственно в сепарабельных
полных метрических пространствах э$> и 0, причем
существует семейство мер |ие, для которого выполняются
условия теоремы 7 и ^- 9 < [х° при всех ае^.
Предположим, что для всякой непрерывной ограниченной
функции 1(х) выражение Г /(х)[га« °{с1х) непрерывно
по а и 0. Обозначим через 91 и © сг-алгебры борелев-
ских множеств в^ив соответственно. Пусть сг(йа, йб) —
некоторая вероятностная мера на 91 X © и мера ц на Э
определяется соотношением
ц(Я) = |^0(Е)а(Ах, М).
Тогда Л1рПм > г*е м*
— множество допустимых
а, О
сдвигов меры [ла' и для аЕ^М0, существуют функ-
а, О
ции ра' е(а, х) и й"(а, 8, х), измеримые по а, 8
относительно 91 X © X 93, для котарых
Р«>Ча, х) = -^(х) (той 11«>%
йхх^ е
& (а, 8, х) = -5-0- (х) (то«Л р,е),
«[А
а рц(а, х) выражается через эти функции по формуле
Г ра' 0и) (а, .V) # (а, 8 (.V), *) а (<*а I 9 (х))
?*(*.*)- ——; , (Ю)
1 8 (а, 9 (*), х) о (йа | 0 (*))
где а (Лх| 8)— условная мера, определяемая
соотношением
|<ф(а, 8)а(йа|8)а(^, с?8)=|ф(а, в).сг(Лх, <*8),
справедливым для всякой измеримой по совокупности
переменных айв функции г|>(а, 8), а в (х) — измеримая
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
545
функция, для которой [лд({х: 9(х) = 9}). Формула (10)
вытекает из следующей цепочки равенств:
]*/(* +а)|а(Л0= \^ 1(х + а)\1^ *{йх)аШ, ад) =
/(*)ра-в(а, х)в(а, 9, х)\хЦах)о(аа\ 9)а(Л, */9) =
-/я.
-Я/
I
/(х)р*-в<*>(а, *)«(<*, 9(Л"), *) X
X О (йа | 9 (х)) р,0 (Лс) а (Л, дЮ) =
Г ра' в(х) (а, л:) ^ (а, 9 (*), л:) о (йа | 6 (х) )
/ (*) -^ ? = \х (с1х)9
] # (а, Э (л:), л:) а Ш | 6 (л:))
а существование функций ра> 9(а, х) и §-(а, 9, х)
доказывается точно так, как существование функции р9(а, х)
в теореме 7.
Как вытекает из формулы (9), функция р^(а, а:) для
меры, выражаемой формулой (8), не зависит от меры сг.
Если [г, и |1Х2 — меры, определяемые соотношением
рк(А)= $ »«(А)о„т
и 0] и Со эквивалентны, то и III! ~ [х2, причем
где 9 (х) —такая функция, что \х®({х: в(х) = 9}) = 1.
Поскольку рЦ](а, *) и р^(а, х) совпадают, то -~ (х — а) =
= ^—(х), что выполняется, если для всех абМй| и
почти всех х выполнено равенство в(х — а) = В{х).
Оказывается, описанная ситуация является до некоторой
степени общей. Предположим, что меры \х и V
эквивалентны и для некоторого а, АйеМ^ при всех
вещественных Я, а рм,(а, *) = р^я, #). Положим <р(х) = -^ (х).
Пусть ^ = {х: ф (*) = /}, а—мера на прямой, для
которой
<7((-оо, /)) = Ц/ЦЯЛ,
I'•< 11 И Гихмлн. А. В. Скороход
546 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
а семейство мер ц' определяется из соотношения
л
справедливого для всех Л<=53 и борелевских множеств Л
на прямой (т. е. \ь* является условным распределением х
на вероятностном пространстве ($?, 93, \х) при условия
<р(л*) = 0- Покажем, что а будет допустимым сдвигом
мер \х* почти для всех I по мере а. Из теоремы 4
вытекает, что меру ц можно представить в следующем
виде:
ц(А>- \\ Т(х98)р(4х)аР(8)9
где ({х, 8) = ~~^г(х + за), Д — мера на подпространстве
<%о = {х: (#, х) = 0}, определяемая соотношением ц(Л) =
= ^(Р"1^), Р — оператор проектирования на <^0, а Р {$) =
= **({*: (а, *)<$}). Аналогично представлению (11) имеем
Д(Л)~/й'(Д)а(Л)
(из того, что ф(Рх) = ф(л:) почти для всех,* по мере \х,
вытекает равенство
А(11^)-=^(^:ф(л:)<0) = ^(^:ф^)<0)==ог((--оо,/)).
Пусть 7(^, *, 5) —измеримая функция, для которой
]{1, х} $) = /(*, 5) при (р(х) = /. Тогда
|х(Л)= Ц* / (/, х, 5) р' {их) а (Л) йР (5) =
| /(*, л:, 5)Д'(^)^(5)"|оЙ).
х+5а^Л ^
Полагая
х + за&А
находим
,х(Л)= ]У'(Л)а(Л).
-а
15]
ДОПУСТИМЫЕ СДВИГИ МНР
547
Значит, для всякого измеримого множества на прямой Л
и непрерывной функции д(х) выполняется равенство
11 § (х) |г' {их) а (М) - 11 е (х) / (их) о (сИ),
Л Л
т. е. | $(х)\х* {йх)>= I §{х)\С {их) для почти всех I по
мере с Но из представления \\*' вытекает, что а является
допустимым сдвигом для этой меры. Заметим,
наконец, что
у(А)= | ч>(х)\1((1х)=*
А
- \ / %а (х) Ф {х) \хг (ах) а Ш) - |* и' {Л) а, Ы1),
где -~ (/) = /. Таким образом, доказана
Теорема 8, Если \х и V — две эквивалентные меры,
для которых М^ = Л1у, причем эти множества — линейные
многообразия, и р^(а, х)=*рх>(а, х), то существует одно-
параметрическое семейство мер \х\ для которых аеМ ;, и
измеримая функция ф(х), для которой \1( ({х: ф(л*) = /})== 1,
а также эквивалентные меры на прямой а и а1 такие, что
ц (А) = [ р* (А) а {Ш), у (А) - | \11 (А) а{ Ш).
При этом функция Ц)(х) для всех а^М^ и почти всех х
по мере \х удовлетворяет равенству ф(л* — а) = ф(л).
Одно достаточное условие допустимости сдвига.
Рассмотрим меру \х на ($?, 5Р). Пусть {еп, я = 1, . . .} —
ортонормированный базис в Ж, ^ — подпространство,
натянутое, на еь ..., еп, Рп~~ оператор проектирования
на это подпространство, \1п — проекция меры \х на Шп.
Будем предполагать, что \хп абсолютно непрерывна
относительно меры Лебега на 8&ю а ее плотность 1п(х)
относительно этой меры положительна. Тогда
^йл /» (х — а Л
^^-Ц^г1' а»-р«а' * = **•
В силу теоремы 1 § 1 почти всюду по мере ц
существует предел
1- !п (Рп (х — а)) , х
Я-»оо 1П\Гпх)
38*
648
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Если йе^, то § (Ху а) = р^ (а, х)у а для того чтобэд
а^Му, необходимо и достаточно, чтобы Г§(х, а)\л((1х) = 1
(см. следствие 2 теоремы 1 § 1). Проверка этого
условия весьма затруднительна. Ниже будут приведены
условия, при которых 1а е М^ Для всех вещественных (к
основанные на замечании к теореме 2 § Д.
Предположим, что плотность !п(х) непрерывно
дифференцируема по х и обозначим через У1п{х)
градиент }п(х), т. е. такой вектор из 36 т для которого
— \п (х + /а) |,_0 = (У/„ (л:), а) для всех ае^. Положим
для всех х е 36 и а ^36
К (*> а) = !п {РпХ) (У?п {Рп*)> Рп&\
Покажем, что функции Нп(ху а) при фиксированном а
образуют по п мартингал на вероятностном
пространстве (36, 33, \х). Обозначим через 93я а—алгебру
цилиндрических множеств с основаниями в 36 п. Пусть ак =
= (я, ек), 1к = (х, ек), 1п{х):=Рп{*и • •-, '«). Тогда
п
Лс = 1 -
Если ф (я)— ^„-измеримая функция, то ф(л:)=Ф(/1,..., <„).
Предположим сначала, что Ф(^, ..., 1п) непрерывно
дифференцируема и отлична от нуля лишь в некоторой
ограниченной области. Тогда
Шп+1(х, а)у{х)=*
и + 1
ХФ(*„ .... ^)Рп + Л^ *п+\)М\ ••• Л« + 1-
= Шп(х, а)ц>(х) + ап+1) ^^- /="„+, (*,, .... *„+,) X
ХФ(/„ .... /„)<«, ... <«„+, = МА„(*. а)ф(*)-
/=-„+, -^ Ф(/„ ..., /„) <«1... Л„+1 -МЛ„(*, а) Ф (*).
-«»+• ]
§21
ДОПУСТИМЫЕ СДВИГИ МЕР
549
Поскольку функции ф(л:) указанного вида всюду плотны
в пространстве всех ограниченных ^„-измеримых
функций, то равенство
Мй„+1(х, а)ч{х)=МНп{х9 а)у(х)
справедливо для всех ограниченных ^„-измеримых
функций. Из последнего равенства и вытекает соотношение
М(йд+1(дг, а) !»„) = /?„(*, а),
т. е. кп(ху а) является мартингалом.
Обозначим через N множество тех а, для которых
81ф к2п(х, а)\х{(1х)<оо.
п ^
Для всех йе N существует почти всюду по мере |л
предел к(х} а) = Пт Нп(х, а), причем {Нх{х, а), .. .
. .., кп(х, а), .. ., И(х, а)} также является мартингалом
на вероятностном пространстве (36, 33, |л) и
Пт | [к (х, а) — кп (х, а)]2 р, {их) = 0.
Легко видеть, что Л/~-линейное многообразие, причем
для каждого вещественного / и для всех а и Ь из А/
почти для всех х по мере \л выполнены соотношения
к (х, 1а) = //г (х, а), /г (х, а + Ь) = /г (,г, а) + /г (х, й).
Следующая теорема дает достаточные условия того,
что аеЛ^ в терминах только что определенной
функции к(х, а).
Теорема 9. Пусть плотности }п(х) положительны
и непрерывно дифференцируемы и при некотором ае^
определено 1г(х, а). Если при некотором 6>0
Г еб1Н&>а^\1{с1х)<со,
то 1а е Мр для всех вещественных I, и справедлива
формула
\ с 1
р (1а, х) = ехр < — А (л: — за, а) из \. (12)
650 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ *МЕР |ГЛ. Ш
Доказательство. Положим
В силу сделанных предположений существует
производная 1'пЦ), причем
1п (0 - - / К (х + 1а, а) ^ + [п (х) их.
Значит,
Воспользуемся теперь следующим неравенством Юнга:
если ^ (0 — функция, определенная при ^0,
непрерывная, строго возрастающая и #(0) = 0, а §~1{{) — обратная
к ^ функция, а>0 и 6>0, то
о о
Взяв ^ ({) = — 1п (1 + /), получим
а&<^1п(1+а) + - -.
Используя это неравенство, будем иметь
1п{1)< /1 М* + 1а, а)\ ^(а) 1п(* + ^)их<
= |/в(0+-[/^|л"и'а,|ц(^).
§2]
ДОПУСТИМЫЕ СДВИГИ МЕР
.551
Из этого дифференциального неравенства вытекает, что
/,Л0<(1+/еб1Л«и-й,1И^))е-
.т'
Поскольку {Н{(х, а), ,.,, Нп(х, а), ..., Н(х, а)} является
мартингалом, то {ехр{6| й, (х, а)\], ..., ехр{б|А(дс, а)\)
будет полумартингалом, так что
|ев1А»(*-в,1ц(^)</ев,*и-в>1ц(^).
Следовательно,
1 1 /я (-V — /Р/гД) //г (X — /Р»«) * / \ * ^-
<8цр-/1п(1+7я^>,яд))/,(х)|^<8ир/<>(0<оо.
Чтобы убедиться теперь в том, что а е М^ остается
применить замечание к теореме 2 § 1.
Приступим теперь к выводу формулы (12). Заметим
сначала, что в силу соотношения
р ((/ + .9) ау х) = р (/а, х) р (яа, х — 1а)
эту формулу достаточно установить для сколь угодно
малых /. С другой стороны, используя однородность
А(х, а) по а, мы можем предполагать, что условие
теоремы выполняется при достаточно больших 6,
например при 6 = 4. Используя определение Ип{х, а), можем
записать
I о )
Поэтому
( с I
р(/а, .«)= Пгп ехр { — Нп{х — $а, а)с18\.
552 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР 'ГЛ. VII
Чтобы убедиться в существовании интеграла
\ Н(х — за> а)с18 почти для всех х по мере цив том, что
о
Пт- Г кп (х — 5а, а) из = Г /г (х — 5а, а) а?5
по мере {А, достаточно показать, что выполнено
соотношение
I
Пт Г| | кп(х — за, а) — кп+т(х — 5а, а) |а?5 ц(а?#) = 0, (13)
(из ^-измеримости к(х, а) вытекает, что к(х — зауа)
является борелевской функцией 5, кп (х — 5а, а) ->
~+к(х — 5а, а) при каждом 5 почти для всех х по мере \х,
значит, в силу теоремы Фубини при почти всех х по
мере II и почти для всех 5 по мере Лебега; из
соотношения (13) вытекает конечность
\\ к{х — за, а) \с1з
о
и равенство
Нхп Г Г | кп (х — 5а, а) — к(х — за, а) \ йз\1 (их) = 01.
П + оо^ * )
о
Имеем
Пт Г Г | кп (х — 5а, а) — /?л+т (я — 5а, а) | Й5р1 (их)
Пт Г Г |йя (*><*)-*«+«(*> а) | X
т-ъоо * *
п+т
Х1п+т(х + зРп+та)й8йх.
Используем уже встречавшееся здесь неравенство Юнга
в такой форме:
аЬК-^—^ + Ь \п(\ + аЬ),
§ 2] ДОПУСТИМЫЕ СДВИГИ МГ.Р 553
Тогда
Г| К (х, а) -Нп+т {к,а) | /^,„(^ + ^+,па) !п ( ^ ^
~ ] [ехр{|Лл(х, а)-кп+т(х, а)\}-1]ц(с1х) +
+ { //п+т(,)1п(1+а/)г+т^^+та)).^.,
Заметим, что
ехр (21 Ьп (х, а) - Ьп+т (х, а) |} <
<~ехр{4|/г/г(л-, а) |} + ~ ехр {41 Н,1+т (х, а)\].
Поэтому интеграл
| (ехр {| Нп (л:, а) - 1гп+т (ху а) | })2 ц (их)
равномерно ограничен, значит, функция ехр{| Л/г(л*, а) —
— 1гп+т(х, а) |} равномерно интегрируема и возможен
предельный переход под знаком интеграла.
Следовательно,
Пт | ехр{| Нп (ху а) - Пп+т (х, а)\}\х (их) = 1,
п, т -> сю «-
так как | /?/г(х, а) — 1гп+т(х, а)|—>0 при дг->оо и т~->оо
по мере [I.
Таким образом,
Пт | | | ЛЛ(лг, а)-Ая4.т(л-, я) | </$р, (</л-)<
/I, !П-><х>
I
г /х\
Поскольку последовательность цп= ,. , р—г является
мартингалом на вероятностном пространстве ($?, 23, \хза)
11 Лоо = Р (— 5а, Л' — $а) = Пт % таково, что Мг)^ =
= ПтМг|,7=1, то эта последовательность равномерно
554 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
интегрируема, значит, в силу теоремы 3 § 2 гл. II будет
мартингалом и последовательность [г\п, я= I, 2, ..., оо].
Поэтому последовательность [т]л1п(1 +ат]п); я=1,2,,.., оо]
будет полу мартингалом, так как §ирМ,пл1п(1 +ацп)<оо
п
(последнее доказывается точно так, как и
ограниченность /„-(/), а при а^1, что нам, собственно говоря,
и нужно, вытекает из ограниченности /„(0)- Поэтому
Мт1„ 1п (1 + ацп) < Мг)^ 1п (1 + а^),
Нт Мцп 1п (1 + ат|я) = Мг)^ 1п (1 + ат|„)
п->оо
(математическое ожидание берется на вероятностном
пространстве (35, 93, \18а))> Так как
МПя 1п (1+ ати) =$Ш\п(1+аГя Д^) их,
ТО
= II 1п (1 +ар(— а$, х — аз)) \18а (их)из.
о
Значит,
г
Игл I \кп(х — за, а) — кп+т(х — за, а)\с1з\х(с1х)^:
^
аз, х— за))\1за{их)из, (14)
- о
Легко видеть, что интеграл
1п (1 + ар (— аз, х — за)) \хза {их)
монотонно стремится к нулю при а | 0. Переходя к
пределу в (14) при а | 0, получаем (13). Теорема доказана.
Следствие. Пусть \х — гауссовская мера со средним
значением 0 и корреляционным оператором В. Тогда
А1 = Ву*т.
§21
ДОПУСТИМЫЕ СДВИГИ МЕР
555
Доказательство. Так как характеристический
функционал меры {1 имеет вид ф(г) = ехр<| — у(Вг, г)>
и ф (г)-> 1 при {Вг, г)->0, то в силу теоремы 2 М^ а Вч*3в.
Обозначим через е[} е2, ... и Л1? Я2, ... соответственно
собственные векторы и собственные значения
оператора В. Если ^ — подпространство, натянутое на
/„ (х) = (2Я)-'2 (Д *Т ехр! -12 -^ 1 •
Поэтому
41 (х* еи) (а> еи)
Легко видеть, что
&=1
%~^| (х б \ (а с \
так что к(х, а) определено и к(х, а)~ — У| —- % >
сю
ли только ^~^гг^~<°°- Так как (#, ей) являются
ее... ^ я
/г-1
независимыми гауссовскими величинами на
вероятностном пространстве {36, 53, ^}, то к(х, а) будет также
гауссовской величиной. Поэтому
Г е1 /I (х, а) | ^ (^д;) <^ | [еН (х, а) + е-Н(х, а)] ^ (^) =
^2ехр{^ \ НЦх, а)1х(ах)}^2ехРи^^^\
1 Л—1 )
Таким образом, в силу теоремы 9 йеМй, если только
ж~ч (а, еЛ2 ,/
2^~—Я^Г""^00' т' е' еслп а^^ ^- Наше утверждение
*-1
656
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
доказано. Из формулы (12) вытекает, что
( оо оо )
[к=1 к=1 )
= ехр{(В-'Чв-,/2х)-1|в-'"аГ}.
Приведем, наконец, пример меры \х, для которой М^
является линейным многообразием, всюду плотным
в 36, и существует такой вектор а, не
принадлежащий М^, что, \ха не ортогонально \х. Рассмотрим гаус-
совские меры \х1 и \х2 со средними значениями 0 и
корреляционными операторами А я В. Будем предполагать,
что собственные векторы у этих операторов совпадают,
обозначим их еи е2, ..., а собственные значения
обозначим соответственно через с^ и р^. Пусть -^-+0 при
Рп
п-+ оо. Легко видетьг что тогда М^ с= М^ и М^ — М^ —
непустое множество. Если а е М^ — М г, то \х2а ~ ц2,
а ^1|х! (см. следствие к теореме 5). Покажем, что
\х1а ± \х2. Величины (х, ек) = 1к на каждом из
вероятностных пространств {36у 23, \х2} и \дВ, 23, ^} являются
независимыми гауссовскими величинами, причем М^ = 0,
0*л = Р* на первом, и Щк = (а, ек), Щк = ак на втором
пространстве. Поэтому
п Л
(х, е^2
Ра
по мере \х2 и
Ы
1
->0
Р&
/8=1
по мере [л^. Ортогональность \х2 и ^ доказана.
Заметим, что из приведенного доказательства вытекает и то,
что \х2 ± [х1. Но тогда в силу теоремы 6 множество,
допустимых сдвигов, меры \х = ^(111 + \х2) совпадает,
с М^ПМуь т. е. с Мцг. Если же ае^-М^, то ца
§ 1] АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР 557
имеет абсолютно непрерывную компоненту ~\&а
относительно меры \х, так что ц удовлетворяет требуемым
условиям.
§ 3. Абсолютная непрерывность мер при отображениях
пространств
Основная задача, рассматриваемая в этом
параграфе, состоит в изучении условий, при которых
отображение гильбертова пространства 36 в себя
переводит меру \х в абсолютно непрерывную относительно ,ц
меру. Если Т (х) — измеримое отображение 36 в 36, т. е.
отображение, для которого Г~ (Л)^23 для всякого
ЛеЗЗ, то мера \к при таком отображении переходит
в меру V, определяемую равенством
Далее будут найдены достаточные условия,
обеспечивающие абсолютную непрерывность V относительно щ
а также выражение для -т— через характеристики меры |1
и отображения Т.
Прежде чем рассматривать меры в
бесконечномерном пространстве, найдем решение указанной задачи
в случае конечномерного евклидова пространства. Пусть
мера \х имеет плотность относительно лебеговой меры:
р (Л) = \1{х)йх,
А
причем / не обращается в пуль. Относительно
отображения Т будем предполагать, что оно взаимно одно
значно и непрерывно дифференцируемо. Тогда для
измеримой ограниченной функции §
^ В{х)'*№ = \ е{т{х))[1{ах)= $е{т{х))!(х)ах =
= $е{у)Цт-1(У))
где —^) якобиан обратного к / отображения,
которое также дифференцируемо в силу сделанных^
РТ~[{у)
<*У*
658 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
предположений. Последний интеграл в этой цепочке
равенств можно записать как интеграл по мере \х:
$8(У)[(Т~1(У))
от-'(у)
оу
а у-
/•
(у)
}{Т~1(у))
Заметим, что
}(т-{(у)) __ /(у(уГ'М))
Ну) Ну.)
Ну)
рт~{(у)
йу
\х (йу).
р(у-т 1(у)> у)>
где р (а, х) — плотность меры \ха относительно меры \1
(мы используем обозначения § 2). Таким образом, в
конечномерном пространстве справедлива формула
/ 8 (х) V (ах) = | е (х) р (х - Г"1 (х), х)
РТ~] (х)
Бх
\л (их).
В таком виде эта формула формально имеет смысл
и в гильбертовом пространстве, если только придать
смысл выражению для якобиана преобразования. Пусть
V — некоторый линейный оператор, для которого V —/,
где / — тождественное преобразование, вполне
непрерывен. Тогда УУ* будет симметричным
неотрицательным оператором, а УУ* — I также вполне непрерывным.
Пусть Хк — последовательность собственных чисел
оператора УУ* (этот оператор имеет полную систему
собственных векторов), А^^О, Ал-*1. Положим
\Ае1У
если это бесконечное произведение либо сходится, либо
расходится к нулю или + оо.
Пусть 5 (х) — некоторое отображение 96 в 9В. Оно
называется дифференцируемым в точке х0, если
существует такой линейный оператор 48 (х0), что выполняется
соотношение
\8(х0 + х)-8 (х0)~ (18 (х0) х | = о (| х |), х е= Я?,
оператор 48 (х0) называется дифференциалом 5 (я)
в точке х0. Если ^ — конечномерное пространство, то
якобиан преобразования 8(х), как легко видеть, совпа-
§3]
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР
559
дает с \Ае1с13(х)\. Последнее выражение имеет смысл
и в гильбертовом пространстве. Итак, мы приходим
к формуле
\ ё (х) V {ах) = |" 8 (х) р (л- - Г"1 (а), х) | <1е* ЛГ ! (х) \ р (</*).
(2)
Справедливость этой формулы для достаточно
широкого класса функций #*приводит к равенству
^ (х) = р (х - Г^1 (л:), а) | с!е* «/Г"1 (х) |. (3)
Исследованию условий, при которых справедлива
формула (3) как в общем случае, так и для гауссовских
мер ц, посвящена остальная часть параграфа. Для того
чтобы формула (3) имела смысл, нужно наложить
некоторые общие условия на меру \х и преобразование Т.
Условие 1. Мера \х имеет линейное многообразие
допустимых сдвигов М и для всякого ортонормирован-
ного базиса {ек} проекция \хп меры \х на 36 п (^„ —
подпространство, натянутое на <?,, ..., еп) имеет
непрерывную плотность 1п{х) относительно меры Лебега на Шп
и для всякого с>0 и конечномерного подпространства
знр
1„(Рп(х-а))
- р (а, х) ; | а \ < с, а е Л' I -> О
1п(РпХ)
по мере [х, здесь Рп~~ оператор проектирования на 86 п,
р{а,х) = &*-(х).
Условие 2. Отображение Т(х) обратимо, обратное
отображение будем обозначать 5 (а), операторы Т (х)
и 5 (а) локально ограничены и непрерывно
дифференцируемы, причем конечны, отличны от нуля, непрерывны
н локально ограничены выражения \Ае\с1Т(х)\
и 1 ее* а8 (а) |.
Теорема 1. Пусть выполнены условия \ и 2 и
существует конечномерное подпространство N в М такое,
что х — Т (а) еЕ Ы, х — 8 (а) е Л' для всех хеЖ, причем,
если Р — оператор проектирования на /V, то РТ(х) =
= Т(Рх), Р(8{х))— 8(Рх). Тогда г~ц и
справедлива формула (3).
560 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Доказательство. Выберем базис еь еъ ... так,
чтобы при некотором т векторы еи ..., ет
образовывали базис в N. Пусть [хп и V" —проекции мер \х и V
на подпространство 36п. Тогда при п>т для всякой
измеримой ограниченной функции^, определенной на 86п,
будем иметь
\ В (х) V" (их) = / 8 (РпХ) V (ЛХ) =^\е (Р„Т (х) ) Ц Ш) =
в» др др
= |§(?' (Рпх)) р № = | § (т (х)) р» (ах) =
ж жп
= I 8{Т(х))Тп(0х)ах.
При наших предположениях отображения Т и 8
переводят дВп в ЗВп при п>пг. Сделав замену переменных
интегрирования х = 8(у), получим
^(Х)уп(ах)= \ ё(х)1п^([х)))\ыа8(х)\1хп(ах).
Поскольку 8(х) = х+ Р{8{х) —х), то матрица Якоби
преобразования 5(х) будет иметь вид /+ К, где V имеет
отличные от нуля элементы лишь в первых гп строках,
причем эти элементы от т не зависят. Таким образом,
при п>т модуль якобиана преобразования 5(лг) от п
не зависит и совпадает с \&е\й8{х)\.
Значит,
#м-да|"«»<«м|-
Очевидно, что меры V" и ц" эквивалентны и
.,11 \Х)
Поэтому
ауп и (X)) - (п (х) ! ае1 Й5 (Г {х))! и (х) | ает йу (х) \,
поскольку по правилу дифференцирования сложной
функции
1 = ах = а[5(т(х))] = а5(т(х))ат(х).
§3]
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР
561
В силу условия 1 существуют отличные от нуля
пределы
Пт1пЩШ= {х_8{х)>х)>
П-*оо 1п\ГпХ)
Ит ^(РпТ(х)) =р{х_т(х)х)
/1->оо 1П\ГпХ)
в смысле сходимости по мере ц (мы пользуемся
тем, что х — 5(х)еЛ/, х-Г(х)еЛ/, локальной
ограниченностью этих функций и условием 1). Остается
применить следствие 1 теоремы 3 § 1. Теорема доказана.
Замечание 1. Мы доказали, что в условиях
теоремы 1 V — [х, и, кроме формулы (3), имеет место
формула
^ (Т (х)) = р (х - Т (х), х) | с!е1 йТ (х) |. (4)
Замечание 2. Формулы (3) и (4) остаются
справедливыми, если для всякого у можно указать такое б
и конечномерное подпространство Ыу а М, что условия
теоремы будут выполняться при |х-~г/|^6, если N
заменить на Ыу.
Теорема 2. Пусть выполняются условия 1 и 2
и существует базис {ек} векторов из М такой, что:
1) для достаточно больших п обратимы отображения
Тп(х) = х + Рп(Т(х) - х), 8п(х) = х + Рп (8(х) - х) и
| с!е± с1Тп (х) | -> | йе! йТ (х) |, | йе1 й8п (х) |->| с!е1 аз (х) \ в
смысле сходимости по мере \х,
2) выражения р(Рп{х — 8 (х)), х) и р (Рп {х — Т (х)), х)
имеют пределы при п—>оо по мере [I, которые мы будем
обозначать р (х — 8 (х)* х) и р (х — Т (х), х) соответственно',
в выражение р(х — 8 (х), х) можно подставить Т(х)
вместо х и
р(Г(х)-х, Т{х))р{х-Т{х), х) = 1.
Тогда меры \х и V эквивалентны и справедливы
формулы (3) и (4). .
Доказательство. Пусть
8%(х) = х + Рп(8(Ртх)-х).
При т>п
8?(Ртх) = Рт8™(х"
562
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Отображение 5™ и обратное к нему удовлетворяют
условиям теоремы 1. Если V™ —мера, определяемая
равенством
V%(А) = ^^(8У(А)^
то
-^ (д) - р(* - 8™ (х), х) | <Ы й8™ (х) I
Заметим, что из условия 1, непрерывности и
положительности !п{х) для всех п вытекает, что р(а, х) является
равномерно непрерывным по а при а е двт, \а\<^.с по
мере \х, т. е.
зир{|р(а„ х)-р(а2, х)\\ \ах\^.с, | а2 Ю, а,, а2<= 95т,
К-а2|<6}->0
по мере \х при 6->0. Так как х — 8™{х)^8вп для всех
т, х — 8% (х) -» х — 5П (х) и х — 3%(х) ограничено по
мере ц, то
р (а: - 8п (х), х)-+р(х--8п (х), х)
по мере \х при га-*оо. Далее очевидно, что Л8%(х) при
всех т имеет вид й8™(х) — 1 + У%(х), где У*(х)
отображает все пространство в Я?л. Можно проверить, что
в том случае, когда У отображает 36 в 8Вп, то
|ае!(/ + 1/)|=|(1е1||((/ + 1/)^^)||1./=1)...)П|,
где \\{{1 Л-У)еь ^/)И//=г1 ...§я — матрица порядка п с
элементом ({1-\-У)еь в}) на пересечении 1-й строки и /-го
столбца. Поскольку для всех г, \
Нт (й5« (х) е19 еЛ = (й5я (*) еи е1),
т->оо
ТО
Нт \&ъ\й$™{х)\ = \Шй$п{х)\.
Таким образом,
Я1->00 Н*
§3]
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МНР
563
*к
в смысле сходимости по мере р,. Используя равенство
х — 8п(х) = Рп(х — 8(х)) и условия теоремы, можем
утверждать, что
сЫ!!(х)
\\т \\ш — — р(х —8(х), х)\({е1с13 (х)\
в смысле сходимости по хмере \х. Значит, можно выбрать
такие последовательности пк и тк, что тк>пк и меры
* = ^\к удовлетворяют соотношению
Ит ~ (х) = р (х - 8 (х), х) | ее! йЗ (х) |
по мере \х.
Пусть теперь Т% (х) = х + Рп (Т {Ртх) — х). Аналогично
убеждаемся, что можно выбрать так
последовательности пк и тк, что для мер
в смысле сходимости по мере р,
Пт ^~(Тк(х)) = р (* - Г(х), х)| с1е* йТ(х) |.
к->со
Наконец,
р(Т(х)-х, Т(х))\йе1(13(Т(х))\р{х-Т(х)9 х)Х
Х\йе1аТ(х)\=1,
так как по правилу дифференцирования сложной
функции
/ = их - й {8 (Т (х))) - с18 (Т (х)) с1Г (х)
и, значит, МсЫ5(Г(;с))|-|(1е<:^Г(х)|=1, а
р(Т(х)-х, Т(х))р(х-Т(х), х)=1
в силу условия 2) теоремы. Значит, можно
воспользоваться следствием 2 теоремы 3 § 1, из которого и
вытекает доказательство теоремы.
Рассмотрим теперь случай, когда мера р является
гауссовской со средним значением 0 и корреляционным
оператором В2. В § 2 было установлено, что в этом
случае М = Вс№, и если а=^ВЬ, ^ — собственные
564 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. УИ
векторы, рй — соответствующие им собственные значения
оператора В, то
V (6' *а) (*» ^ ! , / ,91
и-1 )
Пусть преобразование Г (л:) имеет вид Т(х) = х + ВХ(х),
где Я (л;) —непрерывное и непрерывно
дифференцируемое отображение. Если Т обратимо, то 5 (х) = х + Вк* (х)9
где Х*{х)= — к(8(х)) также непрерывно и непрерывно
дифференцируемо.
Поскольку в случае гауссовской меры 1п /г*1*~ •
является суммой квадратического и линейного
функционалов относительно а, то из сходимости . ~
1п\х)
к р(а, х) вытекает, что эта сходимость равномерна
относительно а при а е 36т, \ а | ^ с, каковы бы ни были
т и с. Поэтому * для гауссовской меры условие 1
теоремы 2 всегда выполнено. Рассмотрим условие 2 этой
теоремы.
Так как
р (Рп{х-Т(х), х) =
■ехр1г|;'иА''»"''>-1|Р,и,)р1,
то существование отличного от нуля предела
1\тр{Рп(х-Т{х)), х)
эквивалентно сходимости по мере ц ряда
оо
к=\ к
и этот предел равен
Р(*-ш, ,)=ехР1-|;^^^-1и(,)р!.
§3]
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР
565
Точно так же Нт р(Рп(х — 5(х), х) существует тогда
Я->оо
и только тогда, когда сходится по мере \х ряд
оо
2>(*),^)-^,
и при этом
( *=1 I
Заметим, наконец, что
Р(Т(х)-8(Т(х)), Т(х)) =
\ VI (Я*(П*)). еЛ(Т(х), е.) 1 )
( й = 1 )
\ у1 (Я (х), ек) (х + Вк (х), ек) I )
= ехр{У-* ^ ^-Т1М*)Р| =
1 V (Л(Х)' ек){Х> €к) ,
Мы доказали следующую теорему:
Теорема 3. Пусть \х является гауссовской мерой
со средним 0 и корреляционным оператором В2; $к и
ек — соответственно собственные числа и собственные
значения оператора В. Если
а) преобразование Т (х) удовлетворяет условию 2 и
имеет вид Т(х) = х + ВХ (х), а 8 (х)=Т~1 (х) = х + ВХ (х),
при достаточно больших п обратимы преобразования
Тп (х) = * + РпВХ (х), 8п (х) = х + РпВХ" (*),
и, наконец,
| йе! аТп (х) | -> | (Ы АТ (х) |, | 6е1 й8п (х) | -> | йе* </5 (л;) I,
566 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
б) почти всюду по мере ц сходятся ряды
V (я (*>> ек) (х> ек) и V (г(*>> **)(*> «»)
^ р* и ^ Р*
&~1 к=\
то меры \х и V эквивалентны, причем
((V , у
-1с1еЫ5(х)1ехр -^ Ц "уЩ*)!2 . (5)
Чтобы иметь возможность проверять условие б)
теоремы 3, рассмотрим некоторые достаточные условия
сходимости рядов, фигурирующих в этих условиях.
Лемма. Если мера ц такая, как в теореме 3,
а к(х) — непрерывное отображение 36 в 36, то для
сходимости по мере \1 ряда
V (М*>' ек)(х, ек)
к=\
достаточно, чтобы выполнялось одно из условий:
1) Существуют такие числа ак, что 2«;<оо и ряд
/5 = 1
2«Г2(Я(д:), ек)2 сходится почти всюду по мере \х.
2) По мере \х сходятся ряды
оо оо
2 (к (х) - к (/>*_,*), е*) -^^-, 5] (Я (Р^х), ^)2.
3) Сходятся ряды
2 /КМ*). е*)(М*)> *,)-(*(*)> *,)(*,(*), е/)]|х(Жг),
где
§3)
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР
567
Доказательство. 1) вытекает из неравенства
/у„.('■«»)' |/ у (>-">■ «.У
2^<^)...>кК2<п?г:К21^
Ра у~\ "к
2
И ТОГО, ЧТО
оо оо
2) Не ограничивая общности, можем считать, что
1М*)12^^' так как сходимость ряда (6) на множестве
{х: \к(х)\2^с} для любого с>0 влечет его сходимость
по мере ц. Обозначим через Нт множество тех л', для
которых
2(л(рл.,х), ^)2<
т.
&»1
Пусть Ат(.г) = Л(*) при ^еЯш, ят(х) = 0 при хШНт.
оо
Так как из сходимости ряда 2 (А(^а-1*)> е/г)2 вытекает,
что (*(#,„)->1 при т->оо, то для сходимости ряда (6)
достаточно, чтобы при каждом т сходился по мере ^
ряд
2(*«(*), ^1Г'
А-1
Но
оо
оо оо
= 2] (л« (х) - Кг (Я*-,*)) ^^- + ^ <Л« (Я*-,*), ек) -^Я
Заметим, что в силу неравенства
оо оо
2 (МЛ*-, Л*). екУ < 2 (Л(РА_,л), е*)2 +
оо оо
+ И (А (/>,*), ^)2 < 2 (^ (/>*-!*). е,)2 + \\{Р1 (х) Р
для всех / и х е //т имеем: Р^г €Е Нт+С. Пусть х е #/Л-^
568
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ.'УН
Тогда
2 (*.« (х) - Хт{Рк-Хх), ек) Щ^- =
к=\
= %(Цх)-\(Рк-1Х), ек)^-,
к=\
а последний ряд сходится по условию. Так как т можно
взять сколь угодно большим, то достаточно установить
^п • (х, ел
сходимость по мере |х ряда^ (Ьт(рк-\х)> ек) ак -
Сходимость этого ряда вытекает из того, что на
вероятностном пространстве {96, 23, \х} его частичные суммы
образуют мартингал, так как (х, ек) — независимые гаус-
совские величины, и кроме того,-
М(%1т(Рь-1х), ек){-^]2 = ЬЛ%кт(Рк^х), ек?(-^ =
= 2 М (К (Рк- .а-"). екУ М ^^- < т.
к = \
3) Покажем, что ряд (6) сходится в среднем квадра-
тическом. Очевидно,
\к=*п /
V Г (*<*>• ек)Чх>ек)2 м ч^
= Ъ) %г——1*(^) +
к=п ~ Р*
+ 2 ^ Л Щ ^*) +
+ 2 5] $[(К (х), е{) (А (х), е,) - (к„ (х), в,) (А„ (*), е,)]Х
п < г < / < т
§31 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР 509
(х, еЛ(х, еЛ { \1 (л (л), е. V (х, е,)2
к~п л
п <С I < / < т
(л', <?/)(*, <?,)
так как
в силу независимости величин л^-(х), (л*, ес), (л\ е^ на
вероятностном пространстве {36, Ъ% \\). Значит,
' т \ 2
при п~>оо и т->оо. Лемма доказана.
Применим теорему 3 к тому случаю, когда
преобразование Т (х) мало отличается от тождественного, Пусть
имеется семейство отображении Тк (х) = л* -Ь ел (л*), тогда
и 5е (х) = х — ел (.г) т О (е2) (мы рассматриваем лишь
члены порядка не выше е). Если <гЩх) имеет конечный
след, то при достаточно малых е
1п | с!е{ с1Те (х) | = V ^— ** 5р № (х)]\
а? -1
Следовательно, ограничиваясь лишь членами порядка
не выше е, можем записать
оо
■$- <*) -1 -. зр [ак (*)] - в 2 <^1^ + о и.
Как видно из этой формулы, основная трудность,
возникающая при использовании теоремы 3 и
заключающаяся в исследовании сходимости рядов в условии 6)
этой теоремы, остается и для преобразовании, сколь
угодно близких к тождественному.
570
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Рассмотрим случай, когда отображение Г линейно.
Теорема 4. Пусть \х — гауссовская мера со
средним значением О и положительным корреляционным
оператором В2. Если линейный оператор Т обратим и имеет
вид Т^1 + ВСВ~\ где 5рСС*<оо, и оператор 1 + С
также имеет ограниченный обратный, то
%(х) = Кехр{Ф(х)}, (7)
еде
К = Пт\^(1 + Оп)\е-5р\ Д„ = Р„ДРП> (8)
Ш(х)= 11т \-(ОВ-1Рпх, В~1Рпх)~
-±\РпОВ-1Рпх\2 + 5рОп]. (9)
Этот предел понимается как среднеквадратическии по
мере [х, Рп — оператор проектирования на 9ВЮ О =
= В~]Т~]В-1.
Доказательство. Оператор Т переводит М в М,
так что й определен по крайней мере на М. Покажем,
что 5р!)Л*<оо. Так как
Г"1 = / - ВСВ~ХТ~\ О - СВ~]Т"1В = С (/ + С)"1 - С1/,
где У — ограниченный оператор, то
оо с»
5р ЯЛ* = 2 Ф'ек, й'ек) = 2 (ГС'е*. УС'ей) <
оо
< I! УУ || 2 I Сек |2 = || УУ || 5р СС\
Из этого соотношения вытекает и ограниченность О.
Положим Оп = Р„РРП. Тогда
5р {О - Оп) {О - БпУ = 5р ОД* - Зр ОпОп =■
-2|^Г-2|^р-
о© оо
= 22 ФЧ, е,у- 2 "2 ФЧ> е,)2 -*о
А=1 /=1 й«1 /=1
при п~~> оо.
§31
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР
571
Покажем существование отличного от нуля предела
НтМе*(/ + Яд)|ехр{-5р/)я}.
П-»оо
Пусть Цп = Оп + /?; + ОпО'п. Тогда
|<1е*(/ + Оя)|ехр{-8рЯ„} =
= 1Л1е1(/ + */„)<Г8р1/''ехр{ у Зр />„/>;}.
Поскольку 5р/)я/>*->5р О/)*, то достаточно показать
существование предела
1ппс1е!(/ + (/„П>~"51"'Ч (10)
П->оо
Положим и==о + о* + оо\
Из условия 5 р (/) — /)„)(/) —/^Г-^О вытекает, что
и 5р (Ц-г/я)((У -г/я)' -*0. Обозначим через к\п\ ..., А(ля)
собственные значения оператора (/„ в ^/2 ({/„
переводит ®вп в <8?„, а его ортогональное дополнение в нуль),
а через /",..., /"—соответствующие им собственные
векторы (считаем, что Я/Г) упорядочены по абсолютной
величине). Из соотношения
V
1-Х
[/р1-}}*у;\><&р((;-(;пу-»0
вытекает, что Я(/Е) —> Аг, /1П)~>//, где ^ — собственные
векторы оператора (/, Аг —соответствующие им
собственные значения. Далее имеем
с!е1 (/ + Цп) <Г5р г'« = [Ю + Я?}) «Г**1' -
\М~\ / \ \к>т I
Поскольку
т \п) т
ПтПО+яГ)^ =П(1+АА)<ГЧ
572
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР \ТЛ. VII
то для доказательства существования предела (10)
достаточно показать, что
оо
т->оо /г->оо т + 1
Но
Пт ит
оо Г т "I
= т+1 пг->оо я->оо [^ /г= 1 ^
= Пт |5р^2-|1л1| = 0.
Существование предела (10) установлено. То, что
предел отличен от нуля, вытекает из соотношения
и того, что 1 + Ай ф 0, так как оператор (/ +О) (/ + /)*)
обратим.
Докажем существование предела (9). Пусть
Тогда в силу формулы (7) § 6 гл. V
|[ГЛ*)-Гт(х)]^№) =
= ] [({я„ + уДЖ-Ят-уЯтА»}^-1*, В~,х) +
+ 5Р (о„ - ят)]2 ц(аХ) = [| 5р .№>„ - /)Ж)]2+
+ 8р\ ^ +——2—; <
< [1 5р (0>„ - 0>т)]2 + ± 8р ({/„ - (/т)2,
последнее же выражение стремится к нулю при л->оо
и т—>оо. Существование предела (9) установлено.
Перейдем к доказательству формулы (7). Пусть
мера Vп определяется равенством чп{А) = ц{Тп1А), где
§3| АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР 573
Г„ ' = В (7 + Дг) В . Тогда из теоремы 3 вытекает, что
\
X ехр: - 2и
1 л«1
(Ог/В~Ч ек)(х,ек) (РпВ-1х. ек)2
Ра 2Р;г
= | с!е1 (/ + Оп) [ехр{ - (ОпВ~1Рпх, В~1Рпх) -
поскольку | с1е1 5 (/ + 0„) В""11 совпадает с модулем
детерминанта матрицы преобразования В(1 + Оп) В~\
рассматриваемого в 36п, записанной в ортонормированием
базисе, то
\йе1 В(1 + Оп) В~1\ = \ Ы(1 + Оп)\.
Таким образом,
^-(л') = /С„ехр{Г„(х)},
где И7ЛЛ') определено выше, а
Л'„-Ие1(/ + /)„)|е-8,>Ч
По доказанному
От -^(л-) = /(ехр{Г(л-)}
в смысле сходимости по мере \х. Пусть теперь мера уп
определяется равенством уп = \х (Г^1 (А)), где Тп = 1 4-
4- ВРпСРпВ^\ Аналогично предыдущему молено
установить, что по мере \х
Пт
й[1
(Тп(*))= К **?№(*%
где /\, Ш определяются формулами (8) и (9), если в них
вместо О подставить С.
Воспользовавшись следствием 2 теоремы 3 § 1,
получаем доказательство теоремы.
574
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
§ 4. Абсолютная непрерывность гауссовских мер
в гильбертовом пространстве
Пусть в гильбертовом пространстве (95, 93) заданы
две гауссовские меры щ и \х2, имеющие средние
значения ах и а2 и корреляционные операторы В{ и В2
соответственно. Ниже находятся необходимые и
достаточные условия, которым должны удовлетворять аи а2,
Ви В2, чтобы мера ц2 была абсолютно непрерывна
относительно \1{. При этом оказывается, что плотность -~-
является всюду положительной, так что абсолютная
непрерывность р,2 относительно \х{ влечет
эквивалентность мер Рч и р-2- Более того, оказывается, что
нарушение условий абсолютной непрерывности приводит
к ортогональности мер, так что две гауссовские меры
либо эквивалентны либо ортогональны.
Тот случай, когда меры отличаются лишь сдвигом,
т. е. Вх = В2, частично исследован в § 2.
Теорема 1. Если В{ = В2 = В, то для того, чтобы
|х2<[11, необходимо и достаточно, чтобы а2 — а{^ В"1г95\
при этом
-^- (х) - ехр{(/Г* (х - а,), В"'А (а2 - а,))
й\хх
~-1|В-1/2(а2~а1)|2}. (1)
Если а2 — а{Ш ВЧг96, то \1{ ± р,2.
Доказательство. Первое утверждение и
формула (1) установлены в § 2. Пусть теперь
у=г{а2-аи ек) = ак,
где Хк — собственные значения оператора В,
а^-соответствующие им собственные векторы. Если а2-~ахШВх,*ёв,
оо
то ^вь^Н"00» Рассмотрим функции
, п \ -1 п
141 абсолютная нетгенямшсть гтссаватх мер $й§
Поскольку
| ёп (*) Й1 №) = 0, ]* #„ (*)Щ■№) - 1»
то ёп "-* О по мере I*! и #л -* I по мере [х2. Отсюда и
вытекает ортогональность щ и \х2. Теорема доказана.
Рассмотрим теперь случай, когда а1 = а2==0.
Предположим, что \х2 <С \^\* Тогда обязательно выражение
(В22, г)/{В{г, г) ограничено при 2е1 Действительно,
если найдется такая последовательность гп> что
- (2 х)
то тогда ~ --*0 по меРе 1*1» а
У (Б2гл, г„)
^11 /(Б2гй, гй) ^ ] / 1^2^ |/|<е ^
значит, —г- =г не стремится к нулю по мере [х9.
V (Б22„, 2П)
Это же противоречит абсолютной непрерывности \х2
относительно р^. Легко видеть, что неограниченность {В22% ,
влечет даже сингулярность мер ц, и \х2. Значит, это
отношение должно быть ограничено снизу
положительным числом. Отсюда вытекает, что области значений
операторов В{2 и В22 совпадают и ограничены
операторы С = В\гВ2'1г и С1 = В12ВТЧ\ Заметим, что из
ограниченности оператора С вытекает, что (г, В!12*) является
измеримым функигшжалом не только по мере \к2 (см,
гл. V, § 6), но и по мере щи так как
(г, В2~,/2^) = (г, СВ^х) = (Сг9 ВТ^х).
Рассмотрим самосопряженный оператор С С = В2{,2В\В21,\
Покажем, что С*С = / + 1), где О — вполне непрерывный
оператор. Для этого достаточно установить, что если
Еь — разложение единицы для оператора Д то
проектирующие операторы Ек при КО и / — Ек при к>0
переводят <% в конечномерное подпространство. Покажем
576
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
сначала, что не существует собственного числа Я Ф О
у оператора О, которому бы отвечало бесконечномерное
собственное подпространство. Если бы это было не так,
то можно было бы указать бесконечную ортонормиро-
ванную последовательность гк в этом подпространстве,
п
для которой ~2д (^> Я"1'**)2-* 1 по меРе М-2 и
п
7Г^ (2*' ^2^х)~> 1 +^ по мере \х{9 так как на каждом
из вероятностных пространств (Я?, 99, и-!) и (^, 93, ^)
величины (гл> В~ч*х) образуют последовательность
независимых гауссовских величин со средними нуль и
дисперсиями соответственно 1+А и 1.
Действительно,
| (*к> В;1'гх)(г,, В;Ч'х)р2(ах) = (гк, 2/) = в„,
1{гк,в;\)(ггв;\)»1(ах) =
= (В,В2-% В;\^(гк, г,) + {йгк, г,)-(1 +Я)б4/.
То, что — V (гл, В~ч*х) сходится к разным постоянным
по мерам III! и \х2У влечет ортогональность мер \х{ и ц2.
Пусть теперь
г^(Еч_гЕКк)%,
где 0 > Я = Я0 > А,! > ... > Аь причем (Яа.л_, — ^) 95 —
непустые подпространства. Тогда {гк, В~ч*х) снова будут
независимыми гауссовскими величинами на
вероятностных пространствах (36, 93, ц,) и (Я?, 93, ц2).
Действительно,
-6*/( 1 + | М(^х2», 2»)
\к
§ 4] АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ ГАУССОВСКИХ МЕР 577
Используя усиленный закон больших чисел, можем
п
утверждать, что 7Г^(гб' В~У2ху~>1 по мере \х2 и что
Л-1
Лй~1
& = 1
по мере ц^. Из этих двух соотношений снова вытекает
сингулярность щ и ^2- Остается заметить, что при КО
подпространство Ек§5 бесконечномерно в том случае,
когда либо некоторому КО отвечает бесконечномерное
собственное подпространство, либо существует счетное
число непересекающихся интервалов на (— оо, Я) таких,
что на каждом из них приращение Ек не равно нулю.
Конечномерность Е%35 при А,<0 установлена. Точно
так же доказывается конечномерность (1-Е))36, Я>0.
Таким образом, оператор В вполне непрерывен.
Пусть еь е2у ... —его собственные векторы, а 6^ — соот-
ветствующие им собственные значения. Покажем теперь,
что из абсолютной непрерывности ^2 относительно м^
вытекает соотношение 2 Й < °°-
оо
Действительно, если 2 б|= + оо, то рассмотрим по-
следовательность функций
ёМ = (Ы'1±бк[(ек,в;\у-1].
Уже отмечалось, что для векторов гк, лежащих в
различных ортогональных собственных подпространствах
оператора Ву величины (гк> В~Чгх) являются
независимыми гауссовскими на вероятностных пространствах
Ш И% И.. Гихман, А, В. Скороход
578 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
($?, 93, ц,) и {36, 93, ц.2)- Из соотношений
П
хЦ**{/(^ в;'^)41г1(^)-[1((^, в;"^)2^ №)]2}=
-2(2**)"я21*Н1+лэ-о^2в*)"')
вытекает, что ^(х)->0по мере \х2 и ^„(л')—> 1 по мере \х{.
оо
Значит, условие 2 &1а + °° влечет ортогональность
мер 1^! и }12. Еще одно необходимое условие, которому
удовлетворяют 6^, вытекает из соотношения
... , , (°Ч'Ч) {В^В^Ч'е,, ек) ,.(В^п.гп)
где гп — такая последовательность векторов из Вг2^-,
что Вх1*гп-*ек. Значит, бл> —1.
Пусть теперь 6к > — 1 и 2 б|< со. Покажем, что
тогда меры III! и \х2 эквивалентны. Для этого рассмотрим
меру Д, определенную равенством
А (А) = / Р (*) Ш (<**)>
где л
§4] АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ ГАУССОВСКИХ МЕР §79
Сходимость ряда
по мере \х{ вытекает из того, что на вероятностном
пространстве ($?, 93, \х{) это ряд из независимых случайных
величин, для которых сходятся ряды из математических
ожиданий и дисперсий:
М [(В;ч% ек)а т^-- 1п (1 + 6,)] = 6,-1п (1 + 6,) = О (б|),
Найдем характеристический функционал меры Д:
% (г) = | е^> *>Д {их) = | е1 <*• х)р (х) ц, (Лс).
Для всякого 2Е^ справедливо соотношение
оо
(*, *) = №, в;Ч')=2(в;/22, ек)(в;ч% ек)9
где ряд справа сходится почти всюду по мере щ.
Используя то, что величины (в~Х1*х, е^ на
вероятностном пространстве ($?, 93, \х{) являются независимыми
гауссовскими со средним нуль и дисперсиями 1+6А,
получаем < <*>
2 (г) = М ехр / 2 (ф, вА) (В7'Ч ек) -
I *-1
оо 1
оо
= Д М ехр {/ (ф, е,) (Я2"Ч еА) -
-тоТб1)(</^^)2}>/тТб;=
11 /2я Л
оо
= Дехр{-^(в;Ч е,)2} = ехр{-1(В2г, г)}.
19*
580 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Поскольку характеристический функционал меры $
совпадает с характеристическим функционалом меры \х2,
то ^2=Д и -щ^{х)=*р{х).
Итак, доказана следующая теорема:
Теорема 2. Пусть \х{ и \х2 — две гауссовские меры
со средними значениями 0 и корреляционными оператор
рами Вк, к= 1, 2. Для того чтобы меры \х{ и \х2 были
эквивалентны, необходимо и достаточно, чтобы
оператор О = В212В\В21% — I был оператором Гильберта —
Шмидта, а его собственные значения 6к удовлетворяли
неравенству 6к > — 1. Если это условие нарушается, то
меры \к{ и \х2 ортогональны. В случае эквивалентности
мер имеет место формула
й\12 __ I 1_
-^--ехр| ~2 л^^х-ч >-*/ 1+0л ---V- • -м\у
^-«р—т2[(в."**- О'-гйс-'"(' +»0] • О)
где ек — собственные векторы оператора В, отвечающие
собственным значениям дк.
Замечание. Пусть \х{ и \х2 — меры такие, как в
теореме 2. Обозначим через 1?(,) и ^?(2) гильбертовы
пространства линейных измеримых функционалов
относительно мер р, и \х2 (см- § 6 гл. V). Если существует
последовательность функционалов {1к{х)> &=1, 2, ...},
принадлежащая обоим пространствам и являющаяся
полной ортогональной системой в каждом из этих
пространств и
№ = | [/* (х)? Ъ (ах), /==1,2, к = 1, 2,
V* / б(1> V
то |Х| —М-2 ПРП условии 6(^>0, 2Д1 - т|Н
2
< ОО И
1 1 \ 6(П
Доказательство этого утверждения совершенно
аналогично доказательству достаточности условий теоремы 2.
Рассмотрим общий случай. Введем, кроме мер щ
и [х2, еще меру цЬ2, у которой среднее значение аь
а корреляционный оператор В2. Покажем, что условие
§ 4) АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ ГАУССОВСКИХ МЕР 531
\х2 «С м-1 влечет соотношение \12 <С И-12 ^ М-ь так чт0
#1 #12 #1 '
причем для вычисления -р^- можно использовать
формулу (1), а для вычисления -1- формулу (2). Доста-
а\12
точно показать, что \х12 <€. м-ь так как в этом случае
\Ь12~Р1 и> значит, ^2 < ^12- Если Д2 — мера со средним
а2 —ах и корреляционным оператором В2, а ^ — мера
со средним 0 и корреляционным оператором Ви то
Д2 <С Д1в Пусть мера Д! определяется соотношением
Д?(Л) = Д. ({х: -хбЛ}). Очевидно, Д* = ДГ Поэтому
Д* <С Д! и, значит, Д2 * Д* < Д} * Дг Легко видеть, что
Д2* Д* — гауссова мера со средним 0 и корреляционным
оператором 2В2, а мера Д! * Д! отличается от нее лишь
корреляционным оператором, равным 2ВХ.
Следовательно, .^2 <С V!, где V^ — гауссовская мера со средним О
и корреляционным оператором Вк. Но тогда и щ2<И1»
так как ц12 и щ получаются сдвигом на ах из мер V2
и V!. Таким образом, в общем случае справедлива
Теорема 3. Если меры щ, ц2 — две еауссовские
меры с характеристическими функционалами
Фл(2) = ехр{/(аЛ|2)-у(ВЛ2,2)}, 6=1, 2,
то для эквивалентности мер \хх и \х2 необходимо и до-
статочно, чтобы выполнялись условия:
1) а2-а{ = Вр} где 6е^;
2) оператор В = В2Х1гВ\В212 — I является оператором
Гильберта —Шмидта и его собственные значения 6к
удовлетворяют неравенству 6к > — 1. Если хотя бы одно
из условий не выполнено, меры \хх и \х2 ортогональны.
Для эквивалентных мер имеет место формула
^(х) = ехр\-±\%(В^(х-а1),.ек)2т^-\п(\+6к)]+
+ (в;1!*(х-а1)9Ь)-±\Ь?}9 (3)
где ек — собственные векторы оператора Д отвечающие
собственным значениям 6&.
б$2 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Рассмотрим некоторые достаточные условия
абсолютной непрерывности гауссовских мер. Приводимые
ниже условия могут оказаться более удобными для
проверки, так как они не содержат дробных степеней
корреляционных операторов. Предположим, что
ограничены операторы В\В21 и В2ВТ1. Положим У = В\В2Х — Т.
Поскольку У^В\гОВ2ч\ то У2 = В^02В21/\ Пусть ^-
ортонормированная последовательность собственных
векторов оператора В{. Тогда
оо сю
5р Л» - ^ (й%, /») = ^ (О2 УК В7% у^ ВЩ -
оо с»
Значит, 8р02<оо» если только конечен ЗрК2.
Поскольку У2—несимметричный оператор, то проверка
условия существования 5рУ2 также может оказаться
затруднительной. Однако используя неравенство
оо с» оо
2 I (У2ек, ек) | = 2 I (Уек, Уек) |< 2 I Уек || Гек |<
к=1 Л=1 /е=1
,/"
< у 21 *Ч I2 • 21УЧI2 = ^зркт-зркг = 8Р \гу
(так как Зр У*У = Зр УУ*), можно сформулировать
условие абсолютной непрерывности уже в терминах следа
симметричного неотрицательного оператора У*У.
Теорема 4. Пусть [х{ и \х2 — гауссовские меры
со средним О и корреляционными операторами В{ и В2.
Если существует ограниченный оператор V,
удовлетворяющий соотношениям
УВ2=В{-ВЪ 5рГК<оо,
и —I не является точкой спектра оператора V, то
Доказательство. Достаточно лишь показать,
что в том случае, если оператор / + У обратим, т. е.
В2В^Х ограничен, то 6Л> — 1. Пусть бт= — 1 при
некотором т. Тогда, полагая г = В>2ет> будем иметь
(1 + V)г = г + В^ВВ^вЪт= * ~ В12ет»О,
§ 4] АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ ГАУССОБСКИХ МЕР 583
т. е. — 1 является собственным значением оператора 1/,
что невозможно по условию теоремы.
,, Отметим еще одну простую формулу для плотности
одной гауссовской- меры относительно другой в том
случае, когда средние равны нулкь Эта формула имеет
смысл при некоторых дополнительных ограничениях,
однако более удобна, так как при её использовании
не нужно искать собственные векторы и собственные
значения оператора О.
Замечание. Если выполнены условия теоремы 4
и определен 8р V (т. е. ряд ^(Уек9 ек) сходится в каждом
ортонормированием базисе), то имеет место формула
^1(х)=^е1(/ + 1/)ехр{-|(ВГ1^, х)}. (4)
Квадратический функционал (ВТ]Ух9 х) измерим по
мере \х{ в силу результатов в § 6 гл. V, так как Зр^
существует и ЗрУУ<оо. Для доказательства
формулы (4) заметим, что из существования ЗрК вытекает
существование 5р2), а, значит, и сходимость рядов
6*
5Х Ц 108(1+**), %{В11х,ек)21+6:г.
Пусть Рп-~ оператор проектирования на
подпространство, натянутое на ел, ..., еп. Тогда
1+6>
оо
- 2 [(ЗГ'Ч ек)2 - (ВГЧ «*) (В7Ч В^ВТ'вЪь)] -
сю
- 2 [(ВТ\, ек? - (ВГ>>Х, ек) (ВНГ1Х, ек)\ -
со
= !>т У ЦРпВ^'х, екУ-(РпВ2'''х, ек) {В^ВТ1х, ек)} =
•** Нт \{РпВгНгх, В2'1'х)-(РпВ7'/гх, В$В71х)]~
= ((В11-ВГ1)хгх) = {В7,Ух,х).
584 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Далее,
21оВ(1+**)-1ог|(1е1(/ + Л)|-
= 1ог | (1е* (/ + В\г ОВ?'2) | = 1о§ | йе* (/ + У) |.
Подставляя полученные выражения в формулу (2),
получим (4),
§ 5. Эквивалентность и ортогональность мер,
соответствующих стационарным гауссовским процессам
Рассмотрим два вещественных стационарных гаус-
совских процесса \х(1) и ^2(0 на промежутке [—7\ Т].
Таким процессам соответствуют гауссовские меры \х{
и (12 на пространстве 3^2[— 7\ Т] всех функций х{1)>
интегрируемых с квадратом на [—Г, Г]. Нам удобнее
рассматривать пространство комплекснозначных
функций со скалярным произведением
г
(х, у)~ \ х{1)Щ(11.
-г
Пусть М|/(0 = Я/(0> а /?/(*) —корреляционная функция
процесса |/(0- Тогда &/(•) будет средним значением
меры [г/, а ее корреляционный оператор В/ определится
соотношением
г г
(В;х,у)= | | К1({-з)хЦ)у!(з)М(1з.
-т -г
Цель этого параграфа — исследование условий
эквивалентности и ортогональности мер \хх и ц2 указанного
специального вида.
Обозначим через Р] (к) спектральную функцию
процесса 1/(():
Пусть процесс ^/(0 имеет такое спектральное
представление:
1/Ю = М0+/еш <**/<*>. (1)
§ 5] ' ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 585
где У1 (А,) — комплексозначный гауссовский процесс
с некоррелированными приращениями, для которого
М|^(Л2)-^(^)|2 = |^(^)-^(М1.
В дальнейшем будет использоваться пространство Жт
функций §(Х), допускающих представление
т
где ф( •) е ^2[~~ Ту Т]. Пространство Жт совпадает
с пространством целых аналитических функций
экспоненциального типа не выше Г, интегрируемых с
квадратом на вещественной оси. В дальнейшем мы будем
рассматривать функции из Жт лишь на вещественной
оси. Через ЖТ(Р{) обозначим замыкание Жт в метрике
Пространство Жт (Р{) — гильбертово пространство со
скалярным произведением
Исследуем сначала условия эквивалентности и
ортогональности мер, соответствующих процессам, у которых
различаются лишь средние значения.
Пусть /?!(0 = /?2(0, МО-0, а2(*) = <*(*).
Теорема 1. Для эквивалентности мер ц, и \х2
необходимо и достаточно, чтобы функция а {I) при /е[ — Г, Т]
имела представление
а(*)= \ е-шЪ{к)йР{{%\ (2)
где Ь (%) е Жт (Р{). Если это условие выполнено, то
■^7 (I. (•)) = ехР {/ ь (я) йух (л) -1 \ | ь (Х)Г ар, Ц; (3)
ух (А,) — функция, входящая в спектральное
представление %!(/) по формуле (1).
Доказательство. Предположим сначала, что
М-1~Н-2- Как вытекает из теоремы 1 § 4,
|И1(*) = ехр {/(*)-<:},
586 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
где / (х) — измеримый линейный функционал по мере ц{,
а с — некоторая постоянная. В § 6 гл. V установлено,
что всякий измеримый линейный функционал 1(1[(-))
от стационарного гауссовского процесса %х{1) на [■—7\Г]
представим в виде
/(1,(-))=/&а)^,(я),
где Ь (Я) е Жт (Рх). Чтобы найти связь между а{1), Ь (Я)
и величиной с, запишем характеристическую функцию
величины |2(0 (при фиксированном /):
ехр{ш(02-4^1(0)}=М^^^ = М^^^^Й1(-))-
- М ехр{|[& (Я) + 1ге^\ Лух (Я) - с}.
Воспользуемся формулой М^ = ехр \ у М^2 \ при М| = О,
справедливой для всякой гауссовской (в том числе и ком-
плекснозначной) величины. Заметим, что из
вещественности \ (/) вытекает, что йу (Я) = йу (—Я) и йР (—Я) = ^ (Я);
поэтому
м{/[ИЯ) + /г^]^(Я)}2-
- М | [* (Я) + й*'*] йух (Я) | [6 (Я) + 1геЩ йух(-К) -
- М | [6 (Я) + 1ге™] йух (Я) ]"[&(- Я) + 1ге~Щ 1уЖ) =
- \[Ь (Я) + &*"*] [6 (- Я) + йе-»*] <*/?, (Я) =
- | 6 (Я) 6 (- Я) ЙЛ (Я) + 2/2 | 6 (Я) е-«* ^ (Я) - г2*, (0).
Наконец, из вещественности I{%[{-)) вытекает, что
| Й-(Я) йух (Я) = | Щ) ЙЫЛ) - / Й~=Т) ^, (Я).
Поэтому 6 (Я) - Ъ ( - Я), Й(~Я)=У(Я) и
| 6 (Я) 6 (- Я) <//?, (Я) - 11 * (Я) р ЛРХ (Я).
Таким образом,
ехр {1га (/) - { /?, (0) г2} = ехр { - с + у 11 6 (Я) |2 <*/>, (Я) +
+ 1г ] е~ш 6 (Я) <*Л (Я) -1 х2Кх (0)}
$Щ ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 58*
и, значит,
с = 11 | Ь (К) \2йРх(Я), а({)=$е~шЬ {X)йР{(%).
Мы установили и необходимость условий теоремы и
формулу (3).
Перейдем к доказательству достаточности условий
теоремы.
Пусть выполняется формула (2). Введем меру ц,
абсолютно непрерывную относительно меры \х{ и
имеющую плотность —^-, совпадающую с правой частью
равенства (3). Покажем, что меры ^2 и Д совпадают.
Для этого сравним их характеристические функционалы
(характеристические функционалы мер \х и \х( будем
обозначать % и %1 соответственно). Очевидно,
Х2(*) =
, т т т ,
= ехр|/ ]" а(/)г(0Л-у | | /?(' - $)г{1)г{$)(Ис18 \.
Далее,
Х(*НМехр{/ $г№Л*)**]-^Ы-)) =
М ехр
И
- \ |1 * {%) \ЧР{ (X) \ = ехр ! -1]*1 Ь (Я.) |2^, (Я) +
/г г -,
+ уМ !П &(*■) + ' ]*г(/)е'ЛЛ
#1 (Я)
= ехр { \ / г (0 / 16 (X) *-«*+&(_ Я,) в'л] йР1 (А) Л +
' -г
Т Т ч
+ 4/ /г(0*'ЛЛ |г(8)в-'ЛЛ^,(й,) }-Хг(г)
-Г -Г . '
Так как Хг —х» то 1-4 •= (*• Теорема доказана.
588 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Следствие. Из теоремы 1 вытекает, что если при
некотором Т меры ^[ и \х%, соответствующие процессам
61(0 и 11(0 +я (0 на отрезке [ — Т, Т], эквивалентны, то
всегда существует такое продолжение функции а (I) на
всю прямую, что меры \х™ и р,~, соответствующие
указанным процессам на (— оо, оо), также эквивалентны.
В качестве такого продолжения можно взять правую
часть равенства (2) для всех значений /.
Предположим, что для спектральной функции /^ (Я)
существует спектральная плотность ?\(к). Пусть а°°(0 —
указанное выше продолжение а{1), для которого меры у.™
и \х% эквивалентны. Если а (Я) — преобразование Фурье
функции а°°(0, то
а(Я) = 2яй(Я)/1(Я).
Поэтому для эквивалентности мер \1\ и \х2 (это исходные
меры, которые рассматривались в теореме 1) небходимо
и достаточно, чтобы существовало такое продолжение
функции а(1) на ( — оо, оо), что преобразование Фурье
этого продолжения а {к) удовлетворяет соотношению
Тогда в качестве Ь(Х) можно взять 2а} ,1, .
Рассмотрим теперь процессы §у(0 со средними
значениями, равными нулю, и различными корреляционными
функциями #{ (0 и /?2(0- Обозначим через Ж2Т
пространство функций Ь(а, р), представимых в виде
т т
Ь (а, р) - | | в«а-М> ф (а, р) (И аз,
-г -т
где ф —функция, интегрируемая с квадратом на [ — Г, Г]Х
X [— Т, Т]. Через Ж%(Р\) обозначим замыкание Ж%
6 метрике, порожденной скалярным произведением
(*ь Ь2) - / / *, (а, р) М^р) ^, (а) <Н>, (р).
Теорема 2. Ясли N^/(0 = 0, /=1, 2, го для эасяи-
валентности мер щ и р-2 необходимо и достаточно, чтобы
§51 ЭКВИВАЛЕНТНОСТЬ II ОРЮГОНАЛЬНОСТЬ> МЕР 589
существовала такая функция Ь (а, р) из Жт{Р{), что имеет
место представление
ЯЛ( -*) - /?1 (*-*)-/ / е-™+** Ь (а, р) ЛРХ (а) йРг (Ь). (4)
При этом
-^(|,(.)) = ехр{//ф(а)р)^1(а)^Ж) + с}1 (5)
где функция Ф(а, р) связана с Ъ (а, р) соотношением
\ Ф (а, р) ЙМУйЛ (Р) = 6 (а, V) - Ф (а, V), (6)
а
с = - 1п М ехр{ \\ Ф(а, р) ^ (а) 3^(Р) }• (7)
Доказательство. Необходимость.
Предположим, что \х{ ~ \х2. Тогда совпадают лространства
линейных измеримых функционалов по мерам III! и \х2:
5?(\х{) = 3?(\12) (относительно линейных измеримых
функционалов см. § 6 гл. V). Как уже упоминалось, для
стационарного гауссовского процесса |у (*) с М|/(0 = 0
каждый измеримый линейный функционал /(!/)
представим в виде
' (6/) = /§(<*) аУ1 (а).
где §^ЖТ (Т7/). При доказательстве теоремы 2 § 4 была
построена последовательность измеримых функционалов,
образующая полную ортогональную систему в 3?(\\.{)
и З7^) одновременно (это функционалы (В2 я, е*) =»
— /л (я), где ^ — собственные векторы оператора /)).
Пусть
МБ/)*8 \ ёк^Лу^а).
Из ортогональности /& по мерам \х{ и [х2 вытекает, что
О = М | §к(а) 4у, (а) |. #т (а) йу1 (а) -
- \ ёк («) бю (а) АР/ (а), & =^ т.
590 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Снормируем §к так, чтобы
.[|Ыа) №(«)=!,
и пусть при этом
||^(«)Р^2(а)=1+с,.
оо
Из теоремы 2 § 4 вытекает, что 2^<оо. Положим
а=ч п
оо
Ь(ау $) = Цск§к(а)ёк(®
А=1
и покажем, что Ь(а, $) будет удовлетворять
соотношению (4). Рассмотрим функцию
= I [ е-(аШЩ (а, р)^ (а)й/?1 (р) + К}Ц __ 5) _ #2(/-5).
Если г(а)= I е~шц{1)(Н, то
-V
г г
-г -т
= \\ г (а) ^) й (а, 0) ^, (а) «//?, (р) +
+ /|г(а)Р(^,(а)-^2(а))«
оо оо
"21**1/ *(*)е№лр1 (а) Г + 21 / 2(«)Й *Р\ (а) |2 -
А-1 А-1
оо
- / 2 | Л (а) / ЫР) 2 Ф) ^1 (Р) |2 ^ (а) =
А-1
оо
=2<1+с*-Л**(а>№М1г(а)^^,(а)Г=0-
А-1
Используя равенство ф(*, 5) = 1|)($, /)> убеждаемся, что
1|э (/, 5) = 0. Необходимость доказана.
§ 51 ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 59*1
Достаточность. Переходим к доказательству
достаточности условий теоремы и выводу формулы (5).
Предположим, что существует функция Ь(,,.)^Жт(Р\),
удовлетворяющая соотношению (4). Рассмотрим
интегральный оператор
Если Ь(.^)^7^т{Р\), то тогда этот оператор будет
переводить Жт (Р{) в Жт {Р\). В этом легко убедиться,
заметив, что
^.еУг, если 6(.,)еГг
для всякой ограниченной функции §, и что
\\У\\ = ]\\Ь(а^)\>йРМйРЛ$)-
Таким образом, оператор V на У(РТ{РХ) является
ограниченным самосопряженным оператором. А из того, что
он является интегральным с квадратически интегрируем
мым ядром, вытекает, что он вполне непрерывен и
является оператором Гильберта — Шмидта. Обозначим
через §к(а) полную ортонормированную
последовательность собственных функций оператора V, а через Я&
соответствующие им собственные значения. Тогда
оо оо
Ь (а, р) = 2 Хк<§к (а) в* (р), 2 ^ < оо.
По построению функции §к{а) ортогональны в ЖТ(Р{).
Покажем, что они будут ортогональны и в Жт (Р2).
Пусть ф*(/)— последовательность функций из 3?2[ —?\ Т]
такая, что г
\е-*мч№)(И-»8кЫ
при п->оо в смысле сходимости в ЖТ{Р\)> Тогда
т т
| //?2(<-5)ф2(/)^(5)Л^-
- | /л,('-$)ф«(0ф7(5)Л^«
-т -т
т т
= Л Ь(а, р) | <р» ({)е-™сИ \ <р»(8)в-'Р»^ йР{ (а) ЛР1 <р),
-г -г
692
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
Из этого равенства получаем, переходя к пределу
при п->оо:
/ 8к («) Я/(а) ЛР2 (а) ~ $ 8к (<*) Я/(а) ^Л (а) =»
= / / *(<*, Р)«Г/ (а)й!<Н>, (а) ЛРХ (р).
Так как при & =И=/
/ / Ь(а, Р) Я/ (а) ЫР№ (а) <*Л (Р) = О,
то при кф] имеет место равенство
/ 8к (<*) в! («) ^2 (а) я / Я* («) «Г/ («) ^1 («) =» 0.
Таким образом, последовательность ^(а) является
одновременно ортогональной в обоих пространствах
ЖТ{Р\) и З^гС^)- Из формулы (4) вытекает, что й(а,р)
можно выбрать так, чтобы Ь{а, р) = Ь {— а, — р); тогда
#&(<х) можно выбрать так, чтобы #*(а) = ^( —а). При
выполнении этого условия функционалы ^(«)^/(а)
будут вещественными линейными функционалами от
процессов |/(0- В силу замечания к теореме 2 § 4
Н<1 ~ И2 И
0^2
м^(-))=ехР ^^[-^^^^(^р-^а+я,)]
Л-1
Заметим далее, что в силу формулы (15) § 6 гл. V
имеет место формула
Л-1
где
ф(^р)=2таг^<а)^(Р)
Л-1
§ 5] ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 593
Остается заметить, что
/
Ф(а,у)Ь(у,®аР1(у) =
= 1цТхГ^(а)ёкф) = Ь(а, Р)-Ф(о, Р).
6=1
Теорема доказана.
Приведем некоторые достаточные условия
эквивалентности мер в предположении, что существуют
спектральные плотности // (Я) = -тг- Т7/ (Я). Нам понадобится один
вспомогательный результат об ортогональных базисах
в ЖТ(Р\), когда Рх имеет специальный вид.
Лемма. Пусть /, (к) = | ф0 (Я) |2, где ф0 е Ж% и #л (Я) —
произвольный ортонормированный базис в Жт (Р^. Тогда
оо
2|^(Я)Р<^. (8)
Доказательство. Поскольку Жт всюду плотно
В ^г (Л)» то достаточно установить неравенство (8.) для
того случая, когда §А(1)е3^г. При этом
предположении йЪ (Я) фо (А) е ^г+5, следовательно,
Г + 5
-Г-5
где ^(/)е5'2[-Г-5, Г + я]. Так как
оо оо
\ 8к (Л) Фо (Я) Я/(Л) Фо (Л) с?Я = | ^6 (Я) ^7Ш Л (*) ^,
— оо —оо
то в силу равенства Парсеваля
Г + 5
-Г-5
Значит, |^2яфй(0 образуют ортонормированную
систему функций в . &2[— Т-8, Т + 8]. Поэтому из
594 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. V*!
неравенства Бесселя вытекает, что
2я^
или
Т + з
-Т~3
2 Г+$
\ е-ш%{1)с1(\ < | \е~ш\2(11^2Т + 28,
-Т-з
2яЕ|^МФо(^)12<2(Г + 5).
Лемма доказана.
Теорема 3. Пусть \х{ и \х2 — меры, соответствующие
стационарным гауссовским процессам !/(/), Мё/(0 = 0,
имеющим спектральные плотности //(Л). #сла
существует функция ф0(А,)еЖ% а постоянные с{ и с2 такие,
что выполнено неравенство
^1Фо(^)12</1(Я)<с21Фо(Я)|2, (9)
и, кроме того,
я
Пт№<--
то леерь< Ц| и ц2 эквивалентны, каково бы ни было Т.
Доказательство. Положим
Г|(Я,) = с,|фо(Я,)Р,
М) 1Ы*); М*.)<Ы*).
т \ Г, (Я) + Ы*) - /, (X); /2 (Л) > /, (Я.),
М) \ /2(Я); /2(Я)</,(Я),
г |Ма.)-Г,(А); /2^)>А(Я);
М I 0; М*ХМ*).
Обозначим через Д/5 / = 1, 2, 3, 4, меры, соответствующие
гауссовским стационарным процессам на [— Г, Т],
имеющим соответственно спектральные плотности ^ (X).
Поскольку \Х; = Д/+1 * р,4, /=1, 2 (при сложении незави-,
симых процессов спектральные плотности складываются),
то для доказательства эквивалентности ц,, и ц2
достаточно показать, что &2 ~ Й-з или что Д/ ~ |Х1э / = 2, 3.
$Щ ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 5§5
Последнее соотношение одинаково доказывается Аля
/ = 2, 3. Обозначим через Р У(Я) спектральную функцию,
имеющую спектральную плотность //(Я). Пусть^{^(Я)}—
произвольный ортонормированный базис в ЖТ{РХ). Тогда
Ъ (Я) -/, (Я) ...
на основании леммы, полагая -—~ = п (Я), получим
Л (Я)
[) \8кМГаР1(к)-\\8к(х)\ЧР1(*.)]2
к=1
12
*=1
оо
*~1
|;[/|л(л)р^/(л)-/|Л(л)р'^|(А.)]а
11[/и*шрл(я)71(л)^]2
Ё /! ** (я) Р а2 (я) Г] (я) <а • 11 ** (я) р 7, (я) с?я=
оо
= / 21 г* (а.) Р А'МЙ (я)<*я< -^ | л2(я)йя<
так как | к (Я) |< ^ | ^ ^""щ Щ | • Пусть К -
симметричный оператор в Жт (Р{), для которого
Мы установили, что для всякого ортонормирован-
ного базиса {^(Я)} в ЖТ(РХ) выполняется соотношение
оо
Из этого соотношения вытекает, что оператор V — I
является оператором Гильберта — Шмидта.
Пусть §к — последовательность собственных функций
оператора V — /, а ак — соответствующие им
собственные значения. Тогда функция
оо
Ь{а, р)-2 <**$»(<») я* (Р)
к-1
596
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
определена и принадлежит ^°\{РХ\ так как 2<^<°°-
Обозначим через Кк корреляционную функцию процесса
со спектральной плотностью /й, а через г|),(А,)
функцию еш, |/|^Г (она принадлежит У^Т(Р\))- Тогда
#, (*-*)- & (*-*) = / *" <'-*> (<//*, (Я) - <//?, (Я) ) -
оо
= ([V -1) Ъ, *,) = 2 ([V - /] Ф*. Ы (й, *.) ="
оо
= 5] «А (Ф<, 5») (в*. Ф») =
/г = 1
ОО
== 2 «* | е»аЫ^ <//?, (а) | е-'**» (р) <//?, (Р) =
= | [ г«а-^ (а, р) ЙЛ (а) ЛРХ (Р).
Остается воспользоваться теоремой 2. Теорема доказана.
Замечание. Неравенство (9) может нарушаться
на множестве Д конечной меры, для которого
А
Действительно, в этом случае можно ввести меру р,*,
соответствующую стационарному гауссовскому процессу
со спектральной плотностью Гх{к)> уже
удовлетворяющей неравенству (9) так:
Г МД ША,
''*А' 1 с,|ф0(Л)'р, ЛеЛ.
Тогда
г Г /, т-!\<*) I2 .„ ^ г Г/2(я) -/;(Л) т
<оо,
Так ЧТО \1{ ~ \1{1 \12 ~ \1{ И \Х{ ~ \1Г
Найдем достаточные условия ортогональности мер щ
и |х2 в предположении, что /г (%) ^/1 (Л). Рассмотрим
§ 5] ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 597
сначала частный случай, когда /Г{Л)= 1 ^2 . Пусть
меры \хг и \х2 эквивалентны. На основании теоремы 2
можем утверждать существование такой функции
Ь (а, Р), что
/?2 (*-«)- /?1 ('-«)- // е-'^+'^й (а, р)т^?-т
+ Р2
Я^^ТТ^ТТ!
Поскольку функция
Ь(а, Р)-^ &-
5-<оо.
1 + а2 1 + р2
интегрируема с квадратом, то существует производная
а2
д1дз
и
[/?2(^-5)-/?,(/-5)]
■^-[/?2(/-5)-/?,(/-5)] =
= Ие~Ш+*$ 1+«> 1+Рр2Н«,РМа^.
1+а2 1+Р2
Полагая /? (О = /?2 (0 — #1 (/)> находим, что
Г Г 2Г
/ /[/?"(г-$)]2^^==-^ / [/?,,(0]212Г-П^<
-Г -Г -2Г
Используя соотношение
2Т
| [/?"(/)]2|2Г-г|й/ =
-2Г
со оо
698
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
а также равенство . т = 1 + Я2, находим, что в слу-
чае /1 (Я) = . , ^2 эквивалентность мер влечет
неравенство
оо оо
зш»Г(а-р) Ма)-Ма) Мр) -/, (Р)
] ] (а-р) М«) /, (Р) м
— оо —оо
Значит, если при некотором Г>0
со со
Г Гзт'Г(а-Р) /2(а)-Л(а) /, (Р) - /, (р) , .,
} }—т*чГ) ш ш~^^= + °°.
— оо — оо
то меры \х{ и \х2) соответствующие стационарным
процессам на [— Т, Т] при условии, что /д (Я) = { ^ ,
будут ортогональны.
Все предыдущие рассуждения остаются в силе, если
при некоторых с{ и с2 выполняется неравенство
Тн^^М^Т+Т*"-
Пусть теперь Ф0(Я) — целая аналитическая функция
экспоненциального типа не выше 5, для которой
) тгт
ах .
< оо.
^)|Фо(Я)|
— оо
Пусть спектральная плотность МЯ) при некоторых с{
и с2 удовлетвовяет неравенству
( 1 + Л») |ф0 (Я) |2 < Л М < ( ! + Я2) ^ Щ |2 •
Рассмотрим процессы
оо
1/(0= 1ем<р0Щау,{1),
§ 5] ЭКВИВАЛЕНТНОСТЬ И ОРТОГОНАЛЬНОСТЬ МЕР 599
где У! (к) взято из представления (1). Легко видеть,
что фоЕ!3^,), поэтому, взяв последовательность
ФяМ— \ /гп(и)еаийи9 сходящуюся к ф0(А) в ЖТ{Р\\
— 3
будем иметь
1у (0 - Ига | еш | е аиНп (и) йи йу, (Я) =
= Нт I %1 (/ + и) Нп (и) йи.
— 3
Таким образом, процесс |у(/) на [—Г, Г]
определяется по значению процесса §/(*) на [ — Г —5, Г + 5].
Спектральная плотность процесса \\{1) равна ^(Х) =
= //(Я)|Фо(Я)|2, так что -г^<^1(я)<т^г.
По доказанно!му меры Д, и р,2 ортогональны, если
СГ8»п»Г(а-Р)Ма)-Ыа)Ыр)-Ыр) . •.» , оп /1{Л
Л (а-р)2 Ш МРГ~ " Р~+ * *'
} — г Т Т
так как ——^^.^А___11_# Но тогда будут ортогональны
/1 А
и меры \х{ и ц2*). Заметим, наконец, что функция
(1 +/А)<Ро(А) будет также целой экспоненциального типа
не выше 5. Итак, доказана
Теорема 4. Если \Х[ и ц2—меры>,
соответствующие стационарным гауссовским процессам на [—Г, Т]
со спектральными плотностями //(Я), /= 1, 2, и средними
значениями О, причем существует целая аналитическая
функция экспоненциального типа не выше 8 <Т такая,
что при некоторых с{> 0 и с2 > 0 выполняется
неравенство с{ ^ | ф0 (Я) |2 /} (А,) ^ с2, то соотношение
Л Л (а-р)2 /,(а) /,(Р) м
влечет ортогональность мер \х{ и \х2.
*) Считаем, что щ соответствуют процессам |/ (/) на отрезке
[-Г-5. Г+5].
600 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ4 УЦ
Замечание. Для всякого а > 0 функция
где т>а+1, такова, что
0< |?'(|*<«1*ТЙ1?г) к Ч'О^ТТпИ < "•
Функция Ф0(Я) целая, экспоненциального типа не
выше те. Функции такого вида можно использовать
при проверке условий теоремы 3 и 4.
Следствие. Если 1{(К) и Ы^)~ дробнорациональ-
ные функции, то необходимым и достаточным
условием эквивалентности мер \1{ и \х2 является условие
Доказательство. Если !\(Х)>0, то для МЯ) вы~
полнено условие как теоремы 3, так и теоремы 4 с
функциями ф0(Я) вида, указанного в предыдущем
замечании. Если
ИтШ=1, то Щ^ГШ.=,0(Х-1)
Л->оо /1 (А) М \А)
и можно воспользоваться теоремой 3. При нарушении
этого условия применима теорема 4. Если /^(А,)
обращается в нуль, то вместо }{(Х) можно рассмотреть !\(Х)
такое, что /[(Я) > 0 и Нт /, (Я)//; (Я) = 1.
§6. Общие свойства плотностей мер,
соответствующих марковским процессам
Пусть на некотором числовом множестве Т заданы
два случайных процесса ^(О и %2(0 со значениями из
некоторого пространства 96 с а-алгеброй измеримых
множеств 91. Обозначим через |иТ меры,
соответствующие случайным процессам ^(/), определенным на а-ал-
гебре §т, порожденной цилиндрическими множествами
над (— оо, х)[)Т. Через ]х1 будем обозначать \х™.
Предположим, что |л2<^1 и р(|1(-)) = -5~-(|1(-))- ТогДа
§ 6] ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР 601
для всех т будет также ^ <С |л*, причем
Р,(1«(-)) = -7т(11(-)) = М(р(|,(.))1?1т).
где условное математическое ожидание берется на
вероятностном пространстве {ЗГТ(36)> 8^, щ), а ?ГТ{Щ~-
пространство всех функций на Т со значениями из 36.
Легко видеть, что процесс {рт, $т} является
мартингалом, удовлетворяющим условию Мрт=1. С другой
стороны, всякий неотрицательный мартингал {рт, §т},
удовлетворяющий условию Мрт=1, может в'ыступать в
качестве плотности \1Х2 относительно \к[ для некоторой пары
процессов 1\(-) и |2(*)' Этот результат, справедливый
для любых процессов, мало содержателен. Более
интересные результаты получаются, если предположить,
что %1 (I) и 12 (0 являются процессами из некоторого более
узкого класса процессов. В этом параграфе
рассматривается случай, когда оба процесса являются
марковскими.
Пусть %х{1) и %2(0 — марковские процессы,
определенные на интервале [а, Ъ) и принимающие значения из
сепарабельного метрического пространства {36, 31),
(21—а-алгебра борелевских множеств). Через @~[а, н будем
обозначать пространство всех функций со значениями
из 36, определенных на [а, р], а через §[а, р] —а-алгебру
подмножеств ^~[а, р], порожденную цилиндрическими
множествами. Пусть р*х [а И(Л) — мера на §[а> м, построенная
по переходным вероятностям процесса ^ (*) при условии,
что ^(а) = #. Из марковского характера процесса
вытекает, что для цилиндрических множеств ■ Л вида
А = Ах П Л2 П Л3, где А{ и Л3 — цилиндрические множества
из §[0} с] и §[С, ь) соответственно, а Л2 — цилиндрическое
множество из §[С], т. е. множество вида {х(-):х(с)&Е}9
справедлива формула
Р*[а. ьЛА) = \ |х[в1 с] (Л,; ау)^уЛСя Ь){А3), (1)
где \х1[а с] — мера, соответствующая марковскому
процессу 6,(0 на [а, с] (это мера на §к с]), а ^ С](Л2; Л2) -
602 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
мера, определяемая равенством
(по А2 это мера на §[С]). Заметим, что под ЛтОЛгГМз
мы понимаем цилиндрическое множество из $[а, ьъ
содержащее все те функции *(•), ограничения которых на
[а, с], [с, с] и [с, Ь) соответственно принадлежат А{, А2
и Л3. Аналогично определяется и АХ{]А2. Установим
один вспомогательный результат. Напомним, что
а-алгебра 6 называется сепарабельной, если существует такая
последовательность множеств Ль Аъ ..., что €
совпадает с минимальной а-алгеброй, содержащей все
множества Ак.
Лемма. Пусть {35, 93) и (<3/, (&) — два измеримых
пространства, \Х[ и \12 — вероятностные меры на 35 и для
каждого х е 35 заданы вероятностные меры VI (х, С) и
ч2{х, С) на 6 такие, что \к{х, С)Ъ-измеримо для всех
Се 6. Определим меры пк на 33 X 6 равенством
пк(ВХС)=\рк(йх)чк(х, С), ДеЭЗ, Се!
в
Если л2 <С щ и существует сепарабельная а-алгебра -
©о, пополнение которой по мере У\(ху С) содержит К
почти для всех х по мере щ , то \х2 «С \1\ и почти для
всех х по мере \\.2 также V2 (х, • ) <^ у{ (х, •).
Доказательство. Положим
Тогда для всех В е 33 и С е 6 имеем
п2 (В X С) = | | р (а:, */К (*, </*/)
и{ (ах) =
X
[|р(*>#0М*, ^/ОЗМ^)- (2)
§6]
ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР Ш
Взяв С = 3^ находим, что
&(х)~-\?{х,у)ъ(х.<1у). (3)
Используя (2) и (3), получаем
пг(В X С) = | V2 {х, С) \12 (ах) «||р(х,г/) V! (х, йу) |х2 {их),
В ВС
где
Р (*, У) = Р (*, #) Г / р (х, у') чг{х, а;/)] , (4)
Значит, для почти всех х по мере ц2 Для каждого С
выполняется соотношение
V2 (х, С) =^] р (*, у) V, (л:, йу). (5)
Пусть Сл — последовательность множеств,
порождающих й0. Тогда можно указать такое множество /Гс=33,
что 112(В*)=1 и для ^бй* и всех Ск справедливо
соотношение
V2 (X, Ск)=* | р (^, у) V! (*, ^).
Но тогда и для всех СеК0 будет также выполняться
равенство (5), а значит, это равенство выполняется и
для всех С из пополнения К0 по мере V! (х, •). Лемма
доказана.
Заметим, что для стохастически непрерывных
процессов со значениями из сепарабельного пространства
всегда молено указать такую сепарабельную а-алгебру §°
(это а-алгебра, порожденная цилиндрическими
множествами над счетным, всюду плотным в области,
определения множеством значений аргумента процесса), что
пополнение §° по мере, соответствующей процессу,
содержит Й- Применяя доказанную лемму к мерам \х1[а ь],
представленным равенством (1), убеждаемся, что почти
для всех х по мере, являющейся распределением %2(с)>
^1, (с, ь) < ^х, [с, ьу ПУСТЬ Р[а, с] обозначает плотность
меры \1*а с] относительно \11[а с]9 если в качестве
аргумента в эту плотность подставить ^(0 (мы считаем, что
604 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
процессы ^(0 заданы на некотором фиксированном
вероятностном пространстве {й, 23, Р}). Аналогично
через ру, [с, ъ] обозначим плотность меры \& [с Ъ)
относительно \\}у [с Ъ] с тем же аргументом. Тогда из формулы (1),
леммы и формулы (4) вытекает соотношение
Р[а, Ь) ^ Р[а, с] Р§, (с), [с, Ь] • (Щ
Обозначим через 33[0, ед подалгебру в вероятностном
пространстве {й, 23, Р}, порожденную величинами ^ (() при
/<=[а, р]. Величины р[а с] и р^(с) [с ь] измеримы
соответственно относительно 23[а с] и 93[с ь). Возьмем
произвольное разбиение отрезка [а, ^]:а = ^^<^^ < ... <^к = I. Из
формулы (6) вытекает, что
р[в''1 = р['.''.] Ц,рЧ>уИ^+Т (7)
Используя формулу (6), докажем теорему.
Теорема 1. Если %г (/) и |2 (0 являются стохастически
непрерывными марковскими процессами, то составной
процесс {^ {1)\ р[а Л также является марковским.
Доказательство. Достаточно показать, что для
всякой непрерывной ограниченной функции 1{х,з) двух
переменных х^^ и 5ЕЙ1 выполняется при а<1х<1
соотношение
ЩЫИ 9[а, ,)\%, *,,) = Щ№*)> Рю. ^ВД. Р[в. .])' <8>
Поскольку Р[в1 п = р[а1 ^р^ ^ ф то
'(М')> Р[а, *}) = Ф(Б1(0. Р[в, *,]• Рб,Ю. №.«)'
где ф(х, 51? 52) —непрерывная ограниченная функция на
36 X Й1 X 1Й1. Предположим сначала, что ф(х, 5!, 52) =■
= ф(^, 52)'ф(51). Тогда, используя измеримость ф(|](0>
Н\Щ, [/, *]) отн°сительно 23^ п и марковский характер |, (0,
будем иметь
" * (Р[«. *,]) М (Ф & О- Рб, №>. [*,. «) 1*1 С)) =
- М (* (Р[а, /41) Ф & (0, Р5, (<1), р,, д) | II (',). Р[в. ,^
*6]
ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР
605
Так как I входит в формулу (8) линейно, а линейными
комбинациями вида
можно аппроксимировать любую непрерывную
функцию ф(л:, 5Ь 52), то этим формула (8) установлена и
теорема доказана.
Замечание. Предположим, что для всех I е [а, Ь]
и разбиений отрезка [а, I] выполняется формула (7), где
р[а г] и р^ {1 V ги и , некоторые величины, измеримые
относительно 23[а,*] и 23[/г */+1]« Тогда, если %х(1) является
марковским процессом, то таким будет и процесс |2(0.
причем вероятности перехода процесса ^2(0
определяются равенством
Р(2)(*„ х, 12, Л)-М(Хд(61(/0.)рв1(<1)1р(1Л||6,('|))В1ОТ-,.
Действительно, для любого набора множеств Аи ..., Ак
из % имеем
МхлДШ)---х^(12('й)) =
к
- м^, & в)) р,в. /,, Д хА, (I, (*,)) р61 <,,_,,, [,,_,. ,у1 х
ХМ(Ч(Б.(М)Ре1Л_1,.р.-1.'ь1|8[^.-,])-
хр(2)й-Л1(и4, лк).
Из этого соотношения и вытекает утверждаемое.
Рассмотрим построение функции р[а п по
вероятностям перехода процессов ^{{1) и |2(0- Вместе с тем
найдем некоторые достаточные условия абсолютной
непрерывности мер, соответствующих этим процессам. Из
леммы вытекает, что абсолютная непрерывность \х2
относительно \х{ влечет абсолютную непрерывность
вероятности перехода Р{2)Ц, х, 8, А) процесса |2(0 (как функ-
606 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ.'VII,
ции Л).относительно цероягности перехода Р(1) (/, х, $, А)
процесса ^ (/) почти для всех х по мере, являющейся
распределением 6г(0- Положим
(если Р(2) для данного л: не абсолютно непрерывно
относительно Р(1), то р обозначает производную
абсолютно непрерывной компоненты Р{2) относительно Р(1)).
Пусть далее ра{у) обозначает плотность распределения
величины 12(а) относительно распределения величины
%{ (а). Если а = /0 < 1{ < ... < 1п = Ь — некоторое
разбиение [а, Ь], то
Р«(Ы«))Пр(<А. ^1 С*). '* + !> М'а-ц))
будет совпадать с плотностью меры [х2п) относительно ц{й),
где ц|я) — сужение меры ц, на а-алгебру §л , аЛп-
конечное множество значений аргумента I: Лп =
= {/0, '1, ...» *«}• Если ЛЛс:ЛЛ+1, то существует предел
Нтр*=Ит—$з- <&,(•))
(с вероятностью 1). Если Л = ^Л„ всюду плотно на
п
[а, 6], а процесс \х (/) стохастически непрерывен, то
пополнение §А по мере \х1 будет содержать §[а Ь] и,
значит, Нт рп будет совпадать с р{а Ь].
Теорема 2. #г/сгб Я(1)(/, я, 5, А), /=1,2, — ве-
роятности перехода двух марковских процессов ^ (/) и
6»(0» определенных на [а, 6]. .Села выполняются условия:
а) распределение 12(а) абсолютно непрерывно
относительно распределения %х (а) с плотностью ра (х);
б) <Эля всех х^.36, а^/<5^6 >^ра Р(2) (/, я, $, •)
абсолютно непрерывна относительно меры Р(1) (/, 5,5 •)
с плотностью р(/, я, 5, у);
в) существует такая постоянная с> что
| 1од'р (/, *, 5, у) Р(2) (/, л:, 5, йу) < с (5 - /),
*§!
ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР
6)7
то мера \12 абсолютно непрерывна относительно щ и
= Нт Ра(1Ла))Т[р(1пн, 1х(1ян), и+и Ь ('«*+!)). (Ю)
где а=1п0< ... </лл = й и множества Лп — {{пк9 к = 0,..., /г}
удовлетворяют условиям: Ллс:Лл+1 & ^Л,г всюду плотно
п
в [а, 6].
Доказательство. Введем процесс 5з(/), у
которого вероятности перехода совпадают с вероятностями,
перехода процесса !&0О» а распределение ^3(^)
совпадает с распределением %\(а). Пусть ^ — мера,
соответствующая процессу !3@), а у^9 как и выше, сужение
меры р. на а-алгебру 8Л * если \^{^п^ ^ — О» •••» п)-
Тогда, как легко видеть,
2 (Ы-)) = Ра(Ыа)),
^6
1 к««
IX— 1
Очевидно, что
"т^з-<{,{«))-Р««з(«)).
С вероятностью 1 существует и предел
п-1
Обозначим его р'. Для выполнения соотношения ц3 <С*ц
достаточно, чтобы Мр' = 1.' Для этого в силу замечания
к теореме 2 § I достаточно, чтобы было ограниченным
выражение
п-\
1а- М ПрСл* II ('„*), '«* + !. б1(*я* + 1))Х
А«0 .
п-1
X 10« ПйСя*. &1 ('«*)* '/!* + !. 51<'/ИЬ + 1) )•
А=0
608
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР |ГЛ* VII
Используя равенство
м(р(^, ьли), и+и м^+1))1и^))~1,
находим
п—1
/Л=М Др(*яЛ, &('«*). *„* + !, Ы^-н))Х
X 2 1оВР('/1*. М'п*)> 'иЛ + 1» 1\{*пк + \)) =
= М 21 Цр('яЙ1 Ё1 ('ял)э 'яЛ + 1, ?1 (^ + 1>) X
X | 1оер(/«/, ?,('«/), '„ж, У)Р{2Чи 1Л*ш)> *ы+1> ЛУ)<
д-1
/«о
Следовательно, М'З^М-ь Из ^ Из- Значит, м^^Ма-
Формула (10) является следствием соотношения
Теорема доказана.
Рассмотрим вопрос о построении марковских
процессов |2(0> для которых соответствующая мера ц2
абсолютно непрерывна относительно меры \хи
соответствующей данному марковскому процессу ^ (/).
Теорема 3. Пусть а = /л0< ... <{пп =
Ь—последовательность разбиений промежутка [а, Ь\ для которой
множества Ап = \1пк, & = О, ..., п) образуют
возрастающую последовательность и \^Ап всюду плотна на [а, Ь].
п
Пусть для каждого п определена измеримая по х, у
функция апЦ> х, $, у), х,.у^9в, а^^<5^6,
удовлетворяющая условиям'.
1) существует предел в смысле сходимости по
вероятности
Т)= Нт ЦаЛи %\Упк)> *пк+и 1Л*пк+1))1
п+оо А—0
§6]
ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР
609
2) равномерно по х
\еа^х'8'у)апа, х, з, у)Р{Х)(и х, 5, ау)-0(8-Ъ
3) для всех п, &, х
Тогда мера \х2, определенная на %[а,ь] равенством
\12(А)=М%А(1Л'))е\
будет соответствовать некоторому процессу Маркова
на [а, Ь].
Доказательство. Убедимся сначала, что мера р,2
является вероятностной, т. е. что Ме^ = \. Пусть
п-\
Тогда из условия 3) теоремы вытекает, что
МЛ* = | Р& (а)е=ах0} Д | А^' **• '«*+!■ **+!> X
6=0
X Р 1) (1пк> хк> *пк+Ь Лхк+1)= 1.
С другой стороны, в силу условия 2),
&=о 7=0
X «л СлЬ #Ь 'п* + 1> */г + 1)^ ('пй> хк> ^пк+Ъ ^хкЛ-\)'
Таким образом, М^МпА ограничено, значит, е*п
равномерно относительно п интегрируемо и в соотношении
МеУ]п = 1 можно перейти к пределу под знаком
математического ожидания. Чтобы убедиться, что мера \х2
соответствует процессу Маркова, рассмотрим функцию
Г](0= Нт 2 ап(*пк> ЬЛ*пк)> *пк + 1> ЪхУпк+д)
п^°° *пк<*
1/2%® и- и- Гихман. А. В. Скороход
610 АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ МЕР [ГЛ. VII
(предел понимается в смысле сходимости по
вероятности). Покажем, что этот предел существует для всех
^е[а, Ъ] и совпадает с величиной
1пМ(ег,|33[0,,1)=Пт1пМ(^|33[о,^)
(предельный переход под знаком математического
ожидания возможен в силу равномерной интегрируемости А).
При /еул„ имеет место равенство
Поэтому при /е(^Ля Нтт]п существует. Если же
п
1п!<1<1Ш+ъ то
1пк<г
= 1п М (АС"/' ^^ ^' |1(^+1})|%^
Из условий 2) и 3) вытекает, что
МеМЧг^(М' 'лу+гМ'лу+1) х
ХО„(<п/, &1('п/)> *п/ + Ь ^1(^/+1))->0
при п—>оо равномерно относительно /. Используя то,
что величина ехр{аЛ(/п/> & ('*/)> *л/+1> &, Упц.х))
равномерно интегрируема относительно /, а также сходимость
этой величины к 1 по вероятности, находим, что в смысле
сходимости по вероятности
1п М (А ('«У *1 Спу)» 'пу+г *1 Спу+1)) 123[а д) _> о.
Существование г|(0 доказано. Пусть а<с<Ь и
р[в1 с] = ехр (л (с)}, 9[с> Ъ] = ехр {т|(6) —л (<0>- Очевидно, р[с ^
измеримо относительно 35[С> ^. Воспользовавшись
замечанием к теореме 1, и получаем доказательство теоремы.
Рассмотрим тот частный случай, когда ^ (<) и ^2(0
являются стохастически непрерывными процессами с
независимыми приращениями, определенными на [а, Ь],
^(а) = 0. Пусть для промежутка [а, р] с [а, Ь] Д^й
обозначает меру, соответствующую процессу ^ (0 — ^ (а)
при ^е[а, Р]. Тогда соотношение Ц2 ^ Ш влечет
соотношение Д|2> р] <С Д[^ м. Пусть 23[а р, обозначает а-алгебру,
§6]
ОБЩИЕ СВОЙСТВА ПЛОТНОСТЕЙ МЕР
611
порожденную величинами II {*) — 1\ {а) при *е[а, р]
Величина
^6м (1( и
является 93^ ^-измеримой. Возьмем произвольное
разбиение отрезка [а, Ь]: а = /0<*1< • • • <^=86. Рассмотрим
произведение измеримыхпространств(^"[^|^+1]>§рА>^])>
а на нем произведение мер
Из того, что процессы ^ (/) являются процессами с
независимыми приращениями, вытекает, что эти
произведения переходят в меры \хь при взаимно однозначном
измеримом отображении произведения указанных
пространств В (&~[а, Ь], 5[а, Ь)) ПО формуле
* (0 = 2 ** С*) + *т+1 (0, *т < * < (
Лг=1
т+1>
Поэтому
Сомножители в правой части независимы между собой.
Предположим, что меры III! и \х2 эквивалентны. Тогда
плотности положительны и последнее произведение
можно логарифмировать. Из вышесказанного вытекает
следующая
Теорема 4. Для того чтобы
были плотностями для эквивалентных мер,
соответствующих процессам с независимыми приращениями,
рассматриваемыми на [а, I], необходимо и достаточно,,
чтобы составной процесс {^ (I), 1п р[а Л был процессом
с независимыми приращениями, р, . было &
^-измеримо и выполнялось равенство Мр[а ^ = 1.
7220*
ГЛАВА VIII
ИЗМЕРИМЫЕ ФУНКЦИИ НА ГИЛЬБЕРТОВЫХ
ПРОСТРАНСТВАХ
§ 1. Измеримые линейные функционалы и операторы
на гильбертовом пространстве
Рассмотрим измеримое гильбертово пространство
(36, 23), на котором определена мера \х. Всякий
непрерывный линейный функционал /(л:), определенный на 36,
очевидно будет 23-измерим. Известно, что если
последовательность непрерывных линейных функционалов 1п(х)
сходится к некоторому пределу/(я) для всех х, то этот
предел также будет непрерывным линейным
функционалом на 36. Дело меняется, если требовать, чтобы 1п{х)
имело предел не для всех х, а лишь на множестве й
таком, что ц(0)=1. Естественно функции 1{х),
являющиеся такими пределами, назвать ©-измеримыми
линейными функционалами. Как пределы
последовательности измеримых функций они также будут 23-изме-
римыми. Из соотношений
Нт 1п {ах + $у) = а Нт 1п (х) + р Нт 1п (у)
вытекает, что область определения Вг функционала 1(х)
(мы считаем, что он определен всюду, где существует
соответствующий предел) является линейным
многообразием и что 1(х) на /)/ является линейным
(аддитивным и однородным) функционалом. Будем
рассматривать в дальнейшем невырожденные меры ц, для которых
\х(Ь) = 0 для всякого собственного подпространства!
пространства 36. Поскольку ^(0/)== 1, то Ь/ плотно в 36.
Таким образом, если /(л:) —измеримый в указанном
смысле функционал, то: 1) он определен на 23-измеримом
§ 1] ИЗМЕРИМЫЕ ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ОПЕРАТОРЫ 613
линейном многообразии Вг таком, что \1{Оь)= 1; 2) 1{х)
является ^-измеримой функцией; 3) 1{х) линейно на Ьь.
Оказывается этих условий и достаточно, чтобы 1(х)
было ^-измеримым. Это вытекает из следующей теоремы.
Теорема 1. Если функция I (х) удовлетворяет
условиям 1) — 3), то существует такая последовательность
непрерывных функционалов 1п{х), что
I (х) = Нт 1п (х) (тос! м^)-
Доказательство. Построим последовательность
непрерывных функционалов 1п(х), которая бы сходилась
к 1{х) по мере |1. Поскольку из такой
последовательности можно выбрать подпоследовательность, которая
будет сходиться почти всюду по мере \х, то тем самым
теорема будет доказана. Пусть 5, = {х: | / (х) | < с}.
Поскольку Нт |лф/ —5<.) = 0, то для каждого е>0
можно указать такое с и компакт К с: $,, что ц(/)/ —/С)<е.
Не ограничивая общности, можно считать К выпуклым и
симметричным, поскольку $<, такое же. Обозначим через
5? линейную оболочку множества К и введем в 3? норму
так, чтобы К стало единичной сферой. Выберем К так,
что 3? с такой нормой (в отличие от нормы в $В будем
обозначать ее | • \к) будет полным и сепарабельным.
Функционал 1(х) — ограниченный линейный функционал
на 3 и, следовательно, он непрерывен в норме | • \к.
В силу 23-измеримости К вытекает, что 23-измеримыми
будут все борелевские множества 3!. Обозначим 33'
а-алгебру борелевских множеств 5?, а через ц' сужение
меры \х на ЗУ. Можно указать такой компакт К\ в 3,
для которого К\<^К и \х(К — К})<г. Покажем теперь,
что 1{х) на К\ является функцией, непрерывной в
обычном смысле. Пусть хп->х0 и хп^К\. Тогда эта
последовательность компактна в 3 и имеет единственную
предельную точку х0. Значит, хп->х0 в Й7, а поэтому
и / (хп) -> I (х0). Из непрерывности 1{х) на компакте К\
вытекает равномерная непрерывность, поэтому для
всякого р>0 можно указать такое 6>0, что при х,
у^К\ из\х — у\<6 вытекает неравенство! 1{х) — 1(у) |<р.
Пусть N — такое конечномерное подпространство, что
Ы[\К\ образует б-сеть в К{. Обозначим через 1м(х)
продолжение 1{х). с N (на всяком конечномерном
20 И. И. Гихман, А. В. Скороход
614
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
подпространстве N аЗ? 1(х) непрерывно) на все 96 без
увеличения нормы (такое продолжение существует по
теореме Хана —Банаха). Очевидно, такое продолжение
сохраняет модуль непрерывности, значит, 11^(х) — 1ы{у) I <Р
при | х — у | < 6. Поэтому для х е К\
\1мМ-Нх)\<\1мМ-1м(х')\ + \Пх)-Пх')1
где /б]У таково, что | л: — я'|<6, следовательно, при
х^ К\ 11м (х) ~ I (х) I ^ 2р. Для данных е > 0 и р > 0 мы
построили непрерывный линейный функционал, для
которого
\х({х: \1ы{х)-1{х)\>2р})<2е.
Теорема доказана.
Следствие. Если I(х) — измеримый функционал и
3?п — последовательность конечномерных подпространств
такая, что 3?п^01 и [)3?п плотно в 35, а Рп —оператор
проектирования на 3?п, то 1{Рпх) сходится по мере \х
к 1(х). Это вытекает из того, что в качестве
подпространства Ы9 указанного в доказательстве, можно
выбирать подпространства из последовательности 3?п, а
продолжение без увеличения нормы можно строить как1(Рпх).
Чтобы построить пространство всех ^-измеримых
функционалов, удобно использовать характеристический
функционал Ц)(г) меры \х. Пусть последовательность
непрерывных функционалов (гп, х) сходится по мере \х
к некоторому измеримому функционалу 1(х). Тогда для
всякого вещественного I
Нт ехр {«(г„ - гт, л:)} = 1.
п, т-»<»
Значит, и
Нт ср(*(2я-гт)) =
п, т->оа
= Нт I ехр{И(гп — гт9 х)}\х(с1х)= 1. (1)
Пусть
§ 1] ИЗМЕРИМЫЕ ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ОПЕРАТОРЫ 615
Тогда необходимым и достаточным условием
существования предела по мере \х у последовательности (гп, х)
является условие
Нт к(гп — 2т) = 0.
п. т-»°°
Необходимость этого условия вытекает из (1) и
теоремы о предельном переходе под знаком интеграла.
Чтобы установить достаточность, заметим, что
= я |(1-*-1<*.*>1)|1(Жс).
Поэтому для всякого е>0
^({*: I (гп- гт х) \>е})< — к{гп-гт)(1 - е~*)~\
откуда и вытекает сходимость (гп, х) по мере [х.
Поскольку
к (г, + г2) = я | (1 - е~\ (*■ *)+(*. *> I) ^ (Лс) <
<я |(1-е-1^ь*)1-1(а.*)1)^(^)<я; |(1-е-1(г..*)1)^(^) +
+ я | (1 - е-'<*■ х")\1 {ах) = 6(г{) + к(г2),
то 36 можно рассматривать как метрическое
пространство с метрикой
г(х, у) = к(х-у).
Пусть 36 обозначает пополнение 36 в метрике г.
Каждый элемент из 36 можно сопоставить некоторому
^-измеримому функционалу 1(х): х «—> /, если существует
последовательность гп в 36, для которой г(гп> л;)->0
и (гпУ х)->1(х) по мере \х. Обозначим пространство всех
^-измеримых функционалов через 2>(\х). Будем
отождествлять функционалы, которые совпадают почти всюду
по мере \х. Тогда соответствие 5 между 36 и 3?{\1)
взаимно однозначно. Если ввести в 3?{\*) расстояние
20*
616
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
то тогда приведенное выше соответствие является
изометрическим. Поэтому естественно пространства 36
и 3? (\1) просто отождествить, что мы всегда и будем
делать в дальнейшем.
Отхметим еще одну особенность пространства 36
с метрикой г. Характеристический функционал меры \х
может быть продолжен по непрерывности в метрике г
на все 36. Это продолжение можно записать в виде
Ф (/) = Г е1^х)\л{йх)
(здесь / — измеримый функционал, рассматриваемый как
элемент §6 = 36{\х)). Покажем, что $ является в
некотором смысле наиболее широким пространством, на
которое продолжается ср(г) по непрерывности.
Пусть Щ — некоторое линейное метрическое
пространство с метрикой р, причем р(л:, у) = р(0, х — у) и ф(г)
непрерывно в метрике р на 36 и продолжимо по
непрерывности на Щ. Поскольку ф непрерывно в метрике р,
то для всякого е>0 можно указать такое 6>0, что
Ке (1 — ср (г)) < в, если р (0, г) < 6. Тогда, используя
неравенство
1Ф(21)-Ф(22) К / I 1 -**-*■*> 111 (<**)<
<]/ |2(1-со5(21-22, *)|л(ЛсХ Уг2Ке(1-ф(21-22)),
находим, что при Ке(1 — <р{г)) <е
п
Ке (1 - ф (пг)) < 2 | ф ((к - 1) г) - ф (кг) | < п \2г.
Поэтому при р(0, г)<6
со
к(г)= | Не(1-Ф(^))-т^- =
— со
• 1*|<я I Ц>п
§ 1] ИЗМЕРИМЫЕ ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ОПЕРАТОРЫ 617
Значит, если р (гп, гт) -> 0, то к {гп — гт) -> 0, так что Щ
может быть изометрически вложено в некоторое
подмножество 95.
Пространство 95 существенно шире 96, так как
содержит, например, пространства $??, получаемые
пополнением 96 в скалярном произведении (х, у)„ = (Вх> у),
где В — такой ядерный оператор, что ср(х) непрерывен
в скалярном произведении (Вг, г).
Наряду с пространством всех измеримых
функционалов 35 \\л) можно рассмотреть пространство 35^2){\1)
всех квадратично интегрируемых линейных
функционалов. Однако это пространство может состоять из
одного нуля. Если у меры \х существует конечный
корреляционный оператор С, то 2?® (р) будет содержать
пополнение 96 в скалярном произведении {Сх, у), но не
обязательно будет совпадать с этим пополнением.
Более того, может случиться, что (х, г)2 \х(с1х)= + оо
для всех гфОу а в то же время 35{2)(\х) может содержать
отличные от нуля элементы.
В качестве примера рассмотрим меру ц, являющуюся
распределением случайного элемента | вида
с»
к-1
где {ек} — ортонормированный базис, ^ —
последовательность одинаково распределенных независимых
случайных величин с устойчивыми распределениями:
Ме^-ехр{/у5-Ма}.
Пусть сначала у = 0> а>1. Тогда (^, г) Ихмеет
устойчивое распределение с тем же показателем а. Поэтому
и для всякого функционала 1(х) из 35 {\л)
Значит, I I2 (х) \х {их) < оо лишь в том случае, когда
1(х) = 0.
Если а>1, у=^=0, то, взяв последовательность
п п
х^ И^ТГе^ бУдем иметь: & гп)=* ^ 2 %• Поэтому
/г-1 к~\
618
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
с вероятностью 1, т. е. почти всюду по мере \х,
существует предел
Нт {х, гп)=Щк = у.
Очевидно, что 1(х) = \\т(х, гп) принадлежит 3?{2)(\1).
П->оо
С другой стороны, (г, х) будет иметь устойчивое
распределение с показателем а и, значит,
Г {г, х)2 \х{их) = + оо при гфО.
Эти примеры показывают, что в общем случае
пространство 56{2){\х) рассматривать неестественно.
Измеримые линейные операторы. Как и в случае
измеримых функционалов, измеримые линейные
операторы естественно определять как пределы по мере \х
последовательности непрерывных операторов. Поскольку
можно рассматривать либо сильную либо слабую
сходимость последовательности Апх, то и измеримость
можно определять сильную или слабую. Таким образом,
оператор А называется сильно (слабо) измеримым
относительно меры |и, если существует последовательность
непрерывных линейных операторов Ап такая, что Апх
сильно (слабо) сходится к Ах (той \х). Очевидно, сильно
измеримый оператор является и слабо измеримым.
Пусть А слабо измерим. Обозначим через Ол
множество тех х, для которых существует слабый предел
последовательности Апх. Тогда, обозначая через N
некоторое счетное плотное в 36 множество, будем иметь
Оа= [х: зир| Л„лг |< оо; существует-Нт (г, Апх), геМ.
Отсюда видно, что ВА измеримо. Очевидно также, что
ВА — линейное многообразие. Для всех хе^
существует слабый предел Ах = \\тАпх, причем А(ах + $у) =
П->оо
= аАх + $Ау для всех вещественных а и р и х, у^йА.
Наконец, |и(Ол)==1. Покажем, что выполнения
перечисленных условий достаточно даже для того, чтобы
оператор А был сильно измерим; тем самым докажем, что
понятия сильной и слабой измеримости эквивалентны.
Теорема 2. Пусть на измеримом линейном
многообразии 0А) для которого \х(Оа)= 1, определена
измеримая функция Ах со значениями из 36, удовлетворяющая
§ 1] ИЗМЕРИМЫЕ ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ОПЕРАТОРЫ 619
для всех х, у^йА и вещественных а, р соотношению
А {ах + $у) = аАх + $Ау. Тогда существует
последовательность непрерывных линейных операторов Ап таких, что
Ах = Пт Апх (той ц).
Доказательство. Заметим, что \Ах\ является
измеримой функцией. Поэтому
Нт \х{{х: | Ах\>с}) = 0,
и значит, для всякого е>0 можно указать такой
компакт /С, что | Ак|<с при х^К и \1(Я? — К)<г. Этот
компакт можно считать выпуклым центрально
симметричным множеством. Определим пространство 2 с
нормой | • \к точно так, как в доказательстве теоремы 1,
точно так же выберем компакт К\ в 3;\ для которого
К\<^К и \х(К — К\)<е. Оператор Л будет непрерывным
на ^ в норме | • \к и непрерывным на К\ в метрике $?.
Значит, для всякого р>0 можно указать такое 6>0,
что \ Ах — Ау\<р при \х — у\<6, х, у&К\. Пусть N —
конечномерное пространство Ь такое, что Ы[\К\
образует 6-сеть в К\. Построим оператор Аы следующим
образом: при х^Ы Аых = Ах, если же ортогонально Ы,
то Аыу = 0. При таком продолжении А с N на все 9В
мы не увеличиваем модуля непрерывности Л. Поэтому
(ср. доказательство теоремы 1) | Аых — Ах | <^ 2р при
#е К\- Значит,
ц({|Л^-Лл:|>2р})<28.
Выбирая последовательности е->0 и р->0, построим
последовательность ограниченных линейных операторов,
которая сходится к Л по мере, а из такой
последовательности можно выбрать последовательность,
сходящуюся почти всюду. Теорема доказана.
В дальнейшем будем использовать просто термин
«измеримый линейный оператор» без указания сильный
(слабый).
Рассмотрим понятие абсолютно измеримого
линейного оператора. Измеримый линейный оператор Л
называется абсолютно измеримым, если для всякого
измеримого линейного функционала 1{х) выражение
/ (Ах) будет также измеримым линейным функционалом.
620
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Последнее утверждение можно понимать двояко. Во-
первых, поскольку существует такая последовательность
гПУ что к(1 — гп)->0, под 1(Ах) можно понимать предел
по мере \х последовательности измеримых
функционалов 1п(х) = (гп, Ах). Во-вторых, 1(Ах) можно понимать
как обычную суперпозицию двух измеримых функций.
Она также будет измерима. Условие аддитивности и
однородности в области определения для этой функции
выполняется. Областью определения этой функции
будет множество {х: Лхе/)/}, где /)/ — область
определения 1(х). Если Дл обозначить область значений
оператора Л, то для того, чтобы 1(Ах) было измеримым
функционалом, необходимо и достаточно, чтобы
выполнялось равенство
А так как в качестве Вг можно взять любое измеримое
линейное многообразие Ь, для которого ц,(1)=1,то
должно выполняться условие \х(А~1(кА ()Ь)) = 1, если
\1(Ь)=*1. Используя теоремы 1 и 2, можно убедиться
в эквивалентности обоих подходов К измеримости 1(Ах).
Опишем строение абсолютно измеримого оператора.
Заметим, что для всякого абсолютно измеримого
оператора А сходимость по мере \х последовательности
измеримых линейных функционалов 1п(х) к 1(х) влечет
сходимость по мере \х последовательности 1п(Ах) к 1(Ах).
Чтобы в этом убедиться, достаточно рассмотреть вместо
сходимости по мере сходимость почти всюду. В этом
случае можно указать такое линейное многообразие Ь,
]и(/,)=1, что 1п(х)-+1{х) при хе[. Значит, 1п(Ах)-+
-+1(Ах) для всех х, для которых Ах&Ь, а это
множество имеет меру единица в силу абсолютной
измеримости оператора А. Таким образом, с абсолютно
измеримым оператором А можно связать оператор Л*,
переводящий §6 в §} и действующий по формуле
[Л7] (х) = / (Ах). Из вышесказанного вытекает, что этот
оператор будет непрерывен в метрике г, так как
сходимость функционалов в этой метрике эквивалентна
их сходимости по мере \х. Покажем, что справедливо
и обратное: если Л —измеримый линейный оператор,
для которого оператор Л*, определенный
соотношением А*г(х) = (г} Ах) для всех 26^, продолжается по
§ I] ИЗМЕРИМЫЕ ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ И ОПЕРАТОРЫ 621
непрерывности в метрике г на все 96, то А — абсолютно
измеримый оператор. Если А* продолжимо по
непрерывности на 96, то ц>(А*г) будет /--непрерывным
положительно определенным функционалом. Поэтому почти
всюду по мере \х сходится ряд
со
Ах=2[А'ек](х)ек,
/2 = 1
каков бьГни был ортогональный базис {ек}, причем ф(Л*,г)
будет характеристическим функционалом так
определенной величины Ах. Пусть / — измеримый функционал,
{1к} — ортонормированный базис в Оь, Тогда
со со
Пусть Рд —оператор проектирования на подпространство,
натянутое на }и ..., ?п. Покажем, что 1(РпАх) сходится
по мере \х к некоторому пределу. Действительно,
аЧ,иГ,)Т,
/-1
(*),
ЦРяАх)-2(А% х)1(!,):
и поскольку I 2 1{{))//. х) = 1(Рпх) сходится по мере ц
к 1{х) на основании следствия из теоремы 1, то
(х)->(А'1)(х)
[А' 2 /(//)//
по мере \х в силу непрерывности А* в 96. Значит,
1(Ах)~[АЧ](х)
является измеримым линейным функционалом, каков бы
ни был линейный функционал /. Абсолютная
измеримость А доказана.
Рассмотрим измеримые линейные отображения одного
гильбертова пространства 96 в другое гильбертово
пространство °у.
Будем рассматривать лишь сильно измеримые
отображения. Оказывается, что изучение таких
отображений просто сводится к изучению измеримых
отображений 36 в 96, т. е. измеримых линейных операторов.
622
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Действительно, пусть /? — изометрическое взаимно
однозначное отображение Щ на 36 (мы считаем оба
пространства сэпарабельными). Пусть У — измеримое
отображение 36 в Щ, тогда можно указать
последовательность непрерывных линейных отображений V\ такую,
что Упх->Ух (в Щ) по мере \х. Но ВУп будет уже
последовательность непрерывных линейных
отображений 36 в 36, которая будет сходиться по мере \х к НУ.
Значит НУ является измеримым линейным оператором.
Наоборот, если I] — измеримый линейный оператор,
переводящий 36 в 36, то 11ВГ1 является измеримым
линейным отображением 36 в Щ. Тем самым все
измеримые линейные отображения 36 в Щ полностью описаны.
Обозначим через V меру, определенную в Щ
соотношением ч(Е) = \х[У~1 (Е)), где У — измеримое линейное
отображение 36 в Щ. Найдем характеристический
функционал меры V. Для этого понадобится понятие
сопряженного к У преобразования. Пусть О — область
определения отображения У, |и(1)) = 1. Выражение (Ух, у)
определено для всех //е^ йхеО и является
измеримым линейным функционалом на О. Поэтому
существует такой элемент /уе1, что (Ух, у) = 1у{х).
Положим 1У = У*У', У*у задает однородное и аддитивное
отображение Щ в 36, непрерывное в следующем смысле:
Г(У*У\1 У*У2)~>® при \У\ — У21->0. Это отображение V*
и называется отображением, сопряженным к У.
Особенно интересен тот случай, когда У* можно
рассматривать как измеримое относительно меры V
отображение Щ в 36. Пусть {^ — некоторый ортонормированный
базис в 36. Чтобы У*у принадлежало 36, необходимо
и достаточно, чтобы
Уу-ЖУу, ек)ек=%(у, Уек)ек
и ряд 2 (Уу У&к)2 почти всюду сходился по мере V. По-
к
следнее условие эквивалентно сходимости почти всюду
по мере \х ряда 2 (Ух> У&к)2- Найдем, наконец, ^(у) —
к
характеристический функционал меры V. Будем через
§ 2] ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 623
Ф^(/) обозначать продолжение характеристического
функционала фДг) на ЗБ по непрерывности. Тогда
Щ (У) - / *' <* У*)р (с(х) - / е< <^. *)ц (^) = % (Ту).
§ 2. Измеримые полиномиальные функции.
Ортогональные полиномы
Хотя уже для линейных измеримых функций мы
в предыдущем параграфе убедились в принципиальном
различии пространств измеримых и квадратически
интегрируемых функций, тем не менее при рассмотрении
полиномиальных функций высших степеней мы
ограничимся лишь квадратически интегрируемыми функциями,
возникающими как среднеквадратические пределы
непрерывных полиномиальных функций. Это ограничение
объясняется, с одной стороны, сложностью строения
даже квадратическои измеримой функции, с другой
стороны — удобством квадратически интегрируемых
функций при различных аналитических приложениях,
в частности при построении ортогональных разложений.
Однако для того, чтобы обеспечить существование
нетривиальных квадратически интегрируемых
непрерывных полиномов, на меру \х приходится накладывать
некоторые ограничения.
Будем обозначать через Мп класс мер [х, для которых
| \х\п\х (ах) < оо
и ^оо = П^- Примером меры из М^ является гаус-
п
совская мера. Для мер из М^ каждый полином
степени п будет принадлежать 2>2[\1] — пространству
измеримых функций, интегрируемых с квадратом по мере \х.
Если \х & М^у то в 1У2 М входят все непрерывные
полиномы.
Напомним определение полиномиальной функции или
полинома. Функция Ф(л:), представимая в виде
Ф(х) = Н(х, ..., х)}
624
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
где Н(хи ..., .*;„)--/г-линейная форма на $?, называется
однородным полиномом степени /г, а функции вида
/г-0
где Фк — однородный полином степени к, называются
полиномом степени п. Для каждого однородного
полинома Ф степени к существует 6-линейная непрерывная
симметричная функция Н (хь ..., хк), порождающая
полином (соответствующая полиному). Такая функция
определяется однозначно. Пусть {^ — некоторый орто-
нормированный базис в $В. Числа
*,.....«*-# к. •■•■ *о -
называются коэффициентами функции Н и формы Ф
в этом базисе. Форма Ф выражается через свои
коэффициенты следующим образом:
ф(*Н 2 *,.....'*(*■'О ••■(*•**)■
Ч 1к
Рассмотрим выражение интеграла Г Тп (х) Т'п, (х) \х {их),
где Тп и Т'п,— полиномы, через характеристики меры \1.
Поскольку Тп(х)Т'п,{х) является полиномом, то
достаточно уметь определять интегралы от одного полинома,
а для этого достаточно определять интегралы от
однородных форм. Пусть \1 е Мп и Ф(х) — однородная форма
степени п. Обозначим через Н соответствующую я~ли-
нейную непрерывную функцию. Если Р — оператор
проектирования на некоторое подпространство, то
\Ф(х)-Ф(Рх)\ = \Н(х, ..., х)-Н(Рх9 ..., Р*)|<
<2|Я(*. ..., *, Рх, ..., Рх)-
*-1 1
- Н (х, ..., х, Рх, ..., Рх)\=*
к-\
п
= 2 I Н {х, ..., х, х - Рх, Рх Рх) | <
*-• —к=\—
<лС|*-Лс||*|п~|,
§ 2] ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 625
где С = $ир[Н (х{, ..., хп)\ 1л^|^1]. Поскольку Ф(л;) —
— Ф (Рх) -> 0 при Р->1 и ограничено величиной 2пС \ х \п,
интегрируемой по мере \ху то
[Ф{х)\1{ах)=*ит [ Ф(Рх)\х(ах).
' Р + 1 *
Выберем произвольный ортонормированный базис {ет}
и обозначим через Рт оператор проектирования на
подпространство, натянутое на еи ..., ет. Тогда
Г Ф (х) \1 (ах) = Нт С Ф (Ртх) \х (их).
Если щ ..., \п — коэффициенты формы Ф в этом базисе,
то
Ф(РтХ)= 2 а',.-.*я(*' ^...(я, *0
6=1, .... л
И
^Ф{Ртх)\х{(1х) =
1кКт
к=\, ..., п
Пусть
5^ (2ь ..., гп) = | (*, г,) ... (*, гя) м- (с?*)
м-я моментная форма для меры \х. Тогда
5^ (в119 ..., е(п) = | (*, ^) ...(*, ^п) [г (<**)
— коэффициенты этой формы в базисе {ек}.
Следовательно,
[ф(х)11{(1х)= Нт 2 ач, ....^(^ ..., */).
1к<т
А—1, ..., /г
626
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Чтобы убедиться, что выражение справа является
суммой сходящегося ряда, заметим, что выполнено
соотношение
Г Ф{х)\х((1х)= Нт Г Н(Ртх,. ..9Ртх)\1(ах) =
•* т1-+оо, ...,тл->оо •*
Нт 2 ... ^ Я (* ..., ^я) 5(ця) (е, , ..., е^).
А это и означает сходимость ряда
. 2 "К е1п)^\е1х,...,е1п). (1)
*1' "•' 1П**1
Если для двух м-линейных симметричных непрерывных
функций Я и 5^ в любом ортонормированном базисе
сходится ряд (1), то сумму этого ряда (она не зависит
от выбора базиса) будем обозначать 5рЯ*5,Г) и
называть следом произведения этих форм. Таким
образом, установлена формула
|ф(*)|х(ЛсН5рЯ*5|!,)| (2)
где Я — м-линейная форма, соответствующая
однородной форме Ф, а 5^ — моментная форма меры \х.
Построение ортогональной системы полиномиальных
функций. В дальнейшем предполагается, что мера \х
принадлежит М^. Под измеримым полиномом степени
не выше п будем понимать среднеквадратическии
предел непрерывных полиномов степени п. Чтобы построить
все измеримые полиномы, удобно использовать
ортогональные системы полиномов. Пусть $п— множество
всех измеримых полиномов степени не выше п\
&п является подпространством в гильбертовом
пространстве -2*2 М- Очевидно, Ф§ а&{ а ... с:^я.
Обозначим через &п подпространство &ю являющееся
ортогональным дополнением к &п-{. Подпространства ^0,
3*ь ..,&*„ ортогональны между собой и
называются ортогональной системой полиномов. Всякий
измеримый полином представим однозначно в виде
§ 2] ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 627
2 ск8ь (х), где §к е &к. Для построения всех
измеримых полиномов достаточно построить все
подпространства Фк. Такое построение естественно проводить
индуктивным образом.
Пусть Т (х) — однородная форма степени м,
порожденная симметричной м-линейной функцией Я. Тогда
Т(х) = РЛН, х)-%(!к(Н9 х), (3)
/г=0
где Рп{Н, х)<==РП) (}к{Н9х)*=&к. Очевидно, Рп{Н,х)
и С}к(Н, х) линейно зависят от Я. Обозначим через Фп
пространство всех м-линейных непрерывных функций.
Введем в Фп скалярное произведение
(Я, Н')п = / Рп (Я, х) Рп (Я', х) IX (ах) (4)
и пополним Фп в этом скалярном произведении.
Полученное гильбертово пространство обозначим Фд, его
элементы будем называть обобщенными формами.
Заметим, что соответствие Я <-> Рп (Я, х) изометрично,
поэтому его можно продолжить на все Фп.
Соответствующую ЯеФ" функцию из 3>п будем также
обозначать через Рп{Н, х). Функции (?&(Я, х) в формуле (3)
представимы в виде <2к{Н, х) = Рк (Нк, х), где Нк^Фк.
Линейный оператор, переводящий ЯеФл в ЯАеФй
обозначим через Vпк. Таким образом, из (3) получаем
Рп(Н,х) = Т (х) + 2* Рк (УпкН, х). (5)
Последняя формула показывает, что для определения
Рп(Н, х) при ЯеФл достаточно знать операторы Упк,
а чтобы затем Рп(Н,х) продолжить на Фд, нужно
знать ('у')п- Если эти характеристики будут известны,
то (5) позволяет свести нахождение Рп(Н,х) к
нахождению Рк(Н,х) при к^п.
Для ЯпеФй и ЯАбФй обозначим через НпХНк
(п + ^-линейную форму Нп(хх, ...,*хп)Нк(*л+1, .. , хпп)
(она несимметрична). Из формул (2), (4), (5) вытекает
628
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
следующее рекуррентное соотношение
(Я, Н\ = 5р (Я X Н' * 5Н - 2 (УпкН, УпкН')к. (6)
Для определения Упк введем билинейные формы
Апк{НюНк), определенные при Я^еФ", Нк*=Фк:
Апк (Я, Нк)=\т(х)Рк(Нк, х)р (йх)9 (7)
где Т (х) — однородная форма степени /г, Н еФ"-
соответствующая /г-линейная функция. Для определения Апк
имеем еще одно рекуррентное соотношение
Апк (Я„, Нк) = 5р (Я„ X Я, * 5{ГЙ)) + 2 Л„/ (Я„, Ук1Нк), (8)
вытекающее из (5) и (7). Наконец, для определения V'пН
имеем следующее равенство, справедливое для всех
ЯеФ* и Нк е= Ф*:
Аяк(Н,Нк)=-{УпкН,Нк)к, (9)
которое получается из (5) умножением на Рк(Нк,х) и
интегрированием. Если \Нкт, т== 1, 2, ...} — некоторый
ортонормированный базис в Ф*, то
со
УпкН=- ЕЛгДЯ, Я*) Я*. (10)
т = 1
Соотношения (6), (8), (9) позволяют последовательно
определить (-,•)<), А10) 1/10> (-,->ь 4го» ^20, Ль ^21 и т. д.
В качестве примера рассмотрим построение
подпространств Рп для гауссовской меры |л со средним 0 и
корреляционным оператором В. Все формулы существенно
упрощаются, если использовать скалярное произведение
{х,у)+ = {В~1х, у)
и в этом скалярном произведении считать следы.
В скалярном произведении (•,•)+ очень простой вид
имеют моментные формы меры \х: 8п(г\,...9 гп) = 0
при п нечетном, а при п четном
/1/2
5/1" («1 гп) = 2 П (г1к9 г!к) ,
§ 2] ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 629
где сумма берется по всем возможным разбиениям
чисел 1, 2, ..., п на п/2 пар (1к> ]к). Последняя формула
вытекает из равенства
Оп (2\, . . ., 2п) —
*к
№ (йх)
= 1
дп
дах ... дап
ехр - у (2 акгк, 2
_<*>кгк
1 ' +
а =0
^м
Следы в скалярном произведении (•,■)+ будем
обозначать 5р+. Введем отображение Фп в Фп~2, определяемое
формулой
8р2+Я(г1> ..., г„_2) = 2 Я(вл> *л> *р ..., гя_2),
где {^ — некоторый ортонормированный в скалярном
произведении (•,•)+ базис. Будем искать
последовательно операторы V'пк и скалярные произведения (•»•)«•
Вычислим
5р+(Я„ХЯ,*5„++й).
Эта величина равна нулю при п + к нечетном. Пусть
п + к = 2т. Заметим, что для подсчета Зр+(Ял+^*5^+й),
где Н п+к — (п + ку линейная форма, нужно аргументы Нп+к
разбить на всевозможные пары, свернуть по каждой
паре (т. е. подставить вместо этой пары аргументов
одинаковые векторы из ортонормированного базиса и
просуммировать по базису) и результаты сложить.
Пусть аргументы Нп X Нк так разбиты на пары, что
имеется 5 пар, в которые входят и аргументы Нп и Нк.
Сворачивая по остальным парам каждую форму в
отдельности, получим
№)
п — з
2 н.
и (5Р2+ЛЧ-
630
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Таких разбиений будет
0(й-1) ... (А —5+ 1)(/г —в— 1)!!(Л —в— 1)!! =
п\к\
Следовательно, полагая —— = /, —^—= г, находим
5! (п -5)!! (Л-5)!!
2 ~~ '
5р+(#„ХЯй*5„++,) =
Используя эту формулу, можем определить
^,о^=-(2"-»)!!(Зр2+)пЯ2я,
^+1.,^+1 = -(2«+1)П(Зр2+)пЯ2„+1.
Далее
К,, (Я*. #2) - тайн" 5Р+ ((5Р2+)"*1 я2. X я2) +
+ (2«- 1)!!(5р2+)пЯ2„(5р2+Я2)-Л2„0(Я2„, У20Я2) =
Следовательно,
^2л,2 (2л-2)1! 2 ^ Р+' 2«'
По индукции можно проверить, что
\, ш("а, Я2,) = -^^^ 5р+ ((8р»+Г* Н2п X Я2,),
<Я2„Я2,)2й = (2й)!5р+Я2ИЯ2й
и, следовательно,
Л/ тт (2л)! /о 9 \П-к тт
у2п,2кп2п (2п~2к)\\{2к)\{°Р+) 2л-
Точно так же
у тт (2л + 1)! /сп2 \п~к и
у2П+\,2к+\п2п+\ (2л-2*)!! (2*+1)1 V Р+/ п2П+г
§ 2] " ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 631
Таким образом, окончательно находим
О, п+ к нечетно,
п—к
~ {п-№к\ (8р+) 2 Я»' л + * четно>
Выясним вопрос, когда измеримые полиномы всюду
плотны в 2'2[\1]- Достаточное условие для этого дает
следующая лемма.
Лемма. Если характеристический функционал ф (г)
меры \х таков, что для всякого г функция ф (1г) является
аналитической функцией I в некоторой окрестности нуля,
то множество измеримых полиномов плотно в 3?2[\1].
Доказательство. Обозначим замыкание
множества всех измеримых полиномов через ^. Покажем,
что е1 (*'г) как функция х принадлежит .^. Для этого
достаточно доказать, что для некоторой
последовательности полиномов <7л(0 вещественной переменной
Нш \\еЧ***-Чп((г,х))?р(ах) = 0. (11)
Я-»оо *
Обозначим через Р (I) функцию распределения
Р(Ь) = \1({х: (г,х)<К}).
Соотношение (11) эквивалентно следующему:
Нт \\е**—дп(К)?<1Р(К) = 0. (12)
Поскольку
<р(г*) = \е1*йР(К),
то из аналитичности этой функции в окрестности нуля
вытекает, что при некотором б>0
]>1М^(Я)<оо.
Пусть ^ — пространство комплекснозначных
функций #(А), для которых Г | /г (К) \2с1Р('а)< оо со скалярным
произведением
/Ы^)ЫЯ)^(Я).
УпкНп =
632
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Пусть З7' — замыкание в 2 множества всех полиномов,
а §(К) — проекция функции еа на «2?/. Тогда для всех гС^О
Используя неравенства
т
у (Ш)"
<е»-1'1, 2
7ТС
<«*-*<ч>2;^
<
<|^-#(Я)|2 + е1Мб
при | /Ку, находим
Дифференцируя это соотношение по I, убеждаемся, что
при |/|<у
|(ел-г(Я.))Ля^(Л) = 0.
Следовательно, при |/|<^ и \и\<-^
. °°
0= |(^-г(А))е^2-^^(Я,) =
I
0 = ^ {еа-8(Х))ешс1Р(Х) при |/|<6.
Продолжая предыдущие рассуждения, убеждаемся,
|(^-#(Я))еш^(Я)==0
при всех I. Полагая 1= — 1, получим
|(е'х-г(Л))е-^^(А) = 0,
или
что
§ 2] ИЗМЕРИМЫЕ ПОЛИНОМИАЛЬНЫЕ ФУНКЦИИ 633
что совместно с равенством
/(^-в(А))вЩ^(Л)) = 0
приводит к соотношению
из которого вытекает (12).
Покажем, что множеству & принадлежит любая
измеримая ограниченная функция. Пусть [(х) — такая
функция. Выбере„м компакт К такой, что \*.фб — К)<ь.
Функция !(х) равномерно напрерывна на К и, значит,
для каждого е>0 можно указать такое 6>0, что
\!{х)-!Ш<* при \х-у\<Ь.
Пусть Ы — конечномерное подпространство,
являющееся 6-сетью в К> оператор проектирования на N
обозначим Р, Кг — проекция К на N. Существует
тригонометрический полином на N такой, что | / (Рх) — Т (х) | < 8
при х^К' и не превосходящий по абсолютной
величине зир|/(л:)|. Легко убедиться, что
х
1\1(х)-Т(Рх)\^(йх)=0(г).
Значит, множеству 9* вместе с тригометрическими
полиномами принадлежат все ограниченные непрерывные
функции, а значит, и ^Мс^ так как они образуют
плотное множество в ^М- Лемма доказана.
Приведем пример, показывающий, что даже на
прямой существует мера, для которой все полиномы
интегрируемы с квадратом, но не полны в ^М- Пусть
мера (я на 0$ определяется плотностью
/(*)
1 1 ~\о?х .
? 2 , х>0,
У2п х
О, х<0.
Рассмотрим функцию @(х) из ^М-"
[.ехр{е1о^2л;}5т:п;(1 — 2е)1о^л:, л:>0,
21 И. И. Гихман, А. В. Скороход
634
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Для всех целых к имеет место равенство
* \ 2я *>
— ОО
ОО
= ^у^ / ехр{(Л + /я(1-2в))/-у(1-2е)/8}л-
— ОО
ОО
-•^р- /ехр{(й-/я(1-2в))/-1(1-2е)^}л-
— ОО
2/У 1-2е \1 . 2(1-2е) /
~еХР{ 2(1-2в) })-°-
Таким образом, функция #(л:) ортогональна всем
полиномам.
§ 3. Измеримые отображения
Пусть 36 и Щ — два гильбертовых пространства
с а-алгебрами борелевских множеств 91 и 23
соответственно. Функцию Н(х)у определенную на ^-измеримом
множестве Ок и принимающую значения из Щ, будем
называть измеримым отображением 36 в Щ, если для
всех Вб8, #~1 (В)^%. Такое отображение будем
называть \х-измеримым или измеримым относительно
меры |я, если \х(Ок)=1. Далее в этом параграфе под
измеримыми отображениями всегда будут пониматься
отображения, измеримые относительно соответствующей
меры. Если отображение /? ц-измеримо, то оно
преобразует меру \х в некоторую меру V на (^/, 23),
определяемую формулой
V(В) = ,^(^Г,(В)).
Вычисление интегралов по мере V сводится к
вычислению интегралов по мере р: для всякой 23-измёримоа
функции !(у)
\!{у)ч№=1НШ)М*х),
§ 3] ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ 635
если только хотя бы один из этих интегралов
определен. Важным вопросом, особенно в различных
приложениях, является вопрос об определении характеристик
меры V (характеристического функционала или момент-
ных функций) по известным характеристикам меры \х.
Простейшим примером измеримого отображения
является непрерывное отображение В в Щ.
Нижеследующая теорема указывает на связь между
непрерывными и измеримыми отображениями.
Теорема. Для всякого \х-измеримого
отображения Я(х) можно указать последовательность
непрерывных отображений #п(х) такую, что
К{х)= Нт #п(х) (тоёц).
Доказательство. Достаточно показать, что для
всякого е>0 можно указать такое непрерывное
отображение #(х), 36 в <У, что
\х({х: \~К(х)-К(х)\>е))<е.
Обозначим через V меру на (^, 93), в которую
переходит \х при отображении /?. Пусть К — такой
компакт в Щ, что V Щ — К) < -|-. Обозначим через Дг/
прообраз К при отображении /?. Тогда \1(3/ — /С')<у.
Пусть N — конечномерное линейное подпространство
в <У, являющееся -|-~сетыо в /(, уи ..., ут— базис в N.
Тогда для всех х е К
КЫ-^(Ш,Ук)Уъ
^ 2
Поскольку (К(х)9 ук) является измеримой функцией по
мере \х, то существует такая непрерывная функция фл(л:),
что
*({х:\ъ(х)-(Н(х),уЛ\>±})<^.
21*
636
ИЗМЕРИМЫЕ ФУНКЦИИ
ГГЛ. VIII
Тогда
V | \х: \К(х)-1^Ч)к(х)ук\>г)\<
<ц({*: и(х)-^(Н(х\ ук)ук\>^\) +
т
+ %»({х: |(ВД,У*)-Ф*(*)1>-^-}).
Остается заметить, что отображение Я(х)= ]%<рк(х)ук
является непрерывным. Теорема доказана.
При изучении- измеримых отображений 36 в Щ
достаточно рассматривать измеримые отображения 36
в 36, так как всякое измеримое отображение 36 в Щ
представимо суперпозицией измеримого отображения 36
в 36 и непрерывного отображения 36 в Щ.
Полиномиальные отображения. Будем
рассматривать отображения 36 в 36, Отображение /? называется
полиномиальным, если (К(х), г) является полиномом
по х при любом г. Если при любом г выражение
(#(х),2) является однородной полиномиальной формой
степени п, то будем говорить, что #(х) является
однородным полиномиальным отображением степени п. При
изучении однородных полиномиальных отображений
важную роль играют некоторые стандартные
отображения, рассматриваемые ниже.
Обозначим через 36^к пространство 6-линейных
симметричных непрерывных форм 5, удовлетворяющих
условиям
Зр 5 * 5< оо.
Пространство 36^ со скалярным произведением
(5, Г)=5р5*Г
является сепарабельным гильбертовым пространством.
Через 23* будем обозначать а-алгебру борелевских мир-
§3}
ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ
637
жеств из $ок. Рассмотрим отображение 36 в §в0к,
определяемое соотношением
к
х <--> Тх (г,, ..., гк) = П («/, х).
/-1
Это отображение является непрерывным, так как
8р(ГЯ1-ГЛ)«(ГЯ1-ГЛ)-
= 2
Л /-1 к Л2
Г/ к к Л2
Г Аг /—1 к
2 2 П(*1. е/у)(*1-*2. */,) П (х2>е{)
<
< б2 и, - х212 тах {| х, |2/~2 +1 х2|2/~2}.
/<&
Следовательно, оно будет измеримым. Введем меру [\ок
на ®6^к с помощью формулы
1хок(А) = 1х{Т~1(А)).
Меру |110А; будем называть 6-й степенью меры \х.
Заметим, что \х0к является распределением случайной
величины Тх со значениями в Зд^к на вероятностном
пространстве ($?, 33, |х).
Обозначим через Ф&(Г) характеристический
функционал меры \хок. Тогда
Ф*
(5)= ]* е1^т*8\хок(с1Т) = | е<*5(*> •■•• х)\х((1х),
так как 5рГЛ*5 = 5(л:, ..., х). Таким образом, ф&(5)
определяется мерой \х, а значит, и характеристическим
функционалом ф (г) меры \л. Укажем некоторые способы
вычисления срЛ(5) по ф(г). Пусть Уи ..., ик — форма
к
из Жш вида Уиг .... «Л(2,, ..., г*)=П(и/» 2У). Тогда
( к • 1
ф* (Уи{, .... ий) = | ехр | / ЭД (*, иу) | ^ (Лк).
Для вычисления интеграла в правой части заметим, что
ф(^!+ ... + (кик) является совместной характеристик
638
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. Ш1
ческой функцией величин {х, и{), ..., (х, ик), а
[ ехр| /$ТТ(*, «/) \\х{йх)
* ( 1 I
является характеристической функцией величины
к
П (*» «/) на вероятностном пространстве ($?, 93, |х). Если
/-1
функция ф(^1«1 + ..• + *кик) абсолютно интегрируема
по ^, ..., 1к, то
X Ф (^«1 + ... + {кик) сН{ ... Лл й$\ ... я?^. (1)
Если интеграл в (1) вычислять с помощью некоторой
регуляризации (например, ввести под интегралом
множитель ехр{—е2^/}> а затем перейти к пределу при
е-*0), то формула (1) справедлива для любых
характеристических функционалов ф.
Рассмотрим совместный характеристический
функционал
Чк,Лт> *) = / ехр.{/Г(*, ..., *) + /(*, х)}\1(ах).
Предположим, что Г | х \к\х{йх)< оо. Тогда для всякой
формы 5 из 8ВШ справедливо соотношение
5р<йф/е, \(Т, г)*5 =
= 1к [ 8(х, ..., х) ехр {1Т (х, ..., х) + 1 (г, х)} \х {их),
где й%кщ 1 (Г, г) 6-й дифференциал функции срл,, (Г, г)
по г (такой дифференциал является 6-линейной
формой). С другой стороны,
/|5(хь ..., л:)ехр{/Г(х, ..., х) + 1{г, х)}\х(с1х) =
где Лтсркг, (Г, г) — первый дифференциал функции
Ф*,1(7\-г) по Г.
§31
ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ
639
Таким образом, функция ф^,! удовлетворяет
дифференциальному уравнению
1к-1*т<Ркш1(Т,г) = а&кш1(Т,г). (2)
Отметим еще, что щ, \(УиГ ..*., «Л, <г) можно вычислить
по формуле (1), если подставить в ее правую часть
ф(г + 1{их + ... + 1киь) вместо уЦ{их + ... + 1кик).
Пусть V — любое измеримое линейное отображение
36ш в 36. Суперпозицию отображений ,
будем называть измеримым полиномиальным
отображением степени к. Пусть 7? (х) — такое отображение.
Тогда (К(х), г) для каждого г является однородным
полиномом степени к или пределом таких полиномов
по мере \х.
Действительно, если Я(х) = УТх, где V — измеримое
линейное отображение 36т в 36, то (/?(*), г) = Уг(тх)9
где У* — сопряженное к V отображение (см. § 1) (оно
переводит измеримые линейные функционалы на 36
в измеримые линейные функционалы на 36ш\ ^ —
функционал на 360к, в который переходит функционал (г, •)
на 36, У* (5) —результат применения функционала У*г
кХе зе*\
Если Уг — непрерывный функционал, то У2(ТХ)
является однородным полиномом степени к. Если же V*
является пределом по мере ц0% непрерывных линейных
функционалов §п> определенных на 3?0к, то §п{Тх)-+
^^гС^х) по меРе М-» а 8п(Тх) является однородным
полиномом степени к. Покажем обратное. Предположим,
что Н(х) — однородное полиномиальное отображение 36
в 36. Обозначим через 8г ту 6-линейную форму, для
которой
(/?(*), г) = Зг(х) ..., х).
Если Тх — элемент из 36^к, определяемый равенством
Тх(*\> •••> **) = (*» гх)"-(х> гк),
то (/?(*), г) = 5р 52* Тх. Очевидно, что 82 является
линейным отображением $/в ^°*, обозначим его Ц: 8г = Цг.
640
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. УШ
Тогда
(ВД, г) = 5р*/2-*Гя = (2, Ц*ТХ)9
где V* — сопряженный к V оператор. Значит, Я(х)*=11*Тх,
где {У* — непрерывное линейное отображение 3?ок в 9В.
Пусть теперь Я{х) является пределом по мере \х
непрерывных отображений #п (х) степени 6. Тогда 'Нп{х) =
= УП7,ЛГ и /?„(*) сходится почти всюду по мере \х.
Поэтому существует измеримое линейное отображение V
-пространства <Я?0Й в Я?, к которому сходятся VпТ по
мере \10к и /? (*) = УТХ.
С помощью функции фА(Г) легко найти
характеристическую функцию меры V, в которую переходит мера \х
при измеримом полиномиальном отображении К(х)
степени к:
V(ЛН^(/Г104)).
Действительно,
Фу (г) = / е1 {г' *{х) V (с1х) = | *' <* ^) ц (Лс) =
= |вМ^.г,|1о*(йГГ) = фл(^ (3)
Разложение измеримых отображений по
ортогональным системам полиномов. Пусть мера \х такова, что
множество всех полиномов плотно в ^М» а /?(*)
—измеримое отображение $В в 36 удовлетворяет условию
\\Я(х)\21х(с1х)<оо.
Тогда для всякого зе! выражение (/?(*), г) можно
разложить по ортогональным подпространствам &кУ по-
строенным в § 2: (/?(*), *)= 2 Ль(2» *)> гДе рк(г> х)^
е ^. Очевидно, что Я& (г, а:) зависит от г линейно.
Возьмем некоторый ортонормированный базис {ек} в $?.
Тогда
оо оо
1 = 1 /=1
§31
ИЗМЕРИМЫЕ ОТОБРАЖЕНИЯ
641
Значит, сходится по мере ц ряд
оо
2Р*(^ х)е1 = Кк(х)
1 = 1
Рк (г> *) = 2 ^ {е1у х) {г, еь) = {Як (х), г).
Таким образом, при сделанных предположениях
измеримое отображение Я{х) может быть представлено
в виде
оо
/г=1
где каждое из отображений Як является измеримым
полиномиальным отображением степени к и ряд
сходится в среднем квадратическом. При к ф I
отображения Як и #1 ортогональны в следующем смысле: для
всякого ограниченного оператора В выполняется
равенство
\№к(х), /?;(*) Ы^) = 0.
Действительно,
оо
| (ВКк (х), КЛх))ц {их) = 12 (В*ь (*>>е/) (*/• Ь М) Iх <<**) =
/-1
ОО
= / %Шх), Ве1)(Я((х)> *,),! (<**) = О,
/-1
так как (/?*(*), г)* и (/?,(л:), и) ортогональны при кфг.
Поэтому
ОО '
11/? (*) |2 И^х) = 2 Л Я6 (*) I21* (<**)
И
оо
\ (/? (х), г? ц (</*) = 2 { [Як (х), г)2 р (</*). (4)
6-1
Формула (4) дает возможность вычислять
корреляционный оператор меры V, в которую переходит мера \х при
отображении Я{х).
042
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
§ 4. Вычисление некоторых характеристик
преобразованных мер
В этом параграфе приводятся результаты,
позволяющие определять характеристические функционалы
и некоторые другие характеристики мер, получаемых
из заданной с помощью измеримых отображений.
Некоторые результаты подобного рода встречались и ранее.
Так, в § 3 гл. VII найдена формула для плотности
преобразованной меры относительно исходной, в § 1
настоящей главы приводится формула для характеристического
функционала меры, полученной из данной измеримым
линейным преобразованием, а в § 3 —измеримым
полиномиальным однородным преобразованием. Конечно,
рассматриваемые ниже результаты не дают возможности
решать все задачи, возникающие в теории измеримых
преобразований вероятностных мер, однако для многих
практически важных задач на основании этих
результатов можно построить вычислительные алгоритмы
получения решений.
Группы преобразований. Пусть в гильбертовом
пространстве 36 определена группа преобразований /?/(*),
зависящая от вещественного параметра ^у определяемая
дифференциальным уравнением
-~Ъ(х) = 9Шх)), (1)
где ^ (л;) —непрерывное отображение 36 в 36,
обеспечивающее существование и единственность решения
уравнения (1), удовлетворяющего начальному условию
Я0(х) = х для всех х<^3?. Тогда при всех I К%{х) также
будет непрерывным'отображением 36 в 36. Пусть ^ —
некоторая вероятностная мера на {36, 23), а V* —мера,
в которую переходит мера [х при отображении /?*(*)•
Через щ{г) и ф(г) обозначим характеристические
функционалы мер V, и \х. Тогда
Ф, (г) =/*'<**'(х))Ц (<**)• (2)
Предположим, что | 9 (/?* {х)) | ц {их) < оо. Тогда
интеграл в правой части (2) можно дифференцировать
§ 4] ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАННЫХ МЕР 643
ПО I И
± ср, (г) = / / (г, 9 (Я, (х))) е1 ^ **{х) )ц (<**) -
При некоторых дополнительных предположениях
относительно 9{х) правую часть последнего равенства можно
выразить через %{г). Пусть
9{х) = 91(х) + 92(х)9
где 9{{х) является полиномиальным отображением,
а 92(х) допускает следующее представление:
92(х)=\еЧ«'*)9{аи), (3)
где р(с1и) — некоторая счетно-аддитивная функция
множества, определенная на ($/, 33) и принимающая значения
из дд% имеющая ограниченную вариацию. Тогда, если
(9{{х)9 2)-2Я^ х),
где Н1(хь ..., хк) — непрерывные ^-линейные формы, то
п
\ (9{ {х)9 г) е1 {х' х) V, (ах) - ^ Г* Зр д> % (г) * Н\.
С другой стороны,
$(г992{х))еЧ*-*)ч1(ах)-
| е1 (и. х) е1 {г, х)(г9р (^)) ^ ^х) =
| [ | еЦи+г. х)ъ(ах)](г, р(А*) = | <&(« + *)(*, Р (<*«)).
Таким образом, при сделанных предположениях %(г)
удовлетворяет следующему интегро-дифференциальному
уравнению
■/|ф*(и + г)(г,р(Ж/)). (4)
&=0
Преобразования, мало отличающиеся от линейных.
Представление отображений с помощью преобразований
644 ИЗМЕРИМЫЕ ФУНКЦИИ [ГЛ. VIII
Фурье по счетно-аддитивной функции ограниченной
вариации со значениями в 9В можно использовать Для
определения характеристического функционала
преобразованной меры, если преобразование близко к
линейному. Пусть 7? {х) = Ух + г<§2 (#), где V — непрерывный
линейный оператор, е— достаточно малое число, а ^2~"
представимо по формуле (3). Тогда ^2 ограничено и,
следовательно,
^ (г) = | е1 <*• *> V (их) = | е1 <*• ^+8^2 <*» ц (их) =
оо
дГ^^»(г^(х))'е<(<|Уж)1|(^н
^ к = 0
оо
Используя представление (3), находим
(г,92(х))* = [/е'<».*>(2>р(Ж*))]* =
= / ... / е1 <"'+ - +в* 2)(г, Р(ащ)) ... (2, р(</«*)).
Значит,
= | ... |ф(1/*2; + и1+ .... +^)(г, р№,)) ... (г, р(А*л)).
Окончательно получаем
°° -к к * Г
^Ф = 2п^~ .1 '•• ] Ф(^*г + и,+ ... +мй) (г, р(йщ))...
к==0 ' ъ—-^ >
к раз
...(г,р((1ик)). (5)
Заметим, что при наших предположениях этот ряд
сходится при всех е и является целой аналитической
функцией относительно е. Весьма существенное
сокращение формулы (5) можно получить, положив /е = Я и
предполагая, что Я>0, а (г, р(с1и)) — неотрицательная
мера. Пусть пг(йи) — мера в Я/, являющаяся* безгра-
§ 4] ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАННЫХ МЕР 645
нично делимой и имеющая характеристический
функционал
| е1 <**- «) лг (Ли) = ехр { А | (е1 <**■ «> - 1) (г, р (А/))}.
Тогда
2*11 / • • • / ф(Гг + «!+■■• + "*)(*, Р(Ж*,)) • • •
... (г, р (</кЛ)) = ] ф(К*г 4- х) лг (ах).
Очевидно, что меры р,могут быть заданы не на самом $?,
а на некотором его расширении, на которое по
непрерывности может быть продолжено ф(г).
Формула взаимности и другие разложения по
малому параметру. При вычислении различных
интегралов по мерам в гильбертовом пространстве (в частности,
по мерам, соответствующим квадратически
интегрируемым процессам) иногда удобно использовать весьма
простую формулу, сводящую интегрирование по одной'
мере к интегрированию по другой. Пусть ^ и т| — две
независимые случайные величины со значениями в дв,
\х и V распределения этих величин, ср^и щ — их
характеристические функционалы. Вычисляя интеграл Ме1{^^ =
= \ \ е1{х'у)\ь{(1х)ч((1у) в различном порядке, находим
| Фл; (*) |1 (ах) === / Фр, (у) V №/). (6)
Эту формулу и будем называть формулой взаимности.
Частным случаем этой формулы является, например,
следующая: ( е 2 ' \х(йх)= I %(у)ч(ау), где V —га-
уссовская мера с корреляционным оператором В.
Формулу (6) весьма удобно применять, когда мера V
является безгранично делимым распределением. Пусть
Н(х) функционал, имеющий вид — 1о^^(г), где V —
безгранично делимое распределение. Введем сехмейство
случайных величин %, имеющих характеристический
функционал еиш = Ме'<г'Ч Тогда Меша\ где
&~случайная величина со значениями в $?, имеющая распре-
№
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
деление ц, можно вычислить по формуле (6):
Ме'^-Мф^Ы. (7)
Эта формула справедлива лишь для />0; для
отрицательных I (или для комплекснозначных I в случае
преобразования Лапласа) можно пользоваться
аналитическим продолжением полученного выражения по I.
Формулу взаимности можно использовать для
получения разложений по степеням малого параметра для
характеристических функций функционалов от
случайной величины ^е, если известно разложение по степеням е
характеристического функционала величины |8. Пусть
М*'<*•*«) = <?,(*) = 2 в'х*(*), (8)
и нужно вычислить характеристическую функцию
величины Л(^е), где к таково, что справедлива формула (7).
Тогда Ме1{Н(*е) = ^гкЬЛ%к(г\^. В качестве примера
применения этой формулы рассмотрим' тот случай, когда
Н(х).= (Вх, х), где В —положительно определенный
оператор. Имеет место равенство ?2{Вх, х) = 1од МеНх> ц\
где г| — гауссовская величина с корреляционным
оператором В (заметим, что она может быть определенной
в некотором расширении пространства 36). Поэтому
Ме" («*• **) = М/77 <*«• *) = МФе (]/| т,) •
Последняя формула справедлива, если <ре(/г) является
целой аналитической функцией /. Если в эту формулу
подставить я = #, то получим преобразование Лапласа
величины (В1е, |е):
Пусть семейство случайных величин 1е, зависящее
'от положительного параметра е, таково, что 1&->0 по
вероятности при е->0. Предположим далее, что для
характеристического функционала <р8(.г) величины ^8 =
= —18 справедливо разложение (8). Пусть далее функ-
§ <] ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАННЫХ МЕР 647
ционал Н(х) представим в виде к (х) = 2 ?к(*)> где
&=1
Рк (х) — однородный полином степени к, Нк —
порождающая его й-линейная форма. Найдем разложение
по степеням е для характеристического функционала
величины — /г(|8) в предположении, что разложение (8)
можно дифференцировать почленно сколько угодно раз.
Имеем
м ехр I т 2р^ 1= м ехр {/5 II е"-~]р» (& I=
оо г- оо
= М ехр {1зР1 (и)} 2 7ГГ <5 2 е%-'П(1е)
гс=0 [_ /г=2 ]
= М ехр {1$Р{ О Л еп ^ <2^ (У гпк («).
л-0 Л«0
Здесь <Э„й (#) — однородные полиномы степени 6, гпк(1)~-
числовые полиномы степени не выше к/2. Эти полиномы
однозначно определяются с помощью соотношений
2/г / со
2 Япк (*) ^ло=•§&ехр I '2 8^~1р* м
Предположим, - что Р{ {х) = (а, а:), где а ^ О, (}пк (х) =
= ГлЛ,(^, ..,, х), где Г„& — й-линейная форма. Тогда
М ехр {18РХ (У) <Эпк (У = Ме1$ (^ °)Г„Й (|е, .... У =
= Гк 5р Ае (5а) * Тпк = Г* 2 ет Зр й\т(за) * Г„*.
т
Следовательно,
Мехр{-^Л(1е)} = .
оо . 2/г оо
=2е" 21г«* (й)Г* 2ет 8р ^ (5«) *Т^ <9)
п=0 6=0
т=о
648
ИЗМЕРИМЫЕ ФУНКЦИИ
[ГЛ. VIII
Разложение (9) нужно переписать, собирая коэффициенты
при одинаковых степенях е. Таким же образом можно
найти и конечное разложение с оценкой остаточного
члена, если вместо ряда в (8) будет конечное
разложение с остаточным членом, а
Ь(х)=-%Рк(х) + о(Тя+1(х)),
к=\
ГЛг + 1 —однородный полином степени #+1.
Формулу, аналогичную (9), можно использовать для
нахождения характеристического функционала
преобразованной меры, если преобразование %(х) представимо
в виде
оо
ВД= 2 Д*(*), (Ю)
где Кк (х) — однородные полиномиальные
преобразования степени к. Пусть Ук — линейное отображение 36
в 36ш, переводящее г в форму Vк(г), порождающую
полином {кь{х)> г). Тогда
оо I оо V п
= \ е,{Улх)^-^(^(уЛг,х,...,х)\ мах).
п==0 \ к=2 1
Если обозначить через фу характеристическую функцию
меры V, то
оо
ФV(2)=2 5рА^(У12)*ГI, (И)
где Т% — ^-линейная форма вида
г* = 2 2- -5ТГ7ТГ ^'<2) ■ • ■ у?^г>*)' (12)
Разложение (11) имеет смысл, если мера ^ удовлетво-
*) Через К обозначается V ... V.
к раз
§ 4] ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАННЫХ МЕР 649
ряет условиям: для всех т и /
|оо I
2 кк (х)
\ ^ т \\к(йх)< со.
Применение ортогональных полиномов. Пусть \х —
некоторая мера, для которой построены ортогональные
полиномы Рк(Нк, х) (см. § 2). Посмотрим, как это
обстоятельство помогает найти характеристический
функционал фу меры V, полученной из ц
преобразованием #(х). Предположим, что удалось разложить
функцию е1{г>*{х)) в ряд по ортогональным полиномам:
е1 (г, * (х)) = 2 Рк (#|, х). Тогда Фу (г) = Г е1 {г' *ш\х {их) -
= Ро(Но). Значит, задача о разложении е'(*.*(*)) не
проще, чем нахождение фу(г). Более естественно
использовать ортогональные полиномы в том случае, когда V
абсолютно непрерывно относительно \х и плотность
-^(х) = р(х) принадлежит 2?2[\х]. Предположим, что
известно разложение р(лг) по ортогональным полиномам
оо
рМ=2^№.4 Тогда
оо
«М*) = / е' <*■ *>р (х) |1 (ах) = / в"* *> 2 Рк {Нк, хЫйх) =
оо
Очевидно, что где ($ — некоторый
полином, легко выражается через ^(г) в виде
дифференциального оператора вида
2-^зр^Ч(2)*я6.
Поэтому можно считать определенными функции
Ък{Нь>г)=1е^*»Рк{Нк,х)р{ах),
650
ИЗМЕРИМЫЕ ФУНКЦИИ
{ГЛ. VIII
через которые ^(г) выражается по формуле
оо
<Мг) = 2х*(Я*,г). (13)
А—0
Выражения для плотности преобразованной меры
относительно исходной приведены в § 3 гл. VII. Эта
плотность выражается через функцию р (а, х) —
плотность сдвинутой меры ра относительно исходной меры \х.
Укажем метод нахождения разложения р(а, х) по.
ортогональным полиномам. Предположим, что
оо
р(а,х)=21Рк{н1х), (14)
где Н% — некоторая 6-линейная форма, зависящая от а.
Тогда для всякого полинома Рг{Них) из 0>х (см. § 2)
выполняется соотношение
$ Рк (ЯА, х) Рк {Н1 х) [х {их) = | Рк {Нк, х) р (а, х) \л {их) -
= \ Рк(Нк,х + а)р(йх) = 8а(Нк).
Линейный функционал 8а{Нк) на Фк легко вычислить,
разлагая полином Рк{НкУ х + а) по формуле Тейлора
и используя разложение каждого полученного полинома
по ортогональным полиномам. Очевидно, что линейная
функция 8а{Нк) на Фк может быть представлена
скалярным произведением
8а{Нк) = (Нк,Н1)к
(см. § 2). Из этого соотношения Нк определяются
однозначно и р(а, х) после этого определяется формулой (14),
Для того чтобы р(а, х) существовало и принадлежало
^2М» необходимо и достаточно, чтобы ряд (14)
сходился, т. е. чтобы выполнялось неравенство
ПРИМЕЧАНИЯ
Нижеследующие примечания содержат некоторые указания на
литературу по затронутым вопросам и не преследуют своей целью
дать полную библиографию или осветить историю основных идей
теории случайных процессов. Во многих случаях- мы позволили себе
не ссылаться на оригинальные труднодоступные работы, а отсылали
читателя к более поздним учебникам и монографиям, содержащим
библиографию по соответствующим вопросам.
Глава I
§ 1. Изложение основано на общепринятой в настоящее время
теоретико-множественной аксиоматике теории вероятностей,
предложенной А. Н. Колмогоровым в 1929 г. и изложенной в его
монографии [29], [102]. По поводу используемых результатов теории меры
и интеграла см. книги А. Н. Колмогоров и С. В. Фомин [37], П. Хал-
мош [66], И. И. Гихман и А. В. Скороход [14], Ж. Неве [44], П.Мей-
ер [106].
§ 2. Общий закон «0 или 1» установлен А. Н. Колмогоровым [29].
§ 3. Теория условных вероятностей и условных математических
ожиданий была предложена А. Н. Колмогоровым [29]. Дальнейшие
усовершенствования принадлежат Дж. Дубу [21]. См. также М. Лоэв
[40], Ж. Неве [44].
§ 4. Основная теорема принадлежит А. Н. Колмогорову [29].
Глава II
§ 2. Мартингалы рассматривались разными авторами, но их
систематическая теория многим обязана Дж. Дубу [21]. Ему
принадлежат основные неравенства для мартингалов, теорема о
существовании предела, понятие полумартингала и другие результаты. Больше
сведений о мартингалах можно найти в цит. монографиях Дж. Дуба,
М. Лоэва и П. Мейера.
§ 3. Основные идеи и результаты этого параграфа принадлежат
А. Н. Колмогорову и А. Я. Хинчину [81] и А. Н. Колмогорову [100].
Более подробно ряды независимых случайных величин рассмотрены
в монографиях Дж. Дуба [21], М. Лоэва [40], А. В. Скорохода [60].
§ 4. Цепи Маркова с конечным числом состояний* были введены
{1906 г.) и изучены А. А. Марковым [42]. Общее определение цепи
и процесса Маркова принадлежит А. Н. Колмогорову [31]. Более
общие точки зрения развиты в монографиях Е. Б. Дынкина [23], [24],
652
ПРИМЕЧАНИЯ
§ 5. Цепи Маркова со счетным числом состояний впервые
изучались в работах А. Н. Колмогорова [104], [30], В. Деблин [85] и в
дальнейшем многими авторами. См. В, Феллер [65], Чжун Кай-лай
[72], Е. Б. Дынкин и А. А Юшкевич [25], Кемени, Снелл, Кнапп[98].
§ 6. Случайные блуждания изучались многими авторами и в этой
области получено много результатов. См. В. Феллер [65], Е. Б.
Дынкин и А. А. Юшкевич [25], А. В. .Скороход и Н. П. Слободенюк [61],
Спитцер [63].
§ 7. Впервые локальные предельные теоремы для решетчатых
одномерных распределений рассматривал Б. В. Гнеденко [16]. См.
Б. В. Гнеденко и А. Н. Колмогоров [18], И. А. Ибрагимов и Ю. В. Лин-
ник [26], А. В. Скороход и Н. П. Слободенюк [61].
§ 8. Возникновение эргоднческой теоремы связано с проблемами
статистической механики. См. по этому поводу книгу А. Я. Хин-
чина [69]. Первые эргодические теоремы Дж. Неймана и Дж. Бирк-
хоффа послужили началом интенсивного развития теории. Обзор
первого периода развития эргоднческой теории содержится в
монографии Е. Хопфа [70]. Простое доказательство теоремы Биркхоффа—
Хинчина предложено А. Н. Колмогоровым [32]. Дальнейшее развитие
эргоднческой теории освещено в книгах П. Халмоша [67], К. Якоб-
са [95], П. Биллингсли [77].
Глава III
§ 1. Многомерное обобщение центральной предельной теоремы
впервые было указано С, Н, Бернштейном [76]. Процессы с
независимыми приращениями систематически начал изучать Б. Финетти [90].
А. Н. Колмогоров [101] нашел характеристическую функцию
процесса с независимыми приращениями в случае конечного момента
второго порядка, а П. Леви [105] в общем случае (одномерный
случай). По поводу определений марковских процессов см. примечания
к § 4 гл. II.
§§ 2, 3. Возможность построения случайного процесса,
стохастически эквивалентного данному, выборочные функции которого
удовлетворяют определенным условиям регулярности, впервые
рассматривали Е. Е. Слуцкий и А. Н. Колмогоров (см. работу Е. Е.
Слуцкого [62]). В дальнейшей разработке возникающих здесь вопросов
и разных вариантов аксиоматического определения случайной
функции много существенных результатов принадлежит Дж. Дубу.
Ссылки на первоначальные работы содержатся в его монографии [21].
Основные теоремы §§ 2, 3 принадлежат Дж. Дубу [21]. См. также
Е. Е. Слуцкий [62].
§ 4. Теорема 1 в несколько более слабой формулировке была
доказана Н. Н. Ченцовым [71], теорема 2 — Дж. Кинни [99] (для
марковских процессов). Отсутствие разрывов второго рода у
стохастически непрерывных процессов с независимыми приращениями
установил П. Леви [105]. Свойства выборочных функций
мартингалов рассматривал Дж. Дуб [21].
§ 5. Теорема 2 доказана независимо Е. Б. Дынкиным [22] и
Дж. Кинни [99] (для марковских процессов). Несколько более
слабый вариант теоремы 6 принадлежит А. Н. Колмогорову и впервые
опубликован в работе Е. Е. Слуцкого [62]. Локальные свойства га-
уссовских процессов изучал Ю. К. Беляев [3, 75]. См. также
монографию Г. Крамера и М. Ледбеттера [84].
ПРИМЕЧАНИЯ
653
Глава IV
§§ 1—2. Понятие процесса стационарного в широком смысле
было введено А. Я. Хинчиным [68]. В этой же работе было указано
спектральное представление корреляционной функции стационарного
в широком смысле процесса. Спектральное представление
положительно определенной последовательности получили Ф. Рисе и Г. Герг-
лотц в 1911 г., а положительно определенных функций — С. Бох-
нер [4] в 1932 г. Спектральное представление однородного и
изотропного случайного поля в евклидовом и гильбертовом
пространстве содержится в работе Шенберга [111].
§ 3. Е. Е. Слуцкий [113], М. Лоэв [40].
§ 4. Теорию стохастических интегралов предложил Г. Крамер
[82]. А. Н. Колмогоров впервые выяснил связь между
стохастическими интегралами, спектральными представлениями и методами
теории гильбертовых пространств [35]. См. также Дж. Дуб [21].
§ 5. Теорема 1 принадлежит К. Карунену [96], теорема 2 —
Г. Крамеру [82].
§ 6. С помощью теории фильтров нетрудно получить
спектральное разложение стационарных процессов (А. Блан-Лапьер, Р.
Форте [78]). Более общую теорию линейных преобразований случайных
процессов можно построить с помощью теории обобщенных
случайных процессов, предложенной И. М. Гельфандом и К. Ито
(И. М. Гельфанд и Н. Я. Виленкин [10], К. Ито [94]).
§ 7. Основные результаты для случая стационарных
последовательностей получены А. Н. Колмогоровым [35], а для процессов с
непрерывным временем К. Каруненом [97] (см. Д. Дуб [21],
Ю.А.Розанов [52]).
§ 8. Общая формулировка задачи линейного прогноза (для
стационарных последовательностей), ее связь с геометрией
гильбертова пространства и сведение к задаче теории функций принадлежит
А. Н. Колмогорову [35]. Н. Винер [116] развил методы эффективного
решения задач линейного прогноза и фильтрации для процессов с
непрерывным временем. Метод А. М. Яглома с большим числом
примеров можно найти в его обзорной статье [74].
§ 9. Теорема о разложении стационарной последовательности и
понятия детерминированного и недетерминированного процессов
принадлежат Г. Волду. Общее решение задачи о прогнозе стационарной
последовательности по всему прошлому получено А. Н.
Колмогоровым [35], для процессов с непрерывным временем — М. Г. Крейном
[38], [39]. Задачу о прогнозе векторной стационарной
последовательности рассматривали Ю. А. Розанов [50], Н. Винер, П. Масани [117].
Подробности о прогнозе процессов с непрерывным временем можно
найти в книгах Дж. Дуба [21], 10. А. Розанова [52].
Глава V
Построение меры в функциональном пространстве впервые было
осуществлено в работе Н. Винера [115]. Общий метод построения
таких мер был предложен А. Н. Колмогоровым [29]. Меры в
банаховых и полных метрических пространствах изучались в работах
А. Н. Колмогорова, Э. Мурье [107], Ю. В. Прохорова [47], К. Р. Пар-
тасарати [108].
654
ПРИМЕЧАНИЯ
§ 3. Построение расширения исходного пространства, на
котором существует мера, имеющая характеристическим функционалом
заданную положительно определенную функцию, принадлежит
Л. Гроссу [92], теорема § 3 установлена Э. Мурье [107].
Теорема § 5 установлена В. В. Сазоновым [55] и Р. А. Мин
лесом [43], обобщенные меры в гильбертовом пространстве ввел
Ю. А. Далецкий [19].
§ 6. Общая теория гауссовских мер в линейных пространствах
построена А. М. Вершиком [6], им же изучены линейные и квадра-
тические функционалы, измеримые относительно таких мер. Кратные
стохастические интегралы построены К. Ито [93], общий вид
линейных и квадратических функционалов от стационарного гауссовского
процесса нашел Ю. А. Розанов [54].
Глава VI
§ 1. Доказательство достаточности условий теоремы 1
принадлежит Ю. В. Прохорову [47].
§ 2. Условие слабой компактности мер в гильбертовом
пространстве установлено К. Р. Партасаратн [108], гл. VI, § 2.
§ 3. Общий вид безгранично делимого распределения и
условия сходимости к нему распре/Селений сумм независимых случайных
величин со значениями в гильбертовом пространстве найдены
С. Р. С. Варадханом [114]. Условия сходимости к гауссовскому
распределению изучали Н. П. Канделаки и В. В. Сазонов [27].
Довольно полное изложение этих результатов имеется в книге К. Р.
Партасаратн [108].
§ 4. Исследования по общим предельным теоремам для
случайных процессов начаты М. Донскером [86], его результат
сформулирован в теореме 4. Теоремы 1—3 принадлежат Ю. В. Прохорову.
§ 5. Первая предельная теорема для процессов без разрывов
второго рода установлена И. И. Гихманом [12]. Пространство О[оп
и предельные теоремы для процессов в этом пространстве изучались
А. В. Скороходом [57]. Сходимость в Г>^ ц рассматривалась
А. Н. Колмогоровым [35] и Ю. В. Прохоровым [47]. Интересная
предельная теорема была найдена Н. Н. Ченцовым [71], теорема 3
является небольшим видоизменением этой теоремы. Сходимость
процессов с независимыми приращениями и марковских процессов
изучалась А. В. Скороходом [57], [53], [59]. Применение предельных
теорем к задачам статистики имеется у М. Донскера [87] и "И. И. Гих-
мана [13].
Глава VII
Различные общие вопросы абсолютной непрерывности мер в
функциональных пространствах изложены в статье И. И. Гихмана и
А. В. Скорохода [15].
§ 2. Меры со всюду плотным множеством допустимых сдвигов
рассмотрел В. Н. Судаков [64]. Структура множества допустимых
сдвигов изучалась Питчером [109]. Теорема 4 сформулирована в
работе А. М. Вершика [7].
§ 3. Абсолютная непрерывность винеровской меры при
различных преобразованиях изучалась Камероном и Мартиным [79], [80].
ПРИМЕЧАНИЯ
655
Некоторые результаты по абсолютной непрерывности гауссовскои
меры в гильбертовом пространстве при нелинейных преобразованиях
содержатся в работе В. В. Баклана и А. Д. Шаташвили [2].
§ 4. Условия абсолютной непрерывности и формула для
плотности гауссовскои меры при сдвиге получены У. Гренандером [91].
Общие условия абсолютной непрерывности и сингулярности для
гауссовских мер получены в работах Я. Гаека, Дж. Фельдмана и
Ю. А. Розанова [9], [88], [89], [53].
§ 5. Теоремы 1 и 2 принадлежат Ю. А. Розанову. Основные
результаты в этой области изложены в книге Ю. А. Розанова [54].
§ 6. Абсолютно непрерывные преобразования некоторых классов'
марковских процессов рассматривали И. В. Гирсанрв [11], А. В.
Скороход [59]. Общие теоремы об абсолютной непрерывности мер,
соответствующих процессам с независимыми приращениями, и
марковских процессов изложены в статье И. И. Гихмана и А. В.
Скорохода [15].
Глава VIII
§ 1. Измеримые линейные операторы и линейные функционалы
изучались в книге Г. Е. Шилова и Фан Дык Таня [73].
§ 2. Ортогональная система полиномов для винеровской меры
построена в работе К. Ито [93], различные применения этих
полиномов указаны в книге Н. Винера [8]. Ортогональные полиномы для
гауссовскои меры построены А. М. Вершиком [6].
ЛИТЕРАТУРА
1. А х и е з е р Н. И., Г л а з м а н И. М., Теория линейных
операторов в гильбертовом пространстве, «Наука», 1966.
2. Баклан В. В., Ш а т а ш в и л и А. Д., Перетворення гаус-
С1вських М1р при нелшшних перетвореннях в пльбертовому
просторе Доповш АН УРСР 9 (1965), 1115—1117.
3. Б е л я е в Ю. К., Локальные свойства выборочных функций
стационарных гауссовских процессов, Теория вероятн. и ее при-
мен. 5 (1960), 128—131.
4. Бохнер С, Лекции об интегралах Фурье, Физматгиз, 1962,
5. В е р ш и к А. М., К теории нормальных динамических систем,
ДАН 144 (1962), 9—12.
6. В е р ш и к А. М., Общая теория гауссовских мер в линейных
пространствах, УМН 19 (1964), 210—212.
7. В е р ш и к А. М., Двойственность в теории меры в линейных
пространствах, ДАН 170 (1966), 497—500.
8. Винер Н., Нелинейные задачи в теории случайных процессов,
ИЛ, 1961.
9. Гаек Я., Об одном свойстве нормальных распределений
произвольных стохастических процессов, Чехосл, матем. журн. 8
(1958), 610—618.
10. Гельфаыд И. М., Виленкин Н. Я., Некоторые
применения гармонического анализа. Оснащенные гильбертовы
пространства, Физматгиз, 1961.
11. Г и р с а и о в И. В., О преобразовании одного класса
случайных процессов с помощью абсолютно непрерывной замены
меры, Теория вероятн. и ее примен. 5 (1960), 314—330.
12. Г и х м а н И. И., Об одной теореме А. Н. Колмогорова, Научн.
зап. Киевск. ун-та, Матем. сб. 7 (1953), 76—94.
13. Г и х м а н И. И., Процессы Маркова в задачах математической
статистики, Укр. матем. журн. 6 (1954), 28—36.
14. Г и х м а н И. И., Скороход А. В., Введение в теорию
случайных процессов, Физматгиз, 1965.
15. Гихман И. И., Скороход А. В., О плотностях
вероятностных мер в функциональных пространствах, УМН 21 (1966),
83—152.
16. Гнеденко Б. В., О локальной теореме для предельных
устойчивых распределений, УМЖ 1 (1949), 3—15.
17. Гнеденко Б. В., Курс теории вероятностей, изд. 3-е,
Физматгиз, 1961.
18. Гнеденко Б. В., Колмогоров А. Н., Предельные
теоремы для сумм независимых случайных величин, Гостехиздат,
1949.
ЛИТЕРАТУРА
657
19. Д а л е ц к и й Ю. Л., Бесконечномерные эллиптические
операторы и связанные с ними параболические уравнения, УМН 22
(1967), 3—54.
20. Д а н ф о р д Н., Шварц Дж. Т., Линейные операторы. Общая
теория, ИЛ, 1962; Специальная теория, ИЛ, 1966.
21. Дуб Дж., Вероятностные процессы, ИЛ, 1956.
22. Дынкин Е. Б., Критерий непрерывности и отсутствия
разрывов второго рода для траекторий марковского случайного
процесса, Изв. АН СССР, сер. матеьц 16 (1952), 563—572.
23. Д ы н к и н Е. Б., Основания теории марковских процессов,
Физматгиз, 1959.
24. Дынкин Е. Б., Марковские процессы, Физматгиз, 1963.
25. Д ы н к и н Е. Б., Юшкевич А. А., Теоремы и задачи о
процессах Маркова, «Наука», 1967.
26. И б р а г и м о в И. А., Л и н н и к Ю. В., Независимые и
стационарно связанные величины, «Наука», 1965.
27. К а н д е л а к и Н. П., Сазонов В. В., К центральной
предельной теореме для случайных элементов, принимающих
значения из гильбертова пространства, Теория вероятн. и ее при-
мен. 9 (1964), 48—52.
28. Колмогоров А. Н., Общая теория меры и исчисления
вероятностей, Труды Комм, акад., разд. матем., 1 (1929), 8—21.
29. Колмогоров А. Н., Основные понятия теории вероятностей,
ОНТИ, 1936.
30. Колмогоров А. Н., Цепи Маркова со счетным числом
возможных состояний, Бюлл. МГУ 1, № 3 (1937), 1—16.
31. К о л м о г о р о в А. Н., Об аналитических методах в теории
вероятностей, УМН 5 (1938), 5—41.
32. К о л м о г о р о в А. Н., Упрощенное доказательство эргодиче-
ской теоремы Биркгофа — Хинчина, 5 (1938), 52—56.
33. К о л м о г о р о в А. Н., Кривые в гильбертовом пространстве,
инвариантные по отношению к однопараметрической группе
движений, ДАН 26 (1940), 6—9.
34. К о л м о г о р о в А. Н., Спираль Винера и некоторые другие
интересные кривые в гильбертовом пространстве, ДАН 26
(1940), 115—118.
35. К о л м о г о р о в А. Н., Стационарные последовательности в
гильбертовом пространстве, Бюлл. МГУ 2, № 6 (1941), 1—40.
36. К о л м о г о р о в А. Н., О сходимости Скорохода, Теория
вероятн. и ее примен. 1 (Ш56), 239—247.
37. Колмогоров А. Н., Фомин С. В., Элементы теории
функций и функционального анализа,, изд. 2-е, «Наука», 1968.
38. К р е й н М. Г., Об одной интерполяционной проблеме А. Н.
Колмогорова, ДАН 46 (1944), 306—309.
39. К р е й н М. Г., Об основной аппроксимационной задаче теории
экстраполяции и фильтрации стационарных случайных
процессов, ДАН 94 (1954), 13—16.
40. Л о э в М., Теория вероятностей, ИЛ, 1962.
41. Л ю с т е р н и к Л. А., Соболев В. И., Элементы функцио*
нального анализа, «Наука», 1965.
653
ЛИТЕРАТУРА
42. Марков А. А., Распространение закона больших чисел на
величины, зависящие друг от друга, Изв. физ.-матем. о-ва при
Казанском ун-те (2) 15 (1906), 135—156.
43. М и н л о с Р. А., Обобщенные случайные процессы и их про*
должение до меры, Труды Моск. матем. о-ва 8 (1959), 497—518.
44. Неве Ж-, Математические основы теории вероятностей, «Мир»,
1969.
45. Пи иске р М. С, Информация и информационная
устойчивость случайных величин и процессов, М., 1960.
46. Привалов И. И., Граничные свойства аналитических функ- '
ций, Гостехиздат, 1950.
47. П р о х о р о в Ю. В., Сходимость случайных процессов и
предельные теоремы • теории вероятностей, Теория вероятн. и ее
примен. 1 (1956), 177—238.
48. Прохоров Ю. В., Сазонов В. В., Некоторые результаты,
связанные с теоремой Бохнера, Теория вероятн. и ее примен.
6 (1961), 87—93.
49. П р о х о р о в Ю. В., Фиш М., Характеристическое свойство
нормального распределения в гильбертовом пространстве 2
(1957), 475—477.
50. Роз а и о в Ю. А., Спектральная теория многомерных
стационарных процессов с дискретным временем, УМН 13, № 2 (1958),
93—142.
51. Розанов Ю. А., О плотности одной гауссовской меры
относительно другой, Теория вероятн. и ее примен. 7 (1962), 84—89.
52. Розанов Ю. А., Стационарные случайные процессы, Физмат-
гиз, 1963.
53. Р о з а н о в Ю. А., О плотности гауссовских распределений и
интегральных уравнениях Винера — Хопфа, Теория вероятн. и
ее примен. 11 (1966), 170—179.
54. Розанов Ю. А., Гауссовские бесконечномерные
распределения, Тр. матем. ин-та им. Стеклова СУШ (1968), 1 —136.
55. С а з о н о в В. В., Замечание о характеристических
функционалах, Теория вероятн. и ее примен. 3 (1958), 201—205.
56. Скороходе А. В., Предельные теоремы для случайных
процессов, Теория вероятн. и ее примен. 1 (1956), 289—319.
57. С к о р о х о д А. В., Предельные Теоремы для случайных
процессов с независимыми приращениями, Теория вероятн. и ее
примен. 2 (1957), 145—177.
58. Скороход А. В., Предельные теоремы для процессов
Маркова, Теория вероятн. и ее примен. 3 (1958), 217—264.
59. С к о р о х о д А. В., Исследования по теории случайных
процессов, Изд. Киев, ун-та, 1961.
60. Скороход А. В., Случайные процессы с независимыми
приращениями, Физматгиз, 1963.
61. Скороход А. В., Слободенюк Н. П., Предельные
теоремы для случайных блужданий, Наукова думка, 1970.
62. С л у ц к и и Е. Е., Несколько предложений к теории случайных
функций, Тр. Ср.-Аз. ун-та, сер. матем., (5), 31 (1949), 3—15.
63. С п и ц е р Ф., Принципы случайного блуждания, «Мир», 1969.
64. Судаков В. Н., Линейные множества с квазиинвариантной
мерой, ДАН 127 (1959), 524—525.
ЛИТЕР АТУРД.
659
65. Ф е л л е р В., Введение в теорию вероятностей и ее
приложения, том I (1964) ИЛ, том II (1967) «Мир». .
66. X а л м о ш П., Теория меры, ИЛ, 1953.
67. X а л м о ш П., Лекции по эргодической теории, ИЛ^ 1959.
68. X и н ч и н А. Я., Теория корреляции стационарных случайных
процессов, УМН 5 (1938), 42—51.
69. X и н ч и н А. Я-, Математические основания статистической
механики, Гостехиздат, 1943.
70. Хопф Е., Эргодическая теория, УМН 4, № 1 (1949), 113—182.
71. Чепцов Н. Н., Слабая сходимость случайных процессов с
траекториями без разрывов второго рода, Теория вероятностей
и ее применения 1 (1956), 154—161.
72. Чжун Кай-Лай, Однородные цепи Маркова, «Мир», 1964.
73. Шилов Г. Е., Фан ДыкТань, Интеграл, мера и
производная на линейных пространствах, «Наука», 1967.
74. Яглом А. М., Введение в теорию стационарных случайных
функций, УМН 7, № 5 (1955), 3—168.
75. Ве1ауеу Зп. К., СогилпиИу апс! НбЫег'з сопшЧюпз Гог зат-
р1е ШпсИопз оГ зЫюпагу Оаизз1ап ргосеззез. Ргос. ЦшгШ
Вегк. 5 утр. оп МаШ. §1а1. ал<1 РгфаЫШу 2, (1961), 23—33.
76. Вегпз1е1п 5., Зиг Гех1епзюп ди Шёогёте НпиЧе .с!и са1си1
(1ез ргоЪаЫШёз аих зоттез с!е ^апШёз ёерепс1еп1ез, МаШ.
Апп. 97 (1926) 1—59 (русский перевод: УМН 10 (1944), 65—114).
77. В 11 П п д з 1 е у Р., Ег^ош'с Тпеогу апс! 1пГогтатдоп. N. V.,
1965.
78. В 1 а п с - Ь а р 1 е г г е А., Р о г 1 е 1 К., Тпёопе с1ез ГопсИопз
а1ёа1о1гез, Рапз, 1953.
79. К. Н. С а т е г о п, №. Т. М а г 11 п, ТгапзЬгтаНопз о! Мепег
1"п1е^га1з ипйег а &епега1 с1азз 1гапзГогта1юп, Тгапз. Атег.
МаШ. Зое. 58 (1945), 184—219.
80. К. Н. Сатегоп, \У. Т. М а г I! п, ТгапзГогтаНоп о? М'епег
шт,едга1з Ьу попПпеаг тгапзГогтаИоп, Тгапз. Атег. МаШ. Зое,
66 (1949), 253—283.
81. С Ь 1 п I з с Ь 1 п А. Ла.к Ко 1 то дого Г! А. Ы,, 11еЪег Копуег-
депг уоп КеШеп с!егеп ОНейег (Зигсп йеп 2иГа11е ЪезНтт* шег-
(!еп, Матем. сб. 32 (1925), 668—677.
82. Сгатег Н., Оп Ше Шеопе оГ гапёот ргосеззез, Апп. МаШ.
41 (1940), 215—230.
83. Сгатег Н., Оп зШспазНс ргосеззез \упозе гга]'ес1опез Ьауе по
ШзсоптлпиШез о! Ше зееопс! Кто1, Апп. ш" Ма^етатюа (гу) 71
(1966), 85—92.
84. С г а т е г Н., ЬеадЬеПег М. К., ^51атюпагу апс! 1а1ес1 з!о-
сЬазИс ргосеззез, N. I., 1967.
85. ОоеЬНп \У., 5иг 1ез ргорпе1ёз азутрЬ^иез* с!е тоиуетеп!
гё^1з раг сег1атз гурез с!е сЬагпез 51*тр1ез, Ви11. МаШ. Зое. Коит.
5с1. 39 (1937), № 1, 57—115, № 2, 3—61.
86. Оопзкег М., Ап Шуапапсе ргтар1е !ог сегЫп ргоЬаЫШу
НтИ Шеогетз, Мет. Атег. МаШ. Зое. 6 (1951), 1—12.
87. Оопзкег М., Ко1то§ог©1! — Зтггпоу Шеогетз, Апп. МаШ.
51а*. 23 (1952), 277—281,
88. Л. Р е 1 с1 т а п, Е(|шуа1епсе аш! регрепсПси1ап1у о! Саизз1ап
ргосеззез, РасН. Лоигп. МаШ. 8 (1958), 699—708.
660
ЛИТЕРАТУРА
89. Л. Р е 1 с! т а п, Зоте с1аззез оГ е^и^Vа1еп^: Оаиззтп ргосеззез
оп т!егуа1, РасИ. Лоигп. МаШ. 10 (1960), 1211—1220.
90. Р 1 п п е И В., ЗиЛе Гшшот а тсгетеп1о а1еа1опо, Непс1. Ассаё.
N32. Ппсе1, С1. 5а. Из.-Ма*. N31. (6), 10 (1929), 163—168.
91. Сгепапйег II., 5т.оспазНс ргосеззез апс! з1а1лз11са1 тГегепсе,
Агк. Ма*., Уо1. 1 (1950), рр. 195—277.
92. О г о з з Ь., Нагтотс апа1уз1з оп НПЬей зрасе, Мет. Атег.
Магп. Зое. 46 (1963), 1—62.
93. По К., МиШр1е УУ1епег т*едга1, Лот. Ма1п. Зое. Ларап 3
(1951), 157—169.
94. По К., 51а1юпагу гапс!от (ПзШЬиИоп, Мет. СоН. За. 11шу.
КуоЬ 28 (1954), 209—223.
95. Л а с о Ь з К., №иеге Мет.пос1еп ипс! Ег^еЬшззе с!ег Егдойеп-
Шеопе, Зрпп^ег Уег1ад, 1960.
96. КагЬипеп К., ШЬег Нпеаге Ме1пос1еп т йег ^апгзспет-
Псгйгесппип^, Апп. Асас1. За. Репшсае, Зег. А, Ма1Ь. РЬуз. 37
(1947), 3—79.
97. КагЬипеп К., ОЬег (Не 51гик1иг з1ат.юпагеп хиШ^ег Рипк-
Иопеп, Агк. МаШ. 1 (1950), 141 — 160.
98. Кете пу Л. С, ЗпеП Л. Ь., Кпарр А. XV., ИепитегаЫе
Магкоу спатз, Уап №з1гапа\ N.-7.—Ь. 1966.
99. К1 п п е у Л. Н., СопИпиНу ргорегИез о! затр1е !ипс!юпз о!
Магкоу ргосеззез, Тгапз. Атег. Ма1п. Зое. 74 (1953), 280—302.
100. Ко1то^огоН А., ИеЬег с!1е Зиттеп дигеп с!еп 2и!а11 Ье-
зглпйег ипаЪпап^дег Огоззеп. МаШ. Апп. 99 (1928), 309—319;
100 (1929), 484—488.
101. Ко1то^огоН А., 5и11а Гогта ^епега1е (Н ип ргосеззо з!о-
- сазИсо ото^епео, АШ Ассас!. Ппсе1 15 (1932), 805—808; 866—
869.
102. Ко1то^огоН А., СгипсИэе^гШе бег ^апгзспетПспкеиз-
гееппипд, ВегПп, 1933,
103. Ко1то^огоН А., Ьа 1гапз!огтаИоп (Зе Ьар1асе с!апз 1ез
Ппёа1гез, Сотр*. Кепо1. Асаа\ 5а. (Рапз) 200 (1935), 1717.
104. Ко1то^огоН А., Ап!ап^з^гйпйе (Зег ТЬеопе с!ег МагкоН-
зспеп Ке11еп п\И ипепсШспеп У1е1еп тб^Пспеп 2из1апс1еп, 1
(1936), 607—610.
105. Ь ё у у Р„ Зиг 1ез т1е^га1ез сЗоп! 1ез ё1ётеп(з зоп! без уапаЬ-
1ез а1ёаЫгез тс!ерепс1еп(ез, Апп. 5сио1а N0™. Р1за 2. № 3
(1934), 337—366.
106. Меуег Р. А., РгоЪаЫШу апс! РокпИак, И5А, 1966.
107. М о и г 1 е г Е., Ё1ётеп1з а1ёа!о1гез (1апз ип езрасе сЗе ВапасЬ*
Апп. 1пз*. Не Ротсагё 13 (1953).
108. Раг1пазагат.пу К. К-, РгоЪаЫШу Меазигез оп Ме*пс
Зрасе, Асайетю Ргезз N.-7.—Ь. 1967.
109. РЦсЬег Т. 5., ТЬе асЗгшззиМе теап уа1иез о! зТ-осЬазИс рго-
сезз, Тгапз. Атег. Ма*Ь. Зое. 108 (1963), 538—546.
ПО. РгоЬогоу Ли. V., ТЬе теШоа" оГ сЬагасТ-епзИс ГипсНопаЬ,
Ргос. 4*ь ВегЫеу зутр. 2 (1961), 403—419.
111. 5 сп 6 п 1 е г & Л. Ь., Ме1пс зрасез ала" сотр1еге1у топо!опе
1ипс«оп$, Апп. МаШ. 39 (1938), 811—841.
И 2. 5 ко го Иод А. V., Оп Ше депзШез о! ргоЬаЫШу теазигез
т 1ипс«опа1 зрасе. Ргос. 51*1 Вегк1еу зутр. 2 (1965), 163—182,
ЛИТЕРАТУРА
661
113. 5 1 и 1 з к у Е. Е., 5иг 1ез ГопсНопз еуеп1ие11ез сопИпиез, 1п(ё-
дгаЫез е! с!епуаЬ1е5 с!ап5 1е зепз зЬсЬаз^ие, Сотр1ез Кепс1из
Аса<1. за. 187 (1928), 370—372.
114. Уагас1Ьап 5. К. 3., 1лтИ Шеогетз Гог зитз оГ тберепйеп!
гапс!от уапаЫез \уИЬ уа1иез т а НПЬег! зрасе, ЗапкЬуа 24
(1962), 213—238.
115. \\Пепег Ы., ОШегепИа1 зрасе, *1. МаШ. РЬуз. Мазз. 1пз1. ТесЬ.
2 (1923), 131—174.
116. \У1епег Ы., Ех1гаро1а1лоп, т1егро1аНоп ап(1 зтооШтд оГ з1а-
Иопагу Нте зепез, N. У., 1949.
117. ХУЧепег N., Мазапу Р., РгеШсИоп Шеогу оГ тиШуапа(е
зЬсЬазКс ргосеззез, Ас1а МаШ. 98 (1957), 111—150; 99 (1958),
93-137.
УКАЗАТЕЛЬ
Алгебра 1Г
— тривиальная 11
0-алгебра 11
— борелевская 16, 23, 188, 373
»-, порожденная классом случайных
величин 37
—, — случайным временем 32
*-, элементом 17
— сепарабельная 602
Белый шум 318
Блуждание возвратное 152, 157
* вполне неприводимое 157
— на решетке 147, 151, 155
•- невозвратное 152, 154, 157
*- случайное 147
Величина случайная 13
дискретная 16
Величины случайные независимые 36,
453, 485
— — ортогональные 2Г
— — эквивалентные 13
Вероятность 12
— первого возвращения 118
*~ ■— попадания П8
— перехода 108, 133, 199, 509
•— регулярная 51
— условная 46, 222
Время случайное 32
Задача фильтрации 325
•— экстраполяции 325
Закон больших чисел 94, 153, 178,
270
— 0 и 1 39, 41, 179
Замыкание субмартннгала 82, 83
Значение собственное 300
•— среднее 241
— — меры 405
— функции граничное 313
Индикатор события 15
Интеграл Лебега 270
•— Лебега—Стилтьеса 280
— Стилтьеса 285
*- Фурье 27, 260, 321
Класс возвратный 123
Классы событий независимые 34
Ковариация 22, 241, 267
Компактность семейства мер 26» 429.
440, 448
Лемма Фату 156. 173. 259
Мартингал 73, 84, 89, 228
Математическое ожидание 18
— — условное 45, 50
Матрица стохастическая 116
— структурная 290
Мера 12
— внешняя 368, 379
— гауссовская 414, 417, 554. 565, 570,
574, 580
—, допустимый сдвиг 528, 539, 547
— инвариантная 112
— Лебега 287, 321
— обобщенная 401, 421
—, соответствующая случайному
процессу 365, 380
— спектральная 256
■— стохастическая векторная 292
*- — ортогональная 284, 288
*- — спектральная 296
— — стандартная 318
»— элементарная 281
— — стохастическая векторная 290
Меры абсолютно непрерывные 518, 557,
574
*- взаимно сингулярные 518
►- ортогональные 518, 539, 584
— эквивалентные 518, 539, 584
Метод Винера 330
— Яг л ом а 334
Множество непрерывности меры 434
— сепарабельности 203, 370
— измеримое 11
*~ инвариантное 174
г- цилиндрическое 17, 64, 174, 382, 402
Момент 29
Моментная форма 404
Независимость событий 34, 36
Непрерывность в среднем
квадратичном 245
Неравенство Гёльдера 78, 89
«— Колмогорова 454
— Чебышева 21, 235, 408
Оператор абсолютно измеримый 619
^~ Гильберта—Шмидта 446, 591, 595
— измеримый линейный 618
*- корреляционный 405
»- переноса 528
»- сдвига времени 358
*- ядерный 406, 411
Операция сдвига времени 299, 307, 345
УКАЗАТЕЛЬ
663
Отображение дифференцируемое 558
— измеримое 527, 634, 639
— полиномиальное 636, 639
— — однородное 636
— случайное 59
Период восстановления 129
— цепи 125
Плотность вероятности условна» 46
-- меры 518, 600
— распределения 67
— — совместная 57
"— -- условная 58
— спектральная 256, 311, 360
Поле изотропное 261
— однородное 256, 265
— случайное 69
Полином 624
— измеримый 624
— однородный 620
— ортогональный 626, 650
Полумартингал 73, 89, 228
Порядок момента 30
Последовательность
некоррелированная 248
~- разбиений исчерпывающая 85
— фундаментальная 19
Поток а-алгебр 32
Представление семейства
распределений 64, 66
— — — естественное 72, 166
— спектральное 253, 345, 348
Преобразование Лапласа 334
— метрически транзитивное 175
— обратимое 166
—, сохраняющее меру 166
— Фурье 27, 163, 179, 259, 263, 336
— эргодическое 175
Производная меры 518
Пространство вероятностное 12
полное 202, 267
—- измеримое 11
— — гильбертово 401, 409, 414, 452,
528, 574, 612
— фазовое 71
Процесс авторегрессии 250
— без разрывов второго рода 215, 221,
227, 230, 496, 506
— броуновский 196, 278
•- винеровский 196, 237
— восстановления апериодический 129,
130
— — периодический 129
— гауссовский 180, 182. 233, 238, 239,
424, 513, 584, 594
— дифференцируемый 673
— измеримый 626
— марковский 108, 199, 248, 494, 503,
604, 606, 600
— — в широком смысле 200
— — стационарный 112, 143
-- непрерывный 230, 478, 492, 494
•-, подчиненный потоку а-алгебр 223
— пуассоновский 196, 197, 245
— с дискретным временем 59, "?[
— с. к. дифференцируемый 273
— скользящего суммирования 249
— случайный 59
*- с независимыми приращениями 188,
190, 226, 232, 492, 512
Процесс стационарный 165, 248
* в широком смысле 246, 275
»- — детерминированный 347, 359
*- — недетерминированный 347, 349
359, 363
— — регулярный 347, 359
— — сингулярный 347, 359
— стохастически непрерывный 190,
395, 604
— Хинчина 246
— эргодический 176, 181
Процессы стационарно связанные 247
Равенство Парсеваля 259, 260, 313,
320, 333. 593
Распределение безгранично делимое
460, 467
— начальное 108, 188
инвариантное 180
— регулярное условное 52
— случайного элемента 23
— стационарное 136
Распределения согласованные 61, 403
— частные 60, 63, 71, 221, 482, .485, 514
Решетка 147
— вырожденная 147
— невырожденная 147
Свертка ядер 103
Семейство распределений
согласованное 403
С. к. предел 22
— — производная 273
След оператора 406
Событие элементарное 9
События независимые 34
Составляющая процесса регулярная
348
сингулярная 348
Сосюяние возвратное 118, 135
— достижимое 116
»~ начальное 188
— невозвратное 118, 135
— несущественное 117
— нулевое Г35
— положительное 135
— существенное 117
Состояния сообщающиеся 116
Стохастический интеграл 280, 282, 285,
292
Субмартингал 73, 82
Супермартингал 73, 229
Сходимость в среднем квадратичном
21. 22
— мер слабая 25, 429, 434, 433, 450,
479
— по вероятности 19
— почти неверное 14
Табу-вероятность 141
Теорема Абеля 130, 132
— Дини 276. 482
*— Вейерштрасса 27, 255
>— Биркгофа—Хинчина 170, 172, 178
— Бореля—Кантелли 40, 92, 122, 456
— Колмогорова 65, 90, 108, 183, 189,
201. 365
— Лебега <$, 38, 100, 173, 269
> -о тцех рядах 91, 445
— Минлос!—Сазонова 407, 415
664
УКАЗАТЕЛЬ
Георема Радона—Никодама 50, 57,
85, 518
— Римана—Лебега 131
— Фубини 39, 211, 214, 268, 391, 397
— Хана—Банаха 614
— эргодическая 165
для цепей Маркова 134
— — максимальная 170
Уравнение авторегрессии 250
*- Фредгольма 330
— Чеимена—Колмогорова 93, 109, 112,
199
Условие Колмогорова непрерывности
процесса 235
— Линдеберга 486
— Липшица 237
— перемешивания 177, 179, 180
•— иол у аддитивности 282, 284
— согласованности 61, 66, 403
— физической осуществимости
системы 301
— фундаментальности по вероятности
19
Фактор-группа 386
Факторизация 322. 324, 333
Фильтр 304, 305, 308
— оптимальный 337
— полосовой 306
— физически осуществимый 310
Форма обобщенная 627
Формула взаимности 646
— Иенсена 89, 314
Функции случайные эквивалентные
316
Функционал 366, 374
— измеримый 421, 612
— — линейный 419, 424
— — квадратический 421, 424
— характеристический 381, 390, 402,
407, 453, 457, 631
— центрированный 421
— цилиндрический 366, 380
— — непрерывный 366
Функция Бесселя 261
— борелевская 14, 27, 255
— восстановления 129
— Грина блуждания 153
— измеримая 13
Функция импульсная переходная 299,
300
— корреляционная 241, 244 253
— — взаимная 243
— — матричная 243, 246, 265, 267, 275
— — стационарного процесса 246
— полиномиальная 623
— положительно-определенная 247, 265
— простая 281
*— распределения 23
— случайная в широком смысле 63
■ гауссовская 182, 186, 328
гильбертова 240, 245, 267
*— — измеримая 211, 612
— — сепарабельная 203
*- — симметричная 454
•~ — стохастически непрерывная 208,
209
>_ ограниченная 208
— ~ подчиненная 316
— собственная 300
*- спектральная 256
— структурная 281
— характеристическая 26
— цилиндрическая 402
Характеристика фильтра частотная
305, 308
Цепь Маркова 108, 115, 136, 509
апериодическая 125, 141
— — неприводимая 117, 134, 136, 144),
181
нулевая 136, 138
*- — обратная 144
' однородная 111
* периодическая 125
•- — положительная 136, 140, 181
Число пересечений полуинтервала 78
Эквивалентность стохастическая 61,62
Элемент случайный 16
*- — обобщенный 421
Ядро положительно-определенное 183,
241
— — матричное 243
*- полустохастическое 99
— стохастическое 99