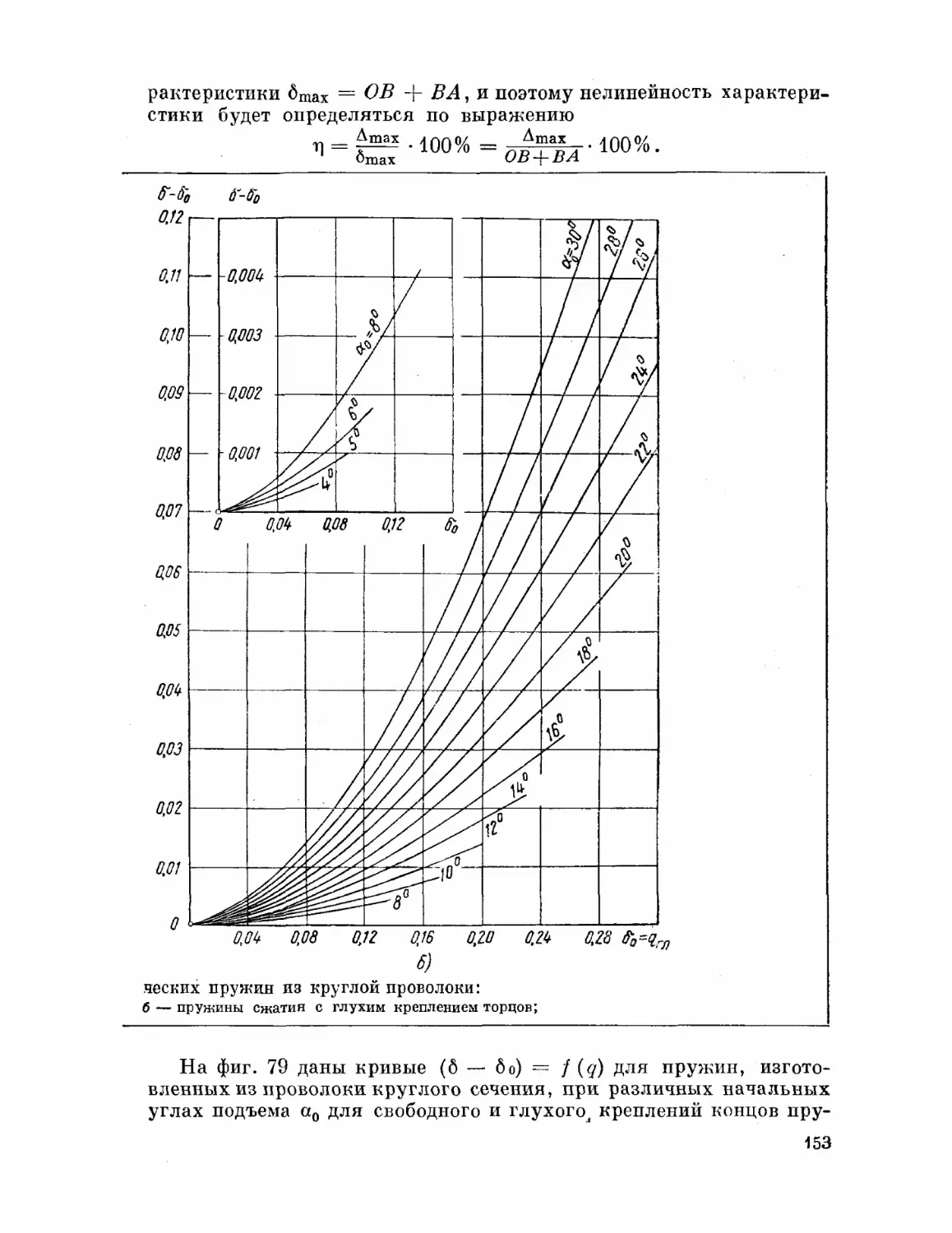
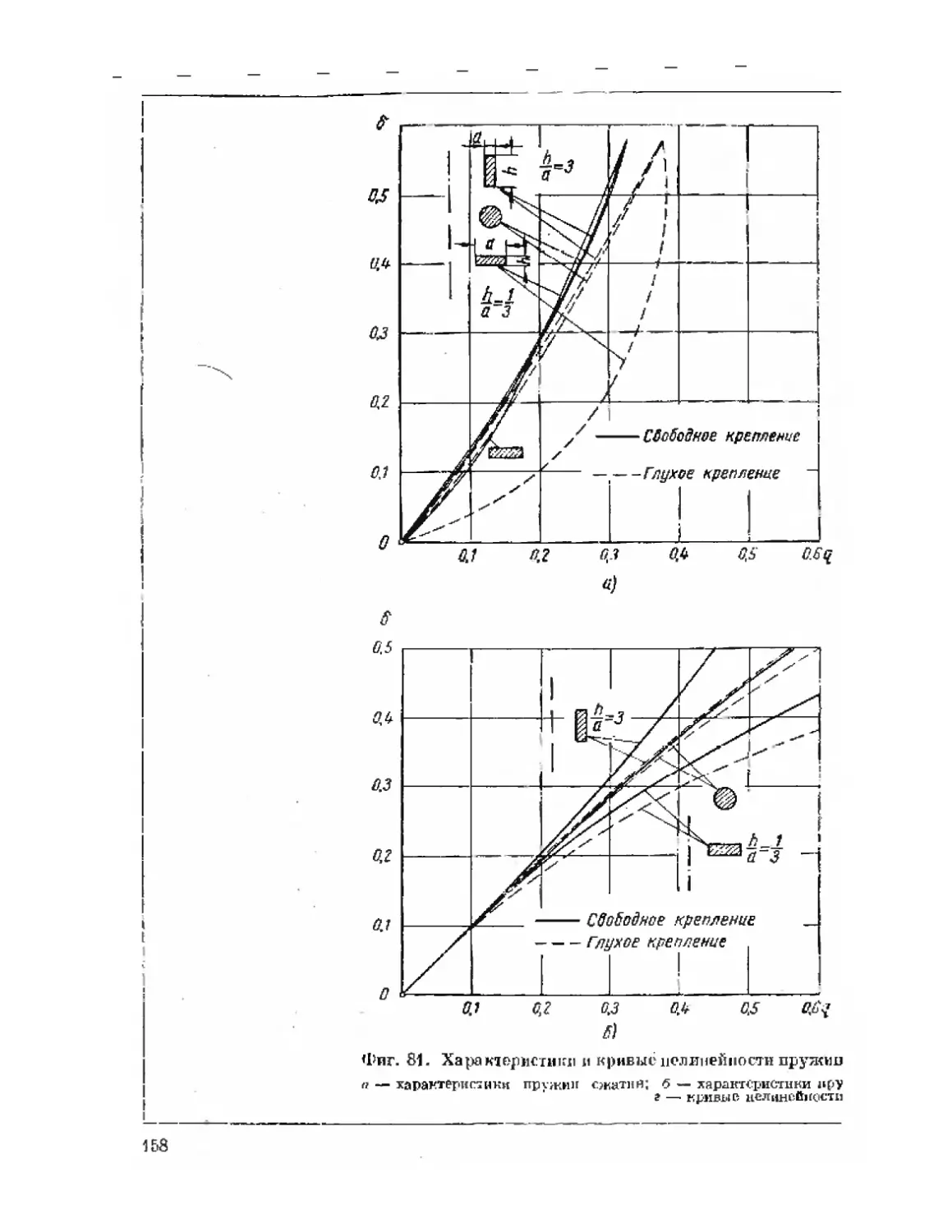
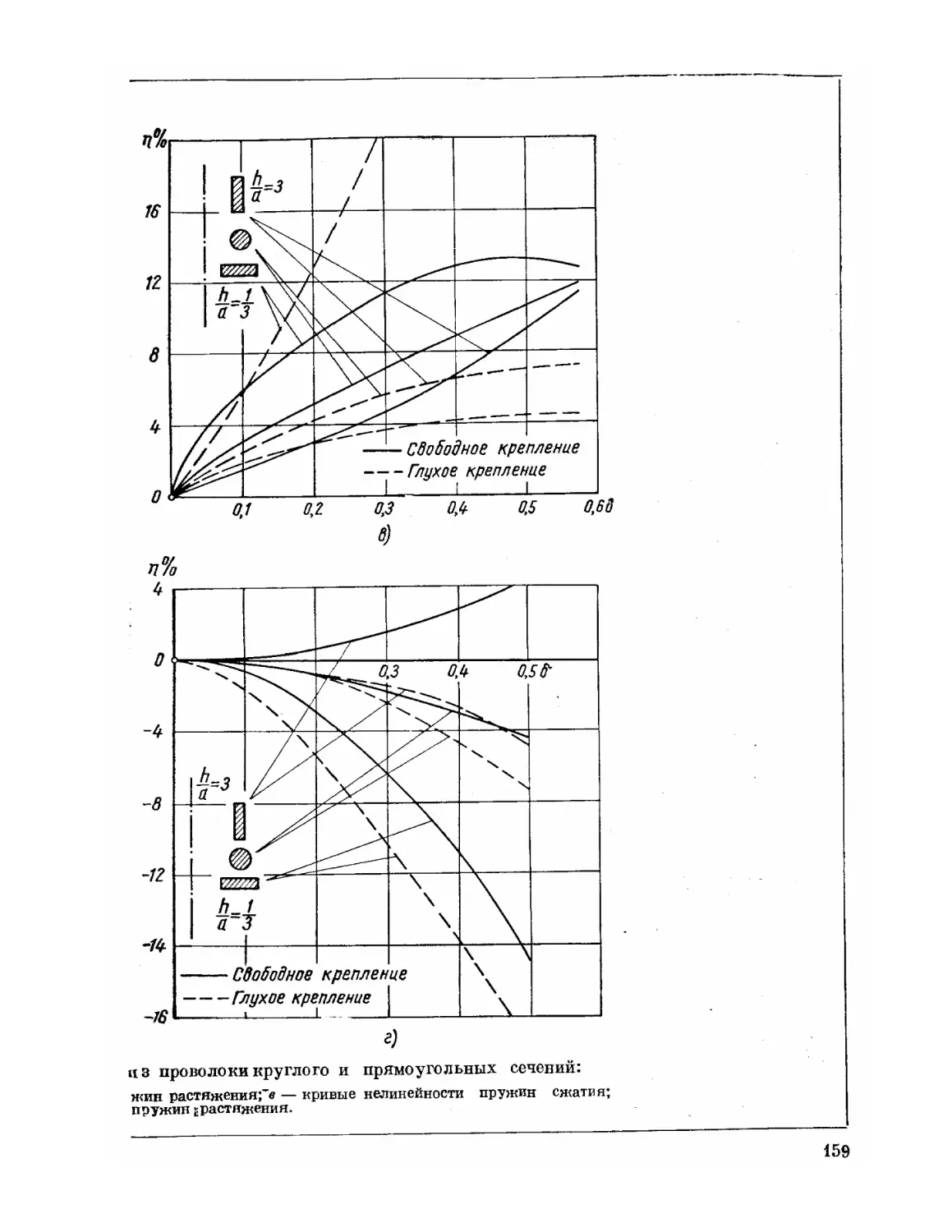
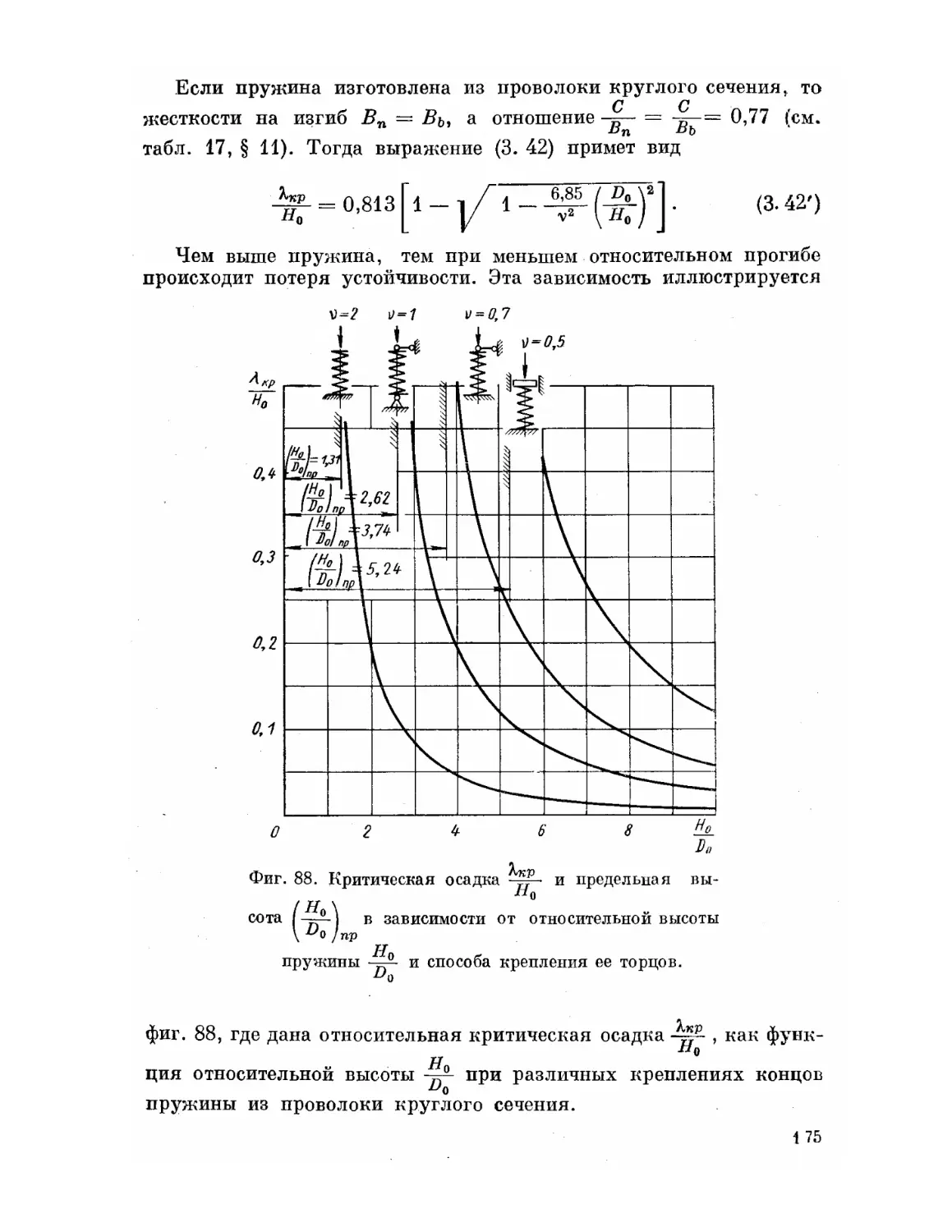
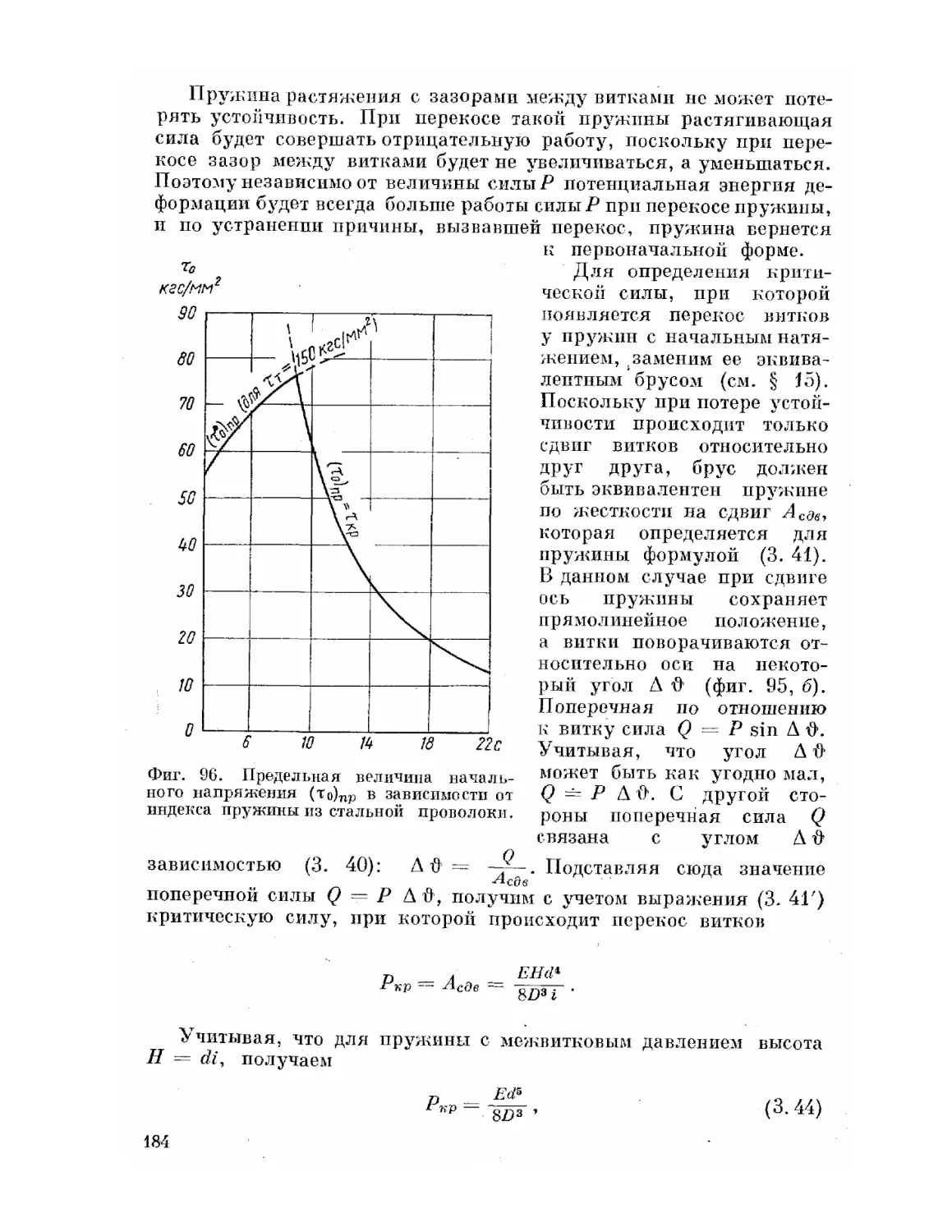
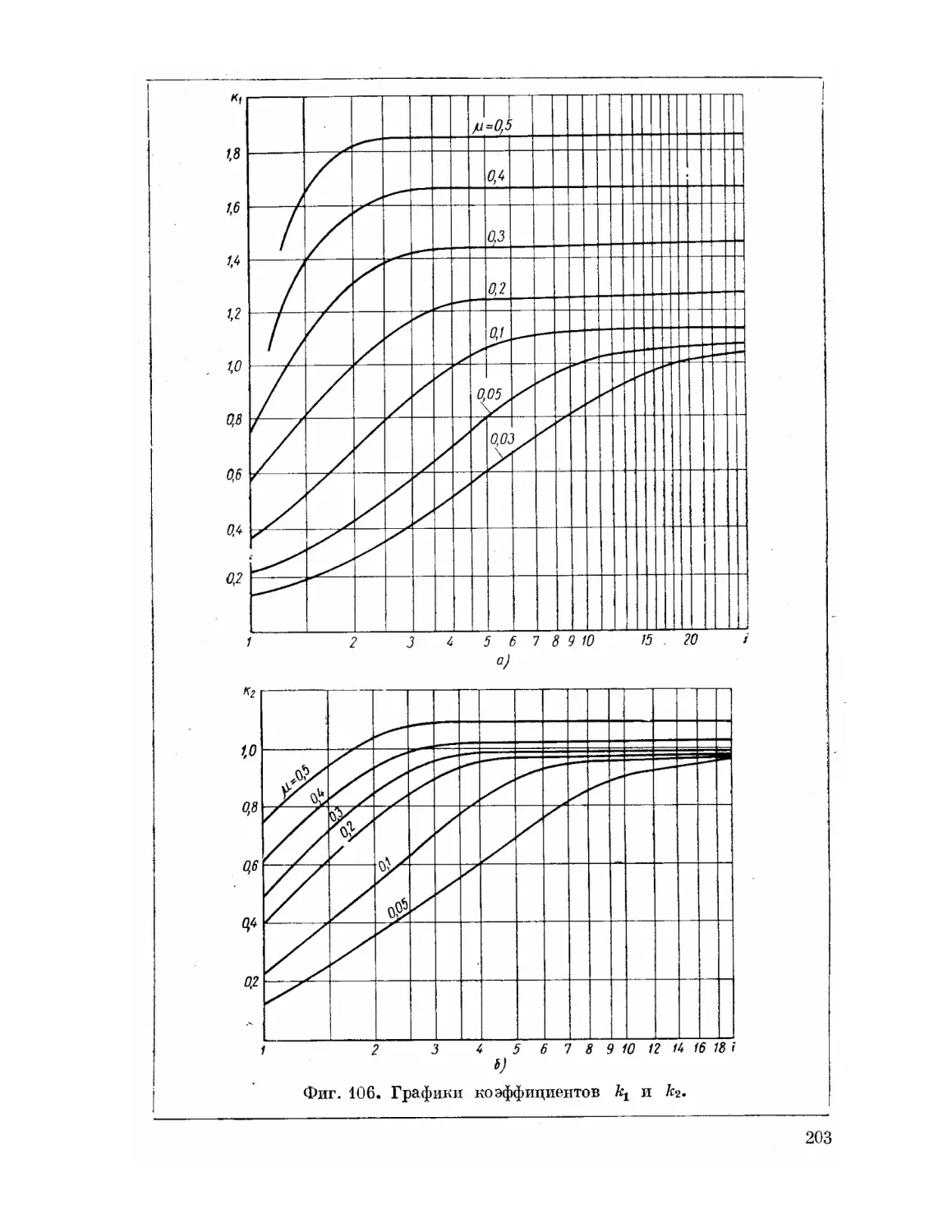
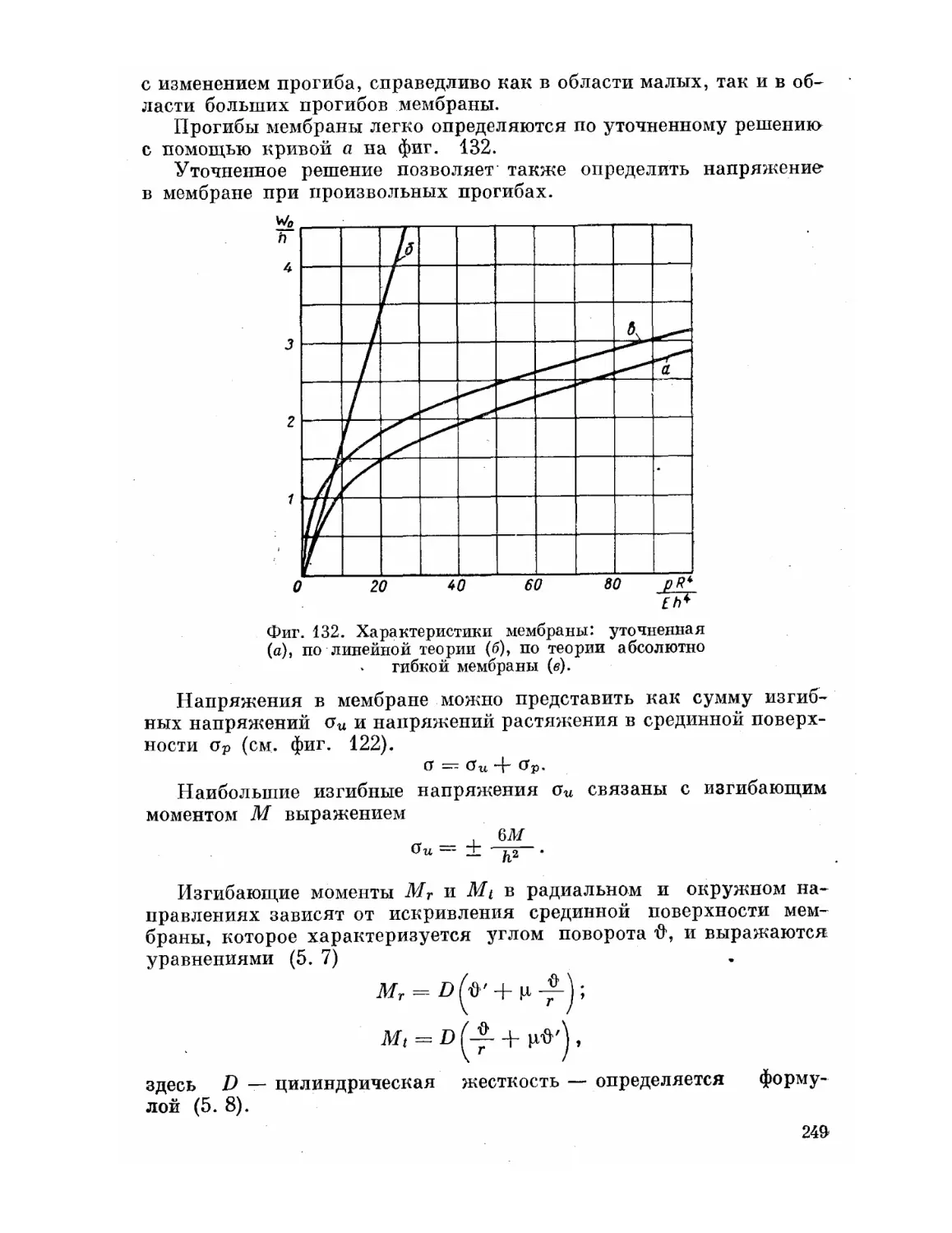
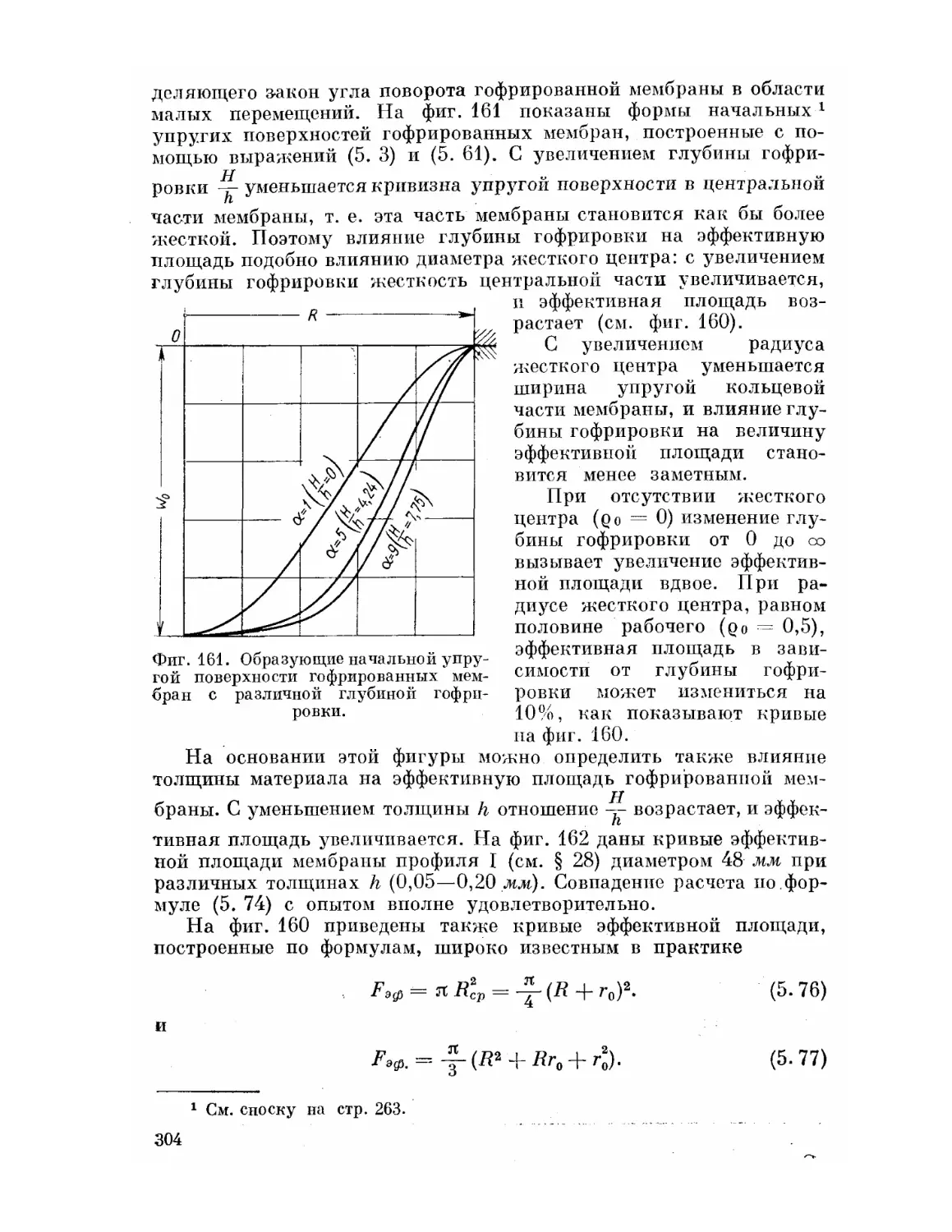
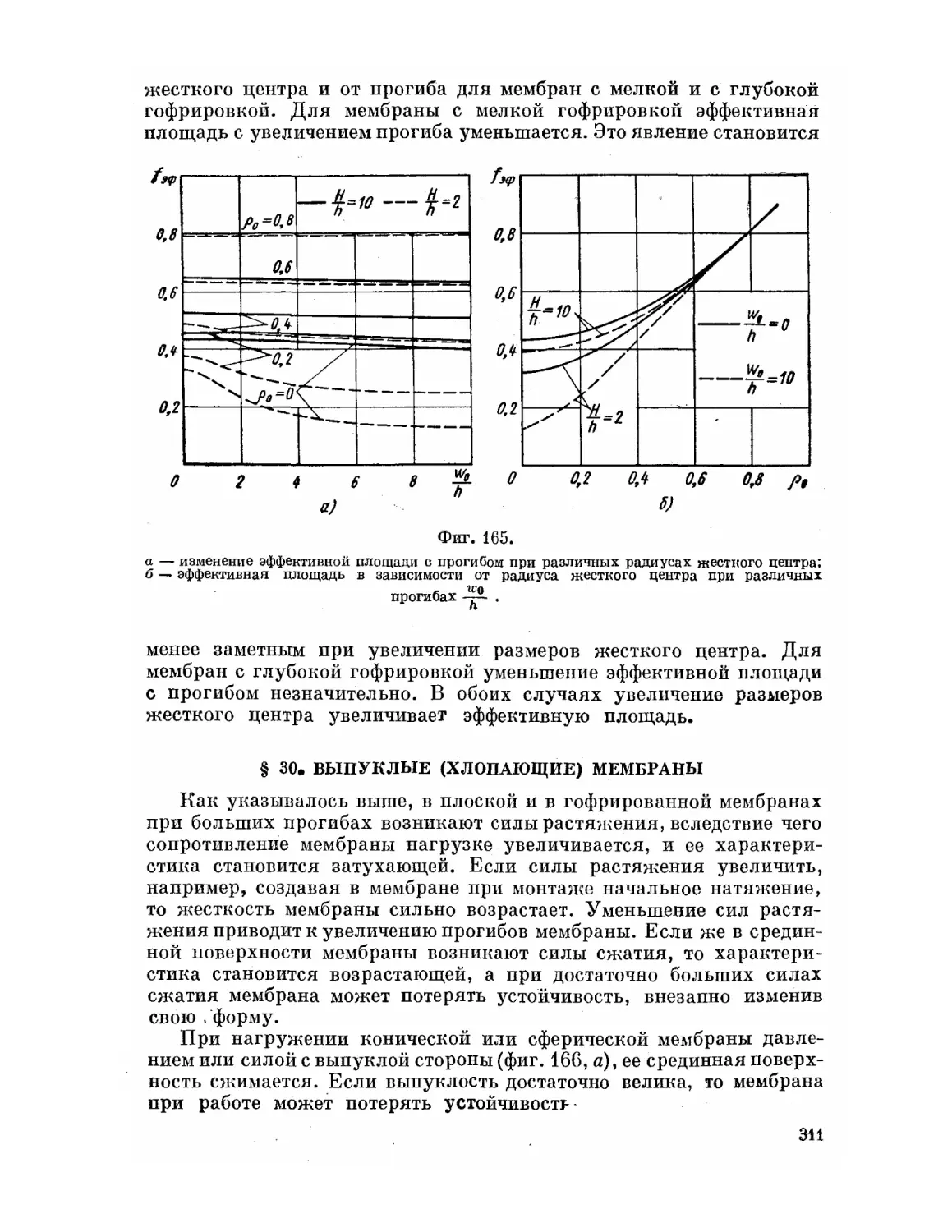
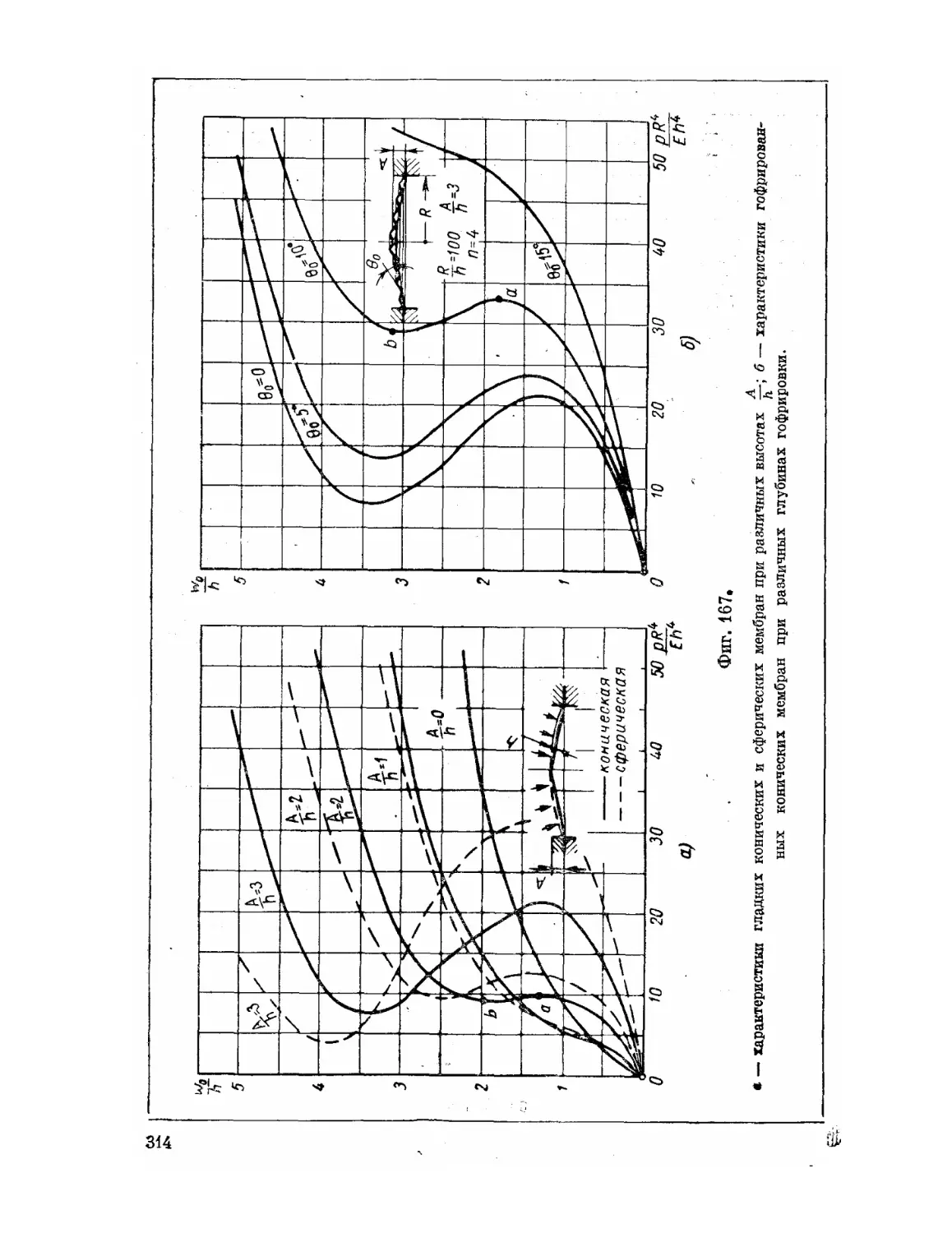
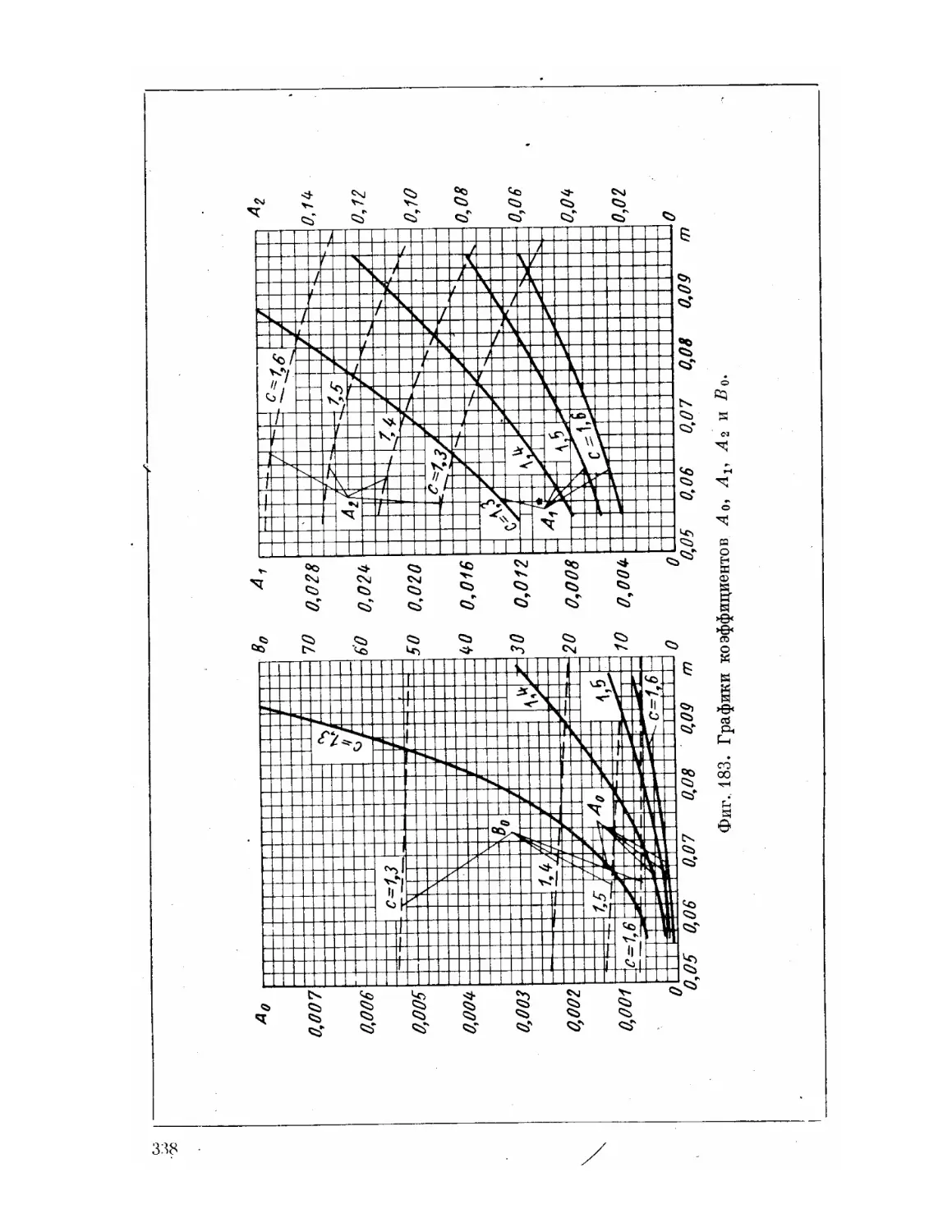
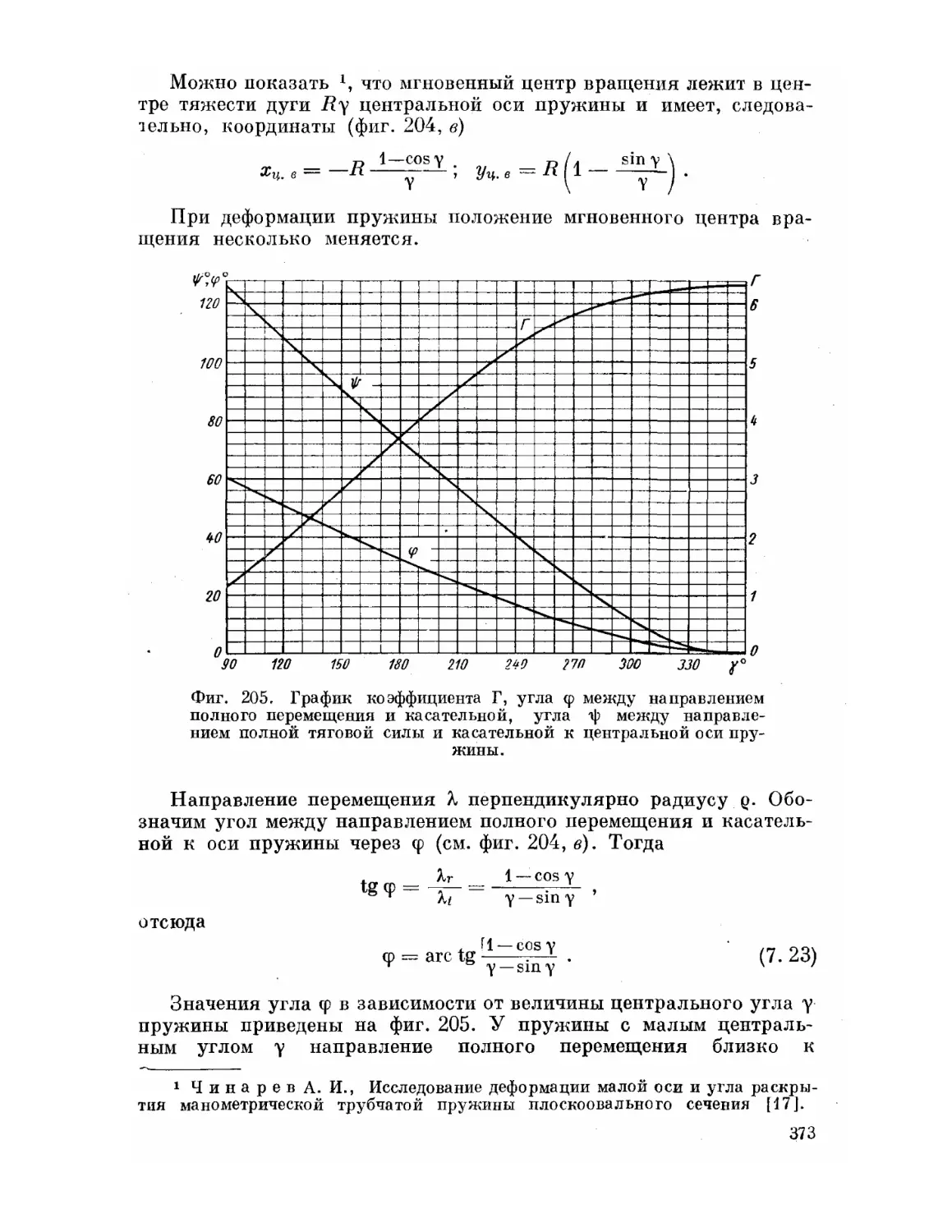
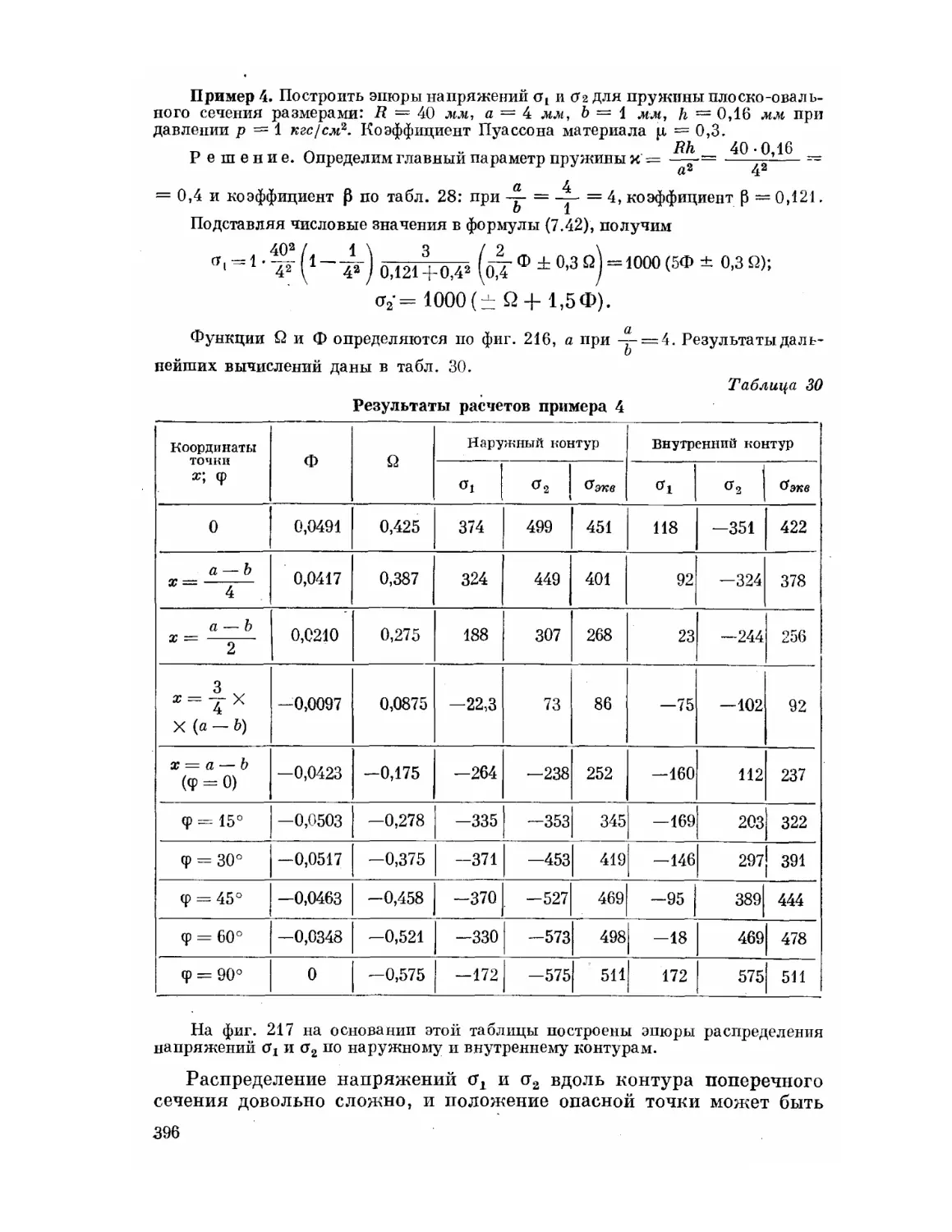
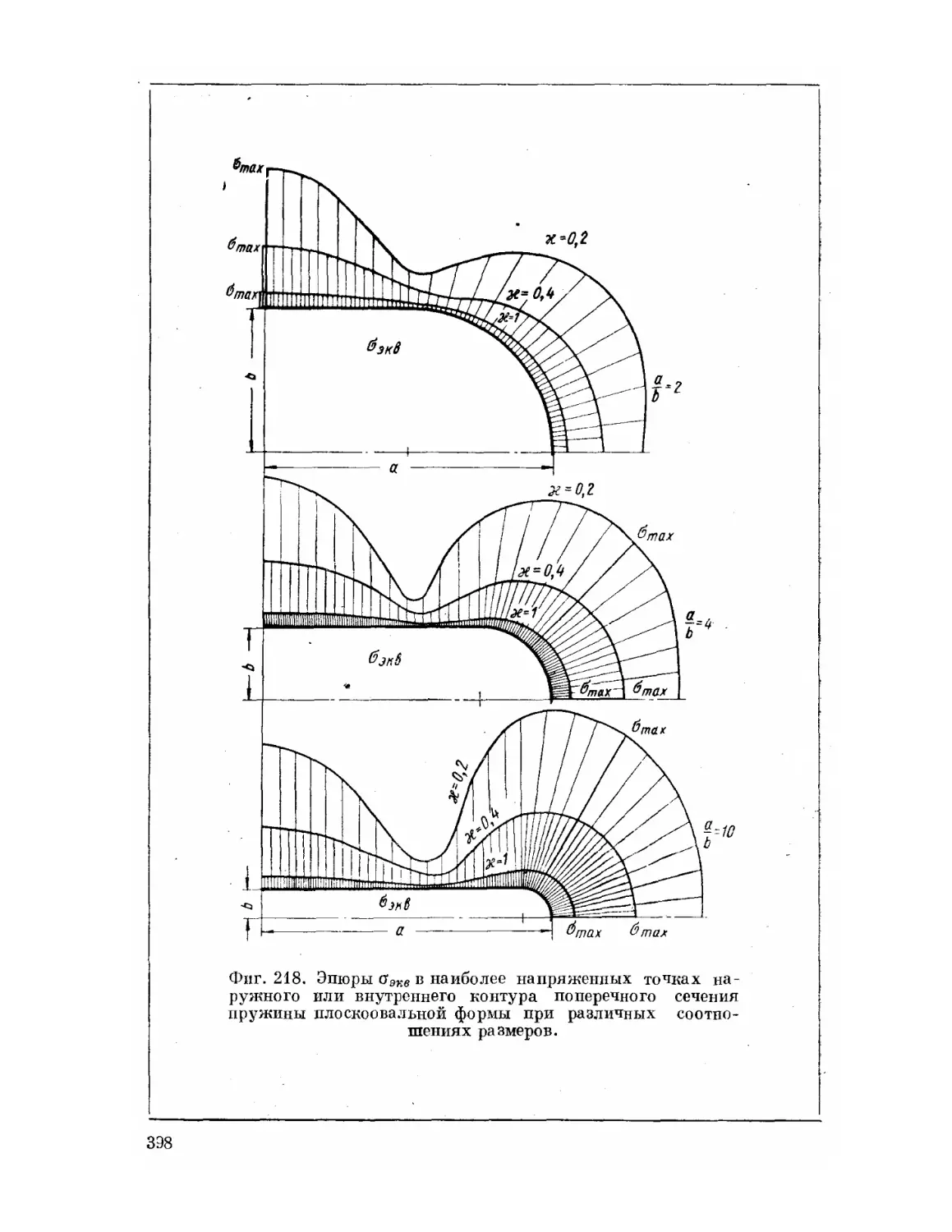
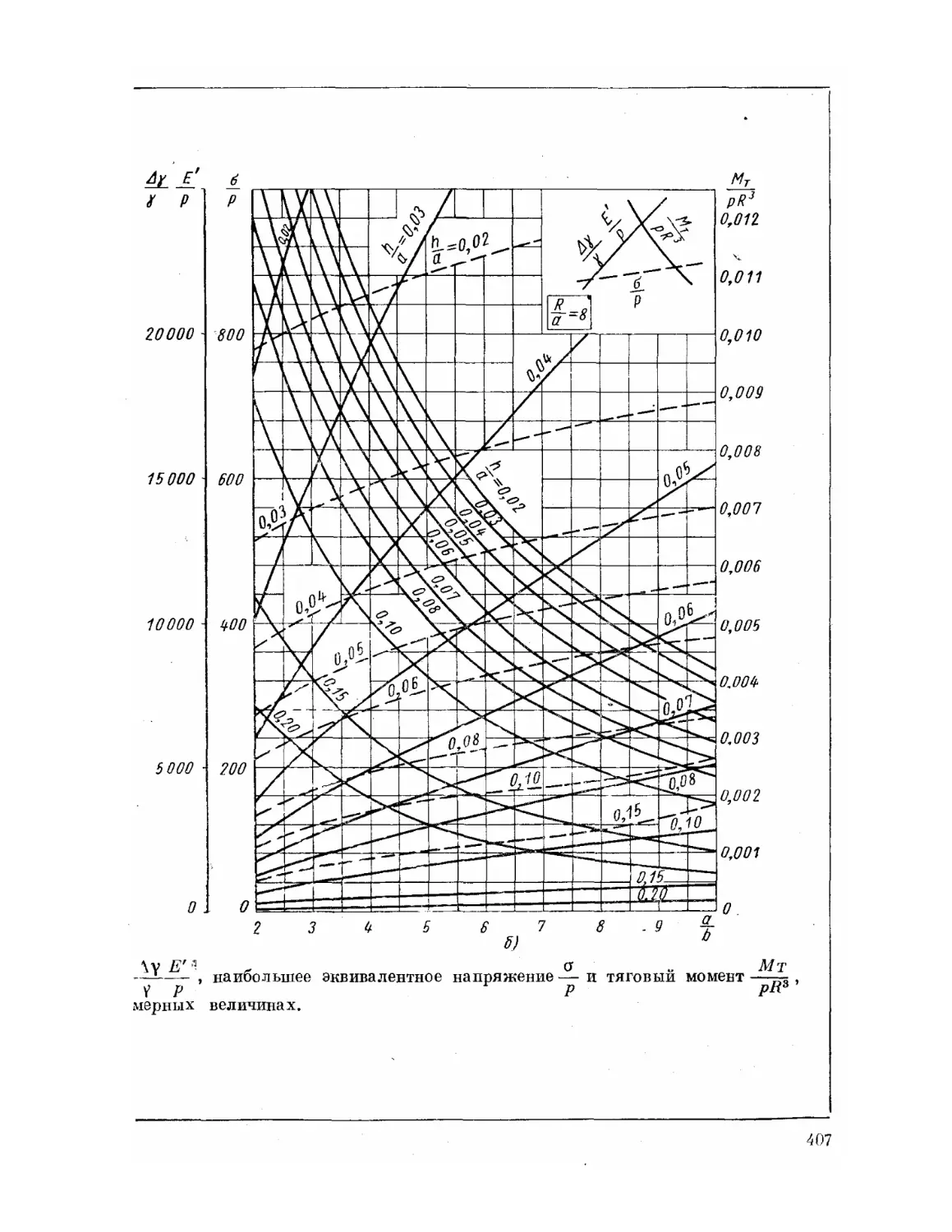
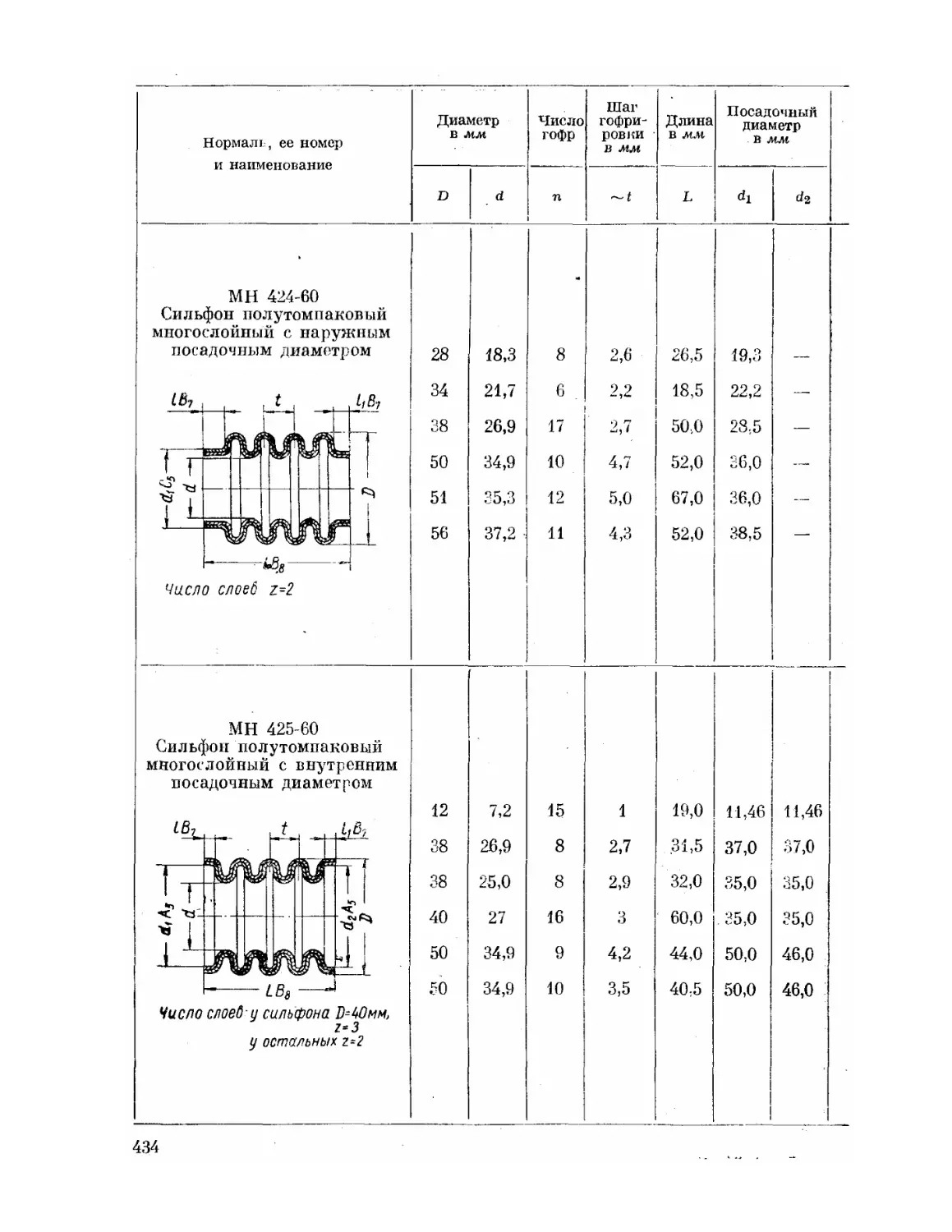
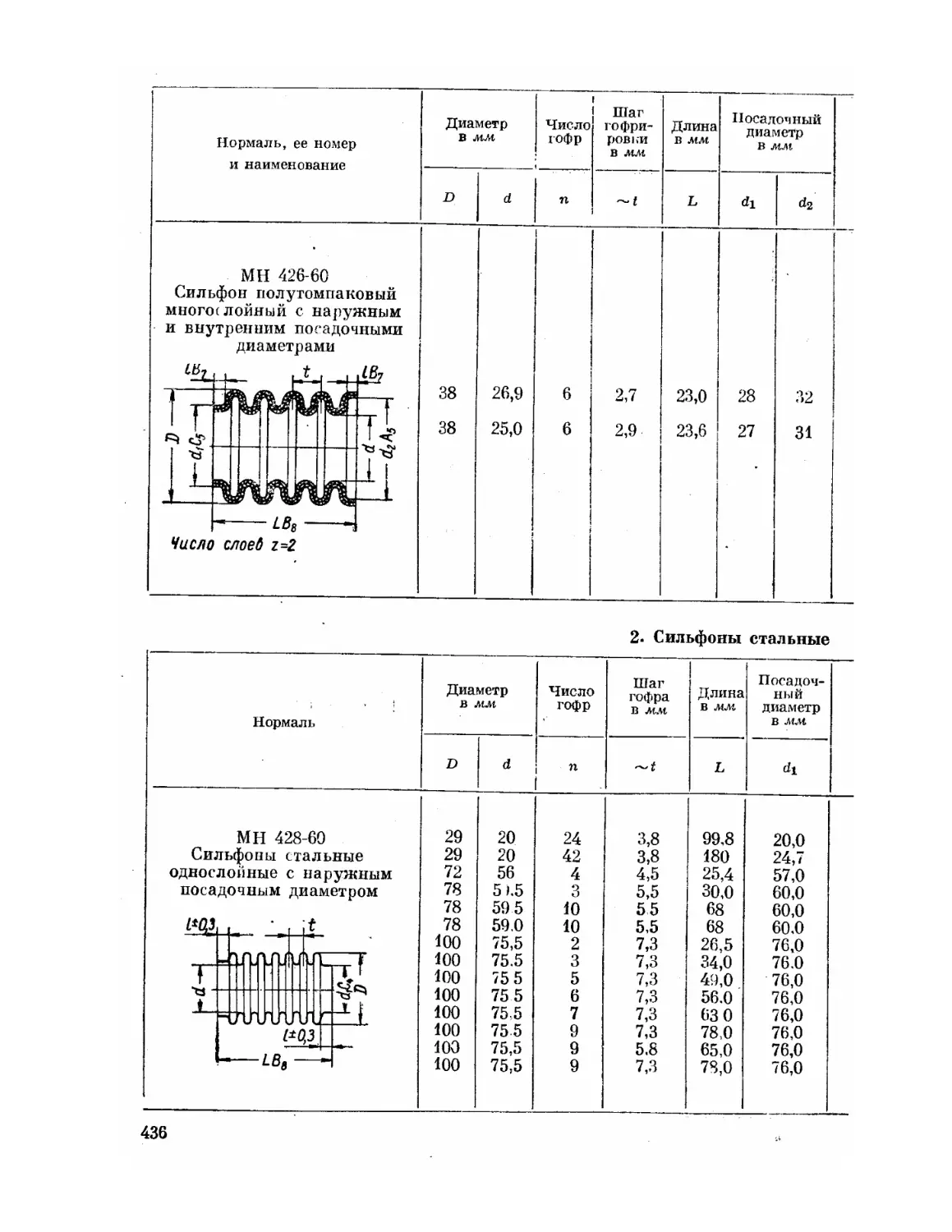
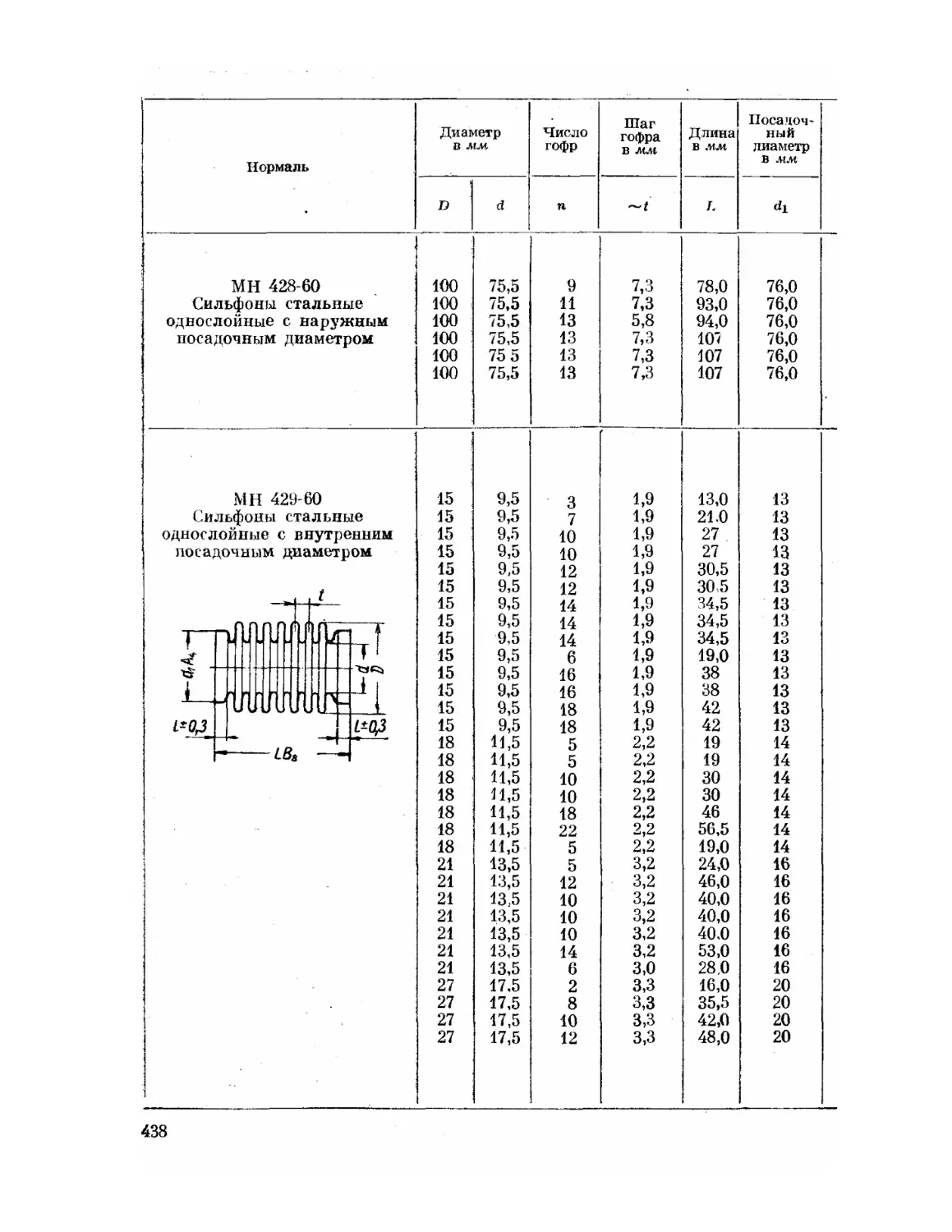
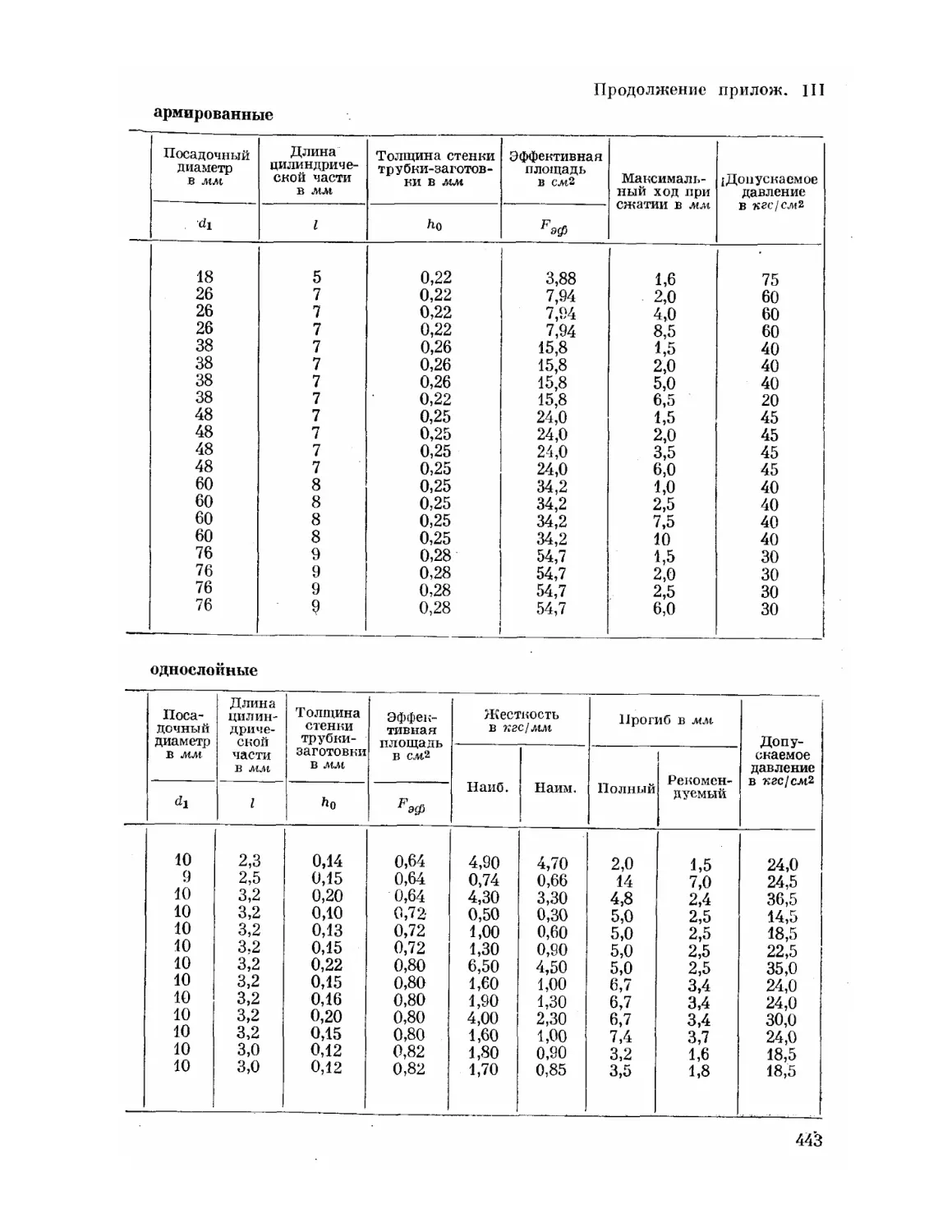
Текст
Л. Е. АНДРЕЕВА
УПРУГИЕ ЭЛЕМЕНТЫ
ПРИБОРОВ
Под редакцией
д-ра техн, наук проф. В. И. ФЕОДОСЬЕВА
МАШГИЗ
ГОСУДАРСТВЕННОЕ НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МАШИНОСТРОИТЕЛЬНОЙ ЛИТЕРАТУРЫ
Москва 1962
6П5. 8
A 65
АНДРЕЕВА Л- Е.
Упругие элементы приборов М.,
Машгиз, 1962. 456 стр. с илл.
В книге изложены теория и расчет упругих
элементов приборов: плоских, винтовых, биметал-
лических пружин, мембран, сильфонов и мано-
метрических трубчатых пружин. Рассмотрены
различные конструкции упругих элементов и их
применение, а также применяемые материалы
и некоторые вопросы технологии.
Книга рассчитана на инженеров-приборостро-
ителей и студентов приборостроительных
факультетов вузов.
Рецензент д-р техн, наук Г. О. Фридлендер
Редактор д-р техн, наук В. И. Феодосгев
Редакция литературы по средствам автоматизации
и приборостроению
Зав. редакцией инж. Н. В. ПОКРОВСКИЙ
ПРЕДИСЛОВИЕ
Упругие элементы являются необходимыми деталями многих
приборов. Они используются в различных целях: для создания
определенного натяга между деталями, аккумулирования механиче-
ской энергии, как элементы передачи движения, упругие опоры,
амортизаторы и т. д. Особенно ответственна роль упругих элемен-
тов в измерительных приборах, если они применяются в качестве
чувствительных элементов, воспринимающих измеряемую величину.
В этих случаях точность и надежность работы прибора во многом
зависит от качества чувствительного упругого элемента.
Развитие и внедрение автоматизации в металлургию, химиче-
скую промышленность, в атомную энергетику, ракетную технику
и в другие области народного хозяйства связано со значительным
повышением технических требований к приборам. Современное
состояние электроизмерительной, радиоэлектронной, счетно-вычи-
слительной и других отраслей приборостроительной техники позво-
ляет осуществлять преобразования измеряемой величины с весьма
высокой степенью точности. Однако если при этом измеряемая
величина воспринимается упругим чувствительным элементом низ-
кого качества, то как бы ни была высока точность дальнейших пре-
образований, погрешность упругого элемента будет ограничивать
точность прибора в целом.
Хотя упругие элементы являются простыми механическими
деталями, и многие виды упругих элементов известны и широко
применяются в течение многих десятков лет, их рабочие харак-
теристики часто не удовлетворяют современным требованиям, что
тормозит создание приборов высоких классов точности.
Одной из причин неудовлетворительного качества упругих чув-
ствительных элементов является недостаточное внедрение теории
и расчета в практику конструирования приборов, что было отме-
чено в решениях Всесоюзной научно-технической конференции по
упругим чувствительным элементам, состоявшейся в Москве в 1960 г.
Многие ответственные упругие элементы подбираются чисто опыт-
ным путем, что затрудняет поиски оптимального для данных требо-
ваний упругого элемента. Это вызвано отсутствием теории некото-
рых типов упругих элементов (например, манометрических витых
и сварных пружин) или недостаточно полной ее разработкой (напри-
1*
3
мер, мало исследована статическая и динамическая прочность мано-
метрических упругих элементов). Однако и в тех областях, где
теория упругих элементов разработана подробно, проектирование
их также часто осуществляется опытным путем, что приводит к из-
лишним материальным затратам и не дает оптимального результата.
Такое положение может быть отчасти объяснено отсутствием
широкой информации о методах расчета упругих элементов. Фун-
даментальная монография В. И. Феодосьева [1], посвященная мано-
метрическим упругим элементам, стала в настоящее время библио-
графической редкостью.
Чтобы восполнить этот пробел, в настоящей книге изложены
основы теории и расчета наиболее распространенных типов упругих
элементов: винтовых, плоских, биметаллических и манометрических
пружин. Для большей наглядности, а также для облегчения
расчета и проектирования теоретические результаты иллюстриро-
ваны графиками, номограммами и числовыми примерами. Выводы
большинства формул даны в сокращенном виде, главным образом
за счет математических выкладок. В приложении приводятся сведе-
ния из нормалей на некоторые типы манометрических упругих
элементов.
Поскольку книга посвящена в основном теории и расчету упругих
элементов и лишь частично затрагивает их конструкцию, техно-
логию, применяемые для изготовления материалы, она не может
дать исчерпывающие ответы на все вопросы, связанные с конструи-
рованием и производством упругих элементов. Эти вопросы должны
быть рассмотрены в специальной литературе.
Пользуясь случаем, автор приносит глубокую благодарность
тем товарищам, которые оказали ему помощь в работе над книгой.
ВВЕДЕНИЕ
В процессе работы детали прибора в большей или меньшей сте-
пени деформируются. В большинстве случаев деформации деталей
нежелательны, так как они могут нарушить правильность работы
прибора. Например, деформации корпуса и рычагов механизма
могут привести к изменению передаточного отношения, увеличению
трения или люфтов в подвижной системе, искажениям в оптических
системах и пр. Поэтому детали прибора конструируются обычно
по возможности более жесткими.
Вместе с тем существует обширная группа деталей, деформации
которых полезны и используются в работе прибора. Такие детали
называются упругими элементами или пружи-
нами. Обладая достаточной гибкостью, упругие элементы спо-
собны заметно изменять свои размеры и форму под нагрузкой,
что является их основным рабочим свойством.
Упругие элементы применяются в приборах в различных целях,
и по этому признаку их можно разделить на несколько групп.
Весьма ответственную роль выполняют в приборах измери-
тельные пружины.
В большинстве механических и электрических приборов в про-
цессе измерения происходит ряд преобразований измеряемого
параметра. Эти преобразования обычно сопровождаются перемеще-
нием некоторого элемента, например стрелки, передвигающейся
по шкале показывающего прибора, управляющего элемента дистан-
ционной передачи и т. п. При этом во многих случаях измеряемый
параметр преобразуется в усилие, которое деформирует измеритель-
ную пружину и уравновешивается возникающими в ней упругими
силами. По деформации пружины можно судить о величине вызвав-
шей ее силы, следовательно, и о величине измеряемого параметра.
Так, например, в магнито-электрических измерительных при-
борах момент сил, возникающих при взаимодействии тока с магнит-
ным полем, уравновешивается упругим моментом спиральной пру-
жины — волоска (фиг. 1, а). С увеличением момента электрических
сил деформация волоска возрастает, и соответственно увеличивается
перемещение связанной с ним стрелки прибора.
Если измерительная пружина непосредственно воспринимает
и преобразует измеряемую величину, то она является также чу в-
ствительным элементом прибора. Упру г и е чувствитель-
ные элементы широко применяются в различных приборах,
особенно, в манометрических. Так, измерение давлений жидкостей
или газов часто производится с помощью упругого чувствительного
элемента в виде тонкостенной оболочки, способной деформироваться
под действием давления (фиг. 1,6).
Точность работы приборов во многом зависит от качества изме-
рительных пружин. При одном и том же значении измеряемого
параметра (силы тока или давления в рассмотренных примерах)
показания прибора будут изменяться, если упругие свойства пру-
Фиг. 1:
а — спиральная измерительная пружина магнито-электрического при-
бора; б — манометрический упругий элемент Как измеритель давления.
жины изменятся по какой-либо причине (например, вслед-
ствие изменения температуры окружающей среды или с течением
времени). Поэтому к рабочим качествам измерительной пружины,
в особенности к стабильности ее упругих свойств, предъявляются
высокие требования. Если в приборе установлена измерительная
пружина низкого качества, то повышением качества других деталей
нельзя существенно повысить точность работы прибора.
В качестве источника энергии многих переносных приборов
используются пружинные двигатели, главной деталью которых
является заводная пружина обычно спиральной формы.
Заводная пружина похожа по форме на измерительную спираль-
ную (см. фиг. 1, а), однако требования, предъявляемые к ним, раз-
личны. Для заводных пружин стабильность упругих свойств не
имеет такого значения, как для измерительных. Основным, что
определяет качество заводной пружины, является ее способность
создавать момент требуемой величины при достаточно большом
угле поворота рабочей оси прибора.
6
Упругие элементы применяются также в качестве кинемати-
ческих устройств: упругих опор, направляющих, гибких свя-
зей. Отсутствие трения и люфтов в этих элементах позволяет значи-
тельно улучшить качество прибора.
Почти в каждом приборе имеются натяжные пружины разно-
образных форм, предназначенные для осуществления силового кон-
такта между деталями прибора, для выбора люфтов в кинематиче-
ской цепи, удержания детали в заданном положении и т. д.
Упругие элементы применяются также и в других целях, напри-
мер: в амортизаторах, фрикционных и храповых муфтах, в качестве
разделителей различных сред, упругих выводов и пр.
Конфигурация упругих элементов разнообразна и зависит от
назначения и конструкции прибора. При этом одинаковым требо-
ваниям могут удовлетворять упругие элементы разных форм и,
наоборот, упругие элементы одинаковой формы могут выполнять
в приборе различные функции. Так, например, и спиральная пружина
применяется и в качестве измерительной, и заводной, и натяжной.
Из большого количества упругих элементов различных конструк-
тивных форм можно составить несколько групп, в которые упругие
элементы объединяются основными геометрическими признаками.
Прежде всего их можно разделить на две основные группы: стерж-
невые упругие элементы, изготовляемые из проволоки или ленты,
и упругие элементы в виде оболочек, которые выполняются
из листового материала. Стержневые пружины предназначаются
для восприятия главным образом сосредоточенных сил и моментов;
упругие элементы в форме оболочек при работе обычно нагружаются
давлением.
Стержневые пружины имеют две основные конструктивные
формы: винтовую и плоскую.
Винтовые пружины (фиг. 2, а) способны получать большие
осевые перемещения под действием растягивающих или сжимающих
сил или взаимный поворот торцов под действием моментов.
Плоские пружины могут иметь различные очертания
(фиг. 2, б, в), но они объединяются тем общим признаком, что ось
пружины располагается в одной плоскости.
Упругие элементы в виде оболочек, реагирующих на изменение
давления, называются манометрическими. К ним отно-
сятся мембраны, сильфоны и трубчатые пружины.
Мембрана (фиг. 2, г) представляет собой гибкую пластинку,
перемещение центра которой определяется величиной действующего
на нее давления.
Сильфон (фиг. 2, д) является гофрированной трубкой, спо-
собной под нагрузкой получать большие осевые или угловые пере-
мещения.
Манометрическая трубчатая пружина
(фиг. 2, ё) представляет собой тонкостенную трубку, ось которой
является дугой окружности; под действием давления пружина раз-
гибается.
Многие из пружин перечисленных форм могут выполняться
в виде биметаллических —двухслойных. Материалы слоев
биметаллических пружин имеют разные по величине коэффициенты
линейного расширения, поэтому при изменении температуры пру-
жина изгибается-.
Выбор метода расчета упругого элемента определяется в основ-
ном его геометрической формой, величиной перемещении, при кото-
рых он работает, и желаемой точностью расчета.
Так как упругий элемент представляет собой гибкий стержень
или гибкую оболочку, то он может под нагрузкой сильно изменять
свои размеры и форму.
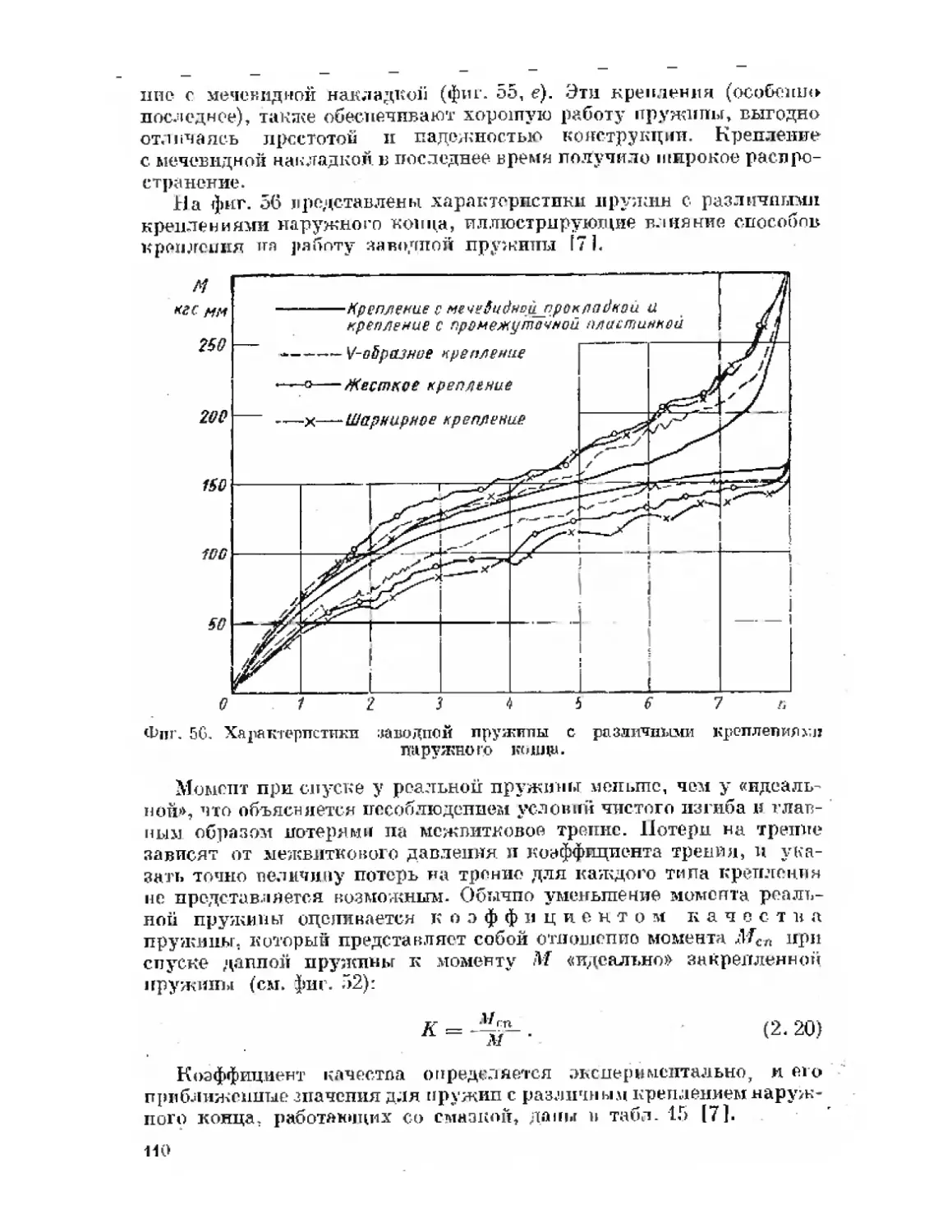
Фиг. 2. Упругие элементы:
а — винтовая пружина; б — кривая плоская’ пружина; в — прямая пло-
ская пружина; г — мембрана; 0 — сильфон; в — манометрическая трубча-
тая пружина.
В начале нагружения, когда изменение размеров упругого эле-
мента еще незначительно, напряжения и перемещения возрастают
прямо пропорционально нагрузке. В этом случае при расчете могут
быть использованы принципы неизменности начальных размеров
и независимости действия сил, значительно упрощающие расчет и
широко принятые в сопротивлении материалов; поведение упругого
элемента в области малых перемещений достаточно хорошо описы-
вается линейной теорией.
С увеличением нагрузки форма и размеры упругого элемента
могут изменяться так сильно, что приходится отказаться от прин-
ципа неизменности начальных размеров. В этом случае зависимость
между перемещениями и нагрузкой становится нелинейной, что зна-
чительно усложняет расчет.
Установить точно границы применения линейной и нелинейной
теорий невозможно. В каждом конкретном случае вопрос решается
8
в зависимости от поведения упругого элемента под нагрузкой
и от той точности, которую требуется получить при расчете.
Теория упругих элементов довольно сложна, и их исследованию
посвящено много работ. Одной из первых в этой области явилась
книга С. Пономарева [2], посвященная конструкциям и расчету
винтовых цилиндрических пружин.
Нелинейная теория винтовых цилиндрических пружин произ-
вольного угла подъема изложена в трудах Н. А. Чернышева
[3], [4].
Вопросы посадки фасонных витых пружин были рассмотрены
Е. П. Поповым [5], которому принадлежит также фундаментальная
работа по нелинейной теории изгиба гибких стержней [6].
Конструкции, теории и расчету пружинных двигателей посвя-
щена книга Т. А. Гевондяна [7].
Основы теории манометрических упругих элементов — трубча-
тых пружин, сильфонов и мембран — разработаны в трудах
В. И. Феодосьева [1], [8] и [9].
Большой интерес представляют монография Узла [10], посвя-
щенная в основном стержневым пружинам, ряд статей Xарингса
по расчету винтовых пружин [11], сильфонов [12] и мембран [13],
а также работы Бюста [14], [15] в области расчета манометрических
трубчатых пружин.
Кроме того, имеется большое количество статей в периодической
литературе, в отчетах и трудах научно-исследовательских институ-
тов, авторы которых внесли значительный вклад в теорию упругих
элементов.
ГЛАВА I
ОСНОВНЫЕ СВОЙСТВА УПРУГИХ ЭЛЕМЕНТОВ
§ 1. МАТЕРИАЛЫ, ПРИМЕНЯЕМЫЕ ДЛЯ ИЗГОТОВЛЕНИЯ
УПРУГИХ ЭЛЕМЕНТОВ
Требования, предъявляемые к материалу упругих элементов
Материал упругого элемента должен удовлетворять многим тре-
бованиям в зависимости от назначения упругого элемента и усло-
вий работы. Он должен обладать высокими упругими свойствами,
достаточной прочностью и выносливостью. Его механические
характеристики должны быть стабильны во времени и в условиях
переменной температуры.
Если упругий элемент будет использоваться при рабочих темпе-
ратурах в несколько сотен градусов, то материал должен быть
термостойким. В тех случаях, когда упругий элемент соприкасается
с агрессивной средой, он должен иметь достаточную коррозионную
стойкость.
В ряде случаев существенно требование высокой или, наоборот,
низкой электропроводности.
Упругие элементы электроизмерительных приборов в большин-
стве случаев изготовляются из немагнитных материалов, однако
если упругий элемент является частью магнитопровода, то его
материал должен иметь достаточную магнитную проницаемость.
Материал должен обладать высокой пластичностью, поскольку
упругие элементы обычно изготовляются из полуфабриката в виде
листов, лент или проволоки, при прокатке или протяжке которых
возникают большие пластические деформации. Изготовление самих
упругих элементов, особенно манометрических, также требует
значительной пластичности материала.
Во многих случаях при изготовлении упругого элемента возни-
кает необходимость сварки или пайки, тогда материал должен обла-
дать соответствующими свойствами и в этом отношении.
Удовлетворить всему комплексу многообразных и нередко про-
тиворечивых требований, предъявляемых к материалу упругого
элемента, сложно, и выбор наиболее подходящего материала часто
встречает большие трудности.
10
Очень немногие материалы, обладая высокими упругими и проч-
ностными характеристиками, имеют в то же время достаточную
пластичность. Еще меньше материалов, способных сохранять свои
упругие свойства в условиях высоких температур (порядка несколь-
ких сотен градусов) и в условиях сильно агрессивных сред. Жаро-
прочные сплавы применяются в машиностроении при температурах
до 800—1000° С, однако, они не пригодны для изготовления из них
упругих элементов, так как их пластические и упругие свойства
недостаточны.
В связи с большим многообразием предъявляемых требований
при выборе материала часто приходится ограничиваться удовлетво-
рением лишь наиболее важным требованиям. Так например, проти-
воречивым оказывается требование сочетания термостойкости и
высокой электропроводности, предъявляемое к упругим элементам
некоторых электроизмерительных приборов. Термостойкость мате-
риала можно повысить путем легирования, но это снижает его
электропроводность. Чистые металлы или слабо легированные
сплавы обладают достаточной электропроводностью, но в то же
время низкой термостойкостью. В большинстве случаев требование
достаточной термостойкости оказывается. более важным, поскольку
повысить электропроводность можно не только соответствующим
выбором материала упругого элемента, но и другими путями. По-
этому в таких случаях обычно приходится выбирать высоколегиро-
ванный термостойкшг материал, хотя его электропроводность и
недостаточно велика.
Механические свойства материалов
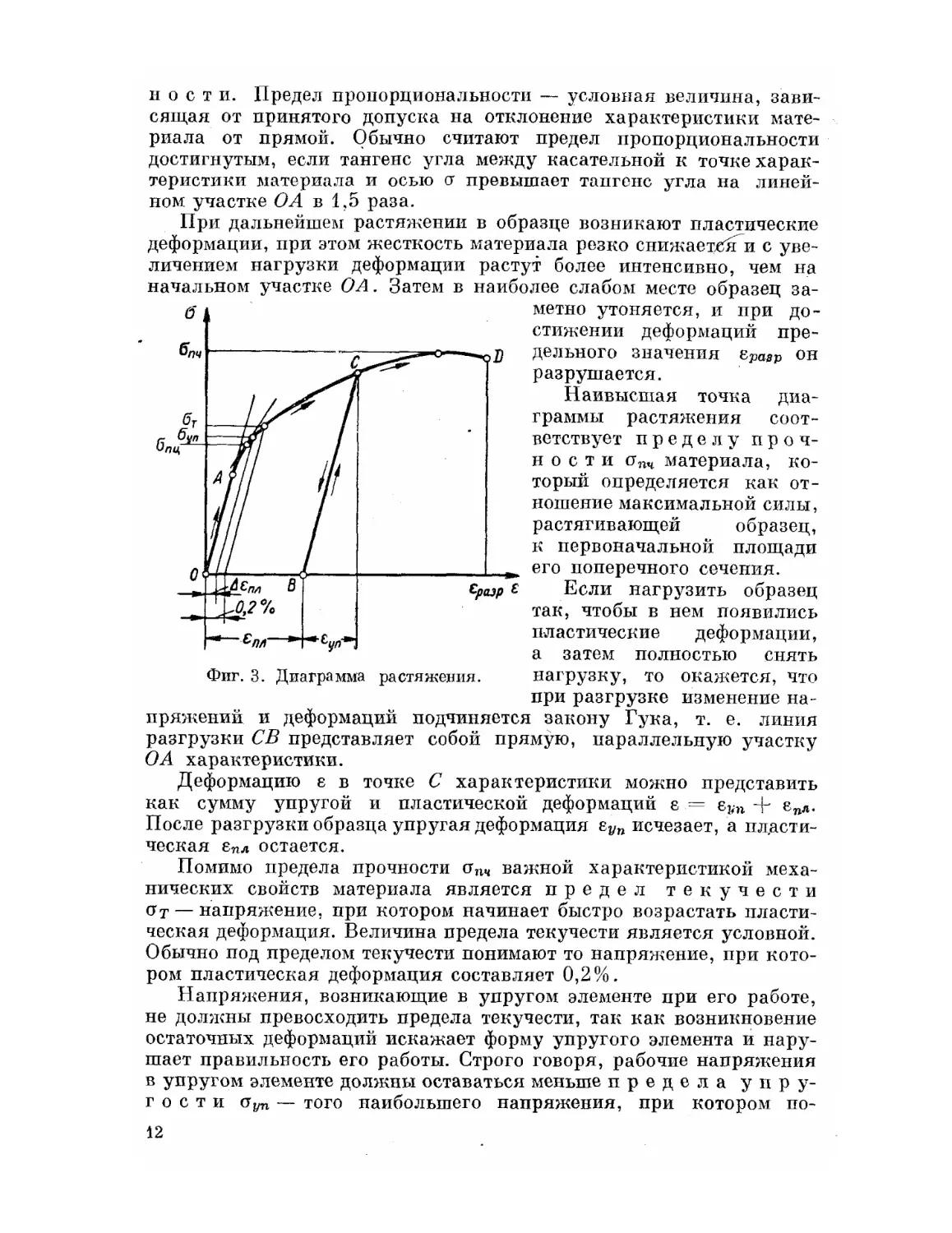
Механические свойства материала наглядно характеризуются
диаграммой, получаемой при испытании на растяжение (фиг. 3).
По оси ординат диаграммы откладывается напряжение <у = -=г (Р —
* о
растягивающая сила, Fq — площадь поперечного сечения образца
до его нагружения), а по оси абсцисс — деформация е ~ (А I —
‘о
удлинение образца, 1о — его первоначальная длина).
При приложении к образцу растягивающих сил он удлиняется
вначале прямо пропорционально силе, что отражается на графике
прямой О А. Линейная зависимость между напряжениями о и дефор-
мациями е выражается законом Гука, который при одноосном напря-
женном состоянии может быть записан в виде
о = Ег,
(1.1)
где Е — модуль упругости материала, характеризующий его
жесткость.
То наибольшее напряжение ппги до которого еще справедлив
закон Гука, называется пределом пропорциональ-
11
Фиг. 3. Диаграмма растяжения.
и о с т и. Предел пропорциональности — условная величина, зави-
сящая от принятого допуска на отклонение характеристики мате-
риала от прямой. Обычно считают предел пропорциональности
достигнутым, если тангенс угла между касательной к точке харак-
теристики материала и осью о превышает тангенс угла на линей-
ном участке О А в 1,5 раза.
При дальнейшем растяжении в образце возникают пластические
деформации, при этом жесткость материала резко снижаетсяГи с уве-
личением нагрузки деформации растут более интенсивно, чем на
начальном участке О А. Затем в наиболее слабом месте образец за-
метно утоняется, и при до-
стижении деформаций пре-
дельного значения gpcwp он
разрушается.
Наивысшая точка диа-
граммы растяжения соот-
ветствует пределу проч-
ности <тпч материала, ко-
торый определяется как от-
ношение максимальной силы,
растягивающей образец,
к первоначальной площади
его поперечного сечения.
Если нагрузить образец
так, чтобы в нем появились
пластические деформации,
а затем полностью снять
нагрузку, то окажется, что
при разгрузке изменение на-
пряжений и деформаций подчиняется закону Гука, т. е. линия
разгрузки СВ представляет собой прямую, параллельную участку
ОА характеристики.
Деформацию е в точке С характеристики можно представить
как сумму упругой и пластической деформаций е = е](П -р епЯ.
После разгрузки образца упругая деформация еУп исчезает, а пласти-
ческая 8ПЛ остается.
Помимо предела прочности опч важной характеристикой меха-
нических свойств материала является предел текучести
(Ут — напряжение, при котором начинает быстро возрастать пласти-
ческая деформация. Величина предела текучести является условной.
Обычно под пределом текучести понимают то напряжение, при кото-
ром пластическая деформация составляет 0,2%.
Напряжения, возникающие в упругом элементе при его работе,
не должны превосходить предела текучести, так как возникновение
остаточных деформаций искажает форму упругого элемента и нару-
шает правильность его работы. Строго говоря, рабочие напряжения
в упругом элементе должны оставаться меньше предела упру-
гости (ТуП — того наибольшего напряжения, при котором по-
12
являются лишь незначительные остаточные деформации. Величина
предела упругости так же, как и предела текучести, определяется
по допуску А Епл (см. фиг. 3) на остаточную деформацию; но если для
предела текучести этот допуск составляет 0,2%, то для предела
упругости он значительно меньше, например, 0,001, 0,003 или
0,005%.
Если при расчете большинства деталей машин и приборов доста-
точно располагать двумя характеристиками прочности материала:
(7ПЧ и <Тт, то для правильного проектирования упругих элементов
желательно знать величину предела упругости оуп, чтобы гаранти-
ровать работу пружины в обла-
сти упругих деформаций.
Величина предела текучести
повышается при наклепе материа-
ла. Если нагрузить материал за
пределами упругих деформаций,
разгрузить и вновь нагрузить,
то линия вторичного нагружения
будет совпадать с линией раз-
грузки, и характеристика будет
изображаться линией BCD
(см. фиг. 3).
Если вторичное нагружение
производится в ту же сторону,
что и предыдущее, то упругий учас-
ток характеристики возрастает,
поэтому говорят, что материал по-
Фиг. 4. Эффект .Баушингера.
лучил «упрочнение», «нагартовку».
Наоборот, предварительное нагружение за пределами упругих дефор-
маций снижает предел текучести материала, если оно противоположно
по знаку последующему нагружению. Так, растяжение образца за
пределами упругих деформаций вызывает снижение предела теку-
чести материала при сжатии от величины <?тсж1 Д° °тсж2 (Фиг- 4).
Это явление известно под названием эффекта Баушин-
гера. Упрочнение, т. е. увеличение упругих свойств нагружением
за пределами упругих деформаций, может быть получено только
в том случае, если знак последующих рабочих нагрузок совпадает
со знаком первичного нагружения.
Помимо перечисленных важным показателем качества материала
является предел выносливости — наибольшее напря-
жение, при котором образец не разрушается при любом большом
числе циклов изменения напряжений во времени.
Известно, что детали, способные длительно работать при до-
вольно больших постоянных во времени напряжениях, могут бы-
стро разрушиться при меньших, но переменных напряжениях.
Однако, если напряжения в материале не превосходят предела
выносливости, то такая деталь может работать, не разрушаясь, в тече-
ние любого отрезка времени.
13
Величина предела выносливости (предела усталости) зависит
не только от свойств материала, но и в большой степени от характера
изменения напряжений во времени, от состояния поверхности
детали и наличия в ней концентраторов напряжений.
Наиболее опасным оказывается симметричный цикл изменения
напряжений (фиг. 5, а). Упругие элементы часто работают в режиме
«нагружение — разгрузка», такой цикл называется пульсацион-
ным (фиг. 5, б). Если упругий элемент предварительно поджат,
то при изменении рабочей нагрузки напряжения в нем иззйеняются
по некоторому асимметричному циклу (фиг. 5, в).
Фиг. 5. Циклы изменения напряжений:
а — симметричный; б — пульсационный; в — асимметричный.
Если поверхностные слои детали нагартованы, а сама поверх-
ность гладкая, не имеет трещин, царапин, рисок и следов механиче-
ской обработки, то выносливость такой детали повышается. Наобо-
рот, плохое состояние поверхностных слоев, особенно при наличии
коррозии, резко уменьшает прочность детали при переменных
напряжениях.
Усталостная прочность также падает вследствие концентрации
напряжений, возникающей в местах резких изменений формы
детали.
Материал упругого элемента должен обладать не только доста-
точно высокими упругими и прочностными свойствами, но и по-
стоянством этих свойств во времени и при изменении условий работы
прибора. Особенно трудно добиться стабильности свойств в том
случае, когда упругий элемент работает при повышенных темпера-
турах.
Изменение температуры оказывает влияние на величину модуля
упругости большинства материалов, что приводит к изменению
жесткости упругого элемента, а следовательно и к появлению тем-
пературной погрешности. При нагреве материала модуль упруго-
сти уменьшается, а при охлаждении — увеличивается.
В некотором интервале изменения температур зависимость
модуля упругости от температуры можно выразить формулой
(1.2)
14
где Ео — модуль упругости при растяжении в условиях нормальной
температуры;
Et — модуль упругости при увеличении температуры на /;
уЕ — температурный коэффициент изменения модуля упругости.
Модуль упругости при сдвиге G связан с температурой анало-
гичной зависимостью
где yG — температурный коэффициент модуля упругости при сдвиге.
Так как в действительности модуль упругости нелинейно зави-
сит от температуры, то значения коэффициентов уЕ и у различны
в разных интервалах изменения температуры.
Определение величины температурного коэффициента модуля
упругости представляет большие трудности, и поэтому в справоч-
ной литературе можно найти числовые значения уЕ и у только
для некоторых материалов.
Большое значение для измерительных пружин имеют несо-
вершенства упругих свойств, присущие в большей
или меньшей степени всем реальным материалам.
Точные измерения показывают, что даже при напряжениях,
меньших пределах упругости, реальные материалы не имеют той
строго линейной и однозначной зависимости между напряжениями
и деформациями, которая выражается законом Гука (1. 1). Кривые
нагружения и разгрузки материала в пределах упругих деформаций
в действительности не совпадают, образуя так называемую «петлю
гистерезиса» (фиг. 6, а). Ширина петли гистерезиса очень
мала и может быть обнаружена только при весьма тщательных изме-
рениях. Явление гистерезиса не имеет существенного значения для
работы большинства деталей \ но для упругих чувствительных эле-
ментов величина гистерезиса является одной из важнейших характе-
ристик, поскольку она целиком входит в погрешность прибора,
определяя разницу в его показаниях при прямом и обратном ходе.
Явление гистерезиса сложно, и природа его в настоящее время
еще недостаточно изучена. Известно, что с увеличением напряжений
петля гистерезиса увеличивается. Большое влияние на величину
гистерезиса оказывают химический состав и структура материала,
определяемая его механической и термической обработкой. Вели-
чина гистерезиса уменьшается с увеличением предела упругости,
т. е. с ростом сопротивления малым пластическим деформациям [16].
Отклонение от законов совершенной упругости материала выра-
жается также в том, что при постоянной нагрузке возможно измене-
ние деформаций во времени. При нагружении основная часть дефор-
мации происходит практически мгновенно, а затем деформации
1 В тех случаях, когда деталь работает в условиях интенсивных вибраций,
целесообразно применять материалы с большой петлей гистерезиса, что облег-
чает гашение вибраций.
15
продолжают нарастать по резко затухающему во времени закону
(кривая ОаА на фиг. 6, 0. При снятии нагрузки деформации исче-
зают также с некоторым запаздыванием во времени (кривая АвВ).
Явление изменения деформаций во времени при постоянной нагрузке
называется последействием. Если после снятия нагрузки
деформации по истечении некоторого времени исчезают полностью,
то такое последействие называется упругим.
Шадцгд
Момент
приложения
нагрузки
Момент
снятия
нагрузки
а — петля
и
5)
Фиг. 6. Несовершенства упругих свойств материала:
гистерезиса; б — изменение деформаций во времени; в — гистерезис
упругое последействие; г — пластическое последействие.
Являясь причиной отставания по фазе деформаций от величин
напряжений при нагружении и при разгрузке упругого элемента,
последействие, складываясь с гистерезисом, увеличивает разницу
в показаниях прибора при прямом и обратном ходе (фиг. 6, в).
Чем медленнее изменяется измеряемая величина (соответственно
и напряжения в упругом элементе), тем меньше проявляется упру-
гое последействие: разница между деформациями при нагружении
и при разгрузке уменьшается, а петля стремится к петле «чистого»
гистерезиса (фиг. 6, а). При измерении переменных весьма быстро
изменяющихся величин упругое последействие также мало сказы-
вается, так как за короткие промежутки времени процесс упругого
16
последействия не успевает развиться. Наиболее сильно про-
является упругое последействие при некоторых средних скоростях.
Стабильность рабочих свойств упругого элемента во- времени
может быть нарушена вследствие пластического тече-
ния материала (так называемой ползучести), кото-
рое может возникнуть при нормальной температуре и сравнительно
небольших напряжениях (меньших предела упругости), но проте-
кает более интенсивно при больших напряжениях и высоких темпе-
ратурах.
Возникновение пластического течения при напряжениях,, мень-
ших предела упругости, связано с неоднородностью структуры
материала и появлением в его микрообъемах остаточных напряже-
ний при изготовлении. Поэтому при нагружении детали напряжения
в отдельных местах могут превзойти предел упругости материала
(хотя среднее значение напряжений остается меньшим предела
упругости), в результате чего в этих местах могут возникнуть пла-
стические деформации. Процесс пластического течения происходит
в течение некоторого времени и приводит к изменению размеров
и перераспределению напряжений в материале детали. При нагреве
ползучесть значительно ускоряется и при достаточно больших на-
пряжениях может привести не только к изменению упругих свойств
детали, но и к ее механическому разрушению.
Ползучесть металлического упругого элемента протекает интен-
сивно, если он работает при температурах порядка нескольких
сот градусов; упругие элементы из неметаллических материалов
(например, из фторопласта, резины) подвержены ползучести при
нормальных или слегка повышенных температурах.
Пластическое течение материала во времени может проявляться
в форме пластического последействия и релаксации.
В отличие от упругого последействия, при пластическом
последействии некоторая часть деформации в детали со-
храняется при полной ее разгрузке по истечении любого отрезка
времени (фиг. 6, г). В результате пластического последействия
размеры упругого элемента могут измениться, что приведет к иска-
жению показаний прибора.
Если в испытываемом образце создать некоторую деформацию
и оставить ее неизменной во времени, то окажется, что в результате
пластического течения напряжения будут уменьшаться. Это связано
с тем, что пластическая деформация с течением времени увеличи-
вается. Так как полная деформация состоит из упругой и пластиче-
ской, то увеличение пластической деформации приводит к уменьше-
нию упругой деформации, а следовательно, напряжения в мате-
риале образца будут также уменьшаться. По истечении достаточно
длительного времени напряжения в образце могут полностью исчез-
нуть. Ослабление напряжений с течением времени при условии
постоянной деформации называется релаксацией напряжений.
Интенсивная релаксация напряжений в упругом элементе мо-
жет быть причиной полного нарушения работы прибора. Например,
2 Заказ 24.
17
при длительном хранении прибора с заведенным пружинным двига-
телем напряжения в пружине в результате релаксации могут сни-
зиться так сильно, что она при раскручивании будет отдавать энер-
гию, недостаточную для приведения в движение механизма прибора.
Точно также в результате релаксации ослабевает со временем дей-
ствие натяжных и контактных пружин.
Для уменьшения влияния релаксации и последействия на рабо-
чие качества упругого элемента, последний подвергается специаль-
ной технологической операции — стабилизации, во время которой
процесс пластического течения почти полностью закацчивается.
Стабилизация упругого элемента заключается в его многократном
нагружении или в выдержке в нагруженном состоянии в течение
достаточно длительного времени. Так как процесс пластического
течения значительно ускоряется при нагреве детали, то стабилиза-
цию упругого элемента часто проводят при повышенных темпера-
турах.
Явления гистерезиса, упругого и пластического последействия,
релаксации, а также изменение модуля упругости с температурой
для материалов упругих элементов изучены в настоящее время
недостаточно вследствие сложности эксперимента. Часто эти свой-
ства изучаются не на образцах материалов, а на готовых упругих
элементах.
При выборе материала для упругих элементов приходится руко-
водствоваться не только теми свойствами, от которых зависят
рабочие качества упругих элементов, но и теми, которые опреде-
ляют большую или меньшую сложность процесса их изготовления.
Так, например, желательно, чтобы материал обладал достаточной
пластичностью. О пластичности материала принято судить по
величине остаточного удлинения б или относительного сужения яр,
которые определяются при разрыве образца.
Материалы для упругих элементов
Упругий элемент заданной (иногда довольно сложной) формы
можно изготовить только из достаточно пластичного материала.
Однако для изготовления упругого элемента пригоден не любой
пластичный материал, а лишь такой, который в результате после-
дующей механической или термической обработки способен приоб-
рести высокую упругость и прочность.
Многие материалы, обладая высокой пластичностью в отожжен-
ном состоянии, в результате нагартовки, возникающей
во время изготовления упругого элемента, значительно повышают
свои упругие свойства. Технология изготовления упругих элемен-
тов из таких материалов относительно проста, так как обычно не '
требует специальной термообработки отформованного упругого эле-
мента. Эти материалы особенно широко применялись* в начале раз-
вития приборостроения.
Физико-механические свойства и химический состав таких мате-
риалов приведены в табл. 1. К таким материалам относятся латуни.
18
Пластичность латуней в мягком состоянии так велика, что, напри-
мер, из латуни Л90 легко формуются сильфоны, процесс изготовле-
ния которых сопровождается весьма глубокой вытяжкой. Однако
упругие свойства латуней невысоки, а гистерезис, последействие,
ползучесть весьма значительны. Нередко большие остаточные на-
пряжения, которые возникают при изготовлении латунных упругих
элементов по истечении некоторого времени приводят к растрески-
ванию материала. Упругие свойства латуни могут быть повышены
в результате низкотемпературного отжига, в процессе которого
также уменьшаются остаточные напряжения. Несмотря на это
и на дешевизну, латунь не имеет перспектив для использования
при изготовлении измерительных упругих элементов приборов
высоких классов точности
Лучшие упругие свойства по сравнению с латунными имеют
упругие элементы из нейзильбера, кремнемарганцевой, оловянно-
цинковой и оловянно-фосфористой бронз. Так же, как и латуни,
эти материалы немагнитны, хорошо свариваются и паяются. Они
стойки на воздухе, в пресной и морской воде. Эти материалы также
приобретают упругие свойства в результате холодной пластической
деформации, и поэтому, хотя прочность их относительно высока,
большие несовершенства упругих свойств являются существенным
недостатком таких материалов.
К числу материалов, приобретающих упругие свойства при
нагартовке, относится элинвар, основным достоинством которого
является постоянство модуля упругости в интервале температур
от —50 до 4-80° С.
Нержавеющая сталь 1Х18Н9Т широко применяется при изго-
товлении сильфонов, мембран и других элементов, работающих
в агрессивных средах (например, в морской воде, окислительных
средах, слабых щелочах) и при повышенных температурах (до
400° С). Эта сталь немагнитна, хорошо сваривается, но плохо паяется.
Низкие упругие свойства ограничивают ее применение в измери-
тельных упругих элементах.
Особо высокой коррозионной стойкостью в большинстве агрес-
сивных сред, например, в 98 %-ном растворе азотной кислоты,
обладает титан ВТ1-1. Он хорошо поддается точечной сварке, удо-
влетворительно — аргоно-дуговой. Упругие элементы, изготовлен-
ные из титана, имеют низкие упругие свойства и поэтому исполь-
зуются в основном в качестве разделителей сред.
Основными недостатками перечисленных выше материалов
являются низкие упругие свойства и нестабильность их во времени.
Причина этого кроется в значительных остаточных напряжениях,
возникающих в материале при изготовлении упругого элемента.
Наличие остаточных напряжений усиливает процессы последействия
1 Ж у к о в с к и й Н. И., Качество приборов с упругими чувствительными
элементами общепромышленного применения [17] и Нагаткин А. Г.,
Упругие чувствительные элементы московского завода «Манометра
2* IS
Таблица 1
Физико-механические свойства и химический состав материалов, упрочняемых нагартовкой
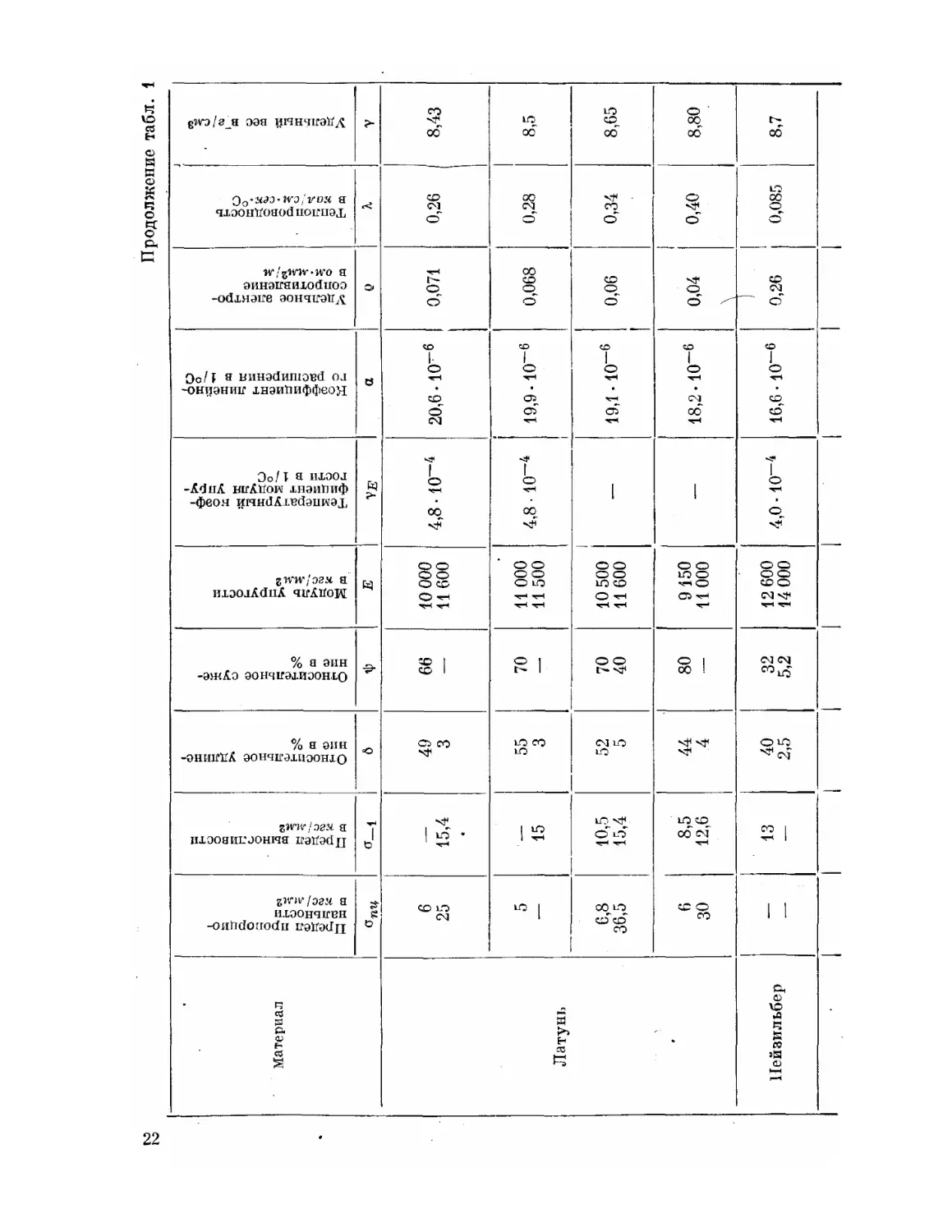
. : Материал Марка, ГОСТ или ТУ Химический состав в % Термообработка перед наклепом (ориентировочно) Состояние материала Твердость : в кес/лшй Предел прочности в кзс 1мм2 ft Предел текучести в кгс/лш2 П редел упругости в кгс/лшЗ j
НВ «пч ,°Т °уп
Латунь « f Л62 ГОСТ 1019-47 60,5—63,5 Си; примеси 0,5; остальное Zn Отжиг t = 6004-700° С Мягкая Твердая 56 140 33 60 11 50 8 42
Л68 ГОСТ 1019-47 67—70 Си; примеси 0,3; остальное Zn Отжиг / — 6004-700° С Мягкая Твердая 55 150 32 66 10 52 50
Л80 ГОСТ 1019-47 79—81 Си; примеси 0,3; остальное Zn Отжиг t = 6804-750° С Мягкая Твердая 53 145 31 64 12 52 8 42
Л90 ГОСТ 1019-47 88—91 Си; примеси 0,2; остальное Zn Отжиг t = 650 4- 720° С Мягкая Твердая 53 130 26 60 13 40 7 38
Нейзильбер МНЦ15-20 ГОСТ 492-52 18—22 Zn; 13,5—16,5 Ni +Со; остальное Си Отжиг / = 700 4-750° С Мягкий -Твердый 70 165 40 67 14 60 10
j 1 1
1 1 1
Бронза кремниево- марганцевая Бр. КМцЗ-1 ГОСТ 493-54 1—1,5 Мп; 2,75-3,5 Si; примеси 1,1; остальное Си Отжиг 600 <-680°C 1 Мягкая Твердая 80 180 55 90 14 54 12
Бронза оловянно- цинковая Бр. ОЦ4-3 ГОСТ 5017-49 3,5—4,0 Sn; 2,7—3,3 Zn; примеси 0,2; остальное Си Отжиг г=600°С Мягкая Твердая 60 160 35 55 " 4» —
1 * Бронза оловянно- фосфорная Бр. ОФ 6,5-0,4 ГОСТ 5017-49 6—7 Sn; 0,3—0,4 Р; примеси 0,1 остальное Си Отжиг t 600 <- 650° С Мягкая Твердая 80 180 40 75 i 22 62 *
Бр. ОФ 4-0,25 ГОСТ 5017-49 3,5—4 Sn; 0,2—0,3 Р; примеси 0,1 остальное Си Отжиг Л ---= 600 -4- 650 ° С Мягкая Твердая 62 170 34 60 54
Элинвар ЭИ-278 1 0,7-0,8 С; Si <0,6; 2-3 Мп; 7—9Сг; 33—35 Ni; 3—4 W, остальное Fe —
Сталь хромоникелевая и 1Х18Н9Т ГОСТ 5632-51 С < 0,12; Мп < 2, Si < 0,8; 17—20 Сг; 8—11 Ni; 0,8 Ti Закалка t = 1050 — 1120°С 155 55 20
Технический титан 1 ВТ1-1 АМТУ 388-57 Fe <0,3; N <0.04; Si <0,15; O<0,15; C < 0,1; II < 0,015; остальное Ti ч. г — 52 4
гг
•Я со S Латунь * • . Материал
F т
Ч* 40 Сп 00 Си 00 О £ Предел пропорцио- нальности в кгс!мм2
1 1 rj~i
1 с LC to 00 ЧЛ О Сл . 10,5 15,4 д i 15,4 « 1 1^ •4 Предел выносливости в кгс / лш2
Сл < +х 4^ Сп Сп ГО С,Э СП h Со с Сх Относительное удлине- ние в %
32 5,2 j g 70 40 | 1 с J»1 Относительное суже- ние в %
t3 9150 11000 1 1 10 500 11600 UUJ к V 000 н 009 И Z4 Л л АТ Модуль упругости В кгс/мм2
-л 1 1, 1 j 00 » 1 ч» 00 • to Температурный коэф- фициент модуля упру- гости в 1 / °C
Ч» « 1 18,2 • 10~6 19,1 • 10“6 i 1 19,9-10~6 to -J * съ Q Коэффициент линейно- го расширения в 1/°С
Ч> ГС ) 0,04 0,06 0,068 С Удельное электро- сопротивление в ом*мм^/м
а * “1 ) 0^‘0 1 0,34 0,28 <-• LC j*1 Теплой роводность в кал;см-сеК'°С
ОС -> ) оо о 8,65 00 СП ОС чв } fa. Удельный вес в"а/слгЗ
Продолжение табл.
Бронза кремниево- марганцевая 8 12,6 21 50 1 75 10400 12 000 15,8 • 10“6 0,15 0,10 8,4
Бронза оловянно- цинковая — н 36 4 к 8 500 12 400 4 18•10-6 1 1 [ 0,087 0,20 8,8 ’ 1
•Бронза оловянно- фосфорная • 10 45 ч * 65 10 И 200 4,8 • 10~4 17,1 • 10“6 0,176 0,18 8,8
35 35,5 ’52 8 10 000 4,0 • 10“4 17,6 • 10“6 0,091 0,20 8,9
Элинвар -—« - ' — —— ———ч— 1 14 500 0,60 ’ ' 1 8,0 •
Сталь хромоникелевая и № 1 I 1 40 55 20 300 3,5 • 10~4 0,75 0,039 7,9
Технический титан * • 25 л 45 11500 — 8,6 • 10-6 0,039 4,5
Таблица 2
Минимальные механическйе свойства полуфабрикатов из материалов,
упрочняемых нагартовкой
Сплав гост или ТУ 1 Полуфабрикаты Предел прочности ч в кг с / л иг2 ч Относительное удлинение 6 в %
м пт т | ОТ М пт от
Л62 ГОСТ 931-52 Листы И ПОЛОСЫ 30 35 42 60 40 20 i 1 10__ . 2,5
Л62 ГОСТ Ленты h ~ 0,05 4- 4-2,0 мм
2208-49 30 38 42 60 35 20 i 10 2,5
♦ Проволока d = 0,10 4- 0,18 мм 35 85 1 г 18
Л62 ГОСТ d ~ 0,20 4-0,50 мм 35 45 82 1^-^— 20 5 — *
1066-58 d — 0,55 4-1,0 мм 35 45 80 —1— 26 5 —
d = 1,10 4— 4,8 мм 35 40 70 —г— 30 10 —
fZ = 5 4- 12 мм 32 36 65 34 12 —
ГОСТ
Л 68 931-52 и ГОСТ Листы, полосы и лепты 30 35 40 50 40 25 1 5 4
А 2208-49 1
Проволока
ГОСТ d = 0,10 4- 0,18 мм 38 82 20 ——
Л 68 1066-58 d — 0,20 4- 0,75 мм d = 0,80 4- 1,40 мм 35 32 40 38 82 70 25 30 5 10 —
d = 1,50 4- 12 мм 30 35 1 65 1 1 40 1 15
Л80 ТУ ЦМО 1001-53 Ленты 27 — - - 50 —V -* ——-
ЛЯП ГОСТ Трубки для силь-
dlOV 5685-51 фонов
Л90 ЦМТУ 2079-49 Ленты и полосы 27 * 35 —
Л90 ЦМТУ 2678-50 Ленты и полосы - 34 40 1 7 - —
МНЦ 15-20 ГОСТ 5063-49 Ленты и полосы 35 —-—— 55 35 1 —
ГОСТ Проволока »
МНЦ 15-20 d — 0,2 4- 0,5 мм 35 —- 55 20 0,5 J 1
5220-50 d = 0,6 4—1,0 мм 35 45 55 25 3 0,5
d — 1,1 4- 5,0 мм 35 45 55 — 30 5 1 ,5 —
24
Продолжение табл. 2
Сплав 1 гост пли ТУ f Полуфабрикаты Предел прочности в кгс/лш2 Относительное удлинение 6 в %
м пт от М пт ОТ
Бр. КМцЗ-1 гост 5222-50 Проволока </ = 0,14-2,6 d = 2,8 4-4,2 d = 4,5 4-8.0 ММ мм мм 9.0 85 83 . ▼ ( 1 • 1 ),5 1,0 1,5 —
d = 8.l 5 4-10,С 1 мм — 78 - - 2,0 ‘
Бр. ОЦ4-3 ГОСТ 5221-50 Проволока <2 = 0,14-2,5 </ = 2,8 4-4,0 d = 4,54-8,0 (2 = 8,5 4-12 . мм мм мм И.И »— — 1 90 85 83 78 ( С ),5 1,0 1,0 2,0
► Бр. ОЦ4-3 ГОСТ 1761-50 Лента 30 — 55 65 38 • • 5
г
Бр. ОФ6,5-0,4 ЦМТУ 3352-53 Проволока 1 1 90 • - • 0,5 ! Г
Бр. ОФ6,5-0,4 ЦМТУ 3383-53 Лента * —— — 75 ——— 1 — 1 5 г
Бр. ОФ4-0,25 ГОСТ 2622-44 Трубки манометри- ческие 33 50 i 40 —— 2 1 1 "
Примечание. М — мягкий, ИТ — полутвердый, Т—твердый, ОТ — особо
твердый.
и релаксации, что приводит к нестабильности показаний прибора
во времени. Кроме того, из-.за низкого предела упругости гистере-
зис оказывается весьма значительным.
Рабочие температуры упругих элементов из нагартовываемых
цветных сплавов невысоки (до 100—200° С), так как при значитель-
ном нагреве нагартовка снимается, и упругие свойства резко сни-
жаются. При формовании элемента из этих материалов происходит
упругая отдача, величина которой зависит от размеров элемента,
сообщаемой материалу деформации и от исходного состояния мате-
риала. В . связи с большой неоднородностью свойств упругие
элементы, изготовленные даже из одной партии материала, полу-
чают весьма большой разброс характеристик.
В табл. 2 приведены некоторые механические свойства полу-
фабрикатов в виде листов, лент и проволоки из материалов, упроч-
няемых нагартовкой.
Для изготовления винтовых и плоских пружин широко приме-
няется высокоуглеродистая стальная пружинная проволока (ГОСТ
9389-60), подвергаемая специальной термообработке (патентиро-
Таблица 3
Предел прочности стальной углеродистой пружинной проволоки
(ГОСТ 9389-60)
1------------------
Диаметр в мм
Предел прочности ст,, u
в кгс/мм%
Класс I Класс II
0,14; 0,15, 0,16; 0,18; 0,20; 0,22; 0,25; 0,28; 0,30
0,32; 0,36; 0,40; 0,45; 0,50; 0,56; 0,60
0,63; 0,70; 0,75; 0,80
0,85; 0,90
1,00
1,10
1,20
1,30; 1,40
1,50; 1,60
1,70; 1,80
2,00
2,20; 2,30
2,50
2,80
3,00
3,20
3,40; 3,50; 3,60
4,00
4,50; 5,00
5,60; 6,00
6,30; 7,00; 8,00
270—310
265-305
260-300
255-290
250-285
240-275
240—270
230-260
220-250
210-240
200-230
190-220
180-205
175-200
170-195
170-195
165—190
160-185
150-175
145-170
225—270
220-265
215—260
210=255
205—250
195-240
195—240
190—230
185—220
180—210
180-210
170-200
165—195
165—195
165-195
155-185
155-180
150-175
140-165
135-160
125—145
В результате этого
ванию) и последующему сильному наклепу.
материал приобретает высокую прочность и в то же время сохра-
няет пластичность
достаточную для дальнейшей механической
Таблица 4
Механические свойства ленты
пружинной холоднокатаной
термически обработанной
(закалка и отпуск)
по ГОСТ 2614-55
Группа
прочности
П редел
прочности
, в кгс/млг2
Относи-
тельное
удлине-
ние б в %
130—160
161—190
> 190
3,0
обработки. Пружины, изготовленные
из такой проволоки, как правило,
не подвергаются дополнительной тер-
мообработке, кроме проводимого иногда
небольшого нагрева для снятия оста-
точных напряжений. В табл. 3 приве-
дены данные из ГОСТ 9389-60 на*меха-
нические свойства стальной углеро -
диетой проволоки.
Для изготовления упругих элемен-
тов используются также материалы,
повышающие свои упругие свойства
в процессе термической о б-
В табл. 4 даны основные меха-
нические свойства пружинной ленты, изготовляемой из сталей У8А—
У12А, 65Г, 60С2А, 70С2ХА и ХО5. Из ленты изготовляются упругие
элементы простой формы, например, некоторые плоские пружины.
Упругие элементы более сложной формы изготовляются из мате-
риала в отожженном состоянии, а затем требуемые упругие свойства
'придаются закалкой на мартенсит с последующим отпуском. Дан-
ные по материалам, упрочняемым закалкой, представлены в табл. 5.
К этим материалам относятся углеродистые стали, стали леги-
рованные кремнием, марганцем, никелем, хромом, ванадием и т. п.
Такие стали отличаются высокой прочностью и применяются для
пружин, работающих при высоких напряжениях.
Марганцовистые стали дешевы по сравнению с другими легиро-
ванными сталями, но склонны к хрупкости при перегревах во время
закалки. Кремнистые стали склонны к обезуглероживанию и обла-
дают небольшой прокаливаемостью.
Высокими механическими свойствами, особенно в отношении уста-
лостной прочности, обладают хромомарганцевые, хромованадиевые
н хромомарганцевокремнистые стали. Благодаря своим высоким ка-
чествам они применяются для пружин ответственного назначения,
работающих в условиях переменных напряжений. Стали 50ХФА и
4X13 могут работать и при повышенных температурах (до 400° С).
Стали, указанные в табл. 5, имеют высокие прочностные и упру-
гие свойства. Однако недостаточная пластичность этих материалов
после упрочняющей термической обработки не позволяет изгото-
вить из них упругие элементы сложной формы, которую, например,
имеют сильфоны или гофрированные мембраны. Кроме того, при
термообработке возможно коробление изделия, что также препят-
ствует изготовлению упругих элементов сложных форм в предва-
рительно отожженном состоянии, когда пластичность велика. Не-
достатком этих сталей являются плохая свариваемость и низкие
коррозионные свойства: они нестойки, например, в питьевой, в мор-
ской воде и в кислотах. Исключение представляет хромистая сталь
4X13, обладающая высокой коррозионной стойкостью: она стойка
во влажной атмосфере, в пресной воде, в паре, в слабых растворах
кислот, солей и щелочей. Эта сталь удовлетворительно сваривается
в отожженном или нагартованном состоянии. Хромованадиевая
сталь 50ХФА хорошо сваривается дуговой сваркой и удовлетвори-
тельно — остальными видами сварки. Все перечисленные в табл. 5
стали магнитны.
Наилучшим сочетанием технологических и эксплуатационных
свойств обладают так называемые дисперсионно-твер-
деющие сплавы (табл. 6), которые также приобретают упру-
гие свойства в результате термообработки. В отличие от указанных
в табл. 5 сталей, дисперсионно-твердеющие сплавы весьма пластичны
в закаленном состоянии, значительное повышение их упругих
свойств достигается в процессе отпуска.
Высокая пластичность дисперсионно-твердеющих сплавов в за-
каленном состоянии позволяет изготовлять из них упругие эле-
менты почти любой сложной формы. При этом процесс формования
элемента не сопровождается заметной упругой отдачей, и пружины
одной партии получают идентичные форму и размеры.
27
82
S
Твердость в
кгс/мм2
Предел прочности
в кгс/мм2
Предел текучести в
кгс / мм2
Предел усталости
в кгс/мм2
Относительное удли-
нение в %
Относительное су-
жение в %
Коэффициент линей-
ного расширения в
1/°С
Удельное электросо-
противление в
ом • мм2 /м
Теплопроводность
в кал/см • сек °C
Удельный вес в
г/смэ
и
S
3
S
и
S
S:
g
S
g
О
6S
Сталь хромомар- ганцевая Сталь кремнистая Материал
50ХГА, ГОСТ 2052-53 2052-53 60С2 А, ГОСТ 60С2, ГОСТ 2052-53 « । Марка, ГОСТ
0,46—0,54С; 08-1,0 Мп; 0,17—0,37 Si; 0,95—1,2 Сг; Ni<0,4 0,6—0,9 Мп; 1,6—2 Si; Сг<0,3; Ni<0,4 0,56-0,64 С; J_X .X . J г т L ..... ! 0,57-0,65 С; 0,6—0,9 Мп; 1.5—2 Si; Сг<0,3; Ni<0,4 Химический состав в %
§ о 3 1g ’Ж с S 3 taan — 870 о to 2 § 3 и 11 00 05 о Термообра- ботка в °C (ориентиро- вочно)
1 1 400 СО to НВ Твердость^в кге/мм*
1 i 130 3 Предел прочности в кге/мм2 :
го Предел текучести • в кге !мм^
Q х Предел усталости в кге/мм2
J-! ^31 Относительное \ удлинение в %
1" о. . 1 Си t Относительное су- жение в %
20 000 \ ** 20 500 Мод упру В KSC
8000 0008 к Н * ta h-i н-м
1 j р Коэффиициент ли- нейного расширения в 1/°С
I 1 j Удельное электросо- противление в QM • ММ2/М
J Теплопроводность в ’ кал (см • сек °C
1 -М . 1 Удельный вес в г/см3
Продолжение табл. 5
ое
1 Хромистая сталь я ииаыррими- | кремнистая f Сталь п ^"Ч 'rt' т -w*. Л Ж V хромована- диевая / 1 3 1 - I f -1 , О • , 1 V 1 .1 ’ Сталь материал * ь Г..’
0004-01 12-14 Сг; от"ТПл * Ni<0,6 ~,-,3ии /V4Q 0,35 0,45 С; . —1050“ ^13, Мне 0,6; ‘’“«Zlioo ГО.С?. Si<0,6; '"‘'nn. 500 168 140, 0,61—0,69 С; 1 п^гопд 0,/0 1,0 Мп, ГОСТ 1,50—2,0 Si; t3aK-= 850 ,qn 17П’ „ Сг<0,3; *огпп=420 ~ 190 1/0 Ni<0,4; 0,80-1,20 W i I 9пК>\ч 0,8—1,1 Сг; tomn =520 480 ldU Ni<0,4; 0,1—0,2 Va i i 1 i L_L_J_L 0,46-0,54 C; 'idXdjA 0’*^ 0,8Mn, 0,17-0,37Si: i4rtK = 850 400- H § s Термообра- и 2 и* Марка, Химический ботка в °C Й ГОСТ состав в % (ориенти- © ч ч ровочно) ^4 ST? r_J w f-Ч h-Г Н к К д К и t-Г Гй? CJ т
00 С г -3 ' SV 01 zs 1 /К ! n ii-Tj л Предел усталости в кге/мм* Относительное ** удлинение в % , Относительное г сужение в %
- 1 22 300 19 000 IX 3 5 t И <3 а; S £ Й 4J £ О й ь 3 ₽ Коэффициент линей- 2 ного расширения в 1/°С ~ Удельное электро- > сопротивление в ом • мм*/м Теплопроводность в кал/см • сек °C
8690 — 0,59 0,069 1 i । । - — — 0S8A1 vr i u, ' У Л 8300 12,4-IO-6 0,23 —
1 1 1 Удельный вес в г/см^
Продолжение табл.
В процессе отпуска, который иногда называют старением или
облагораживанием, отформованный упругий элемент получает высо-
кую прочность, не уступающую прочности упомянутых выше сталей,
закаливаемых на мартенсит.
Рабочие температуры этих сплавов ниже температуры отпуска
(старения) и для некоторых сплавов могут достигать значений
300-1350° С.
По сравнению со сплавами, повышающими свои упругие свой-
ства и результате наклепа (см. табл. 1) или при закалке на мартен-
сит й отпуске (см. табл. 5), дисперсионно-твердеющие сплавы имеют
малые несовершенства упругих свойств, что объясняется практи-
чески полным снятием остаточных напряжений в процессе отпуска
упругого элемента и более равномерным по объему упрочне-
нием.
К дисперсионно-твердеющим сплавам относятся бериллиевые
бронзы Бр.Б2 и Бр.Б2,5, применение которых обеспечивает упру-
гим элементам высокую упругость, прочность, выносливость при
незначительных величинах гистерезиса, упругого последействия
и ползучести. Для некоторых упругих элементов важно то, что бе-
риллиевая бронза обладает высокой электропроводностью, немаг-
нитна, стойка против коррозии- во многих средах (например, на
воздухе, в пресной и морской воде), хорошо сваривается, паяется
и может быть использована до температур 100—150° С.
В табл. 7 даны некоторые механические свойства полуфабрика-
тов из бериллиевых бронз.
Бронза БНТ, отличающаяся от предыдущих марок дополнитель-
ным введением титана, близка к ним по своим свойствам, но из-за
меньшего содержания бериллия дешевле предыдущих 1 2.
Дисперсионно-твердеющий сплав МНМц 20-20 обладает доста-
точно высокими механическими свойствами после термической
обработки, но по сравнению с бериллиевой бронзой — меньшей
усталостной прочностью. Он значительно дешевле бериллиевой
бронзы, нетоксичен, но склонен к растрескиванию под воздействием
коррозионных сред кислотного характера 2.
Сплав К40НХМ нуждается в значительной предварительной
нагартовке, после чего его упругие свойства могут быть повышены
в результате дисперсионного твердения. Этот сплав имеет понижен-
ную пластичность и поэтому, несмотря на исключительно высокую
прочность и выносливость, способность работать при температурах
до 350—400° С, а также высокую коррозионную стойкость (напри-
мер, в морской воде, плавиковохг кислоте), сплав К40НХМ
1 Чипиженко А. И., Зависимость выносливости и упругого гистере-
зиса бериллиевой бронзы от содержания бериллия и других элементов [17]»
а также Ч и п и ж е н к о А. И., Изучение влияния химического состава берил-
лиевой бронзы на качество пружин [18].
2 Бобылев А. В., Медные сплавы для чувствительных элементов
[17], а также [19]; Г р а д у с о в П. И. и МухинН. И., Применение
сплава МНМц 20-20 в упругих элементах манометров [18].
31
Физико-механические свойства и химический
* Материал 1 1 л Марка, ГОСТ или ТУ Химический состав в % Термообра- ботка (ориен- тировочно) 1 Состояние материала Твердость в кгс/лшЗ
НВ
Б ронз а бериллие- вая Бр. Б2, ГОСТ 493-54 0,2—0,5 Ni; 1,9—2,2 Be; примеси 0,5; остальное Си Закалка t=760-ь -4-780° С Отпуск t = 320° С 2 часа Закалка Закалка-)- отпуск Закалка-)- нагартов- ка-)-отпуск 81 350-400 400
Бр. Б2,5, ГОСТ 493-54 0,2—0.5 N1; 2,3—2,6 Be; примеси 0,5; остальное Си ^3CLK 760“ -1- 780° С ^017171 = 320° С 2 часа Закалка Закалка-)- отпуск Закалка-)- нагартов- ка-f- отпуск £8 390 Hv*=400 1
Закалка
Бр. БНТ1,9
ГОСТ 493-54
0,2—0,4 Ni;
0,1—0,25 Ti;
остальное Си
Никельти-
тановая
бронза
^зак — 760 .
-4-780° С
1<утп~320°
2 часа
отпуск
Закалка-)-
нагартов-
ка-)-отпуск
Бр. БНТ1,7
ГОСТ 493-54
0,2—0,4 Ni;
0,1—0,25 Ti;
остальное Си
Закалка
Закалка-]-
отпуск
Закалка-)-
нагартов-
ка-)-отпуск
Марган-
цевый
мельхиор
МНМц
20-20
19,5-21,5 Мп;
19,5-21,5 Ni;
примеси 0,5;
остальное Си
^ак=650° С
^077171=400° С
8 час.
Закалка
Закалка -)-
отнуск
Закалка-}-
нагартов-
ка4-отпуск
Ну = 137
Ну = 400
Ну = 440
32
Таблица б
состав дисперсионно-твердеющих сплавов
* I СП g о И tr о (Я й 3 о £ йД с? и И g о ф Ег К Ф К < ф □ и ф Q. ° Лг с « Предел упругости в кгс] мм2 Предел пропорциональ- ности в кгс/лш2 Относительное удлине- fa 1 Модуль упругости в кгс/ммъ о4* я ф д Температур- ный коэффи- циент модуля упругости в 1/°С Коэффициент линейного расширения в 1/°С Удельное электросо- противление в ом-мм%1 м 1 Теплопроводность в кал/см-сек-^С Удельный вес в г/слсЗ
&пч (У j' °у 5 Е G ye а Q X У
50 125 135 I 30 128 6,2 77 96 5,5 4 75 0 И 700 3 13100 - 13 500 3,1 10~4 16,6 • 10~6 — 0,1 0,068 0,20 0,25 8,23
1 56 130 135 15,7 128 5,1 79 97 - 3 — 1 ,0 — ,5 13 300 3,5 • 10“4 16,6.10“6 0,1 0,08 0,20 0,25 1 8,23
.. 125 135 1 • 42 1115 р 125 1 1 77 96 с — с ““ 1 >0 - >,7 12 800 3 13 000 I — I 1 ч d Г ч
70 91 Е ю — 7 12 800
55 120 135 27 114 124 84 — 2 77 1 98 Ю 12 700 4700 [2 14 400 5000 з — — 19 • 10-6 17,3- 10“6 0,047 0,077 8,29
3 Заказ 24.
33
1 Материал Марка, ГОСТ или ТУ * Химический состав в % 1 Термообработ- ка (ориенти- ровочно) Состояние материала Т вердость в кгс'ммЯ
НВ
Сплав К40НХМ ЧМТУ 5164-55 0,15 С; 2,0 Мп; 20 Ст; 7,0 Мо; 15 Ni; 0,15 Ti; 0,03 Al; 0,03 Be; 40 Co; осталь- ное Fe £заК"1Ю0 • -г-1150° С ^omn=500-j- -г 550° С I Закалка Закалка-]- нагарт. Закалка-f- ! пагартов- 1ка 4-отпуск Hv = 600
Сплав Н41ХТ ТУ 4679-54 41—43 Ni; 5,0-6,0 Cr; 2,2—2,8 Ti; 0,05 C; 0,3-0,8 Si; 0,4—0,8 Mn; 0,4-0,8 Al; остальное Fe ^зак=950о С tomn — 700° С 3 часа Закалка Закалка-р отпуск Закалка-}- нагартов- ка-{-отпуск 145 345 395
V Сплав * ЭИ702 (Н36ХТЮ) ЧМТУ 5834-57 C<0,05; 0,8—1,2 Mn; 0,5—0,7 Si; 12,5—13,5 Cr; 34—36 Ni; 2,8—3,2 Ti; 0,9—1,1 Al; примеси 0,04 остальное Fe ^«=950° С ^ОТПП— /00° С 3 часа * Закалка Закалка-{- отпуск 150 340
Сплав ЭП52 (Н36ХТЮМ8) ЧМТУ 372-60 To же, но 7 — 9 Mo гзак=Ю15°с tomn— /00° С 3 часа Закалка Закалка-р отпуск 222 435
Сплав 1 г ЭП51 (Н36ХТЮМ5) ЧМТУ 372-60 1 4 To же, но 4—6 Mo • 1 75° С iomn=700° С 3 часа Закалка Закалка-}- отпуск * 208 ‘ 410
* п, г — твердость по Виккерсу.
Ф> о
СП ГО ГО -J
О СП 1 СО о о co
СП ел го to **чЗ
1 1 J 1 1
• 1 1 1 1
со to CO
О tO О to О Cn
ГО to to
H. 00
1 о о
о о о
1 1 1 I
J 1
£ ht>
-* СП Си to
» f
•
сь °?
ч*
£> rf>*
1 1
1 1 1
> ГС > о г ( \Э К в $ i о о 3 Л Предел прочности в кгс/лш2
ГО 00 гс СП О Од с » 1 <1 м Q Предел текучести в кгс 1 мм^
1 1 1 1 j J Предел упругости в кгс 1мм%
1 4 w * я Е‘ОГ с в ' 1 Q 3 Предел пропорциональ- ности в кгс/мм^
3 Of * о ( ’с О ] 1л ‘ Относительное ние в % у длине-
1» ши /ши 19 000 7000’ 17 000 7000 Л Л Х“ч Л Л Л ZX УЧ ГС о > о упругости в кгс1мм^ ? иЧ 4
1 0,2 -10“4 t4 1 ! Температур- ный коэффи- циент модуля упругости в . 1 / °C
8,0 • 10~6 1 ♦ [ о Коэффициент линейного расширения в 1/°С *
М С£ > Удельное электросопро- тивление в om-mm^Iм
1 1 Теплопроводность в кал1см-сек-°C
1 * ОС bJ ч Удельный вес в г слЗ
Продолжение табл.
о
Таблица 7
Механические свойства полуфабрикатов из бериллиевых бронз
Марка бронзы ГОСТ или ТУ Полу фабрика ты Предел прочно- сти ст в кге 1мм% Относитель- ное удлине- ние б в %
М т о М о
Бр. Б2 Бр- БНТ1,9 Бр. БНТ1, 7 ГОСТ 1789-60 ГОСТ 1789-60 ГОСТ 1789-60 X Полосы и > ленты «h — 0.25:6,0 мм 40-60 >65 >60 115— 120 / 120 110 30 2,5 2,5 2,5 2—1,5 1,5 1,2
Бр. Б2 ЦМТУ 673-41 Проволока d=0,03 -г-12,0 мм </=0,03 0,1 мм </=0,12 0,2 мм (/=0,35-4-1,0 мм (/=5,5 -г-12 мм 50 75 95 НО 125 132 30 1 1,5 1,0 1,0 0,5
Примечание. М — мягкая, Т — твердая, О — облагороженная.
применяется для изготовления упругих элементов лишь сравни-
тельно простой формы, например, плоских, спиральных и винто-
вых пружин Ч
Высокие механические свойства после закалки и отпуска и доста-
точную пластичность в закаленном состоянии имеют сплавы H4IXT
и Н36ХТЮ (ЭИ702), которые превосходят бериллиевую бронзу
в отношении коррозионной и термической стойкости [21].
Особенностью сплава Н41ХТ является незначительное измене-
ние модуля упругости при нагреве до 150е С 1 2. Сплав Н36ХТЮ
имеет высокий предел упругости и стабильность упругих свойств
во времени. 3 Эти сплавы находят применение для изготовления
многих упругих элементов сложной формы, работающих при высо-
ких напряжениях и в довольно агрессивных средах. Сплавы могут
работать при повышенных температурах (до 200° С).
Добавление к сплаву Н36ХТЮ молибдена повышает его термо-
стойкость 4. Чувствительные элементы из сплавов Н36ХТЮМ5
(ЭП51) и Н36ХТЮМ8 (ЭП52) могут быть использованы до темпера-
тур 300 и 350° С соответственно. Благодаря хорошей коррозионной
1 Болеух А. С., Белова Э. П. и Сольц В. А., Применение
сплава К40НХМ для заводных пружин [20], а также [21].
2 Ч о мо в а Н. Г., Сплавы для упругих чувствительных элементов с ма-
лым температурным коэффициентом модуля упругости [17], а также [20] и [22].
3 Соловьева Н. А. и Сольц В.А., Новый немагнитный коррози-
онно-устойчивый сплав для пружин [22], а также С о л ь ц В. А., Немагнитные
коррозионностойкие сплавы для упругих чувствительных элементов [17].
4 С о л ь ц В. А. и НосаньЛ. Т., Влияние молибдена на свойства
сплава Н36ХТЮ (ЭИ702) [221 а также [17].
и термической стойкости и высоким упругим свойствам эти сплавы
являются особенно ценными для изготовления чувствительных
упругих элементов точных приборов, предназначенных для работы
в условиях повышенных температур и агрессивных сред.
Все сплавы, перечисленные в табл. 6, немагнитны (за исключе-
нием сплава Н41ХТ), хорошо паяются и свариваются.
Таблицы 1—7, где приводятся физико-механические свойства,
химический состав и режимы обработки материалов, используемых
для изготовления упругих элементов, составлены на основе сведе-
ний, сообщаемых в работах [17]—[29].
В тех случаях, когда упругие элементы должны иметь особо
малую жесткость, их изготовляют из немет а л л и ч е с к и х
материалов: кварца, резины, пластмасс, модуль упругости
которых значительно меньше, чем у металлов. Большое значение
имеет также то, что некоторые из этих материалов имеют высокую
стойкость в агрессивных средах.
Кварцевое стекло отличается особенно высокими упругими
свойствами, исключительно малым гистерезисом, постоянством
модуля упругости с температурой и коррозионной стойкостью Ч
Из кварца могут быть изготовлены упругие элементы различных
форм: плоские и винтовые пружины, мембраны и манометрические
трубчатые пружины. Однако хрупкость этого материала ограничи-
вает его применение.
Весьма широкое применение для изготовления манометрических
упругих элементов нашли разные сорта резины. Резина приме-
няется в качестве герметизирующего материала в сетчатых кон-
струкциях упругих элементов (см. § 31). Она имеет очень малую
жесткость, и относительное удлинение резины может доходить до
сотен процентов при малых остаточных деформациях.
Основным недостатком резины, как материала для упругого
элемента, является ее значительное старение, в результате кото-
рой упругие свойства существенно изменяются с течением времени.
Значительное возрастание гистерезиса и последействия и изме-
нение модуля упругости при нагреве служат причинами того, что
резиновые упругие элементы могут применяться в узких интерва-
лах температур. Лишь специальные жаростойкие резины могут?
работать при температурах до 100°—140° С, а морозостойкие —
до —45 (—50) °C. Появившиеся в последнее, время различные новые
сорта синтетических резин значительно расширяют эти темпера-
турные пределы. Так например, полисилоксановая резина может
работать при температурах от —60 до Н~ (250 —300)° С [30].
Коррозионная стойкость обычных сортов резины сравнительно
невысока, но в то же время резина по сравнению с некоторыми
металлами лучше сопротивляется агрессивному действию многих
кислот и щелочей. При длительном использовании во многих сре-
1 Поддубный С. А., Кварцевое стекло как материал для упругих
элементов и новая технология прецизионных кварцевых работ [17].
37
00
I
t
Физико-механические свойства неметаллических материалов
Таблица 8
Материал. Нормаль или ТУ ► Твердость Предел прочности В К2С/лиц2 Относи- тельное удлине- ние в % Модуль упругости В 'KZCjMMZ Коэффициент линейного расширения в 1/°С Удель- ный вес в 3/cjvt3 Интервал рабо- чих температур в °C
при растя- жении при сжа- тии
°пчсж 6 а Y t
Стекло кварцевое - 12 197 —~ 70000 5 • 10~7 2,2 До 1000
Резина листовая невул- канизированная HIT-148-55: а) кислотостойкая б) теплостойкая . . . в) морозостойкая г) масло- и бензо- стойкая .... д) повышенной масло- бензостойкости По Шору 60-80 65-90 60-80 55-85 70—90 1 1 0,45 0,50 0,50 0,55 0,90 1 200 100 175 180 100 1 \, I (—30)-~(+50) (-30)4- (4-90) <-45)->(+50) (-30)-Н4-50) (-30)-4-(4-50)
Фторопласт 4 .... В ТУ ФГ14-59 Я7?=Зч-4 кгс /мм? Iй •1,6-м ,8 2,0 250-4-350 НО (8 4-25) • 1О‘~5 2,14-2,4 (-60) ч-(+250)
Фторопласт 3 .... ВТУ 518-54 ЯВ=Ю-ь 13 кгс/мм2, . 3,04-3,5 5,0 ч-5,7 • 204-40 163 (84-25) • 10~5 2,114-2,16 (-195)4^+100)
дах резина склонна к набуханию и нестойка в органических раство-
рителях. Для работы с бензином и маслами применяются специаль-
ные сорта бензо-маслостойких синтетических резин.
Исключительно высокой коррозионной и термической стойкостью
обладают фторопласты [31]—[33]. Фторопласт 3 и фторопласт 4
находят в последнее время применение для изготовления эластич-
ных мембран и даже сильфонов.
Механические свойства фторопластов несколько повышаются
при закалке — быстром охлаждении после нагрева при 330° С.
При этом, если фторопласт 4 легко подвергается закалке, то фторо-
пласт 3 можно закалить только в виде тонких пленок вследствие
его малой теплопроводности.
Фторопласт 4 —- наиболее химически стойкое вещество из всех
известных пластиков. Он не растворяется и не разрушается под
действием кислот, щелочей, окислителей, паров ртути и других
агрессивных сред. Фторопласт 4 сохраняет прочность при нагреве
до 250° С.
Фторопласт 3 менее термостоек, чем фторопласт 4, и, кроме того,
набухает в некоторых органических средах, но имеет большую
механическую прочность, и из него могут быть изготовлены изделия
сложной формы прессованием или литьем под давлением.
Сильная ползучесть и заметное изменение модуля упругости
с температурой препятствуют широкому использованию фторопла-
стов в качестве материала для упругих элементов.
Механические свойства некоторых неметаллических материалов
даны в табл. 8 [21], [30]—[33].
Вследствие склонности к ползучести и больших упругих несовер-
шенств элементы из резины и пластмасс применяются главным обра-
зом как разделители, к которым не предъявляются высоких требо-
ваний в отношении упругих свойств. Функцию упругого элемента
в таких случаях выполняет плоская или винтовая металлическая
пружина, работающая совместно с неметаллическим разделителем.
§ 2. ВОПРОСЫ ИЗГОТОВЛЕНИЯ УПРУГИХ ЭЛЕМЕНТОВ
Упругие элементы изготовляются из полуфабриката (листового
материала, тонкостенных трубок, проволоки или лент), который
должен иметь надлежащие механические свойства и достаточно точно
выдержанные размеры для обеспечения требуемого качества упру-
гих элементов. Трудоемкость технологического процесса обычно
определяется не столько трудностями изготовления упругого эле-
мента из заготовки, сколько сложностью получения самой заго-
товки. Например, получение тонкостенных трубок с малыми допу-
сками на толщину стенки более трудоемко, чем последующее изго-
товление из них чувствительных элементов — сильфонов или мано-
метрических трубчатых пружин.
Технология упругих элементов разнообразна и зависит как
от конструкции элемента, так и от свойств материала. Однако в тех-
нологии различных упругих элементов есть много общего.
29
Процесс изготовления пружин можно разделить на два основных
этапа: образование формы упругого элемента и придание ему тре-
буемых рабочих свойств.
Формование упругого элемента может производиться штампов-
кой, вытяжкой, гибкой, навивкой. Проектирование инструмента
для формовки упругих элементов из материалов, которые сильно
нагартовываются, усложняется тем, что при определении размеров
инструмента следует учитывать упругую отдачу материала.
Если материал пружины получает требуемые упругие свойства
при термообработке, то в этом случае появляется опасность коробле-
ния, так как пружина обычно представляет Собой длинный тонкий
стержень или тонкостенную оболочку. Для предотвращения или
уменьшения коробления упругие элементы при термообработке
закрепляются в специальных прокладках. Как правило, термообра-
ботка проводится в печах с защитной атмосферой во избежание
окисления и появления окалины. Чтобы получить упругий элемент
требуемого качества, режимы термообработки должны выполняться
с высокой точностью.
Ответственной операцией процесса изготовления является соеди-
нение деталей упругого элемента друг с другом или с арматурой
при помощи сварки или пайки. Сварка или пайка не должна иска-
жать форму упругого элемента и снижать его свойства. Здесь не-
пригодны такие способы сварки или пайки, которые связаны с дли-
тельным нагревом материала до температур структурных превраще-
ний. Широко применяются точечная и шовная коротко-импульсная
сварка, когда упругий элемент нагревается только вблизи самого
шва, а вся его основная масса не успевает прогреваться. Сварной
шов должен обеспечивать плотность соединения; шов манометриче-
ских элементов должен быть герметичным.
Качество сварки зависит от правильного подбора свариваемых
между co6oii материалов. Желательно, чтобы материал свариваемых
деталей был одинаковым, но возможна сварка и различных материа-
лов. Большие трудности встречаются при сварке материалов раз-
ных толщин, например, при соединении тонкостенного упругого
элемента с арматурной деталью большой толщины. В этом случае
для осуществления возможности сварки на арматуре приходится
иногда делать специальные проточки.
Качество сварного шва во многом зависит от режима сварки.
В настоящее время для сварки материалов с небольшими толщинами
наибольшее распространение получила роликовая коротко-импульс-
ная сварка на сварочных машинах с игнитронным прерывателем \
Более высокое качество сварного соединения обеспечивает конден-
саторная шовная электросварка* 2. Упругие элементы из материалов
х Петров В. А., Оборудование для сварки упругих чувствительных
элементов [17].
2 Каганов Н. Л., Конденсаторная сварка тонких и ультратонких
деталей упругих элементов приборов [17].
40
толщиной выше 0,4—0,6 мм чаще свариваются аргоно-дуговой
сваркой.
Следует иметь в виду, что наличие сварного шва снижает корро-
зионную стойкость упругого элемента.
Пайка деталей упругого элемента производится на более про-
стом оборудовании, чем сварка, но качество паяного упругого эле-
мента снижается за счет меньшей прочности самого шва и ухудше-
ния упругих свойств пружины, более длительно прогреваемой при
пайке. Наибольшая температура, при которой может работать
паяный упругий элемент, ниже, чем у сварного. Применение флюсов
при пайке может вызвать коррозию материала упругого элемента.
Пайка упругих элементов производится как мягкими, так и
твердыми припоями. Температура плавления мягких оловянистых
припоев сравнительно низка (200—260° С), и пайка мягкими при-
поями мало снижает упругие свойства основного материала упругого
элемента. Однако качество упругого элемента в целом ухудшается
за счет низких упругих и прочностных свойств самого шва, и, вслед-
ствие этого, пайка мягкими припоями должна производиться в слабо
напряженных местах упругого элемента. В противном случае для
увеличения прочности соединения приходится прибегать к спе-
циальным конструктивным мерам, усиливающим место соединения.
Пайка твердыми серебряными припоями более надежна, обеспе-
чивает достаточную прочность шва, но ввиду высоких температур
плавления этих припоев (720—780° С) происходит нежелательный
прогрев и изменение структуры материала упругого элемента вблизи
шва.
Заключительным этапом изготовления упругого элемента
является его стабилизация, которая заключается в пуль-
сационном нагружении (так называемая «раскачка») или в длитель-
ной выдержке упругого элемента под статической нагрузкой, превы-
шающей максимальную рабочую.
Как правило, при первом нагружении в наиболее опасных точ-
ках упругого элемента напряжения превосходят предел упругости,
и поэтому после первого нагружения форма элемента не возвра-
щается полностью к первоначальной. В процессе стабилизации
происходит упрочнение материала, после некоторого количества
циклов нарастание пластических деформаций заканчивается, и даль-
нейшая работа элемента сопровождается только упругими деформа-
циями.
На фиг. 7, а показано перемещение % некоторой точки упругого'
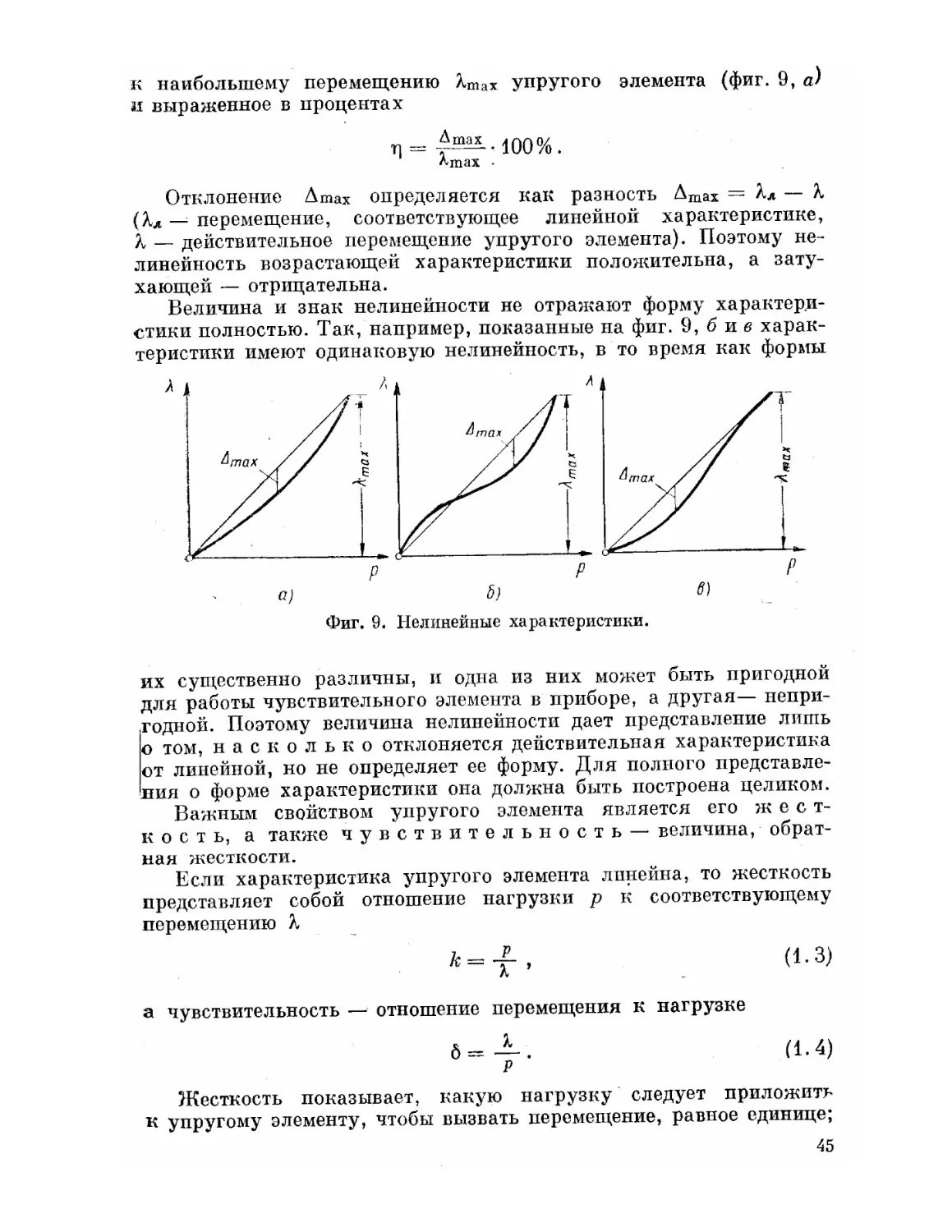
элемента в зависимости от нагрузки р в процессе стабилизации
переменным нагружением. При снятии нагрузки после первого
нагружения упругий элемент сохранил остаточное перемещение ве-
личиной АХортП1. С увеличением числа 7V циклов нагружения прирост
остаточного перемещения АХ0СГГ1 уменьшается (фиг. 7,6) и после
некоторого числа циклов прекращается. Если же упругий элемент
но подвергался стабилизации, то пластическое течение материала
изменит свойства упругого элемента со временем.
41
Если перегрузить упругий элемент свыше нагрузки стабилиза-
ции, то в нем вновь возникнут пластические деформации и появится
остаточное перемещение. Поэтому операцию стабилизации обычно
проводят нагрузками, на 10—20% превышающими рабочие. Для
ускорения процесса пластического течения упругий элемент стаби-
лизируют часто в условиях несколько повышенных температур,
но они должны оставаться значительно меньше температур струк-
турных превращений. Температура стабилизации выбирается в за-
висимости от материала и режимов его термообработки и превышает
рабочие температуры упругого элемента на 10—50° С.
«4/ ост
Фиг. 7. Стабилизация упругого элемента:
а — первые циклы нагружения; б — уменьшение остаточных деформаций
при стабилизации.
Выбор оптимального режима стабилизации (температуры, вре-
мени, характера нагружения, числа циклов и пр.) должен произво-
диться с учетом упруго-пластических свойств материала и условий
работы упругого элемента С В настоящее время не существует
«единого мнения о преимуществах того или иного способа стабилиза-
ции, и на разных предприятиях этот вопрос решается по-разному
на основе опыта и традиций.
Для измерительных упругих элементов операция стабилизации
•обязательна. Натяжные и мало ответственные пружины могут не
подвергаться стабилизации.
Стабилизацией упругого элемента заканчивается процесс его
изготовления
Полезно отметить, что по величине остаточного перемещения АА,0Ст1 после
первого нагружения упругого элемента (фиг. 7, а) можно получить представле-
ние о некоторых его рабочих свойствах. Большой остаточный ход АЛ0Ст1 может
указывать как па слишком большую величину напряжений вследствие несовер-
шенства конструкции упругого элемента (например, наличия в нем концентра-
торов напряжений), так и на снижение механических свойств материала упру-
1 Фролов Г. Н., Вопросы проектирования технологических процессов
изготовления пружин и мембранных упругих элементов [17].
42
того элемента из-за несоблюдения режимов термообработки, сварки или пайки.
Опыт1 показывает, что упругие элементы одной партии, давшие большее оста-
точное перемещение ДХ0Ст1. чем остальные, будут при работе иметь больший
гистерезис и меньший запас прочности, чем остальные упругие элементы этой
же партии.
Как указывалось, особенность технологии упругого элемента
состоит в том, что она должна обеспечить достаточную точность
упругих свойств элемента. Следует отметить, что в большинстве слу-
чаев небольшие отклонения в некоторых размерах упругого эле-
мента вызывают значительные изменения его упругих свойств.
Так, например, жесткость к винтовых цилиндрических пружин,
изготовленных из проволоки диаметром (7, связана с модулем упру-
гости G материала, средним диаметром D пружины и числом i
рабочих витков соотношением к =
Gd*
8D3i
. Так как в этом случае жест-
кость зависит от диаметра d проволоки в 4-й степени, а от диаметра D
пружины — в 3-й степени, то даже небольшие отклонения по этим
размерам могут вызвать значительное изменение жесткости. При
существующих допусках на диаметр проволоки и точность навивки
разброс по жесткости винтовых цилиндрических пружин может
достигать 120% 2.
Большой разброс по жесткости получается также при изгото-
влении других упругих элементов: сильфонов, манометрических
трубчатых пружин, мембран и др., так как их жесткость зависит
в большой степени от толщины материала, допуск на кото-
рую трудно выдержать в достаточно узких пределах. Поэтому
целесообразно назначать относительно широкие допуски на жест-
кость упругого элемента, предусматривая в конструкции прибора
возможность ее регулировки.
В тех случаях, когда необходим узкий допуск на жесткость
упругого элемента, а уменьшать допуски на его геометрические
размеры нецелесообразно, следует при разработке технологического
процесса предусматривать возможность компенсации отклонения
одного геометрического размера упругого элемента соответствую-
щим изменением другого. Например, для цилиндрической винтовой
пружины отклонение по диаметру d проволоки может быть скомпен-
сировано соответствующим изменением диаметра D пружины или
числа i витков и т. д.
Для того чтобы получить упругий элемент требуемого качества,
недостаточно проверить его геометрию и свойства в готовом виде,
необходимо проводить контроль на ответственных этапах техноло-
гического процесса. Так, обязательной является проверка механи-
ческих характеристик материала и размеров заготовки. В процессе
1 Бородко И. С., Новое в технологии производства чувствительных
элементов. Информационный научно-технический бюллетень № 6 НИИТепло-
прибора, Москва, 1956.
2 Фролов Г. И., Вопросы проектирования технологических процессов
изготовления пружин и мембранных упругих элементов [17].
43
формовки, термообработки, сварки и т. д. также нужен контроль
правильности выполнения технологических режимов.
Готовый упругий элемент контролируется по прочности, упру-
гим свойствам, гистерезису, а также в зависимости от назначения
и предъявляемых требований и по другим показателям: по ползу-
чести, виброустойчивости, усталостной прочности, герметичности г
частоте собственных колебаний, по температурным погрешностям
и т. д. Контроль упругих свойств и особенно параметров, характе-
ризующих погрешности измерительного упругого элемента (гисте-
резис, нелинейность, температурная погрешность), следует прово-
дить на аппаратуре, точность которой существенно выше точности
проверяемого чувствительного элемента.
§ 3. ОСНОВНЫЕ СВОЙСТВА УПРУГИХ ЭЛЕМЕНТОВ
Упругая характеристика, жесткость, чувствительность
Упругой характеристикой называется зависи-
мость между перемещением % определенной точки упругого элемента
и величиной нагрузки р. Характеристика упругого элемента может
быть представлена в виде уравнения, в табличной или графической
форме.
Р
Фиг. 8. Характеристики
упруго го элемента:
Ч.
с— линейная; б — затухаю-
щая; в — возрастающая.
В зависимости от конструкции и спо-
соба нагружения упругого элемента его
характеристика может быть линейной к
нелинейной: возрастающей или затуха-
ющей (фиг. 8).
Упругая характеристика является
основным показателем свойств упругих
элементов, особенно измерительных пру-
жин. Если известна упругая характери-
стика пружины, служащей для измере-
ния некоторого параметра, преобразуе-
мого в силовую нагрузку, то может
быть построена характеристика упру-
гого элемента по измеряемому пара-
метру: расходу, температуре, высоте над уровнем моря
и т. д.
Обычно при проектировании измерительного упругого элемента
стремятся к тому чтобы .характеристика его по измеряемому пара-
метру была линейной, так как в этом случае можно получить линей-
ную шкалу прибора при несложном передаточно-множительном
механизме.
Отклонения от линейной зависимости между нагрузкой и переме-
щением оцениваются величиной нелинейное.ти характери-
стики.
Нелинейностью ц характеристики называется наибольшее откло-
нение Дщах действительной характеристики от линейной, отнесенное
44
к наибольшему перемещению Хтах упругого элемента (фиг. 9, а)
и выраженное в процентах
Л шах
^тах
•100%.
Отклонение Атах определяется как разность Атах ~
(ХЛ — перемещение, соответствующее линейной характеристике,
Л — действительное перемещение упругого элемента). Поэтому не-
линейность возрастающей характеристики положительна, а зату-
хающей — отрицательна.
Величина и знак нелинейности не отражают форму характери-
стики полностью. Так, например, показанные на фиг. 9, б и в харак-
теристики имеют одинаковую нелинейность, в то время как формы
а) 5) в)
Фиг. 9. Нелинейные характеристики.
их существенно различны, и одна из них может быть пригодной
для работы чувствительного элемента в приборе, а другая— непри-
годной. Поэтому величина нелинейности дает представление лишь
о том, насколько отклоняется действительная характеристика
от линейной, но не определяет ее форму. Для полного представле-
ния о форме характеристики она должна быть построена целиком.
Важным свойством упругого элемента является его жест-
кость, а также чувствительность — величина, обрат-
ная жесткости.
Если характеристика упругого элемента линейна, то жесткость
представляет собой отношение нагрузки р к соответствующему
перемещению X
(1.3)
а чувствительность — отношение перемещения к нагрузке
(1.4)
Жесткость показывает, какую нагрузку следует приложить
к упругому элементу, чтобы вызвать перемещение, равное единице;
45
чувствительность численно равна перемещению, совершаемому упру-
гим элементом под действием единичной нагрузки.
Размерность жесткости может быть выражена в следующих
единицах: кгс/мм, кгс/см^/мм, кгс.см /рад и пр. в зависимости от
того, нагружен ли элемент силой, давлением или моментом, и какое
перемещение упругого элемента измеряется: линейное или угловое.
Размерность чувствительности обратна размерности жесткости.
Понятия жесткости и чувствительности совершенно равно-
правны, и использование того или иного определяется только вопро-
сами удобства. Например, понятие «жесткость» чаще используется
по отношению к натяжным пружинам, которые должны при работе
обеспечивать определенную силу, а поня-
тие «чувствительность» обычно приме-
няется по отношению к упругим чувстви-
тельным элементам, которые должны
давать определенное перемещение под
действием рабочей нагрузки.
При нелинейной характеристике же-
сткость и чувствительность упругого
элемента меняются с нагрузкой и опреде-
* ляются следующим образом:
Фиг. 10. Жесткость и чув-
ствительность упругого эле-
мента с нелинейной харак-
теристикой. На
dp
нальна
Для всех упругих элементов
фиг. 10
tg а
величина жесткости или чувстви-
жесткость пропорцио-
а чувствительность — tg 6.
тельности представляет собой один из наиболее важных параме-
тров, определяющих рабочие качества упругого элемента. Обычно
желательно, чтобы измерительная пружина обладала возможно
большей чувствительностью; заводные пружины будут удовлетво-
рять предъявляемым к ним требованиям, если отдаваемое ими уси-
лие постоянно на рабочем ходе. Это означает, что идеальная завод-
ная пружина должна иметь нулевую жесткость. Жесткость натяж-
ной пружины должна быть достаточной для обеспечения требуе-
мой силы натяжения при данном перемещении упругого эле-
мента.
Высокая податливость весьма желательна для пружин, работаю-
щих в качестве кинематических элементов механизма при-
бора.
Если несколько упругих элементов постоянной жесткости соеди-
нены параллельно (фиг. 11, а) и начинают одновременно ра-
ботать, то их прогибы X будут равны между собой, а общая на-
грузка Р будет равна сумме усилий, воспринимаемых каждым из
упругих элементов
...+А+... + Рп =
46
Так как сила каждого элемента
КОСТИ кг на Прогиб к (Pi = кг • ,
равна произведению его жест-
то из выражения (а) получим
Следовательно, жесткость к
жесткостей элементов
всей системы будет равна сумме
п
к~ к
Учитывая, что чувствительность есть величина, обратная жест-
кости, получим
где б г — чувствительность г-того элемента
всей системы.
а б — чувствительность
Фиг. 11. Соединение упругих элементов:
6)
а — параллельное; б — последовательное; в — характеристика упругих элементов при
неодновременном включении их в работу.
Аналогично можно показать, что при последователь-
ном соединении упругих элементов (фиг. 11, 6} чувствительность
всей системы равна сумме чувствительностей элементов
п
В этом случае жесткость
г= 1
47
При неодновременном включении параллельно сое-
диненных упругих элементов характеристика получается ломаной,
и жесткость на каждом участке определяется суммой жесткостей
вступивших в работу упругих элементов. При увеличении числа
включаемых элементов характеристика получается затухающей
(фиг. 11, в).
Тяговые усилия и эффективная площадь
Деформируясь под действием рабочей нагрузки, упругий элемент
обычно встречает сопротивление со стороны механизма прибора
в виде, например, сил трения, противодействия различных пружин
механизма и пр. В этом случае правильность работы прибора будет
во многом определяться способностью упругого элемента преодоле-
вать это сопротивление. Такое свойство упругого элемента удобно
оценивать величиной перестановочного или тяго-
вого усилия, с которым упругий элемент будет воздейство-
вать на препятствие, ограничивающее его перемещение.
Величина перестановочной силы зависит от рабочей нагрузки,
размеров упругого элемента и расположения упора. С увеличе-
нием расстояния между упором и упругим элементом величина
перестановочной силы уменьшается. Если это расстояние так велико,
что при работе элемент не достает до упора, то перестановочная
сила будет равна нулю.
Величина перестановочной силы является важной характеристи-
кой упругого элемента. Ею определяется порог чувствительности
прибора, следовательно, возможность применения упругого чув-
ствительного элемента в конкретном приборе.
Особенно часто используется понятие перестановочных или тяго-
вых усилий по отношению к манометрическим упругим элементам,
для которых рабочей нагрузкой является давление.
В тех приборах, где манометрический упругий элемент служит
для преобразования давления в перемещение, он должен развивать
перестановочную силу, превышающую силу сопротивления меха-
низма прибора.
В других случаях манометрические упругие элементы исполь-
зуются для преобразования давления не в перемещение, а в пропор-
циональное давлению усилие. При таком использовании основной
рабочей характеристикой манометрического элемента, определяю-
щей качество прибора, будет зависимость между давлением и тяго-
вым усилием.
Способность манометрического элемента развивать перестано-
вочную силу удобно характеризовать удельной тяговой силой
~ , соответствующей единице давления. Так как удельная тяговая
сила имеет размерность площади, то принято представлять ее в виде
так называемой эффективной площади.
Поясним понятие эффективной площади на примере мембраны
(фиг. 12). Равнодействующая сил давления на мембрану равна
48
pFn, где Fn = л R2 — полная площадь мембраны рабочего радиуса
R. При свободном перемещении мембраны равнодействующая pFn
целиком уравновешивается силами реакции, возникающими в за-
делке. Если же перемещение центра мембраны ограничено упором, то
только часть равнодействующей сил давления будет восприниматься
закреплением по контуру, а остальная часть — упором. Площадь,
передающая силу давления на упор, является эффективной пло-
щадью мембраны.
Предположим, что мембрана ложится на упор при давлении р,
имея при этом прогиб w (фиг. 12). Для того чтобы определить вели-
чину ее эффективной площади при
этом прогибе, мысленно уберем упор
и увеличим давление на малую вели-
чину А р. При этом прогиб мембраны
увеличится на A w. Приложив с про-
тивоположной стороны сосредоточен-
ную в центре силу А <?, вернем центр
мембраны к прогибу ш. Тогда эффек-
тивная площадь при данном прогибе
упругого элемента может быть опре-
делена как отношение приращения
перестановочного усилия к соответ-
ствующему приращению давления
__ А<2
ф~ Ьр 9
Переходя к пределу, получим
, _ dQ
Величина эффективной площади
зависит от размеров манометриче-
ского упругого элемента и харак-
(1.5)
Фиг. 12. Определение эффек-
тивной площади мембраны.
тера его деформаций под нагрузкой.
Если упругий элемент имеет характеристику, линейную
п о давлению (сильфон, манометрическая трубчатая пру-
жина, мембрана с глубокой гофрировкой), то его эффективная
площадь практически остается постоянной на всем участке рабочего
хода (фиг. 13, а). В этом случае ее можно определять как отношение
конечного приращения силы к соответствующему приращению
давления при условии постоянства прогиба, причем величина при-
ращения силы может быть любой в пределах линейного участка
характеристики.
Обозначая к^ и к — жесткости
Q р
и по давлению, получим приращения
соответствующие изменению прогиба
упругого элемента по
силы и давления A Q и
на А ip в виде
силе
Ар,
Д <2 — kQ* hw и А р = к * A ip,
4 Заказ 24.
49
По выражению (1. 5) эффективную площадь можно представить
как отношение жесткости по силе к жесткости по давлению
(1. 5')
1 '
При неподвижном жестком упоре величина перестановочной
силы будет определяться произведением давления на эффективную
площадь
Q-=pFs<f>. (1.6)
Фиг. 13. Зависимость эффективной площади от прогиба
для упругих элементов с различными характеристиками.
Если жесткий упор установлен на расстоянии а от ненагружен-
ного упругого элемента, то при давлении р перестановочная сила
равна
<? = (р — Ро) Гч». (1.6')
где р0 — давление, при котором упругий элемент вступил в контакт
с упором
Ро а.
Если на пути манометрического элемента расположен упругий
упор, то перестановочная сила, равная в этом случае упругой силе
упора, определяется по выражению
Q — к,, (w — а),
где ку — жесткость упругого упора;
w — перемещение манометрического элемента;
а — расстояние от ненагруженного элемента до упора.
50
Перемещение w можно представить в виде
-wQ, (б)
Здесь Wp — перемещение манометрического элемента под дей-
ствием давления р при отсутствии упора
элемента в обратную сторону под действием силы Q. Обозначая
жесткости элемента к
wr. — перемещение
получим
^р = ±~ ;
IV
Ро
Решая совместно уравнения (а), (б) и (в) и учитывая соотношение
(1. 5'), получим величину перестановочной силы
/э — /« \ р ку „„
Если характеристика манометрического элемента нели-
нейна, то эффективная площадь его меняется с изменением про-
гиба. При этом, если характеристика затухает по давлению, то эф-
фективная площадь с увеличением прогиба уменьшается и, наобо-
рот, при возрастающей характеристике эффективная площадь
с ростом прогиба увеличивается (фиг. 13, б и в). Перестановочная
сила упругого элемента с переменной эффективной площадью опре-
деляется на основании уравнения (1. 5)
Ро
>0 — давление, при котором
р — полное давление.
произошла посадка на упор;
Фиг. 14. К определению изменения объема манометрического элемента.
Для того чтобы можно было воспользоваться формулой (г),
нужно предварительно найти зависимость между величиной эффек-
тивной площади и давлением. Этот вопрос обсуждается в § 29,
посвященном эффективной площади мембран.
Понятие эффективной площади удобно также при вычислении
изменения объема манометрических упругих элементов
под действием нагрузки. В качестве примера рассмотрим мембрану
и предположим, что ее характеристика линейна. Под действием
Давления р центр мембраны совершит перемещение под дей-
ствием силы Q — перемещение ivQ. Если сила Q = pF' то переме-
щение и?® ~ w — w. Обозначим объем между начальной и упругой
поверхностями мембраны во втором случае нагружения через
(фиг. 14).
4*
51
На основании принципа взаимности работ [34] работа давления
на соответствующих перемещениях, вызываемых силох! Q, т. е.
р • ДУ равна работе силы Q на перемещении вызванном давле-
нием: р • AFq “ <2 • №р. Отсюда изменение объема A мем-
браны, нагруженной сосредоточенной силой Q = р . Fs$, равно
произведению эффективной площади на перемещение центра
A V = — w ~ F • w.
Q р Р эф
(1.7)
Коэффициенты запаса и допускаемое напряжение
Поскольку возникновений-Заметных пластических деформаций
при работе упругого элемента совершенно недопустимо, вели-
чина напряжений должна оставаться меньше предела упру-
гости аУп.
Если упругий элемент работает при переменных напряжениях,
то величина допустимых напряжений выбирается с учетом усталост-
ных характеристик материала и требуемой долговечности упругого
элемента.
В некоторых случаях опасность представляет потеря устойчи-
вости, которая может произойти при напряжениях, меньших пре-
дела текучести и даже предела упругости. Очевидно рабочие напря-
жения не должны превосходить величины критического напряже-
ния окР, соответствующего наступлению потери устойчивости.
При работе упругого элемента в условиях повышенных темпера-
тур опасной может быть ползучесть материала. В этом случае вели-
чина наибольших допустимых напряжений должна определяться
в зависимости от свойств материала с учетом времени эксплуатации
упругого элемента.
В общем случае величина наибольшего напряжения Отах в упругом
элементе должна быть с некоторым запасом меньше предельного
напряжения опр, при котором упругий элемент достигает предель-
ного состояния, недопустимого для его нормальной работы. Предель-
ное состояние, в зависимости от условий работы, может наступить
в результате появления пластических деформаций, разрушения
от усталости, ползучести, в результате потери устойчивости
и т. п.
Для правильно спроектированного упругого элемента наиболь-
шее рабочее напряжение не должно превышать птах — —— , где п —
72
коэффициент запаса.
Необходимая величина коэффициента запаса обусловливается
многими соображениями: ответственностью и требуемой надеж-
ностью упругого элемента, условиями и длительностью его работы,
достоверностью данных о механических свойствах материала,
вероятной точностью расчета напряжений и т. д.
Величина коэффициента запаса зависит также от того, по какому
из предельных напряжений он определяется. Для большинства
52
упругих элементов желательна работа в пределах упругих дефор-
маций, и тогда коэффициент запаса следует выбирать по отношению
к пределу упругости п = - . Однако ввиду недостаточности све-
шах
дений о величинах предела упругости для многих материалов часто
приходится исходить из величины предела текучести <тт. Для того
чтобы гарантировать работу упругого элемента в пределах упругих
деформаций, коэффициент запаса по текучести пт = —— соответ-
1 ^тах
ственно увеличивают. Если же для данного материала известна
только величина предела прочности опч, то запас прочности ппч =
= °т следует выбрать еще большим.
^тах
Коэффициент запаса по пределу упругости сгУп может быть близ-
ким к единице, а по пределу текучести ат и пределу прочности апЧ —
больше в соответствии с соотношениями между о"Уп, от и для дан-
ного материала.
Коэффициент запаса по устойчивости, равный отношению крити-
ческого напряжения акр к наибольшему рабочему, пУст, = - °кр
^тах
обычно принимается достаточно большим. Это объясняется тем,
что незначительные отклонения от идеальной формы упругого
элемента (начальная кривизна оси сжатого стержня или винтовой
пружины, вмятина на тонкостенной оболочке и пр.), неточное при-
ложение нагрузки, неоднородность материала и другие случайные
причины могут резко (иногда в несколько раз) снизить величину
критического напряжения о,кр, при котором происходит потеря
устойчивости. Все эти случайные отклонения трудно учесть расчетом,
поэтому приходится выбирать достаточно большой коэффициент
запаса по устойчивости.
Если упругий элемент работает при переменных напряжениях,
то он должен иметь необходимый коэффициент запаса по выносли-
в ости пЁЫН = ---, где о> — предел выносливости при данном цикле
о'шах
изменения напряжений.
Итак, для одного и того же упругого элемента коэффициенты
запаса по различным предельным состояниям будут иметь разные
значения. Величина каждого коэффициента запаса определяет
наибольшее напряжение, допускаемое для данного предельного
состояния. Наименьшее из этих напряжений и будет допускаемым
напряжением [ст] для упругого элемента. При работе упругого эле-
мента ни в одной из его точек напряжения не должны превышать
величины допускаемого напряжения: сгтах "С 1<т].
Следовательно, выбор коэффициентов запаса определяет и вели-
чину допускаемого напряжения.
Следует отметить, что выбор величины допускаемого напряжения
по рекомендациям, приводимым в справочной литературе, не дает
обычно представления о действительных коэффициентах запаса,
53
так как не учитывает все многообразие условий работы данного
упругого элемента.
При проектировании упругого элемента часто выбирают вели-
чину допускаемого напряжения, исходя из соображений прочности,
т. е. [о]
-- или [ст] ~ .
Тогда расчеты на устойчивость,
усталость, ползучесть и пр. должны проводиться как поверочные.
В некоторых случаях отсутствуют необходимые методы расчета
упругого элемента (например, расчеты на усталость и на долговеч-
ность манометрических элементов, на устойчивость гофрированных
мембран, на прочность манометрических трубчатых пружин некото-
рых профилей и т. д.), кроме того, иногда неизвестны некоторые
механические характеристики материала (например, предел упру-
гости, предел выносливости, кривые ползучести и др.). Тогда вели-
чина предельной нагрузки, при которой происходит потеря рабочих
свойств упругого элемента, находится экспериментальным путем.
Погрешности чувствительного упругого элемента
Чувствительный упругий элемент, как и всякий другой, должен
иметь достаточную прочность и требуемую жесткость. Однако основ-
ным критерием его качества является та точность, с которой произ-
водится преобразование измеряемого параметра в перемещение
или усилие.
Одним из источников погрешностей упругого элемента является
несовершенство его упругих свойств (стр. 15).
В результате пластического течения материала упругие элементы
могут со временем изменить свои свойства. Для уменьшения этой
погрешности, как уже указывалось, все чувствительные упругие
элементы проходят операцию стабилизации. Если путем стабилиза-
ции можно уменьшить непостоянство упругих свойств во времени,
то снизить величины гистерезиса и упругого последействия значи-
тельно сложнее.
Гистерезис упругого элемента проявляется в несовпадении
величин перемещений при прямом и обратном ходе упругого эле-
мента (фиг. 15, а).
Величина гистерезиса определяется как наибольшая разность Г
между перемещениями при одинаковой нагрузке при прямом и
обратном ходе, отнесенная к наибольшему перемещению Лщах упру-
гого элемента. Обычно гистерезис выражается в процентах
у = 100%.
Лтах
Разность между перемещениями при прямом и обратном ходе
зависит также от величины упругого последействия, которое про-
является в запаздывании перемещений упругого элемента по отно-
шению к приложенной нагрузке. Так, например, в результате упру-
54
гого последействия стрелка прибора после сброса нагрузки не сразу
возвращается на нуль.
Упругое последействие, складываясь с «чистым» гистерезисом,
дает увеличение петли гистерезиса (фиг. 15, б).
Так как обычно имеет место одновременное проявление «чистого»
гистерезиса и упругого последействия, то в практике, как правило,
их не разделяют, и результат их совместного действия называют
«практическим гистерезисом» или просто гистерезисом.
Гистерезис зависит от величины действующих напряжений.
С уменьшением напряжений гистерезис уменьшается, поэтому
в ряде случаев величина допускаемого напряжения устанавливается
а)
Фиг. 15. Гистерезис
а — «чистый»; б -
б)
упругого элемента:
«практический».
не коэффициентом запаса по разрушению или текучести, а исходя
из допустимой величины гистерезиса. Так например, из этих сооб-
ражений для пружин весоизмерительных приборов рекомендуется
величина допускаемого напряжения в одну десятую от предела
текучести Ч
При конструировании упругих элементов следует по возможности
избегать резких изменений в форме упругого элемента, чтобы пред-
отвратить появление концентрации напряжений, увеличивающей
гистерезис. Технологические операции, которые связаны с измене-
нием свойств материала (например, термообработка), должны
проводиться с тщательным соблюдением оптимальных режимов.
Чрезмерный и длительный нагрев упругого элемента при пайке
или сварке может привести к местному ухудшению механических
свойств материала и, как следствие, к увеличению гистерезиса.
На величину гистерезиса существенное влияние оказывают свойства
самого шва: сварные упругие элементы имеют меньший гистерезис,
чем паяные.
1 Феликсов Е. И., Исследование несовершенств силоизмерительных
пружин, Сб. «Весоизмерительные приборы и испытательные 'машины», № 1,
Машгиз, 1959.
55
В условиях переменной температуры изменение модуля упру-
гости материала и линейных размеров упругого элемента приводят
к температурным погрешностям элемента.
Зависимость модуля упругости от температуры выражается
формулой (1. 2):
Et = (а)
Относительная температурная погрешность гц упругого элемента
равна
(б)
Л
где АЛ/ — температурное изменение перемещения упругого эле-
мента .
Перемещение упругого элемента постоянной жесткости, равное
1 Р
л. = , можно представить, как
поскольку жесткость к упругого элемента прямо пропорциональна
модулю упругости Е материала (с — коэффициент пропорциональ-
ности) .
Приращение прогиба упругого элемента при изменении темпе-
ратуры на t равно
ДМ =
dk
dt
Дифференцируя выражение (в) по температуре
симости (а), получим
d к р Ye
dt с Е
t с учетом зави-
(д)
Подстановка выражений (г) и (д) в формулу (б) дает относитель-
ную температурную погрешность упругого элемента постоянной
жесткости в виде
= (1-8)
Температурная погрешность, связанная с изменением модуля
упругости, будет наименьшей у упругих элементов, выполненных
из материалов с малым температурным коэффициентом уЕ модуля
упругости (элинвар, см. табл. 1, сплав Н41ХТ, см. табл. 6).
Температурная погрешность может возникнуть также в результате изме-
нения линейных размеров при нагреве упругого элемента. Если обозначить
через I размер упругого элемента в направлении рабочего перемещения, то из-
менение температуры вызовет дополнительное перемещение, равное a 11, где
56
a — коэффициент линейного расширения. Следует отметить, что обычно на вели-
чину температурной погрешности изменение линейных размеров упругого эле-
мента оказывает значительно меньшее влияние, чем изменение модуля упругости.
На величину температурной погрешности может оказать некоторое влия-
ние и изменение при нагреве или охлаждении тех размеров упругого элемента,
от которых зависит его жесткость, например, диаметра винтовой цилиндриче-
ской пружины, рабочей длины плоской пружины, диаметра мембраны и т. д.
Изменение линейных размеров упругого элемента при нагреве может также
привести к возникновению температурных усилий, влияющих на перемещение
упругого элемента. Например, бронзовая мембрана, зажатая в стальном корпусе,
будет при нагреве сжиматься в радиальном направлении, что может существенно
снизить ее жесткость по давлению. Для уменьшения этой температурной погреш-
ности следует подбирать материалы упругого элемента и корпуса с одинако-
выми коэффициентами линейного расширения.
Уменьшение температурной погрешности может быть достигнуто с по-
мощью различных компенсаторов, которые, однако, усложняют конструкцию
прибора.
ГЛАВА II
ПЛОСКИЕ ПРУЖИНЫ
§ 4. КОНСТРУКЦИЯ И ПРИМЕНЕНИЕ ПЛОСКИХ ПРУЖИН
В приборостроении широко применяются прямые, кривые, спи-
ральные пружины различных форм и размеров. Они называются
плоскими, если оси этих пружин представляют собой плоские
кривые.
Плоской пружине при изготовлении почти всегда может быть
придана такая форма, которая в каждом конкретном случае наи-
более удобна для размещения пружины в корпусе прибора. При
этом пружина обычно занимает небольшое место. Плоская пружина
может иметь весьма малые размеры в направлении перемещения.
В этом отношении она более удобна, чем винтовая, однако, как
правило, максимально допустимые перемещения плоской пружины
значительно меньше, чем у винтовой.
Плоские пружины могут быть очень жесткими или очень подат-
ливыми в зависимости от формы и размеров. Особенностью ленточ-
ной плоской пружины является то, что она податлива на изгиб
только в одном направлении — в плоскости минимальной жестко-
сти — и имеет большую жесткость на растяжение и па изгиб в дру-
гом направлении. Поэтому плоские пружины успешно используются
в качестве измерительных, направляющих, упругих подвесов под-
вижных частей прибора и пр.
Плоскую пружину можно изготовить из любого пружинного
материала (см. табл. 1—7). Выбор материала определяется только
назначением и условиями работы пружины.
Плоские пружины могут изготовляться из круглой проволоки,
но чаще они штампуются из пружинной ленты. Простота изгото-
вления плоских пружин является их существенным достоинством.
Крепление концов плоских пружин осуществляется пайкой,
сваркой или защемлением между прокладками. Первые два способа
более просты в отношении конструкции и технологии и создают
падежный электроконтакт, но не всегда применимы, так как при
нагреве в процессе пайки или сварки упругие свойства материала
пружины могут ухудшиться, а само крепление является нераз-
борным.
58
Широко применяются плоские пружины в различных э л е к-
троконтактных устройствах. Наиболее распространена
здесь одна из самых простых конструктивных форм плоской пру-
жины в виде прямого консольно закрепленного стержня. В качестве
примера на фиг. 16, а изображена контактная группа одного из элек-
тромагнитных реле. Контактные пластинки должны иметь малое
электросопротивление, поэтому они изготовляются из фосфористой,
кремнемарганцовистой, алюминиевой, бериллиевой бронз, латуней,
нейзельбера и значительно реже из пружинных сталей. Благодаря
плоской форме пружин можно собрать пакет контактных групп
в небольших габаритах.
Фиг. 16. Контактные пружины:
а контактная группа электромагнитного реле; б — перекидной контакт;
в — скользящие контактные пружины.
С помощью плоской пружины просто может быть выполнен пере-
кидной контакт, обеспечивающий быстрое включение и выключение.
Как контактная, так и перекидная пружины могут штамповаться
из одного куска ленты (фиг. 16, б). Перекидная пружина устана-
вливается с начальным натяжением, поэтому среднее положение
контактной пластины неустойчиво, и при ее переходе из одного
крайнего положения в другое контакты быстро замыкаются или раз-
мыкаются.
Плоские пружины применяются в электроконтактных устрой-
ствах также в качестве скользящих контактов (фиг. 16, в). Необхо-
димая сила контактного давления обеспечивается упругостью пру-
жины. Большая жесткость контактной пружины в направлении
перемещения определяет достаточно точное положение контактов.
В целях хорошего прилегания при перекосах такие скользящие
59
контакты часто выполняются в виде набора пружин, или концевой
участок одной пружины разрезается на несколько узких полосок.
Плоские пружины получили большое и разнообразное приме-
нение в роли кинематических элементов приборов;
упругих опор и направляющих, гибких связей и деталей переда-
У
4
Фиг. 17.
Упругие
опоры.
сплошного
точно-множительных механизмов.
Упругие опоры и н а п р а в л яющие, изготовлен-
ные из плоских пружин, практически не имеют трения и люфтов,
не нуждаются в регулярном уходе, смазке, не боятся загрязнений
и обладают большей надежностью, чем, например, призматические
опоры. Недостаток упругих опор и направляющих заключается
в ограниченности величин линейных
и угловых перемещений.
В качестве опор для вращательного
движения иногда применяют наиболее
простую конструкцию в виде пло-
ской пружины, одним концом закре-
пленной на неподвижной части при-
бора, а другим — на подвижной. На-
пример, на такой опоре подвешивается
маятник часов \ подвижные элементы
весоизмерительных приборов [35].
Эти опоры выполняются из стальной
пружинной ленты, к которой присо-
единяются накладки для крепления
(фиг. 17, а), или фрезеруются из
ластипки с утолщениями по концам
(фиг. 17, б). Последним способом можно при желании получить
опору с двумя степенями свободы (фиг. 17, в).
При проектировании механизма с упругой опорой необходимо
знать положение центра вращения подвижного элемента, подвешен-
ного на этой опоре.
Для опоры в виде плоской пружины (фиг. 18, а) расстояние
от конца пружины до центра вращения при малых перемещениях
опоры можно приближенно определить, как
__ V V
(2.1)
где v и й — прогиб и угол поворота конца пружины.
Применение линейной теории изгиба плоских пружин (см. § 5)
позволяет просто определить положение центра вращения при раз-
личных схемах нагружения упругой опоры [35]. Так, например,
при чистом изгибе пружины (фиг. 18, б) где / — длина
рабочей части пружины. При поперечном изгибе пружины (фиг. 18, в)
1 Аксельрод 3. М., Часовые механизмы, ГНТИ, 1947.
60
2 гь
гг, в.= -5- k при совместном действии поперечной силы Р и момента М
0
м
I 2+3 ш
(фиг.. 18, е) в. = ----— •
О J W
1+2 Р1
Если опора работает на изгиб и сжатие (фиг. 18, д) или на изгиб
ch a Z — 1
ИЛИ ‘ = ~ а sh а f
где S — продольная
сила, а В — жесткость пружины на изгиб (см. § 5).
и растяжение (фиг. 18, е), то z4.e
соответственно. В этих
1 — cos а I
а sin а I
а)
а}
Фиг. 18. Центр вращения упругой опоры.
Точность работы механизмов приборов обычно связана с постоян-
ством положения центра вращения подвижных частей. Выражение
(2. 1) определяет положение центра вращения только в начале
нагружения опоры. С увеличением нагрузки положение центра
вращения меняется, и его зависимость от характера и величины
нагрузки может быть найдена точно из решения задачи с учетом
больших перемещений (см. § 6).
Значительное изменение положения центра вращения при изме-
нении нагрузки является недостатком плоской упругой опоры.
Этот недостаток меньше проявляется в крестообразной конструк-
ции упругой опоры (фиг. 19, а). Такие опоры нашли применение
61
в весоизмерительных приборах, в контрольно-измерительных при-
борах и автоматах для измерения линейных и угловых размеров
деталей 1, теплоэнергетических 2, сейсмометрических 3 приборах и
и пр. Крестообразные опоры собирают из 3—4 пластин, что обеспе-
чивает высокую жесткость опоры в поперечном направлении.
Радиальная упругая опора (фиг. 19, б) более сложна конструк-
тивно, но имеет практически постоянный центр вращения подвиж-
ной части опоры и воспринимает радиальные усилия в любом напра-
влении. Ее недостаток заключается в том, что она работает при
весьма ограниченных углах поворота и имеет жесткость, возрастаю-
щую при увеличении поворота.
Фиг. 19. Упругие опоры:
а — крестообразные; б — радиальная.
Ленточные пружины применяются также, как направляю-
щие деталей прибора. Упругие направляющие имеют разнообраз-
ные конструкции, определяемые особенностями каждого конкрет-
ного механизма прибора. Некоторые типы упругих направляющих
даны на фиг. 20. Строго поступательное движение обеспечивает
конструкция из двух одинаковых, параллельных друг другу пло-
ских пружин (фиг. 20, й). Однако, помимо рабочего перемещения
в продольном направлении, деталь будет получать небольшие пере-
мещения в поперечном направлении. Этот недостаток не свойственен
упругой направляющей, изображенной на фиг. 20, г. Перемещение
по некоторой криволинейной траектории дает упругая направляю-
щая, указанная на фиг. 20, б. Направляющая в виде криволиней-
1 ВалединскийА. С., Пружинные шарниры и механизмы в измери-
тельных приборах, Сб. «Расчеты деталей и механизмов точных приборов»,
Машгиз, 1950.
2ЗаседателевС. М,, РухадзеВ. А., Дифманометры — датчики
с пневматической силовой компенсацией, «Системы, устройства и элементы
пневмо- и гидро автоматики», Изд. АН СССР, 1959.
3 Ио р ишЮ, И., Измерение вибраций, Машгиз, 1956.
62
ной пружины (фиг. 20, в) обеспечивает осевое перемещение стержня,
допуская в то же время некоторый его перекос. Для направления
движения катушек, якорей и других подвижных деталей электро-
механических приборов применяются упругие направляющие в виде
прорезных шайб (фиг. 20, д').
г)
Фиг. 20. Упругие направляющие.
же время они оказывают
Фиг. 21. Ленточные подвесы:
а ~ подвес рамки электроизме-
рительного прибора; б — подвес
зеркала гальванометра осцилло-
графа.
Очень тонкие ленточные пружины используются также в качестве
подвесов высокочувствительных элементов измерительных
приборов (фиг. 21). Эти подвесы обеспечивают жесткость подвиж-
ной системы в осевом направлении и в
малое сопротивление вращению под-
вижной системы при почти полном
отсутствии трения.'
Передача движения с помощью
гибкой связи, основным эле-
ментом которой является плоская
ленточная пружина (фиг. 22), имеет
преимущества по сравнению с другими
типами передач, например, зубчатой
или шарнирно-рычажной. Эти пре-
имущества заключаются в значительно
меньшем трении, отсутствии люфтов
и в плавности работы. На фиг. 22, а
показана ленточная связь между двумя
рычагами. Такая конструкция обеспе-
чивает хорошую передачу движения
при малых углах качания рычагов.
Гибкие связи могут быть использо-
ваны для передачи вращательного
движения, заменяя зубчатую передачу,
когда угол поворота меньшего колеса
не превышает 270—300° (фиг. 22, б), а
вращательного движения в поступательное, заменяя передачу «зуб-
чатая рейка — трибка» (фиг. 22, в).
С помощью плоских пружин можно осуществить простые и
надежные передаточно -множительные меха-
также для преобразования
63
ном ы. На фиг. 23, а показан пружинный передаточный меха-
низм, применяемый в миниметрах. При поступательном перемеще-
нии измерительного стержня верхний конец пружины 7, скрепленный
перемычкой 3 с пружиной 2, вследствие изгиба пружин поворачи-
вается и перемещается в поперечном направлении. При этом конец
стрелки 4, жестко соединенной с перемычкой 5, получает переме-
щение, во много раз превышающее измеряемое перемещение X.
d_______________ Изменением расстояния между пру-
~Н[ ~ ' жинами можно регулировать чув-
ствительность механизма.
Фиг. 22. Гибкие связи в механиз-
мах.
Фиг. 23. Пружинные передаточно-мно-
жительные механизмы.
Увеличение перемещений может быть получено при боковом
выпучивании сжатой плоской пружины (фиг. 23, б). Небольшие
перемещения в продольном направлении преобразуются в боковые
перемещения со значительным увеличением. Такая схема переда-
точного механизма применяется в различных электроконтактных
устройствах.
Плоские пружины выполняют функции измерения в вибро-
графах, акселографах, тахометрах, манометрах, тягомерах и в дру-
гих приборах. При этом плоские пружины обычно используются,
когда требуются сравнительно небольшие перемещения. При значи-
тельных перемещениях характеристика плоской пружины может
иметь большую нелинейность; в этом случае предпочитают приме-
нять винтовые пружины.
В некоторых приборах, например в тягомерах1, плоская пру-
жина используется как элемент выпрямления шкалы прибора.
Необходимая для этого характеристика пружины достигается по-
садкой пружины на ряд неподвижных упоров (фиг. 24, а) или на
лекало определенного профиля [36]; при этом изменяется рабочая
длина пружины, следовательно, и ее жесткость.
Плоские пружины применяются также как элементы настройки
нуля шкалы прибора; в этом случае натяжение пружины обычно
регулируется винтом (фиг. 24, б).
Фиг. 24. Плоские измерительные
пружины:
а)
а — пружина с нелинейной характери-
стикой; б — пружина настройки нуля;
в — волосок.
Значительные угловые перемещения допускает измерительная
пружина спиральной формы — волосок (фиг. 24, в).
Волоски широко применяются во многих показывающих элек-
троизмерительных приборах. Иногда эта же пружина служит для
подвода тока, и в этом случае она выполняется из материала с малым
электросопротивлением.
Волоски используются в большинстве спусковых регуляторов
часовых механизмов в качестве упругого элемента колебательной
системы. Для правильной работы часового механизма важно, чтобы
центр тяжести пружины при ее деформации не перемещался. Для
этого концу волоска придается специальная форма (по так называе-
мым кривым Филлипса)2.
Допустимая величина угла закручивания ограничивается не
только прочностью волоска, но и потерей устойчивости плоской
1 Преображен ск ий В. П., Теплотехнические измерения и приборы,
Госэнергоиздат, 1953.
2 Аксельрод. 3. М., Часовые механизмы, ГНТИ, 1947»
5 Заказ 24
65
формы изгиба при достаточно больших углах закручивания («спуты-
вание» волоска) 1.
Во многих приборах волоски используются и как натяжные
пружины, предназначенные для выбора люфтов передаточного
механизма прибора.
Спиральную форму имеют также заводные пружины,
которые выполняют роль двигателя механизма приборов. Вопросы,
связанные с конструкцией и расчетом этой обширной группы пру-
жин, излагаются в § 7.
Фиг. 25. Плоские натяжные пружины:
а — пружина храпового механизма; б — пружина фик-
сатора; в — пружина шаровой опоры; г — кольцевая
пружинная шайба.
Плоские пружины применяются также как н а т я ж н ы е.
В качестве примеров натяжных пружин на фиг. 25 показаны пру-
жина храпового механизма (фиг. 25, а), пружина фиксатора
(фиг. 25, б), пружина регулируемой шаровой опоры (фиг. 25, в) и
кольцевая пружинная шайба (фиг. 25, г).
Если перемещения пружины малы по сравнению с ее размерами,
то при расчете можно воспользоваться обычной линейной теорией
изгиба стержней, известной по курсу «Сопротивление материалов»
Обычно такой расчет не представляет большого труда. Если же
пружина работает в области больших перемещений, то ее расчет
является значительно более сложным и может быть произведен
с помощью нелинейной теории изгиба гибких стержней, разрабо-
танной Е. П. Поповым [6].
х Дятлов А. В., Устойчивость спиральных пружин,
Машиностроение», Изд. «Советская наука», 1962, №2.
66
«Известия вузов.
связывающей
моментом М\
§ 5. РАСЧЕТ ПЛОСКИХ ПРУЖИН В ОБЛАСТИ МАЛЫХ ПЕРЕМЕЩЕНИЙ
Теория изгиба стержней основана на зависимости,
изменение кривизны Ди оси стержня с изгибающим
М
относительно
где B = EJX — жесткость стержня на изгиб;
Е — модуль упругости материала ь,
Jx — момент инерции поперечного сечения
нейтральной оси х.
Выражение (2. 2) справедливо как при малых, так и при боль-
ших перемещениях в пределах упругих деформаций.
Наибольшее напряжение
определяется по формуле
________________А/щах
Oniax
где Л/щах — наибольший изгибаю-
щий момент;
Wx— момент сопротивления
сечения.
Для прямоугольного сечения
Wx = -к- (Ь — ширина,
сечения); для круглого
Л dA ТТ7 nd3 , 1
= -6F’ (d -
Ра
11
м
Фиг. 26. Определение прогиба
конца плоской пружины.
Т __ bh*
Jx 12 ’ а
h — высота
сечения Jx
диаметр).
Для определения прогибов стер-
жня в области малых перемещений
удобно пользоваться интегралом
Мора, если ось стержня криволинейна, и правилом Верещагина
для прямолинейных стержней [34].
Пример 1. Определить перемещение конца А плоской пружины при нагру-
жении ее силой Р (фиг. 26, а), если размеры и материал пружины заданы.
Решение. Для определения перемещения точки А воспользуемся пра-
вилом Верещагина. Для этого построим эпюру изгибающего момента Мр от
заданных сил (фиг. 26, б) и изгибающего момента Мг от единичной силы, при-
ложенной в точке А в направлении искомого перемещения (фиг. 26, в, г).
Прогиб точки А определим, перемножая эпюры Мр и Mt по правилу Вереща-
гина :
где Qp — площадь эпюры
М1с — ордината на эпюре М±, расположенная под центром тяжести С пло-
щади эпюры Мр.
__ _ ___ ¥
1 Если поперечное сечение стержня сильно вытянуто вдоль оси ж, то вместо
модуля упругости Е следует пользоваться величиной
Пуассона) [37].
(|i — коэффициент
Перемножение производится отдельно по участкам. В данном случае =
1 сс
^(Ра) -а, М1С = I----— , следовательно, прогиб в точке А будет
Если в этом выражении принять I = а, то прогиб будет
PZ3
Этот случай соответствует нагружению пружины силой на конце,
как это часто бывает. По такой схеме нагружена, например, пружина
фиксатора (см. фиг. 25, б) и одна из электроконтактных пружин (см.
фиг. 16, а).
Фиг; 27. Определение угла поворота конца криволинейной плоской
пружины.
Пример 2. Определить угол поворота конца криволинейной плоской
пружцны, закрепленной и нагруженной так, как показано на фиг. 27, а.
Решение. На конце пружины для определения угла поворота прикла-
дываем ' единичный момент (фиг. 27,6). Определим изгибающие моменты Мр
и Afj в произвольном сечении пружины.
Участок I: Мр — Рх; Мх =1 (0 < х < а);
участок II: Мр — Р (а + R sin ср); =1 10 < (р <
Угол поворота найдем с помощью интеграла Мора
(2. 4)
гце ds — длина элемента пружины; ds = dx на участке I и ds = Rd ср на уча-
стке II.
Подставляя значения моментов Мр и и интегрируя в пределах каждого
участка, получим величину угла поворота О ,
68
Если помимо поперечных сил, стержень нагружен продольными
силами, то его прогибы увеличиваются при сжатии и уменьшаются
при растяжении (фиг. 28).
Фиг. 28. Влияние осевой силы на прогиб
стержня.
Прогиб vn—n при продольно-поперечном изгибе можно
лить по приближенной формуле Тимошенко [34]:
опреде-
эил
где vn — прогиб под действием одних поперечных сил, S — про-
дольная сила [если 5 — сила растяжения, то в формуле берется
знак плюс (+), при сжатии — знак минус (—)]. Эйлерова сила $эйл
определяется по формуле
_ nzEJ
эйл ~ (v Z)2 ‘
(2.6;
Здесь v — коэффициент, зависящий от способа крепления концов
пружины. Его значения даны
Для того чтобы получить более
точные значения перемещений при
продольно-поперечном изгибе сле-
дует прибегать к интегрированию
дифференциального уравнения
изогнутой оси стержня, которое
может быть получено из выраже-
ния (2. 2), если принять Ах —
1
что имеет место при
Таблица 9
Значения коэффициента v
Схема закрепления
Коэффи-
циент v
О
малых перемещениях. (Здесь —
кривизна нагруженного, перво-
начального прямого стержня, i
стержня.)
Тогда из выражения (2. 2) следует, что
— прогиб произвольной точки
By" = М.
(2.7)
69
Пример 3. Определить начальный центр вращения плоской упругой опоры,
нагруженной и закрепленной по схеме, приведенной па фиг. 29.
Решение. Рассмотрим положение стержня после деформации и про-
ведем оси yOz, совместив начало координат О с подвижным концом стержня.
Изгибающий момент в произвольном сечении стержня будет равен
M=-(MQ±Sy),
(а)
(Знак момента определяется по знаку кривизны упругой линии стержня; в дан-
ном случае кривизна стержня отрицательна).
Фиг. 29. Определение центра вращения упру-
гой опоры.
Подставляем выражение момента (а) в дифференциальное уравнение (2. 7)
упругой линии стержня:
By'r——(MQ-\-Sy), (б)
обозначив
напишем уравнение (б) в виде
т/"-]-а2 у —
Общий интеграл этого уравнения будет
у = a sin a z -j-6 cos а z
s •
Постоянные интегрирования а и Ь найдем из граничных условий. В данном
случае при z = 0 величина у = 0 и при z — I угол поворота й1 = у' =0. Это
дает следующие значения постоянных:
а=—^-tgaZ и = ,
О о
и уравнение (г) упругой линии будет
Л/л /. 7 . \
у = —(tg a I • sin az-pcosaz— 1),
JL>
Начальное положение центра вращения определяется по выражению (2. 1)
z =.
М- в tg ’
где vo и б'о — прогиб и угол поворота конца О пружины.
70
В данном случае
Мо . Л/о 1 — cos al
$o = yz==j=—z~(tga l -sma Z-rCOs al~ 1)=—-----------—
1 1 S S coscU
/ Mtt a . Mn
tg ^0 = yz=0 = —Gg a J cos a з— sin a z) 0 — —— alga/.
О о
Следовательно начальное положение центра вращения
1 — cos a I
a • sin a I
Пример 4. Определить контактное усилие микро контакта (фиг. 30, а).
Размеры плоской контактной пружины 1 и U-образной перебрасывающей пру-
жины 2 заданы: для пружины 1 длина I — 10 мм, сечение Ьг X hx = 2 X
X 0,08 jut2; для пружины 2 радиус г — 1,0 мм, Ь% X /г 2 — 4,0 X 0,12 мм2,
в)
Фиг. 30. Определение контактного усилия микро контакта.
Перебрасывающая пружина 2 имеет начальное поджатие Л = 0,5 мм. Полный
ход контакта w = 0,4 мм. Материал пружин — оловянно-фосфористая бронза
Вр.ОФ4-0,25 (табл. 1), модуль упругости Е = 1 • Ю4 кгс/мм2.
71
Решение. Определим усилие начального натяжения перебрасывающей
пружины 2. Для этого можно рассмотреть половину U-образной пружины
(фиг. 30, б) и с помощью интеграла Мара (2. 4) найти соотношение между силой
Р и прогибом — половины пружины.
Изгибающие моменты Мр и Мг на каждом участке равны:
I участок:
I участок:
Мр = Р(2г + г • sin <р);
Тогда по формуле (2. 4)
2т
2
(24-sin <р)а d <р =
о
О
20 .
ргз
9л \
рг3
2
откуда
2
Найдем изгибную жесткость В % пружины 2
О 77 ^2^23 Л ЛЛ4 4 • 0,123 г _р 9
В2—Е —~— — 1 • 104 —— =0,76 кгс, мм2.
Следовательно сила Р по выражению (а) Р —
0,5 • 5,76
27,5
= 0,105 кгс.
Сила Р направлена по линии А В (фиг. 30, в). Разложим ее по вертикаль-
ному и горизонтальному направлениям. Поскольку точка А пружинырасполо-
жена близко к контакту, примем ее перемещение равным w. Тогда угол а можно
приближенно определить как а
w _ 0,2
2 • 2г 2
Составляющие силы Р равны:
Ру = Р sin a ss Р а ss 0,105 -0,1 = 0,0105 кгс.
Рх — Р cos а Р = 0,105 кгс.
Конец контактной пружины 1 нагружен продольной силой Рх и поперечной
силой Рп, равной разности между составляющей Ру и реакцией упора, которая
и является искомым контактным давлением Рк:
Рп — Ру--Рк- (б)
Определим силу Рп, необходимую для сообщения концу пружины прогиба
~2~ . Поскольку пружина находится в условиях продольно-по перечне го изгиба,
то воспользуемся для этого формулой Тимошенко (2. 5)
72
В рассматриваемом примере прогиб под действием продольной силы S ~ Р
и поперечной Рп равен vn_n=-^~ = 0,2 мм. Прогиб под действием одной по-
перечной силы Рп определяется по формуле (2. 3)
Здесь изгибная жесткость Вг равна
В^Е
Ъ h3
1 1
12
2 • О 083
= 1 • 104 —= 0,853 кгс - дьм2.
Величину Эйлеровой силы находим по выражению (2. 6)
= л2 Вг = л2 -0,853
эйл— 02 — 102
= 0,021 кгс,
где коэффициент v находим по табл. 9, откуда v = 2.
Подставляя числовые значения в формулу (в), находим величину силы Рп
0,105
0.021
Следовательно, искомая контактная сила в соответствии с выражением
(б) Рк == Ру — Рп = 10,5 — 3,1 = 7,4 г.
Во многих случаях пружина бывает закреплена так, что для
определения ее характеристики необходимо сначала раскрыть стати-
ческую неопределимость.
Пример 5. Определить начальную жесткость кольцевой пружины, нагру-
женной силами Р (фиг. 31, а).
Решение. Для раскрытия статической неопределимости этой рамы
разрежем ее по сечению А. Взамен отброшенных связей приложим внутренние
силовые факторы: изгибающий момент и нормальную силу, равную — . По-
перечная сила из условия симметрии кольца равна нулю (фиг. 31, б).
Изгибающий момент Хг определим из условия равенства нулю взаимного
угла поворота сечений Л, которое удобно записать в форме канонического-урав-
нения [34]:
^1бц + б1Р = 0, (а)
где б
— взаимный угол поворота сечений А под действием заданных сил;
— угол поворота под действием моментов
— угол поворота сечений А под действием единичных моментов
Коэффициенты б
можно
найти с помощью интеграла Мора (2. 4)
MpM^ds
Г Mds
(б)
73
Для этого найдем значения изгибающих моментов М
следует, что
р и Из фиг. 31, в, г
он увеличивает
крс-
Л/р =~2~ (1 — coscp); 1; /о < <р
(Изгибающий момент считается положительным, если
визну, и отрицательный!, если уменьшает ее.)
г)
Фиг. 31. Определение жесткости кольцевой пружины.
Поскольку рама имеет четыре одинаковых участка
жеьии (о) можно проводить в пределах */4 рамы:
то интегрирование выра-
(1 —cos ф)
(—1) 7?(?ф = —
2РК-
В
о
Из уравнения (а) находим момент
0,182 PR.
Суммарный изгибающий момент М в произвольном сечении
М = Л/р Н- • Л/! = 0,5 PR (1 - cos ф) — 0,182 PR =
= PR (0,318 —0,5 cos ф).
(в)
В соответствии с этим выражением построена эпюра изгибающего момента М
(фиг. 31, д).
Чтобы определить жесткость пружины, равную к , найдем взаимное
Л
перемещение X точек В. Для этого приложим к раме единичные силы (фиг. 31, е).
Поскольку в этом случае условия нагружения рамы отличаются от заданных
только величиной сил, то изгибающий момент М\' в произвольном сечении рамы
определяется выражением (в), где Р = 1
М' = 1 • R (0,318 — 0,5 cos ф).
Тогда в соответствии с выражением (2. 4) перемещение X равно
0,148 PH3
В
(0,318—0,5 cos ф)2 г/(р
Следовательно начальная жесткость к ~
R3 ‘
р
Пример 6* Определить начальные значения жесткости к =—и передаточ-
ного отношения i =—
пружинного множительного механизма, схема которого
дана на фиг. 32, а.
Решение. Выберем расчетную схему пружинного механизма в виде
рамы, закрепленной, как показано на фиг. 32, б. Поскольку рама обратно сим-
метрична, то горизонтальные реакцииХг = 0, а момент Xj находится непосред-
ственно из условия равновесия Хг=
Таким образом, статическая неопре-
делимость раскрыта.
Для определения начальной жесткости к —
найдем перемещение X. Для
этого в точке А приложим силу, равную единице, и построим эпюру изгибающего
момента Мг, которая будет иметь такой же вид, как и эпюра Мр от действия
силы Р. Перемножим эпюры по правилу Верещагина
, 2 / Pal а \ Pa2l , ч
Л. = —----------I =------ , (а
В \ 2 2 ) 2 В v
2В
отсюда начальная жесткость к = —.
аЧ
Для определения начального передаточного отношения следует найти пере-
мещение $ конца стрелки. На фиг. 32,в показана эпюра моментов М от еди-
75
ничной силы, приложенной к концу стрелки в направлении перемещения s.
Перемножая эпюры М-р и М'^
Pal (2£-Н)
в соответствии с выражениями (а) и (б), получаем '
s _ 2L+Z
X 2 а
Таким образом, чувствительность механизма возрастает с увеличением
длин стрелки и пружин и с уменьшением расстояния а между пружиня ми.
Фиг. 32. Определение жесткости и
передаточного отношения пружин-
ного множительного механизма.
1
в)
«Л
Следует иметь в виду,что найденные значения жесткости и передаточного отно-
шения'справедливы только в области малых перемещений. Изменение жесткости
пружины с увеличением прогиба можно определить с помощью теории изгиба
в больших перемещениях.
§ 6. РАСЧЕТ ПЛОСКИХ ПРУЖИН В ОБЛАСТИ БОЛЬШИХ ПЕРЕМЕЩЕНИЙ
ПО МЕТОДУ Е. П. ПОПОВА
Плоская пружина из тонкой ленты или проволоки может при •
изгибе получить большие перемещения, соизмеримые, например,
с длиной пружины. Большие перемещения сопровождаются значи-
тельным изменением кривизны оси пружины; В тоже время, если тол-
щина h пружины достаточно мала, то ее деформации могут оставаться
76
малыми и упругими, поскольку наибольшая деформация Етах
прямо пропорциональна толщине
— изменение кривизны оси
пружины .
При больших перемещениях, в отличие от малых, принципы
неизменности начальных размеров и независимости действия сил
неприменимы; направление действия сил и место их приложения
могут существенно изменяться в процессе изгиба.
Дифференциальное уравнение (2. 7) By" = М упругой линии
первоначально прямого стержня в области больших перемещений
теряет силу, так как оно основано на приближенном представлении
1 /
кривизны как второй производной прогиба — у . При определе-
нии кривизны сильно изогнутого стержня приходится исходить из
точного выражения
1 _ У"
[1+(!/')г]2
Все это значительно осложняет расчет пружин в области больших
перемещений.
Общий метод решения задач об упругом изгибе стержня в боль-
ших перемещениях разработан Е. П. Поповым [6], [38]. Краткое
изложение сущности этого метода и его применение к решению
некоторых задач даны также в работах [39] и [40].
Рассмотрим стержень АВ, изгибаемый силами Р так, как пока-
зано на фиг. 33, а. Из этого стержня можно выделить бесчисленное
77
множество отрезков разной длины; они будут нагружены по концам
силами Р и различными по величине моментами М. Форму упругой
линии каждого из этих отрезков легко можно найти, если известны
форма упругой линии стержня А В, а также положение начальной
и конечной точек отрезка на стержне АВ. Иначе говоря, решение
задачи об изгибе стержня АВ включает в себя решения бесконечного
множества задач об изгибе других стержней, отличающихся по своим
размерам и по величинам нагрузок, если изогнутые оси всех
этих стержней являются частями упругой линии стержня АВ.
Изменяя величины сил Р, получаем новые очертания изогнутой
оси стержня АВ (фиг. 33, б). Е. П. Попов показал, что упругую ли-
нию стержня АВ можно представить как часть некоторой бесконеч-
ной периодической кривой, форма которой меняется с увеличением
нагрузки.
Упругая линия любого стержня при изгибе его произвольными
силами и моментами, приложенными по концам, оказывается подоб-
ной какому-то участку одной из периодических упругих кривых.
Геометрическое подобие форм упругих линий определяется тем, что
в соответственных точках рассматриваемого стержня и периодиче-
ской упругой кривой угловые размеры одинаковы, а линейные —
пропорциональны. Условия подобия упруго изогнутых стержней
выражаются в определенных соотношениях размеров стержней
и величин нагрузок (стр. 85).
Если известно решение всего семейства периодических упругих
кривых, т. е. известны их формы, то для отыскания упругой линии
любого конкретного стержня надо лишь найти тот участок периоди-
ческой кривой, которому подобна упругая линия рассматриваемого
стержня.
Уравнения семейства периодических упругих кривых были
получены Е. П. Поповым в безразмерных координатах, удобных для
применения условий подобия стержней. Конечные формулы включают
эллиптические интегралы, и в каждом конкретном случае решение
можно провести с помощью таблиц эллиптических интегралов, что
несколько неудобно для практического пользования. С целью упро-
щения Е. П. Попов составил таблицы и построил диаграммы так
называемых упругих параметров, которые представляют
собой выраженные в безразмерной форме линейные и угловые коор-
динаты и кривизну в каждой точке периодической упругой кривой.
Упругие параметры полностью характеризуют периодическую кри-
вую, следовательно, и изогнутую линию любого конкретного стер-
жня. Используя условия подобия упруго изогнутых стержней,
можно от безразмерных координат (упругих параметров) перейти
к размерным координатам нагруженного стержня и наоборот.
При решении любой задачи о плоском изгибе стержня по извест-
ным данным всегда можно найти некоторые из упругих параметров
в начальной и концевой точках изогнутой оси рассматриваемого
стержня. По значениям этих параметров находится отображение
упругой линии стержня на диаграмме упругих параметров, после
78
чего определение значений всех остальных упругих параметров в лю-
бой точке стержня не представляет труда. По величинам упругих
параметров с помощью простых формул можно найти все искомые
величины: перемещение, кривизну, напряжение в любой точке
стержня, его упругую характеристику, потенциальную энергию
деформаций и т. д.
Метод, разработанный Е. П. Поповым, может быть применен
к любым задачам о плоском изгибе гибких стержней, но диаграммы
упругих параметров составлены только для задач так называемого
Фиг. 34. Примеры стержней основного класса.
основного класса. К основному классу относятся системы,
имеющие следующие ограничения:
1. Стержень нагружается только по концам сосредоточенными
силами и моментами.
2. Начальная форма стержня представляет собой прямую или
дугу окружности.
3. Жесткость стержня постоянна по длине.
На фиг. 34, а—е приведены примеры изгиба стержней основного
класса.
К основному классу можно привести также задачи изгиба стержня,
каждый участок которого находится в условиях основного класса.
Например, к основному классу можно привести стержень, если он на-
гружен сосредоточенными силами и моментами в промежуточных точ-
ках (фиг. 34, ж, з, /г, ж), а также, если начальная кривизна или
поперечное сечение стержня изменяются ступенчато (фиг. 34, н, л).
7&
При решении задач, сводящихся к основному классу, каждый
участок рассматривается как отдельный стержень основного класса,
а на границах участки связываются силовыми и геометрическими
условиями.
Таким образом, основной класс задач (включая задачи, которые
могут быть сведены к основному классу) весьма обширен и охваты-
вает большинство практических случаев изгиба гибких стержней.
В работах [6] и [38] дано также решение задач, не сводящихся
к основному классу. К ним относятся задачи изгиба стержней плавно
изменяющейся кривизны или жесткости или нагруженных распре-
деленными силами. При решении этих задач стержень разбивается
на бесчисленное множество малых участков, каждый из которых
находится в условиях основного класса.
Ограничимся здесь только кратким изложением метода решения
задач основного класса, обратив основное внимание не на теорию
этого вопроса, а на его использование в решении конкретных задач.
Вывод уравнения упругой линии гибкого стержня
Рассмотрим равновесие первоначально прямого гибкого стержня
постоянной жесткости В, длиной Z, нагруженного по концам силами
и моментами (фиг. 35). Поместим начало координат в точку О
стержня, направив ось л? по линии действия силы Р.
Фиг. 35. К выводу уравнения упругой
линии изогнутого стержня.
Изменение Ах кривизны
в произвольной точке стерж-
ня можно определить как
a
Ах = —— ,
их
где £ — угол наклона каса-
тельной к оси л:, as — дуга,
отсчитываемая от точки О.
С другой стороны изме-
нение кривизны изгибаемого
стержня связано с момен-
том и жесткостью извест-
ным соотношением (2. 2).
Ах
М
/о г-
1В — £ — для узких полос или
ких полос [37]). Таким образом
д/г3
— для широ
d s ~ В *
Изгибающий момент М в произвольной точке стержня (фиг. 35)
М = Мо —Ру,
80
Подставляя значение М в предыдущую формулу, получаем
dt Мр-Ру
ds В
Исключим переменную у, дифференцируя последнее выражение
по $ и учитывая при этом, что ~ — sin £. Тогда
t* О
р • у / ч
rfs3 в Sln£* <а)
Выражение (а) можно представить в безразмерной форме, умно-
жив обе части его на Z2 и вводя безразмерный параметр нагрузки
Тогда уравнение (а) примет вид
12 = -Р2 sin I-
Это выражение является дифференциальным уравнением изогну-
той оси стержня. Первый интеграл уравнения можно записать
в виде
Z4r = 2p/_ (б)
где D — постоянная интегрирования.
Выражение (б) в безразмерной форме связывает кривизну -~-
в каждой точке упругой линии с величиной угла £ наклона касатель-
ной в этой точке к оси х, т. е. к линии действия силы Р.
Различным значениям постоянной D соответствуют различные
очертания упругой линии стержня. Из выражения (б) следует, что по-
стоянная D не может быть меньше | sin2 — наибольшего значе-
\ /наиб
г
ниязш2-|- для данной упругой линии. Если постоянная D =
*
(bin2 , то кривизна упругой линии в той точке, где sin2 ~
\ 4 /наиб 2
— (sin2-—^ , равна нулю I= о\ т. е. в этом месте упругая
\ /наиб \ J
линия имеет точку перегиба. Упругие линии, для которых постоян-
ная D находится в интервале (sin2 -|Л < D < 1, относятся к
\ /наиб
формам перегибного рода.
Если постоянная D 1, то упругая линии не может иметь точек
перегиба, так как в этом случае ни в одной точке упругой оси стержня
кривизна не будет равна нулю в соответствии с уравнением (б).
6 Заказ 24. 81
Поэтому упругие линии, которые описываются у равнением (б) при
1 < D < со, относятся к формам бесперегибного рода.
В случае, когда D — 1, упругая линия имеет переходную
форму, лежащую на границе между формами перегибного и беспере-
гибного рода.
Изогнутая ось стержня, помимо точек перегиба (т. п.), может
иметь и другие характерные точки: точки сжатия (т. с.) и точки
растяжения (т. р.) (фиг. 36). В этих точках внутренние силы приво-
дятся к нормальной силе растяжения или сжатия. Касательная
к упругой линии стержня в точках растяжения или сжатия парал-
лельна линии действия силы. Следует отметить, что точки растяже-
Фиг. 36. Характерные точки изо-
гнутой оси.
ния могут быть только на кривой
бесперегибного рода.
Дальнейшее интегрирование
уравнения (б) производится раз-
лично для перегибных и беспере-
гибных форм равновесия упругой
линии. При этом форму переход-
ную можно рассматривать как
предельный случай двух преды-
дущих .
Прежде, чем интегрировать
уравнение (б), производим следую-
щую замену:
для форм перегибного рода
(Д < 1)
D = к2 и sin = Asin ф;
(2. 8)
для форм бесперегибного рода (D >> 1)
. С
sin — sin ф.
л
В результате этой замены уравнение (б) для форм перегибного
рода принимает вид
1-^- = р У 1 — Aasin2v ,
После интегрирования получим
р = F (ф) - F Ш. (2.9)
Аналогично решается уравнение для форм бесперегибного рода
Р-f-= Л: [/’(ф)
(2.9')
82
Здесь
есть эллиптический интеграл первого рода, значения которого в за-
висимости от его модуля к и эллиптической амплитуды гр даются
в таблицах эллиптических интеграловя.
Величина модуля к постоянна для данной упругой линии стержня.
С изменением модуля к форма упругой линии будет меняться. По-
скольку 0 < к < 1, то в некоторых случаях модуль удобно предста-
влять в виде к — since, где а — модулярный угол (0 < а < 90°) <
Эллиптическая амплитуда ф связана соотношением (2. 8) с углом
£ наклона касательной к произвольной точке упругой линии стержня
(см. фиг. 35) и переменна вдоль его оси. Обозначим фо и фг — зна-
чения эллиптической амплитуды в начальной О и концевой 1 точках
стержня. Так как в концевой точке дуга $ == /, то из выраже-
ния (2. 9) следует, что
₽ = Р Wi) — F Wo)
и тогда уравнение (2. 9) можно записать в виде
F (Ф) = IF (Ф1) “ F (ф0)]
г + ш
Это выражение показывает, что если известны модуль к и эллип-
тические амплитуды ф0 и фг в начальной и концевой точках стержня,
то можно определить эллиптическую амплитуду ф в произвольной
точке стержня. Далее с помощью выражения (2. 8) можно найти угол
С наклона касательной в произвольной точке и, следовательно,
определить форму упругой линии стержня. Величины же к, фо и ф\
можно считать известными, так как по заданным условиям для кон-
кретного стержня их всегда можно найти.
Решая задачу аналитическим способом, приходится прибегать
к таблицам эллиптических интегралов. Далее рассмотрим только
графо-аналитический способ решения с помощью диаграмм упругих
параметров.
Периодические упругие кривые
Уравнения (2. 9) могут быть использованы для построения семей-
ства периодических упругих кривых в безразмерных координатах
I И ц:
| = Р^ИП = Р-Г' (2Л°)
1 Я н к е Е, и Эмде Ф., Таблицы функций, Физматгиз, 1959.
6* 83
начало которых помещаем в той точке периодической упругой кри-
вой, где эллиптическая амплитуда гр — 0. Здесь х и у — координаты
вид в; 90°>а>0°
Фиг. 37. Периодические упругие кривые.
произвольной точки кривой, I — ее длина. Величина 0 определяется
выражением
При этом длина X дуги в произвольной точке периодической упру-
гой кривой, отсчитываемая от начала координат, будет
(2.11)
84
Задавшись каким-либо значением модуля /с, который представим
как к = sin а (0 а 90°), и меняя эллиптическую амплитуду ф
в пределах от —90° до 4~оо, можно построить периодическую упру-
гую кривую на основании формул (2. 8) и (2. 9) с помощью таблиц
эллиптических интегралов. Такое построение можно провести для
различных величин модуля к (или модулярного угла а), в результате
чего будет получено семейство периодических упругих кривых
(фиг. 37).
Бесконечное множество форм периодических упругих кривых
разделяется на девять видов, каждый из которых соответствует
определенному числовому значению модулярного угла а или опреде-
ленному интервалу значений а.
Виды 1—6 относятся к формам перегибного рода и описываются
уравнениями (2. 9); виды#, 9, 8а и 9а — к бесперегибному роду
и соответствуют уравнению (2. 9').
Точки А, С, Е и т. д. периодической упругой кривой являются
точками сжатия; точки В, D, F и т. д. — точками перегиба на кри-
вых перегибного рода и точками растяжения на кривых бесперегиб-
ного рода. Переходная кривая 7 не имеет ни точек перегиба, ни точек
растяжения.
Все участки (NA, АВ, ВС, CD, DE и т. д.) периодической кривой
имеют одинаковые размеры и форму. Участок АВ называется глав-
ной ветвью. Все ветви периодической кривой при наложении
совмещаются с главной ветвью. Точки разных ветвей, совпадающие
при этом друг с другом, называются соответственными точками.
Чтобы полностью определить всю периодическую упругую кривую,
достаточно определить главную ветвь.
Использование периодической упругой кривой для решения кон-
кретных задач основано на условиях геометрического подобия стерж-
ней.
Условия геометрического подобия стержней
Стержни разных геометрических размеров и нагруженные различ-
ными силами и моментами в результате деформации могут получить
геометрически подобные формы упругой линии. Условия геометриче-
ского подобия стержней заключаются в равенстве угловых размеров
и пропорциональности линейных в соответственных точках: две
кривые а и. б (фиг. 38) подобны, если длины дуг si и S2 пропорциональ-
ны радиусам кривизны 7?1 и/?з в соответственных точках (например,
точках Bi и В2), а угол между касательными в точках Bi и Ci одной
кривой равен углу между касательными в точках В 2 и С 2 другой
кривой.
Достаточным условием подобия изогнутых стержней являются
равенство в соответственных точках трех так называемых коэф-
фициентов подобия:
1) углового коэффициента подобия, представляющего собой
угол £ между направлением линии действия силы Р, приложенной
85
в начально!! точке стержня, и касательной к его оси в рассматривае-
мой точке (см. фиг. 35);
2) моментного коэффициента подобия
(О —
(2.12)
где М — изгибающий момент в рассматриваемом сечении стержня;
1
-д — начальная кривизна стержня;
В — жесткость на изгиб;
3) силового коэффициента подобия
(2.13)
Угловой и моментный коэффициенты подобия имеют определенные
значения в каждой точке упругой линии стержня. Силовой коэффи-
циент подобия не зависит от положения точки на стержне и опреде-
Фиг. 38. Подобные изогнутые стержни.
ляется соотношением (2. 13) между силой Р, длиной I и жесткостью
В стержня. Угловой и моментный коэффициенты подобия в началь-
ной 0 и концевой 1 точках стержня £о, £i, coo, «и, а также силовой
коэффициент р называются главными коэффициентами
подобия.
По условию задачи всегда можно найти три из пяти главных
коэффициентов подобия. Например, для стержня, изображенного
на фиг. 39 известны сила Р, длина I и жесткость В на изгиб. По
этим данным можно определить следующие главные коэффициенты
подобия:
1) поскольку известны величины Р, I и В, подсчитываем силовой
коэффициент подобия по формуле (2. 13) р == 1/^^-;
2) изгибающий момент в концевой точке 1 равен нулю, начальная
кривизна - = 0, поэтому моментный коэффициент подобия по
выражению (2. 12) Wj = 0;
86
3) в начальной точке 0 известен угол между касательной к оси
стержня и направлением силы Р: £о = 90°.
Изогнутая ось стержня основного класса при любых величинах
и соотношениях нагрузок принимает форму, подобную некоторому
участку одной из периодиче-
ских упругих кривых. При
этом каждой точке упругой
линии стержня будет соот-
ветствовать определенная
точка участка периодической
кривой. Индексами 0 и 1
будем отмечать точки пери-
одической упругой кривой,
соответствующие начальной
и концевой точкам упругой
линии стержня.
В соответствии с выра-
П
Фиг. 39. К примеру определения коэффи-
циентов подобия.
жением (2. 11) длина уча-
стка периодической кривой, отображающего упругую линию
стержня, равна силовому коэффициенту подобия
(2.14)
Угловой коэффициент подобия £ в произвольной точке периоди-
ческой упругой кривой равен углу наклона касательной в этой точке
к оси
Можно показать, что кривизна в любой точке периодической
упругой кривой равна моментному коэффициенту подобия для этой
dt
ТОЧКИ (0 — i
Диаграммы упругих параметров
Упругими параметрами называются безразмерные координаты,
длина дуги, кривизна и угол наклона касательной к оси £ для про-
извольной точки главной ветви А В периодической упругой кривой.
При отсчете от начала А главной ветви упругие параметры обозна-
чаются и', К', (д' и Ё', а при отсчете от конца.В главной ветви —
х\" и V (фиг. 40).
Упругие параметры, соответствующие точке В, обозначаются
Е'о, ц'о, *. На основании фиг. 40 справедливы следующие соотно-
шения:
G — Вэо - £ ’ Л — Лэо Л ’ — ^80 • (2» 15)
Зная упругие параметры, можно найти величины т), %, со и £
в произвольной точке периодической упругой кривой на любой ее
* В точке В эллиптическая амплитуда ф — 90°.
87
ветви, а затем с помощью коэффициентов подобия определить все
неизвестные величины. Так, координаты х и у точки упругого стержня
связаны с координатами | и т] соответствующей точки периодической
упругой кривой выражениями
х — х0 --- -g- (£ — |0); у~у0 = ~ (ц — т}с). (2.16)
Здесь силовой коэффициент подобия ₽, равный длине дуги отрезка
01 периодической кривой, связан с длиной I стержня, его жесткостью
В и нагрузкой Р соотношением (2. 13)
р _ Xi
Р
В '
С
Изгибающий момент в произвольном
'Сучении стержня может быть подсчитан
с помощью выражения (2. 12)
м=4- - 4-) - <2-17>
а напряжения — по формуле о = ~~ .
™ из
В случае необходимости могут быть
Фиг. 40. Главная ветвь не- построены характеристика стержня, тра-
риодической упругой кри- ектория любой его точки и пр. Нено-
вой и упругие параметры, торые из этих построений будут рассмат-
риваться при решении примеров.
Таким образом, если значения упругих параметров найдены, то
с их помощью легко определяются значения всех искомых величин.
На фиг. 41 (см. вклейку) представлены диаграммы упругих па-
раметров, заимствованные из работ Е. П. Попова.
На этих диаграммах в некоторых координатах а — (р* проведены
кривые одинаковых значений упругих параметров 1/, %', о/,
Г', Л" и V'.
Как следует из фиг. 37, каждой форме периодической упругой
кривой соответствует определенное значение а. Диаграмма упругих
параметров разделена вертикалью а = 90° на две половины: слева
даны линии упругих параметров для периодических кривых перегиб-
ного рода, справа — для кривых бесперегибного рода.
Положение точки на главной ветви АВ периодической упругой
кривой определяется величиной <р, причем в начальной точке Л ср —
= 0, а в конечной точке В <р = 90°.
При решении задачи об изгибе стержня нужно-найти на диаграмме
упругих параметров отображение отрезка периодической кривой,
* Параметр а представляет собой а = arc sin к, где к — модуль эллипти-
ческого интеграла в уравнении (2. 9); (р— табличная эллиптическая амплитуда,
связанная с амплитудой ф выражением ф = п • 180° ± ср, причем 0 90°
и п — 0; 1; 2 и т. д.
88
подобного изогнутой оси стержня. Главная ветвь АВ периодической
кривой (фиг. 42, а) отображается на диаграмме упругих параметров
вертикалью АВ, а некоторый отрезок 01 периодической кривой —
соответствующим отрезком 01 на диаграмме (фиг. 42, б). Если отре-
зок QD1 периодической кривой располагается на двух ветвях, то его
отображением на диаграмме будет двойная линия 0D1 (фиг. 42, в).
На диаграмме упругих параметров легко определяются отображе-
ния характерных точек: точки сжатия располагаются на оси абсцисс
диаграммы (<р = 0), точки перегиба — на левой половине верхней
Фиг. 42. Отображение на диаграмме упругих параметров
отрезков периодической упругой кривой.
горизонтали (<р = 90°), а точки растяжения — на правой половине..
Поэтому, если положение характерных точек на изогнутой линии
стержня можно указать заранее, то решение задачи значительно упро-
щается.
При определении положения на диаграмме некоторой точки
периодической упругой кривой необходимо выяснить, к какому
роду — перегибному или бесперегибному — относится эта кривая
и затем вычислить значения двух любых упругих параметров в этой
точке. Положение любой другой точки кривой будет определяться
значением только одного параметра, так как первая точка уже дала
положение вертикали.
Найденное на диаграмме отображение отрезка периодической
упругой кривой позволяет определить для каждой точки стержня
величины всех восьми упругих параметров. Затем, используя условия
-подобия, можно найти все неизвестные по формулам, часть которых
была приведена выше (2. 16) и (2. 17).
Следует отметить, что решение по методу Е. П. Попова является
точным. Погрешности, возможные при решении задач, обусловли-
89
ваются только точностью техники вычислений. Например, некоторые
неточности могут возникнуть при отыскании по диаграммам числовых
значений упругих параметров.
Порядок и правила решения задач с помощью диаграмм
упругих параметров
При решении задач по методу Е. П. Попова следует придержи-
ваться определенных правил выбора координат, знаков отсчета
угловых и линейных величин и т. д., чтобы получить правильное
а) б)
Фиг. 43.
4
а — оси координат; б — определение знаков угла go и кривизны — .
Оо
Оси координат проводятся так, чтобы ось х была параллельна
линии действия силы Р, приложенной в начальной точке 0 стержня,
и направлена по этой силе (фиг. 43, а). Если при изгибе линия
действия силы Р поворачивается, то вместе с ней поворачиваются
и оси координат хОу.
Угол Со наклона касательной в начальной точке 0 изогнутого
стержня считается положительным, если при отсчете от оси х к каса-
тельной угол направлен против часовой стрелки в правой системе
координат или по часовой стрелке в левой системе (фиг. 43, б). При
этом угол Со берется в интервалах 0 < Со < л или 0 > Со —л,
а затем вдоль изогнутой оси угол С меняется непрерывно.
принимается положительной, если угол С с увели-
чением дуги s, отсчитываемой от начальной точки увеличивается.
Кривизна будет отрицательной, если с увеличением s угол С умень-
шается (фиг. 43, б).
90
Изгибающий момент в произвольном сечении стержня считается .
положительным, если он увеличивает положительную кривизну или
уменьшает отрицательную.
Для того чтобы определить ветвь периодической упругой кривой,
на которой находится отображение начальной точки 0 стержня,
следует пользоваться табл. 10.
Таблица 10
Определение ветви периодической кривой
1 i Знак кривизны в началь- ной точке 0 изогнутой оси Знак угла в начальной точке 0 изогнутой оси Ветвь периодической упругой кривой, на которой располо- жено отображение точки 0 (фиг. 37)
тч О/ Л а А<Г° с 3 ф NA АВ
V ° к Л 1 ВС CD 1
Для произвольной точки любой ветви периодической упругой
кривой координаты g и ц, длина дуги X, угол наклона g касательной
к оси g и кривизна со могут быть выражены через упругие параметры
g', rf, X', g', св', g", ц"и X" соответствующей точки главной ветви
АВ. Например, для точки Т% (см. фиг. 40) дуга X может быть вычи-
слена как X = 2 Х'о + X', координаты g = 2 g80 4- g' и ц —
2 т|ао — т|' (где Ха0, g*0 и Т1ао — значения главных параметров
в точке В, а V, g' и rf—главные параметры в соответствующей
точке Т главной ветви АВ периодической кривой). Такие формулы
перехода к упругим параметрам для различных ветвей периодической
кривой даны в табл. 11.
При решении задач по методу Е. П. Попова следует прежде
всего выяснить, находится ли рассматриваемый стержень в условиях
основного класса. Затем нужно наметить примерную форму изогну-
той линии стержня, отметить на ней, если это возможно, характер-
ные точки (перегиба, растяжения или сжатия). Через начальную
точку 0 стержня, которая может быть выбрана на любом конце
стержня, проводятся оси х и у, причем ось х должна совпадать по
направлению с полной силой Р в точке 0 стержня.
По условиям задачи всегда можно найти три главных коэффи-
циента подобия или соотношения между ними. Затем, с помощью
формул (2.12)—(2.14) и табл. 11 можно определить три упругие пара-
метра в начальной 0 и концевой 1 точках отрезка периодиче-
ской кривой, подобного упругой линии данного стержня. Для этого
предварительно определяются знаки кривизны и угла g в начальной
точке 0 стержня с тем, чтобы по табл. 10 найти ту ветвь периодиче-
ской кривой, на которой расположено отображение точки 0.
91
Та блица 11
Формулы перехода к упругих параметрам
Характер примых Параметры ]$етнь периодической упругой кривой (фиг. 37)» на которой расположена данная точ на
ЛТЛ АВ и CD DE
Все кривые /и = -К -1 к 2^91) 'Т^' Ug.j- Л' 4\Э0 -7^-'
£= -V -г s' 9р' -£' ^90 fe 2^0-1-^' 1 fpff СО * 1 ч ^90 П S'
Кривде перегибного рода Г)-= +п' + >f 2т1м-Пл' ^90 “'Г -J-Tj' I »/
{" _£' tS- _+5' -г Н'
(О ~ -L(A' +ф' — со' ( У -40' |
7 Крипые бсс- псрссибного рода положитель- ной кривизны 1 1 1 и' H-n' Н' +л' +1- +Ч- )
с= — tz тС' и' 2л 4- 4л-Г 1а-[ Г
<0 = 4-(о' + ® Ч-со -I- (О' 4-со' [ со'
отрицатель- ной кривизны 1 1 4 е —п' — Ti -ч' _,Г -г/ i
; 2«+Г 1 Г' ть -< -(2л-Г) -(2я-г-Г)
1 (О — -°' г S i 11 - (!)' — 1ЙГ — о/
По найденным величинами упругих параметров находятся отобра-
жения точек 0 и 1 на диаграмме упругих параметров. Упругие пара-
метры для любой точки отрезка периодической упругой кривой,
подобного изогнутой оси рассматриваемого стержня, можно теперь
легко найти по диаграмме. По формулам перехода, приведенным
в табл. 11, определяются безразмерные величины £, rj, Z, £и©,апо
ним — с помощью формул (2. 16), (2. 17) — все остальные неиз-
вестные.
Фиг. 44. К решению примера 1.
Пример 1. Для стальной пружины, размеры и первоначальная форма
которой указаны на фиг. 44, а, определить перемещение конца, наибольшее
напряжение и форму упругой линии при силе Р — 100 е. Оценить погрешность
расчета по линейной теории. Модуль упругости материала Е — 2,1-104 кгс!мм2.
Решение. Поскольку жесткость В на изгиб стержня и его начальная
кривизна постоянны, и стержень нагружен сосредоточенной силой на конце, то
задача удовлетворяет условиям основного класса.
Выберем начальную точку О в заделке, а концевую точку 1— на свободном
конце и проведем через точку О оси х и у, направив ось х по линии действия силы
Р в точке О. Наметим примерную форму изогнутой оси пружины (фиг. 44, б).
Точка 1 является точкой перегиба, поэтому в ней моментный коэффициент
подобия ©д = 0. Для начальной точки известен угловой коэффициент подобия
£; поскольку касательная к упругой линии в этой точке составляет 90° к оси х,
то £0 = 90°. Кроме того, можно подсчитать силовой коэффициент подобия р.
bh9
Для этого найдем сначала изгибную жесткость пружины В — Е -у— —
А и
= 284 кгс • мм2. В соответствии с выражением (2. 13) сило-
= 2,1
вой коэффициент подобия [3 = I
При принятой левой системе координат кривизна / — и угол в на чал ь-
\ Q /о
ной точке О положительны (см. фиг.43), поэтому отображение точки О упругой ли-
93
нии стержня располагается в соответствии с табл. 10 на главной ветви АВ перио-
дической упругой кривой (фиг. 44, в). При этом точка перегиба 1 совпадает
с точкой В главной ветви.
По величине трех главных коэффициентов подобия go, и р находим
с помощью табл. 11 и соотношений (2. 14) и (2. 15) значения трех упругих пара-
метров
<=°; £'=90°.
Л*
о
По значениям двух упругих параметров в точке О (g'o = 90°
= 1,5) находим отображение точки О на диаграмме упругих параметров. Так как
упругая линия стержня имеет точку перегиба, то отображение следует искать-
fl левой половине диаграммы упругих параметров. Точка О отображается на диа-
грамме точкой пересечения кривых £' = 90° (фиг. 41, б) и V = 1,5 (фиг. 41, а)
и имеет координаты <х = 69° и <р = 49°. Отображение точки 1 — точки пере-
гиба — лежит на пересечении вертикали и = 69° с верхней горизонталью
ф = 90° (фиг. 44, г).
Теперь можно найти все упругие параметры для любой точки отрезка 01
на диаграмме, а по ним — все неизвестные, подлежащие определению.
Координаты концевой точки 1 стержня в осях х и у можно найти из выра-
жений (2. 16). При л-0 = уй — 0
®1 =
У1-------О---
6 соответствии с соотношениями (2. 15) и табл. 11
Отсюда получим
Zi = -y-Z и =
(а)
Находим по диаграммам на фиг. 41, в, г упругие параметры в точке О:
== —0,80 и т)о = 1,21. Координаты концевой точки!,определяемые выраже-
ниями (а), будут
—0,80-80 _ /9fi
г--------— —42,6 мм,
1,5
1,21-80 _/с
t/i =----—-----— 64,5 мм.
1,5
Перемещения точки 1 в горизонтальном и вертикальном направлениях
Угор = I ~ Vi — 80 — 64,5 = 15,5 мм й veepm = | хг | = 42, 6 мм.
Если подсчитать перемещения балки по линейной теории, то получим игор —
=0, и в соответствии с формулой (2. 3) veep~ = 60 мм; ошибка
ос о•284
линейной теории составляет в этом случае соответственно 100% и 41%.
Напряжение o’шах возникает в заделке, где изгибающий момент имеет наи-
большее значение Л/тах = Pyt — 0,1 -64,5 = 6,45 кгс-мм. Следовательно, на-
пряжение O'max = ™ах- = — — 71,6 кгс/мм*.
W on*
94
Расчет по линейной теории дает
Р1 0,1.80-6 _оп . 2
°тах j.y 6 (0,3)2 ыс} мм ,
что составляет расхождение с точным решением около 24%.
Построим упругую линию стержня. Для этого в соответствии с выражениями
(2. 16) определим значения упругих параметров %' и if для нескольких произ-
вольных точек на отображении 01 стержня на диаграммах. Результаты после-
дующих расчетов представлены в табл. 12.
Таблица 12
Результаты расчета примера 1
ф° £' Г| ' 4 о Ш) n'—V X в мм У в мм
90 —0,22 1,86 -0,80 1,21 —42,6 64,5
85 —0,08 1,73 —0,66 1,08 -35,2 57,6
80 +0,10 1,56 -0,48 0,91 —25,6 48,5
75 0,26 1,40 —0,32 0,75 —17,1 40,0'
70 0,38 1,24 —0,20 0,59 —10,7 31,5
65 0,47 1,09 —0,11 0,44 -5,86 23,5
60 0,53 0,93 -0,05 0,28 —2,67 14,9
55 0,55 0,80 -0,03 0,15 —1,60 8,0
49 £>0,58 0,65 0 0 0 1,1
Форма упругой линии построена на фиг. 44, д.
Пример 2. Определить перемещения конца пружины, размеры которой
приведены на фиг. 44, а, при нагружении ее продольной силой Р = 150 г.
Решение. Эта задача, как и предыдущая, находится в рамках задач
основного класса. При нагружении стержня достаточно большой продольной
силой он может потерять устойчивость. Величина критической силы, при кото-
рой происходит потеря устойчивости, находится по формуле Эйлера (2. 6):
кр
л2В
(V/)2
В данном случае коэффициент v — 2 (см. табл. 9). При решении предыду-
щего примера была определена жесткость пружины В = 284 кгс-мм2. Следо-
вательно,
л л2-284 Л,,л
Ркр~(2.80)2 -°’110 кгс*
Указанная в условии сила Р = 150 г > Ркр, и устойчивая форма равно-
весия стержня будет изогнутой (фиг. 45, а).
Проведем оси х и у и отметим точки 0 и 1. Точка 1 является точкой пере-
гиба, точка 0 — точкой сжатия. Касательная к точке 0 совпадает с осью х. Это
определяет величины двух главных коэффициентов подобия: (0j = 0 и £о — 0.
Силовой коэффициент подобия находим по формуле (2. 13)
₽=(1/4=80/°^=ш.
Так как в соответствии с принятым правилом знаков (см. фиг. 43) кривизна
в точке <?(—-) > 0, a to = 0, то из табл. 10 следует, что упругая линия стержня
\ Q /о
95
отображается пя главной ветви АВ периодической упругой кривой. При этом
отображение точки сжатия О совпадает с точкой 4 главной ветви, гдо упругие
параметры А/ — — tj* == О, а отображение точки перегиба 1 — с точкой В.
Отрезок 07 отображается на левой половине диаграммы упругих параметров
(форма стержня исрегибного рода) вергп1и1<тьным отрезком, начало О которого
лежит на нижней горилпнтольной линия, где £' = О, а конец 7 — на верхней
горизонтовьной лпнии, где со' — 0 (фиг* 45» £). Положение этого отрезка можно
Фиг. 45. К решению примера 2
найти с помощью склопого коэффициента подобия, который в wiwwh с вы-
ражением (2. 14) равен длине дуги периодической упругой кривой, отображаю-
щей данный отрезок упругий лилии стержня
₽=’•>-И-*
По диаграмме (фиг. 41, а) находим, что значению упругого параметра
Z — 1,84 (юотвотстаует а — 45". Положенно отрезка 07 на диаграмме опре-
делено полно стыо.
Для нахождения координат a?t и концевой точки 7 стержня найдем упру-
гие- параметры Е' и i]' но диаграмме (фпг. <1, в, г}: — 0,85 и т/ ~ 1,41. Тате
как упругие параметры в точке О — ц* = 0, то формула (2. 16) примет птгп
f г
*1 = - J- 1 и Vi = - j- /,
откуда
0*85
= -ij4"a;=37 AW4
JI
1,41 ч
У1 —- ,£и = 61,4 *илс.
На фиг. 45, * показал вид упругой линии стержня при нагрузке Р — 150 г.
Задаваясь различными значениями силы /\ можно построить
характеристику стержня, нагруженного во схемам, приведенным на
фч1г. 44у б и 45, а. Результаты этих решений даны на графиках
фиг. 46 [40]т ври пользовании которыми молено значительно
OS
упростить решение многих задан для стержней, находящихся в про-
стейших условиях поперечного и продольного изгибов.
Пример 3. Определить силу Р
п перемещение %, при котором
произойдет замыкание контактов
пружинного множительного ме-
ханизма (фиг. 47, а). Материал
пружин — бериллиевая бронза
Бр. Б2, £' = 1,35-104 кгс/льч2
(табл. 6).
Решение. Каждая пру-
жина механизма работает по
схеме, указанной на фиг. 47, б.
Две точки перегиба (т. п) делят
верхнюю и нижнюю половины
пружины па две равные части.
Рассмотрим нижнюю четверть пру-
жины (фиг. 47, в). Поскольку
момент в точке перегиба равен
нулю, то конец этого участка
пружины нагружен только про-
дольной силой Рг = -у- , что со-
ответствует схеме, приведенной
на фиг. 46, 6. Длина этой части
пружины I = 10 мм, а гори-
б)
Фиг. 46. Графики перемещений конца стержня.
зоптальное перемещение, которое получит ее конец 1 при замыкании
а 12 о
контактов ц, = — -г-— о мм.
У1 4 4
По графику фиг. 46, б при — JL= 0,3 находим ^2,53 и —2-яа#0,95«
7 Заказ 24.
97
Определил! пзгибную жесткость пружины
Ы?3 4 . О Об3
В = Е = 1,35 • 104 4 у» =0,972 кгс - мм2.
12 12
Фиг. 47. К расчету пружинного
механизма.
Искомая сила Р будет равна
Р = 2Pt = = 2,53Wq9/2 = 0,0246 кгс 25 г.
Перемещение точки 1 пружины в вертикальном направлении при замыкании
контактов
10 (1—0,95) =0,5 .ил/.
Фиг. 48. К решению при-
мера 4.
Следовательно, перемещение % s 4-0,5 =
= 2 Л1Л4.
Пример 4. Определить силу Р, удерживаю-
щую первоначально прямую пружину в поло-
жении, указанном па фиг. 48.
Р е in е н и е. Указанному на фиг. 48 положе-
х,
нию соответствует координата точки 1
По графику,
ходим при
прпведенному на фиг. 46,
откуда
— 0.
б, на-
сш.а
Пример 5. Определить траекторию движения измерительного стержня
укрепленного на упругой направляющей, которая представляет собой., две
одинаковые плоские пружины. Стержень нагружен вертикальной силой Р.
Размеры плоских пружин указаны на фиг. 49, а. Материал — сталь 70, Е —
2,1 -104 кгс{мм2 .
Решение. Рассмотрим одну из пружин упругой направляющей. Конец 1
р
пружины натружен силой — и изгибающим моментом М. При движении измс-
рательнбго стержня этот конец перемещается, не поворачиваясь, и упругая
98
линия стержня имеет вид, показанный на фиг. 49, б, где отмечена точка пере-
гиба 2.
Направим ось х по силе —
в точке 0 и ось ?/, как показано на фиг. 49,6.
В соответствии с правилами знаков (см. фиг. 43) £о > 0и(—) > 0, поэтому
\ Qo /
начальная точка 0 пружины отображается на главной ветви АВ периодической
упругой кривой (см. табл. 10). Отображение точки перегиба 2 совпадает с точ-
л мм
Фиг. 49. К решению примера 5. |
i
кой перегиба В периодической упругой кривой, следовательно, отображение |
точки 1 попадает на следующую ветвь ВС периодической кривой (фиг. 49,в). |
Определим главные коэффициенты подобия. В точках 0 и 1 касательные |
к упругой линии пружины параллельны друг друг и составляют угол £ ~45° ;
к оси х. Следовательно, в этих точках угловые коэффициенты подобия = j
— = 45®. В соответствии с табл. 11 упругиепара метры в этих точках будут!./
Г = £ о= 45° и — 45°. В точке перегиба 2 моментный коэффициент
подобия со = 0, и эта точка отображается на верхней горизонтали ср — 90°
левой половины диаграммы упругих параметров. Следовательно, упругая линия
пружины отображается на диаграмме двойным отрезком 021, причем отображе-
ния точек 0 и 1 совпадают и лежат на кривой £' = 45° (фиг. 49, г).
Для построения траектория точки 1 нужно определить ее координаты
и уг при различных значениях силы Р, т. е. при различных значениях силового
коэффициента подобия р — I -r- • Величины и у1 связаны с безразмер-
ными координатами £ и г] формулами (2. 16), где я о = у о = 0:
(а)
В соответствии с табл. 11 величины | и ц в точках 0 и 1 выражаем через
упругие параметры: ёо -= Цо —5i = 2 £'о — = 2 — ц/.
Так как отображения точек 0 и 1 на диаграмме совпадают, то упругие параметры
в этих точках равны между собой: 51 = с и цо = ц . Учитывая выражения
(2. 15), получаем
&о = 2 (5<д) 5g) =25о • 41 Ло = 2Цо •
Силовой коэффициент подобия по формуле (2. 14) [3 ~ — Ло или учи"
тывая, что X = Л. , в соответствии с формулами табл. 11, получим
Тогда формулы (а) принимают вид
При изменении величины силы Р, а следовательно и коэффициента подобия
р — 2 Л , отображение 021 перемещается по диаграмме упругих параметров
так, что точки 0 и 1 скользят по кривой £' “ 45°, а точка 2 — по верхней го-
ризонтали ф = 90° (фиг. 49, г). Отметив на кривой = 45° несколько точек,
записываем их координаты ф и а в таблицу и затем по диаграммам
(фиг. 41, а, в, г) находим упругие параметры л , L и ц . В табл. 13 даны ре-
зультаты дальнейших вычислений.
Таблица 13
Результаты расчета примера 5
ф° * а Xq" 5о" 4о" V 1 Xj в мм уу в мм
60 26 0,58 0,39 0,43 26,9 29,6
55 27 0,67 0,44 0,51 26,4 30,7
50 29 0,78 0,48 0,62 24,6 31,8
45 33 0,81 0,46 0,79 . 20,2 34,7
40 37 1,04 0,47 0,92 18,1 35,4
35 43 1,20 0,35 1,12 11,7 37,3
30 51 1,40 0,20 1,34 5,7 38,3
25 65 1,86 —0,34 J 1,64 -7,3 35,2
toe
Траектория конца 1 пружины и положения измерительного стержня по-
казаны на фиг. 49, д.
Пример 6. Построить упругую характеристику стальной кольцевой пру-
жины, размеры и способ нагружения которой указаны на фиг. 50, а. Модуль
упругости Е — 2-104 кгс/мм2.
Решение. Данная задача относится к тем задачам, которые могут быть
сведены к основному классу, так как кольцо можно разделить на участки (по
вертикальной оси симметрии), каждый из которых будет находиться в условиях
основного класса.
О) 5) 4 в)
Фиг. 50. К решению примера 6.
Из условий симметрии каждая четверть кольца (фиг. 50, б) нагружена
одинаково. В точке 1 приложены сила
2
и изгибающий момент (горизонталь-
ная сила равна нулю из условия равновесия правой или левой половины кольца).
При выбранной системе координат касательная к упругой линии в точке
0 параллельна, а в точке 1— перпендикулярна к оси х. Следовательно, угло-
вые коэффициенты, подобия £о = 0 и = 90°.
В соответствии с табл. 10 точка 0 отображается на главной ветви АВ перио-
дической упругой кривой, причем, поскольку точка 0 является точкой сжатия,
то отображением ее является точка А периодической упругой кривой.
Упругая линия стержня относится к перегибному роду, так как при нагру-
жении пружины на упругой линии появляется точка перегиба 2. Поэтому ото-
бражение точки 1 попадает на участок ВС периодической упругой кривой
(фиг. 50, в). На основании формул табл; 11 упругие параметры в точках 0 и 1
101
будут £0 — £о — 0 и £ = £х = 90°. Таким образом, отрезок 01 отображается
на диаграмме упругих параметров вертикальным двойным отрезком, начало
0 которого находится на нижней горизонтали (£' = 0), точка перегиба 2 — на
верхней горизонтали (со' = 0), а конец 1 — на кривой t,' — 90° (фиг. 50. г),
В задаче требуется построить характеристику пружины, т. е. определить
зависимость между силой Р и сближением v точек М и IV пружины. Будем за-
давать силе Р разные значения, меняя этим величину силового коэффициента
подобия р. Для отрезка 01 пружины силовой коэффициент подобия равен
₽=г1/ч
(а)
где 1\ = . При изменении коэффициента р отображение 021 будет переме-
^4
щаться по диаграмме упругих параметров вдоль оси а, причем точка 1 будет
скользить по кривой £' = 90°, точка.#'— по нижней, а точка 2 —по верхней
горизонтали (фиг. 50, г). /
Коэффициент подобия Р связан с безразмерной дугой X периодической упру-
гой кривой зависимостью (2. 14) Р — Лх — Хо. Так как точка 0 отображается
точкой А периодической упругой кривой, тоАо=?о — 0. Отображение точки
1 находится на ветви ВС, поэтому в соответствии с табл. 11
Xi—2Xg0 Xt—Р;
Здесь V и |,д0 — главные параметры в точке В периодической упругой
кривой, где (р = 90°.
Тогда координата по выражению (2. 16) будет равна
С.
(в)
Характеристика пружины может быть записана с помощью выражения (а)
в параметрической форме
= 5 иге - мм2,
bhs 3•0
где жесткость на изгиб равна В ~ Е 2-104-----------------
12 12
I — . Представляя в предыдущее выражение числовые значения, получаем
Здесь величины и Р определяются формулами (б) и (в);
в граммах, перемещение v в мм.
Результаты расчета примера 6^
сила Р получается
Таблица 14
<р° а° V ^90 Рв г Ь' £90
90 45 1,84 1 1,84 1,84 23,8 0,85 1 0,85
i С7 50 1,32 1,92 2,52 44,8 0,74 0,67
59 55 1,17 2,02 2,87 58,0 0,68 0,50
51 60 1,08 2,15 3,22 73,2 0,63 0,27
52 65 1,00 2,30 3,60 91,4 114 0,60 0-
49 J -J 70 0,97! 2,50 4,03 0,574 * —0,3
I 1 -ч Ci JJLP (М в мм V в мм
0,85 17,4 13,2
0,60 8,98 30,1
0,32 4,20 39,6 i
—0,09 —1,05 50,1
-0,60 -6,29 60,6
—1,17 —10,95 70,0
102
Задаваясь рядом положений отображающих отрезков 021 на диаграммах
(фиг. 41, а, в), находим упругие параметры Л , л , В и £ , необходимые для
решения задачи. Результаты вычислений записаны в табл. 14.
На фиг. 50, д построены характеристика пружины и для сравнения — прямая,
соответствующая решению по линейной теории (см. пример 5, § 5).
§ 7. СПИРАЛЬНЫЕ ЗАВОДНЫЕ ПРУЖИНЫ
Общие сведения
Спиральные пружины часто используются в приборах в качестве
пружинных двигателей. Схема заводной спиральной пружины пока-
зана на фиг. 51. Внутренний конец пружины закреплен на валике,
а наружный крепится к корпусу прибора (фиг. 51, а) или к барабану
(фиг. 51, б), внутри которого в этом случае размещается вся спираль-
ная пружина.,
При заводе валик вращается
относительно корпуса или бара-
бана, при этом пружина изги-
бается вокруг валика и, когда
витки плотно навиваются на ва-
лик, процесс завода оканчивается.
В заведенном состоянии пружина
обладает некоторым запасом
потенциальной энергии. При
спуске она способна совершать
определенную работу, вращая
барабан или валик.
Заводные спиральные пружины
Фиг. 51. Схема спиральной завод-
ной пружины.
удобно компонуются в приборе,
надежны в работе, имеют сравнительно небольшой вес, не боятся
динамических нагрузок и широко применяются в качестве пружин-
ных двигателей приборов времени, в механизмах привода диаграм-
мных лент и в других приборах. Пружинные двигатели особенно
удобны в переносных приборах.
От любого двигателя, в том числе и от пружинного, требуется
создание определенного момента па рабочей оси. Момент, развивае-
мый спиральной заводной пружиной, пропорционален взаимному
углу поворота концов пружины, поэтому при спуске пружины обычно
используется только часть ее возможных оборотов. Иначе в начале
завода момент будет слишком малым, а в конце завода большой
момент может вызвать перегрузку механизма и нарушение хода.
Поэтому всегда желательно, чтобы момент, отдаваемый пружинным
двигателем при спуске, оставался постоянным. Способы получения
от пружинного двигателя мало изменяющегося момента при большом
числе оборотов оси рассмотрены ниже (стр. 126).
Заводные спиральные пружины изготовляются из плоской пру-
жинной ленты. Для мелких пружин с толщиной ленты h < 0,1 4-
- 0,3 мм обычно применяется сталь У8А—У12А (табл. 4), для пру-
жин крупных размеров при толщине ленты h — 0,3 мм и больше —
103
сталь 70С2ХА (ЭИ-142)* (ГОСТ 2283-57). Пружины, предназначен-
ные для работы в агрессивной среде или при повышенных темпера-
турах, изготовляются из дисперсионно-твердеющего сплава
К40НХМ** (табл. 6).
В процессе изготовления пружины лента навивается на валик,
виток на виток, и в таком тугозаведенном состоянии она стабилизи-
руется в течение 2—10 дней. Иногда стабилизация пружины произ-
водится при переменном нагружении, для чего пружине сообщается
некоторое количество циклов нагружения в режиме «завод — спуск».
В некоторых случаях для ускорения операции стабилизации пружину
нагревают до 100—120° С.
При первой же навивке на валик пружинная лента пластически
деформируется, и по окончание процесса стабилизации пружина
приобретает форму спирали. Форма и размеры спирали (например,
число ее витков) зависят от размеров пружинной ленты и заводного
валика, а также в большой степени от упруго-пластических свойств
материала ленты. Значительное влияние на свойства материала,
а следовательно, и на форму спирали оказывает режим термообра-
ботки пружинной ленты. Число витков пружины в зависимости от
термообработки пружинной ленты может отличаться в несколько раз.
Если пластические свойства ленты упали в результате неправильной
термообработки, то это может привести к хрупкому разрушению пру-
жины в процессе стабилизации или во время работы. Чрезмерное
увеличение пластичности материала при неправильно!! термообра-
ботке также недопустимо. В этом случае в результате малой упругой
отдачи материала пружина «сядет», т. е. будет иметь слишком боль-
шое число витков. При заводе и при спуске такая пружина слабо
деформируется и развивает меньший, чем требуется момент.
Момент, развиваемый пружинным двигателем, определяется дефор-
мацией пружины при ее работе, а величина деформации будет тем
больше, чем больше разница между числом витков пружины в туго-
заведенном и в свободном состояниях. Для расчета пружинного
двигателя необходимо знать форму спирали, которую приобретает
пружинная лента в свободном состоянии после стабилизации. Спо-
собы решения этой задачи описаны ниже (стр. 114).
Характеристика спиральной заводной пружины
Если пружина находится в состоянии чистого изгиба, то ее харак-
теристика, т. е. зависимость между числом п оборотов валика и разви-
ваемым ею моментом М линейна, и может быть получена из основного
уравнения (2. 2) изгиба стержней
* К о л ч и н К. П., К вопросу о выборе стали для пружинных лепт,
Сборник научно-технических работ Ленинградского отделения ВНИТОМ,
издание ГНТИЛ по черной и цветной металлургии, вып. 1, 1949.
** Б о л е у х А. С., Белова Э. П. и Сольц В. А., Применение
сплава К40НХМ для заводных пружин [20].
104
где I — длина рабочей части пружины;
В = EJ — жесткость на изгиб;
Е — модуль упругости материала;
т bh3
J — ~~- — осевой момент инерции поперечного сечения пружинной
ленты шириной b и высотой h;
Ф — 2 л п — взаимный угол поворота концевых сечений ленты.
На фиг. 52, а сплошной линией показана характеристика спи-
ральной свободной заводной пружины (без барабана).
В конце завода пружины происходит постепенная посадка витков-
на валик, рабочая (деформируемая) длина пружинной ленты умень-
шается, что приводит к увеличению жесткости пружины. Поэтому
в конце завода характеристика пружины становится нелинейной
(участок ВС на фиг. 52, а). Точке В соответствует начало посадки
витков, точке С — тугозаведенное состояние пружины, когда ее
дальнейшая деформация практически невозможна. Начальная точка О
характеристики соответствует свободному состоянию пружины, при
котором число витков равно гсе. Это число можно показать на гра-
фике, если представить, что пружина нагружена некоторым момен-
том Мо, обратным по знаку моменту на рабочем участке. Величина мо-
мента такова, что пружина, разгибаясь под его воздействием, раз-
вернется, и ее центральный угол станет равным нулю (точка D на
фиг. 52, а). Число оборотов валика в этом случае будет равно числу
витков свободной спирали ice. Число витков тугозаведенной пружины
iT определится на графике отрезком db, что следует из сопоставления
развернутого положения пружины (точка D) с тугозаведенным
(точка В). Так как нелинейный участок ВС является нерабочим, то
можно считать пружину полностью заведенной в положении В, тем
более, что на участке ВС, где происходит посадка витков, число
оборотов валика мало по сравнению с рабочим числом оборотов Прав.
В некоторых случаях пружину защищают от перегрузки при заводе-
с помощью специальных ограничителей вращения заводного валика,-
которые не допускают захода на нелинейный участок характеристики
ВС. В качестве ограничителя часто используют мальтийский меха-
низм [41 ].
Наибольший Afmax и наименьший Л/min моменты на рабочем
участке АВ характеристики определяются с помощью формулы
(2. 18). Наибольший момент 7Итах, возникающий в полностью заве-
денной пружине, соответствует числу оборотов «тах валика, необхо-
димому для перевода пружины из свободного в тугозаведенное состоя-
ние. Из фиг. 52, а следует, что «тах = *т — *се- Число оборотов «тц>
валика меньше «тах на число Праб рабочих оборотов: «min ~ «max —
— п^б = ir — Чв — Прав- Тогда в соответствии с формулой (2. 18)/
моменты Л/max и Mmin будут равны
ЛЛпах = —у—2<ГС (iy— ice)} (2- 19)’
vr - EJ
Al min — —i~
105
I
I "I
dOG
Фиг. 52. Характеристика заводной спиральной пружины:
а — беа барабана; б — в бара&глсь
Поскольку момент, развиваемый пружинным двигателем, не
должен быть меньше Afmin, то при работе начальный участок О А
характеристики не используется. Для ограничения деформации
пружины при спуске на нерабочем участке ОА устанавливают спе-
циальные упоры. Они ограничивают габариты пружинного двигателя,
я пружина при спуске не сможет чрезмерно увеличивать свои размеры
п мешать работе других деталей механизма. Для этой цели часто
используется барабан (см. фиг. 51, б), к которому крепится наруж-
ный конец пружины. Такая конструкция позволяет также при
необходимости снимать момент не с заводного валика, а с барабана.
Это упрощает кинематику прибора, а двигатель может заводиться
без остановки механизма прибора.
Характеристика заводной пружины в барабане
показана на фиг. 52, б. Точка 0t соответствует спущенному состоя-
нию пружины, когда большая часть витков пружины прижата
к барабану. При заводе витки постепенно отходят от барабана,
рабочая длина пружины увеличивается, и жесткость ее падает
(участок 0±А характеристики). На рабочем участке АВ пружина
работает всей длиной, поэтому здесь характеристика линейна. В точке
В начинается посадка витков на валик, как и в рассмотренном выше
случае работы пружины без барабана.
Если освободить пружину от барабана, то она развернется и при-
мет положение свободной спирали (точка 0 характеристики). Так же,
как и в предыдущем случае, на фиг. 52, б можно показать число
витков ic& свободной спирали и число витков i? в тугозаведенном
состоянии, отсчитывая их, как число оборотов, от точки D, соответ-
ствующей развернутому положению пружины.
Если наложить характеристики, снятые при работе пружины
в барабане и без него, так, чтобы совпали точки 0, соответствующие
свободному состоянию пружины, то рабочие участки полностью
совместятся. Число пх холостых оборотов, необходимых для дости-
жения рабочего участка АВ, определяется у пружины без барабана
отрезком Оа, а у пружины в барабане — отрезком 0±а. В первом
случае число холостых оборотов будет значительно больше.
Поскольку рабочий участок А В характеристики пружины в бара-
бане совпадает с рабочим участком для пружины без барабана, то
уравнение этого участка по-прежнему описывается формулой (2. 18),
а наибольший и наименьший рабочие моменты — выражениями
(2. 19).
Способы крепления концов пружины
При работе пружины ее витки располагаются эксцентрично
(фиг. 53). В тех местах, где витки соприкасаются, возникает меж-
витковое трение, которое увеличивается к концу завода при посадке
витков па валик. Характеристики, показанные на фиг. 52, а и б
сплошными линиями, построены без учета потерь на трение. В дей-
ствительности кривые завода и спуска не совпадают, образуя петлю,
107
площадь которой соответствует потерям энергии на трение. При этом
гистерезисные потери материала пружины малы по сравнению
с потерями на межвитковое трение.
Для уменьшения межвиткового трения необходимо, чтобы витки
пружины перемещались концентрично. Это может быть достигнуто,
если пружина находится в условиях
Осуществление чистого изгиба зависит в основном от конструкции
крепления наружного конца пружины. При чистом изгибе крепление
должно передавать
близких к чистому изгибу.
Фиг. 53. Эксцентрич-
ное расположение
витков.
креплении возникает
то пружина нахо-
конец пружины будет
радиальном направ-
на пружину только момент. «Идеальным» с этой
точки зрения было бы крепление, выполненное
по схеме, изображенной на фиг. 54,\ а. При
таком креплении невозможен поворот и допу-
скаются линейные перемещения конца пру-
жины. Поскольку
только изгибающий момент
дится в условиях чистого изгиба. Можно по-
казать, что при этом
перемещаться лишь
лении.
Однако практическое осуществление такого
«идеального» крепления наружного конца
пружины связано с усложнением конструкции
пружинного двигателя и увеличением его габаритов. Так, например,
наружный конец может быть закреплен на планке, свободно переме-
щающейся в радиальном направлении (фиг. 54, б). «Идеальное»
крепление может быть получено также при совместной работе двух
одинаковых пружин, включенных параллельно (фиг. 54, в) или
последовательно (фиг. 54, г), но из-за большой сложности эти кон-
струкции не
получили распространения.
заводной пружины, обеспечиваю-
витков.
а)
Фиг. 54. Схемы крепления наружного конца
щие концентричность
Широкое применение нашли другие способы крепления наружного
конца пружины. Эти способы, хотя и не соответствуют идеальной
схеме, но технологически и конструктивно просты, не увеличивают
габаритов двигателя и надежны в работе.
Часто, особенно для пружин без барабана, применяется одно из
наиболее простых креплений — «шарнирное» (фиг. 55, а). Его основ-
408
пой недостаток заключается в большой эксцентричности витков
пружины при работе. Вследствие возникающего межвиткового тре-
ния уменьшается момент, отдаваемый пружиной при спуске. Однако
и при отсутствии трения момент пружины при шарнирном креплении
конца был бы несколько меньше, чем в «идеальном» случае, поскольку
шарнирное крепление не обеспечивает чистого изгиба пружины.
Такой тип крепления применяется в дешевых пружинных двигате-
лях, используемых, например, в будильниках, заводных игрушках
и т. п.
Фиг. 55. Применяемые схемы креплений наружного конца
заводной пружины.
Лучшие результаты дает «жесткое» крепление (фиг. 55, б). В та-
ком креплении величина реактивных сил меньше, чем в шарнирном.
Поэтому, несмотря на то, что эксцентрицитет витков при работе
остается, межвитковое давление, а следовательно, и трение имеют
в данном случае меньшие значения, чем при шарнирном креплении.
Чаще всего в пружинных двигателях применяются различные
конструктивные варианты «упругого» крепления, когда наружный
конец пружины имеет возможность радиально перемещаться при
затрудненном повороте, что приближает его крепление к «идеаль-
ному». К «упругому» креплению можно отнести V-образное крепле-
ние (фиг. 55, в), крепление с промежуточной пластинкой (фиг. 55, г).
Последний тип крепления наиболее близок к «идеальному» и обусло-
вливает практически концентричное распускание витков.
К «упругому» креплению можно отнести также крепление пру-
жины на шарнире с промежуточным штифтом (фиг. 55, д) и крепле-
109
пне с мечевидной накладкой (фиг. 55, е). Эти крепления (особенно
последнее), также обеспечивают хорошую работу пружины, выгодно
отличаясь простотой и надежностью конструкции. Крепление
с мечевидной накладкой, в последнее время получило широкое распро-
странение.
На фиг. 56 представлены характеристики пружин с различными
креплениями наружного копна, иллюстрирующие влияние способов
крепления па работу заводной пружины (71.
Фиг. 56. Характеристики
заводной пружины с различными крепления мп
наружно со концы.
Момепт при спуске у реальной пружины меньше, чем у «идеаль-
ной», что объясняется несоблюдением условий чистого изгиба и глав-
ным образом потерями па межвитковое трепне. Нотерн на трепне
зависят от межвиткового давления и коэффициента трепал, п ука-
зать точно величину потерь на трение для каждого типа крепления
не представляется возможным. Обычно уменьшение момента реаль-
ной пружины оценивается к оэффи циенто м к а ч е с т в а
пружины, который представляет собой отношение момента Л7СЛ при
спуске даппой пружины к моменту ЛГ «идеально» закрепленной
пружины (см. фиг. 52):
К = . (2. 20)
Коэффициент качества определяется экспериментально, и его
приближенные значения для иружип с различным креплением наруж-
ного конца., работающих со смазкой, даны в табл. 15 [7].
110
Таблица 15
Коэффициент К качества пружины
Тип крепления к т-
Шарнирное 0,65—0,70
i j Штифтовое 0,72-0,78
V-образнос • . . . *! F 0,80-0,85
С промежуточной пластиной г 1 1 1 0,90-0,95
4 С мечевидной накладкой 0,90-0,95 _ _ -- _ 1
{конца. Конструкция крепления внутреннего конца пружины должна
.лишь обеспечивать надежную передачу момента от пружины к завод-
ному валику. При неправильной конструкции крепления увеличи-
вается вероятность поломки внутреннего конца пружины, так как
в этом месте пружина наиболее сильно деформируется при изгото-
влении.
Внутренний конец пружины отжигается, и ему примерно на длине
одного витка придается форма, плотно облегающая заводной валик.
Во избежание поломки пружины вследствие концентрации напряже-
ний переход от отожженного участка к закаленному должен быть
постепенным.
Различные конструкции крепления внутреннего конца пружины
показаны на фиг. 57. Выбор того или иного типа крепления опреде-
ляется главным образом технологическими соображениями и требо-
ваниями надежности крепления. ,
Нормальная заводная пружина
Число оборотов пружинного двигателя при заданных размерах
барабана, заводного валика и сечения пружинной ленты зависит от
длины заводной пружины. Если длина пружины мала, то и число
оборотов двигателя будет небольшим. С увеличением длины пружины
число оборотов пружинного двигателя возрастает и достигает макси-
мального значения при некотором оптимальном соотношении между
длиной пружины и размерами барабана и валика. При дальнейшем
увеличении длины пружинной ленты число оборотов вновь падает и
становится равным нулю, если лента настолько длинна, что пру-
жина сплошь заполняет всю внутреннюю полость барабана.
Если длина пружины удовлетворяет оптимальному соотношению,
при котором достигается максимальное число оборотов двигателя,
то такая заводная пружина называется нормальной.
Особенность нормальной пружины состоит в том, что внутренний
радиус пружины в спущенном состоянии равен ее наружному радиусу
в тугозаведенном состоянии (фиг. 58, я, б). Докажем, что при этом
условии пружина действительно даст максимальное число оборотов.
Для простоты будем считать, что концевые участки АВ и CD пру-
жины, не прилегающие к валику при заводе и к барабану при спуске,
малы по сравнению с рабочей длиной пружины. Тогда число витков
нормальной пружины в тугозаведенном и в спущенном состояниях
определяется соответственно по формулам
Гг—. R — Ггг, /л
iT = JL-—L и 1сп =---L., (2. 21)
h h <
здесь В — радиус наружного витка в спущенном состоянии;
гт — радиус внутреннего витка в спущенном состоянии или
наружного витка в заведенном положении;
Го — радиус внутреннего витка в заведенном положении;
h — толщина ленты. Радиус R определяет размер барабана,
а радиус г о — размер валика.
Полное число оборотов валика при переводе нормальной пружины
из спущенного состояния в заведенное равно
п = iT — iCn. (а)
Предположим, что длина пружинной ленты меньше, чем это тре-
буется по условию нормальной пружины. В этом случае между на-
ружным радиусом заведенной пружины и внутренним радиусом
спущенной остается зазор шириной Ат + Дсп (см. фиг. 58, в), где
Дг — уменьшение радиуса наружного витка укороченной пружины
при заводе, а ДСЛ — увеличение радиуса ее внутреннего витка при
спуске по сравнению с радиусом гт нормальной пружины. Очевидно,
Г
Фиг. 58. Нормальная заводная пружина:
а —- в спущенном и б — в заведенном состояниях; в — спущенная и заведенная пружина,
длина которой меньше нормальной.
что Ду Дсп, так как средний радиус кольца шириной Ду меньше,
чем средний радиус кольца шириной Дсп, а их площади должны быть
одинаковыми и равными \lh, где Д2 — разность между длинами
нормальной и укороченной пружин; h —- толщина ленты.
Число витков укороченной пружины в заведенном и спущенном
состояниях будет соответственно
где г'у и icn — число витков нормальной пружины, определяемое
в соответствии с выражением (2. 21).
Число оборотов пг укороченной пружины
^cni ‘ *СП
или с учетом соотношения (а)
п, = п
8 Заказ 24*
— &СП
h
ИЗ
Так как Ат > Дсп, то число оборотов пх укороченной пружины
меньше числа оборотов п нормальной пружины: nt < п.
Аналогичным путем можно доказать, что пружина более длинная,
чем нормальная, также дает меньшее число оборотов.
Итак, увеличение или уменьшение длины пружины по сравнению
с нормальной, при которой радиус наружного витка при заводе
равен радиусу внутреннего витка при спуске, приводит к уменьше-
нию числа оборотов пружинного двигателя.
Поскольку при одних и тех же габаритах двигателя нормальная
заводная пружина дает наибольшее число оборотов, то она особенно
часто используется в малогабаритных пружинных двигателях. |
Радиус гт (фиг. 58) нормальной пружины определим из условий
постоянства объема пружины при работе. Объем V пружинной лентН,
равный Ihb (b — ширина ленты), в тугозаведенном состоянии может
быть выражен по формуле
V = л b (гт
ГО2)
а в спущенном состоянии
V = лЬ(Я2 — гт).
Из условия постоянства объема получим равенство
lh = л (г2т — го) = л (7?2 — гт),
(2. 22)
откуда находим выражения для радиуса
(2.23)
и для длины пружинной ленты
-rS).
(2. 24)
Число оборотов нормального пружинного двигателя при заводе
определяется с помощью выражений (а), (2. 21) и (2. 23).
« = 4- [Уг(/?2 + г?) -(Я + г0)].
11
(2. 25)
Определение формы спиральной пружины после "“стабилизации
Форма спирали, которую приобретает пружинная лента в резуль-
тате стабилизации, зависит от деформации ленты при навивке и от
упруго-пластических свойств материала.
При изгибе прямой пружинной ленты по дуге радиуса г деформа-
ция, возникающая в наиболее удаленных от нейтрального слоя волок-
114
нах, определяется в соответствии с гипотезой плоских сечений по
формуле
е = 4-, (а)
ч
где h — толщина ленты.
При стабилизации лента навивается на оправку виток на виток.
Радиус кривизны1 * * * навитой ленты будет переменным вдоль ее оси,
увеличиваясь от радиуса г о внутреннего витка до радиуса г? наруж-
ного витка навитой пружины. Радиус кривизны г в произвольной
точке, положение которой можно характеризовать угловой коорди-
натой <р, отсчитываемой от внутреннего конца пружины, определяется
по выражению
г = г« + й-^- <б>
Деформация е переменна вдоль оси навитой ленты. Наибольшая
деформация возникает у внутреннего витка егаах = .ч—, наимень-
zj’q
h
шая — у наружного emin = .
-гт
Пластические деформации появляются в том случае, если дефор-
мация е превышает деформацию 8Уп, соответствующую пределу
упругости оуп материала ленты (фиг. 59, а). Обычно соотношения
размеров ленты и валика при навивке заводной пружины таковы,
что даже наименьшая деформация Етщ У наружного витка превы-
шает деформацию 8Уп и поэтому пружинная лента по всей длине под-
вергается пластическим деформациям.
В результате пластических деформаций, возникающих при на-
вивке и стабилизации, пружина сохраняет остаточную кривизну и по-
лучает форму спирали. Для определения формы свободной пружины
можно использовать различные способы.
Если известна диаграмма растяжения материала ленты, то поль-
зуясь теорией упруго-пластического изгиба [34], можно определить
радиус кривизны гсе в произвольной точке оси свободной пружины
с помощью уравнения, основанного на законе разгрузки
1 _ _1____М
гсв г EJ
Зная радиус кривизны гсв в каждой точке оси свободной пру-
жины, можно легко построить ее форму. Получение уравнения сво-
бодной спиральной пружины таким путем изложено в работах [42 ],
[43], где диаграмма растяжения материала схематизировалась,
ломаной линией.
1 Так как толщина ленты мала по сравнению с радиусом оправки (h г0)г
то можно считать, что радиус кривизны совпадает с радиусом-вектором оси
навитой пружинной ленты.
8*
115
При определении формы свободной пружины можно исходить
также из диаграммы изгиба пружинной ленты (фиг. 59, б), которую
получают построением диаграммы растяжения или непосредственным
испытанием ленты-на изгиб на специальном приборе [7].
Откладывая по оси абсцисс значения — в различных точках нави-
той пружины, начиная от кривизны
наружного
витка и кончая
1
кривизной — внутреннего витка пружины, проводим вертикальные
го
прямые до пересечения с кривой изгиба. Значения остаточной кри-
а — диаграмма растяжения; б — диаграмма изгиба пружинной ленты.
визны, которая сохраняется после снятия пружины с оправки,
находим на основании закона разгрузки, проводя прямые парал-
лельно ynpyroii части ОА диаграммы. Определив таким образом ряд
радиусов гсв в различных точках оси пружины, можно построить
ее форму.
Для приближенного расчета пружинного двигателя достаточно
знать число витков 1св свободной пружины, не производя полного
определения ее формы. Число витков ice можно найти весьма просто
по методу, предложенному Т. А. Гевондяном [7], без использования
диаграмм растяжения или изгиба материала.
На фиг. 60, а показан бесконечно малый элемент ds пружины
при навивке и в свободном состоянии. Центральный угол элемента
при навивке равен dtp = —. Вследствие упругой отдачи материала
радиус кривизны элемента в свободном состоянии увеличится и ста-
нет равным гСв, и остаточный центральный угол </фсв будет равен
с?Фсв = —— • Так как длина оси элемента ds остается неизменной,
Г св
то г . d ф — гсв . d фсв.
В качестве меры остаточной кривизны можно принять отношение
остаточного центрального угла элемента к его центральному углу
116
при навивке. Обозначив этот относительный остаточный угол через
0, получим
d фее _ г
«'ф ~ гсв
(в)
Если изогнуть участок ленты по дуге окружности с центральным
углом в один радиан, то остаточный угол этого участка после раз-
грузки и будет равен 0. Величина относительного остаточного угла 0
зависит от деформаций, которые возникают при навивке, т. е. в соот-
ветствии с выражением (а), от отношения — .
Фиг. 60.
а — элемент пружины при
навивке и в свободном со-
* стоянии; б — график от-
носительного остаточного
угла; в — навивка образца
пружинной ленты.
Из выражения (в) следует, что остаточный угол элемента пружины
d фее — 0 d ф. Следовательно, полный центральный угол стабилизи-
рованной пружины в свободном состоянии
2
фее = J 6 • d ф,
0
где i'T — число витков в тугонавитом состоянии и 2 л i т — полный
центральный угол пружины при навивке.
Число ВИТКОВ ice пружины в свободном состоянии определяется
следующим образом:
2лг f
117
Из формулы (б) следует, что dr — d ср. Переходя к перемен-
ной г, получим число витков свободной пружины в виде
dr
h
ленты при различных соотноше-
(например, навивая несколько образцов пружинной ленты
h
можно воспользоваться специ-
го
Испытывая образцы пружинной
ниях 4-
h
постоянной толщины h на оправки различных радиусов г), можно
построить кривую зависимости остаточного угла 0 от отношения
(фиг. 60, б). Остаточный угол0 возрастает с уменьшением отношения
поскольку при этом увеличивается деформация е = — ленты.
В соответствии с выражением (г), заштрихованная площадь графика
будет соответствовать искомому числу витков ice.
Для получения кривой 0 =
альным прибором [71. На этом приборе образец изгибается вокруг
оправки на угол <р = л. После стабилизации многократным изгибом
образец получает остаточную кривизну — и остаточный угол срсв
Г св
(фиг. 60, в), который измеряется по шкале прибора. Относительный
угол 0 находим по формуле
ч
л Фев фев
Экспериментальную кривую 0 =
можно аппроксимиро-
вать гипероолои
Г \ 2 *
h I
(д)
h
Здесь коэффициенты А, В и С зависят от упруго-пластических
свойств ленты.
При достаточно большом радиусе г оправки остаточный угол 0
будет равен нулю. Это означает, что при изгибе на оправке в мате-
риале ленты не возникают пластические деформации. Тот наимень-
ший относительный радиус
будут чисто упругими, можно определить из соотношения (a)
, при котором деформации ленты
уп.
h
= — -— , где еугг — деформация, соответствующая пределу упругости
4 буи
оРп (см. фиг. 59, а).
118
Таким образом, уравнение (д) справедливо при
h
h
yn.
остаточный угол 0=0.
yn
h
И ри -г
h
Для различных материалов пружинной ленты величины коэффи-
циентов А, В и С были определены экспериментально и даны в работе
[7] в табл. 17, где обозначены Хо
Используя уравнение (д)
для относительного остаточ-
ного угла, можно получить
выражение для ice в алгебра-
ической форме. Произведя
интегрирование по формуле
(г), получим
h
'о 'Т
Учитывая, что
— h. (е)
о
для на-
витой пружины справедливо
гт — го
соотношение (2. 21)---— —
= 1?. и введя обозначение
(2. 26)
2
Фиг. 61. Число ВИТКОВ ice свободной пру-
жины в зависимости от числа витков
туго заведенной пружины.
т = -г
Л
преобразуем формулу (е)
в виде
m
(2.27)
m2
\m I
образом, число витков ice свободной стабилизированной
зависит от упруго-пластических свойств материала, от
пружины при навивке и отношения т радиуса
Таким
пружины
числа витков 1Т
внутреннего витка к толщине ленты.
Так же как и уравнение (д), выражение (2. 27) справедливо
в области пластических деформаций, когда наибольший относитель-
, то наружный
Уп
. Если -г-
уп h
h
ныи радиус пружины -г
I V
конец пружины остается упругим и по окончании процесса стабили-
зации выпрямляется. Центральный угол такой пружины и число
ее витков 1св будет определяться только по тому участку, который
после стабилизации получил кривизну, поэтому при дальнейшем
увеличении длины пружины (т. е. при увеличении числа ir витков
при навивке), величина 1св остается постоянной. Это видно из фиг. 61,
119
где в соответствии с выражением (2. 27) построены кривые зависи-
мости 1се от iT для некоторых материалов ленты при т = ~ = 15.
Проектирование нормальной заводной спиральной пружины
Задача проектирования спиральной заводной пружины, как и
любого упругого элемента, имеет не единственное решение. Заданные
требования могут быть удовлетворены при различных соотношениях
размеров. Из всех возможных вариантов следует выбрать наивыгод-
нейший.
Фиг. 62. Кривая спуска заводной пружины.
Работа £7, которую отдает пружинный двигатель при спуске,
пропорциональна площади аАВЬ на фиг. 62, так как
(М"\п + М™х)
2Л TlpaQ.
Для обеспечения плавной работы механизма желательно, чтобы
наибольший момент A7^ax (в начале спуска) лишь незначительно
превышал наименьший момент (в конце спуска), т. е. чтобы
отношение
(2. 28)
было близко к единице. Этому требованию может удовлетворить
пружина малой жесткости с пологой характеристикой.
Снижение жесткости пружины при заданном моменте возможно
в основном за счет увеличения ее длины, что приводит к увеличению
габаритов пружинного двигателя. У заводных пружин большинства
часовых механизмов коэффициент т, характеризующий пологость
характеристики, имеет значения ш = 1,4 3 17].
Приступая к проектированию заводной спиральной пружины,
прежде всего необходимо выбрать ее материал. Материал заводной
120
пружины должен обладать высокими упруго-пластическими свой-
ствами: достаточно большим относительным удлинением Сразр при
разрыве, поскольку в процессе навивки ленте сообщаются большие
пластические деформации, и высоким пределом текучести (Jy, так как
материал заводной пружины работает при высоких напряже-
ниях.
Поэтому для заводных пружин используются высококачествен-
ные пружинные материалы: углеродистые стали У8А—У12А, крем-
нистая пружинная сталь 70С2ХА (ЭИ-142) [7], сплав К40НХМ
(табл. 4—6).
Стремление получить пружинный двигатель малых габаритов
и веса, что особенно важно для переносных приборов, приводит
к использованию прочностных свойств материала до предела.
Пружина получает при изготовлении большие пластические де-
формации. От их величины зависит долговечность пружины, поэтому
коэффициент запаса пружины следует определять не по напряже-
ниям, а по деформациям, как отношение относительного удлинения
при разрыве &ра3р (см. фиг. 59, а) к наибольшей деформации Emax-
Наибольшие деформации возникают при изготовлении во внутрен-
нем витке пружины, где, как правило, и происходит поломка завод-
ных пружин.
Наибольшая деформация етах может быть подсчитана по выраже-
h 1
нию Emax = -к— — -5— , где в соответствии с формулой (2. 26) т =
___ г0
h *
Тогда коэффициент запаса заводной пружины пе — =28pa8J)?n-
етах
Таким образом величина т характеризует прочность заводной
пружины, изготовленной из данного материала. С увеличением т
прочность заводной пружины повышается, но при этом увеличивается
радиус заводного валика и габариты всего пружинного двигателя.
Поскольку заводная пружина работает при переменных напряжениях
в режиме «завод — спуск», то выбор величины т следовало бы производить
с учетом усталостных характеристик материала. Для этого необходимо иметь
зависимость между величиной предельной относительной деформации еп/э и
числом циклов, при котором наступает разрушение пружинной ленты при пере-
менном нагружении. Задавшись коэффициентом запаса по выносливости в виде
пвын ~ -~пр - = 2 епр т и определив предельную деформацию епр по заданному
етах
числу циклов работы пружины, можно из последнего выражения найти величину
т. Однако в настоящее время справочные данные об усталостных характеристи-
ках пружинных лент отсутствуют, поэтому величина т выбирается на основании
накопленного опыта по работе с данным пружинным материалом. Многолетней
практикой проектирования и изготовления заводных пружин часовых механиз-
мов принято для пружин из углеродистых сталей тп = 15 4-16 (7]. При этом
пружинным двигателям обеспечивается долговечность до 30 —40 лет (примерно
8—10 тысяч циклов).
Выбрав материал пружины и задавшись в зависимости от его
свойств и требуемой долговечности отношением ш, можно перейти
124
к определению размеров пружинного двигателя. Ограничимся здесь
рассмотрением задачи проектирования нормальной заводной пру-
жины.
На основании заданных условий — рабочего числа оборотов пРаб,
моментов в начале и конце спуска М^ах и ML— можно построить
рабочий участок АВ характеристики (фиг. 62}. Уравнение характе-
ристики пружинного двигателя при «идеальном» способе крепления,
когда осуществляется чистый изгиб пружины, выражается форму-
лой (2. 18)
л# В в п
М — -г- (р = —у— 2 л п.
Отсюда легко получить уравнение характеристики реальной
пружины при спуске, если вспомнить, что момент при спуске связан
с моментом «идеальной» пружины коэффициентом качества К пру-
жины, значения которого были приведены в табл. 15 в зависимости
от способа крепления наружного конца пружины. Таким образом
Мсп = КМ = К-^-2лп.
Продолжая рабочий участок характеристики пружины до пересе-
чения с осью абсцисс, получаем точку О, соответствующую свобод-
ному состоянию пружины, в котором число витков пружины равно
zC6. Так как в тугозаведенном состоянии число витков равно г'т, то
отрезок Од — iT — ice. Число оборотов, которое необходимо создать,
чтобы перевести пружину из свободного в тугозаведенное состояние,
равное iT — ice, выразим через заданные величины, рассматривая
подобие треугольников ОВЪ и АВК (фиг. 62)
.и
уитах праб
Мсп — Мсп.
max min
или учитывая выражение (2. 28), получим
» •
1т — Ice ~
1П • праб
m—-1
(2.29)
Величина 1? — ice представляет собой упругую отдачу материала
после стабилизации пружины, выраженную в числах витков. Выше,
когда рассматривались способы определения числа ice витков сво-
бодной пружины, была найдена зависимость гсв = /(гт), выражен-
ная формулой (2. 27) и графиком на фиг. 61. На основании этой зави-
симости легко построить кривые i? — iCe ~ f (*т) для различных
материалов пружинных лет при выбранном значении т. Такие кри-
вые построены на фиг. 63 при т = 15.
Определив по формуле (2. 29) величину i? — гсе, находим по
кривым на фиг. 63 число витков Zy, которое должна иметь пружина
в тугонавитом состоянии.
122
Для нормальной заводной пружины справедливо соотношение
th — л (г% — го) = л (Я2 — Гу), (а)
Заменяя радиусы г? = го + г’тй и го = mh по формулам (2. 21)
и (2. 26), получим из равенства (а) относительную длину.пружины
h 1
и относительный радиус барабана
h
123
1Т при
Таким образом относительный радиус барабана и относительная
длина ленты для нормальной заводной пружины определяются
в зависимости от числа ее витков г-р в тугозаведенном состоянии и от
коэффициента прочности т. Для облегчения расчета на
I R
построены кривые — и - - в зависимости от числа витков
п Г1
т — 15.
Толщина ленты находится из уравнений (2. 19) и (2. 20)
д/ .___ ^max EJ о х
Л/ max — --т?-- = --— ZJl (It — Ice) —
Ebh3
121
~ Iceh
Заменив здесь -г- выражением (б) получим
1£
6Л/СП
и max
(2. 30)
Таким образом, расчеты при проектировании заводной пружины
сводятся к следующему. По формуле (2. 29) находится разность
/т — ?св, затем по графику на фиг. 63 определяются значение i?
I п
и соответствующие ему относительные размеры пружины и ,
по которым вычисляются длина пружины I и радиус барабана R.
Толщина h определяется по формуле (2. 30).
Длина 13 заготовки пружины должна быть больше рабочей
длины I на длину отожженных концевых участков, которые служат
для закрепления пружины. Длина внутреннего и наружного нерабо-
чих участков пружины выбирается [7] из соотношений
05-
(2.31)
где го — радиус внутреннего витка пружины, определяемой по
выражению (2. 26),
Го = mh. (2. 32)
Длина заготовки пружины l3 = I + 1в 4~
Отожженный участок пружины плотно прилегает к валику при-
мерно на одном обороте, поэтому радиус валика будет равен
Число оборотов двигателя при заводе находится из соотношения
h
Число холостых оборотов определяется, как разность
Tlx — Пзав — Праб •
124
Пример 1 *. Спроектировать пружинный двигатель для часов, если из рас-
чета механизма известны минимальный момент спуска = 0,65 кгс • мм,
отношение моментов спуска
СП
max
Мсп-
л min
— 1,45 и число рабочих оборотов
ш =
М
Праб= 4. Наружный конец пружины крепится с помощью мечевидной на-
кладки. Материал пружины — сталь У8А, модуль упругости £=2,0 -104 кгс!мм2
(табл. 5).
Решение. Находим по формуле (2. 29) разность между числом витков
пружины в туго зав еденном и в свободном состояниях
. _. __ m праб _ 1,45 • 4 _
ice — 1,45 — 1
Задаваясь отношением т — 15, находим по графику 1Т — 17 и соответ-
ственно 4— = 2550 и = 43 (см. фиг. 63).
Л Л
Толщину h ленты находим по выражению (2. 30}, где наибольший момент
при спуске = ш • Л/^п ~ 1 »45 ‘0>65 = 0,943 кгс.мм. Из табл. 15 находим
коэффициент качества К. При креплении мечевидной накладной К ~ 0,9.
Зададимся шириной ленты b ~ 1,44 мм. Тогда толщина h будет
6-МсюУ*т.(2ш-Мт)
KEb (jT — ice)
6-0,943-17 (2-15+ 17)
0,9 • 2,0 • 104 • 1,44 • 12,9
= 0,12 мм.
Затем находим радиус г о внутреннего рабочего витка пружины, радиус
R барабана и рабочую длину I пружины: го = mh — 15-0,12 = 1,80 мм;
R = 43д = 43.0,12 = 5,16 мм; I = 2550Л = 2550 -0,12 = 306 мм.
Длину отожженных концевых участков находим по соотношениям (2. 31)
1в = 3 л го — 3 л -1,80 ~ 17 мм; 1Н 1,5 л г о ~ 8 мм. Следовательно, длина
заготовки для пружины 1з ~ I + + 1н~ 306 + 17 + 8 = 331 мм.
По выражению (2. 33) находим радиус валика гв = г0 — 1,5h — 1,80 —
— 1,5-0,12 = 1,62 мм.
Число оборотов двигателя при заводе определим по формуле (2. 34)
V 2(Я2 + ^)-(Л+г„)
Пзав - h
/2 (5,162 +1,802)~ — (5,16 +1,80)
Число холостых оборотов по формуле (2. 35) пх — пзае — праб ~ 6,5 —
— 4 = 2,5.
Пример 2. Пружинный двигатель часов марки АЧХ имеет следующие
размеры: R ~ 13,6 мм, h = 0,32 мм, b ~ 6,75 мм, I ~~ 840 мм. Число рабочих
оборотов Праб — 5, число оборотов при заводе пзав = 6,25. Материал пру-
жины — сталь 70С2ХА (ГОСТ 2283-57), £ = 2,1 • 104 кгс!мл^. Минимальный
тчгсп. nr. max л о
момент спуска 20 кгс • мм, отношение моментов спуска m = ---— 1,8.
II1LU дтСТТ
ш min
Наружный конец пружины крепится-мечевидной накладкой (коэффициент ка-
чества К = 0,9).
* Условия примеров 1 и 2 взяты из работы [7].
125
Как изменятся размеры барабана и пружины, а также число оборотов при
заводе, если с целью выравнивания кривой спуска уменьшить отношение щ
до значения m = 1,1. При этом величины M^in, Краб, Ъ и материал оставить
прежними.
Решение. По выражению (2. 29) находим
Ш-Лраб 1,1-5 _г
гт-^=-Н=Г=-04~=55
и по графику на фиг. 63 определим
iT = 62; 4- = 17 800; = 108. (а>
1 h h
Максимальный момент спуска = ш • = 1,1 -20 = 22 «гс-лль
Толщина пружины в соответствии с выражением (2. 30) будет
6-22-62 (30 + 62)
0,9 2,1 • 104 - 6,75 • 55
= 0,327 мм.
Учитывая, что т — ~ = 15, получим по соотношениям (а) размеры пружи-
ны и барабана I = 5820 мм, R = 35, 3 мм, г© = 4,76 мм.
Число оборотов при заводе в соответствии с выражением (2. 34), равно
_ /2 (35,.+ + 4++~(35,3 + 4,76) _
Паа‘ ~ 0,327 —31,6.
Число холостых оборотов по формуле (2. 35) пх — naae — п^аб = 31,5 —
— 5 = 26,5.
Приведенный пример показывает, что получение пологой характе-
ристики пружинного двигателя с коэффициентом щ, близким к еди-
нице, сопряжено со значительным увеличением его размеров. Так,
уменьшение тп от 1,8 до 1,1 вызвало увеличение длины пружины
в 7 раз, диаметра барабана в 2,6 раза, при этом число холостых
оборотов возросло в 21 раз. Для получения пологой характеристики
пружинного двигателя существуют другие более рациональные
методы.
Пружинные двигатели с пологой характеристикой
В ряде случаев, особенно для точных часовых механизмов,
требуется пружинный двигатель с практически постоянным момен-
том.
Решение этого вопроса с помощью различных дополнительных
устройств приводит к существенному усложнению механизма. Рас-
смотрим, например, так называемую «улитку» (фиг. 64), которая при-
меняется с целью выравнивания момента в ряде хронометров. Улитка,
с оси которой снимается момент заводного двигателя, представляет
собой спиральный кулачок, соединенный цепочкой или гибкой лентой
с заводным барабаном. Завод производится вращением оси улитки,
при этом на нее наматывается цепочка. При спуске заводной пру-
жины цепочка наматывается на барабан, сматываясь с улитци.
126
Момент на барабане, а следовательно, и усилие в цепочке при
спуске пружины падают, что компенсируется увеличением плеча
усилия, т. е. расстояния от оси улитки до той точки, где цепочка
сходит с улитки. Поэтому момент на оси улитки может поддержи-
ваться постоянным.
aininiiuiril
IWMMIIIIIllIlll
МП—111111ИННГ
j । i friillilHWhr
Фиг. 64. Механизм «улитки».
IIH4IIIIIII1W1HIHIIIIIHI1111
Выравнивание спускового момента может быть получено не только
введением подобных дополнительных конструктивных элементов, но
также путем изменения конструкции заводной пружины.
Фиг. 65. Зависимость момента заводной пружины от ее формы в сво-
бодном состоянии.
Так, уменьшение кривизны в свооодном состоянии при сохране-
нии всех остальных размеров пружины приводит к увеличению мо-
мента, поскольку при этом увеличивается число оборотов валика
при переводе пружины от свободного до тугозаведенного состояния
(фиг. 65).
Большое увеличение спускового момента может быть достигнуто,
если в свободном состоянии пружина будет изогнута в обратную
сторону, т. е, будет иметь отрицательную кривизну. Из фиг. 65
видно, что уменьшение кривизны свободной пружины дает при общем
127
увеличении^ моментов на рабочем участке уменьшение отношения
Мсп
tn = -юах. .
Мсп.
min
Изготовить пружину, имеющую в свободном состоянии отрица-
тельную кривизну по всей длине ленты, оказывается невозможным.
При изготовлении такой пружины она должна навиваться сначала
на вспомогательную оправку, получая отрицательную кривизну.
При последующей навивке на заводной валик внутренние витки пру-
жины деформируются так сильно, что в них появляются остаточные
деформации. Отрицательная кривизна
Фиг. 66. S-образная пру-
жина.
сохраняется только у наружных витков,
которые при навивке на заводной валик
деформируются меньше, и поэтому пру-
жина получает S-образную форму
(фиг. 66).
Наружные витки пружины S-o б р а з-
н о й формы при работе деформиру-
ются более интенсивно, чем у обычной
спиральной пружины. Число оборотов
S-образной пружины при переводе от
свободного до тугозаведенного состоя-
ния будет больше, чем у обычной пру-
жины при тех же размерах ленты. Поэтому
S-образные пружины при спуске разви-
вают на рабочем участке большие по
величине моменты при более пологой
характеристике.
Большую пологость
отдаваемого момента имеет
(фиг. 67, а).
характеристики при увеличении
также желобчатая пружина
Желобчатая лента более жестка на изгиб, чем плоская. При неко-
тором критическом значении изгибающего момента желобчатая лента
теряет устойчивость: поперечное сечение внезапно выпрямляется,
и желобок на пружине исчезает. Так как момент инерции прямоуголь-
ного сечения меньше, чем желобовидного, то потеря устой-
чивости сопровождается падением изгибной жесткости ленты.
На фиг. 67, б представлена характеристика желобчатой ленты при
изгибе.
При выпрямлении сечения желобчатой ленты в ней возникают
поперечные деформации еу удлинения в верхней половине и укоро-
чения — в нижней (фиг. 67, в). В точках верхней поверхности
еу ~~~ (h — толщина ленты, а — первоначальный радиус кривизны
желобка). Продольные деформации ех связаны с деформацией еу
коэффициентом Пуассона ех = —реу, вследствие чего лента при
выпрямлении желобка изменит свою кривизну в продольном напра-
влении, как показано на фиг. 67, в. Чтобы выпрямить ось ленты,
128
потребуется некоторый момент Мо. Его величину можно найти по
выражению
bh1 2
где a* — продольное напряжение в точках
наружной
поверхности.
Л/4
Фиг. 67.
(ж}
(п)
Желобчатая заводная
пружина:
а — желобчатая лента; б — характери-
стика при изгибе желобчатой (ж) и
плоской (п) ленты; в — изменение кри-
визны элемента желобчатой ленты и
возникающие в ленте деформации при
выпрямлении желобка; г — перемеще-
ние желобчатой пружины в барабане
плотным кольцом; д — диаграмма
заводной желобчатой пружины.
По закону Гука при двухосном
1—
В плоском состоянии ленты е
напряженном состоянии
h
2~- , следовательно
-р,
h
2а
Отсюда момент
Мо — Р*
а
2
Л т ЬЬ8
где Jv =
9 Заказ 24.
129
Таким рбразом, для создания одной.и той же кривизны в закрити-
ческой области к желобчатой ленте должен быть приложен изгибаю-
щий момент Мж, отличающийся от момента Мп плоской пружины на
величину 7И0:
Мм — Мп + М$*
(а)
Здесь Мп =
поперечном сечении
— — изгиоающии момент, возникающий в
первоначально плоской пружины при ее
изгибе по дуге радиуса Q. Знак «минус» в выражении (а) соответ-
ствует изгибу желобчатой пружины в сторону увеличения кривизн^!,
возникающей при исчезновении желобка, а знак «плюс» — изгибу
в противоположном направлении (фиг. 67, б).
Заводная пружина из желобчатой ленты конструируется так,
чтобы она работала в закритической области, т. е. на участке А^В
характеристики (фиг. 67, б). В свободном состоянии ось такой пру-
жины близка к прямолинейной, и на рабочем участке характеристики
она развивает при спуске больший момент, чем обычная спиральная
пружина. При этом уменьшается отношение
Мсп
max
m —__________
Л/сп.
min
Особенность желобчатых пружин состоит в том, что при заводе
и спуске пружинная лента перемещается в барабане плотным кольцом
(фиг. 67, а). Прямая лента при чистом изгибе должна получить
постоянную кривизну. Однако в ленте, изогнутой в спираль, только
средний виток будет иметь кривизну, соответствующую величине
приложенного изгибающего момента; наружные витки имеют мень-
шую, а внутренние — большую кривизну, и, стремясь принять
кривизну среднего витка, они давят Друг на друга. Величина этого
давления и пропорционального ему межвитков ого трения будет
наибольшей в полностью заведенной пружине; по мере спуска пру-
жины межвитковое трение уменьшается. Такой характер изменения
межвиткового трения способствует еще большей пологости кривой
спуска. Это дает возможность получить пружинный двигатель
с почти нулевой и даже отрицательной на некотором участке жест-
костью (фиг. 67, д).
Пружины S-образной формы при спуске также перемещаются
плотным кольцом, что увеличивает пологость их характеристики.
Некоторым недостатком таких пружинных двигателей является
зависимость кривой спуска от коэффициента трения, который не
остается постоянным при различных условиях работы и меняется
в течение срока службы двигателя.
Методы расчета S-образных и желобчатых пружин изложены
в работах [44], [45] и [7].
ГЛАВА III
ВИНТОВЫЕ ПРУЖИНЫ
§ 8. ТИПЫ ВИНТОВЫХ ПРУЖИН, СПОСОБЫ ИЗГОТОВЛЕНИЯ,
ПРИМЕНЕНИЕ
Винтовая пружина обычно навивается из проволоки в виде про-
странственной спирали. Наибольшее применение имеют винтовые
цилиндрические пружины (фиг. 68, а), как самые простые
в изготовлении и эксплуатации. К винтовым пружинам относятся
также и спиральные фасонные пружины: конические, парабо-
лоидные (фиг. 68, б, в). Изготовление этих пружин более сложно,
и они применяются реже.
Фиг. 68. Типы винтовых пружин:
« — цили дрическая; б — коническая; в — параболоидная; г — пружина,, изготовленная
точением и фрезерованием
Пружина способна получать значительные взаимные перемещения
торцов при малых упругих деформациях проволоки. Винтовые пру-
жины компактны и обычно легко размещаются в механизме
прибора.
Все сечения винтовой цилиндрической пружины нагружаются
одинаково (за исключением концевых витков), что в сочетании с вы-
сокими качествами пружинной проволоки обеспечивает хорошую
стабильность упругих свойств и надежность винтовых пружин
в работе.
9*
131
Простота изготовления винтовых пружин определяет их низкую
стоимость к^к в крупносерийном, так и в единичном производстве.
Пружина может навиваться на оправке на обычном или специально
приспособленном токарном станке.
Диаметр оправки должен быть меньше внутреннего диаметра
готовой пружины, так как при снятии навитой пружины с оправки
ее диаметр увеличивается вследствие упругой отдачи материала.
Диаметр оправки обычно подбирается после ряда пробных навивок
пружины на оправках различных диаметров или после навивки на
пологой конической оправке. Предварительно он может быть прибли-
женно рассчитан по методике, изложенной в работах [46], [47].
Навивкой на оправке пружина может быть быстро изготовлена
почти на любом предприятии, поскольку для этого не требуется
специального оборудования.
Значительно более производительна навивка пружин на спе-
циальных пружинно-навивальных автоматах, где проволока подается
на штифты, которые придают ей форму винтовой линии. Процесс
навивки может производиться непрерывно с оформлением концевых
витков и периодической отрубкой готовых пружин. На пружинно-
навивальных автоматах изготовление фасонных пружин и пружин
с начальным натяжением проще, чем на оправке.
Навивка пружин из тонкой, достаточно пластичной, проволоки
производится в холодном состоянии. Если диаметр проволоки пре-
вышает 10—12 мм, или отношение диаметра пружины к диаметру
проволоки меньше 5—6, или материал проволоки имеет низкие пласти-
ческие свойства, то навивка пружины производится с нагревом про-
волоки.
В некоторых случаях применяются пружины с прямоугольным
.сечением витка (фиг. 68, г), изготовляемые из трубки токарно-
фрезерной обработкой. Таким способом может быть изготовлена
пружина из материала с высокими упругими и прочностными свой-
ствами, если его низкая пластичность не позволяет получать из него
пружины навивкой. Трудоемкость изготовления таких пружин
оправдывается в том случае, когда к качеству пружины предъявля-
ются особенно высокие требования.
Материал винтовой пружины подбирается в зависимости от
назначения пружины, требований к ее качествам и условий работы.
Для изготовления многих пружин применяется специальная
термообработанная пружинная проволока (например, проволока
по ГОСТ 9389-60, см. табл. 3). Технология изготовления пружин
из такой проволоки проста, так как нет надобности в термической
обработке навитой пружины. Иногда такие пружины проходят
операцию старения при невысоких температурах нагрева с целью
уменьшения остаточных напряжений, возникших при навивке.
Для пружин ответственного назначения, которые должны обла-
дать более высокими упругими свойствами, применяются закаливае-
мые стали (см. табл. 5) и дисперсионно-твердеющие сплавы (см.
табл. 6). После навивки пружины, изготовленные из этих материалов,
132
проходят термообработку, в результате чего материал получает высо-
кие упругие и прочностные свойства.
Для предотвращения коррозии поверхность пружин защищается
различными покрытиями. Для этого применяются фосфатирование,
цинкование, хромирование и другие способы защиты 1. При кон-
струировании пружины следует учитывать возможность изменения
ее упругих свойств в результате применения покрытий2.
Вопрос выбора типа покрытия, а также другие вопросы техноло-
гии пружин подробно освещены в специальной литературе [48]
и [49].
Жесткость винтовой пружины определяется упругими свойствами
материала и следующими геометрическими параметрами: средним
диаметром пружины D, размерами поперечного сечения проволоки
и числом рабочих витков i. Отношение среднего диаметра пружины
к диаметру проволоки с = (фиг. 68, а) называется индексом пру-
жины. При некруглом сечении проволоки индекс определяется как
D
с = —, где а — толщина проволоки в направлении радиуса витка
(фиг. 68, г). Варьируя этими параметрами, можно изменять жесткость
пружины в очень широких пределах. Поэтому сравнительно легко
спроектировать пружину требуемой жесткости в пределах заданных
габаритов* При необходимости можно получить ряд пружин разных
жесткостей при одних и тех же габаритных размерах. Это позволяет
использовать сменные пружины в различных диапазонах работы
прибора при сохранении его конструкции.
По условиям нагружения винтовые пружины можно разделить на
пружины растяжения, сжатия, кручения и изгиба (фиг. 69).
Благодаря простой и компактной конструкции, хорошим рабочим
качествам, простоте изготовления, винтовые пружины находят
широкое и разнообразное применение в приборах.
Высокие упругие свойства обусловливают успешное применение
винтовых пружин в качестве измерительных, преобразую-
щих измеряемое усилие в перемещение. Измерительные винтовые
пружины широко применяются в манометрических приборах со-
вместно с разделительными элементами в виде сильфонов или эластич-
ных мембран (фиг. 70, п), в качестве силового элемента настройки
нижнего или верхнего предела измерения, например, в манометре
с безнулевой шкалой (фиг. 70, б). Винтовые пружины используются
в качестве измерительных в прецизионных хронометрах3.
В последние годы появились измерительные пружины, предназ-
наченные для преобразования линейного перемещения в угловое.
1 Г р и н б е р г А. М. и Го рина А. П., Антикоррозионная защита
стальных пружин, Судпромгиз, 1958.
2Феликсон Е. И., Исследование упругих несовершенств метроло-
гических пружин, подвергнутых защитным антикоррозионным покрытиям,
Труды НИКИМП, 1958.
3 Дроздов Ф. В., Детали приборов, Оборонгиз, 1948.
133
Фиг. 69. Винтовые пружины:
а — растяжения; б — сжатия; в — кручения; г — изгиба-
Фиг. 70. Примеры применения винтовых пружин:
а — в сильфонном измерителе давления; б —-в манометре с безнулевой
шкалой; в — в передаточном механизме барометра; а — в муфте односторон-
него вращения.
134
Они представляют собой тонкую металлическую ленту, каждая поло-
вина которой навита в противоположном направлении по винтовой
линии большого угла подъема. При осевой деформации такой пру-
жины ее среднее сечение получает значительные угловые перемеще-
ния (до 7—10 оборотов). Такие пружины могут быть использованы
в высокочувствительных весах, в приборах для измерения линейных
размеров, в микроманометрах и барометрах (фиг. 70, #) и в других
приборах Ч
Винтовые пружины используются особенно часто в качестве
натяжных, обеспечивая необходимую силу натяга между дета-
лями прибора. Иногда они применяются как пружинные дви-
гатели, например, в фотозатворах, в механизмах привода различ-
ных счетных и регистрирующих приборов и пр.
Винтовые пружины используются и в других более специальных
целях. В качестве амортизатора часто применяются конические
пружины. Пружины кручения находят применение как тормозы,
муфты одностороннего вращения (фиг. 70, г) и т. д.
§ 9. КОНСТРУКЦИЯ ВИНТОВЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
РАСТЯЖЕНИЯ — СЖАТИЯ
+
В условиях работы пружин растяжения и пружин сжатия разли-
чие заключается лишь в направлении действия осевой силы. Только
это и определяет разницу в их конструкции.
В ненагруженном состоянии пружины сжатия должны иметь
зазор между витками, достаточный для получения рабочей осадки
Фиг* 71. Концевые витки и зацепы винтовых цилиндрических пружин.
пружины. У пружин растяжения межвитковый зазор либо мал, либо
вовсе отсутствует. Кроме этого, пружины растяжения отличаются от
пружин сжатия оформлением концевых витков, через которые
пружине передается нагрузка.
Для предотвращения изгиба пружины сжатия при неосевом
приложении силы (фиг. 71, а) в большинстве случаев достаточно
навить концевые витки (1—2 витка) без зазора между ними и затем
►
1 Мануйлов К. И., Цилиндрическая ленточная пружина как переда-
точный механизм, Труды НИИГМП, № 8, 1959, а также [17].
135
сошлифовать их по плоскости, перпендикулярной оси пружины на
длине от 3/4 до 1 витка (фиг. 71, б). Пружина сжатия легко центри-
руется буртиком или выточкой в опорной плоскости (фиг. 71, в).
Концй пружины растяжения приходится оформлять в виде заце-
пов. Наиболее часто применяемые формы зацепов показаны на
фиг. 71, г—з.
Зацеп, получаемый отгибом последнего витка (фиг. 71, г) техно-
логически наиболее прост. Однако такой зацеп при работе сильно
деформируется и создает эксцентрицитет нагрузки, что приводит
к искажению характеристики пружины. Изготовление зацепов по
фиг. 71, д сложнее, но они обеспечивают большую точность передачи
усилия по оси.
Зацепы усложняют изготовление пружин и часто являются их
слабым местом. Прочность зацепа повышается при постепенном
уменьшении диаметров последних витков пружины (фиг. 71, е).
Измерительные пружины должны иметь стабильную характери-
стику и минимальные потери на трение, что следует учитывать при
конструировании пружин приборов повышенной точности. Таким
требованиям удовлетворяет, например, пружина с зацепом, указан-
ным на фиг. 71, ж. Такой зацеп хорошо фиксирует место приложения
растягивающего усилия. С этой точки зрения еще лучше крепление
приваркой проволоки, отогнутой по оси пружины (фиг. 71, з).
Выполнение указанных требований для измерительных пружин
сжатия сложнее, поскольку здесь приложение нагрузки происходит
не в точке, а по плоскости, что затрудняет передачу усилия точно но
оси. Кроме того, характеристика дополнительно искажается вслед-
ствие изменения рабочей длины проволоки при посадке концевых
витков. Для повышения точности в пружинах сжатия иногда прива-
ривается перемычка между последним рабочим и опорным витками
(фиг. 71, и). Этим уменьшается деформация концевых витков при
сжатии пружины. С такой же целью применяют фиксатор винтовой
формы (фиг. 71, к), который твердым припоем впаивается между
концевыми витками. В весьма хороших условиях работают концевые
и опорные витки пружин, изготовляемых из трубки (см. фиг. 68, г).
Во многих случаях желательна регулировка жесткости пружины
путем изменения числа рабочих витков. Для этого обычно применяют
крепление концов пружин (как растяжения, так и сжатия) на резь-
бовых пробках (фиг. 71, л). Недостаток такого крепления заклю-
чается в его сложности. Кроме того, между пробкой и прилегающей
к ней проволокой возникают силы трения, а в случае жесткого кре-
пления пробки силы на пружину передаются нецентрально.
Более простую конструкцию по сравнению с резьбовой пробкой
имеет пластинка с отверстиями, применяемая для пружин растяже-
ния (фиг. 71, м). Однако она хуже обеспечивает, чем резьбовая
пробка, передачу усилия по оси пружины.
Пружина сжатия практически нечувствительна к перегрузкам,
если она сконструирована так, что при предельной нагрузке витки
пружины смыкаются. В этом случае пружина приобретает форму
135
жесткого цилиндра, работающего на сжатие. Лишь при большом
индексе возможна потеря устойчивости полностью сжатой пружины,
проявляющаяся в выскальзывании отдельных витков в боковом
направлении.
Для защиты от перегрузок пружин растяжения приходится
использовать специальные упоры и ограничители.
Пружины сжатия по сравнению с пружинами растяжения кон-
структивно проще, дешевле в изготовлении и надежнее в работе.
Однако при требовании малой жесткости пружины растяжения
имеют преимущество перед пружинами сжатия. Уменьшение жестко-
сти пружины может быть достигнуто за счет увеличения индекса
и числа витков, но это приводит к росту габаритов пружины и паде-
нию ее изгибной жесткости. Для пружины сжатия рост высоты
увеличивает опасность потери устойчивости. Увеличение же числа
витков пружины растяжения ограничивается только габаритными
условиями.
Очень часто пружины растяжения выполняются с начальным
натяжением (межвитковым давлением). Они отличаются от обычных
пружин тем, что до тех пор, пока растягивающая сила не достигнет
определенной величины, она не вызывает деформации пружины.
Вопросы изготовления и расчета пружин с начальным натяжением
изложены в § 71.
§ 10. ГЕОМЕТРИЯ ВИНТОВОЙ ЦИЛИНДРИЧЕСКОЙ ПРУЖИНЫ
На фиг. 72 показаны винтовая линия пружины и ее развертка
на плоскость. На фигуре обозначены: Н — высота рабочей части
пружины; D — средний диаметр; I — рабочая длина проволоки,
из которой навита пружина; ф — центральный угол пружины;
i — число рабочих витков; а — угол подъема винтовой линии.
Зная высоту Н, диаметр D и число витков i, можно легко вычи-
слить и остальные размеры пружины. Угол подъема а можно найти
из соотношения
= ^ЪТ •
137
Длина проволоки равна
Н _ лш
sin a cos а
7
V
Центральный угол пружины определяется по выражению
cos а .
Прежде чем перейти к расчету на жесткость винтовой пружины,
напомним некоторые понятия, связанные с геометрией винтовой
линии как пространственной кривой.
На фиг. 73, а показаны три взаимно-перпендикулярные прямые,
проведенные в точке А винтовой линии: касательная t, главная
нормаль п и бинормаль Ь.
Фиг. 73. Геометрия винтовой линии:
а — касательная, нормаль и бинормаль винтовой линии; б — нормали и бинормали плоской
кривой; в — к определению кривизны и кручения винтовой линии.
Касательная t и бинормаль Ъ расположены в плоскости bAt,
касательной к поверхности цилиндра, на котором находится винто-
вая линия. Эта плоскость касается цилиндра по образующей А В.
Касательная t и главная нормаль п лежат в соприкасающейся
плоскости nAt винтовой линии. Соприкасающуюся плоскость можно
представить как плоскость, проходящую через три бесконечно близ-
кие точки линии. Главная нормаль, будучи перпендикулярна каса-
тельной плоскости, пересекает ось цилиндра 00 под прямым углом.
Бинормаль Ъ и главная нормаль п лежат в плоскости, нормальной
к винтовой линии. Угол между бинормалью и образующей АВ
цилиндра равен углу подъема винтовой линии а, т. е. углу между
касательной t и плоскостью, перпендикулярной оси ОО.
В частном случае плоской кривой главная нормаль распола-
гается в плоскости кривой и называется просто нормалью. Бинор-
маль же будет перпендикулярна плоскости кривой (фиг. 73, б).
138
Геометрия пространственной линии характеризуется кривизной
и кручением. Кривизна характеризует изменение направления кри-
вой линии при перемещении вдоль этой линии. Проведем к двум
близким точкам М и N касательные t и tr (фиг. 73, в). Через точку М
проведем прямую р параллельно касательной t'. Обозначим угол
между t и t' через dtp, а дугу MN — ds. Тогда кривизна х опре-
делится как предел отношения угла между касательными t и t'
к соответствующей дуге
_ <Др
ds
Понятие кручения аналогично понятию кривизны. Если кривизна
характеризует отклонение кривой линии от прямой, то кручение
определяет отклонение пространственной кривой от плоской. На
фиг. 73, в показаны две бинормали b и bf в точках М и N кривой.
В точке М проведем прямую q параллельно бинормали Ъ', угол
между этой прямой и бинормалью b обозначим через tip. За меру
кручения принимается предел отношения угла
Ъ и Ь' к соответствующей дуге: ~ .
Бинормали в каждой точке плоской кривой
собой (фиг. 73, б), и кручение плоской кривой
Кривизна и кручение винтовой линии выражаются через ее
параметры
между бинормалями
параллельны между
равно нулю.
по формулам
2 cos2 а
(3-4)
(О =
sin 2 а
(3.5)
При растяжении пружины ее высота Н и угол подъема а увели-
чиваются, при этом кручение винтовой линии возрастает, кри-
визна уменьшается, и торцы пружины получают взаимные линейные
и угловые перемещения.
В области малых перемещений изменение А Н высоты пружины
может быть получено как дифференциал высоты Н, которую по
соотношению (3. 2) можно представить в виде Н — I sin а. Поскольку
длина I проволоки остается неизменной, то
А Н — I cos а • Да.
(3.6)
Изменение Аф центрального угла ф получим, дифференцируя
выражение (3. 3). Учцтывая, что при деформации пружины могут
изменяться как угол подъема а, так и диаметр Z), получим
А ф —-------(A a sin а 4“
(3. 7)
cos а;
1 Выгодский
издат, 1949.
М. Я., Дифференциальная геометрия, Гостехтеор-
139
Изменения угла наклона а и диаметра D пружины А а и AZ2
можно связать с изменениями Ах и Дю кривизны и кручения, диф-
ференцируя выражения (3. 4) и (3. 5) по а и по D
ь 2 sin 2а, 2 cos2 а ,
Ах —------н Да---------г—— Д /Л
D D*
А 2 cos 2 а Л sin 2 а А
До =2 ------Да —-----—— Д D.
D D~
Решая эти уравнения относительно Да и A Z), получим
D
2
Да
Д D
D-
(Дю — Дх tg а);
4А — tg2a) — Дев tg а.
(3. 8)
Заменяя с помощью формул (3. 8 ) в уравнениях (3. 6) и (3. 7)
величины Да и ДР, выразим приращения высоты Н пружины
и центрального угла ф через изменения кривизны и кручения
А Г у Jt У)2 Г j л Л J \ 1
Д Н — —~— (До — Дх tg а); [
Дф — п Di( Дх -р До tg а). J
(3.9)
Из анализа этих выражений следует, что высота Н пружины
возрастает при увеличении кручения о и при уменьшении кривизны
х. Для пружины с малым углом подъема а изменение кривизны Дх
влияет на изменение высоты пружины в меньшей степени, чем изме-
нение кручения До.
Центральный угол ф при повороте торцов пружины возрастает
с увеличением как кривизны х, так и кручения о винтовой линии,
причем для пружин с малым углом подъема а изменение Д ф будет
зависеть в основном от изменения кривизны Дх.
§11. РАСЧЕТ НА ЖЕСТКОСТЬ ПО ЛИНЕЙНОЙ ТЕОРИИ [2], [39]
Жесткость пружины зависит от ее размеров, материала и способа
закрепления концов. При расчете будем рассматривать два типа
крепления торцов пружины:
1) свободное крепление, при котором торцы пружины могут сво-
бодно поворачиваться вокруг ее оси, и при нагружении пружины
число витков может изменяться;
2) глухое крепление, при котором торцы не могут поворачи-
ваться. При таком креплении число витков пружины в процессе
ее нагружения не меняется; в заделке появляется реактивный мо-
мент, препятствующий повороту торцов пружины вокруг ее оси;
Креплением, близким к свободному, обладают пружины растя-
жения с зацепами и пружины сжатия, если опорные плоскости мо-
гут поворачиваться относительно друг друга (например, если один
из торцов пружины упирается на подпятник, как показано на
140
фиг. 74, а). К этому же типу крепления следует отнести пружину
с противоположной навивкой на ее половинах (фиг. 74, б). При ра-
стяжении или сжатии такой пружины ее торцы вследствие симмет-
рии не стремятся поворачиваться относительно друг друга, по-
этому в опорах не возникают силы трения. При этом среднее сече-
ние может свободно поворачиваться относительно концевых.
Глухое крепление осуществляется у пружин растяжения и сжа-
тия при жестком креплении резьбовых пробок, а также у большин-
ства пружин сжатия #за счет сил трения, воз-
никающих между пружиной и основанием
(см. фиг. 71, б, в, к, л).
Следует отметить, что реальные конструк-
ции крепления многих пружин не соответ-
ствуют вполне свободному или глухому креп-
лению, а являются промежуточными, более
или менее приближающимися к тому или
иному типу.
Осадка пружины X, т. е. взаимное переме-
щение ее торцов вдоль оси пружины, равна
изменению А Н высоты пружины. Угол пово-
рота 6 одного торца пружины относительно
другого вокруг ее оси равен изменению Аф
центрального угла пружины. Осадка % и угол
а) б)
Фиг. 74.
а — пружина на шпиле-
вой опоре; б — пружина
с противоположным на
правлением навивки.
поворота 6 зависят от изменений кручения и кривизны А<о и Ах
винтовой оси пружины в соответствии с выражениями (3. 9).
(3.10)
здесь/? — средний диаметр пружины;
i — число рабочих витков (полное число витков на 2—3 больше
за счет нерабочих концевых витков);
а — угол подъема винтовой оси.
В свою очередь изменения кручения и кривизны А со и А х свя-
заны с изгибающим и крутящим моментами, возникающими в по-
перечном сечении проволоки при нагружении пружины, уравнениями,
основанными на законе Гука [34]
Д<о = -^-; Дх = -^- ,
О л
(3.41)
здесь А х — изменение кривизны и А о — изменение кручения
винтовой оси пружины при ее деформации, В = Е Jb и С — G JK—
жесткости проволоки на изгиб и на кручение соответственно, Е
и G — модуль упругости первого и второго рода, Jb — осевой мо-
мент инерции поперечного сечения проволоки относительно бинор-
мали Ъ; Jk — геометрическая характеристика, определяющая жест-
кость сечения при кручении.
141
Крутящий и изгибающий моменты могут быть выражены через
внешние силы с помощью метода сечений.
При глухом креплении пружина растяжения-сжатия нагру-
жается, помимо осевой силы Р, реактивным моментом 9)?, возникаю-
щим на торцах пружины в плоскости, перпендикулярной ее оси
(фиг. 75, а). Рассмотрим этот общий случай нагружения пружины
растяжения-сжатия.
Из условия равновесия части пружины, отсеченной плоскостью,
нормальной к винтовой линии, момент внутренних сил в осевой
PD
плоскости пружины будет равен —к—(фиг. 75, б). Торцовый момент Эл
уравновешивается моментом, лежащим в плоскости, перпендикуляр-
ной оси пружины. Кроме того, в сечении возникает сила Р напра-
вленная вдоль оси пружины. Для нахождения крутящего и изги-
бающего моментов рассмотрим фиг. 75, в, где показаны проекции
PD
моментов и У.ч на нормальную и на соприкасающуюся к винто-
вой линии плоскости. Крутящий момент представляет собой момент
внутренних сил относительно касательной t к винтовой линии
« PD
и равен сумме проекций моментов —и 9ft на плоскость попереч-
ного сечения проволоки, т. е. на нормальную плоскость
PD
Мк — ?— cos а + 9ft sin а. (3. 12)
^4
142
Изгибающий момент — сумма моментов внутренних сил отно-
сительно бинормали b — определяется, как сумма проекций момен-
PD сто
тов —- - и 9/с на соприкасающуюся плоскость
PD
Ми = 9ft cos а — -—к— sin а.
(3.13)
Сила Р может быть разложена па нормальную силу (проекция
на касательную if) и на поперечную силу (проекция на бинормаль 6),
однако они мало влияют на осадку пружины по сравнению с изги-
бающим и крутящим моментами, поэтому исключим их из дальней-
шего рассмотрения.
При сжатии или растяжении пружины ее диаметр D и угол подъ-
ема а изменяются. Поэтому крутящий и изгибающий моменты в соот-
ветствии с выражениями (3. 12) и (3. 13) нелинейно зависят от на-
грузки. Следовательно, и деформация проволоки пружины, пропор-
циональная в пределах закона Гука изгибающему и крутящему
моментам, будет нелинейно связана с нагрузкой. Этим объясняется
то, что характеристика винтовой пружины, вообще говоря, нели-
нейна.
Если при выводе уравнения характеристики пренебречь влиянием
изменений размеров пружины в процессе ее деформации на величины
изгибающего и крутящего моментов, то зависимость между осадкой
пружины и нагрузкой окажется линейной. Нелинейность характе-
ристики может быть определена с помощью нелинейной теории,
учитывающей изменение размеров пружины под нагрузкой.
Рассмотрим сначала линейную теорию расчета пружин растяже-
ния-сжатия. Для этого примем в уравнениях (3. 12) и (3. 13) а — а о
и D = Do. Индексом «о» отмечены начальные значения угла подъема
и диаметра пружины.
Мк — 9?tsin а0 4- cosa0;
Ми = 9ft cos а0-----sin а0.
(3. 14)
Заменяя в геометрических уравнениях (3.10) изменения кривизны
и кручения Д х и Д со через изгибающий Мъ и крутящий Мк мо-
менты по выражениям (3. 11), а последние из условий равновесия
(3. 14) — через внешнюю нагрузку Р и 9ft, получим следующие
зависимости осадки X и угла поворота 6 от нагрузки
л D*l
о о
4 В cos a0
cos2 a0
sin2 a
В
1 sin2a0 ; (3.15)
PDQ
fl Dfjio
В cos a0
sin2 a0 4- cos2 a0
(3. 16)
143
Определим перемещения пружины для двух указанных выше
способов закрепления торцов пружины.
1. Свободное крепление. В этом случае торцовый реактивный
момент 9Л = 0.
Тогда из выражения (3. 15) получим следующее уравнение ха-
рактеристики пружины растяжения-сжатия при свободном крепле-
ний торцов
Л PD3i
_____о о
4С cos «о
cos2 а0
sin2 а0
(3.17)
С
В
В соответствии с уравнением (3. 16) взаимный угол поворота
торцов пружины будет
л
_____о о
4В cos а0
— 1 sin 2 а0.
(3.18)
2. Глухое крепление. При глухом креплении угол взаимного
поворота торцов 0 — 0.
Тогда из выражения (3. 16) реактивный момент 9R в заделке
. будет
sin 2 а0
sin2 а0 4- cos2 а0
(3.19)
Подстановка последнего выражения в уравнение (3. 15) дает
характеристику пружины растяжения-сжатия при глухом крепле-
нии концов
л PD3t
______0_0
ЬС cos ай
(3.20)
sin2 a04-cos2 ас
Если пружина имеет небольшой угол подъема витков (ао <5
< Ю ч- 15°), то при приближенном расчете можно принять а о = 0,
и тогда уравнения (3. 17) и (3. 20) принимают следующий вид, оди-
наковый для обоих типов крепления
л PD3i
\ ,_____о о
Л0- 4С »
(3. 21)
Если сечение проволоки круглое, то жесткость на кручение
с = GJ„ = G --«х-, и тогда при «о — 0 получаем известную формулу
8 PD3i
_____о о
Gd*
(3.24')
144
Жесткость С на кручение проволоки прямоугольного сечения
определяется как С = GJK, где геометрическая характеристика
жесткости сечения при кручении (см. фиг. 68, г).
или
Л = Р a3 h при а < h
JK— fiah? при а > h.
(3. 22)
Коэффициент 0 определяется по табл. 16 в зависимости от отношения
сторон прямоугольного сечения.
Значения коэффициента 0
Таблица 16
a h -z— или п а 1 1,5 1,75 2 2,5 3 4 6 8 10
р 0,141 0,196 0,214 0,229 0,249 0,263 0,281 0,29£ ) 0,307 0,313 0,333
Формулы (3. 17) и (3. 20) удобно представить в виде
л PD3n I
Х — т -—-°—— = т Ло,
4 О
(3.23)
где щ — коэффициент, зависящий
а0 и способа крепления
Ло — прогиб пружины с углом
муле (3. 21).
от начального угла подъема
пружины;
н0 = 0, определяемый по фор-
Коэффициент т показывает, во сколько раз увеличивается про-
гиб пружины с начальным углом подъема а о =# 0 по сравнению
с прогибом пружины при «о = 0. Из выражений (3. 17), (3. 20)
и (3. 23) следует, что коэффициент т равен:
1) при свободном креплении концов пружины
с
в
тсв ~ cos а0 -j-
sin2 а0
cos а0
(3. 24)
2) при
глухом креплении
т8Л —-----------------------------
cos3 а0 + sin2 a0cos а0
(3- 24')
,, С
Отношения -н-----жесткости проволоки на кручение к жесткости
Л
на изгиб — для проволоки различных форм поперечного сечения при-
ведены в табл. 17. При этом принято отношение модулей упругости
Е
материала [34] = 2 (1 4- п) 2,6, что соответствует коэффи-
О
циенту Пуассона р, ~ 0,3.
10 Заказ 24.
145
Форма
сечения
Отношение
а
h
h
а
Таблица 17
при разных формах сечения
0 0,135 0,264 0,403
0,651
0,77
В зависимости от формы поперечного сечения проволоки пружина
большого шага может иметь как большую, так и меньшую жесткость,
чем пружина малого шага.
Пружины, изготовленные из проволоки круглого сечения, с уве-
личением шага увеличивают свой прогиб; из выражения (3. 24)
следует, что коэффициент т для них больше единицы, при любом
угле подъема а о =# 0, но не превышает при а о 30° величины 1,1.
Поэтому расчет начальной жесткости пружины с углом подъема
«о < 30°, изготовленной из проволоки круглого сечения, по упро-
щенной формуле (3. 21) может дать погрешность не свыше 10%.
Для пружине ао < 30°, изготовленных из проволоки прямоуголь-
ного сечения, расчет начальной жесткости по формуле (3. 21), не
учитывающей угла подъема винтовой линии, дает погрешность,
не свыше 10%, если при свободном креплении торцов отношение
С с
жесткости-g- <0,8, а при глухом —0,5 < — < 0,85. В соответ-
ствии с табл. 17 первый случай соответствует квадратному и прямо-
угольному сечению, вытянутому вдоль радиуса пружины, при лю-
бом отношении сторон, а второй — прямоугольному сечению при
отношении сторон 1,2 < -Д < 0,7.
§ 12. ОПРЕДЕЛЕНИЕ НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИКИ ВИНТОВОЙ
ЦИЛИНДРИЧЕСКОЙ ПРУЖИНЫ РАСТЯЖЕНИЯ-СЖАТИЯ
Как уже указывалось выше, с изменением угла подъема а и
диаметра D пружины изменяются как крутящий момент Мк, рав-
ный для пружины со свободным креплением торцов (3. 12)
так и изгибающий (3. 13)
Мь —----—sm а.
Для пружины сжатия, изготовленной из проволоки круглого сече-
ния, изгибающий момент в значительно меньшей степени влияет
на осадку, чем крутящий. Крутящий момент в соответствии с выра-
жением (а) возрастает быстрее, чем осевая сила Р. Следовательно,
осадка пружины, определяемая в основном скручиванием проволоки,
также будет нелинейно расти с нагрузкой. В результате этого харак-
теристика пружины сжатия из проволоки круглого сечения будет
возрастающей (фиг. 76).
При растяжении такой пружинь
крутящий момент будет возрастать
медленнее, чем нагрузка, так как
с увеличением растяжения пружины
ее диаметр будет уменьшаться,
а угол подъема витков — увеличи-
ваться. Поэтому характеристика
пружины затухает с увеличением
растягивающей нагрузки.
Величина нелинейности характе-
ристики зависит от геометрических
параметров пружины, формы попе-
речного сечения проволоки и рабо-
чей осадки пружины. Обычно не-
линейность винтовых цилиндриче-
Фиг. 76. Характеристика пру-
жины сжатия (а) и растяжения (б).
ских пружин невелика, поэтому уточненные расчет характеристики
с учетом ее нелинейности требуется в основном только при про-
ектировании измерительных пружин точных приборов.
Нелинейность характеристики может быть определена с помощью
теории больших перемещений винтовой цилиндрической пружины,
разработанной Н. А. Чернышевым [3] и [4]. Отличие этой теории
от линейной состоит прежде всего в том, что уравнения равновесия
составляются не для начального, а для деформированного состоя-
ния пружины. Поэтому в уравнениях равновесия (3. 12) и (3. 13)
Мк — W sin а
Мъ = 9Л cos а —
PD
—— cos а;
PD .
- — sin а
величины а и D означают угол подъема и диаметр пружины в нагру-
женном состоянии.
Далее, поскольку задача решается с учетом больших перемеще-
ний, осадку % и угол 0 взаимного поворота торцов следует считать,
конечными величинами. Поэтому их нельзя определять как беско-
нечно малые приращения высоты Н и центрального угла ф пружины
дифференцированием выражений (3. 2) и (3. 3), как это выполнялось
10*
147
в линейной теории. Осадка X определяется здесь разностью между
конечным и начальным значениями высоты пружины. В соответ-
ствии с выражением (3.2) получим
к — Н— = — sina0). (3.25)
г ' - Л Г* - ' ".
О взаимного поворота торцов по выражению (3.3) будет
л . I q 7 / cos a cos a01 /q oc\
0 = ip — ipo = 2 Ц—p--------D^/• (3.26)
здесь I — длина проволоки пружины; индексом «о» отмечены на-
чальные параметры пружины.
Изменения кривизны и кручения Дх и Дю также определяются
разностью между конечными и начальными значениями кривизны
и кручения.
Используя выражения (3. 4) и (3. 5), получаем
. 2 cos2 a 2 cos2 a0
sin 2 a0
дм = x — x0 —----—
. sin 2 a
Дю = ю —- юс — --~—
(3. 27)
Так как рассматриваются только упругие деформации пружины,
то уравнения (3. 11), связывающие изменения изучения и кривизны
с крутящим и изгибающим моментами, остаются в силе
А М К А - . Ь /.. \
Приравнивая правые части выражений (в) п (3. 27) и заменяя
Мь и Мк через внешнюю нагрузку с помощью уравнений (б), полу-
чим
cos2 a cos2 a0 \
~~D )
< sin 2 a sin 2 a0
_- ___
Уравнения (3. 25), (3. 26) и (3. 28) позволяют получить характе-
ристику пружины.
Определим, как и в линейной теории, уравнения характеристики
пружины при двух способах крепления торцов; свободном и
глухом.
1. Свободное крепление. Полагая' торцовый момент 9)7 = 0,
исключим из уравнений (3. 28) диаметр D. Полученное уравнение
совместно с выражением (3. 25) дает характеристику пружины
в параметрической форме
cos2 a0
cos a
о
к — I (sin a —sin a0),
148
Длина проволоки I может быть найдена по уравнению (3. 2)
£ Яр Д Л)* О
sin а0 cos а0
крепление. В этом случае угол
следовательно, в соответствии с
О поворота торцов
выражением (3. 26)
из уравнений (3. 28) торцовый
2. Глухое
равен нулю,
D = Do-^-
v cos а0
Исключив
характеристику пружины растяжения-сжатия
торцов
гч 4 С cos2 а
момент ЭД, получим
при глухой заделке
па — sin а0
л cos а»
sin а 1-------------5
\ cos а
о
О/’
Для того чтобы построить характеристику пружины, следует
задаться рядом значений угла а и подсчитать соответствующие зна-
чения прогибов X и нагрузок Р по формулам (3. 29) или (3. 31) Если
пружина работает в области растяжения, то X и Р положи-
тельны. Если же пружина работает в области сжатия, то X и Р отри-
цательны. Введем безразмерные параметры
X
(3. 32)
Относительный прогиб б пружины определяется в соответствии
с геометрическими соотношениями (3. 25) и (3. 30) по выражению
6 = sin_g~ sin а0 ,
cos а0 ' '
Безразмерный параметр q нагрузки определяется по формуле
(3. 29) или (3. 31) для свободного и глухого креплений концов пру-
жины
Цсе
cos2 а0
cos а
sin а • sin а0
(3. 34)
sin2 а
дгл — cos2 а0 (sin а — sin а0)
sin а 1 —
cos а0
cos а
(3. 34')
Параметры б и q в соответствии с выражениями (3. 33) и (3. 34)
зависят только от угла подъема винтовой линии пружины до и после
В
нагружения (а о и а) и от отношения жесткостей ™ проволоки пру-
О
жины на изгиб и на кручение. Поэтому представляется воз-
можным для определенных соотношенийпостроить в безраз-
мерных координатах б — q семейство характеристик пружин с раз-
ными начальными углами ао для того, чтобы упростить построение
149
нелинейной характеристики каждой конкретной пружины. Зная
размеры пружины, можно легко с помощью выражений (3. 32)
перестроить характеристику пружины из безразмерных координат
б и q в размерные: X = jtZ?o г0 6 и Р = ^-q.
Построим в качестве примера характеристику пружины из про-
волоки круглого сечения с начальным углом подъема а0 = 15°
при растяжении и сжатии. Для круглого сечения отношение —
= 0,77 (см. табл. 17). Примем крепление концов пружины свобод-
ным.
Результаты вычислений по формулам (3. 33) и (3. 34) приведены
в табл. 18.
Таблица 18
Нелинейная характеристика пружины
а 0° 5° 10° 15° 20° . 25° 30°
—0,233 -0,160 -0,0825 0 0,0892 0,187 0,294
б -0,268 -0,178 -0,0882 0 0,0861 0,170 0,250
При изменении угла подъема а от 15° до 0° пружина работает
на сжатие, а в интервале 15° < а < 30° — на растяжение.
Фиг. 77. Характеристика пру-
жины с начальным углом
подъема ао = 15° при сжатии
(а) и при растяжении (б) по
нелинейной теории и по линей-
ной (в).
Полученная характеристика пру-
жины построена по абсолютным зна-
чениям б и q на фиг. 77.
Как указывалось выше, при рас-
тяжении жесткость пружины из круг-
лой проволоки увеличивается, при сжа-
тии — уменьшается.
Действительно, характеристика
затухает при растяжении пружины
(кривая а) и возрастает при ее сжатии
(кривая б).
На фиг. 77 проведена прямая в,
представляющая собой линейную
характеристику (3. 21) в безразмерных
координатах q — б.
Формула (3. 21) была получена по
линейной теории в предположении,
что начальный угол а0 подъема винтовой
линии пружины равен нулю и может быть записана в виде
150
или, учитывая обозначения (3. 32),
з» =
(3. 35)
1
----относительный прогиб пружины с начальным
где до-
углом подъема а0 = 0. В соответствии с выражением (3. 35) прямая
€ проходит под углом 45° к осям координат.
По характеристике пружины можно легко
нелинейность.
определить ее
Для этого следует конечную точку Л рабочего
участка характеристики соединить прямой с началом координат
(фиг. 78, а).
Наибольшее отклонение Ащах характеристики от этой прямой,
отнесенное к наибольшему прогибу dmax, и будет определять вели-
чину нелинейности
Т|= 4™". юо%.
Отах
(3.36)
Точное определение отрезков Агаах по кривым в координатах
6 — q затрудняется тем, что в большинстве случаев нелинейность
пружин мала. Величина нелинейности может быть определена более
точно, если перестроить кривые из координат д — q в координаты
(д — до)— q, т. е. откладывать по оси ординат разность между
относительным прогибом б пружины с начальным углом подъема «о
и прогибом 6о, определяемым формулой (3. 21) линейной теории
в предположении, что а о = 0. В этом случае можно значительно
Фиг. 79. Кривые <5 — <50 = / (д) винтовых цилиндрв
а — пружины сжатия со свободным креплением торцов;
увеличить масштаб по оси ординат (фиг. 78, б). Так как q — до по
равенству (3. 35), то полный прогиб д будет изображаться на фи-
гуре суммой координат (д — до) + q = д. Для конечной точки ха-
152
рактеристики 6max = OB
BA, и поэтому нелинейность характери-
стики будет определяться по выражению
= Атах . 1ооо/о = Атах . 100»/о .
Ощах иВ + В А
На фиг. 79 даны кривые (б — бо) — f (д) для пружин, изгото-
вленных из проволоки круглого сечения, при различных начальных
углах подъема а0 для свободного и глухого, креплений концов пру-
153
ж ины. Использование этих кривых значительно облегчает задачу
построения нелинейной характеристики пружины и определения
ее нелинейности.
Пример. Определить прогиб и нелинейность характеристики пружины
при сжатии силой Р = 30 кгс, если средний диаметр пружины Do — 16,5 лсж,
диаметр проволоки d = 2 мм, число рабочих витков i0 = 5, высота рабочей
части Но = 55 мм, модуль упругости материала О = 8103 кгс! мм2.
Крепление концов пружины — свободное.
Фиг. 79. Кривые б — б0 = / (q) винтовых циливд
в — пружины растяжения со свободным креплением торцов;
Решение. Определим безразмерный параметр qce по выражению
(3. 32) при Р = 30 кгс.
_ _ РРо8 __ зо • 16,52 • 8
в 4С Gitd1 8 103 • 3,14 • 24
го кРивойна Фиг- 79’ а При начальном угле подъема а0, равном по формуле
55
= 0,163.
а0 = arc tg------5-^— = arc tg
л Doia
= агс tg 0,212 s 12°,
154
находим разность б — до = 0,013. Отсюда с учетом равенства (3. 35) относи-
тельный прогиб д = до + (д — до) = 0,163 + 0,013 = 0,176.
По соотношению (3. 32) находим осадку пружины Л при силе Р = 30 кгс
Х = лП010 б =3,14-16,5-5-0,176=45,6 мм.
Нелинейность характеристики определим графическим путем по кривой
(осо = 12°) на фиг. 79, а. Для этого при q = до = 0,163 находим точку А,
соответствующую концу характеристики пружины, и соединяем ее прямой с на-
рических пружин из круглой проволоки:
г — пружины растяжения с глухим креплением торцов.
чалом координат. Измеряем по вертикали наибольшую разность между этой
прямой и кривой ОА : Лтах = 0,0025. Нелинейность характеристики в соот-
ветствии с выражением (3. 36) будет
п _ Лтах . 100% а
дщах
0,0025 • 100
0,176
% 1,42%.
В том случае, если задана не рабочая нагрузка, а осадка X,
следует сначала определить по выражению (3. 32) относительный
155
прогиб б, а соответствующая этому прогибу точка на кривой фиг. 79
находится подбором так, чтобы сумма ее координат была равна б.
После этого так же, как и в рассмотренном примере, может быть опре-
делена нелинейность характеристики.
Если требуется определить нелинейность пружины, установлен-
ной с начальным поджатием, то на фиг. 79 определяется положение
Фиг. 80. Кривые нелинейности для пружин из круглой проволоки:
а — пружины сжатия со свободным креплением торцов; б — пружины сжатия с глухим
креплением торцов; в — пружины растяжения со свободным креплением торцов; г — пружины
растяжения с глухим креплением торцов.
точек, соответствующих началу и концу рабочего участка (точки А
и В). Наибольшую разность Атах между характеристикой и прямой
АВ (см. фиг. 78, в) следует поделить на рабочую осадку пружины
йРаб} которая в этом случае равна бРаб = (OB' -f- В'В) ~ (ОА' -|-
+- А'А).
С помощью кривых на фиг. 79 построены графики нелинейности
(фиг. 80) для пружин из проволоки круглого сечения в зависимости
от величины относительной осадки б (3. 32) при разных начальных
углах подъема а0 винтовой линии. Эти кривые показывают,
156
что нелинейность возрастает с увеличением осадки. При одинаковых
прогибах нелинейность пружин растяжения меньше, чем нелиней-
ность пружин сжатия. Нелинейность пружин из проволоки круглого
сечения мало зависит от способа крепления торцов пружин.
По кривым, приведенным на фиг. 80, можно при проектировании
пружины сразу оценить ее нелинейность, а по графикам на
фиг. 79 — построить при необходимости уточненную нелинейную
характеристику пружины.
Приведенное в предыдущем примере решение задачи об определении пели-
ценности проводится значительно быстрее с помощью кривых, показанных на
фиг. 80. После определения относительного прогиба б = 0,176, нелинейность
находится непосредственно по кривым на фиг. 80, а: при 6 = 0,176 и угле
«о — 12° нелинейность ~ 1,45%.
§ 13. ВЛИЯНИЕ ГЕОМЕТРИИ И СПОСОБОВ КРЕПЛЕНИЯ ПРУЖИНЫ
НА ФОРМУ ЕЕ ХАРАКТЕРИСТИКИ
Форма характеристики пружины и величина ее нелинейности
. - С
в большой степени зависят от отношения — жесткости проволоки
на кручение к жесткости на изгиб, т. е. от форумы поперечного сечэ-
ния проволоки. На фиг. 81 даны характеристики и кривые нелиней-
ности пружин растяжения и сжатия при одинаковых прогибах:
пружины растяжения растягиваются от начального угла подъема
= 0 до а — 30°, а пружины сжатия сжимаются от а0 — 30°
до а = 0. Проволока этих пружин имеет одинаковую жесткость С
па кручение и разные жесткости В на изгиб относительно бинор-
мали (см. фиг. 73, а). Формы сечений показаны на фиг. 81. Кривые
на этой фигуре наглядно иллюстрируют влияние формы поперечного
сечения на характеристику пружины.
При одинаковой нагрузке большие прогибы получает пружина
из проволоки с сечением, вытянутым вдоль оси пружины и, наоборот,
меньшие прогибы имеет пружина, если сечение вытянуто вдоль ра-
диуса пружины (фиг. 81, а, б). Это можно объяснить, представив
себе характер деформации пружины.
Осадка пружины получается в результате изменения кручения
и кривизны проволоки под действием нагрузки. Если сечение про-
волоки сильно вытянуто вдоль радиуса пружины (жесткость В на
изгиб проволоки относительно бинормали значительно больше
жесткости С на кручение), то кривизна проволоки будет изменяться
мало, и осадка пружины будет определяться в основном изменением
кручения, т. е. величиной крутящего момента.
Пружина из проволоки с малой изгибной жесткостью (сечение
вытянуто вдоль оси пружины) получает дополнительные прогибы
за счет изменения кривизны проволоки под действием изгибающего
момента. При одинаковой нагрузке прогибы второй пружины
(В <Z С) будут больше, чем у первой (В ^>С).
Характеристика пружины с сечением, сильно вытянутым вдоль
радиуса пружины, имеет наибольшую нелинейность (фиг. 81, в, г).
157
Фиг- 81. Характеристики и кривые нелинейности пружмв
п — характеристики пружин окати я; б — характеристики мру
г — кривые нелинейности
158
и з проволоки круглого и прямоугольных сечений:
яшн растяжения;’^ — кривые нелинейности пружин сжатия;
пружин ^растяжения.
159
Прогибы такой пружины, как уже отмечалось, обусловлены в основ-
ном изменением кручения. Для пружины со свободно закре-
пленными торцами крутящий момент равен в соответствии с выраже-
нием (3. 12)
PD
Мк — -х- cos а. (а)
Величина крутящего момента нелинейно связана с нагрузкой
вследствие изменения угла подъема а и диаметра D при нагружении
пружины. У пружины сжатия величина крутящего мо-
мента растет быстрее, чем нагрузка,
особенно в начале характеристики,
Фиг. 82. Нелинейность пружины
в зависимости от начального
ПОДЖатИЯ Ъцач-
когда угол подъема велик, и по-
этому характеристика пружины
сжатия более искривлена в начале
и близка к прямой в конце характе-
ристики при а —> 0 (фиг. 81, а).
Если проволока пружины обла-
дает малой жесткостью на изгиб,
то действие изгибающего момента
выпрямляет характеристику. Это
можно объяснить тем, что изгибаю-
щий момент, равный для пружины
со свободными торцами
Мь =
PD .
— sin а
(б)
вначале, с увеличением силы Р,
сжимающей пружину, возрастает,
а затем, когда угол подъема
а винтовой линии становится малым
он начинает уменьшаться и исчезает при полном сжатии пружины,
при а 0*. Изгибающий момент при сжатии пружины увеличивает
кривизну проволоки. Это приводит к дополнительной осадке пружины
на начальном участке характеристики в соответствии с законом из-
менения изгибающего момента от нагрузки, в результате чего нели-
нейность характеристики уменьшается.
Поскольку характеристика пружины сжатия в конце нагруже-
ния ближе к прямой, чем в начале, то пружина, предварительно
поджатая, будет иметь меньшую нелинейность, так как рабочий
участок характеристики смещается в этом случае к концу. В каче-
стве иллюстрации на фиг. 82 даны кривые нелинейности для пру-
жины сжатия с начальным углом подъема «о — 30° из проволоки
прямоугольного сечения с отношением сторон — 2. Крепление
* В действительности угол подъема полностью сжатой винтовой цилиндри-
ческой пружины всегда больше нуля. Если высота сечения проволоки равна h,
h
то при полном сжатии пружины а = - — •
160
торцов — свободное. Кривые построены в зависимости от начальной
осадки при рабочих прогибах брав = 0,1; 0,2; 0,3.
Следует отметить, что величина полной осадки пружин сжатия
до а = 0 определяется только жесткостью проволоки на кручение,
так как при а == 0 изгибающий момент Мь в соответствии с выра-
жением (б) равен нулю. Поэтому пружины из проволок с одинако-
выми жесткостями на кручение и разными жесткостями на изгиб
сжимаются до а = 0 одинаковыми силами (фиг. 81, а).
Рассмотрим влияние формы сечения на нелинейность характери-
стик пружин растяжения (фиг. 81, б). Пружины растя-
жения с большой жесткостью В в начале нагружения (пока углы а
малы) имеют линейную характеристику. Затем по мере увеличения
угла а характеристика пружины растяжения становится затухаю-
щей, поскольку величина крутящего момента Мк будет расти медлен-
нее силы Р в соответствии с выражением (а).
Пружины из проволок с разными жесткостями В на изгиб, но
с одинаковыми жесткостями С на кручение на начальном участке
характеристики имеют одинаковые прогибы, так как здесь дефор-
мация пружины определяется в основном величиной скручивания
провлоки. Затем при увеличении угла а появляется изгибающий
момент и, в соответствии с выражением (б), он будет расти быстрее,
чем нагрузка. Изменение кривизны вызывает дополнительные про-
гибы, которые могут компенсировать (если проволока пружины до-
статочно податлива на изгиб), уменьшение прогиба из-за падения
роста крутящего момента с увеличением угла а. Чем меньше жест-
кость В проволоки на изгиб относительно бинормали, тем меньше зату-
хание характеристики. При В = С (прямоугольное сечение с отно-
шением сторон — 1,7) характеристика свободно закреплённой
пружины растяжения с начальным углом подъема а0 = 0 будет
линейной. При В << С характеристика пружины растяжения ста-
новится возрастающей (фиг. 81, б, г).
При глухом креплении торцов форма сечения проволоки
оказывает особенно сильное влияние на характеристику пружин
сжатия. Пружины с сечением, вытянутым вдоль радиуса, имеют
сильно возрастающую характеристику (фиг. 81, а). При сжатии
пружина стремится раскрутиться и уменьшить число витков. Однако
глухое крепление не допускает взаимного поворота торцов. Поэтому
изменение кривизны и кручения у пружины с глухим креплением
торцов будет меньше, чем у пружины со свободными торцами, и
это увеличивает ее начальную жесткость (фиг. 81, а, б).
Для пружины с глухим креплением торцов крутящий момент
равен в соответствии с формулой (3. 12)
PD
Мк — cos а + sm а,
где гОс — реактивный момент, возникающий в местах крепления
торцов пружины.
11 Заказ 24.
161
С увеличением прогиба и уменьшением угла а слагаемое S02 sin а
в выражении крутящего момента падает, сдерживающее влияние
реактивного момента на величину осадки пружины исчезает,
что приводит к возрастанию характеристики пружины. Это возра-
стание будет проявляться тем сильнее, чем больше отношение жестко-
. В
стеи -7Т- .
Пружины сжатия с жестко защемленными торцами при доста-
точно большом отношении могут терять устойчивость, что выра-
жается в потере несущей способности пружины при некото-
Фиг. 83. Характеристика пружины
сжатия из проволоки прямоуголь-
ного сечения с отношением сторон
1 : 6 при глухом креплении торцов.
ром критическом значении на-
грузки [3]. В момент потери
устойчивости пружина скачком
изменяет свой прогиб, склады-
ваясь до соприкосновения вит-
ков. При такой форме потери
устойчивости ось пружины
остается прямолинейной
На фиг. 83 построена харак-
теристика пружины с отношением
а
сторон
= 6. В точке А харак-
h
теристики нагрузка достигает наи-
большего значения дКр. Дальней-
шее увеличение прогибов происхо-
дит при уменьшении нагрузки.
Практически пружина в момент потери устойчивости изменит свой
прогиб скачком на отрезок АВ. При разгрузке пружина вернется
на начальную ветвь также скачком (отрезок CD).
В критическом состоянии пружины нагрузка qKp максимальна
(точка А характеристики), при этом производная -~=0. Исполь-
Cl Ct
зуя выражение (3. 34') для параметра дгЛ нагрузки при глухом креп-
лении торцов, получим
В
С
= cos2 а0
аа °
cos а —
cos а —
cos а0
cos2 а
Потеря устойчивости произойдет при угле авр подъема винтовой
линии пружины, который можно найти из равенства — О
cos3 акр =
cos а0
1 Для пружин сжатия более известна другая форма потери устойчивости,
сопровождающаяся искривлением оси пружины; этот случай рассматривается
в § 16.
162
Для пружины с отношением сторон прямоугольного
проволоки
а0 = 30°
и при начальном угле
сечения
подъема
cos3 аКр =
относи-
откуда акр = 15°. Это соответствует по выражению (3. 33)
тельному прогибу
х sin акр — sin а0 sin 15° —sin30° А п_о
6кр-------соБа^---=-----соБзср---= “ °’278
(знак «минус» указывает на сжатие пружины).
Пользуясь формулой (3. 34'), можно определить при желании
и критическую нагрузку дКр.
§ 14. НАПРЯЖЕНИЯ В ВИНТОВОЙ ЦИЛИНДРИЧЕСКОЙ ПРУЖИНЕ
РАСТЯЖЕНИЯ-СЖАТИЯ
При навивке в пружине возникают большие пластические дефор-
мации, что приводит к изменению механических свойств материала,
а также, к появлению в пружине остаточных напряжений. И то и
другое влияет на прочность пружины. Учесть это влияние при рас-
чете довольно трудно, поэтому изложенная ниже оценка прочности
пружин является приближенной.
При осевом нагружении в пружине круглого сечения и малого
угла подъема а возникают касательные напряжения т, эпюра рас-
пределения которых по сечению дана на фиг. 84, а. Поскольку во-
локна элемента на внутренней стороне витка короче, чем на наруж-
ной, то углы сдвига при деформации пружины, а следовательно,
и напряжения в точке А будут больше
Наибольшее напряжение ттах возникает в точке А, расположен-
ной на внутренней стороне витка, и его величина может быть опре-
делена по формуле
чем в точке В.
tmax — К, (а)
где коэффициент К зависит от индекса пружины с — Коэффи-
циент К показывает, во сколько раз напряжение во внутренней
м
точке витка А больше, чем напряжение-^, определяемое теорией
W р
кручения прямого бруса. Величина К возрастает с уменьшением
индекса с пружины. Если индекс пружины с >> 10, то пружину
можно рассматривать как брус малой кривизны, и тогда К 1.
Для пружин с углом подъема а = 0 крутящий момент Мк =
1 зт
полярный момент инерции круглого сечения Wp — —
мула (а) принимает вид
2 ’
и фор-
8PD
jt d3
(3.37)
11*
163
Коэффициент К дан на фиг. 84, б в зависимости от индекса пру-
жины.
6)
Фиг. 84. Напряжения в пружине растяжения-сжатия:
а — эпюра касательных напряжений т в поперечном сечении витка пружины из проволоки
круглого сечения; б —* график коэффициента К; в — опасные точки в пружине из проволоки
прямоугольного сечения; а — эквивалентные напряжения в опасной точке пружины из про-
волоки круглого сечения в зависимости от угла подъема ао.
Его можно также вычислять приближенно [39 ] по формуле
4с 4-2
4с —3
Если пружина имеет прямоугольное сечение, то напря-
жения в точке А (фиг. 84, в) определяются по формуле
хА = К
PD
a2h *
Значения коэффициента К' даны в табл. 19 в зависимости от
D h
индекса с = —- пружины и отношения сторон— сечения.
164
1Ш
Значения коэффициента К'
Таблица 19
D а -се/ t / 1 3 1 2 0,8 1,0 1,25 1,5 2,0 3,0
4 6,16 4,53 3,47 3,16 2,93 2,78 2,58 < 2,35
5 5,80 4,28 3,29 3,01 2,80 2,67 2,48 2,40 2,25
6 5,55 4,10 3,18 2,90 2,70 2,58 2,19
7 5,37 3,98 3,09 2,84 2,65 2,52 2,35 2,15
8 5,24 3,83 3,76 3,03 2,78 2,60 2,48 2,31 2,10
10 5,06 2,94 2,70 2,53 2,41 2,26 ! 2,06 1
У пружин с индексом с
— 6 при отношении сторон прямо-
угольного сечения
0,8 опасной может Сказаться точка В,
* tat
напряжения в которой определяются по фор-
муле
Таблица 20
Значения
коэффициента К"
Здесь коэффициент К" зависит только от отно-
шения сторон сечения, и его значения даны
в табл. 20.
Если при расчете напряжений учесть угол а подъема витков, то величина
касательных напряжений т окажется меньшей, поскольку крутящий момент
Мк, пропорциональный cos а, с увеличением угла а уменьшается. Однако,
кроме крутящего момента, в сечении проволоки пружины возникает изгибающий
момент Мъ, пропорциональный sin а, а следовательно, и нормальные напря-
жения а. Для оценки прочности пружины в этом случае следует определить
эквивалентное напряжение, пользуясь какой-либо теорией прочности. Напри-
мер, по энергетической теории прочности эквивалентное напряжение опреде-
ляется по формуле
= /а2 + 3т2 .
На фиг. 84, г показаны кривые адкв
Wp
PD
в зависимости от начального угла
наклона ао для пружины из проволоки круглого поперечного сечения со свобод-
ным креплением торцов. При расчете были использованы формулы напряжений
пит, полученные с учетом угла подъема витков [4]. Из графиков видно, что
для пружин с начальным углом подъема ао = 30° и ао = 0° расхождение в ве-
личинах эквивалентных напряжений не превышает 5%. Таким образом, угол
ао подъема винтовой оси проволоки оказывает небольшое влияние на прочность
пружины, поскольку уменьшение касательных напряжений т компенсируется
появлением нормальных напряжений а. Поэтому приведенные выше формулы
для пружин с углом а о, близким к нулю, можно использовать и для расчета па
прочность пружин с конечным углом Со-
Итак, расчет на прочность пружин растяжения-сжатия может
быть произведен по формуле
165
где [т] — допускаемое напряжение на кручение. Его величина вы-
бирается в зависимости от материала и условий работы пружины.
Некоторые соображения о выборе величины допускаемого напряже-
ния [т] излагаются в § 18.
§ 15. ИЗГИБ ВИНТОВЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
Расчеты винтовых пружин, работающих в условиях изгиба, не-
обходимы, например, при анализе работы высокочувствительных
тензометров
где пружина закрепляется и нагружается по схеме
консольной балки (см.
п
Фиг. 85. Определение деформаций витка пружины:
а — винтовая цилиндрическая пружина в условиях изгиба; б — нагружение
витка пружины и внутренние силовые факторы в поперечном сечении
витка; в — деформации витка под действием момента М; а — деформации
витка под действием силы Q; д — нагружение витка единичными силовыми
факторами.
Определим перемеще -
ния пружины, изгибае-
мой поперечной нагруз-
кой в осевой плоскости
(фиг. 85., а). Для этого
рассмотрим деформации
витка, выделенного из пружины сечениями, совпадающими
с плоскостью действия нагрузки. В концевых сечениях витка возни-
кают моменты М и силы Q, показанные на фиг. 85, б. Их величины
186
можно определить из условий равновесия части пружины, располо-
женной с одной стороны от рассматриваемого витка. Ограничимся
сначала изучением пружины с малым углом подъема винтовой
линии и при определении деформаций будем считать каждый виток
пружины плоским.
Моменты М вызывают скручивание и изгиб проволоки вокруг
радиуса витка, вследствие чего концевые сечения витка поворачи-
ваются относительно друг друга на величину О в осевой плоскости
пружины (фиг. 85, а).
Силы Q изгибают проволоку витка в его плоскости, и концевые
сечения смещаются относительно друг друга по радиусу витка на
величину w (фиг. 85, а).
Перемещения й и w могут быть легко определены с помощью
интеграла Мора [34]:
/»" ^MnMniRd<p
0 0
/MbMfa Rdq
В~Ъ ’
О
здесь Мк — крутящий момент, Мп и Мъ — изгибающие моменты
относительно главной нормали п и бинормали Ъ (фиг. 85, б) в произ-
вольном сечении ф под действием внешней для витка нагрузки 71/
и Q-
MKt, МП1 и 71/Ь1 — крутящий и изгибающий моменты для еди-
ничного состояния витка (фиг. 85, д)\ С, Вп и Въ — жесткости про-
волоки на кручение, изгиб относительно главной нормали и бинор-
мали соответственно.
Интеграл Мора, определяющий угол поворота й*, состоит из двух
слагаемых, соответствующих скручиванию проволоки и ее изгибу
относительно главной нормали п. Перемещение w определяется
только изгибом проволоки относительно бинормали &, поэтому в ин-
теграле Мора сохраняется одно слагаемое.
Из условия равновесия части витка, отсеченной под углом ф
к плоскости разреза (фиг. 85, б), определим внутренние силовые
факторы под действием моментов М и сил Q
Мк — М cos ф; Мп — Мsin ф; 71/ь = QB. sin ф.
При определении угла поворота й* в концевых сечениях витка
прикладываем единичные моменты, при определении перемещения
w —- единичные силы (фиг. 85, д). Внутренние силовые факторы,
соответствующие этим единичным состояниям, будут
= 1 • cos ф; Мпх — 1 • sin ф; Мъг = 1 • 7? • sin ф. (в)
167
Подставляя выражения (б) и (в) в интеграл Мора (а) и произведя
вычисления, получим взаимный угол поворота концевых сечений
витка
< - г
М л D
2С
и взаимное смещение их по радиусу
Q лЯ9
8Въ
(д)
При чистом изгибе, когда поперечная сила Q равна нулю,
каждый виток пружины находится в одинаковых условиях, по-
скольку момент М будет одинаков для любого витка. Представим,
в соответствии с предположением о малости угла подъема, пружину
как набор плоских витков, расстояние между которыми равно
шагу h пружины (фиг. 86, а). В результате поворота витков от-
носительно друг друга на угол й ось пружины принимает форму
дуги окружности (фиг. 86, б), радиус q которой в соответствии
с выражением (г) будет равен
h _ h
й М л D
Если пружину уподобить некоторому прямолинейному брусу
длиной, равной высоте пружины И, эквивалентному пружине в от-
ношении жесткости на изгиб, то кривизна этого бруса в условиях
чистого изгиба (фиг. 86, в) в соответствии с известной формулой
сопротивления материалов равна
1 _ М
Q -А-из
(3.38)
где Аиз — жесткость эквивалентного бруса на изгиб. Из сопоставле-
ния выражений (е) и (3. 38) определим величину изгибной жесткости
эквивалентного бруса
Айз —
л Di
h ’
(3. 39)
здесь число раоочих витков i ~
Если пружина изготовлена из проволоки круглого
подставляя в выражение (3. 39) С = GJP к Вп — Ejn
соотношение между модулями упругости G
, Hd* Е
сечения, то
и учитывая
2Ж ’ получим
us° 32£>i 2+p *
Используя модель
угловое или линейное
эквивалентного бруса, можно легко найти
перемещение любого сечения пружины при
168
—1ZIH
I
I
Фиг. 86. Определение жесткостей пружины на изгиб и на сдвиг:
а — пружина в ненагруженном состоянии; б — пружина при чистом изгибе;
в — эквивалентный брус; з — к примеру на определение перемещений при
чистом изгибе пружины; д — сдвиг витков при поперечном изгибе; е —
к примеру на определение перемещений при поперечном изгибе пружины;
эя, — изгибная жесткость Аи и жесткость на сдвиг Ас^е в зависимости
от начального угла подъема «о-
169
чистом изгибе. Например, вертикальное перемещение v конца
пружины (фиг. 86, г), можно найти по правилу Верещагина, решая
подобную задачу для эквивалентного бруса. Строя эпюры моментов
от заданных и от единичной нагрузок и перемножая их, получим
ЗДЯ2
При достаточно большом изгибающем моменте витки пружины на одной
стороне сомкнутся. Дальнейший изгиб пружины сопровождается поворотом
витков вокруг касательных к точкам их соприкосновения. При этом изменится
изгибная жесткость пружины, и поэтому формулы (3. 39) становятся недей-
ствительными. Определим момент, при котором витки на сжатой стороне
пружины начинают смыкаться. В этом случае взаимный угол поворота двух
2Д
соседних витков равен
где Д — зазор между витками (см. фиг. 86, а).
Соответствующее изменение кривизны оси будет равно
1 -2A==2AL
q “ Dh DH ’
где h —
— шаг пружины.
Приравнивая правые части выражений (ж) и (3. 38), получим момент SER
при котором смыкаются витки пружины:
f сп>___ 2 Д
/ HD *
При поперечном изгибе пружины, когда сила Q не равна
нулю, помимо поворота на угол й, появляется сдвиг витков относи-
тельно друг друга в результате изгиба проволоки витка в его плоско-
сти под действием сил Q (см. фиг. 85, б, г). Это смещение вызывает
дополнительный прогиб оси пружины. При изгибе бруса массивного
сечения влияние поперечных сил на прогиб мало, и им обычно пре-
небрегают. Винтовая пружина значительно податливее на сдвиг
в поперечном направлении, чем сплошной брус, и это необходимо
учитывать при расчете.
Представим снова пружину как набор плоских витков (фиг. 86, а).
Взаимное смещение двух соседних витков в вертикальном направле-
нии на величину w вызывает дополнительный поворот оси пружины
на угол ДО = (фиг. 86, д), где h — шаг пружины. Заменяя w
JС-
н
по выражению (д) и учитывая, что h = — , получим
I
Ай-
Q л D3i
8НВъ
S
[ При замене пружины эквивалентным брусом в случае попереч-
ного изгиба необходимо, чтобы этот брус был равноценен пружине
не только по изгибной жесткости (как при чистом изгибе), но и по
жесткости на сдвиг. Для эквивалентного бруса дополнительный угол
170
поворота оси, вызываемый деформациями сдвига, может быть опре-
делен по выражению
^сЗв
(3. 40)
где Асое — жесткость бруса при сдвиге. Из равенства выражений
(з) и (3. 40) следует
. _ 8НВь
Асдв л D4 *
(3.41)
Для пружины, изготовленной из проволоки круглого поперечного
сечения, жесткость при сдвиге будет
. EHd* /о ..
"сЭво • (о- 41 )
Пользуясь схемой эквивалентного бруса, можно легко опреде-
лить перемещения пружины при любых поперечных нагрузках.
Для этого удобно использовать интеграл Мора, который будет в дан-
ном случае состоять из двух слагаемых соответственно перемеще-
ниям, связанным с изгибом и со сдвигом эквивалентного бруса
н
/*
./ А из
о
И
Г QpQ^
^сдв
0
здесь Мр и Qp, Mi и Qi — изгибающие моменты и поперечные силы
в произвольном сечении бруса в заданном и в единичных состоя-
ниях. Жесткости эквивалентного бруса на изгиб Аиз и на сдвиг
Асав определяются по формулам (3. 39) и (3. 41).
В качестве примера определим вертикальное перемещение конца пружины,
нагруженной и закрепленной, как показано на фиг. 86, е.
Вычислим интеграл Мора (и), перемножая эпюры в заданном и в единич-
ном состояниях по правилу^Верещагина. Тогда искомое перемещение
из
Д(ря-1)=
PH3 PH
3^4 из -^сдв
Аналогично решается задача об определении перемещений пружины при
чистом и поперечном изгибе в случае, когда угол подъема витков не равен нулю.
Различие в выводе состоит лишь в том, что вырезая отдельный виток пружины
для определения его деформаций, получаем пространственный брус, и опреде-
ление внутренних силовых факторов становится несколько более сложным.
Конечные формулы для определения приведенных жесткостей пружины на изгиб
и на сдвиг имеют вид
sin2a -|-
жиз
2НС cos а
Л Di
cos2 а +
Въ
171
При круглом сечении проволоки пружины формулы упрощаются
__ Н Ed* cos а
' из<>" "32 t (2 4-р cos2 а) ’
_ HEd*
Асдв0— 8р3.
sin2 а
На фиг. 86, ж приведен график, иллюстрирующий изменение жесткостей
на изгиб и на сдвиг пружины из проволоки круглого сечения в зависимости от
угла а подъема витков пружины.
§ 16. УСТОЙЧИВОСТЬ ВИНТОВЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИЩ
СЖАТИЯ [3], [И]
При сжатии винтовой пружины достаточно большой высоты может
наступить потеря устойчивости так же, как и при сжатии гибкого
стержня, и ось пружины при некоторой критической нагрузке вне-
запно искривится. Потеря устойчивости недопустима для нормаль-
ной работы пружины, так как при этом ее характеристика сильно
искажается, запас прочности уменьшается, а при недостаточно
надежном креплении концов пружина в момент потери устойчивости
может вообще вылететь со своего места.
Для определения критической нагрузки воспользуемся расчет-
ной схемой пружины в виде прямого стержня, эквивалентного пру-
жине в отношении жесткостей на сжатие, изгиб и сдвиг. При этом
угол подъема витков пружины примем равным нулю.
Прежде, чем достигнуть критического состояния, пружина со-
вершает осевое перемещение Лкр. При критической силе Ркр ось
пружины сохраняет равновесие в положении, слабо отклоненном
от прямолинейного (фиг. 87, а). Поперечный прогиб оси пружины
можно представить как сумму
V — Vug Ч”
здесь vU3 и рСдв — части прогиба, связанные с деформациями изгиба
и сдвига эквивалентного бруса. Поскольку прогиб v мал, то вторая
производная от него по координате z (фиг. 87, б) представляет собой
кривизну оси пружины; ее также можно представить как сумму
у = v-цз —}— (а)
Составляющая кривизны vU3i связанная с деформациями чи-
стого изгиба, находится по формуле (3. 38)
" 1 м
из
(б)
&иЗ --
где жесткость на изгиб эквивалентного бруса определяется выраже-
нием (3. 39).
172
Изгибающий момент в произвольном сечении z равен М — —Pv
(знак «минус» соответствует отрицательной кривизне оси при ука-
занном направлении осей координат). Подставляя его значение
в формулу (б), получим
f t
^из
из
Так как кривизна vcoe является первой производной угла ново-
рота а угол поворота, вызываемый деформациями сдвига,
определяется подформуле (3. 40)
Vc9° - Л&- ® ,
то соответствующая
составляющая кривизны будет
dQ
>f ___ dz
vcde A A *
s*cde
Поперечная сила Q в произвольном сечении z равна Q = Pfi
(фиг. 87, в), где О’— угол поворота сечения эквивалентного бруса.
Фиг. 87. Потеря устойчивости винтовой цилинд-
рической пружины сжатия:
а — пружина до и после потери устойчивости; б — расчет-
ная схема пружины; в — к определению поперечной силы Q.
Так как при сдвиге поперечные сечения смещаются параллельно
друг другу, не поворачиваясь (см. фиг. 86, <?), то угол поворота 'О’
связан только с изгибными деформациями бруса и поэтому он равен
ф = ^8. Тогда поперечная сила может быть представлена в виде
Q = Р • vu3.
(д)
173
Составляющая кривизны vcoe, связанная с деформациями сдвига,
с учетом выражений (в), (г) и (д) определится как
" PVU3 P*V , .
^c9e — ~~л — ~д ~л------• (е)
Асде Аиз • Асдв
Заменяя в уравнении (a) vu3 и vCQe по формулам (в) и (е), полу-
чим дифференциальное уравнение изогнутой оси пружины
Введем обозначение
Тогда уравнение (ж) примет вид
v" 4- — 0.
Решение этого уравнения можно представить как
v = а • sin kz + b • cos kz,
if
Постоянные интегрирования а и b находятся из граничных
условий. Если пружина закреплена так, что ее торцовые сечения
могут свободно поворачиваться в осевой плоскости (шарнирное
крепление), то граничные условия будут: при z — 0 и при z — Н
прогиб v ~ 0. Из первого условия постоянная Ъ = 0, а из второго
условия получаем равенство cl sin кН = 0, которое может иметь
место при к Н = л. Используя формулу (з) для величины к, полу-
чим уравнение
Р2 + АсдеР - Аиз Асда ~ = 0.
Здесь высота пружины в момент потери устойчивости Н = Но —
—ккр. Решая уравнение с учетом формул (3. 39), (3. 41) и (3. 21) >
получим выражение для критической осадки
где Но и/)о — высота и диаметр пружины в начальном состоянии;
С, Вп тл. Вь — жесткости проволоки пружины на кручение, на из-
гиб относительно главной нормали и бинормали
(см. фиг. 73, а} соответственно;
v — коэффициент, зависящий от способа крепления кон-
цов пружины. Его значения приведены в табл. 9, § 5,
стр. 69.
174
Г
Если пружина изготовлена из
жесткости на изгиб Бп = а
табл. 17, § 11). Тогда выражение
проволоки круглого сечения, то
С с
отношение — ~п—= (см.
(3. 42) примет вид
Акр
н0
0,813 1 —
Чем выше пружина, тем при меньшем относительном прогибе
происходит потеря устойчивости. Эта зависимость иллюстрируется
________ * -------- --- -- - 1 1 *
Z7 2 4 6 8 0°.
Л
Фиг. 88. Критическая осадка
л о
и предельная вы-
(Нй\
сота I в зависимости от
\ /пр
относительной высоты
пружины и способа крепления ее торцов.
фиг. 88, где дана относительная критическая осадка , как функ-
•“0
н
ция относительной высоты -=р~ при различных креплениях концов
пружины из проволоки круглого сечения.
1 75
Если отношение высоты пружины к ее диаметру
мало, то пружина устойчива при любой величине прогиба. В этом
случае подсчет по формуле (3. 42) дает мнимое значение критической
осадки. Предельная высота
— достаточно
о
/ Но \
пружины, при которой потеря
\ ^0 /пр
устойчивости еще не происходит, определяется из условия равенства
нулю подкоренного выражения в формуле (3. 42)
Яр
пр
Для пружин из проволоки круглого сечения
о
о
пР
Значения предельной высоты
О
при различных условиях
\ ^0 /пр
закрепления торцов пружины указаны на фиг. 88.
Для того чтобы оценить устойчивость конкретной пружины,
следует подсчитать относительную высоту и сравнить ее с пре-
н
1“пд » определяемым по формуле (3. 43).
\ ° /пр
, то пружина устойчива при любом прогибе.
пр
то пружина может потерять устойчивость
пр
при прогибах, достигающих критического значения X
Оценка устойчивости пружин из круглой проволоки производится
весьма просто по фиг. 88.
Пример. Оценить устойчивость винтовой цилиндрической пружины раз-
мерами Do ~ 18 мм, d = 2,2 мм, i = 10, На = 46 мм при двух вариантах кре-
пления торцов: в первом случае один торец закреплен на плоскости, другой на
шарнире; во втором случае один торец закреплен на плоскости, другой свободен.
Решение. Определим отношение высоты пружины к ее диаметру:
Для первого способа крепления пружины коэффициент
дельным значением
Если
Если >►
КР
^ = — = 2,51
Do 18
заделки v — 0,7
а предельная относительная высота
\ ” /пр
, то эта пружина устойчива при лю-
пр
оои осадке.
Для второго способа крепления торцов, когда один из них свободен, коэф-
фициент v — 2 и
следовательно, пружина при критическом прогибе потеряет устойчивость.
176
(см. фиг. 88). Так
как ~
о
о
= 1,31 (фиг. 88). В этом случае -=^
пр
о
о
и,
пр
Находим при
Но
D„
2,56 по кривой v = 2 относительную критическую осадку
Акр
Яо
^кр
— 0,11. При высоте пружины Но
- 0,11 Но = 0,11 -46 = 5,06 мм.
= 46 мм
критический прогиб будет
Полная осадка пружины равна разности между начальной и конечной
высотой пружины X = Но — di0 = 46 — 2,2-10 = 24 мм.
Таким образом, на одной пятой от полного прогиба пружина потеряет
устойчивость.
§ 17. ВИНТОВЫЕ ЦИЛИНДРИЧЕСКИЕ ПРУЖИНЫ С НАЧАЛЬНЫМ
НАТЯЖЕНИЕМ (МЕЖВИТКОВЫМ ДАВЛЕНИЕМ) [50], [51]
Пружина с начальным натяжением навивается плотно, без за-
зоров между витками и так, что витки давят друг на друга. Растя-
гивающая сила, приложенная к такой пружине, не вызовет ее де-
формации до тех пор, пока нагрузка не достигнет некоторой опре-
деленной величины, которая называется силой начального натяже-
ния. Если растягивающую силу продолжать увеличивать, между
витками пружины появятся зазоры, и дальнейшая деформация пру-
жины с начальным натяжением будет происходить так же, как и
у обычной пружины. В сечении проволоки возникнут крутящий мо-
PD
мент М = -у- и поперечная сила Q = Р (фиг. 89, а) (угол подъема
витков не учитываем, так как он мал у пружин с начальным натя-
жением). При разгрузке пружины зазор между витками будет умень-
шаться, и витки сомкнутся, когда сила Р уменьшится до величины
силы начального натяжения Ро. В этот момент внутренние силовые
факторы в поперечном сечении проволоки будут иметь значения
Мо = и Q = Ро (фиг. 89, б).
Если продолжать уменьшать растягивающую силу Р, то витки
пружины начнут давить друг на друга. Пренебрегая смятием в местах
соприкосновения витков, можно считать, что в проволоке сохранятся
те деформации, следовательно, и внутренние силовые факторы, кото-
рые она имела в момент соприкосновения витков при Р = Ро
(фиг. 89, в).
При полном снятии внешней нагрузки в пружине с начальным
Р D
натяжением сохраняются остаточный момент Мо = и попереч-
ная сила Q = Ро (фиг. 89, г).
Сила начального натяжения Ро определяется величиной остаточ-
ного крутящего момента Мо, получаемого проволокой при навивке.
Пружины с начальным натяжением изготовляются навивкой
со скручиванием проволоки или навивкой с отгибом.
При навивке со скручиванием проволока, поступаю-
щая на оправку, скручивается в сторону уже навитой части пружины,
как показано на фиг. 90, а. При этом в проволоке фиксируется
приложенный к ней момент. Большая часть его, оставшаяся
12 Заказ 24.
177
в проволоке после снятия навитой пружины с оправки, и определяет
величину силы начального натяжения.
Этот способ навивки применяется лишь при изготовлении корот-
ких пружин из тонкой проволоки с небольшим начальным натяже-
нием, когда скручивание может быть произведено вручную без
• Фиг. 89. Внутренние силовые факторы в пружине
с начальным натяжением.
применения сложных приспособлений. Существенным недостатком
такой навивки является больше!! разброс по длине пружины силы
начального натяжения.
Навивка с отгибом проволоки более проста и надежна и
обычно производится с помощью несложных приспособлений.
При навивке с отгибом проволока, подаваемая на оправку, отги-
бается в сторону навитой части пружины на некоторый угол а
(фиг. 90, б). Если бы проволока не была связана с уже навитой
частью пружины, то она и навивалась бы по винтовой линии с углом
подъема а (эта линия показана пунктиром). Начиная навиваться
по этой линии, проволока затем подтягивается навитой частью пру-
жины и при этом скручивается, так как изменяется кручение ее,
как пространственной кривой. В проволоке возникает крутящий
178
момент, который частично сохраняется в готовой пружине и создает
необходимый натяг между витками. Пружины, изготовленные этим ме-
тодом, имеют достаточно постоян-
ное и стабильное межвитковое да-
вление. Способ навивки с отгибом
позволяет получать пружины
с большим начальным натяже-
нием.
По схеме навивки с отгибом
происходит и навивка на штиф-
тах (фиг. 90, в). Проволока,
выходя из направляющей втулки,
попадает на два штифта, которые
и придают ей необходимую форму.
Как и при навивке с отгибом,
проволока, проходя между втул-
кой и штифтами, получает форму
винтовой линии, показанную
пунктиром. При отгибе проволоки
в сторону уже навитой части она
скручивается и в ней образуется
остаточный крутящий момент.
Способ навивки на штифтах
наиболее производителен, так
как может выполняться по авто-
матическому циклу.
Пружины с начальным иатя-
Фиг. 90. Схемы навивки пружин
с начальным натяжением:
о. — навивка со скручиванием', б — на-
вивка с отгибом; в — навивка на штифтах.
жением должны изготовляться
только из термообработанной про-
волоки. После навивки пружины
термообработка ее недопустима,
так как она приведет к снятию
а следовательно, и начального натяжения.
остаточных напряжений,
Фиг. 91. Характеристики обычной пружины
растяжения ((^ ab) и пружины с начальным
натяжением (ОаЬ).
Измерительные пружины
могут подвергаться обыч-
ной стабилизации при не-
высоких температурах
нагрева.
Анализ способов на-
вивки [49] — [51] пока-
зывает, что наибольшее
остаточное напряжение за-
висит от индекса пружины,
но, как правило, не пре-
вышает 0,4—0,5 от пре-
дела текучести при сдвиге
хт материала проволоки.
На фиг. 91 показаны характеристики пружин обычной и с началь-
ным натяжением. Первая изображается прямой Ot ab, вторая —
12*
179-
ломаной ОбФ.Сила начального натяжения обозначена Ро. Если нужно,
чтобы пружина на рабочем участке аЪ характеристики незначительно
меняла свое усилие, обычной пружине приходится давать большое
предварительное растяжение Хо, которое в несколько раз может
превышать рабочий ход ХрОб- В этом случае пружина с начальным
натяжением дает существенную экономию, занимаемого места:
в рабочем состоянии ее длина будет меньше по сравнению с длиной
обычной пружины на величину отрезка ОХО.
В приборостроении пружины с начальным натяжением широко
используются в качестве натяжных, измерительных и заводных.
Можно считать, что большинство пружин растяжения изготовляются
с начальным натяжением.
v
Фиг. 92. Пассик.
На фиг. 70, б показано применение пружины с начальным натя-
жением в манометре с безнулевой шкалой. Стрелка прибора при-
ходит в движение, начиная с того давления, при котором тяговая
сила манометрической пружины 1 превысит силу начального натя-
жения винтовой пружины 3 и оторвет ее от упора 2.
Известно применение пружины с начальным натяжением в ка-
честве так называемого «пассика» — тросика, передающего движе-
ние между-двумя шкивами (фиг. 92). Особенностью такой передачи
является то, что она одновременно выполняет роль муфты трения.
Пружинный тросик устанавливается с некоторым натягом. При по-
явлении момента сопротивления на ведомом шкиве ведущая ветвь
пассика натягивается, а ведомая — ослабляется, и ведомый шкив
нагружается моментом, пропорциональным разности натяжения вет-
вей. Когда усилие натяжения ведомой ветви падает до нуля, начи-
нается проскальзывание пассика, и увеличение передаваемого им
момента прекращается.
Пружина с переменным по длине межвитковым давлением при
растяжении увеличивает число рабочих витков (фиг. 93), поэтому
ее жесткость будет падать по мере растяжения пружины. Такие
пружины могут быть использованы в приборах с нелинейной харак-
теристикой механизма для исправления шкалы прибора. Пружину,
навитую с переменным начальным натяжением из проволоки с высо-
ким электросопротивлением, можно использовать как датчик со-
противления при измерении усилий или перемещений.
180
Характеристику «, состоящую из двух отрезков прямой (фиг.
94, а), может иметь только «идеальная» 1 пружина с начальным
натяжением. Реальная пружина будет иметь плавную характери-
стику б (фиг. 94, а).
При приложении к пружине растягивающей силы концевые витки
и зацепы деформируются. За счет этого пружина удлинится, и на-
чальный участок характеристики получает некоторый наклон
(фиг. 94, б).
Фиг. 93. Пружина с переменным по длине меж-
витковым давлением.
Так как при изготовлении пружины невозможно выдержать
строгое постоянство межвиткового давления, то при работе витки
пружины размыкаются неодновременно: сначала начинают дефор-
мироваться те витки, которые при навивке получили наименьшую
силу начального натяжения, последними размыкаются витки
с наибольшим межвитковым давлением. Таким образом, число ра-
бочих витков постепенно увеличивается, и характеристика пружины
вместо излома при Р~Р о имеет плавную кривую (фиг. 94, в).
Третьей причиной отличия действительной характеристики
от «идеальной» является некоторое смещение линии действия растя-
гивающей силы от оси пружины. При неосевом растяжении
1 Под «идеальной» понимается такая пружина, которая навита с постоянным
по длине межвитковым давлением, концевые витки и зацепы пружины не де-
формируются, а растягивающая сила приложена точно по оси.
181
пружина нагружается, помимо растягивающей силы, изгибающим
моментом. Когда этот момент достигает определенной величины,
витки пружины на одной стороне расходятся, за счет этого длина
пружины увеличивается, и характеристика пружины получает
нелинейный участок (фиг. 94, г).
Для того чтобы рабочий участок характеристики попал на пря-
мую АВ (фиг. 94, а)у пружину при установке в прибор растягивают
на величину 'кмонт. Величина монтажной вытяжки кмОпт зависит как
от размеров пружины, так и от точности ее изготовления и условий
работы и составляет обычно несколько процентов от начальной
длины пружины 149].
а) ё) б) г)
Фиг. 94. Монтажная вытяжка пружины с начальным на-
тяжением:
. а — «идеальная» (а) и реальная (б) характеристики; б — влияние на
характеристику деформаций концевых витков и зацепов; в — характе-
ристика пружины с неодинаковым межвитковым давлением по длине
пружины; г — характеристика пружины при неосевом растяжении.
Расчет на жесткость и прочность пружин с начальным натяже-
нием ничем не отличается от расчета пружин с зазором между вит-
ками. Для пружин с начальным натяжением угол подъема сс0 можно
считать равным нулю, что упрощает расчет.
Жесткость к пружин с начальным натяжением в соответствии
с выражениями (1. 3) и (3. 21) равна
Gd*
8D3i '
Наибольшее касательное напряжение определяется по формуле
Ттах = К
8PD
л с/з ’
где К — коэффициент, зависящий от индекса пружины. Его вели-
чина может быть взята с графика, показанного на фиг. 84, б.
Пружины, навитые с начальным натяжением, в отличие от обыч-
ных пружин растяжения, при некоторых условиях могут терять
182
устойчивость при растяжении [52]. Эта потеря устойчивости выра-
жается во внезапном перекосе витков. На фиг. 95, а показана пру-
жина, потерявшая устойчивость на среднем участке, где она была
навита с большей силой начального натяжения, чем на верхнем и
нижнем участках.
Потеря устойчивости возможна у пружин большого индекса,
навитых с достаточно большим начальным натяжением. Явление
потери устойчивости можно
объяснить с энергетических
позиций. Предположим, что
пружина нагружена растяги-
вающей силой Р, меньшей
силы начального натяжения
Р о. Тогда витки пружины
Фиг. 95. Потеря устойчивости пружины растяжения с начальным
натяжением:
а — пружина, потерявшая устойчивость на среднем участке; б —' участок пру-
жины до и после потери устойчивости.
останутся прижатыми друг к другу, длина пружины не изменится и,
следовательно, сила Р не совершит работу. Если некоторой посторон-
ней причиной вызвать перекос витков, то длина пружины увеличится,
и сила Р произведет работу. При перекосе витков проволока
изгибается, и витки пружины приобретают потенциальную энергию
деформаций. Если работа силы Р, возникающая при перекосе
витков, будет больше, чем потенциальная энергия деформаций, то
по устранении причины, вызвавшей перекос витков, пружина не
сможет восстановить свою первоначальную форму, и витки оста-
нутся перекошенными; пружина потеряет устойчивость.
Описанное явление потери устойчивости возможно только для
пружин с начальным натяжением.
183
Пружина растяжения с зазорами между витками не может поте-
рять устойчивость. При перекосе такой пружины растягивающая
сила будет совершать отрицательную работу, поскольку при пере-
косе зазор между витками будет не увеличиваться, а уменьшаться.
Поэтому независимо от величины силыР потенциальная энергия де-
формации будет всегда больше работы силыР при перекосе пружины,
и по устранении причины, вызвавшей перекос, пружина вернется
Фиг. 96. Предельная величина началь-
ного напряжения (То)Пр в зависимости от
индекса пружины из стальной проволоки.
к первоначальной форме.
Для определения крити-
ческой силы, при которой
появляется перекос витков
у пружин с начальным натя-
жением, заменим ее эквива-
лентным брусом (см. § 15).
Поскольку при потере устой-
чивости происходит только
сдвиг витков относительно
друг друга, брус должен
быть эквивалентен пружине
по жесткости на сдвиг АСдв,
которая определяется для
пружины формулой (3. 41).
В данном случае при сдвиге
ось пружины сохраняет
прямолинейное положение,
а витки поворачиваются от-
носительно оси на некото-
рый угол А О (фиг. 95, б).
Поперечная по отношению
к витку сила Q = Р sin А й.
Учитывая, что угол А й
может быть как угодно мал,
Q = Р А й. С другой сто-
роны поперечная сила Q
связана с углом А й
О
зависимостью (3. 40): Ай = . Подставляя сюда значение
поперечной силы Q = Р Ай, получим с учетом выражения (3. 41')
критическую силу, при которой происходит перекос витков
Ркр — Асдв ~
БН<Р
8D3i ’
Считывая, что для пружины с межвитковым давлением высота
Н = di, получаем
кр 8D3
(3.44)
184
ценку устойчивости иногда удобнее производить, сравнивая
начальное напряжение То
величиной каса-
тельных напряжений ткр. Напряжение тКр можно выразить через
силу РКр с помощью формулы (3. 37), где коэффициент К при индек-
сах с 10 можно считать равным единице
Ed*
Из выражения (3. 45) следует, что потеря устойчивости опасна для
пружин больших индексов. Для таких пружин предельная величина
начального напряжения (т0)пр ограничивается возможностью потери
устойчивости и рав i критическому напряжению ткр, которое
быстро уменьшается с увеличением индекса (фиг. 96).
Для пружин малых индексов (с < 8 4- 10) величина предель-
ного начального напряжения (т0)пр определяется возможностями
навивки и составляет, как показали исследования [49] и [50],
0,4—0,5 предела текучести тт. Характер изменения предельного
начального напряжения для пружин малых индексов также
указан па фиг. 96.
§ 18. ПРОЕКТИРОВАНИЕ ВИНТОВЫХ ЦИЛИНДРИЧЕСКИХ ПРУЖИН
РАСТЯЖЕНИЯ — СЖАТИЯ
Характер задач, решаемых при проектировании пружин, зави-
сит от их назначения. Наиболее трудоемко проектирование измери-
тельных пружин, требования к рабочим качествам которых более
высоки, чем для .натяжных, заводных пружин, пружин-аморти-
заторов и пр.
При проектировании измерительной пружины основным требо-
ванием является обеспечение заданной жесткости. При этом жела-
тельны минимальные гистерезис и нелинейность характеристики,
которые не должны во всяком случае превышать заданных допусти-
мых значений. Необходимо также обеспечить определенные коэффи-
циенты запаса по текучести, усталости и по устойчивости. Кроме
того, к пружинам нередко предъявляются дополнительные требова-
ния, например, требование одинаковых габаритов у нескольких
сменных пружин при различной жесткости, требование минималь-
ного веса, определенной частоты собственных колебаний и т. д.
Процесс проектирования измерительной пружины обычно состоит
из нескольких этапов. Сначала размеры пружины ориентировочно
определяются с помощью приближенных формул или по номограм-
мам, а также из конструктивных соображений. Затем эти размеры
уточняются при последующих поверочных расчетах.
При проектировании обычно исходят из заданной жесткости,
максимальной нагрузки и рабочего хода пружины.
Прежде всего выбирается материал в соответствии с требованиями,
предъявляемыми к пружине.
185
В зависимости от механических свойств выбранного материала
пружины и условий ее работы назначается величина допускаемого
напряжения [т]. Поскольку условия работы и требования к измери-
тельным пружинам в отношении точности, гистерезиса, стабильности
могут быть самыми разнообразными, то дать точные рекомендации
по выбору величины допускаемого напряжения для всех случаев
не представляется возможным. В каждом конкретном случае, оце-
нив условия работы и требования к пружине, и исходя из механи-
ческих свойств выбранного материала, следует выбрать коэффи-
циент запаса п, определяя этим величину допускаемого напряже-
ния. Обычно коэффициент запаса определяется по текучести, и тогда
допускаемое напряжение будет равно [т] = —
тг — пре-
где
дел текучести при сдвиге \ При выборе допускаемого напряжения
[т] следует учитывать, что предел прочности и предел текучести
пружинной проволоки одной и той же марки зависят от диаметра
’ проволоки (см. табл. 3, § 1, стр. 26).
Определение размеров пружины удобно начать с выбора индекса
пружины с, величина которого редко бывает меньше 4 и больше 20.
Пружины меньших индексов обычно не применяют по следующим
причинам. Опасными точками в винтовой цилиндрической пружине
растяжения-сжатия являются точки, расположенные на внутрен-
ней стороне витка (см. § 14). Напряжения в этих точках тем больше
по сравнению с напряжениями в остальной части поперечного сече-
ния витка, чем меньше индекс пружины (см. фиг. 84, а, б). Следо-
вательно, с уменьшением индекса (с< 4 ~ 6) резко возрастает
неоднородность напряженного состояния пружины, что всегда
нежелательно с точки зрения рационального использования мате-
риала.
Кроме того, при заданной жесткости с уменьшением индекса
приходится увеличивать число витков пружины. При этом возра-
стает высота пружины и появляется опасность потери устойчивости
для пружины сжатия.
Необходимо также иметь в виду трудности навивки пружин
малых индексов как на оправке, так и на пружинно-навивальном
автомате.
Однако нежелательно и чрезмерное увеличение индекса пружины.
Прежде всего увеличение индекса приводит к сильному возрастанию
диаметра пружины, что может быть недопустимо по габаритным
условиям. Кроме того, при увеличении индекса падает жесткость
пружины на сдвиг [§ 15, формула (3. 41)], что может вызвать потерю
устойчивости пружины растяжения, навитой с начальным натя-
жением (§ 17), а у пружин сжатия — потерю устойчивости, выра-
1 В справочной литературе для пружинных материалов приводятся, как
правило, значения пределов текучести при растяжении от. Предел текучести
при сдвиге приближенно можно определить по соотношению тт = (0,54-0,6)от
[34].
186
жающуюся в боковом выскальзывании витков при полном сжатии
пружины.
Навивка пружин больших индексов также встречает технологи-
ческие трудности, поскольку с увеличением индекса отклонения
в режиме навивки могут вызывать значительную неравномерность
упругой отдачи пружины и, следовательно, разброс по диаметру
витков в готовой пружине.
Выбрав материал пружины, величину допускаемого напряжения
и индекс пружины, из расчета на прочность и на жесткость опре-
деляем ее диаметр, размеры поперечного сечения проволоки и число
витков. Б качестве первого приближения при определении размеров
пружины можно воспользоваться формулами (3. 21) и (3. 37) линей-
ной теории, в которд с угол подъема витков считается равным нулю.
Для пружины, навитой из проволоки круглого поперечного сечения,
эти формулы можно записать в виде
______/V- 8Ршах
tmax — Л
краб
здесь Pffiin и Ртах — наименьшее
31 У (а
max — 1 min Gd
~~ 8D3 i~ 8c3i ’
а наибольшее рабочие усилия
краб — рабочая осадка пружины;
D — средний диаметр пружины;
d — диаметр проволоки;
/ — число рабочих витков;
D
с = -г- — индекс пружины;
к — жесткость пружины;
тгаах — наибольшее рабочее напряжение;
[ т ] —допустимое напряжение;
G — модуль упругости материала при сдвиге;
К — коэффициент увеличения напряжения
ренней точке витка (см. фиг. 84, б).
Из выражений (а) определяются диаметр проволоки
витков пружины
во внут-
и число
л [т] ’
№
I
В правых частях формул (б) и (в) находятся заданные и уже выб-
ранные величины: Ртах, к, [т], G, с.
Расчеты можно упростить, используя номограммы [17 ]. Например,
на фиг. 97 (см. вклейку) представлена номограмма, верхняя часть ко-
торой дает значение диаметра d проволоки в зависимости от индекса с
при различных соотношениях допускаемого напряжения материала
к наибольшей рабочей нагрузке Dl •- в соответствии с выражением (б).
* max
187
Нижняя половина номограммы построена на основании фор-
мулы (в), где отношение числа рабочих витков к диаметру про-
G
волоки указывается в зависимости от индекса с и величины -г-
/С
(G — модуль упругости материала при кручении, к — жесткость
пружины).
Расположение кривых в верхней части номограммы показывает,
[Т1 7
что при данном отношении ------ диаметр проволоки а возрастает
*тах
медленно с увеличением индекса пружины, и заданным требованием
прочности удовлетворяют 4—7 стандартных значений диаметров d
проволоки в интервале индексов с от 4 до 20.
Подбор числа витков и индекса пружины легко осуществить из
расчета на жесткость с помощью нижней половины номограммы.
«задаваясь каким-либо значением индекса с, соответствующим по
[Т]
Р шах
кривой
стандартному диаметру проволоки, определяем по
кривой
5- отношение
К
из которого находим число витков i. При
этом нужно иметь в виду, что жесткость пружины зависит от индекса
в большей степени, чем от числа витков [см. выражение (в) ]. Поэтому
при проектировании пружины удобнее добиваться получения задан-
ной жесткости изменением индекса с, а не числа витков г. Число
витков для пружины растяжения органичивается габаритами пру-
жины по высоте, для пружины сжатия, кроме того, возможностью
потери устойчивости. С другой стороны слишком малое число витков
также нежелательно, так как это может увеличить нелинейность
характеристики пружины вследствие большого влпяния посадки
концевых витков. Варьируя индексом с пружины, можно подобрать
подходящее число витков г.
Полная высота Нп пружины сжатия равна
dfn — dd 4“ ^тах Н- А»
здесь Хгаах — наибольшая осадка пружины; величина А зависит от
высоты концевых витков и учитывает также зазор между витками
при наибольшей осадке Хтах пружины. Этот зазор необходим для
того, чтобы на рабочем участке характеристики не происходила
посадка отдельных витков. Величина зазора зависит от допуска
на шаг пружины.
Высота пружины растяжения, навитой без зазора между витками,
равна
И п — d i —A,
где в этом случае А — высота концевых витков и зацепов.
Спроектированную таким образом пружину следует проверить
по габаритным условиям, по жесткости с учетом угла подъема витков,
по нелинейности и устойчивости. При необходимости оценивается
прочность пружины при перегрузках, усталостная прочность и пр.
188
При проведении этих расчетов выбранные размеры пружины уточ-
няются.
Проектирование натяжных пружин производится более просто,
так как для них имеет значение только величина усилия натяжения
при сохранении достаточной прочности пружины. Обычно желательно,
чтобы это усилие изменялось по возможности меньше в пределах
рабочего хода, поэтому жесткость
достаточно малой
мое усилие
предварительным
нием или сжатием пружины.
, Таким требованиям хорошо
удовлятворяет пр. кина рас-
тяжения с начальным на-
тяжением.
пружин натяжения выоирается
В
Pl
Ртах
О
, а треоуе-
достигается
растяже-
^гтп
A.paS
Фиг. 99. Пружина динамометра.
**-------Л max
Фиг. 98. Характеристика пружины.
При проектировании заводных пружин необходимо учитывать
энергию, которую должна отдавать пружина при работе. Энергия
U деформаций пружины может быть определена как работа, совер-
шаемая силой Р на рабочем участке Л В характеристики, и равна
площади аАВЬ на фиг. 98.
А-раб-
Учитывая, что Р
— жесткость пружины), по-
лучим
к
(Р max
2
Пример. Crfpoоптировать пружину динамометра на 2 кгс (фиг. 99). Осадка
пружины должна быть не менее 40 ж. Габаритные размеры пружины по высоте
не более 60 лглг, по диаметру — 20 мм. Пружина должна обладать коэффици-
ентом запаса по текучести 1,5. Материал — стальная пружинная прово-
лока; предел текучести Ту = 110 кгс! мм2, предел прочности Тпч = 130 кгс/мм2,
189
предел выносливости т_. = 100 кгс/.хл^2, модуль упругости G = 8,1 -103 кгс/мм’.
Сечение проволоки — круглое.
Определить нелинейность характеристики пружины, оценить ее устойчи-
вость и усталостную прочность.
Решение. Определим допускаемое напряжение [т]=-----------------=—
пт 1,5
= 73,3 кгс/мм2 и жесткость пружины к — — — = 0,05 кгс/мм.
Найдем отношение допускаемого напряжения к наибольшей силе Рит-:
[т] _ 73 ,3 „л р кгс/мм?
- — - о О, О в
тях KZC
кгс/мм?
кгс
ТТ “ [т]
По кривой ~ -
Р шах
верхней части номограммы (фиг. 97)
устанавливаем, что изменению индекса с от 4 до 20 соответствуют диаметры про-'
волоки d = 0,7 4-1,2 мм. Выберем диаметр d = 1,1 мм при индексе с = 16.
При этом средний диаметр пружины будет D = d-c — 1,1 -16 == 17,6 мм,
а наружный DH = D 4~ d = 17,6 + 1,1 = 18,7 .илг, что соответствует заданным
габаритам.
Подсчитаем отношение модуля упругости к жесткости пружины
8,1 Ю3
0,05 "
__ Jr п .л4 кгс /мм __ „ „
— 1Ь,2-104—-— ------- и по соответствующей кривой
Л-' 2 С У
нижнеи
части номограммы при с = 16 находим = 5-------- Отсюда число рабочих
d мм.
витков i= 5 d = 5 -1,1 = 5,5.
Высота пружины Нп = d-i + А.юах 4- А. В величину А входят высота
концевых витков, которую примем равной 2,5-d = 2,5-1,1 s 3 мм, и суммар-
ный зазор между витками в конце рабочего хода, оставляемый во избежание
преждевременной посадки витков. Если допуск на шаг пружины назначить
±0,5 мм, то достаточно принять суммарный зазор, равным 3 мм. Тогда высота
пружины Нп — 1,1 -5,5 -J- 40 4~ (3 4~ 3) = 52 мм, что также удовлетворяет
заданным условиям по габаритам.
Определим угол ао подъема витков и уточним жесткость пружины. В со-
ТУ
ответствии с формулой (3. 1), tg «о = —где высота Но рабочей части пружи-
ны равна полной Нп за исключением высоты концевых витков:
- 3 = 49 Тогда tg а„ =
Для оценки нелинейности характеристики пружины обратимся к фпг. 79.
Подсчитаем относительную осадку 6о по выражению (3. 35)
= 0,161, т. е. угол ао 9° 10'.
0,007. Следо-
По фиг. 79, а находим при — 0,132 разность б — до =
вательно, относительный прогиб д, уточненный по нелинейной теории, будет
д = 0,132 4- 0,007 = 0,139. Нелинейность rj характеристики определяется по
фиг. 80, а: при а,о ~ 9° 10' и д = 0,139 ц 1%.
Оценка устойчивости пружины может быть произведена по фиг. 88. Для
На 49
этого подсчитаем относительную высоту пружины: . =
Крепление торцов пружины не допускает поворота их *в осевой
кости (фиг. 99), следовательно, коэффициент крепления v = 0,5.
тированная пружина устойчива при любом прогибе, так как
устойчивости при таком креплении возможна только 'при —— >5,24i
плос-
Спроек-
потеря
о
190
Определим запас выносливости по формуле [34]:
----1 ~-
та тпг
^пч
Напряжения в пружине динамометра меняются при работе по пульсацион-
ному циклу (см. фиг. 5, б), следовательно, амплитуда напряжений та и среднее
_______________________________________________________ 73,3 пр q /2
— —-—= 36,6 кгс/ммл.
Тогда коэффициент запаса по выносливости составит
Пв = 36,6 _j_ 36,6 = 1,55 ’
100 • 130'
напряжение тт цикла будут равны то = тт= —
§ 19. ФАСОННЫЕ ВИТЫЕ ПРУЖИНЫ
Фасонные пружины, например, конические или параболоидные
(см. фиг. 68, б, в) могут быть получены путем навивки на пружинно-
навивальных автоматах с перемещающимися в процессе навивки
штифтами или навивкой на специальных оправках.
Фасонная пружина может быть спроектирована так, что при
сжатии ее витки садятся друг на друга или на опорную
поверхностней постепенно выключаются из работы. В этом случае
характеристика фасонной пружины будет затухающей, что исполь-
зуется в тех приборах, где требуется нелинейная характеристика
упругого элемента.
Применение фасонных пружин позволило создать ряд конструк-
ций равночастотных амортизаторов, где с увеличением нагрузки
жесткость пружины возрастает так, что в широких интервалах
изменения нагрузки удается поддерживать постоянной частоту
собственных колебаний амортизируемого объекта 1.
Фасонная пружина может иметь такую форму, что при ее пол-
ном сжатии витки расположатся в одной плоскости, и высота пру-
жины будет равна диаметру проволоки. При жестких требованиях по
габаритам такая фасонная пружина имеет преимущество перед
цилиндрической.
Характеристика фасонной пружины сжатия при посадке витков
имеет вид, показанный па фиг. 100. На участке ОА деформируются
все рабочие витки пружины, и характеристика линейна. В точке А
характеристики начинается посадка витков, в точке В процесс
посадки заканчивается, и при дальнейшем увеличении сжимающей
силы Р осадка пружины X = не изменяется. На этой фигуре
Рн и — сила и осадка пружины, соответствующие началу посадки
витков, Рк и —- сила и осадка в конце посадки. При посадке
на плоскость — Н о.
1 И о р и ш Ю. И., Защита самолетного оборудования от вибраций, Оборон
гиз, 1949.
191
0 РРк Р
Фиг. 100. Характеристика фасонной пружины.
Фиг. 101. Геометрия фасонной пру-
жины :
а — образующая поверхности вращения и
спираль в плане; б — коническая пружина
постоянного шага.
192
Выведем уравнение характеристики фасонной пружины [5].
Ограничимся при этом рассмотрением пружины с малым углом
подъема витков.
Геометрия фасонной пружины полностью определяется формой
образующе!! поверхности вращения и формой спирали, которая
получается при проектировании витков пружины на плоскость,
перпендикулярную ее оси (фиг. 101, а).
Уравнение образующей ненагруженной пружины можно записать
в виде
где zo и г — координаты д. осевом и радиальном направлениях
произвольной точки оси проволоки;
Но — высота ненагруженной пружины;
т\ и г2 — наименьший и наибольший радиусы витков пружины
Для нагруженной пружины уравнение образующех! записывается
.аналогично
z z (г) (а')
но здесь Ни z — высота и осевая координата пружины после на-
грузки.
Уравнение спирали в плане запишем в виде
г = г (<р) (0^Сф-<2л i), (б)
где <р угловая координата, отсчитываемая от наименьшего радиуса
до текущего радиуса г, i — число рабочих витков.
При осевом нагружении пружины малого угла подъема ее проек-
ция в плане остается неизменной, поэтому уравнение (б) спирали
в плане сохраняется и в нагруженном состоянии пружины.
В качестве примера напишем уравнения образующей и спирали в плане
для конической пружины постоянного шага (фиг. 101, б). Для такой пружины
образующая является прямой, уравнение которой можно представить в виде
. (в)
Г2 — Г1
Проекция в плане этой пружины является Архимедовой спиралью
г = (г)
где t = — . —1---шаг спирали в плане.
Будем считать, что шаг t спирали в плане больше ширины а
поперечного сечения проволоки (или диаметра проволоки d, если
сечение круглое). В этом случае при сжатии пружины ее витки,
не задевая друг друга, будут садиться на опорную поверхность,
13 Заказ 24.
которую примем плоской. Таким образом, полностью сжатая пру-
жина представляет собой плоскую спираль.
Обычно посадка происходит, начиная с витка наибольшего
радиуса, поскольку он наиболее податлив. Затем посадка постепенно
распространяется на витки маныпих радиусов, заканчиваясь посад-
кой витка радиуса гг.
Случай, когда посадка начинается с витка меньшего радиуса,
возможен, если шаг витков малых радиусов достаточно мал по
сравнению с шагом витков больших радиусов. Такой процесс
посадки мы рассматривать не будем.
Сначала найдем уравнение характеристики пружины на линей-
ном участке ОА, когда сила Р <. Рн (фиг. 100).
Осадка пружины может быть определена с помощью интеграла
Мора
% = f си , (д)
Z
где Мкр = Р • г и МК1 — 1 . г — крутящие моменты от заданной
силы Р и от единичной силы в произвольном попереч-
ном сечении проволоки;
С — жесткость проволоки на кручение;
ds = гб/ф — длина элемента проволоки.
Так как при Р <С Рн работают все витки пружины, то интеграл (д)
следует брать по всей длине I проволоки или по радиусу г в пре-
делах от до г2. Связь между переменными г и ср устанавливается
уравнением (б) спирали в плане.
В качестве примера, определим линейный участок характеристики кони-
ческой пружины с постоянным шагом (фиг. 101, б). Дифференцируя уравнение
2л
(г) спирали в плане, получим d ср = —dr.
Интегрирование выражения (д) дает
Г2
Если пружина изготовлена из проволоки круглого сечеиия, то жесткость
л
па кручение С — GJP— G — , и уравнение характеристики на линейном
32
участке будет
16 Pi
(i+4) (г24-Г1).
Найдем теперь уравнение характеристики пружины на нелиней-
ном участке АВ, где происходит посадка витков при Рп < Р < Рк.
На фиг. 102,а линия LM изображает образующую zo = zo (г)
поверхности вращения, на которой располагаются витки пружины
до нагружения. В результате сжатия пружины некоторой силой
194
Р > Рн точка К образующей перейдет в положение К', точка М
в положение, М'\ образующая займет положение LK’М\ показан-
ное пунктиром. Отрезки КК' и ММ' = X изображают перемещения
точек К и М пружины и направлены параллельно оси пружины,
поскольку угол а подъема оси проволоки предполагается малым.
При нагружении пружины силой Р происходит посадка пружины
в точке К. Радиус до этой точки обозначим гп и назовем «поса-
дочным» радиусом.
Для определения силы Р рассмотрим развёртку оси проволоки
пружины в начальном (кривая LM на фиг. 102, б) и нагруженном
(кривая LK'M') состо шях.
Фиг. 102. Посадка пружины:
а — образующая до нагружения и после начала посадки витков;
б—развертка оси проволоки до нагружения и после начала посадки
витков.
Угол наклона оси проволоки в точке К в начальном состоянии
равен а; при нагружении пружины этот угол уменьшается и ста-
новится равным нулю, когда посадка витков доходит до точки К'.
Соответственно этому изменяется и кручение (§ 10) оси проволоки
в этой точке. Кручение в точке /Г, находящейся на радиусе гп от
оси пружины, в начальном состоянии равно в соответствии с фор-
мулой (3. 5)
sin 2а
или при малом угле а
СО 0 =
а
гп
Кручение в точке К' нагруженной пружины равно нулю (со — 0),
поскольку эта точка принадлежит плоской кривой LK', где про-
изошла посадка витков.
Таким образом при нагружении пружины силой Р кручение
в точке К изменилось на
Д(0 — со — (Оо = — соо = —.
' гп
13*
195
Из фиг* 102, б следует, что угол а ввиду его малости можно пред-
ставить как
Производную можно определить, если известны уравнения
CL (J)
(а) и (б) образующей и спирали в плане.
Из двух последних выражений следует, что изменение кручения
в точке К, расположенной на радиусе г = гп, равно
dz0
</ф
С другой стороны изменение кручения связано с крутящим
моментом Мк уравнением (3. 11)
= (з)
О
Из выражений (ж) и (з) с учетом того, что в точке КМк — Р • гп,
получим
(3.46)
’п той точки пружины, в ко-
Уравнение (3. 46), называемое уравнением посадки, устанавли-
вает связь между силой Р и радиусом гп той точки пружины, в ко-
торой происходит посадка.
Посадка витков начинается в точке L пружины на радиусе г — г2
при силе Р = Рн, которую можно найти из уравнения посадки
dzG
8
r«r2
Заканчивается посадка
на радиусе г —
при
силе
Р - Рк в точке М пружины
о
//
Для определения осадки X пружины представим ее состоящей
из двух участков: LK — упругого и КМ — абсолютно жесткого.
Сначала под действием силы Р произойдет посадка витков на участке
LK, и точка К пружины перейдет в положение К'. Участок КМ,
перемещаясь, как жесткое целое, займет положение К'М", и осадка
пружины будет равна (фиг. 102, б)
ММ" = КК' = H0—z0 (гп),
где zo (гп) — координата точки К в начальном состоянии пружины.
196
Однако в действительности участок КМ деформируется и дает
дополнительную осадку Я/, равную взаимному осевому смещению
точек К и М. Ее можно найти с помощью интеграла Мора (д), кото-
рый следует брать в пределах участка КМ пружины, т. е. от гх
до гп
гп
. , ” Prsd
== ~~с
Г1
Таким образом, осадка пружины равна сумме X = К К' + К
(фиг. 102, б). В соответствии с выражениями (и) и (к) получим
о
(3. 47)
С помощью уравнений (3. 46) и (3. 47) можно построить харак-
теристику пружины на нелинейном участке А В (фиг. 100). Если
из этих уравнений исключить посадочный радиус гп, то полученное
выражение будет давать непосредственную связь между силой Р
и осадкой X. Выполним это для конической пружины постоянного
шага.
Для того чтобы найти производную входящую в уравнение посадки
(3. 46), исключим из геометрических уравнений (в) и (г) переменную г, в резуль-
тате чего получим осевую координату zo произвольной точки пружины как функ-
цию угловой координаты ф : zo = -„ - ф, отсюда - — v. . Уравнение
t tt ср e-
посадки (3. 46) получит вид
(л)
Определим величины сжимающих сил Рн в начале и
в соответствии с выражениями (3. 46') и (3. 46")
Рк в конце посадки
(м)
, _ сн.
К-- п
2л irj
о
2л 1гп
Осадка X определяется по зависимости (3. 47)
Подставляя сюда радиус гп из выражения (л) и учитывая соотношения
(м), получим после преобразований уравнение характеристики конической
пружины
197
Как и следовало ожидать, полученная зависимость между Л и Р при посадке
пружины нелинейна. Отметим, что уравнение (н) справедливо только при Рн <
<2 Рк. Если Р «С то характеристика конической пружины описывается
линейным уравнением (е). При силе Р = Рк осадка X = Но и остается неизмен-
ной при дальнейшем увеличении силы Р > Рк.
Оценка прочности фасонной пружины из проволоки круглого
сечения производится по формуле (3. 37)
8PD
где К — коэффициент, определяемый в зависимости от индекса с
пружины по фиг. 84, б.
В отличие от цилиндрической винтовой пружины, в которой при
осевом нагружении все сечения витков равноопасны, в фасонной
пружине положение опасного сечения зависит от формы пружины
и может изменяться с нагрузкой.
Если пружина нагружена силой Р < Pw, т. е. посадка
витков еще не началась, наибольший крутящий момент Мк
появляется в сечении витка наибольшего радиуса гг, и тогда
к 16 Рг2
Тщах - Л я d3 ,
где при определении коэффициента К под индексом с следует
2^*
считать с ----- —~ .
После того как началась посадка витков (Рн < Р Рк), часть
витков на участке LK (фиг. 102) выключилась из работы, и напря-
жения в них остаются неизменными при дальнейшем увеличении
нагрузки. В этом случае наибольшие напряжения возникают в сече-
нии К', расположенном на посадочном радиусе гп.
Например, для рассмотренной выше конической пружины при Р > Рн
максимальное касательное напряжение в соответствии с формулой (л)
Ттах
16 Ргп „ 8СН0
л с?3 Л nW
1 = GHnd
гп lrn
Отсюда следует, что с уменьшением посадочного радиуса гп напряжение ттах
возрастает и достигает наибольшего значения, когда гп — г15 т. е. когда посадка
заканчивается
Ттах— А"
4л ir
Вопросы расчета пружин при посадке на опорную поверхность
и проектирования фасонных пружин по заданной характеристике
изложены в работах Е. П. Попова [5], [53], где также рассмотрены
цилиндрические пружины с переменным шагом как частный случай
фасонных пружин.
198
§ 20. ПРУЖИНЫ КРУЧЕНИЯ
Конструкция и применение
По внешнему виду пружины кручения отличаются от пружин
растяжения-сжатия только конструкцией концевых витков и заце-
пов, которые должны обеспечивать возможность нагружения пру-
жины торцовыми моментами. Жесткие пружины, работающие при
небольших углах закручивания, нагружаются силами, приложен-
ными к отогнутым концам (фиг. 103, а, б). При больших углах закру-
чивания такое нагружение пружины может привести к ее перекаши-
ванию, в результате чего появляется трение между витками пружины
и валиком. Пружина кручения не будет перекашиваться, если
к ее зацепам приложить не силы, а моменты. В этом случае пружина
а) $ 6) г) о)
Фиг. 103. Пружины кручения.
по всей длине будет находиться в условиях чистого изгиба и сохра-
нит свою цилиндрическую форму. Такое нагружение пружины
можно осуществить, жестко закрепляя концы пружины в поворачи-
вающихся деталях так, чтобы ось пружины совпадала с осью враще-
ния деталей (фиг. 103, в).
В некоторых случаях для уменьшения перекоса изготовляются
пружины с двойной навивкой (фиг. 103, г).
Пружины кручения большой длины иногда имеют переменный
диаметр для того, чтобы обеспечить достаточные зазоры между
пружиной, валиком и втулкой, как например, у пружины шторного
фотозатвора (фиг. 103, д).
Применение пружин кручения удобно, если нужно приводить
в движение или создавать натяжение между деталями, поворачи-
вающимися вокруг некоторой оси. В приборах пружины кручения
используются в качестве заводных, натяжных, муфт одностороннего
вращения (см. фиг. 70, г) и пружинных тормозов.
199
Расчет на жесткость и на прочность
Расчетом на жесткость устанавливается зависимость между
углом 0 поворота торцов пружины и приложенным моментом 9)7.
Результат решения этой задачи был дан в § 11, когда рассматри-
валось нагружение винтовой цилиндрической пружины осевой
силой Р и торцовым моментом 9)7. Для угла закручивания 0 было
получено выражение (3. 16). Так как у пружин кручения осевая
сила отсутствует, то формула (3. 16) принимает вид
В cos а0
sin2 а0
cos2 а
здесь/)оиго— средний диаметр и число рабочих витков ненагру-
женной пружины;
В и С -— жесткости проволоки на изгиб и на кручение;
о0 — начальный угол подъема витков пружины.
Пружины кручения обычно навиваются. из проволоки круглого
сечения с небольшим зазором между витками, поэтому угол подъема
а0 можно считать равным нулю. Так как жесткость на изгиб круг-
лой проволоки равна
то формула (а) будет
я d4
“64“’
(3. 48)
Если при работе пружина не должна касаться валика, то его
диаметр De должен оставаться меньше внутреннего диаметра нагру-
женной пружины: De<Z D — d. Определим диаметр D пружины
при ее закручивании моментом 9)7. Из условия неизменности длины I
проволоки пружины в процессе нагружения получим
(б)
где D — средний диаметр пружины после нагружения;
фо = 2лг‘о — центральный угол ненагруженной пружины;
ф + 0 — центральный угол пружины после нагружения;
0 — угол закручивания пружины.
Из выражения (б) следует
Где угол 0 определяется формулой (3. 48).
Проволока пружины кручения малого угла подъема работает
на изгиб, и в ее поперечном сечении возникают нормальные напря-
жения, распределение которых по сечению показано на фиг. 104, а.
Эпюра имеет гиперболический характер, поскольку пружина пред-
200
ста ляет собой брус большой кривизны, и деформации внутренних;
волокон а — а при изгибе витка пружины будут больше, чем дефор-
мации наружных волокон б — б. С увеличением индекса пружины;
кривизна витка уменьшается, и эпюра принимает более линейный,
характер.
Фиг. 104. Напряжения в пружине кручения:
а — эпюра нормальных напряжений о в поперечном сечении прово-
локи; е — график коэффициента К.
Напряжения в опасной точке а могут быть определены по
формуле, полученной на основе теории изгиба бруса большой кри-
визны [34], [39]
Сщах — А
Ми
Wu
л d3
здесь коэффициент К можно определить по приближенной формуле-
Ас _______|
К . Числовые значения коэффициента К даны на,
*Ж 'г* -Ж
фиг. 104, б для пружины из проволоки круглого сечения в зависи-
D
мости от индекса пружины с — .
Расчет пружинного храпового механизма (пружинного тормоза) [54J
В некоторых механизмах пружины кручения используются
в качестве пружинного тормоза. Пружина надевается на валик,,
диаметр которого больше внутреннего диаметра пружины. При
этом создается некоторый натяг. Его величина выбирается так, чтобы
валик мог вращаться только в одном направлении. Па фиг. 105, а
это направление указано стрелкой. При движении валика в обрат-
ном направлении пружина силами трения затягивается вокруг
валика и останавливает его. Таким образом, пружина выполняет
функцию храпового механизма.
201
Расчет пружинного тормоза изложен в работе [54]. Расчетом
устанавливаются значения момента трения Mmp, возникающего
при прямом направлении вращения (по стрелке, показанной на
фиг. 105, а) и предельного тормозного момента Мпр, препятствующего
вращению валика при обратном движении. Эти моменты зависят
от натяга пружины
Д = £ —£>0,
где Do — диаметр свободной пружины, a D — диаметр пружины,
надетой на валик.
Фиг. 105. Пружинный тормоз:
а — схема пружинного тормоза; б — нагружение концевого участка пружины при неподвиж-
ном валике; в — элемент пружины; г — нагружение концевого участка при вращении валика.
Определим изгибающий момент Мо в пружине, надетой на валик.
В соответствии с основной формулой (2. 2) теории изгиба бруса
момент Мо равен
Мо = EJX Ах,
(б)
где осевой момент инерции поперечного сечения проволоки
т л dl А
Jх — • g, , а А х — изменение кривизны проволоки:
202
1 2 3 4 5 6 T g 9 10 12 И !б 18 f
Фиг. 106. Графики коэффициентов и к2.
203
Подставляя выражение (в) в формулу (б) и учитывая соотношение
(а), получим
__ 2EJXE
О ^9
Пружина плотно охватывает валик по всей длине за исключением
концевых участков, где между пружиной и валиком остается зазор
на дуге с центральным углом (фиг. 105, б). Рассматривая условия
равновесия элемента (фиг. 105, в), выделенного из прилегающей
к валику части пружины, получим соотношение между равномерно
распределенными силами q и нормальной силой N‘, N = qR. Силы
(?i, возникающие в местах контакта пружины с валиком, и нор-
мальная сила N, а также угол <р находятся из трех уравнений равно-
весия, которые можно составить для участка АВ пружины, а также
из того условия, что взаимное перемещение диаметрально противо-
положных точек А и D равно величине натяга Д.
Аналогично решается задача, если учесть силы трения, возникаю-
щие при вращении валика. При этом, если вращение происходит
по стрелке (фиг. 105, г), то силы трения р, р, Q2 и р, q' будут
раскручивать пружину, в результате чего контактные силы умень-
шатся до величины Qu q . Момент трения для этого случая
может быть определен по формуле [54] Мтр ~ кгМо. Здесь М о
определяется выражением (г), а коэффициент к1 зависит от числа i
витков пружины и коэффициента трения р, и дан на фиг. 106, а.
При изменении направления вращения валика силы трения
меняют свой знак, затягивая при этом пружину вокруг валика.
Наименьший момент МпР, при котором валик еще не проворачивается,
определяется выражением [54] Мпр = к2М0е2лгц. Значения коэф-
фициента къ даны на фиг. 106, б.
ГЛАВА IV
ТЕРМОБИМЕТАЛЛИЧЕСКИЕ ПРУЖИНЫ
§ 21. ОСНОВНЫЕ СВОЙСТВА И ПРИМЕНЕНИЕ
Термобиметаллическая пружина состоит из двух металлических
полосок, материал которых имеет различные коэффициенты линей-
ного расширения (фиг. 107, а). Эти полоски соединяются между
собой сваркой или пайкой. Слой термобиметалла, обладающий боль-
шим коэффициентом линейного расширения, называется активным
в отличие от инертного слоя с меньшим коэффициентом линейного
а)
Фиг. 107. Термобиметаллическая пружина при нор-
мальной температуре (а) и при нагреве (б).
расширения. При нагреве биметаллическая полоса изгибается в сто-
рону инертного компонента (фиг. 107, б). Входным параметром
термобиметалла является температура, а выходным — перемещение.
Благодаря простоте, дешевизне и надежности в работе термоби-
металлы широко применяются в различных приборах и устройствах.
Термобиметаллическая пружина часто используется, например,
как чувствительный элемент биметаллического термометра. В этом
случае термобиметалл должен обладать высокой чувствительностью
для обеспечения достаточно большого перемещения. Перемещение
термобиметалла возрастает с его длиной; для увеличения длины
чувствительного элемента при сохранении малых габаритов ему
обычно придается спиральная или винтовая форма.
Применение термобиметаллов не ограничивается задачей измере-
ния температур. Часто они используются для измерения других
параметров, преобразуемых в температуру. Так, например, для
измерения силы и мощности тока используются биметаллические
амперметры и ваттметры. Измерительная система биметалличе-
ского амперметра показана на фиг. 108, а. Чувствительный элемент
205
представляет собой биметаллическую спираль 7, которая нагревается
током. С увеличением силы тока деформация спирали возрастает,
и стрелка поворачивается. Монометаллический волосок 2 служит
для подвода тока к поворачивающемуся концу биметаллической
спирали, а дополнительная биметаллическая пружина 3 необходима
для введения поправки при изменении температуры окружающей
среды. Волосок 2 и пружина 3 отделены от основной спирали 1
экраном 4, который защищает их от нагрева со стороны спирали 1.
Фиг. 108. Применение термоби-
металлических пружин:
а — измерительная система биметал-
лического амперметра; б — термо-
биметаллические элементы в системе
дистанционной передачи перемещений;
в — термобиметаллическое реле; г —
термобиметаллический контакт быст-
рого срабатывания.
Высокочувствительные термобиметаллические элементы при-
меняются в приборах для измерения лучистой энергии, например,
в некоторых конструкциях радиационных пирометров [55].
Известно применение термобиметаллов в качестве чувствитель-
ных элементов теплоэнергетических приборов, измеряющих расход,
давление, плотность газов [56].
Большое распространение получили системы дистанционных
передач перемещений с использованием термобиметаллических эле-
ментов (фиг. 108, б). Перемещение X контакта 1 датчика пропор-
ционально дистанционно передаваемому параметру. При замыкании
с этим контактом контакта 2 термобиметаллического элемента 3
датчика по цепи проходит ток, нагревающий одновременно и одина-
ково термобиметаллические элементы датчика и вторичного при-
бора. Эти элементы получат одинаковые перемещения. Температура
нагрева, а следовательно, и перемещение биметаллических элементов
3 и 4 зависят от положения контакта 7. Чувствительный элемент 3
датчика будет периодически замыкать и размыкать контакты 1 и 2Г
поддерживая температуру около некоторого значения, определяе-
мого положением контакта 1,
Более широко, чем в измерительных приборах, термобиметал-
лические пружины используются в различных релейных устрой-
ствах, предназначенных главным образом для защиты электрических
цепей и аппаратов от перегрева, а также в элементах простейших
регуляторов температуры. Биметаллические защитные реле и регу-
ляторы температуры широко используются и в бытовых аппаратах
(в холодильниках, утюгах, стиральных машинах), и в промышлен-
ных системах (реле защиты электродвигателей, регуляторы тем-
пературы в электропечах небольшой мощности). На фиг. 108, в-
представлена схема биметаллического реле, реагирующего на изме-
нение окружающей температуры. Биметаллическая пластинка 1
нажимает на контактную пружину 2, разрывая контакт между
пружиной 2 и контактным винтом 3. Положением этого винта уста-
навливается температура срабатывания реле.
Недостатком термобиметаллических контактных устройств
является медленное замыкание и размыкание контактов. Для устра-
нения этого недостатка применяются пружинные или магнитные
перекидывающие устройства, конструкции которых подобны пере-
кидывающим устройствам в обычных контактных механизмах. Тот же
результат может быть достигнут применением биметаллических
элементов специальной конструкции, которые способны давать
скачкообразные перемещения в результате потери устойчивости
при нагреве. Такие элементы выполняются или в виде биметалличе-
ских выпуклых мембран1, или в виде биметаллической полоски
в форме пологой арки (фиг. 108, г).
Биметаллические пластинки могут быть использованы не только
в релейных устройствах, управляющих электрическими цепями,
но и для непосредственного управления регулирующими органами,
например, дроссельными заслонками трубопроводов2. В этих слу-
чаях применяются достаточно мощные биметаллические пластинки.
Весьма широкое применение получили биметаллы в качестве
температурных компенсаторов самых различных приборов.
В некоторых манометрических приборах с изменением темпера-
туры меняется чувствительность прибора вследствие изменения
модуля упругости материала манометрического упругого элемента.
В этом случае одним из наиболее простых средств уменьшения тем-
пературных погрешностей является термобиметаллическая компен-
сация кинематического или силового типов3.
1 Лазор и на Е. И., О работе круглых хлопающих биметаллических
мембран, труды Ленинградского института авиационного приборостроения,
№ 24, 1957.
2 Родес Т. Д., Производственные контрольно-измерительные приборы,
Гостехиздат, 1947.
8 Боднер В. А., Фридлендер Г. О. и Чистяков Н. И.,
Авиационные приборы, Оборонгиз, 1960.
207
Кинематическая компенсация (фиг. 09, а) состоит в том, что
•с помощью биметаллической пружины, входящей в состав кинемати-
ческой цепи механизма, изменяется должным образом передаточное
отношение при изменении температуры. При силовой компенсации
(фиг. 109, б) биметаллический элемент создает дополнительное уси-
лие, пропорциональное как изменению температуры, так и пере-
мещению манометрического упругого элемента.-
От биметаллических компенсаторов не требуется больших пере-
мещений или усилий, поэтому пружины компенсаторов имеют
небольшие размеры и обычно прямолинейную или U-образную форму.
Фиг. 109. Термобиметаллические компенсаторы:
<а — кинематическая и б — силовая компенсация температурной погрешности манометри-
«теского упругого элемента; в — регулировка чувствительности биметаллической пружины
изменением положения натяжного винта; г — регулировка поворотом биметаллической
пружины вокруг ее оси; д — термобиметаллические компенсаторы электролитического
датчика.
Регулировка чувствительности термобиметаллической пружины про-
изводится либо изменением ее рабочей длины или положения натяж-
ного винта (фиг. 109, б), либо поворотом пружины вокруг ее оси,
чем изменяется составляющая Кх перемещения X в заданном напра-
влении х (фиг. 109, г).
Термобиметаллические компенсаторы в виде биметаллических
изогнутых или спиральных пружин используются в электроизмери-
тельных приборах (например, биметаллическая пружина 3 в ампер-
метре по схеме, показанной на фиг. 108, а):
Биметаллические компенсаторы используются в электролити-
ческих датчиках, изменяя взаимное положение электродов при
•изменении температуры (фиг. 109, д).
208
Одним из наиболее известных и давних применений термобиметал-
лов является компенсация изменения упругости волоска в спуско-
вом регуляторе «баланс-спираль» часовых механизмов при нагреве *.
Материалы слоев термобиметалла должны обладать большой
разницей между коэффициентами линейного расширения для обеспе-
чения достаточной чувствительности. Для получения линейной
характеристики термобиметалла желательно, чтобы коэффициенты
линейного расширения его компонентов не изменялись с температурой
или же изменялись одинаково.
Материал термобиметалла должен иметь высокий предел упру-
гости, чтобы при работе в нем не возникали остаточные напряжения.
С другой стороны желательна высокая пластичность материала,
позволяющая прокатывать биметаллические полосы до малых тол-
щин. Компоненты биметалла должны хорошо свариваться или
спаиваться.
Если биметалл работает в условиях высоких температур, то
материал его должен быть достаточно термостойким.
Сплавы на медной основе имеют большой коэффициент линейного
расширения, но могут применяться в качестве одного из компонентов
биметалла только в небольшом интервале температур: главным
образом в устройствах, предназначенных для измерения или ком-
пенсации температуры воздуха, окружающего прибор.
Высокими упругими свойствами обладает биметалл, состоящий
из инвара и хромо-никелевых сталей. Малый коэффициент линейного
расширения инвара обеспечивает достаточную чувствительность
таких биметаллов, а высокая прочность и хорошая термостойкость
позволяют использовать их при высоких напряжениях и повы-
шенных температурах (до 200—225° С).
Если термобиметалл применяется в устройствах, предназначен-
ных для измерения или ограничения величины тока, и нагревается
проходящим током, то величина удельного электросопротивления
материала биметалла не должна быть слишком малой. Для этого,
как правило, используются «черные» биметаллы, компоненты кото-
рых выполнены на основе железных сплавов.
Физико-механические свойства основных типов биметаллов по
ГОСТ 5198-50 даны в табл. 21 и 22 [21], [24].
Слои биметалла свариваются в полосы, которые прокатываются
до требуемой толщины. Биметаллу придается нужная форма путем
механической обработки. Для снятия остаточных напряжений
проводится температурная стабилизация, во время которой биметалл
нагревают до температуры на 10—20% выше максимальной ра-
бочей.
Если чувствительный элемент предназначен для работы в широ-
ком диапазоне температур, то подбор компонентов термобиметалла
производится с учетом изменения коэффициентов линейного расши-i
рения при нагреве. i
1 Аксельрод 3. М., Часовые механизмы, ГНТИ, 1947.
14 Заказ 24.
209
Таблица 21
Свойства термобиметаллов
ИСХОД! Пассив- ный слой 1 1ые материалы Активный слой г* с > tg Пассивный слой „ « h S ° О + + о 0^ W § а Активный слой £ 2 я Б5 Температура в °C 2 к « S GJ й Б & S s о 9 Удельное электриче- ское сопро- тивление Q при соотно- шении толщин 1 : 1 Интервал рабочих темпе- ратур в °C Максимальная темпера- тура в °C
Разность ko8(J линейного ра( (ai—аг) -106 для темпера- туры в °C Q в ом • мм2 / м
Инвар Н36 Хромоникеле- вая сталь 15 000 22 000 100 18 20 0,79 От —60 до 4-200 225 225
Инвар Н36 1 Никельмолиб- деновая сталь 15 000 20 000 50 100 200 18,2 18,2 16,0 20 100 200 305 0,79 0,83 0,86 0,96 От —60 до 4-200
h Плати- нит Н42 1 Монель-мо- талл 16 600 17 600 W0 9,7 1 20 0,54 От —60 до +315 325 i
200 300 11, 7 12,( г *
Плати- нит Н42 Никельмолиб- деновая сталь 16 600 20 000 300 j 12 20 100 200 300 0,68 0,70 0,73 0,82 От —60 до +375 400 i i
Плати- нит Н42 Хромонике- левая сталь 16 600 22 000 100 13,5 1 1 20 0,6 ( От —60 до +375 400 200
Инвар Н36 1 1 i 1 Латунь Л68 15 000 11 500 100 150 200 18,7 18,5 18,< > 20 0,159 От —60 до +185
1 Инвар Н36 Латунь Л62 15 000 10 700 100 200 19,1 17, ? 1 5 20 0,16 От —60 до +185 200
Инвар Н36 Латунь ЛЖН 60-1,5-1,0 15 000 1 10 600 1 100 19,i 20 1 0,18 От —60 до +185 200
Инвар Н36 Латунь ЛОС 60-0,7-0,2 15 000 11000 100 150 19,9 19,8 20 С 0,16 От —60 до +185 200
Инвар Н36 Латунь ЛМц 58-2 15 000 10 500 100 195 Г 20 0,17 От —60 до +185. 200
Инвар изб Бронза алюми- ниевая Бр. А5 15 000 13 400 100 14,1 * 20 0,29 От —60 до 4-185 200
Инвар НЗб Бронза берил- лиевая Бр. Б2 1 15 000 12 500 150 200 15,1 14,5 1 * 20 0,157 От —60 до +200 225
210
Таблица 22
Свойства термобиметаллов
Марна
термобиме-
талла
Разность
коэффициен-
тов
(cii— а2)-106
ТБ-1
ТБ-2
ТБ-3
ТБ-4
ТБ-5
ТБ-6
ТБ-7
21
8
20
12
19
19,5
18,0
Удельное
сопротивле-
ние в
ojvt,
0,58—0,68
0,56—0,64
0,75-0,83
0,14—0,20
0.08-0,14
0,14—0,20
0,14—0,18
Температура, соответствую- щая пределу упругой дефор- мации в °C Интервал температур в °C, где коэффициент (ai — a2) постоянен
530—550 430—450 450-470 410—430 180—200 230—250 290-310 От » » » » » » —60 до - -50 » Н -50 » Н —60 » q —50 » - —50 » —50 » - Н(190- 210) -{320—340) -(190-210) г(190—210) l-(180—210) h(190—210) h(210—230)
§ 22. РАСЧЕТ ТЕРМОБИМЕТАЛЛИЧЕСКИХ ПРУЖИН
При расчете термобиметалла нужно располагать формулами,
определяющими перемещения и напряжения в биметалле при его
нагреве. Если помимо температурного воздействия, биметалл на-
гружен внешними силами, то в этом случае напряжения и переме-
щения можно легко определить суммированием, если известны также
результаты решения при чисто силовом нагружении биметалла.
Теория биметалла разработана достаточно полно в работах
[571-161].
Определение перемещений термобиметалла при нагреве
Рассмотрим элемент, выделенный двул!я поперечными сечениями
из узкой биметаллической пружины (фиг. 110), свободной от внеш-
них силовых нагрузок.
Фиг. 110. Элемент биметалла до и после нагрева.
Обозначим а1? Ег и А<>, а2, Е% — толщину, коэффициент
линейного расширения, модуль упругости активного и пассивного
слоен биметалла соответственно.
14* 211
Деформацию 8 произвольного слоя биметалла при нагреве можно
представить как сумму температурной 8/ и упругой еу деформаций
8=8/ + 8у.
При изменении температуры на величину t биметаллическая
полоса искривляется, сечения элемента, оставаясь плоскими, пово-
рачиваются относительно друг друга на угол и полное относи-
тельное удлинение 8 произвольного волокна АВ, находящегося на
расстоянии у от слоя спая, будет
, dft
г = +
= «о + У Аи,
где ео — деформация слоя спая,
dz
изменение его
кривизны.
Упругая деформация 8У волокна определяется в соответствии
с выражениями (а) и (б) как
8у = 80 + у Ах — 8/,
температурная деформация 8/ = a t, тогда
8,, — е0 + у Ах — a t.
Напряжения, связанные законом Гука с упругими деформациями,
равны
о = Е Еу = Е (80 +
у Ах — at)
(4.1)
причем в активном слое
<т1 = (80 4-у Ах — a, t)
а в инертном слое
^2 (80 + У' Ах
(— /г2<?/<0),
Величины 8 о и Ах найдем из условий равенства нулю нормаль-
ной силы и изгибающего момента в поперечном сечении биметалла,
подверженного только тепловому воздействию:
W = f dF + f a„dF = 0;
Kl 2^2
M = f <BydF J' a2ydF — 0,
Fl F2
здесь ~ bhi и Ft — bh% — площади поперечных сечений слоев
биметалла; b — ширина пружины.
212
В результате интегрирования получим следующие два урав-
нения:
откуда, исключая со, получим выражение, определяющее изменение
кривизны биметалла при нагреве,
Знаменатель этого выражения будет мини-
мальным, если-
£1^?
пли
В этом случае биметалл будет обладать
наибольшей чувствительностью. Биметалл,
удовлетворяющий условию (4. 4), называется
нормальным. В соответствии с выра-
жениями (4. 3) и (4. 4) изменение кривизны
нормального биметалла будет
Фиг. 111. К приме-
рам 1 (а) и 2 (б).
Дх =
где толщина биметалла h + h2-
Зная изменение Д х кривизны, можно определить перемещения
биметалла с помощью интеграла Мора (2. 4), который принимает
с учетом выражений (2. 2) и (4. 5) вид
л з
А | Дх Mrds — ~ (ах — а2)
J “ «
(4.6)
здесь Mi — изгибающий момент от единичной нагрузки, приложен-
ной в направлении искомого перемещения; I — длина биметалла.
Пример 1. Определить прогиб конца биметалла (фиг. 111, а) при его на-
греве на С, если материал и размеры биметалла известны.
Решение. Приложим к концу биметалла единичную силу. Изгибающим
момент Мг, в произвольном сечении равен Мг = 1-2. Тогда согласно выраже-
нию (4. 6) прогиб конца биметалла равен
(4. 7)
213
Пример 2. Найти угол поворота концевого сечения U-образной биметал-
лической пружины (фиг. 111, б) при ее нагреве.
Решение. Для определения угла поворота прикладываем к концу
пружины единичный момент, тогда в произвольном сечении Мг - 1, и искомый
угол поворота равен в соответствии с выражением (4. 6):
О
где длина пружины L = 2 I - Ь л г.
Формула (4. 5) была получена для узкой биметаллической пру-
жины, ширина Ъ которой значительно меньше ее длины I. Если
ширина биметалла соизмерима с его длиной, то при нагреве прогибы
биметалла будут несколько больше рассчитанных по формуле (4. 5).
Расхождение между расчетом и опытом для биметалла, ширина
которого равна его длине (Z = 6), может быть около 25%; если Ь--,
то расхождение будет приблизительно 15%, а при b = -^-расхожде-
ние не превышает 10% [60]. Таким образом, формула (4.5) дает
для большинства практических расчетов вполне удовлетворитель-
ную точность, если ширина биметаллической пружины не больше
1/з от ее длины.
При нагреве широкой биметаллической пружины ее прогибы
увеличиваются по сравнению с прогибами узкой пружины по следую-
щей причине. При нагреве биметаллической пружины ее материал
расширяется как в продольном, так и в поперечном направлениях.
При этом поперечные деформации узкой полосы происходят свободно,
а поперечные деформации широкой полосы стеснены соседними слоя-
ми, и поэтому в поперечном направлении возникают упругие деформа-
ции еу, которые в свою очередь вызовут изменение продольной
деформации ех на величину р,еу, где ц — коэффициент Пуассона.
При этом продольные деформации в активном слое будут увеличи-
ваться больше, чем в инертном, что и приводит к увеличению про-
гибов нагретой широкой биметаллической полосы по сравнению
с прогибами узкой полосы.
Уточненный расчет биметаллической широкой полосы дан в ра-
ботах [60], [61] и [45].
Изгиб биметаллической пружины внешними силами
Рассмотрим чистый изгиб внешними моментами М пружины из
нормального биметалла в условиях постоянной температуры. По-
прежнему будем считать справедливой гипотезу плоских сечений.
Предположим, что нейтральный слой смещен на величину е по
отношению к слою спая (фиг. 112). Тогда относительная деформация
волокна АВ, отстоящего от слоя спая на расстоянии у, будет равна
где
= {у + е) Ах,
кривизна нейтрального слоя.
214
На основании закона Гука напряжения в слоях биметалла
Hi = Е^у + е) Ах
о2-Д(?/-Н)Дх
(О < у < hxY
(—h'z < г/ < 0).
(4. 8)
Найдем положение нейтрального слоя из условия равенства
нулю нормальной силы N в поперечном сечении:
hi о
N^fc^dF-}- f o2dF = 0,
0 —h2
откуда
Е, (Е| + 2ehL) +
+ Ег (- h?. + 2еЛ,) - 0
или
Фиг. 112. Элемент биметаллической
пружины, находящейся в условиях
чистого изгиба.
Так как для нормального биме-
талла справедливо условие (4. 4)
Е
’ то> следовательно, е — 0. Это означает, что нейтральный
^2 h
1
слой при изгибе нормального биметалла внешними силами совпадает
со слоем спая.
Найдем теперь изменение кривизны из уравнения моментов
hl о
М = b [ f G±ydy -f- f o2ydy] =
и —h2
Изменение кривизны равно
Ах --
зм
ь‘
1
Ethf + E2h»
(4.9)
При определении перемещений биметаллическую пружину удобно
заменить эквивалентной полоской тех же размеров, но с некоторым
так называемым «приведенным» модулем упругости, одинаковым
для обоих слоев [57].
Изменение кривизны этой полоски
М
ЕЕ ’
Здесь Е — приведенный модуль упругости материала эквивалент-
bh?
-----осевой момент инерции ее сече-
< W
ной пружины, a J
НИЯ.
215
Приведенный модуль упругости Е определяется из условия
равенства изменения кривизны у эквивалентной и биметаллической
пружин, нагруженных одинаковыми моментами М. Приравнивая
правьте части выражений (4. 9) и (в); получим после преобразований
£’=4-(£’1/г? + Е2А1).
Отсюда, учитывая соотношение (4. 4) для нормального биметалла,
получим
_____^EjE2____
i'M, .
(4.10)
Таким образом, задача определения перемещений биметалли-
ческой пружины под действием внешних сил приводится к простой
задаче нахождения перемещений в эквивалентной однородной
пружине.
Если биметаллическая пружина одновременно нагревается и
нагружается внешними силами, „то действие температуры удобно
заменить эквивалентным изгибающим моментом Mt, величина
которого находится из равенства изменений кривизны пружины
под действием температуры и под действием момента Mt. В соответ-
ствии с выражениями (4. 5) и (в) получим
i _ J£t
h “ EJ ’
откуда
Л/f 3 , \ . EJ
Mt = у (ax — a2) t •—
(4.11)
Здесь EJ — изгибная жесткость эквивалентной балки, а при-
веденный модуль упругости Е определяется выражением (4. 10).
Пример 3. Определить расстояние а до упора А (фиг. 113), исходя из ве-
личины чувствительности
6= —=6,005 мм/ °C
t
нормальной биметаллической
пружины (Л — перемещение концевой точки В пружины при нагреве ее на
i° С). Компоненты биметалла: инвар—латунь JI68, разность коэффициентов
линейного расширения щ — ct2 = 18 10“® 1/°С (табл. 21). Размеры пружины:
I = 30 мм, h ~ 1 мм, b ~ 6 мм. Упор А поджимает пружину так, что в рабо-
чем интервале температур пружина не отрывается от упора.
Решение. Заменим действие температуры эквивалентным изгибающим
моментом Mt соответственно выражению (4. 11)
ЛЛ =
t
h
(а2—а2)
EJ
(г)
и найдем прогиб конца пружины под действием момента Mt. Для этого раскроем
статическую неопределимость пружины из условия равенства нулю прогиба в
точке А, которое запишем в форме канонического уравнения
+ dip =0.
216
На фиг. ИЗ построена эпюра Мр от момента Mt и эпюра Мх от единичной
силы.
Перемножая эпюры по правилу Верещагина получим коэффициенты
Mta3 rr
1р = -----— . Из канонического уравнения находим реакцию»
2EJ
_ _1?> = -—- и строим эпюру суммарного момента М.
Si-, 2 а
3EJ
упора =
Для определения прогиба точ-
ки В приложим к основной системе
единичную силу, построим эпюру М1
и, перемножая ее на эпюру М, по-
лучим
л Л/Д2
a
2EJ
а2 '>
2^1
или, заменив момент Mt по выраже-
нию (г)
й2
212
Подставим в
еловые значения,
условию задачи —
в результате чего
ное уравнение
это уравнение чи-
учитывая, что по
= 6=0,005 лом/°С,
получим квадрат-
а2—90а+ 1060=0, (д)
откуда искомое расстояние а, опре-
деляющее положение упора, равно
а ~ 14 мм. [Второй корень уравне-
ния (д) a s 76 мм не имеет смысла
в данной задаче].
Пример 4. Определить толщину h
нормальной биметаллической пру-
жины 7, предназначенной для сило-
вой компенсации температурной по-
грешности манометрического упру-
гого элемента 2 (фит: 114, а). За-
даны длина I, ширина Ъ биметал-
лической пружины, закрепленной
на жестком основании 3, длина L
игл 4, жесткость по силе мано-
метрического элемента, а также
материалы биметаллической пру-
жины и манометрического элемента.
Решение. Рассмотрим более
подробно принцип действия сило-
во й ко мпенса ции.
Фиг. 113. К решению примера 3.
При сборке биметаллические пружины 1 устанавливаются с натягом так,
что иглы 4 с некоторой силой прижаты к штоку 5 манометрического элемента 2.
При отсутствии рабочей нагрузки (давления) на элемент, когда его прогиб
w = 0, иглы находятся в горизонтальном положении. Под действием давления
Р упругий элемент получает прогиб w, и иглы поворачиваются на угол <р (фиг.
114, б). Силы N сжатия игл дают в этом случае вертикальную составляющую <?,
которая будет дополнительно нагружать манометрический элемент, увеличи-
вая его прогиб.
Если убрать иглы, то при изменении температуры окружающей среды
появится температурная погрешность манометрического чувствительного эле-
мента: модуль упругости материала элемента снижается при нагреве, и за счет
.этого прогиб w будет возрастать.
Действие силовой компенсации проявляется в следующем. Биметалли-
ческие пружины устанавливаются так, что активный слой обращен к манометри-
ческому элементу, а инертный расположен снаружи (фиг. 114, а). При увели-
чении температуры окружающей среды концы биметаллических пружин стре-
мятся разойтись. Но поскольку пружины были установлены при сборке с до-
статочным начальным натяжением, то они и при нагреве продолжают сжимать
мглы, но уже с меньшей силой. Падение величины сил А вызывает уменьшение
At
Фиг. 114. К решению при-
мера 4.
вертикальной составляющей Q и соответствующее уменьшение прогиба мано-
метрического элемента. Параметры биметаллической пружины могут быть подо-
браны так, что при изменении температуры окружающей среды прогиб w чув-
ствительного элемента не изменится, т. е. температурная погрешность элемента
будет равна нулю. Для этого увеличение прогиба за счет изменения модуля
упругости материала чувствительного элемента должно быть равно уменьшению
прогиба вследствие падения сил АГ, что связано с деформациями биметалли-
•ческой пружины при нагреве.
Аналогичная картина имеет место при уменьшении температуры окружаю-
щей среды.
Так как перемещение ш мало по сравнению с длиной L игл, то угол <р повс-
w
рота игл можно считать равным <р ~ —-
будет
. Тогда вертикальная составляющая Q
Q = 2N sin <р 2N
(«)
Относительная температурная погрешность манометрического упругого
элемента, вызываемая изменением модуля упругости при изменении температуры
на t определяется по формуле (1. 8)
A tct
*ф =------=
iv 1
где у — температурный коэффициент модуля упругости. При нагреве прогиб
.манометрического элемента увеличивается на A
Л w = y tu?. (б)
Эта температурная погрешность будет скомпенсирована, если прогиб
уменьшится на Д им, причем
I A u?q I = | A wt\,
(в)
здесь A Wq — уменьшение прогиба при падении силы Q на Д Q.
Равенство (в) выражает условие компенсации температурной погрешности
манометрического упругого элемента.
Уменьшение прогиба Д iVq можно определить по формуле
A iv
(г)
где Aq — жесткость манометрического элемента по силе.
В соответствии с равенствами (б), (в) и (г) величина Д(? должна быть равной
(д)
Изменению Д(? вертикальной составляющей Q соответствует падение сил
N сжатия игл на величину ДХ. Согласно равенству (a) AN = AQ ^или,
учитывая выражение (д), получим
Д ,N =
kQLyt.
(е)
2
Остается связать изменение Д N сил сжатия игл с деформациями биме-
таллических пружин при нагреве.
Если бы биметаллические пружины не были прижаты к иглам начальным
натяжением, то при нагреве концы их получили бы перемещения в направлении
от штока 5 манометрического элемента на величину /•/ (фиг. 114, в). Перемещение
Я,/ нормальной биметаллической пружины можно определить по формуле (4. 7):
, 3 ( ч t I* . .
= (а, - «2) -h- • (ж)
Однако в действительности биметаллические пружины были установлены
с начальным натяжением, поэтому и при нагреве они сжимают иглы с силой
N — AN. Уменьшение Д N силы сжатия иглы можно найти из равенства
(з)
где X/ — перемещение, которое получила бы свободная биметаллическая пру-
жина при нагреве;
1 — перемещение в обратном направлении под действием усилия Д N.
Равенство (з) выражает условие неподвижности концов биметаллических
пружин, прижатых к иглам, при нагреве.
Поскольку угол ф поворота игл мал, будем пренебрегать влиянием вер-
тикальной составляющей N" на прогиб биметалла, а горизонтальную составля-
ющую N' = N cos ф будем приближенно считать равной N' ~ N (фиг. 114, б).
Заменяя биметаллическую пружину однородной эквивалентной, получим
величину в соответствии с формулой (2. 3)
AN ~‘
bNl3
3EJ
(и)
219
здесь Е — приведенный модуль упругости биметалла — определяется выраже-
нием (4. 10); J — момент инерции поперечного сечения биметалла
т ЪЮ
J=a- . (к>
Подставляя в равенство (з) Xf и из формул (ж) и (и), получим с учетом
выражений (к) и (е)
Q / 72 kf)L у tl3 • 12
(а. — а2) _ ~ Ч г__________,
2 h 2 2 • 3 • Ebh3
откуда находим искомую толщину h биметаллических пружин
/ Яко У IL
h = l / -___-------
I/ 3/?(«! — а2) Ь
А
Температурные напряжения в нормальном термобиметалле
Если биметалл мысленно разрезать по слою спая и нагреть,
то в нем появятся лишь температурные деформации е« = at
(фиг. 115). При совместном изгибе в поверхности спая деформации
инертного и активного слоев биметалла будут одинаковыми и рав-
ными Ео, а по высоте биметалла деформации е будут изменяться по
линейному закону в соответствии с гипотезой плоских сечений.
Фиг. 115. Температурные напряжения в биметалле.
Если из полной деформации е вычесть температурную е^, то в резуль-
тате получим чисто упругую деформацию еу, эпюра которой имеет
вид, показанный на фиг. 115.
Этой деформации соответствуют напряжения о, которые будут
возникать в биметалле при его нагреве. Их можно найти, умножая
деформации еу на модуль упругости Е. Изображенный на фигуре
биметалл имеет толщину Лэ < поэтому в соответствии с усло-
вием (4. 4) для нормального биметалла модуль упругости нижнего
слоя Ё2 ^>Ei и, следовательно, наклон на эпюре о2 будет больше,
чем на эпюре ог (фиг. 115).
Знакопеременный характер распределения напряжений о по
сечению соответствует условиям равенства нулю нормальной силы
и изгибающего момента, что имеет место при нагреве свободного от
220
внешней силовой нагрузки биметалла. Из условия равенства нулю
изгибающего момента можно легко показать, что точки попереч-
2
ного сечения, где о = 0, лежат на расстояниях уг — и у2 =
Напряжения, возникающие в биметаллическом элементе при его
нагреве, связаны с упругой деформацией формулой (4. 1).
<з=Е еу ~Е (80-]~г/ Ах—а£). (а)
Изменение кривизны при на-
греве нормального биметалла
определяется выражением (4. 5)
Деформация ео слоя спая
при нагреве биметалла может
быть найдена из первого ура-
внения (4. 2) с учетом выраже-
ния (4. 5) для изменения кри-
визны Ахи соотношения (4. 4)
для нормального биметалла
80 = (0^2 4- «2^1)4” • (б)
Подставляя значения изме-
нения кривизны Ах (4. 5) и
относительного удлинения Ео (б)
слоя спая в уравнение (а), по-
лучим значения температур-
ных напряжений в биметал-
лическом элементе
Фиг. 116. Биметаллический термометр.
Наибольшие температурные напряжения возникают в точках,
расположенных вблизи слоя спая, где у — О
шах — —Ел (cii — ct2) t ;
O'2 max — (ttj — a2)
Пример 5. Определить толщину биметаллической двухзаходной винтовой
пружины термометра (фиг. 116), измеряющего температуру в интервале от
О до 100° С. Шкала прибора имеет 270° С. Из расчета на прочность найти пре-
дельную температуру нагрева. Компоненты биметалла: инвар — латунь Л68
(табл. 21). Для латуни аг = 20 • 10~6 1/°С, Е± ~ 1,2 • 104 кгс(мм2, ат-
= 15 кгс/мм2', %ля. инвара «2 = 2 • 10~6 1/°С, Еъ ~ 1,5 • 104 кгс/мм2, и^, -
= 20 кгс/мм2. Из габаритных условий известно, что диаметр наружного участка
пружины Dx = 8 мм и число витков = 10, диаметр внутреннего участка
Z>2 = 6 Л1ЛГ ПрИ П2 “ 8.
Р е ш е н и е. Угол поворота й концевого сечения пружины равен
й = Ах/, (а)
где I — длина всей пружины. Если пренебречь углом подъема винтовой линии, то
I s it D2n2). ((у
Изменение кривизны Ах пружины при ее нагреве определяется выражением
(4. 5)
Ах = (сн —а2) 4“ . (в)
По условию задачи угол поворота Й должен быть равен 270° или
л.
(г)
Подставляя выражения (б), (в) и (г) в уравнение (а), находим толщину h
пружины
h = (зц - а2) (Z)^ + П2п2) t = 18 • НП6 • 100 (8 • 10 + 6 • 8) =0,23 мм
Для нормальной биметаллической пружины справедливо условие (4. 4), по-
h
это му
1,5 • Ю4
1,2 104
^2
й<2 F Ег
h
— 2,12 йг, то толщина инварного слоя h‘> = ^0,11 мм, а толщина латун-
ного слоя hi = 0,12 мм.
Наибольшие напряжения, возникающие при нагреве биметаллической
пружины на 100° С в точках слоя спая, определяются по формулам (4. 12').
Для латуни
<Т1 max — — +1— а2) t
= -1,2 • 104 • 18 • 10-6 • 100 “
для инвара
-max
= 12,9 кгс/мм2.
Коэффициент запаса по текучести для латунного слоя будет
для инварного слоя
Следовательно, опасными будут точки латунного слоя, распедаженцые
в слое спая, и коэффициент запаса биметаллической пружины будет пт = 4,33.‘
222
При повышении температуры в 1,33 раза по сравнению с наибольшей рабочей
в латунном слое возникнут пластические деформации. Таким образом, предель-
ная температура в данном случае равна tnp — 100 • 1,33 = 133° С.
Напряжения при изгибе биметалла внешними силами
Напряжения в биметаллической пружине, возникающие при
внешнем силовом воздействии, определяются ’ выражениями (4. 8).
Выше доказывалось, что для нормальной биметаллической пружины
Фиг. 117. Напряжения при ^изгибе биметаллической
пружины внешними силами
нейтральный слой совпадает со слоем спая, т. е. е = 0. Тогда выра-
жения (4. 8) принимают вид
щ = Ev у- Ли (0<у<А1);
о2 = Егу- (—Л2<У<0).
Изменение кривизны при изгибе биметаллической пружины
моментом М определяется по формуле (4. 9)
Учитывая соотношение (4. 4) для нормального биметалла, полу-
чим
„ _ ЗМг/ . п _ ЗМу
Q1 “ “ “1.2” •
bh h bh h
1 2
На фиг. 117 показан характер распределения деформаций е
и напряжений о при изгибе биметаллической нормальной пружины
внешними силами. Наибольшие напряжения возникают в крайних
волокнах при у = hA и у — —hz.
__ ЗЛГ . ________ЗМ
^max bhhx ’ ^тах bhh<>
Если биметалл находится при одновременном воздействии тем-
пературы и силовой нагрузки, то полные напряжения можно
определить путем алгебраического суммирования температурных
напряжений и напряжений при изгибе внешними силами.
ГЛАВА V
МЕМБРАНЫ
§ 23. ОБЩИЕ СВЕДЕНИЯ
Во многих манометрических приборах в качестве упругого
элемента применяется мембрана1 — гибкая круглая пластинка,
получающая значительные упругие прогибы wo под действием
давления р (фиг. 118).
Мембраны широко применяются в качестве чувствительных
элементов манометрических приборов высоких классов точности.
При помощи мембран можно измерять давления от сотен атмосфер
до нескольких миллиметров водяного столба. Кроме того, мембраны
могут использоваться как разделители двух сред и как гибкие
уплотнители для передачи перемещений из области давления или
разрежения.
Фиг. 118. Деформация мембраны под давлением.
Рабочий диаметр2 мембраны определяется заданными габаритными
размерами, необходимой величиной эффективной площади, необ-
ходимым прогибом центра, запасом прочности и другими техни-
ческими требованиями, предъявляемыми к мембране. Диаметр
мембраны может иметь различные величины, но обычно не менее
10—15 мм п не более 200—300 мм.
1 В теории упругости под термином «мембрана» понимают пластинку с исче-
зающе малой жесткостью на изгиб. Однако в приборостроительной промышлен-
ности понятие «мембрана» используется более широко. Мембраной называют
любую тонкую пластинку, способную значительно деформироваться под нагруз-
кой, независимо от того, работает ли она на изгиб или на растяжение. Этим
значением термина «мембрана» мы и будем пользоваться в дальнейшем.
2 Рабочим называется диаметр мембраны по контуру крепления.
Мембраны изготовляются из высококачественных пружинных
сталей и бронз и из неметаллических материалов: резины и пласт-
масс, армированных в некоторых случаях тканью из капроновых,
стеклянйых или металлических нитей.
Толщина мембраны выбирается в зависимости от требуемой
чувствительности и прочности мембраны, от свойств материала
и обычно составляет около 0,06—1,5 мм для металлических мембран
и 0,1—5 мм для неметаллических.
б) ‘ г)
Фиг. 119. Характеристики мембран:
а — плоской; б — гофрированной; в — выпуклой; г — неметал-
лической с винтовой пружиной.
В зависимости от геометрии мембраны могут иметь как линей-
ную, таки нелинейную характеристику по давлению. Эта особенность
позволяет успешно использовать мембраны в приборах, измеряющих
параметры, нелинейно связанные с давлением.
Металлические мембраны изготовляются штамповкой из листо-
вого материала. Такой способ изготовления позволяет выдерживать
узкие допуски на толщину материала и на размеры мембраны.
Поэтому мембраны одной партии могут иметь сравнительно неболь-
шой разброс по характеристике.
Наиболее просты по форме плоские мембраны, характери-
стики которых сильно затухают по давлению в области больших
прогибов (фиг. 119, а).
Нанесение кольцевых волн увеличивает рабочие прогибы гоф-
рированной мембраны (фиг. 119, б). Появляется возможность,
15 Заказ 24.
225
изменяя форму и размеры гофрировки, управлять характеристикой
мембраны. Поэтому гофрированные мембраны применяются зна-
чительно чаще плоских.
В различных реле и сигнальных устройствах находят применение
выпуклые (сферические или конические) мембраны (фиг. 119, в).
При нагружении такой мембраны с выпуклой стороны происходит
потеря устойчивости: мембрана скачком изменяет свой прогиб. Это ис-
пользуется, например, для включения или выключения контактор.
Неметаллические мембраны имеют весьма малую жесткость
и поэтому, как правило, работают совместно с измерительной винтовой
пружиной, выполняя преобразование давления в усилие, воспринима-
емое упругим элементом— пружиной (фиг. 119, г). 1
§ 24. ПЛОСКИЕ МЕМБРАНЫ t
Применение и свойства |
Плоские мембраны имеют затухающую характеристику, поэтому
в качестве рабочего участка используется обычно небольшая часть
возможного хода мембраны. В показывающих и регистрирующих
приборах металлические плоские мембраны применяются редко.
Плоские мембраны находят применение там, где от мембраны тре-
буется небольшой ход, причем сама мембрана нагружается только
Фиг. 120. Примеры применения плоских мембран:
а — в емкостном датчике давления; б — в датчике давления элек-
троконтактного сопротивления.
б)
рабочим давлением, не испытывая противодействия со стороны
механизма прибора, как, например, в емкостных (фиг. 120, а), индук-
тивных, тензометрических датчиках Ч Мембраны этих датчиков,
благодаря высокой чувствительности преобразователя, работают
как упругие элементы с относительно большой жесткостью, совершая
1 Т у р и ч и н А. М., Электрические измерения пеэлектрических величин,
Госэнергоиздат, 1959. Сотсков Б. С., Элементы автоматической и теле-
механической аппаратуры, Госэнергоиздат, 1950.
226
незначительные перемещения. Они нередко представляют собой
толстые пластины, конструктивно выполненные за одно
целое с корпусом преобразователя.
Кроме того, плоские мембраны используются в качестве преобра-
зователей давления в усилие, которое затем воспринимается
датчиками электросопротивления (фиг. 120, б), пьезоэлектрическими,
магнитоупругими, частотными или другими датчиками, имею-
щими такую высокую жесткость, что мембрану можно считать
практически неподвижной. В этих схемах находят применение тонкие
металлические и неметаллические мембраны.
Высокая частота собственных колебаний таких датчиков позво-
ляет использовать их для измерения переменных давлений с частотой
до нескольких сотен и тысяч герц.
Фиг. 121. Плоская мембрана, натягигаемая при установке
в прибор.
Изготовить идеально плоскую мембрану из тонкого листового
материала очень трудно, так как из-за несовершенств материала
и технологического процесса изготовления мембрана может получить
некоторое коробление. Нагружение такой мембраны давлением
будет сопровождаться «хлопками», возникающими в покоробленных
местах. В этом случае характеристика мембраны становится неста-
бильной. Чтобы избежать этого, мембрану при закреплении в корпусе
прибора обычно натягивают по контуру (фиг. 121). Иногда такое
предварительное натяжение производится для изменения характе-
ристики, поскольку, меняя величину начального натяжения, можно
в больших пределах увеличивать или уменьшать жесткость мембраны.
Рассмотрим плоскую мембрану, закрепленную по контуру и
нагруженную давлением (фиг. 122). Характер деформации мембраны
зависит от величины прогибов, которые она получает под нагрузкой.
При малых прогибах перемещения мембраны возникают в.ос-
новном в результате изгибных деформаций. Срединная плоскость 1
мембраны почти не удлиняется, и можно считать, что мембрана имеет
линейную характеристику. При расчете мембраны в области малых
перемещений можно воспользоваться линейной теорией изгиба круг-
лых пластинок.
1 Срединной называется плоскость, равнсотстояшая от поверхностей мем-
браны.
15* 227
При последующем увеличении нагрузки прогибы мембраны ста-
новятся соизмеримыми с толщиной. Срединная плоскость мембраны
получает значительные удлинения, что приводит к появлению на-
пряжений растяжения <тр в срединной плоскости, соизмеримых с из-
гибными напряжениями аи. Прогибы мембраны при этом увеличи-
ваются медленнее, чем нагрузка, и характеристика становится
затухающей. Расчет мембраны в области больших перемещений
должен быть основан на нелинейной теории, учитывающей как изгиб,
так и растяжение мембраны в срединной поверхности.
Фиг. 122. Характеристика плоской мембраны и возникающие в ней напряжения.
Дальнейшее увеличение прогибов происходит в основном в ре-
зультате растяжения мембраны. В этом случае расчет может произ-
водиться по теории абсолютно гибкой мембраны без учета жесткости
на изгиб.
Если мембрана достаточно тонка, она может получать большие
прогибы при упругих деформациях материала. В мембранах же
большой толщины могут возникнуть пластические деформации и
в области малых перемещений.
Форма упругой поверхности мембраны по мере увеличения про-
гиба-меняется [1]. На фиг. 122 показаны формы упругой Поверх-
ности мембраны на различных этапах нагружения. С увеличением
прогиба точка перегиба на линии осевого сечения мембраны сме-
щается к контуру, и форма упругой поверхности приближается
к сферической.
Это изменение формы упругой поверхности мембраны является
основной причиной сложности получения точного решения, охва-
тывающего как область малых, так и область больших перемещений.
228
Приближенное, но хорошо совпадающее с результатами опыта,
решение этой задачи дано В. И. Феодосьевым [1], [47]. Простое
решение, вполне удовлетворительное по результатам, можно по-
лучить методом «наложения», который впервые был предложен
А. Фепплем \ Прежде, чем перейти к рассмотрению этих решений,
необходимо вспомнить линейную теорию изгиба круглых пластин.
Плоская мембрана в области малых перемещений
Теория изгиба круглых пластинок разработана и изложена до-
статочно полно во многих работах, например, [47], [62], [63].
Определим прогибы и напряжения в круглой пластинке радиуса
R и толщиной h, защемленной по контуру и нагруженной давлением
р (фиг. 123, а). Этой схеме соответствует плоская мембрана, изме-
ряющая давление.
Фиг. 123. Внутренние усилия в пластинке:
а — пластинка под давлением; б — элемент пластинки; в — центральная
часть пластинки.
Пластинка под нагрузкой изгибается как в радиальном, так
и в окружном направлениях. Возникающие при этом моменты по-
казаны на гранях элемента, выделенного из пластинки двумя осе-
выми и двумя цилиндрическими сечениями (фиг. 123, б). Здесь Мг
и Mt — изгибающие моменты, приходящиеся на единицу длины,
.в радиальном и окружном направлениях, Qr — поперечная сила
на единицу длины.
Рассматриваемая пластинка имеет полярную симметрию отно-
сительно оси z\ силовые и геометрические факторы постоянны вдоль
окружности и могут изменяться только по радиусу. Поэтому ок-
ружные моменты Mt на противоположных гранях элемента одина-
ковы, а радиальные моменты Мг и поперечная сила Qr на радиусе
1 Феппл ь А., ФеппльЛ., Сила п деформация, Гостехиздат, 1933.
г + dr получают приращения. Поскольку в этом разделе мы рас-
сматриваем только малые прогибы пластинки (w С h), то учитывать
силы, растягивающие срединную плоскость пластинки, не будем.
Напишем условия равновесия элемента. Равенство нулю суммы
моментов относительно оси у всех сил, приложенных к элементу,
приводит, после пренебрежения малыми высших порядков, к урав-
нению
Mt - (М/г)' + Qrr - 0;
(5.1)
здесь
Поперечная сила Qr в уравнении (5. 1) может быть выражена
через давление р, если рассмотреть равновесие центральной части
пластинки радиуса г (фиг. 123, в). Проектируя силы на ось z, по-
лучим
Уравнение равновесия (5. 1) содержит две неизвестные: Мг
и Mt, и для решения задачи необходимо составить дополнительные
уравнения.
Рассмотрим элемент осевого сечения пластинки до и после де-
формации (фиг. 124, а). При малых перемещениях можно считать,
что точки срединной поверхности пластинки не смещаются в радиаль-
ном направлении и получают только вертикальные прогибы w. По-
скольку растяжение срединной поверхности при этом не учитывается,
полагаем, что длина отрезка АВ при деформации не изменится, т. е.
АВ = А'В' = dr. Как и в теории изгиба балок, прогиб w пластинки
связан с углом поворота б1 нормали п—п (см. фиг. 123, а) соотноше-
нием
dr
(5-3)
которое может быть получено из треугольника А'В'К (фиг. 124, а).
*
Определим радиальную и окружную деформации ег и 8? в произ-
вольной точке пластинки. При этом на основании гипотезы неизмен-
ности нормали, принятой в теории оболочек, будем считать, что
нормаль п—п, поворачиваясь на угол б1, не искривляется и остается
нормальной к деформированной срединной поверхности; на фиг 124, а
п—п' — нормаль к точке В' срединной поверхности после дефор-
мации.
Для определения радиальной деформации 8Г найдем удлинение
произвольного волокна CD, расположенного на расстоянии z от
срединной поверхности. Так как абсолютное удлинение волокна
CD равно zdft, то относительная деформация 8Г будет
z б'.
(5.4)
230
231
Окружная деформация Et в точке D определится путем сравнения
длин окружностей, на которых находилась точка D до и после • на-
гружения пластинки. До нагружения окружность точки D имела
радиус г, после нагружения точка D переходит в положение D',
определяемое радиусом г 4 z О. Тогда относительное удлинение
Ei в окружном направлении
El = z
(5.5)
В теории оболочек напряжения сжатия в направлении оси z
не учитываются ввиду их малости, поэтому напряженное состояние
пластинки считается плоским (фиг. 124, б). На основании закона
Гука напряжения в радиальном и окружном направлениях выра-
жаются через соответствующие деформации по формулам
— 1 _\j2 (s* + H£r)
1 г
или с учетом формул (5. 4) и (5. 5) получим
(5.6)
Свяжем теперь изгибающие моменты с углом О поворота нормали.
Сумма моментов внутренних сил, распределенных по цилиндриче-
ской площадке высотой, равной толщине h пластинки, и шириной
равной единице (фиг. 124, в), равна радиальному изгибающему мо-
менту Мг
Подставляя сюда напряжения из выражений (5. 6) и произведя
интегрирование, получим для радиального момента Мг и анало-
гично для окружного момента Mt следующие выражения:
здесь
(5.7)
(5-8)
232
Величина D называется цилиндрической жесткостью.
Заменяя моменты Мг и Mt в уравнении (5. 1) выражениями
(5. 7), получим дифференциальное уравнение равновесия круглой
пластинки при изгибе
(5. 9)
где поперечная сила Qr в рассматриваемом случае определяется
выражением (5. 2).
Интегрируя уравнение (5. 9), найдем угол поворота й нормали
к срединной поверхности
(5. 10)
Постоянные интегрирования Ci и С2 находятся из граничных
условий. В центре пластинки (г = 0) и у заделки (г -Я) угол по-
pR2
ворота V = 0 (см. фиг. 123, а), отсюда С2 = 0 и Ci — —.
Подставляя Ci и С2 в решение (5. 10), получим
(г2 — №).
(5. И)
Зная угол поворота й, можно найти прогиб с помощью выра-
жения (5. 3)
w = С3 + J й dr.
Подставляя сюда угол й в соответствии с формулой (5. 11) и про-
изведя интегрирование, получим
1QD
Постоянная Сз определяется из того условия, что у заделки
(г = R) прогиб w — 0. Отсюда Сз —
640 '
Тогда уравнение упругой поверхности плоской мембраны при
малых перемещениях примет вид
W 640
Прогиб wo центра мембраны (г = 0)
pR*
W° ~ ”С4О~ ’
Заменяя величину цилиндрической
(5. 8), получим при н = 0,3
равен
(5.13)
жесткости D по формуле
pR* __ 16 ip0
Eh* = 3 (1 —р2) X
5,86
(5. 13')
Уравнение (5. 13') выражает
ристику плоской мембраны, нагруженной давлением р
малых прогибов. Эта характеристика линейна.
Изгибные напряжения распределяются по толщине стенки по
значения опреде-
в безразмерно!! форме характе-
в области
линейному закону (фиг. 125, а); их наибольшие
г
Напряжения в круг-
Фиг. 125.
лой пластинке при малых пере-
мещениях:
о. и радиальные о
б — эпюра
а — окружные и
напряжения в пластинке;
напряжений и ог по радиусу; в —
напряженное состояние в центре и на
краю пластинки.
_ 3[P(u}pR
8)
h
ляются выражениями (5. 6) при z = i
ражения угол поворота й из формулы (5. 11), получим
। 3 pR2 Г/о \ г2 J
. Подставляя
ЭТИ вы-
ft
h2
Л2
(Зц+1)~
(5.14)
На фиг. 125, б представлены эпюры напряжений в верхних слоях
пластинки
вдоль радиуса, а также напряженное состоя-
ние точек L и М (фиг. 125, в). Эквивалентное напряжение аэкв в этих
точках можно определить, пользуясь какой-либо теорией прочности.
Например, по теории энергии формоизменения для плоского на-
пряженного состояния
где oi и а2 — главные напряжения.
В центре мембраны (точка L) главные
3(1 + и) р7?2
= о2 = —— — , следовательно
напряжения равны
_ 3(1+Ю р^
Оэкв 8 h2
При р = 0,3 эквивалентное напряжение
э 0,488 4Ц- .
На краю мембраны (точка ЛГ)
J
3 pR2 3 pR2
ai — °r — , °2 — Gt - - LI дТ
Л
м тогда
3 pR2 , /д---------------------------------,
Оэкв = I 1 — H + H2.
При p 0,3
Лг.,= 0,666-^ .
(5. 15)
Таким образом, опасной будет точка М у заделки мембраны.
Величина допускаемого давления определится из условия
(Тэкз
= 0,666^- < [о],
f t
где [cf]—допускаемое напряжение.
Отсюда допускаемое давление будет
Рдоп
1,5 [cf]
(5. 16)
Величина рзоп возрастает с увеличением толщины пластинки
и с уменьшением ее рабочего радиуса.
Найдем связь между величинами напряжений в пластинке и ее
прогибом. Для этого давление р в формулах (5. 14) выразим через
прогиб центра шо с помощью уравнения (5. 13). Радиальные и ок-
h
2
ном контуре (г = 7?) будут равны
на наруж-
ружные напряжения в точках у поверхности I z = ±
— I
О р —1 ДЗ
(Tf — [LtCF**
(5. 17)
и в центре мембраны (г
0)
2iu0Eh
235
Напряжения в пластинке связаны с прогибом линейно. Вели-
чину допускаемого прогиба можно найти, исключая из выражений
(5. 13) и (5. 16) давление р
( ^0 ) б on
0,256 [а]-%-
Прогиб (wo)don увеличивается с уменьшением толщины и уве-
личением рабочего радиуса пластинки.
Пример 1. Определить коэффициент запаса по текучести пластинки, за-
щемленной по контуру и нагруженной давлением р — 60 кгс 1см2. Размеры пла-
стинки R = 15 лслц h = 1 мм. Материал — сплав Н36Х.ТЮ, Е = 2,15 х
X 106»гс/с.на, сГу = 95 кгс 1мм2,
Как следует изменить размеры пластинки, чтобы увеличить вдвое коэффи-
циент запаса при сохранении той же жесткости?
Решение. Определим наибольшее эквивалентное напряжение в точках
наружного контура по формуле (5. 15)
с? же =0,666
pR2 0,666 • 60 • (1,5)2
h (0,1)2
= 9000 кгс/см2=§0 кгс/мм2.
Следовательно, коэффициент запаса по текучести будет
Жесткость пластинки равна в соответствии с выражениями (1.3) и (5. 13')
к = ~Г-
w0
5,86 • 2,15 • 10е (0,1)3 0/пп кгс/с.
-----/Х-\4------------= ^490 ------------
(1,э)4 см
Теперь требуется изменить рабочий радиус и толщину пластинки так, чтобы
коэффициент запаса увеличился вдвое до пт = 2,11 при сохранении прежней
жесткости. Обозначим искомые радиус и толщину пластинки 2?! и Для уве-
личения коэффициента запаса эквивалентное напряжение должно быть вдвое
снижено
Р-Н?
О’эКв = 0,666 —х-=4500 кгс[см2. (а)
Л1
Жесткость пластинки должна остаться прежней
к = 5,86 Е
= 2490 К-^-
СМ
(б)
Подставляя численные значения р = 60 кгс!см2 и £ = 2,15 • 106 кгс/см2,
получим из уравнения
(а) = 112,5,
h2
1
откуда
Уравнение (б) дает
(в)
(г)
7?! = 10,6 hv
=1,975- 10~4J?f.
Решая уравнения (в) и (г) совместно, получим 7?х = 4,24 мм и = 0,4 мм.
Таким образом, по сравнению с прежними размерами рабочий радиус пластинки
должен быть уменьшен в 3,54 раза, а толщина — в 2,5 раза.
* «
236
Расчет пластинки с жестким центром радиуса го, нагруженной
давлением (фиг. 126, а), может быть также произведен с помощью
уравнения (5. 10). Постоянные интегрирования Ci и Сг в этом слу-
чае имеют другие значения в соответствии с новыми граничными
С)
Фиг. 126. Пластинка с жестким центром:
а — пластинка с жестким центром, нагруженная давлением; б — пластинка, нагруженная
в центре сосредоточенной силой.
условиями: на наружном и внутреннем контурах пластинки угол
поворота Ф равен нулю
при г — R
при г = г0
0 = 0;
0 = 0-
(5.18)
В остальном решение проводится аналогично изложенному и при-
водит к следующим результатам. Перемещение wo жесткого центра
мембраны определяется уравнением
дй4
Eh? ’
(5.19)
здесь коэффициент Ар зависит от отношения с рабочего радиуса
R к радиусу го жесткого центра с = —-
го
16
с4 — 1—4с2 In с
(5. 20)
Радиальные напряжения в точках у поверхности на наружном
и внутреннем контурах равны
где
_ _ _ R EhlV0
„ CJ/’H---Zl2 -tip Д2 ’
(5. 21)
(5. 22)
Окружные напряжения в этих точках определяются как at —
— [хсгг. Числовые значения коэффициентов Ар и 2?рданыв табл. 26,
стр. 333.
В об ласти малых перемещений также просто может быть решена
и задача о расчете плоской мембраны, нагруженной сосредоточенной
237
в центре силой Q (фиг. 126, б). В дифференциальном уравнении (5. 9)
поперечная сила Qr будет в этом случае равна Qr — —— .
Если мембрана имеет жесткий центр, то как и в случае дей-
ствия давления граничные условия выражаются зависимостями
(5. 18).
Произведя интегрирование уравнения (5. 9), получим переме-
щение жесткого центра мембраны в виде
где
л QR2
~ aq ею
In2 с
?2—1
(5. 23)
(5. 24)
Наибольшие напряжения в точках
контуров определяются выражениями
наружного и внутреннего
т
н
Ehw0
(5. 25>
н
здесь коэффициенты Вп и /? равны
D „ 2 С2 (с2-1—21ПС) . ч
&Qh 1 — р2 (с2 — I)2—4с21п2с ’
о „ 2 с2 (2с2 In с — с2+ 1)
Qe 1— р2 (с2—I)2—4с2 In2 с
(5. 26)
Их численные значения
зависимости от
в табл. 26, § 33.
R
с — —
го
даны
Так как в области малых перемещений плоская мембрана имеет линейную
характеристику, то ее эффективная площадь может быть определена, как
(§3, стр. 48):
пли, используя выражения (5. 19) и (5. 23), получим
здесь коэффициенты А и определяются формулами (5. 20) и (5. 24).
Более подробно вопрос об эффективной площади мембран рассматривается
в § 29. Там, кстати, показывается, что при малых прогибах плоской мембраны
расчет эффективной площади с достаточной точностью может быть произведен
по более простой приближенной формуле
R ^Rcp'
ср — средний радиус мембраны, равный НСр =
о
238
Мембрана не всегда нагружается при работе осесимметрично.
Например, если мембрана служит упругим выводом углового пере-
мещения (фиг. 127, а), то силы, действующие на нее, можно приве-
сти к изгибающему моменту, приложенному к жесткому центру
(фиг. 127, б). Решение такой задачи более сложно, так как упругая
поверхность мембраны не будет обладать полярной симметрией.
Поэтому в осевых и окружных сечениях мембраны помимо изгибаю-
щих моментов Мг и Mt и поперечных сил QT и Qt будут возникать
крутящие моменты Мъ (фиг. 127, <?). Внутренние силовые факторы,
5;
Фиг. 127. Плоская мембрана, изгибаемая внешним мо-
менте м:
а — мембрана в качестве упругого вывода углового перемеще-
ния; б — схема нагружения мембраны; в — внутренние силовые
факторы.
деформации и перемещения будут изменяться не только вдоль ра-
диуса мембраны, как в случае осесимметричной нагрузки, но и вдоль
окружности.
Угол поворота жесткого центра мембраны, изгибаемой внешним
моментом, равен [47], [62]
здесь
. М
— ф Eh9
(5. 27)
(5. 28)
Наибольшие напряжения в точках наружного и внутреннего
контуров равны
Фе
(5. 29)
239
где
^<рн —
^Фв — Вц>нС'
(5. 30)
Числовые значения коэффициентов Лф, 2?Фк и В^в при различных
размерах жесткого центра даны в табл. 26 (§ 33).
Уравнения плоской мембраны в больших перемещениях
Отличие задачи о больших перемещениях плоской мембраны от
изложенной выше линейной теории малых перемещений состоит
в следующем.
Фиг. 128. Мембрана, работающая в области больших перемещений:
а — внутренние силовые факторы; б — элемент мембраны до и после нагружения.
1. Для случая малых перемещений был применен принцип неиз-
менности начальных размеров: при составлении уравнений равно-
весия рассматривался элемент, вырезанный из пластинки в неде-
формированном состоянии (см. фиг. 123, б). В области больших пе-
ремещений принцип неизменности начальных размеров теряет силу
и, составляя уравнения равновесия, следует учитывать изменение
формы мембраны под нагрузкой. Элемент, выделенный из мембраны
после ее нагружения, показан на фиг. 128, а. Здесь й — угол, на
240
который поворачивается нормаль к произвольной точке срединной
поверхности мембраны при ее деформации.
2. Помимо моментов Мг и Mt и поперечной силы Qri возникаю-
щих при малых перемещениях (см. фиг. 123, б), в мембране при
больших прогибах появляются растягивающие силы Тг и Tt, ко-
торые необходимо учитывать.
3. При анализе изгиба мембраны в области больших перемещений
нужно учитывать удлинение еР срединной поверхности и радиальное
перемещение v (фиг. 128, б). В остальном ход вывода дифферен-
циальных уравнений мембраны в больших перемещениях аналогичен
изложенному ранее. Поэтому, перенося выкладки в приложение I,
приведем здесь только конечные результаты.
Дифференциальные уравнения плоской мембраны в больших пе-
ремещениях были получены В. И. Феодосьевым [1], [64] в виде
(5.31)
г
где р = — относительный радиус мембраны; г — текущий, а К—
рабочий радиус; й — угол поворота нормали в произвольной точке
срединной поверхности.
Безразмерная функция ф связана с растягивающей силой Тг
выражением
TrQ
Eh 9
(5.32)
Цилиндрическая жесткость D определяется формулой (5. 8).
Символ ( )* означает ( )’ = .
' ' ' ' dp
Из уравнений (5. 31) можно получить дифференциальное урав-
нение (5. 9) круглой пластинки при малых прогибах, если поло-
жить функцию ф растягивающего усилия равной нулю.
Уравнения (5. 31) нелинейны относительно неизвестных й и ф
и решаются приближенными методами.
Используем эти уравнения для решения абсолютно гибкой мем-
браны.
Абсолютно гибкая мембрана
Тонкую мембрану, работающую при весьма больших прогибах
(и?о^> Л), можно рассматривать как абсолютно гибкую. В такой
мембране напряжения растяжения будут значительно больше из-
гибных, и при расчете изгибной жесткостью можно пренебречь.
Уравнения абсолютно гибкой мембраны можно получить из
16 Заказ 24.
141
уравнений (5. 31) плоской мембраны в больших перемещениях,
полагая в них цилиндрическую жесткость D — 0:
.-11- v v .
еФ + ф — v = -j-;
У
(5. 33)
Для решения этих нелинейных уравнений применим приближен-
ный метод Бубнова—Галеркина [65], [66] и [39].
Фиг. 129. Абсолютно гибкая мембрана:
а — форма упругой поверхности; б — радиальные <УГ и окружные напряже-
ния; в— эпюры распределения напряжений ог и вдоль радиуса.
Под действием давления абсолютно гибкая мембрана принимает
форму, близкую к сферической (фиг. 129, а), и поэтому закон угла
поворота можно выбрать в виде
й = Со,
здесь С — постоянная, подлежащая определению по методу Буб-
нэва—Галеркина. Подставляяй в первое уравнение системы (5 . 33),
242
после интегрирования получим функцию ф растягивающего ради-
ального усилия
С2 / ъ \
“ ЧТ (е3 + "° + т) ‘ <5-35-
Постоянная интегрирования Ъ — 0, так как в центре мембраны
(е = 0) растягивающее усилие имеет конечную величину (ф^со).
Постоянная а зависит от способа закрепления мембраны по наруж-
ному контуру. Если радиальное смещение невозможно, то окружная
деформация на контуре равна нулю. Величина ef связана с уси-
лиями Тг и Tt законом Гука в соответствии с формулой (8. 5), при-
веденной в приложении I,
Ег = ~~ (а)
Граничное условие |е/| = 0, выраженное с помощью формул (а),
(5. 32) и (8. 1) в безразмерных величинах, получает вид
Ф’-м4- =о. (5.36)
Q |Q=1
Из этого равенства находим постоянную а = — .
Подставляя угол поворота '0 (5. 34) и функцию ф растягиваю-
щего усилия Тг (5. 35) во второе уравнение (5. 33), умножаем его
на р в соответствии с методом Бубнова—Галеркииа и интегрируем
в пределах изменения q, т. е. от 0 до 1. В результате получим
С3 7—р pR
24 1 —р Eh '
Это уравнение связывает постоянную С с давлением р, геометри-
ческими и физическими параметрами мембраны.
С Другой стороны, постоянную С можно выразить через прогиб
if о центра мембраны. Прогиб wo можно определить, интегрируя
выражение (5. 3)
о
wQ = f 'О dr.
и
Подставляя сюда значение Ф из формулы (5. 34), получим
о
w0 = CR
(5.37)
Используя значение С = —
2^0 о /
, найдем из выражения (б) урав-
нение характеристики абсолютно гибкой мембраны
pR*
Eh*
/ — p
3(1—p) h? ‘
16*
243
При р = 0,3 зависимость (5. 38) примет вид
dR4
Еу: . — з 1 q_— •
Eh* — О,1У &
(5. 38х)
Точное решение этой задачи, выполненное Генки [67], дает числовой коэф-
фициент 3,45 в выражении (5.38). Однако в этом решении была допущена арифме-
тическая ошибка, замеченная и исправленная Цянь Вэй-чаном [68]. Исправле-
ние привело к коэффициенту 3,58, и поэтому точное уравнение характеристики
абсолютно гибкой мембраны будет
(5. 38")
Формула (5. 38) показывает, что в области весьма больших про-
гибов, когда мембрана работает в основном на растяжение, сопро-
тивление мембраны внешней нагрузке возрастает с увеличением
прогиба по кубическому закону, а не по линейному, как при изгибе
пластинки [см. формулу (5. 13)].
Напряжения растяжения в абсолютно гибкой мембране равно-
мерно распределены по ее толщине (фиг. 129, б). Их можно опре-
делить с помощью уравнения равновесия (8. 1) и формулы (5. 35),
где в соответствии с выражениями (5. 32) и (5. 37)
„I,_ Тг q х,___________ 2и>0
_ __ и С - .
Тг X
Радиальное напряжение о> = -у- будет равно
Еи>1
4R*
2
Or =
(5.39)
Окружное напряжение
ai==-h
Of равно
^0 I
(5.39')
На фиг. 129, в показаны эпюры ог и
возникают в центре мембраны, где
Of. Наибольшие напряжения
Or —
4Я3 *
(5.40)
Отметим, что напряжения растяжения в абсолютно гибкой мем-
бране возрастают пропорционально квадрату прогиба, тогда как
изгибные напряжения в пластинке возрастают пропорционально
прогибу [см. формулу (5. 17) ].
Вели абсолютно гибкая мембрана имеет жесткий центр (фиг. 130,а),
то ее характеристика может быть получена аналогичным путем. Раз-
личие в решении будет определяться только разницей в граничных
244
<1?иг. 130. Семейства характеристик абсолютно
гибких мембран:
а — с разными размерами ;т;есткого центра; б — с раз-
личными величинани начального ьатяи^пцн.
условиях. Для мембраны с жестким центром радиуса г о радиальное
смещение, а следовательно, и окружная деформация st не только
на наружном (р = 1), но и на внутреннем (р = ро — -£-) контуре
отсутствует. Эти граничные условия приводят к выражениям, ана-
логичным (5. 36)
Из решения этих уравнений находим постоянные а и Ъ в выра-
жении (5. 35)
3 —р
1-Р
(1 + ео); ъ = -
3 —р
1-Нр
Следуя в остальном изложенному выводу, можно получить урав-
нение характеристики абсолютно гибкой мембраны с жестким цен-
тром
pR*
Eh*
(5.41)
где
7— р .. . 9 , л, . (3 — р)2 о
3 (1 + т-Qq) + Qo __
(1—Н) (1—Qo) (Wo)a
(5-42)
На фиг. 130, а показано семейство характеристик абсолютно
гибких мембран при различных размерах жесткого центра.
Если абсолютно гибкая мембрана при установке в прибор натя-
гивается, например, способом, показанным на фиг. 121, то ее расчет
на жесткость также может быть получен на основании уравнений
(5. 33).
Предположим, что при натяжении мембраны точки ее наружного
контура получили радиальное смещение иг (фиг. 130, б). Затем мем-
брана закрепляется так, что при нагружении давлением величина
радиального смещения на контуре остается неизменной. Характе-
ристика мембраны с начальным натяжением может быть получена
таким же путем, как и для мембраны без начального натяжения.
Разными будут лишь граничные условия. Для мембраны с началь-
ным натяжением окружная деформация в/ на контуре (г — R) бу-
дет равна е/ — ~ . Заменяя деформации через усилия с помощью
с
формул (а), (5. 32) и (8. 1), получим условие на контуре в виде
Подставляя сюда функцию ф из выражения (5. 35), определим
постоянную интегрирования а
___ 3 — р щ 16
а “ — 1 —р R СЧГ^) '
246
Дальнейшие преобразования ничем не отличаются от изложенных
выше. Они приводят к следующему уравнению характеристики аб-
солютно гибкой мембраны с начальным натяжением:
рД4 7-н “’о ч
Ей4 3(1—JLL) й3
4 ЩИ
1—р, h h1 2
(5. 43)
На фиг. 130, б построено семейство характеристик мембран при
различных величинах начального натяжения. С увеличением на-
тяжения мембрана становится более жесткой, а нелинейность ха-
рактеристики уменьшается.
Уточненный расчет плоских мембран
при произвольных прогибах
В предыдущих разделах были изложены решения задачи о про-
гибах плоской мембраны для двух предельных условий ее работы:
в области малых перемещений, когда прогибы значительно меньше
толщины мембраны, и в области весьма больших прогибов, превос-
ходящих толщину мембраны в 10 и более раз, когда мембрана ра-
ботает практически как абсолютно гибкая.
Для полного решения задачи о плоской мембране необходимо
располагать методом расчета, справедливым при произвольных про-
гибах *. Как указывалось выше, с увеличением прогиба мембраны
форма ее упругой поверхности изменяется (см. фиг. 122). Сложность
решения в области произвольных прогибов и состоит в том, что оно
должно учитывать это изменение формы. Изложим кратко резуль-
таты решения этой задачи по В. И. Феодосьеву [47].
В основу решения положены дифференциальные уравнения пло-
ской мембраны в больших перемещениях (5. 31), интегрирование
которых проводится по методу Бубнова—Галеркина. При этом урав-
нение для угла поворота нормали выбирается в виде
й-С(рг-р), (5.44)
здесь С и z — параметры, определяемые по методу Бубнова—Га-
леркина, р = ---относительный радиус до произвольной точки
мембраны.
Параметр z учитывает изменение формы упругой поверхности
с прогибом. В соответствии с зависимостью (5. 3) уравнение упругой
поверхности может быть получено интегрированием выражения
(5. 44) для угла поворота
w — [ft dr-}-cv.
1 Следует иметь в виду, что при достаточно больших прогибах возможна
потеря устойчивости мембраны, выражающаяся в появлении радиальных
складок. Определение критических прогибов, при которых наступает потеря
устойчивости мембраны, дано в работе [1].
247
Произведя интегрирование и определяя постоянную сг из того
условия, что в заделке (г = В) прогиб w — 0, получим
w == w0
1) Q2] + 1
(5. 45)
где wo — прогиб центра мембраны.
При z = 3 выражение (5. 45) преобразуется в уравнение упру-
гой поверхности пластинки в малых перемещениях. Действительно,
Фиг. 131. Изменение формы образующей упру-
гой поверхности мембраны в зависимости от
величины параметра z.
заменяя давление р в уравнении (5. 12) через прогиб wo центра
мембраны с помощью формулы (5. 13), получим
что совпадает с выражением (5. 45) при z — 3.
С увеличением z форма упругой поверхности, описываемая урав-
нением (5. 45), меняется, приближаясь при z со к сферической,
как и для абсолютно гибкой мембраны (фиг. 131).
Характеристика мембраны, полученная в результате решения,
изложенного в работе [47], выражается довольно громоздкими
уравнениями в параметрической форме.
На фиг. 132 эта характеристика дана графически в виде кри-
вой а. Для сравнения здесь же показаны характеристики пластинки
в малых перемещениях (прямая б) и абсолютно гибкой мембраны
(кривая в). В области малых перемещений, когда справедлива ли-
нейная теория, уточненная характеристика а мембраны касается
прямой б.
В области больших перемещений кривая а близко подходит
к характеристике в абсолютно гибкой мембраны. Это означает, что
решение, построенное на выборе закона угла поворота “O’ в виде функ-
ции (5. 44), отражающей изменение формы упругой поверхности
248
с изменением прогиба, справедливо как в области малых, так и в об-
ласти больших прогибов мембраны.
Прогибы мембраны легко определяются по уточненному решению
с помощью кривой а на фиг. 132.
Уточненное решение позволяет также определить напряжение'
в мембране при произвольных прогибах.
Фиг. 132. Характеристики мембраны: уточненная
(а), по линейной теории (б), по теории абсолютно
. гибкой мембраны (в).
Напряжения в мембране можно представить как сумму изгиб-
ных напряжений и напряжений растяжения в срединной поверх-
ности (Ур (см. фиг. 122).
О = <Уи "4" CFp.
Наибольшие изгибные напряжения ои связаны с изгибающим
моментом М выражением
___67W
СГи - ± -^2- .
Изгибающие моменты Мг и Mt в радиальном и окружном на-
правлениях зависят от искривления срединной поверхности мем-
браны, которое характеризуется углом поворота Ф, и выражаются
уравнениями (5. 7)
здесь D — цилиндрическая жесткость — определяется форму-
лой (5. 8).
249
Подставляя в эти выражения угол поворота й по уравнению
-(5. 44), получим изгибные напряжения в радиальном и окружном
направлениях в точках наружных поверхностей мембраны
В точках срединной поверхности изгибные напряжения равны
нулю и меняются по толщине мембраны по линейному закону
(см. фиг. 122).
Для определения напряжений растяжения в срединной поверх-
ности бр,. постоянных по толщине, необходимо найти растягиваю-
щие усилия Тг и Tt в радиальном и окружном направлениях. Тогда
напряжения
Tt
Усилия Тг и Tt связаны с функцией ф (5. 32), которая может
быть найдена интегрированием первого уравнения системы (5. 31).
Приведем конечную формулу для радиальных напряжений в
срединной поверхности
_ Eh2 wq 2 (z-pi)
0rP ~ R2 h2 (z —I)2 X
Окружные напряжения
радиальных.
В центре мембраны сг.
любой точке мембраны меньше
на краю б = |1<тг ,
р
Параметр z, входящий в выражения (а) и (б), зависит от прогиба
мембраны, и его можно определить с помощью графика, показанного
на фиг. 133.
Полные напряжения бг и 6t находятся суммированием выра-
жений (а) и (б).
Определим суммарные напряжения в центре и на краю мем-
браны.
В центре (р = 0)
Eh2
Gr ~
h
(5.46)
На краю (е = 1)
Eh2 w0 1 -f- z ’ 1
R2 h 1 — p, — 1 + p.
u?o______1
h 2(z4-3)
(5.47)
(Ji — р/СУг*
При вычислении напряжений в точках верхней нагруженной
давлением поверхности мембраны (фиг. 134) в выражениях (5. 46)
и (5. 47) следует брать верхний знак «плюс» или «минус», при опре-
делении напряжений в точках нижней поверхности следует брать
в зависимости от относительного прогиба мембраны.
Из формул (5. 46) и (5. 47) следует, что напряжения на краю
мембраны больше, чем в центре. Это объясняется тем, что с увеличе-
нием прогиба мембрана вблизи контура искривляется сильнее, чем
в центре.
На фиг. 134 построены кривые относительных радиальных на-
пряжений в зависимости от относительного прогиба Этим
251
графиком можно пользоваться при расчете напряжений. Из графика
видно, что суммарные напряжения, изображенные толстыми ли-
ниями, в центре мембраны меньше, чем на краю. При малых проги-
бах 2,2) изгибные напряжения в центре мембраны ии пре-
\ / V
восходят напряжения растяжения срединной поверхности
в мембране в зависимости
ст
Фиг. 134. Радиальное напряжение =
от прогиба —
затем, при увеличении прогибов, большими становятся напряжения
растяжения сгр. На краю мембраны изгибные напряжения при лю-
бом прогибе остаются больше напряжений Ор, что объясняется
сильным искривлением мембраны в этом месте.
Для оценки прочности необходимо определить эквивалентное
напряжение <тэкв в опасной точке мембраны с помощью какой-либо
252
теории прочности. В опасной точке (на краю мембраны) главные
напряжения равны:
Oj = dr, d2 — (Т( = dg == 0.
Тогда эквивалентное напряжение в же, определенное, например,
по энергетической теории прочности, будет
(Уже = V df 4- of — dtd2 = dr j/1 — ц + |ia
или при ц
0,3
о&кв = 0,89 dr.
(5.48)
Коэффициент запаса по текучести
о т
пт = —— ,
(Уэкв
где о„ — предел текучести материала мембраны.
На фиг. 133 построены в без-
размерных координатах характери-
стика мембраны, кривая наиболь-
Фиг. 135. К определению объема,
сметаемого упругой поверхностью
мембраны.
шего напряжения , а также
параметр z в зависимости от
относительного прогиба —г- . Поль-
зуясь этим графиком, можно
легко производить расчеты на
жесткость и на прочность плоской
мембраны при любых прогибах.
В некоторых случаях необхо-
димо знать объем, ометаемый сре-
динной^ поверхностью мембраны при изгибе, например, когда мембра-
на используется как разделитель. Объем V между начальной пло-
скостью мембраны и ее упругой поверхностью можно определить
(фиг. 135) как
R
V = f 2л rwdrt
о
где прогиб w в произвольной точке определяется выражением (5. 45)
Произведя интегрирование, получаем
V = л R2ivq
(5.49)
Пример 2. Определить перепад давлений, изменение объема, форму упругой
поверхности и коэффициент запаса разделительной мембраны при заданном
рабочем прогибе центра wq = 2 мм. Материал мембраны — сплав Н36ХТЮ;
модуль упругости Е = 2,1 • 10® кгс/см^ предел текучести от = 9000 кгс! ем?',
рабочий радиус R = 100 мм\ толщина материала h = 0,4 мм (фиг. 136).
253
2
Решение. По фиг. 133 определяем при — 5 величины:
« 0,4
pR^
~ = 450 и z = 16, отсюда перепад давлений
450 £Л4
Р-
450 • 2,1 • 106 • 0,044 по/_ , 2
= 0.242 кгс]см2.
104
Подставляя z в формулу (5. 45), получаем уравнение упругой поверхности1
мембраны при wq = 2 мм
2R=2Q0
136. Разделительная
мем-
w = w0
[2e
_(16 + 1)q2] + 1
Объем V определяем по формуле (5. 49):
К = 3,14-102-0,
Наибольшее радиальное напряжение
на краю мембраны находим по фиг. 133.
При
= 5 относительное напряжении
От/?3 .nQ
равно - 2 = 108, откуда
108 Eh2 _ 108 2,1 • 10е (0,04)
— 3620 кгс!см2.
R2 102
Эквивалентное напряжение находим по формуле (5. 48):
= 0,89 аг = 0,89 • 3620 = 3220 кгс!см2.
Следовательно, коэффициент запаса по текучести будет равен
. = °Т =. 9000 -2 Я
т Сакв -3220
Определение характеристики плоской мембраны
методом «наложения»1
Основная идея метода «наложения» заключается в том, что со-
противление мембраны внешней нагрузке рассматривается как сум-
ма сопротивлений изгибу и растяжению. Сопротивление мембраны
изгибу определяется по линейной теории изгиба круглой пластинки,
а сопротивление растяжению — из расчета асболютно гибкой мем-
браны, которая, как указывалось выше, работает только на растяже-
ние. Искомое решение при произвольной величине прогиба опреде-
ляется «наложением» этих двух решений, т. е. приравниванием
суммы сопротивлений мембраны на изгиб и на растяжение величине
внешней нагрузки. Полученное таким образом уравнение дает ре-
зультаты, близко совпадающие с уточненным решением как в области
малых, так и в области больших перемещений,
1 Ф е п п л ь А., Ф е п п л ь Л., Сила и деформация, Гостехиздат, 1933.
254
Нагрузка на мембрану по методу «наложения» может быть вы
р а жена суммой двух слагаемых
дД4
ЬТг4
рЙ4 \
здесь величина
Рй4
Eh4
характеризует сопротивление мембраны
— сопротивление растяжению.
изгибу, а
Из решения круглой пластинки в малых перемещениях сопроти-
вление мембраны изгибу определяется в соответствии с выражением
(5. 13') по формуле
16 (Со
[3(1— р2) h
Сопротивление мембраны растяжению определяется из [решения
абсолютно гибкой мембраны (5. 38):
IV
(б)
Суммируя выражения (а) и (б), получаем
(5. 50)
[(5.507
Формулу (5. 50') можно улучшить, если вместо коэффициента
3,19 при кубическом члене, который был получен приближенным мето-
дом Галеркина, взять коэффициент 3,58, соответствующий точному
решению Генки (5. 38"). Тогда уравнение характеристики плоской
мембраны будет:
(5.50'7
Характеристика плоской мембраны, построенная по уравнению*
(5. 50), практически совпадает с линией а, соответствующей уточ-
ненному решению, изложенному в предыдущем разделе (см. фиг. 132).
Таким образом, для расчета характеристики плоской мембраны при
любых прогибах можно пользоваться приближенным уравнением
(5. 50) или более точным (5. 50").
Также просто можно получить характеристику плоской мембраны
с жестким центром, поскольку эта задача была предварительно»
255
решена и по линейной теории (5. 19), и по теории абсолютно гибкой
мембраны (5. 41). Путем «наложения» этих решений получаем сле-
дующее уравнение плоской мембраны, охватывающее как область
малых, так и область больших перемещений
pR* _ 1 10о । „
Eh* “ Ар h р h3
здесь коэффициенты Ар и Вр определяются
и (5.42).
выражениями (5. 20)
Особенно эффективным оказалось применение метода «наложения»
к расчету гофрированных мембран, для которых уточненное решение
по способу, изложенному в § 24 (стр. 247), слишком сложно.
Применение метода «наложения» позволило создать простое и вполне
удовлетворительное решение.
§ 25. ПРИМЕНЕНИЕ, КОНСТРУКЦИЯ, СПОСОБЫ ИЗГОТОВЛЕНИЯ
ГОФРИРОВАННЫХ МЕМБРАН
Гофрированные мембраны применяются чаще плоских. Они
тиогут надежно работать при значительно больших прогибах. Б за-
висимости от формы профиля1 характеристика мембраны может
быть линейной, затухающей или возрастающей по давлению. В этом
^отношении гофрированные мембраны в ряде случаев имеют
преимущество перед другими типами манометрических упругих
элементов (сильфонов, трубчатых пружин), характеристики которых
линейны по давлению.
С помощью гофрированных мембран можно легко решать задачи
измерения величин, нелинейно связанных с давлением (например,
расхода жидкости или газа, проходящего по трубопроводу, воздуш-
ной скорости полета самолета, высоты его подъема и пр.). Про-
ектируя должным образом мембрану, можно получить характери-
стику, линейную по измеряемому параметру, и тогда линейность
шкалы прибора достигается при простейшей кинематике механизма.
На фиг. 137 даны схемы некоторых приборов, в которых исполь-
зуются гофрированные мембраны: авиационный высотомер (а),
мембранный дифференциальный манометр (б), манометр с одиночной
мембраной (в), регистрирующий прибор с дисковой диаграммой (г).
К центральной плоской части мембраны прикрепляется так
называемый жесткий центра (фиг. 138), штифт которого
служит для передачи движения от мембраны к механизму прибора.
На фиг. 138 показаны часто встречающиеся формы профилей б
гофрированных мембран: трапецеидальная, пильчатая и синусо-
идальная.
Наиболее удаленная от центра мембраны волна гофрировки
часто имеет форму, отличную от остальных волн, и называется
1 Профилем мембраны называется образующая срединной поверхности.
256
Фиг. 137. Применение гофрированных мембран в приборах.
Фиг. 138. Элементы
гофрированной мем-
бра пы.
17 Заказ 24.
257
краевым гофром в. На фиг. 138 изображены тороидальный
и цилиндрический краевые гофры. Наличие краевого гофра, как
правило, вызывается чисто конструктивными соображениями. На-
пример, он необходим при соединении двух мембран в коробку.
Краевой гофр переходит в плоский г или цилиндрический д буртик,
который имеет небольшую ширину и служит для закрепления мем-
браны.
Одиночные мембраны, закрепленные по буртику в кор-
пусе, применяются сравнительно редко. Для осуществления надеж-
ного крепления одиночной мембраны (фиг. 139, а) ее приходится за-
тягивать, при этом в корпусе могут возникнуть значительные усилия.
В некоторых случаях мембрана крепится к жесткому основанию
пайкой или сваркой (фиг. 139,6). Такой способ крепления освобо-
ждает корпус от усилий при затяжке, но при пайке или сварке мате-
риал мембраны и основания прогревается неравномерно, и возни-
кающие при этом температурные напряжения могут исказить геомет-
рию мембраны, и, следовательно, ее характеристику. Температурные
напряжения будут меньше, если материалы основания и мембраны
имеют одинаковые коэффициенты теплового расширения.
При креплении одиночной мембраны большое значение имеют
конструкция и точность изготовления крепежных колец или основа-
ния, а также правильная форма буртика. Если буртик или посадоч-
ная кольцевая площадка на основании или крепежном кольце не
параллельны друг другу, то при закреплении мембраны по любому
способу буртик будет поворачиваться, что приведет к деформации
мембраны и искажению ее характеристики. Несовершенства краевого
. крепления мембраны сказываются тем больше, чем меньше ее жест-
кость.
Конструкция мембранного узла значительно упрощается, если
две одинаковые мембраны соединены по буртику, образуя м е м-
бранную коробку. По сравнению с одиночной мембраной
коробка имеет преимущество вдвое большего хода. Кроме того,
установка мембранной коробки в прибор значительно проще, чем
одиночной мембраны. К одной из мембран прикрепляется жесткий
центр, а к другой — штуцер, который служит для подвода во внут-
реннюю полость коробки измеряемого давления и одновременно для
крепления коробки к корпусу прибора (фиг. 139, в).
Мембраны соединяются в коробку пайкой или сваркой по бур-
тику. Так как при этом обе мембраны находятся в одинаковы?
условиях, то пайка или сварка не вызывает ощутимых температур-
ных напряжений, как это имеет место при сварке одиночной мембра-
ны с основанием. Сварные коробки более прочны, лучше герметизи-
руются, имеют меньший гистерезис и большую стабильность упру-
гих свойств, чем паяные.
Для увеличения прочности соединения мембраны иногда свари-
ваются друг с другом по грибковой схеме (фиг. 139, г).
Соединение мембраны в коробку сваркой по цилиндрическому бур-
тику обеспечивает также большее постоянство рабочего диаметра
258
мембранных коробок в партии и, следовательно, малый разброс по
эффективной площади.
Если требуется минимальный объем внутренней полости,
применяются с к л а д ы в а ю щ и е с я мембранные коробки
Фиг. 139. Конструкции мембран: одиночная мембрана, закрепленная в корпусе
зажимным кольцом (а), пайкой или сваркой (б); мембранная коробка (в); гриб-
ковая схема мембранной коробки (г); складывающаяся мембранная коробка
(3); блок мембранных коробок (е).
(фиг. 139, д). Они удобны также тем, что не теряют своих свойств
в случае перегрузки наружным давлением. Чтобы обеспечить идеаль-
ное прилегание мембран друг к другу при перегрузках, обе мембраны
формуются вместе на одном штампе.
Для измерения абсолютного давления (манометрами абсолют-
ного давления, барометрами, высотомерами и др.) внутри коробки
17*
259
создается вакуум. -Такие коробки называются анероидными
в отличие от манометрических
торых соединена с измеряемым
*
Фиг. 140. Защита мембран от перегрузки
давлением:
п — защита неподвижным упором; б — дефор-
мация мембранной коробки; в — складываю-
щиеся мембранные коробки с жидкостным за-
полнителем; г — защита одиночной мембраны
профилированными упорами.
внутренняя полость по-
давлением.
Для того чтобы увеличить
перемещения, можно не-
сколько коробок соединить
в блок (фиг. 139, е).
Для защиты мембран-
ной коробки от перегрузки
давлением применяются спе-
циальные упоры, ограни-
чивающие деформацию мем-
бран. При небольшой пере-
грузке достаточно ограни-
чить упором перемещение
верхнего центра коробки
(фиг. 140, а). Если же пере-
грузочное давление велико,
то необходимо ограничить
деформации во всех точках
мембран. Решение этой за-
дачи может вызвать ряд
затруднений. Дело в том,
что при увеличении давле-
ния во внутренней полости
коробки, закрепленной по
нижнему центру, все точки
как верхней, так и нижней
мембран получают переме-
щения вверх (фиг. 140, б).
Ограничить при этом пере-
мещения верхней мембраны
сравнительно легко, поста-
вив на ее пути неподвижный
упор; защитить же нижнюю
мембрану при таких усло-
виях трудно.
Если мембранный чув-
ствительный элемент мо-
жет испытывать при ра-
боте двухстороннюю пере-
грузку давлением (напри-
мер, в дифференциальном
перегрузок применяют блок
манометре), то для защиты от
двух мембранных коробок, заполненный жидкостью (фиг. 140, в).
В этом случае каждая мембранная коробка выполняется в форме
«складывающейся» (см. фиг. 139, д). Такие коробки могут выдержать
перепад в сотни и тысячи раз больше рабочего. Наличие жидкост-
260
ного заполнителя позволяет применять чувствительные коробки
при больших статических давлениях, значительно превышающих
рабочие перепады. Однако такие системы чувствительны к темпера-
туре вследствие расширения рабочей жидкости. Этим недостатком
не обладает конструкция в виде одиночной мембраны, защищенной
с обеих сторон профилированными упорами (фиг. 140, г). Однако
она работает надежно только в чистой рабочей среде, когда простран-
ство между мембраной и упорами не загрязняется.
а — рифление мембраны гидравлическим способом; б — рифление мембраны ме-
ханическим способом; в — прокладки для термообработки мембран^
Для изготовления мембран используется тонколистовой мате-
риал. Обычно он предварительно подкатывается для получения
достаточно высокой точности по толщине, которую не обеспечивают
принятые допуски на толщину исходного листового материала.
Из листов вырубаются кружки, которые и служат заготовкой
для мембран. Рифление мембран (нанесение гофрировки) произво-
дится гидравлическим или механическим способом.
.Рифление гидравлическим способом производится в специальной
камере, где заготовка помещается между матрицей и основанием.
При подаче давления заготовка прижимаемся к матрице и принимает
ее форму (фиг. 141, а).
Механическое рифление мембраны производится между жест-
кими пуансоном и матрицей. Для обеспечения лучших условий
вытяжки материала пуансон и матрица конструируются так, чтобы
соприкосновение их с мембраной осуществлялось не по всей поверх-
ности, а только по контактным площадкам (фиг. 141, б). Мембраны,
изготовленные механическим способом, приобретают более точно
очерченный профиль, и разброс характеристик мембран одной
партии оказывается меньшим, чем при гидравлической штамповке.
Существенным преимуществом механического способа является
261
обеспечение лучших санитарных условий работы. Поэтому несмотря
на большую сложность инструмента для механической штамповки
(при гидравлической пуансон не нужен и изготовляется только
матрица) этот способ получает все большее применение.
Лучшее качество механической штамповки получается при ис-
пользовании гидравлических прессов1. При этом способе можно
точно устанавливать силу, необходимую для рифления мембраны.
При изготовлении мембран необходимо особенно тщательно
выполнять требуемую глубину гофрировки. Для упругих элементов,
имеющих линейную характеристику, отклонение в размерах вызы-
вает лишь изменение жесткости, которое можно устранить при регу-
лировке прибора. Отклонение же по глубине гофрировки мембраны,
кроме изменения жесткости, существенно меняет форму характери-
стики, что исправить регулировкой механизма прибора значительно
труднее. Поэтому в качестве основных материалов для изготовления
мембран используются такие, которые не имеют упругой отдачи
при рифлении, например, дисперсионно-твердеющие сплавы. Для
предотвращения коробления и искажения профиля термообработка
мембран проводится в специальных прокладках (фиг. 141, в).
Такие материалы, как фосфористая бронза и латунь, которые
приобретают упругие свойства при нагартовке, для изготовления
мембран применяются в настоящее время редко. Мембраны из этих
материалов имеют низкие упругие свойства. Кроме того, упругая
отдача при рифлении искажает форму профиля, что приводит к боль-
шому разбросу характеристик мембран.
Высокие упругие свойства обеспечивает мембранам бериллиевая
бронза Бр. Б2,5 и Бр. БНТ1,9 (табл. 6, § 1).
Для мембран, соприкасающихся с различными технологическими
средами, широко используется дисперсионно-твердеющий сплав
Н36ХТЮ, который обладает хорошей коррозионной стойкостью
и достаточно высокими упругими свойствами. Мембраны из этого
сплава могут работать при повышенных температурах (до 150—
200° С).
Соединение мембран в коробку производится в последнее время
почти исключительно сваркой. Сварной шов является весьма ответ-
ственным местом, так как он располагается в наиболее напряженной
части мембраны. Паяные коробки имеют большие несовершенства
упругих свойств по сравнению со сварными.
Операция стабилизации для мембран обязательна и обычно
производится пульсирующей нагрузкой — «раскачкой».
Основные операции технологического процесса изготовления
анероидных коробок такие же, как и манометрических. Вакууммиро-
вание анероидных коробок производится после сварки мембран
через отверстие, запаиваемое затем каплей мягкого припоя. Отверстие
должно располагаться в наименее напряженном месте мембраны,
1 Бородко И. С., Новое в технологии производства чувствительных
элементов, Бюллетень № 6, НИИТепло прибор, 1956.
262
ближе к жесткому центру, так как иначе капля может вызвать
потерю герметичности анероида по истечении некоторого времени.
Микронегерметичность коробки может появиться также при пло-
хом качестве шва.
§ 26. ВЛИЯНИЕ ГЕОМЕТРИИ ПРОФИЛЯ НА ХАРАКТЕРИСТИКУ
ГОФРИРОВАННОЙ МЕМБРАНЫ
Начальная плоскость1 гофрированной мембраны при нагружении
приобретает форму поверхности вращения.
При малых прогибах можно считать, что на первом этапе нагру-
жения начальная плоскость гофрированной мембраны деформируется
без удлинений так же, как срединная плоскость плоской мембраны
в области малых перемещений (§ 24, стр. 229).
Начальная плоскость мембраны искривляется как в радиаль-
ном, так и в окружном направлениях. Мысленно выделив кусок
Фиг. 142. Элемент гофрированной мембраны
и его нагружение.
А
гофрированной мембраны осевыми и окружными сечениями
(фиг. 142), легко представить, что изгиб в окружном направлении
встретит значительно большее сопротивление, чем в радиальном. По-
этому в начале нагружения прогибы мембраны зависят в основном
от величины жесткости на изгиб в окружном направлении. Послед-
няя, в свою очередь, определяется величиной момента инерции осе-
вого сечения мембраны относительно радиуса в начальной плоскости,
т. е. глубиной гофр и толщиной материала. При одной и той же тол-
щине материала жесткость мембраны в большой степени зависит от
глубины гофрировки: с увеличением глубийы жесткость мембраны
быстро возрастает.
До тех пор, пока длина волн гофрировки остается неизменной,
характеристика гофрированной мембраны будет оставаться линей-
ной.
При дальнейшем возрастании прогибов начальная плоскость
мембраны будет удлиняться, т. е. длины волн гофрировки будут
увеличиваться. На этом этапе нагружения, помимо сопротивления
изгибу, существенное влияние на характеристику оказывает
1 Начальной на зовем плоскость, равноотстоящую от вершин и впадин гофр
мембраны.
263
сопротивление гофрированной мембраны растяжению, и характеристи-
ка становится затухающей. Поведение гофрированной мембраны на
этом этапе подобно поведению плоской мембраны в области больших
перемещений (см. фиг. 122).
Так же, как и для плоской мембраны, сопротивление гофрирован-
ной мембраны внешней нагрузке можно представить как сумму
сопротивлений изгибу и растяжению. Сопротивление изгибу пре-
обладает в начале нагружения, сопротивление растяжению про-
является в области больших прогибов. Мембрана с глубокой гофри-
ровкой имеет большее сопротивление изгибу, поэтому ее характери-
стика будет ближе к линейной, чем характеристика мембраны с мел-
кой гофрировкой, у которой растяжение гофр, следовательно, и
нелинейность характеристики проявляется при меньших прогибах.
Плоская мембрана имеет самую малую начальную жесткость и наи-
более сильно затухающую характеристику.
На фиг. 143, и, показано влияние глубины гофрировки Н на
характеристику мембраны с небольшим числом п глубоких гофр;
для мембраны с мелкой частой гофрировкой это влияние показано
на фиг. 143, б. В первом случае с увеличением глубины гофрировки
мембрана становится более жесткой, а характеристика более линей-
ной. Во втором случае увеличение глубины гофрировки вызы-
вает уменьшение прогибов на начальном участке характеристики,
а в конце характеристики влияние глубины гофрировки оказывается
обратным.
Таким образом, в зависимости от конфигурации мембраны и
величины нагрузки увеличение глубины гофрировки может привести
либо к уменьшению, либо к увеличению прогибов. Однако в любом
случае начальная жесткость мембраны с ростом глубины гофрировки
увеличивается, а характеристика становится более линейной.
Сильно влияет на характеристику гофрированной мембраны
и ее толщина Л, особенно в области малых толщин (фиг. 143, в).
Изменение же числа волн п при условии сохранения глубины гофри-
ровки Н мало меняет характеристику гофрированной мембраны
(фиг. 143, г).
Изменение формы профиля оказывает значительно меньшее влия-
ние на характеристику, чем изменение его глубины.
Мембраны мелкого пильчатого профиля (фиг. 144, а) просты
в изготовлении, устойчивы к небольшим перегрузкам и широко
применяются в приборах, где требуется затухающая по давлению
характеристика чувствительного элемента (расходомеры, высото-
меры, указатели скорости). Изготовление мембран глубокого пиль-
чатого профиля (фиг. 144, б) встречает некоторые трудности вслед-
ствие возможности появления разрывов по вершинам и впадинам,
где имеет место концентрация напряжений. Поэтому мембраны с глу-
бокой гофрировкой обычно имеют трапецеидальный или синусо-
идальный профиль (фиг. 144, в, г).
Изготовление мембраны синусоидального или другого профиля
плавных очертаний требует более сложного инструмента, однако,
264
такие профили предпочитают другим при изготовлении мембран из
толстого материала и в тех случаях, когда стремятся уменьшить
концентрацию напряжений.
Фиг. 143. Влияние глубины гофрировки на характеристику мембраны с неболь-
шим числом глубоких волн (а) и мембраны с мелкой частой гофрировкой (б);
характеристики мембран различных толщин (в) и с разным количеством волн (г).
Тонкая плоская мембрана с небольшими тороидальными гофрами
(фиг. 144,5) весьма чувствительна и находит применение при изме-
рении низких давлений, например, в вариометрах. После посадки
265
мембраны на плоскость она способна выдержать значительные одно-
сторонние (с выпуклой стороны гофр) перегрузки.
Иногда профиль мембраны выполняется переменным по глубине.
Это уменьшает жесткость мембраны и в некоторых случаях упро-
щает конструкцию упоров, применяемых при перегрузках (фиг. 144, е).
Если сравнить характеристики мембран пильчатого, трапеце-
идального и синусоидального профилей при одинаковых глубинах Н
гофрировки и числе волн п (фиг. 145), то оказывается, что наибольшей
нелинейностью обладает мембра-
на пильчатого профиля, наимень-
шей — мембрана трапецеидального
профиля с достаточно большой
Фиг. 144. Профили гофрированных
мембран.
Фиг. 145. Характеристики мембран си-
нусоидального, пильчатого и трапецеи-
дального профилей.
шириной а плоского участка. Однако влияние формы про-
филя на характеристику невелико, и поэтому удобнее управлять
характеристикой мембраны путем изменения толщины материала
или глубины гофрировки. Форму профиля и число волн обычно
выбирают из конструктивных или технологических соображе-
ний.
В § 24 было показано, какое большое влияние оказывают на
работу плоской мембраны силы начального натяжения в ее пло-
скости (см. фиг. 130, б). Гофрированная мембрана также очень
чувствительна к силам начального натяжения, особенно мембрана
малой жесткости. Если в начальной плоскости мембраны создать
предварительно силы сжатия, то жесткость мембраны падает, и ха-
рактеристика может стать возрастающей. Наоборот, при началь-
ном натяжении жесткость мембраны увеличивается. Это влияние бу-
дет тем сильнее, чем меньше начальная жесткость мембраны, т. е.
чем тоньше материал и мельче гофрировка. Так например, мембран-
266
ная коробка -мелкого пильчатого профиля с цилиндрическим крае-
вым гофром при подаче давления во внутреннюю полость дает мень-
ший ход, чем под действием того же давления, но приложенного
извне. Это может быть объяснено тем, что силы давления на цилин-
дрический гофр в первом случае вызывают натяжение начальной пло-
скости мембраны, увеличивая ее жесткость, а во втором случае —
сжатие начальной плоскости, что вызывает уменьшение жесткости
и увеличивает прогибы мембраны.
В зависимости от конфигурации краевого гофра, контур сопря-
жения центральной гофрированной части мембраны с краевым гоф-
ром может получить радиальное смещение (фиг. 146). Если это сме-
Фиг. 146. Влияние радиального смещения кон-
тура центральной гофрированной части мем-
браны на ее характеристику.
щение направлено к центру мембраны, то в ней появляются силы
сжатия, увеличивающие прогибы, и характеристика в этом случае
может стать возрастающей. Смещение контура сопряжения в напра-
влении от центра вызывает натяжение мембраны и увеличение ее
жесткости.
Очень резко меняется характеристика мембраны, если ей при
изготовлении придать начальную выпуклость: сферическую или ко-
ническую (см. фиг. 119, в). При подаче давления с выпуклой стороны
жесткость мембраны падает, и характеристика становится возрастаю-
щей на начальном участке. Это тем заметнее, чем больше величина
начальной выпуклости, о которой можно судить по высоте А (см.
фиг. 119, в). При достаточно большой величине А мембрана будет
изменять свой прогиб скачком «хлопать». Такие «хлопающие» мем-
браны находят применение в сигнальных устройствах (см. § 30).
Гофрированным мембранам, применяемым в измерительных при-
борах, придают небольшую выпуклость в тех случаях, когда
267
необходимо уменьшить жесткость на начальном участке характеристи-
ки (например, в мембранах анероидной коробки высотомера, чувстви-
тельность которой должна быть достаточной при измерении больших
высот, где давление меняется очень мало с изменением высоты).
§ 27. РАСЧЕТ ГОФРИРОВАННЫХ МЕМБРАН
Выбор расчетной схемы
Гофрированная мембрана представляет собой оболочку весьма
сложной формы, поэтому расчет ее связан с большими вычисли-
тельными трудностями даже в области малых перемещений [69],
[70]. Эти трудности значительно возрастают при решении задачи
с учетом больших перемещений [1], [9], [71]. Применение при-
ближенного способа, излагаемого здесь, оказалось достаточно про-
Фиг. 147. Выбор расчетной схемы:
а — гофрированная мембрана; б — элемент гоф- ,
рированной мембраны; в — элемент плоской мем-
браны.
стым и привело к резуль-
татам, хорошо совпадающим
с опытом [72]—[74].
Рассмотрим гофрирован-
ную мембрану периодиче-
ского профиля произволь-
ной формы, нагруженную
равномерно распределенным
давлением (фиг. 147, а). Вы-
режем из гофрированной
мембраны элемент конечных
размеров (фиг. 147, б) и
сравним его с элементом пло-
ской мембраны (фиг. 147, в).
Элемент плоской мембраны
при ее нагружении изги-
бается и растягивается в ра-
диальном и окружном на-
правлениях. Если жесткость плоского элемента одинакова в ра-
диальном и окружном направлениях, то геометрическая форма
гофрированного элемента такова, что его жесткости в этих двух
направлениях будут различными: в радиальном направлении элемент
будет оказывать значительно меньшее сопротивление изгибу и растя-
жению, чем в окружном. Таким образом, гофрированная мембрана
обладает свойствами анизотропии, обусловленными особен-
ностями ее геометрической формы. Это позволяет выбрать расчетную
схему гофрированной мембраны в виде плоской анизотропной мем-
браны.
Определение приведенных коэффициентов анизотропии
Упругие коэффициенты анизотропного материала определяются
из равенства жесткостей на растяжение и на изгиб анизотропной
пластинки соответствующим жесткостям гофрированной мембраны.
268
При этом толщину анизотропной мембраны примем равной толщине
гофрированной мембраны.
Обозначим через ЕГр и Et упругие коэффициенты, характери-
зующие жесткость материала анизотропной мембраны на растяже-
ние в радиальном и окружном направлениях; ЕГи и Et — упругие
коэффициенты, характеризующие изгибную жесткость анизотроп-
ной мембраны в тех же направлениях.
Жесткость на растяжение в радиальном направлении гофрирован-
ной мембраны значительно меньше, чем жесткость плоской изотроп-
ной мембраны, а жесткость при изгибе в том же направлении отли-
чается незначительно. Поэтому Ег < ЕГи. Точно так же и в окруж-
ном направлении упругие коэффициенты, связанные с изгибом и рас-
тяжением, будут различными, а именно, Et < Etu.
Таким образом, материал эквивалентной плоской мембраны
должен обладать двойной анизотропией: в одном и том же направле-
нии модули упругости материала при растяжении и изгибе должны
быть различными.
Модули упругости анизотропного материала эквивалентной мем-
браны можно представить в виде
Еч к‘»Е’ Et* -kt*E'
(5.51)
где коэффициенты к > 1. Их можно определить приравниванием
жесткостей полосок, одинаковым образом выделенных из гофрирован-
ной и из плоской анизотропной мембран.
Определим модуль упругости Ег при растяжении в радиальном
направлении. Для этого вырежем вдоль радиуса гофрированной
и анизотропной мембран полоски и приравняем их удлинения под
действием одинаковых растягивающих сил Q (фиг. 148, а).
Удлинение §А~Б гофрированной полоски можно найти с помощью
интеграла Мора:
bh3
Здесь J ~ - момент инерции поперечного сечения полоски
шириной b и толщиной h]
F = bh — площадь поперечного сечения;
Е — модуль упругости материала гофрированной
• мембраны;
S — длина гофрированной полоски Л В,равная длине
дуги одной волны профиля мембраны.
Величина второго интеграла, учитывающего деформации растя-
жения, будет тем меньше по сравнению с первым, чем глубже
269
4
гофрировка. При пологой гофрировке второй интеграл становится
соизмеримым с первым, поэтому его необходимо учитывать.
Значения изгибающих моментов и нормальных сил от заданной
и единичной нагрузок будут
Мр = Q-y\ М± — 1 • у; TVp — Q cos 9; — 1 cos 0.
Подставляя их в формулу (а), получим
S S
(б)
где 0 — угол наклона касательной в произвольной точке.
Фиг. 148. Элементы гофрированной и плоской анизотропной мембран, вырезан-
ные в радиальном (а) и в окружном (б) направлениях; к определению момента
инерции J* (в).
Для каждого вида профиля гофрировки эти интегралы легко
вычислить аналитически или графически.
Удлинение анизотропной полоски длиной I и площадью попереч-
ного сечения F = bh, растягиваемой силами Q, с учетом соотноше-
ния (5. 51) равно
А—в QI _
“ ~ EF ‘
лг
Приравнивая правые части выражений (б) и (в), находим коэф-
фициент кг
S S
к? = f y2ds + “Г f cos2erfs
I
b 6
где I — длина волны профиля гофрированной мембраны^
270
Коэффициент кг характеризует жесткость на растяжение в ра-
диальном направлении и показывает, во сколько раз уменьшается
жесткость прямой полоски, если на ней нанести волны гофрировки.
Приравнивая удлинения полосок, вырезанных в окружном
направлении (фиг. 148, б), получим коэффициент kt, характеризую-
щий жесткость на растяжение в этом направлении;
Рассматривая изгиб этих же полосок, определим коэффициенты
кг и kt , характеризующие изгибные жесткости в радиальном и
в окружном направлениях.
Для гофрированной полоски, вырезанной в радиальном напра-
влении (см. фиг. 148, а), взаимный угол поворота сечений Я и В
будет
а для плоской анизотропной
Ж1кти
EJ
Из равенства правых частей этих выражений следует, что
Приравнивая взаимные углы поворота концевых сечений поло-
сок, вырезанных в окружном направлении (см. фиг. 148, б), можно
показать, что коэффициент к^ определяющий изгибную жесткость
в окружном направлении, равен
где
— момент инерции поперечного сечения гофрированной
1№
12
полоски относительно радиуса г;
— момент инерции сечения плоской полосы.
Момент инерции бесконечно малого элемента сечения гофрирован-
ной полоски относительно оси г равен (фиг. 148, в).
dj'T = dF • у2 dJv cos2 б — y2hds 4- —75— cos2 9.
Следовательно,
271
В соответствии с соотношением (ж) коэффициент ktu будет
, s s
*»« = -JT = wj y2ds + т-fcos2 °ds-
b о
(3)
Из выражений (г) и (з)
енты попарно равны
и (е) следует
что найденные коэффици-
р
к.; кг
(5. 52)
— к
и
где
к
~ I
h*1 J
о
2
cos2 6 ds.
о
Отметим, что коэффициенты kL и к2 зависят только от геометрии
профиля гофрированной мембраны и ее толщины, причем коэффи-
циент кг немного больше единицы. Коэффициент к%, равный отноше-
нию моментов инерции относительно радиуса осевого сечения гоф-
рированной и плоской мембран, быстро возрастает с увеличением
глубины гофрировки и может быть значительно больше единицы.
Выражения коэффициентов к± и к2, найденные по формулам
(5. 53) и (5. 54), для некоторых профилей мембран (см. Приложе-
ние I, п. 3) даны ниже в табл. 23 (стр. 276).
После определения приведенных жесткостей на изгиб и на растя-
жение можно перейти к определению прогибов мембраны в зависи-
мости от давления. При этом используем так же, как и при решении
задачи о плоской мембране, метод «наложения» (§ 24, стр. 254).
Характеристика гофрированной мембраны, как и плоской, опи-
сывается кубическим уравнением
р= Awq -f- Bwl,
где линейный член соответствует сопротивлению мембраны изгибу
и может быть найден из решения задачи о прогибах мембраны в об-
ласти малых перемещений. Кубический член характеризует сопро-
тивление мембраны растяжению, для его определения необходимо
рассмотреть ,задачу об абсолютно гибкой анизотропной мембране.
Уравнения мембраны при малых прогибах и уравнения абсолют-
но гибкой мембраны можно получить, как предельные случаи, из
дифференциальных уравнений плоской анизотропной мембраны
в больших перемещениях.
Дифференциальные уравнения плоской анизотропной мембраны
в больших перемещениях
Вывод уравнений для анизотропной мембраны во многом совпа-
дает с ранее изложенным выводом для плоской изотропной
мембраны.
272
Одинаковы уравнения равновесия и геометрические уравнения
для анизотропной и изотропной мембран. Различие имеет место
только в выражениях, связывающих деформации с напряжениями.
При этом, поскольку эквивалентная плоская мембрана обладает
«двойной» анизотропией, необходимо составлять уравнения связи
между напряжениями и деформациями отдельно для растяжения:
{Цр О'/»
% = ~Ё7Р ~ ;
= Ет~ ’
Ф тр
и для изгиба:
_ ®ти $tu .
&rU Et ’
<*U Cru
е'“="Ё7Г-Иг“аГ ’
(5.55)
(5.55')
здесь ш и p/u — коэффициенты, связывающие деформацию в ра-
диальном и окружном направлениях при одноосном растяжении
элемента анизотропной мембраны в окружном направлении. Легко
убедиться, что = р (р — коэффициент Пуассона),
так как растяжение в окружном направлении гофрированной мем-
браны вызывает такое же относительное укорочение в радиальном
направлении, как и для обычной плоской мембраны.
Коэффициенты цг и не будут равны коэффициенту Пуас-
сона ц: растяжение в радиальном направлении гофрированной по-
лосы будет очень мало изменять ее поперечные размеры.
Величины коэффициентов цг и рГи находятся из того условия,
что согласно закону Гука для анизотропных материалов справед-
ливы равенства
Р/р Р-Гр Pfu P'f’u*
£/р Егр И Etu Еги
Дальнейший ход вывода аналогичен изложенному выше для
изотропной плоской мембраны, и с ним можно ознакомиться в рабо-
тах [72], [73] или в приложении I, п. 2.
Уравнения плоско!! анизотропной мембраны в больших переме-
щениях получают вид:
РФ” 4- ф* — а2 ;
qO” 4-0’
2 Л = Г_ Ehk+ ДД. е2
о и т 2
(5.56)
* Эти равенства можно также получить с помощью теоремы взаимности
работ ([47] стр. 292).
18 Заказ 24.
273
ЗдесьФ — угол поворота нормали. Функция ф радиального усилия Тг
равна
“ EhRkv '
Относительный радиус мембраны р =
жесткость D определяется по выражению
Eh3
Цилиндрическая
где Е и р,— упругие постоянные .материала;
h — толщина мембраны.
Безразмерный параметр а связан с геометрическими коэффициен-
тами кг и кг'.
а2 = Zcj < к2.
(5. 59)
Коэффициенты ki и кг определяются выражениями (5.53) и (5.54).
/- / v d( )
Символ ( ) означает производную " -.
Если гофрировка на мембране отсутствует, то коэффициенты кг — кг = 1,
следовательно, по выражению (5. 59) а = 1, и уравнения (5. 56) совпадут с урав-
нениями (5. 31) плоской изотропной мембраны в больших перемещениях.
Построение характеристики гофрированной мембраны
Используем уравнения (5. 56) для определения линейного и
кубического членов характеристики гофрированной мембраны.
Линейный член характеристики определяется из решения за-
дачи о малых прогибах мембраны. Полагая для этого случая в ура-
внениях (5. 56) функцию растягивающего усилия ф = О, получим
следующее дифференциальное уравнение плоской анизотропной
мембраны
рй* ’ 4- 'й*
где параметр нагрузки Ар =
- а2 — =
е 4
pRzkx
2D '
(5. 60)
Решение этого линейного уравнения запишем в виде
(а)
Постоянные интегрирования сг и dx определяются из следующих
граничных условий: в центре (р — 0) и на контуре (р = 1) угол
поворота "0 = 0. Отсюда сг = и = 0.
<7 И
274
Подставляя постоянные а и di в выражение (а), получим угол
поворота для гофрированной мембраны в малых перемещениях
О = —-— Го3 — оа)
9—а2\У U Л
(5. 61)
где а — параметр, зависящий от формы гофрировки в соответствии
с выражением (5. 59).
Относительный прогиб центра мембраны вычисляется по формуле
(5. 3)
1
Подставляя сюда угол поворота из формулы (а) получим ту часть
давления, которая определяет сопротивление мембраны изгибу
2(3-|-а) (14-д)
h
(б)
Кубический член характеристики соответствует сопротивлению
мембраны растяжению, которое имеет место при весьма больших
прогибах. В этом случае поведение гофрированной мембраны может
быть описано уравнениями абсолютно гибкой анизотропной пла-
стинки, которые получатся из системы (5. 56), если положить в ней
изгибиую жесткость D — 0
рф" + ф' — а2
(5. 62)
фА = Дрр2,
здесь параметр нагрузки Др =
pR
2ЕКкг
Уравнения (5. 62) решаем методом Галеркина, задаваясь таким
же законом угла поворота, как и для абсолютно гибкой изотропной
мембраны [ср. выражение (5. 34) ]
А - Ср.
В результате решения, аналогичного изложенному выше для
плоской изотропной мембраны (§24, стр. 241), находим кубический
член характеристики
/ pR* \ __ 32 kt Г 1_____3—р.
у 9 — а2 6 (а±3) (а—р,)
Суммируя выражения (б) и (в), получим уравнение характери-
стики гофрированной мембраны
(5. 63)
18*
275
В этой формуле коэффициенты а и b равны
2 (3 ct) 0 Ч- ®)
3 — р .
(а — р) (а + 3)
(5.64)
w0— прогиб центра мембраны;
р — давление;
Е — модуль упругости;
р — коэффициент Пуассона;
h — толщина материала мембраны;
R — рабочий радиус.
В соответствии с выражением (5. 59) величина а = у кх • к2. Коэф-
фициенты кх и к2 зависят от формы профиля мембраны и в общем слу-
чае периодического профиля определяются выражениями (5- 53) и
(5.54). Для наиболее часто встречающихся форм профилей значения
коэффициентов кг и к2 даны в табл. 23. Выражения для этих
коэффициентов для глубокого синусоидального профиля даны в при-
ложении I, п. 3.
Таблица 23
Профиль
Трапецеидальный
Коэффициенты и к.2
Я2
Л2 cos 90
+ cos 90
3 Я2
2 №
276
Коэффициенты а и входящие в уравнение (5. 63) характери-
стики мембраны, могут непосредственно определяться по графикам,
построенным по выражениям (5. 64) на фиг. 149, а~г, в зависимости
от относительной глубины гофрировки и угла наклона0О для пиль-
чатого профиля, или в зависимости от относительного параметра -у
для синусоидального профиля (Н — глубина гофрировки, I — длина
волны, h — толщина материала).
(н \ / н \
] и b = b / | указывает на то,
h 1 In/*7
что основными факторами, определяющими форму характеристики
мембраны, являются глубина гофрировки Н и толщина материала h,
Y Y 7 Н
так как коэффициенты аио зависят главным образом от параметра т- •
Форма гофрировки и число волн (длина волны I или угол наклона 0О)
при неизменной глубине Н влияют на характеристику значительно
меньше. Приведем примеры построения характеристики при задан-
ных размерах мембраны.
Пример 3. Построить характеристику мембраны синусоидального прсфиля
(фиг. 150, а). Размеры мембраны: R — 25 мм; Н ~ 0,75 мм, h — 0,22 мм;
I = 6,6 мм. Модуль упругости Е -- i . 10е кгс/см2.
Р е hi е н и е. Подсчитаем параметры = -2’It = 3,41 и -24г =
_ ft 0,22 I 6,6
= 0,1135 и по кривым на фиг. 149, б находим коэффициенты а = 25,9 и Ъ —
= 0,249. Подставляя коэффициенты а и Ъ и числовые данные мембраны в формулу
5. 63), пел учим уравнение се характеристики
Eh з 1 • Юб • 0,22 0.
р 7Й4 (ah w<> + Йо) =-----(25Й— (25,9' °’222 ’+ °’249 =
- 0,706 u’0 -Ь 0,140 и?,
здесь р в кгс>см2 и в мм.
Дальнейшие вычисления удобно вести в табличной форме (табл. 24).
Таблица 2
Результаты расчета примера 3
'Ц/Q В Л4А1 0,706 wo wo 0,140 wJJ р в к^с/с№ 4L 1
0,2 0,141 0,008 0,001 0,142
0,4 0,282 0,064 0,009 0,291
0,6 0,424 0.216 0,030 0,454
1 1 0,8 0,565 0,512 0,072 0,637 1
На фиг. 150, в приведены расчетная характеристика и характеристика,
полученная в результате испытаний. Они расположены весьма близко друг
к другу.
277
278
»/
Фиг. 149, б. Графики коэффициентов а и Ъ при-,-—2,8 4-5,5.
1 4-
{
279
6 7 8 9 10 4-
h
Фиг. 149, в. Графт ки коэффициентов а и Ъ при — = 5,5 — 11.
280
Я 12 13 15 16
Фиг. 149, г. Графики коэффициентов а и Ъ при — = И -=-17.
281
Пример 4. Построить характеристику мембраны пильчатого профиля
{фиг. 150, б). Материал мембраны — бериллиевая бронза Бр. Б 2,5; Е = 1,35Х
Х106 кгс/см2. Размеры мембраны: R = 24 мм, Н = 0,141 мм, h = 0,101 мм,
0о = 8°45'.
при
Решение.
И _ 0,414
h 0,101
По графикам па фиг. 149, б находим для пильчатого профиля
= 4,1 и 6 о = 8°45' коэффициенты а = 25,3 и b = 0,257.
Фиг. 150. К решению примеров 3 и 4.
Уравнение (5. 63) характеристики после подстановки числовых величин
принимает вид
Р =0,106 wQ4-0,1055 и>* , (а)
здесь размерности р в кгс/см2 и wq в мм»
Подсчитанная по выражению (а) характеристика, а также характеристика,
полученная из опыта, приведены на фиг. 150, г. При и?о = 1,8 мм, когда отно-
Wn
гиенпс прогиба к толщине -j— »17,8, погрешность составляет около 9%.
Проектирование гофрированной мембраны по заданной
характеристике
С помощью уравнения (5. 63) можно спроектировать мембрану,
если задана ее характеристика. Аппроксимируя характеристику
уравнением,
Р = Aw0 4- (5. 65)
находим коэффициенты А и В.
282
Сопоставляя выражения (5. 63) и (5. 65), устанавливаем соотно-
шения между коэффициентами этих уравнений
A — B~-^rhb,
R* ’ J?4
(5. 66>
Исключив из выражений (5. 66) толщину
а _ А / Е \2
Ь3 “ Ж (ДГ ) •
/г, получим
(5. 67)
В соответствии с условиями работы мембраны выбирается
материал, чем устанавливается значение модуля упругости Е.
Диаметром ’2R мембраны задаются из габаритных условий. Таким
образом правая часть равенства (5. 67) содержит известные величины.
Коэффициенты а и b связаны с геометрией профиля мембраны урав-
нениями (5. 64), по которым построены графики на фиг. 149. Поль-
зуясь этими графиками, можно построить также кривые отношения г3
н
в зависимости от параметра относительной глубины гофрировки
Кривые -Д
даны на фиг. 151, а — г в полулогарифмической сетке.
Определив отношение -Д-из формулы (5. 67), находим по фиг. 151
- - h ‘
для пильчатого и синусоидального профилей
h
относительную глубину гофрировки-г- проектируемой мембраны,
f t
а затем по фиг. 149 — коэффициенты а и Ь.
Далее по одной из формул (5. 66) вычисляется толщина мем-
браны А, после чего построение формы профиля мембраны не пред-
ставляет затруднений. Следует иметь в виду, что спроектированная
таким образом мембрана удовлетворяет только требованиям задан-
ной жесткости. Для полного проектирования мембраны должны быть
дополнительно оценены прочность, эффективная площадь и другие
рабочие параметры.
Если мембранный чувствительный элемент предназначен для
измерения параметра, нелинейно связанногос давлением, то прежде
всего необходимо при проектировании построить упругую характе-
ристику этого элемента по давлению. Это удобно сделать с помощью
графического построения (фиг. 152).
В координатах W —П строится требуемая характеристика (кри-
вая а) по измеряемому параметру П.
Предположим, что связь между параметром П и давлением р
изображается кривой б.
Для ее построения можно использовать аэродинамическую таблицу или
таблицу стандартной атмосферы если параметр П является воздушной
1 Браславский Д. А., Логунов С. С., Приборы на самолете,
Оборонгиз, 1947, а также Браславский Д. А., Логунов С. С.,
П е л ь по р Д. С., Расчет и конструкция авиационных приборов, Оборонгиз,
1954.
283
284
285
1
/7 XT "
Фиг. 151, e. Графики отношения при — = 5,5 — 11.
Ьл h :
Г
д
286
М.Л *!4W4W
a
28?
скоростью или высотой над уровнем моря. При измерении температуры мано-
метрическим паро-жидкостным термометром кривая б определяется по термо-ч
динамическим таблицам
При изменении расхода дроссельным методом построение кривой б основано
на уравнении, связывающем расход G с перепадом давления на дроссельном
устройстве, G — с р, где с — постоянная, зависящая от размеров трубопро-
вода и дроссельного устройства, плотности среды ит. д. 1 2 *
Характеристика чувствительного элемента по давлению (кри-
вая в) может быть легко построена по кривым а и б), как показано
на фиг. 152.
Фиг. 152. Построение упругой ха-
рактеристики.
Фиг. 153. К решению примера 5.
Если чувствительный элемент
состоит из N мембран, то
про-
гиб wo одной мембраны находится делением полного прогиба W на
W
число мембран:
W0 ~
Пример 5. Спроектировать мембранную коробку манометра на 1 кгс/см2
по характеристике (фиг. 153), форма которой определена из расчета кинематики
механизма и обеспечивает линейность шкалы манометра.
Рабочий диаметр мембраны должен быть не больше 50 мм, материал —
бериллиевая бронза Бр. Б2,5 (Е = 1,33 • 106 кгс/см2).
Решение. Так как прогиб мембраны вдвое меньше прогиба мембранной
коробки, то характеристика мембраны может изображаться той же кривой
на фиг. 153, если на оси ординат нанести шкалу прогибов в половинном мас-
штабе.
1 Теплотехнический справочник, Госэнергоиздат, 1957.
2 Преображенский В. П., Теплотехнические измерения и приборы,
Госэнергоиздат, 1953.
288
Проведем касательную ОВ к характеристике в начале координат.’ Ее наклон
определяет величину линейного члена характеристики (5.65) : р = Л^'о, где
р и w0 — координаты произвольной точки на касательной ОВ. Например, для
конечной точки В : wo — 2,92 мм и р — 1 кгс/см2. Тогда коэффициент А при
линейном члене характеристики А = ~~ =—-— = 0,342 кгс^см .
Wo 2,92 мм ’
Для определения кубического члена подставим в уравнение (5. 65)
р — Awq^- Bw
(а)
координаты произвольной точки характеристики мембраны, например, точки
С : р = 1 кгс/см2 и wo — 2,5 мм. Тогда
откуда В — 0,00928
1 = 0,342 • 2,5 + В • 2,53,
кгс/см2
Л1313
Для проверки следует построить характеристику мембраны по уравнению
(а), подставив в него найденные значения коэффициентов А и В, и сравнить ее
с заданной. При значительном расхождении полученной и заданной характери-
стик можно повторить расчет, изменив положение произвольной точки С при
определении коэффициента кубического члена. Для этого следует сдвинуть
точку С к тому месту кривой, где получилось наибольшее расхождение.
В рассматриваемом примере уравнение (а) при найденных значениях коэффи-
циентов А и В достаточно хорошо совпадает с заданной характеристикой.
Определим по формуле (5. 67) соотношение между коэффициентами а и 6,
задавшись рабочим радиусом R — 25 мм
0,342
(0,00928)3
Выберем профиль мембраны в виде синусоидального с отношением
,3. По кривой ~
на фиг. 151, в находим при Л- — 4,97 • 106 от-
II
ношение глубины гофрировки к толщине материала
10,1. Затем по кривым
(фиг. 149, в) коэффициенты а = 146 и
6 — 0,031. Толщина h материала мембраны определится из равенства (5.66)
определяем
0,00928.(25)4
“ Ойо *
Е 0,031 • 1,33 • 10е
j/дет Я — 10,1 • h = 0,89 мм. При принятом соот-
= 2,96. Если принять
Глубина гофрировки
Н о
ношении = 0,3 длина
радиус плоской центральной части мембраны г0 = 7 мм, то число волн гофри-
- Я — г0 25 — 7
ровки будет п = -----—- = — S 6.,
I . 2,9b
Пример 6. Спроектировать мембранную коробку расходомера с характери-
стикой, линейной по расходу G на участке от Gq ~ 2 т!час до Gmax== 10 т/час.
Расход G связан с перепадом давлений р уравнением
волны равна I = г
2,96
Н
h
h =
з
о
(а)
где для данного случая коэффициент с = 10,8 т/час см2/кгс.
19 Заказ 24»
289
Материал — сплав Н36ХТЮ (ЭИ702), Е = 2,15 • 10е кгс/см2. Рабочий диа-
метр коробки 2 R = 80 мм, максимальный рабочий прогиб ТУтах — б мм.
Начальный нерабочий прогиб, соответствующий расходу Go, не должен превы-
шать 10% от VVmax-
Решение. На фиг. 154 дано графическое построение упругой характери-
стики. Для этого по известным координатам начальной и конечной точек про-
водим заданную характеристику, линейную по расходу (прямая а). При этом
учитываем, что для одной мембраны прогиб вдвое меньше, чем для коробки,
а начальный прогиб if о = 0,1 icmax = 0Л • 3 = 0,3 мм. Затем с помощью урав-
нения (а) строим кривую б, связывающую расход G с перепадом давлений р.
По кривым а и б находится характеристика мембраны по давлению (кривая в).
Выбираем на кривой & две произвольные точки 1 и 2, разделяющие характе-
ристику на три примерно одинаковые участка. Координаты точек 1 и 2 равны
рг — 0,28 кгс/см2, и\ — 1,5 мм и ра = 0,62 кгс!см2, w^, = 2,5 мм.
Подставим значения р1? рг, и в уравнение (5. 65) характеристики
мембраны •
0,28 = Л • 1,5 +В- (1,5)3;
0,62 = Л .2,5 +В - (2,5)3.
Из решения этих уравнений находим величины А — 0,152
кгс} см2
мм
и В = 0,0153
KZcjCM?
мм3
Характеристика, построенная пр уравнению (5. 65) при А = 0,152 и В «*
= 0,0153, совпадает удовлетворительно с заданной характеристикой.
290
После подстановки числовых значений в выражение (5. 67) получим соот-
ношение между коэффициентами а и Ъ <
а _ 0,152 / 2,15-10е \2 =
Ь3 “ (0,0153)3 404 J
Выбирая форму профиля в виде пильчатого с углом Оо — 30°, находим
И
h
по
криво й *
а
&
на фиг. 151, в
= 6; при этом коэффициенты
в = 46 и 6 = 0,117 (фиг. 149, в).
По формуле (5. 66) определяем толщину материала мембраны
В Я4 = 0,0153
b Е 0,117
245^ = 01156 ММ
Тогда глубина гофрировки будет
Длина волны равна (см. фиг. 151)
Н = 6 • h — 6 ’ 0,156 = 0,935 мм.
27/ 2 • 0,9г
tg60~ 0,577
—— 3,24
При радиусе плоского центрального участка
Го = 8 мм число волн гофри-
ровки будет
40 — 8
3,24
s 10.
Учет влияния жесткого центра на характеристику гофрированной
мембраны [75]
Большинство гофрированных мембран имеет припаянный или
приваренный к средней части плоский металлический диск, назы-
ваемый жестким центром (см. фиг. 138). Если размеры жесткого
центра невелики, то его влиянием на прогибы мембраны можно
пренебречь, и тогда при расчете можно использовать формулу (5. 63),
выведенную для мембраны без жесткого центра. Однако, если центр
имеет большие размеры, его влияние необходимо учитывать.
Так же как и для мембраны без жесткого центра, вывод формул
для мембраны с жестким центром основан на дифференциальных
уравнениях (5.56). При выводе уравнения характеристики также
используется метод «наложения». Вся разница в выводе заклю-
чается лишь в написании граничных условий, которые в этом случае
имеют следующий смысл. При решении линейной задачи на наруж-
ном (q — 1) и внутреннем (р = р0) контурах угол поворота Ф — 0.
При решении задачи об абсолютно гибкой мембране радиальное
смещение принимается равным нулю на тех же контурах, fЗдесь
—относительный радиус жесткого центра].
В результате решения получим уравнение гофрированной мем-
браны с жестким центром [75]:
Eh* Лр «р h
(5. 68)
19*
291
. Здесь коэффициенты av и Ьр определяются формулами (5. 64),
а поправочные коэффициенты и зависят не только от геометрии
гофрировки, по и от радиуса ро жесткого центра
(i —eg+3)g (е?-е’)2 11
(a — p)(3~f-a) (а-рр.) (3 — а) ]'
Числовые значения коэффициентов тц и даны в табл. 25.
Таблица 25
Расчетные формулы для гофрированных мембран с жестким центром
и значения поправочных коэффициентов ц , £ и L
На фиг. 155, а и б с помощью формулы (5. 68) построены семей-
ства характеристик для мембран двух типов:
с мелкой
Н
7Г
жесткого центра.
гофрировкой при различных размерах
*
Фиг. 155.
Влияние
браны с мелкой
жесткого центра на характеристику
мем-
Н
и глубокой
гофрировкой.
Из этих графиков видно, что для мембран с мелкой гофрировкой
жесткий центр мало влияет на характеристику, если его относитель-
ный радиус не превышает о о = 0,2 -ь 0,3. В этом случае при расчете
можно пользоваться формулой (5. 63), выведенной для мембраны
без жесткого центра. Для мембран с глубокой гофрировкой жесткий
центр слабо влияет на характеристику до величины Qo - ~ 0,4 — 0,5.
Дальнейшее увеличение ро приводит в обоих случаях к резкому воз-
растанию жесткости мембраны, и тогда расчет по формуле (5. 63)
даст большие погрешности.
Чем глубже гофрировка, тем меньшее влияние оказывает жесткий
центр на характеристику мембраны. Это можно объяснить тем,
что вообще центральные гофры деформируются значительно слабее,
чем краевые, и поэтому замена центральных гофр жестким центром
мало изменит характеристику, если глубина гофр достаточно велика.
Расчет гофрированной мембраны, нагруженной сосредоточенной
в центре силой [75]
При работе в приборе гофрированная мембрана помимо давления
часто нагружается сосредоточенной в центре силой Q (см. табл.*25),
например, силох! трения в механизме прибора, силой упругости
винтовой или плоской пружины, компенсирующей силой в при-
борах силовой компенсации и т. д.
Характеристика мембраны, нагруженной в центре сосредоточен-
ной силой, может быть получена теми же методами, что и в случае
нагружения мембраны давлением. С решением этой задачи можно
ознакомиться в работе [75] или в приложении I п. 4.
Зависимость- между прогибом wo центра мембраны и сосредото-
ченной силой Q выражается кубическим уравнением
л Eh4 ~~ aQ /г'!” ’
где коэффициенты aQ и bQ равны
(1+а)2 ? Г 1
аО ~ / р2 \ ~ а2 — 1 2
1 —Р-___
(а —р) (а 4-1)
(5.71)
(Остальные обозначения в этой формуле даны на стр. 276).
Если мембрана имеет жесткий центр, то уравнение характерис-
тики получает вид
Л Eh4 ~ ^Q aQ h~ Л» ’
Здесь поправочные коэффициенты определяются выражениями
_____________________(1 — а)2 _________________
(1 +«2) (1 - ф + [4eJ+a - (1 + е?°) d +姻
1 — е 0
(5.73)
294
В табл. 25 приведены значения поправочных коэффициентов
и L в зависимости от относительного радиуса ро жесткого центра
и параметра а, характеризующего глубину гофрировки мембраны
[см. выражение (5. 59)].
Семейства характеристик по силе Q для мембран с мелкой
h
£- = 10 (гофрировкой при различных размерах
— 21 и глубокой
жесткого центра даны на фиг. 155, в и г.
§ 28. МЕМБРАНЫ ПРОФИЛЯ I,-ХАРАКТЕРИСТИКИ КОТОРЫХ ЛИНЕЙНЫ
ПО ДАВЛЕНИЮ
Линейную по давлению характеристику будет иметь мембрана
любого достаточно глубокого профиля. В приборостроении часто
применяются мембраны, профиль которых состоит из двух глубоких
трапецеидальных волн, сопряженных с краевым тороидальным гоф-
ром. Размеры профиля такой мембраны, выраженные через рабочий
диаметр D, указаны на фиг. 156, а.
В дальнейшем будем называть мембраны профиля, указанного
на фиг. 156, а, мембранами профиля I.
Мембраны профиля I решают наиболее распространенную за-
дачу — измерение давления. Они обладают хорошими качествами
в отношении линейности характеристики, стабильности показаний,
постоянства эффективно!! площади и пр., и поэтому широко исполь-
зуются в различных манометрических приборах.
Подробные экспериментальные исследования этих мембран поз-
волили создать графо-аналитический метод расчета [76], на основе
которого была разработана нормаль1 (см. приложение II).
При исследовании был широко использован принцип подобия,
который состоит в том, что геометрически подобные мембраны
(подобные не только по профилю, но и по толщине) после нагруже-
ния одинаковым давлением остаются подобны друг другу.
Принцип подобия позволяет по поведению одной мембраны пред-
сказывать, как будет вести себя другая мембрана, геометрически
подобная первой, и поэтому применение его значительно сокращает
экспериментальные работы.
Для мембран с линейной характеристикой по давлению чувстви-
тельность 6 определяется по формуле (1. 4)
6 = ^-.
Р
Отношение чувствительности 6 к рабочему диаметру D назовем
относительной чу в’с т в и те льностью
6 _ J£o
D pD •
1 Проект нормали был разработан под руководством инж. А. Г. Лебедевой.
a ~~ мембрана профиля I; б — график относительной чувствительности.
296
На фиг. 156, б показана кривая относительной чувствительности
построенная в зависимости от безразмерного параметра мембраны
h
5
где h — толщина материала. Эта кривая получена в результате
экспериментального исследования манометрических коробок, сва-
прогиб центра одной
репных из двух мембран профиля I. По оси ординат отложена отно-
сительная чувствительность коробки
мембраны). Материалом мембран являлась бериллиевая бронза
Бр. Б2,5 (таблица 6, § 1 гл. I). При построении кривых чувствитель-
ность определялась на начальном участке характеристики, где
нелинейность не превышала 1 %.
По кривой относительной чувствительности легко проводить
расчеты на жесткость мембран профиля I: определять
прогиб при заданном давлении или по заданно!! чувствительности
подбирать размеры мембраны.
На основании испытаний мембранных коробок профиля 1 на
разрушение, г и ст ерезис и нелинейность ха-
рактеристики построены кривые, представленные на фиг. 157.
Кривая разрушающего давления p-разр, построенная в зависимости
от толщины Л, разделяет поле графика на две области: ниже и правее
кривой разрушения находится зона осуществимых давлений, выше
и левее — зона разрушения. Кривая разрушения проведена пункти-
ром на том участке, где коробки не доводились до разрушения, но
испытания прекращались вследствие большого искажения харак-
теристики в результате появления пластических деформаций.
В этих же координатах построены еще три кривые давлений
Р1%, р2% 11 Рз%-> соответствующих нелинейности ц = 1%, 2% и 3%.
Кроме того, на графике нанесены кривые гистерезиса у. Величины
гистерезиса измерялись недостаточно точно и поэтому могут ис-
пользоваться только как ориентировочные. График разрушения,
нелинейности и гистерезиса позволяет определить допускаемое да-
вление для данной мембранной коробки или получить представление
о поведении мембранной коробки при заданном давлении.
Для расчета манометрических коробок промежуточных диамет-
ров можно пользоваться обобщенным графиком, который дан на
фиг. 158. Этот график построен в координатах р
на основании
h
принципа подобия.
Анероидные коробки из мембран профиля I можно прибли-
женно рассчитывать на жесткость также по кривой относительной
чувствительности (см. фиг. 156, б). Для изготовления анероидной
коробки можно использовать мембраны с толщиной Лпнп и выше.
Если толщина мембран слишком мала, то при вакууммировании
анероида мембраны теряют устойчивость, на гофрах появляются
вмятины.
График на фиг. 159 дает значения Лпнп
различных диаметров, изготовленных из
для анероидных коробок
бериллиевой бронзы.
297
Фиг, 158. Обобщенный график разрушения и не-
линейности манометрических коробок.
299
Для грубого подсчета эффективной площади можно использовать
формулу
где R — рабочий радиус;
го — радиус жесткого центра.
Для мембран профиля I радиус г0 = -у- (см. фиг. 156, а),
поэтому формулу (а) можно представить в этом случае в виде
Я2 = 0,344 Я2.
Для более точного определения эффективной площади следует
пользоваться формулой (5. 74) (см. § 29).
Приведенные результаты исследований мембранных коробок
профиля I дают возможность проводить достаточно полный расчет.
Пример 7. Блок, состоящий из трех манометрических коробок диаметром
D = 53 мм, при изменении давления от рх — 12 мм рт. ст. до р2 — 715 и рт. ст.
должен давать ход W — 6,8 мм.
Определить толщину h, эффективную площадь Fs$, нелинейность ц и коэф-
фициент запаса по разрушению п.
Материал — бериллиевая бронза Бр. Б2,5.
Решение. При изменении давления на р — р-2 — Pi= 715 — 12 —
— 703 мм рт. ст. = 0,956 кгс!см2 блок, состоящий из трех коробок, совершит
ход И7 — 6,8 мм, а каждая коробка дает 2и?о = —- =. 2,27 мм. Опреде-
лим относительную чувствительность коробки
2^0 2,27
pD Q,956 53
0,0448----
кгс! см1
По кривой относительной чувствительности (фиг. 156, б) определяем —
Л
~ 390, откуда h = —0,136 мм *.
Эффективную площадь подсчитываем по формуле (а)
Т'эдз = 0,344 D2 = 0,344 • 5,32 = 9,65 см2.
Нелинейность ц найдем по обобщенному графику на фиг. 158. Точке с ко-
ординатами -у— = 390 и р = 715 мм рт. ст. = 0,971 кгс] см- соответствует не-
линейно сть т] = 1,8 %.
Коэффициент запаса п определим как отношение разрушающего давления
к наибольшему рабочему
„ _ Рразр.
£> _ Р2
При —т---- 390 разрушающее давление рразр = 2 кгс/см2 (фиг. 158), тогда коэф-
2
фициент запаса по разрушению будет п = -------- 2,1.
0,971
* Известно, что для этих блоков найденная опытным путем толщина соста-
вляет 0,13 мм. Расхождение равно 4,6%.
300
Необходимо напомнить, что графики на фиг. 156—159 построены
на основании исследований мембранных коробок из бериллиевой
бронзы Бр.Б2,5. Пользоваться этими графиками для расчета коро-
бок из других материалов нельзя. Исключение представляет кривая
относительной чувствительности. Для коробки из другого материала
относительная чувствительность может быть определена как
2^о
гДе = С35 . 10< кгс!мм2 — модуль упругости бериллиевой
бронзы Бр.Б2,5;
Е — модуль упругости материала рассчитываемой коробки;
. _ k *
относительная чувствительность, найденная по кри-
о
вой на фиг. 156, б;
2w0
pD
искомая относительная чувствительность.
§ 29. ЭФФЕКТИВНАЯ ПЛОЩАДЬ МЕМБРАН
Размеры мембраны обычно выбираются, исходя из требуемых
чувствительности и прочности, и ограничиваются габаритами при-
бора. В ряде случаев не менее важно требование достаточной эффек-
тивной площади мембраны, и тогда для правильного проектирования
упругого элемента необходимо знать, какие параметры мембраны
влияют па величину эффективной площади, как она изменяется
с перемещением и нагрузкой.
В § 3 главы I отмечалось, что если манометрический упругий
элемент имеет линейную характеристику, то его эффективная
площадь остается практически постоянной при любом про-
гибе. Постоянную эффективную площадь имеют мембраны профиля
I (§ 28) и другого профиля, достаточно глубокого для получения
линейной характеристики мембраны. Расчет эффективной площади
таких мембран может быть произведен с помощью формул (1. 5)
или (1. 5')
Величины жесткости к® по силе Q и kv но давлению р можно
легко найти с помощью формул (5. 68) и (5. 72), где для мембраны
с линейной характеристикой кубический член будет мал по сравне-
нию с линейным и, следовательно,
, Q л Eh3 7 р Eh3
' Q ~ aQ /?2 И ~ R4 '
301
" <1
л Л2 '
Произведя подстановку kQ и к в выражение (а), получим фор-
мулу Для относительной эффективной площади гофрированной мем-
браны с линейной характеристикой
• <5- 74>
Лр av
Относительная эффективная площадь показывает, какую часть
от полной площади составляет эффективная
(5. 75)
Выражения коэффициентов а , и ц даны в формулах
(5. 64), (5. 69), (5. 71) и (5. 73).
Формула (5. 74) позволяет проанализировать влияние гофри-
ровки и размеров жесткого центра на величину эффективной пло-
щади. При этом следует иметь в виду, что эти зависимости будут
справедливы только на линейном участке характеристики: 'для
мембран с глубокой гофрировкой — практически на всем участке
рабочего хода, а для мембран с мелкой гофрировкой или для плоских
мембран^— на начальном участке, где нелинейность характеристики
мала.
Используя табл. 25 и формулы (5. 64) и (5. 71), построим с по-
мощью выражения (5. 74) величину относительной эффективной
площади Ддз в зависимости от относительного радиуса Qo жесткого
центра и от параметра а. Параметр а связан с геометрией гофри-
ровки формулой (5. 59), него величина зависит в основном от отно-
Н
сительной глубины гофрировки-г-. На фиг. 160, помимо значений
fl
параметра а, в скобках указаны соответствующие значения относи-
тельной глубины гофрировки ~ для мембран
с углом наклона гофрировки 0о = 30°.
Кривые на фигуре показывают, что при
диаметре эффективная площадь увеличивается
центра и глубиной Н гофрировки и уменьшается с ростом толщины h
материала.
Если жесткий центр мембраны находится на упоре, то на послед-
ний будет передаваться та часть давления, которая приложена
к жесткому центру и к некоторой прилегающей к жесткому центру
кольцевой площади упругой части мембраны. Окружность Z, огра-
ничивающая эту кольцевую площадь, проходит примерно посредине
между контурами закрепления мембраны в заделке и в жестком
центре. Радиус этой окружности гэ$ и определяет размеры эффектив-
ной площади F= л г2эд5.
С увеличением диаметра жесткого центра окружность I передви-
гается к заделке, и эффективная площадь мембраны возрастает.
Форма упругой поверхности гофрированной мембраны зависит
от глубины гофрировки, как это следует из выражения (5. 61), опре-
302
пильчатого профиля
одинаковом рабочем
с радиусом жесткого
О 0,2
Ро
Фиг. 160. Относительная эффективная площадь^ /эф —
Рэф
л Я2
в зави-
г0
симости от относительного радиуса жесткого центра Qo = ~ и глу-
п
н
оины гофрировки -т— . -
деляющего закон угла поворота гофрированной мембраны в области
малых перемещений. На фиг. 161 показаны формы начальных1
упругих поверхностей гофрированных мембран, построенные с по-
мощью выражений (5. 3) и (5. 61). С увеличением глубины гофри-
ровки уменьшается кривизна упругой поверхности в центральной
части мембраны, т. е. эта часть мембраны становится как бы более
жесткой. Поэтому влияние глубины гофрировки на эффективную
площадь подобно влиянию диаметра жесткого центра: с увеличением
глубины гофрировки жесткость центральной части увеличивается,
и эффективная площадь воз-
растает (см. фиг. 160).
С увеличением радиуса
жесткого центра уменьшается
ширина упругой кольцево!!
части мембраны, и влияние глу-
бины гофрировки на величину
эффективной площади стано-
вится менее заметным.
При отсутствии жесткого
центра (@о = 0) изменение глу-
бины гофрировки от 0 до со
вызывает увеличение эффектив-
ной площади вдвое. При ра-
диусе жесткого центра, равном
половине рабочего (ро — 0,5),
эффективная площадь в зави-
симости от глубины гофри-
ровки может измениться на
10%, как показывают кривые
па фиг. 160.
Фиг. 161. Образующие начальной упру-
гой поверхности гофрированных мем-
бран с различной глубиной гофри-
ровки.
На основании этой фигуры можно определить также влияние
толщины материала на эффективную площадь гофрированной мем-
н
браны. С уменьшением толщины h отношение -г- возрастает, и эффек-
тивная площадь увеличивается. На фиг. 162 даны кривые эффектив-
ной площади мембраны профиля I (см. § 28) диаметром 48 мм при
различных толщинах h (0,05—0,20 мм). Совпадение расчета по.фор-
муле (5. 74) с опытом вполне удовлетворительно.
На фиг. 160 приведены также кривые эффективной площади,
построенные по формулам, широко известным в практике
л. = я 4,=4 (в+Г[1 р.
= -f- (Я« + Rr„ + .
(5. 76)
(5.77)
См. сноску на стр. 263.
304
Относительная эффективная площадь fa# соответственно выра-
жению (5. 75) будет
(1 + бо)1 2
(5. 76')
(1 + 2о + Qo)-
(5. 77')
Формула (5. 76) является эмпирической; формула (5. 77) может
быть выведена весьма приближенным способом, если предположить,
что мембрана может свободно
поворачиваться в местах кре-
пления по наружному и внут-
реннему контурам, а окруж-
ными изгибающими моментами
можно пренебречьх.
Построенная по формуле
(5. 76') кривая а (см. фиг. 160)
почти полностью сливается
с линией, соответствующей пло-
ской мембране (Н = 0). Следо-
вательно, для плоской мем-
браны в области малых пере-
мещений, где характеристика
линейна, можно приближенно
определять эффективную пло-
щадь по простой формуле (5. 76).
Этой же формулой пользуются
и при расчете эффективной пло-
щади сильфонов (гл. VI, § 34).
Кривая б, построенная по
формуле (5. 77'), проходит при-
Фиг. 162. Эффективная площадь мем-
бран профиля I различных толщин.
мерно посредине семейства
кривых. Для мембран с различной глубиной гофрировки погреш-
ность формулы (5. 77) не превосходит 30% при ро = 0 и ± 6%
при ро = 0,5. Этим и объясняется широкое применение формулы
(5. 77) для приближенного расчета эффективной площади гофри-
рованных мембран.
Расчет по формулам (5. 76) и (5. 77) эффективной площади мем-
бран профиля I различных толщин (см. фиг. 162) дает постоянные
значения эффективной площади, так как эти формулы не учитывают
ни глубину Н гофрировки, ни толщину h материала.
Для уточненного расчета мембран с характеристикой, линейной
по давлению, следует пользоваться формулой (5. 74) или непосред-
ственно графиком на фиг. 160.
1 См., например, Боднер В. А., Фридлендер Г. О.,
ков Н. И., Авиационные приборы, Оборонгиз, 1960.
Чистя-
305
20 Заказ 24.
Рассмотрим теперь общий случай когда мембрана имеет нели-
нейную характеристику. Опыты показывают, что если мембрана
имеет затухающую характеристику,
Фиг. 163.
а — изменение эффективной
мембраны с перемещением
б — равновесие центральной
е — изменение эффективной
"W 'F*
площади гибкой
жесткого центра;
час'1И мембраны;
площади с давле-
‘нжем при неизменном положении жесткого
центра.
то ее эффективная площадь
с ростом прогиба умень-
шается; если характери-
стика мембраны возрастает,
то эффективная площадь
увеличивается (см. фиг. 13).
Изменение эффективной
площади с ростом прогиба
связано с изменением формы
упругой поверхности мем-
браны.
Наиболее наглядно можно
представить себе изменение
эффективной площади на
примере абсолютно гибкой
мембраны, установленной
в корпусе с начальным рас-
слаблением. Если жесткий
центр установить на одном
уровне с наружным конту-
ром закрепления и подать
малое давление Ар, то мем-
брана примет некоторую
равновесную форму, а в упо-
ре появится реакция Л(Э
(фиг. 163, а).
В материале абсолютно
гибкой мембраны возникают
только растягивающие силы
Т (фиг. 163,6). Эффективная
площадь будет определяться
радиусом гЭф той окружно-
сти, где силы Т направлены
перпендикулярно оси вра-
щения упругой поверхности
мембраны, т. е. радиусом
окружности I наивысших
точек упругой поверх-
ности.
Из условия равновесия
центрально!! части мембраны
радиуса гВф реакция Д(? =
= Дрлг® , а так как эффек-
тивная площадь г9ф — -
[формула (1. 5)], ТО/’аф^ЯГ®
306
Переместим жесткий центр в новое положение. При действии
того же малого давления Др форма упругой поверхности мембраны
изменится: радиус гэ$ до наивысшей точки Z, определяющий вели-?
чину»эффективной площади, будет уменьшаться при перемещении
жесткого центра вверх и увеличиваться при перемещении вниз
(фиг. 163, а). Чем выше будет расположен жесткий центр, тем
меньше эффективная площадь.
Таким образом, эффективная площадь абсолютно гибкой мемб-
раны, которая имеет затухающую характеристику, уменьшается
с увеличением прогиба.
Металлическая плоская или слабо гофрированная мембрана
также имеет затухающую характеристику, и форма ее упругой
поверхности изменяется с прогибом. Поэтому уменьшение эффек-
тивной площади с ростом прогиба будет иметь место и для таких
мембран, хотя и в меньшей степени, чем для абсолютно гибкой мем-
браны.
Определение эффективной площади в общем случае, когда
чувствительный элемент имеет нелинейную характеристику, ослож-
няется еще тем, ч'то при одном и том же прогибе величина эффектив-
ной площади может меняться с изменением давления. Для пояснения
этого рассмотрим абсолютно гибкую мембрану в некотором рабочем
положении (фиг. 163, в). Если увеличить давление, сохраняя при
этом неизменным положение жесткого центра, то вследствие растяже-
ния мембраны ее упругая поверхность будет вытягиваться. Окруж-
ность I точек упругой поверхности, где прогиб максимален, будет
смещаться к заделке, следовательно, величина эффективной пло-
щади будет расти. Это явление может иметь место лишь в том случае,
если упругая поверхность способна растягиваться. Если материал
мембраны нерастяжим, то форма упругой поверхности и эффективная
площадь останутся неизменными при любом давлении р и непод-
вижном жестком центре.
Итак, эффективная площадь сложно зависит как от прогиба, так
и от нагрузки, оставаясь функцией упругой поверхности мембраны.
Нелинейность характеристики связана с появлением сил растяжения
или сжатия в начальной поверхности мембраны, и в этом случае
эффективная площадь может изменяться с прогибом и нагруз-
кой.
Если мембрана имеет линейную характеристику, то ее начальная
поверхность деформируется, изгибаясь, но не растягиваясь. В этом
случае величина эффективной площади остается постоянной на линей-
ном участке характеристики.
Требования, предъявляемые к эффективной площади, зависят
от назначения мембраны.
Если мембрана используется для преобразования давления
в усилие (например, в приборах силовой компенсации, в пьезо-
электрических, частотных преобразователях, датчиках электрокон-
тактного сопротивления и пр.), то перемещение центра мембраны
ничтожно мало. В этом случае важно, чтобы мембрана имела строго
20*
Ж
постоянную эффективную площадь. Несмотря на то, что жесткий
центр мембраны остается практически неподвижным, изменение
эффективной площади может иметь место при достаточно большом
давлении, когда появляется растяжение начальной упругой поверх-
ности. Расчет мембраны с неподвижным жестким центром должен
быть весьма точным, чтобы уловить изменение эффективной площади
•с изменением давления, которое может быть очень малым. Однако
в таких приборах изменение эффективной площади даже на доли
процента может быть существенным для точности прибора.
При решении этой задачи не могут быть применены те прибли-
женные методы, которые использовались выше при определении
жесткости мембраны. Чтобы получить достоверный результат, реше-
ние должно достаточно точно установить изменение формы упругой
поверхности с давлением. Эта задача сложна и в настоящее время
еще не решена.
Пользуясь формулой (5. 74), можно рассчитать лишь начальное
значение эффективной площади, но не изменение ее с ростом
давления при неподвижном жестком центре.
Если мембрана служит для преобразования давления в п е р е -
м е щ е н и е, она должна обладать достаточной эффективной пло-
щадью, чтобы успешно преодолевать сопротивление со стороны
механизма прибора. На рабочем участке характеристики эффектив-
ная площадь должна оставаться больше некоторого минимального
значения, необходимого для нормальной работы прибора. В этом
случае достаточна приближенная оценка величины эффективной
площади и ее изменения с прогибом. Эта задача решается при помощи
расчетных формул (5. 68) и (5. 72).
При данном прогибе wo эффективная площадь мембраны может
быть определена по формуле (1. 5).
dQ
dQ _ dwQ
dp dp
dw0
Используя выражения (5. 68) и (5. 72), получим
*1Q aQ + 3£q bQ
(5. 78)
T]p «;n-]-3£p bp
здесь — относительная эффективная площадь — определяется
выражением (5.75).
Если мембрана имеет линейную характеристику, то кубический
член в выражении (5. 78) исчезает, и тогда эта формула будет совпа-
дать с полученной ранее (5. 74).
308
Пример 8. Определить эффективную площадь мембраны, размеры которой
указаны на фиг. 164, в рабочем диапазоне давлений 0 4- 650 мм рт. ст. Ма-
териал — бериллиевая бронза Бр. Б2,5; Е — 13 500 кгс!мм2.
О—--- и.......... п - । । ........
О 0,25 0,50 0,75 р ™с/смг
Фиг. 164. К решению примера 8.
Решение. Для определения коэффициентов в формуле (5. 78) нужно
с 1ачала найти геометрические коэффициенты кх и к%. По формулам, приведен-
ным в табл. 23 для пильчатого профиля, вычислим
—— г ”* — — CIO A Z Г / ' 1,09,
cos6o cos 23 °45
Н2 (0 412
^2 “ гг;-----г + C0S °0 ” /Л АоТЯ + 0,91 5 = 10,5
h2 cos 60 (0,135)2 • 0,915
По выражению (5. 59) определяем параметр а = Укх • кг = • 10,5 =
= 3,39.
По фиг. 149 и с помощью выражений (5. 71) определяем коэффициенты
ар, O.Q и Ьд, входящие в формулу (5. 78). Для пильчатого профиля с углом
309
0 4
=+’+-= 2,96
0,135
Ъп = 0,0468.
наклона 0O = 23° 45' и относительной глубиной гофрировки -г-
f С
эти коэффициенты равны: а = 17,3; Ьр= 0,419, Лф = 5,9
По табл. 25 находим поправочные коэффициенты т] и £, учитывающие на-
личие жесткого центра. При а = 3,39 и относительном радиусе жесткого центра
d 9 5
v- = -77+- — 0,192, находим по таблице: np = 1,02, — 1,12, ти =
QO =
Q
Подставляя найденные коэффициенты и толщину h = 0,135 мм в формулу
(5. 78) и учитывая соотношение (5. 75), получим эффективную площадь мембраны
в зависимости от прогиба ее центра в виде
1 + 2,57^
0,136 + 0,594
где F3$ в cjw2; и?0 в мм.
Характеристика мембраны по давлению определяется уравнением (5. 68),
которое после подстановки числовых величин примет вид:
р=0,156 ir0+ 0,228i?; (б)
(р в кгс/смг'} Wq в мм).
Задаваясь рядом прогибов wo, строим по уравнению (б) характеристику
мембраны. Удваивая прогибы, получаем характристику коробки, она хорошо
совпала с экспериментальной (фиг. 164, а).
При этих же прогибах wo находим величины эффективной площади Fa$
с помощью выражения (а) и строим кривую эффективной площади на рабочем
участке давлений (фиг. 164, б).
В приведенном примере расчет по формуле (5. 78) дал удовлетво-
рительное совпадение с результатами опыта. Однако при исполь-
зовании формулы (5. 78) следует иметь в виду, что ее вывод основан
на результатах двух отдельно полученных решений: при нагружении
мембраны давлением р и при нагружении силой Q.
Сложение этих решений возможно, строго говоря, только в обла-
сти малых перемещений, когда применим принцип независимости
действия сил. Если же характеристика мембраны нелинейна, то для
более точного определения эффективной площади следует рассматри-
вать мембрану при совместном действии давления р и силы Q.
Такое решение, созданное В. И. Феодосьевым для абсолютно гибкой
мембраны [1 ], весьма сложно. Для гофрированных мембран подобное
решение очевидно будет еще более громоздким.
Итак, формулой (5. 78) можно пользоваться для определения
эффективной площади мембран, имеющих характеристику, близкую
к линейной. Для мембран с нелинейной характеристикой эта формула
может быть использована для определения эффективной площади
при малых прогибах, когда нелинейность незначительна. Более
точные пределы применимости формулы (5. 78) должны быть устано-
влены дальнейшими исследованиями.
С помощью формулы (5. 78) построены графики на фиг. 165, а и б,
иллюстрирующие зависимость эффективной площади от радиуса
310
жесткого центра и от прогиба для мембран с мелкой и с глубокой
гофрировкой. Для мембраны с мелкой гофрировкой эффективная
площадь с увеличением прогиба уменьшается. Это явление становится
Фиг. 165.
а — изменение эффективной площади с прогибом при различных радиусах жесткого центра;
б — эффективная площадь в зависимости от радиуса жесткого центра при различных
_ W0
прогибах ,
менее заметным при увеличении размеров жесткого центра. Для
мембран с глубокой гофрировкой уменьшение эффективной площади
с прогибом незначительно. В обоих случаях увеличение размеров
жесткого центра увеличивает эффективную площадь.
§ 30. ВЫПУКЛЫЕ (ХЛОПАЮЩИЕ) МЕМБРАНЫ
Как указывалось выше, в плоской и в гофрированной мембранах
при больших прогибах возникают силы растяжения, вследствие чего
сопротивление мембраны нагрузке увеличивается, и ее характери-
стика становится затухающей. Если силы растяжения увеличить,
например, создавая в мембране при монтаже начальное натяжение,
то жесткость мембраны сильно возрастает. Уменьшение сил растя-
жения приводит к увеличению прогибов мембраны. Если же в средин-
ной поверхности мембраны возникают силы сжатия, то характери-
стика становится возрастающей, а при достаточно больших силах
сжатия мембрана может потерять устойчивость, внезапно изменив
свою . форму.
При нагружении конической или сферической мембраны давле-
нием или силой с выпуклой стороны (фиг. 166, а), ее срединная поверх-
ность сжимается. Если выпуклость достаточно велика, то мембрана
при работе может потерять устойчивости
311
Рассмотрим более подробно работу выпуклой мембраны. При
нагружении мембраны давлением р ее прогиб Wo на начальном
участке О А характеристики возрастает монотонно. Затем при некото-
ром критическом давлении ркР1 мембрана теряет устойчивость
и скачком изменяет свой прогиб, переходя на участок характери-
стики DC (фиг. 166, б). При дальнейшем увеличении давления
прогибы мембраны будут снова нарастать плавно.
При разгрузке мембрана также скачком, но при меньшем давле-
нии (Ркр2 <С Pkpi), возвращается на ветвь ОА характеристики.
б Ркрг Ркр{ Р
6)
Фиг. 166.
а — коническая и сферическая мембраны; б — харак-
теристика выпуклой мембраны.
При хлопках возникают колебания, и мембрана рассеивает боль-
шое количество энергии.
Потеря устойчивости выпуклой мембраны может происходить
в области упругих деформаций, если мембрана достаточно тонка,
и материал имеет высокие упругие свойства.
Способность выпуклых мембран изменять скачком свой прогиб
используется в различных реле, где необходимо быстрое замыкание
и размыкание контактов.
В измерительных приборах потеря устойчивости мембраны
обычно недопустима, поэтому если измерительной мембране при-
312
дается небольшая выпуклость, то это преследует лишь цель умень-
шения жесткости на некотором участке характеристики, причем
отношение2^ столь мало, что потеря устойчивости не наступает.
Л
В некоторых случаях небольшая конусность придается анероидам
высотомеров с целью увеличения прогибов на больших высотах, где
с изменением высоты давление изменяется незначительно.
Расчет гладких выпуклых мембран основан на уравнениях
пологой оболочки в больших перемещениях, которые могут быть
получены таким же путем, как и уравнения (5. 31) плоских мембран
(§24, стр. 240). Эти уравнения были получены В. И. Феодосьевым [1]
[47], [64] в виде
где 0 — угол подъема оболочки (фиг. 166, а), а остальные обозначе-
ния такие же, как и в уравнениях (5. 31).
Решение этих уравнений производится методом Галеркина. При
этом форма упругой поверхности предполагается такой же, как
и у плоской пластинки в области малых перемещений (5. 11). Это
решение не учитывает изменения формы упругой поверхности с про-
гибом, и от него нельзя ожидать хорошего совпадения с опытом при
прогибах свыше 2—3 толщин.
Характеристика выпуклой мембраны [1], [77], [78] имеет вид
pR* , %
Eh* ~ h - h2
(а)
здесь знак «плюс» соответствует нагружению мембраны давлением
с вогнутой стороны, знак «минус» •— с выпуклой.
При р, = 0,3 коэффициенты а, Ъ и с для мембран с глухим защем-
лением по контуру имеют следующие значения:
для сферических мембран
для конических мембран
а = 5,86+ 3,46 41
6=6,524;
с = 2,76.
313
co
*
Фиг. 167.
♦ — характеристики гладких конических и сферических мембран при различных высотах б — характеристики гофрирован-
ных конических мембран при различных глубинах гофрировки.
На фиг. 167, а с помощью уравнения (а) построены характери-
стики конических и сферических гладких мембран при различных
величинах выпуклости. Характеристика плоской мембраны
монотонно затухает. Характеристика выпуклой мембраны имеет
участок оа, где прогибы wo возрастают более быстро, чем давление р.
При достаточно большой выпуклости
1,6 для сферической
---- V ---------
1,85 для конической мембран ) на характеристике появляет-
ся участок отрицательной жесткости ab, где прогибы возрастают при
падении давления. Равновесие мембраны на этом участке неустой-
чиво, и она скачком изменит свой прогиб «хлопнет». Потеря устой-
чивости сферической мембраны происходит при меньшей вынукло-
Наличие гофрировки на выпуклой мембране увеличивает ее
устойчивость [78]. На фиг. 167, б представлены характеристики
конических гофрированных мембран с одинаковой выпуклостью
/ = 3 ] при различных глубинах пильчатой гофрировки, характе-
ризуемых углом наклона гофрировки 0О. Участок отрицательной
жесткости ab, где происходит «хлопок», с увеличением глубины гоф-
рировки уменьшается, и в данном случае при 10° < 0о 15° исчезает.
§ 31. НЕМЕТАЛЛИЧЕСКИЕ (ЭЛАСТИЧНЫЕ) МЕМБРАНЫ
Применение, конструкция, материалы
При требованиях весьма малой жесткости или больших пер сме-
щений приходится применять мембраны большого диаметра или
малой толщины. Однако, изготовление металлических мембран
толщиной менее 0,03—0,05 мм встречает значительные трудности.
Поэтому, если диаметр мембраны ограничен, то для получения
мембраны малой жесткости следует переходить к неметаллическим
материалам, модуль упругости которых в сотни и тысячи раз меньше
модуля упругости металлов.
Возможность получения больших перемещений от неметалличе-
ских мембран обеспечивается весьма высокими упругими деформа-
циями некоторых неметаллических материалов, во много раз пре-
восходящими допустимые упругие деформации металлов. В некото-
рых случаях важно, что определенные сорта неметаллических мате-
риалов более стойки к коррозии, чем металлы.
Такие материалы, как кожа и различные органические пленки,
которые использовались раньше для изготовления эластичных мем-
бран, сейчас почти совсем не применяются ввиду их высокой чувст-
вительности к влажности, быстрого старения и плохой герметичности.
315
В настоящее время широкое применение имеют высокоупругие
сорта резины и пластмасс. В зависимости от условий работы для
изготовления мембран применяются бензо-маслостойкие, а также
морозо- или жаростойкие сорта резины. Некоторые сорта синтетиче-
ских резин можно использовать при весьма высоких температурах,
например, полисилоксановую резину — до 300° С. При требованиях
высокой коррозионной стойкости мембраны изготовляются из фто-
ропластов. Краткие сведения и механические свойства некоторых
неметаллических материалов приведены в табл. 8 (гл. I, § 1).
Однако эластичные мембраны имеют и ряд недостатков, и поэтому
они применяются лишь тогда, когда удовлетворить техническим
требованиям при помощи металлической мембраны не представляется
возможным. Модуль упругости неметаллических материалов сильно
изменяется с температурой, прочность, как правило, значительно
ниже, а упругие несовершенства проявляются в большей степени,
чем у металлов. Неметаллические материалы, особенно резина,
подвержены весьма интенсивному старению. Например, у некоторых
сортов резины в течение нескольких месяцев модуль упругости
значительно возрастает, и способность упруго деформироваться
резко падает. Пластмассы склонны к ползучести при повышенных
и даже при нормальных температурах.
В некоторых лабораторных приборах нашли применение кварце-
вые мембраны, которые могут быть изготовлены с очень малой тол-
щиной, что обеспечивает их высокую чувствительность х. Кварцевые
мембраны обладают высокими упругими свойствами и малым гисте-
резисом, однако хрупкость этих мембран ограничивает их приме-
нение в промышленйых условиях.
Эластичные мембраны часто используются при измерении малых
давлений порядка десятков или даже всего нескольких миллиметров
водяного столба. Вместе с тем эластичные мембраны внедряются
и в область измерения давлений от десятых долей атмосферы до
нескольких атмосфер. Для таких давлений эластичные мембраны
слишком податливы, и жесткость чувствительного элемента при-
ходится увеличивать с помощью дополнительно!! винтовой пру-
жины. Мембрана в этом случае служит уже не упругим элементом,
преобразующим давление в перемещение, а разделителем. Она
воспринимает измеряемое давление и преобразует его в усилие,
сжимающее пружину. Пружина имеет значительно большую, чем
мембрана, жесткость и по существу служит упругим элементом.
В такой схеме чувствительного элемента упругая характеристика
эластичной мембраны не имеет существенного значения. Более
важными показателями чувствительного элемента являются вели-
чина и стабильность эффективной площади.
Эластичные мембраны, работающие совместно с пружиной,
широко применяются в механических манометрических приборах
1 ЩукаревС. А. и Новиков Г. И., Изготовление чувствительных
прочных (стеклянных) мембран, «Заводская лаборатория», т. 21, № 1, 1955.
316
и в электрических реостатных и индуктивных датчиках, в мембранно-
пружинных сервомоторах и в других приборах, где от чувствитель-
ного элемента требуются относительно большие перемещения.
Кроме того, эластичные мембраны получили большое распростри- •
нение в качестве преобразователей давления в усилие в тех приборах,
где чувствительный элемент почти не перемещается, как например,
в пьезоэлектрических, магнитоупругих, струнных частотных датчи-
ках, в приборах, работающих по схеме силовой компенсации и т. д.
Мембрана, применяемая в подобной «силовой» схеме, должна
иметь минимальную жесткость. Эластичная мембрана обеспечивает
это в гораздо большей степени, чем металлическая.
Эластичные мембраны также используются в качестве раздели-
телей, защищающих чувствительный, элемент прибора от действия
агрессивной среды. В часто применяемых схемах с жидкостным
заполнением использование эластичных мембран особенно полезно,
так как их высокая податливость позволяет почти полностью исклю-
чить погрешность прибора при температурном расширении жидкости
Конструкции эластичных мембран обычно весьма несложны.
В отличие от металлических, неметаллические мембраны почти
исключительно применяются как одиночные; мембранные коробки
из неметаллических материалов крайне редки, так как их изгото-
вление связано с рядом конструктивных и технологических труд-
ностей. Высокая податливость материала позволяет широко исполь-
зовать плоские мембраны; неметаллические мембраны с периоди-
ческой гофрировкой практически не применяются.
Как правило, неметаллические мембраны имеют большой жесткий
центр, диаметр которого обычно составляет 0,75—0,85 от рабочего
(фиг. 168,а). Кольцевая упругая часть мембраны выполняется пло-
ской или тороидальной. Плоская мембрана более проста, но при
перемещении жесткого центра эффективная площадь такой мем-
браны может значительно измениться (см. § 29). Эффективная
площадь эластичной мембраны определяется обычно, как для абсо-
лютно гибкой, РЭф — nr*#, где г3ф — эффективный радиус, т. е.
радиус окружности наивысших точек упругой кольцевой части
мембраны.
Мембраны с тороидальным гофром, отформованным при изгото-
влении, по сравнению с плоскими имеют более стабильную эф-
фективную площадь, но изготовление мембран с таким гофром
сложнее. Иногда плоскую мембрану устанавливают в корпусе
с расслаблением, а при работе она под действием давления натяги-
вается и приобретает тороидальную форму (фиг. 168,6). Однако
стабильность таких мембран по эффективной площади значительно
ниже, чем у мембран с гофром, отформованным при изготовлении.
Податливость материала, обеспечивающая мембранам малую
жесткость, является в то же время серьезным препятствием к при-
менению эластичных мембран при давлениях порядка атмосферы
и выше. При таких давлениях гофр сильно вытягивается, что при-
водит к изменению эффективной площади. Кроме того, при таких
317
давлениях прочность материала часто оказывается недостаточной.
Увеличение прочности при сохранении малой жесткости может
быть достигнуто применением сетчатой конструкции мембран.
Сетчатая мембрана представляет собой оболочку, выполненную
из нитей, промежутки между которыми заполнены эластичным
материалом (резиной, пластмассой) (фиг. 169,а). Наполнитель обе-
спечивает герметичность и передает нитям рабочую нагрузку.
Жесткость нитей значительно выше жесткости наполнителя, поэтому
Фиг. 168. Неметаллические мембраны:
а — с тороидальным гофром, отформованным при изготов-
лении б — плоская мембрана до нагружения и после, уста-
новленная в корпусе с расслаблением.
они и являются несущим элементом конструкции. Так как при
нагружении мембраны длина нитей практически остается неизмен-
ной, то изменение формы мембраны под нагрузкой связано с дефор-
мациями сдвига в материале наполнителя: каждая ячейка сетки
перекрашивается при сохранении длины ее сторон (фиг. 169,6).
Сетчатая оболочка обладает анизотропными свойствами, опреде-
ляемыми структурой сетки. Например, в прямоугольной сетке
жесткость материала в направлении нитей будет максимальной,
а под углом 45° к направлению нитей — минимальной (фиг. 169, в).
Если нити сетки не перпендикулярны друг другу, то жесткость
в различных направлениях меняется по закону, показанному на
фиг. 169, г. Если три системы нитей перекрещиваются- под углом
60° (фиг. 169,6), то свойства такой сетки будут близки к изотроп-
ным. Трикотажное плетение (фиг. 169, е) нитей обеспечивает малую
жесткость во всех направлениях в начале нагружения; когда же
нити натянутся (фиг. 169, ж), то жесткость в направлении нитей
резко возрастает.
Из анизотропной сетчатой оболочки можно создать чувствитель-
ную и достаточно прочную мембрану. Если при этом профилю мем-
браны придать такую форму, которая будет мало меняться в зависи-
мости от давления при неизменном положении жесткого центра,
318
то это обеспечит высокую стабильность эффективной площади.
Чтобы мембрана была чувствительной, она должна иметь малую
изгибную жесткость и быть податливой при растяжении в окружном
направлении. Тогда при перемещении жесткого центра точки мем-
браны будут свободно перемещаться в осевом и радиальном напра-
влениях. В то же время материал мембраны должен быть достаточно
г)
е) *)
Фиг. 169. Сетчатые конструкции мембран:
а — сетчатая оболочка; б — деформация сетчатой оболочки; в — прямоугольная сетка
и ее жесткость в различных направлениях; г — косоугольная сетка и ее жесткость; д —
равноугольная сетка; е — трикотажное плетение до нагружения; ж — трикотажное плетение
после нагружения.
жестким на растяжение в радиальном направлении (точнее — в мери-
диональном направлении). При этом длина профиля будет оставаться
неизменной, что важно для получения стабильной эффективной
площади.
Этим требованиям удовлетворяет мембрана с радиальным распо-
ложением нитей (фиг. 170, а). Но такая структура ткани неустойчива,
так как под действием давления нити могут раздвинуться, и прочность
мембраны нарушится. Этого можно избежать, направляя нити под
углом к радиусу, как показано на фиг. 170, б. Мембраны с такой
структурой ткани не изготовляются нашей промышленностью^ но
можно предположить, что они будут обладать высокими рабочими
параметрами и стабильной эффективной площадью.
819
Фиг. 170. Конструкция
анизотропных
мембран:
а — с радиальным распо-
ложением нитей; б — с ни-
тями, направленными под
одинаковым углом к ради-
усу; л — из ткани с прямо-
угольной сеткой; г — мемб-
рана, составленная из сек-
торов.
Наибольшее распространение имеют
в настоящее время сетчатые мембраны
из ткани с прямоугольной сеткой как
наиболее простые в изготовлении
(фиг. 170, в). Однако эти мембраны
имеют ряд существенных недостатков.
При формовке гофра происходит не-
одинаковое натяжение нитей. Нити,
направленные по касательной к окруж-
ному направлению, сильно вытягива-
ются, а иногда даже обрываются. Нити,
расположенные под углом 45° к ради-
усу,-находятся в более благоприятных
условиях. Отсутствие осевой симмет-
рии мембраны, изготовленной из ткани
с прямоугольной сеткой, обусловли-
вает сложный характер деформаций
при перемещении центра мембраны.
Ткань имеет наибольшую жесткость
на растяжение в радиальном и окруж-
ном направлениях по сечениям а и Ъ
и минимальную жесткость по сече-
нию с. Поэтому равновесная форма
гофра под давлением будет различной
в сечениях а и с. С изменением давле-
ния форма гофра меняется, что при-
водит к изменению эффективной пло-
щади. Иногда из ткани вырезаются сек-
торы, ориентированные вдоль нитей
основы, затем из них склеиваются
кольца, из которых и формуются мем-
браны (фиг. 170,г). Однако такие мем-
браны обладают большой жесткостью
в окружном направлении.
Основа в виде ткани полотняного
или саржевого переплетения наиболее
проста в изготовлении, но мембраны
из таких тканей не имеют высоких
рабочих параметров. Объясняется это
тем, что в местах переплетения нитей
ткани при работе мембраны появля-
ются силы трения, значительно уве-
личивающие гистерезис мембраны.
С этой точки зрении несомненными пре-
имуществами обладают мембраны из
кордной ткани, где нити различной
ориентации располагаются в разных
плоскостях и не переплетаются.
Эластичную плоскую мембрану наиболее просто изготовить выруб-
кой из мембранного полотна — ткани, обрезиненной с обеих сторон.
Толщина мембранного полотна, предназначенного для изготовления
чувствительных мембран на малые давления, может быть меньше
0,1 мм\ вместе с тем для мембран силовых устройств, работающих
при повышенных давлениях, тканевая основа может быть много-
слойной с общей толщиной до 3—5 мм. Рабочий диаметр мембран
может доходить до 500—600 мм.
Жесткий центр образуется двумя металлическими дисками,
между которыми зажимается часть мембраны. Чтобы при работе
мембрана меньше вытягивалась из жесткого центра, ее обычно
приклеивают к дискам. По на-
ружному контуру мембрана за-
жимается в корпусе и удержи-
вается силами трения. Для
пропуска крепежных болтов по
окружности делаются отверстия
обычно одновременно с вы-
рубкой мембраны.
Мембраны с гофром, формуе-
мым при вулканизации в пресс-
форме, крепятся так же, как и плоские. Однако при таком способе
крепления возможно вытягивание материала из мест крепления мем-
браны к жесткому центру и к корпусу, что приводит к большому
гистерезису и нестабильности рабочих свойств. Для надежного
уплотнения требуется точное изготовление колец и крепкое при-
жатие их друг к другу. Кроме того, такой способ крепления уве-
личивает габариты мембранного узла и не дает гарантии в точном
центрировании мембраны в корпусе.
В последнее время стали применять более совершенные способы
крепления мембран, например, с отформованным при изготовлении
кольцевым буртиком (фиг. 171). Такой способ крепления обеспечи-
вает надежное центрирование мембраны в корпусе, герметичность
и отсутствие смещений мембраны на контуре.
Крепление, центра может быть также осуществлено с помощью
буртика, но лучшие результаты дает приваривание жесткого центра
мембраны при ее вулканизации, когда слои резины охватывают
жесткий центр с обеих сторон (фиг. 171). Этим достигается также
защита от коррозии и хорошее уплотнение в месте крепления штока.
Очень большие перемещения может совершать так называемая
манжетная мембрана. Она представляет собой цилиндрическую обо-
лочку из кордной ткани, нити которой расположены под небольшим
углом к образующей цилиндра (фиг. 172, а). Такая ткань имеет
большую жесткость в осевом и малую жесткость в окружном напра-
влениях. Часть цилиндрической оболочки вывертывается (фиг. 172, б)
и прикрепляется концами к неподвижной втулке и к жесткому
центру, который имеет вид поршня (фиг. 172,в). При перемещении
поршня мембрана перекатывается с поршня на втулку или наоборот.
21 Заказ 24.
321
При этом большая часть оболочки остается прижатой давлением
к стенкам втулки п поршня, и только небольшая часть выполняет
роль эластичной мембраны.
Так как для растяжения манжетной мембраны от диаметра
поршня до диаметра втулки необходимо определенное давление,
то она может работать только начиная с какого-то минимального
давления, когда окончательно устанавливается форма гофра. При
дальнейшем изменении давления форма гофра не меняется, и по-
этому эффективная площадь остается постоянной.
а) 5)
Фиг. 172. Манжетная мембрана.
При перемещении штока потенциальная энергия деформаций
гофра не меняется. Следовательно, жесткость этой мембраны практи-
чески равна нулю.
Манжетные мембраны используются при весьма больших переме-
щениях и там, где требуется высокое постоянство эффективной
площади.
О расчете' неметаллических мембран
Неметаллические изотропные мембраны рассчитываются на жест-
кость и прочность так же, как и металлические. Как правило, неме-
таллические мембраны имеют малую жесткость на изгиб, поэтому
их можно считать абсолютно гибкими и для расчета можно восполь-
зоваться формулами, приведенными в § 24, стр. 241.
Инженерные методы расчета резино-тканевых и резино-кордных
мембран в настоящее время еще не созданы, хотя методы расчета
резино-кордных облочек разработаны достаточно полно В. Л. Би-
дерманом и А. А. Лапиным в работах 179,], [80], [47]. Теория
резино-кордных оболочек основана на предположениях о нерастя-
жимости нитей и о малости напряженийв резине по сравнению с напря-
жениями в нитях. При расчетах усилия N, возникающие в нитях,
заменяются с помощью уравнений равновесия эквивалентными уси-
лиями Тт и равномерно распределенными по граням элемента
(фиг. 173, а). При симметричной деформации усилия определяются
по выражениям
г,„ = Л-2УСО82₽; Ti = -5-JVsin2p, (а)
V £
здесь п — число слоев корда;
Р —угол между направлением нитей и меридианом оболочки;
t — расстояние между соседними нитями.
Из уравнений (а) следует соотношение между силами Тт и Tt
Tt = Tm tg2 p.
(6)
Рассматривая равновесие части мембраны, вырезанной пилинд-
рическим сечением радиуса гЭф (фиг. 173,6) и коническим сечением
с углом <р между осью мембраны и образующей конуса, получим
Фиг. 173.
а — элемент резино-кордной оболочки; б — равновесие части мембраны.
2г sin ф
Второе условие равновесия дает уравнение Лапласа [34]:
Tt sin <р
(г)
где р — радиус кривизны меридиана в произвольной точке;
Мп ф
— радиус кривизны в окружном направлении, равный
длине образующей секущего конуса.
Решая совместно уравнения (б), (в) и (г), можно найти ту равно-
весную форму, которую примет мембрана под нагрузкой, и величину
усилий Тт и Tt. Зная форму мембраны, легко определить ее эффек-
тивную площадь по радиусу гЭф. По усилиям Тт и Tt с помощью
уравнения (а) можно найти усилия N в нитях и произвести оценку
прочности мембраны.
Однако такое решение приводит к уравнению, которое приходится
интегрировать численным или графическим путем. Поэтому для
определения равновесной конфигурации симметричных резино-корд-
ных оболочек, нагруженных внутренним давлением, в работе [80]
(см. также [47 ]) даны номограммы, значительно упрощающие расчет.
Подобные номограммы могут быть разработаны и применительно
к расчету резино-кордных мембран, но пока это еще не выполнено.
12*
ГЛАВА VI
СИЛЬФОНЫ
§ 32. ПРИМЕНЕНИЕ, КОНСТРУКЦИЯ, ТЕХНОЛОГИЯ
Фиг. 174. Сильфон.
Сильфон представляет собой тонкостенную цилиндрическую обо-
лочку с поперечной гофрировкой (фиг. 174). Под действием давления
или осевой силы сильфон удлиняется или укорачивается. Если к нему
приложены поперечные силы, создающие изгибающие моменты, то
он получает соответствующие перемещения в осевой плоскости.
Сильфон способен давать значительные пе-
ремещения при характеристике, близкой к ли-
нейной, и постоянной эффективной пло-
щади. Эти свойства обеспечили сильфонам
широкое применение в различных областях
техники, в том числе и в приборостроении,
несмотря на то что технология изготовления
сильфонов довольно сложна.
В приборостроении находят применение
сильфоны диаметрами от 7—10 до 120—150 мм
с толщиной стенки 0,08—0,3 мм.< Чувствитель-
ность тонкостенных сильфонов большого
диаметра настолько велика, что они могут
использоваться при давлениях порядка десят-
ков миллиметров водяного столба. Толсто-
стенные сильфоны малых диаметров могут
работать при давлениях в сотни атмосфер.
Сильфоны часто применяются в качестве манометрических чувст-
вительных элементов в различных приборах: манометрах, маномет-
рических термометрах, дифференциальных манометрах, в пневма-
тической регулирующей аппаратуре и пр.
На фиг. 175 показана схема сильфонного дифференциального
манометра-пневмодатчика, в котором сильфон 1 преобразует
измеряемое давление в усилие, сильфон 2 служит бессальниковым
уплотнителем, а сильфон 3 — силовым элементом обратной связи.
Сильфоны могут развивать значительные перестановочные уси-
лия, что обеспечивает малый порог чувствительности приборов
324
и позволяет использовать сильфоны в качестве элементов силовых
приводов.
Благодаря большим изменениям объема, сильфоны используются
как элементы гидравлических дистанционных передач.
Сильфоны служат в различных приборах также компенсаторами
температурного расширения жидкости, что объясняется их высокой
податливостью и способностью значительно изменять объем.
Возможность получения сильфонов малой осевой и изгибной
жесткости позволяет успешно применять их в качестве разделителей
и элементов бессальниковых выводов в приборах Г Любопытным
примером подобного использования является применение стеклян-
ных сильфонов в качестве упругого крепления подвижного элект-
рода механически управляемых электронных ламп1 2.
2
Фиг. 175. Схема механизма сильфонного дифмано-
метра с пневматической силовой компенсацией.
Как правило, металлический сильфон изготовляется из тонко-
стенной цельнотянутой трубки, получение которой при малых
допусках на толщину представляет значительные технологические
трудности.
Гофрирование сильфона производится гидравлическим или меха-
но-гидравлическим способом. При изготовлении по первому способу
трубка-заготовка закрепляется в зажимах специального станка
(фиг. 176, а). На определенном расстоянии друг от друга вдоль
трубки устанавливаются разъемные кольца. В трубку подается
масло, под давлением которого она начинает выпучиваться в про-
межутках между кольцами. Затем при постоянном давлении трубка
сжимается в осевом направлении. При этом кольца сдвигаются
и заготовка принимает форму сильфона (фиг. 176,6).
1 РухадзеВ. А., Упругие элементы в качестве бессальникового уплот-
нения в приборах теплового контроля [17].
2 Гончарский Л. А., Механически управляемые электронные лампы,
Госэнергоиздат, 1957.
325
Большую глубину гофра, меньший разброс характеристик гото-
вых сильфонов и меньшее количество брака дает механо-гидравличе-
скйй способ Б Этот способ отличается от предыдущего тем, что сна-
чала трубка-заготовка обкатывается роликом на специальной оправ-
ке, и при этом на ней наносятся углубления на определенном рас-
стоянии друг от друга (фиг. 176, в). Затем трубка устанавливается
на гидравлическом станке, и происходит формование сильфона под
давлением, как и по первому способу.
£)
Преимущество механо-гидравлического способа состоит в том, что
вытяжка материала происходит как внутрь (при механической
обкатке), так и наружу (при гидравлическом формовании), поэтому
утонение материала на гребнях гофр получается меньшим, чем при
гидравлическом способе, при котором вся вытяжка происходит
в одну сторону — наружу. Кроме того, механо-гидравлический
способ дает возможность получить сильфоны с более точно выпол-
ненными размерами, что и обусловливает меньший разброс жестко-
сти сильфонов.
Сильфоны из дисперсионно-твердеющих сплавов подвергаются
последующей термообработке, а сильфоны из нагартовываемых мате-
риалов — операции обжатия, при которой происходит дополнитель-
ный наклеп материала и повышаются упругие свойства сильфона.
Трубка-заготовка весьма малой толщины (порядка сотых мил-
лиметра) может быть получена методом прецизионной шариковой
1 Ра зин В. А.,
прибора № 5, 1956.
326
Новое в технологии сильфонов, Бюллетень НЙИТепло
раскатки1. Цельнотянутая трубка надевается на цилиндрическую
оправку и обкатывается вращающимися в обойме шариками (фиг. 177).
Относительно шариков трубка имеет большую окружную скорость,
осевая подача производится с меньшей скоростью. При таком спо-
собе за один проход толщина стенки может быть уменьшена в 4—5
раз (например, с h = 0,30 мм до h = 0,08 -? 0,05 мм).
Вследствие того, что получить тонкостенные цельнотянутые
трубки точных размеров очень трудно, и некоторых случаях предпо
читают трубки-заготовки для неответственных сильфонов изготов-
лять сваркой из листового материала. Это значительно удешевляет
производство, однако наличие
продольного сварного шва
ухудшает прочность, коррози-
онную стойкость и упругие
свойства сильфонов.
В процессе изготовления
материал сильфона претерпе-
вает большие пластические
деформации. Поэтому для изго-
товления сильфонов из цельно-
тянутых трубок широко при-
меняются такие материалы,
как полутомпак Л 80, фосфо-
ристая бронза Бр. ОФ 6,5-0,4.
Фиг. 177. Прецизионная шариковая
раскатка трубки.
(табл. 1, § 1, гл. I). Однако низ-!-
кие упругие свойства этих материалов определяют низкие качества
получаемых из них сильфонов. Так, у полутомпаковых силь-
фонов гистерезис при рабочих прогибах может доходить до
3-5% [81].
Сильфоны из нержавеющей стали 1Х18Н9Т (см. табл. 1) приме-
няются при работе в агрессивных средах или при повышенных
температурах (до 400° С). Упругие свойства этих сильфонов также
невысоки (гистерезис при рабочих прогибах достигает 2—4% [81]),
поэтому как измерительные упругие элементы они имеют ограничен-
ное применение или используются совместно с винтовой пружиной
высокого качества.
Высокую точность и стабильность упругих свойств имеют силь-
фоны из дисперсионно-твердеющих сплавов; бериллиевых бронз
марок Бр.Б2, Бр.Б2,5, Бр.БНТ1,9 и сплава Н36ХТЮ (ЭИ702)
(см. табл. 6, гл. I, § 1), пластичность которых в мягком состоянии
допускает глубокую вытяжку, а хорошие упругие свойства после
термообработки обеспечивают высокое качество сильфонов. Гистере-
зис сильфонов из дисперсионно-твердеющих сплавов не превышает
0,5—1% в пределах рабочего участка характеристики [81].
Большие трудности изготовления бесшовных цельнотянутых
трубок явились одной из причин появления сильфонов, сваренных
1 Коновалов Б. О., Метод изготовления трубчатых заготовок попе-
речной шариковой раскаткой с помощью специальной портативной головки [17].
327
из отдельно отштампованных кольцевых пластин1 (фиг. 178, а).
Такой сильфон представляет собой по существу блок мембранных
коробок, составленный из мембран с большим диаметром отверстия.
Сварные сильфоны могут быть более чувствительны, чем бесшовные,
так как их можно изготовить с большей глубиной гофр. Кроме того,
упругие свойства и эффективная площадь сварных сильфонов имеют
меньший разброс, поскольку их размеры можно выдержать в более
узких допусках, чем у бес-
шовных сильфонов.
Высокую точность вели-
чины эффективной площади
можно получить, сваривая
мембраны, отштампованные
с цилиндрическим буртиком
(фиг. 178,6). В этом случае
величина эффективной пло-
щади практически не будет
зависеть от положения свар-
ного шва.
♦ Сильфоны, сваренные по
грибковой схеме (фиг. 178,в),
выдерживают большую пе-
регрузку наружным давле-
нием.
Сварные сильфоны могут
быть изготовлены из мате-
риалов с хорошими упру-
гими свойствами и невысо-
кой пластичностью, так как
при изготовлении сварных
сильфонов материал испы-
Фиг. 178. Сварные сильфоны. тывает меньшую вытяжку,
чем при формовании бес-
шовных сильфонов.
Увеличение ширины плоского участка может привести к появле-
нию местной потери устойчивости («хлопкам») из-за возможного
коробления материала. Для устранения «хлопков» мембранам, из
которых сваривается сильфон, иногда придается при штамповке
или при термообработке небольшая конусность или же на плоских
участках наносится гофрировка (фиг. 178, г). Сильфоны, сваренные
из гофрированных мембран, имеют, кроме того, меньшую нелиней-
ность характеристики и больший допустимый ход.
Существенным недостатком сварных сильфонов является пони-
жение коррозионной стойкости из-за наличия большого количества
сварных швов.
1 Сычев И. А., Сварные упругие чувствительные элементы (сильфоны
и манометрические пружины) [17].
328
Сильфон часто устанавливается в приборе вместе с винтовой
цилиндрической пружиной (см. фиг. 70, а). Пружина обеспечивает
требуемую жесткость упругого элемента при сохранении малой
толщины стенки сильфона. Повышать жесткость упругого элемента
за счет увеличения толщины стенки сильфона нерационально, так
как материал сильфона работает в основном на изгиб, и при одинако-
вом прогибе напряжения будут тем больше, чем больше толщина.
Таким образом, увеличение толщины сильфона снижает допустимый
ход, и при требовании повышенной жесткости упругого элемента
удобнее ввести дополнительную пружину, а сильфон оставить
тонкостенным.
Кроме этого, винтовые цилиндрические пружины вводятся в узел
чувствительного элемента для того, чтобы повысить его упругие
свойства, если сильфон изготовлен из материала с низкими упругими
свойствами (полутомпак, нержавеющая сталь). В этом случае вин-
товая пружина изготовляется из высококачественного материала,
и чтобы упругие свойства пружины определяли свойства чувстви-
тельного элемента в целом, ее жесткость должна быть в несколько
раз выше жесткости сильфона.
Дополнительная пружина обычно размещается внутри сильфона,
чтобы не увеличивать габаритов узла чувствительного элемента.
При весьма больших давлениях, когда прочность Тонкостенного
сильфона оказывается недостаточной, применяют многослойные
сильфоны, которые изготовляются из многослойной трубки. Напря-
жения в многослойном сильфоне меньше, а чувствительность выше,
чем у однослойного при той же толщине и при одинаковых прогибах.
Однако в многослойных сильфонах резко увеличивается гистерезис
вследствие трения между отдельными слоями.
Многослойные сильфоны применяются также для защиты от
коррозии. В этих случаях слой, соприкасающийся с агрессивной
средой, выполняется из коррозионно-стойкого материала.
Иногда в целях защиты сильфона от перегрузочных давлений
он армируется наружными профильными кольцами (фиг. 179).
Соединение сильфона с арматурой, т. е. с дном и с основанием,
производится обычно сваркой или пайкой. Крепление по цилиндри-
ческому буртику (фиг. 180,а) дает лучшие результаты, чем крепление
по плоской части гофра (фиг. 180,6), где возникают большие напря-
жения при работе сильфона.
Полутомпаковые сильфоны соединяются с арматурой пайкой
мягкими припоями (ПОС-40, ПОС-60) с бескислотными флюсами.
Сильфоны из нержавеющей стали 1Х18Н9Т и сплава ЭИ702 соеди-
няются с арматурой роликовой коротко-импульсной сваркой. Силь-
фоны из бериллиевой бронзы могут как припаиваться, так и привари-
ваться к арматуре, однако пайка менее желательна, поскольку она
ограничивает интервал рабочих температур.
При конструктировании приборов сильфоны устанавливаются
так, чтобы они работали , на сжатие. Сильфон при нагружении
снаружи может выдержать давление в 1,5—2 раза выше, чем при
329
нагружении изнутри. Кроме того, при ограничении осевого переме-
щения сильфон под действием внутреннего давления может потерять
устойчивость прямолинейной формы оси (см. § 36), что невозможно
при нагружении его внешним давлением.
Характеристика сильфона линейна лишь в первом приближении.
В действительности она имеет некоторую нелинейность, увеличиваю-
щуюся с прогибом сильфона, особенно при его растяжении. Гоф-
рированные сварные сильфоны имеют более линейную характе-
ристику Г
Фиг. 179. Сильфон, арми-
рованный наружными коль-
цами.
Фиг. 180. ^Соединение сильфона
с^арматурой.
Сильфоны обладают высоким постоянством эффективной площади,
что особенно ценно, когда сильфон используется как преобразова-
тель давления в усилие.. Постоянство эффективной площади объяс-
няется малыми прогибами, которые получает каждая кольцевая
пластинка сильфона при его работе, и сравнительно небольшой
разницей между наружным и внутренним диаметрами сильфона.
В этом отношении сильфон близок к мембране с большим жестким
центром, у которой эффективная площадь также практически не
изменяется с прогибом (см. § 29, фиг. 165).
В приложении III приведены основные сведения из нормалей
на полутомпаковые, стальные и бронзовые сильфоны [81]. Эти нор-
мали созданы без достаточного теоретического и экспериментального
исследования и имеют ряд недостатков1 2.
§ 33. РАСЧЕТ СИЛЬФОНОВ НА ЖЕСТКОСТЬ
Бесшовные сильфоны одной партии имеют очень большой (до
50% и выше) разброс по жесткости, о величинах которого можно
судить по данным нормалей (см. приложение III). Такой разброс
объясняется трудностями получения цельнотянутых трубок-загото-
1 С ы ч е в И. А., Результаты предварительных лабораторных исследований
сварных сильфонов, «Научно-технический бюллетень НИИТеплоприбора»,
№ 5—6, 1957, а также [17].
2 Бурцев К. Н., Применение сильфонов в арматуростроении [17].
330
вок с достаточно узкими допусками на толщину. Разница в толщи-
нах трубок обусловливает различие в условиях вытяжки материала
при формовании сильфонов, следовательно, и увеличение разброса
по толщине и другим размерам изготовленных сильфонов.
Большой разброс по свойствам бесшовных сильфонов оправды-
вает применение приближенных методов расчета на жесткость.
Расчет сварных сильфонов может быть произведен более точно
по сравнению с бесшовными, поскольку геометрия и толщина свар-
ного сильфона может быть установлена с большей точностью. Однако
малочисленность экспериментальных данных по сварным сильфонам
не позволяет пока установить пределы применимости той или иной
расчетной формулы.
Ниже излагаются два метода расчета сильфонов: на основе
теории круглых пластин [82], [47] и по методу Ритца [1], [83]
и [84].
Определение осевой жесткости сильфонов на основе теории изгиба
круглых пластин [82]
В основу этого метода расчета положены следующие допущения:
1) радиусы го закругления гофр малы по сравнению с глубиной
волн RH — R6 (фиг. 181,а). Это допущение дает основание пренебре-
Фиг. 181.
« — геометрические размеры сильфона; б — расчетная схема по теории
изгиба круглых пластин; в — условия закрепления и нагружения каждой
пластины.
гать деформациями закругленных участков по сравнению с деформа-
циями плоских участков;
2) рассматриваются неуплотненные сильфоны, для которых
угол а^О.
331
Таким образом расчетная схема сильфона сводится к набору
кольцевых пластин, жестко соединенных друг с другом по наружно-
му и внутреннему контурам (фиг. 181,6). Этой схеме больше соответ-
ствуют сварные сильфоны, чем бесшовные (ср. фиг. 174 и178,«).
Поскольку прогибы каждой пластинки малы, расчет может быть
произведен по линейной теории изгиба круглых пластин. На допу-
стимость этого предположения указывает то, что характеристика
сильфона на рабочем участке весьма близка к линейной.
На фиг. 181, в показана схема закрепления и нагружения каждой
пластинки при осевом сжатии сильфона силой Q. Такая задача была
рассмотрена в § 24, гл. V.
। Прогиб каждой пластинки может
__ * быть определен с помощью фор-
Z- мулы (5. 23), а перемещение X дна
2 ___ | сильфона, равное сумме прогибов
______ - i h____________всех пластин, будет в 2 п раз больше
_________________________| ° (п — число рабочих гофр сильфона).
Таким образом получаем следую-
( и- I щую формулу для расчета сильфона
__пГ на жесткость
JiLiJ ' • QR«
Г-----' Rt Х = (6-D
здесь коэффициент Hq равен в соот-
ветствии с выражением (5. 24).
Фиг. 182. Толщина стенки бес-
шовного сильфона.
41п2с'
с®-——~Г
Его числовые значения даны в табл. 26.
В выражении (6. 1) RH и Нв — наружный и внутренний радиусы
сильфона;
с — безразмерный параметр сильфона, равный
(6. 2)
h — толщина стенки сильфона.
Для бесшовного сильфона, изготовленного гидравлическим или
механо-гидравлическим методом, толщина стенки во внутренних
точках на радиусе Rв (фиг. 182) примерно равна толщине ho трубки-
заготовки. С увеличением расстояния от оси сильфона толщина
уменьшается. На основании опытных данных для сильфонов, изго-
товленных гидравлическим методом, установлено, что толщина
стенки в произвольной точке обратно пропорциональна расстоянию
г до оси и, следовательно, можно принять следующий закон изме-
нения толщины [ 1 ]:
h = ha (6. з)
332
Таблица 26
Формулы и значения коэффициентов для расчета сильфонов
X = 2пАр
Eh3
ф - ^nA(p Eh3
— n qEhe
™ "<P« 2nRH
„ (pEhn
гн пфн 2nRH
с ' BQs ^Qh ВР ф н в
1,10 0,000122 411 386 0,000326 399 0,000249 хк со СО 401
1,15 0,000344 202 184 0,000944 194 0,000782 170 195
1,20 0,000731 120 107 0,00193 119 0,001729 75,5 93,0
1,25 0,00129 88,9 76,6 0,00327 82,6 0,003154 66,5 83,1
1,30 0,00201 67,7 56,9 0,00493 62,1 0,00508 48,2 62,6
1,35 0,00290 54,4 44,6 0,00687 49,2 0,00755 36,8 49,7
1,40 0,00394 45,5 36,4 0,00905 40,6 0,01056 29,3 41,1
1,45 0,00510 39,0 30,5 0,0114 34,5 0,01408 24,1 34,9
1,50 0,00640 34,3 26,2 0,0139 29,9 0,01812 20,3 30,4
1,55 0,00782 30,6 22,9 0,0166 26,4 0,0226 17,4 26,9 24,2
: 1,60 0,00933 27,7 20,3 0,0193 23,7 0,0276 15,1
1,65 1,70 0,01093 25,5 18,3 0,0221 21,5 0,0331 13,4 22,0
0,01261 23,6 16,6 0,0249 19,7 0,0389 11,9 20,3
1,75 0,01436 22,0 15,2 0,0277 18,2 0,0451 10,9 18,8
1,80 0,01616 20,7 14,0 0,0305 17.0 0,0517 9,76 17,6
1,85 0,01800 19,6 13,0 0,0334 15,9 0,0586 8,93 16,4
1,00 0,01991 18,6 12,2 0,0362 15,0 0,0658 8,22 15,7
1,95 0,02182 17,8 11,4 0,0390 14,2 0,0732 7,61 14,8
! 2,00 0,02377 17,0 10,8 0,0417 13,5 0,0810 7,08 14,2
В соответствии с формулой (6. 1) жесткость сильфона зависит
от куба толщины h3. Осредненное значение куба толщины можно
приближенно найти как среднее арифметическое из кубов толщин
сильфона в нескольких точках, отстоящих на различном расстоянии
333
от его оси. Например, толщины в точках 7, 2 и 3 (фиг. 182) будут
в соответствии с принятым законом (6. 3) равны
ht = Ло; h., = h„ ' h3 = A, .
Осредненная величина h3 будет определяться по выражению
Используя обозначение (6. 2), получим
(6.4)
Таким образом, при пользовании формулой (6< 1) для расчета
бесшовных сильфонов следует предварительно подсчитать осреднен-
ный куб толщины h3 по выражению (6. 4).
ч. Для сварных сильфонов толщина h одинакова во всех точках
(в пределах допуска), и ее значение непосредственно подставляется
в формулу (6. 1) для определения жесткости сильфона.
Пример 1. Определить жесткость сварного сильфона размерами 27? м =
= 58 мм, 27?в = 40 мм, h — 0,1 мм, п — 9 (п — число рабочих гофр), изго-
товленного из сплава Н36ХТЮ (ЭИ702); £ = 2,15 • 104 кгс/мм2, р = 0,3.
Решение. Жесткость сильфона в соответствии с формулой (6.1) равна
(а)
Вычисляем отношение
радиусов сильфона по выражению (6. 2)
По .табл. 26 находим при с = 1,45 коэффициент — 0,0051. Подста-
вляя числовые значения в выражение (а), получим жесткость сильфона
2,15 • 104 - (0,1)3
2-9-0,0051 (29)2
= 0,278 кгс/мм.
Опыт 1 дает к — 0,291 кгс!мм. Расхождение составляет 4,5%.
Пример 2. Определить жесткость бесшовного сильфона размерами 2ВИ =
= 52 мм, 2Rg = 37,5 мм, п = 9, толщина стенки трубки — заготовки ho —
= 0,22 мм.
Материал: сталь 1Х18Н9Т, £ = 2,03 104 кгс!мм2.
Решение. Так как для бесшовного сильфона толщина вдоль меридиана
переменна, определим сначала ее осредненное значение по формуле (6. 4),
2/?н 52 . оог
где с = —— = = 1,385,
ZRq 37,5
= 0,00698 мм3.
1 С ы ч е в И. А.,
сварных сильфонов,
№ 5—6, 1957.
Результаты предварительных лабораторных исследований
«Научно-технический бюллетень НИИТепло прибора»
334
По табл. 26 находим при с — 1,385 коэффициент Aq — 0,0036.
Тогда жесткость сильфона по формуле (6. 1)
. Eh3 * 2,03 • 104 • 0,00698 _ по
— 2 — О П Л ПЛОЯ 3)23 К&С/ММ*
2пАп R7 2’9* 0,0036 (26)2
Значение замеренных жесткостей бесшовных сильфонов указанных размеров
колеблется в пределах (см. нормаль МН 429-60 в приложении III) к = 3,75 -4-
-4- 1,70 кгс!мм- Расхождение между расчетным и средним экспериментальным
значением жесткости, равным к = 2,73 кгс!мм, составляет ~ 18%. ‘
В приведенных примерах формула (6. 1) дала более точные
результаты для сварного сильфона, чем для бесшовного, как это
и следовало ожидать.
Результаты сопоставления расчета с опытом для нескольких
бесшовных сильфонов, данные которых взяты из нормалей [81 ]
(см. приложение III), представлены в табл. 27.
Таблица 27
Сопоставление экспериментальных значений жесткостей сильфонов
с расчетными
Нормаль Материал * ад II з *=? ад и <ю со 111 и 5? Ч и О' 3 л а 1 £ Жесткость в кгс/. к им
Эксперимент * Расчет по формуле (6. 1) Расчет по формуле (6. 5)
МН 421-60 Латунь Л80 51,0 35,6 0,12 0.85 15 0,195—0,100 0,144
МН 422-60 Е= 1,16 X 44,5 31,72 0,14 0,425 17 0,385-0,157 0,310 —
ХЮ4 кгс/мм? 79,0 55,0 0,20 1,35 13 0,400-0,200 0,304
МН 428-60 Сталь 72,0 56,0 0,15 1,125 4 2,00—1,00 2,64* к.
МН 429-60 1Х18Н9Т 18,0 11,5 0,14 0,55 10 2,80—1,33 2,40 1,76
Е= 2,03 X 38,0 25,5 0,16 1,05 12 0,80—0,40 0,937* 0,787
X104 кгс{мм^ 38,0 25,5 0,22 1,00 10 2,20—1,20 2,91* 2,04
52,0 37,5 0,22 1,125 9 3,75—1,70 3,23 2,42
< 63,0 47,5 0,22 1,275 9 2,80—1,70 3,39* •——
МН 418-60 Бронза 28,0 17,5 0,11 0,825 5 0,90-0,40 0,557 0,540
Бр. Б2 28,0 17,5 0,12 0,825 9 0,62—0,35 0,402 0,363
Е = 1,35 X 28,0 17,5 0,16 0,825 10 1,35—0,60 0,861 0,645
X104 кгс/мм3 35,0 23,5 0,11 0,875 И 0,40-0,20 0,262 0,244
38,0 25,5 0,14 0,75 5 1,40—0,70 1,01 0,790
38,0 25,5 0,12 0,75 6 0,80—0,40 0,531 0,428
52,0 33,5 0,14 1,00 8 0,50—0,25 0,256 0,221*
52,0 37,5 0,18 1,00 14 0,63-0,47 0,770* 0,585
63,0 47,5 0,27 1,20 8 3,50-3,00 4,690* 2,930*
100,0 75,5 0,18 1,525 8 0,60—0,50 0,552
335
Определение осевой жесткости сильфонов энергетическим
методом [1], [47]
По этому методу прогиб сильфона-под действием осевой силы
определяется из условия минимума полной потенциальной энергии
сильфона в положении статического равновесия.
Полная потенциальная энергия упругой системы равна сумме
потенциальной энергии деформаций и энергии положения внешних
сил.
Для тонкостенной осесимметричной оболочки потенциальная энер-
гия деформаций определяется по формуле
/22
\®тп ~I- ~Н dV•)
где Е и р, — упругие постоянные материала;
ет и et — линейные деформации в меридиональном и в окружном
4 направлениях;
dV — объем элемента сильфона.
Работа внешних сил при осевом нагружении силой Q равна
T = QX,
где X — перемещение дна сильфона.
Если энергию положения внешних сил в ненагруженном состоя-
нии считать равной нулю, то в деформированном состоянии силь-
фона она будет равна-(—71). Тогда полная потенциальная энергия
Э определится как сумма
S = L/4-
(-D-
Деформации ет и из чисто геометрических соображений можно
связать с линейными и угловыми перемещениями бесконечно малого '
элемента осевого сечения сильфона.
В свою очередь эти перемещения определяются законом искрив-
ления среднего контура осевого сечения сильфона, которым при
решении приходится задаваться. Закон искривления гофр сильфона
принимается таким, как для рамы, имеющей форму контура осевого
сечения сильфона и находящейся в соответствующих условиях
нагружения (см. фиг. 182).
Приняв закон искривления гофр, можно связать деформации ет
и е; с углом поворота нормали и Радиальным смещением внутрен-
ней точки 1 сильфона.
Эти параметры являются неизвестными, определяемыми по методу
Ритца из условия минимума полной потенциальной энергии Э [39],
[65], [66].
Опуская подробности вывода, с которым можно познакомиться
в работах В. И. Феодосьева [1] и [84], приведем конечную
336
формулу, связывающую перемещение X дна сильфона с осевой
силой Q
здесь п — число рабочих гофр сильфона;
/го — толщина стенки трубки — заготовки;
Е и р — модуль упругости и коэффициент Пуассона;
А о, Л1, Л 2 и Во — коэффициенты, зависящие от геометрии сильфона.
Их значения можно определить по графикам [1], представленным
на фиг. 183, где тис — безразмерные параметры сильфона (см.
фиг. 181, а)
Г у
' г о
т = ~ и
в
(6.6)
Отметим, что при расчете все размеры сильфона должны опре-
деляться по среднему контуру осевого сечения.
Если угол уплотнения сильфона а = О, то формула (6. 5) при-
нимает более простой вид
Если угол уплотнения а =/= 0, то его можно выразить через па-
раметры сильфона (см. фиг. 181, а) по формуле
4г0 - Т
2 - Л„ - 2г0) ’
здесь Т — шаг волны гофрировки сильфона.
Формула (6. 5) выведена для сильфона с толщиной /г, меняю-
щейся по закону (6. 3), следовательно ее можно применять только
для бесшовных сильфонов, изготовленных гидравлическим или ме-
хано-гидравлическим способом.
Поскольку при определении жесткости сильфона энергетиче-
ским методом учитываются деформации закругленных участков, то
следует ожидать, что расчет по формуле (6. 5) даст более точные
результаты, чем по формуле (6. 1), при выводе которой закруглен-
ные участки принимаются абсолютно жесткими.
Некоторые неудобства пользования формулой (6. 5) вызываются тем, что
кривые коэффициентов А о, Во, Ах и Л 2 (фиг. 183) построены через слишком
большие интервалы параметра с, и это затрудняет точное определение величин
коэффициентов. Кроме того, номограмма охватывает сильфоны с парамет-
рами 1,3 < с < 1,6 и 0,05 < т < 0,10, хотя встречаются сильфоны с парамет-
рами т < 0,05 ис > 1,6.
22 Заказ 24.
337
Фиг. 183. Графики коэффициентов Л о, Лг и Во.
Пример 3, Определить жесткость сильфона, основные [юзмсры которого
даны в условии примера 2- Радиус закруглении гофр по среднему контуру rL«—
— 1,125 лык, угол уплотнения а = 0.
Решение. Определим безразмерные параметры с и т сильфона по вы-
ражениям (6. 6)
с
2НК = 52
2Л, 37,5
= 1,385:
1,125
18,75
= 0,06.
т =
По 183 нА ходим коэффициенты Л« 0,0003 и #о = 3U. Исходя из
формулы (6. 5')? определим жесткость сильф >на
2,03 • 10* • 0,22 n nAn~ . Qn / 0,22 \з" 9 . „ .
-(1- 0:Зг)“ 0’0003 + 30 (18^1 == 2>42
Сроднее значение экспериментально замеренной жесткости сильфонов
указанных размеров (см, пример 2) равно к ~ 2,73 кес/мм. Расхождение
с расчетом составляет Расчет по формуле ((5. 1) этого сильфона да л
погрешность
В табл. 27 приведены результаты сравнения экспериментальных
значении жесткостей сильфонов, данные которых взяты из нормалей,
приведенных в приложении III, с рассчитанными ио формулам
(6. 1) и (6. 5).
Из 19 случаев расчет но формуле (6. 1), основанной на теории
круглых пластин, дал в 13 случаях результаты в пределах замерен-
ных жесткостей.
В остальных 6 случаях (отмечены в табл. 27 звездочкой) резуль-
таты расчета жесткости оказались завышенными.
Но формуле (6. 5), полученной энергетическим методом, были
также рассчитаны 13 сильфонов (остальные 6 имели параметры с
и т, не охватываемые графиком нафиг. 183). Из них в 11 случаях
результаты расчета совпали с экспоримсптальпыми.
Из табл, 27 также следует, что формула (6. 1) дает завышенные
значения жесткости по сравнению с формулой (6. 5). Это объясняется
тем, что при выводе формулы (6. 1) деформации закругленных уча-
стков пе учитывались.
С помощью формулы (6. 5) можно проследить влияние геометри-
ческих размеров на жесткость сильфона.
На фиг. 184 построены графики зависимости жесткости выражен-
ной в безразмерных величинах, от относительного радиуса закруг-
ления тотношения наружного радиуса сильфона к вну-
треннему с =-- и относительной толщины-— .
**6 Л<в
Из фиг. 184, а и б следует, что с увеличением радиуса закругле-
ния жесткость сильфона возрастает, причем более заметно для тонко-
/ ft. 4
стенных сильфонов [д5-— 0.002) с мелкими гофрами (с = 1,3). Влия-
22*
339
кие радиуса закрут лепия мало для толстостенных сильфонов =
— 0,02), особенно при большой глубине гофрировки (с = 1,5 1,6).
4Л.
С увеличением глубины гофр, о которой можно судить по отно-
R
тению радиусов с — , жесткость сильфона быстро падает
(фиг. 184, «).
§ 34. ЭФФЕКТИВНАЯ ПЛОЩАДЬ СИЛЬФОНА
Выше отмечалось, что особенностью сильфона является постоян-
ство аффективной площади па рабочем участке характеристики. Хо-
рошее совпадение расчета с опытом дает широко известная в приборо-
строении эмпирическая формула для определения эффективной пло-
щади
= л Кер = (Ке -S- ад, (6.7)
D I О
здесь средний радиус сильфона 1?ср= 2 ' '
Пользуясь теорией, круглых пластин, можно теоретически опре-
делить эффективную площадь сильфона. В соответствии с выраже-
нием (1. 5 ) (стр. 50)
», &G
/ , (а)
/кр
340
где = — — жесткость сильфона по силе, определяемая по
формуле (6. 1);
— жесткость сильфона по давлению. Ее можно найти
из решения задачи об изгибе круглой пластинки, нагруженной да-
влением [см. формулу (5. 19)].
Значения эффективной площади, подсчитанные по выражению
(а), практически совпадают с тем, что дает эмпирическая формула
р
Согласно понятию эффективной площади (см. § 3, стр. 48) пе-
ремещение сильфона под действием давления р равно перемещению
под действием сосредоточенной силы
Поэтому для расчета на жесткость
нагруженного давлением р, можно
ваться формулами (6. 1) или (6. 5),
силу Q заменить
только осевую
нием pFa$. .
сильфона,
воспользо-
где нужно
произведе-
Изменение объема внутренней полости силь-
выраже-
фона вычисляется в
нием (1. 7)
соответствии
Фиг. 185. Схема
сильфонного регу-
лятора давления.
Пример 4. Определить изменение давления Др,
поддерживаемого сильфонным регулятором (фиг. 185),
при перемещении клапана из одного крайнего положе-
ния в другое. Полный ход клапана X = 8 мм.
фиг. 181, <z). 27?^ 80 мм, 27?в 50 мм, го == 2,5 мм, — .,
а = 4° 46'. Размеры винтовой цилиндрической пружины, работающей совместно
с сильфоном, следующие: средний диаметр пружины D = 40 мм, диаметр про-
волоки d = 5 мм, число рабочих витков i— 8. Материал сильфона — латунь
Л80, Е — 1,16 • 104 кгс/мм2, ц = 0,3; материал пружины — пружинная сталь
70, G = 7,95 • 103 кгс/мм2.
Перемещению клапана X соответствует изменение давления
*
здесь F9$ — эффективная площадь сильфона, определяемая по формуле (6. 7):
Размеры сильфона (см.
ho = 0,2 мм, п = 7,
на сильфон
(4,0+2,5)2 =
33,2 см2‘,
к — суммарная жесткость по силе сильфона и пружины
Жесткость сильфона кс в соответствии с формулой (6. 5) равна
ь ____
Лг* 1 1 , t
h«
о
По фиг. 183 при с = ~
R& 25
ляем коэффициенты Л о = 9 • 10—4,
1,6 И т Re 25
Во— 7, + = 130 • 10~4
= 0,1 опреде-
Л 2=1300.10-4-
341
Угол уплотнения а = 4°46'= 0,0834 рад. В этом случае жесткость сильфона
будет
1,16 -104- 0,2
(1 — 0,32) • 7
9 • 10“4 - 0,0834 • 130 • 10“4
+ (0,0834)2 • 1300 • 10“4 +
(0,2)2
(25)2
= 0,427 кгс/мм.
Жесткость пружин определяется по формуле (3. 21')
= Gd* _ 7,95 • 103 * 54
п 8Р3г 8 • 403 • 8 “
кгс/мм.
Суммарная жесткость
&= 4-fcn = 0,427+ 1,21 =1,64 кгс/мм.
Следовательно изменение давления Др, соответствующее полному ходу
клапана X, будет равно
0,4 кгс/см2.
§ 35. ОПРЕДЕЛЕНИЕ ИЗГИБНОЙ ЖЕСТКОСТИ СИЛЬФОНА
* *
Если сильфон при работе нагружается поперечными силами или
моментами в его осевой плоскости, например, когда он является
элементом вывода углового перемещения (фиг. 186), то его рабочие
свойства зависят от .величины изгибной жесткости. Для определе-
Фиг. 186. Дифференциальный манометр, в котором сильфон
служит для вывода углового перемещения.
ния жесткости сильфона на изгиб удобно выбрать такую же расчетную
схему, как и при определении его осевой жесткости (§ 33, стр. 331),
т. е. в виде кольцевых пластинок, жестко соединенных друг с дру-
гом по наружному и по внутреннему контурам [82]. При нагруже-
нии сильфона моментом М в его осевой плоскости каждая кольце-
вая пластинка будет находиться в условиях закрепления и на-
гружения, показанных на фиг. 127, б. В § 24 даны результаты
342
решения такой задачи. Угол попорота A(f жесткого центра пластинки
связан с величиной момента Jf зависимостью (5. 27)
* М
Д<Р-
где Е — модуль упругости материала;
h — толщина;
Лф — коэффициент, равный в соответствии с выражением (5. 28)
-3-”- Й/Ье-
3t I
о i{K
здесь с -- —- — отношение наружного
Ле
нему }{е (фиг. 181, а);
р — коэффициент Пуассона.
Значения коэффициента Л,у даны
в табл. 26.
Поскольку' сильфон состоит нз 2п
кольцевых пластинок (п — число рабочих
гофр? сильфона), то угол поворота дпа
сильфона равен
л/
<6*9'
радиуса Пи к внутрен-
Фиг. 187. Сильфон, нагру-
женный поперечной силой.
При решении различных задач изгиба сильфона поперечными
силами удобно заменить сильфон балкой, эквивалентной сильфону
в отношении изгибпой жесткости. Угол поворота балки под дейст-
' писм приложенного па конце момента равен
где Виз — жесткость балки на изгиб.
Сравнивая выражения (6. 9) и (а), получим изгибную жесткость
сильфопа в виде
<в-10>
где L — длина рабочей гофрированной части сильфона.
Для того чтобы найти, па пример, перемещение я дна сильфона
под действием поперечной силы Р (фиг. 187), достаточно восполь-
зоваться известной формулой (2. 3) для прогиба консольной балки,
Р/Я
нагруженной га конце силой: v -—, здесь жесткость Виз па
О™ US
изгиб определяется выражением (6. 10).
Следует иметь в виду, что расчет по формуле (6. 10), выведенной
без учета деформаций закругленных участков, будет давать завышен-
ные значения нагибной жесткости сильфона.
343
§ 36. УСТОЙЧИВОСТЬ СИЛЬФОНА /
л
I
При осевом сжатии силой Q достаточно гибкий сильфон может
так же, как и сжатая стойка или винтовая' цилиндрическая пру-
жина, внезапно изогнуться, потеряв устойчивость прямолиней-
ной формы равновесия. При этом в поперечном сечении сильфона
сила создает изгибающий момент, равной Qv, где v — отклоне-
ние оси сильфона от первоначального прямолинейного положения
(фиг. 188, а).
Фиг. 188. Потеря устойчивости сильфона при нагружении осевой
силой (а) й внутренним давлением (б).
Для определения критической силы QKp заменим сильфон экви-
валентной стойкой, и тогда критическую силу можно приближенно
определить по формуле Эйлера (2. 6):
из
где Виз — изгибная жесткость сильфона, определяемая по формуле
(6. 10);
L — длина рабочей гофрированной части сжатого сильфона;
v — коэффициент, зависящий от способа крепления концевых
сечений. Величины коэффициента v даны в табл. 9, стр. 69.
Подставляя в формулу Эйлера величину изгибной жесткости Виз
(6. 10), получим
л2 Eh3
v2 £ 2пЛ '
(6. И)
344
Если концевые сечения сильфона закреплены так, что не могут
поворачиваться, то v — — (см. табл. 9), и критическая сила будет
определяться выражением
п _ 2л2 Eh3
Qkp~ A^nL *
Потеря устойчивости сильфона может наступить также при на-
гружении его внутренним давлением р, если осевое перемещение
дна сильфона ограничено неподвижным упором (фиг. 188, б). Если
упор отстоит на некотором расстоянии от дна сильфона, то при на-
гружении сильфона давлением р, реакция со стороны упора будет
равна
Q = (Р — Ро) (а)
где ро — давление, при котором дно сильфона дошло до упора;
F9$ — эффективная площадь сильфона.
Если реакция Q достигает величины критической силы QKP, то
сильфон потеряет устойчивость. При этом критическое давление
Ркр в соответствии с выражениями (а) и (6. И) будет равно
п _ VKP
^-^7
Л2 Eh3
Ро ..2 л ч~^~г
Если с начала нагружения дно сильфона находится
то ро = 0 и тогда
на упоре
Ркр —
л* Eh3
•пн:
ективную площадь ее выражением
Заменяя здесь э
лучим для сильфона с неповорачивающимися концевыми
(6. 7), по-
селениями
ср
где RcP — средний радиус сильфона, равный НСр — —'н'ТЛв t
коэффициент берется из табл. 26.
При расчетах на устойчивость следует иметь в виду, что рас-
четная критическая нагрузка обычно получается завышенной по
сравнению с действительной. Причиной этого является наличие
у реального сильфона некоторой начальной кривизны его оси, от-
клонений от правильной осевой симметрии за счет различия в раз-
мерах гофр, в толщине материала и др. Чем больше несовершенств
в форме сильфона, тем при меньшей нагрузке произойдет потеря
устойчивости. Кроме того, формула (6. 12) дает завышенные зна-
345
чения критического давления еще и потому, что в расчетной схеме
(фиг. 181, б) не учитывалась податливость закругленных участков.
Если сильфон нагружен наружным давлением, то потеря устой-
чивости прямолинейной формы равновесия его оси невозможна, так
как силы внешнего давления не создают изгибающего момента в осе-
вой плоскости сильфона при отклонении его от первоначальной пря-
молинейной формы оси. Поэтому по устранении причины, вызвав-
шей отклонение, сильфон примет первоначальную форму, как бы
ни было велико наружное давление, если только оно не вызовет
разрушения оболочки сильфона или местной потери устойчивости
в виде вмятин на гофрах.
Возможность потери устойчивости сильфона под действием вну-
треннего давления является одной из причин того, что в большинстве
случаев сильфоны устанавливаются в приборе так, чтобы они на-
гружались наружным, а не внутренним давлением.
Пример 5. Определить критическое давление для сильфона, жестко за-
крепленного по концам и нагруженного внутренним давлением. Размеры силь-
фона известны: RH — 19,7 мм, Re = 13,3 мм, толщина стенки трубки-заготовки
ho = 0,16 мм, L — 166 мм, п= 55. Материал латунь Л90, Е =1, 1 • 10е кгс/см2.
R 19 7
Решение.] Отношение радиусов сильфона с — = 1,48.
Re 13}3
Т*ак как сильфон изготовлен вытяжкой из трубки, то определим его осреднен-
ную толщину h по формуле (6. 4)
I з
ho
MMS.
По табл. 26 находим при с — 1,48 коэффициент А = 0,0165. Средний
19 7 -4- 13 3
радиус сильфона Rcp = —-—к------~— = 16,5 мм
ш
Критическое давление находим по формуле (6. 12')
_ 2л Eh3
Рк р -
2-3,14-1,1-106-0,0025 _.ъ . ,
о —==—77Гг.- rso =0,42 кгс смй.
A^nLR^ 0,0165-55-166-(16,5)2
Опыт дает ркр = 0,29 кгс/см2 [12].
§ 37. ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В СИЛЬФОНАХ
Использование теории оболочек для определения напряжений
в сильфонах приводит к результатам, сложным для практического
применения [83]. Напряжения, определенные энергетическим мето-
дом [1], хорошо совпадают с тем, что дает точное решение, но ко-
нечные результаты также не имеют удобной для пользования формы.
Весьма грубая оценка напряжений, возникающих в сильфоне
при работе, может быть произведена на основе теории изгиба круг-
лых пластинок, если расчетную схему сильфона выбрать в виде
кольцевых пластинок, последовательно соединенных друг с другом,
как показано на фиг. 181, б [82].
В § 24 были приведены формулы (5. 21), (5. .25) и (5. 29) для
определения напряжений в круглых пластинках с жестким цен-
346
тром при различных условиях нагружения. С помощью этих формул
легко перейти к определению напряжений в сильфоне. Соответст-
вующие выражения для определения наибольших (по абсолютной
величине) меридиональных напряжений в точках на наружном (г =
— RH) и внутреннем (г = Re) радиусах при разных условиях на-
гружения сильфона приведены в табл. 26 на стр. 333. Там даны
также числовые значения входящих в формулы коэффициентов,
а также формулы для определения перемещений сильфона.
Окружные напряжения О/ на радиусах г = RH и г = Re свя-
заны с меридиональными напряжениями <эг зависимостью Ot — |ior.
В табл..26 использованы следующие обозначения:
* Q — осевая сила;
р — давление;
М — момент в осевой плоскости сильфона;
X и ф — линейное и угловое перемещения дна сильфона;
(Угв и Grr — наибольшие меридиональные напряжения при г = Re
и г ~ RH соответственно;
Е — модуль упругости;
RH и 7?в — наружный и внутренний радиусы сильфона;
hH и he — толщина материала в точках г = RH иг- Re,
п — число рабочих гофр.
Коэффициенты А и R зависят от отношения с ~ в соответ-
Лв
ствии с формулами (5. 20) — (5. 30) и их числовые значения
даны в табл. 26.
Для сварных сильфонов толщина стенки одинакова во всех точ-
.ках: he — hH = h. Для сильфонов, изготовленных гидравлическим
способом, толщина стенки при г = Re равна he = ho, т. е. толщине
стенки трубки — заготовки. В точках при г = RH толщина стенки
в соответствии с принятым законом (6. 3) изменения толщины равна
й„ = — = .
с с
Формулы, приведенные в табл. 26, получены в предположении
малости радиуса г о закругленных участков по сравнению с шири-
ной кольцевого участка RH — Re (см. фиг. 181, а), и поэтому ре-
зультаты подсчета по этим формулам будут давать худшие резуль-
таты для сильфонов с неглубокой гофрировкой и с большим радиу-
сом закругленных участков.
Если сравнить напряжения, возникающие в круглой пластинке,
жестко защемленной по контуру (фиг. 189, а) с напряжениями в пла-
стинке, края которой упруго защемлены (фиг. 189, б), то при оди-
наковых прогибах большее искривление срединной поверхности,
а следовательно, и большие напряжения будут возникать в жестко
защемленной пластинке. На основании этого можно предположить,
что напряжения, рассчитанные по формулам табл. 26, будут завы-
шенными для сильфонов, плоские участки которых в действи-
тельности сопряжены с упругими закругленными участками, а не
защемлены жестко, как в расчетной схеме по фиг. 181, б.
347
Фиг. 189. Изогнутая круглая
пластинка с жестко (а) и
упруго (б) защемленными кра-
ями.
Из формул, приведенных в табл. 26, следует, что при одинако-
вом осевом перемещении X напряжения в сильфоне прямо пропор-
циональны толщине стенки и обратно пропорциональны квадрату
рабочего радиуса. Если в этих формулах заменить прогиб X через
силу Q или давление р, то окажется, что при одинаковой нагрузке
напряжения с увеличением толщины стенки уменьшаются обратно
пропорционально квадрату толщины, поскольку прогибы сильфона
обратно пропорциональны кубу толщины.
Установить влияние радиуса г о закругленных участков сильфона
на его прочность с помощью приведенных выше формул невозможно,
так как их вывод был основан на
замене закругленных участков жест-
кими ’ кольцами. Исследование напря-
женного состояния сильфона с помощью
энергетического метода показывает, что
при постоянном прогибе с увеличе-
нием радиуса закруглений прочность
сильфона возрастает [1].
Некоторые сведения о характере
распределения напряжений в сильфо-
нах можно найти в работах [85]—[88],
где приводятся результаты экспери-
ментального исследования напряжен-
ного состояния линзовых компенсато-
ров — оболочек, близких по геометри-
ческой форме к сильфонам. .
Если концевые сечения сильфона закреплены неподвижно, то при
достаточно большом давлении может произойти разрыв стенки силь-
фона по наружному закруглению. Давление Рраар, при котором
наступает разрушение, определить по приведенным выше формулам
невозможно, так как они основаны на законе Гука и справедливы
до тех пор, пока напряжения не превысят предела упругости ма-
териала. Давление Рраар можно приближенно определять по без-
моментной теории, как рекомендуется в работе [47], по формуле
Рразр = ~ > где впч — предел прочности материала, hH — тол*
щина стенки на наружном радиусе RH сильфона.
Ввиду больших погрешностей, которые могут дать приведенные
в табл. 26 формулы для определения напряжений в сильфоне, их
нельзя рекомендовать для решения задачи о проектировании силь-
фона, пока экспериментально не установлены пределы их примени-
мости. Эти формулы могут быть полезны для установления качест-
венных закономерностей влияния того или иного параметра сильфона
на его прочность, а также для очень грубой количественной оценки
возникающих в сильфоне напряжений.
Задача расчета на прочность сильфона на основе достаточно
точных и в то же время удобных для пользования формул еще ждет
своего разрешения.
ГЛАВА VII
МАНОМЕТРИЧЕСКИЕ ТРУБЧАТЫЕ ПРУЖИНЫ
§ 38. ОСНОВНЫЕ СВОЙСТВА, КОНСТРУКЦИЯ И СПОСОБЫ
ИЗГОТОВЛЕНИЯ
В манометрических приборах широко используется свойство по-
лой трубки деформироваться под действием давления.
Обычно манометрическая трубчатая пружина представляет собой
тонкостенную кривую трубку вытянутого поперечного сече-
0)
Фиг. 190. Пружина Бурдона и характер ее деформаций.
ния (фиг. 190, а). При подаче давления во внутреннюю полость во-
перечное сечение трубки деформируется, принимая форму, пока-
занную пунктиром на фиг. 190, б. При этом продольное волокно аа
349
трубки переходит на дугу большего радиуса, а волокно ЪЪ — на
дугу меньшего радиуса. Поскольку волокна стремятся сохранить
свою первоначальную длину, поперечные сечения трубки, изобра-
женной на фиг. 190, а, будут поворачиваться против часовой стрелки
(фиг. 190, в). Пружина будет разгибаться, и ее конец получит не-
которое перемещение Л. Это перемещение передается на стрелку
прибора через передаточный механизм, который можно компактно
разместить в центральной части, ограниченной пружиной.
Манометрические трубчатые пружины чаще всего выполняются
в виде одновитковых (пружин Бурдона), ось которых
представляет собой дугу окружности с центральным углом
200-270° (фиг. 191, а).
Фиг. 191. Разновидности манометрических трубчатых пружин:
а — одновитковая (пружина Бурдона); б — винтовая; е — спиральная; г — S-образная.
ъ
*
Можно считать, что пружина Бурдона является наиболее рас-
пространенным типом манометрических упругих элементов. Она при-
меняется не только в показывающих, но и в регистрирующих и ре-
гулирующих манометрах, в термометрах, вакуумметрах, уровне-
мерах, расходомерах и других манометрических приборах.
По сравнению с сильфонами или мембранами трубчатые пружины
обладают малой тяговой силой. В большинстве случаев это является
недостатком трубчатых пружин, но иногда (например, при измере-
нии высоких давлений по схеме силовой компенсации), слишком
большая величина тяговой силы усложняет конструкцию прибора.
В этом случае вместо сильфона или мембраны целесообразнее ис-
пользовать трубчатую пружину.
В приборах, где требуются большие перемещения упругих эле-
ментов, используются многовитковые трубчатые пружины:
винтовые (геликсы) или спиральные (пружины Бойса), по-
казанные на фиг. 191, б и в. Технология изготовления этих пружин
сложнее, чем одновитковых, однако они способны развивать боль-
шие перемещения, что значительно упрощает конструкцию пере-
даточно-множительного механизма прибора.
Спиральные пружины имеют компактную форму и занимают в ме-
ханизме прибора примерно столько же места, что и одновитковые
пружины; они применяются во многих промышленных приборах.
350
Также широко используются и винтовые пружины. Применение
последних особенно целесообразно там, где диаметр пружины огра-
ничен, как например, в глубинных манометрах, измеряющих да-
вление в нефтяных скважинах. Весь механизм такого прибора дол-
жен быть смонтирован в трубе небольшого диаметра при практиче-
ски неограниченной длине *.
У пружин Бурдона используется линейное перемещение конца,
а у спиральных и винтовых пружин — угловое.
В некоторых случаях хорошее конструктивное решение прибора
может быть получено при применении так называемой S-образной
трубчато!! пружины (фиг. 191, г), конец которой перемещается по-
ступательно. S-образная пружина используется при измерении вы-
Фиг. 192. Поперечные сечения трубчатых
пружин.
соких давлений в качестве чувствительного элемента жидкостных
манометрических термометров, а также как элемент компенсаторов
давления в различных промышленных приборах [89].
На фиг. 192 изображены наиболее часто встречающиеся формы
поперечных сечений одно- и многовитковых трубчатых пружин.
Обычно поперечное сечение бывает плоскоовальным (фиг. 192, а),
эллиптическим (фиг. 192, б) или D-образным (фиг. 192, в). Пружина
эллиптического сечения несколько сложнее в изготовлении, но при
одинаковых габаритах обладает большей чувствительностью. Пру-
жины D-образного (сегментообразного) сечения имеют меньшую чув-
ствительность, но более технологичны.
В тех приборах, где упругий элемент должен обладать мини-
мальным начальным объемом (например, в манометрических термо-
метрах), используются трубки с формой сечения, указанной на
фиг. 192, г.
1 Ломоносов И. Г., Чувствительные элементы из прецизионных
сплавов в нефтяном и газовом приборостроении [17].
351
Пружины с сечением в форме «восьмерки» (фиг. 192, д) более
прочны и применяются для измерения повышенных давлений (по-
рядка десятков кгс/см2).
Для измерения высоких давлений (порядка сотен кгс/см2) при-
меняются толстостенные пружины плоскоовального сечения
(фиг. 192, е). Принцип работы толстостенных пружин, так же как
и тонкостенных, основан на деформации поперечного сечения под
действием давления. При этом в точках А и В сечения возникают
высокие напряжения, что ограничивает возможность использова-
ния таких пружин для измерения весьма высоких давлений.
а)
Фиг. 193.
а— внешний вид пружины Нагаткина А. Г.; б — поперечные сечения; в — к определению
изгибающего момента; г—струнный частотный датчик давления.
Для измерения давлений порядка тысяч и десятков тысяч кгс/см2
целесообразно переходить к трубчатым пружинам, работа которых
основана на другом принципе, например, к пружинам конструкции
инж. А. Г. Нагаткина [90]. По внешнему виду эти пружины мало
отличаются от пружин Бурдона (фиг. 193). Разница состоит лишь
в том, что внутреннее отверстие пружины Нагаткина расположено
эксцентрично относительно наружного контура поперечного
сечения (фиг. 193, б).
Если пружина Бурдона изменяет свою кривизну из-за деформа-
ции поперечного сечения, то пружины Нагаткина разгибаются по-
тому, что под действием давления в поперечном сечении возникает
изгибающий момент (который, как это будет показано ниже, в пру-
жине Бурдона отсутствует).
Равнодействующая Р сил давления р, приложенных к отсечен-
ной части пружины (фиг. 193, в), равна Р = pF о (F о — площадь
отверстия) и проходит через центр О отверстия. Приведя ее к центру
352
Поэтому пружины
Фиг. 1S4. Витая труб-
чатая пружина и
формы ее поперечных
евченин.
тяжести С поперечного ссчспия, получим изгибающий момент Л£ —
= Ре и нормальную силу Л -— Pt здесь е— расстояние между точ-
ками О и С (фиг. 193, б и <?). Изменение кривизны оси пружины бу-
дет лропорциупальло изгибающему моменту Л/, следовательно, и
величине давления р.
Весьма массивное поперечное сечение такой пружины деформи-
руется под действием давления незначительно, и напряжения рас-
пределяются более равномерно, чем, например, в толстостенной пру-
жине нлоскоовалиного ссчспия (см. фиг. 192, е)
Пагаткина обладают большей прочностью,
чем пружины Бурдона.
Для измерения высоких давлений может
быть использован струпный частотный датчик
(фиг. 193, а), упругим элементом которого
является прямолинейная трубка с эксцент-
ричным каналом. Под действием давления
в поперечном сечении этой трубки так же, как
и » пружине Игн аткина, возникает изгибаю-
щий момент. Искривление трубки изменяет
натяжение струны, а следовательно, и частоту
ее собственных колебаний.
В последнее время в манометрических
приборах высокого давления (порядка со-
тен кгс/сл-2) зашла применение так ня выкае-
мые «в и ты е » трубчатые пружины, представ-
ляющие собой естественно закрученную труб-
ку: ее внешний вид в применяемые формы се-
чений показаны на фиг. 194. Принцип работы
витой пружины, как и пружины Бурдона, осно-
ван па деформации поперечного сочспия под
действием давления. Продольные волокна
витой пружины располагаются по винтовым
линиям. При деформации поперечного сечения
изменяются расстояния между центральной осью пружины и про-
дольными волокнами, что приводит к измепспию длины волокон.
Стремление колокол вероуться к первоначальной длине приводит
к раскручиванию пружины вокруг ее оси. Применение витых пру-
жин позволяет получать приборы компактной конструкции с про-
стым передаточным механизмом.
Для изготовления трубчатых пружин на невысокие давления и
при отсутствии жестких требований ио гистерезису широко при-
меняются латуни Л62 я Л 68 и фосфористая бронза Бр. ОФ4-2,5
(табл. 1, § 1).
Для пружин высокого давления применяют стали 50ХФА (табл. 5)
и 18ХНВА (ГОСТ 454348).
Высокой прочностью, малым гистерезисом, стабильными но вре-
мени свойствами обладают пружины, изготовленные из бериллие-
вых бронз Бр. Бр2,5; Пр. БНТ '1,9 и из мельхиора МНМц20-20
23 Заказ 34.
353
(табл. 6). Хотя применение этих материалов усложняет технологи-
ческий процесс операцией облагораживания, во время которой про-
исходит дисперсионное твердение, однако это окупается высоким
качеством получаемых пружин. Пружины из этих материалов могут
работать при повышенных температурах (до 100—150° С), мало сни- '
жая свои упругие свойства.
Для работы в условиях высоких температур (до 200—300° С)
и агрессивных сред стали применяться в последнее время пружины
из высококачественных сплавов Н36ХТ (ЭИ702), Н41ХТ (табл. 6).
Наибольшее распространение имеет способ изготовления мано-
метрических трубчатых пружин из цельнотянутых профилированных
трубок, получаемых волочением.
Профиль трубки-заготовки дол-
жен соответствовать форме попе-
речного сечения пружины. Изгиб
трубки производится прокаткой
на роликах. Для предотвращения
искажения поперечного сечения
трубка заполняется мелкой пова-
ренной солью, песком, канифолью,
легкоплавкими металлами и пр.
После изгиба трубки • на оправке
• по дуге заданного радиуса запол-
Фиг. 195. Навивка трубчатой- пру- тель удаляется.
жилы с металлическим сердечником. Более производителен способ
навивки с металлическим сердечни-
ком (фиг. 195). При вращении валика трубка, прижимаемая к валику
роликом, изгибается по дуге круга и стягивается с сердечника.
Пружины с сечениями, показанными на фиг. 192, в, г и е, а также
> ' : л стостенные пружины на высокие давления (фиг. 193) могут из-
готовляться без применения сердечника или наполнителя.
Навитая трубка приваривается или припаивается к держателю,
а на другом конце таким же образом укрепляется наконечник. До-
статочно простое и надежное крепление получается при навивке
пружины из круглой трубки с одновременным профилированием
сечения. Оставшийся круглым хвостовик трубки приваривается
к держателю (фиг. 196, а).
Пружины высокого давления часто изготовляются не из цельно-
тянутой, а из точеной трубки с нарезанной на концах резьбой, слу-
жащей для присоединения к трубке наконечника и держателя
(фиг. 196, б).
Навивка спиральных, винтовых и S-образных пружин произ-
водится на специальных приспособлениях (см., например, [89]) спо-
собами, мало отличающимися от способов навивки одновитковых
пружин.
Изготовление цельнотянутой трубки-заготовки для тонкостен-
ных манометрических пружин весьма трудоемко. Вытяжка тонко-
стенных трубок при малых допусках на толщину производится на
сложном оборудовании при большом числе переходов с промежуточ-
ными отжигами.
Иногда трубку-заготовку получают сваркой из лнстовойо ма-
териала (фиг. 1.97, а и б). Разброс характеристик пружин одной
Фиг. 10В. Кропления концов пружины.
партии при атом может быть снижен, поскольку листовой материал
можно получить с более узкими допусками по толщине по сравне-
нию с допусками ла цельнотяну-
тые трубки.
Расположение сварных швов
по концам большой оси ссчспия
(фиг. 197, <? и с) упрощает техноло-
гию: получаемые штамповкой про-
филированные полосы спариваются,
затем производится навивка пру-
жины. Иногда для того, чтобы
уменьшить искажение сечения, про-
изводится сначала изгиб профилиро-
ванных полос по отдельности, а за-
тем они свариваются в трубку.
Э ксперимептальпыс исследования
[91] показали, что сваренные по
схеме па фиг. 197, в и г пружины
обладают более высокой чувстви-
тельностью, чем бесшовные из цель-
нотянутых трубок.
Применяя сварку, можно изго-
товить трубчатые пружины из ма-
териала прочного и упругого, по
Фиг. 107. Сечения сварных труб-
чатых пружин.
23*
355
в то же время недостаточно пластичного, чтобы из него можно
было тянуть бесшовные трубки.
Применение сварки позволило создать новые конструкции мано-
метрических трубчатых пружин ’. При сварке трех и более полос
получаются двух-и много пол ости ые трубчатые пружины (фш . 197, <9),
Перемещение конца такой пружины зависит от совокупности давле-
ний, подаваемых в каждую полость. С помощью многополостпых
пружин можно решить задачи снижения даишший.
Путем сварки можно изготовить биметаллические трубчатые пру-
жины 191]. Соответствующим подбором материалов полос, образую-
щих пружину, можно частично компенсировать температурную по-
грешность прибора.
Недостатком снарпых пружин является пониженная коррозион-
ная стойкость сварного шва.
Расчету пружин Бурдона посвящено значительное количество
работ [14], [15], [921 —[95]. Наиболее полно теория пружин Бур-
допа разработана в трудах В. И. Феодосьева [1], [8].
Расчет па жесткость пружин массивного поперечного сечеппя
с эксцентричным. каналом (см. фиг. 193) изложен в статье [90]
Л, Г. ТТагаткина.
Витые пружины (см. фиг. 194), которые стали применяться не-
давно, еще не имеют удовлетворительного метода расчета,'хотя не-
которые попытки в этом направлении предпринимались 1 2. Значи-
тельный интерес представляет статья 3, где приведены результаты
йкспоричентального исследования витых пружин
§ ЗОх ВЛИЯНИЕ ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ ЦА ЧУВСТВИТЕЛЬНОСТЬ
И ПРОЧНОСТЬ ПРУЖИНЫ БУРДОНА
Tfa фиг. 198, а изображены пружина Бурдона п со сочепне. Здесь
показаны:
Н — радиус кривизны центральной оси;
у — центральный угол рабочей части пружины;
а и b — большая и малая полуоси поперечного сечения пружины,
отсчитываемые по среднему контуру (в плоскости кри-
визны оси пружины располагается малая ось сечения);
h — толщина стенки трубки.
1 Сычев II. А.г Сварные упругие чувствительные элементы (сильфоны
и манометрические пружины) [17].
г С h и - С he и, A theory of twisted bourdon tubes, Proc. First U. S. Nat.
Congr. Appl. Meeh., Publ. .Amer. Son. Meeh. Engrs., N. Y>, 1952.
Арефьев Б. А., Осесимметричный чувствительный элемент манометри-
ческих приборов. Труды Ленин градского пп-та авиационного приборостроения,
1957, 24.
в Ф о й г е .ч ь Л. А., III е х г <> р 3. X,. Э л ю х и м С. В., Исследование
зависимости упругих характеристик питых трубчатых пружин от геометри-
ческих размеров, «Приборостроение», Л’е 4, 1959.
356
Один конец пружины укрепляется в неподвижном штуцере, а дру-
гой соединяется с механизмом прибора. Под действием давления
пружина разгибается, и ее свободный конец совершает ход X.
Рассмотрим более подробно деформации, возникающие при ра-
боте пружины.
а — геометрия пружины Бурдона; б — элемент пружины; е— деформация поперечного
сечения пружины, эпюры перемещений w и продольных деформаций ti; г — равновесие
отсеченной части пружины.
При подаче давления во внутреннюю полость поперечное сече-
ние пружины деформируется, стремясь к окружности. Если бы по-
перечные сечения пружины не поворачивались, то произвольное
волокно А В элемента пружины, выделенного двумя близкими по-
перечными сечениями, перешло бы в положение A'D (фиг. 198, б).
При этом радиус волокна АВ увеличится с R + у до В + у + w,
где w — проекция перемещения точки А поперечного сечения на
ось у (фиг. 198, в). Волокно АВ удлинилось бы на величину
отрезка CD.
357
В действительности продольные волокна, стремясь сохранить
свои первоначальные размеры, повернут поперечные сечения пру-
жины, и волокно АВ займет положение А'В'. Относительная дефор-
мация волокна АВ будет равна (фиг. 198, б).
СВ' — CD—DB' w>d^-(y-^w)dft
АВ~ “ АВ (7? 4-i/)rf6
Для большинства манометрических пружин радиус кривизны R
значительно больше малой полуоси b сечения, поэтому и у R.
В области малых перемещений w у, следовательно
w — У
Поскольку все участки пружины Бурдона находятся в одинако-
вых условиях (кроме мест креплений), относительный угол пово-
d ft г. Ду
рота элемента оудет равен относительному углу поворота —-
концевого сечения пружины (фиг. 198, «) — -=-^- .
Поэтому выражение для продольной деформации можно пред-
ставить в виде
(7. 1)
- Самые большие перемещения w, следовательно, и наибольшие
удлинения получают волокна I (фиг. 198, в), расположенные вблизи
концов малой оси сечения. Поворот сечений пружины связан именно
со стремлением волокон I — «активных» волокон — сохранить свою
начальную длину. Волокна II вблизи концов большой оси — «пас-
сивные» волокна — перемещаются в основном в направлении оси
х, и их длина при деформации сечения изменяется незначительно.
Поэтому, стремясь сократиться до прежних размеров, «активные» во-
локна встречают сопротивление со стороны «пассивных» и, сжимая
их, сами остаются растянутыми. В нижней половине сечения «ак-
тивные» волокна будут сжаты, а «пассивные» — растянуты. Рас-
пределение продольных деформаций имеет знакопеременный ха-
рактер, показанный на фиг. 198, в.
Продольные напряжения а1? возникающие при работе пружины
Бурдона, распределены по сечению примерно по такому же закону,
как и деформации ег
Из условия равновесия части пружины, отсеченной по некото-
рому поперечному сечению (фиг. 198, г), можно доказать, что при
нагружении пружины давлением в сечении возникает только нор-
мальная сила N = pF о (F о — площадь, ограниченная внутренним
контуром сечения), а изгибающий момент отсутствует. Таким обра-
зом, напряжения в поперечном сечении пружины самоуравнове-
шены.
358
Итак, главным условием работы пружины Бурдона является
искривление контура поперечного- сечения.
Чем больше это искривление, тем больше угловое Ду и линейное л
перемещения конца пружины, тем больше ее чувствительность.
Очевидно с уменьшением толщины h и увеличением радиуса
кривизны R чувствительность пружины возрастает.
Весьма сильно влияет на чувствительность манометрической пру-
жины отношение осей поперечного сечения. Пружина круглого
сечения практически не чувствительна к давлению, так как ее се-
чение не искривляется под действием давления. Чем больше вытя-
нуто сечение, тем сильнее оно искривляется под действием давления
и тем выше чувствительность пружины.
Фиг. 199.
а — формы поперечного сечения пружин с разной чувствительностью:
1 — наибольшей, 4 — наименьшей; б — сечения сварной и цельнотянутой
пружин.
Большое влияние на чувствительность оказывает форма сече-
ния при одинаковых размерах осей 2а и 2Ъ.
Наивысшую чувствительность будет иметь пружина такой формы
поперечного сечения, когда деформации в продольном направлении
одних волокон не будут стеснять деформации других. В этом слу-
чае все продольные волокна, перемещаясь под действием давления,
смогут сохранить свою первоначальную длину, и угол поворота Ду
концевого сечения будет наибольшим. Для выполнения этого усло-
вия необходимо, чтобы перемещения w были прямо пропорциональны
расстоянии у до оси х. Тогда в соответствии с выражением (7. 1) и
из условия отсутствия изгибающего момента в поперечном сечении
пружины,
= 0. При
пружины
полуоси Ъ
Наибольшее приближение к этому условию можно получить
в конструкции сварной пружины 1 (фиг. 199, а). Однако для боль-
шинства сварных и бесшовных пружин условие пропорциональ-
ности перемещений w расстояниям у не соблюдается, так как по кон-
цам большой оси сечения имеются закругленные участки II большего
нагруженной давлением, продольная деформация =
этом относительный угол поворота концевого сечения
Av w ггп
будет ——- = — — ~ , где wo — увеличение малой
сечения.
359
или меньшего радиуса. В этих местах точки сечения получают не-
большие перемещения w при значительных величинах у.
Очевидно, чем большую часть сечения занимают «пассивные»
участки II и чем больше расстояния у на этих участках, тем значи-
тельнее сопротивление, которое будут встречать «активные» волокна I
в своем стремлении повернуть сечения пружины. Сечение эллип-
тической формы 2 имеет меньшие расстояния у вблизи концов боль-
шой оси, чем плоскоовальное 3, и этим объясняется большая чувст-
вительность пружин эллиптического сечения. Пружины 4 с выпук-
лыми участками по концам большой оси обладают наименьшей чув-
ствительностью.
Опыт подтверждает большое влияние формы «пассивного» участка
сечения на чувствительность пружины. Так, одинаковые по раз-
мерам пружины, отличающиеся только формой сечения вблизи кон-
цов большой оси (фиг. 199, б), имеют весьма ощутимую разницу
по чувствительности, причем большей чувствительностью обладает
сварная пружина, форма которой показана на фиг. 199 пунктиром С
Кроме продольных деформаций в манометрической пружине
возникают поперечные деформации е2, связанные с изгибом стенки
пружины в поперечном направлении.
Если обозначить изменение кривизны в произвольной точке А
средней линии поперечного сечения через Ди, то относительная
деформация в точке В волокна.ев, отстоящего на расстоянии z от
средней линии (фиг. 200, д), будет равна
е2 — z- Ан.
При этом деформации, обусловленные растяжением среднего кон-
тура поперечного сечения, не учитываются вследствие того, что они
малы по сравнению с изгибными деформациями. Это подтверждается
тем, что пружина круглого сечения практически не изгибается под
действием давления.
В соответствии с выражением (7. 2) деформации е2 меняются
по толщине стенки по линейному закону.
Распределение деформаций е2 вдоль контура поперечного сече-
ния пружины можно представить, вырезав двумя близкими попе-
речными сечениями участок пружины. Под действием некоторой
равномерно распределенной нагрузки д полученная замкнутая рама
будет искривляться, примерно по такому же закону, что и контур
поперечного сечения пружины Бурдона (фиг. 200, б). Нафиг. 200, в
показан вид эпюры поперечных деформаций е2 в точках внутрен-
него контура поперечного сечения пружины. Знаком «Ц-» отмечены
деформации удлинения, знаком «—-» — укорочения.
Kai? правило, разрушение пружин Бурдона происходит с образо-
ванием продольных трещин, и это дает основание предполагать,
1 Сычев И. А., Сварные упругие чувствительные элементы (сильфоны
и манометрические пружины) [17].
360
что поперечные деформации е2 оказывают большее влияние на проч-
ность пружины, чем продольные деформации ех.
Напряжения в пружине возрастают с уменьшением толщины
стенки h, увеличением радиуса R и отношения полуосей сечения .
— оj
б)
Фиг. 200. Поперечные деформации е2 в пружине Бурдона:
а — распределение деформаций eg по толщине стенки; б — искривление поперечного сечения
• — эпюра деформаций eg в точках внутреннего контура поперечного сечения пружины.
Если сравнить пружины, формы сечений которых указаны на
фиг. 199, то наиболее прочной окажется самая жесткая пружина
а наименее прочной — самая чувствительная пружина I, в стенках
которой возникают высокие напряжения в точках по концам большой
оси сечения.
§ 40. РАСЧЕТ НА ЖЕСТКОСТЬ ТОНКОСТЕННЫХ ОДНОВИТКОВЫХ
ПРУЖИН
Основные допущения
В основу теории тонкостенных трубчатых пружин, разработан-
ной В. И. Феодосьевым [1], [8], положен приближенный энерге-
тический метод Ритца, с которым можно подробно ознакомиться
в книгах [65], [39].
Равновесное положение пружины Бурдона, нагруженной давле-
нием, определяется из условия минимума полной потенциальной
энергии, которая равна сумме потенциальной энергии деформаций
и энергии положения внешних сил.
Величина потенциальной энергии деформаций зависит от искри-
вления контура поперечного сечения пружины и относительного
угла поворота поперечного сечения.
Энергия положения сил определяется произведением давления
на изменение объема внутренней полости пружины, которое в свою
361
очередь также зависит от величины искривления контура попереч-
ного сечения.
Из условия минимума полной потенциальной энергии можно
найти связь между нагрузкой и деформациями пружины Бурдона
и определить перемещение ее конца.
Приближенность этого решения состоит в том, что при исследо-
вании на минимум выражения полной потенциальной энергии ме-
тодом Ритца принимается приближенный закон деформации кон-
тура сечения.
Решение поставленной задачи проводится в рамках следующих
гипотез и допущений:
1. Все участки пружины, выделенные сечениями, нормальными
к центральной оси, находятся в одинаковых условиях. Таким обра-
зом, не учитывается влияние концевых заделок пружины х.
2. Справедливы обычные в теории оболочек гипотезы о ненада-
вливании слоев и о неизменности нормали.
3. Предполагается, что осевая линия трубки не растягивается.
4. Толщина стенки пружины мала по сравнению с малой полу-
осью сечения (h Ь) 1 2, а полуось b мала по сравнению с радиусом R
кривизны центральной оси (Ь В).
5. Сечение пружины симметрично относительно осей х и у (см.
фиг. 198, в).
Определение потенциальной энергии деформации
Двумя нормальными сечениями выделим участок пружины
(фиг. 201, а) с центральным углом dQ. Продольными сечениями вы-
делим из него бесконечно-малый элемент (фиг. 201, б), который, со-
гласно гипотезе о ненадавливании волокон, находится в плоском
напряженном состоянии. Удельная потенциальная энергия и при
двухосном напряженном состоянии выражается через компоненты
деформаций [34]:
Е
2(1—р)
здесь Е] и е2 — относительные деформации в направлении главных
осей 1 и 2;
Е — модуль упругости;
р — коэффициент Пуассона материала пружины.
Потенциальная энергия бесконечно малого элемента равна dU =
= и • dv, где, в соответствии с допущением 4, объем элемента dv =
— RdQdsdz.
1 О влиянии концевых участков на работу пружин см. работу Чина рева А. И ,
Исследование деформации малой сси и угла раскрытия манометрической труб-
чатой пружины плоскоовального сечения [17].
2 О расчете толстостенных манометрических пружин см. § 44.
362
Потенциальная энергия деформации U пружины Бурдона с цен-
тральным углом у определится интегрированием величины dU по
объему пружины:
h
♦
где h — толщина стенки, S — длина дуги средней линии контура
поперечного сечения.
Фиг. 201. К определению
потенциальной энергии де-
формаций:
а — участок пружины; б —
напряженное состояние эле-
мента.
Продольная и поперечная деформации определяются выраже-
ниями' (7. 1) и (7. 2):
Ду
Подставив их в уравнение (а) и произведя интегрирование по
переменной z, получим
^=2ттаЛ("-^)а+^(Аи)2Ь (7-3)
о
263
Вычисление энергии ^положения внешних сил
В рассматриваемой задаче внешними для пружины Бурдона бу-
дут силы давления, поэтому работа Т внешних сил на возможных
перемещениях будет равна в данном случае произведению давления
на изменение объема . внутренней полости пружины
Т = р- A V.
Изменение объема AF можно подсчитать как произведение из-
менения А/ площади, ограниченной средней линией контура, на
длину Ry центральной оси пружины.
Если обозначить / — площадь, ограниченную средней линией кон-
тура до деформации, и Д — площадь после деформации,
(см. фиг. 198, в), то увеличение площади будет равно А/ — Д —/,
а изменение объема
AF = А//? у.
Энергия положения внешних сил равна работе Т, взятой с об-
ратным знаком, если, считать энергию положения в ненагруженном
состоянии равной нулю:
(~7) = ~р. А/-2?у.
>
(7.4)
Определение полной потенциальной энергии
ж.
Полная потенциальная энергия определяется как сумма потен-
циальной энергии деформаций и энергии положения внешних сил,
т. е.
Заменяя U и (— Т) выражениями (7. 3) и (7. 4), получим полную
потенциальную энергию пружины в виде
g J~У ^)2 + -4^(Д^]^-рД/Лу. (7.5)
и
Уравнение (7. 5) содержит четыре неизвестных:
Ду
—5---относительный угол поворота концевого сечения пру-
Y ж ины;
w — перемещение произвольной точки контура поперечного
сечения в направлении малой оси сечения;
Ах — изменение кривизны в произвольной точке среднего
контура сечения;
А / изменение площади, ограниченной средней линией кон-
тура.
364
Перемещение w, изменения кривизны Ах и площади А / опре-
деляются деформацией контура поперечного сечения;, между ними
можно найти связь и уменьшить число неизвестных в уравнении (7.5).
В соответствии с методом Ритца зададимся приближенно фор-
мой искривления контура поперечного сечения пружины. Примем,
что поперечное сечение пружины Бурдона деформируется по тому же
закону, что и контур прямолинейной трубки, находящейся под дей-
ствием внутреннего давления.
Если из прямой трубки двумя близкими сечениями выделим
элементарное кольцо, то получим замкнутую раму, нагруженную
некоторой распределенной нагрузкой q (фиг. 202, а). Раскрывая
Фиг. 202. К определению формы искривления поперечного сечения.
статическую неопределимость этой рамы, можно перемещение w,
изменение кривизны Ах и увеличение площади А/ выразить через
нагрузку q. Однако более удобно характеризовать величину искри-
вления контура не нагрузкой q, а увеличением гг0 малой полуоси
рамы, прямо пропорциональным q. Величины w. Ах и А/, входя-
щие в уравнение (7. 5) свяжем с перемещением шо, которое примем
за меру искривления контура.
В результате раскрытия статической неопределимости рамы по-
лучим выражение изгибающего момента в произвольном сечении В
рамы
м = -1)Й, (а)
где Q — функция дуги $ контура, зависящая только от очертания
оси рамы, т. е. от формы поперечного сечения пружины Бурдона.
Перемещение iv0 точки
грала Мора (2. 4)
А рамы можно найти с помощью инте-
1Г0
М-Мг ,
—7.- - as
где Mi — изгибающий момент в произвольном сечении В рамы от
единичной силы, приложенной в точке А (фиг. 202,6),
В — жесткость рамы на изгиб.
365
В результате интегрирования получим
^0 = -оТГ (а2 — Ъ2) т,
(б)
здесь т — коэффициент, зависящий от формы рамы.
Перемещение w произвольно!! точки В в вертикальном напра-
влении определится по формуле
S
4
Г М>М • ds
__
о
здесь момент М от заданных сил определяется выражением (а);
— изгибающий момент в произвольном сечении от единичной
силы, приложенной в точке В (фиг. 202, в).
Заменяя в выражении (а) момента нагрузку q через перемеще-
ние и\} с помощью уравнения (б), получим после интегрирования
перемещение w в виде
т
где со — функция дуги s -контура.
Для определения изменения кривизны в произвольной точке В
рамы воспользуемся известным уравнением изгиба стерж-
ня (2. 2).
Ах
(В — жесткость рамы на изгиб).
Заменяя в выражении (а) момента М нагрузку q через переме-
щение п?0, получим из последнего выражения
_^о_
та2
(7.7)
Увеличение А/ площади, ограниченной осью рамы, при ее де-
формации можно найти с помощью интеграла Мора
Здесь М определяется выражением (а), а М1инт— момент от рав-
номерно распределенной нагрузки интенсивностью, равной единице
366
(фиг. 202, г). Его значение может быть получено из выражения (а)
при q — 1 .
М1ияот = 4(-^--1')й. ‘ (г)
Величину
перемещение
А/ можно так же, как и предыдущие, выразить через
Wq точки А рамы, в результате чего получим
(7-8)
где п — коэффициент, зависящий от очертания рамы.
Приближенно можно принять, что выражения (7. 6), (7. 7) и (7. 8)
определяющие вертикальное перемещение ip, изменения кривизны
Ах и площади А/ для рассмотренной рамы, справедливы и для пру-
жины Бурдона, если контур ее поперечного сечения совпадает с осью
рамы. Неизвестным в этих выражениях остается величина ip0, ко-
торая была выбрана в качестве меры искривления контура.
Формулы для функций Q и id, коэффициентов т и п, входящих
в выражения (7. 6)—(7. 8), даны в приложении IV для пружин Бур-
дона эллиптической и плоскоовальной формы сечения.
Произведя подстановку выражений (7. 6)—(7. 8), в формулу (7. 5),
получим
S
д _ Eh у f
“ 2 7? (1 — и2)
О
Теперь в выражение полной потенциальной энергии входят только
две неизвестные: — увеличение малой полуоси сечения и
------относительный угол поворота концевого сечения. В со-
ответствии с методом Ритца эти величины определяются из условия
минимума полной
обозначения
потенциальной энергии.
Предварительно введем
Кроме того
ab J
о
y~ds.
3 abz J
0
из выражений (в), (г) и (7. 8) следует, что
Q2
•у
о
о
*
?
8
367
Интегралы Alf А2 и А3 могут быть вычислены, если форма по-
перечного сечения пружины Бурдона задана.
Тогда выражение (д) примет вид
где и — главный параметр пружины Бурдона
Eh
(7. 10)
' Определение угла поворота конца пружины
В соответствии с методом Ритца [65], [39] величины iv0 и
нужно подобрать так, чтобы они обращали энергию Э в минимум
дэ _ as
\ Y /
Выполняя дифференцирование, получим уравнения
Ду
дЭ ______ 2 Eha у
д / Ду \ — /?(1 —ц2)
\ Y /
2Ь*А3
(7. 11)
2Ь^-А2
т
Совместное решение уравнений (7. 11) приводит к следующей
формуле, определяющей относительный угол поворота конца пру-
жины под действием давления р,
Ду 1 — ц2 S2 /. ___ Ь2 \ а
у — Р Е ЬйД1 a2 J₽+x2 ’
(7- 12)
здесь х — главный параметр пружины, определяемый выражением
(7. 10); размеры 7?, а, Ъ и h указаны на фиг. 198, а.
Коэффициенты а и Р имеют следующие значения:
(7.13)
368
Для пружин эллиптического и плоскоовального сечения число-
вые значения коэффициентов аир даны для различных соотноше-
Линейные перемещения конца пружины
Перемещение произвольной точки криволинейного
удобно вычислять с помощью интеграла Мора (2. 4)
стержня
мрм
который можно представить в виде
так как в соответствии с формулой (2. 2) изменение кривизны стержня
-------==—£ (В и Ri — радиусы кривизны оси стержня до и
24 Заказ 24.
369
-J
Коэффициенты a, |3.
Форма поперечного сечения а ь 1 "А 1,5 2
1 |И 1 • • - —- t Плоскоовальная 1 । i a ₽ п с 0,637 0,096 0,149 0,0833 0,811 ч 0,594 0,110 0,167 0,0848 0,713 0,548 0,115 0,166 0,0815 0,65'2 0,4 0,1 o;i о,с 0,5
Т Л
,Д| 9 /у 1
1 1 i —
Эллиптическая
a i 0,750 0,636 0,566 0,4
0 0,083 0,062 0,053 0,0
п 0,197 0,149 0,142 0,1
£ 0,0982 0,0775 0,0662 0,0
0,833 0,662 0,584 0,4
^0 ^2 0,785 0,726 0,705 0,6
Таблица 28
* ’ ё ® -^0 -^2
3 4 5 6 7 8 9 10 ОС
80 0,437 0,408 0,388 0,372 0,360 0,350 0,343 0,267
21 0,121 I1 0,121 0,121 0,120 0,119 0,119 0,118 0,11.4
52 0,140 0,132 0,126 0,121 0,118 0,115 0,113 0,089
>743 0,0690 0,0652 0,0624 0,0602 0,0585 0,0571 0,0560 0,0444
i91 0,552 0,524 0,504 0,488 0,476 0,467 0,459 0,296
93 0,452 0,430 0,416 0,406 0,400 0,395 0,390 0,368
45 0,044 0,043 0,042 0,042 0,042 0,042 0,042 0,042
21 0,111 0,106 0,102 0,100 0,098 0,097 0,095 0,089
1565 0,0515 0,0480 0,0465 0,0460 0,0455 0,0450 0,0445 0,0409
:99 0,459 0,439 0,429 0,423 0,416 0,410 0,404 0,381
180 0,675 0,671 0,670 0,670 0,670 0,670 0,669 0,667
после деформации), а длина элемента оси ds = RdQ (dQ — централь-
ный угол элемента).
Поскольку изменение кривизны равно отношению взаимного угла
поворота d'Q двух сечений к расстоянию ds между ними
1 1
7?г R ~ R • t/О ’
(7-14)
то выражение (а) для X можно переписать в виде
X- f
е
(7. 15)
Изменение кривизны центральной оси пружины Бурдона по-
стоянно по ее длине, так как все участки пружины, нагруженной
давлением, находятся в одинаковых условиях. Изменение кривизны
можно представить как
Ду
R у
(7.16)
(А у —- поворот концевого сечения пружины, Ry — длина централь-
ной оси).
Отсюда взаимный угол поворота для двух бесконечно близких
поперечных сечений пружины Бурдона d\] = dQ. Тогда вы-
ражение (7. 15) для перемещения X концевого сечения пружины
Бурдона примет вид
(7. 17)
здесь Mi — изгибающий момент в произвольном сечении пружины
от единичной силы, приложенной в направлении искомого переме-
щения. Относительный угол поворота пружины под дейст-
вием давления находится по формуле (7. 12).
Для определения радиальной составляющей перемещения конца
пружины приложим единичную силу в направлении радиуса
(фиг. 204, а), и вычислим момент М\ от этой силы в произвольном
сечении трубки
Л/; = 1-Д-sine.
Тогда
у
/.r = -AL R [ Sin о d 6;
у -/ * ’
о
Xr = R (1 — cos у). (7.18)
24*
371
Аналогично можно определить перемещение конца пружины в на-
правлении касательной (фиг. 204, б):
X, =Я (у - sin у). (7.19)
Полное перемещение конца пружины (фиг. 204, в) определится
как
: % = у Д= -у- я г, (7- 2о)
где коэффициент Г равен
Г = }/(1 — cos у)2 + (у—sin у)2.
Значения его приведены на фиг. 205 в зависимости от величины
центрального угла у пружины.
Фиг. 204. К определению перемещений конца трубчатой пру-
жины.
Заменяя в формуле (7. 20) относительный угол поворота --
выражением (7. 12) через давление р, получим перемещение конца
пружины в виде
Ыг
(7-21)
Чувствительность пружппы Бурдона по давлению
(7. 22)
Для правильного проектирования механизма прибора нужно
знать положение мгновенного центра вращения аконца пружины и
направление полного перемещения.
Радиус вращения Q можно .определить как отношение полного
линейного перемещения X (7. 20) к углу поворота Ду конца пру-
жины
372
Можно показать \ что мгновенный центр вращения лежит в цен-
тре тяжести дуги Ry центральной оси пружины и имеет, следова-
тельно, координаты (фиг. 204, в)
ту 1—cosy , ту / л sin у \
Хц. в — —R — 1 Уц. в — R f 1 ——) •
При деформации пружины положение мгновенного центра вра-
щения несколько меняется.
Фиг. 205. График коэффициента Г, угла <р между направлением
полного перемещения и касательной, угла ф между направле-
нием полной тяговой силы и касательной к центральной оси пру-
жины.
Направление перемещения % перпендикулярно радиусу р. Обо-
значим угол между направлением полного перемещения и касатель-
ной к оси пружины через <р (см. фиг. 204, в), Тогда
Л 1 —cosy
X/ — у —sin у ’
отсюда
<Р
— аге
tg
[1 — cos у
у —sin у
(7. 23)
Значения угла <р в зависимости от величины центрального угла у
пружины приведены на фиг. 205. У пружины с малым централь-
ным углом у направление полного перемещения близко к
1 Чина рев А. И., Исследование деформации малой оси и угла раскры-
тия манометрической трубчатой пружины плоскоовального сечения [17].
373
радиальному. С увеличением угла у направление перемещения конца
трубки приближается к касательному.
Итак, расчет на жесткость тонкостенной пружины Бурдона, на-
груженной давлением, может быть произведен полностью с помощью
формул (7. 12), (7. 18)—(7. 23).
Пример 1. Определить перемещение конца пружины Бурдона плоско-
овального сечения при давлении р = 7 кгс!см2. Размеры пружины: радиус
центральной оси R = 52,3 мм, толщина стенки h =0,66 мм, полуоси поперечного
сечения по среднему контуру а = 10,5 мм, Ъ — 3,22 мм, центральный угол
у — 240° (см. фиг. 198, а). Материал — латунь Л62, модуль упругости Е =
== 1,16 10е кгс!см2, коэффициент Пуассона jx = 0,3.
Требуется также выяснить, как изменится чувствительность этой пружины,
если ее сечению придать эллиптическую форму при сохранении указанных
выше размеров.
Решение. Перемещение конца пружины найдем по формуле (7. 21).
Для этого сначала определим коэффициенты а, Р и Г- Из фиг. 203 следует, что
а 10 5
при — — • ’ - = 3,26 для плоско овальней формы сечения а = 0,467, р = 0,121.
о 3,22
Коэффициент Г находим по кривой на фиг. 205: при у = 240° Г = 5,3.
Главный параметр трубки вычисляем по формуле (7. 10)
Rh _ 52,3-0,66
. а2 10,52 ' '1'
Тогда перемещение л в соответствии с выражением (7. 21) равно
. • 1-ц2 оз / ь2 \ Г-сс
bh
_ 1 — 0,32 52,33 / 1
‘ ‘ 1,16 - 10е 3,22-0,66 ( 1 3,262
5,3-0,467 _
0,121 Ч-(0,313)2 3,/8 '
Если пружина имеет эллиптическое сечение, то коэффициенты а и Р будут
иметь следующие значения (см. фиг. 203): а = 0,481, р = 0,045. Прогиб такой
пружины в соответствии с формулой (7. 21) будет X = 5,96 мм.
Таким образом, чувствительность пружин эллиптического сечения будет
в данном случае в 1,58 раза выше, чем чувствительность пружины плоскооваль-
пого сечения.
§41. ИЗМЕНЕНИЕ ОБЪЕМА ВНУТРЕННЕЙ ПОЛОСТИ
МАНОМЕТРИЧЕСКОЙ ПРУЖИНЫ
Для расчета жидкостных манометрических приборов нужно знать
на сколько изменится объем внутренней полости пружины Бурдона
под действием давления. Изменение объема определится как произ-
ведение изменения площади А/, ограниченной средней линией кон-
тура поперечного сечения, на длину Ry центральной оси пружины
Изменение площади А/ может быть выражено через изменение
wо малой полуоси сечения с помощью формулы (7. 8)
62 \
2ы?0
т
п.
Величина w0, в свою очередь, связана с относительным углом
-^- поворота сечения вторым уравнением системы (7. 11):
__ ЬА3 Ду
m А2 у
или, учитывая соотношение (7. 13), получим
ш0 _ 6 Ъ Ду
т а у *
Относительный угол поворота в
деляется формулой (7. 12).
Ду __ 1 — р2 7?2 /. Ь2 \ а
у $ Е bh [ а2уР-ри2 ’
Решая совместно эти четыре
уравнения, получим следующую
формулу изменения объема внут-
ренней полости пружины в зави-
симости от давления р:
(7- 25)
Значения коэффициента п даны
в табл. 28 (стр. 370).
Изменение объема ДУ можно
выразить с помощью формулы
(7. 12) через относительный угол
Ду
поворота —~
зависимости от давления опре-
Фиг. 206. Манометр с разделитель-
ным сильфоном.
Д V = 12 Rab у 0 — -
у 1 I а2 / а
(7. 24)
(7. 25')
или по формуле (7. 20) через перемещение к конца пружины
ДУ = 12Ля6у 1
п
«Г ’
(7.25")
Пример 2. Измеряемое давление р передается в пружинный манометр через
разделительный сильфон (фиг. 206). Определить ошибку в показаниях манометра
которая будет иметь место, если предварительно не провести тарировки мано-
метра с учетом жесткости сильфона. Система заполнена жидкостью, которую
можно считать несжимаемой.
Размеры пружины Бурдона: R = 40 мм, а = 10 мм, b = 2 мм, h =0,4 мм,
у = 270° (см. фиг. 198, а). Сечение — плоскоовальное. Материал — бериллие-
вая бронза Бр. Б2,5; Е = 1,35 10е кгс]см2, р = 0,3.
Жесткость сильфона кс = 0,520 кгс/мм, эффективная площадь F3$ =
— 800 мм2.
375
Решение. Из схемы включения манометра ясно, что он измерит давле-
ние жидкости plt которое вследствие жесткости сильфона несколько меньше,
чем давление р измеряемой среды. Перепад давлений р— pj на сильфоне являет-
ся искомой ошибкой.
Относительная ошибка равна
т]--=-—— > 100%.
Р
Так как жидкость несжимаема, то объем, вытесненный сильфоном, равен
увеличению объема пружины Бурдона
ДИС = Д Уп.
(б)
Изменение объема сильфона определяется в соответствии с формулой (6. 8)
А У с — Fэф * А,
где А — перемещение дна сильфона, a F3$ — его эффективная площадь.
Перемещение X под действием разности давлений р — рп равно
(р — pt)
здесь кс — жесткость сильфона по силе.
Изменение объема пружины Бурдона находим по формуле
можно представить в виде
ч
*
Д Рп=^Р11
(7. 25), которую
где
(в)
Тогда в соответствии с равенством (б) получим
(Р ~ Pi)
кс
откуда относительная погрешность i] по выражению (а) будет
(г)
Вычислим коэффициент А по формуле (в). Из табл. 28 при
2-=5
находим: п = 0,115;
(7. 10)
р = 0,121. Главный параметр х подсчитаем по формуле
Rh
40 • 0,4
102
= 0,16.
Следовательно
Л = 12
1 - (0,3)2
1,35-104
1 \2 0 115
2б) 0,124(0,16)^4400
376
Ошибка измерения равна в соответствии с выражением (г)
11 - Г - -44^0-. 0,52^)100% S 'loo% S °’3s%
\ 1+ (800)3 /
§ 42. ИЗГИБ ПРУЖИНЫ БУРДОНА ВНЕШНИМИ СИЛАМИ [1]
Пружина Бурдона часто нагружается не только давлением р,
но и сосредоточенной силой или моментом, приложенными к ее
концу со стороны механизма прибора. Расчет пружины, находящейся
в таких условиях, можно произвести, пользуясь принципом неза-
Фиг. 207. Изгиб пружины Бурдона внешним моментом.
висимости действия сил. Например, перемещение конца пружины
Бурдона можно представить как сумму
где Хр — перемещение под действием давления р;
— перемещение, вызываемое действием сосредоточенной
силы Q;
км — перемещение под действием момента М.
Расчет пружины Бурдона, нагруженной давлением, изложен
в §40. Рассмотрим теперь пружину Бурдона, изгибаемую сосредо-
точенной силой Q и моментом М. Давление р примем равным нулю.
Начнем с наиболее простого случая нагружения пружины внеш-
ним изгибающим моментом М (фиг. 207, й). Попытка использовать
/ 1 1 \
для определения изменения кривизны ---------оси пружины из-
вестную формулу изгиба (2. 2)
М
приводит к большому расхождению с опытом. Расчет по формуле
(а) дает сильно заниженные результаты. Дело в том, что попереч-
ное сечение тонкостенной кривой трубки при изгибе деформируется,
377
это приводит к дополнительному увеличению кривизны трубки, не
учитываемому формулой (а).
Вырежем участок кривой трубки, изгибаемой внешним момен-
том (фиг. 207, б). Верхние волокна трубки растягиваются, нижние
сжимаются. Вертикальные составляющие Т упругих сил вызывают
сплющивание поперечного сечения (фиг. 207, в). При этом внутрен-
ние силы в трубке перераспределяются. При сплющивании сечения
наружные волокна перемещаются на дуги меньших радиусов (на-
пример, волокно ЛА переходит в положение А 'А'), при этом волокна
укорачиваются, и напряжения растяжения в них уменьшаются.
Аналогично рассуждая, можно показать, что в волокнах, располо-
женных ближе к центру кривизны трубки (например, в волокне В В),
напряжения сжатия также уменьшаются в результате сплющивания
сечения. Если предположить, что кривизна трубки при этом не
изменится, то момент внутренних сил стал бы меньше внешнего
изгибающего момента М, что невозможно. Следовательно, трубка
должна увеличивать свою кривизну до тех пор, пока не наступит
равновесие между внешними и внутренними силами.
При изгибе кривого бруса сплошного поперечного сечения также возникают
силы, которые стремятся сплющивать поперечное сечение. Однако деформация
сечения в этом случае настолько мала, что обычно ее не учитывают и изменение
кривизны бруса соответствует формуле (а).
Изменение кривизны оси тонкостенной трубки при изгибе ее
внешним моментом может быть найдено с помощью энергетического
метода так же, как и в случае действия давления. Различие в вы-
воде будет только в подсчете потенциала внешних сил, который
в этом случае равен — Мй (й — угловое перемещение концевого се-
чения пружины, где приложен внешний момент М). Решение этой
задачи было получено В. И. Феодосьевым [1], и конечная формула
имеет вид
пружины
здесь Jx — осевой момент инерции поперечного сечения
Бурдона, который равен
s
(7.27)
где 5 — длина среднего контура поперечного сечения;
h — толщина стенки;
у — расстояние от оси х до бесконечно малого элемента дуги ds
(см. фиг. 198, в).
s
4
Вычисляя f y2ds, получим для пружины плоскоовального се-
b
чения
Jx = ibsh(-^- — 1 + -5.) (7.27')
378
и для пружины эллиптического сечения
Jx — 4ab2h (10 — /2).
(7. 27")
Разность эллиптических интегралов /о—1г дана
(стр. 370).
в табл. 28,
Коэффициент К учитывает увеличение изменения кривизны пру-
жины за счет сплющивания поперечного сечения и может быть
определен по формуле
Rh
а2
главный
здесь коэффициенты Р
параметр пружины.
При чистом изгибе
кривизны ----
пружины Бурдона моментом М изменение
в каждой точке оси пружины одинаково, и отно-
сительный угол поворота концевого сечения определяется в соответ-
ствии с соотношением (7. 16)
пли с учетом выражения (7. 26)
Ду MR
у В
где В — жесткость пружины Бурдона на изгиб
(7. 29)
(7. 30)
Линейные перемещения конца пружины могут быть выражены
Ду
через относительный угол -у- поворота концевого сечения с по-
мощью тех же геометрических зависимостей (7. 18)—(7. 20), что
и в случае нагружения пружины давлением р.
Если изгиб пружины Бурдона происходит под действием внеш-
ней силы приложенной к еэ концу (фиг. 208, а), то в произволь-
ном сечении изгибающий момент — Q-x, где х — плечо
силы Q.
В этом случае изменение кривизны, пропорциональное изгибаю-
щему моменту, будет переменным по оси пружины. Для определения
перемещения конца пружины в некотором направлении АА можно
воспользоваться геометрическим соотношением (7. 15)
у
% =
о
379
где Mi — момент от единичной силы, приложенной к концу пружины
Бурдона в направлении искомого перемещения (фиг. 208, б). Угол
поворота dft в соответствии с выражениями (7. 16) и (7. 29) равен
Фиг. 208. Изгиб пружины Бурдона внешней силой Q.
Подставляя с?О из формулы (б) в выражение (а),
Y
* = 4,/; MQMxd е.
6
получим
(в)
Разложим силу Q на составляющие QT и Qt, направленные по
радиусу и по касательной к оси пружины в концевой точке. Тогда
в произвольном сечении изгибающий момент от сил Qr и Qt будет
= QrR sin 0 4" QtR (1—cos 9). (г)
Для определения радиальной составляющей полного переме-
щения конца пружины следует единичную силу направить по радиусу.
Изгибающий момент от нее в произвольном сечении равен
= 1 • R sin 6. (д)
Подставляя значения моментов MQ и Мг из формул (г) и (д)
в выражение (в) и интегрируя, получим
Хг = 4(<?гвгг + ^вг.-). (7.31)
Аналогично можно определить составляющую перемещения
в направлении касательной
(Qr $tr + Qt &it)’
(7. 32)
380
В выражениях (7. 31) и (7. 32) коэффициенты податливости
равны
. v f
огг = I sin2 0 d 0 = -к- (у — sin у cos у);
о
V .
6f{ = = j sin 0(1 — cos 0) d 0 = 1 — cos у — s п2 у; •
о 2
v 1
d/e = I (1—cos О)2 tZO = — (Зу — 4sin у-j-sin у cos у).
о.
(7. 33)
Полное перемещение % = 1/".
§ 43. ПЕРЕСТАНОВОЧНЫЕ (ТЯГОВЫЕ) УСИЛИЯ
Важной характеристикой манометрической пружины является
величина перестановочных или тягбвых усилий, которые развивает
пружина под действием давления, когда перемещение ее к ониа
встречает сопротивление со стороны механизма прибора.
Если свободный конец пружины Бурдона закрепить неподвижно
и подать в нее давление, то кривизна центральной оси пружины не
изменится, а момент, с которым она будет воздействовать на за-
делку, будет равен величине тягового момента.
Поскольку тяговый момент вызывает такое же изменение кривизны
оси пружины, что и давление, то он может быть найден на основа-
нии равенства
7
здесь
— изменение кривизны центральной оси пружины
Б урдона под
кривизны под
Изменение
мул (7. 12) и
действием давления р, а —----
\«i
действием внешнего момента М
кривизны
(7. 16)
— изменение
] определяется с помощью фор-
/р
Ду
? bh
«2
от действия внешнего момента равно в со-
Изменение кривизны
ответствии с формулами (7. 26) и (7. 30)
/ 1 1\ Мт
384
Приравнивая выражения (а) и (б), получим для тягового мо-
мента формулу
Мт — QApRab
(7- 34)
Коэффициенты £ и £ зависят от формы поперечного сечения
и указываются в табл. 28, приведенной на стр. 370.
Если конец пружины Бурдона может поворачиваться и пере-
мещаться в направлении оси 2, а перемещение в направлении оси 1
невозможно (фиг. 209, а), то под действием давления пружина
Бурдона будет развивать тяговую силу направленную по оси
1 (фиг. 209, б).
Фиг. 209.- К определению тяговой силы при ограничении перемещения
в одном направлении.
Определим тяговую силу Qr на конце пружины в радиальном
направлении (фиг. 209, в). Радиальное перемещение от действия
давления р по абсолютной величине должно быть равно перемещению
•в этом же направлении от действия силы Qr
^rQ
Перемещение Лг от давления р определяется с помощью формул
(7. 12) и (7. 18)
. г> Ду /л \ 1 — u,2 7?3 /л Ъ2 \ а /л ч
Лг = R —— (1 — cos у) = р ——гг 1----------------г 5-7--»- (1 — cos У)-
р у v bh \ /р-|-ха ' 1'
Перемещение от силы Qr определим по выражению (7. 31),
положив в нем Qt = 0. Тогда
Подставляя величины и АГ(^ в равенство (в),
преобразований следующее значение тяговой силы
n L Л Ь2 \ £ГГ МТГГ
х \ а2 247?
получим после
Qr
(7. 35)
332
Аналогично можно вычислить тяговую силу Qt, которую будет
развивать пружина, если невозможно
касательной к оси пружины:
линейное перемещение по
Qt = pab 1
MTVt
~24R
(7. 36)
Коэффициенты Гг и Г/ зависят от величины центрального угла у
пружины и определяются выражениями
48 (1 — cos у)
у — sin у • cos у ’
48 (у — sin у)
4sin у -f- sin у • cos у ’
Их числовые значения можно определить по фиг. 210.
Фиг. 210. График коэффициентов Гг, Г/, qr и qt.
Коэффициенты £ и | зависят от формы поперечного сечении
пружины и даны в табл. 28.
383
Определим тяговую силу, которую будет развивать пружина,
если ее конец закреплен шарнирно, т. е. может только поворачи-
ваться, но не перемещаться в каком-либо направлении (фиг. 211,а)
Если освободить пружину и нагрузить ее давлением, то ее конец
получит некоторое перемещение (фиг. 211, б). Сила QT, равная
тяговой и приложенная в противоположном направлении к концу
свободной пружины, вызовет перемещение == к (фиг. 211, <?).
Величину тяговой силы можно найти из условия соответственного
равенства проекций перемещений % и на направления радиуса
и касательной.
Фиг. 211. К" определению тяговой силы при шарнирном креплении конца
пружины.
Согласно выражению (7. 18) проекция полного перемещения на
радиус пружины равна
а проекция перемещения на это же направление в соответствии
с выражением
(7. 31) будет
A R3
(д)
где QT и QTt — проекции тяговой силы QT на радиальное и каса-
тельное направления;
бгг и 6rt — коэффициенты податливости, определяемые форму-
лами (7. 33).
Приравнивая выражения (г) и (д) и составляя аналогичное урав-
нение из условия равенства проекций перемещений к и на
направление касательной, получим из совместного решения этих
уравнений проекции полной тяговой силы Q?
(7. 37)
384
Полная величина тяговой силы равна
(7- 38)
Угол ф между касательной к оси пружины и направлением
полной тяговой силы (фиг. 211, в) определится выражением
(7. 39)
В этих выражениях
Значения этих коэффициентов даны на
фиг. 210.
Угол ф, определяющий направление
полной тяговой силы, а также угол ср,
определяющий направление полного пере-
мещения конца пружины при его свобод-
ном движении под действием давления,
представлены на фиг. 205 в соответствии
с выражениями (7. 23) и (7. 39) в зави-
Фиг. 212. Схема мано-
метра с безнулевой
шкалой.
симости от центрального угла у пружины.
Для пружин с небольшим центральным углом у угол ф примерно
вдвое больше угла <р. С увеличением у разница в направлениях
перемещения и тяговой силы уменьшается, и для трубки с централь-
ным углом у = 360° эти направления совпадают.
Если пружина Бурдона под действием давления сначала пере-
мещается свободно, а затем при некотором давлении р0 встречает
упор, то возникающая при дальнейшем увеличении давления тяго-
вая сила может быть вычислена по формулам (7. 35), (7. 36) или
(7. 38) в зависимости от того, в каком направлении ограничивает
упор дальнейшее перемещение конца пружины. Однако в эти фор-
мулы вместо давления р следует подставлять разность р — ро.
В том случае, когда конец трубки Бурдона закреплен упруго
(например, он соединен с плоской или винтовой пружиной) тяговая
сила, с которой трубка Бурдона будет воздействовать на пружину,
зависит от жесткости и расположения последней и может быть
определена из условия равенства перемещений трубки Бурдона
и пружины.
Пример 3. Определить величину начального натяжения винтовой цилинд-
рической пружины, необходимую для того, чтобы пружина манометра с безну-
левой шкалой начала работать при давлении ро = 30 кгс 1см2 (фиг. 212). Размеры
пружины Бурдона: R = 35 мм, а — 7 мм, Ъ = 1 мм, k = 0,5 мм, у — 270°.
Сечение плоскоовальное. Материал —латунь Л62; Я— 1,16.10е кгс/см2,
25 Заказ 24.
385
р = 0,3. Жесткость винтовой пружины кп = 0,13 кгскмм. Определить также пе-
ремещение конца трубки Бурдона по направлению касательной к ее оси при уве-
личении давления до рг = 40 кгс]см\
Решение. Начальное натяжение Со винтовой цилиндрической пружины
должно быть выбрано так, чтобы при давлении р < ро трубка Бурдона остава-
лась неподвижной, т. е. чтобы тяговая сила Ст, развиваемая трубкой Бурдона,
была меньше силы Qo начального натяжения винтовой пружины. Тогда конец
трубки Бурдона будет прижат к неподвижному упору с силой, равной Qo — Qt.
При р = ро величина тяговой силы равна силе предварительного натяже-
ния цилиндрической пружины; конец трубки Бурдона еще неподвижен, но сила
контакта между трубкой и упором равна нулю, т. е. Qo — Qt — 0. Из этого
условия и находим силу Qo предварительного натяжения цилиндрической вин-
товой пружины
Qo ~ IQ т1р=ро'
При давлении р>ро тяговая сила'становится больше силы натяжения пружи-
ны, трубка Бурдона отрывается от упора и совершает ход.
Так как винтовая цилиндрическая пружина ограничивает в данном случае
перемещение конца трубки Бурдона только по касательной к центральной оси
трубки, то для определения тяговой силы следует воспользоваться выраже-
нием (7. 36):
Qt — pab
Коэффициенты £ и £ находим по табл. 28: для пружины плоскоовального
сечения при
Г> определим по фиг. 210, где при у — 270° Г/ = 15,1.
Главный параметр и трубки Бурдона определяется по выражению (7. 10)
_ Rh 35*0,.5 _ п ок*?
х - у2 0,357.
Подставляя в выражение (е) р = ро, находим величину начального натяже-
ния винтовой цилиндрической пружины
— 7 коэффициенты £ = 0,488 и £ = 0,0602. Коэффициент
Со = 30 ♦ 0,7 • 0,1 1
1 \ 0,0602*15,1 =s
72 ) 0,488+ (0,357)2
Определим перемещение X; конца пружины по направлению касательной
при увеличении давления до рх. Винтовая пружина при этом растягивается
также на величину kt. В конечном положении на трубку Бурдона действуют
давление и сила Q± натяжения винтовой пружины, которую можно предста-
вить в виде
Ci=Co + ^ti kt, (ж)
где кп — жесткость винтовой пружины.
Величина кп . kt представляет собой увеличение
цилиндрической пружины при ее растяжении на kt.
Перемещение X/ трубки Бурдона равно
kt=ktp~ ktQ,
упругой силы винтовой
(3)
где kt — перемещение по касательной конца трубки Бурдона при изменении
давления от ро до рх; ktQ — перемещение при изменении силы
от Qo до Qx.
Если обозначить чувствительность по давлению трубки Бурдона в направ-
лении касательной через д/ , а по силе dfQ, то перемещения ktp и ktQ будут
Х/р = dtp (pi — Ро)
и X/q —dtQ (Qi Со)*
(и)
386
Подставляя выражения (и) в равенство (з), получим
&tO — Фо)-
kt=&tp (Pl —Po)
Заменим здесь по формуле (ж)
Отсюда искомое перемещение X/ равно
(Pi — Ро)
Чувствительность б/ по давлению в направлении касательной определится
в соответствии с выражением (7. 19) и (7. 22)
1 — ц2 Н3
kt =
bh
a2
sin у)
X2
Коэффициенты а п [3 находим по табл. 28: при ~г~— 7 « = С,372 и ₽ -
= 0,120. Тогда чувствительность по давлению
fP “ 1,16.106 1-0,5
0,120 + 0,3572
— 0,564 —
кгс/см L
/
Чувствительность 6/Q трубки Бурдона по силе можно определить с по-
мощью выражения (7. 32), где радиальная составляющая силы Qr = 0,
• kt 7?36fr
6,о - 07 = ~ •
следовательно,
Однако в данном случае чувствительность по силе можно определить более
простым путем. При давлении р = р о на трубку Бурдона действует сила Qo
начального натяжения винтовой пружины, равная тяговой силе Qt (е). Так как
при этом конец трубки Бурдона остается неподвижным, то
перемещения от давления ро и от тяговой силы Qo равны
б/
откуда
Ро
?О
30
Подставляя найденные числовые значения в выражение (к),
мое перемещение конца пружины Бурдона:
, (40 — 30) • 0,564
получим и CKO-
§ 44. РАСЧЕТ ТОЛСТОСТЕННЫХ МАНОМЕТРИЧЕСКИХ ПРУЖИН
СИЛЬНО ВЫТЯНУТОГО ПЛОСКООВАЛЬНОГО СЕЧЕНИЯ
Приведенные в § 40—43 расчетные формулы были получены для
тонкостенных пружин Бурдона, у которых толщина стенки h зна-
чительно меньше малой полуоси сечения Ъ. Однако для многих
25*
387
манометрических пружин это условие не выполняется, и тогда при
выводе расчетных зависимостей необходимо учитывать соизмери-
мость толщины h с полуосью Ъ. Такое решение для пружин толсто-
стенных с сильно вытянутым плоскоовальным сечением (фиг. 213,а)
дано в работах [1], [14] и [39]. Расчетная схема пружины выби-
рается в виде двух цилиндрических оболочек, соединенных жестко
по краям; деформации закругленных участков не учитываются. Это
допущение вносит некоторую погрешность в расчет, тем меньшую,
чем более вытянуто сечение.
Решение этой задачи, проводимое энергетическим методом [1],
[14] или по теории цилиндрических оболочек [39], приводит к почти
одинаковым результатам. Приведем расчетные формулы, получен-
ные В. И. Феодосьевым в работе [1].
Относительное изменение центрального угла пружины Бурдона
определяется по формуле
Ду __ 1—р2 К2 1 — %
~у~ "" Р Е bh А , h2 *
X + . о г 2
12 о2
(7.40)
здесь коэффициент % представляет собой
1 sh2 са 4- sin2 са
са sh са • ch са 4- sin са • cos са ’
где а — большая полуось, а параметр с =
R2h2
Величину х можно также определять по графику, приведенному
на фиг. 213, б.
Для определения линейных перемещений конца пружины
Бурдона можно воспользоваться геометрическими соотношениями
(7. 18) — (7. 20), полученными в § 40.
В табл. 29 приведены результаты сопоставления расчета по
формуле (7. 12) для тонкостенных и по формуле (7. 40) для толсто-
стенных пружин с результатами опыта [96]. Подсчитанные примеры
показывают, что формула (7. 12), выведенная для тонкостенных
пружин, дает удовлетворительное совпадение с опытом в широком
интервале геометрических соотношений пружин. Лишь для послед-
них четырех пружин расчет по формуле (7. 40) дал
лучшие результаты, чем по формуле (7. 12), так как эти пружины
имеют сильно вытянутое
и толстостенное
h
~ 0,8 -г 1,2) сечение.
Вывод формул для тягового момента и тяговых
сил толстостенных пружин производится таким же путем, как
и для тонкостенных. Для толстостенных пружин тяговый момент
равен
; ’ . Мт =' kpRdb (1 — X)• (7.41)
388
Jh.
Фиг. 213.
a — толстостенное сечение; б — график коэффициента X.
389
со
Таблица 29
Сопоставление экспериментальных значений чувствительности трубчатых пружин с расчетными
Бца по [96] + ? о Материал R в мм у0 4 h в мм а в мм ъ в мм * а Ь h b
Си и
со
а
ф га
% Л -
22
25
26
29
30
46
47
50
51
53
250
251
252
253
2,11
4,22
4,22
7,03
7,03
141
98,5
352
352
281
7.03
14,06
28,12
42,18
255 56,24
256 56,25
тт Av Е
Чувствительность —1-----------
V Р(1—Ц2)
Фосфори-
стая бронза
Берил-
► лиевая
бронза
Фосфори-
стая бронза
к Нержа-
I веющая
I сталь
52,3
41,1
52,3
41,1
,52,3
18,3
18,0
18,3
18,8
20,8
19,9
19,9
19,9
19,9
19,9
19,9
241
228
241
228
241
245
250
250
250
300
1800
1800
1800
1800
1800
1800
0,381
0,431
0,534
0,534
0,660
0,559
0,559
0,812
0,812
0,762
0,305
0,407
0,508
0,610
0,407
0,610
10,4
10,4
10,4
10,5
10,5
3,30
3,42
3,04
2,92
2,97
4,70
4,70
4,62
4,57
4,57
4,44
3,05
3,02
3,17
3,12
3,22
0,914
0,584
0,890
1,17
1,22
0,685
0,635
0,584
0,508
0,381
0,508
3,40
3,44
3,28
3,36
3,26
3,62
5,85
3,42
2,50
2,44
6,86
7,40
7,91
9,00
12,0
8,74
0,125
0,143
0,168
0,171
0,205
0,612
0,957
0,913
0,694
0,625
0,443
0,639
0,869
1,20
1,07
1,20
7200
4000
3800
2400
2300
230
360
57
39
53
3440
1890
1030
665
5870
3380
3340
2460
2280
250
402
66
44
54
3240
1980
1260
880
18,5
15,5
12,1
—2,5
0,87
-8,7
—41,7
—15,8
—12,8
—2,3
5,8
—4,8
—22,4
-17,3
4550
2760
2210
1860
1620
153
275
39
27
32
2470
1410
864
584
37
31
42
22,5
30
33,5
29
31
30
39
28,2
25,4
16,3
12,2
2335
654
2900
810
—24,2
—23,8
1980
542
15,2
16,9
Тяговая сила при ограничении линейного перемещения в направ-
лении касательной [ср. с формулой (7. 36) ] равна
Qt = раЪ (1
Мт г/
24К ’
а в радиальном направлении
4 Мт Г
Q, = pab (1 - %) Г, = .
§ 45. О РАСЧЕТЕ НА ЖЕСТКОСТЬ МНОГОВИТКОВЫХ
ТРУБЧАТЫХ ПРУЖИН
Винтовые
пружин ы
(см. фиг. 191,
б) обычно имеют малый
угол подъема центральной оси, и если принять его равным нулю, то все расчет-
ные формулы, выведенные для пружины Бурдона, остаются в силе. Угол у для
винтовой пружины равен у = 2л i , где i— число витков.
Расчет винтовых пружин с учетом угла подъема винтовой линии в настоящее
время еще не разработан.
Спиральные и S-образные пружины (см. фиг. 191, в и г) не имеют расчета
в законченной инженерной форме, хотя он может быть создан на основе теории
пружин Бурдона.
При расчете спиральной пру-
жины нужно учитывать переменность
радиуса кривизны оси пружины. Для
бесконечно малого элемента кривизну
можно считать, постоянной, тогда взаим-
ный угол поворота сечений элемента в соот-
ветствии с формулами (7. 12) и (7. 16)
будет
dfi=p
bh
где dQ —центральный угол элемента.
Если пружина имеет толстостенное
вытянутое сечение (см. фиг. 213, а), то
при определении d й следует исходить из
формулы (7. 40).
Угол поворота концевого сечения
спиральной пружины
Фиг. 214, К определению пере-
мещений S-образной пружины.
Ду =
^й =Р
Ь'2 \ а /’ R2d 6
а2 j bh J 0-|-х2
1 о
Зная форму спирали, можно определить интеграл в этом выражении гра-
фическим или аналитическим путем.
При расчете S- о б р а з н о й пружины ее можно представить как
несколько последовательно соединенных пружин Бурдона. Если перемещеттие
конца пружины Бурдона определяется формулой (7. 17)
У г/
о
391
то для S-образной пружины оно равно
/Ду\ „ „ „
здесь — относительным взаимный угол поворота концевых сечении i-ro
участка, определяемый формулой (7. 12) или (7-4©);
Мг— момент от единичной силы, приложенной к концу пружины
в направлении искомого перемещения;
п — число участков.
Чтобы определить полное перемещение Л конца S-образной пружины, сле-
дует найти сначала вертикальную и горизонтальную составляющие Х е и Хг
(фиг. 214), а затем
§ 46. НАПРЯЖЕНИЯ, ВОЗНИКАЮЩИЕ В МАНОМЕТРИЧЕСКИХ
ТРУБЧАТЫХ ПРУЖИНАХ
Приближенный метод Ритца при определении напряжений дает
худшие результаты, чем при определении перемещений. Поэтому
формулы этого параграфа могут быть использованы только для
приближенной оценки величин напряжений, возникающих в мано-
метрической пружине под действием давления. Следует также иметь
в виду, что в манометрической пружине сохраняются остаточные
напряжения, появляющиеся при изготовлении пружин. Эти напряже-
ния могут оказать существенное влияние на прочность пружины.
Формулы, приводимые ниже, не учитывают этого влияния и, по-
видимому, они будут более пригодны для расчета на прочность
пружин из дисперсиоино-твердеющих сплавов, чем для пружин из
нагартовываемых материалов, в которых сохраняются высокие
остаточные напряжения.
Пределы применимости приводимых здесь формул пока не устано*
влены из-за отсутствия экспериментальных работ по определению
напряжений в манометрических трубчатых пружинах.
В трубчатой пружине, нагруженной давлением, возникает двух-
осное напряженное состояние (фиг. 215,а). Осевое и поперечное а
напряжения связаны с соответствующими деформациями е
законом Гука
2
и 8<*
(а)
Деформации ех и е2 определяются выражениями (7. 1) и (7. 2)
w
и е2 = z • Ах.
Здесь w — перемещение произвольной точки контура попереч-
ного сечения в направлении оси у (см. фиг. 198, в) — может быть
определено по формуле (7. 6):
Относительный угол поворота
(7. 12)
_____ 1—р.2 в2
~у“ — Р Ё~ ~bh
т
Ду
определяется выражением
52
2
Фиг. 215.
а — напряжения в пружине Бурдона; б — координаты произвольной
точки для пружины плоскоовального ив — эллиптического сечений.
Изменение кривизны Дх контура поперечного сечения согласно
формуле (7. 7) равно
Дх =Q.
та 2
После подстановки указанных величин в формулы (а) напря-
жения ог и ст2 в произвольной точке наружного или внутреннего
контура поперечного сечения можно представить в виде
(7. 42)
где р — рабочее давление;
7? — радиус центрдльной оси пружины;
а и b — полуоси сечения;
Rh
х — —g- — главный параметр пружины;
Л
h — толщина стенки;
393
Q и Ф = о-----cos ф — функция положения точки на контуре,
определяемого координатами х и ф (фиг. 215, б и г).
Формулы для величин Q и Ф даны в приложении IV, а числовые
а — плоскоовального и
значения — на фиг. 216. Коэффициент 0 приведен в табл. 28.
Знак «плюс» (+) в выражениях (7. 42) соответствует наружному
а знак «минус» (—) внутреннему
контуру
поперечного сечения пружины (фиг. 215,6).
394
Напряжения, возникающие в пружине, постоянны по ее длине,
если постоянна кривизна о’си пружины (пружина Бурдона, винто-
вая пружина), поэтому все сечения таких пружин равноопасны (не
считая мест закреплений).
б — эллиптического сечений.
При определении напряжений в пружинах переменного ради-
уса R (например, в спиральных) следует рассматривать опасное
сечение, которое будет гам, где радиус R достигает наибольшего
значения.
395
Пример 4. Построить эпюры напряжений и сгг для пружины плоско-оваль-
ного сечения размерами: R — 40 мм, а = к мм, Ъ — 1 мм, h ~ 0,16 мм при
давлении р = 1 кгс/см2. Коэффициент Пуассона материала ц =0,3.
Решение. Определим главный параметр пружины х — -
Rh 40-0,16
= 0,4 и коэффициент 0 по табл. 28: при ~
= 4, коэффициент р — 0,121.
Подставляя числовые значения в формулы (7.42), получим
1 4а ) 0,121 + 0,42 (о,4 Ф ± 0,3 —1000 * 0,3
сг2' = Ю00 (± Q + 1,5Ф).
Функции Q и Ф определяются по фиг. 216, а при -|- = 4. Результаты даль-
нейших вычислений даны в табл. 30.
Таблица 30
Результаты расчетов примера 4
Координаты точки х; ф Ф Q Наружный контур Внутренний контур
04 02 01 02 0ЭК8
0 0,0491 0,425 374 499 451 118 —351 422
1 0,0417 0,387 324 449 401 92 —324 378
а — b X = 2 0,0210 0,275 188 307 268 23 —244 256
3 X (а — &) —0,0097 0,0875 —22,3 73 86 —75 —102 92
е II а —0,0423 -0,175 —264 —238 252 —160 112 237
Ф = 15° —0,0503 —0,278 —335 —353 345 —169 322
ф - 30° —0,0517 —0,375 —371 —453 419 -146 297 [ 391
Ф = 45° —0,0463 —0,458 —370 —527 469 -95 389 444
Ф — 60° —0,0348 —0,521 -330 —573 498 -18 469 478
Ф = 90° 0 —0,575 —172 —575 511 172 575 511
На фиг. 217 на основании этой таблицы построены эпюры распределения
напряжений 04 и <т2 по наружному и внутреннему контурам.
Распределение напряжений 04 и ст2 вдоль контура поперечного
сечения довольно сложно, и положение опасной точки может быть
396
в различных местах поперечного сечения в зависимости от соотноше-
ния размеров пружины.
При расчетах на прочность нужно определить величину эквива-
лентного напряжения. Воспользуемся для этого энергетической
теорией прочности, по которой эквивалентное напряжение при
двухосном напряженном состоянии может быть вычислено по
формуле
(7-43)
На фиг. 217 построены эпюры оэкв по наружному и по внутреннему конту-
рам поперечного сечения пружины, размеры которой указаны в примере 4;
числовые значения эквивалентных напряжений для этой пружины приведены
в табл.30.Опасными в данном случае оказались точки А и В по концам большой
осп сечения, где о9кв = 511 кгс/см*.
Фиг. 217. Эпюры напряжений Оа ^.(Уэкв по наружному и внутреннему кон-
турам поперечного сечения. *
Зная предел текучести материала пружины, можно определить
от
коэффициент запаса пружины пг= --------.
1 (Уэкв
Положение опасной точки зависит от соотношений размеров
пружины. На фиг. 218 построены эпюры оЭКе в наиболее напряжен-
ных точках наружного или внутреннего контура поперечного плоско-
овального сечения при различных отношениях полуосей сечения
/ “ = 2; 4 и 10Х Bh
и при главном параметре пружины и ~ —-
Cv
Эпюры Оже показывают, что для трубки с отношением осей
-т- — 2 опасные точки располагаются по концам малой оси сечения
независимо от величины параметра %. При увеличении вытянутости
а
сечения, которая характеризуется отношением у, положение опас-
ной точки смещается и при ^>4 и к >>0,4 опасная точка будет
располагаться по концам большой оси сечения (ср = 90°). Поскольку
397
a
Фиг. 218. Эпюры стэкв в наиболее напряженных точках на-
ружного или внутреннего контура поперечного сечения
пружины плоскоовальной формы при различных соотно-
шениях размеров.
398
коэффициент Ф при ф — 90° равен нулю, то формулы (7. 42) для
подсчета напряжений в точках А п В {см. фиг. 215) упрощаются:
/ ь2 \ 3
^2 ~ ± Р I 1 ) R !_у2 О'1 ~ Р°2’
Тогда напряжение о же в точках А и В при р = 0,3 будет
„ В2 /, b2\ 2,66 о ‘ //х
(Уже р 2 (п2 I g_рх2 ’ ' (7.44)
Здесь коэффициент Q берется по абсолютной величине из фиг. 216
или для пружин плоскоовального сечения из табл. 31.
Таблица 31
Значения коэффициента Q при ср — 90° для пружин плоскоовального
сечения
а ь 1,5 2 ч 3 4 5 1 1 6 7 8 9 10
я —0,446 —0,494 —0,547 —0,575 —0,593 —0,605 —0,613 —0,620 —0,625 —0,629
В соответствии с выражениями (а) и (б) распределение напря-
жений сг2 по толщине стенки имеет линейный характер. Следует,
однако, иметь в виду, что при достаточно большой кривизне закруг-
ленных участков сечения характер распределения напряжений
изменяется. Напряжения ст2 на внутреннем контуре будут больше,
чем на наружном и так же, как в брусе большой кривизны,
эпюра напряжений по толщине стенки становится гиперболической
(см. фиг. 215, б). Можно весьма грубо учесть увеличение напряже-
ний во внутренней точке закругленного участка, как .
(Сэке) max
(7.44')
где коэффициент К зависит от отношения радиуса кривизны Q сред-
него контура сечения в точке С (см. фиг. 215, б, в) к толщине стенки h
и определяется по формулам кривого бруса [34]. Радиус о для
плоскоовального сечения равен малой полуоси Ь, а для эллипти-
Ъ2
ческого сечения радиус кривизны в точке С равен— . Значения
коэффициента К в зависимости от отношения даны в табл. 32.
Таблица 32
Значения коэффициента К
Q h 0,6 0,7 0,8 0,9 Jh 1,0 1,2 1,4 1,6 1,8 2,0 3,0 4,0 5,0
2,89 2,10 1,80 1,63 1,53 1,39 1,32 1,26 1,23 1,20 1,13 1,10 1,09
399
Итак, из анализа эпюр в9ке для пружин плоскоовального сече-
ния следует, что если отношение осей сечения > 4, а главный
параметр пружины х 0,4, то расчет на прочность может произ-
водиться по формуле (7. 44) или с учетом поправки на кривизну се-
чения в месте закругления — по формуле (7. 44').
Если отношение -у < 2, то опасными являются точки по концам
малой оси, где х = 0 (фиг. 215, б).
Для пружин с отношением осей 2 < -т- < 4 и главным пара-
метром и <Z 0,4 прежде
чем производить расчет на
прочность,
необходимо определить положе-
ние опасной точки, для чего
с помощью зависимостей (7. 42) и
(7. 43) следует построить эпюру
оэкв по контуру поперечного сече-
ния.
Более просто значения наи-
больших эквивалентных напря-
жений в пружинах плоскооваль-
Фиг. 219. Схема жид-
костного манометри-
ческо го термо метра.
ного сечения можно определять с
помощью номограмм (см. фиг. 224),
которые также могут служить
целям проектирования трубчатых
пружин (см. § 47).
Пример 5. Пружина Бурдона жид-
костного манометрического термометра
(фиг. 219), измеряющего температуру
в интервале от 0 до 300° С, имеет сле-
дующие размеры: радиус кривизны оси
пружины R = 19,2 мм, большая и малая
полуоси плоскоовального сечения а =
= 4,8 мм и 6=0,8 мм, центральный угол
материал пружины сплав Н36ХТЮ (ЭИ702); модуль упру-
104 кгс/.мл2, предел текучести ит = 100 кгс!мм2. Коэффициент
пружины у = 270°
гости Е = 2,1 .
линейного расширения [материала термобаллона а/ = 11,7 .10—6град.~Б Объем
। мм3. Заполняющая систему жидкость — ртуть,
1,81 . 10“4 град-1.
термо балле на V = 585
объемный коэффициент расширения которой 0/ =
Определить полный ход пружины и подобрать толщину стенки из расчета
на прочность, обеспечив коэффициент запаса по текучести не менее 1,8.
Решение. При нагреве термобаллона на Д t ртуть расширяется на
Р/ VД t, а термобаллон увеличивает свой объем на За/ - РД2. Следовательно,
при нагреве из термобаллона будет вытесняться ртуть объемом
ДЕ = (Р/-За/) V . Д t =(1,81 • 10~4 —3 • 11,7 • 10“6) X
X 585 • 300=26,6 мм3.
На столько^же увеличит прижина Бурдона объем своей внутренней
полости. При этом конец пружины совершит ход, величина которого связана
с изменением объема зависимостью (7. 25")
ДЕ = 12Л абу 1 —
400
При -г- = ~q = 6 коэффициент а = 0,388 и.п = 0,126 (см. табл. 28 на
О U j О
стр. 370). Из фиг. 205 следует, что при у = 270° коэффициент Г = 5,8. Следова-
тельно, перемещение конца пружины будет
A V • аГ • 26,6 • 0,388 - 5,8
/ ъ2\ з 7 ГТ-------------- “
12«& у (1----2” п 12-4,8-0,8- —л (1 — —-1-0,126
\ <2 / Z \ oz I
' \ /
= 2,25 мм.
Так как отношение осей сечения ~г-~ 6, то можно предположить, что опас-
ная точка расположена по концам большой оси сечения, где угол <р = 90°
(фиг. 215, б). После определения толщины стенки h это предположение можно
проверить, подсчитав главный параметр х.
Эквивалентное напряжение в точке (р = 90° определяется по формуле
О'экв ~
W
2,66
2
Здесь давление р заполняющей систему жидкости связано с перемещением
X соотношением (7. 21)
1 —|ц2 ' 62 \ Га
Е bh Г а2/ р + х2 ‘
Исключая из последних двух выражений давление р, определим толщину h
1 —p,2 Ra2 о'экв Га
“ё Ь 2,66 [ Q |
Примем коэффициент запаса по текучести ит= 2,5. Тогда в опасной точке
°т 100
^экв — ---— -х — 40 кгс!см2. Коэффициент Q находим по табл. 31: при
6 и ф = 90° коэффициент Q = —0,605. Подставляя числовые значение
в последнюю формулу, получим
_1 — 0,32 19,2-4,82 40 5,8-0,388 _
~2,1 • 104 0,8 2,25 2,66 - 0,605 =
Определим теперь главный параметр х
Rh = 19,2 -0,6 _ 0
а2 4,82
скольку при этом-г- > 4, опасная точка пружины действительно будет рас-
положена по концам большой оси (см. фиг. 218).
Уточним величину напряжений во внутренней точке контура с помощью
выражения (7. 44')
эке) шах = К
Отношение радиуса кривизны р контура к толщине h будет ~ =
1,33. При этом коэффициент к = 1,35 (табл. 32). Следовательно,
(с?экв)тах = 1>35 • 40 = 54 кгс/мм*
и коэффициент запаса
gT = 100
(Оэхе)тах 54
26 Заказ 24.
401
Пример 6- Как изменится прочность пружины, размеры которой указаны
в условии примера 4, если изменить ее сечение: вместо плоскоовальной придать
сечению эллиптическую форму.
Решение.
Для эллиптического сечения при отношении осей
коэффициент Р = 0,044 (см. табл. 28), и формулы (7. 42) для напряжений и
<т2 после подстановки числовых значений примут вид
<у1==1380(5Ф ± 3Q);
о2 = 13S0 (± Й-Н,5 Ф),
здесь коэффициенты Ф и Q берутся из фиг. 216, б. Эпюра эквивалентных на-
пряжений сгэкв, подсчитанных по энергетической теории прочности в наиболее
напряженных точках наружного или внутреннего контура, дана па фиг. 220.
Наибольшие напряжения появляются в точках Л и В (фиг. 215, в), где они
достигают значения 775 кгс/см2. Для пружины плоско овально го сечения наи-
большее напряжение было равно 511 кгс/см2. Таким образом, пружина эллипти-
ческого сечения в 1,5 раза менее прочна, чем пружина плоско овально го сечения
при данных размерах.
Разница в величинах расчетных напряжений получится еще большей, если
учесть увеличение напряжений во внутренних точках закругленных участков.
При одинаковых размерах полуосей а и Ь радиус q кривизны в точке А контура,
равный для эллиптического сечения—, будет меньше, чем для плоскоовального
0, _ Л
сечения, в — раз. Подсчитаем напряжения в точках А
коэффициента К увеличение напряжений. Для плоскоовального сечения при
р _ b
~h
тического
Q _ Ь2
= 6,25 коэффициент К
учитывая с помощью
0 16 ___г___’___ — - 1 (см. табл. 32); для пружины эллип-
сечения отношение радиуса кривизны в точке А к толщине равно
1,27. Отношение напряжений
4 • 0,16
= 1,56 и при этом К
h ah
в пружинах эллиптического и плоскоовального сечений будет в этом случае
(о’тах)эл
(^тах) ПЛ
1,27 • 775
1-511
Если манометрическая трубчатая пружина нагружена внешними
сосредоточенными силами и моментами, то напряжения в ней
402
можно подсчитать с помощью следующих формул, вывод которых
аналогичен приведенному выше для случая действия давления [1}
— м
— М
°2 &abh
а
п (0-|-И2)
а
п (р -рИ2)
(7. 45)
здесь М — изгибающий момент в опасном сечении пружины. Вели-
чины со и Q даны на фиг. 216 и 221 в зависимости от формы
сечения и координаты (р или х точки на контуре. Коор-
Фиг. 221. График коэффициента <а.
дината у = b cos <р для эллиптического сечения; для плоскооваль-
ного сечения у — b на прямолинейном и у — b cos ср на закруглен-
ном участке. Коэффициенты а, (3, п, £ и £ даны в табл. 28.
Положение опасной точки при изгибе манометрической пружины
внешним моментом зависит от соотношения размеров пружины.
ti Uh /
Вели параметр х — —* велик (толстостенная пружина малой
Gs №
26*
403
Фиг. 222. Эпюра при изгибе цру-
жины внешним моментом.
кривизны), то опасной, как и в брусе сплошного сечения, будет
точка, наиболее удаленная от нейтральной оси х (фиг. 222). При
уменьшении параметра х, т. е.
с увеличением кривизны тон-
костенной пружины эпюра
продольных напряжений ст±
становится криволинейной и
может стать знакопеременной
при достаточно малом х. Такой
характер изменения напряже-
ний связан со сплющиванием
сечения при изгибе тонкостен-
ных пружин большой кривизны
(см. § 42). Если пружина одно-
временно нагружена давлением
и внешними силами, то по формулам (7. 42) находим напряжения от
давления, по формулам (7. 45) — от момента, и результаты сум-
мируем с учетом знака напряжений.
§ 47. ПРОЕКТИРОВАНИЕ МАНОМЕТРИЧЕСКИХ ТРУБЧАТЫХ ПРУЖИН
Для успешного проектирования трубчатой пружины, как и лю-
бого упругого элемента, необходимо знать влияние различных
геометрических параметров на ее жесткость и прочность. Некоторые
соображения о влиянии толщины h, радиуса R кривизны пру-
жины, отношения -г- осей сечения и его формы на чувствительность
и прочность манометрических пружин были изложены в § 39.
С помощью формул, приведенных в § 40, 43 и 46, на фиг. 223
построены семейства кривых, иллюстрирующих влияние отношения
полуосей сечения и относительной толщины — на жесткость, проч-
ность и величину тягового момента пружин плоскоовального сече-
ния. Графики построены для пружин при двух значениях относи-
R
тельного радиуса кривизны — == 4 и 8. По оси ординат отложены
tt1
безразмерные величины
и
Величина Е
У Р
характеризует
Мт
pR3
чувствительность
Относительный угол поворота
формулой (7. 12); упругая постоянная
концевого сечения
определяется
пружины.
пружины
материала
— рабочее давление.
Отношение -у- определяет величину наибольшего напряжения,
возникающего в пружине. Здесь через о обозначено наибольшее
эквивалентное напряжение (сгэке)тах,
(7. 44) с учетом поправки (7. 44').
вычисляемое по формулам
404
В безразмерную величину входит тяговый момент Мт,
который вычисляется по формуле (7. 34). Величина момента М
связана выражениями (7. 35) и (7. 36) с тяговыми силами Qr и Qt.
Расположение кривых на фиг. 223 указывает, что с увеличением
отношения 4
Ъ
быстрее, чем меньше относительная толщина
в большой степени зависит от отношения —• ,
о
чувствительность и напряжения возрастают, и тем
h
— . Тяговый момент
а
быстро убывая с уве-
личением вытянутости сечения (при — = const), и значительно
меньше Зависит от относительной толщины -у . Сопоставление
кривых на фиг. 223, а с кривыми на фиг. 223, б показывает, что
R
с увеличением относительного радиуса — чувствительность и на-
Л
пряжения возрастают почти пропорционально изменению радиуса.
Как указывалось в § 39, существенное влияние на свойства
манометрических пружин оказывает форма поперечного сечения.
Например, пружина эллиптического сечения более чувствительна,
но менее прочна, чем пружина плоскоовального сечения (см. также
примеры 1 и 6). Пружина с сечением в виде «восьмерки» обладает
наибольшей прочностью и жесткостью (см. фиг. 199, а). В каждом
конкретном случае можно подобрать формусечения, наивыгоднейшую
как по требуемой чувствительности, так и в отношении прочности.
Для полного решения этой задачи необходимо располагать расче-
том пружины произвольной формы сечения*. Однако в настоящее
время расчетные формулы созданы только для пружин плоскооваль-
ного и эллиптического сечений, хотя разработанный В. И. Фео-
досьевым метод £1 ] применим к любой форме сечения.
С помощью фиг. 223 построены номограммы (фиг. 224) для приб-
лиженного расчета и проектирования пружин плоскоовального
сечения с относительным радиусом центральной оси — — 2; 4;
Л
6 и 8. По оси абсцисс отложены отношения осей сечения, а
h
ординат — относительные толщины —
по оси
и построены три семейства
Ду Е'
const, прочности
линии: постоянной чувствительности
ст . Мт
— = const и тягового момента —=
р pR
Если размеры пружины известны, то с помощью номограмм на
фиг. 224 можно легко провести поверочный расчет трубчатой пру-
жины плоскоовальной формы поперечного сечения.
const.
Пример 7. Определить угол поворота, тяговый момент и запас прочности
винтовой трубчатой пружины глубинного манометра на 80 кгс/см2. Размеры
пружины R — 10 мм, а — 4,8 мм, b == 0,53 мм, h — 0,7 мм, число рабочих
витков i = 20. Сечение имеет плоско овальную форму. Материал пружины —
405
У P
12000-
11000-
10 000
9000
8000
7000
6000
5000-
№
4000 -
3000 -
2000 -
1000 -
о.
Фиг. 223. Влияние геометрических параметров пружины на чувствительность
выраженные в безраз
406
мерных величинах.
407
Фиг. 224. Номограмма для проектирования трубчатых пружин плоско овально го сечения.
бериллиевая бронза Бр. Б2,5; модуль упругости Е — 1,35 . 10е кгс; см2; предел
текучести <jt = 11 000 кгс} см2.
Решение. Определим относительные размеры пружины
При этих значениях находим по номограмме на фиг. 224, а
р ’ у Р ’ р№ ’ ’
откуда после подстановки числовых значений р = 80 кгс/см2,
= 360° • 20 = 7200°
_ 1,35 • 106
= 360°•i =
= 1,48 . 106 кгс/см2 получим
о=4960 кгс/см2, Ду = 175° и Л/т = 5,44 кгс. см.
Запас прочности
пружины равен
_ ст __ 110G0
(Оэкв) щах 4960
Также просто с помощью номограмм может быть произведен
подбор размеров пружины по заданным величинам чувствитель-
ности, прочности и тяговых усилий. Однако при этом следует иметь
в виду, что такой расчет является весьма приближенным, особенно
в части определения напряжений, и окончательно размеры пружины
должны быть уточнены по результатам испытания опытных образцов.
Пример 8. Подобрать размеры пружины Бурдона для манометра на давле-
ние 5 кгс/см2, если по диаметру она не должна быть больше 100 ллг,а по ширине —
18 мм. При наибольшем давлении р перемещение конца пружины должно быть
5 мм. Пружина должна развивать в радиальном направлении тяговую силу не
менее 0,63 кгс. Коэффициент запаса по текучести пт > 3. Материал — сплав
Н36ХТЮ (ЭИ702), модуль упругости Е = 2,15 . 10е кгс/см2, предел текучести
о У = 9500 кгс/см2.
Решение. Из габаритных условий зададимся радиусом оси пружины
R = 48 мм и большой полуосью сечения а= 8 мм.
Центральный угол у примем равным у = 270°.
Подсчитаем по заданным условиям безразмерные величины чувствительно-
Ду Е' а Мт
сти —- — , напряжения — и тягового момента ——3 .
По величине полного перемещения конца пружины X = 5 мм находим по
формуле (7. 20) относительный угол поворота конца пружины гДе
коэффициент Г определяется по фиг. 205: при у = 270° Г = 5,80. Следовательно
Ду 5 пп.ол
— — и тогда относительная чувствительность равна
7
Ду
Т~
= 0,0180
Е
(1 —р,2)р
=0,0180
2,15 • 10»
(1- 0,32) • 5
= 8500.
Допускаемое напряжение [ст ] находим по заданному коэффициенту запаса
по текучести
9500
— —-— = 3160 кгс/см2
410
п тогда относительное наибольшее напряжение будет
ст 3160 _
Мт
Определим теперь относительный тяговый момент - 3- . Тяговое уси-
лие Qr, развиваемое пружиной (если исключено перемещение ее конца в ра-
диальном направлении), выражается через тяговый момент с помощью форму-
лы (7. 35):
МТГГ
Ог = - - - .
V 24Л ’
где при у = 270° коэффициент Гг = 10,2 (см. фиг. 210).
Отсюда
мт = Qr- 24
р№ pH2. Гг
0,63 -24
5 • 4,82 • 10,2
= 0,0129.
По номограмме на фиг. 224, в (для —
„ Мгг
8500 и
находим точку пересе-
Ду Е' _
чения кривых ————— —
h а - -
—. 0,05 и -г- = 5,5,
а малая полуось сечения b
—д3- = 0,0129. Координаты этой точки равны
следовательно, толщина h = 0,05 • 8 = 0,4 мм,
8
- = 1,4 мм. При этом — 3UU, что соответ-
Р
ствует наибольшему напряжению а = 300 • 5 --- 1500 кгс!см2. Коэффициент запаса
9500
по текучести равен пт =
условию задачи. Таким образом в данном случае можно, скользя по кривой
Ду Er f-
—L —— = 8500 влево, остановиться на [пружине с меньшей толщиной h и
большим размером полуоси Ъ. Такая пружина будет развивать большую тяго-
вую силу при меньшем коэффициенте запаса по текучести.
= 300,
= 6,3, т. е. вдвое больше, чем требуется по
ПРИЛОЖЕНИЕ I
I
ВЫВОДЫ НЕКОТОРЫХ ЗАВИСИМОСТЕЙ К ГЛАВЕ V
1. Вывод уравнений плоской мембраны в больших перемещениях [1], [47]
Составим уравнения равновесия для элемента, вырезанного из деформиро-
ванной мембраны (фиг. 225,а). При этом будем считать угол тЭ1 поворота нормали
достаточно малым и поэтому примем cos$ 1 и sin "О*
Начало координат поместим в центре тяжести 0 элемента, ось | направим
по касательной к меридиану элемента, осьм — по нормали, ось £ — перпенди-
кулярно плоскости £0v.
Спроектируем все силы на ось v
— (Trrdy)]
4~ Ф *4“
d (Qr <7ф) ] — Ttdrdy ф — Tyrdq —
— Qrd ф — prdrd ф = 0.
Отсюда, пренебрегая малой высшего порядка
d(TrrdV)
получим
(Ттг) + (Qr)'+рг=0.
(а)
Здесь ( )' означает производную —.
Составляя сумму моментов относительно оси £ и пренебрегая малыми
высших порядков, получим
[Myrd ф d (Mrrd ф)] — Mfdrd ф — Mrrd ф—
откуда
— Qrd (pdr = О,
Mt — (Мгг)/ + (?г = 0.
(б)
Поперечную силу Q определим, рассматривая равновесие центральной
части мембраны (фиг. 225, б). Проектируя все силы на ось симметрии, получаем
— Q2n г + Тг2я г О р № =0,
откуда
412
Подставляя последнее выражение и его производную в уравнения равнове-
сия (а) и (б), получим
(Tzr)'-Tz=0; (8.1)
(Mr.r)'-Mt==-?£-+T,r$. (8.2)
Для составления уравнений совместности перемещений рассмотрим линей-
ный элемент АВ осевого сечения серединной поверхности до и после нагру-
жения (фиг. 225, в).
5}
Фиг. 225. К выводу уравнений пло-
ской мембраны в больших переме-
щениях:
а — внутренние силовые факторы; б — рав-
новесие центральной части; в — элемент
срединной поверхности мембраны до и
после нагружения.
В результате деформации элемент АВ получает относительное удлинение
еГр. Длина деформированного элемента будет dr(l -J- еГр). Обозначим ip и v —
составляющие перемещения в осевом и радиальном направлениях. Спроектируем
замкнутый многоугольник на радиус г
v-\-dr (1 +Srp) cos О — (v4-dv)— dr=Q.
Подставляя cos О как 1 —
й2
Проекция многоугольника на ось z
w-\-dr (14-вгр) й — (ip + dw) = О
413
приводит, если пренебречь еГр по сравнению с 1, к известному соотношению
(5. 3) между прогибом и углом поворота тЭ — w'.
Относительная деформация растяжения срединной поверхности в окружном
. направлении efp определится как отношение приращения длины окружности,
на которой находится точка В, к первоначальной длине.
2л (г + v) — 2л'г
8/₽ ~ 2л г
или
v
(8. 3)
Подставляя значение v = е/ . г в уравнение совместности
(в), получим
деформаций
(8.4)
Напряжения растяжения срединной поверхности связаны с усилиями соот-
ношениями
__Тг ________ Tt
GrP~~ h ’ h
(h —толщина стенки мембраны).
На основании закона Гука выразим деформации еГр и е/ через усилия
в срединной поверхности Тг и Tt
р) —
Eh
(8. 5)
Eh
(Tr-pTty,
(Tt-fiTr).
Заменяя в уравнении совместности деформаций (8. 4) относительные де-
формации е, и по формулам (8. 5) и учитывая соотношение (8. 1), получим
Л 2
_г (ТггГ - (Тгг)‘ + Тг = —- Eh.
(8. 6)
Уравнение (8. 6) содержит две неизвестные величины: радиальное растя-
гивающее усилие Тг и угол поворота 'О*.
Второе необходимое для решения уравнение можно получить на основании
уравнения равновесия (8. 2), где изгибающие моменты Мг и Mt связаны с углом
поворота ft соотношениями (5. 7), которые были получены в § 24 при рассмо-
трении изгиба пластинки
Mr — D
Mt=D (
здесь D — жесткость оболочки на изгиб — определяется выражением (5. 8).
Заменяя в зависимости (8. 2) моменты Мг и Mt выражениями (г), получим
второе уравнение, связывающее неизвестные 77 и "ft
(8. 7)
414
Теперь осталось привести уравнения (8. 6) и (8. 7) к безразмерной форме.
В этом виде уравнения (5. 31) плоской мембраны в больших перемещениях даны
в § 24.
2. Вывод уравнений плоской анизотропной мембраны
в больших перемещениях
Уравнения равновесия и уравнения совместности деформаций для ани-
зотропой мембраны будут такими же, как и для изотропной [см. уравнения
(8. 1) — (8. 4)]. Различными будут лишь уравнения, связывающие деформации
с усилиями. Для анизотропной мембраны связь между деформациями и напря-
жениями выражается уравнениями (5. 55).
Напряжения растяжения срединной поверхности определяются через уси-
лия 7\. и Tt (см. фиг. 225, а) по выражениям
h ’
Gt? h
(h — толщина стенки мембраны).
Подставляя выражения сгг и <Т/р в уравнения (5. 55) и учитывая соотно-
шения (5. 51) и (5. 52), получим деформации срединной поверхности анизотроп-
ной мембраны
р ___ ^2 /гр Ц гр \ .
Сгп--- >7. U Г----J I >
м v “ / (8.8)
е‘р= k.Eh
где а2 — кг . к2 (5. 59).
Заменяя в уравнении (8. 4) относительные деформации 8Г и 8|р по форму-
лам (8. 8) с учетом выражения (8. 1), получим
— г (Т1гУ' — (Тгг)'
(а)
Второе уравнение можно получить из выражения (8. 2), где соотношения
между изгибающими моментами Мг и Mt и углом й1 находим так же, как и для
изотропной мембраны, но с учетом уравнений (5. 55'), связывающих деформации
изгиба анизотропной мембраны с напряжениями.
Подставляя в уравнения (5. 55') выражения (5. 4) и (5. 5) изгибных дефор-
маций ег и efu через угол й поворота нормали
л
eru = zft' и e/ti = z— ,
получим с учетом соотношений (5. 51); (5. 52) и (5. 59)
к
Н
2
а2
Решим эти уравнения'относительно изгибных напряжений о?и и (Т/и-
415
Изгибающие моменты определяются (см. фиг. 124, в) по выражениям
h
2
o'/,. zdz.
Vv
Л/г _ J а г0?г.
В результате интегрирования получим выражения, аналогичные формулам
(5. 7)хдля изгибающих моментов изотропной пластинки,
(8-9)
* I г а-
здесь D — цилиндрическая жесткость для анизотропной пластинки — опреде-
ляется выражением (5. 58).
Заменяя в зависимости (8.2) моменты Мг и Mt выражениям! (8. 9), получим
второе уравнение, связывающее неизвестные Тг и'й
г D
(б)
Уравнения (а) и (б) осталось преобразовать в безразмерный вид, в котором
они и даны формулами (5. 56) в § 27.
3. Вычисление упругих коэффициентов кг и к2 для нокоторых
профилей мембран
Трапецеидальный профиль
профиля длина дуги одной волны
(фиг.
226, а). Для этого
следовательно, по формуле (5. 53) коэффициент кг равен
л 2а
5_______L_1_^
I cos0o I
Вычисление интеграла в формуле (5. 54) можно производить в пределах
одной четверти волны, увеличивая затем результат в 4 раза. Значения перемен-
ных у и 0 по участкам профиля будут
а
у—з sin0o;
о.
0=0;
416
Подставляем эти значения в формулу (5. 54)
Фиг. 226. Трапецеидальный (а),
пильчатый (б) и синусоидальный
(в) профили.
После преобразований, учитывая выражение (а) и то, что—-— tg6» =
2
== Н, получим
//2
cos 0о
(в)
Пильчатый профиль (фиг. 226, б). Выражения коэффициентов
для этого случая можно получить из формул (б) и (в), рассматривая пильчатый
профиль как частный случай трапецеидального, когда а == 0. Таким образом
получаем
COS 0Q ’
*i=fcJ^3?r+cose»-
27 Заказ 24.
417
Синусоидальный
профиля будет в этом случае
профиль (фиг. 226, в). Уравнение линии
Н . 2л х
rsm ~г
Дифференцируя его, получим
cos
2л х
Учитывая, что cos 0 =
и введя обозначения
а =
и
приводим выражения (5. 53) и
(5. 54) для коэффициентов и /<2 к виду
здесь Ео и Fo — полные эллиптические интегралы I и II рода
a2 sin2 а • da\
2
d а
J У 1 — л2 sin2 а
о
Их числовые значения можно найти в книге Янке Е. и Эмде Ф1.
Пологий синусоидальный профиль. Если глубина II
гофрировки значительно меньше длины волны ZI по крайней мере II < —I У
1 Янке Е., Эмде Ф., Таблицы функций, Физматгиз, 1959.
418’
то в уравнениях (5. 53) и (5. 54) можно положить cos б— 1. В этом случае выра-
жения коэффициентов значительно упрощаются я
^ = 1;
А?., =
3 я2
2 ~fe2
Сводная таблица формул для коэффициентов и приведена в табл. 23
§ 27.
; . I
4. Получение характеристики гофрированной мембраны,
нагруженной в центре сосредоточенной силой
Так же как и в случае нагружения давлением, гофрированная мембрана
заменяется плоской анизотропной. Дифференциальные уравнения анизотропной
мембраны, нагруженной в центре сосредоточенной силой Qt могут быть полу-
чены таким же путем, как и для случая действия давления р. Эти уравнения
отличаются от выражений (5. 56) только грузовым членом и имеют вид
|-ф*— а2
(8. 10)
Для получения линейного члена характеристики мембраны положим в ура-
внениях (8. 10) функцию растягивающего усилия ф = 0. В результате этого
получим дифференциальное уравнение анизотропной мембраны в малых пере-
мещениях.
QRk}
Это уравнение имеет следующее решение
Постоянные интегрирования а и Ъ определяем из граничных условий: угол
поворота # = 0 как на внутреннем (при q = Qo), так и на наружном (q = 1)
контуре (q о —относительный радиус жесткого центра). Отсюда
1 е0-~е0а
а = — ---=- -------- ;
е?-еГ
-
1 е0-е“
eS-era '
♦
Относительный прогиб центра вычисляем на основании формулы (5. 3)
Q0
(8.11)
tt
1
27*
419
В результате преобразований получим ту часть нагрузки, которая соответ-
ствует сопротивлению мембраны изгибу
/ QR2 \ wQ
дГЁАГ
\ / tv
(а)
Определим теперь кубический член характеристики мембраны, соответствую-
щий сопротивлению растяжению. В этом случае поведение мембраны может быть
описано уравнениями абсолютно гибкой анизотропной пластинки, которые
получатся из системы (8. 10), если принять изгибную жесткость D == 0
О1|)" -гЧ1" — И2
(8. 12)
где Д^ ~ -.. —~ .
Q 2Ehk1 л R
Уравнения (8. 12) будем решать по методу Галеркина. При нагружении мем-
браны сосредоточенной силой можно представить, что ее упругая поверхность
будет близка к конической. В соответствии с этим зададимся выражением угла
поворота О’ = С.
Постоянную С с помощью формулы (8. И) можно выразить через прогиб
центра как С= —
Подстановка $ = С в первое уравнение системы (8- 12) и его интегрирование
дают
и?о 1
R 1-QO
г<а
Ч>0 = До,
Постоянные А и В находим из следующих граничных условий: при q — Q*
и при q — 1 — ц —— = 0, что соответствует отсутствию радиального смеще-
ния на внутреннем и наружном контурах мембраны. Отсюда получим
1—ц * ~~ Qq + 1
Х (1-«2)(а-Ю 1-е2«
. Л«+1 — п2а
1—и ер Qo
(l-a2)(a-hp) *
Интегрирование уравнения Галеркина
у н
/ — Ал) dQ == 0.
Q0
420
приводит к Значению нагрузим, соответствующей растяжению мембрану
(?Д2 ' __ , “?0
л Eh* Iр Q Л»
(6)
Суммируя по методу «наложения» выражения (а) и (б), получим уравнение
характеристики гофрированной мембраны с жестким центром, нагруженной
сосредоточенной силой С>
(?i?3 _ “’о.гь Ш0
л Eh* ’VO h fts '
Значения ке^фпциентов Пд, 3g л bq даны гыражеш ями (5.‘71 ) и '5.73\
приложение II
i i ' ~
МАНОМЕТРИЧЕСКИЕ МЕМБРАННЫЕ КОРОБКИ ПРОФИЛЯ I,
ЛИНЕЙНЫЕ ПО ДАВЛЕНИЮ, ИЗ БЕРИЛЛИЕВОЙ БРОНЗЫ Бр. Б2,5
(из отраслевой нормали АН-1671)
№
мембран-
ной
неробки
! Рабочий
диаметр
D в мм
Эффек-
тивная
площадь
РЭф в см2
Толщина h
в мм
допускаемое
отклонение
±0,002 мм
Давления о/ и рдо/о
при нелинейности
характеристики
1>ра3р — разрушающее
давление
Прогиб
2ги0
центра
неробки
в ли*
в кгс/сл12
1 F 24 1,98 1 0,04 р1% рз% Рразр 0,190 0,381 0,544 0,400 ’ 0,800 1,100
2 I ! 0,06 Pi% рз % Р разр 0,558 1,129 1,701 0,600 1,300 1 1,900 1
3 0,08 pi% рз% 1,197 2,245 0,900 1,600
4 0,10 ‘а СО н* 2,857 4,762 1,460 2,400
№ 5 * 28 2,70 0,04 Р1% рз% Рразр 0,150 0,272 0,367 0,450 0,830 1,100
6 0,06 Pi% рз% Рразр 0,367 0,748 1,088 1 0,600 1,200 1,800
422
Продолжение прилож. II
V -• -Г * . л л_ _ , - - - f _ -м. - -г -
а. Давления Р1% и Рз%
№ мембран- ной коробки Рабочий диаметр D в мм > Эффек- тивная площадь ,р „j. В CJU2 Толщина h в мм допускаемое отклонение при нелинейности ха рактеристики в 1% и 3%; ^разр ~ разрушающее Прогиб 2w0 центра коробки
1 • ±0,002 мм давление * в мм
1 1 1 1 в кгс/слг2
ь * । i i । и 0,08 Р1% 0,803 0,900
7 * . i 1 b Р3% 1,524 1,630
I- 28 2,70 F > Рразр 2,585 ' 2,800
. 8 1 7 « 0,10 pi% i 1,487 1430
? . * Рз% 2,789 2,100
i- * i . 1 1 J < Pi% 1 i 0,259 0,600
9 1 , 0,06 ‘ рз% 0,517 1,200
1 I4-! “ » " Рразр 0,748 1,700 " ъ
- 1 и * J- i pi% 0,558 0,800
10 0,08 рз% 1,129 .1,700
- 32 3,52 Рразр 1,701 2,600 Гг-
11 0,10 pi% 1,020 » 1,100
р3% 1,905 2.000
J : 12 0,12 pi% 1 1,837 1,500
* * р3% 3,129 2,500 + -
1 F "1 1 р1% 0,190 " ' . Т 0,600
13 - 0,06 рз% 0,381 1,100
i < - 1 к Рразр 0,544 1,700
14 1 i 1 J | 1 36 1 4,46 0,08 Р1% рз% 0,408 0,816 0,800 1,600
’ i 1 1 р. о/ 0,748 1,100
15 < ' - 0,10 * /Q рз% 1,429 2,000
ф 16 - г 0,12 р1% рз% 1,197 2,245 1,300 2,400
423
Продолжение при лож. II
№ мембран- ной коробки Рабочий диаметр D в мм 1 Эффек- тивная площадь Рэ09 в см2 ► Толщина h в мм допускаемое отклонение ±0,002 мм Давления Pj% и Рз% ’ при нелинейности характеристики в 1% и 3%; Рра3р ~ разрушающее давление - Прогиб 2W центра коробки В Л1Л1
- В КЗС/С.И2
17 36 4,46 0,14 р1% рз% 1,973 3,537 1 1,600 3,000
18 0,06 4 /О рз% Рразр 0,150 0,286 0,408 0,600 1,100 1,600
19 0,08 Р1% Р3% Рразр 0,313 0,612 0,898 1,270 2,500 3,600
20 _ _ 40 5,50 0,10 Р1% Рз% L 0,558 1,129 1,000 2,100 Г 1
21 0,12 Р1% Рз% 1 0,912 1,728 1,300 2,400
22 г 0,14 4 р1% р3% 1,401 2,612 1,560 2,900 ' 1
г 23 1 1 0,16 ♦ pi% рз% 2,245 3,810 1 ! 1,980 2,000
24 1 _ 1 L 0,06 Pi % Рз% Рразр 0,136 0,231 0,286 0,900 1,500 1,900
25 48 । с / 7,93 0,08 pi% рз% Рразр 0,190 0,381 0,544 0,800 1,600 2,300
1 > 9 26 3 г ► ч i 1 ♦ :- 'i 0,10 J4 pi% рз% 0,327 0,680 : 0,960 2,000
424
Продолжение прилож. II
№ мембран- ной коробки Рабочий диаметр D в мм j Эффек- тивная площадь Рэф в см2 Толщина h в мм допускаемое отклонение ±0,002 мм Давления Р[% и р$°/о при нелинейности характеристики в 1% и 3%: Рразр — разрушающее давление в кгс j с.м.2 Прогиб 2 wo центра коробки в лш
27 1 i 48 1 1 7,93 0,12 pi% рз% 0,558 1,129 1,260 2,500
28 0,14 pi% Рз% 0,844 1,605 1,480 2,800
29 0,16 pi% p3% 1,197 2,245 1 Г 1,700 5,200 у
30 0,18 pi% p3% 1,837 3,129 2,200 3,800
31 0,20 pl% P3% 2,857 4,762 2,900 4,870
32 54 . 10,03 0,06 pl% P3% Рразр 0,122 0,190 0,231 1,100 1,700 2,100 J
3< J ‘ 0,08 1- -1 х.^| -- - - Pi% ! P3% Pразр 0,150 0,272 0,395 0,800 1,500 2,200
1 34 j 0,10 Pi% Рз% Pразр 0,245 0,490 0,721 0 970 1,900 2,860
35 L 0,12 J Pi% p3% i i 0,408 S 0,816 1,230 2,460
* . - • -- ' 1 0,14 Pi% p3% 0,612 1,211 1,480 2,900 *
Продолжение прилож. II
№ мембран- ной коробни ч Рабочий диаметр D в мм Эффек- тивная площадь ?Эф В См2 1 - Толщина Л. в мм допускаемое отклонение ±0,002 мм Давления Р\% и Рз% при нелинейности характеристики в 1% и 3%; Рразр ~~ разрушающее давление Прогиб 2 wq центра кйробки В ММ
J __ 1 - в кгс/сл12 । г
“ • - л 37 -* - . ц.... 0,16 . pi% - рз% 0,884 1,673 1 1,700 3,200
38 |_ - - - *. . - * Я J 54 10,03 V L 0,18 р1% рз% 1,197 2,245 1,900 3,650
*39 - у • 0,20 р1% рз% 1,673 2,993 2,300 4,100
ЧО - 0,22 р1% Р3% 2,449 4,082 2,860 4,780
,41 ч г % । 0,08 Лз *6 СО со 0х 0,136 0,245 0,313 0,990 1,790 2,290
, 1 • _ f J - I 1 ; 42 4 г ' [ г » 0,10 р1% рз% Рразр 0,190 0,381 ; 0,544 0,990 1,980 2,800
" ’ И | " J ". 43 60 12,38 0,12 pi% рз% 0,313 0,612 1,200 2,400
44 I 1 0Д4 Р1% рз% 0,463 0,939 1,400 2,900
ь 45 1 1 i ч 0,16 -н р1% р3% 0,667 1,306 1,700 3,300
ч 46 • d 1 0,18' р1% рз% 0,912 1,728 " 1,900 3,650
426
Продолжение прилож. II
Хе • мембран- ной ; коробки Рабочий диаметр JD в мм Эффек- тивная площадь F30 в см2 Толщина h в MM допускаемое отклонение ±0,002 мм Давления Pi % и Pg% при нелинейности характеристики В 1% И 3%; Рразр ~ разрушающее давление Прогиб 2wq центра коробки в мм
в кгс / см%
1 47 < > * 1 60 w 1- 12,38 I 0,20 ’ р1% рз% 1,197 2,245 2,100 4,000
• 48 ! л -ЧЧЧ 1 1 ! 1 ' ' 0,22 р1% р3% 1,605 2,966 2,500 4,600
* j i 49 С г f 1 л i 0,24 - р1% .. р3% 2,245 3,810 2,900 5,000
t * * <j Л" р ч j 50 т i я J Й . <' Ч '«! - ... i- Ь- ь ; Hi j 4 d 4 72 1 h A 1 Ar ? 17,83 1 1 i 0,08 р1% рз% - -- Рразр 0,122 0,190 0,231 1,500 2,300 2,800
! i 51 i t F 0,10 -1- Р1 % рз% Рразр 2» 1 0,136 0,259 0,340 1,100 2,000 2,800 |
* f b !’ 52 F I ! t ; 0,12 р1% ^3% 0,190 0,381 1,200 2,400
! L r J i 53 ? 1 0,14 Р1% рз% 0,286 0,571 1,400 2,700
1 i 54 i * 0,16 pi% рз% 0,408 0,816 1,600 3,300
55 j- •i * 0,18 Рл% рз% 0,558 1,129 1,900 3,800
56 il 1 0,20 р1% рз% 0,748 1,429 2,500 4,800
427
Продолжение прилож. 1I.
№ мембран- ной коробки * Рабочий диаметр D в мм Эффек- тивная площадь в сл<2 Толщина h в ММ допускаемое отклонение ±0,002 мм Давления и Р^% при нелинейности характеристики в 1% И 3%; Рразр —разрушающее давление Прогиб 2wo центра коробки В мм <
1 в кгс/сл<2
57 . 4 0,22 pi% Рз% 0,952 1,796 2,400 4,450
58 , .—. — - 0,24 р1% рз% 1,197 2,245 2,600 4,900 S
59 . 72 17,83 0,26 р1% р3% 1,537 х 2,844 2,900 5,400
60 0,28 pt% рз% 1,973 3,537 3,300 6,000 1 ;
61 * 0,30 Р1% рз% 2,857 4,762 4,300 7,300
62 * 0,10 Pt% 1 /О рз% Рразр 0,109 0,163 0,204 f 2,000 3,000 3,770
63 0,12 Р1% рз% Рразр 0,136 0,231 0,286 1,800 3,050 3,770
64 96 31,7 0,14 р1% рз% Рразр 0,150 0,272 0,381 1,500 2,740 3,840 '
65 ч - 0,16 J Р1% рз% Рразъ 0,190 0,381 0,544 1,580 3,170 4,500
66 < 0,18 pi% рз% Рразр 0,259 0,517 0,748 1 " <" " " " 1,780 3,570 5,170
428
Продолжение прилож. II
№ мембран- ной коробки Рабочий диаметр D в мм Эффек- тивная площадь РЭф в с*2 Толщина А в мм допускаемое отклонение ±0,002 мм Давления рр/ и Рз% при нелинейности характеристики в 1% и 3%; Рразр — разрушающее давление Прогиб 2wo центра коробки в лш
в кгс/см^
67 * * F 1 d 31,7 0,20 р1% Р3% 0,327 0,680 1,900 4,000
68 0,22 р1% рз% 0,449 0.898 • 2,280 4,560
69 0,24 р1% Р3% 0,557 1,129 3,100 5,000 «
70 0,26 pi% р3% 0,694 1,361 2,790 5,470
71 0,28 pi% рз% 0,844 1,607 2,970 5,660
72 0,30 р1% Р<)о/ /О 1,020 1,901 3,300 6,180
1 " 73 0,32 pi% Рз% 1,197 2,245 3,460 6,490 *
74 0,34 р1% Р3% Л 1,429 2,667 3,700 7,000
75 0,36 р1% рз% 1,837 3,129 4,400 7,600
76 0,38 pi% рз% 2,177 3,673 4,700 8,000
77 0,40 pi% рз% 2,857 4,762 5,800 9,700
429
ДАННЫЕ НА
(из нормалей маши
1. Сильфоны полу
Нормаль, ее номер и наименование "| ! Диаметр В ММ Число гофр Шаг гофри- ровки в мм Длина в ММ Посадочный диаметр В ММ <
D d п -1 L di
МН-419-60
Сильфон полутомпаковый
однослойный с наружным
посадочным диаметром
МН 420-60
Сильфон полутомпаковый
однослойный с внутренним
посадочным диаметром
28,5 18,76 8 * 2,0 21,5 19,3 — г < > J ? * 1
34,0 21,70 6 2,2 18,5 * 22,2 ! л i 4 t J 1
12 7,50 15 1,00 19 11,5 11,5 -
16 9,50 7 1,20 12,9 12,3 15,8 ! i
16 9,50 20 1,20 27,7 12,3 15,8
28 18,76 16 1,80 36,0 27,5 27,5. '
28,5 18,76 И 2,75 36,5 21,0 21,0
34 21,7 12 2,20 31,0 32,5 32,5> i 4 1 !
47 31,7 3,50 22,8 46,8 46,8
60 37 И 4,80 62,0 59,6 59,6
МН 421-60
Сильфон полутомпаков ып
однослойный с наружным
в внутренним посадочным
диаметром
20,0 I i 11,5
28,5 18,76
28,5 18,76
51,0 i 35,6
i i 4 _ - J 1 -
13 2,2 33,5 14,0 X : I .•1 18,00
7 3.0 24,0 19,0 28,50
9 2,6 26,0 19,0 28,25
15 3,4 60,0 35,8 50,00
1
430
ПРИЛОЖЕНИЕ lit
СИЛЬФОНЫ
построения [81])
томпаковые (Л80)
Длина ци- линдрической части в лил Толщина стенки трубки- заготовки В ММ Эффек- тивная площадь В CAl2 Жесткость В К8С/ММ I Прогиб в мм Допу- скаемое давление в кгс/сл(2
i 1 Z1 1 Наиб. Наим. Полный Рекомен- дуемый
1 3,0 0,12 < I 4,4 * 0,907 0,228 J * Jf ь 4,0 а 2,0 ’ 6,5 £. F
! 3,6 • 1 0,15 6,1 1 1 1,120 0,340 3,5 F / ч . 1,8 3,2
1,9 0,14 0,75 3,200 0,700 2,8 1,4 10,3
2,0 1 — 0,09 1,27 0,741 0,402 3,4 1,7 7,5
2,0 — 0,09 1,27 0,286 0,080 6,0 3,0 1,2
3,0 0,12 4,30 0,535 0,128 9,3 4,6 3,3
2,5 0,12 4,40 0,695 0,173 9,0 4,5 6,5
1,4 0,15 6,10 0,565 0,170 9,5 4,8 3,2
1,7 — 0,14 12,20 0,870 0,312 4,2 2,1 2,1
3,5 — 0,18 18,50 0,286 0,128 18,0 9,0 1,2
2,0 1,5 * 0,11 1 1 1 1 ч 1,96 0,450 0,250 1 7,6 3,8 Г 2,2
1,5 1,5 0,12 4,40 1,100' 0,275 9,7 4,9 6,5
1,5 1,5 0,12 4,40 0.850 f 0,210 9,5 4,8 6,5
6,0 г 3,0 0,12 15,0 0,195 <1 L 0,100 ч- 7,3 л 1 1 8,7 И • ?- * ; ; 1,8 4
43©
Нормаль, ее номер и. наименование Диаметр В JHAl Число гофр Шаг гофри- ровки В AIJW Длина в мм f) Посадочный диаметр в мм
D d п t di
MH 422-60
Сильфон полутомпаковый
однослойный с наружным
посадочным диаметром
и дном
Для сильфонов]
В-79мм и Т
В=100мм I,
iob}
lb9 —
1 ч 17,0 9,4 12 1,5 26,0 9,7 10,0
32,0 19,2 11 3,3 47,0 22,0 20,0
38,0 25,6 8 2,9 28,7 25,8 26,0
38,0 25,6 10 2,9 45,0 25,8 25,8
44,5 31,72 17 1,9 41,0 32,0 32,0
51,0 35,6 16 3,5 72,0 36,0 36,0
79 55 13 5,4 96,2 55,4 56,0
100 76 И 6,2 86,0 76,4 76,4
МН 423-60
Сильфон полутомпаковый
однослойный с внутренним
посадочным диаметром
и дном
IB, t
LBa
16 9.5 21 1,2 33 12,3 10,5
18 12,5 5 1,5 it 14,4 15,0 13,0
24 15,76 13 1,8 35,0 19,0 17,0
28,5 18,76 И * 2,8 38,8 21,0 19,0
28,5 16,6 7 2,5 24,0 28,2 17,5
57 34,6 12 4,7 68,2 37,5 36,0
432
Продолжение прилож. Ill
Длина цилиндриче- ской части в мм Т олшина стенки трубки- заготовки в мм Эффек- тивная площадь В CJH2 Жесткость в mcj мм Прогиб В АШ Допу- скаемое давление в
1 Z1 ho Наиб. Наим. Полный Рекомен- дуемый
2,5 6 1 . 0,13 1 1,35 Г 0,716 I- 0,270 4,0 2,0 4,9
6,0 6 0,12 5,15 0,330 0,094 12,0 6,0 2,8
1,5 6 0,11 8,00 0,490 0,175 7,5 3,8 1,0
6,0 И 0,11 7,95 0,420 0,170 12,0 i 6,0 1,15
1 3,5 6 0,14 11,40 0,385 0,157 9,3 4,7 1,50
6,0 12 . 0,12 15,0 0,183 0,080 17,0 8,5 1,80
8,0 8 0,20 35,0 0,400 0,200 20,0 10,0 1,60
6,0 1 8 0,20 60,7 0,570 0,304 к i 24,0 12,0 1,60
i 1 1 1 1
2,0 6,0 0,09 1,27 0,274 0,070 6,7 3,4 1,2
2,0 5,0 0,07 1,83 1,750 0,250 2,4 1,2 5.0
2,5 7,5 0,12 3,10 0,820 0,189 7,2 3,6 4,5
2,5 6,0 0,12 4,40 0,695 0,173 9,0 4,5 6,5
1,5 6,0 0,09 4,00 0,260 0,082 4,4 2,2 1,2
3,5 8,0 0,18 16,5 0,276 0,108 18,0 9,0 1,2
•
28 Заказ 24.
433
Нормаль, ее номер и наименование Диаметр в мм Число гофр Шаг гофри- ровки в мм ч Длина в мм Посадочный диаметр в мм
D d п t di С?2
MH 424-60
Сильфон полутомпаковый
многослойный с наружным
посадочным диаметром
число слоев z=2
28 18,3 Ч- 8 2,6* 26,5 19,3
34 21,7 6 . 2,2 18,5 22,2
38 26,9 17 2,7 50,0 28.5 —
50 34,9 10 4,7 52,0 36,0 — !—ЧИ
51 ос о * V ) 12 5,0 67,0 36,0
56 37,2 •. 1 И 41 52,0 1 38,5
МН 425-60
Сильфон полутомпаковый
многослойный с внутренним
посадочным диаметром
Число слоев-у сильфона
z*3
у остальных г=2
12 ч. 7,2 15 1 19,0 11,46 1 11,46
38 26,9 8 2,7 .31,5 37,0 1 , 37,0
38 25,0 8 2,9 32,0 35,0 35,0
40 27 16 3 60,0 . 35,0 35,0
50 34,9 9 4,2 44,0 50,0 46,0
50 ! 34,9 10 3,5 40,5 50,0 46,0
434
Продолжение при лож. III
Длина цилиндриче- ской части В ММ Толщина стенки трубки- заготовки в ММ Эффек- тивная площадь в см2 Жесткость в кгс /мм Прогиб В .НЛ Допу- скаемое давление в кгс/см2
1 -'1 — 1 /го рэф Наиб. Наим. Полный Рекомен- дуемый
1
3,0 3,5 0,24 4,29 2,500 0,500 7,0 3,5 • 13,6
3,0 3,0 0,24 6,10 1,360 0,365 3,5 1,8 • 7,0
2,5 2,5 0,30 8,20 0,995 •4 0,394 11,0 5,5 7,3
4,0 4,0 0,28 14,1 1,060 0,400 12,0 6,0 1,9
3,0 3,0 0,24 14,7 0,790 0,210 12,0 6,0 1,6
3,5 3,5 0,40 17,1 1,245 0,472 10,0 5,0 2,0
1,9 1,9 0,28 0,75 5,25 1,20 2,2 1,1 13,0
4,5 4,5 0,30 8,20 2,74 0,815 3,4 . 1,7 7,3
4,5 3,0 0,22 7,95 0,60 0,25 7,6 3,8 2,0
5,0 5,0 0,51 8,80 1,52 0,74 10,0 5,0 10
1,5 1,5 0,28 14,2 1,13 0,39 9,0 4,5 1,9
1,5 1,5 0,28 14,1 0,970 0,385 11,0 5,5 * 1,9
28*
435
Нормаль, ее номер
и наименование
МН 426-60
Сильфон полутомпаковый
многослойный с наружным
и внутренним посадочными
диаметрами
Диаметр в мм Число гофр . i _ __ _ _ 1 Шаг ГОфрИ’ ровки в мм Длина в мм Посадочный диаметр в мм
п d п t i di
ь 38 38 26,9 25,0 1 1 1 6 6 ! 1 2,7 2,9 • 23,0 23,6 р г 28 27 * 32 31
2* Сильфоны стальные
4 J ’ ! ч Нормаль Диаметр в ММ Число гофр и' Шаг гофра в мм Длина В Л4Л4 Посадоч- ный диаметр в мм
- D d 1 п t di
МН 428-60
Сильфоны стальные
однослойные с наружным
посадочным диаметром
29
29
72
78
78
78
100
100
100
100
100
100
100
100
20
20
56
51.5
59 5
59.0
75,5
75.5
75 5
755
755
755
75,5
75,5
24
42
4
10
10
2
5
6
7
9
9
9
3,8
3,8
4,5
5,5
55
5,5
7,3
7,3
7,3
7,3
7,3
7,3
5.8
7,3
99,8
180
25,4
30,0
68
68
26,5
34,0
49,0
56.0
63 0
78,0
65,0
78,0
20,0
24,7
57,0
60,0
60,0
60.0
76,0
76.0
76,0
76,0
76,0
76,0
76,0
76,0
436
Продолжение прилож. Ill
Длина цилиндриче- ской части В Л1М Толщина стен ни трубим- ая готов ни в мм Эффек- тивная площадь в сл<2 Жесткость в кгс 1 мм Прогиб в мм Допу- снаемое давление в кгс/см2
1 11 ho ^эдЗ Наиб. Наим. Полный Рекомен- дуемый
• 3 1 1 0,30 8,20 3,65 1,08 3,8 Г 1,9 7,3
3 0,22 7,95 L 1,00 ♦ 0,30 7 3,5 4,1
(1Х18Н9Т) однослойные
Длина цилиндри- ческой части в мм Толщина стенки трубки- заготовки в ММ Эффек- тивная площадь в СМ2 Жесткость в кгс!мм Прогиб в мм 1 ч Ч Допу- j Скаемое давление В КЙС/СМ2
1 fto ^эф Наиб. Наим. Полный Рекомен- дуемый
5 0,22 4,71 1 1 10.80 7,80 25 12,5 ч 12.5
5 0,16 4,71 3,70 2,00 46 23 12,5
6 0,15 32,04 2,00 1,00 3,6 1,8 3,0
—т / 0,16 37,2 3,30 1,03 2,4 1,2 3,2
7 0,16 37,2 0,98 0,40 10,8 5,4 3,2
7 0,24 36,8 2,90 1,20 10,8 5,4 4,5
7 0,16 60.0 3,50 1,40 1,7 3,4 0,8 2,4
7 0,16 60,0 2,50 1,00 1,7 2,4
7 0,16 60,0 1,68 0.60 6,8 3,4 2,4
7 0,16 60,0 1,40 050 8,4 4,2 2,4
7 0,16 60.0 0,96 0,45 10,0 5,0 2,4
7 0,14 60.0 0,70 0,22 13,5 6,7 2,2
7 0,14 60,0 0,53 0,17 11,5 5,8 2,4 ‘
7 0,16 60,0 0,90 0,35 13,5 Ж 6,8 2,4 . *
437
л
Нормаль I 1 w Диаметр В JVtAt _ , » Число гофр Шаг гофра в мм Длина в мм Посадоч- ный диаметр в мм
t D ’ d п ~t J" <h
I i '' ii1- MH 428-60 г 100 75,5 9 1 7,3 78,0 76,0
Сильфоны стальные 100 , 75,5 11 7,3 5,8 93,0 76,0
: однослойные с наружным 100 75,5 13 94,0 76,0
посадочным диаметром 100 : 75,5 13 7,3 107 76,0
100 75 5 13 7,3 107 76,0
- 1 * 100 75,5 13 7,3 107 76,0 ♦
! МН 429 60
Сильфоны стальные
однослойные с внутренним
посадочным диаметром
qfiws
'--ЖЖ
h-—LBa -
1 S 1 15 15 15 ’ 9,5 9,5 9,5 3 7 10 1,9 1,9 1,9 13,0 21.0 27 13 13 13
15 9,5 10 1,9 27 13
15 9,5 12 1,9 30,5 13
15 9,5 12 1,9 305 13
15 9,5 14 1,9 34,5 13
15 9,5 14 1,9 34,5 13
15 9,5 14 1,9 34,5 13
15 9,5 6 1,9 19,0 13
15 9,5 16 1,9 38 13
15 9,5 16 1,9 38 13
15 9,5 18 1,9 42 13
15 9,5 11,5 18 1,9 42 13
18 5 2,2 19 14
18 11,5 5 2,2 19 14
18 < 11,5 10 2,2 30 14
18 11,5 10 2,2 30 14
18 11,5 18 2,2 46 14
18 11,5 22 2,2 56,5 14
18 11,5 5 2,2 19,0 14
21 13,5 5 3,2 24,0 16
21 13,5 12 3,2 46,0 16
21 13,5 10 3,2 40,0 16
21 13,5 10 3,2 40,0 16
21 13,5 10 3,2 40,0 16
21 13,5 14 3,2 53,0 16
21 13,5 6 3,0 28,0 16
27 17,5 2 3,3 16,0 20
27 17,5 8 3,3 35,5 20
27 17,5 10 3,3 42,0 20
27 17,5 12 3,3 48,0 20
438
Продолжение при лож. III
Длина цилиндри- ческой части в ММ Толщина стенки трубки- заготовки в ММ Эффек- тивная площадь в см2 Жесткость в кгс/мм Прогиб в лш Допу- скаемое давление , в кгс1см% f ' 1 * t л t
1 Ло Наиб. Наим. Полный Рекомен- дуемый
! 1 ! 7 7 7 7 7 ' 7 <г * . '0,22 0,16 0,16 0,16 0,22 0,24 60,0 60 0 60,0 60,0 60,0 60,0 1,60 0,75 0,55 0,70 1.20 1,50 0,80 0,26 0,20 0,24 0,С0 0,60 13,5 16,5 17,0 20,0 20,0 20,0 6,8 8,2 8,5 10,0 10,0 10,0 1: г р Ъ 9 г 2,4 1 2,4 ‘ 2,4 3,2 5,5 > I hi
l ’ 3,5 • 3,5 3,5 3,5 . 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 3,5 4,5 4 4 4 4 0,12 0,12 0,12 0,14 0,12 0,14 0,12 0,14 0,18 0,18 0,12 0,14 0,12 0,14 0,12 0,14 0,12 0,14 0,18 0.18 0,22 . 0,12 0,14 0,18 0,12 0,14 0,14 0,10 0,14 0,16 0,16 0,16 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,18 1,70 1,70 1,70 1,70 1,70 1,70 1,70 2,34 2,34 2,34 2.34 2,34 2,34 2,34 3,88 3,88 3,88 3,88 । 8,00 3,50 2,40 3,40 2,00 2,83 1,75 2,43 5,30 12,0 1,50 2,13 1,35 1,89 3,80 5,30 1,90 2.80 3,00 2,50 9,50 3,50 2,05 4,70 1,65 2,20 2,00 1.70 8,00 2,80 2,60 2,70 : * 2,50 1,10 0,70 1,37 0,65 1,00 0,55 0,98 2,00 1 4,60 0,48 0,86 1 0,43 0,76 1,50 2,20 0,60 1,33 1,00 0,80 5,50 1,50 0.55 2,00 0,85 1,05 0.70 0,40 2,80 1,10 1,50 1,70 оо со Ф cq сч ф О Ф оо 00 Ф со ос оо Ф о сч сч TH ТТ 0,4 1,2 1,8 1,8 2,2 2,2 2,6 2,6 2,6 1,0 3.0 3,0 3,4 3,4» 1,1 1,1 2,9 2,9 5,4 6,7 1,3 1,5 3,9 3,6 3,6 3,6 4,7 2,2 0,5 2,6 3,6 4.8 4 Г w 17,0 17,0 17,0 21,5 17,0 21.5 17,0 21,5 30,0 30,0 i 17,0 ; 21,5 t 17,0 21,5 15,0 18,5 ! 15,0 18,5 27,0 27,0 31,0 11,5 [ 16,0 ; 20,7 ? 11,5 ; 16,0 i i6,o ; 8,0 • 14,5 16,0 16,0 16,0 !
439
i s Нормаль * ,1 hi 1 | - MH-429-60 Сильфоны стальные I однослойные с внутренним » посадочным диаметром * * । и J р Диаметр в мм Число гофр Шаг гофра в мм Длина в мм 1 Посадоч- ный диаметр В МЛ1 г 1
D 27 27 27 38 38 38 38 38 33 38 38 38 33 38 33 38 40 45 45 45 45 45 45 45 52 52 52 52 52 52 52 52 52 63 63 63 63 63 63 63 63 65 78 _| d 17,5 17,5 17,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 25,5 29,0 33,5 33,5 33,5 33,5 33,5 33,5 33,5 37,5 37,5 37,5 37,5 37,5 37,5 37,5 33,5 33,5 47,5 47 5 45,5 47,5 47,5 47,5 47,5 47,5 50,6 55,5 п 1 8 10 12 2 3 3 6 6 10 10 12 12 7 8 10 16 12 2 6 6 6 8 8 17 3 6 9 9 14 14 17 14 14 6 8 8 9 9 9 15 15 4 10 3,3 3,3 3,3 4,2 4,2 4,0 4,2 4,0 4,5 4,5 4,2 4,0 4,0 4,0 4,0 4,0 4,0 3,7 3,7 3,7 3,7 3,7 3,7 3,7 4,5 4,5 4,5 4,5 4,5 4,5 4,5 6,2 6,2 5,1 5,1 4,0 5,1 5,1 5,1 5,1 5,1 5,0 7,1 ' чь 35.5 42,0 48.5 18,0 22,0 22,0 35,0 34,0 55.0 55,0 60,0 58,0 38,0 41,5 49,5 73,5 60,0 19,0 33,5 33,5 33,5 41,0 41,0 74,0 25,0 3j,0 52 52 75 75 88 99 99 42,5 53 44,0 58 58 58 88,5 88,5 36,0 87,5 <h 20 20 20 32 32 32 32 32 32 32 32 32 32 32 32 32 35 39 39 39 39 39 39 39 45 45 45 45 45 45 45 38 38 55 55 48 55 55 55 55 55 57,5 60,0
440
Продолжение прилож. Ш
Длина цилиндри- ческой части в мм Толщина стенки Трубки- заготовки в мм Эффек- тивная площадь В СЛ12 Жесткость в кгс]мм Прогиб в мм ч Допу- скаемое давление в кгс/смЪ
1 ho Наиб. Наим. Полный Рекомен- дуемый
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 7 7 0,14 0,14 0,14 0,16 0,16 0,22 0,16 0,22 0,12 0,14 0,16 0,22 0,22 0,22 0,22 0,22 0,22 0,22 0,16 0,18 0,22 0,18 0,22 0,22 0,16 0,22 0,16 0,22 0,16 0,22 0,16 0,14 0,16 0,16 0,22 0,26 0,16 0,22 0,26 0,16 0,22 0,30 0,16 Г 3,88 3,88 3,88 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 7,94 9,42 12,0 12,0 12,0 12,0 12,0 12,0 12,0 15,8 15,8 15,8 15,8 15,8 15,8 15,8 14,4 14,4 24,0 24,0 23,1 24,0 24,0 24,0 24,0 24,0 26,1 35,2 1,95 1,55 1,30 5,00 3,20 8,00 3,60 4,00 0,70 0,90 0,80 2,00 3,50 3,00 2,20 1,80 3,20 28,0 4,50 5,50 8,92 4,20 7,30 3,15 5,50 5,80 1,75 3,75 1,13 2,40 0,93 0,50 0,60 2,20 3,30 3,50 1,50 2,80 4,80 0,93 1,70 12,0 0,70 0,70 0,55 0,45 2,50 1,60 4,00 1,80 2,00 0,15 0,30 0,40 1,00 1,70 1,50 1,20 0,80 2,70 14,0 1,80 2,20 4,30 1,30 2,90 1,52 2,00 2,30 0,55 1,70 0,35 1,10 0,30 0,16 0,17 0,95 1,00 1,40 0,60 1,70 2,30 0,35 1,00 3,0 0,20 5,8 6,5 7,9 1,2 2,2 2,0 5,6 4,8 10 10 12 10,6 5,8 6,7 8,6 14,4 8,8 1,0 5,0 5,0 5,0 6,4 6,4 12,8 2,2 5,6 8,9 8,9 14,5 14,5 17,9 21,0 21,0 6,0 8,4 9,5 9,6 9,6 9,6 18 18 3,6 15,7 2,9 3,3 3,9 0,6 1,1 1,0 2,8 2,4 5,0 5,0 6,0 5,3 2,9 3,3 4,3 7,2 4,4 0,5 2,5 2,5 2,5 3,2 3,2 6,4 1,1 2,8 4,5 4,5 7,3 7,3 9,0 10,5 10,5 3,0 4,2 4,8 4,8 4,8 4,8 9,0 9,0 1,8 7,9 14,5 12,5 12,5 11,5 11,5 16,0 11,5 16,0 7,5 8,3 11,5 16,0 16,0 16,0 16,0 16,0 12,0 13,0 9,0 10,5 13,0 10,5 13,0 13,0 13,0 11,5 8,0 11,5 8,0 11,5 8,0 4,0 4,0 6,5 9,5 10,5 6,5 9,5 10,5 6,5 9,5 11,0 5,5
441
Нормаль
3. Сильфоны стальные
Диаметр в лик Число гофр Шаг гофра в мм Длина в мм
D d п
МН 430-60
Сильфоны стальные
однослойные, армирован-
ные кольцами
LBe-----Ч
27
38
38
38
52
52
52
52
63
63
63
63
73
73
73
73
92
92
92
92
17,5 6 3,6 32,0
25,5 5 4,3 34,0
25,5 8 4,3 46,0
25,5 15 4,3 77,0
37,5 4 5,8 34,5
37,5 5 5,8 40,5
37,5 10 5,8 69,5
37,5 12 5,8 81,0
47,5 5 4,5 36,0
47,5 6 4,5 40,5
47,5 10 4,5 58,5
47,5 15 4,5 81,0
59,0 4 4,5 32,0
59,0 7 4,5 45,0
59,0 17 4,5 90,0
59,0 16 5,85 103
75,0 4 5,85 39
75,0 5 5,85 45
75,0 6 5,85 50
75,0 12 5,85 1 85
Нормаль
МН 418-60
Сильфоны бронзовые
однослойные
4. Сильфоны бронзовые
Марка материала Диаметр В ММ Число гофр Шаг гофра в лш Длина в мм
D d п J J
Бр. БИТ 1,9 11,6 6,4 4 1,70 11,5 ±0,5
То же 11,6 6,4 30 1,75 58,0±1,2
» 11,7 6,4 16 1,9 37,5±1
» 12,7 6,4 17 1,7 36,5±1
» 12,7 6,4 6,4 17 1,7 36,5±1
» 12,7 17 1,7 36,5±1
» 12,7 7,5 17 1,7 36,5±1
» 12,7 7,5 22 . 1,7 44,5 ±1
» 12,7 7,5 22 1,7 44,5 ±1
» 12,7 7,5 22 1,7 44,5±1
» 12,7 7,5 24 1,7 48,0±1
Бр. Б2 13,0 7,5 11 1,7 25,0±0,84
То же 13,0 7,5 12 1,7 26,5 ±0,84 1
442
Продолжение прилож. III
армированные
Посадочный диаметр в ММ Длина цилиндриче- ской части В Л1М Толщина стенки трубки-заготов- ки в ММ Эффективная площадь в слг2 Максималь- ный ход при сжатии в мм {Допускаемое давление в кгс/см2
1 ho ^эд5
18 5 0,22 3,88 1,6 • 75
26 7 0,22 7,94 2,0 60
26 7 0,22 7,94 4,0 60
26 7 0,22 7,94 8,5 60
38 7 0,26 15,8 1,5 2,0 40
38 7 0,26 15,8 40
38 7 0,26 15,8 5,0 40
38 7 0,22 15,8 6,5 20
48 7 0,25 24,0 1,5 45
48 7 0,25 24,0 2,0 45
48 7 0,25 24,0 3,5 6,0 45
48 7 0,25 24,0 45
60 8 0,25 34,2 1,0 40
60 8 0,25 34,2 2,5 40
60 8 0,25 34,2 7,5 40
60 8 0,25 34,2 10 40
76 9 0,28 54,7 1,5 30
76 9 0,28 54,7 2,0 30
76 9 0,28 54,7 2,5 30
76 9 1 0,28 54,7 6,0 30
однослойные
Поса- дочный диаметр в мм Длина цилин- дриче- ской части в мм Толщина стенки трубки- заготовки в мм Эффек- тивная площадь в см2 Жесткость в кгс/мм Прогиб в мм Допу- скаемое давление в кгс/см2
Наиб. Наим. 1 Полный Рекомен- дуемый
1 ho F эдО
10 2,3 0,14 0,64 4,90 4,70 2,0 1,5 24,0
9 2,5 0,15 0,64 0,74 0,66 14 7,0 24,5
10 3,2 0,20 0,64 4,30 3,30 4,8 2,4 36,5
10 3,2 0,10 0,72 0,50 0,30 5,0 2,5 14,5
10 3,2 0,13 0,72 1,00 0,60 5,0 2,5 18,5
10 3,2 0,15 0,72 1,30 0,90 5,0 2,5 22,5
10 3,2 0,22 0,80 6,50 4,50 5,0 2,5 35,0
10 3,2 0,15 0,80 1,60 1,00 6,7 3,4 24,0
10 3,2 0,16 0,80 1,90 1,30 6,7 3,4 24,0
10 3,2 0,20 0,80 4,00 2,30 6,7 3,4 30,0
10 3,2 0,15 0,80 1,60 1,00 7,4 3,7 24,0
10 3,0 0,12 0,82 1,80 0,90 3,2 1,6 18,5
10 3,0 0,12 0,82 1,70 0,85 3,5 1,8 18,5
_Л - ” _ч . _ - -1 - . • • _ .
Нормаль F । Л Марка материала Диаметр В ЛЬИ Число гофр Шаг гофра в мм Длина в мм
D d п ~ t
МН 418-60 Бр. Б2 15 9,5 6 2,5 23,0±0,84
Сильфоны бронзовые Бр. БНТ 1,9 15 9,5 6 2,5 23,6 ±0,84
однослойные Бр. Б2 15 9,5 8 2,0 22,0±0,84
То же 15 9,5 16 2,2 41,0±1,0
» 15 9,5 16 2,5 46,6 ± 1,0
» 21 13,5 8 2,1 24,0 ±0,84
Бр. БНТ 1,9 21 13,2 13 3,0 46,5±1,0
Бр. Б2 21 13,5 15 2,1 38,5 ±1,4
То же 24 15,5 7 2,6 22,0 ±0,84
» 24 15,5 6 2,6 24,2±0,84
- » 24 15,5 6 2,6 24,2 ±0,84
Бр. БНТ 1,9 26 17,2 12 3,5 50,5 ±1,0
* Бр. Б2 28 17,5 4 3,3 23,0 ±0,84
ч То же 28 17,5 5 3,3 26,0 ±0,84
- » 28 17,5 6 3,3 29,5 ±0,84
< 28 17,5 8 3,3 36,0±1,0
j' ч » 28 17,5 5 2,5 21,0±0,84
« » 28 17,5 9 3,3 39,0 ±1,0
Бр. БНТ 1,9 28 17,5 10 2,5 34,0±1,0
Бр. Б2 28 17,5 10 3,3 43,0±1,0
- То же 28 17,5 12 3,3 49,0±1,0
» 35 23,5 И 3,5 43,0±1,0
» 38 25,5 5 3,0 24,5±0,84
.. т » 38 25,5 6 3,0 27,0±0,84
» 38 25,5 6 3,0 27,0±0,84
» 38 25,5 6 3,0 27,0±0,84
• Бр. БНТ 1,9 38 25,5 6 3,0 27,0 ±0,84
Бр. Б2 38 25,5 8 3,0 32,0±1,0
То же 38 25,5 8 3,0 32,0±1,0
Бр. БНТ 1,9 38 25,5 9 3,0 36,5±1,0
Бр. БНТ 1,9 38 25,5 17 3,0 61,0±1,3
Бр. Б2 45 33,5 6 3,3 29 ±0,84
То же 45 33,5 6 3,3 29 ±0,84
» 45 33,5 9 3,3 39±1,0
» 52 33,5 6 3,2 31±1,0
» 52 33,5 8 4,0 44 ±1,0
» 52 33,5 9 3,2 36 ±2,0
f » 52 37,5 10 4,0 51±1,2 1 4 А
» 52 33,5 14 3,2 54+*’ — 2,0
- » 52 37,5 14 4,0 68±2,5
63 47,5 8 4,8 51±1,2
» 100 75,5 8 6,1 66 + 2,0
♦
444
Продолжение прилож. Ill
Поса- дочный диаметр В Л1Л1 Длина цилин- дриче- ской части в ММ Толщина стенки трубки- заготовки в мм Эффек- тивная площадь В СЛ(2 Жесткость в кгс/мм Прогиб в мм
Наиб. Наим. Полный Рекомен- дуемый
<*1 1 Ло
Допу-
скаемое
давление
в кгс/см2
13
13
13
13
13
16
16
16
23
18
18
20
20
20
20
20
20
20
20
20
20
32
28
28
32
28
28
32
32
32
32
38
38
38
38
38
38
45
38
45
50
80
3,5 0,10 1,18
3,5 2,5 0,13 1,18
0,10 1,18
2,5 0,11 1,18
2,5 0,12 1,18
3,0 0,11 2,34
3,0 0,33 2,34
3,0 0,12 2,34
1,5 3,5 0,12 3,06
0,09 3,06
3,5 0,11 3,06
4,0 0,32 3,36
4,0 0,16 4,06
4,0 0,11 4,06
4,0 0,12 4,06
4,0 0,12 4,06
4,0 0,12 4,06
4,0 0,12 4,06
4,0 0,12. 4,06
4,0 0,16 4,06
4,0 0,16 4,06
1,5 0,11 6,72
4,0 0,14 7,94
4 0,11 7,94
4 0,12 7,94
4 0,14 7,94
4 0,16 7,94
4 0,16 7,94
4 0,12 7,94
4 0,20 7,94
4 0,22 7,94
4 0,10 12,0
4 0,12 12,0
4 0,12 12,0
5 0,16 14,4
5 0,14 14,4
4 0,10 14,4
4 0,22 15,8
5 0,13 14,4
5 0,18 15,8
5 0,27 24,0
7 0,19 60,0
2,40
4,50
2,00
1,15
1,50
1,20
14,04
0,80
1,30
0,60
1.30
8,80
3,10
0,90
1,10
0,70
1,25
0,62
0,70
1,35
1,00
0,40
1,40
0,67
0,80
1,20
1,70
0,90
0,45
1,90
1,50
0,75
1,20
0,80
1,00
0,50
0,20
2,50
1,14
0,63
3,50
0,60
0,80
2,95
0,90
0,50
0,60
0,50
10,00
0,34
0,70
0,25
0,50
6,00
1,50
0,40
0,45
0,40
0,75
0,35
0,40
0,60
0,50
0,20
0,70
0,30
0,40
0,70
0,85
0,80
0,40
1,20
0,80
0,30
0,70
0,40
0,60
0,25
0,16
1,9
0,10
0,47
3,00
0,50
4
4
4,5
10
10
5,0
8,0
10
5,8
4,8
4,8
9,0
3.6
4,8
6,0
8,4
2,6
9,6
5,8
10,8
13,2
12
4,2
5,2
5,0
5,0
5,0
7,5
7,5
8,5
17
4,0
4,0
9,0
5,0
10
9,0
13
14,6
19,0
11,0
14,0
2
2
2,3
5,0
5,0
2,5
4,0
5,0
3,0
2,4
2,4
4,5
1,8
2,4
3,0
4,2
1,3
4,8
2,9
5,4
6,6
6,0
2,1
2,6
2,5
2,5
2,5
4,0
4,0
4,3
8,5
2,0
2,0
4,5
2,5
5,0
4,5
6,5
7,3
9,5
5,5
7,0
10,0
12,5
10,0
10,5
12,0
7,5
45
7,5
8,0
3,5
6,0
32
10
6,0
7,0
7,0
7,0
7,0
7,0
10
10
6,0
6,0
4,0
4,5
6,0
7,0
7,0
4,5
10
11
2,0
3,0
3,0
5,5
4,5
2,5
8,0
4,0
6,0
7,0
2,8
445
ПРИЛОЖЕНИЕ IV
Выражения для коэффициентов т, /г, Q, <о и Ф, входящих в расчетные формулы для манометрических
трубчатых пружин
Плосноовальное сечение
Продолжение прилож. IV
Коэффи-
циент
t
ЛИТЕРА ТУРА
1. Феодосьев В. И.,
Оборонгиз, 1949.
2. Пономарев С. Д.,
1938.
3. Чернышев Н. А.,
Устойчивость пружин сжатия,
1946.
Упругие элементы точного приборостроения,
Расчет и конструкция витых пружин, ОНТИ,
Сжатие и кручение пружин малой жесткости;
сб. «Новые методы расчета пружин», Машгиз,
4. Ч е р н ы ш е в Н. А., Напряженное состояние и деформация цилиндри-
ческих пружин, свитых из круглого прутка, Сб. «Динамика и прочность пружин»,
изд. АН СССР, 1950.
5. По по в Е. П., О расчете осадки нецилиндрических спиральных пружин,
«Прикладная математика и механика», АН СССР, т. IV, вып. 1 и 4, 1940,
а также т. 1, вып. 2, 1941.
6. Попов Е. П., Нелинейные задачи статики тонких стержней, Гостех-
издат, 1948.
7. Г е в о н д я н Т. А., Пружинные двигатели, Оборонгиз, 1956.
8. Феодосьев В. И., Расчет тонкостенной трубки Бурдона эллипти-
ческого сечения энергетическим методом, Оборонгиз, 1940.
9. Ф е о д о с ь е в В. И., О больших прогибах и устойчивости круглой
мембраны с мелкой гофрировкой, «Прикладная математика и механика», т. IX,
вып. V, 1945.
10. Wahl А. М., Mechanical springs, Penton publishing Co, 1944.
11. H а г i n g x J. A., On highly compressible helical springs and rubber
rods, and their application of vibration — free mountings, «Philips Research
Reports», v. 3, N 6, 1948 a. v. 4, N 1, 1949.
12. H a r i n g x J. A., Instability of bellows subjected to internal pressure,
«Philips Research Reports», 7, 1952.
13. Ha ring x J. A., Design of corrugated diaphragms, «Trans, of the
ASME», v. 79, N 1, 1957.
14. Wuest W., Der EinflufJ der Querschnittsform das Verhalten von
Bourdonfedern, «Ingenieur-Arcniv», Bd. 20, N 2, 1952.
15. Wuest W., Theorie der Hochdruckrohrenfeder, «Ingenieur Archiv»,
Bd. 24, 1956.
16. РахштадтА. Г. и ШурД. M., Свойства и термическая обра-
ботка сплавов для упругих элементов приборов, Сб. «Термическая обработка
и прочность металлов и сплавов», Труды МВТУ, Машгиз, 1958.
17. Сборник «Перспективы развития упругих чувствительных элементов»,
Центральный институт научно-технической информации электротехнической
промышленности и приборостроения, 1961.
18. Сборник «Металловедение цветных металлов и. сплавов», Металлург-
издат, 1960.
19. Б о б ы л е в А. В., Марганцовистый мельхиор — высокопрочный мед-
ный сплав, «Приборостроение» № 3, 1958.
20. Прецизионные сплавы, Сборник трудов ЦНИИЧМ, вып. 22, Метал-
лургиздат, 1959.
21. Справочник по машиностроительным материалам, т. 1, 2, 4, Машгиз, 1959.
448
22. Прецизионные сплавы, Сборник трудов ЦНИИЧМ, вып. 15, Метал-
лу ргиз дат, 1956.
23. Справочник машиностроителя, т. 4, 6, Машгиз, 1956.
24. Справочник металлиста, т. 2, 3, Машгиз, 1960.
25. С мир яг ин А. П., Промышленные цветные металлы и сплавы,
Металлургиздат, 1956.
26. Шмыков А. А., Справочник термиста, Машгиз, 1956.
27. Keulegan G. Н., Houseman М. R., Temperature coefficient
of the moduli of metals and alloys used as elastic elements, U. S. Bureau of Stan-
dards, «Journal of Research», v. 10, 1933.
28. Brombacher W. G., Melton E. B., Temperature coefficient
of the modulus of rigidity of aircraft instrument, NACA Report N 358, 1933.
29. Feder aus Kupfer und Kupferlegierungen, «Metall», N 7, 1953.
30. Гольдберг M. M., Захаров В. А., и др., Неметаллические
материалы и их применение в авиастроении, Оборонгиз, 1958.
31. Пластические массы органического происхождения, Комитет стандартов,
мер и измерительных приборов, 1959.
32. Пластические массы в машиностроении, Сборник трудов уральского
совещания по пластмассам, изд. АН СССР, 1955.
33. Фторопласты, Гостехиздат, 1954.
34. Феодосьев В. И., Сопротивление материалов, Физматгиз, 1960.
35. Д у б о в Б. С. и Ж а в о р о н к о в М. С., Упругие опоры весоиз-
мерительных приборов, Машгиз, 1954.
36. Феодосьев В. И., К вопросу выпрямления шкалы прибора посред-
ством плоской пружины, Сб. «Теоретические и экспериментальные исследования
пружин», изд. МВТУ, 1947.
37. Бидерман В. Л., Чистый изгиб тонкой полоски, Сб. «Расчет
оболочек и пластин», изд. МВТУ, 1947.
38. Попов Е. П., Теория и расчет гибких упругих деталей, ЛКВВИА,
1947.
39. Пономарев С. Д., Бидерман В. Л., Лихарев К. К.
и др., Расчеты на прочность в машиностроении, т. 1, Машгиз, 1956.
40. Справочник машиностроителя, т. 3, Машгиз, 1955.
41. ГевондянТ. А. и Киселев Л. Т., Детали механизмов точ-
ной механики, Оборонгиз, 1953.
42. Лихарев К. К., Пономарев С. Д. и Феодосьев В. И.,
Расчет плоских спиральных пружин с учетом упрочнения при их заневоливании,
Сб. «Теоретические и экспериментальные исследования пружин», изд. МВТУ,
разд. I, 1947.
43. Чернышев Н. А., Пономарев С. Д., Лихарев К. К.
и Лопухин А. Г., К расчету спиральных пружин, Сб. «Новые методы рас-
чета пружин», Машгиз, 1946.
44. Wuest W., Die quergewolbte Biegefeder, «Z. Vereines deutsch. In-
genieurs», 96, N 6, 1954.
45. Wuest W., Einige Anwendungen der Theorie der Zylinderschale
«Z. angew. Math. Meeh», Bd. 34, N 12, 1954.
46. Малинин H. H., Холодная навивка цилиндрических пружин,
Сб. «Новые методы расчета пружин», Машгиз, 1946.
47. Пономарев С. Д., Бидерман В. Л., Лихарев К. К.
и др., «Расчеты на прочность в машиностроении», т. 2, Машгиз, 1958.
48. Батанов М. В. и Петров Н. В., «Стальные пружины», Машгиз,
1950.
49. Сб. «Вопросы проектирования, изготовления и службы пружин»,
Гостехиздат, 1956.
50. Заседателев С. М., Навивка пружин с начальным натяжением,
Сб. «Расчеты на прочность элементов машиностроительных конструкций»,
Труды МВТУ, Машгиз, 1955.
51. Заседателев С. М., Винтовые пружины с начальным натяжением
и их расчеты, Сб. «Расчеты на прочность в машиностроении», Труды МВТУ,
Машгиз, 1955.
29 Заказ 24.
449
52. Заседателев С. М., Потеря устойчивости пружин растяжения,
Сб. «Расчеты на прочность элементов машиностроительных конструкций», Труды
МВТУ, Машгиз, 1955.
53. Попов Е. П., Методы проектирования витых пружин с криволи-
нейной характеристикой, Сб. «Динамика и прочность машин», изд. АН СССР,
1950.
54. Б и д е р м а н В. Л. и Бояршинов С. В., Расчеты храпового
механизма пружинного типа, «Вестник машиностроения», № I, 1947.
55. Воробьев А. И. и Кацнельсон О. Г., Термобиметалл и его
применение в приборостроении и автоматике, Госэнергоиздат, 1951.
56. Агейкин Д. И., Костина Е. Н. и Кузнецова Н. Н.,
Датчики систем автоматического контроля и регулирования, Гостехиздат,
1959.
57. Панов Д. Ю., О некоторых вопросах биметалла, Труды ВВИА
им. Жуковского, 274, 1948.
58. Панов Д. Ю., Об устойчивости биметаллической оболочки при
нагреве, «Прикладная математика и механика», XI, вып. 6, 1947.
59. Григолюк Э. И., Тонкие биметаллические оболочки и пластины,
«Инженерный сборник», т. XVII. 1953.
60. Аксельрад Э. Л., Расчет неоднородных по термоупругим свой-
ствам оболочек и его применение к биметаллическим элементам приборов,
Труды Ленинградского института авиационного приборостроения, т. XXIV, 1957.
61. Ко рол.ев В. И., Тонкие двухслойные пластинки и оболочки,
«Инженерный сборник», т. XXII, 1955.
62. Тимошенко С. П., Пластинки и оболочки, Гостехиздат, 1948.
63. В о л ь м и р А. С., Гибкие пластинки и оболочки, Гостехиздат, 1956.
64. Фе о дось ев В. И., Расчет пружин Бельвилля, Сб. «Новые методы
расчета пружин», Машгиз, 1946.
65. Пратусевич Я. А., Вариационные методы в строительной меха-
нике, Гостехиздат, 1948.
66. Лейбензон Л. С., Вариационные методы решения задач теории
упругости, Гостехиздат, 1948.
67. Н е пс к у Н., Uber den Spannungzustand in kreisrunden Platten mit
verschwinden Biegungssteifigkeit, «Zeitschrift fur Mathematik und Physik»,
Bd., 63, Hf. 3, 1914.
68. Цянь Вэй-чан, Теория круглых пластинок большого прогиба,
сб. «Теория гибких круглых пластинок», Издательство иностранной литера-
туры, 1957.
69. Haringx J. A., The rigidity of corrugated diaphragms, «Applied
Scientific Research», A 2, 1950.
70. D re ssle r R. F., L 1 о у d E. C., W i 1 d h a c k W. A., Investi-
gations of the properties of corrugated diaphragms, «Trans, of the ASME», v. 79,
№ 1, 1957.
71. Панов Д. Ю., О больших прогибах круглых мембран со слабым
гофром, «Прикладная математика и механика», т. V, вып. 2, 1941.
72. Андреева Л. Е., Расчет гофрированных мембран как анизотроп-
ных пластинок, «Инженерный сборник», АН СССР, т. XXI, 1955.
73. Андреева Л. Е., Расчет гофрированных мембран, Сб. «Расчеты
на прочность в машиностроении», МВТУ, Машгиз, 1955.
74. Андреева Л. Е., Расчет характеристик гофрированных мембран,
«Приборостроение», № 3, 1956.
75. А и д р е е в а Л. Е., Определение характеристики и эффективной
площади гофрированной мембраны с жестким центром, «Научные доклады
высшей школы», серия «Машиностроение и приборостроение», изд. «Советская
наука», № 1, 1958.
76. Андреева Л. Е. иЛе б едева А. Г., Исследования мембран, ха-
рактеристики которых линейны по давлению, «Информационный бюллетень
НИИТеплоприбора» № 5, 1956.
77. Феодосьев В. И., К расчету хлопающей мембраны, «Прикладная
математика и механика», т. X, вып. 2, 1946.
78. Андреева Л. Е., Расчет конических и сферических гофрированных’
мембран, Сб. «Расчеты на прочность, жесткость и ползучесть элементов машино-
строительных конструкций»; МВТУ, Машгиз, 1953.
79. Б и д е р м а н В. Л. и Л а п и н А. А., К определению характеристик
резино-кордовых оболочек, «Инженерный сборник, XIV, изд. АН СССР, 1953.
80. Лапин А. А., Графический способ расчета резино-кордовых оболо-
чек, Труды МВТУ, вып. 16, Машгиз, 1952.
81. Сильфоны нолутомпановые. Сильфоны стальные однослойные. Силь-
фоны бронзовые однослойные. Нормали машиностроения СССР, Стандарт-
на, 1960.
82. Королев В. И., Расчет сильфонов, «Вестник Московского универ-
ситета», № 9, 1954.
83. Феодосьев В. И., К расчету гофрированных коробок (сильфонов).
«Инж. сборник», АН СССР, т. IV, вып. I, 1947.
84. Феодосьев В. И., Расчет гофрированных коробок (сильфонов)
методом Ритца, Сб. «Теоретические и экспериментальные исследования упругих
элементов приборов и машин», изд. МВТУ, 1947.
85. Палатников Е. А., Расчет осевых компенсаторов, вводимых
в трубопроводы, Оборонгиз, 1957.
86. ВолошинА. А., Податливость и прочность линзовых компенса-
торов трубопроводов, «Вестник машиностроения» № 4, 1958.
87. Р у ч и м с к и й М. Н., Экспериментальное исследование компен-
сирующей способности линзовых компенсаторов (трубопроводов), Труды Все-
союзного научно-исследовательского института по строительству объектов
нефтяной и газовой промышленности, вып. 6, 1954.
88. Turner С. Е., FordH., Strees and deflextion studies of pipeline
expansion bellows, «Proc. Inst. Meeh. Engrs», N 15, 1957, а также «J. Meeh. Engng.
Sci», 1, N 2, 1959.
89. Сычев И. А., Новые S-образные пружины для манометрических
приборов, «Измерительная техника» № 11, 1959.
90. Н а г а т к и н А. Г., Манометр высокого давления с трубчатой пружи-
ной нового типа, «Приборостроение» № 5, 1956.
91. Сычев И. А., Разработка сварных манометрических пружин, «Бюл-
летень НИ ИТепло прибора», 1960.
92. В i е n z е п о С. В., KochJ.J., On the elactic behavior of the as —
called «Bourdon» pressure gauge, «Proceedings Koninklijke Nederlandsche Aka-
demie Van Wattenschappen», v. 44, 1941.
93. Wo lf A., An elementary theory of the Bourdon gauge, «Journal of
applied Mechanics», v. 13, N 3, 1946.
94. Clark R. A., Reissner E., Deformations and stresses in Bourdon
tubes, «Journal of applied Phisics», v. 21, N 12, 1950.
95. J e n n i n g s F. B., Theories on Bourdon tubes, «Trans, of the ASME»,
v. 78, Nl, 1956.
96. Mason H. L., Sensitivity and life data on Bourdon tubes, «Trans,
of the ASME», v. 78, N 1, 1956.
ОГЛАВЛЕНИЕ
Предисловие ........................................ ............... 3
Введение ......................................................... 5
Глава I. Основные свойства упругих элементов....................... 10
§ 1. Материалы, применяемые для изготовления упругих элементов 10
Требования, предъявляемые к материалу упругих элементов . . 10
Механические свойства материалов.............................. И
Материалы для упругих элементов.............................. 18
§ 2. Вопросы изготовления упругих элементов.................... 39
§ 3. Основные свойства упругих элементов....................... 44
Упругая характеристика, жесткость, чувствительность ......... 44
Тяговые усилия и эффективная площадь......................... 48
Коэффициенты запаса и допускаемое напряжение............ . . 52
Погрешности чувствительного упругого элемента ........ 54
/
Глава II. Плоские пружины ....................................... 58
§ 4. Конструкция и применение плоских пружин.................... 58
§ 5. Расчет плоских пружин в области малых перемещений .... 67
§ 6. Расчет плоских пружин в области больших перемещений по ме-
тоду Е. П. Попова ............................................ 76
Вывод уравнения упругой линии гибкого стержня................ 80
Периодические упругие кривые ................................ 83
Условия геометрического подобия стержней..................... 85
Диаграммы упругих параметров................................ 87
Порядок и правила решения задач с помощью диаграмм упругих
параметров .................................................. 90
§ 7. Спиральные заводные пружины .............................. 103
Общие сведения ............................................. 103
Характеристика спиральной заводной пружины.................. 104
Способы крепления концов пружины............................ 107
Нормальная заводная пружина.................................. 112 ’
Определение формы спиральной пружины после стабилизации . . 114
Проектирование нормальной заводной^спиральной пружины . . 120
Пружинные двигатели с пологой характеристикой............... 126
452
Гл ава III. Винтовые пружины..................................... 131
§ 8. Типы винтовых пружин, способы изготовления, применение . . 131
§ 9. Конструкция винтовых цилиндрических пружин растяже-
ния-сжатия ................................................... 135
§ 10. Геометрия винтовой цилиндрической пружины .............. 137
§ 11. Расчет на жесткость по линейной теории.................. 140
§ 12 Определение нелинейности характеристики винтовой цилиндри-
ческой пружины растяжения-сжатия............................'. 146
§ 13. Влияние геометрии и способов крепления пружины на форму
ее характеристики.......................................... 157
§ 14. Напряжения в винтовой цилиндрической пружине растяжения-
сжатия ....................................................... 163
§ 15. Изгиб винтовых цилиндрических пружин.................... 166
§ 16. Устойчивость винтовых цилиндрических пружин сжатия . . 172
§ 17. Винтовые цилиндрические пружины с начальным натяжением
(межвйтковым давлением) ....................................... 177
§ 18. Проектирование винтовых цилиндрических пружин растяже-
ния-сжатия .................................................... 185
§ 19. Фасонные витые пружины.................................. 191
§ 20. Пружины кручения ................................... 199
Конструкция и применение.................................... 199
Расчет на жесткость и на прочность.......................... 200
Расчет пружинного храпового механизма (пружинного тормоза) 201
Глава IV. Термобиметаллические пружины ......................... 205
§ 21. Основные свойства и применение.......................... 205
§ 22. Расчет термобиметаллических пружин...................... 211
Определение перемещений термобиметалла при нагреве.......... 211
Изгиб биметаллической пружины внешними силами............... 214
Температурные напряжения в нормальном термобиметалле . . . 220
Напряжения при изгибе биметалла внешними силами............. 223
Глава V. Мембраны .............................................. 224
*
§ 23. Общие сведения ' ............................. 224
§ 24. Плоские мембраны ....................................... 226
Применение и свойства .................. ,.................. 226
Плоская мембрана в области малых перемещений................ 229
Уравнения плоской мембраны в больших перемещениях .... 240
Абсолютно гибкая мембрана................................. 241
Уточненный расчет плоских мембран при произвольных прогибах 247
Определение характеристики плоской мембраны методом «наложе-
ния» ....................................................... 254
§ 25. Применение, конструкция, способы изготовления гофрирован-
ных мембран ................................................... 256
§ 26. Влияние геометрии профиля на характеристику гофрирован-
ной мембраны...................., ,...................... . . 263
453
§ 27. Расчет гофрированных мембран , . ........................ 268
Выбор расчетной схемы....................................... 268
Определение приведенных коэффициентов анизотропии........... 268
Дифференциальные уравнения плоской анизотропной мембраны
в больших перемещениях..................................... 272
Построение характеристики гофрированной мембраны........... 274
Проектирование гофрированной мембраны по заданной характе-
ристике .................................................... 282
Учет влияния жесткого центра на характеристику гофрированной
мембраны ................................................... 291
Расчет гофрированной мембраны, нагруженной сосредоточенной
в центре силой ........................................... 294
§ 28. Мембраны профиля I, характеристики которых линейны по
давлению ...................................................... 295
§ 29. Эффективная площадь мембран.......................... . 301
§ 30. Выпуклые (хлопающие) мембраны........................ . 311
§ 31. Неметаллические (эластичные) мембраны.................... 315
Применение, конструкция, материалы.......................... 315
О расчете неметаллических мембран.......................... 322
Глава VI. Сильфоны ............................................. 324
§ 32. Применение, конструкция, технология...................... 324
§ 33. Расчет сильфонов на жесткость............................ 330
Определение осевой жесткости сильфонов на основе теории изгиба
круглых пластин ............................................ 331
Определение осевой жесткости сильфонов энергетическим методом 336
§ 34. Эффективная площадь сильфона............................ 340
§ 35. Определение изгибной жесткости сильфона.................. 342
§ 36. Устойчивость сильфона.................................... 344
§ 37. Определение напряжений в сильфонах....................... 346
Глава VII. Манометрические трубчатые пружины ..................... 349
§ 38. Основные свойства, конструкция и способы изготовления . . 349
§ 39. Влияние геометрических размеров на чувствительность и проч-
ность пружины Бурдона.......................................... 356
§ 40. Расчет на жесткость тонкостенных одновитковых пружин . . . 361
Основные допущения ........................................ 361
Определение потенциальной энергии деформации................ 362
Вычисление энергии положения внешних сил.................... 364
Определение полной потенциальной энергии.................... 364
Определение угла поворота конца пружины..................... 368
Линейные перемещения конца пружины.......................... 369
§ 41. Изменение объема внутренней полости манометрической пру-
жины .......................................................... 374
§ 42. Изгиб пружины Бурдона внешними силами.................... 377
§ 43. Перестановочные (тяговые) усилия......................... 381
§ 44. Расчет толстостенных манометрических пружин сильно вытя-
нутого плоскоовального сечения................................. 387
454
§ 45. О расчете на жесткость многовитковых трубчатых пружин . . 391
§ 46. Напряжения, возникающие в манометрических трубчатых пру-
жинах ................................................... 392
§ 47. Проектирование манометрических трубчатых пружин .... 404
Приложение!. Выводы некоторых зависимостей к главе V . . . 412
1. Вывод уравнений плоской мембраны в больших перемещениях . . 412
2. Вывод уравнений плоской анизотропной мембраны в больших пере-
мещениях ............................................... 415
3. Вычисление упругих коэффициентов кх и к» для некоторых профи-
лей мембран ............................................. 416
4. Получение характеристики гофрированной мембраны, нагружен-
ной в центре сосредоточенной силой...................... 419
Приложение II. Манометрические мембранные коробки профиля I,
линейные по давлению, из бериллиевой бронзы Бр. Б2,5 (из отрасле-
вой нормали АН-1671) ............................... 422
Приложение III. Данные на сильфоны (из нормалей машино-
строения [81])......................................... 430
1. Сильфоны полутомпаковые (Л80) 430
2. Сильфоны стальные (1Х18Н9Т) однослойные............... 436
3. Сильфоны стальные армированные...................... 442
4. Сильфоны бронзовые однослойные........................ 442
Приложение IV. Выражения для коэффициентов, входящих в рас-
четные формулы для манометрических трубчатых пружин..... 446
Литература ................................................. 448
Редактор издательства А. Г. Акгькоеа
Технический редактор В. Д. Элькикд
Корректор Л. 2tf_ Усачева.
Переплет художника А- Я- A/tmitUofici
Стало в производство s;i 1962 г.
Подписано к печати gf-V 1962 г. Т-02766.
Тноам< 8000 эна. Исч- л. 29,25 (2 вклЛ.
Бум- л- 14,63- Уч.-ызд. л. 27,65.
Формат 60 х 90/16- Заказ 24 >
Цепа 1 р. 5 8 к.
типография «Красный Печатник» г
Ленинград, моснопстшй проспект, 9J.
ЗАМЕЧЕННЫЕ О ] I ЕЧ А Т К И
Страница Строка Напечатано Должен быть
113 8-я снизу (ГТ Др — h (?-j. - Ду} Гд h
337 Формула (6. 5) v £fto Miv
Зан. 24. Андреева □. Е.
i/d
1/мм
— Линии п'= Const --------Линии г}”-const
г>
Заиаз 24.
Фиг. 41 в и е. Диаграммы
упругих параметров.
— . Линии Е'= const -------Линии t,r~ const
I
ot
- Линии uj'= const
ex
——Линии £ const
Фиг. 41 а и б. Диаграммы упругих параметров.