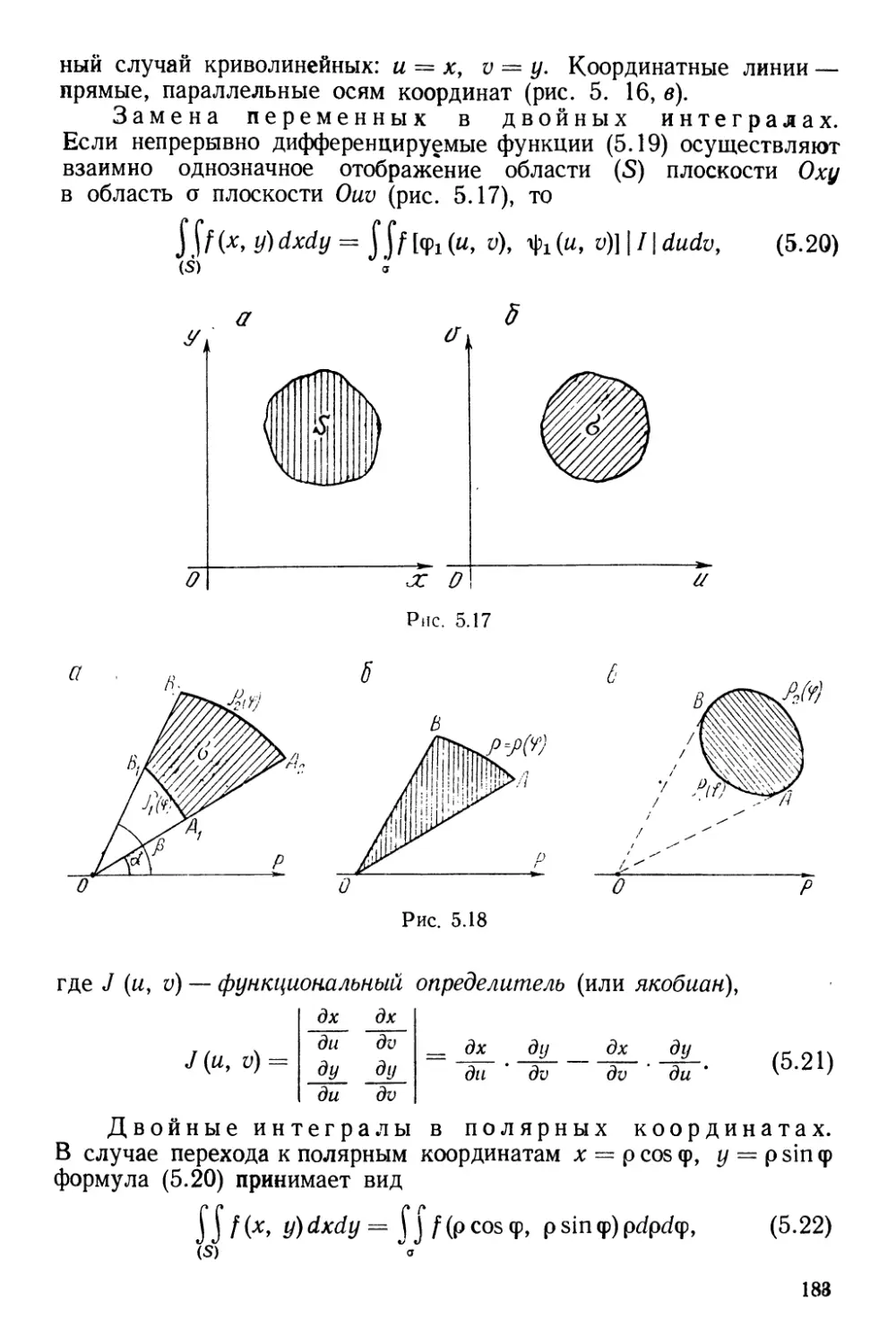
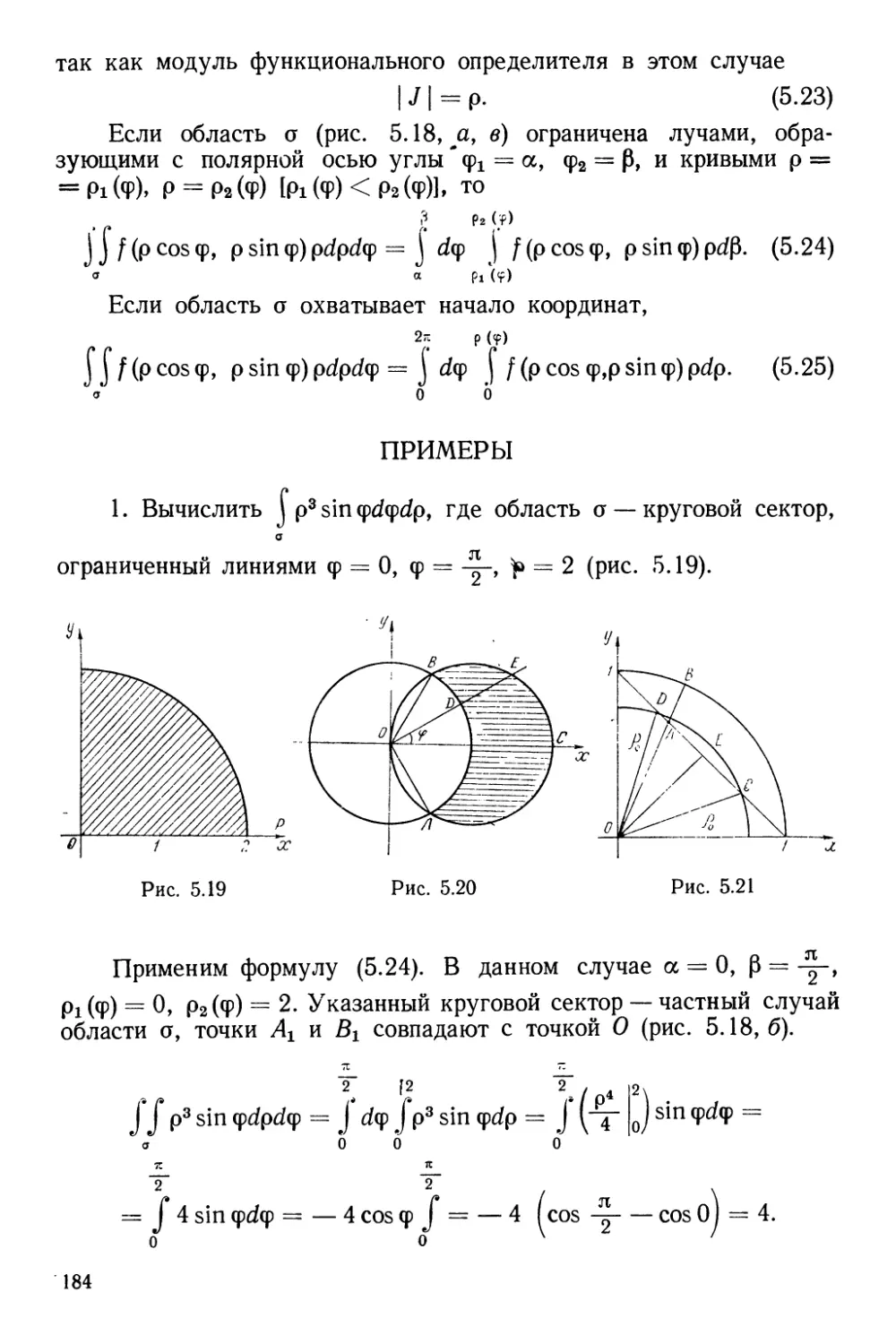
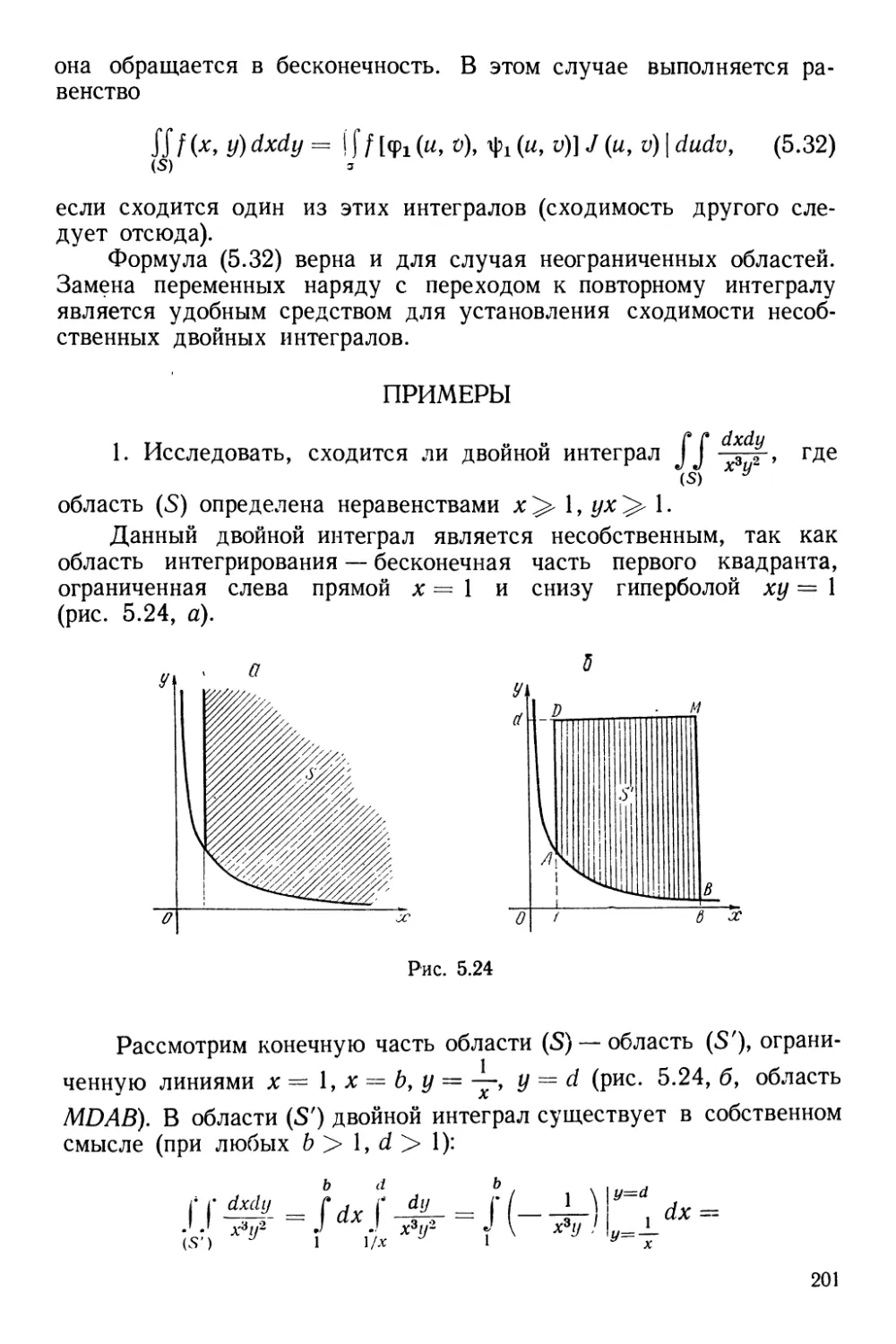
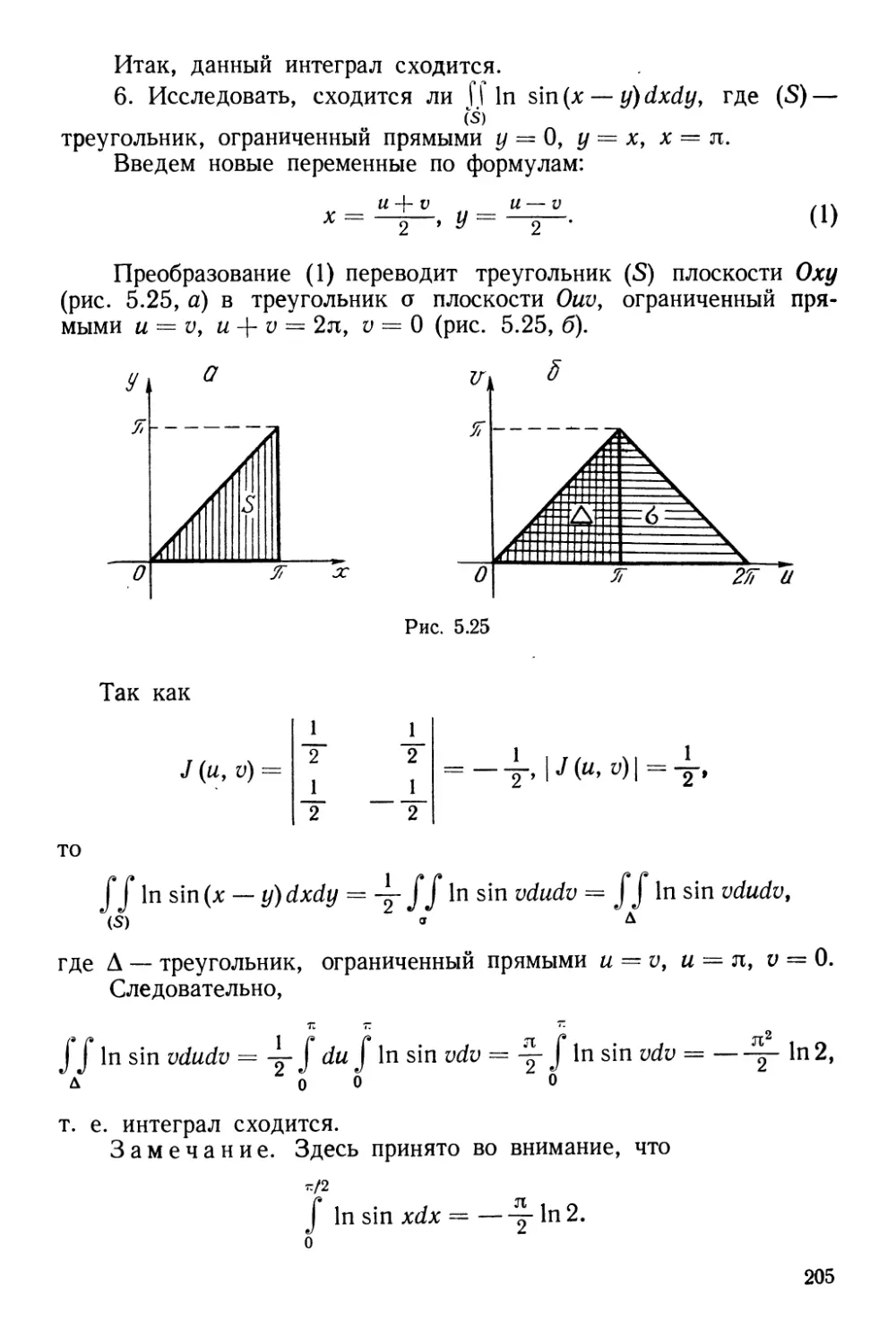
Текст
Α. Α. ГУСАК
РЯДЫ
И КРАТНЫЕ
ИНТЕГРАЛЫ
ИЗДАТЕЛЬСТВО БГУ им. В. И. ЛЕНИНА
МИНСК 1970
Гусак Α. Α.
Γ 96 Ряды и кратные интегралы. Мн., Изд. БГУ, 1970.
384 с. с илл. 9300 экз. 1 р. 03 к. В перепл.
Пособие содержит краткие теоретические сведения, основные
формулы, задачи по следующим разделам программы высшей математики·
числовые и функциональные ряды, двойные, тройные, криволинейные
интегралы и интегралы по поверхности, приложения указанных
интегралов.
В пособии свыше 2400 задач, седьмая часть их дана с решениями.
Предназначено для студентов технических вузов, а также для
геологических и химических факультетов университетов
2-2-3 517
45-70
Алексей Адамович Гусак
РЯДЫ И КРАТНЫЕ ИНТЕГРАЛЫ
Редактор Н. Доркина. Художник В. Козлов. Худож. редактор В. Л а-
пицкий. Техн. редактор В. Безбородова. Корректор Т. Писаренко.
AT 29147, Сдано в набор 19/Ш 1970 г. Подписано к печати 22/ViI 1970 г.
Формат 60 Χ 907ιβ· Бумага типографская № 2. Печ. л. 24. Учетн.-изд. л. 25.
Тираж 9300 экз. Цена 1 руб. 03 коп. Заказ 820.
^Издательство Белорусского государственного университета им. В. И. Ленина.
Минск, Кирова, 24.
Типография издательства ЦК КП Белоруссии. Минск, Ленинский пр-т, 79.
Светлой памяти брата Сергея
посвящает эту книгу автор
ОТ АВТОРА
Сборник задач и упражнений по рядам и
кратным интегралам составлен в соответствии с
программами по указанным разделам высшей
математики для технических вузов, а также для
геологических и химических специальностей
университетов.
В книге содержатся основные теоретические
сведения и формулы, относящиеся к двойным,
тройным, криволинейным интегралам, интегралам
по поверхности и их приложениям, к числовым
рядам с действительными и комплексными членами,
рядам Фурье, степенным рядам и их приложениям
к приближенным вычислениям и интегрированию
обыкновенных дифференциальных уравнений.
Пособие содержит свыше 300 примеров и задач
с решениями, необходимое количество задач для
аудиторных занятий, домашних заданий и
контрольных работ.
Автор выражает глубокую благодарность
доцентам: П. Н. Князеву (Минск), Η. Μ. Матвееву
(Ленинград), Н. В. Поповой (Минск), А. С. Фе-
денко (Минск) за критические замечания и советы;
И. Ф. Метельской — за проверку ответов к
задачам глав 1—4, 7—9, В. А. Прокоше-
вой — за проверку ответов к некоторым задачам
глав 5, 6.
В создании книги большая роль принадлежит
брату Сергею, который уделял много
внимания вопросам преподавания в высшей школе.
Беседы с ним, его советы ускорили начало работы
над рукописью, они содействовали ее быстрейшему
завершению.
Сергей Адамович Гусак (18/Ш 1930—19/ХИ
1969 гг.) всю свою короткую жизнь отдал делу
среднего и высшего образования. Окончив с
отличием филологический факультет Бе л
госуниверситета, он работал учителем сельской средней школы,
завучем средней школы, заведующим Высоковским
районо, научным сотрудником
Научно-исследовательского института педагогики МП БССР,
начальником учебно-методического отдела Министерства
просвещения БССР, доцентом кафедры белорусской
литературы и заместителем декана
филологического факультета БГУ имени В. И. Ленина, ректором
Брестского педагогического института.
I. РЯДЫ
Рядом называется выражение вида
00
2 ик = и1 + и* + Из + . . . + ик + . . . ,
где иъ иъ и3, . . . , ukJ ... — последовательность чисел или функций.
Слагаемые иъ и2, иг, ... , uk, ... называются членами ряда.
Если все члены ряда являются числами, ряд называется числовым,
если члены ряда — функции, ряд называется функциональным.
Глава 1
ЧИСЛОВЫЕ РЯДЫ
§ 1.1. ОСНОВНЫЕ ПОНЯТИЯ. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ
Рассмотрим числовой ряд
00
2 ak = αι + а* + аз + · · · + ak + . . . (1.1)
k=\
Ряд (1.1) задан, если известен его общий член
ak = q>(k),
т. е. известно правило, по которому каждому номеру k(k= 1,2,
3, ...) ставится в соответствие вполне определенный член ряда.
Сумма η первых членов ряда называется его п-и частичной
суммой:
Sn = ах + a2i+ a3 + . .. + ап. (1.2)
5
Конечный или бесконечный предел частичной суммы при
η -> оо называется суммой ряда:
S-limS^. (1.3)
η—>оо
Ряд, имеющий конечную сумму, называется сходящимся.
Если предел частичной суммы не существует или бесконечен,
ряд называется расходящимся.
Ряд, члены которого неотрицательны, называется
положительным. Положительный ряд всегда имеет сумму; эта сумма будет
конечной (и, следовательно, ряд — сходящимся), если его
частичные суммы ограничены сверху, и бесконечной (а ряд —
расходящимся) в противном случае (основная теорема).
Если в ряде (1.1) отбросить первые т членов, получится ряд
00
% = <Wl + ат+2 + flm+З + · · . , (1.4)
называемый остатком ряда (1.1) после т-го члена.
Некоторые теоремы для числовых рядов:
1. Если сходится ряд (1.1), сходится и любой из его остатков
(1.4); из сходимости остатка (1.4) вытекает сходимость исходного
ряда (1.1).
2. Если ряд (1.1) сходится, сумма ат его остатка (1.4) после
т-го члена стремится к нулю при т -> оо.
3. Если члены сходящегося ряда (1.1) умножить на один и тот
же множитель с, его сходимость не нарушится (а сумма лишь
умножится на с).
4. Два сходящихся ряда
00
2 ak = ах + а2 + а3 + ... ;
00
2 bk = Ь1 + Ь2 + Ь3 + · · '
можно почленно складывать и вычитать, так что ряды
00 00
сходятся и их суммы равны соответственно A -f- В, А — В, где А
и В — суммы исходных рядов.
5. Необходимый признак сходимости. Если ряд (1.1) сходится,
его общий член стремится к нулю, т. е.
lim ak = 0. (1.5)
Следствие. Если общий член ряда к нулю не стремится, ряд
расходится.
6
2
ПРИМЕРЫ
1. Написать первые шесть членов ряда, общий член которого
задан формулой
Полагая в данной формуле k = 1, 2, 3, 4, 5, 6, получаем:
а2 =
а3
а4 =
а5
Uq —
*1 =
(-
= (■
:(-
= (-
= (-
(-1)
1)2-1 .
-1)3-
1)4-1
-1)5-
1)6-1
1-1 1
2-1 —
1
2-2—1
-ι L_
23— 1
1
2-4— 1
ι
2-5—1
1
2-6—1
1
= (-
- = (-
= ("
= ("
= ("
(-ΐ)°τ =
4 4—1
_ i)2 ! :
4 6— 1
пз—!— =
4 8—1
_ ΐ)4 ! =
4 10-1
' 12-1
= 1;
1 .
3 '
1 .
" 5 '
1 .
7 '
1
9 '
1
11 *
Таким образом, данный ряд можно записать так:
оо
jLAK } 2k—\ 3^5 7^9
fc=i
_1. ι (~1)fe~1 ι
Π -г · · · -г 2k— l ~t~
2. Написать первые четыре члена ряда с общим членом ak =
ь \ з / ·
Полагая в формуле для общего члена k=l, 2, 3, 4,
получаем:
1/ΊΥ —JL -lil^2 2 - 1 I2
— .л. — — — — __ ι Υ* — ι — ι ί2ϊ3 — 8
ai~~iiQ/ ~ q» fl2- 9 1 зj ~9,аз_" з \з/ — "вР
1 /2\4 4
Й4 4 \3/ "81 *
Итак,
1 /2^
У1(2)* = 1 + -2+1 + 1+ +1(.
jLA k\3J 3^9^81^81^*^fc\3
3. Найти формулу для общего члена ряда
1,1 1,1
1
3-2 ^ 54 7-8 ^ 9-16
считая, что каждый его член получается по тому закону, по
которому образованы записанные члены.
Можно заметить, что члены ряда — дроби, числитель каждой
из которых равен единице I первый член тоже можно представить
так: 1 = у), а знаменатель есть произведение нечетного числа
2k— 1 на соответствующую степень числа 2 (для первого члена
это тоже верно: 1 = ττ^ό)· Далее> так как члены ряда имеют
чередующиеся знаки, нужно ввести множитель вида (— l)k~l, чтобы
получить искомую формулу
"'^"^'ёГ^ <*= 1.2,3,...).
4. Написать формулу для общего члена ряда
1 + 1 + 1 + A + _1+_L + J_ +
считая, что последующие члены получены по тому же закону, по
которому образованы выписанные члены.
Каждый член ряда представляет собой дробь ak = —, ЧИСЛИ-
тель которой равен единице для членов с нечетными номерами
и трем для членов с четными номерами, а знаменатель —
соответствующей степени числа 2. Следовательно, числитель можно
представить формулой pk = 2 + (— 1)*, а знаменатель — формулой
qk = 2k~x, поэтому
2+ (-!)*
2k
ак= 'ΤΤΓι (*= 1.2,3, ...).
5. Найти сумму ряда
00
jLi(c+k)(c + k+\) <c+l)(c+2) ^
оо
' 1
(c+k)(c + k+l) (c+i)(c+2) ' (с + 2)(с + 3)
+ ! + + '
ι in _J_ Ί\ ίη _ι_ л\ I · · · Γ
(с + 3)(с + 4) ' ··· ' (c+k)(c + k+\) ' ···'
где с — постоянная величина (с φ — k, k — 1, 2, 3, ...).
Составим n-ю частичную сумму данного ряда:
ς ' ι ' - ' , ,
(c+I)(c + 2) ^ (c + 2)(c + 3) f (с + 3)(с + 4) ^ · · · "Г
+
(с+п)(с+п+\)·
Чтобы упростить выражение для Snt преобразуем формулу
для общего члена ряда, разлагая ak на элементарные дроби.
Положим
1 А в
(c-\-k)(c + k+ 1) ~~ \c + k "·" с + £+1 '
отсюда
1 (А + В) k + (Л + В) с + А
(c + k)(c + k+\) - (c + k)(c + k+\)
Сравнивая коэффициенты при одинаковых степенях k в
числителях обеих частей равенства, получаем:
А + В = 0, (А + В)с + А=1,
откуда А = 1, В = — 1, поэтому
1 = 1 1
(c + k)(c + k+\) ~ c + k c + k+\ '
Выражение для Sn принимает вид
5" = \7+Т 7+Т/ + [с + 2 ~ 7+Т/ + 1τ+Τ~7ΤΤ/ + · * * +
, (_J U,(J ! )
^{c + n^-l c + n J "i" \c + n c+n+\r
Приводя подобные члены, получаем
с = _J L_
п с+\ с + η+1 *
Переходя к пределу, находим
1
lim S
η—>оо
Следовательно,
п с+ 1
J-d (c + k)(c+k + 1) C+l
Л=1
(1.6)
Замечание. В частных случаях, при с = О, с = 1, с = )/"2,
с = π, по формуле (1.6) получаем соответственно:
00
А=1
оо
_ 2' .—J|
^J(*+I)(* + 2) 2' ^(,/2 + *)(|/2 + &+1) V2+1
^mJ (a + k)(n + k+\) π+1
6. Найти сумму ряда
00
V ι
1
+
1
ft=l
(c + k + 2) (c+i)(c + 3) ^ (c + 2)(c + 4)
1 1
+
(с + 3) (с + 5)
··· +
(с + k)(c + k + 2)
где с — постоянная величина (с φ — k, k = 1, 2, 3, .. .)·
Разложив общий член afe на элементарные дроби, получим
1 1
1
(c + k) (c + k + 2) ~ 2 \c + k c+k + 2)'
Составим п-ю частичную сумму данного ряда и преобразуем ее:
1,1,1,
5„ =
+
+
+
(с+1)(с+3) ' (с + 2)(с + 4) ^ (с + 3)(с + 5)
+
1
1
1
. \ + ι ι
1
(с+п)(с + п + 2) 2 [Дс+1 с + 3) l \c + 2 с + 4
+ .·· +
с + 3 с + 5/ ' ·'· ' \с + п — 2 с
/ Ι ι \, / ι ι
\С + Π
h)
+
\с + η — 1 с
-1—WP-
с + η+ 2/У
1 1 1
я 2\с+\ ' с + 2 с + л + 1 с + я + 2/·
Следовательно,
S = limS„ l l l · *
/г—>оо
т. е.
ι
2 \с^-\ ' с + 2
2с+ 3
2 (с+1)(с + 2) *
В частном случае, при с = О,
6 = 1
Σ-
7. Найти сумму ряда
1
{c + k-\)(c + k)[c + k+\)
1
k(k + 2) 4 *
(1.8)
(1.9)
(с = const, с φ — &, & = 1, 2, 3, .. .)·
Разлагая общий член ряда на элементарные дроби, получаем
1
(c + k-\){c + k)ic + k + \)
2 \с + Л-
+
1 c + k ' с-}- k+ l
10
Составляя п-ю частичную сумму и преобразуя ее, находим
с(с+1)(с+2) "*" (с+1)(с+2)(с + 3) "*"
1 (С + 2)(с + 3)(с + 4) ' •••τ- (с + л_1)(с + „)(с + л + 1)
= -L\(A ?_ . —!_) _1_ /_! 2 I '
2 \\ с с+1"гс + 2/~1~\с+1 с + г'Гс + З
1 2 , 1 \ , , / 1 2
ст +··■ + (;
, с + 2 с + 3~с + 4/~'"~\с + п — 3 с + п-
1 1 ) , / 1 2__ , 1 \ / 1_
1 )] = J-(-L ! !_ + .
/J 2 \ с ^ > ι - ' - ^
с + я ' с -f- лг -}- 1/J 2\с с+\ с + п ' с + п+\
Переходя к пределу, получаем
в-.'Й*-т(4—«Тт)· S = 4-7fW·
Следовательно,
,Zj(c + fc-l)(c + fc)(c + fc+l) 2c (с+1) ' (1.10)
В частности, при с = 1 из последней формулы находим
Σ-
1 1
£(£+1)(£ + 2) 4
/е = 1
8. Исследовать, при каких q сходится ряд
оо
2daqk~x = а + aq + αφ + ag3 + .. . + α^_1 + . ..
k=\
Данный ряд является геометрической прогрессией со
знаменателем q. По определению
Sn = a(l+q + f + q*+... + qrl). (1)
Умножая почленно равенство (1) на q, получаем
Snq = a (q + q* + g3 + . . . + <f ^ + φ). (2)
Вычитая почленно равенство (2) из равенства (1), находим
S„(l-<?) = a(l-<?»).
11
Если <?=£ 1,
sn-^p- (3)
Из равенства (3) видно, что наличие или отсутствие предела
п-и частичной суммы данного ряда зависит от величины q, a
именно:
1) при \q\ < 1 \imqn = Q, поэтому lim Sn = γ-^—;
/ι-»οο η—>οο *■ Я
2) при I q | > 1 lim qn = oo, поэтому lim Sn = oo, ряд расхо-
/i—>oo n—►oo
дится;
3) в случае q = 1 ряд принимает вид
1 + 1+1 + ...,
поэтому Sn = π, lim S^ = oo, ряд расходится. В случае q = — 1
/г—>оо
ряд принимает вид
1-1+1-1+1-...
Для него S2m+i = 1, S2m = 0, поэтому не существует предела
его частичных сумм; ряд расходится.
Следовательно, геометрическая прогрессия сходится тогда и
только тогда, когда \q\ < 1.
со
9. Доказать, что ряд 2j— = ι + ~γ + ~^-+ ~j-+ · · · ^Рас"
k=\
ходится. (Данный ряд называется гармоническим.)
Составим п-ю частичную сумму, где η = 2т:
52. = ι + 4-+4-+4-+4+-δ-+-Γ+1+···+
+ ! + ! + ..+ 1
Г лт—1 ι 1 ' от—1 ι О Г * * * ~
2т—1 + 1 2т_1 +2 2т '
Сгруппируем члены этой суммы следующим образом:
+(
ι ι ι
2т~1 4- 1 + 2m—l + 2 + * * * "ι 2^"
„m—1
2 членов
Так как
_Li_L^J_i_L_ J_ _Lj_J_ , _L . J_\
3~Γ4'^4~1~4~ 2' б^б^У'в^
^8 r 8 ^ 8 ^ 8 2 ' * * ' '
12
1,1, , _L^J_ ,_L, ι 1 ".
2m—1 ι J "τ" 2m-l 4-2 ' * ' 2m ^ 2m "" 2Ш ' ' * * ·" 2m
m—1 членов
_1_
2 '
s 2m > ι+\+(4-+4-+· · ·+4-)= 1+■
m—1 член
Из неравенства S2m > 1 Η—о" ВИДН0» что частичные суммы
не могут быть ограничены сверху. Применяя основную теорему
для положительных рядов, заключаем, что данный ряд имеет
бесконечную сумму, т. е. гармонический ряд расходится.
Замечание. Общий член аЛ = — гармонического ряда
стремится к нулю, т. е. lim ak = lim -r- = 0. Пример гармонического
ряда показывает, что условие lim ak = 0 не является достаточным
£->оо
признаком сходимости ряда.
10. Выяснить, сходится или расходится ряд
— + — + — + — + — + + —+
2 ^ 3 ^ 4 ^ 5 ^ 6^^£+1^
Общий член этого ряда выражается формулой ак = ^ц. Так
как
lim α^ = lim т-г-т = lim г— = 1,
i+-
fc
т. е. общий член к нулю не стремится, то на основании
следствия из необходимого признака заключаем, что данный ряд
расходится.
11. Доказать расходимость ряда
1 + —+ — + — + —+ +-L- +
т. е. ряда
]β*> а*+1="^~' ai = S!=l.
*=1
Общий член данного ряда выражается формулой
ak = -^— (ft = 2, 3, ...).
13
Предположим, что данный ряд сходится. Тогда в силу
необходимого признака lim ak = 0. Так как Sk-\= , то lim S^_i==oo,
т. е. предел частичных сумм не является конечным; ряд
расходится. Полученное противоречие доказывает наше утверждение.
12. Выяснить, сходится или расходится ряд
ι
arccos-^"
k=l
Общий член ряда
1
ak = arccos-^-.
Так как lim ak = lim arccos-нт- = arccos 0 = -г-, т. е. предел
fc->oo k—>oo Ш 1
общего члена не равен нулю, на основании следствия из
необходимого признака сходимости заключаем, что данный ряд
расходится.
ЗАДАЧИ
Написать первые пять членов ряда по заданному общему
члену:
ι Ιο I о Ь
г* (2Л — I) (2Л + Ι)" А" "*~ (2^-1)3^ ' к 2*(Л+1)"
4· а*= 1к+\ ' 5· fl* = if. гДе *1 = 1-2-3 ... Л(Л = 1, 2, 3, ...).
β /г _ (2fe— 1)ΐ! 1 ((2k- 1)11 = 1-3-5-7... (2fe- 1)Λ
* 2*П ." fc.2*+i l2>fe!! = 2-4.6-8 ... 26 j*
7- a, = (-l)*+i^. 8. «»== 3+^'>* .
9. ал = (-1)—2--£г(* = 0, 1,2,...).
fe (fe-l) (fe-2) j
10. ал = (-1) S _^_(ft = 0f 1,2,...).
В каждой из задач 11—20 найти формулу для общего члена
ряда, считая, что каждый последующий член получается по
тому же закону, по которому образованы выписанные члены:
1Ь Т"+ ~ζ^+ "3^+ ~4^~ + * * *
12# 2 In 2 + 31п3+ 4 In 4+ 5 In 5 +" " #
14
ι°· 3 ^ 6 ^ 11 ^ 20 ^
14 1 I 4 I 9 I 16 I 25 I 36 I
14. 1 + 2 + g + 24 + ,20 + 720 ' * · ·
ις ι l 4- l l л. l ' .
,6. 1—JU+ » ' · » »
/2 Π Κ4 V 5 Кб
17. i-fJ L__L + _L + J ! L.
"' ' r 2 3 4 ^ 5 ^ 6 7 8 ^
is. -1 L + -L + -! ! L+ > ·
4 ' 9 ' 16 25 36 ' 49 ' * * *
19. i+4-+4--4-+4-+4-+^-i+...
'"' 2 ^ 5 ^ 8 11 ^ 14 ^ 17 ^ 20 23 ' "·
В каждой из задач 21—30 найти сумму ряда, считая, что
последующие его члены образованы по усматриваемому правилу:
и. 1 + 4+4+4-+^- + ···
22. 1-4-+4—^ + 4" + · ··
23· (е + 1)(в + 2) + (е + 2)(е + 3) + (е + 3) (е + 4) +'··
24 ———5—= ι = ! _| ! = l
(Y3+l)(V 3+2)Т(КЗ+2)(1/ 3+3) ^ (К 3+3)(>^3+4) ^'"
25.
26.
1,1,1, 1
2-4 ' 4-6 ' 6-8 г 8-10
1,1,1,1
1-3 ' 3-5 ' 5-7 ' 7-9
27· (с + 2)(с + 4) + (с + 4)(с + 6) + (с + 6)(с + 8) +'
(с = const, с ±. — 2k (k = 1, 2, 3, .. .))·
28. ! + 1,1,
(c+l)(c + 3) ' (c + 3)(c + 5) ' (c + 5)(c + 7)
(с-const, c:£ — (2k— 1) (*= 1, 2, 3, . ..))·
2k + 1
29' Ь4 + 49 + 9-16 + 16-25 +*" +
fc2(fc + l)2
5 ' 12 ^ 21 r * * " ^ fc2 —4
15
Найти суммы следующих рядов (с = const, с = φ — k,
k=\,2, 3,...):
31.
33.
1 ХЛ 1
il Цс + k) (с + k + 3) · 32· ^ (с + А) (с + k + 4) ·
ft=l ft=l
оо оо
i*(fc+I)(fc + 2)(fe + 3)· 34· 2jl
I (c+ft-I) (с+Л) (c+k+l) (c+k+2)
DO OO
όό· ^J L2fc3(fc+1)3 · *&· ^j fc4(fc+l)*
fc=l k=l
С помощью следствия из необходимого признака доказать,
что каждый из следующих рядов является расходящимся:
2k + 4 · 38· 2.1 Ы + 1 · 39· ^j C0S 2fc
*=1 fc=l ft=l
40. 2*sinX· 41·2(1+Τ")· 42 ^
ОТВЕТЫ
4-)'
1 1 1 1 1 1111
Ιβ 3 + 15 + 35 + 63 + 99 + * * * * 2· l + 9 + 45 + 189+729 + · · · ·
1 J_ _3_ J_ _5_ J^ t J3_ _5_ 7_ _9_
3· Τ + 6 + 32 + 20 + 192 + '''' 4* 5 + 17 + 37 +65 + 101 + ''' '
JL JL J*L -*L 243 L- 3 is
5* 1 + 2 + 6 + 24 + 120 +*·· · 6* 2·1-22 + 8·2·23 + 48-3-24 +
105 945 J_ , J_ __L JL
*+ 384-4-25 + 3840-5-26 ' 7* l ~ 4 + 9 ~" 16 + 25 +' *' ' 8* l +
4 1 _4_ J_ ο ι _i_ iL J_ JL _L
+ 1" + "2"+ 5 + 3+···· 9*1+ 2 ""4 ~~ 8 + 16 + 32 -
1 1 1 J_ _1_ _1_ J_ _2_
— П64— 128 + 256+···· 10. 1+ 2 + 5 - ю + 17 + 26 +
»3. аЛ = 2)Г+1 (6=1,2,3, ...). Η. σΛ=-Η-(Λ = 1, 2, 3, .. .)· 15. α* =
= (-1)^2^=1 (*=1'2,3, ...)· 16. аЛ = (-1)*~у=(Л = 1,2,3, ...).
16
k(k-l) k (fe+D j
17. αΛ = (-1) 2 yqrj (* = 0, 1,2,3, ...). 18. αΛ = (-1) 2 ηρ- (Λ =
fe (fe-1) (fe-2)
= 1,2,3,...)· 19. σΛ = (—1) 2 -^py(^ = 0, 1,2,3, ...)· 20. a*=
fc (Λ-1) (k-2)
2 fc+ 1 3 tt -
= (—1) 3fe4-2 (fe = 0> *' 2' 3, ...).21.-y. Указание. Данный
1 3 9q 1
ряд является геометрической прогрессией, q = -ό~. 22.-τ— ζ°· . j .
Указание. См. пример 5. 24. —= . Указание. См. пр имер 5.
25. —г- Указание. а^ = —г- · , (< , ... См. замечание к примеру 5.
2β·Τ· 27· 2(с+2)· Указание. . а* = (c + 2*_ i)(c + 2* + 1) =
1 ( l ' .). 28. '
. Указание, α^ =
29. 1. Указание.
~2\с+2&— 1 c + 2k+l J 2(c+l)
1 L/ ι ι
(с + 2*)(с + 2Л + 2) - 2 ^ c + 2* "с+ 2*+2,
2fe+ 1 1 1 25 1
a*~ #>(fc+l)2 _ #> ~~ (k+l)2' 30* 48' Указание· aft- £2__4
1 \ on 1 / 1
4 \c+.l
+
Указание. ак = {c + k)(*+k + 3) = ^{^~ c+ \ + 3) 32'
1 1 1 \ ., 1 1/1
4- «-4- «4- · Указание, a* = — =__ .—
^ c+2^ с + Ъ^ с + А) * (c + k)(c + k + 4) 4 \c+k
J Υ 33. JL. 34. — . ! 35 —· Указание.
k + 4/ 18 3 c(c + l)(c + 2)' όό' 2
c + k-
W + M+l _WjL_ ! I 36. 1. Указание. ak =
==4fe3 + 6^ + 4fe + l+/jL_ ! \ 37. Расходится, так как
1 3
lim ak = 38. Расходится, так как lim a^ = 39. Расходится, так как
£->оо 2 £->оо 2
lim а^ = 1. 40. Расходится, так как lim a^ = 1. 41. Расходится, так как
k -*oo к—>оо
lim aft = е. 42. Расходится.
k »оо
17
§ 1.2. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ. ПРИЗНАКИ СХОДИМОСТИ
Признаки сравнения. Интегральный признак Коши
Рассмотрим числовые ряды с положительными членами:
оо
2 а* = 01+ 02 + ^8 + ···; (1.Ц)
00
2&, = &1 + 62 + &з+... (1.12)
Первый признак сравнения. Если для k^>k0
*k<h (1.13)
и ряд (1.12) сходится, то сходится также и ряд (1.11).
Если для k^>k0
ak>bk (1.14)
и ряд (1.12) расходится, то расходится и ряд (1.11).
Второй признак сравнения. Если существует конечный и
отличный от нуля предел
lim-^- = /£0, (1.15)
то ряды (1.11) и (1.12) сходятся или расходятся одновременно.
Интегральный признак Коши. Если / (х) — неотрицательная
невозрастающая функция при χ > О, то ряд
00
2w) ο·16>
сходится или расходится одновременно с интегралом
00
\f{x)dx. (1.17)
ι
Замечание. Нижним пределом интегрирования в интеграле
(1.17) может быть любое другое положительное число из области
существования функции f(x).
ПРИМЕРЫ
1. Выяснить, сходится или расходится ряд
2 22 23 2k
1 + ι + 22 + 1 + 24 + 1 + 26 + · " · + ! + 22* "^ " '
Все члены данного ряда положительны, общий член
2^
ak = г-.
* 1 + 22k
18
Сравним данный ряд с геометрической прогрессией
1 + -2- + -22- + -23-+·.. + -££-+·.·> bk= -ψ-
Так как
2" <Sr = 4r (°k<bk9 ft = 0, 1, 2, 3, ...),
1 _[_ 22* 22fe 2*
00
1
— СХОДИТСЯ
т. е. выполнено условие (1.13), и ряд \\—— сходится (геомет-
рическая прогрессия, для которой q = — <^\\, то на основании
первого признака сравнения заключаем, что исходный ряд также
сходится.
2. Выяснить, сходится или расходится ряд
i+_^ + _L_ + _J l._L_ +
Сравним этот ряд с гармоническим рядом
который, как известно, расходится (см. пример 8 § 1.1). Так как
в данном случае
1 6* = 4" (*=1, 2, 3, ...)
VT ' к k
1 >!
т. е. выполнено условие (1.14), то из расходимости гармонического
ряда следует расходимость данного ряда.
3. Выяснить, сходится или расходится ряд
у ι ^ ι , ι , [_ , !_ .
jZj sk — k 3—I"1" З2 — 2 "^ З3 — 3 ^ З4 — 4 1" · · · ·
Сравним данный ряд с геометрической прогрессией
2и~1* ~~"Т + ~з2~ + "зз- + ^4-+ ··· (О
k=\
В данном случае
ι , ι
ak~ &-k ' bk~W
19
Так как
lim -ξ*- = lim ('—J—: A-) = ton - 3*
Л 3* — i"
bk ^oo I 3* - k ' 3* 7 *-><*> 3*
ft_oo \ 3" — Л 3* / fc->oo
lim !-т-= 1,
ft—>00
fc
3*
т. е. выполнено условие (1.15), и геометрическая прогрессия (1)
сходится, то сходится и данный ряд.
4. Выяснить, сходится или расходится ряд
,=1 kkV-k + 2VY + 3ΪΓ3 + 4ίΤ + "'
Сравним данный ряд с расходящимся гармоническим рядом
S4--»+4-+4-+4-+-4-+·-·
Поскольку
lim -£*- = lim (—. _ : -г-) = lim —τ-ζ=Γ = lim —г = 1
\imi/T= 1, применено правило Лопиталя к функции \пу η =
Inn \
= ~~7Г~I, т. е. выполняется условие (1.15), то из расходимости
гармонического ряда следует расходимость данного ряда.
5. С помощью интегрального признака Коши доказать
сходимость ряда
V * _ 1- , * , 1 , 1 ,_
^-J ^2 _|_ ! ! _j_ j "Г 22 + 1 "*" 3*fc+ 1 "ί" 42 + 1 "Г · · · ·
k=\
Общий член данного ряда определяется формулой
<*» = /(*)= ^ (*=1, 2, 3, ...)·
Записывая в этой формуле χ вместо k, получаем функцию
f(x) = —2ΐΐ · Эта функция удовлетворяет условиям
интегрального признака Коши: она принимает положительные значения
и убывает с возрастанием х.
Докажем сходимость интеграла (1.17) для данного случая:
j-^fi~^arctgx
ι
оо
ι = lim arctgx — arctg 1 = -^ τ- = 4"
1 *->00 Δ Ъ Ъ
20
Так как интеграл сходится, то сходится и соответствующий
ряд (1.16), т. е. данный ряд.
6. С помощью интегрального признака Коши исследовать,
сходится или расходится ряд \^A+J
Функция / (#) = —-ξ— удовлетворяет условиям интегрального
признака Коши. Поскольку
р*^-;(-т+4-)<Н'«-4
00
= оо.
т. е. интеграл вида (1.17) расходится, то расходится и данный
ряд.
00
7. Исследовать, сходится или расходится ряд ^j ил„и.
Общий член ряда определяется формулой ak = f (ft) =
Обратим внимание на то, что суммирование начинается
с k = 2 (при k = 1 соответствующий член не определен, так как
в знаменателе содержится множитель lnl = 0).
Из формулы для общего члена ряда находим фунцию /(*) =
= г (*>2).
х\пх \ ^ >
Принимая во внимание замечание к формуле (1.17), получаем
00
\ *— = In In а:
j xlnx
00
= ос.
2
Так как интеграл вида (1.17) расходится, то расходится
и данный ряд.
8. Исследовать, при каких ρ сходится ряд Дирихле
Если ρ ^ О, то общий член ряда не стремится к нулю,
поэтому ряд расходится (на основании следствия из необходимого
признака сходимости).
В случае ρ > 0 применим интегральный признак Коши.
Функция / (х) = —р- положительна и не возрастает при #>1.
Рассмотрим сначала случай, когда О < ρ < 1. Положим ρ = 1 — h,
где h — достаточно малое положительное число.
Так как
00 00 00
dx f dx (' h-\ * xh |0°
dx
xp J xl-h J h
= oo,
1
т. е. интеграл вида (1.17) расходится, то при 0<р< 1
расходится и данный ряд.
Пусть ρ > 1. Положив ρ == 1 + h (h > 0), получим
00 00
dx ι dx
J χΡ J xi+h hxh
'= limf.
ι \ ι
hxh I \ h I h
Поскольку интеграл вида (1.17) сходится, то сходится и ряд
Дирихле.
Если ρ = 1,
00
dx
= \пх
оо
lim In a: = эо. (1-19)
л-->оо
Интеграл расходится, поэтому расходится и ряд Дирихле
(при ρ = 1 получаем гармонический ряд, расходимость которого
установлена ранее более длинным путем).
Итак, ряд Дирихле сходится при ρ > 1 и расходится при
Р<1.
Замечание 1. Сходимость многих рядов может быть
исследована сравнением с соответствующим рядом Дирихле.
Замечание 2. Вопрос о сходимости ряда.
00
V Pm(k) ^щ
^J Qn(k)
где Рт (k) — многочлен от k степени т\
Qn (k) — многочлен от k степени п,
решается сравнением с рядом Дирихле 7i-ттгу где р = т — п.
При этом целесообразно применять второй признак сравнения.
00
9. Доказать сходимость ряда J7j
(3fc—l)3fc '
22
Преобразуем формулу для общего члена данного ряда:
_ ι ι ι =
Uk ~ (3k — 1)3* ~~ / ι \ ~~ / ι
(эд2!1--^) И1--й-)
1 1
9k2
Х~ 3k_
Рассмотрим ряд с общим членом bk = -^-. Ряд ^К-щ^-
00 00
--g-^-jfeT сходится, ибо это ряд вида ^j-pr, где ρ = 2.
Так как
lim-^- = lim
/г—>оо "к /г-»оо
1 1 1
№ ' j_\ ■ 9k2 ]-Л^ j
1 = lim l——= 1,
т. е. выполнено условие (1.15), то данный ряд также сходится.
00
10. Доказать сходимость ряда Zj м + к£ j_ Ц2 + 7 ·
Это ряд вида (1.20), причем Рт (k) = k2 + 2k — 3, tn = 2,
Qn (k) = № + 5k3 + 4&2 + 7, η = 4. Так как ρ = m — η = 2 — 4 =
00
—- —2, сравним данный ряд с рядом ^ ]-ТГ> который является
рядом Дирихле и сходится, ибо р> 1.
Поскольку
Г _?!*-= Г / fe2 -г 2^ — 3 _J_\ __ v k* + 2k* — 3k2 _ 1
т. е. выполнено условие (1.15), данный ряд сходится.
ЗАДАЧИ
Исследовать, сходятся или расходятся следующие ряды:
1 II3,32,33, , & ,
Ь 1+ 1+32 + 1 + 3* + 1 + 3* + · · · + ι _■_ 32k + · · · ·
2· 1 + 1"+-ТГ+-Зб-+-85"+ ЗМ-5 +·'·+ 3k + k +··· ·
4^7^12^19^***^£2+3 ι ··· ·
2 "ί" 9 "*" 28 "τ" 65 "ί" * * * "Γ" k* + 1 "Γ · · · ·
23
С» 00 00
00 00 00
^ fe 1^ А: 4- 1 ^ lOfe3 + 4*2+5 ^-J
Π. |>1η*Γ>. 12.2-^j^» (6>0). 13.|]-^^-.
1
(In In ^)ln л
(a + ta)*7
/г=2 k=k0 ν /ι=2
oo 3 oo oo
14. y\^LIL, is. V__> . ,6. V.
00 00
/г=2 Л==3
*=1 /г=1
ОТВЕТЫ
1. Сходится. 2. Сходится. Указание. а& < ^ = —£-. 3. Сходится.
Указание. а^<^Ьк = ~ш~- 4. Сходится. 5. Расходится. Указание.
1 1
~k~ ^ In А» » так как & > In &. 6. Расходится. Указание. Сравнить с
гармоническим рядом. 7. Расходится. Указание. V k (k +3) < }^(& + З)2 = k + 3,
oo oo
1 1 V4 1 VI 1
УЩ+Щ >ТТЗ> 2jT+~3=2jT' 8-Сх°Дится- Сравнить с рядом
/е=1 /е=4
00 00
9. Сходится. Указание, &3 + 4£2 + 5 >&3,
V»+tf + 5 <ТГ >0· Сходится. Указание. у==<
< о = —γ,— · П. Сходится при /?> 1, расходится при ρ < 1. 12. Сходится
при /?> 1, расходится при ρ < 1. Указание. Сравнить с рядом Дирихле.
13. Расходится. У к а з а н и е. η + Υ η < 2/2. 14. Сходится. Указание. η2 +
+ л/1г~+/л2>л2. 15. Сходится. Указание. 1n k = ^ln ln ^ ' < ^Г
для А; > £„· 16. Сходится. Указание. ^ 1η Λ = ^п щ in λ < "jfei" Аля
k^k0. 17. Сходится. Указание. Применить интегральный признак Коши:
24
/ Μ = —Γ~ΰΠί—» F (χ) = — ' ο , * · 18- Расходится. Указание. Приме-
л; ln1-r χ о In л:
нить интегральный признак Коши: / (χ) = ν In л: In In л: ' ^(χ) = ^η^ηχ· 19.
Расходится. Указание. См. замечание 2 к примеру 8. 20. Сходится.
Признак Даламбера. Признак Коши. Другие признаки
Рассмотрим числовой ряд с положительными членами
00
2α* = αι + α2 + <*8+..· + α*+... · О·21)
/е=1
Признак Даламбера. Пусть для ряда (1.21)
lim g*+i =q. (1.22)
/г->оо ak
Если q< 1, ряд (1.21) сходится; если <7> 1, ряд расходится.
Замечание 3. Если q = 19 вопрос о сходимости ряда
остается открытым.
Признак Коши. Пусть для ряда (1.21)
ь
lim |/ ak = q. (1.23)
k—Ю0
Если q < 1, ряд сходится; если q > 1, ряд расходится.
Замечание 4. Если q = 1, вопрос о сходимости ряда
остается открытым.
Признак Раабе. Пусть для ряда (1.21)
lim&
_ίί*-_1) = ρ. (1.24)
fc->oo V "Дг+1 /
Если р> 1, ряд сходится; если р< 1, ряд расходится.
Признак Гаусса. Пусть для ряда (1.21)
fl*+i = Р + М""Ч- + ^ (1 25)
αΛ km+Cikm-\ + m+Cm·
Если сх — 6i > 1, ряд сходится; если сх — &ι < 1, ряд
расходится.
ПРИМЕРЫ
11. Доказать сходимость ряда
2 "Г 22 ·" 23 "■" 24 "■" 2б "Г · · · ·
25
Общий член ряда определяется формулой ак = ^ fe .
Заменяя в этой формуле k на k+ 1, получаем последующий член
УЪ+ϊ
ak+\ = 2fe+1 ■
Составим отношение последующего члена к предыдущему:
а,
k+\
Vk+\ . Vk _ Vk+\-2k _ >/Т+1
flfe 2/г+1 2* |/ k -2k+] 2γ k
Найдем предел (1.22):
lim "*+. =iimJ^EL = 4-iiml/i+-i- = 4-i = 4-·
Так как gr = —< 1, то на основании признака Даламбера
2
заключаем, что ряд сходится.
00
5*
И
12. Доказать расходимость ряда 7 г ^ ·
Применим признак Даламбера. Поскольку
_ 5* _ 5*+!
а* ~ ~W~' а^+! ~ (*+1)5 ;
α* ~ (/г+1)5 * *5 "~ 5*(fc+l)* "" (^+1)5
1
lim ^±L = lim 5fe5 = 5 lim (χ^τ) = 5 lim - .
Λ-oo ak k-+oo (k+l? fe->ooU+l/ Λ->οοΙ 1+J_
= 5-1 = 5> 1,
ряд расходится.
13. Доказать сходимость ряда ^j
00
2k-
Так как
2k - 1 _ 2(fe+l)—l 2fe+l
2k— 1 2fc + 1
αΛ (Λ+ 1)! * &I (2fc- \)(k+\)'
,. α*+ΐ ι· 2fc+ 1 ,. 2fc+ 1 π / ι
lim ^ = Ьттдт—η/»,, η = нт 9fe2 ,—Γ — О < 1,
то, согласно признаку Даламбера, ряд сходится.
26
14. Доказать сходимость ряда
i4--L_j__L._i.J_ ,
1 ' 22 ' З3 ^ 44 ^ 5s ^ ' * *
Применим признак Коши. В данном случае
1 ι ι _ 1
а* = --г-, \ak\ =
k k / j j
lim у | аЛ | = lim I/ —— = lim —- = 0,
т. е. g = 0 < 1, поэтому ряд сходится.
Замечание 5. Сходимость данного ряда можно
установить и с помощью признака Даламбера:
lim --——- = lim -τ—-: —- = lim
Λ_>οο АЛ Λ->οο\ (Λ+1)Λ+1 ' kk Γ k-^a, (k+\)k+l
00
15. Доказать сходимость ряда ^jfe*sin*-
2fc
fe=l
Применяем признак Коши. Поскольку
ak = kk sin* ---, /αΛ = ft sin -^-,
1 1
/— 1 sln~2F 1 sm~2k~ 1
lim у ak = lim&sin-r— = lim i ^lim-—· : = -—,
£->oo fc-^oo ^* fe->oo _L fc-*oo ^ 1 z
k 2k
т. e. 9— —-< 1, ряд сходится.
Замечание 6. Сходимость данного ряда можно установить
с помощью признака Даламбера.
16. Исследовать, сходится или расходится ряд
J_ _3 J_ 1-3-5 _1_ 1-3-5-7 \_ (2k—\)\\ J_
2 + 2-4* 2 + 2-4-6 ' 3 + 2-4-6-8 ' 4 +* * * + (2£)!! ' k ~^ " ' '
Общий член данного ряда определяется формулой
_ (2k— 1)!! 1
йк ~ (2k)!! k '
Заменяя здесь k на k + 1, получаем
[2(6+1)-!]!! _ (2fe+l)ll
"*+1 (*+i)[2(*+l)]ll (k~\-\) (2k + 2)!! *
27
Составляем отношение последующего члена к предыдущему:
ak+\ _ (2fe+l)ll . (2k-\)\\ (2k + 1)!! (2k) И k
(£ + 1)(2Л + 2)!1 * k(2k)\\
(2fc + \)k
(2k + 2)(k+\) ~
Находим предел (1.22):
r ak+\ ,. 2k2
! ι m .... — 11 m
(26-
2£2-Ь
2fc2 + 4k
+ k
11111 — 11111 n,9 . л1 ; ~ ■ —
1)!!
£
+ 2
2
2
(2Λ + 2)ΙΙ(Λ+1)
_ j
Поскольку q=l, признак Даламбера не дает ответа на
вопрос о сходимости ряда.
Обратимся к признаку Раабе. Найдем предел (1.24):
\\т ul ak Л г и! 2fc2 + 4fc + 2
\\mk —-* 1 = \\mk\ J~2 ι Τ— _ ι
,;mW 2fc2 + fc + 3fc + 2 Λ ,. ./, , 3fc + 2 «
,. ,3£ + 2 .. 3/s2-{-2fe 3
3
Так как в данном случае ρ = -у > 1, на основании признака
Раабе заключаем, что ряд сходится.
Замечание 7. Сходимость ряда можно установить с по-
аы-1 2k2 A- k "· 2
мощью признака Гаусса: -±-= 2k2 + 4k + 2 = ' k2 + 2k+\ '
Ci — 6ι = 2 2" = "2" > 1; РЯА СХ°АИТСЯ·
17. Исследовать, сходится или расходится ряд
1+ —+—+—+- +
Составляем отношение последующего члена к предыдущему:
ak+\ _ ^ * · * = 2^-1
~к r2k+\'2k—\ 2k + 1 *
Поскольку
lim ——- = lim 0, , f — -~- = 1,
α£ 2k-±\ 2
вопрос о сходимости ряда с помощью признака Даламбера решить
нельзя.
28
Применяем признак Раабе. Так как
(2 \ 2 2&
то и признак Раабе не дает ответа на вопрос о сходимости ряда.
Обращаемся к признаку Гаусса. Находим выражение (1.25):
β*+ι 2Λ— I *~~~2~
я* 2* + 1 . , 1 "
В данном случае т = 1, 6Х= ^", сх = -γ. Так как сх — Ьх =
= ~ ί §-] = 1, ряд расходится.
18. Исследовать условия сходимости гипергеометрического
ряда
αβ α(α+1)β(β+1) , α(α+1)(α +2)β(β+1)(β + 2)
1γ ^ 1·2γ(γ+1) "*" 1·2·3γ(ν+1)(ν + 2) "t" · · · "t"
α (α+1)... (a+k-1) (a+k) β... (β + k)
"*" (Λ+ΐ)!γ(ν + ΐ)...(ν + Λ)
где α > 0, β > 0, γ > 0.
Общий член данного ряда определяется формулой
α(α+1)...(α + *-1)Ρ(Ρ+1).--(β + *---1)
k Л! у (у + 1)... (у + Л — 1)
Поскольку
_^ α(α+1)...(α + ^-1)(α + ^)Ρ(Ρ+1).-.(Ρ + ^-1)(Ρ + ^)
Ш (Л+ 1)!Υ(Υ+1)-..(Υ + Λ— 1)(ν + k)
TO
(а + к)ф + к) _ fe2 + (a+p)fe + ap
Из последнего выражения видно, что применение к данному
ah
ряду признака Даламбера бесполезно ( lim fe+1 = 1 .
Примени—>оо ak I
ним признак Гаусса. Так как в данном случае 6χ = α + β,
Cx = γ + 1, то при сх — 6Х =г γ -f 1—α — β> 1 ряд сходится, при
Οχ — {>! = у + 1 — a — β <. 1— расходится. Преобразуя
полученные неравенства, заключаем, что ряд сходится при γ — a — β > 0
и расходится при γ — a — β <; 0.
29
Замечание 8. Вопрос о сходимости данного ряда с
помощью признака Раабе полностью решить нельзя. В самом деле,
ak fe2 + (Y+l)fe + Y ^<:2 + (« + β)/; + αβ + (ν+1--«-β)/; + ν--»β
ak+l *» + (α + β)* + αβ *» + (α + β)Λ + οβ
. (Y+l-a-p)fe + T-c0.
1^ /ι2 + (α+β)^ + αβ
ft^oo I flft+i / fe-,οο £2 + (α+β)£ + αβ
= Υ + 1-α-β.
Ряд сходится при γ + 1 — a — β > 1 и расходится при
γ+1— α — β<1. Если γ-j-l— α — β=1, ο сходимости ряда
ничего нельзя сказать (по признаку Раабе).
19. Исследовать, сходится или расходится ряд
У 2<-')*-* =J_ + _L + J_4--!_ + -L_ + _L +
^^ * 22 ' 21 ' 24 ' 23 ' 26 * 25 ^~ * * * *
Применяем к данному ряду признак Даламбера. Так как
аА = 2(-'>Ч ak+i = 2(-1)Α+Ι ~«+\
ТО
- 2
(_ i)^+l — <— 1)Λ— 1
Предел этого отношения не существует, потому что при
k = 2m — 1 (m=l, 2, 3, ...) оно принимает значение 2, а при
k = 2т значение, равное 2_3. Следовательно, признак Даламбера
не решает вопроса о сходимости ряда.
Применим признак Коши. Поскольку
(- \)k — k (— \)k — k
V~ak = 2 k , lim/a^ = lim2 k = -i-<l,
fc->oo l
данный ряд сходится.
20. Исследовать, сходится или расходится ряд
00
>£ 2(-!>*-* = 2а + 21 + 24 + 28 + 2е+ 2Б+... .
k=\
Этот ряд расходится, так как его общий член к нулю не
стремится (следствие из необходимого признака).
Данный ряд также является примером ряда, к которому не
применим признак Даламбера, но применим признак Коши, так
как предел отношения (п+ 1)-го члена к п-му не существует, а
k-(-\)K
lim/a* =lim2 * = 2 > 1.
ft—>00 &—Ю0
30
Замечание 9. Признак Даламбера и признак Коши
связаны между собой: если существует конечный или
бесконечный предел lim k+l = /, то существует и равен ему предел
£
lim у ak = /.
k -»оо
ЗАДАЧИ
С помощью признака Даламбера исследовать, сходятся или
расходятся ряды:
91 1 1 8 1 27 1 б4 1 125 1 216 ι
£ΐ. ι -г 2 -Г 6 -1- 24 -1- 120 -1- 720 -f · · · ·
99 * , 16 I 81 . 256 ' ι 625 Ι
££л 3 "^ 9 "ί" 27 ' 81 "^ 243 "^ * * * *
23. У _* 24. У * 25. 2-^- 26. У *
С помощью признака Коши исследовать, сходятся или
расходятся ряды:
С помощью признака Даламбера или признака Коши выяснить,
сходятся ли ряды:
00 00 00 ,
- - (2*)! «о V k 11 V 5*
«· Σ-Шг- 32. 24"· 33. 2-*
Исследовать, сходятся или расходятся ряды:
ОО 00
1 оК V (2*-1)11 1
37· 2| (2fe-l)52*-1 · 38' £ (2*)» k-2k+l ■
«.5(1-4-)*. 4o-i *
Λ=1 х " / k=\ ( 1 + —
4..|-ϊ±ί=*-. 4, |(iiL
31
С помощью признака Раабе или признака Гаусса исследовать,
сходятся или расходятся ряды:
43 У-L 44 У (2*~1)!! !
4ύ· ** 2k · чч' jfd (2k) U 2k+\ ■
Л=1 k=\
* 2-5-8 ...(3/г —4) лл V / 1-3... (2fe— 1)
45 У 2-5-8...(3fe-4) у
47 V «(«+l)(« + 2)...(« + fe-D ία>0 β>0,
О β(β+1)(β + 2)...(β + *-Ι) (α>υ' Ρ>υ)·
48 Ια. 2 > , 2·4 ' ι 2-4-6 1 ,
Исследовать, сходятся ли ряды:
00
* k=l D k=\
-f- 1,1,1,1,1. 1, _ 1
"33Г + "32" + "35" "r -34- "r -37 Г ~зб~ "Г···» ufe 7^- При
* = 2/n - 1, a, = -^ ПРИ * = 2m- 56· 2^Г 57' 2%T)il "'
ОТВЕТЫ
21. Сходится. Указание. a^= тг. 22. Сходится. Указание. а^ = -т.
23. Расходится. 24. Сходится. 25. Сходится. 26. Расходится. 27. Сходится.
28. Сходится. 29. Сходится. 30. Сходится. 31. Расходится. 32. Сходится. 33.
Расходится. 34. Сходится. 35. Расходится. 36. Сходится при Ь<^е, расходится при
6> е. 37. Сходится. 38. Сходится. 39. Расходится. 40. Расходится. 41.
Сходится. 42. Сходится. 43. Расходится. 44. Сходится. 45. Сходится. 46. Сходится
при a > 2, расходится при a < 2. 47. Сходится при β>1+α, расходится
при β< 1 -fa. 48. Расходится. 49. Сходится при <х> 1. 50. Сходится. 51.
Расходится. 62. Сходится. 53. Сходится. 54. Расходится. 55. Сходится. 56.
Сходится. 57. Расходится.
§. 1.3. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ
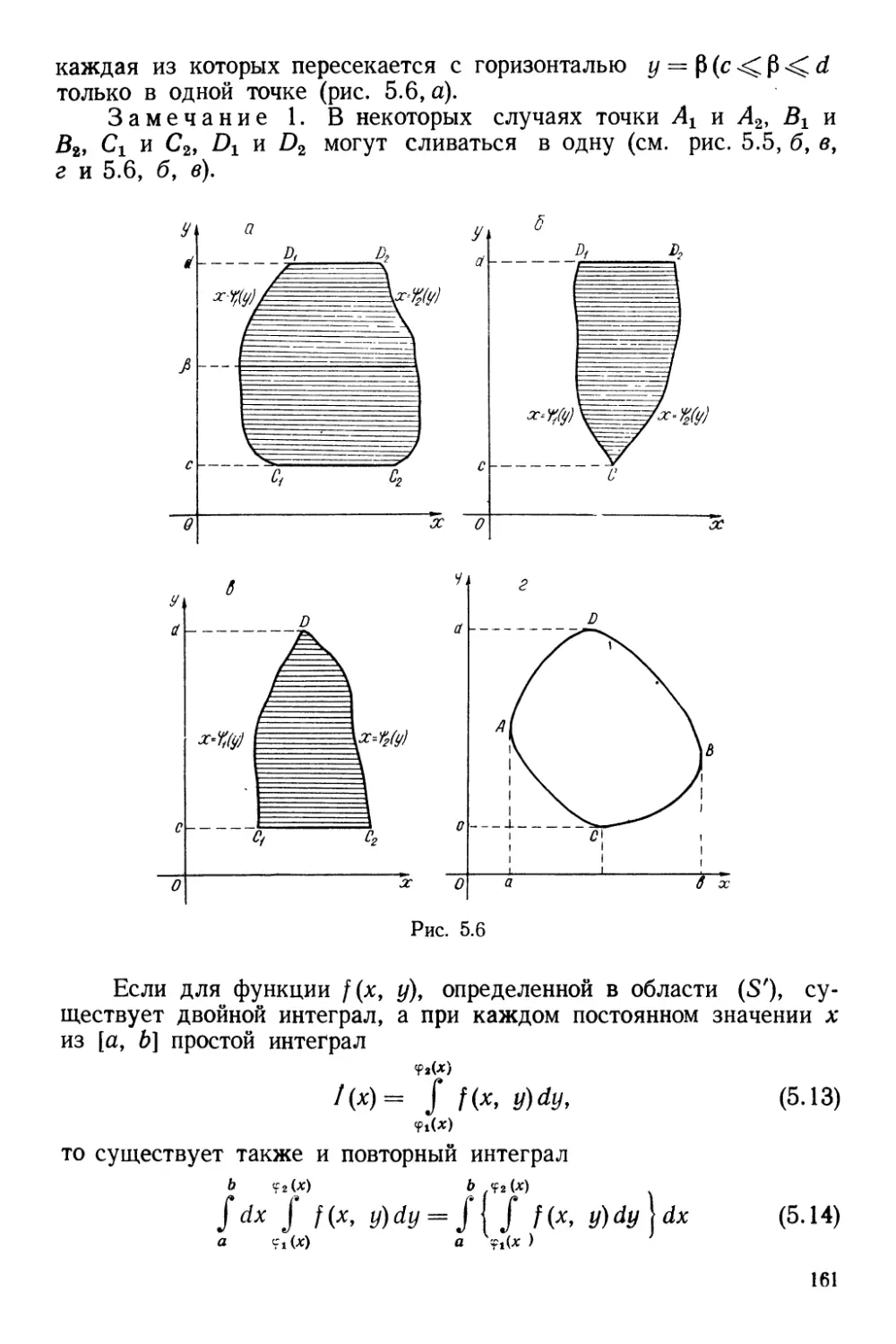
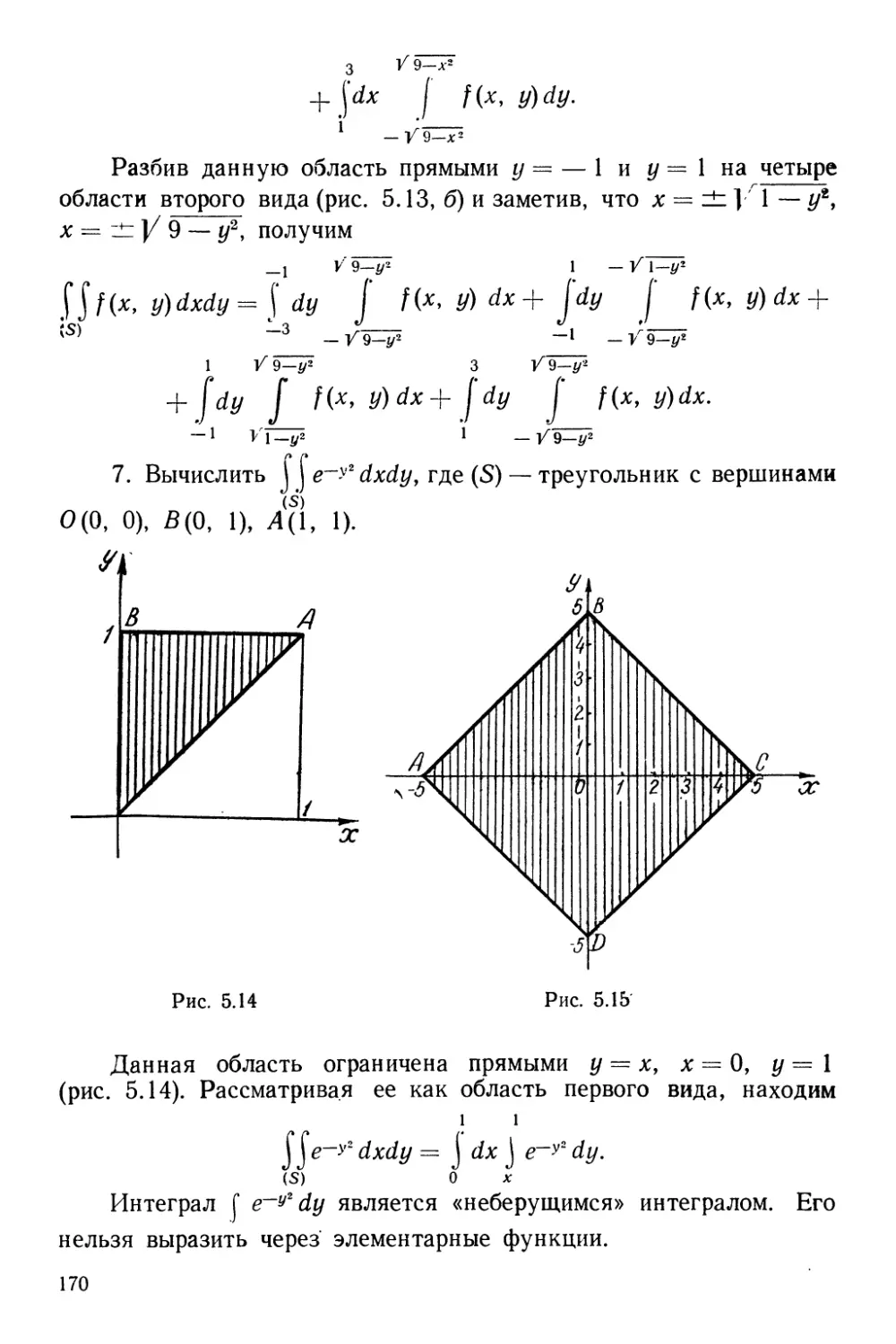
Ряд, содержащий как положительные, так и отрицательные
члены, называется знакопеременным.
Знакопеременный ряд
00
32
сходится, если сходится ряд, составленный из абсолютных
величин его членов, т. е.
00
Σ\^\ = \^\+\^\ + \^\ +... + \Ьк\ + ... . (1.27)
k=\
Ряд (1.26) в этом случае называется абсолютно сходящимся.
Сумма абсолютно сходящегося ряда не зависит от порядка
слагаемых.
Если ряд (1.26) сходится, а ряд (1.27) расходится, ряд (1.26)
называется условно (неабсолютно) сходящимся. Сумму условно
сходящегося ряда путем перестановки его членов можно сделать
равной любому данному числу {теорема Римана).
Ряд (1.27) является рядом с положительными членами,
поэтому для исследования вопроса о его сходимости можно
применять ранее рассмотренные признаки (признаки сравнения,
интегральный признак, признаки Коши, Даламбера и др.).
Замечание 1. Из расходимости ряда (1.27) в общем
случае не следует расходимость ряда (1.26).
Ряд, у которого любые два соседних члена имеют разные
знаки, называется знакочередующимся.
Признак Лейбница. Знакочередующийся ряд
00
2 (— 1)*+1 Ч = % — а2 + а3 — а4 + а6 — ... +
+ (-1)*-Ч+ ...(а*>0) (1.28)
сходится, если выполнены условия:
ak>ak+i (k=\, 2, 3, ...) (at > а2 > а3 > а4> ...); (1.29)
limaft = 0. (1.30)
k -*■ 00
При замене суммы сходящегося знакочередующегося ряда
суммой η его первых членов ошибка не превышает абсолютного
значения первого из отброшенных членов, т. е.
|Я„|<а«+1· (1-31)
Признак Дирихле. Знакопеременный ряд
2*А (1.32)
η
т. е.
сходится, если: 1) частичные суммы Bn=^bk ограничены,
k=\
|5„|<с (п=1, 2, 3, ...); 2) числа ak(k=l, 2, 3, ...)
образуют монотонную последовательность, стремящуюся к нулю.
Замечание 2. Признак Лейбница является частным
случаем признака Дирихле. В самом деле, если ak, монотонно убы-
33
вая, стремится к нулю, a bk = (— Ι)*-1, то ряд (1.32) принимает
00
вид^ (— \)k~xak, для которого выполнены условия признака
k=\
Лейбница.
Признак Абеля. Ряд (1.32) сходится, если: 1) сходится ряд
00
2j bk\ 2) числа ak(k= 1, 2, 3,...) образуют монотонную и
Огранила Ι
ченную последовательность.
ПРИМЕРЫ
1. Исследовать, сходится или расходится ряд
,1111111. (__1 )*(*-!)
1 + ~з "з2 зз~ + ~з*~ + 1^ "3*"""" W^ " ' "^ ρ ^'-' ·
Составляем ряд из абсолютных величин членов данного ряда:
14- — + - + — +—+ + —+
^ 3 ^ 32 ^ 33 ^ З4 ^ · " " ^ з* " '
Последний ряд сходится, как геометрическая прогрессия со
знаменателем q — -q-< 1· Следовательно, данный ряд также
сходится; он является абсолютно сходящимся рядом (в соответствии
с определением абсолютной сходимости ряда).
00
2. Доказать сходимость ряда ^-^S—·
iS k
Составим ряд из абсолютных величин членов данного ряда,
т. е. ряд
00
Σ| sin k I _ 1 sin 1 I 1 sin2 1 , [ sin 3 | , , |sinfe| ,n
£з — f3 Η ψ 1 зз г · · · Ί £з h · · · (Ч
Так как: |sin&|< 1, каждый член последнего ряда не
превышает соответствующего члена сходящегося ряда
00
_ "£Г = "ρ" + "23" + ^ + · · · . (2)
00
(ряд (2) является рядом Дирихле, т. е. рядом вида V —, где
р = 3>1).
Согласно первому признаку сравнения, ряд (1) сходится.
Поэтому сходится и данный ряд, причем абсолютно.
34
3. Исследовать характер сходимости знакочередующегося ряда
i__L . J L.J L , _L_ ι (-0fe+1 ι
Поскольку ряд, составленный из абсолютных величин членов
00
данного ряда, т. е. ряд^^=, расходится (см. пример 2 § 1. 2),
то о сходимости исходного ряда пока ничего нельзя сказать (см.
замечание 1). Применим к данному знакочередующемуся ряду
признак Лейбница. Условия признака Лейбница здесь выполнены:
1>-L>-L>4=> ··· > Hm-L = 0.
"У2^УЗ J/4 *->ооК*
Следовательно, этот ряд сходится. Так как ряд из
абсолютных величин расходится, данный ряд сходится условно
(неабсолютно).
4. Сколько нужно взять членов ряда
У /_η*-ι_1__ i_4_L + -! L, ι <- ')*"' ι
^у \ l) fo3 1 23 З3 43 ' ' ' ' ' k3 ' ' ' '
чтобы вычислить его сумму с точностью до 0,001?
Данный ряд является знакочередующимся рядом,
удовлетворяющим условиям признака Лейбница:
1>^г>-^г>^г> ··· > ^Ί?" = 0·
Следовательно, данный ряд сходится, причем абсолютно, так
как ряд
00 00
У L _i)*-i_L| = У_1_
сходящийся (ряд Дирихле, ρ > 1).
Чтобы вычислить сумму ряда с указанной точностью,
необходимо найти такой член, абсолютная величина которого меньше
0,001, т. е.
4-< 0,001 или -!■< И
Последнее неравенство выполняется, когда k3 > 1000, т. е.
k> 10.
Следовательно, нужно взять 10 членов данного ряда. Так
как αη = -ryg- < -ггр- = 0,001, по формуле (1.31) получаем
следующую оценку для остатка ряда:
#ιο<αιι < °>001 ·
35
5. Исследовать, сходится или расходится ряд
У 2—I /2+1 /3-1 /3+1 "' Vk—\
Общий член данного ряда стремится к нулю при &-><*>, но
условие (1.29) здесь не выполнено: члены убывают не монотонно:
> —, а —= < —p=z и т. д. Монотонность
V 2 — 1 νΛ2+1> J/2+1 УЗ—1
нарушается при переходе от члена -= к члену ^ .
Исследуем сходимость этого ряда, пользуясь основными
определениями. Составим частичную сумму из 2п его членов:
л+1 / ι ι \ V!1 2 п 1
2 ( γτ- ι ~~ γΊ+ 1/2 1=Т ^22~*~·
Так как гармонический ряд расходится, причем
ΗΐΉ 2ίγ
ОС,
гс—> 00
/г=1
то
"+1,. j
»^2(тггг
' °° fc=2 γι.
Следовательно, данный ряд расходится.
Замечание 3. Для сходимости знакочередующегося ряда
недостаточно, чтобы его общий член стремился, к нулю. Условия
(1.29) и (1.30) означают, что знакочередующийся ряд сходится, если
абсолютная величина общего члена стремится к нулю монотонно.
6. Исследовать, сходится или расходится ряд
i_J_.J L.-J-- ι * L_ ,
1 23 "*" З4 43 ^ 54 # * * ^ (2k — I)4 (2kf ^ · · · ·
Общий член данного ряда стремится к нулю при fe-*oo,
/, ^ 1 1^1 1^1
хотя и не монотонно 1 >-ψ-, -ψ-> -^r» ~з^<~^ги т· д-> °Днако
этот ряд сходится и притом абсолютно, так как сходится ряд
1 + —·+— + — + — +
а -Г 2з ^ З4 ^ 43 ^ 54 ^ " * * '
каждый член которого не превосходит соответствующего члена
00
сходящегося ряда 2"Тз~ (РЯА Дирихле, ρ > 1).
36
Замечание 4. Для сходимости знакочередующегося ряда
выполнение условий признака Лейбница не необходимо. Как
показывает данный пример, знакочередующийся ряд может сходиться,
когда абсолютная величина его общего члена стремится к нулю
не монотонно.
7. Исследовать, сходится или расходится ряд
|(- .>'-(. + 4·)'.
В данном случае ak = 11 + -£-·) . Поскольку
l\mak = lim(l+—-) = е,
fc->00 Jfe--»Oo\ П J
т. е. общий член ряда к нулю не стремится, ряд расходится
(не выполнен необходимый признак сходимости).
00
8. Показать, что знакочередующийся ряд \ (— I)*-1 —
сходится условно и что от перестановки его членов меняется
сумма ряда.
Данный ряд удовлетворяет условиям признака Лейбница:
1>-γ>-γ>4-··,·.4Ϊ™-τ = °·
Следовательно, ряд сходится. Так как ряд, составленный из
абсолютных величин членов исходного ряда, расходится, как
гармонический ряд, то данный ряд сходится условно.
Переставим члены данного ряда, расположив их так, чтобы
за каждым положительным членом были два отрицательных:
ι J L.J ! L.J ! L. . ι
1 9 A ~T Я fi Я Τ * 1Π ίο "Γ · · · "Γ
2 4^3 6 8 ' 5 10 12 ^ · · · π- 2η— 1
~~ An — 2 Τη" "Ί" " " " * Ο
Покажем, что ряд (1) сходится и его сумма равна-^- S, где
S — сумма исходного ряда, т. е.
]k-\
k - = 5· (2)
В самом деле, обозначая частичную сумму ряда (1) через ση,
а частичную сумму данного ряда — через Sn, для η = Зт получаем:
— / ι Μ 1_1 1_1о
37
«■- -+)-i+(i-i)-i=-;-i+4-i
— σ3 + -£ δ~ — ~9- S4;
j L — J_
6 8 ~~ 2
I\ _L. /J U___L . /J. _J_\ ι
2 j 4 "*" (χ 3 6 j 8 "♦■ [ 5 10 / 12 ~~
= J L.J L.J L_a , J L_ ι с
2 4^6 8 ^ 10 12 °6 -I- ш 12 — -g-^e.
Замечая, что
1 _ J_ _ J_ l l ι ι ι ι
2 2 ' 3 6 6,*··'2η—1 4/2 — 2 ~~ 4/2 — 2 '
находим
σ3*=(~2 4") + (^ 8")+ ··· +(Ί^2~2"~-4^"
откуда
σ3η = ~2-^ 2"+"3 Γ + ··* + 2η— 1 2л~) = ~2"S^*
Поскольку
Hm S2/2 - S,
i
TO
>2Л
Π -» 00
Hm σ3„ = Hm -~- S2„ = -=- S.
П—> 00 П— > GO
Таким образом, последовательность частичных сумм ряда (1) с
номерами, кратными трем, сходится к -γ S. К этому же пределу
сходятся и σ3η_|-ι, Оз,г+2- Действительно,
lim σ3η+ι = lim Ισ3η + 9 ) - 4"S;
lim σ3Λ+2 = Hm (σ3„+ι — An_A = 4"S-
/г-> oo /г-> oo v 4n 2 / 2
Следовательно,
lim σΛ = -s- S,
/г—> oo Δ
где п произвольным образом стремится к бесконечности.
Итак, σ^-^-S, т. е. в результате ^указанной перестановки
членов сумма данного ряда уменьшилась вдвое.|^
Покажем, что другая перестановка членов^ряда приводит к
з
ряду, сумма которого равна, например, -o-S. Умножим обе части
38
равенства (2) на множитель -γ и полученный ряд напишем под
исходным рядом:
i_J- + -L_JL + J__J_ + _L_J_+ =s.
J L J Li -_ί_ς
2 4i"6 8 -f- . . . — 2 ύ.
Сложив эти ряды, получим
А^3 2 ^ 5 ^ 7 4 ^ 9 ^ 11 6 ^ "·· 2 °"
Легко видеть, что последний ряд можно получить из
данного ряда перестановкой его членов.
9. Исследовать характер сходимости ряда
i,±_±__L,_L,J ! L_i_ . {-\)Hk'x\
1 ~Г о о а \ К ~Г с 7 Я « " " " ~Г
2 3 4 ^5 ^6 7 8 ' * * * г k τ· · · ·
Ряд, составленный из абсолютных величин членов данного
ряда, является гармоническим рядом, который, как известно,
расходится. Сравнение данного ряда с гармоническим не решает
вопроса о его сходимости (см. замечание 1).
Применим признак Дирихле. Данный ряд можно представить
в виде
00
где αΛ = -£-(£- 1, 2, 3, ...);
(k-\)(k-2)
bk = (-l) 2 (k = 1, 2, 3, ...),
r. e.
&i = 1, b2 = 1, &з = — 1» 64 = — 1, &5 = 1, bQ= I, b7 = — 1,
fib = -lf ... .
Поскольку ak монотонно стремится к нулю/1 > -2"->-3" >· · ·
η
lim ak = О], частичные суммы Дг=^ 6Λ ограничены (5Л<^2 (л=
fe-*00 / Λ==1
= 1, 2, 3, ... ), так как Вх = 1, В2 = 2, 53 = 1, #4 = О, В5 = 1,
β6==2, β7= 1, 58=0» · · · > В4к-з= 1, £4^-2=2, &ifc_i = 1, β^ ■■=(), ...),
то, согласно признаку Дирихле, ряд сходится. Так как ряд из
абсолютных величин его членов расходится, данный ряд сходится
условно (неабсолютно).
39
oo (fe-1) (fe-2)
10. Доказать сходимость ряда 2 (~ 1) 2
з*(1+4)й
Применим признак Абеля. Этот ряд можно записать в виде
00
^J аФк>
г*е а* = ~—ι-τνΓ*
(fe-l) (fe-2) j
6* = (-l) 2 "5Г (*=1, 2, 3, ...).
00 / 00 \
Поскольку ряд^ bk сходится (так как сходится ряд^—- I
а числа ak образуют монотонную ограниченную
последовательность Мр < ак < 4". Ч > ak+u ибо (1 + 4") < f 1 + 3 Х
ез ^ »k ^ 4 ' "* ^ И'Л+1' ж"~ \х ' >fe у V * + 1
lim afe = 5—зг = —згЛ» то» согласно признаку Абеля, дан-
k~> 00
('■ьт)
lim 1+ΊΓ
3 \Л "" е3
ныи ряд сходится.
ЗАДАЧИ
Исследовать, сходятся или расходятся знакопеременные ряды
ι. i + -L ! L + _L+J ! L +
Τ 2 22 23 ^ 2* ^ 25 2е 27 ' " " ' '
о , ■ J L_i__L_j_J L4-
* τ 2! 3! "т" 4! "ι" 5! 6! ~*~ " ' "
00 ΟΟ 00
sin k a
β V/ \\к(л 5 Γ τ V cosfca β Χ? sinfc
6· Jii-OMi—xj. 7W. 8·2—
k=\ \ ι k=i k=\
00 00
9. 2 (-!)*£. 10. 2 (-!)*]/£.
Исследовать, абсолютно или условно сходятся ряды:
00
el ν*5 ίέΐ * к* Bi lnk
40
и. 2-ЩР- is. 2-ВД±. 16. 2-ь^.
ifi 2* *=i * £ί (2*-1)3*
17
00 00 . .
~ "~P. 18. У (-1)
ί=ί *·5*
V / П4 1-3-5.,.(2fe-l)
*dK l) \ 2·4-6. ..2k
k=l L
С точностью до 0,01 вычислить суммы рядов
19 У (-1) 90 У (-1*
(-Ι)*-1 оо V (-1)*-'
^'- S-^iF- и· 2
6=1 5 6=1 ^
Сколько нужно взять членов, чтобы с точностью до 0,001
вычислить суммы следующих рядов?
0° и ι °° Ь ι °° h ι
23. 24Й4· 24. 2-ЧР-. 25. 2-Ь
А=1(2й-1)!· -^ з* · · £ V*
(-if~' 97 V (-if'1 9o V (-if
— ^—k\—· 27· ^—ρ—· 28· 2j—г ·
k=\ k=\ k=l
С помощью признака Абеля или признака Дирихле
исследовать, сходятся или расходятся ряды:
2Q ι . Л* \ L·4-_L· + -ί ! !_4-
^ У2 Уз VI ^ V5 ^ У~6 VT У8 ■*" '" '
зо. 1+4+4—г- 4—г+ ····
о, V (-1)* / 1 + 3fe* \ „9 V (-1)* 1
6=1 * \ 1 6=2
»■!<-■) ! ^(l-i).34 |(-1) ■ ^1-4
ι - 4-1*.
6=1 \ / 6=1
ОТВЕТЫ
1. Сходится. 2. Сходится. 3. Сходится. 4. Сходится. 5. Расходится. 6.
Расходится. 7. Сходится. 8. Сходится. 9. Расходится. 10. Расходится. 11. Сходится
абсолютно. 12. Сходится абсолютно. 13. Сходится условно. 14. Сходится
условно. 15. Сходится абсолютно при р> 1, сходится условно при р<; 1. 16.
Сходится абсолютно. 17. Сходится абсолютно при р>2, сходится условно при
0<рс2. 18. Сходится абсолютно. 19. 0,46. 20. 0,95. 21. 0,16. 22. 0,79. 23. Зчле-
на. 24. 6 членов. 25. 7 членов. 26. 6 членов. 27. 31 член. 28. 999 членов.
Замечание. Задачи 23—28 показывают, что одни ряды сходятся быстрее, дру-
00
гие — медленнее. Ряд задачи 28 сходится очень медленно, ряд 7х^ '— схо-
6=1 Vk
дится еще медленнее. 29. Сходится. 30. Сходится. 31. Сходится. 32. Сходится.
33. Сходится. 34. Сходится.
41
§ 1.4. ДЕЙСТВИЯ НАД РЯДАМИ. РАЗНЫЕ ЗАДАЧИ
Суммой двух рядов
00
2 ak = αι + а2 + аз + ... +ak+ ... ; (1.33)
00
2 bk = bi + b* + h + ... + bk + ... (1.34)
k=\
называется ряд
00
2 (fl* + bk) = (ai + bi) + (β2 + b2) + . . . + (ak + bk) + . .'. . (1.35)
Аналогично определяется разность двух рядов.
Произведением рядов (1.33) и (1.34) называется ряд
00
2е* = ci + ^2 + ^з + · · · + ск + . . . , (1.36)
где
ck = axbk + афк-х + ... + akbx (к = 1, 2, 3, ...). (1.37)
Ряд (1.35) сходится, если сходятся оба ряда (1.33) и (1.34);
его сумма равна сумме данных рядов.
Если ряды (1.33) и (1.34) сходятся абсолютно, ряд (1.36)
также сходится абсолютно; его сумма равна произведению сумм
данных рядов.
Замечание. Если из двух сходящихся рядов (1.33) и (1.34)
хоть один сходится абсолютно, их произведение — сходящийся
ряд.
ЗАДАЧИ
00 00 .
1. Составить сумму рядов 2л—k— и 2л и * ^хо"
дится ли полученный ряд?
(-i)fe
2. Найти сумму ряда ^ ——
3. Что можно сказать о сумме двух рядов, из которых:
1) один ряд сходится, а другой расходится? 2) оба ряда
расходятся?
00
4. Составить разность расходящихся рядов 2л и
00
2^ 2k . Сходится ли полученный ряд?
k=\
42
5. Сходится ли ряд, являющийся разностью рядов Zj-t- и
2-
00
6. Подобрать такие два ряда,-чтобы сумма сходилась, а
разность расходилась.
7. Составить произведение двух рядов:
2 + 2 + 22 + 23+ ... +2*+ ... (ft=l, 2, 3, ...);
- 1 + 1 + 1 + 1 + ... + 1* + . . . (k = 2, 3, .. .).
Сходится ли полученный ряд?
00 00
8. Составить произведение рядов 2flfe и^^Ч· В ка-
ком случае все члены, начиная со второго, равны нулю?
00
9. Сходится ли произведение рядов 2 — и 2—F=T~^
00
10. Показать, что квадрат сходящегося ряда ^ k_x есть
// оо \2 оо оо \
ряд сходящийся 11 2 ak I = 2 ak * 2d ak \
k=\ / fc=l fc=l
о»
x ' есть
ряд расходящийся.
12. Доказать, что произведение сходящихся рядов Л- —
-—\ (β > 0) есть ряд сходящийся, если α + β > 1,
и расходящийся, если α-}-β< Ι.
00 00
13. Доказать, что если ряды 2dak и 2d^k СХ°ДЯТСЯ> то РЯД
оо
Ζλ akbk абсолютно сходится.
/e=l
оо
14. Доказать, что если ряд ^ ak абсолютно сходится, то и
00
ряд 2 —t— ak абсолютно сходится.
43
15. Доказать, что ряд ^ kP\n«k : ^ сходится при произ-
вольном q, если ρ > 1, и при q > 1, если ρ = 1; 2) расходится
при произвольном <7> если р< 1, и при 9 < 1, если р= 1.
Исследовать, сходятся или расходятся следующие ряды:
ifi у fe2 + 3fe + з 17 у ι+fe to v_JH_i_
S Λ(Λ+1)(Λ + 2)(Λ + 3) · jg{ 1+*2" j£{ fc2(fc+l)2 ·
00 00 00
,tF· ^ ft(ft + 2)· *"' fa (2ft-l)2(2ft+1)** ίΧ· fax 3ft-1 ·
oo oo
22. ^arctg 2 , * . , . 23. T]tg-£--.
^J to л2 + л + 1 ^ b 4&
6=1 k=l
(-*)* or V (-1)'
k—\
00 . 00
94 У <=i£ 25 У
0 (2ft + 1) (2ft + 2) (2ft+ 3)(2ft+ 4) " ΔΟ' fak (2ft + l)(2ft + 2)(2ft + 3)"
00 00
26. 2 arctg-^r-. 27. 2arctg (2fe-!i)i-·
00 00 00
28· 2 «/J. .»· 29· 2 / ' 30· 2
-*J ft3ift 4- Π3 ^J i/n ' ot ^J
*3(*+·)3· · a Kft*T2T · · £/. , MVt_J-f
Λ=1 v ' ' *=1 Г * ~Γ^ £=!£ +
4)>-i)
31· Στ Γ\Ϊ7 Г-з-· 32· 24" О'*" + k+l-Vk*-k+\).
З3.|(-!^)2· 34· larctf-L. 35. |(-,)*arctg1Ff±^T
oo oo
sin ft α
36. 2sin^T- 37· 2arcsin*-T· 38· Σ
39· 1^'п-й- 40· Ι*™**-*
ОТВЕТЫ
00
1. у * ' J—, сходится. 2. —. 3. 1) расходится; 2) может как сходиться,
Jmd ok 6
k=\ Δ
так и расходиться. 4. Сходится условно. 5. Расходится. 7. — 2 + 0 + 0 + ...+
+ 0^ + ... (& = 2, 3, .. .) (в данном примере произведение двух
расходящихся рядов есть абсолютно сходящийся ряд). 8. с^= {ak [а -\- (Ь0 — \)(а — Ь)] —
— Ьк[Ь + (\ — а0)(а — Ь)]} /(а — b) (k = 1, 2, 3,...) ck = О, если а = (1 — Ь0) (а —
44
—b), b == (a0 — 1) (a — b)\ если при этом а и b связаны равенством а — b = 1, то
а0 и Ь0 вычисляются по формулам а0 = b + 1 = α, 60 = 1 — α = — 6. 9. Сходится.
И. Указание. Пользуясь тем, что функция γ(\ + х) (k + 1 — *) на замк-
нутом промежутке [0, k] достигает максимума при x = — t получаем \сь\ =
111 12
VWk + x^ V2Vk ~"~ VzVk-i +'"+ Vk + \VT> k + 2 +
2 +···+ A20 = 2(^o1) >1(£ = 0, 1, 2, ...). 16. Сходится,
k + 2 k + 2 k+2
о
S= 17. Расходится. 18. Сходится, S=\. 19. Расходится. 20. Сходится,
ό
1 π
S = 21. Расходится. 22. Сходится, S = 23. Расходится. 24. Сходится,
8 4
= 5-π-21η2 2$ с тс s = 3π-61η2-5 26 Сходится> s =
12 18 АЛ
/1 Я Я
= arc tg ι ι , S = -τ-. 27. Сходится, о = -о-. 28. Сходится, 5 = 10 — я2.
29. Расходится. 30. Сходится, S = я2 — 8. 31. Сходится, S = 32 — Зя2. 32.
Расходится. 33. Сходится. 34. Сходится. 35. Сходится. 36. Расходится. 37. Сходится.
38. Сходится. 39. Сходится. 40. Сходится.
Глава 2
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
§ 2.1. СХОДИМОСТЬ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Пусть дан функциональный ряд
00
2 ЩΜ = ^ι Μ + и2(х) + и3(х) + ... + uk(χ) + ... , (2.1)
k=l
т. е. ряд, члены которого uk (χ) = fk (χ) — некоторые функции от χ.
При каждом фиксированном значении χ = х0 функциональный ряд
(2.1) становится числовым рядом
00
2 ик (*о) = "ι (*о) + и2 (*о) + ^з (*о) + · · · · (2·2)
k=\
Если ряд (2.2) сходится, значение аргумента χ = х0 называется
точкой сходимости ряда (2.1). Совокупность всех точек
сходимости χ функционального ряда (2.1) называется его областью
сходимости, а функция
η
S(x)= WmSn(x) = lim 2 Μ*)— (2-3)
П—ЮО П—*Οθ£_ι
суммой данного ряда. Функция
Rn(x) = S(x)-Sn(x) (2.4)
называется остатком ряда (2.1).
45
Если ряд (2.2) расходится, значение χ = х0 называется
точкой расходимости ряда (2.1).
В простейших случаях для определения области сходимости
ряда (2.1) можно применять к нему известные признаки
сходимости, считая χ фиксированным. В частности, при применении
признака Даламбера или Коши случай, когда q = I, исследуется
особо, с помощью других признаков сходимости.
Функциональный ряд (2.1) называется равномерно сходящимся
в некотором промежутке, если, каково бы ни было ε > 0, можно
найти такое Ν, не зависящее от х, что при п> N для всех χ
из данного промежутка выполняется неравенство
|Я„(*)1<е, (2.5)
где Rn (x) — остаток ряда.
Признак Вейерштрасса. Функциональный ряд (2.1) сходится
абсолютно и равномерно в некотором промежутке, если существует
сходящийся числовой ряд с положительными членами
00
"Σα*==αι + α2 + α3+ ... +а*+ ··· (2·6)
k=\
такой, что
\uk(x)\<ak (*=1, 2, 3,...) (2.7)
для всех χ из данного промежутка. Ряд (2.6) в этом случае
называется мажорантным для ряда (2.1).
Свойства функциональных рядов:
1. Сумма равномерно сходящегося ряда функций, непрерывных
в замкнутом промежутке [а, Ь], есть функция, непрерывная в
данном промежутке [а, Ь].
2. Если члены сходящегося ряда (2.1) имеют непрерывные
00
производные при а < χ < b и ряд ^ Uk (x) сходится равномерно
в замкнутом промежутке [а, Ь], то ряд (2.1) в этом промежутке
можно дифференцировать почленно, т. е.
[00 η, 00 ρ Г П . Π
2(м*) =2α*(*)или lim'2^w = lim 2 м*)· (2.8)
Ь=1 J *=1 U-»00£, ι J n-+0Oh=}
k=\ J k=l
3. Если члены ряда (2.1) непрерывны при α <;#<;& и ряд
этот сходится равномерно в замкнутом промежутке [a, ft], то его
можно интегрировать почленно в данном промежутке, т. е.
t оо ., оо Ь
J 2uhм\dx=2 ίuhμdx- (2·9)
46
4. Если ряд (2.1) сходится равномерно в некоторой области
и каждый член ряда имеет конечный предел lim uk (x) = ck, где
χ—>α
α — точка сгущения данной области, то к пределу можно перейти
почленно, т. е.
00
lim
2 uk м = 2lim uk w = 2 ck· (2·10)
ПРИМЕРЫ
X — 1 t / * — ! \2 t
1. Найти область сходимости ряда —ίγγ ' (ЗГ+Т/ '
*-INi· ... +f^=J-r+
Данный ряд представляет собой геометрическую прогрессию
со знаменателем q = —ϊπτ~· Как известно, геометрическая
прогрессия сходится тогда и только тогда, когда | q |< 1. Следовательно,
I х— 1 '
данный ряд сходится лишь в случае, когда
< 1. Послед-
х+\
нему неравенству равносильны неравенства
Если (х + 1) > 0, то — х— 1 < χ — 1 < л: + 1, т. е.
— л: — 1 <л: — 1 их— 1 < χ + 1.
Второе из этих неравенств выполняется для всех х, первое
верно только для χ > 0.
Если (л; + 1) < 0, то — χ — 1 > χ — 1 > χ + 1, т. е.
#+ 1 < # — 1 их— 1 < — χ — 1.
Первое из полученных неравенств противоречиво, второе
выполняется при χ < 0. Но при # < 0 | q | > 1.
Таким образом, ряд сходится при χ > 0, т. е. областью его
сходимости является открытый промежуток (0, + °°)· (При χ = О,
как и следовало ожидать, получаем расходящийся ряд —1 + 1 —
-1+ ···)
X X2
2. Найти область сходимости ряда 2 2 + -γη—г + . .. +
.k
2 + χ2
Общий член данного ряда определяется формулой uk (χ) =
+ ^r +
Y2k
Так как
2 +г
•2&
vfc I
<|*|* при |*|<1
x2k
47
и ряд Jdl*|* сходится при |*|< 1, то и данный ряд сходится
1 v^ I I v^
для μ|<1. Поскольку
и ι <J—и = г при \х > 1
оо
и ряд ^ | * |~* сходится при | χ | > 1, то данный ряд сходится и для
\х\> 1. Если χ = 1 или χ = — 1, то | ыЛ(1) | = —; ряд
расходится. Итак, данный ряд сходится при всех х, кроме χ = — 1
и х=1.
оо
3. При каких # сходится ряд \ (1 -f- —г-) 2kx?
Применим к данному ряду признак Коши, для чего найдем
предел:
lim v \uk\ = q.
ft-*0o
Так как
"а
= (l + 4-)V, kv'\uk\ ={1 + ^)2*,
ТО
Wmfy \uk\ = lim (1 + 4") 2х = 2х.
k- 00 fc->oo \ * /
Найдем те значения χ, при которых этот предел меньше
единицы, для чего решим неравенство 2*<1, которое
выполняется для χ < 0. Случай, когда 2·*= 1, т. е. л: = 0, исследуем
оо
особо. При χ = О данный ряд принимает вид ^ ( 1 + -γ) · Этот
ряд расходится, так как для него не выполнен необходимый
признак сходимости (общий член к нулю не стремится: lim ak =
= lim (1 + -V-) = е). Итак, ряд сходится при #<0.
4. Найти область сходимости ряда
1,1.1,1
у ~г ДуЗ ~f~ 5*з + 7*7 <~ * * * *
3*з τ 5^5 -г 7дл "Γ · · · -г (2Aj_ 1)χ2Λ-ι
48
Применим к данному ряду признак Даламбера, для чего
найдем предел:
lim
fe—>oo
*k+l
= ч-
Так как
иь =
(2k-\)x2k~l ' Uk+l (2k+l)fk+l '
то
uk+\
1
(26+ \)x2k+l
(2k — \)x
2k— 1 J_
; 2k + 1 " x2
2k—\
x2k~x(2k — 1)
x2k+l (2k + 1)
Считая χ фиксированным, получаем
lim
k—>oo
Найдем значения а:, при которых этот предел меньше единицы.
Неравенство —г< 1 выполняется при |а:|> 1, поэтому, согласно
признаку Даламбера, ряд сходится при |*|>1. Случай, когда
1, х=1, исследуем дополнительно. При
1 !
--г= 1, т. е. χ
х= 1 получаем расходящийся ряд ^loi. , (см. пример 17 § 1.2).
При а: = — 1 также получаем расходящийся ряд
оо оо
£^2k—\ = ~ 2j2k— Г
fc=l fe=l
Таким образом, данный ряд сходится при |а:|>1, т. е. его
областью сходимости является совокупность двух бесконечных
интервалов ( — оо, —1), (1, + оо)·
00
5. Найти область сходимости ряда Zu^2k(3x+ 2)2*-1.
k=\
Применяем признак Даламбера, считая χ фиксированным.
В данном случае:
ик = 42* (За: + 2)2*"1, uk+l = 42 <*+ι> (3* + 2)2 <*+»> - ' -
- 42*+2 (За: + 2)2*-1;
42fe+2(3* + 2)2fe+1
42fe (3* + 2)'
L2fe-1
42(3a:+2)2, lim
£—>oo
«*+i
«A
42 (3x + 2)2
49
Найдем, при каких значениях χ полученный предел меньше
единицы. Решая неравенство 42 (За: + 2)2 < 1 или | 4 (За: + 2) | < 1,
получаем — 1 < 4 (За: + 2)< 1, т. е. — -i- < За: + 2 < -^-,
_2_-L<3*<4-2, -\<х<-Т-ш
о
Рассмотрим случай, когда 42 (За: + 2)2 = 1, т. е. χ = —j-,
7 3
χ = jy. При х = j- получаем ряд
S 4- [з (- i)+»f" - s *· [=£р - _ s < -»- -4.
Этот ряд расходится (каждый член ряда равен — 4). При
00
χ = j2~ снова получаем расходящийся ряд 2 I2*-1 -4=4+4+
/г=1
+ 4 + ... . Следовательно, областью сходимости ряда является
интервал ( - А —-У.
6. Исследовать, равномерно ли сходится ряд ?ι
оо
cos kx
3* '
Так как |cosfe#| < 1 для всех χ (на всей числовой оси), то
cos k χ
3*
<-^ (k=l9 2, 3, ...),
т. е. каждый член данного ряда не превышает соответствующего
оо
члена сходящегося числового ряда ^^— (геометрическаяпрогрес-
сия, q = — V Последний ряд является мажорантным для данного
ряда. В соответствии с признаком Вейерштрасса заключаем, что
данный ряд сходится абсолютно и равномерно для всех х, т. е.
на всей действительной оси.
00
7. Доказать, что сумма ряда ?: snu9x является непрерывной
k=l
функцией при всех х.
Каждый член данного ряда uk(x) = —^— (Л= 1, 2, 3, ...)
есть функция, непрерывная при всех χ (на всей числовой оси).
Ряд сходится равномерно при всех х. В самом деле, поскольку
Isin kx I 1 «»
< -ψу для данного ряда существует мажорантный ряд
50
^V ι
7iTj—сходящийся числовой ряд с положительными членами
/е=1
(ряд Дирихле, ρ = 2 > 1). Согласно свойству 1 функциональных
рядов, сумма данного ряда есть функция, непрерывная при всех χ
(как сумма равномерно сходящегося ряда непрерывных функций).
00
8. Можно ли почленно дифференцировать ряд ^ ϊ smUA x в об-
k=\
ласти его сходимости?
sin kx
Каждый член данного ряда есть функция uk (χ) = ,4 , диф-
' k COS kx COS kx
ференцируемая при всех jc, причем uk = —^ = ~~£з—· Соста-
00
вим ряд производных χ, C0SU3X · Каждый член нового ряда — не-
fc = l
прерывная функция иЛ (#) =
I cos kx I
cos &*
. Так как
I uk (χ) I
£з
<-^ (k=l, 2, 3, ...),
для него существует мажорантный ряд ^j-sr·
k=\
Следовательно, ряд производных равномерно сходится при
всех х, поэтому, согласно свойству 2, исходный ряд можно
дифференцировать почленно. По формуле (2.8)
00 * -, , 00 г- -, , 00
Σ sin kx I _ 'V4 sin kx _ V^
k=\
k=\
cos kx
k*
k=l
9. Можно ли почленно дифференцировать ряд ?t
sin 2knx
k=\
2k
Этот ряд сходится равномерно для всех х, ибо для него
существует мажорантный ряд
^J 2k
так как
sin 2клх
2&
<
2*
fe=l
sin 2 ttγ
Каждый член ряда uk (χ) = — есть функция дифференци-
2k
00
руемая, причем uk (χ) = я cos 2knx. Ряд производных π^ cos2*ju:
расходится в каждой точке, ибо ни в одной точке не выполняется
необходимый признак сходимости (общий член к нулю не
стремится).
51
Следовательно, исходный ряд почленно дифференцировать
нельзя.
00
1
10. Можно ли почленно интегрировать ряд 2—;
k=l
2 + k*
Каждый член данного ряда uk = χ2 , fe2 есть функция,
непрерывная для всех х. Данный ряд сходится равномерно на всей
числовой оси. Действительно, так как для всех χ выполняется
неравенство хгл-& ^ ~W' для данного РяДа существует мажо-
00
рантный ряд Zj тг-
k=\
Таким образом, согласно свойству 3, данный ряд можно
интегрировать по любому промежутку из его области сходимости,
в частности по промежутку [0, х). Интегрируя, получаем
О k=\ /г=1 О
оо оо
= 24" arct§ ΊΓ I = 2 ΊΓ arctS ΊΓ
ЗАДАЧИ
Найти области сходимости функциональных рядов:
х + 2 , (х + 2\2 , /* + 2х3
* + 3 г \х + 3/ ' \* + 3,
) +
2 -J^+-LpU2 + _LpL_)3 + ... .
ζ· л: + 1 ^ 2 U+1/ ^ 3 \ дс + 1 / ^ * * *
оо оо оо
5. ^(\5-x2)k. 6. 2χ2*cos*χ. 7· 2sin^"
00 00 ^
8. 2 fe4 9· 2 <*-l)<*-2)...(*-*) (* ^ fe>
52
l5· 2 (й+2нз!!-1)* · |6· 2^1 (-έ+r) ·
Исследовать, равномерно ли сходятся следующие ряды:
00 00
17. ^akcosk2x (\a\< 1). 18. ^aksmbkx (\a\< 1).
fc=l fe=l
00 00 00
19. Σ—4· 20. V-ji-^. 21. У-^.
22. Ss-H^. 23. Σ^4· 24. Υ**-1.
Исследовать, непрерывны ли суммы следующих рядов:
25 У ** 26 У (~Р**2* 27 V (-!)*-' .
^J 2^ (1 + x2k) ' ^ 3* (1 + ***) ' ' ^Ll x* + k ш
98 V (-l)fe-^2 29 V_J_
k=\ &=l
X
80-т±т + 2лгг
1+* r^J [!+(*+!)*](!+**) *
/e=l
Исследовать, непрерывны ли суммы следующих рядов на
замкнутом промежутке [0, 1]:
оо
31. ^ 2х [ft2.?-*2*2 - (ft - 1) е- <*-'>2*2 ].
fc=l
32.
* l V Г * ί_1
Η л2 т ^J L ι + (k + ΐ)2χ2 l + fe2*2/
м.х+2с»«-^). 34.2[T^5r_Tj^Bl].
fc=l fe=l
00
35. У [arctg fex — arctg (k — 1) л:].
л-1
53
36.
_L_)
Можно ли почленно дифференцировать следующие ряды
в области их сходимости?
37
00 00 00
sin Зклх
. 2^. 38. Στ· 39. 2-
3fe
k=\ k=\ k=l
00 00
40. ^S™*™Lu 41. 2^-(fe-1)2x2-^fe2x2b
k=l k=\
00
42. 4-ln(l + ^) + 2{J^ln(l + fe2x2)- 2(fe'_1)ln[I +
k=2
+ (*-l)V]}.
Можно ли почленно интегрировать следующие ряды в области
их сходимости?
00 00
cos kx
43. 2·^· 44. 2:
k=\ k=i
00
45. 2 2x №e-k2x° -{k-\fe~ <*-»·**].
46.2
k=\
00
1+£2χ2 1 + (^— 1)2^2
ОТВЕТЫ
5 1 r—
1. *> — "2". 2. *>—-y. 3. |jc|>1. 4. jc>1. 5./l4 0<4, — 4<
<"*<— V14. 6. |x|<l. 7. | a; | < +°° (сходится для всех *). 8. χ < 0.
9. Сходится для всех я, кроме л: =/г (k = 1, 2, 3, ...). 10. Сходится для
всех х, кроме χ = k (k=0, 1, 2, 3,...). 11. | jc | > 2, | χ |< -у. 12. |х|< 1.
2
13. Сходится для всех дс. 14. —1<х<1. 15. *>"~з~*· 16. х>0.
17—22. Сходится равномерно для всех х. 23. Сходится для всех х, но
неравномерно. Указание. Остаток ряда выражается формулой Rn (χ) = 5 (χ) —
χ2
χ2 χ2 я2 (1 + χ2)η^~ι
~SnW= {1+χ*γ*+1 + {l+x2f+2 +(1+^)1+3 + ···= —j—=
1 ~~ 1 + л:2
54
= л -l 2\η· При любом фиксированном nRn(x)-> 1 при *->0 (поэтому не
может выполняться неравенство | Rn (χ) | < ε для всех χ при любом ε, на-
13 4 \
пример при ε = -γ , ε = -j-, ε = -g- и т. д.). 24. Сходится в интервале
(—1,1), но неравномерно. Указание. Остаток выражается формулой
χη + Ι 1
Rn(x)=:- . При фиксированном η получаем lim \Rn(x)\ = -^-i
1 х х->—1+0 z
lim Rn(x) = оо. Оба соотношения показывают, что осуществить нера-
х- 1—0
венство \Rn(x)\ <ε (если ε < ~о~) одновременно для всех χ невозможно.
Замечание. Сходимость данного ряда будет равномерной на любом
отрезке, лежащем внутри интервала (— 1, 1). Обозначим этот отрезок через
[ — 1 + δ, 1 — δ], где δ > 0. На этом отрезке | я | < 1 — δ, |1 — * | > δ,
(1—б)л+1
следовательно, | Rn (χ) \ < τ . Задав ε>0, потребуем, чтобы
(1 б)*+1<8> откуда (η+1)ΐη(ΐ-δ)<1η(εδ), т.е. (п + 1) > /"{8б>
о In (1—о)
1η(εδ)
(так как In (1 —δ)<0), η > ι ,, ^ — 1. В качестве /V можно взять меньшее
In (εδ)
из двух целых чисел, между которыми заключено число . ,, ^ — 1, или
само это чис^о, если оно целое. При η>Ν неравенство | Rn (χ) | < ε
выполняется одновременно для всех χ из отрезка [—1 + δ, 1—δ]. 25. Сумма
ряда — функция непрерывная. Указание. Данный ряд непрерывных функций
сходится равномерно. 26 — 29. Сумма ряда — функция непрерывная. 30.
Разрывна при χ = 0. Указание. Частичная сумма определяется формулой
2 1 2
Sn W = Т+Т — 1 + пх> 0ТКУда 5 Μ = lim Sn (χ) = ι + χ при χ φ 0; если
я = 0, το Sn (0) = 1, 5 (0) = 2. 31. Непрерывна. Указание. Частичная
сумма определяется формулой Sn (χ) = 2п2 хе~η*χ2, S (χ) = lim Sn (χ) = 0. 3 a-
/ 1 \ 2л
м е ч а н и е. Ряд сходится неравномерно, Sn I — = -у-. 32. Непрерывна.
χ
Указание. Sn(x)= } , 2 2 , 5 (х) = lim Sn (χ) = 0. 3 а м е ч а н и е. Дан-
1 -\- П X η-*οο
ный ряд сходится равномерно. 33. Разрывна в точке х=\. Указание.
Sn (χ) = хп, S(x)= lim Sn (χ) = lim xn = 0, если χ < 1, 5 (1) = 1. 3 а м е ч а-
п—юо п—>оо
н и е. Ряд сходится неравномерно в промежутке [0, 1]. На рис. 2.1
изображены графики функций Sn (χ) при п= 1, 2, 4, 10, 30. 34. Непрерывна.
Указание. Sn (χ) = ι _L „2v2 > 5 W = lim 5« W = °- 3 а м е ч а н и е. Ряд
сходится неравномерно. На рис. 2.2 изображены графики функций
Sn(x) при м=1, 2, 4. Для каждой функции найдется точка
χ = , в которой у = Sn (—) = -иг (горб). Наличие таких
горбов мешает равномерной сходимости к нулю функций Sn (x).
35. Разрывна в точке * = 0. Указание. Sn (χ) = arctg nx, S (χ) =
55
= lim Sn{x) = ~K-, если *>0, 5 (0) = 0. На рис. 2.3 изображены графики
функций Sn(x) при п=1, 2, 4, 10. 36. Непрерывна. Указание. Sn(x) =
= , , S (я) = lim S„(*) = 0. На рис. 2.4 изображены графики функций
* ' " /г->оо
Sn(x) при η = 2, 3, 5, 10, 20. 37. Можно. Указание. Члены ряда —
дифференцируемые функции, ряд производных сходится равномерно, так как
Sfom
Рис. 2.3
для него существует мажорантный ряд.
38. Можно. 39. Нельзя. Указание.
1
Ряд производных расходится во всех точках, кроме точек х =
(*=1.
3*-2
2,3,...). 40. Нельзя. 41. Нельзя. Указание. Sn(x)=\— е"п*х*t S(x)=\,
если χ φ 0, 5 (0) = 0. Если продифференцировать этот ряд, получится ряд задачи
31. Этот ряд сходится к нулю во всех точках, в том числе и в точке х~ 0,
но неравномерно. С другой стороны, сумма исходного ряда в точке χ = 0
производной не может иметь (она разрывна в этой точке). 42. Можно.
Указание. Sn(x) = тгг In (1 + п2х2), S (х) = 0 для всех х. Если продиффе-
56
рейдировать этот ряд, получится ряд задачи 34, который сходится к нулю
во всех точках, т. е. 5' (6с) — 0. Следовательно, почленное дифференцирование
повсюду приводит к верному результату. Замечание. Ряд производных
сходится неравномерно. Этот пример показывает, что условие равномерной
сходимости в свойстве 2 (формула (2.8)) не необходимо. 43. Можно. 44. Можно.
ι ι
45. Нельзя. Указание, lim Sn(x)dx = lim 2п2хе η*χ2άχ= lim (1—
n~>0° ω η~>0° ή л->оо
l l l
— е~п*)=\\ \ lim Sn(x)dx=\ 0dx=0, т. е. lim f Sn (χ) dx Φ
·' ГС-»00 «/ П—>О0 J
1
φ \ lim Sn (x) dx. Равенство (2.9) в этом случае не выполняется. Замеча-
J п—*оо
н и е. Ряд сходится неравномерно. 46. Можно, хотя ряд и сходится неравно-
Г пх , ln(l + n2)
мерно. В самом деле, lim « , 2v2 dx— lim к~ = 0;
п->ю .) ι ~т п х п->оо Δη
ι ι
\ ^т ι ι „2у2 dx — \ 0dx = 0. Замечание. Этот пример показывает,
что условие равномерной сходимости в свойстве 3 (формула (2.9)) не необходимо.
§ 2.2. СТЕПЕННЫЕ РЯДЫ. ДЕЙСТВИЯ НАД СТЕПЕННЫМИ РЯДАМИ
Степенным рядом называется функциональный ряд вида
00 00
2^ uk (χ) = 2^ак (х — a)k = а0 + ах (х — а) + а2 (х — а)2 +
+ ... + ak(x-a)k+... , (2.11)
где ak (/5 = 0, 1, 2, 3, ...) —числа, называемые
коэффициентами ряда.
При а = О ряд принимает вид
00
2 я*** = ^о + αι* + а2*2 + аз*3 + · · · + а*** + . . . . (2.12)
fc=0
Радиусом сходимости ряда (2.12) называется число R такое,
что при | χ | < R ряд сходится, а при | χ | > R — расходится.
Интервал (-—/?, /?) в этом случае называется интервалом сходимости
указанного ряда (рис. 2.5, а). На концах промежутка [ — R, R]
ряд может или сходиться, или расходиться.
Теорема Абеля. Если степенной ряд (2.12) сходится при χ = R,
его сумма сохраняет непрерывность при указанном значении х:
00 00
lim 2 ak*k = 2 α*#*·
57
Если степенной ряд (2.12) сходится на всей числовой оси,
полагают R = оо; если он сходится только при χ = О, полагают
R = 0. Степенной ряд сходится абсолютно и равномерно на любом
отрезке, принадлежащем интервалу сходимости.
Замечание 1. Аналогично определяется радиус и интервал
сходимости для ряда (2.11): если при |лг — а| </? этот ряд
сходится, а при | χ — а | > R расходится, то R — радиус его
сходимости, (a — R, α + R) — интервал сходимости (рис. 2.5, б).
α δ
-R О R ос \ О a-R a a+R cc
Рис. 2.5
Радиус сходимости степенного ряда находится с помощью
признака Даламбера или признака Коши.
Радиус сходимости можно вычислить по одной из формул:
-д-= lim у \ак\; (2.13)
/?- lim
k—* оо
k - 00
(2.14)
если соответствующий предел существует.
Простейшим примером степенного ряда является
геометрическая прогрессия 1 + х + *2 + хг + ... + xk + ... . Этот ряд
сходится при |<7| = 1*1 < 1. Следовательно, для данного ряда
радиус сходимости /?=1, а интервалом сходимости является
интервал (— 1, 1). Сумма этого ряда равна S(x) = , __ (в
соответствии с формулой S = . °_ , а = 1, i/ = jn, поэтому для
функции S (х) = -г—— имеем следующее разложение в степенной ряд:
1
= 1 + X + х2 + х3 + X* + хь + · · · + *k +
1 — χ
+ ...(М<1), (2.15)
т. е. представление ее в виде суммы указанного ряда.
Действия над степенными рядами. Рассмотрим
степенные ряды:
00
2 ак(х — a)k = α0 + αί(χ — α) + а2(χ — а)2 +
+ ... + Μ*-α)*+...; (2.1 Г)
58
2М*- a)k = &о + Μ* - α) + b2(x - af +
+ ... + bk(x-a)k+... (2.16)
с общим интервалом сходимости (a — R, a+R).
Сумма (разность) рядов (2.1 Г) и (2.16) определяется
формулами:
00 00 00
2М*- а)* + 2 bk (* - а)Л = 2 (а* + 6*) (* ~ a)k> (2.17)
k=0 k=0 k=0
oo oo oo
2 ak(x - af - 2 h(x - Of = 2 (a* - 6») (я- а)*, (2.18)
fe=0 k=0 k=0
а их произведение — формулой
2 ak (χ—°)k 2 bk (*—α)* = 2 ^ (*—α)*>
(2.19)
&=o
k=0
k=0
где
^ = a0bk + axbk-{ + a26fe_2 + .. . + akb0. (2.20)
Ряды (2.17) —(2.19) имеют тот же радиус сходимости R.
В частном случае, если ряды (2.1 Г) и (2.16) совпадают,
формула (2.19) обращается в формулу для возведения ряда
в квадрат:
2 ak (* - °)k
k=0
2 oo
= 2i (a0ak + ахак-\ + a2ak-2 +
+ ... + aka0) xk.
(2.21)
Степенной ряд в пределах промежутка сходимости можно
возводить в степень с любым натуральным показателем т.
Степенной ряд (2.11) внутри его промежутка сходимости
можно почленно дифференцировать и интегрировать:
2M*-flH =2(*+ 1)αλ+ι(*-α)*;
(2.22)
00
k=0
ak
2 ak (x - a)k dx = 2мПГ (χ — α)*+1 + с. (2.23)
k=0
k=0
Ряды (2.22) и (2.23) имеют тот же радиус сходимости, что
и ряд (2.11).
Единственность разложения функции в
степенной ряд. Если ряды (2.1 Г) и (2.16) в окрестности точки
χ = а имеют одну и ту же сумму, они тождественны, т. е.
ак = Ьк(к = 0, 1, 2, ...)·
59
ПРИМЕРЫ
1. Найти радиус сходимости степенного ряда
1 + Зх + 9л:2 + 27л:3 + 81л:4 + ... + Ъкхк +
Это степенной ряд вида (2.12), все коэффициенты его
отличны от нуля. Воспользуемся формулой (2.13). Так как
ak = 3*, lim V 3* = 3, χ = 3,
fe->00
радиус сходимости данного ряда R = -γ. Интервалом
сходимости является интервал ( «-, -х-
Замечание 2. Данный ряд является геометрической
прогрессией со знаменателем q = Зх. Геометрическая прогрессия, как
известно, сходится при |ί/|<1, τ. е. при |3*|<1 или при
~Т<Х<Т'
2. Найти радиус и интервал сходимости степенного ряда
00
2 (kx)k = х + 4*2 + 27х3 + 256л;4 + ... + (kx)k + ... .
Это также степенной ряд вида (2.12), все коэффициенты, за
исключением а0, отличны от нуля. Применим формулу (2.14).
Поскольку
ak _ kk _ kk\ _ / k k 1
ak+l ~~ (k+\)k+l ~ (k + \)k(k+ 1) ~~ U + 1 j ^ + 1 '
lim _^i_ = lim / Ц_γ 1 = J_.0 = 0,
радиус сходимости ряда равен нулю. Ряд сходится в
[единственной точке χ = 0.
Замечание 3. Тот же результат можно получить и по
формуле (2.13):
lim kT**i= lim k = оо, -^ = оо, # = 0.
fc-,οο ' ' Λ -*оо *
3. Найти радиус и интервал сходимости степенного
00
60
Так как
lim
k—>co
ak
= lim
и/M-i
k -*oo
1
k\
1
• (k + \)\
= lim
k ->oo
(ft -f 1)!
ft!
= lim (k+ 1) = oo,
/г -*оо
то /? = oo. Ряд сходится при всех х9 т. е. в интервале (— оо, + °°)·
4. Найти область сходимости степенного ряда
fc=
(я-2)2*-1
fc3
Т~ · · · !
* —2
1
- 2)2*-1
(л:-2)« (ж-2)»
Q "Г 07 1
27
+ .·
Чтобы ответить на вопрос задачи (определение области
сходимости см. в § 2.1), достаточно найти интервал сходимости
ряда и исследовать сходимость числовых рядов, получающихся из
данного ряда при χ = — R и χ = R. Данный ряд является рядом
вида (2.11). Применим к нему признак Даламбера, для чего
найдем предел:
lim
fc-»oc
*k+l
uk
я-
В данном случае:
_ (x-2)2k-1
k*
Uk+\
(x-2f<k+"-
(x — 2)2k+l
lim
k—»00
(x — 2)2fe+1 β {χ__
(ь +1)3 :
(Л+1)Э (*+l)3 '
2)2k~l_ = (x-2)2k+lP _
(x-
k*
■ 2)2Λ_1 (k + l)3
= (x — 2)2
#»
*k+\
uk
= lim (#
&-* 00
(6+1)3 '
k
2)
£ +
г) = (*~2)2
Так как при (* — 2)2 < 1 или | χ — 2 | < 1 ряд сходится,
а при (я — 2)2 > 1 или | χ — 2 | > 1 расходится, в соответствии
с определением радиус сходимости данного ряда /?=1.
Неравенство | χ — 21 < 1 равносильно неравенствам — 1 < χ — 2 < 1
или 1 < χ < 3; интервалом сходимости является интервал (1, 3).
(Этот интервал можно найти, полагая в общем выражении
(a — R, a+R) a = 2, #=1.) Исследуем поведение ряда на
концах промежутка [1, 3]. При χ = 3 получаем ряд
(3 — 2)2*-1
£3
k=\
00
61
Ряд сходится (ряд Дирихле, ρ = 3 > 1). При χ = 1
00 00 00
V (l-2)2fe~1 V ( — 1) 2fe—1 ^ _^J_
k=\ k=\ k=\
Этот ряд также сходится. Следовательно, данный ряд
сходится при 1 <^ χ < 3, т. е. областью его сходимости является
замкнутый промежуток [1, 3].
Замечание 4. Применять формулу (2.14) здесь нельзя,
так как бесконечное множество коэффициентов ряда равно нулю
(а именно a2k = 0, ибо отсутствуют члены с четными степенями
(х-а)).
Замечание 5. Формулу (2.13) также применять нельзя,
но можно пользоваться формулой Коши — Адамара
-^=Мт^\ак\, (2.13')
где lim у \ak\ — верхний предел последовательности (j/ak }.
k—»оо
00
V"! (χ _±_ 3)2&
5. Найти область сходимости степенного ряда ,>, и '—#
k=\
Это также ряд вида (2.11), для которого а = —3, a2k-\ = 0.
Применяем признак Даламбера. В данном случае:
(* + 3)2<*+]> (x + 3)*k
"н-1= —ь~+-\ '» uk= k ;
(χ + 3)2fe+2 (x + 3)*k _ k(x + 3)2fe+2 fc
«Λ k+\ ' ^ (£ + 1)(a: + 3)2fe b+\
(* + 3)2;
lim
fc—>oo
"fe+l
"Λ
lim
&->oo
т^г(х + з)2
U + 3|
2
Поскольку при (# + З)2 < 1, т. е. при | χ + 31 < 1, ряд
сходится, а при (х + З)2 > 1, т. е. при | л: -f- 3 | > 1, расходится,
радиус сходимости данного ряда /?= 1. Интервалом сходимости
является интервал (— 4, — 2). Исследуем сходимость ряда на
концах промежутка [ — 4, —2], т. е. при х = —4, х = —2. При
χ = — 4 получаем ряд
00 00 00
Σ (_4 + 3)2fe _ у (— \)2k _ Vi_L
k ~ jL· k ~ Zj k -
Этот ряд расходится (гармонический ряд). При χ = — 2
00
также получаем расходящийся гармонический РЯД^-^-· Следо-
62
вательно, областью сходимости данного ряда является интервал
<~4' -2)·
VI (х + 2)k
6. Найти область сходимости ряда ^j &(5*+1) '
k=\
Применяем признак Даламбера, считая χ фиксированным.
Поскольку
(х + 2)fe+1
uk+\
»k \ I (k+ 1)(5*+1 + 1)
(* + 2)fe+1&(5fe + 1)
(* + 2)*(fc+l)(5*+1 + l)
. (a: + 2)fe
fc(5fe + l)
|s + 2|fe(5*+l)
(^ -|- 1) (δ^^1 + 1) '
TO
lim
k ->oo
4fc+l
«Λ
,. fc(5* + 1) | , ol
= hm —Txr \x + 2 =
= lim
fc ->oo
1 +
__ (1+5-*)
_L ' (5 + 5-*)
■|* + 2| -
|* + 2|
Ряд сходится, когда полученный предел меньше единицы, т. е.
ι χ _L 2 I
■' "Г ' < 1 или | χ + 2 | < 5. Так как при | χ + 2 | < 5 ряд
сходится, а при | χ + 2 | > 5 расходится, радиус сходимости R = 5.
Интервал (— 7, 3) является интервалом сходимости. Исследуем
поведение ряда на концах промежутка [ — 7, 3]. При χ = —7
получаем знакочередующийся ряд
(-7 + 2)fe
£ (5* + 1) ·
(-5*)
k{bk + 1)
-S(-i)·
£(1-
fe=l k=\ k=\
Этот ряд удовлетворяет условиям признака
поэтому он сходится. При χ = 3 получаем ряд
00 . 00 . 00
Σ(3 + 2)* _ yi 5fe _ γ,
fc(5*+l) ~ 2u k(5k+\)%~ Za
Лейбница,
k=\
ι
k=\
k=\
k(\+b~*)
Полученный ряд расходится, так как каждый его член больше
члена расходящегося гармонического ряда
соответствующего
00
^Т+Т, т. е.
>
£(1+5-*) k+\'
так как k (1 + 5~k) < k + 1. Следовательно, областью сходимости
данного ряда является полуоткрытый промежуток [»— 7, 3).
63
7. Разложить в ряд по степени χ функцию f(x) — . , .
Воспользуемся разложением (2.15). В формуле
T-L_ = 1 + χ + χ2 + χ3 + χ* + хъ + .. . + xk + ...
напишем (— л;) вместо х:
—^)=1 + (-х) + (-х)*+(-Х)*+(-Ху +
+ ... +(-*)* + ....
Таким образом, получено следующее разложение данной
функции в степенной ряд:
1 — χ + х2 — х3 + х* — .. . + ( - 1 )*+ι** + . .. (2.24)
\ + х
Этот ряд сходится при | χ | < 1.
Замечание 6. Формулу (2.24) можно получить и другим
путем. Ряд 1— χ + х2 — х3 +... + (— \)k+xxk + ... является
геометрической прогрессией со знаменателем q = —χ; он сходится
при |*|< 1, его сумма S(x)= , (получено по формуле S =
-- 1, q = —х).
8. Разложить в ряд по степеням χ функцию f(x) = . _ 2.
В формуле (2.24) вместо χ напишем — х2:
J-L-2 =1 + х» + ^ + д«+... + х8*+... (2.25)
Полученный ряд сходится при \х\< 1.
Замечание 7. Этот пример можно решить и другим
способом. Так как
' '■ · ■+■
1-х2 2 \ 1 + χ
то в соответствии с разложением (2.15) и (2.24) по определению
суммы степенных рядов (формула (2.17)) получаем
1 =4-[(ΐ-*+*,-*8+*4-...)+
1-х* 2
= -§- К1 + !) + (- х + χ) + (*2 + х*) + ( - *3 + *3) +
+(х*+**)+...]=4- (2+2*2+2χί+■ ■ ·) =
= 1 + χ2 + χ* + ... + x2k +
64
9. Разложить в ряд по степеням (х + 2) функцию
f <*) = т^г-
Преобразуем данную функцию следующим образом:
1 1 = 1 =
1-х ~ 1— (а;+ 2)+ 2 "" 3 — (а;+ 2) ""
1 _ J_ 1
"3
3 1
χ +2
1
х + 2
Введем новую переменную t, полагая x + 2 = t. Воспользуемся
разложением (2.15), записывая в нем -г- вместо х:
/М =
1-х
1
х + 2
1
-И'+*+т+т)+- + (
или
1
3
['+-Г
1 1
1 —
χ 3
+
(1)
1+±+± + 1* + *
х + 2
т. е.
+(
х + 2 (х + 2)2 (* + 2):
(2)
1—л: 3 + З2 +
З3
+
З4
+ ... +
(х + 2)k
3^+1
(3)
Ряд (1) сходится при \-γ < 1, т. е. при |ί|<3, или при
—3</<3, а ряд (3) сходится при —3<#-f 2<3 или при —5<
<х< 1.
10. Разложить в ряд по степеням χ функцию f(x) =
4
(1+*)(1-Зд)·
Разлагая данную функцию в сумму элементарных дробей,
получаем
4 1 3
(1 + х)(1 — За;) ~~ \+х + 1 — За;*
= ι _ χ + х*-.хз + χ*_хь + _г + (_ 1)*+!^* + ...; (4)
Так как
1
1 +х
5 А. А. Гусак
65
_L_ =1+3χ+ (3д)2 + (3л.)3 + {3x)i + {3х)Ь +
+ ... + (3x)k +..., (5)
по формуле (2.17)
4
2(_ 1)*х*+з2(зх)*«
(1 + x)(l — 3x)
00
= 2к-1)* + з*+ч**. (6)
k=0
Ряд (4) сходится при | χ | < 1, ряд (5) — при | χ | < -у, поэтому
ряд (6) также сходится при | * | < -g-, т. е. в интервале ( х-, -j-j.
11. Найти разложение в степенной ряд функции f(x) = arctg*
с помощью степенного ряда для ψ(χ) = 2.
Напишем степенной ряд для функции φ (χ). Записывая
в формуле (2.15) х2 вместо (— #), получаем
у-1^ = 1 - χ2 + χ4 - χ6 + xs - .. . + ( - I)**2* + ... . (2.26)
Этот ряд сходится при 1*1 < 1, т. е. в интервале (—1, 1).
Следовательно, его можно интегрировать почленно по любому
промежутку, содержащемуся в указанном интервале. Интегрируя
ряд по промежутку [0, х], где 0<х< 1, находим
X X
f "гЬ5 dx = ί[1 ~~ χ2 + χί ~ *6 + *8 ~~'''+ (~ X)k*2k + "^dx =
О О
х3 хъ х1 хд и л:2^-1
= X з~ + ~5 Г + ~9 ·.. + (— 1) 2F+T+ " " " '
X
Поскольку 1 * 2 = arctg x, то
о
, Л? . X5 X1 , X9
arctgx = x--T + ^ _ + __
Ряд (2.27) имеет радиус сходимости /?= 1. На концах
промежутка [—1, 1] ряд также сходится. В частности, при χ = 1
получаем ряд
-Г'1—Г + 4—Г + 4- + ···· (2·28>
66
12. Найти разложение в ряд по степеням χ для функции
f Μ = (1+х)2'
Данная функция является производной функции φ(#) =
= 1 . ν» Аля которой при |χI < 1
- j^j = -1-*+χ2-χ* + χ*-... + (- \)кХк +
+ ... = — 1 + х — хг + х3 — ... + (— 1)*+ι** +
Почленно дифференцируя этот ряд, получаем
(—fir)' = 1_1 + χ~χ2 + χΖ~ ■ · ■ + (-1)*+'** + · · ·]',
т. е.
(1+Χ)2 = 1-2λ:+3λ;2-4λ:3+5χ*- ...+
00
+ (— ΐ)*-1^*-1 + ... = 2(— ΐ)*-1*^*-1.
ft=l
Замечание 8. Последний ряд можно получить и
возведением исходного ряда в квадрат по формуле (2.21):
1
= (ттт)2 = (1-х + х2-х3 + х*-хь + х«+...)2
(1 + х?
= 1 + [1(-1) + (-1)1]х+[Ы + (-1)(-1)+Ы]х2+...=
= 1 - 2х + Зх2 — ... + (— Ι)*-1***-1 + ... .
ЗАДАЧИ
Найти радиусы и интервалы сходимости степенных рядов:
1. 1 + Τ + ΊΓ + -2Γ+··· · 2. l-3x + 9x2-27x3+....
3. 1 + 5χ+2·25χ2 + 3·125χ3+... _ 4 ι _i__]_*._i£ + ... .
00 00 00
5. ^klxk. 6. 2ΐ**· 7· Σ^****·
ft=l ft=l k=\
*Σ£*· «-si*· ·*ί:(' -if"·
fc=l fc=l fc=l
«■S^ и·^-*·. >3.Jt^!i.
67
00
κ2*ΐ?· |5-2(^)Т- .е.21^(С>о).
/?=1 Л=1 Л=1
Найти области сходимости рядов:
17
*-I klH й*^*+1"
fc=l *=1 *=1
Разложить в ряды по степеням χ следующие функции:
23. / (х) = у4^· 24. / (χ) = Τψ1?· 25. / (χ) = -^.
ae./W = rb· 27. fW = rpr,· 28./W = rra-
29· / W = (l-xHl-4») · 30· / W = (1+.H1+5*) ·
«•/(х) = 7ТГЙ + б·· 32./(Х)=,21-Д2- 33. /(Χ) = 27Τ3·
34. / (x) = з^Г-4. 35. / (χ) = ^. 36. / (χ) = ^.
37· / (*) = (11χ)2- Ι 38. / (χ) = (arctg χ)2.
Разложить по степеням (χ — 1) следующие функции:
39. /(*) = ! 40. /(*)=-^. 41. /W = ^x-. 42./(*) = ^
Разложить по степеням (# + 3) следующие функции:
43. /(х) = 4:- 44. /(х) = ^. 45. /(х) = г^. 46./(х) = ^.
47. Разложить по степеням (х — а), где а > О, функцию
/■<*> = тЪ·
48. Разложить по степеням (# -f α)> гАе α > О, α =^ 1, функцию
Найти производные степенных рядов:
v»2 v3 у4 у#
49. x-iL + 4r-^-+... + (_l)*+iir + ...(|x|<l).
y2 уЗ y4 уЛ
50. 1 + х + 4г+4г + -^Г + --- + ^Г+··· ·
В промежутке [0, х] проинтегрировать степенные ряды:
51. 1— х+х2 —х3+х4 — ... + (— 1)*х*+... (|х| < 1).
52. 1 + χ + л? + *3 + *4 τ ··· + **+·· · (|х| < 1).
68
ОТВЕТЫ
ι. н=з, (-3, з). 2. *=4-. (-4-. 4} *·*=4· (-4-· τ)·
4. # = 2, (— 2, 2). 5. Я = 0. 6. /? = 0. 7. # = 0. 8. Я = оо. 9. Л =—
(——. —)· Ю. R = e, (-e, е). 11. /? = 1, (2,4). 12. Я=1, (3,5).
13. #= ^2, (— 1— ^"2, — 1+|/"2). 14. /? = 2, (—5,-1). 15./?=—·
/——. —)· 16- Л = оо при с<1, /?=1 при с=1, /? = 0 при с> 1.
17. [—6, —4]. 18. [—9, 5). 19. [1, 3]. 20. [—/3 + 4, |^3 + 4].
21. Г-±, -U. 22.'(-/2в, 1/Ъ). 23. 1+λ;3 + λ;6 + *9+_ (|*|<1).
24. л: — *4 + *7 — *ю + ... (| χ |< 1). 25. 1 — *4 + л:* — х12 + . . . (| χ |< 1).
26. jc + jc» + jce + jc«+... (|*|<1). 27. 1 — 4* + (4*)2 — (4*)3 + ... Μ χ |< —V
00
28. l+5^ + (5^ + (5x)3 + ...^|<^_j. 29. ^(1+4л+1)х* (l^K-J")·
oo
Указание. 5 = —+ 4 ■ 30. VW+1—1)(—1)*]WU|<1
°° /
fc=0
31.
1
*fe (| a: |< 2). Указание.
1
1
1
32.
k=0
oo
k=\
00
3Л+1/ X1 ' ^ x2_5^ + 6 2 —л; 3 —л;
1 \ jfe/,„. ^14 v„ _ 3-2.V
2*+V
) *fe( | χ I < 1). Указание.
33.
35
00
-Σ-
fc=0
00
2*
3*+i
,|<A. 34. -У
■ 2 / —*
= _1_ + _Ι_.
x2 — 3a;+ 2 1 — jc 2 — χ
00
■Л I
k=0
3k
4M-1
;('"<4-)
bkxk
0*+'
*|<
36.
I](-l)fe
bkxk
aW
k=0
x\ <
37.
^te*-!(|*|<l). Указание. * ^ = (yj^)'- £38· /(*) = *2~
fc=l
3 n
, *5
τ —^— —
- 23 x°-
*7
-4- + ··
105
.) . 39
x8 + ... (I * |< 1). Указание. /(*)=* — _ +
ι. 5j(— !)*(*—1)*(|*—1 |<1). Указание. JL
fc=0
= ! 40. — V (χ — \)k (I x — 1 |< 1). У к а з а н и е 1 =
fc=o
69
= - .-(Li)' 4,-2(-1)ft(-lHT-ft(^-,1<4)· Указа„ие.
k=0
1
г + х
(*-l) + 4
■{"■•■τ
-. 42
• 2j^+t-(U~1|<2)· Указа"
k=o
3 — Χ ι γ .
2 1· *
ние. т = .
1
i_(*+3)1
ние.
1
д: + 4 ~ 1 + (а: + 3)
—. 43. 2(_1)(^W"(|X + 3I<3)· Указа"
00
. 44. V(_ i)^(^ + 3)fe(|A: + 3|<l).
Указало
3* .—J—4*+1 (I* + 3I<4)· Указание.
л=о
1-х
2-х
з а н и е.
4fl-^+_3
. 46. ^У (* + 3)* (|* + 3|<5). Указание
1
fc=0
оо
5(l-* + 3
1
1 + *:
2(-d*
. 47. ^'/-i^·
5 / 'k=o
1
(a; — α)*
(1 + ауН-1 (|*-α|<1+α). У к а-
00
(1 + α) (1
. 48. VI (* + a)k
(1 +a)k+l
х-а\ ^ /t , „jh-1 - 49· l-* + *2-
1 + a/ ^=0
-*3+ ... = —!— 50. S'(x) = S(x), (1 +Α;+ί!+^1+ίί + ...ί^ + ...) =
1 + * \ 2! ^ 3! ^ 4! ^ W. J
v»4 v^ \ v*2 v«* v4 v5
-^ + _ + ..._ + .... 51. л; —_ + — —_ + _+... +
2! ' 3! ^ 4! ^ W. j 2^3 4^5^^
+ (-i)*+1^ + ...(U|<i). 52· ^ + ΐ + :?- + ··· + ^ + ··· (ι χ I < υ-
A;
§ 2.3. РЯД ТЕЙЛОРА. РЯД МАКЛОРЕНА
Формулой Тейлора для функции /(*) называется формула
f(x)=f(a) + ^f^(x-ar + rn(x),
(2.29)
fc=l
где гп (х) — остаточный член, который может быть выражен,
например, в форме Лагранжа
/C+Dfa + θ (* — a)] r, ч ..
(2.30)
70
где О < θ < 1, или в форме Коши
гп {х) = ί{η+1)ία + β{χ-α)] {1_Θ)η{χ_ α)η^ {2Ж)
где 0<Θ< 1.
Если функция f(x) разлагается в степенной ряд
/ (х) = Со + сг (х — а) + с2 (х — а)2 + . .. + ck (χ — a)k + . ..
в некоторой окрестности точки а, т. е. в интервале (a — h, a + Л),
то коэффициенты этого ряда определяются по формулам:
c0 = f(a), Ck = -^-(k=\,2,3, ...)· (2.31)
Следовательно,
/'(") ,v „\ , Г (а)
/ (х) = f(a) + J-*L(x-a) + Ιψ-(χ-α)*+... +
+ i?jM-{x-a)k+.... (2.32)
Ряд, стоящий в правой части формулы (2.32), называется рядом
Тейлора для функции f(x) (независимо от того, сходится ли он
и имеет ли своей суммой* /(х)).
Равенство (2.32) выполняется (ряд Тейлора сходится к f(x)
в интервале (а — h, a + h)), если остаток ряда Тейлора
г η (х) =
/(*)-/(α)-2-π[τ-(*-α)*
V^(,-^l
стремится к нулю при неограниченном возрастании /г, т. е.
\\тгп(х) = 0 (2.33)
П->О0
при всех χ из интервала (а —Л, а + А).
Достаточное условие разложимости функции
в ряд Тейлора. Если функция /(#) имеет производные любого
порядка в интервале (a — h, a -}- Л) и эти производные равномерно
* Может оказаться, что ряд Тейлора для функции / (х) сходится в
некоторой окрестности точки х = а, но его сумма не равна f (х). Например, для
функции
f(x) = \ e х'г при хфО,
{ 0 . при χ = О
сумма ряда Тейлора равна нулю при всех χ (так как все коэффициенты этого
ряда равны нулю), а сама функция обращается в нуль лишь в точке χ = 0.
71
ограничены в данном интервале, т. е. существует такое
положительное число L (не зависящее от п), что
|р>(*) |<L (n =1,2,3, ...) (2.34)
при всех л: из (а — h, a + h), то имеет место разложение (2.32)
во всем интервале (а —Л, a + fi).
Формула (2.32) в частном случае, при а = О, определяет
разложение функции в ряд Маклорена
№) = i(0)l», + ^f + aW... + ^ + .... (2.32')
При разложении функций в степенные ряды'часто используются
формула (2.15) и разложения в ряд Маклорена следующих функций:
00
+ -£ + ...(|х|<оо); (2.35)
(- ^-'"(Ж^Т)! = *~ ЗГ + -5Г-· · · +
у2*-1
+ (- l^k~lw=w + · · · d*i< <*)-. (2·36)
00
cos * = 1 + 2j (- 1)* -щ- = 1 - -и" + ТГ ~ Ж + · · · +
+ (-1)к-щг + ---(\х\<°°У, (2-37)
00
ΐη(ΐ + χ)=2(-ι)""'χ=χ-4+4-ΐ+ ··· +
+ (- Ι)*"1 £+...(- 1< * < 1); (2.38)
α(α— 1) 2 α (α— 1)(α — 2) 3 ι
i 21 Χ Η 3! Χ + · ·· +
+ «(«-ΐ)(«-2).^α-(*-1)Ι χ, + (_ t < χ < ц> (2 39)
где α — действительное число.
72
Подстановка ряда в ряд. Рассмотрим функцию y=f (x)'
которая в промежутке (—R, R) разлагается в степенной ряд
00
У
/м = 2
akxK
(2.40)
k=0
Пусть, кроме того, дана функция φ (у), также разлагающаяся
в степенной ряд,
00
<р(У) = ^КУт(-р\<У<Р)- (2.41)
т=0
Если \а0\ = |/(0) | < р, сложную функцию φ (/(*)) в
окрестности точки χ = 0 можно разложить в ряд по степеням х, для
чего нужно подставить в равенство (2.41) вместо у ряд (2.40),
возвести в степень и объединить затем подобные члены.
[ПРИМЕРЫ
1. Разложить в ряд Маклорена функцию y = s\ix.
Гиперболический синус (sh#) определяется равенством
sh* =
Заменяя в формуле (2.35) χ на (—а:), получаем
Следовательно,
sh'x = -γ I
1 4- — 4- — 4- —-
'21 3! +
+ Ц2 +
k\
+ Ж+1
v3
- 1
3! + 5! +
+ ..·
- — +
1! ^
· +
Jim— 1
+ '
(2m — 1)!
Итак,
shx
V x2m~x
jL· (2m— .
m=\
(2m—1)! *
Полученный ряд сходится при всех χ, как и ряды для функций ех
и ег
2. Разложить в ряд Маклорена функцию f(x) = $>mx (т. е.
убедиться в справедливости формулы (2.36)).
73
Функция / (χ) = sin χ разлагается в ряд Маклорена,
сходящийся при всех х, ибо все производные ее равномерно ограничены
|Р>(*)|<1 (*= 1,2,3, ...)
при всех х, так что условие (2.34) выполнено при любом h.
Находим производные данной функции и их значения при χ = 0:
f(x) -sin χ, /(0) = 0;
Ρ (χ) = cos χ = sin (χ + -5-), /ι (0) = 1;
/π (χ) = _ sin χ = sin (χ + π), /» (0) = 0;
/πι (Χ) = _ cos χ = sin (χ + -^-), Ζ1" (0) - — 1;
/ιν (χ) = sin λ: = sin (χ + 2π), /ιν (0) = 0;
/<*> (χ) = sin [χ + k -f j, /<*> (0) - sin Ik -J-);
Подставляя полученные значения в формулу (2.32), находим
У^ Х^ Х~ X® X
sin χ = *__ + ___+__... + (_l)*-i w-w + ... .
Полученный ряд сходится при всех х.
3. Разложить функцию /(*) = In * в ряд по степеням (х — 1),
т. е. в ряд Тейлора, в окрестности точки х=\.
Находим производные данной функции:
ρ (χ) = 4-· fuw = -i-'f111 w = -k>
Ρ (χ) = —1£ f(ft) W = (- O*"1 (±^r~.
Вычисляем значения функции и ее производных при х= 1:
/(1)-In 1-0, Я(1)=1, /п0) = -1. ··· .
/(*) (1) = (— Ι)*—ι (fe — 1)!
Подставляя эти значения в формулу (2.32), получаем искомый
ряд Тейлора:
In * = (л: — 1) — 2 + з 4 + * * * +
+ (_l)*JiLzi)i + ... .
74
С помощью признака Даламбера можно убедиться, что ряд
сходится при | χ — 1 | < 1. Действительно,
lim
ft —>оо
uk+\
"ft
= lim
ft—>oo
(*__ i)^+i ^ (X__ if
= lim
ft—»00
(*-
ft-
= lim
ft->oo
— Ι λ: — 11 lim
(χ- 1)*+^
(χ—1)*(Λ+ 1)
И.
= U
Ряд сходится, если | χ — 1 | < 1, т. е. при 0 < χ < 2. При
jc = 2 получаем знакопеременный ряд, удовлетворяющий условиям
признака Лейбница. Отметим, что при χ = О функция не
определена. Итак, областью сходимости ряда является полуоткрытый
промежуток (0, 2].
Покажем, что сумма ряда при фиксированном значении χ равна
соответствующему значению данной функции (ряд сходится к
данной функции), для чего убедимся в справедливости равенства (2.33).
Формула (2.30') в данном случае принимает вид
/(«+D ρ + θ(χ— ΐ)ΐ
\гп(х)\
(1 - Θ)"
(1-©)"(*- l)*+i
\х- \\п+\
[1 +θ (χ— \)]η+ι
откуда видно, что при \х— 1| < 1 lim rn(x) = 0, что и требовалось
п—>оо
показать.
1 4- х
4. Разложить в ряд Маклорена функцию /(*) = 1пуз—»
использовав разложение функции φ(x) = In(1 —л:).
Найдем разложение в степенной ряд функции φ (χ) = In (1
Записывая в формуле (2.38) — χ вместо х, получаем
yft
χ).
In (1 — λ:)
хъ
5
хк
Полученный ряд сходится при
получаем знакочередующийся ряд,
признака Лейбница,
- 1 <х < 1. Если
удовлетворяющий
. . (2.38')
χ = — 1,
условиям
In 2- 1
+
и
{ Л- χ
Так как In 1 _ = In (1 -} χ) — In (1 — χ), с учетом формул
(2.38) и (2.38') находим искомое разложение:
In
1-х
— — +
9 ^
л:*
— 4-
^
5
X*
τ
75
In
1 + * r>/ x
= 2(τ + ΊΓ + ΊΓ+··· + ί£γ^Τ + ···)· (2·42)
Этот ряд сходится в интервале (—1, 1).
5. Разложить в ряд Маклорена функцию /(*) = 1п(* +
+ |/ 1 + *2), использовав разложение функции φ (л:) = .
у\ + х2
Находим предварительно разложение функции φ (л:) в ряд
Маклорена, используя биномиальный ряд, определяемый форму-
\_
лой (2.39). Так как = (1 + х2) 2 , то, записывая в ука-
Vl + χ2
занной формуле х2 вместо χ и полагая а = ~-, получаем
2
■4- -'-ι
i + \—L)x*+ { 2> 02—^ +
+
т. е.
4)
1 1-4—2
_2 / V 2
1-2-3
ΜΙ , J_ 2 , J_^_ 4 1-3-5 6 1-3-5-7 8_
у\ 4- χ2 9^2-4 2-4-6 ^ 2-4-6-8
+ (-1)*-ι ^У" х"+... . (2.43)
Полученный ряд сходится в интервале (—1, 1). На концах
промежутка [— 1,1] он также сходится (знакопеременный ряд,
удовлетворяющий условиям признака Лейбница). Интегрируя ряд
(2.43) по промежутку [0, х], где 0 < χ < 1 (что можно делать, так
как ряд сходится равномерно), находим
dx _ Ι*/! _ JL Г2 . 1± Y4 _ ЬЗ-5 б 1-3-5-7 8 _
|/Г+Т2 ] \ 2 * "*" 2-4 * 2-4-6 X "^ 2-4-6-8 * * * "1"
0
^ I *' (2fc)!! -\- ...jax — x 2 3+2.4 5
1-3-5 λ:7 1-3-5-7 л»
2-46 ' 7 + 2-4-6-8 9 · · · +
, /_ 1U-1 (2fe-l)!l *2fe+1 ■
^^ ^ (2fc)!! 2fc+l ^
76
Поскольку
χ
С dx
J ΚΙ + χ2
о
= ln(x+Vl + x*),
из двух последних равенств получается искомое разложение:
ΐπ(χ+ι/ττ^) = ^-4-·4 + 4τ·τ-""··· +
fe ЬЗ.5. ..(2*-1) χ2**1
^ V ' 2-4.6.. .2k ' 2fc + 1 "t" · · · ·
Последний ряд сходится при |*|<; 1.
6. Разложить в ряд Маклорена функцию / (л:) = arcsin jc,
использовав разложение функции φ (χ) =
1
Найдем разложение в ряд Маклорена функции φ (χ) = -
К 1 — χ2
для чего воспользуемся формулой (2.39). Записав в этой формуле
2 !
— jr вместо χ и положив α = ^", получим
|^1 х2 2 2-4 ' 2 · 4 · 6 ' '
+ |.,5.б(М-„^+ ^ (244)
Этот ряд сходится при \х\ < 1. Интегрируя его по промежутку
[О, х], где 0 < * < 1, находим
b о
ЬЗ.5...(2^-1) ν8Λ>?_ Ь , J *3
^ 2.4-6. ..2k X -Г '•·)αχ-χ-ϊ- 2 3 ф
1-3 x5 1-3.5 *7 l-3-5...(2fe—1) χ2*4"1 .
+ 2-4* 5 + 2·4·6 ' 7 +···+ 2-4-6. .. 2Λ ' 2fc + 1 + * * *
Так как
dx
= arcsin χ,
TO
0
, 1 *3 , 1-3 a;5 . 1-3-5 x1 . .
arcsin χ = χ + τ·— + —. — + ^4^-·— + ... +
l-3...(2/g—1) *^+1
2-4... (2fc) 2k+\
+ ... . (2.45)
77
Полученный ряд сходится при |*|< 1. Положив в формуле
(2.45) χ = ——, получим
iL = J_ . J L_ . -Li l ι _i_
4 /2 ^ 2-3 2/2 2-4 5.22Κ2^",_Ι~
1
2-3
(2fc-
1
2/2
-1)!!
...
(2*)" (2*+1)2*/2
ИЛИ
οι/·οΓι ,11.1-31, 1-3-5 1
2^6 ' Ί^Ψ + · · · +
(2k — 1)!!
(2*)" (2*-Η)2*
+ l""-'J" i Ι 1
' /9MM ,π, , tv nb I · · · l·
7. Разложить вряд Тейлора функцию f(x) =—, положив
а = —2.
Данную задачу можно решить с помощью формулы (2.32),
для чего нужно найти производные данной функции и их
значения при χ = —2. Однако можно получить искомое разложение
проще, воспользовавшись формулой (2.15) и положив в нейг"Г )
вместо х. Действительно,
j_^ 1 __ 1 1__ __
χ (х + 2)-2 2-(х + 2) Г (х + 2
i'-m
1 + ^+№Г+-+(^Г+
...],
т. е.
1 1 х + 2 (х + 2)2 (x + 2f (* + 2)*
х — 2 22 23 24 * ' * 2k+l " ' '
I х + 2 I
Этот ряд сходится, если -—^—L < 1, т. е. при — 2 < χ +
+ 2 < 2 или при — 4 < л: < 0. Полученный ряд и является рядом
Тейлора для данной функции (это следует из единственности
разложения функции в степенной ряд).
8. Разложить в ряд Маклорена функцию / (х) = х3 cos x.
Используя формулу (2.37), получаем:
(х2 х4 а;6 хв
1 2! ' ~4! 6! ^ ~8! · · · +
x2k , \ , х5 . х7 х9 , хг
W + '
x2k+3
+ ^ *)* (2k)\ +·--) — х 2! + 4! 6! "*" 8! · · · +
_l ί \\k
(2*)!
+ (-Vk^m- +
78
ХЪ χ7 χ9 gZk+3
χ8 cos χ = χ8--35- +-41 _+... + (_ 1) к-щГ^
+ ... (\x\<oo).
9. Написать первые три члена разложения функции f(x) =
= sec x в ряд Маклорена.
В точке χ = 0 функция определена и имеет производные
любого порядка. Предположим, что разложение ее в степенной ряд
имеет вид
sec χ = а0 + ахх + а2х2 + а3х3 + а±х* + · · · ·
Так как
1 л
sec χ = , sec χ cos χ = 1,
cos χ'
cos χ — l 2 + 24 720 ■+- .
ΤΟ
1 = sec χ cos χ = (α0 + αχχ + α2*2 + α3χ3 +
+ α4χ4 + ...) (1 - 4" + "Й" - 4ο + * * *) = α° + αι* +
+ (α2-^)^ + (α3-^)^ + (-^_^ + α4)^+... .
Сравнивая коэффициенты при одинаковых степенях х,
получаем уравнения:
а0=1, fli = Of α2-^- = 0, α3-^- = 0, -g--^ + a4 = 0,
из которых находим:
а0 = 1, ах = 0, а2 = -?>-, α3 = 0, ^ = -g^-·
Следовательно, получены первые три члена разложения в
ряд данной функции:
sec χ = 1 + -γ- + —χ4 + . .. .
Ряд сходится при |х|<-^-(при χ = ±:-5-функция не
определена).
10. Найти первые пять членов разложения функции f{x) = tg л:
в ряд Маклорена.
Функция / (х) = tg χ непрерывна в точке х = 0 и имеет
производные всех порядков. Так как данная функция нечетная, ее
разложение в ряд Маклорена содержит только нечетные степени х.
79
Коэффициент при x2k~l в искомом разложении возьмем в форме
72Fh)P П0ЭТ0МУ
00
\(2k—\)\ x'
2k-\
Поскольку tg χ cos x = sin *, с учетом формул (2.36) и (2.37)
(2Л-1)!
2k \ Ч^, 1N ', )?k~
Σ^ύ^ΰϊ \ι+Σ(-^4τ =Σ<-!>
(2* — Ι)! *
Коэффициент при х в правой части равен единице, поэтому
Ьх— I. Для определения других чисел 6^, приравнивая
коэффициенты при одинаковых степенях χ слева и справа, находим
уравнения вида
bk , Ьк-\ _]_ , bk-2 J , 14fc_i 1
(2fc—1)! ^ [(2k — 3)! ' 2! ^ (26 — 5)! '4! ·,β ^ *' (2£—1)!*
Умножив эти уравнения почленно на (2k— 1)!, получим
Ък - С|л_1&Л_1 + С^_!^_2 -... = (_ 1)*-1.
Положив в последнем уравнении k = 2, найдем:
&2 - Сзбх = (— I)2-1, Ь2 = 2 (так как 6Х = 1, С§ = 3).
Аналогично находим другие коэффициенты:
Ь3= 16, 64 = 272, 65 = 7936.
Таким образом, получены первые пять членов искомого
разложения:
tg*=*+4-*3+-t*5+w*7+w*3+---(M<^)·
11. Найти несколько первых членов разложения функции
f(x) = -i-(l + х)х в ряд Маклорена.
Данную функцию можно представить в виде
Так как при | χ | < 1
х2 jc3 а;4
\П(1 + Х) = Х 2~+-з 4" + *·· »
80
то
1 ι ,, ι ч 1 ( 'хг х3 хА , \ ί. χ , χ2 χ3 , \
ее е
_ Χ_ , 'χ* fl ι _ _£_ _|_ _ί!_ ίΐ _L
= -Lee 2 + 3 4 +---=e 2 + 3-4 +■-
e
Применим формулу (2.35), переписав ее так:
У . У2 , У3 , #4 , У ,
1 ^ 2 "^6 ^ 24 ^ 120 "τ* · · · τ- ^
^ 1* 1 ^ 9 ^ fi ^ 94 ^ 19П ' · * * ^ Ы "Г··· ·
Воспользуемся последней формулой, считая у = о"+
Я2 λ3
+ ~о τ- + · · · (осуществим подстановку ряда в ряд):
1 Π ! ιΛ*- Л 2 3 4 1 I / * I *2 ** I \ I
"rL24 V 2 "^3,- 4 "Γ·· ^ "Γ 120V 2,7.3 4 ~1~* # 7 "^ * * *""
— 1 2 *+ 24 * 16 ^"Γ*··
ЗАДАЧИ
Можно ли разложить в ряд Маклорена функции, указанные
в задачах 1—8? Если да, ответить на вопрос, сходится ли
соответствующий ряд к данной функции:
1. /(x) = sh-g-. 2. /(x)=_L-I. з. /(д) = |*|. 4. f(x) = \nx.
_
Ιδ. /(χ) = cosecχ. 6. f(x) = VΊό. 7. /(χ) = ctgχ*8. f(x) = e x\
/(0) = 0.
С помощью биномиального ряда разложить в ряд Маклорена
следующие функции:
9. f(x) = (l—x): 10. f(x)= \ 1-х.
И. /(*) = )/5"+^ (α >0). 12. /(x) = -7=L=.
У 1 — χ
|3·/(х) = νττΤ <α > °)· ,4· /<*> = /ι -*2·
15. / (χ) = }/а"+х*(а > 0)· 1в. / (*) = j/1 + JC3.
81
17. /(χ) = з, ' ■ 18. f (χ) = , ' ,
«9· /(*) = 5- ' · 20. /(χ) = "7==-·
Разложить в ряд Маклорена следующие функции:
21. f(x) = chx. 22. / (χ) = sh 2*. 23. / (χ) = In (χ + 3).
24. f (χ) - e-*\ 25. f (x) = sin2*. 26. f (x) = cos2*.
"·η*)=*%¥+2· 28. /W= ,.17Д12 ■
Разложить в ряд Тейлора данные функции в окрестности
указанных точек:
29. / (х) = х* + 2х3 — 5х2 + 2х + 4, л: = —3.
30. Дх) = х5 — 7х4 + 6х3-10х2+4х + 16, л: = 1.
31. f(x) = ex, х = — 4. 32. f(x) = ]/J^, *=1.
33-/W = -TT7' * = ~2. Si.f(x)=7^J, х = Ъ.
Разложить в ряды по степеням χ следующие функции:
35. / (х) = хег\ 36. / (х) = х2 sin χ. 37. / (χ) = -L sin x.
38. / (χ) = -L In y^. 39. / (χ) = 1 arctg χ. 40. / (χ) = i£/q^).
41. /(χ) = e*sin χ. 42. / (χ) = e* cos x.
43. /(χ) = -J- In 4^ —у arctg χ. 44. f(x)=x arctg χ + Ιη/йЦЗ?.
45. / (χ) = χ arcsin χ + Vх 1 — χ2.
46. ^(χ) = ΐ/ΓΤ^2_ χ In (χ +/ΪΤ**)·
47. /(χ) = ΐη^-(ΐ + /Γ+^).
48. /(χ) = УТ+1?1п(х + ΚΤΤ^)·
49. f(x)=V T^x2 arc sin χ. 50. f (χ) = -i- arcte * 1η T=~P
Написать несколько первых членов разложения в ряд
Маклорена следующих функций:
51. / (х) = έ*05х. 52. f (χ) = esin *. 53. /(χ) = th χ. 54. / (χ) =-^—.
1η
55. / (χ) = β*β λ. 56. / (χ) = In cos χ. 57. / (χ) = 1η
82
1-х
sin*
ОТВЕТЫ
1. Да. Сходится. 2. Да. Сходится. 3. Нет. Указание. В точке χ = О
функция не имеет производной. 4. Нет. Указание. В точке χ = 0 функция
не определена. 5. Нет. 6. Нет. Указание. В точке χ = О не определена
производная (/' (0) = ос). 7. Нет. 8. Да. Сходится лишь в точке χ = 0.
Указание. Все коэффициенты разложения этой функции в ряд по степеням
χ равны нулю, поэтому и сумма ряда в любой точке равна нулю, а сама
функция отлична от нуля (она равна нулю в единственной точке χ = 0). 9. 1 —
_ α q(q-l) α(α-1)(α-2)
1 ~τ~ 1·2 χ 1·2·3 * ^~ '*' ~"~
+,-„.«,»-,,...,<,-,*-.,!>t+ (UI<|) ,,,^,-ή-
1-3 χ* 1-3-5 *4 1-3-5 ... (?k — 3)xk
~ 24 * 6 "~ 246 ' 8 "~ ■"·"" 2-4-6 ... (2£—2)26 "~ '·· "χ Ι < !)'
^2 α 8 α2 ^ 16 α3 128 α4 ^ ι Ι4;
Г5"(
JL L? 2 13·5 3 1-3-5-7 4 ( - (2fe — 1)!!
2^ + 2-4х + 2-4-6 * + 2-4-6-8 * + ···+ (26)!) x +
1 Λ 1 д: , 13 > 1-3-5 *3 , Ь3-5-7 χ*
χ*
6
1
1-3-5
2-4-6 '
χ*
Xs
8
5
(\x\<l).\5.Va (/ + — ·~-ΤΧ
(|*|<^ΊΓ). 16. 1 + 4-*·-
(|*Ю)· ,3·^ Τ'"Η" + Τ4"'^^ 2^6 '^" + 2^678 '^Γ +
. 1-3 ... (2/г — \)xk 1 „ 1 χ*
13 χβ 13 5 χ» ... ... ,_ /, , 1 ^_ 1
~~ 2-4
x α2 + 16 a3 128 a4 / v' ' ^ r ' ^ 2
-'Γ*β + ΊΤ*',-'ϊ28*" + ··· <И<1)· 17· 1-4"^ + ~Й_хв--- +
. 1-4-7 ... (3k — 2) , , 11-3
+ <-') 3-6-9 ... 3fe x + ··· (I^K')· 18· '--2-*4+-2T*8-
1-3-5 1 3 11
-TTW* + ••■U*\<1)· ,9· 1-"Г**+"2Гдс4"-Тй"дсв+·· <Ι*Ι<1)·
1 1 я2 1-3 a;4 1-3-5 χβ
™-—--Τ·-3Γ + ΎΤ·^τ-Ύ^-4τ+ -(\χ\<α)- 21.1 +
00 00
MW(UI<+«>.*2.2r-j2riTr(l*l< + ~>. »>"* + f -
-4- · -S-+^(тЬ:'+<- >ГЧ-(4-)'+ - <-·<-<»
Λ- . *2 *4 У* t, y2fe
24· l--^+^|--^|-+ ··· + (-l)*^_ + ...<|*|<+~).
25·Ζ(~1) i2r(|Jc|< + ^ 26· H42(_1)*W(l*l<+~}·
(2fc)!
83
k=\
1 1
■3
27. 4 + 2(-1)"(1 + lir)^(l^<l). Указание. _*HJ
00
Г. 28. ^ + 2(ΐάτ + ΐάτ-)^ (l*K3)< Указа-
1 +χ τ 2 + х'
1
7 — 2л; 1
ние· *«-7*+12= 3=7 + Τ=7" 29. -20-22(* + 3) + 31(* + 3)2-
— 10(χ + 3)3 + (χ + 3)4 (|jc|<+oo). 30. 10 — 21 (л:— 1) — 24 (χ— Ι)2
— 12 (χ— Ι)3— 2 (*— 1)4 + (χ— 1)5 (|jc|< + oc). 31. е-4 J
1+ * + 4 +
1!
(* + 4)2 (* + 4)3 (χ + 4)4 1
f Τι + Τι + 41 + ···] (l*l< + °°)· 32·^
- J \Λ+ι
2!
3!
, -L\(x-d4- ! . (*-*)2 ι J*±JL ,
+ 2 [{Χ υ+-2" 91 -Τ * *ϊ + ···
21 4
00
3!
. 33,
Σ
*=0
(*+
+ 2)*(-5<*<1). 84.-ξ-+Σ~ '>* ^^ (- 3 < χ < 9). 35.χ-_ί-+
(*-3)V
*=ι
6*+'
+ (-!)*
K2ft+1
... (|*|<+ ос). 36. χ3-
3! 5!
(2ft — 1)!
.+ ...(| χ |< оо). 37. 1
3!
+ (- 1)'
А—1 *'
2А-2
(2ft-1)1
+ ... <|*|< + оо). 38. 1 + -2"
5!
... +.
1!
• ··· +
• ··· +
Ji-l
+ ...(|х|<1). 39.1
+
·..+(-!)
k-l X"
+ ... (|*|<1). 40. ^(_1)"-'(1
k
41.
OU
S
00
22 sin
trn
k_
43
χ
Ik
k\
xk (|*l< + °°)· 42,
■s
2 z cos
kn
k\
2ft +1 f
*ft (-I<*<1).
^-(UKl). 44. 4 ,.-(4.+ _|-)^+ (-»--4.)
(^+4)^+... + (-1Г(^=г+-±#И+-"<1*1
4S..+4- + 5] (2fe-l)H.2ft+2 (U|<1).
2 ^ (2ft + 2)!! 2ft + 1 ^ ' '
46. 1— _jc2 +
2
84
1 χ* 13 χ6 1-3-5 χ8
+ 2-4 ' 3 — 2-4-6 ' 5 + 2-4-6-8 ' 7 ' + " · +
, щ.| (2*-1)!!χ2*+2 (|J|<1) 47 1 ■ χ - Ь3 · ** +
+ (-!) (2fe + 2)!!2fe+l +···<Ι*Ι<1>· χ — -2Τ- Τ+
1-3-5 χ* χ3 2 χ5 2-4 χ7
+ ~2^Π6"·~6~- ··· (Ι*1<1)· «· * + —-"3" ^~+Τ^_-~7~-
jc3 2 λ:5 2-4 α;7
— ... (|*|<1). 49. χ: — —3— · -χ ·—5~"-"3^5"·Τ""~ ··· 0*1 < 0·
so. *2 + Λ_._Ι_ + 1_)_ί!_ + (\ — — + 1 — 1 + 1)-?£L+ ··· (Ι χ Ι <ΐ).
\ 3^5/3 V 35 7^9/5 u ι ^ /
2 . *4 \ eo ι ι Χ ι *2 ι cq v *3
51. βίΐ— — + — — .... 52. 1 +JL+Z—+ .... 53. χ — χ ,
^2^6 / '1^2^ 3 +
2л* 111
54. 1 — —ο" α; — —πτ~ α:2 — ол λ^— .... Указание.
15 -τ ... . ο·», ι— 2 Λ— 12 Λ 24
α; χ
-jfi = " ^2 ^з · Приме-
Inyfrj^ *-j-^- + —+ ... 1+_ + _ + -_+ ...
1 1
нить способ, использованный в примере 8. 55. 1 + χ + -у х2+ — дс3 + ... .
Cfi у2 у4 уб С7 v2 у4 уб
ΰο. 2 χ {2х 45 jc .... о/. 6 a; lg()* 2g35* ... .
§ 2.4. РЯДЫ ФУРЬЕ
Рядом Фурье функции f(x) называется тригонометрический
ряд
00
-Y- + ^d(akcoskx + bksmkx); (2.46)
коэффициенты которого определяются формулами.
afe = JL J /(*) coskxdx (k = 0, 1, 2, 3, ...); (2.47)
— π
6ft = -L <if(x)smkxdx (k = 1, 2, 3, .. .)· (2.48)
—π
Если ряд (2.46) является рядом Фурье функции /(#), то
пишут
00
/ (*) ~ -tjt + \] (ak cos kx + bksin ft*). (2.49)
Замечание l.He для всякой функции можно построить ее
ряд Фурье (нельзя написать ряд Фурье функции, для которой
85
интегралы в формулах (2.47), (2.48) не существуют). Не всякая
функция является суммой ее ряда Фурье, даже если он сходится.
В формуле (2.49) вместо знака соответствия можно
поставить знак равенства, когда функция / (х) удовлетворяет условиям
теоремы:
Если функция f (χ) с периодом 2тс кусочно-дифференцируемая
в промежутке [—л, π], то ее ряд Фурье сходится в любой
точке х0 и имеет сумму
s {Хо) = /(*о-о)-г/(*.+о^ (2 50)
В частности, в точке непрерывности функции f(x) значение
суммы ее ряда Фурье совпадает со значением самой функции f(x).
На концах промежутка [— л, л] имеем:
S(—π)=/(—π), S(ji)=/(ji),
если функция f(x) непрерывна в точках ±п, и
S(±l) = iHJ±iM)
если функция f(x) рзраывна в точках it: л.
В дальнейшем предполагаем, что рассматриваемые функции
удовлетворяют условиям этой теоремы.
Ряд Фурье четной функции (т. е. функции, для которой
/(—x) = f(x)) содержит только члены с косинусами:
00
/(*) = ^ + ^akcoskx, (2.51)
где
ak = — ^ f (x) cos kxdx {k = 0, 1, 2, 3, ...). (2.52)
о
Ряд Фурье нечетной функции (т. е. функции, для которой
/(—х) =—/(*)) содержит только члены с синусами:
00
f(x) = ^bkSinkx, (2.53)
k=l
где
6A = !T.(fMsin**d* <fe=1' 2' 3' ···)· (2·54)
о
Кусочно-дифференцируемая функция, заданная на полупериоде
[О, л), может быть продолжена в промежуток [—л, 0] либо как
четная, либо как нечетная, в соответствии с чем ее можно раз-
86
ложить в ряд Фурье или только по косинусам, или только по
синусам кратных дуг.
Ряды Фурье периода 21. Если функция f(x) и ее
"производная /' (х) в промежутке [—/, /] длины 21 либо непрерывны, либо
имеют лишь конечное число точек разрыва первого рода, то во
всех точках непрерывности этого интервала справедливо
разложение
00
/(*) = -£ + 2(** cos-^Г + ** sin Пг)> (2·55)
где
ak = ^§f(x)cos-^j-dx (ft = 0, 1, 2, 3, ...); (2.56)
—/
/
bk = -^\f{x)un-^-dx (k=l, 2, 3, ...). (2.57)
-/
В точках разрыва функции f(x) и на концах х— ±:1
промежутка [—/, /] сумма ряда Фурье определяется формулой (2.50).
В случае разложения функции f (х) в ряд Фурье в
произвольном промежутке [а, а + 21] длины 2/ пределы интегрирования
в формулах (2.56), (2.57) следует заменить соответственно через
а и а -f- 21.
Замечание 2. Ряд (2.46) является частным случаем ряда
формулы (2.55), он получается из последнего при / = я. Формулы
(2.47) и (2.48) получаются соответственно из формул (2.56) и
(2.57) при / = я,
ПРИМЕРЫ
1. Разложить в ряд Фурье периодическую периода 2я
функцию, заданную на промежутке [— я, я] формулами:
ί 1 при — я <; χ < О,
/(*) = ( _ J при 0<*<л.
Данная функция удовлетворяет условиям теоремы, при
которых ряд Фурье функции сходится к ней во всех точках
непрерывности, а в точках разрыва и на концах промежутка [—я, я]
сумма ряда определяется формулой (2.50). Функция эта непрерывна
во всех точках промежутка (— я, я), за исключением точки χ = 0.
Находим коэффициенты ряда Фурье данной функции по формулам
(2.47) и (2.48):
π - 0 π
α° = 4" j'f W cos °xdx = ΊΓ if {x) dx = ~k ЦЫх + lT.fί" *> dx=
—π —- —π Ь
87
= — \dx \dx = —*x
Я J Я J Я -
X
τ Я
*= J-
o я
π
[θ-(-π)]·
— (π — 0) = — — — = 0;
ak==~n~ /Μ cos kxdx = -£■ cos kxdx — *— I cos kxdx =
—ic —π 0
1 sin kx Ρ 1 - sin kx
k —- Я
B=0 (ft=l, 2, 3, ...);]
bk = — \ f (x) sin &*dx = — \ 'sin kxdx \ sin kxdx =
π ι' x 7 я J >· я J
& |0
0
1 cos kx
--] Я
1 cos kx
'== _ EJ_(cos 0 — cos fort) +
) . nk
+ ~L·- (cos kn -cos °)= -hr (cos fejT - cos °) = ~i K—I1)* -1].
Я&
Таким образом, 6^ = 0 [при"(& четном, т. е. при [& = 2п
(п = 1, 2, 3, ...), 6fe = —£ при & [нечетном, тЛ[е. при k =
= 2/г—1 (л = 1, 2, 3, ...). Следовательно,
ak = 0, 62/г = 0, ЬъГ\ =
π (2л — 1)'
ου
w \ 4 "V sin!(2n—1)*1 41/ . , sin3x
/2 = 1
+ -i-[sin5*+ .Λ].
Полученный ряд сходится к функции /(*) во всех точках ее
непрерывности. В точке х = 0 равенство f(x) = S(x), где S(x) =
00
4 ^ sin(2n— \)x ,
=- — — /ι 2л — l—' нарушается (сумма ряда равна нулю, а
п—\
значение функции отлично от нуля). При χ = О получаем:
S(0)=o, /(-0) + /(+0) ^.Ш
1)
/(-0) + /(+0)
2 - 2 -О, S(0)_ g ,
т. е. сумма ряда в этой точке определяется формулой (2.50). При
χ = — π, χ = π получаем соответственно:
<?(-π) = /(-π-0) + '(-π + 0) = 0;
88
S(n)
/(π-0) + /(π + 0)
= 0.
3fHa рис. 2.6, α изображен график функции/(л:), на рис. 2.6/6 —
графики частичных сумм ее ряда Фурье: Si(x), S2(*), S3(x).
2. Разложить в ряд Фурье функцию / (л;) = π ~х- в
промежутке (0,2π).
а
-Я
У\
0
-1
1
я
X
Рис. 2.6
Данная функция непрерывна в указанном промежутке
длины 2π. Найдем коэффициенты ее ряда Фурье, для чего
воспользуемся формулами (2.47) и (2.48), предварительно заменив в них
пределы интегрирования на 0 и 2π соответственно:
2π
1 Γπ
-* , 1 ( *2
2κ
0;
89
2π
2π
α* = 4" J-V* cos **** = ΈΓ.ί <π - χ) d №г) =
Ο Ο
2η
1 , ν sin&A: |2~ . 1 Γ . , , 1 Γ/ 0 ч sin 2/
_ (я_ Χ)__ I + _J 5,„Ых = ^-[(π - 2π) —
■ (π — 0)
sin 0
]·
cos kx
26л
2£2л
cos0) = 0 (k= 1, 2, 3, ...);
2п
6* = it J-V5 sin Шх = "йг ί <π - x) d
(cos 2&π
cos &x
2к
2π
1 , ν cos kx
(n-x) j—
2* \_C
о 2/гл J
cos kxdx
l
2π) cos 2kn — (π — 0) cos 0]
1
1
2*л (sin2to-sin0)= 2πΛ
Итак,
2£2л
2л Ι
sinfejc
2nk
1
ΐ(π
2л£
(—π—π)—
2k2n
0=4- (*=1. 2, 3, ...).
π — *
sin&*
(0 < χ < 2π).
(2.58)
Λ=1
При χ = 0 / (0) = -J, S (0) = 0, где S (jc) = 2 -^χ5-. п°это-
МУ /(0)^5(0), т. е. равенство (2.58) нарушается. При л: = 2π
указанное равенство также нарушается, не будет выполняться
это равенство и вне данного промежутка. (Этот пример
показывает, что два аналитических выражения могут совпадать в
некотором промежутке, не совпадая при этом всюду.)
График суммы ряда S(x) изображен на рис. 2.7 (он состоит
из бесчисленного множества параллельных отрезков с
исключенными концами и ряда отдельных точек на оси Ох).
Примечание. Разложение данной функции в
тригонометрический ряд (см. формулу (2.58)) впервые получил Эйлер в 1744 г.
3. Разложить в ряд Фурье функцию / (х) = еах (а Ф 0) в
промежутке (— π, π).
90
По формулам (2.47) и (2.48) находим:
— \eaXdx
π J
1 еах
"ϊΓ" α
= (еак — е~аг)
-π απ ν '
2 shan
2 e'
απ
,απ .—απ
απ
Рис. 2.7
β*
e°* cos &#йл;
1 acos kx -\~ k sin £*
ΊπΓ' α2 + £2
βα*
= (-1)*
2α
π * α» + £2
-shan (Λ = 1, 2, 3, ...);
*-4-ί
eax sin &#d# =
(-i)
fe-1.
1
2fc
π a* + k2
Следовательно, для — π < χ < π
00
9 сЬ /тгтг I 1
eax
1 a sin Λα; — & cos kx
~л ' a2 + fc2
shan (k= 1, 2, 3, .. .).
= 2"ЬлаП i +Σ i2 + i2 <acosfe*- ftsinM · (2·59)
В частных случаях, при a= 1 и а = — 1, соответственно
имеем:
е*
(00 Ϊ
4- +Σ !"+'£ (cosb-fesinfex)j; (2.59')
,-,= 2shn _L+J>] (~+'^ (cos foe+ fe sin foe) 1. (2.59")
Б I.
91
4. Разложить в ряд Фурье функцию f(x) = x2 в промежутке
[—л, л]. С помощью полученного разложения показать, что
00 00
V<J__ _л^_ \1 (— 1)*+1 _ π2
jL· k2 ""' 6 ' jL· k* ~ 12 *
По формулам (2.47) и (2.48) находим:
2Λν —
x2dx
π ' 3
α* = — \ χ2 cos kxdx = — \ x2d
* π J π J
2 f . - , 2 f , / cos kx
^[яЗ-(-Я)31= 3π
2π3 2л2
3 '
sin kx \ 1 2 s*n kx
k Ι ~ π &
cos &*
nk
2 f 2
ρ- ] cos kxdx = —Tg- [л cos &π — (— л) cos k (— π)]
2 sin &x
tecosto =(_!)«* (/fe=if 2, 3, ...);
π£2
6^ = — \x2s\nkxdx — — \A:2d
1 9 cos &x
—x *:—
π k
+
+ —τ- I x cos ^xdx = — [π2 cos &π — (— π)2 cos k (— π)] -f
JX/2 ,/ 3l·
πΛ J
xd
sin kx \ 1
j =.- —(π2 cos kn — л2 cos kn) -| ρ- λ: sin &л;
2 f . , * 2 cos kx
ш \Smkxdx = 1^-—i—
—ψ [cos kn — cos k (— π)] = 0.
Итак,
2π2
a0 = ^, α* = (- l)*-^, 6* = О (* = 1, 2, 3, . . .),
поэтому для — л <; χ < л
*· = .χ+42]<-1>*^-·
&=1
(2.60)
92
При χ = О
о=4+<5]^
*=i
ИЛИ
т. е.
я2 _ , у (- р*
k=l
12
-Σ
(-1)'
*2
,*+»
ft=l
ι\
l\
1 \ j
i 4/
\ST -#/"
A
/' \
/ '\
' 1 \
1
ι
-.'//
VV/
/|\
/l\
/ ι
1
I
•7/
У,
#
ι
/ '
Jl
27,
\\
1 1
1
3/i
477
\\
\
/ 1
/ 1
i
077 "ос
Рис. 2.8
VI 1 л2
При л: — π находим 7 \~ut — —q~ » что и требовалось показать.
На рис. 2.8 изображен график суммы ряда Фурье, состоящий
из бесконечного числа параболических дуг.
Замечание 3. Данная функция является четной, поэтому
она разлагается в ряд только по косинусам, т. е. все коэффициенты
ее Ък — О и их можно не вычислять.
5. Разложить в ряд Фурье функцию / (х) = cos ах в
промежутке [—π, π] (здесь а Ф k, где k = 1, 2, 3, ...).
Данная функция является четной (/(—л;) = /(*))> поэтому все
коэффициенты bk = 0. Вычислим коэффициенты ak по формуле
(2.52):
а0 = -Mcos axdx = A.iiiL^h J_(sinajt_ sin 0) = 2sinajl ;
π .' πα |0 απ \ / απ
τ π
afe = — j cos ax cos kxdx = — \ [cos (a -f- &) # + cos (a — k) x] dx =
93
1 # sin (α — k)
a-\-k |o π
1 sin (α -\- k)x
π
a — k
1 Γ sin (a + fe) π ,
sin (a __£) π "I _ l [ 2a sin απ cos kn _ (— 1 )fe 2a sin απ
"^ o~=l J~~' a2-*2 "~ n(a*-k*) ·
Следовательно,
cosox;
sin απ
fc=i
6. Разложить в ряд Фурье функцию f(x) = x в промежутке
(—π, π).
Эта функция нечетная (/ (— х) = — /(*)), поэтому все ak = 0.
Коэффициенты bk найдем по формуле (2.54):
π π
bk = — j a: sin &#d* = — J *d
cos &л:
2 ^ cos &л:
.+
π
+ Jj_j" coskxdx = —-^ [ncosbi — OcosO] +
2 sin &*
π&-' &
2 „(_i)* = (_l)M-i-|- (£=1,2,3,...)·
π&
Итак,
00
sin£*
Рис. 2.9
Рис. 2.10
График суммы полученного ряда Фурье изображен на рис. 2.9.
На рис. 2.10 представлен график частичной суммы
0 , ч Л / . sin 2л; . sin Зх
S5 (χ) = 2 (sinχ 2 ' з—
sin 4л: , sin 5л:
л 1 Ε
94
7. Разложить в ряд Фурье функцию
χ при — я<л:<0,
О при 0 < χ < π.
С помощью полученного разложения показать, что
/(*) =
8 ""^.'
1
fc=l
(2£—Ι)2
i+_L ι _i_
^ З2 ' 52
По формулам (2.47) и (2.48) находим коэффициенты ряда
Фурье:
π 0 -
fl0 = — \ f(x)dx = — I — xdx + — \0dx = · 4- =
—π —π 0
_ π2 _ π .
~" "2iT ~~ "F;
π Ο π
αΛ = — I f (x)cos kxdx = — \ —#cos£*d*H \0dx =
=4-4ΐ
1 cos /гх
nk
#sin£#
π/г
υ
ί
sin kxdx =
jt£
π£2
2" (COS 0 — COS kn) =
= -L (cosfoi-cosO) = -L- [(- i)*_ 1],
т. e. <v
π£2
2
—ρ- при k нечетном; ak = О при & четном;
О π
^ = — J / (л;) sin kxdx = — j — л: sin &л;£/л; Η j 0 sin &#£/# =
-π -π 6
о о
--ί'
π J
cos&a:
1 cos kx
— x —г—
π k
cos&a:
dx ■=
■^ [0 cos 0-(-я) cos *(-*)] —^-^
π cos &π (— 1 )fe
π&
Таким образом,
uu ου
f/ ν π 2 ^1 cos(2fc — 1)* , ,V4, ..k s'mkx , . ^ ч
fc=l
96
При χ = О получаем
00
U— 4 π jiL· (2k— 1)2
ИЛИ
fc=l
π2 V^ 1
8 AU(2k— l)2'
fc=l
что и требовалось показать.
График суммы ряда изображен на рис. 2.11.
У
-37Г
-27Г
-УГ
О
зг
237 ЗЯ X
Рис. 2.11
8. Функцию / (х) = χ в промежутке [О, π] разложить по
косинусам.
Заметим, что в данном случае требуется получить
разложение функции в промежутке [О, π] длины π (а не 2π). Продолжая
функцию в промежуток [— π, Ο] четным образом, заключаем, что
ее разложение в ряд Фурье содержит только косинусы, т. е. все
bk = 0. Коэффициенты ak находим по формулам (2.52):
а0 — — \ xdx = — χ2
0 π J π
— η
ο π
π;
2 , , 2 ,/ s'mkx
ak = — \ χ cos kxdx = —Ι χα \
Ι π
sinu*
-г— ι sin kxdx = —£ [π sinkn — Osin 0] + —^—co^
о
= T2~ lcos ^π ~ cos 0]
£2π
[(-!)*-lb
т. e.
a2„ = 0, «2n-i =
(2/1— l)2 π
(л=1, 2, 3, ...).
96
Следовательно,
χ =
2 π jL·'
/ι=1
COS(2tt— \)Х
(2n—l)2
(0<*<π). (2.61)
График суммы ряда изображен на рис. 2.12.
На рис. 2.13 представлен график частичной суммы
с> / \ я 4 / .1 0 . cos 5*
S5 (χ) = "2 I cos * + -32- cos 3* Η ρ—
Замечание 4. Из разложения (2.61) можно получить
последний результат примера 7.
Замечание 5. Из разложений (2.60) и (2.61) можно
получить следующий результат:
00
За;2 — 6шг+ 2π2 V*4 cos &*
12
fc2
(О < л: < π).
9. Разложить в ряд Фурье функцию f(x) = ex в
промежутке (-1, 1).
97
Функция задана в промежутке (—1, 1) длины 2(2/, где
/= 1). По формулам (2.56) и (2.57), полагая /= 1, находим:
ι
aQ = \ exdx = ех \_х = / — е~х\
—Ί
ι
ι' , , kn sin knx + cos /mx J1
afe = ] g* cos #π #α# = . , 2 2 g*|
-1
1 + k2n2 * l-i"
1
== ,,,22 [β (&π sin kn + cos £π) — g_1 (— &π sin kn + cos &π)] =
(β cos &π — β-1 cos kn) =
1+'
ттй-^-^1) (*=Ь 2, з, ...);
f „ . - , smknx — kn cos knx J1
) exsm knxdx —
1
g* =
1 + k2n2 l-i
= | ι jl2 2 Ie (sm kn — kn cos kn) — g-1 ( — sin kn — kn cos kn)]
(— e kn cos &π + g-1 kn cos &π) = « , , 2 2 {e"x ~ e)
~ 1+£2JT2V ^-«^ол^-Г-о *<* wo *„,,,- 1+^2π2
= - "T^ ^-0-^(~^2+1^-^) (*= 1.2,3,...).
Таким образом, в соответствии с формулой (2.55) искомое
разложение имеет вид
00
+ (g-O^ \+]£п* COsfejtX +
00
+ π (e - g-1) Jj \ + ^π, sin far* -
00 00
= (g - β"1) Ц" + Σ 1 (+ίπ2 C0S kUX + π Σ ΐ'+^π» Sinbt*}·
10. Разложить в ряд Фурье функцию fix) = χ3 в промежутке
(-ι. ί)·
Данная функция является нечетной, поэтому разложение
(2.55) будет содержать только члены с синусами, все ak = 0 (k —
= О, 1, 2, 3, ...). Коэффициенты bk в этом случае можно
определять по формуле
о (* knx
bk = —\f (χ) sin -7— dx
о
98
или
1
bk = 2 j χ3 sin kn xdx (k = 1, 2, 3, .. .)·
Найдем эти коэффициенты:
bk = 2\x*d(-™knx) = -2x*
cos /гшс
kn
ι
= τ— (1 cos kn — 0 cos 0) + -τ— J x2d
s'mknx \ 2(—1)*
kn
kn
+
k2n2
x2 sin knx
ι 12 С
ο (Λπ)« J
л: sin knx dx = (— 1)*+1 -τ f-
fi 19
+ ^2^2- (1 sin kn - 0 sin 0) + η^ρ
II
о
1
\xd
cos fort*
- (— 1)*+»
12
&JT
&3π3
• # cos &π#
12
1
•f-
£π
cos &πχ
&2π2 J &π
о
dx =
^-^Tsr + t-^w-
(- D*+1 ιέ- + та- (J cos ы ~ °cos °> - -ШГ-
= (-1)fe^r(-1 +
ι, np:
oo
s
sin knx
kn
k2n2
Следовательно, при — 1 < χ < 1
00
χ3 = 2
(— Ι)*"»"1 , (— l)fe6
- + ·
k=
00
(fe=l, 2, 3, ...)·
■ sin knx =
4|^ + Н^]з1
sin knx.
ЗАДАЧИ
В промежутке (—π, π) разложить в ряды Фурье следующие
функции:
1. f(x) = 2x+3. 2. /(х) = 2 — Зх.
3. / (#) = cos χ + 2 cos 2x + 3 cos 3*.
4. / (#) = sin x + sin 2л: + sin 3*.
5. /(я) = |*|. 6. /(*) = л: + х2. 7. /(χ) = | sin χ \.
8. /(*) = [ cos *|. 9. / (л;) = sin ax. 10. / (л:) = ch ax.
11. / (jf) = sh ajc. 12. / (χ) = χ cos χ. 13. / (л:) = χ sin л:.
99
14. f(x) =
15. /(x) =
16. /(*) =
17. /(*) =
18. /(*)-
19. f(x) =
*
20. /(*) =
21. /(*)=■
0, если — π < α: <ζ 0,
sin jc, если 0 < χ < π.
2
— χ + 1, если — π < а: <С 0,
о
jc + 1 у если 0 < χ < π.
0, если — π < а: < О,
1, если 0<; χ < —,
— 1, если -^- < χ <; π.
1, если — π < χ < О,
2, если 0 < χ < π,
-н-, если а: = О, χ = — π, χ = л.
О при — π < а: < О,
-j- ла: при 0 < χ < л.
-4- при — π < χ < О,
-^- (пх — 1) при 0 < χ <! л.
-τ- χ при — π <; χ <; О,
-τ- (π — а:) при 0 < χ ^ π.
Η1 +ir)при ~~п<х<°>
при 0 < χ < π.
Показать, что справедливы следующие равенства:
00 00
22.
24.
26.
1 - 1 23
4£2 — 1 2 * *°"
(- 1)*+'
2k— l
π
Τ"
λ? 12
(-Dfe+1 __ 1 м
£2 + 1 2 ! *
οο
25.
j^i & ~ 6 *
Λ=1
π
sh π
100
В промежутке (0, π) разложить в ряды по косинусам
следующие функции:
27. f(x) = x. 28. f(x) = eax. 29. f(x)= sin ax. 30. f(x) = \cosx\.
1 при 0 < χ <; с,
31. /(*)={ η"'" ; ;' 32. /W = iA 2с при0<х<2с.
I 0 при с < χ < π. | о при 2с < χ < π.
1-
33. f(x).
34. f(x).
-^-x при 0<а:<-~,
[-γ(π—χ) при "2~ < χ < π.
cos л: при 0<л:<;-^-,
- cos χ при -у < л: < π.
В промежутке (0, π) разложить в ряды по синусам
следующие функции:
35. / (х) = х. 36. / (х) = х2. 37. / (х) = еах. 38. / (х) = cos ax.
В промежутке (— 1, 1) разложить в ряды Фурье следующие
функютиГ
ί— 1 при — 1 < χ < О,
39. /(*)= in ι 40. fix) = |χ|.
1 v ' [ 1 при 0^х< 1. ' v ' ' '
41. f(x) = x\ 42. / (л:) = а:4.
В промежутке (—/, /) разложить в ряды Фурье следующие
функции:
( 1 при — / < χ < 0, (0 при — I < χ < О,
43· f(*)=(_ 1 при 0<*</. 44-/(*)==ЬприО<*</.
45. /(*) = *. 46. f(x) = ex.
ОТВЕТЫ
оо ор
1. з + 4 V(-l)*+' slnkkx. 2. 2 + 6 V(--l)fesin^. 3. cosx + 2cos2x +
00
+ 3cos3x. 4. sinx + sin2* + sin3x. 5. JL - _L V CQS(2" ~ *> *. 6. -*L +
^ 2 π ^ (2n — l)2 3 ^
л=1
00
■ΣΙ-
Λ=1
_j_4 ^j (— l)fecosfeA: (—ir+1sinifejc
fc2
2k
_2___4_ VI cos 2n л:
7 π π ^J 4n2 —1
л=1
101
8. A +_i_ V ("Ρ"*1 cos 2/ιχ. 9. 2sinj™ V (-Q^sfaife*
π π ^U 4η2 — 1 π ^J fc2 — α2
/ι=1 /г=1
00
10> shan 2sh«i V(_|)fe a cosfex. U. 2sh"» χ
πα π ^^ a2 + k2 π
00 00
x^(_,)*+i_jL_sinb, 12.-^ sin*+ 2^-1)*^sin**.
fc=l fc=2
13. l_J_cos*-2 Υ,(-1)*£^. 14. -L + -Lsinx-lVcos2^.
2 jiiv ' fc2 — 1 π ^ 2 π ^J 4/i2 — 1
00 00
15 8 X^ cos(2n—1)л: j6 2 X^ / ря+l cos(2n — 1)л: j- 3 .
π2 ^ (2/i—l)2 ' π Zji 2n—1 ' 2 "t"
л=1 /z=l
00 00
, 2 ХЧ sin (2/1—1)* 1λ π2 _ 1 X^ cos (2n — 1) χ (— 1)" π sin nx
~^~~n~£i 2iT=T ' ~Ϊ6~ Τ JLil (2n — l)2 + 2n J'
/г=1 /г=1
oo
π2 _ V^ Γ cos(2/z — Ι) χ Ι π 1 \ sin (2/г — 1)*
16 2UY 2(2n — l)2 "" \ 4 ~~ n) 2/1—1 +
19
8n
sin /гх
00 00
20 V Г cos(2/z—l)x _π_ sin (2/г — 1)* 1 21 J_ V
'^L (2n— l)2 + 2 2n—l J' 'π ^ &
л=1 fc=l
22. Указание. Воспользоваться разложением в ряд Фурье функции задачи
14, положить в этом разложении χ = 0. 23. Указание. Воспользоваться
00
разложением — = X sin^ '* (0<χ<π), положить в этом равен-
п—\
π
стве χ = -л~. (Данное разложение можно получить из разложения примера 2,
полагая в последнем 2х вместо χ и вычитая найденное разложение, обе части
которого разделены на 2, из исходного.) 24. Указание. Воспользоваться
разложением в ряд функции / (х) = х2 (см. пример 4) в промежутке (—π, π),
положить в этом разложении χ = 0. 25. У к а з а н и е. В разложении в ряд
Фурье функции f> (χ) = χ2 положить χ = π. 26. У к а з а н и е. Воспользоваться
разложением в ряд Фурье функции f(x)=eax при а= 1 (см. пример 3),
положить в этом равенстве χ
00
π 4 ХГ1 cos (2/ι—1) χ /Λ ^ , ч
= 0. «7.*=.-g— -~2j (2K-D2 &<*<*)·
00
Σ
28. e°* = - ! + -^- V —,o о cos^ ° < * < π ·
απ π j^ k2 + a2 v ^
fc=l
00.
1 + cos απ
— χ
/ι=1
102
X
> , cos ' n '—— (0<Α;<π), где а не является целым числом;
^j а2 — (2п — Ι)2 ν
/ι=1
если α — целое число, то при а = 2т и а = 2т—1: sin2mx =
= .^У ™{2η~1)* .sin(2m-l)^=A|-L_ + 2(2m-l)X
π ^hJ (2m)2 —(2n—Ι)2 π [ a
/ι=1
00 00
>П cos 2nx 1 _!_[_!_ ΛΓ^ f— η""1 cos 2η χ 1
^J (2m -Ι)2 -(2η)2 J' Ж π L2 +^Jl ' 4η2- 1 J'
/ι=1 п=1
*'·^[4-+|]^4· --Н^+ЗЗИ?-)"·"*·]·
fc=l k=\
00 00
VI costo «Д 4 ( 1 , V^ , n*_i cos2fo: \
Zi~~k 3*'—{-2- + 2d{-l) 4*2-l Γ
fe=l · fe=l
2 N. (—1) sin kx. · 36. д;2 = 2 ^ sin kx> гДе V = — —» 62/г-1 =
TT2
33. -4V- —
fc=l
2л 8 37i
e« = A V [1 - (- 1)» О _^_ sin nx
π ^J η2 + α2
2n—1 π(2η— l)3 л ^J ' η2 +1
/ι=1
00
(0<*<π). 38. 1(У[2/|(1ГС08аЯ) sin2nx + Vn-W+cosan)x
K ^ ^ ' π UeJL 4n2 —a2 ^ (2n — l)2 — a2
л=1
Xsin(2/i-l)*|\. 39. 1+JL У sin (2m-1) π* 40.JL-
J J π ^^ 2я — 1 2
n=l
—i-У cos(2n-l)n, 41.А + А,У (-О* созпя*.
π2 ^J (2n—Ι)2 3 ^ π2 ^il η2
/ι=1 /ι=1
00
42 1 4- 8 "УГЛ— 3 \ cos2mrx , / 6 ' _ Л
' 5 π2 JmJ[\ 2η2π2 / 4n2 ^ \ (2n— 1)2π2 /
n=l
X cos (2л-1) я* Ί 43 _1V 1 Sin (2я-1) πχ 44. jL-
(2n— l)2 J n^J 2n~l / 4
/z=l
— 2LV[ 1 2 cos <2"-l> Я.+ (-1}/ϊ sin "** 1.
л=1
00
45.-г. >:>-■' sin^i^. 46. '-■ +!(.'-«-■) >:,'-;;п, х
fc=l /г=1
_ Sin
' + <
/7 = 1
103
Глава 3
ПРИЛОЖЕНИЯ РЯДОВ
Ряды широко используются в приближенных вычислениях.
С помощью рядов с заданной точностью можно вычислять
значения корней, тригонометрических функций, логарифмов чисел,
определенных интегралов. Ряды применяются также при
интегрировании дифференциальных уравнений.
§ 3.1. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ФУНКЦИЙ
Если неизвестное число А разложено в ряд
A = f1an = a1 + a2 + a3 + ... , (3.1)
k=\
где аъ аъ а3,... — некоторые числа,
К = ах + а2 + а3 + . .. + ап, (3.2)
то погрешность при замене А на Ап выражается остатком
ап - αη+χ + ап+2 + ^+з + ·.. . (3.3)
При достаточно большом η эта погрешность станет сколь
угодно малой, так что Ап выразит А с любой заданной точностью.
Если рассматриваемый ряд оказывается знакопеременным
и притом с монотонно убывающими по абсолютной величине
членами, остаток имеет знак своего первого члена и по
абсолютной величине меньше его.
В случае ряда с положительными членами необходимо найти
00
новый ряд *Sbk с большими членами (bk^>ak), который бы легко
суммировался, и в качестве оценки для остатка ап взять величину
остатка β„ этого нового ряда (ап < β^).
Обычно ищется десятичное приближение числа Л, в то время
как члены ряда (3.1) могут и не быть выражены десятичными
дробями. При обращении этих членов в десятичные дроби
округление их служит источником новой погрешности, которую также
следует учесть.
Значения тригонометрических функций можно вычислять,
пользуясь формулами (2.36), (2.37) и другими (см. примеры 9, 10
§ 2.3).
104
Для вычисления натуральных логарифмов чисел применяется
формула
2N+1
ln-
- + ■
IV
1
3
-1-
N
-i In
1
(2N + Ι)3
(N+l)
-4- l ·
+ 5
— lnN =
1
(2N + 1)5
2[ 2N+\ + 3 ' (2iV+l)3 + 5 ' (2W+1)5 + ' ''}> (3*4)
1
которая получается из формулы (2.42) при χ = 9Ν , . ·
Формула (3.3) для погрешности в данном случае принимает
вид
= рГ 1 1 , 1 1 ,
а" \2п+\ (2Ν+\)2η+{ 2п+3 " (2N+\fn^ +
Очевидно,
+ ! ! +
2 1
(3.5)
1
ап<Рп 2/1+1 ' (2УУ+П2" + 1 |1+ (2ЛГ+1)* +
(3.6)
(2Ν + ΐ)2η+1
1 +...
1 (2Ν + Ι)4
или
а» < 2(2п+1) (2N+\fn~{ ЩЛГЙГ' (3,7)
В основе вычисления корней лежит биномиальный ряд (2.39).
Предположим, что нужно вычислить jf А, причем уже известно
приближенное значение а этого корня (по недостатку или по
д
избытку), но требуется улучшить его. Если —w = 1 + *,
где \х\ — небольшая правильная дробь, то можно преобразовать
корень следующим образом:
ΐ~Α = αΥ·4τ = α(1 + χ)" (3.8)
и использовать биномиальный ряд (2.39) при а = —.
ПРИМЕРЫ
1. С точностью до 0,00001 вычислить sin 1.
Замечание. Число а является приближенным значением А
с точностью до 10~~л, если абсолютная погрешность
А = |Л —α К-^г.
В формуле (2.36)
Sin X — X 3| + 5I 7! + 9i · · · + I 4 @k — 1)! "^ ' " '
105
положим х = 1. Тогда
• ι ι 1,1 1,1
8,п1 = 1--зГ + -5Г--7Г+1Г
6 ' 120 5040 ~ 362880 * * * *
Полученный ряд знакочередующийся и удовлетворяет уело
виям признака Лейбница, поэтому, погрешность при замене ег<
суммой первых η членов не превысит первого отброшенного члена
Так как 362880 ^ 0,000003 (< 0,00001), достаточно взять сумм]
первых четырех членов, чтобы получить искомое значение с за
данной точностью. Следовательно,
sinl^l-4 + -r^-w^0'84147·
2. Вычислить sin 20° с точностью до 0,0001.
Чтобы можно было пользоваться формулой (2.36), т. е. разло
жением функции f(x) = unx в степенной ряд, необходимо выра
зить значение аргумента в радианной мере. Получаем χ =
0,3491. Подставляя значение χ в формулу (2.36)
π
= ~9~
находим
. _л_ _ _л 1_ /_π_\3 _1^_ (_л_\ь 1_ /jrx
Sln 9 ~ 9 3! V 9 / + 5! { 9 / 7! [ 9
^ 9! \ 9 / ^ * * * ^ (2k — 1)! \ 9 / "Г · · · ·
Так как
^-(^-)5< 0,00004 «0,0001),
то, ограничиваясь первыми двумя членами, получаем
sin^- ~ JE J_ (-|-j3^ 0,3491 - 0,0070 = 0,3421.
3. С точностью до 0,000001 вычислить In 2.
Воспользуемся формулой (3.4). Положив в ней N = I,
получим
1° 2 = 2 [ "з" + з-з3 ~*~ 5-35 + 7-з7 + · · · +
+ ! +
Формула для оценки погрешности (3.7) при N = 1
принимает вид
*"< 2(2/1+1) * з2*-1 ' Ь2 4 (2/1+1) β2"-1 *
106
В соответствии с условием задачи выберем η так, чтобы
остаток был меньше 0,000001, т. е. ап < 0,000001. Возьмем η
таким, чтобы
4(2n-f 1)32"-1 ЮОООО *
Последнее неравенство выполняется начиная с η = 6, так как
при этом значении η
1 1 1 <тппкйп= 0,000001.
4(2-6+ 1)326_3 413-311 9211644 ^ 1000 000
Следовательно, в формуле (3.4) можно ограничиться шестью
слагаемыми, чтобы получить значение 1#п2 с заданной точностью:
In 2 ^ 2 Γ-L + —L- 4- -JL- + —*- + -L_ + 1 1 -
iii^ ^ ^ 3 -г 3 Зз -у- 5 35 -|- ? 3? -г 9>39 -Г п.311 J —
2,2, , 2
' i" Q. ОЗ !"··· +
з ^ з-з3 ^ · · · ^ ц.з" ·
Вычислим значение каждого слагаемого (с одним лишним
знаком):
\ да 0,6666667; -^з- — 0,0246914; -^- да 0,0016461;
0,0001306; ^V ~ 0,0000113; ,Λη ж 0,0000010.
? 3? ν,,ν^ν,^ν^, g 39 ~~V,v,v,*,V**„, п зп
Итак,
In 2 ж 0,6931471.
4. Вычислить |/17 с точностью до 0,0001.
Преобразование (3.8) в данном случае принимает вид
\_
16"'
]/17 = /16 + 1 = ]/l6 (l + -^j = 4(l + -π
Воспользуемся биномиальным рядом (2.39). Полагая в нем
1 " 1
= -Tg-, α = -γ9 получаем
"^ 1-2-3 \ 16/ "^ 12.34 А
т. е.
Ί+ — i2=i + _J ! + '
1 i 1 β / х ' 9 . 1 fi 93.1Α2 \
16 / ' 2-16 2М62 ' 24163 27164
107
Полученный ряд (если не принимать во внимание первый
член) знакочередующийся и удовлетворяет условиям признака
Лейбница. Погрешность при вычислении его суммы не превышает
первого отброшенного члена. Так как
1 * <-uL·-- ο,οοοι,
24·163 66 536 ^ 10 000
достаточно взять сумму первых трех членов ряда, чтобы получить
искомое значение корня с заданной точностью:
УП^4{\+^- 2^W")~ 4>1230·
з^ ·
5. Вычислить у 124 с точностью до 0,0001.
Применим преобразование, аналогичное преобразованию (3.8):
V А
ат
где —г- = (1 + у), и воспользуемся биномиальным рядом, положив
а = . Для данного случая
1
γ/ 125 \ '124/
V ~Ϊ2<
124
-5
/ 1 N 1 \ ~3~/ \ ~3~ / /' 1 \2
U I l Q ΙΟ/Ι Τ Q2 1CM2 *··/ U Q 1 O/l "T
3-124 ~ 3M242 '") 3-124 ~ 32·1242 ·" '
Так как полученный ряд является рядом лейбницевского
типа и
Ш 5 5 <-т^ = 0,0(Ю1,
32-1242 9-124-62 69 192 ^ 10 000
с заданной точностью находим
5
/124 ^ 5 - -^ » 5,0000 - 0,0134 = 4,9866.
ЗАДАЧИ
С точностью до 0,001 вычислить значения функций:
1. ^37- 2. V69. 3. ]Л5. 4. уТ. 5. £'60. 6. νΠΌ20.
108
С точностью до 0,0001 вычислить значения функций:
7. sin 11°. 8. cos20°. 9. sin 15°. 10. cos25°. 11. sec 10\
12. tg5°. 13. arctgO.l. 14. V e. 15. In 1,2. 16. In 1,5.
С точностью до 0,000001 вычислить значения функций:
17. 1пЗ. 18. In 5. 19. In 6. 20. In 10.
ОТВЕТЫ
1.2,059. 2.8,307. 3.3,873. 4.2,080. 5.3,915. 6.1,999. 7.0,1908.
Указание. Выразить аргумент в радианной мере, χ = 0,1920. 8.0,9397.
9. 0,2588. 10. 0,9063. 11. 1,0154. 12. 0,0875. Указание. Воспользоваться
формулой примера 10 § 2.3. 13. 0,0997. Указание. Применить формулу
(2.27). 14. 1,6487. Указание. Применить формулу (2.35), положить в ней
χ = -о-. 15.0,1823. Указание. Воспользоваться формулой (2.38).
16.0,4055. 17.1,098612. 18.1,609438. 19.1,791759. 20.2,302585.
§ 3.2. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
С ПОМОЩЬЮ РЯДОВ
Многие определенные интегралы не могут быть вычислены
с помощью формулы Ньютона — Лейбница, так как ее
применение связано с нахождением первообразной, последняя же не
всегда выражается в элементарных функциях. Нередко
первообразная является или достаточно сложной функцией, или
нахождение ее связано со значительными трудностями. В этих случаях
целесообразно приближенное вычисление определенного интеграла.
Если подынтегральная функция разлагается в степенной ряд,
а пределы интегрирования принадлежат области сходимости этого
ряда, соответствующий определенный интеграл можно вычислить
с заданной точностью.
ПРИМЕРЫ
_1_
4 .
1. Вычислить интеграл f ^ψ~άχ с точностью до 0,00001.
о
Соответствующий неопределенный интеграл J dx не
может быть выражен в элементарных функциях, т. е. представляет
собой «неберущийся интеграл». Применить формулу Ньютона —
Лейбница здесь нельзя. Вычислим интеграл приближенно. Разделив
почленно ряд для sin л: на х, получим
X3 X5
sin* _ *~~ЗГ +~5Г~ —··' _ 1 _ J^_ *4 χβ
χ ~ χ ~ [ 3! "^ 5! 7! + " " " "
109
Интегрируя этот ряд почленно (это возможно, так как
пределы интегрирования принадлежат интервалу сходимости данного
ряда), получаем
Г sin χ ι Γ ι л х2 .
3-3!
1
1
4 χ5
ο +ΊΓ5Γ
1
5!
J_
4
7!
dx =
о 7-7!
J 1
45
1
4 3-3! 43 ' 5-5! 4* 7-7! 47 ' + · · · ·
Ограничиваясь первыми двумя членами этого ряда, находим
j ^ψ- dx^-\ 3 3| 43 да 0,25000 - 0,00087 - 0,24913.
о
Погрешность не превзойдет первого отброшенного члена
ι ι 1.1
5·5!·45
5·120·1024
2
614 400
<
100 000 "
2. Вычислить интеграл J \/ 1 + x3dx с точностью до 0,001.
о
Подынтегральная функция разлагается в степенной ряд
VT
(Ι + χΫ =1+·
l^+ir-
128
(|Х|<1).
Интегрируя этот ряд почленно в промежутке
_1_
2
j )/T+~>?dx = (x + -!j-
16
0,
л7
56
+
5а;13
160
= _L + _L._L
2^8 24
Поскольку
56-27
_2_ _[_
56 ' 27
1 1
160 ' 2Х°
1664
5
1
56-128
7168
+ ·
_1_
1664 ' 213
< 0,001,
находим
ПО
для вычисления данного интеграла с указанной точностью
достаточно взять два первых члена полученного ряда, т. е.
/|Л+д^х«^+-[1г«0>508.
о
3. Найти длину дуги эллипса
*2 и2
iL- + JL-=l {а>Ь),
лежащей в первой четверти.
Рассмотрим параметрические уравнения эллипса:
x = as'm((, у = Ъcos φ.
Очевидно, точка описывает дугу эллипса, лежащую в первой
четверти, когда φ меняется от 0 до -о-. Так как dx = a cos φ d<p,
dy = — b sin φ<ίφ, формула для дифференциала дуги dl —
= Ydx2 + dy2 принимает вид
dl = j/я2 cos2 φ + 62 sin2 φ dtp = Υ α2 (1 — sin2 φ) -f- b2 sin2 φ <ίφ ~
= Υ a2 — (a2 — b2) sin2 φ d(p.
Интегрируя равенство dl = Υ α2 — (α2 — 62) sin2 φ άφ по
промежутку
О —
• 2
, находим
I = f Yа2 — (а2 — b2) sin2 φ dq>.
Итак, вычисление длины дуги эллипса свелось к нахождению
так называемого эллиптического интеграла. В элементарных
функциях эллиптический интеграл не выражается. Вычислим его
приближенно, предварительно преобразовав подынтегральную функцию
и разложив ее в степенной ряд. Поскольку
Υ а2 - (а2 - b2) sin2 φ = у а21 1 - ( а* q2 b* ) sin2 φ
ι
Г. / а2 — Ь2 \ . п 1
= а
L \ w /
1
fl2fl262 )sin2(p =αίΐ —-у- ε2 sin2 φ — y^ ε4 sin4 φ —
jg- ε6 sin6 φ — .
Υ а2 — б2
где ε = ~ эксцентриситет эллипса,
111
то
2 / ν 2
Г/ ε2 ε4 ε6 \ л
α(1 2"Sin2(P g~sin4<P jg- sin6 φ — . . .) ίίφ = α J dtp —
ί. ί. Δ
/#ε4 Γ Αεβ /*
sin2 φ dtp g— J sin4cpd(p j^-J sin6cpd(p. .. .
αε*
2 _ . _ _
ooo
С помощью метода интегрирования по частям можно показать,
что
/^"φ^^.^-ΊΓ (π= 1.2.3,...).
т. е.
2
ьз
J sin2 φί/φ = -х- · -5-, J sin4 φ^φ
π
2 2 ' J ~"ж γ~τ — 2-4 2
J sin6 ψάφ
1·3·5 π
2·4·6
ο
Таким образом,
π αε2 π αε4 3π αε6 5π
/ = α-
2 2 4 8 16 16 32
πα (* ε2 3ε4 5εβ
·)·
2 \ 4 64 256
Замечание. Длина всего эллипса определяется формулой
/ о (л ε2 3ε4 5ε6 \ /0 ЛЧ
/ = 2πα(1--ϊ й gg- - ... J. (3.9)
В частном случае, при а = b = R, получаем формулу для
длины окружности / = 2nR.
4. Вычислить длину эллипса -|g- + -fg- = 1·
Найдем предварительно эксцентриситет эллипса и
воспользуемся формулой (3.9). Так как а = 5, 6 = 4, с = 3, ε = 3/s> no
указанной формуле получаем
,_„..[, _4(4)·-έ-(4·)'—·]·
112
Ограничиваясь первыми тремя членами ряда, находим
ЗАДАЧИ
С точностью до 0,0001 вычислить интегралы:
1 · Х 4 1 1
1. Г ir~dx. 2. t^Ldx. 3.fsmx*dx. 4. fcosx2dx.
δ о ° Ь
JL _L _L
2 3 6
dx η С ι/1—;—л j - [' dx
о о ' '
ι ι ι
8
4 ^ 2 ^ 8
j f ** . 9. f "* . 10. fl/b=T2djc.
/ 3/TT^ J V25 + * J
о о
2
П./г—Лс. \2. j-™*&L-dx.
0 0
Вычислить длины эллипсов (с точностью до 0,01):
13. Jj- + ^L = 1. м. -£- + Jf-= 1. 15. 6х2+16*/2 = 96.
16. 5х2 + 9г/2 = 45.
ОТВЕТЫ
1.0,2491. 2.0,4931. 3.0,2339. 4.0,9045. 5.0,4926. 6.0,3337. 7.0,1664
8.0,2497. 9.0,0998. 10.0,1247. 11.0,7468. 12.0,4872. 13.26,38. 14.7,68.
15. 20,86. 16. 16,58.
§ 3.3 ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С ПОМОЩЬЮ РЯДОВ
Интегрирование многих дифференциальных уравнений не
приводится к квадратурам, а их решения не выражаются в
элементарных функциях. Решения некоторых из этих уравнений могут
быть представлены в виде степенных рядов, сходящихся в
определенных интервалах. В таких случаях ряд, являющийся
решением дифференциального уравнения, можно найти или способом
неопределенных коэффициентов, или способом, основанным на
применении ряда Тейлора (Маклорена).
из
Способ неопределенных коэффициентов особенно удобен в
применении к линейным уравнениям, т. е. уравнениям вида
Уп + Pi (х) Уп~х + р2 (х) Уп~2 + · · · + Pn-i (х) У* +
+ Рл(*)У = /М. (3.10)
и состоит в следующем. Если все коэффициенты его pk(x)(k = 1,
2, 3, ... , η) и свободный член f(x) разлагаются в ряды по
степеням (л: — а), сходящиеся в некотором интервале (a — h, a + h)>
искомое решение у = у(х) также представляется в виде
степенного ряда
У(х) = с0 + с1(х — а) + с2(х — а)2 + .. . + сп(х — а)п + ... , (3.11)
который сходится в том же интервале. Подставляя в уравнение
(3.10) функцию (3.11) и ее производные, приравниваем
коэффициенты при одинаковых степенях (х — а). Из полученных при этом
уравнений (и начальных условий, если они заданы) находим
коэффициенты с0, cl9 c2, с3, ... .
Способ, основанный на применении ряда Тейлора (Маклорена),.
заключается в последовательном дифференцировании данного
дифференциального уравнения. Это дает возможность найти значения
производных, входящих в выражения для коэффициентов ряда,,
являющегося решением уравнения, т. е. ряда
У(х) = У(а) + У' (а)(х ~а) + ^- (х - af + ... +
+ -^(х-аУ+... . (3.12)
Замечание 1. Если для данного дифференциального
уравнения я-го порядка заданы начальные условия: у = у0, у' = г/0, ... ,
уп-\ = уп—\ ПрИ χ = а, в ряде (3.11) нужно положить:
- _А _ w
со — Уо> с1 Уо> с2 2! * * * ' * Сп п\ > * * * *
ПРИМЕРЫ
1. Найти с помощью ряда решение дифференциального
уравнения у' — у = 0, удовлетворяющее условию у = 1 при χ = 0.
В данном случае а = 0; решение ищем в виде ряда
У = Со + сгх + с2х2 + с3х3 + с4х4 + . .. + спхп + ... . (1)
Находим производную функции (1):
у' = сг + 2с2х + Зс3х2 + 4с4х3 + · · · + пспхп~{ + ... . (2}
114
Подставляя разложения (1) и (2) в данное уравнение,
получаем
с0 + сгх + с2х2 + с3х3 + с4х4 + ·. . — (сг + 2с2х + Зс3х2 +
+ 4с^х3 +...) = О
или
с0 + схх + с2х2 + с3х3 + с4*4 -h ... =
= сг + 2с2х + Зс3х2 + Ас^х3 + ... .
Сравнив коэффициенты при одинаковых степенях χ в
последнем равенстве, получим систему уравнений:
х°
X1
х2·
Xs
X*
хп
С0 — Οχ
С1 — бС^
С% = оСз
с3 = 4с4
с4 — ос5
сп = ("+ !)c«+i
(3)
Используя начальное условие у(0) = 1, из равенства (1)
находим с0= 1. Решая систему (3), получаем:
i 1
1» с2 — ~2~» сз —
1
1
2-3 '
СА =
1
2-3-4'
2-3-4-5
2-3 ... η
Следовательно, искомое решение представляется следующим
рядом:
У=1+-
+
2!
+
л3
3!
+ .·.+
х"
+ .
(4)
Этот ряд сходится при всех х.
Замечание 2. Непосредственное интегрирование данного
уравнения дает решение у = ех, которое разлагается в ряд (4).
2. Найти общее решение уравнения у" = —у в виде
степенного ряда.
Пусть искомое решение является сходящимся степенным рядом
у = с0 + с1х+ с2х2 + с3х3 + с4*4 + съхъ + cQx6 + с7х7 + ... ,
где с0, cl9 c2, с3, ...—постоянные, подлежащие определению.
Находим производные функции у:
у' = Cl + 2с2х + Зс3х2 + 4c4jc3 + 5с5х*'+ 6с6х5 + 7c7xQ + ...;
у" = 2с2 + 2-Зс3х + ЗЛс^х2 + 4-5с5*3 + 5-6с6х4 + 6-7с7х5 +
115
Подставляя выражения для у и у" в уравнение у'1 =—у,
получаем
2с2 + 2·Зс3х + 3-4с4*2 + 4·5с5х3 + 5-6с6*4 + 6·7с7хь + . .. =
— Cq — С±Х СъХ — С$Х — С^Х — С§Х
Приравняв коэффициенты при одинаковых степенях χ в обеих
частях последнего уравнения, получим систему:
Решая ее, находим:
Со =
Сз =
с* =
2с2 =
2-Зс3 =
3-4с4 =
4-5cs =
5 · 6с6 =
6-7с7 =
ψ.
С2 __
— с0
—Сг
— с.
— с3
— Ci
— Со
Со
3-4
2-3-4
4!
Са = —
5-6
л? ' · · · ' c*k \ ч Qk)\ "г · · · »
6!
2-3
_£l_ _
3! ' Съ ~
сз __ _£ι_ г __ j£i_
4-5 5! ' 7 7!
C2* + I = (-l)*
(2Л+1)! '
Следовательно, общее решение определяется формулой
Y2k 1
+ *[*-4ι+ΊΓ-ΤΓ+-+(-1^1
(2k)\
„24-1
(2k— 1)!
+
...].
где с0, cx — произвольные постоянные.
Замечание 3. Непосредственное интегрирование данного
дифференциального уравнения, как уравнения второго порядка
с постоянными коэффициентами, приводит к общему решению:
у = сх cos χ + с2 sin χ. Это решение совпадает с решением,
полученным способом неопределенных коэффициентов. (Чтобы
убедиться в этом, необходимо подставить в функцию y = c1cosx +
+ c2s'mx разложения в ряды для shut, cos* и ввести
обозначения сх = Со, с2 = сг.)
3. Найти в виде степенного ряда частное решение уравнения
у" — 2у'-\-у = ех, удовлетворяющее начальным условиям у = О,
у' = 1 при χ = 0, т. е. у(0) = 0, у' (0) == 1.
116
Пусть искомое решение представляется сходящимся
степенным рядом
у (х) = с0 + схх + с2х2 + с3х3 + с4*4 + съхъ + ... + спхп +
Дважды дифференцируя этот ряд в его интервале
сходимости, получаем:
у' (х) = сг + 2с2х + Зс3х2 + 4с4*3 + Ьсъх* + ... + ncnxn~{ + ...;
у" (х) = 2с2 + 2- Зс3х + 3 · 4с4*2 + 4 · Ъсъх3 +
+ ... + п(п-1)спх«-2+... .
При χ = 0 имеем #(0) = с09 у' (0) = сг. Принимая во
внимание начальные условия у(0) = 0, у' (0) = 1, находим два первых
коэффициента разложения для у(х): с0 = 0, сх = 1. Подставив
в данное дифференциальное уравнение выражения для у(х),
У* (*). #"(*) и разложение в ряд функции в*, получим
2с2 + 2-Зс3* + 3-4с4*2 + 4-5с5*3 + . · · + п(п— \)спхп~2 +
+ ...—2(1 + 2с2х + Зс3х2 + 4с4*3 + 5с5х* +
+ ... + /гсЛхя—! + ...) + χ + с2*2 + с^3 + с4л:4 +
1
л:3
1! ~"~ 2! "^ 3! ·" 4! ~^
х5
5!
+ съхь + ... + слх* + ..
или
(2с2 - 2) + (2-Зс3 - Ас2 + 1) χ + (3- 4с4 - 2-Зс3 + с2) х2 +
+ (4-5с5 - 2-4с4 + с3) х3 + (5-6с6 - 2 5с5 + с4) х4 + .. .
+ .
+ ...
х?
+ 1! + 2! + 3! + 4! + *
п\
+
Приравнивая коэффициенты при одинаковых степенях χ
в обеих частях этого равенства, получаем систему уравнений для
определения коэффициентов с2, с3у ...:
2с2 — 2 = 1
2 · Зс3 — 4с2 + 1 1
■II
3 · 4с4 — 2 · Зс3 + с2
1
2!
4.5с5 — 2.4с4 + £з = "зГ
5-6с6 — 2-5с5 + с4 = —
Решая эту систему, находим:
_ 3
с2 — ~2~> сз
1.
1
и* ~~ 12 ' 5 ~~ {
Таким образом, имеем частное решение:
У
x + ±x* + x* + -Lx* + -L*>
хъ+
117
Замечание 4. Решая это уравнение как линейное
неоднородное · с постоянными коэффициентами, получаем у = хех +
+ -к- х2е*- Подставив в это равенство разложение в ряд
функции е\ найдем
ί, = χ+(ΐ+4-)χ»+(4- + 17ϊΓ)'" +
1" \~W "I" 0.91 Iх + ~ΊΓ "Γ 9.QI * +
\ 3! ' 2-2! ) ~ ' \ 4! ' 2-3!
J_
1)! ' 2 (/ι —2)!
Li'1 η' '" ом . * ~τ"
т. е. тот же результат.
4. Найти первые пять членов разложения в ряд решения
уравнения у' = х2 + У2, удовлетворяющего условию у = —
при χ = 0.
Искомое решение запишем в виде ряда Маклорена:
+ -^L^+...+^b^+.... (i)
Найдем выражения для трех последующих производных
дифференцируя исходное уравнение:
-у" = 2х + 2уу\ у™ = 2 + 2у,г + 2уу\ у™ = 4*/У +
+ 2у'у" + 2yyf" = бу'у" + 2ууг".
Вычислим значения этих производных при χ = 0, принимая
во внимание начальное условие у (0) = -х-. Имеем: у1 (0) = 0 +
+ -^=4; ^(0) = 2·0+2·4-·-1-=-Γ; УН1 = 2 + 2· -jL +
4-2·-!- _L = Ji. „iv__L+JL+i9- = ii
^ 2 ' 4 8 ' * 4 ^ 8 ^ 8 4 -
Подставляя эти значения в формулу (1), получаем
5. С помощью степенного ряда проинтегрировать уравнение
(1 — х) у" + ху' — у = х2 — 2х + 2.
Пусть ί/ = с0 + сгх + с2х2 + с3*3 н- с4*4 + ^о*5 + · · · · Тогда
У' = ci + 2c2# + Зс3*2 + 4c4#3 + Ьсъх* + ... ;
//' - 2с2 + 2-Зс3* + 3-4с4*2 + 45с5х3 + . .. .
118
Подставляя выражения для у, у\ у" в данное уравнение,
получаем
(1 — х) (2с2 + 23с3х + ЗАс±х2 + 4-5с^3 + ...) +
+ χ(θχ + 2с2х + Зс3х2 + 4c4*3 + 5c5*4 +···) —
— (с0 + схх + с2х2 + с3х3 + с^ + съхъ + ...)
2х + 2
или
(2с2 - с0) + (2-Зс3 — 2с2 +с1 — с1)х + (3-4с4 - 2 Зс3 +
+ 2с2 — с2) х2 -f (4-5с5 — 3-4с4 + Зс3 — с3) х3 + (5-6с6 —
— 4 · 5с3 + 4с4 — с4) *4 + . .. = х2 — 2х + 2.
Так как # — решение уравнения, последнее равенство
выполняется тождественно. Коэффициенты при одинаковых степенях χ
в обеих частях равенства равны между собой:
2с2-
2-Зсо
с0 = 2
— 2с« = —2
3 4с± — 2-Зс3 + с2 = 1
4-5с5 — 3-4с4 + 2с3 = 0
5 6с6 — 4 · Ъсъ + Зс4 = О
(п+ 1) (п+2)сп+2~п(п+ l)cn+i + (n—l)cn = 0 J
Решая эту систему, находим:
_2 + с0 _
с2 — о —
4!
^ 2
Со
120
Сз
^0
5! '
сь со
~ 6 "" 3! '
Сб 720 ~~
Q
24
Таким образом, все коэффициенты начиная с с2 выражены
через коэффициент с0, который остается произвольным; остается
произвольным и сх (этот коэффициент не входит в полученную
систему). Следовательно, искомое решение представляется рядом
У
со + сгх + [ 1 + -f J χ2 + ^ χ3 + -bf- χ* +
^ 5! ^ 6! * ^ * * * '
сходящимся при всех х.
Это решение является общим:
*3
ί/ = ^ο 1 + -П-+1Г+1Г + ··· +(с1- со)* + **
3!
119
или
у = Οχβ* + С2х + #2,
где Сх = С0, с2 = Сх — с0 — произвольные постоянные.
Замечание 5. Коэффициенты ряда можно найти и другим
способом. Действительно, из выражений для у, у\ tj' при χ = О
имеем:
у(0) = с0, ί/'(0) = ^, у»(0) = 2с2.
Из исходного уравнения при χ = О находим новое выражение
для у" (0): у" (0) -1/(0) = 2, т. е. ί/"(0) = 2 + г/(0) = 2 + с0.
Сравнивая два выражения для г/"(0), получаем
2с2 = 2 + с0 или с2 = 1 + -тр.
Далее, при л: = 0
ί/'»(0) = 2-ЗСз, ί/ιν (0) = 2-3-4с4, г/V (О) -
= 2-3-4-5с5 i/<")(0) = n!c„, .... (1)
(Эти значения получены из выражений для ут(х), у™(х), ... ,
г/<") (х), ... , которые здесь не были написаны.)
Дифференцируя исходное уравнение, получаем
— у» + (1 - х)ут + г/1 + ху» -yi = 2x-2
или
(1-χ)ί/"·-ι/» + χί/" = 2χ-2,
т. е.
(1-х) (г/1"-у») = 2*-2. (2)
Продифференцируем несколько раз уравнение (2):
- (У111 - Уи) + (1 - х) (yw ~ Ут) = 2 или (1 - χ) (у™ -
-ί/«>) = 2 + (ί/"1-ί/«); (3)
- (У]У ~ Ут) + (l-x)(yv- у™) = (y]V - Ут) или (1 -
-χ)(ί/ν-ί/ιν) = 2(ζ/'ν-ί/ΐΗ); (4)
- (ί/ν ~ Уп) + (1 ~ х) (ί/νι - ί/ν) = 2 (ί/ν - ί/Ιν) или (1 -
■-x)(yvl-yv) = 3Utv-ylv). (5)
Для n-й производной уравнения (2)
(.1 - χ) (у"+3 - ι/"+2) = η (г/"+2 - */"+>) (η = 2, 3, 4, ...). (6)
Из уравнений (2) — (5) при χ — 0 получаем:
ут -у» = — 2, ί/'ν - ί/'" = (ί/'« - ί/") + 2, у* - yiv =
= 2 (y'v - j/Ш), i/vi _ yv = 3 (yv _ y.V). (7)
120
Так как у11 (0) = 2 + с0, из первого уравнения системы (7)
следует, что уш (0) = с0. Далее, из первых двух уравнений
системы находим, что ί/Ιν — ут = 0, поэтому остальные два
перепишутся так:
yv-y™ = 0, yv*-yv = 0. (8)
Принимая во внимание соотношения (8) и уравнение (6),
заключаем, что все производные начиная с третьей равны:
ут ==yiv = yw = uu9 = у(п) = .. . = Со.
Из системы (1) находим:
3 ~~ 3! ' 4 ~~ 4! ' 5 5! ' * ' " ' п ~ п\ ' * * * '
Следовательно,
У = с0 + с1х+(\ + ^)х*+^х*+^х*+^х*+....
6. Найти первые шесть членов разложения в степенной ряд
решения дифференциального уравнения 27х3ут — Юу = 0, удов-
1 2
летворяющего условиям: у= 1, у1 = —, уп = д- при х= 1.
Поскольку jc0 = 1, решение будем искать в виде ряда по
степеням (х—~ 1):
Первые три коэффициента определяются начальными
условиями:
</(1) = 1, </'(!) = 4' ί/"(1) = Г·
При χ = 1 из уравнения 27χ3ί/ΠΙ — Юу = 0 находим:
27.1».уш _ ю-1 = 0, т. е. у'" (1) = ^ = -£.
Чтобы найти значения t/IV(0) и t/v(0), предварительно
продифференцируем исходное уравнение:
27-ЗхУ" + 27*VV - ΙΟί/1 = 0;
27.3-2хуш + 2.27·3ΛΓ2ί/,ν + 27χ3ι/ν — 10ι/" = 0.
Из первого уравнения при χ = 1 получаем
27·3·12·^-+27·ΐνν—10-^ = 0,
121
откуда
27ί,ιν = -I- - 30, ί/ΐν = __«!_ T. e. y.v(1) = _-g.
Второе уравнение дает возможность найти yv(l):
27·3·2·1~ + 2·27·3·12(-|γ-) + 27·13ί/ν- 1θ( —-§-) = 0,
откуда
27^ = 160-60-^- = ^, т. е. f/v(l) = ^.
Следовательно,
ί/(1)= 1, f/!(l) = 4-· |/"(1) -р-. 0Ш(1) =
10 τν/14 80 ν/14 880
= "зг. У1У (!) = - зг» ί/ν (!) = ιτ·
Подставляя значения функции и ее производных в
разложение у(х), получаем шесть членов искомого решения:
</«= 1 + -1- <*- D+ (- 4г)ж1'- »* +
+ #-ά-ί*-4·+(-ϊ)>-')· + ¥·1(«-1)·+·...
т. е.
«/(*)= ι + 4- (χ-ΐ)-^(χ-Ψ + -§г(х- i)s -
10 99
-зНх-1)4 + !и*-1)5+...
Замечание 6. Это решение можно получить и с помощью
метода неопределенных коэффициентов, полагая у = с0 + сх (х —
— 1) + с2 (х — I)2 + с3 (х — I)3 + . .. и замечая, что х3 = 1 +
+ 3 (х — 1) + 3 (х — I)2 + (л: — I)3. Подставляя эти разложения
в данное уравнение и приравнивая коэффициенты при одинаковых
степенях (л: — 1), получаем систему, из которой определяются
коэффициенты ск (k = 0, 1, 2, 3, .. .)-
ЗАДАЧИ
Найти с помощью рядов решения дифференциальных
уравнений, удовлетворяющие при χ = 0 указанным условиям:
1. у1 — 2у = 0, у= 1. 2. ylcosx + у sin χ = 1, у = — 1.
3. у11 + 4у = 0, у = 1, у1 = 0. 4. у» - 2у] + у = 0, у = 0, у1 = 1.
122
5. уп(\ + 2х)-2у*-у(3 + 2х) = 0, у = О, у'=1. 6. уп + ху =
= 0, у=1, ί/ί-Ι.
7. лгу» + 2е/' + Л/ = 0, [ι/=1, (/' = 0. 8. ху" + 2yl + ху = О,
у=\, у' = 0.
9. у» + ху1 + У = 0, 0 = 0, (/'=1. 10. £/" + x2t/= 0, у=\,
У'=1.
Найти с помощью рядов решения дифференциальных
уравнений, удовлетворяющие данным начальным условиям; указать
области сходимости полученных рядов:
11. (I ~ х) у + у — χ — I = 0, у = 0 при χ = 0.
12. у' -f у = л: + 1, у = 1 при χ = 0.
13. у'χ In л: — у = 0, у = 0 при л: = 1.
14. у' -\- 2ху = 2*е-*2, у = 0 при χ = 0.
15. ху" + у' + ху = 0, у = 1, у' = 0 при χ = 0.
16. (sin л: — cos χ) у" — 2у' sin χ + (cos л: + sin χ) у = 0, у = 1, у' = 2
при χ = 0.
17. ху" + у = 0, у = 0, у' — 1 при * = 0.
18. (cos χ + sin л;) у" — 2у' cos* + (cos χ — sin x) у = 0, у = 2, #' = 1
при л: = 0.
С помощью степенных рядов проинтегрировать следующие
дифференциальные уравнения:
19. (sin χ + cos χ) у" + 2 sin ху' + (sin χ — cos χ) у = 0.
20. (cos χ — sin л:) у" + 2 cos у' + (sin χ + cos χ) у = 0.
21. (1 + χ2) у" + 2*у' - б*2 + 2.
22. (χ2 — 2х + 2) у" — *V + 2ху' — 2у - 0.
23. у" + ху = 0. 24. у" + ах2у = 0. 25. ху" + 2у' + х2у = 0.
26. х(1 — х)у* — (1 - 2х)у' + (1 - 3* + х2)у = — х2(1 - х)2.
Найти несколько первых членов разложения в степенной ряд
решений дифференциальных уравнений при указанных начальных
условиях:
27. у' = у2 — х2у у = 0 при χ = 0.
28. у' = х2 + у2, у = -1. при χ = 0.
29. cos2 л:-у' + cos*-у — sin л: = 1, у -= 1 при χ = 0.
30. у' = у2 + х3, у = 4~ при χ = 0.
31. у" = 2уу', у = 0, у' = I при л: = 0.
32. 4xY+y = 0, у = 1, У' = ~^ при * = 1.
33. ху' = у2 — Зу + 4х2 + 2, у = 2 при л: - 0.
123
34. xy' = x2y* — y-\-\,y=l при χ = 0.
35. (1— x)y" + y = 0, y = y' = 1 прих = 0.
36. у" + xy' - (2x2 +l)y=l, y = y'=l при л; = 0.
ОТВЕТЫ
1. у = 1 + 2х + 2л? + γ- * + -§- * + -^*+ ... +-£■*+ ... (1/ =
я2 я3 я4 х5 „ ,, х"
= *2Х)· 2^ = -1+^ + -2Γ--3Γ--¥· + -5Γ+···+(-1)+ -ы" +
22 24 26
+ ... (ί/ = sin χ — cos *). 3. у = 1 — -gf x2 + ~ξ|- л;4 — -gj- л;6 +
28 χ2 а? л;4 a£
+ "gf *8 — · · · (y = cos 2x). 4. i/ = χ + -η- + ~2p + "зр + -ξρ +
x^ #3 #4 x^
+ · · · + (n_i)i + · ■ · (0 = **л")· 5. i/ = A: + A:2+-2r + -3Jr+-4J- +
xn x3 2x* 4 2-5
+ ..· + („_!)! + .... 6· У=1+х-Ж--Ж + -оГ xQ + -WS-
4-7 2 2-5 2-5-8
--9f *·+ .... 7. ί/= ι — "4Г ^ + 7Γ *6-~~ϊοΓ*9 + ···· 8· #=1~
*2 л;4 λ'6 л:3 л:5 л;7
~~1Й~ + ~5!~—7Г + 9· у==х~~3~+ 1-3.5 "" 1 -3-5-7 +
+ . . . + i -1 ί + . . . . 10. у = 1 — ό-Τ + о Л 7 Q —
1 -3-5... (2^— 1) * \ 3*4^ 3-4-7-8
χ12 (—\)kx*k \ / д;5
~~ 3-4-7-8-11 -12 -г··· -г 3-4-7-8 ... (4£—1) 4£ ^ '' ') "^ ^л ~~ 4-5
, *9 *13 , (-ΐ)ν^1
"г α. .ς.я.о л. к. я. о. 19.1 я "г · ■ ·"+" . г о л Λί. ,Λί. , ιχ— ~t~
...).
4·5·8·9 4·5·8·9·12·13 τ ■ ■ ·τ 4·5·8·9 ... 4*(4ft+l)
11. </ = *+£2 + ^3+^4+··· + (k-l)k + ■■■ (-»<*<!)· 12. ί/ =
#2 дЗ χ4 д-5 (д 1)2
= 1 + "2Г— ~ЗГ+ ~4!~~~"5Г+ ··· (|*1<<*)· 13. ί/ = л: — 1 — ^ +
(а;—I)3 (* — I)4 fe, , (χ— \)k
+ 3 " 4 + ··· +(-!)+ fe + --.(0<*<2). 14,y=
_ _^ί_ *6 х8 а:10 а:12 л+1 x2k
-х2- v + 21 —- з! +4! " 5! +■··+(—О (Л—1)1 +
д-2 д-4 д;6
+ ... (|*|<оо). 15. ί/= 1 — -ψ- +22Τ42— 22·42·62 + ·■· (\χ\<°°Υ
2χ χ2 χ* 2хь χβ χ8 2χ9
16. ί/=ι + ιτ + -^ + -4Γ + -5Γ+'6Γ + -8Γ + "9Γ+··· (Ι*Ι<°°). 0 =
λ:2 ( α:3 α:4 λ:5
= ^ + sinA;. 17. y = χ— ^jj22 + (21)23 ~~ (3!)24 + (4Vf5 "~
χ Xs 2χ4 χ5 χΊ 2jc8
-... (Ι χ |< 00). 18. г/ = 2+ -ТГ + -1Г + ТГ+ Ы- + -7Г + -8Г +
124
+ ... (I χ |< оо), у = е* + cos χ. 19. у = с1 + (съ — с1)х + с1-^-—(с1 +
у8 у4 %Ь j^6 j^7
+ ^2). ~sT+ci "5Г + (с2 — ^ι)"5Γ + ci "gf '— (Ci + c2) ~fr + 20. у =
χ2 χ3 χ* хъ
= ci + c2 — cix + (ci — c2) ~~2\~ — ci ~зР + (ci + c2) 4j~~ — ci 5j + (ci —
y6 j^7 yS / j^5 j^7
~~ ca) "6Г ~~ Cl ТГ + 21# ^ = °2 + Cl* + ** ~~ Cl Τ + Cl ("5" "" ~T~ +
a;9 \ /
+ -9- + · · · I. У = с1 arctg x + c2 + x2. 22. у = cQ + (c0 + ^) a; + I c2 +
c0 \ / x3 x* а;5 \
+ —21—) *2 + co ("зГ +"4Г + ~5Г+···)' # = *«*"* + ClX + C2* * 23# У =
1 x3 1-4 1-4-7 \ / 2 o 2-5
= c° (1~-"зГ+~бГ xQ~ 9! *9 + · · ή + W ^ — —ξΓ Xs -\--γΓ x* ~
2·5·8 \ _ Ι αχ* α2χ8 α3χ12
— ϊό! *9+ ---,· 24. y-co^l— 34 + 3.4-7-8 — 3·4.7-8-11-12 +
α"*4* \ / _α^ α2*9 .
+ ··· +(— Х)П 3-4.7.8 ... (4/2—1)4/2 + ···) +^ι (* — 4-5 + 4·5·8·9~~
α*χ™ апхАп+х \ _
~" 4·5.8.9·12.13 +···+(— Χ> 4·5·8·9 ... 4η(4/2+1) + · · ·| 25· 0 ~
с0 / л? Ь4 1-4-7 \ / 2 2-5
= TL(1—3Γ+-6Γ^6--9Τ^+···)+^ ,1—4Γ^+~ΤΓ-^6-
— —Г7Г.— α:9 + .·.). Указание. Полагая ху — и, получаем и" -{-хи = 0,
т. е. уравнение того же вида, что и в задаче 23. 26. у = сх — 1 + (сх — 1) χ -\-
+ (-ΐ- + τ)*6+···· 27'У = -^хЪ + ^гх1-^ёбГх11+
13 1 1 1 19
+ ц.21.63.15 χ15-'" ' 28· y = —+ — * + — x2 + -Wx3 +
11 х2 5 / π \
+ ~96~А;4 + ··* * 29. ί/= 1 + —+ -24~*4+ ··· 1*1<—· Замеча-
111 1
н и е. Решение: . у = sec χ. 30. ί/ = -g- + -5- Jt + -g- x2 + -т~- а;3 +
9 Й « 1 o 2 17 62
+ 32"^ + ... · 31. y = x+-^-xS + _д5 + _-х7 + __ *, + ... (| я ι <
<-yJ. Решение: y = igx. 32. j/= 1 + —^—- v 8 ; + v ^ ' -
b(x— l)4 7 (a;— l)5
— j2g + —256 ~~ Решение: у = γ χ. 33. у = 2 + 4α;2 +
128 34-128 / , π \
а:4 + -[5~ α:6 + 315 * + '·· Ν<τί' Решение: y = 2xig2x +
125
1 2 17 62 / π \
+ 2. 34. ί/=1+ — *2 + 15Х*+-ШХ° + Ш5ХЙ+ ■■■ (l* К "г")·
tg χ χ2 χ3 χ* 7
Решение: у = —γ. 35. у = 1 + χ — —γ- — —^- — -g- — -у^- л;5 — ... .
36. у=\+х + -¥х2 + -^х* + 1йх* + -4хх«+ ....
Глава 4
РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
§ 4. 1. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексным числом называется выражение вида а -\- ib, где
а и b — действительные числа, / = Υ — 1 — мнимая единица.
Число а называется действительной, число b — мнимой частью
комплексного числа. Обозначая а + ib через с, будем писать:
a = R(c), b = I(c),
где R — начальная буква латинского слова real is (действительный);
/ — начальная буква слова imaginarias (мнимый).
Комплексные числа сх = ах + ibx, с2 = а2-\- ib2 считаются
равными тогда и только тогда, когда порознь равны их
действительные и мнимые части, т. е. ах = а2, 6Х = Ь2.
Каждое комплексное число с = а + /6 может быть изображено
на плоскости Ол:{/ точкой Μ (а, 6), координатами которой являются
действительная и мнимая части данного числа
(рис. 4.1). В этом случае рассматриваемую
плоскость называют плоскостью комплексной
переменной ζ или просто комплексной
плоскостью.
Действительные числа а = а + / -0
изображаются точками на оси Ох, а чисто мнимые
числа /6 = 0 + ib — точками на оси Оу, при
f ~Q Зг этом первую ось называют действительной, вто-
' рую — мнимой.
Рис. 4.1 Сохраняя за абсциссой и ординатой точки
привычные обозначения χ и у, будем записывать
комплексные числа в виде ζ = χ + iy.
Сложение, вычитание, умножение и деление комплексных чисел
ζχ = χχ _|_ iyu z2 = x2 -f iy2 производятся по формулам:
Zl + z2 = (*х + iy±) + (x2 + iy2) = (χχ + *8) + i {yx + y2)\ (4.1)
Zi ~ ^2 = (*i + Wi) - (*« + ^2) = (*i — *2) + I (У1 — i/2); (4.2)
126
ΖιΖ2 - (*ι + iyx) (*a + 4/2) - (*i*2 — У1У2) + i (Х1У2 + *2i/i); (4.3)
Jl_ _ *1 + 4/2 _ *1*2 + j/li/2 , · *2*/l — Х1У2 (Л л\
z2 - ь + iy* 4 + £ ±l xl + yl ^Λ)
(последнее в предположении, что (х2 + iy2) Φ 0, т. е. Х2 + у\ Φ 0).
Для комплексных чисел соблюдаются все обычные свойства
действий, не связанные с понятиями «больше» и «меньше» (эти
понятия для комплексных чисел не устанавливаются).
Если ζ = χ + iy, то
ζη = (χ + iyf = xn + пх»~Чу + ~{\~X) xn'2(iyf +
+ ... + №n, (4.5)
где η — натуральное число.
В полученном выражении надо заменить степени / их
значениями:
/2 = _ lf /з = _ΐ9 μ = lf /5 = i9 uuu ^
и в общем случае
•tAk = 19 Цк+l = l9 iAk+2 = _ 1, /4^+3 = _/.
Полярные координаты ρ, φ точки Μ (см. рис. 4.1) плоскости Оху,
служащей изображением комплексного числа ζ = χ -f- iy,
называются соответственно модулем (или абсолютной величиной)
и аргументом комплексного числа z\ для них вводятся следующие
обозначения:
р = \г\, φ = Argz,
причем угол φ определен с точностью до слагаемого 2kn (k — целое
число). То из значений аргумента ζ, которое удовлетворяет
неравенствам — π < φ <π, называется главным значением аргумента
и обозначается argz. Сохраняя обозначение φ только для главного
значения аргумента, получаем
Arg z = arg z + 2kn = φ + 2kn. (4.6)
Соотношения между модулем и аргументом комплексного числа
г = х+ iy и его вещественной и мнимой частями определяются
формулами:
# = pcoscp, у = ρ sin φ, (4.7)
поэтому
Ρ
cos φ
sin φ
127
1*1
χ
_у_
I*
V χ2 + f
V x2 + i
Ι ν** + <
(4.8)
Заменяя χ и у в записи комплексного числа ζ = х + iy их
выражениями через ρ и φ, получаем так называемую
тригонометрическую форму комплексного числа:
ζ = ρ (cos φ + i sin φ). (4.9)
Два комплексных числа ζ = χ + iy к ζ = χ — iyf у которых
вещественные части равны, а мнимые отличаются знаком,
называются сопряженными. Для сопряженных
^ комплексных чисел (рис. 4.2)
.«м? Ι Ζι | = \z21, arg zx = — arg z2.
У'У \ Если комплексные числа заданы в три-
Ь^Л У/ гонометрической форме:
1 " Ζχ = ρχ (cos φχ + / sin φχ);
. , w % = p2 (cos φ2 + i sin φ2),
Рис 42 то умножение и деление определяются
следующими правилами:
ZiZ2 = P1P2 [cos (φ + φ2]) + i sin (φχ + φ2)] (4.10)
(модуль произведения равен произведению модулей множителей,
а аргумент произведения — сумме аргументов множителей);
Т~ = ΊΓ [cos (Φι " Φ») + 'sin (Φι ~" Φ«)1 (4·**)
^2 Κ2
(модуль частного равен частному модулей делимого и делителя,
а аргумент частного — разности аргументов делимого и делителя).
Если ζ = ρ (cos φ -f i'sincp), возведение в степень и извлечение
корня л-й степени (п — целое положительное число)
осуществляются по формулам:
zn _ р/г (cos Πφ _j_ / sin Αίφ); (4.12)
V'z^Vp (cos-ЗЦ^ + ism i±^j (4.13)
(£ = 0, 1, 2, ..., л-1).
В частности, из формулы (4.12) получаем
(cos φ + i sin φ)Λ = cos шр + / sin ηφ.
Формула эта называется формулой My αβρά.
ПРИМЕРЫ
1. Найти сумму, разность, произведение и частное двух
комплексных чисел: ζχ = 5 + 2/, ζ2 = 3 — 4/.
128
По формулам (4.1) —(4.4) соответственно находим:
Zi + z2 = (5 + 2/) + (3 - 4/) = (5 + 3) +"(2 — 4)/ = 8 — 2/;
Ζι - Za = (5 + 20 - (3 - 40 = (5 - 3) + (2 - ( - 4)] i = 2 + 6/;
ZiZ2 = (5 + 20 (3 - 40 = [5-3 - 2( - 4)] +
+ [5(-4) + 2-31/ = 23— 14/;
*2
5 + 2t ^ (5 + 20 (3 + 4t) _ (15 — 8) + (20+6) i
3 — 4/
(3-40(3 + 40
16
"" 25 + 25 U
2. На комплексной плоскости построить
точку, изображающую число ζ = 3 — 3/.
Найти модуль и аргумент этого числа,
представить число в тригонометрической форме.
Для данного числа вещественная часть
χ = 3, а мнимая у = — 3, поэтому ему
отвечает точка Μ (3, — 3). Выбрав систему
прямоугольных координат, построим точку Μ
[рис. 4.3).
По формулам (4.8) находим модуль и
аргумент данного комплексного числа:
У
12 3 4
' ' I '
-Л
Рис. 4.3
X
p = |z| = |/^ + ^=[/32 + (-3)a
cos φ = —
Ύ Ρ
3 J/ 2
у —з
sinq) = — = =
Ύ Ρ 3^2
= ^9 + 9= |/ 18 = 3^2;
1 /"2
V 2 " 2 * _
1 /"2 .
К "2 2 '
Argz= — -J- + 2fot (fe = 0, 1, 2, ...)·
— -χ-. В тригонометрической
Главное значение аргумента φ
форме это число имеет вид
3 — 3/- 312
cos
■ —) + iesin ( -
г/]·
3. Найти ζ5, где 2 = 2 + /.
Применяя формулу (4.5), находим
(2 + О5 - 25 + 5-24 + 10-28? + 10-22/3 + 5-2/4 + /5.
Подставляя в это выражение значения степеней /:
1, Ρ
■ι, г
1, ? = i,
получаем - ■ '
(2 + О5 = 32 + 80/ - 80 - 40/ + 10 + ί = —;38 + 41/.
4. Выразить cos4cp и sin4<p через cos φ и sin φ.
129
Воспользуемся формулой Муавра в случае η = 4:
(cos φ + i sin φ)4 = cos 4φ + i sin 4φ.
Преобразуем левую часть этого равенства:
(cos φ + i sin φ)4 = cos4 φ + 4 cos3 φ / sin φ + 6 cos2 φ (/ sin φ)2 +■
+ 4 cos φ (/ sin φ)3 + (/ sin φ)4 = cos4 φ + 4/ sin φ cos3 φ +
+ 6/2 cos2 φ sin2 φ + 4/3 cos φ sin3 φ + /4 sin4 φ =
— (cos4 φ — 6 cos2 φ sin2 φ + sin4 φ) + i (4 sin φ cos3 φ —
— 4 cos φ sin3 φ).
Следовательно,
(cos4 φ — 6 cos2 φ sin2 φ + sin4 φ) + / (4 cos3 φ sin φ —
— 4 cos φ sin3 φ) = cos 4φ + i sin 4φ.
Так как комплексные числа равны тогда и только тогда, когда
равны соответственно их действительные и мнимые части, то
cos 4φ = cos4 φ — 6 cos2 φ sin2 φ + sin4 φ;
sin 4φ = 4 cos3 φ sin φ — 4 cos φ sin3 φ.
5. Найти все значения -\ί — 1 -J- /.
Представим данное число в тригонометрической форме:
- 1 + i = V 2 (cos 135° + i sin 135°)
и применим формулу (4.13) в случае η = 3:
γ — 1 + ι = у V 2 (cos j f ι sin ~ J (k = 0, 1, 2).
Следовательно, получаем три значения данного корня:
з
6, -
/ —l + i = Y 2 (cos 45° + i sin 45°);
V — 1 + i = γ"2 (cos 165° + /sin 165°);
/ — 1 + / = j/2 (cos 285° + i sin 285°).
6. Решить уравнение г6 — 1 = 0.
Задача сводится к нахождению всех шести значений корня
6-й степени из единицы г=у 1.
Представляя число 1 = 1 + 0/ в тригонометрической форме
1 = 1 (cosO+i'sinO)
и применяя формулу (4.13), находим
ζ = * Τ = Vl~+W= ^I(cos0 + /sin0) = ^l(cos °\2Ы +
+ /sin °+62fejl) (k = 0, 1, 2, 3, 4, 5).
130
Следовательно,
zt = 1 (cos 0 + i sin 0) = 1;
z4 = 1 (cos π + ι sin π) = — 1 + Ю = — 1;
ζ*=1 (cos—+ *sin -5-] = —ι—;
ζ6 = 1 (^cos — + ί sin —J = -^ ι —2~.
ЗАДАЧИ
Найти сумму, разность, произведение и частное следующих
комплексных чисел:
1. гг = 1 + 2/, z2 = 2 + 3/. 2. ζχ = 2 — /, ζ2 = 3 — 4/.
3. ζχ = 4 + 3/, ζ2 = 5 — 2/. 4. ζχ = 1 — /, ζ2 = 1 + *·
Произвести указанные действия над данными комплексными
числами:
5. -^-, Zl = 2 + /, z2 = 2 - /, 28 = 4 - 3/.
6. uZL&f Zl = 3 + 4/, z2 = 2 + 4/, z8 = 5 — 6/.
гз
7. —^—, Ζχ = 10 — 8/, ζ2 = 6 + 5/, ζ3 = 4 + 5/.
г2 "Г г3
8. -77-, Ζι = 1 + /, ζ2 = УЗ + /, ζ3 = 1 + i |/3.
Ζ2Ζ3
Привести к тригонометрической форме следующие
комплексные числа:
9. 1) 1, 2) /, 3)-1, 4) /.
10.5-5/. 11. 3 + 3/. 12. -2-2/. 13. 1— i γЪ.
14. [/3 — /. 15. 1 + ι|/*3. 16. 1 + sin α —/cos α.
Вычислить следующие выражения:
17. (2- З/)3. 18. (3 + 2/)4. 19. (1 - 2/)5. 20. (1 + /)6.
Найти все значения указанных корней:
21. УТ. 22. | 3 - 4/. 23. ]/ - 11 + 60/. 24. уТ
25. 1/8+6/. 26. у"^64. 27. у 64. 28. ^7.
131
Где лежат точки, изображающие комплексные числа, для
которых:
29. φ = 45°. 30. ρ = 3. 31. R(x) > 0. 32. Ι (χ) < 0.
Решить следующие уравнения:
33. 1) х2 + (5 — 2ί)*+5(1 — ϊ) = 0; 2) х2 — (3 — 2ι) χ + (5 - 5/) = 0.
34. 1) χ2 + (1 — 2ί) χ — 2/ = 0; 2) (2 + i) χ2 — (5 — i)x + (2 - 2ί) = 0.
35· (4йг)я - т^Ш- 36· d <*+^+<* - ^ - °;
2) χ3 + 8 = ο; 3) jc4 — 81 = 0; 4) χ6 + 64 = 0.
Выразить через cos φ и sin φ следующие функции:
37. sin 3φ, cos 3φ. 38. sin 5φ, cos 5φ.
С помощью формулы Муавра вычислить:
39. (cos 9° + i sin 9°)10. 40. (cos 4° + i sin 4°)45.
41. ( V 32+ ' J''. 42. (cos 10° +/sin 10°)27.
Найти геометрическое место точек, изображающих числа г,
удовлетворяющие неравенствам:
43. | ζ | < 3. 44. | ζ + i | < 2. 45. | ζ — 11 < 4. 46. ] ζ + 1 - i1< 3.
47. | ζ — 2 + i I > 5.
48. Доказать тождество \ζλ + ζ2 \2 + \ζί — ζ2|2=2 (| ζλ |2+Ы)2.
49. При каких условиях модуль суммы двух комплексных
чисел равен: а) сумме модулей слагаемых; б) разности модулей
слагаемых?
50. Доказать теорему: Если в результате конечного числа
рациональных действий (т. е. сложения, вычитания, умножения
и деления) над числами ζχ, 22, ... , ζη получается число и, то
в результате тех же действий над сопряженными числами ζ[,
22, ... , ζη получается число и, сопряженное с и.
ОТВЕТЫ
2 Q ι
1. ζ1 + ζ2 = 3 + 5ι\ ζ1 — ζ2 = — \ — ίί zz2 = — 4 + 7i, -γ- = -^ — -γ^-ί.
ζ 9 1
2. ζ1 + ζ2 = 5 — 5/, ζχ — ζ2 = — 1 +3/, ζίζ2 = 2— 11/, -γ- = -g- + -g- /.
3. гх + ζ2 = 9 + /, z1 — z2 = —1+5/, г1г2 = 26 + 7/, -j- = -^ + -g^- /.
Л *i 4 3 5 6
4. ζχ + 22 = 2, ζχ — z2 = — 2ι, z^ = 2, — = — /. 5. -j- + — L 6. gj + gy /.
11 /π
7. 0,1— 0,9ί. 8. -j- — -j- /. 9. 1) 1 = I(cos0 + /sin0), 2) /=l cosy +
132
+ ί sin-g-J, 3)— 1 = 1 (cos л + /sinji), 4) — / = 1 cosi — у) + ί sin | — ~2~)l·
10. 5/2"jcosi—^J + tsini—-^-jl Π. 3 ]/2 icos -|- + / sin -j-).
,-/ 5 5 \ / 2π 2ns ( 11 π
12. 2 К 2 cos —j-π + /sin—τ- лЛ 13. 2 cos —5— + /sin у I. 14. 2 cos-g- +
11π\ „ / π . π \ Λ /π α \ Γ /α
+ / sin —g— 1. 15. 2 cos-у + t siny ). 16. 2 cos -τ- — -ψ I cos у —
— y)+/sin(y — yj . 17. —46 — 9/. 18. —119+120/. 19. 41 + 38/.
20. —8/. 21. + 7- · 22' =(2—20· 23. ±(5 + 6/). 24.—/, ±± ^
V 2 2
25. ±(3 + t). 26. 2(cos<p + isinq>), φχ = 30°, φ2 = 90°, φ3=150°, φ4 = 210°,
φ5 = 270°, φ6 = 330°. 27. 2 (cos φ+ /sin φ), φχ = 0, φ2 = 60°, φ3 = 120°,
φ4 = 180\ φ5 = 240°, φ& = 300°. 28. cos 22°30' + / sin 22°30' = 0,9239 +
+ 0,3827/, cos 112°30' + / sin 112°30' = — 0,3827 + 0,9239/, cos 202°30' +
+ / sin 202°30' = — 0,9239 — 0,3827/, cos 292°30' + i sin 292°30' = 0,3827 —
— 0,9239t. 29. На биссектрисе первого координатного угла. 30. На окружности
радиуса R = 3 с центром в начале координат. 31. Справа от оси Оу. 32. Книзу
от оси Ох. 33. 1) χ1 = — 2 + ί, х2= — 3 + /; 2)^ = 2 + /, х2 = 1 — 3/.
4 — 2/ j α + kn
34. 1)^ = 2/, х2 = — 1; 2) х1 = 1 — /, х2 = —ε—. 35. xk = tg —-— (k =
2^+ 1
= 0, 1, 2, ... , η — 1). 36. 1) xk =ctg 2n n(k = 0, 1, ... , /2—1).
37. sin 3φ = 3 cos2 φ sin φ — sin3 φ, cos 3φ = cos3 φ — 3 cos φ sin2 φ. 38. sin 5φ =
= 5 sin φ cos4 φ — 10 sin3 φ cos2 φ + sin5 φ, cos 5φ = cos5 φ — 10 cos3 φ sin2 φ +
+ 5 cos φ sin4 φ. 39. /. 40. —1. 41. 1. 42. —/. 43. Множество точек, лежащих
внутри круга радиуса R = 3 с центром в начале координат. 44. Множество
точек, лежащих внутри круга радиуса R = 2 с центром в точке Λί(0, —1)
и на его границе. 45. Множество точек, лежащих внутри круга радиуса R = 4
с центром в точке Λί(0, 1) и на его границе. 46. Множество точек, лежащих
внутри круга радиуса R = 3 с центром в точке Μ (—1, 1). 47. Множество
точек, лежащих вне круга радиуса R = 5 с центром в точке Л1(2, —1).
48. Указание. Положить ζχ = х± + iy^, ζ2 = х2 + iy2. Тождество выражает
известную теорему геометрии: Сумма квадратов диагоналей равна сумме
квадратов его сторон. 49. а) если разность аргументов этих чисел равна 2&π (k —
целое число); б) если разность аргументов этих чисел равна π + 2/гл (/г—целое
число),
§ 4. 2. ЧИСЛОВЫЕ РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
Пусть дана последовательность комплексных чисел
Ζ\9 ^2, Ζ$, . . . , Ζη> . . . ,
где гп =хп + iyn {η - 1, 2, 3, ...).
Число с = а + ib называется пределом последовательности
гъ z2, z3, ··· » zn> ··· » если Для Л1°бого сколь угодно малого
числа ε > 0 существует такой номер Ν, что для всех значений ζη
с номерами п> N выполняется неравенство \ζη — с\ < ε.
133
©бозначения предела последовательности:
lim zn — с, zn->c при η -> ос.
η—>αο
Необходимое и достаточное условие существования предела
последовательности комплексных чисел: число с = α + ib является
пределом последовательности комплексных чисел
Χι + ьУи *2 + *>Уъ *з + Ч/з, · · · > ** + ^, . . ·
тогда и только тогда, когда
lim хп = a, lim #л = 6.
п~>оо /ζ—»оо
Рассмотрим последовательность комплексных чисел
соь ω2, ω3, ... , ω„,
где ω„ - ип + wn (n = 1, 2, 3, .. .).
Числовым рядом с комплексными членами называется
составленное из этих чисел выражение
оо
ωι + ω2 + ω3+ . . . + ω„ + ... = 2«V (4.14)
/г=1
Сумма
Sn = ωχ + ω2 + ω3 + . . . + ω„ (4.15)
называется п-й частичной суммой ряда с комплексными членами.
Ряд с комплексными членами называется сходящимся, если
последовательность его частичных сумм имеет предел:
S = lim Sn. (4.16)
η —>оо
Число S называется суммой ряда.
Необходимым и достаточным условием сходимости ряда
с комплексными членами
00 00
2ω»==2("»+/ο») (4·17)
к сумме S = S' + /S" является сходимость в отдельности рядов
из действительных и мнимых частей его членов и выполнение
равенств:
%n = S', 2i»„ = S". (4.18)
/г=1 /г= 1
Ряд (4.17) сходится, если сходится ряд, составленный из
модулей его членов, т. е. ряд
2к1 = 2К«Гь* <4Л9>
л=1 л = 1
134
Ряд (4.17) в этом случае называется абсолютно сходящимся.
Для рядов с комплексными членами справедливы следующие
признаки сходимости:
1) если существует сходящийся ряд с положительными чле-
00
нами 2j ап такой, что | ωη \ <; ап для всех /г, ряд с комплексными
00
членами ^ со„ сходится, причем абсолютно;
2) если
00
υ/ι+1 '
/, при / < 1 ряд ^ ωη абсолютно сходится
п=\
00
(признак Даламбера);
3) если У] ωη | -> /, при / < 1 ряд ^ ωη абсолютно сходится
(признак Коши).
ПРИМЕРЫ
1. Выяснить, сходится или расходится ряд 2л \~W "^ *~3/*~K
л=1
Рассмотрим два ряда с вещественными членами:
00 00
Каждый из этих рядов является геометрической прогрессией:
1
первый — со знаменателем qx = -^-, второй — со знаменателем
<?2 = -3-; оба ряда сходятся (так как |<7ι| < 1, |<7г|< 1)» причем
00 00
V-L = i У-*---!-
п=\ п=\
т. е.
и 1
S'=~P = 1. S" =
1-9ι Λ· \-q2 2·
Следовательно, данный ряд с комплексными членами также
сходится и его сумма
S = S' + iS"= 1 + -i-i.
2. Показать, что ряд ^ \- Jn—ч расходится.
/1=1
135
Рассмотрим ряды, составленные из действительных и мнимых
частей данного ряда;
00 00
vij_ у (-1)"+1
—J η ' jLA 2* '
η=\ /ι = 1
Первый из этих рядов является гармоническим рядом,
который, как известно, расходится. Таким образом, исходный ряд
является расходящимся.
Замечание. Второй ряд сходится (как геометрическая
прогрессия со знаменателем q = =-], но для сходимости
исходного ряда с комплексными членами этого недостаточно.
00
о г, 'V sin n + * cos η
3. Выяснить, сходится или расходится ряд ^ —$ .
/2=1
Составим ряд из модулей членов данного ряда. Так как
sin η + i cos n Ι 1
sin η + i cos η , ,
ω„ = ^ и ω„ =
η*
получим ряд
00
Σ
п=\
Этот ряд сходится (ряд Дирихле 2 ~^т ПРИ Р>1)> поэтому
/1=1
рассматриваемый ряд сходится абсолютно.
00
4. Показать, что ряд γ к—— расходится.
Преобразуем общий член данного ряда:
— 1 _ Vn — i = Vn — i =
ω"~ Vn + i ~ {Yn+i){Vn-i)~ "-ι*
_ Vn — i _ Vn i
~ n-fl ~~ n+1 η + 1
Следовательно,
00 00
ΓΙ / V η i
—4 ι η + i ~ 2u \
I rt+i —J \ n+1 n+1
л=1 л=1
136
Рассматриваемый ряд расходится, так как расходящимся
является ряд
00
1
Σ
п + 1
п=\
00 / П
5. Выяснить, сходится или расходится ряд^ (—ί-ί-i .
/z=l
Так как 1 + *· = 1^2 (cos-^-+ / sin -χ-), общий член в
тригонометрической форме
fcosJL + isin — |
\ 4 4 / 1 / л/2 . . . πη \
ω*= WW ~ = ~^~ \ ~ +1 sin ~';
l<oJ = '
2я/2 "
00
Следовательно, ряд ^ | ω„ | сходится (как геометрическая
прогрессия), поэтому сходится и данный ряд.
ЗАДАЧИ
Выяснить, сходятся или расходятся следующие ряды с
комплексными членами:
оо .. . . _ _Р?_ „
\я+1
1# JLI 2п + 3* V 2· ^ [_ 5я
/2=1 /ί=1
00 00
yl-^ + iJL·)
_ νι / cos η2 , . sin η α\ ^ Γ 2" ι / 1 1
η 1 Χ / « 1
Π=\ λ ' /2=1
οο , __ „ οο
п. У>{п~Уп +ϊ "~*η) 12· Σ ( "+1 + *
~, \ η2 - η ^1 η*—η)' £4 \ 2η + 4 ^ '
3η — 1 \
^ \ η2 — η ' η3— η )' ;£" \ 2η+ 4 ' 2η+ 1 /'
137
л=1
/ι=1 L J
JK у η (2 + 0"
ίο. ^ 2"
η=1
1β.
19.
00
.4.2
π n(2i-\)n
2d зл
00 .
ОТВЕТЫ
ηη
n\(e — i)n ·
00 1
1 7· 2d (η+ i) Vn ·
л=1
00 .„
1. Сходится. 2. Сходится. 3. Расходится. 4. Расходится. 5. Сходится. 6.
Сходится. 7. Сходится. 8. Сходится. 9. Сходится. 10. Расходится. 11. Расходится
12. Расходится. 13. Сходится абсолютно. 14. Сходится. 15. Сходится. 16. Схо-
дится абсолютно. 17. Сходится абсолютно. 18. Расходится. 19. Сходится
абсолютно. 20. Сходится условно.
§ 4.3. РЯДЫ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ.
СТЕПЕННЫЕ РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ
Рассмотрим две комплексные переменные величины: ζ = χ +
+ iy и ω = и + /ϋ, где χ, у, и, υ — действительные переменные.
Если каждому значению переменной ζ из некоторого
множества соответствует одно значение переменной ω, то говорят, чте
ω есть функция от ζ:
ω = / (ζ) = и (х, у) + iv {x, у). (4.20)
Здесь и (х, у) и υ (χ, у) — действительные функции от χ и у,
так что задание одной функции от одной комплексной
переменной означает задание двух действительных функции от двух
действительных переменных.
Комплексным рядом функций называется ряд вида
00
2 "„(*) = "ι (z) + u2(z)+...+un(z) + ..., (4.21)
члены которого являются функциями комплексной переменной.
Значения 2, при которых ряд (4.21) сходится, называются
точками сходимости. Множество всех точек сходимости
называется областью сходимости этого ряда. Для каждого числа ζ
из области сходимости справедливо соотношение
limS„(2) = S(«), (4.22)
η—►»
где Sn (z) — частичная сумма ряда (4.21);
S (г) — его сумма.
138
Степенным рядом с комплексными членами называется ряд
вида
где
2а» (* - χο)η>
(4.23)
п=0
ζ — комплексная переменная;
20 — данное комплексное число;
an{n = Q, 1, 2, ...) —данные комплексные числа, называемые
коэффициентами.
В частном случае, при z0 = 0, получаем комплексный
степенной ряд, расположенный по степеням ζ:
op
2 W* = Яо + ^ζ1 + α222 + .. . + ajP + · · ·
(4.24)
л=0
Для каждого степенного ряда (4.23) существует круг радиуса R
с центром в точке М0 (т. е. |z —z0|</?), внутри которого
данный ряд сходится, а вне его расходится (т. е. при \г — г0\ > R).
Этот круг называется кругом сходимости (рис. 4.4). Его радиус
называется радиусом сходимости степенного ряда (R = оо, если
степенной ряд сходится во всей плоскости; R = 0, если он
сходится лишь в центре круга, в точке М0). Во всех точках внутри
круга сходимости степенной ряд абсолютно сходится.
X
Рис. 4.4
Рис. 4.5
Рис. 4.6
При отыскании радиуса сходимости степенного ряда могут
применяться признаки сходимости Даламбера и Коши. В
частности, радиус сходимости степенного ряда (4.23) можно
вычислить по формуле
R= lim
Я"+1
(4.25)
Показательная и тригонометрические функции комплексной
переменной определяются равенствами:
е*= 1
ζ
ТГ
2!
_
3!
+ .·.
ИГ
+ ... ;
(4.26)
139
sin г
г-1Г + 1Г-1г + - + (-1),(Ь)Г + ···; (4·27>
ζ4 г» , , , 1Ч„ ζ*"
C0SZ=1-ir + Tr--ir+--- + (-1)nw + ··· (4·28)
Ряды, стоящие в правых частях формул (4.26) — (4.28),
сходятся для всех комплексных ζ (R = сю).
Связь между этими функциями устанавливает формула Эйлера:
ё2 = cos ζ + i sin z. (4.29)
Из приведенных определений и формулы Эйлера следует:
cos г -^ , sin z = 2ϊ ; (4.30)
eziez2 _ ezi+z2^ ez+2r.i _ ^ вг _ ^(cos ί/ + /sin г/); (4.31)
г - геЧ (4.32)
Замечания: 1. Вторая из формул (4.31) означает, что
функция ez имеет период 2π/.
2. Формула (4.32) представляет комплексное число ζ = χ + iy
в показательной форме (г — модуль, φ—аргумент).
3. Формулу e~iz = cos z — i sin ζ и формулу (4.30) также
называют формулами Эйлера.
ПРИМЕРЫ
00
1. Найти область сходимости ряда ^ζ4 и его сумму.
/ι=0
Составим ряд из модулей членов данного ряда
00
2Н"= 1 + ϊζ| + |ζ|2+... + |ζ|"+...
/ι=0
Полученный ряд является рядом с действительными членами
и представляет собой геометрическую прогрессию. Следовательно,
этот ряд сходится, когда \ζ\< 1, т. е. в круге радиуса R = 1
с центром в начале координат.
Таким образом, исходный ряд также сходится в круге \ζ\ < 1,
который и является его областью сходимости (рис. 4.5).
Так как частичная сумма ряда выражается формулой
/2=0
и ζη -> 0 при п-> oc(\z\ < 1, zn = |z|"(cos η φ + / sin η φ)), то сумма
ряда
S(z) = UmStt(z) = T±T.
/!-► 00 * c
140
Итак, получено разложение
%п (\г\<1).
п=0
оо
2. Найти область сходимости ряда ^—„- и его сумму.
/1=0
Рассмотрим ряд, составленный из модулей членов данного
ряда:
1+-
μι
и
2 Ч^ ι у |3 I
И3
77Г + ··
Этот ряд является геометрической прогрессией со
знаменателем q = —:—р. Он сходится при |ί/|<1, т. е. при —>—г- < 1,
или при |ζ | > 1.
Итак, областью сходимости является совокупность точек,
лежащих вне круга радиуса R = 1 (рис. 4.6).
Сумма данного ряда
S(2)
то
1 —ζ'
/г=0
3. Найти радиус сходимости степенного ряда 2и η\{ζ — ί)η
Для данного ряда имеем:
ап = /г!, ап+\ = (п + 1)!
По формуле (4.25)
R= lim
Π—>ΌΟ
"я+1
= lim
/l—> 00
η!
(η+1)!
= lim —г-z-
η~>οο "+1
0.
Ряд сходится в единственной точке ζ0 = ι.
00
4. Найти радиус сходимости степенного ряда ^ -^-.
Так как
1
/1=0
1
2п
А/г-Н
о/Ж
# = lim
я—> оо
u/i+l
= lim
/г—>оо
2 л ' 2/г~^"^
2.
Итак, радиус сходимости данного ряда R = 2.
00
5. Найти область сходимости ряда 1 + ^ —г
/i-fl
141
Поскольку
а =
п\
йп+\
1
(я + 1)1 '
то
β„+1 η\ ' (п+1)!
л + 1
Я- lim
Л—юо
u/i+l
lim (η -f 1) = оо.
Данный ряд сходится на всей комплексной плоскости.
6. Найти сумму cos χ + cos 2x + cos Зх + ... -f cos я*.
Используя первую из формул (4.30), получаем
cos kx =-s~ {ekxi + e~kxi\
поэтому
S (χ) = COS * + COS 2X + . . . + COS ШГ = ^COS kx ■■
*=1
2*" +Σ
e-J
/ы
Суммируя геометрические прогрессии, находим
Λη+\)χΙ
SM=i[4
+
e—xi __ e—(n+l)xt
1-е
—xi
Разделив почленно первую дробь на е , вторую — на е
получим
а:/
ад = -
xl (/i-hl) '
■у- */ - («+т) */
е — г
откуда
S(x) =
J_
J Я
2
(*+i-) jf/ - (я+γ·) xi
J_
2t
^'Y/_e-T
e — e
2i
sin(n+4)·
2 sin —ψ χ
2 *
142
Итак,
sin (η + _L) χ
2j cos kx =
Λ=ι 2sin-o-A:
7. Пусть ζ = re1'* = r(cosφ + /sinφ). Из разложения
00
_ = 2^ (Ι2Ι < 1) получить следующие:
00
1 — г cos φ VJ „
π—о . τ- = Z^ r cos n Φ»
1— 2 r cos φ + г2 *** т
Ύ /ι=ο
оо
г sin φ V „ ·
—-.—=- = Λ Гл Sin Π φ.
COS φ -+- Γ2 ^" τ
1 — 2r cos φ ,
Данное разложение получено в примере 1. Подставив в него
выражение ζ = г (cos φ + i sin φ), найдем
1
2 гП cos η φ + *2 ^ sin η φ.
(1 — r cos φ) — ir sin φ
ν Ύ/ Ύ η=ο /ι=0
Преобразуем левую часть данного равенства:
1 _ (1 —г cos φ) + ir sin φ
(1 — r cos φ) — ir sin φ [(1 — r cos φ) — ir sin φ] [(1 — r cos φ) + ir sin φ]
(1—r cos φ) -\-ir sin φ 1—r cos φ , . r sin φ
~~ (1 — r cos φ)12 — i2r2 sin2 φ ~~ 1 — 2r cos φ -j- r2 ' 1 — 2r cos φ + r2
Следовательно,
1 — r cos φ ,. r sin φ
1 — 2r cos φ + r2 1 — 2r cos φ -f r2 ~~
oo oo
= 2 r" cos яф + *" 2 '" s*n n Ф'
/г=0 /i=0
откуда
oo oo
1 — r cos φ χι „ r sin φ V1 „ ·
т я=0 γ ' /ι=0
8. Выразить через тригонометрические функции кратных дуг
функцию f(x) = sin6 л:.
Применяя формулу Эйлера, получаем
• 6 ( eix-e~
sin°
\ 21 )
143
Преобразуя правую часть с помощью бинома Ньютона,
находим
sin6 χ = ~^г (е6** — бе4'* + 15е2<* — 20 + \5e~2ix — 6e~4ix + е~Ых)
или
1 rg6f* + <?-6l* ^ (β«χ + e-4te) ( ^e2ix+e-2ix
32 L 2
Следовательно,
sin6x = _JL[e6'^0e "" -6 v~"V -> +15e""te "" -10l
sin6 χ = — "32"(cos 6* — 6 cos 4# + 15 cos 2 a: — 10).
9. Выразить через тригонометрические функции кратных дуг
функцию / (х) = sin3 χ cos4 χ.
Применяя формулы Эйлера, находим
/ eix-e~ix \3/ еи + е-1х V
Sin3*cos^ = ( й ] ( 2 J = .
= ~ψϊΓ №χ - e'ix) (eix + e'U)? (eix + e~ix) =
1
128t
1
. (#lx _ e-2ixy^eix _|_ e-ix}
128/
1
(e6/x _ 3^2/* _j_ 3g-2/x __ £-6**) (gi* _|_ £-/*)
_ (β7^_|_β5^_3β3.^_3^_|_ %e-ix _|_ 3e-3/x __ β—5/АГ — β—7/jc)
128t
= gj- (sin 7 χ + sin 5* — 3 sin 3* — 3 sin x).
10. Число 1 записать в показательной форме.
Применяя формулу
ei(p = cos φ -\- i sin φ,
находим
1 = 1 + / .0 = cos 2π + / sin 2π = е2гЛ.
ЗАДАЧИ
Найти области сходимости следующих рядов:
оо оо „ оо
з. 2<-iy--^. 4.2-^ + 2-S-·
144
Найти радиусы сходимости указанных степенных рядов:
Б. J?-£=*£. 6·!^^· 7. 2я!(г-1-0«.
/г=1 /г=1 гс=1
00 00 00
8. 2 «'г (г + 2 - 30". 9. 2 "('7"2θ) · 10· Σ 3"ζ"·
/г=1 п=0 гс=0
00 00 00 00
11.2"$-^· 12· Σ"1""2"· 13· 2гЛ 14· 2cos//i·**·
,t=l
00
15. ^(n + an)zn.
л=1 л=1 л=0 я=0
00
я=0
• Найти следующие суммы:
η η
16. 2sin(2£— I)*· 17. 2^cos(2^+ !)^·
fc=l fc=0
/г
18. 1 + ^ 2α* cos β φ.
k=l
Написать действительные и мнимые части следующих
функций (х и у — действительные числа):
19. cos/у. 20. sin и/. 21. sm(x+iy). 22. cos(x+4/)·
23. ln(x + /i/). 24. arctgix.
Вычислить значения следующих функций:
25. в2 \ 26. еЧ 27. е2 "\ 28. *К 29. In (—2). 30. In (—в).
31. Ы. 32. Ιη-ί-У-. 33. 2'. 34. ΪΚ 35. Ц^Ш"'. 36. tg-^-.
V 2 I /2 / δ 2
Выразить через тригонометрические функции кратных углов
следующие функции:
37. cos3 φ. 38. sin3 φ. 39. cos4 φ. 40. sin4 φ. 41. cos5 φ.
42. sin5 φ. 43. cos6 φ. 44. sin7 φ. 45. sin2* φ. 46. cos2* φ.
47. sin2**1 φ. 48. cos2*-1 φ.
49. Пусть ζ = r (cos φ + / sin φ). Из разложения
ln(l-z) = -24- (И<1)
п=\
получить следующие:
41п(1-2гсовФ + г«) = -2^-^£-;
/1=1
145
arete rsiny = V rn s{nn<?
ъ 1 — r cos φ ^d η
50. Показать, что
00 OO
ιη0οίη Φ V^ cos αϊ φ π —φ χ* sin η φ /Λ ^ . ч
/г=1 η=1
ОТВЕТЫ
1. Вся плоскость, за исключением точки ζ = 0, т. е. при | ζ \ > 0. 2. Кольцо
1 < | г |< 3. 3. Расходится в любой точке плоскости (| ζ | < оо). 4. Кольцо
1 < I г | <5. 5. R = 1. 6. R = 1. 7. /? = 0 (ряд сходится в единственной точке
сходится в единственной точке ζθ = 3i — 2).
R = e. 12. Д=1. 13. R=\. 14. Я = —.
1 , sin2 η χ
R= τ^Γ при |fll>L 16· sin* -
х. _., -artflcos(2n + 3)A: + a/t+2cos(2Ai+ \) χ
17· 1 — 2α cos λ; + α2
1 _ α2 _ 2α*-Η cos (η + Ί) φ + 2α"+2 cos η φ
18. 1_2асо5<р + а2 ' 19· ^s ly = ch у (т. е.
действительная часть и (х, у) = ch ί/, мнимая часть и (χ, ί/) = 0). Указание.
Применить формулу Эйлера. 20. s'miy = ishy. 21. sin (A;-f-t£/)=sin л: chi/+/ cos л: sh г/.
z0 = 1 + ί).
9. R = 2.
15. tf=l
8. Я = 0 (ряд
ίο. /? = -з~. ii
при | α |< 1,
(1 — α) cos л; —
У
22. cos (χ -f ty) = cos л; ch ί/ — t sin л; sh у. 23. In / χ2 -f- у2 -f / arctg — + 2/гш.
/ *
Указание. Воспользоваться определением логарифмической функции.
Число 2, удовлетворяющее уравнению е2 = ω, называется натуральным
логарифмом ω и обозначается символом ζ = Ln ω. Если ζ = χ -\~ iy и ω = r (cos φ+
+ sin<p), уравнение ez = ω (с учетом третьей из формул (4.31)) приводим
к таким уравнениям: ех = г, cos # = cos φ, sin у = sin φ, откуда я = ln r,
ί/ = φ + 2kn (/г—целое). Таким образом, логарифм ω (при ω φ 0) всегда
существует и равен
1η ω = In |·ω | + i Arg ω = 1η | ω | + ί arg ω + 2/гш. (4.33)
При k = О получаем так называемое главное значение логарифма
In ω — ln I ω | -j- i arg ω, которое характеризуется тем, что его мнимая состав-
1 , \—х
ляющая содержится в промежутке (—π, π). 24. -kj- In , , -f- &π· 25. /.
Указание к задачам 25—28. Применить формулу Эйлера. 26. — 1. 27. — и
28. 1. 29. \n2-\- (2k -{- \)ni. Указание. Воспользоваться формулой (4.33).
30. 1 + (2k + 1) ш. 31. (4k + 1) ™ . 32. (8k + 1) ^р. 33. β- 2* π + *1η 2 .
Указание. Воспользоваться определением степенной функции. Пусть а и
Ь — комплексные числа, причем а Ф 0. Тогда по определению
аЪ = еЫпа = е& (In а + 2k г. ί) {k _ целое) (4 34)
146
При k — 0 получаем так называемое главное значение степени аь = еь 1п а.
- (4* + 1) |- 2Л π + i- π
34. е £ . 35. е . 36. / th -у. У к а з а н и е. Воспользоваться
sin г 1 / eiz — e~iz \ 1 Л
определением tg г - C0S2 = — ^ eiz + е-и ) > * =£ (А +^-) я.
1 1 Л . . ' 1
37. — (3 cos φ + cos 3 φ). 38. -j- (3 sin φ — sin 3φ). 39. -g- (3+4cos2<p+cos4(p).
40. —g—(3 — 4 cos 2φ + cos 4φ). 41. —τ^—(10 cos φ + 5 cos 3φ + cos 5φ).
42. -Tg- (10 sin φ — 5 sin 3φ + sin 5φ). 43. -oo"(cos6(p + 6 cos 4φ + 15cos2(p+10).
1 (— \)k Γ
44. — -gj-(sin 7φ — 7 sin 5φ -f- 21 sin 3φ — 35 sin φ). 45. —^-ί— cos 2&<Р —
Λ. ,Λ, „ 2^(2^—1) (— 1)Л 2£(2£-1)...(Н-1)1
-2fccos (26-2)φ+ γ2 cos (2fc - 4) φ + ... + ^-γ- · ι.2·3..Λ '
(— \)k Γ (2fc-fl)2fc
47. ν22fe sin(2fe + 1)φ — (2k + l)sin(2As—1)φ-τ γγ sin(2fc—3)φ+
. (2k + l)2k...(k + 2) Ί
+ ... + (— \p j-72 jL sin φ . 50. У к а з а н и е. Воспользоваться
разложениями задачи 49, перейти в них к пределам при г-^1—0.
II. КРАТНЫЕ ИНТЕГРАЛЫ
Глава 5
ДВОЙНОЙ ИНТЕГРАЛ
§ 5. 0. НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ПОНЯТИЯ
Приведем определения, которые будут необходимы в
дальнейшем. Рассмотрим непустое множество Ε точек некоторой плоскости.
Открытый круг радиуса ε с центром в точке Μ (т. е.
совокупность всех точек плоскости, расстояния которых до точки Μ
меньше ε) называется г-окрестностью или просто окрестностью
точки М.
Точка Μ называется предельной для множества £, если любая
ее окрестность содержит бесконечное множество точек,
принадлежащих Е. Предельная точка множества Ε может или
принадлежать, или не принадлежать этому множеству.
Множество Ε называется связным, если при любом его
разбиении на два непустых множества £Ί и Е2 по крайней мере одно
из них содержит предельную точку другого.
Множество Ε называется открытым, если для каждой его
точки существует окрестность, все точки которой принадлежат
множеству Е, .
Открытое и связное множество называется областью. Примеры
областей: множество всех точек, лежащих внутри некоторого
круга (точки ограничивающей его окружности исключаются!), вся
плоскость. Например, совокупность точек, координаты которых
удовлетворяют условию #2 + #2<1> есть область (рис. 5.0,а).
Множество, состоящее из двух открытых кругов х2 + у2 <С 1 и(# — 2)2 +.
+ у2<1> не является областью: оно открыто, но не связано
(рис. 5.0, б).
Открытое множество является областью тогда и только тогда,
когда любые две точки его можно соединить непрерывной линией;
целиком принадлежащей данному множеству.
Точка Μ называется граничной для множества £, если любая
ее окрестность содержит точки, как принадлежащие, так и не
принадлежащие множеству Е. Сама граничная точка может или
148
принадлежать, или не принадлежать множеству Е. В частности,
открытое множество не содержит ни одной своей граничной
точки. Совокупность всех граничных точек множества называется его
границей. Множество, содержащее все свои граничные точки ^
k
^ΙΙ^Ι'ί''
Ж
„ишии
,fe
Рис. 5.0
называется замкнутым. Присоединив к некоторой области G все
ее граничные точки, получим множество, называемое замкнутой
областью G.
Множество называется ограниченным, если его можно
поместить внутрь некоторого круга достаточно большого радиуса.
149
Ограниченная область G называется односвязной или
многосвязной в зависимости от того, является ли ее граница связным
или несвязным множеством. Множество точек, лежащих внутри
круга радиуса R, является простейшим примером односвязной
области. Множество точек, лежащих между двумя
концентрическими окружностями радиусов R1 и R2 — круговое кольцо (точки
окружностей исключены!),—пример многосвязной области. Эта
область называется двусвязной. Граница этой области состоит из
двух окружностей радиусов /?х и R2 (рис. 5.0, в). Если внутри
некоторой области G выделить п— 1 (п>1) замкнутых областей
Gu G2,..., G„_b попарно не имеющих общих точек, то
множество всех точек исходной области G, не принадлежащих ни
одной из указанных областей, представляет собой η-связную
область. Ее граница состоит из η линий: линии γ, ограничивающей
область G, и линий yk, ограничивающих области Gk (k =
= 1, 2, 3, ... , η— 1; (на рис. 5.0, г, д изображены четырех-
связные области).
Пусть Ε — ограниченное множество. Расстояние между двумя
его произвольными точками Мх и М2 обозначим через ρ {Мъ М2).
Представим, что точки Мх и Л42, независимо друг от друга,
пробегают все множества Е. Очевидно, множество всевозможных
расстояний ρ (Л4Ь М2) ограничено сверху (расстояние не может
быть больше диаметра круга, в котором помещается множество Е).
Точная верхняя грань чисел р(Л1ь М2) называется диаметром
d(E) множества Ε (см. рис. 5.0, е\ диаметром здесь является
наибольшая хорда данного множества).
Плоской фигурой называется некоторое ограниченное множество
точек плоскости.
Аналогично определяются понятия области и фигуры в
пространстве. (В этом случае г-окрестностью точки Μ называют
открытый шар радиуса ε с центром в точке М.)
Определение двойного интеграла
На плоскости Оху рассмотрим область (S) площади S,
ограниченную замкнутой кривой γ (рис. 5.1). Пусть в области (S)
определена функция ζ = f (х, у). Разобьем область (S) сетью линий на
конечное число областей (Sx), (S2), ... , (Sn), площади которых
Si, S2, ... , Sn (рис. 5.2). В каждой ι'-й элементарной области (S,·)
выберем произвольно точку Mi (xi9 yt)y значение функции в этой
точке f(xh у ι) умножим на площадь S,- соответствующей области
и все произведения сложим. Полученная сумма
η
называется интегральной суммой функции f(x, у) в области (S).
150
Двойным интегралом функции /(*, у) по области (S)
называется конечный предел / интегральной суммы ση при λ —»0, где
λ — наибольший из диаметров элементарных областей (S,):
η
Рис. 5.1 Рис. 5.2
Двойной интеграл обозначается одним из символов:
/= ff/(x, y)dS', (5.3)
1= fJ/(*, ίΟ</**Λ (5.4)
'(S)
Функция z = f(x, y)y для которой предел (5.2) существует и
конечен, называется интегрируемой. Если функция ζ = f(x, у)
непрерывна в области (S), она является интегрируемой в этой
области.
Геометрический смысл двойного интеграла.
Если / (*, у) > 0, то двойной интеграл от функции ζ = f(xy у) по
области (S) равен объему тела, ограниченного сверху поверхностью
z = f(x, у), с боков — цилиндрической поверхностью, образующие
которой параллельны оси Oz, а направляющей служит граница γ
области (S), снизу — плоскостью 2 = 0 (рис. 5.3).
Физический смысл двойного интеграла.
Двойной интеграл от функции ζ = f(x, у) > 0 по области (S)
представляет собой массу пластинки (S), если подынтегральную функцию
/(*, у) считать плотностью этой пластинки в точке М(х, у).
Свойства двойного интеграла:
1· J J cf {x, y)dS = c$\f (χ, у) dS (с = const).
(S) (S)
151
2. j f [/ (χ, у) it g (*, y)] dS = f f / (x, </) dS ± \ \g (x, y) dS.
(S) (S) \S)
3. Если / (χ, у) < g (xy у), то f J / (χ, у) dS < j j g (x, y) dS.
\s)
4. |Jj7(*. y)ds|<jf|/(x, y)|dS.
(S)
(S)
(S)
Рис. 5.3
$ jc
5. ]\f(x, y)dS= §][(х, y)dS+ §\f(x, y)dS, где (S') и
(S) (Sr) (S")
(S") —области, на которые разбита область (S) некоторой кривой.
6. Если в (S)m</"(*,#) <Λί, то mS<j j/(x, y)dS^MS,
откуда j ) / (χ, y)dS = μΞ (m < μ < Λί).
(S)
5 5.1 ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА В ПРЯМОУГОЛЬНЫХ
КООРДИНАТАХ
Приведение двойного интеграла к повторному в случае
прямоугольной области
Пусть область (S) является прямоугольником со сторонами,
параллельными осям координат (рис. 5.4). Обозначим его так:
(S) = [а, Ь\ с, d]9 т. е. а<*<6, c<#<d.
Если для функции f(x, у), определенной в прямоугольнике
(S) = [а, Ъ\ с, d], существует двойной интеграл
/= \\f(x, y)dS, (5.5)
(S)
152
а при каждом фиксированном значении χ из [а, Ъ\ — простой
интеграл
d
Ι (χ) = \ f (x, y)dy (α < * < 6), (5.6)
с
то существует также повторный интеграл
Ъ d Ь d
\ dx \ f (χ, у) dy ^ \ {J" / (х, у) dy) dx, (5.7)
ас ас
причем выполняется равенство
Ь d
[\f(x, y)dS = $dxjjf(x, y)dy. (5.8)
'(S) а с
Если существует двойной интеграл (5.5), а при каждом
постоянном значении у из [с, d] — простой интеграл
ь
Hy) = if (*. У)ах (с<у < d\ (5.9)
а
то существует также повторный интеграл
d Ь d Ь
J ^ ,f / (*. У) dx = J ) 1 / (χ, </) dx) Λ/, (5.10)
причем
d b
Jj/(*, y)dS = Jdyj/(xf »)d*. (5.11)
(S) с α
Если вместе с двойным интегралом (5.5) существуют оба
простых интеграла (5.6) и (5.9), то выполняются одновременно
равенства (5.8) и (5.11), откуда
Ь d d b
j dx] f(x, y)dy = \ dy]f{xy y)dx.
а с с а
ПРИМЕРЫ
e 5
1. Вычислить повторный интеграл J dy J -^ dx.
1 3 У
В соответствии с формулой (5.10)
е 5 е 5
1 3 у 1 3 у
153
Вычислим сначала интеграл, стоящий в фигурных скобках (он
называется внутренним интегралом). Считая у постоянным,
находим
— dx — — \ xdx
у у i
У 2
λ-=5
x=S
i(52-32> = T
Вычисляем внешний интеграл, для чего полученную функцию
интегрируем по у в пределах от 1 до е:
е 5 е е \е
j dy j — dx = j -ρ dy = 8 f -^- - 8 In J = 8(lne - In 1) = 8.
13^ ι lJ ι У |i
2 1
dy
2. Вычислить повторный интеграл \ dx )-τ-χ
В соответствии с формулой (5.7)
(х + у + 2)2
Δ 1
\dX\~
dy
(х + у + 2)2
-Я'
dy
ι о
(х + У + 2)2
dx.
Вычисляем внутренний интеграл, считая χ постоянным:
dy
{x + y + 2f
■У + 2
*/=о
1
1
1
х+1+2 *+0+2
1
до 2:
2 1
* + 2 * + 3*
Полученную функцию проинтегрируем по χ в пределах от 1
dy
(х + у + 2)*
(■
1
1
*+2 х+ 3
dx
J * +
1 '
2)
rf(* + 3).
х + г
= In (χ + 2) j' - In (χ + 3)|* = In 4 - In 3 - (In 5 - In 4) - ln-|J-.
ι ι
3. Вычислить повторный интеграл J dx J ex+y dy.
о о
He выписывая отдельно вычисление внутреннего интеграла,
находим
I 1 1 \у=\ 1 1
[ dx\ ех+У dy = J ех+У dx = j (ex+l — e?) dx = J e*+l d (x + 1) —
0 0 0 |r/=0 0 θ
J exdx =
,x+l
(e_e°)-^-2^+ 1 -(β— l)2.
154
4. Вычислить J J xydxdy, где область (S) является прямоуголь-
V)
ником [4, 8; 1, 2].
Задача сводится к вычислению повторного интеграла с
помощью формулы (5.8). По этой формуле интегрирование выполняется
сначала по у в пределах от с до d при произвольном постоянном
jc, а потом —по χ в пределах от а до Ь. Формула (5.8) в данном
случае примет вид
8 2
) J xydxdy = J dx J *j/rfj/.
\S) 4 1
Так как
J *ί/^ί/ = *
= JL(4-l) = -f-*,
= 4-(64— 16) - 36.
то
8 2 8 8 li
J d* J* ATi/dj/ = / -ή"*d* = "2"/ *d* = "2" "T"
4 14 4 |4
Следовательно,
j J xydxdy = 36.
(S)
Замечание. Тот же результат можно получить и по
формуле (5.11):
J j xydxdy = J rfi/ J *i/d*.
(S) l 4
Действительно,
J xydx =
»■
-f (64-16) = 24у,
12 (4-1) = 36.
поэтому
2 8 2
j dy J xydx = J 24 ί/Λ/ = 12i/2
1 4 1
5. Доказать, что если функция f(x, у) в прямоугольнике (S) =
= [а, 6; с, d] может быть представлена в виде произведения
функции только от χ на функцию только от у: / (х, у) = φ (*) ψ (у), то
двойной интеграл этой функции по прямоугольнику (S) равен
произведению двух простых интегралов:
Ь d
SS Φ W Ψ to)d*^ = / Φ Μ d* / Ψ (») аУ' (5·! 2)
(S) α с
155
Действительно, при интегрировании по у функцию φ (χ) можно
рассматривать как постоянную и вынести за знак интеграла. При
d
интегрировании по χ интеграл J ^(y)dy есть постоянная, поэтому
с
ее также можно вынести за знак интеграла:
ь d ь а
/J* Φ (х) ty(y)dxdy = Jj /φ (*) ψ (if) dy \dx = J φ (x)j^(y)dy\ dx =
(S) а с ' ii с )
d b b d
= Jty(y)dy fq>(x)dx = J <p(x)dx fty(x)dy.
с а а с
6. Вычислить двойной интеграл J J x2ysdxdy, где (S) — прямо-
\s)
угольник [1,3; 2,4].
Подынтегральная функция представляет собой произведение
функции только от χ на функцию только от у, т. е.
*Υ = φ(*)Ψ(!/),
где у(х) = х2, гр (г/) = t/3,
поэтому при вычислении двойного интеграла можно пользоваться
формулой (5.12):
3 4 3 4
J J x2y3dxdy = J d* J x2y*dy — J *2djt J i/3dy =
"(S) "l 2 ί 2
= -|- (27 - 1) (64 - 4) - -L.26 60 = 520.
7. Вычислить JT У 3/2 > где (S) = [0,1; 0,1].
(S) I * ~t~ * ТУ)
По формуле (5.11)
_ _ Π 4-
(S)
1 1
Яхахау ρ /· *d*
Так как
J"
xdx
1
(1+r
2 t /72\3/2
]Л + *» + i/2
x=l
x=0
Vi + ι + i/2
1
')
1
1
TO
V\ + y2 J Vy2 + \ Vy2 + 2 '
1
1 1
Яхахау __ > /
(1 +^2 + ί/2)3/2 ■ J ^
γιβ + \ Vy* + 2
^jdy
156
= 1п(у + уУ+ 1)
ln(t/+|/V + 2)
ln(l + у 2) — In 1 —
— [ln(l +Κ3)-1ηΓ2] = 1η(1+ V 2)+ In J/2 —ln(l + ]/3)
2 + V2
ln-
1 + ^3
Замечание. Можно воспользоваться и формулой (5.8):
xdxdy 3/2 = Г*** Г ^
(S) (1+*2 + ί/2)3/2 ·' J Π 4-,
Поскольку
#7
S
dy
1
TO
(\ + х2 + у2Г
xdxdy
,3/2
1 +x2 /i+x2 + i
0=1
y=0
1
(1+a:2)]/2 + a:2 '
-/-
xdx
(S) 0+*2 + i/2)3/2 ^ (l + x2)/2 + **
1 . V2 + x2— 1
-о- In .
2 1/2 + χ* + 1
2 (|/3+l)(|/2-l)
Полученный ответ отличается от предыдущего только по форме.
Действительно,
1 1п (V3-1) (У2 + 1)
2 (γ3+1) (/2-1)
1 1п (/3- 1) (/3- 1) (|/2_+ 1) (V2+ 1)
2 (|/з+1)(^3-1)<К2-1)(К2+1)
In
_ 1 ■ (УЪ-\)*(У2+\)*
2 (3—1) (2—1)
(У1-\)(Уъ + \)(\ 2+1)
У2(УЗ+1)
In
(1/3-I) (I/2+1)
У2
In 2</2±'>
J/2(t'3+l)
УТ
1 + 1/3
Однако в этом случае интегралы оказались более сложными
(для нахождения второго интеграла применена подстановка
1/2 + х2 = О·
8. Доказать неравенство
ь ь άχ
Jf(x)dxfj^->(h-aY,
где f(x) — положительная непрерывная функция.
Не ограничивая общности, полагаем, что а < Ь. Так как
величина определенного интеграла не зависит от обозначения
переменной интегрирования и в любом из интегралов χ можно заме-
157
нить на у, левую часть неравенства с учетом результата примера 5
можно представить так:
где S = [а,й; а,Ь].
Следовательно,
2 i) L /^ + /W J У U 2/w/(y) ^ay·
Поскольку 2αδ^α2 + /?2, то ^fjtw!^ > *·
J 2f(x)f(y) ^
В силу свойства 6 двойного интеграла
1>{Ь-а)\
что и требовалось доказать.
ЗАДАЧИ
Вычислить следующие повторные интегралы:
5 1 14 6 2 14
1. J dx J ΛΓί/^ί/. 2. J di/ J A:y2d*. 3. J d* J х2уЛ/. 4. J d*J *i/3di/.
30 6*2 30 02
6 9 4 2 6 e 12
5. jdyj x2y2dx. 6. fdxjx3ydy. 7. JdyJ-γάχ. 8. f dx j x3y2dy.
3 6 2 0 4 1 0 1
2 4 2 6 4 8
9. J dx j x2y3dy. 10. J di/J -ψ dx. 11. J Λ/J ~& dy.
12 14 2 6
3 4 2 1 * Ь ( χ* 2 *
12. idyfjsdx. 13. fdxj(x3 + y3)dy. \4. f dxf (ηρ-+ ^Uy.
12 10 Ь 0 '
α 6
15. ) dy J (x3 + y3 — Зсху) dx.
о о
Вычислить двойные интегралы по указанным
прямоугольникам (S):
ie.ffy-dxdy, (S) = [l,2; 4,8]. 17. Jfxydxdy, (S) - [2,4; 1,2].
(S) (S)
18.//(x—»)^й»,(5) = [1,4; 1,3]. 19. ff(x+y)dxdy, (S)=[3,5; 0,2].
(S) (S)
20. ff(x + y2)dxdy, (S)=[2,3; 1,2]. 21.//(x2+y)^dy,(S)=[l,2;0,l].
158
22. Jf(# + !f)dxdy, (S) = [0,1; 0,1].
(S)
23. fj(x* + y*)dydx, (S) = [l,2; 0,1].
(S)
24- Я ,,+;%. (5) = HA 0,1]. 25. Я^^, <S) = [0,1; 0,1].
(S) v ' * ~ } (S)
26. JJ(3yx2-2x3)dxdy, (S) = [0,1; 1,2].
(S)
27. JJsm(x + y)dxd»9 (S) = \o,^-; 0, -J-1
(S) L J
X I/
28. Доказать, что если F(x9 у) = J J /(w, v)dvdu, f(x, у) — не-
прерывная функция в S = [а, 6; с, d], (x, у) — ^любая точка из
указанного прямоугольника, то —=— = J /(χ, u)du, ^х^у —/(*> У)·
с
1 1 1
29. Доказать, что J J (xyf^axdy = J jfvdj/.
δο о
30. Доказать неравенство Буняковского: J f(x)g(x)dx <
<; J /2 (χ) dx J g2 (χ) dx, где f(x) и g (χ) — интегрируемые функции.
b b
31. Доказать неравенство ЧебышеваJ p(x)f(x)dxj p(x)g(x)dx^
a a
b b
^ J p(x)dx J ρ (χ) / (χ) g (χ) d*, где ρ (χ) — положительная инте-
грируемая функция; /(χ) и g(x) — монотонно возрастающие
функции.
ОТВЕТЫ
7 1
1. 4. 2. 2. 3. 126. 4. 30. 5. 10 773. 6. 120. 7. 10. 8. -утр. 9. 140. 10. 5. 11. -j-.
2 ab I a2 b2 \ ab
12. 2-д-. 13.4. 14. -у- —r _j- -^г). 15.—ξ- (α3 + Ь8 — Забс). 16.9.17.9.
5 5 2 1 9 л
18. 3. 19. 20. 20. 4-g-. 21. 2-у. 22. —. 23. 4-^. 24. In-у. 25. -j-. 26. 1.
27. 2. 28. Указание. Воспользоваться формулой F (х, у) = \du I / (и, у) dp и
159
теоремой о производной интеграла с переменным верхним пределом. 29.
Указан и е. При вычислении внутреннего интеграла применить постановку ху = t
(при у = const). 31. Указание. Рассмотреть интеграл
/=JJ lf(x)g(y)-f(y)g(x)]2dxdy, />0
Приведение двойного интеграла к повторному в случае
криволинейной области
Различают два основных вида области интегрирования:
1) область первого вида (S'), т. е. область АхА2В2Ви
ограниченную слева и справа прямыми χ = α, χ = b(a < b) соответ-
/ χ
S Χ
ственно, снизу — кривой у = φχ (я), сверху—кривой у = φ2 (χ) [φ2(*)>-
Ξ^ΦιΜΙ» каждая из которых пересекается с вертикалью χ =
= α(α<;α<;&) только в одной точке (рис. 5.5, а); .
2) область второго вида (S"), т. е. область ΟχΌχΌ^Ο^
ограниченную снизу и сверху прямыми у = с, у = d соответственно,
слева — кривой χ = ψχ (у), справа — кривой χ = ψ2 (у) [ψ2 (ί/)> Ψι(ί/)]>
160
каждая из которых пересекается с горизонталью у = $(c^Cfi<Cd
только в одной точке (рис. 5.6, а).
Замечание 1. В некоторых случаях точки Ах и Л2, Вг и
β2, Сх и С2, Al и D2 могут сливаться в одну (см. рис. 5.5, б, в,
г и 5.6, б, в).
У
tf
0
0
г
а[
\
1\
ι \
ι \
1
X
а
D
Р\
I
V
/1
у \
1
^ X
Рис. 5.6
Если для функции f(x, у), определенной в области (S'),
существует двойной интеграл, а при каждом постоянном значении χ
из [а, 6] простой интеграл
/(*)= / /(χ, i/)di/, (5.13)
Ψι(Χ)
то существует также и повторный интеграл
Ь Vr2U) ί> <?г(х)
jdx f f(x, y)dy = j{ J f(x, y)dy\dx (5.14)
α ΐι{χ) a Kvt(x ) ;
161
и выполняется равенство
///(*, y)dS' = Jdx J f{x, y)dy. (5.15)
В случае области второго вида (S")
d ЫУ)
JJf (χ, у) dS" = f dy J f (x, y) dx (5.16)
(5") с Ыу
в предположении, что наряду с двойным интегралом существует
простой интеграл по χ при постоянном у.
Если область (S) можно рассматривать как область первого
вида (S') и как область второго вида (S") (см. рис. 5.6, г), то при
выполнении указанных условий применимы обе формулы (5.15) и
(5,16), поэтому
Ь φ2(λ) d ψ2(ΐ/)
J dx J f(x, y)dy = J dy J /(x, y)d*. (5.17)
Если область интегрирования не принадлежит к
рассмотренным выше видам, ее стараются разбить на части, каждая из которых
относится к одному из этих видов (рис. 5.7, а, б, в). Тогда двойной
Рис. 5.7
интеграл, в соответствии со свойством 5, равен сумме двойных
интегралов.
Замечание 2. В повторном интеграле (5. 14)
интегрирование производится сначала по у, при этом χ считается постоянным;
пределы интегрирования φχ (χ) и φ2 (χ) представляют собой правые
части уравнений линий г/ = φχ (л:), у = φ2(*), ограничивающих
область (S') снизу и сверху соответственно. Другими словами,
Φι (*) — эт0 значение ординаты у, при котором прямая χ = а
«входит» в данную область (S'), φ2 (*) —значение ординаты у, при ко-
162
тором эта прямая «выходит» из указанной области (см. рис. 5.5, а).
В результате интегрирования получается функция от х, которую
потом интегрируют по χ в постоянных пределах а и 6, являющихся
правыми частями уравнений прямых χ = а и χ = Ь, ограничивающих
область (S') слева и справа соответственно.
Замечание 3. В повторном интеграле (5.16) интегрирование
производится сначала по χ от % (у) до ψ2 (у), при этом у считается
постоянным, затем полученную функцию от у интегрируют по у
в пределах от с до d (линии χ = ψχ (у), χ = ψ2 (ί/))*> прямые у = с,
у = d ограничивают область (S"); ψχ (у) — это «* входа» прямой
ί/ = β в область (S"), ψ2(ί/)— «* выхода» из нее (см. рис. 5.6, а).
Замечание 4. В повторном интеграле (5.15) нижний предел
интегрирования по χ равен наименьшей абсциссе точки границы
области (S') (см. рис. 5.5^, верхний предел b равен наибольшей
абсциссе точки границы области (S').
Замечание 5. В повторном интеграле (5.16) постоянные
пределы интегрирования с и d являются наименьшей и
наибольшей ординатами точек границы области (S") (см. рис. 5.6).
ПРИМЕРЫ
1 ~ 2—*2
1. Вычислить повторный интеграл J dx J (x + у) dy. Напи-
0 χ'
сать уравнения линий, ограничивающих область интегрирования
соответствующего двойного интеграла.
Напишем уравнения линий, ограничивающих область
интегрирования. В соответствии с замечанием 2 имеем: χ = 0, χ = 1 —
уравнения прямых, ограничивающих область интегрирования слева
и справа; у = х, у = 2 — х2 — уравнения линий, ограничивающих
эту область снизу и сверху (рис. 5.8).
Переходим к вычислению повторного интеграла. Вычислим
внутренний интеграл, считая χ постоянным:
2Ч . (2 —*2)2 1
2-х'
J (x+y)dy =
Χ
-(» + £)-
-(>у+-т)
у=2—х*
x(S
--2х — х3 + 2 — 2х2 + ^-
7
2
- х2 + 2х -
f 2.
Следовательно,
2—*2
/dx f (X + y)dy = f (^- - χ» - 1-х* + 2x+ 2)dx =
163
= (-£—τ—г*+ χ2 + 2χ}
10
+ 1 +2
101
60
2. Расставить пределы интегрирования в повторном интеграле,
к которому сводится двойной интеграл
(S)
где (5) — область, ограниченная линиями у2 = * + 2, у — * — 0;
дх> у)— функция, непрерывная в данной области.
Рис. 5.8
Рис. 5.9
2 ос
Построим область (S) (рис. 5. 9). Первая линия — парабола,
симметричная относительно оси Ох с вершиной в точке А ( — 2,0);
вторая линия — прямая, проходящая через начало координат
(биссектриса первого и третьего координатных углов). Найдем точки
пересечения этих линий. Решая систему уравнений у2 = χ + 2 и
у — χ = 0, находим: хг = — 1, Уг = — 1, Ч = 2, #2 = 2; получены
точки Λίχ(—1, —1), М2(2, 2). Область интегрирования является
областью второго вида (см. рис. 5.6). В данном случае χ = ψχ(ί/) =
— 2 — у2 (найдено из уравнения линии у2 = χ + 2, ограничивающей
область слева) и χ = ψ2 (У) = ί/ (найдено из уравнения линии у —
— jc = 0, ограничивающей область справа), с = — 1, d = 2
(наименьшая и наибольшая ординаты точек границы области; см.
замечание 5). Следовательно, в соответствии с формулой (5.16)
2 К
S!f(*> y)dxdy= f dy f f(x, y)dx.
(S)
— 1
2-i/2
164
Область (S) можно рассматривать также как сумму двух
областей первого вида АВМ1 и Μχθ^ (см. рис. 5.9), так как линия,
ограничивающая снизу криволинейную фигуру АВМ2МгА, на
различных промежутках определяется различными уравнениями, а
именно: если — 2 <; л: <; — 1, то у = — Υ χ + 2; если — 1 <; χ ^ 2,
то у = х. Сверху криволинейная фигура ABM2MiA ограничена
кривой у = Ух+2. Итак, с другой стороны,
— 1 Ух~+2 2 Yx+2
j!f(x, y)dxdy= J dx J /(χ, i/)dy+ j dx J f(x, y)dy.
(S) —2 — |/^q=2 -1 *
Таким образом,
2 у —1 >^^+2 2 /*+2
fdy J /(x, j/)dx= Jdx / f(x, y)dy+ fdx j f(x9 y)dy.
-1 2-i/2 _2 _ yjj~2 — 1 x
Замечание. Последняя формула определяет перемену
порядка интегрирования в заданном интеграле.
3. Переменить порядок интегрирования в'повторном интеграле
1 —λ:2+2
J dx J f(x, y)dy,
-1 '' 2_
3
χ
где /(#, у) — функция, непрерывная в данной области.
И
А
Рис. 5.10
Рис. 5.11
Область интегрирования ограничена линиями х3 = х2, у =
= —х2 + 2 (рис. 5.10), пересекающимися в точках Мх(— 1,1),
^2 (1,1), т. е. представляет собой криволинейную фигуру ΟΛίΧ;4Λί2, где
А (0,2) — точка пересечения параболы у = —х2 + 2 с осью Оу. Эта
область является областью первого вида (S') (см. рис. 5.5). Ее
можно рассматривать также как сумму областей второго вида (Si)
165
и (Si) (см. рис. 5.6, г), т. е. областей ОМ1М2 и М1АМ2 (см.
рис. 5.10). Область (S[) ограничена слева дугой ОМх графика
_з_
функции χ = ψχ (у) = — у2 (получено из уравнения *3 = х2) и
справа — дугой ОМ2 графика функции χ = ψ2 (у) = у3/2 (получено из
того же уравнения) при любом фиксированном у из промежутка
[0,1]. Область (Si) при любом у из [1, 2] ограничена слева дугой
МгА, справа — дугой ЛМ2, т. е. дугами графиков функций χ =
= — Vе! — у, х= Ϋ 2 — у соответственно (эти уравнения
получены из уравнения у = —х2 + 2).
Следовательно, в соответствии со свойством 5
1 2-х» 1 уЧ2 2 /2=5
/d* J /(a:, t/)dt/= J dy / /(χ, t/)d* + I dy J /(*, y)dx.
-1 *2/3 0 _^3/2 1 _/2=F
4. Вычислить J J x2ydxdy, где (S') — область, ограниченная ли-
Ъ)
ниями у = —χ2, χ = у2.
Данные линии пересекаются в двух точках — 0(0, 0), Μ (1, — 1)
(рис. 5.11). Область (S) можно рассматривать как область
первого (S') и второго (S") вида. Рассматривая ее как область
первого вида, получаем следующие пределы интегрирования: а = 0,
b = 1, у = φχ (х) = — |/лг, # = q>2 (*) = — *2· По формуле (5.15)
ι — х2
\ ) x2ydxdy = J d# J *2ydi/.
*& δ J)-
Так как
—X2
/ x2ydy = -^f-
-Vx
у= —χ2
y= — Yx
χ2 (— χ2)2
χ2 (— Ух )2
χ*
2
ΤΟ
-χ2
Χ'
IT"
8
/ dx S x2ydy = /(-*-- -*-) d* =
о __^ о \
J 1__ 3_
^ 14 8 ~" 56
Следовательно,
f f x2y dxdy = —
\S)
Замечание. Рассматривая данную область как область
второго вида, находим следующие пределы интегрирования:
3
56
с = — 1, d = 0, а: = ψχ (t/) = ί/2, χ = ψ2(ί/)
166
поэтому
V) -i I/2
Вычислив повторный интеграл, получим тот же результат.
5. Вычислить fj(x + 2y)dxdy, где (S) —трапеция с верши-
в(5)
нами А(-2, -2), S(-l, 2), С(3, 4), D(6, 2).
Составим уравнения прямых, на которых лежат стороны АВ,
ВС, CD, AD данной трапеции:
4х — у+ 6-0 (АВ),
х — 2у + 5 = 0(ВС),
2х+3у- 18 = 0 (CD),
x — 2y-2=--0(AD).
Область интегрирования ABCD
(рис. 5.12) прямыми χ =— 1,
χ = 3 разбивается на три области
первого типа: ABM, BCNM,CND,
а прямой у = 2 — на две области
второго типа: ABD и BCD.
Воспользуемся вторым
разбиением, так как в этом случае
нужно вычислять два повторных
интеграла, а не три. Для области
ABD найдем пределы интегрирования:
шая и наибольшая ординаты точек), χ = ψι (у) = -j- у ■
чено из уравнения прямой АВ), χ = ψ2 (У) = 2у-\-2 (получено из
уравнения прямой AD)\ для области BCD имеем соответственно:
с = 2, d = 4 (наименьшая и наибольшая ординаты точек), χ =
з
= ψχ (у) = 2ί/ — 5, χ = ψ2 (у) = 9 2" t/ (получено из уравнений
прямых ВС и CD).
Рис. 5.12
2, <Г
1
(наимень-
"2" (П0Лу-
Следовательно,
2У+2
*-Ь
M(x+2y)dxdy= fdy j (x+2y)dx+fdy j x + 2y)dx.
1/4 0—;
Так как
2ί/+2
(jc + 2y) rfjc -
ί
2xy
2y+2
1
(2y + 2)2
167
+ 2{/(2г/+2)
1 / 1
+ Ц-ту—т)
= (2? + Ау + 2) + 4у2 + 4у - [\- (-^-V - 4" У + 4") +
, 1 2 о 1 175 „ , 91 ,7
+ -J" У2 ~ 3i/j = -32-ί/2 + -g- ί/ + -у,
ТО
2 2ίί+2 2
-2 _Ly_i- J 2
-(■
175 φ
32
91 j£
8 2
Х*
2
—2
175
96
7_
2 ~~ 6
[8-(-8)]-f
+ -u-«-<>+-i-B-<-'w-!r-+-i--!!L-S-.
Поскольку
I
2y-5
(# + 2ί/) d*
2xy\
)Гт"=\-
I \2y-5 L
9--2- У +
+ 2у(9 - А у)] - [-i- (20 - 5)» + 2ί/(2ί/ - 5)] =.· -ί- (δΐ - 27у +
+ 4 У2) + 18f/ - Зу2 - [-i-(4f/2 - 20ί/ + 25) + (4</2 - 10</)] =
то
4 S"I»
jdi/ f (x + 2y)rfx= |*7
2y-5
iy2 + 4i/ + 4 Ui/ = 7(-l^ +
+4-^2+4^)|2=7[-4(б4-8)+1-(1б-4)+4(4-2)]=
= 7(—21 +21 +8) = 56.
Таким образом,
j j(x + 2y)dxdjr = -f- + 56 = -ψ- = 88-f-·
(S)
168
6. Расставить пределы интегрирования в двойном интеграле
J J f(x* У) dxdy, где область интегрирования (S) определена нера-
(5)
венствами: х2 + у2 !> 1, х2 + у2 <; 9.
Область (S) есть круговое кольцо, ограниченное
окружностями радиусов R± = 1, /?2 = 3 с общим центром в начале координат
рис. 5.13, а). Она не принадлежит ни одному из двух основных
Рис. 5.13
видов областей (так как прямые χ = α, — 1 <; α <; 1, г/ = β,
— 1 <;β<; 1 пересекают каждую окружность в двух точках).
Для расстановки пределов интегрирования в данном
интеграле разобьем область (S) прямыми χ = — 1, χ = 1 на четыре
области первого вида (Si), (S2), (S3), (S4) (см. рис. 5.13, а).
Из уравнений окружностей
х2+у2= 1, х2 + у2 = 9,
ограничивающих данную область, находим:
У = ±У 1-х2, у = ± V9-X2.
Следовательно,
JJ/(a:, у)dxdy = jf f(x, у)dxdy + \\ f(x, у)dxdy +
(si) ($
+ J J / (х, У) dxdy + f j /(*, у) dxdy = jdx J f (χ, у) dy +
(5з) (S4) -3 _/§=ΞΪ
1 — ΫΤΞ& 1 V"9=^
+ jd* J f(x, y)dy + Jdx j f(x, y)dy +
-1 — |Л9_А:2
KT=I"2
169
Υ 9-A"2
+ \dx j f(x, y)dy.
Разбив данную область прямыми у = — 1 и у = 1 на четыре
области второго вида (рис. 5.13, б) и заметив, что χ = ztz 11 — ί/2,
а: = it: |/ 9 — ί/2, получим
_j V" 9-*/*- 1 - Υ l-y2
]*]*/(*, y)dxdy=§ dy J f(x, У) dx+ Jdy j f(x, y) dx +
{S) _3 -Vl=^ -1 ->;9=^
1 /9=4?* 3 YT^fi
+ fdy f f(x, y)dx+ j dy J f(x, y)dx.
— 1 > i_yz 1 _ /gZ^i
7. Вычислить j J e~y2 dxdy, где (S) — треугольник с вершинами
O(0, 0), β(0, 1), Α{\, 1).
Η
у
ίδ
Рис. 5.14
Рис. 5.15
Данная область ограничена прямыми у = χ, χ = 0, у = 1
(рис. 5.14). Рассматривая ее как область первого вида, находим
ι ι
j j е~Уг dxdy = J dx J e-^2 dy.
(S) 0 *
Интеграл Г е~у2 dy является «неберущимся» интегралом. Его
нельзя выразить через элементарные функции.
170
Переменив порядок интегрирования, получим
! у
\\e-y'dxdy= \dy\e~y2dx.
(S)
Так как
у
j е~У2 ах = хе-У2 \У = уе~У2 — 0е~У2 = уе~У2,
то
о
1
о 2е ' 2 *
]\е-У2 dxdy = j уе-У2 dy = — ± е~У2
(S) О
Интегрирование в этом случае выполнено, вычисление про-
изведено в элементарных функциях.
8. Вычислить ^xdxdy, где (S) — область, ограниченная осью
(5)
Ох и аркой циклоиды χ = a (t — sin t), у = а (1 — cos /) (0 < t < 2π).
Особенность данной задачи в том, что кривая,
ограничивающая область интегрирования, задана параметрическими"
уравнениями. Однако ордината у точки циклоиды представляет .собой
однозначную и непрерывную функцию абсциссы χ: у = у(х).
Заметив, что χ = О при t = 0 и χ = 2па при t = 2π, получим
2га у (дс) 2га
J | jcdjcdi/ = j dx J jcdi/ = J A:i/djc.
(S) 0 0 0
Чтобы освободиться от неизвестной нам функции у = у(х) и
вернуться к известным функциям, сделаем подстановку: x = a(t —
— sinί), у = а{\ — cost). Тогда dx = а(1 — cos /)Л, новые пределы
интегрирования: а = 0, β = 2π.
Следовательно,
2га 2г
) дч/dx = | α (ί — sin t) a (1 — cos ί) α (1 — cos t) dt =
о
2π 2r
= a3 j(1 — cosf)2(t — sin/)Λ = a3 \ (t — 2tcost + tcos2t — sint +
ο ό
+ 2 sin t cos ^ — sin t cos2 ^) df.
2π 2π
Так как J tdt = 2π2, ) ί cos2 fdf = π2, а интегралы от всех дру-
-° ' δ
гих функции равны нулю, то
2га 2л 2г
\ ] jtdxdi/ = j xydx = a3 j fdf + a3 j f cosHdt = 3π2α3.
(S) 0 0 0
171
9. Оценить двойные интегралы:
Г Г dxdy * __ Г Ρ dxdy
Л = JJ /25·-a*-^' 2~ J J 25 + sin2 (* + */) +cos2*/*
д;2+у2<1б \х\+\У\<5
Воспользуемся свойством 6 определенного интеграла: если
/п</(д:, у)<УИ в данной области (S), площадь которой S, то
mS<iJf/(jc, y)dxdy^MS.
(S)
Оценим первый интеграл. Областью интегрирования является
круг радиуса R = 4, площадь которого S = 16π. Так как в
данной области функция
/(*> у) = —,
удовлетворяет соотношениям:
1 < '
]/25 — 0 1/25 — х2 — у2 % Г 25—16*
J_ 1 J_
Τ· β· 5 ^ ^/25_X2_i/2 < 3 '
то
16 ^ / / 16
-_π</1<-Γπ.
Переходим к оценке второго интеграла. Областью
интегрирования является квадрат с вершинами А(—5, 0), 5(0^5), С (5, 0),
D(0, — 5) (рис. 5.15). Длина его стороны а = 5 ]/ 2, а площадь
S = 50. Поскольку
27 ^ 25 + sin2 (x + y) + cos2у ^ 25 '
ТО
1,85 £/2 L 2.
ЗАДАЧИ
Вычислить повторные интегралы, написать уравнения линий,
ограничивающих области интегрирования соответствующих двойных
интегралов:
4 х2 3 χ 6 [х
1. ) dxjj xdy. 2. J dx j ydy. 3. J dx J — dy.
1 0
2 0
4 лг-f-l
4. j dx \ i-dy-
2 1
172
1 0
3 *2+5
5. [dx f ·
Г' 2"
У- 4 г8 УС dx
Ι» . г» л л г с* dx
dy \ Vydx. 8. J dy J -ψ- dx. 9. J dy J ~^ϊ
За;
_2_
1 ί,3 5 ^"y 3 уЪ
10. f dy (j/ ΪΓώκ. 11. j di/ j *W*. 12. \dy\-frdx.
ό ό i ό i о
Расставить пределы интегрирования в повторных интегралах,
к которым сводятся двойные интегралы 1 | f(x, y)dxdy от функ-
\s)
ции f(x, у), непрерывной в указанных областях (S):
13. (S) ограничена линиями у2 = лс, * = 1.
14. (S) ограничена линиями jci/ = 6, л: + ί/ — 7 = 0.
15. (S) ограничена линиями у = х2 + 1, л: — ί/ + 3 = 0.
16. (S) ограничена линиями х2 — у2 = 1, # = —2, у = 2 ((S)
содержит начало координат).
17. (S) ограничена линиями у2 — х2 = 16, л: = —3, л: = 3
((S) содержит начало координат).
18. (S) ограничена линиями у = х, У = V 3 χ, χ2 -\- у2 = 8
(х>0,у>0).
19. (S) ограничена линиями х2 + у2 = 4, у = 2а: — χ2, χ = 0
(χ>0, у>0).
20. (S) — прямоугольник с вершинами Л(2, 4), 5(5, 4),
С(5 ,-2), D(2, -2).
21. (S) — прямоугольник с вершинами Л(1, 1), 5(5, 5), С(7, 3),
£>(3, -1).
22. (^ — треугольник с вершинами А(— 2, —2), 5(—1, 2),
С (6, 2).
23. (S) —квадрат с вершинами А(— 1, 3), 5(4, 3), С (4, —2),
0(-1, -2).
24. (S) — квадрат с вершинами Л(0, 3), 5(4, 7), С (8, 3),
D{4, -1).
25. (S) —трапеция с вершинами А(— 2, η 5(1, 4), С(5, 4),
D(—2, -3).
26. (S) — параллелограмм с вершинами А(—2, 1), 5(2, 4),
С(3, 1), D(-l, -2).
27. (S) — круговой сектор ABC с центром в точке Л(1, 1), у
которого концы дуги 5(4, 2), С (2, 4).
28. (S) — круговое кольцо, ограниченное окружностями
радиусов Rt = 2, £2 = 3 с общим центром в точке О (0, 0).
Расставить пределы интегрирования в повторных интегралах,
к которым сводятся двойные интегралы J \f(x, у) dxdy, где / (χ, у)—
(S)
непрерывная функция в указанных областях (S), определяемых
неравенствами:
173
29. 1) 2<χ<3, 4<ί/ <5; 2) α<χ<6, c<*/<d.
30. α<χ<6, φχ (χ) < у < φ2 (χ).
31. c<y<d, ψχ(г/) < χ< ψ2(ί/).
32. 0<χ< 1, χ<*/<3χ. 33. 0<χ< 1, χ2<ί/<χ.
34. 1 < χ < 3, χ — 2 ч. г/ < χ + 1.
35. 1 < у < 2, ί/ + 3 < α: < ί/ + 5.
36. α:2 + ί/2 < 4, χ f ί/>2. 37. χ>0, г/>0, χ — ί/<3.
38. -^- + -^-<1· 39. χ2+ί/2<2χ.
40. χ2 + ί/2< 1, x2 + 2*/2> 1.
Расставить пределы интегрирования в повторных интегралах,
к которым сводятся следующие двойные интегралы:
41. И/(х, y)dxdy, (S) ограничена линиями ух = —1, χ =
(S)
5
= sin(ju/), y2(x) = (x+ 1)2(-[2"^+ 1].
42. J J f(x, y)dxdy, (S) ограничена линиями χ2 -f у2 = α2,
(S)
χ2 + 4ί/2 = α2.
43. J J / (χ, у) dxdy, (S) ограничена линиями χ2 + у2 = α2, ί/ =--
(S)
= αχ — a:2 (χ>0, ί/>0).
Записать в виде одного повторного интеграла следующие
выражения, предварительно изобразив на чертеже области
интегрирования:
44. \dy j/(x, y)dx+\ dy j/(x, y)dx.
ό у_ 2 JL
2 2
45. J di/ Γ /(χ, i/)tfx + jdi/ f /(a:, */)d*.
—Vx/—ι -*V-i
-1 4*-j-6 6 2
46. \dx \ f(x, y)dy+ §dx j / (χ, */) d#.
-2 1, -11,
12 2 2
47. f di/ [/(x, i/)di/+ jdf/j/(*, y)dx.
JL _L 'l y
2 у
174
*+5 _2_
3 2 6 3*
f(x, y)dy+ \dx j f(x, y)dy.
— 12 3 2
.! VT 4 v~y
49. J Λ/ j /(a:, i/)dx + j'di/ j/(*> y)dx.
2 2 1 l—l^r^i"
50. j dy j /(a:, y) dx + j di/ J f(x, y) dx +
1 У^_ Q j/2
2 2
1 2
+ jdi/ j /(χ, */)dx.
0 i-fvT=^
ι \-VT^y ι il^y*
51. \dy \ f(x, y)dx + §dy J f(x, y)dx +
Ό ο о \+V\=-y
2 1 1—г/2
+ J di/ f /(*, i/)dx.
1 0
Переменить порядок интегрирования в следующих повторных
интегралах, предварительно изобразив на чертеже области
интегрирования:
2 4 а V
а У а*—х2
52. fdxff(x, y)dy. 53. Jdx j /(χ, у) dy.
—2 χ2 0 a—x
r ι У~у ι v^T
54. j dy j f (x, y) dx. 55. J dy J f (x, y) dx.
0y 0 y2
1 3-х 2 2x
56. J dx J f(x, y)dy. 57. J dx J /(x, i/)di/.
—2 jt*-fl 0 ϊ
2 л: 2 х+2
58. J dx //(χ, y)dy. 59. J dx J f(x, i/)di/.
i J_ —ι χ2
a:
4 2/~
*+6
8 7
60. jdx J f(Xf y)dy. 61. fdx f f(x, y)dy.
-6 J_ ° VAx-
3
175
6 7—Χ α γα2_χ2
62. J dx J /(χ, y)dy. 63. Jdx / /(jc, y)dy.
1 _Ё_ О ал:—л:2
Вычислить двойные интегралы:
64. J I xydxdy, (S) ограничена линиями у = α:2, */2 = jc.
(S)
65. J J xdxdy, (S) ограничена линиями лгг/ = 6, χ -f ί/ — 7 = 0.
(S)
66. J] x2ydxdy, (S) ограничена линиями y = x2, у = 4.
(S)
67. J J y2xdxdyf (S) ограничена линиями *2+ί/2=4, λ'+ί/—2 = 0.
(S)
68. J J x3ydxdy, (S) ограничена линиями у = α:2, ί/ = jc + 2.
(S)
69. J J x^ydxdy, (S) ограничена линиями ху= 1, у—jc =0, jc=2.
(S)
70. J J (jc+ί/) dxdi/, (S) определена неравенствами 0<ί/<π,
(S)
0<a: <sini/.
71. J J (лгу + y) dxdyf (S) определена неравенствами 0< у < 1,
(sn
у < χ < 2 — у.
72. JJ (лгу2 + l)dxdy, (S) определена неравенствами 0 <; χ < 2,
(S)
73. J j ex+ydxdy, (S) ограничена линиями у = ex, χ = О, у = 2.
(5)
74. j J |/ xy — y2dxdyf (S) определена неравенствами 1 < у < 2,
(S)
i/<x< 10{/.
75. Вычислить JJ (a: + 2y) dxdy по указанным областям (S):
(S)
1) (S) ограничена прямыми у = 4а: + 6, у = -у #— 1, а: = — 1;
2) (S) определена 'неравенствами — 1<!а:<3, у *— 1<;
2
176
3) (S) — треугольник с вершинами А(3, 4), 5(6, 2), с(з,у).
76. Вычислить J J (2х + у) dxdy по указанным областям (S):
(S)
1) (S) — треугольник с вершинами А (— 2, —2), 5(— 1, 2),
c(-,,-i);
2) (S) —параллелограмм с вершинами А(—1, 2), 5(3, 4),
с(з,4-). D(-b
J3_
2 7*
9 1
3) (S) ограничена прямыми у = —^-л: + 6, у = -~- х— I,
ι з
4) (S) определена неравенствами -j- */ 9-<Α:<2ί/·+2,
— 2<{/<2;
5) (S) — треугольник с вершинами Л (— 1, 2), 5(3, 4), С (6, 2);
6) (S) ограничена прямыми χ — 2*/ + 5 = 0, 4х — ί/ -f 6 = О,
2jc + Зу — 18 - 0, а: — 2у — 2 = 0.
77. Вычислить j J (x2 -f ί/2) dxdi/ по указанным областям (S):
(S)
1) (S) — треугольник с вершинами Л(0, 0), 5(|/2, 1/ΊΓ),
C(|/Tf/"6);
2) (S) ограничена линиями а: = j/2, у = х, х2 + У2 = 8 (х >0,
У>0);
3) (S) ограничена линиями у = х, у = УЗх, л:2 + у2= 8(х >- 0,
У>0).
78. Вычислить двойные интегралы ^ydxdy и ^y2dxdy, где
(S) (S)
(S) — область, ограниченная аркой циклоиды χ = a (t — sin /),
г/ = α(1 — cos/) (0</<2π).
79. Вычислить J J xydxdy, где (S) — область, ограниченная
(S)
осями координат и частью астроиды χ = a cos3 /, у = α sin3 /
(o<«-f).
80. Оценить следующие двойные интегралы:
1) Д = // К 2Ь - х2 — у2 dxdy\
Х2+У2<9
2)/,= Я ^ ·
16 + sin2 * +cos2 (* + #)'
177
Яахау
*)а- Я
V 10000— 16хг —25(/4 '
5) А= Я (9 + *2+*/2)<Ш*/; 6)/β= if ^
Χ2 V2
25 ^ 16 ^
у2 j иг ·
*2+y2<l *2-fi/2>4 ^ ^
А'2+У2<9
ОТВЕТЫ
1. 60, х = 2, л; = 4, у = 0, # = л:2. 2. 4-^-, л; = 1, χ = 3, у = 0, у = χ. 3.8.
4.5. 5.4. 6.1. 7. 4, 0= 1, ι/= 3, х = 0, x = V~J. 8. 2,j/ = 1, у = 2,
12 ι /*
* = 0, * = у3. 9. 1. 10. -у. 11. 2О-3-. 12. 13. 13. ΐ dx Г /(л;, у) dy =
о -/Т
1 1 6 7—л: 6 7—у
= j dy j f(x, y)dx. 14. J d* | /(л;, y)dy = j dy J f (x, y) dx.
— 1 y2 1 _6_ 1 _6_
2 лт+З 2 УуЗ] 5 ^"y^T
15. j dx J f(x, y)dy=Jdy j f(x, y)dx+j dy j f (x, y) dx.
-1 *4-i 1 -Yf=\ 2 У-3
2 /"y^H —1 2 —1 — /*2— 1
16. Jdy f f(x9y)dx= j dx J f(x,y)dy+ J dx f f(x,y)dy+
-2 _У7Щ _/5" /i^i -VW -2
1 2 V~T 2 /ΊΓ —/*^T
+ Jd* j f(x, y)dy+ j dx j f(x, y)dy+ J dx J f(x, y) dy.
-1 -2 1 y^ l -2
3 V хЧ-16 —4 — /ι/2—16 —4 3
17. J ^ J / (*, y) dy = Jdy J / (*, y) dx+ Jdy J f (x, y) dx +
-3 -Υχϊ+Ϊ6 ~5 -3 _5 Yy^Tb ·
4з 5 -/yTZie 5 3
+ J dy jjf(x, y)dx+ fdy f f(x, y)dx+ J dy J /(*, y)d*.
—4 —3 4—3 4 /y2—16
/"2" νΤ* 2 /8^F 2 у
18. J dx j f(x, y)dy+ J dx J /(*, y)dy=fdy j f(x, y)dx +
0 * /*2~ * 0 у
ντ
178
ΥΎ V8—у2 2 Υ Α—χ2 1 \-V\—y
+ J dy J f(x,y)dx. 19. J d* J f(x,y)dy=fdy J f(Xty)dx+
2 у
x4-i/2
5 4
2 /4-y2
+ J^i/ J f(x> y)dx+ Jdy J f(x, y)dx. 20. J* d* J /(*. У) dy =
0 1+νϊ=ί 10 2-2
4 5 За: 5 а:
= J dy J f(x, y)dx. 21. J d* J / (χ, y)dy+ Jdx J f (x, y) dy +
—2 2 1 2—a: 3 a:—4
7 10—a: 1 y+4 3 £/+4
+ J d* J /(a;, y)dy = J dy j f (x, y) dx + Jdy J f (*, #) d* +
5 a:—4 —1 2—£/ Ι ί/
5 10—у 2 2y+2 —1 4л:+6
+ Jdi/ J /(*, */)d*. 22. Jdi/ J f(x, y)dx=Jdx J /(*, y)dy +
3 У
6 2
—2 1 3
4 3
-2 1
a:—1
+ | d* J /(λ, */) dy. 23. J d* J/(a:, y)dy = j dy J f (x, y) dx.
-1 1
a: —1
-1 -2
8 11—a:
-2 —1
4 a:+3 8 11—a: 3 Б+у
24. J dx J f(x, y)dy + Jdx j f (x, y) dy = J dy J f (x, y) dx +
0 3—a: 4 x—5 —1 \ 3—у
7 11—у 1 дс+З 5 4
+ Jdy J f(x, y)dx. 25., Jdx J f(x, y) dy+ J dx J /(*, y) dy
3 у-Ъ
ι y+\
3,5
2 T*+T
-2 a:-1
4 0+1
1 i/—3
3 10—3a:
1 a:-1
3 , 5
-1 TX+T
= Jdy J f(x, y)dx+ J dy J f(x, y)dx. 26. Jdx J f(x, y)dy +
-2 -5-3*
4</+5
1 3
+ Jdx J f(x, y)dy + Jdx J f(x,y)dy = Jdy J f(x,y)dx +
-13 5
10— у
4 3
2 3 5
TX~T
2 3a:—2
-2 y+5
3
4 i_f- /ц+2а:—*2
+ Jdjj J f(x, y)dx. 11. Jdx J f(xty)dy+Jdx j f(*,y)dy =
1 4y—10 1 £+2 2 £+2
3 3 3
2 3i/—2 4 1+/11—y2+2y —2 Vg—x2
= Jdy J f (x, y) dx +Jdy J f (x, y) dx. 28. Jdx J f(x, y) dy+
1 У+2 2 y±2 -3 _/g=F
3 3
179
2 Y9—X2 2 — Υ 4—χ2 3 V9—x2
+ Jdx J /(χ, */)d// + Jdjc J /(x, y)dy+jdx J f(x, y)dy =
-2 ^4=^ -2 -/9=72 2 _K9=Ji
—2 1/9— i/2 2 — /4—y2 2 /θ"^
= Jdy J /(x, */)dx + J d</ J /(x, */)dx + Jdy J /(x, y)dx +
-3 _ /9=72 -2 —Y$Z^t -2 /4^2
3 /9=^2 3 5 b d
+ Jdy J f(x, y)dx. 29. 1) fdxff(x, y)dy; 2) f dx f f (x, y) dy.
2 _/§Ζ£β 2 4 ас
b φ2 (at) Д* ψ2 (У) 1 3*
30. I'djc f /(x, */) d//. 31. fdi/ Γ /(χ, */)dx. 32. fd* f f (x, y) dy.
α <pt (дг) с ψ4 (ί/) 0 *
1 л: 3 л:+1 2 у+Ь
33. fd* Г /(χ, y)dy. 34. Г ^л: Г /(л;, у) dy. 35. fdi/ Г /(л;, у) dx.
о *2
2 /4—хг
1 л:—2
3 О
1 0+3
36
39,
о *—з
j*djc J /(*> #)% 37. Jdx J/(χ, y)dy. 38. fax J f (x, y) dy.
Уф^х~2
и
ι/ΊΞ*!
ι V\—xz 1 V 2
. Jdx J f(x, y) dy. 40. Jdx J f(x, y)dy+ jdx J / (x, */) dy.
—1 /I=F '
Κ τ-
1 уг (χ) 0 sin (r.y)
0 —a:+2
2 /2a:—x2
/j
- /2a:—a:2
— V 1—a:2
41. J J /(*, y)dxdy= J dx J f(*.y)dy+ J dy f f(x,y)dx +
S _3 _! _i _!
0 y2 (x) 1 sin (iti/)
+ Jdx J /(x, y)dy+ jdy J /(*, */)dx. 42. J J /(x, y)dxdy =
-1 0
а ' /а2—а:2
0 0
(S)
а "Ка2^2
Jdx J /(x, y)dy + Jdx J f(x,y)dy.43.fdx J f(x,y)dy=
—a Y^^x~z —a __ /a2_ *2
О яа:—x2
a2
4
l/a2-
a2 a l/ a2
= Г dy J f(x, y)dx+ J dy J f(x,y)dx+
0 0 ° fl|1A^
2"+Κ Τ -^
Уа2-у
2 2x
1 3—л:
-f/dj, J /(x, y)dx. 44. Jdx J /(x, i/)di/. Qil? Jdx J f(x, y)dy.
0 a:
—2 a:2+1
180
2 χ
4 »-ТУ
46 j dy j fix, y) dx 47 j d* J / (*, */) djf. 48.J\fc J / (χ, у) dx.
—2 J_ 3_ 1 J[ 2 2i/—5
4^2 a:
2 x+2 2 V2x 2 /4=F
(£9 fdx J f(x, y)dy. bO.jdx j fix, y)dy. Ы, jdx j f(x,y)dy.
-1 a:2
4 Y~y
0 K2a:—a:2
α Уаг—у2
О 2лг—л:2
1 χ
52. jdy j fix, y)dxi &i jdy j f{x, y)dx. 54. J dx J fix, y) dy.
О —Y~y~ Ο α—ί/ О л:2
1 Y~x~ 2 l^^l 5 3—у
55. fdx j f(x9 y)dy. M.jdy j fix,y)dx+Jdy j fix, y) dx.
2 у 4 2 12
57. J <ty J /(*, y)dx+ J dy j fix, y)dx. 58. j Ж, J /(a:, */) dx +
О _y_ 2 _y_ J_ i_
2 2 2 i/
2 2 1 /У 4 /У
+ jdy jf(x, y)dx. 59. jdy j fix, y) dx + J <ty J /(a;, */) dx.
\ у о —/"7 ι у-2
О у3 2 ί/3 4 4
60. j dy j /(x, y)dx + jdy j fix, y)dx. 61. Jcty j fix, y)dx +
Ъг— —6
-j/ 6
0 7y-6
2 4
2 J^_
4
7—a:
2 2-YA-y* _ _
+ jdy j f(x, y)dx+j dy j fix, y) dx. 62. jdx J / (*, ί/) dy =
о j/?_ о г+К^^у1 *
6 7-i/
a Ϋa*—xz
— a λί^Τ
4 у-К Т+У
= j dy j fix, y)dx. GS.jdx j fix, y)dy = jdy ΐ fix,y)dx +
1 *? Λ ..О Г\ V
1 JB_
У
a2
4
О я*—a:2
/a2-
/a2—y2
+ J dy j fix, y)dx+ j dtj j fix, y)
0 а лГИГ
γ-V —
dx. 64.
12
-+y
19
65. 20 -g-. 66. 24 "2j-. 67. 1-g. 68. 10 -^. 69. 7-gp 70. -j-π. 71.-3-.
47 1 3 13
72. -j^-. 73. e. 74. 42. 75. 1) — 4-j7>-; 2) 49; 3) 43 -f. 76. 1) — δ-^;
4 4
2) 45-y; 3) 53-g-; 4) 37 -g-; 5) 56; 6) 93-3-. 77. 1) 2/3 — -5-; 2)-^-π —
181
4 4
2 ΥΎ + -о-; 3) -5- π.
78. 1)-ή-πα3; 2)
< Λ < 45π; 2) 1,77 < /2 < 2; 3) 4π < /3 <
5) 9π < /5 < ΙΟπ; 6) -g- π< /β <~τ~ π.
35πα4
12 "
ΙΟπ
v~r
79. -gQ. 80. 1) 36π^
π . π
5 ^ *^ 2Κ 6
§ 5.2. ЗАМЕНА ПЕРЕМЕННЫХ В ДВОЙНЫХ ИНТЕГРАЛАХ.
ДВОЙНЫЕ ИНТЕГРАЛЫ В ПОЛЯРНЫХ КООРДИНАТАХ
Криволинейные координаты на плоскости.
Рассмотрим непрерывно дифференцируемые функции и и ν
прямоугольных декартовых координат χ и у:
α = φ(*, у), υ = ψ(χ, у). (5.18)
Предположим, что уравнения (5.18) однозначно разрешимы
относительно χ и у:
х = Ч>х(и, υ), у = Цг(и, υ), (5.19)
где φι (и, υ), ψχ (и, υ) — непрерывно дифференцируемые функции
и и v.
Придавая поочередно и я υ различные· (возможные для них)
постоянные значения, получаем два семейства линий на плоскости
jfcCMSt
Рис. 5.16
(рис. 5.16, а); эти линии называют координатными линиями.
Положение точки Μ на плоскости определяется парой чисел (#, у)
или парой чисел и, υ> где и и υ выражены формулами (5.18). Пара
чисел и, ν называется криволинейными координатами точки Μ на
плоскости.
Примером криволинейных координат являются полярные
координаты, в этом случае и = г, ν = φ. Координатные линии —
концентрические окружности и полупрямые, исходящие из начала
координат (рис. 5.16, б). Прямоугольные координаты — также част-
182
ный случай криволинейных: и = χ, υ = у. Координатные линии —
прямые, параллельные осям координат (рис. 5. 16, в).
Замена переменных в двойных интегралах.
Если непрерывно дифференцируемые функции (5.19) осуществляют
взаимно однозначное отображение области (S) плоскости Оху
в область σ плоскости Ouv (рис. 5.17), то
, у)dxdy = /[φι(и, ν), ψχ{и, ν)] Ι/1dudv, (5.20)
(S) *;
у
о
σ
σ
JT D\
Рис. 5.17
a
ρ=χψ)
Рис. 5.18
J (и, υ) =
__ дх ду
ди ' dv
£-г- («о
где J (и, ν) — функциональный определитель (или якобиан),
дх дх
ди dv
ду ду
ди dv
Двойные интегралы в полярных координатах.
В случае перехода к полярным координатам χ = ρ cos φ, у = ρ sin φ
формула (5.20) принимает вид
J J /(*> У) dxdy = JJ /(p cos φ, psinq>)pdpdcp, (5.22)
(S) σ
183
так как модуль функционального определителя в этом случае
| J | = р. (5.23)
Если область σ (рис. 5.18, β, в) ограничена лучами,
образующими с полярной осью углы * φχ = α, φ2 = β, и кривыми ρ =
= Pi (φ), ρ = Ρ2 (φ) [ρι (φ) < ρ2 (φ)], το
? p2 {?]
JJ/(pcos(p, ρ sin φ) pdpc/φ = J άψ \ /(ρ cos φ, ρ sin φ) ρ(ίβ. (5.24)
σ α Ρι (φ)
Если область σ охватывает начало координат,
2* ρ (φ)
J J / (ρ cos φ, ρ sin φ) ράρώρ = ^ dtp J / (ρ cos φ,ρ sin φ) pdp. (5.25)
ПРИМЕРЫ
1. Вычислить J p3sincpd(pdp, где область σ — круговой сектор,
ограниченный линиями φ = 0, φ
-, γ = 2 (рис. 5.19).
Рис. 5.19
Рис. 5.20
Рис. 5.21
Применим формулу (5.24). В данном случае α = 0, β = -^-,
Pi (φ) = 0, р2 (φ) = 2. Указанный круговой сектор — частный случай
области σ, точки А1 и Вх совпадают с точкой О (рис. 5.18, б).
jj ρ3 sin φώρώφ = / dtp /ρ3 sin φφ = j [-ξ- [J sin φ^φ =
σ 0 0 θ'
Τ ~*~ / π \
= J 4 sin tpdtp = — 4 cos φ J = — 4 ί cos -^ cos 0) = 4.
184
2. Вычислить jj pcoscpdpdcp, где область σ ограничена окруж-
σ
ностями ρ = α, ρ = 2α cos φ и лежит вне первой окружности
(рис. 5.20, область ABC).
Область имеет вид, изображенный на рис. 5.18, β (частный
случай области ΑχΑ^ϋ^, изображенной на рис. 5.18, а, точки
Лх и А2 совпадают, точки 5Х и В2 — также).
Найдем пределы интегрирования. Выясним, в каких границах
меняется угол φ, для чего определим координаты точек А и В,
являющихся точками пересечения данных окружностей. Решая
систему уравнений ρ = α, ρ = 2α cos φ, находим а =» 2а cos φ,
1 — я я; тт я 0 я
откуда cos φ = -g-, Φι = ——, Фг = -у· Итак, а = —^-, β = —.
При фиксированном φ из указанного промежутка —^-, -^
ρ будет меняться от ρχ = а до р2 = 2а cos φ (луч ОЕ,
соответствующий данному значению φ, пересекает первую окружность
в точке Д вторую —в точке Е). Следовательно, Ρι(φ) = α,
р2 (ф) = 2а cos φ.
Таким образом, по формуле (5.24) получаем
π
. ~3~~ 2а cos φ
I I ρ cos φάράφ = I dtp /ρ cos q>dp =
г а
З"
3 3
С ίο2 |p=2acostP\ 1 С
= cos φ -ν dcp = "ο" [(2α cos φ)2 — a2] cos (pd<p
3
π
Ύ
= 2α2 I cos2 φ cos φ<ίφ — ~2~ I cos φ<ίφ =
"~ Τ "~ΊΓ
Τ" Τ"
= 2α2 1(1— sin2 ф) cos tpdtp — -у I cos tpdtp =
~~Τ ~~ΊΓ
Τ" Τ
= ~2~α2 Ι coscpdip —2a2 I sin2 φ<ί (sin φ) =
185
= "4~ α2 sin φ
2α2
а2 УЗ.
3. В двойном интеграле J j f(x, y)dxdyy где (S) ограничена
(S)
окружностью х2 + у2 = 1 и прямой χ -\- у = 1, перейти к полярным
координатам и расставить пределы интегрирования в том и другом
порядке.
Область интегрирования является сегментом круга х2 -f- у2 = 1,
отсекаемым прямой л: + у = 1 (рис. 5.21). В прямоугольных
декартовых координатах данный двойной интеграл сводится к повторному
ί = /J / (*> у)dArd^= /dx J / (*> у) dy·
(S) 0 1— χ
Перейдем к полярным координатам χ = ρ cos φ, у = ρ sin φ.
Напишем уравнения линий, ограничивающих область (S), в
полярных координатах. Уравнение окружности х2 + У2 = 1 перейдет
в уравнение ρ = 1, уравнение прямой χ -{- у = 1 примет вид ρ (cos φ+
+sin φ)= 1 или 2psin-j- cos I—.—φ] = 1, т. е. рcos f — φ
= ——. Угол φ меняется от 0 до -γ. При фиксированном
значении угла φ (θ < φ < -у) соответствующий луч О В пересекает
границы области в точках А и В (сначала в точке Ау
принадлежащей прямой, затем в точке В, принадлежащей окружности),
__(-г-ф)
1
т. е. ρ меняется от pi = ■■" _ — ^ = -=— до р2
Следовательно,
/ = j dtp J f (p cos φ, ρ sin
see (-£-<?)
VT
Поменяем порядок интегрирования в данном интеграле.
Пределы интегрирования можно установить следующим образом.
Зададим такое значение ρ = р0, чтобы окружность радиуса р0
проходила внутри области (S). Она пересечет хорду сегмента
186
в точках Си Д значения координаты φ для которых определяются
из уравнения хорды
Полагая в этом уравнении ρ = р0, получаем
φχ = -Ц arc cos j=r-, φ2 = -χ- -г arc cos τ=·
Ψ 4 Ρο V 2 Ψ2 4 Ρο V 2
Эти значения и являются пределами переменной φ во
внутреннем интеграле, причем индекс при ρ можно опустить.
Во внешнем интеграле ρ будет меняться от наименьшего значения
ρ = -р=, равного длине отрезка ОЕ, до ρ = 1.
Таким образом,
Г d<p Г /(pcoscp, ρ sin φ) pdp =
sec ( j—φ)
1
-—\- arc cos
4 ρ ντ
= Γ dp Γ /(ρ cos φ, psincp)pd(p.
1 π ι
τ^-χ- ~* arc cos =ι
1 2 4 ρ /2
4. Перейдя к полярным координатам, вычислить J j (x2 -f
(S)
+ ί/2) dxdi/, где область (5) ограничена линиями у = х, у = КЗл
и дугой окружности а:2 + У2 = 8, лежащей в первой четверти.
Применим формулы (5.22), (5.24), предварительно выразив
уравнения границ области и подынтегральную функцию в
полярных координатах.
Так как x^pcoscp, у = ρ sin φ, уравнения границ области
принимают вид:
pcoscp = psin<p, tg(p= 1, φχ = -f-;
ρ sin φ = У Зр cos φ, tg φ = j/3, φ2 = JL;
ρ2 cos2 φ -- ρ2 sin2 φ = 8, ρ2 = 8, ρ = γ%.
187
Подынтегральная функция χ2 -f у2 = ρ2 cos2 φ + ρ2 sin2 φ = ρ2;
вместо dxdy нужно подставить pdpdtp:
Χ2 + y2) d^di/ = J ώρ J p2pdp = Ji/φ J* ρβφ =
(S)
'«Ι-Ϊ—τ—ί-·
Замечание. Вычисление данного интеграла в
прямоугольных координатах сопряжено с гораздо большим объемом
вычислительной работы.
9 L
Г
/[
Ч
5
III IIII||| ЩИII
jlll
/
9 U
Рис. 5.22
5. Перейдя к полярным координатам, вычислить
SSV
(S)
1 + _*ч-_£
α2
- dxdy,
где область (S) ограничена линиями (χ2 + у2)2 = 2а2ху, у =
= х(х>0, у< х).
Область интегрирования ограничена дугой лемнискаты Бер-
нулли и отрезком прямой у = χ (рис. 5.22, область ОАВ).
Границы области в полярных координатах # = pcoscp, у —
= ρ sin φ:
ρ2 = a2sin2cp, ρ = aV'sin2(p, tg φ = 1;
пределы интегрирования:
Φι = 0, φ2 = -j-, ρχ = 0, р2 = a |/sin 2φ;
188
подынтегральная функция
По формуле (5.24) получаем
4 a /sin2f
V1+^r dxdy=-r!d(f S Уа2+ρ2ρφ·
(S) О О
Вычислим внутренний интеграл:
a Ysin 2φ a Ysin 2φ JL
о о
3
_ J_ (a2 + ρ2) 2 |β /Sin 2φ _ J
lo " 3W"
_ ^ -4-/1* sin 9nri2 __^21==
0
2 _3_
2
3
TO
= f-[(a2 + a2sm2<p)z ~(a2)z]
--^[(1+8ίη2φ)2 -1].
Так как
1 + sin 2φ = 1 + cos (-J- — 2φ) = 2 cos2 ί-5- — φ),
(1 + sin 2φ)~*~ = [2 cos2 (-*- _ φ)]^ = 2 |/^cos3 (^ - φ),
поэтому
4 a Vsin2?
-i-Jdcp J W + pVp =
0 0
Τ
= ^/[21/2со8з(^--ф)-фФ =
О
π
4~
= 4-/[2У2со^(^—Ф)сов(^—φ)-ΐ]<ίφ =
О
π
Τ"
,= 4-/{2Κ2(ΐ-8ίη»(^-φ)]α»(-^-φ)-ΐ}Λρ =
189
= 4[-2/23ίπ(^-φ) + ^5ίη3(^-φ)_φ]
*.2/2sIn4—
2 12 . з π
-^-Sin-4"
з
= t(*-t-t)-w(»-**
Следовательно,
Я V
1 +
*2+*/2
dxdi/= iL(20 — 3π).
(S)
6. В двойном интеграле ^ f(x, y)dxay, где область (S) огра-
(S)
ничена линиями х = 0, у = О, # + у = 2, перейти к новым
переменным г/, у по формулам:
ы = х + У, ϋ =
2у
(1)
Найдем функции φχ(ί/, у), ψι(ί/, у), определяемые
формулами (5.19), т. е. выразим из уравнений (1) χ и у через гг, у:
_ и (2 — ϋ) _ Ht>
# о » У ~9~·
(2)
Область (S) плоскости Оху при преобразовании (2) перейдет
в некоторую область σ плоскости Ouv, границы которой будут:
и = О, и =* 2, ϋ = 0, г; = 2. Эти равенства получены из уравнений
χ = 0, |/ = 0, х + у = 2 и формул (2). Действительно, если л: = О,
то и (2 — ν) = 0, откуда г/ = 0, у = 2; если у = 0, то и = 0, у = 0;
если *+У = 2, то и = х + у = 2, и = 2. Область σ в плоскости
Ouv является прямоугольником (рис. 5.23, а, б).
Найдем выражение для якобиана преобразования (2). Так как
дх \
ди ^~
Ι — υ
2 '
е (5.21)
, ϋ) =
2 —υ
2
υ
~2~
дх
dv
и
~~2~
и
~2
и ду ν ду и
2 ' ди 2 ' dv 2 '
2 — у к , и ν и
~ 2 "2 ' 2 ' 2 ~~ 2
190
Таким образом, в соответствии с формулой (5.20)
/'/ f (χ, у) dxdy = / da J / [ϋ^, f ] JL dv =
(S) Ό Ό
2 2
= -γ I wda I f (u, v) dv,
где Τ7 {а, у) — / j
м(2-
l>) UV 1
7. Вычислить | ί у k2 — —2— -^- d*di/, где (S) — область,
(5)
ограниченная линиями
+ ■
= 1,
+ ·
= 1 (* > 1).
k2a2 ^ k2b2
Для вычисления данного двойного интеграла введем так
называемые обобщенные полярные координаты:
— ρ cos φ, -τ- = ρ sin φ или χ = ар cos φ, у = ftp sin φ (3)
Найдем якобиан данного преобразования (считая ρ = и, φ = ν).
Так как
дх дх · ду , . ду ,
-^ = acos<f>, ау=— apsincp, ^ = 6 sin φ, -^-^fcpcoscp,
по формуле (5.21)
/(Р> Ф) =
I Зд:
dp
3l/
1 aP
дх 1
дф
a» I
дф
a cos φ — αρ sin φ
j b sin φ bp cos φ
afrp.
Подынтегральная функция и уравнения границ области (S)
примут вид:
v>
-У=У1г2-р2 (cos2 φ + sin2 φ) = J/k2 - ρ2;
-J + -p- = p2eos2(p + P2sin2(p = p2, p* = i, Pl = i;
!.£ + £ = *■. p2 = k2, p2 = k.
k2a2
+
k2b2
Итак, преобразование (З) переводит область (S), ограниченную
эллипсами, в круговое кольцо, ограниченное окружностями
радиусов ρ = 1 и ρ = k с центром в точке О. Угол φ меняется от 0
до 2π.
191
По формуле (5.25) находим
JJ ]Л2 - -£- - -g- dxdy = JJj ¥^ab9dpd<p
(S)
2π fc
2π fc
= об] Лр J Vk2—P2pdp=ab f { / (&2 - p2)2 [ - \d{k2 - ρψφ
ΌΊ δ #1
0 — (^2 — 1)" |αδφ
2π
2πα6
(*2-D
ЗАДАЧИ
Вычислить повторные интегралы в полярных координатах:
т. π
2~ 2 π 4 Τ 3
1. Г <ίφ fpcoscpdp. 2. Γ<ίφ fpsincpdp. 3. Γί/φ fp2cos2qxip.
οο οο οο
π
г 2 Ύ a /2~cos~2?
4. J dcp J ρ3 sin 3φφ. 5. J dcp J p3dp.
0 1 π 0
R cos с
4 а У2 cos 2φ
6. j*dq> Г>#2-р2рф. 7. J £ίφ J pscosq>dp.
i? COS φ
8. Γ ί/φ Γ k #2 —ρ2ρ2 cos φφ.
Вычислить двойные интегралы в полярных координатах по
указанным областям σ:
9. J J pdpdcp, σ определена неравенствами 0 < φ <; -ψ,
σ
α < ρ < &.
10. J J cos2cpdpd(p, σ определена неравенствами 0 <φ < -^-,
2<p<4.
192
11. J J psincpdpdq), σ — полукруг 0<p</?, лежащий выше
σ
полярной оси.
12. J J p cos tpdpdtp, σ — круговой сектор, ограниченный ли-
σ
ниями ρ = R, φ = 0, φ = -γ.
13. J J p2 cos cpdpdcp, σ — половина круга радиуса R с центром
σ
в точке N Ы, -4р), расположенная справа от этой точки.
14. jjp3 sin ydpdtp, σ — половина круга радиуса R с центром
σ
в точке M(R, 0), расположенная выше полярной оси.
15. I J р2 sin tpdpdtp, σ ограничена линиями ρ = 1, ρ = 2 + cos φ,
полярной осью и расположена выше этой оси.
16. J J p3sincp<ipd(p, σ ограничена полярной осью, линией
σ
ρ = 1 f cos φ и расположена выше полярной оси.
Расставить пределы интегрирования в двойных интегралах по
указанным областям:
17. σ ограничена окружностями ρ = R, p = 2R sin φ и
находится выше первой окружности.
18. σ ограничена линиями ρ = 1, ρ = 2 + cos φ.
19. σ ограничена окружностью ρ = R.
20. σ ограничена окружностями р = Rx, p = R2(Ri < R2)·
В двойном интеграле J | / (χ, у) dxdy перейти к полярным коор-
(S)
динатам, положив x = pcoscp, у = ρ sin φ, и расставить пределы
интегрирования в случае указанных областей (S:)
21^ (S) ограничена линиями х2 + у2 = 1, х2 + у2 = 4, у = х,
У=\~Ъх.
22. (S) ограничена линией х2 + у2 = 27?*.
23. (S) ограничена линией х2 + У2 = 27?у.
24. (S) ограничена линией (л:2 + У2)2 = я2 (*2 — У2)·
25. (S) ограничена линией (л:2 + У2)2 = 2а2ху.
Переменить порядок интегрирования в следующих интегралах,
заданных в полярных координатах:
2 a cos ~ 2 а У sin 2φ
26. f d<p J '/(ρ, φ)dp (α>0). 27. Jdcp J /(ρ,φ)dp
(a > 0).
193
28. Jd(pj7(p, φ)Φ (0<α<2π).
ο ο
Перейдя к палярным координатам, заменить двойные
интегралы однократными:
29. J J f (χ2 + у2) dxdy, (S) - круг х2 + у2 < Я2.
(S)
30. iff (—) dxdy, (S) - кольцо α2 < χ2 + у2 < b2.
(S)
Вычислить двойные интегралы, введя полярные координаты:
31. I I х х у , (S) ограничена линиями х2 + у2 = 4, х2 +
+ ί/2 = 16 (х>0, у>0).
32. I I / х у , (S) ограничена линиями л:2 + У2 = 1, *2+
(S) ' *2 + #2
+ У2 -9 (if>0).
33. [J&'+y'dxdy, (S)-Kpyr *2 + #2<1.
34. J J V^x2 + y2dxdy, (S) определена неравенствами х2 +
(S)
+ y2^2Rx (y>0).
Я cos l^ a;2 4- ί/2 π2
—7=^=^-dxdyf (S) определена неравенствами -V<!
(S) 1/a;2 + ^2
<χ2+ί/2<4π2.
36. Μ cos γ χ2 -f y2dxdy, (S) определена неравенствами
(S)
i£- < χ2 + ί/2 ^ 4π2
37. J/ I/ 25 — x2 — y2dxdy, (S) — круг χ2 + у2 < 9.
(S)
38. ff ахаУ (S)-Kpyr x2 + y2<16.
«/ ·' У 25 — л;2 — у2
(S) *
39. J J (χ2 + у2) d*dy, (S) ограничена линиями х2-\-у2=\,
(S)
40. J J (x2 + y2) dxdy, (S) ограничена линиями (х2 + у2)2 =
(S)
= a2(x2_y2)f y==0 {x>Qy y>Q)
194
41. j j (x* + 2x2y2 + у4) dxdy, (S) определена неравенствами
(S)
x2 + y2>l, х2 + У2<4.
42. J J (x« + 3x*y2 + 3*Y + y6) d*dy, (S) - круг χ2 + у2 < 4.
(S)
43. J J (x2 — y2) dxdy, (S) ограничена лемнискатой {х2 + у2)2 =
(S)
= α2 (λ:2 — ί/2).
44. J J xydxdy, (S) ограничена лемнискатой (х2 -f ί/2)2 = 2а2ху.
(S)
45. J j (χ2 + у2) dxdy, (S) ограничена линией (χ2 + у2)2 = 8 ху.
(S)
46. I I — , (S) ограничена линиями χ = 0, у = О,
?(5) <* + Лт
* + У = 1, * + У = 2.
47. УУ (# + У) dxdy, (S) ограничена линиями х2 + У2 = 1, *2 +
(S)
+ У2 = 4 (у>0).
48. УУ xydxdy, (S) — круг х2 + У2 < а2·
(S)
49. ff VR2 — х2 — y2dxdy, (S) — круг х2 + у2 ^а2 (а< R).
(S)
50. // χ γ R2 — х2 — y2dxdy, (S) определена неравенствами
<S)
x2 + y2^CRx, у>0.
51. J J YR2_^xi_y2> (β) ограничена линиями х2 + у2 = α2,
(S)
x2 + y2 = b2(a<b<R), y = x, y = J/3* (x > 0, у > 0).
52. ff (a:8 + 4χψ + 6χψ + 4x2y6 + у8) dxdy, (S) — круг χ2 +
(S)
+ У2<1.
53. ff(x10 + 5x8y2 + 10*У + 10x4y6 + 5*2y8 + y10) dxdy, (S)—
(5)
круг *2 + y2 < 1.
В двойном интеграле fff(x, у)dxdy по данным областям (S)
(S)
осуществить указанные замены переменных, изобразить на чертеже
каждую область (S) и соответствующую ей область σ
плоскости Ouv:
54. (S) определена неравенствами #>(), у>0, ^х + у^Са;
замена переменных: χ + У = и, яу = и^·
13* 195
55. (S) ограничена линиями ху = ρ, ху = q (0<p<q),
у = ах, у = bx (О < а < 6); замена переменных: ху = и, у = ш;.4
56. (S) ограничена линиями ху = р, ху = q (О <р <q), у2 = ах,
у2 = Ьх (О < а < 6); замена переменных: ху = а, у2 = их.
57. (S) ограничена линиями у2 = рл;, у2 = qx (0 < ρ < g),
л:2 = ш/, л:2 = 6ί/ (0 < а < 6); замена переменных: у2 = ал:, л:2 = ш/.
58. (S) ограничена линиями у — + у -γ = Ι, χ = 0, у = 0;
замена переменных: χ = аи cos4 υ, у = bu sin4 v.
С помощью надлежащей замены переменных вычислить
следующие двойные интегралы:
С Г ι ί "5? W х2
59. Μ у 25 —[б" ~" 25" dxdy, (S) ограничена линией т^- +
у*
5
60.
(S)
4--2- = 1
^ 25 *
(S)
\ \ у R2 — —г— η^- dxdy, R > 1, (S) ограничена линией
^ Л2 1в
61 - V 1 —Г д.2 2,» (S) ограничена линией
У25 ""~"55~~Тб~
25
16 ь
Я dxdy
г χ2 8, с> 1, (S) ограничена линией
Г ^ ~~ ~^~ "" "62"
(S)
£l_L^l- 1
α2 "Г b2 — Ь
63. I / ( |/ -|- + у -γ-) dxdy, (S) ограничена осями коор-
(S)
динат и линией у -|- + у -у- = 1·
64. ff xydxdy, (S) ограничена линиями у == ах3, у = Ьх39
(S)
у2 = рх, y2 = qx (0 < а < Ь, 0 < ρ < ί/).
65. У/ xnyndxdy (n — натуральное число), (S) ограничена
(SL _
линией У χ + Υ у = 1 и осями координат.
66. У/ xydxdy, (S) ограничена линиями *2 = ау, х* =
(S)
= by (0 < α < 6), ί/2 - рх, y2 = qx (0 < ρ < ?).
196
67. f f (χ2 + у2) dxdy, (S) ограничена линиями xy = ρ, xy = q,
\s)
y = ax, y = bx (0 < ρ < q, 0 < a < b, χ > 0, у > 0).
68. ff Уху dxdy, (S) ограничена линиями xy = ρ, xy = q
\s)
(0 < ρ < ?), у2 - αχ, у2 - bx (0 < α < 6).
69. f f (x2 + у2) dxdy, (S) ограничена линиями у2 = px, у2 =
(S)
= qx (0<p<q), у = ах, у = bx (0 < a < 6).
70. /У xydxdy, (S) ограничена линиями у2 = px, у2 = qrjc
(S)
(0<p<q), y = ax, y = bx (0 < a < 6).
71. Доказать, что /У xnymdxdy = 0, где (S) — круг х2 +
'(S)
+ ί/2 <; Я2; η, т — натуральные числа и по меньшей мере одно из
них является нечетным.
72. С помощью замены переменных доказать тождество
2 2 2
| ] cos (2г sin φ sin θ) dtpdQ = | ) cos (2 sin λ) ώλ
b b ό
(при любом ζ = const).
ОТВЕТЫ
. 1 1 πα4 1 ί π 2 \ πα5
1. 2. 2. 16. 3. 4 -γ. 4. 2 -у. 5. -j-. 6. -3- /?з /-— __^-j. 7# __# yKa3a.
Τ j3_
η и е. При вычислении интеграла 1(1—2sin2 φ) 2 cos φ<ίφ положить Ϋ~2 sin φ =
о
= sin/. 8. -35-. 9. -^- (62 - α2). 10. 1. 11. /?2. 12. -у-. 13.-|- Д».
14. -у- /?*. 15. 6. 16. 1 -j-. 17. фж =-?"· φ2 = "β" π, Ρι = /?, pr,
= 2/? sin φ. 18. фх = 0, φ2 = 2π, Ρι (φ) = 1, ρ2 (φ) = 2 + cos φ. 19. φχ = 0,
φ2 = 2π, р! = 0, р2 = /?. 20. φ1==0, φ2 = 2π, pi(q>) = #lf ρ2 (φ) = #2.
21 · Ψι=1". ^2 = 3"» Ρι^1' Ρ2 = 2· 22· Ψι = — "2". φ2 = -=2~, Ρι = 0,
ρ2 = 2/? cos φ. 23. φι = 0, φ2 = 2π, ρχ = 0, ρ2 = 2/? sin φ. 24. φχ = — -j-,
π 3 5
Φ2 = -4". Ρι = 0, ρ2 = α ]/cos2<p, φ3 = -4"π, φ4 = "4-π, ρ3 = 0, ρ4 =
r π *
= a]/cos2<p. 25. ф! = 0, φ2=^-, Ρι = 0, ρ2 = a psin2q>, φ3 = π, φ4 =
197
ρ
arccos —
a
= ~o~ π> Рз —0, Ρ4 = α J^sin2<p. 26. ./ dp J f (ρ, φ) d<p.
π . ρ»
arcsin -ί—
2 α2
#
27. f dp / /(ρ, φ)Λρ. 28. /dp//(ρ, φ) Λρ. 29. 2π / / (ρ2) pdp.
Ο i_ arcsin-4 Ο ρ О
2 α2
2π
30. ^^- J /(ctgq>)d(p. 31. 6. 32. 8. 33. n(e— 1). 34. !*!£!. 35. — 2π.
ο 9
122 15 πα4
41. 21π.
44.
36. 2π —π2. 37. -у π. 38. 4π. 39. -у- π. 40. -gy 41. 21π. 42. 64π.
Указание. χ« + 3*V + 3*У + */6 = (χ2 + */2)3 = ρ6. 43. —. ■„. 6
14 α4 2π 2 /?*
45. 2π. 46.1. 47.—. 48. -у. 49. -у- [/?3 — (Я2 — α2) ]. 50. -yp
51. -7S- (Κ /?2 — α2 — / /?2 — 62). 52. -у. У к а з а н и е. х8 + 4*У + 6*У+
12
+ 4*У + </8 = (*2 + Л4 = Ρ8· 53. -у. 54. -Μ ^ | / [ Ц(аа Р) .
6 о
<? 6 q Ь
~^ udu. 55. 4 J Λι J/ (]/-iL, Vw) %-■ 56. ^ Jd« j) ψ£,
pa pa
π
q b Ι Ύ
Vuo ) -y-. 57. -j- ] du I f Wuv2, V u2v) do. 58. 4a6 I du I f (aw cos4 u,
pa 0 0
3
бы sin4 v) и sin3 ϋ cos3 vdv. 59. -y^ (125 — /243). 60. —y— [R3 — (R2 — 1)2 ].
5 _A _A
61. 40π (5 — γ 24). 62. 2πα6 (с — Vс2 — 1). 63. 2. 64. -^ (а ъ —Ь 5 ) χ
Х(?Т-рТ). 65. (,+ 1)(У2)1)!.(4,+ 3)' 66'-il·- ^2-α2) (^-Λ·
(д2_р2){Ь_а){аЬ+1) 2 7 ,_ „_ Ь
67.
4а6
68. -у- (qVq -pVp)\n—t
аа Ч*-Р* ibl~al , bb~Qb \ ™ (^4-p4) (Q6-^)
ΊαΊ& ^ 5a5£5 У '"' 24a666
198
§ 5.3. НЕСОБСТВЕННЫЕ ДВОЙНЫЕ ИНТЕГРАЛЫ
Интегралы, распространенные на неограниченную область
Рассмотрим функцию / {ху у), определенную в неограниченной
области (S). Предположим, что функция / (а:, у) интегрируема в
любой конечной части (S') области (5), т. е. существует двойной
интеграл
fj f (x, у) dxdy. (5.26)
(S'>
Кривую γ, отсекающую область (5'), всеми ее точками станем
удалять в бесконечность так, чтобы наименьшее расстояние R ее
точек до начала координат неограниченно возрастало, а отсекаемая
ею переменная область (S') постепенно охватывала все точки
области (S).
Несобственным интегралом от функции / (а:, у) в
неограниченной области (S) называется предел (конечный или бесконечный)
интеграла (5.26) при R -> сю:
Jf / (χ, у) dxdy = lim j*f / (χ, у) dxdy. (5.27)
(S) R-*>oo(S')
В случае существования конечного предела интеграл (5.27)
называется сходящимся, в противном случае — расходящимся.
Функция, для которой интеграл (5.27) сходится, называется
интегрируемой (в несобственном смысле) в области (S).
Приведение двойного интеграла к повторному
Пусть функция / (а:, у) задана в неограниченной области любого
вида. Полагая ее равной нулю вне этой области, всегда можно
свести дело к случаю неограниченной прямоугольной
области—одному из прямоугольников: Pi = [а, Ъ\ с, оо], Р2 = [а, оо; с, d],
Ρ = [а, оо; Ь, оо] или к сумме некоторых из этих прямоугольников.
Если в каждом конечном прямоугольнике [а, Ь\ с, d] (при любых
b > α, d > с) существует в собственном смысле двойной
интеграл от данной неотрицательной функции /(а:, у) и
простой интеграл по у, то
Я/(х, у)dxdy = fdx J f(x, y)dy9 Ρ = [α, оо; Ьу оо], (5.28)
Р ас
где
ldx]f(x, y)dy = lim \dx]f{x, y) dy, (5.29)
b—>QO
d-*oo
в предположении, что повторный интеграл сходится.
199
Если функция / (а:, у) меняет знак в бесконечной области (S),
формула (5.28) верна при дополнительном условии сходимости
повторного интеграла от абсолютной величины данной функции
]dx°°\\f(x,y)\dy. (5.30)
а с
Двойные интегралы от неограниченных функций
Пусть функция f(x, у) задана в ограниченной области (S), но
оказывается неограниченной в окрестности некоторой точки Μ (χ, у),
а в любой части области (5), не содержащей этой точки, она
является интегрируемой в собственном смысле.
Выделим особую точку М0, окружив ее кривой γ0. Если
удалить из области (S) окрестность, имеющую площадь и
ограниченную кривой γ0, получим область (5'), для которой существует
двойной интеграл
Nf{x,y)dxdy. (5.26')
<s')
Станем «стягивать» кривую γ0 в точку М0 так, чтобы
диаметр d области, ограниченной γ0, стремился к нулю.
Несобственным интегралом от неограниченной функции f (x, у)
по области (S) называется предел интеграла (5.26') при d ->· 0:
Я /(х, У)dxdy = lim Jf / (x, У)dxdy. (5.31)
(S) d->0(S')
Если указанный предел существует и конечен, интеграл (5.31)
называется сходящимся, в противном случае — расходящимся.
Аналогично определяется несобственный интеграл в случае,
когда имеется несколько отдельных особых точек или указанные
точки заполняют особую линию.
Замена переменных в несобственных двойных интегралах
В плоскости Оху и Ouv рассмотрим ограниченные области (S)
и σ, связанные формулами преобразования:
χ = φι (и, υ), ί/ = ψχ (и, υ)
или обратными им:
и = У(х,У), ν = ψ(χ, у),
с соблюдением условий, о которых шла речь в § 5.2 (см.
формулы (5.18) и (5.19)).
Пусть в области (S) задана функция f(x, у), непрерывная всюду,
за исключением конечного числа отдельных точек или кривых, где
200
она обращается в бесконечность. В этом случае выполняется
равенство
Я/ (х, У) dxdy = I f / [φχ {и, ύ), ψχ (и, υ)] J (и, ν) \ dudv, (5.32)
(S) я
если сходится один из этих интегралов (сходимость другого
следует отсюда).
Формула (5.32) верна и для случая неограниченных областей.
Замена переменных наряду с переходом к повторному интегралу
является удобным средством для установления сходимости
несобственных двойных интегралов.
ПРИМЕРЫ
1. Исследовать, сходится ли двойной интеграл
(S)
dxdy
х3у2 '
где
область (S) определена неравенствами χ > 1, ух ;> 1.
Данный двойной интеграл является несобственным, так как
область интегрирования — бесконечная часть первого квадранта,
ограниченная слева прямой χ = 1 и снизу гиперболой ху = 1
(рис. 5.24, а).
б JC
Рис. 5.24
Рассмотрим конечную часть области (S) — область (S'),
ограниченную линиями x=l,x = b, y = —, y = d (рис. 5.24, б, область
MDAB). В области (S') двойной интеграл существует в собственном
смысле (при любых Ъ > 1, d > 1):
ι Ϊ
.U χψ ~ J axJ χψ J [ xsy
(5') J 1 \/x 1
y=d
dx =
ly=—
201
b,
b, Α
ι Γ ώ2
-/1-ά"·-^-/#-4-/^-(-τ)
-(-т+')+т(^-')-('-т)+4(^-')·
Поскольку подынтегральная функция положительна во всей
области (S), то в соответствии с формулами (5.28) и (5.29)
ъ
f№ = Cdxf jy_ = \[m idx г dy =
'is [(>-i)+4 (ΐ-■)]-'·
6-00
rf-00
Следовательно, данный несобственный двойной интеграл
сходится и равен единице.
2. Исследовать, сходится ли J j —- х у —, где (S) — круг
V) J R2 — χ2 — у2
χ2 + у2 < R2·
Данный двойной интеграл является несобственным, так как
подынтегральная функция не ограничена в данной области (на
границе области, т. е. на окружности х2 + У2 = R2, она обращается
в бесконечность).
Для решения вопроса о сходимости интеграла перейдем к
полярным координатам по формулам χ = ρ cos φ, у = ρ sin φ:
1 _ 1 .( ) =
VRZ — x2-if ~~ У /?2 — ρ2 ' Ι®' φ' Ρ'
пределы интегрирования:
α = Ο, β = 2π, р! (φ) = Ο, ρ2 (φ) = 7?.
Формула (5.32) в данном случае примет вид
Л /Я2-*2-/ ~ «'J К^=У2
Так как
J J |//?2_p« J YJ )//?2_p2
2.t 4- . „ 2-
p=0
1 J* (Я»--р*) йф = fRdV = 2nR,
202
то
dxdy
= 2nR,
{S) У&-х*-ф
т. е. двойной несобственный интеграл сходится и равен 2nR.
dxdy
3. Установить, при каких α и β сходится
(S)
х /у
(а>0,
β > 0), где область (S) определена неравенствами у ]> 1, ху >- 1.
Областью интегрирования является бесконечная часть первого
квадранта, ограниченная прямой у = I и гиперболой ху=\.
Рассмотрим конечную часть (S') данной области, ограниченную
линиями х = —, χ = Ь, у = 1, у = d(b > 1, d > 1). Двойной интег-
у
рал по области (S') существует. Действительно,
d b d b d
ι ι x У ι
-α-t-l
-Sir"
U—+1.
-τ)
-a+1
a+1
x=b
dy=
-a + 1
= i(&s^
1
■β+α-1
^^,.;1(1.g)H!/=
+
-3+a
<α-1)(α-β)
Следовательно,
ι ι/y x У
a—1
6—+i
(l-a)(l-
6-°+'
(1-α)(1-β)
^ = т=1г
(<*-?+· — 1) +
-P+i
β+1
+
β)
(d-
(ο-1)(ο-β)·
-3+1
1) +
,,-?+«
(ο-1)(α-β)·
Предел этого интеграла при Ь -* <х>, d -> σο существует, когда
— а+ 1 < 0, — β + α<0, т. е. а > 1, β > а.
Итак, получены условия сходимости: β > α > 1. При
выполнении этих условий
Я-Л-У — lim I dy I —^г = lim —т.—Ц-^—-ir-^ +
ίί-»0Ο
<ί-οο
-ι- (a_i)(a_P)J
(ο-1)(α-β) (β-α)(α-1)·
4. Установить, при каких m сходится ))тш
где (S) — круг л:2 + у2 < Я2.
- х2 — у2)"
(т>0),
203
Подынтегральная функция определена во всех точках круга,
за исключением его граничных точек. На границе круга (т. е. на
окружности х2 + у2 = R2) она обращается в бесконечность.
Для выяснения условий сходимости данного несобственного
интеграла перейдем к полярным координатам χ = ρ cos φ, у = ρ sin φ.
Получаем
^ R _,, 2,
Яахау — С И Г РФ 1_ (/?2 — p2)~m+1
{S) (R2 -х2- У2)т ~ J Φ j (R2-P2)m ~ 2 ' - m + 1
—и
ι I" (tf2- /^2)~m+1 - (R2 - o)~m+1 12π
1
Из последнего выражения видно, что интеграл сходится при
т < 1 и расходится при т >- 1.
В случае 0 < m < 1
ГГ__ахау___ Л (D2\\-m
J J (R~ — χ2 — y2)m \ — mK*'
(S) K υ '
Итак, интеграл сходится при m< 1.
Замечание. При т <; О интеграл существует в собственном
смысле.
5. Исследовать, сходится ли Г Г г х уп , где об-
х*
ι/ ι —
(S)
1/1 ^1 ML
У 1~ а2 ~ Ь2
ласть (S) определяется неравенством —г + тг^ 1·
Подынтегральная функция определена во всех точках, находя-
а:2 и2
щихся внутри эллипса -^- + ~|г = 1 · На границе области она
обращается в бесконечность. Для выяснения вопроса сходимости
интеграла перейдем к новым координатам по формулам:
— = ρ cos φ, -|- = ρ sin φ
или
χ = ар cos φ, у = 6ρ sin φ (0 <; ρ <; 1, 0 < φ <; 2π).
Получаем
2- 1
dxdy _ С' f abp
(s) К ^^-^
2t 1 1
= /ЬгЧг^ = ^/*Ь^ =
у ι-ρ* r τ J vjyi-p*
= abj dq>/(l -p*)"T[—Ld(l -p2)]
i-ii 2*
6(1 — ρ2)2 / ίίφ = 2πα6.
|0ό
204
Итак, данный интеграл сходится.
6. Исследовать, сходится ли fl In sin (χ — у) dxdy, где (S) —
(S)
треугольник, ограниченный прямыми у = О, у = χ, χ = я.
Введем новые переменные по формулам:
и-\- ν и — ν
X 9 ' У 9 '
(1)
Преобразование (1) переводит треугольник (S) плоскости Оху
(рис. 5.25, а) в треугольник σ плоскости Ouvy ограниченный
прямыми и = υ, и + υ = 2π, у = 0 (рис. 5.25, б).
JT jt
27F U
Так как
У(и, υ) =
1
Τ
1
2
1
2
1
2
ТО
(S)
= * |7(Μ>ϋ)|== *
In sin (χ — у) d*di/ = -γ J J In sin усЫу = J J In sin vdudv,
где Δ — треугольник, ограниченный прямыми и = υ, и = π, ι; = 0.
Следовательно,
/ In sin ydacfo = -ί- J rfw / In sin νάυ = γ J In sin ycfo = y- In 2,
о о
т. е. интеграл сходится.
Замечание. Здесь принято во внимание, что
тг/2
J In sin #d* = 2~1η2·
205
Этот интеграл (называемый интегралом Эйлера) вычислен с
помощью замены переменной. Полагая χ = 2t, получаем
π/2 π/4
/ = J In sin xdx = 2 J In sin 2tdt.
о о
Так как
In sin 2/ = In 2 sin / cos / = In 2 + In sin / + In cos /,
то
π/4 π/4
1 = -J- In 2 + 2 f In sin tot + 2 J In cos /Λ.
о о
Последний интеграл с помощью подстановки t =-χ и при-
π/2
водится к виду 2 J In sin udu, поэтому
/ = JL in 2 + 2/ или / = - \ In 2.
7. Исследовать, сходится ли JJ cos (#2 + ί/2) d#dy, где область (S)
определена неравенствами л: >- 0, у > 0.
Рассмотрим квадрант круга радиуса R с центром в начале
координат, обозначим его через Кя- Вводя полярные координаты
по формулам χ — ρ cos φ, у = ρ sin φ, получаем
π/2 # π/2 Я
J J cos (x2 + y2) dxdi/ = J ί/φ Γ cos p2pdp = J dcp J cos p2 -^ d (p2) =
кя о о oo
π/2
= i-/sinp2
о
« 1
dq> = γ (sin /?2 — sin 0)-y = — sin #2
Так как sin R2 при R -> oo предела не имеет, данный интеграл
расходится.
00 _
8. Доказать, что j e-*2dx = γ π.
—00
Этот интеграл интересен как пример несобственного интеграла
от функции, первообразная которой неизвестна (не выражается
в элементарных функциях).
Рассмотрим двойной интеграл
(S)
где (S) — круг х2 + y2<CR2.
206
Переходя к полярным координатам, получаем
2тс R 2тс
Ir = J d(f f e-92pdp = — -i- e-P21 / dcp = π (1 — е-*2).
!° о
Квадрат — /?<#<#, — /?<#<# содержит внутри себя
круг х2 + у2 < R2 (О < ρ < R) и сам содержится в круге х2 + у2 <
<; 4/?2 (О < ρ <; 27?), а подынтегральная функция всюду
положительна, поэтому
R R
π (1 - е-*г) = /* < J dx I е-х2~Угау < /2* = π (1 - е"4*2).
-я -я
Принимая во внимание формулу (5.12) (см. пример 4 § 5.1)
и независимость величины определенного интеграла от обозначения
переменной интегрирования, рассматриваемый двойной интеграл
можно записать в таком виде:
R R J R \ / R \ / R \2
)" dx j e-x2-y2dy = [ \ e-x2dx)( J e-y2dy) = ( | e-*2dx).
—7? —R \—R I \—R j \—R
Следовательно,
π(1-Η2)< J e~x2dx) <π(1 — e'AR2\
Переходя к пределу при R -> ос, получаем
00 _
j" e-x2dx = \/ π,
—оо
что и требовалось доказать.
ЗАДАЧИ
Исследовать, сходятся ли двойные несобственные интегралы:
*· / I ~i*~r> (^) определена неравенствами ί/> 1, *у> 1.
ft(s>
2· II ~ίγγ> (5) определена неравенствами #;> 1, ху^\.
3. ffз_^_, (З)-круг *2+ί/2<1·
•У У'*2 + </2
; I /д.2 f ^з > (S) определена неравенством #2+ί/2> 1.
4
(S)
5. fT^fk' (S)-KPyr^ + i/2<l.
(S)
207
(S)
+ ί!»=1(*>0).
(S)
х + У>1
I I дзл/2 > (S) ограничена линиями у = О, i/ = jc2, χ2 -f-
(S)
1 (χ > 0).
7· 1 j (χ + ί)*'' №) определена неравенствами 0<jt<l,
(S)
E/>1.
8. Г Г ^ , (<?)-Круг*2 + У2<1.
V) /l-*2-</2
9· Ι Ι τ _\У_ 2 > (S) ограничена линиями л: = 0, у = 0,
(S)
10. f J sin (л;2 + у2) d#dy, (S) определена неравенствами *>0,
(S)
if>0.
Установить условия сходимости следующих интегралов (α>0,
6 > 0, т > 0):
11. II ~т ——w?r, (S) определена неравенством -^—Ь
- ('-■£-■£-)
12. I I р-^—Γν*"' ^ определена неравенством -^—Ь
■<* ΐ'-ί-fr
#
2
* Л2 ^ А*
(S)
х + у> 1.
13. / / —^-, (S) определена неравенствами #> 1, t/*< 1.
(S) *
14. Μ (х^_У)Гп у (S) определена неравенствами 0<*<;1,
(S)
>1.
15· ίίί^ψ^ (5)-круг *2+ι/2<1.
*(S>
"*- Ι / /д.2 _f Уг\т* (5) определена неравенством *2 + y2> 1.
(S)
"^· Ι / —a X Уь m y №) определена неравенствами jt>-0, t/>0,
(S)
*α + ί/*< 1.
208
*8, I I a 1 Уь\т >(^) определена неравенствами χ>0, ί/>0,
(S) (* + y }
19. I x y —, (S) определена неравенствами л:>0,
(S) ^ —Х—У)т
if>0, xe + y*<l.
20. I | * y ^ ^ , (S) определена неравенствами #>0,
t/>0, jc« + i/6> 1.
Вычислить следующие двойные интегралы:
21. \§ е-(х+УЫхс1у, (S) определена неравенствами 0<л:<у.
(S)
22. I — х у , (S) определена неравенством л:2 + У2 < *·
(i) V^ + y2
23. Jj е- (*2+*>2> cos {χ2 + ί/2) rfjcrfi/, (S) — вся плоскость Оху.
(S)
гг -(lL+yL) X2
24. J J e \a- b% ι dxdy, (S) определена неравенством —г +
(S) a
~ A2 ^ x·
25. ff In .J— rf^if. (S) - круг x2 + У2 < 1.
(S) V*2 + i/2
26. ί dx ί dy (a > 0).
•J j/ }Г(а-х){х-у)
1 С
27. Jdxjy a2 — x2 — (c2 — x2)y2 Vc2 — x2dy, где 0 < с < α.
о о
28. Показать, что интеграл I I * 7" ^2 ^*Ф расходится,
J J \χ ι У )
л:>1
00 00 00 00
хотя повторные интегралы J dx J (*2 ~у2)2 dy, J dy J (*2^2)2 dx
ii Ί ι
сходятся.
29. Пусть функции f(x) и φ (у) абсолютно интегрируемы:
первая — в промежутке [а, Ь], вторая — в промежутке [с, к] (каждый
из этих промежутков может быть как конечным, так и
бесконечным). Доказать, что тогда сходится и двойной интеграл
Ь d
Я f (*) Φ (У) ахаУ = ί f Μ dx J Φ (У) dy>
(S) а с
где (S) = [α, b\ с, d].
209
30. Доказать следующий признак сходимости. Если в
область (S) функция / (*, у) может быть представлена в виде / (х, у) =
= (x2 + yi)m , гДе <р(х,у) ограничена в области (S), то двойной
интеграл от функции / (х, у) сходится:
1) при т < 1 в ограниченной области (S), содержащей начало
координат;
2) при т > 1 в бесконечной области, не содержащей начала
координат.
31. Показать, что интеграл )\ sin (x2 -f у2) dxdy расходится,
хотя сходятся повторные интегралы
00 00 00 00
[ dx j sin (χ2 + у2) dy, I dy ( sin (x2 + y2) dx.
bo oo
ОТВЕТЫ
1 3 π
1. Сходится. 1. 2. Сходится. -у. 3. Сходится, "о" π. 4. Сходится. -ψ. 5.
Расходится. 6. Сходится. Указание. Перейти к полярным координатам. 7.
Сходится. 8. Сходится. 9. Сходится. 10. Расходится. 11. т< 1. 12. га> 1. 13. а >
1 1
>6>1. 14. /п>1. 15. га<1. 16. /л>1. 17. — + -g->m. Указание.
Ввести новые координаты по формулам χ = ρ α cos α φ, ί/ = ρ ^ sin β φ. 18. —+
+ ~ь<т- 19· m< L 20· m> L 2!· ~2' 22*2· 23* ΊΓ 24* ~α^ 25* Τ"' 26* πα·
_з_
27. -β- [α3 — (α2 — с2) 2 J. Указание. Ввести новые переменные по формулам
ν ии
j/l+w2 J Yc2(\+u2)-v2 У '
Глава 6
ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ
§ 6.1. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ОБЛАСТЕЙ
Площадь S плоской области (S) равна двойному интегралу от
дифференциала площади dS, распространенному на область (S):
S= (JdS. (6.1)
\S)
В прямоугольных координатах элемент площади dS
выражается формулой dS = dxdy, поэтому
S= ((dxdy. (6.2)
210
Так как в криволинейных координатах элемент площади dS =
= | J (г/, ϋ) I dudv, где «/ (и, ν) — якобиан преобразования χ = φ (и, ν),
у = ty(u, υ), переводящего область (S) в область σ, то площадь
последней
с = j j \ J (и, v)\ dudv.
(6.3)
В частности, в полярных координатах
σ = /J pdpcUf.
(6.4)
ПРИМЕРЫ
1. Вычислить площадь области, ограниченной линиями * =
= у* + 1, χ = 5.
Данная область ограничена параболой χ = у2 + 1 и прямой
х = 5 (рис. 6.1). Решая систему уравнений χ = ί/2+ 1, у = 0,
находим, точку Л(1, 0) пересечения параболы с осью О*. Из системы
уравнений jc = y2-f 1, л: = 5 находим две точки пересечения
параболы с прямой д: = 5 — β (5, 2), С (5, —2). Область ABC является
как областью первого вида, так и областью второго вида.
Рис. 6.1
Рис. 6.2
Применяя формулу (6.2) и рассматривая область ABC как
область первого вида, находим
5 Ух—I
S = jjdxdy = J dx J dy = Jt/
d# =
211
" О
Μ
Г| (5-1)^ - (1 - 1)
2 — — == 10 —
J - з ш з
Замечание. Рассматривая область ABC как область
второго вида, получаем
2 5 2 2
S= jdy J dx= j'(5-y*-l)dy = J(4-y*)dy =
уЧ-i
4f/
—2
3
—2
16
16
3
32
3 *
2. Вычислить площадь области, ограниченную линиями у =
= 2 — а:2, у8 = #2. Область, ограниченная указанными линиями,
изображена на рис. 5.10 (область OM^/lAig).
По формуле (6.2)
2-х2
S= §dx \ dy= J{2 — x2 — x3)dx = 2x
—1 2 —1
3
—Τπ|-ι =2(1 -Ы) —4"(! + !) —-|-(1 + 1) = 4 —
3 5 15 ^ 15 *
3. Вычислить площадь фигуры, ограниченной линией
(χ2 + ι/2)2 = 2α2(χ2 —ί/2).
В силу симметрии кривой относительно осей координат
(рис. 6.2), достаточно вычислить площадь одной четверти данной
фигуры (например, расположенной в первом квадранте).
Переходим к полярным координатам, полагая χ = ρ cos φ, у = ρ sin φ.
Полярное уравнение лемнискаты
ρ2 = 2α2 cos 2φ или ρ = а |/ 2 cos 2φ.
Для указанной части фигуры имеем:
Φι = 0, ф2 = -j-, Pi = 0, р2 = а У2 cos 2φ.
212
Обозначая площадь этой части через Sl9 по формуле (6.4)
получаем
4 α Ϋ2 cos 2s Α α Ϋ2 cos 2? 4
Si = J dcp j pdp = j -ί. | ^φ = α2 f cos 2φ<ίφ =
β2 · η I «2
= -2-sm2<p = -«-.
ο Δ
Следовательно, площадь всей фигуры
S = 4S, = 2а2.
4. Найти площадь фигуры, ограниченной линией (х2 + у2)3 =
= а2 {х* + у4).
Линия симметрична относительно координатных осей. Начало
координат является изолированной особой точкой (координаты
χ = О, у = О удовлетворяют уравнению, но вблизи начала
координат других точек линии нет; в самом деле, при χ > у > 0 из
уравнения кривой получаем (2*2)8> 2а2х*, откуда х>-|-).
Рис. 6.3
Рис. 6.4
Линия лежит в ограниченной части плоскости. Действительно,
при χ > у χ* < 2а2*4, х2 < 2а2, J χ |< а |/ 2"; аналогично при у > а:
*/6 < 2α2ι/4, у2 < 2а2, | у |< а ] г 2. Кривая имеет вид, изображенный
на рис. 6.3.
В полярных координатах уравнение кривой запишется так:
р2 = a2 (cos4q> + sinJcp).
213
Принимая во внимание симметрию кривой, по формуле (6.4)
π т.
2 а V cos49+sin49 2
S = 4 j dcp j pdp = 2α2 J (cos4 φ + sin4 φ) dtp =
= 2a2 j cos4cpd(p -f 2a2 jsin4cpd(p.
о о
Вычислим каждый из полученных интегралов:
Ύ Τ Ί~ Τ
J cos*tpdtp -J (cos2 φ)2 dcp = J (1+02Ο82φ) ώρ = i-f (1 + 2cos2(p +
0 0 0 / 0
+ cos2 2φ) dcp = -J- ί (l + 2cos 2(P + ^g0549) dcp =
1 Γ 1 /
= -g- J (3 + 4 cos 2φ + cos 4φ) dtp = — [ 3φ ~f 2sin 2φ +
+ -j-Sin
4
ίη4φ)
2 — * , Q π
16
π.
Аналогично вычисляется второй интеграл:
2 4 2 2
f Sin*cpdcp = j (sin2φ)2Λρ = J /1-cos2<P]2d(p = 1 Г /3
-f- cos 4φ J dtp --
Следовательно,
Ύ
-g- ί 3φ — 2sin 2φ + -χ*sm 4ф
- 4 cos 2φ -f
3
Тб"я·
S - 2α2 j (cos4cp + sin4cp) dtp - 2a2 (-^- π + -Α- π) = -|"
παώ.
5. Найти площадь фигуры, ограниченной линией (χ2 + ί/2)2 =
= 2αχ3(α>0).
Из уравнения видно, что линия симметрична относительно
оси Ох (уравнение не меняется от замены у на — у). Линия
проходит через начало координат (х = 0, у = О удовлетворяют
уравнению) и целиком расположена справа от оси Оу (х не может
принимать отрицательных значений, так как левая часть уравне-
214
ния неотрицательна). Линия расположена в ограниченной части
плоскости (из уравнения видно, что х* <; 2ах3, поэтому χ <; 2α,
а поскольку и у4 < 2ах3, то также и | у | <; 2а). Кривая пересекает
ось Ох при χ = О и χ = 2а (рис. 6.4).
Введем полярные координаты. Тогда
ρ = 2а cos3(p ( γ < φ < -~-
Учитывая симметрию кривой, по формуле (6.4) находим
la cos3^
S = 2 j dy j pdp = 4α2 f cosGcpd(p - 4α2 j (cos2(p)3 ώφ
= 4fl2i(-
1 -j- cos 2φ Νι
Γ
| <ίφ = 4α2-
8 V 8
5 3
φ + 2 sin 2φ + -^- sin 4φ —
sin3 2φ
= 4α2
32
πα*
6. Вычислить площадь, ограниченную астроидой х3 + у =
_2_
- а 3 (см. рис. 8.8 § 8.2).
Параметрические уравнения астроиды:
х = a cos3/, у = a sin3/ (О <; / ^ 2π).
Если заменить α на α (0<ia<;a), получим семейство
подобных астроид, заполняющих данную фигуру:
х = и cos31, у = и sin3 /.
Воспользуемся этими формулами как формулами
преобразования, т. е. перейдем к новым, криволинейным координатам и, ^
(координатными линиями здесь будут астроиды и полупрямые, исходящие
из начала координат). Найдем якобиан преобразования:
J (и, /) =
дх
ди
ду_
ди
дх
~дГ
_ду_
dt
cos3/
sin3/
■ 3u cos2/ sin /
3u sin2/ cos /
3u sin2 /cos2/.
С учетом симметрии кривой относительно осей координат по
формуле (6.3) находим
•S = 4 J du j Зи sin2 / cos2 tdt = 12 J* ^<fo J sin2 / cos2 /rf/ =
215
12 —
1Z 2
a С Г 3
sin21 cos2 tdt = 6a2 \ sin2 ^ cos2 tdt = -^- πα2.
7. Найти площадь фигуры, ограниченной линиями у2 = рх,
у2 = qx, у = ах, у = bx{0<p<q, О < α < 6).
Фигура представляет собой криволинейный четырехугольник,
ограниченный двумя параболами и двумя прямыми, проходящими
через начало координат (рис. 6.5).
!/.
(и-
(/■■ах
<^у:
!С
■-дх
-рх
X
ίΤ'Φ%
р*рх
Рис. 6.5
Рис. 6.6
Введем новые криволинейные координаты и, υ, связанные с
координатами хну формулами:
и =
У*
χ
(p<u<g, α<ϋ<&).
(1)
Эта замена переменных подсказана видом области
интегрирования (в качестве новых переменных взяты параметры, входящие
в уравнения линий, ограничивающих данную фигуру). Из
уравнений (1) выражаем χ и у через и и ν:
χ =
и
"U2
7)2 у У υ '
(2)
Находим якобиан преобразования (2):
J (и, ν) =
дх
ди
ду_
ди
дх
dv
ду
dv
1
υ2
1
V
_2и_
~v*~
и
2м
216
По формуле (6.3)
S = Г Г-£- dudv = j" Ж> j -£-<*" = Г
ο
<?2 — ρ2 1 / 1
ь
<?2 —Ρ2 λ
2υ*
Ρ
3 \ ϋ3
Ь_ д*-рг( ι 1 \ {ς2_ρ2)φ3_αη
\α 6 \ 63 ' α3 / 6α3#>
8. Вычислить площадь криволинейного четырехугольника,
ограниченного линиями у2 = рх, у2 = qx, χ2 = ay, χ2 = by, где
0<p<q, 0<a<b (рис. 6.6).
Сделаем замену переменных по формулам:
у2 = их, х2 = иу (р < и < q, а < υ < 6), (3)
т. е. перейдем к криволинейным координатам α, υ (и и и
сохраняют постоянные значения вдоль парабол у2 == их, х2 = vy\ эти
параболы являются координатными линиями).
Из уравнений (3) выражаем χ и у через и и υ:
О О
χ = J/W*, у = |/ г/2и.
Так как
то
2 2
7Г-=4-« Зу3'
ди 3
J {и, υ)
Ιο формуле (6.3)
6 —<
"~ 3
11 11
дх 2 з з ду 2 з з
di> 3 ' дм 3
2 2
dv 3 '
= — χ, 1 У (α, ϋ) Ι = -g-.
= 4~ ί du j Λ> - 4" ί (6 "" α)da =
ρ α ρ
2-(q-p)= (Ь-аНЯ-Р)
9. Вычислить площадь фигуры, ограниченной линией
I х* у2 \2 χ//
1 а2 г ^2 / с2 '
Линия эта ограничена, симметрична относительно начала
координат, так как уравнение ее не меняется при одновременной
замене χ на — χ и у на —у, проходит через начало координат (эта
точка является единственной точкой пересечения с осями
координат), две симметричные петли ее лежат: одна — в первом коорди-
217
натном угле, другая — в третьем (ибо только в этих четвертях
ху^О и только при этом условии уравнение имеет смысл).
Введем новые координаты («обобщенные» полярные
координаты), которые связаны с декартовыми формулами:
χ = ар cos φ, у = bp sin φ.
Уравнение кривой в новых координатах:
9 ab
рг = —— sin φ cos φ.
Учитывая симметрию кривой и принимая во внимание, что
J (и, υ) = αδρ, по формуле (6.3) находим
_L l/ab . JL
2 γ -7i-sin<pcosf 2
С (* a2b2 С a2b2
S = 2 J dcp abpdp = —— J sin φ cos cpdcp = —^r-
о о ° о
10. Найти площадь фигуры, ограниченной линией I—- + -г-) =
_к* ιβ_
h2 k2
(χ > 0, у > 0).
Введем новые координаты по формулам:
χ = ар cos2 φ, у = 6р sin2 φ.
(Это возможно, так как л: > 0 и у > 0.) Уравнение кривой примет
вид
Р4 = Р2 [-%- cos4 Φ ~ -gr- sin4 Φ
Исключая двойную точку в полюсе (р2 = 0), находим
Р2 = -Jr cos4 Φ — 1Г" sin'φ*
Полученное уравнение, как и исходное, свидетельствует о том,
что равенства возможны, когда правые части уравнений
неотрицательны, т. е. -р |г-^0> -^2~С084Ф £2~sin4<p>0.
Из последнего неравенства находим:
tg'qX-pjp-' tg9<|/·
Ж"*
Это означает, что в задаче рассматривается та дуга кривой, ко-
ά соответс
Так как
г—г"
торой соответствует изменение угла φ от φχ = 0 до cp2=arc tg l/ -|т-
j (ρ, φ) = 2abp sin φ cos φ,
218
по формуле (6.3)
к lAak~\/ a2 ; F2 ~7
arctgK ш V wcosi—wsin*
S = jj\ «/(ρ, φ) Ι (Ιράφ = J j 2a&psincpcos(pd(p=
*TCi*Vw
if a2 b2 \
( -p- cos4 φ £2~ sin4 φ j sin φ cos φ<ίφ
о ^
= ab[—6^С05ф--6^-5Ш «ρJ|o bh --&?
-■^cos«(arctg]/-g-)-|^sin6(arctg |/-g-
Чтобы упростить полученный результат, положим
arct§ Уж = α·
Тогда
tg α = J/ -g£-, cos α
Kl +tg2a " Vak + bh '
tg a V a&
sin a = ,. & — = —A
V\ + tg2 a /afc + bh
Итак,
a36 aty b3h? ab* a*k* _ a*bk(ak + 2bh)
s =
6h2 6h2 * (afc + bhf 6k2 ' (ak + Μ)3 6/ι2 (afc + bh)2
11. Вычислить площадь, ограниченную эллипсом (αχ + by +
+ с)2 + (ax* + Μ + Cx)2 = /ι2, a&i — αχ& Φ 0.
Введем новые переменные по формулам:
и = ах + by + с, и = αχ* + &j# + Съ
откуда
Ьги — bv — bxc + foi «у — ο,λίΐ — ас1 + агс
Х ~~ nh n.h > У —
ab1 — axb ' v abx — агЬ
Эллипс плоскости Оху преобразуется в окрубкность и2
-j- v2 = h2 плоскости Ouvy якобиан преобразования
J (и, υ) = — г> I J (и, υ) I = -—г гт ·
219
Переходя к полярным координатам в плоскости Ouv, получаем
5 = ]] dxdy = jj , abi '!_ ° b | = J J -щ^гщ- =
(S) ι °'
2π h 2-
— .)a4>J \ab1 — a1b\ = \ab1 — a1b\ J 2 "Ψ = Ι α^ — axb Γ
0 0 0
ЗАДАЧИ
Вычислить площади фигур, ограниченных линиями:
1 · У = Ху У = *2. ' 2. у = х2 + 1, л: — у + 3 = 0.
3. у = х, у = 3х, х = 2. 4. х2 + 1 — у = 0, у — 5 = 0.
5. л; -f у — 7 = 0, ху = 6.
6. х2 + у2 = 4, ί/ = 2л: — х2(л: > 0, у>0).
7. у = J/2ax, у = ]/2ал: — х2, х = 2а.
8. х2 -f у2 = а2, л: + у = а.
9. χ — у + 3 = 0, * _ у _ ι = о, χ + 2 = О, у — 4-0.
10. 2х + Зу — 18 = О, χ — 2у — 2 = 0, χ — 2у + 5 = 0, 4х —
— у + 6=_0.
11. V x + Vy = Va, x + y = a.
L· L· А
12. х3 +у3 = а3, х+у = а.
13. х2 = 2Ьу — Ь2, х2 = 2ау — а2 (а>Ь> 0).
Вычислить площади фигур, определяемых неравенствами:
15. |х| + |у|<а. 16. -£- + -g-<l.
17. χ2 + у2 < х. 18. х2 + у2 < 2у.
Перейдя к полярным координатам, найти площади фигур,
ограниченных линиями: '
19. х2 + у2 — 2ах = 0, х2 + у2 — 2Ьх = 0 (О < а < 6).
20. х2 + у2 - а2, х2 + у2 — 2ах - 0, у - 0.
21. х2 + у2 — 2ах = 0, х2 + у2 — 2ау = 0.
22. (х2 + у2)2 = 2а2 (х2 - у2), (х - а)2 + у2 = а2.
23. (х2 + у2)2 = 2а2ху. 24. (х2 + у2)2 - а (х3 + у3).
25. х4 + у4 = 2а2ху.
Вычислить площади, ограниченные петлей кривой:
26. х3 + У3 = аху. 27. (х + у)4 = ах2у.
28. (х + у)3 = аху. 29. (х + у)5 = ах2у2.
Вычислить площади фигур, ограниченных линиями:
чп ( χ2 д- у2 У- χ2 у2 41 ( χ2 · у2 У- *2
220
«•(-S-+-£-)'-^ ». (-5-+-£-)'-"·+*·
Введя обобщенные полярные координаты ρ и φ по формулам
χ = ар cosacp, у = bp sin'cp (ρ > 0), где a, b, a — надлежащим
образом подобранные постоянные и якобиан J (p, 9) = aa6pcosa_19sina-^,
найти площади, ограниченные следующими линиями (параметры
считаются положительными):
34-(i+lbi--f^>°)· 35· (-£ + !)3=-^>°)·
36· (1 + у)4=^+|н*>0'*>>0)· 374+ΐ=| + |·
Произведя надлежащую замену переменных, найти площади
фигур, ограниченных линиями:
38. χ -\- у = а, х + у = Ь, у = kx, у = hx (0 < а < b, 0<fe</i).
39. ху = а, ху = Ь, у = kx, у = hx (0 < а < 6, 0 < fe < /ι).
40. у2 = рх, у2 = qx, ху = а, ху = 6, (0 < ρ < g, 0 < а < 6).
41. ху = а, ху = Ь, у = т, у = η (0 < а < 6, 0 < т < л).
42. (х+2у—1)2 + (2χ + ί/—2)2-9.
= c2(0<t;1<t;<i;2, χ > 0, у > 0).
ОТВЕТЫ
1 1 32 35 4 / о тт \
1. χ. 2.4-2". 3·4· 4·—' 5.—-61п6. β. π—5-. 7. (|-f)^.
8. (iZLl]a2. 9.20. 10.21. П.-^-. 12. _^!_(16— 3π). 13. 1 (a — b) \ Ж
π
14. α2 (π— 1). 15. 2a2. 16. nab. 17. -j-. 18. π. 19. π (62 — a2).
20. JLa2^ « ^
25.
.1 21. a2 \JL — A 22. (π— 1)α2. 23. a2. 24. JiL a2.
26. —g—. Указание. Ввести новые переменные по формулам
2 \ 3 2
πα2 αΓ
a2 Q2 fl2
λ; = ρ cos2<p, у = ρ sin2<p. 27. 21Q . 28. 6Q . 29. 126Q . 30. ah.
π α36 π a5b? razft aft 1 a5ft
31. -g- · ^2". 32. -^ ' -^T-. 33. -2~ (a2 + ft2). 34. -^ 35. -^ . ^.
36. J*, f JL + -JLY 37. *"*. (-*_ + _ϋΛ 38. (^-а2)(/г2-^)
6 U2T ^2/ ' 4 \ Л2 ^ Л» j β" 2(1+Λ)(1+Λ) "
1 Л 1 q η
39. -g-(6 — a) In-у. 40. ~γφ — α) In -*-. 41 (ft —a) In—. 42. 3π.
с2
43. —-ξ- [(ν2 — Vi) (sh 2u2 — sh 2ux) — (u2 — Wi) (sin 2v2 — sin 21^)].
221
§ 6.2. ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ
Объем цилиндроида, ограниченного сверху непрерывной
поверхностью z = f (х, у), снизу плоскостью ζ = Ο я с боков прямой
цилиндрической поверхностью, вырезающей из плоскости Оху
область (S) (см. рис. 5.3), вычисляется по формуле
V= Iff(x, y)dxdy. (6.5)
(S)
Вычисление двойного интеграла, стоящего в правой части
формулы (6.5), в некоторых случаях упрощается при переходе к
новым координатам.
ПРИМЕРЫ
1. Вычислить объем тела, ограниченного плоскостями х-\-2у —
— ζ = 0, 2х + Зу — 18 = 0, χ — 2у — 2 = О, χ = 3, ζ = 0.
Данное тело ограничено сверху плоскостью χ + 2у — ζ = 0
или
ζ = х + 2у9
с боков — плоскостями
2х + Зу — 18 = 0, χ — 2у — 2 - 0,
3,
(1)
(2)
параллельными оси Οζ (уравнения не содержат координаты ζ) и
снизу — плоскостью ζ = 0 (плоскость Оху). '
У
3
2
1
И
I
/
/
с
7
In
1
~2 3 4~~*
Ρ
ис. 6.7
]$>β
в
Χ
11
А
?.,
Z = OL
*Z+</J<^V4
/a
Рис. 6.8
0
7
К
β r
У
В плоскости Оху (ζ = 0) уравнения (2) являются уравнениями
прямых, по которым плоскости (2) пересекают плоскость Оху.
Решая каждые два из них, находим три точки пересечения:
Л(3, 4), 5(6, 2), Ci3,-jf). Следовательно, плоскости (2)
вырезают в плоскости Оху область (S), которая является
треугольником ABC (рис. 6.7). На плоскости (1) точкам Д 5, С будут соот-
222
ветствовать точки Р(3, 4, 11), Q(6, 2, 10), R (З,-^-, 4)
—вершины данного тела.
Так как в данном случае ζ = f(x, у) = χ + 2у, пределы
интегрирования по я: *! = 3, х2 = 6; пределы интегрирования по у:
2 1
ί/χ = 6 тг-х, у2 = —х — I (получено из уравнений прямых АВ
и ВС), то по формуле (6.5) находим
б— ·
V = j j (χ + 2у) dxdy = jdx f (χ + 2y) dy =
(S)
Ύχ-ι
J(*y+y2)
У=Ь-тх
y= —x-1
άχ = j Iх № 3" x) + (6 —3- *
•[x(^x-l) + (-l-x-l)2]}dx= Д35
6
= 35/(l--g-))te = 35
X3
36-3
35
36 л
175
d#
2. Вычислить объем тела, ограниченного поверхностью х2 +
+ у2 — ζ = 0, координатными плоскостями и плоскостями # = а,
у = 6 (а > 0, Ъ > 0).
Данная поверхность является параболоидом вращения с
вершиной* в начале координат и осью, совпадающей с осью Οζ. Тело,
ограниченное этой поверхностью и указанными плоскостями,
изображено на рис. 6.8. Область (S), вырезаемая плоскостями
χ = 0, χ = а, у = 0, у = Ь, является прямоугольником ОАСВ.
Так как ζ = χ2 + У2, по формуле (6.5)
v = И (*2 + у2) d^y = Jd* JV + ^ = / (х2у +
(S)
α
С
у=0
<±к =
С ( ъи ι P\j ( b& . ^ Π ba* + b*a ab I 2 , , Λ
3. Найти объем тела, ограниченного поверхностью ζ = с2 —
— χ2 — у2 и плоскостями χ — ^ζα, у = ^zb (а2 + Ь2 < с2).
Поверхность, ограничивающая цилиндрическое тело сверху,
является параболоидом вращения с вершиной в точке Л(0, 0, с)>
область интегрирования — прямоугольник со сторонами 2а, 26 и
центром в начале координат (рис. 6.9).
223
Объем тела
а Ъ
у=Ь
V= fdxf(c2-x2-y2)dy = f(c2y-x2y:
—а —b —a X
= 2 / (с2Ь - х2Ъ - -^-) ах = 2 (с2Ьх
—а
= 4 [c2ta - -^- (α2 + б2)] - -^- [з<:2 - (а2 + б2)].
d# =
*3& б3* \ Г
Рис. 6.9
Рис. 6.10
Замечание. Исходя из соображений симметрии, данный
объем можно найти по формуле
V = 4Jdxf(c2 - x2-y2)dy = 4 J 1Л> — х26
b*
dx
\ah
[Зс2-(а2 + 62)].
4. Вычислить объем тела, ограниченного поверхностью х2 +
+ у2 + ζ — 4 = 0 и плоскостью г = 0.
Разрешая первое уравнение относительно г, получаем ζ -— 4 —
— χ2 —у2. Это уравнение определяет параболоид вращения с
вершиной в точке Л (0, 0, 4), являющейся высшей точкой поверхности
(рис. 6.10). Параболоид ζ = 4 — χ2 — у2 и плоскость г = 0
пересекаются по окружности, уравнение которой в плоскости Оху
имеет вид х2 -f у2 = 4.
224
Формула (6.5) в данном случае запишется так:
V = ff(A-x*-y*)dxdy,
(S)
где область (S) ограничена окружностью х2 + у2 = 4.
Чтобы вычислить интеграл, перейдем к полярным
координатам, полагая # = pcos(p, y = psir\(f. Так как
4 — х2 — у2 = 4 — р2, J (ρ, φ) = ρ, pi = 0, р2 - 2, φχ = 0, φ2 = 2π,
Рис. 6-11
Рис. 6.12
ТО
2π 2 2к
//(4 - r> - t/2)Жи& = /dq> J*(4 - ρ2) рф = / (2ρ2 - 4
(S) 0 0 0 λ 7
ί/φ = 8π.
5. Вычислить объем тела, ограниченного поверхностями χ2 -f
+ у2 — ζ + 1 = 0, г2 + ί/2 + 3ζ — 7 = 0.
Данное тело ограничено двумя параболоидами (рис. 6.11).
Линия пересечения параболоидов определяется системой их
уравнений: ζ= I + х2 + у2, 3ζ = 7
у2. Исключая из этих
уравнений ζ, получаем х2 + у2 = I. Из первого уравнения при х2 +
-|- у2 = 1 имеем ζ = 2.
Итак, линией пересечения является окружность
(пересечение прямого кругового цилиндра х2 + у2 = 1 и плоскости
г = 2).
Проекция этой линии на плоскость Оху также является
окружностью
X*+tf = 1, ζ=0.
15 А. А. Гусак
225
Искомый объем равен разности объемов двух цилиндрических
тел с одним основанием и ограниченных сверху и снизу
соответственно поверхностями:
г = ±(7-х?-у*), z=l + x* + y\
т. е.
V = Уг - V2 = J/4- (7 - х2 - У2) dxdy - fj\ l + x2 + y2) dxdy,
(S) (S)
где (S) — круг χ2 + ί/2 < 1.
Переходя к полярным координатам, находим
V = /<*рЯг<7 - Р2) РФ - Jd«P / (Ρ + Ρ3) Φ = ^ я·
0 0 0 0
6. Вычислить объем тела, вырезанного цилиндром х2 -f у2 = Rx
из сферы х2 + у2 + z2 = R2.
На рис. 6.12 изображена половина тела, объем которого
нужно найти (вторая половина находится под плоскостью Оху).
В силу симметрии
V = 4 /JV#2 - *2 - #2 dxdy,
(S)
где (S) —полукруг в первом квадранте плоскости Оху,
ограниченный линиями у = 0, #2 + у2 = /?#.
Переходим к полярным координатам,. полагая χ = ρ cos φ,
ί/ = ρ sin φ. Поскольку окружность χ2 + у2 = Rx в полярных
координатах имеет уравнение ρ = R cos φ, то ρ меняется от 0 до
Rcostp при фиксированном φ. Далее, в области (S) φ меняется
от 0 до-о-. Заметив, что
V R2 - χ2 - у2 = К Я2 - ρ2,
получим
π/2 7? COS φ
V = 4 J ώρ J I//?2 — ρ2 pdp.
ο δ
Так как
^ COS φ R COS <p J_
о о
Γ Slices <p ,
= -^--XL(^2-P2) Jo =-Γ*·(1-8ίη»φ),
226
то
Но
π/2
π/2
π/2
V = -^-R3 /(1—5ίη3φ)β(φ=-|-π^3- "Γ^3 J"sirfV<P·
it/2
J sin3 φ<ίφ = — J (1 — cos2 φ) d cos φ = —cos φ
π/2
cos3<p
π/2
О
поэтому
V = -±- π/?3
3 3 A l 2 3
7. Вычислить объем тела, ограниченного эллипсоидом
-sl-+iS- + -3- = i («>о. ^>о. с>о).
Разрешая это уравнение относительно г, находим
ζ
f ν*
Рис. 6.13
Рис. 6.14
Вычислим половину указанного объема, т. е. объем тела,
ограниченного поверхностью ζ
_
-и плоскостью
ζ = О и представляющего часть эллипсоида, расположенную над
плоскостью Оху (рис. 6.13).
По формуле (6.5)
'г-cJSV
-Is- dxdy,
227
где область интегрирования (S) ограничена эллипсом — -j- -^- = 1,
г = 0 (получено из уравнения поверхности).
Для вычисления интеграла переходим к обобщенным поляр-
ным координатам, полагая χ = ар cos φ, у = bp sin φ. Так как
ν
1 2 тг = V I — Ρ2, «/ (р» ф) = abp, φ меняется от 0 до 2π,
от 0 до 1, то
2- 1
Vl = с I f У ! ^-4rdxdy = с /dcp/ ^ 1 - р2а6рф =
2- 1 J_ 2π
:/^/(1_р«)2й(1-р^ = —^J*
d<p= -^-·2π.
о т 3
= -f-Ρφ /(1 -р>)2 d(l-tf = -ψ J^f
οο ο -γ·
Следовательно, объем всего эллипсоида V = 2l/x = -^— abc.
4
В случае а = b = с = R получаем объем шара V = -«- π/?3.
Замечание. Объем 1/х можно вычислить по формуле
*/2 1
о о
8. Вычислить объем тела, ограниченного поверхностями
х2 + у2 — ζ = 0, χ + у — ζ = 0.
Данное тело ограничено сверху плоскостью ζ = χ + У,
проходящей через биссектрису второго и четвертого координатных
углов плоскости Оху, а снизу — параболоидом ζ = χ2 + У2· Объем
его равен разности объемов двух цилиндроидов с общим
основанием на плоскости Оху. Это основание ограничено линией,
представляющей собой проекцию на плоскость Оху линии пересечения
данных поверхностей. Уравнение указанной проекции получается
исключением ζ из данной системы уравнений:
z = x2 + y2, z = x + y
и имеет вид х2 + у2 = χ + У, ζ = 0. Это уравнение окружности
--г)2+(у--г)2=-1-' г = 0'
ограничивающей область интегрирования (S).
Следовательно,
v = №+у) dxdy -№2+у2) шу = Я(*+у -
(S) (S) (S)
- х- - л «ω* - - // [(χ - J-)2+ („ - .f )·_ 4]*^.
(S)
228
Переходим к полярным координатам, полагая
χ
Получаем
1 1
ψ = ρ cos φ, у — -γ = ρ sin φ.
Ρ*
и
—/(4-
1
ΥΎ
jpdpdcp
άψ f (ρ
pdp =
1
/Τ
^=/(-Г ϊΗ^ΊΓ
9. Найти объем тела, ограниченного поверхностями г = х2 +
+ У2, ху = р, *y = q, у = ах, у = bx9 z = 0{0<p<qt О < а < 6,
*> 0, */>0).
Указанное тело ограничено параболоидом ζ = χ2 + */2,
гиперболическими цилиндрами ху = ρ, #ί/ =-- q9 плоскостями у = αχ,
ί/ = 6х, координатной · плоскостью Оху и расположено в первом
октанте. Цилиндры и плоскости вырезают в первой четверти
плоскости Оху криволинейный четырехугольник ABCD (рис. 6.14).
Объем тела
V = J ((х2 + y2)dxdy,
где (S) — четырехугольник ABCD.
Чтобы вычислить этот интеграл, введем криволинейные
координаты по формулам:
[ху = α (ρ < α < <?), у = νχ (α < ν < Ь).
(Эти формулы подсказаны видом уравнений цилиндров и
плоскостей.)
Так как
uv
х = У ^, У = V м, х2 + у2 = -£- +
2 V и'
и + ми2 ,
У (^ ϋ):
дм dv
ду_ ду_
ди dv
2 Yuv
V τ, W^r
2ν
TO
(S) j pa
-\-liv2
dv ■
229
--*-/*■/(-$- +«)*--rf(~i- + »)
v=b
du =
2 J
+ *·
4
udu
- + — -*- u>b — ua) du
a J
1 (b — a)(ab+\) u2
2 ab '2
2 \ α b ^
<* (b-a)(ab+\) (
ρ 4ab l
•(^-p2).
ЗАДАЧИ
Изобразить тела, объемы которых выражаются следующими
двойными интегралами:
1 χ 4 3
1. fdxf-^-p — x — y)dy. 2. fdxf{\6-x2)dy.
3. ff (9 —χ2- y2) dxdy, (S) - круг χ2 + у2 < 4.
'<S>
4. J J j/"*2 + У2 dxdi/, (S) ограничена линией (χ2 + у2)2 = 8(х2 — у2).
(S)
Вычислить (и изобразить на чертежах) объемы тел,
ограниченных указанными поверхностями:
5. χ + 2у — ζ = 0, χ — 2у + 5 = 0, 2х + Ъу — 18 = 0, г - 0.
6. 2* + У — ζ = 0, 2л:+ 3ί/— 18 = 0, * — 2у — 2 = 0, 2 = 0.
7. 2х + # — г = 0, χ — 2у + 5 - 0, 2х + Ъу — 18 = О, г - 0.
8. х2 + ί/2 — ζ - 0, χ — 3 - 0, ι/ — 2 = 0, * = 0, у = 0, 2 = 0.
9. *2 + у2 + 4_г = о, ■*:— 2-0, ί/— 3 = 0, χ = О, у = 0,г = 0.
10. х2 + */2 + с — 2 = 0, χ — α = 0, ί/— 6 = 0(α>0, 6 > 0, с> 0),
х = 0, у = 0, ζ = 0.
И. 2= 16 —х2 —у2, х = :±:3, */= ±3, 2 = 0.
12. 2 = α2 — г2, у = 6, ί/ = 0, 2 = 0.
13. χ2 + у2 + 2 — 4 = 0, χ2 + ί/2 — 2г + 2 = 0. '
14. у = г2, χ = у2, 2=12 + */ — *2·
15. 2=-^ + -f-(P>0, 9>о), χ = α, χ = 6(0<α<6), ί/= с,
у = d(0< с < d), 2 = 0.
Перейдя к полярным координатам, вычислить объемы тел,
ограниченных следующими поверхностями:
16. 2 = }/х2 + у2, х2 + у2 = а2, 2 = 0.
17. 2 = х2 + у2, х2 + у2 = а2, 2 = 0.
18. 2 = х4 + ί/4 + 2х2*/2, χ2 + ί/2 = а2, 2 = 0.
19. 2 = χ2 — у2, {χ2 + у2)2 = 4 (χ2 — ί/2), 2 = 0.
20. 2 = χι/, (χ2 + ί/2)2 = 8χι/, 2 = 0.
230
21. ζ = χ2 + у2, (χ2 + у2)2 = 4ху, 2 = 0.
22. 2 = χ2 - у2, (χ2 -ι- y2f = a2 (x2 - у2), 2 = 0.
23. 2 = xy, (χ2 + у2)2 = 2a2xy, 2 = 0.
24. 2 = χ2 + у2, (х2 + у2)2 = 2а2ху, 2 = 0..
25. αζ = χ2 + ι/2, л:2 + ί/2 = 2αχ, 2 = 0.
26. 2 = 1 — χ2 — г/2, у = χ, ι/ = j/"3"Je, 2 = 0.
27. χ2 + ί/2 + ζ2 = α2, (χ2 + ί/2)2 = α2(χ2 — ι/8), 2 = 0.
28. χ2 + у2 + 22 = 2α2, л:2 + г/2 = α2, 2 = 0.
29. χ2 + ί/2 = ζ2, χ2 + ί/2 = 2г/, 2 = 0.
30. г2 = 2*1/, (χ2 -f ί/2)2 = 2а2ху, 2 = 0.
31. ζ = χ2 + у2, ζ2 = xy, 2 = 0.
32. αζ = χ2 + г/2, {χ2 + у2)2 = α2 (χ2 — у2), 2 = 0.
33. χ2 + у2 = 2алг, 2 = for, 2 = 0.
34. z = x + y, (x2 + у2)2 = 2ху, 2 = 0, (χ > 0, у > 0).
Вычислить объемы тел, ограниченных указанными
поверхностями (параметры считаются положительными):
35. -4- + i£-= 1, — = -^- + -4-(с>0).
а2 ' б2 с р2 q2 v 7
36. -J- + -fj- = 1, cz = xy (с > 0, χ > 0, t/ > 0).
37. * + » +-i_ = 1,
a2 ' 62 ' c2 '
38. ^- + -f- +-V=L * = 0, */ = 0, 2 = 0.
\ a2 ^ 62 / ^
39. (4^+-|5-)+-i-=l, 2 = 0.
40. 4r + 4-+4r- =1,
X*
41,
£2 I C2 ' V Я2 ' 62 / rt2 62 "
(■£++)'+-5--'· (■* + *)'-£w>.<>..><».
С помощью надлежащей замены переменных вычислить
объемы тел, ограниченных поверхностями:
42. z = х2 + у2, ху = а2, л# = За2, у = — χ, ί/ = 4л:, ζ = О (* > О,
</>0).
43. г = ху, х2 = у, χ2 = Зу, у2 = х, у2 = Зх, ζ = 0.
44. ζ = χ2 + ί/2, ί/2 = Зх, ί/2 = 4л:, у = χ, ί/ = 2*, г = 0.
45. г2 = *ί/, xy = 1, **/ = 9, ί/2 = χ, ί/2 = 5*, ζ = 0.
46. г = ху, у2 = 2χ, у2 = 3х, у = χ, у = 2χ, ζ = 0.
47. cz = xt/(c > 0), χ2 = ш/, χ2 = 6ί/(0 < α < 6), ί/2 = ρχ,
y2 = qx{0<_p<q), ζ = 0.
48. ζ - | дн/, χί/ - ρ, χί/ = ^ (0 < ρ < q), ί/2 = αχ, у2 =
= bx{0<a<b), z = 0.
49. ζ = ху, у2 = ρχ, у2 = qx (О < ρ <q), y = ax, у = bx(0 <
< a < b), ζ = 0.
231
50. ζ = x2y, xy = ρ, xy = q, у = ах, у = bx, ζ = 0 (0 < ρ < q,
0 < а < b, л: > 0, у > 0).
51. ζ = jc2i/, у = рх3, y = qxs, у = ах, у = bx, z = 0(0<p<q,
О < α < 6, χ > 0).
52. г - х2 + у2, у2 = рл-, у2 = qx(0 < р < q), у = ах, у =
^bx(0<a<b), z = 0.
53. Доказать, что объем тела, ограниченного цилиндром х2 +
+ у2 = R2 и плоскостями z = ax -\- by + с, ζ = 0, равен л/?2с.
54. Доказать, что объем тела, ограниченного поверхностями
*2 + У2 = с2, ζ = 0, ζ [φ (χ) + φ (*/)] = αφ (*) + &<ρ (у), где φ (χ) —
любая положительная интегрируемая функция, а > 0, 6 > 0, равен
±-пс2(а + Ь).
ОТВЕТЫ
5 1 1
1. См. рис. 6.15. 5. 388-^р. 6. 160-|ё-. 7. 58-у. 8. 26. 9. 50. 10. аЬс +
ab _________ 4 _ ,569 _ (6—a) (d—с)/а2+а6+62 ^
+ -з"(а2 + ^2). П. 360. 12. -^аЧ. 13. Зл. 14. у^· 15.
')(a2+ab-
Л Ρ
+ С2 + jd + d2 \ ^
Ltd*. 17. ϋ*.
3 2
18.
_. 19.
16
3
20.
21. Λ
Рис. 6.15
α4 α4 πα4 3π rt π
22.— 23. -g-. 24. -g-. 25. -2" Λ 26. -3-
2 , r— 32
27. -Q- α3 (3π + 20 -
r—ν ζ / Γ— ν ύζ πα° π
16^2). 28. ~3-πα3(2) 2—1). 29. —. 30. —. 31.^. 32.
8
33. jt£q3. 34.
8 ·
35.
-abc
Указание. Ввести новые
232
координаты по формулам χ = αρ cos φ, у = bp sin φ. 36. —«—. См. указание к
задаче 35. 37. -^шЬс (2 — ]Л<Г). 38. ^р 39. ~^abc. 40. -§ аЬс (Зл+
+ 20—16 У 2). 41. —g—. 42. 15α4. Указание. См. решение примера 9.
лп 4 лл 7515 л 52 1365 1
43· Τ' 44·~5Ϊ2"· 45· "Г In 5. 46. —gj2—. 47. -^(62 - α«) (<?*- /Я).
-. 4(,w-,k-p),»|. · *■-*£-->■ s..!^pvt-
§ 6.3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПОВЕРХНОСТЕЙ
Случай явного задания поверхности. Площадь S
гладкой поверхности ζ = г (*, */) выражается формулой
s=//y ^^W-f-)'^· ад
где Ρ — проекция данной поверхности на плоскость Оху.
Если поверхность имеет уравнение вида у = у(х, ζ), то
W//'+(-£)'+(тв'**· №7>
где Ρ — проекция поверхности на плоскость Охг.
Если поверхность задана уравнением χ = х(у, ζ), то
где Ρ — проекция поверхности на плоскость Oyz.
Случай неявного задания поверхности.
Площадь S поверхности, заданной уравнением F (х, у} ζ) = 0,
выражается интегралом
S-
f (V№ (■£№)'
dF
dz
dxdy, (6.9)
где Ρ — проекция поверхности на плоскость Оху.
Случай параметрического задания
поверхности. Если уравнения поверхности заданы параметрически:
х = х(и9 υ), у = у(и, υ), z = z(u9 v), (6.10)
233
где (и, υ) ζ Ρ и Р — ограниченная замкнутая квадрируемая
область, в которой функции ху ί/, ζ непрерывно дифференцируемы, то
где
+
дх
да
S =
\"5ίΓ/
дх
' '~dv~
Ρ
^ Ι ди
4- JL·
^ ди
:0 — F1
■)'■■»-
* dv "1"
ПРИМЕРЫ
dudv
I dx
\ dv
dz
da '
-h
dz
dv
\ dv j
•
(6.11)
' ( дг )г
(6.12)
1. Вычислить площадь поверхности шара радиуса R.
В системе прямоугольных декартовых координат с началом в
центре шара уравнение поверхности его имеет вид х2 + у2 + ζ2 =
= R2 или х2 + у2 + z2 — R2 = 0.
Поверхность здесь задана неявным уравнением F (х, у, ζ) — 0,
где F(x, ί/, ζ) = χ2 + у2 + ζ2 — R2- Воспользуемся формулой (6.9).
Так как
VI
(-
lL-2x — -'
дх ' ду '
1 то
2у,
dF
дг
22,
= 2 У х2 + у2 + z2 = 2R,
= 2ff-Ydxdy (z>0)
или
dxdy
S = 2R\\-=J^
V VR2-x''
Рис. 6.16
где Ρ — круг χ2 + у2 < R2 (рис. 6.16).
Для вычисления полученного
несобственного интеграла перейдем к полярным координатам χ =
= pcos φ, у = ρ sin φ. Находим
2tzR
о г! ν*
pdp
J J I/ R2 _ p2 J У R2 — p2
- 4π/?2.
234
2. Вычислить площадь боковой поверхности кругового конуса
с радиусом основания R и высотой Н.
Начало прямоугольной декартовой системы координат
поместим в вершине конуса, а ось Oz направим по оси конуса
(рис. 6.17).
Уравнение конуса примет вид
Η
ζ = -^- К *2 + У2-
Рис. 6.17
Рис. 6.18
Рис. 6.19
Поверхность в данном случае задана уравнением вида ζ ■■
ζ (χ, у). Вычислим по формуле (6.6) ее площадь. Поскольку
дг Η χ dz Η у
~дх~~ ~#~" V х* + у* ' ~W ~~R" Ух2-\-у2 '
ιΛ+(ΐ№/=]
/
1 +
Я3
+ —·
* D2
Г
R2 x2-\-y2 ^ R2 х2 + у2
-V77
Н2
R2
то
S = ny\+-^dxdy,
где Ρ — круг х2 + у2 <! R2.
Следовательно,
S = SJYn--g-dxdy=yi + J^fjdxdy=Yl+^nR2=
= nR]/R2 + H2\
3. Вычислить площадь поверхности части цилиндра х2 + у2 —
= R2, отсеченной плоскостями ζ = О, ζ = Н.
235
Уравнение данной поверхности не содержит 2, поэтому
применить формулу (6.6) здесь нельзя. Так как данное уравнение
разрешимо относительно у и относительно х, то можно
воспользоваться либо формулой (6.7), либо формулой (6.8). Применим
формулу (6.8). Уравнение половины цилиндра, находящейся впереди
плоскости Ozy (рис. 6.18), имеет вид
VR* - У2·
Так как
VR2
** - . У. -*L-o l/i « /J!L\2_l/^LV
ду ' VR2 — У2 ' дг ~ ' У 1 ~т~ [ду ) ' { дг )
то поверхность цилиндра
s = 2SJvw=wdydz>
где Ρ — прямоугольник, — #< у < #, О < 2 < #.
Итак,
" 3 /?^ = 2/у/ |? <fr = 2^Яагс51п _
4. Найти площадь части поверхности цилиндра х2 + у2— Rx — О,
заключенной внутри сферы *2 + у2 + z2 = R2 (боковая поверхность
«тела Вивиани», см. рис. 6.12).
В данном случае нельзя воспользоваться формулой (6.6), так
как уравнение поверхности цилиндра не содержит 2. Применим
формулу (6.7). Поскольку цилиндр разделяется плоскостью Οχζ на
две равные части, можно вычислить половину искомой площади
поверхности.
Найдем площадь той части поверхности, уравнение которой
R
= 2nRH.
-R
у = У Rx-χ2.
Для определения области интегрирования Ρ следует
спроектировать на плоскость Οχζ линию пересечения поверхностей,
уравнение которой находится исключением у из данных уравнений.
Вычитая одно уравнение из другого, получаем z2 = R2 — Rx. Это
уравнение параболы, лежащей в плоскости Οχζ, с вершиной на оси
Ох на расстоянии R от начала координат и пересекающей ось Οζ
в точках z= R, z = — R. Дуга указанной параболы вместе с
соответствующим отрезком оси Οζ составляет границу области.
Так как
ду R — 2х ду
дх 2YRx-x2' дг
О,
236
ν
4Rx — 4л:2 + R2 — 4/?jc + 4л:2
4 (Rx — л:2)
2 YRx -
TO
Я 1 R*-Rx β
0 _ν/?2__^
dxdz
/? ΐ ι
2 J /#* —**
о
VR*-Rx
dx
-Vrz—Rx
= R
Итак,
VR* — Rx
Yr
i Vr*
dx = R f~ rfx - 2/? VR Vx
я
-, 9E>2
2/?2.
— 4Z?2
4R2.
5. Вычислить площадь поверхности конуса х2 -f- ί/2 — ζ2 = 0,
заключенной внутри цилиндра *2 -f- ί/2 — 2ах = 0.
Цилиндр отсекает на поверхности конуса две части,
симметричные относительно плоскости Оху. На рис. 6.19 изображена только
верхняя часть (ζ^>0). Вычислим площадь S этой части, проекция
которой на плоскость Оху есть круг х2 + У2 <С 2а*.
Так как для рассматриваемой части конуса ζ = Υ χ2 + у2 и
dz = * ^ = У ι/1 . ι дг \* ι дг γ __ ^
дх γχ2 + у2 > ду ухг + у2 ' \ А i- ( dx J + ^ ду J — У 2
по формуле (6.6) получаем
Sx = ff\/2dxdy,
ρ
где Ρ — круг χ2 -f- у2 — 2α* < 0.
Переходя к полярным координатам, находим
π π \2α cos с
2 2ί/ cos ψ
Sx=V2$d4 S pdp = 2/2/4-P'
<ίφ = J/ 2 J 4a2 cos2 φ<ίφ
о
= 2a2 j/2 f (1 + cos 2φ)Λρ - 2a2 γ 2 (φ + 4~sin 2ф)
= 2a2 V2 \Л- + -Lsin π ) = πα2 \ί2.
Следовательно, вся искомая площадь S = 2SX = 2πα2 Υ2.
6. Найти площадь поверхности, вырезанную цилиндром х2 +
+ ι/ = г2 из сферы х2 + У2 + г2 = Я2 (г < #).
237
Цилиндр вырезает из сферы две части, верхняя из них
изображена на рис. 6.20. Вычислим площадь Sx поверхности этой части
сферы. Для верхней полусферы:
dz
г=* VR2 — x2 — y2,
dz _ —У
дх ук2_х2_у2' ду у^__хг_у2
R
■ V*+W+ffl-
У ^2 _ χ2 _ у2
Следовательно,
Sx = (f-7=JL==dxdy,
1 J *> l/ 02 v° ° Ό
p VR2-x2 — y2
где Ρ — круг χ2 + у2 < г2.
Рис. 6.20
Рис. 6.21
Рис. 6.22
Переходя к полярным координатам, находим
*=Ws-yih?**=*s**h* - р2И- 4 w - р2)Ь
о о r A ^ оо L J
= -RJ\r2-92)
d<p = -2nR[(R2-r2Y -R]
Итак,
2nR(R-VR2-r2).
S = 2SX = 4π#(# - l/#2 - z-2)·
7. Вычислить площадь части поверхности эллиптического па-
χ2 „2 у2
2а ~r"W
раболоида ζ = -^—\- -|т-, находящейся внутри цилиндра -^- + т-2
г2
с2 (рис. 6.21).
238
Так как
dz
дх
по формуле (6.6)
где Ρ — область -^- + -|г < с2·
Введем новые координаты по формулам л: = ар cos φ, у =
= fepsinqp. Тогда
S - J"d<pJ V^T+У раМр = 2παδ/(1 + ρ2)2 ~γά{\ + ρ2) =
= nab 3
~2
0+Ρ2)2 2 ,r/1 , 24Τ tl
о
8. Вычислить площадь частей сферы х2 + У2 + ζ2 = /?2,
вырезанных из нее цилиндром х2 + у2 = Rx, воспользовавшись
параметрическими уравнениями сферической поверхности:
χ = R sin и cos υ, у = R sin и sin υ, ζ = /? cos г/
(О < и < π, 0 < υ < 2π).
Здесь идет речь о вычислении площади верхнего и нижнего
оснований «тела Вивиани» (см. рис. 6.12) (в примере 4 необходимо
было вычислить его боковую поверхность).
Воспользуемся формулой (6.11), для чего предварительно
найдем коэффициенты Еу G, F. Так как
&х η ду г» · дг г» ·
-з— = a cos и cos у, -=2_ = Rcosu sin у, —г- = — /< sin г/,
-λγ = —/? sin ί/ siny, -32- = R sin tt cos у, -з—= О,
по формулам (6.12) находим:
£ = Я2, f = 0, G-/?2sin2i/.
Следовательно,
j/£G — /* = /?» sin и.
Ограничимся рассмотрением четверти изучаемой поверхности,
лежащей в первом октанте. Для точек «кривой Вивиани», т. е.
кривой пересечения сферы и цилиндра (в пределах первого октанта),
239
u + v = -γ. Действительно, подставляя выражения χ и у через и
и и в уравнение цилиндра х2 + у2 = Rx, получаем sin и = cos vf и
поскольку для рассматриваемых точек, очевидно, 0<;г/<;-^-,
О < ν < -£-, то отсюда следует, что и + υ = -^-.
Установив на основании сказанного пределы изменения и и
υ, по формуле (6.11) получим
S = 4R2 Г dv f sina<fo = 4#2 f(— саш)
0 0 0
= 4^(^-1)
t 2
dv = AR2 f(l—sinr;)di;=
9. Найти площадь части сферы х2 + У2 + ζ2 = /?2, заключен-
ной между плоскостями χ = ζίζ -^-, # = —-у·
На рис. 6.22 изображена восьмая часть поверхности, площадь
которой требуется вычислить. Для верхней полусферы:
дг
дх
VR2-
— χ
-х2-
=?·
Ζ = у R2 — χ2 — ί/2,
дг _ — у
дУ V R2 — х2 — у2'
_ R
/dz 2
VR2-x2 — y2'
поэтому
о 6 δ
Интегрируя по частям, получаем
R
Г R R 2<« * R
jA2-^" ο/1"
4 (Я2 — χ2)
Χ τ~άχ
(R2-x2)2
1 = 4#Гагс8т-1=-Г хЧ; 1.
J [ V3 J (R*-x*)y^-R2-x2\
240
Для вычисления интеграла переходим к новой переменной φ,
яУг . ~
полагая χ = —^— sin Φ· Тогда
a R1· з" , о . ι
а# = —2—coscpacp, sinq^^O, sin(p2 =——,
V 3
откуда
Φι = 0> Φ2 = arc sin ——-.
Итак,
ί 7 4"δίη1Φ ] ί ν^45ίη2φ-0+1 Ι
S = 4/?JVa— -i-з dq> =4/? <ρ2- \\1 ί άψ =
1 — sin2©
4
ь ! - τsin2 φ
\ / Г2
«* Γ·-/ιτχ-^ -«■ Κ-ί:
1 3
-sin2 φ / \ ^ 1 cos2©
4 - V \ 04^4 τ
<?2 , <?2
0 0
Полагаем tg φ = и. Тогда
"ι = 0, u2 = tg φ2:
1
sin φ2 _ Уъ _ 1
соБф2 -./* ι γ2'
Υ Τ
Следовательно,
ι
ντ
S = 8*'(arc tg-i= - 2 j ^) = SP (arc tg-^ - arctg^)
0
1
8R2 arc tg V2 , 2]^2 - 8/?2 arc tg -LA
l ι
Г У 2 У 2
10. Найти площадь части параболоида вращения х2 + У2 =
= 2аг, заключенную внутри цилиндра (л:2 + У2)2 = 2а2ху.
Направляющей данного цилиндра является лемниската
Берну лли, оси симметрии которой совпадают с биссектрисами
координатных углов плоскости Оху. Исходя из симметрии, можно
вычислить -j- искомой площади, проектирующейся на область Ρ —
половину лепестка лемнискаты (см. рис. 5.22).
241
Так как
dz χ dz у
дх а ' ду а '
то по формуле (6.6) получаем
Но
^ Y~J^L dxdy = -g- (20 - 3π)
(см. пример 5, § 5.2), поэтому
S = -^-(20 —3π).
ЗАДАЧИ
Изобразить на чертежах и найти площади частей следующих
поверхностей:
1. Плоскости x + y-\-z = 2a, отсекаемой плоскостями χ = 0,
у = 0, х = а, у = а.
2. Конуса ζ2 = 2хуу отсекаемого плоскостями χ + У = я, х = 0,
у = о.
3. Цилиндра л:2 + у2 = /?2, отсекаемого плоскостями г = 0,
ζ = kx.
4. Плоскости χ + у + ζ = 2α, вырезаемой цилиндром χ2 +
+ У2 = «2.
5. Гиперболического параболоида ζ = ху(х> 0, у > 0),
вырезаемого цилиндром г2 + У2 = #2·
6. Гиперболического параболоида яу = аг, вырезаемого
цилиндром (х2 + У2)2 = 2а2ху.
7. Конуса у2 -f- z2 = χ2, отсекаемого цилиндром χ2 + у2 = а2.
8. Конуса ζ2 = 2ху, отсекаемого плоскостями # = α, у = b.
х = о, у - 0.
9. Цилиндра я2 + У2 = 4*, отсекаемого плоскостью Ояу и
конусом г* + у2 = ζ2.
10. Параболоида у2 + ζ2 = 2х, отсекаемого параболическим
цилиндром у2 = χ и плоскостью а: = 1.
11. Цилиндра х2 + у2 = 1 (* > 0, у > 0), отсекаемого
плоскостями #+y + z = 2, 2 = 0.
12. Параболоида х2 + у2 = 2аг, вырезаемого цилиндром (х2+
+ у2)2 = а2(х2-у2).
13. Конуса х2 + У2 = ζ2 (ζ > 0), вырезаемого цилиндром (х2 +
+ у2)2 = 2ху.
14. Цилиндра λ'2 -f у2 = α2, вырезаемого цилиндром я2 -f ζ2 = α2.
242
Вычислить площади частей поверхностей:
15. — + -у- = 2z внутри цилиндра —г + -фг = 1.
16. -^ £- - 2г внутри цилиндра -ij- + Jj- == ι (при
z>0).
17. 4" + 4- = 22 внутри цилиндра (4г + -fr)" =
18. Найти площадь поверхности, образованной вращением
кривой у = f(x) вокруг оси Ох (а < χ < b, / (*) > 0).
19. Найти площадь поверхности вращения χ = φ (α) cos v, у —
= φ (α) sin у, ζ = ψ(ί/) (α<α<β, 0<υ<2π).
20. Вычислить площадь части сферы x = Rcosucosvy y =
= R cos и sin у, ζ = /?sin w между параллелями г/ = иъ а = гг2 и
меридианами υ = и1э t; = ϋ2.
21. Вычислить площадь части поверхности тора χ — (Ь +
+ α cos α) cos у, у = (b + β cos гг) sin у, г = α sin гг (0 < а < 6),
ограниченной меридианами υ = vlt v = v2vl параллелями и = иъ и = и2.
Чему равна поверхность всего тора?
22. Найти формулу для вычисления площади общей винтовой
поверхности χ = φ (и) cos ν, у = φ (и) sin υ, ζ = ψ (u) + cu.
23. Вычислить площадь обыкновенной винтовой поверхности:
# = и cos у, у = и sin у, ζ = cv, вырезанной из нее цилиндром х2 -\-
+у2 = а2 и плоскостями 2 = 0, ζ = 2яс (0 < υ < 2π).
24. Вычислить площадь винтовой поверхности χ = tg г/ cos и,
ί/ = tg w sin υ, ζ = 0sln " + In "I/ 1 + sin ц _|_ ^ отвечающей изме-
z cos и у cos M
нению параметров 0<α<;-^-, 0<υ<.2π.
25. Найти формулу для вычисления площади поверхности
x = r(u, v) sin и cos ν, у = г(и, υ) sin ί/ sin υ, z = r(uy ν) cos и.
26. Вычислить площадь поверхности (х2 + у2 + г2)2 = а2 (х2 +
+ У2).
27. Вычислить площадь поверхности (х2 + у2 + ζ2)2 = 2а2л:у.
28. Найти площадь части поверхности х2 + У2 + ζ2 = 2/?г,
содержащейся внутри конуса г2 = ах2 + by2.
29. Вычислить площадь поверхности тела, являющегося общей
частью двух цилиндров х2 + у2 = R2, у2 + z2 = R2.
30. Доказать, что площадь S любой фигуры, лежащей на верх-
χ2 ι φ 22
ней полости конуса вращения —-^ г = 0, пропорциональна
площади ее проекции на плоскость Оху.
31. Найти площадь части поверхности параболоида вращения
χ2 + У2 = αζ, ограниченной плоскостью г = 2а.
32. Найти площадь части поверхности ζ = arc sin (sh # sh у),
ограниченной плоскостями л: = α, # = 6 (0 < а < 6).
243
ОТВЕТЫ
V2
3
\.α2Υ?>. 2. ^ . 3. 2kR2. 4. πα2 КЗ 5. -g- [(1 + Я2) — 1].
2 / 10 л \ 4 Γ 1 ,__
6. -у α2 -у- — -γ\ 7. 2πα2. 8. -у-(α + 6) |^2α6 . 9. 32. 10. -g-jx(3j/3— 1)
α2 r- 2 ,_
11. π —2. 12. -<ρ(20 — 3π). 13. 2^2. 14.8α2. 15. ~γ nab(V 8 — 1).
b
16. -j-(VS— 1) α& arc tg ]/-£-. 17. —аЬ. 18. 5 = 2π f / (*) ~\f\ + [f(*)I2 d*.
α
Указание. Уравнение поверхности вращения имеет вид у2 + г2 = [/(я)]2,
а уравнение верхней половины ее ζ — У72 (*) — У2- Область интегрирования на
плоскости Оху ограничена линиями χ = а, х—Ь, у = /(χ), # — — /(я). 19. 5 =
β
= 2π Г φ (и) |/[φ' (w)]2 + №' Ш2 du. 20. (ι>2 — vt) (sin н2 — sin ux) R2. 2\.a(v2 —
a
— vi) [b (w2 — их)-\- a (sin u2 — sin иг)], 5 = 4n2ab. (Поверхность тора описывается
при вращении окружности χ = b + α cos и, ζ = α sin и, т. е. (χ — b)2 + ζ2 = α2,
вокруг оси Οζ.) 22. 5 = J j V {[y(u)]* + c*} ([φ'ΜΡ+ΙΨ'ΜΡΗ^ΙΨ'ί")]2 Λ"*ο,
ρ"
2* α
где Ρ — область изменения и и t». 23. 5 — Ι Ι Υ и2 + с2 aWu = 2π -ί- j^fl2 _j_ c2 _j_
+ f ,„i±j2S]. η. |, 2, ^иУ[,.+(1)']»,п.„+(1р*
где Ρ — область изменения и, у. Указание. Воспользоваться формулой (6.11)*
/ дг \2 дг дг ( дг \2 о о π2α2
£-(^г) +г2> /7=-ЖГ-лГ· G = (^) +^sin2"· 26. π2α2. 27. —·
Указание. Воспользоваться формулой задачи 25 и полярным уравнением
/ l/Г / дг \21 " / дг \2 α sin и
поверхности: г = α sin и Vsin2y, J/ |^2 + J-^-j J sin2 и + [-^J =-y==-.
3nR2
28. —, Указание. Воспользоваться формулой задачи 25
У (а+1)0+1)
и полярным уравнением сферы: г = 2/? cos и. 29. 16/?2. 30. Воспользоваться фор-
13 shb
мулой (6.6) и явным уравнением поверхности. 31. —γ-πα2. 32. πΐη « .
Указание. Область интегрирования определяется условиями: α ^ χ ^J 6,
I sh л:, sh ί/1 < 1. Ввести новые перемен ные: sh χ = и, sh ί/ = v.
§ 6.4. ПРИЛОЖЕНИЯ ДВОЙНЫХ ИНТЕГРАЛОВ К МЕХАНИКЕ
Масса и статические моменты пластинки*. Если
(S) — область плоскости Оху, занятая пластинкой, а γ (χ, у) — по-
* Под пластинкой понимается некоторая область, по которой распределена
масса плотностью γ = γ(Λ;, у).
244
верхностная плотность пластинки в точке Р(х, у), то ее масса Μ
выражается формулой
Л1 = JJy(jc, у) dxdy, (6.13)
(S)
а статические моменты Мх и Λί^ относительно осей Ох и Оу
определяются двойными интегралами
мх= \ f ί/ϊ (AV У)d^» Му = 1ί Λ' V (*> У) d^i/· (6·14)
\S) (S)
Если пластинка однородна, то γ (χ, у) = const; эту постоянную
часто полагают равной единице.
, Координаты центра тяжести пластинки. Если
С (х0, У о) — центр тяжести пластинки, то
му мх
где Μ — масса пластинки;
Мх, Му — ее статические моменты относительно осей координат,
определяемые соответственно формулами (6.13) и
(6.14).
Если пластинка однородна, γ (χ, у) = const. Тогда формулы
(6.15) с учетом формул (6.13) и (6.14) принимают вид
Jj xdxdy \ j ydxdy
Χ°=Ζ'~ΊΓΤ * Уо = ~тгп · (6.16)
\ J dxdy J J dxdi/
(*S) (S)
(В формулах (6.16) знаменатели дробей — площадь пластинки, центр
тяжести которой отыскивается.)
Моменты инерции пластинки относительно осей Ох
и Оу соответственно определяются формулами:
Ix = ifi/2Y(*> У) dxdy, Iyl= \\x2y(x, у) dxdy. (6.17)
(S) ' '(S)
Момент инерции пластинки относительно начала координат
/о = f f (x2 + У2) Υ (х, У) dxdy = /, + / (6.18)
(S)
Полагая у (х, у) = 1 в формулах (6.17) и (6.18), получаем
геометрические моменты инерции плоской фигуры.
Координаты центра тяжести тела. Если С (x0i y0i
ζ0) — центр тяжести однородного вертикального цилиндрического
245
тела, имеющего своим основанием область (S) на плоскости Оху
и ограниченного поверхностью z = f(x, у), то
МУ2 Mxz мх
где Λί — масса тела;
М)г, УИ^, УИху — статические моменты тела относительно
плоскостей Oyz, Oxz, Oxyf определяемые формулами:
Му2 = \\ xzdxdy }
(5)
МХ2 = \\ yzdxdy
\S)
Mx=±-\\z2dxdy
1 \s)
(6.20)
Моменты инерции цилиндрического тела.
Моменты инерции цилиндрического тела, ограниченного поверхностью
ζ = / (χ> #)> ее проекцией (S) на плоскость Оху и проектирующим
цилиндром с образующими, параллельными оси Ог, относительно
этой оси и относительно плоскостей Ozx, Oyz выражаются
формулами:
Ig= \\{x2 + y2)zdxdy\ (6.21)
I2X = J ) yhdxdy, Iyz = J J x2zdxdy. (6.22)
(S) (S)
При вычислении двойных интегралов в формулах (6.13) —
(6.22) во многих случаях целесообразно перейти к полярным
координатам.
ПРИМЕРЫ
1. Найти массу круглой пластинки радиуса /?, если
поверхностная плотность γ (а:, у) материала пластинки в каждой точке
Р(х, у) пропорциональна расстоянию точки Ρ от центра круга.
Начало прямоугольной декартовой системы координат поместим
в центре круга. Тогда координаты любой его точки
удовлетворяют соотношению х2 + У2 <^ R2> Расстояние точки Р(х, у) до
начала координат определяется формулой d = Vχ2 + У2, поэтому в
соответствии с условием γ (χ, у) = k Υ χ2 + у2, где k —
коэффициент пропорциональности.
По формуле (6.13)
Μ = \ j k V χ2 + У2 dxdy,
Is)
где (S) - круг χ2 + у2 < R2.
246
Переходя к полярным координатам, находим
2- R 2тг
M=jd(fjkppdp = kj -~-
о "о о
А №*
2-
= -±-£π/?3.
2. Найти статические моменты Мх и Μ фигуры, лежащей
X2 И2
в первой четверти, ограниченной эллипсом —г + -^~ = 1 и
координатными осями, если в каждой точке фигуры плотность
пропорциональна произведению координат этой точки.
По условию γ (χ, у) = kxy, где k — коэффициент
пропорциональности, поэтому формулы (6.14) для данного случая примут
вид:
Мх = JJ kxy ydxdy, Μ = \[ kxy xdxdyy
(S) " (S)
где (S) — область, ограниченная дугой эллипса у = — ]/ α2 - χ2
(# > 0, ί/ ;> 0) и координатными осями.
Найдем сначала статический момент данной фигуры
относительно оси Ох:
а f Va>-x>
Μχ = || kxy2dxdy = Γ ( f kxy2dy) dx.
(S) * V
Так как
kxy2dy = kx -y-
o о
if \a kx b*
4-(|/*2-*2)3,
TO
Mr
j'%-£(V*=]tydx=g-Jx(*-x*)*dx =
a 3
=^/(α2-^2)τ[-4-^α2-^]
kb* (а2—д:2)2
6a3
kb*a2
15
Аналогично находим статический момент фигуры относительно
оси Оу:
ь г
а — уа2 Х2
Му = JJ &*i/ *d#dy = (J kyx2 dxdy = f (|a kyx2dy) dx =
(S) (S) 0 0
247
=JW
0 Δ
b
a
0
a
0
Va°— x2
dx =
a
[ kx2 b2 f о
0
\a
kb2 x3
2 ' 3
kb2 хъ
2a* ' 5
0
a
0
- x2) dx =
kbV
2-3
0
kb2a* kb2a*
2-5 ~ 15
3. Найти центр тяжести фигуры, указанной в примере 2.
Координаты центра тяжести плоской фигуры определяются
формулами (6.15). Статические моменты Μχ1 Му найдены в
примере 2, осталось вычислить массу данной фигуры.
По формуле (6.13)
α Τ Ϋ**-
Μ = ^ kxydxdy = J (j'
(S) 0 0
b
,2
kxydy) dx =
0 z
- Va*—x2
dx
~J 2
b2
(a2 — x2) dx
и и
[kb2 , Γ kb2 ,.
J — xdx — J -^rx*dx
Так как
kb2
2
_
kb2
2a2
kb2a2
Mv
kb3a2
15
Mx,
то по формулам (6.15)
Μ,
kb2a*
15
Λί "~" 15 й> Уо
■Mr
Μ
= -τΗ·
4. Найти центр тяжести однородной фигуры, ограниченной
параболой у2 = \ах + 4а2 и прямой у = 2а — х.
Воспользуемся формулами (6.16), для чего вычислим
предварительно входящие в них двойные интегралы.
Найдем интеграл, стоящий в знаменателе; он выражает
площадь данной фигуры. Решая совместно уравнения у2 — \ax-\- 4а2,
у = 2а — х, находим точки А (О, 2а), В (8а, — 6а) пересечения
параболы и прямой (рис. 6.23).
#у2 4/7
В области ABC при фиксированном у χ меняется от -^—-
(абсцисса точки М) до 2а — у (абсцисса точки Ν\ выражения для
абсцисс точек Μ и N получены из уравнений линий решением
248
относительно χ), а у меняется от —6а (ордината точки В) до 2а
(ордината точки А). Следовательно,
2а
\ \ dxdy = \ \ dxdy = ί ί 2α — у
(S) —6α у2—4α2 —6α
μ2 — 4α2
4α
Jdx
64
4α
Вычисляем интегралы,
стоящие в числителях формул (6.16):
2а 2а—у
\ \ xdxdy = J J xdxdy =
(S) —6а у2—4а2
4а
2а
/' 1
2а-у
dy
у2—4а2
4а
2а
4-]'(3α2-4αί/+4ί/2-
— 6а
У*
dy
256
16а2 ')"* ~ 5
2а 2а—у
У
\
аШ
c\=l
-J
6а
\
Φ
±Яа .
δα
^^Ч-
χ
■а*;
Рис. 6.23
128
2а 2а—у 2а
J J ydxdy = J J ydydx = J [bay — y2 — -^j dy =
(S) —6a f/2—4a2 —6a
4a
По формулам (6.16) находим координаты центра тяжести:
256
128
64
12
-у а, у о
64
•2а.
3 и з и-
5. Найти центр тяжести одного однородного лепестка
лемнискаты
(*» + У2)2 = 2α2 (χ2 — ί/2).
В силу симметрии ясно, что центр тяжести находится на оси
Ох, т. е. у0 = 0. Вычисляем Му = Π xdxdy, переходя к полярным
(5)
координатам по формулам x^pcoscp, у = ρ sin φ. Уравнение
кривой в полярных координатах имеет вид
р2 = 2a2 cos 2φ £- < φ < -£- ,
249
поэтому
Τ α Υ2 cos 2? Τ" α /2cos2f
Λί,
I jxdxdy = I J pcoscppdcpdp = | ( / coscpp2dp)d(p:
(S)
4 4
- Г 3 - T 3
a3 I cos φ cos 2 2φ dtp = —^— a3 / (1 — 2 sin2cp)2 cos φ dcp.
о
4
Полагаем |/2"sinq) = sin/. Тогда
Ύ
My = i-a3 Г cos4/d/ - -^-a3,
о
Τ
так как I cos4tdt = -τττ-π (см. пример 4 § 6.1).
о
Поскольку площадь одного лепестка S = а2 (см. пример 3
§ 6.1), окончательно имеем
π з
Ч = —-2 = -j-<*> Уо = 0.
6. Найти моменты инерции однородной полукруглой пластинки
0 ^ У ^С VR2 — *2 относительно осей Ох и Оу.
По первой из формул (6.17), полагая у(х, у)=1, находим
момент инерции относительно оси Ох:
я
-я
я Уя2—хг
Ix = J jy2 dxdy = J [ J y2dyjdx ■
(S) -Я 0
VR2-xz * 3
= / 4 dx=4"/ (R2 ~ *2)2 dx=■§■/{R2 ~ χ2)2(ΐχ·
о -я о
Полученный интеграл вычислим с помощью подстановки
χ = Rsm t (dx = R cos tdt, новые пределы: a = 0, β = -^-1:
Я _з_ Τ _з_
4 = 4"/ (Λ8 — ^8)2 ^ =-|- J (#2 —#2sin2n2 Rcostdt =
ο Ό
250
2
■ Я4 [ (cos2/)2 cos /Л - -|- Я4 [
2 пЛ^2л2-^„_ 2 miC0S4irfi= 2^ 3 я== я*4
0 0
Аналогично вычисляется момент^ инерции относительно оси Оу:
R >А#2-лг2 " #
/у = JJx2dxdy = J ( J x2di/)dx - J χ2 VR2-x2dx =
(S) -R 6 -tf
= 2 ) jc2Vr/?a-r-Jc2djc = 2 |' Я2 sin2 / ]//?2 - R2 sin21R cos tdt =
Ό ό
π π π
Ύ Ύ Ύ
= 2tf* f sin- * cos* tdt = 2R*j si"242/ Л = -у" f ^f^ Л =
ο Ό ο
π/?4
8
Итак,
г _ π/?4 , , π/?4
8 *
7. Найти момент инерции однородного лепестка лемнискаты
(х2 + У2)2 = 2а2 (л:2 — у2) относительно начала координат.
Полагая γ (χ, у) = 1, по формуле (6.18) получаем
/0 = Я (*2 + ^2)dA:^'
(S).,
где (S) — область, ограниченная одной петлей (х1^ 0) лемнискаты
(х2 + у2)2 = 2а2 (х2 — г/2).
Для вычисления интеграла перейдем к полярным
координатам по формулам * = pcoscp, у = ρ sin φ. Так как полярное
уравнение лемнискаты имеет вид р2 = 2а2 cos 2φ ί j- <; φ < -^)»
a jc2 + y2 = p2 и /(ρ, φ) = ρ, то
π
Τ" α νΥοοΓ2ψ
/Q=[Ux* + y*)dxdy= f( Γ ρ2Ρίίρ)ίίφ =
(5) ^\ J Ι
4
С Ρ4 |« * 2 cos 2? f , 2 0 , πα4
= | -ξ- dcp = \ α4 cos2 2φ αφ = —^—.
4
251
8. Найти момент инерции однородной фигуры, ограниченной
параболой у2 = ах и прямой χ = α, относительно прямой */ = — а:
Формулами (6.17) здесь пользоваться нельзя, так как прямая
у = — α не является координатной осью. Введем новую систему
координат, для которой прямая у = —α будет осью 0ХХ, ось C^F
совпадет со старой осью Оу
(рис. 6.24). Формулы
преобразования:
х = X, у = Y — а
или .*;
X = х, F = г/ + а.
В новой системе координат
Ix = ftY*dXdY,
(S)
где (S) — область ОАВ; Л (а, а),
Л (а, — а) — точки пересечения
параболы у2 = ах и прямой л: =а.
В старой системе координат
а а
J J (y + a)2dxdy =
—a yz
-£>-т«*·
9. Вычислить момент инерции однородной пластинки,
ограниченной гиперболой ху = 4 и прямой а: + у = 5, относительно
биссектрисы первого координатного угла.
В данном случае также нельзя непосредственно пользоваться
формулами (6.17). Эту задачу можно решить, как и предыдущую,
с помощью преобразования координат (взяв биссектрису в
качестве новой оси ОхХ).
Укажем другой способ решения. Гипербола ^ = 4и прямая
х-\-у = 5 пересекаются в точках Л(1, 4), β(4, 1) (рис. 6.25).
Расстояние точки Ρ (χ, у) до прямой χ — у = О (биссектриса
первого координатного угла) d = ,-У, поэтому момент инерции
площадки Ахку, содержащей точку Р, относительно этой прямой
равен -—2 Ал: Ау (с точностью до бесконечно малых высшего
порядка). Суммируем сначала моменты инерции элементарных
площадок, расположенных в полосках, параллельных оси Оу; вдоль
252
ц
(?\
о\
\
-а\
~Щ
У
А^^^
U
1
*ЩЦ|
Ή
^L
6 ^^^-^
X
X
Рис. 6.24
U
j (у + af [a -
такой полоски, содержащей отрезок RS, у изменяется от —
(ордината точки R) до 5 — χ (ордината точки S). Затем суммируем
моменты инерции всех таких полосок, соответствующие
значениям χ от 1 (абсцисса точки А) до 4 (абсцисса точки В).
Рис. 6.25
Переходя к пределу, получаем
4 5-* 4
у f Г J^y)Ldxdy= Γ4-(125-162χ+60χ2~7χ3~
ι д i
χ
__6|_ + JL)dx==i61n2-9^-.
χ3 ' a; / 8
10. Найти центр тяжести однородного тела, вырезанного
цилиндром х2 + у2 = Rx из сферы х2 + у2 + z2 = R2 («тело Вивиа-
ни», см. рис. 6.12 к примеру 6 § 6.2).
Из соображений симметрии ясно, что центр тяжести лежит
на оси Ох, поэтому у0 = 0, ζ0 = 0. Остается найти координату х0
с помощью первой из формул (6.19). Вычислим статический момент
тела относительно плоскости Oyz. Первая из формул (6.20) в
данном случае примет вид
Му2 = 4f j xzdxdy = 4 Jf x VR2 - λ'2 - У2 dxdy,
(S) (S)
где (S) — полукруг в первом квадранте плоскости Оху,
ограниченный линиями χ = 0, х2 + У2 = Rx-
253
Рис. 6.26
Вычислим этот двойной интеграл, перейдя к полярным
координатам по формулам x = pcoscp, у = ρ sin φ:
π
~2~ R COS φ
Μνζ = 4 j j χ VR2 — χ2-у2 dxdy = 4 j cosydy J YR2 — p2p2dp.
(S) 0 0
Так как
7? COS φ
j УЯ2-р2р2:Ф= [χ(2ρ2-/?2)^^Γρ2 +
o
Я4 Ρ 1 |P=^cosa o4 Г Я 1
+ — arcsin-^-J J =o = — ^cos φ (2 cos2 φ — 1) sin φ + -^ φ j,
то
π
Ύ
μ = -*!
■ j (2 cos4 φ — cos2 φ) sin φ + I-^ φ j cos φ d<p
о
-51
2
2 _ * , 1 о , / π \ . ||2 2
_cos59 + -o-cos39+ ^—φ sincp — coscp = τ* Я4.
Остается вычислить массу тела. Она равна объему V этого
тела (тело однородно, поэтому γ (χ, ί/, ζ) = const. Эту постоянную
можно положить равной единице). Но V = — Rs[-k о" I
(см. пример 6 § 6.2), поэтому
Щг 3
■/?.
"°~ V - 5(3π-4)
11. Найти общее выражение для момента инерции пластинки
(S) произвольной формы относительно любой оси Ои,
составляющей с осью Ох угол φ (рис. 6.26).
Примем ось Ои и перпендикулярную к ней ось Ου за новые
координатные оси. Тогда
и = a: cos φ + у sin φ, ν = —xsincp + у cos ψ. '(1)
Момент инерции фигуры (S) относительно оси Ои выразится
формулой
Iu=\$v2ydS.
(S)
Преобразуем этот интеграл, используя вторую из формул (1):
Iu = jj v2 у dS = J[' (— х sin φ + у cos φ)2 γ dS =
(S) (S)
= sin2 φ [f χ2 у dS — 2 sin φ cos φ [j xy у dS + cos2 φ j j у2 у dS. (2)
(S) (S) (S)
254
Коэффициентами при sin2 φ и cos2 φ являются моменты
инерции /у и 1Х относительно старых осей координат Ох и Оу.
Величина
Kxy = S\xyydS
(S)
называется центробежным моментом.
Итак,
1и = Ix cos2 φ — 2Кху sin φ cos φ + Iy sin2 φ. (3)
Замечание. Для наглядной иллюстрации изменения
момента инерции фигуры при вращении оси Ои поступают
следующим образом. На оси Ои откладывают отрезок ON = ■
(см. рис. 6.26) и рассматривают геометрическое место полученных
точек N. Если координаты точки N обозначить через х, у, то
п\т cos φ л,т . sin φ
χ = ON cos φ = rjL , у = ON sin φ = —-=-.
Ψ Via Ψ Via
Разделив соотношение (3) на 1и9 получим [уравнение
геометрического места:
1лх*-2Кхуху + 1уУ2=1. (4)
Распространяя неравенство Буняковского на случай двойных
интегралов, легко видеть, что
IJy-Kxy>0,
поэтому линия (4) есть эллипс. Его называют эллипсом инерции.
Если Кху = 0, уравнение (4) принимает вид
В этом случае оси координат служат осями эллипса инерции
(главными осями инерции).
ЗАДАЧИ
1. Найти массу пластинки, имеющей форму круга
радиуса R, если плотность в любой точке Ρ обратно пропорциональна
расстоянию ее до центра круга.
2. Вычислить массу кругового кольца, если в каждой точке
его поверхностная плотность обратно пропорциональна квадрату
расстояния ее до центра кольца.
3. Найти массу круговой пластинки радиуса R, плотность
которой в каждой точке равна расстоянию этой точки от контура
круга.
255
4. Вычислить массу квадратной пластинки со стороной а,
в каждой точке которой поверхностная плотность пропорциональна
сумме ее расстояний до диагоналей квадрата.
5. Найти массу квадратной пластинки со стороной а, если
плотность ее в каждой точке пропорциональна расстоянию этой
точки от одной из вершин квадрата и равна γ0 в центре
квадрата.
6. Пластинка ограничена параболой у2 = 2рх и ее хордой,
проходящей через фокус перпендикулярно к оси параболы. Найти
массу пластинки, если в каждой точке ее поверхностная
плотность обратно пропорциональна расстоянию точки до директрисы
параболы.
7. Вычислить массу прямоугольной пластинки со сторонами а
и bt в каждой точке которой поверхностная плотность
пропорциональна квадрату расстояния ее до одной из вершин
прямоугольника.
В задачах 8—11 найти статические моменты относительно
осей Ох и Оу однородных пластинок, имеющих формы:
8. Полукруга 0 < у < VR2 — *2.
9. Прямоугольника О^х^а, О^у^Ь.
10. Треугольника с вершинами Л(0, 0), В (а, 0), С(0, Ь).
И. Прямоугольника — а^х^а, — b^y^b.
12. Найти статические моменты однородной пластинки, огра-
X2 И2
ничейной эллипсом —τ + -^ = 1, координатными осями и
лежащей в первой четверти.
13. Пластинка имеет форму прямоугольного треугольника
с катетами ОБ = а, ОА = Ь, причем плотность ее в любой точке
равна расстоянию точки от катета О А. Найти статические моменты
пластинки относительно катетов ОА и ОБ.
В задачах 14 — 21 найти центры тяжести однородных
пластинок, ограниченных линиями:
14. х = ±:а, у = ±Ь. 15. χ = 0, χ = α, у = 0, у = b.
16. у — χ = 0, χ + у — 4 = 0, χ — 2у — 4 = 0. 17. у = х2,
х + У = 2._ _
18. \/х+ \/у= 1, х = 0, у = 0. 19. у= VR2-x2, у = 0.
20. p=l + coscp, φ = 0. 21. x = t — s\nt, y=l— cost
(0<ί<2π), y = 0.
22. Доказать, что центр тяжести однородной треугольной
пластинки находится в точке пересечения медиан.
23. Доказать, что статический момент однородной пластинки
относительно некоторой прямой равен Sh, где S — площадь
пластинки, h — расстояние ее центра тяжести до прямой.
В задачах 24 — 30 найти моменты инерции относительно осей
координат Ох, Оу однородных пластинок, ограниченных линиями:
256
24. χ = О, л:=я, y = 0, y = b. 25. jc = —a, x = a,y = b,
y = -b.
26· -F + 4- = 1. *
О, у = 0. 27. -£- + ■
1.
28. (χ — a)2+(i/-a)2-a2, jc = 0, у = 0 (0<x<fl).
29. *i/ = a2, xj/ = 2a2, x = 2y, 2x = у (х>0, y> 0).
30. x4 + j/4 = a2 (a:2 + i/2).
В задачах 31 — 34 найти моменты инерции относительно
начала координат однородных пластинок, ограниченных линиями:
31. χ = 0, * = а, у = 0, у
33. ρ = 2а cos φ.
6. 32.
а2 г б2
34. p = a(l-
Найти центры тяжести однородных тел:
35. Конуса ζ = 1
в плоскости Оху.
= 1.
cos φ).
Vx2 + y2, основание которого лежит
36. Треугольной пирамиды, ограниченной плоскостями
х+2у — ζ— 1 -0, х = 0, у-0, z = 0.
37. Полушара х2 + у2 + г2 < R\ z > 0.
Рис. 6.28
38. Шарового слоя, заключенного между сферой х2 + у2 +
_|- ζ2 = /?2 и плоскостями а: = а, л: = 6.
39. Найти центр тяжести однородного тела, отсеченного
плоскостями ζ = 0, ζ = &у от цилиндра л:2 + #2 = α2 (это тело
называется цилиндрическим отрезком; рис. 6.27).
40. Найти центр тяжести однородного тела, ограниченного
χ2 φ г2
эллипсоидом —2~ + -|з- Η 2~ = 1» плоскостями координат и
содержащегося в первом октанте (рис. 6.28).
41. Для однородного кругового цилиндра высоты Η и
радиуса R найти момент инерции относительно любой плоскости,
проходящей через его ось.
257
42. Вычислить момент инерции однородного цилиндра
высоты Η и радиуса R относительно одной из образующих его
поверхности.
43. Найти момент инерции Ιζ для однородного тела, ограни-
χ и ζ2
ченного эллипсоидом —γ- + -ττ- Η т~ = 1 ·
44. Найти центр тяжести однородного тела, ограниченного
х2 и2
эллиптическим параболоидом ζ =-^ Ь-§—» координатными
плоскостями и плоскостями χ = а, у = Ь.
45. Однородное цилиндрическое тело имеет в основании
плоскую фигуру (S), а сверху ограничено плоскостью (Р). Доказать,
что объем У указанного тела равен произведению площади
основания S на длину d перпендикуляра к основанию, проходящего
через центр тяжести тела до пересечения с плоскостью (Р).
ОТВЕТЫ
1. 2nkR, где k — коэффициент пропорциональности. 2. 2nk\n~n~, где k —
коэффициент пропорциональности; R2, Ri— радиусы окружностей, ограничи-
π ka -ι/~2 ynas
вающих кольцо (R2 > RJ. 3. -у R3. 4. —^—. 5. -+J- [2 + \ 2 In (1 -f /2)]..
,_ &α& 2 аб2
6. kp У 2 (4 — π). 7. 3 (а2 + Ь2). 8. А^ = -у Я3, Му = 0. 9. УИХ = —-g—,
а26 аб2 а26 аб2
Му=—. 10. Λί* = -§-, iMj,= -g-. 11. Мх = Му = 0. 12. Жх = —J-,
а2Ь сРЬ а2Ъ2 ία Ь \
Му=—. 13. Mx = -j£-, Afy=-24". И. С(0, 0). 15. С (-^", -γ\.
„. с(4-,-4) п. c(-j-.-l-> <··'(+. !■)■'»'(·.£>
/ 5 16 \ / 5 \ аЬ3 а3Ь 4
20· с(-б-· -лг]· 21· СЬ τ)·24· 7*=-τ· 7>=—·25· ^=^-«*3·
4 а/33 а36 шЬ3 лсРЬ
/у = -гЛ. 26. /χ =-12", 'у=Т2~· 27. /л'=-4~, ^ = —4"· 28* 7* =
а4 9 Зла4
= /, = 1б"(16-5л). 29. /, = /,,= -g-o*. 30. /x = /v = -^j7=. 31. /0 =
а6(а2 + 62) лаб о ,о r 3 4 пл т 35 πα4
= — з ■ 32· 7°= Т"(а + * >· 33* 7°= Т~πα · 34* 7°= —Гб~~ ·
35. С [θ, 0, -ξ-). 36. Cl-j-, -g-, -у). 37. С (θ, 0, -g- j. 38. *0 =
3 (а + 6) (2/?2 — а2 — б2) Λ οΛ 3
= 4 (3/?2 _ а2 - b2 — ab) ' *Ό - ". *o - "· «"· *ο - «. </ο - 16
20 = -30- л/ш (/г = tg а, см. рис. 6.27). Указание. Mzx = \ \ yzdxdy =
(S)
a Ya2—x2 a 3
у2 dxdy = — Ι (α2 — *2)2 dx = -j" &*4> М*у = ~2~ 1] 22ίω# =
ооо (S)
258
= ΊΓ) \yzdxdy = ^r
(S)
2
отрезка V = -q~ ka3. 40. x0
π jtfe2a4
8 ka = 16
Myz = 0. Объем
3 3
цилиндрического
с. Указание.
Μ
1
ху-
^dx j (l-^--^)rfi/--^f(«2-A:2)2^==^a6c2,
π π
V =
о
■ ate. 41. Указание. В качестве
1Уг— 16 и<я" /ri^~ 16 ' б
плоскости Олег взять данную плоскость, а ось 0z направить по оси цилиндра.
π
IX2= -7-HR*. 42. Указание. Ось Oz направить по данной образующей,
а ось Ох — по диаметру О А основания конуса. Перейти к полярным координа-
3 4
там. 1г = —γ π HR*. 43. Iz = Ixz + /yz = -rr π абс (а2 + b2). Указание.
Можно ограничиться одним октантом эллипсоида (см. рис. 6.28), полученный
результат умножить на 8. В этом случае область (S) ограничена дугой эллипса
б2
= 1(х>0, у>0)
координатными осями Ох и Оу.
•V·
ML
/ 7 2
/« = 8 fy*zdxdy = -ξ- j r/2^ j у я2 (l - -fr) - *2 ^ =
(S) 0 0
Г / У2\ 4 4
= 2яас I i/2 I 1 — -£2 I rfi/ = -jg- π ab3c, Iyz = -^ π α3 6c.
3a2q+2b2p a
Рис. 6.29
2a2q+3b2p
44. *0- ^ + 6ap ' 4 . #o - a2q + b2p ' 4
Zo=
9aV+10fl262/?(7+964p2
cz2<7 + 62p
X
X
1
60/?i7
45. Указание. Если в прямоугольной декартовой системе
(рис. 6.29) уравнение плоскости имеет вид ζ = ах + by-\- с, то V= \\ (ах +
(S)
+ by + с) rfS = a f[ jcdS + ^ [J ^5 + с J f rfS = (αχ0 + fo/0 + с) S = Srf.
(S) (5) (S)
259
Глава 7
ТРОЙНЫЕ ИНТЕГРАЛЫ
§. 7.1. ВЫЧИСЛЕНИЕ ТРОЙНЫХ ИНТЕГРАЛОВ В ПРЯМОУГОЛЬНЫХ
ДЕКАРТОВЫХ КООРДИНАТАХ
Рассмотрим замкнутую пространственную область (V) и
функцию f(x, у, ζ), определенную в этой области. Область (V)
разобьем произвольно на η элементарных областей (Vi),(K2), · · · , (Vn)
с диаметрами dl9 d2, ... , dn и объемами AVlf AV2, ... , &Vn.
В каждой элементарной области (Vk) возьмем произвольную точку
Pk {xk9 yk9 zk) и образуем произведение / (хк, yk, zk) AVk.
Интегральной суммой для функции f(x, у, ζ) по области (V)
η
называется сумма вида ^ / (xk9 yk, zk) AVk.
k=\
Тройным интегралом от функции f(x, ί/, ζ) по области (V)
называется конечный предел интегральной суммы при условии,
что тахб4->0 (я-voo):
ffj/(xf у, z)dV= lim j?f(xk9 yk9 zk)AVk. (7.1)
Если функция f(x, у, ζ) непрерывна в области (I/), то
указанный предел существует и конечен (он не зависит от способа
разбиения области (V) на элементарные и от выбора точек Pk).
Основные свойства тройных интегралов аналогичны свойствам
двойных^; интегралов.
В прямоугольных декартовых координатах тройной интеграл
обычно записывают в виде
J J J f (x> У' z) dxdydz (так как dV = dxdydz).
(V)
Если область интегрирования (V) определяется неравенствами:
Х\ -^, X <С %2 I
йМ<КйМ (7.2)
*1 (*. У)<2<М*> у) J
где у г (х), у 2 (х)9 ζί (χ, у), ζ2 (χ9 у) — непрерывные функции своих
аргументов,
то тройной интеграл вычисляется по формуле
с х* Уг(х) г2(х,у)
JJJ/(*, У, z) dxdydz = j dx \ dy J f(x9 y9 z) dz. (7.3)
W *i уЛ*) zt{x,y)
260
Область (V) ограничена сверху поверхностью z = z2(x, у),
снизу —- поверхностью г = гг {х, у), а с, боков — цилиндрической
поверхностью с образующими, параллельными оси Oz (рис. 7.1),
вырезающей ца плоскости Оху область {Sxy), определенную
неравенствами х1 < χ < х2, ух (х) ^: у < у2 (х).
ι шш
I
'х.у>
щ
ш
1
z--z/x,yj
9
Рис. 7.1
Рис. 7.2
Отметим, что порядок интегрирования может быть изменен;
тройной интеграл можно вычислить шестью различными способами
(в формуле (7.3) первое интегрирование совершается по 2,
второе — по у, третье — по х\ оставив первое интегрирование по 2,
можно поменять местами второе и третье; далее, можно совершить
первым интегрирование по х, а также по у).
В частном случае, если функции yL(x), у2(*)> гг (х, у)
и Мх> У) являются постоянными yl9 y2, zl9 ζ2, то область
интегрирования представляет собой прямоугольный параллелепипед
и формула (7.3) принимает вид
х2 Уг ?2
) \ \ f (х, у, z) dxdy = j dx \ dy J / (x, y, z) dz. (7.3')
{V) Xi Ui zt
Для вычисления тройного интеграла в прямоугольных
координатах применяется также формула, которая иногда упрощает
вычисления:
х2
J J J / (*> У* z) dxdy = J dx \\ f (χ9 y9 z) dydzf (7.4)
(V)
Xl (Sv>
где область (Sx) — проекция на Oyz сечения области (V)
плоскостью, параллельной плоскости Oyz и проходящей через
произвольную точку интервала (хъ х2).
261
ПРИМЕРЫ
1. Вычислить тройной интеграл
13 2 13 2
j dx j dy j (x + y + z)dz = j{ J [ J (x + y+z)dz] dy } dx.
0 0 0 0 0 6
Это интеграл вида (7.3'). Пределы интегрирования в каждом
из интегралов являются постоянными. Область интегрирования —
прямой прямоугольный параллелепипед (рис. 7.2) с измерениями
а = 1, Ь — 3, с = 2, одна из вершин которого находится в начале
координат.
Вычисляем внутренний интеграл, находящийся в квадратных
скобках, считая χ и у постоянными:
) (х + У + г) dz = [xz -f yz + -^-
2x + 2y +
2=0
~2 = 2(x + y + 1).
Второй интеграл, находящийся в фигурных скобках,
принимает вид
3 2 3
\[§{х + у + г)аг]ау = $2(х+у+1)ау =
0 0 0
= 2§(х + у+ \)dy.
2
Находим этот интеграл, считая χ постоянным:
3
2 j*(* + у+ 1) dy = 2 (ху+ ^ + у) [Го = 2 (3*+ 4 + 3) =
о
= 6* + 15.
Вычисляем внешний интеграл:
13 2 1
Л \[§(* + y + z)dz\dy}dx= f (6x+ 15)dx =
о о о Ь
= {3х2+ 15х)[ = 18.
Итак,
ι з 2
j d* j dy j (* + ί/ + ζ) dz = 18.
0 0 0
262
Замечание. Интегрировать можно и в другом порядке.
В частности,
2 3 1
2 3
J dz J dy j (χ -f у + ζ) dx = J dz j (y -f г + -^-) dy =
0 0 0 0 0
2
= j(6 + 3z)dz= 18.
о
2. Вычислить j И ydxdydz, где (I/) — треугольная пирамида,
(V)
ограниченная плоскостью 2х -\- у -\- ζ — 4 = 0 и плоскостями
координат (рис. 7.3, а).
Рис. 7.3
Расставим пределы интегрирования. Плоскость 2х + у + ζ—
— 4 = 0 пересекает плоскость Оху по прямой 2х + у + ζ — 4 = 0,
ζ = 0 или 2* + у — 4 = 0, ζ = 0. В плоскости Оху эта прямая,
проходящая через точки А и В (рис. 7.3, б), определяется
уравнением 2х + у — 4 = 0. Треугольник 0Л5 и его внутренние
точки являются областью (Sxy) изменения переменных χ и у (в эту
область проектируется данная пирамида на плоскость Оху).
Очевидно, л: изменяется в промежутке [0, 2], т. е. 0<;л:<;2, при
фиксированном л: из этого промежутка (абсцисса точки М) у будет
изменяться от 0 (ордината точки М) до 4 — 2л: (ордината точки Л";
получена из уравнения прямой 2х + у — 4 = 0). При
фиксированных χ и у из области (Sxy) ζ будет изменяться от 0 до 4 — у —
— 2х (получено из уравнения плоскости 2* -j- у + ζ -— 4 = 0).
Таким образом,
4—2*
\ 1 | ydxdydz
4—0—2*
I dx | dy | ydz.
263
Поскольку
4—у—2х
j ydz = yz
2=4—0—2*
2=0
у(4 — у — 2х) = 4у — уй — 2xyt
J (4ί/ - У2 - 2ху) dy = (2ί/2 - 4 ~ xy2) |
4—2jc
Vfe—g--*
0=4—2*
0=0
(4-2x)2 2-
i/=4—2*
0=0
4 —2a:
(*-4-ΐΗ
- (4 - 2*)2 (2 - -i" + \x -χ) = (4 ~ 2*)2 (
= J-(4-2*)3,
1
a: =
TO
4— 2x 4—0—2*
\dx j dy j ydz = \-±-{4-2x)*dx =
DO 0 0
2
-^§(*-2x)3d(4-2x) = -±(^^
12 " 4 ~~ 3 '
Замечание. Тот же результат можно получить, меняя
порядок интегрирования. В частности, проектируя пирамиду на
плоскость Oyz, сводим данный тройной интеграл к следующему:
4—ί/—ζ
4 4-2 2^
J ) J ydxdydz = \ dz ) dy J yd*.
(V) -
о о
Так как
4—у—2
2
j #d* =
ух
4-0-
*=0
,(!={=;)_»»-4.
2 '
4—2
i(*-4-f)*-(«■-■«-ΐ)
= i*(l-
0=4—2
4 / |0=O
2 \ 1
" 12
= (4-z)2(l
(4-г)3,
0=4—2
0=0
4 —г
264
то
^ydxdydz = j -^ (4 - ζ)3 dz = —i- J (4 - 2)3d (4 - z) =
0
(4 - zY
№
48
о
о 3 '
3. Вычислить j j j ^*2*xz\v r^e область (l/) определена
(V)
неравенствами 0 <; # < 1, 0 <; ί/ <C 1 — χ, 0 <; г <; 1 — л: — у.
В соответствии с формулой (7.3)
1 1—д: 1-х—у
dz
■x + y + z)*
ШоТ^ЙЬгН'^Ь ί ,Τ
(V)
Поскольку
о о
1—Хт-у
i-x-y
J {1+х1У+ф<Ь = J (1 + ^ + ί/ + 2)-4^(1 +*+ί/ + ζ) =
о
= _L_[ ! _Ll·
3 L(l-M+</)3 8 J'
(1+х + у+г)-
2=1—χ—у
2=0
1-*
J 3 |_(1 + а; + ^)з S\dy~ з[ 2(1+* + */)*
3
JL 1 Γ=Ι"* = J_ Г ! 1-a: , 1 1
8 ^|ί/=ο 3 [ 2·22 8 ' 2(1+л:)2 J
= J_ Γ 1 _ 2 —л:]
3 L 2(1+ х)2 8 J'
TO
1 1—л: I—x—у
Г» /»
j dx \ dy J -
dz
(l+x + y + zy
* ,) 3 1.2(1+*)2 8 J
dx ■■
-if
d*
(1+*)2
' 12" j dA: + "24" ] *d*
1
6(1 + x) |o 12
0+ 48
0
12 ^ 6
12 ^48 48*
4. Вычислить J j J zdxdydz, где (I/) — область, ограниченная
(V)
*2 ί/2 Σ2
верхней половиной эллипсоида —Г + jj- + — = 1 и плоскостью
Оху (см. рис. 6.13).
265
Проекцией тела V на плоскость Оху является область (Sxy)
χ2 и2
ограниченная эллипсом —^ + -"к- = 1. В этой области пределами
изменения χ являются числа —а и а. При постоянном χ у изме-
няется от У а2 — х2 до Η \ а2 — х2 (получены из
уравнения эллипса).
При фиксированных χ и у из области (Sxy) пределами измене-
ния г служат 0 и с I/ 1 г "~ "έτ (получены из уравнения
ζ = О плоскости Оху и уравнения эллипсоида).
По формуле (7.3)
+ ^^ cl/"l-^l—^
α α ψ а- о2
J J J zdxdydz = \ dx J rfy | zdz =
(V) -a b 0
α
—α 6
— — Υα*—χ2
. 6
-α 0
= С J^l1—ST-^jL ^ = ^з~ J(a2-*2) dx =
\у=о
а
46с2
За3
о
f (а2 - χ2)2 d* = -J- afec2
Здесь использованы равенства
, ft г , b ,
+ — /α2—χ2 + -τ 1 α2—λ2
νΌ2—χ2
α
3 /» 3
/-» о г» о
\ (α2 - χ2)τ dx = 2 J (α2 - *2)τ rfjc,
-α 0
верные для четной подынтегральной функции. Последний интеграл
вычислен с помощью подстановки x = as\nt.
266
Замечание. Данный интеграл можно вычислять и другим
путем, используя формулу (7.4). Меняя в этой формуле роли
переменных χ и ζ, получаем формулу
J J j / (х, У, ζ) dxdydz = J dz j J / (x, y, z) dxdy, (7.4')
(V) zx (Sz)
где (Sz) — проекция на Оху сечения области (V) плоскостью,
параллельной плоскости Оху, проходящей через
произвольную точку интервала (zl9 z2).
В данном случае формула (7.4') принимает вид
с с
J J J zdxdydz = J dz j \ zdxdy = J zdz J J dxdy.
(V) 0 (S^) 0 (Sz)
Область (SJ ограничена эллипсом, проекция которого на
плоскость Оху имеет уравнение
Η т^·—Г7 = 1 (ζ фиксировано!),
*(■-Я "(■--£)
т. е. также представляет собой эллипс с полуосями
поэтому площадь области (SJ есть S2 = παφχ = πα& 11 — -^-).
Следовательно,
j I dxdy = παί? (1 —^-)
1 ] \ zdxdydz = nab \ ζ
1_4)ώ = -^.
(V)
5. Вычислить \ \ j ydxdydz, где область (I/) ограничена кону-
л2
сом у2 = -иг (*2 + ζ2) и плоскостью у = /ι (рис. 7.4).
Применим второй способ решения предыдущей задачи, для
чего перепишем формулу (7.4). Меняя в этой формуле роли
переменных χ и у, получаем
j jj / (х, ί/, г) dxdydz = j di/ J J / (x, y, z) dxdz, (7.4")
(V) Ух (Sy)
267
где (Sy) — проекция на Oxz сечения области {V) плоскостью,
параллельной плоскости Oxz, проходящей через
произвольную точку интервала (уи у2).
В нашем случае формула (7.4") имеет вид
] J J ydxdydz = \ dy \\ ydxdz = \ ydy \ \ 'dxdz,
о (Vv) о
(V)
<S )
Рис. 7.4
Рис. 7.5
Ry
где (Sy) — круг радиуса г = -т- (см. рис. 7.4, выражение для
радиуса г получено из подобия соответствующих
треугольников).
Так как двойной интеграл ) J dxdz выражает площадь области
(Sy)9 которая равна л г2
Следовательно,
nR2y2
h2
<sv)
, то
I \ dxdz = ~~J[2~.
(Sy)
η η
j j 1 ydxdydz = j ydy \ \ dxdz = \^/~ dy = £^ί.
(V) Ό (Sy) о
6. Вычислить / / / ί-^2—ί—^—Ь~ тг) dxdydz, где область (I/)
' (V)
λ"2 Ι/2 Ζ2
ограничена эллипсоидом —г + -тг Η—г = 1 ·
268
Так как тройной интеграл от суммы функций равен
соответствующей сумме тройных интегралов от слагаемых, то
III й"+-£■ + -5-) dxdydz = fff 5-dxdydz ■
(V) ' (V)
-f j j J -fr dxdydz +11J -^- dxdydz.
(V) ' (V)
К первому интегралу применяем формулу (7.4), ко второму —
формулу (7.4"), к третьему — (7.4'). Получаем
J J ^r dxdydz = I -ζ-dx J J dydz = J -Jr S^x =
(V)" -a \s'x) -a
a a
= \^лЬс{\-^ах = Л4 fx*(l-$)dx =
J a2 \ α2 ι a2 J \ a1 ;
—a
nbc x3
nbc xb
2 2 4
= -ζ- nabc =- nabc = -р- παί?£.
ο ο Ιο
Здесь принято во внимание, что двойной интеграл от единицы
по области (Sx) есть площадь Sx этой области, равная площади,
ограниченной эллипсом
= 1 (л: фиксировано!)
с полуосями .
а2
\ = Ъу 1—-§г и ^i = ^ j/l—"5"
(см. пример 4).
Аналогично находим два других интеграла:
ь ъ
iff ~Й~ dxdydz = J ΐ~dy ff dxdz = J^nac(1-- irjdy
(V) -b <SV) -b
-yg- nabc,
j J j -^dxdydz = J ^-dz j j dxdy =
с
I z2 I z2 \ 4
J 7Г nab (l — 72-j^ = 15-nabc-
(V)
с
269
Следовательно,
ίίί (ΐ+ΐ+4) dxdydz - 4 шЬс-
(V)
7. Вычислить I I I -pr dxdydz, где (К) — область, ограничен-
а;2 и2 ζ2
ная конусом -^г + 4г г = О (* > О» у > 0), плоскостью г = с
и координатными плоскостями (рис. 7.5).
Будем интегрировать сначала по х\ затем по у и, наконец,
по ζ, для чего воспользуемся формулой
*2 Уг (2) *2 (У, Z)
.//./ '(*' у'г) ^yute = i dz j dy ί f (χ> y' ζϊ dx> (7·3")
(V) \ yt(z) XiiV.z)
аналогичной формуле (7.3) для случая области (V), определяемой
неравенствами:
zx<ζ<ζ2, у1 (ζ)<у<у2(г), *х (у, ζ)<χ<х2(у, г).
Рассматриваемая область (I/) проектируется на плоскость
Oyz в виде треугольника, ограниченного прямыми у = 0, г = с,
^ с
Эта область определяется следующими неравенствами:
поэтому в соответствии с формулой (7.3")
JJJfLdxdydz-JjLfydy f xdx.
- V ζ J V z
(V) Y О Г 0
Так как
fc2
о о
г4,
то
270
\Jjf?dXdydz = ^-SzTdz = ^**)Tc.
(V) г о
ЗАДАЧИ
Расставить (всевозможными способами) пределы
интегрирования в тройном интеграле Μ I / (χ, у, ζ) dxdydz для указанных
(V)*
областей (V):
1. (V) — область, ограниченная эллипсоидом -^- + -|г + ^т == 1 ·
2. (V)- шар х2 + у2 + z2 < R2.
Расставить (в каком-нибудь порядке) пределы интегрирования
в тройном интеграле I I I f(x, У, z) dxdydz для указанных обла-
(V)
стей (V):
3. (V) — треугольная пирамида, ограниченная плоскостью
*+2ί/ + 3ζ — 6 = 0 и координатными плоскостями.
4. (V) — область, ограниченная цилиндром у2 + ζ2 = R2 η
плоскостями л: = 0, χ = α.
5. (V) — область, ограниченная поверхностью г = 4 — л:2 — у2
и плоскостью ζ = 0.
д-2 22 φ
6- (V)— область, ограниченная конусом -γ- -\—г = j^r и
плоскостями у = 0, у = Ь.
Вычислить следующие интегралы:
111 21 λγ+2ι/
7. | ώκ J dy j (Зх + у + 2z) dz. 8. \ dx \ dy j dz.
bob ooo
1 χ ϊΐϊ+ΰ* 3 2x Vx~y
9. fdxfdy j zdz. 10. f dx f dy f zdz.
boo ooo
Вычислить следующие тройные интегралы по указанным
областям:
П. Jff (2x+y — z)dxdydz, (У) — куб:0^х^1, O^y-tCl,
0<ζ<1.
12. I I / (x + У + z) dxdydz, (V) — параллелепипед: 0 < χ < α,
0<У<Ь9 0<z<c.
13. J if (χ + 2y + 3z + 4) dxdydz, (I/), 0 < χ < 3, 0 < у < 2,
(V)
0<ζ<1.
271
14. \))(4x+3y+2z+l)dxdydz, (V): 0<*<1, 0<y<2,
V)
Q<2<3.
15. J J J (Ax -f By + Cz + D) dxdi/dz, (I/): 0 < χ < α, Ο < у < 6,
0<2<с.
16· JJJ(1+f+f-r^ (Ю:0<х<3,0<у<2,0<2?<1.
(Ю
17. JJJ xdxdydz, (V) ограничена плоскостями χ = 0, у = О,
(V)
z=r 0, у = h, х + z = a.
18. J J J xyzdxdydz, (V) ограничена поверхностями х = О,
у = 0, ζ = 0, д:2 + у2-|-22= 1 (х>0, у>0, 2>0).
19. j J J zdxdydz, (V) определена неравенствами 0 <; χ <; -γ-,
(V)
х<у<2х, 0<г<У 1 — χ2 — у2.
20. J J J (3x + Ay) dxdydz, (V) ограничена поверхностями
(V)
ζ = χ2 + у2, у = χ2, 2 = 0, у = 1.
21. j ) J z2dxdydz, (V) — общая часть двух шаров: х2 -f у2 +
(V)
+ ζ2 < Л2, *2 + У2 + z2 < 2Rz.
22. J J J У χ2 + y2dxdydz, (V) ограничена поверхностями χ2 +
+ У2 = 22, 2 = 0, 2= 1.
2**· J J J (χ2 + У2 + χ2) dxdydz, (V) определена неравенствами
(V)
0<jc<a, 0<у<6, 0<2<с.
24. Jjj xyzdxdydz, (V) ограничена поверхностями у = χ2,
(V)
χ = у2, 2 = ΛΓί/, 2 = 0.
25. JJJ z3dxdydz, (V) ограничена конусом —^ 1 |g— =
ζ2
= —г (# > 0, у > О, 2 > 0), плоскостью 2 = с и координатными
плоскостями.
272
26. I I I (χ + у + ζ)2 dxdydz, (V) ограничена поверхностями
(V)
2αζ = χ2 + y2f x2 + y*-\-z2 = За2.
27. \ \ \ x2dxdydzy (V) ограничена конусом —^ + -^ = ■
(V)
(#>0, у>0, 2>0), плоскостью z^=c и координатными
плоскостями.
28. (х2 + у2 + z2) dxdydz, (V) — шар х2 + у2 + z2 <>/?2.
(V)
29. I I I xyz dxdydz, (V) определена неравенствами
J J J V x2 + y2-\-z2
(V)
x2 + y2 + z2<R\ *>0, У>0, ^>0.
30. Показать, что формула для вычисления объема
цилиндрического тела, ограниченного поверхностью z = f(x,y), V =
= \ \ f(x> y)dxdy и формула объема тела по поперечным сече-
(S)
ниям V = \ S (x) dx являются следствиями основной формулы
(V) (V)
ОТВЕТЫ
Ъ г , ΐ/\ χ2 у2
1- I dx \ dy j f(x, у, z)dz =
-a -4-vra -<УЧ^
b +ϊπ=* + «/·-■£-£
= \ dy \ dx \ f{x,y,z)dz =
b V a2 b2
—b
+ — Va2-x2 + b]/l-^-- JjL
a a * а2 сг
j dx j ' dz j f{Xi y, z)dy:
a V ~2 7^
273
с с г а2 с2
= \ dz \ dx J /(*, у, z)dy =
с г α2 с2
+ .f V^^=i5 + β J/ , ... £_ *_
■αγ\
-ί* ί
62 C2
<fc
6 +f/sc*
■±YW=?
j /(*, у, z)dx^=
■K-S-S-
ζ-
Τ2 Τ2"
Λ! + V R2—χ2 + VR2—x°—y2
2. [ dx f ί/ί/ Γ /(*, ί/, г)с?г =
—# _ у^д2—χ2 — У R2—x2—y2
R + YR2—x2 + V^tf2—x2-z2
= j <** J ώ J /(*, У, z)dy =
— R _ У ^2_X2 _ yr^2_x2_22
Д + YRZ-yZ + YR3_x2__y2
= \ dy j dx J /(a;, i/, e)rfz =
—# _ YR"—y2 — 1Λ^2_χ2...ι/2
# + Vl^/5 + YR2-y2-z2
- I dy j Λ j f(Xt y, z)dx^
—R _ YR*-y
— Yr2-
■y'—z*
R + VR2-z2 4- YR*—y*—z*
= I dz I d# I f(x, y, z)dx =
—R _ Yr*—z* — Yw-yi—z2
R 4. YR2^!2 4- У^-д^-г2
= j dz j dx j /(χ, ί/, z)di/.
—^ — YW^ — Yr-—x2-z2
6—λ: 6—χ—2y
6 2
3. $ dx \ dy I /(*, i/, e)i/z. 4. \ dx \ dy \ f(xt y,z)dz.
0 0 0 0 — R _ Yr£Z&
a R
ί
R
2 Ya—x2 \—x2—y2
5. \ dx \ dy \ f (x> У> z) dz.
-2 _ γϊ=τχ
о
274
-2- УЫ
а
6· ί dx ί
dz
V a*—x2 b
V— + -
V az с2
f(x, y, z)dy. 7. 3. 8. 4. 9. -~-
81 „ « „ obc abc
10. —. 11. 1. 12. —(a + b + c). 13. 54. 14. 54. 15. — (Aa + Bb'+ Cc +
41 α3/ι 1 7 160
+ 2D). 16. w. 17. -g- 18. -jg-. 19. w 20. -gg-.
59
21. Ж„Я·.
22.
абс
23. -~- (а2
.„ 1 л; обе4
b2 + с2У 24·"96· 25·^-
6 '
26.
97
\ π 4
} 27· "80"а3^· 28-~
πα5/ /—
^(18/3-
π/?5. 29.
40
§ 7.2. ЗАМЕНА ПЕРЕМЕННЫХ В ТРОЙНЫХ ИНТЕГРАЛАХ
Если ограниченная замкнутая область (V) пространства Oxyz
взаимно однозначно отображается на область (V') пространства
O'uvw с помощью непрерывно дифференцируемых функций
х = х(и, v, w), у = у(и, υ, w)f z = z(u, υ, w)
и якобиан J в области (V) не обращается в нуль:
У =
то справедлива формула
дх дх дх
ди dv dw
ду ду ду
ди dv dw
dz dz dz
du dv dw
Ф0,
\\\f(x, y?z)dxdydz =
(V)
= \Hf[x(u, υ, w), y(u, v, w), z(u, υ, w)]\J \dudvdw. (7.5)
(V)
В частности, при переходе от декартовых координат х, у, ζ
к цилиндрическим координатам ρ, φ, ζ (рис. 7.6), связанным
с х, у, ζ формулами:
χ = ρ cos φ, у = ρ sin φ, ζ = ζ
(0 < ρ < + οο, 0 < φ < 2π, — οο < ζ < + οο),
якобиан преобразования J = ρ, поэтому
Ш / (х> У» z) dxdydz = fff/ (p cos φ, ρ sin φ, ζ) pdpdtpdz. (7.6)
(V) (V"v)
275
При переходе от декартовых координат х, у> ζ к сферическим
координатам ρ, φ, θ (рис. 7.7), связанным с х, у, ζ
соотношениями:
χ = ρ sin θ cos φ, у = ρ sin θ sin φ, ζ = ρ cos θ
(0<р< + сс, 0<φ<2π, 0<Θ<π),
якобиан преобразования / = ρ2 sin Θ, и формула (7.5) принимает вид
III/ (х, у у ζ) dxdydz =
\v)
= f 11 / [ρ sin Θ cos φ, ρ sin Θ sin φ, ρ cos θ] ρ2 sin Θάράφάθ. (7.7)
Μ (ΡΧΖ)
Рис. 7.6
Рис. 7.7
Замечание 1. Наименование «цилиндрические координаты»
связано с тем, что координатная поверхность ρ = const (т. е.
поверхность, все точки которой имеют одну и ту же координату р)
является цилиндром, прямолинейные образующие которого
параллельны оси Oz (рис. 7.8). (Координатной поверхностью φ = const
является полуплоскость, проходящая через ось Oz, координатной
поверхностью ζ = const является плоскость, параллельная
плоскости Оху.)
Замечание 2. Наименование «сферические координаты»
связано с тем, что координатная поверхность ρ = const (т. е.
поверхность, все точки которой имеют одну и ту же координату р)
является сферой (рис. 7.9). (Координатной поверхностью θ = const
является круговой конус с осью Oz и вершиной в точке О, а
координатной поверхностью φ = const служит полуплоскость,
проходящая через ось Oz.)
Замечание 3. Сферические координаты иначе называются
полярными координатами в пространстве.
276
ПРИМЕРЫ
1. Вычислить тройной интеграл \ \ \ (х2 -\- у2 + z2) dxdydz, где
"(V)
область (V) есть шар х2 + у2 + z2 < R2.
Перейдем к сферическим координатам:
# = psin6cosq\ у = ρ sin θ sin φ, 2 = pcos0.
(1)
J У
i\
\
1--ГШ-Л
Рис. 7.8
Рис. 7.9
В области (V"), являющейся образом области (V) при
преобразовании (1), переменные ρ, φ и θ меняются в следующих
пределах: ρ от 0 до /?, φ от 0 до 2π, Θ от 0 до π. Так как
подынтегральная функция х2 + у2 + ζ2 = р2 sin2 Θ cos2 φ -f ρ2 sin2 θ sin2 φ+
+ ρ2 cos2 θ = ρ2 sin2 Θ -f ρ2 cos2 Θ = ρ2, а якобиан преобразования (1)
равен ρ2 sin Θ, то по формуле (7.7)
R г. 2-
\)\ {х2 + У2 + г2) dxdydz = Ϊdp f d® ί р2р2sinθ</ψ -
"(V) обо
R г. 2-
= I p«dp \ Sin6d6 j dcp = i^-.
2. Вычислить
Χί/Ζ
dxdydz, где область (I/) ограни-
(V)
чена снизу плоскостью ζ = 0, а сверху поверхностью (х2 + У2 +
+ г2)2 = α2*ί/.
Переходим к сферическим координатам по формулам (1)
(см. пример 1). Уравнение поверхности принимает вид
р2 = a2 sin2 θ sin φ cos φ,
277
а подынтегральная функция
xyz ρ3 sin2 θ cos θ sin φ cos φ
ρ2 sin2 θ
= ρ cos θ sin φ cos φ.
х2 + У2
По формуле (7.7), с учетом симметрии области
относительно оси Ог,
(V)
2 2 a sin θ V sin φ cos φ
- 2 I d<p I d<d
0 0 О
\ d(f \ d& Ι ρ3 sin Θ cos Θ sin φ cos φ<ίρ.
Так как
a sin θ У sin с cos ;
ρ3 sin θ cos Θ sin φ cos cpdp
sin Θ cos Θ sin φ cos φ
ρ=α sin и У sin φ cos .
p=0
= -τ- sin5 Θ cos Θ sin3 φ cos3 φ;
ί-
sin50cos0d6= I sin5 Ш (sin Θ)
sin6©
2 ^_1_
η ~ 6
2 2
sin3 φ cos3 φί/φ = I sin3 φ (1 — sin2 φ) d (sin φ) =
то
sin4 φ 2 sin6 φ
2 _ J_
(Ю
#+ιβ dxdydz = 2
4 ' 6 ' 12 144
3. Вычислить J11 zdxdydz, где (V) — область, ограниченная
(V)
верхней частью конуса —^— = -тт- и плоскостью ζ = /ι (/ι > 0).
278
Введем цилиндрические координаты по формулам:
х = ρ cos φ, у = ρ sin φ, ζ = г.
Уравнение конуса принимает вид
(2)
Ра
ИЛИ 2
ΊΓΡ·
Новые переменные в области (V) изменяются в следующих
пределах: ρ от 0 до /?, φ от 0 до 2π, ζ от -^- ρ до Л.
По формуле (7.6)
/? 2π /г /? /г
\l\zdxdydz = f dp f d<p f pzdz = | { [ f pzdz] dcp } dp =
"(V) 6 0 h_
R p
Я 2π . Я 2-
ΊΓΡ
ill
г2
ρ Τ"
z=ft
dcp
* = j|j(-T-^5P2)pdcp}dP =
πΛ2
/?2
(Я2 - ρ2) pdp = ηΚ
-^2 Ρ!
π /ι2 ρ4
/?2 ' 4
πΛ2#2
4. Вычислить Ι Ι Ι у \ —^ — -fa— -^2" dxdydz, где область
(I/) ограничена эллипсоидом
"Г „2
1.
α2 ^ 62
Введем так называемые обобщенные сферические координаты
по формулам:
χ = ар sin Θ cos φ, у = bp sin Θ sin φ, ζ = cp cos Θ. (3)
Якобиан преобразования (3), определяемый формулой
дх дх дх I
dp dS dtp I α sin Θ cos φ αρ cos Θ cos φ — αρ sin Θ sin φ
ΊΓ~ ~Ш~ ~7Γ~ = ^ sin Ο sin φ 6ρ cos Θ sin φ 6ρ sin Θ cos φ
_dz_ Jz_ _dz_\ I^COS© — cp Sin θ 0
dp dS dtp I
равен a6cp2sin0. Подынтегральная функция по формулам (3)
преобразуется к виду
/ =
ν
X'
а*
V\
р\
а уравнение эллипсоида запишется так: р2 = 1 или ρ = 1.
В области (V) переменные ρ, Θ, φ изменяются в следующих
пределах: ρ от 0 до 1, Θ от 0 до π, φ от 0 до 2π.
279
По формуле (7.5)
ШУ
^r-Ίβ-^ϊ dxdydz =
ι
\ d<p \ άθ \ I 1 — ρ2 abcp2 sin θφ -
(V)
2- ~ 1
О
2г
= abc \ d(p \
sinΘάθ \V I— ρ2p2dp.
о
С помощью подстановки ρ = sin ^ находим первый интеграл:
1 2 2
\ γ\ — ρ2 p2dp — 1 cos / sin2 / cos tdt = — I
b 6 4 ό
Далее,
if d-cos4t)rft = ^.
jsin6d©-2,
поэтому
2-
я2а&с
(V)
/χ2 и2 ζ2 π Γ
1 — -^τ — -ψ — ~c2- dxdydz = abc ш -2 dip =
5. Вычислить \\\ χ2dxdydz, где область (V) ограничена поверх-
'(V)
ностями ζ = 4у2, г = 9у2 (у > 0), г = 2х, г = Зх, ζ = 9.
Введем новые (криволинейные) координаты по формулам:
ζ = "ί/2Ι(4<ί/<9);
г - ш: J (2 < ν < 3); %
2 = а>Ж'(°<а><9)·
Разрешив эти уравнения относительно х, у, ζ, получим:
х = —,У= У—, г = ю.щ (4)
Найдем частные производные функций (4) и вычислим якобиан
данного преобразования. Так как
дх _ г. дх_ _ w дх_ _ 1
Ж" ' ~δϋ ~ IF9 Έΰ~~ϋ~;
280
ду_
ди
" 2 Г u3 ' dv ' dw 2 Vuw'
dz ^ dz ~ dz 1
TO
a/
.J-1/JL о -U
2 Г и3 2К«ш
2 Г MV > I J I 2 Г u304 '
0 1
2
По формуле (7.5), с учетом пределов изменения ы, ό, w,
находим
9 3 9
x4xdydz = \du \ dv J J- · -±- y-^dw =
4 2 0
3 9
(П
= -γ I dw / da I w 2 ^~"4^2 dw =--
4 2 0
9 3 3 9 ? _J_
■ и" du\ υ~4υ wTdw = -^- - ^-
9 -3
0 ό
и -з
9
з y
2 A
_2
27 V 3
I L) /'J LW ъ-Щ
3 2 Μ 27 8 )υ ° 8 *
6. Исследовать, сходится ли
J J J VW-
(V)
dxdydz
-x* — y*
ν ™e (V)
шар χ2 + у2 + ζ2 < R2.
Данный интеграл является несобственным, так как
подынтегральная функция не ограничена в рассматриваемой области (она
обращается в бесконечность на границе области, т. е. на сфере
x2 + y2 + z2 = R*).
Выражаем этот интеграл в сферических координатах:
χ = ρ sin θ cos φ, у = ρ sin θ sin φ, ζ = ρ cos Θ.
Так как в данном случае 0 < ρ < R, 0 < θ <; π, 0 < φ < 2π,
то по формуле (7.7)
dxdydz
(V)
V /?2 — χ2
<ν*
ρ2 sin SdpdydS
281
2т: R
С ρ2Φ ΐ С С р2ф
Последний интеграл (несобственный) вычислим с помощью
подстановки ρ = R sin t:
r Τ Τ
f-^L^ Γ у ^2sin2/ - Rcostdt= (>sin«fdf =
J /Я2 —ρ2 J ^ /?2 — Я2 sin2 t J
0 0 0
~2~
= _|L (\-Cos2t)dt = -^-
o
Итак,
Y-^-sm2t
2 _ R2n
о " 4
R
Μ ο
Следовательно, данный несобственный интеграл сходится
и равен π2/?2.
г* г* г*
7. Исследовать, сходится ли I \ \ χ2χ у' * ^2">где (Ю—
(V) * — ~^2-_ ~W~~ Τ2"
Χ2 ί/2 Ζ2
область, ограниченная ^эллипсоидом ~т + η*τ -Α τ — 1 ·
Перейдем к обобщенным сферическим координатам по
формулам:
χ = ар sin Θ cos φ, у = 6ρ sin Θ sin φ, 2 = cpcos6. (1)
Так как якобиан преобразования (1) J = abcp2 sin Θ, 0<ρ<; 1,
0<;Θ<;π, 0<^φ<;2π, то по формуле (7.5)
dxdydz
ζ·
'οι - 2-
(V)" ] ~ а2 ~~ Ь2 с2 ' (V'~)
J J J yine^^
Γ ρ2 Γ Γ Γ ρ2
== а&с ι ] _„2 dp I sin θί/θ ι d<p = 4π абс Ι ι __ρ2 dp
οδό ο
= 4яа6с P'^t1 Φ = 4ла6с !~(^~,ρ>) ф =
282
Γ Φ Г
Anabc I j _p2 — 4яа6с \ dp = —
о о
ι
— 4nabc -γ In
P + i
— Anabcp
о
Поскольку
p-1
limln
00,
P+l
то данный интеграл расходится.
8. Оценить тройной интеграл I \ I х у z где
(V) χ у г
область (V) определена неравенствами х2 + у2 + ζ2 > 9, χ2 +
+ ί/2 + ζ2<16.
Для тройного интеграла верны следующие оценки:
mV^Wf(χ> У> г)dxdydz<AW, (2)
где V — объем области (V);
т и Μ — соответственно наименьшее и наибольшее значения
функции f (х, у, ζ) в области (V).
В данном случае область (V) ограничена двумя сферами:
*2 + У2 + ζ2 = 9, х2 -\- у2 + ζ2 = 16, ее объем равен разности
объемов двух шаров радиусов R± = 3 и i?2 = 4 с центрами в
начале координат:
у = у2 - Уг = 4" π/Й - 4"«/?? = χ π (43 - З3) = ψ π.
Подынтегральная функция принимает наибольшее значение на
сфере х2 + у2 + ζ2 = 16, причем
К 25—16 3
а наименьшее — на сфере х2 + У2 + ζ2 = 9,
ι ι
m = r = -г-.
■^25 — 9 4
Следовательно, в соответствии с соотношениями (2)
1 148 . Г С С а
(V)
dxdydz ^ \ 148
— v<C . ТС
у 95 — у2 _ „2 _ ?2 ^ 3 3
или
ГГГ <^г 148π
J J J /25 - χ2 - у2 - ζ2 9
37_
3
(V)
283
ЗАДАЧИ
Перейдя к сферическим координатам, вычислить следующие
тройные интегралы:
1. | IJ V х2 + У2 -г z2 dxdydz, (V) - шар х2 + у2 + ζ2 < Я2.
2. 11J (л:2 + у2 + г2)2 dxdydz, (V) — верхняя половина шара
'&)
x2 + y2jr z2 < R2. '
3. 11 j zdxdydz, (V) — часть шара х2 + у2 + ζ2 < #2, находя-
щаяся в первом октанте.
4. JJJ |/х2 -\- у2 + г2 dxdydz, (V) ограничена поверхностью
(V)
x2 + y2jrz2 = у.
5. jjj j/ \ + {x2 + y2 + z2y dxdydz, (1/)-шар χ2 + у2 +
(V)
+ 22<1.
6 Г Г С xyzdxdydz (α>β>γ>0), где (^)-часть
шара χ2 -f- у2 -f ζ2 <; /?2, расположенная в первом октанте.
Перейдя к цилиндрическим координатам, вычислить
следующие тройные интегралы:
7. И \ ζ ]/ х2 -f у2 dxdydz, (V) ограничена поверхностями х2 +
W
+ у2 = 2х, ί/ = 0, 2 = 0, 2 = 3.
8. \\\ (х2 — у2)dxdydz, (V) ограничена поверхностями х2 + У2 —
= 2z, 2 = 2.
9. И (\(х2 + у + 22)3 dxdydz, (V) ограничена поверхностями
"(V)
x2 + z2 = 1, */ = 0, у=1.
10. И ) ζ j/*2 + у2 dxdydz, (V) ограничена поверхностями у2 =
\v)
= SX — X2, 2 = 0, 2=2.
С помощью надлежащей замены переменных вычислить
следующие тройные интегралы:
11. \\\ x2dxdydz, (V) ограничена поверхностями ζ = у2, 2 =
= Ay2, z = χ, 2 = 2л:, 2 = 3.
284
12. ШхЧхйуаг, (V) ограничена поверхностями ζ = pyz, z = qyz,
у > 0 (0 < ρ < q), z = ax, z = bx (0 < a < 6), г = с (с > 0).
13. \\\ xyzdxdydz, (V) расположена в первом октанте и огра-
"(V)
ничена поверхностями х2 + у2 = г, х2 -f у2 = 2z, л:у = 1, л:у = 4,
ί/ = х, У = 2х.
14. \\\ xyzdxdydz, (V) расположена в первом октанте и огра-
(V)
ничена поверхностями ζ = -ζ-, ζ = ——, ху = а2, ху = б2,
у = ах, ί/ = βΑ: (0 < α < 6, 0 < α < β, 0 < m < η).
ОТВЕТЫ
2 π/?4 π 8π „
1. π/?4. 2. -у- π/?7. 3. -jg-. 4. -j^-. 5. -g— (/ 2 - 1).
ft #5 αβ + αγ + βγ
6. —jg— · (α -|_ p) (a _j_ γ) (β -J- γ) · Указание. В полученном интеграле
16π 3
ввести новые переменные: sin2 φ = υ, sin2 Θ = и. 7.8. 8. -«-. 9. ~о~ π.
10. 24. 11. ^Σ. 12 2 ^^/ 1 1 W 1 ^ Μ 13. J*
-ξ— - 27 " ' * ^з ~ аз у ^- ^-| - 512
+ 16Ш2). 14. ^(_1__^ (^-ιι·)[(β»-^)(ΐ + ^) + 41η4].
§ 7.3. ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ
Объем V области (V) выражается формулой
V = $$$ dxdydz. (7.8)
В сферических координатах этот интеграл имеет вид
V = f И' Р2 sin θώρώθΛρ, (7.8')
"(V)
а в цилиндрических координатах
V= \\\pdpd<pdz. (7.8")
Если тело занимает объем V и γ = γ (χ, у, г) — плотность его
в точке Λ4(λ;, ί/, ζ), то жасш тела
Л« = Шт(*. У> z)dxdydz. (7.9)
(V)
285
Координаты центра тяжести тела вычисляются по
формулам:
х° = ~wj J J yxdxdydz> y* = ~W J J J Wdxdydz, z0 =
(10 (V)
= -^j J J yzdxdydz, (7.10)
(V)
где Μ — масса тела.
Если тело однородно, в формулах (7.10) можно положить
γ = 1. Тогда Μ = У, где V — объем тела.
Моменты инерции тела относительно координатных
плоскостей определяются интегралами:
Iху = Ц\y&dxdydz, fxx = fflyy*dxdydz, /v, = \\\yx4xdydz. (7.11)
im (h '" \v)
Момент инерции тела относительно некоторой оси Ои
определяется интегралом
tu = Nhr*dxdyd2, (7.12)
(V)
где г — расстояние точки N (х, у, ζ) тела от оси Ои.
В частности, моменты инерции тела относительно
координатных осей Ox, Oy, Oz определяются формулами:
tx = Nh(!f + *)dxdydz
{V)
/v = jjfv (x2 + ζ2) dxdydz
(V)
4 = JiJv(*2 + У2) dxdydz
(V)
(7.13)
Момент инерции тела относительно начала координат
определяется формулой
А> = Ш Υ (х2 + У2 + г2) dxdydz. (7.14)
(V)
Очевидно, имеют место следующие соотношения:
* х ~ *ху "Т" 'xz> 'у * ух ' *yzi *z 'ζχ "Γ * zy> 'О ' ху \ * yz \ ' zx'
Ньютоновым потенциалом тела в точке Ρ (ξ, η, ζ)
называется интеграл
и {Ι, η, Е) = ///т(*. У. г) -^-, (7.15)
(V)
286
где V — объем тела;
У (х, У у ζ) — плотность тела;
г = Y{x-lf + {у - Άγ + {ζ-ζ)\
Материальная точка массы т притягивается телом с силой,
проекции которой Fx, Fv, F2 на оси координат 0ху Оуу Oz:
Fx = km-^- = km I ι Ι γ *~s dxdydz I
(V)
Fy = km^ = kmJ J J γ^11 dxdydz > (7.16)
Fz = km-^ = km \ Ι Ι γ г~^ dxdyd*
(V)
где fe — постоянная закона тяготения.
ПРИМЕРЫ
1. Вычислить объем тела, ограниченного поверхностями by —
= x2 + z2, y = b (b> 0).
а в у
Рис. 7.10
Рис. 7.11
Данное тело ограничено слева параболоидом by = χ2 -f г2,
справа плоскостью у = b и проектируется в круг х2 + z2 -< b2
плоскости Oxz (рис. 7.10). Принимая это во внимание, по
формуле (7.8) получаем
Ь Yb°—x2 Ь
V = fffdxdydz = J dx f dz f dt/.
ь
(V)
287
Так как
,ί dy = -\- (б2-χ2-ζ2);
Χ2+22 U
Υ&—Χ*
ί (&2-
- Vb2—χ2
b
- χ2 — ζ
ζ= Vb2—x*
4
_L· {Vb2-X2)\
36
TO
V= f 4b(Vb2-x2)3dx = 4b J (K62-&2sin2/)36cos^
= 4-63 ^„„atf = _«.*, _|_я = ^.
2
Замечание. Здесь принято во внимание, что
j cos4 tdt = (-|-φ + -i- sin 2φ + -^ sin 4φ
3
2
(См. пример 4 § 6.1.)
2. Найти объем тела, ограниченного поверхностями х2 + у2 +
+ ζ2 = α2, χ2 + у2 + ζ2 = b2 (0 < a < 6), χ2 + ί/2 = г2 (г > 0).
Данное тело ограничено сферами радиусов а и b с центрами
в начале координат и конусом с вершиной в начале координат
и осью, совпадающей с осью Oz. Тело расположено над
плоскостью Оху. Сечение этого тела плоскостью Ozy изображено на
рис. 7.11.
Для вычисления объема тела перейдем к сферическим
координатам по формулам:
χ = ρ sin Θ cos φ, у — ρ sin θ sin φ, ζ = ρ cos Θ.
Уравнение сферы χ2 + у2 + ζ2 = а2 примет вид ρ = α, так как
x2 + y2 + z2== p2 sin2 Θ C0S2 φ _μ p2 sin2 θ sin2 φ + Ρ2 cos2 Θ =
= ρ2 sin2 θ (cos2 φ + sin2 φ) + ρ2 cos2 θ = ρ2 (sin2 θ + cos2 θ) = ρ2.
Аналогично преобразуется уравнение второй сферы: ρ = b.
Уравнение конуса χ1 + у2 — ζ2 примет вид Θ = -^-, потому что
д;2 + у2 = р2 <цП2 θ> χ2 = р2 с0<,2 θ> р2 sjn2 @ = р2 CQS2 Q>
288
откуда
tg2e= ι.
По формуле (7.8')
т.
ь Τ ^ Р-а*
V = JJJ ρ2 sin θάράψάθ = J p2dp I sin θάθ \ dq> = ~з~ (2 - J/ 2) π.
(Ρ) α '
3. Вычислить объем
тела, ограниченного
поверхностями х2 + У2 + ζ2 = 4, х2 +
+ ί/2 = 3*.
Данное тело ограничено
сферой л:2 + f/2 + г2 = 4 и
параболоидом вращения х2 +
+ у2 = Зг. Сечение тела
плоскостью Oyz изображено на
рис. 7.12.
Для вычисления объема
тела перейдем к
цилиндрическим координатам по
формулам:
χ = ρ cos φ, у = ρ sin φ, ζ = ζ.
В цилиндрических
координатах получаем: ρ2 -f ζ2 =
= 4 (уравнение сферы); ρ2 = Зг (уравнение параболоида).
Отметим, что при постоянных значениях ρ и φ внутри тела ζ
Р2
изменяется от ζ = -^т- Для точки N пересечения с поверхностью
параболоида до ζ = У А — р2 для точки Μ пересечения с верхней
частью поверхности сферы (см. рис. 7.12).
При постоянном φ ρ изменяется от нуля (для точек, лежащих
на оси Οζ) до наибольшего значения в точках линии пересечения
данных поверхностей, так как с возрастанием г ρ для поверхности
параболоида возрастает, а для шара убывает (что видно из
уравнений поверхностей).
Для линии пересечения поверхностей х2 + у2 + ζ2 = 4
и х2 + у2 = Зг имеем: ζ2 + Зг — 4 = 0, откуда гг = 1, г2 = 4
(второй корень дает мнимые значения для р). Следовательно, для
точек линии пересечения ζ= 1, ρ = J/ 3; внутри тела ρ
изменяется от 0 до |/3. Заметив, что φ изменяется от 0 до 2π, по
формуле (7.8") получим
l/ = jd<P ί Pdp J <fe = i<ftp J (ρΐ/4-ρ2 --|-Ц> =
0 0 _£»_ 0 θ \ ° /
3
Рис. 7.12
289
^ 3
л
1 (4-P2)2 p4
1_з 19
3 v ^ ' 12
о
4. Вычислить объем тела, ограниченного эллипсоидом
X2 И2 22
— А- — 4-—- = 1
а2 "Г £2 "Г С2
ΑΧ
2
При наличии выражения "^г + тг + -^- в уравнении
поверхности полезен переход к обобщенным сферическим координатам по
формулам:
χ = ар sin θ cos φ, у = bps'm θ sin φ, 2 = cpcos6,
якобиан в этом случае равен J = абср2 sin θ.
Уравнение данной поверхности в новых координатах примет вид
ρ = 1 (ибо ^2~ + 4г + ^2" = Р2 sin2 θ cos2 φ + ρ2 sin2 θ sin2 φ +
+ ρ2 cos2 Θ = ρ2), поэтому для данного тела р изменяется от О
до 1. Заметив, что 0<;θ<!π, 0<]φ<;2π, по формуле (7.8)
с учетом формулы (7.5) получим
2- π 1
V = fjj dxdydz = j dy J άθ J abc p2 sin Qdp =
(Ю 0 0 0
2- π 2π
abc I dtp Ι -γ sin ΘάΘ = γ abc I (— cos Θ)
oo о
3
dtp = -5- nabc.
ο Ύ 3
4
Итак, V = -ο- πα&ε. Β частном случае, при α = 6 = с = /?,
получаем объем шара х2 + у2 + г2 <: R2, V = -^-π/?3.
з
Замечание. Поскольку эллипсоид симметричен относительно
координатных плоскостей, можно найти объем γ части данного
тела. При вычислении интеграла нужно иметь в виду, что в этом
случае 0 < ρ <; 1, 0 < θ < γ, 0 < φ <; γ, τ. е. верхние пределы
интегрирования по θ и φ отличны от предыдущих.
5. Найти массу шара х2 + у2 + z2 < 2Rz> если плотность
в каждой точке обратно пропорциональна расстоянию ее до начала
координат.
Пусть N (ху у у ζ) — произвольная точка данного шара. Тогда
ее расстояние d до начала координат выражается формулой d =
= Yx2 + y2 + z2. Плотность γ, в соответствии с условием задачи,
определяется формулой
290
γ (χ, у, ζ) = =-,
у χ2 + У2 + ζ2
где k — коэффициент пропорциональности.
По формуле (7.9)
Μ == I I I — =-— dxdydz,
(V) v г у ι
где область (V) ограничена сферой х2 + У2 + ζ2 = 2/?г.
Для вычисления данного интеграла перейдем к сферическим
координатам по формулам:
χ = ρ sin θ cos φ, у = ρ sin θ sin φ, г = ρ cos θ;
якобиан преобразования J = ρ2 sin θ.
Подынтегральная функция
k _k_
V x2 + y2 + z2 ~ Ρ '
а уравнение сферы χ2 + У2 + ζ2 = 2/?2 примет вид ρ = 27? cos θ.
По формуле (7.7)
(V) r ~» ^ (y)
π тс
2κ ΊΓ 2/? COS θ 2π ΊΓ
= k f dtp f άθ f ρ sin ©dp = ft [ ώρ ( 2/?2 cos2 θ sin 6d6 =
ο ο ο ο Ό
= 2/?2ft ( (- ^-^j |o ώφ = -|- Я2* f d<P = 4 ****·
о о
6. Найти центр тяжести шара χ2 + У2 + ζ2 < 2#2, если
плотность в каждой точке его обратно пропорциональна расстоянию до
начала координат.
Воспользуемся формулами (7.10). Масса Μ была определена
в примере 5. Из соображений симметрии следует, что х0 = 0,
Уо = 0. Найдем ζ0:
_ 1 f [ f kzdxdydz , - ν
3- м JJJ ух% + # + # "· V>
(У) ψ ' ν '
Вычислим этот интеграл, перейдя к сферическим координатам:
2т: ~2~ 2/? cos Θ
III tWfwβ*/ "ф/de I |p2sin0pcosedp^e=
(У) о о b
291
2т. 2 2R cos θ
k Γ dtp Γ sin θ cos ΘάΘ Γ p2dp =
о о
2г. Τ
Sd4'
2 г.
dcp I cos4 6d (cos Θ)
о
2г. 2
ft Г Лр Г SR3 cos3 Θ sin Θ cos ΘάΘ
.0 О
2-- ~2
_ _ 8fc/?3
3
о
8kR* ' ι cos5 θ
■д
Следовательно,
2·^ Τ
3
о
о ^Ф^Тб"^^3·
1 С [' С kzdxdydz _ 1 16 , рз _ 4 η
Замечание. Тот факт, что х0 = 0и у0 = 0, можно
установить с помощью первых двух формул (7.10). Действительно,
_ J_ Г Г Г kxdxdydz _
Хо~ м JJJ Vx* + y> + z> ~
(V)
IT 2R cos Θ 2г.
= Α |· d0 f dp [ Ρ* ""βΡ^η θ cos φ d(f =
0 0 0
~2~ 2/? cos θ 2r.
= Ίλ Ι άΘ ί dp ί ρ2 sin2 θ cos ψάψ = °"
boo
Аналогично показывается, что у0 = 0.
7. Найти центр тяжести однородного тела, ограниченного
эллиптическим параболоидом 2л:2 + У2 = 4г и плоскостью г = 2.
Из соображений симметрии следует, что х0 = у0 = 0. Так как
тело однородно, можно считать γ = 1. Координата ζ0 в
соответствии с (7.10) выразится формулой
zo = -\r J J J zdxdydz,
(V)
292
где V = f Π* dxdydz.
(V)
Вычислим каждый из тройных .интегралов. Область (V)
ограничена параболоидом 2л:2 -J- у2 = \z и плоскостью ζ = 2. Проекцией
тела на плоскость 0#ί/ является эллипс, уравнение которого в этой
плоскости имеет вид 2л:2 + у2 = 8. Укажем пределы
интегрирования: г изменяется от -j- (2x2 -f у2) до 2, при фиксированном χ у
изменяется от — ]/ 8 — 2*2 до 4- ]/ 8 — 2л:2 (получено из
уравнения 2*2 + у2 = 8), χ изменяется от — 2 до 2 (получено из того же
х2 и2 \
уравнения: -γ, -f- -у- = 1, а2 = 4, а = 21.
Таким образом,
У 8-2л-
I/ = J f f dxdj/dz = J dx Г dy J9
dz.
(V)
^8-2·ΐ2 -j" <2λ'2+^2>
Так как
ί dz = 2-x(2r4-i/2);
+ /8-2a:2
Г
ί
- l/8=2T2
■ (2х2+У2)
2--^{2х2 + у2)
dy =
2у
12
/-_= > 8—2л:2
,= _ У8-2х2
ТО
I/
= 4 j/A8 — 2*2 - х2 \' 8 - 2х2 - 4- (18 - 2х2)3,
f U УЪ — 2х2 — х2 \ 8 - 2х2 —\{\/Ъ — 2х2У
dx.
Для вычисления полученного интеграла применим подстановку
χ = 2 sin /. Тогда dx = 2 cos tdt, новые пределы интегрирования:
л β д
« = —2-, Р = ^-.
ι/
= J J4/8 — 8 sin2/ — 4 sin2M''8 — 8 sin2/
293
"^(|/8 — 8 sin3 /)s 12 cos tat = ί (δ V 2 cosi — 8 sin2<^2 cosi —
(2 J/ 2)3 cos3/12 cos tdt=\bV"2 f cos2 Ли ■
16/2 / sin2 < cos2 tdt --^-p- J cos4Wi
= 161/2 J cos2<(l-sin20
Л-
16^2
s
COS4 /itf
^-/ cos«idf = 32V'2 3
3 8
—5-π = 4 1' 2 π
/ cos* tdt = 2 I cos* tdt = 2 -j^-π = -^-π; см. пример 4 § 6.1
_3_ _ J3_
16 π "~ 8
Аналогично вычисляется и второй интеграл:
2 /гРЫ2 2
zdxdydz = j dx J di/ J zdz.
(V)
Поскольку
2
-2 _ /8_2χ2 ^ (2;c2+i/2)
/
zdz = ~2~
- (2*2+i/2)
■ (2*2+i/2)
V 8 8 32/'
V8—2x2
/
2_^__ X2^ */* \
8 8
-Ы dy = 2y -
8 24
Ϋ&—2χ2
294
160
у= V 8—2х2
\у=— /8—2x2 4
--±- *2 (V8^~272)3 —^ (|/ 8 = 2?)»,
то
J [J zrfjotydz = J U |/ 8 — 2jc2 - -i- *4 ]/8 — 2jc2 -
(V) -2
_ _L *2 d/8^272)3 - -I- (|/8^2^)5] ^-||/2л.
Этот интеграл также вычислен с помощью подстановки
χ = 2 sin/.
Следовательно,
(V) г
т. е. С(0, 0, -ψ) — центр тяжести данного тела.
8. Вычислить момент инерции однородного куба относительно
одного из его ребер.
Начало прямоугольной декартовой системы координат поместим
в одной из вершин куба, а оси направим вдоль его трех взаимно
перпендикулярных ребер (рис. 7.13). Обозначим через а ребро
куба и найдем его момент инерции относительно оси Ozy
воспользовавшись формулой (7.12) или третьей из формул (7.13). Так как
куб является однородным, то в указанных формулах можно
положить γ = с (с = const).
/z = cJjJ(x2 + у2) dxdydz = c J f f(x2 + y2) dxdydz
(V) ο Ό ο
a a a a a
= c f dxj dy J (x2 + y2) dz = ca f dx J (x2 + y2) dy =
0 00 00
a a
= ca J (x»y + 4-) |^ dx = ca J (ax* + ^-)dx =
0 0
/ x3 . a3
a 2 .
A = -τ ca°.
0 3
295
ЗАДАЧИ
Найти объемы тел, ограниченных следующими поверхностями:
1. 2х + Зу+4г = 12, χ = 0, у = 0, ζ = 0.
2. — + 4" + — = 1. х = 0, у - 0, г - 0.
3. αχ = у2 + ζ2, л: = а.
4. 2г - х2 + у\ ζ = 2.
5. χ2 + у2 + ζ2 — 2r/ = 0, χ2 + ζ2 = 2 — у.
6. ζ = ^ χ2 + у2, г = χ2 -4- у2.
7. у2 = 4 — 3*, у2 - *, г = ±9.
8. ζ = 6 — χ2 — у2, г = |/ χ2 + У2·
9. χ2 + г2 - 4у, χ2 -f ί/2 + ζ2 = 12.
10. αζ = α2 — χ2 — ί/2, г = а —λ: —ί/, * = 0, у = 0, ζ = 0(α>0).
11. г2- 1 — χ — у^ χ = 0, у = 0, г = 0.
12. χ2 4 у2 + ζ2 = 16, х2 + У2 + г2 — Sx = 0.
ίο У2 , г2 2л:
13. 4*· -\—=- = —, х = а.
14. (г- l)2 = x2-f-y2, х>0, у>0, 1>г>0.
15. г2 = qx(q> 0), у2 + г2 - б2, χ = 0.
16. χ2 + У2 = 2ах, х2 + у2 = 2αζ, ζ = 0.
Перейдя к цилиндрическим или сферическим координатам,
вычислить объемы тел, ограниченных поверхностями:
17. х2 + У2 = Rx, x2 + y2 + z2 = R2, г = 0.
18. χ2 + у2 + ζ2 = 4, у2 + ζ2 = 3χ.
19. χ2 + у2 + г2 = α2, г = j^#2 + у2 (внешний по отношению
к конусу).
20. х2 + у2 + z2 = R2, χ2 + У2 + z2 = 2Rx.
21. χ2 + у2 = 2az, x2 + y2 + z2 = За2.
22. x2 + y2 + z2 = R2, у2 = х2 + г2(У>0).
23. (χ2 + У2 + ζ2)2 = а3х. 24. (χ2 + У2 + ζ2)2 = αζ (χ2 + у2).
25. (χ2 + у2 + ζ2)3 = 3xyz. 26. χ2 + у2 + ζ2 = 2αζ, χ2 -f У2 <г2.
С помощью надлежащей замены переменных вычислить объемы
тел, ограниченных поверхностями:
97 [*-+£-+ *_\ -£_+t_
^ * I 02 "Г £2 "Г С2 / а2 "Г 62 ·
9« *2 л. 11 а. г2 - 1 ^.jl У2 - ζ
29. х2 + у2 = г, х2 + у2 = -|-, ху = а2, ху = 2а2, х — 2у== Θ,
2* — y = 0(x>0, y>0).
30. (* + ? + *)* = -**-.
I у2 /72 \П 7ЧП ~ ί у2 ,,2 \«—2
32. {axx + Ьгу + cxzf + (а2х + b2y + c2zf + (а3х + b^y + c3z)2 = /ι2,
если
αι ^ι cx I
a2 b2 c2 \φΟ.
#з b3 c3 I
В каждой из задач 33—42 найти массу тела, ограниченного
данными поверхностями, при указанной объемной плотности:
33. R2z2 = h2 (χ2 + у2), ζ = h, у (χ, у, ζ) = kz.
34. Прямоугольного параллелепипеда, определенного
неравенствами:
0<х<а, 0<у<6, 0<2<с, γ (χ, у, ζ) = k{χ2 + у2 + ζ2).
35. 2* + ζ = 4, χ Η- ζ = 2, у2 = 2х(у> 0), γ (*, у, г) = Ay.
36. α:2 + У2 + ζ2 = За2, χ2 + у2 = 2αζ (α > 0), у (χ, у, ζ) =
= k(x + y + z)2.
37.
38.
39.
x2 + y2+z2 = R2, χ2 + y2 + z2 = 2Rzf у (х, у, ζ) = kz2.
χ2 + ζ2= 1, y = 0, y = 1, т(*,У,г) = /ф2 + у+г2)3.
*2 + у2 + Z2 = R2f χ2
У2 + г2 = 4/?2, γ (χ, у, ζ) =
Ϋ x* + y2 + z2
a2
У*
+ 7Г= 1» γ (χ, ί/, ζ) = fe (-^г +
У*
+ С2
41. *2 + у2 + z2 = R2 (t/ > 0), у2 - χ2 + ζ2, Υ (*, y,z) = k (x2 +
+ У2 + ζ2).
42. ζ = ху, у = χ, χ = 1, г = 0, γ (я, у, г) = kxy2z3.
43. Найти массу шара х2 -\- у2 + ζ2 <^ *, если плотность в
каждой его точке пропорциональна расстоянию этой точки до начала
координат.
44. Вычислить массу тела, ограниченного параболоидом
вращения х2 + У2 = 2ζ и плоскостью ζ = 2, если плотность
пропорциональна сумме квадратов двух первых координат данной точки
М(х, у, ζ).
45. Найти массу призмы, ограниченной плоскостями χ = 0,
у = 0, ζ = 0, у = 6, # + ^ = а, если плотность в каждой ее точке
пропорциональна абсциссе χ данной точки М(х, у, 2).
46. Вычислить массу тела, ограниченного конусом у =Υ χ2 + ζ2
и плоскостью у = bt если плотность в каждой его точке
пропорциональна ординате этой точки.
В каждой из задач 47 — 60 найти координаты центра тяжести
©днородного тела, ограниченного указанными поверхностями:
47. * = 0, у = 0, 2=1, 2 = 3, 2х + у = 3.
48. χ + ί/ + ζ = α, χ = 0, у = 0, 2 = 0.
49.
50.
ь2
+
х* + 2у2 = 4г, 2 = 2.
297
51. χ2 + у2 + ζ2 = 1, χ2 + у2 + ζ2 = 2у.
52. ζ2 ='jm/, л: = а, у = b, z = 0.
53.
54.
55.
56.
57.
58.
59.
60.
x + y=l, x2 -f y2 = z, χ = 0, у = 0, ζ = 0.
*2 + У2 + ζ2 = 3, χ2 + у2 = 2ζ.
^ + ζ» = j:, л: -f У + 2 = 0.
л:2 + ζ2 = 2ι/, χ + ζ = г/.
χ2 _l φ _|_ ζ2 = 256, χ2 + ί/2 — ζ2 = 0.
0* +2« = 2χ, Χ= 1.
x==3 — y2-z2(x>0), x = 0.
χ2 . ι/2 . ζ2 .χ2 if , г2 η , . m
1Γ + ^- + 7Γ=1. -52--^τ7τ = 0(ί/>0).
61. Найти координаты центра тяжести куба 0<.*<; 1, 0<;
<1у<1 1, 0<^2<; 1, если плотность в каждой точке Μ (χ, у> ζ)
2α-1 26-1 2с-1
у(х9у,г)=х1-ау1-ьг1-с9
где 0<α< 1, 0< Ь< 1, 0 < с < 1.
В каждой из задач 62—67 найти моменты инерции
относительно координатных плоскостей однородных тел, ограниченных
поверхностями:
62. χ + у + ζ = 1, χ = 0, у = 0, ζ = 0.
63· ΊΓ + Τ + "Г = *' * = °' у = °' ζ = °·
64. x2 + y2 + z2 = 1.
Χ2 Ζ/2 22
65· ^ + ΐ2- + 12-=1·
66.
"б2"_t~ T2" — "i?
b2 с2 a ' b l с а
Найти моменты инерции относительно оси Ох однородных тел,
ограниченных поверхностями:
68. —+ Т- + —= 1, х = 0, у = 09 г = 0.
a l b * с * 'У *
•o.^ + f + 5-ι. *.(тГ+ (-ff + (4-f-·
Найти моменты инерции относительно оси Оу однородных тел,
ограниченных поверхностями:
71. Ь2 (х2 + г2) = а2у\ 0<у<6.
72. х2 + У2 + ζ2 = 2, χ2 + ζ2 = у2 (у > 0).
73. х2 -)- ζ2 = ί/, χ + г = it 1, χ — ζ = ± 1, ί/ = 0.
Найти моменты инерции относительно оси Οζ однородных тел,
ограниченных поверхностями:
74. ζ2 = 2ах9 х2 + у2 = αχ, г = 0.
75. χ + у + ζ = 2, χ2 + У2 = 2, г - 0.
76. (х2 + у2 + ζ2)2 = ah.
298
В задачах 77—79 найти моменты инерции данных однородных
тел с массой М:
77. Прямоугольного параллелепипеда с ребрами а, 6, с
относительно каждого из ребер и относительно центра тяжести.
78. Шара относительно касательной прямой.
79. Прямого круглого цилиндра (высота Я, радиус
основания R) относительно диаметра основания и диаметра его среднего
сечения.
80. Найти момент инерции неоднородного шара х2 + у2 + z2^CR2
массы Μ относительно его диаметра, если плотность шара в
текущей точке Ν (χ, у, ζ) пропорциональна расстоянию этой точки до
центра шара.
81. Доказать равенство Iu = Illo + Md2, где 1и — момент инерции
тела относительно некоторой оси и, IUo — момент инерции тела
относительно оси и0, параллельной и и проходящей через центр тяжести
тела, Μ — масса тела, d — расстояние между осями.
82. Доказать, что момент инерции тела, занимающего объем V,
относительно оси а, проходящей через его центр тяжести О(0, 0, 0)
и образующей углы α, β, γ с осями координат, Iu = Ix cos2 a +
+ 1у cos2 β -f- I2 cos2 γ — 2Kxy cos α cos β — 2ΚΧΖ cos α cos γ —
— 2Kyz cos β cosy, где Ixf /v, I2 — моменты инерции тела
относительно осей координат, /( = \\\ хуу (х9 у,z) dxdydz, KX2 = f I j* xzy (x,
"(V) "(V)
у, ζ) dxdydz, Kvz = i IJ yzy (x9 y, z) dxdydz — центробежные моменты.
'(V)
83. Определить высоту Н и радиус основания R однородного
цилиндра так; чтобы эллипсоид инерции для этого цилиндра
обратился в сферу.
84. Определить высоту Η и радиус основания R однородного
конуса так, чтобы эллипсоид инерции для этого конуса обратился
в сферу.
ОТВЕТЫ
1 да3 7 д. 32 8
1. 12. 2. frabc. 3. -γ. 4. 4л. 5. ηγ. 6. у. 7. 32. 8. ул. 9. у π (6 J 3—5).
а3 4 80 л л&4 3
10. 2j(3π — 4). 11. jg. 12. — л. 13. nabc. 14. jg. 15. -^-. 16. -j- πα3. Реше-
_^ Х2-\-У2 _£_ r2 π
2а /2ах—χ2 2а 2 2а cos φ 2а 2 2а cos с
ние. V = 2 | dx I dy I dz = 2\ αφ Γ rdr I de=2J d<p ί — =
£^ Λρ = ! ла3. 17. ** (Зл - 4). 18. !? π. 19. 2™*V~2. 20. ^.
4 Ύ 4 9 ν ' 6 3 12
299
πα3 - „ π/?3 ,Α- πα3 ла3 1 „ π2
21. -g-(6 КЗ— 5). 22. -у- (2 — /2). 23. -у. 24. -gg-. 25. γ. 26. πα3. 27.-j-abc.
ЪпаЬс ,- ' 9 4π β π2 α^2 4π/ι3 knR2h2
28. -jj-o-V5). 29. χα*. 30. -g- α3. 31. -.—. 32. —- 33. —j-.
3nsin— ύΙ^Ι
ΑΙ
34. 2^ (α2 + 62 + с2). 35. ϋ 36. ΞΣ^Λβ КЗ —-5Ζ-Υ 37. 5?* π/?». 38. ^
3ν^; 3 5 \ 6 / 480 2
4 fot#3 ,- k kn \6kn kcflb
39. 6nkR2. 40. -g- fcrmte. 41. -у (2 — V 2). 42. yg 43. yg. 44. —g-. 45. -g- ,
. knb* An η ί I
k—коэффициент пропорциональности. 46.?™-. 47. С (_, 1, 2 I. 48. С l±, —, iL
4 \ 2 / \ 4 4 4
49. С (2 С, 0, θ) . 50. С (θ, 0, 1) . 51. С (θ, Ι, θ) . 52. С р, Ъ± f 9J^.
53. С /2,2Д). 54. С (θ, О, 5(61_1+5)\ ^ с /_5_, _2_,-_L). 56. С Л
\ 5 5 30/ V 83 / _ \ 6 2 2 / V
2, Г». 57. С (0, 0, 3(2 + ) 2)). 58.c(^2±2L2, 0, θ). 59. С(1, 0, 0). 60. С (θ,
6+?/2 Ь, 0J. 61. С (α, 6, с). 62. /χν = /V2 = Ixz = 2. 63. Ixy = _^2, /v, =
a36c a63c 4π 4 4
= "go"» !χζ = "60"' 64' 7*> = 7>'<? = 7« = Ϊ5- 65' 7*v = 15 ла^> ^= Ϊ5 na36c,
4 Tiabc3 ncPbc яаЬ3с 4
7ac = Ϊ5 πα^. 66. /xy = -2o~, /yz= —5—, /** = —2o~- «7. /ху=^лак3,
7 4 abc АлаЬс ЗпаЬс <о
/W="2* /zx= ynato. 68. -gg- (62 + c2). 69. -y^-^ + c2). 70.-^gg- (62 +
+ c*). 71. U^-. 72. 12.(4 /2-5). 73. ii. 74. 32 ^ q». 75. 4π. 76. iiiifL.
^ ; 10 15 V ' ' 45 135 140
1 Μ Μ Ι 7
77. -jM(b2 + c*), "з-(с2 + а2), -y^ + fc2), -jg-Λί(а2 + б2 + с2). 78. -g- MR2.
79. Λί(22+ ^!), 21(я2 + з/?2)· 80.2 м/?2. 83. я = я/з. 84. з/?|/з=яу1>.
\ 4 3 / 12 9
Ш. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ.
ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
Глава 8
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 8.1. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
Рассмотрим пространственную кусочно-гладкую* кривую L,
ограниченную точками А и В (рис. 8.1), и определенную на ней
непрерывную функцию f(x, у, ζ)=/(Λ1), где М(х, у, ζ) — точка
кривой. Дугу АВ разобьем точками Мъ М2, ... , Мп-\ на η
элементарных дуг Λ1/_ιΛ1/(ί= 1, 2, 3, ... , η, Μ0=Α,Μη = Β),
длины которых обозначим соответственно через А/ь Δ/2, ... , ΔΙη.
На каждой из элементарных дуг Λί,-ιΛί,- выберем произвольно
точку Mi(xh yif Ζι) и составим сумму
η
s„ = 2/&. у» ^·)Δ/<·' <8Л)
ι=1
называемую интегральной суммой по кривой L функции / (х, у, г).
Криволинейным интегралом первого типа от функции / (лс, у, г)
по кривой L называется предел интегральной суммы (8.1) при
п->оо и max Δ /, -> 0:
η
\ f (χ, у, ζ) dl = lim S„ = lim ^f(xi, y~t, zt)Alt. (8.2)
На кривой L, целиком лежащей в плоскости Оху, функция /
от координаты ζ не зависит, поэтому по определению
η
\ f (χ, у,) dl = lim 2 / Й- Й)Δ/-· (Щ
I max Δ^.-*0^1 ^
* Кривая называется гладкой, если в каждой ее точке существует
касательная, непрерывно изменяющаяся вдоль кривой. Кривая, состоящая из
конечного члена гладких дуг, называется кусочно-гладкой.
301
Если подынтегральную функцию / > 0 рассматривать как
линейную плотность кривой интеграции L, то криволинейный
интеграл первого типа представляет собой массу кривой L.
Вычисление криволинейного интеграла первого типа сводится
к вычислению определенного интеграла.
Если пространственная кривая L задана параметрическими
уравнениями
x = x(t), y = y(t), z = z(t) (ίι<^</2),
у\
3
2
1
Д
0
ι
/
^в
2 3 4
Рис. 8.2
ОС
то
и
J/(*, У, z)dl= §f[x(t), У®, z{t)]Yx'2 + y,2 + z'2dty (8.4)
L tx
так как в этом случае дифференциал дуги dl=y χ'2 + у'2 + ζ'2 at.
Если кривая L лежит в плоскости Оху, то
и
/ / (х, У) dl = jf [х (О, У (01 К*'2 + У'2 dt. (8.5)
L h
В частности, для плоской кривой, заданной уравнением
у = у (л;), где а < χ < Ьу имеем dl = у 1 + у'2 dx, поэтому
ъ
J / (х, У) Л = ί / [х, У (*)] Kl + y'2dx. (8.6)
Если плоская кривая задана уравнением ρ = ρ (φ) (α < φ <; β)
полярных координатах, το dl = у ρ2 + ρ'2 dq> и
в
302
§f(x, y)dl = j/(ρ cos φ, Ρ5ίπφ)Κρ2 + ρ,2^φ. (8.7)
L a
Основные свойства криволинейного интеграла
первого типа:
1) по самому определению криволинейный интеграл первого
типа не зависит от направления пути интегрирования:
то
J/(M)d/= f f(M)dl;
АВ ΒΑ
2) j [h (Μ) ± /, (Μ)] dl=\h (Μ) dl ±: j U (Μ) dl;
L L L
3) \ cf (Μ) dl = c§f (Μ) dl (c = const);
L L
4) если путь интегрирования L разбит на части Lly L2, ... , Ln,
j f (Λί) dl = j / (M) dl + f / (M) dl + ... + j / (M) dl.
ПРИМЕРЫ
1. Вычислить криволинейный интеграл J xy2dl, где L — отре-
L
зок прямой между точками Л (0,0), β (4,3).
Прямолинейный отрезок АВ лежит в плоскости Оху (рис. 8.2),
на нем задана функция / (лс, у) = ху2. Уравнение прямой АВ имеет
3 3
вид у = — х. Так как у' = -j-, то
dl = yi+y'2dx= 1/ 1 +(4") ^ = 4"djc·
По формуле (8.6) получаем
4 4
ί ХУ41 = Jx (4 *j 4 d* = J Ж" *3βί* = 1Г · ΊΓ
L 0 О
- 64 4 ~40·
2. Вычислить j (χ5 + 8д:у) d/, где L — дуга кривой Ay = χ4
между точками, для которых χ = 0, χ = 1.
Поскольку у' = χ3, dl = У I + a:6 dx и на дуге кривой 4у = л:4
функция f (jc, у) = (χ5 + 8ху) = хь + \у 2х = х5 + Jt4 2x = За:5, то
по формуле (8.6)
303
1 1 I
J (xb + Sxy)dl = j 3jc5 V\ + x*dx = 3/(1 + x*)T -i-d(1 + x«)
θ
з_
J_ (1+*6)2
2 * _3_
2
1 1
-T(2K2-1).
3. Вычислить j у Vy2 + 1 dl, где L — дуга кривой х = \пу
L
между точками, для которых у = 1, ι/ = 4.
Так как кривая задана уравнением χ = φ (у), то дифференциал
ее дуги выражается формулой
dl = |/1 + х'2 dy.
Криволинейный интеграл вычислим по формуле
d
j / (χ, y)dl=\f [φ (у), у] V\ + χ'2 dy. (8.8)
L с
В данном случае с = 1, d = 4, л: = φ (у) = In ί/, л:'= —,
dl = V\ + x'2dy = γ 1 + -Ldy = -у VY+ldy, поэтому
4 4
J yVVTTdi = f у у'уМП" -L VTTTdy - j (у2 + ΐ) rfir =
ϊ У 1
Νί+4)-(4-+■)-£+«--!-->-«·
4. Вычислить J (2л: + у) d/, где L — контур треугольника ABO
(рис. 8.3) с вершинами 4(1,0), 5(0,2), 0(0,0).
В соответствии с четвертым свойством криволинейного
интеграла первого типа
j (2х +y)dl= j (2x + y)dt+§ (2x + у) dl + j (2x + у) dl.
L АВ ВО ОА
На отрезке АВ у = — 2х + 2, поэтому у' = — 2, dl =
= Vl + y'2dx = V~5dx.
На отрезке ВО χ = 0, χ' = 0, d/ = К1 + χ'2 dj/ = dy, на
отрезке ОА у = 0, у' = 0, d/ = I'' 1 + #'2 d* = dx. Принимая во вни-
.304
L
[1Г+У
мание первое свойство криволинейного интеграла и используя
формулы (8.6) и (8.8), получаем
1 ? 1 I1
j (2х + y)dl= f 2 ΫΤάχ + j ydy + J 2xdx = 2 |/"5x | +
+
+ x
1 X
Рис. β.3
Рис. 8.4
5. Вычислить J (χ + у) dl, где L — лепесток лемнискаты
l
p = a]/sin2(p, расположенный в первом координатном углу
(рис. 8.4).
Линия L задана уравнением в полярных координатах, поэтому
здесь целесообразно воспользоваться формулой (8.7).
Так как
1 no a cos 2φ
cos 2φ 2 =- -JL—
ρ = a-
2 V sin 2φ
TO
dt= [/fl2sin2<p + ******* dq>-
sin2q> Ύ ]/δίη2φ
α2άψ _ α2άψ
Ys'm 2φ
dtp =
a V sin 2φ Ρ
Заметив, что 0<φ <-£-, т. е. a = 0, β = -^-, по формуле
(8.7) получим
"2" У
J (jc -|- у) d/ = J (ρ cos φ + Ρ sin φ) φ = a2 | (cos φ + sin φ) dtp =
= a2 (sin φ — cos φ)
-2α2.
305
6. Вычислить \ xdl, где L — первая арка циклоиды
L
x = a(t— s'mt), у = a(l —cost) (a > 0).
Применим формулу (8.5). Для первой арки циклоиды (рис. 8.5)
0 < t < 2π, т. е. tL = О, t2 = 2π.
Поскольку
x'f = а (1 — cos t)y y't = a sin t
Рис. 8.5
И
dl = Yxt2 + y't2 dt=Va2(l— cos tf + a2 sin21 dt =
= aV2 — 2costdt = a "[/2·2sin2-^-Λ = 2α sin-g-Λ,
по формуле (8.5)
\ xdl = ) a (t — sin i) 2a sin -у Л = 2a2 ) ί sin -γ dt—
2-
— 2a2 1 sin ^ sin -γ-dt = 8πα2,
о ^
так как
2π
2π 2п |2κ 2π
ft sin -5-Λ - — 2 j id (cos -g-j - — 2^ cos -Η + 2 f cos -5-Λ -
о о
|2n
о
= — 2 (2π cos π — 0 cos 0) + 4 sin -γ
ζπ 2г. 2г.
Jsinisin-^-di = 2 j sin-ψ cos-γ-s\n-γ dt = 2 j sin2 γ 2d ( sin у J =
η η Ο
И
2π
-4
sin»-g-
-0.
306
7. Вычислить J (2х + Ay — Az + 7) dly где L — отрезок прямой
между точками Мг (8, 9, 3), Л42(6, 10, 5).
Составим сначала уравнения прямой, проходящей через точки
Мг и Λί2:
л —8 _ у — 9
г —3
ИЛИ
* —8 _ ί/ —9 _ 2 — 3
( = 0-
6 — 8 ~~ 10 — 9 ~~ 5 — 3 —2 ~~ 1 ~~ 2
Таким образом, получены параметрические уравнения прямой:
х = 8 — 2U y = 9 + t9 ζ = 3 + 2ί;
точка Λί пробегает отрезок MjMg, когда t изменяется от 0 до 1,
т. е. tx = 0, t2= l.
. Так как х' = — 2, у' = 1, г' = 2, то
= |/4+ l + 4df=3df.
По формуле (8.4)
j (2л: + Ау — Az + 7) dl =
L
= J [2 (8 - 2Q + 4 (9 + О - 4 (3 + 2t) +
о
1
+ 7]3df = 3j(47 — &f)'dt =
= 3 (47* - At2)
-3(47-4)= 129.
Рис. 8.6
8. Вычислить \ xydl, где L — дуга винтовой линии χ = a cos ί,
L
y = asmt, z=bt (рис. 8.6), ограниченная точками, для которых
< = о, < = -£-.
Применяем формулу (8.4). Поскольку
х' = — a sin t, у' = a cos *, г' = Ь,
то
d/ = Υ χ'2 + у'2 + z'2 dt = V а2 + b2 dt
ΊΓ Ύ
J χί/d/ = j a cos * b sin * )/a2 + b2dt = ab \ra2 + fr2 j cos ί sin / d/
307
ab Va2 + b2 f sin t d (sin t) = ab У a2 + b2 -5^
= ^V^TT\
9. Вычислить \ Yx2 + 2z2 dl, где L — окружность χ2 -f у2 -f-
+ г2 = R2, у = ζ.
В данном случае линия задана пересечением двух
поверхностей: сферы и плоскости.
Составим параметрические линии, положив ζ = t. Тогда у = t>
а л: = ± VR2 — 2t2 (получено из уравнения х2 + у2 + ζ2 = /?2
с учетом равенств у = ζ = t).
Из параметрических уравнений линии
находим:
поэтому
# =
±ζ}//?2-2/2, j/ = f, ζ = ί
1, ζ' = 1,
2/
|/ R2 — 2t*
-, у
Л = ι/ *'2 + у'2 + г'2 Л = ]/ R2^2t2 + ι + ι dt =
/2/?
/Я2 — 2/2
■Л.
Из равенств * = ± l^/?2 — 2^2 определим пределы изменения t,
положив χ = О, или /?2 — 2t2 — 0, откуда ίχ
— /
/"2
Ι/Τ'
Заметив, что на данной линии χ + 2г2 = /?2 или 1^#2 + 2Ζ2 = R,
по формуле (8.4)
R R
d(f2t) _
f*
^2 + 2z2d/ = 2 j R /2Rdt
L R
Vr*—w
2R2 —.
A v.
-= 9E>2
2R2 arc sin
1^2"
У 2t
R
= 2R2 [arc sin 1 — arc sin (— 1)] =
R
ΥΎ
= 2R2(^r+^-) = 2nR2.
ЗАДАЧИ
Вычислить криволинейные интегралы первого типа по
указанным плоским кривым, заданным уравнениями вида у = f(x) или
* = <Р(0):
308
1. J x2y2dly L —отрезок АВ прямой, где Л (О, 0), 5(2, 1).
2. \ xdl, L — дуга кривой у = λ'2 -f- 1 между точками Л(0, 1),
В(\, 2).
3. \ У 1 + х2 d/, L — дуга кривой 2у — х2 = 0 (1 < χ < 3).
L
Г X3
4. \ —2~dl, L — дуга кривой л:*/ = 1 между точками Л(1, 1),
5. J yd/, L — дуга кривой у = χ3 между точками Л(0, 0),
'.6. ί]Λ + *4Λ, L —дуга кривой Зу = х3 (1<х<2).
L
7. Ι Υ1 + *6 d/, L — дуга кривой 4у = л;4 между точками
А(0, 0), S(1,4)·
8. \y2dl, L — дуга кривой х = 1пг/ между точками Л(0, 1),
β(1, е).
fcos^x
- - d/, L — дуга синусоиды у = sin χ (0 < χ < π).
К 1 + cos2*
fc j rj3y
— - d/, L — дуга косинусоиды у = cos χ
j/ 1 -f sin2*
(o<x<L-j-).
11. J Υ1 + cos4* d/, L — дуга тангенсоиды ί/ = tg χ
(0<x<4).
12. I sin χ I' 1 + sin4xd/, L — дуга кривой у = ctgjc
/ π π
13.
Ρ 1/14- cos2*
os* ^ ^ ~~ Д^га синусоиды у = sinjc
L
(o<*<4)·
14. J sin4 .v cos xd/, L — дуга кривой у = In sin л: ί^- <; jt<; -ΐ-
309
15. J sin2 χ cos3 xdl, L — дуга кривой у = In cos χ ί 0 < χ < -^-).
16. I sin4 x cos2 xdl, L — дуга кривой у = lncosecjc
(x<x<—;.
17. J cos4 л: sin2 xd/, L —дуга кривой у = In sec л: (θ <*<;-£-
Вычислить криволинейные интегралы первого типа по
указанным плоским кривым, заданным уравнениями в полярных
координатах:
18. J xdl, L — дуга окружности ρ = R, лежащая в первой
четверти.
19. \ y2dl, L — верхняя полуокружность ρ = R.
20. f \ί χ2 4- у2 + a2 dl, L — дуга спирали Архимеда ρ = αφ
L
(a > 0) между точками А(0, 0), β (α2, α).
21. Jj/x2+i/2d/, L — верхняя половина кардиоиды
ρ = а(\ + cos φ).
22. J γ χ2 + у2 dl, L — дуга лемнискаты ρ = а |/ cos 2φ
L
23. j (*2 + у2)z dt, L — дуга лемнискаты ρ = a Υ sin 2φ
(θ«Ρ<-=-)·
24. J l/x2 + y2 arctg-|-d/, L — дуга лемнискаты ρ = aY co$2q
(о <ф <-=-)·
25. J ^x2 + y2 iarctg ^-) dl, L — дуга кривой ρ = α|/Ιϊη2φ
(o«p<^-).
Вычислить криволинейные интегралы первого типа по
указанным кривым, заданным параметрическими уравнениями:
26. \ xy2dl, L — дуга окружности χ = Rcost, у = Runt, ле-
жащая в первой четверти.
310
27. \ 1/ -Τ2~ί/2 + -^-x2dl, L —дуга эллипса x = acost,
L
y^bsmt (o<i<-|-J.
28. J ydl, L — первая арка циклоиды χ = 3 (t — sin /),
у = 3(1 — cost).
29. j (χ + у + 2) d/, L — отрезок прямой между точками
Л(0, 0, 0), 5(1, 1, 1).
30. j (х+ 2у — Зг) d/, L — отрезок прямой между точками
Л(1, 3,-1), 5(3, 5, -1).
31. | (За: — 5у + z+ 2)dly L — отрезок прямой между точками
Л (4, 1, 6), 5(5, 3, 8).
32. j (Ax + By + Cz -f D) dl, L — отрезок прямой между точ-
L
ками М1(хъ уъ zx) и М2(х2, уъ z2).
33.. \ |/1 +-^-dl, L — дуга кривой jc = #sin2i,
у = #sintcost,z = Rcost (θ < ί < -^-
34. j]/l + 4t/+ 9xzdt, L — дуга кривой х = ty у = t2, z = t3
(0<ί<1).
35. j (jc2+л/2 + г2) d/, L —отрезок прямой между точками
Л(1, 1, Ι), 5(3, 0, 3).
Вычислить следующие криволинейные интегралы первого типа:
36. \ye~xal, L — дуга кривой х = ln(l + f2), y = 2arctgi —
— ^ -f 8 между точками, для которых / = 0, t = 1.
37. j (а:2 + у2) d/, L — дуга кривой х = a (cos / + t sin f),
у - a (sin t — tcost) (0 < f < 2π).
38. fjo/zd/, L — дуга кривой χ = -Lf2, y = t, z = -^-V8t3
(0<ί<1).
39. j (a:2 + y2 + z2) dl, L — дуга винтовой линии χ = α cos ί,
i/ = asini, * = « (0<ί<2π).
40. j jct/d/, L — дуга эллипса χ = a cos t, у = b sin t, лежащая
в первом квадранте.
311
41. J zdl, L — дуга конической винтовой линии χ = t eos t,
у = ts'mt, z = t (0< t< π).
42. 1 —, L —дуга гиперболической спирали ρφ = 1
J (*2 + </2)Τ
L
от φ = / 3 до φ = 2 V~2.
43. j γ χ2 + у2 dl, L — окружность χ2 + у2 = #лг.
44. J J/ 2x2 + i/2 d/, L — окружность χ2 + у2 + ζ2 = α2, г = χ.
L
45. j χ2 dl, L — окружность χ2 + у2 + г2 = /?2, jc + У + ζ = 0
46. Izrf/, L-
до β^α, α, α|/"2)
46. \zdl9 L — дуга линии χ2 + у2 = ζ2, if = αχ от А (0, 0, 0)
ОТВЕТЫ
1- 4 5 б · 2.-^ (δ/Τ-Ι). 3. -3-· 4. ~(\7\/n-~2V'2).
π
5.-^(10/10-1). β. -у-. 7.-у"· 8. 4-[(l-ref)2 -21
2 1 5 Ϋ~2 π 3π /ΊΓ
10. -γ. 11. -g-(10 + ji). 12. j2— — In tg -g~. 13. In tg -g- + -^~
5 π 33/3—17 17 α
14·"64· 15·^2· 16· 480 ' 17·-48δ~· 18·*2· ^Τ-*··
20. α» Λ*1 + Λ 21. J5- α2. 22. **π . 23. α·. 24. _^ΐ!_. 25. q2ji° .
\ 3 / 3 4 32 24
Я4 π ЗУТ ,_
26.-3-. 27. ^-(α2 + 62). 28.96. 29. ^ · 30. 26 |/ 2.
■Z1L 32. Κ (χ2 - *x)2 + (|/2 - //Ο2 + (г, - *ι)2 Γ(Λ*ι + *ifr + Czx + D) +
■+■ § } 33' "Τ π/?· 34' ~Ϊ5~ ·
π2 1п2 0 16 γ"2
35. 27. 36. -jg- — — + 2π. 37. 2π2α3 (1 + 2π2). 38. ш .
31.
2л / . ab (α2 + ob + b2) 1 17
39. — (За2 + 4π^) >V + ЬК 40. l 3(fl + *) ' 4К ~3~ Ц2 +
\2 —1 19 2 а2 / —
+ л2) — 2 2 J. 42. -у. 43. 2Я2. 44. 2яя2. 46. -j-jtfl3. 46. — ( 100 V 38 —
25 + 4/38 \
— /2— 17 In jy I.
312
§ 8.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
Пусть дана дуга пространственной кусочно-гладкой кривой L,
ограниченная точками А и В (см. рис. 8.1), и определенные на
ней непрерывные функции Р(х, у, z), Q(x, у, z), R(x, у, ζ).
Дугу АВ разобьем точками Ml(xl, yl9 zx), М2(х2, Уг> za), ··· »
Af/,—ι (jc«—ι, уп-\, Zn-\) на η элементарных дуг Λ4/_ι МД/== 1, 2,
3, ... , η, Μ0 = Α, Μη=.Β). На каждой дуге Λί,-ιΛί,- выберем
произвольно точку Mi(xi, yt, zt), и значения функций в этой точке
Р(хг, у,, ^)=Р{Щ, Q(*„ у,, i,) = Q(Ai,), /?(ϊ„ у„ ^ξξ/^ΛΪ,)
умножим не на длину дуги Λί/_ι Μ,- (как это было в случае
криволинейного интеграла первого типа), а на проекции этой дуги
соответственно на оси Ox, Оу, Oz, которые обозначим через
Ах{, Δί/·, Δζ„ причем Αχ. = χ. — ^_ь Ayt = yt — у,_ь Azt = г{ — Ζ|_ι.
Из полученных произведений составим сумму
η
Τ п = Σ 1ρ (Μι) Δ *, + Q (ΛΪ,) Ayt + R (Щ Δ Ζ/ΐ, (8.9)
называемую интегральной суммой по координатам для функций
Р(х, у, z), Q(x, у, ζ), /?(*, у, ζ).
Криволинейным интегралом второго типа, взятым по кривой L
или по пути АВ, называется предел интегральной суммы (8.9) при
η -> оо, max | Axt | -► 0, max | Ayt | -> 0, max | Δζ,1 -> 0:
j"P(x, у, z)dx + Q(x, у, z)dy + R(x, у, z)dz = \\mTn =
L . я—voo
ГС
= Hm2[/>(Af/)Ajc/ + Q(A?<)Ai// + /?(A}()Az/] (8.10)
max I Δχ. | -* 0
max | Ayi | -*■ 0
max | Δ ζ. | -> 0
На кривой L, целиком лежащей в плоскости Охуу функции
Р, Q, /? не зависят от ζ, Δζ,- = 0, dz = 0, поэтому
/г
J Ρ (χ, у) dx + Q (χ, у) dy = lim 2 [Ρ (Д) Δχ, + Q (Μ,) Ay,]. (8.11)
L ί=ι
max Ι Δχ. | -♦ 0
max I Ayi \ -> 0
Если функции Ρ, Q, 7? рассматривать как проекции некоторой
переменной силы F на координатные оси, то криволинейный
интеграл второго типа выражает работу силы F \P, Q, R}, точка
приложения которой описывает кривую L.
313
Криволинейный интеграл второго типа зависит от выбора
направления обхода кривой; если изменить направление обхода, то
интеграл меняет знак:
f Pdx + Qdy + Rdz = — \ Pdx + Qdy + Rdz. (8.12)
AB BA
Вычисление криволинейного интеграла второго типа также
сводится к вычислению определенного интеграла.
Если линия L задана параметрическими уравнениями
* = *(<)> y = y(t), z = z(t) (ti<t<t2)
и значению tx соответствует точка Л, значению t2 — точка В, то
\ Ρ (χ, у, z) dx + Q (χ, у, z)dy+ R (χ, у, ζ) dz =
AB
U
= J' {Ρ[χ(0, y(t),z(t)]x'(t) + Qlx(t), у (0, z(t)]y'(t) +
h
+ R[x(t), y(t), z(t)]z'(t)}dt. (8.13)
В частности, для кривой L, лежащей в плоскости Оху,
$Р(х, y)dx + Q(x, y)dy = $[P[x{t), y(t)]x'(t) +
AB tx
+ Qlx(t), y(t)]y'(t)}dt. (8.14)
Если плоская кривая L задана уравнением у = у(х) (a^x^b),
то
Ρ (χ, y)dx + Q(x, y)dy-=
AB
b
= J [P[x, У (x)] + Q[x, У (x)]У' (х)} dx. (8.15)
a
ПРИМЕРЫ
1. Вычислить криволинейный интеграл второго типа
\ х2 dx + ху2 dy,
1
где L — отрезок прямой от точки Л (О, 1) до точки 5(1, 2).
Уравнение прямой, проходящей через точки А и 5, имеет вид
у = χ -f- 19 поэтому на отрезке AB dy = dx.
Подставляя в подынтегральную функцию вместо у его
выражение через х(у = х+ 1) и замечая, что при перемещении от А
к В χ меняется от 0 до 1, по формуле (8.15) получаем
1 1
\x2dx+^xy2dx= \x2dx+x(x+ \fdx= f [x2 + χ (χ2 +
L 0 0
314
+ 2x + \)]dx = [(x* + 3x* + x)dx = (^ + x3 t-4")
2. Вычислить J (л:3 + у) dx + (χ + у3) dy, где L —ломаная ЛБС
(рис. 8.7), причем A (I, 1), 5(3, 1), С(3, 5).
Так как контур интегрирования L состоит из отрезков АВ
и ВС, то
J (χ3 + у) dx + (χ + у3) dy = J (χ3 + у) dx + (χ + у3) dy +
L АВ
+ $(x3 + y)dx + (x + y*)dy.
ВС
I
^
4»
J
2
/
0
I
л
1
2
Рис.
С
В
3 ОС
8
7
Рис. 8.8
На отрезке АВ, уравнение которого у=\, dy = 0; на
отрезке ВС, уравнение которого χ = 3, dx = 0, поэтому
з
/(x3 + i/)dx + (* + #3)^ = /(*3 + l)d*+(* + 1)0 +
L 1
5 3 5
+ f(Z* + y)0 + (3 + y*)dy = f(x*+l)dx + f(Z + y*)dy =
+ x
+ (3ί/ + ^τ
- 190.
fx2
3. Вычислить I x2dx-\ 1-, где L — дуга кривой л: = -γ-
ι \
от точки А (1, 1) до точки В(4, -j-j.
Линия L задана уравнением вида л: = φ (у) (c^y^d). В этом
случае вместо формулы (8.15) целесообразно применить формулу
315
fP(x, y)dx + Q\x, у)ау = ${Р[<р(у),у]<р'(у) + (3[у(у),у]\ау.
L с
Поскольку в данном примере с = 1, d = -j-, α'χ = If-, то
А
1 \
\ x2dx Η—γ = I —it- =-) Η—5- ki/ =
ί у2 Ί L у2 \ у2 J у2 } *
1 ^4 = 18.
Замечание. Здесь можно пользоваться и формулой (8.15),
так как уравнение линии L записывается в виде у = —,
причем 1 < χ <; 4:
4 4
i*d* + -$r= J[^ + ^(-^r)]dx = J(x»-l)
\dx ■■
<)
18.
4. Вычислить J yd* + *di/, где L — дуга астроиды * = a cos3/,
у = α sin3/ от точки M1(t1) до точки /М2(/2)> для которых /х = О,
*а = Нг (Рис. 8.8).
Применим формулу (8.14), так как плоская кривая здесь
задана параметрическими уравнениями. Из уравнений линии находим
dx = — За cos2/ sin tdt, dy = 3α sin2/ cos /d/.
Следовательно,
j ydx + xdy = I [asin3/(—3acos2/ sin /)-f a cos3/ 3a sin2/ cos/] Л =
i- о
τ τ
- 3a2 Γ (cos4/ sin2/ — cos2/ sin4/) Λ = 3a2 ( sin2/ cos2/ (cos2/ —
sin2 2i
3a2
sin2/) Λ = 3a2 J ^^- cos 2/d/ = -^- f sin2 2/d (sin 2/) =
3a2 sin3 2t
\T a-
316
с о [(У3 — х2) dx + (х3 + у2) dy ,
5. Вычислить J ' 2 ' 2 , где L — дуга окруж-
ζ, ' ^
ности а: = 7?cos/, у = Runt (θ<;/<-|Μ, пробегаемая в
направлении возрастания параметра /.
Замечая, что dx=—Rsin tdt, dy = Rcostdt, /x = 0, /2 = —?>-, no
формуле (8.14) находим
Г (j/3 - X2)rf* + (Д8 + y2)dy
L Х2 + У2
С (Rhlrtt — R2cosH)( — Rsintdt) + (/?3cos3/ -f R4'm2t)Rcostdt
j/ /?2 cos2/ + #2 sin2/
π
ΊΓ
Γ fl4 cos4/+/?3 sin2/ cos t+R3 cos2; sin t—R* sin4/ ,, _
о
π
Ύ
(#2cos4 / — R2 sin4 / + # sin2 tcost + R cos2 / sin t) dt
0
- R2 J cos4 /d/ - Я2 f sin4 tdt + # J sin2 id (sin /) — /? J* cos2 td (cost) =
0 0 0 0
_ ρ sin3 /
у- ρ cos3;
0 ό
2 = JL#
о А·
0 J
3
Замечание. Здесь принято во внимание, что
Ύ Ύ
Г з С з
I cos4 /d/ = -rg- π, \ sin4 tdt = -r~- л;
о Ь
(см. пример 4 § 6.1).
6. Вычислить J i/2dx + (*2 + ζ) Л/ + (* + ί/ + ζ2) dz, где L —
L
отрезок прямой в пространстве от точки Л(1, 0, 2) до точки
В(3, 1, 4).
Составим уравнения прямой, проходящей через точки А и В:
χ — 1 у —о _ г — 2 , ,ν
3—1 1—0 4 — 2 I *'"
Из параметрических уравнений прямой
χ = Ц- 2/, у = /, ζ = 2 + 2/
получаем
dx = 2d/, di/ = d/, dz = 2d/.
317
Из этих же уравнений видно, что при перемещении от -Точки
А к точке В параметр t меняется от 0 до 1, т. е. пределы
интегрирования в формуле (8.13), которой здесь нужно пользоваться,
соответственно fx = 0, ί2 = 1.
По формуле (8.13) находим
ι
Jy2dx + (x2+z)dy + (x+y + ζ2) dz = ft2 2dt + [(1 + 2t)2 +
L 0
+ (2 + 2t)\ dt+[(l+2t) + t + (2+ 2t)2] 2dt =
ι
--= f[2t2 + (1 + At + 4t2+2 + 2t) + 2 (1 + 3/ + 4 + 8t + At2)]dt =
m
95
3 "
= / (Ш2 + 28t + 13) dt = (-^- + Ш2 +
7. Вычислить J (y2 + z2) dx — yzdy + xdz, где L — дуга винто-
L
вой линии χ = ty y=2cost, z = 2smt (()</<;-^4.
Поскольку dx = dt, dy = — 2 sin tdt9 dz = 2 cos tdt, то
J (i/2 + z2) dx — yzdy + xdz =
L
π
= Γ (4 sin2/ + 4 cos2/) Л — 4 sin t cos < (— 2 sin fdf) + 2/ cos tdt =
о
π _π_ π
Τ 2 2
= C(2t cos ί + 8 sin21 cos f + 4) Λ = 2 J/ cos tdt+ 8 J sin2 id (sin f) +
0 0 0
π π π π π
τ τ τ γ τ
+ 4 С dt = 2tsmt + 2cosi! Ι + -4-sin8* + 4Μ = 3π + -=-.
J I I ^ I I ^
Замечание. Интеграл С t cos tdt вычислен с помощью
метода интегрирования по частям:
!2
Г / cos tdt = (* /d (sin /) = / sin t\2 — Г sin ίΛ = t sin /
2 +cos/
о
318
8. Вычислить
ί-
a3dx
xy
+ zdy + adz, где L—дуга линии
пересечения поверхностей xyz = аи (χ2 + у2)ζ2 = α4.
Составим сначала параметрические уравнения данной линии.
Возведя в квадрат обе части первого уравнения, получим x2y2z2 = α6.
Разделив почленно второе уравнение на x2y2z2 = α6, найдем
1
ι
— /»2
Из этого уравнения видно, что можно положить
χ =
cos t
-. у = -
s'mt
Из уравнения xyz = α3 находим ζ — aunt cos t.
Итак, получены следующие параметрические уравнения линии:
χ = ■
~г, У = —г—г, ζ = aunt cos t.
и ' ν sin/ '
Принимая во внимание, что
, a s'mt ,, ,. a cost ,, , Λ,_/,
αχ = —γτ- at, du = r-5-7- αί, dz = a cos 2ш/,
cos2 / ' ^ sin2 / ' '
по формуле .(8.13)
С a3dx ,1,1 if cfias'mt sin / cost , . , ./ α cos Л .
cos2 /
sin/
+ cos2t)dt =
+ aacqs2t)dt = a2 ί(-^γ
2 f/l — cos2 / 1—sin2/ . 0Λ ,, 2/7 1
= α I 1 7 —..7 l· cos 2nd/ = a2 ■ 7
J \ cos/ sin/ ' / J \ cost
In
tg(^-+4
~ cos t + sin ί + cos 2t)dt = a2
— s'mt -4- ~2~ sin 2/ — cos t\ I.
In
sin/
tg-9"
ЗАДАЧИ
Вычислить криволинейные интегралы второго типа, взятые
вдоль данных плоских кривых в указанных направлениях:
1. 1хЧх + x2dy, L — дуга кривой у = х2 от А (1, 1) до β (3, 9).
319
2. J cossxd# + ydyy L — дуга кривой t/=sin χ от x=0 до x= -£-.
3. \cos2xdA: + -yf-, L—дуга кривой f/=tg* от *=-т- до лг=-^-.
4. J (дс2 + t/2) dx + xydy, L — дуга кривой у = e* от Л (0, 1)
до θ(1, е).
5. I sin3*d;H |-, L—дуга кривой y=ctg χ от *=0дох= -£-.
J У о
6. ( (а:3 — у2) dx + xydy, L — дуга кривой у = а* от Л (0, 1)
до 5(l,La).
Вычислить криволинейные интегралы второго типа, взятые
вдоль указанных плоских кривых в направлении возрастания
параметра:
7. J xydx + i/2di/, L — дуга кривой χ = t2f у = t (1 < / <; 2).
8. J x2i/d# + y2xdyy L — дуга кривой χ = /, у = /3 (0 <; / <; 1).
9. J (* + i/) d* + (x — У) dy, L — дуга окружности х = R cos t,
10. f i/2d# + ΛΓί/di/, L — дуга эллипса х = a cos f, ί/ = b sin f
11. J i/dx — xdi/, L — дуга астроиды x = a cos3 i, у = a sin3 /
L
12. f i/2d:v + jc2di/, L — первая арка циклоиды χ = a (t — sin f),
L
j/ = a(l — cos0(a>0).
Вычислить криволинейные интегралы второго типа, взятые
вдоль указанных пространственных кривых в направлении
возрастания параметра:
13. ( yzdx + xzdy + xydz, L — дуга кривой x = t, y = t2,
z = f8(0<f<l).
14. f ydx + x2dy + zdzy L — дуга кривой x = t, у = ts, ζ = t5
(0<f<l).
15. J хЧх + i/2di/ — zdz, L — дуга кривой χ = /3, j/ = f, ζ = t2
(0</<l).
320
16. J (χ2 + у + ζ) dx + z2di/ + (χ + у2) dz, L — отрезок прямой
от точки Л (2, 1, 0) до точки 5(4, 3, 1).
17. J zdx + x2dy + y*dz, L — дуга кривой x = t2, у = t, ζ = ts
(0</<Ί).
18. \yzdx + z2di/ + (* — */) dz, L — отрезок прямой от точки
А{\, 0, 2) до точки 5(2, - 1, 0).
19· J (у + z) dx + (χ + ζ) dt/ + (jc + у) dz, L—дуга кривой *=ί2,
У = *4, ζΓ^6(0<^<1).
20. J x2dx + {x + z)dy+ xydz, L — дуга кривой х = sin t,
у = sin2*, г = sin3* (θ < f < -|Λ
21. J *yd* + zdi/ + (a:2 + i/2) dz, L — дуга винтовой линии
L
x = acost, y = as\nt9z = bt[0<CtK-Y
22. jzd* + j/dj/ + (x2 — y2) dz, L — дуга кривой x = ach t,
y = asht, z = tt(0<f < 1).
23
. I zdx + xdy y-dz, L — дуга кривой χ = tcost,y = I sin /,
24. Доказать, что если / (и) — непрерывная функция и L —
кусочно-гладкий замкнутый контур, то § f (χ4 + ί/4) {x3dx + y3dy) = 0.
25. Доказать, что для криволинейного интеграла справедлива
следующая оценка: |\Pdx + Qdy + Rdz\ <Ш, где / — длина
дуги L, Μ = max V Ρ2 + Q2 + Я2 на дуге L.
26. Оценить интеграл IR = (J) J'+~Х*+Уу2у > гДе L ~
окружность а:2 + у2 = R2. Доказать, что lim /# = 0.
R—κ»
ОТВЕТЫ
1.60. 2.4". з. ^ + _^1_+-^. 4.4-^2 + nl·· 6-4—^·
β 1 α2 3(1—α2) 221 1 об2
6·^Γ + — + 4ΐηα - 7·-Τ^· 8·— · 9·-^2· 10·--3-·
3 27 1 95
П. — -χ6~πα2· 12· «3^(5 —2π). 13. 1. 14. -gg-. 15. -g-. 16. -у.
321
11 17 nab α3
17· ~Ϊ0~* 18# —3~~* 19* a 20* l* 21* 2 (\+а) — аЬ——т£-
22. α6 (ch 1 — sh 1) + -y- sh2 1 -f a26. 23. -~- _ — π -|- 1.
§ 8.3. ФОРМУЛА ОСТРОГРАДСКОГО—ГРИНА. УСЛОВИЯ НЕЗАВИСИМОСТИ
КРИВОЛИНЕЙНОГО ИНТЕГРАЛА ОТ ПУТИ ИНТЕГРИРОВАНИЯ
Если L — кусочно-гладкий контур, ограничивающий на
плоскости Оху область (S), а Р_(х, у)у Q(x, у)—функции,
непрерывные в замкнутой области (S) и имеющие в ней непрерывные
частные производные, то справедлива формула Остроградского—Грина
§ Ρ (χ, y)dx + Q (χ, у) dy = jj (-*?- - ^-) dxdy, (8.16)
где обход контура выбирается так, чтобы область (S) оставалась
слева.
Криволинейный интеграл
Jp(x9 y)dx + Q(x, y)dyf (8.17)
L
где контур L целиком лежит внутри некоторой односвязной
области S, в которой функции Ρ (χ9 у) и Q (х, у) непрерывны вместе
со своими частными производными, не зависит от пути
интегрирования тогда и только тогда, когда
В этом случае подынтегральное выражение представляет собой
полный дифференциал некоторой функции
Ρ (χ, y)dx + Q (χ, у) dy = dU {χ, у)
и
J Ρ (χ, у) dx + Q (x, y)dy = U (x2, y2) - U (xlt уг), (8.19)
L
где Λίχ (xlt ί/χ) — начальная; M2 (х2, у2) — конечная точки пути
интегрирования.
В частности, криволинейный интеграл по замкнутому контуру
в этом случае равен нулю:
§Р(х, y)dx+Q(x, y)dy = 0. (8.20)
L
Криволинейный интеграл
lP(x, yy z)dx + Q(x, у, z)dy + R(x, у, z)dz, (8.21)
L
322
где L — контур, целиком лежащий в односвязной области V9 в
которой функции Р(х, у, г), Q(x, у, г), R(x, у, ζ) непрерывны
вместе со своими частными производными, не зависит от пути
интегрирования тогда и только тогда, когда выполняются
равенства:
dQ = _дР_. _dR_ = _dQ_. д^_ ^ _dR_ ,g ™
дх ду ' ду dz ' dz дх \ · /
В этом случае подынтегральное выражение представляет собой
полный дифференциал некоторой функции:
Р(х, у, z)dx + Q(x, у у z)dy + R(x, у, z)dz = dU (χ, у, ζ)
и
(*2. Уз. г2)
j Pdx + Qdy + Rdz = U (x2, y2, z2) - U (xl9 yl9 гг). (8.23)
В частности, криволинейный интеграл по замкнутому контуру
в этом случае равен нулю:
j)Pdx + Qdy + Rdz = 0. (8.24)
L
Криволинейные интегралы первого и второго типов связаны
формулой
\Pdx + Qdy + Rdz = \(Р cos α + Q cos β + R cos γ) d\9 (8.25)
L L
где α, β, γ — углы между осями координат и направлением
касательной, соответствующим направлению
интегрирования для интеграла левой части.
ПРИМЕРЫ
1. Вычислить криволинейный интеграл второго типа
/ = J(4xjr + 5у3) dx + (2х2 + \5ху2) dy
L
в каждом из следующих случаев:
1)1 — отрезок прямой у = χ от точки О(0, 0) до точки 5(1, 1);
2) L — дуга параболы у = х2 между точками О (0,0), 5(1,1);
3) L — дуга параболы у2 = χ между теми же точками;
4) L — дуга кривой у = х3 между теми же точками (рис. 8.9).
В первом случае уравнение прямой, проходящей через точки
О и Bt имеет вид у = х9 поэтому dy = dx и
323
1
A = f(4AT£/ + 5y3) dx -f (2x2 -f I5xy2) dy = fj(4x2 + 5x3 + 2x2 +
L 0
+ 15л:3) dx = j(6x2 + 20x3) dx = (2x3 + 5x4) Г - 7.
о 1°
Во втором случае у = χ2 и dy = 2xdx, поэтому
1
/2 - j [Axx2 + 5 (x2)3] dx + [2x2 + 15* (χ2)2] 2xdx =
Рис. 8.9
Рис. 8.10
f (4л:3 + 5л:6 + 4л:3 + ЗОх6) dx = j (8л:3 + 35л:6) dx =
= (2л:4 + 5л:7)
= 7.
В третьем случае у2 = xt dx = 2ydy, следовательно,
ι
U = ί (4ί/2ί/ + 5ί/3) 2^у + (2*/4 + \Ъу2у2) dy =
= j (18ί/4 + 17ί/4) dy = j 35i/4dy = 7y5 = 7.
Наконец, в четвертом случае у = χ3, dy = 3x2dx, поэтому
ι ι
/4 = f (4χ* + 5л:9) dx + (2л:2 + 15х7) 3x2dx = f (10х4 + 50х9) йл: =
5 6
= (2л:5 + 5л:10) Г = 7.
324
Замечание. Во всех рассмотренных случаях получено одно
и то же значение криволинейного интеграла. Этот результат не
является случайным. Действительно, в данном примере
Р(х, у) = \ху + 5у3, Q (х, у) = 2х2 + 15ху2]
ду ~ 4* + [*У > дх ~ qX ' 1Di/ ' ду ~ дх >
т. е. выполнено условие (8.18) и криволинейный интеграл не
зависит от пути интегрирования.
2. Вычислить криволинейный интеграл второго типа
К = \(3х2у — 7х3) dx + (6* - 1lx2y2) dy
L
в каждом из следующих случаев:
1) L — отрезок прямой у = χ от точки О (0, 0) до точки 5(1, 1);
2) L — дуга кривой у = х4 от точки О(0, 0) до точки 5(1, 1).
В первом случае
1 1
Кг = j (Зх3 — 7а:3) dx + (6* + 11л-4) dx - Ц11х4 -f- 6л: — 4х3) dx =
о о
-У- л:5 -Ь Зх2 — jcj ) Г = -^-.
5 / Ιο 5
Во втором случае у = х4, dy = 4x3dx, поэтому
ι ι
К2 = f (Зх6 — 7х3) dx + (6х + 11л:10) 4x3dx = f (Зх6 — 7х3 + 24х4 +
ό о
11 927
лл ^ j /За;7 7л;4 , 24х5 , 44*14
О 140
Замечание. Этот интеграл зависит от пути
интегрирования, так как условие (8.18) не выполняется:
дР _ д (Зх*у — 7х3) _ ~ 2 _^0_ _ д (6* + 11*2/72) _
д// д# ' дх дх
3. Вычислить криволинейный интеграл по замкнутому контуру
yxdx + ydi/,
L
где L — эллипс -?L + -£- = ι.
α2 ' я2
Воспользуемся параметрическими уравнениями эллипса
х = α cos ί, ί/ = 6 sin / (0 < / < 2π).
Так как dx = — asmtdt.dy = b cos tdt, то
325
(j) xdx + ydy = \ a cos t (— a sin tfdi) + bsmt (b cos frW) =
l d
2n 2-
= a2 J cosW(cos0+ 62 I sin/d(sin/) =
9 COS2/
a~2-
л +6 —o—
2n
= 0.
о
Замечание. Условие (8.18) здесь выполнено fтак как
-т— = 0, -р- = 0), подынтегральное выражение является полным
X2 + ί/2
дифференциалом функции U (х, у) = <^~:
xdx + ί/di/ = dy\y2 J,
поэтому по формуле (8.19)
§ *** + у^ = 4" [(4 + yl) - (4 + уо)1 = о,
L
где М0(х0, ί/0) — произвольная точка эллипса.
4. Вычислить (6 ^Γ:^ν ,
J a:2 -t- ί/2
L
где L — окружность χ2 + у2 = R2.
Используя параметрические уравнения окружности
x = Rcost, y = Rsmt (0<*<2π),
получаем
2π 2π
£ xdy — ydx _ Γ R cos t R cos tdt— Rs'mt(—Rsint)dt f,, _ ~
J *2 + </2 - J /?2 cos2 * + R2 sin2 * ~ J ln"
0
Замечание. Функции Ρ (χ, у) =* & + у* > Q (*> ί/) =
2 , 2 удовлетворяют условию (8.18), так как
% г У
дР у2 —х2 dQ у2 —χ2
ду χ2 + у2 ' д* χ2 + ί/2 '
подынтегральное выражение является полным дифференциалом
функции
326
d(jL
xdy — ydx \ χ
1-ЬМ-
-^-2-=rffarctg^-
y \ \ χ
однако интеграл по замкнутому контуру не равен нулю. Это
объясняется тем, что функции Р(х, у) и Q(x, у) не являются
непрерывными в точке О(0, 0), лежащей внутри области S,
ограниченной линией L (область непрерывной дифференцируемое™
функций Ρ и Q не односвязна!).
5. Показать, что криволинейный интеграл
h
{у2 — 21 ух2) dx + (2ху — 7х3 + 6у2) dy
L
не зависит от пути интегрирования L с началом в точке О(0, 0)
и концом в точке 5(1, — 1). Найти функцию U(x, у), полным
дифференциалом которой является подынтегральное выражение,
вычислить значение этого интеграла.
Рассмотрим любую односвязную область S, которой
принадлежат точки О и 5 (рис. 8.10).
В области (S) функции
Ρ (х, У) = У2- 21x2i/, Q (х, у) = 2ху - 7х3 + 6у2
непрерывны вместе со своими частными производными.
Так как
^--2и~2\х2 ^--2и-2\х2 1L--W.
ду - Zy ZiX , θχ - Zy Δ\Χ , ду - δχ ,
то условие (8.18) выполнено. Следовательно, данный
криволинейный интеграл не зависит от пути интегрирования.
Подынтегральное выражение в этом случае представляет собой
полный дифференциал некоторой функции U(x, у):
dU (χ, у) = (у2 — 21 х2у) dx + {2ху — 7х3 + 6у2) dy.
С другой стороны,
dU(x, y) = — dx+ -gj-dy.
Сравнивая два последних выражения для dU (x, у), заключаем,
что
^- = у*-2\х2уу *L = 2xy-7x* + 6y2. (1)
Итак, функция U (х, у) содержится в множестве
«первообразных по х» выражения у2 — 2\х2у, т. е. эту функцию можно
представить в виде
χ
U{x, У) = J (У2 - 21 х2у) dx + с.
о
327
В качестве нижнего предела интегрирования можно было бы
взять любую другую постоянную х0. Постоянная интегрирования
С постоянна по отношению к переменной χ но может зависеть
от у; поэтому в дальнейшем вместо С будем писать φ (у):
х
U (х, у) = / (у2 - 21 х2у) dx+ψ (у).
о
Выполнив интегрирование, получим
U(x, У) = У2х-7х5У+<р(у). (2)
Теперь нужно выбрать функцию φ (у) так, чтобы
выполнялось и второе из равенств (1), т. е.
-*L = 2xy-7xs±6y\ (3)
Из равенства (2) получаем
-|^- = 2*{/-7х3 + ср'(у). (4)
Из равенств (3) и (4) находим, что
2ху - 7х3 + 6у2 = 2ху - 7х* + φ' (у),
т. е. φ' (у) = 6у2, откуда φ (у) = 2у3 + С
Следовательно,
U(x, у) = у2х-7х*у + 2у* + С.
По формуле (8.19) вычисляем значение данного
криволинейного интеграла:
/(у2 — 2lx2y)dx + (2ху - 7xs + 6у2) dy = U (1, — 1) - U (О, 0) = 6.
L
Замечание. Данный криволинейный интеграл можно
вычислить по любому пути L, соединяющему точки О(0, 0) и 5(1, —1).
Например, если L — отрезок прямой у = —χ (и dy = —dx), то
ι
f(y2 — 21 x2y)dx + (2ху — 7χ3 + 6y2)dy = J(x2 -f- 21 χ3) dx +
l δ
ι
+ (_ 2x2 — 7 χ* + 6x2) (— dx) = f (— 3x2 + 28x3) dx =
δ
Π
-(7л:4 — Xs) \ =6.
v ' 0
328
6. С помощью формулы Остроградского—Грина вычислить
криволинейный интеграл второго типа
j)V^TV2 dx + у [ху + In (x + V^T?)] dy,
L
где L — контур прямоугольника с вершинами Л(3, 2), 5(6, 2),
С (6, 4), D(3, 4).
Преобразуем сначала этот интеграл по формуле
Остроградского—Грина. Поскольку
dQ_
дх
д [у [XIJ + In (X + Υχ*-±-ΐβ)\) = (уУХ2^у2+] у
дх
дР __ д {Ух2 + if)
ду ~ ду
Υ χ2 -i- if
Ух2 -;- f '
по формуле (8.16) имеем
(j) Vx^Ff dx + y [xy + In (x + V^TJ2)] dy =
у Vx^Tf - 1
9
/;
D
2
//
4 <!
^
9
.2
Я
(5)
/χ2 + ί/2
j/ λ:2 + ί/2
dxdy = \ J y2dxdy,
Рис. 8.11
где (S) — область, ограниченная
контуром L, в данном
случае прямоугольник
ABCD (рис. 8.11).
Вычислим полученный
двойной интеграл по
прямоугольнику ABCD:
л 56
ах — —5-
2 3
-56.
\ J tfdxdy =\dx} y2dy = j -|
V S 3 2 3 3"
7. Вычислить криволинейный интеграл второго типа
\(12ху + 4z2) dx + (6х2 — I5y2z) dy -f {8xz - 5*/3) dz
L
по пути L с началом в точке О(0, 0, 0) и концом в точке 5(1, 1, 1),
предварительно установив, что он не зависит от пути
интегрирования.
Это интеграл вида (8.21), для которого
Р= 12ху+ 4z2, Q = бх2 — \5tfz, R = 8xz — 5t/3.
329
Так как
ду ΐχΧ'
-£-■*.
дР _ dQ
ар
ду ~
дР
' дх dz
- 15ίΑ
5/? dQ dR
дх ' дг — ду '
= - 15ίΛ
ТО
т. е. выполнены условия (8.22).
Следовательно, интеграл не зависит от пути интегрирования.
Вычислим его по отрезку прямой, проходящей через точки О и В.
Параметрические уравнения прямой имеют вид:
x = t, у = t, z = t,
поэтому dx = at, dy = at, dz = dt. Так как на отрезке OB О < t < 1,
то
\(\2ху + Az2) dx + (6x2 - 15y2z) dy + {8xz - 5*/3) dz =
L
1
f(12/2 + At2 + 6/2 -I5t3 + 8t2 - bt*)dt - j(30i2 - 2№)dt
L
1
(10^3— 5/f4)
Замечание. Этот пример можно решить и с помощью
формулы (8.23). Действительно, так как выполнены условия (8.22), то
подынтегральное выражение является полным дифференциалом
некоторой функции
dU(χ, у, ζ) = (12*1/ + 4z2) dx + (б*2 — \by2z) dy + {8xz - 5y3) dz.
С другой стороны,
λιίι \ dU , , dU , , dU ,
dU (χ, y, z) = -^dx+-dfdy + -^- dz.
Сравнивая два выражения для dU, получаем:
~™-=l2xy + 4z2, -|J- = 6A'2-15i/2z, ™_ = 8xz-by\
Из первого равенства, считая у и ζ постоянными, находим
U = 6х2у + Αζ2χ + С;
постоянная интегрирования С является постоянной по отношению
к х, но она зависит от у и ζ, т. е. С = φ (у, ζ).
Итак,
U =, 6х2у + 4ζ2χ + φ (у, ζ).
330
Находя частную производную по у от функции U
дЦ
-7ПГ = 6х2 + у'у(у, ζ)
и сравнивая с выражением -^— = 6л:2 — 15*/22, получаем
6л:2 + <р'у(У, ζ) = 6л:2 — 15y2z,
откуда
q>y(f/, z) = — \by2z,
т. е.
φ(ί/, ζ) = —5y3z+ ψ (г),
поэтому
U (л:, у, г) = 6л:2у + 4г2л: — ЪуЧ + ψ (ζ).
Поскольку
_^_ = 8хг-5у3+г|/(г) и ^ = 8^_5у35
то
ψ' (г) - 0, т. е. ψ (г) = С. -
Следовательно,
ί/ (χ, у, ζ) = 6х2у + 4г2* — 5у3г + С.
По формуле (8.23)
j( 12ху + 4z2) dx + (6л:2 — 15y2z) dy + (8xz — 5у3) dz =
L
= г/(1, ι, ι,) —ί/(ο, ο, ο) = 5.
ЗАДАЧИ
Проверить, зависят ли от пути интегрирования следующие
криволинейные интегралы:
1. j (χ3 + Зх2у2) dx + (ί/3 + 2х*у) dy.
L
2. ^(x2-4Xy+x*)dx + (y*-2x2 + y)dy.
L
3. j (x + 2x3y2 — i/4) dx + {y2 — Зл:2*/3 + 4xy) dy.
L
4. f (4л:3 — I2x2y) dx + (5y4 — 4x3) dy.
L
5. \ (л-ί/3 + x2 — 2y2) dx + (y5 — 3x3y2 + *4) dy.
L
331
6. j (За-2 + 3z3 -f- Юху) dx + (5a-2 — 8yz) dy + (9xz2 - 4y2) dz.
L
7. f уЧЧх + x2z2dy + x2y4z.
L
8. j (6x2z + Wx) dx + (4г/3 - 6z2y) dy + (2a-3 - 6zy2) dz.
L
9. f (y2 + z2) d* + (a-2 + z2) dy + (a-2 + у2) dz.
L
10. J (2jc - 3z3 + 15λ'2ί/) dx + {Ayz + 5x3 - 3*/2) dy + (2y2 -
— 9xz2 — 8z)dz.
Установить, зависят ли от пути интегрирования следующие
криволинейные интегралы (без предварительной проверки условия
(8.18) или условий (8.22)):
11. j xdx + ydy. 12. f ydx + xdy. 13. J x2dx + y2dy + z2dz.
L L L
14. J jcd* + ydy + zdz. 15. \ yzdx + xzdy -f xydz.
L L
Вычислить данные криволинейные интегралы в каждом из
следующих случаев:
16. \(y + z)dx + {x + z)dy + (x+y)dz:
L
1) L — отрезок прямой от точки А (0, 0, 0) до точки 5(1, 1, 1);
2) L — дуга кривой x = t, у = /2, ζ = /3 (0 < / < 1);
3) L — дуга кривой χ = t, у = /3, ζ = /5 (0 < / < 1);
4) L — дуга кривой χ = sin/, у = sin2/, z = sin3/ ( (k< / <; -γ
17. \ x2dx + (x + z) dy + *f/dz:
1) L —отрезок прямой от точки Л(0, 0, 0) до точки 5(1, 1, 1);
2) L —дуга кривой x = sin/, у = sin2/, z = sin3/i0 < / <-^ );
3) L — дуга кривой χ = /, у = /2, ζ = /3 (0 < / < 1).
Вычислить следующие криволинейные интегралы,
предварительно определив функции U (х, у), соответствующими полными
дифференциалами которых являются подынтегральные выражения:
18. \{?>x2y-Axy2)dx-\-{x*-Ax2y + ?>y2)dy, где Л(— 1, — 1),
АВ
В{\, 1).
332
19. § (Зу2 + 4y)dx + (бху + 4x — Ay)dy9 где Л(0, 1), 5(1, 2).
АВ
(1. 3)
20. f (4xy — 1Ъх2у) dx + (2л:2 — 5л:3 + 7) dy.
(θ" 2)
(1^1)
21. j (4х3 — Зу2 + 5i/) dx + (5л: — 6j«/ — Ay) dy.
(О, 0)
(2Ч1)
22. j [(*+!/ + 1)e* — вУ]£/д: + [β* — (χ + у + l)^]dy.
(1. 0)
(6, 8)
С xdx + ί/di/
23. Ι у 2 ι 2~ (вдоль путей, не проходящих через начало
(1. 0)
координат).
(1. 0)
24. \ */^_Ζ" ^2* (вдоль путей, не пересекающих прямую
(О, -1)
у = х).
Проверив, что подынтегральное выражение является полным
дифференциалом, вычислить следующие криволинейные интегралы:
(1, 1, 1)
25. f 2xy2z3dx + 2x2yz3dy + 3x2y2z2dz.
(0, 0, 0)
(1, 1, 1)
26. J (2xy + у2 + yz2) dx + (xz + 2xy + xz2) dy + 2xyzdz.
(0, 0, 0)
(i. ι. i)
27. j · χ (y2 + z2) dx + y (x2 + z2) dy + ζ (χ2 + у2) dz.
(0, 0, 0)
(1, 0, -1)
28. J (Axy + 1 2λ:2ζ) dx + (2x2 — 3z3) dy + (4л:3 — 9yz2) dz.
(-i. i. 2)
(1. 0. 2)
29. j (6z2 + I8xy3—I5yx2z2) dx+ {27x2y2 — 5x3z2 — Hyz)dy+
+ (l2xz — 7y2— I0x3yz)dz.
(5, 3, 1)
ол Г xzdy + xydz — yzdx ,
30. j (x ___ г\2 (вдоль путей, не пересекающих
(7, 2, 3)
поверхность χ = yz).
Применив формулу Остроградского—Грина, вычислить
следующие криволинейные интегралы:
333
31 (f) (2* ~ у2 Vx2 + 4ί/3) ^ + (l2j/2 + χ2 ^*2 + 4^3) ^ L-контур
прямоугольника с вершинами Л (α, с), B(by с), С (6, d), D(a, d),
причем 0 < a < 6, 0 < с < d.
32. j> (1 — χ2) ydx + л: (1 + У2) dy, £ — окружность χ2 + у2-/?2.
L
33. ψ(χ + y)dx — (x — у) dy, L — эллипс -^- + -|^- — 1.
34. (j) e~ (*2-*>2) (cos 2xydx + sin 2xy) dy, L — окружность χ2 +
+ У2 = A
35. ф(л:у + x+y)dx + (xy-j-x — y)dy, L — эллипс—г + р-= 1.
36. φ (xy + л: + у) dx + (xy + χ — у) dy, L — окружность х2 -f-
L
f#2
+ yz = ax.
37. Какому условию должна удовлетворять
дифференцируемая функция Т7 (х, у), чтобы интеграл J F (χ, у) (y2dx+ x2dy) не зави-
L
сел от вида пути интегрирования?
38. Показать, что при выполнении условия -ч— = —р- выра-
х у χ
жения U = J Ρ (χ, у) dx + J Q (x0> ^) dy и У = ] Р(д:, y0) dx-\-
Xo Уо хо
У
+ J Q (*» У) dy представляют собой одну и ту же функцию.
Уо
39. Доказать, что J [Ρ cos (χ, ή) + Qsin (χ, η)] dl --=
= / /Id—'"ΊΓ") ^*^» где чеРез (*» η) обозначен угол между осью
Ох и внешней нормалью к замкнутому контуру L, ограничивающему
область (S).
40. Показать, что (J)cos(a:, ri)dl = 0, где d/— дифференциал
L
дуги, (*, п) —- угол между осью Ох и внешней нормалью к
замкнутой линии L.
41. Вычислить значение криволинейного интеграла y[xcos(x, я)+
L
+ У sin (χ, /i)]d/.
334
ОТВЕТЫ
1. Не зависит. 2. Не зависит. 3. Зависит. 4. Не зависит. 5. Зависит. 6. Не
зависит. 7. Зависит. 8. Не зависит. 9. Зависит. 10. Не зависит. 11. Не
зависит. Указание, xdx -j- ydy — —ψ d (χ2 -f- у2). 12. Не зависит. 13. Не
зависит. Указание. x2dx -f y2dy -~ z2dz = -тг- d (x3 -f у3 -{- г3). 14—15. Не зави-
5
сит. 16. 3 (во всех случаях). 17. 1) -g-; 2)1, 9; 3) 1, 9. 18. 2. (У (χ, у) = х3у —
—2x2if -\-у3 + с. 19. 14. U(x, у) = Зх2у + 4х*/ — 2//2 + с. 20. — 2. U (х, у) =
= 2*2*/— 5χ3ί/ +7ί/+ с. 21. 1. 22. Зе2 —4e-f 1. 23. 9. 24. 1. 25. 1. 26. 3.
3
27.-2". 28* 26' ^(А;' #' г) = 2х2у ~~ 3yZ* + 4Λ + с· 29* 31· ^(*' У> г) =
9 (6 — a)(rf—c)(a + 6 + c+d)
= Зхг* — 7ί/22 + 9x2y3 — Ъх3уг2 + с. 30. - -γ. 31. V - 2 '
π/?4 πα3 д \y2F (χ, у)] д [x2F (x, у)]
32. —у-. 33. — 2nab. 34. 0. 35. 0. 36. —-g-. 37. li/ '—— = ——^——·
38. Указание. Сравнить частные производные функций U и V по χ и у.
39. Указание. Применить к данному интегралу формулу Остроградского—
Грина и формулу J*P dx + Qdy — f [— Ρ sin (χ, η) -j- Q cos (χ, η)] dl, где
l l
(χ, η) — угол между положительным направлением оси Ох и внешней
нормалью к линии L. Эта формула получена из формулы (8.25) f Pdx + Qdy =
L
= f (Ρ cos a + Q sin a) dl, связывающей криволинейные интегралы обоих ти-
L
пов (а — угол между осью Ох и касательной к линии L). 40. Указание.
Если считать, что направление касательной совпадает с направлением положи-
dy
тельного обхода контура, то cos (χ, n) = cos(y, t) = —77- (t — касательная).
41. 25, где 5 — площадь, ограниченная контуром L.
§ 8.4. ПРИЛОЖЕНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
Длина I дуги АВ плоской или пространственной линии
вычисляется по формуле
I = fdl. (8.26)
АВ
В частности, если пространственная линия задана
параметрическими уравнениями:
x = x(t), y = y(t), ζ = z(0 (*i<f<f2),
то
/ = / Vx* _|_ y>* + z'2 dt. (8.26')
335
1
m
L
Площадь S фигуры, расположенной в плоскости Оху'и
ограниченной замкнутой линией L,
S = -±-$)xdy — ydx. (8.27)
Масса т материальной дуги L определяется формулой
т = л(у(*> У> z)dl, (8.28)
L
где γ (х, у, ζ) — линейная плотность вещества в точке Μ (χ, у, ζ)
этой дуги.
Прямоугольные декартовы координаты центра тяжести
материальной дуги L находятся по формулам:
j ху(х, у, z)dl, Уо = -£г)УУ(х> У> г)М, г0 =
■ L
=---Ι-|ζγ(*, у, z)dl (8.29)
где т определяется формулой (8.28).
Если F = X (х, у, z)i + Υ (χ, у, ζ) j + Ζ (χ, y,z)~k —
переменная сила, совершающая работу Ψ вдоль пути L, и функции Χ, Υ, Ζ
непрерывны, то
W= § Х{х, У, z)dx + Y(x, у, z)dy+Z(x, у, z)dz. (8.30)
L
В случае, когда сила F имеет потенциал, т. е. если
существует функция U(x, у, ζ) (потенциальная или силовая функция)
такая, что
dU _ у Ш_ _ v dU__ 7
то работа, независимо от пути L,
(*2, У2> 2Г2) (*2, У2, 2-г)
• W= J Xdy+Ydy + Zdz= j dU = U(x2> y2, z2) —
(Xu 'Уи z,) (*i, У1, 2t)
—U{*b Уъ Zi), где М1{хи уъ гг) — начальная точка пути;
Μ2 (х2, у2, г2) — конечная.
Функцию U (х, у, ζ) можно найти по формуле
х У ζ
U {χ, у, ζ) = f X (х9 у, z)dx+] Y(x0i у, z)dy+\ Z(x09 у0, z)dzy
Хо Уо го
336
где М% (х0$ у0, г0) — некоторая фиксированная точка в области V,
в которой функции Χ, Υ, Ζ непрерывны вместе
со своими частными производными и в
которой содержится линия L.
Замечание. Если линия L — плоская и лежит в
плоскости Оху, то формулы (8.26), (8.28)—(8.30) упрощаются
(соответствующие функции не зависят от ζ).
ПРИМЕРЫ
1. Найти длину дуги винтовой линии
χ = 4а cos /, у = 4а sin /, z = 3α/ (0 < / < 2π).
Замечая, что
χ' = — 4а sin /, у' = 4α cos t, z' = 3α, /χ = 0, /2 = 2π,
по формуле (8.26')
2я 2-
/ = J |/ 16α2 sin2/ + 16α2 cos2/ + 9α2Λ - / V I6a2 + 9a2dt =
о > ό
2г.
= 5α J dt = ΙΟπα.
2. Вычислить площадь фигуры, ограниченной астроидой
χ = a cos3/, у = α sin3/ (0 < / < 2π).
Запишем выражения для dx и dy:
djc = — За cos2/ sin /, dy = 3a sin2 / cos /.
По формуле (8.27)
2π
S = -κ- φ xdy — yd* = -γ I a cos3/ 3a cos / sin2/d/ + a sin3/ X
l 6
2-
X 3a cos2/ sin tdt = -γ f (3a2 cos4/ sin2/ + 3a2 sin4/ cos2/) Λ -
6
2π 2г.
= J|L f cos2/ sin2/ (cos2/ + sin2/) Л = Щ- J cos2/ sin2 /Л =
о 6
2т: 2"
f sin2 2* ,, 3a2 Г 1 — cos4i .
"J—Г-Л = —J—2—Л =
2
ο ό
_3a!_
16 '
2r- 3a2 sin 4^ Ι2' 3α2π
16 4 о
337
3. Найти площадь, ограниченную петлей листа Декарта
г5 + у3 = Заху, а > 0 (рис. 8.12).
Составим параметрические уравнения данной линии, для чего
положим у = tx. Подставляя это выражение для у в данное
уравнение, получаем х3 + t3x3 = ЗахЧ. Отсюда х(1 + /3) = За/.
Итак,
χ =
3at
1 -f ί3
У
3at2
поэтому
ах =
За(\ — 2Ρ)
(1 - t*f
__ 3a(2t — t*)
dt, dy =
dt.
(l + t*f
Из геометрических
соображений ясно, что петля кривой
описывается при изменении
параметра t от 0 до оо (так как t = -^-
или t = tga, где 0<α<-|-).
По формуле (8.27)
оо
S = 4"^ xdy — ydx = -Щ- Г ■
Рис. 8.12
l(2t — t*) — t2{\ — 2t3) _
(1+'3)3 ~~
9а2
t2 + t5
2 J (1
. о
ί3)3
dt =
9а2
2 J (1
о
t2
За2
ί3)2
1 + ί3
= -тг-а
4. Найти м&ссу материальной дуги кривой 2у = х2 между
точками Л(0,0), βίΐ, -о-), если линейная плотность вещества в
точке М(х, у) пропорциональна абсциссе этой точки.
Применим формулу (8.28), для чего сначала найдем
выражения линейной плотности γ (а:, у) и дифференциала дуги dl. Из
условия следует, что линейная плотность выражается формулой
V (х, у) = kx,
где k — коэффициент пропорциональности.
Из уравнения линии у = —х2 находим у' = ху поэтому
dl = |/ 1 + У'2 dx = У 1 + χ2 άχ.
338
Согласно формуле (8.28),
m = / γ (χ, i/)d/ = /йа:|/1 + а:26(а:=:й((1+а:2)2 -i- d (1 + jc*) =
k (1 -1-х2)2
o=^(2]/2-l).
5. Найти центр тяжести дуги винтовой линии
A: = acos^, y = asin^, г = btio^t <-?Н»
если линейная плотность в точке М(х, у, ζ) пропорциональна
произведению первых двух координат.
Так как
х' = — a sin t, у$ = a cos ty ζ' — b,
то
dl
-уГ*
Я , .Л , _/2
+ ίΓ + ζ"dt = у a2sin21 + a2cos2t + ЬЛ dt =
= Va2+b2dt.
Согласно условию, линейная плотность
γ (χ, у, ζ) = kxyy
где k — коэффициент пропорциональности.
По формуле (8.28) находим массу данной дуги:
ΊΓ
т = j γ (*, у, z)dl = J kxy dl = J &a2 cos f sin t У a2 + ft2d/ =
sin2^
= ka2 Va2 + b2) sin td (sin 0 = ka2 У a2 + b2 2
о
Итак,
2 £a2 »^a2 + 62
m =
£a2 V a2 + 62
Вычислим интегралы, стоящие в числителе каждой из формул
(8.29); обозначим их через Д, /2, /3 соответственно:
Д = J гу (*, у, г) d/ = ] xkxydl = k J x2t/d/ =
339
= kf a2 cos2* a sin t γ α2 + b2 dt = — &a3 ]/a2 + ft2 J" cos2^ (cos t) =
о
cos3^
= — ka3 \ a2 + b2
2 _
a*k V a2 -f- 62
A = J УУ (x, У\ z)dl= j ykxydl = k \ xy2dl =
1 ί L
Ύ Ύ
= k^ a cos ta2 sin2* \ a2 -\-b2 dt = a3£ ΫάΡψΈ* / sin2 /d (sin /) =
a3£ I' a2 + b2
sin3 /
a3£ V a2 + 62
/3 = J ζγ (л% у, г) d/ = jzkxydl = k j xyzdl =
= £ J a cos ta sin f&f у a2 +b2dt
ka2b V a2-r-b2
ka2b V a2 + b2 ( t cos 2t
+
sin 2^
J * sin 2tdt
ka2b V a2-\-b2 π
По формулам (8.29) находим координаты центра тяжести:
Х(\
_ _Д__ аЧ V а2-\-Ь2 а2к V а2 + Ь2
ί/ο = — =
^υ /72
W 3
/2 a3k[/~a2~-
2а .
3 '
a2£ |/ a2 + б2
2а .
3 '
_ /8 _ л£а26 / о2 - б2 . а2^ / а2 + Ь2 = _nb_
Z°~ т ~ 8 * 2 "~ 4 '
Таким образом, искомый центр тяжести находится в точке
Ρ I 2а 2а nb
L° \"з~' ~з"' ~Т~
6. Найти работу, производимую силой Г = 4а:6/ + xyj вдоль
дуги кривой у = х3 от точки О(0, 0) до точки 5(1, 1).
Проекции силы X и Υ на координатные оси равны:
Х(х, у)=-Ах\ Y(x, у) = ху.
Чтобы найти работу, необходимо воспользоваться частным
случаем формулы (8.30):
W = fX(x, y)dx+Y{xy y)dy.
340
Для данного случая по этой формуле
1 1
W = j АхЧх + xydy = / (4a'g -f хх3 Зх2) dx = / 7хЧх = λ'7
l δ о
7. Найти работу, производимую силой
F = ί(ί/2 — ζ2> λ-, уг | или F = (у2 — г2) / + х/ + уг/г
вдоль дуги гиперболической винтовой линии
х = Ы, у = α ch /, г = α sh ί (0 <; t <; 1).
Проекции силы X, F, Ζ на координатные оси равны:
X (х, У, г) = у2 — г2, Г (л-, у, ζ) = *, Ζ = (χ, у, ζ) = yz.
Искомую работу найдем по формуле (8.30):
ι
W = f (у2 - z2) dx + xdy + yzdz = f [(α2 ch21 — a2sh2t) b -+
L 0
1
-j- 6ta sh / + α ch f α sh f α ch /] Λ = J (α26 + aW sh t +
δ
ι ι ι
+ a3 ch2 f sh t)dt = J a2bdt + J abt sh /Λ + / a3 ch2 f sh tdt =
ι
= 1.
о
=: Λ*
a2bt
1 Η - α6 (ί ch t — sh 0 Γ + a3 -^ Γ = a2b +
ο ν ' |o 3 |o
+ ab{ch 1 - sh l) +-^-(ch*l - 1).
Замечание, ft sh tdt = f'td (ch t) = t ch /— /ch /Л = / ch I—
— sh / + с
ЗАДАЧИ
Вычислить длины указанных дуг следующих линий:
1. у = -γΧ V х — I х (между точками пересечения линии
с осью Ох).
2. у = In sin x(jr <jc<Jl). 3. y= I*2 — у ln*(l<jt<4).
4. χ = a (cos t + ts\nt), у = a (sin i — t cos t) (0 < / < β).
5. a: = t — -i-sh 2/, у = 2 ch * (0 < t < 2).
6. χ = a(t — sin /), у = α( 1 — cos /), ζ = 4α cos-у (между двумя
точками пересечения линии с плоскостью Oxz).
7. χ = cos3/, у = sin3/, z = cos 2/ (длину всей кривой).
341
8. x = acht, y = asht, ζ = at (0</<β).
9. x = at, y = ai Yin /, ζ = -£- (1 < / < 10).
10. x3 = 3a2y, 2xz = а2 (между плоскостями у = -|-, у = 9a).
В каждой из задач 11—24 вычислить площадь фигуры,
ограниченной данной линией:
11. χ = a cos/, у = 6sin/ (эллипс).
12. χ = a(2cos/ — cos2/), У = α(2sin/ — sin2/) (кардиоида).
13. (χ -j- у)2 = a* (a > 0) и осью О*.
14. Площадь сектора, ограниченного осью Ох, дугой
гиперболы x^ach/, y = bsht до точки Αί0(^0, у0) и отрезком ОМ0.
15. Площадь сектора, ограниченного дугой Λί1Αί2 астроиды
x = acos3/, y = as\x\H и отрезками прямых ОМъ ОМ2
(исходящими из начала координат).
16. χ = (Я + Ό cos/ — rcos^±Lty у=(R+r) sin t—rsin^tl/
(эпициклоида 7? = nr, где η — натуральное число; рассмотреть
частный случай R = r, при котором получается кардиоида).
17. а: = (7? — г)cos/ + ^cos——/, #=(/?—г) sin/-f sin——/
(гипоциклоида /? = nr, где η — целое число, п > 2; рассмотреть
частный случай R = 4г, при котором получается астроида).
18. (х2 + У2)2 = 2а2 (х2 — у2) (лемниската).
19. Петлей кривой (х + у)3 = аху.
20. Петлей кривой (х + у)4 = x2y.
21. Петлей кривой (х + у)ъ = х2у2.
22. Кривой х3 -f у3 = х2 + у2 и осями координат.
23. Петлей кривой (\/ χ + V уУг = *у.
24. Петлей кривой (-^)2"+1 + (^т)^ = с (-f)" (-f^Wo,
6 > 0, с> 0, η > 0).
В каждой из задач 25—34 найти массу материальной дуги
данной линии при указанной линейной плотности у(х, у, ζ):
25.ху=1 (1<у<2); у(х, у, ζ) = ^-.
26. Зу = х3 (0 < χ < 1); γ (χ, у) = kx3.
27. у - χ4 (0 < χ < 1); γ (*, у) = to5.
28. х = \пу (1<У<2); γ(χ, у) = У3^У2+ 1.
29. у = In sin χ (-ί- < χ < -ί-1; γ (a, y) = & sin3*.
30. у = In cos χ ίθ< *<^-F-h γ(*> У) = k sin a cos2*.
31. у = lncosec *(-r- < #< -j-j; γ (a, y) = & sin3* cos χ.
32. у = In sec χ (о<л:<;-^-); у (χ, у) = k sin2* cos2*.
33. χ = t3, у = t, ζ = t2 (О < / < 1); γ (χ, y,z) = k |Λ+4ζ+9*ι/.
34. x=Rcost, y=Rs'm2t,z=Rs'mt cosnO < / <-^-); γ(χ, t/,z) =
35. Найти координаты центра тяжести однородной дуги
циклоиды χ = a (t — sin /), у = α (1 — cos f) (0 <; / < 2л).
36. Найти координаты центра тяжести однородной дуги
винтовой линии χ = α cos tf, у = aunt, z = bt (0 < / < β).
37. Найти координаты центра тяжести однородной дуги
кривой χ = е* cos tf, у = et sin /, г = е' (— оо < t <; 0).
38. Найти координаты центра тяжести дуги винтовой линии
x = acost, у = a sin/, z = bt (0</<я), если в каждой ее точке
линейная плотность пропорциональна аппликате этой точки.
39. Вычислить статический момент первого витка конической
винтовой линии * = /costf, y = tsint, z = t относительно
плоскости Оху, если плотность пропорциональна квадрату расстояния
точки до этой плоскости.
40. Вычислить моменты инерции первого витка винтовой ли-
. . . h
нии χ = a cost, у = asmty ζ = -γ- ι относительно координатных
осей.
В каждой из задач 41—52 найти работу, производимую силой
F = {X, У, Ζ) вдоль указанного пути L (в направлении
возрастания параметра):
41. F = | jc, -уз— J, L — дуга кривой ху = 1 (1 < χ < 4).
42. F={sin2A:, у2}, L — дуга линии у = cos л- (0<л-<л).
43. F = {х2 + у у х + У2 К ^ — отрезок прямой от точки.Л(—1, 1)
до точки 5(0, 2).
44. F = '{ — у, х), L — дуга астроиды χ = a cos3/, у = α sin3 /
(o</<-f
45. Ζ7 = {у, л-}, L —отрезок прямой от точки А (а, 0) до точ-
46. F = { — у2, ху), L —дуга эллипса x = aco$>t, y = 6sin^
(o</<J-'
47. F = {у — г, л-2, л'2|, L — отрезок прямой от точки Л (0, 2, —1)
до точки 5(2, 1, 0).
343
48. F = {ζ3, х, у2}, L —дуга линии * = t3, y = t2, z = t
(0 < t <_0·
49. F={y2 + z2, — i/z, a:}, L — дуга линии x = bt, y = acost,
z = asmt (o<i<-y-j.
50. ? = I HL9x9y\ L —дуга линии x = t, y=tcost, z = ts'mt
(0 < t <_2π).
51. F = [x2, t/, г2), L — дуга линии x = t, у = t2, ζ = /3
(0<*<J).
52. F = {yz, xz, *y}, Lx — дуга кривой χ = t2, у = /4, ζ = /6
(0<;/<;i), Lo —отрезок прямой от точки Л(0, 0, 0) до точки
В(1, 1, 1).
53. Найти работу, производимую силой тяжести, когда точка
массы т перемещается из положения Мх (хъ уи ζχ) в положение
М2{х2, Уъ 22) (ось Οζ направлена вертикально вверх).
54. Найти работу упругой силы, направленной к началу
координат, величина которой пропорциональна удалению точки от
начала координат, если точка приложения силы описывает против
часовой стрелки четверть эллипса-^—h -гг~ = 1» лежащую в
первом квадранте.
В задачах 55—60 показать, что работа, производимая силой
F= {X, У, Z), не зависит от пути с началом в точке Мх и
концом в точке Λί2; вычислить величину работы:
55. F= (2л-у, х2\у Мх(0, 0), Af2(l, 1).
56. F= \ху2, х*у\, Λίχ(0, 0), Λί2(2, 2).
57. F={3jc2+4jci/, 2*2-Зу2!, Λίχ(0, 0), Αί2(1, 1).
58. f ={χ, ί/, -ζ], Μχ(1, -1, -2), Λί2(6, 4, -4).
59. F = {5y2 + 4*ζ, Юху - 3ζ2, 2χ2 - 6*/ζ}, Λίχ (1, 0, 2),
Λί2(2, 1,J).
60. f = [2y — 10*ζ — 3y2z3, 2x -f 7z2 — 6*yz3, 14yz — 5*2 —
-9;q/2z2}, Mx(l, 1, 0), /И2(0, 1, 1).
61. С какой силой притягивает масса Λί, равномерно
распределенная по верхней полуокружности х2 + У2 = я2 (У Ξ> 0),
материальную точку массы т, занимающую положение О(0, 0)?
62. С какой силой масса Λί, распределенная с постоянной
плотностью на окружности х2 + у2 — α2, ζ = 0, воздействует на
массу т, помещенную в точке Л(0, 0, Ь)?
ОТВЕТЫ
1. 21/ΊΓ. 2. \пУ~3. 3. 4"(-^- + 1η 4)· 4· — Ρ2· 5· — (ch4— 1). 6. 8aVT.
344
a
,2
7. 10. 8. aV2shfi. 9. 9,9α. 10. 9α. 11. nab. 12. бла2. 13. -g~.
14. γ ab arcch -£-. 15. -jg- U — -j-sin4/J| 16. π (R -f r) (R + 2r), 6л/?2
при /? = г. 17. л (/? — г) (R — 2г), блг2 при /? = 4г. 18. 2а2. Указание.
Положить у = χ tg φ ί — _ϋ_ < φ < —). 19. —— Указание. Положить
\ 4 4 / 60
y = tx(0<tiK). 20. -±-. 21.-^. 22. -L + _i=n. 23 J_ .
Указание, у = xt2. 24. g (gyi t 25. -g-(l7r 17-2 j/ 2 ). 26. -g-(2 ]/" 2 - l).
27'Ш(17/17-1). 28. ig. 29. -| (-=-+■)■ »■ £ 81.^(3/3-2^2).
32. A>_2. 33. _*U 34.JL*n*. З5.*0 = ла, у0 = J_ а. 36. *0 =i™£,
а (1—cos β) 6β _Ji _ _L _L /_ 4α
Уо — β > ζο = 2 * *° — 5 ' ^° == 5 ' 2° = 2 * *^' ° ν "π2"'
-^-.-f**)· 39· ?^[(Зя2-1) (2л2+1)^+1]. 40./Wv=(4 +
-μ—) ΐ/4π2α2 + Λ2, /2 = α2 Κ 4π2α2 + h2. 41.—. 42. Л — JL 43. ϋ.
^ 3 / - ^ 2 2 23 3
3 α2 17 πα6
44. -Jg-яа2. 45.-g-. 46. ab2. 47. -3-. 48.1,1. 49. —g—(1 + а)+
+ αί-^_-Α 50. πί-1-π2 + 4π + 4-)· 51'4" 52, L 53-m*(*i-*i)·
54. -о- (а2 — б2), где k — коэффициент пропорциональности. 55. 1. 56. 8.
57. 2. 58. 19. 59. 11. 60. 5. 61. Проекции силы на оси координат: * = 0,
2kmM kmMb
у = —~2~ , где к — постоянная тяготения. 62.
ш2 , .^ п. „v,v..v,,„„«„ .,„v,.w.„„. ...
К (α2 + b2f
Глава 9
ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ
§ 9.1. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ПЕРВОГО ТИПА
Пусть дана функция f(x, у, ζ), непрерывная на некоторой
гладкой поверхности (σ). Разобьем поверхность (σ) сетью
произвольно проведенных кривых (рис. 9.1) на ряд частей (ах), (σ2),
... , (σ„). В каждой из этих частей (σ,) выберем произвольно
точку Mt (xi9 Vi, zt·), вычислим значение данной функции в этой
точке и, умножив его на площадь σ, соответствующей части
поверхности, составим сумму всех таких произведений
η
345
называемую интегральной суммой. Обозначим через d (σ,·) диаметр
элементарной части поверхности (S,·), т. е. расстояние между ее
наиболее удаленными точками; max d (at) — наибольший из
указанных диаметров.
Поверхностным интегралом первого типа от функции
/ (*, У, ζ) по поверхности (σ) называется предел интегральной
суммы (9.1) при maxd(ai)-^0:
η
\\f(x, У, z)da = lim У f{xi9 yi9 zt) σ·. (9.2)
Рис. 9.1
Рис. 9.2
Поверхностный интеграл первого типа обладает свойствами,
аналогичными свойствам криволинейных интегралов первого типа.
Если / (х, у, ζ) > 0 и функцию / рассматривать как
поверхностную плотность массы материальной поверхности (σ), то
интеграл (9.2) определяет массу этой поверхности.
Предположим, что поверхность (σ) однозначно проектируется
на какую-либо координатную плоскость, например на плоскость
Оху, и область (S) является ее проекцией. Тогда элемент
поверхности
do =
dxdy
I cos γ (Μ) Ι
где у (Μ) — угол между нормалью к поверхности в точке Μ (χ, ί/, ζ)
и осью Οζ.
Если поверхность задана уравнением ζ = ζ(χ, у), то
*>=Vi+ (■£)*+(■%■)'**
(9.3)
346
и интеграл (9.2) вычисляется по формуле
<*) (5)
= j j / [χ, у, ζ (χ, у)] γ ι + (_|_)2+ (|_)2 dxdy. (9.4)
Если (σ) — кусочно-гладкая двусторонняя поверхность
х = х(и, υ), у = у (и, υ), ζ = ζ (и, υ) ((и, υ) ίζ Q),
а функция /(*, у, ζ) определена и непрерывна в точках
поверхности (σ), то
Я/(*. ί/. z)do =
- \\f[x(u, ν), у (и, υ), г (и, υ)]]/EG — F2 dudv, (9.5)
где
°- Ш+(*■)'+(■£■)'= м
г, дх дх ду ду dz dz
~ ди dv * (5α ду "^ дм di>
Формула (9.4) является частным случаем формулы (9.5) при
ζ = ζ(χ, у).
ПРИМЕРЫ
1. Вычислить интеграл по поверхности первого типа
JJ V1 + 4л:2 + 4у2 do, где σ — конечная часть поверхности ζ = 1 —
σ
— α:2 —ί/2, отсеченная плоскостью ζ = 0 (рис. 9.2).
Поверхность задана уравнением, разрешенным относительно 2,
т. е. уравнением вида ζ = ζ(χ, у), поэтому можно применить
формулу (9.4). Так как
— = — 2х —-—2ί/
дх Δ ' ду - zy>
то по формуле (9.3)
da = Vl + (— 2х)2 + (— 2у)2 dxdy.
Проекцией рассматриваемой части данного параболоида
вращения ζ = 1 — χ2 — у2 на плоскость Ох у является область,
ограниченная окружностью х2 + У2 = 1 (получено из уравнений
поверхности и плоскости). Следовательно, областью (S), фигурирующей
в формуле (9.4), является круг *2 + у2<!1.
347
В соответствии с формулой (9.4) получаем
^ у 1 + 4х2 + 4у2do = Jf К 1 + 4х2 + 4i/2 J/ l + 4х2 -}- 4у2 d*dj/ =
(?) (5)
= ii(l + 4x2 + 4i/2)dxdy.
(S)
Для вычисления полученного двойного интеграла перейдем
к полярным координатам χ = ρ cos φ, у = ρ sin φ. Замечая, что
в области (S) φ меняется от 0 до 2π и ρ — от 0 до 1, находим
2-1 2-1
Ж1 + 4.V2 + 4у2) dxdy = J άψ J (1 + 4p2) pdp = j dq> J' (p + 4p3) ф =
(S) 0 0 0 0
2π 2-
j'fr+p4)|>=4J^=3*·
2. Вычислить J J (χ2 + у2 + г) do, где σ — верхняя половина
сферы х2 + у2 + z2 = R2 (рис. 9.3).
Разрешая данное уравнение поверхности относительно 2,
получаем ζ = :±ζ |/ Я2 — х2 — у2. По условию нужно взять знак «плюс»
(рассматривается верхняя половина сферы). Таким образом,
поверхность σ задана уравнением ζ = УR2 — х2 — у°\ Поскольку
dz χ dz у
ОХ ~ у %2_х2_у2' ду ~ γ Д2 _ χ2 _ у2 '
то
do = )/l + R>_Xl*_y> + R*S_y*dxdy =
Rdxdy
ι / R2
= К R2_X2_y2dxdy= у————
По формуле (9.4)
J J (*2 + У2 + ζ) do = J J (*2 + y2 + y7?-**-!/* -
Rdxdy
s VR2 — x2 — у2
s
где (S) — проекция полусферы на плоскость Оху, т. е. круг
х + у<Я2.
Переходя к полярным координатам χ = ρ cos φ, у = ρ sin φ,
находим
(S) (S) 0 0
348
2π
2- R
2* R
+ R j'dcp ^prfp = /? jrfcp f v^—-2dp + /? fdcpj'pdp
о о
о о
= 2nR~R* + 2nR-^- = -i"π/?4 + л/?3·
Замечание. Первый двойной интеграл вычислен с помощью
подстановки ρ = R sin tf:
./ К/?2 —о2 r ./
/?3 sin3 f
К/?2 — p2 .' //?2—/?2sin2i
о о
-r
R cos tdt = R3s'm3tdt =
Рис. 9.3
Рис. 9.4
Рис. 9.5
■Ζ?8 Ι (1— cos2i)d(cos0 = — #3cos/
δ
— Τ?3 — ^3 — JL_ 7?з
+ /?
,з cos3 *
3. Вычислить $$x{y + ζ) do, где σ — часть цилиндрической
поверхности χ = \гЬг — у2, отсеченной плоскостями ζ = 0, ζ =
= с (с>0).
Уравнение данной поверхности не содержит 2, поэтому
применить здесь формулу (9.4) не представляется возможным.
Так как поверхность задана уравнением, разрешенным
относительно jc, необходимо воспользоваться формулой
///(*> У> z)do = ffflx(yf ζ), у, z\yi +
где (Sx) — проекция поверхности σ на плоскость Oyz.
дх_у , (дх
ду ) ~^\дг
-J dydzt
349
Поскольку
дх
дх
Υ b2 — у2 ' dz
О,
то
do
-Φ
£)'+(■#■)'«*
dz
V
1 +
b2-y*
dydz
dydz
■ dydz.
Vb2-y2
Заметив, что в данном случае область {Sx) представляет собой
прямоугольник ABCD (рис. 9.4), определяемый неравенствами
— Ь-^Су^СЬ, 0<г<с, по указанной формуле найдем
j j * (У + ζ) do = j j χ (у + ζ) \-dydz = b j j (y + z) dydz =
(Si)
(Si)
= bj dyj (y + z)dz = bj [yz + -ξ-) \Jody = b J(cy + £-)dy =
-b
b
--be
J ydy+^j- J dy=-^-y2
-b -b
—b
be2
—y
&r2
b2c
4. Вычислить Jj (3x2 + 5y2 + 3z2 — 2) do, где σ — часть
поверхности у = Ι7χ2 -f- г2, отсеченной плоскостями у = 0, у =
= Ь (Ь > 0).
Поверхность задана уравнением, разрешенным относительно
у. Для вычисления интеграла по поверхности первого типа
воспользуемся формулой
jjf(x, у, z)da=^f[x, у (χ, z), z] }/'i + (Λ-J + (*L.J dxdz,
где (S2) — проекция поверхности σ на плоскость Οχζ.
Поскольку
ду _ χ ду _ г
J/*2
72 ' дг
У х2 + г2
то
«<>-/' t^M-H-)'<<*«* =
-/
1+.
dxdz = "j/2 dxdz.
χ2-\-ζ2 ~ χ2-}-ζ2
Проекцией (S2) данной поверхности на плоскость Οχζ является
круг χ2 + ζ2 = Ь2 (рис. 9.5), поэтому при переходе к полярным
координатам x = pcoscp, 2 = psincp получим 0<^φ<;2π, 0<]ρ<;&.
350
По указанной формуле находим
JJ (Зх2 + 5ί/2 + 3ζ2 - 2) do = IT [3 (χ2 + г2) +
s2
2- b
5 (χ2 + ζ2) - 2] К 2 djwfe - К 2 J Лр j (8p2 - 2) pdp
о о
2r.
dcp =
V 2 J <ίφ j (8p3 - 2p) ф = V 2 j (2p4 - p2)
δ ό ο
2-
- V 2" j (264 - ft2) dcp - 2 I/ 2"π (264 — ft2).
5. Вычислить (l (x2 + у + г2 — 1) da, где σ — конечная часть
σ
поверхности 2у = 9 — χ2 — ζ2, отсеченной плоскостью у = 0.
Применяем формулу, приведенную в примере 4. Находим
частные производные функции у по χ и по г, а также элемент
площади do:
ду
ду
д = —х, -р- = — 2, da = ]/Ί + χ2 + г2 dxdz.
По указанной формуле
+
(Si)
+ ζ2 - 1) V 1 + χ2 + г2 d*dz = j f (-£- + -f- +
+ 4") Vх"! + ^2 + z2 dJtdz = j j
(St)
^_(Х2 + г2+1) +
+ 3 1 V 1 + χ2 + ζ2 dxdz.
Перейдем к полярным координатам в плоскости Oxz:
χ = ρ cos φ, 2 = psin(p. Область (S2) в этой плоскости представит
собой круг х2 + г2 <; 9, поэтому 0 < φ <; 2π, 0 < ρ < 3.
Следовательно,
й ["Г (χ2 + ζ* + V + 3] ^1 + *2 + ζ2 ^ -
2π 3
= Jdq>/[4-(Ρ2 + 1) + 3] j/Г+р"2prfp =
0 0
2π 3 2π 3
= 4- / dyj (ρ2 + 1) УТ+? pdp + 3 J dq> J* /TTp2 pdp -
351
2π
4-/<ίφ/(1 + Ρ2)2 ±d(l+p*) +
2π
О О
1
+ 3/ίίφ/(1+ρ2)24^(1 + Ρ2) = 42π£±ί
У
О О
+ -§-*·^
= " (Ю2 _ΐ) + 2π(102 _1) =
= -£-(200 Ι 10-11).
6. Вычислить I I ]/ 1 +^T" + -^2_rfo. где σ —часть
поверхности 2 =
\ Р2 + ?
Так как
2/? 2</
|— (ρ > 0, <7 > 0), вырезанная цилиндром
(х>0, д>0).
л: dz
ТО
В соответствии с формулой (9.4)
■IIV
1 +
-do
(S)
1 +
X
(S)
где (S) — область, ограниченная линией I —g- + -V-) =α(—
Введем обобщенные полярные координаты, положив χ = ρ ρ cos φ,
у = q p sin φ. Тогда
-|- = pcoscp, -|- = psinq>f -^- + ^2- = P2.
Уравнение линии, ограничивающей область S, в новых
координатах примет вид
р2 = a2 cos 2ср или ρ = a j/cos 2φ.
352
Итак,
a /cos 2f
(S) X H Ч ' \. 0
а У cos 2φ
w
jd<p j (p + p»)dp = WJ (x+x)
α > cos 2φ
dcp
4 *
С (a2 cos 2φ , α4 cos2 2φ \ , a2pq С лл 0 , ,
= P?J ( 2^ p^-l^^-f-J cos2(pd(p +
. a*pq f 1 + cos 4φ , a<
+ —p- —9—- d4> = —
pq
sin2cp
+
32
sin4cp
• а*РЯ
+ -Р-Ф
npqa*
+
16
ЗАДАЧИ
Вычислить следующие интегралы по поверхности первого типа:
1 · J J (χ2 + У2 + 3z2) da, α — часть поверхности ζ — J/*2 + У2,
σ
отсеченная плоскостями ζ = О, ζ= 1.
2. J J ( χ2 -f У2 + ^ 2~) ^σ» σ—конечная часть поверхности
σ
2ζ = 2 — χ2 — ί/2, отсеченная плоскостью Оху.
3· Яг (χ + ί/) ^σ> о» — часть поверхности ζ = j/9 — χ2, отсечен-
σ
ная плоскостями у = О, у = 2.
4· Я (г2 + *2 + У3) ^α, σ — полусфера ί/ = |/ R2 — χ2 — г2.
σ
5. J J |/ 1 + 4x2 + 4г2 da, σ — конечная часть поверхности у =
= 2
г2, отсеченная плоскостью у = 0.
6- Я(7У2 — З*2 — 3z2) da, σ — часть поверхности у = У χ2 + ζ2,
σ
вырезанная цилиндром χ2 + ζ2 = 2а:.
7. ] J ί λ: + ί/2 + г2 2~) da, a — конечная часть поверхности
х = 2
-, отсеченная плоскостью χ = 0.
353
χ =
8. J J (5л:2 + 3ί/2 + 3ζ2 + 4) do, о — часть поверхности
з
= V У2 + г2> отсеченная плоскостями х = О, л: = 2.
9. JJ |/1 + У2 + z2 da, σ — часть поверхности л: = ζί/,
вырезанная цилиндром (ζ2 + у2)2 = 2zy.
10. JI (x4 + У4 + 2χ2ί/2 + г2) da, σ — часть плоскости χ + у +
_f- ζ = α, вырезанная цилиндром х2 + У2 = #2·
11. J J \ 1 -f *2 + ζ2 da, a — часть поверхности у = —^ о—»
вырезанная цилиндром (χ2 + ζ2)2 = 4 (ζ2 — χ2).
12. fj V 1 + 4ί/2 + 4z2 da, σ — конечная часть поверхности
з
х = 4 — у2 — ζ2, отсеченная плоскостью χ = 0.
13. J J (^2 + ί/ + ζ2 — 2) da, σ — конечная часть поверхности
з
2у = 9 —~ х2 — ζ2, отсеченная плоскостью у = 0.
14. j J(2z2 — χ2 — у2) do, a — часть поверхности ζ — γ χ2 -f- у2,
3
вырезанная цилиндром χ2 + У2 = 2х.
15. f J ί/ (г + *) da, α — часть поверхности у = |/~ с2 — ζ2,
отсеченная плоскостями л; = 0, * = а.
16. fj*V 1 + 9х2 -}- 9z2da, a — часть поверхности у = Зл-z, вы-
резанная цилиндром (г* + ζ2)2 = 8χζ.
17. J J (х2 + 2ί/2ζ2 + У4 + ζ4) da, α —часть плоскости х + у +
3
_f- ζ = 2, вырезанная цилиндром у2 -\- ζ2 = 1.
18. j*J V 1 + с2χ2 + c2i/2 da, a — часть поверхности ζ =-- cxy(c > 0,
*i>0, y>0), вырезанная цилиндром (χ2 -f- у2)2 = 2а2ху.
19. \ \ 1/ 1 + -^2~ + -~2~^σ> σ — часть поверхности χ =
= "Τ Ir^ > °> г > °)> вырезанная цилиндром (-^- + -^-j -
20. И (— 1 —rZ + bjdo, a — часть поверхности z =
3
= — 1— (а > 0), вырезанная цилиндром (х2 + У2)2 = а2 (*2 — у2).
21. f j (x2 + У2) do, о — граница тела ]/ х2 + у2 ^Cz^C 1 ·
354
da
22. j| (\+х + у + г)* » σ — граница тетраэдра л: + у + ζ < 1,
*>0, ί/>0,'ζ>0.
23. JJzda, σ — часть поверхности геликоида x = ucosv,
σ
у = и sin vy z = v(0<u<a, 0 <υ < 2π).
24. JJ 22da, σ — часть поверхности конуса # = г cos φ sin α,
ί/= rsincpsina, 2 = rcosa (0<><;α), 0<^φ<2π, α = const
(■
0<a<-^-
25. Jj* (л:2у2 -f- x222 + y2z2) do, о — поверхность, отсеченная от
σ
верхней части конуса г2 = k2 (χ2 + у2) цилиндром х2 + у2 — 2ах = 0.
26. Г С з " » σ ~~ поверхность
•V <*+*+w*/-£-+-£-+-£-
эллипсоида -^- + -^ + -^- =-1 (а > 6 > с > 0).
27. Доказать формулу Пуассона Я/ (a* + by -\- cz) da =
σ
1
= 2π J f (и Υ α2 + b2 + с2) du, где σ — поверхность сферы χ2 +
—ι
+ y2 + z2=L
ОТВЕТЫ
1.2/Υπ. 2, -i-(9/"3—1). 3.36. 4. π (— /?4 + J?l). 5. 10 π.
6. 6 /Τπ. 7. -тг- (25 К "5"— 1). 8. 80 У Τ π. 9. -у (π + 8). 10. (JUL. +
+ -^- + α2/?2)π|/3. 11. 2(2 +π). 12. 36 π. 13. JL (500 j/10—23).
^ Ιο
3 Ϋ~2 ο ο 29 ,_ а2 с2а*к
14. 2 π· 15· α с · 16· 2 (2 + 9 π). 17. — ^ 3 π. 18. -γ + jg—
π^4π 8α3 20 πα2 (3α — 56) π , .—
19. <7^2 + ^8~~* 2°· ~75~+~9~α6 + Л5 ' 21. -g-(1 +/2).
3 γ "з" '
22. 2 +(Κ 3— 1)1η2. 23. π2[α)Λ + α2 + 1η (α + |Λ + α2)]
ηΛ ла4 / π \ 1 г
24· — sin a cos2 α (^0 < α < -g-). 25. -^ (80 £2 + 7) πα6 /ΐ + £2. 26. 4π
27. Указание. Перейти к новой системе координат Ouvw: взять плоскость
ах -\- by -\- cz = 0 в качестве плоскости Ovw, ось Ow направить перпендикулярно
/ ax + by + cz\ n
к этой плоскости тогда и = — =- 1. Параметрическое уравнение
сферы взять в виде: и = и, ν—У \ — и2 cos a, w = У 1 —- w2sina (— 1 <н<1,
0 <. a < 2л).
355
§ 9. 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ ВТОРОГО ТИПА
Пусть в точках двусторонней поверхности σ задана
непрерывная функция f(x, у, ζ). Выберем на поверхности определенную
сторону. Разобьем поверхность σ сетью произвольно проведенных
кривых на части σχ, σ2, ... , оп. В пределах каждой части σ^
выберем произвольно по точке Mt(x£i yt ζχ·), вычислим в ней
значение данной функции. Это значение f(xh yL zL) умножим на
проекцию (S) части аг на плоскость Оху (а не на площадь σ,,
как это было в случае поверхностного интеграла первого типа).
При этом числу St приписывается определенный знак, а именно:
если в точках σ,- нормаль, отвечающая выбранной стороне
поверхности, составляет с осью Οζ острый угол, то через Sz обозначаем
площадь проекции σ,, взятую со знаком «плюс»; если же
упомянутая нормаль составляет с осью Οζ тупой угол, то под S,-
будем понимать площадь этой проекции, взятую со знаком
«минус». Составим сумму всех таких произведений:
η
7'»=2/(JC/· У1· z')Si- (9·7)
Поверхностным интегралом второго типа называется предел
суммы (9.7) при maxdto)->0:
η
ίί/to У, z)dxdy= lim 2/(*,, ft, z,.)S„ (9.8)
V max </(*.)-0-Ξι
где d(o) — диаметр oL.
Аналогично определяются интегралы
jj /(χ, у, z)dxdz, ^fi*, У, z)dydz, (9.9)
3 3
причем для выбора знака проекции элемента служит угол между
нормалью, отвечающей выбранной стороне поверхности, и осью Оу
или Ох.
Наиболее общим видом поверхностного интеграла второго типа
служит интеграл
[J (a-, i/, z)dydz + Q(xt у, ζ) dxdz + R(x, ί/, z)dxdy, (9.10)
з
где Р, Q, R — функции от ху у, 2, определенные и непрерывные
в точках двусторонней поверхности σ.
Поверхностный интеграл второго типа обладает всеми
свойствами поверхностного интеграла первого типа, за исключением
одного: при изменении стороны поверхности интеграл (9.10)
меняет знак.
356
Поверхностные интегралы второго типа вычисляются
следующим образом. Если поверхность σ однозначно проектируется
в область (Si) плоскости Оху и z = f(x, у) —ее уравнение, то
JJ/?(at, */, ζ) dxdy = ^z\§R[x, y, f(x, y)]dxdy, (9.11)
(Si)
где знак «плюс» берется в том случае, если на выбранной
стороне поверхности cos γ > 0, и знак «минус» — если cos γ < 0.
Аналогично, если σ однозначно проектируется в область (S2)
или (S3) на плоскости Oxz или Oyz, т. е. может быть задана
уравнением у = у(х, ζ) или х = $(у, г), то
§§Q(X> У> z)dxdz= ± ]J Q[x, φ (χ, z),z]dxdz\ (9.12)
(S2)
JJP(*, у, z)dydz= ζ± ]|Ρ[ψ(ί/, ζ), у, z]dydz, (9.13)
(S3)
где в случае (9.12) берется тот же знак, что и у cos β, а в случае
(9.13) — знак cos а.
Для вычисления интеграла общего вида (9.10) используются
те же формулы (9.11) — (9.13), если поверхность σ однозначно
проектируется на все три плоскости. В более сложных случаях σ
разбивается на части, обладающими указанными свойствами,
а интеграл (9.10) —на сумму интегралов по этим частям.
Поверхностные интегралы обоих типов связаны формулой
\ J Pdydz -f Qdxdz + Rdxdy =
3
= \ j (P cos α + Q cos β + R cos γ) do, (9.14)
где cos α, cos β, cosy — направляющие косинусы нормали,
направленной в ту сторону поверхности, по
которой берется интеграл второго типа.
ПРИМЕРЫ
1. Вычислить поверхностный интеграл второго типа \\ (у2 +
3
+ z2) dxdy, где σ — верхняя сторона поверхности ζ = У а2 — χ2,
отсеченной плоскостями у = 0, у = Ь (рис. 9.6, а).
Нормаль η в точке Λί, соответствующая указанной стороне
поверхности, составляет с осью Οζ острый угол (точнее 0 < a<i-S-)»
поэтому в формуле (9.11), которой следует воспользоваться,
нужно взять знак «плюс». Проекцией (Sj) данной поверхности на
плоскость Оху является прямоугольник ABCD (рис. 9.6, б),
определяемый неравенствами — α <;л;<;α. 0 <; ί/ < &.
357
По формуле (9.11) находим
ί f {У2 + ζ2) dxdy = f J [у2 -!- (Va2 -χ2)2] dxdy =
° (Si)
b
-a 6
j dx\(y2 + a2~x2)dy = \ [JL· + a2y-x2y)\ dx =
!i/=o
a
ί (ίγ + a2& ~λ'26)dx = (τ- A' +fl2ft* -b ύ)
= -±-a&(&2 + 2a2).
£
<?
^l
-«
Ί
11
Ί
<?
1
|
I
/?
\A
a x
Рис. 9.6
Замечание. Если бы рассматривалась нижняя (внутренняя)
сторона поверхности, то нормаль, соответствующая ей,
образовывала бы с осью Oz тупой угол, в формуле (9.11) нужно было бы
взять знак «минус».
2. Вычислить J J (ax2 -f by -f cz2) dxdz, где σ — внутренняя сто-
σ
рона поверхности χ2 = 2ру (р> 0), отсеченной плоскостями у = 2р,
г = 0, ζ = q (рис. 9.7, а).
Проекцией (S2) данной поверхности (части параболического
цилиндра) на плоскость Oxz является прямоугольник ABCD
(рис. 9.7, б), определяемый неравенствами — 2р<^л:<;2р,
0<z<<7.
Так как нормаль η в произвольной точке Μ данной
поверхности, соответствующая ее внутренней стороне, образует с
положительным направлением оси Оу острый угол, то в формуле (9.12)
нужно взять знак «плюс». Замечая, что у
2р
(следует из
уравнения поверхности), по указанной формуле находим
Я {ах2 + by + cz2) dxdz = \\ (a*2 + b^- + cz2) dxdz
(Si)
2p
358
—2р О
I к«+i) a+ΐ]> - J [, (.+i)*■+*μ=
2ρ
ί.
-2ρ
- [4+£)4 -:-4 «]|!;:f λ(·+£)+4 «··
# <r
Рис. 9.7
3. Вычислить 1 j (χ2 + ζ2 + ay2) dxdz, где σ — внешняя сторона
поверхности у = j/л;2 + ζ2, отсеченной плоскостями у = 0, у = &
(рис. 9.8).
Нормаль к поверхности в точке Μ образует с осью Оу тупой
угол, поэтому в формуле (9.12) следует взять знак «минус».
Проекцией (S2) данной поверхности на плоскость Oxz
является круг х2 -+- ζ2 < δ2. По формуле (9.12)
if (*2 -rz2 + ay2) dxdz = - |ϊ [χ2 + ζ2 + α{γχ2 + ζ2)2] dxdz =
(S2)
= — ί ί (*2 + ζ2) (α + 1) dxdz = — (fl -ι- 1) f f (χ2 + ζ2) dxdx.
(S2) (Й)
Переходя к полярным координатам χ = ρ cos φ, ζ = ρ sin φ,
находим
2- b 2r.
jj (χ2 + ζ2) dxdz - j dcp j р2рф = J 4
(S2) 0 0 0
dq> =
2π64 лб4
359
Следовательно,
f j (χ2 + г2 + ay2) d*rfz =
σ
- (a + i) J J (χ2 + 2») л*** = - π(α;τ1)64.
(SS)
Рис. 9.8
Рис. 9.9
4. Вычислить jj {αχ2 + 6ί/2 + fe2) dydz, где σ — внутренняя
σ
сторона части полусферы χ = ]//?2 — у2 — г2, вырезанной конусом
х = lV + z2·
В формуле (9.13), которой надлежит пользоваться, следует
взять знак «минус», так как нормаль, соответствующая
выбранной стороне поверхности, составляет с положительным
направлением оси Ох тупой угол:
Я [ах2 + by2 + bz2] dydz = - Я № (Я2 - У2 - ζ2) +
is,)
+ by2 + bz2) dydz = — Я [яЯ2 +iP~a) {у2 + ζ2)] dydz.
(S·)
D2
Так как (S3) есть круг ί/2 + ζ2 < -=- (получено из
уравнений χ = YR2 — у2 — ζ2, х= у у2 + ζ2), то, вводя полярные
координаты, находим
R
Я laR2 + {Ь-а) (у2 + z2)] dydz = \ dq> J [atf2 + (b-a) p2] pdp =
(S3)
R
V2
R
V2
= U<f UaR*p + (b-a)9*]d9= j [fl# £ + (ft - fl) ^ dtp =
= 2π[ί£ +(6-α)4]-^(& + 3^
360
Итак,
j J (αχ2 + by* + fe2) di/dz = — ^ (b + 3a).
5. Вычислить \ \ (^y- -f- -|з- + &z) dxdy, где σ — внешняя сто-
д-2 f,2 22
рона нижней половины эллипсоида —2-+T2-H—г = 1 (Рис· 9.9).
Нижняя половина эллипсоида
.--ОЛ~£~
б2 "
Проекцией (Sx) этой половины эллипсоида на плоскость Оху
является эллипс
_^!_ _i.iL- ι
а2 ' ^ ~~ 1в
Так как нормаль я, отвечающая внешней стороне
поверхности, составляет с осью Οζ тупой угол, то
·£ + -J - *с γ ι - £ - £) «ω» -
(St)4
Вводя новые координаты по формулам
χ = ap cos φ, у = bp sin φ,
находим
(St)
= 2παδ
jj („c j/i _!-_!-_!-_»1)_„_0=
2п 1
= J *Ф j (to J/ 1 - ρ2 - ρ2) a&pdp =
о о
2- 1
ч /-»
= ab J d<p J (&ф К 1 — Ρ2 — Ρ3) dp =
J |o
(SO
2- 1
0 0
^ (1 — ρ2) 2
6. Вычислить J J x2dydz + y2dzdx + z2dxdy, где σ — внешняя
сторона сферы (χ — a)2 + (ί/ — bf 4- (ζ — с)2 = Τ?2.
361
Этот интеграл представляет собой сумму трех интегралов.
Вычислим первый из них:
I1 = $$x*dydz.
Уравнение сферы будет
х — а=± YR2-{y-b)2-{z-c)\
где знак «плюс» отвечает одной полусфере (ближней), «минус» —
другой (дальней). Подынтегральную функцию представим в виде
х2 = {х — а)2 + а2 + 2а (х — а).
Обозначим через σχ внешнюю сторону ближней полусферы
ABDEFi (рис. 9.10, а), через σ2 — внешнюю сторону дальней
полусферы ABDEF2, через (S3) — проекцию каждой полусферы на
плоскость Oyz (это круг, ограниченный окружностью (у — Ь)2 +
+ (z-c)2 = #2, рис. 9.10,6).
Принимая во внимание, что выражение х — а меняет знак
при переходе от одной полусферы к другой, по формуле (9.13)
находим
h = Л x?dydz = Я U* - аТ + а2-г 2а (х- a)] dydz -
— \\ [(χ — а)2 + α2 — 2а {χ — a)] dydz =
= 4а JT (x-a)dydz = 4a \[V R2 - (y -bf - (z- cf dydz =
(Ss) (53)
2- d
= 4o J </φ ,f /#2 - ρ2ρφ = ^-naR3.
362
При вычислении двойного интеграла осуществлен переход
к полярным координатам по формулам
у — Ъ = ρ cos φ, ζ — с = ρ sin φ.
Аналогично вычисляются и другие два интеграла:
/2 = \ J ψά,ζάχ = -f- nW?3, /3 = J j 22i/i/ciJC = -|" яс#3.
з σ
Следовательно,
JJ A-2dt/iiz + y2dzdx + zMxdy = 1г + /2 + /, = -|- π#3 (α + b + с).
7. Вычислить / = |j (ί/ — ζ) dydz + (ζ — χ) άχάζ + (χ — y) dxdy,
где σ — верхняя сторона поверхности, вырезанной цилиндром
jc2 + у2 = 2ах из сферы х2 + у2 + ζ2 = 2#х (/? > а, 2 > 0).
Воспользуемся формулой (9.14), связывающей поверхностные
интегралы обоих типов. По этой формуле
t = Ji [(У — z) cos а + (z — х) cos β + (χ — У) cos Vl do.
Далее, поскольку
cosa =
dF
дх __ 2x~2R _ χ— R.
R '
cos β =
d# _ j_.
R '
l/idFY /dF\* /dFX
V (-dx-)^(-w) +(-*■)
dF
dz
cosy
dF \2 tdF 2 R '
У (w) + (-asr) + N
TO
/= Я (г-У)da.
σ
Так как поверхность симметрична относительно плоскости 0*2, то
И ydo = 0,
3
а
/ = jjzffa.
з
363
Переходя снова к интегралу второго типа, получаем
7 = J J Т^У dxdy = "7" dxdy = R J j dxdy = nRa2'
* R
ЗАДАЧИ
Вычислить следующие поверхностные интегралы второго типа:
1. J J (Ъх2 4- 5ί/2 + ζ2) dxdy, σ — внешняя сторона части верхней
σ
полусферы ζ = Υ\ — χ2 — у2, вырезанной конусом ζ = Vχ2 -\- У2·
2· Я (*2 + У2 + Зг2) dxdy, σ — внешняя сторона поверхности
ζ — У х2 -\- у2, отсеченной плоскостями ζ = 0, г = 2.
3. J J (л:4 + у4 + 2г2) dxdi/, σ — внутренняя (нижняя) сторона
поверхности ζ = ху (х > 0, у > 0), вырезанной цилиндром (х2 +
+ ί/2)2 = 6^ί/.
4. I I (-^-+ -^r) dxdy, σ —нижняя (внутренняя) сторона по-
σ
X2 II2
верхности 2 = 4 —rg- —^-, отсеченной плоскостью 2 = 0.
5. JJ (.ν2 — 2ί/2 + 6г) dxdi/, σ — нижняя (внешняя) сторона по-
3
верхности у2 = 6г, отсеченной плоскостями 2 = 6, χ = 0, χ = 3.
6. Μ (-^- -+- -^- + 2z) dxdi/, σ — верхняя (внешняя) сторона
поверхности ζ = 1 — 4 4"» отсеченной плоскостью ζ = 0.
7. JJ (2а: + 3ί/ + 4z) dxdy, σ — верхняя сторона плоскости χ -f-
2 ,,2
+ {/+2 — 6 = 0, вырезанной цилиндром — + \- = 1 ·
8. /M-T"+-f-+z+lj d^rfi/, σ — верхняя сторона поверх-
σ
х2 и2 ί х2 и2 \2
ности г = -7 -у- (У > °)' вырезанной цилиндром (-γ + ^-1 =
»(.£-4)·
*· Я(*г + z2)dydz, σ —внешняя сторона поверхности х =
= \/9 — у2, отсеченной плоскостями 2 = 0, 2 = 2.
10. JJ (2л:2 + ί/4 + z*)dydz, σ — внешняя сторона поверхности
χ = yz (ί/> 0, 2> 0), вырезанной цилиндром (ί/2 + ζ2)2 = 262ί/2.
364
11. / | ί-^2~ + ~τ) dxdz, σ — внутренняя сторона поверхности
σ
Χ2 Ζ2
у = b2 2 2~> отсеченной плоскостью у = 0.
12. jj (л:2 + У2 + ζ2) dxdz, σ — внешняя сторона части
полусферы у = I/ 1 — х2 — г2, вырезанной конусом у = |^*2 + ζ2.
— внутренняя сторона
поверхности χ = Υ у2 -\- г2, отсеченной плоскостями χ = 0, λ' = а.
14. I I \х + -^ + a dydz, о — внешняя сторона по-
σ
у2 ζ2 „ / ί/2 , г2 \2
верхности χ = -^ г» вырезанной цилиндром \Т2~ + -^2~/ =
и [ ъ2
15. II 1^2- + -тг + kzjdxdy, σ —внешняя сторона поверх-
/у2
я -jj-, отсеченной плоскостью ζ = 0.
16. | \ (-4- + "L· + ζ + k) dxdy, σ — внешняя сторона поверх-
σ
(#Ξ>0), вырезанной цилиндром! ~^- -\- -~- ) =
ности г —
а2 Ъ2
С \ α2 ί
17. JJ xdydz + у^Ыл: + zdxdy, σ — внешняя сторона сферы
*2 + ί/2+σζ2 = /?2.
ίο Γ Γ% ^^г . dzdx . djtdi/
I I —^ 1 1 —, σ —внешняя сторона эллип-
σ
х2 и2 ζ2
соида -Γ+^. + _=ι.
ОТВЕТЫ
1. 16я. 2. —32л. 3. — 3. 4. — 96π. 5.324. 6. 9π. 7.144л. 8. 6(1+π).
о ш in b° 11 лаМс to n iq (Л + Д)а*л 1Л (я+ 1) лисп*
9.88. 10. -g-. 4· — 2 12· Τ- ,3· 2 · ,4· 8 .
яабс4 ,, , ,, . лаАс4 лаЫгс2 4я
15. —2~ (1 + к). 16. —— + —γ—. 17. 4лЯ3. 18. -j- (cfib2 + b2c* + с2а2).
365
§ 9.3. ФОРМУЛА СТОКСА. ФОРМУЛА ОСТРОГРАДСКОГО — ГАУССА
Если функции Р = Р(х, у, z), Q = Q(χ, у, ζ), R = R(xf у, ζ) —
непрерывно дифференцируемы и L — замкнутый кусочно-гладкий
контур, ограничивающий конечную кусочно-гладкую двустороннюю
поверхность σ, то справедлива формула Стокса
fP(x, у, z)dx + Q(x, у, Z)dy+R(x, у, z)dz =
=#[(3—£)»-+(■*—£)«»+
* (9.15)
+ (-§-—w)cosv]d(J>
где cos α, cos β, cos γ — направляющие косинусы нормали к
поверхности σ, причем направление нормали
определяется так, чтобы со стороны
нормали обход контура L совершался бы
против часовой стрелки (в правой системе
координат).
Формула Стокса может быть записана в следующем
символическом виде:
f Pdx + Qdy + Rdz = jj
cos α cos β cos у
д_ д_ д_
дх ду dz
Ρ Q R
da. (9.15')
Если σ — кусочно-гладкая поверхность, ограничивающая
объем V, и Р = Р(х, у, z), Q = Q(χ, у, ζ), R = R(х, у, ζ) —
функции, непрерывные вместе со своими частными производными
первого порядка в области (V) -\- σ, то справедлива формула
Остроградского — Гаусса
я
(Р cos a + Q cos β + R cos γ) do =
(V)
где cos α, cos β, cos γ — направляющие косинусы внешней нормали
к поверхности σ.
ПРИМЕРЫ
1. С помощью формулы Стокса вычислить криволинейный
интеграл / = $ ydx + zdy + xdz, где L — окружность χ2 + у2 +
4- ζ2 = α2, χ + у + ζ = 0> пробегаемая против часовой стрелки,
если смотреть с положительной стороны оси Ох. Проверить
результат непосредственным вычислением.
366
В данном примере Ρ (χ, у, ζ) = у, Q (χ, ί/, ζ) = ζ, R (χ, ί/, ζ) = χ,
поэтому
_2*.-η _^_-ΐ _^-η _^--ΐ JUL-η _^L - ι
di/ ~~ ' dz ~~ *' dz ~~ U' дх ~~ *' их ~~ U' % ~~ 1#
По формуле (9.15)
§ ydx + 2di/ + xdz = JJ( — cos α — cos β — cos γ) do,
L σ
где σ — часть плоскости χ + у + 2 = 0, ограниченная данной
окружностью.
Приводя уравнение плоскости χ + ί/ + ζ = 0 к нормальному
виду, находим
cos α = cos ρ = cos γ = —г=.
Таким образом,
<$> ί/d* + zdy + *^2 = — JJ da = — πα2 j/3,
L )' 3 j
где а — радиус круга, ограниченного указанной окружностью.
Проверим полученный результат непосредственным
вычислением данного криволинейного интеграла, для чего предварительно
линию L представим параметрическими уравнениями. Из уравнений
*2 + У2 + & = a2> x + y + z = 0 получаем
ζ = — х — у, х2 + У2 + ( — х — У)2 = а2,
откуда
X2 + у2 + Ху = -ηρ
Из последнего уравнения находим у как функцию от х:
ν = ζΛ±ψΞΚ. (1)
Следовательно,
—x±V2a2—Зх2 — χ + /2α2 — Зх2 /оч
^= — ^ — ί/= —^ 2 = ~2 " ^
Отметим, что в выражениях для у и ζ знаки выбираются
верхние или нижние (одновременно).
Так как рассматриваются только действительные значения
координат, подкоренное выражение в полученных формулах для
у и ζ не может быть отрицательным, т. е.
2а2-3*2>0или — fl]/-|.<jc<fl|/r-|-. (3)
367
Полагая χ = t, мы могли бы получить параметрические
уравнения кривой L. Введем другую параметризацию, положив
* = α ]/-у sin f. (4)
этом случае пр
а 1/ — sini ± α Ϋ2 cost ,-
V 3 aV2
Формулы (1) и (2) в этом случае принимают вид:
/~
_ sin t ~т- aV I cos t
2
-η
2
sin ^ -f α V 2 cos /
2 13
(— sin ^±: ]/3 cos 0; (5)
α 1/2
4- (— sinfzp|/3casf). (6)
2 2 J/3
Принимая во внимание соотношения (З), заключаем, что
--£-<«-}. (7)
Окружность L разобьем на полуокружность L', лежащую выше
плоскости Оху, и на полуокружность L", лежащую ниже указанной
плоскости. В соответствии с данным направлением обхода кривой
пределы интегрирования в первом случае (по пути L') будут -5-
и — -~-, во втором случае (по пути L") 9~ и "о"·
Из равенств (4)—(6) получаем:
dx = а 1/ -γ cos tdt;
dy = -^i(_cos ί zp J/3 sin ft Λ;
* 2^3V '
rfz = -^L (— costzlz V 3 sini) Λ.
2}/3 '
Следовательно,
(j) yd* + zdi/ + *dz = \ ydx + zdi/ + xdz + J i/dx + zdy + xdz =
-j
2 ._
a^2 (_sin^+ V/3cos0-£~^-cos^ +
2J/3 V ^ r ' }/3
2
+ ^^(_$ш^-1/Зсо50^3-(-со5^--)/35т0 +
^ 2 /3 2 ^ 3
368
+ -^Д-sin *.-^J- (— cos t+ γ 3 sin *)
dt +
+ j ргЙ-(— sint — V3cast)2£L cos* +
2 ]/3
V3
a V2
αγ2
+ ^(-sint +V3 cost)-^ (-cost + V 3sint) +
Η T^r-sin * —^ (·— cos *
J/ 3 sin /) Л =
π
~~ Ύ
= -4- j (— 2 sin * cos * + 2 |/ 3 cos2 * + sin * cos * +
π
Ύ
+ ]/3sin2* + |/ 3 cos2*+ 3 sin/ cos* —2 sin/ cos* +
T
+ 2|/3sin20d/ + -^- J (—2 sin* cos* — 2 ^3 cos2* +
π
— Τ
+ sin * cos * — ]/3 cos2 * — J/ 3 sin2 * + 3 sin * cos * — 2 sin * cos * —
~T
— 2/3sin2*)d*-^|^ J (cos2* + sin2*)dt—
Vs
°-1 <■
cos2* + sin2*)d* = ^-a2*
/3 a2
— na2 V 3.
Итак, получен тот же результат (но более длинным путем;
преимущества первого пути очевидны).
2. С помощью формулы Остроградского — Гаусса вычислить
J J (χ2 cos α + ί/2 cos β + ζ2 cos γ) do,
369
где σ — часть конической поверхности х2 + у2 = ζ2 (О < ζ <; Л);
cos a, cos β, cos γ — направляющие косинусы внешней нормали к
этой поверхности.
Формула Остроградского — Гаусса применима в случае
замкнутой поверхности. Чтобы получить замкнутую поверхность,
присоединим к поверхности конуса соответствующую часть плоскости
ζ = A (χ2 + y2^Cz2). Обозначая эту часть плоскости через аь по
формуле Остроградского — Гаусса можем написать:
] J (x2 cos α -f у2 cos β + ζ2 cos γ) do + J ] (χ2 cos α + у2 cos β +
+ ζ2 cos γ) dor = J J f (2* + 2ί/ + 2z) djofydz.
Чтобы решить задачу, достаточно вычислить второй и третий
интегралы. В случае области σχ cos α, cos β, cos γ — косинусы углов
с осями координат нормали к плоскости ζ = А, а именно: cos α = 0,
cos β = 0, cosy = 1, поэтому
j j {χ2 cos α -f у2 cos β + ζ2 cos γ) da = J J ζ2 cos Yda =
= Jj h4o = Λ2π/ι2 = лЛ4,
так как на плоскости ολ ζ = /ι и двойной интеграл равен площади
круга радиуса А, получающегося при пересечении конуса плоскостью.
Вычислим третий интеграл, произведя в нем сначала
интегрирование по ζ от ζ = \х2 + у2 до ζ = А, а затем вычислив двойной
интеграл по области (S) в плоскости Оху (эта область является
кругом x2-|"i/2<ft2, z^-0; она получается проектированием объема
(V) на плоскость Оху).
Таким образом,
Jf j {2* + 2у + 2z) dxdi/dz = 2 j J j (x + y+z)dz
dxdy =
(V)
(S) L ^^сЧ1^
! jj [(-+i/> 3+^];rV
(S)
d*dy =
*2+*/2
= 2 jf [(* + У) (h - V*2 - У2) + 4 (Λ2 - x2-У2)] dxdy.
(S)
Обозначая последний интеграл через / и переходя к полярным
координатам по формулам χ = ρ cos φ, у = ρ sin φ, находим
370
2rr h
I = 2 j j l^p (cos φ + sin φ) (/ι — p) + -^-/i2 — -^p2Jpdpd<p =
о о
= 2J [^(οοβφ + βίηφ) —-^(cos9 + sinf) + -^- —-^-]ίίφ =
0
2n
о
Γ Λ4 / · ч . Λ4φ 1 |2π πΑ4
= [^(^φ —α*φ)+-^]|ο =—.
Итак,
\ \ (*2 cos α + У2 cos β -f ζ2 cos γ) do = -^ я/ι4 =
π/ι4
2 *
ЗАДАЧИ
По формуле Стокса преобразовать следующие криволинейные
интегралы:
1. (|) ydx + zdy + xdz. 2. (j) x2y3dx + dy + zdz.
L l
3. (j)jcd* + ί/dy + zdz. 4. ^(y2 + z2)^ + (^2+z2)dy+(^2+i/2)dz.
L L
По формуле Остроградского — Гаусса преобразовать
поверхностные интегралы:
5. J J xdydz + ydzdx + zdxdy. 6. j J xydxdy + yzdydz -\- zxdzdx.
σ 3
7. J j У χ2 + у2 + ζ2 (cos α + cos β + cos γ) do, где cos α, cos β,
σ
cos γ — направляющие косинусы внешней нормали к поверхности.
8. j j x2dydz + y2dzdx + z2dxdy.
9. j j (xs + ys+ z3) {dydz + dzdx + dxdy).
σ
10. J j -|£ dydz + ^ dxdz + -|j- сЫг/.
С помощью формулы Стокса вычислить следующие интегралы,
проверить результаты непосредственным вычислением:
371
11. φ (у + ζ) dx + {ζ + χ) dy -f (χ + у) dz, L — окружность х2 +
+ y2 + z2 = a2y x + y + z = 0.
12. (ρ t/d* + zdi/ + xdz, L — окружность χ = 7? cos2 f, ί/ =
sin 2^, г = R sin2t.
V2
13. у (у — ζ) dx + (ζ — *) dy + (χ — у) dz, L — эллипс χ2 + У2 =
L
= β2, — + -у- = 1 (β > 0, с > 0), пробегаемый против часовой
стрелки, если смотреть с положительной оси Ох.
14. φ (у2 + г2) dx -f (χ2 + г2) dy + (χ2 + y2) dz, L - кривая х2+
L
+ У2 + ζ2 = 2Rx, χ2 + у2 = 2rx (О < г < /?, г > 0), пробегаемая так,
что ограниченная ею на внешней стороне сферы х2 + у2 -f- ζ2 = 2/?а:
наименьшая область остается слева.
С помощью формулы Остроградского — Гаусса вычислить
следующие поверхностные интегралы:
15. J j xdydz -f ydzdx + zdxdy, о — внешняя сторона поверх-
σ
X2 Ц2 Ζ2
ности эллипсоида -т + ~тт -\—τ = 1.
а2 Ъ1 х с-
16. \\ x2dydz + y2dzdx + z2dxdy, σ — внешняя сторона гра-
σ
ницы куба 0<*<α, 0<*/<а, 0<2<а.
17. J J x3dydz+ y3dzdx + z3dxdy, σ — внешняя сторона сферы
х2 + У2 + ζ2 = R2.
18. И x2dydz + y2dzdx -f- z2dxdy, σ — полная поверхность ко-
σ
нуса ^+|--|- = 0(0<г<6).
19. J J xdydz + ydxdz + zdxdy, о — поверхность цилиндра χ2 +
+ y2 = a2(—h^Cz<h).
20. Доказать, что объем тела, ограниченного поверхностью σ,
V = -γ Ι Ι (λ: cos α + У cos β + ζ c°s ν) ^σ, гДе cos α> cos β> cos Υ ■
направляющие косинусы внешней нормали к поверхности σ.
21. Доказать, что объем конуса, ограниченного гладкой
конической поверхностью F (х, у, ζ) = 0 и плоскостью Ax+By+Cz +
-f Ό — 0, V =-ο- Shf где S — площадь основания конуса,
расположенного в данной плоскости, h — его высота.
372
22. Доказать тождество
д2и
дх2
д2и
ду2
J dxdy = ]
ϋιι
Ш
dl, где
ди
дп
производная по
L — контур, ограничивающий область σ,
направлению внешней нормали.
23. Доказать вторую формулу Грина J \ \ (vAu—uAv) dxdydz =
ж
(V)
υ——u-^-jdo, где объем (V) ограничен поверхностью σ,
дп
п — направление внешней
нормали к поверхности σ, а функции
и = и(х, у, г), ν = ν (χ, у, ζ)
дважды дифференцируемы в области
(V + σ). Символы Аи и Αν обознача-
А д2и . д2и , д2и А
ют: Au = -^r+w + -j-r, Av =
d2v , d2v . д2и ~
='-d#+W+~3*" ЭТИ ВЫРаЖе"
ния называются операторами
Лапласа в пространстве.
24. Доказать тождество
/ | I Audxdydz = I j η£ do, где
Рис. 9.11
(V)
Аи
д2и д2и
д2и
дх2 ^Ту2^-^ (°пеРат°Р Лапласа).
25. Функция и = и (х, у, г), имеющая непрерывные
производные второго порядка в некоторой области, называется гармониче-
скоц в этой области, если Δα = -^2- + -g-g- + -^р- = 0. Доказать,
что если α (jc, ί/, г) — гармоническая функция в конечной замкнутой
области (I/), ограниченной гладкой поверхностью σ, то I I -g^-da = 0.
ОТВЕТЫ
1. — W dxdy-\-dydz-\-dzdx, где σ —область, ограниченная замкнутой линией L.
2. — 3 J J x2y2dxdy. 3. 0. 4. 2 JJ (л — */) dxdy + (у — ζ) dydz + {ζ — χ) dzdx.
σ σ
Jtf 3rf«f^ = 31/. 6. 0. 7. /// у?^Д, ^ 8· Ш2 (х + У+z)dV-
(V)
(V)
rx2 + y2 + *2
(V)
9. 3JJJ (jc2 + i/2 + г2) dxdi/dz. 10. ί I I i
(V) {V)
d>u , ^ f Л\^& Пш 0β
dz2 /
(9a:2
a//2
373
nR2 12
12. ——τ=·. 13. — 2ла(а + с). 14. 2лЯг2. 15. 4ла&\ 16.3а4. 17. -у- π/?5.
πα262
18. —о—· ^· 6ла2й. 20. Указание. Применить формулу ОстроградскЪго—
Гаусса. 21. Решение. Не ограничивая общности, можно считать, что вершина
конуса находится в начале координат (рис. 9.11). В этом случае функция
F(x, у у г) будет однородной. По формуле задачи 20 объем конуса выразится так:
1'=— / I (х cos α -j- у cos β ~ ζ cos y) do, (1)
где о1 — боковая поверхность конуса;
σ — его основание.
Интеграл (1) разобьем на два интеграла. Так как первый берется по
поверхности конуса F(x, у, z) = 0, то с учетом выражений для cos a, cos β,
cos γ (см. решение примера 7 § 9.2) получим
(х cos α + У cos β 4- ζ cos γ) do ■
dF dF ι dF
x dx ~riJ dy ^z dz
" do.
Применяя к функции F(x, у, ζ) теорему Эйлера об однородных функциях
dF dF dF
где k—степень однородности функции F, находим, что
dF dF dF
х^х-^У~Щ}~+гЖ = 0>
ибо на поверхности конуса F(x,y,z) = 0. Следовательно, первый интеграл
равен нулю.
Переходим к вычислению второго интеграла по области о плоскости Ах +
-f- By + Cz + D = 0. Поскольку
где знак корня противоположен знаку D, второй интеграл принимает вид
±_СС, , о „, _,_ 1 С С Ах + Ву + Сг
С С о [ С С Лх -г оу + Uz
•jJ(^cosa + i/cosfi + zcosY)da = -3-jJ-p=8 + JBa + ca da =
я
D (V D
do = —
3 У Α2 -Ι- ^2 -г С2 J J 3 VA2 + Б2 + С2
3
(Здесь принято во внимание, что на данной плоскости Ла: -[- Л// -f- Cz = — D.)
D
Так как величина — — выражает длину перпендикуляра,
У Α2 -γ- В2 -|- С2
опущенного из начала координат на данную плоскость, т. е. высоту конуса h, то
374
l/ = TJJ(Kosa+!/cosP+ZcosT)da = - 3уАг + в>. + сГа=~ Ησ'
что и требовалось доказать.
22. Ρ е ш е н и е:
ζ ' L
= \ [-Υ cos(s, х)+ X sin(s, x)]dl,
L
где (s, χ) — угол между касательной к контуру L и осью Ох.
Если через (/г, х) обозначить угол между нормалью к тому же контуру
и осью Ох, то sin(s, χ) = cos (η, χ), cos(s,x) = — sin (η, χ).
Следовательно,
С С ^J)X_ _,_ jftM dxdtj = j* [χ cos (П}Х) + У sin (/2 f ^] ^/
ди ди
Полагая X = -τ-, Κ = -ν-, получаем
if(S-<-$-)**- Д#~<..->+£*.<-.4
Л.
дм dw дм
Так как по определению -т- = -т- cos(n, χ) + -gr sin (я, χ), то
dhi д2и
Выражение -π- -f- ηττ" называется оператором Лапласа.
23. В формуле
Ш1дХ + W^dZ\ dxdydz = Г Г[Х cos (Л| Л) + к Cos (n,y) + Zcos (n, 2)] do
\ дх ду dz I J J
[V) σ
положим Χ = νιιχ — ιινχ, Υ = vu' — uv , Ζ = vu2 — iwr
Тогда
дХ dY dZ „ „ „ „ „ „
~dT+~di + 'dz~==v K* + пуу + w«> - " (*>xx + ϋ^+ ϋ ζζ) = **" - «Δ»;
X cos (η, λ;) + У cos (λ · У)-г Ζ cos (η, г) = ϋ [и^. cos (η, χ) +
+ ы' cos (/г, //) + м^ cos (я, ζ)] — и [νχ cos (η, χ) -j- ι> cos (я, ζ/) {-
+ р2со5(я,г)1=»ж-«ж.
375
Итак,
ШivAu -uAv) dxdydz=Я [υΐη -и ж) "σ·
(V)
24. Указание. В формуле задачи 23 положить ν = 1. 25. Указание-
Воспользоваться тождеством задачи 24.
§ 9.4. ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ ПО ПОВЕРХНОСТИ
Площадь σ поверхности (σ) вычисляется по формуле
° = ffdo· (9.17)
(')
Если γ = у (χу уf z) — поверхностная плотность массы
материальной поверхности (σ), то масса всей этой поверхности
определяется интегралом
т = ffy{x, У, z) do. (9.18)
(')
Координаты центра тяжести С0{х0, у0У г0) поверхности (σ)
вычисляются по формулам:
х°= ~irj J ху (χ> у>ζ) άσ> Уо== ~ίγ] J yy (χ> y>z) do>
3 3
σ
где m определяется формулой (9.18).
Моменты инерции /х, 1Г 1 г относительно координатных осей
Ох, Оу, Ог находятся соответственно по формулам:
1Х = // (г2 + if) γ (χ, у, ζ) da;
К = IS (χ2 + z') Υ (*» У> 2) do' (9.20)
/, - // (ζ2 + у2) γ (χ, у, ζ) da.
з
Моменты инерции Ixy, 1хг, /у2 относительно координатных
плоскостей Оху, Oxz, Oyz вычисляются соответственно по
формулам:
fxy = f/z2y (Λ'> у> z) da;
3
l*z = /fy2Y (x, У> z) da;
f>*= ffx*4 (*· У' z)do-
3
376
Для однородной поверхности, т. е. в случае, когда γ (χ, у, ζ) =
= const, вычисление интегралов в формулах (9.18) — (9.21)
значительно упрощается.
ПРИМЕРЫ
1. Найти массу полусферы х= \^R2 — у2 — ζ2, если
поверхностная плотность в каждой точке пропорциональна квадрату
расстояния точки до начала координат.
В силу условия функция γ (χ, у, ζ), фигурирующая в
формуле (9.18), имеет вид
у(х, у, z) = k(x2 + y2 + z2),
где k — коэффициент пропорциональности;
Υх2 -f у2 -f z2 = R — расстояние точки М (ху уу ζ) до начала
координат.
По формуле (9.18)
т = ffk (*2 + У2 + z2) do>
σ
где σ — данная полусфера.
Так как
^ = у 1 + (-f^f + -wfdydz = 4- dydz,
= f \k (χ2 + уг + ζ2) da = k f \r2 -£- dydz =
σ
J 1 VR2 — y2
TO
m
(S)
_
(S) *
где (S) — круг у2 + г2 < R2 на плоскости Оуг.
Переходя к полярным координатам у = ρ cos φ, г = ρ sin φ,
находим
2π R
P<*P _
J J уф — у* — г* J φ.; Κ/?2 — ρ2
(S) О О
2, Л
= _Jd«pJ"(/?»-p*) 2-Ld(tf2-p2) =
о о
_1_
ι (£2-р2)2 2π
2
о
377
Следовательно,
m = kR3f J
dydz
(S)
VR2 ~ IJ2 — Z2
= kR32nR = 2nkR*.
2. Вычислить массу части поверхности ζ = ху (*> 0, у > 0),
вырезанной цилиндром (х2 -f- У2)2 = 8ху, если "поверхностная
плотность γ (χ, ί/, ζ) = V1 -f *2 -г У2·
Так как
то
дг
г/, -^- == л-, da = У 1 + *2 + У2 d*dt/,
- /У Kl-^2 + i/2 V\ + x* + t?dxdy
(S)
= //(l + ^ + i^)d^,
(S)
Рис. 9.12
^ где (S) — лепесток лемнискаты (х2 + у2)2 =
= 8ху, для которого χ > 0, у >0
(рис. 9.12).
В полярных координатах x = pcos<p,
у = ρ sin φ уравнение границы области
имеет вид ρ = 2|/sin 2φ (θ <; φ < -у-), поэтому
*(S) 0
2 2 Vrsin2f
dtp
(1 + Ρ2)ΡΦ =
2 lAsin2^
0
2
2 Ksin 2^
dq> =
ί^φ j (P + P8)dp=j
oo b
j· (-ίίΒϊ- + !5i!£*l) ίφ = 2 f sin 2ф J- <f (20 +
+ \f
1 — cos 4φ
dcp
cos 2φ
+ 2φ
sin 4φ
2 + π.
Следовательно,
т = π + 2.
378
3. Найти массу части цилиндрической поверхности y=Y§—ζ2,
отсеченной плоскостями χ = О, χ = 2, если поверхностная
плотность γ (χ, ί/, ζ) = ky (χ -f ζ).
По формуле (9.18) находим
я* = if *# С* + У) do = k \\y (x -ft/) — d#dz =
(S) У
Zk \ dz\(x^-z)dx=Zk \(*+хг
—3 Ό —з ^ l
= 3* | (2 -f 2z) rfz = 36 (2z + z2)
dz
36&.
—3
4. Вычислить момент инерции относительно оси Oz части
однородной поверхности сферы х2 -f у2 + z2 = R2, для которой
х>0, у> О, ζ>0.
Так как поверхность однородная, т. е. γ (χ, у, ζ) = const, то
в формулах (9.20) можно положить γ = 1.
Третья из формул (9.20) принимает вид
/2=--tf(x2 + y2)do.
σ
Поскольку в данном случае
F(x, у, z) = x2 + y2 + z2-R2;
dxdy V ЬИ + (~WJ'+ Ьг) , .
do = -Щу= df dxdlJ>
dz
TO
d = *4χ2 + 4y2 + 4*2 = RdxdlJ
~ 2Z ~ yR2 — X2—y2
Следовательно,
к2 + у2) dxdy
'·= "+ΛΑ = ί1ΐ7
VR2
(S)
где (S) — четверть круга χ2 + у2 = /?2 при л: > 0, #]> 0.
Переходя к полярным координатам χ = ρ cos φ, ί/ = ρ sin φ,
получаем
π π
Ύ R Ύ R
π/?3
(S) 0 0 0 0
379
(Последний интеграл вычислен с помощью подстановки
p = Rsmt; см. замечание к примеру 2 § 9.1.)
Итак,
* р Г Г (x* + if)dxdy - л/?3 _ л/?*
Z J J VR*-x*-tf K 3 3 '
(S)
ЗАДАЧИ
В каждой из задач 1 — 14 найти массу поверхности при
указанной поверхностной плотности γ (.ν, у, ζ):
1. 2 = у 4 — χ2, отсеченной плоскостями у = 0, у = 5;
Υ(*, 1/, 2) = kz{x+y).
2. г/= 2χζ (χ>0, ζ>0), вырезанной цилиндром (χ2+ζ2)2·=■- 8χζ\
Υ (*, У, 2) = V 1 + 4χ2 + 4ζ2.
3. λ: = -| γ, вырезанной цилиндром (у2 + ζ2)2 = 4 (ί/2 — ζ2);
Υ(*, |/, ζ) = "|Λ + ι/2 + ζ*.
2
4. ζ—-^—4-, вырезанной цилиндром (-j-+-^-) =2(_4~
y(jc. у- ζ) = ~|/ι + 4-ь тг
5. 6г = χ2 — у2, вырезанной цилиндром (х* + У2)2 = 9 (х2—г/2);
γ (л:, у, ζ) = -ξ- + -3- + г + 4.
6. ΛΓ+ί/+ζ=4, вырезанной цилиндром jc2-f г2 = 4; γ (л:, у, ζ)~
= *4 + г4 + 2л:222 + j/2·
7. 2 = У Ρ? - л:2 - t/2; γ (χ, у, г) = ж2 + у2 + г3.
8. у = ]/#2 — г2 — г2; γ (χ, у, ζ) = χ2 + л:2 + ζ2.
9. jc = У"/У - у2 - г2; γ (χ, у, z)=x + y2 + z2.
10. ί/== 1 χ2 + ζ2, отсеченной плоскостями у = 0, у = b;
γ (χ, г/, 2) = алтМ-ог2 + су2 + d (а > 0, b > 0, с> 0, d > 0).
1!. x=|/i/2 + 22, вырезанной цилиндром (ι/— α)2 + 22 = α2;
γ (χ, у, 2) = 5χ2 - 2у2 - 2ζ2.
12. г = 2ху{х > 0, </>0), вырезанной цилиндром (х2 + У2)2=
= 4ху; у (х, у, ζ) = ]Л + 4л;2 + 4ι/2.
13. ί/ = -£ £-, вырезанной цилиндром [JL-+ Jj-j8 =
14. 2г = 9 — χ2 — г/2, отсеченной плоскостью 2 = 0; γ (χ, у, ζ) =■-
= x* + y2 + z-2.
15. Найти массу части поверхности г—\/Гх2 + у2,
вырезанной цилиндром (л: — о)2 + у2 = а2, если поверхностная плотность
380
в каждой точке пропорциональна квадрату расстояния этой точки
до начала координат.
16. Найти массу поверхности куба 0<x<;i, 0<;#<1,
О С 2 < 1, если поверхностная плотность в каждой точке
пропорциональна произведению ее координат.
17. Найти массу сферы радиуса R, если поверхностная
плотность в каждой точке равна расстоянию этой точки до некоторого
фиксированного диаметра сферы.
18. Найти массу поверхности 2г = х2 + У2 (О <С ζ <; 1), если
плотность в каждой точке пропорциональна аппликате этой точки.
В каждой из задач 19 — 25 найти координаты центра тяжести
указанной однородной поверхности:
19. xZ + y* + z2 = R2 (*>0, */>0, г> 0).
20. х2 + y2 + z2 = R2 (h < ζ < R).
21. г- VR2 — χ2 — у2 (*>0, #>0, * + у<#).
22. χ = и cos v, y = usmv, z = hv (0<!α<α, О^и^л).
23. ζ = Υχ2 + у2, вырезанной поверхностью χ2 + у2 = ах.
24. Зг = 2 (л: j/x + У Vу), ограниченной плоскостями χ = 0,
ι/ = 0, а: + У = 1-
25. 2 = Ух2 + ί/2, отсеченной плоскостями 2 = 0, 2 = /г.
26. Найти координаты центра тяжести верхней половины
сферы х2 + У2 + г2 = /?2, если поверхностная плотность в каждой
точке равна расстоянию этой точки до оси Οζ.
27. Найти координаты центра тяжести верхней половины
сферы х2 + У2 +- ζ2 = /?2, если поверхностная плотность в каждой
точке равна квадрату расстояния до оси Οζ.
В каждой из задач 28 — 31 найти момент инерции
относительно оси Οζ указанной части однородной поверхности:
28. jc2 + i/2 + 22 = /?2 (2>0).
29. Л2 {х2 + у2) = а2г2 (0 < 2 < /ι).
30. x2 + #2+z2 = #2 (ft<z<#).
31. х2 + #2 = 2α2 (0<2<α).
32. Вычислить момент инерции однородной конической обо-
х2 и2 ζ2
лочки —^- + -|g ^- = 0 (0 <г < Ь) относительно прямой
χ = t, у = 0, 2 = Ь.
33. Найти моменты инерции относительно координатных
плоскостей поверхности однородного конуса, ось которого совпадает
с осью Οζ, а вершина лежит в начале координат.
ОТВЕТЫ
/ π \ 22 33 280 -
1. 100/г. 2. 4π + 2. 3. 4 Ητ+ΐ]. 4. 3(4 +л). 5. 88-gg- — "5" π. 6. -у π J/3.
4 1 4 _ Γ 64 Ι
7. -^-π/?4 + -2~π#5. 8. 2π/?4. 9. ^π#4 + π#3. 10. /2π (α + с) -γ + db2 .
381
11. 9^2 πα*. 12. π+1. 13. ас (b2 + -ηρ\ 14. -jg- (500 К 10— 23).
,_ 3
15. 3 К 2nka4, где /г — коэффициент пропорциональности. 16. -j-fc. 17. π3#3.
Указание. Воспользоваться сферическими координатами. 18. π^ ~*~—-—ίζ·
15
R R R I RA-h \ I R
19. x0 = ~2-, y0=~2-, ζ0=-γ. 20. C0 \0, 0, -$ j. 21. C0 ί—ρ=,
Я # ._ \ 4 u3 — Λ3 π/t
ΤνΤ· -5Γ-<^2 + 1))· 22.^ = 0,^=3^. -мПГ-го=—'·
где «2 = α2 + Λ2. 23. C0i-f-, 0, -^-α). 24. *0 = у0 = 2&~^V'2 ,
^"(^+1). 25. Jo.0. J-*). 26. C0(o,0, JLA
/2+1) °\ 3 / °\ 3π /
_ 61/2
г°~~ 96 (/2+1)
27. C0(o, 0, -§-*)· 28· — nR*' 29· — Уа* + h2' Ж —nR(R-h)2(2R+h).
\ 8 / 3 2 3
55 + 9/3 πα(3α2+262) ^ά^Τ2
• 65 α2σ> где σ ~~ ПлощаДь поверхности. 32. тк ·
π/Λ2/? π/Я3
33. /^у = —о—» ' у ζ = 'jc^ — —Ζ—' где ^ — высота конуса, R — радиус
основания, / = ΫR2 + К1 — образующая конуса.
ОГЛАВЛЕНИЕ
I. Ряды
стр.
От автора 3
Глава 1. Числовые ряды 5
§ 1.1. Основные понятия. Необходимый признак сходимости .... —
§ 1.2. Ряды с положительными членами. Признаки сходимости . . 18
§ 1.3. Знакопеременные ряды 32
§ 1.4. Действия над рядами. Разные задачи 42
Глава 2. Функциональные ряды 45
§ 2.1. Сходимость функциональных рядов —
§ 2.2. Степенные ряды. Действия над степенными рядами .... 57
§ 2.3. Ряд Тейлора. Ряд Маклорена 70
§ 2.4. Ряды Фурье 85
Глава 3. Приложения рядов 104
§ 3.1. Приближенное вычисление функций —
§ 3.2. Приближенное вычисление определенных интегралов с
помощью рядов 109
§ 3.3. Интегрирование дифференциальных уравнений с помощью рядов 113
Главах4. Ряды с комплексными членами 126
§ 4.1. Комплексные числа и действия над ними —
§ 4.2. Числовые ряды с комплексными членами 133
§ 4.3. Ряды функций комплексной переменной. Степенные ряды с
комплексными членами 138
II. Кратные интегралы
Глава 5. Двойной интеграл 148
§ 5.0. Некоторые вспомогательные понятия —
§ 5.1. Вычисление двойного интеграла в прямоугольных координатах 152
§ 5.2. Замена переменных в двойных интегралах. Двойные интегралы —
в полярных координатах 182
§ 5.3. Несобственные двойные интегралы 199
Глава 6. Приложения двойных интегралов 210
§ 6.1. Вычисление площадей плоских областей —
§ 6.2. Вычисление объемов тел 222
§ 6.3. Вычисление площадей поверхностей 233
§ 6.4. Приложения двойных интегралов к механике 244
383
Глава 7. Тройные интегралы 160
§ 7.1. Вычисление тройных интегралов в прямоугольных декартовых
координатах —
§ 7.2. Замена переменных в тройных интегралах 275
§ 7.3. Приложения тройных интегралов 285
III. Криволинейные интегралы. Интегралы по поверхности
Глава 8. Криволинейные интегралы 301
§ 8.1. Криволинейные интегралы первого типа —
§ 8.2. Криволинейные интегралы второго типа 313
§ 8.3. Формула Остроградского-Грина. Условия независимости
криволинейного интеграла от пути интегрирования 322
§ 8.4. Приложения криволинейных интегралов 335
Глава 9. Интегралы по поверхности 345
§ 9.1. Поверхностные интегралы первого типа —
§ 9.2. Поверхностные интегралы второго типа 356
§ 9.3. Формула Стокса. Формула Остроградского-Гаусса .... 366
§ 9.4. Приложения интегралов по поверхности 476
P.I
ι,„.