Автор: Каплан И.А.
Теги: интегралы дифференциальное исчисление аналитическая геометрия высшая математика
Год: 1967
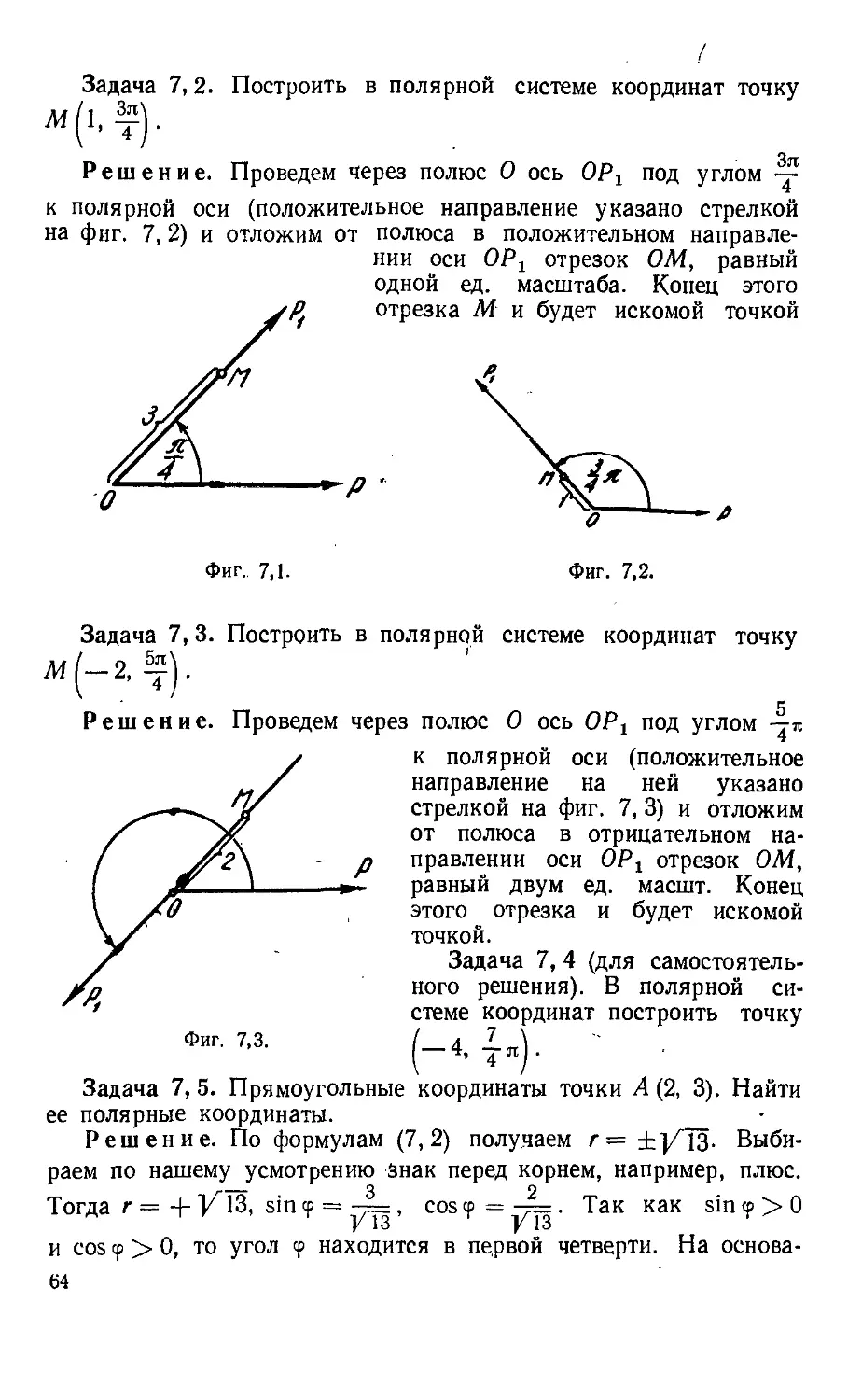
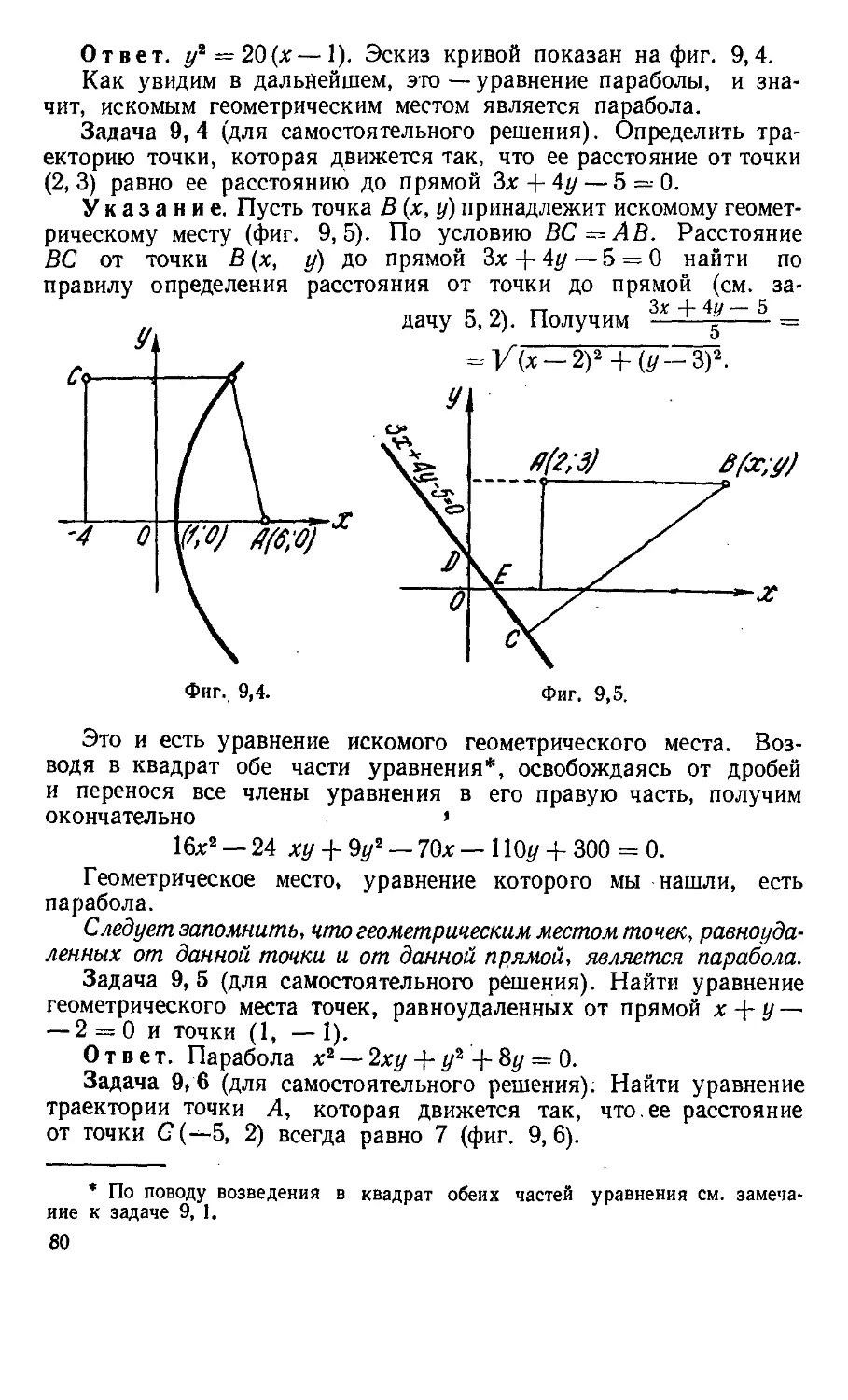
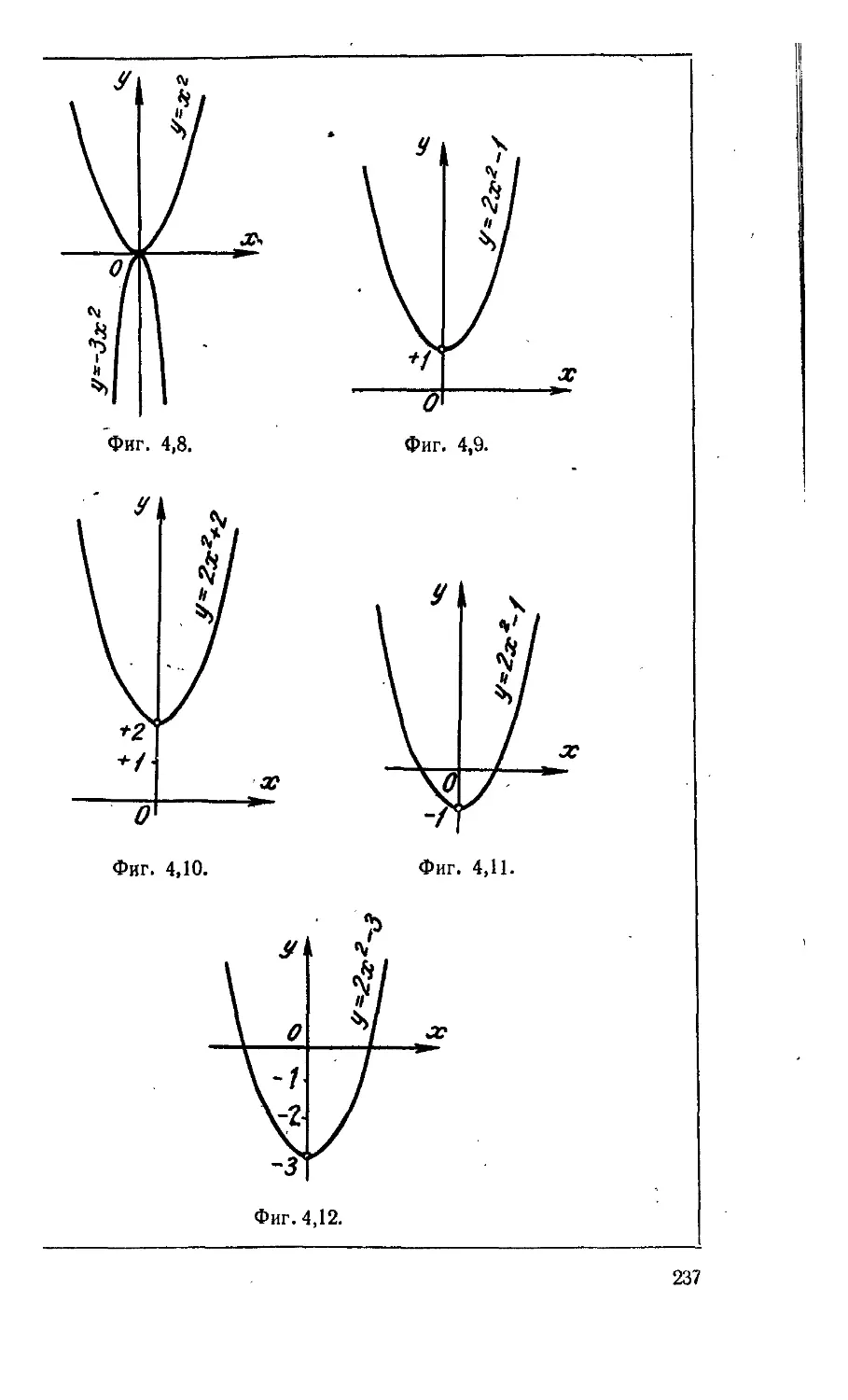
Текст
И. А. КАПЛАН
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО
ВЫСШЕЙ МАТЕМАТИКЕ
(АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
В ПРОСТРАНСТВЕ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
' ФУНКЦИЙ ОДНОЙ И МНОГИХ НЕЗАВИСИМЫХ
ЕРЕМЕННЫХ, ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ, ИНТЕГРИРОВАНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ)
Третье издание
Допущено Министерством высшего и среднего специального
образования в качестве учебного пособия для студентов
высших технических учебных заведений УССР
.;;<г Кп. Пед. Ич-та fsfe
ИЗДАТЕЛЬСТВО
ХАРЬКОВСКОГО ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА имени А, М. ГОРЬКОГО
арьков 1967
517@7)
K20
В книге разобраны и подробно решены типовые задачи по аналитической
геометрии на плоскости и в пространстве, дифференциальному н интегральному
исчислениям и по интегрированию дифференциальных уравнений.
Из задач, помещенных для самостоятельного решения, многие снабжены
указаниями, промежуточными результатами и ответами.
Книга рассчитана на студентов высших технических учебных заведений,
может быть полезна также преподавателям, ведущим практические занятия.
Ответственный редактор первой части кандидат физико-математических
наук доцент Д. 3. Гордевский.
Ответственный редактор второй и третьей части кандидат физико-мате-
физико-математических наук доцеит Р. В. Солодовников.
2—2—3
13-67Р
ПРЕДИСЛОВИЕ
В этой книге объединены три ее части, изданные в прошлые
годы отдельными книгами. В нее вошли практические занятия
по аналитической геометрии на плоскости и в пространстве,
дифференциальному исчислению функций одной и многих неза-
независимых переменных, по неопределенным и определенным инте-
интегралам и их приложениям к задачам геометрии, механики и гид-
гидравлики и по интегрированию обыкновенных дифференциальных
уравнений и систем дифференциальных уравнений.
Цель книги — помочь студенту научиться самостоятельно ре-
решать задачи по указанным разделам курса высшей математики
в высших технических учебных заведениях. Она рассчитана
прежде всего на студентов, обучающихся заочно и по вечерней
системе, но может быть полезной и студентам стационарных выс-
высших технических учебных заведений, а также преподавателям,
ведущим практические занятия.
Книга написана в полном соответствии с новой программой
по высшей математике.
Весь учебный материал разделен на отдельные практические
занятия. Перед каждым занятием помещены основные сведения
из теории, относящиеся к этому практическому занятию, теоремы,
определения, формулы и подробное решение типовых задач раз-
различной степени трудности с полным анализом решения, причем
большое количество этих задач решаются различными способами
и целесообразность этих способов сравнивается. Каждое практи-
практическое занятие содержит большое число задач для самостоятель-
самостоятельного решения, многие из них снабжены методическими указа-
указаниями к решению и промежуточными результатами.
Такое построение книги предоставляет студенту широкие воз-
возможности для активной самостоятельной работы и экономит его
время. Студент, пользующийся этим пособием, должен перед
каждым практическим занятием выучить относящийся к нему
раздел теории, внимательно, с выполнением всех действий на
бумаге, разобрать решенные задачи, и только после этого при-
приступить к решению задач, предложенных для самостоятельного
решения.
Для удобства пользования книгой перед первой и второй
частью помещен указатель рекомендованных учебников и пара-
параграфов в них, которые должны быть изучены перед каждым
практическим занятием.
Книга написана так, что она допускает не только последо-
последовательное проведение всех практических занятий, но и исполь-
использование их в выборочном порядке.
Автор приносит глубокую благодарность рецензенту этой
книги доктору физико-математических наук профессору Г. М. Ба-
Баженову и ее ответственным редакторам кандидатам физико-мате-
физико-математических наук доцентам Д. 3. Гордевскому и Р. В. Солодов-
никову, ценные советы и замечания которых, "учтенные автором,
способствовали значительному улучшению книги.
Автор признателен также сотрудникам кафедры высшей
математики Харьковского инженерно-строительного института
В. Г. Александрову, Э. Б. Александровой, В. М. Аветисовой,
И. М. Каневской, Ю. В. Князеву, 3. Ф. Паскаловой и Л. В. Олей-
ник, проверившим ответы к задачам и Р. А. Ежовой за помощь
в оформлении рукописи.
ЧАСТЬ 1
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
1ЛОСКОСТИ И В ПРОСТРАНСТВЕ
¦у—b,i.-ua;=fc ?::
I
Указатель учебников и параграфов, которые должны быть изучены перед
каждым практическим занятием
X та
оз со
Си О
&§ к
^ q^ S
fe СР Н
1
2
3
4
5
6
7
8 и 9
10
11
12
13
14
15
16
17
18
19
20
Из учебника И. И. Привалова
«Аналитическая геометрия»
Гл. 1, § 1-5
Гл. I, § 6, 10
Гл. II, § 1—4
Гл. III, § 1—6, 14, 15'
Гл. III, § 7—13
Из гл. III повторить все ра-
ранее изученные параграфы
Гл. III, § 16
Гл. I, § 11; гл. II, § 16
Повторить из гл. I § 11
и из гл. II § 1—6
Гл. IV, § 1, 2, 3, 8
Гл. IV, § 4, 5, 9, 10, 17
Гл. V, 1, 2, 6, п. 3
Гл. V, § 3, 6, п. 2
Разобрать страницы 29, 33 по
книге «Высшая математика. Ме-
Методические указания и конт-
контрольные задания», 1959 г.
Гл. VI, § 1—8
Ч. II, гл. I, § 1—4
и гл. II, § 1—15
Ч. II, гл. III, § 1—3
и гл. IV, § 1—10
Ч. II, гл. V, § 1—5
Ч. II, гл. V, § 6—10
Ч. II, гл. III, § 4—6,
гл. VI, § 1—12
Из учебника Н. В. Ефимова
«Краткий курс аналитической
геометрии»
§ 1, 2, 3, 5
§ 6, 7
§ 11—13, 16, 17, 19, 20, 22
§ 18, 23
Повторить § 6—23
§ 22
§ 4, § 11-15
Повторить § 4 и § И—15
§ 24, 25, 26
§ 14, 30—32, 35, 36
§ 10, 43, 45
§ Ю, 45
То же самое
Приложение, § 1—6
§ 46—61
§ 62, 66, 67, 68, 71
§ 69-71
§ 69-71
§ 64, 65, 72—76
ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Координаты точки на плоскости. Расстояние между
двумя точками.
На первых двух практических занятиях мы будем решать
задачи, связанные с применением первоначальных формул ана-
аналитической геометрии на плоскости. Сюда относятся такие задачи:
1) определение расстояния между двумя точками на пло-
плоскости;
2) деление отрезка прямой в заданном отношении;
3) определение площади треугольника по координатам его
вершин.
На этом и последующих практических занятиях по анали-
аналитической геометрии будут применяться только две системы коор-
координат: прямоугольная система на плоскости и в пространстве и
полярная.
Когда в условии задачи будет сказано «дана точка», то это
значит, что координаты точки известны. Если же в задаче будет
поставлено требование «найти точку», то это означает, что сле-
следует определить ее координаты.
Фраза «дан отрезок прямой» означает, что координаты концов
этого отрезка известны. Если известны координаты концов от-
отрезка прямой, то тем самым положение отрезка на плоскости
вполне определено. Координаты точки записываются в скобках
рядом с названием точки, причем всегда на первом месте в пря-
прямоугольной системе координат записывцется абсцисса точки, а
на втором — ее ордината. Например, если хг — абсцисса точки
А, а ух— ее ордината, то это записывается так: A {xlt yj.
У точки, лежащей на оси абсцисс, ордината равна нулю;
у точки, лежащей на оси ординат, абсцисса равна нулю. Обе
координаты начала координат равны нулю.
1. Расстояние d между точками A (xlt уг) и В (х2, и2) пло-
плоскости определяется по формуле
d = У(х2-Х1J + (У2-Уг)г. A, 1)
Задача 1,1- Построить точку С B, 4).
Решение. Абсцисса точки С равна 2, а ее ордината равна 4.
Выберем единицу масштаба и возьмем на плоскости прямоуголь-
прямоугольную систему координат. Отложим на оси Ох вправо от начала
координат О отрезок ОА длиною в 2 ед. масштаба, а по оси Оу
вверх от начала координат — отрезок ОВ длиною 4 ед. масштаба.
Из точки А восстановим перпендикуляр к оси Ох, а из точки
В — перпендикуляр к оси Оу. Пересечение этих перпендикуляров
и определит искомую точку С (фиг. 1,1).
?N,0)
r1-
J -2-l\
f
?
1
1
3
4
4
Ч в{2,
1
i
t
i
t г
Фиг. 1,2.
Задача 1,2 (для самостоятельного решения). Построить точ-
точки А (-2, 4); 5B,3); С(-1, -2); D@, -5); ?(-3, 0)
(фиг. 1,2).
Задача 1,3. Построить точку, симметричную точке А (х, у)
относительно: а) оси Ох, б) оси Оу, в) начала координат.
Решение. Две точки Мг и М2 называются симметричными
относительно прямой, если отрезок МгМ2 перпендикулярен этой
прямой, причем его средина лежит на этой прямой.
Две точки Mj и М2 называются симметричными относительно
точки О, если точка О является срединой отрезка М1М2. Эти
определения следует иметь в виду при решении задач 1,3
и 1,4.
а) Точка В, симметричная с точкой А (х, у) относительно осп
Ох, имеет абсциссу такую же, как и точка А, а ординату, равную
по абсолютной величине ординате точки А, но противоположную
ей по знаку. Значит, точка В имеет координаты х и —у:
В{х,—у) (фиг. 1,3).
б) Точка С, симметричная с точкой А (х, у) относительно оси
Оу, будет иметь ординату такую же, как и точка А, а абсцисса
точки С будет по абсолютной величине равна абсциссе точки А,
9
но противоположна ей по знаку. Значит, точка С имеет коор-
координаты —х и у: С{—х, у) (фиг. 1,3).
в) Точка D, симметричная точке А {х, у) относительно начала
координат, будет иметь абсциссу и ординату, равные по абсо-
абсолютной величине абсциссе и
ординате точки А, но про-
противоположные им по знаку,
т. е. координаты точки D
будут равны —х и — у:
D(-x, -у) (фиг. 1,3).
Задача 1,4 (для самосто-
самостоятельного решения). Дана
точка А C, —4). Построить
точки, симметричные ей от-
относительно: а) оси абсцисс,
б) оси ординат, в) начала
координат.
Ответ. а) В C, 4);
б) С(—3, -4); в) D(—3,
+4).
Задача 1, 5. Какое соотношение существует между координа-
координатами точки, если она лежит: а) на биссектрисе первого и тре-
третьего координатных углов;
б) на биссектрисе второго и
четвертого координатных
углов.
Решение, а) Биссектри-
Биссектриса первого и третьего коор-
координатных углов делит эти
углы пополам и с положи-
положительным направлением оси Од:
составляет угол в 45°. Если
из любой точки А (х, у) этой
Фиг. 1,3.
aj
Фиг. 1,4.
биссектрисы опустить перпендикуляр на ось Од:, то треугольник
ОАВ будет равнобедренным прямоугольным треугольником, и
потому его катеты О В и А В между, собою равны (фиг. 1,4 а).
Так как катет ОВ есть абсцисса точки А, а катет АВ — ее ор-
ордината*, то заключение состоит в том, что абсцисса и ордината
любой точки этой биссектрисы между собою равны, причем это
верно независимо от того, находится ли точка А в первом коор-
координатном углу или в третьем, так как в каждом из них абсцисса
* Координатами точки могут быть не только числа, ио и отрезки, изме-
измеренные единицей масштаба.
10
и ордината точки имеют один и тот же знак. Итак, для координат
точек этой биссектрисы имеет место равенство х = у.
б) для точек биссектрисы второго и четвертого координатных
углов мы, рассуждая так же, придем к заключению, что абсцисса
и ордината любой точки на этой биссектрисе также равны между
собою по абсолютной величине, но противоположны по знаку,
что следует из таблицы знаков абсциссы и ординаты во второй
и четвертой четвертях:
Четверти
IV
0
/
8
/i\
У i /
>^
ч
\
<
Фиг. 1,5.
X
У
Таким образом, для координат
точек, лежащих на этой биссек-
биссектрисе, выполняется равенство
х = — у.
Задача 1,6. Точка А (а, в)
находится внутри Первого коорди-
координатного угла. Определить координаты точки В, симметричной
с точкой А относительно биссектрисы этого координатного
угла.
Решение. Так как точка В симметрична точке А относи-
относительно биссектрисы первого координатного угла, то она лежит
с точкой А на перпендикуляре к ОС и АС = СВ (фиг. 1,5).
Учитывая это, а также то, что в треугольниках ОАС и ОСВ
катет ОС — общий, заключаем, что эти прямоугольные треуголь-
треугольники между собою равны (фиг. 1,5).
Рассмотрев теперь треугольники О BE и OAD, мы придем к
заключению, что и они равны, так как, будучи'прямоугольными
они имеют равные гипотенузы и равные острые углы AOD и ОВЕ.
Почему?
Из равенства треугольников ОВЕ и OAD заключаем, что
0D = BE, a AD'= 0E. Так как по условию абсцисса 0D точки
А равна а, а ее ордината AD = в, то мы приходим к заключе-
заключению, что точка В имеет абсциссу ОЕ = AD = в, а ординату
BE = 0D = а. Итак, координатами точки В служат числа в
и а: В (в, а).
Задача 1,7 (для самостоятельного решения). Найти коорди-
координаты точки В, симметричной точке А (—12, 4) относительно
биссектрисы третьего координатного угла.
Ответ. В D, —12).
11
В
-7-6-54-3-2-1 О
Фиг. 1,6.
Задача 1,8 (для самостоятельного решения). Найти коорди-
координаты точки В, симметричной точке А B,4) относительно биссек-
биссектрисы второго и четвертого координатных углов.
Ответ. В(—4, —2).
Задача 1,9. Точки А (—4, 2) и В(х, у) лежат на прямой, па-
параллельной оси Ох,
причем расстояние меж-
ду ними равно 2 ед.
масштаба. Определить
—х координаты точки В.
Решение. Задача
допускает два решения:
точка В может находи-
находиться как слева, так и справа от точки А. Так как в каждом
из этих случаев точка В лежит на прямой, параллельной оси
Ох, то ордината ее у в обоих
случаях будет равна ординате
точки А, т. е. у = 2. Абсцисса
же ее в том случае, когда она
находится слева от точки А, бу-
будет равна —6, а когда она на-
находится справа от А, будет рав-
равна — 2. Итак, В( — 6, 2), а
Вх(—2, 2) (фиг. 1,6).
Задача 1, 10 (для самостоятель-
самостоятельного решения). Точки ,Л (— 5, 2) и
В (х, у) лежат на прямой, парал-
параллельной оси Оу. Найти коорди-
координаты точки В, если она находит-
находится от точки А на расстоянии 6 ед. масштаба. Построить чертеж.
Ответ. Вг(—5, 8) и ?2(— 5, —4).
Задача 1,11. Точки А E, 5) и В (х, у) лежат на биссектрисе
первого координатного угла. Расстояние между ними равно 4 ед.
масштаба. Найти координаты точки В.
Решение. Так как точка 5 лежит на биссектрисе первого
координатного угла, то ее абсцисса, и ордината между собою
равны (задача 1,5). В равнобедренном прямоугольном треуголь-
треугольнике ABC (фиг. 1,7) гипотенуза АВ = 4, а АС = ВС. Тогда по
теореме Пифагора
АС2 + ВС2 = АВ2 и 2ЛС2 = 16, АС2 = 8; АС = ВС = 2/2.
Таким образом, абсцисса искомой точки (а значит, и ее ор-
ордината) получится из абсциссы точки А, если к ней сначала
прибавить, а потом из нее вычесть 21/ 2, и задача имеет два
решения:
В E+ 21/2, 5 + 21/2). и В1 E-2/2, 5-2/2).
12
Фиг. 1,7.
Задача 1,12. Найти расстояние между точками А (А, —5) и
В G, -1).
Решение. По формуле A, 1) для расстояния d между двумя
точками, если взять в ней хг = 4; х2 = 7; у1 = —5; г/2= — 1.
получаем
d = VG — 4J + [— 1 — (—5)]2; d= 5 ед. масштаба.
Задача 1, 13 (для
лить расстояние между
А (-3, 9) и В C, 1).
Ответ. d= 10 ед. масштаба.
Задача 1,14 (для самостоя-
самостоятельного решения). Найти длину
отрезка А В, соединяющего точки
А (-11,5) и В A,0).
Ответ, d— 13 ед. масштаба.
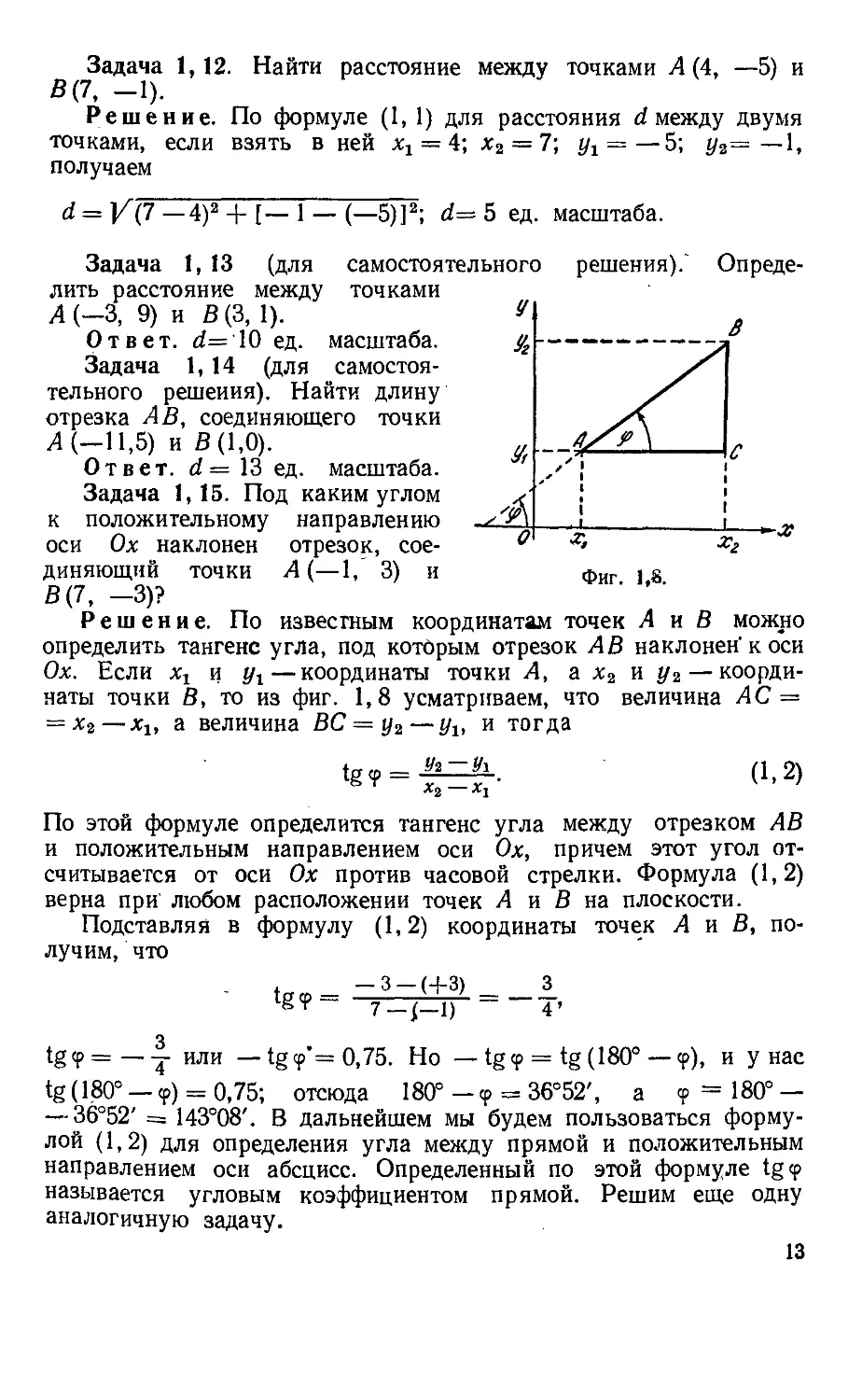
Задача 1,15. Под каким углом
к положительному направлению
оси Ох наклонен отрезок, сое-
соединяющий точки Л (—1, 3) и
В G, -3)?
самостоятельного
точками
решения)." Опреде-
ОпредеУ
У,
0
1
i
В
С
*, X,
¦X
Фиг. 1,8.
Решение. По известным координатам точек Лив можно
определить тангенс угла, под которым отрезок АВ наклонен" к оси
Ох. Если хг и Ух—координаты точки Л, а х2 и у2 — коорди-
координаты точки В, то из фиг. 1,8 усматриваем, что величина АС —
= х2—хг, а величина ВС = у2—ylt и тогда
= ^f. A,2)
По этой формуле определится тангенс угла между отрезком АВ
и положительным направлением оси Ох, причем этот угол от-
считывается от оси Ох против часовой стрелки. Формула A,2)
верна при любом расположении точек Л и В на плоскости.
Подставляя в формулу A,2) координаты точек Л и В, по-
получим, что
_ — 3 — (+3) _ 3
g?== 7-1-1) ="~Т'
tgcp=— — или — tg<p'=0,75. Но — tg<p = tgA80° — <p), и у нас
tg A80° — <р) = 0,75; отсюда 180° - <р = 36°52\ а <р = 180° —
— 36°52' = 143°08'. В дальнейшем мы будем пользоваться форму-
формулой A,2) для определения угла между прямой и положительным
направлением оси абсцисс. Определенный по этой формуле tg cp
называется угловым коэффициентом прямой. Решим еще одну
аналогичную задачу.
13
Задача 1,16. Отрезок АВ соединяет точки А(—6, 7) и
5A,—2). Определить длину этого отрезка н угол между ним
и положительным направлением оси Ох.
Решение. По формуле A, 1), полагая в ней хх =—6, х2 =
= 1, уг = 7, у2 = — 2, получаем, что длина АВл^ 11,4 ед. мас-
масштаба (знак ж означает, что имеет место приближенное равенство).
Теперь по формуле A,2) находим угловой коэффициент отрезка
АВ: tgср = —у- Перепишем это равенство в виде — tg<p =
д
— у. Отсюда следует, что tg A80° — <р) = 1,2857, и по таблицам
найдем, что <р= 127°52'.
Задача 1,17 (для самостоятельного решения). Найти длину
отрезка АВ, соединяющего точки А(—4, 5) и В(—6, 7) и угол
между этим отрезком и положительным направлением оси Ох.
Ответ. АВ = У% ед. масштаба; <р = 135°.
Задача 1,18. Найти периметр треугольника, если координаты
его вершин известны: А{—3, —6); В D, —1); С E, —2).
Ответ. АВ ж8,6 ед.,масштаба;
АС^и 8,9 ед. масштаба;
ВС я^ 1,4 ед. масштаба;
периметр треугольника А В + АС + ВС zz 8,6 + 8,9 + 1,4 =
= 18,9 ед. масштаба.
Задача 1, 19 (для самостоятельного решения). Найти периметр
треугольника с вершинами А(\, 3), В (А, 5), С(—5, —7).
Ответ. Периметр треугольника приближенно равен 30,3 ед.
масштаба.
Задача 1,20. Доказать, что треугольник, вершины которого
Л B, 3); В F, 7); С(—7, 2)—тупоугольный.
Решение. 1) Определяем длины сторон и находим, что
АВ — |/л32 ед. масштаба;
АС — У82 ед. масштаба;
ВС = >^194 ед. масштаба.
Значит, ВСг > АВ2 + АС2 A94 > 32 + 82); треугольник действи-
действительно тупоугольный.
Замечание. Из элементарной геометрии известно, что если
квадрат одной стороны треугольника равен сумме квадратов двух
других сторон, то треугольник — прямоугольный; если квадрат
большей стороны треугольника меньше суммы квадратов двух
других сторон, то треугольник — остроугольный; если же квад-
квадрат большей из сторон треугольника больше суммы квадратов
двух других сторон, то треугольник — тупоугольный. Пользуясь
этим замечанием, решите самостоятельно следующую задачу.
Задача 1,21. Определить вид треугольника, если координаты
его вершин известны:
А B, -5); В (-7, -4); С(-1, 6).
14
Ответ. Треугольник — остроугольный, так как длины сто-
сторон равны:
АВ = J/82; АС = /156; ВС = /Ж
Задача 1,22 (для самостоятельного решения). Доказать, что
треугольник ABC — прямоугольный, если координаты его вершин
Л @, 0); В D, 2); С (-2, 4).
ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Деление отрезка в заданном отношении. Координаты
середины отрезка. Определение площади треугольника по известным коорди-
координатам его вершин.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Если хг и у1— координаты точки А, а х2 и t/2 —коорди-
—координаты точки В, то координаты х и у точки С, делящей отрезок
АС
А В в отношении X = ^, определяются по формулам
_
х ~
Если Х=1, то точка С(х, у) делит отрезок АВ цополам,
и тогда координаты х и у средины отрезка А В определятся по
формулам
ЦЬ Ь+. B,2)
2. Плошадь треугольника по известным координатам его вер-
вершин А {хи yi), В{х2, у2), С(х3, у3) вычисляется по формуле
S = у [(*i — *з) (Уа — Уз) — (*2 — ха)(у1 —Уз)]. B, 3)
Полученное с помощью этой формулы число следует взять по
абсолютной величине.
v Задача 2,1.-Найти координаты точки С — средины отрезка,
соединяющего точки А (—2, 4) и В (—4, 10).
Решение. Воспользуемся формулами B,2). Запомните, что
каждая координата средины отрезка равна полусумме соответ-
соответствующих координат его концов.
В формулах B,2) возьмем хг = — 2; х2 = —4} ух = 4; у2 =»
= 10. Тогда абсцисса средины отрезка АВ
_-2 + (-4) -6 о
2 ~-Т=—д'
15
а ордината средины отрезка А В
и - у^ + у* - 4+10 _ 14 _ 7
Итак, средина отрезка А В — точка С(—3,7).
Задача 2, 2 (для самостоятельного решения). Найти коорди-
координаты точки С — средины отрезка АВ, если координаты концов
отрезка известны: А(—7, 5); В A1, —9).
Ответ. х = 2; у=— 2; СB, —2).
Задача 2,3. Найти координаты конца В отрезка, если дру-
другой конец отрезка — точка А (—5, —7), а средина отрезка —
С (-9, -12).
Решение. В формулах B,2) координаты средины отрезка
обозначены через х и у. По условию задачи х=—9; у =—12.
Координаты одного конца отрезка точки А в этих формулах
х'г = —5; г/j = — 7. Координаты точки В (другого конца от-
отрезка) — величины неизвестные, которые мы обозначим через х2
и г/2- Тогда по формулам B,2) для определения этих неизвестных
получаем два уравнения:
—У - g, 2
Отсюда
— 18 = —? + *а и *, = —13,
_24 = —7 + г/2 и у, = -17.
Задача 2,4 (для самостоятельного решения). Один конец от-
отрезка Д(—4,2), средина отрезка С(—6,5). Найти координаты,
точки В другого конца отрезка.
Ответ. хг = —8; г/2 = 8.
Задача 2,5 (для самостоятельного решения). Даны вершины
треугольника:
Л (-7, 4); В (-5, 2); С F, -3).
Найти координаты средин его сторон.
Ответ. Если обозначить средину стороны АВ буквой Е, сре-
средину стороны АС буквой F, а- средину стороны ВС буквой К,
то координаты этих точек: ?(—6,3); W— у; ±\; К l-j, — j).
Задача 2, 6 (для самостоятельного решения). Даны вершины
треугольника:
Л (—4, 6); В (—8, 9); С E, —6).
Найти координаты точек Е, F и /С средин сторон ЛВ, ЛС и ВС.
Ответ. ?(-6; ^;/^-}-±; о); *(-¦|; |) •
16
Задача 2,7. Даны координаты средин сторон треугольника:
?G,8); F{—4, 5); КA, —-4). Определить координаты вершин
треугольника.
Решение. Пусть точки А, В и С — вершины треугольника,
точка ? —средина стороны АВ, точка F — средина стороны АС,
а /(—средина стороны ВС. Требуегся найти координаты точек А,
В и С.
Обозначим чере'з хА и уА — координаты вершины А,
» хв и ув — координаты вершины В,
* хс и Ус — координаты вершины С.
По формулам B, 2) имеем
у* =
Подставляя в эти формулы координаты точек ?, F и К, мы
для определения неизвестных получим следующие уравнения:
а) Уравнения, отмеченные (*), после подстановки в них коор-
координат точки Е запишутся так:
7 _ ХА + ХВ о _ У А + У В ,
/ - 2 ' °- ~2 '
или
«д + а:в = 14; . уА + ув — 16.
б) Уравнения, отмеченные (**), если подставить в них коор-
координаты точки F, запишутся в- виде
л _ха + хс. г_У_а±Ус
— 2 ' — 2 '
или хА + хс = — 8; t/д + г/с = Ю.
в) Если же в уравнения, отмеченные (***), подставить коор-
координаты точки К, то эти уравнения запишутся так:
, _*в + хс л _Ув + Ус
2 '• —4 - 2
или хв + хс = 2, ув + ус = —8.
Итак, для определения шести неизвестных мы получили такие
две системы уравнений:
Первая система Вторая система
уравнений уравнений
Xa + хв = 14
xA + хс = — 8
Хв + Хс = 2
2 И.
А. Каплан
Уа + Ув = 16
Уд + г/с = Ю
У в + Ус = — 8
Складывая почленно уравнения первой системы, будем иметь
Ха + хв + хА + хс + хв + хс = 8.
После приведения подобных членов и деления обеих частей урав-
уравнения на 2 получим
ха + хв + хс = 4. B, 4)
Так как на основании третьего уравнения первой системы
хв + хс = 2, то из B,4) получаем хА + 2 = 4, а хА = 2; исполь-
используя второе уравнение первой системы хА + хс = — 8, получим
хв — 8 = 4; хв = 12; на основании первого уравнения первой си-
системы ха + хв = 14, и уравнение
B, 4) примет вид
хс + 14 = 4; а *с = — Ю.
Итак,
*л = 2; хв = 12; д;с = — 10.
Поступая так же, найдем из вто-
второй системы уравнений
Уа =17; ув= — 1; ус = —Т.
Вершины треугольника имеют та-
такие координаты:
•s-5ч-з-г-f о Тг
Фиг. 2,1-
Л B, 17); В A2, -1); С(—10, -7)
(проверить правильность полученного решения по условию задачи).
Задача 2,8 (для самостоятельного решения). Координаты сре-
средин сторон треугольника Е(—4, 6); F B, —6); К@, _4). Найти
координаты вершин треугольника.
Ответ. Ха + хв + хс= — 2; хА — — 2; хв = — 6; хс = 6;
г/л + Ув + Ус = — 4; г/д = 4; t/B = 8; ус = — 16.
Координаты вершин треугольника: Л (—2, 4); В(—6, 8); С F, —16).
Задача 2, 9. Точки А B, 4), В (—3, 7) и С(—6, 6) —три вер-
вершины параллелограмма, причем Л и С — противоположные вер-
вершины. Найти четвертую вершину.
Решение. Требование задачи: «найти четвертую вершину»
означает, что следует найти ее координаты. Решение задачи облег-
облегчит чертеж (фиг.. 2, 1).
Известно, что диагонали параллелограмма в точке пересечения
делятся пополам. Поэтому координаты точки Е — пересечения
диагоналей найдем как координаты средины отрезка АС. Обозна-
Обозначая их через Хе и Уе, получим, что
2 4- (—6) о
хе = ^Ч>—-; хЕ = —2;
4 + 6
Уе = -j-;
?(—2, 5).
= 5.
18
Зная координаты точки Е—средины диагонали BD и коорди-
координаты одного из ее концов В (—3, 7), по формулам B, 2) легко
определим искомые координаты вершины D параллелограмма.
В формулах B, 2) надо положить х = — 2; у = 5; хх = —3; ух =
= 7. Искомыми будут xd и г/г> — координаты точки D. Получаем
такие уравнения:
— 2 = к—— ; —4 = —3 + xd) xd = — 1.
Итак, вершина D (—1,3).
Задача 2, 10 (для самостоятельного решения). Три вершины
параллелограмма имеют координаты А (—6, —4); В (—4, 8);
С(—1,5), причем А и С — противоположные вершины. Опреде-
Определить координаты четвертой вершины параллелограмма.
Ответ. Координаты точки Е пересечения диагоналей
Е (—s", к) . Координаты четвертой вершины параллелограмма
D(-3, -7).
Теперь решим несколько задач, связанных с делением отрезка
АВ в данном отношении (формула B, 1)). Если точка С делит
отрезок АВ в отношении X, то это следует понимать так: Х = ^.
Числитель этой дроби есть длина отрезка," начало которого на-
находится в точке А—в начале отрезка АВ, а конец в точке С,
делящей этот отрезок. Знаменатель дроби есть длина отрезка,
имеющего начало в точке С, а конец в точке В — в конце от-
отрезка АВ. Это замечание, разъясняющее смысл числа X, поможет
избежать ошибок. В формулах B, 1) в числителе X является
множителем при координатах конца отрезка.
Задача 2,11. Отрезок АВ, соединяющий точки /1B,5) и
В (А, 9), разделить в отношении 1:3.
Решение. Условие задачи требует найти координаты точки
С, делящей отрезок АВ в отношении Х = 4-.
3
Точку А B, 5) будем считать началом отрезка, а точку В (А, 9)—
ее концом. В формулах B, 1) х и у — искомые координаты точ-
точки С, хх и ух — координаты точки А, х2 и у2 — координаты точ-
точки В; X = -g-. Значит, у нас хх = 2; х2 = 4; уг = 5; yz = 9. Итак,
по формулам B, 1)
_2+1Л _2 + ±_ 5
х - ; х j— ; х — —;
о*
i 19
у =
5+3"'9.
—
у =
5+3
Точка С имеет координаты С[-^, 6).
Задача 2,12. Концы отрезка АВ имеют координаты: А (—4, 8),
В F, —2). Найти координаты точек С и D, делящих отрезок А В
на три равные части (фиг. 2, 2).
Решение. Отрезок АВ разделен. на три равные части, а
у точка С делит отрезок АВ в отношении
Л * X = ^ • Так как &С = у СВ, то от-
отсюда следует, что
, _ АС_ 1
СВ~ ?•
-4-з-г-/., /Z3J\.B
Фиг. 2,2.
5 S В первой из формул B, 1) следует поло-
жить
= 6;
*с — искомая абсцисса точки С.
Во второй из формул B, 1) надо положить, что
Ух = 8;
Уч. = —^»
ус — искомая ордината точки С.
Итак,
-4 +-§¦-6
1
8 + -g- • (-2)
Ус = ^—; ус = —з
—4 + 3 .
О 1
8 — 1
2
2 14\
Координаты точки С найдены: С( —-j, -gj
20
14
Координаты точки D можно определить просто, как коорди-
координаты средины отрезка СВ. Пользуясь формулами для определения
координат средины отрезка, получаем
> XD — "з" >
•з-2.
2 '
Задача 2,13 (для самостоятельного решения). Найти коордит
наты точек, делящих отрезок „
с началом в точке А (—6, 10)
и концом в точке В (—2, —6)
в отношениях:
1) X = 1; 2) ;
=4; 4) Х = |.
= 2; 3) X =
Ответ.
1)
2)
4)
10- -^ •
~3' 3J'
Фиг. 2,3.
(-5' 5,1-
Задача 2,14. Найти координаты центра тяжести однородной
пластинки, имеющей форму треугольника, вершинам которого
соответствуют координаты: А (хъ Ух), В {х2, уа)> С (х3, у3) (тол-
(толщину пластинки не учитывать).
Решение. Центр тяжести треугольника, указанного,в усло-
условии задачи, находится в точке пересечения его медиан. Из эле-
элементарной геометрии известно, что три медианы треугольника
пересекаются в одной точке, причем эта точка делит медианы
в отношении 2:1, считая от вершины треугольника. Обозначим
эту точку буквой Е, ее координаты — хе и Уе (фиг. 2,3).
Рассмотрим медиану, проведенную из вершины А. Один ее
конец А имеет координаты (х1У yj, а координаты другого ее конца
получим, как координаты средины отрезка ВС, концы которого
имеют известные координаты: В(хг, уг), С (х3, у3). Координаты
точки D обозначим через хо и t/д и по формулам B,2) для
определения координат средины отрезка получим
Ч + х3 . .. _Уг_
2 ' yD ~
°ГЖ
2 )
Теперь, зная координаты начала А и конца D отрезка AD
и то, что точка Е (хЕ, уЕ) делит этот отрезок в отношении X = 2,
по формулам B, 1) получаем
Г 2 ¦*!+*« + *» ¦ Y
? 1+2 3 ' ХЕ ~
Полученный результат приводит к выводу, что координаты
центра тяжести однородной треугольной пластинки, если не
учитывать ее толщину, равны среднему арифметическому одно-
одноименных координат ее вершин.
Задача 2, 15 (для самостоятельного решения). Найти центр
тяжести однородной треугольной пластинки, вершины которой
имеют координаты (толщиной пластинки пренебречь): А B, —3);
Б(-3, 6); С(-7, 0).
Ответ, х =—-j ; у = 1.
Задача 2,16. Найти площадь треугольника, вершины которого
находятся в точках А B, —3), ВA, 1), С (—6, 5).
Решение. Задачу очень просто решить, воспользовавшись
формулой B, 3), в которой нужно взять
хг = 2, х2 = 1, х3 = — 6; уг = —3, #2 =1, у3 = 5.
Подставляя эти числа в B,3), получим
S = ±{[2-(-6)] .A-5)-[1-(-6)] .(-3-5)} =
= 1 {B + 6) • (-4) -A + 6) ¦ (-8)} = -i [-32-(- 56)] =
= 1. (-32+ 56) = 1.24 =12;
S= 12 кв. ед.
Решение задач, в которых требуется определить площадь тре-
треугольника по координатам его вершин, не представляет труд-
трудности, а потому можно ограничиться самрстоятельным решением
еще одной задачи.
Задача 2,17 (для самостоятельного решения). Координаты
вершин треугольника: А (—2, 4), В (—6, 8), С E, —6). Опреде-
Определить площадь этого треугольника.
Ответ. S = 6 кв. ед.
Задача 2,18. Доказать, что три точки Л A, 8), В (—2, -^7),
С (—4, —17) лежат на одной прямой,
22
Решение. Если три точки А, В и С лежат на одной пря-
прямой, то треугольник ABC обратится в отрезок прямой, а потому
его площадь должна быть равна нулю. Полагая в формуле B,3)
S = О, получим условие, при котором три точки лежат на одной
прямой
(*i — *з) {Уг — Уз) — (*» — х3) (f/j — у3) = О,
или
(*1 — *3) (У2 — Уз) = (*2 — Х3) (Ух — У3).
В более удобной форме условие, при котором три точки лежат
на одной прямой, можно записать так:
*i — *з _ j/i — у г B д\
Ч— Ч 1/2—1/3 ¦ К ' '
Подставляя сюда координаты данных точек, получим, что левая
часть B, 5) будет равна
а правая часть
УхцУ? = Л
Уг-Уз 2*
Требование B,5) выполнено:
А — 1
2 ~~ 2 *
и, значит, три данные точки лежат на одной прямой.
Задача 2, 19 (для самостоятельного решения). Проверить, что
три точки: А{1, 5), В(—5, —1), С (—8, —4) лежат на одной
прямой.
ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Различные виды уравнения прямой. Исследование общего
уравнения прямой. Построение прямой по ее уравнению.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
В прямоугольных координатах уравнение прямой на плоскости
задается в одном из следующих видов:
1. Уравнение прямой с угловым коэффициентом
y = kx + b, C, 1)
где k — угловой коэффициент прямой, т. е. тангенс того угла,
который прямая образует с положительным направлением оси
Ох, причем этот угол отсчитывается от оси Ох к прямой против
часовой стрелки, b — величина отрезка, отсекаемого прямой на
оси ординат. При Ь = 0 уравнение C, 1) имеет вид у = kx, и
соответствующая ему прямая проходит через начало координат.
23
Уравнением C, 1) может быть определена любая прямая на
плоскости, не перпендикулярная оси Ох.
Уравнение прямой с угловым коэффициентом разрешено отно-
относительно текущей координаты у.
2. Общее уравнение прямой
Ах + Ву + С = 0. C,2)
Частные случаи общего уравнения прямой:
а) Если С = О, уравнение C, 2) будет иметь вид
Ах + By = О,
и прямая, определяемая этим уравнением, проходит через начало
координат, так как координаты начала координат х — О, у = О
удовлетворяют этому уравнению.
б) Если в общем уравнении C,2) В = 0, то уравнение при-
примет вид
Ах + С = 0, или х— —-г-.
Уравнение не содержит переменной у, а определяемая этим урав-
уравнением прямая параллельна оси Оу.
в) Если в общем уравнении прямой C,2) А = О, то это урав-
уравнение примет вид
Q
Ву + С = О, или у = — g-;
уравнение не содержит переменной х, а определяемая им прямая
параллельна оси Ох.
Следует запомнить: если прямая параллельна какой-нибудь
координатной оси, то в ее уравнении отсутствует член, содер-
содержащий координату, одноименную с этой осью.
г) При С = О и А — 0 уравнение C, 2) принимает вид By = О,
или у = 0.
Это уравнение оси Ох.
д) При С =. 0 и В — 0 уравнение C,2) запишется в виде
Ах= 0 или х = 0.
Это уравнение оси Оу.
3. Уравнение прямой в отрезках на осях
где а — величина отрезка, отсекаемого прямой на оси Ох;
b — величина отрезка, отсекаемого прямой на оси Оу.
24
Каждый из этих отрезков отложен от начала координат.
Особенности этого уравнения такие: в левой части уравнения
между дробями -стоит знак плюс, величины аий могут быть как
положительными, так и отрицательными, правая часть уравнения
равна единице.
4. Нормальное уравнение прямой
jecosa + t/sina—р = 0. C,4)
Здесь р—длина перпендикуляра, опущенного из начала коор-
координат на прямую, измеренная в ед. масштаба, а a — угол, ко-
который этот перпендикуляр образует с положительным направ-
направлением оси Ох. Отсчитывается этот угол от оси Ох против часо-
часовой стрелки. Для приведения общего уравнения прямой C,2)
к нормальному виду обе его части надо умножить на нормиру-
нормирующий множитель.
N= ± 1 , C,5)
причем перед дробью следует выбрать знак, противоположный
знаку свободного члена С в общем уравнении прямой C, 2).
Особенности нормального уравнения прямой: сумма квадратов
коэффициентов при текущих координатах равна единице, свобод-
свободный член отрицателен, а правая часть его равна нулю.
ПОСТРОЕНИЕ ПРЯМОЙ ПО ЕЕ УРАВНЕНИЮ
Прямая вполне определена, если известны две принадлежа-
принадлежащие ей точки. Для того, чтобы построить прямую по ее урав-
уравнению, надо, пользуясь этим уравнением, найти координаты двух
ее точек. Твердо следует помнить, что если точка принадлежит
прямой, то координаты этой точки удовлетворяют уравнению
прямой.
При практическом построении прямой по ее уравнению наибо-
наиболее точный график получится тогда, когда координаты взятых
для ее построения двух точек — целые числа.
1. Если прямая определена общим уравнением Ах + By + С —
= 0 и С Ф 0, то для ее построения проще всего определить точки
пересечения прямой с координатными осями.
Укажем, как определить координаты точек пересечения прямой
с координатными осями. Координаты точки пересечения прямой
с осью Ох находят из следующих соображений: ординаты всех
точек, ^ расположенных на оси Ох, равны нулю. В уравнении
прямой полагают, что у равно нулю, и из полученного уравне-
уравнения находят х. Найденное значение х и есть абсцисса точки пе-
пересечения прямой с осью Ох. Если окажется, что х = а, то коор-
координаты точки пересечения прямой с осью Ох будут (а, 0).
25
Чтобы определить координаты точки пересечения прямой с
осью Оу, рассуждают так: абсциссы всех точек, расположенных
на оси Оу, равны нулю. Взяв в уравнении прямой х равным
нулю, из полученного уравнения определяют у. Найденное зна-
значение у и будет ординатой точки пересечения прямой с осью Оу.
Если окажется, например, что у — Ь, то точка пересечения прямой
с осью Оу имеет координаты (О, Ь).
Пример. Прямая 2х + у — 6 = 0 пересекает ось Ох в точке
C,0). Действительно, взяв в этом уравнении у~0, получим для
определения х уравнение 2х — 6 = 0, откуда х = 3.
Чтобы определить точку пересечения этой прямой с осью Оу,
положим в уравнении прямой х = 0. Получим уравнение у — 6 =
= 0, из которого следует, что у — 6. Таким образом, прямая
пересекает координатные оси в точках C,0) и @,6).
Если же в общем уравнении прямой С = 0, то прямая, опре-
определяемая этим уравнением, проходит через начало координат.
Таким образом, уже известна одна ее точка, и для построения
прямой остается только найти ее еще одну точку. Абсциссу х
этой точки задают произвольно, а ординату у находят из уравне-
уравнения прямой.
Пример. Прямая 2х — 4г/=0 проходит через начало коорди-
координат. Вторую точку прямой определим, взяв, например, х = 2.
Тогда для определения у получаем уравнение 2-2 — 4у = 0;
4# = 4; у = 1. Итак, прямая 2х — 4г/= 0 проходит через точки
@, 0) и B, 1).
2. Если прямая задана уравнением C,1) с угловым коэффи-
коэффициентом, то из этого уравнения уже известна величина отрезка Ь,
отсекаемого прямой на оси ординат, и для построения прямой
остается определить координаты еще только одной точки, принад-
принадлежащей этой прямой. Если в уравнении C, 1) k ф0 v. b Ф0,
то легче всего определить координаты точки пересечения прямой
с осью Ох. Выше было указано, как это сделать.
Если же в уравнении C,1) b — 0, то прямая проходит через
начало координат, и тем самым уже известна одна принадлежа-
принадлежащая ей точка. Чтобы найти еще одну точку, следует дать х лю-
любое значение и определить из уравнения прямой значение у, соот-
соответствующее этому значению х.
Пример. Прямая у=-^х проходит через начало координат и
точку B, 1) так как при х= 2 из ее уравнения г/ = у • 2 = 1.
Построение прямых, параллельных координатным осям, за-
затруднений не вызывает.
Теперь будем строить прямые по их уравнениям.
Задача 3. 1. Построить прямые: а) х + 2у — 4 = 0; б) 2х —
— 3</ + 6 = 0; в) у = Зл; + 2; г) у =—2х; д) 2лг + Зу = 0;
26
e) 1+1=1; ж) |-|=1; з) А л:-±</-4 = 0; и) г/= 2;
к) х + 3 = 0.
а) Определим точки пересечения прямой х -\-2у — 4=0 с коор-
координатными осями. Взяв в этом уравнении сначала у = 0, найдем
у
\У
0
Фиг. 3,1.
из него, что точка А пересечения прямой с осью Ох имеет абс-
абсциссу х = 4. Координаты точки А D, 0). Положив теперь в урав-
уравнении х = 0, найдем, что точка В пересечения прямой с осью Оу
имеет ординату у — 2. Координаты точки
В @,2). Построив эти точки, соединим
их прямой (фиг. 3,1а). Эта прямая и
соответствует данному уравнению.
б) Определим точки пересечения пря-
прямой 2х — Ъу + 6 = 0 с координатными ося-
осями: при у = 0 получаем 2х + 6 = 0, х =
=—3. Точка А пересечения прямой с
осью Ох имеет координаты (—3,0); при
х = 0 имеем —2>у + 6 = 0; у — 2, и прямая
пересекаетесь Оу в точке В @, 2). Построим
эти точки, соединим их прямой и полу-
получим прямую, соответствующую данному
уравнению (фиг. 3,16).
в) Прямая у = Ъх + 2 задана уравнением с угловым коэффи-
коэффициентом. Из уравнения видно, что прямая отсекает на оси ординат
отрезок, величина которого Ь = 2 (фиг. .3,2). Значит, точка А
@, 2) принадлежит прямой. Найдем еще одну точку на этой пря-
прямой. Как указано выше, легче всего определить точку пересече-
пересечения прямой с осью Ох. Взяв в уравнении прямой равным ну-
лю, получим 0 = Зх + 2, ах— — у, и точка В пересечения пря-
—jj-, 0). Построив точки @,2)
B \
— j, 0J и соединив их прямой, получим прямую, соответ-
соответствующую этому уравнению.
27
Фиг. 3,2.
Фиг. 3,3.
г) Прямая у = —2х проходит через начало координат (Ь = 0),
а поэтому для ее построения достаточно найти еще только одну
точку, принадлежащую ей.
Взяв х = — 1, получим, что у——2 • (—1) = 2 и, значит,
точка А(—1,2) принадлежит прямой. Проведя прямую через на-
начало координат и точку (—1,2), мы получим прямую, соответ-
соответствующую данному
уравнению (фиг. 3,3а).
д) Прямая 2х + Зу ==
— 0 проходит через на-
начало координат, так
как ее уравнение не
содержит свободного
члена. Найдем^ еще од-
одну точку, принадлежа-
принадлежащую прямой. Возьмем,
например, на прямой
точку с абсциссой х — 2. Подставляя в уравнение прямой х —
— 2, получим для определения ординаты этой точки уравнение
2 • 2 + Ъу = 0; Зу = -4; у = - 1
Таким образом, прямой принадлежит и точка А B, —А- Пря-
Прямая, проведенная через
начало координат и точку
А12,—-А, и будет соот-
ветствовать данному урав-
уравнению (фиг. 3,3 6).
е) Уравнение ?¦ + ¦§¦ =
= 1 — уравнение прямой в
отрезках на осях. Из . Фиг. 3,4.
него сразу усматриваем,
что прямая отсекает на осях Ох и Оу отрезки, величины
которых а = 4, b = 5 (фиг. 3,4 а).
ж) Уравнение |-—- -f-= 1 преобразуем к виду C,3). Запом-
Запомните, что в уравнении прямой, в отрезках на осях в левой
его части, между дробями должен быть знак плюс. На основании
этого замечания данное уравнение перепишем в виде
О
lo;s)
\
\
тогда а — 2, а Ь = — 4. Прямая, соответствующая этому урав-
уравнению, показана на фиг. 3,46.
28
з) Для построения прямой -?х— -=• 4 = 0. Определим точ-
точки пересечения ее с координатными осями. Положив в ее урав-
нении у — 0, найдем, что -=¦ х — 4 = 0, а отсюда х = -к-, и точка А
О О
пересечения прямой с осью абсцисс имеет координаты A /-g-, 0).
Взяв в уравнении прямой х = 0, найдем, что и — — 5 и точ-
точка В пересечения прямой с осью Оу име-
имеет координаты В @, —5). Проводим через
эти точки прямую. Она и соответствует
данному уравнению (фиг. 3,5).
и) Уравнение у = 2 определяет пря-
прямую, у которой все точки имеют ордина-
ординату, равную 2 ед. масштаба. Эта прямая,
очевидно, параллельна оси Ох, находится
над ней и проходит через точку @, 2)
(фиг. 3,6).
к) Уравнение х -\- 3 = 0 перепишем в
виде х— —3. Это уравнение определяет
прямую, у которой все точки имеют абс-
абсциссы, равные —3. Ясно, что эта прямая параллельна оси Оу,
находится слева от нее на расстоянии 3 ед. масштаба и про-
проходит через точку (—3,0) (фиг. 3,7).
9.
А
/iff.oj
Фиг. 3,5.
(-3,0)
Фиг. 3,6.
Фиг. 3,7.
Задача 3,2. Общее уравнение прямой Ах — Зг/+ 12 = 0 пред-
представить в виде: 1) с угловым коэффициентом; 2) в отрезках на
осях и 3) в нормальном виде. Построить эту прямую.
Решение. 1) Уравнение C,1) прямой с угловым коэффици-
коэффициентом имеет вид у = kx + b. Чтобы заданное уравнение преобра-
преобразовать к этому виду, разрешим его относительно у: Ъу = 4Jc + 12,
У = з"х + 4.
Сравнивая с уравнением C, 1), видим, что здесь угловой коэф-
коэффициент прямой ^ = —, а величина отрезка, отсекаемого прямой
29
на оси ординат, 6 = 4 (если уравнение прямой дано в общем виде
C, 2), то ее угловой коэффициент легко получить, если разделить
коэффициент _при х на коэффициент при у и взять полученное
А*
частное с обратным знаком k = — ¦„-.
2) В отрезках на осях уравнение прямой имеет вид C,3)
а ' Ь
Чтобы определить величины отрезков, отсекаемых заданной
прямой Ах—3i/+ 12 = 0, поступим так: в уравнении прямой по-
положим у — 0. Получаем Ах + 12 = 0, а х =—3. Значит, наша
прямая пересекает ось Ох в точке с координатами (—3,0), и в
уравнении C, 3) величина отрезка а = — 3.
Полагая в нашем уравнении х = 0, определим ординату точки
пересечения прямой с осью ординат. Будем иметь
—Ъу + 12 = 0; у = 4.
Точка пересечения прямой с осью ординат имеет координаты
@,4), и в уравнении C,3) величина отрезка Ь = А**.
Таким образом, наше уравнение в отрезках на осях будет
иметь вид
—3^4
3) Чтобы привести уравнение к нормальному виду, обе его
части следует умножить на нормирующий множитель C, 5), вы-
выбрав перед корнем знак, противоположный знаку свободного члена
в общем уравнении прямой. В нашем случае свободный член в
общем уравнении прямой равен +12, а поэтому перед корнем в
нормирующем множителе должен быть выбран противоположный
знак, т. е. знак минус, и так как
А =4, В = — 3, то
5*
Умножая на —=- обе части уравнения
О
4Х — Зу+ 12 = 0,
приведем его к нормальному виду
4.3 12
* В дальнейшем вместо фразы «возьмем прямую с уравнением, например,
Ах + By + С — 0» мы будем употреблять более короткую: «возьмем прямую
Ах+ В(/ + С = 0». Мы обращаем на это внимание потому, что Ах -\- By +
+ С = 0 есть уравнение прямой, но не сама прямая.
** В дальнейшем вместо термина «величина отрезка» употребляется термин
«отрезок».
30
Запомнить: В нормальном уравнении прямой сумма квадратов
коэффициентов при текущих координатах должна быть равна
единице, а свободный член должен быть отрицательным. Эти два
требования в полученном нами последнем уравнении, как легко
проверить, выполнены. В пункте 2 решения мы получили урав-
уравнение прямой в отрезках на осях: а = —3, 6 = 4. Зная эти от-
отрезки, мы легко построим кашу прямую (фиг. 3, 8).
Задачи 3,3 и 3,4 решаются так же, как и задача 3,2. По-
Поэтому приводятся только ответы. Эти задачи должны быть решены
самостоятельно.
Задача 3, 3 (для самостоятельного ре-
решения). Уравнение прямой 6х + 8у — 15=
=0 представить в виде:
1) с угловым коэффициентом, 2) в от-
отрезках на осях.
Построить эту прямую.
Ответ. 1) Уравнение прямой с угло-
угловым коэффициентом %»¦/>) ' л\—' *~х
3 . 15
2) Уравнение прямой в отрезках на осях
2,5 М,875
Задача 3, 4 (для самостоятельного решения). Те же требова-
требования, что и в задаче 3,3 для прямой \2х — Ъу + 26 = 0.
п 12 . 26 х , у ,
Ответ, у = -*+yj3+^= 1.
6 "
Задача 3, 5. Под каким углом прямая у = х + 2 пересекает
ось 0x7
Решение. Прямая задана уравнением с угловым коэффици-
коэффициентом в виде C, 1). Сравнивая данное уравнение с уравнением
у = kx + Ь, получаем, что k — 1. Нам известно, что k —угловой
коэффициент прямой, т. е. k—это тангенс того угла, который
прямая составляет с положительным направлением оси Ох. Этот
угол мы обозначим буквой ср. Значит, k = tgср. У нас k = 1, т.е.
tgcp= 1; следовательно, ср = 45°. Этим заканчивается решение за-
задачи.
Задача 3, 6 (для самостоятельного решения). Под каким углом
прямая у = 2х + 3 пересекает ось Ох?
Указание. При решении задачи воспользуйтесь таблицами
тригонометрических функций.
Ответ, tg ср = 2; ср = 63°26'.
31
Задача 3,7. Найти уравнение биссектрисы первого и третьего
координатных углов.
Решение. Уравнение прямой с угловым коэффициентом в том
случае, когда прямая проходит через начало координат, имеет
вид
У = kx, C, 6)
так как в этом случае отрезок 6, отсекаемый прямой на оси Оу,
равен нулю. Биссектриса первого и третьего координатных углов
составляет с положительным направлением оси Ох угол в 45°.
Величина k в уравнении C, 1) есть тангенс этого угла, т. е. k =
= tg45°=l. Подставляя это значение в уравнение C,6), полу-
получим у = х.
Это и есть уравнение биссектрисы первого и третьего коорди-
координатных углов, его следует запомнить. Оно может быть записано
также р виде х — у — О.
Задача 3,8 (для самостоятельного решения). Найти уравнение
биссектрисы второго и четвертого координатных углов.
Ответ. у = —х, или х-\-у = 0.
Задача 3, 9. Прямая проходит через точку B, —3) и отсекает
на оси ординат отрезок 6 = 3. Найти ее уравнение.
Решение. Будем искать уравнение прямой в виде C,1) с
угловым коэффициентом. Это целесообразно сделать потому, что
в задаче задан отрезок, отсекаемый прямой на оси ординат, а в
уравнение прямой с угловым коэффициентом входит этот отрезок.
Итак, в уравнении у = kx-\-b нам известно, что 6 = 3. Подставим
в него это значение и получим
у = kx + 3. (А)
Следовательно, теперь осталось определить только угловой коэф-
коэффициент k. По условию прямая проходит через точку B, —3).
Если линия проходит через точку, то координаты этой точки
удовлетворяют уравнению линии. Подставим ь последнее уравне-
уравнение 2 вместо х и —3 вместо у. Получим уравнение для определе-
определения k: —3 = 2k + 3. Решая уравнение, находим, что k — —3.
Подставляя это значение k в (А),, получим искомое уравнение
прямой у = — Ъх + 3.
Задача 3, 10 (для самостоятельного решения). Найти уравне-
уравнение прямой, проходящей через точку (—1, —3) и отсекающей на
оси ординат отрезок 6 = 4. Эта задача решается так же, как
и 3,9.
Ответ. у = 7х + 4.
Задача 3,11. Написать уравнение прямой, отсекающей на ко-
координатных осях Ох и Оу отрезки а = 3 и 6 = 4.
Решение. В уравнение прямой в отрезках на осях
32
подставим а = 3 и 6 = 4. Получим искомое уравнение в виде
Задача 3,12 (для самостоятельного решения). Построить пря-
прямые, заданные уравнениями
1) х + 2у — 6 = 0; 2) х —Зг/ + 9 = 0;
3) Ъх — у = 0; 4) х + 2г/ = 0;
5) х— 4 = 0; 6) 2у —3 = 0.
Решим теперь две задачи, связанные с исследованием общего
уравнения прямой.
Задача 3,13. Указать особенности в расположении относительно
координатных осей прямых
1) 2х — Ъу = 0; 2) Ъх — 2 = 0;
3) 1у + 12 = 0; 4) 5х = 0;
Ъ)Ъу=О.
Решение. 1) Прямая 2х — 5у = 0 проходит через начало
координат, так как ее уравнение не содержит свободного члена.
2) Прямая Ъх— 2 = 0 параллельна оси Оу (ее уравнение не
содержит текущей координаты у).
3) Прямая 7г/+12 = 0 параллельна оси Ох (ее уравнение
не содержит текущей координаты х).
4) Прямая Ъх = 0 совпадает с осью Оу (ее уравнение можно
переписать в виде х = 0).
Задача 3,14 (для самостоятельного решения). Указать особен-
особенности в расположении прямых
1) Ъх + Ъу = 0; 4) Ъу = 0;
2) 4г/ + 8 = 0; 5) 7х = 0.
3) Ъх - 16 = 0;
Ответ. 1) Проходит через начало координат;
2) параллельна оси Ох;
3) параллельна оси Оу;
4) совпадает с осью Ох;
5) совпадает с осью Оу.
Задача 3,15. Уравнение прямой х + Ъу — 4 = 0 привести к
нормальному виду.
Решение. Нормирующий множитель определяется по фор-
формуле
+ в2
Здесь Л = 1; В — 3. Перед корнем надо выбрать знак, противо-
противоположный знаку свободного члена в заданном уравнении, т. е.
знак плюс. Тогда нормирующий множитель'
N = ' N = -i=r;
/2 2 /10
33
после умножения обеих частей- уравнения на
мет вид
1.3 4 Л
= X + -7=. У 7= = О-
10 /10 /10
уравнение при
Задача 3,16. Привести к нормальному виду уравнение пря-
прямой Ъх — 12^ + 26 = 0.
Ответ. -*.х*
Из сравнения с уравнением C, 4) видим, что р = 2; cos a =
5 . 12
; 51
Задача 3,17 (для самостоятельного решения). Уравнение пря-
прямой 7х + У— 3 = 0 привести к
нормальному виду.
Ответ. —т=х-\ -р=ц —
5/2 5/2 а
3
Р =
5/Т'
sin a
cos а = ——:
5/2"'
5/2 "
фиг. з,9. Задача 3, 18 (для самостоя-
самостоятельного решения). Привести к
нормальному виду уравнение прямой 6х — 8у — 15 = 0.
3 4 3
Ответ, -д-л;—-^у — 1,5 = 0; р=1,5; cosa = -g-;
sina = —=-.
О
Задача 3,19. Найти длину перпендикуляра, опущенного из
начала координат на прямую Ъх — 6у + 5 = 0, а также коорди-
координаты основания этого перпендикуляра.
Решение. Приведем данное "уравнение к нормальному виду:
N = —
1
/З2 + 6а> /45 3 / 5 '
После умножения на нормирующий множитель уравнение при-
примет вид
'/"
/5
Из сравнения с C, 4) заключаем, что р = Ц- .
Для определения координат основания этого перпендикуляра
из фиг. 3, 9 получим формулы
х — р cos a,
у = psina
34
(эти формулы верны при любом расположении прямой относи-
относительно координатных осей).
1 2
Как видно из уравнения C,4), cosa = —, sina^-^
У 5 У 5
и искомые координаты основания перпендикуляра равны
1_ __2
X — д. У — д.
ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Уравнение прямой, проходящей через данную точку
в данном направлении. Уравнение прямой, проходящей через две данные
точки. Угол между двумя прямыми. Условие параллельности и перпендикуляр-
перпендикулярности двух прямых. Определение точки пересечения двух прямых.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Уравнение прямой, проходящей через данную точку
А (хъ у,) в данном направлении, определяемом угловым коэф-
коэффициентом k,
У — yi^kix — xJ. D,1)
Это уравнение определяет пучок прямых, проходящих через
точку А (хг. Ух), которая называется центром пучка.
2. Уравнение прямой, проходящей через две точки: A (xlt уг)
и В (лг2, t/г), записывается так:
Угловой коэффициент прямой, проходящей через две данные
точки, определяется по формуле
fe^f^f. D,3)
*2 — *1
3. Углом между прямыми а и Ь называется угол, на который
надо повернуть первую прямую а вокруг точки пересечения
этих прямых против движения часовой стрелки до совпадения
ее со второй прямой Ь.
Если две прямые заданы уравнениями с угловым коэффи-
коэффициентом
у = kxx + Ьи
y^=k2x + Ь2, D,4)
то угол между ними 0 определится по формуле
35
Следует обратить внимание на то, что в числителе дроби из
углового коэффициента второй прямой вычитается угловой коэф-
коэффициент первой прямой.
Если уравнения прямых заданы в общем виде
Са = 0, D,6)
угол между ними определяется по формуле
4. Условия параллельности двух прямых:
а) Если прямые заданы уравнениями D,4) с угловым коэф-
коэффициентом, то необходимое и достаточное условие их параллель-
параллельности состоит в равенстве их угловых коэффициентов:
kl = kt. D/8)
б) Для случая, когда прямые заданы уравнениями в общем
виде D, 6), необходимое и достаточное условие их параллельности
состоит в том, что коэффициенты при соответствующих текущих
координатах в их уравнениях пропорциональны, т. е.
тг = к- D>9)
5. Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями D, 4) с угло-
угловым коэффициентом, необходимое и достаточное условие их пер-
перпендикулярности заключается в том, что их угловые коэффициенты
обратны по величине и противоположны по знаку, т. е.
Это условие может быть записано также в виде
Mi = -1- D,11)
б) Если уравнения прямых заданы в общем виде D,6), то
условие их перпендикулярности (необходимое и достаточное)
заключается в выполнении равенства
ЛИ2 + ад. = 0. D,12)
(х Координаты точки пересечения двух прямых находят,
решая систему уравнений D,6). Прямые D,6) пересекаются в том
и только в том случае, когда
АхВг -A2B^0.
^ Задача 4,1. Найти уравнение прямой, проходящей через две
точки: (— 1, 2) и B, 1).
36
. Решение. По уравнению D,2), полагая в нем* хх = — 1,
уг = 2, хг — 2, уа,= 1, получим
у-2_х+1 у-2_х + 1.
r=2~2+T ^=T~~3~'
после упрощений получаем окончательно искомое уравнение в
виде
х + Ъу — 5 = 0.
Задача 4,2. Найти уравнение прямой, проходящей через
точки Л B, 1) и В (—5, 1).
. Решение. Эта задача не отличается от предыдущей. Под-
Подставляя координаты точек Л и В в уравнение D,2), получаем
х — 2 _у—\
— 5-2~ 1 — 1 '
или ^?у- = ^—, а отсюда заключаем, что у—1 = 0, или
у = 1 (см. объяснения в учебнике И. И. Привалова «Аналити-
«Аналитическая геометрия». 1957, гл.- III, § 12).
Задача 4,3 (для самостоятельного решения). Найти уравне-
уравнения сторон треугольника, вершины которого Л A, — 1); ВC, 5),
С(-7, 11).
Указание. Эта задача решается точно так же, как и две
предыдущие. Используя формулу D,2), получим уравнения сто-
сторон:
(АВ) Ъх— у— 4 = 0,
{ВС) Ъх + Ъу — 34 = 0,
{АС) Зх + 2у— 1 = 0.
Задача 4, 4. Стороны треугольника заданы уравнениями:
{АВ) 2х + 4у+ 1=0,
{АС) х— у+ 2 = 0,
{ВС) Зх + 4у~ 12 = 0.
Найти координаты вершин треугольника.
Решение. Координаты вершины А найдем, решая систему,
составленную из уравнений сторон А В и АС:
2х + Ау + 1 = 01
х— 0 + 2 = О].
Систему двух* линейных уравнений с двумя неизвестными ре-
решаем способами, известными из элементарной алгебры, и полу-
получаем
— _! -1
X — 2 '» У 2 *
* Безразлично, какую точку считать первой, а какую — второй.
37
Вершина А имеет координаты
Координаты вершины В найдем, решая систему из уравнений
сторон А В и ВС:
2х + 4у+ 1 = 0
Ъх + Ау — 12 = 0
27 / 27\
получаем х = 13; у =—-г ; В [13, —т- .
Координаты вершины С получим, решая систему из уравне-
уравнений сторон ВС и АС:
х— у+ 2 = 0
Вершина С имеет координаты С [у, у).
Задача 4,5 (для самостоятельного решения). Найти коорди-
координаты вершин треугольника, стороны которого заданы уравне-
уравнениями:
(AB) х+ у— 5 = 0,
(ВС) 2х- у + 4 = 0,
(AC) Ъх — Ъу + 14 = 0.
Ответ. Л/-г-, -=-); в/т, -^
Задача 4,6 (для самостоятельного решения). Найти коорди-
координаты вершин треугольника, стороны которого заданы уравне-
уравнениями:
(АВ) 2х+ у— 5 = 0,
(ВС) 2х— у+ 4 = 0,
(AQ Ъх — 8у+ 14 = 0.
Ответ А№ ^\- В/1 1\- С(-^
итвет. л ^21, 2Jj, d ^4 , 2j, ц п,
Задача 4,7. Найти уравнение прямой, проходящей через
точку А B, Ъ) параллельно прямой Ъх — 4г/ -f- 15=0.
Решение. Докажем, что если две прямые параллельны, то
их уравнения всегда можно представить в таком виде, что они
будут отличаться только свободными членами. Действительно,
из условия D,9) параллельности двух прямых следует, что
38
Обозначим через t общую величину этих отношений. Тогда
а отсюда следует, что
A^AJ, B1 = Bat. D,13)
Если две прямые
параллельны, условия D, 13) выполняются, и, заменяя в первом
из этих уравнений Аг и Вг по формулам D, 13), будем иметь
A2tx+ B2ty + C1 = 0,
или, разделив обе части уравнения на t ФО, получим
. А2х + В2у+^ = 0. D,14)
Сравнивая полученное уравнение с уравнением второй прямой
Агх + Вгу + С2 = 0, мы замечаем, что эти уравнения отличаются
только свободным членом; тем самым мы доказали требуемое.
Теперь приступим к решению задачи. Уравнение искомой пря-
прямой запишем так, что оно будет отличаться от уравнения данной
прямой только свободным членом: первые два слагаемые в иско-
искомом уравнении возьмем из данного уравнения, а его свободный
член обозначим через С. Тогда искомое уравнение запишется в
виде
Ъх — 4у + С = 0, D,15)
и определению подлежит С.
Придавая в уравнении D, 15) величине С всевозможные дей-
действительные значения, мы получим множество прямых, парал-
параллельных данной. Таким образом, уравнение D, 15) представляет
собой уравнение не одной прямой, а целого семейства прямых,
параллельных данной прямой Ъх— 4у -\- 15 = 0. Из этого се-
семейства прямых нам следует выделить ту, которая проходит
через точку А B, 5).
Если прямая проходит через точку, то координаты этой
точки должны удовлетворять уравнению прямой. А поэтому мы
определим С, если в D, 15) подставим вместо текущих коорди-
координат х и у координаты точки А, т. е. х = 2, у—Ъ. Получаем
3.2 — 4- 5 + С-О и С = 14.
Найденное значение С подставляем в D, 15), и искомое урав-
уравнение запишется так:
3* — Ау+ 14 = 0.
Ту же задачу можно решить и иначе. Так как угловые
коэффициенты параллельных прямых между собою равны, а для
39
данной прямой 3* — 4r/ -j- 15 = 0 угловой коэффициент k =
3 / А \
= —, Ik = —п")> то и угловой коэффициент искомой прямой
3
также равен -у.
Теперь используем уравнение D, 1) пучка прямых. Точка
А B, 5), через которую проходит прямая, нам известна, а потому,
подставив в уравнение пучка прямых у — уг — k (х — хг) значе-
значения k = -j\ хг = 2; у1 = 5,
получим
у~5 = ^(х-~2); Ау — 20 = 3* — 6,
или после упрощений
Зх — 4у + 14 = 0,
т. е. то же, что и раньше.
Задача 4,8 (для самостоятельного решения). Найти уравнение
прямой, проходящей через точку C, —4) параллельно прямой
2х + 5у-7 = 0.
Указание. Задача решается так же, как и предыдущая.
Решение проведите двумя способами.
Ответ. 2х + &У+ 14 = 0.
Задача 4, 9. Найти уравнение прямой, проходящей через точ-
точку А E, —1) перпендикулярно к прямой Зх — Ту + 14 = 0.
Решение. Мы знаем, что если две прямые
перпендикулярны, то выполняется равенство D, 12)
A^a + B&^O,
или, что то же,
AlAt = —BlB,,
а отсюда следует, что
^2 _ Ё1
Вх~ Ах-
Общее значение этих отношений обозначим через t.
Тогда %—% = *-¦
откуда следует, что
Аг = Btt, 5a = — Att.
40
Подставляя эти значения А2 и В2 в уравнение второй пря-
прямой, получим
или, деля на t обе части равенства, будем иметь
Сравнивая полученное уравнение с уравнением первой прямой
замечаем, что у них коэффициенты при х и у поменялись мес-
местами, а знак между первым и вторым слагаемым переменился на
противоположный, свободные же члены различны.
Приступим теперь к решению задачи. Желая написать урав-
уравнение прямой, перпендикулярной к прямой Зх — 7у+Ы = 0,
мы на основании только что сделанного заключения поступим
так: поменяем местами коэффициенты при х и у, а знак минус
между ними заменим знаком плюс, свободный член обозначим
буквой С. Получим 7х + Ъу -f С = 0. Это уравнение есть урав-
уравнение семейства прямых, перпендикулярных прямой 2>х—7у-\-
-J- 14 = 0. Мы определим С из условия, что искомая прямая про-
проходит через точку А E, — 1). Известно, что если прямая прохо-
проходит через точку, то координаты этой точки должны удовлетво-
удовлетворять уравнению прямой. Подставляя в последнее уравнение 5
вместо х а — 1 вместо у, получим
7 . 5 + 3 • (— 1) -f С = 0;
С = — 32.
Это значение С подставим в последнее уравнение и получим
7х + 3у — 32 = 0.
Решим ту же задачу другим способом, использовав для этого
уравнение D, I) пучка прямых
У—У1 = к{х — х1).
Угловой коэффициент искомой прямой мы найдем из условия
D, 10), т. е. он должен быть обратен по абсолютной величине
и противоположен по знаку угловому коэффициенту данной
прямой.
Угловой коэффициент данной прямой Ъх — 7у+ 14 = 0
«1 — 7 >
тогда угловой коэффициент прямой, ей перпендикулярной,
41
Подставив в уравнение пучка прямых k2——-^, а
и ух координаты данной точки Л E, —1), найдем {/ —(—1) =
= — j(x — 5), или Зу + 3 = — 7х + 35, и окончательно 7* +
-f- Зу — 32 = О, т. е. то же, что и раньше.
Задача 4, 10 (для самостоятельного решения). Через точку
А (— 3, 2) провести прямую, перпендикулярную прямой 7х +
+ Ау— 11 = 0*.
Ответ. 4х — 7у + 26 = 0.
Задача 4,11 (для самостоятельного решения). Через точку
пересечения прямых
х + у— 1 = 0 и 2* + Зу + 4 = 0
провести прямую: 1) перпендикулярно прямой Ъх — у + 7 = 0;
2) параллельно этой прямой.
Ответ. 1) х + 3у+ 11 = 0; 2) Зх — у— 27 = 0.
Задача 4, 12 (для самостоятельного решения). Сторонами тре-
треугольника являются координатные оси и прямая, проходящая
через точку А C, 4). Найти уравнение этой прямой при усло-
условии, что площадь треугольника равна 9 кв. ед.
Указание. 1. Написать уравнение пучка прямых, проходя-
проходящих через точку А C, 4).
2. Найти величины отрезков, отсекаемых этой прямой на ко-
координатных осях. Получится
а = 3-^-4, 6 = 4-3*.
3. Использовать формулу для определения площади прямо-
прямоугольного треугольника S= ± -z-ab, где а и Ь — катеты, и для
определения k получатся уравнения
16 = 0 и 9А8—6А + 16 = 0.
Корни второго уравнения комплексны и должны быть отбро-
отброшены. Подставляя найденные из первого уравнения значения k
в уравнение пучка прямых, полученное в п. 1, окончательно
найдем, что требованию задачи удовлетворяют две прямые:
Задача 4,13. Даны две противоположные вершины квадрата
А B, 1) и С D, 5). Найти две другие (фиг. 4, 1).
Решение. Обозначим буквами В и D искомые вершины:
В (х2, у2) и D (Xi, yi). Надо найти числа х2, Уг и xit r/4. Для
* Это условие следует понимать так же, как и условие задачи 4,9.
42
определения каждой пары этих чисел необходимы два уравнения,
связывающие их.
Первое из них мы найдем, определив расстояние АВ и при-
приравняв его к расстоянию ВС (АВ — ВС, так как стороны квад-
квадрата равны между собой):
Отсюда следует, что
Возводя обе части этого равен-
равенства в квадрат, после упроще-
упрощений получим первое уравнение,
связывающее х2 и у2,
х2 + 2у2 = 9.
Для получения второй свя-
связи между х2 и у2 найдем угло-
угловые коэффициенты прямых А В
и ВС. Так как эти прямые пер-1
пендикулярны, то произведение
их угловых коэффициентов рав-
равно — 1 (см. формулу D, 11)).
У
5
4
3
г
/ 2 3 4 5
Фиг. 4,1.
Угловой коэффициент прямой, проходящей через две данные
точки (хъ z/x) и (хг, уг), определяется по формуле
«1
Ц нашем случае хх = 2, ух = 1. Для прямой А В угловой коэф-
коэффициент
и.
Для прямой ВС угловой коэффициент, учитывая координаты
точки С, будет равен
, _ уг — 5
1 х2 — 4
Из условия перпендикулярности двух прямых D, 11) следует,
что
— 1 г/2 —5
= — 1.
хг — 2 *2 — 4
Умножая обе части этого равенства на (х2 — 2) • (х2 — 4), получим
(У2 - 1) (Уш — 5) = - (*, - 2) (х, ~ 4),
пли (г/2 — 1) (г/? — 5) + (*» — 2) (*, — 4) = 0;
43
раскрывая скобки, будем иметь
*! + §?—6х, — б0,+13 = 0.
Это второе уравнение, связывающее х2 и у2.
Его можно получить и проще: 1) координаты точки Е пере-
пересечения диагоналей квадрата найдутся, как координаты средины
диагонали АС:ЕC, 3). Из условия BE = АЕ получаем преды-
предыдущее уравнение. Таким образом, для определения х2 и у2 мы
имеем такую систему уравнений:
х2 + 2уг = 9
xl + yt — 6x2 — 6у2 + 13 = 0
Из первого уравнения находим, что х2 = 9 — 2у2. Подставля-
Подставляем это значение во второе уравнение и, решая относительно у2
полученное квадратное уравнение, найдем, что
Ы1 = 4, (у2J = 2,
а {х2I = 1, (х2J= 5.
Значит, вершиной В могут служить точки с координатами
A, 4) и E, 2). Проделайте самостоятельно точно такую же ра-
работу относительно второй искомой вершины; получите
= U Мг = 4.
Следовательно, вершина D имеет координаты E, 2) или A, 4).
Задача 4, 14. Найти угол между двумя прямыми
У = 2х + 4;
0 = 3*-1.
Решение. Поставим перед собой задачу найти острый угол
между данными прямыми. Воспользуемся формулой D,5), так
как прямые заданы уравнениями с угловым коэффициентом, при-
причем поскольку нас интересует острый угол, правую часть фор-
формулы D, 5) возьмем по абсолютной величине:
У нас
3 — 2
По таблицам тригонометрических функций находим, что G = 8°8'.
Задача 4, 15 (для самостоятельного решения).
Найти угол между прямыми
г/=_2л; + 3 и у =
Ответ. 0= 135°.
44
Задача 4, 16. Найти угол между прямыми
Зх+4у— 7 = 0 и
Ах — 2>у + 8 = 0.
Решение. Воспользуемся формулой D,7), так как уравне-
уравнения прямых заданы в общем виде.
У нас Ах = 3; Вх = 4; А2 = 4; В2 = — 3;
tee =
— 9—16
12—12
tgO =
— 25
и так как деление на нуль невозможно,
Угол 9 = 90°, т. е.' прямые перпенди-
перпендикулярны. Их перпендикулярность мож-
можно было усмотреть и сразу, соста-
составив выражение D,12) Ау_А2-\- B^i и
убедившись, что оно равно нулю.
Задача 4,17 (для самостоятельного
решения).
Найти острый угол между прямыми
Зх + 5у — 7 = 0 и* — у+5 = 0.
то
не существует.
Фиг. 4,2.
воспользуйтесь табли-
Ответ. tg9 = 4; 8 = 75°58'.
Указание. Для определения угла
цами тригонометрических функций.
Задача 4, 18. Найти уравнения прямых, проходящих через
точку А C, 4) под углом в 60° к прямой 2х + Зу + 6 = 0.
Решение. Для решения задачи нам следует определить
угловые коэффициенты прямых I и II (фиг. 4,2). Обозначим
эти коэффициенты соответственно через kx и k2, а угловой коэф-
коэффициент данной прямой — через k. Очевидно, что k = — \.
О
На основании определения угла между двумя прямыми
(стр. 35) прн определении угла между данной прямой и прямой
I следует в числителе дроби в формуле D, 5) вычесть угловой коэф-
коэффициент данной прямой, так как ее нужно повернуть против ча-
часовой стрелки вокруг точки С до совпадения с прямой I.
Учитывая, что tg60° = VA3, получаем
tg 60° -
¦т1*.
_24-13угЗ
Определяя же угол между прямой II и данной прямой, сле-
следует в числителе той же дроби вычесть угловой коэффициент
прямой II, т. е. k3, так как прямую II следует повернуть про-
тив часовой стрелки вокруг точки В до совпадения ее с данной
прямой:
1-3*8
Задача 4,19. Через центр тяжести треугольника, вершины
которого Л B,3), В(—1,4), С E, 5), провести прямую, параллель-
параллельную стороне Л С, и прямую, перпендикулярную стороне АВ.
Решение. Прежде всего определим координаты центра тя-
тяжести М треугольника. Известно, что каждая координата центра тя-
тяжести площади треугольника есть средняя арифметическая одно-
одноименных координат его вершин. Значит, если вершины треугольника
имеют координаты (xlt yt), (х2, у2) и (х3, у3), то координаты его
центра тяжести хс и ус будут
*1+*а+*з .. _ Ух + Уа + Уз
з , УС— з
В нашем случае
Центр тяжести треугольника М имеет координаты B,4). Урав-
Уравнение стороны АВ будет х -\-Зу— 11 = 0; уравнение стороны АС
будет 2х — Зу + 5 = 0 (мы нашли эти уравнения, воспользовав-
воспользовавшись уравнением прямой, проходящей через две точки).
Теперь так же, как в задачах 4,7 и 4,9, определим уравне-
уравнение прямой, проходящей через точку М параллельно стороне АС
и перпендикулярно стороне А В. Получим соответственно
2х — 3z/ + 8 = 0 и 2>х — у — 2 = 0.
ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Расстояние от дайной точки до данной прямой.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Расстояние точки А (хъ у^) до прямой Ах \- By + С — 0 есть
длина перпендикуляра, опущенного из этой точки на прямую.
Она определяется по формуле
E,1)
у а- -у и-
46
Правило. Чтобы определить расстояние от точки А (хъ у^
до прямой Ах -\- By + С — 0, нужно привести уравнение прямой
к нормальному виду, взять левую часть полученного уравнения и
подставить в нее вместо текущих координат координаты данной
точки. Абсолютная величина полученного числа и даст искомое
расстояние.
Расстояние от точки до прямой есть всегда величина положи-
положительная. Кроме расстояния от точки до прямой, рассматривается
еще так называемое отклонение точки от прямой.
Отклонение 8 данной точки от данной прямой есть расстояние
от этой точки до прямой, которому приписывается знак плюс,
если точка и начало координат находятся по разные стороны от
прямой, и знак минус, если точка и начало координат находят-
находятся по одну сторону от прямой (см. учебник И. И. Привалова,
гл. III, § 16, или § 22 учебника Н. В. Ефимова).
Расстояние от точки до прямой есть абсолютная величина
отклонения этой точки от прямой.
Задача 5,1. Найти расстояние от начала координат до прямой
х+ г/ — 2 = 0 (см. также задачу 3, 19).
Решение. Приведем уравнение прямой к нормальному виду.
Нормирующий множитель
дг= ' N--L
У 1* + I2 VT
В нормальном виде уравнение прямой запишется так:
JL-j-J^ ^ = 0
/2 /2 /2
Свободный член в нормальном уравнении прямой, взятый по
абсолютной величине, дает искомое расстояние р = Y% ед«
масштаба.
Задача 5, 2. Найти расстояние от точки B, 5) до прямой
6х + 8у — 5 = 0.
Решение. Приведем уравнение прямой к нормальному виду.
Нормирующий мцржитель
10 '
] +
Уравнение прямой в нормальном виде запишется так:
б* + 8у - 5 _
—w
Согласно правилу стр. 47, возьмем теперь левую часть этого
уравнения ^ и подставим в нее координаты данной точ-
47
ки. Абсолютная величина полученного числа и даст искомое рас-
расстояние
6-2+8-5-5
— 4,7 ед. масштаба.
10
Итак, d = 4,7 ед. масштаба.
Задача 5, 3 (для самостоятельного решения).
Найти расстояние от точки C, — 1) до прямой Зх+5у +
+ 8 = 0.
Ответ. d = jj]/34 ед. масштаба.
Задача 5,4. Найти расстояние между двумя параллельными
прямыми
Зх + Ау— 12 = 0,
3* + Ау + 13 = 0.
Решение. Искомое расстояние мы найдем, как расстояние
от произвольной точки первой прямой до второй прямой. Возь-
Возьмем на первой прямой произвольную точку, например, точку с
абсциссой х = 0. Ее ордината будет у = 3.
Итак, на первой прямой выбрана точка А @,3). Найдем те-
теперь расстояние этой точки до второй прямой так же, как и в
задачах 5, 2 и 5, 3, и получим
d = 5 ед. масштаба.
Задача 5, 5. Найти уравнение прямой, проходящей через точ-
точку (—4,3) и удаленной от начала координат на расстояние 5 ед.
масштаба.
Решение. Уравнение искомой прямой, как проходящей че-
через точку (—4,3), запишется на основании уравнения D,1) в
виде
После упрощений оно примет, вид
kx-y + (Ak + 3)=0.
Теперь приведем его к нормальному виду. Нормирующий
множитель будет равен
-¦-yir+T1
и уравнение в нормальном виде будет выглядеть так:
k ! -. | 4fe + 3 =n
Сравнивая это уравнение с нормальным уравнением прямой,
видим, что прямая удалена от начала координат на величину
48
которая по условию равна 5. Значит, для определения k полу-
получаем такое уравнение:
I 4A + 3 | = R
а после возведения в квадрат обеих частей этого уравнения для
определения k будем иметь квадратное уравнение
9А2 — 24А +16 = 0,
откуда
4
&! = А2 = з-.
Следовательно, искомое уравнение запишется так:
4
и после упрощений получаем
4*—3i/ + 25 = 0.
Задача 5,6. Через точку (—1,2) провести прямую, расстоя-
расстояние которой от точки C, — 1) равно 2 ед. масштаба.
Решение. Уравнение искомой прямой, как прямой, прохо-
проходящей через точку (—1,2), запишется так:
у — 2 = k(x+ 1), или kx — у+ (k + 2) = 0. (А)
Приведем его к нормальному виду. Нормирующий множитель
1
N = ±
После приведения уравнения (А) к нормальному виду око запишется
в виде
Вспомним теперь, что расстояние между точкой и прямой опре-
определяется по формуле
d = Axi + Byi'
V л2 + в2
В нашем случае следует определить расстояние от точки
C, — 1) до прямой. У нас xt = 3; у1 = — 1; d = 2; подставляя эти
значения в предыдущую формулу, будем иметь
3k + 1 + k + 2
2 =
2 =
ИЛИ
2VT+T2 = \4k + 3|, 4 A + /fe2) = 16Л;2 +- 24Ar + 9,
3 И. А. Каплан 49
и для определения k получаем уравнение
№* + 24k + 5 = О,
откуда находим, что
«2
g •
Подставляя эти значения в (А), заключаем, что есть две пря-
прямые, удовлетворяющие условию задачи:
Задача 5,7. Через точку М1A,2) провести прямую, расстоя-
расстояния до которой от точек Мг B, 3) и М3D,—5) были бы равны.
Решение. Так как искомая прямая проходит через точку
Mj(l,2), то ее уравнение запишется так:
y-2 = k(x-l), (В)
илн
kx-y-k + 2 = 0,
а после приведения его к нормальному виду
kx — у — k + 2 _ 0
- ±УТ+?
Используя формулу E, 1) для длины перпендикуляра, опу-
опущенного из точки на прямую, и подставляя в нее сначала коор-
координаты точки Мг: х2 — 2; уг = 3, а потом координаты точки М3:
xs = 4; у3 — — 5, получим
По условию dr—d2, а отсюда следует,* что имеют место два ра-
равенства:
k — i _ 36 + 7 6 — 1, 3fe + 7
2
Из первого fe = —4, а из второго ^ = т • Итак, искомых прямых
две, и уравнения их получим из (В), подставляя в него сначала
k = — 4, а потом k = — g •
Искомые прямые: '4* + # — 6 = 0 и Зх + 2# — 7=0.
Задача 5,8. Дана прямая 4х + Ъу + 1 =0. Найти уравнение
прямой, параллельной данной и отстоящей от нее на 3 ед. мас-
масштаба.
50
Решение. Очевидно, что искомых прямых будет две. Откло-
Отклонение 8 точек одной из искомых прямых от данной будет равно
+ 3, а другой — 3; 8 = ± 3.
Уравнение семейства прямых, параллельных данной, будет
таким:
Из этого семейства требуется отобрать две искомые прямые. По-
После приведения его к нормальному виду получим
Q
± 5
(два знака в знаменателе мы удерживаем пока потому, что знак
С нам неизвестен). Возьмем на данной прямой произвольную точ-
точку, например, Л @, —^А . Подставим ее координаты в левую
часть последнего уравнения и, учитывая, что отклонение точек
данной прямой от искомых равно ± 3, для определения С полу-
получим уравнения
На основании этого Сг = 16, С2 = «~ R. Подставляя эти значе-
значения С в уравнение семейства пряирх; 4* + Ъу + С = 0, получим,
что искомых прямых две:
4х + Зу + 16 = 0 и 4х + Ъу — 14 = 0.
Решение допускает простую проверку, которую рекомендуется
сделать.
Задача 5,9 (для самостоятельного решения). Уравнения сто-
сторон треугольника ABC известны:
(АВ) х + у—1 =0,
{АС) 2х — у — 5 = 0,
(ВС) Ъх + у = 0.
Найти длины высот этого треугольника и их уравнения.
Указание. Определить координаты вершин треугольника и
воспользоваться формулой для определения расстояния от точки
до прямой.
С —1 С—1 С —1 С—1
* Четыре случая: 3 = —н— ; 3 = _g-; — 3 = —g— ; — 3 = ^
С —1 С — 1
сводятся к двум: 1) —г— = 3; 2) —g—*»,т- 3, откуда Сх =? J6; С8 = — 14.
3* 61
Ответ. Уравнение высоты hBc x — 3# —5 = 0;
уравнение высоты hAc 2л: + 4у — 5 — 0;
уравнение высоты Иав х — у — 4 = 0;
hBC —
з/5 .
2 '
3/2
ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Уравнение биссектрисы угла между двумя прямыми.
Задачи повышенной трудности.
На этом практическом занятии мы будем решать задачи по-
повышенной трудности, однако такие, которые не потребуют каких-
либо дополнительных сведений из
теории прямой линии. Научимся
прежде всего находить уравнение
биссектрисы угла между двумя
прямыми.
Задача 6,1. Найти уравнения
биссектрис углов между прямыми
12* + 9у —'17 = 0 и Зх + 4у +
+ 11 = 0.
Решение*. Приведем подроб-
подробное решение этой задачи. Из эле-
элементарной геометрии известно, что
биссектриса угла между двумя
прямыми есть геометрическое ме-
место точек, равноудаленных от
Фиг. 6,1.
сторон угла. Обратимся к фиг. 6, 1. Отклонения Вх и Ва точки А
биссектрисы от сторон угла CDE имеют знак плюс, так как точ-
точка Л и начало координат лежат по разные стороны как от пер-
первой, так и от второй прямой, т. е. Ьг = В2. Возьмем точку В на
биссектрисе смежного угла CDF. Точка В и начало координат
лежат по разные стороны от прямой EF, поэтому отклонение 84
имеет знак плюс (84 >»Q), Отклонение 83 точки В от прямой CL
имеет знак минус, так как точка В и начало координат лежат с
одной и той же стороны от прямой CL, т. е. 83 < 0. Значит, 83
и 84 в этом случае равньь-по абсолютной величине, но противо-
противоположны по знаку, и имеет место равенство
* Прежде чем решать эту задачу, еще раз повторите рассуждения о знаке
отклонения точки от прямой по учебнику Н. В. Ефимова (§ 67) или по учеб-
учебнику И. И. Привалова (§ 16, гл. III).
62
Обозначим через X и У текущие координаты точки на бис-
биссектрисе и рассмотрим отклонения этой точки от сторон угла.
Для биссектрисы одного угла эти отклонения равны, а для бис-
биссектрисы смежного угла они равны по абсолютной величине, но
противоположны по знаку. Пусть уравнения сторон угла имеют
вид
Агх + Вгу + Сг = 0 и А2х + В2у + С2 = 0.
Приведем эти уравнения к нормальному виду, и тогда, для слу-
случая, когда 8Х = 82, уравнение биссектрисы будет иметь вид
А V I D V I Г* А V" I D V I /~*
ЛУА ¦+- B\i j- ^i _ Л2Л -f- Д2Г -\- 12 ( Л\
Для случая же 83 = —84 уравнение биссектрисы получим в
виде
AX + BY + C AX + B
Замечание. При решении задачи нет надобности обозначать
текущие координаты точки на биссектрисе через X и У. Их мож-
можно обозначить через х и у, так как это не меняет этих уравне-
уравнений.
Объединяя уравнения {А) и (В) и используя только что сде-
сделанное замечание, будем иметь уравнения двух биссектрис в виде
А^Х ~\~ В^у -у* Cj A<%x -р В%у -у* Cg
— = ^ ~"— — . (
Теперь решение нашей задачи не составит труда.
Для нашего случая уравнения биссектрис запишутся так:
х + 4г/ + 1
УЗ2 + 42
или
12х+9у—17 | Зх+Ау+П
1-5 — "¦"" 5
И
f—17
15 ~ 5
Окончательно уравнения биссектрис получаем в виде
21лг + 21у+ 16 = 0,
3* — Ъу — 50 = 0.
Легко проверить, что найденные две биссектрисы перпендику-
перпендикулярны. Действительно, условие перпендикулярности двух пря-
прямых Л1Ла + В152 = 0 выполняется (проверьте!)*.
* На этом примере мы получили подтверждение известной из геометрии
теоремы: биссектрисы двух смежных углов перпендикулярны.
S3
Задача 6, 2 (для самостоятельного решения). Найти уравнение
биссектрисы угла между прямыми
4х + 2у + 7 = 0 и 2х — 4у + 15 = 0.
Ответ. Уравнение биссектрис получаем в виде
Ах + 2у + 7 , 2х — 4у+ 15
/20 ~ tB
После упрощений получаем уравнения биссектрис в виде
х + Зу — 4=0,
Зл:— +11 = 0.
Задача 6, 3 (для самостоятельного решения). Найти уравнения
биссектрис внутренних углов треугольни-
треугольника, "заданного вершинами
А @,0); В C,-1); С D,7).
Указание. Найдите сначала уравне-
уравнения сторон треугольника. Получите та-
такие уравнения:
(А В) х + Зу = 0, {АСOх- Ау «= О,
(ВС)8х — у-25 = 0.
. Уравнение биссектрисы угла Л:
Фиг. 6,2. (? ^- ^g-^ ^4 yj^+ 3 ^gE^ 0
Уравнение биссектрисы угла S: (8|^10 -f-K65)^ +
—/ТО) у —25/ТО = 0.
Уравнение биссектрисы угла С: Зл: — у — 5 = 0.
Задача 6,4. Даны две смежные вершины квадрата Л A,4) и
В D, 5). Найти две другие (фиг. 6,2).
Решение. Очевидно, что задача допускает два решения, так
как искомые вершины могут находиться по разные стороны отрезка
АВ. Уравнение стороны квадрата АВ будет таким: х — Ъу + 11 = 0, а
ее длина равна/10. Теперь через точки А A, 4) и Б D, 5) проведем
прямые, перпендикулярные А В, и на каждой из этих прямых опреде-
определим по две точки, расстояние которых от АВ равно/10 (у квадрата
все стороны равны). Координаты этих точек и будут искомыми.
Уравнения прямых, перпендикулярных к АВ и проходящих
через концы отрезка АВ, будут такими:
{ADKx + y— 7== 0, {ВС)Ъх + у— 17 = 0.
На каждой из этих прямых найдем две точки, находящиеся от
АВ на расстоянии, равном ]/ 10, причем для одной из точек откло*
нение от АВ будет положительным, для другой — отрицательным.
54
Обозначим координаты точки D через хх и yv Так как эта
точка лежит на прямой AD, то ее координаты удовлетворяют
уравнению этой прямой, т. е. имеет место уравнение
3*1 + г/1-7 = 0. {А)
Второе уравнение, связывающее хх и уи найдем, определяя
отклонение этой точки от прямой АВ. Приведя уравнение АВ к
нормальному виду и взяв отклонение равным ± 1^10, получим
а отсюда будем иметь два уравнения:
*i — ЗУг + 1 = 0 и хх — Зг/j + 21 = 0.
Объединяя каждое из этих уравнений с уравнением {А), по-
получим две системы уравнений:
Из первой системы уравнений хх — 2;ух — 1; из второй — хг —
= О*. Ц\ = 7. Таким образом, вершина D может иметь координа-
координаты @,7) или B, 1).
Точно так же найдем, что четвертая вершина С квадрата мо-
может иметь координаты E,2) или C, 8)
Эту задачу можно решить и иначе. Используйте указания,
которые даются ниже, и самостоятельно решите задачу другим
способом:
1) Найдите длину d стороны АВ.
2) Диагональ квадрата BD будет равна dY2.
3) Напишите формулу для определения расстояния от точки
D до точки Л и от точки D до точки В. Вы получите два урав-
уравнения, из которых и определятся координаты точки.D.
4) Найдите координаты средины диагонали BD.
5) Зная координаты этой точки и координаты точки А, поль-
пользуясь формулами для определения координат точки, делящей
отрезок пополам, определите и координаты точки С.
Задача 6,5. Найти уравнение прямой, параллельной прямой
2х + Зу + 6 = 0
и отсекающей от координатного угла треугольник, площадь которого
равна 3 кв. единицам.
Решение. Обозначим отрезки, отсекаемые искомой прямой
на координатных осях Ох и Оу, соответственно через а и Ь. Тогда
имеем
3 —g-afe, илиа& = 6. • (А)
55
Уравнение семейства прямых, параллельных данной, запишет-
запишется в виде 2х + Зг/ + С = 0. Отрезки, отсекаемые этой прямой на
осях координат, равны
С С
Подставляя а и & в (А), получим
откуда
-
= —6,
и искомая прямая имеет уравнение 2х + Зг/ + 6 = 0, или 2х -f
+ Зу — 6 = 0. Среди только что
найденных прямых есть данная:
2х + Зг/ + 6 = 0. Таким образом,
данная прямая удовлетворяет
требованию задачи; этому требо-
требованию удовлетворяет также и най-
найденная прямая 2х + Зг/ — 6 — 0.
Задача 6, 6. Даны уравнения
двух сторон параллелограмма
2х
+1 = 0 (АВ)
— 3 = 0 (AD)
и точка пересечения его диаго-
диагоналей Л/A,2). Найти уравнения
фиг> 63. Двух других сторон этого парал-
параллелограмма (фиг. 6,3).
При решении, замечая, что данные стороны параллелограмма
не параллельны, будем следовать такому плану:
1) найдем координаты точки А пересечения данных сторон;
2) зная координаты точек А и N, найдем координаты точки
С, что мы легко сможем сделать по формуле определения коор-
координат средины отрезка;
3) через найденную точку С проведем сначала прямую, парал-
параллельную AD, а потом прямую, параллельную АВ.
4) Определим координаты точки А, как точки пересечения
прямых А В и AD, и получим, что
5
V
т. е.
56
(I. -Л
1з • з
5) Формулы для определения координат средины отрезка в
данном случае запишутся так:
_ хА + хс _Уа+Ус
Xn — —2 ' УМ — 2 *
По этим формулам получим
__]_ _ 17
Хс — з , Ус — з •
Итак, точка С\— 3. -jI •
6) Через точку С проведем прямую, параллельную AD, и по-
получим, что уравнение стороны ВС будет таким:
2х + у — 5-0.
Уравнение стороны CD
х + 2у— 11 = 0.
Задача 6,7. Найти координаты точки Р, равноудаленной от
точек М1{4, — 3) и М2{2, — 1) и отстоящей от прямой 2х + у —
—1 = 0 на расстоянии, равном 2 ед. масштаба.
Указание. Обозначим координаты искомой точки Р через
хх и ух; из условия, что МХР = М2Р, получаем
Это первая зависимость между лгх и yv Вторую же зависимость
между ними найдем из условия, что искомая точка находится на
расстоянии 2 ед. масштаба от прямой 2х-\-у—1 = 0; получим
о _ 2*t + У1 — 1
±/5
Отсюда два уравнения, связывающие хг и уъ имеют вид
или
2*1 +г/i-1+2/5 = 0.
Каждое из этих уравнений следует решить совместно с pajjee
полученным уравнением хх — ух = 5. Задача допускает два реше-
решения:
г/i =-
или
57
Задача 6, 8. Даны уравнения высот треугольника 2х—Зу +
+ 1=0 и * +г/= 0 и координаты одной из его вершин А A,2).
Найти уравнения сторон треугольника.
Решение. Точка А(],2) не принадлежит данным в условии
высотам треугольника, так как ее координаты не удовлетворяют
их уравнениям: 2-1 — 3-2+ I фО и 1 -f- 2 =И= 0. Отсюда следует,
что высоты, данные в задаче, проведены из двух других вершин
треугольника В и С (фиг. 6,4).
Назовем их CD и BE, CD ± AB, BE ± АС. Пусть высота CD
имеет уравнение х + у = 0, а уравнение высоты BE 2x — Зу-\-
+ 1 = 0. Так как AC ± BE, то урав-
уравнение АС мы найдем из уравнения
семейства прямых, перпендикуляр-
перпендикулярных BE, приняв во внимание, что
искомая прямая проходит через дан-
данную точку А A, 2).
Сторона АС имеет уравнение
Зх + 2г/ — 7 = 0. Уравнение прямой
А В найдем, как уравнение прямой,
проходящей через точку А A,2) пер-
пендикулярно CD. Оно ^имёет вид
Фиг. 6,4. Х—у+ 1 =0.
Теперь следует найти координаты точек В и С:
хв = — 2; у в = — 1;
хс = 7; ус = — 7.
Уравнение стороны ВС 2х + Зу + 7 = 0.
Таким образом, уравнения всех трех сторон треугольника най-
найдены.
Задача 6, 9 (для самостоятельного решения). Даны две верши-
вершины треугольника А B, 1) и В D, 9) и точка пересечения его высот
NC,4). Найти уравнение сторон треугольника.
Ответ.
(АВ) 4х — у — 7 = 0,
* (ВС) х + Зу — 31 = 0,
{АС) х + 5у — 7 = 0.
Задача 6.10 (для самостоятельного решения). Даны координа-
координаты средин сторон треугольника — А A,2), В G, 4), СC, — 4). Най-
Найти уравнения сторон треугольника (фиг. 6,5).
Ответ. 1) 2х— у = 0; 3) х — Зу— 15=0.
* 2) Зх + у-25=0;
58
Задача 6,11. Даны уравнения сторон треугольника х-}-у —
— 1 = 0(АВ) и у -+- 1 = О (ВС) и точка N (— 1,0) пересечения его
медиан. Найти уравнение третьей стороны АС (фиг. 6,6).
Ответ, х — # + 3 = 0.
Решение задач, которыми заканчиваются упражнения, по теме
«Прямая линия», связано с уравнением пучка прямых. Перед ре*
шением этих задач следует изучить § 23 из учебника Н. В. Ефи-
Ефимова или § 11 главы III учебника И. И. Привалова.
Задача 6,12. Найти уравнение прямой, проходящей через точ-
точку пересечения прямых х — у — 1 = 0 и х + 2у — 2=0 и точку
М(—1, 1), не находя точки пересе-
чения данных прямых.
Фиг. 6,5.
Фиг. 6,6.
Решение. Уравнение пучка прямых, проходящих через точ-
точку пересечения данных прямых Ах -f By + С = 0 и Агх-\- В^у +
+ Cj = 0, записывается так:
Ах + Ву + С+ЦА^ + Вл + СД^О-, F,1)
в нашем случае оно будет иметь вид
х-у~1 + \{х + 2у-2) = 0. (А)
Из этого пучка надо выделить прямую, проходящую через точку
М{—1,1). Подставляя в уравнение (Л) координаты точки М
вместо текущих координат, получим X = — 3.
Подставив это значение X в уравнение (Л), будем иметь
л:-г/-1-3(л: + 2г/-2)=0.
Раскрывая скобки и делая приведение подобных членов, на-
находим уравнение искомой прямой
2х + Ту — 5 = 0.
Задача 6, 13. Найти уравнение прямой, которая проходит че-
через точку пересечения прямых х + У—1=0 и х-\- 2# + 1 = 0
и отсекает на отрицательной части оси Оу отрезок в 2 ед. мас-
масштаба. " .
Решение. Уравнение пучка прямых, проходящих через точ-
точку пересечения данных прямых, имеет вид F, 1).
59
В нашем случае оно запишется так:
х + у—1+\(х + 2у+1) = 0. (В)
Так как прямая на отрицательной части оси Оу отсекает отрезок
в 2 ед. масштаба, то прямая проходит через точку @, — 2).
Подставляя координаты этой точки вместо текущих координат в
(В), получим Х= — 1, а уравнение искомой прямой будет иметь
вид
Задача 6,14. Найти уравнение прямой, проходящей через точ-
точку пересечения прямых х-\-2у—11 = 0 и 2х^-у — 2 = 0 на
расстоянии 5 ед. масштаба от начала координат.
Решение. Уравнение пучка прямых с центром пучка в точ-
точке пересечения данных прямых имеет вид * + 2у—11+ХBл; —
-*/-2)=0,
или
(\ + 2Х)х + B — Х)у — A1 + 2Х) = 0. (А)
Нормирующий множитель равен
1
1
Умножая на нермирующий множитель уравнение (А) и принимая
во внимание, что в нормальном уравнении прямой абсолютная
величина свободного члена равна расстоянию прямой от начала
координат, для определения X получаем уравнение
N1 + 2X1 с , 2
==== = 5. откуда Х = п.
Искомое уравнение: Зх + Ау— 25 = 0.
Задача 6,15 (для самостоятельного решения). Найти уравне-
уравнение прямой, проходящей через точку пересечения прямых 2х -+-
+ 5z/ + 8 = 0 и Ъх — Ау — 7 = 0 под углом в 45° к прямой у =
= Ах + 3.
Ответ. 69*— 1\5у — 199 = 0 и 115* + 69у + 99 = 0.
Задача 6,16 (для самостоятельного, решения). Через точку
М(\, —1) провести прямую так, чтобы средина ее отрезка меж-
между параллельными прямыми х + 2у— 1 = 0 (I) и х + 2у — 3 = 0
(II) лежала на прямой х — у— 1 =0 (фиг. 6,7).
Ответ. Ах — у—5 = 0.
Задача 6,17 (для самостоятельного решения). Луч света, про-
проходящий через точку С-B,3), отражается от прямой (АВ)
х + у + 1 -- 0 и проходит после этого через точку (Ы)- Найти
уравнения падающего и отраженного лучей (фиг. 6,8).
Ответ. Уравнение падающего луча
5дг — Ау+ 2 = 0;
60
уравнение отраженного луча
4х— Ъу + 1 = 0.
Задача 6,18 (для самостоятельного решения). Луч света, про-
проходящий через точку С A,2), отражается от прямой (АВ)
х -f-5#+ 1 = 0 и проходит через точку F (—1,3).
Найти уравнение луча падающего и отраженного.
В
Фиг. 6,7. Фиг. 6,8.
Ответ. Уравнение отраженного луча
уравнение падающего луча
62л; — 41 у + 20 = 0.
Этим мы заканчиваем упражнения, связанные с теорией пря-
пряй
мой линии на плоскости.
СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Полярная система координат. Переход от полярных
координат к декартовым и обратно. Построение кривой, определяемой урав-
уравнением в полярных координатах.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это практическое занятие посвящается полярной системе ко-
координат, упражнениям на переход от декартовой системы коорди-
координат к полярной и обратно, а также на построение кривой по ее
уравнению в полярных координатах.
В полярной системе координат основными постоянными эле-
элементами, по отношению к которым определяется положение точ-
точки на плоскости, являются точка О — полюс и ось ОР, которая
называется полярной осью.
61
Если М — произвольная точка плоскости, не совпадающая с
полюсом О, то ее положение на плоскости вполне определено
заданием двух чисел: г — ее расстояния от полюса, выраженного
в ед. масштаба, и ср —Угла, на который следует повернуть по-
полярную ось против часовой стрелки, чтобы она совпала с лучом
ОМ. Числа г и 9 называются полярными координатами точки М.
Из них первой координатой считается г, а второй ср. Координа-
Координата г называется полярным радиусом точки М (иногда радиусом-
вектором точки М), а координата ср— ее полярным углом*. По-
Полярные координаты точки записываются в скобках справа от
обозначения ее, причем на первом месте в скобках записывается
координата г, а на втором — координата ср. например, М (г, ср).
Полярный угол ср считается положительным, если он отсчнтыва-
ется от полярной оси против часовой стрелки, и отрицательным,
если он отсчитывается от полярной оси по часовой стрелке.
В определенной таким образом полярной системе координат
полярный радиус г — всегда величина положительная или рав-
равная нулю (г > 0), так как под г понимается расстояние от полю-
полюса О до точки М, а расстояние, как и всякая длина, не может
быть отрицательным.
Однако на практике удобнее пользоваться такой системой
полярных координат,, в которой полярный радиус г, может при-
принимать и отрицательные значения. Система полярных координат,
в которой полярный радиус г может принимать любые значения
(положительные, отрицательные и равные нулю), называется
обобщенной системой полярных координат. Этой системой мы
и будем пользоваться.
Если точка М имеет координаты -(-г и ср: М {+г, ср), то
она имеет также и координаты —г и ср ~Ьтс". М (—г, ср + тс)>
так как угол ср + я характеризует направление полярного радиу-
радиуса, прямо противоположное тому, которое соответствует углу ср
(см. задачи 7,3 и 7, 4).
Отметим, что какой бы из этих двух систем полярных коор-
координат мы ни пользовались, всегда паре чисел г и ср соответствует
на плоскости единственная точка.
Если полюс полярной системы координат находится в начале
прямоугольной системы координат, а положительная полуось Ох
совпадает с полярной осью, ось же Оу перпендикулярна оси Ох
и направлена так, что ей соответствует полярный угол ср = -^,
то по известным полярным координатам точки ее прямоугольные
координаты хну вычисляются из формул
х = г cos ср, у = г sin ср**. G, 1)
* Полярный угол измеряется в радианах.
** Везде в дальнейшем, если не будет оговорено, предполагается именно
такое расположение полярной и прямоугольной систем координат.
62
Если же известны прямоугольные координаты х и у точки, ее
полярные координаты определяются по формулам
G,2)
tgcp = -g- • G,3)
Как видно из G,2), у корня в формуле для определения г
стоят два знака — плюс и минус, что соответствует обобщенной
системе полярных координат, а потому и в формулах для опре-
определения sin ср и cos ср перед корнем стоят два знака (рекомендует-
(рекомендуется ознакомиться в учебнике И. И. Привалова с замечанием
к § 11, гл.' 1). Два знака в формуле для определения г появи-
появились потому, что г находится из выражения г2 = х% + у%. Если
за г оставляется право быть только величиной положительной
или нулем, то г — -f- Yx2 + у2. Если^же г, как это имеет место
в обобщенной системе полярных координат, может быть и отри-
отрицательной величиной, то из г2 = дс2+У2 следует, что г —
В заключение укажем, как вести вычисления по форму-
формулам G,2), чтобы по известным прямоугольным координатам
точки найти ее полярные координаты. Прежде всего следует оп-
определить г, выбрав перед корнем любой знак, затем вычислить
sin cp и cos ср, сохранив перед корнем в формулах G,2) уже вы-
выбранный знак, и по знакам sin 9 и cos 9 установить четверть, в
которой находится полярный угол 9- Само вычисление угла 9
по таблицам тригонометрических функций следует вести по фор-
формуле G,3).
Укажем также, как следует в полярной системе координат
построить точку М по ее полярным координатам г и 9- По за-
заданному полярному углу 9 строим ось, проходящую через полюс
под углом 9 к полярной оси, причем положительное направле-
направление построенной оси должно совпадать с тем направлением, ко-
которое имела бы полярная ось, если бы ее повернули против ча-
часовой стрелки на угол 9- На этой оси откладываем отрезок дли-
длиной | /• | от полюса О в положительном направлении построенной
оси, если г > 0, и в отрицательном — если г < 0.
Задача 7,1. Построить точку М с координатами C, -f т) в
полярной системе координат (фиг. 7, 1).
Решение. Проведем через полюс О ось ОРг под углом ^|[-
к полярной оси ОР (положительное направление указано стрел-
стрелкой) и отложим от полюса в положительном направлении оси ОРг
отрезок ОМ, равный трем единицам масштаба. Конец М этого
отрезка и будет искомой точкой..
63
Задача 7,2. Построить в полярной системе координат точку
Решение. Проведем через полюс О ось ОРг под углом -г-
к полярной оси (положительное направление указано стрелкой
на фиг. 7, 2) и отложим от полюса в положительном направле-
направлении оси OPt отрезок ОМ, равный
одной ед. масштаба. Конец этого
отрезка М и будет искомой точкой
Фиг. 7,1.
Фиг. 7,2.
Задача 7,3. Построить в полярной системе координат точку
Решение. Проведем через полюс О ось OPt под углом -тк
к полярной оси (положительное
направление на ней указано
стрелкой на фиг. 7, 3) и отложим
от полюса в отрицательном на-
направлении оси ОРг отрезок ОМ,
равный двум ед. масшт. Конец
этого отрезка и будет искомой
точкой.
Задача 7, 4 (для самостоятель-
самостоятельного решения). В полярной си-
системе координат построить точку
Фиг. 7,3. /_ 47 L А .
Задача 7, 5. Прямоугольные координаты точки А B, 3). Найти
ее полярные координаты.
Решение. По формулам G,2) получаем г— ±]/ТЗ- Выби-
Выбираем по нашему усмотрению знак перед корнем, например, плюс.
Тогда г = + у 13, sin ср = -—, coscp = -r=. Так как sincp>0
и cos ср > 0, то угол ср находится в первой четверти. На основа-
64
о
нии формулы G,3) tg ср = у; по таблицам находим, что ср = 0,98.
Полярные координаты точки А найдены: г = УТЗ, ср = 0,98 или
А {У\Ъ\ 0,98). Постройте точку. Если бы перед корнем был вы-
выбран знак минус, то тогда г = — У13; sin ср = — ~j=; cos ср = —
о
—j=, и так как sincp<0 и coscp<0, то угол ер находится в
о
третьей четверти. Зная, что tg ср = -— , получаем ср = 4,12, а точ-
точка А имеет полярные координаты г=—]/ТЗ, ср = 4,12:
А (—1^13, 4,12)- Постройте точку по этим координатам и убе-
убедитесь, что она совпала с ранее построенной.
Задача 7, 6 (для самостоятельного решения). Найти полярные
координаты точки А, прямоугольные координаты которой
(-1.-1).
Ответ. A(V2, -§-*) или А (— j/2, ~
Задача 7,7 (для самостоятельного решения). Прямоугольные
координаты точки А B, —2). Найти ее полярные координаты.
Ответ. Л B1/2, -?«) или А(—2\/Ъ, -|тс).
Задача 7,8. Найти прямоугольные координаты точки А, по-
полярные координаты которой B, -^ тс).
Решение. По формулам перехода G, 1)
х = г cos ср. У = г sin ср
получаем
Задача 7,9. Найти прямоугольные координаты точки, поляр-
полярные координаты которой А(—3, -тА.
Решение.
х = г cos 9, г/ = г sin <p,
х = — 3 cos -г ic, у = — 3 sin -j- ic,
2 2
Задача 7,10 (для самостоятельного решения). Найти прямо-
прямоугольные координаты1 точки А, полярные координаты которой
Ответ. х=0;у = — 2.
65
Задача 7, 11. Составить уравнение прямой линии в полярных
координатах.
Решение. Поместим полюс полярной системы координат в
начало прямоугольной системы координат, полярную ось сов-
совместим с положительной полуосью абсцисс (фиг. 7, 4).
Возьмем уравнение прямой в нормальном виде
х cos a -f у sin а — р — 0.
Формулы перехода G, 1) имеют вид '
х = г cos 9, y=rs'm<?.
У
N
О
Фиг. 7,4. Фиг. 7,5.
Подставив в это уравнение значения х и у из формулы
G, 1), получим г cos 9 • cos a + г sin 9 • sin а — р = 0,
или г (cos9 • cosa + sin9 • sina) — р — 0,
откуда г cos (9 — a) = р,
и окончательно г =
cos (ф — а)"
В этом уравнении постоянными величинами являются р и а,
величины же г и 9 — переменные: это текущие полярные коорди-
координаты точки на прямой (последняя формула может быть получена
также из чертежа).
Задача 7,12. Построить кривую r = acos29 и найти ее урав-
уравнение в прямоугольной системе координат.
Решение. Будем давать значения полярному углу 9 от
9 = 0 до 9 = 2« через промежуток a = -о- и вычислим соответ-
соответствующие значения г. Найденные значения поместим в таблицу.
Примем произвольный отрезок за единицу масштаба, которой
мы будем пользоваться при построении г. По значениям г и 9
из таблицы построим точки, соответствующие каждой паре чисел
г и 9. и соединим их плавной кривой.
66
ф
0
я
я
т
Зл
8
я
5я
8
Зя
4
7я
8
я .
2Ф
0
я
т>
я
2"
Зя
т
я
5я
4
Зя
2
7я
4
2я
г = a cos 2ф
а
V2
ат
0
—а
V?
-а —
0
VT
ат
а
ф
9я
8
5я
4.
\\п
8
Зя
2
13я
8
7я
4
15л
8
2л
2?
9я
4
5я
2
Ня
4
Зя
'Зя
4
7я
2
15я
4
4я
г = а cos 2ф
•?
0
V2
— а
VT
0
ут
а-J-
а
Фиг. 7,6.
Фиг. 7,7.
Построение кривой показано на фиг. 7,5—7,12.
На фиг. 7,13 кривые, построенные на различных этапах, сое-
соединены в одну. Полученная кривая называется четырехлёпестко-
вой розой.
67
(a;x)
Фиг. 7,8.
Фиг, 7,9.
hi*)
Фиг. 7,10.
Фиг. 7,П.
Фиг.7,12.
Фиг. 7,13.
68
Теперь найдем уравнение четырехлепестковой розы в прямо-
прямоугольной системе координат, причем напоминаем, что начало
прямоугольной системы координат помещено в полюс полярной
системы координат, а ось абсцисс направлена вдоль полярной
оси.
Учитывая, что cos 2ср = cos2 cp—sin2 cp, уравнение четырехле-
четырехлепестковой розы г — a cos 2<р перепишем в виде г = a (cos2 cp —
— sin2 cp). Подставляя сюда формулы перехода G,2), получим
или
Отсюда
= а
+ у2 = а
'¦-У
—Р
Фиг. 7,14,
Возводя обе части последне-
последнего уравнения в квадрат, полу-
получим окончательно
(х* + у*K = а2 (х2 — у2J.
Задача 7,13 (для самостоя-
самостоятельного решения). Построить
кривую
г — 4 cos Зср
и найти ее уравнение в прямоугольных координатах при условии,
что начало прямоугольных координат совпадает с полюсом поляр-
полярной системы координат, а положительная полуось абсцисс совпа-
совпадает с полярной осью.
Указание. Углу ср придавать значения от 0 до 2it через про-
промежуток а = -ф т. е. значения
/ч Я Я Я
U> 12' Т' Т' " *
Постройте точки с координатами (г, ср) и соедините их плавной
кривой (фиг. 7, 14—7, 18). Точки кривой для значений it < ср < 2it
(фиг. 7, 16 и 7, 17) совпадут с построенными на фиг. 7, 14 и 7, 15.
Кривая г =4 cos Зср называется трехлепестковой розой (фиг. 7, 18).
Для преобразования уравнения этой кривой к прямоугольным ко-
координатам надо выразить cos Зср через coscp:
cos Зср = cos Bcp -f- cp) = cos 2cp • cos cp — sin 2ср • sin cp
(использовать, что cos 2cp = cos2 cp — sin2 cp, sin 2cp = 2 sin cp • cos cp,
и учесть, что sin2 9 = 1—cos2cp). Окончательно
cos Зср = 4 cos3 cp — 3 cos cp.
• 69
Фиг. 7,15.
Фиг. 7,18.
70
Уравнение кривой r = 4cos3cp перепишется теперь в виде
г = 4 D cos2 ср — 3 cos ср),
или
г = 16 cos3 ср — 12 cos ср.
Применить формулы G, 2).
Ответ, {х2 + у2J = 4х {х2 — Зу2).
Задача 7, 14 (для самостоятельного решения).
Построить кривую г = 5 sin Зср и найти ее уравнение в прямо-
прямоугольной системе координат, полагая, что начало прямоугольной
системы координат совпадает с по-
полюсом полярной системы координат,
а положительная полуось абсцисс —
с полярной осью.
Задача 7,15 (для самостоятель-
самостоятельного решения). Построить лемниска-
лемнискату Бернулли
г2 = 6sin2cp
и найти ее уравнение в прямоуголь-
прямоугольной системе координат при распо- —
ложении осей координат, указанном
в предыдущей задаче.
Ответ. Кривая изображена на
фиг. 7,19.
Задача 7,16. Построить кривую Фиг. 7,19.
Указание. Найти полярное уравнение кривой. Поместить
полюс в начало прямоугольной системы координат, а полярную
ось совместить с положительной частью оси абсцисс. Воспользо-
Воспользоваться формулами G, 1). Уравнение данной кривой в полярных
координатах имеет вид
г = 2а cos3 ср.
Из рассмотрения данного уравнения мы заключаем, что при лю-
любых значениях х и у его левая часть не отрицательна, так как
она содержит квадрат суммы х2 + У%- Значит, и правая его часть
2axs(a> 0) не может быть отрицательной, т. е. х не может при-
принимать отрицательных значений. Это говорит о том, что вся кри-
кривая будет расположена вправо от оси Оу.
Так как замена в данном уравнении у-на —у не изменяет
уравнения, то очевидно, что кривая расположена симметрично
относительно оси абсцисс. Значит, достаточно построить кривую
в первой четверти, а затем симметричную ей часть — в четвертой
четверти. Эти соображения говорят о том, что полярному углу ср
в уравнении данной кривой г = 2а cos3 ср следует придавать зна-
значения только от ср = 0 до ср = -2. Таким образом, это простое
71
исследование помогло нам значительно упростить вычисления, так
как теперь, вместо того, чтобы придавать полярному углу ср зна-
значения от ср = 0 до <р = 2те, мы ограничимся значениями для ср
только из первой четверти (кривая изображена на фиг. 7, 20).
Задача 7,17 (для самостоятельного решения). Построить кри-
кривую
*в = А(х4 — у*).
Указание. Прежде всего усматриваем, что замена х на —х
и у на —у не изменяет уравнения кривой. Это говорит о том,
что кривая расположена симметрично относительно координатных
осей. Поэтому достаточно построить кривую только в первой
четверти, а потом, учитывая симметрию ее относительно коорди-
% • натных осей, построить ее в трех
/ остальных четвертях.
Фиг. 7,20.
Фиг. 7,21.
Перейдем к полярной системе координат, расположив ее так,
как было указано в предыд>мцей задаче. Используя формулы G, 1),
получим уравнение кривой в полярной системе координат
cos 2<p
cos8?
Так как полярный радиус г может принимать только действи-
действительные значения, то cos 2ср,-стоящий под знаком корня в полу-
полученном уравнении, ие может быть отрицательным, т. е. должно
быть cos 2<р > 0. Это значит, что угол 2ср должен находиться или
в первой, или в четвертой четверти. Но мы уже выяснили, что
достаточно построить кривую только в первой четверти, а поэтому
будем рассматривать значения 2<р, удовлетворяющие условию
0 < 2ср < —. Отсюда следует, что для построения кривой в пер-
первой четверти углу ср следует придавать значения от <р = 0 до ср =
=-J-. Эскиз кривой показан на фиг. 7,21.
Задача 7, 18 (для самостоятельного решения). Построить спи-
спираль Архимеда г = аср (а > 0).
72
Задача 7, 19 (для самостоятельного решения). Построить кар-
кардиоиду
г = 2аA +coscp) (а> 0).
Задача 7, 20 (для самостоятельного решения). Построить ги-
гиперболическую спираль
ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Составление уравнения кривой по ее геометрическим свой-
свойствам.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Составить уравнение линии на плоскости в выбранной систе-
системе координат — это значит составить такое уравнение с двумя
переменными, которому удовле1
творяют координаты любой
точки, лежащей на этой линии,
и не удовлетворяют координа-
координаты точек, которые на этой ли- /х*""^ Г \0 Р
нии не лежат (это определение О\
следует усвоить, так как оно
неоднократно в дальнейшем ис-
используется).
. Для вывода уравнения ли-
линии поступают так:
1: Выбирают на плоскости Фиг. 8,1.
систему координат.
2. На линии, уравнение которой выводится, берут произволь-
произвольную точку. Координаты этой точки обозначают через х и у, если
уравнение линии выводится в прямоугольных координатах, или
через г и <р. если оно выводится в полярных координатах. Осно-
Основываясь на заданном свойстве всех точек, лежащих на линии,
составляют уравнение, связывающее координаты произвольной
точки с некоторыми постоянными величинами, данными в задаче.
Найденное уравнение и будет искомым.
Задача 8, 1. Составить уравнение окружности, проходящей
через полюс системы координат, центр которой С лежит на по-
полярной оси, а радиус равен R (фиг. 8, 1), и найти уравнение
этой окружности в прямоугольных координатах.
Для вывода уравнения'окружности, указанной в задаче, возь-
возьмем на окружности произвольную точку А (г, tp) и соединим ее с
точкой В — концом диаметра. Угол ОАВ — прямой, а потому,
так как диаметр равен 2R, из прямоугольного треугольника АОВ
получаем <
г = 2R cos ср.
73
Это и будет искомое уравнение. Теперь преобразуем это уравне-
уравнение к прямоугольным координатам. Используя формулы перехода
G, 2), будем иметь
Умножая обе части уравнения на ± Ух2-\-уг, получим
х2 + г/2 = 2Rx, или х2 -f- у2 — 2Rx = 0.
Задача 8, 2 (для самостояаельного решения). Найти уравнение
окружности радиуса R, проходящей через полюс, центр которой С
лежит на прямой, перпендикулярной полярной оси и проходящей
через полюс (фиг. 8, 2). Найти урав-
уравнение этой окружности в прямоуголь-
ных коордииатах.
/I
О
Фиг. 8,2.
В
Фиг. 8,3.
Ответ. Искомое уравнение в полярной системе координат
г = 2/? sin ср.
Уравнение этой окружности в прямоугольных коордииатах
2*2R 0
+yy
Задача 8, 3 (для самостоятельного решения) Найти уравнение
окружности радиуса а, центр которой находится в полюсе. На-
Написать уравнение этой окружности в прямоугольной системе ко-
координат.
Ответ, г = а; в прямоугольной системе координат
Задача 8, 4. Отрезок А В неизменной длины 2/ скользит своими
концами по сторонам прямого угла. Из вершины угла на этот
отрезок опущен перпендикуляр ОС. Найти геометрическое место
оснований таких перпендикуляров. Построить кривую и иайти ее
уравнение в прямоугольных координатах.
Решение. Поместим полюс полярной системы координат в
вершину прямого угла, а полярную ось направим по одной из
сторон прямого угла — например, по стороне ОВ (фиг. 8,3).
74 " •
Пусть точка С имеет полярные координаты г и ср. Тогда
BC = rtgcp
АС == г ctg <p
но
а отсюда
ВС + AC = 21 и г (tgcp -j- ctgcp) = 21,
sin?
sin2 ? +cos2 у = 2^
sin <j> • cos v '
r . _ ¦- ~ 21, или r = / sin 2<p.
tj- sin 2f
Это и есть искомое уравнение.
Значит, наше геометрическое место
имеет уравнение
г— /sin 2cp,
Кривая — четырехлепестковая роза (фиг. 8,4).
Теперь постройте кривую (полярному углу ср придавать значе-
значения от ср = 0 до ср = 2те через промежуток а = -5-V Найдем урав-
уравнение этой кривой в прямоугольной системе координат. Уравне-
Уравнение кривой перепишем в виде г = 2/sincp • coscp (sin2cp == 2 sin cpx
x coscp). Используя формулы G, 2) для перехода от полярной си-
системы координат к прямоугольной, получим
Фиг. 8,4.
± !/*¦
= 2/
а отсюда, возводя в квадрат обе части равенства, будем иметь
окончательно
(г8 + уу - Я*х*у\
Сравнивая уравнение нашей кривой в прямоугольных коорди-
координатах с ее уравнением в полярных координатах
г = / si-n 2cp,
мы усматриваем, что последнее значительно проще. Кривая по-
получается поворота» на 45е кривой, изображенной на фиг. 7, 13.
Задача 8,5. Найти уравнение геометрического места точек,
произведение расстояний которых до двух данных точек А и В
есть величина постоянная, равная <Д Длину АВ считать рав-
равной 2а.
7S
Решение. Проведем вывод уравнения в прямоугольных ко-
координатах. Направим ось Ох по прямой, соединяющей Л и Б,
как обычно, вправо, начало координат поместим в средине от-
отрезка АВ, ось Оу направим вверх по перпендикуляру к оси Ох.
Длина отрезка АВ по условию равна 2а(АВ = 2а); тогда точки
А и В будут иметь координаты: А (—а, 0); В (а, 0). Пусть точка М
принадлежит кривой. Ее координаты обозначим через л; и у
(фиг. 8,5).
Из условия задачи AM -ВМ = а2. По формуле расстояния
между двумя точками
AM = V(x + аJ + у2, ВМ = V(x—aJ±y*.
Значит,
или
^_х Возведем обе части этого урав-
3{а;0) нения в квадрат:
Фиг. 8,5. __а41
[(х* + У2 + а2) + 2ах] [(х2 + у2 + а2) -2ах] = а4;
Упрощая, получаем
Это и есть искомое уравнение.
Преобразуем теперь это уравнение к полярным координатам,
поместив полюс полярной системы координат в начале прямо-
прямоугольной системы координат, а полярную ось направим по поло-
положительной полуоси Ох. Подставляя в последнее уравнение зна-
значения х и у из формул перехода G, 1), будем иметь
г4 = 2aV2 (cos2 ср — sinacp).
Замечая, что cos2cp—sin2 ср = cos 2cp, и сокращая на г2, полу-
получим окончательно V
Кривая, определяемая этим уравнением, называется лемниска-
лемнискатой Бернулли. Постройте теперь эту кривую.
Так же, как в задаче 7, 12, составьте таблицу значений г по
известным значениям ср, имея в виду, что так как полярный ра-
радиус может принимать только действительные значения, то кривая
не может быть расположена в тех секторах, где полярный ра-
радиус имеет мнимые значения.
76
Это будет иметь место для значений сротср=-^доср = -5-тс
5 7
и от <p = -4"'t до ? = j«i а поэтому в этих секторах точек кри-
кривой нет. На фиг. 8, б эти секторы заштрихованы, а кривая изо-
изображена на фиг. 8, 7.
Фиг. 8,6.
Фиг. 8,7.
ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений в составлении уравнений
лин ий.
Это практическое занятие является продолжением предыду-
предыдущего. Мы будем составлять уравнение линии по извест-
известному свойству, общему всем ее точкам.
Задача 9,1., Найти геометрическое
место точек, равноудаленных от двух
данных! точек."
Решение. Возьмем прямоуголь-
прямоугольную систему координат и пусть две
данные точки В и С лежат на оси
абсцисс и имеют координаты (xlt 0) и
(х2, 0) (фиг. 9, 1). Пусть точка А при-
принадлежит искомому геометрическому
месту. Обозначим ее координаты через
х и у: 4.(х, У).
На основании формулы для определения расстояния между
двумя точками
АВ = У(х-х^ + у*, AC = V(x-x2)* + y\
и значит, так как по условию АВ — АС, мы можем лаписать,
что
У
0
в
I
С
(х,:Ш
Фиг. 9,1.
V(x - Xlf + у* = V(x - x2)s + у\
Это и есть уравнение искомого геометрического места.
Возводя в квадрат обе части последнего равенства, будем
и меть
77
После очевидных упрощений получим
2х (х2 — х,) = {х2 — л;,) (х2 + X,);
сокращая на х2 — хх (х2 — ххф0), имеем
2х = хх + х2,
или
Это уравнение прямой; перпендикулярной оси Ох и про-
проходящей через середину отрезка ВС.
Итак, искомым геометрическим местом является прямая, пер-
перпендикулярная к отрезку ВС, соединяющему данные точки, и
проходящая через его средину.
Замечание. При решении задачи нам пришлось уничтожить
радикалы в уравнении искомого геометрического места
V(x-Xiy + y* = V(x-Xi)* + y*, (A)
в результате чего было получено уравнение
*1 -f- Х2 / п\
х — —g— • \В)
Из алгебры известно, что возведение обеих частей уравнения
в квадрат может привести к уравнению, которое не равносильно
(не эквивалентно) исходному. Это значит, что уравнение, полу-
полученное от возведения в квадрат обеих частей исходного уравнения,
может иметь решения, не удовлетворяющие исходному уравнению,
т. е. иметь так называемые «посторонние» корни. Поэтому всегда
в тех случаях, когда обе части уравнения приходится возводить
в квадрат, следует ставить вопрос об эквивалентности получен-
полученного и исходного уравнений.
В интересующем нас случае вопрос ставится так: не содер-
содержит ли линия (В) точек, которых нет на линии (А), т. е. таких,
координаты которых не удовлетворяют уравнению (А) и таким
образом не удовлетворяют исходному условию АВ = АС.
Чтобы убедиться в том, что линия (В) не содержит точек,
которых нет в линии (А), надо показать, что уравнение (В) мо-
может быть преобразовано в уравнение (А).
Произведя в обратном порядке операции, с помощью которых
было получено уравнение (В), мы придем к уравнению
(х-Х1Г+у2 = (х-хяу + у*,
откуда следует, что
У(-Х1г + у* = ± V(x-Xt)' + y; (о
т. е. что АВ = ±АС; отсюда видно, что или Л5 — ЛС = 0, или
ЛВ + ЛС 0
78
Но А~В>0 и Л С> 0, а следовательно, А В + АС фО, так
как сумма двух положительных величин не может быть равна
нулю, а потому остается только одно равенство А В —
—ЛС=0, т. е. АВ = АС, и знак минус перед корнем в правой
части уравнения (С) должен быть отброшен. Поскольку из урав-
уравнения (Л) получается уравнение (В) и обратно — из уравнения
(В) следует уравнение (Л), то эти уравнения равносильны (экви-
(эквивалентны). Таким образом, поставленный нами вопрос решен:
линия (В) не содержит таких точек, которых нет на линии (Л).
У
Bfx.-ff)
Фиг. 9,2'.
Фиг. 9,3.
При решении следующих задач этого практического занятия
нам придется часто обе части исходного уравнения возводить
в квадрат. Учащийся должен знать, что всякий раз в таком
случае перед ним должен возникать вопрос об эквивалентности
полученного и исходного уравнений. Однако мы во всех по-
последующих задачах этим заниматься не будем, а заметим только,
что эквивалентность исходного и окончательного уравнений в этих
задачах действительно имеет место.
Задача 9, 2 (для самостоятельного решения). Найти уравнение
геометрического места точек, одинаково удаленных от начала
координат и от точки А (—3, 4) (фиг. 9, 2).
Ответ. 6* — 8# + 25 = 0.
Проверьте, что эта прямая перпендикулярна отрезку АО и
проходит через его середину.
Задача 9,3 (для самостоятельного решения). Найти геомет-
геометрическое место точек, одинаково удаленных от прямой х — —4
и точки Л F, 0).
Указание. Пусть точка В (х, у) принадлежит искомому геомет-
геометрическому месту (фиг. ^9,3). По условию расстояния от точки В
до прямой х = — 4 и до точки Л (б, 0) между собою равны, т. е.
АВ — ВС. По формуле для определения расстояния между двумя
точками
АВ = VJx^WT^
^WT^, а ВС = х + 4
V(x — бJ + у2 = х + 4.
79
Ответ. у2—20(х—1). Эскиз кривой показан на фиг. 9,4.
Как увидим в дальнейшем, это — уравнение параболы, и зна-
значит, искомым геометрическим местом является парабола.
Задача 9, 4 (для самостоятельного решения). Определить тра-
траекторию точки, которая движется так, что ее расстояние от точки
B, 3) равно ее расстоянию до прямой Зх -f- 4у — 5 =-¦ 0.
Указание. Пусть точка В (х, у) принадлежит искомому геомет-
геометрическому месту (фиг. 9,5). По условию ВС — АВ. Расстояние
ВС от точки В(х, у) до прямой Зх + 4у-- 5 = 0 найти по
правилу определения расстояния от точки до прямой (см. за-
задачу 5, 2). Получим
(
3* + 4у - 5
!|
0
6fa#)
у
K
Фиг. 9,4.
Фиг. 9,5.
Это и есть уравнение искомого геометрического места. Воз-
Возводя в квадрат обе части уравнения*, освобождаясь от дробей
и перенося все члены уравнения в его правую часть, получим
окончательно '
16а:2 — 24ху + 9г/2 — 70* — 1 Юг/ + 300 = 0.
Геометрическое место, уравнение которого мы нашли, есть
парабола.
Следует запомнить, что геометрическим местом точек, равноуда-
равноудаленных от данной точки и от данной прямой, является парабола.
Задача 9,5 (для самостоятельного решения). Найти уравнение
геометрического места точек, равноудаленных от прямой х -\- у —
— 2 = 0 и точки A, —1).
Ответ. Парабола х2 — 2ху + г/2 + 8г/ = 0.
Задача 9, 6 (для самостоятельного решения): Найти уравнение
траектории точки А, которая движется так, что.ее расстояние
от точки С(—5, 2) всегда равно 7 (фиг. 9,6).
* По поводу возведения в квадрат обеих частей уравнения см. замеча-
замечание к задаче 9, 1.
80
Ответ. Траектория — окружность л:2 -f у2 -f- 10х — 4у— 20 = О
с центром в точке С (—5, 2) и радиус ее R = 7.
Задача 9,7. Найти траекторию точки А, которая движется
так, что ее расстояние до точки 6B, 4) в два раза меньше, чем
и до точки С(—6, 2).
Фиг. 9,6.
Фиг. 9,7.
Указание. Обозначить координаты точки А, как всегда,
через х и у (фиг. 9,7). По условию АС — 2АВ.
АС = V(x + 6J + (y — 2f\ АВ = V(x — 2f +{y — 4J.
Значит, из АС = 2ЛВ получаем,
что
О
Фиг. 9,8.
Ответ. Траекторией является
окружность Зх2 + Зу2 — 2&с —
— 28t/ + 40 = 0 с центром в точке
[j, jj, а ее радиус /-^5,5.
Задача 9,8 (для самостоятель-
самостоятельного решения). Точка А дви-
движется так, что отношение ее рас-
расстояния до точки В B, 3) к ее
расстоянию до прямой х-\-2у — 4 = 0 равно-к-. Найти уравнение
траектории точки.
Указание. Обозначить координаты точки А через х и у
(фиг. 9,8). Расстояние точки А (х, у) до точки В B, 3) АВ —
= V{x — 2J + (у — ЗM, а ее расстояние АС до прямой *-f 2y —
— 4 = 0 будет равно
ЛВ 1
по условию дс = -j.
4 И. А. Каплан
81
Отсюда
итсюда
1.
2
V5
•-JT
Фиг. 9,9.
Ответ. Уравнение траектории
19ха — Аху + 16уа - 72* — №у + 244 = 0.
Задача 9, 9 (для самостоятельного решения). Найти уравнение
геометрического места точек, сумма расстояний которых от точек
FtB, 3) и FaD, 5) есть величина постоянная, равная 10
(фиг. 9,9).
Ответ. 24ха — 2ху + 24г/2 — 136х — Шу +1=0 (эллипс).
Задача 9,10 (для самостоятельного решения). Найти уравнение
геометрического места точек, расстояние каждой из которых от
данной прямой А В в два раза мень-
меньше расстояния от данной точки С, не
лежащей на этой прямой.
Указание. Направить ось Ох по
данной прямой А В, а ось Оу по пер-
перпендикуляру к оси Ох, проходящему
через данную точку С. Координаты точ-
точки С пусть будут @, b) (b ф 0).
Ответ, х2 — Зу2 —• 2Ьу + Ь2 = 0 (ги-
(гипербола).
Следует иметь в виду,что уравнение
геометрического места в выбранной систе-
системе координат может оказаться более или
менее сложным в зависимости от расположения координатных осей
в выбранной системе координат. В данном случае, если бы мы
направили ось Оу не через точку С, то абсцисса точки С уже
была бы равна не нулю, а скажем, а, и уравнение геометри-
геометрического места оказалось бы более сложным. : Следует, однако,
помнить, что в зависимости от того или иного расположения ко-
координатных осей может измениться только уравнение линии, но
не сама линия.
Задача 9,11 (для самостоятельного решения). Найти геоме-
геометрическое место оснований перпендикуляров, опущенных из на-
начала координат на прямые, проходящие через точку (а, Ь).
Ответ. Окружность х2 -j-j/2 — ах — by = 0.
ДЕСЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Кривые второго порядка: окружность, эллипс.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Окружность. Окружностью называется геометрическое место
точек, равноудаленных от одной и той же точки.
Уравнение окружности имеет вид
(х — а)* + (у — Ь)*=>г\ A0,1)
82
где а и Ь — координаты центра окружности, а г — радиус ок-
окружности.
Если же центр окружности находится в начале координат, то ее
уравнение имеет вид
x2+j'»=rl. A0,2)
2. Эллипс. Эллипсом называется геометрическое место точек,
для которых сумма расстояний до двух данных фиксированных
точек (фокусов) есть для всех точек эллипса одна и та же по-
постоянная величина (эта постоянная величина должна быть больше,
чем расстояние между фокусами).
Простейшее уравнение эллипса
где а — большая полуось эллипса,
Ь — малая полуось эллипса.
Если 2с — расстояние между фокусами, то между а, Ь и с (если
а > Ь) существует соотношение
а2 — Ьг = с2. A0,4)
Эксцентриситетом эллипса называется отношение расстояния
между фокусами этого эллипса к длине его большой оси
в = А A0, 5)
У эллипса эксцентриситет е < 1 (так как с<С.а), а его фокусы
лежат на большой оси.
Задача 10,1. Написать уравнение окружности с центром в
точке С B, —3) и радиусом, равным 6.
Решение. По уравнению A0,1), полагая в нем а = 2, Ь =
= — 3, г = 6, сразу имеем (х — 2)а -f (у -f 3J = 36, или
х* + у* —4х + 6у —23 = 0.
Задача 10, 2. (для самостоятельного решения). Написать урав-
уравнение окружности с центром в точке (—4,7) и радиусом, рав-
равным 7.
Ответ, (х + АJ + (у— 7J = 49,
или
х2 +уг + 8х — Ну + 16 = 0.
Задача 10, 3. Показать, что
*2+у2 + 4х-6г/-3 = 0
есть уравнение окружности. Найти ее центр и радиус.
Решение. Заданное уравнение преобразуем к виду A0,1).
Выпишем члены, содержащие только х, и члены, содержащие
только у. Легко проверить (сделайте это!), что
*«-|-4* = (х + 2)*—4, :
ВЗ
Левая часть уравнения запишется теперь так:
х2 -f- Ах у2 — 6у
или отсюда
(х + 2J + (</-3J=16. (А)
Сравнивая уравнение (А) с A0, 1), заключаем, что это уравнение
определяет окружность, центр которой имеет координаты С(—2, 3),
г2 = 16, а г = 4.
Задача 10, 4. Найти координаты центра и радиус окружности
х2 +у2 — х + 2у — 1 =0.
Решение. Преобразуем уравнение к виду A0,1).
Соберем члены, содержащие только х и только у:
j
Заданное уравнение перепишется в виде
-т+&+!)•-1-1 =-0.
х2-х у2+2у
или
2
и окончательно в виде
М2
Следовательно, из сравнения с уравнением A0, 1) заключаем,
что центр окружности находится в точке /у, —1), а радиус ра-
равен |.
Задача 10,5 (для самостоятельного решения). Найти коорди-
координаты центра и радиус окружности
х2+у*+3х-7у—1=0.
Ответ. (-1; |), г = 4.
Задача 10,6 (для самостоятельного решения). Найти коорди-
координаты центра и радиус окружности
хг +у*+х-у = 0.
о,..,. (-1,1), ,~Ц.
84
Задача 10,7. Найти точки пересечения окружности (х—IJ +
-\- (г/ — 2J = 4 и прямой у — 2х.
Решение. Координаты точек пересечения должны удовле-
удовлетворять обоим указанным уравнениям, так кай эти точки нахо-
находятся как на одной, так и на другой линии. Решим систему урав-
уравнений
')¦
у = 2х
Подставляя в первое уравнение 2х вместо у и раскрывая скобки,
получим
х* _ 2х + 1 + 4xz — 8* -f 4 = 4,
или
5х2 — 10х + 1 = 0,
а отсюда
_ 5 + 2/ 5-2^5"
Хг- g , Хч— g .
Подставляя эти значения во второе уравнение у = 2х, получим
10+4J/T 10 — 4/5"
</i = 5 ' ^2 = 5 *
Искомыми точками пересечения будут А (х1г у-^), В (х2, Уг).
А E + 2У~Ь 10+4Vt\ R /5-2^5
А \ 5 ' 5 ) И ° \ 5
Задача 10,8. Написать уравнение окружности, проходящей
через три точки: @, 1); B,0); C,—1).
Решение. Искомое уравнение имеет вид (х — аJ + (у — бJ =
= г2. Поскольку окружность проходит через указанные точки,
координаты каждой из этих точек удовлетворяют уравнению
окружности. Подставляя поочередно в искомое уравнение коор-
координаты данных точек, получим три уравнения для определения
a, b и г. Вот эти уравнения:
B —аJ + 62=г2
C-аJ + (-1-6J =
Возьмем уравнения первое и второе, а потом первое и третье.
Правые части этих уравнений между собой равны, значит, равны
и левые их части, и мы получаем
Раскрывая скобки и упрощая, будем иметь
4а—2fe=3|
6а — Ab = 9J*
85
3 9
Отсюда а — — у, b = —у. Подставляя эти значения аи b в
первое из уравнений системы, получим г2 = -=-. Искомое уравне-
ние имеет вид
или после упрощений х2
+ У2 + Зх + 9у — 10 = 0.
Задача 10, 9. Найти уравнение окру-
окружности, касающейся оси Ох в начале
координат и пересекающей ось Оу в
точке А @, 10) (фиг. 10, 1).
Решение. Известно, что диаметр
окружности, проведенный в точку ка-
касания, перпендикулярен касательной.
Это значит, что диаметр О А' окружно-
окружности направлен по оси Оу, центр окру-
окружности находится в точке С @,5), а
радиус окружности г = 5. Искомое урав-
уравнение имеет вид
х2 + (у — 5J -= 25, или х2 + у2 — Юг/ = 0.
Задача 10, 10 (для самостоятельного решения). Найти уравне-
уравнение окружности, касающейся оси Оу в начале координат и пере-
пересекающей ось Ох в точке (—12, 0).
Ответ.1 х2 + уг + 12л: = 0.
Задача 10,11. Составить простейшее уравнение эллипса, зная,
что: а) полуоси его а — 6, b = 4; б) расстояние между фокусами
2с = 10, а большая ось 2а — 16; в) малая полуось 6=4, и рас-
расстояние между фокусами 2с == 10; г) большая полуось а = 12, а
эксцентриситет е = 0,5; д) малая полуось b ~ 8, а эксцентриситет
е = 0,6; е) сумма полуосей а + b = 12, а расстояние между фоку-
фокусами 2c = *bV~2.
Решение, а) Простейшее уравнение эллипса имеет вид
^г + тг = 1- Подставляя сюда а — 6, 6 = 4, получим
36 "^ 16 ~ 1'
б) У нас 2с =10; с = 5;
2а = 16; а = 8.
Чтобы написать уравнение эллипса, следует найти малую по-
полуось Ь. Между величинами а, Ь и с у эллипса существует зави-
зависимость о2 — Ь2 = с2, или Ь2 = а2 — с2. В нашем случае Ь2 — 64 —
— 25 = 39, и уравнение эллипса будет иметь вид
64
„a
»
39
86
в) Решите самостоятельно.
Ответ. ? + Й = 1. -
г) а = 12; е — 0,5; известно, что е = —; в этой формуле не-
неизвестно с. Для его определения получаем уравнение
0,5 = j^; отсюда с = 6.
Теперь, зная, что а = 12, с = 6, пользуясь соотношением а2 —
— с2 = ft2, найдем, что Ьг = 144—36 = 108; а2 = 144.
Уравнение будет щ + щ = 1-
д) 6 = 8; е = 0,6; ^ — —> отсюда — = 0,6, с = 0,6а. Напишем
соотношение а2 — с2 = Ь2 и подставим в него с = 0,6а; Ь = 8.
Получим а2 — 0,36а2 = 64; 0,64а2 = 64; а2 = 100.
Уравнение эллипса будет иметь вид
100 '64
е) а+ 6= 12, 2с =
Для определения уравнения эллипса надо знать а и Ь. Нам
известно, что с = 3 "j/1; с2 = 18; а2 — Ьг = cV
Поэтому (а -f 6) • (а — 6) = 18. Подставляя сюда а + Ь = 12,
найдем, что а — 6=1,5.
Решая систему уравнений
а + Ь = 12)
a — 6 = l,5j'
получим, что а = 6,75, b — 5,25.
Уравнение эллипса запишется в виде
^Lj-^L 1
6,75* "^ 5,252 ~ ь
Задача 10,12. Найти длины осей, координаты фокусов и экс-
эксцентриситет эллипса
4х2 + 9у2 = 144.
Решение. Преобразуем это уравнение к простейшему виду
"т + р = 1- Разделив обе части заданного уравнения на 144, по-
Отсюда заключаем, что а2 = 36, Ь2 = 16. Значит, а = 6, 2а =
= 12; Ь =4; 2Ь = 8. Таким образом, длины осей равны соответ-
соответственно 12 и 8.- Зная а и Ь, из соотношения а? — с2 =i b2 най-
найдем с. Подставим а = 6; b = 4 и получим, что с — 2 У" 5. Коор-
87
динаты фокусов будут B|^5,0) и (—2 ]/" 5, 0). Эксцентриситет
эллипса
Задача 10, 13 (для самостоятельного решения). Найти длины
осей, координаты фокусов и эксцентриситет эллипса
16л:2 + 9у2 = 144.
Указание. Фокусы эллипса лежат на его большой оси.
Большая ось заданного эллипса лежит на оси Оу, как вы легко
усмотрите, получив простейшее урав-
уравнение эллипса.
Ответ. Большая ось равна 8,
малая 6. Координаты фокусов
Задача 10, 14. Отрезок ВС посто-
постоянной длины / движется своими кон-
концами по сторонам прямого угла ВОС.
Какую линию опишет на этом отрезке
точка А, разделяющая его в отно-
отношении X I j^. = X)?
Решение. Стороны прямого угла, о котором идет речь в
задаче, примем за оси прямоугольной системы координат (фиг. 10, 2),
Если мы обозначим через тип отрезки, отсекаемые отрезком
ВС соответственно на координатных осях Ох и Оу, то во все вре-
время движения будет сохраняться равенство
т2 + п2 = /2.
Координаты точек В и С будут В @, п), С (т, 0), Координаты
точки А обозначим через хну. Тогда по формулам B, 1) для
определения координат точки, делящей отрезок в данном отноше-
отношении, получаем
О+Х/л Хт п + Х • 0 п
x m
X ~ 1 + X' у ~ 1 + Х-
Возведем обе части каждого из этих равенств в квадрат и по-
почленно их сложим. Получим
Т* + У" = о + X)" •
вспоминая, что /п2 + /г2 = /2, имеем
* 4- ,fl - р
\г-ГУ - A + хр
а отсюда,, деля обе части этого уравнения на его правую часть,
запишем искомое уравнение в виде
Искомым геометрическим местом является эллипс с полуосями*
__
и &=
ОДИННАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Кривые второго порядка: гипербола, парабола.
Основные сведения из теории
Гипербола. Гиперболой называется геометрическое место точек,
разность расстояний которых от двух данных фиксированных
точек (фокусов) гиперболы есть одна и та же постоянная вели-
величина. Предполагается, что эта постоянная величина не равна нулю
и меньше, чем расстояние между фокусами.
Простейшее уравнение гиперболы
Здесь а — действительная полуось гиперболы, Ь — мнимая
полуось гиперболы.
Если 2с — расстояние между фокусами гиперболы, то между
a, b и с существует соотношение
а2 + Ь*=с\ A1,2)
При b = а гипербола называется равносторонней. Уравнение
равносторонней гиперболы имеет вид
х* — ф = а*. A1,3)
Фокусы гиперболы лежат на ее действительной оси.
Эксцентриситетом гиперболы называется отношение расстояния
между фокусами этой гиперболы к длине ее действительной оси
е=с-. A1,4)
Асимптоты гиперболы —две прямые, определяемые уравне-
уравнениями
*
Напомним, что асимптотой кривой, имеющей бесконечную
ветвь, называется прямая, которая обладает тем свойством, что
когда точка по кривой удаляется в бесконечность, ее расстояние
до этой прямой стремится к нулю.
Парабола. Параболой называется геометрическое место точек,
каждая из которых одинаково удалена от заданной фиксированной
точки и от заданной фиксированной прямой. Точка, о которой
идет речь в определении, называется фокусом параболы, а пря-
прямая — ее директрисой.
Простейшее уравнение параболы
^ A1,6)
Входящая в это уравнение величина р называется параметром
параболы. Параметр параболы равен - расстоянию от директрисы
параболы до ее фокуса.
Координаты фокуса F параболы A1,6) Wy , О). Уравнение
директрисы параболы A1,6)
* = -?. (Н.7)
Эксцентриситет параболы е = 1.
Гипербола
Задача 11,1. Составить простейшее уравнение гиперболы,- если
расстояние между вершинами ее равно 20, а расстояние между
фокусами 30.
Решение. Вершины гиперболы ле#сат на ее действительной
оси. По условию 2а =20; 2с—30. Значит, а = 10; с— 15;
а2 = 100; с2 = 225.
Величины а, Ь и с у гиперболы связаны соотношением A1,2)
а2 + Ь% = с2;
отсюда Ь2 = с2 — а2 = 225 — 100; 6а = 125.
Значит, уравнением гиперболы будет
f!__il_ 1
100 125 *
Задача 11,2. Действительная полуось гиперболы равна 5,
эксцентриситет е = 1,4. Найти уравнение гиперболы.
90
Решение. У нас а = 5, а2 = 25; е=^-=1,4; с=1,4а =
= 1,4 • 5 = 7, с2 = 49; б2 = с2 — а2 = 49 — 25 = 24, Ь2 = 24; иско-
искомым уравнением будет
25 24 '
Задача 11,3. Г.ипербола проходит через точки C, —^—) и
(—21/5, 3). Найти уравнение гиперболы.
Решение. Уравнение гиперболы A1, 1) может быть запи-
записано так:
ЬЧг— агу2 = а2Ь2. A1,8)
Определению подлежат а2 и б2. Подставим в это уравнение ко-
координаты первой точки и получим
4562 — 12а2 =
Подставляя в уравнение гиперболы A1,8) координаты второй
точки, получим
2062 — 9а2 = а2ЬК
Решим систему уравнений
2062 — 9а2 =
4562 — 12а2 = )
Умножая первое уравнение на 4, а второе на 3 и вычитая из
втор&го первое, получим а2 = 5. Подставим а2 = 5 в первое урав-
уравнение н получим 2062 — 45 = 562, откуда Ьг = 3. Подставляя
найденные значения а2 и б2 в A1,8), получим, что искомое урав-
уравнение имеет вид
Зд;2 — 5г/а = 15.
Задача 11,4. Найти уравнение асимптот гиперболы
2х2 — 3t/8 = 6.
Решение. У гиперболы- две асимптоты, определяемые урав-
уравнениями A1,5). Следует найти а и Ь.
Приведем уравнение гиперболы к простейшему виду, разде-
разделив обе его части на 6. Получим
*• у* .
Отсюда заключаем, чт а2 = 3, а — Y%; Ьг = 2, Ь — ]/2. Подстав-
Подставляя эти значения а и Ь в уравнения асимптот A1,5) получаем
— }/Иу = 0 и 1/2*+1/30 = 0.
91
Задача 11,5 (для самостоятельного решения). Дана гипербола
Найти уравнения ее асимптот.
Ответ. Уравнения асимптот
у = тх и г/= —jx.
Задача 11, 6. Найти эксцентриситет гиперболы 25дс2—36у2=900.
Указание. Привести уравнение гиперболы к простейшему
виду A1,1)- Окажется, что а = 6; Ь = Ъ; из A1,2) следует, что
с = |/1. Эксцентриситет е = —, е = J-g- .
Задача 11,7. Уравнения асимптот гиперболы у=^х и # =
= — -jx> a расстояние между фокусами 2с = 10. Найти уравне-
уравнение гиперболы.
Решение. Уравнения асимптот гиперболы имеют вид A1,5).
Из условия задачи следует, что: 1) — = -^ и а = 2Ь\ 2) с = 5.
Подставляя в соотношение A1,2) значения а =2Ь и с = 5, полу-
получим B6J + Ь2 = 25; б2 = 5; а = 26, а потому а2 = 4й2 = 20. Иско-
мым уравнением гиперболы будет ^—{=¦ = !•
*2 «2
Задача 11,8. На правой ветви гиперболы 55 — Т ~ ^ наити
точку, расстояние которой от асимптоты с отрицательным угло-
угловым коэффициентом было бы в два раза больше, чем расстояние
ее от асимптоты с положительным угловым коэффициентом.
Решение. Так как у нас а2 =25; а = 5; Ь2 = 9; b = 3, то
на основании A1,5) уравнение асимптоты с отрицательным угло-
вым коэффициентом запишется в виде у = —-^х, или Зле + 5у—0,
а уравнение асимптоты с положительным угловым коэффи-
коэффициентом
у = — х, или Ъх — Ъу = 0.
Возьмем на правой ветви гиперболы точку А с координатами
хну. Ее расстояние dx до асимптоты Ъх + Ъу = 0, определен-
определенное по правилу нахождения расстояния от точки до прямой,
будет dx =
Зх+5у
/34
Расстояние d2 этой точки до асимптоты
Ъх — 5у = 0
2~ /34
92
По условию dx = 2й?2, или
3* +__5f
/34
Отсюда или
о чл. — чу
~ 1зТ
= 2 3* ~ 5j
Зх -f 5у _ о Зх - 5у
ум ~ ум
или
Из (А) следует, что
Зх + 5у=—6х+10у; * = |«/.
Из (В) вытекает, что
3* + Ъу = 6х — Юу; Зх— 15t/ = 0; х = Ъу.
Полученные соотношения х — Ьу и х — -^у есть зависимости
между абсциссой и ординатой искомой точки. Подставим сначала
х = 5г/ в уравнение данной гиперболы. Из условия задачи sg — -§¦ = U
= Ъу, т. е. л:х =
15/2"
7
15/2
1
= — ^J^; У нас
Но по условию задачи точка лежит на правой ветви гипер-
гиперболы. Значит, абсцисса ее положительна, и значение х% = ¦——
должно быть отброшено. Ордината точки на правой ветви гипер-
гиперболы может быть как положительной, так и отрицательной. Но
из того, что х = Ъу, следует, что у должен иметь такой же знак,
как и я, а потому, так как абсцисса х положительна, ордината
/1Г
должно
не может быть отрицательной. Значение у2 =
быть отброшено, и окончательно
_
х
15/?
_3/2~
У— ~ •
Убедитесь самостоятельно, что зависимость х — ¦=¦ у приводит к
мнимым значениям у. На этой гиперболе нет точки, для которой
5 /15/*2 3/~2\
х — -^у. Таким образом, есть только одна точка I—|—, ——),
удовлетворяющая условию задачи.
Задача 11,9 (для самостоятельного решения). Найти острый
угол между асимптотами гиперболы, если ее эксцентриситет
равен 2.
93
Указание. Воспользоваться формулой A1,4) и заменить в
ней с по формуле A1,2), откуда должно получиться соотношение
4аг = а2 + Ь2,
За2 = Ь\ Ь = ± аУЪ, - = ± 1/3.
a
Подставляя это значение — в уравнения асимптот гиперболы
A1,5), получим
Угол между асимптотами найдем по формуле
где kx — 1/3, k2 = —]/3~. Отсюда заключаем, что угол <р = 60°*.
Задача 11,10. Дана равносторонняя гипербола х2 — у2 = 8.
Найти уравнение эллипса, фокусы которого находятся в фокусах
гиперболы, если известно, что эллипс проходит через точку
А D, 6).
Решение. Уравнение гиперболы преобразуем к простей-
простейшему виду и получим у — ^- = 1, а2 = Ь2 = 8. Из соотношения
A1,2) получаем, что с = 4. Значит, координаты фокусов гипер-
гиперболы F2(—4,0) и Ft D,0). В этих точках находятся фокусы эл-
эллипса. Обозначим большую и малую полуоси эллипса через аг
и Ьг. Расстояние между фокусами эллипса такое же, как и рас-
расстояние между фокусами гиперболы. Поэтому половину этого
расстояния по-прежнему обозначаем через с. Но у эллипса
т. е. 4 = У а\ - Ь\ и а? —6?-= 16- (А)
Для определения аг и Ьх нужно найти еще одно соотношение,
связывающее их. Искомое уравнение эллипса запишется так:
Поскольку точка А D, 6) лежит на эллипсе, ее координаты
должны удовлетворять уравнению эллипса. Подставляя в послед-
* Угол между асимптотами может быть найден также из таких сооб-
соображений: угловой коэффициент одной асимптоты kx = Уъ, а другой — ?2 ==
= —УЪ. Это значит, что асимптоты составляют с положительным направле-
направлением оси Ох углы в 60 и 120°, а следовательно, острый угол » между ними
равен 120-60° =60°.
94
неё уравнение х — 4, у =6, получаем, что 36at -f 166, = a\b\-
Присоединяя уравнение (А) к этому уравнению, получаем для
определения а? и b\ систему уравнений
а\ -Ь\ =16
36at
= а\Ь\
откуда а? = 64; b] = 48. Подставляя эти значения в E), находим
искомое уравнение щ + %$= 1-
Парабола
Простейшее уравнение параболы имеет вид у2 = 2рх(р > 0).
Вершина этой параболы находится в начале координат, ее ось
направлена по оси Ох. Фокус этой параболы находится в точ-
точке F (^, 0], а директриса АВ имеет уравнение х = — у. Пара-
Парабола у2 = 2р* расположена ^
так, как указано на фиг. 11,1
(запомните, что фокус пара-
параболы лежит на ее оси сим- / р \
метрии). 12'у
Задача 11,11. Как распо- —
ложена относительно коор-
координатных осей линия у2 =
= — 2рх (р > 0)? Какая это
линия?
Решение. Прежде всего
замечаем, что эта кривая про-
проходит через начало координат, так как координаты точки @, 0)
удовлетворяют ее уравнению.
Левая часть уравнения при любом вещественном значении у
положительна, значит и правая часть также должна быть поло-
положительной. Так как величина р > 0 по условию, то это будет
иметь место только тогда, когда величина х не является поло-
положительной, т. е. когда х. < 0. Значит, х не может принимать
положительных значений. Из уравнения у2 = —2рх видно, что
при замене в нем у на — у оно не изменится. Это говорит о том,
что кривая расположена симметрично относительно оси Ох. Ка-
Какая это кривая линия?
Возьмем параболу у2 = 2рх. Замена в этом уравнений х на
— х переводит параболу в кривую у2 =— 2рх. Следовательно,
рассматриваемая кривая уг = — 2рх расположена симметрично
параболе у2 = 2рх относительно оси Оу. Значит, кривая у2 =
= —2рх—тоже парабола. Ее фокус и директриса симметричны
95
Фиг. 11,1.
фокусу и директрисе параболы у2 — 2рх относительно оси Оу:
фокус имеет координаты F(—-?-., 0), а директриса определяется
уравнением х = у (фиг. 11,2).
Составим теперь уравнение параболы, исходя из известного
определения этой кривой, выбрав такое расположение коорди-
координатных осей: примем за ось Оу прямую, проходящую через фо-
фокус параболы перпендикулярно к ее директрисе, а за положи-
положительное направление на ней возьмем направление от директрисы
F
S
Фиг, 11,3.
к фокусу. Начало координат поместим в точку, делящую по-
пополам расстояние между фокусом и директрисой. Ось Ох на-
направим, как обычно (фиг. 11,3). Итак, АВ—жданная прямая,
F — данная точка.
Если FC =р, то фокус F имеет координаты @, -§¦). Пусть
точка М (х, у) принадлежит параболе. Тогда из определения
параболы (см. стр. 90) следует, что FM = MD. По формуле
расстояния между двумя точками FM = Л/ х2 + (у — ¦§-) »
MD = 1/ (у + -п-) ; координаты любой точки кривой удовлетво-
удовлетворяют уравнению
и после очевидных упрощений будем иметь х2 — 2ру. Если раз-
разрешить это уравнение относительно у, то получится, что
1
2р
Обозначим g- = а (а > 0), так как по условию р > 0. Уравнение
параболы в этом случае будет иметь вид
у=ах2 (а>0).
96
Исследуем теперь расположение этой параболы относительно
координатных осей.
1. Точка с координатами @, 0) лежит на параболе, так как
из уравнения параболы усматриваем, что при х = 0 и у = 0,
т. е. парабола у = ах2 проходит через начало координат, являю-
являющееся вершиной параболы.
2. При замене х на — х уравнение у=--ах2 не изменяется.
Это значит, что парабола у = ах2 расположена симметрично отно-
относительно оси Оу.
-X
Фиг. 11,4.
Фиг. 11,5.
3. Так как по предположению а > 0, то при любом х, как
положительном, так и отрицательном, будет у > 0. Это значит,
что кривая расположена над осью Ох.
4. При возрастании х по абсолютной величине будет воз-
возрастать и у. Парабола у =. ах2 (а > 0) имеет вид, указанный
на фиг. 11,4. Координаты фокуса этой параболы найдем так:
у нас OF = -{j-, или с учетом того, что g- = а, получим р =
= .-, — — j-. Итак, фокус параболы у — ах2 имеет коорди-
координаты @, j-j • Если в уравнении параболы у = ах2 у заменить
на —у, то мы получим кривую, которая расположена симмет-
симметрично параболе у = ах2 относительно оси Ох. Значит, кривая
у — — ах2 — тоже парабола. Расположение ее показано на фиг. 11,5.
На фиг. 11,6—11,9 изображены параболы
у2г=2рх (фиг. 11,6)
у2=-2рх(фиг. 11,
= ах2 (фиг. 11,8)
--ох2 (фиг. 11,9)
97
Параболу, определяемую уравнением у = ах2, называют восхо-
восходящей, а параболу, определяемую уравнением у = — ах2,—
нисходящей.
Расположение этих парабол следует хорошо запомнить.
Задача 11,12. Парабола у2 = 2рх проходит через точку А B,4).
Определить ее параметр р.
Решение. Подставляем в уравнение параболы вместо теку-
текущих координат координаты точки А B, 4). Получаем
42 = 2р-2; 16 = 4р; р = 4.
У
Фиг. 11,6.
Фнг. 11,7.
Задача 11, 13. Составить уравнение параболы, зная, что вер-
вершина ее находится в начале координат и расстояние от фокуса
до вершины равно 4 единицам длины, а осью симметрии слу-
служит ось Ох.
О
Фиг. 11,8.
-JT
Фиг. 11,9.
Решение. Так как осью симметрии параболы служит ось
Ох, а вершиной — начало координат, то парабола может быть
определена одним из уравнений у2 — 2рх и у2 = '— 2р*. Параметр
параболы р есть расстояние от директрисы параболы до фокуса.
Расстояние от фокуса до вершины равно половине параметра.
Значит, у нас у — 4, р — 8. Подставляя это значение р в каж-
каждое из только что написанных уравнений, получим
у2 — 16* и у2 — — 16л:.
9$
Эскизы парабол указаны на фиг. 11, 10 и 11, П.
Задача 11, 14. Парабола симметрична относительно оси Ох,
проходит через точку Л D, —1), а вершина ее лежит в начале
координат.' Составить ее уравнение.
О
Фиг. 11,10.
Фиг. 11,11.
Решение. Так как парабола проходит через точку А D, —1)
с положительной абсциссой, а ее осью служит ось Ох, то урав-
уравнение ' параболы следует искать в виде у2 = 2рх. Подставляя
в это уравнение координаты точки А, будем иметь
1 = 8Р, р = 1» 2р = т;
искомым уравнением будет
Эскиз этой параболы показан на фиг. 11, 10.
ДВЕНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Преобразование прямоугольных координат. Параллель-
Параллельный перенос координатных осей без изменения их направления.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Преобразованием системы координат называется переход от
одной системы координат к другой.
При такой замене надо установить формулы, позволяющие по
известным координатам точки в одной системе координат опреде-
определить ее координаты в другой.
Главной целью преобразования координат является определе-
определение такой координатной системы, в которой уравнение;данной
линии становится наиболее простым. Удачным расположением ко-
99
ординатных осей можно добиться того, чтобы уравнение кри-
кривой приняло наиболее простой вид. Это имеет важное значение
для исследования свойств кривой.
Преобразование уравнения кривой второго порядка к простей-
простейшему виду достигается в общем случае 1) параллельным перено-
переносом координатной системы без изменения направления осей и
2) поворотом осей.
Если имеются две системы прямоугольных координат с раз-
разными началами, оси которых параллельны и одинаково направле-
направлены, то между координатами одной и той же точки в этих систе-
системах координат существует зависимость
= х1+х0
=У1 + Уо
(
где х, у — координаты точки в первоначальной системе коорди-
координат, хъ уг — ее координаты в новой системе координат, а х0,
у0 — координаты нового начала Ог в первоначальной системе ко-
координат.
Эти формулы позволяют определить первоначальные координа-
координаты точки х и у, если известны ее новые координаты и координаты
нового начала в первоначальной системе координат.
Для обратного перехода от первоначальных к новым служат
формулы
*1 = * —*б1 A2i2)
Первоначальную систему координат иногда называют исход-
исходной, иногда — старой.
Задача 12,1. Координаты точки относительно некоторой си-
системы координат х = 2, у= — 1. Чему будут равны координаты
этой точки, если, сохраняя направления осей, перенести начало
координат в точку:
а) G,-4); б) D,-2); в) B,-1); г) (-1,-4).
Решение, а) По формулам A2,2), полагая в них х = 2,
хо = 7- У = — 1, Уй = ~ 4> получаем хг = 2 — 7; уА = — 1 — (— 4),
отсюда новые координаты точки хг=—5; уг = 3.
Случаи б), в) и г) решите самостоятельно.
Ответ, б) (-2,1); в) @,0); г) C,3).
Задача 12,2. Относительно двух систем координат хОу и х^О^,
имеющих одно и то же направление осей, координаты некоторой
точки A2,-7) и @, 15). Чему равны координаты начала каждой
из этих систем относительно другой? Сделайте чертеж.
100
¦решение. По формулам A2, 1), полагая в них х — 12, х1=0,
у = — 7, уг= 15, получаем координаты нового начала в системе
координат хОу:
j2 = q _i_ х % =12
— 7= 15+г/о, г/о = —22.
В системе координат х1О1у1 координаты точки О — начала ко-
координат в системе хОу получим, поменяв местами х с хг и у с
Ух в предыдущих формулах. Бу-
Будем иметь У/ У
0= 12 + *о,
15 = _ 7 +
= — 12,
|/о = 22.
Здесь х'о и г/о — координаты то-
точки О в системе координат х1О1у1.
Задача 12,3 (для самостоятель-
самостоятельного решения). Две системы коор-
координат имеют одинаковые направ- фиг. 12,1.
ления осей. Координаты начала
первой системы относительно второй (8, — 4). Чему равны коор-
координаты начала второй системы координат относительно первой
(фиг. 12, 1)?
Ответ: (—8,4).
Задача 12,4 (для самостоятельного решения). Как изменятся
координаты любой точки А (х, у), если за ось абсцисс принять
ось ординат, а за ось ординат — ось абсцисс?
Ответ. Абсцисса и ордината точки поменяются местами.
Геометрический смысл квадратичной функции:
у — ахг + Ьх + с.
Задача 12, 5. Уравнение у = ахг + Ьх + с преобразовать так
чтобы в преобразованном виде оно не содержало члена <; первой
степенью х и свободного члена.
Решение. В учебнике Привалова на стр. 113 проведено ис-
исследование кривой, определяемой уравнением у = ах2 + Ьх + с
(а ф 0), и показано, что это уравнение определяет параболу.
Указанный в учебнике Привалова способ решает поставлен-
поставленную нами задачу. Мы укажем здесь другой прием, основанный
также на параллельном переносе системы координат, который по-
помогает проще решить эту задачу.
Заданное уравнение у — ахг + Ьх + с преобразуем так: у пер-
первых двух слагаемых в правой части уравнения вынесем за скоб-
скобки а (афО). Теперь
(А)
101
Из выражения хг -)— х, стоящего в скобке, выделим полный
квадрат суммы двух слагаемых. Запишем это выражение в виде
х + ^ ' 2ах-
г-, * /Ь\2
Прибавим к нему и вычтем из него In- , отчего выражение
\ ]
не изменится. Получим, что
Легко усмотреть, что сумма первых трех подчеркнутых сла-
слагаемых равна (* + 2"| , а потому окончательно
Тем самым мы из х2 + —х выделили полный квадрат суммы
двух слагаемых: \х + к^\ '
Теперь выражение (А) может быть переписано так:
»-«[(*+?)'-?]+«¦
Если раскрыть скобки в правой части этого равенства, то по-
получим
или
. 6\2 Аас — б2
4а
а отсюда следует, что
Аас — Ь* ../.. , 6\2
У In =
Сделаем параллельный перенос координатных осей без изме-
изменения их направления в точку О! с координатами
Ь 4ас — Ь2 .л.
Подставляя эти значения х0 и у0 в формулы A2, 1), получим
b _ Aac — 62
xi~2a> У — Ух Л la '
ИЛИ
102
В новой системе координат уравнение (В) перепишется так:
Ух = axl * (Е)
Этим и заканчивается преобразование исходного уравнения.
Легко заметить, что полученное уравнение (Е) действительно
значительно проще исходного: в нем нет первой степени текущей
координаты хг и нет свободного члена.
Таким образом, требование задачи выполнено: 1) преобразо-
преобразованное уравнение не содержит члена с первой степенью абсциссы
и 2) оно не содержит свободного члена.
Полученное уравнение уг — ах\ есть уравнение параболы, вер-
вершина которой находится в новом начале координат — точке
/ Ь Аас — *2\
О А — 2а > —4а—) • Мы можем сделать такое заключение:
. Графиком квадратичной функции у — ахг + Ьх + с при аФО
—2а'
ш'~ j, а ее ось симметрии параллельна оси Оу. Для построе-
построения этой параболы следует:
1)' определить координаты ее вершины 0х;
2) точку 0г принять за новое начало координат и через нее
провести координатные оси б1х1 и Otyv параллельные первона-
первоначальным осям координат и одинаково с ними направленные;
3) в новой системе координат построить параболу уг —- ах\.
Не следует запоминать координаты вершины параболы — фор-
формулы (С), а проделывать каждый раз указанные простые выклад-
выкладки. Решение последующих задач основано на выделении полного
квадрата из квадратного трехчлена, а потому эта операция дол-
должна быть хорошо усвоена. После решения нескольких задач
эти преобразования не будут вызывать никаких затруднений»
Решенная нами задача иногда формулируется иначе: уравне-
уравнение кривой у — ахг -\- bx -f- с (а ф 0) упростить так, чтобы в нем
отсутствовал член с первой степенью текущей координаты и сво-
свободный член, а иногда и еще короче: привести уравнение кривой
у — ах2 -f- Ьх + с к каноническому виду. В дальнейшем мы будем
пользоваться и этими формулировками. После того как показано,
что уравнение у — ахг + Ьх -\- с определяет параболу, можно за-
заключить: упрощение этого уравнения достигнуто параллельным
переносом первоначальной системы координат так, что новое нача-
начало координат находится в вершине параболы, а новая координат-
координатная ось Огуг совпадает с осью симметрии параболы.
Следует также иметь в виду, что если в уравнении у = ахг -f
-\- bx -\- с коэффициент а положителен, то ветвь параболы направ-
направлена вверх (так называемая «восходящая» парабола), а при отри-
отрицательном а — вниз («нисходящая» парабола).
103
_s
Форма параболы определяется только коэффициентом а. Чис-
Числа же b и с на форму параболы влияния не оказывают, и изме-
изменение их при одном и том же а влияет только на расположение
параболы на плоскости. Заметим также, что чем больше а по аб-
абсолютной величине, тем сильнее парабола прижата к оси симме-
симметрии; наоборот, чем меньше а по абсолютной величине, тем «ши-
«шире» будет парабола.
Решим теперь ряд задач с числовыми значениями a, b и с и
начертим эскизы нескольких
парабол (с построением эски-
эскиза параболы по ее уравнению
приходится очень часто встре-
встречаться, например, при изу-
изучении сопротивления матери-
материалов).
Задача 12,6. Упростить
уравнение параболы у — хг —
-, —7х 4- 12, найти координаты
' ¦ ^ »у ее вершины и начертить эскиз
*/ кривой.
Фиг. i2t2. Решение. Выделим в
правой части уравнения у =
= хг — 7х -f- 12 полный квадрат по способу,указанному в преды-
предыдущей задаче, и получим
или
Положим
х —х — - — 4--
Отсюда из сравнения с формулами A2,2) координаты нового
начала, т. е. вершины параболы, будут х0 = „-, у0 — — j . Пос-
/7 1\
ле переноса начала координат в точку OJtj-—4) уравнение па-
параболы примет наиболее простой вид ух = х\. Эскиз кривой пред-
представлен на фиг. 12, 2.
Задача 12, 7. Привести к простейшему виду уравнение пара-
параболы
у =- 2*2 + 4* + 5
и найти координаты ее вершины.
104
Решение. Уравнение у = 2х2 -\- 4х -{- 5 преобразуем, выде-
выделив в правой части полный квадрат:
-5, у = 2[(*+ IJ — 1]+5, у = 2(х + 1J+3,
пусть теперь х1~х-\-1,у1 = у—3. Из сравнения с формулами
A2,2) координаты нового начала: х0 = —1;
у0 = 3. Уравнение параболы примет вид уг = УЛ У
— 2х\. Эскиз параболы показан на фиг. 12, 3.
Задача 12,8 (для самостоятельного реше-
решения). Уравнение параболы у — — Ъхг +8х—9
преобразовать к простейшему виду и начер-
начертить ее эскиз.
Ответ. Вершина параболы находится в
точке (^-, —у). Преобразованное уравнение
будет иметь вид уг — — Ъх\. Знак минус у
коэффициента при х\ указывает на то, что
парабола — «нисходящая» (фиг. 12,4).
Самостоятельно решите несколько аналогичных задач и обя-
обязательно начертите эскизы этих парабол.
Задача 12,9 (для самостоятельного решения). Преобразовать
к простейшему виду уравнения парабол: 1) у = 5х2 -f- 4* — 3
¦f- Ъх -j- 1; 3) у = 2лг + Ъх; 4) у — —х* + 2х;
5) у — 3xz -}-9х — 1. Начертить эскизы этих
парабол.
Ответ. Координаты вершины:
2) «/==-<
У
[ 5 > Ь}>
4) A, 1); 5) (_!,_!
иг" ' *
Задача 12, 10. Из точки О под углом
а к горизонту брошена материальная точка с начальной ско-
скоростью v0. Найти: 1) уравнение траектории полета, 2) высоту
подъема; 3) дальность полета (сопротивление воздуха в расчет
не принимать).
Решение. Прежде всего определим траекторию полета. Пусть
в начальный момент t = 0 точка находилась в начале координат
105
(фиг. 12, 5). Проекции начальной скорости на оси прямоугольной
системы координат равны:
Vox — Vo COS Я,
vOy — yosina.
По прошествии / секунд точка в горизонтальном направлении
пройдет путь * = y0cosff-f (так как скорость ее в горизонталь-
горизонтальном направлении vqx — постоянна и равна y0cosa). В вертикаль-
вертикальном направлении точка пройдет за
то же время t путь, который мы
получим, если из пройденного в
вертикальном направлении пути
v0 sin я • t отнимем ^ — расстояние
на которое опустится точка под
действием силы притяжения земли.
х Значит, в вертикальном направле-
направлении за время t будет пройден путь
Уравнения х = у0 cos я • t, у = у0 sin я • / — ^
и являются уравнениями траектории полета точки. Мы замечаем,
что обе координаты х и у выражены здесь через одну и ту же
переменную величину /. В этом случае говорят, что мы имеем
параметрические уравнения траектории* (у нас параметром явля-
является время t). Желая найти зависимость между координатами
х и у, исключим из этих уравнений параметр t. Из первого урав-
уравнения следует, что / = р *qs(^ . Подставим это значение / во вто-
второе уравнение и получим
р qs(^
v0cos a
или
Положим
и тогда
у = — ахг 4-
* С параметрическими уравнениями Зшний мы будем часто встречаться в
математическом анализе. В учебнике Привалова это вопрос освещен в § 5
гл. II.
106
Легко усмотреть, что это уравнение параболы и, следовательно,
траекторией точки является парабола. Так как в ее уравнении
отсутствует свободный член, то парабола проходит через начало
координат. Найдем теперь высоту полета точки. Для этого оп-
определим ординату вершины параболы. Так как коэффициент при
я2 отрицателен, то парабола — «нисходящая», а вершина параболы
будет ее наивысшей точкой.
Из уравнения траектории у = —ах* + Ьх найдем, что абсцисса
вершины х0 — я- •
Подставляя сюда
2g „ , b=tga,
cos2 a
получим
После подстановки этого значения х0 в уравнение траектории
(А) получим ординату вершины параболы и тем самым высоту
полета
vl sin2 a
Как легко усмотреть, дальность полета / равна удвоенной абсцис-
vо sin 2a
се вершины, т. е. / = 2х0, или / = .
Дальность полета I будет наибольшей, если sin 2а, входящий
в выражение /, будет иметь наибольшее значение, т. е. при
sin 2а = 1, а тогда а = 45°.
Задача 12.11. Упростить уравнение кривой
Указание. Привести уравнение к виду
и поступить так же, как в предыдущих задачах.
Ответ. Кривая — парабола у\ — — н- хг; вершина параболы
в точке hr,—j\ (фиг. 12,6). Ось параболы параллельна оси
абсцисс. *
Задача 12, 12 (для самостоятельного решения). Упростить
уравнение кривой х + Ъу2 + 8у + 2 = 0 и начертить ее эскиз.
107
Ответ. Простейшее уравнение кривой. у\ = —^хг, координа-
координаты вершины параболы О1 (у, — ~\. Ось параболы параллельна
оси абсцисс.
Мы выполнили ряд упражнений на упрощение уравнения па-
параболы у = ах2 + Ьх + с и видели, что упрощение этого уравне-
уравнения- достигается параллельным переносом координатных осей без
изменения их направления так, что но-
новое начало координат находится в вер-
вершине параболы. Этим же преобразова-
преобразованием координат (т. е. параллельным пе-
переносом) можно привести к простейшему
(каноническому) виду уравнение любой
линии второго порядка, если это урав-
уравнение не содержит члена с произведе-
произведением текуших координат. Сейчас мы
выполним ряд таких упражнений.
Задача 12, 13. Привести к простей-
простейшему виду уравнение
5х + 4у — 6 = 0.
Фиг. 12,6.
Решение. Соберем члены уравнения, содержащие одну и ту
же переменную величину, и получим
(х2 — 5х) + Bу2 + Ау) — 6 = 0.
Из второй скобки вынесем коэффициент при у2, после чего
предыдущее уравнение примет вид
(х2-5х) + 2(у2 + 2у) -6 = 0.
В каждой из скобок выделим полный квадрат и получим
ИЛИ
откуда следует, что
(Л)
Произведем теперь такую замену: положим, что
*1=*—2", 01 = 0+1.
Произведенная замена представляет собою не что иное, как
преобразование координат всех точек плоскости параллельным
108
переносом координатных осей без изменения их направления.
Сравнение последних соотношений с формулами A2,2) показыва-
показывает, что новое начало координат находится в точке 0г I-^-, — 1),
а уравнение (Л) принимает вид
57
Разделив обе части этого уравнения на -т , получим канони-
канонический (простейший) вид данного уравнения
57^57 ~
4 8
Заданное уравнение определяет эллипс с полуосями а — ^~
b = —гтт=, центр которого находится в первоначальной системе
координат в точке OW-g-,—1). Таким образом, упрощение
уравнения этой линии достигнуто параллельным переносом начала
координат в ее центр.
Задача 12,14 (для самостоятельного решения). Упростить па-
параллельным переносом координатных осей без изменения их
направления уравнение линии хг — Зу2 -\-4х — Ъу -f I — 0.
Ответ. Линия — гипербола. Центр ее находится в точке
Otl—2, —тг]. Ее каноническое уравнение
12 36
Задача 12,15 (для самостоятельного решения). Упростить
уравнение кривой
Ответ. Кривая—эллипс с центром в точке Ol j-j , —-Л
в исходной системе координат. Простейшее уравнение кривой
х2 и2
И^~ J = *"
48 72
Задача 12, 16 (для самостоятельного решения). Привести к ка-
каноническому виду уравнение линии
4х2—у2 — 8х — 6у — 9= 0.
109
Ответ. Линия—гипербола с центром в точке О^ A, — 3)
в исходной системе координат. Каноническое уравнение линии
В задачах 12, 14 —12, 16, как и в задаче 12, 13, упрощение
уравнений линий достигнуто параллельным переносом начала
координат в центр этих линий.
ТРИНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Преобразование координат поворотом координатных
осей без изменения начала координат.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Если ср—.угол поворота, х и у— первоначальные координаты
точки, хх и ух— координаты той же точки в новой, повернутой
системе координат, то имеют место формулы
.?--=*! COS ср — ^Sincpl
у = хх sin ср + f/i cos cpj '
и
х-, = х cos cp -f у sin ср 1
. A3,2)
ух = —xsincp 4- г/coscp )
Задача 13,1. Чему будут равны координаты точки А A^3, 2),
если повернуть оси координат на угол+ 60° без изменения на-
начала координат.
Решение. Воспользуемся формулами A3,2). Тогда так как
cos60°=y, a sin 60° = *—"
f+ 2; л = Ч- -
Задача 13,2. Координатные оси прямоугольной системы коор-
координат- переносятся без изменения направления осей в точку
Ох C, — 1) и поворачиваются на угол 30°. Найти новые коор-
координаты точки А, если старые ее координаты были А C, 4)
(фиг. 13,1).
1) Сначала перенесем параллельно координатные оси, не из-
изменяя их направления, в точку C, — 1). По формулам A2,2)
получаем хг — 0; уг = 5.
ПО
2) Повернем теперь оси координат х1О1у1 на 30°; координаты
точки в системе координат хг0гуг найдутся по формулам A3, 2),
в которых надо заменить xt на хг, У\ на г/2. х на х1ч а у на уг.
Получаем
х2 — хг cos tp + г/i sin cp,
t/г = — Х\ sin cp -f- г/г cos ср.
Подставляя в эти формулы sin <р = sin 30° = 4-; cos cp = cos 30° =
Фиг. 13,1.
Фиг. 13,2.
= 1-i ; ^x = 0; t/x = 5, будем иметь искомые координаты точки
5 .
Определение. Гипербола, определяемая уравнением х? — у2 =
= а2, называется равносторонней.
Задача 13,3. Какой вид примет уравнение равносторонней ги-
гиперболы хг—уг = аг, если оси координат певернуть на угол
ср = —45° (фиг. 13,2)?
Решение. Так как ср = — 45°, то
sincp
V~2
— xx ¦ *y- + yx
= — ig-; coscp^i^-;
Подставляя эти значения х и у в уравнение гиперболы
л;2—у2 = а2, будем иметь
111
или
Отсюда получим
1
-о (xi + У1 — У1+ *i).(*i + У1+У1 ~хг) = а?,
О
Фиг. 13,3.
Фиг. 13,4.
окончательно
2х1у1 = а2, или ^
Это и есть искомое преобразованное уравнение равносторонней
гиперболы. Так как у равносторонней гиперболы b =a, то урав-
уравнения ее асимптот у= — х и у = х при Ь=а примут вид
у=.х и у = — х.
Эти прямые перпендикулярны и являются биссектрисами 1-го
и 2-го координатных углов. Значит, если асимптоты равносторон-
равносторонней гиперболы принять за координатные оси, то уравнение рав-
равносторонней гиперболы (если опустить индексы у хх и ух) примет
вид
Это уравнение носит название уравнения равносторонней гипер-
гиперболы относительно ее асимптот (фиг. 13, 3). Его следует запомнить.
Если бы мы сделали поворот осей не на —45°, а на +45°
(фиг. 13, 4), то уравнение гиперболы приняло бы вид
а2
с?
Опуская индексы в уравнении хху\ = —о", мы получили бы
уравнение равносторонней гиперболы относительно ее асимптот
112
в виде ху — — -g . Запомните, что ветви гиперболы ху = %-
расположены в первой и третьей четвертях (фиг. 13,3), ветви
же гиперболы ху = — у находятся во второй и четвертой чет-
четвертях (фиг. 13, 5).
Геометрический смысл дробно-линейной функции
(А)
называется дроб-
О
Фиг. 13,5.
__ах-\* Ъ
" ex -\- d
Определение. Функция вида у —
но-линейной (предполагается, что ad —
— ЬсфО, так как, если ad — be — 0, то
ad — be, и тогда -г ~ d)' Обозначая об-
общую величину этих отношений через t,
мы имели бы
?.-? - t
Ъ ~~ d
откуда а — Ы, c — dt. Подставляя эти
значения а и с в уравнение (А), мы по-
получили бы, что
___ Ых -f- Ь __ Ь (tx -f- 1) b
У ~" dtx+ d ~~ d(tx+ 1) — ~d'
и уравнение не содержало бы х. Уравнение (А) определяет рав-
равностороннюю гиперболу, асимптоты которой параллельны коор-
координатным осям. Ниже даются упражнения на преобразование
уравнения (А) к уравнению, в котором нет членов первого изме-
измерения.
Преобразованное уравнение может получить вид либо
ху — ^ > либо ху = — ^ •
Напомним, что уравнение ху = -^ определяет гиперболу, асим-
асимптоты которой служат координатными осями, а ветви располо-
а2
жены в первой и третьей четвертях; уравнение ху = — ^-опреде-
^-определяет гиперболу, у которой асимптоты служат координатными
осями, а ветви расположены во второй и четвертой четвертях.
Задача 13,4. Преобразовать дробно-линейную функцию
2.x -4- 3
у = 7^ так, чтобы в преобразованном виде она не содержала
членов первого измерения, и начертить эскиз кривой.
Эту задачу мы решим более простым способом, чем тот, ко-
который указан в учебнике. Числитель дроби 2х -j- 3 в правой
5 И. А. Каплан
113
части уравнения разделим на ее знаменатель Ъх + 4 по правилам
деления многочленов:
2х +3
Злг
Таким образом,
2х + 3
Зх + 4
Зх
В знаменателе второй дроби в правой части этого равенства вы-
вынесем за скобки 3 и получим, что правая часть данного уравне-
уравнения может быть записана так:
2 , 1
9 * + -?-
Зх + 4
а данное уравнение приобретает вид
*~'г' 2,1
¦X У == *
или г/ — -^ =
1
Фиг. 13,6.
9 * + 4
Обозначим теперь хг~х-{- -*¦; Ух=У—к • Тогда из сравне-
сравнения этих соотношений с формулами A2, 2) получаем, что х0 =
4 2
= —3 , г/0 = -3-,ав преобразованном виде данное уравнение
запишется так:
Ух = ^-, . или д^ = j (фиг. 13,6).
Этим же способом преобразуйте уравнение
а ~~ ex + d
так, чтобы в упрощенном виде оно не содержало членов первого
измерения (при этом преобразовании считать с Ф 0). Должно
получиться
а Ьс —ей 1
114
а полагая х + — = xt и у — ^ = уъ будем иметь
_ Ьс — cd \
Новое начало координат находится в точке с координатами
_ d __ a
х° ~~ ~ ' У® ~ ~с '
Задача 13,5 (для самостоятельного решения). Уравнение
Ъх Л~ 2
у — преобразовать так, чтобы в преобразованном виде оно
if.
\
Фиг. 13,7.
\)
О
42)
о,
Фиг. 13,8.
не содержало членов первого измерения, и начертить эскиз кри-
кривой.
Ответ. хгуг = -j .
Это уравнение равносторонней гиперболы, отнесенной к асимп-
асимптотам. Ветви кривой находятся в первой и третьей четвертях
новой системы координат. Новое начало координат находится в
точке (I, |)-фиг. 13,7,
Задача 13,6 (для самостоятельного решения). Дробно-линей-
Дробно-линейную функцию у = 3 _- преобразовать так, чтобы в преобра-
преобразованном виде уравнение не содержало членов первого измере-
измерения, начертить эскиз кривой и найти уравнения асимптот.
Ответ. xxyi = — -у ; х0 — 2, у0 = 2.
Кривая—равносторонняя гипербола, ветви которой располо-
расположены во второй и четвертой четвертях новой системы коорди-.
нат. Эскиз кривой представлен на фиг. 13,8. Уравнения асимптот:
х = 2 и у = 2.
5* П5
Задача 13, 7 (для самостоятельного решения). Преобразовать
дробно-линейные функции
2) y =
3) У =
х+2'
2 — 2*
так, чтобы в преобразованном виде они не содержали членов
первого измерения, найти уравнения асимптот и начертить эски-
эскизы кривых.
Ответ.
Преобразованные
уравнения кривых
1) *i«/i = -3;
2) Xjf/! = 4;
3) *i«/i = — 5;
Координаты нового
1 начала
хо = -2; (/„ = 1;
*о = —1; Уо = — 2;
х0 = — 2; ;/„ = 3;
Уравнения
асимптот
х = 2; (/ = 1;
х = _1; (/=—2;
х = — 2; (/ = 3.
ЧЕТЫРНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Упрощение общего уравнения кривой второго порядка
На двух последних занятиях мы достигали упрощения урав-
уравнения кривой параллельным переносом (задачи 12,4—12, 16), а в
задаче 13,3 уравнение кривой было преобразовано поворотом ко-
координатных осей без изменения начала координат.
Общее уравнение линии второго порядка имеет вид
Ах2 + 2Вху + Су2 + Dx + Еу + F = 0.
Задача упрощения этого уравнения состоит в том, чтобы чв пре-
преобразованном уравнении были устранены: 1) член, содержащий
произведение текущих координат, и 2) члены, содержащие первые
степени двух координат или, по крайней мере, одной из них.
Новая программа по высшей математике для машинострои-
машиностроительных, приборостроительных, механических, энергетических и
строительных специальностей втузов не предусматривает изложе-
изложения в общем виде вопроса об упрощении уравнения кривых второго
порядка и изучения инвариантов.
116
Поэтому мы приведем решение только нескольких задач. Из
них учащийся уяснит методы, с помощью которых достигается
упрощение уравнений линий второго порядка.
Случаи упрощения уравнения кривой второго порядка, когда
оно не содержит произведения текущих координат, были разобра-
разобраны раньше.
В том случае, когда уравнение линии второго порядка содер-
содержит произведение текущих координат, упрощение его следует на-
начинать с поворота осей без изменения
начала координат и надлежащим выбо-
выбором угла поворота добиться того, что-
бы из преобразованного уравнения«был
устранен член, содержащий произведе-
произведение текущих координат. Преобразова-
Преобразование координат в этом случае будем
вести по формулам
X = Хг COS ср — yl sin cpl
i/ = A:1sincp+ г/jcoscpj'
Если после устранения из преобразованного уравнения члена
с произведением текущих координат в нем останутся члены с
первыми степенями текущих координат, то последующим парал-
параллельным переносом осей можно, как это было показано, привести
уравнение к каноническому виду.
Координатную систему, полученную в результате поворота
первоначальной системы координат, будем обозначать через хг0уъ
а систему координат, полученную от параллельного переноса ко-
координат системы хх0уъ — через ХчРгуъ (см. фиг. 14, 1).
Задача 14,1. Привести к простейшему виду уравнение кривой
5л:2 + 4*j/ + 8t/2- — 32л: — 56г/ + 80 = О
и найти координаты центра в первоначальной системе координат.
Решение. Начнем с поворота осей. Целью этого преобразо-
преобразования, как вы уже знаете, является уничтожение в преобразо-
преобразованном уравнении члена, содержащего произведение текущих
координат. Формулы преобразования координат поворотом осей
без изменения начала координат имеют вид
х — хх cos ф — у1 sin ср,
у = х1 sin ср + i/i cos ср.
Подставляя эти значения х и у в заданное уравнение, будем
иметь
4 (л^ cos ср — у1 sin ср) . (х1 sin cp -f
ух cos срJ — 32 {хг cos ср — г/х sin ср) —
cp 4- У\ cos ср) + 80 = 0.
117
5 (хг cos ср —ух sin срJ
4~ ух cos ср) + 8 (хх sin ср
Раскроем скобки и получим
Ъх\ cos2 cp — К)*!*/! sin cp • cos <р + %? sin2 cp -f- 4х* sin cp ¦ cos cp —
— 4x1y1 sin2 cp + 4^^! cos2 cp — 4«/f sin cp cos cp +
+ 8*2 sin2 cp + 16*г1/г sin cp • cos cp + 8y2t cos2 cp —
— 32-iqcoscp + 32^/jSincp — ббд^этср —
— 56г/! cos cp + 80 = 0. .
Сделаем приведение подобных членов:
E cos2 cp + 4 sin cp cos cp + 8 sin2 cp) x\ + F sin cp cos cp — 4 sin2 cp -f
+ 4 cos2 cp) xxyx + Esin2cp —4 sin cpcoscp + 8cos2cp) y\ —
— C2 cos cp + 56 sin cp) xx + C2 sin cp —
— 56coscp)«/1 + 80=0. (
Выберем теперь угол поворота ср так, чтобы коэффициент при хху±
обратился в нуль. Приравнивая этот коэффициент нулю, получаем
уравнение для определения значения угла ср, при котором этот
коэффициент обратится в нуль: ^
6 sin cp cos ср — 4 sin2 ср + 4 cos2 cp = 0.
Разделим обе части этого уравнения на cos2 cp (cos ср ф 0, так
как если coscp=0, то sincp= ± 1, и тогда это уравнение не
имеет места, ибо получается, что — 4 = 0. Это замечание следует
помнить и при решении последующих задач). После деления по-
получим
6 sin у cos у . sin2 у . . »
cos2 у cos2 у *"
или после упрощений
2 tg2 ср — 3 tg ср — 2 = 0.
Отсюда получаем для тангенса угла ср поворота координатных
осей такие значения:
или
(tg<p)! = 2 И (tg<pI = —I.
Эти два значения tg cp соответствуют двум взаимно-перпендику-
взаимно-перпендикулярным направлениям, так как произведение этих тангенсов рав-
равно— 1. Из (tgcp)=2 следует, что угол поворота ср может нахо-
находиться в первой или третьей четвертях, а из (tg ср) = — — следу-
следует, что угол поворота ср может находиться во второй или чет-
118
вертой четвертях. Условимся всегда брать для tg <p из двух воз-
возможных значений — положительное, а угол поворота ср—впервой
четверти @<ср<-^-). Таким образом, из двух возможных зна-
значений тангенса берем tgcp = 2. Определим по известному tg ср ве-
величину sin ср и cos ср. Это нам нужно для того, чтобы определить
коэффициенты при х\, у\, хх и ух в уравнении (А).
Так как у нас tgcp>0, а угол ср находится в первой чет-
четверти, то по известному tg ср функции sin ср и coscp могут быть
определены следующим образом:
tg ср ,1
sin ср = -f- -——==, cos ср = Н—- '
тл • .2 1
Из этого следует, что sin ср = —=¦, coscp = ,
у 5 У 5
• 2 4 , 1 2
Sin2 ср = -g-, COS2 ср = -g-, Sin ср • COScp — —.
При найденных значениях sin ср и coscp коэффициент при д^ ра-
равен 9, коэффициент при х1у1—нулю, при у\ равен 4, коэффициент
144 8
при хх равен -= , а при уг равен . Подставляя эти значения
У 5 У 5
в уравнение (Л) и -поступая так же, как в задаче 12, 13, получим
Выделяя в скобках полные квадраты, имеем
откуда
576
или
9 („-?)'+ 4(„ + ?!г)'..эв. да
Сделаем теперь параллельный перенос координатной системы
Oj/! (фиг. 14, 1).
Формулы преобразования, аналогичные формулам A2, 1) и
A2, 2), запишем так:
X-i = Хъ ~т~ Хл\
\ A4,1)
f/i = f/a Ч- f/oJ
и
•^2 == %1 -^л) i
° 14,2)
У2 = У1 — У о)
119
Теперь в уравнение (В) введем обозначения:
о »
Х2 — х1— -р=; уъ = у-i + -т=; из сравнения с формулами A4, 2)
Q ]
заключаем, что х0 = + -==, уо = —— а уравнение (В) пере-
перепишем так:
После деления обеих частей равенства на 36 получим данное урав-
уравнение в каноническом виде:
о о
4 ~1~ 9
Итак, данное уравнение опре-
определяет эллипс. Он вытянут вдоль
оси Ojt/2- Эскиз кривой показан
на фиг. 14, 2. Докажите, что точ-
точка Ог — центр эллипса в исходной
системе координат имеет коор-
координаты B, 3)*.
Ниже помещено для самостоя-
самостоятельного решения несколько за-
задач с подробными ответами и ука-
указаниями. Эти задачи следует ре-
решать так же, как и задачу 14, 1. При решении их следует
считать, что угол поворота находится в первой четверти, и, зна-
значит, из двух возможных значений tgtp надо брать положительное.
Учащимся рекомендуется ознакомиться не только с приведен-
приведенным, но и с более совершенным методом упрощения общего
уравнения кривой второго порядка, изложенным в учебниках
И. И. Привалова и Н. В. Ефимова.
Задача 14,2 (для самостоятельного решения). ,
Упростить уравнение кривой
Фиг. 14,2.
Ответ. Кривая — гипербола. Каноническое уравнение ее
^1-Х-1 = \ (фиг. 14,3).
* Принимая do внимание, что х = xY cos у — уг sin у; у = х1 sin у + у1 cos у,
а хг = х2 + х0; (/j — yt + у0, получаем, что
х = (хг + х0) cos ч> — («/а + Уо) sin 9;
у = {х2-\- х0) sin </+(у2+ Уо) cos <f.
120
Указание. Уравнение для определения tgtp имеет вид
2tg2cp — 3tgcp — 2 = 0, tgcp = 2, 0°<cp<90°. После поворота
первоначальной координатной системы на угол, для которого
tg ср = 2, уравнение приобретает вид
В системе координат х1Оу1 ко-
координаты центра гиперболы
Ul\V5' ~уьГ
Задача 14, 3 (для самостоятель-
самостоятельного решения). Упростить урав-
уравнение линии
х2 — 4ху + 4у2~2х — 6у + 2 = 0.
Ответ. Кривая — парабола.
Ее каноническое уравнение у\ ~
= -^—х2 (фиг. 14,4). Для опре-
определения tg tp получим уравнение
2 tg2cp
tg tp — 2 =¦- 0; tg<p== i-
Фиг. 14,3.
0° < tp < 90°. После пово-
рота первоначальной координатной системы на угол, для кото-
</ рого tgtp = ", уравнение приобретет
вид 5у2] j=. хх —-~= ух~\- 2 = 0.
В системе координат х1Оу1
координаты вершины параболы
Задача 14,4 (для самостоятельно-
самостоятельного решения). Упростить уравнение
кривой
х2 — 2ху + у2 — 6х — 2у + 9 = 0
Фиг. ]4,4.
и найти координаты фокуса в исходной системе координат.
Ответ. Кривая — парабола. Ее каноническое уравнение
у2 — 2|/2л;2 (фиг. 14, 5); tgtp = 1; ср = 45°. После поворота перво-
первоначальной координатной системы на этот угол уравнение при-
примет вид
4/2*,+ 21/20,+9 = 0.
[21
В системе координат х1Оу1 вершина параболы имеет коор-
динаты 011У2, ——-J, координаты фокуса в исходной системе
координат F B, 1).
Задача 14, 5. Привести к простейшему виду уравнение
9.
Уг
Фиг. 14,5.
9х2 + 24 ху + 16у2 + 50л; —
— 100*/ +25 = 0. ¦
Найти уравнение директрисы
и координаты фокуса в пер-
первоначальной системе коор-
координат.
Ответ. Кривая — пара-
парабола. Ее каноническое урав-
уравнение у\ — 4*2 (фиг. 14, 6).
В первоначальной системе
координат фокус параболы
имеет координаты Fl—-g-, —V а уравнение директрисы 4х
— Ъу — 5 = 0.
Задача 14, 6. Упростить уравнение кривой
8*2 — 4ху + 5г/2 + Ах — №у — 319 = 0.
Фиг. 14, 6.
Ответ. Кривая — эллипс. Его каноническое уравнение
х\ 1/|
gy +- gg = 1. В системе координат х1Оу1 центр эллипса имеет
/ 2 1
координаты О1 1-^=, —j (см. фиг. 14,7).
122
У
щ
1
ФИ1
У
/
1
Фиг
ь
/
Фиг
/'
г- II mi 7*
14,7.
^-^
9
14,8.
it
У
^ •¦¦
14,9.
123
Задача 14,7. Упростить уравнение линии
34л:2 — 12ху + 18г/3 + 24л: — 72у — 504 = 0.
Найти в первоначальной системе координат уравнения осей
симметрии.
Ответ. Кривая — эллипс. Его каноническое уравнение
5g + 7g = 1 (фиг. 14,8). Уравнение осей симметрии
Зл: — у + 2 = 0; х + Зг/ — 6 =--- 0.
Задача 14, 8. Упростить уравнение линии
бху + 8г/2 — 12л: — 26г/ + 11 = 0.
Ответ. Кривая — гипербола. Ее каноническое уравнение
*Л-Ц = \ (фиг. 14,9).
ПЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Определители и системы линейных алгебраических
уравнений.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Вычисление определителей основывается на их известных свой-
свойствах, которые относятся к определителям всех порядков. Вот
эти свойства:
1. Если переставить две строки (или два столбца) определи-
определителя, то определитель изменит знак.
2. Если соответствующие элементы двух столбцов (или двух
строк) определителя равны или пропорциональны, то определи-
определитель равен нулю.
3. Значение определителя не изменится, если поменять ме-
местами строки и столбцы, сохранив их порядок.
4. Если все элементы какой-либо строки (или столбца) имеют
общий множитель, то его можно вынести за знак определителя.
5. Значение определителя не изменится, если к элементам
одной строки (или столбца) прибавить соответствующие элементы
другой строки (или столбца), умноженные на одно и то же число.
Для определителей третьего порядка это свойство может быть
записано, например, так:
, 4- ka<> b, 4- kb2 с, + kc^
аг Ъх сх
а2 Ь2 с2
а3 Ь3 с3
c2
с3
124
6. Определитель второго порядка вычисляется по формуле
I1 Чг =^aib2—a2bx. A5, 1)
ох о2
7. Определитель третьего порядка вычисляется по формуле
ах Ьх сх
2 2 2
а3 Ь3 с3
= axb2c3 + аф3сх + a3bxc2 - a3b2cx — A5, 2)
— a2bxc3 —axb3c2
Фиг. 15,2
Существует удобная схема для вычисления определителя третьего
порядка (см. фиг. 15, 1 и фиг. 15, 2).
По схеме, приведенной на фиг. 15, 1, произведения соединен-
соединенных элементов берутся со своим знаком, а по схеме фиг. 15, 2 —
с обратным. Величина определителя равна алгебраической сумме
полученных шести произведений.
В определителе порядка п алгебраическим дополнением эле-
элемента, стоящего на пересечении й-го столбца и 1-й строки, на-
называется определитель порядка (п—1), получаемый из данного
вычеркиванием в нем строки и столбца, на пересечении которых
стоит этот элемент, причем к этому определителю присоединяется
множитель (—71)*+', где {k -\-1) — сумма номеров вычеркнутой
строки и столбца. Алгебраическое дополнение элемента, рассмат-
рассматриваемое без множителя (—l)ft+;, называется минором этого эле-
элемента.
Пример. В определителе 5-го порядка
аг Ъх сх йг ех
Ъ2 с? d2 e2
а3 b3 c3 d
3 d3
A5, 3)
алгебраическим дополнением, соответствующим элементу d3, будет
определитель 4-го порядка
ах Ъх сх ех
(-
Ъ2 с2 е2
«5 Ъъ сь еь
125
Здесь в показателе степени у (— 1) три — номер строки, че-
четыре—номер столбца, на пересечении которых стоит элемент d3.
8. Определитель равен сумме произведений каждого элемента
некоторой строки (или столбца) на его алгебраическое дополнение.
Условимся обозначать элементы определителя маленькими
буквами, а их алгебраические дополнения — соответствующими
большими буквами с теми же индексами. Так, алгебраическое
дополнение элемента а3 будем обозначать через А3, алгебраи-
алгебраическое дополнение элемента d4 — через D4 и т. д. На основании
свойства (8) определитель A5,3) может быть представлен, напри-
например, в таком виде:
D = а3А3 + Ь3В3 + csC3 + d3D3 + e3E3.
Это равенство представляет собой разложение определителя по
элементам третьей строки. По свойству 8 вычисление определи-
определителя порядка п сводится к вычислению определителей поряд-
порядка (п— 1).
9. Если все элементы какого-нибудь ряда определителя, кро-
кроме одного, равны нулю, то .определитель равен этому не равному
нулю элементу, умноженному на его алгебраическое дополнение.
С помощью указанных свойств можно вычислить определитель
любого порядка.
Задача 15,1. Вычислить определители
2 7
4 1
2)
1 2
О 1
3)
4 5
— 1 6
Решение. По формуле A5, 1) имеем
= 2 • 1 — 4 • 7 = — 26, .
= 1 - 1 —0-2=1.
Задача 15,2 (для самостоятельного решения).
Вычислить определители
1)
2)
2
4
1
0
7
1
2
1
1)
2 —7
-4 —2
2)
1—4
2 — 5
3)
—2 —3
3 2
Ответ. 1) —32; 2) 3-, 3) 5.
Задача 15,3. Вычислить определители
1)
1
0
4
3
2
1
5
1
2
; 2)
2
7
3
4
3
1
— 1
2
—2
; 3)
2
3
1
1
2
4
1
1
—3
126
2)
3)
Решение. С помощью формулы A5,2) получаем
1 3 5
О 2 1
4 1 2
2 4 —1
7 3 2
3 1 —2
+
— 1 .1.1=4
+ 4-3.1— 4-2-5 — 0-3-2 —
0+12 — 40 — 0—1= — 25.
= 2-3- (—2) + 7 • 1 • (— 1) + 3 - 4 • 2 — 3 ¦ 3(— 1) —
— 7 • 4 • (—2) — 2 • 1-2 = — 12 — 7+24 + 9 +
+ 56 — 4 = 66.
2 1 1
3 2 1
1 4—3
=. 2 • 2 ¦ (—3) + 3-4-1+1-1-1—1-2-1 — Зх
Х1 .(—3) —2-4- 1 =—12+ 12+1 — 2 + 9 — 8 = 0.
Задача 15, 4 (для самостоятельного решения).
Вычислить определители
1)
2
—4
3
4
2
1
— 1
1
5
; 2)
4
2
8
7
3
1
1
—4
3
; 3)
3 1 —2
1 2 —3
2-1 4
На каждом из этих определителей проверить, что сумма
произведений элементов какого-нибудь ряда на алгебраические
дополнения, соответствующие элементам параллельного ряда,
равна нулю.
¦ Ответ. 1) 120; 2) —236; 3) 15.
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. Система двух линейных уравнений с двумя неизвестными
Система двух линейных уравнений с двумя неизвестными
имеет вид
Определителем этой системы называется определитель, со-
составленный из коэффициентов при неизвестных. Этот опреде-
определитель
I к\ 05.5)
будем обозначать буквой D.
. 1. Если определитель системы не равен нулю, то система A5, 4)
имеет единственное решение, которое находится по формулам
х ~
«1
а2
У =
а2
A5,6)
12?
В этом случае говорят, что система — совместная или опреде-
определенная.
Определители, стоящие в числителях этих дробей, будем
обозначать соответственно через Dx и Dy.
Итак, значение неизвестного системы ~ A5,4) равно дроби,
знаменатель которой есть определитель системы, а числитель
есть определитель, получающийся из определителя системы
заменой в нем столбца из коэффициентов при определяемом не-
неизвестном столбцом свободных членов.
2. Если же определитель системы D равен нулю, но, по
крайней мере, один из определителей Dx и Dy в числителях
формул A5,6) не равен нулю, то система решений не имеет.
В этом случае говорят, что она противоречива, или несовместна.
3. Если же равен нулю не только определитель системы, но
и определители Dx и Dy, а хотя бы один из коэффициентов при
неизвестных не равен нулю, то одно из уравнений системы яв-
является следствием другого, и система A5,4) двух линейных
уравнений с двумя неизвестными приводится к одному уравне-
уравнению, всякое решение которого является одновременно и реше-
решением второго уравнения. В этом случае система допускает
бесконечное множество решений, и о ней говорят, что она не-
неопределенная.
II. Система трех линейных уравнений с тремя неизвестными
Система трех линейных уравнений с тремя неизвестными имеет
вид
bxy + схг = dx
ахх
a2x
a3x
b2y
=d2
A5,7)
Определитель
D =
A5,8)
b3y + c3z = d3
ax bx cx
a2 b2 c2 ,
a3 b3 c3
составленный из коэффициентов при неизвестных, называется
определителем системы.
1. Если определитель системы D Ф 0, то система A5,7) имеет
решение, и притом единственное. Это решение находится по
формулам
d\
d2
d3
ax
a2
a3
bx cx
b2 c2
b3 c3
Ьг с{
b2 c2
b3 c3
У =
«1
а2
а3
ах
а2
а3
dx
d.
d3
Ьг
ь2
ь3
сг
c2
c3
c2
b\ dx
b2 d2
b3 d3
ax bx cx
a2 b2 c2
a3 b3 c3
A5,9)
Из этого заключаем, что значение неизвестного системы A5,7)
равно дроби, знаменатель которой есть определитель системы,
128
а числитель есть определитель, получающийся из определителя
системы заменой в нем столбца из коэффициентов при опре-
определяемом неизвестном столбцом свободных членов.
Определители, стоящие в числителях дробей A5,9), мы будем
обозначать соответственно через Dx, Dy, Dz.
2. Если D = О, но, по крайней мере, один из его миноров
и хотя бы один из определителей Dx, Dy и D2 не равен нулю,
то система A5,7) решений не имеет. В этом случае говорят, что
она противоречива, или несовместна.
3. Если D = 0 и все определители, стоящие в числителях
дробей A5,9),—Dx, Dy, Dz — равны нулю, т. е. если
D = Dx = Dy = Dz = О,
но хотя бы один из миноров в определителе D не равен нулю,
то одно уравнение системы A5,7) является следствием двух дру-
других, и система трех уравнений A5,9) приводится к двум урав-
уравнениям, причем решения этих двух уравнений удовлетворяют
третьему. В этом случае система A5,9) имеет бесконечное мно-
множество решений и называется неопределенной.
4. Если же все миноры в определителе D равны нулю, но хотя
бы один из миноров в каком-нибудь из определителей Dx, Dy,
Dz не равен нулю и хотя бы один из коэффициентов при не-
неизвестных не равен нулю, то система несовместна и решений не
имеет.
5. Если в определителях D, Dx, Dy, D2 все миноры равны
нулю, но хотя бы один из коэффициентов при неизвестных
нулю не равен, то два уравнения системы являются следствием
третьего, и система трех уравнений приводится к одному урав-
уравнению, является неопределенной и имеет бесконечное множество
решений, причем решения этого третьего уравнения удовлетво-
удовлетворяют первому и второму уравнениям.
Задача 15, 5. Решить систему уравнений
х + 2у = 8
Злг — у = 3
Решение. Прежде всего вычисляем определитель D системы,
стоящий в знаменателях дробей формул A5,6):
1 2
3 —1
= —7.
Так как D Ф 0, то заданная система — совместная и опре-
определенная, т. е. допускает единственное решение. Формулы для
определения х и у запишем по A5,6) так:
х =
8
3
1
3
2
— 1
2
— 1
> У
1
3
1
3
8
3
2
—1
Dx =
8
3 -
1
3
2
-1
8
3
= -14;
= —21.
129
Определитель, стоящий в знаменателях двух дробей, уже вычислен
и равен D = — 7;
DX -14
о. о.
Задача 15, 6. Решить систему уравнений
Зд: — 2у = 1 |-
Решение. Вычисляем определитель системы
1 —1
3 —2
= 1;
так как D ф О, то система — совместная и определенная, т. е.
допускает единственное решение. Неизвестные х и у найдутся
по формулам
3 —1
1 —2
1 —1
3 —2
1 3
3 1
1 —1
3—2
3 —1
1 —2
1 3
3 1
= —8.
Знаменатель этих дробей D = 1 был вычислен раньше:
у- х Ъ *>• г-
X — -g- — -у — — О, Л —
Задача 15,7 (для самостоятельного решения).
Решить систему уравнений
+ гу = —2\
~у= 7J-
Ответ. х= 1,9; г/= — 1,3.
Задача 15, 8 (для самостоятельного решения). Решить системы
уравнений:
1)х + 4«/=12 1 2) 13л:— 12у = — 9[ 3) Зд: + 5у = 121
Зд: — 2у = — 6/> 2д:+ Зу = 18/ 2х + 7у=Щ-
Ответ. 1) х = 0; t/= 3; 2) х = 3; у = 4; 3) х = — 1; у = 3.
Задача 15, 9. Решить систему уравнений
2х + 3у = 5\
Ах + 6у =
130
Решение. Составляем определитель системы D —
2 3
4 6
= 0.
Так как D — О, то система или несовместная, или неопределен-
неопределенная. Составляем определители, стоящие .в числителях дробей
формул A5, 6):
5 3
7 6
= 9=^0.
Так как D — 0, a Dx ф 0, то система несовместна, т. е.- решений
не имеет. Геометрический смысл нашего* заключения состоит в
том, что уравнения, входящие в систему, есть уравнения двух
параллельных прямых, а так как параллельные прямые не пере-
пересекаются, то решений предложенная система не имеет (прямые
2д; + 3(/ — 5 = 0и4л:+6у— 7 = 0 параллельны, так как коэф-
коэффициенты при соответствующих текущих координатах пропорцио-
2__ 3_\
4 ~ 6/'
Задача 15, 10. Решить систему уравнений
нальны:
бдг — 81/ = 10 )•
Решение. Составляем определитель системы
~ 3-4
6 —8
= 0.
Так как определитель системы равен нулю, то может ока-
оказаться, что система или вовсе не имеет решений, т. е. несо-
несовместна, или является неопределенной, т. е. допускает бесчис-
бесчисленное множество решений (напоминаем, что система уравнений
называется совместной и определенной, когда она имеет решение,
и притом единственное). В нашем случае D — 0. Вычислим
D, и Dy:
5 ~4
10 —8
3 5
6 10
- — 40 + 40 = 0; Dx = 0;
= 30 — 30 = 0; Dy = 0.
Таким образом, D — 0, Dx = 0 и Dy — 0. Это значит, что система
неопределенная. Действительно, если обе части второго уравне-
уравнения разделить на 2, то получится первое уравнение, и система
двух уравнений сводится к одному уравнению с двумя неизвест-
неизвестными, а именно:
131
и имеет бесчисленное множество решений, заключающихся в фор-
формуле
, 3*-5
У —•
Давая произвольные значения неизвестному х, получим со-
соответствующие значения у.
Задача 15,11 (для самостоятельного решения). Решить системы
уравнений:
1) 15л; — у = 14 1 2)Ъх—Ъу=\\
12л: + 13t/ = 25 j; бд:— lOt/ = 5 J;
Ответ. 1) лс = «/= 1; 2) система несовместна; 3) система яв-
является неопределенной.
Задача 15,12. Решить систему уравнений
xi ~\~ 2*a — х% = — 3
2л;х -f- Здг2 -f- дс3 == — 1 .
Х\ — х% — xs = 3
Решение. Составляем и вычисляем определитель системы:
12—1
23 1
1 —1 —1
Это значит, что система совместна и определенна, т. е. имеет
решение, и притом единственное. Формулы A5,9) для опреде-
определения неизвестных дают
-3 2 -1
-1 3 1
ч 1 i
1 2 -1
2 3 1
1 —1 —1
; х% =
1
2
1
1
2
1
—3
—1
3
2
3
—1
—1
1
—1
—1
1
—1
1 2 -3
2 3—1
1 —1 3
1 2 —1
2 3 1
1 —1 —1
Определитель, стоящий в знаменателях этих дробей, нами
уже вычислен. Он равен 9. Dx — 18; Du = — 18; Dz = 9.
Xl ~ ~D - 9" ~ A
D
9
Задача 15, 13. Решить систему уравнений
5л: — у — г = 10
х — у + 52 = — 12
132
Решение. Вычислим прежде всего определитель системы
3 1 1
5 -1 -1
1 —1 5
= — 48.
Поскольку этот определитель не равен нулю, система имеет ре-
решение, и притом единственное.
Приступаем к определению неизвестных по формулам A5,9):
2
10
-12
3
5
1
1
—1
—1
1
—1
—1
1
—1
5
1
—1
5
У =
3
5
1
3
5
1
2
10
—12
1
J
—1
1
—1
5
1
—1
5
3
5
1
3
5
1
1
—1
—1
1
—1
—1
— 2
10
— 12
1
— 1
5
Определитель, стоящий в знаменателях этих дробей, нами
уже вычислен. Он равен — 48. Вычисляем определители, стоящие
в числителях этих дробей:
—2 1 1
10 —1 —1
— 12 —1 5
3 —2 1
5 10 —1
1 —12 5
3 1 —2
5 —1 10
1 —1 —12
= -48; Dx = ~
= 96;
= 144;
Dy = 96;
D2 = 144
X~~D~
—48 _ ,
л я — »
У - D - _48
?г_ И1
z ~ D - _48
Z _ —
Задача 15,14 (для самостоятельного решения). Решить си-
систему уравнений
2хх -\- х2 — х3 = 0 1
хх — х2 — ох3 = lo v
Зхх — 2х2 + 4х3 = — 15 j
Ответ. хх = — 1; х2 — — 2; х3 — — 4.
Задача 15,15 (для самостоятельного решения). Решить си-
системы уравнений:
1) *! +Зл:2-Зл:з= 13 \ 2) 2хх — х2 + х3 = — 4
\хх — 2д;2 + Зл:3 = — 7
133
3) 2xx + x3 = 6
Ответ. 1) xx = 1; x2 = 3; лс3 = —1; 2) ^ = — 1; л:2 = 3;
^ v 1 . O\ v V -и 9
Л3 ^^ 1 , Oj Xj — Л2 —¦ A3 — л.
Задача 15, 16. Решить систему уравнений
х + Зу- 42 = 5
2х — Зу + 62 = 11
8л: — 3t/+ 102 = 21
Решение. Вычисляем прежде всего определитель системы
1 3—4
D =
2—3 6
8 —3 101
= О
Итак, определитель системы равен нулю.
Минор этого определителя, стоящий в левом
13 Л . „ ,
верхнем углу,
Д =
2 —3
Это обстоятельство указывает на то, что третья строка опре-
определителя является линейной комбинацией двух первых. И дей-
действительно, если элементы первой строки умножить на 2, а вто-
второй — на 3 и сложить, то получатся элементы третьей строки
(проверьте!).
Вычислим теперь определители Dx, Dy и Dz, и если окажется,
что хотя бы один из них не равен нулю, то из этого будет
следовать, что система не имеет решений, т. е. она несовместна,
или противоречива.
5 3 4
D,= И -3 6 = — 132.
21 —3 10
Таким образом, по пункту 2 (стр. 129) правил исследования
системы уравнений получается, что система несовместна. Если
умножить левую часть первого уравнения на 2, а второго —
на 3 и полученные произведения сложить, то получим левую
часть третьего уравнения
2(х+ Ъу — 4г) + ЪBх — Ъу + 6г) = 8л: — Зу + Юг.
Отсюда заключаем, что она является линейной комбинацией ле-
левых частей первого и второго уравнений. Но если правую часть
первого уравнения умножить на 2, а второго — на 3, то полу-
получится 2-5 + 3- 11 =43, тогда как правая часть третьего урав-
уравнения не 43, а 21. Отсюда и произошла противоречивость си-
системы.
Итак, предложенная система уравнений решений не имеет.
134
Задача 15,17 (для самостоятельного решения). Решить си-
систему уравнений
7jc — у + г= 17
Ответ. Система несовместна (см. п. 2, стр. 129) и решений
не имеет.
Задача 15,18. Решить систему уравнений
Л1 -р ОЛ2 лз — UI
2xj — х2 + Зл:3 = 1 }.
7*! + 7х2 + Злг3 = 2 J
Решение. Прежде всего вычисляем определитель системы
и находим, что D — 0.
Один из миноров определителя
1 3
Д =
-1
= — 7 Ф 0.
Это указывает на то, что один из рядов определителя D яв-
является линейной комбинацией двух других рядов (проверьте,
что если сложить утроенные элементы первой строки с соответ-
соответствующими удвоенными элементами второй строки, то получатся
соответствующие элементы третьей строки).
Теперь вычислим Dx, Dy и D2 и получим, что Dx — Dy —
= Ог = 0.
Итак, не только D = 0, но и Dx ~ 0; Dy = 0 и Dz = 0. Из
того, что все эти определители равны нулю, а минор Д ф 0,
на основании пункта 3 (стр. 129) следует, что одно из урав-
уравнений системы является следствием двух других, и система не-
неопределенна. Действительно, третье уравнение мы получим, если
первое умножим на 3, второе — на 2 и почленно сложим.
Отсюда уже заключаем, что третье уравнение удовлетворяется
решениями первых двух
Х\ -р ох% — х$ — О
и система приводится к двум уравнениям с тремя неизвестными.
Из того, что
1 3
2 —1
Ф0,
следует, что эта система может быть разрешена относительно
хг и х2. "
Перепишем уравнения последней системы в таком виде:
Х\ + Злг2 ~ х3 1. '
2% — х% = 1 — Ъх3 J •
135
Теперь по хорошо известным формулам получаем
К л —-
1-3*з-
1
2
1 xs
2 1—3*з
1 3
2 —1
3
1
3
-1
л:2 —
3 — 8*3 .
5*,- 1
Давая неизвестному х3 произвольные значения, будем полу-
получать соответствующие значения для х1 и х2. Предложенная си-
система уравнений имеет решения, и этих решений бесконечное
множество.
Задача 15, 19. Решить систему уравнений
у~ ?Хъ
_ з
= 1
= 13
Ответ. Система неопределенна: хх = —д—¦
Задача 15, 20. Решить систему уравнений
х + Зу — 4г = 3
7 у — 7г = 1
2х — у — 2 = 5
Ответ. Система неопределенна: х =
Х2 — -ё" Х3-
У =
1+72
7 • * - 7 •
Давая неизвестному 2 произвольные значения, будем полу-
получать соответствующие значения х v. у. Предложенная система
уравнений имеет решения, и этих решений бесконечное множество.
Задача 15,21. Решить систему уравнений
х — 2у+ 2 = 3
2х — Ау + 2г = 5
Ъх — 6у + Зг = 9
Решение. Вычисляем определитель системы
1—2 1
2
3
D=
2—4
3—6
= 0.
К этому заключению мы приходим немедленно, замечая, что
элементы первого столбца равны соответствующим элементам
третьего столбца.
Исследуем миноры определителя D:
1 —2
2 —4
= 0;
1 1
2 2
-0;
—2 1
—4 2
= 0.
136
Из этого следует, что коэффициенты при соответствующих
неизвестных первого и второго уравнений пропорциональны.
Оказывается, что и
1 — 2
3 — 6
= 0;
1 1
3 3
= 0"
¦2 1
¦ 6 3
= 0.
Это показывает, что соответствующие коэффициенты при не-
неизвестных в первом и третьем уравнениях также пропорцио-
пропорциональны.
Определитель
Dx
3 —2
5 —4
9 —6
Минор же этого определителя
3 —2
5 —4
= — 2 =? 0.
Таким образом, определитель системы D и все его миноры
равны нулю, один из коэффициентов при неизвестных нулю не
равен; оказалось, что и один из миноров определителя Dx не
равен нулю. На основании пункта 4 (стр. 129) заключаем, что
система несовместна (противоречива) и, значит, решений не имеет.
Всего этого исследования, можно было бы и не производить,
если заметить, что коэффициенты при неизвестных во втором
уравнении получаются из коэффициентов при неизвестных в пер-
первом уравнении умножением на 2, а свободный член второго
уравнения не получается из свободного члена первого уравнения
умножением его на 2. Отсюда сразу можно было сделать заклю-
заключение о противоречивости системы.
Задача 15, 22. Решить систему уравнений
х — 4у + 3z = 5
2х— 8у + 6г= 10
Ъх — \2у + 9г=^ 15
Решение. Определитель системы
1—43
2 — 8 6
3 —12 9
D=
-0,
поскольку имеет место пропорциональность соответствующих
элементов, например, первого и второго столбцов (свойство 2).
5-43
10 — 8 6
15 —12 9
= 0,
13?
так как легко усмотреть пропорциональность соответствующих
элементов, например, первой и второй строки (свойство 2).
1 5 3
Dy= 2. 10 6=0,
3 15 9
так как сразу усматриваем, что элементы первого столбца про-
пропорциональны соответствующим элементам второго и третьего
столбцов (свойство 2).
На том же основании сразу заключаем, что
1—4 5
2 — 8 10
3 —12 15
=0.
Легко проверить, что все миноры определителей D, Dx, Dy,
Dz также равны нулю. И так как один из коэффициентов при
неизвестных нулю не равен, то система неопределенна, имеет
решения, и решений будет бесконечное множество (см. пункт 5
на стр. 129).
Мы легко усматриваем, что второе и третье уравнения си-
системы получаются из первого умножением соответственно на 2
и на 3, т. е. второе и третье уравнения являются следствиями
первого, а потому решения первого уравнения удовлетворяют
второму и третьему.
Значит, система трех уравнений в нашем случае приводится
к одному первому уравнению
х — 4у + 32 = 5,
откуда
* = 5 + 4t/ — 32.
Давая у и г произвольные значения, получим соответствую-
соответствующие значения х. Система имеет бесконечное множество решений.
Задача 15, 23 (для самостоятельного решения).
Решить системы уравнений:
2хх — Ъх2
3)
Ъх3 = — 7
i х3 = — 4
5хг + Зд;2 — 4лг3 =11
2xt + Зх2 — Ах3 = — 4
3*! + 2х2 + Ьх3 = 22
2) 2хг — Ъх2 + 4л:3 = 11
7хх — Здг2— х3 — 17
4) 2х + у— 2 = 11
3* + 2у — 4г = 15
5) 2х + Зу— 5г= 4
4х+ 6у— Юг = 8
8л: + 12у— 202= 16
Ответ. 1) *i = 1; л:2 =—2; х3 = — 3.
2) Система несовместна.
о) *j :^=: 1) Х2 =^ Z\ X$ = О.
138
4) Система неопределенна. Она допускает бесконечное мно-
множество решений: х = 7 — 2г; у — — 3 + 5г.
5) Система неопределенна. Она допускает бесконечное мно-
3 5
жество решений: х = 2 — уу -f- -кг.
ШЕСТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Векторная алгебра.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это занятие посвящается векторной алгебре, имеющей очень
большое значение для механики, электротехники и других техни-
технических дисциплин. Напомним основные сведения из векторной
алгебры.
Различают два рода величин: скалярные и векторные.
¦*"#
Фиг. 16,1.
1. Если некоторая величина вполне определяется ее число-
числовым значением, то ее называют скалярной. Примерами скаляр-
скалярных величин могут служить масса, плотность, работа, сила тока,
температура. Скаляры являются алгебраическими величинами
и с ними можно производить любые алгебраические действия:
сложение, вычитание, умножение, деление, возведение в сте-
степень и т. д.
2. Если при определении некоторой величины для ее полной,
характеристики, кроме числового значения, надо знать и ее
направление, то такая величина называется векторной, или век-
вектором. Примерами векторных величин являются скорость, уско-
ускорение, сила. Длина вектора называется также его модулем, или
абсолютной величиной.
3. Вектор обозначается графически отрезком прямой, на ко-
котором ставится стрелка, указывающая направление вектора
(фиг. 16, 1). Мы будем вектор обозначать одной буквой с черточ-
черточкой над ней, например, а, а модуль этого вектора — той же бук-
буквой, только без черточки над ней, т. е. а. Модуль вектора а
часто обозначается \а\.
Вектор мы будем также обозначать АВ, где А— начало и
В — конец вектора, а его модуль —теми же буквами, нр без
черточки наверху.
13»
4. Вектор равен нулю, если его модуль равен нулю. Такой
вектор называется__нулевым.
5. Два вектора а и b называются равными, если 1) равны их мо-
модули, 2) они параллельны и 3) направлены в одну и ту же сторону.
Два вектора с равными модулями, лежащие на параллельных
прямых, но противоположно
направленные, называются
противоположными. Вектор,
противоположный вектору а,
обозначается через— а.
6. Сложение векторных ве-
личин производится по пра-
правилу параллелограмма: сумма
двух векторов а и Ь, приведен-
Фиг. 16,2.
ных к общему началу, есть третий вектор с, длина которого
равна _длине диагонали параллелограмма, построенного на век-
векторах а и Ь, а направлен он от точки А к точке В (фиг. 16,2)
а + Ь = с.
Модуль вектора с вычисляется по формуле
с = |/а2 + b2 + 2ab cos (a, ~b). A6,1)
В
Фиг. 16,3.
7. Сумму нескольких векторов, например а, Ъ, с и d, строят
так: берут произвольную точку О плоскости и из нее строят
вектор О А, равный вектору а; из точки А _проЕодят вектор
АВ, равный вектору е, из точки В—вектор ВС, равный век-
вектору с и, наконец, из точки С строят вектор CD, равный век-
вектору d., Вектор OD, замыкающий полученную ломаную линию
OABCD, и будет суммой векторов а, Ь, с и d (фиг. 16,3):
Ш) ^a + b + c+d.
140
По такому же правилу строится и сумма любого числа век-
векторов .
8. Разностью двух векторов а и Ь называется такой третий
вектор с, который равен сумме векторов аи —Ь (фиг. 16,4).
Вектор — Ъ параллелен вектору Ъ, равен ему по модулю, но
противоположно направлен: .
А
Фиг. 16,4
Фиг. 16,5.
9. При умножении вектора а на скаляр k получается вектор
6, модуль которого равен модулю вектора а, умноженному на
k, т. е. b = ak: Направления векторов а и Ъ совпадают, если
k > 0, и они противоположны, если k < 0. Имеем
k-a = b, или а = ~ Ъ (k Ф 0).
10. Два вектора, лежащие на параллельных прямых, неза-
независимо от того, направлены они одинаково или противоположно,
называются коллинеарными.
11. Единичным вектором, или ортом данного вектора, назы-
называется вектор, совпадающий по направлению с данным вектором
и имеющий модуль, равный единице.
12. Проекцией вектора а на ось I называется длина отрезка
А'В', заключенного между проекциями начала и конца вектора
на эту ось. Этой длине приписывается знак плюс, если направ-
направление отрезка А'В' совпадает с направлением оси, и знак минус,
если его направление противоположно направлению оси.
Проекция вектора на ось есть скалярная величина, равная
произведению модуля проектируемого вектора на косинус угла
между положительными направлениями оси и вектора (фиг. 16, 5).
Проекция вектора а на ось / обозначается через щ или пр;а,
а угол между осью I и вектором а будем обозначать так: A,~а).
Таким образом,
сц = пр*а — acos 9. A6, 2)
141
Если а, р и 7 — углы, ' образованные вектором а с коорди-
координатными осями Ох, Оу и Ог прямоугольной системы координат,'
то проекции вектора а на координатные оси будут равны
ах — a cos а |
aj, = acosp|. A6,3)
az — a cos т )
В дальнейшем предполагается, что система координат — прямо-
прямоугольная.
Модуль вектора через его проекции на оси прямоугольной
системы координат вычисляется по формуле
а = У~ах + 4 + а\, A6,4)
т. е. модуль "вектора равен арифметическому значению квадрат-
квадратного корня из суммы квадратов его проекций.
Вектор равен нулю, если все три его проекции равны нулю
(этим положением пользуются, например, в механике при вы-
выводе необходимых и достаточных условий равновесия тела под
действием системы сил, проходящих через одну точку).
Если векторы с, и а2 равны, то равны и их проекции:
а\х — а2х; aw — aw\ аи=а2г. A6,5)
Если для вектора а известны координаты его начала
А(хъ ylt гг ) и координаты его конца В(х2, у2, г2), то проекции
вектора а на координатные оси определяются по формулам
ах = хя — Хх\ ау^у^ — у-^, аг = г2 — г1, -A6,6)
а модуль вектора в этом случае определится по формуле
a = V (x2-Xiy + (y2 - уг? + (г, - ггJ. A6,7).
Очевидно, что по формуле A6,7) следует вычислять и рас-
расстояние между точками А (х1У уъ гг) и В (х2, у2, z2).
13. Проекция суммы векторов на какую-нибудь ось равна
алгебраической сумме проекций этих векторов на ту же ось.
Из векторного равенства
a = al+'ai + aa + ...+an A6,8)
следуют такие три скалярные равенства:
ах = а1х + а2х + азх + ... + <W,
аи = aw + a2y + asy + ...+ any; A6,9)
аг = а1г + а2г + агг + . .. + апг.
14. Если i, i и k — векторы, по модулю равные единице
и направленные по координатным осям Ох, Оу и Ог, то разло-
142
жение вектора а по трем координатным осям выражается фор-
формулой
а = ах1 + а„1 + агЪ, . A6,10)
где ах, ау и аг — проекции вектора а на координатные оси Ох,
Оу и Ог.
Величины ах, ау и аг — проекции вектора а на координатные
оси — называются координатами вектора*. Если вектор а имеет
начало в начале координат, а его конец А имеет координаты х,
у и z, то тогда его проекции на
координатые оси равны координа-
координатам его конца:
ах — х; ау = у; az — г.
В этом случае вектор а назы-
называется радиусом-вектором точки А.
Радиус-вектор точки обозначается
обыкновенно через г (фиг. 16,6)
~г = хТ+у7+г?, A6,11)
а модуль радиуса-вектора точки
А (х, у, г) вычисляется по фор-
формуле
+-22. A6,12)
Фиг. 16,6.
15. Углы, образуемые вектором а с координатными осями
Ох, Оу и Ог, определяются из формул A6,3) и A6,4):
х
а
cos? =4 =
ау
A6, 13)
а2 а
COS т = — = .
а У4+4 + 4
Косинусы, определяемые по этим формулам, называются на-
направляющими косинусами вектора а.
Для направляющих косинусов вектора имеет место формула
cos2 a-f-cos2 р + cos2 7 = 1, A6,14)
т. е. сумма квадратов косинусов углов, образуемых вектором
с тремя взаимно-перпеидикуля рными осями, равна единице.
* Если вектор а имеет координаты ах, а^, аг, то это обозначается так:
а {"х, ау, az\.
143
Если | а | = 1, т. е. если а — единичный вектор, обозначаемый
обыкновенно через а0, то его проекции на координатные оси вы-
вычисляются по формулам
a° = l-cosa; a°=l-cosC; a° = l-cos?, A6,15)
т. е. проекции единичного вектора а0 на оси прямоугольной
системы координат Ох, Оу и Ог равны соответственно направ-
acosff
Фиг. 16,7
'ляющим косинусам этого вектора. Имеет
место формула
а0 — i ¦ cos a + / cos p + k ¦ cos 7. A6, 16)
16. Если даны два вектора
а = ах ¦ i + ау ¦ j + аг ¦ k,
Ъ — Ъх ¦ i -\- by • j + bz -~k,
то a±b = (ax± bx) i + (ay ± bv) i +
+ (az ± bz) k
{a ± b)x = ax± bx\ [a ± b)y = ay ± bu; {a ± b)z = az ± bz. A6, 17)
17. Скалярным произведением двух векторов а и Ъ называет-
называется число, равное произведению их модулей на косинус угла между
ними. Скалярное произведение векторов а и Ъ обозначается сим-
символом а • В. Если обозначить угол между векторами а и Ъ через
G, для скалярного произведения будем иметь
a-6 = a6cos6. A6,18)
Из формулы A6, 18) следует, что скалярное произведение двух
векторов а и b — это произведение модуля одного из них на
проекцию второго на направление первого вектора (фиг. 16,7):
а -Ъ =а ¦ ba = b -ab, A6, 19)
откуда пр-6 = —^—; пр^а = —-т— • Скалярное произведение двух
перпендикулярных векторов равно нулю, так как в этом случае
л
cos ~ = 0.
cos(a, b)
Скалярное произведение имеет свойства, аналогичные свой-
свойствам произведений чисел:
а -Ъ = Ь • а
(переместительное свойство умножения);
(а+ b) -с = а -~с + Ъ -с
144
(распределительное, или дистрибутивное свойство произведения).
Если векторы а и b заданы проекциями на координатные оси
то их скалярное произведение вычисляется по формуле
а • b = axbx + ayby + a2bz, A6,20)
а косинус угла 9 между этими векторами определяется по
формуле
cos 9=
Если углы, образуемые вектором а с координатными осями,
обозначить через а, р и f, а углы, образуемые вектором b с ко-
координатными осями, —через olt (Зг и ?!> то косинус угла 8
между векторами а и b определяется по формуле
cos б = cos а • cos 04 -f cos {3 • cos (^ -f- cos 7 • cos ft. A6, 22)
Если векторы а и Ъ перпендикулярны, то их скалярное произ-
произведение равно нулю, и тогда
axbx + ajby + агЬг = 0, A6,23)
или
cosa • cosoti -f cos^ • cospx -f cosy • cosyi =: 0. A6, 24)
18. Векторным произведением векторов а н b называется век-
вектор с, который определяется следующими условиями:
1) Его модуль равен ab • sin 9. где ср — угол между вектора-
векторами а и Ъ.
2) Вектор с перпендикулярен к плоскости, определяемой пе-
перемножаемыми векторами а и Ь.
3) Вектор с направлен так, что наблюдателю, смотрящему
с его конца на перемножаемые векторы а и Ь, кажется, что для
кратчайшего совмещения первого сомножителя со вторым первый
сомножитель нужно вращать против часовой стрелки (фиг. 16, 8).
Векторное произведение векторов а и Ь обозначается символом
а х b:
\с\=\а х Ь| = а-6 sin (аГ 6), A6,25)
или
\а х &| = пл. О ABC. A6,26)
б И. А. Каплан 145
Основные свойства векторного произведения:
1) Векторное произведение а х Ъ равно нулю, если векторы
а и Ь коллинеарны или какой-либо из перемножаемых векторов
является нулевым.
2) При перестановке местами векторов сомножителей вектор-
векторное произведение меняет знак на противоположный (фиг. 16,9):
а хЪ = — b ха
а*6
а
Фиг. 16,8.
Фиг. 16,9.
Векторное произведение не обладает свойством переместитель-
переместительности .
3) (а + Ъ) х с = а Хс + b x с (распределительное свойство).
Выражение векторного произведения а х Ь через проекции
векторов а и Ъ на координатные оси прямоугольной системы ко-
координат дается формулой
а X Ъ = (ауЬг—~агЬу)Т+ (a2bx — axbz)J+ {axbu —ауЬх)Ъу A6,27)
которую можно записать с помощью определителя
k
а х b —
I
ax
j
A6,28)
Проекции векторного произведения на оси прямоугольной си-
системы координат вычисляются по формулам
(а X Ь)х = aybz — агЬу
( )
агЬу
A6, 29)
( ) y у
(а х Ь)у = azbx — ахЬг
(а X b)z = axby — aybx
и тогда на основании A6,4)
\аХ Ь\= V(aybz — azbyy + (агЬх — axbzf + (axby — aybxf. A6,30)
Механический смысл _ векторного произведения состоит в сле-
следующем: если вектор F — сила, а вектор г есть радиус-вектор
146
точки приложения силы, имеющий свое начало в точке О, то
момент силы F относительно точки О т0 (F) есть вектор, равный
векторному произведению радиуса-вектора г точки приложения
силы на силу F, т. е.
т0 (F) = г X F.
19. Векторно-скалярное произведение трех векторов а, Ъ и с
или смешанное их произведение вычисляется по формуле
ах ау а
а • (b x с) —
Сг
A6,31)
Абсолютная величина векторно-скалярного произведения равна
объему параллелепипеда, построенного на векторах а, Ъ и с.
Объем пирамиды, построенной на векторах а, В и с, получим по
формуле
ах
Ьх
V - + —
» пир — X с
Cz
A6,32)
причем знак перед определителем должен быть выбран так,
чтобы объем V был положительным*.
20. Три вектора а, Ь и с называются компланарными, если
они лежат в одной плоскости или параллельны одной и той же
плоскости. Для того, чтобы три вектора были компланарны, не-
необходимо и достаточно, чтобы их смешанное произведение было
равно нулю.
Задача 16,1. Найти равнодействующую двух сил ~FX и F2,
модули которых равны Fx = 5, F2 — 7, угол между ними 6 — 60°.
Определить также углы аир, образуемые равнодействующей
с силами Fi и F2 (фиг. 16, 10).
Решение. По формуле A6, 1) находим
/? = ¦
+ Т + 2 • 5 • 7 • cos 60°,
пли
R = У 25 + 49 + 35 яз 10,44.
Углы аир находим из треугольника ABC, пользуясь теоремой
синусов F = a -f- p):
sin
sin а " sin A80° — 6) *
* Предполагается, что векторы а, Ъ и с не лежат в одной плоскости.
6* 147
Но
н тогда
sin a =
sin p=
sin A80° — б) = sine,
= —±. =0,581; <x = 35°30';
=LL^Ei = 0,415; |J=24°30'.
Контроль: (я + р =
Фиг. 16,11.
Задача 16,2. (для самостоятельного решения). Найти равно-
равнодействующую R сил Fx и F2, а_также углы « и р, составляе-
составляемые равнодействующей с силами Ft и ?2, если \FX\ = 15; \F2\ =
= 10; угол между силами ?г и ?2 е = 45°.
Ответ. /? = 23,173; я = 17°46'; р=,27°14'.
Задача 16,3. Определить координаты точки С — средины век-
вектора а по известным радиусам-векторам его концов А н В
(фиг. 16,11).
Решение. Пусть радиусы-векторы точек А и В соответ-
соответственно равны г\ и г2. Средина отрезка А В будет находиться на
пересечении диагоналей параллелограмма, построенного на век-
векторах гх и г2, и тогда точка С определится радиусом-векто-
радиусом-вектором г, который равен полусумме векторов гх и г2, т. е.
_
h
A6,33)
Координаты точки А обозначим через xlt yx и гх координаты
точки 5 — через *2> f/г и 2г. а координаты точки С—через х,
у и г.
148-
Спроектируем векторное равенство A6,33) на оси координат
по формулам A6,9). Так как векторы г, гг и г2 являются ради-
радиусами-векторами точек А и В, то их проекции на координатные
оси будут равны
гх = х\ гу = у; гг = г; ги — хх\ пУ ¦¦= ух\ г1г = гг;
Тчх = Х%, f2y = Уг, Гчг = 22.
Тогда векторное равенство A6,33) заменится такими тремя
скалярными равенствами, определяющими координаты средины
отрезка по известным координатам его концов,
X —
„ __ У1 + У2 . , _
У— о • г~
A6, 34)
Задача 16,4 (для самостоятельного решения). Вектор а
задан координатами своих концов Л B,4 — 3) и В(—4,4 — 5).
Найти координаты средины отрезка АВ.
Ответ. * = —1; у = 4; z — — 4.
Задача 16,5 (для самостоятельного решения). Три вектора
a, b и с расположены в одной и той же плоскости. Даны их
длины: |а[ = 3; |б| = 2; |с| = 2. Известно, что векторы Ъ и с
составляют с вектором а углы в 60°. Определить угол а между
векторами Ъ и с и длину суммы s = а + Ъ-\- с.
Ответ. я = 0 или я = 120°. В первом случае \s\ — У~37, во
втором | s | = 5.
Задача 16,6 (для самостоятельного решения). Три вектора а,
b и с попарно взаимно-перпендикулярны, а длина их соответствен-
соответственно равна 2, 3 и 6. Найти длину суммы s этих
векторов и направляющие косинусы вектора s
(фиг. 16, 12).
— —''v— 2
Ответ. (s | = 7; cos (s, a) = у;
cos (s, Л6) « 5. ;
cos (s, с) = - .
Задача 16,7. Даны два вектора:
а = 2i+ 2>j— Ak и Ъ = — 3? + 2/ +
с 1
Г
А
/
У
Фиг. 16, 12.
Найти проекции на координатные оси суммы и разности этих
векторов.
149
Решение. Составим сумму и разность этих векторов:
а + 5 = B_3)Г+-C + 2)/ + (-4 + 5)Л.
а — Ъ == B + 3) Г + C — 2) / + (— 4 — 5) k.
Ответ, а + Ъ = — i + 5/ + k; а — Ь" = 5/ + / — 9&;
(a + b)x = — \; (a + b)y = 5; (a + ft), = 1;
(a — ft), = 5; (a — b)y = 1; (a - ft), = — 9.
При решении задачи можно было сразу воспользоваться фор-
формулами A6, 17).
Задача 16,8 (для самостоятельного решения). Найти сумму и
разность векторов
a = 27 + 3/ — 4/г и 5 = 37 —4/+6Л,
а также проекции а + b и а — Ьна координатные оси.
Ответ, а + В = Ы — / + 2k;
а~Ъ = _ Г+ 7/— 10/fe;
(a + %=5; (a + b)y = — 1; (Б + ft), = 2;
E_5), = —1; J5—ft)» = 7; (a—ft), = —10.
Задача 16, 9. Вектор a задан координатами своих концов А и
В: А B, 1-4); 5A,3,2). _
Найти проекции вектора а на координатные оси и его направля-
направляющие косинусы.
Решение. Проекции вектора а на координатные оси нахо-
находим по формулам A6, 6). ах = —1; ау = 2; а2 = 6;
а = ]/(_ 1J + 22 + б2 = 1/41.
Направляющие косинусы определяем по формулам A6, 13):
1 о 2 б
cos a = — ; cos В — -= ; cos т = ——..
Задача 16. 10 (для самостоятельного решения). Проекции век-
вектора а на координатные оси равны: ах — 2; ау = 3; а2 — —4. Найти
направляющие косинусы вектора а.
Q О А
От вет. cos a— —= ; cosB = -r=; cost— 7=.
/29 Г /29 ' /29
Задача 16,11. Найти проекцию вектора
а = axi + ayj + a2fe
на ось L, которая составляет с координатными осями углы X, a
и v.
150
Решение. Обозначим через ср угол между положительными
направлениями вектора а и оси проекций L, а через а, р и f —
углы, составляемые вектором а с координатными осями Ох, Оу и
Oz. Тогда по формуле A6, 22), учитывая, что по условию ось L
составляет с теми же координатными осями углы X, р и v, мож-
можно написать, что
cos ср = cos а • сое X -{- cos р • cos p + cos 7 • cos v. A6, 35)
По формуле A6,2) проекция
aL — a cos ср.
Подставляя сюда значение coscp из A6,35), получим
UL — й (COS а • COS X -f- COS P • COS (i -f- COS 7 • COS v).
Раскрывая в правой части этого равенства скобки и замечая,
что
a cos а = а/, а cos р = ау\ a cos 7 — а2.
получим окончательно для проекции aL вектора на ось выраже-
выражение
aL = a, cos л -f ay cos p + а2 cos v. A6,36)
Задача 16,12. Дан вектор a = 2i + 5j +~k. Найти его проек-
проекцию аь на ось L, составляющую с координатными осями равные
острые углы.
Решение. По условию направляющие косинусы оси проек-
проекций между собою равны:
cos X = cos ji = cos v.
Но сумма квадратов направляющих косинусов какого-либо на-
направления равна 1, а потому
COS2 X -f COS2 (i -f- COS2 v = 1,
и так как в этой сумме все слагаемые между собой равны, то
3cos2 Х- = 1; cos2 >. = g-; cos X = — ;
тогда
cos X = cos № = cos v = —=
V3
(знак плюс перед корнем взят потому, что по условию углы X,
I* и V —острые, а значит, косинусы их положительны). Так как
по условию а* = 2; а^ = 5, а2 = 1, то по формуле A6,-36) полу-
получаем
151
Задача 16,13. На точку. действуют три силы: Fx> F2 и F3,
проекции которых на оси прямоугольной системы координат таковы
X
Y
Z
2
1
5
4
-3
1
F3
—5
4
2
Найти величину и направление равнодействующей^
Решение. Равнодействующая R = /^ -f F2 + F3. Обозначим
проекции равнодействующей через X, Y, Z, а проекции сил
F\, F2, ^з — соответственно через Хх, Yv Zlt X2, Yz, 22 и Х3,
Y3, Z3.
По формулам A6, 9) имеем
X = Xj -f-л2 4" -^s> X = 1,
По формуле A6, 4) величина равнодействующей R будет рав-
равна корню квадратному из суммы квадратов проекций #" на коор-
координатные оси:
По формулам A6, 13) находим направляющие косинусы равнодей-
равнодействующей
cos {R, х) — -т= ; cos (R, у) = -7= ; cos (R, г) = -= .
v ; /69 v *' /69 v V&
Задача 16,14 (для самостоятельного решения). На точку дей-
действуют четыре силы: Fu F2, F3, Fit проекции которых на коор-
координатные оси прямоугольной системы координат даны в таблице:
X
Y
Z
Fy .
1
2
1
F2
—5
3
—2
F,
4
4
-3
Ft
—1
5
4
Найти величину и направление равнодействующей.
Ответ. #=1/197; cosa = L;
/197
14
152
Задача 16,15. Два вектора а и Ь определены своими проек-
проекциями а {7,2,—1} и Ь{1,2,—3}. Найти скалярное произведение
этих векторов и угол между ними.
Решение. По формуле A6,20)
а • Ъ = axbx + ауЬу
подставляя сюда проекции данных векторов, получим
a- JT=14;
по формуле A6, 18)
а • b =abcos6,
откуда
cos в = ill.
ab
Таким образом, для определения cos 6 нам осталось определить
модули векторов а и Ь.
По A6,4)
а = ]/ах±а1 + гг; Ь = ]/ bl + b2v +b~l;
отсюда
а = 1/54; а = 7,348;
Ъ = УП\ Ь = 3,742;
получаем, что
cos6= 14 ¦
27,496 '
cos 8 = 0,509; 9 = 59°24'.
Задача 16,16 (для самостоятельного решения). Векторы АВ и
CD заданы координатами своих концов
А {1,-3, -4); В {-1,0,2}; С{2,-4,-6}Г Я {1,1,1}.
Определить угол между этими векторами.
Ответ, cos6 = 0,973; 9=13°21'.
Указание. (АВ)Х = — 2; (АВ)У = 3; (АВ)г = 6;
(CD), = -l; (CD), = 5; (CDJ = 7;
АВ = 7; CD = 8.660
Задача 16,17. Определить угол между векторами а и ? за-
заданными своими проекциями а {2,1,—2}, Ь{\,—4,2}.
153
Решение. По формуле A6,21)
ab
Все величины, стоящие в числителе этой дроби, известны из ус-
условия задачи. Неизвестными являются модули векторов а и b
а = У~а2х + аи + а2г; а = ]/9; а = 3.
b = Ybl + Ь2и + Ь\\ 6 = 1/21; Ь = 4,582.
Подставляя в A6, 21), числа получим cos 8 = 13 746;
cos9 = —0,436; 9=115°51'.
Задача 16,18 (для самостоятельного решения). Два вектора
а я b определены своими проекциями а {2,4, — 3} и b {6,—4,2}.
Определить: 1) их скалярное произведение; 2) угол между
ними; 3) проекцию вектора а на направление вектора Ь.
Ответ. 1) а~Ь = —10; 2) cos9=—0,248; 9=104°21.
3) аь =—1,336.
Задача 16, 19 (для самостоятельного решения) Два вектора
а я Ъ определены своими проекциями а {4, — 1,—2} и Ъ {2, 1,2};
Определить: 1) скалярное произведение этих векторов; 2) -угол
между ними; 3) проекцию аь вектора а на направление вектора Ь;
4) проекцию Ьа вектора b на направление вектора а.
Ответ. 1) а-Ь~=3; 2) G=77°24'; ab = 1; ba = 0,655.
Задача 16,20. Найти площадь параллелограмма, построенного
на векторах
а = 57— 4] + 76,
Ь~ = Г+ /"— 26.
Решение. По определению векторного произведения двух
векторов модуль/ векторного произведения равен площади парал-
параллелограмма, построенного на этих векторах. Поэтому для реше-
решения задачи найдем сначала векторное произведение а х Ъ, а по-
потом его модуль. Согласно A6, 28) имеем
96,
1 1—2
а модуль
154
1 X
а х
6 =
ft| =
i
5-
1
1/12
la x
/'
4
1-
+
ь\
k
7
о
= i +
172 4- 92 =
19,26.
Искомая площадь параллелограмма
S = 19,26 кв. ед.
Замечание. Векторное произведение а хЪ можно было
сразу определить по формуле A6,27), в которой следует взять
ах = 5; ау = —4; аг = 7;
Ь,= 1; Ь„ = \; 62 = -2.
Задача 16, 21 (для самостоятельного решения). Найти вектор-
векторное произведение векторов
а = 7J+ 2]— 36
Ъ - 2Г— 2] + 4k
и его модуль.
Ответ. а х 6 = 21 —34/—18&; |ахЬ| = 38,52.
Задача 16,22 (для самостоятельного решения). Векторы а иЬ
определены своими проекциями а(—1, 2, 4} и Ь{2,—1, —4}.
Определить их векторное произведение и его модуль.
Ответ. ахЬ = — п + 4/ — 3&'. \а х Ъ| = 6,4.
Задача 16,23. Векторы Л В и CD определены координатами
своих концов: Л B, 4,5); В(— 1,— 3, — 2); СD, 1,7); D (—2,3,
10). Найти: 1) векторное произведение ЛВ х CD; 2) его модуль;
3) направляющие косинусы векторного произведения.
Решение. 1) - Найдем прежде всего проекции векторов
АВ и CD на координатные оси по формулам A6, 6):
(АВ)Х = -3; (CD)X - -6;
(АВ)у = -7; {CD)U = 2;
(ЛВJ = -7; (CD), = 3.
Итак, АВ {-3,-7, -7}; CD{-6,2,3}.
Тогда по формуле A6,27)
АВ х CD = [ — 7 • 3 — (—7) . 2]Г+ [— 7 • (—6) — (—3) ¦ 3] f +
+ [-3-2-(-7). (-6)] Г.
ЛВ х CD - — 77 + 5lJ— 48fe.
2) Модуль векторного произведения по его известным проек-
проекциям найдем по формуле A6,4):
\ГВ X CDJ = У{—7J+512-Ь(—48J;
| AS х CD | = /4954 = 70,3847.
155
3) Направляющие косинусы векторного произведения найдем
по формулам A6, 13):
—7 о _ 51 —48
COSa-7O3847; COSP~0^847; COS T = 703847 ;
cos a = — 0,099; cos p = 0,724; cos f = —0,682.
Задача 16, 24. Найти площадь треугольника, координаты вер-
вершин которого известны:
А (-2, 1,2); В C,-3,4); С A,0,9).
Решение. Рассмотрим векторы АВ и АС. Площадь треуголь-
треугольника ABC есть половина площади параллелограмма, построенно-
построенного, на векторах АВ и АС. Площадь параллелограмма, построен-
построенного на векторах АВ и АС, есть, модуль векторного произве-
произведения АВ х АС, а потому площадь треугольника А ВС есть
-sabc=\\JbxJc\-
Найдем векторное произведение АВ х АС, а потому половину
его модуля.
Проекции векторов А В я АС на координатные оси найдем по
формулам A6, 6),
(ЛВ), = 5; (ЛС), = 3;
(АВ)у =-4; (АС)у = -1;
= 2; (ЛС)г = 7.
ЛВ= 6,708;
ЛС =--1/1)9; АС = 7,681.
По формуле A6,27) для векторного произведения векторов най-
найдем, что _
АВхАС = —261— 29/ +7 А.
Модуль вектора Afi"x ЖГнайдем по формуле A6,4):
| ЛВ х АС | = 1/1566; ЙВ х ЛС | = 39,573;
S^bc - ^| ЛВ х ЛС| = j • 39,573;
Ялвс = 19,787 кв. ед.
Задача 16,25. Дана сила F{3,4,—2} и точка ее приложения
Л B,—1,3). Найти момент силы относительно начала координат
и углы, составляемые им с координатными осями.
Решение. Момент силы относительно начала координат ра-
равен векторному произведению радиуса-вектора точки Л приложе-
приложения силы на силу F, т. е. т0 (F) = г х У.
156
Проекции радиуса-вектора точки А на координатные оси равны
координатам точки А—формула A6, 11):
„ гх =х = 2; гу =у = — 1; г2 = z = 3;
г = 21 — / + 36.
Проекции X, Y, Z силы F на координатные оси нам также из-
известны из условия задачи:
X = Z; Y = 4; Z = — 2,
и тогда формула A6, 27) даёт
mo(F)=rxF = [—l-(— 2)-3-4]Г+[3-3-2-(-2)]-/-Ь
+ [2-4 —(—1).3]Л;
т0 (F) = — ЮТ + 13J+ 1 life.
Отсюда
тх = — 10; ту — 13; тг =11;
и модуль момента
т - Vtn\+m* + m\'= У (— 10)г + 132 + И2; m = /ЗЭО;
m = 19,748.
Направляющие косинусы вектора mo(F) равны
i °>506' «Н
а углы, составляемые моментом силы с координатными осями,
следующие:
a = 120°24'; р = 48°51'; т = 56°9'.
Контроль: должно быть cos2a + cos2(J + cos2-j = 1. У нас
cos2 a + cos2 p + cos2 т = 0,999.
Задача 16, 26 (для самостоятельного решения). Найти момент
силы F {5, 6, —7} относительно начала координат, если точка ее
приложения А{\, 1, 1). Определить также направляющие коси-
косинусы момента.
Ответ.
mo(F) =
i ] k
1 1 1
5 6—7
т-^УШ;
; nix = — 13; niy = 12; n%z = 1;
\ cosS ; cost
/314* V /314' ' /314*
157
Задача 16,27. Найти объем пирамиды, если координаты ее
вершин
А1(хи ух, zx); Л2 (х2, у2, z2); Л3 (х3, у3, z3);
А 4 {xii У it ^4).
Решение. Рассмотрим векторы А1А2, АгАа и ЛХЛ4, на ко-
которых построена пирамида.
Зная координаты начала и конца каждого вектора, найдем
проекции этих векторов на оси прямоугольной системы коорди-
координат:
— Zj); A1A3{x3 — xv у3 —#i,z3 —г^;
для объема пирамиды получаем на основании формулы A6,32)
V=
+-
- 6
xs — xi Уз'— Ух гз
xt — хг уi — yx z4 —
Задача 16,28. Даны координаты вершин пирамиды ЛхE, 1,
—4), Л2 A,2,-1), Л3C, 3, —4) и Л4 B, 2, 2). Определить ее
объем.
Решение. Рассмотрим три вектора: АгАг, АгА3 и ЛХЛ4. По-
Поступая так же, как и при решении задачи 16,27, по формуле
A6, 32) найдем объем пирамиды, построенной на этих векторах.
Для применения формулы A6,32) нам надо знать проекции век-
векторов на оси прямоугольной системы координат. Записывая про-
проекции вектора рядом с его названием, получаем ЛХЛ2{—4, 1,3};
Ли; {-2, 2,0}; ДИ4{—3, 1,6}; и тогда
1
= ±'(-24).
—4 1 3
-2 2 О
—3 1 6
V = 4 куб. ед.
В правой части выбран знак минус, так как определитель отри-
отрицателен.
Задача 16,29 (для самостоятельного решения). Найти объем
пирамиды по известным координатам ее вершин:
ЛхB, 1, -2); Л2C, 3, 3); Л3A, 1, 2); Л4(-1, -2, -3).
Ответ, -g- куб. ед.
158
СЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Основные задачи на плоскость.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это практическое занятие посвящается основным задачам, свя-
связанным с плоскостью. Напомним основные формулы.
1. Общее уравнение плоскости
¦ Ax + By+Cz + D = 0. A7,1)
Если в этом уравнении D — О, то плоскость проходит через
начало координатой ее уравнение будет таким
Ax + By + Cz = 0. A7,2)
При С =0 уравнение A7, 1) примет вид
Ах +By + D = 0, A7,3)
и плоскость параллельна оси Oz. При В — О уравнение A7, 1)
запишется в виде
Ax + Cz+D = 0. A7,4)
В этом случае плоскость параллельна оси Оу, а при А = 0 урав-
уравнение A7,1) приобретает вид
Bi/ + Cz + D = 0, A7,5)
и плоскость параллельна оси Ох.
Вообще следует запомнить, что если плоскость параллельна
какой-нибудь координатной оси,. то в ее уравнении отсутствует
член, содержащий координату, одноименную с этой осью. Если
в уравнениях A7,3), A7,4) и A7,5) окажется, что D = 0, то эти
уравнения имеют вид
Ах+Ву--^0; A7,6)
Ax + Cz = 0; A7,7)
By + Cz^0. A7,8)
Уравнение A7,6) — уравнение плоскости, проходящей через коор-
координатную ось Oz; A7,7) — уравнение плоскости, проходящей через
ось Оу, а A7, 8) — уравнение плоскости, проходящей через ось Ох.
Если в уравнении A7, 1) А — 0 и В = 0, то оно приобретет вид
Cz + D = 0, A7,9)
и плоскость параллельна координатной плоскости хОу. При В = 0
и С = 0 уравнение A7, 1) запишется в виде
Ах + D = 0, A7, 10)
159
а определяемая им плоскость, параллельна координатной плоскости
уОг. При А = 0 и С = О получаем из A7,1)
By + D = 0, A7,11)
и плоскость A7,11) параллельна координатной плоскости хОг.
Если окажется, что в уравнениях A7,9), A7,10) и A7,11)
D = 0, то эти уравнения примут вид
z = 0, A7,12)
х = 0, . A7, 13)
У = 0 A7, 14)
и будут уравнениями самих координатных плоскостей, соответ-
соответственно хОу, уОг и хОг.
2. Уравнение плоскости в нормальном виде
х cos а '4- У cos р -f z cos 7 — р = 0, A7,15)
где а, р и т — углы между координатными осями Qx, Ot/ и Ог
и перпендикуляром, опущенным из начала координат на плос-
плоскость, а р— длина этого перпендикуляра.
3. Для приведения общего уравнения плоскости A7, 1) к нор-
нормальному виду A7, 15) обе его части следует умножить на нор-
нормирующий множитель
выбрав перед корнем знак, противоположный знаку свободного
члена в уравнении A7, 1).
4. Уравнение плоскости в отрезках на осях
? + Т+7 = 1' <17'17)
где a, b и с — величины отрезков, отсекаемых плоскостью на коор-
координатных осях.
5. Уравнение связки плоскостей, проходящей через точку
М (хь уг, z-ij, имеет вид .
А (х-хх)+В(у-У1) 4- С(г-г1) = 0. A7, 18)
Давая коэффициентам Л, Я и С в уравнении A7, 18) различные
значения, мы получим различные плоскости, проходящие через
точку М (xlt yu гг).
6. Угол между двумя плоскостями
A1x + B1y-\-C1z + D1 = 0 и A2x + B2y + C2? + D2 = 0 A7, 19)
«
определяется по формуле
cos ср = ± ЛА + ВА + СА A7 20)
VA*+B* + qyAi + B* + c*
160
7. Условие перпендикулярности двух плоскостей A7, 19) имеет
вид
А1Аг + В1В2 -l-CxC-O. A7,21)
8. Условие параллельности двух плоскостей A7, 19) имеет вид
9. Расстояние от точки N (хъ уъ гг) до плоскости Ах -\- By -f
-f Сг -f D = 0 определяется по формуле
х1 + Вуг + Сг, + D
10. Нам часто придется решать систему двух линейных одно-
однородных уравнений с тремя неизвестными
ах -f by -f сг = 01
A7>24)
В учебнике Привалова решение этой системы подробно разо-
разобрано (см. ч. I, гл. VI).
Мы же для ссылок приведем относящиеся сюда формулы:
х =
b с
t; y =
с а
t\ г =
aj Ьг
¦ t, A7, 25)
где t — произвольное число, а, по крайней мере, один из опре-
определителей, входящих в A7,25), не равен нулю.
11. Уравнение плоскости, проходящей через три данные точки
А (*i> l/v Zi), & (*2. Уъ г2), С (х3, у3, г3). имеет вид
х —х1 у —ух г — гх
= 0.
A7,26)
Прежде всего решим ряд задач, связанных с исследованием
общего уравнения плоскости.
Задача 17,1. Найти уравнение плоскости, параллельной оси
Ог и проходящей через точки Л B,3, — 1) и В (—1,2, 4).
Решение. Уравнение плоскости, параллельной оси Ог, имеет
вид A7,3)
Ах + By + D = О
(так как плоскость по условию задачи параллельна оси Ог, то
в ее уравнении отсутствует координата г).
Если плоскость проходит через точку, то координаты этой
точки удовлетворяют уравнению плоскости. Подставляя коорди-
координаты точек Л и Б в уравнение A7, 3), получим два уравнения:
2A + 3B+D =0
—A + 2B+D
= 0,
= 0Г
161
Для определения коэффициентов А, В и D мы имеем систему
двух однородных линейных уравнений с тремя неизвестными.
Составляем матрицу коэффициентов этих уравнений
1-4 2 \
Тогда по формулам A7,25) получаем
А =
• t; В =
•t;D =
2 3
— 1 2
t;
1 2
1 —1
A =t\ B = — 3t; D = 7t.
Подставляя найденные значения Л, Б и С в A7, 3), получим
tx — 3ty + It = 0.
После сокращения на t уравнение искомой плоскости приоб-
приобретет вид
х — Зг/ + 7 = 0.
Проверьте правильность решения подстановкой в полученное
уравнение сначала координат точки А, а потом координат точки
В. Каждый раз в левой части должен получиться нуль.
Задача 17, 2 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через точки А B, —3,2) и
Б G, 1,0) и параллельной оси Ох.
Ответ, у + 2г~ 1 = 0.
Задача 17, 3 (для самостоятельного решения). Найти уравнег
ние плоскости, параллельной оси Оу и проходящей через точки
А B, 1,-2) и В(-7,-2, 1).
Ответ, х + Зг + 4 = 0.
Задача 17, 4. Найти уравнение плоскости, параллельной плос-
плоскости хОу и проходящей через точку Л A,2,—4).
Решение. Уравнение плоскости, параллельной плоскости
хОу, имеет вид A7,9): Cz + D = 0
Подставляя в него координаты точки А, получим —4С +
+ D = 0, или D = 4С. Подставляя это значение в A7, 9), получим
Cz + 4С = 0,
а сокращая на С, будем иметь окончательно
2 + 4=0.
Задача 17, 5. Составить уравнение плоскости, перпендикуляр-
перпендикулярной оси Ох и проходящей через точку А C,7,—1).
Решение. Так как плоскость перпендикулярна оси Ох, то
она параллельна плоскости yOz, а потому ее уравнение имеет
вид A7, 10)
A
162
Подставляя в это уравнение координаты точки Л, получим, что
D = —ЗЛ. Это значение D подставим в A7, 10) и, сокращая
на А, будем иметь окончательно х— 3 = 0.
Задача 17, 6 (для самостоятельного решения). Найти уравне-
уравнение плоскости, параллельной плоскости xOz и проходящей через
точку Л B, —3, 4).
Ответ. г/ + 3 = 0.
Постройте эту плоскость.
Задача 17,7. Найти уравнение плоскости, проходящей через
ось Ох и через точку А B, 1,3).
Так как искомая плоскость проходит через ось Ох, то ее
уравнение имеет вид By + Cz = 0 A7,8). Подставим в это урав-
уравнение координаты точки А, через которую плоскость проходит.
Получаем В + ЗС = 0, откуда В = — ЗС.
Это значение В подставляем в A7,8) и получаем, сокращая
на С, Ъу — z = 0.
Задача 17,8 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через ось Ог и точку А (—2,4, —4).
Ответ. 2х + у = 0.
Задача 17,9 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через точку А B, —5,4) и через
ось Оу.
Ответ. 2х — 2 = 0.
Задача 17,10. Какие отрезки на координатных осях отсекает
плоскость
2х + Ъу — 5z + 30 = 0?
Решение. У точки, лежащей на оси Ох, координаты у и г
равны нулю.
Полагая в уравнении плоскости у = г = 0, получим для опре-
определения величины отрезка, отсекаемого плоскостью на оси Ох,
уравнение 2х + 30 = 0, или х = — 15.
Для определения величины отрезка, отсекаемого плоскостью на
оси Оу, полагаем в уравнении плоскости х = 0 и г = 0 и получаем
Ъу + 30 = 0, или и = — Ю. Наконец, величину отрезка, отсекаемо-
отсекаемого на оси Ог, найдем, положив в уравнении плоскости х = 0 и у —
= 0. Получим —5z + 30 = 0 и 2 = 6.
Этим заканчивается решение задачи. Можно было бы посту-
поступить и проще, преобразовав данное уравнение к виду в отрезках
на осях A7, 17). Для этого перенесем в правую часть равенства
свободный член. Данное уравнение запишется в виде 2лг + 3t/ —
— 5г = — 30. Разделим теперь обе его части на —30 и получим
—15+ —10 + 6 ~~ 1ш '¦
Величины отрезков, отсекаемых на координатных осях, равны:
а = - 15; Ь =¦- - 10; с - 6.
163
Задача 17,11 (для самостоятельного решения). Найти величины
отрезков, отсекаемых плоскостью х—10t/ + 2z— 12 = 0 на коор-
координатных осях.
Ответ. а=12; Ь=—g- и с = 6.
Задача 17,12. Уравнение плоскости 2х-\-2>у— 4г + 24 —0
преобразовать к виду A7, 17) в отрезках на осях.
Решение. Перенесем свободный член 24 в правую часть
уравнения и получим 2х-\-Ъу — 4г = — 24. Разделим теперь обе
части уравнения на —24 и получим
JL-A-JL -L-1- 1
_12 + _8~т 6 •
Задача 17, 13 (для самостоятельного решения). Уравнение
плоскости 3* — 4у -f 5г — 24 = 0 преобразовать к виду в отрезках
на осях.
Ответ. | + X + i_=1.
Задача 17,14. Уравнение плоскости Ьх+1у — 34z-f-5 = 0
привести к нормальному виду.
Решение. Для приведения общего уравнения плоскости
A7, 1) к нормальному виду A7, 15) надо обе его части умножить
на нормирующий множитель A7, 16), выбрав перед корнем знак,
противоположный знаку свободного члена в общем уравнении
плоскости. В нашем случае перед, корнем следует выбрать знак
минус. У нас А = 5; В — 7; С = — 34, и для N получаем
/ 52 + 72 + (—34J' /1230 '
а уравнение принимает вид
5 x 7 u, 34 г_ 5 =p
/1230 /1230^/1230 /1230
Задача 17,15 (для самостоятельного решения). Привести к
нормальному виду уравнение плоскости 2х -f- 9у — 6г + 33 = 0.
Задача 17,16. Найти длину перпендикуляра, опущенного из
начала координат на плоскость 10*-f- 15t/ — 6z —380 = 0, и углы,
образуемые этим перпендикуляром с координатными осями.
Решение. Приведем уравнение плоскости к нормальному
виду.- По формуле A7, 16) находим, что нормирующий множитель
N — уд. Обе части уравнения данной плоскости умножим на
•jg и получим уравнение плоскости в нормальном виде
164
из которого усматриваем, что р =- 20; косинусы же углов обра-
образуемых этим перпендикуляром с координатными осями, будут
10 0 15 6
cos a = -jgj cos p = jg-, cos т = — jg-
Дроби в правых частях последних равенств превратим в деся-
десятичные и получим, что
= 0,5263; <х= 58°15';
p= 0,7895; р= 37°52';
cosT = — 0,3158; ? = Ю8°25'.
Контроль: cos2a + cos2р + cos27 = 1 (значения углов най-
найдены с помощью таблиц тригонометрических функций).
Задача 17,17 (для самостоятельного решения). Привести к
нормальному виду уравнение плоскости
3jc — 4t/ + 5z — 14 = 0.
3 4.5 14 n
Ответ. ^=х-^+г 0
Задача 17,18 (для самостоятельного решения). На плоскость
Ьх — t/ + 3z + 12=0 из начала координат опущен перпендикуляр.
Найти его длину и углы, образованные им с. координатными
осями, а также координаты основания этого перпендикуляра.
12 5 1
Ответ, р — -р=; cosa = —-=•; cos В =¦-==, cost =
Н /35 /35 V /35 '
3 / 12 12 36
= —у=.. Координаты основания перпендикуляра! — у> 35.—
Указание. Координаты основания перпендикуляра найдите
по формулам
jtj — р cos a; yt = р cos Р", гх =» р cos f.
Задача 17,19. Найти расстояние от точки А B, 3, —1) до
плоскости 1х— 6у — 6г -f 42 = 0.
Решение. Расстояние от точки до плоскости определяется
по формуле A7,23,) в которой следует положить А =7; В — — 6;
С — —6; лгх = 2; ух — 3; гх = — 1. Подставляя эти значения в
формулу A7,23), будем иметь
d== 17-2 + (—6) • 3 + (—6) • (—1) + 42
(-6J+(-6J
14—18 + 6 + 42
11
= 4.
Задача 17, 20 (для самостоятельного решения). Найти расстоя-
расстояние от точки А B, —4, 2) до плоскости 2х + 11 у + 10z — 10 = 0.
Ответ. d = 2.
Задача 17,21 (для самостоятельного решения). Найти расстоя-
расстояние от точки ЛC, +4, —1) до плоскости 3* + 4у — 5 = 0.
Ответ, d = 4.
165
Задача 17, 22. Найти расстояние между параллельными пло-
плоскостями
Ьх+Зу— 4z + 15 = 0;
15л: -Ь 9г/— 12z — 5 = 0.
Решение. Возьмем на какой-нибудь из этих плоскостей
произвольную точку. Например, на первой плоскости возьмем
точку, для которой у = 0; г = 0, и определим абсциссу х этой
точки. Получим 5* + 3-0 — 4-0+15 = 0; х = — 3. Итак, на
первой плоскости взята точка (—3,0,0). Определив ее расстоя-
расстояние до второй плоскости по формуле A7,23), получим
Найденное расстояние d и будет расстоянием между данными
плоскостями.
Задача 17,23 (для самостоятельного решения). Найти рас-
расстояние между параллельными плоскостями
2х— 3t/+6z — 14 = 0
2Х - Ъу + 6z + 28 = 0.
Ответ, d — 6.
Задача 17,24. Через точку М B, 3, —1) провести плоскость,
параллельную плоскости
2х — Ъу + Ъг — 4 =0.
Решение. Уравнение связки плоскостей, проходящих через
данную точку, имеет вид A7, 18). В нашем случае оно будет
таким:
А(х — 2) + B(y — 3) + C(z + l) = 0.
Из условия A7,22) параллельности двух плоскостей получаем
Т--3- 5 (-R)-
Заменяя в последнем уравнении А, В и С величинами, им про-
пропорциональными, будем иметь
2k (х — 2) — ЗА (у — 3) + Ыг (г + 1) = 0.
или окончательно после упрощений \
2х — Ъу + 5z+ 10 = 0.
Можно решить задачу и иначе: если плоскости параллельны,
то их уравнения можно преобразовать так, что они будут отли-
отличаться только свободным членом. Тогда уравнение семейства
плоскостей, параллельных данной „плоскости, запишется так:
2х — 3j/ + 5z + D = 0. (A)
166
Подставляя в это уравнение вместо текущих координат х, у
и 2 координаты точки М B, 3, —1), через которую проходит
плоскость, получим уравнение, содержащее одно неизвестное D:
2 • 2 — 3 • 3 + 5 • (— 1) + D = О, D = 10. Это значение подставляем
в (Л) и получаем то же, что и раньше:
2х — 3i/ + 5z + 10 = 0. .
Задача 17,25 (для самостоятельного решения). Через точку
М{—4, —1, 2) провести плоскость, параллельную плоскости
Зх + 4у — г — 8 = 0.
Ответ. 3* + 4t/ —2+18 = 0.
Задача 17,26 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через точку B, 5, —1) и парал-
параллельной плоскости
* + 3t/ —4г + 5 = 0.
Ответ. х + Зу — 42 — 21 = 0.
Задача 17,27 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через точку A, —3, 2) параллельно
плоскости
7х — 4y + z-~ 4 = 0.
Ответ. 7х — 4y + z — 21 = 0.
Задача 17,28. Через точки М A, 2, 3) и N (—2, —1, 3) про-
провести плоскость, перпендикулярную плоскости
х + 4у — 22 + 5 = 0.
Решение. Уравнение связки плоскостей, проходящих через
точку, имеет вид A7, 18).
Подставляя в A7, 18) вместо хъ уг и гг координаты точки М,
получим
А(х— 1) + В(у— 2) + СB-3) = 0. (А)
Определению подлежат А, В и С.
Так как данная плоскость проходит и через точку N(—2,
—1, 3), то координаты этой точки должны удовлетворять урав-
уравнению плоскости. Подставим в (А) координаты точки N вместо
текущих координат и получим
А (—2 — 1) + В (—1 —2) + С C —3) = 0,
откуда
—ЗЛ — W ---- 0, или А + В =-- 0. , (В)
Используем теперь то, что искомая плоскость перпендику-
перпендикулярна данной. Условие перпендикулярности двух плоскостей
167
A7,21) с учетом того, что из данного уравнения At = 1, Вх =
= 4, Cj = — 2, запишется так:
1 . Л + 4 • Б — 2.С = 0.
Соединяя (Л) и (Б), получим систему двух однородных ли-
линейных уравнений с тремя неизвестными:
А+ Б= 0
А+4В — 2C = J
Решаем эту систему по формулам A7,25) и получаем
Л= — 2t; B = 2t; C = 3t.
Подставляя эти значения А, Б и С в (Л) и сокращая на t,
будем иметь
-2{х—1) + 2(у-2) + 3(z-3) = 0.
Откроем скобки, сделаем приведение подобных членов и окон-
окончательно получим искомое уравнение в виде
2х — 2у — Зг+ 11 =0.
Задача 17, 29 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через точки М(—1, 2, —3) и
#A, 4, —5) и перпендикулярной плоскости Ъх + Ьу— бг-f
+ 1=0.
Указание. Для определения коэффициентов А, В и С
получится система уравнений
А+ В— С = 0\
ЗА + 5В — 6С = 0 /'
из которой на основании формул A7, 25) А — — t; В = 3t; С = 2t.
Ответ. *—'Зу —2г+ 1 =0.
Задача 17, 30. Найти острый угол между двумя плоскостями:
5* — 3t/-f-4z — 4 = 0, (I)
Зх — 4у — 2z + 5 = 0, (LI)
Решение. По формуле A7,20) получим, если учесть, что на
основании (I) А1 = Ь; В1 = — 3; Ct = 4, а из (II) Л2 = 3; Б2 =
= —4; Сг = — 2,
М5+12 —8
19
cos <p =
cos <f = 0,4990; <f = 60°04'.
В формуле A7, 20) следует взять абсолютную величину правой
части, так как надо найти острый угол между плоскостями и,
значит, cos <p > 0.
168
Задача 17,31 (для самостоятельного решения). Найти острый
угол между плоскостями
5л: — Ъу + Ъг + 5 = 0 и х— 2у + Зг— 5 =, 0.
Ответ, cos9 = 0,9046; ср = 25°14'.
Задача 17, 32. Выяснить геометрический смысл коэффициентов
Л, В и С в общем уравнении плоскости A7, 1)
Ах + By + Cz + D = 0. • (Л)
Решение. 1. Рассмотрим вектор л с проекциями на коор-
координатные оси, соответственно равными А, В к С, т. е. п{А, В, С].
2. Возьмем на плоскости (Л) две произвольные точки: М (хг,
уъ гг) и N (х2, уг, г2) и рассмотрим вектор MN. Этот вектор
лежит в плоскости (Л). Его проекции на координатные оси со-
соответственно равны хг — хг, у2 — Ух, г2 — гх и MN [хг — х1г
Уг — Уъ г% — 4\-
3. Так как точки М и N лежат в плоскости (Л), то имеют
место равенства
A
и
Л*2 + Ву2 + Сгг + D = 0.
Вычитая первое уравнение из второго, получим
А (х2-хх) + В(у2-y1) + C(z2-z1) = 0. (В)
Скалярное произведение вектора п {А, В, С) на вектор
MN \х2 — xv у2 — уг, z2 — zx) равно
А (х2 ~.Xl) + B(y2 — yt) +C (z2 — гх).
Так как на основании (В) это скалярное произведение равно
нулю, то вектор п перпендикулярен вектору MN, а тем самым
и той плоскости, в которой лежит этот вектор, т. е. вектор
п{А, В, С} перпендикулярен плоскости Ах + By + Cz + D = 0.
Заключение. Геометрическое значение коэффициентов Л,
В и С в общем уравнении плоскости A7, 1) состоит в том, что
они являются проекциями на координатные оси Ох, Оу, Ог
вектора, перпендикулярного этой плоскости.
Задача 17,33. Найти следы плоскости Зл: + 2у — 4z + 5 = 0
на координатных плоскостях.
Решение. Уравнение прямой, по которой данная плоскость
пересекается с плоскостью хОу, мы получим как уравнение гео-
геометрического места точек, координаты которых одновременно
удовлетворяют уравнению данной плоскости и уравнению пло-
плоскости хОу. Так как плоскость хОу имеет уравнение г =< 0, то
уравнение искомого следа получим, положив в уравнение данной
плоскости z = 0.
169
Окончательно уравнения искомого следа данной плоскости на
плоскости хОу имеют вид
Зх + 2у + 5 = О
0
Периое из этих уравнений изображает плоскость, пар'аллельную
оси Oz, а второе указывает на то, что на этой плоскости рас-
рассматриваются точки, принадлежащие плоскости хОу (в плоскости
хОу первое из этих уравнений определяет прямую линию).
Уравнение искомого следа на плоскости yOz получим, учи-
учитывая, что плоскость yOz имеет уравнение х = 0. Положив в
данном уравнении х = 0, получим уравнения следа плоскости на
плоскости уОг
2у — 42 + 5 = 0 \
х = 0 }¦
Первое из этих уравнений есть уравнение плоскости, параллель-
параллельной оси Ох, а второе указывает на то, что в этой плоскости
рассматриваются только точки, принадлежащие плоскости уОг
(в плоскости уОг первое из уравнений определяет прямую линию).
Наконец, след данной плоскости на плоскости хОг, уравнение
которой у -- 0, мы получим, положив у = 0 в уравнении данной
плоскости. Уравнения этого следа
Ъх — 4г + 5 =
причем первое из них — уравнение плоскости, параллельной оси
Оу, а второе указывает на то, что на этой плоскости рассматри-
рассматриваются только точки, лежащие в плоскости хОг (первое уравне-
уравнение в плоскости хОг определяет прямую линию).
Задача 17,34 (для самостоятельного решения). Найти следы
плоскости 5лг + 3г/ + 2г—12 =--0 на координатных плоскостях и
построить эти следы.
Ответ. Уравнение следа на плоскости хОу
5х + 3у— 12 = 0 л
уравнение следа на плоскости yOz
2>у + 2г — 12 = 0
х = 0.
уравнение следа на плоскости хОг
С v | О— 1 Q (Л
\
Задача 17,35. Найти уравнение плоскости, проходящей через
точки ЛМ1, 2, —1); М2(—1, 0, 4); М3(—2, — 1, 1).
170
Решение. На основании уравнения A7,26) можно уравне-
уравнение искомой плоскости написать в виде
х—1 у—2 z -J- 1
— 2 —2 5=0.
— 3 —3 2
Вычисляя этот определитель, получим
— 4(х—1)—15@ —2) + 6(z+l)+15(x—1) +
+ 40/ —2) —6(z+l) = 0.
Раскрывая скобки, делая приведение подобных членов и сокра-
сокращая на 11, получим окончательно х— г/+1 = 0. Это уравнение
определяет плоскость, параллельную оси Ог.
Задача 17,36 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через три точки: /И1A, —3, 4);
ЛЫО, -2, -1); М3A, 1, -1).
Ответ. \Ъх— Ъу— 4г—14 = 0.
Задача 17,37 (для самостоятельного решения). Найти урав-
уравнение плоскости, проходящей через точки Мх П, —2, —Л\
М2B, 1, 3); М3@, -1, -1).
Ответ. 5х + Зг/ — 4z — 1 »= 0.
ВОСЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Основные задачи на прямую в пространстве.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это практическое занятие посвящается прямой линии в
пространстве. Напомним основные формулы:
1. Канонические уравнения прямой линии в пространстве,
или уравнения прямой с направляющими коэффициентами,
имеют вид
х ~~~ Xq у ~~" ijq z — Zq
т
A8, 1)
где д:0, у0, г0 — координаты точки, через которую проходит пря-
прямая, а т, п и р— направляющие коэффициенты прямой, кото-
которые являются проекциями на координатные оси Ох, Оу, Ог на-
направляющего вектора прямой.
Если а, Ри-f — углы между прямой и координатными осями
Ох, Оу и Ог, то
cos а. = ± Г т —; cosS=4 " ;
171
cos a, cosfB и cos? называются направляющими косинусами пря-
прямой. Направляющие коэффициенты т, п и р можно рассматри-
рассматривать как проекции на координатные оси вектора, параллельного
прямой, причем т, п и р не могут быть одновременно равны нулю.
Уравнения A8,1) могут быть записаны также в виде
х Хд у — |/о z г0 _ ,.п о\
cos a ~ cos p cos у ' К ' >
2. В параметрическом виде уравнения прямой линии в про-
пространстве записываются так:
x = xo + mt\ y=-yo + nt; z = zo + pt, A8,4)
где t— параметр.
3. Общие уравнения прямой:
Каждое из уравнений A8,5) — уравнение плоскости, и таким
образом прямая в пространстве может рассматриваться как пере-
пересечение двух плоскостей, причем плоскости эти предполагаются
непараллельными, т. е. соотношение
i; = ^ = c7
не имеет места.
4. Условие параллельности двух прямых в пространстве:
X — *0 У — У0 __ * — Zo .jg g^
т п Р ' '
х — *i ^У—Ух =г — гх
Щ «1 Pi
имеет вид
ъ=к=к- A8>7)
5. Условие перпендикулярности двух прямых A8,6) имее?
вид
ттх + ппг Н- ррх = 0 A8,8)
6. Угол между двумя прямыми A8,6) определяется по фор-
формуле
™^^ ~ш /~ 9 I 9 1 9 *Ш /^ О О О
7. Уравнения прямой, проходящей через две данные точки
!*i» #i» zi) и ^(^2. «/г, z2), запишутся в виде
172
Задача 18,1. Найти углы, которые прямая
х — 5 _ у+ 1 _ г— 4
2 ~~ 3 ~~ 6
составляет с координатными осями.
Решение. По формулам A8, 2), полагая в них т = 2, п = 3,
р = 6, будем иметь
2 2 2
cos а = ± — = ± —я=. или cos а = ± ¦=-;
/2a + 32+6a J/49 7
cos p = ± -=-; cos f = ± у.
Проверьте, что cos2 a -j- cos2 p + cos2 f — 1.
Острые углы, составляемые прямой с координатными осями,
равны: a = 73°24'; p = 64°37'; f = 31°l' (эти значения определены
по таблицам тригонометрических функций),
Задача 18,2. Общие уравнения прямой
2х— у+ z — 4 =
преобразовать к каноническому виду A8, 1).
Наметим такой план решения задачи: из системы (А) исклю-
исключим сначала у и выразим z через х, потом исключим х и выра-
выразим г теперь уже через у.
1) Для того, чтобы, из системы (А) исключить у, умножим
второе из уравнений системы (А) на 3 и сложим его почленно с
первым. Получим, что 7х — z — 7 = 0, откуда z = 7х — 7,
X— 1
т
2) Умножая первое уравнение из (А) на —2 и складывая
почленно со вторым, получим, исключая х из системы (Л),
— 7у + 9z — 14 =-.= 0,
откуда
9z = 7y 4- 14;
._ 7 (у+ 2)
Z ~~ 9 '
ИЛИ
Z- g^ .
7
Сравнивая найденные значения z, получаем уравнения прямой
в каноническом виде
173
Умножая теперь все знаменатели на 7, окончательно получим
х—\у + 2 г — о
В учебнике Привалова указан и другой способ преобразова-
преобразования общих уравнений прямой A8,5) к каноническому виду
(стр. 250).
Рекомендуем внимательно изучить этот способ. В связи с тем,
что в учебнике не указаны окончательные результаты, приведем
их здесь.
Если общие уравнения прямой записываются в виде A8,5)
= 0
то уравнения прямой с направляющими коэффициентами имеют
вид
х х у у z г /, о ...
X — Xa
B2 С„
у-
с1
~Уа
к
г —
А1
Вг
где х0, у0 и 20 — координаты одной из точек, через которую пре-
преходит прямая A8,5)
Из уравнений A8, 11) усматриваем, что направляющие коэф-
коэффициенты прямой и, пир определяются по формулам
m —
В« Се
Г, л =
t\ p =
А2 В
• t, A8, 12)
в которых можно положить t = 1 (на основании указаний в учеб-
учебнике эти формулы рекомендуется получить самостоятельно).
Решим нашу задачу по этому способу. Определим одну из то-
точек, через которую проходит данная прямая (А). Дадим коорди-
координате z значение нуль (z = 0). Для определения абсциссы х и ор-
ординаты у этой точки получим систему уравнений*
2х— у — 4 =
или
2х— г/=
из которой х— 1; у — — 2. Итак, одна из точек, через которую
проходит прямая, известна. Ее координаты A, —2, 0). Чтобы
определить направляющие коэффициенты прямой по форму-
формулам A8, 12) в которых взято t— 1, составляем матрицу из коэф-
коэффициентов уравнений системы (А):
/1 3-4\
12-1 1/
174
3
— 1
— 4
1
n =
— 4
j
1
2
. P =
1
2 —
3
1
и получаем
m =
m = — \; n = — 9; p = — 7.
Уравнения прямой (Л) в каноническом виде с учетом того, что
прямая проходит через точку A, —2, 0), примут вид
х — I у + 2 г —0
— 1 ~~ —9 =~~ —7 •
Умножая все знаменатели на —1, получим окончательно
х — 1_у + 2_г—О
Задача 18,3
прямой
1 ~ 9 ~ 7
самостоятельного
Уравнения
(для самостоятельного решения).
x — 4y + 5z—\=0]
2х + 3у+ г -H9-0J
преобразовать к каноническому виду и определить углы, обра-
образуемые этой прямой с координатными осями.
Указание. Воспользоваться вторым способом, указанным в
предыдущей задаче.
1. Определите одну из точек, принадлежащую данной прямой.
Координате г этой точки дайте произвольное значение, например,
z = 0. Для определения координат х и у получите систему урав-
уравнений
х — 4у = 1
2х + Зу = — 9
Отсюда х — — 3; у — — 1.
Итак, определена точка (—3, —1, 0), через которую прохо-
проходит прямая.
Воспользовавшись дляj определения т, п и р формула-
формулами A8, 12) при t — 1, получим
т = --19; п = 9; р = 11.
Искомое уравнение в виде A8, 1) запишется так:
х+3 _у+1 _г-0
9
-19 - 9 11 •
Углы, образованные этой прямой с координатными осями, опре-
определяем по формулам A8,2), в которых т, п и р имеют только
что найденные значения:
i ^ = ±0,374;
cos? = ¦±-7У== ±0,464.
1 /563
175
Контроль: cos51 a + cos2(J + cos2f = 1. По известным коси-
косинусам углов находим углы а = 143°14'; р = 67°44'; у = 62°2Г (при
определении углов из двух возможных знаков у косинусов выб-
выбран верхний знак).
Уравнения прямой получились бы в другом виде, если бы
вместо точки (— 3, —1, 0) на прямой взяли какую-либо другую
точку. Числители дробей в (А) изменились бы,, но знаменатели
остались теми же. Если же решать эту задачу по способу пер-
первому, указанному в предыдущем номере, то в знаменателях могли
бы получиться числа, пропорциональные тем, которые стоят в
знаменателях дробей (А).
Задача 18, 4 (для самостоятельного решения). Привести к ка-
каноническому виду общие уравнения прямой
х — 2у + 3г — 4 = 0,
2х + Ъу — 4z + 5 = 0.
Ответ. Один из возможных видов канонических уравнений
прямой
2 13
*~Т_..У + 7 г-0
—1 ~ 10 7 '
Задача 18,5 (для самостоятельного решения). Преобразовать
к каноническому виду уравнения прямой
2z + 8 = 01
Ответ. Один из возможных видов канонических уравнений
прямой
х — 4 у + 6 г —1
—1 ~~ 4 ~ — 5
Задача 18, 6 (для самостоятельного решения). Найти углы кото-
которые прямая
х+у+г—1=0
образует с координатными осями.
Ответ, cos a = ± 0,60470; cos p = =F 0,77747;
cos? = ±0,17277.
Контроль: cos2 а + cos2 p + cos2 у = 1.
Задача 18,7. Найти уравнения плоскостей, проектирующих
прямую
3x-4y + 5z+ 7 = 01
х + 2у + Ъг + 11 = 0 J W
на координатные плоскости.
176
Чтобы найти уравнение плоскости, проектирующей прямую
(А) на плоскость хОу, надо из системы (А) исключить коорди-
координату г. Умножая первое уравнение этой системы на —3, а вто-
второе на 5 и складывая полученные уравнения, будем иметь
— 4л; -f 22у + 34 = О, а сокращая на — 2, получим искомое урав-
уравнение в виде 2х — lit/ — 17 = 0.
Уравнение плоскости, проектирующей прямую (А) на плос-
плоскость хОг, получим", исключая из системы (А) координату у.
Умножая второе уравнение в системе (А) на 2 и складывая с
первым, получим искомое уравнение в виде
5х + llz + 29 = 0.
Уравнение плоскости, проектирующей прямую (А) на плоскость
yOz, получим, исключая из системы (А) координату х. Умножая
второе уравнение в системе (А) на —3 и складывая с первым,
получим искомое уравнение в виде
Ъу -f 2г + 13 = 0.
Задача 18, 8 (для самостоятельного решения). Найти уравнения
плоскостей, проектирующих прямую
х — 2у— г — 1 =0\
Зх — y + z — 2 = 0 J
на координатные плоскости.
Ответ. Уравнение плоскости, проектирующей прямую на плос-
плоскость yOz,
Ъу + 4г + 1 = 0.
Уравнение плоскости, проектирующей прямую на плоскость
хОг,
5х + Зг — 3 = 0.
Уравнение плоскости, проектирующей прямую на плоскость
хОу,
4^ — Зу —3 = 0.
Задача 18,9. Определить следы прямой
Sx + 3y-4z+8 = 0\
х — y + z + 5 = 0/ И)
на координатных плоскостях (следом прямой на плоскости назы-
называется точка пересечения прямой с плоскостью).
Решение. Уравнение плоскости xOy:z = 0. Положив в си-
системе (A) z=0, получим систему из двух уравнений
7 И. А, Каплан 177
Решая эту систему, найдем х и у:
v_ 23- ,,_17.
и след прямой (А) на' плоскости хОу имеет координаты
B3 17 \
— IF'T' г '^леды пРямой на плоскостях yOz и л;Ог найдите
самостоятельно.
Координаты следа прямой на «плоскости yOz будут @, 28, 23).
(9ft I7\
— Т ' *"*' —"9 )•
Задача 18, 10 (для самостоятельного решения). Найти коорди-
координаты следов прямой
х — 2 у + 3 г —4
1 ~ 2
на координатных плоскостях.
Ответ. A, -5, 0); (|, 0, К)); @, -7, -4).
Задача 18, 11. Найти острый угол между двумя прямыми
х — 2 "у— 1 г —3
— 1
2 ~ 4 ~ — 2 "
Решение. Угол <р между двумя прямыми определяется по
формуле A8,9), в которой надо взять
т =3; п =— 1; р = 2;
пц = 2; «! = 4; рг = — 2.
3-2 + (—1)-4 + 2 • (—2)
COS <р = ± —, I
Т /За + (—IJ + 22 • /2а + 4а + (-2;2
cos ф = ± ~2r- ; cos ф = =F -4= = =F 0,1091.
Y /14 /24 Т 2/21
Так как нас по условию интересует острый угол между этими
прямыми, мы должны соэф взять положительным: cos ср = 0,1091.
Теперь, пользуясь таблицами тригонометрических функций, на-
находим, что ф = 83°44'.
Задача 18, 12. Найти острый угол между прямыми
x—y+z =0
и
2x + y— г--5 = о)
178
Решение. Чтобы воспользоваться формулой A8,9) приведем
заданные уравнения прямых к каноническому виду A8,1) и по-
получим
*±1 _ У±1 _ ?и° (Л)
1 — 6 ~ 5 * (Л)
х—Зу+1 г —О ,R
Пользуясь этими уравнениями прямых, по формуле A8,9)
определим, что cos <р = 0,9445, а ср = 19°1Г
Задача 18,13. Через точку Л C, —1, 4) привести прямую,
параллельную оси Oz.
Решение. Уравнения оси Oz можно записать в виде
х—о_У—0_г—0
0 0 1
(ось Oz проходит через начало координат, а ее направляющие
косинусы равны cosa = 0, cos [3 = 0; cosf = l). Так как прямая
проходит через точку А C, —1, 4), то ее уравнения запишутся
в виде
х — 3_ у+1 _ г—4
т n p
Числа т, п и р в этих уравнениях из условия A8,7) параллель-
параллельности двух прямых должны быть пропорциональны числам 0,0
и 1 в уравнениях оси Oz. Заменяя поэтому в последних урав-
уравнениях числа tn, n и р им пропорциональными, получим иско-
искомые уравнения в виде
х — 3 у+1 г — 4*
0 0 ~" 1 *
Из этих уравнений следует, что
д:_3 = 0\
У + 1 = 0 }
и искомая прямая может быть определена и,этими уравнениями.
Задача 18,14. Через точку А(\, —1, 2) провести прямую,
параллельную прямой
х — Ч _ у — 3._ г+1
1 ~" 3 ~ 2 "
Решение. Напишем уравнение прямой, проходящей через
точку А:
г —2
* Эту запись, содержащую нули в знаменателях, понимают ' условно,
так, как это указано в учебнике Привалова (см. § 13 гл. 11, а также разъяс-
разъяснения на стр. 247).
7* 179
Из условия A8,7) параллельности двух прямых т, па р в этих
уравнениях должны быть пропорциональны направляющим коэф-
коэффициентам 1, 3 и 2 данной прямой. Заменяя т, п и р числами,
им пропорциональными, получим уравнения прямой в виде
д; — 1 _у+1 _ г — 2
1 ~~ 3 ~~ 2 •
Задача 18,15 (для самостоятельного решения). Через точку
B, —1, 3) провести прямую, параллельную оси Ох.
1/4-1=01 х-2 y+l г-3
Ответ. 2_3 = 0/ или ~Т~ = -~0~ ~ ~о~¦
Задача 18,16. Найти уравнения прямой, проходящей через
точки ЛA, 2, —1) и 5@, 3, —4).
Решение. Согласно A8, 10) имеем
х—1_у—2_г+1
—1 1 —3 »
или, умножая все знаменатели на —1,
х—1_у—2_г+1
Т~~~2 ~ 3 '
Задача 18,17 (для самостоятельного решения). Найти урав-
уравнения прямой, проходящей через точки А C, 0, 4) и
В (—1,-2, 3).
л х — 3 у —0 г —4
Ответ. _ = ?_ = _.
ДЕВЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Задачи на прямую и плоскость.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это практическое занятие содержит упражнения по разделу
«плоскость и прямая». Приводим основные формулы.
1. Острый угол между прямой
х — а у—Ь_ г—с
т п р
и плоскостью
Ах + By + Cz + D = 0
определяется по формуле
Ат + Вп + Ср \
sin 9 =
у А* + В2 + Са • Vт2 + п2 + Ра I'
A9, 1)
180
2. Условие параллельности прямой и плоскости имеет вид
Ат + Вп + Ср = 0.
3. Условие перпендикулярности прямой и плоскости имеет вид
4. Уравнение пучка плоскостей, проходящих через данную
прямую
Ах + By + Cz + D = 0
A
имеет вид
Ах+ By + Cz + D+l {Агх + Вху + Qz + Dx) = 0, A9,4)
где X — любое действительное число.
Задача 19,1. Найти острый угол между прямой
х—\' _ у+2 _ г —1
2 ~ 1 ¦ ~~ 2 f
И ПЛОСКОСТЬЮ
2х + у — 2 + 4 = 0.
Указание. Задача решается с помощью формулы A9,1),
в которой надо положить А = 2; 5=1; С = — 1; m = 2; п = 1;
Ответ. Угол ср = 24°5'.
Задача 19,2.,Найти острый угол между прямой
х + у+ z-4 = 0
2х — и + 4г
= 0|
= 0}
и плоскостью х -f- У + 3z — 1 =0.
Решение. Уравнения прямой нет надобности преобразовы-
преобразовывать к каноническому виду. Достаточно определить направляющие
коэффициенты и, пир этой прямой (см. задачу A8,2)). Состав-
Составляем матрицу из коэффициентов уравнений (А)
/1 1 1\
[2 -1 4)
и, полагая / = 1 в формулах A8, 12), получаем
т =
1 1
j 4
= 5; п= 4 2
1 1
2 —1
= —3.
Из уравнения плоскости заключаем, что А = 1, 5=1, С = 3,
и тогда для определения острого угла <р между прямой и плос-
плоскостью по формуле A9, 1) получаем
sin ср =
— 6
УТ\\-
181
Задача 19,3. Найти уравнение плоскости, проходящей через
точку РA, 2, —1) перпендикулярно прямой
х — 3 _ у —2 _ г+1
1- "^ —3 ~ 4 *
Решение. Уравнение плоскости, проходящей через точку
Р{1, 2,—1), напишем иа основании уравнения A7,18) в виде
А(Х- 1) + В (у -2) + С (г + 1) = 0.
Пользуясь условием A9,3) перпендикулярности прямой и
плоскости, заменив в последнем уравнении величины А, В я С
им пропорциональными величинами т, п и р из уравнений пря-
прямой, т. е. числами 1, —3 и 4, и получим
а после упрощений будем иметь
х — Зг/ + 4г + 9 = 0..
Задача 19,4 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через точку Р B, —4, —2) перпен-
перпендикулярно прямой
x — 4y + 5z—\ =0
2х+ у +3 =
О т в е т. 5* — Щ — 9z — 68 = 0.
Задача 19,5. Через точку B, 1, 6) провести прямую, перпен-
перпендикулярную плоскости х — 4«/ -f- Ъг—1—0, и определить направ-
направляющие косинусы этой прямой.
Решение. Напишем прежде всего уравнения прямой, про-
проходящей через данную точку:
х — 2 _у—1 г — 6
т п р '
На основании формул A9,3) числа т, п и р пропорциональны
числам Л, В и С из уравнения плоскости, а потому, заменяя
в последнем уравнении т, п и р соответственно числами 1,
—4, 5, получим искомые уравнения в виде
х — 2 у— 1 _ г — 6
1 ~ —4 5 "
Направляющие косинусы этой прямой определим по форму*
лам A8,2):
cos а = ± ; cos а = ± -—;
182
Задача 19,6 (для самостоятельного решения). Найти уравне-
уравнение перпендикуляра к плоскости
Ъх — у — 5г — 8 = 0,
проходящего через точку A, —1, 2).
Ответ х-=1 - l±l - i=2
итвет. -д---zr - г=Г •
Задача 19, 7. Найти точку пересечения прямой
х — 1 _ у+1 _ г —2
3 ~ — 1 ~~ +5
С ПЛОСКОСТЬЮ
х+у — 2z — 4 = 0.
Решение. Представим уравнение прямой в так называемом
параметрическом виде. Пусть каждое из отношений, входящих
в уравнение прямой, равно t:
Т - =Г — Т (~ *>'
или
х — 1 _,. у+1 _ f. г — 2 _ .
откуда
x = 3t+-l\ y = — t—\; z = 5t + 2. (A)
Это и есть параметрические уравнения данной прямой. Так как
координаты точки пересечения прямой и плоскости должны удов-
удовлетворять уравнениям прямой и уравнению плоскости, то, под-
подставив значения х, у и г из (А) в уравнение плоскости, будем
иметь
3/ + 1 + (— / — 1) — 2 E* -Ь 2) — 4 = 0.
Из него следует, что t — —1. Это значение / есть значение па-
параметра в точке пересечения прямой и плоскости. Подставим
это значение в уравнения прямой (А) и получим: х = —2, у = 0;
z = — 3. Итак, координаты точки пересечения данных прямой и
плоскости будут (—2, 0, 3).
Задача 19,8 (для самостоятельного решения). Найти уравнения
перпендикуляра к плоскости
х + Зу — 4г— 13 = 0,
проходящего через точку B, — 1, 3), и определить координаты
основания этого перпендикуляра.
Ответ. Уравнения перпендикуляра к плоскости
х — 2 _ у + 1 г — 3
1 ~ 3 — —4 \
Координаты основания этого перпендикуляра C, 2, — 1).
183
Задача 19,9 (для самостоятельного решения). Найти коорди-
координаты основания А перпендикуляра к плоскости х — Зг/ + 4г +
+ 5 = 0, проходящего через точку B, 1, —1).
Ответ. А B, 1, —1).
Задача 19,10. Найти точку пересечения прямой
*—1_у+2_г—1
5 ~~ 4 ~~ — 1
и плоскости
гх — 4у — z + 5 = 0.
Решение. Поступаем, как обычно: уравнения прямой за-
запишем в параметрическом виде:
* —1 ,. + 2 1
5 -*.
Отсюда получаем
Подставляя эти значения х, у и z в уравнение плоскости, бу-
будем иметь
3 E/ + 1) — 4 D/ — 2) — (— / + 1) + 5 = 0.
После раскрытия скобок и приведения подобных членов получим
15/ — 16/ + t + 15 = 0, что можно представить в виде
0-/+15 = 0.
Конечного значения t, удовлетворяющего этому уравнению,
не существует. Значит, наша прямая не пересекает плоскости.
Легко проверить, что прямая параллельна плоскости. Действитель-
Действительно, условие A9, 2) параллельности прямой и плоскости здесь выпол-
выполняется. У нас А = 3; В = — 4; С = — 1; т = 5; п = 4; р ~ — 1
и Л/я + Ял+ Ср = 3-5+ (— 4)-4 + (— 1)-(— 1) = 0.
Если бы это было замечено сразу, можно было бы не решать
задачу.
Задача 19,11 (для самостоятельного решения). Найти точку
пересечения прямой
х _ у—\ __ г + 2
2 ~ — 1 ~ 1
И ПЛОСКОСТИ
х + у — 2 + 5 = 0.
Ответ. Прямая параллельна плоскости.
Перед тем как решать следующую задачу, усвойте по учеб-
учебнику условия, при которых прямая *-^ = ^^ — г-^- лежит в
плоскости Ах + By + Cz + D = 0. Эти условия имеют вид
fAa + Bb + Cc + D=.O, A9,5)
[Am + Bn + Ср = 0. ' A9,6)
184
Задача 19,12. Проверить, что прямая
2 - 1 - з ^
лежит в плоскости
х + у — z — 6 = 0. (В)
Решение. Здесь а — 2, & = 3, с = — 1;
m = 2, л = 1, р = 3;
Л = 1, 5 = 1, C = — I, D= —6.
Проверьте, что условия A9,5) и A9,6) здесь выполнены, а это
значит, что прямая (А) лежит в плоскости (В).
Задача 19,13 (для самостоятельного решения). Найти точку
пересечения прямой
* —2 у _г+\
3 ~~5 ~~ 9
и плоскости
2х — Ъу + z — 3 == 0.
Ответ. Прямая лежит в плоскости.
Задача 19. 14. Составить уравнение плоскости, проходящей
через прямую
3* + у — 4г + 5 = 01
х — у -\-2z- 1 =0}
и точку М A, —1, 2).
Решение. Уравнение пучка плоскостей, проходящих через
данную прямую, на основании A9,4) может быть записано так:
Ъх + у — iz + 5 + l{x — y + 2z— 1) =0. (А)
Из этого пучка плоскостей нам требуется выбрать ту, которая
проходит через точку МA, —1,2).
Если плоскость проходит через точку, то координаты этой
точки должны удовлетворять уравнению плоскости. Подставляя
в уравнение (А) координаты "точки М, получим уравнение для
определения X: 5Х — 1=0; X = г • Подставляя это значение X в
о
уравнение (Л), получим
8х + 2у — 9г + 12==0.
Задача 19,15 (для самостоятельного решения). Составить урав-
уравнение плоскости, проходящей через точку М B, — 1,0) и прямую
Ответ. х — 7у+ Viz — 9 = 0.
185
Задача 19, 16 (для самостоятельного решения). Составить урав-
уравнение плоскости, проходящей через точку A.1.—2) и прямую
х — 1 у —3 _ г
~Т~ — 1 ~ 5 •
Ответ. 2д:+ t/ — z —5 = 0.
Задача 19, 17. Найти уравнение плоскости, проходящей через
прямую
За: —t/ + 2 —5 = 01
¦ x + 2y-z+2 = 0\
параллельно прямой
Решение. Уравнение пучка плоскостей, проходящих через
прямую (А), имеет вид
Ъх — у + г — 5 + Цх + Чу- г + 2) = 0,
или иначе
(S + X)x + B\—l)y + (l—X)z — 5 + 2X = 0. (С)
Из этого пучка плоскостей должна быть отобрана плоскость, па-
параллельная прямой (В), и потому должно выполняться условие
A9,2) параллельности прямой и плоскости. На основании урав-
уравнения (С) А = 3 + ^. В = 2\ — \л С — 1 — X, а из уравнения (В)
следует, что m = — 1, и = 2, р = 2. Тогда условие параллельности
прямой и плоскости запишется в виде
C + Х)(-1') + BХ-1).2 + A-Х).2 = 0,
или
_3 —Х + 4Х—2 + 2 —2Х = 0; Х = 3.
Подставляя это значение X в (С), получаем
6* + 5«/ — 2г + 1 = 0.
Задача 19,18. Найти уравнение плоскости, проходящей через
прямую
<х-\ у + 2 г А
1 - 1 ~2 V*'
перпендикулярно плоскости
Sx — y + 2z — 2 = 0. (В)
Решение Уравнения прямой запишем в виде
х-1 у+2
2 1
х— 1 _ г_
2 ~ 2
186
или после упрощений
*_z—1=о
Уравнение пучка плоскостей, проходящих через эту прямую,
имеет вид
х — 2у — 5 + Х(х — 2— 1)=0,
A+Х)* —2t/ —Хг —5 —Х = 0. (С)
Из этого пучка плоскостей отберем ту плоскость, которая
перпендикулярна плоскости (В). Условие перпендикулярности двух
плоскостей имеет вид A7,21). В нашем случае
Л1==3; 5! = -1; С1==2;
Л3 = 1 +Х; В2= — 2; С2 = — X,
а потому указанное условие примет вид
3A + Х) + (-1)(-2) + 2(-Х) = 0.
Раскрывая скобки, получаем
З + ЗХ + 2 —2Х = 0
и
Х = —5.
Подставляя это значение X в (С), получаем уравнение искомой
плоскости в виде
4* + 2у — Ъг = 0.
Задача 19,19 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через прямую
3* + 2«/ + Ъг — 5 = 0,
* + «/ + z —4 = 0
параллельно прямой
х — y + 2z+ 1 =0
2х + у— 3z + 2 = 0
Ответ. 7х — 4«/+7г + 49 = 0.
Задача 19, 20 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через прямую
х — 2«/ + Зг— 1 =01
х — y + z + 5^0 )
перпендикулярно плоскости 2х + 2у — г + 5 = 0.
Ответ. 4х — 3г/ +22+ 26 = 0.
Задача 19,21. Найти уравнение плоскости, проходящей через
две параллельные прямые:
2 ~ 3 ~ 4 •
х+2_у.+ \ _ г-1
187
Решение. Уравнения первой прямой запишем в виде
х— 1 __ у — з
2 - з
х— 1 г
2 ~~4
или после упрощений
3* — 2г/ -{-3 = 0,
2х — г— 2 = 0.
Уравнение пучка плоскостей, проходящих через эту прямую,
запишется так:
Ъх — 2у + 3 + ХBх— \г — 2) = 0,
или
C + 2Х)л: —2г/— Хг + 3 — 2Х = 0. (Л)
Из этого пучка выделим ту плоскость, которая проходит че-
через вторую прямую. Вторая прямая, как видно из ее уравнения,
проходит через точку М(—2,— 1, 1), а потому и плоскость, про-
проходящая через вторую прямую, должна содержать эту точку.
Подставляя в (А) координаты точки М(—2,— 1, 1) вместо теку-
текущих координат, получим для определения X уравнение
C + 2Х)(— 2) — 2 • (— 1) — X . 1 + 3 — 2Х = 0; Х = —у.
Подставляя это значение X в уравнение (А), получим
19*— 14«/+ 2 + 23 = 0.
Задача 19, 22 (для самостоятельного решения). Найти уравне-
уравнение плоскости, проходящей через две параллельные прямые: •
х + 2 _ у — 1 __ г
4 ~ — 1 ~Т'
' х—1 у г+ 1
4 — 1 ~ 3 *
Ответ. 4х+ \3у — z —5 = 0.
ДВАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Поверхности второго порядка.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Это практическое занятие является последним по курсу ана-
аналитической геометрии. Оно посвящается поверхностям второго
порядка.
Поверхностью называется геометрическое место точек, коорди-
координаты которых удовлетворяют уравнению вида F (х, у, г) = 0.
188
Если это уравнение можно разрешить относительно 2, то полу-
получим уравнение поверхности в виде z = f(x, у). Уравнение поверх-
поверхности может и не содержать всех трех переменных: х, у и z.
1. Сфера. Сферой называется геометрическое место точек
пространства, равноудаленных от одной и той же точки, назы-
называемой центром сферы.
а) Уравнение сферы имеет вид.
(х - а)а + (у- Ь? + (г - cf = R\ B0, 1)
где а, Ь и с — координаты центра сферы, a R — ее радиус.
б) Уравнение сферы с центром в начале координат
хг + у2 + za = Я2.
B0, 2)
Задача 20,1. Составить уравнение сферы радиуса R = 5 с
центром в начале координат.
Решение. Подставляя в уравнение сферы B0, 2) R = 5, по-
получим
хг + Уг -V za = 25.
Задача 20,2. Составить уравнение сферы радиуса R = 3 с
центром в точке С(— 1,2, — 3).
Решение. Подставляя в B0,1) а = — 1, b = 2, с = —'3 и
R =. 3, будем иметь
или
Задача 20, 3 (для самостоятельного решения). Написать урав-
уравнение сферы радиуса R = 8 с центром в точке СA, 1, — 1).
Ответ. *а + t/2 + z2 — 2х— 2y + 2z — 61 = 0.
Задача 20, 4 (для самостоятельного решения). Составить урав-
уравнение сферы радиуса R = 6 с центром в точке С(— 1, —2, —4).
Ответ. хг -I-t/2 + za + 2* + 4«/+ 8z — 15 = 0.
Задача 20, 5. Определить координаты центра сферы и ее радиус
г/а
za — 6х + 8у + Юг + 25 = 0.
Решение. Представим это уравнение в виде B0, 1) для чего
1) объединим в группы члены, содержащие одноименные ко-
координаты;
2) выделим в этих группах полные квадраты (мы так же по-
поступали и при определении координат центра окружности и ее
радиуса). Поступая, как указано, получим
х* — 6* + t/a + 8у + z2 + Юг + 25 =• 0.
L1 'I Ч'
189
Выделяя полные квадраты в подчеркнутых группах, получим
f 1 f I \ I
I IV Ш
а упрощая, будем иметь
(*_3J + (t/ + 4J+(z + 5J-25 = 0.
и окончательно
Сравнивая с B0, 1), имеем
а = + 3^ Ь = — 4; с = — 5; R2 = 25.
Итак, центр сферы — точка С C, — 4, — 5), R — 5.
Задача 20, 6. Определить координаты центра и радиус сферы
4*2 + Ауг + 4г2 — Ах + \2у — 16г + 1 = 0.
Решение. Для приведения этого уравнения к виду B0,1)
разделим обе части данного уравнения на коэффициент при х2 и
получим
Xs + у2 + г*-х + Ъу-Аг + I = 0.
Будем следовать плану, намеченному в предыдущей задаче.
Объединяя в группы члены, содержащие одноименные координа-
координаты, и выделяя в каждой такой группе полный квадрат, получим
Отсюда уже получаем уравнение сферы в виде
Центр сферы С имеет координаты С (j, — ^ , 2], а ее радиус
Р 5
Задача 20,7 (для самостоятельного решения). Определить ко-
координаты центра и радиус сферы
х2 + У2 + 22 + х — у + z = 0.
2 ' 2 ' 2/ ' х — 2 '
Задача 20, 8 (для самостоятельного решения). Найти радиус и
координаты центра сферы
х2 + у2 + г2 — Ах — 5 = 0.
Ответ. СB, 0,0); R = 3.
190
Задача 20,9 (для самостоятельного решения). Определить ко-
координаты центра и радиус сферы
Х2 _|_ у2 _|_ 2г _|_ 2ах + 2Ьу + 2cz -f d = 0.
Ответ. С(— а, — Ь,— с); R = Va% -Ь Ь2 + с2-^Z
При этом предполагаем, что а2 + Ь2 + с2 — d > 0. Если бы
оказалось, что а2 + Ь2 + с2 — d < 0, то сфера называлась бы
мнимой; при а2 + Ьъ + с2 — d = 0 сфера имела бы радиус # = 0.
Задача 20,10. Сфера проходит череа точку А (— 2,3,5), а ее
центр находится в начале координат. Составить уравнение сферы.
Решение. Радиус сферы легко определить, как расстояние
от центра сферы (начала координат) до точки А на сфере. По
формуле для определения расстояния между двумя точками в
пространстве получаем
Подставляя это значение R в уравнение B0,1), будем иметь ис-
искомое уравнение сферы
. х2 + t/2 + z2 = 38.
Задача 20,11 (для самостоятельного решения). Сфера имеет
центр в точке С E,7, — 1) и проходит через начало координат.
Найти ее уравнение.
Ответ. x2+ye + z*— Юх— 14y.+ 2z = 0.
2. Цилиндрические поверхности. Цилиндрической поверх-
поверхностью, или цилиндром, называется поверхность, описанная
бесконечной прямой (образующей), которая движется, оставаясь
все время параллельной данной прямой и пересекая данную кри-
кривую (направляющую).
Мы будем рассматривать только такие цилиндрические по-
поверхности, у которых образующие параллельны одной из коорди-
координатных осей, а направляющей является плоская кривая, лежащая
в одной из координатных плоскостей.
Уравнения таких цилиндрических поверхностей содержат
только две переменные величины. В них будет отсутствовать пе-
переменная, одноименная с той координатной осью, которой парал-
параллельны образующие цилиндрической поверхности.
Так, всякое уравнение вида
F(x, у)-0 или {/ = /(*), B0,3)
содержащее только две переменные х и у, определяет цилиндри-
цилиндрическую поверхность, у которой образующие параллельны коор-
координатной оси Oz, а направляющая леяйй^в плоскости хОу, причем
ее уравнение есть одно из уравнений B0,3). Всякое уравне-
уравнение вида
или F(x, z) = 0, B0,4)
191
содержащее только две переменные х и z и не содержащее
переменной у, определяет цилиндрическую поверхность, у которой
образующие параллельны оси Оу, а направляющей является ли-
линия, лежащая в плоскости хОг и имеющая своим уравнением
одно из уравнений B0,4).
Точно так же всякое уравнение вида
F(y, 2)-0 или z=f{y), B0,5)
содержащее только две переменные у и г и не содержащее пере-
переменной х, определяет цилиндрическую поверхность, у которой
г образующие параллельны оси Ох, а на-
jt правляющей служит линия, лежащая в
плоскости yOz и имеющая своим урав-
уравнением одно из уравнений B0,5).
Задача 20,12. Какую поверхность
определяет уравнение
Л;2 -f у* = л2?
Решение. Данное уравнение содер
жит только две переменные х и у и
определяет в пространстве на основании
уравнений B0,3) цилиндрическую по-
поверхность, у которой образующие па-
параллельны оси Oz, а направляющей
служит окружность х2 4- у2 =-= г2, лежа-
лежащая в плоскости хОу.
^LJ
Фиг. 20,1.
Приводим более подробные разъяснения полученного заклю-
заключения. В плоскости хОу данное уравнение определяет окружность
радиуса г с центром в начале координат. Пусть эта окружность
является направляющей цилиндра, а его образующие параллель-
параллельны оси Oz. Возьмем на цилиндре (фиг. 20,1) любую точку А с
координатами х, у, z — A (x, у, г) и спроектируем ее на пло-
плоскость ' хОу. Ее проекция—точка В с координатами л;, у и 0
находится на окружности, которая служит направляющей, а по-
потому координаты х и у точки В удовлетворяют уравнению окруж-
окружности х2 4- у2 — г2. Но так как абсцисса и ордината точки
А (х, у, г) на цилиндрической поверхности такие же, как абсцисса
и ордината точки В(х, у, 0) на окружности, то, учитывая, что
уравнение окружности х2 -\- у2 = гг не содержит переменной г,
можно сказать, что этому уравнению удовлетворяют и координа-
координаты любой точки А (х, у, z), лежащей на цилиндре.
Таким образом, данное уравнение х2 -f у2 — г2 определяет в
пространстве прямой круговой цилиндр, у которого образующие
параллельны оси Oz, а направляющей служит эта окружность,
лежащая в плоскости хОу.
Задача 20,13. Какую поверхность определяет уравнение
192
Решение. Данное уравнение содержит только две переменные
х и у и на основании B0,3) определяет в пространстве цилиндри-
цилиндрическую поверхность, образующие которой параллельны оси Oz,
а направляющей является эллипс. Такой цилиндр называется
эллиптическим. К этому же выводу можно прийти, повторяя
рассуждения предыдущей задачи.
Задача 20, 14 (для самостоятельного решения). Какую поверх-
поверхность определяет уравнение у2 = 2рх (фиг. 20,2)?
Ответ. Уравнение г/2 = 2рх определяет параболический цилиндр
с образующим, параллельными оси Oz. Направляющей цилиндра
служит парабола у2 = 2рх, лежащая в
плоскости хОу.
г
О
*-x
\
\
Фиг. 2,02
Фиг. 20,3.
Задача 20, 15. Какую поверхность определяет уравнение
Уг *2 „
Ответ. |з — H5^ — уравнение цилиндра, образующие кото-
которого параллельны оси Oz, а направляющей служит данная ги-
гипербола, лежащая в плоскости хОу (фиг. 20,3). Такой цилиндр
называется гиперболическим.
Задача 20,16. Какие поверхности определяют уравнения
1)*? + 22 = 16; 2) ? + ?=1; 3) х = 222; 4)^-^=1?
Решение. Каждое из этих уравнений содержит только две
переменные х и г и определяет на плоскости xOz кривые: 1) ок-
окружность; 2) эллипс; 3) параболу; 4) гиперболу.
В пространстве же каждое из них определяет цилиндрическую
поверхность с образующими, параллельными оси Оу, так как эти
уравнения не содержат переменной у. Направляющими этих ци-
цилиндрических поверхностей служат указанные кривые: •
1) х2 -f г2 = 16 — уравнение прямого кругового цилиндра;
193
X2 „г
2) -g- + -г = 1 — уравнение эллиптического цилиндра;
3) x = 2z2 — уравнение параболического цилиндра;
г2 х2
4) -? — •=- = 1—уравнение гиперболического цилиндра.
Задача 20,17. Какие поверхности определяют уравнения
1) уг = Ъ, 1) у = бг2, 3) f + г2 = 9, 4)"{? -Ь J = 1?
Ответ. 1) уг— Ь — уравнение гиперболического цилиндра;
2) у = 6г2 — уравнение параболического цилиндра;
3) у2 -J- 22 = 9 — уравнение прямого кругового цилиндра;
4) |г + -г" = 1 — уравнение эллиптического цилиндра.
Образующие всех этих цилиндрических поверхностей парал-
параллельны оси Ох.
Задача 20,18 (для самостоятельного решения). Какую поверх-
поверхность определяет уравнение
Ответ. В пространстве уравнение определяет прямой круго-
круговой цилиндр, для которого данная окружность служит направля-
направляющей. Образующие цилиндра параллельны оси Oz, причем сама
ось является одной из образующих, так как данная окружность
проходит через начало координат. Постройте эскиз цилиндра.
Задача 20,19. Какую поверхность определяет уравнение
Ответ. Прямой круговой цилиндр, образующие которого па-
параллельны оси Ох.
Задача 20, 20. Какую поверхность определяет уравнение
Решение. Перепишем данное уравнение в виде
что в свою очередь может быть записано так:
Каждое из этих уравнений определяет плоскость, проходящую
через ось Оу, причем ось Оу является прямой пересечения этих
плоскостей.
3. Линия в пространстве. Линия в пространстве может рас-
рассматриваться как пересечение двух поверхностей. Если уравне-
194
ния этих поверхностей F (х, у, г) = 0 и Ft (л;, у, г) = 0, то эти два
уравнения
F(*'iA2)==Oi B0 6)
Fl(x,y,z)=0\ ^U'b)
и являются уравнениями линии в пространстве. Таким образом,
линия в пространстве есть геометрическое место точек, коорди-
координаты которых удовлетворяют системе B0, 6).
Решим несколько задач, связанных с линиями в пространстве.
Задача 20, 21. Какая линия изображается системой уравнений
= 61
Решение. Первое из уравнений системы^определяет сферу,
а второе—плоскость, параллельную плоскости хОу. Так как
данная плоскость пересекает данную сферу, то линией пересече-
пересечения будет окружность. Значит, линия, о которой идет речь в
задаче,— окружность лежащая в плоскости z =^ 6.
Запишем уравнение этой окружности в другом виде. Исклю-
Исключим г из данной системы уравнений. Сделать это надо так: в
первое уравнение системы подставить значение 2—6. Получим
2 =
ИЛИ
2 =
Окончательно
2 =
Первое уравнение определяет в пространстве прямой круговой
цилиндр, у которого осью служит ось 02, а второе — плоскость,
параллельную плоскости хОу. Первое уравнение этой системы
х2 + у2 = 15 на плоскости хОу определяет окружность, являю-
являющуюся прямоугольной проекцией той окружности, которая опре-
определяется заданной системой уравнений.
Задача 20, 22. Какую линию определяет система уравнений
2 = 5
Решение. Первое уравнение этой системы определяет в про-
пространстве эллиптический цилиндр, а второе — плоскость, парал-
параллельную плоскости хОу. Линией их пересечения будет эллипс,
лежащий в данной плоскости. Его прямоугольной проекцией на
195
плоскость хОу будет эллипс, определяемый первым из уравнений
системы.
Задача 20, 23. Какая линия определяется системой уравнений
"*=Э:
Решение. Первое из данных уравнений определяет в про-
пространстве параболический цилиндр, а второе — плоскость, парал-
параллельную плоскости yOz. Эта плоскость пересечет параболический
цилиндр по параболе. Итак, линия, определяемая заданной си-
системой уравнений,— парабо*ла, лежащая в плоскости х = 5. Про-
Проекцией этой параболы на плоскость yOz будет парабола, опреде-
определяемая первым уравнением данной системы.
Задача 20, 24 (для самостоятельного решения). Какая линия
определяется уравнениями
Г
2-9
Ответ. Окружность, лежащая в плоскости г — 9, параллель-
параллельной плоскости хОу. Проекцией этой окружности на плоскость хОу
будет окружность
2 2 = 91
2= О)' - '
Второе из этих уравнений указывает на то, что окружность,
определяемая первым уравнением, лежит в плоскости хОу, урав-
уравнение которой 2 = 0..
4. Поверхность вращения. В учебнике Привалова на страни-
странице 269 выведено простое правило, позволяющее по известному
уравнению вращающейся линии получить уравнение поверхности
вращения.
Приведем здесь это правило и дадим к нему разъяснения.
17р авило. Чтобы получить уравнение поверхности, обра-
образованной вращением линии L, лежащей в плоскости yOz, вокруг
оси Оу, нужно в уравнении этой линии заменить z на ± Ух2 + г2.
Разъясним это правило.
Уравнение линии, лежащей в плоскости yOz, содержит в общем
случае две переменные величины: у и г и имеет вид
Уравнение же поверхности в общем случае содержит три теку-
текущих координаты: х, у и г.
Уравнение вращающейся линии надо преобразовать так,
чтобы оно стало уравнением поверхности вращения Правило
указывает, что в уравнении вращающейся линии / (у, г) = 0 те-
текущая координата z должна быть заменена на ± ]/х2 -f- г2. Это
196
надо понимать так, что в этом уравнении вторая текущая коор-
координата у, одноименная с осью вращения Оу, должна быть остав-
оставлена без изменения.
Таким образом, преобразованное уравнение' в общем случае
будет содержать три текущих координаты: х, у и г.
Если бы вращение линии f (у, г) = О происходило не вокруг
оси Оу, а вокруг оси Oz, то, чтобы получить уравнение поверх-
поверхности вращения, следовало бы в уравнении кривой текущую ко-
координату г, соответствующую оси вращения Oz, оставить без
изменения, две же другие текущие координаты хну ввести, за-
заменив в уравнении кривой у на ± Yx* + У2-
Аналогично поступают в случаях, когда происходит вращение
линии, лежащей в плоскостях хОу и xOz. Ниже рассматривается
ряд задач на применение этого правила.
Задача 20,25. Окружность х2 -\- у2 — г2 вращается вокруг оси
Ох. Найти уравнение поверхности вращения (сферы).
Решение. Чтобы написать уравнение поверхности вращения,
полученной от вращения заданной окружности вокруг оси Ох,
следует в уравнении окружности переменную х, соответствующую
оси вращения, оставить без изменения. Вторую же переменную у
в уравнении окружности заменить на ± корень квадратный из
суммы квадратов двух остальных переменных — у и г, т. е. на
± Yy2 + z2'» тогда уравнение поверхности вращения запишется
так:
т. е. в виде
x* + y* + z2=r2 (сфера).
Задача .20, 26. Прямая х = z вращается вокруг оси Oz. Найти
уравнение поверхности вращения (конуса).
Решение. Так как в уравнение линии входят только пере-
переменные л: и 2, то линия лежит в плоскости xOz.
Для написания уравнения поверхности вращения в уравне-
уравнении прямой переменная z должна остаться без изменения, так
как она соответствует оси вращения Oz. Вторая же переменная х
в уравнении прямой должна быть заменена ± корнем квадрат-
квадратным из суммы квадратов двух остальных переменных х и у, т. е.
± Y*2 + У2- Уравнение поверхности вращения запишется так:
Возведя обе части последнего равенства в квадрат, получим
окончательно уравнение поверхности вращения в виде
х2 + у3 = z\
или
х2 + Уг— г2 = 0 (конус).
197
Вершина этого конуса находится в начале координат, а так как
прямая х = z является биссектрисой координатного угла хОг, то
угол в,осевом сечении этого конуса равен 90° (фиг. 20,4). Сле-
Следует запомнить, что уравнение х*-\-у2 — z2=0 определяет конус
с вершиной в начале координат и углом в осевом сечении, равным
90°. Осью этого конуса является ось Oz. Если бы вращение пря-
прямой х = z происходило не вокруг оси Oz, а вокруг оси Ох, то
мы получили бы уравнение поверхности вращения, оставив в этом
уравнении без изменения переменную х и заменив переменную z
на ± УФ -f- z2. Уравнение поверхности вращения приняло бы
вид
х = ± Ууг + г2,
а после возведения обеих частей равен-
равенства в квадрат х2 — у2 + z2, или окон-
окончательно уг + г2 — л;2 = 0.
Задача 20, 27 (для самостоятельного
решения). Прямая y — z вращается во-
вокруг оси Оу. Найти уравнение поверх-
поверхности вращения (конуса).
Ответ, х2 -f- z2 — уг = 0.
Задача 20,28 (для самостоятельно-
самостоятельного решения). Определить уравнение по-
поверхности вращения, образованной вра-
вращением прямой у — Зх вокруг оси Ох (конус).
Ответ, у2 + г2 — 9л;2 = 0.
Задача 20,29. Определить уравнение поверхности вращения,
образованной вращением эллипса \ -\- |j = 1
1) вокруг оси Ох;
2) вокруг оси Оу.
Решение. 1) Уравнение кривой содержит координаты х и у,
значит, кривая лежит в плоскости хОу.
Для определения уравнения поверхности, образованной вра-
вращением эллипса вокруг оси О*, надо в уравнении эллипса пере-
переменную х, соответствующую оси вращейия, оставить без измене-
изменения, а вторую переменную у в уравнении эллипса заменить на ±
корень квадратный из суммы квадратов двух остальных перемен-
переменных, т. е. на ± Ууг + z2.
Искомое уравнение поверхности вращения будет выглядеть так:
Фиг. 20,4.
(± Уу^Г?? 1
или
х i У -г* _ 1
Эта поверхность называется эллипсоидом вращения.
198
2) Если же вращать данный эллипс вокруг оси Оу, то «пере-
«переменную у, соответствующую оси вращения, в уравнении эллипса
следует оставить без изменения, а переменную х заменить на
± yV + г2.
В этом случае уравнение поверхности вращения будет таким:
, у2 _ 1
~Т Ьг~ '
ИЛИ
*'+г2
у2 .
Эта поверхность также называется
эллипсоидом вращения.
Фиг. 20,5.
Фиг. 20.6.
У
Задача 20, 30 (для самостоятельного решения). Найти уравне-
уравнение поверхности, образованной вращением эллипса
вокруг 1) оси Ох; 2) оси Ог.
Ответ. 1) % + г ¦ д— = 1 — эллипсоид вращения;
2)
хг i
—-JJ5
аа + Т2 = * —эллипсоид вращения.
Задача 20,31. Найти уравнение поверхности, образованной
вращением гиперболы
дг —72= 1
вокруг 1) оси Ох; 2) оси Ог.
Ответ. 1) у-^ j = — 1 (двухполостный гиперболоид вра-
вращения, фиг. 20, 5).
2) * ау— ~г — 1 (однополостный гиперболоид вра-
вращения, фиг. 20,6).
199
Задача 20, 32 (для самостоятельного решения). Парабола уг =
= 2pz вращается вокруг оси Oz. Написать уравнение поверхно-
поверхности вращения.
Ответ. Полагая ^- — at получим z = а (х* + у2). Эта поверх-
поверхность называется параболоидом вращения.
Задача 20,33 (для самостоятельного решения). Найти урав-
уравнение поверхности, полученной от вращения параболы у2 = х во-
вокруг оси Ох.
Ответ. x=yi-\-zi (параболоид вращения).
Задача 20, 34 (для самостоятельного решения). Найти уравне-
уравнение поверхности, образованной вращением. прямой х-\-z — ] во-
вокруг оси Oz.
Ответ. х2 + у2 — (z—lJ = 0.
Поверхность — конус с вершиной в точке С @,0, 1). Угол в
осевом сечении этого конуса равен 90°.
В заключение решим несколько простых задач, связанных с
поверхностями второго порядка, заданными простейшими уравне-
уравнениями. Приводим для справок простейшие уравнения поверхно-
поверхностей второго порядка.
1. Трехосный эллипсоид
B0'7>
(а, Ь и с — полуоси эллипсоида).
2. Однополостный гиперболоид
„2
. ? = !• B0,8)
В пересечении поверхности однополостного гиперболоида с
координатными плоскостями получаются кривые:
1) с плоскостью xOy(z = 0) — эллипс -^2 + jrj- = 1, который
называется главным;
х2 z2
2) с плоскостью хОг — гипербола -^ — ^ = 1;
V2 г2
3) с плоскостью yOz — гипербола-|г — -? — 1.
Вершины главного эллипса (иногда он называется горловым)
называются вершинами гиперболоида, а оси этого эллипса —
поперечными осями гиперболоида. Их длины равны 2а и 26. Ось
гиперболоида B0,8), расположенная по оси Oz и равная по
длине 2с, называется его продольной осью.
В случае, когда продольная ось однополостного гиперболоида
расположена но оси Ох, уравнение его поверхности запишется
в виде
200
для случая же, когда продольная ось" однополостного гипербо-
гиперболоида находится на оси Оу, его уравнение имеет вид
i! + ?1 _ |1 =: 1. B0,10)
3) Двухполостный гиперболоид
|-+!i--;4=-i. Bо,п)
Плоскость хОу не пересекает поверхности двуполостного
гиперболоида B0, 11). Плоскости xOz и yOz пересекают поверх-
поверхность B0, 11) соответственно по гиперболам
х2 г2 . у2 г2 ,
а2 с2 ~ ~~ Ъг с2 '
которые называются главными гиперболами. Отрезок длиною 2с,
расположенный по оси Oz, называется продольной осью дву-
двуполостного гиперболоида B0, 11), а отрезки длиною 2а и 2Ь,
расположенные соответственно по осям Ох и Оу, называются его
поперечными осями.
У двуполостного гиперболоида
4 + т—й- = —1 B0,12)
CL С Ь
продольная ось расположена по оси Оу, а у двуполостного гипер-
гиперболоида
-Й + ?-5-=--1 B0,13)
она расположена по оси Ох.
4. Действительный конус второго порядка
B0,14)
Вершина этого конуса находится в начале координат, он состоит
из двух частей, расположенных по обе стороны от вершины.
Одной из возможных направляющих этого конуса является эллипс
Z — C
У конуса
Г2 72 ,Л
т* + ?-&- = о B0'15>
вершина находится в начале координат, он состоит из двух
частей, расположенных по разные стороны плоскости xOz. Одной
из возможных его направляющих является эллипс
X2 7г
20L
У конуса же
-? + ?—-J--0 B0,16)
вершина находится в начале координат, а две его части рас-
расположены по разные стороны плоскости уОг. Одной из возмож-
возможных его направляющих является эллипс
5. Эллиптический параболоид
* = ?+?• B0.17)
Ось Oz называется его осью.
У эллиптического параболоида
Х% Z2
У = тг + о~ B0, 18)
/р 1х
осью служит ось Оу, а у эллиптического параболоида
осью служит ось Ох.
6. Гиперболический параболоид
*-?-&• B0>20)
Задача 20, 35. Найти главные сечения эллипсоида
25 "l"l6"t" 4 — !»
определить координаты их вершин и длину осей.
х* Ф г2
Решение. Главными сечениями эллипсоида -^ + |r -h ж — *
называются линии, по которым эллипсоид пересекается с коор-
координатными плоскостями. Плоскость хОу имеет уравнение г = 0.
Полагая в уравнении эллипсоида z = 0, получим уравнение ли-
линии пересечения эллипсоида с плоскостью хОу
25 ^ 16 М
которое в плоскости хОу определяет эллипс. В сечении данного
эллипсоида плоскостью у = 0 (координатная плоскость хОг) полу-
полулается эллипс
25
2С2
:'Л
Координатная же плоскость yOz, уравнение которой х — О,
пересекает данный эллипсоид по эллипсу
Таким образом, главные сечения данного эллипсоида определены:
это эллипсы, лежащие в координатных плоскостях.
Координаты вершин этих эллипсов и определят координаты
вершин эллипсоида. Вершивы эллипсоида, лежащие в плоскости
хОу, имеют координаты E, 0, 0), (—5, 0, 0), @, 4, 0) и @, —4, 0);
вершины эллипсоида, лежащие в плоскости xOz, имеют коор-
координаты E, 0, 0) (—5, 0, 0) @, 0, 2) и @, 0, —2); вершины эл-
эллипсоида, лежащие в плоскости yOz, имеют координаты @, 4, 0),
@, —4,0); @, 0, 2) и @,0, —2). Соединяя эти результаты, приходим к
такому заключению: у эллипсоида всего 6 вершин и их коорди-
координаты: АХ{Ь, 0, 0), Л2(—5, 0, 0), Л3@, 4, 0), Л4@, -4, 0),
Аь@, 0, 2) и Лв@, 0, —2).
Сравнивая уравнение данного эллипсоида с уравнением эл-
эллипсоида B0, 7), заключаем следующее:
а2 — 25; полуось а = 5, а ось эллипсоида, расположенная вдоль
оси Ох, будет 2а — 10;
Ь2 = 16; полуось Ь = 4, а ось эллипсоида, расположенная вдоль
оси Оу, будет 1Ъ = 8;
с2 = 4; полуось с = 2, а ось эллипсоида, расположенная по
оси Oz, равна 2с = 4.
Задача 20,36 (для самостоятельного решения). Определить
главные сечения эллипсоида
64 49 25 " '
а также координаты его вершин и длину осей.
Ответ.
1) Уравнения главных сечений:
2) Длина осей: 2а = 16; ЪЪ = 14; 2с = 10.
3) Вершины эллипсоида: Л1(8, 0, 0), Л2(—8, 0, 0),
А3@, 7, 0), Л«@, -7, 0), Л,@, 0, 5) и Л,@, 0, -5).
Задача 20,37. Найти линии пересечения поверхности гипер-
гиперболоида
У2 „2 -2
27 ^ 18 9
С координатными плоскостями и с плоскостями
z = 2, х = 3.
203
Ответ, а) Уравнение линии пересечения данного гипербо-
гиперболоида с координатной плоскостью хОу
27" "*" 18" = 1 (эллипс);
2 = 0 J
б) с плоскостью yOz гиперболоид пересекается по
18 9 ~ [ (гипербола);
х — 0 )
в) с плоскостью xOz — по линии
2У —"9 = 1 (гипербола).
линии
Уравнение линии пересечения гиперболоида с плоскостью
= 2
щ- + sg- = 1 I (эллипс, лежащий в
z = 2 ) плоскости z = 2)
Уравнение линии пересечения с плоскостью х = 3
?._!!.=. 1 ]
12 6 > (гипербола).
х = 3 J
Задача 20,38. Какие поверхности определяются уравнениями
1) х2+у2 — z2=0; 2)z = ^ + «/2;
У2 ,.2 72 >>2 -2
7) г = -(*»+ */¦); 8)г=1-^2-г/2.
Ответ. 1) Круговой конус, у которого осью является ось Oz.
2) Параболоид вращения, у которого осью является
ось Oz.
3) Круговой конус, у которого ось вращения совпа-
совпадает с осью Ох.
4) Двухполостный гиперболоид вращения, у которого
ось вращения совпадает с осью Оу.
5) Из сравнения с B0, 10) заключаем, что это одно-
полостный гиперболоид, ось которого совпадает
с осью Оу.
6) Конус, у которого ось совпадает с осью Ох.
7) Параболоид вращения.
8) Параболоид вращения.
204
Задача 20, 39. Какие поверхности определяются уравнениями
1) 2х2-5г/2-8=--0;
2) 4л:2 — 8у2 + 16z2 = 0;
3) 8л;2 — 4у2 + 24z2 — 48 = 0;
4) у2 = 6л:-4;
5) 2л;2 — уг — 22=0;
6) Зх2 + Ъуг =-- 12г;
7) л:2 + V — 8 = 0;
8) г2 — 4х = 0;
9) 2л;2 — Зг2 = — 12у;
Ю) 4л;2—12уг —6га = 12.
Ответ. 1) Гиперболический цилиндр с образующими, парал-
параллельными оси Oz.
2) Из сравнения с B0, 15) очевидно, что это конус.
3) Из сравнения с B0, 10) заключаем, что это одно-
полостный гиперболоид, продольная ось которого
расположена по оси Оу.
4) Параболический цилиндр с образующими, парал-
параллельными оси Oz.
5) Перепишем уравнение в виде
• у2 + z2 — 2л;2 = 0,
ИЛИ
откуда видно, что это круговой конус, у которого
ось совпадает с осью Ох.
6) Переписав уравнение в виде
можем заключить, что это эллиптический парабо-
параболоид B0, 17)..
7) Эллиптический цилиндр с образующими, парал-
параллельными оси Oz.
8) Уравнение содержит две координаты. Это цилинд-
цилиндрическая поверхность. Перепишем уравнение в
виде
z2 = 4х (парабола).
Уравнение определяет параболический цилиндр с
образующими, параллельными оси Оу.
9) Уравнение перепишем в виде
— !i _ х*
у ~ 4 6"
205
Из сравнения с B0, 20) заключаем, что это гипербо-
гиперболический параболоид.
10) Перепишем уравнение в виде
ИЛИ
Из сравнения с B0, 13) заключаем, что это дву-
полостный гиперболоид, ось которого совпадает
с осью Ох.
ЧАСТЬ II
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПО ДИФФЕРЕНЦИАЛЬНОМУ
ИСЧИСЛЕНИЮ
ФУНКЦИЙ ОДНОЙ И МНОГИХ
НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ
Указатель параграфов, которые должны быть изучены перед каждым практическим занятием
8
Номер
практи-
практического
занятия
1
2
3
4
5
6
7
8
9
10
И
12
13 .
14
§
§
§
§
§
§
§
§
§
§
В. И. Смирнов. Курс
высшей математики
1, пункт 1, 2, 3
1, пункты 5, 6, 7
1, пункты 9, 10,
18, 19, 22, 23, 24
1, пункты 10, 11,
1, пункты 20, 21,
1, пункты 23, 24
1, пункты 23, 24
То же
1, пункт 20
2, пункт 25
2, пункты 25, 26,
2, пункты 25,26,
Те же параграфы,
для предыдущего
ческого занятия
Глава 1, § 2, пункт
8
12, 16,
14, 19
22
27, 28, 29
27, 28, 29
что и
практи-
32
Автор и название учебника
А. Ф. Бермант. Курс
математического анали-
анализа, ч. I
Введение
2, 3, 6
Глава I,
Глава I,
Глава I,
Глава 1,
Глава I,
См. два
иятия
§ 3, пункты 1,
§ 1. 2
§ 2, 3
§4
§5
§6
предыдущих за-
См. предыдущие практи-
практические
Глава I,
Глава II,
Глава II,
Глава II,
Глава II,
Глава II,
33, 34
занятия
§ 5; § 3 пункт 15
§ 1
§2
§ 1 и 2
§ 1 и 2
§ 2, пункты 32,
Г. П. Толстов. Курс мате-
математического анализа, т. I
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
1, § 1, 2, 3, 4, 12, 13
Н, § 1, 2, 3
И, § 1, 2, 3
И, §4
", § 4
И, § 4
И, §4
I, §3
Н, § 16
I, § 7, 8, 9
И, §8
П, § 8
См. предыдущее практиче-
практическое
Глава
занятие
II, § 7, 8, 9, 10
Н. С. Пискунов. Диффе-
Дифференциальное и интеграль-
интегральное исчисления
Глава
Глава
Глава
Глава
Глава
Глава
Те же
I, § 1, 2
I, § 3, 4, 6, 7
I, § 3, 4, 6, 7
I, § 8, 9, 10
I, § 8, 9, 10
I, § 8, 9, 10
параграфы, что и
к предыдущим двум за-
занятиям
Те ж«
: параграфы, что и
к занятиям шестому и
седьмому
Глава
Глава
Глава
Глава
Глава
Глава
Ш, § 13, 14
II, § 1, 2, 3, 4, 5
II, § 1, 2, 3, 4, 5
II, § 1, 2, 3, 4, 5
II, § 1, 2, 3, 4, 5
II, § 1, 2, 3, 4
(Продолжение указателя)
Номер
практи-
практического
занятия
15
16
17
18
19
20
21
22
23
24
25
26
27
28
В. И. Смирнов. Курс
высшей математики
То же, что и на предыду-
предыдущем практическом заня-
занятии
Глава
Глава
Глава
33,
Глава
Глава
Глава
Глава
48,
Глава
48,
Глава
48,
Глава
48,
Глава
Глава
54,
Глава
I,
I,
1,
39
1,
I,
И,
II
49
II.
49
и,
49
П
49
11,
И,
55
и,
§ 2,
§2,
§
§ 2,
§ 2,
§ з
, §
§
§
§
§3
§
§ 4
пункт 33
пункт 38
2, пункты
пункты 36,
пункты 34,
, пункты 45,
3, пункты
3, пункты
3, пункты
3, пункты
, пункт 50
4, пункты
32,
37
35
46
47,
47,
47,
47,
53,
Автор и название учебника
А. Ф. Бермант. Курс
математического анали-
анализа, ч. I
Глава
Глава
Глава
См. f
Глава
Глава
Глава
42,
Глава
46,
Глава
46,
Глава
46,
Глава
46,
Глава
Глава
Глава
II §
II, §
и, §
, 2
4, пункт 40
4, пункт 41
федыдущее занятие
II, §
И. §
Ш. §
43, 44
Ш,
47, 48
III,
47, 48
ш,
47, 48
ш,
47, 48
I", §
III, §
III. §
4, пункт 39
3
1, пункты
§ 2, пункты
, 49
§ 2, пункты
, 49
§ 2, пункты
49
§ 2, пункты
, 49
2
3, 4
5
Г. П. Толстов. Курс мате-
математического анализа, т. I
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
И,
И,
Н,
И,
11
И,
III
III,
III
III,
III,
III,
III
III,
§ 7, 8, 9, 10
§ 11
§ И
§ 10, 11
§ 22
§ 12, 13, 14,
S 1, 2, 3, 4
§ 1, 2, 3, 4,
§ 1, 2, 3, 4,
§ 1-6
§ 1—6
§ 1-6; § 19
§ 9, 10, 11
§ 15, 16, 17
15
5
5,
5,
6
6
6
H. С. Пискунов. Диффе-
Дифференциальное и интеграль-
интегральное исчисления
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
Глава
И,
II,
И,
И,
Н,
И,
III
III
III
III
III
III
III
HI
§
§
§
§
§
§
§
>§
§
§
§
§
§
§
1. 2, 3, 4, 5
6
7, 8
7, 8
11
9, 10
1—3
4—9
6, 10
14
8, 12
11
20, 21
22, 23, 25
29
30
31.
32
33
34
35
36
37
38
39
40
41
42
43
Глава
Глава
Глава
Глава
59,
Глава
59,
Глава
72,
Глава
59,
71,
Глава
79,
Глава
Глава
ва
Глава
156
Глава
Глава
Глава
II, § 4, пункты 65, 66
II, § 4, пункты 6J
II, § 5, пункт 57
И, § 5, пункты
60, 61
II, § 5, пункты
60, 61
И, § 6, пункты
73
>,66
58,
58,
71,
11, § 5, пункты 58,
60, 61; § 6, пункты
72, 73
II, § 6, 71, 77,
80, 81, 82, 83, 84
II, § 6, пункты 6/
II, § 6, пункт 69,
V, пункты 151, 152,
VI, § 15, пункты
То же
VI, § 15, п. 157
VI, § 16, п. 162
VI, § 15, п. 160
78,
, 85
',68
гла-
153
155,
Глава IV, § 4 пункт 73
Глава IV, § 4 пункт 73
Глава IV, § 1
Глава IV, § I, пункт 62;
§ 3, пункт 70
Глава IV, § 1, пункт 62;
§ 3, пункт 70
Глава IV, § 3, пункты
71, 74
Глава IV, § 4, пункт 35
Глава IV, § 6
Часть II, глава X, § 1,
2, 3
Часть II, глава X, § 4
Часть II, глава X, § 5
Часть II, глава X, § 3
Часть II, глава X, § 4
Часть II, глава XI, § 1
Часть II, глава XI, § 3,
пункт 166
Глава IV, § 7
Глава IV, § 7
Глава IV, § 12
Глава IV, § 13, 14
Глава IV, § 13, 14
Глава IV, § 15, 16
Глава IV, § 17
Глава V, § 1—9
Часть II, глава XI, § 1—6;
глава XII, § 1, 2, 3
Часть II, глава XII, § 6, 7
Часть II, глава XII, § 10
Часть II, глава XIV
Часть II, глава ХШ, § 1
Часть II, глава XIV, § 1, 2
Часть II, глава XII, § 5
Глава IV, § 4, 5
Глава IV, § 4, 5
Глава V, § 1, 2
Глава V, § 3, 4, 5, 6, 7
Глава V, § 3, 4, 5, 6, 7
Глава V, § 9, 10
Глава V, § 11, 12
Глава VI, § 1—7
Глава VIII, § 1, 2, 3, 4,
5, 7
Глава VIII, § 10
Глава VIII, § 12
Глава VIII, § 13, 14, 15
Глава VIII, § 11
Глава VIII, § 17, 18
Глава IX, § 6
ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содерж ан ие: Интервал, отрезок, промежуток. Абсолютная величина
числа. Свойства абсолютных величин.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Интервал, отрезок, промежуток
1. Если а и Ь — действительные числа и а меньше b(a<b),
то совокупность всех действительных чисел х, подчиняющихся
условию а<х<Ь, образует интервал. Левым концом интервала
является число а, а правым его концом — число Ь. Обозначается
интервал символом (а, Ь).
С геометрической точки зрения интервал (а, Ь) представляет
собой совокупность всех точек прямой, находящихся между точ-
точками а и Ь, причем концы этого отрезка а и Ъ в интервал не
включаются.
На фиг. 1,1 представлен интервал. Стрелки показывают, что
точки а и Ъ не принадлежат интервалу (а, Ъ).
Фиг. 1,1.
2. Если к интервалу (а, Ь) присоединить числа а и Ь, то
получим отрезок ab, который обозначается символом [а, Ъ].
Таким образом, под отрезком [а, Ь] понимается совокупность всех
действительных чисел х, подчиняющихся условию а < х < Ъ.
Геометрически отрезок [а, Ь] есть отрезок прямой с концами
в точках а и Ь.
Различие между интервалом (а, Ъ) и отрезком [а, Ъ\ состоит
в том, что в случае интервала (а, Ъ) числа а и Ъ ему не принад-
принадлежат, а в случае отрезка [а, Ь] числа а и Ъ ему принадлежат.
На фиг. 1,2 представлен отрезок [а, Ь].
Фнг. 1,2.
212
3, Под символом [а, Ь) следует понимать совокупность всех
действительных чисел х, подчиняющихся условию а < х <cb, т. е.
рассматриваются все действительные числа, содержащиеся между
числами а и Ь, причем число а рассматривается, а число Ъ — нет
{фиг. 1,3).
Под символом же (а, Ь] понимается совокупность всех дей-
действительных чисел х, подчиняющихся условию а < х < 6, т. е.
<*х д
Фиг. 1,3.
рассматриваются все действительные числа, содержащиеся между
числами а и Ь, причем число а ,не рассматривается, а число b
рассматривается (фиг. 1,4).
Фиг. 1,4.
Каждая из совокупностей чисел (а, Ь] и [а, Ь) называется
полуотрезком *.
4. В том случае, когда безразлично, принадлежат ли гра-
граничные точки а и Ъ рассматриваемым совокупностям или нет,
вместо терминов «интервал* и «отрезок» употребляется тер-
термин «промежуток».
Пример 1. Интервал E,9) есть совокупность всех действитель-
действительных чисел х, удовлетворяющих условию 5 < х < 9.
Пример 2. Отрезок [—1, +2] есть совокупность всех действи-
действительных чисел х, удовлетворяющих условию —1<лс< +2.
Пример 3. Совокупность всех действительных чисел х, для
которых — 1<л:<1, есть полуотрезок [—1,1).
Пример 4. Совокупность всех действительных чисел х, подчи-
подчиняющихся условию —2 < х < 2, есть полуотрезок (—2, +2].
5. Если рассматривается совокупность всех действительных
чисел, то это записывается так: — oo<*<-f-oo или {— со, +оо).
Под записью а<*<+оэ, или (а, Н-оо) следует понимать,
что рассматривается совокупность всех действительных чисел х,
больших, чем а, а под записью а<л:<+оо, или [а, +оо), по-
понимается совокупность всех действительных чисел х, не мень-
меньших а (когда мы говорим «число, не меньшее числа а», то это
значит, что это число или больше, или равно а).
* Некоторые авторы, например Г. П. Толстов в учебнике «Kypq матема
тического анализа», называют эти совокупности чисел не «полуотрезками»
а «полуинтервалами».
213
Запись —со < х < b или (—co,b) означает, что рассматри-
рассматриваются все действительные числа х, меньше числа Ь, а запись
—оо < х < Ь или (—со, Ь] следует понимать так, что рас-
рассматривается совокупность всех действительных чисел х, не боль-
больших числа b (когда говорят, что число не больше числа Ь, то
это означает, что оно или меньше, или равно числу Ь). Интер-
Интервалы, рассмотренные в этом пункте, называются бесконечными.
2. Свойства абсолютных величии "
С абсолютными величинами чисел в математическом анализе
приходится часто встречаться. Мы напомним относящиеся сюда
определения и теоремы и сделаем ряд упражнений.
1. Абсолютная величина числа а обозначается символом \а\.
Пусть а — действительное число. Если оно положительно или
равно нулю (а > 0), то его абсолютной величиной называется оно
само, а если оно отрицательно (а < 0), то его абсолютной вели-
величиной называется число — а.
Итак, если а > 0, то | а | = а; если а < 0, то | а | = —а.
Чтобы перейти к абсолютной величине числа, имеющего в циф-
цифровой записи знак минус, надо этот знак отбросить.
Если а = 5, то | а \ = | 51 = 5; если а = 0, то | а | = 0.
Если а = — 3, то | а | = | —31 = —(—3) = 3.
2. Если |*| <е (е > 0), то это означает, что х удовлетворяет
неравенствам (фиг. 1,5);
-е<*< + е. A,1)
-е О +?
Фиг. 1,5.
Пример 1. Если |а|<3, то имеют место неравенства
-3<а<+3.
Пример 2. Если ] у | < ~, то у удовлетворяет неравенствам
— у < У < + |- (фиг. 1,6).
Фиг. 1,6.
Задача 1,1. Определить числовую величину выражения M
при х = 2.
214
Решение. При х — 2
2-2+5
2л-+5
7 — 2*2
2 2г
4 + 5
-1-91-9.
Задача 1,2. Определить числовую величину выражения
2л-3 — 4 Л
при х = 0.
5 —л-
Решение. При х = 0 имеем
2л-3 — 4
5 —л-
2-0 — 4
5 — 0
—4
5
_4_
5 '
Задача 1,3 (для самостоятельного решения). Определить при
х = 4 числовую величину выражения
Ответ, уу.
Задача 1,4 (для самостоятельного
5 —л-3
величину выражения
5 —л-3
решения). Найти числовую
при: 1) х = 0; 2) х = 2; 3) х = —3.
1—л-
Ответ. I) 5; 2) 3; 3) 8.
Задача 1,5. Определить, при каких значениях х будет спра-
справедливо неравенство | х — 31 < 2.
Решение. Согласно формуле A,1) данное неравенство может
быть записано так: —2 < х — 3 < 2. К каждой части этих не-
неравенств прибавим по 3 и получим —2 + 3<х<2 + 3, откуда
следует, что 1 < х < 5.
Заключение: неравенство | х — 3 | < 2 выполняется для всех
значений х из интервала A,5).
Задача 1,6. Определить, при каких значениях х выполняется
неравенство \х — а | < е.
Решение. Поступая так же, как и в предыдущей задаче,
получаем, что — е < х — а < + е, а отсюда, прибавляя а к каждой
части этих неравенств, имеем а — е < л: < а 4- г.
Заключение: неравенство \х — а| < s выполняется для всех
значений х из интервала (а — е, а + е).
Задача 1,7 (для самостоятельного решения). Определить, при
каких значениях х выполняются неравенства: 1) | х — 11 < 3;
2) |х + 3|< 1; 3) \х+ 1|>3.
Ответ. 1) —2<х<4; 2) — 4 < х < — 2; 3) х < — 4
и х > 2.
Указание к третьему примеру: из того, что \х\> а(а>0),
следует, что х> +а и л: < — а. В нашем случае из того, что
| х + 11 > 3, заключаем, что *+1>3 и #+1< —3; отсюда
и следует указанный ответ. ,
Задача 1,8. При каких значениях х корень )/9 — х2 будет
иметь действительные значения?
215
Решение. Корень У 9 — хг будет иметь действительные зна-
значения, если подкоренное выражение не является отрицательным,
т. е. когда 9 — х2 > О, а дс2 < 9.
Многие совершают грубую ошибку, делая на основании не-
неравенства х2 < 9 заключение, что х < ±3, т. е. х < +3 и х < —3.
В действительности же верно только, что х < +3, а неравенство
х < —3 является в данном случае ошибочным. Правильными ре-
решениями неравенства х2 < 9 являются х > —3 к х < +3, т. е.
—3<*<+3, или |*|<3, ибо для всех значений х из интер-
интервала (—3, -}-3) выполняется неравенство х2 < 9. Если же при-
принять, что х < —3, то числа, удовлетворяющие этому неравенству,
будучи возведены в квадрат, дадут числа ббльшие, чем' 9 (на-
(например, —4 < —3 и (—4J = 16 > 9).
Итак, решением деравенства х2 < 9 является —3 < х < +3,
или |* | < 3.
Задача 1,9 (для самостоятельного решения). При каких зна-
значениях х корень Ухг — 9 будет иметь действительные значения?
Ответ. *< —3 и х > +3, т. е. Ух2 — 9 имеет действитель-
действительные значения для значений х, удовлетворяющих неравенствам
— со < х < —3 и 3< х < +оо.
3. Теоремы об абсолютных величинах
Теорема 1. Абсолютная величина суммы нескольких слагае-
слагаемых не больше суммы абсолютных величин этих слагаемых, т. е.
например, \х + у + z\<\x\-\- \у\ + \z\, причем знак равенства
имеет место только в том случае, когда числа х, у и z имеют
один и тот же знак.
Теорема 2. Абсолютная величина разности двух чисел не
меньше разности абсолютных величин этих чисел, т. е. | х — у | >
>\х\-\у\.
Теорема 3. Абсолютная величина произведения нескольких
сомножителей равна произведению абсолютных величин этих со-
сомножителей. Например, в случае двух сомножителей \ху\ =
= 1*1Ы.
Теорема 4. Абсолютная величина дроби равна абсолютной
величине числителя, разделенной на абсолютную величину знаме-
знаменателя, т. е.
У\ \У\'
Задача 1,10 (для самостоятельного решения). Проверить тео-
теорему 1 этого параграфа для
1) *= —5; г/= 4; z = 5; и = —1.
2) х - -4; у = 5; z = -2.
3) х = 4; у = 2; z=--7.
4) *=5; г/=-3; z = -6.
216
Задача 1,11 (для самостоятельного решения). Проверить тео-
теорему 2 этого параграфа для чисел
1) *= 7; 0=-4; .3) х= 5; у = 7;
2) * = -4; у = -8; 4) дс = -10; у = 4.
1^ j |
2. . 3, — -g- < 0,01 (*>—з).
Решение. Упростим выражение, стоящее под знаком абсо-
абсолютной величины:
х—1 1__ 5* — 5 — 2х — 6 _ 3*—11
2(* + 3) 5~ 10 (х + 3) 10 (л- + 3) *
и данное неравенство запишется в виде
Ъх — П
10 (дг + 3)
1
Too*
Освобождаясь от знака абсолютной величины, получаем:-
1_ Ъх—11 _1_
100 "^ 10(^+3) + 100'
а отсюда уже имеем два неравенства:
п 1 За- — 11 „, Зл-— И 1
' 100*^10(^ + 3)' МО (х + 3) "^ ТОО '
Так как по условию х > —3, то дс + 3 — величина положи-
положительная, и первое неравенство после умножения обеих его час-
частей на х + 3 дает
—1 • (дг + 3) <:ЗОдг — 110; -*-3<30*-110; х > ^
(* -f 3 > 0, а поэтому смысл неравенства от умножения обеих
его частей на х + 3 сохраняется).
113
Из второго неравенства получаем, что х < -gg-. Итак, данное
107 ИЗ
неравенство выполняется, если -щ- < х < -sk- .
ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Величины постоянные и переменные. Функция. Область
существования функции. Основные элементарные функции.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1., Постоянные величины. Абсолютные постоянные и параметры.
Величина называется постоянной, если она всегда или только
в условиях данной задачи сохраняет одно и то же числовое
значение.
Постоянные величины разделяются на абсолютные постоян-
постоянные величины и параметры. Величина, которая сохраняет одно
217
и то же значение при всех условиях, называется абсолютной пос-
постоянной (примерами абсолютных постоянных являются: все
числа, сумма внутренних углов треугольника, число тс; скорость
света в пустоте).
Параметром называется такая постоянная величина, кото-
которая лишь в условиях данной задачи (данного исследования) сохра-
сохраняет постоянное, вполне определенное числовое значение, но с из-
изменением условий задачи принимает уже другое, хотя опять-
таки определенное числовое значение.
2. Переменные величины. Величина называется переменной,
если она в условиях данной задачи принимает различные число-
числовые значения.
3. Независимые переменные. Две переменные величины назы-
называются независимыми, если значения, принимаемые одной из них,
не зависят от значений, принимаемых другой.
(Пример: в формуле для определения объема цилиндра V = -kR2H
величины R и Н — независимые переменные, так как значения,
принимаемые высотой Н цилиндра, не зависят от значений R,
которые принимает радиус цилиндра).
4. Функция. Переменная величина у называется функцией от
переменной величины х, если каждому рассматриваемому значе-
значению х по известному правилу или закону соответствует одно
определенное значение у. * Если переменная величина у является
функцией переменной величины х, то это обозначают так:
У = f(x). ' .. B,1)
Эта запись читается: «игрек есть функция от икс», или «игрек
равен эф от икс».
В записи B,1) х называется аргументом или независимой пе-
переменной, а у — функцией, или зависимой переменной.
5. Задание функции. Функция B,1) считается заданной, если:
1) Указана совокупность всех рассматриваемых значений ар-
аргумента х.
2) Указан закон, который позволяет по заданному значению
аргумента х находить соответствующее ему значение функции у.
6. Частным значением функции называется то ее значение,
которое соответствует частному значению аргумента х = х0.
Для обозначения частного значения функции при х = х0 упот-
употребляется символ f (хп) или у(х0).
7. Область существования функции. Если функция задана
аналитически, то областью существования функции (иначе, об-
областью определения функции) называется совокупность тех дей-
действительных значений аргумента, при которых аналитическое
выражение, определяющее функцию, не теряет числового смысла
и принимает только действительные значения.
* Многозначные функции нами не рассматриваются.
218
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ
Задача 2,1. Период малых колебаний Т математического ма-
маятника вычисляется по формуле Т =-. 2тс 1/ —, где / — длина ма-
маятника, g — ускорение силы тяжести.
Какие из величин, входящих в эту формулу, являются абсо-
абсолютными постоянными, параметрами, переменными?
Ответ. 2 и тс — абсолютные постоянные; g — параметр; зна-
значение этой величины постоянно только в данной точке земной
поверхности, но изменяется при переходе от одной точки земной
поверхности к другой; / и Т — величины переменные.
Задача 2,2. Согласно закону Бойля-Мариотта, в изотермиче-
изотермическом процессе pV — C, где р — давление газа, а V — занимаемый
им объем. Указать в этой формуле переменные величины и па-
параметр.
Ответ. Величины р и V — переменные; величина С — пара-
параметр, так как она сохраняет постоянное значение только для
данного газа и для данной температуры.
Задача 2,3. В случае свободного падания тела в пустоте прой-
пройденный им путь S вычисляется по формуле S = ^-.
Какие из входящих в эту формулу величин являются абсо-
абсолютными постоянными, параметрами, переменными?
Ответ. 2 является абсолютной постоянной величиной (следует
помнить, что в^е числа.— абсолютные постоянные величины); g —
параметр (см. задачу №2,1); s и t — переменные величины.
, Задача 2,4. Объем усеченного конуса вычисляется по фор-
формуле
Указать, какие из величин, входящих в эту формулу, явля-
являются переменными, абсолютными постоянными, параметрами.
Ответ. Величины тс и 3 — абсолютные постоянные; V, Я, R
иг — переменные величины.
Ни одна из величин, входящих в эту формулу, не является
параметром.
ОПРЕДЕЛЕНИЕ ЧАСТНЫХ ЗНАЧЕНИЙ ФУНКЦИИ
Для того чтобы найти частное значение функции по задан-
заданному частному значению аргумента, надо в аналитическое выра-
выражение функции подставить вместо аргумента его частное зна-
значение.
Задача 2,5. Дана целая рациональная функция f (х) ~ Зле2 —
2Х 1
Вычислить: 1)/B); 2) /(-2); 3) /A); 4) /@); 5) f(a + 2);
6)f(-*).
219
Решение. 1) f B) = 3 - 22 — 2 • 2 — 1 = 3-4-4-1 = 12-
-4-1=7.
2) /(—2) = 3(—2K — 2(—2) — 1 = 3-4 + 4-
-1 = 12 + 4-1 = 15.
3) f(l)-3- 12-2 -1-1 =0.
4) f@) = 3 -0а-2 -0-1 = -1.
5) f(a + 2) = 3(a + 2)a-2(a + 2)-l=3(a2 +
+ 4а + 4) — 2а - 4 - 1 = За2 + 10а + 7.
6) f(-x) = Z(—xf-2{—x)-\ = Зл:2 + 2*-1.
Задача 2,6 (для самостоятельного решения). Дана целая ра-
рациональная функция f (г) = 2г3 — г2 + г — 1.
Вычислить: 1) /(¦!); 2) /B); 3)/(-1);
Ответ. 1) -1; 2) 13; 3) -5; 4) *
-- а" — 7д2 + За — 5
Задача 2,7. Дана дробная рациональная функция
Вычислить: 1) Да); 2),/(^); 3) /B);.4) /@).
Репине. 1) На)-«?!&1. 2) /(l) -
_ 4 — 7а^ + 2д« „ , „ _ 4 • 22 — 7 ¦ 2 + 2 _ 16—14 + 2 _ _4_ .
"" 5а*+ 3 ; d''W~ 3-22 + 5 ~ 12 + 5 ~ 17'
4) /= @) = А •
Задача 2,8 (для самостоятельного решения). Дана функция
/(г) = 5т~'. Вычислить: 1) f(l); 2) /B); 3) /(-2); 4)/(|).
Ответ. 1) /A) = 1; 2) /B) = -Ь 3) /(-2) =^-_; 4) /Ш=
= 52.
Задача 2,9. Дана дробно-линейная функция f (х) — %_х •
Найти: 1) <р (Зх); 2) ? (л;3); 3) 3^ (л); 4) [у (д:)]3.
Решение. 1) Чтобы найти fCx) следует в выражении для
f (х) заменить х на Зле. Получаем ср (Зд:) = -g_^^.-" = 2—"зу •
220
2) Заменяя в выражении для <р (х) х на х3, получим
3) Следует отличать f (Зх) от 3<р (х), f (х3) от [<р (*)]3. Было
найдено в 1), что <р B>х) = 2_J^. , a3?W 3 ± J^
~ 8—15
Задача 2,10 (для самостоятельного решения). Дана функция
Найти:
1) ФB6); 2) 2ФF); 3) ФF2); 4) [ФF)]а.
Ответ. 1) ФB6) = lg|^|; 2) 2Ф@) = lg
; 4) 1Ф@)Р = 1^ —•
Задача 2,11 (для самостоятельного решения). <р (х) = lg sin x.
Доказать, что <р (а) + f(b) — lg(sina • sinb).
Задача 2,12 (для самостоятельного решения). F (x) — sinx. До-
Доказать, что F (Зх) = 3f (х) — 4 [F (х)}3.
Задача 2,13. Доказать, что если f (х) = ^2ii t то f (—x) = —/ (х).
Решение. f(—*)= _х ' = — = — {(х).
Задача 2,14 (для самостоятельного решения). f(a) = tga. До-
Доказать, что /Bа) = 1 _р(а\'
Задача 2,15 (для самостоятельного решения). Доказать, что
если f(x) = s~, то f (—x) = / (х).
Ос с
Задача 2,16. Вычислить f (х) =-¦ -j + х2 в точках, где —|-
ос /а \2
Решение. ~ + х2 = 1—\-х) — 12, а так как по условию
Л \ X I
- 4- х = 5, то Щ + х2 = 52 - 12 = 13.
Задача 2,17. Дано, что f (х) = х2 + х -| Ь т • Доказать, что
? (j) = ? (*)•
221
Решение. Т A) = (±) +1 + -J-+ ' =^ + ±
Задача 2,18 (для самостоятельного решения). Дана функция
7 — х2
Ответ.
. Вычислить: ф — и —;-?.
7Л-2-1 1 5 — л- + д-2
ОБЛАСТЬ СУЩЕСТВОВАНИЯ ФУНКЦИИ
Задача 2,19. Найти область существования функции
<р = 3*3 + 5л:2 — 7* + 2.
Решение. Заданная функция — целая рациональная функ-
функция. Ее областью существования является бесконечный интервал
(—оо, +оо), или в другой записи —оо<д;<4-оо.
Задача 2,20. Найти область существования функций:
1) y = -j'> 2) У^т^х'' 3) у = 77^24
Решение. 1) Функция у — дробная рациональная функ-
функция. Она существует при всех значениях независимой перемен-
переменной х, кроме тех, которые обращают в нуль ее знаменатель,
т. е. в данном случае кроме х = 0. Область существования этой
функции состоит из двух бесконечных интервалов (—оо, 0) и
@, -f00), или в другой записи —со<*<0 и 0<*<+со.
2) Функция у = . _ также определена при всех значениях
х, кроме того его значения, при котором 1 — х = 0, т. е. кроме
х— 1. Область существования состоит из двух бесконечных ин-
интервалов (—оо, 1); A, +оо), или в другой записи (—оо < х < 1);
A <Х< +оо).
о
3) Решив уравнение 7х — 2 = 0, найдем, что х = у. Область
существования функции у = ' состоит из двух бесконечных
/ 2\ /2 \ /
интервалов I— оо, у I; ly , -f-ool, или в другой записи I—<
:т)и(т<*<+оо).
Задача 2,21 (для самостоятельного решения). Определить об-
область существования функций:
X2 — 1
Ответ. 1) (—оо, —1); (—1, +оо), или — оо<л:<— 1
И — 1 <*< + ОО.
2) (-со, 2); B, +оо),
или—со<*<2 и 2<*<+оо.
Задача 2,22. Найти область существования функции у =
х—1
— хг _ 7л- + 12 '
Решение. Заданная функция — дробная рациональная функ-
функция. Она определена при всех действительных значениях х, кроме
тех, при которых знаменатель дроби х2— 7х + 12 равен нулю,
т. е. кроме значений х = 3 и х = 4 (эти значения найдены из
уравнения х2 — 7х + 12 = 0). Область существования заданной
функции состоит из трех интервалов: (—оо, 3); C,4) и D, + оо),
или в другой записи: —оо < х < 3; 3 < х < 4; 4 < х < + °°-
Задача 2,23 (для самостоятельного решения). Определить об-
область существования функций:
П — 5л — 7х+12. _ 7л-8 + х — 1
Ч У — хг—\ > У — Зл-2 — 8Л- + 4"
Ответ. 1) Область существования состоит из трех интервалов:
(-со, -1); (-1, +1); (+1, +оо).
2) Область существования состоит из трех интервалов:
Задача 2,24. Найти область существования функции у =
л-2 +. х 4-1 •
Решение. Приравняв нулю знаменатель дроби х2 + х + 1
и решив квадратное уравнение хг -\-х +1=0, убедимся, что его
корни — комплексные числа: х = —^ ± i ^~. Ни при одном
действительном значении х многочлен х2 + х + 1 в нуль не обра-
обращается. Поэтому заданная функция определена при всех дей-
действительных значениях х. Ее областью существования является
бесконечный интервал (—оо, +оо).
Задача 2,25 (для самостоятельного решения). Найти область
существования функций:
5 ¦
х 4- 5' "> * ~ л-2 + 1 •
223
Ответ. 1) Бесконечный интервал (—со, +со).
2) Бесконечный интервал (—со, -Ь00)-
Задача 2,26 (для самостоятельного решения). Найти область
существования функций:
i9
(знаменатель дроби х3 — 1 имеет один действительный корень
х = 1);
0 _ 2л-3— 1
Ответ. 1) Функция существует в двух бесконечных интерва-
интервалах: (—со, 4=1) и (+1. +со)> т. е. при любом значении х,
кроме х=\. 2) Знаменатель дроби х3 -\- 1 имеет один действи-
действительный корень х = — 1. Функция существует в двух бесконеч-
бесконечных интервалах: (—со, —1) и (—1, +со), т. е. при любом
значении х, кроме х— — 1.
Задача 2,27. Найти область существования функций:
1) у = У 2-х; 2) у = уТ+Т
Решение. 1) Для того чтобы функция у принимала только
действительные значения, величина 2 — х, стоящая под корнем,
не должна принимать отрицательных значений, т. е. должно
быть 2 — х > 0, откуда х < 2. Областью существования функции
является совокупность действительных значений х, меньших или
равных 2, т. е. полуотрезок — со<*<2.
2) Чтобы определить область существования функции, соста-
составим неравенство х + 4 > 0, из которого получаем, что х > —4.
Область существования функции полуотрезок —4 < х < + со
[-4, +со).
Задача 2,28 (для самостоятельного решения). Найти область
существования функций ]) у = УЬ — х и 2) у = У х — 3.
Ответ. 1) Полуотрезок — оо<х<5.
2) Полуотрезок 3 < х < +со.
Задача 2,29. Найти область существования функций
» i-7T=i> 2> »-иЬ' 3) »-*«=¦
Решение. 1) Выражение Ух —2 принимает действительные
значения, когда х — 2 > 0, т. е. когда х > 2. Но при х = 2
имеем л — 2 = 0, знаменатель дроби обращается в нуль, дробь
теряет числовой смысл, а потому значение х — 2 не может вхо-
входить в область существования функции. Значит, функция суще-
существует при значениях х > 2, область существования представ-
представляет собой бесконечный интервал B, +со).
224
2) Областью существования функции является бесконечный
интервал (—оо,4).
3) Область существования состоит из двух бесконечных ин-
интервалов (—оо, 8) и (8, +°°)- Это же заключение можно записать
с помощью неравенств: —со<д;<8 и 8<*<-foo.
Задача 2,30 (для самостоятельного решения). Определить об-
область существования функций:
Ответ. 1) Два бесконечных интервала ¦(-— оо, 3); C, +°°)
2) Бесконечный интервал (— оо; 3,5).
Бесконечный интервал E, +°°)-
ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений в определении области существо-
существования функции.
Задача 3,1. Найти область существования функций 1) у —
= Ух*=Т, 2) у = VT±*J/
Решение. 1) Для того чтобы функция у = Ух2 — 1 прини-
принимала только действительные значения, надо, чтобы х2 — 1 > 0,
т. е. х2 > 1. Это неравенство выполняется тогда, когда х < — 1 и
х> 1, и, таким образом, область существования функции состоит
из двух полуотрезков: (—оо, —1] и [+1. +°°). или в другой
записи —оо < х <—1 и 1<лс + оо.
2) Должно выполняться неравенство 4 — хг > 0, т. е. х2 < 4.
Отсюда следует, что х > —2 и *<-f2.
Областью существования функции является отрезок [—2, +2].
Это можно записать иначе: —2<д:<+2.
Задача 3,2 (для самостоятельного решения). Найти область
существования функций:
4) «/ =
Ух2 —16'
Ответ. 1) Отрезок [—3,+3], иначе — 3 < х < +3. 2) Два
полуотрезка (—со, — j/б] и [+1/6, +оо), иначе — оо<д:< —
— 1/6 и + УЪ < х < +оо. 3). Интервал (- УЪ, УЪ), или(- УЬ <
<х<У5) (значения х= ±УЪ отбрасываются, так как при х =¦-¦
— ±УЬ знаменатель дроби обращается в нуль и дробь, теряет
числовой смысл). 4) Два иетервала (—оо, —4) и D, -fco), или
— оо < х < —4 и 4 < х < -)-оо (значения х — ±4
225
отбрасываются, так как при х= + 4 знаменатель дроби обраща-
обращается в нуль и тем самым дробь теряет числовой смысл).
Задача 3,3 (для самостоятельного решения). Определить об-
область существования функции у = 1/ jzzr\ ¦
Указание. Должно выполняться неравенство > 0. Для
определения тех значений х, при которых это имеет место сле-
следует решить системы неравенств:
1) х+ 1 >01 и 2) х+ 1 <01
* —1>OJ ж—1<OJ"
Из решения этих неравенств следует, что областью сущест-
существования является полуотрезок (—оо, —1) и интервал A , +оо).
Это можно записать иначе: — оо < *< — 1 и 1<*<+°°. Зна-
Значение х = 1 рассматриваться не может, так как тогда х — 1=0
х А- I
и дробь _ . теряет числовой смысл.
Задача 3,4 (для самостоятельного решения). Найти область
существования функции у = У (х — 2) (л; + 3).
Указание. Рассмотреть неравенство (л; — 2){х + 3) > 0.
Ответ. — оо < л: < —3 и 2 < х < +оо.
Задача 3,5. Найти область существования функции у — lg(* —
-5).
Решение. Учитывая, что если основание логарифмов поло-
положительно, то ни нуль ни отрицательные числа логарифмов не
имеют, область существования данной функции найдем из требо-
требования, чтобы х — 5 > 0, откуда следует, что должно быть х > 5.
Функция существует для значений 5 < х < + <х>, т.е. на беско-
бесконечном интервале E, +°°)-
Задача 3,6 (для самостоятельного решения). Найти область
существования функций:
lH=lgB-x); 2) y=\g(x*-3).
Ответ. 1) —оо<л;<2; 2) —оо<д:< —l/З и УЗ < х <
Указание. В случае 2) рассмотреть неравенство х2 — 3 > 0.
Задача 3,7 (для самостоятельного решения). Найти область
существования функции у = lg*4.
Ответ. (—оо<л;<0) и @<х<+оо), т.е. функция опре-
определена при любом значении х, кроме х = 0.
Задача 3,8. Найти область существования функции у =
= sin Bх + 3).
Решение. Функция у = s'mx определена при любом значе-
значении аргумента х. Значит, выражение 2х + 3, стоящее под знаком
синуса, может принимать любое значение, откуда следует, что
226
х может принимать любое значение. Областью существования
функции является бесконечный интервал (—оо, +°°)- Это заклю-
заключение можно написать и иначе: —со < * <-|-оо.
Задача 3,9 (для самостоятельного решения). Найти область
существования функции у =-¦ sin — .
Ответ. Все действительные числа, кроме х — О. (— оо < х <
<0) и @<*< +oo).
Задача 3,10. Найти область существования функции у = ig2x.
Решение. Функция y = \gx определена при всех действи-
действительных значениях х, кроме х = Bk -f- l)-<r • где k — любое целое
число. Значит, в нашем случае величина 2х, стоящая после зна-
знака тангенса, не должна быть равна BА +1)у, т. е. 2х ф
Ф Bk + 1)у. а х Ф Bk-\- I)-^ . Таким образом, область сущест-
существования функции у ~ tg2x состоит из всех действительных чисел,
кроме значений х = Bk -\- \)-г, где k — любое целое число.
Задача 3,11 (для самостоятельного решения). Найти область
существования функций: 1) i/ = ctg-j-, 2) г/ = tg 4х; 3) j/ = sec-g-
и у = cosec 2>x.
Ответ. 1) Множество всех действительных чисел, кроме зна-
значений х — ЪЫ. 2) Множество всех действительных чисел, кроме
значений х = Bk -f- 1) -g-. 3) Множество всех действительных чисел,
кроме х = Bk + От- 4) Множество всех действительных чисел
кроме х — ^ (всюду k — любое целое число).
Задача 3,12. Найти область существования функции у =
= arcsin Eл; — 8).
Решение. Областью существования функции у =¦¦ arcsin x
является отрезок [—1, +1]. Поэтому область существования
данной функции указывается неравенствами —1 < 5х — 8< + 1.
Прибавляя ко всем частям этих неравенств по 8, получаем
7 < 5л: < 9, откуда уже следует, что функция существует для
„ 7 9
значении -г- < х < -=-.
Задача 3,13 (для самостоятельного решения). Найти область
существования функций:
I х \
1) у = arcsin I у — 1); 2) у — arccos (Зл: — 6).
Ответ. 1H<л:<4; 2)-|<*<-|.
227
Задача 3,14 (для самостоятельного решения). Найти область
существования функций:
1) у = arctg Bл: — 5); 2) у = arcsin
Ответ. 1) — оо <*< +оо; 2) -~-< х < 1.
Задача 3,15 (для самостоятельного решения). Найти область
существования функции у —¦ arcsin (х2 + 2).
Ответ. Данное аналитическое выражение не определяет ни-
никакой функции, так как ни при одном значении х не имеют
место неравенства — 1 < х2 + 2 < -}-1.
Указание к решению задач 3,16—3,23.
Если требуется найти область существования алгебраической
суммы нескольких функций, то надо поступить так:
1) Определить область существования каждой из слагаемых
функций:
2) Определить часть, общую для всех найденных областей. Эта
общая часть и будет искомой.
Если такой общей части у областей, найденных в п. 1), не
окажется, то заданное аналитическое выражение, представляю-
представляющее алгебраическую сумму нескольких функций, не определяет
никакой функции в области действительных чисел.
Это указание распространяется также на произведение не-
нескольких функций и на частное двух функций, причем при опре-
определении области существования частного двух функций должны
быть исключены точки, в которых знаменатель дроби обращается
в нуль.
Задача 3,16. Найти область существования функции у —
= \og2(x-]) + x\
Решение. Областью существования функции ух = log2 (х — 1)
является совокупность всех значений х, удовлетворяющих нера-
неравенству х — 1 > 0, т. е. интервал A, +оо).
Областью существования степенной функции у4 = *а является
интервал (—оо, +°о)-
Общей частью этих двух интервалов является интервал
A, +со). Таким образом, данная функция существует для значений
1 <х< -foo.
Задача 3,17. Найти область существования функции г/ =
= уь — х + ух + г. —
Решение. Функция ух = У5 — х существует для значений
— со < д; < 5. Функция г/г = К*+3 существует для значений
—3<Х< +оо.
Общей частью найденных двух областей является отрезок
[—3, +5], а поэтому данная функция существует для значений
—3<х< +5.
228
Задача. 3,18 (для самостоятельного решения). Найти область
существования функции у = У А — х — Ух + 2.
Ответ. — 2<*<4, т.е. отрезок [—2,4].
Задача 3,19 (для самостоятельного решения). Найти область
существования функции у = У 4 + х — Ух + 2 + У15 — х.
Ответ. [—2,15], т.е. — 2 < х < 15.
Задача 3,20 (для самостоятельного решения). Найти область
существования функции у = 2х3 + lg (* — 1) + jzri •
Ответ. Функция существует для значений 1 < х < 3 и
3<х<+оо, т.е. в интервалах A,3) и C,+оо).
Задача 3,21 (для самостоятельного решения). Найти область
существования функции у = 2х tg x.
Ответ. Функция существует при всех значениях, х, кроме
значений х — Bk + 1) ~, где k — любое целое число.
Задача 3,22. Найти область существования функции у =
sin х
Решение. Функция #1 = sinje существует в бесконечном
интервале (—оо, +00)-
Функция y—[g(x2 — 4) существует в интервалах (—оо, —2)
и B, +оо). Но следует иметь в виду, что функция lg(*2 — 4)
стоит в знаменателе дроби, а потому из этих двух интервалов
надо исключить точки, в которых эта функция обращается в
нуль, т. е. точки, для которых lg (хг — 4) = 0, или х2 — 4 = 1,
а х = ±УЪ. Таким образом, функцию lg (л:2 — 4) следует рас-
рассматривать в интервалах: 1) (—оо, —УЪ); 2) (—У~5, —2); 3) B, |Лэ)
и 4) 0/5,+ оо).
Общей частью, принадлежащей бесконечному интервалу
(—оо, +оо), в котором определена функция sinx, и только что
найденным интервалам являются именно эти интервалы, а потому
данная функция существует в интервалах: 1) (—оо, —1/5);
2) (-/5, -2); 3) B, ^5); 4) (УЪ, +оо).
Задача 3,23 (для самостоятельного решения). Найти область
существования функции у = lg х г~ 'Т^ -
Ответ. Два бесконечных интервала: (—оо, 2) и C, +оо).
ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержавие: Построение графиков функций.
Это практическое занятие посвящается упражнениям на по-
построение графиков функций, заданных аналитически.
В инженерной практике с построением графиков функций
приходится встречаться очень часто. При изучении таких пред-
229
метов, как сопротивление материалов, теория упругости, гидрав-
гидравлика, электротехника, радиотехника, к построению графиков
функций приходится прибегать буквально на каждом шагу.
Поэтому студенту следует с исключительной серьезностью от-
отнестись к этому практическому занятию.
К построению графиков более сложных функций мы еще воз-
возвратимся на практическом занятии № 35 и используем для этого
уже аппарат дифференциального исчисления.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Определение 1. Графиком функции у — f (х) называется сово-
совокупность всех точек плоскости, абсциссы которых есть значения
аргумента, взятые из области существования функции, а орди-
ординаты, соответствующие этим значениям аргумента, — значения
функции.
Согласно этому определению, для построения точного графика
функции нам следовало бы построить все точки, принадлежащие
графику, а это, как правило, сделать невозможно так как,
вообще говоря, график функции содержит бесконечное множество
точек.
Для построения графика функции у = f (x) обычно поступают
так: дают аргументу несколько частных значений и пользуясь
аналитическим выражением функции, вычисляют соответствующие
значения функции. Если, например, взяты значения аргумента
х = Ху, х = x^\ х = х3, ... , х — хп, то соответствующими им
значениями функции будут
0i = f (*i); у* = f to); Уз = f to); • • •; yn = f (*»)•
Эти значения сводят в таблицу такого вида:
После этого берут прямоугольную систему
координат, выбирают масштабную единицу и
строят точки
М1(х1, ух), Мг(хъ, уг), М3(х3,.у3), ... ,
Мп(хп,уп).
Полученные точки соединяют плавной кривой.
Эта кривая дает эскиз графика функции (при-
(приближенный график). Прежде чем приступить
к составлению таблицы числовых значений
функции, очень полезно выяснить вопрос
о симметрии графика функции.
Если функцию можно отнести к классу четных или нечетных
функций, то построение ее графика значительно облегчится.
Приведем относящиеся сюда определения.
Определение 2. Область существования функции называется
симметричной, если вместе с числом х этой области принадле-
принадлежит и число —х (на геометрическом языке это значит, что
230
X
Ч
ч
х?
хп
У
У\
У2
Уг
Уп
симметричная область существования функции расположена сим-
симметрично относительно начала координат).
Определение 3. Функция у — f (x) называется четной на
симметричной относительно начала координат области, если
для каждого значения аргумента х из этой области имеет место
равенство
f(-x) = f(x). D,1)
Таким образом, если функция — четная, то изменение знака
у аргумента не меняет значения функции, а потому в случае
четной функции каждой точке ее графика с абсциссой х и орди-
ординатой у соответствует точка, имеющая абсциссу —х и ту же ор-
ординату у.
Это приводит к выводу, что график четной функции распо-
расположен симметрично относительно оси Оу.
Таким образом, если функция четная, то ее график мы будем
строить так:
1) Построим только часть графика этой функции, расположен-
расположенную справа от оси Оу, т. е. при составлении таблицы числовых
значений функции будем давать аргументу только положитель-
положительные значения и значение, равное нулю, если это значение при
надлежит области существования функции.
2) Построим «зеркальное отображение» относительно оси Оу
графика, полученного в п. 1).
Определение 4. Функция у — f(x) называется нечетной на
симметричной относительно начала координат области, если
для каждого значения аргумента х из этой области имеет место
равенство
D,2)
Таким образом, у нечетной функции изменение на противо-
противоположный знака аргумента изменяет на противоположный и знак
функции, не изменяя ее абсолютной величины.
Поэтому график нечетной функции расположен симметрично
относительно начала координат, так как если графику принад-
принадлежит точка А (х, у), то ему же принадлежит и точка В,
(—х, —у).
Для построения графика нечетной функции надо: 1) построить
только ту часть графика, которая расположена справа от оси Оу,
т. е. часть, соответствующую положительным значениями аргумента
(и значению х — О, если нуль принадлежит области существова-
существования функции); 2) построить кривую, симметричную относительно
начала координат кривой построенной в п. 1).
Эти свойства четных и нечетных функций будут использованы
при построении графиков функций.
Задачи 4,1—4,12 являются упражнениями, связанными с опре-
определениями четной и нечетной функций.
231
ПРИЕМЫ, ОБЛЕГЧАЮЩИЕ ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
4
Укажем приемы, облегчающие построение графика функции
в ряде случаев, которые часто встречаются в практике
4.1. Для того чтобы по известному графику функции у —
— f (х) построить график функции y — f(—х), надо построить
линию, симметричную линии у = f (x) относительно Оу.
4.2. Для того чтобы по известному графику функции у —
= / (х) построить график функции у — —/ (х), надо построить
линию, симметричную линии у = f (х) относптельно оси Ох.
4.3. Если известен график функции y — f (x), то, чтобы
построить график функции у= f (х + с), надо перенести график
функции у = f (x) вдоль оси Ох на с единиц масштаба вправо,
если с <0, и влево, если с>0 (предполагается, что ось Ох направ-
направлена вправо).
4.4. График функции у — f (x) -f- В получается из графика
функции у — f (х) переносом этого графика на В единиц мас-
масштаба вверх, если В >О, и вниз, если В <0 (предполагается,
что ось Оу направлена вверх).
4,5 График функции у = Af (x) получается из графика функ-
функции у =¦- f (x) умножением всех его ординат на А при сохранении
величины соответствующих абсцисс.
4,6. График функции y — f (kx) (k > 0) получается из графика
функции y — f (x) делением всех абсцисс этого графика на k,
если k> 1, и умножением их на -^, если 0 <k < 1, при сохра-
сохранении величин соответствующих ординат.
Применяя последовательно эти приемы, можно, зная график
функции у = f (x), построить график более сложной функции
вида
Упражнения, связанные с понятиями четной и нечетной
функции.
Задача 4,1. Доказать, что функция f (x) — 2х* — четная.
Решение. Вычислим f(—x). Если окажется, что f(— х) =
= / (х), то из определения 3 будет следовать, что функция f (х) —
= 2х* — четная:
Равенство D,1) выполняется, а потому заданная функция—
четная.
Задача 4,2. Доказать, что функция /(*) — ^~нечетная-
232
Решение. Вычислим, f (—х) и если окажется, что f (—x) —
= ¦—/(*)» то из определения 4 будет следовать, что заданная функ-
функция действительно нечетная:
Задача 4,3 (для самостоятельного решения). Доказать, что функ-
ция f (х) -— v T^ — четная.
Задача 4,4 (Для самостоятельного решения). Доказать нечет-
нечетность функций: 1) f (*) = _?_; 2) f (x) = *??+~ * •
Задача 4,5 (для самостоятельного решения). Доказать четность
функций: 1) f (х) = ^5: 2) / (х) = ** +/' 7 * •
Задача 4,6. Выяснить, является ли функция /(х) = —^-т четной
или нечетной.
Решение. Вычислим/(—х):
f/ уч —-у + 1 -у — 1
Отсюда заключаем, что изменение знака у аргумента изме-
изменило абсолютную величину функции; ни равенство D,1), ни ра-
равенство D,2) не выполняются, а потому данная функция не мо-
может быть отнесена ни к числу четных, ни к числу нечетных
функций.
Читателю необходимо уяснить, что функция не
обязательно должна быть либо четной, либо не-
нечетной.
Задача 4,7 (для самостоятельного решения). Показать, что
функции f (x) = smx + cosx и <?(х) — 2л:+ 7 нельзя отнести ни
к четным, ни к нечетным функциям.
Задача 4,8. Доказать, что сумма или разность двух четных
функций есть функция четная.
Решение. Пусть у (х) = /х (х) ± \г (х), причем функции fx (x)
и /2 (х) — четные. Тогда 7i (—х) = fx (x), a U (—х) = \г {х) D,3).
Вычислим ср (—д): <р (—х) = /х {—х) ± /2 (—х).
На основании равенств D,3) ср (—х) = f1 (x) ± ft (x), и тре-
требуемое доказано: <р (—х) = ср (х).
Доказанное предложение распространяется на алгебраичес-
алгебраическую сумму любого конечного числа слагаемых (предполагалось,
что функции /х (х) и \г (х) рассматриваются в одной и той же
симметричной области).
Задача 4,9 (для самостоятельного решения). Доказать, что
сумма или разность двух нечетных функций есть функция не-
нечетная (предполагается, что функции рассматриваются в одной
и той же симметричной области).
233
Задача 4,10. Доказать, что произведение двух четных или
двух нечетных функций есть функция четная.
Решение. Пусть функции fA (x) и f2 (x) — четные. Тогда
fi (—х) = fi (х)> а h (—х) — \ч (х)- Составим их произведение: <р (х) =
=: h (х) !г (х), и тогда <р (—х) = ft (—х) f2 (—х) = U (x) f2 (х) = <р (х);
тем самым доказано, что произведение двух четных функций —
функция четная.
Теперь самостоятельно докажите, что произведение двух
нечетных функций есть тоже функция четная.
Задача 4,11 (для самостоятельного решения). Доказать, что
произведение функции четной на нечетную есть функция не-
нечетная.
Задача 4,12 (для самостоятельного решения). Выяснить, какая
из функций 1) f (х) =¦¦ х* + sec х; 2) у— х2 + ^z 3) f (х) =
— х2 cos х; 4) f (х) = х sin х; 5) f (х) = х2 tg х; 6) f (х) = х3 sin x;
7) y — x&smx является четной, а какая нечетной.
Ответ. Функции 1), 2), 3), 4), 6), 7) — четные, 5) — не-
нечетная.
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
Графики целых рациональных функций
Задача 4,13. Построить графики функций: 1) у = Ъх — 5;
2) г/--2х + 3; 3) у = 4х— 1; 4) у = -Зх+ 1.
Решение. 1) Данную функцию нельзя отнести ни к четным,
ни к нечетным функциям: у (—х) = — Зх — 5.
Ее областью существования являет-
является бесконечный интервал (—оо, -j-oo).
Функция — линейная (это хорошо изве-
известно читателю из аналитической геоме-
геометрии). Ее графиком является прямая
линия, для построения которой доста-
достаточно знать только
две ее точки. Возь-
Возьмем два произволь-
произвольных значения аргу-
аргумента х и вычислим
соответствующие им
значения функции у.
Построим на пло-
плоскости точки А1B,\) и Л2 (—3, —14).
Прямая изображена на фиг. 4,1.
Графики остальных функций по-
постройте самостоятельно. Фиг. 4,1.
234
X
2
—2
У
1
— 14
Задача 4,14. Построить график функции у = х2.
Решение. Заданная функция — четная. Ее график сим-
симметричен относительно оси Оу. Поэтому достаточно построить
часть графика для значений х > 0, а потом дополнить эту
часть ее «зеркальным отображением» относительно оси Оу. Так
будет получен полный график этой функции. Так как функ-
функция определена при любом значении х, составим таблицу ее
значений при произвольных значениях х > 0 и построим на
плоскости точки Ах(О, 0); Л2A, 1); Л3 B, 4);
Л4C, 9).
Соединим эти точки плавной кривой (фиг. 4,2).
Построим теперь «зеркальное отображение»
этой кривой относительно оси Оу и получим
полный приближенный график данной функции
(фиг. 4,3). Очевидно, что графиком функции
является парабола.
Задача 4,15. По известному графику функ-
функции у = х2 построить графики функций: 1) у =
х_ -
0
1
2
3
У
0
1
4
9
= Зх2; 2) у*=-
у = 4*2;4) у - -*2; 5) у = -ъх\
Фиг. 4,2.
Фиг. 4,3.
Указание. Учесть указание 4,5 (стр. 232). Пользуясь гра-
графиком функции у = х2 (фиг. 4,3), сохраняя величины абсцисс,
в первом случае надо увеличить все ординаты в 3 раза (фиг. 4,4),
во втором случае уменьшить все ординаты в 2 раза (фиг. 4,5),
в третьем — уменьшить их в 3 раза (фиг. 4,6). В случаях чет-
четвертом и пятом использовать указание 4,2 стр. 232 (фиг. 4,7
и 4,8).
Задача 4,16 (для самостоятельного решения). По известному
графику функции у = 2х2 построить графики функций: у = 2х2 +
+ d при d= 1, 2, —1, —3.
235
Указание. 1) Построить график функции у = 2х*, исполь-
использовав график функции у = х2. Учесть указание 4,4 (стр. 232).
Графики этих функций показаны на фиг. 4,9 — 4,12.
Например, график функции у = 2х2 — 3 получается из гра-
графика функции у — х2 так: увеличив все ординаты этого графика
X
Фиг. 4,4.
Фиг. 4,5,
в два раза при сохранении величины соответствующих абсцисс,
получим график функции у = 2Л Если этот график опустить
на 3 ед. масштаба, тр получим график функции у = 2*2 — 3.
X
Фиг. 4,6.
Фиг. 4,7-
Задача 4,17. По известному графику функции у — х2 построить
графики функций: 1) у -^ (х -f 1J, у = (х — 2J.
Решение. 1) График функции у = (х+ IJ получается из
графика функции у — хг переносом его на 1 ед. масштаба вдоль
оси Ох "влево — фиг. 4,13а и 4,136 (см. указание 4,3, стр. 232).
236
* >
Фиг. 4,8.
237
2) График функции у ¦-¦ (х -~ 2J получается из графика функ-
функции у = х2 переносом его вдоль оси Ох на 2 ед. масштаба впра-
вправо—фиг. 4,14а и 4,146 (использовать то же указание).
У
\
-/ о
1
/
б)
ос
Фиг. 4,13.
Задача 4,18 (для самостоятельного решения). По известному
графику функции у — х2 построить графики функций:
1) у = 2(х + 2J; 2) у = \{х-\)\
Фиг. 4,14.
Задача 4,19. Пользуясь графиком функции у = х2, построить
график функции у = х2 + 2х + 2.
Решение. Заданную функцию представим в виде у = (х -f
+ 1J+ 1- Исходя из графика функции у = х2, построим сначалаг
график функции y = (x-j- 1J, а потом этот график перенесем на
1 ед. масштаба вверх (фиг. 4,15) —см. указание 4,4 стр. 232.
Задача 4,20 (для самостоятельного решения). Пользуясь гра-
графиком функции у — х2, построить график функции у = \х2 +
+ 8х+ 12.
238
Указание. Заданную функцию записать в виде у — 4(х +
4-1J + 8 и вести построение в такой последовательности:
1) г/ =--ха; 2) */=(*+1)а; 3) у = 4(*+ IJ; 4) у - 4 (ж + IJ + 8.
Фиг. 4,15.
Задача 4,21 (для самостоятельного решения). Построить гра-
графики функций:
\) у=—х2 + 2х + 2; 2) г/ = — 2х2 + Зх — 4;
3) г/ = 5х2 + 4х„+ 7; 4) у = 2х2 + 4х;
5) у = —Зл;2— х.
Найти также точки пересечения этих парабол с осью Ох.
ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений в построеиии графиков функ-
функций. Графики показательной и логарифмической функции.
Задача 5,1. Построить график кубической параболы у = ха
(график этой функции, так же как и график параболы второй
степени, надо хорошо запомнить). •
Решение. Функция у = х9 определена прн всех значениях х
(—т<х< +оо). Функция эта нечетная (у(—х) = — х3 = —у (х))
239
Поэтому мы построим сначала ту часть ее графика, которая со-
соответствует значениям х > О, а затем для построения полного
графика воспользуемся указанием к построению графика нечет-
нечетной функции (стр. 231). Так как данная функция определена при
Фиг, 5,1.
Фиг. 5,2.
Фиг. 5,3.
X
0
1
2
3
. У
0
1
8
27
любом значении х, то мы можем составить таблицу числовых
значений функции для нескольких произвольных значений аргу-
аргумента.
1) Построим точки ^@, 0),.Л,A,- 1), Л, B, 8), Л4C, 27) и
соединим их плавной кривой. Построим после этого кривую,
симметричную этой кривой относительно начала координат.
Вся полученная кривая и будет приближен-
приближенным графиком функции у = х3 (фиг. 5,1).
Задача 5,2 (для самостоятельного решения).
Зная график функции у = х3, построить гра-
графики функций:
)ух;
3) y=-(x
5) у = -±
Указание. Построение этих графиков сле-
следует выполнить на основании указаний 4,1 —
4,6 стр. 232 "(см. фиг. 5,2 - 5,6).
Задача 5,3 (для самостоятельного решения).
Построить график параболы четвертой степени
* пользуясь им, построить графики
у = х* и,
функций:
2) у
; 5) у
7) У =
fi; 3) у =
:4; 6) у=(х-
1L-2
IL
Фиг. 5,4.
240
(графики удобно строить на одном чертеже, используя указания
4,3-4,7 стр.). •
Задача 5,4. Построить график функции у = — (функция у —
т
— — выражает закон обратной пропорциональности между пере-
i i
Фиг. 5,5.
Фиг. 5,6.
менными х ну, а ее график называется графиком обратной про-
пропорциональности) .
Решение. Прежде всего замечаем, что заданная функция —
нечетная, так как у{—х) = — — у{х).
Функция У — ~ определена при
всех значениях х, кроме х — 0.
Её область существования состоит
из двух бесконечных интервалов
(-ОО, 0) И @, + СО).
Построим часть графика дли зна-
значений х > 0, а полный график функ-
функции получим на основании указания
для, построения графика нечетной
функции (стр. 231). Составим таблицу
числовых значений функции для по-
положительных значений аргумента.
Фиг. 5,7.
9 И. А. Каплаи
241
X
1
T
1
1"
1
т
1
2
3
4
У
4
3
2
1
1
2
1
1
4
Построим на
3
плоскости точки
Мт-4
~. 2
AtB, I),
3
3, -g-j, Л7 И, -г-), соединим их плавной
кривой линией. Теперь построим кривую, сим-
симметричную ей относительно начала координат,
и получим приближенный полный график функ-
функции (фиг. 5,7)
_ j_
У О *
Эта кривая, как известно читателю из ана-
аналитической геометрии,— равнобочная гипербола
(иногда говорят равноосная гипербола).
График этой функции был уже рассмотрен
в первой части этого пособия. Там же был
рассмотрен и график дробнолинейной функции
вида
У
cx + d
Числителю рекомендуется повторить относящиеся сюда вопросы.
ГРАФИКИ ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЙ
Задача 5,5. Построить график функции у = 2х.
Считая этот график исходным, построить график функций:
1) у = 2-х; 2) у =-2*;
3) у = —2-*.
Решение. Показательная
функция у = 2х определена при
всех значениях х. Ее областью
существования является беско-
бесконечный интервал (— со, + °°)-
Составим таблицу числовых зна-
значений функции, давая аргумен-
аргументу произвольные значения.
Построим на плоскости эти
точки, соединим их плавной кри-
кривой линией и получим прибли-
приближенный график данной функ-
функции (фиг. 5,8а).
1) График функции у—2~х
Фиг. 5,8 симметричен графику функции
242
у = 2х относительно оси Оу (фиг. 5,86), т. к. если у(х) = 2х, то
у(—х) = 2~х (см. указание 4,1 на стр. 232).
2) График функции г/— — 2х симметричен
графику функции у — 2х относительно оси Ох —
см. указание 4,2, стр. 232 (фиг. 5,8е).
3) График функции у — —2~х симметричен
графику функции у = 2~х относительно оси Ох
(фиг. 5,8г) — см. указание 4,2, стр. 232.
Задача 5,6 (для самостоятельного решения).
X
—5
^
—3
—2
— 1
0
1
2
3
4
у
1
32
1
16
1
8
1
4
1
2
1
2
4
8
16
Построить график функции У-¦[-§¦} и> считая
его исходным, построить графики функций:
(Г Ш* (Г
(Г Ш Г
Задача 5,7. Построить график функции у —
= 22Х, считая исходным график функции у — 2х.
Решение. Для построения графика функ-
функции у = 22К по исходному графику у = 2х сле-
следует воспользоваться указанием 4,6 (стр. 232).
Сначала построим график функции у = 2х.
На этом графике выбираем несколько точек.
На том же чертеже построим точки, ординаты
которых равны ординатам выбранных точек,
но с абсциссами в два раза меньшими, чем у них (на фиг. 5,9
на графике функции у = 2х выбраны точки А, В и С). Получен-
Полученные точки соединим плавной кривой линией, которая и будет
приближенным графиком функции у — 22х.
Задача 5,9 (для самостоятельного решения). Считая исходным
JL
график функции у = 2х, построить график функции у — 22.
243
Задача 5,9 (для самостоятельного решения). Построить график
функции у = У и, считая его исходным, построить графики
функций:
1) г/= 1 + 3*; 2) у = 3х-2; 3)г/=г=3*-2;
4) г/=--¦ З"з~*.
Указание. При построе-
построении графиков функций 1) и 2)
использовать указание 4,4 (стр.
232), а при построении графика
функции 4) использовать указа-
указание 4,6 стр. 232.
Задача 5.10. Построить гра-
график функции y=\og10x.
Решение. Заданная функ-
функция определена только для зна-
значений х > 0. Составим таблицу
числовых значений функции при
Z 3 4 5 6 7 8 х
Фиг. 5,10.
у
нескольких произвольно выбранных положительных значениях
аргумента. Построим на. плоскости точки, абсциссы которых рав-
равны значениям аргумента, а ординаты — соответствующим им зна-
значениям функции.
Построенные точки соединим плавной кри-
кривой линией и получим приближенный график
данной функции (фиг. 5,10).
Задача 5,11 (для самостоятельного реше-
решения). Зная график функции y=\ogl0x, по-
построить графики функций 1) y=log10x3;
2) у=1о&о(*-1); 3) y~\og10(-x); 4)г/ =
Указание к 4): logi0y == log101 — Iog10 л:=
— log10*.
Использовать также указание 4,2 (стр. 232).
X
1
ЮО
1
10
1
2
3
4
У
—2
—1
0
0,3010
0,4771
0,6021
ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Построение графиков тригонометрических и обратных
тригонометрических функций.
ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Задача 6,1. Исходя из графика функции y = s'mx, построить
график функции y — cosx.
244
Решение. Функцию y = cosx представим в виде
у = sin I -=¦ + х). График этой функции получится из графика функ-
функции y = sinx (фиг. 6,1), перенесением его вдоль оси Ох влево
на — ед. масштаба (фиг. 6,2).
у=since
г
-х\ У о
Ч
Фиг. 6,1.
Фиг. 6,2.
Задача 6,2 (для самостоятельного решения). Считая извест-
известным график функции у — cos x (фиг. 6,2), построить график функ-
функции у — sin *.
У
Z
-Л"
i
I
i
Фиг. 6,3.
Задача 6,3 (для самостоятельного решения). Исходя из графи-
графика функции y=tgx построить график функции у — ctgx.
Указание, ctg * = tg [~ — jej. 1) Построить график функ-
функции y=-igx (фиг. 6,3);
245
2) Пользуясь им, получить график функции у — tg (—х) и по-
потом с помощью сдвига вдоль оси Ох получить график функции
График функции г/ —ctgJt представлен на фиг. 6,4.
Фиг. 6,4.
Задача 6,4. Исходя из графика функции y=sinx, построить
график функции z/=—sinjc.
Решение. Если построить кривую, симметричную относи-
относительно оси Ох графику функции у = sin*, то она и будет являться
Фиг. 6,5.
графиком функции у = —sin х (фиг. 6,5). График функции у =
= sin(—х) совпадает с графиком функции у— —sinjc. Почему?
Задача 6,5 (для самостоятельного решения). Начертить график
функции y=\sinx\ (фиг. 6,6).
Задача 6.6. Начертить график функции у — 2 sin x, исходя из
графика функции y — s\nx.
Решение. Начертим одну волну графика функции y = sinx
на отрезке [0,2тс] (график этой функции можно срисовать из учеб-
учебника). Выберем на этом графике несколько точек. Построим теперь
246
на том же чертеже точки с абсциссами, равными абсциссам выбран-
выбранных точек, но с ординатами, увеличенными в два раза. Соединив
эти точки плавной кривой линией, получим приближенный график
функции г/ == 2 sin j: (фиг. 6,7).
У,
у-/$1/7 3}/
Фиг. 6,6.
Теперь, пользуясь периодичностью этой функции (ее период
равен 2тс), продолжим построенный график в соседние интервалы.
Фиг. 6,7.
Задача 6,7 (для самостоятельного решения). Построить гра-
графики функций:
2) г/ =-jsi
Задача 6,8. Построить график функции у = sin (х — 1), исходя
из графика функции y = s\nx.
Решение. Чтобы построить график функции у — sin(х — 1),
начертим' сначала одну волну графика функции у = sinx на отрез-
отрезке [0,2ir] и перенесем ее вправо на 1 ед. масштаба. Зная, что
247
заданная функция имеет период, равный 2тс, продолжим построен-
построенный график в соседние интервалы (фиг. 6,8).
Задача 6,9 (для самостоятельного решения). Построить графи-
графики функций: 1) у — cos(* + 2) и 2) у = sin (х + 3), исходя из гра-
графиков функций y = cosx и у = sin х.
Фиг. 6,8.
Задача 6,10. Построить график функции у - s\n2x.
Решение. Используем указание 4,6, стр. 232. Чтобы построить
график функции у = sin 2x, построим сначала одну волну синусо-
синусоиды г/ = sin jc на отрезке [0,2n].
Фиг. 6,9.
Выберем на построенной кривой несколько точек и построим точ-
точки с ординатами, равными ординатам выбранных точек, но с
абсциссами, уменьшенными в два раза. Полученные точки соеди-
соединим плавной кривой. Пользуясь периодичностью заданной функ-
функции у— sin2x (фиг. 6,9) (ее период Т = тс) продолжим получен-
полученный график в соседние интервалы (и, 2и), Bтс, Зи), (—и, 0),
(—2ir, —и), находящиеся справа и слева от интервала @,-тс).
248
Задача 6,11 (для самостоятельного решения). Исходя из гра-
графиков функций у = cos х и у = sin х, построить графики функций:
1) z/ = sin3* и 2) у — cos -g- x.
Задача 6,12. Построить график функции у = cos -g- x.
Решение. Построим на отрезке [0,2ц] сначала график
функции z/ = cosje (фиг. 6,10). Используем указание 4,6 стр. 232.
Выберем на этом графике несколько точек и построим точки
с ординатами, равными ординатам выбранных точек, но с абсцис-
абсциссами, в два раза большими, чем абсциссы выбранных точек.
Фиг. 6,10.
Построение кривой показано на фиг. 6,10. Функция
у — cos н-х — периодическая. Ее период равен 4тс. Пользуясь перио-
периодичностью этой функции, ее график, построенный на отрезке [0,4тс],
продолжим в соседниеч интервалы Dи, 8и); (8и, 12тс); (—4ir, 0);
-Задача 6,13 (для самостоятельного решения). Построить гра-
графики функций: 1) у = sin у; 2) y = cos-j; 3) y = s\n-j-
Задача 6,14. Построить график функции у — 2 sin 3-е.
Решение. Будем исходить из графика функции y — s\nx.
Построим одну волну этого графика на отрезке [0,2ц]. Поль-
Пользуясь этим графиком, построим график функции у = sin 3*. Для
этого, как уже известно читателю, следует на кривой z/ = sin*
выбрать несколькб точек и построить точки с ординатами, равны-
равными ординатам этих точек, но с абсциссами в три раза меньши-
меньшими, чем абсциссы выбранных точек. Построенные точки соединим
плавной кривой линией.
После того как построена кривая у — sin Зя, на основании
указания 4,5 стр. 232 построим кривую у —2 sin 3jc. 3tq надо
сделать так: оставив абсциссы построенных точек без изменения,
построить точки, ординаты которых в два раза больше, чем орди-
249
наты построенных точек. Построения показаны на фиг. 6,11.
После этого построенную кривую следует продолжить в соседние
интервалы (|«; ?я); (А*;, |я); (-|*;о) (--J-*; --?«)
и т. д., используя то, что заданная функция — периодическая
о
с периодом Г — -я-тс.
о
Фиг. 6,11.
Задача 6,15 (для самостоятельного решения). Построить гра-
графики функций: 1) г/ = -i-sin 2л:; 2) у = 3 cos 2л;; 3) г/ = -i- tg ~ х.
Указание. При построении графика функции у — -jtg-jx
следует исходить из графика функции y—tgx. Пользуясь этим
графиком, построить график функции г/ = -g- tg л:, а потом уже
кривую y = \ig~x.
Задача 6,16 (для самостоятельного решения). Построить гра-
графики функций: 1) у = —sin 2х; 2) у = — 3 cos ~; 3) у = —2 sin ~.
Задача 6,17 (для самостоятельного решения). Построить гра-
график функции у~ 2sin(x— 1).
Указание. 1) Исходя из графика функции у — sin я по-
построить график функции у = sin (л; — 1). 2) Зная график функции
у = sin(x — 1), построить график данной функции у = 2 sin (л: — 1).
Задача 6,18. Построить график функции у = sin Bх + 3).
Решение. Представим заданную функцию в виде у —
— sin 2 \х + -jj и будем вести построение графика в таком порядке:
250
1) Построим на отрезке [0,2^] график функции y = si
2) Выберем на этом графике несколько точек и построим точки
с ординатами, равными ординатам выбранных точек, но с абсцис-
абсциссами, уменьшенными в 2 раза. Построенные' точки соединим плав-
плавной кривой линией. Эта кривая линия будет графиком функции
у — sin 2x.
3) Перенесем этот график влево вдоль оси Ох на -^ ед. мас-
штаба и получим график функции у — sin 21 х + у I, т. е. график
заданной функции у — sin Bя + 3) (фиг. 6,12).
Следует предостеречь читателя от одной распространенной
ошибки. Эта ошибка состоит в том, что для построения графика
Фиг. 6,12.
функции у — sin [шх + 9) иногда поступают так: из графика функ-
функции у — sin х получают график функции у = sin ш, и этот график
переносят вдоль оси Ох на у ед. масштаба, вместо того, чтобы
его перенести на — ед. масштаба.
Чтобы избежать этой ошибки, надо функцию вида у = sin (шх -f
+ ?) представить в виде y = sinu>\x + -^\, т. е. сделать так, что-
чтобы в скобках под знаком синуса коэффициент при х был равен 1.
Из рассмотрения функции у = sin со (х + —) сразу видно, что пе-
перенос вдоль оси Ох должен быть сделан не на <j> ед. масштаба,
а на -? ед. масштаба.
О)
Задача 6,19 (для самостоятельного решения). Построить графи-
ки функции: 1) у — sin D* + 8); 2) у = sin ly — 31;
3) у = -sin Bx - 4).
Задача 6,20. Построить график функции у = 3 sin {2x —, 4).
Решение. Представим заданную функцию в виде у =
= 3 sin 2 (х — 2). Построим одну волну синусоиды на отрезке [0,2^).
251
Считая этот график исходным, построим график функции
у = sin 2х.
Если перенести эту кривую вдоль оси Ох на 2 ед. масштаба
вправо, то получим график функции у = sin 2 (х — 2). Выберем на
этом графике несколько точек и, не изменяя абсцисс этих точек,
увеличим их ординаты в три раза. Соединив полученные точки
плавной кривой линией, получим приближенный график данной
функции у = 3 sin 2 (л; — 2). Зная, что заданная функция перио-
Фнг. 6,13.
дическая и что ее период Т — тс, продолжим полученный график
в соседние интервалы, как мы это делали в предыдущих задачах
(фиг. 6,13а)
Задача 6,21 (для самостоятельного решения). Построить гра-
графики функций:
1) «/ = 2cosC*+ 1); 2) «/ = 2cos3*= 1;
3) у = — 2 sin Bx — 1); 4) у; = — 3 cos C* + 1);
5) у = | sin 2лг |.
-х
2
y-arcsinx
Фиг. 6,14.
Задача 6.22. Построить график функ-
функции у = arcsin 2x 2х, считая исходным гра-
график функции у — arcsin x.
Решение. График функции у =
= arcsin* представлен на фиг. 6,13,
перечертите этот график. Выберите на
нем несколько точек.
Постройте точки с ординатами, равны-
равными ординатам выбранных точек, то с абс-
абсциссами, уменьшенными в два раза. По-
252
y=arcsi/>2x
строенные точки соедините плавной кривой линией, которая и бу-
будет приближенным графиком функции у = arcsin 2x (фиг. 6,15).
Задача 6,23 (для самостоятельного ре^
шения). Пользуясь графиком функции
# = arcsinx (фиг. 6,14), постройте графи-
графики функций: 1) у — arcsin -j; 2) у —
— arcsin (л; + 1); 3) у = arcsin (* — 1); 4) у —
= 2 arcsin х; 5) у = arcsin х — 1; 6) у —
— — arcsin х.
Задача 6,24 (для самостоятельного ре-
решения). Пользуясь графиком функции
у = arccos х (фиг. 6,16), построить
графики функций: 1) у =— arccos x;
2) у = arccos (— х)\ 3) у =* arccos ~;
/ . , Фиг. 6,15.
4) у — arccos (~ + 1); 5) у — 2 arccos 2я.
Задача 6,25 (для самостоятельного решения). Исходя из гра-
графика функции г/= arctg* и #= arcctg* (фиг. 6,17 и 6,18), по-
построить графики функций: 1) у = 2arctg*; 2) у =— arctg*;
3) = arctg ~; А) у= arcctg * + 2; Ъ) у = ~ arcctg *.
\
y=arccosx
Фиг. 6,16.
Фиг. 6,17.
253
СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Построение графиков функций, заданных несколькими
аналитическими выражениями. Построение графика суммы, разности и произ-
произведения нескольких функций.
Определение функции, данное в кратких сведениях по теории
предпосланных второму практическому занятию, не предполагает,
что функция обязательно задается одной формулой. Может
оказаться, что на различных участках изменения аргумента
функция задана различными формулами.
С таким способом задания функции приходится встречаться
и в математических исследованиях, и в таких науках, как сопро-
сопротивление материалов, теплотехника, радиотехника и др. Поэтому
этот способ не следует считать чем-то надуманным.
Задача 7,1. Функция задана следующими равенствами:
У =
2, если х < — 1,
х + 3, если — 1 < х < О,
— х-\-3, если 0<х< 1,
2, если х> 1.
Построить график.
Решение. Если х < — 1, то функция задана равенством у =
= 2 и ее графиком будет полупрямая, параллельная оси Ох
(фиг. 7,1а). На участке —1 <я<0 функция задана равенством
у = х -\- 3. Графиком этой функции является прямая линия, на
которой надо взять отрезок ее, соответствующий значениям аргу-
аргумента х из отрезка [—1,0] (фиг. 7,16).
На участке 0 < х < 1 функция у = — х -f 3, ее график — пря-
прямая линия, на которой следует взять отрезок, соответствующий
значениям аргумента из отрезка [0,1] (фиг. 7,1 б) и для значений
х > 1 функция у = 2 и ее графиком будет полупрямая, парал-
параллельная оси Ох (фиг. 7,1 г).
В «собранном» виде график заданной функции представлен
на фиг. 7,1 д.
Задача 7,2. Построить график функции, определяемой равен-
равенствами
у = х2, если х < 0;
у = х, если х > 0.
Решение. Графиком функции у — х2 для значений х < 0
является часть параболы, расположенная во втором квадранте
(фиг. 7,2 а).
Графиком функции у = х для значений х > 0 является полу-
полупрямая — биссектриса первого координатного угла (фиг. 7,2 б).
На фиг. 7,2 в график заданной функции представлен в «собран-
«собранном» виде.
254
н !?„_ (
•¦1 ,
-¦А
1? ^ 7'
1
¦к
Н
• и о-- --- ^
t
7,2.
е
ц
;$• J> ч
ч
е
;
255
Перед решением приведенных ниже задач введем такое условие:
если на кривых линиях или на полупрямых поставлены стрелки,
то это означает, что концы этих линий, на которых находятся
стрелки, не принадлежат графику функции.
Задача 7,3. Построить график функции
/ +2 для х < 0;
У ~ { — 2 для х > 0.
Решение. См. фиг. 7,3.
У
0
-г
2
. X
Фиг. 7,3.
Задача 7,4 (для самостоятельного решения). Построить график
функции, определяемой равенствами
—х, если х < О,
х, если х > 0. f
Фиг. 7,4.
(график этой функции представлен на фиг. 7,4). Эта функция
может быть задана одним аналитическим выражением: у—\х[,
где | х | — абсолютная величина х.
Задача 7,5. Построить график функции
х, если х Ф 2,
\5, если х = 2,
256
Решение. График функции состоит из всех точек прямой
у — х, кроме точки B,2). Эта точка удалена из прямой («изъята»,
«вырвана»). Она помещена в точку B,5). Это изолированная точка
графика функции (фиг. 7,5).
Задача 7,6 (для самостоятельного
решения). Построить графики функций,
определяемые равенствами:
2х + 2 для 0 < х < 3
8 для 3 < х < 6
х + 2 для х > 6
_ 1х — 1 для л;<0
*¦' У'~\ Ъх для х > О
(не забывайте на прямых проставлять
стрелки, если они нужны на основании
сделанного выше условия. В примере 2)
они нужны).
—2х — 1 для х < 2
3) у = | 3 для х = 2
2х — 9 для х > 2
Фиг. 7,5.
+ 1 для х < О
О для .х = О
— 1 для х > О
а:
Фиг. 7,6
Задача 7,7 (для самостоятель-
самостоятельного решения). Построить графи-
графики функций, определяемых равен-
равенствами
1)
{—2я —2, если х<— 1;
—У 1 — г8, если — 1<ж1;
2^ — 2, если я > 1.
Указание. График функции
у = — V. 1 — х2 — часть окруж-
окружности х2 + г/2 = 1, лежащая в ниж-
нижней полуплоскости (фиг. 7,6).
2) «/ =
3) У-
х, если < —2;
3, если — 2 < х < 2;
л;2, если я > 2.
1 1
—, если 0<*<-s-;
х 2
2, если -g- < х < 6;
У—32+ 12л; —л;2, если 6 < х < х < 8.
257
Задача 7,8 (для самостоятельного решения). Построить графики
функций:
' (фиг. 7,7 а и 7,76)
1) 0=1*» —1|;
2) у = 2-|дс!;
3) у = | *2 - 7х + 121.
л) у
б)
О
X
Фиг. 7,7.
Задача 7,9. Построить график функции у = х-\- s'mx.
Решение. Построим на одном чертеже графики слагаемых
функций (фиг. 7,8): у = х и у = sinx.
•-.г
</=sinx
Фиг. 7,8.
Проведем ряд вертикальных прямых, пересекающих графики
этих функций, и пометим на них точки, ординаты которых равны
сумме' ординат слагаемых функций. Каждая из точек, построен-
построенных на этих вертикальных прямых, имеет абсциссу такую же,
как и соответствующие точки обоих графиков. Соединяя получен-
258
ные точки плавной кривой, получим график данной функции
у — х + sin х (конечно, полученный график будет приближенным).
Задача 7,10 (для самостоятельного решения). Построить гра-
графики функций:
1) у = 2* + sin x;
2) у =34- cos х;
3) у = sin ж + cos*;
4) у = sin2x + 2cos*;
5) г/ =
Указание. При построении графика функции y = xs\nx
(пример 5) учесть, что: 1) эта функция четная, а потому ее гра-
график симметричен относительно оси Оу. 2) Учитывая, что х умно-
умножается на sin х, который по абсолютной величине не больше
единицы, заключаем, что абсолютная величина произведения х sin x,
т.е. |#sinx|, не больше \х\, т. е. |xsin#| < |х|, а потому гра-
график функции y = xsmx расположен между двумя биссектрисами
координатных углов у — х и у — —х. В точках х= ±-s-, ±-к",
5л , Bп + 1)л , .
+ Y , • • . , ±-—к—¦— график функции у = xsmx касается этих
биссектрис, а в точках О, +и; ±2ir..., график пересекает ось Ох.
Задача 7,11 (для самостоятельного решения). Построить гра-
графики функций
I \ /I уЗ 1 Qv2«
ЧУ — Л Т^ &л ,
2) у — х + cos x;
о) у = х -—g- х ,
4) у — х3 cos x;
5) у = х2 + ~.
ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Решение уравнений с помощью графиков (графическое
решение уравнений).
Если не требуется большой точности, то можно корни различ-
различных уравнений находить при помощи графиков функций. Для
этого поступают так:
Способ 1, Все члены уравнения переносят в его левую часть
(правая часть оказывается при этом равной нулю), обозначают
левую часть через f(x), и тогда уравнение приобретает вид
f(x) = O. После этого строят график функции y = f(x), где
f(x)—левая часть уравнения. Абсциссы точек пересечения этого
графика с осью Ох и будут корнями уравнения, так как ё этих
точках у = 0.
259
Фиг. 8,1.
Способ 2. Члены уравнения разбивают на две группы, одну
из них записывают в левой части уравнения, а другую — в правой.
Уравнение приобретает вид f (х) =
, = f i (x). После этого строят гра-
графики двух функций у = f (x) и у =
— fI (x) • Корнями данного уравне-
уравнения будут абсциссы точек пересече-
пересечения этих графиков? Так, если точка
пересечения графиков имеет абсцис-
абсциссу х0, то в этой точке ординаты
графиков между собой равны, и тогда
f(xo)=fi(xo)- Это равенство по-
показывает, что х0 — корень уравне-
уравнения. Второй из указанных спосо-
способов предпочтительнее первого; он
особенно удобен, когда одна из ча-
частей уравнения является линейной
функцией.
Задача 8,1. Решить графически
уравнение х3 — Зл: + 2 = 0 первым
и вторым из указанных способов.
Решение. 1-й способ. Построим график функции у — х3 —
— Зх 4- 2 (фиг. 8,1) и определим абсциссы точек пересечения этого
графика с осью Ох : хх = —2; хг = х3 — 1.
Кривая касается оси Ох в точке х = 1,
а потому уравнение имеет.кратный корень
х — 1 (следует иметь в виду, что уравнение
третьей степени с действительными коэффи-
коэффициентами имеет или один действительный
корень или все три его корня — действи-
действительны. Так как кривая пересекла ось Ох
в одной точке и коснулась ее в другой,
то в той точке, где имеет место касание,
будет кратный корень. В данном случае
таким двукратным корнем является 1).
2-й способ. Перепишем данное урав-
уравнение в виде jc3 = Зх — 2. Построим гра-
графики функций у — х3 и у — Зх — 2 (фиг.
8,2). Найдем абсциссы точек пересечения
этих графиков. Получим xL = —2, xg= 1.
В точке хг — 1 прямая у = Зх — 2 касается
графика функции у = х3.
Задача 8,2 (для самостоятельного ре-
решения). Решить графически уравнение
Задачу решить двумя способами.
Фиг. 8,2.
Ответ. Один действительный корень х = 1.
260
Указание. Прежде чем решать заданное уравнение вторым
способом его выгодно сначала упростить. Общий вид кубического
уравнения записывается так:
а0х3 + аху? + агх + а3 = 0 (а0 Ф 0). (А)
После деления обеих частей равенства на а0 оно преобразуется
к виду х3 + btx2 + Ьгх rf- b3 = 0.
Если теперь сделать подстановку
<=у-%, (В)
то оно приведется к виду
ya + py + q = 0. (С)
Этот вид кубического уравнения называется приведенным. Оно
не содержит квадрата неизвестной величины. Уравнение (С) ре-
решить графически проще, чем исходное уравнение (А), т. к. здесь
дело сведется к построению графика кубической параболы и пря-
прямой (см. предыдущую задачу), в то время как графическое реше-
решение уравнения (А) потребовало бы построения графиков кубиче-
кубической параболы и параболы второй степени (уравнение (А) следо-
следовало бы переписать так: uqX3 — —а,*2 — а^х — а3).
После того как решено уравнение (С), надо воспользоваться
подстановкой (В) и найти неизвестное данного уравнения (А).
Задача 8,3 (для самостоятельного решения). Решить графи-
графически уравнения:
1) х3— 6л:2 + Пд: — 6 = 0;
2) х% — хг — 10* - 8 = 0.
Указание. Перейти к приведенному виду (С) кубического
уравнения, использовав указание предыдущей задачи.
Ответ. 1)^=1; хг — 2; х3 = 3;
2) Ла=-2; xt = —1; *з = 4.
Задача 8,4. Найти графически вторым способом положитель-
положительный корень уравнения xi — х — 1 =0.
Указание. При построении графиков функций у — х* и
у = х + 1 масштабную единицу по оси Оу уменьшить в 5 раз.
Ответ. 1,22.
Задача 8,5. Найти графически наименьший положительный
корень уравнения х — tg* = 0.
Указание. 1) Переписать уравнение в виде tg* = x. 2) На-
Начертить графики функций y^igx и у =± х (фиг. 8,3). Графики
261
пересекаются в бесконечном множестве точек. Уравнение имеет
бесчисленное множество корней.
Ответ. Наименьший положительный корень ^«4,5 (более
точное вычисление дает хг == 4,4934).
Задача 8,6 (для самостоятельного решения). Найти графически
наименьший корень уравнения tg* — 0,5л: = 0.
Ответ. д;:^;4,3.
Задача 8,7 (для самостоятельного решения). Найти графически
наименьший положительный корень уравнения 0,2л: — sin х = 0.
Фиг. 8,3.
Указание. Искомый корень является наименьшей положи-
положительной абсциссой точки пересечения прямой у = 0,2л: и синусои-
синусоиды у = sin х.
Ответ, л:^2,6.
Задача 8,8 (для самостоятельного решения). Найти наимень-
наименьший положительный корень уравнения *tg* = 0,3.
0 3
Указание. Переписать уравнение в виде \gx— —
и по-
0,3
строить графики функций t/=tgJC и У =-у
ги-
(равноосная
пербола).
Ответ. 0,52.
Задача 8,9 (для самостоятельного решения). Найти наимень-
наименьший положительный корень уравнения х sin х — 1.
Ответ, л:^; 1,1.
Задача 8,10 (для самостоятельного решения). Решить графи-
графически уравнения:
1) х — 2sin>t = 0 (найти положительный корень).
2) совл:—л:2 = 0.
Ответ. 1)л:^1,9; 2) х = ±0,824.
262
ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Обратная функция и ее график. Периодические функции.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Обратная функция и ее график
Если функциональная зависимость у от х задана аналити-
аналитически уравнением y~f(x), из которого можно определить х как
функцию от у уравнением х — <р (у) так, что каждому значению
у соответствует единственное значение х, то функция, опреде-
определяемая уравнением х = <р (у), называется обратной по отноше-
отношению к функции у = f (х), которая в этой связи называется прямой.
В уравнении y=f(x) величина х — независимая переменная, а
у — функция. Для того чтобы сохранить стандартные обозна-
обозначения, в которых х обозначает независимую переменную, а у —
функцию, в уравнении х = ф (у) следует заменить у буквой х,
а х — буквой у. Именно так полученную функцию у = <?(х) мы
и будем считать обратной по
отношению к функции y = f(x).
График обратной функции у =
= <р (х) симметричен графику пря-
прямой функции у = f (х) относи-
относительно биссектрисы первого и
третьего координатных углов.
Задача 9,1. Найти функцию,
обратную функции у — Зх — 1,
и построить ее график.
Решение. Находим из дан-
данного уравнения х в зависимости
от у:
V+1
Фиг. 9,1.
Заменяя в этом равенстве х на у, а у на х, получаем окончательно
»-'-?¦
Графики заданной функции и ей обратной представлены на
фиг. 9,1.
Задача 9,2. Найти функцию, обратную функции у = х2
(—со <л:< +оо).
Решение. Из уравнения у = я2 видно, что значения функ-
функции у заполняют полуотрезок [0, +°°)- Если это уравнение раз-
разрешить относительно х, то получим уравнение х — -+Vy,
из которого видно, что каждому значению у из полуотрезка
[О, +оо) соответствует не одно, а два значения х из интервала
263
(—оо, +оо). Отсюда мы заключаем, что если функцию у = х2 рас-
рассматривать на интервале (—оо, + оо), то для нее обратной функции
не существует (jc через у выражается не однозначно).
Если будем рассматривать данную функцию у — я2 только для
положительных значений х и х = 0, т. е. значений х из полу-
полуотрезка [0, +°°), тогда х-=-\-~Уу, и каждому значению у>0
соответствует не два, а только одно значение х, обратная функция
теперь существует и определяется уравнением у = -\-~\f х (фиг. 9,2).
Если данную функцию
у = х2 рассматривать только
для значений х < 0, то она
и в этом случае будет иметь
обратную функцию. Действи-
Действительно, _в этом случае х =
==. — У у, каждому значению
у > 0 соответствует единст-
единственное значение х, и обрат-
обратная функция определяется
уравнением у = — Ух.
Задача 9,3 (для самостоя-
самостоятельного решения). Убедить-
Убедиться, что на интервале (—оо,
-f-oo) функция у = sin х не
Фиг. 9,2.
имеет обратной функции, а на
р фу
Г к к]
отрезке — -^, -j\ —
имеет.
Задача 9,4. Найти функцию, обратную функции #=lg-g-
(*>0).
Решение. 1) Находим х в зависимости от у:
i = 10»; х = 5 • 10».
2) Заменим в последнем выражении х на у, а у на х и полу-
получим у — 5 • 10*. Это и есть функция, обратная данной.
Задача 9,5 (для самостоятельного решения). Найти функции,
обратные данным:
\) У = sinC* — 1),
2) у = arcsin ~
где
где —3 < к < 3;
где (—оо <jt <
Ответ. 1) # = -iA4-arcsin*);
2) i/
оо).
i
264
При каких значениях х могут рассматриваться эти функции?
Задача 9,6 (для самостоятельного решения). Найти функцию,
обратную функции у = х3, и построить ее график, пользуясь свой-
свойством графика обратной функции.
Задача 9,7 (для самостоятельного решения). Определить функ-
функции, обратные следующим функциям:
1) г/= х2 - 2* + 4; 2) у - ?=± ; 3) у = 2^;
.4)# = 5'е*; • 5) y = 3sinx; 6) у = cos2* — sin2x.
Указание. Заданную функцию 1) рассмотреть сначала для
значений х> 1, а потом для значений я < 1.
Ответ. 1) г/= l + VrJ^r3,^= 1—1/J^3 (jc> 3);
2* 4- 1
2) у ~ o^-rrj, область существования — два бесконечных ин-
интервала: ( — со < х < — -g-j; f—•-д-<л:< + ooj;
3) У — 1 °§2^ , , область существования — интервалы @<jc<2)
и B < х < +2сю);
ig*
4) у = 10lg 5, область существования — @ < х < + оо);
5) у = arcsin j|^, {^- < д: < 3J
6) г/ = -jarccosл, (—1<*<1
ПЕРИОДИЧЕСКИЕ ФУНКЦИИ
Основные сведения из теории
Определение. Функция f (х) называется периодической, если
существует такое число Т, отличное от нуля, что для всех зна-
значений х, принадлежащих области существования функции, вы-
выполняется равенство f (x) = f (х + Т).
Обыкновенно наименьшее из чисел Т, обладающее таким свой-
свойством, называется периодом функции.
Если Т — период функции, то ее периодом будут также и
числа kT, где k — любое целое число.
Из определения периодической функции следует, что если
точка х принадлежит области определения функции, то ей при-
принадлежат также и точки х + kT, где k — любое целое число
(k=±l; ±2; ±3;...).
Построение графика периодической функции облегчается тем,
что можно ограничиться построением его части только для'тех
точек области определения функции, которые находятся на полу-
265
отрезках [х0, хо + Т) или (х0, хо+Т], и. последующим периоди-
периодическим повторением построенной части графика*.
Тригонометрические функции у = sinx, y = cosx, у— secx и
у = cosec х имеют период Т—2п: sin (х-\-2к)=г$,\п х, cos (x + 2п) =
—cos х, sec (x + 2тс) = sec x, cosec (x -f 2tcJ = cosec х.
Кроме числа 2к периодом этих функций являются также и
числа вида 2-nk, где k — любое целое число. Число In — наимень-
наименьший период этих функций.
Функции же у — tg.v и у — ctgx имеют период Т = тс.
Число к является наименьшим периодом этих функций. Во-
Вообще же периодом этих функций являются числа вида тс/г, где
k — любое целое число.
Задача 9,8. Доказать, что функция у = sin (шх -f- <p), где ш и
<р — действительные числа и ш ф 0, имеет наименьший период
Т — —
ш
Решение. Прибавим к аргументу х данной функции число
~ 2к / 2л -
/ = — I здесь следует уяснить, что — прибавляется не к а«, а к д:
и покажем, что функция от эгого своей величины не изменит.
Этим мы и докажем, что число — является периодом этой функ-
функции:
Г / 2л\ 1
sin \ш (х + — 1 + <р = sin (шх -\- 2тг -f- <p) =
== sin [(шх 4- <р) + 2тг] = sin (шх -f <p). ;
Таким образом, требуемое доказано. i
Следует запомнить, что функция sinoxx: имеет период Т —
— -? (шфО). Примеры: . г
1) функция - у = sin -g- имеет период Т = ~ — бтс; >
2) функция г/ = sin 2х имеет период Т1 = ^ = тс; |
3) функция у = sin 4х имеет период Т — -т- = ^ • |
Задача 9,9 (для самостоятельного решения). Доказать, что если |
функция f(x) имеет наименьший период, равный- Т, то функция [
/ (ах), где а — любое действительное, не равное нулю число, имеет !
Т
наименьший период Тг = — (предполагается, что точки х и ах'
принадлежат области определения функции).
Указание. Использовать определение периодической функ-
функции.
Здесь х0 — произвольная точка области определения функции, а Т —
период функции.
266
Задачи 9,10 (для самостоятельного решения). Доказать, что
функция у — cos2 х имеет период Т = тс.
Задача 9,11. Показать, что если функции и и v — периодичес-
периодические функции х с одним и тем же периодом Т, то и и + v, uv и
-^- периодические функции с тем же периодом.
Указание. Удобно, например, ввести обозначение
<р (х) = и (х) ± v (х); <р (х + Т) = и (л: + Т) ± v (х + Т)
и использовать свойство периодичности данных функций:
ДЕСЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Последовательности.
ОСНОВНЫЕ СВЕДЕНИЯ.ИЗ ТЕОРИИ
Если функция рассматривается только при целых и положи-
положительных значениях аргумента, то она называется функцией на-
натурального аргумента. Множество ее значений образует числовую
последовательность: каждому целому положительному числу со-
соответствует число хп — член последовательности, имеющий но-
номер п. Это значит, что
*„ = /(/»).
Определение. Числовой последовательностью называется
множество значений функции f(n), определенной на множестве
натуральных чисел.
Член хп называется общим членом последовательности.
Последовательность с общим членом хп содержит бесконечное
множество чисел и обозначается {хп}.
Последовательность считается заданной, если дан способ вы-
вычисления любого ее члена по его известному номеру.
Задача 10,1. Зная общий член последовательности хп — п, на-
написать ее первые десять членов.
Решение. Давая п значения 1, 2, 3, ... , 10 получим:
хг= \; Хг = 2\ х3 =• 3; я4 = 4; xt — 5; х6 = 6;
Х<] == (\ JCq =;= oj Xq z= yj Xiq '==r- 1U.
Эта последовательность из 10 членов запишется так 1, 2, 3,
4, 5, 6, 7, 8, 9, 10.
Вообще же последовательность с общим членом хп = п запи-
запишется так: 1, 2, 3, ...,«,...
Задача 10,2. Написать первые десять членов последователь-
последовательности, если ее общий член хп = , „ •
267
Решение. Вычисляя значение дроби ^г-% ПРИ значениях п,
равных 1, 2, 3, ... , 10, получим:
-5- ,
i.. _ 9 • _1°
10 ' Хд — 11' ^10 ~~ 12 '
Вообще же последовательность с общим членом х — —р-= за-
пишется так:
i А А га
3"' 4' 5'-"""'п + 2'*ф'
Задача 10,3 (для самостоятельного решения). Написать после-
последовательности с общими членами:
't Хп —
sinwt
1 m ~~2~
(Зга—1)(Зга+1)' "' " " га '
~ для п нечетных; ... ,.„
"в .Ю)Х/| = 1±1-^.
—г-т для п четных; z
га + 1
Задача 10,4. По данным первым членам последовательности
_6 9 14 21 30
7 ' Й5' 15' 22' 31'
написать ее общий член.
Решение. Прежде всего отметим, что заданием нескольких
первых членов последовательности не определяется вся последо-
последовательность. Однако условимся считать, что как написанные
члены последовательности, так и все следующие за ними состав-
составлены по одному и тому же закону соответствия между .натураль-
.натуральными числами и членами последовательности.
В нашем случае нетрудно усмотреть, что числитель каждой
дроби равен квадрату номера плюс пять, т. е. п2 + 5, а знамена-
знаменатель каждой дроби на единицу больше числителя, т. е. равен
п2 + 6. Итак,
*" ~ п2 + 6 •
268
Задача 10,5 (для самостоятельного решения). Написать фор-
формулу общего члена последовательности по данным ее первым
членам:
п 1 1 1 I 1
4 3 ' 6 ' 9 ' 12' 15' " " " '
Z; 3 ¦ 4 ' 5-6' 7 ¦ 8 ' 9 • 10 '
оч J_ ± X 15 11 '
&) 6 ' 11 ' 16' 21 ' 26 ' ' " " '
.v 3_ ]_ ]}_ 15 19
^ ' 8 ' 11 ' 14* 17' " * '
Ь> 3 ' 9 > 27' 81 ' 243' 729
6^ 0 1 1 1 1 А
' ' 3 ' 4 * 5 ' 6 ' 7 < • •
7\ — — ~ ~ —
' 5 ' 17 ' 37 ' 65 ' 101 ' ' * * •
Ответ. 1)*„ = з^; 2) хп=
Bп+1)Bп + 2)'
3/г~2 ^ _. 4/г~} сч _ !
Г1 ^Ж" ~ З/г + 2 ' ' Хп ~ 3^'
7\ у — 3"'
п хп- 4п2 + 1 ¦
Монотонные последовательности .
Последовательность называется монотонно возрастающей, если
при всех п каждый ее член больше предшествующего, т. е. если
хп+1 >хп, и-монотонно убывающей, если каждый ее член меньше
предшествующего, т. е. если хп+1 < хп.
Примеры монотонных последовательностей:
1) Последовательность натуральных чисел
1, 2, 3, ... , п, ... — монотонно возрастающая.
2) Последовательность чисел хп — —, обратных натуральным,
1, у, "з".-^", ••• . —. .-• — монотонно убывающая.
Если переменная величина хп изменяется не монотонно, то ее
называют колеблющейся.
Ограниченные последовательности
Последовательность называется ограниченной, если все ее члены
находятся в конечном интервале (—М, -\-М) и М > 0, т. е., если
|#„|<М для любого номера п.
/ 269
Примеры ограниченных последовательностей:
1) Последовательность {л;„}, где хп есть n-й десятичный знак
числа У5, ограничена, так как |х„|<9.
2) Последовательность | ¦" . \ ограничена, так как |х„|<1.
Замечание. Ограниченная последовательность не обязатель-
обязательно монотонна, а монотонная последовательность не обязательно
ограничена.
Последовательность с общим членом хп = \Г , в которой
хх — 0, хг — 1, х3 = О, лг4 = 1, ... ограничена, но не монотонна,
а последовательность натуральных чисел 1, 2, 3, ... , п, ...
монотонна, но не ограничена.
Задача 10,6 (для самостоятельного решения). Привести примеры:
1) возрастающей ограниченной последовательности;
2) возрастающей неограниченной последовательности;
3) убывающей ограниченной последовательности;
4) убывающей неограниченной последовательности.
Задача 10,7. Доказать, что последовательность с общим чле-
членом хп = 2 " ¦ — монотонно возрастающая.
Решение. Найдем хп+1, заменив п на (п + 1) в выражении хп:
я +1 _п+1
Xfl+1 "
Xn+i — 2 (л + 1) + 1 ' Xfl+1 " 2л + 3 '
г, , „ ¦ Л Я + 1
Сравним величину дробей хп = 2 , t и л:„+1 = „ ' „, для чего
приведем эти дроби к большему знаменателю:
_ (я+1)Bя+1) . я Bя + 3)
Х"+'~Bп + 3)Bл+О' " Bл + 3)Bл+ 1)-
Теперь знаменатели дробей равны.
Числитель первой дроби равен 2п2 + Зп + 1, а числитель вто-
второй дроби 2п2 + Зп и ясно, что 2п2 + Зп + 1 > 2п2 + Зп. Мы знаем,
что из двух положительных дробей с одинаковыми знаменателями
та дробь больше, у которой числитель больше. Значит, хп+1 > хп
и данная последовательность — возрастающая.
Задача 10,8 (для самостоятельного решения). Доказать, что
последовательность с общим членом хп — . _3 — монотонно убы-
убывающая, а с общим членом хп — ?— монотонно возрастающая.
Задача 10,9 (для самостоятельного решения). Доказать, что
последовательность |—-^|— ограниченная и монотонно возраста-
B«4-11
ющая, а последовательность { ^ | — ограниченная и монотонно
убывающая.
270
Задача 10,1.0 (для самостоятельного решения). Показать, что
последовательность с обшим членом хп = 2" — неограниченная и
монотонно возрастающая.
ОДИННАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Предел последовательности.
Это практическое занятие отводится для упражнений, связан-
связанных с определением понятия предела последовательности. Отыски-
Отыскивать предел последовательности на этом занятии не придется.
В задачах предел последовательности будет задан, а учащийся
на основании определения предела последовательности должен до-
доказать, что заданное число действительно является пределом этой
последовательности.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Определение предела последовательности
Число а называется пределом последовательности {хп}
Xi, Xi, Х3, . . . , Хп, ... A1,1)
(пределом переменной хп или пределом функции f (п.)), если ка-
каково бы ни было наперед заданное положительное' число е, всегда
можно найти такое натуральное число N*, что для всех членов
последовательности с номерами п> N будет выполняться нера-
неравенство
\а-хп\<в. A1,2)
Это неравенство равносильно таким двум неравенствам:
a — е < л;„ < а + е.
Число /V зависит, вообще говоря, от выбранного е.
Если уменьшить число е, то соответствующий ему номер N
увеличится.
Для последовательности (или для переменной хп) необязатель-
необязательно иметь предел, но если этот предел есть, то он единственный.
Если число а есть предел последовательности {хп} с общим
членом xn~f{n) или переменной величины, хп, то это символи-
символически записывается так:
\\тхп = а. A1,3)
Вместо записи A1,3) употребляется также запись
хп-*-а,
которая читается так: <«„ стремится к а».
* Натуральными числами называются все Целые положительиые числа.
271
В том случае, когда переменная величина хп (последователь-
(последовательность (И,1) имеет предел, равный а, говорят, что эта пере-
переменная величина или что последовательность [хп] сходится к а.
Последовательность, не имеющую предела, называют расходя-
расходящейся.
Переменная величина хп может стремиться к своему пределу
различными способами: 1) оставаясь меньше своего предела, 2) оста-
оставаясь больше своего предела, 3) колеблясь около своего предела и
4) принимая значения, равные своему пределу.
Выбор числа е произволен, но после того как оно выбрано,
никаким изменениям в дальнейшем оно не должно подвергаться.
Задача 11,1. Доказать, что последовательность с общим чле-
членом хп — . . имеет предел, равный 1.
Решение. Выберем произвольно положительное число е и
покажем, что для него можно определить такое натуральное
число N, что для всех номеров п>N будет выполняться неравен-
неравенство A1,2), в котором надо взять а= 1; хп ~ ¦ " . , т. е. нера-
неравенство
1 -
я+1
После приведения в скобках к общему знаменателю получим
A1,4)
я+1
я+1
Но если
1
< е, или
1
1
е, то и .¦ <е. Из последнего неравенства
я+1
1* 1
следует, что м + 1 > —, п> 1.
Значит, если номер N больше, чем -—1, то неравенство
A1,4) будет выполняться. Теперь надо решить вопрос о числе N,
о котором идет речь в определении. За число N можно принять
наибольшее целое число, содержащееся в числе 1.
Наибольшее целое число, содержащееся в числе х, обозна-
обозначается знаком Е(х).
На основании этого наибольшее целое число, содержащееся
в числе — — 1, надо обозначить так: Е (-— 1 j.
Итак, можно принять
tf = ?-L-l (П.5)
* Если а <Ь. то — > -т-
а Ь
272
(предполагается, что El-—П>0, иначе N не будет натураль-
натуральным и его надо брать равным 1).
Заключение: По произвольно заданному положительному числу
s мы нашли такое натуральное число N, что для всех номеров
п > Л7 неравенство A1,4) действительно выполняется, а этим и
доказано, что 1 является пределом последовательности с общим
членом
п
х
Теперь приведенные вычисления проиллюстрируем числовым
примером.
Пусть, например, е = jgo • Тогда при г = -щ полУчаем из
A1,5)
N = e(-\ Л = ?A00-1) = 99; N = 99.
Ы )
Таким образом, для членов последовательности с номером боль-
большим, чем 99, выполняется неравенство
|1-*„1<Т50' О1'6)
п 97
Пусть п — 97; тогда, так как хп = ¦^ц~]-{, х„7 = щ,
97
98 ' Э 98 ^ 100 '
если п = 98, то
J
_9_9 I. _ 98
~~ 99 ' И 99
1- 1-. 1
99' 99 > 100 *
Из этих расчетов видно, что когда номер п члена последова-
последовательности меньше 99(n = 97, n = 98) неравенство A1,6) не выпол-
выполняется: вместо того чтобы |1—хп\ была меньше щ, мы получа-
получали, что \\ —хп\>-щ. Если взять п > 99, т. е., например, п =
1АА 100 м ,1, 100 1101 — 100
-100, тогда^„ = ш и |1_хЛ! = |1- I
аТоТ<:Тоо> Неравенство A1.6) будет выполняться для всех номе-
номеров п, которые больше, чем 99. Так как е ~ -щ, а п > 99, то
все члены последовательности, начиная с сотого, будут лежать
на интервале f 1 —-jog, 1+тбо)' т> е# на интеРвале @,99; 1,01)
(теперь возьмите для е значение, меньшее у^, например, е =
Найдите N и убедитесь, что оно увеличится).
Ю И. А. Каштан 273
Полученный результат можно записать так: lim——-г = 1.
Иначе можно сказать, что последовательность {хп} —
сходится к 1.
Мы употребили запись п-*-оо, которую следует понимать так:
переменная величина п становится все большей и большей и не
существует предела для ее возрастания.
Какое бы большое число мы не задали, п в процессе своего
возрастания его превзойдет. Для того чтобы коротко описать этот
характер изменения п, принято говорить «п стремится к бесконеч-
бесконечности» и записывать это так: п->оо. Символ оо произносится
«бесконечность» и применяется для сокращенной записи слова
«бесконечность».
Символ оо ни в коем случае не может рассматриваться как
число, а потому бессмысленной является запись п= оо, так как
п может равняться числу и не может быть равно символу, вве-
введенному только для сокращенной записи и сокращенного произ-
произношения фразы, которой заранее был придан определенный,
указанный выше, смысл.
Очевидно, что последовательность | " | может быть записа-
записана так:
.1 1. Л 90 п
2 . у. 4 ' •• • ' ТОО' ' • ' ' п+ 1 ' ••*
и легко усмотреть, что она стремится к своему пределу 1, воз-
возрастая и оставаясь меньше 1.
Задача 11,2. Доказать, что последовательность с общим членом
хп — „ _|_ 1 имеет предел, равный 2.
Решение. Повторим подробно все рассуждения, приведенные
в предыдущей задаче. Выберем произвольно положительное число
е и покажем, что для него можно подобрать такое число N, что
для всех значений номера п, больших этого числа N, будет вы-
выполняться неравенство A1,2), в котором надо взять а = 2, хп =
An *
= „ . , т. е. будет выполняться неравенство
Из этого неравенства после приведения в скобках к общему
знаменателю получаем
2 —
An
2п+ 1
An + 2 — An
2п+ 1
2п+1
2л -f 1 ¦
о
и неравенство A1,7) запишется так: 2 . < е.
274
Отсюда следует, что ~~ > — (см. сноску на стр. 272)
или
Таким образом, если номер п больше, чем к-, то нера-
неравенство A1.7) будет выполняться.
За N примем наибольшее целое число, содержащееся в числе
— — "о, т. е.
A1,8)
Таким образом, мы сумели по произвольно заданному поло-
положительному е определить такое натуральное N, что неравенство
A1,7) выполняется для всех номеров n>N. Этим и доказано,
что 2 есть предел последовательности с общим членов хп = » ^
(предполагается, что е{ ~j)'>®' так как иначе ^ не будет
натуральным числом. Если Е ( ~\ окажется отрицательным
то следует взять N = 1).
Теперь, чтобы лучше уяснить приведенные рассуждения, при-
приведем числовой пример: пусть выбрано e = gg. Тогда из A1,8)
следует, что
50 )
число содержащееся в 49-к-
так как наибольшее целое число содержащееся в 49-к-, есть 49.
Значит, для всех номеров п, больших, чем 49 при е= щ, не-
неравенство A1,7) будет выполняться. Начиная с пятидесятого чле-
члена все члены последовательности будут лежать в интервале
B — gg, 2 + j^J, т. е. в интервале A,98; 2,0 2). Убедимся сначала,
что при п < 49 неравенство A1,7) не выполняется. Пусть, напри-
Atx
мер, п — 47. Тогда, так как хп = 2 {, получим, что xi7 =
Л А7 1ЯЙ
= -^- и левая часть неравенства A1,7)
2 . 47 + 1 ~ 95
188
95
95-
2 1
На основании A1,7) -^ должно быть меньше, чем е = ^, а фак-
2 1 1
тически не не меньше gg, а больше нк и, значит, неравенство
A1,7) не выполняется,
10» 275
4-48 192
При п = 48 имеем хп = 2 . 48 + 1 ~ "97"
2
2 —
1
]92
97
2
97
И ОПЯТЬ
1
неравенство A1,7) не выполняется, т. к. и „у > щ, а не меньше щ.
200
101
Если же взять, например; п = 50, то хп = -щ и
^, а -1§1<5б' и неравенство A1,7) выпо.
для всех номеров п, которые больше, чем 49.
Теперь примите, за е число, меньшее, чем щ, например ^,
и убедить, что N увеличится.
Итак, lim о " , = 2 (можно сказать иначе: последовательность
| - " | сходится к 2).
Замечание 1. В решенных двух задачах мы находили наи-
наименьший номер N, фигурирующий в определении предела после-
последовательности, такой, что начиная с него, неравенство A1,2)
выполняется. Однако учащийся должен уяснить, что 1) если это
неравенство выполняется, начиная с номера JV, то оно будет вы-
выполняться и подавно при всех номерах Nlt больших, чем JV;
2) заданием число е номер N определяется неоднозначно и 3) для
доказательства того, что lim xn = а, вовсе нет необходимости среди
всех номеров N искать наименьший. Так, в задаче 11,1, уста-
установив, что неравенство A1,4) выполняется для всех п> 1,
мы могли дальше не вести никаких рассуждений.
Замечание 2. Выше было указано, что если последователь-
последовательность- имеет предел, то этот предел — единственный: двух раз-
различных пределов последовательность иметь не может.
В последней задаче мы доказали, что пределом последователь-
последовательности |—^—| является 2.
Покажем, что, например, число 3 не может быть пределом этой
последовательности.
Рассмотрим абсолютную величину разности-
о
_4я_
2n+l|
6«+ 3 — An
2п+ 1
2/г + З | 2« + 3
2п + 11 2/г + 1
2п+3 ^
и решим относительно п неравенство „ . ^ < г.
При любом целом и положительном п (а номер п может быть
только чиелом целым и положительным) число „ ~Т t > 1, а по-
поэтому оно не может быть меньше произвольно заданного поло-
положительного числа е. Этим мы показали, что число 3 не может
служить пределом последовательности 1„ ¦ Л.
276
Теперь самостоятельно решите простую задачу.
Задача 11,3 (для самостоятельного решения). Доказать, что
переменная хп = — имеет предел, равный нулю (следует запом-
• j
нить, что lim — = 0).
Произносится эта запись так: «предел —, когда п стремится
к бесконечности, равен нулю». Вместо того чтобы писать lim — = 0.
можно употребить запись >-0 при п->оо, которую следует
читать так: «— стремится к нулю при п, стремящемся к беско-
бесконечности». Из того, что lim— = 0, следует, что
«-(¦00 П
lim (\ + 1) = 1 и limfl — -)= 1.
Сокращенно это можно записать так:
1 -\ >-1 при п -»- оо, 1 »-1 при п -*¦ оо.
Задача 11,4. Доказать, что последовательность q, q2, q3, ... , q"...
сходится к нулю, если абсолютная величина q меньше 1, т. е.
если | q | < 1.
Решение. Чтобы доказать требуемое, возьмем произвольное
положительное число е и убедимся, что можно будет определить
такое N, что для всех номеров п, больших N будет выполняться
неравенство
|0-<Л<е A1,9)
(в неравенстве A1,2) надо взять а = 0, xn — qn).
Учитывая, что по условию |<7|<1 можно заключить, что
-.—: > 1, т. е. можно полагать, что у—-. равно 1 + а, где а — число
положительное.
1 + па + п{п~1) о? + ... + а" > 1 + па,
а потому j^ > 1 + па, или |^|Л<___.
Выберем п так, чтобы знаменатель дроби 1 -\- па. стал больше,
чем — ¦. Тогда окажется, что и подавно \q\n<-r, т. е. |<7"|<е,
? »
И неравенство A1,9) будет выполняться, так как из него следует,
277
1 Г'1
что j q |" < e. Но если 1 + па > — , то п > -^—. Значит, можно
в качестве N выбрать наибольшее целое число, содержащееся в
l-i /1-Л
числе — , т. е. взять N — Е 1 I, и при этом неравенство
A1,9) будет выполняться при всех номерах n>N. "Таким обра-
образом доказано, что lim qn = 0.
П-юо
Надо запомнить, что если \q\ < 1, то \imqn = 0 (lim9", когда
\q\>l вычислен в задаче 13,1).
Если, например, о = -=-<1, то последовательность запишется
О
так: "т > ij" > §7 ' 81' • • • дн • • • . и переменная р -> 0, монотонно
убывая (здесь каждое следующее значение переменной меньше
предыдущего).
Если q — —9 > то последовательность запишется так:
1 1 _1 1
' 4 • 8 ' 16
И эта последовательность, как доказано, сходится к нулю (| q | < 1).
Однако здесь уже переменная величина I — -^\ стремится к свое-
своему пределу — нулю, принимая значения, то меньшие нуля, то
большие его. Можно сказать, что переменная в данном случае
колеблется около нуля.
Запишем эту последовательность в виде
Ln * п -1 0-i.fl
2 1 и» -?, и, g- , и, jg, и, . ..
% Ясно, что и эта последовательность сходится к нулю, но те-
теперь она содержит бесконечное множество членов, равных нулю.
Это тот случай, когда переменная, стремясь к пределу, становится
равной ему, причем это имеет место бесконечное множество раз.
Задача 11,5. Доказать, что последовательность 3, З2, 3s,
З4, ... , 3" ... не имеет предела.
Решение. Мы докажем требуемое, если установим, что об-
общий член этой последовательности хп = 3" превзойдет любое на-
наперед заданное число.
Пусть А такое число. Возьмем п > А — 1. Тогда п + 1 > А;
3" = A + 2)" > 1 + 2п, и подавно 3">п+1, или Ъп>А. Тем
самым показано, что 3" может превзойти любое число А. Если бы
существовал предел переменной хп — 3", и был бы равен а, то для
любого s > 0 можно было бы подобрать такое/*/, что при номерах
п> N выполнялись бы неравенства « — е < хп < a -j- e, т, е,
278
a — e < 3" < a + e, а это противоречит доказанному, так как 3"
при п>А — 1 превзойдет любое число А, а тем самым и число
а + е, меньше которого оно должно оставаться. Это противоречие
и доказывает, что последовательность {Зл} предела не имеет. Этот
пример иллюстрирует утверждение: не всякая последовательность
имеет предел.
Задача 11,6. Доказать, пользуясь определением предела по-
последовательности, что последовательность с общим членом хп —
--. *г— - имеет предел а = 1.
Решение. Подставим значения а и хп в неравенство A1,2)
и получим
\-yZ^l^1 <e. A1,10)
1 —
VV+1
+1
+ 1 — 1 — Yn* + 1 — 1
n* +1 —
Вместо неравенства A1,10) теперь имеем неравенство:
Решим это неравенство относительно п:
? -ш /~ Л , 4
.(|+ l) — 1.
Таким образом, если п удовлетворяет последнему неравенству,
то неравенство A1,10) будет выполняться при любом е > 0. Тем
самым мы доказали, что lim —===^~ = 1, а за N можно при-
.2
нять N —
Определим из этого равенства значение N при е = 0,01
и е = 0,001. Если е = 0,01, то N = е(]/ (^ + lV— l) =
= ?(У201«— 1) = 200.
Значит, при всех номерах п > 200 будет выполняться неравен-
уп + + <-о,О1, т. е. при п > 200 все числа задан-
ство
Vni+l-l
ной последовательности будут лежать на интервале @,99; 1,01).
Если s =., 0,001, то N = Е (У20012 - 1) - Е A/404000) = 2000 и
279
для всех членов последовательности с номерами п > 2000 будет
выполняться неравенство
1 —¦
< 0,001, а для номеров
+ 1 — 1
п > 2000 все члены последовательности будут лежать на интер-
интервале @,999; 1,001).
Задача 11,7 (для самостоятельного решения). Пользуясь
определением предела последовательности, доказать, что
5) i™ «^ПГТТ^ 1; 6)
Задача 11,8 (для самостоятельного решения). Пользуясь опре-
определением предела последовательности, доказать, что
2) lim
П-юо
3) lim 2 + (~1)n = 0; 4) lim
П-Ю0 Я П-юо
Задача 11^9 (для самостоятельного решения). Составить после-
последовательности: 1) возрастающую и сходящуюся к нулю; 2) убываю-
убывающую и сходящуюся к 3; 3) колеблющуюся и сходящуюся к 1;
4) колеблющуюся и расходящуюся; 5) убывающую и расходящуюся.
ДВЕНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Бесконечно малые и бесконечно большие величины.
Дальнейшие упражнения в определении предела последовательности.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
На предыдущем занятии мы задавали число и проверяли, яв-
является ли оно пределом переменной величины хп (последователь-
(последовательности {хп}).
Теперь мы займемся отысканием числа, являющегося пределом
переменной величины (последовательности).
Вычисление предела переменной величины основывается на
определениях и теоремах, помещенных ниже.
Бесконечно малые величины
12,1. Если переменная величина хп имеет своим пределом нуль
lim хп = 0, то она называется бесконечно малой. Это же опре-
определение можно высказать и в другой формулировке:
280
Переменная величина хп называется бесконечно малой, если для
всякого наперед заданного положительного числа е можно ука-
указать такое натуральное число N, что |jcnf<e для всех номе-
номеров п, которые больше N.
Ни одно число, кроме нуля, не может быть отнесено к бес-
бесконечно малым величинам.
12.2. Алгебраическая сумма нескольких бесконечно малых ве-
величин есть также величина бесконечно малая. (Алгебраической
суммой называется такая сумма, члены которой присоединяются
друг к другу не только при помощи знака плюс, но и при по-
помощи знака минус).
12.3. Разность двух бесконечно малых величин есть величина
бесконечно малая.
12.4. Произведение ограниченной переменной величины на бес-
бесконечно малую есть величина бесконечно малая.
Отсюда следует:
A. Произведение постоянной величины на бесконечно малую
есть также бесконечно малая величина.
B. Произведение переменной величины, стремящейся к пре-
пределу, на бесконечно малую есть величина бесконечно малая.
C. Произведение двух бесконечно малых величин есть величина
бесконечно малая.
12.5. Отношение двух бесконечно малых величин не обяза-
обязательно есть величина бесконечно малая.
Отношение двух бесконечно малых величин может быть величиной
конечной, бесконечно малой и даже бесконечно большой величиной.
Об отношении двух бесконечно' малых величин иногда говорят,
- „ О
что оно представляет собой «неопределенность» вида -^.
Вычисление предела отношения двух бесконечно малых часто
О
называется также раскрытием «неопределенности» вида -д-.
Бесконечно большие величины
12.6. Переменная величина хп называется бесконечно большой,
если для любого наперед заданного числа М >0 можно указать
такое натуральное число N, что для всех номеров п, больших N,
выполняется неравенство \х„\>М. Короче: переменная величина
хп называется бесконечно большой, если, начиная с некоторого
номера, она становится и остается при всех последующих номе-
номерах по абсолютной величине больше любого наперед заданного
положительного числа М. Если хп есть величина бесконечно боль-
большая, то это записывается так: Нтл:„= со, или хп-*-оэ.
Следует обратить внимание, что из определения бесконечно
большой величины следует, что знак хп роли не играет, а требует-
требуется лишь, чтобы абсолютная величина х„, т. е. \хп\, могла быть
сделана больше любого наперед заданного положительного числа.
281
Бесконечно большая величина хп называется положитель-
положительной бесконечно большой величиной, если, начинная с некото-
некоторого номера, она становится положительной. В этом случае
уже нет надобности писать, | хп\ > М, знак абсолютной величины
(прямые скобки) можно опустить и писать хп > М. В случае,,
когда хп — положительная бесконечно большая величина, пишут
Птл:п= + со, или х„-*¦-{-со, и произносят: «хп стремится к
плюс бесконечности».
12.7. Переменная величина хп называется отрицательной
бесконечно большой величиной, если для любого числа М < О
можно указать такое натуральное число N, что для всех номе-
номеров п больших N, выполняется неравенство хп < М. В случае,
когда хп — отрицательная бесконечно большая величина, пишут
\\тхп --¦ — со, или хп-*- — оо, и произносят.«хп стремится к ми-
минус бесконечности».
12.8. Надо помнить, что символы со, + оо, — со отнюдь не
являются числами, а вводятся только для упрощения записи и
для сокращенного словесного выражения того факта, что пере-
переменная величина является босконечно большой, положительной бес-
бесконечно большой и отрицательной бесконечно большой. Следует
твердо запомнить, что никаких арифметических действий над
этими символами производить нельзя.
12,9 Бесконечная большая величина предела не имеет.
12.10. Переменная, принимающая значения, обратные по ве-
величине Соответственным значениям бесконечно малой величины,
есть величина бесконечно большая.
12.11. Переменная, принимающая значения, обратные по вели-
величине соответственным значениям бесконечно большой величины,
есть величина бесконечно малая (хотя в некоторых учебниках и
применяются условные записи — = 0 и -д- = оо, но их следует вся-
всячески избегать, так как 1) делить на нуль запрещено, 2) делить
же на оо тоже нельзя, ибо оо не число, а символ, делить же на
символы бессмысленно).
12.12. Если А постоянная величина, не равная нулю, то про-
произведение А на бесконечно большую величину есть величина бес-
бесконечно большая.
12.13. Произведение двух бесконечно больших величин есть ве-
величина бесконечно большая.
12.14. Отношение бесконечно большой величины к бесконечно
малой есть величина бесконечно большая.
12.15. Сумма двух бесконечно больших величин одинакового
знака есть бесконечно большая величина того же знака.
12.16. Отношение двух бесконечно больших величин не обя-
обязательно есть бесконечно большая величина.
Это отношение может быть 1) величиной бесконечно большой,
2) величиной конечной и даже 3) величиной бесконечно малой
282
(см. задачи 12,1 — 12,9). Об отношении двух бесконечно больших ве-
величин говорят, что оно представляет собой «неопределенность» ви-
оо
да—, а отыскание этого отношения называется «раскрытием неопре-
неопределенности».
Действия над сходящимися последовательностями
12.17. Последовательности складываются, вычитаются или
умножаются путем сложения, вычитания или умножения их со-
соответствующих членов. Если есть две последовательности:
аи аг, а3, ... , а„, ... {ап}
и
Ьо, Ьг, Ь3, . .. Ьп {Ьп}
то получим их сумму в виде
(аг + Ьх), (аг + Ьг), (а3 + Ь3) (ап -\- Ьп), ... , {ап) -\- {Ьп}
разность в виде
(ai — bi), (аг — Ьг), (а3 — Ь3), ... , (а„ — Ьп) Л . , {ап} — {Ьп}
а их произведение в виде
(«1 bi). (аг Ьг), (а8 Ь3), . . . , (а„ Ьп), ... {ап} ¦ {Ь„}
Частное от деления двух последовательностей получим как
частное от деления членов последовательности {ап} на соответ-
соответствующие члены последовательности {Ьп) при условии, что в по-
последовательности {Ьп) нет членов равных нулю.
Предел суммы, разности, произведения и частного
двух последовательностей
12.18. Если две последовательности {х„} и {уп} имеет пре-
пределы, равные соответственно а и Ъ, то:
A) Последовательность {хп ± уп) имеет предел равный а±Ь,
т. е.
lim (хп ± уп) = lim xn ± lim уп = а ± Ъ.
fl-i-co П-юо И-1-со
Это свойство распространяется на случай любого фиксированного
числа слагаемых.
B) Последовательность {хп уп) имеет предел, равный ab, т. е.
\\т(хп ¦ уп) = \imxn ¦ \imyn = ab.
П-юо ft-*-oo П-юо .
' Это свойство распространяется также на случай любого
фиксированного числа сомножителей.
283
Постоянный множитель можно выносить за знак предела
Ит/гл:„ = k \\mxn при любом постоянном k.
С) Последовательность \—\ имеет предел, равный ~, т. е.
lim хп
„ lim yn b
при условии, что все уп не равны нулю и \\туп — Ь ф 0.
Теоремы о последовательностях, расходящихся к ± со
Если для последовательности {хп} Птл:„ = + со, то говорят,
И-то
что последовательность {хп} расходится к плюс бесконечности.
Если для последовательности {хп} Птл:„= — со, то говорят,
что последовательность {хп} расходится к минус бесконечности.
Символы + со и — со имеют смысл, о котором было сказано в п. 12,8.
12.19. Если последовательность {х^} ограничена, а последова-
последовательность {уп} расходится к + оо: Пту„ = + со, то
а) Пт (*„ + уп) = + °о; б) Пт (хп -«/„) = - со;
rt-юо Л-»-оо
в) Пт— = 0 при условии, что у Ф 0 для всех п.
«->со Уп
12.20. Если последовательности {хп} и {уп} расходятся к плюс
бесконечности:
\\гахп = + со и l\myn'— + со, то
«->со П-юо
lim(xn + уп) = + со; lim(хп ¦ уп) = + со.
П.-+0О /1-»-оо
12.21. Если Птл:„ = +. со, а Пту„= — со, то
П-+оо П-+оо
а) Пт (хп - уп) = + со; б) Пт (хп ¦ уп) - - со.
12.22. ?слы Птл:„ = аиа^0, а Птуп = + со ы а — дейст-
вительное число, а не один из символов -f- со ылы — со, то
co' если а
со, еслы а
12,23. ?слы Птл;„ = а(а# 0), а limyn = 0 и уп > 0, то
11
?(+ . а>0;
Уп\ — оо, если а<0.
284
) Теоремы о предельном переходе
12,24. Если переменная хп (последовательность {хп)) имеет
конечный предел, то для любого действительного а имеет место
равенство
«a A2,1)
в предположении, что степени хап и (\\тхп)* имеют смысл. Ко-
И-юо
роче: можно переходить к пределу в основании етепени с любым
действительным показателем.
12.25. Если переменная хп имеет конечный предел, то имеет
место формула
\1тУТа = ут7а, A2,2)
П-i-co Л-юо
т. е. можно переходить к пределу под знаком корня (в случае
четного т предполагается, что хп > 0 и корень берется ариф-
арифметический).
12.26. Если а > 0, а хп принимает только положительные
значения и имеет предел, не равный нулю, то имеет место формула
lim loga xn = loga (Нтх„). A2,3)
П-t-eo /1-»-со
Короче: можно переходить к пределу под знаком логарифма.
-'• 12,27. Если а > 0, а переменная хп имеет конечный предел,
то имеет место формула
\\mxn
limaxn = a"-M . A2,4)
It-*- оо
Короче: при фиксированном основании можно переходить к пре-
пределу в показателе степени.
Теперь приступим к решению типовых задач на отыскание
предела переменной хп (предела последовательности {хп}).
Задача 12,1. Найти предел переменной —
2»*
Последовательность {п2} расходится к + оо, а значит и после-
последовательность {2п2} расходится к + оо, (п. 12,22). На том же
основании последовательность {Ъп) расходится к + со, а потому
последовательность {Зп + 2п2} расходится к + со и на основании
п. 12,19 последовательность A+Зп + 2п2) также расходится к
+ со и limA + Зп + 2п2) = + со. Можно было бы рассуждать и
п-
иначе: при п -*¦ оо величина п — бесконечно большая, ее квадрат,
как произведение двух бесконечно больших величин, есть вели-
величина бесконечно большая (п. 12,13). На основании п. 12,12 про-
285
изведение 2п2 есть бесконечно большая величина, как произведение
постоянной, не равной нулю, на бесконечную большую величину.
На том же основании величина Зп — бесконечно большая. Так
как Зп и 2п2 — бесконечно большие одного и того же знака, то
и сумма их (Зп + 2п2) есть величина бесконечно большая того
же знака, потому и 1 + (Зп + 2п2) — бесконечно большая величина,
как сумма постоянной величины 1 с бесконечно большой и снова
lim A + Зп + 2п2) = + со. Что касается знаменателя 1 — п2,
при п -*- со последовательность {п2} расходится к + со, и на ос-
основании п. 12,19, б получаем, что последовательность A — п2}
расходится к — оо и знаменатель дроби A2,5) — тоже бесконечно
большая величина.
Таким образом, дробь A1,5) есть отношение двух бесконечно
больших величин, о котором без исследования ничего определен-
определенного сказать нельзя. Здесь также нельзя применить теорему о
пределе частного, так как в условии этой теоремы предполагает-
предполагается, что пределы числителя и знаменателя существуют, а в нашем
случае ни числитель, ни знаменатель дроби предела не имеют
(см. п. 12,9). Данную переменную A2,5) преобразуем, чтобы
к ней можно было применить теоремы о пределах. Обыкновенно
в этом случае поступают так: числитель и знаменатель дроби
делят на наивысшую степень п, встречающуюся в членах дроби*.
Тогда
-4 . 3 , „
( }
2.
л»
Отыскивая теперь предел последней дроби, мы сможем при-
применить теорему о пределе частного, так как теперь числитель и
знаменатель дроби имеют пределы: величины -$ и — есть вели-
величины бесконечно малые, как величины обратные бесконечно боль-
большим п2 и п, а потому
lim -^=0, lim —=.0.
В-» Я* В-» Я
о
Величина — есть тоже бесконечно малая, как произведение
1 3
постоянной величины 3 на бесконечно малую — и lim — — 0
(п. 12 4А), и тогда существует предел числителя:
lim (~+~ + 2] = l\m-. + Um- + Um 2 = 0
(предел постоянной величины 2 равен ей самой).
* Деление на п допустимо, так как предполагается, что п Ф 0.
286
Предел знаменателя -j—1 дроби A2,6) также существует и
равен — 1, так как
lim (~—\) = lim i — lim 1 = 0—1 = —1; \шх. = Лг= -2.
После этих подробных рассуждений укажем, как следует распо-
расположить записи:
1+Зл + 2л2 ,. ~п* + ~п+2
lim -^Ц—^— -- lim —j =
в-» ! —"' в-» Л 1
lim (-L -l J* л. 21 lim JL j_ lim — _i_ lim 2
lim(-L_ 1) lim JL— lim 2
«Л-»»\П3 / «->со /I2 B-^co
(Здесь применена теорема о пределе дроби. Это можно
было сделать только после, того, как мы убедились, что
существуют пределы числителя и зиамеиателя).
0 + 0 + 2 _ _ 2 _ о
Такие подробные записи в последующем, когда выработается
определенный навык, можно сократить.
Задача 12,2. Найти lim 1п. + 2лп~1.
„_„5иа —4п + 4
Решение, lim
(числитель и знаменатель данной дроби
разделен иа па)
lim 7+ lim -i— lim — 7+2 lim — — 3 lim —
П-+ОО /I-»-00 fl tl-*-CO tl^ A-b.OQ fl tl-*-OQ tl I
lim 5 — lim -i + lim -1 5 — 4 lim J. + 4 lim -L
«->co B-l-co tl /!->¦» W8 B-^co /1 B-^oo И8
(применена теорема о пределе дроби).
Задача 12,3 (для самостоятельного решения). Найти
' — An + 2
' п^оо 5ns-4/i+17
Ответ. 1) ~; 2) 0.
287
Задача 12,4 (для самостоятельного решения). Найти
Cn-l)Bfl
Ответ. Последовательность расходится к -f- °° • Можно упо-
употребить символическую запись и написать, что
y-''-+«¦•
Указание. В числителе перемножить двучлены, разделить
числитель и знаменатель на п3 и воспользоваться п. 12,23.
Задача 12,5 (для самостоятельного решения). Найти предел
переменной хп = з^ + я + 1 '
Указание. Известно, что сумма квадратов чисел натураль-
натурального ряда 1* + 28 + 32+ _ +П2^ Щп+1П2п+1)^
Ответ, -д-.
Задача 12,6 (для самостоятельного решения). Найти
ча — п 4- 1
:
4) lim
Ответ. 1) -I; ' 2I; 3) оо; 4) 0.
Задача 12,7. Доказать, что если п-»-оо, то 1) п*-*- + '°°»
когда ft > 0; 2) п* -*• 0, когда ft < 0; 3) п* -*-1, когда ft = 0.
Решение. 1) Пусть ft > 0, а М — любое заданное положи-
положительное число.
Чтобы доказать, что nfe->--f-oo, мы должны показать, что
можно найти такое натуральное число N, что пк > М при
n>N.
Так как пк должно быть большим, чем М, то это равно-
равносильно тому, что должно быть п > У'М., и за N можно принять
N > у М\ тем самым доказано, что п -»- + оо при ft > 0. Например,
если ft — 3, а М = 1000, то должно выполняться неравенство
п3 > 1000 для всех п> N, причем следует взять N > у^ЮОО, т. е.
принять N> 10. Значит, начиная с п— 11, неравенство п3 > 1000
будет выполняться.
Если взять М — 1000 000, то должно выполняться нера-
неравенство п3 > 1000 000 для всех п> N, и следует взять
N > У 1 000 000 = 100 (N > 100) и при п > 100, т. е. начиная
с п= 101 неравенство п3 > 1000 000 будет выполняться.
288
Доказательство пунктов 2) и 3) предоставляется читателю.
При доказательстве п. 2) и 3) выгодно взять k = —/(/> 0), и тогда
пк = —; при доказательстве п. 3) учесть, что если k = 0, то
всегда пк = 1 при любом п.
Результат проведенных вычислений можно записать и так:
{+ со, если k > 0,
0, если k< 0, A2,7)
1, если k = 0.
В задачах 12,1 — 12,6 мы рассматривали пределы отношения
двух целых рациональных функций от п в частных случаях.
После решения предыдущей задачи мы можем рассмотреть вопрос
об отношении двух целых рациональных функций в общем виде.
Задача 12,8. Найти предел при п-»-со
_ аопР + сцпР-1 + а2»Р-а -j \-ар
* + Vi9~a + • • • + bq '
причем а0 ф 0, Ьо Ф 0.
Решение. Перепишем A2,8) в виде
Xn =
Теперь предел
lim xn = lim
Предел второго сомножителя равен ?-°, так как в числителе
и знаменателе предел каждого слагаемого, кроме первых (а0 и
Ьо), равен нулю. Что касается первого сомножителя, то его предел
зивисит от знака разности р — q:
1) Если р — q > 0, т. е. р > q, то на основании A2,7)
\\тпР-ч= +оо, и тогда, в соответствии с п. 12,22, заключаем,
что \\тхп = + со.
2) Если р — q < 0, т. е. р < q, то из A2,7) следует, что
limnp-'? = 0; тогда искомый предел равен нулю: Птл:л = 0.
289
3) Если же р — q — О, т. е, р = q, то lim пр~ч = 1 или lim хп=
-¦¦ ^. Соединяя полученные результаты, приходим к выводу, что
( + со, если р >q;
О, если p<q\ Попч
* если p = q. { '*
Таким образом, при п -> со предел отношения двух целых
рациональных функций от п равен 1) отношению коэффициентов
при высших степенях п, если степени этих функций между со-
собою равны; -2) нулю, если степень числителя меньше степени
знаменателя и 3) +со> если степень числителя больше степени
знаменателя.
Заключения, полученные при решении задач 12,1 — 12,6, совпа-
совпадают с только что сделанным.
Задача 12,9. Найти Jim {??+? ~ ]2J •
Решение. Воспользуемся указанием п. 12.24, заметив, что
основание степени имеет предел
Задача 12,10 (для самостоятельного решения). Найти
. /Зя8 — 4«2 + 5«\з
07
Ответ. =7.
64
Задача 12,11. Найти lim('l +—)B — —Y(~— l) .
Решение. Применяя теорему о пределе произведения (это
мы имеем право сделать, так как каждый сомножитель имеет
предел) получаем последовательно:
290
3 1
т. к. lim — = 3 lim -- = 3-0 = 0, ибо если п -*¦ оо, то величина
Л-1-оо П П-ьоо П
ей обратная бесконечно малая (lim — = 01. 4
6п+2
Задача 12,12. Найти НтЗ3"-4.
И-*- во
Решение. Воспользуемся указанием п. 12,27 о переходе к пре-
делу в показателе степени Iim33n~4 = 3"-°°3" 4=3
«->00
Urn (б + —\
П-*е°{ П I
= 33 з2 9
Задача 12,13 (для самостоятельного решения). Найти:
3n JL. п~1_
1) lim 76"-5: 2) lim { ; Iim5"!+2.
Ответ. 1) 1/7; 2)|; 3) 1.
lOg
о„
lOga
j
Решение. На основании формулы A2,3), допускающей пере-
переход к пределу под знаком логарифма, имеем:
= logfl|=Ioga-g-=-loge2.
Задача 12,15 (для самостоятельного решения). Найти:
lim ч ", "^—п=,-
Ответ. —Ig3.
ТРИНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Определение предела последовательности (задачи повы-
повышенной трудности).
Задача 13,1. Найти lim qn, если 1) q > 1; 2) q < —1,3) q= 1,
4) q=-\.
1 /1 \n
Решение. 1) Если q > 1, то 0 < — < 1, и тогда lim — =0
Q л-»» \"}
i. задачу
меньше 1).
(см. задачу 11,4 — основание степени — по абсолютной величине
291
Значит, -jj — бесконечно малая величина, а потому обратная
ей величина q" — бесконечно большая величина; так как при
q> 1 ил, стремящемся к +оо, переменная величина qn прини-
принимает только положительные значения, то lim?4"— -{-со.
«->со
. 2) Если же q< —1, то переменная величина qn при п-*- -{-со
делается попеременно то положительной, то отрицательной, неогра-
неограниченно возрастая по абсолютной величине, а потому
lim qn = со, если q < —1.
3) Если q = 1, то q" = 1, при каждом п, а потому при q = 1
будет linn?" = 1.
Л-ио
4) Если же q = — 1, то переменная величина ^" не. стремится
ни к какому пределу, потому что когда п пробегает значения
1, 2, 3, 4, ... величина (—1)" делает скачки от —1 к +1 и
обратно.
+ со если q > 1;
0, если \q\ < 1;
1, если <7= 1; A3,1)
не существует, если q — — 1;
. со если q < — 1.
Прежде чем решать следующие задачи, укажем на очень
важные теоремы, выражающие признаки существования предела
переменной величины.
Теорема 13,1. Если переменная величина хп монотонно воз-
возрастает вместе с л, но остается меньше некоторого числа К, то
хп стремится к пределу, и этот предел не больше К, т. е. меньше
или равен К. — '
Теорема 13,2. Если переменная величина хп монотонно убы-
убывает с возрастанием п, но остается больше некоторого числа L,
то хп стремится к пределу и этот предел ие меньше L, т. е.
больше или равен L. Теорема 13Л и 13,2 можно объединить в
одну, которая коротко формулируется так:
Каждая ограниченная монотонная последовательность схо-
сходится.
Эти теоремы будут использованы в задачах 13,2—13,4 кото-
которые будут решаться по такому общему плану:
1) прежде всего мы докажем, что данные последовательности
монотонны;
2) после этого установим, что они ограничены.
Убедившись в7выполнении этих двух требований, и тем самым
в существовании предела последовательности, мы будем отыски-
отыскивать этот предел.
292 ¦
Задача 13,2. Доказать, что если а —любое положитель-
положительное число, то
1шУо=1. A3,2)
П~* со
Решение. Допустим сначала, что число а > 1. Тогда после-
последовательность a, Yа> V а> V а • • • является монотонно убываю-
убывающей. Но эта последовательность и ограничена, так как уга>1.
Поэтому на основании теоремы 13,2 эта последовательность имеет
предел L, и этот предел не может быть меньше, 1, т. е. L> 1.
Покажем, что предположение I > 1 приводит к противоречию.
Действительно, так как рассматриваемая последовательность —
монотонно убывающая, то даже при сколь угодно большом п
имеем, что
V~a>L.
Отсюда a>Ln. Так как L>1, то при п->со величина V —
бесконечно большая. Но это противоречит условию задачи, со-
согласно которому а — число и тем самым не может быть величиной
бесконечно большой. Таким образом, предположение что L > 1
привело нас к противоречию и должно быть отброшено и остается
только заключить, что L = 1.
Читателю предлагается самостоятельно доказать что и при с
положительном, но меньшем I имеет место соотношение A3,2).
Указание. Воспользоваться теоремой 13,1. В этом случае
последовательность а, ~\^ а, У a, j^ а, ... — возрастающая (и огра-
ограниченная, т. к. У а< 1). Пределом будет число К < I. Доказа-
Доказательство должно привести к тому, что случай К < 1 является
невозможным. Останется единственно возможное заключение К — 1,
а это и требуется.
Задача 13,3. Показать, что если Z>1, то lim- = + oo,
т. е. что последовательность {хп} = — расходится к +°°-
Решение. Так как / > 1, то можно записать, что / = 1 + а,
где а > 0. Тогда
I"- 1 , , п— 1 , , («— 1)(«— 2)
:==Т + а+-Га +" 5Т "
Теперь переходя к пределу при п -> со, получаем
i i я—1 я i (я—1)(я —2) „ ,
т. е. переменная хп — — при / > 1 — бесконечно большая.
293
Поэтому можно также утверждать, что для достаточно больших п
Г > п, если />1. Результат этой задачи приводит также к
выводу, что
lim 4 = 0 при /> 1.
Задача 13,4. Показать, что
WmV~n=\. A3,7)
Решение. При вычислениях, связанных с числом е, полу-
A п I 1 \п
1 -\ 1 < 3 при любом п. Значит, 1-(
tt } \ ft I
меньше любого числа, которое больше 3 или равно 3, т. е. для
всех чисел п > 3 имеет место неравенство A —j 1 < п. Из этого
следует, что
< п, {-^±р1 <п, (п+ 1)" < пп\ (п + 1)" < л»+1.
Извлекая теперь из обеих частей неравенства корень степени
п(п-\-\), получаем, что
или
Мы установили это неравенство для того, чтобы показать,
что последовательность {jfn} — убывающая, когда п возрастает
от значения, равного 3, т. е. \Г 3, i/~ 4, j/~ 5, т/~ 6, ... — убы-
убывающая последовательность. А так как при любом целом п > 0
всегда |/ п > 1, то эта убывающая последовательность ограни-
ограничена. Значит, последовательность |>^л}, будучи убывающей и
ограниченной, необходимо стремится к пределу, причем этот
предел не меньше I. Обозначим этот предел через L. Так как
этот предел не меньше I, то L> 1. Покажем, что предположение
L > 1 приводит к противоречию и тем самым для L останется
единственная возможность быть равным I. Действительно, так как
рассматриваемая последовательность — монотонно убывающая, то
даже при сколько угодно больших п будет yfn>L, а потому
п > Ln. Это неравенство находится в противоречии с неравенством
Ln > n полученном в последнем абзаце предыдущей задачи при
тех же условиях: L> I, a n достаточно велико.
Таким образом предположение L > 1 привело к противоречию
и должно быть отброшено. Для L остается только одна возмож-
возможность быть равным I и тем самым соотношение A3,7) доказано.
294
Отсюда можно получить следствие:
lim т/Т =1, A3,3)
rt-*-co Г fl
Т. К.
lim V/T = lim -L = —!— = -{-=1
Задача 13,5 (для самостоятельного решения). Найти:
1) lim у^Еп; 2) lim^/F; 3) li
4)limy^; 5) lim^.
Указание. 1)y/~5n — УъУп. Применить теорему 12,18п.fl
о пределе произведения и использовать задачи 13,2 и 13,4. 2)у/7г4—
= (\^пу. Использовать задачу 13,4.
Ответ. 1) 1; 2) 1; 3) 1; 4) 1; 5) 0.
Для решения дальнейших задач полезна
Теорема 13,3. Если для трех переменных х„, уп и zn, начиная
с некоторого номера п, выполняется соотношение
xn<zn< уп,
а хп и уп имеют равные пределы, то тот же предел имеет и zn.
Задача 13,6. Найти предел Нгп|/3л + 2.
П-+ со
Решение. Для п > 2 выполняются неравенства
но
а поэтому на основании последней теоремы 13,3 заключаем, что
искомый предел равен 1:
Задача 13,7 (для самостоятельного решения). Найти:
1)¦ limУЪЛ~Ъ; 2) limп-/~(п + 2) ¦
Ответ. 1) 1; 2) 1.
Задача 13,8. Найти lim (Yn + 2 — V п). При вычислении этого
П-ио
предела мы не можем применить теорему 12,18 п. Л о пределе
разности двух переменных, ибо эта теорема верна только в том
295
случае, когда обе переменные имеют предел. В нашем случае ни
У п + 2, ни У л предела не имеют, так как на основании соот-
соотношений A2,7) при п->'со у^л-^-оо, а вместе с ним и
( )
( )
Здесь мы имеем дело с разностью двух положительных бес-
бесконечно больших величин. Без специального исследования об этой
разности нельзя сказать ничего определенного. Такие разности
называют «неопределенностями» вида оо — оо (запись оо — со —
есть символическое обозначение «неопределенности» такого вида,
а не вычитание символов). Данную переменную преобразуем,
умножив и разделив ее на У п + 2 + У п ¦ Это преобразование
мы делаем для того, чтобы перенести иррациональность в зна-
знаменатель:
== 2.0 = 0,
ибо У« + 2 н}^п при л -»- со есть положительные бесконечно
большие величины, их сумма Yn + ^ + Yn есть тоже положи-
положительная бесконечно большая величина, а величина," обратная ей,
есть величина бесконечно малая. Предел же бес-
бес^=
конечно малой величины равен нулю.
Задача 13.9. Найти Iim (У 2п + 3 — У п — 1).
Я-»-оо
Решение. Здесь снова мы имеем дело с разностью двух
босконечно больших величин (см. 12,7) («неопределенность» вида
со—со), и без специального исследования никакого заключения
о пределе их разности мы сделать не можем.
Как и в предыдущих двух задачах, перенесем иррациональ-
иррациональность в знаменатель, и тогда
разделим числитель и
знаменатель иа п
= Hmп
»
2. +1+1/1 + 1
так как при л-> со предел числителя равен 1, а знаменатель есть
величина бесконечно малая, как сумма двух бесконечно малых
296
величин. Значит, мы имеем дело с величиной, которая обратна
бесконечно малой, а такая величина — бесконечно большая.
Задача 13,10 (для самостоятельного решения). Определить
lim У~п (УТ+Т - V л) •
П-»-°о
Указание. Здесь снова фигурирует разность двух беско-
бесконечно больших величин Yn + I —Vп, а множитель ]/ п преде-
предела не имеет. Поэтому теорему 12,18 (пункты А я В) применить
нельзя. Для решения задачи надо выражение, стоящее под зна-
знаком предела, умножить и_разделить на у^/г + 1+/п и в полу-
полученном выражении , —j= произвести деление числителя
V п-\-\ +у п
и знаменателя дроби на ]/ п. ~
Отве т. у.
Задача 13,11 (для самостоятельного решения). Определить
П-оо П-\- 1
Указание. Здесь мы имеем дело с отношением двух беско-
бесконечно больших величин, о котором без специального исследования
ничего определенного сказать нельзя. Также нельзя применить
и теорему о пределе частного A2,18 пункт С), так как для ее
применения требуется, чтобы числитель и знаменатель дроби
имели пределы, а в данном случае ни числитель, ни знаменатель
дроби предела не имеют (они величины бесконечно большие).
Для решения задачи Следует числитель и знаменатель дроби
разделить на п.
Ответ. 1.
Задача 13,12 (для самостоятельного решения). Найти
Указание. Здесь мы опять-таки встречаемся с отношением
двух бесконечно больших величин. Теорему 12,18 (пункт С) при-
применить нельзя (числитель и знаменатель дроби предела не имеют).
Для решения задачи числитель и знаменатель дроби разделить
на л. . *
Ответ. 1.
Задача 13,13 (для самостоятельного решения). Найти:
1) lim (yV + п + 1 - Vn* - п + 1);
2) lim (V (п + a) (n + b) -n).
Ответ. 1) 1; 2) ^.
297
Указание. При решении каждого из этих примеров мы
имеем дело с разностью двух бесконечно больших величин. Тео-
Теорема о пределе разности и в первом и во втором случае непри-
неприменима, так как переменные не имеют предела. Перенести
иррациональность в знаменатель, после чего числитель и знаме-
знаменатель дроби разделить на п.
Задача 13,14. Найти:
Указание. 1) Воспользоваться формулой A2,2), переписать
данное выражение в виде
»? У вйгнг
lim
lim,
~ п + 1
2 + п + 3
и учесть результат задачи 12,8.
2) lim
5п
6
Ответ. 1) у! 2) Ij)
Задача 13,15 (для самостоятельного решения). Найти
¦. у п? + 5л
urn -_ . 9 .
Указание. Числитель и знаменатель дроби разделить на п.
Можно поступить и иначе: представить данную дробь в виде.
воспользоваться формулами A2,2) и A2,9).
Ответ. 0.
Задача 13,16 (для самостоятельного решения). Найти
lim
1—24-3 —
— 64- • ¦ ¦ — 2п
yni + 1 + у 4«а — 1
Указание. Числитель дроби записать так:
1-2 + 3-4 + 5-6+ 2л = [1+3 + 5 +
-[2 + 4 + 6+-..+2л].
298
Каждую, из сумм, стоящую в скобках, вычислить как сумму
членов арифметической прогрессии. После этого числитель и зна-
знаменатель дроби разделить на л.
Ответ. —т .
Решение трех следующих задач основано на применении фор-
формул (а — Ь) (а2 + ab + Ь*) = а3 - Ь3 и (а + Ь) (а2 - ab + Ь2)=а3+Ь3.
Задача 13,17. Найти lim(j/ 1 — п3 + л).
Л-к»
Решение. Здесь в скобках стоит разность двух бесконечно
больших величин. Полагая у1 1 — п3 ~ а; л = Ь, умножим и раз-
разделим выражение, стоящее под знаком предела, на а2— ab + Ьъ
и получим
lim (у 1 — п3 + п) ¦•= lim
(у/ I — Л8J — Л |/1—Л8 +
= 0,
так как знаменатель дроби при п ->- оо есть сумма трех положи-
положительных бесконечно больших величин, а потому на основании
п. 12,20 заключаем, что это величина положительная, бесконечно
большая. Величина же обратная бесконечно большой есть вели-
величина бесконечно малая, и ее предел равен нулю.
Задача 13,18 (для самостоятельного решения). Найти
lim[(n+l)8 — (л —I)8].
Указание. Здесь мы снова имеем дело с разностью двух
_2_ _2_
бесконечно больших величин. Полагая (п-\- IK — а, (п — IK =b
умножить и разделить на а2 -\- ab + Ьг. После приведения подоб-
подобных членов в числителе получится 4л. После этого .числитель и
знаменатель дроби разделить на наивысшую степень п, встречаю-
встречающуюся в членах дроби, т. е. на л3 .
Ответ. 0.
Этим заканчиваются упражнения, связанные с определением
предела последовательности.
Задачи для дополнительных упражнений учащийся может
взять из хорошо зарекомендовавшего себя задачника для втузов
под редакцией Б. П. Демидовича «Задачи и упражнения по мате-
математическому анализу»,
ЧЕТЫРНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Предел функции.
Определение предела функции.
Число А называется пределом функции f (х) при х, стремя-
стремящемся к а (или в точке а), если для любого наперед заданного
положительного числа е (хотя бы и как угодно малого) можно
найти такое положительное число 8, что для всех значений х,
входящих в область определения функции, отличных от а и
удовлетворяющих условию \х — а | < 8, имеет место неравенство
\f(x)-A\<*.
Короче: число А называется пределом функции f(x) при х,
стремящемся к а, если выполнение неравенства 0<|д; — а\<Ь
влечет за собой выполнение неравенства \ f (х) — А | < е, где
в > О — наперед заданное число, а 8 соответствующим образом
подобрано.
В определении предела функции следует обратить внимание
на то, что вовсе не требуется, чтобы функция / (х) была непре-
непременно определена в точке а. Для того чтобы функция f(x) имела
возможность стремиться к пределу при х-*-а, необходимо лишь
чтобы в области ее существования были точки, как угодно близ-
близкие к а и отличные^ от а.
Прежде чем приступить к непосредственному вычислению пре-
предела функций, приведем основные сведения из теории:
14,1. Бесконечно малые и бесконечно большие функции.
а) Функция f (х) называется бесконечно малой при х-*-а, если
0. A4,1)
b) Функция f(x) называется бесконечно большой при х-*-а
если имеет место одно из равенств
limf(jc) = со; \\rnf (х) — +оэ; Нт/(д;) = — оо.
х-уп х-+а х-уп
c) Функция f (х) называется ограниченной при х -*¦ а, если
существует такое положительное число А, что для всех значв'
ний х из окрестности числа а выполняется неравенстве
\f(x)\<A.
14,2. Свойства бесконечно малых функций.
a) Если функция f(x) бесконечно мала при х-*-а, то их
—f(x) также бесконечно мала при х-*-а.
b) Если функции fi(x) и ft (x) бесконечно малы при х-*-а,
то сумма их, а также и разность их: f^(х) + !г(*) и fi{x).—
— h (х) бесконечно малы при х-*- а (это утверждение распро-
распространяется на любое фиксированное'число функций).
300
с) ?сли при х-*-а функция f(x) бесконечно мала, а функция
9 (л:) — ограничена, то их произведение f (х) ср (л:) есть функция
бесконечно малая.
14,$. Свойства бесконечно больших функций.
Если при х-*-а функция f(x) имеет конечный предел
(lim / (х) = b), а функция <р (л:) — бесконечно велика (lim <р (л:) =
х-*а х-*-а
=¦¦ со), то
а) сумма их — бесконечно велика, т. е. \\m[f(x) + <р (*)] = °°.
хч-а
предел отношения f(x) к <р (x) равен нулю:
b) если lim f (x) — b (b > 0), a lira f (x) — 0, причем <р (д;)
x-*a x-t-a
f (ХЛ
положительна в окрестности точки а, то Пт-*-^ = +°°-
с). При положительном k, если limf (дс) = +оэ, то
хю
d) Произведение двух бесконечно больших функций есть функ-
функция бесконечно большая, т. е. если limf (дс) = да« lim <р (л;) = со,
х-ю х-ю
то и lim f(x) = оо.
х-ю
14,4. Связь между бесконечно большими и бесконечно малыми
функциями:
а) Если f(x) при х-i-a — бесконечно большая функция, то
функция 77^ бесконечно мала.
1(л)
1()
Ь) Если при х-*-а функция <р(х) бесконечно мала, то функ-
функция —Ту: — бесконечно большая, причем предполагается, что в
окрестности точки а функция <р (л:) в нуль не обращается.
14,5. Правила предельного перехода.
а) Були при х-*-а функции f(x) и <р(х) имеют конечные
пределы, то и алгебраическая сумма их f(x)±f (x) имеют пре-
предел, который равен сумме их пределов, т. е. если \imf(x) = b,
х-*а
a lim <? (х) =_Ьи то lim [f (х) ± <р (л:)] = lim f (x) ± lim <p (л:) =
= b±bt.
Короче (но не совсем точно): предел алгебраической суммы
нескольких функций равен алгебраической сумме пределов этих
функций. ,
Ь) Если при х-*-а функции f(x) и <р (л:) имеют пределы, то
их произведение f (x) <р (х) также имеет предел, который равен
301
произведению их пределов, т. е. если lim/(x) — b, а \\т<?(х) = Ьи
х-+а х-ю
mo\\mf(x)<f(x) = Vim f (x) lim (f (x) = bb^
х-ю х-ю х-ю .
Короче (но не совсем точно): предел произведения двух
функций равен произведению пределов этих функций. Свойства
а) и Ь) распространяются на любое фиксированное число функ-
функций.
с) Если при х-*-а функции f(x) и <? (х) имеют пределы и
предел функции <р (х) не равен нулю, то предел их частного
существует и равен частному от деления их пределов, т. е.
если
Umf(x) = b, a lim <р (х) = bL (Ьг ф 0),
х-+а х-ю
то
Короче (но не совсем точно): предел частного равен частному
пределов, если предел знаменателя не равен нулю.
14.6. Предел целой рациональной функции.
Если
Р (х) = а9хп + аХ'1 + агх"-* +¦¦¦+ ап_хх + ап,
то
ПтР(х\ = Р(а), A4,2)
Х-Уп
т. е. при отыскании предела целой рациональной функ-
функции можно в аналитическом выражении функции заме-
заменить аргумент его предельным значением.
14.7. Предел дробно-рациональной функции.
Если
F (V\ - а°хп + aiX"~l + агДГ"~~2 + '' - + а"-1дг + а" = ЕМ
Г W - boxm + b^m-i _)_ Ь2хт-* -\ 1- Ьт_хХ + Ьт Q{x) '
то
limF (х) ='Ш = F (а), если Q (а) Ф 0, A4,3)
т. е. при отыскании предела дробно-рациональной
функции можно в аналитическом выражении функции
заменить аргумент его предельным значением, если при
этом предельном значении знаменатель не обращает-
обращается в нуль.
Задача 14,1. Найти lim (x2 —7х + 4).
х-+3
Решение. Функция f (х) — хг — 7х + 4 — целая рациональ-
рациональная. Для отыскания ее предела применима формула A4,2), Заме-
302
ним ;в аналитическом выражении функции х его предельным зна-
значением и получим
lim (х2 — 7х + 4) = З2 — 7 • 3 4- 4 =-- —8.
Х-уЗ
Задача 14,2 (для самостоятельного решения). Найти
1) lim B*3-7л:2+ 4* 4-2); 2) \\mi\-x* ~х + 2\.
Ответ. 1) -2, 2) 30.
Указание. Воспользоваться формулой A4,2).
Задача 14,3- Найти lim *?tf+2
Решение. Здесь отыскивается предел дробно-рациональной
функции. Прежде чем применить A4,3), надо проверить, не обра-
обращается ли в нуль знаменатель дроби при х — 3. Проверяем:
З2 4- 2 • 3 + 8 = 23 Ф 0:
!4 2*4-8=^33 4-2-34-8 = 23*
Задача 14,4 (для самостоятельного решения). Найти пределы:
, ч ,. л-2 — Зх + 2 о. ,. л-2 — х 4-1
1) lim—т-г——г', 2) lim si „ ¦, .¦ л.
Указания: 1) Проверить, что знаменатель дроби в первом
примере при х = 1, а во втором при х — — 1 не обращается в
нуль; 2) воспользоваться формулой A4,3).
Ответ. 1) 0; 2) —-|.
„3
Задача 14,5. Найти lim -с
Л — 8
Решение. Знаменатель дроби <? обращается в нуль при
X — ^
хъ g
х = 2, а потому функция f{x) = 5- при х = 2 не существует.
ДГ"~~
Теорему о пределе дроби A4,5 п. с) применить нельзя, так
как предел знаменателя равен нулю. По той же причине нельзя
применить и формулу A4,3). Но определение предела функции
содержит существенную оговорку: при отыскании предела функ-
функции f (х) при х-*-а значение функции f(a) при х = а может не
рассматриваться. От функции f (x) это определение не требует,
чтобы точка х — а входила в область существования функции.
Поэтому значение х = а может нами не приниматься во внима-
внимание. Именно 'эти соображения и дадут возможность решить1 за-
задачу. В нашем случае мы должны считать, что х, стремясь к 2,
303
никогда не становится равным 2, а потому значение функции
хз g
5" ПРИ х = 2 нас не интересует.
При х = 2 и числитель, и знаменатель дроби обращаются
в нуль. Мы имеем в данном случае отношение двух бесконечно
малых функций, о котором без специального исследования ничего
определенного сказать нельзя. Для решения задачи разделим
числитель и знаменатель дроби ^- на х—2. Мы имеем право
это сделать потому, что значение х — 2 не рассматривается и,
значит, х — 2 ф О,
Если бы указанной оговорки в определении предела функции
не было и мы должны были бы рассматривать и значение х = 2,
то разделить числитель и знаменатель дроби на х — 2 мы не
смогли бы, так как такое деление означало бы деление числителя
и знаменателя дроби на нуль, что, конечно, недопустимо. После
сокращения дроби на х — 2 получим *
**-8 _ (лг-2)(дг»
7=" 7=
и нам придется отыскивать предел не данной функции, а функ-
функции х2 + 2х -{- 4. Тогда перед учащимся должен возникнуть такой
вопрос: тождественны ли функции ^ и *а + 2а; -f- 4. Этот
вопрос имеет положительный ответ:» функции тождественны,
если не рассматривать значения х = 2. Следует иметь в виду,
что две функции тождественны, если они удовлетворяют таким
двум требованиям:
1) их области существования совпадают и
2) при одном и том же значении аргумента, взятом из обла-
области существования функции, численные значения функций равны.
В нашем случае эти два требования будут выполнены, если
не рассматривать значения х = 2, но ведь 'оно и не рассматри-
рассматривается. Таким образом,
х-*2 х — 1 х^-2 х 1 х->-2
= 22 + 2 • 2 + 4 = 12,
так как функция х2 + 2х + 4 — целая рациональная функция
и для определения ее предела на основании формулы A4,2) сле-
следует в аналитическом выражении функции заменить аргумент
его предельным значением.
Можно указать такое
Правило. Для того чтобы определить предел дробно-рацио-
дробно-рациональной функции в случае, когда при х-*-а числитель и знаме-
знаменатель дроби имеют пределы, равные нулю, надо числитель и
знаменатель дроби разделить на х — а и перейти к пределу»
304
Если и после этого числитель и знаменатель новой дроби имеют
пределы, равные нулю при л: -> а, то надо произвести повторное
деление на х—а (это правило основывается на известном из
элементарной алгебры следствии из теоремы Безу, согласно ко-
терому, если многочлен обращается в нуль при х = а, то он де-
делится без остатка на х — а).
Теперь для самостоятельного решения будет предложен ряд
задач на определение предела дробно-рациональной функции.
Задача 14.6 (для самостоятельного решения). Найти
il™ 2*1-9* +<Г
Указание. При х = 3 числитель и знаменатель дроби —
функции бесконечно малые, пределы их равны нулю. Об их от-
отношении без специального исследования ничего определенного
сказать нельзя. Теорему 14,5 п. с о пределе дроби применить нельзя,
так как предел знаменателя равен Нулю. Следует применить
указанное правило; разделить числитель и знаменатель дроби на
х — 3. Повторить рассуждения предыдущей задачи о допустимо-
допустимости такого деления.
Ответ. т.
О
Следует не только запомнить тот или иной прием, но глав-
главное — понять, на чем основано его' применение', и каждое дейст-
действие проводить совершенно сознательно, а не автоматически, «по
правилам». Применяя правило, надо понимать те положения, из
которых оно выведено.
Задача 14,7 (для самостоятельного решения). Найти
Указание. Здесь опять-таки функции, стоящие в числителе
и знаменателе дроби, бесконечно малы при х-*-1. Для решения
вопроса о пределе их отношения следует разделить числитель
и знаменатель дроби на х — 1. Полученные после этого деления
функции при х -> 1 будет опять-таки бесконечно малыми. Снова
каждую из них следует разделить нал;—1. Этим указанием вос-
воспользуетесь и при решении двух следующих задач.
2
Ответ, -к-
Задача 14,8 (для самостоятельного решения). Найти
.. Ьх3-Ьх*
™4xs + 2x* + x*-
Ответ. —6.
Задача 14 4 (для самостоятельного решения).
Ответ, у.
П И. А Каплан * 305
Задача 14,10. Найти lim^—f(m и п —целые положитель-
ные числа).
Решение. При х -*¦ 1. числитель и знаменатель дроби имеют
предел, равный нулю, а поэтому это функции бесконечно малы.
Для решения вопроса о пределе их отношения следует числитель
и знаменатель дроби разделить на х—1. Допустимость такого
деления подробно была объяснена в задаче 14,5. Повторяем,
что х, стремясь к 1, не становится равным 1, а потому х— 1 ф
Ф 0, и деление на х — 1 имеет смысл.
Функция п__ . при х = 1 не существует, но значение х = 1
нашему рассмотрению и не должно подлежать. Воспользуемся
известной формулой алгебры
ат — Ьт = (а- Ь) (а" + ат~2Ь + f- abm-* + b'1). A4,4)
Полагая здесь а — х, a b — I, в нашем случае получим
*-,! лл — 1 x^.t {X — 1) {Xn~l + Xn~* + ••• + X + 1)
m раз
1 + 1 + 1 + • • ¦ + t т.
1+1 + 1+..- + 1 я
n раз
Задача 14,11. Найти fim1"^3
Решение. При х -*• — 1 числитель и знаменатель дроби имеют
пределы, равные нулю, а потому это функции — бесконечно ма-
малые. Чтобы можно было применить формулу A4,4), с помощью
которой была решена предыдущая задача, следует сделать под-
подстановку х — у85, где показатель степени 35 — наименьшее крат-
кратное показателей корней.
Если х = у35, то у/~х~ у&. a frx = у7, и тогда 1 + ^ = ]
l + \fx l
причем у-*-—I, когда х-*-—1, и задача перепишется так:
*—i
Теперь следует разделить числитель и знаменатель дроби на
У применить формулу A4,3).
Ответ, у.
306
Задача 14, 12 (для самостоятельного решения). Найти:
1) liml-t/* 2) lim 1 ~ ^*
2"'
Ответ. ,1) -|: 2) ~.
Задача 14, 13. Найти Нт-г-2дг
Решение. При х -*¦ 3 имеем
предел числителя:
lim Ba;-5)= 1;
предел знаменателя:
lim (л:2 - 7х + 12) = О
Теорема A4,5 п. с.) о пределе дроби неприменима. Рассмот-
рим обратную дробь — _"Г— . и ее предел при х ->- 3
л-2 —7л-+12 О Л
llm 9*-5 = т ^ °
(здесь теорема о пределе дроби применима, так как предел зна-
знаменателя 2х — 5 не равен нулю). Так как предел функции
—„ __~Г—равен 0, то эта функция при х->-3 бесконечно малая,
о у. с:
а потому, функция -г—=—г-н; при х -*¦ 3 — бесконечно большая,
2Х 5
и тогда ее предел lim-^—7 ¦ .» == °° (мы воспользовались тео-
ремой 14,4 пункт (б.).
Задача 14, 14 (для самостоятельного решения). Найти
,. хг + х + 1
lim , » ', о-
Ответ, со
Задача 14,15 (для самостоятельного решения). Найти
*>о
Ответ, п.
Задача 14, 22 (для самостоятельного решения). Найти
Указание. Произвести вычитание дробей.
Ответ, со.
Задача 14, 16 (для самостоятельного решения). Найти
J з\
-л- !-*•]•
liml
Ответ. —1.
U* 307
Ук а з а н и е. После приведений к общему знаменателю ока-
окажется, что при х -v — 1 числитель и знаменатель — функции бес-
бесконечно малые. Воспользоваться указанным на стр. 304 правилом.
ПЯТНАДЦАТОЕ. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений на нахождение предела
функции.
Решим несколько задач на нахождение предела дробно-ра-
дробно-рациональной функции при л:->-оо.;
Задача 15,1. Найти htn
3xi_ix_. i •
Решение. Для того чтобы можно было применить теорему
о пределе дроби, надо, чтобы числитель и знаменатель дроби
имели пределы и чтобы предел знаменателя не был равен нулю.
В данном случае эта теорема неприменима, так как пределы чис-
числителя и знаменателя дроби не существуют. При х -»- со и чис-
числитель, и знаменатель дроби функции бесконечно большие (см.
теоремы 14,4 о свойствах бесконечно больших функций. Рекомен-
Рекомендуется еще раз повторить эти теоремы). Значит, мы имеем дело
с отношением двух бесконечно больших функций. Об этом отно-
отношении, так же как и об отношении двух бесконечно малых
функций, ничего определенного без специального исследования
сказать нельзя. Для решения задачи следует применить прием,
знакомый из решения задачи 12,1 (полезно также возвратиться
к задаче 12,8): дроби разделить на высшую степень х, встречаю-
встречающуюся в членах дроби, а после этого перейти к пределу.
Итак,
Злг» + х 1
lim
lim
2 +
3 +
3 +
lim
lim
1
X2~
i
lim
lim
5
xs
1
л-3
2
3 '
так как при х-*- со — — величина бесконечно малая, а потому
и -j, ~з и -J—величины бесконечно малые (см. теоремы 14,4);
1 11 1 111 5 с 1
^^YT' ?=-77Т' а ^ = 5Р и пРеДелы этих величин
равны нулю, когда д;->-оо.
После деления числителя и знаменателя на х3 оказалось воз-
возможным применить теорему о пределе дроби, так как теперь
308
и числитель, и знаменатель дроби имеют пределы, равные соот-
соответственно 2 и 3, и предел знаменателя не равен нулю.
Для самостоятельного решения предлагается несколько ана-
аналогичных задач.
Задача 15,2 (для самостоятельного решения). Найти:
9\ \\т
' *4+ л-— 11
3 .г, ]_
5
Ответ. 1) 5; 2) 0; 3) со; 4) -|; 5)
Задача 15.3 (для самостоятельного решения). Найти
Указание. Произвести вычитание дробей.
Ответ, ^g.
Задача 15,4 (Для самостоятельного решения). Найти
lim
Х-юо
Ответ, -s-.
Задача 15,5 (для самостоятельного решения). Найти
Ответ. 16.
Решение остальных задач этого практического задания осно-
основано на применении теоремы:
При постоянном показателе степени можно переходить
к пределу в основании степени при условии, что предел основания
степени существует, т. е.
A5,1)
где k — постоянная величина (для случая, когда k -^ целое число,
мы этой теоремой пользовались неоднократно* так как она прямо
следует из теоремы о пределе произведения),
309
Из формулы A5,1) следует, что при любом нечетном т всегда
lira у77ф= У\\т!(х). A5,2)
х-ю хч-а
Если же и-четное число, то эта формула верна только
тогда, когда функция f (*) —неотрицательна, т. е. когда f(x) > 0.
Выполним сначала ряд простых упражнений на применение
этой теоремы.
Задача 15,6. Найти: 1) lim Ух; lim Ух.
X-+Z7 х-*—243
Решение. На основании формулы A5,2) имеем:
хч-27
2) lim ух = У lim х = f-243 = -3.
*.*_243 х-*—243
Задача 15,7. Найти lim ]/2*2 + 7.
Решение, lim]/2*2 + 7 = /limB*2 + 7) = ]/2 • 22 + 7 =
2 2
Задача 15,8. Найти при нечетном /п
1)
; 2) lim-Ц; З) W
т. е. при х ->¦ оо функция —- бесконечно мала;
1
3) lim у х — lim —г— = оо,
Ш/
ух
так как по результатам второго примера этой задачи при
х -*¦ оо функция —- бесконечно мала, потому функция Ух —
бесконечно велика.
Задача 15,9. Найти lim L±±i—L.
х-+0 Х
Решение. Когда х -*- 0, числитель и знаменатель имеют
своим пределом нуль, а потому они бесконечно малы:
lim (У\+х — 1) =-- l^lim(l+jc) - 1 =--• 1 — 1 = 0.
Для того чтобы решить вопрос о пределе их отношения, пере-
перенесем иррациональность в знаменатель, умножив для этого чис-
числитель и знаменатель дроби на (]/l + * + 1). Будем иметь
Так как * ->¦ 0, не становясь равным нулю, то деление на к
числителя и знаменателя дроби возможно.
При решении задачи мы вместо предела функции f (х) =
i/l i * 1 1
— -—— отыскали предел функции у (х)= —z ; здесь
х V1+*+1
должен быть затронут вопрос о тождественности этих функций
(подобно тому как этот вопрос возник при решении задачи 14,5).
О функциях <? (х) и / (х) мы можем сказать, что они тождест-
тождественны (хфО).
Таким образом, замена функции f(x) при отыскании предела
функцией <р (х) является законной.
При отыскании предела дроби, содержащей иррациональные
выражения, в большом числе случаев приходится с помощью
преобразований переходить от заданной функции к другой функ-
функции, и у учащегося должен возникнуть вопрос о тождественности
заданной функции и той, которая получается в результате пре-
преобразований. Во всех дальнейших примерах исследованием этого
вопроса мы заниматься не будем, предоставляя это читателю.
¦ Теперь, после решения этой задачи, укажем правило для ре-
решения задач, в которых требуется определить предел дроби, со-
содержащей иррациональные выражения в случае, когда ее числи-
числитель и знаменатель — бесконечно малые функции, т. е. когда их
пределы равны нулю.
Правило. Чтобы найти предел дроби, содержащей иррацио-
иррациональные выражения в случае, когда предел и числителя, и зна-
знаменателя дроби равен нулю, надо перенести иррациональность
из числителя в знаменатель или из знаменателя в числитель
и после этого сделать необходимые упрощения, (приведение по-
подобных членов, сокращение и т. д.) и перейти к пределу.
Задача 15, 10. Найти lim Vx%' + *'~3 .
Решение. При х -*- 2 числитель и знаменатель дроби имеют
предел, равный нулю. Перенесем иррациональность в знамена-
знаменатель, для чего умножим числитель и знаменатель на У хг -f 5 + 3.
311
Получим
lim!
Л--2
U-
+ 5 + 3)
= lim
*—Г " — а _ i: * ~ t
¦ 2) (/?П+~5 + 3) ~ х^(х-Ч){Ух^+~Ъ + Ъ
x^t (л--2)(/
_ 2 + 2 _ J
Задача 15,11 (для самостоятельного решения). Найти пре-
пределы:
3)
4) lim
Л-+2
У 5=1*— 2
1— х
Ответ. 1I; 2) 1; 3) |; 4) 1;
Задача 15,12. Найти И
-/2, + ю
К4а-+13-/л- + 22
Решение. При х ->- 3 числитель и знаменатель дроби имеют!
предел, равный нулю. В этой задаче придется сначала числитель,
и знаменатель дроби умножить на
10, а по-Ц
том на У~4х+ 13 + Ух+ 22 или сразу умножить числитель;
и знаменатель дроби на (/3* 4-7 4- V%x + Щ (У 4* + 13 4-|
4- Ух + 22). Используя это указание, получаем1
lim
13 — /л-+ 22
= lim
(/4л- + 13-/* + 22) (УЪх + 7 + /2а- + 10)(/4л- + 13 + /* +22)
- Нт (Зл- + 7 - 2л- - 10) (/4Т+ТЗ"+ /7+22) =
х-+з Dа- + 13 — х — 22) (/зТ+~7 + /2а-+10)
= lim^
З(
(лг~
im
->3 (Зл- —9)(/Зл-
—3)(/Зл- + 7+/2л-+10)
-lim
к~г 3(/За- + 7 + /2а-+10) 12
Задача 15,13 (для самостоятельного решения). Найти Пре-
Пределы:
1)
2) lim
312
4)
5 — 3
3
Ответ. 1) ?; 2H; 3) ^; 4) »
Указание. В третьем примере одним из множителей чис-
числителя будет Зд:2 — х — 44. Корни этого квадратного трехчлена
хх = 4; Хг — — -д-, вследствие чего Зл:2 — * — 44 = 3 (* — 4) (х + ~).
Задача 15,14. Найти lim-
х — 7 '
Решение. Здесь и предел числителя, и предел знаменателя
равен нулю. Перенесем иррациональность из числителя в знаме-
знаменатель. Воспользуемся известной формулой алгебры (а — Ь) (а2 +
+¦ ab +Ь2) — а3 + Ь3. Положим а = у/~х — 6, b'— 1. Значит, для
того, чтобы получить в числителе разность кубов, надо его
умножить на \/ (х — бJ -f уОс — 6 + 1. Умножая и знаменатель
на эту величину, получаем
= lim
_ 6>в -}- ^ — 6 + 1)
х~7
Задача 15,15
решения). Найти
Ответ.
Задача
Ответ.
Задача
—
15,
—
15,
9 *
16
17
lim
(ДЛЯ
х-*\
(ДЛЯ
lim
самостоятельного решения). Найти
л- — 1 — У Ъх — 2
/4Т=~3-1
самостоятельного решения). Найти
7л- -
Ответ.
21
313
Теперь мы рассмотрим задачи, в которых требуется опреде-
определить предел функции, содержащей корни в том Случае, когда
аргумент стремится к оо или к ± со.
Задача 15,18. Найти, lim (Ух — 2 — Ух).
Решение. Здесь непосредственно теорема 14,5 не может
быть применена, так как при х -»--f-oo пределы слагаемых не сущест-
существуют: мы имеем дело с разностью двух бесконечно больших
величин, о которой ничего определенного без специального иссле-
исследования сказать нельзя.
Умножим и разделим данное выражение на сопряженное с ним
и получим
lim (Ух
Х-г+е*
=¦- lim
так как при х ->¦ + оо знаменатель дроби, стоящей под знаком
предела, есть функция бесконечно большая (см. задачу 15,8C)),
а потому дробь г т= есть величина бесконечно малая,
ух—2+ух
а ее произведение на —2 есть также бесконечно малая величина.
Задача 15,19. Найти lim х (У х2 + 1 — х). Когда je-»--f-oo,
выражение, стоящее в скобках, есть разность двух бесконечно
больших величин, о которой без специального исследования
нельзя сказать ничего определенного. Умножим и разделим функ-
функцию, стоящую под знаком предела, на выражение, сопряженное
с Ух2 + 1 — х, т. е. на У х2 + 1 + х, и получим
так как lim -^ = 0.
х-*+™ х
Теперь рассмотрим случай, когда х -»— оо. Выражение, стоящее
в скобках, им%ет в этом случае положительное значение и неогра-
неограниченно возрастает по абсолютной величине, множитель же х,
стоящий за скобкой, неограниченно возрастает по абсолютной вели-
величине, но сохраняет отрицательное значение. Поэтому все выражение
314
x(Vx2 -f- 1 —x) при х -*¦ — oo неограниченно возрастает по абсо-
абсолютной величине, сохраняя отрицательное значение и
lim х(Ух2+ 1 — х) = — оо.
Задача 15,20 (для самостоятельного решения). Найти
lim (|/x2 + 4 — Vx% — 4).
Ответ. При л: ->- + °° и при х -*• — оо искомый предел равен 0.
]/ ха 4- 4
Задача 15,21. Найти lim -—~-.
Решение. I) Рассмотрим сначала случай х-*- -\-оо:
T+T.
Так как х > 0 при дг -»--)- оо, а мы рассматриваем арифметическое
значение корня, то j/P = + х и J/*2 + 4 = -f х |/ 1 + т ,
а потому lim к Г1" =. lim —^ r-= lim ^-= 1.
¦*"
2) Пусть х -v — оо. По-прежнему |/хМ-~4 = ]/'Р 1/ 1 + ^ , но
теперь Yip = —х, так как х < 0, а мы рассматриваем ариф-
арифметическое значение корня, и У~х* + 4 = — х 1/ 1 4- -$ , а
lim Ц^= lim —f jT" = - lim -1 ^-=-1.
Задача 15,22 (для самостоятельного решения). Найти
lim (Vx2 + x+ 1 -Ул:2-л:+1).
*-±и _
Указание. Учесть, что при х > 0 имеем )Л:2 = х, а при х < 0
тот же "|/р = —х.
Ответ. При х-*--\-со искомый предел равен +1» а при
х-*-—оо искомый предел равен —1.
Задача 15,23 (для самостоятельного решения). Найти
lim {Ух2 + 2 — х).
Ответ. 0 при х-*- -)-со; + оо при х -*- — оо.
315
Задача 15,24 (для самостоятельного решения). Найти 1
lim[(x + 1K -(х- IK].
Указание. Выражение, стоящее под знаком предела, умно-
1 1 1 ¦ ±
жить и разделить на (к+\K + (х + IK • (х — IK-\-(х—IK ,
чтобы получить в числителе разность - кубов. После упрощении >
под знаком предела будет находиться выражение
4*-
Знаменатель дроби представить в виде
и сократить дробь на х,
Ответ. 0.
Задача 15,25 (для самостоятельного решения). Найти
1 1
lim [д;3 -(л;2- IK].
Указание. Выражение, стоящее-под знаком предела, умно-)
1. — 1 — I
жить и разделить на *3 + л:3 (х2 — 1K + (х2 — 1) 3 и полученную %
дробь сократить на а;2. ]
О т в е т. 0. I
ШЕСТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Определение пределов тригонометрических функций
н упражнения на использование предела lim 5!5_? .
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
При определении предела тригонометрической функции можно
независимую переменную заменить ее предельным значением, если
оно принадлежит области существования функции:
limi sin x = sin a\ limcosjc= cos a; limtg*=tga;
x-*a x-*a x-*a
lim ctg x = ctg a; lim sec x —• sec a; lim cosec x = cosec a.
x-*a хч-а х-*а
316
Примеры:
1) 11m sin л: = sin 5-== y; 4) lim tgx = tg~ == 1.
2) lim sin л: = sinO = 0; 5) limtg*— не существует, так
«x-0 x
3) limcosx = cosO = 1; *"
0
как tg-н- нельзя приписать ника-
никакого числового значения.
Задача 16,1. Найти lim ' ~s8inAf.
х C0S Х
Х~* 2"
Решение. На основании приведенного выше правила для
отыскания предела тригонометрических функций lim sin * =
* X
"Sin-|-=1, а потому, когда *-»-у, 1—sin*-*-0; lim cos2 * =
— cos2 y — О И мы имеем дело с отношением двух бесконечно
малых функций. Требуется, как уже хорошо известно чита-
читателю,, специальное исследование, чтобы решить вопрос о пре-
пределе. Зная, что cos2* =1 — sin2* =¦ A — sin*)(l + sin*), имеем
= lim г—,—• — =
x l +smx
Задача 16,2 (для самостоятельного решения). Найти
i
I/
Ответ.
Задача 16,3 (для самостоятельного решения). Найти:
1 — 4 sin2 х
lim
cos Здг
Указание. Под знаком предела находится при *->¦ -g-
отношение двух бесконечно малых функций. Следует числитель
разложить на множители:
317
1 — 4 sin2 * = 4 Ц- — sin2 xj-= 4 (~ — sin*j (у -f sin A
Знаменатель дроби
/ 3 \
cos Зх — 4 cos3 х — 3 cos x = 4 cos x I cos2 x — -jJ =
=-- 4cos*(cos*—^j-IIcosa; + -5-1.
Если под знаком предела имеется сумма или разность три-
тригонометрических функций, часто бывает полезным преобразовать
их в произведение по известным формулам тригонометрии.
Учесть, что ~ = sin 30°; ^ = cos 309.
ОТВет. -
Задача 16,4. Найти lim Vte*
х-*а y^sin x — у sin a
Решение. При *->-а и числитель, и знаменатель дроби —
функции бесконечно малые:
lim (V^tgjc — V^tga) = lim Ktg^ — lim V^tga = ]/limtg-V —
limx- "|/tg« =
Аналогичные рассуждения провести и по отношению к знаме-
знаменателю. Имеем
3
f/sin д: —
a • sin x
sm* a) =
sin x
— *g «)
+ ^/"sin x ¦ sin a + i^sTn^T) _
a) (sin д: — sin a)
x '
- —a)
VW* + ViT*
cos ^ cos a 2 cos
t-sln —
* а Ф Bk ~\-])-^-, где А —любое целое число. Если не сделать этой ого-
оговорки, то, например, при a = ~ будет tga = tg-H-, а tg-^- не имеет число-
числового смысла.
318
n . X — a X — a
2 sin —?;— cos —=r—
COS AT COS a 2 COS ——- sin —~
2 2/tga COS8 a'
Задача 16,5 (для самостоятельного решения). Найти
~ • 2
Ответ, -о- -
sin х — У sin a
При решении остальных задач этого практического занятия
следует иметь в виду, что
lims-^=l. A6,1)
*-о х
Задача 16,6. Найти lim , (k — величина постоянная).
х-*0 х
Решение. Иногда при отыскании предела полезно произвести
замену переменной с тем, чтобы упростить отыскание предела
и использовать уже известные пределы.
Если под знаком предела делается замена переменной, то все
величины, входящие под знак предела должны быть выражены
через эту новую переменную, и из равенства, выражающего зави-
зависимость между старой переменной и новой, должен быть опре-
определен предел новой переменной.
Для решения предложенной задачи сделаем такую подста-
подстановку: kx = у. Из этого равенства следует, что у -*- 0, когда х ->- О,
у т 1- sin kx ,. sin и . • ksiny ,,• sin w ,
а х = -f-. Тогда lim = lim—- = hm = k lim—- ~ k,
X-+0- x ' y-+0 jL_ y-+Q ¦ У у~*0 У
k
так как lim 5iM == i.
У-+0 У
Следует запомнить, что
lim
х-+0
Задача 16,7. Найти li
l^ = fe. A6,2)
х
sinfey jjm sin kx
Решение, lim ^= lim JL- = !z°* = * .
x_osmlx ^n sin Ix ,.m sin Ix I
x x^o x
Мы разделили числитель и знаменатель дроби на х. Это
можно было сделать, так как значение х = 0 не должно рас-
319
сматриваться. При вычислении предела числителя и знаменателя
последней дроби использована формула A6
Задача 16,8 (для самостоятельного решения). Найти lim ¦¦¦- - .
О т в е т. -g-. . /
Задача 16,9. Найти lim^. /
л-0 х ¦
г. ,. te Лдг , ¦ sin kx/ .. sxftkx s. 1
Решение, lin-s—= tim—J=\\m lim—r =
J *_L
lim cos 6* "" cos(lim/fejr) ~ cosO
Задача 16,10 (для самостоятельного решения). Найти П
Указание. Числитель и знаменатель дроби разделить на х
и перейти к пределу. Использовать решение предыдущей задачи.
Ответ. ~.
Задача 16,11 (для самостоятельного решения). Найти lim
sin* ах
Указание. Дробь, стоящую под знаком предела, записать
так:
sin' ax sin ax sin ax
х* ~ х х
Использовать теорему о пределе произведения*.
Ответ, а2.
Задача 16,12. Найти
Х-+0
х
Решение. При дс -»- 0 числитель и знаменатель дроби — беско-
бесконечно малые функции. Воспользуемся тем, что 1— cosmx =
= 2sin2— и тогда
тх . тх .' тх
-^- Sin -rr- Sin-рг
^2 1
|мы использовали формулу A6,2). В нашем случае k = ~\
Задача 16,13. Найти lim (secx — tg*).
Решение. При х -*- ~ функции sec* и \gx — бесконечно
большие функции; таким образом, под знаком предела находится
sln ахI = (limsln axI =a2
X I \x-rO X ]
320
разность двух бесконечно больших функций. Теорему A4,5а
о пределе разности ^применить нельзя, так как не существует
конечных пределов каждой из функций sec* и tgjc при х-*-^ .
Преобразуем эту разность так:
, 1__ sii\A- _ 1 — sin x _ A — sin x)(l -f sin x)
SeC*~tg coT*~~cosS," cos* ~ cos a-A-f sin*-) ~
] ^— Sin2*" _ \ COS8* COS*
~ cos x(l -f- sin *) ~ cbs*.(l -f- sin дг) ~~ 1 -f sin x '
После этого получаем '\
Хт*~2 Х "*.Т I
К последней дроби можно было применить теорему о пределе
дроби, так как предел знаменателя равен 2, а числитель дроби
имеет конечный предел 0.
Задача 16, 14 (для самостоятельного решения). Найти
,. cos kx — cos/дг
lim 7% .
Хч-0 *
Указание. Числитель дроби равен — 2sin —jpjc-sin -^- x;
использовать также формулу A6,2).
„ ' /а — &
Ответ. —g—.
Задача 16, 15 (для самостоятельного решения). Найти lim^ctg*.
Указание. При х->-0 функция ctgjc —бесконечно большая,
ах — величина бесконечно малая. Значит, мы имеем произведе-
произведение функции бесконечно большой на величину бесконечно малую
и требуется специальное исследование, чтобы определить предел
этого произведения.
лг , cos дг , cos* тт
Учесть, что ctgjc = -:—-, а поэтому х ctg х — х -.—. На осно-
sin х ' sin X
вании формулы A6, 1) lim-Д— = 1.
osmjr
Ответ 1.
Задача 16, 16 (для самостоятельного решения). Найти
lim sin (° + у) ~sin (g ~ ¦*•)
х -+0 х
Указание, sin (а + дг) — sin (a~ x)~2 cos a sin x.
Ответ. 2 cos а.
Задача 16, 17 (для самостоятельного решения). Найти
!4
lim I—
I— 2 cos л-
32J
Указание. Представить числитель в виде
2 sin D- —-г-
а знаменатель
1 — 2 cos х = 21 -j — cos x) ==,2 (cos ~ — cos x) =
Сократить дробь и перейти к пределу
Ответ. -у=.
Задача 16, 18. Найти lim(l — х) tg ^.
д; -> 1 z
Решение. При дг-*-1 не существует предела tgy, а потому
нельзя применить теорему A4, 5 е) о пределе произведения. Сде-
Сделаем в нашем примере подстановку: 1—х — у. Когда х-*-1, то
новая переменная у-*-0, так как limy = lim(I — х) — 0. Если
*-.! х -<¦ 1
1 —х = у, то х = 1 —г/; выражение, стоящее под знаком предела,
перепишется так:
к
COS "тр U
sm -g- (/ sin у у
поэтому
lim A — х) tg^ = lim —-— lim cos —у =
= lim_L_==>2
У y->0\ ,y
Задача 16, 19 (для самостоятельного решения). Найти
,. tg дг — sin дг
lim ~^ •
sin дг
sin дг
Указание. 1) tgje = . Преобразовать дробь к виду
COS X
— sin дг
Ig x — sin дг cos дг sin дг A—cos*) _ 1 sin дг 1 — cosx
x3 F ~ xs cos x " cosT x Ja
О т в е т. y •
322
' \
\
\
Задача 16, 20 (для самостоятельного решения). Найти
\
cos~-\sin ~ V'TTlgx- /l-tg*
1) lim 2cos^ 2; 2) lim .+ sin; g~'
% cos дг , x _ 0
* "" 2
Указания. 1) В первом примере умножить числитель и
знаменатель дроби на cos у Ц- sin ~, сократить дробь и перейти
к пределу. 2) Во втором примере перенести иррациональность в
знаменатель, сократить дробь на sin* и перейти к пределу.
Ответ. 1) ^?; 2) 1.
Задача 16,21 (для самостоятельного решения). Найти
к ^, о1Х -г s'n йх
Ответ. 1) --1; 2) 1; 3) i-.
Указание. В первом примере числитель и знаменатель дроби
разделить на х, во втором положить arcsin.* = z, в третьем при-
примере 1 + cos™ = 2cos2 ~5^H
к 2
~; tgvJc = 5^H .
2 ' ь cosiur
СЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Число е.
Это практическое занятие отводится для упражнений, связан-
связанных с числом е.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
= e; A7,1)
A7,2)
lim (I + kx) " = eft. A7,4)
о
о
Нам придется также пользоваться теоремой о переходе к пре-
пределу в показателе степени при постоянном основании. Эта тео-
теорема формулируется так:
323
Если существует \\mf(x), то при постоянном Ь имеет место
х -г а ¦
формула
limf (x) ,
Ь / A7,5)
Короче (но менее точно): при постоянном основании можно
переходить к пределу в показателе Степени.
При отыскании пределов вида/lim [/(дг)]*(JC) в случае, когда
i ->¦ а
существуют конечные пределы \\mf(x) и timcp(jc), имеет место
х *¦ а х •*¦ а
формула
lim cp (*)
lim [/(*)]*<*> = [Нт/(*)]*-» . A7,6)
х — а х -+ а
Замечание. В формуле A7,6) а может обозначить и число,
И ОДИН ИЗ СИМВОЛОВ со, + со И — со.
Если в этой формуле lim<$>(*)= ± со, a lim/(я) конечен, но
х •* а X -<¦ а
не равен 1, то вопрос о пределе lim [/ (x)]f <*> затруднений не вы-
х ч- а
зывает (см. например, задачу 17,10). Случай, когда lim/ (лс) = 1,
х —¦ а
a lim <p (jc) = ± со, рассмотрен в задачах 17,13—17,25, а соответ-
ствующие указания даны на стр. 326.
Сначала мы выполним упражнения, связанные с применением
формулы A7,5).
2х
Задача 17, I. Найти lim 4
х -2
2х ,. 2х 2-2 _?
Решение, lim 4*^* = Ах™2*+Х = 4Fpr = 4 3 =
Х-+2
Зх
Задача 17,2. Найти lim 2*+2.
з
Зх lim JL lim _2_
Решение, lim 2Х+2 = 2^^х+2= 2*4" х = 23 = 8.
Х-+ оо
Y2+X-2
Задача 17,3 Найти lim а х~2 (а > 0).
Х-+2
lim
W lim + lim li
Решение, lima *~2 = ax^2 "~2 = а*~2<*-2>(/2+*+2)=
lim-
1
4 г-
324
Задача 17,4 \ (для самостоятельного решения). Найти
\
\ iim 2 2
Указание. Ввести замену переменной: положить-=- — я =*= г.
При л -> -?- переменная г-*-0. Перейти к пределу в показателе
степени.
О'твет. 2.
/ 1V
Задача 17,5. Найти lim 1 — — .
и»\ хI ¦
Решение. Полагая в формуле A7,3) k~ — 1, получим
()'
Задача 17,6 (для самостоятельного решения). Найти:
-~)Х; 2) lim(l + ^)X; 3) li
4) lim (I + xfx.
х-0
Ответ. На основании формулы A7,3) получаем:
JL ' ч
1) е-*; 2) е3;
на основании формулы A7,4):
j_
3) е2; 4) е*\
Задача 17.7 (для самостоятельного решения). Найти
Ответ. ех (здесь п — величина переменная, a jc — постоянная).
Задача 17,8 Найти 1) lim(l + 5 tg3хK с'в!*;
2) lim(l +2sinxKcosec*.
х->0
Решение. 1) Для того чтобы решение первого примера
свести к известной формуле A7,4), сделаем замену переменной,
положив tg2лс = г.
Теперь следует и ctg2*, стоящий в показателе степени, выра-
выразить через г. Так как ctg2x= t-j-, то ctg2v= —. Таким обра-
зом, и ctg2 л; выражен через новую переменную. Осталось решить
вопрос о пределе новой переменной, когда старая переменная х
стремится к нулю. Из равенства tg2*~2 следует, что lim г —
х-*0
325
= lim tg2jc = 0, а потому новая переменная г-*-0, когда
Записи расположатся так:
= lim A + 5гKт= [Mm A + 5г)т]3=(е5
применить формулу
A7,4).
2) При решении второго примера сделать подстановку sinjc=2.
Из этого равенства следует, что новая переменная г -*¦ 0, когда
*-*¦().
Ответ. ев.
Теперь выполним ряд упражнений, связанных с использова-
использованием формулы A7,6).
х
11 V+1
Задача 17,9. Найти lim I-,)
Решение. На основании формулы A7,6)
lim
x-t-u i \
lim A
поэтому
lim -Jr == О1 = 0.
Задача 17,10 (для самостоятельного решения). Найти
lim
х+\^х
Ответ. 0 (воспользоваться формулой A7,6); lim 0 , q = -Л.
Задача 17,11 (для самостоятельного решения). Найти
2Х-1
4 v ч 2
Ответ. -2g (предел основания степени равен -g-, а предел
показателя степени равен 2).
Задача 17,12 (для- самостоятельного решения). Найти
2»+5
Ответ, -д- (воспользоваться формулой A7,6)).
В формуле A7,6) мы исключили из рассмотрения случай,
когда lim <р (х) — ± оо, a lim / (х) =-- 1 (см. замечание к этой формуле).
к—-а х-+а
Теперь выполним несколько упражнений, связанных с отыска-
отысканием lim [f (x)]f w в случае, когда lim/(x) — 1, a lirnf (х) = +оо.
326
В этом случае формула A7,6) неприменима, так как выражение
1°° не имеет смысла («неопределенность» вида 1"). Существует
общий прием для отыскания предела в этом случае. Прием этот
состоит в следующем: функцию / (х) представляют в виде f (х) =
= 1 + [/(•*)— П- Показатель степени <р (х) запишем в виде:
1
и тогда
Mm [/(*)]*<*> = lim [l + (f(*)-l)]fM-'
1
== {lim [1 + (f (x) — 1)]M*)-' }**a . A7,7)
х-» а
Сделаем подстановку: f (л;) — 1=2. Так как по предположению
при х-+-а f (х)-*-I, то lim [f{x) — 1] = 0, т. е. г -*¦ 0, когда
л: -> а. На основании предыдущего равенства
1 lim if W- l)?(x)
Следует иметь в виду, что а может быть и числом и одним
ИЗ СИМВОЛОВ оо, -f- оо ИЛИ — оо.
Теперь все дело сведется к вычислению lim [/(я) — 1] <?(х).
\ x-ta
Это общее указание использовано при решении задач 17,20—
17,25.
Этим же указанием можно воспользоваться и при решении
задач 17,13—17,19. Однако в этих задачах использование общего
приема приведет к ненужным осложнениям и мы их решим проще.
Задача 17,13. Найти Iifc)
у I I
Решение. Здесь основание степени / (х) — -——г -*- 1, когда
х-+са, а показатель степени л:-»-оо. Здесь, таким образом,
имеет место рассматриваемый случай «неопределенности» вида 1".
Покажем, что применение общего приема, указанного выше,
приведет к более сложным выкладкам.
327
У нас
X — 1 X—\'
Таким образом,
а потому показатель степени должен быть представлен на осно-
основании формулы A7,7) так:
х— 1 2
X о v 1 '
id Л ~~^ 1
и теперь
х—\ 2 зс—1 2*
Теперь ясно, что общий прием оказался сложнее.
Задача 17,14 (для самостоятельного решения). Найти
Указание. Числитель и знаменатель дроби разделить на
2х, применить теорему о пределе дроби и формулу A7,3). В чис-
числителе в этой формуле k = — у, в знаменателе k = 2.
Ответ.
Задача 17,15. Найти lim ^^Н
Решение. Разделив числитель и знаменатель дроби на х,
получим
G \2х+4 / 7\2* / 7\*
1 + т) Лт»A + т) ЛтA+т)
lim 1 + - lim l+~
Пт|г-т-н1 =Нт
К-ч-оо
lim
— • 1
— (е5J е10
так как lim f 1 +-)*= 1 и lim f 1 + -Y= 1.
328
Можно было бы сразу записать
+ 5/ ~\x + 5J U + 5/
и, учитывая, что предел второго сомножителя
отыскивать только предел первого множителя liml ]Г-1 , что
упростило бы записи.
Задача 17,16 (для самостоятельного решения). Найти
Указание. Числитель и знаменатель дроби разделить на 3jc
и перейти к пределу. Для упрощения записей полезно предста-
представить выражение, стоящее под знаком предела, в виде
Зх + 4\*/Зг + 4\3
Зх + 5/ \3х -f 5/
и учесть, что предел второго сомножителя равен 1.
Ответ, е 3 .
Задача 17,17 (для самостоятельного ч решения). Найти
- fo-l\to+2
Указание.
Учесть, что предел второго сомножителя равен 1, а для опре-
определения предела первого сомножителя числитель и знаменатель
дроби нужно разделить на Ах и перейти к пределу в числителе
и знаменателе дроби: ± ~.
Ответ. е~3.
/ о, \Х+3
Задача 17,18. Найти lim U-^ .
v , Зх \х+3 I Зх VI Зх
Указание. ' ' ' ' '
+ 2/ •
Предел второго сомножителя равен 1, а при определении пре-
предела первого сомножителя нужно числитель и знаменатель дроби
разделить на Зх.
_ 2
Ответ, е "э".
329
Задача 17,19 (для самостоятельного решения). Найти
х \2*+3
)
Ответ, е2.
Задача 17,20. Найти lim f** +3 2х f Т-
х-к» \ х' + а. /
Решение. Воспользуемся указаниями стр. 326. Здесь
** + 2* + 2
*2 + 3 '
Перепишем наш пример так:
lim Iх + Х7 I = Hm11 + Г "t „ - 1) = lim (l+Ц1
У нас / {x) — 1 = y, , з, а потому ^,_ } = **—l' Ha 0CH0"
вании формулы A7,7) показатель степени ^ = ^ j^ -x,~ U,
а потому
/ 2л-— Лх
1
)
= ех— +3
так как
= е, a lim тпр" = 2
(если j^g = г, то ^i-j = — , z -*¦ 0, когда ¦*-»¦ оо и
lim (l + J^r' = lim(l + г)т= в).
Задача 17,21 (для самостоятельного решения). Найти
+ х +
330
Указание (см. указание на стр. 326).
* + *±2. ftx) i=
+ x
показатель степени
9(х) зх1 + +
(см. пояснения к предыдущей задаче).
Ответ, е3.
1
Задача 17,22. Найти lim (?-
Решение. Предел lim ^~ = 1, а показатель степени j-—
неограниченно возрастает по абсолютной величине, когда х-*-а.
Решение примера проведем на основании указаний стр. 326. У нас
„ х -\- а . х—а
2 cos —i— sin —=—
f , . sin л- г, ч , sin x . sin x — sin a22
1slna Ша
На основании формулы A7,7) показатель степени запишем
в виде
. x-\- a . x — a
2 cos —я— sin —ft- i
sin a 2 2 1
x — a n x 4- a . x—a sin a x — a
2 cos —¦— sin —=—
и тогда
X -4- a X a\o *+a x~a sin a x—a
2 cos —k~ sin —^- \2 cos ~T sin ~T
|
1 * I 1
= lim 1 1
x-a ^ Sina
, 2 cos —i-sin—r— ,
sin a "i ,, 2 2 1
lim -
2 cos
liu»|i + ^^
lim ;
= e = cctg a
331
sin a
2cos —k— sin —=— \2cos —*-sln "IT
та как lim I 1 -\ -. J
2 cos —я— sin =—
2 l
. .r — a
Sin
2 л- -4- a Sin 2~~ 2 1
= -— lim cos -?- lim = -— cosa ¦ -^ = ctga.
S!n a x-*a ^ ж^.в л- — a sin a 2 ь
2
Объяснение: 1) постоянная величина ^-^ вынесена за знак
предела;
2)
х-*а Z Z
. х — а
sin—g—
3) Для вычисления предела lim——— применена подста-
х-*а х "
новка х — а = z и г -*-0, когда х-*-а.
. х — а . г
sin—g— sin у j
lim = lim = -я-
t „ х — а _ п г 2
на основании формулы A6,2). ч
I \т
Задача 17,23. Найти lim cos — .
Решение. Здесь опять-таки следует использовать указания
стр. 326, так как f (т) — cos — , причем х следует рассматривать
как величину постоянную. Предел
lim f (m) = lim cos — = 1,
а показатель степени т неограниченно возрастает по абсолютной
величине. Составим
Показатель степени преобразуем по формуле A7,7):
? {т) = т = —Ц_ (-2 sin* {A
2т
и тогда
332
cos— = lim I + cos—— 1 =
ml „,-+«, l \ tn /J
i / x \
I —2 sina r— \m
I 2 sin2 — v '
I 2m
x
~2sm22^J
= lim
«-«¦eo
Sin2 75 Sin т;—
так как lim m sin2 ~—= lim—=— = limsin^— hm
m
Если т -v со, то ~ -v 0 и sin -y- -*- 0.
sin -=—
Для вычисления второго предела Hm —:— сделаем подста-
т
новку ~ == z, тогда г -»- 0, когда т-*- со а — = —, и полу-
получим, учитывая, что х — величина постоянная
sin =—
• . 2т ,. sin г х ... sin z jr. . лс
hm —j— = lim -x- = -s- hm -— = T • 1 = -y
m x
и, значит,
limmsin2^ = 0 • ~ = 0, a e«= 1.
Задача 17,24 (для самостоятельного решения). Найти
1
1\тх1~х.
Ответ. е~г.
Задача 17,25 (для самостоятельного решения). Найти
lim (cosx)cts*x.
1_
Ответ, е 2.
ВОСЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Вычисление пределов выражений, содержащих лога-
логарифмы и показательные функции.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Теорема. Если существует предел \\mf(x) = A и этот пре-
4 х-+а
дел положителен (А > 0), то
lim[logbf(x)] - log* [Hm(/(х)] A8,1)
x-hj хч-a
333
Короче (но менее точно): можно переходить к пределу под зна-
знаком логарифма.
Замечание. Требование теоремы о • том, что \\mf(x) = A
х-*а
должен быть положительным, связано с тем, что число А в пра-
правой части формулы A8,1) стоит под знаком логарифма, а лога-
логарифмическая функция определена только для положительных
значений аргумента.
Между десятичными и натуральными логарифмами сущест-
существует связь, выражаемая формулой
A8,2)
где М — модуль перехода: М = lg е = т—^ = 0,43 429.
Сначала выполним упражнения на непосредственное примене-
применение формулы A8,1).
Задача 18,1. Найти lim lg(*-f 1).
хч-9
Решение. На основании формулы A8,1)
+ 1I = lg Him (*+ 1I = lg 10=1.
Задача 18,2. Найти lim In *'+.*_* 5.
Решение. На основании формулы A8,1) можно записать,
что
Г j J_ j
... , .. , г ....... г ^ ^^
числитель и знамена-
знаменатель разделены иа хг
= 1п1=0.
Задача 18,3. Найти lim In ¦ у ¦х~—j—\-
Решение. Воспользуемся опять формулой A8,1):
lim [in ,JLZ4 ,-] = In [lim ;_1Г -—=1 =
=^ In lim —¦ _— ¦ -—-—=— n=
i I i * \X — 4) (y X —p 4-T— / 8) < r <. ,-¦ / ;—7
= In limv 4.4 — 8 = ^ (К ^ + 4 -
= In 2/8 = In 4/2.
Перейдем теперь к вычислению пределов, которые играют
важную роль в дифференциальном исчислении.
334
Задача 18,4. Найти limlnA+Jf).
дг-0 •*¦
Решение. lim'nA + х) = lim j-ln(l + *) ~ Hm [ln(l+*P 1=
= lnflim(l + *)
Результатом этой задачи нам придется часто пользоваться, а
потому для ссылок запишем его отдельно:
i0±)==L A8,3)
Получите самостоятельно более общий результат:
lim -—±-^ = a. A8,3a)
Задача 18,5. Найти lima ~ , считая, что а — положительная
постоянная величина,.не равная 1.
Решение. Сделаем подстановку:
ах — 1 = г. A8,4)
На основании указания стр. 2Ц9 мы должны: 1) величину х,
стоящую под знаком предела, выразить через г и 2) определить
предел новой переменной г, когда старая переменная х-*¦ 0.
Из подстановки A8,4) следует, чтоа* = 1-fz, х \па = In A + z);
•, a lim 2 = lim {ax — 1) = 0, т. е. при х ->- 0 и z -+¦ 0.
"' ' _i = lim in a =- Ыа -
Vo
In a, г г-*о г
= 1па, так как на основании A8,3) предел знаменателя равен 1,
а предел limlna = lna, ибо а, а вместе с ним In а —величина
постоянная. Итак,
lim^-^ = lna. A8,5)
1 — 1
Если в формуле A8,5) взять х — — , то ах = а у , у = — и
у х
и
= со, и тогда lim
х г/-» L
и
lim г/ = lim— = со, и тогда lim ~ == In а, т. е.
о х L
х-+о г/ L
У
— 1) = \па. A8.6)
335
Если у->-оэ, принимая целые и положительные значения, то
это равенство можно переписать так:
[im п<Уа— 1)= In а. A8,7)
П-+оо
Задача 18,6. Найти
Решение. Решение этой задачи потребует некоторых искус-
искусственных преобразований для того, чтобы можно было использо-
использовать результаты двух предыдущих задач. Выражение, стоящее
под знаком предела, умножим и разделим на х:
х) х _ In A + лг) 1 тяк ' о2* _ о*
^7 ТЭК КЭК д ~У>
и теперь
lim'nA + x) -\\mln{l+x) ' -L
Использовать Использовать
формулу A8,3) формулу A8,5)
Задача 18,7 (для самостоятельного решения). Найти lim
3g-l 3g-ltg* п
Указание. ;— = —т -=— . При отыскании предела
X Tg X X
первого множителя положить tg x = z и воспользоваться резуль-
результатом задачи 18,5.
Ответ. 1пЗ.
Задача 18,8 (для самостоятельного решения). Найти,
НтA+51п*)ПГг.
Указание. Сделать подстановку 5\пх = г и воспользова-
воспользоваться формулой A7,2).
Ответ, е5.
Задача 18,9. (для самостоятельного решения). Найти
urn .
х-+0 х
Указание. В числителе дроби отнять и прибавить 1, запи-
записать дробь в виде
ах — 1 — 6» -f 1 _ ах— 1 — (Ьх— 1)_ ах~ 1 __ 6*—1
X X ~ .* X
и воспользоваться формулой A8,5).
Ответ. In —.
336
Задача 18,10 (для самостоятельного решения). Найти
От вет. а — р.
Задача 18,11. Доказать, что если
lim [In/(x)] = А, то limf(x) — eA.
х-*а х-*а
Доказательство. На основании того, что мы имеем право
переходить к пределу под знаком логарифма, можно вместо
lim [In f (х)] записать In [lim f (x)] = A, r. e. \imf(x) = eA.
х-кх х-*а хч-а
Итак, если \im[\nf(x)] = А, то
x-*a
Umf(x) = eA. A8,8)
Задача 18,12. Найти Hm(l + tg*)~.
Решение. Сделаем подстановку A + tg*)~= у, откуда
3 3
1пг/ = — 1пA + tg*) и limln«/= lim — ln(l + tgx) —
* хч-0 X-+Q X
InA + tgдг) tg*
II
При вычислении первого предела положить tg* — г, исполь-
использовать результат задачи 18,4; получится, что lim (In у) = 3 -1 • 1,"
хч-0
т. е. lim (In у) = 3, и на основании A8,8) lim t/ = е3, а значит,
Х-+0 х->-0
lim(l H-tgx)* ^e3.*
х-*0
Задача 18,13 (для самостоятельного решения). Найти
JL
lim(l-fsinje)* .
дг-+О
Ответ, е6.
_3_ 1 Zigx
* Задачу можно решить и иначе: A + tg х)х = A + tg*)tsr* * =
1 3tg* _з^ j_ Um з tg*
= [A +tgx)tex] x ; HmA + tg*) * = [limA + tg*)*8*)*-o x ^e3
(при вычислении предела в квадратной скобке положить tg х — г, а
12 И. А.Каплав. 337
Задача 18,14 (для самостоятельного решения). Найти
Указание. В числителе дроби заменить 1 на \пе. Тогда
выражение, стоящее под знаком предела, запишется так:
1 *
In —
In л- — 1 In х— In e _ '" е _ , (Л х~е
х-е ~ х-е -Т=~е~ т\е )
и теперь
е
= ln« '=-'-.
ii- /i , *— e\ x—e e . Г.. / л- — e\x—e~\e
= lnlim(l+—j = ln[hm(l + —) J =
Ответ. 7.
ДЕВЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Сравнение бесконечно малых величин.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Пусть f{x) и срix) — бесконечные малые функции при х-*-а,
т. е. lim/(;t) = 0 и limcp(;t) = 0, причем а может быть как чис-
х-*а х-н2
лом, так и одним из символов + °°. —«>, °о. Тогда имеют
место приводимые ниже определения.
Определение 1. Если\\т'-~=0, то функция f(x) назы-
хч-а f {х>
вается бесконечно малой функцией высшего порядка малости, по
сравнению с функцией ср (х), а функция со (х) называется бесконеч-
бесконечно малой функцией низшего порядка малости, по сравнению с
функцией f(x).
Определение 2. Если Нт^, = со, то функция f(x) назы-
вается бесконечно малой функцией низшего порядка малости, по
сравнению с <р(х), а ср (х) называется бесконечно малой функцией
высшего порядка малости, по сравнению с функцией f(x).
Определение 3. Если Ит'-Щ=^А и А Ф 0, то бесконечно
малые функции f (x) и ср (х) называются бесконечно малыми одного
и того же порядка.
338
Определение 4. Если lim t-j- — \, то бесконечно малые
функции f (x) и <р (х) называются эквивалентными, или равносиль-
равносильными. В этом случае пишут: / (л:) — <р (х).
Определение 5. Если lim . ,Хг- — А и А фО, то бесконечно
х-*а 19 W Г
малая функция f(x) называется бесконечно малой k-го порядка
малости, по сравнению с бесконечно малой функцией <р (х) (из этих
определений вовсе не следует, что отношение двух бесконечно
малых функций всегда имеет конечный или бесконечный предел.
Может оказаться, что отношение двух бесконечно малых функций
не имеет ни конечного, ни бесконечного предела).
Теорема (о замене бесконечно маЛых функций им эквивалент-
эквивалентными). Предел отношения' двух бесконечно малых функций не из-
изменится, если каждую из них или какую-либо одну заменить
эквивалентными им.
Задача 19,1. Доказать, что если х->-0, то функция xk, где
k > 1, — бесконечно малая высшего порядка, чем х.
Решение, lim— = Нт^-'= 0, так как по условию & — 1 > 0.
Х-.0 X х-И)
Этим и доказано требуемое.
Задача 19,2. Доказать, что При jc-»-0 функции %тх и \.gx —
эквивалентные бесконечно малые.
Решение. Если мы докажем, что lim^-^ = 1, то тем са-
мым будет доказано, что tgx—sinx при х-*-0.
Действительно, lim ^ = lim ^ = lim cos* = 1.
cos*
Задача 19,3 (для самостоятельного решения). Доказать, что
при х-+0 1) функции sin;t~.r, 2) In A + *)~-*; 3) ех — 1~х;
4) sin kx ~- kx; 5) In A -f kx) ~ kx.
Указание. Рассмотреть lim 5Д Jim illil±^; limlnA+b);*
х-+й x х-*Ъ x x-*0 x
lim ; lim—r— и убедиться, что каждый из этих пределов
х-+0 х х-+0 ^х
равен 1. Полезно запомнить, Что In (I + kx)~kx, sinkx-^kx при
Задача 19,4. Доказать, что при х -*- 0 функции sin kx и
I • x(k ф 0, I фО) — бесконечно малые одного и того же порядка.
Доказательство. Найдем limsi" *и убедимся, что он
равен постоянной величине, отличной от нуля (см. определение 3),
Действительно, lim Щ^- ^=~ф0.
X-+Q 1Х '
*См. Задачу 18,4. ... ~ .
12* 339
В частности, например, sin 2* и 3* при х-*-0 будут беско-
бесконечно малыми одного и того же порядка.
Задача 19,5. Показать, что если х — бесконечно малая пер-
первого порядка, то 1 — cos x — бесконечно малая второго порядка,
по сравнению с х.
Решение. Чтобы показать требуемое, надо на основании
определения 5 показать, что lim ~ ^os x есть величина постоян-
постоянно х
1 — cos х 2 sin* ~2
ная, не равная нулю. Действительно, lim 5— = Hm 5— —
«-•¦о х х-+о х
X . X
sin -s- sin "9" 1 1 - 1
= 21im—llim—i = 2.-J--T = T-
X-t-0 * Jt-t-0 * i. ? &
Замечание. При решении следующих задач полезно знать,
что если x-h-a, то lim*°—1, так как переменная величина,
х-+а
стремясь к а, возводится в степень, равную нулю, а потому со-
сохраняет постоянное значение, равное 1. Предел ее поэтому
равен 1. '
Задача 19,6. Считая, что х — бесконечно малая первого по-
порядка, определить порядок малости функции sin* — tgj;.
Решение. Отличие этой задачи от предыдущей состоит в
том, что в предыдущей задачетюрядок малости функции 1 — cos x
задавался, и требовалось только подтвердить это расчетом. В этой
задаче порядок Малости функции sinx — tgx, не задан, а подле-
подлежит определению. Будем считать, что порядок малости этой
функции равен k и найдем k такое, чтобы lim S1"*T g* имел
дг-+О х
конечное значение, отличное от нуля (см. определение 5 на стр. 339):
sin jf
= -2
\ / x-*0 ж-0
Теперь дело решает предел lim .к3-*. Если предположить, что
дс-t-O
3 — k > 0, то lim*8-* = 0. Если же 3 — k < 0, то lim*3-* = <».
x-t-0 «-t-0
340
Чтобы получить конечный и отличный от нуля lim*3-ft, надо
Х-+0
отбросить предположения 3 — k>0 и 3 — & < 0, так как в пер-
первом случае искомый предел равен нулю, а во втором -— беско-
бесконечности. Только тогда, когда 3 — & ~ О, т. е. когда k = 3, мы
получим, на основании сделанного замечания (см. задачу 19,5),
что \\тх*~к — 1, а искомый предел равен —*-, т. е. имеет ко-
х-+0 z
нечное и отличное от нуля значение. Итак, & = 3 и при х-*-О
функция sin х — tg x — бесконечно малая третьего порядка малости,
по сравнению с х.
Задача 19,7. Считая, что * —бесконечно малая величина пер-
первого порядка, определить порядок малости бесконечно малой
функции
Решение. Будем считать, что искомый порядок малости
равен k и определим k так, чтобы limlnA+f+ дгЭ) имел конеч-
0 X
х-*0 X
ное значение, отличное от нуля.
ц 1п A + * + ,3) = Ы
*-И> Хк Х-+0
Первый предел равен 1 (подстановка: хг + х* — z приводит
к хорошо известному пределу: lim " ^ г' = 1).
Отыщем теперь второй предел:
lim x—tJ? = lim (д«-* 4- x3~k) =» lim *»-* A + x).
J 0 0
Последний предел имеет конечное значение только в том слу-
случае, когда 2 —к —0, т. е. k — 2, так как если k<2, то этот
предел равен нулю, а если k>2, то при х-*-0 хъ~к — величина
бесконечно большая, при k = 2 \\тх*~к = 1.
х-*-0
Таким образом, если k = 2, то lim- » = 1 • 1 Ф 0.
Итак, при л; —»- 0 бесконечно малая функция 1п A +*' + х8) имеет
второй порядок малости относительно бесконечно малой х.
Задача 19, 8 (для самостоятельного решения). Считая, что х —
бесконечно малая величийа первого порядка, определить поря-
порядок бесконечно малой функции
1пA+* + *2).
Ответ. Первого порядка малости {k— 1).
34J
Задача 19,9- Считая, ч*о х — бесконечно малая величина пер-
первого порядка, определить порядок малости бесконечно малой
функции
cps3jt — cos*.
_ ' , -. ,. COS 3jf — COS X
Решение. Определим число к так, чтобы lim
X
имел конечное значение, не равное нулю. Учитывая, что cos3* —
— cos x — —2 sin 2x sin x, искомый предел перепишем в виде
,. cos3* — cos* ,. 2 sin 2 x sin x
lim г = — lim j =
*-*0 Xя x-*0 X*
= -2 lim ^ lim ^ lim i = -2.2-1. lim*2-*.
Если взять k < 2, то lim x*~k = 0, и тогда весь искомый пре-
х-*0
дел будет равен нулю, а мы ищем .такое значение k, при котором
искомый предел был бы конечен, но не равен нулю.
Если взять k > 2, то lim x2r~k = oo, что также не годится,
*-*о
так как тогда искомый предел не конечен. И только тогда, когда
, п1. • > . < о | • COS ЗЛГ — COS X . .
к = 2 limr =1, а искомый предел lim г = —4 • 1 =
0 0 XR
= —4, т. е. имеет' конечное и не равное нулю значение.
Итак, k = 2. При х->-0 бесконечно малая функция «>s3;e —
— cosjc имеет второй порядок малости, по сравнению с х — бес-
бесконечно малой первого порядка.
Задача 19,10 (для самостоятельного решения). Считая, что
х — бесконечно малая величина первого порядка, определить по-
порядок босконечно малой функции cos 2х — cos x.
Ответ. k = 2.
Теперь выполним упражнения, связанные с использованием
теоремы (стр. 339) о замене бесконечно малых функций им экви-
эквивалентными. Эта теорема во многих случаях значительно упро-
упрощает определение пределов.
Задача 19,11. Найти limln A +. Здг) .
sin •**¦
Решение. При х-^-0 числитель и знаменатель дроби — функ-
функции бесконечно малые. Из задачи 19,3 нам известно, что при
х-*-0 бесконечно малая функция In A + 3*)~-.3*, sin Ax ~ 4x, a
потому, используя эту теорему, получаем
,. In A + 3*) ,. 3* 3
lim \ .—- = lim — = —.
х-о sm4x *~о4* 4
Задача 19,12. Найти lim
х^0 х
342
Решение. Так как при х -*¦ 0 бесконечно малая функция
sin3*~-3*, то заменяя sin3* эквивалентной ей бесконечно малой
Зх, получаем
lim .J*, = lim . , 3* , = lim , , ,3* , ,. = 3.
х-*о* +х+х х-*ох+хг + х *-о*(*+*+1)
Задача 19,13 (для самостоятельного решения). Пользуясь тео--
« / оог>\ • I • cos ах — cos an
ремой (стр. 339), найти lim—п*_х%—•
Ответ.
x-m
asm an
Задача 19,14 (для самостоятельного решения). Пользуясь тео-
теоремой (стр. 339), найти lim ("
о
Ответ. ~.
Задача 19,15 (для самостоятельного решения). Используя ту же
теорему, доказать, что
1) lim, *lnx . = —1; 2) limcosec* • ln(l + х) = 1.
Л1п\1~х) х-*0
ДВАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Непрерывность функции. Односторонние пределы.
Точки разрыва и их классификация.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Определение 1. Если предел функции f (x) при х -*¦ а суще-
существует и равен значению функции в точке х = а, то функция
f (х) называется непрерывной при х = а или в точке а, т. е.
для функции f (х), непрерывной при х — а, должно выполняться
равенство
limf(x)=f(a). B0,1)
х-*а
При этом следует иметь в виду, что для непрерывности
функции при х = а равенство B0,1) должно выполняться при
стремлении х к а любому закону.
Для того чтобы согласно этому определению функция была
непрерывной при х = а, требуется выполнение таких трех усло-
условий:
1. Точка а должна принадлежать области определения функ-
функции, так как иначе о значении функции f (а) в этой точке не
имеет смысла говорить. Функция f (x) должна быть определена
не только в самой точке а, но и в некоторой ее окрестности.
343
2. Функция f (x) должна иметь конечный предел при х-*-а
3. Этот предел А должен быть равен значению функции в
точке х = а', т. е. должно выполняться равенство f (а) — А.
Если соотношение B0,1) не имеет места для данной функции
у — f (х) в данной точке х — а, то функция называется разрыв-
разрывной в точке х = а, а сама точка х = а называется точкой раз-
разрыва функции f(х). г
Функция непрерывная в каждой точке некоторой области (ин-
(интервала, отрезка) называется непрерывной в этой области
(в интервале, на отрезке).
Определение 2. Функция f (x) называется непрерывной в
точке х = а, если в этой точке ее приращение Дг/ стремится
к нулю, когда приращение аргумента Ах стремится к нулю, или
иначе: функция f (х) называется непрерывной в точке х = а, если
в этой точке бесконечно малому приращению аргумента соответ-
соответствует бесконечно малое приращение функции, т. е. если
(/ = О. ¦ B0,2)
Дж-t-O
Односторонние пределы функции
а) Левосторонний^ предел функции. Если отыскивается предел
функции f (x) при условии, что х, стремясь к а, может прини-
принимать только такие значения, которые меньше а, то этот пре-
предел, если он существует, называется левосторонним пределом
функции f (х) (или левым пределом функции). Для того чтобы
показать, что х стремится к а, оставаясь меньше а, употреб-
употребляется запись: х-*-а — 0, а левосторонний предел функции обо-
обозначается символами:
1) \\mf(x) или 2) f(a — 0).
б) Правосторонний предел функции. Если отыскивается предел
функции f (х) при условии, что х, стремясь к а, может прини-
принимать только такие значения, которые больше а, то этот предел,
если он существует, называется правосторонним пределом функ-
функции f (х) (или правым пределом функции).
То что х, стремясь к а, остается больше а, обозначается
так: х-*-а-\-0, правосторонний предел функции обозначается
одним из символов:
1) \\mf(x) или 2) f(a + O).
344
Очевидно, что предел функции при х-*-а существует только
тогда, когда существуют и равны между собой ее левосторонний
и правосторонний пределы, т. е. когда f (а — 0) = / (а + 0), Символы
f (а — 0) и f (а + 0) являются только сокращенным, обозначением
левостороннего и правостороннего ^пределов и ничего другого не
обозначают. Их можно применять только в случаях, когда опре-
определяющие их пределы существуют. *
Определение 3. Функция f (x) называется непрерывной при
х = а, если ее левосторонний и правосторонний пределы суще-
ствуют, между собой равны и равны значению функции в этой
точке, т. е. f(a).
Таким образом, для непрерывности функции в точке х = а
требуется, чтобы выполнялись равенства
B0,3)
Точки разрыва и их классификация
Если равенство B0,3) в какой-либо его части не выполняется,
то о точке х = а говорят, что она является точкой разрыва.
1. Точка разрыва первого рода
Определение. Если левосторонний предел функции f (а — 0)
и ее правосторонний предел f(a + 0) существуют, но не равны
между собой, т. е. если
if (а — 0)^/=(а + 0), B0,4)
tfa-ofrfta+o)
-*-х
а
Фиг. 20,1.
то точка а называется точкой разрыва первого рода (фиг. 20,1).
* Символ х -*¦ а означает, что х стремится к а, изменяясь по любому за-
закону. Тем самым этот символ отличается от символов х-*¦ а — 0 и jr-»-a-f-O.
345
2. Точка разрыва второго рода
Определение. Если в точке х = а не существует левосторон-
левосторонний или правосторонний предел функции или оба одновременно,
то эта точка называется точкой разрыва второго рода (фиг. 20,2;
20,3; 20,4). На фиг. 20,4 отсутствует левосторонний предел
О
а
Фиг. 20,2.
а
Фиг. 20,3.
функции; на фиг. 20,3 нет правостороннего предела функции, а
на фиг. 20,4 у функции нет ни левостороннего, ни правосторон-
правостороннего предела. Во всех этих случаях функция в точке х = а тер-
терпит разрыв второго рода
(иначе: точка х = а — точ-
точка разрыва второго рода).
3. Устранимый
разрыв
Если в точке х = а функ-
*~ ция f (х) имеет левосторон-
х ний и правосторонний пре-
фиг 20 4 делЫ и эти пределы между
' ' собой равны, но их значения
не. совпадают со значением
функции в точке а, т. е. со значением / (а), то точка х = а назы-
называется точкой «устранимого» разрыва. Таким образом, в этом
случае
i
B0,5)
Разрыв «устраняется» тем, что полагают f (а) равным f (а — 0)
a f(a + 0), т. е. принимают, что f (a) = \\mf (х).
346
Свойства непрерывных функций
Теорема. Сумма, разность, произведение и частное двух функ-
функций, непрерывных в одной и той же точке а, есть функция не-
непрерывная в той же точке, причем в случае частного предпола-
предполагается, что функция делитель не обращается в нуль при х — а.
(Теорема остается верной для суммы и произведения любого ко-
конечного числа функций).
Упражнения, связанные с первым определением непрерывной
функции
Задача 20,1- Доказать, что функция f (х) = З*3 — Ах + 5 не-
непрерывна при любом значении х, т. е. непрерывна на бесконечном
интервале (—со, +со).
Решение. Заданная функция определена на бесконечном ин-
интервале (—со, -f-со'). Возьмем из этого интервала произвольное зна-
значение х — а. На основании известных теорем о пределе функции
мы можем написать
hmf(x) = ПтCл;3 — 4* + 5) = За8 — 4а + 5.
х-иг х-*а
Но ведь и f(a) = За3 — 4а + 5 и, таким Ьбразом, у нас выполнено
соотношение B0,1): \\mf(x) = f(a), а это и значит, что рас-
х-*а
сматриваемая функция непрерывна при х=-а. Учитывая, что а
произвольное число интервала (—со, -f-oo), мы заключаем, что
заданная функция непрерывна при любом значении х, т. е. на
бесконечном интервале (—со, +оо).
Задача 20,2. Доказать, что любой многочлен
f (х) = а,хп + агхп-1 + агхп-г +¦¦•+ ап_гх + ап
непрерывен при всех значениях х.
Решение. Пусть х = а — произвольное значение х из бес-
бесконечного интервала (—со, +оо), в котором определена заданная
функция.
Докажем, что lim f (x) — f (a).
х-*а
Действительно, на основании известной теоремы о пределе
целой рациональной функции имеем
п~х
lim f (х) = аоап + а1а
х->-а
Но полученное выражение есть не что иное, как значение задан-
заданной функции при х = а, т. е. f (а), и тем самым мы убедились
в том, что выполняется соотношение B0,1) lim/(х) = f(a), а по-
347
тому и заключаем, что многочлен непрерывен всюду, т. е. при
любом значении х.
Задача 20,3. Доказать, что любая дробно-рациональная функция
(Р (х) и Q (х) — многочлены) непрерывна для всех значений х, за
исключением тех из них, при которых знаменатель обращается
в нуль.
Дробно-рациональная функция определена для всех значений х,
кроме тех, которые знаменатель обращают в нуль. Пусть а —
произвольное число, такое, что Q(a)=^0. Из соотношения A4,3)
следует, что lim R (х) = R (а), т. е. соотношение B0,1) выполнено,
и мы заключаем, что дробно-рациональная функция непрерывна
при всех значениях х, кроме тех из них, которые обращают зна-
знаменатель в нуль, т. е. дробно-рациональная функция непрерывна
при всех значениях х, при которых она определена.
Задача 20,4 (для самостоятельного решения). При каких зна-
значениях х непрерывна дробно-рациональная функция
Ответ. Функция непрерывна всюду, кроме значений х = 2п
х — 4, при которых знаменатель дроби обращается в нуль. О не-
непрерывности функции в этих точках не может быть и речи, так
как они не принадлежат области определения функции.
Задача 20,5 (для самостоятельного решения). Исследовать на
непрерывность функцию f(x) = ~.
Ответ. Функция непрерывна при всех значениях х, кроме
х = 0. Значение х = 0 не принадлежит области определения функ-
функции: /@) не существует.
Упражнения, связанные с определением приращения функции
Эти упражнения будут проводиться и на следующем практичес-
практическом занятии. Читатель должен приобрести прочные навыки в оп-
определении приращения функции, так как с необходимостью опре-
определять приращение функции приходится очень часто встречаться.
Задача 20,6. Найти приращение А</ функции f(x) — x2 при
переходе аргумента от значения ^ = 3k новому значению хг = 4.
Решение. Приращение аргумента Ах = х% — xL = 4 — 3 = 1.
У нас f(x) = хг, а потому /(*2) = /D) = 42 = 16, f (xj = f C) =
= З2 = 9, а приращение функции Ay = f (хг) — f (jfx) = f D) — f C) =
= 16-9 = 7.
348
Задача 20,7. Найти приращение Ау функции f (л;) = дс3 при
переходе аргумента от значения х к значению х-{-Ах.
Решение. Ау = f {х + Ах) — f(x). Найдем f (х + Ах). Так как
у нас f (х) = х3, то f(x-{- Ад;) получим заменой х на х + Ах в вы-
выражении функции f (х): f (х + Ах) = (х + Ад;K, а потому
Ду = (* + Дд;)з _ х8 = Xs + Зд;гАд; + ЗхАх2 + Ах3 — х3;
Ау = Ъх*Ах + ЗхАх2 + Ах3.
Пользуясь этой формулой, вычислите, чему равно приращение
Ау функции, когда х от значения хх — 2 переходит к значению
*, = 2,01.
Ответ. 0,120 601.
Задача 20,8 (Для самостоятельного решения). Найти прираще-
приращение Ау функции f (х) — х3 при переходе аргумента от значения
jc, = 2k новому значению хг = 3.
Ответ. Ау = 19.
Задача 20,9. Найти приращение Ау функции f (дг) = sin x при
переходе аргумента от значения х к значению х + Ад;.
Решение. Ay ~ f(x + Ах) — f (х). У нас f (д;) == sinx. Мы
найдем /(x+Ajc), если заменим х на д; + Ах в выражении функ-
функции f(x):
f{x + Ax) = sin (д; + Ад;); Ау = sin (д; + &х) — sin x
и, применяя формулу
i п о + Ь . а— Ь
sin а — sin о = 2 cos —^— sin —к— >
получим
Ау = 2 cos (лг + ^) sin ^. B0,6)
Задача 20,10 (для самостоятельного решения). Найти прира-
приращение Ау функции у = cos л; при переходе аргумента от значения х
к значению х + Ах.
Ответ.. Д(/ = —2sln(*+^) sinЩ. ¦ B0,7)
Задача 20,11 (для самостоятельного решения). Найти прира-
приращение функции f (x) = sin х при переходе аргумента от значения
= -g- к значению
Ответ. -5-.
Задача 20,12. Найти приращение функции у = а^.
Решение. /(х) = а*; /(д; + Аж) = ax+Ux; Ay = /
/() +^д:*(йх1)
Аг/ = а^ (а4* — 1). B0,8)
349
Задача 20,13. Найти Приращение функции у = \пх.
Решение. У нас f (х) — Inх; f (х +АХ) ~ 1П(х + А*);
\y = f(x + \x)-f (х) = In (х + Ах) - In x;
Задача 20,14 (для самостоятельного решения). Найти прира-
приращение AS функции S = y при переходе аргумента от значения t
к значению t + A/.
Ответ. AS ^
Задача 20,15. Доказать, что при *=0 функция sin* непре-
непрерывна.
Решение. Мы должны обнаружить, что lim sin x = sin 0 = 0.
х-+0
Учащийся не должен думать, что мы здесь имеем право просто
подставить под знак минуса нуль вместо х. Это мы имели бы
право сделать, если бы непрерыв-
непрерывность функции sin* при х — 0
была бы уже доказана.
Рассмотрим окружность ради-
радиуса О А = 1 (фиг. 20,4 а). Тогда
Отрезок AD короче дуги АВ,
а потому | sin х
Если те-
теперь угол х уменьшать, делая
его все меньшим и меньшим по
абсолютной величине, мы можем
и синус этого угла сделать по
Фиг. 20,4 а абсолютному значению сколь угод-
угодно малым, а это значит, что при
х ->¦ 0 sin х есть величина бесконечно малая, и ее предел
lim sin x = 0, т. е. lim sin *= sinO.
х-+0 х-*0
И так как здесь выполняется соотношение B0,1): lim/(*)==
х-*а
= f(a), то при х~0 функция sin* действительно непрерывна.
Задача 20,16. Доказать, что функция sinx непрерывна при
любом значении х.
Решение. В задаче 20,9 для определения приращения /(х) —
= sin* была получена формула B0,6), верная при любом значе-
значении *.
350
Воспользуемся теперь вторым определением непрерывной функ-
функции B0,2) и докажем, что МтАу = 0.
д*-*о
На основании результата предыдущей задачи sin -у -»- 0, ког-
когда Ал: -*¦ 0; что касается cos [x + -?), то он величина ограниченная
при любом значении *:|cos*j<l. Произведение же величины
бесконечной малой на ограниченную есть величина бесконечно ма-
малая, поэтому, когда Л*->-0, то Ау-*~0, т. е. lim At/= 0. Так как
Дх->-0
это выполняется при любом значении х, то мы теперь вправе утвер-
утверждать, что функция sin х непрерывна при любом значении х (иначе
говорят: «непрерывна всюду», «непрерывна на всей числовой оси»).
Теперь уже, определяя предел йпх при х-+а, мы вправе с пол-
полным основанием писать:
lim sin* = sin a.
х-ю
Задача 20,17 (для самостоятельного решения). Доказать, что
функция f{x) — cosx непрерывна при всех значениях х.
Указание. Воспользоваться формулой B0,7).
Задача 20,18 (для самостоятельного решения). Доказать, что
функции tgx, ttgx, sec л;, cosecx непрерывны в любой точке своей
области существования.
Указание. Использовать непрерывность всюду функций sinx
и cos л: и теорему о непрерывности частного двух непрерывных
функций.
Упражнения, связанные со вторым определением
непрерывной функции
Задача 20,19. Пользуясь вторым определением непрерывности
функции, доказать, что функция f (х) = Ьх% — Ьх + 2 непрерывна
в произвольной точке х.
Решение. /(х + -Ах) = 5(х + Л*K — 6(х + Ах) +2;
Ау = / (х + А*) — / (х) = ЮхАх — 6Ах + 5Дх2 =••
Найдем теперь предел At/ при Ах-*-.0:
lim Ay = lim [A0* — 6) Ад: + 5Д*2] = 0
Лх-+0 Лл;-»О
при любом значении х, что и доказывает непрерывность заданной
функции при любом значении х.
351
Задача 20,20 (для самостоятельного решения). Пользуясь вто-
вторым определением непрерывной функции, доказать, что функция
1 -4- х
f(x) = iT 2 непрерывна при любом значении х.
Указание. Найти At/,' после чего перейти tf пределу при
Д* -*¦ 0.
Задача 20,21 (для самостоятельного решения). Доказать, что
при х = 3 функция f (x) = j _*2 непрерывна.
Указание. Составить Ау = /C + Д*) — fC) и найти limAt/.
Задача 20,22 (для самостоятельного решения). Доказать, что
функция / (х) = Yx2 + х + 1 непрерывна при любом значении *.
Указание. Определить Аг/, после чего перейти к пределу
при А* ->- 0,
Упражнения, связанные с классификацией точек разрыва.
Задача 20,23. Испытать на непрерывность при х = 1 функцию
f(x) = 2 + Ц_.
Решение. Так как знаменатель 1 — х дроби равен нулю при
х = 1, то f(x) разрывна при х= I. Установим-характер этой точки
разрыва. Найдем сначала левосторонний предел функции \imf(x).
дг-^1—0
Если х -»• 1 — 0, то можно положить х= 1 — а(а>0) и считать,
что а, оставаясь положительной, стремится к нулю. Заменяя х
на 1 — а
Umf(x) = lim B +
так как при a -*- + 0 ^величина — бесконечно большая, 22 также
a
бесконечно велика, 1 + 2a —бесконечно большая величина, обрат-
обратная ей величина j- — бесконечно мала:
1 + 2"
lim —Ц- = О,
"""^ 1 + 2**
а потому lim /2 -j г | = 2.
о*+0 — I
\ 1+2я/
Таким образом,
/A-0) = 2.
352
Теперь определим правосторонний предел функции. Если
х _> 1 -f- 0, можно положить х = 1 + а (а > 0) и считать, что а,
оставаясь положительной, стремится к нулю.
Тогда, заменяя х на 1 + а, получим:
limf (х) = lim [i -J Ц— \ = lim [ч + 1—Л = 3,
1+0 +О( I а-Н-0( |
7 \ 1 + 2 а/
так как при а ->- + 0, — и2а — величины бесконечно большие, то
-- 1
2 а = —— величина бесконечно малая, а поэтому
lim A + 2~~) = 1; lim —1—т = 1; a lim [i -\ 1—г\ = 3
а*+0 а-»+0 —L а^+01 —— I
1 + 2 я \ 1 + 2 а/
и, значит, f A + 0) = 3.
Итак, у функции существуют и левосторонний предел/ A — 0) =
= 2, и правосторонний предел f A + 0) — 3, но между собой они
не равны. Из этого мы заключаем, что точка х— 1 является для
заданной функции точкой разрыва первого рода.
Задача 20, 24 (для самостоятельного решения). Испытать на
2
непрерывность функцию / (х) — — при х — 2.
з + 5^
Указание. 1) Найти левосторонний предел функции lim//*)
*-*2— 0
(положить х = 2 — а(а>0) и найти предел полученной функции
о
при <х-»- + 0). Получится, что /B — 0) = у. 2) Найти правосто-
правосторонний Предел функции lim / (х) (положить х = 2 + а (а > 0) и найти
предел полученной функции при а ->-+0). Получится, что/ B+0)=0.
Ответ. Точка х = 2! — точка разрыва первого рода: / B — 0)
и / B + 0) существуют, но между, собой не равны.
Задача 20, 25 (для самостоятельного решения). Испытать на
непрерывность функцию / (х) — р при х = 0.
Указание, При х = 0 функция терпит разрыв. Левосторон-
Левосторонний предел функции lim/(*) = -^-; /(—0) = -о-.
х-<—о d а
Правосторонний предел функции lim/(*) = 0:/(+0) = 0 (сим-
+0
волы 1) х-+- — Ой 2)х->-+0 означают, что: 1) х стремится к"(нулю,
оставаясь меньше нуля; 2) х стремится к нулю, оставаясь больше
нуля).
353
У
Левосторонний и правосторонний пределы функции существуют
/ (—0) = -о-, f (+0) -- 0, но между собою не равны: / (—0) Ф f D-0).
Заключение. Точка х = 0 — точка разрыва первого рода.
Задача 20, 26 (для самостоятельного решения). Функцию / (х) =
= — j- испытать на непрерывность при х = 5.
2-\-1~*
Ответ. /E-0) = 0, / E 4-0) =-|: f E — 0) Ф E + 0).
Точка х — 5 — точка разрыва первого рода.
Задача 20, 27 (для самостоятельного решения). Какого рода
разрыв имеет функция f (х) = 3*~ в точке х — 0. Начертить график.
Ответ. Разрыв второго рода: f (—0) = 0, f D-0) = 4~ °° •
Задача 20, 28. Какого рода
разрыв имеет функция у — —-
в точке х = 0.
Решение. Левосторонний
предел функции Нш—= — со,
хч—0 х
а ее правосторонний предел
lim — = 4- °°- Таким образом,
х-*+0х<
здесь не существуют ни предел
слева, ни предел справа, а пото-
потому точка х = 0 — точка разрыва
второго рода.
фиг 20,5 Задача 20, 29 (для самостоя-
самостоятельного решения). Ка^го рода
разрыв имеет функция у = —~ в точке х =¦¦ 3 (фиг. 20,5).
X — о
Ответ. Второго рода:
при х ->• 3 не существуют У
ни предел слева, ни пре-
предел справа.
Задача 20, 30 (для са-
самостоятельного решения).
Какого рода разрыв имеет
1
функция у = -2 в точке
О
-Х-
Ответ. Второго рода
(фиг. 20,6). Фиг. 20,6
Задача 20, 31 (для самостоятельного решения) Определить точ-
точки разрыва функции у = а_ и род этих точек разрыва.
354
Ответ. Точка х= —1 и х = + 1 — точки разрыва второго
рода (фиг. 20,7).
Задача 20, 32. Какого рода разрыв в точке х = 0 имеет функ-
функция у = arctg -.
Решение. В точке лс ='
1
не существу-
функция arctg •
ет. Определим левосторонний и
правосторонний пределы функ-
функции: lim arctg—=—5", так
*->—о х
как при * -»- — 0 величина
-U-oo, a arctg^-!; f(-0)=
== — -S-, lim arctg — = + -я- по-
тому, что при jf —>—Н 0 величина
-^ + со, a arctg-^+-р-;
-/
Фиг. 20,7
Таким образом, оба" предела — левосторонний и правосторон-
правосторонний — в точке х = 0 • существуют, но между собою -не равны:
/ (_0) ф f (+0), и точка х = 0 — точка разрыва первого рода
(фиг. 20,8).
-лг
Фиг. 20,8
, , . sin дг
Задача 20, 33. Какого рода разрыв имеет функция f (х) = -j—
в точке х — О?
Решение. В этой точке функция1 разрывна, так как f@) не
существует. Однако нам известно, что при стремлении х к нулю
по любому закону (х ->¦ 0)
hm
sin
= 1
355
и, таким образом, существуют левосторонний предел функции
f (—0), правосторонний предел функции f (+0) и они между со-
собою равны: /(—0) = f (+0) — 1. Но /@) не существует. На кри-
кривой, которая является графиком этой функции, отсутствует точка
(она как бы «вырвана»), абсцисса которой равна нулю. Если ус-
условиться, что при х = 0 функция = 1, то тем самым график
функции станет сплошным (непрерывным), и разрыв будет «уст-
«устранен» (фиг. 20,9).
Заключение: Для функции ^^ точка х = 0 является точ-
точкой «устранимого» разрыва, так как / (—0) = / (+0), и функция
-г* -jt о я -гх
Фиг.- 20,9.
в этой точке может быть доопределена так, что можно взять
Замечание. Термин «устранимый» взят в кавычки потому,
что фактически разрыв функции ^-^ в точке х — 0 ничем устра-
устранить нельзя, так как он существует в действительности. Можно
только условно принять, ч?о значение функции в этой точке
равно 1. Такое соглашение восстановит на кривой отсутствующую
на ней точку @,1).
Это замечание следует иметь в виду и при решении других
задач, в которых разрыв будет «устранимым».
Задача 20,34. Испытать на непрерывность функцию / (х) =
= -х_2 В точке Х — 2.
Решение. Так как при х — 2 функция не существует и тем
самым нарушено первое условие непрерывности, то в этой точке
функция терпит разрыв. Найдем левосторонний и правосторонний
пределы функции
l^^ a + 2x + 4)= 12, /B — 0)= 12;
^оСТД^а + 2^ + 4)=12; /B + 0) =12.
Таким образом, существует и предел этой функции при х -*• 2,
как / B — 0) = / B + 0). В точке х = 2 разрыв можно «устра-
нить», если значение функции в этой точке принять равным 12,
т. е. если условиться, что / B) = lim
х-*2
х — 2
= 12.
Точка х = 2 — точка «устранимого» разрыва. Графиком функции
хз g
f (*) ~ х — 2 является парабола (фиг. 20, 10), на которой нет точки
с абсциссой х — 2. На графике эта точка обозначена кружком и
к ней направлены стрелки. Сплошной
ход кривой в этой точке оборвался. Сле-
Слева и справа от точки х = 2 график
функции — непрерывная линия.
Задача 20, 35 (для самостоятельно-
самостоятельного решения). 1) Исследовать на непре-
jj.2 9
рывность функцию / (х) — 3 и на-
начертить график функции. 2) Чему
должно быть равно /(—3), чтобы по-
пополненная этим значением функция
была непрерывна при х = —3?
Ответ. Точка х = —3 — точка
«устранимого» разрыва. Следует взять
/ (-3) = -6.
Задача 20, 36 (для самостоятельного
решения). 1) Исследовать на непрерыв-
непрерывность функцию / (*) = *_/".¦ и начер-
X —р- 1
тить график функции. Как следует
доопределить эту функцию при х =
— — 1, чтобы при х— — 1 она была
непрерывной?
Задача 20, 37. Доказать, что функ-
функция f(x) = x3 cos2 х + х2 1 непрерыв-
непрерывна при всех значениях х.
Решение. Воспользуемся теоремами о сумме произведении
и частном непрерывных функций. Так как функция cos* непре-
непрерывна при всех значениях *, то и ее квадрат есть функция, не-
непрерывная при всех значениях *, как произведение двух непрерыв-
непрерывных, функций: cos2 * = cos * • cos *.
Функция <р (х) — х непрерывна всюду, а потому и функция
<?i(x) = х3 также всюду непрерывна, как произведение непрерыв-
непрерывных функций: срх (*) = (хK = ***.
Произведение х3 cos2 * — функция непрерывная, как произведе-
произведение непрерывных функций х3 и cos2*.
Второе слагаемое а ¦. — функция непрерывная, как частное
X -f- 1
двух непрерывных функций, причем знаменатель дроби не имеет
357
:/ о
Фиг. 20,10.
действительных корней (уравнение х2 + 1 = 0 не имеет действи-
действительных решений).
Заключение. Заданная функция непрерывна при всех зна-
значениях х.
Задача 20, 38 (для самостоятельного решения). Пользуясь тео-
теоремами о непрерывности суммы, произведения и частного непре-
непрерывных функций, решить вопрос о непрерывности функций:
sin х
Ответ. ]) функция непрерывна при всех значениях*, кроме
значений хг = — 3 и хч = 3.
2) Функция непрерывна для всех значений х, кроме *=1.
3) Функция непрерывна для всех х, кроме х — ги, где п —
любое целое число.
ДВАДЦАТЬ ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Задачи, приводящие к вычислению производной. Не-
Непосредственное вычисление производной из определения. Геометрический
и механический смысл производной.
Это практическое занятие является первым по разделу «про-
«производная и дифференциал функции». К вычислению производной
данной функции мы приходим всякий раз, когда требуется опре-
определить скорость изменения одной величины (функции), в зависи-
зависимости от изменения другой величины (независимой переменной).
Определение 1. Средней скоростью изменения функции у —
— f (x) при переходе независимой переменной от значения х к
значению х-\- Ах называется отношение приращения Ау функции
к приращению Ах независимой переменной:
Определение 2. Истинной (мгновенной) скоростью измене-
изменения функции у при данном значении х называют предел, к кото-
которому стремится средняя скорость изменения функции при стрем-
стремлении к нулю Ах:
V=\imVcp;
)/w- B1,2)
При вычислении этого предела следует х считать величиной
постоянной. Переменной же величиной здесь является Ал: (конечно,
значение х можно выбрать произвольно из области существования
358
функции, но после того как этот выбор сделан, значение х должно
оставаться постоянным, а изменению может подвергаться только Л#).
Найденный из B1,2) предел будет являться функцией х. О ско-
скорости изменения функции при данном значении х имеет смысл
говорить лишь в том случае, когда предел B1,2) существует и
не зависит от того, каким способом Ад; стремится к нулю.
Функция, полученная в результате определения предела B1,2),
называется производной функцией от функциии f(x). Сокращенно
найденная из B1,2) функция называется просто производной.
Определение производной. Производной функции / (х) по
независимой переменной х называется предел, к которому стре-
стремится отношение приращения функции Ау к приращению аргу-
аргумента Ал", когда приращение аргумента стремится к нулю.
Операция нахождения производной называется дифференцирова-
дифференцированием функции.
Производная функции при частном значении х есть число,
если при этом значении х производная имеет конечное значение.
Обозначение производной. Производная обозначается од-
одним из символов: у'х, у', ~, f (x), а ее значение при х~х0 обо-
обозначается так:
Когда мы нашли производную функцию /' (х), тем самым мы
нашли скорость изменения данной функции в точке х.
Механическое значение производной
1. Средняя скорость. Закон движения точки считается задан-
заданным, если ее путь s* есть известная функция времени t, т. е. если
s = /@ B1,3)
(s — расстояние движущегося тела от начала отсчета). Будем счи-
считать, что s > О, если оно находится справа от начала отсчета и
s<0, если оно находится слева от начала отсчета. Средняя ско-
скорость движения 1/Ср за время от момента / до момента t ~\- Ы
вычисляется по формуле
1/ _ As - /(* + AQ-/(Q т д.
Истинная скорость движения в момент времени t по определе-
определению есть предел, к которому стремится средняя скорость Vcp за
промежуток времени А/, когда промежуток времени Д/ -»¦ 0. Или
Предполагается, что точка движется в одном направлении.
359
иначе: скоростью движения в данный момент времени t назы-
называется предел отношения приращения пути As к приращению
времени At, когда приращение времени At стремится к нулю.
Скорость в момент времени / определяется равенствами
1/= lim Кср=ПтД?. B1,5)
д*->о д*-»-о At
Из сравнения B1,5) с B1,2) видно, что скорость точки в момент
времени t есть производная от пути s по времени t.
Геометрическое значение производной
Производная от функции f(x), вычисленная при заданном
значении х, равна тангенсу угла, образованного положительным
направлением оси Ох и положительным направлением касатель-
касательной*, проведенной к графику этой функции в точке с абсциссой х.
Упражнения этого практического занятия имеют целью закре-
закрепить у студента понимание определения производной, ее меха-
механического и геометрического значения.
Мы будем решать задачи, в которых производная вычисляется
не из готовой формулы, как это делается, на следующих практи-
практических занятиях, а непосредственно, исходя из ее определения.
После твердого усвоения определения производной мы перей-
перейдем к упражнениям, которые помогут выработать прочные на-
навыки вычисления производных.
Задача 21,1. Вычислить производную функции у = х2 при х = 3.
Решение. Проведем решение этой задачи двумя способами:
1) сначала найдем производную как функцию х, а потом вы-
вычислим ее значение при х = 3, т. е. у' C).
2) значение производной будем вычислять, исходя из значения
х = 3:
у^х2, т. е. /(х) = х2;
/ (х + Ах) ~ (х + Ад:J = х2 + 2д;Ах + Ах2Г
Теперь найдем приращение функции Ay = f(x + Ax) — f(x)~
= х2 + 2д:Дл: -Ь Ах2 — х2 = 2хДл: + Ад:2 = Bх + Ах) Ах.
Разделим теперь приращение функции Ау на приращение ар-
аргумента Ад::.
Ау Bх+Ах)Ах. Ау „ , .
А~х = Д^ ' А~х ^ 2Х + АХ'
В этом месте мы можем сказать, что найденное отношение -г|
есть не что иное, как средняя скорость изменения данной функ-
функции f(x) = xz в промежутке (х, д: + Ад:).
* Положительным направлением на касательной считается то, в котором
возрастает абсцисса.
360
Для того чтобы найти производную у' этой функции, нужно
найти предел полученного отношения при Ах ->¦ 0. Переходя к пре-
пределу, получаем
у' = lim ^ = lim Bх + Ах) = 2х
(еще раз напоминаем, что здесь при отыскании предела величину
х мы должны считать постоянной).
Итак у' = 2х.
При х = 3 значение производной у' C) = 2 • 3 = 6. Найденное
число 6 есть не что иное, как скорость изменения функции / (х) — х2
при х = 3.
2) Найдем теперь значение производной данной функции при
х = 3, минуя нахождение производной, как функции х.
У нас f(x)=x2; /C) = 32.
Перейдем от значения х — 3 к значению х = 3 + Ах;
= 9;
Ау = / C + А*) - /C) = C + Axf - 9 = 6Дх + (АхJ = F + Дх)Дл;;
Найдя производную у' C), мы нашли и тангенс угла между
положительными направлениями оси Ох и касательной к графику
функции у = х2 в точке с абсциссой д;=3, т. е. угловой коэф-
коэффициент касательной к параболе у = х2 в точке с абсциссой х = 3.
Задача 21,2 (для самостоятельного решения). Вычислить про-
производную функции у = х3 при х = 2.
Дать геометрическое истолкование полученного результата.
Задачу решить двумя способами по примеру решения предыду-
предыдущей задачи. Найти среднюю скорость изменения функции в про-
промежутке от хг = 3 до x<i = 3,1.
Ответ, у' B) = 12; средняя скорость изменения функции на
интервале C; 3,1) vcp = Ъх2 + ЗхАх + Ах2. Подставляя сюда х=\,
Ах =0,1, получим уср = 27,91.
Задача 21,3. Точка движется по прямой по закону S = t3,
где S — путь, измеряемый в сантиметрах, a t — время в секундах.
Найти среднюю скорость точки за время от t = 2 сек до tx =
= B +At) сек, считая, что At = 1; 0,5, 0,01; 0,001. Вычислить
также истинную скорость точки в момент t = 2 сек.
Решение. Согласно результату предыдущей задачи, если
у — х3, то Ау = Зх2Ах + ЗхДл;2 + Ал:3. Так как в/задаче, которую
мы решаем, функция обозначена буквой S, а аргумент буквой t,
то выражение для Ау надо переписать, заменив у на S, а х на V.
AS = 3/2Д* + 3tAt2 + At3,
361
а средняя скорость будет равна
1/ср = ^ = З/2 + 3* Д/ + At2.
Если At = 1 сек, то, приняв, что t = 2 сек, получим
1/ср = 3 • 22 + 3 • 2 • 1 + I2 = 19 он/сек;
при t — 2 сек, а А( = 0,01 сек;
Vcp = 3 • 22 + 3 • 2 • 0,01 + @,01J = 12,0601 см/сек;
при f = 2 сек, а Д( = 0,001 сек;
1/Ср = 3 • 22 + 3 • 2 • 0,001 + @.001J = 12,006 001 см/сек.
Найдем теперь истинную скорость в момент времени t = 2 сек.
У нас
Vcp = ЗР + StM + At2.
Истинная скорость по B1,4) будет равна
V = lim Vcp = Hm (З^2 + 3/А^ + Щ = З/2.
При t = 2 сек получаем I/ = 3 • 22 = 12 см/сек.
Все полученные нами средние скорости отличаются от истин-
истинной, но из рассмотрения полученных значений средних скоростей
мы приходим к выводу, что они тем ближе к истинной скорости
в момент t — 2 сек, чем меньше At.
Задача 21,4 (для самостоятельного решения). Точка'движется
по прямой по закону S = 5/3 — З^2 4- 4, где путь S измеряется
в сантиметрах, а время t — в секундах. Найти среднюю скорость
за промежуток времени от ti — 1 до ti = A + At), считая А^ =
= 0,5; 0,3; 0,1.
Определить также истинную скорость в момент t = 1 сек.
Указание. 1) Найти AS; 2) VcP = f^-
Ответ. При Д? = 0,5 1/ср — 15,25 слисек; при Д? = 0,1 Vcp =
= 10,21 см/сек; 1/= \5t2 -6t, 1/A) = 9 см/сек.
Задача 21,5. Функция У = з7+Г Вычислить производную
при х = 1.
Решение. Сначала найдем производную у' как функцию х,
а потом вычислим у' A).
Наращенное значение функции у + Ау мы найдем, если за-
заменим в аналитическом выражении функции х на х + А#. Имеем
2дг+1_
-
~ [3(x+ Дл-) + 1|(Зл-+1) ' a Ax~ [3(л- + Дл-)+ 1](Зл-+1)
362
Эта формула дает выражение средней скорости изменения дан-
данной функции на интервале (х,х 4- Ах). Чтобы найти производную,
перейдем к пределу, устремляя Ах к нулю:
If—, '
C*4-1J ' a K ' 16"
Найденный результат геометрически истолковывается так:
2* 4- 1
угловой коэффициент касательной к графику функции у — "Г
в точке с абсциссой х = 1 равен — у§; tg 9 = — тг ¦
Если точка движется по прямой по закону У — о Т ¦¦ гделг—
время в секундах, а у — путь в метрах, то найденное значение
производной г/'A) = —-г~ — скорость движения в момент времени
t — 1 сек, а знак минус у скорости показывает, что с увеличе-
увеличением времени расстояние движущейся точки от начала отсчета
пути уменьшается.
Эту задачу можно решить и иначе: вычислить значение про-
производной заданной функции при х=\, минуя определение ее
производной при любом х.
Перейдем от значения х — 1 к значению х = 1 4- А*. У нас
2*4-1 т, f м. 2 • 14-1 3
. ]__ I ГХГЧ7П Т i \\ -. ' — •
_ 2Д* 4- 3 .
в точке х— 1 приращение функции Аг/— /(~1 4-А^) — /A);
. _ 2Д* + 3 Ъ_ —Д* Ау _ 1
У ~ ЗД*4-4 ~Т~ 4 (ЗД* 4- 4) ' Д* ~" ~ 4(ЗД* + 4) '
а
1 1
Таким образом, найдена производная заданной функции при
х = 1 без определения производной как функции х.
Задача 21,6 (для обстоятельного решения). Найти произ-
производную функции у — ух при х = 9.
Ответ. г/'(9) = -^-
Задача 21,7 (для самостоятельного решения). Доказать, что
для линейной функции у — Ы-^Ь отношение ^ есть величина
постоянная.
363
Задача 21,8 (для самостоятельного решения). Пользуясь опре-
определением производной, найти производную функции у = ]/д;2— 1
при х — Yb.
Указания: 1) Дг/ = У(х + АхJ — 1 — Ух2— 1; 2) при опре-
определении lim -г^ следует числитель и знаменатель дроби умножить
Д0ДДГ
на У(
У дг2 — 1
Ответ. 1/ ^
Задача 21,9 (для самостоятельного решения). Закон движения
точки по прямой задан формулой s = t3 — З^2 + Ы + 5 (s — в мет-
метрах, t — в секундах). В какие моменты времени t скорость точки
равна нулю? • "
Ответ. V = St2 — 6* + 3; V = 0 при t = 1 сек.
Задача 21,10 (для самостоятельного решения). Две точки дви-
движутся по прямой по законам &± = t3 — Ы2 + Ш — 4; s2 = ta — St.
В какой момент времени их скорости равны?
Ответ, t = 2 сек A^ = 3*а - 10/ + 17; К, = З*2 - 3).
Задача 21,11 (для самостоятельного решения). Тело, брошен-
брошенное вверх, движется по закону s— — 4,905*2 + 98U + 950 (s —
в метрах, t — в секундах). Найти: 1) скорость тела в любой мо-
момент времени и его начальную скорость; 2) в какой момент вре-
времени скорость тела станет равной4 нулю и какую наивысшую
высоту в этот момент времени достигнет тело.
Ответ. 1I/--9,81* + 981; Vo = 981 м/сек', 2) t = 100 сек;
sA00) = 50 км.
ДВАДЦАТЬ ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Дифференцирование алгебраических функций.
Это практическое занятие отводится для упражнений в опре-
определении производных алгебраических функций. Эти упражнения
продолжаются и на следующем практическом занятии. Операция
определения производной функции называется дифференцирова-
дифференцированием функции.
Вычисление производных мы будем вести не непосредственно,
исходя из определения производной, а по формулам, с выводом
которых читатель уже знаком. Здесь приводится для ссылок и
справок
СВОДКА ФОРМУЛ ДЛЯ ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Во всех приведенных ниже формулах функции и и о счита-
считаются функциями независимой переменной х: и —¦¦ и(х); v — v (x).
Эту таблицу читатель должен твердо выучить наизусть.
' У — Q (с — постоянная); у' — 0 B2,1)
364
(производная постоянной величины равна нулю);
У = х\ у'=\ B2,2)
(производная независимой переменной равна 1)
у = си (с — постоянная); у' — си' B2,3)
(постоянный множитель можно выносить за знак производной)
B2,4)
B2,5)
B2,6)
у = и ± v; у' = u'±v'
у = v ¦ и; у' = u'v + uv'
,. и , u'v — uv'
:' " V ' V*
у = ~; у' === — ~ • и' (а — постоянная величина);
у = и«; у' = пи"-1 -, и'
(п — любое действительное число)
у = аи; у' = а" ¦ \па • «'; у — е"; у' = еии'; а >0, а # 1
г/ = logau; у' = -1
ulna
у = In a;
у =¦ sin u;
у = cos и;
У = tg u;
у = ctg и;
y = secu;
у = cosec и;
у = arcsin ы;
у = arccos ы;
г/ = arctg и;
у = arcctgw;
* и ¦
у' = cosu • ы';
у' = —sinu • и'
и> = 1 ц/.
у cos2u '
1 ,
у' = sec и tg u • и';
у' = _ cosec u • ctg и • и';
y' = 77=L==u';
у' —
У ' =
и';
B2,7)
B2,8)
B2,9)
B2,10)
B2,11)
B2,12)
B2,13)
B2,14)
B2,15)
B2,16)
B2,17)
B2,18)
B2,19)
B2,20)
B2,21)
B2,22)
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Если у = f (и), а и является не независимой переменной, а
функцией независимой переменной х: и =¦¦ у (я), то, таким образом,
V = f(i(x)).
365
Функция у называется в этом случае сложной функцией х.
Переменная и называется промежуточной переменной. Производ-
Производная сложной функции определяется на основании такой теоремы:
Пусть у — f (и), а и — <р (х), причем для соответствующих
друг другу значений х и и существуют конечные производные
у'и и и'х. Тогда сложная функция у = f (<? (х)) имеет конечную
производную по х, и эта производная определяется по формуле
у'х = ylu'S, B2,23)
причем производная у'и вычисляется так, как если бы и было
независимой переменной. Короче: производная сложной функции
равна произведению производной данной функции по промежуточ-
промежуточной переменной на производную от промежуточной переменной
по независимой переменной.
Эта теорема распространяется и на сложные функции, которые
задаются с помощью цепи, содержащей три и более звена. Напри-
Например, если у =-. / (и), й - ср (и), v = <1> (*), т. е. если у = / (<р ([ф (х)]},
то
y'x = y'uu'vv'x. B2,24)
Формулы B2,23) и B2,24) дифференцирования сложной функ-
функции являются очень важными.
Прежде чем приступить к решению задач, сделаем замечание,
которым нам неоднократно придется пользоваться:
Если функция, которую надо продифференцировать, не яв-
является сложной, то мы в формулах B2,3) — B2,22) будем полагать,
что и = х, т. е. и — независимая переменная, а тогда по формуле
B2,2) и'х = 1 (производная независимой переменной равна единице),
и поэтому, применяя указанные формулы, на и' умножать не
придется, так как такое умножение равносильно умножению на
единицу, а, как известно, умножение на единицу не изменяет
произведения.
Сначала решим самые простые задачи.
Задача 22,1- Найти производные функций:
\)у = *\ 2)-у =*=*•; 3) *, = !/*; 4) у=>
Решение. Учитывая замечание, которое только что сделано,
по формуле B2,8), полагая в ней и = х, имеем:
1) В этом примере показатель степени п = 4, а потому у' =
= 4х3;
2) Здесь п = 5, а потому у' — 5лг*;
* Индексы у производных указывают нэ то, по какому переменному про-
производится дифференцирогание.
•злд
3) Если у — у х, то, переписав пример в виде у = х2, пола-
полагая в формуле B2,8) я = -^, получаем у' = у x2 —yx 2 =
/
При решении этого примера можно было сразу воспользоваться
формулой B2,9).
- ¦ 3
4) Пример можно переписать так: у = я4. Здесь я = -г-, а
3 -г-' 3 —j 3
Задача 22,2. Найти производные функций:
1) у = 5х», 2) у = -4х2, 3) у = 7/х; 4) у = ~
Решение. При решении всех этих примеров можно поль-
пользоваться формулой B2,8) и надо учесть, что постоянный множи-
множитель можно выносить за знак производной (формула B2,3)).
1) у' — 5 (х3)' (здесь постоянный множитель 5 вынесен за знак
производной); у' = 5 • Зх2 = 15х2 ((х3)' = Зх*)\
2) у' = —4(х2)' = —4 • 2х = —8д; (постоянный множитель —4
вынесен за знак производной, а (л;2)' = 2х);
¦ 3) У = 7Л ,' = 7(^)' = 74^ = 72l7j = ^F К
стознный множитель 7 вынесен за знак производной, а (д:2)' =
= -~ х 2 . Здесь можно было сразу воспользоваться формулой
B2,9), и тогда, если у = 7 |/"д:, то у' = 7 —j= = —7= .
" Учащемуся рекомендуется запомнить (это очень часто встре-
встречается), что если у = У х, то у' = —7= .
2 у х
4) Перепишем пример в ,виде у = 8х~2, тогда у' = 8 (х~2)' =
= 8(—2л^3), г/'= —^з (постоянный множитель 8 вынесен за
знак производной, а (х-2)' — —2х~2-1 — —2х~3). Можно было
сразу воспользоваться формулой B2,7), взяв в ней а = 8; и = х%,
а и! -- 2х. Здесь уже на и' придется умножить, так как и — не
независимая переменная, а ее функция: и = х2.
О О о г-чч»^^ t ft
Имеем У = ^; у' = — ^j(?/ = — ^2д:= — ^, т. е. то же,
производная
знаменателя
что и раньше, но функцию, данную для дифференцирования, не
пришлось преобразовать.
367
_2
5) Данную функцию перепишем в;. виде у = 4х3; тогда у' —
4 2 "г* о
•у* 3 =
Задача 22,3 (для самостоятельного решения). Найти произ-
производные функций: l)y=7xe; 2) у = 8]/х; 3) У =-^ •
Ответ. 1) у'^42*5; 2) У =4=; 3)y' = -f.
Задача 22,4. Найти производные функции:
Решение. Здесь для решения всех примеров удобно при-
применить формулу B2,7):
п „'Ё (V7Y6 2 •
производная
знаменателя
"I У ,о , .„ IV ¦* I ч. » ' ». Ч —
производная
знаменателя
о
= == (здесь можно было также воспользоваться формулой
Зхух*
_ 2_
B2,8), но данную функцию переписать в виде у = 4х 3, тогда
и' — 4 (х~ ~5\' — 4 A\ х~ з" ~'х~ т
г/_4(^ ;-4^ jx х
3) У' = (~ D?Г - we 4 (^3)' = !§, 3*» = ^ (можно посту-
производная
знаменателя
пить и иначе: данную функцию переписать в виде
Если дифференцируется дробь с постоянным знаменателем,
то применять формулу B2,6) для дифференцирования дроби не
следует, а поступить надо так: взять производную только, от
числителя дроби, а знаменатель оставить без изменения:
и 1 , 1 , и'
v с с ' * с с
368
Следует запомнить: производная от дроби с постоян-
постоянным знаменателем равна производной числителя, раз-
разделенной на тот оке знаменатель.
Использование здесь формулы B2,6) привело бы к ненужному
и , и'с — с'и и'с — 0 • и и'с и' , , Л
усложнению: у = —; у = —?— = —^— = -^ = — (с = О
потому, что производная постоянной величины равна нулю).
Если отыскивается производная от дроби с постоянным чис-
числителем, то также не следует применять формулу B2,6) для
дифференцирования дроби, а надо воспользоваться формулой B2,7)
для дифференцирования дроби с постоянным числителем;
а / a i
У ~~ ~п ' У ~ ~1? и '
Если здесь пользоваться формулой для дифференцирования дроби,
то получим
а-. / а'и — аи' 0 • и — аи' % аи' __ а ,
У ~ ?.' У "~ й5 п5 Ж ~ 1? ~ ~" 1?"
Такой способ вычисления производной тЬ^роби с постоянным
числителем следует считать нецелесообразным.
Задача 22,5 (для самостоятельного решения). Найти производ-
производные функций:
Ответ. l)y'=_-g,: 2) у'= ~; 3) у' =
* . 4л- у^х"
Задача 22,6. Найти производную функции у = Ьх? — Зд:2 + х — 1.
Решение. Заданная функция есть алгебраическая сумма
нескольких функций. Известно (формула B2,4), что производная
алгебраической суммы функций равна такой же алгебраической
сумме производных этих- функций, а потому у' = Eл^)' — (Зд:2)' +
+ х' — A)'. Здесь мы дифференцирование выполним без проме-
промежуточных записей:
у' = 15л-2 - бд; + 1
(производная от х равна 1: лг' == 1, а производная 1 равна нулю,
как производная постоянной величины).
Задача 22,7 (для самостоятельного решения). Найти произ-
производные функций: 1) у = а У~х + х У а; 2) у = \хг — \х^ +
I I? .js _ оve I i. yt. Ъ и — Qx7 ~ - а •
г 5 X" — /.X1 -\- -jX , И) у — УХ л-5 JiT~Jm'
4) у = Зх*Ух-4хУх* + 9Ух*-бУх+4= —•
V* 7х*\Гх
13 И. А. Каплан 369
Указание. Перейти к дробным показателям степеней.
Ответ. 1) у' = -^т= + Va (при дифференцировании второго
слагаемого учесть, что ]/а — постоянная величина, а х' = J);
2) у' = л;2 A — 6л; + 13л;2 — 12л;3 + 4л;4);
о\ ' Ло е . 15 г- 33 *. am
о) У = ®М + ^6 Г ^Тг + Jm+i '
.. , _ s/~ nif~% ,6 3 2,4
4) г/ = 7л; у х — 7 у х3 + —- —-^ — —-^ Н —:.
Задача 22,8 (для самостоятельного решения). Найти производи
о
ные функций 1) г/ — —^ + 30 v^a;Н . Указание. -4г=5л;5;
z; y = zix —~2Х
Ответ. 1) у' = 8^ + ^^ —; 2) г/ = (9л;
-2K^J.
*¦ -к-
Задача 22,9. Найти производную функции у *=. (ELy2 -\-lx-\- 2)*л
Решение. Здесь мы имеем дело со сложнЪй функцией. Поло-
Положим и = 5л;2 -(- 7л; + 2, тогда г/ = ы3. Следует писать так: ,у = ы3;
ы == 5л;2 -Ь 7х + 2.
Для того чтббы найти производную, воспользуемся формулой
B2,23) для дифференцирования сложной функции:
у' =.- Зн2ы' = 3 Eл? + 7л; + 2J^5л;2 + 7х + 2)' =
= 3 Eл;2 + 7л; + 2J • A0л; + 7).
Однако можно обойтись и без промежуточных записей, т. е.
без введения переменной и. Мы настоятельно рекомендуем
читателю пдсле того, как он сделает несколько упражнений,
выполненных при помощи введения вспомогательной переменной,
от введения такой переменной отказаться и дифференцирование
выполнять сразу.
Формула B2,8) должна быть понята так: производная от сте-
степенной функции и", где и есть функция х, равна пи"~1и', т. е.
равна показателю степени, умноженному на ту же функцию и,
но в степени на единицу меньшей, а полученное произведение
надо еще умножить на производную от основания степени и.
В нашем случае получаем: у' = 3 Eл;2 + 7л; + 2J • (Юл; -j- 7)
производная производная
степенной основания
функции степени
370
Выполним еще несколько аналогичных задач, но без столь
подробных пояснений.
Задача 22,10. Найти производную функции у = Eх3 -+- 4л;2 -f-
+ 8)*.
Решение. 1) у — м4, где и = 5л;3 + 4л;2 -f- 8. По формуле
B2,23) у' = 4mV == 4 (бх3 + 4х2 + 8K A5л;2 + 8л;) (производная от
8 равна 0). Проведем решение без введения промежуточной пере-
переменной: у' = 4 Eл;3 + 4л;2 + 8K A5л;2 + 8л;)
производная производная
степени степени
основания
Задача 22,11 (для самостоятельного решения). Найти произ-
производные функций:
1) #=E*»+7)»; 2) # =
Ъ)у = (а + Ьх)т; 4) у =
Найти производные, введя сначала промежуточную перемен-
переменную, а потом минуя ее введение.
Ответ. 1) у' = ЗОхEл;2 + 7J;
2) у' = 5 A + 5л; - 8л;2L E - 16л;);
3) у' =-• Ьт {а + Ъх)т-\
Задача 22,12. Найти производные функций:
2
1) у = /л;2 + 2; 2) г/ = /Зх; 3) г/ = ,-„ .— -,.,.
Решение. 1) Положив н = х2 + 2, получим « = )/м, и
поэтому на основании формулы B2,23)
у' = -1й' = ' Як = *
2/" 2|/"л-2+2 /л-а+2'
Можно было бы сразу воспользоваться формулой B2,9) для
дифференцирования квадратного корня из функции, не вводя
промежуточной переменной и.
Эту формулу следует понимать так: чтобы получить производ-
производную от квадратного корня из функции, надо единицу разделить
на два корня квадратных из той же функции и полученную дробь
умножить на производную от функции, стоящей под корнем.
Следовало поступить так: 1) у = ~\Гхг -\- 2; у' — __ • 2л;
производная производ-
от квадратного ная от
корня из функции,
функции стоящей
под корнем
13* 371
производная квад- производная от
ратного корня функции, стоя-
яз функции щей под корнем
производная дро- производная
, 36 би с постоянным знаменателя
У = - C^-5)* ' числителем
Для упражнения выполним еще один совершенно аналогич-
аналогичный пример, но без введения переменной и.
Задача 22,13. Найти производную функции у — ¦
V лга + х + 1
Решение. По формуле B2,7) у' = - х% + \+х (Ух2 + х + 1/ =
производная производная
дроби ананенателя
дроби
\ W / O/QI i 1 \ "Ш /~
производная производная производная
дроби знаменателя функции, стоящее
под корнем'
Задача 22,14. (для самостоятельного решения). Найти произ-
производные функций: 1) у~УЗх* + 5х+1; 2) у =—==; 3) у
Ю
DХ8 —
Ответ. 1) у'^--- &х+- ; 2)/=
' У 2/Зл-2 + 5л-+Г
5)Ух* + 5
°> У {Ах3 — 5*2 +7л-— 1)*'
Задача 22,15. Найти производные функций: 1) Q = |^3/ — 2/2;,
2) ^ = К
Решение. 1) Перепишем пример в виде Q = (St —
Q' = 4- C* — 2^2) 3 C - 4/). Окончательно Q' = —
s/Ci —
производная производная осио-
степени ваиня степени
2) Перепишем пример в виде S = Btz — t*) 4;
S' = -J B^2 — Р) 4 • {4t —
проиаводная производная осио-
степеии ванн* стгпени
372
Окончательно S' = Зд<D~3<) .
Задача 22,16 (для самостоятельного решения). Найти производные
функций: 1) у = VЬ + 2 УШ + Sx; 2) у = КC + 4 3/2JcK;
Птврт
+ 2 /Здг + Зг)« 8/7* УЗ + 4 8
Теперь решим несколько задач, в которых требуется найти
производную произведения и частного функций. Нам придется
пользоваться формулами B2,5) и B2,6).
Задача 22,17. Найти производную функции у = х2 {5х — 4)в.
Решение. Здесь надо продифференцировать произведение
двух функций. Будем считать, что в формуле B2,5) и = х2, v =
— Eх — 4)'. Каждую из этих функций мы уже умеем дифферен-
дифференцировать, а потому на основании указанной формулы у' — (х2)' х
X Eл; — 4)' + х2 [Eх — 4N]'. Теперь выполним дифференцирование:
у' — 2х Eх— 4)e -f х2 ¦ &i5x — 4M • 5, а после упрощений получим
у' =8хEх — 4)ъEх — 1).
Задача 22,18 (для самостоятельного решения). Найти произ-
производную функции у = Eх2 — 7х -J- 2) (\5х2 + 5K.
Ответ, у = A0х - 7) A5х2 + 5K + 90л; A5л:2 + 5J Eх2-
Задача 22,19. Найти производную функции
у = (Зх2 + Бах — 2а2) Уа2
Решение. По формуле B2,5) имеем при и — Зх2 + Бах — 2а2;
v = ^Ч-Зл:2; / = (Зх2 + 5ал: - 2а2)' • Уа* + 3х2 + (Зх2 + бал; —
){У+)
Выполняя дифференцирование, получим у' — (Ох + 5а) х
X Уа2 + 3*2 -Ь (Зх2 -f 5ал: — 2а2) , ^ ¦ 6х; после упрощений
. производная
производная подкоренного
, 5а8 + ЗОадг2 + 2^Д(* корня выражения
~ Уа* + Зл-2 "
Задача 22,20. Найти производную функции
у = (9а2 — бабх + 5„62л:2) у (а + &еJ.
Решение. Эту задачу мы решим без промежуточных записей
(формула B2,5)):
у' = (-баб -f Ш2х) У{а + bxf + (9а2 - Qabx + ЬЬ*х*) х
г + bx) 3 • Ъ.
производная пер-
первого сомножителя
производная вто-
второго сомножителя
373
Теперь следует сделать упрощения, после которых должно
получиться
406V
У =--, :•
Зу/~а + Ьх
Задача 22,21 (для самостоятельного решения). Найти произ-
производные функций:
1) у = D0 — 12* + ?.г2) УЬ + Зх;
»; 3) «/ = (8х» - 21) f GTW.
2/5 + 3*'
Задача 22,22 (для самостоятельного решения). Найти произ-
производные функций:
1) 0 - (~ - 2х + а;2) /E + 2л;K; 2) t/ = (Зл;* +
Ответ.
2) у' = . 135Jf? ; 3) /=
«А(9^4 з)з
—о
— 9
Задача 22,23. Найти производную функции у =uvw, где и,
v, w — функции л; : « = и {х), v — v (x), w = w (x).
Решение. Запишем данную функцию в виде y'=(uv)w и
применим к ней формулу B2,5):
- у' == (ми)' w + uvw', но (ми)' = м'у + uv',
а поэтому г/ = (u'v -f- uv')w + «шЛ раскрывая скобки, будем
иметь окончательно
#' = м'ую + uv'w + uvw'. B2,24)
Можно указать, что вообще, если у = щиги3 ... ип, то
' + + • • "л +
Этот результат словесно выражается так: чтобы вычислить
производную произведения любого числа функций, надо продиф-
продифференцировать первую функцию и умножить полученную про-
производную на произведение всех остальных функций, затем найти
производную второй функции и умножить ее на произведение
всех остальных функций. ТЬчно так же поступить со всеми
функциями-сомножителями и все полученные таким образом про-
произведения сложить. т
374
Задача 22,23а. Найти производную функции
у = Bа + 36л;) Bа — 36л;J /4а + 66л;.
Решение. На основании формулы B2,24), полученной в пре-
предыдущей задаче,
у' = Bа + 36л;)' Bа - ЗбхJ /4а + 66л: +
+ Bа + 36л;) [Bа — ЗбхJ]' /4а + 66л; +
-f Bа + 36л;) Bа - 36л;J (У 4а + 66л;)'.
Выполняя дифференцирование, получим
у' = 36 Bа - 36л;J /4а + 66л; + Bа + 36л;) • 2 • Bа - 36л;) ¦ (—36) х
X /4а + 66л; + Bа + 36л;) Bа - 36л;J . 1 • 66
2 у 4а -\- 6Ьх
и после упрощений окончательно
y'=Yb (Ш - 2а) B16л; + 2а) /4а + 66х.
Задача 22,24 (для самостоятельного решения). Найти про-
производную функции
у == Dл; — 7) C* + 7) у Ъх + 7.
Ответ.
у' = 28х уЪх + 7.
Задача 22,25 (для самостоятельного решения). Найти про-
производную функции
у =
Ответ.
2а
Задача 22,26. Найти производную функции
= аа — л-2
Решение. Здесь следует применить формулу B2,6) для диф-
дифференцирования дроби. При решении этой задачи и следующей
будем делать подробные записи, а в дальнейшем от них откажемся.
Надо научиться дифференцировать бегло, без промежуточных за-
записей. Здесь и = а2 — х2, v = а2 + л;2;
' — («" — х2)' (а2 + *2) — (а2 + х2)' (а2 — *2)
375
Выполняя дифференцирование в числителе, получим, что
а после очевидных упрощений
Задача 22,27. Найти производную функции
» 5 —
Решение. Применяя формулу B2,6), имеем
* E — З
Выполняя дифференцирование, получим
, C + 2дг) E - Здг + х2) - (- 3 + 2дг) E + Здг + дг^)
у E —
а после упрощений
„'- 6E—л*)
^ E — Зл- 4- *2J'
Задача 22,28 (для самостоятельного решения). Найти про-
производные функций:
1)у = фг',2)у = \±?-,3)у = Aх™х)п.
Ответ.
Задача 22,29. Найти производную функции
х
Решение. По формуле B2,6), считая и = х, v = У 1 -f-
получаем
а выполняя дифференцирование, имеем
1
2^.^ J
после упрощений получим, что
1
376
ДВАДЦАТЬ ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Дифференцирование тригонометрических функций.
Задача 23,1. Найти производные функций:
1) y = s\nkx; 2) y = coslx; 3) y = igpx; 4) y = ctgqx.
Решение. 1) По формуле B2,13), полагая и = kx, имеем:
у = sin и; и = kx; у' = cos и • и'', у' = cos kx • k\ у' = k cos fex.
производная производная
синуса и =• kx
2) По формуле B2,14), полагая
у = cos и; и = 1х; у' = —sin и • и'; у' = —sin lx • I; у' = —I sin lx.
3) По формуле B2,15), полагая
у = tg«; и = р*; у' ^'
производная производная
косинуса u=lx
производная производная
тангенса и=рх
или У = р sec2 дк.
4) По формуле B2,16), полагая
*/ = ctgu; « = «7*; / = ^ ^
производная производная
котангенса u=qx
или «/' = — <7cosec2<7x.
После нескольких упражнений студент сам откажется от вве-
введения промежуточной переменной и, подразумевая ее в тех мес-
местах, где она нужна.
Задача 23,2 (для самостоятельного решения). Найти производ-
производные функций: 1) у = sm3x; 2) у = sirxbx; 3) у = sin 15r, 4) у =
= cos4;e; 5) «/=—cos3x; 6) y = cos9x.
Ответ. 1) y' = 3cos3*; 2) #' = 5cos5*; 3) у' = 15cos 15x;
4) у' = — 4 sin 4*; 5) у' = 3sin3*; 6) у' = ---9sin9;e.
Задача 23,3. Найти производные функций:
; 2) </ = sinl/i; 3) # = tg^; 4) у =
Решение. 1) Мы прежде всего вычисляем производную си-
синуса, а так как синус берется от 2х2, то вычисляем производ-
производную 2х2. Производная данной функции равна произведению этих
производных. Пользуясь формулой B2,13), получаем
у' = cos2;e2 • 4х; у' — 4*cos2;e2.
377
2) При решении этого примера мы также прежде всего должны
вычислить производную синуса, а так как синус вычисляется от
У~х, то надо взять производную от этого корня и полученные
производные перемножить. Формула B2,13) дает
у' = cosV^
3) Здесь прежде всего надо продифференцировать тангенс, но
так как он берется от дроби, то следует найти производную
дроби и эти производные перемножить. По формуле B2,15)
[и = —-
П+xV I 1 • дг — A
и- -
У —
произ-
производная
дроби
1 + * ' х*
cos2—¦—
1 ,1
4) В этом примере следует сначала продифференцировать косинус.
Так как косинус вычисляется от квадратного корня, то вслед за этим
надо продифференцировать корень. Но корень вычисляется от дроби,
а поэтому надо, продифференцировать дробь и все три полученные
производные перемножить. Здесь цепочка из трех звеньев:
у = cos и; и = УЪ\ v = j~
Производная
Окончательно
производная ' ' t * производная
косинуса * ¦ ' дроби
Аналогичное упражнение выполните самостоятельно.
Задача 23,4 (для самостоятельного решения). Найти производ-
производные функций:
1) 0 = sin У y-L- ; 2) у = "
1 ., 1 — sin *
-^ 1 -f- sin.
378
Ответы даются в таком виде, который позволяет проверить
решение. Упрощение ответа сделайте сами.
Ответ.
у = cos /IE ¦ _J^ • [- (Т-У • (-1);
1—*
2) у' = }. .cos*; 3) у' =—Д=- • / V~) • (—sin*);
' У 2/sin* ' * 2l/_L \ /
Г cos *
4) У = — (i _}_ Sin д-)а •
Задача 23,5. Найти производную функции у =р 3 sin2 x.
Решение. Запишем пример так: у = 3 (sin xJ.
Если ы = sin*, то у = Зы2) и тогда v
у' = бии' =
Теперь покажем, как решить задачу, не вводя и. Прежде все-
всего продифференцируем степень, а так как в степень возводится
sin л;, то продифференцируем .и sinx. Найденные производные
перемножим, постоянный множитель 3 вынесем за знак произ-
производной:
#' = 3-2sin;e cos*; у' = 6sin*cos*,
производ- произ-
¦ иая степе- водная
• ии синуса
или
у' = 3 sin 2x.
Задача 23,6. Найти производную функции y = cosex.
Решение. Запишем пример в виде у = (cos*)e¦ и положим
у = и6, а и = cos*; тогда у' — 6и5и' = 6(со§*M • (—sin*); у' = —
— 6 sin * cos5 *.
Теперь ту же задачу решим без введения и.
У нас дифференцируется шестая степень косинуса: сначала
продифференцируем степень, а так как в степень возводится коси-
косинус, то надо найти производную и от косинуса, а затем эти про-
производные перемножить.
Итак,
у = cos6 *; у' = 6 cos5 * • (— sin *);
производная производная
от шестой от cos x
степени ко-
косинуса
у = —6 sin* cos5*.
Теперь самостоятельно, но без введения и (и держать в уме)
решите несколько аналогичных примеров.
379
Задача 23,7 (для самостоятельного решения). Найти производ-
производные функций:
1) у = s.ins Х; 2) у = tgs *; 3) у = ctg4 л:;
4) y = 5cos5*; 5) у = 7tgejc; 6) y = 8sin2A;.
Ответ. 4-) i/r = 3sin2A;cosA;; 2) г/' = 3tg2хsec?х;
3) у' = — 4 ctg3 x cosec2 г, 4) у' = —25 cos4 X sin *;
5) у' = 42 tg5 x sec2 x; 6) у' = 16 sin x cos л: =
= 8 sin 2*.
Задача 23,8. Найти производную функций:
1) у = /sin*; 2) .у = T/sin2A; + 3cosMA;; 3) у = ^f.
Решение. 1) Вычисляем производную от квадратного корня,
а так как корень извлекается из sin;*;, то следует вычислить
производную от синуса и перемножить эти производные. Последо-
Последовательно получаем
cos*.
—4== -cos*.
2 У Sin X произ-
произ2) Здесь корень квадратный извлекается из суммы sin2 x +
+ 3 cos3 4л:. Поэтому сначала вычисляем производную от квадрат-
квадратного корня, а потом умножаем ее на производную от подкорен-
подкоренною выражения:
у' = ,, * [Bsin.KCos;t) + 3 . 3cos24^ • (—sin4л:) • 4].>
2 /sin* к + 3 cos' Ax - . •> ¦ . ¦ . ¦ i-i
~—^-v— : ' производная от произвол- произвол- про-
производная sin" *
корня ¦
3) Сначала возьмем производную дроби, затем вычислим про-
производную от знаменателя дроби и перемножим эти производные:
i 1 о * / • ч 3 sin х
У - - 3cos4(sm*)
производ-
производная от сте-
пеин cos
пронзвод-
пронзводная от
cos ix
про-
извод-
изводная от
4х
^?и^ производная зна-
водная менателя дроби
дроби
Задача 23,9 (для самостоятельного решения). Найти производ-
производные функций:
1) у = sin (px + g);
13 1
2) у = у sin 7х + " sin Ъх + -^ sin Зл: — 5 sin x;
3) У = 4- sin 8л: + l-sin 6* + sin 4л: — 2 sin 2л: — 5л:;
О О
4) у = ¦§- cos 9л: + у cos 7х — ~ cos Зл: — 6 cos x.
380 * '
Задача 23,10. Найти у', если
... . у = x3sin;c4- 3x2cos;c — бдгвтл: — 6cos*.
Решение. Производную от первого, второго и третьего сла-
слагаемых будем искать, как производную от произведения
у' — 3*2sin х + х3 cos x + б* cos х — Зх2 sin х — 6 sin х — бд; cos x +
производная первого производная второго производная третьего
слагаемого слагаемого слагаемого
производ-
ная чет-
четвертого
слагае-
слагаемого
после приведения подобных членов получаем у' — х3 cos x.
Задача 23,11 (для самостоятельного решения). Найти произ-
производные функций:
3) у = tgjf-ctg* — 2х; 4) у = (cos2* + J-)sin3*.
Указан вд. При дифференцировании первого сомножителя
во втором примере учесть решение третьего примера задачи 23,8.
От.ет. О/-^ '" %/4|S?'i
3) у' = tg2x + ctg2д:; 4) у' = 5siri2xcos3дс.
Задача 23,12 (для самостоятельного решения). Найти произ-
производные функций:
1 1 3 4
1) ?/ = -jcosxctgx — -g-cos2xsinд: —g"s^nx —-g-
2) y= ^*4-ct
Ответ. 1) /=S?p; 2)^' = -
Задача 23,13. Найти производную функции
3 cosec х — 2 sin x 16
381
Решение. Первое слагаемое — дробь, а потому при его
дифференцировании должна быть использована формула B2,6):
, _ 1 C cosec х — 2 sin x)' cos5 x — (cos5 x)' C cosec x — 2 sin д-)
У ~~ !> cos10 х
16/ 1
"\" sin2 2х 2}~~
(—3 cosec х ctg x — 2 • cos x) cos5 x — (—5 cos4 x sin x) ¦ C cosec x — 2 sin x) .
— 5 cos10 л- ¦"
32 1
"т " sin2 2л-'
а после упрощений окончательно получим (если заменить
1 , cos дД
cosec х = -.—, a ctg х = -г—1,
sin х • 5 sin х/ '
что
1
ций.
" sin2 х ¦ cos6 x '
ДВАДЦАТЬ ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание; Дифференцирование обратных тригонометрических функ-
Задача 24,1. Найти производные функций:
1) у = arcsin 2х\ ¦ 2) у — arccos^; »
3) у = arctg Vx(x > 0); 4) у = arcctg -^ (х > 0).
V х
Решение. 1) Задачу перепишем в виде
у — arcsin и, и — 2х.
Тогда по формуле B2,19)
1 п. ... 2
про-
извод-
изводная
от
и = 2х
Можно было обойтись и без введения промежуточного аргумен-
аргумента. Присмотритесь к формуле B2,19). Производная от функции
у = arcsin и находится так: единица делится на квадратный
корень из единицы минус квадрат той функции, которая стоит
382 " ^
под знаком арксинуса, и эта дробь умножается на производную
этой функции. Поэтому сразу можно было бы писать:
,/= , ' ¦ 9 = --Д_
ь/ "I/- -4O Т/1 jtn
производи
производ- ная от
иая от функции,
арксинуса стоящей
под зна-
знаком арк-
арксинуса
Таким образом, мы функцию и не ввели, а держали ее в уме.
2) Здесь мы используем формулу B2,20), которая только зна-
знаком отличается от формулы B2,19) и проведем решение с введе-
введением и без введения промежуточного аргумента. Перепишем за-
задачу так:
у = arccos и; и = хт; у' = г -=, ¦ <хт)' =
У 1 —и2
mxm-i
(и — хт, а потому «2 = хгт).
Теперь решим эту задачу, не вводя промежуточного аргумента.
„' _ 1 тги-1
произ- *»
производ- водная от
ная от арк- функции,
косинуса стоящей
под знаком
арккосинуса
3) При решении этого примера будем пользоваться формулой
B2,21). Опять-таки сначала введем промежуточный аргумент и,
а потом проведем решение без этого осложнения.
Перепишем задачу так: у = arctg и; и = Ух;
1 /1/-Ч' 1 1 / л Г- * ч
I/ _____^—_ ( I/ V\ . . _____ ( tqi/ l^CIW // I/ V Т/Ч //в — VI
У —* 1 I n ' 11^ Л I | , у 11 ыД 1\ы<\ W, I/ Д. j l\J 14, •—* Л} •
Запомните, что производная функции у = arctg в равна дроби,
у которой числитель равен 1, а знаменатель равен 1 плюс квад-
квадрат функции, стоящей под знаком арктангенса, и дробь умножа-
умножается на производную этой функции:
у = arctg У х;
, _ 1 1 _• 1
произ- производная
водная от функции,
от арк- стоящей под
тан- знаком арк-
генса тангенса
383
4) Здесь следует воспользоваться формулой B2,22). Поступим,
как и раньше: сначала введем промежуточную функцию и, а по-
потом проведем решение, не вводя ее.
Перепишем задачу:
S/ = arectgu, u = -^;
ух
произ- производ-
водная ная зна-
дроби менателя
дроби
Так как и = г^. то и2 = —, а потому
у =
и окончательно
У' = -
Мы получили такой же ответ, как и в предыдущей задаче.
Этот результат не является случайным, потому что при а > О
имеет место формула arctg а = arcctg —, а в нашем случае
V*'
В дальнейшем нам придется ссылаться на соотношения между
обратными тригонометрическими функциями.
Читателя, интересующегося относящимися сюда выводами,
отсылаем к книге: С. И. Новоселов. Обратные тригонометри-
тригонометрические функции.
Задача 24,2 (для самостоятельного решения). Найти производ-
производные функций:
1) у — arcsin Ъх; 2) у = агс$\пУ~х{х > 0); 3) у — arcsmmx;
4) у — afccos 6л:; 5) у = arccos(l — г8); 6) у =~arccos— .
Ответ. 1)У'= *_; 2)у,
1
384
Задача 24,3 (для самостоятельного решения). Найти производ-
производные функций:
1) у = arctg Ъх; 2) у = arctg ~; 3) у = arctg Зх2;
4) у = /arctgl; 5) у = arcctg тх; ! 6) arcctg jq-^.
Ответ. 1) г/' = у^^г I 2) у' = - -^ ; 3) у' = y-j^;
}1/"l/i?Ht|I 1 + **' )У ~ 1 +
Ь) У —
В двух следующих задачах даны упражнения в дифференци-
дифференцировании степеней обратных тригонометрических функций.
Задача 24,4. Найти производные функций:
1) у = arcsin2*; 2) у = arcsins3*; 3) у = arctg4 У~х.
Решение. 1) Этот пример решим сначала с помощью введе-
введения промежуточного аргумента и. Перепишем задачу так: у =
= (arcsinjcJ.
Пусть у — и2, и = arcsin x.
Поэтому у' — 2ии' — 2 (arcsin д:) (arcsin x)'\
у = arcsin х
Этот же пример решим без введения промежуточного аргу-
аргумента. У нас y = arsin2;c.
Прежде всего следует продифференцировать степень, а так
как в степень возводится arcsin д:, то вслед за этим надо про-
продифференцировать arcsin х и производные перемножить:
у' = 2 arcsinx • . . .
yl — х*
2) Мы настоятельно рекомендуем не вводить промежуточных
аргументов.
а) продифференцируем сначала степень;
в) так как в степень возводится arcsin Зд:, надо взять про-
производную от arcsin Зд:;
с) вычислим производную от Зд: потому, что арксинус вы-
вычисляется от Зд:. Полученные производные перемножим.
Записи расположатся так:
у' =¦ 3 arcsin2 Зд; • ' -3
производная . ПР°-
от степени производная извод-
арксинуса от арксинуса иая **
385
3) Этот пример также решим без введения промежуточного
аргумента.
у' = 4 arctg3 Vx ±т=
производная
степени производная пронз-
арктангенса водная
корня
Задача 24,5 (для самостоятельного решения). Найти произ-
производные функций:
1) у = arcsin3 х2; 2) у — arctg3 -^-; 3) г/ = arccos4 5a:;
4) г/ = arcctg У*5; 5) У = arctg у=? .
Ответ. 1) у'= 3arcsin3*2j7f=i; 2) #' = ~ ;^7агс^ ? .
20 arc cos3 5x
Задача 24,6. * Продифференцировать:
1) у = arcsin У1—х2; 2) у = tg (arcsinж);
о. , cos jr , v ¦ а 4- b cos x
3) « — arctg r-;—: ; 4) у — arctg ¦—- .
' " s 1 + sin x ' v & b + a cos дг
Решение. 1) При дифференцировании не будем вводить про-
промежуточных аргументов:
У' = B)
производная от производная пая под-
арксииуса корня коренного
Еыр1»:ения
У = -
А так как У~х? —\х\=( х, если х> 0;
\—я, если л: < 0,
Л*
то получаем, что при х > 0 г/' = -,—:
; у = f ,
а при л; < 0 у' = — ¦ / ; «' = ' .
В первом случае (х>0) получилась производная, равная про-
производной от arc cos*, а во втором (*<0) производная получилась
* В этой и следующих задачах буквы а и b имеют такие значения, что
содержащие их фуикции вещественны. Неоднозначность знака не указывается.
386
такая же, как от арксинуса. Этот результат не случаен. Из три-
тригонометрии известно, что если 0< * <1, то
arc sin У\ — х2 — arc cos*,
а при значениях — 1 < х < О
arc sin УI — х2 —- ic — arc cos x.
2) у' = sec2 (arc sin x) ¦ , ;
производная тангенса '
производ-
производная арк-
синуся
,, _ 1 —sin х A + s'n х) — cos x ¦ cos x . , 1_
' У "" . COS2A- A + Sin A"J > У — 2 "
> (] _L sin уЛ2 Ч x ; '
^_ ит1*) производная дроби
—6 sin д- (Ь+а cos x)—(—a sin д-) (а + b cos л-) _
производная арк-
арктангенса
г _
(а+ь cos xV ' (&+а cos х)*
a cos д-
, —б2 sin д- + a2 sin Jf
г/ = -77—. .„ , .—r-т гт: и окончательно
* (b + a cos д-J -(- (а -)_ Ь cos д-J
, __ (a2 — b2)sin х
^ ~ (а2 + Ь2) -)- (а2 + Ь2) cos2 д- +. 4аЬ cos x '
Задача 4,7 (для самостоятельного решения). Продифференци-
Продифференцировать:
1) у = arc sin x -f- arc cos*; 2) у = arc tgx + arc ctg*;
и объяснить простоту полученных результатов.
Ответ. 1) 0; L) 0; 3) у' = j-jL^ .
Задача 24,8. Показать, что каждая из функций
^; 2) г/-2arctg
имеет производную, равную —А —- .
Решение. Дифференцирование проведем с подробными запи-
записями, но без введения промежуточных аргументов:
1 1 1
1) у' = 2 •
^~Г1 a— b '
производ-
'¦ — b ная под-
коренного
производная арксинуса "'TodhT13* ВЫраЖеНИЯ
387
В этом примере мы прежде всего дифференцируем арксинус
(постоянный множитель 2 сразу вынесен за знак производной).
Арксинус берется от корня и, следовательно, нужно взять про-
производную корня. Корень извлекается из дроби, а потому следует
вычислить производную дроби (дробь имеет постоянный знаме-
знаменатель а—b, а производная от дроби с постоянным знаменателем
равна производной числителя дроби, разделенной на тот же зна-
знаменатель). Производная заданной функции равна произведению
полученных выше производных.
После упрощений получаем:
2)у~2
_
2 /_Z± а~Ъ V(a~x)(x-b)
а — b У а — Ь
1 (а-х) + (х-Ь)
S
О — ¦*¦ производная под-
коренного выраже-
производная от производная ння
арктангенса корня
Упрощения проведите самостоятельно и получите, что
У =
3) у' = ' . _L_ . 1 -у
/ {2У(а-х)(х-Ь)\* а-Ь 2У(ах)(хЬ)
У
l *(а—х)(* —
(аЬ)*
X
(—2х -f а + Ь) 1 a-j-b — 2x
— x)(x — b) = V(a — bf—4(о — х)(х — Ь) У(а — х) (х — Ь)
Но выражение под корнем в знаменателе первой дроби равно
(а + Ь — 2дсJ, а потому получаем, что у' — , ,
У (а — х) (х — Ь)
Задача 24,9 (для самостоятельного решения). Продифферен-
Продифференцировать функцию
/сскЗлт
Ответ.
^ У cos х cos Zx '
ДВАДЦАТЬ ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Дифференцирование показательной и логарифмической
функций. Логарифмическое дифференцирование.
При дифференцировании показательной и логарифмической
функций мы будем пользоваться формулами B2,10), B2,11) и
B2,12) из основной таблицы формул.
Задача 25,1. Найти производные функций:
1) у = азх (а > 0); 2) у = fx- 3) у = 2";
4) у = 4sin* *' ,. 5) у = е?; 6) у = eVW*+a;
7) у = >ЯНТ. . 8) у = V (х3 - Зх2 + 6* - 6);
9) у = е*в*; 10) r/==^rcsin^_
Решение. 1) По формуле A2,10), если у' — аи(а > 0), то
у' = аи -и' ¦ 1па, , , *
В яаше*м случае, полагая у — а", и=± Зд:, имеем у' = аи 1па-3=
3**\
Здесь снова возникает вопрос о целесообразности введения
промежуточного аргумента и.
Можно" обойтись без этого. Техника дифференцирования у
читателя уже выработалась, а потому все последующие примеры
должны решаться без введения вспомогательных переменных.
Пример первый должен решаться так: у' = аЭх1па(Зх)';
пронзвод- производ-
производная пока- наз пока-
показательной зателя
функции степени
2) Здесь также будем пользоваться формулой B2,10):
у' = 7**
производная
показательной производная
функции показателя
w степени
3) По формуле B2,10) имеем:
у' = 2х' In 2 • Зх2 = Зх22" In 2.
проиэрод- произ-
ная пока, водная
аательной показа-
функции теля
степени
4) По формуле B2,10) имеем
у' = 4sin* х • In 4 • 2 sin x ¦ cos x = 4sIn' * sin 2x • In 4.
производная произ- проиа-
показательной водная водная
функции степени синуса
синуса
389
5) Из формулы B2,10) следует, что производная от функции
у = ех> равна ей же самой, умноженной на производную показа-
показателя степени и. Получаем у' = ех' (х4)' = 4х3ех'.
6) у' = eVx'+x+2 ¦ \ ' ¦ Bх + 1).
* ^г производная
производная подкоренного
корня , выражения
7) Здесь также следует воспользоваться формулой B2,10):
и дУ sin х __^^_^___ яле v
2/sin* -~—
- произ-
производная водная
корня синуса
8) Применим формулу для дифференцирования произведения:
у' = (ех)' (х3 — Зд:2 + бд: — 6) + ех {х3 — За:2 + бд: — 6)' =
=- ех (д:3 — За:2 + бд: — 6) + ех (Зд:2 — бд: + 6);
у' = ех (д-3 - Зд-2 + бд- - 6+Зд-2 - бд- + 6).
Окончательно после приведения подобных членов в скобке
у' — х3ек.
о\ „' _ etg xi\o xY = —
*) у е \щ*> со5ъх •
10) г/'— earcsin2*-2arcsin*—-¦ i
производная
степени производная
арксинуса арксинуса
Задача 25,2 (для самостоятельного решения). Продифференци-
Продифференцировать функции:
1) у = а*?1 (а > 0); 2) у = (а*)> > 0);
5)у=ех; 6)у = е~х.
Ответ. 1) у' =-- а^ ¦ In а • пх"-1; 2) у' = папх ¦ In а;
1 + л-2 ' '' » i* .'
5) у' = — - е7- 64 — — ~х-
X
Задача 25,3. Продифференцировать функции:
1) у = In (ах + Ь); 2) у = !п6 х; 3) у = In sin x;
4) у = In arc tg a:; 5) t/ = д: In x\ 6) t/ = —*;
7) г/ = In (* + ]/l + x\ 8) г/ --= In (In*).
390
Решение. По формуле B2,12), если у — In и, то у' — —и.
Чтобы получить производную от функции In и, где и — функция х,
надо единицу разделить на функцию и, стоящую под знаком
логарифма; полученную дробь следует умножить на производную
этой функции:
и = г-г- (ах + о)= гт о. —
ах + Ь ^ ' "' ах + Ь - - ах + Ь '
2) Здесь дифференцируется степень логарифма, а потому
производная n^^.
степени Еодная
лога-
логарифма
3) у' = -^ • COS X — Ctg X
Sin А" ь.
^троиз^ произ-
производная водная
лога- синуса
рифма
4) Аналогично решается пример 4: у' — —-— ¦ -р-—^.
ЭГС Xg X х —J— X
5) Здесь следует применить формулу для дифференцирования
произведения
у' — х' In х + х (In *)' = In x + л: • — = In x + 1.
6) По формуле для дифференцирования дроби имеем
, _ (In Л-)'а" — X' In X X _ 1 — In A"
У Zi ^2 Zi •
)'
2VT+T*)
производная производная от
логарифма функции, стоящей
под знаком логарифма
После упрощений получим, что у' = у
У 1 +
У ~~
^ » ~ kl А" ' А" ' У ~~ X 1П X '
произ- производная
водная от функции,
лога- стоящей под
рифма знаком лога-
логарифма
Задача 25,3а (для самостоятельного решения). Продифферен-
Продифференцировать функции:
1) у = In A5е* + х2)\ 2) у = 51п«"+*+1).
Ответ. 1) у' - 1^ + 2^ ; 2) у' ¦= 51п(**+*+» In 5 ¦ 32f+' . .
' J \Ъех -\- х ' J л-3 + х +1
391
Задача 25.4. Продифференцировать функции:
*) # 1п;
Решение. Во всех этих примерах прежде чем вычислить про-
производную, целесообразно выполнить логарифмирование.
1) Перепишем пример в виде у = \nx — ln(l — xl), а теперь
^ i
окончательно
у — жA —**)*
2) Перепишем пример в виде у= 1пл:—g-hlO +*2). и тогда
ы' - 1 - i
у ~ х 2
3) В преобразованном виде пример запишется так:
а поэтому
или
Задача 25,5 (для самостоятельного решения). Продифференци-
Продифференцировать функции:
; 2) у =
Указание. Прежде чем вычислять производную, целесо-
целесообразно выполнить логарифмирование.
оч „, -12 , /Ж
^ У — ж F + 7х + 2л-2)! 4) г/ = 7^2 _з
Задача 25,6 (для самостоятельного решения). Продифферен-
Продифференцировать функции;
392
Ук а з а н и е. Под знаком логарифма в первом слагаемом вы-
выгодно освободиться от иррациональности в знаменателе. После
этого дробь сначала прологарифмировать и только потом при-
приступить к дифференцированию. Производная второго слагаемого
найдена в задаче 25,3 (пример 7).
9\ — f x -L 1 1/ * — a
Ответ.1)/=№; 2
2 + л-г
Задача 25,7 (для самостоятельного решения). Продифферен-
Продифференцировать функции:
У к аз а н и е. В каждом примере, прежде чем дифференцировать
первую дробь, надо ее прологарифмировать.
Ответ. 1)/ = ^; 2)/ = ^; 3) у'- i
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
Если требуется продифференцировать произведение несколь-
нескольких функций или дробь, числитель и знаменатель которой со-
содержат произведения, часто представляется выгодным обе части
данного выражения сначала прологарифмировать, по основанию е,
а потом уже приступить к дифференцированию. Этот прием
получил название, логарифмического дифференцирования. Произ-
Производная от логарифма функции называется логарифмической про-
производной.
К этому приему удобно прибегать и при дифференцировании
выражений, содержащих корни из дробей. К нему прибегают
всегда, когда следует продифференцировать функцию вида
т. е. когда и основание степени, и показатель степени есть
функции х.
Способ-логарифмического дифференцирования будет подробно
рассмотрен на ряде примеров.
393
Задача 25,8. Найти производную функций:
1) у =* (х + 5J Bх - 7)Цх -2)(х + 3);
Ух* — Зл-2 + х — 4
"' » - (л-+ 2M (л-+ 4J' -/»~р Сл- + Й-
Решение. Во всех предложенных примерах целесообразно
сначала прологарифмировать по основанию е обе части равен-
равенства, а потом уже дифференцировать.
1) Если у = (х + 5J B* — 7K (* — 2) (х + 3), то In t/ =
= 2 In (д: + 5) +¦ 3 In Bx - 7) + In (x - 2) + In (* + 3).
Будем считать функцию In у сложной функцией переменной
х и найдем ее производную:
Производная функции In у с учетом того, что у есть функция
х, равна —у', а потому, вычисляя производную левой и правой
У
частей равенства, получим
7У ~ а-+ 5 +2л- — 7 '• -^1л- — 2+Л- + 31
Умножая обе части этого равенства на у и учитывая, что у
есть заданная функция, получим
2) Поступая так же, как в первом примере, получим
In у = ~ In (х2 + 7х — 8) + -i- In (x4 - 1) - -g-In (л:3 - Зд:2 + д: - 4).
Считая функцию In у сложной функцией переменной х и диф-
дифференцируя обе части равенства, получим
Умножая обе части этого равенства на г/ и зная, что у есть
заданная функция, получаем окончательно выражение искомой
производной:
7х - 8 ¦ y-^F^l /J 2л-+ 7 , J 4л-3
Зл-а - 6л- + 1
л-3 — Зл-2 + х — 4
394
3) Здесь опять-таки целесообразно сначала прологарифмиро-
прологарифмировать по основанию е обе части равенства, а потом уже дифферен-
дифференцировать:
In у = 2 In (х + 5) -+- 3 In (x — 4) — 5 In (x + 2) — 2 In (x + 4).
Считая, как и в двух предыдущих примерах, In у сложной
функцией переменной х и дифференцируя обе части равенства,
получим:
~уу= x^fl^ ' 7=^4 ' х~+2~ ' JTfl'
а после умножения обеих частей равенства на ^ учитывая, что
у есть заданная функция, получаем окончательное выражение
производной
, __ (х +S)i Or-4)»/ 2 3 5 2_\ ч
у (* + 2M (л- + 4J \д- + 5 "^ * — 4 * + 2 х — 4/ '
4) Прологарифмируем обе части равенства:
In у = -i- [In (a* + b) — In (с* + d)l-
Считая, что In у есть сложная функция переменной х и диф-
дифференцируя обе части равенства, получим:
Г.,
у " 2 [ ад" -j- 6 «r + d
Умножая обе части этого равенства на у = I/ a'Y , ,, получим,
Г СХ -г- и,
№
что искомая производная
/ \ ( п
У = ~2 W+ 6 "~ сд- + d / F cF+" rf '
и после очевидных упрощений окончательно
/ ad — be "I fax_j-_b _
У ~ 2(ax+b) (ex + d) V cx + d '
Задача 25,9 (для самостоятельного решения). Найти произ-
производные функции:
1H = {Ъх - 4)» (х - 2J C - 4*); 2) у =
о\ 5д-2 . „ « .. (л-+ 5O (л-2 — 4л: + 2K
3) У = ^рт • sin'* • cos**; 4) у = +J +^t + &)+
395
Задача 25,10 (для самостоятельного решения). Продифферен-,.^!
цировать функции:
2) у в
E-2*) C*-4)
3) у =
Теперь мы займемся дифференцированием функций вида
Читатель должен обратить внимание на тот факт, что для!
дифференцирования этой функции непригодна ии формула B2,8),|
ни B2,10), так как в первой из них основание степени и есть!
функция х, а показатель степени—величина постоянная, вовто-1
рой основание степени — постоянная величина, а показатель сте-1
пени — функция х. В рассматриваемом случае и основание
степени / (х), и показатель степени 9 (*) — величины переменные —
функции независимой переменной.
В общем виде задача дифференцирования этой функции ре-
решается так:
Прологарифмируем по основанию е обе части равенства и по-
получим
lny = f{x)\nf(x).
Теперь, считая In у сложной функцией переменной х, найдем
производную обеих частей последнего равенства, дифференцируя
правую часть, как произведение
jy' = f' (х) In f(x) + ? (х) -^ Г (x).
Умножая теперь обе части этого равенства на у и учитывая,
что у =¦ [f (х)]*<*>, получаем окончательно
у' = [f (X)]fW j<p' (X) In
Запоминать эту формулу не следует, а вместо этого надо хорошо
усвоить метод вычисления производной от функций рассматри-
рассматриваемого вида.
Задача 25,11. Найти производную функции у = х*(х>0).
Решение. Беря натуральные логарифмы от обеих частей
равенства, получим \пу^х\пх и дифференцируем теперь обе
части равенства, считая Ип у сложной функцией х:
I
396
Умножая теперь обе части равенства на у, который по усло-
условию равен хх, получаем окончательно у' — хх (In х -f- 1)-
Замечание. В условии задачи указано, что х >0 потому,
что х в последующем оказывается под знаком логарифма, а ло-
логарифмы можно вычислять только от положительных чисел.
Задача 25,12. Определить производную функции
Решение. Беря натуральные логарифмы обеих частей ра-
равенства, получаем
In у — cos я» In sin x
(так как sin* стоит под знаком логарифма, то является сущест-
существенной оговорка в условии задачи, что х берется из интервала
@; тс), так как для значений х из этого интервала sinx>0 и
In sin x имеет смысл). Теперь продифференцируем обе части по-
последнего равенства, считая, что In у — сложная функция пере-
переменной х:
— у' — —sin л: ¦ In sin x + cosx • —^ • cos*.
Умножая обе части этого равенства на у, который по условию
задачи равен (sin x)cos x, получаем окончательно, что
у' = (sin x)'°s x {- sin x ¦ In cos x +
ДВАДЦАТЬ ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Гиперболические функции. Дифференцирование гипербо-
гиперболических функций. Дифференцирование неявных функций.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Предыдущие практические занятия убедили читателя в широ-
широком применении при решении разобранных задач показательной
функции ех. Но кроме самой этой функции как в математике,
так и в прикладных науках применяются различные комбинации
ее с функцией е~х.
По определению вводятся такие часто встречающиеся комби-
комбинации функций е* и е~х:
~е— называется гиперболическим синусом х и обозначается
символом shx;
sh x = еХ~/~Х (-оо<х<.+ оо); B6,1)
397
е называется гиперболическим косинусом х и обозна-
2
чается символом ch x
ch х = е* + *""* (- со < х < + со); B6,2)
~ _t называется гиперболическим тангенсом д: и обозна-
обозначается символом th д:
th л; = ~^г(- со < * < + оо); B6,3)
^'—е-* называется гиперболическим котангенсом х и обозна-
обозначается символом cth х
cth x = Z-7-"* (~ °° < х < 0)' @<*< + °°). B6,4)
Производные гиперболических функций вычисляются по фор-
формулам (и = и (х)):
у = sh и; у' = ch и ¦ и; B6,5)
у = ch и; г/' = sh ы ¦ и'; B6,6)
y=thu; у'=,-!-. и'; B6,7)
г/ = сШ«; у' - - ^¦• и'. B6,8)
Эти формулы следует запомнить.
Задача 26,1 (для самостоятельного решения). Доказать, что
функции sh х, th* и cth x — нечетные, а функция ch x — четная.
Указание. В формулах B6,1)—B6,2) заменить х на — х
и убедиться, что sh (—*) = — sh x; th (— x) = — th x; cth (—*)- =
= — cth x, a ch (— х) — ch x\
Задача 26,2. Вычислить производные функций: 1) */ = sh2*;
2) у = th3 х2; 3) у = In sh x; 4) у = cos (ch x).
Решение. 1) Используя правило дифференцирования сложной
функции и формулу B6, 5), получаем, что у' = 2sh*ch*= sh2x
(проверьте, что из определения гиперболических функций дейст-
действительно следует, что 2 sh x ch x = sh 2x)\
2) у' =
произ-
производная производ- произ-
стелени ная гипер- водная
болического *
тангенса -
3) у' = -^y ch x — cth x; 4) у' = — sin (ch *) ¦ sh д:
произвол- пронз-
ная коси- водная
иуса гипербо-
лическо-
косинуса
398
Задача 26,3 (для самостоятельного решения). Вычислить про-
производные функций: l)y=ch3x; 2) у —- shх + -g-sh2x; 3) у =
= ch (sin x); 4) i/ = sin (ch x); 5) г/ = In ch x; 6) г/ = In th x; 7) у =
= cos x ¦ ch a: -f sin x • sh *; 8) у — th д: —g-th8 ж; 9) г/ = ^h * T g°^-
Ответ. 1) г/' = 3ch2xshx; 2) г/' = ch3*; 3) у' = sh(sin*)cosa:;
о
4) г/' — cos (ch x) ¦ sh x; 5) г/' = th x; 6) г/' — sh 2y ; 7) г/' ~ 2sh x cos д:;
оч ' i л гчч 2shA- sin x
8) 0 = sch«*; 9) y= (sh^ + sin^ •
ДИФФЕРЕНЦИРОВАНИЕ НЕЯВНЫХ ФУНКЦИЙ
Если независимая переменная х и функция у связаны уравне-
уравнением вида f(x, у) — 0, которое не разрешено относительно у, то
у называется неявной функцией х.
Несмотря на то, что уравнение f(x, у) = 0 не разрешено отно-
относительно у, оказывается возможным найти производную от у по х.
В примерах, которые рассматриваются ниже, указан прием
для нахождения производной в случае, когда функция задана
неявно. Прием этот состоит в том, что обе части уравнения
f(x, у) — 0 дифференцируются по х с учетом, что у есть функция
х, и из полученного уравнения определяется у'.
Задача 26,4. Найти производную от неявной функции 5х + Ъу —
-7=0.
Решение. Дифференцируя по х обе части равенства и учи-
учитывая, что: 1) у есть функция х и что 2) производная правой
части равенства равна нулю, получаем 5 + 3t/' = 0; Ъу' = — 5;
и'- 5
Задача 26,5. Найдем производную у' неявных функций:-
1) х2 + у2 — 25 = 0; 2) х3 + уа — 3аху = 0.
Решение. 1) При дифференцировании у2 по х получается
% - 2уу.'
Здесь сначала продифференцирована степень у, а потом диф-
дифференцируется по х основание степени у (производная от у по х
есть у'). Обе эти производные на основании правила дифферен-
дифференцирования сложной функции перемножаются.
Дифференцируя обе части равенства, получаем 2х + 2уу' — 0.
Сокращая на 2 и перенося х в правую часть равенства, имеем
у у' = — х; разрешая это уравнение относительно у', находим,
что и' = — — .
У
2) При дифференцировании последнего слагаемого второго
примера надо применить формулу для дифференцирования произ-
399
ведения и тогда (Заху)'х = 3а(у + ху'). Поэтому получаем Зх2 -f
+ Zyty'-3a(y + xyt) = 0.
Сокращаем на 3, раскрываем скобки, переносим члены, не
содержащие у', в правую часть равенства и получаем (t/2 — ах)у' =
= ау — *2, а отсюда у' = рг~; •
Задача 26,6 (для самостоятельного решения). Найти произ-
производную у' неявных функций:
1) Ь*х2 + Фу2 - а262 = 0;
2) * + у*-а = 0.
Ответ. 1) / = -??; 2) </ = --?.
Задача 26,7. Найти производную неявных функций:
Решение. 1) Считая, что у есть функция х, производную
по х от у" находим так:
(у*)' = щГ~1у'.
Дифференцируя обе части уравнения, получаем:
шЛ-V - С1 + f/') (л- — у) — A —;/') (д- + у) = 0
(х — у)*
Умножим теперь обе части последнего равенства на (х — у)г,
раскроем скобки в числителе дроби и получим
п\Г~гу'(х — уJ — х — ху' + у + уу' + х — ху' + у~уу' - 0.
У членов, содержащих у', вынесем за скобку у', а остальные
члены перенесем в правую часть равенства:
у' [пу*-1 (х - у)* -2х] = - 2у;
отсюда уже получаем, что у' = —
Покажем теперь, как использовать условие задачи для того,
чтобы упростить это выражение.
У нас в знаменателе дроби есть у"~г, а потому, если умно-
умножить числитель и знаменатель дроби на у, то в знаменателе
окажется у", который можно на основании условия задачи за-
заменить на 1j^-\ выполним эти преобразования: у'— ~пмх-!>и^—'2
подставим теперь ^— вместо у".
После этого окажется, что
, V 2у*
х + У / v, г, ~ п (д-а — уг) —2ху '
400
2) Указание. В полученном выражении для у' на основании
п
условия задачи заменить хп на xt^_
Ответ, у =-i
4*V
t
Задача 26,8 (для самостоятельного решения). Найти производ-
производные неявных функций: 1) уь — Ъаху + хь = 0; 2) ах — ех~у = 0.
После того как производная у' будет определена, надо учесть,
что из условия задачи следует равенство ах ~ ех~у.
Ответ. 1) у' — йу~ж > 2) #' = 1 — In а.
Задача 26,9. Найти производную неявной функции еу = хх+у.
Решение. В правой части равенства переменными являются
и основание степени х, и показатель степени х -f у, а потому
здесь следует сначала прологарифмировать обе части равенства,
а Лотом уже дифференцировать.
После логарифмирования с учетом того, что 1пе—- 1, получаем
у = (х 4- у) In х. Отсюда у' = A -f у') 1п х + (х + у) — . Раскрывая
скобки, имеем:
'mi 1 ¦
X
''11 1
У У — ~г \ ~г У) ~yi
У - я-A — In л-) '
и окончательно:
, х(\пх+ 1) + у
» "" л- A — In л-) •
ДВАДЦАТЬ СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Параметрическое представление функции. Дифференци-
Дифференцирование функций, заданных параметрически.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
В геометрии и механике часто употребляется так называе-
называемый параметрический способ задания уравнения кривой. Кривую
линию можно рассматривать как геометрическое место последо-
последовательных положений движущейся точки, а~ координаты х и у
этой точки выразить в виде непрерывных функций вспомогатель-
вспомогательной переменной t, которая называется параметром. Плоская
кривая в этом случае определяется двумя уравнениями:
14 И. А. Каплан 401
причем параметр t должен изменяться в таком промежутке,'
чтобы при изменении его в этом промежутке точка с координа-
координатами (х, у) описывала всю кривую или ее рассматриваемую часть.
Предполагается, что каждому значению t соответствует
только по одному значению х и у.
Задание кривой уравнениями B7, 1) называется парамет- г
рическим.
Если из уравнений B7,1) можно исключить параметр t,
у определится, как явная или неявная функция х. Однако
тель должен знать, что исключение параметра t из уравнениЩЗ
B7,1) является в большом числе случаев задачей трудной, а иногд[
и просто неразрешимой.
Задачи B7,1) — B7,9) отводятся для упражнений в исключен
нии параметра. |
В механике уравнения B7,1) называются уравнениями двщ
жения точки. Если из этих уравнений исключить t, то полу->
чится уравнение траектории точки.
Задача 27,1. Исключить параметр t из уравнений
у = I6t2 + 4
и определить линию, определяемую полученным уравнением.
Решенце. Из первого уравнения определим t2 в зависимости
от х:
/2 _
Подставим это значение t2 во второе уравнение, и тогда у —
= 16 ¦ * g + 4; у — 2х -f 18. Линия, определяемая этим уравне-
уравнением, — прямая. Значит, заданные уравнения определяют прямую.
Задача 27,2. Какую линию определяют уравнения
Решение. Если второе уравнение умножить на 2 и вычесть
его почленно из первого, то получим х — 2у = 0, Это уравнение
определяет прямую, а потому и заданные уравнения есть пара-
параметрические уравнения этой прямой.
Задача 27,3 (для самостоятельного решения). Линия задана
параметрическими уравнениями
Определить вид линии.
Ответ. Прямая линия Зх — Ъу = 0.
402
Задача 27,4. Даны уравнения движения точки:
х = от \
y = st | •
Определить траекторию точки.
Решение. Исключим из уравнений параметр t. Найдем из
второго уравнения t и подставим найденное значение в первое
уравнение:
. _ у __ с У*. г _ _?
г — -д-; л: — о • -д-; f/ -- -=- дс;
траектория — парабола. Заданные уравнения — параметрические
уравнения параболы.
Задача 27,5. Какую линию определяют уравнения
х =гcost\
Решение. Для исключения параметра / возведем обе части
каждого уравнения в квадрат и сложим почленно полученные
уравнения:
х2 = г2 cos21,
+ у2 ¦-= г2 sin21,
^2_ (?7,2)
Перед корнем выбран знак плюс потому, что когда t изме-
изменяется на отрезке [0, к], то t/ = rsin/ не принимает отрицатель-
отрицательных значений. Кривая — полуокружность с центром в начале
координат, расположенная в верхней полуплоскости.
Если бы параметр t изменился на отрезке [т:, 2я], то в B7,2)
следовало бы у корня взять знак минус у — —yV2 — х2> так как
в этом случае y = rsmt положительных значений не принимает.
Уравнение у = — ]/г2 — х2 определяет полуокружность с цент-
центром в начале координат, расположенную в нижней полуплоскости.
Если же считать, что параметр t изменяется на отрезке [0, 2к],
то уравнения
X = Г COS t \
у = г s'mt j
определяют две функции: у = ]/г2 — х2; и у = —]/г2 — х2.
Графики этих двух функций в совокупности образуют целую
окружность.
14* 403
Задача 27,6. Кривая задана параметрическими уравнениями^
= acost\
Исключить параметр / из этих уравнений.
Решение. Обе части первого уравнения разделим на a, i
второго на Ь:
Обе части каждого из этих уравнений возведем в квадрат и па
членно сложим:
X2 о ,
--cos2/
^ = sin2/
?! 4- I* - 1
кривая — эллипс. Итак, заданные уравнения — уравнения эллипса
в параметрической форме. Когда параметр t изменяется на от-
отрезке [0, 2т:], точка на эллипсе описывает всю кривую.
Задача 27,7 (для самостоятельного решения). Исключить пара-
параметр t из уравнений и определить вид кривой:
у = 4 cos 1
4) х = .
г/= 4 — 3 sin i
Ответ. 1) Кривая — эллипс, определяемый уравнением х2 -\-
4- 4#2 — 36 = 0. 2) Кривая — окружность хг 4- f/a = 16. 3) Кривая —
окружность х2 4- У2 = 9. 4) Кривая — окружность х2 4- (У — 4J = 9.
Задача 27,8. Исключить параметр t из уравнений:
х--- 2 4-3 cost,
Решение. В первом уравнении из правой части в левую
перенесем 2, а во втором —3. Тогда
х—2 = 3cost\
t/4-3=j
404
Обе части первого уравнения разделим на 3, а второго — на
4, после этого обе части каждого уравнения возведем в квадрат
и сложим их почленно:
(л- — 2J „ ,
v , ' =т cos I
(х — 2J (у + 3)* .
9 + 16 *
Кривая эллипс, центр которого находится в точке B, —3).
Задача 27,9. Исключить параметр / из уравнений
х — a cos31)
у = a sin311'
Решение. Обе части каждого уравнения возведем в степень
2 -
-я- и почленно их сложим:
о
* I
"Г 2 2
у3 = a3 sin2 i
2 2 2
Кривая — астроида.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Производная функции
заданной параметрически, вычисляется по формуле
Й = $ • B7,3)
Ниже предлагаются задачи, в которых требуется найти про-
производную от функций, заданных параметрически, минуя опреде-
определение у как функции х.
Эги задачи не должны вызвать у читателя затруднений, так
как предполагается, что техника дифференцирования у него вы-
выработана хорошо на большом количестве примеров, решенных
на предыдущих практических занятиях.
Поэтому подробно мы рассмотрим решение только двух задач,
а остальные должны быть решены самостоятельно. Формула B7,3)
используется при решении задач B7,9)— B7,13).
405
Задача 27,9 а. Найти производную у'х от функций, заданных
параметрически:
1) х = г
a sin/
+ b cos /
с cos /
1 + 6 cos /
2) x — arc sin;
= arc cos
+
Решение. 1) Находим x't и у] и полученные значения под-
подставляем в формулу B7, 3):
. cos / (I + b cos /) — (-—6 sin /) sin t > a (cos t -\-b)
xt — a A+6 cos/J ' *' ~" A+6 cos 02 '
, _ —sin t A + fe cos t) — (—6 sin t) cos /. / _ — sin t
Уг—с A+6 cos/J ' У* A +6cos02*
Теперь по формуле B7, 3) имеем:
• _ s'n'
У* C
a F + cos t)
находим далее, что и г// = уттг > ПОТОМУ !/.« = 1 •
Замечание. Из тригонометрии известно, что
arc tg t = arc sin , = arc cos
и, таким образом, у нас в задаче
х = arc tg П
у = arc^tg f J'
т. е. у = х, а потому и г/^ = 1.
Если бы это сразу было замечено, то не было бы необходи-
необходимости находить x't и y't .
Задача 27,10. Найти производную у'х от функции, заданной
параметрически,
х = 2 cos / — cos 2t)
y
в точке, где t = -g-.
Решение.
= —2 sin ^ + 2 sin 2/ = 4 cos у sin -5
:,' = —2 sin ^ + 2 sin 2/ = 4 cos у sin -5-;
t/,' = 2 cos t — 2 cos 2< = 4 sin -^ sin у,
406
а потому
yi
7
. . 3t . t
4 sin -~- sin -=-
'. зТТ Г;
4 cos -- sin -=-
ё 2 6 ё 4 '
Задача 27,11 (для самостоятельного решения). Найти при
t = Y производные функций, заданных параметрически:
1) х = аA — t)\ 2) х = sin2H
у = at }' у = sin2t ]'
3) х = cos t + t sin П 4ч _ 11/975
Ответ. 1) y'x=—l; 2) y'x = ~ ; 3) f/; = 0,414; 4) ^ = 0,833.
Задача 27,12 (для самостоятельного решения). Найти произ-
производные функций, заданных параметрически:
1) л: = a cos Л 2) x — a(t — sin ^) \
y — bsintj' у = а(\ — cos 0J'
3) x = acost\ « v_iz
у = aunt у
У =
2t
+ t
Ответ. 1) y'x = -±ctgt; 2) y'x = dg{;
Задача 27,13 (для самостоятельного решения). Найти произ-
производные функций, заданных параметрически:
, ч cos31
sin3
It
„_
У
at
_ 4 (a —
Ответ. I)ri=-tg3*; 2) y> -tgf, 3) y; = *(»
ДВАДЦАТЬ ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Со держание. Дифференциал функции.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
/) Если дана дифференцируемая функция у — f (x), то ее при-
приращение
Ьу = РХх)Ьх + аАх, B8,1)
где, a ->• 0, когда Ах -> 0.
407
2 При Ах -»¦ 0 величина аДх есть бесконечно малая высшее^,
порядка, чем Ах. • Щ
3) Из формулы B8,1) следует, что приращение функции^
которая имеет производную в точке х, не равную нулю, можещ
быть представлено в виде суммы двух слагаемых. В первое слагай
емое f (х) ¦ Ах приращение Ах независимой переменной входит щ
первой степени, т. е. оно, как говорят, линейно относительно Адг|
Это слагаемое является главной частью приращения функции щ
называется дифференциалом функции. 1
Определение. Дифференциалом функции у — f (x) называетсщ
произведение производной этой функции на приращение независщ
мой переменной. Дифференциал функции обозначается символом
dy, и, таким образом, дифференциал функции . 1
dy = Г (х) Ах. B8,2|
Определение. Дифференциалом независимой переменной. нам
зывается ее приращение: dx = Ал:, и поэтому можно сказать, чтл
дифференциалом функции называется произведение еа
производной на дифференциал независимой переменной;
dy = /' (х) dx,. B8,3)
а формула B8, 1) может быть переписана в виде
Ay = dy + аАк. B8,4)
4) Второе слагаемое а.Ах в B8,1) при Ах -*¦ 0 есть величина
бесконечно малая высшего порядка малости чем Ах. Из этого
следует, что разность Ay — dy между приращением функции и
ее дифференциалом, равная о.Ах, есть величина бесконечно малая
высшего порядка, по сравнению с Ах.
5) Для вычисления дифференциала функции необходимо задать
начальное значение независимой переменной х и ее приращение Ах.
6) Если Ах мало, a f (х) Ф 0, то величина о-Ах, входящая в при-
приращение функции, значительно меньше, чем дифференциал функ-
функции dy, причем тем меньше, чем меньше Ах.
Поэтому вычисление Ау приращения функции может быть
с хорошим приближением заменено вычислением дифференциала
функции dy, а вычислить дифференциал функции значи-
значительно проще, так как для этого требуется только
найти производную этой функции и умножить ее на
приращение независимой переменной:
Ay^dy B8,5)
7) Из формулы B8,5), учитывая, что
Ay^f(x + Ax)~f(x), B8,6)
408
следует, что f (х + Ах) — f(x)zz f (x) Ax, а отсюда заключаем,
что наращенное значение функции
f (х) + f (х) Ах. . B8,7)
Эта формула позволяет по известному значению функции и ее
производной в точке х найти приближенное значение функции
в точке х + Ах, близкой к х, и тем самым дает возможность
использовать дифференциал функции для приближенных вычислений.
8) Таблица для вычисления дифференциалов основных элемен-
элементарных функций получается из таблицы для вычисления произ-
производных этих функций путем умножения соответствующей произ-
производной на дифференциал независимой переменной dx.
9) Правила дифференцирования:
d(cu) = cdu, B8,8)
d (и ± v) = du ± dv, B8,9)
d(uv) = udv + vdu, B8,10)
= S*L^?. B8,11)
Задача 28,1. Определить приращение и дифференциал функ-
функции у = х3 при переходе х от значения х = 2 к значению хг = 2,01.
Решение. Решим задачу сначала в общем виде, т.е. опре-
определим приращение заданной функции при произвольных значениях
х и Ах, а потом уже при заданных.
У нас у = х3, а потому, так как у' — Зх2, то
dy = y'dx = 3x2dx; Ау = (х + AxK — x3 =
= д:3 4- 3x3Ax + Зд: (Axf + (AxK — x3;
Ay = ЗлМх 4- 3x (AxJ + (AxK.
Таким образом, дифференциал функции и ее приращение най-
найдены при произвольных значениях х и Ад:.
Подчеркнутое слагаемое Зл:2Адг, линейное относительно Ад:, и
есть dy — дифференциал функции.
Теперь определим Ау и dy при заданных числовых значениях.
Начальное значение х = 2. Приращение аргумента
Дх = Xl — х = 2,01 — 2 = 0,01,
а потому приращение функции
Ьу = 3 • 22 • 0,01 + 3 ¦ 2@,01J + @,01K; B8,12)
Ьу = 0,12 4- 0,0006 + 0,000001 = 0,120601
409
Дифференциал же функции — первое слагаемое в равенстве
B8,12); dy = 3 • 23 -0,12.
Теперь определим погрешность, которую мы допустим, если при-
приращение функции заменим дифференциалом функции dy. Эта по-
погрешность равна Ау — dy = Зх (Л*J + (Л*K, и мы усматриваем,
что она при Ах -*¦ 0 есть величина бесконечно малая более высо-
высокого порядка, чем Ах.
При числовых данных задачи абсолютная величина погреш-
погрешности от замены приращения функции ее дифференциалом
\Ax~dy\ = |0,120601 - 0,121 = 0,000 601.
Относительная погрешность
Ay — dy
0,000 601
0,120 601
= 0,00498^:0,005
в процентах это составляет всего около у % . Подчеркнем еще раз,
что определение дифференциала функции вместо ее при-
приращения дает значительную экономию в вычислениях,
а допускаемая при этом погрешность будет тем мень-
меньше, чем меньше приращение аргумента.
Мы очень подробно разобрали эту задачу и теперь предложим
ряд аналогичных задач для самостоятельного решения.
Задача 28,2 (самостоятельного решения). Дано у = Зх2 +
+ 5х — 4. Определить Ау и dy при произвольных значениях х
и Ах, а потом при переходе х 1) от значения х — 2 к значению
х3 = 1,98; 2) от значения х = 4 к значению хх = 4,03.
Ответ. Ау = Fх + 5) Ах + 3 (АхJ; dy = Fх + 5)dx\ при чис-
числовых данных: 1) Ау = —0,3388; dy = — 0,34; 2)' Ау = 0,8727;
dy = 0,87. Относительная погрешность в процентах: 1) 0,3; 2) 0,3.
Задача 28,3 (для самостоятельного решения). Вычислить при-
приращение и дифференциал функции у = 2х3 — х2 + 3 сначала при
произвольных значениях х и Ах, а затем:
1) при переходе х от значения х = 3 к значению jcx = 3,01 и
2) при переходе х от значения х — 3 к значению лгх = 3,001.
Найти в этих двух случаях абсолютную и относительную погреш-
погрешности.
Ответ. Ау = Fх2 — 2х) Дх + F* — 1) (АхJ + 2 (ДхK;
dy = Fх2 — 2х) dx
при числовых данных: 1) Ау = 0,481 702; dy = 0,48", 2) Ау =
= 0,048 017 002; dy = 0,048; абсолютная погрешность: 1) 0,001702;
2) 0,000017 002; относительная погрешность в процентах: 1) 0,35;
2) 0,03.
Задача 28,4. Показать, что при Дл;->0 с точностью до бес-
бесконечно малой высшего порядка имеет место приближенное ра-
равенство
(I + Ах)п ^ I + пАх.
410
Решение. Рассмотрим функцию f(x) — хп. Тогда Лг/ = (х +
-f- Ал;)" — х"; dy = пх"~1Ах, а так как на основании B8,5) с точ-
точностью до бесконечно малой высшего порядка имеет место при-
приближенное равенство Ду zzz dy, то
(х + Ах)" - хп ж пх^Ах, а (х + Ах)" ж х" + пх"~х Ах.
Полагая здесь х = 1, получаем, что для достаточно малых Ах
имеет место приближенное равенство
A + Axf^l +nAx. , B8,13)
Числовые примеры для приближенных вычислений по формуле
B8,13):
1) A.03M ж 1 + 5 • 0,03 =1,15 (Ах = 0,03; п =¦- 5);
2) VXOOS «1 + 1. 0,005 = 1,0025 (здесь п = ~, а Ах =
= 0,005);
3) ^,998 = у^1—0,012 =1 + у (-°'°12) = 1 - °.°04 = °.
(а = ' ; 4лг =-0,012J
4) >/267 = ^256+11 = |/256 (l + ^) -
=4"К1 + й ~4 (• + т • зУб) = 4 (' + °>0107) =4-0428
4
1 * И
Задача 28,5 (для самостоятельного решения). Пользуясь фор-
формулой B8,13), вычислить:
" 1 • m —L_. ъ 1 ¦
> 0,9988' ' A.003)8'
_. 37 . „ 15,23
^ 0,9997' 0; 1,004' °; 0,999'
Указание. 4) ^~ = 5 ¦ } _ 0'0(ЮЗ = 5A— О.ОООЗ); теперь
надо взять в B8,13) п = — 1: Ах = 0,0003.
Ответ. 1) 0,9995; 2) 1,0012; 3) 0,991; 4) 5,0015; 5) 36,852;
6) 15,246.
Задача 28,6 (для самостоятельного решения). Пользуясь фор-
формулой B8,13), вычислить:
1) VW2; 2) ^щ=8; 3) з7Щ2;4)^0.9843.
Ответ. 1) 2,003; 2) 0,498; 3) 4,997; 4) 0,995.
411
Задача 28,7. При нагревании объем твердого тела растет про-с*
порционально кубу его линейного расширения. Если а — коэффи-у i
циент линейного расширения, р — коэффициент объемного расши*A
рения, а / —г температура, то имеет место формула 1 -f- Р/ = L
Пользуясь формулой B8,13), доказать что имеет место при- i
ближенное равенство р ^ За. ~ ^
Решение. При малых а A -f- atK^z I -f- 3at и значит, 1 -\-%t
-f-p/?s; 1 + За/; $tzz3oLt; р^За, т.е. коэффициент объемного Щ
расширения твердого тела приближенно равен утроенному коэф-Й
фициенту его линейного расширения. щ
Задача 28,8. Высота ртутного столба в барометре при темпе-^
14- a't "Г^
ратура f приводится к 0q по формуле ро = р 1 ~Т. ,. где
коэффициент расширения ртути, а а' — коэффициент расширения
латунной шкалы. Упростить эту формулу так, чтобы она не со-5
держала дробей.
Решение. По формуле B8,13) г^= A + а/)^ 1 — а/,|
а потому р0 — р A + а'О A — а/) == р A + a't — а/ — аа'/). Так как \
а и а' — малы, то последним произведением в скобке можно пре-
пренебречь; окончательно получаем упрощенную формулу
Задача 28,9 (для самостоятельного решения). Ускорение силы
тяжести gh на высоте h над уровнем моря определяется по фор-
формуле
s/l s (R + АJ'
где g — ускорение силы тяжести на уровне моря, a R — радиус
земли. Считая, что h мало по сравнению с R, доказать, что имеет
место приближенная формула
Указание. R + h = R\\+~\.
Задача 28,10. Доказать, что если Ajc — бесконечно малая ве-
величина, то с точностью до бесконечно малой высшего пор-ядка имеет
место приближенное равенство sin Ajc ;=s Ax (Дх — выражается в
радианах).
Решение. Рассмотрим функцию у = sinx. Приращение этой
функции Аг/ = sin (х + Ах) —sin x, а ее дифференциал dy = cos xAx.
На основании формулы B8,5) с точностью до бесконечно малой
высшего порядка имеет место приближенное равенство Ayz^dy,
412
а потому sin (x + Ax) — sin x ?s cos x ¦ Ax, или sin (x + Ax) ж sin x -f-
+ cosx-Ax. Полагая здесь х — 0 и учитывая, что sin 0 = 0, а
cosO== 1, получаем требуемое приближенное равенство
sinAx^Ax. B8,14)
Эта формула показывает, что для малых углов (выраженных
в радианах) синус равен числу радианов, содержащихся в угле.
Например, так как 4° = 0,0698 радиана, то sin 0,0698 ж 0,0698.
Это же значение для sin 4° дают и четырехзначные таблицы (не
забудьте, что при использовании формулы B8,14) следует гра-
градусы переводить в радианы).
Заметим, что формула B8,14) для углов, не больших 3°, дает
величину синуса с четырьмя верными десятичными знаками (для
перевода градусов в радианы и обратно следует пользоваться
справочниками). Для углов же, не превышающих 7°, эта формула
дает значение синуса с тремя верными десятичными знаками.
Задача 28,11 (для самостоятельного решения). Доказать, что
если Ах — величина бесконечно малая, то с точностью до беско-
бесконечно малой высшего порядка имеет место приближенное равенство
tgAx^Ax. B8,15)
Применить это равенство к вычислению tg 3е и сравнить получен-
полученное число со значением tg 3е из четырехзначных таблиц.
Задача 28,12 (для самостоятельного решения). Доказать, что
если Дх — бесконечно малая величина, тосточностью до беско-
бесконечно малой высшего порядка имеет место приближенное равен-
равенство
Указание. Рассмотреть функцию у—\пх. Приращение этой
функции ,
\у= 1п(х + Ах) — \пх = ln(l + ^; dy = \dx.
Из формулы B8,16) следует, что, например,
In 1,007 - In A + 0,007) ss 0,007;
In 1,008 = In A + 0,008)« 0,008.
Задача 28,13 (для самостоятельного решения). Доказать, что
если Ах — бесконечно малая величина, то с точностью до беско-
бесконечно малой высшего порядка имеет место приближенное равен-
равенство
еЛ*^1 + Дх. B8,17)
Получить это же равенство из формулы B8,16).
413
Указание. Рассмотреть функцию у = ех.
Ay=e*(eu*- 1),
dy = exAx.
Пользуясь формулой B8,17), можно получить приближенные
значения ед* при малых значениях Ах. Например, е0'003 як 1 +
+ 0,003 = 1,003; е0009як 1 + 0,009 = 1,009; е004» 1 + 0,04 = 1,04
(все десятичные знаки верны).
Приведем сводку полученных приближенных формул B8,13),
B8,14), B8,15), B8,16), B8,17), причем во всех этих формулах
заменим для удобства Ах, а в последней —-, буквой а:
tg a як а;
In A +а) г» а;
Задача 28,14. Составить таблицу для вычисления значений
функции у = sinx при значениях х, равных 30° Г; 30'; 3093',
имея в виду, что Г = Tg^—go ~ ^,00029 радиана.
Решение. Рассмотрим функцию f(x) — sinx. При переходе
аргумента от значения х к значению х -f- Ax наращенное значение
функции определяется из приближенного равенства B8,7). У нас
/ (х) = sin х. Поэтому f(x + Ах) = sin (x -f Ах), а /' (х) = cos x.
Для заданной функции f(x) = sinx приближенное равенство B8,7)
запишется так:
sin (x-f-Ax) ;=s sin х-f cos х ¦ Дх. B8,18)
Полагая в этой формуле х = 30° = -g-.' Дх = Г = 0,00029, а
sin 30е = 0,50000; учитывая, что cos 309 = Щ- = 0,86602, получим
sin309 Г = 0,50000 + 0,86602 • 0,00029 = 0,50025,
что совпадает точно со значением sin 30* Г по пятизначным таб-
таблицам.
Из формулы B8,18) найдем и sin30е2', учитывая, что теперь
Ах = 2' = 2 • 0,00029 = 0,00058 радиана и по-прежнему х = 30Q.
sin 30s 2' = 0,50000 -f- 0,86602 ¦ 0,00058 = 0,50050
(все десятичные знаки верны).
При вычислении sin 30° 3' воспользуемся той же формулой,
взяв Lx = 3' = 3 • 0,00029 = 0,00087;
sin 30° 3' = 0,50000 -f- 0,86602 • 0,00087 = 0,50075
414
(это значение отличается от табличного на 0,00001 (по пятизнач-
пятизначным таблицам sin30° 3' =¦-¦ 0,50076).
Задача 28,15 (для самостоятельного решения). Составить таб-
таблицу для вычисления функции cosx при значениях х, равных
60° 1'; 60°2'; 60°3' (для справок sinбО5 = 0,86602; cos60° =
= 0,50000; Г =--= 0,00029 радиана).
Полученные значения сравнить со значениями из пятизначных
таблиц тригонометрических функций.
Задача 28,16 (для самостоятельного решения). Вычислить
tg45° Г, tg45°2', tg45°3' и сравнить полученные значения со зна-
значениями из пятизначных таблиц тригонометрических функций.
Задача 28,17. Вычислить натуральные логарифмы чисел 2,001;
2,002; 2,003; 2,004 и сравнить их с табличными значениями
по пятизначным таблицам натуральных логарифмов (для справки:
In 2 = 0,69 315).
Решение. Рассмотрим функцию /(х) = lnx. Чтобы применить
формулу B8,7) надо определить /(х + Ах) и /'(х):
1
f (x -f- Ах) = In (x -f Ax); f (х) = —
Подставляя эти значения в B8,7), получаем
In (х + Ах) ж In x + ~ Ах. ¦ B8,19)
Чтобы найти In 2,001, возьмем в формуле B8,19) х = 2, а Ах =
= 0,001:
In 2,001 = In B -f 0,001) ж In 2 + у ' 0>001 =
= 0,693154-0,00050 = 0,69365.
Аналогично по формуле B8,19) вычисляется In 2,002; In 2,003
и In 2,004: берем по-прежнему х —. 2, а Ах надо взять равным
соответственно 0,002; 0,003; 0,004. Имеем
In2,002 = InB 4- 0,002)х2 + ~- 0,002 = 0,69315 +
+ 0,001 = 0,69415; In 2,003 = In B + 0,003) =s 2 + ~ ¦ 0,003 =
= 0,69315 + 0,0015 = 0,69465; In 2,004 = In B + 0,004) ж 2 +
+ ~ ¦ 0,004 =- 0,69315 + 0,0020 = 0,69515.
Пятизначные таблицы логарифмов дают значения, равные най-
найденным. Решение последних задач показало читателю, как диф-
415
ференциал функции может быть использован для составления^
таблиц тригонометрических функций и логарифмов. Формула B8,7)
позволяет составлять таблицы и других функций.
Мы считаем необходимым обратить внимание на то, что заме-
заменяя во всех предыдущих задачах приращение функции Аг/ ее диф-
дифференциалом dy, мы не интересовались оценкой погрешности,
которую мы при этом допускаем. В последующем, при изучении
раздела «Бесконечные ряды», будут указаны более совершенные
приемы составления таблиц функций и там же указаны формулы,
оценивающие погрешность, возникающую при замене точного зна-
значения функции ее приближенным значением.
Задача 28.18. Прямым измерением найдено, что диаметр круга
равен 6,7 см, причем максимальная погрешность измерения со-
составляет 0,03 см. Найти приближенную относительную и про-
процентную погрешности в вычисленной площади этого круга.
Решение. Относительная погрешность вычисленной площади
8S = —, а ее приближенное значение мы получим, заменив в этом
ds
равенстве As на ds. В таком случае 8S =^ —. Но площадь круга
s = -y7ije2 (х — диаметр), а поэтому ds = -_- тех dx. Таким образом,
1
кх dx и*
8S ^ = 2 • — . У нас х = 6,7 см; dx = 0,03 см, а потому 8s^s
Т™2
zz2 --gy^ 0,009, а умножая эту величину на 100, получим про-
процентную погрешность, которая равна @,009- 100)% =0,9%.
Задача 28.19. Доказать, что приближенная относительная по-
погрешность вычисленного объема шара равна утроенной относитель-
относительной погрешности в измерении его диаметра.
Решение. Объем шара вычисляется по формуле V = -g- ъх3,
где х — диаметр шара. Приближенно погрешность АУ вычислен-
вычисленного объема равна dV — -к ъхг dx. Относительная погрешность
8V^:
ния
JV ~2KX
" V 1
т*1
диаметра с
2 dX
1
о
dx
х '
¦ у ¦ Но .
а потому
^, что и требовалось.
416
Задача 28,20 (для самостоятельного решения). С какой отно-
относительной погрешностью допустимо измерить радиус шара, чтобы
объем его можно было определить с точностью До 2%.
Ответ. 8^ = 0,66%.
Задача 28,21. Период малых колебаний маятника (в секундах)
определяется по формуле
T = 2тг у -, B8,20)
где / — длина маятника в сантиметрах, a g—- 981 см/сек2 — уско-
ускорение силы тяжести.
Доказать, что приближенная относительная погрешность изме-
измеренного периода колебания маятника равна половине относитель-
относительной погрешности его измеренной длины.
Решение. Приближенно абсолютная погрешность периода
колебания AT zzzdT = —?=, а потому относительная погрешность
У gl
Ьтяа — .-= — 8Г_ = -н--т-, а так как относительная погрешность
2*1/ i
Г g
измерения длины маятника 8/ = у, то 8Г ^ -к- 8/( и требуемое до-
доказано.
Задача 28,22 (для самостоятельного решения). Пользуясь фор-
формулой B8,20), установить, насколько следует изменить длину
маятника / — 25 см, чтобы его период Т увеличился на 0,05 сек.
Ответ. dl = ^VTdT; dl = 2,49 см.
Задача 28,23 (для самостоятельного решения). Из формулы
B8, 20) следует, что определение ускорения силы тяжести с по-
помощью колебания маятника может быть сделано по формуле
Определить относительную погрешность в определении g, если
известны:
1) относительная погрешность в измерении / (Т вычислено
точно);
2) относительная погрешность в измерении Т (I вычислено
точно).
Ответ. 1) 8g = 8,; 8g = 28r;
417
ДВАДЦАТЬ ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Производные высших порядков. Формула Лейбница.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Производная от функции у = f (х) в общем случае является
функцией х. Если от этой функции вычислить производную, то
получим производную второго порядка, или, короче, вторую про-
производную функции y = f(x). Таким образом, вторая производная
от первоначальной функции есть производная от первой произ-
производной.
Производная от второй производной называется третьей про-
производной. Производная от третьей производной называется чет-
вертой производной и т. д.
Обозначения- Вторая производная функции у -. f (х)
обозначается одним из символов: у" (читается: игрек два штриха);
-з-| (читается: де два игрек по де икс дважды); f" (x) (читается:
эф два штриха от икс).
Третья производная функции у — f(x) обозначается одним из
символов: у'" (читается: игрек три штриха); f" (x) (читается:
эф три штриха от х); -pj; г/<">.
Производная порядка п есть производная от производной по-
порядка (п — 1). Эта производная обозначается одним из символов:
/<«>(*),
Для обозначения последовательных производных нами приняты
обозначения: у", у3, уD), ... у(п).
Задача 29,1. Найти третью производную функции г/—¦ 5*4.
Решение, у' = 20*3; у" = 60а;2; у'" = 120*.
Задача 29,2. у = З*4 + 5*3 — 4*2 + 8. Найти у<4>.
Решение, у' = 12*3 + 15*2 — 8*; у" = 36*2 + 30* — 8; у<3> =
= 72* + 30; г/<4> = 72.
Задача 29,3. у = sin2*. Найти г/E).
Решение, у' = 2sin*cos* = sin2*; у" = 2cos2*;
у(з) — _4 sin 2*; г/<4> = —8 cos 2*; у<Б> ¦= 16 sin 2*.
Задача 29,4. у = Ух -^ 5. Найти г/<4>.
Решение. Запишем заданную функцию в виде у = (* + 5J.
1 _L I _i ч -?-
Тогда у' = т (* + 5) 2 ; г/" = - -f (* + 5) ¦ ; г/<3> - 4 (* + 5) 2 ;
418
Задача 29,5. Найти у<4> от функции у = In sin х.
Решение. и' — -— cosх = ctgх\ и" = — cosec2*,
г Sin* ь > а >
у<3> = —2cosecjc(—co?ecjc • ctgx) = 2cosec2x • ctg л:;
y(V = 4cosec x (—cosec x ¦ ctg x) ctg x -f- 2cosec2 x (—cosec2 x) —
= —4cosec2 x ctg2 x — 2cosec4 x — — 2cosec2 x Bctg2 x + cosec2 x).
Задача 29,6 (для самостоятельного решения).
1) y = arcsinjr, найти у". 2) y = arctg.r, найти у".
3) г/=1пх; найти г/'4>. 4) у = т-^—; найти г/'3).
Ответ. 1)
2) -
3) -3U-; 4) (Т-
Задача 29,7 (для самостоятельного решения).
1) у = |/je;
найти уD>
Ответ. 1)
найти у
'3);
2) у = -т=-, найти г/C);
У *
3) у =
2)
Ь3/5,
3)
Определить от заданной функции производную порядка п —
значит найти формулу, по которой можно определить производ-
производную любого порядка этой функции. Вообще говоря, для этого
надо вычислить все последовательные производные до п-й включи-*
тельно. Однако этого можно избежать, пользуясь методом ма-
математической индукции. На практике поступают так: находят
несколько последовательных производных, подмечают закономер-
закономерность, по которой они все образовываются, и, считая, что эта
закономерность выполняется для производной любого порядка, со-
составляют выражение для производной порядка п (заметим, что
нулевая производная означает саму функцию).
Мы прежде всего определим производные порядка п основных
элементарных функций.
Задача 29,8. Найти у(п) функции у = хт.
Решение, у' = mxm~x\ у" = т(т— 1)xm~2.
у'" = т(т— \){т-2)хт-\
Здесь нетрудно усмотреть закономерность, которая состоит
в следующем: 1) число множителей перед х равно порядку про-
производной; 2) первый множитель равен показателю степени т, а
каждый следующий — на единицу меньше; 3) в последнем мно-
множителе из т вычитается число, на единицу меньшее порядка про-
производной; 4) показатель степени буквы х равен т минус порядок
производной. Полагая, что для производной порядка п эта зако-
закономерность сохраняется, получаем
у<"> = т (т — 1) (/л — 2) ... (т — п+1) хщ-п.
419
Задача 29,9. Найти */<"> функции у = ах.
Решение. ?/'= ах In а; у" = a* (In аJ; г/3> =.а*AпаK; */<4> =
= а*AпаL.
Здесь уже нетрудно подметить, что каждая из найденных
производных равна произведению ах на In а в степени, равной
порядку производной. Полагая, что эта закономерность сохра-
сохраняется для производной любого порядка, получаем */<"> = a" (In а)".
Задача 29,10. Найти */<"> функции у — ех.
Решение, у' = ех; у" = ех\ */C> = ех; ... ; г/'"> = ех.
Задача 29,11- Найти г/(я) функции у=1пх.
Решение, у' = 1 = (-1)° • 1;«,' = -1 = (-1)» • i,?<3> -
Усмотрим закономерность, по которой составлена каждая из
этих производных: 1) все производные содержат множителем
число —1 в степени, которая на единицу меньше порядка произ-
производной; 2) числитель дроби есть произведение натуральных чи-
чисел, начиная с единицы и кончая .числом, на единицу меньшим
порядка производной; 3) знаменатель дроби есть х в степени, равной
порядку производной. Считая, что эта закономерность сохраняется
для производной любого порядка, получаем
по этой формуле, например, уМ — (— IN -^ .
Задача 29,12. Найти #<"> функции y = s'mx.
Решение.у'^-cosx^s'mix-}- yj. у" ¦=—sinx:=sin(A: -f ~ • 21;
г/О) = _cos х = sin (x + 3 • --) ; г/<4> = sinх = sin (x + 4- -j)-
Легко усматривается закономерность, по которой образованы
все эти производные: у каждой из них под знаком синуса к х
прибавляется произведение — на порядок производной. Считая
что эта закономерность сохраняется для производной любого по-
порядка, получаем, что «/<"> — sinlx + п • ~).
Задача 29,13 (для самостоятельного решения). Найти
функции у = cos х.
Ответ. */<«> = cos[х + п ¦ ~) .
Задача 29, 14 (для самостоятельного решения). Найти
функции У-=-?.
420
Ответ. |,(«) = (_
Задача 29,15. Вычислить «/'"> функции у — Ух, пользуясь
формулой, полученной в задаче 29,8 при т = -^ ,а затем эту же
производную вычислить непосредственно.
Ответ у"».-. Г ип-гУп-т У~х*)
итвет. уу -( 1) Bп-1J« х" "
Задача 29,16 (для самостоятельного решения). Найти г/<п)
функции у — (а + &x)m;
Ответ. ?/(») = m (т - 1) (т - 2)... (т ~ п + 1) Ь" (а + Ьх)т~";
Задача 29,17 (для самостоятельного решения). Доказать на
основании формулы, полученной при решении предыдущей задачи,
что
П /__!__У — (—l)"raib" . о) I 1 Уя) _'
__!__У ) I У
a f ЬХ) ~ (а + Ьдг)л+1' ' \/^+bj) " 2« (а -f
Задача 29,18. (для самостоятельного решения). Доказать, что
= pnsin({px+n~\, 2){cospx)W =pncos
Задача 29,19 (для самостоятельного решения). Показать, что
функции у ~ cxcosx+ Сг&\пх (с1! и сг — постоянные величины)
удовлетворяет уравнению у" + у — 0.
Задача 29,20. (для самостоятельного решения). Показать, что
функция и — сцгАгСг— удовлетворяет уравнению
d4 , 1 du I n
dr2 ' r dr r*
(сг и Cz — постоянные величины).
Задача 29,21 (для самостоятельного решения). Показать, что
функция V = Ci cos ax + с? sin ax -f- с3д: + с4 удовлетворяет уравне-
уравнению К'4) + ааУ = 0(Ci, c2, с3, с4, — постоянные величины).
МЕХАНИЧЕСКОЕ ИСТОЛКОВАНИЕ ВТОРОЙ ПРОИЗВОДНОЙ
Если точка движется по прямой и задан ее закон движения
s = f(t)(s — путь, t — время), то ускорение точки равно второй
производной от пути по времени.
Задача 29,22. Найти ускорение точки, совершающей простые
гармонические колебания по закону s -¦ A sin(u>/ -f- у).
Решение. ~ — А<а cos (utf + <Р); ^ = — Аш2 sin (o>t ¦}- f), но
d2s
так как s = A sin (o>t -f <p), то -775 = — u>2s.
* Символ Bп—1)М означает произведение нечетных натуральных чи-
чисел от 1 до Bге— 1) включительно. Например, 911 = 1 • 3 • 5 • 7 • 9.
421
Задача 29,23 (для самостоятельного решения). Доказать, что
если точка совершает затухающие колебания по закону х =
— Ае~ы sin Ш, то ее ускорение ^4 = — (со2 + k2) x — 2kv; где v —
скорость точки (о — f
Формула Лейбница. Эта формула дает возможность вычислить
производную любого порядка от произведения двух функций, ми-
минуя последовательное применение формулы для вычисления про-
производной от произведения двух функций. Формула Лейбница
записывается так:
(ио)<я> = u^v + Cy-lW + C2nuln-2W + ... + uv<nK B9,1)
Задача 29,24. Найти г/<5\ если у — eixsin 3*.
Решение. Если y — uv, то на основании B9,1)
t/E) = UE)V + c\uWv' + c\uMv" + c^"d<3) + с*«'у'4> + uvW B9,2)
Полагая в заданной функции и = е4лг, у == sin 3^, для приме-
применения формулы B9,2) нам следует найти первые пять последо-
последовательных производных каждой функции и и v:
и' = 4е4*; и" = 16е4дг; ы<3) = 64е4*; ы<4> = 256е4дг; «'5) = 1024е4*;
v' = 3 cos Зх; у" = —9 sin Зх; ы<3> = —27 cos Зх; у<4> = 81 sin Зх;
оE) = 243 cos Зх.
Подставляя эти производные в B9,2), получим
у(Ь) = 1024е4* • sin Зх + 5 • 256e4jt • 3 cos Зх + ^-| 64e4j; (-9 sin Зх) +
+ ffifl 16e4^ (-27 cos Зх) + \ '\ \ \ \ 4е4х ¦ 81 sin Зх + е4* X
X 243 cos Зх; и после упрощений г/E> = — е4* C116 sin Зх + 237 cos Зх).
Задача 29,25 (для самостоятельного решения), у — х*е2х; найти
«/(в).
Ответ. г/F> = 64е2х (х4 + 12х3 + 45х2 + 60х + 22,5).
Задача 29,26 (для самостоятельного решения). Найти произ-
производную порядка п от функции у = х2е*.
Ответ. уЮ = [х2 + 2пх+п(п— 1)]е*.
Задача 29,27 (для самостоятельного решения). Определить г/<4>
от функции у = х3 In —.
Ответ. г/<4) = — .
422
Задача 29,28 (для самостоятельного решения), у = е* cos x.
Найти г/<5>.
Ответ. у& -=
ТРИДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Правило Лопиталя. Предел отношения двух бесконечно
малых и двух бесконечно больших величин I раскрытие «неопределенностей» ви-
видов: _ и — и приводящихся к ннм
О 00 '
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
При вычислении предела отношения -±Ц- может оказаться,
что при х-*-а числитель и знаменатель одновременно стремятся
к нулю или к бесконечности, т. е. являются одновременно беско-
бесконечно малыми или бесконечно большими величинами. Говорят, что
в этих случаях мы имеем дело с «неопределенностями» вида
О ОО J
-к- или — .
U оо
Вычисление предела в этом случае называется «раскрытием
неопределенности» и производится по правилу, указанному фран-
французским математиком Гильомом Лопиталем A661—1704 гг.)
Правило Лопиталя. Если функции f (х) и <? (х) таковы, что:
1) limf (х) = 0 и Нт<р(Х) = 0;
х-*а х->а
или
limf (х) = ± оо и Нт ср (х) ~ ± оо;
х-+х х-ьа
2) они имеют первые производные в окрестности точки х — а
(за возможным исключением самой точки а);
3) существует limMjs. тогда существует также и lim^-j^
и имеем место равенство lim -V4 = lim -A-{.
Х-Ш
Сущность этого правила состоит в том, что в случае «не-
«неопределенностей» вида -^-или— вычисление предела отношения
функций, при соблюдении указанных требований, заменяется
вычислением предела отношения их производных, которое в боль-
большом числе случаев оказывается проще.
В случае, когда и отношение производных приводит к одному
из этих видов «неопределенностей» -к- или —, можно уже к этому
423
отношению применить правило Лопиталя и тем симым исследо-
исследовать отношение вторых производных. Может оказаться, что и
отношение вторых производных дает опять-таки какую-либо из
этих «.неопределенностей». Тогда следует перейти к отношению
третьих производных и т. д. Укажем, что если понадобится
прибегнуть к отношению вторых, третьих и т. д. производных
то прежде чем это делать, следует провести все возможные
упрощения в выражении, полученном на предыдущем этапе.
1. Предел отношения двух бесконечно малых величин
(«неопределенности» вида ~\
Задача 30,1. Найти lim
хп_а„ .
х-*а
Если в заданное отношение подставить вместо х число а, то
получим «неопределенность» вида -д-. Применим правило Лопи-
Лопиталя,. т. е. заменим отношение функций отношением их произ-
производных.
Следует предостеречь читателя от распространенной ошибки:
надо дифференцировать не дробь, а отдельно ее числитель и зна-
знаменатель:
дг — ат );ттхт—1 та-1 т от_„
urnа
|. дг — ат );ттхт1 та1 т от_„
lim— =• = urn—-=?¦ = ——=т- = —а
хп — ап пхп 1 пап 1 п "•
х-*а х-*а
Задача 30,2. Найти lim ^ j?^+ ^ +^
X-f—1
Решение. Если в данную дробь подставить —1 вместо х,
то получится «неопределенность» вида -=-. Применяя правило Ло-
Лопиталя, получим
х3 - 5л-" + 2* + 8 _ Нгп Зл-Д - 10л- + 2 _ 15 _ _5
4 — 2х» - 16л-г + 2х + 15 т4Л:з_6л-г —32л- + 2~24~ 8 •
x-t~ 1 *->—1
Задача 30,3. Вычислить lima~~^a^~~^".
Решение. Если заменить в данной дроби х нулем, то по-
получится «неопределенность» вида -^ • Применим правило Лопи-
таля: заменим числитель и знаменатель дроби их производными
и будем отыскивать предел этого нового отношения:
пг— (С1 — Хп)п ¦ (— «Л-")
,. а — \> ап — хп .. п v '
hm Ц--„ = im ——, .
424
Сокращая дробь на пх"~г и подставляя после этого д:.= О,
1 — — 1 al~"
получим, что искомый предел равен — (а")" = .
Если бы мы не произвели сокращения на пх", то снова
имели бы «неопределенность» вида -д-. Еще раз напоминаем, что
прежде чем решить вопрос о необходимости перехода к следую-
следующим производным, надо сделать все возможные упрощения.
Задача 30,4. Вычислить lim -1 ~ * + 1пх
l
вместо х, то получится «неопределенность» вида ^ . Применим
Решение. Если поставить в числитель и знаменатель 1
есто х, то полу
правило Лопиталя:
11/2» 22х
2 /2л- — л-2
2A-дг)дг
И здесь были сделаны необходимые упрощения. Если бы мы
их не сделали, а в полученную дробь подставили бы х— 1, то
снова получили бы «неопределенность» вида -д-.
Задача 30,5. Найти lim *Г''" *.
Решение. Подставляя в данную дробь х = 0, получим «не-
«неопределенность» вида -г-. Применим правило Лопиталя:
Снова «неопре- Снова «неопре-
«неопределенность» ви- деленность» вн-
0 1 0
да __ ; _. вы_ да _. . В тре.
носим за знак тнй раз прнме-
предела, вто- няем правило
рнчно применя- Лопиталя.
ем правило
Лопиталя.
Теперь предлагается ряд задач для самостоятельного решения.
425
Задача 30,6 (для самостоятельного решения). Найти пределы:
а-2—! 9, .. а-3 — 8а-2 + 17а-— 10
L} i НИ g Оу2 _J_ 9v 1 ' / y4 ^v-3 91*2 _i_ 1 I у 4 *
„л А &Л ~y- &Л I X-*-Ъ "^
-l-4 5a*^ *~l~ 4 x^ * ^)X^ I ¦ 4
3) lim—^— 24 и "m 1— а л *
д-з ^-2 ^^- j-12 . У a, A- x V^2q
f v3 Л v-2 _J_ v _L R * ' \f ~ i ri.. i / ?Г~ *
6) hm к ; . 7) lim—-—
х^а у X — а лг-vO А
8) Hm^ + ^-^^SZ; 9) limri
Указание. В числителе сначала вынести х за скобку, и
тогда
lim-:— ~х.— = limXj-^—-^— = limxlim- У ~
Указание. Разложить числитель на множители и сократить
дробь.
Ответ. 1) 2; 2) |; 3) -§-; }; 4H; 5) ]/}; 6) о/З;
7) 1п|; 8) V~a\ 9) -2; 10) -1.
Задача 30,7 (для самостоятельного решения). Для вычисления
пределов в этой задаче правило Лопиталя придется применять
не менее двух раз. Найти пределы:
1) 1\теХ-е~х-2х; 2) lim8'"
о х — sin дг q s
х->о
х — sin дг
4) Hm
х^0 х—slnX
Указание. Искомый предел равен:
,. 1 ,. (ех — е-*)* .. (в* — е~Л /..
hm limv ъ—- = lim = hm
1im
lim
x
1~C0SA'
Ответ* 1) 2; 2)"|; 3) 1; 4) 4; 5) \±?; 6) oo.
Задача 30,8 (для самостоятельного решения). Найти
+ in- i
2 A-+1
426
Указание. Здесь «неопределенность» вида -^, так как
-т = 1; In 1 = 0; lim arctgx — ~.
Ответ. —1.
2. Предел отношения двух бесконечно больших величин
00
00
«неопределенность» вида —
00
Задача 30,9. Вычислить lini —¦.
X
Замечание. В условии задачи подчеркнуто, что х-*¦ +0; это
указание является существенным, потому что при х-»- — 0, так
же как при х->0, 1пл: не существует, так как отрицательные
числа логарифмов не имеют.
Решение. При х^-+0 числитель и знаменатель данной
дроби — величины бесконечно большие, и мы имеем здесь слу-
„ 00
чаи «неопределенности» вида —.
На основании правила Лопиталя заменяем отношение функ-
функций отношением их производных и отыскиваем предел этого но-
нового отношения:
1
.. In х ,. х ,. хг ,. „
lim -у- — lim —р ¦= — lim — = — limx = 0.
ЛГ-++О — X-++Q L x-v+О ЛГ-++О
X X*
Задача 30,10. Вычислить lim p-gj-
Решение. При х^-^- функции tgЪх и tg5x — величины бес-
бесконечно большие, т. е. мы имеем «неопределенность» вида —.
Применим правило Лопиталя, т. е. заменим отношение функций
отношением их производных и будем отыскивать предел этого
нового отношения:
3
3 cos2 Ъх 3 ,. cos2 Ъх
cos2
Здесь имеет место
«неопределенность»
вида -— . Прежде
чем1 применять пра-
правило Лопнталя,
преобразуем дробь.
427
Предел степени равен
степени предела. При-
Применяем теперь прави-
правило Лопнталя.
3 25/ sin5*\2_ 5/ 1 V _5_
5 ' ? \ „ sEU; ~ з \=Т/ - з •
Задача 30,11 (для самостоятельного решения). Найти lim — .
Ответ. 0.
Задача 30,12. Найти lim ~.
Решение. Здесь имеет место «неопределенность» вида —.
lim e~ =r lim ~ ^ lim ~ = + оэ.
, Х-^+оо *. X-+~ LX Х-Ч-» Z
Здесь «неопре- Здесь уже
деленность» ви- никакой
оо „ «неопреде-
да — . Вторич- лрннгк-ти»
оо ленности»
но применим ис-
исправило Лопи-
таля.
Задача 30,13 (для самостоятельного решения). Найти:
1) lim 4^-; 2) lim |^-
Х-»-0 Lt6 л дг-t-l-O Ш
v
Ответ. 1) 1; 2) 1.
Задача 30,14 (для самостоятельного решения). Найти:
It! (l — ~)
1) lim^j-2) lim V a>; 3) lim
4 У H0
lim ; 3) lim
*-»o-0 • ctg— X-4-H-0 CtgJtJf
Ответ. 1) +oo;) 0; 3) —2.
3. Разность двух бесконечно больших величин
(«неопределенность» вида оо — оо)
Если
limf(x) = + со и lim<p(x) = + со, C0,1)
0
428
то для определения предела lim [/ (х) — ср (х)] надо преобразовать
х-ю
эту разность f(x) — f (x) к такому виду:
J l_ j 1_
/ (х) - <PjM = Ш-Ш.; тогда lim [/ (х) - <р (х)} = lim ?(лг> . f(x).
'х-*а х*а;
Учитывая C0J), заключаем, что теперь мы должны исследо-
исследовать «неопределенность» вида -^, которую мы умеем раскрывать
с помощью правила Лопиталя. *-
Задача 30,15. Найти: Hmf-r-! 1
\1пх Х
Решение. При х -*¦ 1 -.— и г — бесконечно большие ве-
in х х ~~~ 1
личины одного и того же знака, а потому мы имеем здесь раз-
разность двух бесконечно больших величин («неопределенность» вида
ч г, 1 1 ' ДГ — 1 — In X
оо — оо). Разность -, : = -. уг~.—;
.. X — 1 — In Л" .. X
= Hm -. .. ,„ „ — lim —: =
«неопределенность»
вида -— .
1 1
- 0+1 + 1 ~ 2 "
Задача 30,16. Найти lim
2 1
Решение. При х -*¦ 1 дроби -т—г и г — величины беско-
X — 1 X — 1
нечно большие одного и того же знака, а" потому их разность
приводит к «неопределенности» вида с» — оо. Выражение, стоя-
стоящее в скобках, приводим к общему знаменателю и получаем
,. / 2 1 \ ,. 2 — л-— 1 ,. —1 —1 1
hm -:—г—-—rl = hm——г- = hm— = о—г = — тг •
U2 - 1 х-1}~ ;"V х* ~ l ~Lx"t 2х ~ 2 • 1 " 2
«неопределенность»
429
Задача 30,17 (для самостоятельного решения). Найти
Г
lim (-:
Ответ. 0.
Задача 30,18 (для самостоятельного решения). Найти:
() ^
Ответ. 1) 1; 2) ~; 3) -1.
Задача 30,19. Найти Hm fej-+-7-2jz—г, •
Решение. При х->0 имеем
1
Значит, мы имеем «неопределенность» вида со — со.
.. (а-— \){е**— 1) + 2
о
«Неопределенность» вида -г- ;
в числителе раскрываем скоб-
скобки и делаем приведение подоб-
подобных членов.
А'2 (e2jr —
vv
Применяем правило Лопи- Опять «неопределенность» вида
— . Прежде чем вторично приме-
применять правило Лопиталя, упростим
числитель и знаменатель дроби.
1 lim е2Х Vх ~ ') + ' lim 2e2t {2х ~1)+ 2е*Х
о
(х + х2~> + е" О + 2дг) -
Снова применяем правило 0
Лопиталя «Неопределенность» вида — .
Bл- — 1) + 4g2x + ie2x 1 4 _ J_
" 4 2 + 2 + 2 ~" 6
4. Произведение бесконечно малой величины на бесконечно
большую («неопределенность» вида Осо)
«Неопределенности» этого вида могут быть сведены к «не-
«неопределенности» вида j- или —. Действительно, пусть
lim f (x) ---- 0, a lim <? (х) -= со. C0,2)
430
Записав
мы получим,
f (х) <р (х) =
что
JJX)
Ш
\imf(x) • <р(*)
«Неопределенность»
вида 0 - оо
, или
— lim
f(x)?
На основании
C0,2) здесь
«неопределен-
0
(х) = ^,
W)
lim^.
На основании
C0,2) здесь
«неопределен-
= *M , C0,3)
При решении задач в этом случае следует выражение
f (х) ¦ ср (х) записать в одном из видов C0,3).
Задача 30,20. Найти linuclnx (см. замечание в задаче 30,9).
Х-++0
Решение. При х -> +0 Inx — величина бесконечно большая,
а х — бесконечно малая. Поэтому здесь имеет место «неопределен-
«неопределенность» вида 0 • оо. Применяем преобразование, указанное в C0,3):
1
lim х \пх — lim-j- — lim —г- =.- lim (—х) == 0.
дг-»+О *-*+0_L *-»+0 L х-^+0
2
Неопределен-
Неопределенность вида — :
применяем пра-
правило Лопиталя.
Задача 30,21. Найти \\тхе~х.
Решение. При х->+оо имеем lime * = 0, а потому при
х -> + со выражение хе~х — произведение величины бесконечно
большой на бесконечно малую («неопределенность» вида 0 • сю).
Так как е~х — — , то
lim хе~х =¦• lim —х — lim — = 0.
рХ аХ
Задача 30,22 (для самостоятельного решения). Найти:
1) lim (I -x)tg~x; 2) lim x" \nx(n > 0).
Ответ. 1) |-; 2) 0.
431
Задача 30,23 (для самостоятельного решения). Найти:
1) lim A - х) In (I - х); 2) lim?^* tg I* JL\ ¦
*-*l-0 x-*a x \z a/
3) lim sec ^-x • In — .
Ответ. 1H, 2) -1; 3)|.
5. «Неопределенности» видов 1"; oo°, 0Q
«.Неопределенности» этих видов сводятся к «неопределенности»
вида 0 • сю, которая была рассмотрена в предыдущем параграфе.
Это достигается с помощью тождества
[f (*)]?<*> =, efM i« m C0,4)
в предположении, что f(x)>0 (это предположение необходимо
сделать, так как в показателе степени в правой части равенства
f(x) стоит под знаком логарифма). Теперь можно написать, что
Um <?{x) In Цх)
lim [/ (х)ун*> = lim e-p<*> 1пЛ*) = е*-в
и дело сводится к определению предела Нт<р(л;) \nf(x).
х-*а
Задача 30,24. Найти lim Xх («неопределенность» вида 0е).
Решение. На основании C0,4) можем записать, что хх =
= ех 1п *, а потому
lim x\nx
lim xx = lim e*ln* = e*-+° . C0,5)
Найдем теперь lim xlnx (здесь «неопределенность» вида 0 ¦ со):
х-*+0
lim х In л; = lim^= lim —^Ц- = lim (—x) = 0
X-++0 X-++0 _L x-*4-0 _L x-f+0 ^m-^_..
X Л-2
Неопределен-
Неопределенность вида —.
Применяем
правило Лопи- •
таля.
Подставляя этот результат в C0,5), получим, что
432
I
Задача 30,25. Найти limA -f mx)x («неопределенность» ви-
o
Решение. На основании C0,4) имеем A -f- тх)х — е
а потому
1 lim — 1п A -\-tnx)
ПтA + тх)~* - lime~ {+тх) = ех^х ; C0,6)
т
= Пт —;— = т.
«неопределенность» «неопределен-
«неопределенен да 0, во: ~ 0
иость» вида -~.
Подставляя найденное значение в C0,6), получим, что
lim (I + tnx)x =6"".
х-+0
Задача 30,26 (для самостоятельного решения). Найти:
1) lim xx («неопределенность» вида ooQ);
+
2) lim ( —I («неопределенность» вида оо°).
ОтветТ 1) 1; 2) 1.
Задача 30,27. Найти lim I— / («неопределенность» вида 1").
1
Решение. На основании C0,4) (—Г = ех''" * . а потому
lim
—l
1
1 tg*
«неопределен-
«неопределенность» вида
О-*., т. к. ^L?-*l,
когда х-*0
2
1 j. sin2jf
о ' «
г x-*+0 X
15 И. А, Каплаи
Jt-4-O
,„*??
«иеопределеи-
1
и
1 ,. 2х — sin 2x
2 х+_^0 хг ¦ sin 1x
Применяем правило
Лопнталя
1 Иг
1
{ ' sec'
2
2jrsin2.
• sec^-
Чх
<x 2 \
sin 2x)
2 cos 2*
x-\-2x* cos
1
2x
433
, sin 2x -f 2x cos 2x -j- 2дг cos 2л- — 2л-2 sin 2л-
«Неопределенность» вида —. Вторично применяем пра-
еило Лопиталя
1 ,. 4 cos 2л-
_ | ( гт-| ^^_^______^______________,_^_.,^^_^^_-_^^^_^_^______^^_____^_________
2 х" 2 cos 2л- + 4 cos 2л- — 8л- sin 2л- — 4л- sin 2л- — 4л-2 cos 2х
1 4 1
4 ~ 3 #
)"
И тогда lim (*Н)" = ет.
Задача 30,28 (для самостоятельного решения). Найти пределы:
1) lim 4-arctgx @°)
2)Jim (-H-arctg*)* @°)
3) lim (cosax)"' A")
Хч-0
Ответ. 1) 1; 2) e~~; 3) \T
Задача 30,29 (для самостоятельного решения;. Найти пределы:
1) lim (cos axH05"'"* (I00);
2) lim(l+l)* A-);
X-KX> \ * I
4) lim (—\nx)x (oo°);
Ответ. 1) e~w'; 2) e; 3) e; 4) 1; 5) 1.
ТРИДЦАТЬ ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Возрастание и убывание функций.
Краткие сведения из теории
Определение 1. Функция f (x) называется возрастающей в не-
некотором интервале, если для любых двух чисел ху и х2 из этого
интервала из неравенства хг > хх следует неравенство
f(x2)>f(Xl).
434
Если же из неравенства х2 > хг следует нестрогое * неравен-
неравенство f(xi)>f(x1), то функция называется неубывающей в этом
интервале.
Определение 2. Функция f(x) называется убывающей в не-
некотором интервале, если для любых двух чисел хх и хг из этого
интервала из неравенства хг > хг следует неравенство
)f(O
Если же из неравенства хг > хх следует нестрогое неравенство
f () f (Xi), то функция называется невозрастающей в этом
интервале. Функции возрастающие и убывающие, а также функ-
функции певозрастающие и неубывающие называются монотонными.
ПРИЗНАКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИЙ
Следующая теорема выражает важный для практических це-
целей признак строгого возрастания и строгого убывания функции
и указывает правило для определения интервалов, в которых
функция возрастает и убывает (иначе, интервалов монотонности
функции).
Теорема. Если во всех точках некоторого интервала первая
производная f (х) > 0, то функция f (x) в этом интервале воз-
возрастает. Если же во всех точках некоторого интервала первая
производная f (х) < 0, то функция в этом интервале убывает.
Эта теорема выражает достаточный признак возрастания
и убывания функции на интервале.
Замечание, Строгое возрастание или строгое убывание
функции на интервале не исключает возможности обращения
в нуль первой производной функции в некоторых отдельных
точках этого интервала. Слова «отдельных точках» подчерк-
подчеркнуты потому, что в случае строгого возрастания или строгого
убывания функции точки, в которых первая производная обра-
обращается в нуль, не должны сплошь заполнять никакого частичного
интервала, даже малого, ибо если бы это имело место, то функ-
функция в этих частичных интервалах сохраняла бы постоянное зна-
значение и тем самым не была бы строго возрастающей или строго
убывающей на всем рассматриваемом интервале.
Правило. Для определения интервалов строгого возрастания
и строгого убывания функции следует решить неравенства:
f'(x)>0 и f'(x)<0. C1,1)
Следует также рассмотреть, как располагаются в этих ин-
интервалах точки, в которых f (x) обращается в нуль. Если ока-
окажется, что эти точки не заполняют сплошь какого-либо частич-
частичного интервала, то неравенства C1,1) укажут интервалы стро-
строгого возрастания и строгого убывания функции.
* Неравенства вида а < Ь и а> Ь называются строгими, а неравенства
вида а<6 и а > 6 —нестрогими,
15* 435
При решении задач, в которых требуется определить интер •
валы возрастания и убывания функции, следует прежде всего опре-
определить область существования этой функции.
Задача 31,1. Определить интервалы возрастания и убывания
функции
11.
Решение. Областью существования данной функции явля-
является вся ось Ох (функция существует при любом значении х).
Ее производная /' (х) —- Зх2 — 12. Чтобы найти интервалы возрас-
возрастания функции, решим неравенство Зх2 — 12 > 0. Деля на 3 обе
его части, получаем х2 — 4 > 0. Отсюда следует, что х2 > 4,
а х<—2 и х > 2, т. е. |х|>2. Следовательно, данная функция
возрастает в двух бесконечных интервалах: (—оо, —2) и B, + оо).
Чтобы определить интервалы убывания функции, решим неравен-
неравенство Зх2 — 12 < 0 или х2 — 4 < 0, из которого следует, что х2 < 4,
а х < 2, или х > —2, т. е. \х\ < 2. Отсюда заключаем, что функ-
функция убывает на интервале (—2, 2). Производная функция Зх2— 12
обращается в нуль при х — —2 и х = +2. В точке х = —2 функ-
функция переходит от возрастания к убыванию, а в точке х—-~\~2
она от убывания переходит к возрастанию.
Легко усмотреть, что /A) —0, а /@)= 11. Так как /A) = 0,
то х3 — \2х + 11 делится без остатка на х — 1 и мы получаем, что
х3 - \2х + 11 ~{х - 1) (х2 + х - 11).
Приравняв последнее выражение нулю и решая уравнение хг-\-х—
— 11=0, найдем и другие два значения х, при которых / (х) = 0.
Этими значениями являются
х=-~±^~; я^-3,85; х^2,85.
~"~ Полученных данных достаточно, чтобы составить представле-
представление о графике функции. Постройте его эскиз.
Задача 31,2 (для самостоятельного решения). Найти интервалы
возрастания и убывания функции / (х) = Xs — Зх — 2. Построить
эскиз графика.
Ответ. Функция возрастает в интервалах (—оо, —1) и
A, +аэ); /B) = 0; /(-1) = 0; / @)•== -2; /' (х) = 0 при х=-1
И X — 1.
Задача 31,3 (для самостоятельного решения). Доказать, что
функция / (х) = х3 возрастает на бесконечном интервале
(—оо, -j-oo)> а ее производная обращается в нуль при х — 0.
Задача 31,4. Определить интервалы возрастания и убывания
функции
y = s'mx.
436
Решение. Область определения функции — вся ось Ох. На-
Находим у' = cos х. Решаем неравенство cos x > 0.
Это неравенство, выполняясь на интервале I— -j! у), выпол-
выполняется также и на интервалах! — ~ + 2/етг; ~-\-2kv\, где /г —
любое целое положительное или отрицательное число, так как
функция cosх — периодическая, а ее период Т — 2к.
Заключение. Функция y = sinx возрастает на интервалах
, где k = 0, ±1, ±2, ...
Решая неравенство cos x < 0, получаем, что оно выполняется
в интервалах \^- + 2Ы; ~ + 2k% , где k — любое целое ПОДОЖН-
ПОДОЖНУТ Z I
тельное или отрицательное число, а потому приходим к заклю-
заключению, что функция y — sinx убывает в этих интервалах.
Задача 31,4а (для самостоятельного решения). Доказать, что
функция f(x) — igx возрастает во всех интервалах, в которых
она -существует.
Задача 31,5 (для самостоятельного решения). Доказать, что
функция / (х) = ctg х убывает во всех интервалах, в которых она
существует.
Задача 31,6. Найти интервалы возрастания и убывания
функции
Решение. Функция существует при всех значениях х, кроме
х——1 и х=+1, т. е. областью ее существования являются
интервалы: (—оо, ,— 1); (—1,1) и A, +00)-
Находим производную функции
f'(x)-2- 1-*2 + 2*2. f'W = 20+?!)
Числитель и знаменатель последней дроби положительны при
всех значениях х (значения х— —1 и х= -\-\ не должны рас-
рассматриваться, так как при этих значениях не существует и за-
заданная функция). Значит, во всех интервалах, в которых функ-
функция определена, она возрастает.
Задача 31,7 (для самостоятельного решения). Определить ин-
2л"
тервалы возрастания и убывания функции / (х) = . , 2' • Начер-
Начертить эскиз графика функции.
Ответ. Функция возрастает в интервале (—1, +1), убывает
в интервалах- (—оо, —1) и A, +оо); /'(*) = i|L=J^.
437
Задача 31,8. Определить интервалы возрастания и убывания
функции
у == 4х3 — 2\хг + 18л: + 20.
1) Решение. Функция существует при всех значениях х:
у' = 12ха - 42х + 18 = бкх2 ~7х + 3); у' = 6 Bх -1)(х- 3).
Решаем неравенства: 1) у' > 0 и 2) у' <0.
\. Решаем неравенство у' > 0; 6 Bх — 1) (х — 3) > 0.
Произведение двух множителей положительно тогда, когда
они оба имеют один и тот же знак, т. е. когда они одновременно
положительны или одновременно отрицательны. Эти соображения
приводят к двум системам неравенств:
2х — 1 > 0 ( 2х — 1 < 0
х~3 > 0 ^ ^ \ х — 3 < 0 ^
Первое из неравенств (А) дает х > -к-, а второе л; > 3; поэтому
неравенства (Л) приводят к заключению, что х> 3. Из неравенств
(В) получаем: из первого х<.-^-, из второго х < 3; приходим
к заключению, что эти неравенства выполняются при х < —.
Таким образом, функция возрастает в интервалах I—сю, —
и C, +оо).
2) Теперь решим неравенство у' < 0; 6 Bл:— 1) (х — 3) < 0 или
Bл: — 1) (х — 3) < 0. Произведение двух сомножителей отрица-
отрицательно тогда, когда эти сомножители имеют разные знаки. Это
приводит к двум системам неравенств:
2х — 1 > 0 | 2х — К О
л:-3<0 (С) 1 х-3>0 (D)
В системе (С) из первого неравенства х >^' из второго х<3;
на основании этого заключаем, что (С) выполняется для значе-
значений х из интервала -^ < х < 3. Система неравенств (D) дает: из
первого х < -j, из второго х > 3, что противоречиво, так как не
может быть, чтобы одновременно х было меньше о- и больше трех.
Заключение. Неравенство у' < 0 выполняется для значе-
значений y < х < 3; таким образом, данная функция убывает на ин-
438
тервале \-^-, 3). В точке х = у функция сменяет возрастание на
убывание, а в точке х = 3 убывание прекращается и сменяется
возрастанием.
Задача 31,9 (для самостоятельного решения). Найти интервалы
возрастания и убывания функции
у = х6 — 5х4 + 5х3 + 1.
Указание, у' — Ъх2 (х2 — 4х -f 3). Так как х2 > О при всех
л; =? 0, то г/' > 0, когда х2 — 4х + 3 > 0, и г/' < 0 при
х* - 4х + 3 < 0; х2 - 4х + 3 = (х - 1) (х — 3).
Функция возрастает в интервалах (—оо, 1) и C, +°°). а убы-
убывает в интервале A,3). Производная обращается в нуль при х — 0,
но это значение содержится в интервале (— оо, 1) где функция
возрастает. Это пример показывает, что хотя в интервале (—оо, 1)
функция строго возрастает, но ее первая производная обратилась
в нуль в отдельной точке @, 0).
ТРИДЦАТЬ ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
С о д е р ж а н и е: Определение максимума и минимума функций. Наиболь-
Наибольшее и наименьшее значение функции на отрезке.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Определение максимума. Говорят, что функция / (х) имеет
в точке х = х0 максимум, если значение функции в этой точке
больше, чем ее значения во всех точках, достаточно близких к х0.
Иначе: функция f (х) имеет максимум при х = х0, если
для любых Ах — как положительных, так и отрицательных, но
достаточно малых по абсолютной величине.
Определение минимума. Говорят, что функция f (x) имеет
в точке х — хй минимум, если значение функции в этой точке
меньше, чем ее значения во всех точках, достаточно близких к х0.
Иначе: функция f (х) имеет минимум при х = х0, если
f(xo + Ax)>f(xo)
для любых как положительных, так и отрицательных Ах, доста-
достаточно малых по абсолютной величине.
Если в некоторой точке функция имеет максимум или мини-
минимум, то говорят, что в этой точке имеет место экстремум,
а значение функции в этой точке называется экстремальным.
439
Замечание. Следует помнить: 1) Максимум (минимум) не
является обязательно наибольшим (наименьшим) значением, при-
принимаемым функцией. Вне рассматриваемой окрестности точки
х0 функция может принимать большие (меньшие) значения, чем
в этой точке. 2) Функция может иметь несколько максимумов
и минимумов. 3) Функция, определенная на отрезке, может до-
достигнуть экстремума только во внутренних точках этого от-
отрезка.
Необходимое условие экстремума. Если функция f (x)
имеет экстремум при х = х0, то ее производная в этой точке
равна нулю, или оо или вовсе не существует.
Из этого следует, что точки экстремума функции
следует разыскивать только среди тех, в которых ее
первая производная f (х) = 0, f (х) = оо или не суще-
существует. Исследование остальных точек отпадает. Точки, в ко-
которых первая производная функции равна нулю, бесконечности,
а также те, в которых она не существует, но функция сохра-
сохраняет непрерывность, называются критическими.
Следует уяснить, что указанный признак экстремума явля-
является только необходимым, но отнюдь не достаточным: производ-
производная функции может быть равна нулю, оо или не существовать
не только в тех точках, в которых функция достигает экстре-
экстремума. Поэтому, определив критические точки, в которых функция
может достигать экстремума, надо каждую из точек в отдель-
отдельности исследовать на основании достаточных условий существо-
существования экстремума. Укажем два таких достаточных условия.
ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ
ЭКСТРЕМУМА ФУНКЦИИ
Пусть точка х = х0 является критической точкой функции
f(x), а сама функция f (х) непрерывна и дифференцируема во
всех точках некоторого интервала, содержащего эту точку (за
исключением возможно самой этой точки). Тогда: 1) если при
х <х0 производная функции f (х) > 0, а при х > х0 f (x) < О,
то при х = х0 имеет место максимум, т. е. если при переходе
слева направо через критическую точку первая производная функ-
функции меняет знак с плюса на минус, то в этой точке функция
достигает максимума; 2) если при х < х0 f (х) < 0, а при
х> х0 f (х) > 0, то при х =?= х0 имеет место минимум; иначе:
если при переходе слева направо через критическую точку первая
производная функции меняет знак с минуса на плюс, то в этой
точке функция достигает минимума; 3) если же при переходе
через критическую точку первая производная функции не меняет
знак, то экстремума нет.
440
ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА
Если в точке х = х0 первая производная функции f'(x) равна
нулю: f (х0) — О, то при х = х0 имеет место максимум, если
Г (х0) < 0, и минимум, если f" (х0) > 0. Если же f" (х0) = О, то
для заключения об экстремуме в этой точке требуется дальней-
дальнейшее исследование (предполагается, что функция f (х) в окрест-
окрестности точки х = х0 имеет непрерывную вторую производную).
Способ, которым функция исследуется на экстремум с по-
помощью первого достаточного условия (по первой производной),
мы будем называть первым, а способ исследования функции на
экстремум на основании второго достаточного условия (по вто-
второй производной) — вторым.
Правило для исследования функции на экстремум при помощи
первой производной (первый способ)
Для исследования функции на экстремум по первой
производной следует:
1. Hautnu f (x) — первую производную функции.
2. Решить уравнение f(x)~0, а также определить
те значения х, при которых f (х) = оо или не сущест-
существует (короче: найти критические точки функции f (х)).
Пусть этими точками будут точки с абсциссами хи
х2, х3 ..., Хп, которые находятся в интервале (а, Ь).
3. Все критические точки расположить в порядке
возрастания их абсцисс в интервале (а, Ь).
а < хх < х2 < х3 <„ •• • < хп < Ь.
4. Внутри каждого из интервалов (a, xt); (xu х^);
(х2, х3); ... (х^ Ь) взять любую точку и установить в
этой точке знак первой производной функции (произ-
(производная сохраняет знак в каждом интервале между
двумя соседними критическими точками).
5. Рассмотреть знаки /' (х) в двух соседних интер-
интервалах, переходя последовательно слева направо от пер-
первого интервала к последнему. Если при таком переходе
знаки /' (х) в двух соседних интервалах различны, то
экстремум в критической точке есть: максимум будет,
если знак поменяется с + на —, а минимум, если он
поменяется с — на +. Если же в двух соседних интер-
интервалах имеет место сохранение знака первой произ-
производной, то экстремума в рассматриваемой критиче-
критической точке нет.
6. Найти значения функции в точках, где она дости-
достигает экстремума (экстремальные значения функции).
441
Правило для исследования функции на экстремум по
второй производной (второй способ)
Для того чтобы исследовать функцию на экстре-
экстремум по второй производной, следует:
1. Найти /' (х) — первую производную функции.
2. Решить уравнение f (х) = 0.
3. Исследовать знак /" (х) — второй производной
функции — в каждой точке, найденной в п. 2. Если ока-
окажется, что в рассматриваемой точке f"(x)>Q, то в
этой точке будет минимум, а если f"(x) < О, то в ней
будет максимум. Если же окажется, что в рассмат-
рассматриваемой точке /" (х) = 0, то исследование надлежит
провести по первому правилу.
Наибольшее и наименьшее значение функции на отрезке
Если функция f (х) непрерывна на отрезке [а, Ь], тона этом
отрезке всегда имеются точки, в которых, она принимает наи-
наибольшее и наименьшее значения. Этих значений функция дости-
достигает или в критических точках, или на концах отрезка [а, Ь].
Поэтому, чтобы определить наибольшее и наименьшее
значение функции на отрезке, надо: 1) определить кри-
критическое точки функции; 2) вычислить значения функ-
функции в критических точках и на концах отрезка [а, Ь\;
3) наибольшее из значений, найденных в п. 2s, будет
наибольшим, а наименьшее — наименьшим значением
функции на отрезке [а, Ь].
1 2
Задача 32,1. Найти экстремум функции у = -j х* — -j х3 —
g
— -у*2+ 2, а также определить ее наибольшее и наименьшее
значение на отрезке [—2, 4].
Реш ение. Проведем решение сначала по перво-
первому правилу, а потом по второму. Областью существования
функции является весь бесконечный интервал (—оо, +оо).
1. Находим, что
/' (х) = х3 — 2х* — Ъх. C2,1)
2. Решаем уравнение /' (х) = 0, т. е. уравнение
х3 - 2х2 - Зх = 0. C2,2)
Разлагаем левую часть уравнения на множители:
х (х2 — 2х — 3) = 0,
откуда хх = 0; х2 — 2х — 3 = 0, а хг = 3; х3 = — 1.
Производная конечна при любом х (говорят в этом случае,
что производная конечна всюду). Поэтому критическими точками
будут только найденные из C2,2).
442
3. Располагаем критические точки в порядке возрастания
абсцисс: —1; 0; 3.
4. Рассмотрим интервалы
(_09,._1); (-1,0); @,3), C, +оо) C2,3)
Выберем внутри каждбго из этих интервалов произвольную
точку и определим в этой точке знак первой производной по вы-
выражению C2,1). В интервале (—со, —1) возьмем, например, точ-
точку х = -2; /' (-2)=(-2K - 2 (-2J - 3 (-2) = -10 < 0; в интер-
интервале (—1,0) возьмем точку * = — —; /' I — ~) = — > 0; в интер-
интервале @,3) возьмем точку х ~ 1 и вычислим в ней /' (х): /' A) =
= —4 < 0; в интервале C, +со) возьмем точку х = 4: /' D) =
= 20 > 0 (вместо этих точек читатель может в каждом из интер-
интервалов C2,3) взять любые другие). Таким образом, в интервалах
C2,3) первая производная имеет такую последовательность знаков:
mln max min
и мы приходим к заключению, что в критической точке х — —1
имеет место минимум, в критической точке.-л: = 0 — максимум; а
в критической точке х = 3 — минимум. Найдем теперь экстре-
экстремальные значения функции
Эскиз графика представлен на фиг. 32,1.
Теперь проведем решение по второму правилу,
т. е. исследуем функцию на эк-
экстремум с помощью второй про-
производной.
У нас критические точки уже
определены: *i = — 1; х2 = 0 и
хъ — 3. Найдем вторую производ-
производную функции. Дифференцируя
первую производную, получаем
/" (х) ~ Зх2 — 4х —3, и согласно
второму правилу определяем знак
второй производной в каждой
критической точке:
/" (— 1) = 4 > 0; при х = — 1
функция имеет минимум,
/"@)—3<0; при х = 0
функция имеет максимум,
I" C) = 12 > 0; при х = 3
функция имеет минимум. Фиг. 32,1.
443
Читатель должен отметить, что исследование, проведенное по
второму способу, было значительно проще. Однако от исследова-
исследования функции на экстремум по первому правилу при помощи пер-
первой производной отказываться не следует, так как может ока-
оказаться, что в критической точке вторая производная окажется
равной нулю, а в этом случае нельзя сделать никакого заключения
о наличии экстремума.
Поэтому упражнения в нахождении экстремума функции по
первой производной необходимы. Теперь ответим на второй вопрос
задачи: определим наименьшее и наибольшее значение функции
на1 отрезке [—2,4]. Этот отрезок содержит внутри себя все кри-
критические точки. Так как значения функции в критических точках
мы уже вычислили C2,4), то нам осталось вычислить значения
функции на концах отрезка, т. е. /(—2) и / D): / ( — 2) = у;
о
/D) = —о-. Сравнивая эти значения со значениями C2,4) функции
в критических точках, мы видим, что наибольшим из них являет-
является /(—2) = -д~, а наименьшим — /C) = ——, т. е. наибольшего
значения функция достигает на левом конце отрезка при х — —2,
а наименьшего — в критической точке х = 3. Решим подробно еще
одну аналогическую задачу.
Задача 32,2. Определить экстремум функции у ~ х3 — З*2 +
+ Ъх + 2 и найти ее наименьшее и наибольшее значение на отрез-
отрезке [2,5].
Решение. Сначала решим задачу по первому способу, а потом—
по второму. Областью существования функции является весь беско-
бесконечный интервал (— оо, -foo). Находим первую производную функ-
функции: /' (х) = Зх2 — 6х + 3. Решим уравнение Зх2 — 6* + 3 = 0.
Это уравнение имеет только один корень х = 1. Производная конечна
при любом значении х, а потому х = 1 является единственной
критической точкой.
Рассмотрим интервалы ( —оо, 1) и A, +°о).
Внутри каждого из этих интервалов выберем произвольную
точку и определим в ней знак первой производной. Например,
в первом интервале возьмем точку х = 0, во втором х = 2.
/'@) = 3>0; /'B) = 3>0
(читатель вместо этих точек может в каждом из этих интервалов
взять любые другие).
Таким образом, в интервалах (—оо, 1) иA, +оо) имеет место
такая последовательность знаков первой производной: +> +.Из
этого мы заключаем, что первая производная знака не поменяла,
а потому в точке х = 1 экстремума нет.
Если первую производную записать в виде /' (х) = 3 (х — IJ,
то можно сразу заключить, что она положительна при любом
444
значении хф 1, а потому рассматриваемая функция возрастает на
'всем бесконечном интервале (—со, +оо). Эскиз графика представ-
представлен на фиг. 32,2.
Покажем, что по второму правилу с помощью второй произ-
производной исследование провести нельзя. Действительно, f (х) =
= 6* — 6, ив критической точке х = 1 имеем, что f A) = 0. Та-
Таким образом, исследование следует вести по первому правилу, а
на основании его мы уже заключили, что экстремума нет.
Теперь ответим на второй вопрос задачи. Так как отрезок
[2,5] не содержит критической точки, то для определения наимень-
наименьшего и наибольшего значения функ-
функции на этом отрезке следует опре-
определить только значения ее на
концах отрезка: /B) = 4, / E) = 67.
Наименьшего значения на отрезке
[2,5] функция достигает на левом
конце при х — 2, и это наименьшее
значение / B) = 4. Наибольшего
значения функция достигает при
х = 5 — на правом конце отрезка;
это значение f E) ~ 67.
Задача 32,3 (для самостоятель-
самостоятельного рошения). Найти сначала по
первому, а потом по второму пра-
правилу экстремум функции у =
Х4 ХЭ
Фиг. 32,2.
Х4 ХЭ
= -J- — -у — 7*2 + 24а: + 1,
а также наибольшее и наименьшее
значение функции на отрезке [—5,2].
Указание. Уравнение л? — *2 — 14л:-f 24 = 0 имеет корни:
х^ = —4; Х4 = Z\ х$ = о.'
Эти корни могут быть легко найдены на основании следствия
теоремы Безу, известной из алгебры. Можно также уравнение
представить в виде
х3 — 2х2
— 2х — 12* + 24 = 0,
а тогда его левая часть равна (х — 2) (х2 + х — 12).
365
Ответ. При х = —4 минимум; / (—4) = д- ; при х = 2 —
максимум; /B) = -g-; при х = 3 — минимум; /C) = — ; на отрез-
ке [—5,2]: #наиб. = у B) = -д-; г/наим. = у (—4) = — -^, т. е. функ-
функция достигает наибольшего значения в критической точке х = 2,
которая является правым концом отрезка, а наименьшего значе-
значения — в критической точке х — —4 внутри рассматриваемого отрез-
отрезка (в этой точке функция достигает также и минимума).
445
Задача 32,4 (для самостоятельного решения). Найти сначала
по первому правилу, а потом по второму экстремум функции
у = л:4 — 8х3 + 22л:2 — 24* + 12.
Указание. Уравнение х3—6х2 + Их — 6 = 0 может быть
переписано так: х3 — *2 — Ьх2 + Ьх + 6* — 6 = 0, или (* — 1) (х —
— 2) (х — 3) = 0. Корни этого уравнения: хг = 1; хг=- 2; х3 — 3.
Ответ. При * = 1 — минимум; / A) = 3; при х = 2 — макси-
максимум; fB) = 4; при * = 3 — минимум; /C) = 3 (см. фиг. 32,3).
Задача 32,5. Исследовать
У\ на экстремум функцию у = *4+
+ 8*3 + 16л:2, а также найти ее
наибольшее и наименьшее зна-
f2\ I чение на отрезке [—3,1].
Решение. Область суще-
существования — бесконечный интер-
интервал (—оо, + оо). Первая про-
производная /' (х) = 4*3+24*2+32л:.
Для определения критических
точек решаем уравнение
4х3 + 24*2 + 32* = 0.
Перепишем его в виде
* (*2 + 6* + 8) = 0, откуда * =0;
*2 + 6* -f- 8 = 0- Критические
точки: хг — —4; *2 —2; *3 = 0.
Применим первое пра-
правило. Критические точки раз-
разбивают область существования функции на интервалы:
(-ао, --4); (-4; -2); (-2, 0); @, +оо).
В каждом из этих интервалов первая производная сохраняет
знак. Поэтому для "исследования в них знака первой производ-
производной можно в каждом интервале выбрать произвольную точку. В
первом интервале возьмем точку * = —5, /' (—5) = —60 < 0; во
втором интервале возьмем точку * = —3; /' (—3) = +12 > 0; в
третьем интервале выберем точку *=-—1; /'(—1) = —12 < 0;
в четвертом интервале — точку * = +1; /' A) = 60 > 0.
Последовательность знаков первой производной в рассмотрен-
рассмотренных интервалах запишется так:
min max min
Следовательно, при х = —4 имеем минимум, а / (—4) = 0;
при х — —2 — максимум и / (—2) = 16, а при х = 0 — минимум,
446
причем /@) = 0. Эскиз графика представлен на фиг. 32,4. Вторым
способом задачу решите самостоятельно.
Найдем теперь наименьшее и наибольшее значение функции
на отрезке [—3,1]. На этом отрезке ^имеются две критические
точки: х = — 2 и х = 0; /(—2) = 16, /@) = 0. Для решения во-
вопроса о наибольшем и наименьшем значении в нем функции надо
еще рассмотреть значения функции на концах отрезка: /(—3) и
/A). Подсчет показывает, что /(—3) = 9, а /A) = 25. Сравнивая
эти значения функции с ее значениями в критических точках,
приходим к заключению, что наи-
наименьшее значение функции в точ-
точке х = 0, и оно равно 0, а наиболь-
наибольшее значение функция имеет на
правом конце рассматриваемого
отрезка в точке х = 1, и оно рав-
равно 25.
Задача 32,6 (для самостоятель-
самостоятельного решения). Исследовать на
экстремум по второму правилу
90
функцию f (х) = xi - - х3 + 8х2.
Начертить эскиз графика функции.
Ответ. Критические точки:
*! = 0; *2 = 1; х3 = 4. При jcx =
= 0 — минимум; при хг — 1 — мак-
максимум; при х3 ~ 4 — минимум.
Задача 32,7 (для самостоятель-
самостоятельного решения). По второму пра-
правилу исследовать на экстремум
функцию
Фиг. 32,4.
18л: -
1
20.
*2 = 3;
Ответ. Критические точки: хл
максимум, при х — 3 — минимум;
_97. _ __
Задача 32,8. Исследовать на экстремум функцию
при
Решение. Функция определена при всех значениях х. Про-
Проведем решение по первому и второму правилам. Начнем с опреде-
определения первой производной:
f (х) = 3 (х - IJ (х + 1J+ 2 (х + 1) (х - \K =
447
Так как производная имеет конечное значение при любом х,
то критическими точками будут только те, в которых первая
производная равна нулю. Решая уравнение (х—1J(* + 1)E* +
-f 1) = 0, находим критические точки: хх = —1; х2 — — -g-;
Эти точки разбивают интервал (—оо, +оо), в котором суще-
существует заданная функция, на интервалы.
(-оо, -1); (-1, -1); (-1, l); A, -fco).
Теперь мы должны исследовать знак первой производной в
каждом из этих интервалов. Учитывая, что в каждом из этих
интервалов первая производная сохраняет знак, мы можем в каж-
каждом из них рассмотреть любую точку. Возьмем в первом интер-
интервале х = —2; /' (—2) = 81 > 0. Во втором интервале берем х =
= — у; /' (—у) = ~ jg < 0- В третьем интервале берем х = 0;
Г @) = 1 > о.
В четвертом интервале возьмем х = 2; /' B) = 33 > 0 (вместо
этих точек читатель может в каждом из этих интервалов взять
любые другие). Последовательность знаков первой производной
будет такой:
max min
Из рассмотрения этой последовательности знаков заключаем,
что в точке х — —1—максимум, a f(—1) = 0; в точке х = —
— -g- — минимум, а п—-=-] =
,331 ¦
= —1 gj25; в точке х = 1 экст-
экстремума нет: / A) = 0; в интервале
(— -=-, Ч'°°) функция возра-
возрастает, так как ее первая произ-
производная в этом интервале поло-
положительна (эскиз графика пред-
представлен на фиг. 32,5). Теперь
решим эту же задачу по второ-
второму правилу. Находим, что
*E1
Фиг. 32,5.
Поскольку нас интересует только знак второй производной в
критических точках, то нет надобности упрощать это выражение).
Подставляя в это выражение критические значения х, получим:
448
f (—1) = —16 < 0. Значит, при х = —1 функция имеет максимум;
/" (— ~\ — -gg- > 0. Это означает, что при * = — — минимум;
/"A) = 0. Для заключения о поведении функции в этой точке
надо прибегнуть к исследованию по первой производной (оно уже
было проведено выше: в этой точке экстремума нет).
Задача 32,9. Определить экстремум функции f(x) = yrx2.
Решение. Легко находим, что /'(*) = -§-1/—-.
2 3/Т
Уравнение -у 1/ — — 0 не удовлетворяется ни одним конечным
значением х. Рассмотрим значения х, при которых /' (х) = оо или
не существует. Ясно, что таким единственным значением будет
х = 0. Таким образом, имеется
только одна критическая точка
х — 0, которая весь бесконечный
интервал (—оо, +°°) существо-
существования функции разбивает на 2
интервала: (—оо, 0) и @, +°°)-
Исследуем знак первой произ-
производной в любой точке каждого
из этих интервалов. Возьмем, Фиг. 32,6.
например, в первом интервале
п
точку х =—1; /'(—1) = —о-< 0; во втором интервале возь-
2
мем точку х~ 1; /'A) = -д->0. Последовательность знаков пер-
первой производной:
Так как производная меняет знак с — на +, то в критиче-
критической точке х — 0 функция имеет минимум, и f @) = 0. Эскиз гра-
графика представлен на фиг. 32,6.
Исследование заданной функции во второй производной про-
провести нельзя, так как /* (х) не существует в точке х — 0.
ТРИДЦАТЬ ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений на определение максимума и
минимума функций и их наибольшего и наимеиьшего значения на отрезке (необ-
(необходимые краткие сведения из теории помещены в тридцать втором практиче-
практическом занятии).
Задача 33,1. Определить экстремум квадратичной функции
у — ах2 4 Ьх -f с.
449
Решение. Прежде всего находим первую производную
функции
у' — 2ах + 6
и решаем уравнение 2ах + 6 = 0; х = — ^. Бесконечный интер-
интервал (—со, +со) существования заданной функции разбивается
на два:
Ь
-СО' 'Та
Для исследования вопроса о знаке первой производной в этих
интервалах возьмем в каждом из них произвольную точку: на-
например, в первом —точку — 2^—1, а во втором —^+1, и вы-
вычислим первую производную функции в этих точках:
Таким образом мы получаем такую последовательность знаков
первой производной:
при а>0 —, +, при а<0 +, —
min max
Заключение. Квадратичная функция у = ах2 -\-bx-\-с в
точке х— —s~ достигает: минимума, если а >0, максимума при
а < 0. Значение ординаты в этой точке:
/ Ь \ ( Ь\г . ,1 Ь \ . Ь* 6а .. 4ас — Ь*
У\)а[) +Mj+C + C
,Исследование во второй производной значительно проще при-
приводит к этому же результату (у" = 2а), и сразу видно, что в
критической точке х = — н- при а < 0 — максимум, а при а > 0 —
минимум. Читателю известно, что квадратичная функция у = ах2-\-
+ Ьх 4- с определяет параболу с осью, параллельной оси Оу. В
первой части этой книги вершину параболы мы определяли вы-
выделением в правой части уравнения у ~ ах2 + Ьх + с полного квад-
квадрата и последующим параллельным переносом координатных осей.
После разбора этой задачи учащийся получает более простой спо-
способ определения координат вершины параболы у = ах2 + Ьх + с:
надо просто определить экстремум этой функции. Числовые
примеры:
1) Найти вершину параболы у = 2х2 + 6* — 7.
450
3
Решение, г/' = 4* + 6; 4л:+ 6 = 0; * = —=- — абсцисса
вершины.
Так как а = 2 > 0, то в этой точке функция имеет минимум.
Ордината вершины равна
а координаты вершины этой параболы
— —11 —
' 2 ' ~2,
2) Найти вершину параболы у = —5*2 — 4л: + 2.
Решение, у'= — 10* — 4; —10* — 4 = 0; *=—— . Так
как здесь а.~ —5 < 0, то в этой точке функция имеет макси-
! 2\ 14 /2 14\
мум, а « —=-=-=-. Координаты вершины параболы —=-, -=- .
\ ь j a \ ь о /
Несколько аналогичных задач решите самостоятельно. Найти
координаты вершины парабол и начертить эскизы их графиков:
I) у = х2 + х+1; . 2) у= — 4л:2+ 9*— 1;
3) у = —2л:2 + 2л: + 3; 4) у = 4*2 + 6л: —4;
5) у = 6л:2 + 2л:.
Ответ. .)(-!,!); 2) (-|, Ц)
5) (— —, —-\.
Задача 33,2 (для самостоятельного решения). Исследовать на
экстремум функцию / (л:) = sin3 * + cos3 x и начертить эскиз гра-
графика этой функции.
Указания. 1) Функция периодическая, а ее период Т — 2я;
f (х + 2тг) = f(x). Поэтому при определении экстремума можно
ограничиться определением экстремума на отрезке [0; 2«];
2) у' — 3sin*cos*(sin* — cos*). На отрезке [0,2те] уравнение
3sin*cos*(sin* — cos*) = 0 имеет такие корни: 0; -j\ ^; it;
~; ~; 2к, а потому критическими точками будут 0; -|-; у; чг;
5тс Зтс 9
Т' "' *
3) Дальнейшее исследование выгоднее провести по второй
производной, знак которой следует определить во всех критиче-
критических точках.
Ответ. Максимум в точках: 0; -к-; -д-те; 2ъ\ f@) —
451
Минимум в точках: -^, я, -^, a / (j-j =^ V •
(
Задача 33,3 (для самостоятельного решения) Исследовать на
? J.
экстремум функцию f (х) — х3 — (х2— IK.
Сделать эскиз графика функции.
Указания. 1) Область определения функции — интервал
(—сю, +со), 2) первая производная обращается в нуль при х =
V2
= dt-^; 3). /' (jc) = с» при я=—1; *--0; х=+1; 4) крити-
i/o 1/2
ческие точки —1; —-g-; 0; ~ ; 1.
Ответ. При я= +1 экстремума нет; при х = 0 — минимум; при
я = + — максимум.
В следующих четырех задачах, которые должны быть решены
самостоятельно, надо иметь в виду, что если в рассматривае-
рассматриваемом интервале имеется единственный экстремум, то
в критической точке функция достигает наименьшего,
или наибольшего значения, смотря по тому, будет ли
в этой точке минимум или максимум.
Задача 33,4 (для самостоятельного решения). Найти наимень-
наименьшее значение функции у — х2\пх.
Указание. 1) Область - существования функции — интервал
@, +со); производная существует во всем этом интервале; 2) крити-
критическая точка х = -г=. Других критических точек нет. 3) /" (-^^О,
ye We]
и тогда при х — -т= — минимум. Так как заданная функция
Ve t
имеет на интервале @, +со) единственный минимум, то при х —• —=.
У е
функция .достигает наименьшего значения, и это наименьшее
значение
Задача 33,5. Найти наибольшее значение функции y = xl-'nx.
Указание, у' = х1~Ых~A — 2\пх).
Для всех значений х из интервала @, +°°). в котором опре-
определена заданная функция, производная имеет конечное значение
и обращается в нуль, когда 1 — 21пл: = 0, т. е. при \пх — — , и
тогда х = Ye — единственная критическая точка.
Докажите, что в этой точке функция достигает максимума.
Так как эта точка — единственная критическая точка функции, а
452
в ней достигается максимум, то в ней достигается и наибольшее
значение заданной функции:
(/„аиб = y(V7) = (\Tef-\nVt= {V~e) X~ "* = (V~ey =^ё.
Задача 33,6 (для самостоятельного решения). Найти наимень-
наименьшее значение функции У ~ f~-
Ответ, j/наим '-= е лри х = е.
Указание, у' — т*пГх • Область существования функции
состоит из двух интервалов: @,1) и A, +оо). В каждом из этих
интервалов производная имеет конечное значение, причем у' = 0
при \пх — 1 =. 0, т. е. когда 1пд: = 1, а х — е.
Задача 33,7 (для самостоятельного решения). Найти наимень-
наименьшее значение функции у = Xх.
Ответ. Наименьшего значения функция достигает при х =
= е~г и г/наим — уё~х.
Указание, у' = хх (\п х -\- I) и имеет конечное значение при
всех х > 0.
Задача 33,8 (сля самостоятельного решения). Определить экст-
экстремум функции и = 2х -Ь Зу^B — хJ.
,, ,, г- 2B —а-K — 2
Указания: 1) и ---¦ — —j—;
B-хO
2) критических точек две: х = 1 и х = 2;
3) рассмотреть знак первой производной в интервалах (—со, 1);
A, 2); B, +оо).
Ответ. При х == 1 функция имеет максимум: утах = 5; при
х — 2 — минимум, r/min = 4. В интервале B, +°°) функция
возрастает.
Задача 33,9 (для самостоятельного решения). Исследовать на
3 3/
экстремум функцию и = у у Bах — я2L.
Ответ. При я —0 и х — 2а функция имеет минимум:
и @) = 0; и Bа) = 0; при х = а — максимум и и (а) — -к а2 уа2.
Указание к решению задач 33,10 и 33,11. В этом случае,
когда первая производная представляет собой отношение двух
функций, а исследование на экстремум ведется при помощи вто-
второй производной, полезно для упрощения вычислений иметь в
виду следующее: пусть у' — ~, где и и у —функция х.
Тогда
v\u' v'
U'V—UV
453
Сокращая последнюю дробь на у и принимая во внимание,
и I I, и' — u'v'
что — = у , получим у = —^— .
Так как при исследовании функции на экстремум по второй
производной мы определяем знак второй производной при тех зна-
значениях х, которые обращают в нуль первую производную, то в
предыдущей формуле окажется, что у' = 0, и тогда y'v' — 0, а
знак у" будет таким же, как и знак —. Поэтому нет на-
надобности в рассматриваемом случае отыскивать полностью вто-
вторую производную для определения знака второй производной при
значениях х, найденных из уравнения у' = О, а надо эти значения
подставить в выражение —. Составить же это выражение зна-
значительно проще, чем отыскивать вторую производную. Если ока-
окажется, что v > 0, то придется исследовать знак только и'.
Задача 33,10. Исследовать на экстремум по второй производ-
производной функцию
_
У — л-4 _
Решение. Находим прежде всего первую производную:
— 4л-4 — а-8
У
(д-4 _*!>_)_ 1)
2
При всех действительных значениях х производная имеет конеч-
конечное значение. Критические точки найдем из уравнения у' = 0.
Приравнивая числитель дроби нулю, имеем 1 -f 4х2 — 4xi — хъ = 0,
откуда I ~хв+ 4х2A—х2) = 0. Рассматривая 1— хв как раз-
разность кубов, получаем 1—хъ — A — х2)(\ -\-х2 + **)> а уравне-
уравнение перепишется в виде:
A - х2) A + х2 + *4) + 4*2 A - *2) = 0,
или
отсюда получаем два уравнения: 1) 1 — дс2 =v 0; 2) 1 + 5х2 +
+ *4 = 0.
Корнями первого уравнения будут числа х--¦—1; * = +1, а
второе уравнение имеет только комплексные корни, а потому кри-
критическими точками будут только точки х — —1 и х= +1. Для
определения знака второй производной при этих значениях со-
составим, согласно сделанному указанию, выражение — . У нас м=
= 1 + 4х2 — 4х* — л:8; v = (xi — х2 + IJ;
а так как v > 0 при любом х, то надо исследовать знак только
и'= 8х - 16х3 - 6хь; и'(-1)=14>0.
454
Значит, при х ——1 функция имеет минимум, и ут\п = —2.
При*—+1 имеем и' (+1) =» —14 < 0 и, значит, при х=+1
функция имеет максимум, а утах — +2.
Задача 33,11 (для самостоятельного решения). Исследовать, на
. (а- + ЗK
экстремум функцию и — ,v ' ' .
\х ~~г *¦)
Указание, и' = *,\Т91 • Корнями уравнения и' = О будут
jci = —3; Хч — 0; и' = со при * = —2. Но при * = —2 заданная
функция не существует, а потому значение д: = —2 рассмотрению
не подлежит. Критическими точками, подлежащими рассмотре-
рассмотрению, являются Xi — —3 и х2 = 0.
Ответ. При * = —3 экстремума нет; при х = 0 функция
имеет минимум, а итт = м @) = 6~4~.
Теперь мы решим несколько задач, в которых требуется опре-
определить наибольшее или наименьшее значение функции, причем,
в отличие от предыдущих задач, эта функция не дается в гото-
готовом виде, а определяется из условия задачи.
Общее указание. Во всех случаях, когда функция, опреде-
определенная из условия задачи, окажется функцией двух независимых
переменных, надо, используя известные теоремы, одну из этих
переменных исключить.
Задача 33,12. Доказать, что из всех прямоугольников, имею-
имеющих данный периметр 2р, наибольшую площадь имеет квадрат.
Решение. Обозначим длину одной стороны прямоуголь-
прямоугольника через х. Тогда длина другой его стороны будет р — х, а его
площадь s — х(р — х) @ < х < р). Эта функция и есть та, кото-
которая получена из условия задачи и наибольшее значение которой
должно быть найдено:
- - о — 2х- — - -2
Приравняем первую производную нулю. Из уравнения
р — 2х — 0 находим, что х = ~. Так как вторая производная
отрицательна, то при этом значении х функция достигает мак-
максимума, а поскольку в интервале 0 < х < р имеется единствен-
единственный максимум, то он будет и наибольшим значением функции
в этом интервале.
Мы нашли, что наибольшего значения площадь прямоуголь-
прямоугольника достигает, когда одна его сторона х = ~, его другая сто-
сторона равна р —^- = -?-, т. е. стороны его равны, а прямоуголь-
прямоугольна
ник — квадрат: SHaH6 = 4 кв> еД-
455
Итак, из всех прямоугольников, имеющих один и тот же
периметр, наибольшую площадь имеет квадрат.
Задача 33,13 (для самостоятельного решения). Доказать, что
из всех прямоугольников, имеющих данную площадь а2, квадрат
имеет наименьший периметр.
Указание. Если обозначить длину одной стороны прямо-
угольника через х, то его другая сторона равна —, а периметр
>-*&+*)¦
Это и есть составленная из условия задачи функция, наимень-
наименьшее значение которой требуется определить.
Найти ~ и решить уравнение ~ = 0.
Ответ, х = а, т. е. прямоугольник — квадрат.
Задача 33,14. Основание треугольника равно а, а его пери-
периметр 2р. Определить его две другие стороны так, чтобы площадь
его была наибольшей.
Решение. Пусть вторая сторона треугольника Ь —¦ х. Тогда
его третья сторона с — 2р — а — х. Известно, что площадь тре-
треугольника определяется по формуле S = Ур (р — а){р — Ь) (р — с).
а в наших обозначениях S = Ур (Р — <*)(Р — х) [р — Bр — а — х)],
т. е".
S = Ур(р-а)(р-х)(а + х-р). @<х<р)
Таким образом из условия задачи определена функция, наи-
наибольшее значение которой требуется найти. Очевидно, что эта
функция достигает наибольшего значения, когда ее подкоренное
выражение будет наибольшим. В подкоренном выражении первые
два постоянные множителя можно не учитывать, а потому тре-
требуется определить наибольшее значение произведения f(x) —
— (Р — х) (а + х — р). Находим, что /' (х) = — (а + х — р) + (р —
— х) = 2р — а — 2х. Решая уравнение 2р — а — 2х — 0, находим,
что л: = р — у, т. е. b — р — ~ . Третья сторона с = 2р — а —
— ^)~Р —\ ' т< е> ^ ~ с' и РассматРиваемый треуголь-
треугольник— равнобедренный. Так как f"{x) — —2 < 0, то отсюда за-
заключаем, что при х — р — ~ площадь достигает наибольшего зна-
значения (при х — р—5" Функция s имеет максимум, но так как
в интервале @, р) он единственный, то х — р — ~ доставляет функ-
функции наибольшее значение в этом интервале.
456
Задача 33,15 (для самостоятельного решения). В треугольнике
одна сторона а, а противолежащий ей угол а. Определить два
других угла так, чтобы площадь его была наибольшей.
Указание. Второй угол треугольника обозначить через х,
тогда его третий угол тг — (а + х). Площадь треугольника SA =
= у ay sin х, где х — угол, образуемый сторонами any. Функ-
Функция S — функция двух переменных х и у. Используем теперь
известную из тригонометрии теорему синусов
Sin a
у Sin [тс — (а + X)] '
откуда
a sin (а + х)
Sin a
„ 1 a2 sin (a -f- х) sin x
" ШГа '
Теперь уже 5 — функция одной независимой переменной.
Наибольшего значения S достигнет тогда, когда его достиг-
достигнет множитель числителя f(x) — sin(a + *)sinx, производная
/'(*) = sinB* + a).
Уравнение sinBx -f- a) = 0 имеет решение 2х -\- a = i:k . Зна-
Значения fe = 0 и fe > 1 не должны рассматриваться. Остается одно
решение:
2х + a = «, а х = -j (it — a).
Если х = -в-(ir — а), то третий угол равен тг — а — -„-(я — а)=
= уGг — а) и, таким образом, углы, прилежащие к стороне а,
между собою равны, и искомый треугольник — равнобедренный.
Решите самостоятельно вопрос о том, доставляет ли значение
х — -^(т: — а) наибольшее значение функции 5 (докажите, что
/" (х) < 0, когда х = i- (it — a)j .
Задача 33,16. Требуется изготовить закрытый цилиндриче-
цилиндрический бак объемом V. Какими должны быть его размеры, чтобы
на его изготовление .ушло наименьшее количество материала?
Решение. В задаче требуется определить, в каком отноше-
отношении должны находиться радиус и высота цилиндра, чтобы при
заданном объеме V его полная поверхность была наименьшей.
Полная поверхность цилиндра
2*Я2. (R > 0)
457
Наименьшее значение этой функции и следует определить. Но
легко усмотреть, что S является функцией двух независимых
переменных. На основании указания стр. 455 следует одну из
этих переменных исключить."Известно, что объем цилиндра V =
= *R*H.
В задаче V — величина известная. Выразим Н через V:
" = =*• (Д)
С этим значением Н полная поверхность цилиндра
S = 2яД ¦ -4 + 2itjR», или S = Щ. + 2тгЯ2.
Теперь уже S — функция только одной независимой перемен-
переменной R:
и при любом R имеем, что S" (R) > 0. Из уравнения S' (R) — 0
следует что
а Я =
Так как S" (R) > 0, то это значение R доставляет функции S
минимум, а вместе с тем и наименьшее значение.
Подставив в равенство (А) это значение R, получим, что
,т. е.
Таким образом, на изготовление цилиндра заданного объема
будет употреблено наименьшее количество материала, если взять
высоту цилиндра равной диаметру.
Задача 33,17 (для самостоятельного решения). Требуется изго-
изготовить цилиндрический сосуд заданного объема V, открытый
сверху. Определить его радиус и высоту так, чтобы поверхность
была наименьшей.
Ответ.
R-H-V*.
Задача 33,18 (для самостоятельного решения). Какие разме-
размеры должен иметь цилиндр, поверхность которого равна S, чтобы
его объем был наибольшим?
458
Указание. Объем цилиндра
V = *R2H (A)
— функция двух независимых переменных R и Н. Чтобы одну из
них исключить, воспользуемся формулой для вычисления полной
поверхности цилиндра:
S =
из которой следует, что
Это значение Н подставим в формулу (А) и получим, что
у _ SR—2nR*
V - 2
Ответ. # = l/g^; H = 2R, т. е. высота цилиндра должна
быть равна диаметру его основания.
Задача 33,19 (для самостоятельного решения). Доказать, что
прямой круговой конус при заданном объеме имеет наименьшую
боковую поверхность тогда, когда R2: H2:12 ~ 1:2:3.
У к азание. S6oK. конуса = nRl; I = у Н2'+ R2; тогда S =
= r.R ]/Я3 + Rs- Наименьшее значение этой функции требуется
найти. Но она — функция двух независимых переменных. Одну
из них можно исключить с помощью формулы для объема конуса:
V = утгЯ2//, откуда Н =-. ^,
и тогда
¦у-, откуда
следует, что R2: Я2: /2 =1:2:3.
Задача 33,20 (для самостоятельного решения). Чему должны
быть равны радиус основания R, высота Я и образующая I пря-
прямого кругового конуса для того, чтобы при заданном объеме V он
имел наименьшую полную поверхность?
Указание. Учесть указание, данное в предыдущей задаче.
Задача 33,21 (для самостоятельного решения). Чему должны
быть равны высота Я, радиус оснований R и образующая I пря-
прямого кругового конуса, чтобы при заданной боковой поверхности S
он имел наибольший объем?
459
Указание. Объем конуса V = -jvR9H.
Из этой формулы одну независимую переменную следует исклю-
исключить. Используем с этой целью формулу для вычисления боко-
боковой поверхности прямого кругового конуса S = ¦kRI, или, так как
образующая конуса I = У И2 + R2, то 5 = kR УН2 -f R2, откуда
Н — -—~ " , а объем V с этим значением Н становится функ-
функцией одной независимой переменной:
Ответ. Объем конуса будет наибольшим при
откуда следует, что R2: Н2:12 — 1:2 :3.
Задача 33,21а (для самостоятельного решения). При данной
длине прочность балки прямоугольного сечения пропорциональна
ширине и квадрату высоты.
Из цилиндрического ствола дерева диаметром d надо выре-
вырезать балку наибольшей прочности. Определить ширину и высоту
балки.
Указание. Л2 = й2 — х2. Прочность у — kx (d2 — л:2), где k—
коэффициент пропорциональности.
Ответ. Ширина балки # = —=, а ее высота Н—
у 3
Задача 33,22 (для самостоятельного решения). Найти радиус
основания г и высоту h прямого кругового конуса, вписанного
в шар радиуса R так, чтобы его объем был
наибольшим.
Указание. Объем конуса V = -j w2/j.
Исключим одну из переменных, например
г2. На фиг. 33,1 изображено сечение фигу-
фигуры плоскостью, проходящей через ось
конуса. Известно, что в прямоугольном
треугольнике перпендикуляр, опущенный
из прямого угла на гипотенузу, есть сред-
средняя пропорциональная между отрезками
гипотенузы. Поэтому 2R — h ~ Т и r* =
— h B7? — Л), а объем конуса V —
Фиг. 33,1
Ответ. h =
2V2
R.
460
Задача 33,23 (для самостоятельного решения). На какой вы-
высоте следует поместить источник света над освещенной поверх-
поверхностью, чтобы освещение на расстоянии а от основания перпен-
перпендикуляра, опущенного из источника света на освещенную поверх-
поверхность, было наибольшим?
Известно, что освещенность обратно пропорциональна квад-
квадрату расстояния от источника света и прямо пропорциональна
синусу угла между лучом и освещенной поверхностью.
Указание. Освещенность Е = k -тх^а > гДе & ~ коэффици-
коэффициент пропорциональности, h — высота источника света над осве-
освещенной поверхностью, ср — угол между лучом и освещенной по-
поверхностью. Так как sin <р = ,, , то Е = k 3-.
Ответ, h = -—; максимальная освещенность Етах = ¦ g 2 .
Задача 33,24 (для самостоятельного решения). Точка Рх дви-
движется в направлении от Л к Б с постоянной скоростью Vx. В тот
момент, когда Рг проходит че-
через А, другая точка Рг выхо-
выходит из Б и движется с постоян-
постоянной скоростью Vi по направле-
направлению к С. В какой момент вре-
мени / расстояние Р\Р% между
этими двумя точками будет наи-
наименьшим, если принять АВ — а,
/_ ЛВС = ИФиг. 33,2).
Указание. За время / пер-
первая точка, двигаясь с постоян-
постоянной скоростью Vi, пройдет рас-
расстояние V4 и в треугольнике
РхРъВ сторона PiB = а — IV; вторая точка, вышедшая из Б, за
то же время / пройдет расстояние Р%В = V%t, а потому по из-
известной формуле геометрии квадрат стороны PXP2 треугольника
PiPiB равен
(PiPtf - (а - IVJ + (V2/)a - 2 (а - IV) Vtt cos p.
Ответ. Момент времени t, в который расстояние РаР2 между
точками будет наименьшим, определится по формуле
t =
21V.COSP
Задача 33,25. На расстоянии АВ — b от прямолинейной ма-
магистрали ON находится завод В. От какого места D магистрали
461
надо сделать прямолинейное ответвление DB, чтобы стоимость
проводки водопровода к заводу была наименьшей, если известно,
что стоимость единицы длины водопровода по направлениям OD,
DN и DB равна соответственно kb k2 и k3 рублей, О А — а,
ON = / (фиг. 33,3).
Указание. Стоимость водопровода: 1) на участке 0D равна
ktx\ 2) на участке DN равна кг (I — х); 3) на участке DB она
равна k3 Via — хJ + Ьг.
Фиг. 33,3.
Общая стоимость k —¦ kxx + /гг {I — х) -f k3 Via — хJ + b2. Убе-
dk
ДИТЬСЯ, ЧТО -г- = Й! — Й2 —
нения
3 ~
; > определить х из урав-
l
• /(а - а-J + б2
и показать, что при найденном х
Выгодно ввести в рассмотрение угол BDA = а. Из фиг. 33,3
видно, что cos а -= , а~/==. Из уравнения (А) следует, что
т. е.
cos а =
ХТ a
, (А, — А2 < /г3)
з
и, значит, ответвление DB следует вести под углом а, определя-
определяемым из равенства C3,23). Выражение для х получается очень
просто:
(а-
462
и х определяется равенством х = а — b ctg а, в котором а уже
известно из C3, 23).
Задача 33,26 (для самостоятельного решения). Стоимость пере-
перевозки груза на один километр по железной дороге АВ равна kL
рублей, а по шоссе PC — k% рублей (kL < ki). С какого места Р
надо начать шоссе, чтобы возможно дешевле доставить груз из
А в С. Известно, что АВ = а; ВС = Ъ (фиг. 33,4).
Ответ. АР = a — b ctg a, a угол а определяется из соотно-
соотношения cos а = ~. Из последнего равенства усматриваем, что на-
правление, в котором надо вести шоссе, зависит только от отно-
отношения стоимостей и не зависит от положения точки Р. Если,
например, кг — 4klt то cos а =.- ^ — -^, а ал 75Ч.
ТРИДЦАТЬ ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Точки перегиба. Асимптомы.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Определение 1. Говорят, что на интервале (а, Ь) кривая
обращена выпуклостью вниз, если она лежит выше касательной,
проведенной в любой ее точке.
Определение 2. Говорят, что на интервале (а, Ь) кривая
обращена выпуклостью вверх, если она лежит ниж& касательной,
проверенной в любой ее точке.
Дуги кривой, обращенные выпуклостью вверх, в дальнейшем
будем называть выпуклыми, а обращенные выпуклостью вниз,—
вогнутыми.
Дуга кривой y — f{x) выпукла на интервале (а, Ь), если во
всех точках этого интервала f (х) < 0, и вогнута на этом ин-
интервале, если во всех его точках f" (x) > 0.
Правило. Интервалы, в которых дуги кривой выпуклы, опре-
определяются из неравенства /" (х) < 0, а интервалы, в которых
дуги этой кривой вогнуты,— из неравенства /" (х) > 0.
463
Определение 3. Точка кривой, отделяющая ее выпуклую дугу
от вогнутой, называется точкой перегиба.
Определение 4. Точки кривой, в которых f" (х) = 0 или
/" (х) — оо, а также те из них, в которых f" (x) не существует,
называются критическими точками второго рода.
Точки перегиба следует искать среди критических точек вто-
второго рода.
В критической точке второго рода х — х0 перегиб будет
только в том случае, когда при переходе через эту точку f" (x)
меняет знак.
Правило. Для определения точек перегиба кривой надо опре-
определить все критические точки второго рода и рассмотреть знаки
f" (x) в каждых двух соседних интервалах, на которые эти точки
делят область существования функции. В случае, если знаки
/" (х) в двух соседних интервалах различны, критическая точка
второго рода является точкой перегиба. Если же в двух соседних
интервалах f" (x) имеет один и тот же знак, то в рассматри-
рассматриваемой критической точке второго рода перегиба нет. В точке
перегиба кривая пересекает касательную.
Задача 34,1. Определить интервалы выпуклости и вогнутости
и точки перегиба графика функции
у = 5х2 + 20* + 9.
Решение. Область существования функции — интервал
(_оо, +оо); у' = 10* + 20; г/"=10>0,
и так как у" > 0 при любом значении х, то кривая вогнута на
всем интервале (—оо, + оо). Точек перегиба нет./
Задача 34,2. Определить интервалы выпуклости и вогнутости
и точки перегиба графика функции
у^—6х2 + 8х- 11.
Решение. Область существования функции — интервал (— оо
+ )
+ 8; у"=-12-?0.
Так как неравенство у" < 0 выполняется при любом х из об-
_ласти существования функции, то кривая на всем интервале
(—оо, -fсо) выпукла. Точек перегиба нет.
Задача 34,3 (для самостоятельного решения). Определить
интервалы выпуклости и вогнутости, а также точки перегиба
кривых:
1) у =3х* + х + 1; 2) у = —2х* + 8* - 9; 3) у = *2 + х.
Ответ. На всем бесконечном интервале (—оо, -f-oo) кривая
1) вогнута, 2) выпукла, 3) вогнута. Ни одна из этих кривых точек
перегиба не имеет.
464
Задача 34,4. Определить точки перегиба и интервалы выпук-
выпуклости и вогнутости кривой у — х3.
Решение. Область существования функции — интервал (—оо,
-j-oo); у' = Зх2; у" = 6х. Решаем уравнение 6л; = 0 и находим,
что х == 0. Вторая производная' конечна и существует при любом
х, а потому х = 0 — единственная критическая точка второго
рода. Область существования функции она разделяет на два
интервала:
1) (-оо, 0) и 2) @, +оо).
В каждом из этих интервалов у" сохраняет знак. При любом
значении х из первого интервала у" < 0, а при любом х из вто-
второго интервала у" > 0. Таким образом при переходе через точку
х — 0 вторая производная меняет знак. Эта точка является точ-
точкой перегиба. Ее координаты @, 0). В первом интервале (—оо, 0)
кривая выпукла (у"<0), а во втором — вогнута (г/">0).
Задача 34,5 (для самостоятельного решения). Доказать, что
кривая у = х (х2 — Ь2) имеет точку перегиба в начале координат.
Задача 34,6. Определить точку перегиба и интервалы выпук-
выпуклости и вогнутости кривой у — х3 — 12л;2 + х — 1.
Решение. Область существования функции —бесконечный
интервал (—со, +оо). Находим у": у' — Зх2 — 24* + 1; у" =
= 6х — 24.
При любом х вторая производная конечна и существует. Кри-
Критическую точку второго рода найдем из уравнения у" = О, т. е.
из уравнения 6л: — 24 = 0. Такой точкой будет х — 4. Интервал
существования функции она разделяет на два:
1) (-оо, 4) и 2) D, +оо).
В каждом из этих интервалов у" сохраняет знак. При любом х
из первого интервала у" < 0, а при любом х из второго интер-
интервала у">0, а потому точка с абсциссой х = 4— точка перегиба,
а так как в первом интервале у" < 0, то дуга кривой на нем —
выпукла, а во втором интервале у" > 0, и дуга кривой вогнута.
Координаты точки перегиба D, —125).
Задача 34,7 (для самостоятельного решения). Определить точ-
точки перегиба и интервалы выпуклости и вогнутости кривой у =
= — х8 + 15л;2 — х — 250.
Ответ. Точка перегиба E, —5); слева от точки перегиба
кривая вогнута (у" > 0), справа от нее — выпукла (у" < 0).
Задача 34,8 (для самостоятельного решения). Определить точки
перегиба и интервалы выпуклости и вогнутости кривой
у =-. х* + 2ха — 12л;2 — Бх + 2.
16 И. А. Каплан 465
Ответ. Точки перегиба при х = —2 и х= 1; на интервалах
(—оо, —2) и A, +°°) кривая вогнута, на интервале (—2, 1)—
выпукла.
Задача 34,9 (для самостоятельного решения). Найти точки
перегиба и интервалы выпуклости и вогнутости кривой
у =, х* - Ах3 — 18л;2 + 45* — 14.
Ответ. Точки перегиба (—1, —72) и C, —68). На интервале
(—оо, —1) кривая вогнута; на интервале (—1, 3) кривая выпукла;
на интервале C, + оо) кривая вогнута.
Задача 34,10 (для самостоятель-
самостоятельного решения). Определить интерва-
интервалы выпуклости, вогнутости и точки
перегиба кривой у = (х — IL.
Ответ. Кривая на всем беско-
бесконечном интервале вогнута (у" > 0).
Задача 34,11 (для самостоятель-
самостоятельного решения). Определить точки
перегиба и интервалы выпуклости
и вогнутости кривой у = е~х' (кри-
(кривая Гаусса, или кривая вероятностей)
Фиг. 34,1.
Ответ. Точек
перегиба
/2
две:
_Y1 ±) и (У1 ±)
2 ' Vel \ 2 ' УёГ
Слева от точки х = — -^- кривая вогнута, на интервале
/ V2 V2\ /2
I — -Ц- , ^- кривая выпукла, а справа отточки х — -т. вогнута
(фиг. 34,1).
Асимптоты
Определение. Если расстояние d от точки кривой у—-f(x),
имеющей бесконечную ветвь, до некоторой определенной прямой
по мере удаления точки по этой кривой в бесконечность стре-
стремится к нулю, то прямая называется асимптотой кривой.
Различают асимптоты: I) горизонтальные, 2) вертикальные
и 3) наклонные.
1. Кривая у = f (х) имеет горизонтальную асимптоту у = Ь
только в том случае, когда существует конечный предел функции
f (х) при х -э- 4- °° или при х -*¦ —оо,иэтот предел равен Ь, т. е. есл
lim/(х) = Ь или lim/(*) = b.
C4,1)
2. Кривая у = f (х) имеет вертикальную асимптоту х — а,
если при х-*а, х-*-а — 0 или при х -*¦ а + 0, /(х) -*¦ оо. Для опре-
определения вертикальных асимптот надо отыскать те значения аргу-
аргумента, вблизи которых f (x) неограниченно возрастает по абсо-
466
лютной величине. Если такими значениями аргумента являются
аъ a<t то уравнения вертикальных асимптот будут
х = a^f х = #2/ • • •
3. Для определения наклонной асимптоты у — kx -j- b кривой
У — f (x) надо найти числа k и b из формул
= lim
— kx)
C4,2)
C4,3)
(следует отдельно рассматривать случаи л--»--)-со и х->-—со).
Наклонные асимптоты у кривой у — f(x) существуют в том и
только в том случае, когда пределы C4,2) и C4,3) имеют ко-
нечное значение (если окажется, что k = 0, a b имеет конечное зна-
значение, то асимптота будет горизонтальной). При - определении
пределов C4,2) и C4,3) удобно пользоваться правилом Лопиталя.
Задача 34,12. Найти асимптоты кривой у = — (равноосная ги-
гипербола).
Решение. 1) Находим горизонтальные асимптоты по форму-
формулам C4,1):
lim;I=.O; lim - = О,
х^+„ х х->—°° х
и кривая имеет единственную горизонтальную асимптоту у = О,
т. е. горизонтальной асимптотой является ось Ох.
2) Определяем вертикальную асимпто-
асимптоту; для этого находим те значения х, вбли-
вблизи которых f(x)~— неограниченно воз-
возрастает по абсолютной величине. Таким
значением будет х — 0. Вертикальная
асимптота имеем уравнение х — 0, т. е._
это ось Оу (фиг. 34,2).
Задача 34,13. Найти асимптоты гра-
графика функции у = —j—--.
Решение. 1) Для определения гори-
горизонтальных асимптот находим по C4,1)
2
Фиг. 34,2.
lim
= 0 и
lim
Х-*—to '
— 4
= 0.
Горизонтальная асимптота одна: у = 0 (ось Ох).
2) Для определения вертикальных асимптот находим те зна-
чения х, вблизи которых / (х) = ^_4 неограниченно возрастает
467
по абсолютной величине. Такими значениями являются х — —2
и х = -j-2, и вертикальными асимптотами будут прямые х — —2
и л; = +2. Эскиз графика показан на фиг. 34,3.
Задача 34,14 (для самостоятельного решения). Определить
асимптоты графика функции у = -_2 •
Ответ. Вертикальная асимптота х = 2, горизонтальная асимп-
асимптота у — 0 (ось Ох); наклонных асимптот нет.
Фиг. 34,3. Фиг. 34,4.
Задача 34,15 (для самостоятельного решения). Определить
асимптоты графика функции у = ~^т^.
Ответ. Горизонтальная асимптота у = 1;
вертикальная асимптота х = —4;
наклонных асимптот нет.
Задача 34,16. Найти асимптоты кривой г/= arctg*.
Решение. Находим горизонтальные асимптоты по формулам
C4,1) полагая в них f (х) = arctg x.
limarctg* = -?¦;
lim arctgx = —~.
Горизонтальные асимптоты имеют уравнения у = ~и у = — ~.
Вертикальных асимптот нет, так как нет значений х, вблизи
которых функция f{x) = arctgx неограниченно возрастает по
абсолютной величине (фиг. 34,4).
Задача 34,17 (для самостоятельного решения). Найти асимп-
асимптоты кривой y^igx.
Ответ. Вертикальных асимптот бесконечно много. Их урав-
уравнения
* = уBА+1),
где k -¦=-- 0, +1, +2, +3, ... (фиг. 34,5) (это следует из того, что
вблизи точек х = ~ Bk + 1) функция tg* неограниченно возра-
возрастает по абсолютной величине). Других асимптот нет,
468
Задача 34,18 (для самостоятельного решения). Найти асим-
л-2 — ]
птоты кривой у = . .
</=tgx
¦
/
L
1
г 3
z
- 1
/
1
L
У'
I
/
у
г~
., /,.
/
-2-
-3J
/
1
L
4-
/
/
4—
1
/
J-
7
Фиг. 34,5.
Ответ. Горизонтальная асимптота у = 0; вертикальная асимп-
асимптота л; = 0 (фиг. 34,6).
Задача 34,19 (для самостоятельного решения). Найти асимпто-
асимптоты кривой у = t ,-хг.
Ответ. Горизонтальная асимптота
у = 0 (фиг. 34,7). _-=
Задача 34,20. Найти асимптоты кри-
ой =?1+1
Решение. Горизонтальных асимптот
нет. Так как у неограниченно возрастает,
когда х
ъ I з
— j Bх + 3 = 0 при х = — T
то имеется вертикальная асимптота: ее
3
уравнение х =—к, при этом у->—со,
3
когда х-*-— -J— 0 и у-^+со, когда
х -* s" + 0 (эти сведения мы используем
в дальнейшем при построении эскиза гра- фиг. 34,7.
фика).
Теперь определим наклонные асимптоты, уравнение которых
имеет вид у == kx + b, a k и b определяются по формулам C4,2)
и C4,3),в которых надо взять / (х) —
469
Так как hub имеют конечные значения и равные между
собой при х-*- -j-оэ и при х-*- —со, то имеется единственная на-
наклонная асимптота, уравнение которой
У
Чтобы сделать заключение об интервалах, на которых кривая
находится над асимптотой и под ней, надо составить разность
8 = г/кр — уас. На тех интервалах, где 8 > 0, кривая лежит над асимп-
асимптотой, а на тех, где 8 < 0, кривая лежит под асимптотой.
п
В нашем случае укр =
+
13
13
Знак 8 такой же, как и знак двучлена 2х+ 3. Решая нера-
неравенства 1) 2х + 3 > 0 и 2) 2х + 3 < 0, находим, что первое вы-
3 3
полняется при х > — у, а второе — при х < — -=-; поэтому:
3 / 3 \
1) 8>0, когда х> — -н-, а значит на интервале! — -*- -fool
3
кривая лежит над асимптотой; 2) 8 < 0, когда х< — -=- > а эт0 значит,
/ 3\
что на интервале I — оо, —=-1 кривая лежит под. асимптотой.
Набросок графика функции сделан
на фиг. 34,8. ;
Задача 34,21 (для самостоя-
самостоятельного решения). Определить
2х* + х + 3
асимптоты кривой у = —±в ' '
Ответ. Уравнения асимптот:
1) х = —6; 2) у = 2х 11.
Самостоятельно решить вопрос
об интервалах, в которых кривая
лежит над асимптотой и под ней.
Замечание. Следует иметь
в виду, что когда k имеет конеч-
конечное значение, а Ь — бесконечное,
то наклонной асимптоты нет. Этот
случай имеет место в следующей
задаче.
Фиг. 34,8.
Задача 34,22. Найти асимптоты кривой у ==
470
Ответ. Вертикальная асимптота х = —2. Так как 6-*-+оо
когда х-*- +оо, то наклонной асимптоты нет. Так как при х < О
не существует Ух, то пределы C4,2) и C4,3) при х-*- —со не
должны рассматриваться.
ТРИДЦАТЬ ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Общее исследование функции.
Приобретенные на предыдущих занятиях навыки в определении интерва-
интервалов монотонности функции, экстремума функции, интервалов выпуклости и
вогнутости графика функции, его точек перегиба и асимптот позволяют про-
провести полное исследование функции и построить эскиз графика функции, ко-
который, хотя и не будет отличаться большой точностью, но все же даст воз-
возможность усмотреть характерные свойства и особенности исследуемой функции.
Под полным исследованием, функции обычно понимается реше-
решение таких вопросов:
1) Определение области существования функции.
2) Выяснение вопроса о четности и нечетности функции.
3) Определение точек разрыва функции.
4) Определение асимптот графика функции.
5) Определение интервалов возрастания и убывания функции.
6) Определение экстремума функции.
7) Определение интервалов выпуклости и вогнутости графика
функции.
8) Определение точек перегиба.
Полученные данные следует использовать для построения гра-
графика функции. Для большей точности эскиза графика рекомен-
рекомендуется построить еще и отдельные точки графика, давая
значения независимой переменной и определяя соответствую-
соответствующие значения функции. Полезно также получаемые данные сразу
наносить на чертеж.
Учитывая, что на предыдущих занятиях все элементы этой
схемы были полно изучены, мы дадим подробное решение только
трех задач, после чего остальные задачи должны быть решены
самостоятельно. Эти задачи снабжены ответами и необходимыми
указаниями.
Задача 35,1- Исследовать функцию у — тЦхТТр'
Решение. 1. Определим область существования этой функции.
Функция существует при всех значениях х, кроме х— —1, при
котором знаменатель дроби обращается в нуль. Значит, функция
определена в интервалах (—со, —1) и (—1, +<х>).
2. Исследуем вопрос о наличии центра симметрии и оси сим-
симметрии. Проверим для этого выполняются ли равенства /(—х) =
= f{x) и f(-x)~-f(x).
' 471
Непосредственная подстановка убеждает нас, что ни одно из
этих равенств не выполняется, так что ни центра, ни оси сим-
симметрии график функции не имеет.
3. Числитель и знаменатель дроби у = -„, , ^2 непрерывные
функции и, следовательно, функция у будет непрерывной при
всех значениях х, кроме х =—1, при котором знаменатель дро-
дроби обращается в нуль.
4. Переходим к определению асимптот графика.
а) Вертикальные асимптоты найдем, приравняв знаменатель
нулю: 2(х+1K = 0; х=— 1.
Вертикальная асимптота одна: ее уравнение х — — 1.
б) Горизонтальные асимптоты находим так: отыскиваем lim у
lim и — lim
а это означает, что горизонтальных асимптот нет.
в) Наклонные асмиптоты:
= lim -__f_ = |
= у(—2)=—1;
Наклонная асимптоты одна: у = -„х — 1.
5 и 6. Определяем интервалы возрастания и убывания функ-
функции и экстремум функции.
Находим первую производную у' = ^x+iy •
Определим критические точки: 1) Решаем уравнение у' = О,
„2 (у _L tX\
т. е. уравнение 9 / 7~. , = 0 и находим, что хг — —3; хг — 0.
2) Определяем значения х, при которых у — со. Таким зна-
значением является х— — 1. Но эт© значение рассмотрению «е дол-
должно подлежать, так как оно не входит в область определения
функции. Критические точки, подлежащие рассмотрению: хх =
= —3, х2 = 0 и точка х— — 1 —разделяют интервалы существо-
существования функции на такие интервалы:
1) (-со, -3); 2) (-3, -1); 3) (-1,0); @, +°о).
В каждом из этих интервалов производная сохраняет знак: в
первом — плюс, во втором — минус, в третьем — плюс, в четвертом—
472
плюс (в этом можно убедиться, взяв в каждом интервале произ-
произвольное значение х и вычислив при нем значение у'). Последо-
Последовательность знаков первой производной запишется так: +, —,
+ , +• Значит, в интервале (—со, —3) функция возрастает, в
интервале (—3, —1)— убывает, в интервалах (—1,0) и @, +со)
функция возрастает.
При х — — 3 функция имеет максимум и уыакс. = —¦§¦• Так как
знак во втором и третьем интервалах различны, то можно было
бы предположить, что при х = — 1 есть экстремум. Но такое пред-
предположение неверно, так как при х — — 1 заданная функция не су-
существует. Итак, функция имеет единственный экстремум (максимум)
при х = —3. • . •
7 й 8. Определение интервалов выпуклости и вогнутости гра-
графика функции и точек перегиба.
Находим, что у" — . , l j и определяем критические точки
3*
второго рода: 1) решаем уравнение ,у J_n4 = 0 и находим, что
(+)
х = 0; 2) определяем значения х, при котором у" ~со. Таким
значением является х — —1). Как уже было отмечено выше, это
значение рассматриваться не должно, так как при нем не суще-
существует заданной функции.
Критическая точка второго рода х = 0 разделяет интервалы
(—со, —1), (—1, -f оо) существования функции на интервалы:
1) (-оо, -1); 2) (-1, 0); 3) @, +°о).
у=
В каждом из этих интерва-
интервалов вторая производная конеч-
конечна и сохраняет знак: в первом —
минус, во втором — минус,
в третьем — плюс, и мы имеем
такое чередование знаков вто-
второй производной в этих интер-
интервалах: —, —, +.
Значит, в интервалах (—оо,
— 1) и (—1,0) кривая выпукла,
а в интервале @, + оо)— вог-
вогнута. При х — 0 вторая произ-
производная равна нулю, а при пе-
реходе из второго интервала е
третий она поменяла знак. Это указывает на то, что при х = 0,
кривая имеет точку перегиба. Координаты точки перегиба @, 0) —
это начало координат. Все полученные сведения наносим на чер-
чертеж и получаем эскиз кривой (фиг. 35,1).
ФИГ- 35,1.
473
X3
Задача 35,2. Исследовать функцию у — -^, 2х , э.
1. Определим область существования функции. Прежде всего,
определим, при каких значениях х знаменатель х2 -f- 2х + 3 обра-
обращается в нуль. Приравняем знаменатель нулю и решим уравнение
х2 + 2х + 3 = 0; получим, что х = — 1 ± i Y~2. Корни знаменателя
комплексны. Значит, ни при одном вещественном значении х зна-
знаменатель дроби в нуль не обращается. Дробь, представляющая
собой отношение двух непрерывных функций, будет функцией
непрерывной при всех значениях х, за исключением тех, при ко-
которых знаменатель дроби обращается в нуль. В нашем случае
числитель и знаменатель — функции, непрерывные на всей оси.
Следовательно, заданная функция непрерывна при jjjo6om x (мы
выяснили, что ни при одном вещественном х знаменатель в нуль
не обращается), и областью ее определения является вся ось Ох,
т. е. интервал (—оо, +оо).
2. Определим, нельзя ли отнести данную функцию к классу
четных или нечетных функций. Для "этого вычислим /(—х):
f(—х) = ¦ 2 _ „ . Мы заключаем, что f (х) не-равно ни /(—х),
ни — f(x), т. е. нашу функцию нельзя отнести ни к классу
четных, ни к классу нечетных функций, и график функции не
имеет ни оси, ни центра симметрии.
3. Определим теперь асимптоты графика: а) вертикальных
асимптот нет, так как нет тех конечных значений х, при которых
t/->oo; б) найдем горизонтальные асимптоты:
х3
Так как конечный предел отсутствует, то горизонтальных асимп-
асимптот нет; в) находим наклонные асимптоты, уравнение которых
k + b
2*4-3) =
51
Значения k и b как при х->-\- оо, так и при х-*—оо одни
и те же. Наклонная асимптота одна; у — х —2.
4. Теперь определим интервалы возрастания и убывания функ-
цйи и ее экстремум у' =
474
Определим критические точки функции: 1) Решаем уравнение
у' = 0, т. е. уравнение Л , 2х iW — 0. Из него следует, что
л; = 0 и хг + 4х + 9 = 0, т. е. л; = —2 + i УЪ. Значит, производ-
производная имеет один действительный корень х = 0.
2) Ни при одном действительном значении х первая произ-
производная не принимает бесконечно больших значений (из уравнения
х2 + 2х + 3 = 0 следует, что х — — 1 ± i V2). Таким образом, име-
имеется одна критическая точка х = 0. Область существования функ-
функции— интервал (—оо, + оо) она разделяет на два интервала:
1) (—оо, 0) и 2) @, +°о). Выбирая в каждом из них произволь-
произвольные значения х и вычислив при нем у', мы получим такую пос-
последовательность знаков первой производной: -f, +.
Так как в рассматриваемых двух соседних интервалах у' имеет
один и тот же знак, то в критической точке х = 0 экстремума
нет: во всей области существования функция возрастает.
е „ ., „ 2х (х* +18* 4- 27) „
5. Определяем точки перегиба: у = —.v 2 ]_ „ _Д 8 ' . Прирав-
Приравниваем у" нулю:
(х* 4- 2х 4- ЗK
+ 18л; + 27) = 0; л; = 0; х* -\- 18* + 27 = 0;
л;2^-16,2; х,»—1,8.
Ни при одном значении х знаменатель дроби в нуль не обра-
обращается; таким образом, критическими точками второго рода будет
X! як-16,2; х,«—1,8; xs = 0.
Эти точки разделяют область существования функции — интервал
(—оо, +оо) на интервалы 1) (—оо; —16,2); (—16,2; —1,8);
3) (-1,8; 0) и 4) @; +«>).
Для определения знака второй производной в каждом из этих
интервалов достаточно определить ее знак в произвольной точке
этого интервала, так как при всех значениях х из данного ин-
интервала она имеет один и тот же знак. Последовательность зна-
знаков второй производной записывается так: —, +, —, +, и так
как в каждом из двух соседних интервалов вторая производная
имеет различные знаки, то найденные три критические точки вто-
второго рода —точки перегиба графика функции. Их координаты:
1) (-16,2; -18,2); 2) (-1,8; -2,64); 3) @, 0).
Прежде чем приступить к построению эскиза графика функ-
функции, определим взаимное расположение кривой и асимптоты.
475
Выясним, не пересекает ли кривая асимптоту. Для этого решим сов-
совместно их уравнения:
» д-2 _f_ 2Х 4- 3
у= х — 2
Исключая у, получим, что х — 2 =
C5,1)
9у . о. откуда
(х - 2) (х2 + 2л; + 3) = х2; х = -6.
Подставляя это значение во второе уравнение системы C5,1),
получим, что у — ~8. Асимптота пересекает кривую в точке
(-6, -8).
Уас = х —2;
У нас укр. = х2
— Z/кр. Уас — ~г~
2х
/„ 2\
a-8 -f- 2л- -f- 3 *
/ftffpi/к
У=
Так как знаменатель положителен при любом л; (корни его
комплексны), то знак дроби зависит от знака числителя. Он бу-
будет положительным при х + 6 > О,
т. е. при х > —6. Значит, при
х > —6 кривая располагается над
асимптотой.
Разность 8 будет отрицательной,
когда числитель дроби отрицатель-
отрицательный, х -)- 6 < 0, т. е. при х < —6,
а кривая расположена ниже асимп-
асимптоты при х < —6.
Теперь достаточно данных, чтобы
начертить эскиз кривой (фиг. 35,2).
Задача 35,3. Исследовать функ-
функцию у = ~.
1. Определим область существо-
Фиг. 35,2. вания Функции:
Функция существует при всех
значениях х, кроме х = 0. т. е. в интервалах (— оо, 0), @, + оо).
В этих интервалах функция и непрерывна.
2. Исследуем вопрос об оси и центре симметрии кривой.
У нас / (х) = — , a f (—х) = — (ни одно из равенств / {х) =
= f(—x) и /(—*)= — f(x) не имеет места, т. е. у кривой не
существует ни оси, ни центра симметрии).
3. Определим асимптоты графика функции;
а) Значение х = 0 является точкой разрыва функции. Верти-
476
кальная асимптота имеет уравнение х — • 0 и, таким образом, ось
Оу является вертикальной асимптотой кривой. При этом
lim у = lim — = —оо; lim у = lim — ~ +°°-
Х-+—0 Х-+—0 х хч-+0 x-t+0 x
б) Определяем горизонтальные асимптоты:
lim y= -f оо; lim ~-¦= О,
и горизонтальная асимптота имеет уравнение у — 0 (ось Ох яв-
является горизонтальной асимптотой).
в) Определим наклонные асимптоты, уравнение которых у =
= kx -f b. По формуле C4,2)
ki = lim — = +00.
При л; -*- -f- °° наклонной асимптоты нет.
При л;->—оо, k2 —- lim — —• lim -^ = 0, а это опять-таки
Х-*.— ов * хн оо •*
говорит о том, что наклонной асимптоты у кривой нет.
4. Определяем интервалы монотонности функции:
У — Х2 •
Находим критические точки:
1) Из уравнения у' — 0, т. е. *г~ ~ ®> следует, чтох — 1 ==
= 0, а х = 1;
2) у'—оэ при л; = 0, но при х = 0 функция не определена.
Таким образом, функция имеет критическую точку: дс=1.
Область существования функции она разделяет на интервалы:
1) (—со, 0); 2) @, 1); 3) A, +оо). В каждом из этих интервалов
у' сохраняет знак. Беря в них произвольные значения х и вы-
вычислив при них у', получаем такую последовательность знаков
производной: —,—,-{-.
Заключение. В первых двух интервалах функция убывает,
в третьем возрастает. При х — 1 функция достигает минимума, а
Ут1п~УA) = е- Координаты точки экстремума A, е).
5. Теперь определим точки перегиба и интервалы выпуклости
и вогнутости графика функции:
./> - еХ (*2 - 2* + 2)
у - хъ
477
О
Определим критические точки второго рода:
ех (х^ 1х -4- 2^
Из уравнения— ^ ¦ =0, учитывая, что е" ф 0 ни при
одном конечном значении х, должно быть хг — 2х + 2 = 0, т. е.
х — 1 + L Значит, нет действительных значений х, при которых
вторая производная равна нулю.
Определим те значения х, при которых у" — оо. Таким един-
единственным значением является х -— 0. Значит, имеется одна кри-
критическая точка второго рода х = 0. Но точки перегиба при х = 0
не может быть, так как при х = 0 заданная функция не суще-
существует. Итак, точек перегиба график функции не имеет.
Для определения интервалов
выпуклости и вогнутости гра-
графика функции рассмотрим знак
у" на интервалах (—со, 0) и
@, +оо). Выбрав в каждом из
них произвольное значение х и
вычислив при нем у", получим
такую последовательность зна-
знаков второй производной: —, +.
Значит, на интервале (—оо, 0)
кривая выпукла, а на интерва-
интервале @, +Ъэ) кривая вогнута.
Еще раз подчеркиваем, что
Фиг. 35,3. несмотря на то, что переходя че-
через х = 0 вторая производная по-
поменяла знак, точка х = 0 не является точкой перегиба, так как при
х — 0 не существует заданная функция (фиг. 35,3).
Задача 35,4 (для самостоятельного решения). Исследовать функ-
функцию у = зд-2 4-4^ + 4 и П0СТР0ИТЬ эскиз графика.
Ответ. 1) Область- существования функции — бесконечный
интервал (—со, + оо);2) функция непрерывна при любом*; 3) цент-
центра симметрии и оси симметрии нет; 4) вертикальных и горизон-
горизонтальных асимптот нет; наклонная асимптота у — х —„-; 5) экстре-
экстремума нет, функция возрастает на всем интервале существования;
6) критические точки второго рода: а) х1 — —6 — 2"|/б, yt zz —4,5;
б) хг — — 6 + 21^6; у2^ —1,5; в) хг — 0; у3 — 0 является точ-
точками перегиба; 7) на интервале (—оо, —6 — 2^6) кривая вы-
выпукла; на интервале (—6 — 2 ]/б; —6 + 2 У~Ь) кривая вогнута;
на интервале (—6 + 21^6; 0) кривая выпукла, на интервале
@, +со) кривая вогнута.
Задача 35,5 (для самостоятельного решения). Исследовать функ-
функцию у = — и построить эскиз графика.
478
Ответ. 1) Область определения — интервал (—то, -f оо);
2) функция не относится ни к четным, ни к нечетным: график
функции не имеет ни центра, ни оси симметрии; 3) в интервале
(—оо, 0) у < 0 кривая находится под осью Ох, в интервале
@, +°о) кривая расположена над осью Ох, а в точке @, 0) она
пересекает координатные оси; 4) вертикальных и наклонных асимп-
асимптот нет. Горизонтальная асимптота у = 0 — ось Ох; 5) на интер-
интервале (—оо, 1) функция возрастает; на интервале A, + оо) — убы-
убывает. При х = 1 максимум, #max~0,37; 6) на интервале (—оо, 2)
у" < 0 кривая выпукла, на интервале B, +°°)у">0 кривая во-
вогнута. Точка перегиба: х — 2; г/^0,3.
Задача 35,6 (для самостоятельного решения). Исследовать
хг 2х 4- 2
функцию у = р— и построить эскиз кривой.
Ответ. 1) Область определения — два бесконечных интервала:
(—оо, 1) и A, +°о); 2) точка разрыва одна: х — 1; 3) функция не
принадлежит ни к четным, ни к нечетным: кривая не имеет ни оси,
ни центра симметрии; 4) асимптоты: верикальная х = 1; наклонная
у = х — 1; 5) критические точки первого рода: хх = 0; хг — 1; xs =2.
В интервале (—оо, 0) у' > 0 функция возрастает; в интервале @,1)
у' < 0 функция убывает; в интервале A,2) у' < 0 функция убы-
убывает; в интервале B, +.то) у' > 0 функция возрастает. При х —
= 0 функция имеет максимум: утах = —2; при х = 2 функция имеет
минимум: г/min = 2. Экстремальные точки @, —2) и B,2); 6) у" =
2
=-. ггд. Критическая точка второго рода х—\. Перегиба в
ней быть не может, так как в этой точке функции не существует:
точки перегиба нет. При х<\ у" <0: на интервале (— оо, 1)
кривая выпукла; при х>1 у" >0: на интервале A, +то) кри-
кривая вогнута.
Задача 35,7 (для самостоятельного решения). Исследовать
(х — 1 \3
функцию г/ — I—-7-у) и построить эскиз ее графика.
Ответ. 1) Интервалы существования функции (—со, —1);
(-1, +°°);
2) ни оси, ни центра симметрии кривая не имеет;
3) кривая пересекает ось Ох в точке х — 1. В интервале
(—оо, —1) кривая лежит над осью Ох, в интервале (—1,1) —
под осью Ох, а в интервале A, +°°) —над осью Ох;
4) асимптоты: х = — 1 — вертикальная, у ~ 1 — горизонталь-
горизонтальная;
5) критические точки первого рода; х1 = — 1 и хг —- 1. Значе-
Значение х— —1 не должно рассматриваться, так как оно не принад-
принадлежит области существования функции; функция возрастает
в интервалах, где она определена; экстремума нет;
6) критические точки второго рода: xt = —1; Хг— 1; х3 --= 3.
Значение хх — — 1 не должно рассматриваться: у( — 1) не сущест-
479
вует. В интервале ( — со, —1) кривая вогнута, в интервале(—1,1) —
выпукла, в интервале A,3) — вогнута, а интервале C, +«>)—
выпукла. Точки перегиба: х = 1 и х = 3; их координаты: A, 0);
( )
)
¦ Задача 35,8 (для самостоятельного решения). Исследовать
• 2х
функцию у = ¦. а и построить эскиз графика.
Ответ. 1) Область определения — вся числовая ось.
2) функция — нечетная, кривая симметрична относительно на-
начала координат;
3) горизонтальная асимптота у = 0 — ось Ох. Других асимп-
асимптот нет;
4) критические точки первого рода: xL = —1 и хг = 1; в интер-
интервале (—со, —1) функция убывает, в интервале (—1, ^ — возрас-
возрастает, в интервале A, +°°) убывает; при х ——1—минимум,
(Уты — —1); при х = 1 — максимум, утах = 1. Экстремальные точки
(-1, -1) и A, 1);
5) критические точки второго рода
Xi = —
являются точками перегиба.
В интервале (—со, —]/3) у" < 0 — кривая выпукла, в интер-
интервале (—"[/3, 0) у">0 кривая вогнута, в интервале @, ]/3)
у" < 0 — кривая выпукла, в интервале A^3, +со) у" > 0 кривая
вогнута;
6) при х < 0 кривая расположена под осью Ох, а при х > 0 —
над осью Ох.
Задача 35,9 (для самостоятельного решения). Исследовать
функцию у~х\пх и построить эскиз ее графика.
Ответ. 1) Область существования функции — интервал
@, + со): функция определена только при положительных значе-
значениях х;
2) ни оси симметрии, ни центра симметрии нет;
3) асимптот нет;
4) критическая точка первого рода х = ё~х. В интервале
@, е~г) функция убывает, в интервале (е~г, +оо) — возрастает. При
х = е~х минимум: ymia = —е~1 5) у" = — . Критическая точка
второго рода х = 0 не принадлежит области существования функ-
функции. Точек перегиба нет. Во всей области существования функ-
функции у" > 0. Кривая выпукла. 6) Кривая пересекает ось Ох в точке
х = 1. При 0 < х < 1 кривая находится под осью Ох, а при
х > 1 — над осью Ох.
480
ТРИДЦАТЬ ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Геометрические приложения производной: уравнения
касательной и нормали к плоской кривой. Длины касательной и нормали.
Подкасательная и нормаль и их длины. Кривизна, радиус кривизны. Центр
кривизны. Соотношение между радиусом кривизны и длиной нормали. Эволюта
кривой. .
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Касательная к кривой
а) Если кривая определена уравнением у — f (х), то уравнение
касательной к ней в точке М с координатами (хъ уг) имеет
вид
у-у1^у'(х1)(х-х1). C6,1)
б) Если кривая задана уравнением f (х, у) — 0, то уравнение
касательной, проведенной в точку М(хи yj на ней, имеет вид
У-У1=у'(хъ i/i)(*-*i), C6,2)
где у' (хи г/i) есть производная неявной функции f (х, у) = 0, в ко-
которой буквы х и у заменены числами хг и у± — координатами
точки касания.
в) Если кривая задана параметрическими уравнениями
то касательная к этой кривой в точке, соответствующей значе-
значению параметра t = tx, определяется уравнением
y-yi = y'x(tx){x-Xl), . C6,4)
причем y'x{ti) определяется по формуле B7,3), и в полученном
выражении буква t заменяется числом tx. Числа же хг и ух на-
находятся из C6,3), если там заменить букву t числом tx.
2. Нормаль к кривой
а) Если кривая задана уравнением у = f (x), то нормаль к ней
в точке М (xit yL) имеет уравнение
б) Если кривая задана уравнением f (х, у) = 0, то уравнение
нормали записывается так:
y'^ = -wh;){x-Xi)- C6>6)
481
в) В случае, если кривая задана параметрическими уравне-
уравнениями, то нормаль к ней в точке, где параметр t ~ tu имеет
уравнение
У-Ух~--?щ(х-хх). C6,6а)
3. Длины касательной и нормали. Подкасательная
и поднормаль
Определение. Длиною касательной или нормали к кривой
в точке М(хи yL) называется длина отрезка этих прямых от
точки касания до точки их пересечения с осью Ох. Эти длины
обозначаются соответственно буквами Т и N. Подкасательная
и поднормаль являются соответственно проекциями отрезков Т
и N на ось Ох. Их длины будем обозначать: Sr и Sn- Если
кривая задана уравнением у = f (x), то для определения длин
этих отрезков служат формулы:
r= ЛлУ1 + ^у'(х^ ; C6.7)
у ¦
у' (*i)
,r, 1 , .
Ух
У' (xi)
7—vfa
C6,8)
C6,9)
C6,10)
Касательную и нормаль легко построить, если соединить ко-
конец под касательной Т и конец поднормали N с точкой касания М
на кривой. Но для определения поло-
положения на оси Ох точек Т и N — кон-
концов под касательной и поднормали
(фиг. 36) недостаточно знать длины
этих отрезков, определяемые по фор-
формулам C6,8) и C6,10), а необходимо еще
знать направление, в котором надо от-
отложить длины этих отрезков от точки Р
1>(з:,оГм * для получения точек Т и N. Условимся
считать подкасательную РТ и поднор-
Фиг. 36. маль PN положительными или отри-
отрицательными, смотря по тому, будут
ли направления omPKTuomPKN совпадать с положи-
положительным или отрицательным направлением оси Ох. По величине
и по знаку PN = уху' {х{), а РТ = ^- .
Отсюда следует, что РТ и PN имеют противоположные
знаки, так как произведение у.у' (хЛ и частное ~~-.- имеют
У (ХО
один и тот же знак.
482
Если окажется, что РТ > О, то точка Т лежит с положи-
положительной стороны, а точка N — с отрицательной стороны от Р.
Противоположное расположение получим, когда РТ < 0. Иначе:
точка Т лежит с положительной стороны от Р, а точка N —
с отрицательной, если ух и у' (х) имеют разные знаки, а про-
противоположное расположение этих точек имеет место тогда,
когда Ух и у' (хх) имеют одинаковые знаки.
В случае, когда кривая задана параметрическими уравнениями,
для определения величин Т, N, St и Sn следует сначала по за-
заданному в точке касания значению параметра t = tx определить
координаты точки касания хх и уъ вычислить у'х в точке каса-
касания при t — tL, а затем воспользоваться формулами C6,7) —
C6,10), причем в них следует заменить у'(xL) на y'x{ti).
В случае, если уравнение кривой задано в виде f (х, у) — О,
в тех же формулах надо значение производной у' (xj заменить
на у' fo, yj) где хг и г/i — по-прежнему координаты точки ка-
касания.
Если кривая задана в полярных координатах уравнением г =
= /(?). то длиной ее касательной и нормали считается длина
отрезков этих линий от точки касания M(rlt ср^ до точки пе-
пересечения их с прямой, проходящей через полюс перпендикулярно
к радиусу-вектору, проведенному в точку касания. Эти отрезки
называются полярной касательной и полярной нормалью. Проек-
Проекции этих отрезков на указанную прямую называются полярной
подкасательной и полярной поднормалью. Длины этих четырех
отрезков вычисляются по формулам:
C6,11)
w = | Vr\ + [r' (cpi)[21; C6,12)
S'-fr4l: C6ЛЗ)
Sw = |r'(?i)|. C6,14)
Во всех этих формулах гх и <?х — полярные координаты точки
касания.
4. Кривизна и радиус кривизны
а) Если кривая задана уравнением у — f {x), то ее кривизна К
и радиус кривизны R определяются по формулам
К= |Л 3, C6,15)
C6>16)
483
Входящий в эти формулы У\ + у'2 берется со знаком, плюс.
Кривизна и радиус кривизны кривой, по определению ~ вели-
величины не отрицательные.
б) В случае, если кривая задана параметрическими уравне-
уравнениями C6,3), то в точке, для которой параметр t — tu
з
[*" ft) + У'* ft)]^
причем берется только положительное значение корня
V*'*(ti) + y't(ti)-
в) Если кривая задана уравнением в полярных координатах
C6,19)
[rl + r"
) — r1r"(<A)\
3
4<pi)]2
3
Ч?!)]2
где гх и <рх — полярные координаты точки, в которой вычисляют-
вычисляются К и R, аУг\ + г'2(cpi)следует брать со знаком плюс.
5. Круг кривизны. Центр кривизны. Эволюта и эвольвента
Координаты аи^ центра кривизны в точке М(хи ух) кривой
определяются по формулам
a = Xi —
C6,21)
В случае, когда кривая задана параметрическими уравнениями
C6,3), координаты центра кривизны в ее точке М, соответствую-
соответствующей значению параметра t = tlt определяются по формулам
vit\ y't ft) [*/'ft) + y/*ft)] .
Формулы C6,22) применимы и тогда, когда кривая задана
полярным уравнением г = /(<р). Так как в полярных координатах
484
je = rcos<j>, у = r sin?, то, подставляя сюда г = /(?), получим
x = f If) cos <p, у — /(<p)sin f, и параметром теперь является поляр-
полярный угол ср.
Определение. Геометрическое место центров кривизны дан-
данной кривой называется ее эволютой. По отношению к своей
эволюте исходная кривая называется эвольвентой,
Если в формулах C6,21) опустить индекс у хг и ух и заме-
заменить у на f(x), а в формулах C6,22) опустить индекс у t, то
эти формулы можно считать параметрическими уравнениями
эволюты, причем в первом случае параметром является х, во вто-
втором— /.
Исключение параметра х из уравнений C6,21) или парамет-
параметра t из уравнений C6,22) определит эволюту неявным уравне-
уравнением
F(a, р) = 0.
Задача 36,1. Для параболы у2 = Чрх в произвольной ее точке
М (xlt У]) найти уравнение касательной и нормали, длины подка-
сательной и поднормали, длины касательной и нормали, радиус
кривизны, координаты центра кривизны и эволюту.
Решение. Прежде всего из уравнения параболы определим
у' и у" в точке с координатами (xlt уг): 2уу' = 2р; у' = —;
У'(*и У1) = ~> У" = ~~,У'-
Подставляя сюда найденное значение у', получим у" = —^,
У" (xi> Уг) ——т • Подставляя у'(xL, г/х) в уравнение касательной
C6,1), получим
У — У1 = ~ (х — Xj), или уух — у\ = рх — рх!. C6,23)
Так как точка М(хъ уг) лежит на параболе, то ее координаты
удовлетворяют уравнению параболы, а потому
У1 = 2р*>. C6.24)
Используем эту зависимость для упрощения уравнения C6,23)
касательной. Для этого в его правой части прибавим и отнимем
рхх и получим
УУ1 — у\ = рх + рхх — рхх — рхи
или
УУ1 — у\ = Р(х + Xl) ~ 2PXi,
а с учетом того, что у1 = 2рхи уравнение касательной запишется
в виде
485
Подставляя значение производной у'
получим уравнение нормали
y yi*
в уравнение C5,5),
которое после упрощений запишется так:
ух (х — xj + piy — у,) = 0.
Формула C6,8) дает для длины подкасательной
2
C6,25)
Используя равенство C6,24), получим, что ST = \—2x1\,
т. е. длина подкасательной параболы равна удвоенной абсциссе
точки касания. Так как в C6,25) отрицательное число, то
для построения подкасательной ее длину 2xL надо отложить от
основания ординаты точки касания в отрицательном направлении
оси Ох. Соединив конец подкасательной с точкой касания, полу-
получим касательную к параболе.
Из того, что у' — —, следует, что уху' (хх, уЛ = р.
У\
Так как левая часть этого равенства, взятая по абсолютной
величине, на основании C6,10) есть длина поднормали, то мы
заключаем, что у параболы длина поднормали есть величина
постоянная, равная параметру параболы. Так как р>0, то мы
получим поднормаль, если отложим по оси Ох в положительном
ее направлении от основания ординаты точки касания отрезок,
равный параметру параболы. Соединив конец этого отрезка с точ-
точкой касания, получим нормаль к параболе. Получить самостоя-
самостоятельно по формулам C6,6) и C6,9), что длины касательной
и нормали равны *
Т = —
Радиус кривизны определим по формуле C6,16), подставив
в нее у' и у":
D I yll D (у\ + P2J
486
Самостоятельно докажите, что радиус кривизны в любой
точке параболы у2 — 2рх равен кубу длины нормали, проведенной
в эту точку, разделенному на квадрат ее параметра, т. е.
Координаты центра кривизны находим по формулам C6,21)
с учетом найденных значений у' и у":
^-; Р = Ух + —^Г
и после упрощений
Эволюта параболы. В последних уравнениях опустим индексы
у х и у и, учитывая, что из уравнения параболы у2 = 2рх, а
у = ± У~2рх, получим
Р=±2
Отсюда следует, что
Это и есть параметрические уравнения эволюты параболы,
а параметром является х. Чтобы исключить параметр х, разде-
разделим почленно первое уравнение на второе
и получим, что
$* 8 '
а отсюда получается уравнение эволюты
в виде
Текущими координатами здесь являются
аир. Обозначая их, как обычно, через х и
у, получим
Это полукубическая парабола, вершина которой находится
в точке (р, 0) (фиг. 36,1).
487
Задача 36,2. Для эллипса, заданного уравнением
найти в произвольной точке на нем М (хъ Ух):
1) уравнения касательной и нормали;
2) длины подкасательнои и поднормали;
3) радиус кривизны;
4) координаты центра кривизны;
5) эволюту.
Решение. Запишем уравнение эллипса в неявном виде:
ЬЧ2 + а2 у2 — a2b2 = О
и найдем у' и у" по правилу дифференцирования неявных функ-
функций:
2Ь2х + 2а*уу'= 0; y' = -b?; у"=-^1.
В точке касания M(xlt yx)
, „ . Ь*х, „ , . б4
У (*i> Уг) = г" "> У №> Уи — з •
Уравнение касательной по формуле C6,2) запишется так:
У
или
Так как точка М{хъ уг) лежит на эллипсе, то ее координаты
удовлетворяют уравнению эллипса, а потому №х\ -f агу\ — a2b2,
и уравнение касательной запишется так:
агуху = a2b2,
или после деления обеих частей этого уравнения на a2b2
"о* + ~Ь* ~ Y'
Уравнение нормали получите самостоятельно по формуле
C6,6). Оно будет таким:
х\ У\
Длина подкасательнои найдется по формуле C6,8):
ST - _ У* -
488
но а?у\ = a2b2 — ЬЧ\ = b2 (a2 — x\), а потому
и, таким образом, длина подкасательной не зависит от & — малой
полуоси эллипса. Это значит, что у эллипсов, имеющих одну
общую ось 2а, их подкасательные в точках с одинаковыми абс-
абсциссами, равны между собой (фиг. 36,2).
Длина поднормали на основании фор-
формулы C6,10)
По формуле C6,16) определится ра-
радиус кривизны
Фиг. 36,2
а по формулам C6,21) координаты центра кривизны
а = хх —
!
б4
— Л1
Ь*
-1 = и, —
Ух
Теперь получим уравнение эволюты эллипса: в последних
двух формулах для вычисления а и р опустим индекс у х и у
и получим, что
а. — х —
У
Постараемся с помощью-уравнения эллипса исключить из послед-
последних двух равенств хну. Из уравнения эллипса следует, что
= и-&
ш*
aV = аЧ2 — Ь*х\
489
В выражениях для аир заменим а2у2 и Ь2х2 по этим форму-
формулам, в правых частях выполним вычитание, раскроем скобки
и, учитывая, что у эллипса а2 — Ь2 = с2, получим после очевид-
очевидных сокращений, что
Перепишем их в виде
С2*1
с*х3
Ь*
и возведем каждое из этих равенств в степень -^.
Получаем
4 4
(«аK =
2 Т"
и сложим их почленно:
(ао)Т
=сз (? + g
Но из уравнения эллипса следует, что
? 1 У _ 1
а потому
(ао)
Это и есть уравнение эволюты эллип-
эллипса. Здесь аир — текущие координаты.
Если их обозначить через х и у,
то уравнение эволюты перепишется
в виде
= /-3
Фиг. 36,3
Кривая, определяемая этим уравне-
уравнением, напоминает астроиду и получает-
получается из нее растяжением по вертикали
(см. фиг. 36,3).
Задача 36,3 (для самостоятельного решения). Взять парамет-
параметрические уравнения эллипса в виде
y — bsint
490
и доказать, что в точке, соответствующей значению параметра
t = ti, имеют место следующие равенства:
ST — | a sin tt ¦ tg tx |; Sn = — — cos tx
T = | —tg tt V
N = |- V~a3 sin3 /, + b2 cos2 ^ ;
_з_
D (a2 sin2 /j + 6! cos2 <jJ
^ = з ;
a = i~ cos3 ^; p = — ~ sin3 tt.
Пользуясь выражением для радиуса кривизны, доказать, что
в вершинах эллипса it = 0 и t — ~) радиус кривизны
(R)t=-o = -j ; (^). л. = ~ь >
2
а координаты центра кривизны в этих точках:
Задача 36,4 (для самостоятельного решения). Пользуясь ре-
результатами предыдущей задачи, доказать, что у эллипса радиус
кривизны равен кубу нормали, разделенному на квадрат пара-
параметра эллипса.
Указание. Параметром р эллипса называется половина
длины его хорды, проведенной через фокус перпендикулярно
большой оси: р = — .
г а
Задача 36,5. (для самостоятельного решения). Найти уравне-
уравнение касательной и нормали к кривой у = З*4 — 5х2 -\- 4" в точке
* = —1. У = 2.
Ответ. Уравнение касательной:
2х + у = 0.
Уравнение нормали:
х — 2у + 5 = 0.
Задача 36,6. Найти уравнения касательной и нормали к кривой
4х3 - Зхг/3 + 6л:2 - 5*«/ - 8г/2 + 9* + 14 = О
в точке, (—2,3),
49J
Решение. Уравнение.кривой задано в неявной форме. На-
Находим производную по правилу дифференцирования неявной
функции:
12х2 — Зг/3 — бхуу' + 12* — 5г/ — Ъху' — Щу' + 9 = 0;
Зу»+12дг-5у + 9. ,, „ оч 9
У B d>
Уравнение касательной
9д:4-2г/4- 12 =-0;
уравнение нормали
2х — 9г/ + 31 =0.
Задача 36,7. Найти уравнение касательной и нормали кривой
; х = 3* - 5
в точке, где ^ = 3.
Решение. Для того чтобы воспользоваться формулами C6,4)
и C5,6а), надо определить хи г/А и у' (t) при t = 3. Определим
прежде всего д^ и г/х:
*! = 3 ¦ 3 — 5 = 4,
У1 = 3»-4 = 5.
После этого находим г/^ производную в точке, где
t = 3; г/; = 2f, x't = 3; ^ = | ; ^C) = 2.
Уравнение касательной г/ — 5 = 2 (* — 4), или 2х — г/ — 3 = 0.
Уравнение нормали г/ — 5 = — у (* — 4), или д: + 2г/ — 14 = 0.
Задача 36,8 (для самостоятельного решения). Найти уравне-
уравнение касательной и нормали к кривой
' х = 2 cos t + 3 sin t
¦ у = cos t + 2 sin t
в точке, где t = -j.
Ответ. Уравнение касательной д: — 2г/ + 1 = 0;
уравнение нормали 2х + г/ — 8 = 0.
Задача 36,9 (для самостоятельного решения). Найти уравне-
уравнение касательной и нормали к гиперболе
в точке на ней (xL, y^.
Ответ. Уравнение касательной ^ — Щ = 1;
уравнение нормали —*¦ + ^ = с2 (с2 = а2 + б2).
492
Задача 36,10. Для циклоиды
'х = a(t — sin/),
ч I/ = 0A —COS 0
C6,26)
в точке, где t = tlt определить:
1) уравнения касательной, нормали и длину поднормами;
2) доказать, что нормаль в произвольной точке циклоиды
проходит через точку касания производящего круга, а касатель-
касательная — через соответствующую ей высшую точку этого круга;
3) доказать, что у циклоиды радиус кривизны имеет длину
в два раза большую, чем соответствующая нормаль;
4) определить координаты центра кривизны и доказать, что
эволюта циклоиды есть циклоида, конгруэнтная данной*, но пе-
перемещенная на отрезок cm: в положительном направлении оси Ох
и на отрезок 2а в отрицательном направлении оси Оу.
Решение. Если круг радиуса а катится без скольжения
по прямой, то всякая точка, лежащая на его окружности, опи-
описывает кривую, которая называется циклоидой. Уравнения C6,26)
есть параметрические уравнения циклоиды. Примем прямую, по
которой катится круг, за ось Ох.
Если в исходном положении точка, вычерчивающая циклоиду,
находилась в начале координат, а центр катящегося круга был на
оси Оу, то параметр t есть центральный угол, соответствующий
дуге, на которую прокатился круг по оси Ох.
Фиг. 36,4.
Циклоида состоит из конгруэнтных арок, каждая из которых
соответствует одному полному обороту производящего круга.
Расстояние на оси Ох между началом и концом одной арки равно
длине окружности производящего циклоиду круга, т. е. 2ка.
Когда точка описывает одну полную арку циклоиды, параметр t
изменяется от t = 0 до t = 2тс (фиг. 36,4).
1) Пусть при t = tlt x = xt, у — ylt причем
х1 = а (ti — sin ti); yx — a A — cos tj. C6,26a)
* Две геометрические фигуры называются конгруэнтными, если одну из
них можно совместить с другой, изменив только в результате некоторого дви-
движения ее положение на плоскости,
493
Чтобы найти уравнения касательной и нормали на основании
C6,4) и C6,6а), найдем у'х при t = t,:
y't = a sin t\ x't = а A — cos 0;
«/* = ctg j, а в точке, где t = tu y'x (tt) = ctg -?.
Уравнение касательной г/ — г/х = ctg у (х — х,)\
уравнение нормали г/ — г/i = — tg у (* — х,).
Длина поднормали находится по формуле C6,10):
Но у, = аA —«
Sm =
Д а потому
аA — cosfjctgJ?
= | a sin
т. е. длина поднормали равна про-
проекции на ось Ох радиуса произ-
производящего круга (фиг. 36,4).
2) Точка Р касания производя-
производящего круга с осью Ох (фиг. 36,5)
имеет координаты ati и 0: Р (atlt 0).
Покажем, что нормаль в точке М
проходит через эту точку. Для
этого надо доказать, что коорди-
координаты этой точки удовлетворяют
уравнению нормали. Подставляя
координаты этой точки вместо
текущих координат х и у в уравнение нормали, а вместо хх
и ух их выражения из C6,26а), получим в левой части уравнения
Фиг. 36,5.
О — а A — cos t,) = —2а sin2 -|,
а в правой части
-tg | [о^ - a ft - sin /О] = - tg -1 (at, - of
== — a tg -^ sin tx = —2a sin2 -^.
a sin tx) =
Таким образом, координаты точки Р' удовлетворяют уравнению
нормали и, значит, нормаль в точке М проходит через точку
касания производящего круга Р (at,, 0). Касательная же необхо-
необходимо пройдет через противоположную точку N диаметра PN,
так как касательная перпендикулярна нормали, проведенной
в точку касания (в окружности вписанный угол, опирающийся
на диаметр, есть прямой),
494
3) Найдем радиус кривизны циклоиды по формуле C6,18)
и длину ее нормали по формуле C6,9). Из уравнений циклоиды
C6,26) следует, что
х'(*) = аA—cos/); y'(t)
x"(t) = asint; у" (t) — a cost.
Заменяя здесь t на tx и подставляя в C6,18), получим, что
_ [д2A — cos Q2 + a2 sin2^] 2 _ Bа' — 2а2 cos tt) 2
[а« cos
— c°s *i) — а2 sin2
a» {I— cos
= 4a sin
2 Г
C6,27)
По формуле C6,9), полагая в ней t/x = a A — cos fx), будем иметь
Получим, что длина нормали
N = 2a sin3 4r
cosec^l;
N =
sin ¦
C6,28)
Из формул C6,27) следует, что
-тт- = 2, или R = 2N,
т. е. радиус кривизны в произвольной точке циклоиды равен
удвоенной длине, соответствующей нормали.
4) Координаты центра кривизны определяются по формулам
C6,22). Подставляя в них ранее найденные значения x't, x", y't,
у", вычисленные в точке, где t = tu и учитывая C6,26а), полу-
получим, что
а = a(tx + sin^);
Р = —аA — cos^i).
Если в этих формулах опустить индекс у tu то получим уравне-
уравнение эволюты циклоиды
[ а = a(t + sin t),
i = —аA —cos Л.
495
Если теперь взять t = к + т, то уравнение эволюты циклоиды
запишется так:
а = an + а (т — sin -с);
р = — 2a + a(l —cost).
Из этих формул мы заключаем, что эволюта циклоиды есть
циклоида такая же, как данная, но смещенная на отрезок an
в положительном направлении оси Ох и на отрезок 2а в отри-
отрицательном направлении оси Оу.
Циклоида обладает замечательным механическим свойством:
материальная точка, двигаясь по этой кривой, достигает задан-
заданной на ней точки, затрачивая на это одно и то же время, не-
независимо от того, из какой исходной точки кривой началось дви-
движение.
Задача 36,11 (для самостоятельного решения). Найти радиус
кривизны и эволюту астроиды
\х — a cos31
\ у = a sin31
в произвольной ее точке, где < = ^.
Указание. Астроида — кривая, описываемая точкой окруж-
окружности радиуса а, которая катится без скольжения по внутренней
стороне окружности радиуса, в четыре раза большего, т. е. рав-
равного 4а*.
Ответ. R = -^a?>m2tl; а = acos^x A + 2sin2/1); p =
A+2COS2/!).
_?_ JL 1-
Уравнение эволюты (a -j- p)" -f (а — рK = 2а 3.
Если повернуть координатные оси на 45а вокруг начала ко-
координат, то можно усмотреть, что эволютой астроиды является
опять-таки астроида, образованная кругами, радиусы которых в
два раза больше исходных. Докажите это.
Задача 36,12. Найти угол между касательной и радиусом-
вектором произвольной точки спирали Архимеда
г = af.
Решение. Спираль Архимеда представляет собой траекто-
траекторию точки М, которая равномерно движется по прямой ON в
то время, как сама эта прямая равномерно вращается вокруг
точки О (полюса). Предполагается, что в начальный момент дви-
JL .L JL
* Уравнение астроиды в прямоугольных координатах хя +У3 =а3 .
496
жения точка М находилась в полюсе полярной системы коорди-
координат, а прямая ON совпадала с полярной осью (фиг. 36,6).
Известно, что угол ^ между радиусом-вектором произвольной
точки кривой г = г(<р) и касательной к ней в этой точке опреде-
определяется по формуле
" 7M C6'29)
где г есть производная от г по f.
Подставляя в эту формулу из уравнения спирали Архимеда
г =, of и г' - а, получим, что
* _ ОФ „ -_„!._, ,« /ОС ОП\
хй м* ^^ —^== Ф» a и* == arcts ф, (оо,ои)
Число а в уравнении спирали Архимеда называется парамет-
параметром. Полученный результат показывает, что р. не зависит от а.
Это значит, что все спирали Архи-
Архимеда пересекают радиусы-векторы, уъ" ,' "Sx *,
соответствующие одному и тому же '' ^ч ^^
значению полярного угла, под одним
и тем же углом. Интересно подме- \
тить и такую особенность: когда
ф--э-оо, то из C6,30) следует, что
уь -*- -|-, а это означает, что по мере
развертывания спирали она стре-
стремится стать нормальной к своим Фиг. 36.6
радиусам-векторам.
Задача 36,13. Определить полярные поднормаль и подкаса-
тельную спирали Архимёда в произвольной точке спирали (гь «р^-
Решение. По формулам C6,13) и C6,14) находим, что длина
полярной поднормали S# = а, а длина полярной подкасательной
л 2
Из этого заключаем, что полярная поднормаль спирали Архи-
Архимеда есть величина постоянная, равная ее Параметру, и что
концы всех поднормалей лежат на окружности радиуса а с цент-
центром в полюсе. Рассматривая длину полярной подкасательной,
приходим к выводу, что она равна длине дуги окружности ра-
радиуса гъ соответствующей центральному углу, равному <рх. В част-
частности, в точке, где спираль вторично' (после полюса) пересекает
положительное направление полярной оси (в этой точке <Рх = бтс),
длина дрлярной подкасательной равна длине окружности, радиус
которой равен радиусу-вектору этой точки.
Задача 36,14 (для самостоятельного решения). Определить ра-
радиус кривизны спирали Архимеда в произвольной ее точке.
_з_
Ответ. R — —-
17 И. А. Каплан 497
Задача 36,15 (для самостоятельного решения). Доказать, что
подкасательная гиперболической спирали г = — имеет постоян-
постоянную длину, равную а.
Задача 36,16 (для самостоятельного решения). Для логариф-
логарифмической спирали г= а? определить в ее произвольной точке:
1) угол между радиусом-вектором касательной в этой точке;
2) длину полярной подкасательной и поднормали;
3) длину полярной касательной и нормали.
Ответ. 1) Логарифмическая спираль пересекает все свои ра-
радиусы-векторы под одним и тем же углом p.: tg р. = -,— . Напри-
Например, спираль г = е"> пересекает все свои ради усы-векторы под
углом 45°. 2) 5,- = ^; SN = r\na. 3) Г = ]Л + fij^ • Л
N = 1/1 + In2 а • г.
Задача 36,17. Доказать, что радиус кривизны в произвольной
точке логарифмической спирали г — а? пропорционален радиусу-
вектору этой точки и равен R — г|/l -f- ln2a (сопоставляя вели-
величину R с длиной полярной нормали, найденной в задаче 36,16,
приходим к выводу, что радиус кривизны в произвольной точке
логарифмической спирали равен полярной нормали в этой
точке).
Задача 36,18 (для самостоятельного решения). Доказать, что
эволюта логарифмической спирали г = аР есть так же логарифми-
логарифмическая спираль, конгруэнтная данной, но повернутая относительно
ее на некоторый угол.
Указание. С помощью формул, связывающих прямоуголь-
прямоугольные координаты с полярными (* = rcos<p; t/ = rsin <j>), уравнение
логарифмической спирали записать в виде
х. — a"? cosy,
у = Of sin <р
и по формулам C6,22) определить координаты центра кривизны
произвольной точки (ru fi) логарифмической спирали. Получится,
что
a— —ati sin <px In a,
Радиус вектор центра кривизны
п = У о? + р> =
гг — a?» In а.
Если взять lna = af« и опустить индекс у, гг и уь то получим
эволюту логарифмической спирали в виде г = a,ta,f«, или г = af+f».
Эта кривая получается из данной логарифмической спирали г = а*
вращением ее на некоторый угол <ро-
498
Задача 36,19. В какой точке кривая у = \пх имеет наимень-
наименьший радиус кривизны?
Решение. Находим по формуле C6,16), что в произвольной
з
точке А (х, у) этой кривой R = ——
X
Чтобы определить наименьшее значение R, находим производ-
производную
dR _ Bл-2— l)Vl + x*
dx ~ д-2 '
приравниваем ее нулю и решаем уравнение Bхг—1I^1 -\- х2 —
= 0, откуда х = + у У 2. Критической точкой является также
1
и х — 0. Но значения х=— у к 2 и х = 0 должны быть от-
отброшены, так как для значений х<0 функция г/ = 1пд; не су-
существует (на кривой у — Хпх нет точек с абсциссами х < 0).
1
Осталось исследовать значение х = у У 2. Найдите R", подставь-
подставьте в полученное выражение х — -=- У2 и убедитесь, что R" 1-^-j/2 >
> 0. Это доказывает, что радиус кривизны кривой г/=-1пд; бу-
будет наименьшим в точке с абсциссой х = у |^2, т. е. в точке
~ 1/2; -yln2).
Задача 36,20 (для самостоятельного решения). Доказать, что
X _ X
у цепной линии г/ = у(е"^4-е д) радиус кривизны пропорцио-
пропорционален квадрату ординаты (R — — уЧ и что он равен длине нор-
нормали N.
Указание, у' = -^ (е а —е~^): у" = -^.
ТРИДЦАТЬ СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Функции многих независимых переменных. Область су-
существования. Частные производные. Полное приращение и полный дифферен-
дифференциал первого порядка функции нескольких независимых переменных.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Переменные х, у, г, ... t называются независимыми меж-
между собой, если каждая из них может принимать любые значе-
значения в своей области изменения, независимо от того, какие зна-
значения принимают при этом остальные переменные.
17* 499
2. Переменная величина и называется функцией независимых
переменных х, у, z, .. , t, если каждой системе значений этих
переменных в области их изменения соответствует единственное
определенное значение и*. • ,
Символически функция и независимых переменных х, у, z, ... , t
записывается так:
¦y = f(x, у, z t). . C7,1)
3. Областью существования функции f (х, у, z, ... , t) назы-
называется совокупность значений независимых переменных х, у,
z, ... , t, при которых функция определена (т., е. принимает
действительные значения). Область существования функции на-
называется также областью определения функции.
В дальнейшем для упрощения записей все определения и фор-
формулы приводятся только для функций от трех независимых пе-
переменных.
4. Частные приращения функции. Если и = / (х, у, z) и одна
из независимых переменных, например х, получила приращение
Ах, то частным приращением Ахи функции называется разность
Ахи — / (х + Ах, у, z) — / (х, у, z). Соответственно
= \(x, y+ Ay, z) — f (x, у, z),
а
Аги = / (х, у, z + Az) — f (x, у, z)
5. Частные производные. Составим отношение -^~. Если при
стремлении Ах к нулю это отношение стремится к определен-
определенному пределу, то этот предел называется частной производ-
производной функции и — f (х, у, г) по независимой переменной х и обо-
обозначается одним из символов ^, -X, и'х, f'x.
Таким образом,
или в более подробной записи
д1 = Нт /(•*" +А*. у> z) — f(x, У> ^
Аналогично определяются частные производные функции и =
= f (х, у, г) по независимым переменным у и г. Частная произ-
производная по у обозначается одним из символов j-, 4-, и'у, f'y,
|/ = lim *? = Ит f{x.y + Ly.z)-f{x,y,z) У
* Многозначные функции нами не рассматриваются.
500
tip z —одним из символов: ^; -J; u'z; /г'
*¦ ¦¦¦¦ 1 iЦ1
^ lim И lim
дг Дг-0 Аг Дг-»О Аг
Вычисление частных производных функции нескольких незави-
независимых переменных производится по тем же правилам, по кото-
которым вычисляются производные функции одной независимой пере-
переменной, только следует иметь в виду, что при определении
частной производной надо считать постоянными все независимые
переменные, кроме той, по которой вычисляется частная произ-
производная.
Задача 37,1. Найти область существования функции и =
= 1/4 — х2 — г/2.
Решение. Представим функцию в виде и = V 4 — (я2 + г/2).
Очевидно, что функция определена для тех значений х и у,
которые удовлетворяют неравенству х2 + г/2 < 4. На языке гео-
геометрии это означает, что функция определена в точках, лежащих
внутри окружности х2 + уг = 4 и на ее границе, так как для
всех точек, лежащих вне ее, имеет место неравенство хг -\- у2 > 4.
Задача 37,2. Найти область существования функции г =
= \п{х — у).
Решение. Так как отрицательные числа и нуль логариф-
логарифмов не имеют, то должно выполняться неравенство х — у > О,
т. е. у < х.
Точки плоскости хОу, координаты которых удовлетворяют
этому неравенству, расположены под прямой у — х, причем точ-
точки, лежащие на этой прямой; рассматриваться не могут. Короче:
область определения функции — полуплоскость, расположенная
под прямой у = х, причем сама прямая у — х при рассмотрении
не учитывается. ч
Задача 37,3 (для самостоятельного решения), и =-- ~—. Най-
х + У
ти область существования функции.
Ответ. Функция определена во всех точках пространства,
кроме точек плоскости х + у = 0, так как в точках этой пло-
плоскости знаменатель дроби у заданной функции обращается в
нуль.
Задача 37,4 (для самостоятельного решения). Найти область
существования функций: 1) z = ху и 2) z — х2 + у2.
Ответ. Обе функции определены во всей плоскости хОу,
т. е. при любых значениях х и у.
*ч г df df ¦
) Следует иметь в виду, что символы у- . ^г- > • • • нельзя рассматривать
как частные от деления, "например df на дх, так как ни df, ии дх в отдель-
отдельности смысла не имеют.
501
Задача 37,5. Найти область существования функции г —
= arcsin C — х2 — у2).
Решение. Так как функция и = arcsin г определена для
значений аргумента / из отрезка [—1, +1], то искомая область
существования найдется из условия — 1 < 3 — х2 — у2 < 1, от-
откуда следует, что 2 < х2 + у2 < 4 и область существования ,фУнк"
ции заключена между двумя концентрическими окружностями:
х2 -f у2 = 2 и х2 + у2 — 4, причем могут рассматриваться и точки,
принадлежащие этим окружностям.
Задача 37,6 (для самостоятельного решения). Найти область
существования функции z — arcsin Зху.
Фиг. 37,1
Фиг. 37,2
Ответ. Область существования ограничена двумя сопряжен-
сопряженными гиперболами:
и — 5- и у = —V .
а Ъх ¦ Зх
Задача 37,7 (для самостоятельного решения). Найти область
существования функции / (я, у) = arcsin A — х2 — у2) + arcsin 2xy.
Ответ. Областью существования является общая часть об-
областей существования слагаемых функций: 1) arcsinA — х2 —у2)
и 2) arcsin 2xy, т. е. область, изображенная на фиг. 37,1.
Задача 37,8. Найти область существования функции и =
~ *¦-»¦•
х^ Ч- iP'
Решение. Должно выполняться требование: „ > 0. Эта
дробь положительна, когда положителен ее знаменатель, т. е.
когда х2 — у2 > 0, или у2 < хг, а это влечет за собой неравенство
\У\<\*\-
Рассмотрим два случая: 1) х > 0, 2) х < 0. 1) Если х > 0,
то | х | — х, и тогда | у | < х, или —х < у < х. На языке геомет-
502
рии это означает, что область определения есть часть правой
полуплоскости (т. к. рассматриваются значения л:>0), ограни-
ограниченная прямыми у = х и у = —х, причем точки, лежащие на
этих прямых, рассматриваться не могут1 2) Если х < 0, то | Jt | =
= —х, и тогда | у \ < —х, или х < у < — х.
Последние* неравенства определяют ту часть левой полупло-
полуплоскости, которая находится между прямыми у = —х и у = х,
причем опять-таки точки, принадлежащие этим прямым, не долж-
должны рассматриваться (фиг. 37,2).
Задача 37,9 (для самостоятельного решения), и = lnx -f- In г/.
Найти область определения функции.
Ответ. Первый квадрант (*>0, у > О),'причем оси Ох и Оу
исключаются.
Задача 37,10 (для самостоятельного решения), и = 1Лп* + 1пг/.
Найти область определения функции.
Ответ. *>0; у > 0; ху~>\. Область состоит из точек пер-
* 1
вого квадранта, лежащих над гиперболой у = — и на ней.
Задача 37,11- Найти частные производные функций: 1) и =
X
= х2 + Зху + 4г/2; 2) и = sin C* -f- Ъу — 4z); 3) и = е~».
Решение. 1) Функция и — функция двух независимых пе-
переменных —х и у. При определении частйой производной функ-
функции и по независимой переменной х вторая независимая пере-
переменная должна рассматривагься как величина постоянная. По-
Поэтому ^ = 2х + Ъу, так как производная по х от 4г/2 равна нулю,
как производная от постоянной величины.
При отыскании ~ независимая переменная х рассматривается
как величина постоянная, а потому ~ = Зх + 8г/.
2) Функция и — функция трех независимых переменных: х, у
и г. При определении частной производной по каждой из этих
переменных две других следует считать величинами постоянными.
Поэтому ~х = 3 cos Cjc + Ъу — 4г); ^ =- 5 cos C* + Ъу -~ 4г); ~ =
= —4 cos (Зх -\-Ъу — 4z).
3) Заданная функция есть функция двух независимых пере-
переменных хну. При дифференцировании по каждой из них вто-
вторая переменная Должна рассматриваться как величина постоянная.
Поэтому ? = jeT; Ji^-±eTt так как ^ = -, ибо про-
производная от дроби с постоянным знаменателем равна производ-
производной числителя, разделенной на тот же знаменатель, а про-
производная по у от дроби — есть производная от дроби с постоян-
у
503
ным числителем х и переменным знаменателем у. Как известно,
в таком случае
у1у У*'
Задача 37,12 (для самостоятельного решения), Найти частные
ди ди ,
производные ¦=• ^ Ъ~ ФУнкИии:
Ответ. 1) ? = ±-JL-t f?
' дх у x*' ду
n: 3) z = cos (ax + by).
(при дифференцировании по д; производная от у11 равна нулю,
так как у" рассматривается как величина постоянная, а при диф-
дифференцировании по у производная от х" равна нулю, так как хп
считается теперь величиной постоянной).
3) | = - a sin (ах + by); | = - Ь sin (ax + by).
Задача 37,13 (для самостоятельного решения). Найти частные
производные функций: 1) и — ах + by -f- cz; 2) и — ysinx + sin у;
3) и = jcsin у (х> 0); 4) и = z*v (z > 0); 5) и = Ух2 + у2 + г2.
Ответ. 1) -=j^ — a\ ^, — Ь; ^ = с (ПРИ дифференцировании
по х Две другие независимые переменные считаются постоянны-
постоянными, а потому производная по х от by и от сг, как производная
от постоянных, равна нулю. Аналогично при дифференцировании
по у независимые переменные х и z считаются постоянными,
и поэтому производная по у от ах и сг равна нулю и т. Д.)
п, ди ди . .
2) Ыс^У Cos *' ду ~ Sin ¦* + Cos У;
3) — = sin# • л;8'"*'-1; ^ = xsiny ¦ cosy ¦ \пх
(здесь при дифференцировании по х заданную функцию следует
рассматривать как степенную. Основание степени х — величина
переменная, а показатель степени sin у — величина постоянная.
При дифференцировании по у величину х следует рассматри-
рассматривать как постоянную, a sin у — как величину переменную, а по-
потому в этом случае функцию xsiny следует рассматривать как
показательную).
с, ди х , ди у . да
' дх ~ yxz + уг + г* ' ду ~~ ух* _|_ г,а + га ' дг
504
Задача 37,14 (для самостоятельного решения). Найти частные
производные функций: 1) z = excosy — evunx;,
I - V ^ ~r У > ) ^у'
arotg-4. p, .. X
4) z = e x\ 5) и = ,
Ответ. 1) ;Д = e*cosy — eycosд;; ^ = — e^sihy — eysinjc;
г2J
Задача 37,15 (для самостоятельного решения). Известно, что
сторона треугольника а определяется через две другие стороны
и угол а между ними по формуле
тт „ да да да
Найти ш, Тс и й.
= Vb2 + с2 —2bc cos а.
6 — с cos a b—с cos а
:
Ответ. — — =:
дь /Ъ* + с2 — 26с cos а a
да _ с — & cos a да _ be sin а
Зс а ' eta а *
Задача 37,16 (для самостоятельного решения). Сила тока
V д1
согласно закону Ома вычисляется по формуле / = -„-. Найти щ
д! '
и м-
п EL - У- д1 - [
итвет. dR- — #2 ; dV~T?'
Задача 37,17 (для самостоятельного решения). Формула Кла-
Клапейрона pV = RT, где R — величина постоянная, связывает для
идеального газа его объем V, давление р и абсолютную темпе-
температуру Т.
Считая каждую из этих величин V, р и Т функцией, ,а две
другие — независимыми переменными, определить частные произ-
производные этих функций.
505
,, ,, RT dV R dV RT O4 RT
Решение. 1) F=-; ш = -\ щ = - j, : 2) p = -p-;
dji_ R_ dp__ __RT- q\ r _ ?^ • ^1 — Z. • <H-— JL
df ~ V ' 3V ~ V2' ' ~ /? ' <Эр ~ Л ' dV ~" R '
n dp dV dT- ,
Докажите, что ^^^ = - 1.
Задача 37,18. Доказать, что функция z = г/2 sin (х2 — г/2) удо-
удовлетворяет уравнению уг-^--\-xy~ = 2xz.
Решение. ~ = г/2cos(хг — г/2) • 2х
производная функции производная
sin (xa — г/а) по дг функции
х2 — у", стоящей
под знаком синуса
производная производная функ- производная
по ^ первого . ции sin (хг — у*) по у функции
сомножителя *! — у*
Умножая обе части первого равенства на у2, а второго — на
ху и почленно складывая, получим
Но так как z = у2 sin (х2 — г/2), то правая часть последнего
равенства есть 2xz, и тем самым требуемое доказано.
Задача 37,19 (для самостоятельного решения). Доказать, что
функция z = In (x2 + У2) удовлетворяет уравнению
дг dz n
Утх-хд-у = °-
Задача 37,20 (для самостоятельного решения). Доказать, что
если z = arctg —, то имеет место равенство
дх ' а ду
Полный дифференциал и полное приращение функции.
Связь между полным дифференциалом функции
и ее полным приращением
Полное приращение функции u = f(x, у, z) определяется по
формуле
Дм = / (х + Ах, у + Ay, z + Az)-f (x, у, г). C7,2)
где Ад;, Ау, Дг — приращения независимых переменных.
По определению приращения независимых переменных Ах, Ау,
Az и их дифференциалы dx, dy и dz — числа, между собою равные:
Ад; = dx; Ay — dy; Az = dz.
506
Полный дифференциал функции н = /(д:, у, z) обозначается
символом du и вычисляется по формуле
du±%dx + %dy + %dz C7,3)
и аналогично, если z — f (х, у), то
dz = a?dx + %dy. C7,4)
Полный дифференциал du функции есть главная часть ее при-
приращения Аи, линейная относительно Ах, Ау и Дг, т. е. Auxzdu,
причем при бесконечно малых Ах, Аг/ и Аг разность Аи — du —
величина бесконечно малая высшего порядка малости, чем
р = Y(Axf + (Аг/J + (АгJ.
Приближенное равенство Аи st; du на основании формулы/37,3)
может быть записано так:
. ди , , ди , , ди , ,о~ _.
Au^,Txdx + Tydy + Tzdz, C7,5)
или более подробно:
f(x + Ax, у + Ау, z+Az)^f(x,ytz) + ^xdx + d^ydy + ^dz.C7,6)
Это приближенное равенство тем более точно, чем меньше
величины dx, dy, dz.
Вычисление Аи приращения функции представляет собой за-
задачу, значительно более сложную, чем вычисление ее дифферен-
дифференциала du, а потому в практических вычислениях с достаточной
точностью при малых приращениях независимых переменных за-
заменяют вычисление приращения функции вычислением ее диф-
дифференциала.
Задачи 37,21—37,25 являются упражнениями в вычислении
полного приращения и полного дифференциала функции, а также
в применении формулы C7,6) для приближенных вычислений.
Задача 37,21. Найти полное приращение Аи и полный диффе-
дифференциал du функции и (х, у) — 3*2 + ху — у2 + 1.
Решение. Аи — и (х + А*, у + Аг/) — и {х, у) = 3 (* -f Ад;J +
+ (х + Ах) (г/ + Аг/) - (у + Аг/J + 1 - (Зх2 + ху - г/2 + 1);
Ди = Зх2 + Ъх . Ах + 3 (АхJ + ху + У Ах + хАу + Ах ¦ Ау—
- г/2 - 2г/Дг/ - (Аг/J + 1 - З*2 - ху + г/2 - 1;
Аи = (fix + у)Ах + (х- 2у) Ау + г (Ах2) + Ах Дг/ - (Аг/J C7,7)
V -s^. ^ ¦ ' ^ V- '
du при бесконечно малых Ах и Ау—
Ееличина бесконечно «алая
высшего порядка по
сравнению с
y)'
507
Так как ?, = 6* + у, а -^ — х — 2г/, то на основании фор-
формулы C744)
du = Fх + г/) d* + (х - 2у) dy; (Ax^dx; Ay = dy). C7,8)
Разность
Аи — du = 3 (Ад;J + Ад; • Дг/ — (Дг/J*
представляет собой погрешность, которая возникает от замены
приращения Аи функции ее дифференциалом du. В связи с этим
примером решим такой числовой пример; найти для заданной
функции ее полное приращение и полный дифференциал в точ-
точке A,2), если: 1) Ад; = 1, Аг/ = 2; 2) Ад; = 0,1; Аг/ = 0,2; 3) Ад: =
= 0,01; Дг/ = 0,02.
1) Подставляя в C7,7) значения х = 1, у — 2, Ад; = 1, Аг/ = 2,
находим, что
Аи = F • 1 + 2) 1 + A - 2 • 2) 2 + 3 • I2 + 1 • 2 - 22 =
=¦-8-6 + 3 + 2-4 = 3;
подставляя эти же значения в C7,8), получаем, что
du = F • 1 + 2) 1 + A - 2 • 2) 2 = 8 - 6 ^ 2,
а разность
A«-cf« = 3-2= 1. C7,9)
2) Подставим теперь в C7,7) и C7,8) значения х—\, у — 2,
Ах = 0,1, Дг/ = 0,-2, получим:
Аи = F- 1 +2H,1 + A-2-2H,2 + 3@,1J +
+ 0,1 • 0,2 - @,2J - 0,8 - 0,6 + 0,03 + 0,02 - 0,04!
Аи = 0,21,
a i
. d« = F- 1 + 2H,1+ A -2 -2H,2 = 0,8-0,6 = 0,20;
Аи — du- 0,21 -0,20 = 0,01. C7,10)
3) Подставим теперь в C7,7) и C7,8) те же значения хну,
но возьмем Ад: = 0,01, а Аг/ = 0,02;
Аи = F • 1 +2H,01 + A -2-2H,02+ 3@,01J +
+ 0,01 • 0,02 - @,02J = 0,08 - 0,06 + 0,0003 + 0,0002 -
-0,0004 = 0,0201;
du = F • 1 + 2) 0,01 + A - 2 • 2) 0,02 = 0,08 - 0,06 == 0,02,
а
Au — du = 0,0201 — 0,02 = 0,0001. C7,11)
* В выражениях (Дл-)а, (АуJ скобки могут быть опущены, так как
А у рассматриваются как единый символ.
508
Сравнивая . разности C7,10), C7,11) и C7,12) между полным
приращением функции и ее полным дифференциалом, мы усмат~
риваем, что они уменьшаются вместе с уменьшением приращений
Дл; и Ау независимых переменных.
Этот пример иллюстрирует высказанное выше утверждение,
что равенство C7,5) тем более точно, чем меньше приращения
независимых переменных.
Задача 37,22 (для самостоятельного решения). Найти полное
приращение функции и — ЛД и ее полный дифференциал в точ-
точке B,1) при: 1) Ад; = -0,1; Ау =—0,1; 2) Дл: = -0,01; А у =
=—0,01. В обоих случаях сравнивать разности Аи — йи.
Ответ. 1) Аи = -2,4442; йи = -2,8; Аи - du = 0,3558;
2) Аи = —0,2762; йи = -0,2800; Аи -du =» 0,0038.
Задача 37,23. Найти полный дифференциал функции
Решение. Полный дифференциал функции находится по
формуле C7,4). Найдем || и ||:
* = - * . Л Л * ) = ' .
дх х + Ух* + у* [ Vгх* + #2 Vx2 + уа'
дг
Поэтому
Задача 37,24 (для самостоятельного решения). Найти полный
дифференциал функций: 1) z = аУГ~ х; 2) z = arctg —;
Off '^~ CtX X
3) z — хъ'т.у + ysinx; 4) u = x
Ответ. 1) uz~
3)dz=(s\ny+ycosx)йх-р(хcosy+s'mx)dy, 4) du = A + e«) dx
Otrpt >V -% — ^~~g8)(хйУ-У dx) • ow-. __xdy-ydx_
Ответ. 1) uz~ фу_ах)г..—. ^)Й2- х2 + у2 ,
Задача 37,25 (для самостоятельного решения). Найти полный
дифференциал функций: 1) и. = - ' ; 2) ы = у
3) и = ;K>tg —i 4) u = arcsin > т": ; 5) ы = е « + е «¦'.
+ у*
509
Ответ. 1) du = - 'dx + ydy +
(x*
Au _ A +x2)dy2
3) rf«=
у sin — y2 sin —
У У
5) du = — e у dx — [e у ¦ ~ + e~v - ~ )du + fy • — dz.
' у v » \ ^2 yv ? у
Задача 37,26. Для вычисления объема цилиндра были вычисле-
вычислены его высота и диаметр основания. При этом оказалось, что высота
Л = 60 см, а диаметр D — 50 см, и граяицы ошибок, допущен-
допущенных при измерении, АЛ = AD = 0,1 см. 'Йайти границу ошибки
AV в объеме цилиндра, вычисленном по этим данным.
Решение. Объем цилиндра V = —т-.
Считая, что к ^ 3,14 и подставляя сюда числовые данные за-
задачи, получим, что V = 117,75 дм3. Чтобы вычислить границу
ошибки в полученном числе, примем, что AV~dV.
Учитывая,
получаем,
что
что
dV
dV
dD~
= dDdD +
TtDh dV
2 ' a dh
dV
Ж
7
dh.
tD2
4
dV = -g- dD -)- -j- rf/2.
Оценим абсолютную величину rfV:
Подставляя числовые данные из условия задачи, получим,
что граница ошибки равняется 0,7 дм3. Таким образом, AV?t;
?^0,7 дм3. *
Следует иметь в виду, что мы приняли тс = 3,14, что также
внесло ошибку в результат вычислений. Однако ошибка, возник-
возникшая из-за этого, значительно меньше той, которая возникла от
неточности в измерении D и h.
Задача 37,27. Для вычисления удельного веса тела его взве-
взвешивают и измеряют его объем. Оказывается, что вес Р — 326 г,
а объем V = 126 см8; при этом границы ошибок величин Р и V
равны АР = 0,5 г, AV = 1 см3.
510
Определить границу ошибки AD в удельном весе D, вычис-
вычисленном по этим данным.
Р 326 г
Решение. Удельный вес D = у = y^g = 2,59 ^ . Теперь
положим, что
VAP — PAV
V*
_\УАР — РАУ\ ^У\АР\_
\/г ^* уг
Подставляя сюда числовые данные задачи, найдем, что гра-
граница ошибки AD ss 0,024 *—3.
СМ
Задача 37,28 (для самостоятельного решения). Даны две точ-
точки Р(х, у) и Р1{х1, уг). Насколько изменится расстояние S между
ними, если- координаты точек получат приращения dx, dy и dxu
dylf и сколько процентов р от длины S составит это изменение.
Ответ. dS — {dx — dxx) cos a + (dy — dyy) sin аь где а — угол,
образуемый с положительным направлением оси Ох прямой, про-
проведенной из Pi по направлению к Р
jo
Количество процентов р = -g- • 100.
Задача 37,29 (для самостоятельного решения). Решить пре-
предыдущую задачу с такими числовыми данными:
S = 4200 м; а = 349 17'25"; dx = -l м;
dy = 3 м; dx1 = 4 м; dyx — 2 м.
Ответ. Расстояние S уменьшится на 3,65 м, или на 0,087%.
Задича 37,30. Даны две точки Р(х, у) и Pi{xt, yt). Расстоя-
Расстояние между ними равно S, а угол а определяется, как и в задаче
37,29. Точка Рх неподвижна. Насколько изменится угол а, если
координаты точки Р станут равными х + dx, у -f dy.
Указание, tg a = у ~ yi; lntga = In {у — уг) — 1п(а: — ^i).
Отсюда следует, что
tg a COS2 a у — (/x ЛГ — X
1
(xi и ух по условию — постоянные величины). Так как у — ^ =
= Ssina, а х — Jca=Scosa, то отсюда получается ответ
. cos a . sin a .
da. = ~g- • dy ?- dx.
511
Задача 38,31 (для самостоятельного решения). Решить преды-
предыдущую задачу при таких числовых данных: 5 = 3500 м; а =
= 52° 13' 24"; dx = 1 м; йу — 2м. Выразить rfa в секундах.
Указание. В формуле, полученной в ответе предыдущей
задачи, rfa измеряется в радианах. Чтобы получить da в секун-
секундах, следует полученное число умножить на 206264,8, т. е. на
число секунд в одном радиане.
Ответ. 25",6.
Задача 37,32. Вычислить приближенно величину A,03K-001.
Решение. Мы знаем, что 13.= 1. Нам следует теперь про-
произвести вычисления для того случая, когда основание степени .1
получит приращение 0,03, а показатель степени 3 — приращение
0,001. Будем исходить и3'функции f(x, у) = ху и воспользуемся
формулой C7,6).,
Учитывая, что в нашем случае ^- = yxy~l\ J- = xy\nx, полу-
получим (х + kx)y+hy ^ху + ухУ~1 Ах + ху\пх Ау.
У нас х = 1; у — 3; Ах = 0,03; Ду = 0,001, а потому A,03K-001 ^
~1з 4-3 . 13-1 .0,03+ 131п1 -0,001 = 1 +0.09= 1,09, т.к. In 1 =
= 0.
Задача 37,33 (для самостоятельного решения). Вычислить при-
приближенно: 1) @,97J-°2; 2) A,003J-07; 3) /(б.ОЗJ + (8,04J.
Указание. В последнем примере следует исходить из функ-
функции /(*, у) = Ух* + у\
Ответ. 1) 0,94; 2) 1,006; 3) 10,05.
ТРИДЦАТЬ ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Дифференцирование сложной функции от одной и не-
нескольких независимых переменных.
1. Дифференцирование сложной функции от одной независимой
переменной
Формула полной производной. Если z = f(u,v), а и и v
являются функциями независимой переменной х: и = <р (х) v =
= ф (х), то и z является функцией х.
В таком случае говорят, что z есть сложная функция аргу-
аргумента х. Производная от функции z no независимой переменной
х вычисляется по формуле
dz dzdu . dzdv /Qo n
y + C81)
Вычисленная по этой формуле производная называется пол-
полной производной от функции z no независимой переменной х.
512
Аналогично, если z — f(u-, v, w), a u = cp(x), v~ty(x), w =
--= со (х), то полная производная от функции г по независимой пе-
переменной х вычисляется по формуле
dz дг du.dzdv.dz dw_ ,qo r>\
dx Зп dx ' dv dx ' dw dx ^ ' '
Частный случай. Если z = f(x, и, v) а и и v, в свою оче-
очередь, также являются функциями х, т. е. и = <р (л:); v — ф (л:),
то -¦
йг дг , дг йн 5г rfo
Читатель должен обратить внимание на то, что в правой
части формулы C8,3). стоит частная производная *-, вычис-
вычисленная в предположении, что и и v — величины постоянные. Эту
производную следует отличать от полной производной ~, кото-
которая вычисляется в предположении, что кип являются функция-
функциями х. Различие в этих двух производных объясняет также и
различие в их обозначениях.
Задача 38,1. Найти ~, если г = sin Cu 4- 2v — Aw), a u =
= 2x3; v = 3x2; w = л:4.
Решение. Здесь следует воспользоваться формулой C8,2).
Определим производные, входящие в эту формулу:
._ = 3 cos Cu ~j- 2у — 4о>); ^- = 2 cos C« + 2у — 4а>);
dz dti a dx) dxu)
Подставляя эти величины в C8,2), получим
~х = [3 cos C« + 2v — Aw)]6x2 + [2 cos Cu 4- 2v — Aw)] 6x —
— 4 cos Cu + 2у
Вынося в правой части за скобку cos (Зы + 2v — Aw) и заме-
заменяя под знаком косинуса и, v и w их выражениями через х,
получим окончательно
~ = A8л:2 + 12л: - 16л:3) cos Fл:3 + 6л:2 - 4х4).
Задача 38,2 (для самостоятельного решения). Найти полную
производную -^ функции и — sin ~L где х = еи, у = t2.
Указание. Формулу C8,1) следует переписать в виде
du да dx . ди dy
д!~Ъх'' Ш + ду ' dt'
Ответ. ! = (г_2).?.со5?.
513
Задача 38,3 (для самостоятельного решения). 1) и =
п dx
¦ zy; z — sin x; у = ех. Определить полную производную ~ .
Указание. На основании формулы C8,1)
du _ ди йг . ди <fy
dx ~ dz dx ду dx'
2) и = v2 + vy; v = In x; у — e*.
Найти полную производную -^.
Указание. Применить формулу C8,1), переписав ее в виде
du dudv ,dudy
dx ~~ dv dx ' dy dx '
3) Найти полную производную —, если г = / (и, v) и — ах2 -f
+ Ьх + с; v = ах + Ь.
Ответ. 1) ?-=3e3i; + ej:(sinx + cosA;) + sin2A;; 2) d~-=
у du 2 In х + ех , х, оч dz дг ,п , .. , dz
+ t^; Tx j + e\nx; Ъ)^ Ти{2ах + Ь) + ша.
Задача 38,4 Определить полную производную функции
и = еах (у — г); y — as'mx; z = cosx.
Решение. Здесь следует применить формулу C8,3), так как
функция и зависит от х как непосредственно, так и через по-
посредство функций у и г. Определим производные, входящие в пра-
правую часть этой формулы:
— - аеах(и — гУ — - еах- — еах- ^-acosx- ~~ —sinх-
дх-ае (у z), ду-е , & - е , dx - a cos x, dx - sin*,
du ди . dudy . dv dz alc . ~\ .
= + + Т = ^е ax(yz) + e
Задача 38,5 (для самостоятельного решения). Найти -—, если
z =-• f(x, и, v), u~~; v = \пх.
Указание. Применить формулу C8,3).
Otrpt dZ -дг дгЛ -Ldz 1
dx ах ду дг2 dv x
Задача 38,6 (для самостоятельного решения), z — Ух2 + у\
у —¦ sin2 х. Найти ~ и ~.
* dx дх
514
,, dz дг
Указание. Тх =
„ dz x . у . п
Ответ, -г- — -т= + 77= sin2л:.
Задача 38,7 (для самостоятельного решения). Найти ~, если
1) z — и", где « = sin jc; у = tg jc; 2) z = иод>, где « = sin х; v =
= Injc; w= tgx.
Ответ. 1) px = (sm
> dx x-cos* cos2*-
Задача 38,8 (для самостоятельного решения). Найти ~ и ^,
если г = д:4', где у —1пх.
[ у . lnx\
Ответ. 5=-y^;SJClT +
Задача 38,9 (для самостоятельного решения). Найти —, если
X
z = е *, где у = sin3 jc.
Ответ. ~ =—6^A— — sin2 jc cos jc).
Задача 38,10 (для самостоятельного решения). Найти ~, если
1) z = In (jc2 + у2), где у = е**; 2) z = arctgfi?, где «/ = cosjc.
1 — ATI/
Ответ. 1) т? =-^-ц-^A-)-2.^'), а вместо у можно подставить
е«; 2) 1г = -J-j - т_1-! sin jc.
7 djf 1 + л-2 1 + г/2
Задача 38,11. -Движение точки задано уравнениями
*=.-3*«; ^ = Й*; г = 4^6.
С какой скоростью возрастает ее расстояние от начала координат?
Решение. Расстояние г точки от начала координат опреде-
определяется формулой г = ]/jc2 -f у2 -f- г2, где х, у и г — координаты
точки.
Для решения задачи следует найти g = |J + || + g|;
5т х дг у дг
/Ч у + г»
Ответ <fr-'8'
515
2. Дифференцирование сложной функции от нескольких
независимых переменных
Если z — f(u, v) — функция от двух переменных и и v, а каж-
каждая из них есть в свою очередь функция двух независимых пере-
переменных х и у, то и z есть функция независимых переменных к
и у, а ее частные производные по этим переменным вычисляются
по формулам
дг _^ дг ди . дг dv
дх ди дх ' dv дх
дг_^дгди ,dzdv
ду виду' dvdy ¦
Частный случай. Если функция г зависит от х и у не только
через посредство и и v, но и явно, т. е. г = f(x, у, и, v), то имеют
место формулы:
дг /дг Y дгди . dz dv
дх \длт/ ~"~ ди дх dv дх ,оо с\
дг /Зг\ , дг ди . дг ди
ду~[ду)~т~дпду~+''5Ъ'ду'.
причем следует иметь в виду, что производные (^) и 1~\ от
функции г вычисляются в предположении, что и и о —величины
постоянные. г т (
Задача 38,12. Найти |^и ~, если z = \n(u? + v\ a
Решение. Следует воспользоваться формулами C8,4). Опре-
Определим частные производные, входящие в эти формулы:
дг Г о дг. __ 1 9 ди _
«; go ~ «г + уа ' ^ дх~ C0S У;
ди' ¦ dv
xsmy; sinx
Подстановка этих производных в C8,4) дает
| =
у cos х = -^2 (и cos у + vy cos х) -
2
= -;; ;—;—. ¦¦ . ¦¦ (и sin2 x — x2 sin и • cos ы).
дг2 cos2 у + У2 sin2 «¦Vi7 a ai
516
Задача 38,13. Определить ^ и д~-, если z = arctg-^-, a « =
= х sin у, и — х cos г/.
Решение. Здесь опять-таки следует применить формулы
C8,4). Определяем частные производные, входящие в эти формулы:
дг 11 - » дг 1 / и
ди , 5L2 у иг-М2' df 1 и2 \ ц2 ] u2'-\-v2'
du . dv • д« dp
^ = sin#; ^ = cosy; ^-^cosy; ^
Пэтому
^r = о ? . sin и „ " „ cos у = -7—,—; (v sin и — и cos if) =
— x sin y cos у) = 0; з-=1.
Задача 38,14 (для самостоятельного решения). Определить
"if; Jf; Ji ? если ц = In
Указание. Формулы C8,4) в данном случае для определе-
ди
ния, например, -я запишутся так:
ди __ ди дх , ди ду , ди дг
~di '
ди du
и аналогично для гИт-,
Ответ. а? = -^^(^
Задача 38,15. Найти g| и—, если z = f{u,v) a u = x + i/;
Решение. Применяя формулы C8,4), получаем, учитывая, что
5г 5г . , дг , , > дг дг
др ~ Э« + dv(~ > ~ дй dv'
Задача 38,16 (для самостоятельного решений). Найти ^ и ^-,
если г — / (ы, »),аи = д:2 + У2; f/= ^У-
Ответ. !? = 2*?Чу?;? = 2^ + *?.
ддг . ди ' ^ ди ' ду а ди ' dv
Задача 38,17. Доказать, что функция г = уср (лса — у2) удовле-
удовлетворяет дифференциальному уравнению — ^Ч—я~ — ~г-
' 517
Решение. Обозначим х% — у2 = и. Тогда заданная функция
г = yf (и). C8,6)
Легко усмотреть, что z зависит от х только через посредство
и, а от у — как непосредственно, так и через посредство и. По-
Поэтому
% = У9' («)|~ = У?' (и) 2* = 2ху?' (к).
Производная ~ должна быть определена по второй из формул
C8,5). Входящая в эту формулу производная 1^-1 = <р (и), а пото-
потому, учитывая, что ~ = — 2у.
| = «Р (и) + У?' («)| = ?(«)- 2yY (и).
Подставляя найденные выражения ~ и ~ в левую часть за-
заданного уравнения, получим
так как на основании C8,6) <р (и) = —.
Задача 38,18. Доказать, что функция z = ху + л:ср (—) удовле-
\ X /
творяет дифференциальному уравнению х^- + у4- = ху + z.
ох оу
Решение. Обозначим — = «. Тогда заданная функция пере-
перепишется в виде
z = ху + хс? (и) C8,7)
и очевидно, что z зависит от х и у как непосредственно, так и
через посредство и. Поэтому частные производные ^ и ^- сле-
следует отыскивать по формулам C8,5). Учитывая, что
($-'»+*<»• «(в)-*
и, кроме того,
ди у ди
дх ~~ ха ' ду
518
' (и) (-?) = y + <f (и) - |?'
_ дг дг
Подставляя значения ^- и j- в левую часть заданного урав-
уравнения, получим
х| + у~ = х [«/ + <р («) - | ?' (и)] + «/ [х + ?' («)] = ху + хер («)-
- У?' (и) + лгу + У9' (и) = хг/ + *ср (-f-J + ху = ху + г.
Задача 38,19 (для самостоятельного решения). Доказать, что
функция z = х + У + <Р I—) удовлетворяет дифференциальному
уравнению х ~ + у ~ = х + у.
Указание. Обозначить -=«и воспользоваться формулами
C8,5). Учесть, что (|) - 1; (|)=1.
Задача 38,20 (для самостоятельного решения). Доказать, что
функция z = у (х2 -f- У2) + <Р (х — у) удовлетворяет дифференциаль-
дифференциальному уравнению fx + %/
Указание. Обозначить х — у = и и воспользоваться форму-
формулами C8,5), в которых (|) = х; ||) = у.
Задача 38,21 (для самостоятельного решения). Доказать, что
11
функция z = еуу (уе2уг) удовлетворяет дифференциальному урав-
уравнению
_ Указание. Положить уе2у' = и, воспользоваться формулами
C8,5) и учесть, что (|) = 0; (|) = е«. '
Задача 38,22 (для самостоятельного решения). Доказать, что
функция z — ху\~\ — х2 — у* удовлетворяет дифференциальному
уравнению х^ +у~ = z—x2 —
519
ТРИДЦАТЬ ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Производные и дифференциалы высших порядков функ-
функций нескольких независимых переменных.
1. Производные высших порядков
Если задана функция двух независимых переменных z = f (x, у)
и вычислены ее частные производные ? и J?, то они, вообще
говоря, также являются функциями независимых переменных х
и у, а потому от каждой из них можно вычислить производные
как по х, так и по у.
Если вычислить частную производную по х от -j^, то полу-
получим частную производную второго порядка от функции г, взятую
два раза по х. Эта производная обозначается символом з^ и, та-
таким образом, %-[~] = д^2. '
Если вычислить частную производную по у от Л, то полу-
получим частную производную второго порядка функции г,' взятую
сначала по х, а потом по у. Эта производная обозначается сим-
дЧ , д (дг\ д*г
волом Шу и, таким образом, Гу Ц = Шу.
Подобно этдму частная производная по х от -Л даст вторую
частную производную функции г, вычисленную сначала по у, а
потом по х. Она обозначается символом д-4-;
аудх
д_ (дг\ _
дх \ду] ~
дудх '_
а частная производная по у от j- есть вторая частная произ-
производная от функции г, взятая два раза по у. Она обозначается
символом а_;^у ?
Также вводятся частные производные порядка более высокого,
чем второй.
Например, символ =А обозначает производную претьего поряд-
порядка функции z = f(x, у), вычисленную три раза по х.
Символ же з-зд- обозначает, что от функции г взята произ-
производная третьего порядка, причем она вычислялась два раза по х
и от полученной производной ^г вычислена-один раз производная
по у и т. д.
520
Задача 39,1. Найти частные -производные третьего порядка
функции z = л.4 + Зх3у — Ах2у2 + Ьху3 — у*.
Р е ш е н и е. ^ = Ах3 + 9х2у — 8ху2 + Ъу3; C9,1)
- = Зх3 — &х2ц + 15xif - Ау3. C9,2)
Если взять производную по х от— (выражение C9,1)), то
получим, tiTo j~ = 12jc2 + 18лгг/ — 8i/2; если то же выражение C9,1)
продифференцировать по у, то получим
Продифференцируем теперь по л: производную^ (выражение
C9,2) и получим, что
дудх
Читатель должен усмотреть разницу в обозначениях -g-g- и 5-4-1.
Символ т-д- означает, что от функции г сначала была взята про-
производная по х, а результат был продифференцирован по у. Сим-
вол же^-j- показывает, что от функции z была сначала вычис-
вычислена производная по у, а полученный результат продифферен-
продифференцирован по х. Таким образом, производные^- и -j-^ отлича-
отличаются порядком, в котором велось дифференцирование.
Если продифференцировать по .у производную ^-j, то получим
третью производную ^-^- = 18л: — 16г/.
Продифференцировав же по х производную j-4-, получим
если вычислить производную по у от fr-jr-, получим
дхду*
Производная по х otj4- даст ^^ = 18д: — 16г/.
521
Производные
дг dz
наконец, если взять производную по х от ^, то получим -^ =
= 24л: -J- 18г/, а если взять производную по у от s-j-. то получим
Здесь опять-таки следует подметить, что производные
дл%2 ' дудхду'
а также производные
' дхдудх' дудх*
отличаются только порядком дифференцирования.
Оказалось, что
C9>3)
дхду* ~~ дудхуу ~ ду*дх'
Это совпадение не является случайном. Имеет место такая
важная теорема: если частные производные непрерывны,
то их значения не зависят от порядка дифференци-
дифференцирования.
Задача 39,2 (для самостоятельного решения). Найти частные
производные второго порядка функций:
1J = ху; 2) z = eax+bt>\ 3) г = 1п (л:2 + у\ 4) г = е*К
Ответ. 1) ^ = 0; gjgj=l; ^ = 0;
_ _л
¦ дг» -
Задача 39,3. Определить производную дхдудг функции и
= sin (xyz).
522
Решение.
д~ = yz cos (xyz); -щ^ = z cos (xyz) — xyz* sin {xyz);
-д*и ¦ = cos (xyz) — xyz sin (xyz) — 2xyz sin (xyz) — x2y2z2 cos (xyz);
——— —- n — Л И л I Шо ЛШ ^^ ОЛИС Ы11 \Js,yZ)*
oxoyoz '
Задача 39,4. Показать, что функции: 1) z = lnr, где г =
= У (х — *iJ + (У — УхJ и 2) г = arctg — удовлетворяют урав-
уравнению Лапласа ^ + -^ = 0.
Решение. 1) л~ — ~л~- Но так как
дг х — xt х — х1
ТО
дх
дг — iv v\'
— _ {х — xj -? .
Теперь вычислить ^, рассматривая правую часть последнего
равенства как произведение
~~ **
Подставляя сюда найденное выше значение ^ = ^ ~~ **, получим
i!f _ 1 2(^ —^)«
Аналогично находим
бу* г* г»
Подставляя найденные значения ^ и ^-| в левую часть урав-
уравнения Лапласа и учитывая, что если
то (х - XiJ + (y- угу = г2, получим
1 2{x-xtf I
2 2г«. 2 2 -
га г4 г2 г2 ~" '
523
и тем самым доказано требуемое. I
2) * = —i_ /_ JL\ = _ —М— ¦ д*г = У «у.
' дх 1 i ^! \ * / ** "Ь У%' дхг (х* + у"J '
дг 11 л- д2г • *
Подставляя найденные значения ^ и — в левую часть|
уравнения Лапласа, получим |
и требуемое доказано.
Задача 39,5 (для самостоятельного решения). Доказать, что
функция 9 = —, где г = У'хг + У2 + г2 удовлетворяет уравнению
Лапласа:
Задача 39,6 (для самостоятельного решения). Доказать, что
функции 1) v = r cos 6 и 2) у = —j- удовлетворяют уравнению Ла-
Лапласа в сферических координатах:
йг \' дг/ ' sin G 59
Задача 39,7. Доказать, что если функция и = и(х, у, z) удов-
удовлетворяет уравнению Лапласа
д2и . д2и . д2и «
то и функция
дх * ду ' дг
также удовлетворяет этому уравнению.
Указание. Подставить в заданное уравнение вместо и функ-
d2v , d2v . d%v n
цию v и доказать, что -^ + -^ + -^ = О
Ш*[Хд1с1:=2дх* + Хдх[дх*}' 'ду^[Хдх)==ХЫду^==Хдх\ду^
^( ди\ _ д3и _ д_ (
дг* \Хдх) ~~ Х дхдгг ~ Хдх\дг*
524
и, таким образом,
^лдх
так как по условию
д2и . д2и . д2и р.
дх2 ' ду2 ' дг2
Аналогично
ди) . JP_
ду) дг2
д2 I ди) . д2 I ди\ Jf^l ди) ^_ „дЧ
~дх* \ дг) ' 'ду2 [ дг) ' дг2 \ дг) ~*. дг^
Поэтому ^-| + д-^ ^~ Л^ => ^' что и тРебовалось.
Задача 39,8. Известно, что z = f (и, v), а переменные и и v
являются функциями независимых переменных х и у.
« = ?(*, У); У = ф(д:, г/).
Определить g; **.
Решение. На основании формулы C8.4)
дх~ дидх~т~ dvTx'' дх* ~ дх \дх} ~ дх [ди дх + dv дх
±(§гди),д_ (дг dv) __ 'д_ (дг)ди ,d^^u,±(dz)dv,dzd^v
дх \ди дх) + дх [dv дх) ~" дх [ди/дх + ди дх* + ^л- \йу/ дх "^ Л й2
Учитывая, что производные^ и ^ являются, вообще говоря,
функциями мин, имеем, опять-таки на основании формул C8,4),
Ш \д~п) дх + ди [ди) дх ~ ди* дх + dudv дх'
_3_ /йг\ д /дг\ ди . _^ /dz\ йр й2г йи . д2г dv
дх [dv] ~ дй [dvj дх + dv [dv] дх ~ ^
__ \ _^
дх [dv] ~ дй [dvj дх + dv [dv] дх ~ Шп дх~
Подставляя эти значения в предыдущее равенство, получим
окончательно, что
&_z __ (дЧ du . d*z dv) ди dz d*u I d*z du dHdv)dv_ ¦
дхг ~ U«2 дх + dudv dx]dx + du' дх" + [dvdu d~x + dv* дх) Ы( +
, дг d*z d*z (du\* „ d*z du dv ^г /'feX2 ^г 5г» , дгд*у
h [] + + + +
( ^
h 5o oP ~ W [дх] + а«5о йл- дх + аи2 \ax/ + du dx*
Этим же путем найдем, что
() , g d*z du dv d*z IdvJ dz дЧ dz d*v
du2 [dy] + dudv дуду~^~ Ыё^ду) + du dy* + dv dy* '
525
Задача 39,9 (для самостоятельного решения). Вычислить -^- ¦',
дхду *
Функции г = / (ы, v), где и = <р (*, г/); у = ф (*, г/).
Указание. Воспользоваться методом, с помощью которого
была найдена производная ^§в предыдущей задаче, и учесть, что
ду \дх) ~ ду [ди дх """ dv dxj
Ответ:
д2г д2г ди ди . д2г (ди dv . dv du) , дгг dv dv dz d2u , dz d2v
dxdy ~"дп?дх Ty~r~dudv ' \dxd~y ~*~ дх'ду) ~*" d~v*dxdy' du ~дхду ^ dv'dxdy *|
Замечание. Формулы, полученные в последних двух задач
чах, не должны запоминаться. Читатель должен усвоить метод,|
с помощью которого эти формулы были получены.
На применение* этого метода предлагается задача 39,10.
Задача 39,10 (для самостоятельного решения). Найти ^-|,
и ^4 • если z — f(u' у); и — х* 4- У2' v — ХУ-
Указание.
du o du q dv dv d2u o
dx ' dy v dx ?" dy ' dx* '
, Q» _^^_ 0* — Ij» „^-^__ —— (I* __ 1 •
dy2 дх2 ду2 дхду дхду
дг _ dz ди , dz dv dz n- , йг
dz ) _ d (dz9) д (dz' \
dvy) ~ die U / + Ь~х \dvy) =
_ l(dA2x 4- дг 24- ~{дА U = ШдА- + ^Н ¦ 2х 4-
~ 5а: U«/ /Х + дп 1 ^ дх [dvj у [ди \ди) дх ^ dv \ди) дх\ *х +
dz \d (dz\du d(dz\dv] (d*zdu d*z dv) dz
+ dv ' l + [дп [to) die + Щ dv) дх\ у-\ди*дх^ dudvdxj гХ+г
ди д*г dv
+ dx
Подставляя сюда значения частных производных функций и
и v по х, получим окончательно: >
(учтено, что
Ответ.
^
д*г . й2г , о . , . 2Ч 52г . d*z . dz
дхТу = АхуШ + 2{-Х +уIШ+ХУ1кГ* + д;-
526
Задача 39,11 (для самостоятельного решения). Определить
частные производные второго'порядка функции г = <р (и, v), где
и = х + у; v = х — у.
д д д д d d
dxdy du*
du^ dv*
Ответ.
Задача 39,12 (для самостоятельного решения). Доказать, что
функции 1) и = екпН sin nx и 2) и = е~Ын • cos я* удовлетворяют
уравнению теплопроводности
du, _ , d*u
Задача 39,13. Показать что функция
z = f(x — at) + ty(x + at)
удовлетворяет уравнению колебания струны
(функции 9 и ф — какие угодно дважды дифференцируемые функ-
функции).
Решение. Введем обозначения х — at = и; x + at = v.
Тогда заданная функция перепишется так: z = ср (и) +
дг _ 5tp й« *. йу Eр . д^ ди . dty dv
die ди дх ' dv дх ¦" йи Лс "• dv дх ' '
Но так как функция <р не зависит от v, а функция ф — от и,
d<o п дф п
dv ¦ ди
т-. du t dv , dz d<p . дф
Ьсли учесть, что ^- = 1 и^-=1, T05~:=^n"^;
'. d (dz) д (dy йф\ d (д<р\ д (d\i\ d (dtp\du j^
~ dx \dxj dx \du d~v) dx \duj ' dx \dvl ~~ du \dujdx ¦"
d^z
dx*
¦J dx *" du \dvl die ' du \dv! dx du*
г-«»а-*)-
ЛГ йи 5у dz d® , di)
Учитывая, что ^- = — a, a ^ = а, имеем ^ = — a ^ -j- a ^-.
d*z _ d (дг) _ д j df , dty) _ d (dA , d {d^\ _
W ~di[dij~~dl\~adu'j'aduj a&\du}4raTt\dv')-
du \duj dt^adv {dvj dt ~ a du*^ dv* ~~ a [dv* + du*J '
527
Умножая ^-| на а2, убеждаемся, что действительно
что и требовалось.
Задача 39,14 (для самостоятельного решения). Доказать,
функция
z = х? (х + у) + yty (х + у)
удовлетворяет уравнению
д2г „ д2г , д2г п ">
ор дхду "^ ду*
Указание. Положить х + У — и. \
Задача 39,15 (для самостоятельного решения). Показать, что \
функция '
z ===
удовлетворяет уравнению
, дг , дг
дх* у ду*ш
Указание. Ввести замену; xy = u;~ = v.
2. Дифференциалы высших порядков
Аргументы х и у функции z = f(x, у) — независимые пере-
переменные. • •
Дифференциалом второго порядка функции г = f (x, у) назы-
называется дифференциал от дифференциала первого порядка; он обо-
обозначается через d2z. Таким образом d2z = d (dz).
Дифференциал второго порядка вычисляется по формуле
? ? % C9,6)
Дифференциал третьего порядка функции z — f (х, у) есть
дифференциал ее дифференциала второго порядка; обозначается
он символом d3z, т. е. dsz = d (d2z).
Дифференциал третьего порядка вычисляется по формуле
0^ ^ + 0^. C9,7)
Ьсли, условиться над символами ^- и ^- производить все ариф-
арифметические действия по тем же правилам, по которым они про-
производятся над числами, а произведение
дт дп
U
528
дт+пи
заменять частной производной дхтдип . то формулы для вычисле-
вычисления d2z и d3z можно в символической записи переписать так:
C9,8)
, C9,9)
и вообще для дифференциала порядка п функции z = f (х, у)
имеет место символическая формула
йу)аг. ' C9,10)
При вычислении по формуле C9,10) следует применить извест-
известную из алгебры формулу Ньютона для возведения бинома в целую
и положительную степень.
Например, выражение -^ dx3 g-2 dy* ¦ z следует заменить выра-
выражением д „^ г dxzdy%, а выражение ^—2dx2^-dy-z выражением
яг,
йхЧу и т- д- -
Вычисление дифференциалов любого порядка функции z=f (x, у),
где х и у — независимые переменные, по формулам, приведенным
в этом параграфе, не может вызвать у читателя никаких затруд-
затруднений, так как по существу все вычисления сводятся к опреде-
определению частных производных высших порядков, которые читатель
уже умеет" находить.
Мы разъясним при решении задач другой способ нахождения
дифференциалов высших порядков, который даст возможность
определять их, минуя вычисление частных производных, а по
известному выражению дифференциала мы сможем находить и
частные производные.
Задача 39,16. Найти dH функции г = хгуг.
Решение. Первый способ. Воспользуемся формулой C9,6),
для чего определим все частные производные, входящие в нее:
~ - 2хФ- - - 2xV — - 2м2- — - Ахи- — = 2л:2
дх - гху , ду- гх у, дх% - iy , дхду - чху, Qyt - гх .
Подставляя вторые производные в C9,6), находим, что
d*z = 2уЧхг + Sxydxdy + 2хЧуг.
Второй способ. Определим сначала дифференциал первого
порядка заданной функции, опираясь на основные формулы:
dz ¦= уЧ (д:2) + хЧ (у2) = у2 ¦ 2xdx + хг ¦ 2ydy - 2xy2dx + 2x2ydy =
= 2xy(ydx\xdy).
!8 И. А. Каплан 529
Для определения d2z дифференцируем dz, но при этом следует
иметь в виду, что так как хну — независимые переменные, то
их дифференциалы dx и dy — величины постоянные, которые при
дифференцировании выносятся за знак дифференциала. Учитывая
это, получим
d2z = d (de) = d [2хц (ydx + xdy)) = 2 [d{xy) (ydx + xdy) +
+ xy d (ydx + xdy)] --= 2 [(ydx + xdy) (ydx + xdy) +
+ xy ¦ (dydx + dxdy)] = 2[(ydx + xdyJ + xy ¦ 2dxdy] =
# =-. 2 [(y2dx2 + 2xydxdy + x2dy2) + 2xydxdy] =
== 2y2dx2 + 8xydxdy + 2x2dy\ C9,11)
Теперь уже, зная дифференциал второго порядка, можно найти
частные производные второго порядка. Легко усмотреть, что
коэффициент при dx2 равен *—2, коэффициент при dxdy есть
2, , , а коэффициент при dy2 есть ^-j. Это следует из того,
чтб при произвольных dx и dy равенство
. Adx* + Bdxdy + Cdy2 = gdx2 + 2-^-y dxdy + |? dy2
имеет место только при условии, что
д^г _ . 9_^2__ R. &г _ Г
дх* ~~ ' z дхду ~~ ' ду*~ '
Таким образом, из C9,11) заключаем, что
2»
дх* - zy ' dxly~
и совпадает с ранее найденными значениями этих производных.
Сейчас подробно двумя способами будет решена еще одна
задача. *
Задача 39,17. Найти дифференциал" третьего порядка daz
функции 2 = cos-{* + 2у2).
Р еш ен ие./Перьый способ. Воспользуемся формулой C9,7),
для чего прежде всего определим частные производные третьего
порядка, входящие, в эту формулу. '
Производные первого порядка:
~ = - sin (а; + 2у2); | - - \у 5т{х+2у*).'
Производные второго порядка: ,'
д?ъ= — cos (х + 2у2); -щ! -¦= — Ay cos (* + 2у2);
530
0 = - 4 sin (х + 2у2) - 16у2 cos (х + 2у2). C9,12)
Производные третьего порядка
= sin {x -4- 2//2); -з-т!-
; = — 4 cos (а- + 2у2) + 16г/2 sin (at + 2у2);
g = sin {x + 2у*); $% = 4У sin (х + 2у2);
дхду*
р3 = — 16// cos (лт + 2у2) — 32г/ cos (at + 2г/2) + 64f/3 sin (jc + 2y2) =
= — 48г/ cos (a- + 2г/2) + 64f/3 sin (at + 2y2). C9,13)
Подставляя значения третьих частных производных в C9,7),
получим, что
йЧ = sin (л: + 2у2) dx* + 3 • 4г/ sin (л: + 2г/2)
+ 3 [- 4 cos (дс + 2г/2) + 1бг/2 sin (х + 2r/2)]
+ [—48ycos (л: + 2у2) + 64у? sin (x + 2y*)]dya.
Второй способ. Теперь мы вычислим третий дифференциал
d3z тремя последовательными дифференцированиями:
dz — — sin (л- + 2г/2) dx — 4у sin (л; + 2у2) dy;
dz= — sin (* + 2г/2) ¦ (dx + 3ydy). '
Дифференцируя второй раз, следует помнить, что дифферен-
дифференциалы dx и dy независимых переменных должны рассматриваться
как величины постоянные, а потому они должны выноситься за
знак дифференциала
йЧ = d{dz) = d[- sin(x + 2y2) ¦ {dx + 4ydy)] =
= d[-sin {x + 2tf)\ ¦ {dx + 4ydy) + [-sin (x + 2y2)) d {dx + 4ydy) =
= [—cos(л: + 2y2) dx — 4y cos(x + 2y2)dy] ¦ {dx + 4ydy) +
+ [—sin (л- + 2y2)) 4dydy = — cos (* + 2г/2) dx2 —
~4y cos (л- + 2y2) dydx — 4y cos {x + 2ys) dxdy —
— \6y2 cos (л: + 2y2) dy2 — 4 sin (* + 2y2) dy2 = —cos (л: + 2y2) dx* —
—8#cos {x + 2y2) dxdy — [1бг/2 cos (л: + 2г/2) + 4 sin (л: + 2г/2)] dy2.
Читатель легко заметит, что коэффициенты при dx2, dxdy и
dyi равны соответственно ^-2, 1 , , и ^i, которые были
найдены выше в выражениях C9,12).
- Чтобы упростить определение дифференциала третьего порядка,
выражение дифференциала второго порядка перепишем в виде
d2z = —cos (at -f 2y2) {dx2 + bydxdy + 16#W) — 4 sin (x + 2y2) dy2.
18* 531
Тогда
d3z = d (d2z) = d [-cos (x + 2y2) (dx2 + 8y dx dy +
+ d [^-4 sin (л: + 2y2) dy2] = d [-cos (x + 2y2)] (dx2 + 8ydx dy +
+ I6y4y2) + [-cos (x + 2y2)] d (dx2 + 8ydx dy + I6y2dy2) +
+d [—4 sin (* + 2y2)] dy2 = [sin (л; + 2y2) dx +
+ Ay sin (* + 2y2) dy] (dx2 + 8y dx dy + I6y2 dy2) +
+ [-cos (x + 2y2)] (8dy dx dy + 32y dy dy2) +
+ [—4cos(* + 2y2) dx—\6ycos(* + 2y2)dy] dy2 =
= sin (л; + 2y2) dx3 + \y sin (* + 2y2) dx2dy + 8y sin (л: + 2y2) dx2dy+
+ 32y2 sin (л: + 2y2) dx dy2 + I6y2 sin (x + 2y2) dx dy2 +
+ 64г/3 sin (x + 2y2) dy3 — 8 cos (* + 2y2) dx dy2 —
' — 32t/ cos (л; + 2y2) dy3 — 4 cos (* + 2y2) dx dy2 —
— 16t/cos (л: + 2y2) dy3 = sin (* + 2y2) dx3 + I2ysm (x + 2y2) dx2dy +
+ \A8y2 sin (л: + 2y2) — 12 cos (x + 2y2)] dx dy2 +
+ [64y3 sin (x + 2y2) — Щ cos (x + 2y2)] dy3.
Теперь легко усмотреть, что коэффициенты при dx3, dx2dy,
dxdy2 и dy3 равны соответственно: g, 3g^t 3^2 и 0,
значения которых были найдены выше (выражения C9,13)).
Задача 39,18 (для самостоятельного решения). Найти двумя
способами d2z функции z = х3у3.
Ответ. d2z = 6xy3dx2 + \8x2y2dxdy + 6x3ydy2.
Задача 39,19 (для самостоятельного решения). Найти двумя
способами дифференциал третьего порядка функции z = sinBx+y)
при х = ~; г/ = 0.
Ответ. d3z = 8dx3 + ШхЧу + Uxdy2 + dy3.
Задача 39,20 (для самостоятельного решения). Найти диффе-
дифференциал второго порядка функций:
1) z = ex-y*+cosx; 2)z = y\nx;
3) z = ху; 4) z = eax+by; 5) у = e*.
Ответ.
1) d2z = (e*-"* - cos л:) dx2 - iy^-^'dxdy + 2ex~v' By2 - 1) dy2;
2) d2z = -?dx2 + ^dxdy;
3) d2z = 2dxdy; 4) d2z = eax+b« (adx + bdyf;
5) d2z = exyy2dx2 + 2ex« (xy + 1) dxdy + x2exydy2.
Задача 39,21 (для самостоятельного решения). Найти диффе-
дифференциалы третьего порядка функций:
1) 2 = х4г/-хг/4;
2) z = х sin у + У cos x;.
определить все частные производные третьего порядка.
532
Ответ.
. d3zп. Л ,„ , д*г . 0 а дгг
1мху их' иу'
пч даг . даг д3г . д*г
2)^3 = ysinx; _ = -cosx; _ =-sin*/; ^ =-*cost/.
б) Аргументы х и у функции z = f(x, у) являются функциями
одной или нескольких независимых переменных.
Задача 39,22. Вычислить дифференциал второго порядка функ-
функции z = f(x, у), где х = <р (и, v), у = ф (", у).
Решение. Здесь уже л: иг/ — не независимые переменные,
а функции независимых переменных и и v, т. е. заданная функ-
функция является сложной.
Если при вычислении дифференциала первого порядка функции
z — f(x, у) совершенно безразлично, будут ли аргументы незави-
независимыми переменными или функциями других независимых пере-
переменных (свойство инвариантности дифференциала первого по-
порядка), то при вычислении дифференциалов .высших порядков
надо строго различать эти два случая.
Так как z = / {х, у), то dz = ^ их + щ dy.
При повторном дифференцировании мы теперь не можем уже,
как ©то делалось раньше, считать дифференциалы dx и dy вели-
величинами постоянными, потому что х и у — не независимые перемен-
переменные, а функции независимых переменных и и у. Поэтому
д*г , , д*г
д (дг\ . , д (
d (dx) = d2x; d (dy) = dzy.
Подставляя только что найденные величины в предыдущее
равенство, получим, что
Л - (S «* + я
Окончательно после приведения подобных членов получаем
или в другой записи (символической):
1 | C9,14)
533
Сравнивая эту формулу с формулой C9,6) или C9,8) для вы-
вычисления второго дифференциала функции z = f(x, у) в том случае,
когда аргументы х и у являются независимыми переменными, мы
видим, что в рассматриваемом случае появились два дополнитель-
дополнительных слагаемых ^- d2x и -^ d2y.
Заметим что формула C9,6) является частным случаем фор-
формулы C9,14), так как если х и у— независимые переменные, то
dx и dy — величины постоянные, а потому их дифференциалы
d.4 = 0 и d2y — О, добавочные слагаемые становятся равными
нулю и мы получаем из C9,14) формулу C9,6).
Формулу C9,6) вряд ли имеет смысл запоминать. Значительно
важнее уяснить метод, с помощью которого она была получена.
Задача 39,23. Определить d2z, если z — xy, где х = uv; y =
= и -f- v.
Решение. Дифференциал первого порядка
dz = ~ dx + ~ dy = ух»~Чх + ху\п х dy;
<Рг = d (dz) = d (уху~Чх) + d (ху\п xdy)=-d (ух"'1) dx +
+ уху~Ч (dx) + d (xy In x) dy + xy ¦ In x ¦ d (dy) =
= [dy ¦ x"-1 + yd (x1^1)] dx + ух^ЧЧ +
4- [d (xy) \nx + хЧ (In л:)] dy 4- x" In x ¦ d2y.
Нам осталось вычислить дифференциалы d (л*); d (xy) и
d(\nx):
d ('v9~1) = Tx W1) dx + fy (^ dy =
= {y — \)xy~4x 4- л*-Чп xdy;
d (xy) = yxy~ldx 4- xy In xdy;
d(\nx) = ~dx.
Подставляя эти величины в предыдущее равенство, имеем
d2z = {ху-г dy + y [(у— 1) ху~г dx 4- ху~г In x dy]} dx +
4- ух"-1 d?x 4- Uyx"-1 dx + xy In x dy) lnx + x*--jdx jdy +
4- xy In x ¦ d2y = у (у ~ 1) xy-* dx2 + 2 (xy~x 4- Уху~г In x) dx dy +
4- xy In2 x ¦ dy* 4- уху~г d2x + xy In x ¦ d2y. C9,14)
На основании данных задачи надо в последнее выражение
подставить х — uv; у = и -\-v; dx — udv + vdu; dx2 = (udv +
4- vduJ; dy = du + dv; dy2 = (du + dvJ; d2x = dudv + dv du =
— 2du dv; d2y = 0, так как du и dv, как дифференциалы незави-
независимых переменных,— величины постоянные, а значит, их диффе-
дифференциалы равны нулю.
534
Решение задачи можно, конечно, провести сразу по формуле
C9,14), и тогда было бы
дг ,.ц—1 i ,.„и—1 1„ ... 02
ду
Подставляя эти значения в C9,14), получим выражение d2z,
уже ранее найденное. В нем следует сделать замены, указанные
выше.
Задача 39,24 (для самостоятельного решения). Найти диффе-
дифференциал второго порядка функции z = f (и, v), где и = х2 -\- У2',
v = ху.
Указание. Здесь и и у — промежуточные переменные, а х
и у — независимые переменные.
Формула C9,14) должна быть переписана в виде
dU +2tdudV+dV +Tdu+!rdv
du = 2xdx + 2y dy; du* = 4 (x2 dx2 + 2xy dx dy + y2 dy2);
d2u = 2dx2 + 2dy2; d2v = 2dxdy.
Ответ, ч
(д2г . „ . . д2г . o дг , d2z
з~2 4л:2 -f- ixy ¦ -^—^ +2 ч- +
\ди* v ди dv ' ди
,o (д2г . „ . . д2г . o дг , dz Л , 9 .
d z — з~2 4л:2 -f- ixy ¦ -^—^ +2 ч- + %-. ¦ у2) dx2 +
\ди* v ди dv ' ди ' да v / '
Задача 39,25 (для самостоятельного решения). Использовать
результат, полученный в предыдущей задаче, если z = eu cos v, a
и и v имеют те же значения, что и в задаче C9,24).
СОРОКОВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Линни и поверхности уровня. Производная функции по
заданному направлению. Градиент функции.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Физическим полем называется часть пространства, в которой
происходит физическое явление.
1. Скалярное поле
Физическое поле называется скалярным, если физическое явле-
явление, его образующее, характеризуется функцией f = f(x, у, г),
зависящей только от координат точек пространства, в кото-
535
ром это явление происходит. Скалярное поле полностью опреде-
определено заданием одной функции f(x, у, z) трех независимых пере-
переменных*.
Если физическое явление образовало скалярное поле, то каж-
каждой точке Р(хи ylt zx) пространства, в котором происходит это
явление, ставится в соответствие определенное число, характери-
характеризующее это явление в рассматриваемой точке. Это число есть
частное значение функции f(x, у, г), вычисленное в точке
P(xlt ylt zx) {примерами скалярного поля являются: поле элект-
электрического потенциала, давление в атмосфере).
2. Поверхность уровня
Если однозначная функция f(x, у, г) соответствует скаляр-
скалярному полю, образованному физическим явлением, то поверхностью
уровня (иначе эквипотенциальной поверхностью) этого поля
называется поверхность, во всех точках которой функция
f(x, у, z) сохраняет одно и то же значение.
Поверхности уровня имеют уравнение
f(x, у, г) = с, D0.1)
где с—постоянная величина. '
Придавая постоянной с различные числовые значения, получим
семейство поверхностей уровня. Через каждую точку простраН'
ства проходит одна поверхность уровня.
Во всех точках поверхности уровня физическое явление проте-
протекает одинаково.
Уравнение поверхности уровня, проходящей через точку
Р(хи Уъ zi). имеет вид
f{x, у, z) = f(xlt уъ Zl). D0,2)
3. Производная по направлению
Производная от функции f(x, у, г) по направлению (Г) харак-
характеризует скорость изменения функции f(x, у, г) по этому на-
направлению.
Эта производная вычисляется по формуле
% = gcos (/, х) + gcos (I, у) + gcos (/, z). D0,3)
* Предполагается, что функцня f{x, у, г) — однозначная непрерывная
функций х, у, г, имеющая непрерывные частные производные первого порядка
д[ д[ д[
дх ' ду' дг'
536
Производная щ равна нулю по любому направлению,
касательному к поверхности уровня. Она достигает
своего наибольшего значения по направлению нормали
к поверхности уровня-
4. Градиент функции
*
Градиентом скалярной функции f (x, у, г) называется вектор,
проекции которого на координатные оси Ох, Оу и Oz соответ-
df df df
ственно равны ~, ¦+ и -?, т.е.
grad / = д- / -\- jr-j -f- ~a~k. D0,4)
На основании этого определения проекции вектора grad f на
координатные оси запишутся так:
(grad/), = g; (grad/)y = ^; (grad ft, = | D0,5)
(предполагается при этом, что f (х, у, г) — однозначная непре-
непрерывная функция, имеющая непрерывные частные производные).
Модуль вектора grad/ вычисляется по формуле
Щ
Если х — единичный вектор направления (Т),
х = cos (/, х) i -f cos {I, y)} + cos (/, z) k,
mo формула D0,3) запишется так:
% = (gradf.x). D0,7)
Вектор grad/ в каждой точке направлен по норма-
нормали к поверхности уровня, проходящей через эту точку,
в сторону возрастания функции. Скорость изменения
скалярной функции f no некоторому направлению (I)
равна проекции вектора grad / на это направление, т. е.
| D0,8)
В этом состоит основное свойство градиента функции.
Задача 40,1- Скалярное поле образовано функцией
V =
Найти поверхности уровня этого поля.
537
Решение. На основании формулы D0,1) уравнение семейства
поверхностей уровня найдем в виде
VR* - х2 — у2 - z2 = с,
или
#2 _ Х2 _ у2 _ 22 = С2
Отсюда уже получаем окончательно я2 -J- у2 + 22 = R2 — с2.
Поверхностями уровня является семейство концентрических
сфер.
Задача 40,2. Найти поверхности уровня скалярного поля
v = arctg y~
Решение. По формуле D0,1) уравнение семейства поверх-
поверхностей уровня имеет вид
г
: = С.
Отсюда
и окончательно
22 = tg2c(x2 + y2).
Это уравнение семейства круговых конусов с общей вершиной
в начале координат. Их общей осью является ось Oz.
Задача 40,3. Найти производную функции f (х, у) = ха — у3
в точке МA,1) в направлении I, составляющем угол а = 60° с
положительным направлением оси Ох.
Решение. В формуле D0,3)
cos (/, х) = cos a = cos 60° = -5-;
Кроме того,
1/5
cos (/, у) = cos (90 — а) = cos 30а = v~ ; cos (/, 2) = 0.
= 3х2;
ox
Подстановка в D0,3) дает
В точке М A,1) имеем х = 1, у = 1. Подставляя эти значения
х и у в последнее равенство, будем иметь
df __ 1 _ VI 3 .
538
Итак, искомая производная
Задача 40,4. Найти производную функции f(x, у) = Зл:2 —
— бху + у2 в точке Л1—<г;—о") в направлении I, составляю-
составляющем угол а с положительным направлением оси Ох. В каком
направлении эта производная имеет: а) наибольшее значение;
б) наименьшее значение; в) значение, равное нулю?
Найти также градиент этой функции, его модуль и его
направляющие косинусы.
Решение. По условию задачи cos (/, х) = cos а, и тогда
cos (/, у) = cos (90° — а) = sin а.
Дальше: J- = 6х — бг/; -J- = 4« — 6*.
Подстановка в формулу D0,3) дает
¦щ — Fх — бг/) cos a + By—6x) sin а;
в точке А\ —у; —^-1
\ d л /
a/ __ ffi /_
а/ [° " \
т. е. 4-. — cos a + sin а.
Теперь нам надо найти те значения а, при которых ^ имеет
значения: а) наибольшее, б) наименьшее, в) равное 0.
Обозначим и = cos a -|- sin а и найдем экстремум этой функции
и' — — sin a -f- cos а. Из уравнения — sin a -f- cos а = 0 следует, что
tga = 1, a a = -^-+ kit.
Считая, что а может изменяться от 0 до 2л, из последней фор-
формулы получаем
при k = 0 (Xj = ^ при k = 1 <хг = -у, и" = — cos a — sin a, и так
как и" \~) = — cos-^— sin-^- = —1/2, то при а, =-?-
\4/ 4 4 г> ^Х4
достигает максимума, а вместе с тем и наибольшего значения.
Таким образом, производная -X нашей функции имеет наиболь-
наибольшее значение по направлению, составляющему с положительным
направлением оси Ох угол a = -j.
539
При а = -j-k имеем и" (-jk) = у > 0. Производная -щ имеет
наименьшее значение по направлению, составляющему с поло-
жительным направлением .оси Ох угол а = -^-тс.
Ответим теперь на последний вопрос задачи: надо найти то
значение а, при котором ¦— = 0, т. е. при котором cos а + sin а=
= 0. Решая это уравнение, имеем cosa=— sin a; tga = — 1
и для a, содержащегося между 0 и 2тс, получаем
3 7
a = T7t и a = Tit.
Другое решение этой же задачи: мы нашли, что направление
наибыстрейшего роста функции составляет с положительным на-
направлением оси Ох угол a = -j-. Известно, что направление наи-
наибыстрейшего роста функции в данной точке совпадает с направ-
направлением вектора, являющегося градиентом этой функции, который
определяется формулой D0,4), а длина его находится по формуле
D0,6).
Для нашей функции / (х, у) — Зх2 — бху + У2
а в точке А [— -~, — yj (grad /) _ j_= ^ + /.
3
1
Длина вектора grad f в этой точке
а его проекция на оси прямоугольной системы координат равна
(grad/k^l; (gradf)y=\.
Известно, что направляющие косинусы вектора а находятся
по формулам
в нашем случае вектор grad/ в точке Л\—„-, —g-) имеет на-
1/2 D 1 /2 ,
правляющие косинусы cos а = —г= = -у-; cos р = -j~ = -у .
Значит, вектор grad f составляет в точке A[ — -j, —у) с по-
положительным направлением оси Ох угол а = -j. Этого и сле-
540
довало ожидать потому, что этот вектор указывает направление
наибыстрейшего роста функции в данной точке, а мы нашли, что
производная -щ, определяющая скорость изменения функции, до-
достигает своего наибольшего значения именно по направлению /,
составляющему угол а = -j с положительным направлением оси Ох.
Задача 40,5. Определить производную функции
f{x, у, z) = *У + x*z* + y2z2
в точке А '— , — , —I в направлении 7, составляющем с осями
У* У A y~V
прямоугольной системы координат Ox, Oy, Oz углы, соответ-
соответственно равные а, р и 7. градиент этой функции, его величину
и направляющие косинусы.
Решение 1. По формуле D0,3) находим производную ¦?
по указанному в задаче направлению. Чтобы воспользоваться этой
формулой, найдем частные производные
Подставляя эти значения производных в D0,3), получим
^ = 2х (у2 + z2) cos а + 2у (х2 + z2) cos p + 2z (x2 + у2) cos T.
В точке А (—- , -—, —-1 значение ~т найдем, подставив в пре-
\ /~/Г /~~Л /~~А I ^^
дыдущее равенство х = у — z = —
HL\ = cos a + cosp + cos-f.
2. По формуле D0,4)
grad f = 2x (у2 + 22O.+ 2у {х2 + z2) ] + 2z (x2 + у2) k.
В точке A (grad /)л = i + / + k, a его проекции на координат-
координатные оси и его модуль в этой точке равны:
(grad f)x = (grad f)y = (grad /J = 1,
|grad /| = l/la+ 12+ I2 = 1/3. ¦
. Направляющие косинусы вектора grad f в точке А равны:
1 ._„ 1
(Контроль: cos2 ax -f cos2 px -f cos2 f x = 1).
541
Эти направляющие косинусы определяют направление наибы-
наибыстрейшего роста нашей функции в точке А.
Если направление /, о котором шла речь в задаче, совпадало
бы с направлением вектора' grad /, то производная — достигла бы
своего наибольшего значения в этом направлении, и тогда
в точке А
х /з /3 /3 /3
Задача 40,6. Найти |grad«| и направляющие косинусы гра-
градиента в точке A (xOlyOizo), если функция и = у,
где г = l/^e2 -j- i"
22.
Решение. Чтобы воспользоваться формулой D0,6) для опре-
1 ди ди ди „ I
деления grad и, нам надо найти -г-, -г- и ^-. У нас « = —, а по-
потому проекция градиента этой функции на оси Ох
а потому EL =
2л"
2 /л-2 + у2 + г2 г
= Л , и тогда
дх
или д~= —^л ¦
Аналогично (grad —) = -?¦ = — -f-; ( grad —
\fe r jу ду г3 * ь г
Пользуясь формулой D0,6), получаем, что
дг :
«| - у _ + -,. + -_
В точке А |grad и\ = -,, где ¦
-2 2 2
0 — -*-0 + У 0
Направляющие косинусы вектора а =- grad — найдем по фор-
формулам
grad —
cos(a,A;) = ^ = V r
grad -_
grad —
; cos |
; cos (a, z) = ^ =
grad
542
Подставляя в эти формулы найденные значения grad —
(grad ~jx, (grad ^ и (grad ~)г, получим
cos (a, x) = — ? ; cos (a,y) = —^\ cos (a, 2) = — ^ .
Чтобы найти значения направляющих косинусов градиента
нашей функции в точке А, надо в последних формулах заменить
х, у и z соответственно на х0, у0 и z0, а г — на
ro = VSo + yl + zl..
СОРОК ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Дифференцирование неявных функций.
/. Если независимая переменная х и функция у связаны урав-
уравнением
/(*. 40 = 0, D1,1)
неразрешенным относительно у, то говорят, что у есть неявная
функция х (или функция у от х задана неявно). Для того чтобы,
не решая уравнение D1,1) относительно у, найти производную
от у по х, пользуются формулой
д1
y' D12j
Чтобы определить вторую производную от у по х, надо пере-
переписать D1,2) в виде ~- + —¦ у' = О, продифференцировать его
по х и в полученном выражении заменить у' уже найденным зна-
значением D1,2). Точно так же определяется у'" и т. д.
Запоминать достаточно громоздкие формулы для определения
у" и у"' не имеет смысла. На примерах будет показан метод опре-
определения производных высших порядков в рассматриваемом случае.
Задача 41,1. Определить у' и у", если функция у от х задана
неявно уравнением х3 + у3 — Ъаху = 0, где а — величина постоян-
постоянная.
Решение. Обозначим левую часть этого уравнения через
f(x, У)- Чтобы воспользоваться формулой D1,2), найдем J- и -р
Подставляя эти выражения в D1,2), получим после сокраще-
сокращения на 3
543
Чтобы определить у'', перепишем равенство D1,3) в таком виде:
х2 — ау + (у2 - ах) у' = 0. D1,4)
Продифференцируем его по х, помня, что у есть функция от х.
Здесь следует применить правило дифференцирования сложной
функции. Получим
2х - ау' + Bуу' —а)у' + (у2 - ах) у" = 0,
или
2л: - 2ау' + 2уу'* + (у2 -
Подставляя сюда вместо у' его значение из D1,3), получим
Отсюда
•¦ — ax ¦ " \y2 — ax
ИЛИ
„ _ _ 1х (у* — ах)* + 2а (дт" - ау) (у — ах) -f- 2у (дт2 - ау)*
У ~ (у* —ах)*
Если в числителе дроби раскрыть скобки и сделать приведение
подобных членов, то получится выражение 2ху* + 2х*у — 6ах2у2-\-
+ 2а3ху, которое выгодно переписать в виде 2ху (х3 + у3 — Ъаху) +
+ 2а3ху. Так как по условию х3 -{- у3 — Заху равняется нулю, то
окончательно числитель дроби равен 2авху, а
„ 2а*ху я 2ааху
У ~~ (у*—аху ' ИЛИ у ~ (ах — у*K '
Задача 41,2. Функция у от х задана уравнением
х2 — Ъху + 4у2 — 2х + Ъу + 2 = 0.
Определить у', у", у"' при х — 2; у = 0.
Решение. Обозначим левую часть заданного уравнения через
f(x, у). Имеем:
и на основании D1,2)
, _ 2х — 3«/ — 2
У — Ъх + 8у + 3 '
544
Подставляя вместо х и у их значения, имеем
У' B-°) = " ^Й^ОТЗ 'У' B' °) = 4 •
Перепишем D1,5) в виде
2л: - Зу - 2 - (Зх - 7у - 3) г/' = 0.
Продифференцируем это равенство по х, имея опять-таки в виду,
что у есть функция х:
2-Ъу'-(Ъ~ 8у') у' - (Зле - By -3) </" = 0. D1,6)
Подставляя сюда вместо х и у их значения, а вместо г/' —
найденное выше его значение \у' — -А , получим
2 _ з ¦ 4 - (з - 8 • -i)|. - C ¦ 2 - 8 • 0 - 3)/ = 0,
откуда
Для определения г/"' продифференцируем опять'по х равен-
равенство D1,6):
-Ъу" - (-8у") у' - C-8г/) у" - C-8/) у" - C* -Ъу -3) jT = 0.
Подставляя сюда данные значения х и у и уже найденные
значения г/' и у", получим, что
-294 + 243/" = 0, а у"' = ™г
Задача 41,3 (для самостоятельного решения). Кривая опреде-
определена уравнением хг + 2ху + у2 — ix + 2у — 2 = 0.
Определить, в какую сторону направлена вогнутость этой
кривой в точке A,1).
Указание. Направление вогнутости кривой в данной точке
определяется знаком второй производной в этой точке. Поэтому
следует найти у".
Ответ. / = 0; 1 +2у' + у'2 + (х + у+ \)у" = 0; у" = --J-.
Кривая в точке A,1) обращена вогнутостью в сторону отрицатель-
отрицательных ординат.
Задача 41,4 (для самостоятельного решения). Найти у"' функ-
функции, заданной в предыдущей задаче при тех же значениях х и у.
Указание. Продифференцировать по^я полученное при ре-
решении предыдущей задачи равенство 1 + 2у' + у'2 + (х + у +
+ 1)г/" = 0
Ответ. /" = 4-.
О
545
Задача 41,5 (для самостоятельного решения). Функция у от х
задана уравнениями:
1) х sin у — cos у + cos 2г/ = О,
2) у sin х — cos (x — у) = О,
3) sin л: In у + cos г/ In л; = 0.
Найти г/'.
Ответ П // — slny •
uitsci. ЧУ— * cos г/+ sin г/— 2 sin 2г/'
2 ' _ у cos .г + sin (X — у)
' ^ sin (х — у) — sin д- '
cos х In «/ -J cos «/
3),' f
3), = f.
sin г/ In jt sin jt
Задача 41,6. (для самостоятельного решения). Кривая опреде-
определена уравнением
х2 — 2ху + 5г/2 — 2х + Ау + 1 = 0.
В точке (-g-> —2") на не" определить уравнение касательной
нормали, направление вогнутости, а также у"'.
Ответ. Уравнение касательной 2г/+ 1=0; уравнение норма-
нормали 2х — 1=0; у" = 1. Кривая обращена вогнутостью в сторону
положительных ординат; у"' = —3.
Указание 1. Касательная к кривой f(x, у) = 0 в точке
Уо) определяется уравнением у — у0 = у' (х0, уо)(х — х0), а
нормаль
у~Уо==~утТчГу7)(х~~Хо)-
1. Если функция г от двух независимых переменных х и у
задается уравнением
/(*,?, z) = 0, D1,7)
не разрешенным относительно г, то говорят, что г есть неявная
функция переменных х и у. В этом случае частные производные
функции -г по независимым переменным х и у определяются по
формулам
д± dj_
дг __ дх. дг _ ду .
д~х~ ~д}' ду ~W ( ' >
~дг дг
На примерах будет показано, как можно определить в рас-
рассматриваемом случае производные j- и j-, не прибегая к готовым
формулам D1,8).
546
На примерах будет также показан и метод определения част-
частных производных
дх* ' дхду ' ду* '
Задача 41,7. Функция г независимых переменных х и у задана
уравнением х2 + у2 + z2 = а2. Определить ~ и ^.
Решение. Первый способ. Перенесем а2 в левую насть дан-
данного уравнения и обозначим ее через f(x, у, г). Тогда f(x, y,z) =
= х2 + у2 + z2 - а2 =0;
Ё1-2х- df-2v d-t-2z
дх ~ **' ду~ Ly> дг ~ ZZ-
Подставляя эти значения в D1,8), будем иметь:
дг _ 2jt_ х дг 2«/ у^
дх 2г г ' ду 2г г '
Второй способ. Продифферениируем данное уравнение и получим
2xdx + 2ydy + 2zdz = 0,
отсюда
dz = -\dx-^dy. D1,9)
С другой стороны, мы знаем, что дифференциал функции z =
= <р (х, у) вычисляется по формуле
dz = fxdx + pydy. D1Л0)
Сравнивая формулу D1,10) с выражением D1,9), мы заключаем,
что
дг х дг у
дх~ ~~Т' Ь~у~ ~Т]
*
таким образом, мы определили искомые производные, не прибегая
к готовым формулам D1,8).
Задача 41,8. Функция z независимых переменных х и у зада-
задана неявно уравнением 4л;2 + 2у2 — 3z2 + ху — уг + х — 4 = 0. Опре-
Определить -г- и -з-при х = 1; у — 1; г = 1.
Решение. Первый способ. Обозначим левую часть уравнения
через f(x, у, г.) Тогда
По формулам D1,8) получаем
дг
ду 6г + «/' * V-'...;
547
Подставляя сюда значения х— 1; у= 1; 2=1, получим, что*
дх ~ Т' ~ду= Т' ¦ |
Второй способ. Дифференцируя заданное уравнение, получаем!
&«/* + Aydy — 6zdz + xdy + г/Ле — гд/г — zdy -\- dx = 0, ,
или # ^
(8л: + I/ + l)'df* + Di/ + л: — 2) dy -f- (—62 — г/) rf2 = 0, |
откуда I
сравнение с формулой D1,10) показывает, что
дг 8х + у+1 , дг х + 4у — г
djf 6г + У ' ду 6г + г/ '
что совпадает с выражениями D1,11), полученными раньше.
Задача 41,9 (для самостоятельного решения). Функция г неза-
независимых переменных х и у задана уравнениями:
3) ху-\-xz + yz = I.
Определить ^~ и ^-- Решение провести двумя способами.
О1Ч дг сН дг с*у
т r е т. 11 — = : -з- = — т-^ \
о\ §1 — Л.- ~ — Ж.•
> дх~ р ' ду~ q '
п. дг •
'5л- х -{- у' ду х + У'
Задача 41,10. Из уравнения, заданного в задаче 41,7, опре-
определить вторые производные.
5л-2 ' дхду дуг '
Решение. В указанной задаче было получено, что
Поэтому
дг_ х дг у
дх ~ ~г ' ду г
1 дг
\ • Z — -Z- ¦ х
дх
дх*
548
Подставляя сюда значение^ получим, что
дх2 ~ г2 — ¦ г8 *
Дифференцируя по у выражение ^ и учитывая, что при диф-
дифференцировании по у переменная х, стоящая в числителе, рассматри-
рассматривается как величина постоянная (так как х и у — независимые
переменные, то х не зависит от у), получаем
• dsz х дг х I у\_ ХУ
дхду — zs ду ~ г* \ г) г8 *
Аналогично находим, что j\ — — у ^ Z .
Задачи 41,11. Из уравнения f(x,y,z) = 0, в котором х рас-
рассматривается как функция независимых переменных у и z, опре-
дх дх
ДелиТЬ Ту И Ь~г •
Решение. Дифференцируя данное уравнение, получаем
откуда следует, что
ди dz j
дх ¦ дх
С другой стороны, если х есть функция у и z:
. . , дх . , дх ,
х = х (г/, г), то их = Гу dy + Тг dz.
Сравнивая последнее равенство с предыдущим, получим, что
df df
дх ду , дх дг
ду • д[' дг д?'
дх дх
Задача 41,12 (для самостоятельного решения). Из уравнения
F (*> У, z) — 0, в котором у рассматривается как функция незави-
независимых переменных х и г, определить
ду ду
дх И Ъ~г-
д? д?
Ответ-1=-|; 1 = -|-
ду ду
549
СОРОК ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Экстремум функции нескольких независимых переменных.
Наибольшее и наименьшее значения функции двух независимых переменных.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Экстремум функции
Определение 1. Функция и = f(x, у, z, ..., v) при некото-
некоторой системе значений х0, у0, z0, .. ., v0 независимых переменных
имеет максимум (минимум), если приращение функции
Аи = / (х0 + Ах, г/0 + Ay, z0 + Az, ..., v0 + Aw) —
— / (*o, г/о, • • •. v0)
отрицательно (положительно) при всевозможных, достаточно
малых по абсолютной величине как положительных, так и отри-
отрицательных значениях
Ах, Аг/, Az, ... , Av.
Максимум или минимум функции называется ее экстремумом.
Необходимые условия экстремума
Если функция и = f(x, у, z, ..., v) достигает экстремума при
значениях независимых переменных х — х0, у = г/0> z = z0, .. ., v =
— v0 ..., то при этих значениях или выполняются равенства
fi = 0; J = 0; J = 0; . . .; % = 0, D2,1)
дх ду дг ' dv ' v > /
или частные производные при этих значениях не существуют.
Иначе: в точке экстремума первый дифференциал
функции равен нулю или не существует. Количество
уравнений D2,1) равно числу независимых переменных.
Точки, в которых выполняются равенства D2,1),
называются стационарными точками функции.
Равенства D2,1) выражают необходимое, но недостаточное
условие экстремума функции нескольких независимых перемен-
переменных. Это значит, что не при всех тех значениях независимых
переменных, при которых эти равенства выполняются, функция
имеет экстремум.
Достаточные условия экстремума
Для того чтобы решить вопрос, какие из значений независи-
независимых переменных, получаемых из уравнений D2,1), доставляют
функции максимум или минимум, или ни то, ни другое, обраща-
обращаются к исследованию дифференциала второго порядка этой функции.
550
Если при значениях независимых переменных, найден-
найденных из уравнений D2,1), дифференциал второго порядка
функции сохраняет постоянный знак при всевозмож-
всевозможных достаточно малых по абсолютной величине при-
приращениях независимых переменных, то функция при
этих значениях имеет экстремум, причем максимум
будет в том случае, когда дифференциал второго по-
порядка отрицателен, а минимум— когда он положителен.
Если дифференциал второго порядка при значениях
независимых переменных, найденных из системы урав-
уравнений D2,1), не сохраняет постоянного знака, то для
этих значений функция не имеет ни максимума, ни
минимума.
Если же окажется, что при этих значениях дифференциал
второго порядка обратится в нуль, то решение вопроса об экстре-
экстремуме требует исследование дифференциалов порядка выше, чем
второй.
Правило определения экстремума функции двух независимых
переменных
Чтобы определить экстремум функции z =f(x, у),
двух независимых переменных следует:
1) Определить стационарные точки, в которых функ-
функция может достигать экстремума, для чего надо ре-
решить систему уравнений
Определить вторые частные производные
дх2' дхду' ду
3) Вычислить значения вторых частных производ-
производных в каждой стационарной точке, а полученные числа
обозначить соответственно через А, В и С
4) Составить выражение А = АС — В2. При этом,
а) если Д > О, то экстремум в стационарной точке
есть: если А> 0, то будет минимум, а при А < 0 — мак-
максимум;
б) если Д < 0, то экстремума в рассматриваемой
стационарной точке нет;
в) если Д = 0, то имеет место сомнительный случай,
и для заключения об экстремуме надо привлечь к рас-
рассмотрению частные производные порядка выше второ-
второго (этот случай в программу не входит и нами не рас-
рассматривается).
5Б1
Задача 42,1. Исследовать на экстремум функцию
г = 2х3 + 2у3 — Зблт/ + 430.
Решение. Прежде всего определяем ^ и ~:
g = 6ж2 - 36#; | = 6/ _ 36*. D2,2)
Решаем систему уравнений
которая в нашем случае запишется так:
| 6л:2 — Збу = О,
\ 6г/2 — 36л: = 0;
после сокращения на 6 имеем
Из первого уравнения у = -g- . Подставляя его во второе урав-
нение, получим gg — 6л: == 0, или л:4 — 216л: = 0, которое перепи-
перепишем так:
л: (л:3 —216) = 0.
Разлагая на множители выражение в скобках, получим урав-
уравнение х (х — 6) (л;2 + 6л; + 36) = 0.
Отсюда следует, что xt = 0; хъ = 6, а остальные два корня —
комплексные, которые нас не интересуют (это корни уравнения
*2 + 6л: + 36 = 0).
Подставляя эти значения х в равенство у = -=-, получаем, что
Ух = 0; У* = 6- N _
Итак, есть две пары решений системы уравнений D2,3):
1) хх = 0; У1 = 0; 2) л:г = 6; у% =, 6.
Теперь определим число А, для чего найдем
дч
И ду*'
дх*' дхду И ду
Из D2,2) получаем, что
552
Подставим теперь сюда сначала первую пару решений, а потом
вторую и определим числа Л, В, С и Д.
Для первой пары решений:
а потому число А = АС — Б2 = —36.
Так как А < 0, то при х — 0; г/ ==-- 0 функция не имеет ни мак-
максимума, ни минимума.
Для второй пары решений:
?) _ 72. о _ (*г\ _ _ofi. r __ 1дЧ\ _ ?9
Теперь число А = АС — В2 = 72 • 72 — 362 =-- 3888, и так как
оно положительно, то экстремум при значениях х — 6; у — 6 есть.
Учитывая, что А — число положительное, заключаем, что при
этих значениях х и у имеет место, минимум. Чтобы определить
минимальное значение функции, подставим в нее х = 6, у = 6 и
ПОЛУЧИМ Zmin = —2.
Замечание. Из А>0 следует, что АС — В2>0, АС>В%,
т. е. АС > 0, а это означает, что Л и С в случае, когда функция
имеет экстремум, имеют один и тот же знак.
При решении этого примера читатель усмотрел, что не все
значения независимых переменных, которые получаются при ре-
решениях системы D2,1), доставляют функции экстремум. Так,
значения х = 0 и у = 0, хотя и являются решениями системы
D2,1), но при них функция не имеет ни максимума, ни минимума
(экстремума нет).
Задача 42,2. Исследовать на экстремум функцию
2 = Ux3 + 27ху* — 69ж — 54г/.
Решение. Находим прежде' всего т-и т-:
| | 54. D2,4)
Решаем систему уравнений
/ 42л:2 + 27у2 - 69 = 0,
{ Ыху — 54 = 0.
После очевидных сокращений эта система запишется так:
9г/2 = 23,
553
Решая эту систему, получим 4 пары решений, при которых
исследуемая функция может иметь экстремум.
Первая пара: хг = 1; yt = 1; вторая пара: х2 — —~; Уч. = ^-q—;
V14 d
1 1 —3
третья пара: х3= — 1; г/3 = —1; четвертая пара: *4 = -7=;
у И
/и
% = д-.
Теперь определим, какие именно из этих значений доставляют
функции экстремум.
Определим из D2,4) вторые частные производные:
а-.- = 84а:; з—=- = 54г/; s~s =
Для каждой пары значений определим числа А, В и С и
число А.
1. Для хх — 1; ух = 1 имеем
Число А = ЛС - В2 = 84 ¦ 54 - 542 > 0.
Экстремум есть, а так как А > 0, то имеет место минимум
zmin = 14 • 1 + 27 • 1 • 1 - 69 -E4 = -82.
2. Дляжг
, /в«г\ 252
Ух=хг
0=0»
и при х = -у=:; г/ = ^— экстремума нет.
3. Для х3 = —1; г/3 = —1
Л = -84; В = -54; С = -54;
А = ЛС - В2 = (-84) (-54) - (-54K > 0.'
Экстремум есть, и именно максимум, так как А = —84 < 0;
гтах = -14 - 27 + 69 + 54 = 82.
554
4. Для xt = — р== ; г/4 = — ^ имеем
= -Ц; В—18/Д С —$;
Экстремума при значениях а: = аг4 и у = г/4 нет.
Задача 42,3 (для самостоятельного решения). Исследовать на
экстремум функцию
г = f + 2жг/ + у~ - 4х - 5г/.
Ответ. Экстремума нет.
Задача 42,4 (для самостоятельного решения). Исследовать на
экстремум функцию г = х* -f г/4 — 2ж2 + 4жг/ — 2г/2.
Указание. Система уравнений 4- = 0 и ^ — о приведет
к системе уравнений
3 — а: + у = О,
Почленное слежение даст уравнение х3 + У3 ~ О, откуда сле-
следует, что у = —х.
Подставляя в первое уравнение, получим х3 — 2х = 0, откуда
у __ п. у ~\/~O' y = l/~9 я и ==О* и = l/~2* и = Л/ 2
Имеем три пары решений: 1) xt = 0; ух = 0; 2) лг2 =
= - 1/2; 3) xs = — 1/2; у, = V2.
Ответ. zmiH = —8 при х2 — У~2, г/г = — У~2 и при х3 = —
г/3 = V2. Вопрос об экстремуме при х = 0, г/ = 0 остается открытым.
Задача 42,5 (для самостоятельного решения). Исследовать на
экстремум функции: 1) z = xsy2 A2 — * — у); 2) z = ху (ху (х+у—1);
3) z = х3 + г/2 — бжг/ — 39л: + Щ + 20.
Ответ. 1) Максимум при х = 6; г/ = 4; zmax = 6912;
о\ 111
2) минимум при * = -д-; у = -g-; zmin = — 57;
3) минимум при х = 5; г/ = 6; zmin = —86.
Задача 42,6. Найти экстремум функции
и = х2 + г/2 + г2 + ху — х + г/-2г.
Решение. Здесь мы имеем дело с функцией трех независи-
независимых переменных. Определим частные производные:
ди о | ди п . . ди п q
дх~ 1У~'ду~~У^~^~'дг~~
555
и решим систему уравнений:
2х + у— 1 ' = 0,
2у + х + 1 = 0,
2z — 2 = 0;
получаем х = 1; у = —1; z = 1.
Значит, при этих значениях независимых переменных возможен
экстремум.
Для того чтобы сделать заключение, будет ли он, надо об-
обратиться к исследованию дифференциала второго порядка этой
функции. Известно, что дифференциал первого порядка
. ди , ди , ди ,
UU — ^- и X -\- -г- йу -J- ,— dZ.
Дифференциал второго порядка читатель определит самостоя-
самостоятельно и получит, что
^-w^ + didz2 + 2bWydxdy +
' дхдг
У нас
' ду*~г' дг* ~ ' дхду~ ' дхдг ~ ' дудг
а потому
d2u = 2dx2 + 2dy2 + 2dz2 + 2dxdy = 2 (d^:2 + dxdy + d'y2) + 2dz2.
Выражение, стоящее в скобке, не отрицательно при любых
dx и dy: (а2 + Ь2) > — аЬ, а последнее слагаемое положительно.
Таким образом, d2u > 0 при любых dx, dy и dz.
Тем самым мы доказали, что при х=\; у~—1 и z=l
функция и достигает минимума, a umin = —2.
Задача 42,7 (для самостоятельного решения). Определить
экстремум функции и = х2 + у2 -\- z2 — ху + х — 2z.
2 1
Ответ. При * = — -s-; у — —5"; z,= 1 функция достигает
О О
минимума, а ит\п = — -г •
2. Отыскание наибольших и наименьших значений функции
двух независимых переменных в замкнутой области
Функция ограниченная и дифференцируемая в замкнутой об-
обмети достигает в этой области своего наибольшего и наимень-
наименьшего значения или во внутренних точках этой области, кото-
которые являются точками стационарности функции, или на ее
границе.
556
Для того чтобы найти наибольшее и наименьшее значение
функции, надо: 1) Найти стационарные точки функции, для
чего следует решить систему уравнений ^- = 0; j- = 0;
2) вычислить в стационарных точках значения функции;
3) найти наибольшее и наименьшее значение функции на каждой
линии, ограничивающей область; 4) сравнить все полученные зна-
значения . Наибольшее из них будет наибольшим, а наименьшее —
наименьшим значением функции в замкнутой области.
Задача 42,8. Найти наибольшее и наименьшее значение функции
z = х2 — ху + 2у2 + Зх + 2г/ + 1
в замкнутом треугольнике, ограничен-
ограниченном осями координат и прямой х + у +
+ 5 = 0 (фиг. 42,1).
Решение. 1) Находим стационар-
стационарные точки функции:
~ =2х - у + 3; ~ = —х + 4у + 2.
дх " ' ' ду J
Решаем систему уравнений
х + 4у + 2 = 0
N
Фиг. 42,1.
1. Итак,, имеется одна стацио-
и находим, что х — —2; у —
нарная точка (—2,-1).
2) Определяем значение функции в этой точке:
г (-2, -1) = -3
(запись г(—2, —1) означает, что ищется значение функции
z = z (х, у) при х = —2, у — —1).
3) Переходим к исследованию функции на границах области,
которая состоит из отрезка оси Ох, отрезка оси Оу и отрезка
АВ прямой.
а) На оси Ох у = 0, а заданная функция принимает при у = 0
такой вид: z = х2 + Зх + 1 (—5 < х < 0).
Эта функция должна быть рассмотрена на отрезке [—5,0].
Так как на этом отрезке функция z непрерывна, то она дости-
достигает на нем как наибольшего, так и наименьшего своего значения.
Это может произойти или в точках стационарности функции, где
dz n
gj — и, или на концах рассматриваемого отрезка.
Определим прежде всего точку стационарности
dz 3
dx ' 2
557
Определим значение функции при х — —к и на концах от-
отрезка [—5,0]:
г(-|, о) = -|; 2[—5,0] = 11; г [0,0] = 1.
g
Сравнение показывает, что B„анб.)ол = И; Bнаим.Ы = — -j.
б) На оси Оу: х = 0, а данная функция при л: = 0 запишется
так:
г = 2г/2 + 2г/ + 1 (-5 < г/ < 0).
Эта функция — функция одной независимой переменной. Она
должна быть рассмотрена на отрезке [—5,0] (см. фиг. 42,1).
Определим на этом отрезке ее наименьшее и наибольшее значе-
значения, которые в силу непрерывности должны существовать. Прежде
всего определяем точки стационарности функции:
Определим значение функции при у — —к» а также на кон-
концах рассматриваемого отрезка:
Bнаиб.HВ = 41; BНаим.HВ = у •
в) Наконец, исследуем данную функцию на отрезке прямой АВ,
принадлежащем' границе области.
Уравнение прямой АВ х + У + 5 = 0. Поэтому на ней у =
Подставляя это значение у в заданную функцию, получаем
Наибольшее и наименьшее значение этой функции должно
быть определено для значений —5 < х < 0:
g = 8* + 26; 8ж + 26 = 0; х = ~~.
Находим соответствующее значение у. Из у = —х — 5 сле-
следует, что
\ / ° 4 ° 4 '
558
Итак, рассмотрению подлежит точка I — -^, —fj (надо следить
за тем, чтобы исследуемые точки принадлежали рассматриваемой
области):
13 Л 5 z(-5, 0) = 11; z(-5, 0) = 41;
4 > 4/ 4 '
{Zwh6.)ab — 41; BНаим.)АВ = f •
Сравнивая теперь-значение функции г в стационарной точке
(—2, —1) с наибольшими и наименьшими значениями на отрез-
отрезках О А, ОВ и АВ, найденными в пунктах а), б) и в), усматри-
усматриваем, что в заданной замкнутой области
2наиб. =2@, -5) = 41,
2„аим. =2 (-2, -1) = -3;
таким образом, оказалось, что наименьшего своего значения
функция t достигла в стационарной точке (—2, —1), а наиболь-
наибольшего — на границе- области, в точке @, —5).
Задача 42,9 (для самостоятельного решения). Найти наиболь-
наибольшее и наименьшее значения функции z = х2 + Цг ¦*- 6ж + 4г/ -f- 2
в прямоугольнике с вершинами: ЛA, —3); В(\, 2); СD, 2);
D D, -3)
(К х < 4); (-3 < у < 2).
Указания. В стационарной точке C, —2) zC, —2)= —11.
Рассматривая границу области, получаем: 1) На отрезке АВ:
z — z A, у) = г/2 -j- 4г/ ¦— 3. Наибольшего значения на Л В функция
достигает в точке ВA, 2) и BнаИб.)дв = 9, а наименьшее ее зна-
значение на АВ в точке A, —2) и (гншы.)Ав= —7;
2) на отрезке CD: z = zD, у) = у2 + 4у — 6. На CD наиболь-
наибольшего значения функция достигаете точке СD, 2) и (гнаИб.)со = 6,
а наименьшее ее значение в точке D, —2) и (гнаИм.)со = — Ю;
3) на отрезке BC:z = z(x, 2) = х2 — 6ж+ 14; наибольшего
значения функция достигает в точке ВA, 2), а (гнаИб.Ьс = 9;
4) на отрезке AD: z = г (ж — 3) = х2 — 6ж — 1; (г„аиб.)ло = —6;
Bнаим.)ло = —Ю.
Сравнить полученное значение функции в стационарной точке
C, —2) с ее наибольшими и наименьшими значениями на гра-
границе области.
Ответ. В рассматриваемой области функция достигает наи-
наименьшего значения в стационарной точке: 2наИм. = —11. Наиболь-
Наибольшего значения функция достигает на отрезке АВ в точке A, 2)
и 2наиб. = 9.
559
Задача 42,10 (для самостоятельного решения). Найти наи-
наибольшее и наименьшее значения функции г = ху(х-\- у-{¦ 1) в
замкнутой области, ограниченной линиями у = —; х = 1; х = 2;
Ответ. Стационарные точки: (—у, —„¦); @, —1); ( —1, 0);
(О, 0) находятся вне рассматриваемой области. Наибольшего зна-
значения функция достигает на границе области в точке 12, ~ 1; а
2Наиб. — 3,5. Наименьшего значения функция достигает в точке
2, —-S-), а 2наим. = — 4,5.
(
Задача 42,11 (для самостоятельного решения). Найти наиболь-
наибольшее и наименьшее значения функции z =¦ cos x cos у cos (x + у) в
замкнутом квадрате, ограниченном линиями х = 0; х = тс; у = 0,
Указания. 1) После определения частных производных
дг дг
д- и ^- их выгодно представить в виде:
? = - - [sin B* + 2у) + sin 2л;];
щ = - - [sin B* + 2у) + sin 2y).
2) Из системы уравнений
- - [sin Bх + 2у) + sin 2х] = 0 ]
— — [sin Bл; + 2у) + sin 2t/] = 0 j
следует, что sin 2л: = sin 2у, и тогда 2 cos (л; -f у) sin (л: — д) — 0.
Отсюда получаем, что
Х — у — Rtz, (Щ
x + y = ~Bk+ 1), (С)
где /г — любое целое число. Но условие задачи требует, чтобы
выполнялись неравенства 0<л;<тс; 0<г/<тс, а потому должно
быть — тс<л: — г/<тс иО<лт + У<2тс; поэтому в (В) можно брать
k = —1; k = 0 и k = 1, а в (С) & = 0 и k = 1.
л: — t/ = 0, откуда г/ = л;;
л: — г/ = «, » У — X — тс;
ТС ТС
+ 3tc 3rt
560
Подставляя в первое уравнение системы (А) первые три зна-
значения у, получим уравнение sin 4х + sin 2х = О, а подстановка в
это же уравнение последних двух значений у приводит к урав-
уравнению sin 2х — 0.
Из этих уравнений находим стационарные точки:
@,0) @, «):(?!);
(i )(-=•); КО)
(решения, находящиеся вне данного квадрата, отброшены).
3) Теперь следует отобрать из стационарных точек те, кото-
которые лежат внутри квадрата;
4) На прямой у — 0 имеем /(х, 0) = cos2x,
» » у — ъ имеем f(x, ¦k) — cos2x,
» » sx = 0 имеем /@, у) = cos2 у,
» » х — я имеем /(тс, у) = cos2у.
На каждой из этих прямых наибольшее значение функции
равно 1, а наименьшее — нулю. Наибольшее значение функция
имеет в вершинах квадрата, а наименьшее, равное нулю, — в точках
(*.»)¦• (т••);(«¦ тМ- *)•
Ответ.- Наибольшего значения функция достигает в верши-
вершинах квадрата и гнаИб. = 1; наименьшего — в стационарных точках
(п тс
/2 2 \ 1
и It17' ?^ и 2наим- ^~"8'
Задача 42,12. Доказать, что из всех треугольников, имеющих
данный периметр 2р наибольшую площадь имеет равносторонний
треугольник.
Решение. Обозначим стороны треугольника через х, у и г.
По формуле Герона площадь треугольника
S = Ур (р -х)(р- у) (р - г).
Замечая, что z = 2p — х — у, мы получим S как функцию только
двух независимых переменных,
S = Ур{р - х)(р - у)(х + у - р).
Вместо того, чтобы искать экстремум этой функции, будем
искать экстримум ее квадрата
f(х, у) = S2 = р{р — х)(р — у)(х + у — р);
Гх -2х-у); | = р(р -х)Bр -2у-х).
19 И. А. Каплан 561
Решаем систему уравнений
р(р-у)Bр-2х-у) =
p(p-x)Bp-2y-x) =
Эта система приводит к таким четырем системам:
1) р-у = 0\ 2) 2р-2х-у = 0
р — л; = О J • 2р — 2у — л: = О
3) 2р — 2х — у = 0 \ 4) 2р — 2у — х = О
О] 0
Находим стационарные точки:
(р. р); [1р,{р); (р, 0); @, р).
Исследованию подлежит только одна точка М\~^р, -д-р),
так как остальные точки не удовлетворяют смыслу задачи: не
может быть треугольника, у которого сторона равна половине
периметра.
1 /2 2
Исследуем на экстремум точку Mlyp, -к
-(df) - In*
A > 0, а так как А < 0, то в исследуемой точке функция дости-
достигает максимума. Итак, в единственной стационарной точке функ-
функция достигает максимума, а потому и наибольшего значения: та-
2 2
ким образом, при х — -jp, у = -jP функция достигает и наиболь-
шего значения. Но тогда г = 2р — х — у = -^р. А так как х =
= у = г, то треугольник — равносторонний.
Задача 42,13. Канал, подводящий воду к турбине, имеет в
сечении равнобедренную трапецию, площадь которой задана и
равна S. Определить глубину канала и угол а откоса так, чтобы
периметр, смоченный водой, был наименьшим*.
* Периметр, смоченный водой называется «мокрым», Он влияет на трение,
и от его величины зависят расходы на сооружение канала.
562
Решение. «Мокрый» периметр обозначим буквой L, и тогда
(фиг. 42,2) L = АВ + ВС + CD. Так как h = CD sin а, то CD =
, 2Л
Sin a
Учитывая, что ВС ~ а, получаем, что L =а
Sin a
Таким образом, L есть функция трех независимых перемен-
переменных: a, ft и а. Условие задачи позволяет одну из переменных
исключить. Требуется, чтобы площадь сечения была постоянна
и равна S. В трапеции S = BC+AD ft. Но ВС = a, a AD = ВС +
+ 2ED = а + 2ft ctg а, а потому
„ 2а + 2/г ctg а и,
О — п И,
S = {a +hctga)h;
откуда следует, что
а = -j — h ctg а,
и для L получаем формулу
t
Фиг. 42,2
2ft
sin a '
в которой только две независимых переменных — h
(S — величина постоянная).
Находим
и а.
dL
6L
2Л cos a
sin2 а
и решаем систему двух уравнений:
, о 2Л cos a ,,
h cosec2 a ^-5— = 0
Sin2 a
после упрощений эта система запишется так;
S , 2 — cos о
Л* ~ sin о
h A — 2 cos a)
sin8 a
= 0
0
Из второго уравнения следует, что ЛA —2 cos a) = 0, откуда
или ft = 0, или 1 — 2 cos a == 0. Но глубина h не может быть
равна нулю, а потому остается только 1 —2 cos a = или cos a =
1 к
19*
563
Найденное значение а подставим в первое уравнение и полу-
получим
Теперь определим значения производных второго порядка при
найденных значениях а и Л:
d*L _ 2S cW. __ 1 — cos a -f- cos2 a , d*L __ 1 — 2 cos а
Ш~ h? ' da*~Z ilrFS "' <Ш ~~ sin« а •
Находим числа А, В и С:
Значит, экстремум есть, а так как Л > 0, то при найденных
значениях h и а функция L достигает минимума, и Lmin = 2]/5уЛ31
Задача 42,14. Два пункта Рх и Рч отстоят от двух пересе-
пересекающихся под прямым углом прямых, которые принимаются за
оси прямоугольной системы координат Ох и Оу, на расстояния
соответственно равные: *I=a1, S1=b1; хг = а«, Уг = Ьг (все эти
числа положительны). PL и Рг надо соединить телеграфным про-
проводом так, чтобы провод сначала шел к какой-нибудь точке Qlt
на положительной части оси Ох, от нее к точке Q« на положи-
положительной части оси- Оу, а после этого — от Q« к Рг (фиг. 42,3),
где на осях Ох и Оу надо поместить точки Qi и Q«, чтобы длина
телеграфной линии была наименьшей?
Решение. Все обозначения указаны на фиг. 42,3. Длина
телеграфной линии
L =
Z — функция двух независимых переменных — х и г/. Приступаем к
определению стационарных точек:
dL а, — х | х _
s~~V7T v^
OL у
564
Решаем систему уравнений
= 0
Запишем уравнения системы так:
х а1 —.
г + У*
У
+ (а, -
уаг
(А)
0
Фиг. 42,3
Возводя в квадрат обе части каждого уравнения, получим
+ i/2 ь\ + (а, —
Отсюда следует, что
Ь\ + (ах — л-J
(а, - л-J
565
Поэтому.
После очевидных упрощений получаем
ИЛИ
х — х
Перемножая почленно уравнения последней системы, получим
1 =
Отсюда
(о,-х) (*,-«,)' -1 л~Ьг~
g,fea — aty — a
Но из второго уравнения последней системы следует, что
х = ,а^_ . Сравнивая это значение с только что полученным,
имеем
откуда следует, что
— а\У —
или
агу= а А — аху — агЬъ
aty + агУ = а А — афх\
Определите самостоятельно .г, получите Л1 = а' 2~f2 ', причем
ах^г — аг^! > 0, так как х>0 и у > 0 по условию. Значения
jc и г/ можно определить значительно проще, если рассмотреть
геометрическое значение уравнений системы (А) (вообще от та-
такого истолкования никогда не следует отказываться, так как оно
часто приводит к значительным упрощениям).
В первом уравнении системы (А)
а потому
cos ocj = cos
и a, =
566
Второе уравнение системы (А) дает:
¦ , у = cos аа; 2~у =5 cos|32 и а2 = (Зг.
Из этого мы заключаем, что треугольники PiQiRx, QiOQt и
PiQtRi подобны, т. к. они имеют по равному острому углу.
Из подобия треугольников следует, что —!— = — = г~у..
О| —— X X ' Cln
Отсюда уже просто можно найти значения х и у, которые были
найдены раньше.
Теперь самостоятельно докажите, что
1) найденные значения х и у доставляют функции L минимум;
2) кратчайшая длина провода LHaHM. = Vifli + агJ + (bt + Ьг)\
3) для построения точек Qj и Q2 следует поступить так: пер-
перпендикуляры PXRX и PiRt продолжить за точки Ri и R2 на рас-
расстояния, равные этим перпендикулярам, и концы полученных
отрезков соединить прямой линией. Эта линия перееечет ось Ох
в точке Qi, а ось Оу в точке Q« (следует написать уравнение
прямой, проходящей через точки (аь — Ьх) и (—а«, Ьг) и найти
координаты точек пересечения этой прямой с координатными
осями).
Задача 42,15 (для самостоятельного решения). Число а раз-
разделить на три слагаемых так, чтобы произведение этих трех
слагаемых было наибольшим.
п (
Ответ. Каждое слагаемое равно -д-(полУченный результат
допускает простое геометрическое истолкование: из всех прямо-
прямоугольных параллелепипедов, у которых сумма трех измерений
есть величина постоянная, равная а, наибольший объем имеет куб
с ребром, равным
Задача 42,16 (для самостоятельного решения). Требуется изго-
изготовить из жести коробку без крышки в виде прямоугольного
параллелепипеда заданного объема V .так, чтобы затрата мате-
материала была наименьшей. Определить размеры коробки.
Ответ. Основание параллелепипеда — квадат со стороной
а — -^V, а высота его h =
Задача 42,17. Задано п неподвижных материальных точек Pt
с массами тг и координатами Pt(xt, yt) (t=l, 2, 3... , n).
Найти координаты х и у точки Р (х, у), для которой сумма
квадратов ее расстояний от этих неподвижных точек, помножен-
помноженных на массу соответствующих точек имеет наименьшее зна-
значение.
567
Указание. Искомая сумма
Ответ.
mj + m2 + • ¦ • + mn ' У ~ m, -)- m2 -)-¦•• + "*„ ' '1
СОРОК ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Касательная плоскость и нормаль к поверхности. >
Если на поверхности через точку М на ней провести всевоз-:
можные кривые и к ним в этой точке провести касательные
прямые (они называются касательными к поверхности), то ока-
окажется, что все эти касательные лежат в одной плоскости, ко-
которая называется касательной плоскостью к поверхности в точке М,
а перпендикуляр к касательной плоскости, восстановленный к ней
в точке касания М, называется нормалью к поверхности.
\. Если поверхность задано уравнением z = /(x, у), разре-
разрешенным относительно z (т. е. в явной форме), а точка касания
М имеет координаты (х0, у0, z0), то уравнение касательной
плоскости записывается так:
— X(s) ~Т~ 2„ (Xq, t/д) (У — Уд), D3,1)
а нормаль к поверхности в точке М определяется уравнением
х хо У — Уо г го ' /до m
г*(*о. Уо)~ гИ'о. Уо) -1 ' [ ''
Символы г'к (х0, у0) и г'у (х0, у0) означают, что производные
функции г = f (х, у) вычислены при значениях х ~ х0, у — у0.
2. Если поверхность определена уравнением f (х, у, г) = О,
неразрешенным относительно г (уравнение поверхности задано в
неявной форме), а точка касания имеет координаты (х0, у0, г0),
то касательная плоскость определяется уравнением
Гх(х0, у0, zo)(x—xo) + fy(xo, г/0. го)(у — уо) +
+ !'г (*о. Уо- г„) (г - г0) = 0, D3,3)
а нормаль к поверхности в точке М (х0, у0, г0)
х — Xq _ У—Уо _ г— г0 ,До л\
Гх(х<>. Уо, «о) f't,(xo, Уо, г„) П (х0, .у0, г0)" к°'^'
Символы f'x(x0, г/0> z0), f'v(x0, у0, г0), f'z(xu, у0, г0) означают
частные производные функции f (x, у, z) вычисленные для значе-
значений х = хй, у = у0, г = г„.
568
Задача 43,1. Найти уравнения касательной плоскости и нор-
нормали к поверхности г = х2 + Ъуг в точке, для которой х — I;
Решение. Прежде всего определим аппликату точки каса-
касания: гA,1) = 12 + 3 ¦ I2 = 4. Итак, точка касания имеет коорди-
координаты A, 1, 4), т. е. хо=1; уо=1; г0 = 4. Так как уравнение
поверхности разрешено относительно г, то касательная плоскость
и нормаль определяются уравнениями D3,1) и D3,2). Опреде-
Определяем частные производные функции г : г'х (х, у) = 2х; г'у (х, у) =
= 6//. Вычислим теперь значения частных производных в точке
касания: г'х(\, 1) = 2; г'у(\, 1) = 6.
Подставляя эти значения и координаты точки касания в урав-
уравнения D3,1) и D3,2), получим уравнение касательной плоскости
г — 4 = 2 (х — 1) + 6 [у — 1), или 2х + 6у — г — 4 = 0. Уравнение
х — 1 у—\ г — 4
нормали —g— = —g— = ——р •
Задача 43,2 (для самостоятельного решения). Найти уравнения
касательной плоскости и нормали к поверхностям:
1) к эллиптическому параболоиду г = 2х2 + уг в точке A,1, 3);
2) к поверхности z = xl+ 2x2y —xy-\-x в точке A,0, 2);
3) к гиперболическому параболоиду z — ху в точке A, 2, 2).
Ответ.
1) 4x + 2y-2-3 = 0;^=! = ^=-!- = i?^;
2) 5х + У - z - 3 = 0; ?р! = ^5 = i~ ;
^ j у 2 2 2
' ^ ~~ ' 2 ~ 1 ~~ —1
Задача 43,3. Определить уравнения касательной плоскости и
нормали к поверхности
х2 + У2 + г2 — 4л: + 6у — 8г — 1 = 0 в точке М A, 2, 2).
Решение. Здесь уравнение поверхности задано в неявной
форме (оно не разрешено относительно г), а потому касательная
плоскость и нормаль к поверхности определяется уравнениями
D3,3) и D3,4). Обозначим левую часть уравнения поверхности
через f(x, у, г), найдем частные производные этой функции и их
значения в точке касания М:(Р) , (|П и Ш) ,
\dxjM \ду]м \dzjM'
fix, у, г) = л;2 + у2 + г2 - 4л; + 6у - 8г - 1;
©„-*•*+•-«*
8- f^) _ 9 . 9 _ Я — —4
°' Uz/м ~ ~ 4"
569
Подставляя найденные значения частных производных и коор-
координаты точек касания в уравнения D3,3) и D3,4), получим урав-
уравнение касательной плоскости
—2(х — 1)+ 10B/ — 2)— 4(z — 2) = 0, или х — Ъу + 2г + 5 = 0;
уравнение нормали
х — 1 _ у —2 _ г —2
Г~~ — б ~~ 2 "
Задача 43,4 (для самостоятельного решения). Определить урав-
уравнения касательной плоскости и нормали к поверхностям в за-
заданных на них точках:
1) х2 + у2 — х + 2у + 4z — 13 = 0 в точке B, 1, 2);
2) x2 + 2y2-3z2 + xy + yz-2xz + 16 = 0 в точке A, 2, 3);
з) S+S+S=1 в точке (*°- у°' *«)•
Ответ.
x i у 2 г 3
xl
Указание к пункту 3). Воспользоваться тем, что -г
г2
Задача 43, 5 (для самостоятельного решения). Определить
уравнение той касательной плоскости к эллипсоиду — +1^ +
-f ?_ = 1) которая отсекает равные отрезки на координатных осях.
Указание. Воспользоваться уравнением, полученным при
решении предыдущей задачи. Отрезки, отсекаемые этой плоскостью
на координатных осях, равны: —; —; —.
хо Уо го
_ а2 б2 с2
По условию задачи —=— = — .
хо Уо ^о
Обозначив каждое из этих отношений через k, получим
а2 б2 с2
л0 fr > УО k ' k '
Так как точка (х0, у0, z0) — точка касания, то ее координаты
удовлетворяют уравнению поверхности, а потому, подставляя по-
полученные значения х0, у0, z0 вместо текущих в уравнение эллип-
эллипсоида, получим
Я2 б2 С2 I
—\- —\~ — = 1 a k == *Ь v (* ~\~ Ь2 -\- с^'
570
тогда
x» = ± /as + ft2 _|_ cs " Уо ~ ± ]/aa + ba + c2 ' ° ± l/
Подставляя этн значения в уравнение касательной плоскости к
эллипсоиду, полученное в предыдущей задаче, имеем оконча-
окончательно
x + y + z± }/~а2 + Ь2 + с2 = 0.
Задача 43,6 (для самостоятельного решения). В какой точке
эллипсоида ^ 4- р + \ = 1 нормаль к нему образует равные углы
с осями координат?
Указание. Из уравнения нормали к эллипсоиду, получен-
полученного в задаче 43,4, следует, что направляющие косинусы нор-
нормали равны:
где
а« + Ь* + с*
Из условия задачи следует, что
хо Уо го
aM 6M с*А '
ИЛИ
х0 = Aa2k; г/о = Ab2k; г0 = Ac2k,
где k — общее значение написанных выше отношений. Так как
точка М (х0, г/о. zo) — точка касания, то ее координаты удовлет-
удовлетворяют уравнению эллипсоида, а потому
A2a2k2 + A*b*k* + A4*k2 = 1; Ak = 4-
координаты точки, удовлетворяющей условию задачи,
а2 № с2
* ± ; ^ ± ; 2 ±
Задача 43,7. К поверхности х2 -\-Ъу2 -\- г2 — 1 провести каса-
касательную плоскость, параллельную плоскости 2х -\- 4г/ + г = 0.
Решение. Запишем уравнение поверхности в виде / (х, у, г) =
— х2 4- Зу2 + г2 — 1 = 0. Обозначим координаты точки касания
М через х0, г/0. zo- Определим значения частных производных
функции f(x, у, г) в этой точке:
i-
571
Уравнение касательной плоскости запишется в виде D3,3):
х0 (х — х0) + Зг/0 (у — ув) + 20 (г —20) = 0.
Так как точка касания М (х0, у0, г0) принадлежит поверхности,
то х* -f Зг/2 -f г* = 1 и уравнение касательной плоскости может
быть записано так:
хох + Ъуоу + zoz — 1 = 0 (А)
Из условия параллельности этой плоскости и заданной в условии
задачи плоскости 2х + Ay -\- z = 0 следует, что
^о _ %о _ ?о
2 4 1 -
Обозначая каждое отношение через k, получим, что
х0 = 2k; yo = jk; zo = k.
Подставляя эти значения в уравнение поверхности, получим:
Откуда & = + -т= и, значит,
Подставляя это значение в уравнение (А), получим оконча-
окончательно уравнение касательной плоскости:
Таким образом, оказалось, что условию задачи удовлетворяют
две плоскости.
Задача 43,8 (для самостоятельного решения). К поверхности
х2 + 2у2 + г2 = 1 провести касательную плоскость, параллельную
плоскости х — y+2z=0
Ответ, х— y + 2z± |/y =
ЧАСТЬ III
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ПО ИНТЕГРАЛЬНОМУ ИСЧИСЛЕНИЮ
И ИНТЕГРИРОВАНИЮ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Первообразная функция и неопределенный интеграл.
Свойства неопределенного интеграла. Непосредственное интегрирование.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Основной задачей дифференциального исчисления является
определение для заданной функции F (х) ее производной F' (х) ¦-¦=
= / (х) или ее дифференциала F' (x) dx = / (х) dx.
Обратная задача, состоящая в определении функции F (х) по
ее известным производной / (х) илн дифференциалу / (х) dx, пред-
представляет собой основную задачу интегрального исчисления.
Операции дифференцирования и интегрирования взаимно об-
обрати ы.
Определение. Первообразной функцией (короче: первообраз-
первообразной) функции f(x), определенной на отрезке [а, Ь], называется
функция F (х), определенная на том же отрезке и удовлетворяю-
удовлетворяющая условию
F' (х) = / (*) или dF (x) = f (х) dx. A,1)
Процесс нахождения первообразной функции для заданной
функции называется интегрированием.
Если функция F (х) является первообразной для функции / (х),
то и функция F(x) + C, где С — произвольная постоянная вели-
величина, также является первообразной функции f(x). Таким обра-
образом, если функция / (х) имеет первообразную, то она имеет их
и бесчисленное множество, причем все они отличаются одна от
другой только постоянным слагаемым.
Определение. При соблюдении равенств A,1) выражение
F (х) 4- С, где С — произвольная постоянная величина, называется
неопределенным интегралом функции f(x) и обозначается сим-
символом:
)dx. A,2)
Здесь знак j называется интегралом, / (*) — подынтегральной
функцией, а произведение f (x) dx — подынтегральным выражением.
575
Наличие в этой формуле произвольной постоянной величины С
объясняет, почему интеграл J / (х) dx называется неопределенным.
Равенство A,2) дает самый общий вид первообразной функции.
Вопрос о том, имеет ли заданная функция }{х) первообраз-
первообразную, решается основной теоремой интегрального исчисления:
Теорема. Если функция f(x) непрерывна в каждой точке
отрезка [а, Ь], то во всех точках этого отрезка она имеет пер-
первообразную, которая на этом отрезке также непрерывна.
СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. Если а — постоянная величина, то
A,3)
т. е. постоянный множитель можно выносить за знак интеграла.
2. Интеграл от алгебраической суммы конечного числа функ-
функций равен такой же алгебраической сумме интегралов от сла-
слагаемых функций
jf/i(x) + hW-A.(*I dx = jh(x)dx+$f2(x)dx-\h(x)dx. A,4)
3. d^f(x)dx = f(x)dx, / A,5)
т. е. знак дифференциала d и знак интеграла j , когда первый
помещен перед вторым, взаимно погашаются (иногда говорят
взаимно сокращаются нли взаимно уничтожаются).
= F(x) + C, • A,6),
т. е. знаки d и J взаимно погашаются также и тогда, когда
знак интеграла стоит перед знаком дифференциала, но в этом
случае к F (х) нужно прибавить произвольную постоянную.
Формулу A,6) можно переписать так; J F' (x) dx = F (х) -\- С.
5.[[f(x)dx]'=f(x). A,6а)
ОСНОВНАЯ ТАБЛИЦА ИНТЕГРАЛОВ
Во всех формулах под и понимается или независимая пере-
переменная, или произвольная функция любой независимой пере-
переменной, дифференцируемая в некотором промежутке.
Каждая из формул этой таблицы справедлива в любом про-
промежутке, содержащемся в области определения соответствующей
подынтегральной функции.
576
Интегралы, помещенные в таблице, называются табличными.
1. Jo-d* = C. , - A,7)
2. [du = u + C. ' A,8)
С un+1
(n — постоянная величина).
Частными случаями этой формулы являются следующие две:
4.
du
1
1
(п — постоянная величина; пф 1).
5-
6. ]? || +
7. Ja«d« = -]^- + C(a>0> a ^ 1).
8. ]eudu = e" + C.
9. j sin «d« = — cos и + С.
10. j cos udu = sin ы + С.
11. ]tgudu = — ln|cos«| + C.
12. J' ctg «du = In | sin и \ + C.
13- i
16.
19. j sh udu = ch« 4-C.
20. J ch udu = shu + C.
A,11)
A,12)
A,13)
A,14)
A,15)
A,16)
A,17)
"A.18)
A,19)
d.20)
A,22)
0.23)
A,24)
A,25)
A,26)
577
Таблицу формул читатель должен выучить наизусть. Это и
следующие два практические занятия отводятся для непосред-
непосредственного интегрирования, not, которым понимается вычисление
интегралов с помощью таблицы основных интегралов. Навыки
интегрирования приобретаются опытом, а потому рекомендуется
решить как можно больше задач.
1. Упражнения в применении формул A,9) — A,12)
Перепишем формулу A,9) в виде, который более удобен для ее
практического применения.
Если и есть функция независимой переменной х, то du =
= и' dx, и формула A,9) перепишется так:
пи> dx = ?1 + с (л ф -1). A,29)
Следует обратить внимание на подынтегральную функцию
и"и'. Здесь л-я степень функции и умножается на и' — на про-
производную основания степени и. Эта формула верна только при
наличии множителя и'. В правой части формулы функция и на-
находится в степени л + 1, т. е. в степени, на единицу большей,
чем под знаком интеграла, и ип+1 делится на ее показатель сте-
степени л+1. Оговорка п ф—1 существенна, так как если л =
= —-1, то л + 1 = 0, и тогда в правой части формулы знамена-
знаменатель равен нулю. Когда л =—1, следует пользоваться формулой
A,12). В случае, когда и — независимая переменная (например,
х), и' = 1 и формула A,29) переписывается в виде
+ C. A,30)
Первые упражнения связаны именно с этой формулой.
Задача 1,1. Вычислить интегралы: 1) jjxdx; 2) §x3dx;
3) jjx5dx; 4) S^Vxdx; 5) \Ухгйх; 6) I y^ и самостоятельно
проверить дифференцированием полученные результаты.
Решение. По формуле A,30) находим:
^- + C; 2) §x*dx = -?- + C; 3) ^хЫх = ~ + С;
з
4) §Vxdx = §x2dx=^- + C = Yxy* + C' 5)
? +
578
В пятом примере проверка дает
Как и следовало ожидать, мы получили, подынтегральную функцию.
Задача 1,2. Вычислить интегралы: 1) | 7хъйх\ 2) ( З^хЧх;
3) \-^dx; 4) \-й^дг; 5) \ 5dx, и проверить дифференцированием
полученные результаты.
Решение. 1) Вынося за знак интеграла постоянный множи-
множитель 7, получаем: J 7лг5Лк = 7 J Л/* = 7 • ¦— + С;
7
2) Гз V**d* = 3 |*П& =^ 3 ^- + С = у хУх~3 + С;
Т
3) ^±dx =
Замечание. Можно было сразу применить формулу A,10),
положив в ней и = х, du = dx, n = 2.
4)
(см. замечание к предыдущей задаче);
5) ^5dx = 5^dx = 5x + C
(применена формула A,8), в которой взято и = х).
Задача 1,3. Вычислить интегралы: 1) \ (х3 — З*2 + 5* — 4) dx;
Указание. При решении этих примеров следует применить
формулу A,4), выражающую правило интегрирования алгебраиче-
алгебраической суммы, и формулу A,30).
При вычислении интеграла от суммы нескольких функций сумму
произвольных постоянных, которая при этом получается, заме-
заменяют одной произвольной постоянной, обозначаемой обычно бук-
буквой С.
Ответ: 1) ~ — х3 + 5~ — Ах + С;
2) tVx-*-±.±-8Vx-l4Vx* + C.
579
Замечание. В этом примере при вычислении каждого инте-
интеграла можно сразу воспользоваться формулой A,Ю), заменив в ней
и на х.
Задача 1,4 (для самостоятельного решения). Вычислить ин-
интегралы: 1) \У~хйх\ 2) \Vx™dx\ 3) J (ax2 + bx + c)dx.
Ответ. 1) _*/* + С; 2) —^хУ*" + С; 3) т +-у +
+ а: + С.
Задача 1,5 (для самостоятельного решения). Вычислить ин-
]{( )
«гралы: .) ][±-Г'+ +
Ответ. 1) 15f* —-J
О
21
4 л4
о 1С о f Гл« — 3x2 + 5i/"x — 7л; + 6 ,
Задача 1,6. Вычислить интеграл /= 1 ¦—— !—ах.
J ¦ Ух
Решение. Для вычисления интеграла следует разделить мно-
многочлен, стоящий в числителе, на знаменатель. Если это выпол-
выполнить, то получится, что
=
— Зд;3 +5-7л;5 + 6д; 3)йх = ±х3 — ~х3 + 5х —
J + 9x + C = \Tx(lx-jX + bV'x-jX + 9) + С.
Задача 1,7 (для самостоятельного решения). Вычислить ин-
тегралы: 1) f C*-5)»<fc; 2) Г
J
Ответ. 1) ул;7 —27д;б + 75^
Задача 1,8. Какая функция имеет производную 5л:а — 7л:+ 4
и принимает значение, равное 3, при х= 1?
Решение. В задаче требуется найти функцию, для которой
известна ее производная, т. е. требуется найти первообразную
функцию для функции 5л:2 — 7л: + 4.
Из бесчисленного множества первообразных, которые имеет
эта функция, следует отобрать ту, которая равна 3 при х = 1.
580
Если F (x) — какая-нибудь первообразная функция, то в самом
общем виде она на основании формулы A,2) запишется так:
F (х) + С = J Eх2 — 7х + 4) dx;
В условии задачи дано, что F(l)—3, для того чтобы опре-
определить произвольную постоянную. Полагая в последнем равенстве
jc=1, a F (\) = 3, получаем
отсюда С=—g-. Тогда F (х) — 7Г = 1ГЛ:3— -jxiJr^x> а искомая
функция F (х) = -| х3 — ~ х2 + 4х + ~ .
Таким образом, мы нашли функцию F (х), производная кото-
которой равна 5хг — 7х -\- 4, и кроме того F A) = 3.
Задача 1,9 (для самостоятельного решения). Какая функция
имеет производную Зх2 + 2л: + 1 и принимает значение, равное 2,
при х = О?
Ответ. Искомая функция F (х) — х3 + х2 + х -f 2.
Задача 1,10 (для сайостоятельного решения). Какая функция
имеет производную 5—9л: + 4л:2, если известно, что при л:=2 эта
функция равна ,50?
9 4 142
Ответ. Искомая функция F (х) — Ъх — -j х2 + -j х3 + -у •
Задача 1,11 (для самостоятельного решения). Вычислить ин-
интегралы:
2)
J
Указание. В первом интеграле числитель сначала возвести
в куб, полученный многочлен разделить на J/x и после этого
проинтегрировать. Во втором интеграле в числителе перемножить
з
многочлены, произведение разделить на у х2, после чего выпол-
выполнить интегрирование.
Ответ. 1) 2yrx + 3x + 2xVx + ~ + C;
2) |j|
Задача 1,12. Вычислить интегралы: 1) ] (х2 + 5I2хdx;
2) j (Зл-3 + 5л-2 — 8) (9л-2 + 10л-) dx; 3) J /л^Тб • 2л: dx;
4) |Bл-а+ 7Kл-^л-; 5) ^7s~+8x2dx; 6) \Va? — x2xdx.
581
Решение. Все эти примеры решаются с помощью формулы
A,29). Прежде чем применять ее, надо выяснить: 1) какую из
функций, стоящих под интегралом, следует принять равной и и
2) есть ли под интегралом множитель, равный и'.
1) В первом примере следует взять и — х2 + 5. Множитель 2х
является производной функции и, так как (х2 + 5)' = 2х. Поэтому
на основании A,29) при л = 7 имеем
Г (хЧ^O • 2х dx = (lfi + 5)8 + С.
Если бы подынтегральная функция не содержала множитель 2х,
то применить формулу A,29) было бы нельзя. В этом случае сле-
следовало бы вычислить по формуле Ньютона (х2 + 5O и интегриро-
интегрировать полученную сумму функций.
2) Пример второй решается аналогично. Считая, что и = Зх3 +
+ 5л:2 — 8, и замечая, что множитель 9л:2 + Ю* есть производная
функции и, а п = 3, по формуле A,29) находим
dx =
Здесь опять-таки отметим, что наличие множителя 9л:2 -f Юл:,
который на первый взгляд осложнил подынтегральную функцию,
на самом деле облегчило интегрирование, так как если бы мно-
множитель 9л:2 -f- Юл: отсутствовал, то для вычисления интеграла
следовало бы возвести Зх3 -f- 5л:2 — 8 в куб, что потребовало бы
значительно больших выкладок.
3) Этот пример также легко решается, так как подынтеграль-
подынтегральная функция имеет вид ипи'. Действительно, полагая и = хг + 6,
мы замечаем, что множитель 2х равен и', п = у, а потому
Если бы подынтегральная функция не содержала множитель
2л:, то вычисление интеграла j Yx* + 6 dx потребовало бы значи-
значительно большей работы. Еще раз напоминаем читателю, что фор-
формула A,29) применима только тогда, когда подынтегральная функ-
функция имеет вид и"и' или может быть преобразована к этому виду.
582
4) В этом примере подынтегральная функция равна Bл:2 + 7Kх
Если принять, что и = 2л:а -f 7, то и' = 4л:. Множитель 4л: отсут-
отсутствует под знаком интеграла, а потому подынтегральная функция
не имеет вида и"и'.
К такому виду мы легко придем, если запишем подынтеграль-
подынтегральную функцию в виде -у Bх2 -f 7K 4л:, т. е. если умножим и раз-
разделим подынтегральную функцию на 4, отчего ее значение не
изменится. При интегрировании постоянный множитель -j- выне-
вынесем за знак интеграла и применим формулу A,29). Имеем
РBх2 + lfxdx = \ ГBл*+ 7)! •**dx = \B*2 + 7L + С =
16v ~ ' '
В этом примере подынтегральная функция не имела вид ипи',
но умножением на постоянную величину легко была к нему при-
приведена.
5) Подынтегральная функция в этом примере может быть за-
I
писана так: (л? + 8Kл:а. Если принять и ¦= х3 + 8, то и' = Зл:а.
У нас же вместо множителя Зл:а есть множитель л:2.
Умножим на 3 подынтегральную функцию. Чтобы она не из-
изменила своего значения, разделим ее на 3 и получим -^(х3-^
-\- 8K Зха. При интегрировании множитель -=- вынесем за знак
интеграла, а под интегралом окажется выражение вида ипи'
(п — -Л. Применяя формулу A,29), получаем
4-+1
J
= 1 С(х* + 8)т • 3x*dx = 4-(ж3 + 8) h С =
1 • . • т — j 1
+
6) В этом примере опять-таки придется преобразовать подын-
подынтегральную функцию так, чтобы она приобрела вид ипи. Пред-
Представим ее в виде (аа — х2J х. Если принять, что и = а2 — х2,
то и' — —2х. Значит, чтобы под знаком интеграла был множи-
множитель —2х, подынтегральную функцию надо умножить на —2.
583
Выполняя это умножение и деля одновременно на —2, получаем:
- 1 -
(а2 — хгJ х = —2"(°2 — *aJ (—2лг). При интегрировании множи-
множитель —к вынесем за знак интеграла, тогда под интегралом ока-
окажется выражение вида ипи' и формула A,29) может быть приме-
применена. Записи расположатся так:
г* \ J i
/ Y\ П 1*=: —
Г УсР — хех-dx = — ~Г (аа — л-V • (—2
1 /Д
= — v(aa — x2)Va* — л-а + С.
3
Задача 1,13 (для самостоятельного решения). Вычислить инте-
4
тралы: 1) |Eл- +4L?/л-, 2) J(9 + 7x*)*xdx; 3) J (8axa + 9bx3)T x
X A6ал- + 27йл:а) с/л:; 4) J ]Лл:а + 8л: Bл: + 2) ^л:;
Указания. В пятом интеграле: - — G + л:3) 2л:а =
-^GЧ^Гт-Зл_а.
и и'
J_ J_
В шестом интеграле: Y\—х = A — л:J = — A—хJ •(—1).
Ответ. 1)^Eл- + 4M + С; 2) 1 (9 + 7я*)' + С;
3 ]_
3) у (8ал-а + 96л?K + С; 4) -I Dд;а + 8л;) Vх 4л;а + 8х + С;
5) %уГ+# + С; 6) _1A_
Задача 1,14. Вычислить интегралы: 1) j 81
2) JcosM*sin4^; 3) \^ ; 4) J^dr, 5)
6) j tga x seca л: t/л:; 7) J >^
Р 1 П
Решение.. 1) Подынтегральная функция имеет вид и"и'.
Действительно, если и = бшл:, то и' = соэл:, п = 3. Поэтому, при-
применяя формулу A,29), имеем
dx = ^^ + С.
sin3x • cos л:
584
2) В этом примере подынтегральная функция cos5 Ax sin 4л: не
имеет вид ипи', так как если и = cos 4л:, то и' = —4 sin 4л: (п—5).
Значит, недостает множителя —4. Умножая и деля на —4 и вы-
вынося — -J- за знак интеграла, получим:
I cos5 4л: sin 4л: dx = — -j- I cos5 4л: • (—4 sin 4x) dx =
Us /
u
1 cos" 4x . ~ 1 ,, , „
= — -—— + С = — ^cos6 4л- + С.
3) Представим подынтегральную функцию в виде Dл? -f 9)~4л:а.
Возьмем и = Ах3 + 9, тогда и! = \2х2, (п = —4). Чтобы подынте-
подынтегральная функция приобрела вид ипи', её надо умножить на 12.
Умножив и разделив полученное выражение на 12, вынесем мно-
множитель j2 за знак интеграла. Тогда получим
С.
36 Dл;3 + 9K
4) Представим подынтегральную функцию в виде arctg^ x
X , _. а. Положив ы = агЫ?л\ получим ц' = . 7 а. и подынте-
гральная функция будет иметь вид ипи' (п — 3). Поэтому без
дополнительных преобразований можем применить формулу A,29).
Найдем
Г
J
, , 1 , arctg4 х „
arctg3л- • rq—idx = —f- +C.
4
5) Запишем подынтегральную функцию в виде ят~5л:созл:.
Возьмем u — sinx, тогда, w' = cos;e. В таком случае без всяких
преобразований подынтегральная функция имеет вид и"и', а по-
потому на основании формулы A,29) получаем
sin * х . /-. 1 1 . г,
6) Положим, что и = tgx, тогда и' — зес2л: и подынтегральная
функция имеет вид и"и' (п = 2), никаких дополнительных пре-
преобразований делать не требуется. На основании A,29) сразу по-
получаем
tg^ • sei
7) Представим подынтегральную функцию в виде cos3
п
Возьмем и = cosх, тогда и' — —smx, я — —-. Чтобы получить
585
под знаком интеграла выражение вида ипи', но не изменить вели-
величину подынтегральной функции, умножим и разделим ее на —1.
По формуле A,29) получаем
2 —
I i/cos2 х sin х dx = — I cos3 x ¦ (—sin x) dx = —cos * -\- С =
i- "" 3
,3
2* -f- C.
О
Решим еще одну аналогичную задачу.
Задача 1,15. Вычислить интегралы: 1) I — dx;
2) [У^Щь- 3) f *L; 4)
' J Г 1 — х2 ' ' J х In4 л: ' ;
-. Г sin л j сч С sin л: cos л: ,
5) I . -.dx; 6) I у - dx.
' J /5 + cosa; J /3 —sin2x
Решение. 1) Представим — в виде Aпл:) —. Полагая и —
= In х, получим и' — —. Подынтегральная функция — приобре-
приобретает вид ипи' (п = 1), и тогда [~^dx = Г In* ¦ ^dx = l-^
и
1
Считая, что u = arcsin*, имеем ».' = — ш а потому по
V * х
формуле A,29)
arcsin х, С . . .-к- 1 . (arcsinxJ , ^
-j—^- d* = (arcsin *J—==. dx = v—x—^— + С =
= -я- arcsin * У arcsin * + C.
3) Выражение . 4 = (Inx)~4 •—. Если положить ы = In*, то
. 4 = (Inх) •
егральная функци
ипи (п = —4), а потому по формуле A,29)
и' — —, и подынтегральная функция Aпя)~4-— приобретет вид
X X
586
4) Подынтегральную функцию,. можно преобразовать так:
-¦ * = 4- A + *а)~ Г2х. Положим, что и = 1 + хг, тогда и' =
у \ -\-хг 1
= 2х. Если -н- вынести за знак интеграла, то подынтегральная
функция примет вид ипи' и формулу A,29) применить можно:
2
U 2
При решении этого примера можно было сразу воспользоваться
формулой A,11), переписав подынтегральную функцию в виде
du и' dx
Уи~~Уи '
Тогда
" '^ = 2Уп+С. A,31)
и
Заметьте, что числитель дроби под знаком интеграла равен
производной функции, стоящей в знаменателе под квадратным
корнем. Если положить и = 1 + *а> числитель дроби переписать
в виде х — -н- * 2х и вынести -=- за знак интеграла, то окажется,
что числитель дроби равен производной функции, стоящей в зна-
знаменателе под квадратным корнем. На основании формулы A,31)
5) Подынтегральную функцию перепишем так:
j f cos x
—sin*
-r— = . Теперь числитель дроби равен производной функ-
V 5 -[- cos х
ции, стоящей под корнем в знаменателе. Поэтому на основании
формулы A,31) имеем
f sin* , С —sin* , л,/=—; , „
1 , ах = — I f : ах = —2 ]/ 5 -f cos x + С.
J /5+ cosх J /5 + cosх ^ ^
6) Принимая ы = 3 — sinajc, получаем, что и' — —2sinxcosx.
Переписываем подынтегральную функцию в виде sin x cos - =
уз — sin2 х
1 —2 sin д: cos л; ^ , ,, „,.
= —^ . ==¦. Теперь мы можем применить формулу A,31),
так как числитель второй дроби является производной функции,
стоящей в знаменателе под квадратным корнем:
С sin х cos x , 1 С—2 sin x cos x , i n,^s r-r-
I .r dx = — _L ¦,., - dx = -T--L • 21/3 — sinaA: +
J /3 —sin2x 2J /3 —sin^A; 2 K
+ С = —1/3 — sin2A: + С
587
Ниже предлагаются для самостоятельного решения десять
примеров на применение формул A,29) и A,31).
Задача 1,16 (для самостоятельного решения). Вычислить ин-
,, С cos х , п. Г l/^ln а: , оч С х3 dx .ч С arcsin3 x ,
тегралы: 1) j -^dr. 2) j У-^ dx; 3) j F=; 4) J y—^dx;
Ответ. 1) — -i-cosec6* + C; 2) -| In л:V\nx + C;
C; 4) i- arcsin4* -f C;
6) 2
Чтобы закончить это практическое занятие, нам остается вы-
выполнить упражнения на применение формулы A,12). Полагая,
что и есть функция независимой переменной х: и = и (х), a du =
= и' dx, эту формулу можно переписать в виде, более удобном
для применения:
'-Лс = 1п|и| + С. A,32)
Следует обратить внимание на подынтегральную функцию — :
числитель дроби является производной ее знаменателя, а перво-
первообразная функция равна натуральному логарифму абсолютной
величины знаменателя. Если и = х, то и' = 1, и формула A,32)
запишется так:
A,33)
Задача 1,17. Вычислить интегралы: 1) 1 —?-;
^ dr.
dx с. С dx _. Г х2
6)j; 7)J
588
Решение. 1) Подынтегральная функция —, дробь, числи-
л —J— С*
тель которой является производной знаменателя (х + а). Дробь
имеет вид —, а потому на основании формулы A,32) интеграл
равен натуральному логарифму абсолютной величины знамена-
знаменателя
С dx , . , с
J х-\-а — п\х -т~ \-г
2) И в этом примере подынтегральная функция — дробь, числи-
числитель которой есть производная знаменателя: и = х2 + 5, и' = 2х,
дробь имеет вид — , формула A,32) может быть применена:
Здесь х2 + 5 не следует писать под знаком абсолютной вели-
величины, так как хг + 5 > 0 при любом действительном значении х.
„. _, , sin д:
3) Стоящую под знаком интеграла дробь t . cos x можно пре-
преобразовать так, чтобы ее числитель стал равным производной
знаменателя.
„ „ sin х —sin x j-, ,
Действительно, jqrESil = "~ i -f-cos х • Если " = J + cosx< TO
и'— —sin л:, дробь имеет вид ^, формула A,32) применима и
—sin x j i i i
& lnl1
V J Oy
4) Дробь j—-2 = — у • у—^ . Если и = 1 — x*, то и' = —2х,
и числитель второй дроби равен производной знаменателя. Эта
дробь имеет вид —. Поэтому по формуле A,32)
5) Чтобы преобразовать дробь -^Гх к ВИДУ \ • перепишем ее
1 j -
так: я—у = —т, • Если знаменатель дроби а — х = и, то и' =
= — 1, числитель дроби равен производной знаменателя, и по
формуле A,32) получаем
hi^ 1п|а—*| + C.
589
1 X
6) Перепишем подынтегральную функцию в виде —;— = j—
Если взять и = 1п х, то и' — —, и числитель дроби равен произ-
производной ее знаменателя. Поэтому на основании A,32) имеем
7) Подынтегральную функцию можно преобразовать так, чтобы
ее числитель был равен производной знаменателя: *». =
1 9л:2
= "э" 4 -I- Зх3' Принимаем, что и = 4-\-Зх3, тогда и' = 9хг. Вторая
дробь имеет вид ^, и по формуле A,32) получаем
8) Дробь -р4 рациональная, неправильная: степень ее чис-
лителя равна степени знаменателя. С помощью деления можно
из этой дроби выделить целую часть. Действительно, если раз-
разделить х на дс+1, то получится 1 -т-у. Таким образом,
(применены формулы A,8) и A,32), при вычислении второго ин-
интеграла учтено, что числитель дроби 1 равен производной знаме-
знаменателя дроби).
9) Если и = 5 + ех, то и' = ех. Дробь имеет вид —, и по
формуле A,32) получаем
(так как при любом значении х имеет место неравенство: 5 +
+ е* > 0, то выражение 5 -f- ex мы не поставили под знак абсо-
абсолютной величины).
X3
10) Дробь —рз — неправильная, так как степень числителя
больше степени знаменателя. Чтобы выделить целую часть, раз-
делим х3 на х + 2 и получим —т-х = х2 — 2х-\-4 т-х, а по-
X —— ? X —— ?>
тому
590
В этом примере вместо деления х3 на х -(- 2 можно было пред-
представить дробь в таком виде: '
х3 х3 4- 8 — 8
jc-f-2
Аналогично в восьмом примере дробь ~- == *|~ = 1 —
1
Задача 1,18 (для самостоятельного решения). Вычислить ин-
.. (' dx о\ Г х&х о\ Г ^*
тегралы: 1) ^пг^'. 2) 2_fr22; 3) ¦
A -f х2) arctg л:',
4) Г—^-—; 5) Г- ,s'n-y dx; 6) Г-т=
; \ cos2 xtgj;' ' 15+7 cos х ' li/i
Jf2 arcsin x
11) Jtgjcrfjc; 12) ^ctgxdx.
Ответ. 1) iln|a + 6jc| + C
2) —^inla1 —6»*«| + C; 3) In | arctg x \ + C;
4) lnltgjcj + C; 5) -¦
6) In | arcsin л: i 4-С (хфО); 7) — ln| 1 — ln*| + In С = In! j
8) — ~ In 162 cos2 x 4- a21 4- C; 9) —4-C-4-^
10) --^ — ^In12дг + 31 + C; 11) -In|cosa;| + C; .
12) In | sin x | + С
ВТОРОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Интегрирование показательной и тригонометрических
функций.
На этом практическом занятии мы проведем упражнения в не-
непосредственном интегрировании по формулам A,13) — A,20).
1. Интегрирование показательной функции (упражнения в при-
применении формул A,13) и A,14)).
591
Придадим этим формулам вид, который более удобен для при-
применения их на практике: считая и функцией независимой пере-
переменной х: и = и (х), запишем, что du = и' dx, а потому формулы
A,13) и A,14) перепишутся в виде:
V dx = е- + С. B,2)|
Здесь следует обратить внимание на то, что подынтегральная!
функция в этих формулах содержит множитель 'и', являющийся ц
производной функции и, стоящей в показателе степени. Без этогоЦ
множителя формулы B,1) и B,2) не верны. Если х — независимая!
переменная, т. е. и = х, то и' = 1, формулы B,1) и B,2) пере- j
пишутся так:
+ С (а > 0, а Ф 1); B,3)
' dx = ех + С. B,4)
Задача 2,1. Вычислить интегралы: 1) J3*dj*:; 2) \{V2)K dx;
3) J4-Mjt, 4) \e~xdx; 5) §23Xdx; 6) j e5x dx.
Решение. 1) Этот пример не требует пояснений. Он решается
непосредственным применением формулы B,3). Полагая в ней
а = 3, получаем f 3* dx = т^ + С.
J 1П О _
2) Точно так же полагая в B,3) а — Y%, получаем, что
3) Этот интеграл не может быть вычислен по формуле B,3),
так как в показателе степени стоит не х, а —х. Поэтому обра-
обратимся к формуле B,1). Перепишем подынтегральную функцию
в виде 4~х = —4~х - (—1). Такое преобразование нам понадобилось
для того, чтобы ввести множитель —1, который является произ-
производной от показателя степени —х. Теперь уже подынтегральная
функция содержит производную от показателя степени, и мы
получаем при а = 4, полагая, что и = —х:
J 4~х dx^^ —4~х (— 1) dx = — J <Г* ¦ (—1) dx = — -^ + С.
4) Запишем, что е~х — —ё~х (—1) и применим формулу B,2).
Полагая в ней и = —х, имеем
^ • (—1)dx = — е~л + С.
" и'
592
5) При решении этого примера формула B,1) не может быть
применена, так как подынтегральная функция не содержит мно-
множителя и', являющегося производной от показателя степени и =
= Зх. Но так как и' = 3, введем такой множитель, умножив
и разделив подынтегральную функцию иа 3. Тогда можно будет
применить формулу B,1): 23* = -|- • 23* • 3. Поэтому
а" и'
6) Поступая так же, как в предыдущем примере, получаем
по формуле B,2)
Задача 2,2. Вычислить интегралы: 1) fa**dr, 2) \
3) (V'-^dj*:; 4) f *»• * sin x dx; • 5) (V'xdx; 6) (V'jkMjt,
7) Г2<е*Бес*л:^д:; 8) Г е-^+*+3) Cjcs -f 1)^; 9)^e~^dx;
10) J" (e^ + е-*)" ^лг.
Решение. 1) При вычислении этого интеграла следует иметь
в виду, что к-—любое действительное число. Подынтегральная
функция акх не содержит множителя и'. Если и = кх, то и' =k.
Чтобы ввести этот множитель, перепишем подынтегральную функ-
функцию так: в** = -г d"k. Поэтому
2) Применим рассуждения, проведенные в предыдущем при-
примере: е** = -г- е^к, а потому
J<
dx = -!s-\ekx ¦kdx = ^ekx + C.
и и'
Этот результат полезно запомнить. Зная его, сразу получаем,
X X
С CДесь k = ~Т. Т
что например, (V*dj*: = ~е?* + С; [e%dx = 2е% + С ^здесь к
= Т' Т = 2) ;
= —3J, и т.,д.
20 И. А. каплаа 593
3) Здесь показатель степени и — Ух, и' — —-^. Подынте-
2 ух
гральная функция вместо этого множителя содержит множитель -у= ¦
Умножая и деля на -_-, получим 5 —т= = 2 ¦ 5 • —гт=-> а п0"
1 ух 2 ух
тому по формуле B,1) при а = Ъ
4) В примере и — cosa:; и' — —sin л:. Значит, недостает множи-
множителя —1. Подынтегральную функцию представим в виде е008 * sin x =
_—ecosx(—sinx), поэтому по формуле B,2)
f е008 * sin л: с/д: = — f е008 * (—sin x) dx = —ecos * + С.
5) Здесь и = х*\ и' = 2х.
Подынтегральная же функция содержит множитель х. Умно-
Умножая и деля ее на 2, запишем, что 7х'х = -_• • 7*г ¦ 2х, a I 7x'xdx —
7" и'
6) В этом примере функция ы = лс3, ее производная ы' = Зле1.
Подынтегральная же функция содержит множитель л:2. Умножая
и деля ее на три, получим ех'х2 = -5- ex"ix2. По формуле B,2) на-
О
ходим
[ i f С.
= i. f **• . 3?de = j^
7) Этот пример решается без предварительных преобразований,
так как множитель sec^— производная от функции u = tgx —
входит в подынтегральную функцию. По формуле B,1) при а = 2
получаем
2tg*
'г* • sec2xdx = т-тг + C. .
2u и'
8) Полагая здесь и = —(х3 + х +- 3), имеем и' = —(Зле2 + !)•
Вместо этого множителя подынтегральная функция содержит мно-
множитель Злс2+1- Чтобы получить требуемый множитель и', под-
подынтегральную функцию представим в виде e~(*3+*+3) (с$*2 + 1) =
= — е-<*"+*+3> [—C*2+ 1)] и на основании B,2) получим
j) dx = _ j e-u'+x+D [—(За;2 + 1I d* =
U'
= —e-<Jr'+Jf+1' + С.
594
9) Здесь функция и = —, ее производная и' = — -^. Подын-
- 1 -/ 1\
тегральную функцию перепишем в виде ех • ~г ~ —ех I — -^], и
по формуле B,2) найдем
10) {е* + е~хJ = е2к + 2 -f e~2*. Учитывая решение второго при-
примера, получаем
J (в* + e~xf dx = § (e2X +2 + е<) dx = j e2* djc + J 2 dx +
i- «¦« + 2a; - -i- e~2C + С
Задача 2,3 (для самостоятельного решения).
Г Г earcsin х
Вычислить интегралы: 1) I (е — e~ks) ds; 2) I , dx;
3) j e8 *cosjtdj»:; 4) j (e» + 2Ke~ 7 dA;; 5) j 9*'+в*'+з^ (д;«+4д:+1) dx;
dx'< 7) 1 (^ + е"ОДK dy' 8) 1 I
9)
Ответ. 1) ^((** + e-ks) + С; 2) е>"Ып* + С; З)
4) -i eT " + ~ е~2 Х + 144^ * — 32е~ т + С; 5) ^ • 9^3
— е-ау) + С; 8) -i-earcte2* + C; 9) l
2. Интегрирование тригонометрических функций (упражнения
в применении формул A,15) — A,20).
Полагая, что функция и, входящая в эти формулы, есть функ-
функция независимой переменной х: и = и(х), и заменяя дифференциал
2D* 595
этой функции du по формуле du = и' dx, формулы A,15) — A,20)
можно переписать в виде более удобном для практики:
Jsinu •u'dx = — cos u + С; B,5)
\ cos и • и' dx = sin и + С; B,6)
J tgи • и'dx = — In | cosu | + С; B,7)
g«-u'd* = ln|sinu| + C; B,8)
Следует обратить внимание на то, что множитель и', входящий
в подынтегральную функцию во всех этих формулах, есть произ-
производная от той функции и, которая находится под знаком тригоно-
тригонометрической функции. Если и — независимая переменная, и — х,
то «' = 1, и эти формулы перепишутся так:
jsin*d* = ~-cosat + C; B,11)Jctg*dx = ln|sinx|+ C; B,14)
B,12) j-l-^ = tg* +С; B,15)
; B,13) ^jr^dx^-ctgx + C. B,16)
Задача 2,4. Вычислить интегралы: 1) j sin tnxdx; 2) J cos nxdx;
. 5)
Во всех примерах буквы т, п, р, q, k и / — величины постоян-
постоянные, не равные нулю.
Решение. 1) Формулу B,5) можно применить в том случае,
если подынтегральная функция имеет множитель и', являющийся
производной от функции, стоящей под знаком синуса.
В нашем случае функция и = тх, а ее производная и' = т.
Множитель т в подынтегральной функции не содержится. Умно-
Умножим и разделим подынтегральную функцию на т, т. е. предста-
представим ее в виде sin/шс = — sin тх - т; тогда, вынося постоянный
множитель — за знак интеграла, по формуле B,5) получим
I sin tnxdx — — I sin тх ¦ m dx = cos mx 4- С
J m J . , , m
и и'
596
2) Повторяя те же рассуждения, что и при решении первого
примера, получим по формуле B,6)
\ cos nx dx ~ — \ cos nx ¦ п dx — — sin nx + С.
J п j —- _ п
и и'
На основании этих результатов легко вычисляются, например,
такие интегралы: I sin 2xdx — —г- cos 2x + С; \ sin ¦— dx =
= \-cos~ + C = — 3cosi- + C (здесь м-у; и' = у);
Т
f cos V2x dx = 4= sin V2x + C; \ cos Ax dx = j sin Ax + C;
jcos^-d^-msin-^ + C (здесь И = Л; «' = 2.) .
3) Здесь w = ^jc; и' = k. Подынтегральная функция не содер-
содержит множителя k. Чтобы можно было применить формулу B,7),
преобразуем подынтегральное выражение так, чтобы оно содер-
содержало множитель k: умножим и разделим его на k и представим
в виде tg kx = у tg kx • k. Теперь на основании B,7) получаем
\ tg kx dx = ~ \ tg kx ¦ kdx = — ~ In | cos kx \ + C.
и и'
4) Повторяя рассуждения, проведенные в предыдущем примере,
получаем по формуле B,8)
J ctg lx dx = у ctg lx- dx = у In | sin /д; | + C.
Используя результаты, полученные при решении этого и преды-
предыдущего примера, легко вычислим такие интегралы:
Jtg2xdje=.—-J-ln|cos2x| + C; J tg-g-Ле = —51
Jctg3xdx = jln|sin3j»:| + C; [ctg~dx = a In
cos ~
sin —
ctg yd* = 7 In
sin-й- +C.
C;
5) По формуле B,9) получаем
1
dx = —
и
597
(подынтегральную функцию мы умножили и разделили на р,
а постоянный множитель — вынесли за знак интеграла), поэтому,
^пример, J__= tg3x + C; —-=6tgT
Jcosг
п * , п Г dx
=6tgT + C; -
cos-г J
7!
6) На основании формулы B,10), повторяя рассуждения, про-
проведенные при решении предыдущих примеров, получаем
dx = -
q
-^J— qdx = —-ctgqx
sm2 qxZ. ' q
sinz qx q
~— u'
и
(подынтегральную функцию мы умножили и разделили на qt
а постоянный множитель — вынесли за знак интеграла). Полу-
Полученный результат позволяет легко вычислить, например, такие
интегралы:
J
у рр
: J -r^ dx = —j ctg 5x + С; I —х— = —4 ctg ~ + C;
sin2 -г-
Ь
Задача 2,5 (для самостоятельного решения). Вычислить инте-
i\ Г dx о\ Г
гралы: 1) ]г^5Гх; 2)
Указания. 1) 1—cosx = 2sin2-=-; 2) 1 + cosx = 2cos2-g-.
Ответ. 1) -ctg-J + C; 2) tg| + C.
Задача 2,6 (для самостоятельного решения).
Вычислить интегралы: 1) \ s\r\ (х2)xdx; 2) \ cos ?-*dx;
3) jtgB*-3)d*; 4) Jsin(lnjc)ldx; 5) J^? + fc) i
6) fcos(e*)e*dje; 7) f cos (In x) — dx; 8) f. .dx. - ; 9) *" rfj;
J J * J * -j- sin *
in2* Cos2*'.
1 1 — sin *
Указания. В восьмом примере: .-
1 — sin* 1 sin*i
cos2 * cos2 * cos2*'
r> 1 sin2 * + cos2 * 1 , 1
В девятом примере: -г-; ^— = —. , „— = —=—\- -г-?—.
r r sin2 * cos2 x sin2 * cos2 * cos2 * ' sin2 *
Ответ.
1) _1cosjc2 + C; 2) 2sinVx + C; 3) — -I In | cos B* — 3)| + C;
4) -cos In 1 x j+C; 5) 1 tg (ax + b) + C; 6) sin (e*) + C;
7) sin 1п|лг| + С; 8) tgjt — sec* + C; 9) tgjt — ctgx + C;
10) —cosec л:-f C.
Задача 2,7 (для самостоятельного решения). Вычислить инте-
интегралы:
2) [r-^jy; 3) \^dx; 4)
5) f^d*; 6) [s^pdx; 7) fc-^^; 8) [^ dx;
' J sin2 л: ; J cos2 j; ' 7 J sin2 x ' > J cos2 * '
9) J cos (ax+b) dx; 10) J ctg* xdx; 11)
12)
Указания. В седьмом примере: cos2л: = cos2a: — sin2*, после
деления на sin2* заменить ctg2x = cosec2д:—1. В восьмом при-
примере: после деления на cos2jc заменить tg2A: = sec2j»:—1. В при-
примере 10 заменить ctg2 x = cosec2 х—1. В примере 11 числитель
и знаменатель дроби разделить на cos2jc Подынтегральная функ-
sec2*
ция примет вид т-—.
Ответ.
1) —-^ cos Bx +5) С; 2) — tg-1 + C; 3) — In | cos (In*) | + С;
4) jtgx + C; 5) 21n|sinA:| + C; 6) — 2In|cosд:| + C;
7) -cigx — 2x + C;. 8) 2*-tg* + C; 9) i-sin (ax + b) + C;
10) — ctg* — x+C; 11) ln|tg*| + C; 12)—In sinl + C.
Задача 2,8 (для повторения материала первого практического
занятия). Вычислить интегралы: 1) j V^tg 2xsec22x dx (воспользо-
С хг
ваться формулой A,29)); 2) I „ . 3 dx (воспользоваться форму-
формулой A,32)); 3) ^~dx (формула A,29)); 4) ^(ax' + bfxdx
(п Ф -1) (формула A,29)); 5) j^ (формула A,29)); 6) j ^Щ-5 dx
(формула A,32)); 7) j" f~ dx (п Ф —2) (sin 2* = 2 sin x cos x,
599
сократить дробь и воспользоваться формулой A,29)); 8) I "x t dx
f) x у /—j—in x
С dx
(воспользоваться формулой A,31)); 9) I
J( + )] + g
1АЧ С sin 2x , ii4 Г sin* cosx , , ,
l0) J Vf + PMi**' U) j a^x + b^xdx (воспользоватьсяфор
мулой A,32)); 12) f /cosx~csinx^dx; 13) f_J^L; 14) Г|^
15) Г . х3 dx; 16) Г «* f?y; 17) Г _^?_; 18)
' J ^^ ' J ]/9-
7л:а
Указание. В примере 16 разделить ё3" на ^ + 2, получится
Ответ.
3) -1 ctg^ ax + С; 4) щ^ {ах- +
9) /5 + arctg2x + C; Щ ^V as + b2sin2л; + С;
11) j-j^—^\n(acos2x+bsin2x)+C-, 12) 2J/a + b sin * + с cos x+C;
13) _i-ln(aa-*a)+C; 14) 1 In D + 7**) + C;
15) LyETW+-C; 16) le2*_
17) \\n\a + bx\ + C; 18) -
31п'лг
1 г J. _.О .. t 1 „ / 1 t . П\ •« г У-t ЛЛ\ , "
19) Y[arctg2A; + ln(l+^)] + C; 20) — у ]/9 — 7x2 + C.
ТРЕТЬЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Продолжение упражнений в непосредственном интегри-
интегрировании.
1. Упражнения в применении формул A,21) и A,22)
Эти формулы перепишем в виде, более удобном для практики.
Полагая, как и раньше, что функция и, входящая в эти фор-
формулы, есть функция независимой переменной х: и = и (х), заменим
600
ее дифференциал du по формуле du = и' dx и перепишем эти фор-
формулы так:
I ^ = arctg и + С; C,1)
= arcsin " + С- C>2)
Следует обратить внимание на то, что в этих формулах числи-
числитель дроби и' есть производная первой степени функции и, кото-
которая в C,1) находится в квадрате в знаменателе, а в C,2) — в зна-
знаменателе под квадратным корнем.
Прежде чем начать упражнения, выведем более общие формулы,
чем C,1) и C,2), а именно: вычислим интегралы
dx. C,3)
[^—2dx и [——
J a2-)- J уа2 _и?
В первом интеграле преобразуем подынтегральную функцию
так, чтобы можно было применить формулу C,1):
т *ыт~-ыт'
Числитель и зна-
знаменатель дроби
умножен на —
Теперь числитель дроби f-^-j есть производная от первой сте-
степени функции I —I , которая находится в знаменателе, и фор-
формулу C,1) можно применить.
Поэтому, вынося за знак интеграла постоянный множитель —,
получаем
Итак,
"- + С C,4)
0.5)
601
Если ы = х, то и' = 1, и эта формула запишется так:
Подынтегральную функцию второго интеграла C,3) преобразуем
так, чтобы можно было воспользоваться формулой C,2).
У а* — и2
т _ (т)'
Из-под корня
вынесен мно-
множитель а
Теперь числитель дроби (¦—¦) есть производная от первой сте-
- (и\2
пени функции 1 — 1 , которая находится под корнем в знаменателе.
На основании формулы C,2)
dx = arcsin —(- С.
Итак,
Г , "' cfjc = arcsin— + С. C,6)
Если и = x, то и' = 1, и эта формула запишется так:
- + С. ч C,7)
Задача 3,1. Вычислить интегралы:
- 9) I f dx ¦
3dx
Решение. 1) Здесь а2 == 7; a = V'7, по формуле C,5) полу-
получаем / = -i=
2) В этом примере а2 =10; a — VTO, по формуле C,5) полу-
vv
3) В знаменателе дроби находится не х2, а 5л;2. Поэтому фор-
формула C,5) непригодна. Здесь должна быть, применена формула
C,4). Для этого надо в числителе иметь производную функции и,
квадрат которой ы2 = 5х2; и = УЪх. Производная и' = J/5.
602
Формулу C,4) можно применить в том случае, если числитель
подынтегральной функции будет равен и'. Мы этого достигнем,
умножив его на У5, а чтобы не изменилась величина подынте-
подынтегральной функции, разделим ее на /5 и представим в виде
1 =i VI
Учитывая, что а2 = 8, а —2 Y\ п0 формуле C,4) получаем
4) Этот пример ничем не отличается - от предыдущего. Здесь
и2 = 9х2; и — Ъх\ и' — 3. Чтобы можно было применить формулу
C,4), надо образовать в числителе и'. Умножим подынтегральную
функцию на 3, а чтобы не изменилась ее величина, разделим ее
на 3 и представим в виде п,9х2 — -g-11 i /3xji ¦ Теперь формулу
C,4) можно применить с учетом, что а2 ~ 11; а — У^\\\1 —
___ 1 f 3 j.. 1 _А„ За: , „
и
5) Этот пример решим без подробных объяснений: а* = 6;
и2 = 13х2; и = /ТЗл;; а2 = 6; а = Кб; и' = УГз.
Подынтегральную функцию запишем в виде
з _ з ]/Тз
6+13л:2 ~ Т/Т
/= з [_Vbdx= з 1: Кш с
V13 J 6Н-(Т/13лгJ /13/6 S /6
Задача 3,2 (для самостоятельного решения). Вычислить интег-
- 1\ Г dx о\ Г dx ~\ (* Ах .. (* 7rf<
• ; J 5+Тб^; ^ J 12 + 7x2; ^ J 14+15^ ' ^ J 15+19*» ;
5) f 9rfjc
Ответ.
603
Задача 3,3. Вычислить интегралы: 1) / = \ ^^dx; 2) I =
C Г
J
.
_ Г
J
Решение. 1) Подынтегральную функцию запишем в виде
лг + З * , 3
каждую из этих дробей проинтегрируем и интеграл представим
в виде суммы двух интегралов:
(IX 1 * / 9 t Л\ ' t ^
/ _
Умножая числитель на 2,
получим в нем производ-
производную знаменателя
Применить фор-
формулу C,5)
а= У 2
2) Подынтегральную функцию представим как сумму двух
дробей:
3*+2 _ Зх 2
Каждую из этих дробей мы умеем интегрировать. Интеграл пред-
представим как сумму двух интегралов (постоянные множители вы-
вынесены за знак интеграла):
7 =3
Здесь в числителе
получится произ-
производная знаменате-
знаменателя, если числитель
умножить на 10
dx 3
«2-j-7 10
Применить
«'= /5
In Eл:
C,4)
; а =
2 4- 7\
¦г /;
при
/5«"
/7
+ 2 arctg У~= + С. Окончательно / = ^ In Eл:2 + 7) +
3) Этот пример следует решить самостоятельно.
Ответ. |ln(8/« + 9)
Задача 3,4 (для самостоятельного решения). Вычислить интег-
интегралы: 1) \ m^jLn dx> 2) I i^j-зд^ 3) \жлГШЯ и прове-
проверить вычисления, проведенные в примерах 1 и 2, по формуле,
полученной при решении примера 3.
604
Ответ. l)^lnA0*24-ll)+^arctgJ^ + C;
2) 1 In A2*2 + 23) + ^arctg Щх + С;
Задача 3,5. Вычислить интегралы: 1) jg^.^cfo; 2) /=
dx
6) I- jr-j-cos^1
Решение. 1) Если и2 = sin2*, то и = sin*; u' = cos*; a2 = 5,
а = V 5, а потому сразу без дополнительных преобразований по-
получаем по формуле C,4)
2) Возьмем ы2 = х*, тогда и — х2, а и' — 2х.
Чтобы получить в числителе 2х, умножим его на 2, а чтобы
величина подынтегральной функции не изменилась, разделим ее
на 2 и запишем в виде уф-± = -j7 , ^,)g;
Применяем фор-
формулу C,4)
3) Примем и2 = е*х; и — е2х. Тогда и' = 2е2х. Формулу C,4)
можно применить, если в числителе находится функция и' —
производная функции и. Чтобы этого достигнуть, умножим и раз-
разделим подынтегральную функцию на 2, тогда она запишется так:
е2* 1 2е** , 1 Г ге2* , 11 , е2* , „
г* = -9~- -oaTCts-o- + c =
4-f-e4* 2 4-f-(е2жJ' 2
I ф = 4; а = 2
= larctgf+ С.
4) Полагаем, что ы2 = In2* = (In*J; и = In*; ы' = —.
Если мы представим подынтегральную функцию в виде
х E + \пЧ) = 5 + (\п хI' т0 заметим> что в числителе имеется и', а
потому формулу C,4) применить можно (а2 = 5; а = ^
605
5) Здесь и2 = tg2*; « = tg*; «' = sec2*, поэтому без дополни-
дополнительных преобразований получаем (а2 = 9; а = 3):
, _ i sec2*
1 ® -f- (tg Jf)a - —
6) Вычисление этого интеграла связано с некоторыми труд-
трудностями.
Здесь надо догадаться, что интеграл может быть приведен к
виду C,4), если числитель и знаменатель дроби умножить
на sec2*. Выполняя это, получим
1 sec2* sec2* sec2*
1 + cos2* ~~ sec2* + 1 ~ tg2* +1 + 1 ~ tg2* + 2 "
Если теперь положить и2 — tg2*; и — tg*; и' = sec2*, формулу C,4)
можно применить, так как числитель содержит производную
функции и. Тогда
Задача 3, 6 (для самостоятельного решения).
¦ С dx
Вычислить интегралы: 1) ) /5*4- 7)'Vx'
Указание. Представить * = (К*J, взять и — Ух; и =—7= .
COS*rf* -.j 9 L9 • 9 1 • ¦ I
. Указание: и2 = b2sin2*; « = &sin*; и =
а2 + б2 sin2*
= Ь cos*. Умножить и разделить подынтегральную функцию на Ь.
3) \ a i X 2 • Указание: числитель и знаменатель дроби
щ) 4 -j- COS X
умножить иа sec2*. Подынтегральная функция примет вид
4 tgS + 5 (Учтено> что sec*x = tg1* + 0-
.. Г rf* Л.
v \ 5 4- • 2 • Оказание: числитель и знаменатель умножить
на cosec2*. В знаменателе заменить cosec2* = ctg2* + 1.
Ответ. 1) 4= arctS Vt + С; 2) -т arctg (Asin*) + С;
^ 35 \ ^ /
4-С; 4)
Теперь выполним упражнения, связанные с формулами C, 6)
и C, 7).
Напомним еще раз построение этих формул: числитель дроби
есть производная от первой степени той функции, которая в
квадрате стоит под корнем в знаменателе.
Задача 3, 7. Вычислить интегралы: 1) / = Г ,
J F5 —;
Решение. 1) Здесь сразу можно применить формулу C,7),
полагая, что а2 = 5; а — /5. Получаем / = arcsin-^ + С.
2) Здесь также формула C,7) может быть применена сразу:
а2 =10; а = /То, a / = arcsin-?= + С.
3) Применить формулу C, 7) здесь нельзя, так как и" равно
не х2, как в двух предыдущих примерах, а 2х2. Поэтому надо
применить формулу C, 6), полагая и2 = 2х2 = (У2хJ; и = V%x.
Числитель дроби подынтегральной функции должен быть равен
и' = У2. Но так как Y2 в числителе не содержится, то мы ум-
умножим числитель на ]/2, а чтобы выражение не изменило своей
величины, и разделим его на ]/2. Подынтегральная функция
перепишется в виде
4) Здесь и2 = 8л;2; u2 = Bj/2xJ; ы = 2^2л;; и' = 2|/2. Для
того чтобы можно было применить формулу C, 6), надо, чтобы
числитель дроби в этой формуле был равен производной функции и,
т. е. 21/2. Умножим и разделим подынтегральную функцию на
это число и получим
1 __1 2^2
VT=&* ~ 2/2 /7-B/2> '
Теперь уже формулу C, 6) можно применить. Постоянный
множитель ——. вынесем за знак интеграла, получим
| а2 == 7; д = /7; и =
Задача 3, 8. (для самостоятельного решения).
Вычислить интегралы: 1) Г , dx ¦. ; 2) Г _ dx
^ ' J /80 — 11*2 ' ) /36 —
607
Ответ: 1) -i= arcsln ^7^ + С> 2) Т arcsin iх + С>
у 11 4у 5 /о
Задача 3, 9. Вычислить интегралы:
i\ т С cos* , ~ , С sec2* ,
1) / = \-1== ах; 2) / = 1 , = cU;
' J/7 — 3sinax ' J/ll— 5tg2AT
4W=f^
Г
J
Решение. 1) Здесь функция «a = 3sina^, « = 1^3sinx, ее
производная и' = КЗсоэ*.
Для того, чтобы числитель дроби в подынтегральной функции
был равен и', умножим его на V^3, а чтобы дробь не изменила
своей величины, ее надо и разделить на КЗ. Представим подын-
. cos* 1 l/з cos х
тегральную функцию в виде у7=ШГх = щ ут=
Т й б ф
Теперь числитель второй дроби содержит производную функции
V~3sinx, и формула C,6) может быть применена
, If1 v^cosx , 1 . /]/3sin>:\ , п
I = —pz \ -¦ ' ах = -т= arcsin -—у=— + С.
2) Этот пример решается так же, как и предыдущий:
ы2 = 5 tg2*; и = 7^5 tg х\ и' = -/5 sec2 x.
Числитель подынтегральной функции надо умножить на
чтобы ои стал равен и'. Деля одновременно, на jfE, для того,
чтобы не изменить величину подынтегральной функции, преобра-
преобразуем ее к виду
sec2* _ 1 УЪ sec» *
Применяя теперь формулу C,6), получим
, 1 Г ]/5
/ == -7= \ ,
K5J/ii_
secU j I . /Stg*
= ofjc = -= arcsin r .±
K5 /11
608
3) Представим подынтегральную функцию в виде
A +х2) /6—5 arctg" * -/6 - (/? arctg *)*
Здесь и* = 5 arctg2*; и — У'Ъ arctg х; и' = f~ .
Для того, чтобы числитель подынтегральной функции стал равен
и', его надо домножить на /5. Если это сделать и одновременно
разделить на /5, то подынтегральная функция не изменит своего
значения и запишется так:
/5
1 1 1 4- X1
A + x») /6-5 arctg" * /5 /б - (]/g arctg хуГ
Теперь на основании C,6)
/ = 4= \ 1+* = _L arcsin 1ы^И) 4- С.
/5 /6 _ (/5 arctg ху /5 \ /б / ^
4) Перепишем подынтегральную функцию в виде —
Полагаем и2 = 7 In2*, тогда ы == ^/7 In jc, и' = У7 • — . Чтобы
получить в числителе и', умножим его на У1, одновременно раз-
разделим на У7, и подынтегральную функцию представим в виде
1 1 V7-Y
Теперь по формуле C,6) находим
Vl I /15 /^
_dx = arcsin (??
/15-(/7In*)» Vl I /15
5) Умножим и разделим на 1 — х числитель и знаменатель
дроби, стоящей под корнем в подынтегральной функции, и получим
Т~х 1/A-*)A-~^ _ -|/A-*J _ I-*
" г A + ^A _х) - У 1-х* ~ vms
—*J = 1—л;, так как предполагается, что —1
Теперь / = Г ¦?-* dx = [ , dx - Г /rfJC =
= arcsinJC -l- У 1-х2 4- С 1 Применяем
r " I формулу A,31)
609
Задача 3,10 (для самостоятельного решения).
Вычислить интегралы: 1) ( ,х~ dx; 2) Г ¦ ~ х dr. (см.
указание к предыдущему примеру);.
3) I smх ___ дг< 4) Г - -dx\ 5) Г- х -dx;
6)Г ™2х dx; i) f , Sh>r Л.
J К 5 — 3sin4 л- 'jVl — 15 chs л-
Указания. В первом примере: х~ = х —
/7— 2*з'
Каждая из этих дробей может быть легко проинтегрирована:
первая — по формуле A,31), вторая — по формуле C,6).
В шестом примере: к2 = 3 sin4 г, и = "|/3sin2Jt; и' = ]/3~sin 2x.
+ С;
Ответ: 1) — -|/7 -2л:2 — -^
2) JL arcsin Щ + 4 /6^5F + С;
i "
7)'—— arcsin ")/15 ch л:.
2. Упражнения в применении формул A,23) и A,24)
Как и раньше, преобразуем эти формулы к виду, который
более удобен для их применения в практике. Получим формулу
A,23) в более общем виде. Если функция и есть функция неза-
независимой переменной х: и = и(х), то du ?= u'dx. Тогда вместо фор-
формулы A,23) получим
J
1—
: dx = тг 1П
1+и
1-й
+ С, C,8)
а формулу A,24) преобразуем к виду
=^d* = in|« + yriF±7F| + c. C,9)
Отметим построение этих формул: числитель подынтегральной
функции есть производная функции и, квадрат которой нахо-
находится в C,8) в знаменателе, а в C,9) — в знаменателе под квад-
квадратным корнем.
610
Обобщение формулы A,23) состоит в том, что знаменатель
дроби 1 — и2 заменен на а2 — и2.
Теперь можно применить формулу A,23),
так как числитель содержит производную
функции, квадрат которой находится в зна-
знаменателе
и окончательно
и'
а2—и21
а —и
с.
C,10)
Так как под знаком логарифма стоит абсолютная величина
а + и
дроби а_и
можно записать и в таком виде:
перепишется в виде
, то, не изменяя величины этого выражения, его
и + а
и — а
, и тогда формула C,10)
и'
1
а2 —и2'
= ~\n
и + а
и — а
с.
C,11)
Укажем также формулу для вычисления интеграла \ a"_ 3dx\
¦ = -а1п
и + а
= J-ln
2а "' | и - а
Итак, окончательно
и — а
и — а
u + a
с.
1
и — а
и + а
Теперь приступим к упражнениям.
с.
C,12)
Задача 3,11. Вычислить интегралы: 1) /2 = \ ¦ d* ; 2) 12 —
¦ г ^ - J *
; 3) /3 = j 5^—7 ; 4) /4 =
5) 7* =
dx
611
Решение. 1) Здесь к2 = хъ, и — х, и' = 1. Числитель содер-
содержит и' — производную функции м, значит, формула C,10) может
быть применена. Учитывая, что а2 = 5, а = /5, получаем
/j = -U In
1 2/5
/5-;
с.
2) При решении этого примера следует учесть, что и2 = дх2;
и = Зл;; и' = 3.
Числитель подынтегральной функции не содержит и'. Умно-
Умножим и разделим подынтегральную функцию на 3 и запишем, что
1 Г 3
/2 = — \————dx, и = Зл;. Теперь применим формулу C,10) и,
учитывая, что а? = 7, а = |/, найдем
/7-
Зл:
/7—
6/7
In
Зл;
/7-Зх
с.
3) Этот пример отличается от предыдущего тем, что здесь на
первом месте стоит в знаменателе не квадрат постоянной вели-
величины, а квадрат функции и. Поэтому должна быть применена
формула C,12): к2 = 5л;2; м= УЪх. Ее можно применить в том
случае, если числитель будет содержать множитель и' = УЪ, Этот
множитель получим, умножив подынтегральную функцию на УЪ
и одновременно, чтобы не изменилась ее величина, разделив на
У5. Делая это и применяя формулу C,12) с учетом, что аъ — 7;
а—У7, найдем
У5х- /7
/5,'
(/5*)»-7
= -4= In
2/35
— — _i_1n
~/5 2/7Ш
УЪх— У1
/Sx + /7
c.
4) Этот пример решается сразу по формуле C,9): и = х, а
множитель и' = 1 в числителе есть. •
Поэтому /4 = In | * + Ух*+17 | + С.' _
5) Здесь к2 = 19л;2; и =* УШ, и' = /19.
Для применения формулы C,9), надо, чтобы в числителе был
множитель и' = |/Т9.
Умножим и разделим подынтегральную функцию на ]/Т9.
_ 1 Г /19
Тогда
что и
_ /19J (/19л:)»—14
/19, найдем
dx. По формуле C,9), учитывая,
612
Задача 3,12 (для самостоятельного решения).
Вычислить интегралы: 1) Г g _ ^i; 2) ln _f6ja
5) Г / 9dx : 6) Г , ^
J Юл? - 7;
Ответ. 1)
4/6
In
2/2+ /Зх
2/2- /Зх
С;
Применена формула C,10):
:/3
= 8;
1 = 2/2
2>
/ТТ+ /бх
/П-/бл:
/Юл:-/7
4-С; 3) —Uln у"*""'
' 2/70 /10x4-/7
Применена формула C,12):
и = /1бх; м' = /Ш; а = /7.
4)
5) ^1
Применена формула C,9)
6) ±
Задача 3,13 (для самостоятельного решения).
Вычислить интегралы: 1) j^-^; 2) J^-,; 3)
4) Г
J
Ответ. 1)
2ac
In
ал: — с
ax-j-c
+ C; 2) 4 In
3> F?1
36
4> FI1"
— 2/3
C;
C.
Проведенные упражнения позволяют предложить для само-
самостоятельного решения задачи на применение формул A,25) — A,28).
Перепишем эти формулы в виде, который более удобен для их
практического применения. Полагая в них, что и = и (х), du =
= и' dx, получим вместо формул A,25) — A,28) соответственно:
C,13)
. C,14)
C,15)
C,16)
613
j sh и • и' dx = ch и 4- С;
j ch и ¦ и' dx — sh и 4- С;
с(л; = —cth и + С.
sh2 u
Задача 3,14 (для самостоятельного решения).
Вычислить интегралы: 1) \jsh2xdx; 2) I ch-|-t/л:; 3) j A0* +
+ 7)shE*2 + 7*+9)d*; 4) j ch (8* + 7) dx; 5) {^J^dx;
6) f sh,(ff+5); 7) Jsh«*ch*d«; 8) jctM<&; 9) Jth*<&;
10) J
Ответ. 1) -^ch2* + C; 2) 3shi-+C; 3) ch Eл;2 + 7л; + 9) +
C; 4) ~sh(8x + 7) + C; 5JchK* + C; 6) — -J-cth(Зл:2 +
5) + C;' 7)-g-sh'^ + C;' 8) In|shjc| + C; 9) 1п|сЬл;| + С;
10) j In [ ch x21 + С
Этим заканчиваются упражнения, связанные с непосредствен-
непосредственным применением таблицы основных интегралов.
ЧЕТВЕРТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Замена переменной в неопределенном интеграле (метод
подстановки). Интегрирование по частям.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Метод подстановки. Два правила
Если интеграл / = J / (л;) dx не может быть вычислен непо-
непосредственно по основным формулам A,7) —A,28), То введением
новой независимой переменной во многих случаях удается пре-
преобразовать подынтегральное выражение / (л;) dx. При этом интеграл
приводится к табличному или к такому, прием вычисления ко-
которого уже известен. Замена переменной интегрирования и со-
составляет существо метода, называемого методом подстановки.
Укажем два правила подстановки.
1) Независимую переменную заменяют по формуле.
* = ?(*). DЛ)
где <р (z) — дифференцируемая функция.
После этого определяют dx — y'(z)dz, а интеграл ^
приводят к виду / = j / [9 (z)] 9' (z) dz. Цель подстановки будет
достигнута, если окажется, что вычислений этого интеграла проще,
чем исходного. В результате интегрирования получится функция
независимой переменной г. Чтобы возвратиться к переменной х,
614
надо из -уравнения D,1) определить г через х и подставить это
значение вместо z в найденную функцию.
Общего правила, которое указывало бы, как выбрать функцию
<р (z) в D,1), не существует. Умение выбрать эту функцию дости-
достигается опытом. Однако для многих типов интегралов подстановка
D,1) известна и нами будет в соответствующих местах указана.
Обратим внимание читателя на то, что, пользуясь подстановкой
D,1), надо найти множитель dx.
Заметим также, что функция <p(z) в D,1) должна иметь обрат-
обратную. Это необходимо для того, чтобы из подстановки D,1) можно
было определить г как функцию х.
2) Полагают, что
<!>(*) = z. D,2)
Эта подстановка отличается от предыдущей тем, что в D,1)
сама независимая переменная х заменялась новой функцией <f(z),
а здесь не независимая переменная х, а ее функция <|> (*) заменяется
новой переменной г. Из уравнения D,2) находят dx. В результате
этой подстановки подынтегральное выражение заменится другой:
f(x)dx = <o(z)dz.
Подстановка D,2) достигнет цели, если вычисление интеграла
/ = j ш (z) dz может быть выполнено проще, чем исходного. После
интегрирования получится функция переменной г. Для того,
чтобы возвратиться к переменной х, надо подставить в получен-
полученную функцию из D,2) <|> (л;) вместо г.
И здесь умение выбрать функцию ф (х) так, чтобы вычисление
интеграла упростилось, достигается большим числом упражнений.
Для определенного класса интегралов целесообразные подста новки
вида D,2) будут указаны.
Упражнения этого практического занятия не имеют целью
указать подстановки для вычисления определенного класса инте-
интегралов, а предназначены только для приобретения навыков в при-
применении -указанных двух правил подстановки.
Упражнения в применении первого правила подстановки
/1 if ?
Задача 4,1. Вычислить интеграл / = I —> при помощи
r J хУ х2 — а2
подстановки х = ~.
Решение. Здесь применяется правило, первое. Подстановка
имеет вид D,1). Сразу находим, что dx = —^dt и преобразуем
подынтегральную функцию
11?!
х Ух* — о3 а -|/ и2
T2"
615
Поэтому
Чтобы перейти к переменной х, надо из подстановки х — -j
выразить t через х : t = ^-, и тогда
/ = arcsin — •+ С = — arccos — -f С.
(хх ах
Мы здесь заменили —arcsin— на arccos— не потому, что они
X X
равны между собой, а на основании следующих соображений:
из тригонометрии известно, что
arcsin a + arccos а = -?¦; у — arcsin а = arccos а. D,3)
Считая, что С = ~y + Ci, получим
= т (т -arcsin т) + Ci = тarccos т + с>
а Сх мы снова обозначим через С, отбросив у Ct индекс.
Ответ был преобразован путем выделения слагаемого —•\ из
произвольной постоянной. Следует иметь в виду, что за счет тож-
тождественного преобразования ответа, а также в связи с возмож-
возможностью представить произвольную постоянную интегрирования в
разных видах ответы при вычислении неопределенных интегралов
могут получаться различные.
Замечание. Следует иметь в виду, что можно было сразу
написать: —— 1 = —
1
-_ 1 , = — arccos/ + С, так как (arccos/)' =
у 1 <
Задача 4,2. Вычислить интеграл / = Г г х при помощи
J /Чах —ха
подстановки х = а A — /).
Решение. Здесь опять-таки применяется правило первое.
Подстановка имеет вид D,1).
Находим, что dx = —adt; подставляя под корень х — а A — t),
имеем
— х* = \ 2с-сA— /)— а2A — /J =
616
и тогда
= ± arccos t + C.
Верхний знак надо взять при а > 0, а нижний — при а < О, так
как | а | = а, если а > О, и | а | = —а, если а < 0.
Чтобы возвратиться к старой переменной, надо выразить t
через х. Из л; = а A — t) следует, что t = 1 — -^- = ^-р, а потому
Вычислим два интеграла, которые нам часто будут встречаться
в дальнейшем: 1) | sin2 udu и 2) Jcos2KdK.
. о 1 — cos 2м ,
Из тригонометрии известно, что sirr и = g » cosz и =
1 + cos 2и
= , поэтому
sin2udu = |1=^^^м = у|A-cos2«)dM =
= -g- (м — y sin 2м| + С = у (ы — sin и cos ы) + С;
2) jcos2udu =
= " (u + -g" s'n 2") = ^ (M + s'n M cos M) + C*
Выпишем для ссылок полученные результаты:
\ sin2 udu = у (м — sin ы cos и) + С; D,4)
I cos2 udu = ^ (u + s*n " cos M) + ?• D.5)
Задача 4,3. С помощью подстановки jf = asin^ (так назы-
называемая тригонометрическая подстановка) вычислить интегралы:
/,= {Va?-x*dx; L= f r* dx.
Решение. 1) Из подстановки
x = a sin / D,6)
следует, что d* = a cos /d/; V^a2 — *2 = ]/a2 — a2 sin2 f =
== Va? A — sin3/) = У a2 cos2 f = a cos /, а потому
Л = j a cos / (a cos tdt) = a2 j cos2^ = a*^{t + sintcost) +
Применить формулу!
D,5)
617
Чтобы возвратиться к переменной х, надо из D,6) определить
t, sint, cost:
-^-; / = arcsin —; cost —VI — sin2/ =
X V a —-
a a
C.
Окончательно
DJ)
2) Из D,6) следует, что в /2 подынтегральная функция
(выше было вычислено, что Ya% — *2 — a cos г)»
__ a2 sin21
У а2 — л:2 "~ a cost
а потому
/2 = J ^у а cos / Л = а2 J sin2 f Л = а2 у (/ — sin / cos /) + С.
Применить
формулу D,4)
Возвратимся теперь к переменной х.
Подставляя значения /, sin^ и cos?, найденные при вычисле- |
нии 1и получим
или
/2 = ^ arcsin i---i Ка2 - *2 + С.
Задача 4,4 (для самостоятельного решения).
\ ~Ш / 1 ¦ _у
При помощи подстановки *=sin/ вычислить / = \ I/ , dx.
Ответ. / = arcsin^ + Vl—х2 + С.
Задача 4,5 (для самостоятельного решения).
Вычислить интеграл / = I ¦ при помощи подстановки
J V 1 + х*
= Ctg t.
Указание, dx = — -
V 1 +
1 f
dt; у 1 + л;2 = -^-(;
Но
COST
_ 1 + cos t 1_
2 sin — cos^-
618
значит,
ln( + / + ) + C
Задача 4,6 (для самостоятельного решения).
Г* dx
Вычислить интегралы: 1)-/х = I = (подстановка x=z2)\
jEx+7)/x
J fe ( ]
(подстановка к =
Ответ. l^arctg/f + C; 2) -1 In а-+^^ + С.
Указание. Во втором примере после подстановки
Задача 4,7 (для самостоятельного решения). ¦
X
Вычислить интеграл I , с помощью подстановки х =
J Ve'-l
= 21пг.
Указание. ех = е21пг = еШг2 = za; йлг = Щ-.
Ответ. 2\п{е2 Jt-Vex—l) + C.
Упражнения в применении второго правила подстановки. .
С dx
Задача 4,8. Интеграл /= I—. вычислить подстановкой
J х у хг — а2
У1?—& = z. D,8)
Решение. Этот интеграл был уже вычислен нами в задаче
4,1. Указанная новая подстановка имеет вид D,2): ф (х) = z. Подын-
Подынтегральное выражение — : должно быть выражено через
новую переменную z. Из D,8) следует, что
х2 — а2 = г2; х2 = а2 + z2; 2x dx = 2z dz; xdx = zdz.
Деля обе части этого равенства на х2 и заменяя в правой части
равенства х2 на о? + z2, получим
dx zdz dx zdz dz
x
Теперь
Переходим к переменной х: с помощью D,8) получим оконча-
окончательно
Этот ответ отличается от полученного в задаче 4,1. Однако
это только кажущееся различие. Фактически же ответы тожде-
тождественны: легко показать, что arccos — = arctg ' х ~а . Здесь мы
еще раз обращаем внимание читателя на возможность различных
ответов при вычислении одного и того же интеграла.
Задача 4,9 (для самостоятельного решения).
Вычислить интеграл / = I .. подстановкой у х -f 2 = t.
J /л+2 + 3
Решение. Из подстановки ]/ х + 2 = t следует, что х -f 2 =
= t2; x — t% — 2; dx — 2tdt, а потому подынтегральное выражение
dx 2tdt
;
= 2 It — 3In(f + 3)] + C.
Подставляя сюда t — Vх •+¦ 2, окончательно получим
/ = 2[j/x + 2 — 31п|]/л: + 2 + 3|] +С.
Задача 4,10 (для самостоятельного решения).
Вычислить интеграл / = ( —?-=. подстановкой 1 •+¦ Vх = v.
J 1 + ух
Указание. Yx = v — 1; x = (v— IJ; dx — 2{v— 1) dv,
Ответ. I = 2[l + Vx — \n\l + Vx\] + C^2 (
— In11 + V~xI) + С = 2{V~x — In11 + V~x\) + Clt гдеd = 2 + С
С dx
Задача 4,11. Вычислить интеграл /= 1 г при помощи
J у а2 — х2
подстановки
Va* — x* = t(a — x). D,9)
Решение. Этот интеграл иам уже хорошо известен: / =
= arcsin— + С. Мы предложили этот пример для упражнения,
а также для того, чтобы показать еще раз, что вычисление интег-
интеграла может приводить к различным по форме ответам, в зависи-
зависимости от того, какой метод применен при его вычислении. Из
620
указанной подстановки получаем а2 — х2 = t2 (о — хJ. Сокращая
теперь на а — х, имеем о + х = t2 (a — х), отсюда
4at dt r 2at
Так как arcsin -j + у = 2 arctg j/ ^77^. то следует считать,
что полученный ответ только формой отличается от уже извест-
известного, указанного выше.
Задача 4,12. Вычислить интеграл / = Г cosx x— (подстановка
J /6 — sin2х
s'mx — z).
Ответ. / = arcsinfej + С.
Задача 4,13 (для самостоятельного решения).
Вычислить интеграл / = I dx, (подстановка ctg x — и).
J О *"i *¦ 4 Sill л
Указание. —cosec2 xdx = du; cosec2 x = 1 + и2; sin1* =
= т-7—5. Подынтегральное выражение
dx du
Ответ. 1 = 4щ arcct6 ( Vt ct§ x) + C-
Задача 4,14 (для самостоятельного решения).
Вычислить иитегралы:^1) 1Х = \ l ^x (подстановка tg* =г);
(* dx
2) /г = J sin^cos'^ (подстановка tgx = г);
С dx
3) /3 = I ¦ ~ ' . (подстановка ctg х = z).
J sin^/4 sin2* — 9cos2x '
У к a 3 а и и я. Во втором примере: JL « dz; i ^
l+г»1 sin*A:~ г* ~" г* + г2 + Ь
Подынтегральное выражение
/J_ _2_
~" \г* + г2
dx J
dx
В третьем примере: r : =1 =
sin^/4sinaj; —9cos2^ sin2 x y' 4 — 9 ctga x
dz
/4 — 9zs"
621
Ответ. 1) /^-L
2) /2 = tgx — 2ctgx — ~ctg3A
3) /s = I arccos (-| ctg x) + С
\ ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Этот метод, так же как и метод подстановки, который
только что разобрали, принадлежит к числу основных метод»
интегрирования.
Формула интегрирования по частям записывается так:
J и dv = uv—j vdu. D,1
Применение этой формулы предполагает, что в правой час
интеграл J v du может быть вычислен легче, чем исходный и
теграл.
Задача 4,15. Вычислить интегралы: 1) Ix—\xexdx\ 2) /2 •
= J х sin x dx; 3) /3 = jln;ed*; 4) /4 = J arctg*d*; 5) /,
= j arcsin x dx.
Решение. Для вычисления всех предложенных интегралов
применим формулу D,10) интегрирования по частям. При исполь-
использовании этой формулы надо прежде всего установить, какая
функция принимается равной и и что относится к dv. Затем по;
установленному выражению и надо дифференцированием найти|
du, а по известному dv определить интегрированием функцию v.\
Таким образом, для применения формулы D,10) потребуется вы-
выполнить одно дифференцирование для определения du и одно!
интегрирование для- определения v. Следует помнить, что в состав
dv должен обязательно входить дифференциал независимой пере-
переменной.
После этих общих указаний приступим к вычислению пред-
предложенных интегралов:
и
dv
V
=
=
du
X
exdx
du
= dx
и dv
4
¦i
Замечание. При вычислении этого интеграла нецелесооб-j
разно брать и = ех; dv = x dx, так как в этом случае было бы 1
„2 ft
du = ехdx; v = -^-. Применяя формулу D,10), мы получили бы|
J
= J xex
622
Совершенно очевидно, что интеграл в правой части сложнее исход-
исходного Из этого читатель должен сделать вывод, что выбор и и dv
не может быть произвольным. Он определяется требованием, чтобы
интеграл, к которому приводит формула D,10), был проще задан-
заданного.
2) /2= {
dv
и —
dv =
UV
X
sin
xdx
V
du =
du
--dx
V = —COS X
Здесь также надо иметь в виду, что если взять « = sin*;
dv = xdx, то мы придем к интегралу более сложному, чем.дан-
чем.данный.
3) /3 = \\nxdx = x\nx—\XY=:x\nx—\dx = xlnx —
и dv
и = \nx '
dv = dx
. dx
du — —
x
V = X
¦ = хAп*— 1) + С.
4) I arctg xdx — х arctgx — I ог^г dx =
rfx
и dv uv
и = arctg x
dv = dx
V = X
5) I
= л: arctg л:— yln(l + x2) + С
arcsin л: dx — x arcsin л: — I .
_ J/l—X
u dv
и = arcsin x
dv = dx
dx =
1
V = X
— x arcsin x + V1 — x2.
Задача 4,16 (для самостоятельного решения).
Вычислить интегрированием по частям интегралы:
2) /2 = §xs\nxdx;
l7 j
Указание. В третьем примере взять и — arcsinx; dv =
х dx
623
Ответ. 1) Л = хsinx + cosx + С; 2) /2 = ^~ — ¦?• 4- С; ;
3) /3 = — К 1 — х2 arcsin л: + х + С; 4) /4 = ^ + С.
С* j
Задача 4,17. Вычислить интегралы: 1) 1Х = \ ? ;
,) COS а
2) /2 = \ " ^8n ^ d*; 3) /s = J sin x In cos # d*;
Решение. 1) Л
u = л:
= *tg* —
uv
du = d*
o=tgx
du
Применить фор-
формулу A,17)
2) /2
4- In | cos x | 4- C.
x = tgx • \nsinx — jtgxctgxdx =
u = In sin Jt
du = ctg j; dj;
v = tgx
= tg # • In sin # — j dx = tg * In sin x — x 4- С
3) /3 = j sin # • In cos x dx = — cos x In cos x —
и = In cos*
dv = sin Jed*
du = — tg xdx
v = — cos x
— J (—cos x) (—tg x dx) — — cos л: In cos x — j sin xdx —
v du
= —cos x In cos x 4- cos* 4- С — cos#(l — In | cos*D + C.
4) /4 =
- J arct§x -шгх -rhdx = arctgx ln arctgx-.
и = lnarctg*
dv •¦
dx
du ¦
1
1
arctg*
v = arctg x
dx
dx
l+x2
= arctg x • In arctg x — arctg x = arctg x (In a rctg x — I) + C.
624
/5 = jV In (e*
u= ln(e*-f 1)
dv = e* dx
¦dx
l) — ex + \n(ex+l) + C = (ex+ l)ln(e* + 1) — е*
Задача 4, 18 (для самостоятельного решения).
Вычислить интегралы: 1) /х = J cosx • \nsinxdx;
2) ^ = ^Шгах' 3) /. = Jsec»x.lntgxd*; 4) ^^dx;
5) jxenxdx.
Ответ. 1) sinx(Insinx— 1) + С; 2) — * — ctg*Incos*-f С;
3) tg*(lntgx— 1) + C; 4) — ctgx —
Интегралы, для вычисления которых интегрирование по частям
применяется несколько раз
Задача 4, 19. Вычислить интеграл ^(\nxJdx.
Решение. Интегрирование по частям применим дважды:
(In xJ dx = x (In xJ — 2 j In ж dx = x (In *J — 2 (x In x — j dx) =.
«= (In xJ
dv = dx
du = 2 In x — dx
x
u=lnx
dv = dx
du = —t
= x(lnxJ — 2xlnx-f 2x + С = xlnx(lnx — 2) -f 2x + С
Задача 4, 20 (для самостоятельного решения).
Вычислить J ~/x (In xJ dx.
Указание, и — (In xf; dv = V~x dx; du — —^ dx;
v = — x y^'x.
Интегрирование по частям и здесь придется применить дважды.
Ответ, -j-x у^х AпхJ — у Inx •+¦ -g- + С.
Задача 4,21. Вычислить интеграл J (arcsin xJ dx.
Ответ, х(arc sinxJ + 2 Vl —x2arcsinx — 2х + С.
21 И. А. Каплаа 625
Упражнения, в которых двукратное интегрирование
по частям приводит к исходному интегралу
Задача 4,22. Вычислить интеграл / = J eax cos bx dx.
Решение. В этом примере двукратное применение интегри-
интегрирования по частям приведет к исходному интегралу.
С 1 Г
I — \ еах cos bx dx = -г- еах sin bx r eax sin bx dx =
J b 6 J
Вторично применяем инте-
интегрирование по частям:
и — еах Ш = аеах dx
и =
dv
- еах
= COS
bxdx
du-
v =
= аеах
1 .
-г- Sin
О
dx
bx
dv = sin bx dx
v = r- cos bx
b
= j e°* sin bx — ^-l—^tf* cos bx + у j eax cos bx dx\.
Таким образом, двукратное применение формулы интегриро-
интегрирования по частям привело нас к исходному интегралу, который
нами вычисляется.
Раскроем скобки в правой части:
/ = —
sin bx + -J; ex cos bx
? J
eax cos bx dx.
Это вычисляемый ин-
интеграл, который мы
обозначили буквой /
Таким образом,
b Ьг Ьг
Мы получили уравнение с неизвестной величиной /.
Перенося последнее слагаемое в левую часть уравнения,
найдем
2 1 / ч
/ + к- / = -г еах sin bx 4- -г <
Вынесем в левой части этого уравнения / за скобку:
/ —^- = j- eax I sin bx + j cos &к I.
Отсюда следует, что искомый интеграл равен
Аналогичную задачу предлагаем для самостоятельного решения.
626
Задача 4,23 (для самостоятельного решения).
Вычислить интеграл / = J е®* s'mbx dx.
Ответ. / = JT^ (« sin bx — b cos bx) + С. D,12)
Задача 4,24 (для самостоятельного решения).
Применить формулы D,11) и D,12) к вычислению интегралов:
J. X X
sin -н- + cos т
— з _ dx.
i/~ex
Ответ. 1) дBcos3* + 3 sin3*) + С; 2) 2^2^-Зсоз2х.
. х _ л;
„ Sin -тг — О COS -z-
Задача 4,25 (для самостоятельного решения).
Найти интегралы: 1) 1Х = J sin (In x) dx и 2) /2 = ) cos (In x) dx.
Указание. Применение дважды к каждому интегралу фор-
формулы интегрирования по частям приводит к исходному интегралу.
Например,
1г — х sin (In х) —
cos (In x) dx = х sin (In x) — [x cos (In x) +
Снова применить
и нтегрирование
по частям
4- J sin (In л:)
| Исходный интеграл |
Ответ. /i = y [sin (In x) — cos (In x)\ + С; /2 = -| [sin (In x) +
+ cos(\nx)] + C.
ПЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Простейшие дроби. Разложение рациональной дроби на
простейшие.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Простейшие дроби. Простейшими (иначе элементарными) дро-
дробями называются дроби вида:
21* 627
где А, В, а, р и q— действительные числа, а трехчлен х2 4-
-f- рх + q имеет комплексные корни, т. е. не раскладывается на
действительные множители первой степени.
Рациональные дроби. Дробь
называется рациональной, если ее числитель и знаменатель —
многочлены (предполагается, что коэффициенты многочленов дей-
действительные числа).
Дробь E,1) называется правильной, если степень многочлена
Р(х), находящегося в числителе, меньше, чем степень много-
многочлена Q(x), находящегося в знаменателе.
Если же степень числителя равна степени знаменателя или
больше ее, то рациональная дробь E,1) называется неправильной.
Примеры. 1) Дробь * ~^_ „ _ .- — правильная (степень числи-
' теля меньше степени знаменателя).
.. _ , х34-х* — 9 Xй — Зх* + х — 8
2) ДР06" 2*з + 3*'-* + 7 и x* + J+3 неправильные: в
первой степень числителя равна степени знаменателя, а во вто-
второй степень числителя больше степени знаменателя.
Из неправильной рациональной дроби всегда можно выделить
целую часть (многочлен). Это достигается делением числителя
на знаменатель по правилу деления многочленов.
Например, неправильная дробь ~ ^_ ^_^7' может быть
представлена так:
— Зх2 + 5* 4- 4
4-
x2 — 8* 4- 5
х2 4- 8х 4- 56
8х3 — 8х2 + 5х + 4
8xs — 64л2 4- 40*
56л:2 —35*4-4
56s2 — 448* 4- 280
413* —276
и, таким образом,
= хш + 8* + 56
Целая часть
(многочлен)
Правильная I
дробь |
Всякая неправильная рациональная дробь может быть пред-
представлена в виде суммы многочлена и правильной дроби.
Поэтому интегрирование рациональной дроби E,1) всегда мо-
может быть приведено к интегрированию многочлена и правильной
дроби.
628
Корни многочлена. Еслц при х — хг многочлен
Q(x) = a0xn + a1xn~1 + a2xn-*+ ... +an_lx + an E,2)
обращается в нуль, т. е. Q (хх) = 0, то число х1 называется кор-
корнем многочлена.
Разложение многочлена на множители. 1. Если числа хи x2,
х3, ..., хп являются корнями многочлена E,2), то этот многочлен
может быть разложен на множители по формуле
Q (х) = ао(х — хх) (х — х2) (х — х3) ... (х — хп). E,3)
2. Многочлен степени п не может иметь больше, чем п раз-
различных корней.
3. Корень многочлена xL называется простым, если в разло-
разложение E,3) множитель х — хг входит один раз. Если же этот
множитель в формулу E,3) входит о^ раз, то корень хх называется
корнем кратности а.1 многочлена E,2).
Если корень хх имеет кратность <хь корень х2 — кратность <х2,
а корень хр — кратность ар, то формулу E,3) можно заменить
такой:
Q (х) = а0 (* — xtf* (х - ха)" ... (х- хр)'р, E,4)
причем а1 + <х2 + • • • + <*р = п.
4. Если коэффициенты многочлена E,2) — действительные
числа, а его корнем является комплексное число а-\-Ы, то его
корнем будет также и комплексное число а — Ы, сопряженное
с а + Ы.
Если в формуле E,3) перемножить множители х — (о + Ы)
и х — (а — Ы), соответствующие этим корням, то получи-тся квад-
квадратичный множитель вида х2 + рх + Ц, где р и q — действитель-
действительные числа.
В случае, когда а + Ы — простой корень многочлена E,2),
то и а — Ы — также простой корень этого многочлена.
Если же а + Ы — корень кратности k многочлена E,2), то
и корень а — Ы имеет такую же кратность. В этом случае паре
этих комплексных сопряженных корней в E,3) будет соответство-
соответствовать множитель (х2 + рх + q)k.
Если многочлен E,2) имеет не только действительные, но
и комплексные корни, то вместо формулы E,4) имеет место фор-
формула
Q (х) = а0 (х — х^ {х — х,)- ... (х2 + Рхх + q^ (x2 +
+ Р2Х + q2)k' ... (Х2 + pix + qtfi, • E,5)
причем
Ч + «2 + • ¦ • + 2&J + 2k2 + ... + 2ki = п.
Квадратичные множители, входящие в эту формулу, не имеют
действительных корней и на множители первой степени с действи-
действительными коэффициентами не разлагаются.
629
Теорема (о разложении рациональной дроби на простейшие).
Р (х)
Пусть qy\ — правильная, несократимая рациональная дробь, а ее
знаменатель после разложения на множители имеет вид
Q (х) = а0 (х — *!)"• (х — *2)«. ... (х> + рхх + <7t)*« (а:2 + ргх +
+ <72)*. ... (х* + р(х
где хъ х2, ... — действительные числа, а квадратичные множи-
множители не имеют действительных корней.
Тогда дробь ~1 может быть представлена в виде суммы про-
простейших дробей. В этой сумме каждому множителю вида (х — хх)р
в знаменателе, где хх— любой из действительных корней, ар —
его кратность, соответствует выражение вида
Аз
Л. Л.
=2 + • • • Н
а каждому множителю (х2 -\- рх + q)r знаменателя — выражение
вида
, . Brx -f- Cr
|
(X* + РХ+ ЧУ + (х* + РХ+ ?)!-» + (х»
E,7)
где Аи А2 Ар, Въ В2 Вг, Съ С2 ... , Сг — действи-
действительные числа, подлежащие определению.
Теперь мы на нескольких примерах укажем два наиболее рас-
распространенных способа определения коэффициентов, стоящих
в числителях тех простейших дробей, на которые разлагается дан-
данная рациональная дробь. Это способ неопределенных коэффициен-
коэффициентов и способ задания частных значений.
Задача 5,1. Разложить на простейшие дроби рациональную
*{2 4
Решение. Применим способ неопределенных коэффициентов.
Общий вид разложения будет таким:
2* — 4_ Aj , А2 . А3 At
Умножим обе части этого равенства на знаменатель левой
части:
х* + 2х — 4 = Ах{х — 2) (х + 3) (х — 4) + А2(х — 1) (х + 3) (х —4)+
+ А3 (*- 1) (х-2) {х-4) + А, (*- 1) (х-2) (х + 3). E,8)
Левая часть равенства должна быть тождественно равна пра-
правой, т. е. равенство E,8) должно выполняться при любом значе-
значении х. Это будет иметь место только в том случае, когда коэф-
коэффициенты при одинаковых степенях х в обеих частях равенства
будут между собою равны.
630
В правой части E,8) произведем умножение двучленов и по-
получим
Х2 + 2х — 4 = Ах (х3 — Зх2 — 10* + 24) + А2 (х3 — 2х2 — Их + 12) +
+ А3 (х3 — 7л:2 + 14а: — 8) + Ах (х3 — 7х + 6).
Это равенство можно переписать иначе, расположив многочлен
в правой части по убывающим степеням х:
х2 + 2х — 4 = (А1 + А2 + А3 + А4) х3 + (—3AL — 2А2 — 7Л3) а:2 +
+ (—10А — 11Л2 + 14Л3 — 7Л4) х + B4^! + 12Л2 — 8Л3 + 6Л4).
Сравнивая коэффициенты при одинаковых степенях х в левой
и правой частях последнего равенства, получаем систему четырех
уравнений первой. степени с четырьмя неизвестными:
V3 А I А I А _[_ А П
л /lj —\- ™2 ~Т* ™3 I ^Н — ^
v8 ЧА О А 7/1—1
Л/ U/lj idii.2 I /13 — 1
v 1П/1 11 Л _L 1 Л. А 7 Л 9
л:0 24Л, + 12Л2 — 8А3 + 6Л4 = —4
(свободный
член)
Решив эту систему, получим:
А - 1 ¦ А --2 • А --Ь А -10
х~ 12' ^2 ~ Т' 3 — 140' 4~2Г
Теперь определим числа Аъ Аг, А3 и Л4 вторым способом —
способом задания.частных значений.
Так как равенство E,8) — тождество, то оно сохраняется при
любом значении х. Будем давать х такие значения, чтобы в пра-
правой части все члены, кроме одного, обращались в нуль. Такими
«выгодными» значениями являются, очевидно, корни знаменателя,
т. е. значения х = 1; х = 2; х — —3; х = 4.
При х=1 в правой части E,8) все слагаемые, кроме первого,
обратятся в нуль, левая часть равенства х2 + 2х — 4 при х = 1
будет равна—1, и мы получим
-1 = 4, A-2) A+3) A-4); _1 = 12ЛХ; Лх = -^.
При х = 2 левая часть равна 4, а в правой части E,8) все
слагаемые, кроме второго, будут равны нулю:
4= Л, B-1) B + 3) B-4); 4 = -Ш,; А2 = -1.
При х = —3 в правой части E,8) все слагаемые, кроме тре-
третьего, равны нулю:
-1 = Л,(-3-1) (-3-2) (-3-4); —1 140Ла; Аа = ^.
При х = 4 в правой части E,8) все слагаемые, кроме четвер-
четвертого, обратятся в нуль, и мы будем иметь:
20 = А, D- 1) D—2) D + 3); 20 = 42Л4; Л4 = ^.
631
Заметим, что каким бы способом ни вычислялись неизвестные
коэффициенты, мы всегда получим для них одни и те же значе-
значения, так как разложение рациональной дроби на простейшие может
быть осуществлено единственным образом.
Итак, заданная дробь
*2 + 2х — 4 1 2
(х— 1)(х — 2)(*4-3)(* — 4) ~ 12(*—1) Ь(х — 2)~*~
1 . 10
+ 140(х + 3) + 21(х —4)"
Укажем, что способ задания частных значений х для опреде-
определения неизвестных коэффициентов особенно удобен в том случае,
когда знаменатель дроби содержит только действительные мно-
множители первой степени, среди которых нет равных.
В других случаях способ задания частных значений также
дает сокращение вычислений, так как позволяет избежать реше-
решения системы уравнений с числом уравнений, равным числу неиз-
неизвестных.
Однако мы рекомендуем учащемуся овладеть этими двумя
способами.
Задача 5,2 (для самостоятельного решения).
Рациональную дробь (д._ 2И* —3) (*+ 1) Разл0жить на
элементарные. Решение провести двумя способами.
Ответ. _•__»+, *>
—3) 24(*-f I)'
Задача 5,3 (для самостоятельного решения).
Разложить на простейшие дроби следующие рациональные
дроби (применить два способа):
и Пх~4
Указание: знаменатель разложить на множители.
2ла4-41л: — 91 „. З*3 — 24л? — 41*+20
Z> (*-l)(* + 3)(.v-4); 6> (х + 1) (х + 2) (х - 3) (х - 2);
. _. 11*4-40 .
2)(х — 3)' aJ 4(x — 4)(*4-2)'
3*4-23^+28 __
Ответ. 1) » + » ; 2)-!,- 7
оч 17 9 П9_ 67
/ RCi-_L 11 "г irv»-_L9^ \ft(r Я1» "i
—3)Т(* —2)'
7 3
—2 *—3' "' 2(^ — 4)- 4(*4-2)'
L+ 4
% 4 '
632
Задача 5,4 (для самостоятельного решения).
Представить в виде суммы многочлена и простейших дробей
рациональные дроби:
Зх3 — 10**—11*+21 _ х* — хз-. 9*2— Юх— 14.
Ч х2_5д; + 4 ' 1> х*~~ 2* — 8 '
165x3 + 341*8 + 271* + 30
Указание. Выделить целую часть, согласно объяснению на
стр. 60; знаменатели разложить на множители.
Ответ. 1) Зх + 5-^-f + ^li;
*—4'
3) 30л:2 + 105 + - + -5-т +
' * -' *+1 '
+* +
Задача 5,5. Разложить на простейшие дроби рациональную
х3 6а + 9+7
Решение. Разлагая дробь на простейшие, получаем согласно
формуле E,6):
Ая . Aj
(* — 2K (* — 5) (* — 2K "•" (* — 2J + * — 2 + х — 5'
Умножим обе части этого равенства на знаменатель левой
части:
хз _ 6*2 + 9* + 7 = Л х (х — 5) + А 2 (а: — 2) (х — 5) +
+ Л3(а:-2)8(а:-5) + Л4(а;-2K. E,9)
Для определения неизвестных коэффициентов AL, A2, А3 и Л4
применим второй способ — способ задания частных значений в соче-
сочетании со способом неопределенных коэффициентов. Напоминаем,
что написанное равенство является тождеством: оно остается вер-
верным при любом значении х. Принимая х = 5 и х — 2, мы сможем
просто определить два коэффициента. При х = 5 имеем в левой
части 27, тогда 27 = Л4 E — 2K; 27 = 27Л4; Л4 = 1.
При х = 2 получаем в левой части 9.
9 = ^B—5); 9 = —ЗА1\ Лг = —3.
Теперь сравним коэффициенты при xs в левой и правой части
тождества E,9). В левой части коэффициент при х3 равен 1,
а в правой, если выполнить в ней возведение в степень и умно-
умножение, коэффициент при х3 равен А3 + Л4. Таким образом, А3 +
+ ^4 = 1- Но так как Л4 = 1, то А3 = 0.
Сравним теперь свободные члены в левой и правой части E,9).
В правой части свободный член равен —ЪАХ + 10Л2 — 20Л3 — 8Л4,
а в левой 7, т. е. имеет место уравнение
—ЪАХ + 10Л2 — 20Л3 — 8А, = 7.
633
Подставляя найденные значения Аъ А± и А3, получим для
определения А2 уравнение
15 + 10Л2 —8 = 7; 10Л2 = 0; А2 = 0.
Итак, данная дробь
3 1
(Y о^З (у к\ (у 0\s I у г. •
\Л 6) \Л О) \Л ?>) А О
Определение Л2 и А3 можно было провести способом задания
частных значений. Например, при х = 1 и х = 0 получаем систему
уравнений:
7 = — ЪА\ + 10Л2 — 204, —48Л4) '
Подставляя найденные значения А1 = —3, 44 = 1, получаем:
442 — 44, = 0'
i3 и; А2 ¦
Отсюда следует, что А2 == А3 = 0.
Задача 5,6 (для самостоятельного решения).
Разложить на простейшие дроби:
»— Юх2 —8*4-5. с\ —69*3 — 12*2 4- 475.V + 646 .
7 = 15 + 10Л2 — 20Л3 — 81' или А\ — 2Л3 =
(х — 2K (* 4
5х2 + 6*4-9
V-I+t^!'
(дс_4)»(*-2)'
¦ 3)«
. ut
6)
7)
3^ +
(*+1.
^ — 2;
*Й1
са _ 3* + 4
С*-2)*
4) (*г —3*—ГОJ'
Указания. В четвертом примере х* — Зх — 10 разложить
на множители; в седьмом примере представить дробь в виде
А\ . Лг | Лз ¦ Л4
JC2 ~т~ Т + (* — 2J "г" * — 2 "
Ответ П 1 I 42 I 27 ¦ 23
5 (* — 2K ~ 25 (* — 2J ~ 25 (* — 2) ~ 25 (* 4" 3)а
! 9 | J
25(*4-3)' ' 2(*
3) 13
!_ + _? _
4K (* —4J^* —4 * —2'
8 30 2730
4N
' 49 (* — 5J ^ 343 (х — 5) ^ 49 (* 4" 2)г 343 (* + 2) '
гч 8 9_ __4 60_.
; (х + 2)г * + 2 "^ (^ — 3)а * — 3 '
; (*+l)«Tj(+l *+2'
7N J. 4- - * | 3^
' *2 ^ 4* 2 (* — 2J ' 4 (* —2)"
634
Задача 5,7. Дробь . . разложить на простейшие.
Р е ш е н и е. Разложим знаменатель х3 + 1 на множители: х3 -f 1 =
= (х + 1) (х* — х + 1)- Квадратичный множитель х2 — х + 1 дей-
действительных корней не имеет, а потому на основании формул
E,6) и E,7) имеет место разложение
х
х°
(свобод-
(свободй
Умножая обе части равенства на х3 4 1, получаем
Для определения неизвестных AUBY и Сх воспользуемся способом
неопределенных коэффициентов. Выполняя умножение, имеем'
1 = (Лх + ВХ) х2 + (-Л + Сх + Bi) х + Лх + Ct.
Это равенство является тождеством и может сохраняться только
тогда, когда коэффициенты при одинаковых степенях х в левой
и правой частях равенства равны между собой:
А1 + В1 = 0 ' ' A)
А, 4- Сх + Bi = 0 B)
Л + Сх = 1 C)
ный член)
Складывая первое уравнение с третьим и вычитая из полу-
полученного уравнения второе, получаем -
j
I . п
Тогда из уравнения A) Вх = —у, а из уравнения C) Сг = -^
и, окончательно
1 ._ 1 х— 2
*»41 ~~ 3(л:4-1) 3(.ч2 —л:4)'
Задача 5,8. Дробь . _ 4 разложить на простейшие.
Решение. Знаменатель дроби 1—х* = A—*) A + *) A+
4-х2). Поэтому данная дробь может быть представлена в виде
•к2 А, , Л» "
1_л:4 1 —л: ^ 14-л: ^ 14-*2'
После умножения обеих частей равенства на 1 —Xх получим
тождество
х2 = А, A + х) A + *2) 4- А2 A - х) A + х2) + (Л* + А,) A - г>).
E,10)
Для определения неизвестных коэффициентов А1г А2, А3 и Л4
применим сначала способ задания частных значений. При х = 1
635
получаем в левой части 1, а в правой все слагаемые, кроме пер-
первого, обратятся в нуль, а первое слагаемое станет равным 4ЛХ.
Ai найдем из полученного уравнения: 1 = 4АЪ А1 = -^. При х —
= — 1 получаем в левой части равенства 1, а в правой 4Л2,
и тогда 1 = 4Л2, a^ = j.
Теперь сравним коэффициенты при х3 в левой и правой части
равенства E,10). В левую часть этого равенства х3 не входит.
Это означает, что коэффициент при х3 равен 0, а в правой части
коэффициент при ха равен А1 — Ла — А3. Таким образом,
Учитывая, что А1 и А2 уже определены, имеем
а отсюда следует, что Аа = 0.
Нам осталось определить Л4.
Дадим х значение 0. В левой части получим 0, а в правой
А\ + А2 + Л4, и тогда
0 = Ах + А2 + Л4.
Так как At = Аг — —, то 0 = -^ + -j + Ait отсюда At =
__ _ l
Итак, предложенная дробь
л:а 1.1 1
; + ¦
1 — а^ 4A-^)т4A+«) ' 2 A + х*) '
Задача 5,9 (для самостоятельного решения). Разложить на
простейшие дроби:
п 1 . о}
' (а+Ьх)A+х*)' ' (х— 1)(*
3) w+i-
Указание, х4 + 1 = к* + 2xz -f I — 2x2 = (х* + IJ — 2*2 =
= (х» + V2x + 1) (х* - V2x * 1).
Дробь представить в виде
1 Ax-j-B ' Cx + D
- - - +
Otrpt 1ч a — bx ,
4 (x — 1) T 4 (x + 1) T 5 (x — 2) t~ 10 (^* + 1) '
636
Задача 5,10 (для самостоятельного решения).
Рациональные дроби: 1) ?±i и 2) х3 + ^~^х + 4 разложить
на простейшие.
Указание, х3 + х2 + 4х + 4 = х* (х + 1) + 4 (х + 1) = (х +
4)
1Ч 1 / 2 . х+1 \ о. 2
Ответ. l)T^q-T + ^_!l-j-Tj; 2) _
Задача 5,11 (для самостоятельного решения). Разложить на
простейшие дроби: 1) xiJf_xi_2 ; 2) у—^"в-
Указание. 1) Знаменатель разложить на множители. Для
этого решить биквадратное уравнение х* + хг — 2 = 0. Его корни
ху = 1; х2 = — 1; xs = -/^i и х4 = — -/2i, а потому х* + х2 —
— 2 = {х — 1) (х + 1) (* — K2i) (л; + V%i). Перемножая множите-
множители, соответствующие мнимым корням (х — y^2i) (a: + ]/2i), полу-
получим окончательно
2) 1— ^« = A— х3) A + х3) = A — лг) A + л: +
П П 1 1 1
и т в е т. i; - —т — 6
^ 6 1+л:+ 6 1—л:" 6
ШЕСТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Интегрирование простейших рациональных дробей.
Интегрирование рациональной дроби щ-\ приводится к инте-
интегрированию простейших дробей вида:
!) 2) {П>°
4) (х^7ЛяГ
rf* = ln|x-a| + C. F,1)
Задача 6,1. Найти интегралы:
637
Решение. 1) По формуле F,1) J—д=1п|л: —3|-f С;
Числитель равен
производной
знаменателя
Задача 6,2 (для самостоятельного решения).
Найти интегралы: 1) frA-; 2) [ t^oz\ 3) Г^Д
4) ]з=Ж; 5>
Ответ. 1) In |л: — 131 + С;
2) — -j In 115 — Зл:| + С; 3) — у In | 4 — 7x\ + C;
4) — -i-ln|3 — 8x\ + C\ 5) -|ln|4x —9| + C.
Окончательно:
Задача 6,3. Вычислить интегралы:
dx
n /- Г dx ¦ 2W- f
; J (x - 2K' ^ ~ J (x + 3)» '
3) 7 = J (S=T? ; 4) / = J D-J3*)»"
Решение. Для вычисления первых двух интегралов непо-
непосредственно применяется формула F,2):
2)п = 5; / = -1
3) Чтобы можно было применить формулу F,2), числитель
дроби ,2х_ }.4, стоящей под интегралом, должен быть рдвен про-
производной от основания степени знаменателя. Преобразуем дробь
к виду
1 _ 1 2
Bл:— IL ~ У Bл:— IL '
638
и тогда
/ _ _L f 2 лу _ _L [ i ' | I r —
6 Bх—1K
4) Этот интеграл вычисляется как и предыдущий
/ ' Г -3 dx J f i
c-
__L
D -
Для вычисления этого интеграла поступают так:
а) в числителе дроби, стоящей под интегралом, записывается
производная знаменателя, т. е. {2х-\-р). Тождественными пре-
преобразованиями из 2х + р получают заданный числитель Ах + В,
Для этого следует 2х + Р умножить на -у и к полученному
Ар
произведению прибавить В ^-. Очевидно, что
б) Преобразованная дробь а . . имеет вид
и может быть представлена как сумма двух дробей:
R_A?
2
Л 2х+р 2
2 x2 + px+o +
Первая дробь интегрируется просто: в числителе находится
производная знаменателя — интегрирование приводит к натураль-
натуральному логарифму модуля знаменателя. Для интегрирования вто-
второй дроби в знаменателе выделяют полный квадрат:
639
Интеграл от второй дроби приводится к табличному интег-
ралу A,23), если Aq— р2 < 0, и к табличному интегралу A,21),
если 4<7 — р2 > 0.
Замечание. Если в знаменателе дроби вместо квадратич- •
ного трехчлена х2 + рх + q находится трехчлен ах2 -\- bx-\- ch
(а ф 0), то коэффициент а следует вынести за скобку и тем са-
мым свести этот случай к предыдущему. ;
В задачах 6,4 и 6,5 даны примеры вычисления интегралов j
этого типа. ;
Задача 6,4. Найти интегралы:
^='1^+47+14: 2) /. = J;q?
7* = J **-э/+25 ; 5) 7« = J ^IZ
7л;+14'
¦9*+25
Решение. В этом практическом занятии нам часто при-
придется пользоваться формулой C,4). Напомним, что она имеет
такой вид: \
" и'
1) Выделим полный квадрат в знаменателе дроби:
х* + 4х + 14 = (х + 2J— 4 + 14 = (х + 2J + 10.
Применим формулу C,4)
11 J (* + 2J+10 ~" ]/Ш
и = х+2; и' =2
аа= 10; я = /10
2) Выделяем полный квадрат в знаменателе дроби:
+ !;«'-
Т;а = ~
3) Выделим полный квадрат, в знаменателе дроби:
/я =
dx
3V . »s
1 + ?
= -karctg-7==-
/ТВ /15
Формулу
применить:
и' = 1
C,4)
и =
можно
¦с~Ь"о" '•
15.
4'
= -?=arctg^^ + C.
/15 s /15 ^
4) В знаменателе выделяем полный квадрат:
л; ——
2 / + 4
2 2
Формулу C,4) можно
9
применить: и—х —g-;
и'=1; а^ = ^
9 2* Q
= /TlarctgTtT + c-
5) Выделим полный квадрат в знаменателе:
dx.
7
1 \2 , 55
/55
/55
641
Задача 6,5 (для самостоятельного решения).
Найти интегралы:
dx „. f dx оч Г dx
¦¦"I
j\ I "Л Г\ I dX
12 '
Ответ. 1) — arctf
arctgW + C; 3) 7TSarclgTl
Задача 6,6. Найти интегралы:
/ _ Г dX О\ Т _ Г dx
1 — J 5л;а + 7л;+11 ' ^ уа — J
/ _ Г
+ J + +5 '
dx
Решение. Эта задача отличается от предыдущих тем, что
коэффициент при х2 в знаменателе не равен единице. Для того
чтобы свести этот случай к предыдущему, будем этот коэффици-
коэффициент выносить за скобку (см. замечание на стр. 72).
49 _П]_ Л/ | 7\2 171]
' ТОО + 5 J ~ L\ 10/ + TOOJ'
_ р dx_
J 51г+То)
11 Х+10
x-j-.
h = I 77 7Т5 Щ = i-yfn «ctg
TooJ "To
= _2 t_ 10*+ 7
\
2)
2 , 8л: + 1 , „
= -т= arctg ,— + С.
/79 /79
642
3) Зх2-
Задача 6,7 (для самостоятельного решения).
Найти интегралы:
dx .
Зх + 5 '
dx
1) Г d± ; 2) Г 1
3) f *± ; 4) f i ,
; J 9x2 + x + 12 ' ' J 6хг + 7x + 15
Ответ. 1) ^
t
6л:—11
Теперь выполним упражнения в интегрировании дробей вида
Ах + В
Задача 6,8. Найти интегралы:
Решение. На стр. 71 дано указание, как вычислять эти
интегралы. Рекомендуется еще раз ознакомиться с ним.
643
1) Преобразуем дробь
, 1 ,
стоящую под интегралом:
выделим в числителе из Зх + 4 производную знаменателя, равную
2л:+ 7, но чтобы величина числителя при этом не изменилась:
Поэтому
J1~J
Преобразовываем в разность
двух интегралов, причем во
втором интеграле в знамена-
знаменателе выделяем полный
квадрат
-3 Г
2*4-7
Числитель является
производной знамена-
знаменателя. Применима фор-
формула A,32)
dx
*+7Г -X
13
Х~Т~ 2
Ответ. /х =-| In (л* + 7* + 14) — -^L
Замечание. Под знаком логарифма трехчлен х2 -+- 7х + 14
не взят по абсолютной величине, так как корни его комплексны,
коэффициент при х2 положителен, а поэтому при любом значе-
значении х этот трехчлен положителен.
Это замечание следует иметь в виду и в дальнейшем.
2) Из числителя дроби 2х — 3 выделим производную знаме-
знаменателя, равную 2х + 1, и получим 2х — 3 = Bх +1) — 4. Поэтому
72 = j
Представляем как раз-
разность двух интегралов,
а во втором интеграле
в знаменателе выде-
выделяем полный квадрат
В числителе произ-
производная знаменате-
знаменателя. Применить фор-
формулу A,32)
dx
= arctg ^tl _j_ с.
19 s /19 ^
644
3) Поступаем так же. Из числителя дроби 7х— 8 выделяем
производную знаменателя, равную 2х + 5:
= \ In (*• + 5х + 17) —^L arctg 2^У + С.
Задача 6,9 (для самостоятельного решения). Найти интегралы:
х + 7 , „.Г х — 3 ,
dx 3> 3 ^:
4) Г 7х+4 dx; 5) Г 5*-7 d
Ответ. l)|ln(*s +
3) 1 In (x* - 9x + 23) + ф= arctg 2j^ + C;
4. Интеграл вида \ 2.х?, .„, где п>1 и целое, а кории
знаменателя комплексны, сводится к вычислению двух интегра-
интегралов. Это достигается так: в числителе записывается производная
основания степени знаменателя, т. е. производная от х* + рх -\- q,
и так же, как было указано в п. 3, (стр. 71 ), эта производная
преобразовывается в выражение Ах -\- В, стоящее в числителе.
Дробь
/о , ч А , D Ар
1
Интеграл первой дроби вычисляется по формуле A,29).
Вторая дробь
Если обозначить
Q-Pi = P2, ^ + | = Рг F,4)
645
(обозначить q— ^- через Р2 мы имеем право, так как по предпо-
предположению корни трехчлена х2 + рх + q — комплексны, а -потому
q — ^- — величина положительная I, то
[Р2 A + г2)]"
и таким образом интегрирование второй дроби в правой части
F,3) сводится к интегрированию дроби t . 2.„.
Интеграл
F,5)
вычисляется по формуле
где
I _ __| ? |_ 2/г — 3 , ,fi «,
Ч~ 2(я— 1W1 4-2^»-» ^ 2га —2 п-1' ^и> '
(индекс у буквы / равен показателю степени выражения 1 + z2).
Вывод формулы F,6) можно найти, например, в учебйике Н. С. Пис-
кунова «Дифференциальное и интегральное исчисления».
Формула F,6) называется рекуррентной, или формулой приве-
приведения. Она позволяет вычисление интеграла /„ свести к вычисле-
вычислению интеграла 1п_1 с меньшим на единицу индексом.
Упражнения, связанные с применением рекуррентной
формулы F,6)
Задача 6,10. Вычислить интегралы:
П / = Г dz • 2W = Г dx ¦ Ъ I = Г dx
> 3 J A — г2K' ' * J(l+-v2L' ' i)D + *2N'
(Значок при / равен показателю степени выражения, стоящего
в знаменателе).
Решение. 1) Применим последовательно формулу F,6).
Подставляя в F,6) п = 3, получим:
, ____} г 2-3 —3, .
3 ~~ 2C — lXl-fz2K + 2- 3 — 2 2'
/ — 1 г I 3-/
646
Теперь применим F,6) к вычислению /а (положим в F,6) п=2).
Тогда
г I 3 ( ' г 2-2-3Л 1 г
I (
4 A+г2J" 4 \2B—1) A+г2) '2-2— 2
,1A г I l ! ) 1 г I 3 г ¦ It
~f~ 4\2 l+^"i~ 2 yV~ 4A+ г2J "•" 8 1 + г2 т 8 1-
Но /х = I fnrr = агс*ё г + С, а поэтому окончательно
= J (
+г2)з = ТA -f г2J + "8" ТТТ2 + 8"агс^г + С. F,7)
2) Здесь также последовательно применяем формулу F,6)
начиная с п = 4:
/ - ' * д. 2'4~3 / •
'* ~2D — 1)\\+х*)*~1~*~2- А — 2'3'
Но /3 нами было найдено в предыдущем примере, только там
вместо х стояла буква г. Заменяя в F,7) z на х и подставляя
в F,8), получим
5 Г1
6"LT
3 * 3 ,
"8 Г+J? + Т arct8*
Окончательно
3) Формулу F,6) можно применить, если в знаменателе будет
выражение вида A + х2)". У нас же в степень п = 5 возводится
не 1 + хя, а 4 + х2. Полагая х = 2г, получим dx = 2dz; x2 = 4z2
а D + *2M = D + 4г2M = [4A+ г2)]5 = 1024 A + г2N.
Поэтому искомый интеграл
, Г dx = Г Ыг = 1 Г dz _ 11_
J D + л:2M J 1024A +02M 512 J A +г2M-512/5<
Итак, -^ = 512/5 и' пРименяя формулу F,6) при п = 5,
/ - ' Г ' г 2-5-3
512L2E-l)(l+z2)*'i. 5 — 2
т
Подставляя сюда найденное в предыдущем примере /4 (только
в F,9) надо х заменить буквой г), получаем
I = 1 [ 1 г 7/1 г 5 _г_
512 [ 8 A -f- г2L 8 \ 6 A + г2K ^ 24 A -f- г2J Т
647
Раскрывая скобки, будем иметь
г__ . Т_ г _35_ г
A + г2L + 48 A + г2K + Т92 A + г2J
35 г .35 ,
+
Возвратимся к старой переменной х. Мы полагали, что х —
X X
Отсюда г = y ¦ Подставляя в последнее равенство г = -=-, полу«|
чим окончательно
1 — 32 D + х2)* + 768 D + х2K + 12288 D + л;2J +
+ 32768 4 + л? + 65536 аГС1§ 2 + Ь-
Задача 6,П (для самостоятельного решения).
Вычислить интегралы (указания даны на стр. 77 и 78).
2) / =
Eл:2 Н- 2х + 4)
8 '
Г Злг + 5 , .. г _ Г 2л: — 1
' }(x* + 2x+5JUX' q) J Dл:2 + Зл; +
6х + 1 ,12 &4-I , .
&* + х+7) + к7Ш***7&+С-'
± 1 Г 1 . , 15 1 ,
38 L2 Eл;2 + 2л; + 4J ^ 76 Eх2 + 2л; + 4)J *"
5?±
2888/19
21
336 , 8л;+3 , „
7= arctg —т=- + С.
5041]/71 /71
СЕДЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Интегрирование рациональных дробей.
На пятом практическом занятии учащийся на большом числе
упражнений ознакомился со способами разложения рациональной
дроби на простейшие, а на шестом занятии он приобрел навыки
интегрирования простейших рациональных дробей.
Поэтому интегрирование рациональных дробей не должно вызы-
вызывать трудностей. Ограничимся только несколькими подробно разо-
648
бранными примерами, а остальные предложим для самостоятель-
самостоятельного решения.
Мы рассмотрим такие четыре случая:
1. Корни знаменателя — только действительные числа, среди
которых нет равных.
2. Корни знаменателя — только действительные числа, но среди
них есть равные (знаменатель имеет действительные кратные корни).
3. Знаменатель дроби, кроме действительных корней, имеет
и комплексные корни, но среди них нет равных.
4. Знаменатель дроби наряду с действительными имеет и
кратные комплексные корни.
Первый случай.
Задача 7,1. Вычислить / = 1 ,X_^I7_^dx.
Р 6 ш е и и е. Прежде чем приступить к интегрированию ра-
рациональной дроби, следует убедиться в том, что дробь — пра-
правильная и несократимая. В нашем случае дробь, стоящая под
интегралом,— неправильная, так как степень ее числителя (третья)
выше степени знаменателя (второй).
Поэтому прежде всего исключаем целую часть.
Для этого делим числитель х3 + х + 2 на знаменатель
(х — 3) (* — 4) = л:8 — 7х + 12:
X3 + X
-Рл:3 -Ь
7л:2 —
'+7л:2
7л:2
11л:
±4
Т
+
9л:
12*
2
X2
-
— 7л:
_
+
*'
12
38*-
-82
С+12
38л: — 82
Поэтому
в
? 0\ (? ^\ ? , g "Г ? ^ '
Умножая обе части этого равенства на, (л: — 3) (л: — 4), получаем
38л: — 82 = А {х — 4) + В {х — 3).
Здесь коэффициенты проще всего определить способом задания
частных значений: А = —32; В — 70.
дробь (;ЛкА=-д+^- а '=4*2+7*+
1 U * ': = -1-л:2+7л:—32Injл:—3| + 701п|л:—
' (* 2 1 I К
Задача 7,2. Вычислить / = 1 /+Y . dx.
j х (х -\- о) (х Z)
Решение. Дробь, стоящая под интегралом,— правильная.
Разлагаем ее на простейшие:
+5 А , В , С
х(х-\-3)(х— 2) х ^ х + 3^ х~ 2"
649
Умножая левую и правую часть этого равенства на знамена-
знаменатель левой части, имеем
х2 + х + 5 = А (х + 3) (х — 2) + Вх (х — 2) + Сх (х + 3).
И здесь при определении коэффициентов А, В и С наиболее
быстро к цели ведет способ задания частных значений.
(Вообще, если корни знаменателя — числа только действитель-
действительные и разные, этот способ является наиболее целесообразным).
А2- ВП- С11
Задача 7,3 (для самостоятельного решения).
: 1) I .—. , * . . ч; 2) |
; J (a + bx)(c + dx)' ' J
Вычислить
a-\-bx
Ответ-
c + dx
\n\c
Задача 7,4 (для самостоятельного решения).
Вычислить интеграл 1 :
dx
Ответ, g-In
х — а
х*
с.
Задача 7,5. Вычислить:
/= Г 2х+3
„. , С 2х* — 7х + 8 , .. ,
Решение. 1) Разлагаем прежде всего знаменатель на мно-
множители: х2 — 7х + 12 = (х — 3) (х — 4). Дробь
_ 2л;+3 _ А Д ¦ .4 — ~9- Д— 11-
"~ (л: — 3)(х — 4)~х— 3^~х — 4' '
/|n с
' ~ Ш (х- З)» +С>
2) Знаменатель дроби разлагаем на множители:
х3 — 9л;2 + 20* = х (х2 — 9х + 20) = х (х — 4) (х — 5).
Дробь
^ Л Б С
~~ х ' х — 4 '
*3 — 9л:2 -f 20л: ~~ х ' х — 4 ' л: — 5 '
650
Для определения коэффициентов А, В и С с целью упражне-
упражнений примените способ задания частных значений и способ неопре-'
деленных коэффициентов. Окажется, что
л _ 3 . r__27. г_38.
20' 4 ' 5'
(х— 4)«У(х — 4)8
3) Знаменатель дроби разлагаем на множители: приравниваем
знаменатель нулю и находим его корни:
х* — Ю*2 + 9 = 0; xt — 1; х2 = —1; х3 = 3; xt = —3, поэтому
xi _ ш*2 + 9 = (х — 1) (л; + 1) (х — 3) (х + 3), а дробь
2хг — 7л:+8__ А . В . С D
"^ ~T~ +
47
- 1П (X + 1) у (^_1)9(^+3L7 +
4) Здесь мы прежде всего обращаем внимание на то, что дробь,
стоящая под интегралом,— неправильная. Исключаем целую часть:
— 9* +5
А
A ^X 6) \X -j- Of X A О Л -j- О
Определяя коэффициенты любым из указанных способов, по-
получим:
А = — —¦ R — — • Г = — •
Q T Q * Q *
С.
Задача 7,6 (для самостоятельного решения).
Вычислить интегралы:
¦>Г
'5
; —91 , ON Г dA;
, о\ Г d
пХ' 6> J 4** -
;* - 1) (х -f 3) (л— 4) """' ^ J 4л-* - 5л-2+ 1
4) f 1^
' J г3 -f 7г2 + 2г — 40 '
651
i
Указания. В первом примере после исключения целой части*
х -4- 5 • ¦ ¦''
получится дробь -д—=-~—j—=; знаменатель после разложения]
X ~~— ОХ ~~ X -Н— О \Ц
его на множители равен (х + 1) (х — 1) (х — 5). Дробь „_^Д_ i_5=|
В четвертом примере один корень знаменателя zx = 2.
Ответ. 1) (i±^+lln|^+ I |_|ln|^-l |+lln[*-5|+CJ
Второй случай. Корни знаменателя — только действительные;;
числа, но среди них есть кратные. :]
Задача 7,7. Вычислить . ;
J (* —:
¦tdx.
Решение. Заданная дробь — правильная и несократимая.
(На это прежде всего следует обратить внимание).
Представим дробь в виде
А , В , С + D , Е ,, 1Ч
(х— lK(*-f2J (л: —I)8 ~ (х— IJ ' х—1 ' (лг + 2J *+ 2 ' v '
Определение Л, Л, С, D, Е проведем способом неопределен-
неопределенных коэффициентов и способом задания частных значений, кото-
которые целесообразно комбинировать.
Умножая обе части написанного равенства на знаменатель
левой части, получим
2л;2 + 5л; —8 = А (х + 2J + В (х— 1) (х + 2J + С(х— IJ (л;+2J +
+ D (х — IK + Е (х — IK (х + 2).
Напоминаем, что написанное выражение является тождеством,
а потому равенство должно сохраняться при любом значении х.
При х = —2 получаем
2 (—2J + 5 (—2) — 8 = D (—2 — IK,
отсюда определяем коэффициент D:
—10=—27D; D = |5.
При л; = 1
2. 12 + 5- 1— 8 = /1A +2J; — 1 =9-4; А = — -^-.
652
Нам осталось определить еще три коэффициента: 5, С и Е.
Теперь будем сравнивать коэффициенты при одинаковых сте-
степенях х в левой и правой части равенства.
Коэффициент при х* в левой части равен нулю (х* в левой
части отсутствует), а в правой С -f Е. Поэтому С + Е = 0.
Свободный член в левой части равен — 8, а в правой 4Л —
— 45 + 4С — D — 2?. На основании этого получаем второе урав-
уравнение: 4Л — 45 + 4С — D — 2Е = —8, в котором А и D уже
97
известны, а поэтому 25 — 2С + Е — ^.
Мы сравнивали именно свободные члены потому что это можно
сделать, не выполняя умножения и возведения в степень в пра-
правой части равенства.
Для того, чтобы получить третье уравнение для определения
В, С и Е, снова возвратимся к способу, задания частных значе-
значений. При х = 2 получим
8+ 10 — 8= 16Л + 165 + 16C
4E.
G учетом, что А = — -§¦, a D = ^= это уравнение примет вид
Таким образом, для определения В, С и Е имеем систему
уравнений
4В + 4С+ ?'=
В =
29
27:
77
27 I
.— 27' C~27#
Таким образом,
13
10-
13
Очень полезно сделать проверку найденных значений коэф-
коэффициентов. Для этого дадим х произвольное значение, например,
х = —3, получим равенство
-5 = Л —45 + 16С — 64?) + 64?.
65
При найденных значениях коэффициентов оно выполняется.
Отсюда мы заключаем, что коэффициенты определены верно.
I3 _!
27 | 27
27*— 1 27Ш|* '
26*2 + 5*-34 13.
+ 27 In
Задача 7,8 (для самостоятельного решения).
Вычислить интеграл \ х- ' ,—~ / ГЧч^ ^ способами, ко<
J (X Z) (X-f- О)
торые были применены в предыдущей задаче.
Ответ 23 1 42 27 . д,
итвет. ^^^^ __________ -f 2S Ш | х .|
Задача 7,9 (для самостоятельного решения).
Г* г2 _i_ г 1
Вычислить интеграл I „7~_„,2 • dx
"°ТВеТ-
8*2 (I- 2)'
Задача 7,10 (для самостоятельного решения).
С Х2 8* -1- 7 j
Вычислить интеграл / = J (^__3*-ЮJ
Указание. г> — Зл:— 10 = (х— 5) (х + 2).
п _8_ 1 27 1 30 ,
UTBeT> 49х~5~ 49^+2 + 343 Ш
х — 5
С.
x+2
Третий случай. Знаменатель дроби, кроме действительных
корней, имеет и комплексные, но среди комплексных корней нет
равных.
Задача 7,11. Вычислить интеграл / — \ v~
J х
_,5 dx.
Решение. Разложим знаменатель на множители:
х3 — хг + 5х — 5 _ х2 (х — 1) + 5 (х — 1) = (х — 1) (х2 + 5).
Дробь, стоящая под интегралом, — неправильная. Поэтому,
прежде чем разлагать ее на простейшие, исключим целую часть,
Окажется, что она равна
654
„ , 6л-2 4-25л-— 35 „ ,,
Теперь дробь xs_xi<5x_5 разложим на простейшие. Учиты-
Учитывая, что знаменатель дроби равен (х—1) (х2 + 5), получим
6л:2 -f 25л: — 35 _ А Вх + С
(х— 1) (л:2 +5) — х— 1 "¦" л-2-f5 '
Умножая обе части этого равенства на знаменатель левой
части, получим
б*2 4- 25л: — 35 = А (х2 + Ъ) + (Вх + С)(х— 1).
Применим сначала способ задания частных значений. Возьмем
6 • I2 4-25 • 1—35 = А (I2 + 5); — 4 = 6Л; Л = — -§-.
Теперь сравним коэффициенты при одинаковых степенях х.
В левой части равенства коэффициент при х2 равен 6, а в пра-
правой А -\- В.
2 23
Поэтому А + В = 6, а так как А = — -г-, то 5 = •=-.
Свободный член в левой части равенства —35, а в правой
ЪА — С. Поэтому ЪА — С = —35; С = ^.
Итак, дробь
20 95
• QC о 1 Ч *~Г о
(л-— 1)(л-2+5) ~ 3 х— 1+ л:2+5 *
Учитывая это, а также выражение (А), получаем
= ~ + 6х-~\п х-1 +^
Задача 7,12 (для самостоятельного решения).
Вычислить I г~4 •
Указание. 1 — ** = A — х) A + х) A + *2). Дробь запишется
в виде
1 = А В Сх+Р
. 1— х*~ I— ЛГ+1+-« 1+л:2'
Ответ. l
у 1 О
Задача 7,13. Вычислить
х dx
1+х3'
655
Решение. Так как 1 + х3 = A + х) A — х + х2), а корни
трехчлена 1 — х + х2 комплексны, то дробь запишем в виде
х _ А . Вх+С
1 + * + 1 — х+х*'
Задача 7,14 (для самостоятельного решения).
Вычислить I .__ ,.
Указание. 1 _ х3 = A — х) A +х + х2).
о,.„. 1
Задача 7,15. Вычислить/ =^{ + + ^+)
Указание. Учитывая, что корни каждого из' трехчленов,
находящихся в знаменателе,— комплексны, подынтегральную дробь
запишем в виде
х3 Ах + В . Cx + D
1 I "
(Хъ 4- х + 2) (х2 — 2х + 3) л:2 + х + 2 ~ х* — Чх + 3 '
22' °~11' °~2' 22*
Ответ. In У (х2 + х + 2M (л;2 —2х + 3)"+ -—=¦ arctS f±y=i ~
22/7 /7
Задача 7,16 (для самостоятельного решения).
Вычислить I . 2 ¦
1 1 X
Ответ, -j arctg х — -^- arctg у + С.
Четвертый случай. Знаменатель дроби имеет действительные
и кратные комплексные корни.
Задача 7,17. Вычислить J(—-jJ
Указание. Знаменатель дроби имеет кратные комплексные
корни. Если (х2 -J- 4J = 0, то хх = 2г, х2 = —21; х3 = 2i\ xA =
= —2г. Дробь
1 _ А , В м Сх+ D ¦ Ex+F.
! "Т" , 1 I /„2 I /П2 Т
(х— 1J(л:24-4J (х— IJ Т х— 1
L- R- *_• Г--М-- П_ PJ-
25' ° ~ 125' 125 " 125 * 125
-L
125 *
A-L- R- *_• Г--М-- П-_31- P-J--
25' ° ~ 125' 125 " 125 * 125'
656
Ответ 2 ln*a + 4 71^ + 4^+88 I_arctg- + C
итвет. 125 (л:— IJ 1000(х — 1)(*2 + 4) 2000 8 2 + '
Задача 7,18 (для самостоятельного решения). Вычислить ин-
интегралы:
J (jt*-6*-fl3)ld*: 2) J
C +
Указание. При вычислении второго интеграла можно избе-
избежать обычного пути, если ввести подстановку 3 + 2х2 = г. Тогда
Axdx = dz; xdx = f; x* = ^ ; x* = (-^=^ и
Г jfidx _ Г x*xdx _ С (z — 3J dz _ J_ Г г2 — 6г + 9 . _
J C + 2*2)з ~ J C +2*2K ~ J 4-4-z* ~ 16J P dZ ~ -
= ^[in C
С.
Отсюда легко получается и предыдущий ответ.
Замечание.Следует вообще иметь в виду, что интегралы
вида \ , , 2 dx, где т — целое и положительное число, легко
вычисляются с помощью подстановки а + Ьх2 = г. Эта подстановка
1 С (г — а)т .
приводит к интегралу ^m+1 \ zrl' dz, а вычисление его сво-
сводится к вычислению интегралов от одночленов.
Задача 7,19 (для самостоятельного решения). Вычислить
Указание. Подстановка 5 + 4л:2 = г;
Ответ. ±[ln E + 4*2) + 1375 + ^ +1440*4 + С.
512 L v ' ' ' 6 E+4л:2)8 J '
22 и. А. каплан ' 657
ВОСЬМОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Интегрирование выражений, содержащих тригонометри-
тригонометрические функции.
I. ИНТЕГРАЛЫ ВИДА
J sin kx cos lx dx\ J cos kx cos Ix dx\ j sin kx sin Ix dx;
где k и I — действительные числа.
Из тригонометрии известно, что произведения тригонометри-
тригонометрических функций, находящихся под знаками этих интегралов, пре-
преобразуются в суммы по следующим формулам:
sin kx cos lx = y lsm (k — l)'X + sin (k + t)x]\ (8,1)
cos kx cos lx = y [cos (k — /) x -f cos (k + /) x]; (8,2)
sin kx sin Ix = y teos (k — l)x — cos(k + I) x]. (8,3)
Заменив в рассматриваемых-интегралах подынтегральные функ-
функции по этим формулам, легко выполним интегрирование.
Следует также иметь в виду уже известные нам формулы,
которыми часто придется пользоваться. Для удобства мы запи-
запишем их здесь:
\sinnxdx = cosnx + C; (8,4)
i cos nx dx = — sin nx + С; (8,5)
dx
sin*
dx
In
= ln
(8,8)
tg(y-r- t
cos*
Задача 8,1. Вычислить интегралы:
1) lx = f sin бдс cos Ix dx; 2) /2 = f cos 3* cos 9* cfo;
3) /3 = J sin 2^ sin 5* d*.
658
Решение. 1) Заменяя произведение sin6xcos7x по фор-
формуле (8,1), получим
/х = -1 I [sin (—л:) + sin 13л:] dx — у I (-sin^ + sin 13л:) dx =
= -о-(cos* — 75 cos 13л:) + С-
2) Заменим cos Зл: cos 9л: суммой косинусов по формуле (8,2),
найдем
/2 = 1 Г fcos (—6л:) + cos 12л:] dx = у ] (cos 6x + cos 12x) dx =
| cos (—6х) = cos блг j I Применить формулу (8,5) j
=-i-(j sin 6* +1 sin 12х) + С.
3) Заменяя произведение sin2л:sin5x по формуле (8,3), по-
получим
/3 = -i- I [cos (—Зл:) — cos 7x] dx = у (у sin Зл: — у sin 7x) + С. ,
Задача 8,2 (для самостоятельного решения).
Найти интегралы: 1) \ cos Зл: cos x dx; 2) \ sin Ъх sin у dx;
3)
Ответ. 1) ^{^sin2
2) j(_^si
3) -y
Задача 8,3. Найти / = J sin 2л: cos 5л: sin 9л: с(л:.
Решение.
sin 2л: cos 5л: sin 9л: = у [sin (—Зл:) + sin 7x] sin 9л: =
= у (—sin Зл: sin 9л: + sin 7x sin 9л:) = у — у (cos 6х — cos 12л:)
l /
, 1 / о п о iftv\l. / l /sin 12л sin6x . sin2A: sin 1
+ т(cos2x-cos 16*)j; I=-T[—га g~ + 1 Гб
Задача 8,4 (для самостоятельного решения). Найти:
1) f sin x cos 2л: cos Зл: dx; 2) j cos л: cos 2л: cos 5л: dx.
л , ч cos 2x , cos 4лг cos 6x . ^
Ответ. 1) __g^ + _^ 2Г+С;
O\ s^n^x I sin4x , sin блг . sin 8* . _
^ ~"8~ + Тб~ + IT" + 2" + C-
22* 659
II. ИНТЕГРАЛЫ ВИДА
§smmxcosnxdx. (8,10)
(Во всем дальнейшем т — показатель степени синуса, п — пока-
показатель степени косинуса).
Интегралы этого вида вычисляются особенно просто в четырех
случаях: 1) m — нечетное положительное число; 2) п — положи-
положительное нечетное число; 3) m + п = — 2k — четное отрицательное
число; 4) т. + п = 0 (в четвертом случае предполагается, что т
и п — целые числа).
Первый и второй случаи. Показатель степени синуса т — не-
нечетное положительное число: т. = 2k -f 1. В этом случае подынте-
подынтегральное выражение преобразовываем так: из sin* = sin2*+1x,
выделяем первую степень синуса и получаем
sin2*+1* = sin2** sin л: = (sin2 л;)* sin л; = A —cos2*)* sin л:,
а подынтегральное выражение
sin x cos" x dx = A — cos2 x)k cos" x sin x dx.
Теперь применим подстановку
cos* = z. (8,11)
Тогда —sin x dx = dz;
A — cos2 x)k cos" x sin x dx = — A — г2)* zn dz,
и вопрос сведется к интегрированию суммы степенных функций.
Второй случай. Показатель степени косинуса п — нечетное
положительное число:
n = 2k + \.
Из cos" х = cos2*+1 x выделяем первую степень косинуса и по-
получаем
cos2** = cos2* x cos* = (cos2 *)* cos * = A — sin2 x)k cos*.
Подынтегральное же выражение запишется так:
sin* cos" xdx = sinm*(l —gin2*)* cos xdx.
Применим подстановку
sin* = z, (8,12)
cos*d* = dz, подынтегральное выражение примет вид
zm{\— z*)kdz,
и вопрос опять-таки сведется к интегрированию суммы степенных
функций.
Итак, вычисление интеграла (8,10) при указанных значениях
тип сводится к интегрированию многочлена.
Приступим к решению задач.
660
Задача 8,5. Вычислить интегралы:
1) /j = j sin3 x dx; 2) /2 = j cos6 x dx;
3) /3 = fsin7*d*; 4) /4 = Г cos9 жd*.
Решение. 1) Запишем, что sin3* = sin2*sin* ==
= A — cos8*)sin*. Тогда
/1 = j(l — cos2*) sin ж <i*. (8,13)
Применяя подстановку (8,11) cos* = 2, получим
h = —1A -г2) dz = -2 + I + С
Возвращаясь к старой переменной, получим окончательно
Собственно говоря, для вычисления интеграла (8,13) никакой
подстановки не требуется, так как формула A,29)
позволяет сразу написать ответ. Из (8,13) следует, что
/х = jsin*d*—fcosa*sin*d* = —cos*-f
+ Г cos2 x (—sin *) dx = —cos * + c-^- + C.
Это замечание относится и к следующим примерам этого но-
номера. Однако мы все же для упражнений будем прибегать к под-
подстановкам.
2) В подынтегральной функции cos5 * выделим первую степень
косинуса, тогда ¦
cos5 х = cos4 x cos x = (cos2 х)г cos x = A — sin2 xf cos * =
= A — 2sin2* + sin4x) cos*,
a
/2 = f A — 2 sin2 * + sin4 x) cos x dx.
Применяя подстановку (8,12): sin* = 2; cos*d* = d2, получим
I2 = j A -2г2 + г4)dz = z-\ + f + С
Возвращаясь к старой переменной, т. е. заменяя z на sin*, по-
получим окончательно
, . 2sin3х . sin5* r
/2 = sin* g \ g—h C.
И здесь, конечно, можно было обойтись без подстановки,
а вести интегрирование непосредственно при помощи формулы
661
3) Из sin7 л: выделяем первую степень синуса и получим
sin7 л; = sin6 л; sin л; = (sin2 *K sin * = A —cos2*K sin*;
/3 = Г A—cos2 л;K sin х dx.
Подстановка (8,11): cos* — z; —sinxdx = dz
/3 = — j A — z2K dz = — j A — 3z2 + Зг* — гв) dz =
Возвращаясь к старой переменной, т. е. заменяя z на cos*,
получим окончательно
/3 = — (cos * — cos3 * + -g- cos6 * — у cos7 *) + С.
4) Решение проведем без подробных объяснений:
cos9 * = cos8 * cos * = (cos2 *L cos * = A — sin2 *L cos *;
/4 = j A — sin2*Lcos*d* = j A — z2Ldz =
I Подстановка:
sin x = z; cos x dx = dz
= Г A — 4га + 6г4 — 42е + г8) dz = z — -|г3 + -|г6 —
_4-z7 + 4-z9 + C = sin* — i-sin3*+ -| sin5* —
У О
Задача 8,6. Найти интегралы: 1) /й = Г sin4 * cos3 * dx;
2) /2 = f cos2*sin5*dx; 3) /3 = j sin4*cos7*dx.
Решение. Эти примеры решаются так же, как и примеры
предыдущей задачи. У функции, которая под интегралом нахо-
находится в нечетной степени, выделяем первую степень и применяем
указанный выше прием.
1) sin4*cos3* = sin4*cos2*cos* = sin4*(l—sin2*)cos* =
= (sin4 * — sin* *) cos *,
поэтому
/x = T (sin4 * — sin* *) cos * dx = f (г4 — 2е) dz =
I Подстановка: sinx—z;
cos xdx= dz
sin5* sin7*
Заменяем г на
sin*
662
2) Подынтегральную функцию преобразуем так:
cos2хsin5x = cos2xsin4xsinx = cos2* (sin2*Jsin* =
= cos2 л; A — cos2 xf sin x = cos2 x(l — 2 cos2 x + cos4 x) sin x =
= (cos2 x — 2 cos4 x + cos6*) sin x;
/2 = f (cos2 x — 2 cos4 x + cos6 x) sin * d* =
I Подстановка: cos x = z; I
—sin xdx = dz
j Заменяем г на cos x I
/cos^x 2cos6* cos?*\ , /-. ¦
= — (-3 g- + -^ j + C.
3) Подынтегральную функцию запишем так:
sin4 x cos7 x = sin4 л; cos6 л; cos л; = sin4 * (cos2 jcK cos x =
=sin4 * A — sin2 xf cos *=sin4 л; A — 3 sin2 л; +3sin4 л; —sin6 x) cos jc=
= (sin4 x — 3 sin6 jc + 3 sin8 x — sin10 л;) cos x;
I3 =-1 (sin4* — 3sin6;c + 3 sin8* — sin10x)cosxdx =
I Подстановка: s\nx = z; cos xdx=±dz\
I Заменяем z на sin x I
sin5x 3 sin?* sin9 x sin11* . ~
Задача 8,7 (для самостоятельного решения).
Найти интегралы: 1) J sin7*cos6*dx; 2) \ sin2*cos5*dx;
3) \ sin2* cos3* dx; 4) f sin3 * cos2 * dx.
113 1
Ответ. 1) —у cos7 * + -g- cos9 * — jy cos11 * -+- j* cos13 * -+- C;
2) ysin3* — |-sin5* + irSin7* + C;
3) у sin3 * — -g- sin5 * + C;
4) 4-cos5* —4-cos3*''+C.
Задача 8,8. Найти интегралы: 1) /х = \
COS X
663
Решение. 1) sin6 л; = sin4jc sin л; ^ (sin2x)a sin л: ==
= A — cos2*J sin x — A — 2 cos2x + cos* x) sin x;
1
cos4 л;
Подстановка: cos л; = z;
—sin xdx= dz
_
Выполним почленное
деление
--Hi—1+1 <Ь = -(-55 + 4
(Заменяем г на cosxj
12 1
cos x + С = -^ sec3 x — 2 sec лс — cos x + С.
cos x '3 '
= 5—5
3 cos3 x cos x
2) cos3 x = cos2 x cos jc = A — sin2 jc) cos x;
_ f
Подстановка: sin x — z;
cos xdx= dz
__±1 ¦ 1J_ ,
5 г5" З гз"
| Заменяем г на sin* j
l
5 si
3 sins л:
= —=- cosec5 х -\- -г- cosec3 x + С.
О О
3) Числитель sin3 х = sin2x sin х = A — cos2 x) sin x;
Подстановка: cosx = г;
sin xdx= dz
I Заменяем г на cos x j
= h cos л; + С = sec л; + cos x -)- С
cos* ' ' ' '
Задача 8,9 (для самостоятельного решения).
r. 3)
, 7)
Найти интегралы: 1) J>J?->; 2)
8) f-^rdx; 9) fcos8jcy^iit?jcdx; 10) [^SJ
J l/cosx J J ysin
664
Ответ. 1) _™ff_lnicos*| + C; 2) g^ + С;
3) + ln
6) у cos2 л: —2" cos4 л; -+- -j cos6 x — -g-cos8* -+- jgcos10* — In j cosjc|;
?• • о i * • Л
7) 33
8) —
9) 3 j/sin2* Цг sin x — ^ sin3 x + ^ sin5 x) + C;
10) 2VsirTx(l— i-sin2j«;) + C.
Задача 8,10 (для самостоятельного решения).
Найти интегралы: 1) \^xdx; 2) J^
Ответ. 1) -cos^-
Третий случай Сумма т + п показателей степени синуса и
косинуса в интеграле (8,10) — четное отрицательное число:
т + п — —2k (k > 0 и целое).
В этом случае подынтегральная функция может иметь два
вида:
1) Подынтегральная функция — дробь, в числителе которой
находится степень синуса, а в знаменателе — степень косинуса
(или наоборот), причем показатели степени или оба четные, или
оба нечетные. В этом случае говорят, что они одинаковой чет-
четности.
Так как т-\-п — отрицательное число, то отсюда следует,
что степень знаменателя больше степени числителя.
2) Подынтегральная функция — дробь, числитель которой по-
постоянная величина, а знаменатель — произведение степеней синуса
и косинуса одинаковой четности.
В рассматриваемом случае (т + п = —2k) .любая из подста-
подстановок
tgx = z (8,14)
или
z (8,15)
665
преобразует подынтегральную функцию в многочлен или в много-
многочлен, сложенный с целыми отрицательными степенями новой не-
независимой переменной г.
Если подынтегральная функция имеет первый из разобранных
видов, а в числителе находится степень sin x, более удобной из
этих подстановок является (8,14), если же в числителе находится
степень cos*, рациональнее применить подстановку (8,15).
Дроби второго вида с помощью подстановок (8,14) и (8,15)
можно привести к интегрированию степенных функций.
Применяя подстановку (8,14), надо учесть, что из tgx = z
следует:
, dz 1
COS X =
c2xdx — dz- dx -
c xax - az, ax -
dz
dz
= dz )
Если применяется подстановка (8,15), то
dz \
sin л; =
cos л; =
(8,17)
-z*
Задача 8,11. Найти интеграл /= \^^dx.
t) COS X
Решение. Здесь т = 4; n = —8; m + n = —4 — четное отри-
отрицательное число. Подынтегральная функция относится к рас-
рассматриваемому случаю.
Так как в числителе находится степень синуса, то на осно-
основании сделанного указания удобно применить подстановку (8,14):
tgx = z. По формулам (8,16) получаем
Z*
. _
1
I + г2
(/1 + г2)»
_ (V(l + zs)« 1
A ц_ Z2J 1 4. гг
-J!
-J'
Переходим к старой переменной (заменяем г на tgx)
Задача 8,12. Найти интеграл /
л
dx.
Решение. Здесь п=4; т = —6; т -f- п = —2 — четное отри-
отрицательное число, и мы имеем рассматриваемый случай. Так как
в числителе находится степень косинуса, удобна подстановка
(8,15): ctgx = z.
Используя формулы (8,17), получаем
Заменяем г
на ctgx
Задача 8,13. Найти интегралы:
si х и*- о
dx 2
Г
Г cos3 х
Решение. 1) Здесь т = 3; п = —7; т + « = —4 — четное
отрицательное число, т. е. рассматриваемый случай. В числителе —
степень синуса, а потому удобна подстановка (8,14): tgx = z.
Используя формулы (8,16), относящиеся к этой подстановке, по-
получим
г3
л =
- J г3
Vd
¦
Vd
1+22
+ г2K
1
+ г2O
= jV(l
dz Г
l + г2 J
>-
1 I ~2}4 dz
1 *" ' 1 + z2
I 75\ A7 Z
f- Z )U? ^
Заменяем
2 1 С
г на tgj;
2) Здесь т = —9; п = 3; m + n = —6 — четное отрицательное
число, т. е. рассматриваемый случай. В числителе — степень
667
косинуса, удобно применить подстановку (8,15): ctg л: = ц. Исполь-
Используя формул*ы (8,17), относящиеся к этой подстановке, получаем
= — J г3 A + 2г2 + z4) dz = — J (г3 + 2г5 + г1) dz =
I Заменяем г на ctgx
ctg4 д: . ctg8 x ctg8
+ +
Для упражнения к первому интегралу примените подстановку
(8,15), а ко второму — (8,14). Ответы совпадут, но в каждом —
случае придется интегрировать отрицательные степени г, поэтому
интегрирование осложнится.
Задача 8,14 (для самостоятельного решения). Вычислить ин-
интегралы:
1) j 5Щ^ [подстановка (8,15)];
2)
Ответ. 1)— ctg*-lctg3* + C;2)tg* + ltg3A:+C;3)tgA: +
+ ^tg3x + ±tgsx + C; 4) —
5) tg x + tg3 x + ~ tg6 x + ~ tg7 x + С
Задача 8,15 (для самостоятельного решения).
Найти интегралы: 1) \^^dx [подстановка (8,16)];
2) [c^dx; 3)
' J sin8 x ' '
Ответ. 1) _lctg8x + C; 2) _(lctg5x + |ctg' x) + C;
В предыдущих задачах тип были целыми числами. Это тре-
требование не является обязательным. В рассматриваемом случае
необходимо только, чтобы т + п было отрицательным четным
числом. Мы предложим несколько задач, в которых соблюдается
условие т + п = — 2k, но т и п — числа не целые.
Задача 8,16. Найти интегралы:
dx' 2> 7« = 1 УШ dx' 3) '. =1 tg1
Решение. 1)В подынтегральную функцию sin* входит в
1 9
степени т = у, a cos л: — в степени и = — у. Поэтому т + о =
19 8. _
= — -д- = — -я- = — 4 — четному отрицательному числу. Здесь
наиболее удобной будет подстановка (8,14): tgje = z. Используя
формулы (8,16), получим
1 COS2 X
^ (]/l_|_22J
; a _ Л .J | _ J г1
У T
9 3 „ 7 / , , \
4- Г — — fa2 jc -к — t?>2 * -J- <? — 2 Vhfx \ — iPx -\- — \03x\ -U Г
Q
2) В этом примере показатель степени синуса т = — у, а по-
2 . 8.2
казатель степени косинуса п = -,-, а потому m + n = —г + т =
= — 2 — четному отрицательному числу. Здесь уместна подста-
подстановка (8,15) : ctgjc = z. Учитывая связанные с ней формулы (8,17),
получим
2
23
1 + 22 \ 2 !+2!
I Применяем формулы (8,17) I .
= — jY3dz = —1-25 + С = —-|ctgA;3/cTg^ + С.
669
3) Преобразуем подынтегральную функцию к виду, который
соответствует рассматриваемому случаю:
—
13
COS2 X COS2 X
1 13
Здесь m = -?-; n = — у; т + п = — 6 — отрицательному не-
нечетному числу. Применяя подстановку (8,14) и учитывая связан-
связанные с ней формулы (8,16), получим
Применяем формулы (8,16)
= |-22 + у г
Возвращаемся к старой переменной,
заменяя г на tg x
+ 422+C = 4tg2A: + |tg2A: + 4tg2A: + C
= 2 Vt^ A tg jf + T tg3 jf +1 tg5 x) + G.
Задача 8,17 (для самостоятельного решения).
тт „ i\ I 1 / sin* , O\ I -? f si
Найти интегралы: 1) J у -^-dx; 2) J j/ ^
3) J tg2A:sec4A:dA:.
Ответ. 1) |tgAr/tiA: + C; 2) i-tg^tg*+ C;
3) 2 l/igjf (-g-tg2A: + | tg* *) + С
Теперь рассмотрим примеры, относящиеся ко второму виду
дробей (см. стр. 97).
Задача 8,18. Найти: 1) Ix = f . /* . ; 2) /2 = Г . /* , ;
sin7 х cos х '
670
Решение. 1) Здесь т = —3; п = —5; т -f п = —8 — отри-
отрицательному четному числу, а потому подынтегральная функция
относится к рассматриваемому случаю. Для вычисления инте-
интеграла можно применить любую из подстановок: (8,14) или (8,15).
Остановимся, например, на подстановке (8,14): tgx — z и исполь-
используем связанные с ней формулы (8,16)
1 - dz
А
I Заменяем г на tg x|
Для упражнения при вычислении этого интеграла применить
подстановку (8,15) и связанные с ней формулы (8,17).
2) В этом примере т = —4; п = —6; т + п — —10 — отри-
отрицательному четному числу. Подынтегральная функция относится
к рассматриваемому случаю. Для вычисления интеграла, как это
было указано и при решении предыдущего примера, можно при-
применить любую из подстановок: (8,14) или (8,15). Чтобы разнооб-
разнообразить решение, применим подстановку (8,15): ctg;e = z и исполь-
используем связанные с ней формулы (8,17)
Вычисляем A -|-ггL
по формуле бинома
Ньютона
11
41
г3
Возвращаемся к старой переменной,
заменяя г на ctg x
1 1
= Ttg6* + -|tg3A: + 6tgA: —4ctg* —4-ctg3* + C.
67
3) Здесь т — —7; п = —1; т + п = —8. Применим подста-
подстановку (8,14): tgA: = 2. Учитывая связанные с ней формулы (8,16),
получим %
/ _ (* ' dz _ п(\-\- г2K , ___
J3 = I Z7 I ' UfZ2" ~~ I * ^ ~~
J (/т+
Заменяем г на tgx и учитываем,
чт° tb=ctgx
= — \ ctg6 х — ~ ctg* х — -| ctg2 л: + In | tg x | + С.
Задача 8,19 (для самостоятельного решения).
Найти интегралы: 1) I -r-i т- ; 2) \ —
у ' Jsin6xcos6x' ' J sin
С dx ..f dx ,ч f
J sin3 x cos3 x * ' J sin x cos9 jc • ' J sin5 x cos5 x *
с
Ответ. 1) 10(tgAr-
sin х cos3 x
dx
+ 2 In | tg a: | + C; 4) ltg«A: + 4
+ ln|tgA:| + C; 5) -ictg*A:- |
+ 6 In | tg лг | + C.
Четвертый случай. Сумма показателей степени синуса и ко-
косинуса равна нулю: т + п = 0, причем предполагается, что т
и п — целые числа.
Таким образом, # показатели степени синуса и косинуса равны
по абсолютной величине, но противоположны по знаку, а подын-
подынтегральное выражение имеет один из видов:
.. Sinm X п\ COS™ X
l или 1
В рассматриваемом случае интеграл (8,10), если т > 0, при-
приводится к интегралу вида
\igmxdx, (8,18)
а если п > 0 — к интегралу
jctg"*^. (8,19)
672
К интегралу (8,18) следует применить подстановку (8,14):
tgx = z;^x = ~~i. (8,20)
Эта подстановка приведет к интегралу
?z
J 1
К интегралу (8,19) удобно применить подстановку (8,15):
** ctg* = z;
которая приведет его к виду
ctg* = 2; dx = - у— , (8,21)
f zn .
Выполняя деление (в первом случае zm делим на' 1 + z2, а во
втором г" на 1+ z2), придем к выражению, которое непосред-
непосредственно интегрируется.
Задача 8,20. Найти интегралы: 1) /, = \igixdx;
С С С
2) /о = I ctg5.*^*; 3) /3 = \ ctg6xdx; 4) I. = \ tgsxdx.
Решение. 1) Применяя подстановку (8,20), получаем
г4: (г* + 1) = гг— 1 +
1
Заменяем г на igx
= ^~ tgjr 4- arctg (tgjf) + C = ^ —tgjc +
2) В этом случае применяем подстановку (8,21):
?
Возвращаемся к старой перемен-
переменной: г = ctgx
X , Ctg2 X I , 1
-+ 2 -2ХпШ
673
3) Подстановка (8,21) дает
= — (~z5 — j zs + z — arctg 2) + С
Учитывая, что arctg a + arc ctg a =y , a arctg a = у—arc ctga,
получаем
/3 = — ~гъ + i-23 — 2 + arctg г + С =
= — ~ ctg5 x + ~ ctg8 x — ctg x — x + С
(слагаемое -^ отнесено в произвольную постоянную).
4) Подстановка (8,20) дает
-1 tg5 jf + i- tg3 x - tg jf + arctg (tgJf) + С =
= у tg7 X — -g- tg5 Jf + 1 tg3 Jf — tg X + X+C.
Задача 8,21 (для самостоятельного решения).
Найти интегралы: 1) J tg9хеке; * 2) J tg6л:d-t; 3) Jctg3Ard*;
4) Jtg3A:dx; 5)
Ответ/ 1) ±tg5x—^tgsx + tg
2) Itg«*-^tg»* + ln
3) —-i-ctg2^—ln|sinA:|
4) 4-
5) i-
674
III. ИНТЕГРИРОВАНИЕ ЧЕТНЫХ СТЕПЕНЕЙ СИНУСА
И КОСИНУСА
J sin2" х dx, j cos2" х их, п — целое и > 0.
Из тригонометрии известно, что
*** sin2* = -i (I — cos 2лг); (8,22)
cos2 x = ~ A + cos 2x). (8,23)
Применение этих формул позволит снизить степень подынте-
подынтегральной функции в рассматриваемых интегралах.
Задача 8,22. Найти: 1) It— [cos2xdx; 2) /2 = J sin2xdx.
Решение. 1) Заменяя cos2* по формуле (8,23), получим
/= Г-1A + cos2x)dx=-~(x + ^rsm2x\+C.
Итак, i
[ cos2 xdx =~(x +~sm 2x) + С (8,24)
J 2 \ 2 I
2) Поступая так же, найдем
[ sin2 x dx =-!(*— \ sin 2*) + С (8,25)
Задача 8,23. Найти / = J cos4 * dx.
Решение.
cos4 x = (cos2 *J = \~ A + cos 2лг)|2 = -j A + 2 cos 2л: + cos2 2x) =
I К cos2 2x применяем формулу (8,23) I
= l[l + 2cos2x + 1A + cos 4a:)] = i- [l + 2 cos 2x + 1cos4a:].
Поэтому
/ = ~ j" (¦! + 2 cos 2a: + ~ cos 4a:) d* =
Задача 8,24 (для самостоятельного решения).
Найти \ sin4*^*.
Г1 I2
Указание, sin4х = (sin2л:J = -^-A — cos2x) .
Ответ. ^ — -
675
Задача 8,25. Найти / = j cos6 x dx.
Решение.
cos6 х = (cos2 xf = \~ A + cos 2x) I =
| Применить (8,23) j
(l
= ^ h + з cos 2* + 3 • у A + cos 4x) + cos2 2* • cos 2x| =
= ^ U + 3 cos 2л: + -| + -| cos 4x + A — sin2 2л:) cos 2*] =
= i.T|- 4. 4cos2a: + -| cos 4л: — sin2 2л: cos 2л:].
Поэтому
/ = i. j" ^ + 4 cos 2л; + -| cos 4x — sin2 2л; cos 2л:) dx =
= 4" D * + 2sin 2x + I"sin 4л: — "S-si
Задача 8,26 (для самостоятельного решения).
Найти: 1) Гзт6л:^л:; 2) j sin8 л:с?лг.
Указание. Учесть, что cos32л: = cos22xcos2л: =
= A — sin2 2л:) cos 2л: = cos 2л: — sin2 2л: cos 2л:.
Ответ. 1) 4-(|-л: — 2sin2л: +-|-sin 4л: +-isin32л:) + С;
2) rrU-L sin 8л: — 4 sin 6x + 7 sin 4л:—28 sin 2л:)+~
Замечание. Интеграл \sin6*d* получается из рассмотрен-
рассмотренного в предыдущей задаче \cos6xdx заменой х на х + -?-:
cos ix + YJ — — s'n х' cos<i I* + -j) = (— sin *N = sin6л:;
I Sin6 Л:^Л: = I COS6 [x + ^~) dx.
Проверьте, что ответ этой задачи получается из предыдущего,
если в нем заменить х на х -f- -|- •
676
IV. ИНТЕГРАЛЫ ОТ ПРОИЗВЕДЕНИЯ ЧЕТНЫХ
ПОЛОЖИТЕЛЬНЫХ СТЕПЕНЕЙ СИНУСА И КОСИНУСА
(ИНТЕГРАЛЫ ВИДА:
j sin2m х cos2" x dx, где т и п — целые и > 0).
При вычислении «нтегралов этого вида нам придется приме-
применять формулы (8,22) и (8,23).
Задача 8,27. Найти интегралы: 1) It = j sin2 x cos2 x dx; 2) /2 =
= j sin4 л: cos2 л: d*; 3) /3 = j sin4 л: cos4 л: d*.
Решение. 1) Запишем подынтегральную функцию так:
/ 1 \2
sin2 л: cos2 л: = (sin л: cos л:J = I у sin 2x I =
= -^ sin2 2л: = -j --тгС1— cos 4л;). ч
| Применить (8,22) j
Поэтому
\ С 11
h — " \ 0 — cos 4x) dx = -j- x — зд sin 4x + С.
О J О uZ
2) Преобразуем подынтегральное выражение так:
sin4 х cos2 x — sin2 x cos2 x sin2 x = (sin atcos x)z sin2 x —
= (-=- sin 2x I sin2 a; = -j sin22x sin2 * =
К каждому сомножителю применяем
формулу (8,22)
= — ¦ ^ О — cos 4а;) • у A — cos 2х) = jg A — cos 4x — cos 2x +
+ cos 4x cos 2л:) = -^ 1 — cos 4л: — cos 2л: + у (cos 2x + cos 6*) =
| Применяем формулу (8,2) |
= -rz A — cos 4л: — -к- cos 2л: + -о" cos 6л:).
Поэтому
/2 = 1 j A _ cos 4л: — ~ cos 2х + 1 cos 6*)
= В [х ~~ Т sin 4лг ~ Т sin 2х + Т2 sin 6х
677
3) Подынтегральное выражение преобразуем так:
1 \4 i
/1 \ i
sin4 л: cos4 л- = (sin* cos*L = I -^ып2х) = jg (sin2 2л:J =
Тб [тA "" C0S 4лг)Г = §4
= Тб [тA "" C0S 4лг)Г = §4 A ~~ 2 COS 4х + cos2 4лг) =
| Применить (8,23) I
= ^(-| —2cos4* + y
+ 1 sin 8л;) + С = ^g (з* — sin 4* + -i- sin 8*) + C.
Задача 8,28 (для самостоятельного решения).
Найти интегралы: 1) J sin2*cos4*d*; 2) j sin4*cos6*dx.'
Указание.
sin4 x cos6 * = sin4 x cos4 * cos2 x = (sin x cos *L • у A + cos 2*) =
/l • о V ! /i , о ч 1 • do l+cos2x
= Tsin2* • -5- A + cos 2x) = эд sin4 2* -^_ =
2
~~ 32
= sk (sin4 2* + sin4 2* cos 2*).
Jsin42*d* вычисляют как и j sin4*d*, a j sin4 2x cos 2* d* легко
находят по формуле A,29).
Ответ. 1) щ Dх — sin 4х + sin 2* — -j sin блг) -f- С;
xks'm4x + sin8x + 'mi)
Задача 8,29. Найти интегралы:
1) j sin6 * cos4 * dx; 2) j sin8* cos6* dx.
Указание, sin8 * cos6 * = у™ (sin6 2л: — sin6 2* cos 2*).
Вычисление j sin6 2* dx см. задачу 8,26.
Ответ. 1) -LCa:_sjn 4* +-j-sin 8* — 4 sin5 2л:) + C;
2) jQ24 \2X~~ S{n 4X + Тб S'n 8X ~^~ \2 Sin3 4X) ~~
678
V. ИНТЕГРАЛЫ ВИДА
j#(sin*, cosx)dx. (8,26)
Запись R (sin *, V>s *) означает, что над синусом и косинусом
производятся только рациональные операции: сложение и вычи-
вычитание, умножение на постоянные величины, возведение в целые
степени как положительные, так и. отрицательные, деление. Дру-
Другими словами, под символом /?(sin*, cos*) следует понимать
рациональную функцию синуса и косинуса.
Интегралы вида (8,26) приводятся к интегралу от рациональ-
рациональной функции подстановкой
tgf=2 (-*<*<«), (8,27)
которая называется универсальной тригонометрической подста-
подстановкой. Это название подстановка .(8,27) получила потому, что
она во всех случаях приводит функцию R (sin x, "cos x) к рацио-
рациональному виду.
В тригонометрии доказывается, что все тригонометрические
функции выражаются рационально через tg ^-:
sin x = ; cos x =
поэтому универсальная тригонометрическая подстановка (8,27)
приводит к формулам, по которым sin*, cos л: и dx выражаются
рационально через новую переменную г:
^ i dXr=rp? С8-28)
(из tg у = 2 следует, что — = arctg z (—it < x < it), x = 2 arctg z;
rir 2dz
dx
Применяя подстановку (8,27), мы могли бы вычислить все
интегралы этого практического занятия. Однако это привело бы
к значительному усложнению вычислений. В случаях, разобран-
разобранных выше, мы обошлись без этой подстановки.
Укажем еще три случая, в которых легко можно избежать
универсальную тригонометрическую подстановку (8,27).
1. Если R (sin*, cos*) меняет знак при замене sin* на —sin*,
т.е. если /?(sin*, cos*) — нечетная функция от sin*, то подын-
подынтегральное выражение в (8,26) приводится к рациональной функ-
функции подстановкой .
cos*=:z. (8,29)
679
2. Если функция R (sin x, cos x) меняет знак при замене cos x
на —cos*, т. е. если она нечетная функция cos*, то подынтег-
подынтегральное выражение в (8,26) приводится к рациональной функции
подстановкой
sin х = z. (8,30)
3. Если функция R(s'mx, cos*) не изменяется при одновре-
одновременной замене sin* на —sin* и cos* на —cos*, то подынтег-
подынтегральное выражение в (8,26) приводится к рациональному виду
подстановкой
tg* = z. (8,31)
Задача 8,30. Найти / = -^- .
J sin3 х
Решение. Применим универсальную тригонометрическую
подстановку:
tg-?- = z; sin* =
2г
1+г2
dx =
2dz
1+г2
<см. формулы (8,27) и (8,28)).
Поэтому
2dz
Возвращаемся к старой перемен-
X
ной: заменяем г на tg —
х_
~2
= --g-ctg«T+Tln
t?
Задача 8,31 (для самостоятельного решения).
Найти / = I —?- .
J COS3 X
Указан и е. Воспользоваться результатом предыдущей задачи,
заменив * на * + —¦ Так как cos* = sin(х+1.\ т0 j _j?_ =
f* dx
, и в ответе предыдущей задачи всюду вместо *
sin3U + -^
подставить х + у.
Ответ. /=-4ctg'(-l + !) + i
Преобразуйте этот ответ к виду
Задача 8,32. Найти /
¦__ С dx
~ J sin6 х '
. Решение. 1) Здесь опять-таки применим универсальную три
, х . 2г , 2dz
гонометрическую подстановку: tg -5- = z; sin x = . , ..; ах =-
j __
(* Idz
\ i±?L
1 32г"
J (\+z*f
~ 16 j is az — те J
16 V 4
Возвращаемся к старой переменной: заменяем г на tg ~
i In
1
Задача 8,33 (для самостоятельного решения).
Найти I —?-.
J cos6x
Указание. Воспользоваться результатом предыдущей зада-
задачи, заменив в нем х на х + ~.
Задача 8,34 (для самостоятельного решения).
Найти: 1) Г-^-; 2
7 J sin' л;'
681
Ответ. 1) jr-1 -т- tge —|— tg4 —f- -я- tg? -s" 4" 20 In
2 Clg 2 2Clg T 6Clg 2J + ^'
Задача 8,35. Найти /= Г. 5tV^X ^x.
J sin x D 4 3 cos я)
Решение. Применяем универсальную тригонометрическую
подстановку: tgy = z. Используя формулы (8,27) и (8,28)! имеем
12г
5 +
1+г2
J пЫ<+?
1+*
Разложим на простейшие дробь, стоящую под интегралом:
5г24_12г4_5 _ А
отсюда
5гг Н- 12z + 5 = А G + га) + z (Bz + С);
Л=А; В = М. с=12>
Поэтому
Переходим к старой переменной:
, х
заменяем г на tg-jr
Задача 8,36 (для самостоятельного решения).
тт» 1\Г 5+9 sin х ,
Найти интегралы: 1) j J^,**;
Г 4
J sinx
4+5CQS.K
682
Ответ.
2)
т1
I 7 + 3 sin, x
| sinx
12
-77rearctg
7tBTr-
2/10
Задача 8,37 (для самостоятельного решения).
1 -f cos х ^ (подстановка: tg у = zj.
ti» С х-\- s'mx
Наити J
Ответ. *tg-| + C.
Задача 8,38 (для самостоятельного решения).
Найти интегралы: 1) 1 -г-^—:—.; 2) I —=—jt—. г.
у ' J cosx(l — sinx)' ' J cos2 x(\ 4-cosx)
dx
cosx(l
Указание. Подстановка: tg4- = z.
Ответ.
* x
2) tgf
В заключение выполним несколько упражнений на применение
упрощающих подстановок, указанных на стр. 111.
Задача 8,39. Найти интеграл / = I - dx
j }
Решение. Так как синус и косинус находятся в четных
степенях, то изменение знака у каждого из них не изменяет
подынтегральной функции C-й случай, стр. 112). Подстановка
(8,31):
tg х = z; sec2 x dx = dz; A + z2) dx = dz; dx = ytj2 ¦
г s x
Если tg x — z, то sin x =
cos x =
683
Пользуясь этой формулой, можно легко вычислить интегралы:
С dx Г dx
J l + sin2x' J l-
Выполним это так: 1 = sin2 x 4- cos2 x, а потому
Г dx С dx Г dx
J I -j- sin2x~ J sin2 x-j- cos2 x -f- sin2 x ~~ J
sin2 x 4- cos2 x 4- sin2 x J cos2 x-\-2 sin2 x '
'a2=l; 62 = 2|
1
Аналогично легко найдем, что
Рекомендуем вычислить эти два интеграла не по готозой фор-
формуле, а при помощи подстановки tgx = z.
Задача 8,40 (для самостоятельного решения).
тт о Г sin2х cos х ,
Найти I j dx.
J sin x -j- cos x
Указание. Перемена знака у синуса и косинуса не изме-
изменяет подынтегральную функцию, а потому и здесь мы имеем тре-
третий случай, и наиболее удобной будет подстановка: igx = z.
Подынтегральная функция после подстановки примет вид
2
Ответ. -^ In | sin x + cos х | — -j cos л: (sin * 4- cos *) + С.
Задача 8,41. Найти интегралы:
[S°*? 2) /a==
!) ll[dx; 2) /a.
' х J sin4 х ' ' 2 J sin3 x cos2 x
Решение. 1) При замене cos* на —cos* подынтегральное
выражение меняет знак. •
Здесь уместна подстановка: sin х = z (см. стр. 112);
cos х dx = dz; cos* = |A — z2;
Г cos* x cos x
J sin*x
f /A - г2)* . Г A — г2J dz
dX ~ } W— UZ ~ J ?
'.'4_:1 + г + С = — 4- т4- 4- -A- 4- sin л: + С.
3 г3 г ' 3 sin3 x sin x
Возвращаемся к старой
переменной: г = sin x
684
2) При замене sin л: на —sin л: подынтегральная функция ме-
няет знак. Подстановка: cos*=z; см. стр. Ill; simc =1^1—z2',
dz-
— sin x dx = dz; dx — —
"Iv
dz r dz
¦)/l —22>/(l — Z2K Z2 J ('—z2)
Указание. Дробь _ a.a a разложить на элементарные.
1 cosx
Ответ. ^ — 2ijH^ + ~
Задача 8,42 (для самостоятельного решения).
Найти интегралы:
1) 1 —1~ (подстановка: cosx = z);
> J sin х cos4 л; v м ''
dx
sin2 x cos3
Ответ. 1) -L + _l_+ln|tg4
' cos x ' 3 cos3 x | s 2
sin л:
ДЕВЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Интегрирование алгебраических иррациональностей.
I. ИНТЕГРАЛЫ ВИДА
(x«, х?, х\ ...)dx, (9,1)
где а, р, f — дробные рациональные числа;
R (х*, х$, XI) — рациональная функция от аргументов х*, х$, x^•
Это означает, что над этими аргументами производятся только
четыре арифметических действия и действие возведения в целую
степень, как положительную, так и отрицательную. Вообще же
под интегралом находится иррациональная функция.
Интегралы этого вида приводятся к интегралу от рациональ-
рациональной функции подстановкой
х = уп, dx = пуп~Чу, (9,2)
где п — наименьшее кратное знаменателей дробей а, [3, -j-.
Интеграл (9,1) преобразуется к виду
уп\ уп\ .. .)пуп~Ыу,
6S5
но теперь па, пC, щ — целые числа, и тем самым интеграл (9,1)
от иррациональной функции сведен к интегралу от рациональной
функции.
С Vic
Задача 9,1. Найти / = I 5—^r dx.
Решение. Представим интеграл в виде \ dx. Наимень-
1 2
шим кратным знаменателей дробей у, у и — является 6.
_^
Под интегралом находится рациональная функция от Xs, т. е.
от У х. Интеграл относится к рассматриваемому типу (9,1), а так
как наименьшее кратное знаменателей дробей равно 6, то под-
подстановка (9,2) запишется в виде
х = «A dx = 6у5 dy; (9,3)
а интеграл
Выделяем
целую часть
Возвращаемся к старой переменной:
из (9,3) следует, что у = у/~х
Задача 9,2 (для самостоятельного решения1).
Найти: 1) Г—ТЁК— dx; 2) Г ^ dx;
Г
Указание. 1) Первый интеграл приводится к интегралу от
рациональной функции подстановкой х = у6. После этой подста-
подстар фу
новки интеграл переходит в 6 I -~n
686
2) Ко второму интегралу применяем такую же подстановку:
х = г/6 -
3) К третьему интегралу применяем подстановку х = у12, кото-
которая приводит интеграл к такому виду:
Ответ. 1) 6[L \
\n\V'x-\\Uc; 2)\n~^ + C; 3) In
Задача 9,3 (для самостоятельного решения).
Найти интегралы: 1) Г—-—; 2) \Vx + Vx + l/l
Г—-—; 2) \
Указание. Подстановка х = у12 приводит к 121 '[f'^
(выделить целую часть).
Ответ. 1)
2) l2(Yjf* + ±
Задача 9,4 (для самостоятельного решения).
Найти интегралы: 1) \(Х~^~хKdx; 2) Г ? ;
р
Ответ. 1) |3/^-у
2) 4Г—
-i V^5 -ln ]/(^ +1L + c-
687
Ц. ИНТЕГРАЛЫ ВИДА
где а, C, ^ — дроби, a R — рациональная функция своих аргу-
аргументов.
После подстановки
й*". (9'5)
где п — общее наименьшее кратное знаменателей дробей а, C, у,
интеграл (9,4) переходит в интеграл от рациональной функции.
Из (9,5) следует определить х, а по найденному значению х
определить его дифференциал dx.
Отметим, что частный случай интеграла (9,4) получается тогда,
когда вместо дроби °* , , подынтегральная функция содержит
дробные степени линейной функции от х.
В этом случае рационализация достигается подстановкой
.. ах + b = yn, (9,5а)
где п имеет указанное выше значение.
Задача 9,5. Найти / = I , dx.
jVx—l
Решение. Этот интеграл может быть переписан так: / =
dx, и поэтому он относится к рассматриваемому типу
Подстановка: х — 1 = у2; х = у2 -f- 1; dx = 2y dy.
Осуществляя эти замены, получаем интеграл от рациональной
функции:
f 1) dx = 2 -i- г/9 + т #' + Т У5 + Т 0" + » + С =
К старой переменной переходим,
полагая у = Ух — 1
^l] + С = 2 Vx~=~\ [\ (х - 1)
688
Задача 9,6. Найти / = 1х
д.2
Решение. Интеграл представим в виде / = I dx.
'¦J
_
Он относится к рассматриваемому типу. Сделаем подстановку
Ъх + 2 = у2.
Тогда Ых = 2y dy; dx = Щ^-; х = ^=^ .
Подставляя эти значения, получаем интеграл от рациональной
функции:
Зу<*У_ 2 Г (g«-2)» , 2 fg*
5 25J у2 ау J25J
f С.
Задача 9,7. Найти / = I —, х (рассмотреть случаи Ь > О
J xy ах-\-Ь
И Ь<0).
Решение. Подстановка: ах + Ъ = у2; a dx=2ydy; dx^—ydy;
d
Подставляя эти значения в /, получим под интегралом рацио-
рациональную функцию:
/ = Г* Zydy . / =
I а-—-(уг—Ь)у
Если Ь > 0, то Ь = k2, и тогда
-fe2 2ki
I Заменяем k на Y^,
f а у на Yax-\-b
i\n»=V* + c {b 0)_
/6 y+/6^ '
Окончательно, возвращаясь к старой переменной, имеем
/=: ' In-^^S^+C. (9,6)
23 И А. Каплан 689
Если b < О, то Ь = — р2:
ах
(9,7)
Задача 9,8. Найти /=
Решение. / =
Интеграл относится к рассматриваемому типу.
Полагаем, что Зх + 4 = у2. Тогда х = Ц^-
а интеграл преобразуется к интегралу от рациональной функции:
^1
Интегрируем по частям
du — dy;
У
,dy
X) =
-4)
Ответ / = —
, 3,
+ -т-I
4
—2
+ +
Задача 9,9. (для самостоятельного решения).
Найти: 1
Указание. Во втором примере после подстановки удобно
применить интегрирование по частям.
Ответ. 1) ^^^
9. 1 (х — 5)Ух — 5 1 Ух — 5
г> То 7* 20 , х
Задача 9,10. Найти / =
"Г
20/5
Уъ ^
—4'
Решение. Положим д; + 2 = г/2; х = у2 — 2; dx = 2ydy.
Тогда
Выделить целую часть
41 + С.
690
Задача 9,11' (для самостоятельного решения).
Найти Г^
Указание. Подстановка х — 8 = у3.
Интеграл после подстановки примет вид: 3 I -тпгя •
Разложить дробь ^r-g на простейшие.
„ 1 , у2 — Чу + 4 , ]/И , у — 1-
Ответ. -\пу {у+у^ +VarctgyT'
Задача 9,12. Найти / = Г dx
Решение. Здесь подынтегральная функция отличается от
предыдущих тем, что она содержит корни разных степеней (третьей
и второй).
Перепишем интеграл, заменяя корни дробными показателями:
/=Г ^ .
2 1
Общий наименьший знаменатель дробей -и у равен 6. Под-
Подстановка (9,5а) будет такой:
Подставляя эти значения, получим
2
Возвращаемся к старой переменной
2х—1\\+С.
Задача 9,13 (для самостоятельного решения).
„, ..Г dx о. Г ]/FfT+i
Найти: 1) \ _ 2) \ ~-
23*
Теперь найдем несколько интегралов вида (9,1), в которых
подынтегральная функция — дробно-линейная функция в дробной
степени.
Задача 9,14. Найти / =
Решение. Подстановка . . „¦ = у2 приведет к интегрирова-
интегрированию рациональной функции. Из указанной подстановки опреде-
определим х, а потом dx:
5 — 3* =
5 — 4г/а =
Поэтому
Здесь удобно вместо разложения на
элементарные дроби применить интег-
интегрирование по частям:
и= у
dv =7;
У
dy
du = dy
1 1
° = -14-7
и
Возвращаемся к старой переменной: у =
/E — 3jc)D+7x) 47/21
7 147
5 —
692
Задача 9,15 (для самостоятельного решения).
Найти: 1) /х = Jj/fi^; 2) /, =
Ответ. 1) —1^4 — х2 + 2arcsinу + С. (Этот пример можно
легко решить и не пользуясь подстановкой (9,5), если переписать
подынтегральную функцию, умножив ее числитель и знаменатель
на У2 + х. Тогда
J/4 = *
1/C — 4x) (9 — 5x)
+ _^_1п|51-40ж +
20 ]/
4/5C —4дг)(9 —5дг)| + С.
Задача 9,16. Найти интеграл / = j ?±| j/ j^
Решение. Применим подстановку
о
Отсюда определим х и dx:
"ж + 3 == л;^2 — Зу2; 3 + З^2 =
— ж;
dv =
Интегрировать по частям:
У
\dy
du = 3(/2 dy
1 1
V — *— ~тг~ -
2 у2— 1
Ответ. 1 = (х-
Задача 9,17 (для самостоятельного решения).
Найти интегралы: 1) j]/(^K^; 2) j ]/(i±iK dx;
Указание. В первых двух интегралах после подстановки
интегрировать по частям.
693
Ответ. 1) —E + х) I/ I . х + 6arctgT/ -j-r-^-4- С;
г ' -f-л: Г \ -\-х
2) E — ;
о 3
3) [\ ~х^У^—х —
Задача 9,18. Найти интеграл /= Г
J
Решение. Подстановка: х + 4 = у\ dx = 2y dy
Разлагаем на простейшие дробь
У + З _ (/+3 _ А . Ву + С
Отсюда следует, что А = -т; В = — -i;C = — -^;
О О О
Переходя к старой переменной, с помощью равенства у
Ух + 4 окончательно получаем N
4 1п.(УТ+4-0^_ 4
3 л: + 5 + 1/л: + 4 /3
1п^
3 л: + 5 + 1/л: + 4 /3 /3
Задача 9,19 (для самостоятельного решения).
т/14-jt 1/1 х т/1 jt
2) In V-Zli ^т=^ + 2 arctg I/ f-r-f + C.
Указание. После подстановки . = у2 окажется, что
1 -f- X
1 —г/2 , , у dy
Дробь
г/2 _1_ _1 1_ _\ _1_ L
694
Рассмотрим еще несколько интегралов, сводящихся к виду (9,4).
Задача 9,20. Найти /= Г dx .
J ^(*-!)»(* +2)
Решение. Этот интеграл легко приводится к рассматривае-
рассматриваемому типу:
и иначе
Поэтому
Подстановка нам хорошо известна:
= у3. (В)
Отсюда х — 1 = ху3 + 2#3; 2#3 + 1 = * A — У3);
у_2{/3+Г, . 9_2t/3+l 0_ 3
1 — у3 ' 1 — у3 ' 1 — I
Производя замены в (А), получаем / = 3 1--=—^. Разлагаем
на простейшие дробь
1 I А . _Ву + С
1 —у3 ~~ A —у) A -)- у -\-у*) 1 —у
Отсюда
3 Ад. j
Из подстановки (В) следует, что у = 1/ j-r-g, а поэтому по-
получаем
2
= _ 1 Щ р+2-^ у + ^3 arctg 2^ + ^2 с>
Ответ можно несколько упростить, если постоянную величину
-j In 3 присоединить к произвольной постоянной.
695
Окончательно
3 . |3/—:—j; 8/ J-. , -,/т, , 2 л/х — 1 -4- л/х-4- 2
Tln\yx + 2 — yx—l\ + V3arctg у ^у ^
Задача 9,21 (для самостоятельного решения).
dx
Найти интегралы: 1) Г dx ; ) Г
J V(x - ЗУ (х + 1)» J ^(* + 1)» (лс -
3) Г ^
J
Указания. 1) f (*-3)»(а: + IM = ^(л;-З)
Применить подстановку: j^|=^4; x+l = п4рТ
2) ^ + 1)« (х - 2)* = ^|±$ (Jf - 2)« = (х -
Подстановка: j^ = ^3; х= -~^~ ;
У3— 1 (У — 1)а
Подстановка: \^ = у*\ х = у^~^\ 1— ^ = ^qr
Ответ. 1)
3) ^ln^^
III. ИНТЕГРАЛЫ ОТ БИНОМИАЛЬНЫХ ДИФФЕРЕНЦИАЛОВ
Так называются интегралы вида
т{а + Ьхп)рйх, (9,8)
где т, п и р — любые рациональные числа;
а и Ь — какие угодно постоянные, не равные нулю К Подынтег-
Подынтегральное выражение называется биномиальным дифференциалом.
1 Кенечно, предполагается, что числа т, п и р не все целые. Если бы все
они были целыми, то вопрос свелся бы к интегрированию суммы степенных
функций.
696
П. Л. Чебышев доказал, что только в трех случаях этот
интеграл может быть выражен в конечном виде через алгебраи-
алгебраические, логарифмические и обратные круговые функции:
1) р — целое число, которое может быть положительным, отри-
отрицательным или равным нулю. В этом случае применяется под-
Становка х = у\ (9,9)
где s — общее наименьшее кратное знаменателей дробей тип.
Это простейший случай: дело сводится к интегрированию суммы
степенных функций. Нами он рассматриваться не будет.
2) 2L+ целое число. Здесь следует применить подстановку
а + Ьх" = у1, (9,10)
где s — знаменатель дроби р.
3) '—L—\- р — целое число. В этом случае применяют под-
подстановку _
ах -+- о — у , (У.11)
где s — знаменатель дроби р.
Других случаев интегрируемости биномиальных дифференциа-
дифференциалов, кроме перечисленных, нет. Интересно отметить, что они были
известны еще Ньютону, а Эйлер указал приведенные выше под-
подстановки. Однако только П. Л. Чебышев доказал, что эти случаи
интегрируемости являются единственными и что в других случаях
интеграл (9,8) не может быть выражен при помощи элементарных
функций.
Задача 9,22. Найти / =
Решение. Перепишем интеграл в виде
1 1 1
и, сравнивая его с (9,8), получим
т = __; /г=_;р==_.
т -4- 1 2 "^ 2?" *
Составим выражение: = -.— = -у- — 2—целое число.
Т Т
Следовательно, здесь мы имеем второй случай интегрируемости.
Подстановка (9,10) запишется так:
(9,12)
697
Поэтому
Возвращаясь к старой переменной, при помощи равенства
3 / ГТ-
у —у 1 + У х получим
Задача 9,23 (для самостоятельного решения).
Найти
Указание. т = — -=-; п = -я-; р = — ; т~1 =3 — целое
число. Здесь имеем второй случай интегрируемости. Знаменатель
дроби р равен 3. Подстановка (9, 10): 1 -\- х9 = у3. После подста-
подстановки получится
18 $ (у3-I)* у3 dy.
Ответ. 18A +fcjfa + Ух[Ц1 + \Г$-т{1 + У
Задача 9,24. Найти / = г .
Решение. Запишем интеграл в виде / = \ (а + bx2) 2 dx.
Сравнивая его с (9,8), замечаем, что m — 0; п — 2; р = — у.
Составляем числа т'~ и ^t—\- р, чтобы обнаружить, какое
из них — целое (если бы оказалось, что ни одно из чисел не
целое, то от интегрирования мы бы отказались):
m_L-l 0+1 1
_л_ — _х_ = _ — не целое число;
—L—Нр = тг — -о" = — 1 — целое число, и мы имеем здесь
третий случай интегрируемости.
Подстановка (9,11) при п = 2 (знаменатель дроби р равен
также 2) выглядит так:
698
Отсюда следует, что — 2ах 3 dx = 2у dy, a x 3 dx = ydy.
Преобразуем подынтегральное выражение так, чтобы оно содер-
содержало ах~г + Ь (в третьем случае интегрируемости биноминальных
дифференциалов рекомендуется преобразовывать подынтегральное
выражение так, чтобы оно содержало ах~п + Ь). Вынося в
подынтегральном выражении х2 за скобку, имеем
(а + bxT^dx = [х* (? + b)] 2 d* -
-- 1
= х~3(шг2 + b) 2 dx = —-^y~2dy.
Поэтому
, if.., 1 и* . п 1 1 , „
/ = \ у 2dy = ^—г + С = \- С.
a j у v а —1 ' а у
Подставляя сюда
получим окончательно
а уа+Ьх2
Задача 9,25 (для самостоятельного решения).
Найти J Ух C + 4л^) dx.
Указание. Записать интеграл в виде ]хг C + 4ж3J dx;
m — -yr\ п = 3; р = -=-; ^-i—\- р = I — целое число, третий слу-
чай интегрируемости.
Подстановка (9,11): ЗлГ~3 4- 4 = у2. Подынтегральную функцию
представить в виде х2 B>х~3 + 4J. Из подстановки следует, что
Злг3 = у* — 4; х~3 = ^— , а х* = ^~ . Отсюда Зх2 dx =
2 = — (Jy-l)t> и интеграл преобразуется к виду
Вычисление этого интеграла можно выполнить разложением
рациональной дроби на простейшие, но проще применить инте-
интегрирование по частям, полагая
и = у I du = dy
j ydy \ 11
dv = , : у.,„ Iо = — -j jz—i
699
После интегрирования получим
' ln
причем, чтобы возвратиться к старой переменной, надо сюда
подставить
Задача 9,26. Найти интегралы:
1) Г ^Ц-dx; 2)
Ответ. 1)
2) ~E + х2) Dл;2 — 15) ^5~Т* + С.
IV. ИНТЕГРАЛЫ ВИДА
к, У ах2 + Ьх + с) dx, (9,13)
где R — знак рациональной функции.
(Еще раз напоминаем, что это понимается так: над аргумен-
аргументами х и ]^ах2 + Ьх -\- с могут производиться четыре действия
арифметики и возведение в целую степень как положительную,
так и отрицательную).
а) Интегралы вида
dx . (9,14)
Напомним три интеграла, которые нам часто будут встре-
встречаться:
1) J yj^dx = ln\u + ifWTJ* 1 + С; (9,15)
3) ^dx = 2V~u + C. (9,17)
Вычисление интеграла (9,14) производится так:
1) под корнем \а\ следует вынести за скобку, ——за знак
интеграла;
2) после этого под корнем выделить полный квадрат и при-
применить формулу (9,15) (при а>0) или (9,16) (при а<0).
(Если |с| = 1, то вынесение за скобку становится излишним,
и надо только выделить под корнем полный квадрат).
700
Задача 9,27. Найти интеграл / = Г -т=
J у 1х
dx
Решение. Здесь а = 2 > 0; вопрос сведется к применению
формулы (9,15). Вынесем под корнем 2 за скобку, и в остав-
оставшемся выражении выделим полный квадрат:
dx
= -7= 1П
47
Применяем формулу
(9;i5): « = * + -§-;
u'= 1
л; 4- -r-
Выражение, стоящее
под корнем, равно
4
= -pL {In
I") —1п 4
Окончательно, присоединяя j=\n4 к произвольной пос-
постоянной, получаем
/=-^1п|4л-+34-2
4- Зл- + 71 4- С
Задача 9,28 (для самостоятельного решения).
Найти интегралы: 1) I ¦ ; 2) Г
С rix С
3) ¦ ; 4)
Ответ. 1) -L
+ 2л; + 91 + С;
2) In 12л; + 2 +
3) -i_in| 16x4-
4) J. ln| 12л: 4- 5 + 2/бFдс« + 5* + И) | 4- С;
5) y= In 188* 4- 9 + 2 У14 A4л;2 + 9л; 4; 1)|4-C.
701
С dx
Задача 9,29. Найти интеграл / = I , ¦ —- .
J у о + IX ¦ ОХ
Решение. Здесь а = —3 < 0, интеграл может быть вычис-
вычислен по формуле (9,16). Вынесем под корнем за скобку 3, т. е. \а\'
5
¦q~l п~ л.; — г " V о I п"
О о / г О О
Выделяем под корнем
полный квадрат
Для выделения полного квадрата в этом случае поступаем
так: 1) ставим перед' скобкой минус; 2) в скобку вписываем х
и половину коэффициента при х в первой степени с обратным
знаком; 3) выражение в скобке возводим в ква'драт, а квадрат
второго слагаемого в скобке прибавляем к свободному члену.
_7_
r If* dx 1 . Х~Т . п
/ = —т= — =——ЯГГЧ1П 4- (.
1/3 1/109 / 7 \а /3 /109 ^
г* ах
D/1TFI
Применяем (9,16):
7 /109
Окончательно
' - /З^'" /Т09
Задача 9,30 (для самостоятельного решения).
Найти интегралы: 1) i -
dx
2) Г dx 3) Г rfA:
; J /3 + 2*-5*2' ; J /9-a:-a:2 '
/11 + 9л: — 7л:2.'
Ответ. 1) arcsin-T7=r + С; 2)-^arcsin-^— + С;
„V 2л;+1 ^ .. 1 . 14л: — 9 . п
3) arcsin yW + С; 4) у= arcsin y^^ + С.
б) Интегралы вида
Г r Ax + B =dx. (9,18)
J Уах* + Ьх + с '
Интегралы этого вида приводятся к интегралам (9,15) и (9,17),
если а>0, а если а < 0, — к интегралам (9,16) и (9,17). Дос-
702
тигается это так: в числителе дроби, стоящей под интегралом,
записывается производная подкоренного выражения, т. е. 2ах +
+ Ь, которая тождественными преобразованиями преобразуется
в заданный числитель Ах + В.
2a'
и тогда
J V^H^+T J 1
У ах2 -f- bx -\- с
Разлагаем на сумму
двух интегралов
¦dx
А Г
dx
Этот интеграл вычисля-
вычисляется по формуле (9,17):
числитель — производ-
производная подкоренного выра-
выражения
У а*2 4- bx 4- с
Этот интеграл приво-
приводится при а>0 к интег-
интегралу (9,15), при a < О—
по формуле (9,16)
Задача 9,31. Найти интегралы:
Решение.
ол—' _^у. 2) /„= f ^-г-"_
/5л:24-8л:4-1 ' 3/7 4-8л:—:
_ Г A0* + 8L-7-^
h 8л: + 1 J
4(-lte+8 -^-gf
10 J /5*24-8*4-1 5J
Применяем формулу
(9,17)
См. задачу 9,27
= 4 /5л:2 + 8x 4- 1 Цг- In 110л: 4- 8 4- 21/5 Eл:2 + 8x + 1 I + С.
й 5у 5
2)
f
2x4-5
j /74-8*— II*2
1 f 8 — 22*
Г(8_
11
/74-8*—II*2
-I
Применяем формулу
(9,17)
Поступаем так же, как
и в задаче (9,29)
= — -л- у 7 + 8х — 1 1л:2 у= arcsin —-=^ 4- С.
П г 11 /11 У93
703
Задача 9,32 (для самостоятельного решения).
Найти интегралы: 1) ;
о\ Г *+8 о\ f 2 — Зх
2>] /3^ + ^ + 9 '• Ъ)\
+ 2 К 2 Bл;2 + 5х + 3) | + С;
2) ±.
,, f xdx Ks Г 5л: —3 ,
4) J/8-3»-2*'; 5) J /Г- 13»-5***-
Ответ. 1) 1 |/2л:2 + 5* + 3 jL_in|4*
3) -4К4*2-х-7 + Ц1п|8*-
4) _ 1 /8-3^-^-
5) -Kl-13,-5^-
в) интегрирование функций вида R {x, Vax2 + Ъх + с) в общем
случае приводится к интегрированию рациональной дроби и вы-
вычислению интегралов таких трех видов:
Р\х\ dx (P (х) — многочлен); (9,19)
¦ (р — целое число и > 0); (9,20)
(x + kf
—5 —"Г , (т — целое число и т > 0)
(ал:2 + рл: + 7)m]/a*2 + &* + c (ООП
Укажем способы вычисления интегралов вида (9,19) и (9,20),
выполним упражнения на применение этих способов, а затем вы-
вычислим несколько интегралов, в которых подынтегральную функ-
функцию придется преобразовывать так, чтобы вопрос сводился к вы-
вычислению интегралов указанных видов1.,
1. Интеграл вида (9,19) вычисляется по формуле
, К) dx = Q (х) У ах2 + Ьх + с+\\-
(9,22)
где Q(x:) — многочлен степени, на единицу меньшей, чем много-
многочлен Р (х).
1 Интегралы вида (9,21) нами рассматриваться не будут, так как программа
не предусматривает изучение их. Интересующиеся этим видом интегралов могут
обратиться к учебнику Г. М. Фихтенгольца «Курс дифференциального и инте-
интегрального исчисления», т. II, § 272.
704
Коэффициенты многочлена Q (я) и число X подлежат спреде-
спредера dx
лению. Интеграл же I , —- выше уже был рассмотрен.
J Vax2 + bx+c
Для определения коэффициентов многочлена Q (л;) и числа X
поступают так:
дифференцируют обе части равенства (9,22) и получают то-
тождество
= Q' (х) Vax* + bx + c + Q{x)
У
(производная неопределенного интеграла равна подынтегральной
функции).
Умножая обе части этого равенства на Уах2 + Ьх + с, полу-
получаем
Р (х) = Q' (х) (ах2 + Ьх + с) + i-Q (дс) • Bал; + ft) + X.
Неизвестные коэффициенты многочлена Q(x) и число X нахо-
находятся сравнением коэффициентов при одинаковых степенях буквы
х в последнем равенстве.
Подставляя найденные коэффициенты и число X в (9,22) и вы-
вычисляя интеграл, входящий в правую часть этой формулы, нахо-
находим и интеграл (9,19).
Решим несколько относящихся сюда примеров.
Задача 9,33. Найти интеграл /= Г З^3 + 5^ - 7Н-? л
F J У2х*+5х + 7
Решение. На основании формулы (9,22) имеем
Многочлен степени, иа
единицу меньшей, чем
многочлен числителя дро-
дроби, стоящей под интегра-
интегралом
dx
-f 5x + 7'
Определению подлежат неизвестные коэффициенты а, Ь, си
число X.
Дифференцируем обе части последнего равенства и, учитывая,
что производная неопределенного интеграла равна подынтеграль-
подынтегральной функции, получаем
+ (ах2 + Ьх + с) - . 4х + 5 -. + Х
705
При
При
При
При
Xs
X*
X
х°
6= 8аН
10 = 20а Н
—14 = 28а -\
18 = 146 4
(свободный
член)
L 4а.
- 46-
-106-
- Ъс -\
Ь5а
Ь56
-2Х
Умножая обе части этого равенства на 2 ]/^2лга + 5л: + 7, имеем
6л:3 + Юл:2 — 14л: + 18 = Dал: + 26) Bх2 + 5х + 7) +
+ (ах2 + 6л: + с) Dх + 5) + 2\.
Сравнивая коэффициенты при одинаковых степенях буквы х
в левой и правой частях этого равенства, получаем:
A)
B)
4с . C)
D)
Из первого уравнения следует, что а = -=- •
Подставляя а = -_• во второе уравнение, получаем 10 = 10 -j-
5 5
+ 86 + -<р отсюДа Ь = —Tg. При найденных значениях а и 6 из
373
уравнения C) получаем, что с — — -^т-, а из уравнения D) —
. _ 3297
Таким образом,
5О7^\ > 49Q7 /* Av
vt, v о'о\ i/qv2 I Cv _j_ 7 _j_ O?»? ( a*
Id 64 I lzo \
Интеграл
U^ 1 * I л I C I
/2
| См. задачу 9,271
а потому окончательно
/ = Jj C2л:2 — 20л: — 373) К2л:2 + 5л: + 7 +
Задача 9,34 (для самостоятельного решения).
Найти интегралы: 1) Г r x*~4 ±dx; 9) Г 3^-8x±LdY
Указания. В первом примере на основании формулы (9,22)
имеем
Г f x*~4 :dx = (ах + 6) ]/ЗЗс2 + бд: — 5 + ), Г-
J /Зх2+6д:-5 V ; J /з
: —5
Дифференцируем обе части этого равенства, освобождаемся от
дробей и сравниваем в полученном равенстве коэффициенты при
одинаковых степенях буквы х в левой и правой части, получаем
_j_. l__ X — — —
6 ' 2 ' 3
706
Во втором примере по формуле (9,22) йаходим
С Зл:3 — 8x4-5 , , , , . . ,—5 л ^ ¦ ^ Г dx
\ — ' — dx = (ax2 + bx + с) у х2 — 4х — 7 4- X ¦ , —.
J У х2 — Ах — 7 J /*2 — 4л: — 7
Дифференцируя обе части равенства, освобождаемся в получен-
полученном выражении от дробей и, сравнивая коэффициенты при одина-
одинаковых степенях буквы х в левой и правой части, получаем:
а = \\ 6 = 5; с = 36; Х = 112.
1 (y %\ п/Зу^О- fir К - — ,
3/3
Ответ. 1) ~(х — 3) /3^+6л: — 5 — ^^ In | Зл: + 3+
+ /З (Зл:2 + 6л: — 5) 1 + С;
2) (xz + 5x + 36)yx2 — \х — 7 + 112In |л: — 2
+ /л:2 — 4л: — 71 + С.
Задача 9,35 (для самостоятельного решения).
С х^ С
Найти интегралы: 1) \ . rfjc; 2) I
J /+ J
Указание. В первом примере окажется, что
4 а —15, о — 10 ; с — 10; к ~ и.
Замечание. В этих двух примерах X = 0, а потому реше-
решение имеет чисто алгебраический вид.
^ 1
Ответ. 1) ^Bх2 + Зл: + 3I/5л:а-6л: + 3 + С; 2IA1л;3 —
— 77х2 + 105л: — 175) j/л:2 + 6л: + 5 + С.
Задача 9,36. Найти интеграл
bx + с dx.
Решение. Следует иметь в виду, что к интегралам (9,19)
легко приводятся интегралы вида1
P
где Р (х) — многочлен относительно х.
Действительно, перенося иррациональность в знаменатель,
получим
Р (х) у ах2 + bx + cdx= \ \'/ ~ ^ 'dx.
J . J Va* + bx+c
Теперь остается применить формулу (9,22).
Предложенный в задаче интеграл может быть представлен так:
1 г—5 ; ;— j С ах2 4- Ьх 4- с ,
у ах2 + Ьх + с dx = I -r — dx ~
J Vax*+bx + c
\
= (ах + Р) Уах2 + Ьх + с + X Г —
Применена формула (9,22) с другим обозначением
неизвестных коэффициентов
707
Значения неизвестных коэффициентов:
а = Т ' Р ~ 4а ' Л ~ 8а '
и, таким образом, учитывая, что
1 Ь_ _
1Т * + 4а ~ 4а
Г
+ 4ас~6г Г dx . (9,23)
Вычисление же последнего интеграла известно из задачи 9,27 и 9,29.
Задача 9,37 (для самостоятельного решения).
По формуле (9,23) найти интегралы!
+ A:adx; 2) <\jVc — x2dx (c> 0).
Ответ. 1) -|
2) i/ТЗГ? + f arcsin ^= + G.
Задача 9,38 (для самостоятельного решения).
Найти интегралы:
1) j /5 + Зх + 8х2 dx; 2) §Y2x* + 5х + 7 dx;
3) j-f/5—x — 3x*dx; 4) j /7 + 8л: — 5л:2 djc,
не применяя формулы (9,23), а пользуясь указаниями, данными
в задаче 9,36.
Ответ. 1)
6л:+16л:21 + С;
2) 4?±
+ 2 /4х2+ 10л: + 141 + С;
5~2 .61
4) ^/7+ 8*-Б* + Jl_ arcsin^4 + С.
708
2. Интегралы вида (9,20)
подстановкой
dx
(x+k)p
(9,24)
приводятся к интегралу вида (9,19), примеры определения кото-
которого мы уже разобрали.
С dx
Задача 9,39. Найти интеграл / = I
Jx
Решение. Этот интеграл принадлежит к рассматриваемому
типу: & = 0; р = 1; а = 1; 6 = 0; с = 5. Применим подстановку
(9,24), которая в данном случае будет такой: х = —; dx=^—$dy.
У У
Подставляя эти значения в подынтегральную функцию, получим
Возвращаемся к старой переменной:
/5 ,
Окончательно
4=
/5
Задача 9,40. Найти /= Г—г^т-п-.
J х*У7-х*
Решение. Этот интеграл относится к рассматриваемому типу:
k = 0; р = 2; а = —1; 6 = 0; с = 7.
Подстановка:
х у ; х у2;
у2'
709
Возвращаемся к старой переменной:
у
Окончательно
с.
' 7 x
Задача 9,41 (для самостоятельного решения).
С dx С
Найти интегралы: 1) I— ; 2) I-
Ответ. 1) arccos—т^ + С; 2) — ~ --
х/2 '15 х
Задача 9,42 (для самостоятельного решения).
С dx
Найти интегралы: 1) /х = 1 т.
dx
— х2>
2) /я = f
¦ 2K /Зх2 — 8х + 5
Указания. В первом примере использовать подстановку
х — 1 = —, во втором — подстановку х — 2 = — . После подста-
подстановки получится: /2 = — 1 —г=
(9,22).
Ответ. 1) —In
У
JL
dy; применить формулу
¦+С;
2) 6*-13
> 2 (х — 2J
- 8х + 5 - -1 In
2х — 3 + /Зх2 — 8х + 5
х—2
V. ПРИМЕНЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ПОДСТАНОВОК
ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ВИДА
, /ах2 + Ьх + с) dx.
(9,13)
Для вычисления интегралов, не содержащих другой иррацио-
иррациональности, кроме квадратного корня из квадратного трехчлена,
применяются также тригонометрические подстановки, которые
710
приводят интеграл (9,13) к интегралу от рациональной функции
синуса и косинуса.
Чтобы применить эти подстановки, следует поступить так:
Из квадратного трехчлена, находящегося под корнем, надо
выделить полный квадрат, после чего применить линейную под-
подстановку, которая будет показана ниже на ряде примеров. Это
даст возможность получить под корнем следующие выражения:
1) При а > О — сумму квадратов вида
& + У2 , (9,25)
или4разность квадратов вида
г/2 — к*. (9,26)
После того как под корнем окажется выражение вида (9,25),
для уничтожения иррациональности в подынтегральном выражении
следует применить подстановку
y g
dy = k sec2 tdt
¦/k2 + у2 = k sec t
(9,27)
Если под корнем окажется выражение вида (9,26), то для
уничтожения иррациональности в подынтегральном выражении
надо применить подстановку
у = k sec t
dy = k sec t tg tdt
(9,28)
2) При a < 0 под корнем после выделения полного квадрата
и применения линейной подстановки могут оказаться выражения
вида
k2 — у2 (9,29)
или
- /г2 - у\ (9,30)
В случае, когда под корнем окажется выражение вида (9,29),
подстановка
у = k sin /
у = Rsmt \
dy = k cos tdt\ (9,31)
ы2 = k cos t \
освободит подынтегральное выражение от иррациональности.
Случай (9,30) не представляет для нас интереса, так как корень
здесь не имеет вещественного значения ни при одном действи-
действительном значении у.
711
Помещаем для справок основные интегралы рассматриваемого
вида:
dx ._..,_ х , „. ^9>32)
(9,33)
a2 — *2 d* = ±/a2 —
!arcsin_L + C; (9,34)
± a2 ± ^ ln| л; + /д;2 + aa j + С (9,35)
Сначала найдем несколько интегралов, в которых выражение,
находящееся под корнем, имеет один из видов: (9,25), (9,26) и
(9,29), а "после этого — несколько примеров, в которых подкорен-
подкоренное выражение придется приводить к этому виду.
С dx
Задача 9,43. Найти интеграл /= I
V
Решение. Выражение, стоящее под корнем, имеет вид
(9,25) (k = 3). Применяем подстановку (9,27):
х — 3 tg#; dx = 3secaydy
л:3 + 9 = 9 tg2r/ + 9 = 9 (tga у + 1) = 9sec2 у.
Поэтому
= i. Г
a/==f y , = lf^
= i. Г cos r/d«/ = .1 sin r/ + C.
Для того, чтобы возвратиться к первоначальной переменной х,
найдем sini/ через х. Из подстановки
У1+Т
Поэтому окончательно
——— \-Г.
9 /9 + *• ^
Задача 9,44 (для самостоятельного решения).
Найти интегралы: 1) Г , ** : 2) Г dx
Ответ. 1) -j- r-^~ + С; 2) —/ +С
712
Задача 9,45. Найти / = Г ;
dx
Решение. Подкоренное выражение имеет вид (9,26). Под-
Подстановка (9,28) (k2 = 5, k = i/5) должна уничтожить иррацио-
иррациональность подынтегрального выражения. Полагаем
х — j/5 sec./; dx = j/5 sec / tg t dt;
x* — 5 = 5 sec2/ — 5 = 5 tg2 /; y/x* — 5 = /5 tg /.
Тогда
Из подстаьювки л; = y^5 sec t следует, что
4 ^; cos2/=J-
... , 5 x2 — 5 . . /*2 — 5
sin2 t=l—-z = -T3—; sin t == ¦!-— ,
а потому окончательно
Задача 9,46 .(для самостоятельного решения).
Найти интегралы: 1) I ?______ • 2У I ,
F 7 J (дг2 —10)Клг2 — 10 ' J (*»—14)/*» —14
Задача 9,47. Найти интеграл / = I ,. .
J B — *!) 1/2 — х*
Решение. Подкоренное выражение имеет вид (9,29) (k? = 2;
= У^2). Применяем подстановку (9,31):
л: = /2 sin/; dA; = /2cos/d/; 2 — х* = 2 cos21;
¦/2-х2 = /2 cos t;
1 = Г 1^2«»ft» -lfiL-i
J 2cos» ^2cos< ~ 2 J cos4 ~ 2
Но из подстановки л; = y^2 sin / следует, что sin / = ~ ,
tg/ == yr==^t а поэтому окончательно
X
713
Задача 9,48 (для самостоятельного решения).
Найти интегралы: 1) f -—„.^^^; 2) J —
.
1
+ С 2)
Задача 9,49 (для самостоятельного решения).
Найти ( ^т=..
J (x2 + 4)/l-x2
Ответ, гт?
4)dx
Задача 9,50. Найти интеграл
h
(х2 + 2х + 4) /*а + 2л: + 5 '
Решение. В подкоренном выражении выделяем полный
квадрат: х2 + 2х + 5 = (х + 1)а + 4.
Сделаем линейную подстановку, о которой мы упоминали
на стр. 143: х + 1 = у; dx = dy; x2 + 2х + 4 = (х + IJ + 3 =
= г/а + 3; х-{-4 = х+1+3~у + 3, а интеграл
(/+3
/ =
-dy.
Теперь выражение, стоящее под корнем, имеет вид (9,25).
Применим подстановку (9,27) (k2 = 4; k = 2):
^r г/ + 3 = 2tg/ -f 3;
Теперь
| 4 sin21 + 3 cos2 < = 4 — cos2 *
4 sin2 / + 3 cos 21 =
= sin21 + 3
2 + cos
2 — cos <
/з
sin t
2 — cos
-COS I
I Учтен 'знак минус,
I стоящий перед логарифмом |
714
Теперь следует от переменной / перейти к переменной у,
а затем от' у к х.
у . .... 2
Так как */=2tg/, то /?/=-§¦; sin/ =
а потому
/ = i-ln
= >
; cos/ =
2/4 + J/2 + 2
Но так как х + 1 = у, то г/2 + 4 = х2 + 2д: + 5, и окончательно
х+1
1
+ 2л: +5 — 1
+ /3 arct
Ч- 2л: + 5 + 1
Задача 9,51 (для самостоятельного решения).
Найти интегралы: 1) I •
= + С.
dx
Указания. 1) Подкоренное выражение представить так:
4ж2 + Ах + 5 = Bх + IJ + 4.
— -^-dy\
2
Линейная подстановка 2х+ 1 = y\2dx ~ dy;
при-
приведет это выражение к виду у2 + 4. Выражение же х2 + д: + 4 =
4л-2 + 4л:+16 Bх+1J4-15 уг+15 т
= —j—!— = —!—j—!— = —j— . 1еперь следует применить
подстановку i/ = 2tgif; Можно сразу'взять 2х-\- 1 =2igt.
2) Подкоренное выражение х2 -\- 2х + 4 = (х + IJ + 3. Можно
сразу применить подстановку х + 1 = |/ tg t или сначала линей-
линейной подстановкой х -\- \ — у привести подкоренное выражение
к виду г/2 + 3, а потом взять у ~ -/bigt. Вопрос сведется к вы-
вычислению интеграла J cos5 tdt. Из х + 1 =
g / следует, что
sin/ =
х+1
Ответ.
1) _1
; 2/165
,/4л:2 + 4х + 5
/11 Bx+ 0 — /15 Dл:2 4-4x4-5)
х+1
/11 Bх 4- 1) 4- /15 Dх24- 4х 4- 5)
JC+1
27/х2+2х
81\/х2
\/х2+ 2л: + 4,
т+с.
715
ДЕСЯТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Интегральная сумма. Определенный интеграл и его основ-
основные свойства. Вычисление определенного интеграла как предела интеграль-
интегральной суммы.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Интегральная сумма. Пусть на отрезке [а, Ь] (а < Ь) оси Ох
задана непрерывная функция f(x).
Отрезок [а, 6] разделим на п частей, длины которых могут
быть произвольными.
Каждый такой отрезок будем называть частичным.
Абсциссы точек деления обозначим через хь х2, х3, ... хп_1
и будем полагать, что
а < Xi < хг < х3 < ¦ ¦ ¦ < хп_х < Ь. ;
Длину частичного отрезка, равную разности xk — xk_1 (k — 1,
2, ... , п), обозначим через Д
На каждом частичном отрезке выберем произвольную точку,;
абсциссу которой обозначим через lk (k = 1, 2 п), вычислим
/ (?*) — значение заданной функции / (х) в этой точке. Найдем
произведение числа / (lk) на длину Axk отрезка, на котором взята
точка ?А, т. е. f(Zk)bxk.
Составим сумму таких произведений
которую обозначим
? U0.1)
Эта сумма называется интегральной суммой для функции / (я)
на отрезке [а, Ь].
Для заданной функции / (я) на отрезке [а, 6] можно составить
бесчисленное множество интегральных сумм, так как отрезок [а, 6]
может быть разделен на "части бесчисленным числом способов,
а при выбранном способе разделения существует еще бесчислен-
бесчисленное число возможностей для выбора в каждом отрезке точек ?А.
2. Определенный интеграл. Обозначим через / длину наиболь-
наибольшего из частичных отрезков [xk_lt xk] (k = 1, 2, 3, .. . , п) в дан-
данном разделении отрезка [а, Ь] на части (I — max &xk).
Определение. Предел интегральной суммы A0,1)
Km tf(lk)bxk
716
при условии, что / -у О (а значит, число отрезков п неограниченно
возрастает (п->- оо)), если он существует и не зависит ни от того,
каким образом разделен на части отрезок [а, 6], ни от того, какая
точка lk выбрана на каждом частичном отрезке, называется опре-
определенным интегралом функции f(x) на отрезке [а, 6] и обозна-
чается символом (" f (x) dx. Таким образом,
а
Hm Vf(e*)A** = ff(*)d*. A0,2)
i
fe=l
Функция f(x) в этом случае называется интегрируемой на от-
отрезке [а, 6].
Гарантией существования этого предела, или, что то же са-
Ь \
мое, существования определенного интеграла j f(x) dx, и незави-
а
симости его ни от способа деления отрезка [а, Ь] на части, ни от
выбора точек lk на каждом частичном отрезке является непре-
непрерывность функции f(x) на отрезке [а, 6].
Теорема (о существовании определенного интеграла).
Если функция f (x) непрерывна на отрезке [а, $], то предел
интегральных сумм A0,1) при условии, что длина каждого час-
частичного отрезка стремится к нулю, а число частичных отрезков
неограниченно увеличивается, существует и не зависит ни от
способа разделения отрезка [а, Ь] на части, ни от выбора точек
на каждом частичном отрезке.
В символе J / (x) dx числа а и 6 называются соответственно
а
нижним и верхним пределами интегрирования, отрезок [а, 6] —
отрезком интегрирования, а переменная величина х — переменной
интегрирования.
п
Отыекивая предел A0,2) суммы Ц/(^)Дл:4 при условии, что
длина наибольшего из частичных отрезков hxk стремится к нулю,
следует иметь в виду, что каждое слагаемое f (ik) b.xk есть вели-
величина бесконечно малая, так как в этом предельном процессе Lxk —
величина бесконечно малая, а [ (lk) имеет конечное значение, по-
потому что функция f(x) на отрезке [а, Ь] по предположению непре-
ь
рывна. Таким образом, определенный интеграл ^f(x)dx есть
а
предел суммы бесконечно малых величин, количество которых
неограниченно возрастает.
717
3. Формула Ньютона — Лейбница. Имеет место формула
x = F{b)-F(a), A0,3)
где функция F (х) есть какая-нибудь первообразная для подын-
подынтегральной функции f{x).
Формула A0,3) называется формулой Ньютона — Лейбница.
Она является основной формулой интегрального исчисления.
Согласно этой формуле, для вычисления предела интегральной
суммы A0,1) при указанных выше условиях, или, что то же, для
ь
вычисления определенного интеграла J f(x)dx, надо: 1) найти ка-
а
кую-нибудь первообразную функцию F {х) для подынтегральной
функции; 2) вычислить ее значение F (Ь) при верхнем пределе
и вычесть из него ее значение F (а) при нижнем пределе.
Обычно при вычислении определенного интеграла употребляют
такую запись:
с "
)f(x)dx = F(x) =F{b)-F(a).
Формула Ньютона — Лейбница позволяет свести сложную за-
задачу вычисления предела интегральной суммы, для решения кото-
которой отсутствует общий прием, к нахождению первообразной функ-
функции для подынтегральной; тем самым она указывает единообраз-
единообразный и простой способ вычисления предела суммы неограниченно
возрастающего количества бесконечно малых величин и позволяет
заменить бесконечный процесс суммирования хорошо известной
операцией отыскания первообразной функции.
4. Основные свойства определенного интеграла.
1) §dx = b — a. A0,4)
а
2) Постоянный множитель можно вынести за знак опреде-
определенного интеграла
A0,5)
где с — постоянная величина.
718
3) Определенный интеграл от алгебраической суммы несколь-
нескольких функций равен такой же алгебраической сумме определенных
интегралов от слагаемых функций
±fn(x)]dx =
b b
= j f, (x) dx ± j h (*) dx ± ¦ ¦ • + j /„ (ж) dx. A0,6)
4) При перестановке пределов интегрирования знак опреде-
определенного интеграла меняется на противоположный
{x)dx. A0,7)
5) Если нижний и верхний пределы интегрирования р^авны
между собой, то определенный интеграл равен нулю
. A0,8)
6) Переменную интегрирования можно обозначить любой бук-
буквой, не нарушая справедливости формул, т. е.
f (x)dx = jf(y)dy = $f(t)dt = $f (a) da. A0,9)
a a a
7) Имеет место формула
b с b
§ $ (x) dx, A0,10)
которая верна при любом взаимном расположении чисел а, Ь и с.
Если выполняются неравенства a < с < Ь, то из формулы A0,10)
следует, что интеграл по всему отрезку равен сумме интегралов
по частям этого отрезка1.
1. Упражнения на вычисление определенных интегралов непо-
непосредственно из определения, как предела интегральных сумм, и с
применением формулы Ньютона — Лейбница.
Задача 10,1. Составить формулы для вычисления интегральных
сумм для функции f(x), непрерывной на отрезке [а, 6], разделяя
этот отрезок на п равных частичных отрезков.
Значение функции вычислять:
1) в правом конце каждого частичного отрезка;
2) в левом конце каждого частичного отрезка.
1 Дальнейшие свойства определенных интегралов будут рассмотрены на
последующих практических занятиях.
719
Решение. 1) Длина отрезка интегрирования равна b — а.
Длину каждого частичного отрезка для удобства записи обозна-
обозначим не через Длт, как обычно, а через h. Тогда
n
Координаты точек деления равны:
х0 = а; х1 — а + h; x2 — a -\-2h хп_х = а + (п — 1) /г;
xn = b = a + nh. A0,11)
Значения функции в правых концах частичных отрезков будут
f(a + h)\ f(a + 2h); f(a + 3h) f (a + nh).
Умножая каждое из этих чисел на длину h частичного
отрезка и складывая эти произведения, получим интегральную
сумму
Sn = f (a + h) h + f (a + 2A) h + f (а + ЗА) h -\ +f(a + nh)h =
= t>f(a + ih)h = h%f(a + ih). A0,12)
(постоянная величина Л, входящая в каждое слагаемое, вынесена
за знак суммы).
ь
В таком случае J / (х) dx будет пределом этой интегральной
a
суммы, т. е.
Ь п
^f(x)dx = h\\m Yif(a + ih) (!°. 13)
a ft-*0 j—\
2) Значениями функции в левых концах каждого частичного
отрезка будут числа
f(a); f(a+h); f(a + 2h) f[a + {n-\)h].
Умножая каждое из этих значений на длину h частичного
отрезка, получим интегральную сумму
S\ -= f(a) h + f(a + A) A + f (a + 2A) h + ¦ ¦ ¦ +f[a + (n— 1)]A =
1=0 (=0
В этом случае
* л—1
" (a + ih). A0,15)
720
Задача 10,2. Составить формулу для вычисления интегральной
суммы для функции / (х), непрерывной на отрезке [а, Ь] (а < Ь),
разделяя отрезок [а, Ь] на п частичных отрезков так, чтобы
абсциссы точек деления образовывали геометрическую прогрессию
(или, что то же, чтобы длины частичных отрезков разбиения об-
образовывали геометрическую прогрессию).
Решение. Если знаменатель геометрической прогрессии обо-
обозначить через q(q> 1), то абсцисса конца отрезка [а, Ь]
b = aqn. A0,16)
Абсциссы точек деления будут такими:
х0 = а; хх = aq; х2 = aq2; х3 = aq3, . .. , хп = aqn = Ь.
Длины частичных отрезков равны:
Д*1 = *i — х0 = aq — а = a (q — 1); Ьх2 = х2 — х1 = aq2 —pq =
= aq(q— 1)
и вообще
b.xk = xk — хк_г = aqk~l {q — 1).
Вычислим значения функции в левом конце каждого частич-
частичного отрезка и получим числа
f(a); f{aq); f{aq\ .... f(aq"-">.
Умножая эти числа на длину соответствующего отрезка и
складывая полученные произведения, составим интегральную
сумму
f(a).a(q-l)+f(aq)-aq(q-l)+f(aq*).aq*(q—l) + ... +
+ f (aq"-1) ¦ aqn-1 (q - 1) = a (q - 1) S / И') q'. A0,17)
В этом случае
Ь л-1 л-1
)f(x)dx = a lira ? (q — 1)./ (aq').q' = a lim (q - 1) ? / (aq') q<.
л-1 л-1
,o ? (=0
A0,18)
Из A0,16) получаем
<? = j/|, A0,19)
а потому, когда п-*- со, то q-*¦ 1 (см. И. А. Каплан. «Практи-
«Практические занятия по высшей математике», ч. II, задача 13,2).
ь
Задача 10,3. Вычислить определенный интеграл j e* dx как
а
предел интегральной суммы.
24 И. А. Каштан 721
Решение. Разделим отрезок интегрирования [а, Ь] на п рав-
равных частей и составим для функции f (х) — ех по формуле A0,12)
интегральную сумму, выбирая точки в правом конце каждого ча-
частичного отрезка. Так как / (х) = е*, то
f(a+h) = e?+h\ f (a + 2h) = e°+ih f(a + ih)= ef+ih;
f (a + nh) = f (b) = еа+ЛЛ (a+nh = b);
¦ Sn - h<?*h + h(?+ih H + /геа+'Л -\ + h<?+nh;
Sn = he" (eh + е2Л -\ \-eih-\ + «"*)• A0,20)
Выражение в скобках — геометрическая прогрессия, знамена-
знаменатель которой q = ё1.
Известно, что сумма п членов геометрической прогрессии равна
Sn-0-^^. A0,21)
У нас ах — ен; q = e\ а потому A0,20) перепишется так:
Но из A0,11) следует, что а + tih = b, а потому
На основании A0,2) определенный интеграл
ь
=е6—е?
(множитель еъ — е° как постоянная величина, вынесен за знак пре-
предела, а по правилу Лопиталя lim_*_ = limi- = 1, alimeft=l).
ft-.oeft— 1 ft-^oe" h-0 1
Итак,
Вычислите самостоятельно этот интеграл по формуле A0,14),
т. е. разделяя отрезок [а, Ь] по-прежнему на п равных частей,
но выбирая на каждом частичном отрезке (xk_bXk) точку в его
левом конце.
Теперь применим к вычислению этого интеграла формулу A0,3)
Ньютона — Лейбница. Согласно этой формуле
722
где F (x) — первообразная функция для подынтегральной функции
f(x). Поэтому
ь ь
j I '
а а
что совпадает с ранее найденным результатом.
Учащийся легко оценит экономию в вычислениях, которую
дает формула Ньютона—Лейбница: весь процесс сводится к оты-
отысканию первообразной функции для подынтегральной, вычислению
её значений при верхнем и нижнем пределах интегрирования
и определению разности этих значений.
ь
Задача 10,4. Вычислить интеграл \ xkdx, где а и 6 — положи-
а
тельные числа, a <b, k ф —1, рассматривая его как предел инте-
интегральной суммы. s
Решение. Предпримем такое разбиение отрезка интегриро-
интегрирования [а, Ь] на части, чтобы абсциссы точек деления образовали
геометрическую прогрессию. (Это равносильно тому, что длины
частичных отрезков образуют геометрическую прогрессию). Вы-
Вычислять значение функции будем в левом конце каждого частич-
частичного отрезка.
В задаче 10,2 была получена формула A0,18) для вычисления
определенного интеграла при таком способе разбиения отрезка
интегрирования на части. Полагая в этой формуле / (х) = хк,
f (aq1) = (aq')k и учитывая A0,19), получим
Ь . п— 1 л—1
f хк dx = a lim (q — 1) У (aq-)k ql = a lim (q — 1) У akq'^+l> =
a ,0-1, /To ,»-!, /To
n-1
lim (<7 — 1) 2 <7'(*+"- (I0>22)
0-1 ,=0
Под знаком суммы стоит геометрическая прогрессия. Её первый
член cti = 1, знаменатель qk+1. Поэтому по формуле A0,21) сумма
этой прогрессии
_1 ¦ [(?*+')» — Ц _ (g")*+1 — 1
Но на основании A0,19) qn — —, поэтому
24* 723
a A0,22) перепишется в виде
ь
xkdx = ak+xWm{q— 1)'
(Л-*оо)
так как по правилу Лопиталя
^9 q^{+)q
Итак,
ь
\ b " A0,23)
причем на пределы интегрирования а и Ь было наложено ограни-
ограничение 0 < а < Ь, так как при этом предположении проведенное
деление отрезка [а, Ь] на части, длины которых составляют гео-
геометрическую прогрессию, всегда возможно.
Следует отметить, что формула A0,23) верна при любых зна-
значениях а и Ь.
Теперь применим к вычислению этого интеграла формулу
A0,3) Ньютона—Лейбница:
ь ь
J
xkdx =
k+i
k+l
(никаких ограничений на числа а и b не наложено).
Очевидно, что применение этой формулы просто и быстро
дает необходимый результат.
При k = 0 из A0,23) получаем
ь
j dx = b — а,
а
т. е. определенный интеграл от дифференциала равен разности
между верхним и нижним пределами интегрирования.
Эти две задачи приведены с целью упражнения в составлении
интегральной суммы для подынтегральной функции, определении
предела этой суммы при разных способах разбиения отрезка инте-
интегрирования на части, а также для сравнения труда, затрачивае-
затрачиваемого на вычисление определенного интеграла по формуле Нью-
Ньютона—Лейбница и как предела интегральных сумм.
Теперь мы предложим для тех же упражнений несколько за-
задач для самостоятельного решения с необходимыми указаниями,
724
Задача 10,5 (для самостоятельного решения).
ь
Вычислить I — dx(a > 0; b > 0; а < b), составив интегральную
а
сумму для функции f (х) = — на отрезке [а, Ь]. Разбиение отрезка
на части произвести точками, абсциссы которых составляют гео-
геометрическую прогрессию. Вычислить этот интеграл и по формуле
Ньютона—Лейбница.
Указание. Использовать формулу A0,18).
* я-1 п-\
л
ч
Задача сведется к определению предела lim n(q — 1).
(я~«)
Так как согласно A0,19) q — у —, то \nq = — In — , a n =
-j— . Поэтому указанный предел преобразуется в
lim
In —
^ (<7—I) = lnp
(применить правило Лопиталя: «неопределенность» вида
Ответ. In — . По формуле Ньютона—Лейбница
— dx — In x
=ЫЬ — In a = In—.
Требование, чтобы а и b были числами положительными,
является существенным, так как каждое из них оказалось под
знаком логарифма.
Задача 10,6 (для самостоятельного решения).
ь
Вычислить xdx, составив интегральную сумму для функции
а
f (х) = х. Отрезок [а, Ь] разделить произвольным образом на
п частей,
725
Точку, в которой вычисляется значение функции, взять в сере-
середине каждого частичного отрезка:
<k =
Так как / (х) = х, то / (?*) =
Длина частичного отрезка
— хн — xk-i.
Интегральная сумма примет вид
(хк — xk-i) = y 2 (* Jft)
k-l A=l
Ho xn = 6; x0 = а, поэтому интегральная сумма равна
-р-(Ь2 — а2), а ее предел в данном случае, как предел постоянной
величины, равен ей самой
ь
Такой результат, конечно, мог быть получен сразу по формуле
A0,23). При решении этой задачи было произведено не специаль-
специальное разбиение отрезка на части, а произвольное. Точка, в которой
вычисляется значение функции, была выбрана в середине каж-
каждого отрезка. По формуле Ньютона—Лейбница получается, ко-
конечно, то же самое
ь ь
Задача 10,7 (для самостоятельного решения).
ь
Вычислить \ sin х dx как предел интегральной суммы и при-
а
меняя формулу Ньютона—Лейбница.
Указание. Отрезок [а, 6] разделить на п равных частей.
Значения функции sin* вычислить в правом конце каждого
отрезка. ,
По формуле A0,12) интегральная сумма будет иметь такой
вид (с учетом, что h = ——-\:
h [sin (a -f h) + sin (a + 2A) + ... + sin"(a + ih) -f-
+ ... -f sin (a + nh)].
720
Учесть, что 2sin (а + ih) sin -к = cos (а + ih —о") ~ cos (а
ih+~j, а отсюда
sin (a + ih) = —Ц- [cos (а + ih -1) - cos (а + ih + -j
2sin2
(f = l, 2 л).
Подставляя это значение sin (a 4- ih) в интегральную сумму,
после приведения подобных членов получим
Перейти к пределу при Л-»-0 (я-»-оо), но учесть, что a 4-
4- nh — b, a lim г = 1 (применить правило Лопиталя).
h*°2sin4
Ь
Ответ. \ sin х dx = cos a — cos b.
a
По формуле Ньютона—Лейбница
ъ ь
\ sin х dx — — cos x '= — (cos b — cos a) = cos a — cos b.
a a
Заканчивая упражнения на вычисление определенного инте-
интеграла как предела интегральных сумм, отметим еще раз, что
такое вычисление даже в простейших случаях требует больших
усилий.
В заключение этого практического занятия выполним ряд
упражнений на вычисление определенного интеграла по формуле
Н ьютона—Лейбница.
Задача 10,8 (для самостоятельного решения).
Вычислить интегралы:
* * С
1) \ sin х dx; 2) J ekxdx; 3) \ тц-# dx (учесть, что значения
о о ¦ _i ~"~
функции у — arctg х находятся на интервале — ~ > у , arctg 1 =
= т; arctg(-l) = -T; 4) ) г+#\ 5)
Ответ. 1) 2; 2) е—=-^; 3) J-; 4) j ; 5) /2—1.
727
Задача 10,9 (для самостоятельного решения).
Вычислить интегралы:
Ь Ь J 1
(а>0; b>0); 2)Jcos*d*; 3) J Т^З^; 4> "
dx
a a 0 0
а
5) Va2 — x2dx (учесть результат задачи 4,3).
—a
Ответ. 1) ln-^-; 2) sinft — sina; 3) In2; 4) ^ ; 5)^-.
Задача 10,10 (для самостоятельного решения).
Интегралы, вычисляемые в этой задаче, имеют большое зна-
значение в теории тригонометрических рядов.
Доказать справедливость следующих формул, если т и п —
целые числа:
11
1) J sin mx cos nx dx = 0;
2) I sin mx sin nx dx =
vl
0, если | m \ Ф \ n\,
it » m = n,
—ic » m = — n.
У к а з а н и e: sin mx sin nx = -^- [cos (m — n) x — cos (m + ti) x].
3) l cos mx cos nx dx =
0, если | m | ^ | n |,
it » m = ± n,
2it » m = n = 0.
У к а з а н и е: cos mx cos л* = -^ [cos (от + я) х + cos (m — п) х].
Задача 10,И (для самостоятельного решения).
Интегрируя по частям, доказать формулу
j sin2 л; dx = — ^ sin2m-i л: cos л; + ^=^ j sin2 л; dx
и, применяя её при от > 0 и целом, показать, что
2
2т — 1 2т — 3 2m — i
jsi
Sin2 v Ay —
о
728
Задача 10,12 (для самостоятельного решения).
Из формулы A0,24) получить, заменяя х на у — г, формулу
j cos2m x dx = i cos2-1 x sin x + ^^~ f cos2-2 x dx
и, пользуясь ею, доказать, что при т > 0 и целом
om i 2т— 1 2m — 3 2m — 5 3 1 и ,<„ „.-,
cos2xdx — —g— • __2 ¦ » _4 • • • т ' T ' T• (Ю.25)
о
На последующих практических занятиях учащийся сможет
выполнить еще много упражнений, связанных с применением фор-
формулы Ньютона-Лейбница для вычисления определенного интеграла.
ОДИННАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Задачи механики и физики, приводящие к определенному
интегралу. '
Решим несколько задач, в которых для определения искомой
величины требуется сначала составить интегральную сумму, а
затем найти ее предел.
Задача 11,1. Сила тока / является заданной непрерывной
функцией времени t: I = I(t). Определить количество Q электри-
электричества, протекшего через поперечное сечение проводника за время
Т, отсчитываемое от момента начала опыта.
Решение. Считая, что в начале опыта Т = 0, разделим про-
произвольным образом отрезок времени @, Т) на п частичных отрез-
отрезков. Абсциссами точек деления пусть будут числа tx, t2, t3, ¦¦¦, tn-u
а длины частичных отрезков времени tk — tk_x (k = 1, 2, ..., n)
обозначим через Mk
Д/ / / (h 10 t}\
причем подчеркнем еще раз, что прбмежутки времени А^ не обя-
обязательно должны быть между собою равны. В каждом из этих
частичных промежутков времени выберем произвольный момент
времени xk (ft = 1, 2, . .. , п). Этот момент может находиться как
внутри отрезка времени [tk_v tk], так и на любом из его концов.
Сила тока — величина переменная, изменяющаяся во времени.
Однако мы будем считать, что за время Mk сила тока не изме-
изменяется, а имеет в течение всего этого промежутка постоянное
значение, а именно то, которое она имела в момент хк. Таким
образом, для отрезка времени [tk-ъ tk] сила тока, равная / (xk),
считается величиной постоянной.
Известно, что для постоянного тока количество электричества,
протекшего через поперечное сечение проводника, равно произве-
произведению силы тока на время, затраченное на прохождение током
729
этого проводника. Следовательно, за отрезок времени, равный
Ltk, протечет количество электричества, приближенно равное
Ifa)btk (й = 1, 2, .... я).
Произведение / (tft) Atk дает приближенное, а не точное коли-
количество электричества, протекшего за время Ltk, потому что силу
тока в течение всего этого промежутка времени мы считаем вели-
величиной постоянной, в то время как в действительности она изме-
изменяется непрерывно со временем и является величиной переменной.
Давая индексу k значения 1, 2, ..., п и складывая произве-
произведения I fa) itx, Ifa)At2 I(zn)Un, найдем, что количество
электричества Q, протекшего за весь отрезок времени [О, Т],
приближенно определяется суммой
которая является интегральной суммой для функции / (/) на
отрезке [О, Т]. Итак,
Q-S/ЫЛ/а. A1,1)
k=\
За точное значение количества электричества Q принимается
предел этой интегральной суммы при условии, что наибольший
из отрезков времени max Atk стремится к нулю, а значит, число
п этих отрезков неограниченно возрастает, т. е.
lim ? 1ЫЫк. A1,2)
4f0 k\
Когда наибольший из отрезков времени Д/д. стремится к нулю,
то каждое слагаемое / (rk) Ltk — величина бесконечно малая, а ко-
количество п этих слагаемых неограниченно возрастает. Таким
образом, при определении предела интегральной суммы A1,1) мы
отыскиваем предел суммы бесконечно малых величин, когда их
количество неограниченно возрастает.
Из A1,2) следует, что количество электричества, протекшего
за отрезок времени [О, Т], определяется по формуле
J(/)A A1,3)
о
(см. формулу A0,2)).
Таким образом, формула A1,1) определяет приближенно коли-
количество электричества, протекшего через поперечное сечение про-
проводника за время, равное Т секундам. Формула же A1,3) опре-
определяет это количество точно, причем числа, найденные по этим
формулам, тем меньше отличаются одно от другого, чем меньше
отрезки времени Д/А, на которые разделен основной отрезок вре-
времени [0, Т].
730
ю
Q = [ Bt*
о
Напомним, что в технической системе единиц количество
электричества Q измеряется в кулонах, а сила тока / — в ампе-
амперах.
Задача 11,2. Сила тока I = 2t* — 3t + 2.
Определить количество электричества, протекшее через попе-
поперечное сечение проводника за 10 секунд, считая время от начала
опыта.
Решение. щ
ю
3t + 2) dt = (jt3 --|*а + 2*)|'о° = 536-|
о
Задача 11,3. Тело движется по прямой Ох из точки с абсцис-
абсциссой а до точки с абсциссой b (а < Ь) под действием переменной
силы F, являющейся непрерывной функцией абсциссы х: F = F (х),
причем сила параллельна прямой Ох, а ее направление сввпа-
дает с направлением движения тела. Найти работу А, произве-
произведенную силой F (х) на этом перемещении.
Решение. Если бы сила F (х) была не переменной, а постоян-
постоянной, параллельной прямой Ох, и ее направление совпадало с на-
направлением движения тела, то работа А, произведенная ею, была бы
равна произведению модуля силы на пройденный путь, т. е. на
длину отрезка [а, Ь], равную (Ь—а):
A = F{Jb — a).
Но сила переменна, а потому этой формулой для определения
работы мы воспользоваться не можем.
Отрезок [а, Ь] разделим на п отрезков [xk_u xk] (k=l, 2,
3, ..., п). На каждом из них выберем произвольную точку %k.
Определим в этой точке численное значение силы F (х). Получится
число F(Zk). Полагая, что в пределах каждого частичного отрезка
сила не переменна, а постоянна и что ее значение на всем час-
частичном отрезке такое же, как в выбранной точке, будем считать
произведенную этой силой работу приближенно на каждом час-
частичном отрезке равной произведению модуля силы на путь, т. е.
РИА*
Работа силы F{x) на всем отрезке [а, Ь] приближенно равна
сумме работ на всех частичных участках
i4«?fF*)A**. A1,4)
*=i
л
Сумма 2 F (ik) kxk — интегральная сумма для функции F (х)
на отрезке [а, Ь]. По формуле A1,4) мы получим не точное зна-
значение работы, а приближенное, потому что на каждом частичном
731
отрезке мы считали силу постоянной, в то время как фактически
в пределах каждого частичного отрезка она непрерывно изме-
изменяется.
За точное значение работы силы F (х) на отрезке [а, Ь] мы
примем тот предел, к которому стремится интегральная сумма
A1,4), когда наибольший из частичных отрезков t\xk стремится
к нулю, а число их п неограниченно возрастает, т. е.
п 9
Л= lim SF(?*)^,
и согласно формуле A0,2)
ь
$(x)dx. A1,5)
Подынтегральное выражение F (x) dx называется элементарной
работой и обозначается через ЬА.
Работа А есть определенный интеграл от элементарной работы
ЬА = F (x) dx. Таким образом, для определения работы перемен-
переменной силы на прямолинейном пути надо сначала вычислить эле-
элементарную работу ЬА, а после этого интегрированием по формуле
A1,5) найти полную работу.
Приближенное значение работы, вычисленное по формуле A1,4),
будет тем меньше отличаться от ее точного значения A1,5), чем
меньшими будут частичные отрезки t\xk, на которые разбит отре-
отрезок [а, Ь].
При определении предела суммы A1,4) наибольший из отрез-
отрезков t\xk -> 0, каждое слагаемое F (Sft) Kxk — величина бесконечно
малая, а количество их неограниченно возрастает. Поэтому и здесь
определение искомой величины, как и в задаче 11,1 связано с оп-
определением предела суммы бесконечно малых величин, когда их
количество неограниченно возрастает.
Задача 11,4 (работа упругой силы на прямолинейном пере-
перемещении).
К телу прикреплена пружина, другой конец которой закреп-
закреплен неподвижно в точке О. Упругая сила, с которой действует
пружина на тело, подчиняется закону Гука, согласно которому
F =—kx, где k — коэффициент пропорциональности, а х — удли-
удлинение пружины. Найти работу упругой силы на прямолинейном
перемещении по линии действия силы из точки с абсциссой а
в точку с абсциссой Ъ. (Сила — в килограммах, перемещение —
в метрах). Знак минус в выражении силы показывает, что упру-
упругая сила стремится восстановить равновесие.
Решение. Элементарная работа ЬА силы упругости на пере-
перемещении dx равна
ЬА = —kx dx,
732
а потому полная работа на перемещении из точки а в точку b
определится по формуле A1,5)
= jj —kx dx = -k^-
Следует иметь в виду, что работа упругой силы положительна,
если тело движется в сторону убывания модуля упругой силы,
и отрицательна, когда движение происхо-
происходит в сторону возрастания модуля упру-
упругой силы. «
Задача 11,5. Электрический точечный
заряд -\-е1 движется в электрическом поле,
созданном точечным зарядом +е. Согласно
закону Кулона, сила взаимодействия между
двумя точечными зарядами в пустоте
численно определяется по формуле
F ~ —
/* ' К задаче 11,5
Определить работу при перемещении заряда ех из точки А
в точку В, считая, что А и В находятся на прямой, проходя-
проходящей через заряд +е.
Решение. Элементарная работа на перемещении dr равна
ЬА = F dr = — dr, а полная работа определится интегрированием
/i — ei i __ —-
Выражение, стоящее в скобках,— разность потенциалов или
напряжение между точками А и В.
При решении задачи можно было не составлять выражение
элементарной работы, а сразу воспользоваться формулой A1,5),
так как здесь известно аналитическое выражение силы: F — —-.
Это же замечание относится и к предыдущей задаче.
Задача 11,6. Тяжелая цепь длиною L — 200 м поднимается,
навиваясь на ворот. Определить работу силы веса при поднятии
цепи, пренебрегая размерами ворота, если погонный метр цепи
весит 50 кг.
Решение. Пусть к некоторому моменту времени на ворот
навернулся отрезок цепи длиной х. Тогда свешивается его часть
733
длиной L — х. Весит эта часть (L — x) • 50 кг. Элементарная
работа силы веса на перемещении dx будет равна
ЬА = —(L — х) ¦ 50 dx.
(Знак минус поставлен потому, что сила веса направлена проти-
противоположно перемещению). Полную работу найдем по формуле
A1,5) как интеграл от элементарной работы
L
и «\2 L
А=\ —
= —25La =
= —25 • 2002 = —1000000 кгм.
Задача 11,7. На вал, вращающийся с угловой скоростью to,
насажен диск радиуса R, погруженный в жидкость. Считая, что
сила трения окружающей жидкости о поверхность диска пропор-
пропорциональна плотности жидкости р, ква-
квадрату скорости и площади соприкасания,
определить момент сил трения относитель-
относительно оси вала.
Решение. Очевидно, что сила трения
окружающей жидкости о поверхность
диска будет меняться с глубиной. Подсчи-
Подсчитаем сначала элементарную силу трения dF.
На расстоянии г от оси вала рассмотрим
кольцо, внутренний радиус которого г,
а внешний г -f dr. Площадь этого кольца
К задаче 11,7 равна
. те (г + drf — тег2 = 2тсг dr + тс dr2.
При dr, стремящемся к нулю, ndr2 — величина бесконечно
малая высшего порядка малости, чем dr, а потому, пренебрегая
ею, примем площадь кольца равной 2кг dr. Линейная скорость
v = tor. Квадрат этой скорости равен to2r2, плотность жидкости — р.
А потому, принимая коэффициент пропорциональности равным
k, для элементарной силы трения dF на расстоянии г от оси вала
получаем
dF =
а ее момент относительна оси вала
dm = rdF = (&p2w cfrto2r2) r;
dm — 2«&ptoV4dr.
Полный момент сил трения найдем интегрированием этого
выражения от 0 до R:
т =
j г4 dr =
~.
734
Число это следует удвоить, принимая во внимание, что трутся
обе поверхности диска. Поэтому полный момент сил трения
При решении задач 11,8—11,15 следует иметь в виду, что
давление — величина векторная.
Задача 11,8. Определить численное значение силы давления р
ветра на стоящую вертикально цилиндрическую башню высотой
/икс круглым основа-
основанием радиуса а м, если
известно, что сила дав-
давления ветра на 1 м2
плоской поверхности, ..
расположенной перпен- —-
дикулярно к его направ- —-
лению, равна р кг. ' ~
Решение. На чер- ——
теже показано основа- —».
ние башни, направле- —>
ние ветра и расположе-
расположение координатных осей. —-'
Дугу АСВ разделим на п —~
дуг точками Аъ А2, .. . , р
Ак, ... , Ап_х и рассмо-
рассмотрим полоски башни,
опирающиеся на соот-
соответственные дуги. Если
направление ветра не
перпендикулярно по- К задаче 11,8
верхности полоски, то
эта поверхность будет испытывать только часть давления, равную
составляющей силы давления р по нормали к этой поверхности.
Вычислим силу давления, которую испытывает полоска башни,
опирающаяся на дугу AsK. Обозначим через fK угол, который каса-
касательная в точке Ак д,уги'АкАк+1 составляет с направлением ветра.
Тогда составляющая пкАк'Силы давления по нормали равна
\ __ .
Полоска башни, опирающаяся на дугу LsK, имеет площадь,
равную приближенно AAsK м2, а потому она испытывает давле-
давление, равное
~Ерк = р sin <?Kh As*.
735
Обозначим через Д<рк центральный угол, опирающийся на дугу
As*. Учитывая, что радиус окружности основания башни равен а,
получим
а сила давления ветра на полоску башни, опирающуюся на дугу
Крк = р sin ср* ЛаД?*.
Определим проекции этой силы на координатные оси Ох и Оу:
(?Рк)х = {pahsinср*Д<р«)cos \~ — cp«j ,
или
(Ьрк)х = pah sin* <pK&<pK;
(Ар~к)у = (pah sin <$>кДсрк) cos cp« = pah sin срк cos срк Дсрк.
(Учащегося должен заинтересовать вопрос, почему от силы дав^
ления ветра Арк на полоску башни мы переходим к проекциям
этой силы на координатные оси).
Суммы проекций по соответствующим координатным осям да-
дадут приближенные значения проекции на эти оси силы давления
р на всю башню.
п
Pah sin2 сркД<р« = pah ^] sin2 ср«Д<р«
2j pah sin cpK cos ср^Ду* = pah 2j sin fK cos ^кДсрк
K=l
A1,6)
(в обоих случаях постоянная величина pah, входящая в каждое
слагаемое, вынесена за знак суммы).
Угол ср отсчитывается от ОА и изменяется на дуге АСВ от
О до тс, а потому, переходя к пределу в последних равенствах
A1,6) при условии, что число частей деления дуги АСВ на части
неограниченно увеличивается, а все Дер* стремятся к нулю, полу-
получим точные выражения для проекций силы давления на оси Ох
и Оу в виде определенных интегралов:
рх =
= pah
pah
кг;
¦к
py = pa/i I sin cp cos cpdcp = pah -
_lsin2?)
= 0.
Итак, рх =
г; ру = 0.
736
Если известны проекции ах и ау вектора а на координатные
оси, то его численное значение (модуль), как известно, находится
по формуле а = Yа\ + а*, а потому модуль силы давления р на
всю башню равен
Задача 11,9 (о давлении жидкости на погруженную в нее вер-
вертикальную стенку).
В жидкость, удельный вес которой равен 7, погружена верти-
вертикальная стенка. Определить численное значение (модуль) силы
гидростатического давления жидкости на эту стенку (см. чертеж).
Решение. Из гидростатики
известно, что давление жидкости п
на погруженную в нее горизон-
горизонтальную пластинку численно равно
весу столба жидкости, опираю-
опирающегося на эту пластинку, т. е.
произведению площади этой пла-
пластинки на ее расстояние от сво-
свободной поверхности жидкости и
на удельный вес жидкости.
Если площадь пластинки S,
ее расстояние от свободной по-
поверхности жидкости h, а удель-
удельный вес жидкости
силы давления
Е
у
то модуль
ffxj
A1,7)
К задаче 11,9
Но эта формула верна только для пластинки, занимающей в
жидкости горизонтальное положение. Если же пластинка, погру-
погруженная в жидкость, занимает не горизонтальное положение, а,
например, вертикальное, то ее различные точки находятся на раз-
различной глубине, а поэтому о расстоянии всей пластинки от сво-
свободной поверхности жидкости не' имеет смысла говорить, и фор-
формула A1,7) для вычисления модуля силы давления на эту пла-
пластинку непригодна.
Отнесем пластинку ABCD к прямоугольной системе координат
(см. чертеж), причем ось Оу расположим на поверхности жидкости.
Абсциссы точек А и В соответственно равны а и 6, а линия CD
определяется уравнением y = f(x), где / {х) — непрерывная функ-
функция на отрезке [а, Ь].
Разделим отрезок [а, Ь] на п произвольных частей и построим
прямоугольники, как показано на чертеже. Площадь пластинки
EFKH примем приближенно равной площади прямоугольника
EFGH, т. е. произведению f(x^x,-. Чтобы вычислить-прибли-
вычислить-приближенно величину давления на этот прямоугольник, повернем его
737
вокруг стороны EH так, чтобы он принял горизонтальное поло-
положение. Теперь уже к этой площадке применима формула A1,7),
и приближенно величина давления жидкости на прямоугольник
EFGH будет равна
Эта величина тем меньше будет отличаться от истинной вели-
величины давления на пластинку EFKH, чем на большее число п
разделен отрезок [а, Ь].
Поступая так же со всеми прямоугольниками, мы найдем, что
приближенно модуль силы давления определяется интегральной
суммой
л—1
(постоянная величина f входит в каждое слагаемое, а потому вы-
вынесена за знак суммы). При составлении интегральной суммы мы
точку на каждом частичном отрезке взяли в его левом конце. Как
известно, на предел интегральной суммы это не повлияет.
За точное значение модуля силы давления примем предел, к ко-
которому стремится эта сумма, когда наибольший из отрезков Дя,-
стремится к нулю, а число п этих отрезков неограниченно увели-
увеличивается
л—1
Р = 7 Hm
max Д*у-*О
Я-ю»
Так как Д*,—>О, то каждое произведение xtf(x^LXi — вели-
величина бесконечно малая, и здесь опять-таки мы имеем дело с опре-
определением предела суммы неограниченно
в Ше^рш жидкости возрастающего количества бесконечно
* малых величин.
На основании формулы A0,2) мы
можем записать, что модуль силы давления
жидкости на вертикально погруженную в нее
стенку равен
b
Задача 11,10. Прямоугольная пластинка со
х сторонами а дм и h дм вертикально погруже-
К задаче и,*в на в жидкость удельного веса *[• Сторона дли-
длиной а дм лежит на поверхности жидкости.
Определить численное значение силы давления, испытываемого
каждой стороной пластинки.
738
Решение. Применим формулу A1,8). В ней нижний предел
интегрирования нужно взять равным нулю, верхний равен h, f (x)=a,
а потому модуль силы давления
h
Р = ^ 1 axdx = 7укг
(давление получилось в килограммах, так как стороны прямо-
прямоугольника выражены в дециметрах).
При решении задачи значительно большую пользу принесло бы
повторение рассуждений, проведенных в предыдущей задаче, чем
использование готовой формулы A1,8).
Задача 11,11. При условиях предыдущей задачи определить,
на какой глубине надо разделить прямоугольник горизонтальной
прямой, чтобы давления на каждую из двух частей прямоуголь-
прямоугольника были равны между собой.
Решение. Проведем прямую, разделяющую прямоугольник
на глубине с(с< Л). Тогда давление р1 на верхнюю часть прямо-
прямоугольника численно равно
с
Рд =т5 axdx'
а давление р2 на нижнюю его часть
Л
По условию задачи эти числа должны быть между собой равны,
а потому
? \ axdx = т J
О '
т J axdx.
О
Сокращая на аг[ и интегрируя, получим уравнение для опре-
определения неизвестной величины с:
Задача 11,12 (для самостоятельного решения).
Определить численное значение силы давления жидкости удель-
удельного веса if на одну из сторон прямоугольной пластинки, наклонен-
наклоненной к поверхности жидкости под углом а, причем верхняя сторона
739
AD длиной а дм расположена горизонтально на глубине h от по-
поверхности жидкости. Длина другой стороны АВ прямоугольника—
b дм (см. чертеж).
Указание. На прямоугольнике ABCD взять полоску ши-
шириной Ах на расстоянии х от стороны AD. Площадь этой полосы
равна а • Ах, а ее расстояние от поверх-
поверхности жидкости равно h + x sin а. Дав-
Давление, оказываемое жидкостью на эту
полоску, приближенно равно
f (h + x sin a) aAx.
Ответ, р = ^ BЛ + b sin а) кг.
Задача 11,13 (для самостоятельного
решения).
Плотина имеет форму половины
эллипса, малая ось которого 26 лежит
на поверхности жидкости. Большая
К задаче 11,12 ось эллипса — 2а. Вычислить численное
значение давления воды на плотину.
Указание. Если расположить оси, как это сделано на чертеже,
то эллипс определится уравнением -^ + ?5
Вырежем полоску на глубине х шири-
ною Д*. Площадь этой полоски равна 2уАх.
Величину у определить из уравнения
эллипса. Принять удельный вес воды
7 = 1.
Численное значение давления равно
a* — x*dx.
Можно было сразу воспользоваться готовой формулой A1,8), в
которой взять у = — У а% —х%.
Ответ. Если полуоси эллипса выражены в дециметрах, то
численно давление получится в килограммах
Если заменить эллипс половиной круга (а = Ь) то
2
= -^а3 кг.
740
Задача 11,14 (для самостоятельного решения).
Найти численное значение давления воды (f = 1) на треуголь-
треугольные щиты, показанные на чертеже.
Указание, а) Уравнение АВ: «/ = ¦§-— kj.x;
б) уравнение ОС: у = ~ х.
О т в е т. а) р = ¦%-; б) р = %-,
а
г
У
О
\х
К задаче 11,14 а
Задача 11,15 (для самостоятельного решения).
Поперечное сечение стенки резервуара, наполненного водой,
представляет дугу АВ круга-радиуса а дм, центр О которого
лежит на поверхности воды, а цен-
центральный угол АО В равен а. Опре-
делить давление воды на эту дугу
(см. чертеж).
Указание. 1. Дугу АВ разде-
разделить на п частей.
2, Учесть, что давление направ-
направлено по перпендикуляру к поверхно-
поверхности и численно равно произведению
длины элемента As на его глубину
DC и на удельный вес f жидкости.
3. Длина дуги окружности равна произведению ее радиуса на
число радианов, содержащихся в центральном угле, опирающемся
на эту дугу, Т; е.
As
К задаче 11,15
DC = a sin <p; ? = 1, а потому на элемент As дуги АВ численное
значение силы давления Ар приближенно равно
Ар — (a sin <f>) a A f = а2 sin <p Дер.
741
4) Найти проекции ДХ и ДУ силы Др на оси Ох и Оу:
ДХ = (a2 sin <р Д?) cos (90° — <р) = a2 sin2 9 Д<р;
ДУ = а2 sin <p cos 9 Д<р.
а . а
X = J аа sin2 «р d«f; У = J а2 sin <j> cos 9 d<p; p = 7/ X2
о о
Y2.
Как и в задаче 11,9, читателя должна заинтересовать при-
причина, заставляющая перейти от элементарных давлений Др к их
проекциям, затем суммировать не элементарные давления, а их
проекции, и только найдя их, определить численное значение
самого давления.
Ответ. p=^-i/4sin4a-fBa — sin2aJ/c2.
Задача 11,16. Согласно закону Гука, удлинение Д/ стержня
длиной I постоянного сечения F под действием растягивающей
нормальной силы Р определяется формулой
Д* = й. (И.9)
'////////////у
О
где Е — модуль упругости материала, из ко-
которого сделан стержень.
"Определить удлинение свободно подвешен-
ного цилиндрического стержня длиной I см и
поперечного сечения F см? под действием его
собственного веса. Удельный вес материала
стержня f г/сма.
Решение. Разделим стержень на эле-
элементарные цилиндрические стержни. Эти эле-
элементы будут испытывать различные растяже-
растяжения, так как они находятся под действием
различных сил веса.
Вычислим по формуле A1,9) растяжение
элементарного цилиндра высотой Д#, находя-
находящегося на расстоянии х от места подвеса. На него действует
сила веса, равная весу нижележащей части стержня. Длина
этой части равна (/ — х), объем ее — (/ — х) F, а вес — (/ — х) Ff.
Полагая в формуле A1,9) / = Ддс; Р = (I — д:)/^. получим, что ра-
растяжение элементарного цилиндра приближенно равно
х
К задаче 11,16
EF ~ Е
ч Суммируя растяжения этих элементарных цилиндров и пере-
переходя к пределу при условии, что число этих элементарных ци-
цилиндров неограниченно возрастает, а высота Ах каждого из них
742
неограниченно убывает, общее удлинение стержня найдем по фор-
формуле
Ответ.
Задача 11,17 (для самостоятельного решения).
Материальная точка движется по прямой с переменной ско-
скоростью, являющейся заданной непрерывной функцией времени t:
v — v (/). Определить путь, пройденный телом от момента вре-
времени /0 до момента Т.
Указание. Промежуток времени [^0, Т] разделить на л
произвольных частей. Длина каждого промежутка времени '
В каждом частичном промежутке времени выберем произволь-
произвольный момент — xk. (Момент tk может совпадать и с любым из
концов отрезка времени Mk).
Вычислим скорость v в этот момент времени. Получится, число
)
Принимаем, что за время Д/А движение происходит равномерно.
Поскольку при равномерном прямолинейном'движении путь, прой-
пройденный телом, равен произведению скорости на время, путь, прой-
пройденный за время Д/А, будет приближенно равен и(хА)Д/А. Сложим
пути, пройденные за все частичные отрезки времени.
Приближенное значение пути
S ж ? и (**)*'*• (ИДО)
За точное значение пути S следует принять предел интеграль-
интегральной суммы A1,10), когда наибольший из промежутков времени
Д4 стремится к нулю:
S= lim ?е>ЫДгА.
max btk-+O ft=l
На основании формулы A0,2) можно записать, что
т
S = $v(t)dt. A1,11)
и
Таким образом, если задан закон изменения скорости, то путь,
пройденный телом, вычисляется с помощью определенного инте-
интеграла по формуле A1,11).
743
Когда max Mk -> 0, то произведение v (xA) Д^ — величина беско-
бесконечно малая. Определение искомой величины и в этой задаче
свелось к отысканию предела суммы неограниченно возрастающего
количества бесконечно малых величин.
Задача 11,18 (для самостоятельного решения).
Вычислить путь, пройденный свободно падающим в пустоте
телом за Т секунд, если известно, что скорость v свободного па-
падения в пустоте определяется формулой v = gt (начальную ско-
скорость v0 принимаем равной нулю).
Ответ. S = ^- . Если v0 Ф О, то v = v0 + gt, a S = v0T -j- S— _
Задача 11,19 (для самостоятельного решения).
Дан неоднородный тонкий стержень длиной L. Определить
массу этого стержня, зная, что в каждой его точке плотность |х
есть заданная непрерывная функция абсциссы х этой точки: ;х =
= [х (X).
Указание. Если бы стержень был однородным, то плот-
плотность ]1 во всех его точках была бы величиной постоянной, а его
масса, учитывая, что по условию стержень тонкий, была бы равна
произведению плотности [х на его длину L, т. е. m = [xL.
Разделить длину стержня на п произвольных частей. Вычислить
массу каждой части, считая, что плотность каждой из частей
постоянна, сложить полученные массы и перейти к пределу, уст-
устремляя к нулю наибольший из частичных отрезков, на которые
разделен стержень.
Ответ, m = J \*.(x)dx.
ДВЕНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Замена переменной в определенном интеграле. Интегри-
Интегрирование по частям. Теорема о среднем значении.
I. ЗАМЕНА ПЕРЕМЕННОЙ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Краткие сведения из теории
Часто для упрощения вычисления интеграла
dx A2,1)
приходится заменять независимую переменную величину х, пола-
полагая, что
х = ? (О- A2,2)
744
Это приводит к формуле преобразования определенного инте-
интеграла при введении новой переменной
ь 3
J/(*)d* = J/[?(*]?'(О #• A2,3)
а а
При этом предполагается: 1) функция / (х) — непрерывна на
отрезке [а,Ь]\ 2) функция f (t) и ее производная ср' (^) — непре-
непрерывны на отрезке [а, C]; 3) имеют место равенства а = <р (а): 6 =
= у (р); 4) при изменении новой переменной t от а до р функция
л; — <р (^) изменяется всегда в одном и том же направлении от
<р (а) = а до <р (Р) = 6, т. е. функция я = <р (*) на отрезке [а, р]
должна быть монотонной. (Это требование можно заменить другим:
все значения функции <рG) должны находиться на отрезке [а, 6]).
Из этой справки читатель видит, что замена переменной в опре-
определенном интеграле требует осторожности и обязательного выпол-
выполнения всех перечисленных условий, налагаемых на функцию A»2,2).
При соблюдении этих требований важно отметить, что замена
переменной в определенном интеграле приводит в общем случае
к интегралу с новыми пределами интегрирования. Эти пределы
находятся так: в A2,2) подставляется сначала нижний предел а
заданного интеграла и решается уравнение а — <р (t). Значение t,
найденное из него, и будет новым нижним пределом а. Если
этому уравнению удовлетворяет не одно, а несколько значений t,
то за а можно принять любое из них. Затем для определения
нового верхнего предела в A2,2) подставляется верхний предел 6
заданного интеграла и решается уравнение 6 = <р (t). Найденное
из этого уравнения значение t будет новым верхним пределом р.
Если это уравнение имеет несколько корней, то за р можно при-
принять любой из них. Однако свобода выбора чисел аир ограни-
ограничивается требованием, чтобы значения функции <р (t) не выходили
из отрезка [а, 6], в котором определена и непрерывна подынте-
подынтегральная функция f(x) (см. задачу 12,1).
Сделав замену переменной, изменив пределы интегрирования,
после вычисления преобразованного определенного интеграла нет
необходимости переходить к старой переменной, кйк это мы де-
делали при вычислении неопределенного интеграла с помощью замены
переменной.
Еще раз. подчеркиваем, что подстановка A2,2) должна упро-
упростить вычисление интеграла A2,1).
Укажем также, что несоблюдение всех указанных требований,
налагаемых на функцию A2,2), может привести к грубым ошибкам.
Во многих случаях приходится вместо подстановки A2,2), ко-
которая переменную интегрирования х заменяет функцией новой
переменной, вводить новую переменную t как функцию старой
переменной х, т. е. полагать
t = ш (.*).
745
В этом случае новые пределы интегрирования а = ш (а), a C =
= соF). Если соотношение t = ш(х) разрешить относительно х,
то окажется, что х — ср (^), причем необходимо, чтобы для функ-
функции у (^) были соблюдены все указанные выше условия.
Задача 12,1. Вычислить определенный интеграл
J -/а2 — xs dx.
о
Решение. Можно было бы воспользоваться известным из
задачи 4,3 вычислением неопределенного интеграла 1 у/ а2 — х2dx и,
применяя формулу A0,2) Ньютона — Лейбница, найти искомый
интеграл
а
о
/а2 — х2 dx = (i- /а2 — х* + f arcsin ?
а2 . а а8 . , а*к
= ^ arcsin — = -J arcsin I = -j-,
(Первое слагаемое \л^& — х2 обращается в нуль как при
верхнем, так и при нижнем пределах).
Вычислим теперь этот же интеграл с помощью замены пере-
переменной. Введем подстановку
A2,4)
Прежде всего определим новые пределы интегрирования. Когда
х = 0, из уравнения 0 = asin^ получаем, что t — kn. Подстав-
Подставляя же в A2,4) вместо х верхний предел а, получим: a = asint;
sin^ 1; t
Из всех возможных значений t, удовлетворяющих уравнениям
asin/ = 0 и a = asin/, мы возьмем 0 и т потому, что на от-
отрезке 8, ~\ функция # = asin^ удовлетворяет не только первым
трем из указанных требований, что очевидно было сразу, но и
четвертому, так как на отрезке 0, -|- она монотонно возрастает
и ее значения сплошь заполняют первоначальный отрезок интегри-
интегрирования [0, а]. Вместо этих значений можно было бы взять и лю-
любые другие, но такие, чтобы значения функции х = a sin t не вы-
выходили из отрезка [0, а]. В качестве таких значений можно взять,
например, a = 2к, ^ — -^•к. При изменении t от 2тс до у тс функ-
функция jt = asin^ изменяется от 0 до а. Но взять значения a = тс,
746
P = у тс нельзя, так как тогда функция х = as'mt принимает зна-
значения не на отрезке [0, а], на котором ведется вычисление задан-
заданного интеграла, а на отрезке [0, —а].
Подынтегральная функция преобразуется так:
— х2 = |/а2 — а2 sin2t = a cos t\ dx = a cos t dt.
Поэтому
~2
a2-*2d* = J a2 cos21 dt = a2 J
D 0
Ответы, конечно, совпали.
Задача 12,2. Вычислить J у/Г2ах — х3 dx.
Решение. Преобразуем подкоренное выражение
2ах — х3 = а3 — (х3 — 2ах + а3) = а2— (х — аJ
и введем подстановку
х — а = a sin t; x = с -f о. sin t; A2,5)
dx = a cos tdt; -/2ax — x2 = -/a3 — (x — aJ = y/ a2 — a2 sin2 * =
= ya^l — sin2/) = acost.
Подынтегральное выражение будет таким: -/2ах — x3dx =
— a3 cos21 dt.
Теперь надо не забыть определить новые пределы интегриро-
интегрирования: сначала в подстановку A2,5) подставим нижний предел
заданного интеграла х = 0, а потом верхний х = 2а, и получим:
при х = 0 0 = а + a,sint; sftit — —1; / = — —; при х — 2а:2а —
= а + a sin /; 2=1+ sin f; sin / = 1; ' = ¦?¦• Решая уравнения
sin/ = —1 и sin/ = 1, мы остановились на значениях / = — —
и t = ~, так как на отрезке —-5-, — функция A2,5) монотонно
возрастает и остальным требованиям от также удовлетворяет.
747
Таким образом, новыми пределами интегрирования будут —
нижний предел, у— верхний. Поэтому
ТС ТС
2а 2 2
f /2аж — х2dx = а2 f cos2tdt =%¦ f A + cos2/)d^ =
.-?[!-(-*)]-?•
2
Задача 12,3 (для самостоятельного решения).
a
dx
Вычислить
] +
а
У к а з а н и е. х* — 2ах + 2а2 == (х — аJ + а2.
Подстановка: ж — а = г.
Пределы интегрирования: при ж = 0 получаем, г = —а, при
= a z = 0. Таким образом, новая переменная г изменяется на
о
отрезке [—а, 0]. Интеграл преобразуется к интегралу Г
J
а
Ответ. 1п(/2+ О-
Задача 12,4 (для самостоятельного решения).
J г2 + а2"
—а
Вычислить \ ,_.
J l + Vx
Указание. Подстановка: х = г2 (г > 0).
Определяем новые пределы интегрирования:
при лг = 1 1=22;г=1;
» л; = 4 4 = г2; z = 2.
Новая переменная г изменяется на отрезке [1; 2]. Интеграл
2
преобразуется к виду 2 1 ^-т-? . г
g
Ответ. 1 + 1п_-.
1
Задача 12,5. Вычислить
о
Указание. Сделать подстановку: х = cos 6.
748
Пределы интегрирования:
при х = О 0 = cos 6; 6 = ~;;
» х =1 1 = cos 6; 6 = 0. 4
Новая переменная изменяется на отрезке -^-, 0 .
тс
0 Т
Интеграл приводится к виду —2 I sin2yd9 = 2 I sin2-H-d6.
jc О
2
(Перемена местами пределов интегрирования меняет знак опреде-
определенного интеграла на противоположный)
Ответ. ~— 1.
тс 1
Задача 12,6. Вычислить /= f *sm* dx.
ч) i COS X
о
Решение. Сделаем подстановку:
* = 7Г — 2. A2,6)
Новые пределы интегрирования:
при х = 0 0 = ir—2;2 = тг;
» дг = тг тг = тг — z; z = 0.
Таким образом, новая переменная изменяется на отрезке [тс, 0].
Подстановка A2,6) поменяла пределы местами. Учитывая, что из
A2,6) dx = —dz, данный интеграл
0 t
/ — _ Г (к •— г) sin (ti — г) . _ Г (я — г) sin г . _
J~ J l-fcosM^ —г) J l + cos2z
тс 0
sin г , Г г sin г
о о
Но I ^_sln z2 dz равен искомому, потому что по сравнению с ним
о
здесь изменилось только название переменной (г вместо я).
Поэтому последнее равенство можно переписать так:
sin г
f sir
= 7rJnp
749
-j- cos2 г
о
т. е.
1С 1С
sin г j г я Г sin г
о о
= —5" arctg (cos z) Г = — -?- [arctg (cos ir) — arctg (cos 0)] =
Ответ. ' = т*
o»+b»
2
Задача 12,7. Вычислить j/^
i/Зо'+Ь'
Решение. Применим подстановку:
jt2 = a2 cos2 6 + б2 sin2 б, A2,7)
Отсюда следует:
2х dx = — 2а2 cos б sin б d8 -f 262 sin 0 cos 6 db;
xdx= F2 — a2) sin 6 cos 6 db; A2,8)
r> —a2 = a2cosa6 +62sin26—a2 = 62sina8+ a2(cos26 —1) =
= 62 sin2 9 — a2 sin2 8 = (b* — a2) sin2 9;
6* _ X2 = p — a2 cos2 8 — b2 sin2 8 = 62 A — sin2 6) — a2 cos2 6 =
= b2 cos2 в —a2 cos2 9 = (b2 — a2) cos2 8;
! — а2) (б2 — х2) = / (б2 — а2) sin2 8 (b2 — a2) cos2 8 =
= (b2 — а2) sin 8 cos 8.
При учете A2,8) подынтегральное выражение станет равным db.
Теперь определим новые пределы интегрирования. -
При нижнем пределе х = ' aSr имеем из A2,7);
3a8+fca = a2 cos2 8 + Ь2 sin2 8;
За2 + Ь2 = 4а2 A — sin2 8) -f 462 sin2 8 = 4а2 — 4а2 sin2 8 + Ab2 sin2 8;
б2 —а2 = 4 (б2 —a2) sin2 8; sin2 6 = -i-; sin8 = y; 8 = -|.
750
При верхнем пределе х = у а ^ , используя A2,7), получим:
^±^ = a2 cos2 8 +б2 sin2 6;
a2 + b* = 2a2 A — sin2 б) + 26* sin2 6;
a2 + б2 = 2o2 — 2a2 sin2 6 + 262 sin2 6;
62 —a2 = 2 F2 —a2) sin» 6; sin26 = i-; sin6 = 2^;
Таким образом, новая переменная 6 изменяется на отрезке
JL ( JLI а исходный интеграл
/ —
Ответ. / = ~.
4
It 7C
Задача 12,8 (для самостоятельного решения).
Вычислить интегралы:
Указания. 1) Подстановка: х = 4 . Здесь можно вооб-
вообще легко избежать подстановки, если подынтегральную функцию
представить в виде
1 ц-^ — я* 1 -4-х* ** jl__ xs
х 1 4- х1'
Новые пределы интегрирования: 2 и j*',
17
к
2) Подстановка: л: + 6 = г2. Новые пределы интегрирования:
нижний z = 3, верхний 2 = 4; х — 1 = 22 — 7,
751
Ответ. 1) -J-lnff; 2) »ta^^?; 3)|-ln4.
Задача 12,9 (для самостоятельного решения).
Вычислить интегралы:
1
т
х—т= (подстановка: х = г2);
J
13-*&/+*« (п°Дстановка: х3 = z);
Уз
3) j *3>Л + *2^* (подстановка: 1 + x2 = г2),
о
Ответ. 1) -J; 2) g; 3) |.
Задача 12,10 (для самостоятельного решения).
Доказать, что интеграл / = j / (*) dx может быть преобразован
а
в интеграл с заданными пределами аир при помощи подстановки
Ь — а , , "а — и-
Х= о 1 +
— a ( ' H — a
и указать подстановку, которая преобразует этот интеграл в ин-
интеграл с пределами 0 и 1.
II. ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Формула интегрирования по частям для определенных интегра-
интегралов имеет вид
ь ъ ь
] — ] vdu A2,9)
а
в предположении, что функции и и v имеют непрерывные произ-
производные на отрезке интегрирования.
Применение формулы A2,9) мало чем отличается от примене-
применения соответствующей формулы для неопределенного интеграла.
Поэтому мы ограничимся небольшим числом упражнений
Задача 12,11. Вычислить интегралы:
1) J arcsin* dx; 2) J x arctg x dx.
и о
752
i
о
Решение. 1) J arcsinxdx = xarcsinx
dx
1 _ f xdx _
и = arcsin л:
= dx
du =
v = x
= 1 • arcsin 1 — 0 • arcsjn О + у 1 — х2 — -%¦ — 1, так как
о *
arcsin 1 — ~.
1 1
С х2 1 1 Г х2
2) J х arctg х dx=Y arctg x — -^\ f, xi dx =--
о ° о '
и = arctg a:
dv = xdx
du =
dx
1 , , 1 Гjc* + 1 —
7C 1
= -o- — -9- (-V — arctg
тс 1.1 . ,
= T— "о" + "9 arct6 J =
7C
I
Задача 12,12 (для самостоятельного решения). Вычислить ин-
интегралы:
1С
е 2 4 1
1) j In2 х dx; 2) J =¦? Лс; 3) J jc tg2 jc йл;; 4) j (arcsin *J Лс.
1 1 о о
Ответ. 1) e-2; 2)^-^; 3)|-lln2-g;
4)^-2.
III. ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ ФУНКЦИИ НА ОТРЕЗКЕ
Краткие сведения из теории
Вводя понятие об определенном интеграле, мы произвольным
образом делили отрезок интегрирования [а, Ь] на п частей, и в произ-
произвольной точке lj каждого частичного отрезка вычисляли значение
25 и. А Каплан 753
функции / (х). При этом получались числа / (I,). Очевидно, самым
простым способом будет разложение отрезка [а, Ь] на части, рав-
равные между собой. В таком случае длина каждой из них будет
Ъ — а
равна , интегральная сумма примет вид
и ее предел
ь
lim b-=^ [/ (у + / &) + ... + / О = j / (х) Ах,
п-+*> а
ИЛИ
ф - a) lim
Песле деления обеих частей этого равенства на Ь — а получим
lim /&> + /&>+ •••+/<&¦>. = ' / (х) их. A2,10)
Число ^F"Т^^" ' •" +^t^ есть среднее арифметическое чи-
сел /(?!>, /(S2), ..., /(&„), а потому и правую часть ^^j / (x)dx
а
формулы A2,10) называют средним значением функции f(x) на
отрезке [а, 6]. Среднее значение функции / (*) обозначается через
/ (с), и имеет место формула
A2.11)
которая и выражает теорему о среднем значении. При этом пред-
предполагается, что функция f (х) непрерывна на отрезке [а, Ь].
Итак, по определению, среднее значение функции f {x) на от-
отрезке [а, Ь] равно определенному интегралу от этой функции,
вычисленному в пределах от а до b и разделенному на длину
этого отрезка.
Задача 12,13. Найти среднее значение функции t/ = sin3* на
отрезке 0, -^ .
754
Решение. По формуле A2,11), полагая в ней а = 0; 6 =
к
3"
= тг! f (х) — s^n Зх, получим, что среднее значение функции
/(с) = ^— Г sin Зл: ^л: = — ^- • y|
о
= — i-jcos 3 у — cos о] = — 1 (cos u — cos 0) = — 1 (—1 — 1) =
= 1 = 0,6366.
7С
Задача 12,14. На отрезке Л5 длиною а еж взята точка Р.
Найти среднее значение Sm площадей прямоугольников, построен-
построенных на отрезках АР и РВ как на сторонах.
Решение. Примем точку А за начало отсчета. Пусть точка Р
находится на расстоянии х от А. Тогда АР = х, а РВ = а — х.
Площадь прямоугольника, построенного на АР и РВ как на сто-
сторонах равна л; (а — *).
По формуле A2,11), полагая в ней нижний предел равным 0,
а верхний а, находим среднее значение площадей
~~ а ' 6 ~~ 6 '
Итак, Sm = -g- см2.
Задача 12,15 (для самостоятельного решения).
Чему равно среднее значение обратных величин всех вещест-
вещественных чисел, лежащих между а и b (a < 6)? Рассмотреть част-
частный случай: Ь = 2а.
Указание. Обозначить обратную величину вещественного
числа через — , а искомую — через т.
Ответ. т = ^-q In А. При 6 = 2айп = ¦?•.• 0,69315 (In 2 =
= 0,69315).
Задача 12,16 (для самостоятельного решения).
Если тело падает свободно вблизи поверхности земли без на-
начальной скорости, то его скорость вычисляется по формуле v =
= i/2gS, где S — путь, пройденный от начала падения. Найти
среднюю скорость vm на пути 5Ь пройденном от начала падения.
Ответ. уот = J
25* 755
где Vi = V2gS1 — скорость в момент, когда пройденный путь
равен Sj.
Задача 12,17 (для самостоятельного решения).
Найти среднюю длину рт радиусов кривизны одной арки
циклоиды.
Уравнение циклоиды
x = a(t — sint); y = a(l—cost) @<^<2tt).
Указание. Радиус кривизны циклоиды равен 4а
sin-J-
(см. И. А. Каплан. «Практические занятия по высшей математике», ч. II,
стр. 291, формула C6,27).
Ответ. р„ = -.
Задача 12,18. В динамомашине электродвижущая сила пере-
переменного тока выражается формулой
Е = Ео sin у ,
где Т — продолжительность периода в сек;
Ео — максимальное значение (амплитуда) электродвижущей
силы.
Определить среднее значение Ет электродвижущей силы и сред-
среднее значение ее квадрата (Е2)т в течение одного полупериода от
/ = 0 до t = \ . ^
0 т в е т. 1) Ет = 0,6366?0; 2) (?¦)„, = f.
ТРИНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ1
Содержание: Несобственные интегралы по бесконечному интервалу и от
разрывных функций. Принцип сравнения несобственных интегралов с положи-
положительными подынтегральными функциями. .
Краткие сведения из теории
ь
Определенный интеграл \ / (я) Ах во всем предыдущем рассмат-
а
ривался при следующих предположениях: 1) отрезок [а, Ь] инте-
интегрирования конечен и 2) подынтегральная функция на этом отрезке
непрерывна. При таких предположениях этот интеграл называется
интегралом в «собственном смысле», или «собственным» интегралом.
В том же случае, когда отрезок интегрирования бесконечен или
1 Без ущерба для последующего задачи этого практическогр занятия могут
решаться после шестнадцатого практического занятия,
75<?
конечен, но подынтегральная функция на этом отрезке терпит
разрыв, интеграл называется интегралом в «несобственном смысле»,
или «несобственным» интегралом.
Каждый из названных двух случаев рассматривается на этом
практическом занятии.
I. ИНТЕГРАЛ, РАСПРОСТРАНЕННЫЙ НА БЕСКОНЕЧНЫЙ ПРОМЕЖУТОК
(НЕСОБСТВЕННЫЙ ИНТЕГРАЛ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ)
Определение интеграла с бесконечными пределами
В этом разделе считается, что f (х) в промежутке [а, +°°1
непрерывна. Интегралом от f(x)dx между пределами а и +°°
: j f(x)dx . .A3,1)
а
называется предел интеграла от / (*) dx, взятого в пределах а
и N, когда N стремится к -f- оо, т. е.
f f(x)dx= lim \f{x)dx. A3,2)
Интеграл A3,1) с бесконечным верхним пределом — несобственный
интеграл.
Если существует определенный конечный предел в правой
части A3,2), то несобственный интеграл A3,1) называется сходя-
сходящимся, а функция / (я) в этом случае называется интегрируемой
на бесконечном промежутке [а, + оо].
Если же этот предел бесконечен или не существует, то интеграл
называется расходящимся.
а
Интеграл ] / (я) dx определяется аналогично:
00
а а
f f(x)dx= lim \f(x)dx, A3,3)
-co A-*-~ A
а интеграл
f f-(x)dx= lim \f(x)dx, A3,4)
_/» A-*— ~ A
ЛГ-Ч-оо
при этом
4 оо а +°°
j f{x)dx= j f(x)dx+ j f(x)dx, A3,5)
—оо —к а
где а — любое число.
757
Если удается найти первсюбразную функцию F {х) для подын-
подынтегральной /(*), то записи можно расположить так:
f f{x)dx = lim \f(x)dx= lim F (x) N =
= lim [F(N) — F(a)} = lim F(N) — F(a). A3,6)
Очевидно, что несобственный интеграл A3,1) существует, если
существует предел lim F (N).
Введем обозначение lim F (N) — F (+ оо) (и аналогично:
lim F (N) = F (— оо)).
Тогда A3,6) можно переписать так:
+~
f / (д;) dx = lim F(N) — F (a) = F (+ оо) — F (a).
Разность же ^(-1-оо) — F (а) можно записать в виде F (х)
в таком случае вычисления располагают следующим образом:
j f{x)dx = F {x) f" = F (+ оо) - F (a), A3,7)
а
понимая, что F (+ оо) = lim F (х).
Если отыскать первообразную функцию для / (*) трудно или
если она в конечном виде не может быть вычислена, то сущест-
существуют признаки, позволяющие решить вопрос о сходимости или
расходимости интеграла A3,1).
Признаки сравнения
1. Если две функции / (я) и ф (л;) для всех значений х из полу-
полуотрезка [а, + со] не принимают отрицательных значений и к то-
тому же
/(*)<?(*), A3,8)
то ] f(x)dx сходится, если сходится интеграл J <p(x)dx и
а а
-f ОО +00
j ср (*) dx расходится, если расходится J / (*) dx.
а а
2. Если при х ->¦ + оо
Хч-fo i W
758
причем с> 0, с ф со и /(х) ф О для всех достаточно больших х,
то интегралы J / (х) dx и j ср (*) d* либо оба сходятся, либо оба
а а
расходятся.
3. Если сходится j / (*) dx+ то сходится и J kf(x)dx, где Л—
а а
величина постоянная.
+<•
Эти признаки распространяются и на интегралы вида J f(x)dx,
— 00
но относятся только к указанным выше функциям.
4. Для решения вопроса о сходимости интеграла A3,1) в том
случае, когда функция f(х) является знакопеременной в проме-
промежутке [а, + оо), можно применить такую теорему:
+.-
Если несобственный интеграл J \f(x)\dx от абсолютной ве-
а
личины функции f (х) сходится, то сходится и интеграл A3,1).
Задача 13,1. Вычислить
Решение. По определению, применяя запись A3,7), полагая
р ф \, имеем
С dx_ l_ 1 +~ \ I .. _\ Л
|—г, если р> 1;
oo, если p < 1.
Значит, при р > 1 интеграл сходится, а при р < 1 — расхо-
расходится. (Первый ответ получен так: если р > 1, то р — 1 > 0, н
если х ->- + оо, то х"~1 ->- + °°. а дробь ^т ->¦ 0.
Второй ответ объясняется так: если р<1, тор — 1 < 0, а 1 —
— р > 0. Тогда хр~1 ¦= ^гр ->- 0, когда л; ->- + со, т. е. величина
хр~1 — бесконечно малая. Поэтому величина -j=j , которая нас ин-
интересует, — величина бесконечно большая).
Осталось рассмотреть случай р = 1:
dx
= lim In* — In 1 == + 00.
759
Таким образом, при р = 1 интеграл A3,9) расходится. Так
как нам придется обращаться к этому интегралу, то сделаем
общее заключение.
Интеграл \ ^ сходится при р > 1 и расходится, когда р < 1.
1
Этим интегралом часто пользуются, применяя признак срав-
сравнения, для решения вопроса о сходимости интеграла.
Задача 13,2. Вычислить интегралы:
+ оо О
1) j e~pxdx\ 2) j epxdx. A3,11)
о —»
Решение. 1) Интеграл /х = j e~pxdx = е~рх
lim(e-P*_1) = j}, если р>0;
р *-+°° I + оо, если р < 0.
При р > 0 lim e~px =1im -^ = 0, так как ерх -*¦ + оо при
*++оо х-4-4-»
# -»--(- оо. При р < 0 lime~p* = + оо.
Заключение, j e~px dx при р > 0 сходится, а при р < 0 рас-
о
ходится.
2) Второй из интегралов A3,11) сводится к первому подста-
подстановкой х = — у (сделайте это преобразование самостоятельно),
о
а потому J epx dx сходится при р > 0 н расходится при р < 0.
—л»
+~
Задача 13,3. Вычислить I х
,
Решение.
= lim arctg x — lim arctg x =*
Можно было бы записи вести так:
arctg х = arctg (+ оо) — arctg (— оо) = -| — ( — |j =* «.
760
+r
Задача 13,4. Вычислить J sinxdx.
о
+Г +,-
Решение. 1 s'mxdx =—cos* = — limcos#
Ъ о *-+-
о о
Но cos л; при дс->+ оо не стремится ни к какому пределу,
совершая колебания от —1 к +1, а потому интеграл расхо-
расходится. Этот случай отличается от рассмотренного в задаче 13,2
при р < 0 тем, что там имелся бесконечный предел, а здесь его
вовсе нет.
Записи в ^том примере можно было вести и так:
+ » ¦ +»
j sinxdx = —cos* | = — cos(-foo)-fl,
о о
но cos(+oo) числового значения не имеет.
Задача 13,5. Решить вопрос о сходимости интеграла / =
+Г
= \ ё~ах sin bx dx и вычислить его (а>0).
Решение. Вопрос о сходимости этого интеграла решается
+Г
просто. Так как J e~ax dx при а > 0 сходится (см. задачу 13,2),
о
a \e~ax.s\nbx\ <Се~ах, то на основании признака сравнения схо-
сходится и интеграл J \е~ах sin bxdx\. Применяя пункт 4 (стр. 191),
о
заключаем, что сходится и рассматриваемый интеграл. Требуется
не только решить вопрос о сходимости этого интеграла принци-
принципиально, но и вычислить его.
Пользуясь справочником (а этого избегать не следует), или
применяя дважды интегрирование по частям, легко показать, что
для функции е~ах sin bx первообразная функция
р , , a sin bx + b cos bx _ax
Поэтому
/ = _ Hm Qsin b\¦+b™sbxe-"x
так как под знаком предела числитель дроби.— величина огра-
ограниченная, a lime~a* = 0 при а > 0. Величина же есть/7 @).
761
Задача 13,6 (для самостоятельного решения).
Вычислить интеграл J e~ax cos bxdx.
Ответ.
Задача 13,7 (для самостоятельного решения).
+
Вычислить J a
о
Ответ- ш-
Задача 13,8 (для самостоятельного решения).
Вычислить интеграл I т-ггп- '
Указание. Воспользуйтесь справочником для вычисления
неопределенного интеграла \ *. или найдите первообразную
функцию самостоятельно.
Должно получиться
F{x) = Г» in** + *
W L4 1/2 х2 — л:
in +
1/2 х2 — л:/2+1 2/2
+ ^агс1§(,/2-
Ответ.
2/2
Задача 13,9. Вычислить In = J *V* йд; (n > 0 и целое). (Ин-
о
деке п у /„ равен показателю степени буквы дг в подынтеграль-
подынтегральной функции).
Решение. Применим формулу интегрирования по частям
/„ = J х"е~л ах = — х"е~л | + п
о о
и = хп rfu =?' i
= — lim xne~x + nln_v
762
Для вычисления lim^e"* применим правило Лопиталя:
*->+со
1- л -X 1- Хп ,. ПХп~1 ,. П(П~- \)Хп~г
\шх"е х = hm -j- = lim —-j— = hm ——-^ =
,. re! n
— ... = hm -=¦ = 0.
X-. + - ^
Таким образом, In = n/n_i. Применяя последовательно эту
рекуррентную формулу, найдем
In = nln-i = П (П — 1) /П-2 = " (" — 1) {П — 2) /я-з = . . . =
^п{п— 1)(п — 2)(п — 3) ... 2- 1 • /, = я!/,.
Но, как легко видеть, /0 = \ е-л:йд; = —е~х =—limle~*—
Ъ о ^-*+»
— 1] = 1, так как \\те~х = 0.
ДГ-^ + оо
Таким образом,
1 \
Задача 13,10. Доказать, что \ е *'dx сходится.
i
Решение. Этот интеграл имеет важное значение в теории
вероятностей и называется интегралом вероятностей. В данном
случае \ ё~х' dx через элементарные функции не выражается.
Для решения поставленного вопроса используем" признак
сравнения. Для этого рассмотрим выражение хг—2х-\-\. Ясно,
что
х2 — 2х + 1 > 0; — 2*+1> — я2, или — *2 < — 2л;+1. а по-
потому е~хг < е~йх+1, или ё~хх < e~ix • е.
+.-
Из задачи 13,2 следует, что интеграл J е~2ЛГ dx сходится, зна-
о
/»
чит, на основании п. 3 (стр. 191) сходится и интеграл \ e~iX ¦ edx.
_ г °
А так как е х < е 2< ¦ е, то на основании признака сравне-
+с
ния п. 1 (стр. 190) заключаем, что сходится и интеграл J e~x'dx.
о
Заменяя в этом интеграле х на —у, приходим к выводу,
о
что сходится и j е~хгdx (название переменной интегрирования
не изменяет величину определенного интеграла). Из сходимости
763
рассмотренных двух интегралов следует, что сходится также и
интеграл j e~x'dx.
Задача 13,11 (для самостоятельного решения).
I х I х^ dx
Доказать, что интегралы I с»| я ах и \ -а а расходятся.
а а
Указание. Вычислить первообразные функции.
После того как доказана расходимость первого интеграла,
расходимость второго легко показать на основании признака
сравнения.
Задача 13,12 (для самостоятельного решения).
Вычислить интегралы:
TTWdx' 2)
о '
Указание. 1) Интегрировать по частям и принять во вни-
внимание, что —-2(i+x)* =0"
о
2) Положить х = t2. Получится 2 \ .. ,(щ2 и интегрировать
по частям.
%
Ответ. 1) -1; 2) y + f.
Задача 13,13. Доказать, что I arc dx расходится.
Решение. Воспользуемся формулой A3,9). Сравним задан-
ный интеграл с интегралом A3,10) \ ~, в котором подынтег-
подынтегральная функция равна -j.
Полагаем, что в A3,9) <р (х) = arc g*, a f(x) = -p (при х > 1
9 (х) > 0 и /(*)>0 формула A3,9) применима), тогда
arctg х
lim y^- = lim —j— = lim дг^1 • arctg x.
764
Определим теперь р так, чтобы этот предел был конечным
и не равным нулю. Так как lim arctg х = -?¦, то определяемый
предел будет иметь конечное значение, не равное нулю, только
при р— 1=0, т. е. при р — 1 (и этот предел будет равен-|-) ¦
Но при р = 1 функция /(#) = — , а I -^ расходится, а потому
1
расходится и исследуемый интеграл (см. п. 2, стр. 190).
Решим две задачи физики, которые приводят к вычислению
интеграла по бесконечному промежутку.
Задача 13,14. В начале координат О находится масса т, ко-
которая притягивает по закону Ньютона с силой, модуль которой
F = \, материальную точку М единичной массы, находящуюся
на оси Ох на расстоянии х от начала координат.
Вычислить работу А, которую произведет эта сила при пере-
перемещении точки М в бесконечность из положения х — а.
Под перемещением точки в бесконечность следует понимать
удаление ее на такое расстояние, что сила F уже не оказывает
на нее действия.
Решение. Так как сила притяжения направлена к началу
координат, т. е. против движения, то работа будет отрицатель-
отрицательной. На основании формулы A1,5), принимая верхний предел
равным +°°, получаем
т
Задача 13,15. Согласно закону Бно— Савара, модуль силы
F, с которой на магнитный полюс массы / действует конечный
прямолинейный отрезок тока, вычисляется по формуле
J (а2 + s2) 2
где / — сила тока;
а — расстояние от магнитного полюса до прямолинейного от-
отрезка, по которому протекает ток;
ds — элемент тока.
Вычислить модуль силы F в предположении, что проводник
имеет бесконечно большую длину.
765
Решение. Прежде всего сделаем оговорку: проводников бес-
бесконечно большой длины не бывает. Если проводник очень длин-
длинный, то его приближенно можно рассматривать как бесконечно
большой. В этом случае модуль силы F
(a2 + s*J
Легко показать, что подстановка s = a tg t дриведет задачу
к вычислению интеграла
Задача 13,16 (для самостоятельного решения).
Исследовать сходимость интегралов:
dx
Указание. Каждый из интегралов представить в виде
суммы двух интегралов, из которых первый берется по интер-
интервалу @,1), а второй — по интервалу A, +°о).
За интеграл сравнения взять A3,10)х, f(x) = — , а <f(x) —
подынтегральная функция.
з ,
В первом интеграле Ух3 + 5х +3 = х2 1/ 1 -J—^ Н—г» вовт°-
_2_
ром у^х2 + 5 = х3
При отыскании предела A3,9) для первого интеграла ока-
окажется, что он имеет конечное и отличное от нуля значение при
3 2 ,-,
р = -г,-, а для второго интеграла Р = у • Поэтому, используя
интеграл сравнения A3,10) и п. 2 (стр. 191), заключаем, что пер-
первый интеграл сходится, а второй расходится.
1 Поэтому и следует интервал интегрирования @, +оо) представить в виде
суммы двух интервалов: @, 1) и A, +°°).
766
II. ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ
а) Может оказаться, что в интеграле
ь
\f{x)dx - A3,12)
а
функция f (х) неограниченно возрастает, т. е. f(x) -*- ±00 когда
х приближается к одному из пределов интегрирования.
Если это имеет место, когда х ->¦ b, a F (х) — первообразная
ь
для f (х), то )f(x) dx определяется так:
а
Ь Ь~е Ь—г
j / (x) dx = lim j / (х) dx = lim F (x) | =
a гч-fO a e-»-H> a
= \imF(b — ?) — F(a). A3,13)
Аналогично находят этот интеграл и в том случае, когда при
х -*- а подынтегральная функция / (х) -+¦ ± со.
При этом
ь ь ь
J / (х) dx = lim j f (x) dx — Vim F (x)\ =
= f (ft) — lim F (a + e). A3,14)
Если в A3,13) и A3,14) конечные пределы существуют, то
интеграл A3,12) называется сходящимся. Если же эти пределы
бесконечны или вовсе не существуют, то интеграл A3,12) назы-
называется расходящимся.
Таким образом, в обоих рассматриваемых случаях отбрасывают
тот конец отрезка интегрирования, на котором подынтегральная
функция перестает быть, ограниченной, и переходят к пределу.
б) Если подынтегральная функция перестает быть ограничен-
ограниченной внутри отрезка интегрирования, например, при х = с, то эту
точку «вырезают», а интеграл A3,12) определяют в предположении,
что F (х) — первообразная для / (х), так:
Ь с—г Ъ
\f(x) dx = lim \ f (x) dx + lim \ f (x) dx =
= lim F (x) \c~° + lim F (x) \" = lim F (c — t)—F (a) +
E-^-|-0 'a s-t-+O c-H s-^+0
+ F(b) — \\mF(c + t). A3,15)
767
Если пределы в A3,15) существуют и конечны, то интеграл
A3,12) называется сходящимся, в противном случае — расходя-
расходящимся.
Задача 13,17. Вычислить ( -=dx.
J Ух
о
Решение. При х-^-0, т. е. при приближении х к нижнему
пределу, подынтегральная функция тт= неограниченно возрастает.
Здесь х = 0 особая точка. По A3,14) имеем
1 1 1
= 2 • 1 — lim 2/1 = 2.
' X e-*+0j УХ
О t
Интеграл сходящийся.
«¦+0
Задача 13,18. Вычислить I
2
dx
2-х'
о
Решение. Когда х приближается к верхнему пределу
(х ->¦ 2), подынтегральная функция j—^ ->¦ + со. Точка х = 2 —
особая. На основании A3,13) имеем
о о
is- -
= — lim In B— 2 + е) + In 2 = — lim In (+ e) + In 2 = + oo.
E-++0 ЕЧ-+0
Интеграл расходящийся.
Задача 13,19 (для самостоятельного решения).
Вычислить интегралы:
2 1 2
1 \ Г dx Г- dx Г dlC
' J V2=~x' 2) J'7r^; 3) j *ln* *
0 0 1
Особые точки: 1) х = 2; 2) дс = 1; 3) дс = 1.
Ответ. 1) 2^/^; 2) —; 3) интеграл расходится. Первооб-
Первообразная функция In In х.
Задача 13,20 (для самостоятельного решения).
ь ь
Доказать, что интегралы \.—^Цьи \iu * \ъ> г*еа < ^» ap—const,
J\X О)*' J(D — X)V
а а
сходятся при р < 1 и расходятся при р > 1.
768
Задача 13,21. Вычислить /= \\nxdx.
Решение. Здесь особенность при х — 0. Интеграл заменим
по формуле A3,14).
1 1
/ = \ In х dx = lim \ \nxdx = lim [x In x — х] I =
5 =-*+<> \ *->+о |е
= —1 — lim (e In e — е).
+о
Но lim e In е = 0 | применить правило Лопиталя к lim e In e =
е++0 I еч-4-0
1- 1пе\ , .
= lim -j- \, а потому / = —1.
е-+0 1. I
fdx
х У 2х* — х — 1
1
_. , С arcsin х ,
2) I — \ -г, dx.
о
Решение. 1) Когда х приближается к нижнему пределу,
подынтегральная функция . = неограниченно возрастает.
х у 2х2 — х — 1
Особая точка х= 1.
Отыщем первообразную функцию для подынтегральной с по-
помощью подстановки х = —. Окажется, что 1 —-г- , = =
г J х У 2х* — х — 1
+ 2
— arcsin
Зх '
2
= lim Г / dx
l+
= — lim arcsin
. 2 , я
= — arcsin -3- + у •
2) Решите эту задачу самостоятельно.
Ответ, тг-.
Чтобы закончить практическое занятие, рассмотрим пример,
в котором подынтегральная функция неограниченно возрастает
при некотором значении х внутри отрезка интегрирования.
769
27
Г dx
Задача 13,23. Вычислить \з~г--
дух
Решение. Внутри отрезка интегрирования [—8,27] при х->0
подынтегральная функция неограниченно возрастает (х — О —
особая точка). «Вырежем» эту точку, и тогда по A3,15)
°7 ~е 27 2 ~Е 2 27
—8 -8 +?
= -| (lim (—е)з - (-8K") + I- B73" - lira (+ e^) =
2
Задача 13,24. Вычислить /= \-^—-&х.
—2
Решение. Здесь на отрезке интегрирования [—2,2) две
точки: х = —1 и х=-\-1, при приближении к которым подын-
подынтегральная функция неограниченно возрастает. Интеграл надо
расписать так:
— 1—6 1-Е 2
** +lim [-??-. dx.
[
s-H-0 J ~~
-2 —l+e 14-е
Вычислять эти пределы не имеет смысла, так как первообразная
функция In (л:4—1) обращается в бесконечность в особых точках.
Рассматриваемый интеграл расходится.
Задача 13,25 (для самостоятельного решения).
ь
Доказать, что интеграл I , ^ гг расходится, а интеграл
J V-* Я/ \Х О)
а
dx
ЧЕТЫРНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Приближенное вычисление интегралов: формулы прямо-
прямоугольников, трапеций и Симпсона (формула парабол).
Краткие сведения из теории
Известно, что всякая непрерывная функция имеет первооб-
первообразную. Однако это утверждение имеет только теоретическое зна-
значение. Для широкого класса элементарных функций первообраз-
770
ная функция уже не является элементарной и не может быть
определена их конечной комбинацией. К таким функциям отно-
относятся, например,
Sin JC 1 _г 1
В тех случаях, когда первообразная функция для подынте-
подынтегральной, хотя и существует, но не может быть вычислена, поль-
ь
зуются способами приближенного вычисления интеграла I / (х) dx.
а
Программа предусматривает овладение только тремя такими
способами.
1. Способ прямоугольников. Отрезок интегрирования делится
на п равных частей точками деления
х0 = а < хх < хг < ... < xn_i <хп = Ь.
Длина каждой такой части равна h — -~^-.
Эта величина называется шагом интегрирования.
В каждой точке деления вычисляются значения подынтеграль-
подынтегральной функции f(x), т. е. значения
о
Формула для вычисления интеграла J / (*) dx по этому спо-
а
собу называется формулой прямоугольников. Она записывается
так:
ь
&-«,*/.. х , г,..ч , г,..ч ,_ _ +/fe_l)].(H,l)
а
2. Способ трапеций. В этом способе отрезок [а, Ь\ интегри-
интегрирования делится также на п равных частей. С прежними обозна-
обозначениями формула для приближенного вычисления интеграла
выглядит так:
ь
f(x)dx^b~a{f(x0)+f(xn) + 2\
Если Цх = / (*0) + / (хп), а Ц2 = / (*i) + / (*г) + ... + / (*n-i).
то
ь
a
Пх)йхх~^С^ + 2}^. A4,2)
Эта формула называется формулой трапеций.
771
3. Способ парабол (способ Симпсона). Здесь отрезок интегри-
интегрирования делится на четное число равных частей. Обозначим это
число через 2п, точки деления [а, Ь\ — через
Xq = п <С Хх < Х2 < ... <С %2п—2 "^ ^2п—X "^ %2п == ">
а значения подынтегральной функции в этих точках — через
Уо> УU У2 #2га-2> #2п-1> #2/г
Формула для приближенного вычисления определенного ин-
интеграла в этом случае записывается так:
{x)dx^.-^r[{i)
ИЛИ, если Si = У о + Угп\ Из = Ух + Уз + Ун + .-•+ Угп-ъ Из
= Уг + Уа + Ув + •¦• + У2„-г, ТО
A4,3)
Формула A4,3) называется формулой Симпсона. Оценкой по-
погрешности, возникающей при использовании этих формул, мы
заниматься не будем. Отметим, что формула Симпсона дает точ-
точность значительно большую, чем формула A4,2) трапеций при
одном и том же шаге.
Рекомендации. 1) При вычислениях следует пользоваться
не логарифмической линейкой, а арифмометром или электрической
клавишной машиной. Даже в решенных примерах необходимо
выполнять все выкладки, а не пользоваться «готовыми» числами.
2) Следует иметь пятизначные таблицы тригонометрических
функций, натуральных и десятичных логарифмов, значений об-
обратных чисел и их квадратов.
Очень удобными являются «Пятизначные математические таб-
таблицы» Б. И. Сегала и К. А. Семендяева (конечно, можно поль-
пользоваться и другими).
Обозначения. Искомый Интеграл будем обозначать симво-
символом Ik, где индекс k указывает число равных частей, на кото-
которые разделен отрезок интегрирования.
Для того, чтобы оценить точность различных способов, мы
вычислим сначала с помощью указанных способов интегралы,
значения которых известны. Затем уже применим эти способы
к вычислению интегралов, значения которых неизвестны.
Задача 14,1. Вычислить спесеёами прямоугольников, трапеций
1
А Симпсона \ е* dx, вычисления вести с пятью десятичными зна-
знаками. Отрезок интегрирования делить на 8 частей.
772
Решение. Точное значение вычисляемого интеграла с пятью
верными знаками §exdx = exlQ = e—l = 2,71828 — 1 = 1,71828.
о
Теперь посмотрим, что даст каждый из применяемых способов.
Способ прямоугольников (формула A4,1)). Если п = 8, то
-—^ = —^— = 0,125, а точками деления будут:
Xq X Х% Xg X^ X$ Xq Х4
0; 0,125; 0,250; 0,375; 0,500; 0,625; 0,750; 0,875
Значения подынтегральной функции е* в этих точках по таб-
таблицам следующие:
e° =1,00000
/A) е0-125= 1,13315
/ (х2) = е0-250 = 1,284 02
/ (х3) = е0-376 = 1,454 99
/ (ХЛ = е0-500 = 1,648 72
/(АГ»)=е°-в2Б= 1,868 24
/ (xe) = е0-78» = 2,117 00 /«/, = 0,125- 12,90500.
f(x7) = e°-™=: 2,398 88 /,яв 1,61312
S= 12,90500
Полученная точность явно недостаточна.
Применим способ трапеций (формула A4,2)).
Шаг h = — = ~ =0,125.
п о
Множитель -^ перед скобкой в A4,2) равен yto =гб =
- 0,0625.
/ (*e) =/(l)=gi = 2,718 28
2i = 3,718 28
= e0-125 = 1,133 15
= e°-250= 1,284 02
f (x ) = e0-375 =1 454 99
У (xl) = e0'500 = 1,'648 72
/ (x5) = е°-в2Б = 1,86824
/(xe)=e°-750 = 2,117 00
/ (x7) = e0-875 = 2,398 88
2«= 11,90500 2 22 = 23,81000
2i= 3,718 28
2i + 222 = 2 = 27,528 28.
/ « /8 = 0,0625 • 27,528 28
/«1,72052
773
Здесь мы уже значительно ближе подошли к искомому зна-
значению.
Теперь применим способ Симпсона.
Отрезок [0, 1] разделен на 8 частей. Значит, 2п = 8; п = 4.
Вычислим прежде всего множитель перед скобкой в A4,3):
^=L« = L=° 1 = 0,041667.
6n 6-4 24
г/0 = е° = 1,00000
5^ = 3,71828
г/1 = е0125= 1,13315 г/2 = е°-25о = 1,28402
Уа = еОЗ'Б = 1,454 99 yt = е»-ш = 1,648 72
уь = ео,вг5 = j 868 24 Ув = е0-750 = 2,117 00
У7 = «¦¦"' = 2.39888 ?з = 5,049 ?4
S2 = 6,855 26 2 v = 10,099 48
4 ?2 = 27,421 04
/ ж /, = 0,041 667 (Si + 4 S2 + 2 ?з) = 0,041 667 C,718 28 +
+ 27,42104 + 10,09948);
/8^0,041667 -41,23880 = 1,71829.
После запятой здесь уже верны четыре знака, в то время как
формула трапеций давала только один верный знак.
Погрешность по сравнению с точным значением R = 1,71829—
— 1,71828 = 0,000 Q1, что следует признать очень хорошей точ-
точностью.
1
Задача 14,2. Найти число -к, пользуясь интегралом I * а =
о
= arctgx = -т-. (С шестью верными знаками -j = 0,785 3981.
Решение. Отрезок интегрирования разделим на 10 равных
частей точками:
0° 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9.
774
Способ прямоугольников / (х) = 1 . g. Поэтому с помощью
таблиц получаем: /(*0) = 1;
/ (Xl) = / @,1) = j-pLp = щ = 0,990 099
/ (*,) = / @,2) = гт^_5 = _»_ = о,961 538
= / @,3) = ^j-L- = ^д = 0,917 431
= / @,4) = T-pL__ = _J_ = 0,862 069
/ (*.) = / @,5) = j-pL. = _^_5 = 0,800 000
/ (*,) = / @,6) = j-p^j = ^ = 0,735 294
/ (х7) = f @,7) = j^ = A = 0,671 141
/ (*„) = / @,8) = j^, = jL = 0,609 756
/W =/@,9) = r+W' = lil =
S = 7,099814
Применим формулу A4,1). Складывая полученные числа, на-
найдем сумму, стоящую в скобках.
ттт , Ь — а 1 — 0 «,
Шаг А = __ = __. = 0,1.
/ ~ ho = ^ • 7,099 814 = 0,709 98.
(Округление сделано до пяти знаков после запятой).
Сравнивая с точным значением, убеждаемся, что получена
очень незначительная точность.
Теперь применим формулу трапеций A4,2). Для этого надо
довычислить
Множитель перед скобкой в формуле A4,2) равен
^ - 1=-° - I - 0 05
Чп ~ 2 • 10 ~ 20 ~ U'UO-
/(*о) = 1,000 000
f(xlo) = 0,500000
Si= 1,500000
(x.)= 7,099 814
2Ц2 = 14,199 628; ?i + 2^8 = 15,699628
/ « /10 = 0,05 (Si + 2 ?2) = 0,784 981.
775
Если округлить это до трех десятичных знаков после запя-
запятой, то получится 0,785, т. е. три верных знака.
Применим формулу Симпсона A4,3).
Теперь следует считать число частей деления равным 2п =
= 10; п = 5, а множитель перед скобкой в A4,3) равен -g— =
_i — о 1
~ 6 • 5 ~ 30 • . .
уо = 1,000000
у10== 0,500000
^ = 1,500000
у% = 0,961 538 ^ = 0,990099
г/4 = 0,862069 г/3 = 0,917 431
у, = 0,735 294 ул = 0,800000
ув = 0,609756 у7 = 0,671 141 ___
?3 = 3,168657 j/9 = 0,552 486
2^3 = 6,337314 ?2 = 3,931 157
4 Ц2= 15,724 628
/«/„ = 1 (S, + 4^2 + 2Ц3) = ^ A,500000 + 15,724 628 +
+ 6,337 314) = gg • 23,561 942 = 0,785 398,
т. е. получено значение числа ~ с шестью (!) верными знаками.
Задача 14,3. Вычислить по способу трапеций и способу Симп-
Т
сона \ sin х dx.
Ответ. По способу трапеций / = 0,997 94, по способу Симп-
Симпсона /= 1,00006.
Задача 14,4 (для самостоятельного решения).
Вычислить по способам трапеций и Симпсона интегралы:
2 0,8 4 1,7
1) f?; 2) [cosxdx; 3) (Vrfx; 4) Г ~.
io о од
Отрезок интегрирования делить в первых двух интегралах на
10 равных частей, в последних — на 8.
Ответ. 1) Точное значение интеграла 0,69314718...
Приближенное: по способу трапеций 0,69377,
по способу Симпсона 0,693 152,
776 ~ "
2) Точное значение интеграла 0,717 36.
Приближенное: по способу трапеций 0,716 76,
по способу Симпсона 0,71736.
3) Точное значение интеграла 53,59815.
Приближенное: по способу трапеций 54,710 15,
погрешность равна — 1,112 00,
по способу Симпсона 53,616 22,
погрешность равна — 0,01807, что
указывает на значительно более высокую точность.
4) Точное значение интеграла 1,975 12.
Приближенное: по способу трапеций 2,020 18,
погрешность равна — 0,045,
по способу Симпсона 1,98558,
погрешность равна — 0,010.
Задача 14,5 (для самостоятельного решения).
Вычислить по формулам трапеций и Симпсона I arc g x dx. От-
0
резок интегрирования разделить на 10 равных частей.
Указание, при х = 0 arc g* находится как lim arc g* = 1.
Ответ. По способу трапеций 0,915728,
по способу Симпсона 0,915965 (все знаки верны).
1
Задача 14,6. Вычислить по формуле Симпсона j e~x' dx.
Ответ. 0,746825 (все шесть знаков верны).
ПЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Приложения определенного интеграла к геометрии. Опре-
Определение площадей плоских фнгур.
Площадь в прямоугольных координатах
Площадь плоской фигуры, ограниченной непрерывной кривой,
уравнение которой в прямоугольных координатах имеет вид у =
= / (х), осью Ох и двумя прямыми х — а и х = b (a<b), нахо-
находится по формуле
ь *
^ \ A5,1)
777
Отрезок [а, Ь] следует разделить на части, в каждой из кото-
которых функция f (х) сохраняет один и тот же знак. При этом не-
необходимо соблюдать такое правило знаков: площади, находящиеся
над осью Ох, берутся со знаком плюс, а площади, расположен-
расположенные под осью Ох, со знаком минус.
Если площадь ограничена двумя непрерывными кривыми, урав-
уравнения которых в- прямоугольных координатах у = /\ (х) и у =
— /2(х), причем всюду на отрезке [a, b] f2(x)> fi(x)> и двумя
прямыми х = а и х = Ь, то площадь определяется по формуле
ъ
x)-f1(x)]dx. A5,2)
И в этом случае надо соблюдать указанное выше правило знаков.
Интегрирование четных и нечетных функций в пределах,
симметричных относительно начала координат
Если функция / (х) — четная, то
dx. A5,3)
Если же функция f(x) — нечетная, то
A5,4)
а
U
а
J
J
—а
Эти формулы часто оказываются полезными при вычислении
определенных интегралов вообще и, в частности, при вычислении
площадей. Формула A5,3) приме-
применяется в том случае, когда рас-
рассматриваемая фигура симметрична
относительно оси Оу.
2я Задача 15,1. Найти площадь,
~х ограниченную синусоидой у = si n x
на отрезке [0, л] и осью Ох.
К задаче 15,1 Решение. На отрезке [0, ъ\
функция sin л: сохраняет знак,
а потому по формуле A5,1), полагая в ней / (я) = sin х, сразу
находим
п
S = j sin х dx = — cos x ™ = — (cos v — cos 0) =
0
= — (—1 — 1) = 2 кв. ед.
В частности, если единицей масштаба является сантиметр,
то S = 2 см*.
Если требовалось бы найти площадь, ограниченную той же
синусоидой и осью Ох на отрезке [0, 2я], то, применив формулу
778
A5,1) без учета правила знаков, мы получили бы абсурдный ре-
результат: оказалось бы, что площадь равна нулю. Действительно,
2*
s'mxdx ='— cosx
2х
= — (cos 2я — cos 0) = — A — 1) = 0.
Это получилось потому, что на отрезке [0, 2к] функция s'mx ме-
меняет знак. Следовало этот отрезок разделить на два: [0,«] и [«, 2ic],
в каждом из которых функция сохраняет знак (в первом — плюс,
во втором — минус A5,1)).
По правилу знаков, на отрезке [я, 2я] площадь надо было
брать со знаком минус и тогда
2
S — Si — S2 = J sin x dx — J sin x dx = — cos x — (— cos x)
О
= — (COS it — COS 0) + (COS 2ic — COS ic) = — (—1 — 1) + A — (—1)) =
= 2 + 2 = 4 кв. ед.
При вычислении площадей строго
.соблюдайте правило знаков и, прежде
чем интегрировать, убедитесь, что на
отрезке интегрирования функция сохра-
сохраняет знак.
'Задача 15,2. Вычислить площадь,
ограниченную прямой х = 4, кривой
у = Зх2 — 6х и осью Ох на отрезке
[0,4].
Решение. Прежде всего построй-
постройте эскиз графика функции. Кривая —
парабола. Площадь ОАВ расположена
под осью, брать ее надо со знаком
минус, а площадь BCD — над осью Ох,
и взять ее следует со знаком плюс.
Отрезок интегрирования [0,4] должен
быть разделен на два: [0,2] и [2,4].
Поэтому, полагая в A5,1) f(x) = 3x2 —
— 6х, найдем
2
К задаче 15,2
S = —Si + S2 = — J (Зх2 — 6*) dx +¦ J (Зх2 — 6*) dx =
О 2
+ F4 — 48 - 8 + 12) = 4 + 20 = 24 кв. ед.
Если за единицу длины взять, например, дециметр, то площадь
равна 24 дм2.
Если бы правило знаков не было учтено, отрет был бы неверен.
779
Задача 15,3 (для самостоятельного решения).
Найти площадь, ограниченную осью Ох и параболами:
1) у = 2л:2 + Ъх — 9; 2) у = х* + 6х + 5.
Ответ. 1) ЗО-g-KB. ед., 2) 10у кв. ед.
Задача 15,4 (для самостоятельного решения).
Найти площади, ограниченные осью Ох и линиями:
1) у = 2х\ х = 1 и х = 2; 2) у = ~х3 на отрезке [0,2],*=2.
Ответ. 1) 4~ кв. ед.; 2) 1 кв. ед.
Задача 15,5. Найти площадь, ограниченную осью Ох и кри-
кривой у = х3 — 6а:2 + 11л: — 6.
х
К задаче 15,5
К задаче 15,6
Решение. Найдем точки пересечения кривой с осью Ох.
Для этого решим уравнение лг3 — 6л:3 + 11* — 6 = 0. Легко заме-
заметить, что его корнем является хх — 1. После деления левой части
уравнения на х—1, получим л:2 ^5*+ 6, а приравняв это выра-
выражение нулю, найдем: х2 — 2; х3 = 3. Из эскиза графика видно,
что на отрезке [2,3] площадь находится под осью Ох, а потому
2
S = St — S2 = jV3 — 6*2+ 11* — 6)dx —
11л: — %)dx = -i-кв. ед.
Задача 15,6. Доказать, что площадь параболического сегмента,
отсеченного от параболы хордой, перпендикулярной ее оси, равна
-я- произведения высоты h сегмента на его основание Ь.
Решение. Пусть середина указанной хорды — начало коор-
координат, ось Ох направлена по хорде направо, а осъ'Оу вверх по
оси симметрии параболы.
780
Уравнение параболы будет иметь вид у = — ах* + с (а > 0).
Вершина параболы находится в точке @, К), где h — высота сег-
сегмента. Ось Ох парабола пересекает в точках I — у, Oj и (у,0|.
Зная координаты этих точек, найдем значения коэффициентов
а и с в уравнении параболы. Подставляя координаты вершины
в уравнение у = —ах* -\- с, получим h = с. Подставляя же коор-
()
динаты -н-,
имеем:
= — а
—
аЪг
4Л
и уравнение параболы с найденными а и с примет вид у —
= —-j^x2-\-h. Искомую площадь определим по формуле A5,1),
полагая в ней f (х) = —-r^x2-\-h, а так как функция f (x) — четная, то
ь
т
= -jhb кв. ед.
Задача 15,7 (для самостоятельного решения).
Вычислить площадь, ограниченную эллипсом.
Указание. Из уравнения эллипса — -\- ¦— — 1 найти у.
Четверть площади эллипса равна
а
о
а2 — х2 dx. Применить
подстановку лг = a sin z. Новые пре-
пределы интегрирования: 0 и ~ . Под
интегралом окажется cos2 г, который
14- cos 2z
надо заменить на —[—~ .
Ответ. Tzab кв. ед. (Этот ответ
полезно запомнить). При а = b имеем
окружность. Получается, что пло-
площадь круга равна ад2, как это из-
известно из геометрии.
Задача А 5,8. Определить площадь,
ограниченную параболами у2 = 2рх
И*Л Onfi
х — гРУ-
Решение. Найдем прежде всего координаты точек пересе-
пересечения парабол, чтобы определить отрезок интегрирования. Из пер-
781
К задаче 15,8
вого уравнения у = У2рх (у > 0, так как точка пересечения —
X2 r-i
в первой четверти), из второго у = -j- ¦ Приравнивая эти зна-
значения, получим
или
Отсюда ** — 8р3х = 0; х (xs - 8р3) = 0; х(х- 2р) (х2 -f 2px + 4р2) =
= 0, т. е. х = 0; х — 2р = 0; х2 + 2рх + 4р2 = 0. Корни первых
двух уравнений: хх = 0; х2 = 2р. Последнее уравнение имеет
комплексные корни. Значит, параболы пересекаются в начале
координат (х = 0) ив точке А с абсциссой х = 2р. Искомую
площадь найдем по формуле A5,2). Значения у из каждого урав-
уравнения были найдены выше. Принимая в A5,2) /2 (х) = ]/2рлс,
хг
получим
-^г U*= У2р^ ^-
2р
= — р^ кв. ед.
Задача 15,9. Вычислить площадь, ограниченную осью Ох
и линиями у = (х + 2J и # =
Решение. Первая линия —
парабола, вторая — прямая. Отре-
Отрезок интегрирования [—2,4] следует
разбить на два: [—2,0] и [0,4], так
как на этих отрезках линии, огра-
ограничивающие площадь, имеют раз-
различные уравнения. На отрезке
[—2,0] надо у взять из уравнения
параболы, а на отрезке [0,4] — из
К задаче 15,9 уравнения прямой. Поэтому
По)
—2
—2
Задача 15,10 (для самостоятельного решения).
Найти площадь, ограниченную осью Ох и линиями у = (х — 4)а
и у — 16 — х2 (сделать чертеж).
Ответ. 64 кв. ед.
782
Задача 15, И (для самостоятельного решения).
Найти площадь, ограниченную линиями ху = 3 и л: -(- f/ = 4.
Сделать чертеж.
Указание. Разрешить оба уравнения относительно у. Найти
абсциссы точек пересечения линий. Окажется, что х = 1; х = 3.
Применить формулу A5,2), в которой /2(лг) =4 — лг; fi(x)=~.
Ответ. D — In 27) кв. ед.
Задача 15,12 (для самостоятельного решения).
Найти площадь, ограниченную гиперболой ху = а2 и прямыми
х — 1; х = 5; у = 0.
Ответ: а21п5 кв. ед.
О / 5 х
К задаче 15,12
о а х
К задаче 15,13
Задача 15,13. Найти площадь, ограниченную цепной линией,
определяемой уравнением у = ~(е " -\- е а), осями координат и
прямой х = а (а > 0).
Решение. По формуле A5,1)
5 = -=-
= ~ (е — е) = а2 sh 1 кв. ед.
Если заметить, что 4-(еа +е a) = ach—, то задача реша-
ется проще
а
= a[ ch- dx = a2 sh -
J а а
= а2 sh 1 кв. ед.
783
Задача 15,14. Найти площадь, заключенную между кривыми
8 хг
Указание. Первая кривая называется локоном Аньези,
вторая — парабола. Чтобы
определить отрезок интегри-
интегрирования, найдем абсциссы то-
точек пересечения этих кривых.
Ответ. 2
(-*)
кв. ед.
Задача 15,15. Найти пло-
площадь фигуры, ограниченную
К задаче 15,14 * ЛЙНЙЯМЙ У = F ' Х=а (а > °>
и осью абсцисс.
Решение. В формуле A5,1) верхний предел интегрирования
равен + °°. а потому
+
J
= [~dx = —~
J & х
- = -кв. ед.
а а
Интеграл
несобственный
Таким образом, несмотря
на то, что площадь прости-
простирается в бесконечность, в
данном случае ей можно при-
приписать определенное число-
числовое значение.
О а
К задаче 15,15
Задача 15,16. Та же задача для равносторонней гиперболы
1
от-
от— dx = In x
= lim In * — In a — -f- oo,
I Интеграл I
несобственный
т. е. площадь бесконечно велика и никакого числового значения
ей приписать нельзя.
784
Задача 15,17 (для самостоятельного решения).
Найти площадь, ограниченную осью Ох и локоном Аньези,
у
определяемым уравнением у = ; . $.
+» +»
г* 1 Г 1
Указание. S = \ jj-jidx = 2 j j-p
—» о
= 2 lim arctg x.
Ответ. S = ic кв. ед.
= 2arctg
К задаче 15,17
Задача 15,18 (для самостоятельного решения).
Найти площадь, ограниченную линиями у ~ -
осью Ох.
Ответ. Tg кв. ед.
Задача 15,19 (для самостоятельного решения).
= 4 и
X = 1 И
Найти площадь, ограниченную линиями у = — ,
осью Ох.
Ответ. + °°- "
Задача 15,20 (для самостоятельного решения).
Найти площадь, ограниченную кривой у =-?=., осью Оу и
Vх
прямой х — У.
9
Указание. S= \-^dx. При приближении к нижнему пределу
^ oVx
(х -*- + 0) подынтегральная функция неограниченно возрастает,
а потому этот интеграл — несобственный:
9 9
[4= dx = lim fХ^йх = lim2Vx 9= 2 lim (}/9 — l^ej = 6 кв. ед.
0 s
26 И. А. Каплан
785
Вычисление площади, ограниченной кривой, заданной
полярным уравнением и двумя радиусами-векторами
Если кривая, ограничивающая площадь, определяется урав-
уравнением
A5,5)
то площадь, ограниченная ею, вычисляется по формуле
s = —
где а и C (a < C) — пределы изменения полярного угла.
Задача 15,21. Найти площадь, ограниченную кардиоидой
г = 2а A — costp).
Кривая относится к классу эпициклоид и яв-
является траекторией точки, лежащей на
окружности круга радиуса а, который
без скольжения катится по внешней
части окружности круга такого же ра-
радиуса (интересующихся выводом урав-
уравнения эпициклоид, гипоциклоид и их
частных случаев отсылаем к книге
акад. В. И. Смирнова «Курс высшей
математики», том I).
На всей кардиоиде полярный угол <р
изменяется от 0 до 2-к, а потому, учи-
К задаче 15,21 тывая, что г2 = 4a2(I — costpJ:
— cos<pJdcp =
= 2а2 ( A — 2 cos <р + cos2?) d<p = 2а2 I A— 2 cos <р + -
о о
= 2а2 (ср — 2 sin <f + -j <р + -г sin 2<p
= бтга2 кв. ед.,
т. е. площадь, ограниченная кардиоидой, равна ушестеренной
площади круга, который ее производит.
Задача 15,22. Определить площадь, ограниченную спиралью
Архимеда г = а<р и двумя радиусами-векторами, которые соответ-
соответствуют полярным углам <pi и ср2 (срх < <р2).
Решение. Спираль Архимеда — траектория точки, равно-
равномерно движущейся по прямой, которая равномерно вращается
вокруг заданной точки (полюса).
786
По формуле A5,5) имеем г2 = a2f2;
<р2 аг (ср" _ cp8)
¦¦Pi
Из (Л) следует, что площадь, ограниченная полярной осью
и первым витком спирали Архимеда (<рЛ = 0; <р2 = 2it):
кв- ед-
Площадь, ограниченная полярной
осью и вторым витком (ср! = 2тг; <р2 =
= 4тг), на основании (А) равна
S2=| F4*3-8и3) =
6
К задаче 15,22
Разность этих площадей, т. е.
площадь, заключенная между вторым и первым витками спирали
Архимеда:
QQ Л
S2 - Si = f u3a2 - -i ^a2 = 8тг3а2.
Можно показать, что и вообще площадь, заключенная между
двумя последовательными витками спирали Архимеда равна 8тг3а2.
Задача 15,23. Определить площадь, ограниченную лемнискатой
Бернулли, определяемой уравне-
уравнением г2 = 2a2 cos 2<p.
Решение. Лемниската—это
геометрическое место точек, про-
изведение расстояний каждой из
которых от двух фиксированных
точек (фокусов) — постоянная ве-
величина. Ее уравнение в прямо-
прямоугольных координатах
2a2(*2 — у2) = 0.
У
>
\
z
К задаче 15,23
(^2 + f/2J"
Проследим, как изменяется угол f, когда радиус-вектор точки
на лемнискате описывает четверть искомой площади, лежащей
в первой четверти.
При <р = 0 г = а\^2. Определим, чему равен полярный угол <р,
когда радиус-вектор станет равным нулю. Подставляя г = 0 в
уравнение лемнискаты, получим 0 = 2a2cos2<p, откуда cos2<p = 0;
2tp = у ; <р = -т • Таким образом, на одной четверти площади
26* 787
полярный угол <р изменяется в пределах от 0 до —. Поэтому по
формуле A5,5) четверть искомой площади
4
1 -If
4 Ч
a вся площадь
S = 2a2 =
кв. ед.,
т. е. площадь, ограниченная лемнискатой, равна площади квад-
квадрата со стороной а\^2.
v> Задача 15,24 (для самостоятельного решения).
Вычислить площадь, ограниченную петлей декартова листа,
определяемого уравнением
0. A5,6)
Указание. 1) Перейти к поляр-
полярным координатам, положив х — г cos <p,
t/ = rsincp.
Получится уравнение
г =
3a sin у cos у
sin3 «р -|- cos3 «р'
2) Учесть, что так как в уравнение
К задаче 15,24 A5,6) координаты х и у входят симме-
симметрично, т. е. замена х на у, а у на х не
изменяет уравнения, то кривая симметрична относительно биссек-
биссектрисы первого координатного угла у = х. Поэтому искомую площадь
можно рассматривать как удвоенную площадь О AN. Когда радиус-
вектор ОА описывает площадь OAN, угол у изменяется от 0 до -^-.
3) Половина площади
S_ = l G За sin у cos И2 9_ С
2 2 J \sin3y + cos»y/ a? ~~ 2 п J
=!«¦•!
sin2 у cos2 у
*
sin6 у + 2 sin3 у cos3 у -f- cose у
Числитель и знаменатель дроби I
умножить на cos2 у
sin2 у cos4
cos2 у (sin6 у -j- 2 sin3 y cos3 у -)- cose у) ¦
788
Числитель и знаменатель дроби разделить на cos6 <р, получится
It Я
Т f 9 Т tg*
Т = ~2а J cos2 ср (tg6 9 + 2 tg3 9 +~l) "? = " ° J cosa ? (tg3
Подстановка tg <p = г; ^- = &z. Новые пределы интегриро-
интегрирования 0 и /.
S 9 Г
~2~ = ?fl J
l
о
Ответ. S = -2-a2 кв. ед.
Задача 15,25. Вычислить площадь одного лепестка розы, опре-
определяемой уравнением
A5,7)
Решение. Кривые, определяемые уравнением A5,7), а также,
уравнением r = acosfecp, где а и k — постоянные величины, назы-
К задаче 15,25 а К задаче 15,25 6
ваются розами. Если k — четное число, то кривая имеет 2k ле-
лепестков, если же k — нечетное число, то кривая имеет k ле-
лепестков.
Например, кривая, определяемая уравнением г = asin2<p,
имеет 4 лепестка, а кривая г = a sin 5<p — 5 лепестков.
Чтобы найти площадь одного лепестка, определим, как изме-
изменяется полярный угол <р, когда радиус-вектор описывает площадь
одного лепестка. Положим в A5,7) г = 0 и решим уравнение
O = asin&p. Из него следует, что sin/2cp = 0, а отсюда Щ — т.
При п = 0 <р = 0, при п = 1 имеем k<f = тс, а ср = у . Таким обра-
789
зом, угол ф изменяется от 0 до -^-, а площадь одного лепестка по
формуле A5,5) равна
Т
1 9. Г 1
о
,? ?t К тг/v Ч/v
а) Для четырехлепестковой розы г = а sin 2<р площадь одного
лепестка
о теа2 __ яа2
б) Площадь одного лепестка трехлепестковои розы г = a sin 3^>
Площадь плоской фигуры, ограниченной кривой,
уравнения которой заданы в параметрической форме
Если кривая задана параметрическими уравнениями
?
= 4» @
A5,8)
и в точках А и В кривой tx и t2 — значения параметра, то пло-
площадь вычисляется по формуле
1 @ dt. A5,9)
Задача 15,26. Найти пло-
¦Z щаДь, ограниченную осью Ох
и одной «аркой» циклоиды
К задаче 15,26 Ц^ ~ ^ ^ У = ° A ~
Решение. Когда круг, производящий циклоиду, сделает
один полный оборот, абсцисса той точки окружности круга, кото-
которая в начале движения совпадала с началом координат, станет
равной 2ш (а —радиус окружности).
В формуле A5,9) надо взять ^ (t) == у — a (I—cos^); <p' (t)
находят из уравнения у (t) = х = a (t — sin /). Получим ср' (t) •=
790
Пределы интегрирования будут равны 0 и 2it, так как пара-
параметр t при одном полном обороте производящего круга пробегает
отрезок [0,21т]. Поэтому
2it 2it
S= §a(l — cost)a(l — cost)dt = a2§ (l — costJdt =
о
2it
2it
= a2 J A — 2 cos t + cos2t) it = a2 J A — 2 cos / +
о о
/ 1 1 \ I21C
= a2I f — 2 sin t + -j f + -j sin 2Л = a2 B« + «) = Зто2 кв. ед.
Таким образом, искомая площадь в три раза больше площади
катящегося круга.
Задача 15,27 (для самостоятельного решения).
Найти площадь, ограниченную астроидой, определяемой урав-
уравнением: t .
A.5,10)
Параметр t — угол, на который из начального положения повер-
повернулась подвижная окружность. За один полный оборот подвижной
окружности (t изменяется от 0 до 2тс) У
описывается четверть кривой. При
вычислении интеграла
sin4 j cos2 -
подынтегральную функцию предста-
представить в виде
t ( I t /\2
sin4-^ cos2-^-= I sin-^ cos-^-1 x
D
К задаче 15,27
X sin21 = I [sin2 -i - sin2 i- cos^] •
Ответ. S = -д-kR2 кв. ед.
о
Задача 15,28. Найти площадь, заключенную между осью Ох
и верзиеройг, определяемой уравнениями
У =
а»
а2 + Р-
1 Кривая, называемая верзиерой, получается так: берется круг диаметром а
и отрезок BDM такой, что OB : BD = ОС : ВМ. Геометрическое место точек М
и представляет верзиеру (см. А. А. Савёлов «Плоские кривые»).
791
Решение. Кривая симметрична относительно оси Оу. На
всей площади абсцисса точки кривой изменяется от — оо до +оо,
а так как х = t (первое уравнение), то параметр t изменяется
в тех же пределах. По формуле A5,9)
= a2 [arctg (+00) — arctg (—00)] = а2 [f- — (— -)] = ад2 кв. ед.
К задаче 15,28
Эта кривая называется также локоном Аньези.
ШЕСТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Приложения определенного интеграла к геометрии (про-
(продолжение): длина дуги плоской кривой, объем тела вращения, поверхность
тела вращения.
Краткие сведения из теории
1. Длина дуги плоской кривой, определяемой в прямоугольных
координатах уравнением у = / (х), Находится по формуле
VTT!/2dx, A6,1)
где а и Ь — соответственно абсциссы начала и конца дуги.
2. Если кривая задана параметрически уравнениями
причем а < t < р, а функции ср (t) и .<]) (t) имеют непрерывные
производные, то длина дуги
A6,2)
792
3. Если кривая задана уравнением в полярных координатах
' = /(?)>
а полярный угол ср на дуге изменяется от а до [3, то длина дуги
вычисляется по формуле
C
§ + r'2d?. A6,3)
Задача 16,1. Найти длину окружности.
Решение. Возьмем окружность радиуса R с центром в на-
начале координат. Ее уравнение х2 + г/2 = R2. Чтобы применить
формулу A6,1), найдем из этого уравнения у. Окажется, что
у = ±VR2 — я2, причем знак плюс отвечает верхней полуок-
полуокружности, а минус — нижней.
Найдем длину четверти окружности, лежащей в первой чет-
четверти. Возьмем поэтому перед корнем знак плюс. Под интегралом
в формуле A6,1) стоит VI -Ьу'2. Вычислим это выражение
0\ ,,'г х* ¦
2) У =^гр-
3) 1 + У' = 1 + R2_X2 = R2_X2 I
Подставим его под знак интеграла в A6,1) и учтем, что абс-
абсцисса х точки на окружности, находящейся в первом квадранте,
изменяется от 0 до R, а потому четверть длины окружности
R
т — \ г dx = R arcsin -^
4 }yR2_x2 R
R I i
arcsin
arcsin
" — ОI =
о
= R arcsin 1 = R -^ .
Поэтому
В процессе решения задачи становится ясно, что не следует
сразу подставлять у' под знак интеграла в формулу A6,1), а надо
сначала вычислить V1 + у' , определить, как изменяется абс-
абсцисса х точки на дуге, длина которой вычисляется, и после этого
применить формулу A6,1). Это замечание относится и к форму-
формулам A6,2) и A6,3).
. 793
Эту же задачу решим для случая, когда окружность задана
параметрическими уравнениями:
х — R cos / \
у = R sin t)'
Чтобы применить формулу A6,2), вычислим:
х' = — R sin t\ у' = R cos /;
л;'2 = Я2 sin21\ у'2 = R2 cos21;
х'* + у'2 = Я2 sin21 + Я2 cos2 * = Я2 (sin2 / 4- cos21) = Я2;
/*'2 4- у'2 = VW2 = Я.
На всей окружности параметр f (его геометрическое значе-
значение— центральный угол, опирающийся на дугу, начало которой
лежит на положительной части оси Ох) изменяется от 0 до 2it,
а потому по формуле A6,2) длина окружности
L = f Rdt = Rt 2* = 2«R.
о
Еще более простым будет решение этой задачи, если урав-
уравнение окружности задать в полярных координатах. Если центр
окружности находится в начале координат, то она определяется
полярным уравнением г — R
(полярная ось совпадает с положительной частью оси Ох, а поляр-
полярный угол 9. когда точка на окружности пробегает ее всю, из-
изменяется от 0 до 2тс). Поэтому по формуле A6,3), так как г —
величина постоянная, равная радиусу окружности, а г' = 0, по-
получаем, что у г2 4- гл = j^R2 = R и
L= \ Rd<? = R<?\ = 2kR.
о о
Задача 16,2 (для самостоятельного решения).
JL. х
Найти длину цепной линии у = у(еа -\-е а) между точками
с абсциссами 0 и х (х > 0) (см. чертеж к задаче 15,13).
Указание. Применить формулу (L6,1);
dx = $(e«—e <•).
Задача 16,3 (для самостоятельного решения).
Найти длину дуги параболы у = ах2 (а > 0) от вершины до
произвольной точки с абсциссой х.
У казан ие. j/l + r/'2=yA4a2x2+l (применить формулу A6,1))
Ответ. L = j/4а2х2 + I + ~\п {2ах + у/ 4а2*2 + 1).
Задача 16,4 (для самостоятельного решения).
Вычислить всю длину астроиды, определяемой уравнением
2 2 2
х3 -\-у3 = a3
(см. чертеж к задаче 15,27).
IS. 2.
Указание. у3 — а3—х3 ; чтобы найти у, возвести обе
3 - --
части этого равенства в степень -у. Получится у = (а3 —х3)* .
— = ( а~х~ ~ь dx;L — 6a.
Ответ.
Задача 16,5 (для самостоятель-
самостоятельного решения).
Найти длину дуги кривой у — In x
от точки с абсциссой 1 до точки с
абсциссой т/З.
VT , О
Указание. ^- = 1 -——— dx.
Удобна подстановка х = tg z, которая
приведет к вычислению интеграла
К задаче 16,5
J sin г cos2 z
Г sin2 г 4- cos2 г , ( , ,
= ..„Lv.!, <fe= secz + ln
sin г cos2 г
Ответ. 2 — /2 — -g- In 3 — In tg -jj- = 0,920.
Задача 16,6. Вычислить длину дуги линии у — ех от точки
л: = 0 до точки х.
х
Указание. ?=J V^ +
о
Подстановка: 1 + е2* = г2.
Ответ. TT^ i
dx.
795
Задача 16,7 (для самостоятельного решения).
Найти длину одной «арки» циклоиды:
х = a (t — sin t)
у = a (I — cos^)
Указание. Применить формулу A6,2). Пределами интегри-
интегрирования по t будут 0 и 2и (см. задачу 15,26).
Ответ. L = 8а, т. е) длина одной «арки» циклоиды равна
увосьмеренному радиусу производящего ее круга.
Задача 16,8 (для самостоятельного решения).
Определить длину всей кривой Штейнера1.
О
О
Указание.
К задаче 16,8
Ответ. L = 16R.
Задача 16,9 (для самостоятельного решения).
Найти длину всей астроиды:
х = R cos3 -j
t
у = /?j
(см. чертеж к задаче 15,27).
Указание. (См. также указание к задаче 15,27).
Воспользоваться формулой A6,2):
,2 , ,2 ЗД2 t / Л/г~, J2 3R . t
х +у =_sin2Tcos2T; Vx' +y' = -^sinTc
16
4
2it
Ответ. L = 6R.
L 3R Г . t t
-r- = -p\ Sin-rCOS-r
4 4 J 4 4
1 Кривой Штейнера называется гипоциклоида, которая получается в том
случае, когда радиус производящего круга в три раза меньше радиуса непо-
неподвижного круга.
796
Задача 16,10 (для самостоятельного решения).
Определить длину одной ветви эпициклоиды, определяемой
уравнениями:
х = (R + mR) cos mt — mR cos (t + mt)
y=(R+ mR) sin mt — mi? sin (t + mt)
Ответ. 8Rm(\ + m).
Задача 16,11 (для самостоятельного решения).
Найти длину дуги кардиоиды, определяемой уравнениями:
х = 2R cos t — R cos 2t
(см. чертеж к задаче 15,21).
(Эти уравнения получаются из уравнений предыдущей задачи
при т = 1).
Ответ. L(/1) = 4#Jsin-j^ = 16flsin2-^. При ^ = 2« полу-
о
чим, что длина всей кардиоиды L = 16#.
Задача 16,12. Решить предыдущую задачу в случае, когда
кардиоида задана полярным уравнением r = 2a(l — cos 9)
(см. чертеж к задаче 15,21).
Решение. Надо воспользоваться формулой A6,3):
г' = 2а sin f, r' — 4а2 sin2 f;
/-2 _|_ г'2 = 4а2 A — cos <?J + 4а2 sin2 <p =
= 4а2 A — 2 cos 9 + cos2 <p + sin2 cp) = 4а2 B — 2 cos <p) =
= 8a2 A — cos 9) = 16a2 sin2 \;
Когда точка на кардиоиде пробегает всю кривую, ее поляр-
полярный угол изменяется от 0 до 2it.
Поэтому по формуле A6,3)
2*
L= I 4asin-|dcp = — 4a • 2cos-| =
= —8a (cos те — cos 0) = —8a (—2) = 16a.
Мы получили тот же ответ, что и в предыдущей задаче (R = а).
1 Эпициклоидой называется кривая, являющаяся траекторией точки, неиз-
меиио связанной с окружностью, которая без скольжения катится по внешней
стороне неподвижной окружности радиуса R, а т — отношение радиуса по-
подвижной окружности к радиусу неподвижной.
797
Задача 16,13 (для самостоятельного решения).
Найти длину дуги спирали Архимеда г = щ от начала коор-
координат до произвольной точки Р (г, <р) (см. чертеж к задаче
15,22).
Указание. Чтобы воспользоваться формулой A6,3), надо
вычислить
г'
Ответ. Ь = -| [<?
-\- г' . Из г = аср следует, что г' = а;
г2 + г'2 = а2ср2 + а2 = а2 A -Ь <р2);
^ = а j/I +?2d<? (см. формулу A6,3)).
о
+?2 + In K
+
?")].
При <? = 2п: получим длину пер-
первого витка спирали Архимеда.
Задача 16,14 (для самостоятель-
самостоятельного решения).
Найти длину логарифмической
спирали r = af (а > 0, а Ф 1) между
точками (/"о, ?о) и (гь cpi).
Указание. Воспользоваться
формулой A6,3):
К задаче 16,14
г2 + г'2 = а2? + а2? In2 а = а2? A + In2 а);
Ответ. L =
ln2a -
или
Во второй части этой книги (задача 36,15) была определена
длина полярной касательной логарифмической спирали Т =
Запишем полученный в этой задаче ответ в виде
Таким образом, длина дуги логарифмической спирали равна
разности длин полярных касательных, проведенных в конце и на-
начале этой дуги.
798
Задача 16,15 (для самостоятельного решения).
Определить длину дуги гиперболической спирали г — ~ от
точки (гь <pi) ДО точки (г2, ф2)-
Указание, h = а\ -—ii dcp. Подынтегральную функцию
представить в виде ¦
К вычислению \ -
iJtp
У 1 + <Ра
количества:
dcp применить подстановку обратного
: ф = —, а ( - у — табличный.
а.
К задаче 16,15
Ответ
.«.-.['
Задача 16,16. Найти длину дуги циссоиды Диоклеса
COS<p
от точки (rv cpi) ДО точки (г2, ф2) («pi < ф2).
Решение. Кривая задана полярным уравнением. Чтобы при-
применить формулу A6,3), вычислим Vг2 + /"'*:
, _ „ 2 sin <p cos2 у + sin3 У
г ~м cos2 tp
¦ г' = 2а ¦
t
2а
d9.
799
Сначала вычислим неопределенный интеграл
С помощью подстановки Уз cos ср = — придем к интегралу
= 2а У 3 Г -
Первый интеграл вычислим
подстановкой обратного количе-
количества и = -т-, и после интегри-
интегрирования получим
—In (t +
К задаче 16,16
а возвращаясь к старой пере-
переменной ср, найдем, что он равен
—In (Уз cos ср -|- У1 + 3 cos2 ср).
Второй интеграл равен
У\ -\- и3, а после перехода к
старой переменной
' 3 cos* 9
Поэтому искомая длина
1 + 3 cos2 9
¦/Ъ cos <p
L = 2а УЗ [/l+3cos8'p- In (УЗcos? + yi+3cos*?I1".
L у 3 cos <p , J |cp,
Окончательно
L =
y/~3 cos 9а
/ 4-3 cos2 9i
/"З cos ?1
i /3 cos 92 -|- /1 + 3 cos" 921
/3 cos 9i + / 1 + 3 cos* 9XJ
Вычисление длин дуг многих кривых, например, эллипса-
гиперболы, лемнискаты, приводит к так называемым эллипти-
эллиптическим интегралам, которые мы рассмотрим в связи с упраж-
упражнениями по степенным рядам.
800
Объем тела
Если известна площадь S (л:) поперечного сечения тела, то
его объем
ь
S(x)dx, A6,4)
где абсциссы а и Ъ отвечают крайним сечениям.
Объем тела, полученного от вращения криволинейной трапе-
трапеции, ограниченной непрерывной кривой, определяемой уравнением
y = f(x), осью Ох и прямыми х — а
и х = Ь, вычисляется по формуле
ь
у2 dx. A6,5)
а
Площадь поверхности тела вра-
вращения определяется по формуле
ь
A6,6)
Задача 16,17. Найти объем тела,
отсекаемого от прямого круглого ци-
цилиндра плоскостью, проходящей че-
через диаметр основания под углом а
к нему.
Решение. Такое тело назы-
называется цилиндрическим отрезком. К задаче 16,17
Пусть цилиндр, о котором идет речь,
определяется уравнением х2 + у2 — R2. Найдем площадь сечения,
перпендикулярного оси Ох. Сечение — прямоугольный треуголь-
треугольник. Возьмем на оси Ох точку с абсциссой х (\х\ < R). Площадь
сечения будет функцией х:
S(x) = ~MN-NP. '
Но MN — ордината точки N окружности х2 + У2 = R* и
= /Я2 — л:2; NP = MN tg a = /tf2 — л;2 • tg а.
Если обозначить через Н высоту цилиндрического отрезка
(KL = H), то tga = -|, и тогда JL
р
= VR*-x2 -JLt
S(x) - i-
801
Переменная интегрирования х изменяется от—R до +R,
а потому по формуле A6,4)
V = |.-f [ (R* - х*) dx = ± ¦ —¦ ¦ 2^ (R*- х*) dx =
-R
Задача 16,18. Найти объем части однополостного гипербо-
гиперболоида ~ 4- -р— -^- = 1 ,* ограниченного плоскостями z = —Я и
Решение. Вычислим площадь сечения гиперболоида плоско-
плоскостью, перпендикулярной оси Oz при постоянном г.
Площадь эта будет функцией z. В сечении получится эллипс,
который определяется уравнениями
2 = Const
Перепишем первое уравнение так, чтобы можно было сразу
усмотреть, чему равны полуоси эллипса. Для этого обе его части
разделим на правую часть. Тогда уравнения эллипса, получен-
полученного в сечении, будут такими:
z — const
Из первого уравнения следует, что полуоси этого эллипса
равны:
а потому его площадь (см. задачу 15,7)
S (г) = mib1 = каЬ (l + -j).
В формуле A6,4) переменной интегрирования надо взять не х,
а 2, так как площадь поперечного сечения есть функция г, при-
причем на вычисляемом объеме г изменяется от —Н до 4-Я, поэтому
н
V= J TOfe(l +-J-) dz = 2ад& (я +-g) куб. ед.
—н
802
Задача 16,19 (для самостоятельного решения).
Найти объем трехосного эллипсоида, определяемого уравне-
уравнением
Г2 „2 ?2
— 4- •— 4- — = 1
О2 Г 62 Т С2
Указание. Пересечь эллипсоид плоскостью, перпендику-
перпендикулярной оси Оу и проходящей через точку у этой оси (—b < у <
< Ь). При постоянном у из уравнения эллипсоида получим урав-
уравнение эллипса-сечения:
— = 1 — У—
с2 б2
у = const
или
Полуоси этого эллипса:
г/ = const
а его площадь
S (у) =
Теперь в формуле A6,4) надо вести интегрирование не по х,
а по у в пределах от—6 до +6
ь
¦jr)dy
V = ъаЬ [ (l —
куб. ед.
803
Итак, объем трехосного эллипсоида
V = -^- вдбс куб. ед.
О
Этот результат полезно помнить.
Если а~Ь = с, то эллипсоид — сфера, и тогда объем, ею
ограниченный, равен
V = -тгвд3 КУ^' ед>
(Хорошо известная из геометрии формула для вычисления объ-
объема шара).
Задача 16,20 (для самостоятельного решения).
Найти объем тела, ограниченного двумя прямыми круговыми
цилиндрами:
xi + y3 = R3 и х3 + г3 = R2.
Указание. Пересечь тело плоскостью, перпендикулярной
оси Ох и проходящей через
точку с абсциссой х (—R <
< х < R). На чертеже изо-
изображена восьмая часть тела.
В сечении получится ква-
квадрат, сторона которого равна
ординате той точки окруж-
окружности х2 + уг = R3, абциссса
которой равна х, т. е. сто-
сторона квадрата равна у =
— YR2 — х3. Площадь ква-
квадрата будет функцией х, она
равна
К задаче 16,20 ^ М = У2 = #2 — *а-
При вычислении объема восьмой части тела пределами инте-
интегрирования по х будут О и R:
1 fi
Ответ. V = -о-R3 куб. ед.
Задача 16,21 (для самостоятельного решения).
Найти объем пирамиды, зная, что ее высота Н, а основание —
многоугольник, площадь которого равна S.
Указание. Из геометрии известно, что сечение пирамиды
плоскостью, параллельной основанию, есть многоугольник, подоб-
804
ный основанию, причем отношение площади сечения к площади
основания равно отношению квадратов их расстояний от вершины.
Провести сечение на расстоянии h от основания. Обозначить
площадь сечения через S (h). Расстояние этого сечения от вершины
равно Н — h. Поэтому
В формуле A6,4) переменной интегрирования будет h, причем
h изменяется от 0 до Н:
н
= ^-куб. ед.
Мы получили известный из геометрии результат: объем пира-
пирамиды равен одной трети произведения площади ее основания на
высоту.
Задача 16,22 (для самостоятельного ре-
решения).
Найти объем шара радиуса R.
Указание. Пересечь шар плоскостью,
перпендикулярной диаметру. Вычислить пло-
площадь круга, .полученного в сечении. Из чер-
чертежа видно, что радиус этого круга г =
= VR* — Л2- Его площадь есть функция h
и равна S (h) = wa = тс (#2 — h2), причем
h — расстояние сечения от экваториальной
плоскости и изменяется h от —R до +R.
К задаче 16,22
В формуле A6,4) переменной интегрирования надо взять h
R R
V = J S (h) dh = ic J (Я2 — h?) dh =~ %R* куб. ед.
-R
-R
Объемы и поверхности тел вращения
Задача 16,23. Найти объем и боковую поверхность параболоида,
образованного вращением параболы у* = 2рх вокруг оси Ох и огра-
ограниченного плоскостью х = Н.
Решение. Объем тела вычислим по формуле A6,5):
н н н
V ^к
= крН* куб. ед.
805
Боковая поверхность определится по формуле A6,6). Найдем
сначала корень i/i , ц/2, входящий в эту формулу. Если у2 = 2рх,
Так как у2 = 2рх, то у — У 2рх и по формуле A6,6) находим
н н
о
К задаче 16,23
Задача 16,24. Вычислить объем и поверхность шара, рассмат-
рассматривая его как тело вращения.
Решение. Будем полагать, что сфера образована вращением
окружности л:2 + у2 = R2 вокруг оси Ох. Чтобы найти объем шара
по формуле A6,4), найдем из уравнения окружности у2 = R2— х2.
Переменная интегрирования х изменяется от —R до +R, а поэтому
R R
V = тс J уЧх = тс J (#2 — х2) dx=-~ kR3 куб. ед.
-R ~R
Теперь вычислим площадь поверхности сферы по формуле
A6,6). Из уравнения окружности найдем, что «/'=——; к 1 + у'*=
= —, так как х3 + y2=R2. Под-
Подставляя это значение корня в A6,6), получим
R R
S = 2n§yV\+y'2dx~2T:§y -fdx =
S =
-я
кв. ед.
806
Здесь уместно обратить внимание читателя на то, как просто
с помощью интегрального исчисления получены объем и поверх-
поверхность шара. Для того, чтобы это оценить, полезно вспомнить до-
достаточно сложный и гро-
громоздкий вывод этих же
формул в элементарной гео-
геометрии.
Задача 16,25 (для само-
самостоятельного решения).
Найти объем и боковую
поверхность прямогокруго-
вого конуса, рассматривая
его как тело, полученное
От вращения полупрямой,
проходящей через начало
координат и точку (Н, R),
и ограниченное плоскостью
Н
B(H,R)
К задаче 16,25
R
Указание. Уравнение прямой у = ^х. Определив боковую
поверхность конуса, учесть, что его образующая Ь = У Н2 + R2.
Ответ. V = ^~5— ; S = %RL.
О
Задача 16,26 (для самостоятельного решения).
Доказать, что поверхность сферического сегмента равна боко-
боковой поверхности цилиндра с тем же основанием и высотой.
У
К задаче 16,26
О R
К задаче 16,27
Задача 16,27. Вычислить объем и поверхность тора, образован-
образованного вращением круга, уравнение окружности которого х2 -\-
+ (у — аJ = ^2, вокруг оси Ox (a>R).
Решение. Тором называется тело, образованное вращением
круга вокруг прямой, лежащей в плоскости этого круга и не пере-
8J7
секающей его. Это тело напоминает бублик или автомобильную
шину. Из чертежа видно, что объем тела равен разности объемов
тел, полученных от вращения полукруга BCDB и полукруга ABDA
вокруг оси Ох. Чтобы воспользоваться формулой A6,5), найдем
ординаты кривых BCD и BAD. Решим уравнение окружности
относительно у:
(у — a)* = R3-x*; у-а= ± VR3 —
На окружности BCD: yBCD = а + У R3 — х2;
на окружности BAD: yBAD — a — У R2 — х3\
R R
V = Vsco - Vbad = 2* j y\CD dx - 2* j y\AD dx.
(Множитель 2 появился потому, что мы взяли пределами интег-
интегрирования не —R и +R, а О и R, учитывая симметрию тела отно-
относительно оси Оу).
= 2u \la • 2VR* — x*dx = &(№ [У'R2 — xadx = San(iУ R3-x3 +
~ arcsin ~j \= 2k3uR3 куб. ед."
Поверхность тора равна сумме поверхностей, полученных, от
вращения дуг BCD и BAD вокруг оси Ох.
На верхней полуокружности BCD у'~ —, g* g; г/'2 = рг^.^»'»
На нижней полуокружности Bi4D К 1 + г/'2 имеет то же зна-
значение (вычислите его). Поэтому
r r
*=2[2k j Vbcd У 1 + у'* dx + 2те j yBAD У1+УЛ dx] =
R
= 4u J (у BcD -f У bad) У\ + У'2 dx.
Но
У bcd + У bad = 2а; a Vl + у'г = р===
R R
= 4тг f 2а ¦ , R dx = 8im# [ , dx =
arcsin -n
о
= 4n2aR кв. ед.
Задача 16,28 (для самостоятельного решения).
Вычислить поверхность эллипсоида, полученного от вращения
эллипса ^а Ч- ^а = 1: а) вокруг его большой оси (так называемый
вытянутый эллипсоид вращения) и б) вокруг малой оси (сжатый
эллипсоид вращения).
Указание. В случае а) вычисление поверхности сведется к
интегралу ~ j" yV — (а2 — 6a) x* dx.
Следует для упрощения записей ввести а2 — Ь2 = с2, где с —
половина фокусного расстояния, а поэтому
S = ^
и теперь можно воспользоваться формулой D,7).
В случае б) вращение происходит вокруг оси Оу, и задача
сводится к вычислению поверхности по формуле
. A6,7)
(Этой формулой следует пользоваться в том случае, когда по-
поверхность образована вращением вокруг оси Оу).
Ответ, а) S = 2vb(b + ^arc sin-Д
Этот ответ получится, если учесть, что
Задача 16,29 (для самостоятельного решения).
Решить предыдущую задачу, взяв уравнение эллипса в пара-
параметрической форме:
х = a cos t; у = b sin t.
809
Указание. В случае, когда кривая задана параметриче-
параметрическими уравнениями х = 9 @> У =Ф @> объем тела вращения
V — к (* ф2 (t) 9' @ *, A6,8)
и
а поверхность тела вращения
и
S = йс J ф @ /9'2 + f2 Л. A6,9)
При вычислении половины площади поверхности пределами
интегрирования по t будут 0 и |.
В первом случае (вытянутый эллипсоид вращения) получится
2
S — 4каЬ у^1 — е2 sin2 9 co
о
Интеграл легко вычисляется подстановкой es'\nf = z (новые пре-
делы интегрирования 0 и ё), где е=^ ¦ — эксцентриситет
эллипса. Во втором случае (сжатый эллипсоид вращения)
т
S — 4шЪ \ |/l -f- k2 sin2 <f cos <f d<p,
Применить подстановку k sin 9 = г. Новые пределы интегри-
интегрирования 0 и k. Ответы, конечно, должны получиться те же. Дока-
Докажите, что при Ь, стремящемся к а, из обоих ответов получится
площадь поверхности сферы 4ка2.
а2 с
При определении предела — arc sin — представить это выра-
жение в виде а , учитывая, что — = е.
\/ Задача 16,30 (для самостоятельного решения).
Найти объем и поверхность тела, образованного вращением
одной арки циклоиды
х = a (t — sin
;
вокруг оси Ох.
810
Окажется, что
2л
2я
V = ш3j A — cos fK dt = 5u2a3
о
(f (l _costf dt = JA — 3cos t + 3cos2i — cos3/) Л = 5ic) •
При вычислении поверхности надо пользоваться формулой
-A6,9):
2х
S = 8тш2 j sin3 y dt.
64
Ответ. V — 5n2a3 куб. ед.; S = yica2 кв. ед.
Задача 16,31 (для самостоятельного решения).
Найти объем и поверхность тела, образованного вращением
кардиоиды
х = 2R cos t — R cos 2t
у = 2R sin t — R sin 2t
вокруг ее оси (см. чертеж к задаче 15,21).
Указание. При вычислении объема воспользоваться форму-
формулой A6,8), при вычислении поверхности — формулой A6,9).
Ответ. V = ~о kR3 куб- ед.; S = -g-nR2 кв. ед.
Задача 16,32 (для самостоятельного решения).
Найти объем и поверхность тела, полученного от вращения
астроиды
х = R cos3 -j
у= Я sin3 j
вокруг оси Ох (см. чертеж к задаче 15,27).
Ответ, V = щkR3 куб. ед.; S = -^<kR2 кв. ед.
811
СЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание. Дифференциальные уравнения первого порядка.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Дифференциальным уравнением называется соотношение, свя-
связывающее независимую переменную, неизвестную функцию и ее
производные (или ее дифференциалы).
В случае, когда неизвестная функция, входящая в дифферен-
дифференциальное уравнение, зависит только от одной независимой пере-
переменной, дифференциальное уравнение называется обыкновенным.
Порядком дифференциального уравнения называется наивыс-
наивысший порядок производной (или дифференциала), входящей в урав-
уравнение.
Обыкновенное дифференциальное уравнение порядка п в самом
общем случае содержит независимую переменную, неизвестную
функцию и ее производные или дифференциалы до порядка п
включительно и имеет вид
f{x, у, у', у", ..., */<">) = 0. A7,1)
В этом уравнении х— независимая переменная, у—неизвест-
у—неизвестная функция, а у', у", ..., г/(л) — производные неизвестной
функции.
Обыкновенное дифференциальное уравнение первого порядка
имеет вид
f(x,y,y') = O, A7,2)
а если его удастся решить относительно производной, то оно
запишется так:
y' = F(x,y). A7,3)
Задача состоит в определении из дифференциального уравне-
уравнения неизвестной функции, а процесс определения этой функции
называется решением, или интегрированием дифференциального
уравнения.
Решением, или интегралом уравнения A7,3) называется всякая
дифференцируемая функция у = у (х), удовлетворяющая этому
уравнению, т. е. такая, после подстановки которой в уравнение
A7,3) оно обращается в тождество, т. е.
является тождеством относительно я.
Кривая у = <р (х), определяемая решением уравнения A7,2) или
A7,3), называется интегральной кривой дифференциального урав-
уравнения.
Ы2
Общим решением ~ дифференциального уравнения A7,2) или
A7.3) называются соотношения вида -
Ф (х, у, С) = О, или Ф (*, у) = С, A7,4)
включающие одну произвольную постоянную величину и обладаю-
обладающие тем свойством, что решая их относительно у при любых част-
частных значениях произвольной постоянной, получаем функции вида
у = <р(х), являющиеся решениями уравнения A7,2) или A7,3).
Уравнения A7,4) определяют семейство интегральных кривых
уравнения A7,2).
Частным решением дифференциального уравнения A7,2) назы-
называется такое решение, которое получается из общего решения
A7.4) при некотором частном значении произвольной постоянной.
Произвольная постоянная С, входящая в A7,4), определяется
из так называемых начальных условий.
Задача с начальными условиями ставится так: найти решение
у = <р(х) уравнения A7,2) такое, чтобы оно. принимало заданное
значение у0 при заданном значении независимой переменной х =
= х0, т. е. чтобы выполнялось равенство
Уо = У (*о).
С точки зрения геометрии задача с начальными условиями
сводится к тому, чтобы из семейства интегральных кривых A7,4)
выделить ту, которая проходит через точку (х0, у0) плоскости.
Задача Коши. Задача отыскания решения уравнения A7,2),
удовлетворяющего начальным условиям
у = г/0 при х = х0,
называется задачей Коши.
Особое решение. Решение дифференциального уравнения, кото-
которое не может быть получено из общего решения ни при одном
частном значении произвольной постоянной, включая + со, называ-
называется его особым решением.
При решении дифференциального уравнения надо стремиться
к тому, чтобы наряду с определением общего решения были най-
найдены также и особые.
Мы рассмотрим на этом практическом занятии типы диффе-
дифференциальных уравнений первого порядка, предусмотренные про-
программой.
Первый тип. Уравнения с разделяющимися переменными
Этот тип уравнений является самым простым типом уравне-
уравнений первого порядка, но вместе с тем очень важным.
Если.в дифференциальное уравнение первого порядка F(х, у,
у') = 0 производная у' входит в первой степени, то после реше-
решения его относительно у' получится уравнение вида
813
Так как у' — ¦—,, то это уравнение может быть переписано так:
/ (*, у) dx + <р (л;, у) dy = 0.
В частном случае, когда каждая из функций / (х, у) и <р (х, у)
является произведением двух функций, одна из которых — функ-
функция только х, а вторая — только у, т. е. когда
, У) = /i (х) • ft (у), а <р (х,у) = <pi (х) • <г, (У),
уравнение примет вид
h (*)*• h (У) dx + 9l (x) • 9t (у) dy = 0. A7,5)
Уравнение A7,5) называется дифференциальным уравнением
с разделяющимися переменными.
Разделение переменных производится делением обеих частей
A7,5) на произведение ^(х) • /2 (у), в котором /2 (у) — функция
только от у, являющаяся множителем при dx, a <pi (x) — функ-
функция только от х, являющаяся множителем при dy. После деле-
деления на это произведение уравнение A7,5) примет вид
а его общий интеграл запишется так:
I /i (x) j I I <ft (У) ju /-> П7 7\
Особые решения уравнения с разделяющимися переменными
Уравнение A7,5) может быть переписано так:
Поэтому, кроме найденного ранее общего интеграла A7,7) урав-
уравнения A7,5), ему могут также удовлетворять решения, получае-
получаемые из уравнения
?iW-/.(?) = 0. A7,8)
Если эти решения не входят в общий интеграл A7,7), то они
будут особыми решениями уравнения A7,5).
Задача 17,1- Найти общие интегралы уравнений, особые реше-
решения, а также частные решения, удовлетворяющие начальным
условиям:
814
Начальные условия:
1) х2 (у3 + 5) dx + (Xя + 5) у2 dy = O, у @) = 1;
2) хVV+V2dx + у/ТТх~2dy = O, у(/3) = 0;
3) ху dx + (l+ у2) /ТТх~2 dy = O, у (/§) = 1;
4) у' = 5 Vy, У@) = 25;
5) tg у dx — х In х dy = 0, х [~\ = е;
6) y' + f/2= I-
Решение. 1) Приведем уравнение к виду A7,6). Разделим
обе части уравнения на (х3 + 5) (у3 + 5) и получим
л? + 5 у3 + 5 v
Теперь переменные разделены. Интегрируем обе части урав-
уравнения:
(Здесь мы заменили Сх на -j In | С |).
Отсюда общий интеграл запишется так:
(х3 + 5) (у3 + 5) = С.
Следует также рассмотреть уравнение (л;3 + 5) (у3 + 5) = 0.
Но решения этого уравнения не являются особыми, так как они
получаются из общего интеграла при С = 0. (Напоминаем, что
особым решением дифференциального уравнения называется та-
такое его решение, которое не может быть получено из общего ни
при одном частном значении произвольной постоянной С).
Используя начальное условие, найдем С: подставляем х = 0,
у = 1 в общий интеграл:
@ + 5) A + 5) = С; С = 30.
Частное решение, соответствующее начальному условию:
(х3 + 5) {у» + 5) = 30.
2) Приведем уравнения к виду A7,6). Для этого разделим
обе его части на V\ + х2 ¦ У\ + у2. После деления получим
* dx + У dy = 0.
815
Интегрируя обе части этого уравнения, получим общий ин-
интеграл:
Отсюда
^2 + КТТ? = С (С > 0). A7,9)
(С > 0, так как рассматриваются только арифметические значе-
значения корня).
Теперь следует решить вопрос об особых решениях. Для
этого рассмотрим уравнение
Действительных решений это уравнение не имеет, а потому
и нет особых решений.
Частное решение получим из условия у = 0 при х = /3. Под-
Подставляя эти значения х и у в общий интеграл A7,9), получим
1/ТТЗ + УТ+0 = С; С = 3;
и частным решением будет
3) Обе части уравнения делим на г//1
Интегрируя, получаем
или
Чтобы рассмотреть вопрос об особых решениях, надо прирав-
приравнять нулю произведение г//1 +л;2 = 0. Отсюда следует, что у =
= 0, /Г+72 = 0.
Решение у = 0 является особым решением, так как оно удов-
удовлетворяя уравнению не может быть получено из общего решения
ни при одном ^частном значении С. Уравнение же /l + х2 = 0
действительных решений не имеет.
Частное решение получим, подставляя в общий интеграл
/
/Г+~8 + In 1 + I = С; С = ¦?...
816
Частное решение
или
+ х2 + In г/2 + г/2 = 7.
4) Перепишем уравнение в виде j- =
Отсюда, деля обе части уравнения на 5 (А/ и умножая на
их, получим
4
— ах.
5 ?У
Интегрируя, найдем общий интеграл
^У~у = х + С, A7,10)
или
У = *{* + С)\
Чтобы получить особое решение, рассмотрим уравнение
5 Yy = 0. откуда у = 0. Это решение будет особым, так как
оно не может быть получено из общего ни при одном числовом
значении произвольной постоянной С.
Частное решение получим из A7,10), подставляя в него
х = 0, у = 25:
-g- r ~« — 0 + С; С — 2,
и частным решением будет
5) Для того, чтобы разделить переменные, разДелим обе
части уравнения на tgy • Inх, и получим ¦ х^х — ^- ~ 0,
а интегрируя
найдем
In I In л; 1 — In I sin |/1 = ln|C|,
Отсюда
In* r
ИЛИ
mx = Csiny.
27 И. А. Каплан 817
Общий интеграл уравнения
x = eCsiny. A7,11)
Для решения вопроса об особом решении надо приравнять
нулю выражение tgy ¦ х\пх, иа которое мы делим уравнение:
tg у ¦ х In х = 0.
Отсюда tg у = 0; х = 0; In х = 0. Таким образом, у = foe (& = 0,
±1, ±2, ± ...); х = 0; х=1.
Но из общего интеграла при С = 0 получаем л; = 1. Значит,
х = 1 является не особым решением, а частным. При С = —со
имеем х — 0, а потому я = 0 также не особое решение, а част-
частное. При С=+со будет у = kw, что следует из A7,11), и по-
поэтому эти решения не особые, а частные. Таким образом, реше-
решения х — 0; л; = 1 и у = Ы «подозрительные» на особенность яв-
являются попросту частными решениями. Значит, особых решений
уравнение не имеет.
Чтобы найти частное решение, подставим в A7,11) х = е;
у = -7Г , и получим
Поэтому частным решением будет
л; = е81"».
6) Перепишем уравнение в виде
dx v
Разделим обе части уравнения на 1—у2 и умножим на dx.
Получим уравнение, в котором переменные разделены:
1-</2 "л-
Интегрируем обе его части:
, = х + С;
.Ж.
1-у*
1 =
Отсюда
И1
In
1+0
1-У
или Щ = _ е2 (дг+С),
1±J = е (л:+)> или Щ
Рассмотрим каждый из этих случаев в отдельности.
1 j
П — р2 (х+С)- Ц _ 1 = _!
1> I— у~е ' » "" е2 (х+о -f 1 е<*+С) + е-(*+С) *
818
Общий интеграл: у = th (я + С).
0 е е _ е- (дг+С) •
Общий интеграл; у — cth (я + С).
Чтобы решить вопрос об особом решении, приравняем нулю
выражение 1 — у2, на которое мы делили обе части уравнения:
1-г/2 = 0, у=±\.
Эти решения являются особыми, так как не могут быть по-
получены из общего ни при одном числовом значении произволь-
произвольной постоянной С.
Задача 17,2 (для самостоятельного решения).
Найти общие интегралы, особые и частные решения диф-
дифференциальных уравнений:
1) у' = 0; 2) у' = а; 3) у' = 2х2 + Бх + 12; у A) = 1;
4) у'-у2-Зу + 4 = 0;
5) Vl-y2dx + \/l-x*dy = 0; y@) = l;
6) A + у2) dx + (l+ х*) dy = 0; у A) = 2.
Указания. В пятом уравнении произвольную постоянную
выгодно ввести под видом arcsin С, в шестом уравнении — под
видом arctgC.
Ответ. 1) у = С; 2) у = ах + С;
2 5
3) у = -j х3 -(- у х2 + 12л: + С. Частное решение у =
_ 1 + 4е5 <*+с>. _ i-4e5<*+c>
> У~ 1 _ е5 (х+С) '• У j + е5 (л+С) •
Решения г/ = 1иг/ = — 4 — частные. Они содержатся в общем
решении: первое при С = —оо, второе при С= + со.
5) arcsin х + arcsin у = arcsin С, или, беря синус обеих
частей, х V\ — у2 + у У\ — х2 = С. Учесть, что
cos (arcsin x) = Yl — х2
Особое решение у,— ± 1. Частное решение хУ\—у2
6) arctg* + arctg у = arctg С. Беря тангенс обеих час-
частей, это равенство можно записать в виде .* у = С.
Частное решение *_% =—3. Учесть, что tg(arctgx) =
27*
Уравнение вида
у' =f(ax + by + c) A7,12)
приводится к уравнению с разделяющимися переменными с по-
помощью подстановки
ах + by + с = г; а + by' = г'; у' ~ г-^
Уравнение A7,12) принимает вид:
Z=° = f(z); z' = bf{z)+a;
+ a, или ^d
Последнее уравнение — уравнение, в котором переменные раз-
разделены. В общем интеграле следует перейти к старой перемен-
переменной, заменив z на ах -f- by + с. -
Задача 17,3. Найти решения уравнений:
1) У' = ъПГу ; 2) У' (У + х) = 1; 3) у' =
Решение. Первое и второе уравнения этой задачи отно-
относятся к типу A7,12), а третье — уравнение с разделяющимися
переменными.
1) Подстановка: Зх -\- у — z. Дифференцируя, находим: 3 +
+ у'=г'\ y'=z'-3. Поэтому г'-3 = 1; г'=-Ц^; | =
= . Разделяем переменные, умножая обе части последнего
Z /
уравнения на t \zdx. Получаем j4r&dz = dx.
Интегрируя, находим
откуда, вычисляя интеграл, получаем
iZ-lln|l+3Z| = je + C,
а заменяя г на За; + у, имеем
1 (Зл;'+ у) -1 In 19* + Зу + 11 =-^ + С.
2) Подстановка: л; + У = 2.
Ответ, t/ — 1п|л; + г/ + 11 = С.
3) Представить правую часть в виде 33jc+2* = 33д!
Q
Произвольную постоянную выгодно ввести под видом — „. о
Ответ. 3 • 3-2* + 2 • 33* = С.
Задача 17,4 (для самостоятельного решения).
Проинтегрировать уравнения:
1) г/'=3*4-4г/; 2) ^'= 2^ — 3; 3) у' = |/2* + у- 3.
3 3
Ответ. I) у = Ceix — -jx — jQ-,
2) 5а; 4- Юг/+ 4 In 15л; 4- Юг/ —4 | = С—25а;;
3) 2 J/2* 4- У — 3 — 4 In (V2x + у — 3 + 2) = х + С.
Второй тип. Линейные дифференциальные уравнения
первого порядка
Уравнения вида
y' + p(x)y = q(x) A7,13)
называются линейными потому, что искомая функция у и ее произ-
производная у' входят в них в первой степени.
Функции р(х) и q {x) предполагаются непрерывными в про-
промежутке (а, Ь), в котором ищется решение уравнения A7,13).
Если правая часть в A7,13) — функция q (x) тождественно равна
нулю при всех значениях х из (а, Ь), то уравнение принимает вид
У' + р(х)У = 0 A7,14)
и называется в этом случае линейным однородным дифференциаль-
дифференциальным уравнением первого порядка. Оно соответствует уравнению
A7,13), которое при q(x)=?0 называется неоднородным. Отметим,
что линейное однородное уравнение является уравнением с раз-
разделяющимися переменными.
Иногда уравнение A7,14) называется линейным уравнением без
правой части.
Общее решение линейного неоднородного уравнения A7,13)
можно найти с помощью постановки
y = e~SPi*)dxv(x), A7,15)
где и(х) — новая искомая функция. Множитель e~Jp{x)dx—общее
решение линейного однородного уравнения A7,14), соответствую-
соответствующего уравнению A7,13), причем в этом общем решении опущен
множитель С.
Эта подстановка предпочтительнее указанной в учебниках —
у = uv, так как функция и всегда равна выражению е~$"w dx
и ее, собственно, каждый раз отыскивать излишне.
Подстановка A7,15) приводит A7,13) к уравнению с разделяю-
разделяющимися переменными.
821
Задача 17,5. Найти решение уравнения у' + У — ех, удовлетво-
удовлетворяющее начальному условию у @) = 1.
(Прежде всего обратите внимание на то, что уравнение —
линейное, так как искомая функция у и ее производная у' входят
в него в первой степени).
Решение. Сравнивая это уравнение с A7,13), мы видим, что
функция р(х)— коэффициент при у — равна 1.
Чтобы применить подстановку A7,15), вычислим ] p(x)dx,
который при р (х) = 1 запишется в виде J р (х) dx = j dx — х,
a e~$Pi*)dx — е~х. Поэтому подстановка A7,15) имеет вид
y^er'v. A7,16)
Подставим выражение A7,16) в заданное уравнение. Для этого
A7,16) продифференцируем как произведение
у' = e~xv' {х) — v (х) е~
У = v(x)e~
е" = e~xv' (x)
(Складывая в левых частях этих равенств у' + У, мы получаем
правую часть заданного уравнения, т. е. е*).
Получилось уравнение с разделяющимися переменными
dxe ег-
Умножая обе его части на е* dx, получим
dv = <*xdx,
а интегрируя, найдем
Подставляя найденное значение и в A7,16), получим
ИЛИ ' •
y^Gr' + i-e*. ¦ A7,17)
Как доказывается в теории интегрирования линейных неодно-
неоднородных дифференциальных ~ уравнений первого порядка A7,13),
общее решение этого уравнения равно сумме двух слагаемых,
из которых одно является общим решением соответствующего одно-
однородного уравнения A7,14), а другое — его частным решением неодно-
неоднородного уравнения (оно получается из общего при С = 0). В нашем
случае в A7,17) первое слагаемое Сё~х — общее решение однород-
однородного линейного уравнения у' + у = 0, соответствующего заданному,
а второе — ех — частное решение заданного уравнения,
822
Действительно, уравнение у' + у = 0 — уравнение с разделяю-
разделяющимися переменными: --| = —у; ———dx. Интегрируя, получим
Из A7,17) определим произвольную постоянную С, используя
начальное условие у @) = 1:
Подставляя в A7,17) С=-~-, получим частное решение у=-^е~х
1
1 -
+ -o"e*> т. е. частным решением является y = shx.
Задача 17,6. Найти общее решение уравнения у' — 4# = cosa;,
а также частное, удовлетворяющее начальному условию у@) = 1.
Решение. Сравнивая с A7,13), заключаем, что, р(х) =—4
(это коэффициент при у в заданном уравнении). Чтобы приме-
применить подстановку A7,15), вычислим —^p(x)dx, подставляя в него
р(лг) = -4:
—J p (x) dx == —\ —4 dx = 4х,
Поэтому A7,15) запишется так:
A7,18)
Подставляя это значение у в заданное уравнение, получим
1
—4
у' = V'e*x
у = veiX
cos x = и'е4*
(при сложении два последних слагаемых уничтожились). Получи-
Получилось уравнение с разделяющимися переменными:
Умножая обе его части на e~ix dx, получим
dv = e~ix cos x dx.
Интеграл правой части найден в задаче D,22). В формуле
D,11) надо взять а = —4; 6=1.
Поэтому w = -jy-(sinj<; — 4cos*)-|-C, а из A7,18) получаем:
у = ^т=- (sinх — 4cosx) + С\е**;
(sinx 4cosx) A7,19)
823
Здесь опять-таки следует обратить внимание на то, что сла-
слагаемое CeiX есть общее решение однородного линейного уравнения
у'— 4у = 0, соответствующего данному неоднородному, а второе
слагаемое — частное решение всего данного уравнения. Э,то сла-
слагаемое получается из общего решения при С — 0.
Чтобы определить частное решение, подставляем в A7,19)
х = 0; у = 1 и получаем:
поэтому частным решением будет
у = yj B1е4ж + sin х — 4 cos х).
Задача 17,7 (для самостоятельного решения).
Найти общее решение уравнения
х' + ах = еь* (а + Ьф 0).
Рассмотреть также случай а -{- b — 0.
Указание. Здесь искомая функция не у, как было в двух
предыдущих задачах, а х, независимой переменной является /
(это усматриваем из того, что правая часть ebt — функция /).
Вместо интеграла —^p(x)dx в A7,15) надо вычислить
— ]adt = —at. Поэтому подстановка A7,15) будет такой:
x = v(t) e~at.
Ответ, х = Се-°'+-^
Если а + Ь = 0, то х ='Ce~at + te~at.
Указание. Если а -\- b = 0, то b = —а.
В трех последних задачах коэффициент при первой степени
искомой функции в линейном уравнении был величиной постоян-
постоянной (это были числа 1, —4, а).
Теперь мы решим задачу, в которой этот коэффициент есть
функция независимой переменной.
Задача 17,8. Найти решение уравнения
у' -\- у cos х = sin х cos х,
удовлетворяющее начальному условию у @) = 0.
(Уравнение линейное, так как искомая функция у и ее про-
производная у' входят в уравнение в первой степени).
Решение. Сравнивая заданное уравнение с A7,13), заклю-
заключаем, что р (х) = cos х; — \ р (х) dx = —\ cos xdx = —sin x. По-
Поэтому множитель e~Jp^dx в A7,15) равен e~sinx, а подстановка
A7,15) запишется так:
y = v(x)e-siax. A7,20)
824
Подставляя это значение у в заданное уравнение, получим:
1
cos л;
у' = v'e~sin х — ye-sin x cos x
у = ve~sinx
sin л; cos л; =f v'er&inx
Получилось уравнение с разделяющимися переменными
Умножая его обе части на е*Ых, получим
dv = esin x sin x cos x dx,
а
v = \ esin х sin д; cos xdx — esin x sin x — \ esin * cos x dx
и = sin x
dt = esin * cos x
du = cos x dx
= esin * sin x — e?in X + C.
Подставляя это значение v в A7,20), найдем
у = (esin x sin x — esln X + C) e~sin *;
Теперь найдем частное решение. Подставляем в общее решение
начальное условие х = 0; у = 0; 0 = С— 1; С = 1. Частное реше-
решение запишется так:
Задача 17,9 (для самостоятельного решения).
Найти общие и частные решения следующих линейных урав-
уравнений:
1) y'+ytgx = cos*x; y(i) = -j'>
2) У'-^ |
Указания. При решении многих задач придется пользо-
пользоваться формулой e]nN = N. В первом уравнении p(x) = tgx\
—j р (я) dx = — ? tg x dx = In cos x; e ~$p (J?> d* = e]n ^ * = cos *.
Во втором уравнении
825
Сх* I \х I 5
Подстановка: у = v(x)(x + 2). Функция v (x) = \ j. ^ d*=
Ответ. 1) i/ = С cos х + sin x cos а;; частное решение:
у — sin a; cos x;
2) I/ = С (а; + 2) + 2 + (* + 2) In (a; + 2); частное
решение: у — (х + 2) + 2 +(х + 2) In (x + 2);
- 3) х = C(t + 1)" + е? (t + 1)"; частное решение:
х __ gt h _|_ 1\«_
Задача 17,10 (для самостоятельного решения).
Найти общие интегралы и частные решения линейных уравне-
уравнений:
1) у' ¦. у — —coseCA; — sin а;; у(-г) = 1+^г;
1 " sin х cos x" \ 4 / ' 2
2) у' — 2ху = 1— 2х\ у @) = 2;
3) *#' -f У = х* + За; -f 2; i/(l)=^-g-.
Указания. 1) j _|?_ = In tg x; elnt^ = tgA;. Подста-
Подстановка: у = v tg л\
2) р (а;) = —2а;; e~J"<JC) dJC = е*1. Подстановка: у = vex\
3) Обе части уравнения разделить на х. Функция р (а;) = —;
— \p(x)dx = —In x; e~in * = eln *-' = х~г — —. Подстановка:
Ответ. I) у = Ctgx + cosx; у = tgх + cosx;
2) у = Се*г + х; у = 2е*г + х;
3) f/ = 4 + T + f+ 2' ^ = Т + Т + 1 + 2-
Задача 17,11. Найти общий интеграл уравнения
у dx — (х -\-у* sin у) dy — 0.
Решение. Если обе части уравнения разделить на dy, то
получится
У Ту — х~ «/2sinir = 0.
Разделив на коэффициент при т-, получим уравнение
826
в котором искомой функцией является х, независимой перемен-
переменной — у. А так как искомая функция х и ее производная ~
входят в уравнение в первой степени,, то оно линейное. Подста-
Подстановка A7,15) запишется так:
х = v (у) eSp iy) dv = ve~ J ~ 7 d" = ve]a « = vy.
Общее решение: x = Су — у cosy.
Задача 17,12 (для самостоятельного решения).
Найти общие интегралы уравнений:
1) t dx + (x — t sin t) dt = 0;
Указание. Каждое из этих уравнений линейно относительно х
и у. Искомая функция—х, независимая переменная — у. Прежде
чем интегрировать обе части уравнения, разделить на коэффициент
dx
Ту
Ответ. 1) x = Y+SJT-cost> 2) ^ = ^= + уУ3;
,- 2
Х- з
Задача 17,13. Найти общие интегралы уравнений:
Указание. В третьем уравнении при интегрировании по
частям, которое надо будет применить, два интеграла взаимно
уничтожатся. Интегрировать по частям придется только один раз.
Ответ. 1) у = С(х* + х+ 1) +sin*;
2) у = С sin х -f x2;
3) у = С*2 + е*.
Третий тип. Уравнение Бернулли
Если правую часть линейного уравнения A7,13) умножить на
у" при условии, что л — любое действительное число, кроме нуля
и единицы (п Ф 0 и п ф 1), то получим уравнение вида
y' + p(x)y = q(x)y\ A7,21)
Оно называется уравнением Бернулли.
827
Так как пфО и п=/= 1, то это уравнение не является линей-
линейным.
После умножения его обеих частей на у~п и подстановки
у1~п — z, где г— новая искомая функция, оно приводится к ли-
линейному, интегрированием которого мы уже занимались.
Преобразование уравнения Бернулли в линейное будем прово-
проводить в такой последовательности:
1) умножим обе части уравнения на у~п;
2) введем подстановку г/1"" = г. Обе части этого равенства
продифференцируем: A — ri)y~ny' = г'; у~пу' = j~ <
3) полученное уравнение проинтегрируем как линейное с по-
помощью подстановки A7,15), в которой вместо у надо писать г;
4) возвратимся к искомой функции, заменяя г на у1'".
Подробно мы рассматриваем решение только одного уравнения
Бернулли и для самостоятельного решения предлагаем 5 уравне-
уравнений, учитывая большое число упражнений, выполненных при
интегрировании линейных уравнений.
Задача 17,14. Найти общее решение уравнения
ху' — уBу\пх—1) = 0.
Решение. Приведем уравнение к виду A7,21):
(обе части уравнения мы разделили на х и слагаемое, содержа-
содержащее у в первой степени, оставили в левой части уравнения).
1) Обе части уравнения умножим на у~2:
*ГУ +^ = 2^. A7,22)
2) Сделаем теперь подстановку
у-г = г. A7,23)
Дифференцируя обе части этого равенства и помня, что у
есть функция х, получим
-*ГУ = г\ а гУ"=-2'.
Делая эти замены в A7,22), получим уравнение
Z+xZ~Zх >
или
которое линейно относительно гиг'.
Чтобы сделать подстановку A7,15), вычислим сначала входя-
входящий в нее интеграл.
828
У нас р (я) = — —; —
еХп х = х.
Подстановка: z = vx.
±dx = lnx\
г' = v'x
z =
v
vx
' dx
и
dt
= In л;
dx
¦—
X2
du =
t =
1
dx
1
X
г = Сд; + 2Aпл;+1).
Чтобы возвратиться к исходной искомой функции, восполь-
воспользуемся сделанной подстановкой A7,23) и получим
Задача 17,15. (для самостоятельного решения).
Найти общие решения уравнения:
1) *У % + ху3 - а2; 2) ху'-уЧпх + у = 0;
3) У'-^У = -У2; 4) (х*-*)у'-*у = -(х
Указание. Прежде чем делать какие-нибудь преобразования
в уравнениях 1, 2 и 4, следует разделить обе части уравнения
на коэффициент при у'.
Ответ. 1) У3 = 2§Г + 1?; 2)j=l+lnx + Cx;
3) *-$ li±|
5)
829
Четвертый тип. Однородные уравнения
(Эти уравнения не следует смешивать с линейными однород-
однородными уравнениями A7,14), которые рассматривались выше).
Если уравнения у' = f (х, у) или р (х, y)dx + Q (х, у) dy = О
не изменяются при замене х на kx и у на ky, то они называются
однородными. Подстановка
У = их, A7,24)
где и — новая искомая функция, преобразует однородное уравне-
уравнение в уравнение с разделяющимися переменными.
После того как новое уравнение будет проинтегрировано, сле-
следует и заменить на ~.
Задача 17,16. Проинтегрировать дифференциальные уравнения:
= 0; 2) xydy-y*dx = {x + y?e~^ dx.
Ху
Решение. 1) Прежде всего следует убедиться, что это урав-
уравнение однородное. Заменив х на kx, а у на ky, заметим, что
уравнение не изменилось. Это и доказывает, что оно однородное
Сделаем подстановку A7,24): у — их. Тогда у = и'х + и, и урав-
уравнение перепишется так:
их -f и -\—— = 0,
1 ' xux '
или, сокращая на хг:
откуда и'х А— =0; -^-x =
1 ' и dx и
Теперь мы получили уравнение с разделяющимися перемен-
переменными, которое после разделения переменных запишется следую-
следующим образом: •
и , dx
Интегрируя, получаем:
In A + 2Ы2)-1 = 4 In | л: 1 + 4 In | С |,
или, переходя от логарифмов к числам, т. е. потенцируя, находим
830
Заменим теперь и на — и получим
1 -1_ .- 1~ "
Сократим на х2, тогда xt,2y* = Сх2'
Это решение удобнее записать в виде
1
или х2(х2 + 2у2)=-?.
Заменяя -^- на Съ получаем
2) В том, что это уравнение однородное, легко убедиться,
заменив х на kx, а у на ky. Замечаем, что при этом уравнение
не изменилось. Перепишем его для удобства в виде
— JL
1(х + уJе * +y*]dx — xydy = 0
и сделаем подстановку у = их, из которой следует, что
dy = и dx + х du.
Уравнение перепишется в виде
[(х + ихJ е~" + и2х2] dx — их2 [udx + x du) = 0.
Разделив обе его части на х2, получим уравнение
[A + иJе~и + и2] dx — и(иdx + хdu) = 0,
или
[A + иJ е'" + и2 — и2] dx — uxdu = 0.
Это уравнение с разделяющимися переменными. Разделяя их,
получим уравнение
*? udu n П7 9^
Интеграл
Г udu Г ueu'du __ еы
J
Поэтому из A7,25) получаем
или
831
Заменяя и на —, получаем
и окончательно
(х + у) In Сх = хе х .
Помещаем для самостоятельного решения еще 5 однородных
уравнений.
Задача 17,17. Проинтегрировать уравнения:
1) (x + y)dx + (y — x)dy = O; 2) (х2 — ху)dy + у*dx = 0;
3) у' = ё* +Y+U 4) xy'=x.sm± + y;
5) ху' + х cos —— у + х = 0.
Указание. В третьем уравнении \ ы " |- = I —Jqfy—^и=
= и — 1п (е" + 1). Полученное решение разрешить относительно е *.
_у
Ответ. 1) arctg^ = ln(CVx2 + y2y, 2) у = Сех;
3)e*=T^L-x; 4) у = 2*arctgС*; 5)tg|-ln|.
В заключение этого практического занятия решим несколько
задач из физики и механики, которые требуют составления диф-
дифференциального уравнения первого порядка и его интегрирования.
В задачах 17,18—17,21, несмотря на их внешнее различие,
две переменные величины х и время t, участвующие в них, обла-
обладают тем общим свойством, что скорость изменения одной из
них (х) по отношению к другой (t) пропорциональна наличному
количеству величины х в рассматриваемый момент времени.
Учитывая, что скорость изменения величины х есть производ-
производная -Z7, обозначим через к коэффициент пропорциональности.
Тогда дифференциальное уравнение, описывающее этот процесс,
будет иметь вид
| = Ь. A7,26)
Это уравнение с разделяющимися переменными и интегриру-
интегрируется оно очень просто.
832
Разделяя переменные, получим
или
In
di = kdt;
— - to-
х = Cekt. A7,27)
Таким образом, решением уравнения A7,26) является показа-
показательная функция.
Условие задачи должно содержать данные:
1) для определения произвольной постоянной, т. е. значение
х0 величины х в момент времени t = t0: х (t0) = х0;
2) для определения коэффициента пропорциональности k.
Уравнение A7,26) описывает процесс непрерывного роста или
непрерывного убывания величины х, причем, как видно из реше-
решения A7,27), рост имеет место при положительном коэффициенте
пропорциональности k, а убывание—при отрицательном k.
Задача 17,18. Скорость распада радия пропорциональна коли-
количеству нераспавшегося радия. Количество радия в начале процесса
(t = 0) было равно х0. Известно, что за 1600 лет распадается
половина первоначального количества.
1) Через сколько лет количество нераспавшегося радия будет
составлять 80% первоначального?
2) Определить, какой процент радия сохранится через 300 лет.
Решение. Уравнение A7,26) описывает процесс радиораспада.
Определим в A7,27) произвольную постоянную С. Известно из
условия задачи, что в начальный момент, т. е. при t = 0, коли-
количество радия равно х0. Таким образом, начальное условие:
х@) = х0. Подставляя в A7,27) ? = 0; х — хо, получим
Xq == L>6 , и ^^ Xq,
а потому A7,27) перепишется так:
х = V. A7,28)
Задача содержит условие, позволяющее определить коэффициент
пропорциональности k: когда t = 1600, количество радия х равно
половине начального, т. е. х — ~. Подставляя в A7,28) ^вместох
и 1600 — вместо t, получаем у = *0е*'1600. Сокращая на х0, полу-
получим y = е*-1600. Для определения k, прологарифмируем по осно-
основанию е обе-части этого равенства:
1пу"=/г- 1600; In 1 — In2 =/г ¦ 1600; /г = —
833
Теперь решение A7,28) перепишется в виде
In 2
или
-hit
е 'во» . A7,29)
Ответим на первый вопрос задачи. По условию — = 0,8(80%).
Подставляя это значение в последнее уравнение, имеем
In 2 .
0,8 = е 1600
Для определения t прологарифмируем обе части равенства
1пО8 '
отсюда
. 1600 In 0,8 1600 (—0,223 14) С1Г.
t = Щ— = 0,69315- ~515лет-
Чтобы ответить не второй вопрос задачи, найдем из A7,29)
отношение — при / = 300:
хо
Л = е 1боо° и. ± = е 1боо _ в—о.13о ~0,878 = 87,8%.
Xq" Xq
Таким образом, через 300 лет сохранится 87,8% начального
количества радия, а следовательно, распадется за 300 лет 12,2%.
Задача 17,19 (для самостоятельного решения).
Согласно закону Ньютона, скорость охлаждения нагретого
тела пропорциональна разности температур тела и окружающей
среды.
Определить, за какое время тело, нагретое до температуры
х0 = 300°, помещенное в жидкость, температура которой 60°,
охладится до 150°, если считать количество жидкости настолько
большим, что ее температура практически остается без измене-
изменения. При этом известно, что через 10 минут после начала про-
процесса температура тела равна 200°.
Указание. Обозначить через х непрерывно убывающую тем-
температуру тела C00 < х < 60). Разность температур тела и жидко-
жидкости равна х — 60*3. Скорость охлаждения — -?. Если k — коэф-
коэффициент пропорциональности, то дифференциальное уравнение
процесса будет таким:
834
Общее решение имеет вид
х — 60 = Се«. A7,30)
Начальное условие: в начальный момент времени t — 0 темпе-
температура х0 = 300°:
300 —60 = Се*°; С = 240.
Поэтому A7,30) запишется так:
х = 60 + 240е*. A7,31)
Для определения коэффициента пропорциональности k исполь-
используем дополнительное условие в задаче:
при t = 10 мин температура тела равна 200°. Поэтому из
A7,31) при х = 200, t = 10, 200 = 60 + 240е*10. Откуда следует,
что k — —0,053, и тогда уравнение A7,31), связывающее темпера-
температуру х и время t, запишется так:
х = 60 + 240е-°-053'.
Чтобы ответить на вопрос задачи, надо подставить сюда
л: = 150 и определить t.
Окажется, что t =•—оТM3^п?*
- Ответ, t — 18,5 мин.
Задача 17,20 (для самостоятельного решения).
Известно, что изолированный проводник вследствие несовер-
несовершенства изоляции теряет сообщенный ему заряд, причем скорость
потери заряда пропорциональна наличному заряду в данный
момент.
В начальный момент проводнику сообщен заряд 2000 CGSE.
За первые две минуты проводник теряет 150 CGSE. Определить,
через сколько минут заряд проводника станет равным половине
начального.
Указание. Обозначая переменный заряд через х, получим
дифференциальное уравнение процесса
dt - RX-
Его общее решение дается формулой A7,27): х = Се**. Из началь-
начального условия (х — 2000 при t = 0) следует, что С = 2000, и тогда
* = 2000е«. . A7,32)
Так как через две минуты заряд равен 2000— 150 = 1850 CGSE,
то для определения k имеем уравнение:
1850 = 2000е*'; k = -^ In J = —0,039.
835
Поэтому A7,32) перепишется так: х = 2000-0-039'. Подставляя сюда
л: = 1000 — заряд, равный половине исходного, получаем: 1000 =
= 2000е-°.°39', откуда 1 = е-0-039', а< =
Ответ, t^ 18 мин.
Задача 17,21 (для самостоятельного решения).
Предполагая, что скорость прироста населения пропорцио-
пропорциональна его наличному количеству, и зная, что население СССР
на 1 января 1962 года составляло 200 млн. человек (приближенно),
а прирост за 1962 год был равен 2%, определить на основании
сделанного предположения и этих данных количество населения
СССР на 1 января 2000 года.
Указание. Дифференциальное уравнение процесса: -J = kx\
х = Се*'; С = 200, а потому
* = 200е«. A7,33)
По условию за 1962 год прирост населения составил 2%.
Полагая в A7,33) х = 200 + щ • 2, т. е. х = 204, a t = 1, нахо-
109
дим k: k = In щ = In 1,02 = 0,02, а поэтому уравнение A7,33)
перепишется так:
* = 200е0-02'.
На 1 января 2000 года t = 38, так как за начальный момент
приняты сведения на 1 января 1962 года. Отсюда х — 200е0'0238.
Ответ. *2ооо = 428 млн. человек.
Если бы не был принят во внимание непрерывный рост насе-
населения, то за 38 лет из расчета 2% в год прирост населения
составил бы 76% начального, т. е. 152 млн. человек, и на 1 ян-
января 2000 года оно равнялось бы только 200"+ 152 = 352 млн.
человек.
Ошибка была бы в 428 — 352 = 76 млн. человек.
Задача 17,22. Точка движется по прямой с постоянным уско-
ускорением, равным а —г. В начальный момент / = 0, ее скорость
сек
v = v0, а расстояние от начала координат — So, т. е. v@)—v0,
S@) = S0.
Найти закон движения.
Решение. При движении по прямой ускорение есть произ-
dv
водная от скорости по времени, а потому- ускорение а = -г;
dv = adt. Интегрируя, получим v = at -f- Cv Подставляя сюда t — 0,
v = v0, найдем Ct = v0, а потому уравнение, связывающее ско-
скорость и время, перепишется так:
v = at + va.
836
Известно, что скорость в прямолинейном движении — i .
dS
водная от пути по времени: v = -г-,.
Поэтому J7 = at + v0, dS = atdt + vodt, a S = ^~- + vot -f- C2.
Используя начальное условие S = So при t = О, получим, что
C2 = So, и закон движения запишется следующим образом:
S = ^ + vot + So.
Если So — 0, то S = -к- + ^о^ — хорошо известный из физики
закон прямолинейного равномерно-переменного движения.
Задача 17,23. Определить, форму зеркала, отражающего все
лучи, исходящие из одной точки так, чтобы после отражения
они были параллельны
заданному направлению.
Решение. Поме-
Поместим начало координат
в точку, из которой
исходят лучи, а задан-
заданное направление, кото-
которому должны быть па-
параллельны отраженные
лучи, примем за ось Ох
(см. чертеж). " " "л
Пусть точка А при- К задаче 17,23
надлежит зеркалу, а
АР — один из таких лучей. Кривая АК — линия пересечения
зеркала с плоскостью хОу. Согласно известному закону оптики,
лучи падающий, отраженный и нормаль к поверхности, на кото-
которую падает луч, лежат в одной плоскости и составляют с нор-
нормалью равные углы (угол падения равен углу отражения). На
чертеже АВ — нормаль к кривой KL в точке А(х, у), О А — па-
падающий луч, АР — отраженный. Поэтому < ОАВ = < ВАР — а.
Треугольник ОАВ — равнобедренный: О А = ОВ. Сумма углов с
общей вершиной в точке А, расположенных по одну сторону от
МР, равна 180°. Поэтому, так как а + f = 90°, то и а -f p = 90°.
Значит, a-ff = a + p, а f = р. Отсюда заключаем, что треуголь-
треугольник СО А — равнобедренный: ОС = О А.
Если уравнение искомой кривой y = f(x), то tgp = #'(*). Но
с другой стороны, tg Р = пгЦпп ~ пампп • Так как 0А =
= У х2 -f у2, а OD = х, то tg р = ¦ г ¦ . Подставляя сюда
= у', получаем дифференциальное уравнение
837
которое не изменяется от замены х на kx, а у на ky, а потому
оно является однородным. Применяя подстановку у = их, полу-
получим уравнение с разделяющимися переменными
du _ и У\ + ц"
dx ~~ /l-f и« + 1
а после разделения переменных
Иметь в виду, что 1 —, удобно вычислить при помощи
J и 1/1 + «г
подстановки и = -j. Окажется, что он равен — In u ¦
Ответ. у% = С2 + 2Сл; — семейство парабол.
Зеркало должно иметь форму параболоида вращения. Дока-
Докажите, что начало координат'есть фокус параболы.
ВОСЕМНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Дифференциальные уравнения высших порядков, допу-
допускающие понижение порядка.
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Дифференциальное уравнение порядка п(п> 1) имеет вид
fix, У, У', У" #<">) = 0, A8,1)
где по-прежнему х—независимая переменная, у — искомая функ-
функция. Всякая функция у — <р (х), определенная и п раз дифферен-
дифференцируемая в промежутке (а, Ь), называется решением этого урав-
уравнения, если она обращает его в тождество.
Задача Коши. Задача Коши для дифференциального уравне-
уравнения A8,1) порядка п ставится так:
Найти такое решение дифференциального уравнения, чтобы
оно само и его производные до порядка (п—1) включительно
при заданном значении аргумента х = х0 принимали бы заданные
значения, т. е. чтобы это решение удовлетворяло условиям:
у (*„) = Уо, у' (*„) = Уо; у" (*«) = у1; - ; у*~1) fo>) = yf~l\ A8,2)
где х0 и у о, у'0\ у"й\ ... ; yt~X) — заданные числа, которые назы-
называются начальными данными или начальными условиями. Число х0
называется начальным значением независимой переменной, а числа
Уо, Уо> Уо> ¦ ¦ ¦ > У(а~1) — начальными значениями решения и его
производных.
Отличительной особенностью задачи Коши является то, что
значения как искомой функции, так и всех ее производных до
838
порядка (n — 1) включительно задаются при одном и том же
значении независимой переменной х = х0.
Решение уравнения A8,1) имеет в своем составе п произволь-
произвольных постоянных и имеет вид
F (x, Ci, С2, С3 Сп) = 0.
Если произвольные постоянные в это решение входят так,
что задачу Коши можно решить при любых начальных условиях,
то оно называется общим.
Краевая задача. Задача интегрирования уравнения A8,1) назы-
называется краевой, если значения искомой функции у и, возможно,
ее производных задаются не при одном и том же значении неза-
независимой переменной, как это делается в задаче Коши, а на кон-
концах некоторого фиксированного интервала. В более общих случаях
значения искомой функции или ее производных могут задаваться
более чем в двух точках.
Задача Коши иногда называется одноточечной, краевые за-
задачи— двухточечными, а в соответствующих случаях — многото-
многоточечными.
Отметим, что краевая задача не всегда имеет решение, а если
она его и имеет, то оно во многих случаях не является един-
единственным.
На этом практическом занятии будут рассмотрены три типа
дифференциальных уравнений порядка выше первого, которые
допускают понижение порядка и интегрируются в квадратурах.
Первый тип. Уравнения, содержащие только производную
порядка п и независимую переменную
Эти уравнения имеют вид
F (х, уМ) = 0. A8,3)
Если удается это уравнение разрешить относительно у^п\ то
оно записывается так:
</<">-/(*). A8,4)
Общее решение уравнения A8,4) имеет вид
п раз
+ ... +С„*"-Ч A8,5)
Из этого видно, что для получения общего решения уравне-
уравнения A8,4) нужно п раз проинтегрировать функцию / (х) и при-
прибавить к полученному результату многочлен от х степени (п— 1),
коэффициентами которого являются произвольные постоянные.
839
Если задача Коши решается для уравнения A8,4) с ;началь-
ными условиями A8,2), то частное решение уравнения A8,4)
имеет вид
/ (х) dx + i?_ (*_ *0)*
k~2)
(ТгЬг)!
(x - x0)"-2
-x0)+ y0.
A8,6)
(См. В. В. Степанов. «Курс дифференциальных уравнений», стр. 154;
Н. М. Матвеев. «Методы интегрирования обыкновенных дифференциаль-
дифференциальных уравнений», стр. 217).
Уравнения вида у<п> =f(x)
Задача 18,1. Решить задачу Коши при указанных начальных
условиях для уравнений:
2) у" = sin х; у (f) = 1; у' (|) - 2; / (|) = у'" (|) = 0;
3) r/v = е2*; г/ @) = 0; у' @) = -2; у" @) = 3; у'" @) = -1;
ylv@) = 2.
Решение. 1) На основании A8,6) выполним трижды инте-
интегрирование функции — каждый раз в пределах от 1 до х (х0 = 1)
Первое интегрирование:
I
— dx = In x
= In*.
Второе интегрирование:
X X
\ In х dx = х In х г — j dx = x In x — (x — 1).
и
dv
1
= In x
du
V
X
840
Третье интегрирование:
х хх
\[х\пх — (х— \)\dx = I хInxdx — j (x — 1)dx =
u = In x
dv — xdx
du = — dx
x
x
X*
V =
л л:
— -er\ xdx — I (x — l)'dx = %rInx — ~r
(X — IJ _ X2
На основании формулы A8,6), полагая в ней п = 3, имеем:
Уо= 1> У о— "+¦*> У о — —г< хо — 1>
Раскрывая скобки и делая приведение подобных членов, по-
получим
(Проверьте, что начальные условия выполнены).
2) Проинтегрировав четырежды sin* в пределах от 4- до х и
использовав формулу A8,6) при п — 4, при заданных начальных
условиях получим после приведения подобных членов
(Проверьте, что начальные условия выполнены).
3) Проинтегрируем 5 раз функцию ё*х в пределах от 0 до х
(хо = О) и, использовав формулу A8,6) при *п = 5 и заданных
начальйЫх условиях, получим частное решение
у-^ + т^-т^ + т^-Р-т-
(Проверьте, что выполнены начальные условия).
Задача 18,2 (для самостоятельного решения).
Найти общие решения уравнений:
) У"' = 2Ш' 2> VT+*f - 1 = 0;
3) у" = arcsin х; 4) у"' = 27езл: + 120л:3.
Указания. Воспользоваться формулой A8,5).
841
Уравнение 2 представить в виде у" = , д; в уравнении 3
при вычислении J х arcsin х dx воспользоваться справочником.
Ответ. 1) у = In sinx + Ct + С2х + С3х2\
2) у = х\п(х
1 *Ч 'i
3) у = — л:3arcsinx + jxyl— x2 + — arcsinд: + Сг + С2х;
4) у = <?* + х9 + С, + С2х + С2х\
Задача 18,3. В сопротивлении материалов доказывается, что
дифференциальное уравнение упругой линии консоли с постоян-
постоянным поперечным сечением и сосредоточенной на свободном конце
силой Р имеет вид
d4i) Рх
dx*~~"EI'
где w — прогиб консоли в сечении с абсциссой х, a EI — посто-
постоянная величина, так называемая жесткость на изгиб сечения
балки.
Найти решение этого уравнения, удовлетворяющее начальным
условиям:
w @ = 0; о»' (I) == 0.
Решение. Уравнение принадлежит к рассматриваемому типу.
Применив формулу A8,6) при п = 2 и х0 = /, получим
I I
(два последних слагаемых в этой формуле исчезают, так как
имеют место нулевые начальные условия);
, . Р {ХЗ [2Х В
Если не пользрваться сразу готовой формулой A8,6) (хотя
в этом нет ничего предосудительного), то интегрирование .уравне-
.уравнения можно провести так.
Первое интегрирование даст
dx =~Ш
Учитывая второе начальное условие о»' (/) = 0, получаем урав-
уравнение для определения произвольной постоянной
0 = — — — + С- С = — —
Поэтому
dw _ Р х* Р 1*_ Р_ , а ,2,
dx ?7T+?72~~~2l7^X ''
842
Интегрируя вторично, получаем
Используя первое начальное условие, находим
откуда
г _ р13
^2 ~ 3EI'
и поэтому окончательно
_ Р (х3 12 \ Р1*
W '2ElVi~l X)~Wr
что, как легко видеть, совпадает с полученным ранее решением.
Полученное уравнение A8,7)— уравнение упругой линии кон-
консоли. Из него видно, что эта линия — кубическая парабола (па-
(парабола третьей степени).
Задача 18,4 (для самостоятельного решения).
Дифференциальное уравнение изогнутой оси простой балки
постоянного сечения, несущей сплошную равномерно распреде-
распределенную нагрузку интенсивностью q, имеет вид
JL (si _ 2?2N
_ 2V
dx* ~ El \ 2 ~ 2 /
(El имеет прежнее значение, / — длина балки).
Краевые условия (иногда они называются граничными):
при х — 0 w = 0, иначе: w@) = 0;
при х = I w = 0, иначе: w (I) = 0,
т. е. на концах балки прогиб равен нулю.
Указание. Эта задача — краевая, так как заданы условия
не в одной точке, а в двух. Поэтому формулой A8,6) восполь-
воспользоваться нельзя. Можно применить формулу A8,5), найти общее
решение и, пользуясь заданными условиями на краях балки,
определить входящие в общее решение две произвольные по-
постоянные.
Ответ. Общее решение
Первое краевое условие дает С2 = 0, второе — Сх = —
Искомое решение, удовлетворяющее краевым условиям:
843
Задача 18,5. Найти общие решения уравнений:
1) / = 0; 2) у" = а.
Решение. 1) Если у" = 0, то у' — Сь отсюда ~- = Q; dy =
= C,dx;
y = Ctx + C8. A8,8)
2) у" = а; у" dx = adx, но */"<i*— дифференциал у', а потому
dy' = а d*.
у' = ах + С,; g = а* + d;
dy = ах dx + Сх d*;
у = ^ + С^ + С,. A8,9)
Уравнения этого вида часто встречаются в задачах теорети-
теоретической механики, второе из них нам встретится в следующей
задаче.
Задача 18,6 (прямолинейное движение материальной частицы)-
При движении точки по прямой, принимаемой за ось Ох,
основное уравнение движения точки записывается так:
m% = Fx, A8,10)
где т — масса точки; -Л — ускорение, a Fx — проекция действу-
действующей на точку силы на ось Ох.
Найти закон движения точки, падающей под действием силы
тяжести, учитывая, что в начальный момент t — t0 ее координата
х — х0, а начальная скорость равна v0.
Решение. Направим ось Ох вертикально вниз и обозначим
через g ускорение силы тяжести.
Уравнение движения A8,10) запишется так:
т % ^ т$-
Сокращаем на т и получаем
dt* ы'
Умножаем на dt обе части равенства:
Но j?dt — d(~J, поэтому di~\ = gdt. Интегрируя, имеем
-| = gt -f Сi. При t = tQ начальная скорость v = v0. Подставляя
эти значения, получаем
Щ-gto + Cii Cl-v9 — gt0.
844
Теперь
Интегрируя вторично, находим
X — Vot -f- g 2 Г ^2-
Но х = х0 при t == t0, а потому х0 = voto -f С2; С2 = д:0 —
Подставив это значение С2, получим окончательно
X = 0(/ ~j- g 2" Ь х0 — ^0^0-
Если ^0 = 0, то
(Это тот же результат, что и в задаче 17,22, если заменить
х на S, g на а, х0 на So).
Задачу можно было решить сразу по формуле A8,6).
Теперь рассмотрим случаи интегрирования уравнения вида A8,3)
F (х, у(">) = 0, когда решение его относительно у(п) затруднительно
или просто невозможно.
В этом случае полагают, что
х = ?@; y(n) = ty(t). A8,11)
Функции ср (t) и ф (t) должны обращать уравнение _ A8,3)
в тождество.
Дифференциал производной (п — 1) порядка, т. е.
. йу^-^ = [у^-Щ'dx^y^dx. A8,12)
Из A8,11) следует, что dx = ср' @ dt, а потому
dy("-D = ф (/) <р' @ Л.
yW dx
Интегрируя, получим /
yc-i) « J ф (/) 9' (О Л + Сх = фх (/, d).
Теперь рассмотрим
di/C-2) = t/C-D ^д: = ф! (;, Cj) <f' @ Л
и, снова интегрируя, получаем
у(п-2) = j ф1 (^ Ci) f' (/) Л + Q = ь {tt сь С2)
и т. д.
845
В итоге окажется, что
y = *ln{t,Cu С8, .... Сп),
и решение уравнения F (х, у(п)) = О представится в виде
* = 9 @; у *= Ф» (t, си с„ ..., Q.
Иногда выгодно взять
y(n) = t, A8,13)
т. е. принять параметр t равным г/(п).
Задача 18,7. Решить уравнение
(!*• + / = *. A8,14)
Решение. Это уравнение относится к рассматриваемому виду
F (х, //(«>) = 0.
Положим, как это указано выше в A8,13), tf=t. Тогда урав-
уравнение A8,14) перепишется в виде
е* -\-1 == х.
Параметрическое представление заданного уравнения:
x = * + t; y" = t.
На основании формулы A8,12)
dy.' = y"dx — t dx.
Но dx = (e* + i) dt, а потому
dy' = t(e? + l)di.
Интегрируя, находим
у' = J/ (в' + 1) dt = te + t* — j (e* + 0 Л =
= te1 +1* - e* - -J + Ci; у = e'(t - 1) + -? + С
Умножая обе части этого уравнения на Лк:, получим
Но <^лг = (е* + 1) Л, а у' d* = dy. Поэтому
846
Выполнив интегрирование, получаем
а общее решение предложенного уравнения имеет такое парамет-
параметрическое представление:
Задача 18,8 (для самостоятельного решения).
Решить уравнение
(У"Г + *2 = 1.
Указание. Перейти к параметрическому представлению
уравнения, положив х = sint\ у"' = cos/.
Убедиться, что эти значения х и у"' удовлетворяют уравне-
уравнению (cos2 ^ + sin2 ^ = 1).
Учесть, что dx = cost dt, и поэтому
dy" = у"' dx = cos t cos tdt — cos21 dt;
Помещаем промежуточные результаты:
1 3 1
у' = -j t sin t -f -g- cos t — 24 cos & + Cj sin t -f C2.
Учесть, что
sin 2t costdt = — -g- cos 3^ — у cos t\ dy — y' dx ~ y' cos t dt,
a sin t cos t — y sin It
1 3 7 1
Ответ, у = — -g- / cos / + -^ / + щ: sin 2i — -т^ sin 4t —
— ^ cos 2t + C2 sin t + Cs.
Учтено, что
cos 3/ cos tdt — 4- D- sin 4/ + 4- sin'.
Второй тип. Уравнения, не содержащие искомой функции
Уравнение порядка п, не содержащее искомой функции, имеет
такой вид:
fix, У', у", .... #<">) = 0. A8,15)
847
Порядок его может быть понижен на единицу с помощью под-
подстановки ч i
у' = р(х), A8,16)
где р (х) — новая искомая функция.
Эта подстановка приводит к уравнению
f{x, p, р', р", ..., p(«-D) = 0.
Если уравнение A8,15) не содержит ни искомой функции у,
ни ее производных до порядка (k — 1) включительно, т. е. имеет вид
fix, уЮ, */<*+» */<«>) = О, A8,17).
то его порядок может быть понижен на k единиц при помощи
подстановки
&к) = р(х). A8,18)
После определения функции р(х) уравнение A8,17) оказы-
оказывается приведенным к уравнению вида A8,3), интегрирование
которого разобрано выше (см. первый тип).
К этому же типу уравнений относятся и такие, которые содер-
содержат только две последовательные производные, т. е. уравнения
вида
/(уО-О, у<«)) = о. A8,19)
Если это уравнение можно решить относительно г/'">, то оно
принимает вид
у{п) _ «р @<«-1>) A8,20)
и интегрируется подстановкой
?,("-0 = />(*), A8,21)
которая приводит к уравнению
Определив из этого уравнения функцию р (д:) и подставив ее
в A8,21), придем к уравнению вида A8,3).
Задача 18,9. Найти решения уравнений:
1) A-*«)/-*у'= 2; 2) у" = ау'.
(Уравнения не содержат искомой функции у, а потому относятся
к рассматриваемому типу).
Решение. 1) Пусть у' = pix). Тогда у" = %-, и уравнение
перепишется так:
843
dx'
Это линейное уравнение относительно р и J. Разделим его
обе части на коэффициент при ^ и получим
dp х 2
Сделаем подстановку A7,15).
Искомая функция
С x_dx
Подстановка в A8,22) дает:
1
у = 2arcsin x -\-Ci, p = / B arcsin д: + Q).
Ho p — у' = -^, а потому
t/ = arcsin2 x + Cj arcsin д: + C2.
2) Это уравнение относится также к рассматриваемому типу,
так как оно не содержит искомой функции (его можно отнести
и к частному случаю этого типа — к уравнению A8,19)).
Подстановка: у' = р(дс); У" = ¦?•
Уравнение принимает вид
Переменные разделяются: — = adx.
V428 И. А. Каплав
849
Интегрирование дает:
1п? = аж; ?¦ = еах; p =
Но р = j-, а потому —¦ = Схе"*. Снова переменные разделяются:
с с
dy = Схеад; d*; у = —еах -\- С2. Обозначим — —Съ и получим окон-
окончательно
У = Схеах + С2.
Задача 18,10. Найти плоские "кривые, у которых кривизна
постоянна.
Решение. Известно, что кривизна кривой
к = С—,
Найдем решение этого уравнения, полагая, что К — величина
постоянная.
Подстановка: у' = р(х), у"' = ~;
~
dp
dx
A+р2J
Получилось уравнение с разделяющимися переменными. Раз-
Разделяя их, получим:
1 dp _ , 1 р dp ¦ _ г
¦ц у — ах, ^- I у — х -+- Ох.
A+р2J JA + p2J
При вычислении интеграла положить р = tg г; 1 + р2 = sec2 г;
dp = sec2 г dz\
= Г
= Г
2) J (sec2гJ
A+P2) J (sec2г)
p
Но если tg z = p, то sin z = , p a.
850
Поэтому после первого интегрирования получаем
Определим отсюда р:
к тт7*= (х + CiJ; кр2 = {х + CiJ + р'(х
Lp2-p2(x+ CiJ = {х + Ci
= (x + C1f; p=±
Второе интегрирование даст: у + С2 = ± |/ ^ _ (^ 4- Q2.
Заменяя^- — величину, обратную кривизне, радиусом кривизны R
L = R J, получим ответ
(д. + ClJ + (г/ ^ С2)^ = /?».
Полученное уравнение — уравнение семейства всевозможных
окружностей радиуса R.
Таким образом, мы приходим к выводу, что единственными
плоскими кривыми с постоянной кривизной являются окружности.
Задача 18,11 (для самостоятельного решения). Найти частное
решение уравнения у" = 1 + * i _Г^а > удовлетворяющее краевым
условиям: г/@)=1; г/A) = у.
Указание. Подстановка у' =¦ р(х) приведет к линейному
dp х 1 — 2л:2
уравнению —- — t _Л.2 р = . _ а .
Ответ. Общее решение:
i/ = -r^ + Ci arcsin x + С2.
Частное решение:
1 2
г/ = -g- ж2 arcsin x-\- \.
Задача 18,12 (для самостоятельного решения).
Найти общие решения уравнений:
1) у" - 2х (х* - у') = 0; 2) у'у" - /ГТ?1 = 0; 3) г/ = у'.
851
Ответ. \) у — -^xs — * + Ci I e~x'dx + C2, причем входящий
в общее решение интеграл в конечном виде не вычисляется.
2) У = Х~^л/ (x-Ctf -I _lln[(x- Сг) +
Я1 — ( г ^ i с
Задача 18,13 (задача о цепной линии).
Найти уравнение кривой, по которой расположится гибкая нера-
нерастяжимая нить, укрепленная концами в двух данных точках А (х0,
у0) и В(хъ yj, под действием нагрузки, равномерно распреде-
распределенной по ее длине, причем на-
наВ/х„у,)
qc/s
К задаче 18,13
грузка, приходящаяся на еди-
единицу длины, равна q.
Решение. Вырежем на
кривой элемент дуги MN = ds.
На него действуют такие силы:
в точке М — натяжение 7\_в точ-
точке N — натяжение Т + dT и си-
сила тяжести, численно равная
qds. Условия равновесия тре-
требуют, чтобы суммы проекций
этих сил на оси координат были
равны нулю.
Сумма проекций всех сил на ось Ох:
2jX = —Тх + (Г + dT)x = 0 (проекция силы q ds на ось Ох
J] х — Тх + Тх -f (dT)x = 0 равна Нулю).
dTx = 0. A8,23)
Сумма проекций всех сил на ось Оу:
2 У = —Ту + ТУ + (dT)y — q ds = 0,
откуда
dTy — qds = 0. A8,24)
Обозначим для удобства горизонтальную проекцию Тх натя-
натяжения через Я, а вертикальную его проекцию Ту — через V.
Тогда уравнения равновесия A8,23) и A8,24) запишутся так:
dH = 0; dV — qds = 0. A8,25)
Из dH = 0 следует, что Я = const, т. е. горизонтальная проек-
проекция натяжения нити — величина постоянная. Обозначим через а
угол, который касательная к нити в точке М составляет с осью Од;.
852
Второе уравнение в A8,25) преобразуем так:
К. = tg a = у'- V = Ну'; dV = d (Ну') = Ну" dx.
(Величина Н, как постоянная, вынесена за знак дифференциала).
Дифференциал дуги ds — j/~l + у'2 dx. Подставляя эти значения
dV и ds во второе уравнение A8,25), получим
Ну" dx = q У \ +у'2 dx,
и окончательно дифференциальное уравнение искомой линии бу-
будет таким:
Zfi = WV 1+{Tx)- A8-26)
Обозначим ~ = а и введем подстановку ~ = p (x). Тогда
т\ == ~
-т\ == ~ , и уравнение A8,26) станет таким:
Это уравнение с разделяющимися переменными. После разде-
разделения переменных получим
Vl'+P*
Интегрируя это уравнение, найдем
In (р + /1 + р2) = ах + Clt
откуда
р + /1 + р2 = е"х+с'. A8,27)
Из A8,27) надо определить р. Это проще всего сделать так:
умножим обе части A8,27) на р — У 1 + р2 и получим
(р + /1"Тр2) (р - VTT7)
или
—1 = еах+с> (р — уТТр2).
Отсюда, умножая обе части равенства на е~1ах+с*\ получаем
р — VI + р2 = —е-("*4-с,)ш A8,28)
Складываем почленно A8,27) и A8,28):
р = ~
28 и. А. Каплан 853
Правая часть последнего равенства есть sh (ах + 0^, а р =
= y . Поэтому последнее равенство перепишется так: •
j-x = sh (ax + Ci), или dy = sh (ax + Ci) dx.
Интегрируя, находим
у = 1 ch (ax + СО + С2. A8,29)
Перепишем A8,29) в виде
у — C2 = -i-chajx+§] A8,30)
и перенесем начало координат в точку ( -, С2], а новые коор-
координаты точки на кривой обозначим по-прежнему через х и у.
Уравнение A8,29) перепишется в виде
у — — ch ax.
v a
Это уравнение цепной линии. Итак, искомая кривая — цепная
линия.
Третий тип. Уравнения, не содержащие независимой
переменной
Эти уравнения имеют в общем случае такой вид:
f(y, У', У" </<«>) = 0. A8,31)
Понижение порядка на единицу достигается подстановкой у' =
= р (у), где р (у) — новая искомая функция. В этом случае за
независимую переменную принимается не х, а у. Поэтому вторая
и последующие производные должны быть преобразованы так,
чтобы независимой переменной был у:
A8.32)
= (|^ = (l"Il = (?" + ||)^|V + (fp A8.33)
так как ¦? = р\
И Т. Д.
Поэтому уравнение A8,31) перепишется так:
_ n
dy*' ¦"" liF^i ~~
Если удастся найти общее решение этого уравнения, то оно
будет иметь вид
F(y, р, Сь С„ .... Сп^) = 0. A8,34)
854
Так как Р = л|> то A8,34) — уравнение первого порядка, из
которого определится искомая функция у.
Частный случай. Если уравнение A8,31) имеет вид
' f{y, У") = 0 A8,35)
и его удается разрешить относительно у" так, что
'/ = ?&). A8,36)
то интегрирование, кроме указанного приема, можно провести
так: умножим, обе его части на 2у' их и приведем уравнение
к виду
2y'y"dx=2?(y)y'dx, A8,37)
Левая часть этого уравнения 2y'y"dx =' d(y'*), а в правой
части у' dx = dy, поэтому A8,37) перепишется так:
Отсюда следует, что
У'2 = 2 j? (*/) dy + Си у' ~ У2|ф (у) dy + Сх.
Последнее уравнение допускает разделение переменных. Про-
Проинтегрировав его, найдем
т. е. определим х как функцию у.
Следует отметить, что этот прием интегрирования уравнения
A8,35) не дает ничего существенно нового по сравнению с ука-
указанным общим приемом замены у" по формуле A8,32).
К уравнениям вида A8,35) приводятся также и уравнения вида
2>), A8,38)
содержащие только две производные, порядки которых отличаются
на две единицы. В этом случае применяется подстановка
- A8,39)
Задача 18,14. Найти общие решения уравнений:
1) у" = аеу; 2) у'2 +2уу" =0; выделить интегральную кривую,
проходящую через точку A,1) и касающуюся в этой точке бис-
биссектрисы первого координатного угла; 3) у" = --=..
Решение. 1) Уравнение не содержит независимой перемен-
переменной и относится к рассматриваемому типу. Полагаем у' ~р(у).
Вторую производную у" определяем по формуле A8,32):
855
Уравнение запишется в виде
Отсюда
pdp =
Интегрируя, получаем
у = аеу
Находим, что
11 dx
Разделяя переменные, получаем:
~ *
С»
Интеграл / = 1 ¦ ,.„ - .-: вычисляется подстановкой 2аеу +
«= г2; 2^ dy^2zdz; aey dy = zdz\ dy = ~ .Но так как
г2 — d
= —2"^, то
, _ гйг _ 2гйг
2
Поэтому
=2
Окончательно
Г1= \
2) Это уравнение, так же как и предыдущие, не содержит
независимой переменной х, а потому относится к рассматривае-
рассматриваемому типу. Полагаем у' = р(у). По формуле A8,32) у" = ¦? pt
и уравнение запишется в виде
Сокращаем на р (не забудем впоследствии исследовать реше-
решение р = 0):
4
Это уравнение с разделяющимися переменными:
n dp Idp dy O|
2« — = —п: —- = : 2 ш D = -
856
Отсюда, потенцируя, находим, что
2 ^i d , dy Сг
У ' Р ~~ у у ' dx ~~ yjj'
В этом месте мы можем определить произвольную постоянную
d. В условии задачи дано, что кривая в точке A,1) касается
прямой у = х. Следовательно, угловой коэффициент касательной
в этой точке равен у' = 1. Подставляя у' = \; у — 1 в последнее
С
уравнение, получаем: 1 = ~ ; С1=1.
Переписываем уравнение в виде^=-?=и, разделяя перемен-
переменные, имеем
Vy dy = dx.
2 -
Интегрируя, получаем -jу2 = х + С2.
Используем то, что кривая проходит через точку A,1):
а потому
-д- • 1 = 1 + С2; С2 = —j,
1 т т 3*— 1
2
Возводя обе части равенства в степень у, получим окончательно
уравнение искомой интегральной кривой
Исследуйте оставленное решение: р = 0, т. е. -^ = 0; у = С,
Решите вопрос о том, будет ли это решение особым решением
уравнения.
3) Это уравнение также относится к рассматриваемому типу,
так как оно не содержит независимой переменной х. Подстановка,
понижающая порядок на единицу: у' = р (у). По A8,32) у" =
= — о
С этими значениями у' и у" уравнение перепишется так:
dy V"y
Разделяя переменные, получаем pdp = -JL; у = 2Vy + 2C,,;
р2 = 4 Vy + 4Ct. (Произвольную постоянную мы ввели под видом
2Ct с тем, чтобы в последующем извлечь корень из 4);
857
Так как р = -?¦•, последнее уравнение перепишется так:^| =
= 2 к Vу + Cj. Разделяя переменные, получаем — у
2VVS
Интегрируя, получим:
Вычислить интеграл в левой части можно с помощью подста-
подстановки Уу + Ci = г2-
Окончательно получим
х + С2={(Уу-2С1)УУу + С1..
Задача 18,15 (для" самостоятельного решения).
Найти общие решения уравнений:
1) У" =* "jf A + У'9)- Начальные условия у @) = у' @) = 0;
2) УУ" » у'\ 3) уу" — 2уу' In у = у''. ¦
Ответ. 1) у = —a In cos —, или е" cos —= 1;
- 2) у == C2eCi* (здесь положено еСг — С2);
3) у = gc, tjr<c,jt+c,). у = с (особое решение).
Задача 18,16. Найти общее решение уравнений:
Решение. 1) Перепишем уравнение в виде у" — j. Будем
его интегрировать таким приемом: обе части умножим на
2у'dx и получим
2у'у" dx = — -j 2г/' dx. Но у' dx = dy, а потому имеем
d(y") = -±r
Интегрируя получаем:
У 3: у .
Разделяем переменные ± - = dx; интегрируем вторич-
вторично и получаем ± уг V 1 + С±у2 = х + С2. Так как Ci может быть
величиной как положительной, так и отрицательной, то знаки ±
858
перед корнем нет смысла сохранять. Окончательно общее реше-
решение имеет вид '
/1 + с1У* = clX + с2, ¦- ¦-
где С2 = CiC2.
2) Умножаем обе части уравнения на 2у' их и получаем
ЪУ'У" dx = -|— dy (у' их = dy).
или
Интегрируя, имеем
У' =
Разделяем переменные: * у у _— = + dXi
Интегрируем вторично: / = I ' у у, —• и вычисляем / при
помощи подстановки 1 + Ct -/у2 = г2. Отсюда
~5 г2-! зА- Уг2-! 1..-4, гйг
J |_. _ г</г ^, _ Ъ?уг-гйг . А 3(г2—
гпгт1 йу"с,/г;/?=
Поэтому
Окончательно
-2) К 1+С!^=±(х + С2).
859
Задача 18,17 (для самостоятельного решения).
Найти общее решение уравнений:
Указание. 1) Подстановка у' = р(х) приводит к уравне-
уравнению р" = р (уравнение вида A8,36).
2) Подстановка у" = р понизит порядок уравнения на две еди-
единицы и оно примет вид р" = а?р.
Ответ. 1) у = d + С2е* + С3е~х;
2) у = С, + С2х + Cft» + С4е'ах.
Замечание. На следующем практическом занятии эти урав-
уравнения будут проинтегрированы очень просто, как линейные урав-
уравнения.
В заключение этого практического занятия решим две задачи
из теоретической механики.
Задача 18,18. Найти закон прямолинейного движения мате-
материальной точки массы т, которая падает в среде, сопротивление
которой пропорционально второй степени скорости. На-
0<1 чальные условия: в начальный момент движения t = О
координата точки равна х0, а начальная скорость v = v0
(см. чертеж).
Решение. На точку действуют две силы: вес Р и
_ сила сопротивления /. Примем прямую, по которой про-
Р исходит движение, за ось Ох, и направим ее вертикально
вниз.
Основным уравнением динамики точки является урав-
уравнение
mw^Yfk, A8,40)
К задаче ^-,-
18,18 где 2j^fc — равнодействующая всех сил, действующих на
точку.
Так как сила сопротивления по условию пропорциональна
квадрату скорости, то. ее модуль f — k^tnv2, где k?m — коэффи-
коэффициент пропорциональности. Спроектируем на ось Ох действующие
на точку силы:
X
Знак минус перед k?mv2 объясняется тем, что сила сопротивле-
сопротивления всегда направлена в сторону, противоположную движению.
Проекция ускорения w на ось Ох равна 'у~, а проекция ско-
скорости на ту же ось есть ^-, а потому A8,40) перепишется в виде
860
Сокращая на т, получим уравнение
которое является дифференциальным уравнением движения точки.
Это уравнение не содержит искомой функции х и принадлежит
к виду A8,15). Сделаем подстановку: — = р.(/). Порядок урав-
уравнения понизится на единицу и оно перепишется так:
Переменные в этом уравнении разделяются, получается сле-
следующее уравнение:
dP - Aj
g-*2P2
Интегрируя, имеем
dp
или
2k]/g
рость 7r
Так как при t = 0 скорость 7r — p(i) равна v0, то для опре-
определения С, получаем уравнение
1
1
2k Vg Vg~kv0
и уравнение A8,41) запишется в виде
_; ,
Определим отсюда р:
1
~kvo
vj
2k Vg _
Vg-kv0
Vi+kv e2k v-t
=
Vg — kp Vg — H
Решая это уравнение относительно Р = jj- . получим .
dx Vg (Vg + kv0) e2k vtj _ {y-g _ kVo)
kvy K '
861
Умножим числитель и знаменатель дроби на e~k ^. Тогда
V* e~k ^)
dx
dt
V~g VI («* ^ *- e
k
Вводя гиперболические синус и косинус и сокращая на 2,
получим
dx _ Vg Vg sh k Vet + to0 ch k Vet
dt k 'VV V ' ' K ' '
= х0— -g
Если в правой части уравнения числитель умножить на g,
то он станет производной знаменателя. Замечая это, разделяем
переменные и интегрируя получаем
х = -Jj In (-/g ch k Vgt + kv0 sh k Vgt) + Ct.
Определим произвольную постоянную С2.
На основании начальных условий х = хп при t = 0. Поэтому
^i C2 (chO=l;
Окончательно
Уравнение A8,43) дает закон изменения скорости в зависи-
зависимости от времени. Очевидно, что при неограниченном возраста-
возрастании времени (t -*• оо) дробь в правой части
этого уравнения стремится к единице, а
скорость Ь -*• УЛ. Отсюда мы можем за-
заключить, что движение точки асимптоти-
асимптотически приближается к равномерному, ско-
V~g
рость которого равна -f-, причем эта ско-
скорость не зависит от начальных условий.
Задача 18,19 (для самостоятельного
решения).
Материальная точка массы т брошена
из начала координат вертикально вверх
со скоростью v0, и движение происходит
в среде, сопротивление которой пропорцио-
пропорционально квадрату скорости. Определить:
1) высоту h, на которую поднимется точка
и 2) скоррсть и, с которой точка возвратится в исходное поло-
положение.
Считать, что движение происходит по оси Ох, которая на-
направлена вертикально вниз.
7
Р
0
х
К задаче 18,19
852
Указание. Модуль силы сопротивления / = k'mv*, где k*m —
коэффициент пропорциональности. Так как сила сопротивления
направлена в сторону, противоположную движению, то она при
движении вверх направлена вертикально вниз.
Проекции на ось Ох, силы веса и силы сопротивления —
положительны:
Уравнение движения после сокращения на т запишется так:
3F = * + *'(?)'• 08,44)
По условию задачи требуется определить скорость в зависи-
зависимости от положения точки. Поэтому здесь выгодно проинтегри-
проинтегрировать уравнение способом, указанным для интегрирования урав-
уравнения A8,36). Перепишем его в виде
и умножим обе части на 2-^-dt:
odx_dH_
dt dt* JA
Если числитель дроби в левой части умножить на №, то он
станет равным производной знаменателя, а потому, интегрируя,
получим
Определив произвольную постоянную (при ^ = 0 * = (), ^ =
= 1>о) > найдем закон скорости в зависимости от положения точки
в виде
Чтобы найти высоту подъема, надо в этом уравнении взять
dx n
jf = 0, так как подъем точки прекратится в тот момент, когда
ее скорость станет равной нулю. Обозначая высоту подъема
853
через h и подставляя в A8,45) х = h, -^ = 0, получим для опре-
определения высоты подъема h уравнение
тт^:=е2т' AМ6)
отсюда
А = ж In ——
2*2
При движении вниз надо учесть, что начальная скорость
v0 = 0, а х0 = h. Движение вниз описывается уравнением
dt* —8 R \dt
(см. предыдущую задачу). Интегрируя это уравнение тем же спо-
способом, что и уравнение A8,44), получим
Из начальных условий при х0 = h, v0 = 0
-
а потому
или
1°\8 — Ь*[щ~) \~—2k2x-\-\ng
Когда точка возвратится в исходное положение в начало
координат, то х станет равным нулю, а скорость в этот момент
dx
пусть равна и, т. е. -$ = ". поэтому
In [g — k2u2] = ln g + 2/г/е2;
a k2u2 = e'n s+2A*! =
Используя A8,46), получаем
g-k*u* = g- 8
Окончательно скорость, с которой точка возвратится в первона-
первоначальное положение, равна
u = vo~ ' e
834
ДЕВЯТНАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Линейные дифференциальные уравнения высших порядков.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Линейным дифференциальным1 уравнением порядка п на-
называется уравнение вида
У{п) + Pi (х) г/*"-1» + Рг (X) г/(л-2> + . .. + Р;Г, (*) у' +
+ Pn(x)y = f(x), A9,1)
где / (х) — функция независимой переменной х, по которой вы-
вычислены производные.
Отличительной чертой линейного уравнения является то, что
искомая функция у и все ее производные входят в это уравне-
уравнение в первой степени.
2. Предполагается, что функции pt(x) (i = 1, 2, ..., п) и
правая часть уравнения — функция / (х) непрерывны в проме-
промежутке (а, Ь). Случаи а = — со, 6 = -f со не исключаются. Функ-
Функции р,(х) называются коэффициентами уравнения.
3. Задача Коши (см. восемнадцатое практическое занятие)
для этого уравнения при сделанном предположении (п. 2) всегда
имеет единственное решение при любых начальных условиях
A8,2), лишь бы точка х — хй находилась в промежутке (а, Ь)
непрерывности функций р, (х) и / (х).
4. Если в уравнении A9,1) правая часть f{x) тождественно
равна нулю в-промежутке (а, Ь), то уравнение A9,1) принимает
вид
У(п) + Pi (х) #<«-'> + р2 (х) г/<"-2> + ... + р_, (х) у' +
+ Рп (х)У = 0 A9,2)
и называется в_этом случае линейным однородным уравнением,
соответствующим уравнению A9,1). При ?(х)фО уравнение A9,1)
называется неоднородным.
На этом практическом занятии мы будем заниматься только
однородными линейными уравнениями, причем нами будут рас-
рассматриваться два вида этих уравнений: 1) уравнения, в которых
коэффициенты при производных являются функциями независи-
независимой переменной, и 2) уравнения, в которых коэффициенты при
производных постоянны, так называемые линейные однородные
уравнения с постоянными коэффициентами.
5. Если функция ух (х) является решением линейного одно-
однородного уравнения A9,2), то и С^ (*) — произведение ее на
произвольную постоянную величину Сг — также является реше-
решением этого уравнения.
6. Если функции г/х (х) и у2 (х) являются решениями линей-
линейного однородного уравнения A9,2), то и их сумма yL (x) + у2 (х)
также является решением этого уравнения.
865
Если функции ух(х), уг(х), ..., уп(х) являются решениями
уравнения A9,2), то и функция
У = С1У1 (х) + С2у2 (х)+ ... + С„уп (х), A9,3)
где Си С2, ..., Сп — произвольные постоянные, также является
решением этого уравнения. Функции Ух(х), у2(х), .,., уп(х) на-
называются частными решениями уравнения A9,2).
7. Две функции yt (x) и уг (х) называются линейно независи-
независимыми в промежутке (а, Ь), если их отношение ^4-т в этом про-
промежутке не является постоянной величиной.
Если же отношение ^Ц^ — величина постоянная, то эти функ-
Уг \х)
ции называются линейно зависимыми.
8. Если имеется п функций уъ у2,. . ., уп, то они называются
линейно независимыми в промежутке (а, Ь), при условии, что
равенство
<*ii/i + <*2У2 -1 + апУп =0,
где a, (i = 1,2,. . ., п) — постоянные, может выполняться только
тогда, когда все коэффициенты а, равны нулю.
Если же это равенство в промежутке (а, Ь) имеет место, когда
хотя бы один из коэффициентов а не равен нулю, то функции
Уъ У г, • • •> Уп называются линейно зависимыми.
9. Если функции у у, у2,. . ., уп являются решениями уравне-
уравнения A9,2) и в промежутке (а, Ь) они линейно независимы, то
общее решение этого уравнения имеет вид A9,3):
У = Cji/i + С2у2 + Csy3 + ¦ ¦ ¦ + Спуп-
Эта формула определяет структуру общего'решения линейного
однородного уравнения A9,2) порядка п и указывает способ" построе-
построения общего решения. Таким образом, чтобы найти общее реше-
решение линейного однородного уравнения, надо найти п его частных
линейно независимых в (а, Ь) решений, каждое из них умножить
на произвольную постоянную величину и все эти произведения
сложить.
Система линейно независимых решений.уравнения A9,2) назы-
называется фундаментальной.
10. Для того, чтобы функции уь у2 y,i были линейно неза-
независимы в промежутке (а, Ь), необходимо и достаточно, чтобы их
так называемый определитель Вронского
W(x) =
У1
У'х
n
Ух
Уг
У'ш
It
Уг
... Уп
...Уп
п
... Уп
был отличен от нуля хотя бы в одной точке х0 промежутка (а, Ь),
в котором непрерывны коэффициенты уравнения A9,2).
Таким образом, чтобы проверить линейную независимость функ-
функций Уь у2, • ¦ ¦, Уп, надо составить их определитель Вронского
W (х) и убедиться, что хотя бы при одном значении х из промежутка
(а, Ь) он не равен нулю.
11. Уравнение A9,2) имеет л и только л линейно независимых
решений.
12. Если известно частное решение у^{х) линейного однород-
однородного уравнения A9,2), то его порядок можно понизить на единицу
при помощи подстановки
^ A9,4)
где и = и(х) — новая искомая функция.
Полученное в результате подстановки A9,4) уравнение также
будет линейным.
1. Линейные однородные уравнения с переменными
коэффициентами
Задача 19,1. Доказать, что если Ух(х) — частное решение ли-
линейного однородного уравнения второго порядка
y" + Pi(x)y' ±рг(х)у=:0, A9,5)
то второе его частное решение, линейно независимое с первым,
находится по формуле
0.x.
Решение. Подставим A9,4) в данное уравнение, помня, что
(J udx)' = и. Получим v • .
*= У") udx-+ у [и + у[и + ухи'
1
0 = (У"+ Pi (х) У[ + Р* (х) ух) I udx + У1и' + [2У; +¦ Pl (х) yju
Это выражение равно
нулю, так как Ух —
решение данного
уравнения
(для сокращения записей вместо ух (х) мы пишем #х).
867
Получаем уравнение
ухи + {2у[ + р1У1) и = О,
порядок которого понижен на единицу по сравнению с данным.
Оно является также линейным однородным уравнением первого
порядка, допускающим, как известно, разделение переменных.
Разделяя переменные, получим
du = _ 2у[ -f р^ dx
« Ui
Интегрируя, будем иметь
In и = — J ~- dx — J p! dx = — 2 In yt — J px dx.
Отсюда
—2 In #, — f ,p,rf* —?!nft — f p,dx \ny~! — f pirfx л — J p,rfA:
у,
Заменяя в выражении A9,4) у = yt\ udx функцию и только
что найденным значением, получаем
— dx. A9,6)
Найденное значение у и будет вторым частным решением
у2 (х) данного уравнения. Его линейная независимость с первым
видна из того, что отношение — не является постоянной вели-
величиной.
Решение этой задачи показывает, что знание одного частного
решения уравнения A9,5) позволяет найти второе линейно неза-
независимое с первым частное решение при помощи формулы A9,6),
которая требует выполнения двух интегрирований (говорят — двух
квадратур).
Тем самым для определения общего решения линейного одно-
однородного уравнения второго порядка достаточно знать одно его
частное решение.
Ниже предлагаются задачи на применение этой формулы.
Задача 19,2. Найти общее решение уравнения (х—\)у" —
— ху' + у — О, если известно, что его частное решение ух = х
(проверьте, что оно действительно является решением). Найти
частное решение при начальных условиях у@) = 1; у' @) = 2.
Решение. Данное уравнение — линейное однородное уравне-
уравнение второго порядка. Прежде всего приведем уравнение к виду
A9,5), в котором коэффициент при у" равен единице. Получаем
868
Здесь коэффициент при у' — функция р1(х) = —jzzr\- ^ы-
числим прежде всего входящий в формулу A9,6) интеграл —
= х + \п(х— 1)
(произвольную постоянную вводить не следует, так как в после-
последующем она объединится с произвольной постоянной, вводимой
при построении общего решения).
Теперь, входящее в A9,6) выражение
— f р, dx x-t-In (х—1) х In (л; — 1) х
е J =е =е е =е (х— 1),
а формула A9,6) дает
Уг =
1
и = —
д;
dv = exdx
¦J?
du =
v = e
dx\ = x
-idx
x
= x
dx = x
I*
— ex = ex.
X
Итак,
= ех
Умножая ух на Съ у2паС2 и складывая произ-
произведения, получим общее решение заданного уравнения
y = ClX + C2e*. A9,7)
Указание. Чтобы найти частное решение, удовлетворяющее
начальным условиям (т. е. чтобы решить задачу Коши), надо
начальные условия подставить в систему уравнений, которая
состоит из общего решения и его производных до порядка (п—1)
включительно; определить из этой системы произвольные постоян-
постоянные и подставить их значения в найденное общее решение. Полу-
Полученное выражение и будет искомым частным решением.
Дифференцируя найденное общее решение A9,7) один раз (так
как п = 2, то п— 1 = 1), получаем систему
у' = СХ + С2ех
\
J •
подставляем в нее начальные условия: г/@) = 1; у' @) = 2;
l.= d -0 + C2e°\ 1=Са I
2 = Сх + С2 | или 2 = d + CJ ;
/-« 1 . п 1
V-,o — 1, v>i — 1,
искомое частное решение у = х -\- ех.
369
Задача 19,3 (для самостоятельного решения).
Найти общие решения линейных однородных уравнений второ-
второго порядка и их "частные решения по известным первым частным
решениям этих уравнений и заданным начальным условиям:
1) (l-\nW + ±y>-±y = 0; У1-=\пх. *
Начальные условия: у A) = 2; у' A) = 4;
2) y" + tgx -у' + cos2 х ¦ у = 0; уг = cos (sin x);
Начальные условия: у@) = 3; у' @) = 2;
3) y" — ctgx ¦ у' + sin2* • у = 0; ух = cos (cosx);
Начальные условия: у ьи = 0; у' НН = 1;
4) y" + -jy'~^y = 0; У1 = х*;
Начальные условия: уC) = 1; у' C) = -g-.
Указание. Во всех задачах использовать формулу A9,6).
В первом уравнении разделить обе его части на 1 — In x.
Учесть
, что — J рг (х) dx = — J хA_^1пх) = In (In x — 1),
dx
dx
Первый интеграл вычислить по частям. Окажется, что второй
интеграл взаимно уничтожится с тем, который получится при
применении интегрирования по частям к первому интегралу.
Ответ.
№
1
2
3
4
Второе частное
решение
Уг — х
уг = sin (sin x)
i/2 = sin (cos x)
Общее решение
у^С^пх + С%х
У = СХ cos (sin x) +
+ C2sin(sin;t)
У — Сх cos (cos х) +
+ C2sin (cos x) '
у = С1Х* + С2±
Частное решение
у = 2\пх-\-2х
у = 3 cos (sin x) +
+ 2 sin (sin x)
у = — sin (cos x)
870
Задача 19,4 (для самостоятельного решения).
Зная первое частное решение линейных однородных уравнений
второго порядка, найти их общие решения:
1) 4*V + 5«/ = 0; у1 = У~х cos (In x);
2) y>
Указания.Для отыскания второго частного решения при-
применить формулу A9,6).
В первом уравнении разделить обе его части на коэффициент
при у". Учесть, что pL (х) = 0, так как уравнение не содержит у\
a J рг(х) dx = J 0 • dx = С, причем, можно взять С — I, ибо в
последующем произвольная постоянная будет введена.
Интеграл j ж со^Aп х) = tg (In x) (подстановка \пх = г).
Во втором уравнении — j px (x) dx = — I sin x — cos x +
dx = COS * + Sin X + ln (Sin * + COS ХУ>
gcos x + sin x +ln (sin x + cos x) —- gcos x + sin x (sin X -4- COS XY
u - esin , re™x + *inx(sinX+cosx) d _
У* — е J g2 sin * UX —
_ gsln x Г gcos д: - sin *(sjn ^ _|_ cos x) fa = gsin д: (_ gcos x - sin xy.
yt = -**»*.
(Знак минус при написании общего решения ввести в произволь-
произвольную постоянную).
Ответ. 1) у2 = y~xsin(\nx);
общее решение:
у = d Ух cos (In x) + С2Ух sin (In x),
или
у = |/"jc (d cos (ln x:) + C2 sin (ln д;));
2) Уг = ~<?°$х;
общее решение:
у = desin * + Сое005 *.
871
Задача 19,5. Доказать, что если Ух и у2— два линейно неза-
независимых частных решения линейного однородного уравнения вто-
второго порядка
У" + рЛх)у' + Рг(х)у = О, A9,8)
. W (х) , . " [
то
у
где W (х) =
Ух Уг
У'х Уг
= УхУг —
Решение. Так как yv и у2— решения заданного уравнения,
то имеет место система уравнений относительно неизвестных
Pi(x) и р2(х), подлежащих определению:
или
Исследуем определитель этой системы:
Ух
У'г
Ух
Уг
Ух
Ух
У*
Уг
Ух
У'х
Уг
У'г
A9,9)
A9,10)
Строки и Поменяли
столбы местами
поменяли строки и из-
местами меняли знак
перед опре-
определителем
Так как решения ух и у2 по условию линейно независимы,
то W (х) ф 0 и система A9,9) имеет решение и притом единст-
единственное:
Рх(х) =
—Уг Уг _
Ух Ух
Уг Уг
-W{x)
W'(x)
W(x)
На основании
19,10
(Следует иметь в виду, что производная определителя Вронского,
как легко проверить, есть определитель, который отличается от
определителя Вронского тем, что в нем последняя строка содер-
содержит производные порядка на единицу большего, чем в опреде-
определителе Вронского).
Из первого уравнения системы A9,9) следует, что
УхРг(х) = —у" — у1'рх(х),
откуда и получается доказываемое значение р2 (х).
Найденные выражения коэффициентов Pi(x) и р2 (х) урав-
уравнения A9,5) позволяют составить линейное дифференциальное
уравнение второго порядка, если известна его фундаментальная
система решений.
872
2. Линейные однородные дифференциальные уравнения
с постоянными коэффициентами
Характеристическое уравнение. Если в уравнении
A9,2) коэффициенты постоянны, то оно называется линейным
однородным уравнением с постоянными коэффициентами и имеет
вид
yw + aiy{n-i) + а2у(п-2) + ... +an-ly' + a,jj = 0, A9,11)
где все а,¦ — (i = 1, 2, ... , п) — вещественные числа; у — искомая
функция; х — независимая переменная.
Решение этого уравнения ищется в виде
у = е"х. A9,12)
Это приводит к алгебраическому уравнению степени п
kn + ulkn-i + a2k»-2 + • • • + пп-ik + ап = 0, A9,13)
которое называется характеристическим.
Таким образом, чтобы составить характеристическое уравне-
уравнение A9,13), надо в уравнении A9,11) заменить производные сте-
степенями неизвестной величины к, причем степень k должна быть
равна порядку соответствующей производной, а сама искомая
функция у заменена единицей.
1. Если все корни характеристического уравнения ku k2,
k3, ... kn — числа вещественные и среди них нет равных между
собою, то, подставляя значение корней в A9,12), получим п
частных линейно независимых решений уравнения A9,11) в виде
уг = в*.*; уг-= в*.*; у3 = ек'х\ ... ; уп = ek»x. A9,14)
2. Если все корни характеристического уравнения — числа
вещественные, но среди них есть равные, то каждому корню ki
кратности / соответствует / линейно независимых частных реше-
решений уравнения A9,11)
Ух = ek'x; уг = хе!ч*\ Уз = я*^ ... ; Уп = xl~4ki*. A9,15)
3. Если среди корней характеристического уравнения име-
имеются комплексные, но не равные между собой, то каждой паре
сопряженных комплексных корней а + pi и а — Щ соответствуют
два частных линейно независимых решения уравнения A9,11)
вида
e^cosp* и e^sinp*. A9,16)
Если же среди комплексных корней характеристического урав-
уравнения имеются кратные комплексные корни, то корню а + Щ
кратности / (корень а — pi имеет ту же кратность) соответствует
2/ частных линейно независимых решения уравнения A9,11), ко-
которые имеют вид
cos
873
Задача 19,6. Найти решения линейных однородных диффе-
дифференциальных уравнений, удовлетворяющие указанным начальным
условиям:
1) y"-3y' + 2y = 0; у@) = 2; г/' @) = — 3;
2) у"-Ъу'+ 8у = 0; уф)=1; . у'ф) = 0;
3) у* + 9у'+20у = 0;уф) = 0; г/' @) = — 1;
4) У'-У = 0; г/@)=1; г/' @) = 1
5) у"-2у'+у = 0; «/@) = 2; у'@) = 4;
6) у" + 4у' + 4«/ = 0; У B) = 4; у' B) = 0;
7) 1Г-2у' + 2у = 0\ у(к) = -2; г/» = -3;
8) у" + у' + у = 0; у@) = 2; y'(Q)=-j;
9) у" + и*у = 0; у @) = а; у' @) = v0;
Щу: + У' = 0; уф) = 2; у' @) = 5.
Решение. 1) Составляем характеристическое уравнение вида
A9,13), согласно сделанному указанию: заменяем у" на k2, у' на
k, а у на 1.
Получаем &2 — 3& + 2 = 0.
Решая это квадратное уравнение, находим, что kx— I; k2 = 2.
Корни характеристического уравнения — числа вещественные и
не равные между собою. Согласно A9,14) частными решениями
уравнения будут функции: У\ = ех; у2 = е2х. Легко видеть, что
функции эти линейно независимы!—=ех Ф const]. Общим реше-
решением, согласно A9,3), будет
у^С^.+ Сгв2*. (А)
Теперь определим произвольные постоянные Сх и С2 по за-
заданным начальным условиям. Прежде всего найдем производную
у• = С1е* + 2Сге*\ (В)
Пользуясь указанием стр. 301 подставляем начальные усло-
условия в (А) и (В), и для определения Сх и С2 составляем систему
уравнений
2 = С1+ С2
С
Решая эту систему, получаем: Сг = 7, Са = — 5.
Подставляя эти значения в (А), найдем решение заданного
уравнения, удовлетворяющее начальным условиям:
у = 7ех — 5е2х.
2) Характеристическое уравнение вида A9,13) получим, заме-
заменив у" на k2, у' на k, а у на 1. Оно запишется так: k2 — 6k-\-
+ 8 = 0.
874
Решая это квадратное уравнение, найдем, что кг — 2; k2 — 4.
Корни его.— числа вещественные и не равные между собою. Со-
Согласно A9,14), частными решениями уравнения будут функции:
ух = е2х; у2 = е*х. Функции эти линейно независимы, так как
У? = е2х ф const. В соответствии с A9,3) общим решением урав-
уравнения будет
у = Се2* + C2eix. (A)
Чтобы найти решение, удовлетворяющее начальным условиям,
найдем производную полученного общего решения
у' = 2С^Х + 4С2еЧ (В)
В уравнения {А) и (В) подставим заданные начальные усло-
условия и получим для определения произвольных постоянных С и
Са систему уравнений:
1= С + С2
из которой следует, что С = 2; С2 = — 1.
Подставляя эти значения в общее решение (А), находим ре-
решение, удовлетворяющее начальным условиям:
у = 2е2х — е4х.
3) Это уравнение решим без подробных объяснений. Характе-
Характеристическим уравнением будет № + 9k + 20 = 0; кг = —4; k2 =
= —5 (корни — вещественные и разные); частными решениями,
согласно A9,14), — функции yL = e-4x; y2 — e-5x. Общее решение
на основании A9,3): у = Схе~4х + Сф~Ьх. Находим у' = — iCxe~ix —
— 5С2е~5х. Система уравнений для определения произвольных
постоянных на основании начальных условий:
0= Сг+ С2;
-1 = -4Сг-5Сл;
Сх = — 1; С2 = 1. Искомое решение, удовлетворяющее началь-
начальным условиям:
у = —е-4* + е~Ъх.
4) Характеристическое уравнение: k?—1 = 0; корни его &х =
= 1, k2 = —1 — числа вещественные и не равные между со-
собою. Частные решения, согласно A9,14), имеют вид: yL = ex\
у2 — е~х. Общее решение в соответствии с A9,3)
у = С,е* + С2е-Х.
Вместо этого вида общего решения в прикладных науках оно
записывается часто через гиперболические синус и косинус. Так
е*_ е-х ех\е-х
как sh х = —5— > а с" х — —2—' то
ех = ch^ + sh^\
.e-* = ch*-sh*j- A9'18)
875
Подставляя эти значения в общее решение, получим
у — Ci (ch x + sh x) + С2 (ch x — sh x),
или
у = (С2 + С,) ch х + (С, - d) sh x.
Обозначим: С2 + Ci = с^ С2 — Ci = с2, и тогда общее реше-
решение запишется в виде
у — Сх ch х + с2 sh х.
Из начальных условий Сх = 1; С2 = 0. Решение, удовлетво-
удовлетворяющее начальным условиям:
у = ех, или г/ = ch х + sh x.
5) Составляем характеристическое уравнение
k* — 2k + 1 = 0.
Его корни &х = 1, &2 = 1 — числа вещественные, но равные
между собою {kv = k2). Поэтому частные решения надо записать
не в виде A9,14), а в виде A9,15):
У\ = ех\ у2 = хех.
Легко заметить, что в этом случае второе частное решение
получается умножением первого частного решения на независи-
независимую переменную (в данном случае на х). Решения эти линейно
независимы, так как - = х ф const.
У\
Общее решение, согласно A9,3), имеет вид
у = Схех + С2хех, или у = ех (Ск + С2х); (А)
Подставляя начальные условия в общее решение и его про-
производную, получим систему уравнений для определения произ-
произвольных постоянных:
2 = d;
4 = CL + С2;
Сх = 2; С2 = 2. Искомое решение, удовлетворяющее начальным
условиям:
у = 2е* A + х).
6) Характеристическое уравнение имеет вид № + 4& +¦ 4 = 0.
Его корни kx = —2; &2 = —2 — числа вещественные и равные
между собой. Согласно A9,15) в этом случае частными реше-
решениями являются функции
Ух = е-2*; уг = хе-*х.
Общее решение
у = Cie-2* + С2хе~2х,
или
у = е~2х (d + С2х);
у' = е~2х (С, — 2Ci — 2С2х).
Система уравнений для определения d и С2 из начальных
условий:
44 С + 2
О = 2С, + ЗС2
d = —12е4; С2 = 8е~4. Искомое решение
у = 4е*~2* Bх — 3).
7) Характеристическое уравнение запишется так: &2 — 2k +
+ 2 = 0. Его корни &! = 1 -f-1-> ^2 = 1 —J — сопряженные комп-
комплексные числа вида а + Щ- Частные решения имеют вид A9,16),
причем в этих решениях надо взять а = 1; р = 1:
у1 — ех cos х; у% — ех sin x.
Общее решение:
у = Суех cos х + С2ех sin x,
или
y = ex(Clcosx + C2sinx). (A)
Для определения произвольных постоянных из начальных
условий надо найти у':
У' = е* [(С2 + d) cos x + (С2 — СО sin x\. (В)
Подставляя в (А) и (В) начальные условия, получим систему
уравнений для определения произвольных постоянных:
—2 = — е* d
-3 = -<* (d + С2),
Искомое решение, удовлетворяющее начальным условиям, полу-
получим, подставляя эти значения в общее решение (А):
у = ех~п B cos х + sin x).
8) Характеристическое уравнение:
„ , 1 . /3. . 1 /3 .
Его корни: kl = —5" |~ 2 r> 2 = —2~ — ~Т1 — комплексные
1 /~^
сопряженные числа вида а ±Щ\ а — —г"> Р — 2 ' Согласно
A9,16), частными решениями будут функции:
877
(очевидно, что эти функции линейно независимы). Общее решение
в соответствии с A9,3) запишется так:
у = Схе~~" cos & х + С2е~~* sin
_
или, вынося е 2 за скобку:
у = е~~х (d cos *Jх + С2 sin ,^ x). (А)
Чтобы определить произвольные постоянные на основании
начальных условий, найдем у':
C2+^C^m^x]. (В)
Используя начальные условия, из уравнений (А) и (В) полу-
получаем систему уравнений для определения Сг и С2:
отсюда Cx = 2; С2 = КЗ. Подставляя эти значения в общее ре-
решение, найдем искомое решение
9) Это уравнение является уравнением свободных гармони-
гармонических колебаний. Оно имеет очень важное значение в механике
и других прикладных науках.
Характеристическое уравнение имеет вид k2 + u,a = 0; kx = ш;
&2 = —«>t — корни комплексные сопряженные, причем а = 0; [3 = со.
Частные решения, согласно A9,16), имеют вид:
ух = cos соя; у2 = sin соя.
Следует запомнить, что. когда действительная часть комплекс-
комплексного корня характеристического уравнения равна нулю, т. е. когда
корни чисто мнимые, то частные решения содержат только три-
тригонометрические функции, множитель же е°-х при них отсутствует,
так как при а = 0 еах = 1.
Общее решение, согласно A9,3):
у = Сх cos со* + С2 sin соя; A9,19)
у' = —Схи> sin соя + С2со cos соя
(рекомендуется запомнить это общее решение уравнения свобод-
свободных гармонических колебаний. Встречаться оно будет очень
часто).
Определяем Сх и С2 из начальных условий:
878
Отсюда С = а; С2 = —. Подставляя эти значения произволь-
произвольных постоянных в A9^19), получаем искомое решение в виде
у = a cos wx + — sin шх.
Это решение выгодно представить в другом виде. Положим
a = Asin<p; — = Acosf. A9,20)
Тогда
у = A cos <ох sin f + A sin сод; cos o> = Л (cos шх-sin <j> + sin со cos <j>).
Окончательно
у = Л sin (сол: + «р). A9,21)
Возводя в квадрат обе части каждого из равенств A9,20)
н складывая их почленно, получим:
+^
Механический смысл величин Л, со и у: Л — амплитуда коле-
й^ со —частота колебаний; у — начальная фаза.
Движение, определяемое рассматриваемым уравнением у" +
+ <«J# = 0, г- периодическое. Его период Т = —.
10) Характеристическое уравнение: &2 + & = 0. Его корни
ki = 0; fe2 = —1- Корни вещественные и разные. Частные решения
на основании A9,14)
«/i=l; У2 = е~х-
Общее решение в соответствий с A9,3)
- у = СИ- Сге~х.
Решение, удовлетворяющее начальным условиям:
(С1 = 7; С, = -5).
Задача 19,7 (для самостоятельного решения).,.
Найти общие решения уравнений (независимая переменная t):
1)х" — 4х' = 0\ 2)х" — 9л; = 0; 3) х"-7х'+ Юх = 0;
4) х" + 5х' = 0; 5) х" — 16л; = 0; 6) х" + х' + х = 0;
7) х" + 2х' + 4х = 0; 8) х" — 4х'-+4х = 0; 9) л;" + 6л;' + 9л; = 0;
Ю) х"—Ах' + 29х.= 0; 11).х" + Ах = 0; 12) х" + \1х = 0.
Ответ. 1) а: = С1 + С2е«; 2) л; = Qe3' + Сге~3'; 3) д: = Cje2^
+ С2е«; 4) х => d + С2е-5'; 5) лГ= Схе« + С2е-«; 6) х = е~т х
X (схcosi^f + C2 sin^f); 7) x = er*(СгcosVSt + C2sin/3/);
8) x = e2/(Ci + C,0; 9) * = б' (Ct + CO; 10) x = e21 (C cps_5^ +
+ C2sin50j_ 11) x = C1cos2t + C2sin2t; 12) л; = Cxcos|/l7^ +
+ С sin/17/.
879
Задача 19,8 (для самостоятельного решения).
Материальная точка массы т движется по прямой, притяги-
притягиваемая к неподвижному центру силой, прямо пропорциональной
расстоянию точки от центра притяжения. Сопротивление среды
отсутствует. Определить закон движения точки, если в началь-
начальный момент движения / = О, х = х0, v — v0, т. е. х @) = х0,
v @) = v0.
Решение. Прямую, по которой происходит движение точки,"
примем за ось Ох, причем положительным будем считать направ-
направление направо. Начало координат поместим в центр притяжения.
Коэффициент пропорциональности возьмем для удобства после-
последующих выкладок равным k2m. Сила
О х F Д притяжения
здесь \х\ — расстояние точки от на-
начала координат.
. = Определим модуль силы F.
" т Модуль вектора — величина по-
2)х<0 ложительная. Поэтому перед моду-
К задаче 19,8 лем силы надо поставить знак плюс,
когда точка находится справа от
начала координат (х > 0), и знак минус, когда она находится
слева от него (х<0). Таким образом, модуль силы
F = 9±k2mx. (A)
Когда точка находится справа от начала координат (х > 0),
то сила притяжения к началу координат направлена в отрица-
отрицательную сторону оси Ох, а потому составляет с осью Ох угол
в 180°, a cos(x,F) = — 1.
Если же точка находится слева от начала координат (х < 0),
сила притяжения направлена в положительную сторону оси Ох
и составляет с нею угол_в 0°, а потому cos (*, F) == +1.
Таким образом, cos (x,F) = ^p I, причем верхний знак соответ-
соответствует х > 0, а нижний х < 0.
Известно, что проекция вектора на ось равна модулю вектора,
умноженному на косинус угла между вектором и осью. Умножая
(А) на cos (л:, F) = ^1, получаем
Fx = — k*mx, (В)
независимо от того, где находится на оси Ох притягиваемая
точка.
Подставляя это значение проекции силы в основное уравне-
уравнение динамики:
получаем дифференциальное уравнение движения
m •*• — k2my MQ 99*1
и, сокращая на т, имеем
d*x ,„
= — k2x.
dt*
Перепишем это уравнение в виде
d*-x
-ж + к*х = 0. (С)
Это уравнение, как мы уже говорили, называется уравнением
свободных гармонических колебаний. Мы замечаем, что оно яв-
является линейным однородным уравнением второго порядка (иско-
(искомая, функция— х, независимая переменная — /).
Его характеристическим уравнением будет
/2 + Ь2 = 0. (?))
Неизвестное характеристического уравнения мы обозначили
не буквой k, как это было в предыдущих задачах, а /, так как
k входит уже в коэффициент пропорциональности.
Решая уравнение (D), находим, что / — ±ki, а потому част-
частными решениями уравнения (D) будут:
Xi = cos kt; x2 = sin kt,
и его общее решение
х = Сх cos kt + C2 sin kt.
Из начальных условий задачи следует, что Сг = х0; С2 =
= ~- (определите это самостоятельно), поэтому решением задачи,
удовлетворяющим начальным условиям, будет
х — x0coskt +-~sinkt. (E)
Далее удобно поступить так, как это было сделано в задаче
19,6 (9), и тогда решение (Е) запишется так:
х — a sin (co^ +<р),
где
Задача 19,9 (для самостоятельного решения).
Материальная точка массы т движется по прямой, оттал-
отталкиваемая от неподвижного центра силой, пропорциональной рас-
расстоянию. Начальные условия: х (t0) = х0; v {t0) = v0.
Указание. Дифференциальным уравнением движения будет
d4 ,9
т —п^ — k2mx.
Общее решение:
х-= Схеы + С2е-«.
881
Из начальных условий определяем Сх и С2:
или, используя формулы A9,18):
(t —10) + f shk(t — to).
0
f
J a
f
Задача 19,10. Материальная точка массы т движется по пря-
прямой, притягиваемая к неподвижному центру силой F, прямо про-
пропорциональной расстоянию точки от центра притяжения. Сила
сопротивления среды J прямо пропор-
пропорциональна первой степени скорости.
Начальные условия: в начальный
момент движения (t = 0) х @) = х0;
Решение. Эта задача отличается
от задачи 19,8 тем, что здесь учиты-
учитывается сила сопротивления среды. Обо-
К задаче 19,10 значим для удобства последующих вы-
выкладок коэффициент пропорционально-
пропорциональности через 2hm (h > 0). Если точка движется в* положительном на-
направлении оси Ох, то ее абсцисса с течением времени возрастает, а
скорость -? > 0. Если же точка движется в отрицательном направ-
направлении оси, то ее абсцисса убывает с течением времени, а следо-
следовательно, ее скорость ~ < 0. Так как сила сопротивления f всег-
всегда направлена в сторону, противоположную скорости, то / =
= — 2hmV. Таким образом, на точку действует сила притяжения
F = k2mx; J>x = —№тх (см. задачу 19,8) и сила сопротивления
f — —2hmV. Сумма проекций этих сил на ось Ох равна — k2mx —
— 2hm-~j, и дифференциальное уравнение движения, согласно
второму закону Ньютона, запишется так:
d*x _
или
^ . 2Л ^ + k*x = 0. A9,23)
dt2 at
Это линейное дифференциальное уравнение второго порядка.
Искомая функция — х, независимая переменная — t.
882
Характеристическое уравнение, если обозначить его неизвест-
неизвестное буквой s, будет таким:
s2 + 2hs + k* = 0;
s = h±Vhk.
Рассмотрим три елучая: 1) h < k; 2) h = k\ 3) h > k.
1) Если h<k, то ft2 —&2<0. Обозначим /i2 — k2 = — со2.
Тогда s = — h + cot, а дсх = e~ft' cos со/; л;2 = e~ht sin to/.
Общее решение:
x = Cxe~M cos со/ + C2e-ft' sin со/,
или
x = e-ft' (Ci cos со/ + С2 sin to/).
При < = 0 имеем x0 — Cv
Найдем -Jj и определим С2:
~ = e~ht [(C2to — C,A) cos wt — (da) + C2h) sinmt].
При / = 0
v0 = — d^ + C2°»
Подставляя найденные значения Сх и С2 в общее решение, по-
получим решение, удовлетворяющее начальным условиям:
х = e~w (jc0 cos mt + v-^±^- sin wt) .
Если обозначить
xo = asincp; Ed^^acoscp, A9,24)
то предыдущее равенство запишется так:
x = ae~htsin(wt + <?). A9,25)
Возводя в квадрат обе части каждого из равенств A9,24) и
складывая их почленно, получим
Хеш
Наличие в равенстве A9,25) множителя sin^Z + f) указывает
на колебательный характер движения. С увеличением времени /
множитель ё~м уменьшается и стремится к нулю. Когда время
неограниченно возрастает, точка колеблется около начала коор-
координат, неограниченно к нему приближаясь. Движение в рассмат-
рассматриваемом случае является затухающим колебательным, а уравне-
уравнение A9,23) называется уравнением затухающих колебаний.
883
2) Если h> k, то /г2 — k2 > О, ft2 — fe2 = u>2; корни характери-
характеристического уравнения s2 и s2 — числа вещественные и не равныу
между собой:
х = des-' + C2e$'(. A9,26)
Из начальных условий следует, что
Решение A9,26) описывает так называемый апериодический
затухающий процесс движения точки к положению равновесия.
3) При h = k корни характеристического уравнения веществен-
вещественны и между собою равны: sx — s2 = — h:
у (р Л- Г Л о—ft<- /1 о 97"!
И в этом случае, когда /->оо, абсцисса движущейся точки
х -> 0, т. е. точка неограниченно приближается к началу коорди-
координат— положению равновесия, оставаясь с одной стороны от него,
если начальная скорость и0 не очень велика. Движение, описы-
описываемое уравнением A9,26), также называется апериодическим.
Теперь мы решим несколько линейных дифференциальных одно-
однородных уравнений порядка выше чем второй с постоянными коэф-
коэффициентами.
Задача 19,11. Найти общие решения уравнений:
1) У'"-У" -У' + У = 0; 2) у'"-3у" + Зу'-у = 0; 3) у'" + у = 0;
Ч)г/<4>—у"=0; 5)у^-у=0; 6) yW + у=0; 7) г/F>—2у^-у"+2у=0;
10) у^ — ЬуИ) + 12у'" — 16у" + \2у' — 4у = 0.
Независимой переменной во всех примерах, где она не указана,
является х.
Рещение. 1) Характеристическое уравнение имеет вид
k3 — k* — k+\ =0.
Разлагаем левую часть этого уравнения на множители:
k2(k—l) — (k— l) = 0; (k— 1) (/г2— 1) = 0,
или (k — 1) {k— 1) (k + 1) = 0. Отсюда k —1=0; ?—1=0;
k + 1 = 0. Корни: ki=\\ k2 = 1; fe3 = —1. Все корни — веще-
вещественны, но среди них есть два равных: kx = k2.
Частными решениями уравнения на основании A9,14) и A9,15)
будут:
Ух — б , у2 — хе , у3 — е .
Общее решение:
у = Схех + С2хех + С3е~~\
884
2) Характеристическое уравнение: k3— 3&2 4-3&—1=0, его
/ёвая часть равна (k— IK. Поэтому kx =1; кг — 1; k3 = 1. Корни
гещественны и все между собою равны.
Частными решениями уравнения в соответствии с A9,15) будут:
fl лД- • // , YO 11 » \^О
mi —— с ) У2 — л(/ ) */3 — л с j -.
а общее решение запишется так:
у = Ctex + С2хех + С3х*ех, или у = ех (С, + С2х + С3 х2).
3) Характеристическое уравнение: ks + 1 = 0. Разлагая левую
часть на множители, получаем: (k + 1) Ф2 — k 4- 1) = 0; k 4- 1 = 0;
k2 — & 4- 1 = 0. Корни: ki = —1; k2,3 = у + -у Л Корню ^=—1
соответствует решение г/х = е~*, а корням k2 a k3 (а = у, Р =
на основании A9,16) — решения:
Общее решение:
окончательно
у = Cie~x 4- е2^ (С2 cos -у л: 4- С3 sin ^-.
4) Характеристическое уравнение: &4 — ^2 = 0; k2 (k2 — 1) = 0.
Корни: kx = 0; k2 — 0; ^3 = 1; &4 = —1- Первым двум веществен-
вещественным и равным между собою корням соответствуют на основании
A9,15) частные решения: ух = \; у2 = х, а корням k3 и fe4 — ре-
решения у3 = ех и г/4 = е~*.
Общим решением уравнения будет
г/ — с>1 -(- с>2^ -
5) Характеристическое уравнение: &4—1=0.
Разлагая левую часть этого уравнения на множители, полу-
получаем: (k2 — 1) (k2 + 1) = 0, или (k —l)(k+ 1) (k2 + 1) = 0. Корни:
&j = 1; k2 — —1; &3i4 = ± i. Первым двум корням в соответствии
с A9,14) отвечают частные решения уравнения: yi = ex; y2 =е~х,
а мнимым корням k3 и &4 (а = 0; р = 1) на основании A9,16) —
решения: y3 = cosx; у4 — 5\пх.
Общее решение:
у = С^ + С2е~х 4- С3 cos д; + С4 sin л:.
6) Уравнение встречается при определении уравнения" изогну-
изогнутой оси балки, лежащей на упругом основании.
29 и. А. Кап лав 885
Характеристическое уравнение: k* + 1 = 0.
Решение этого двучленного уравнения вызовет некоторые за-
затруднения. Прибавим в его левую часть и одновременно вычтем
из нее 2k2, отчего уравнение не изменится. Получим:
/г4 + 2/е2 + 1 — 2k2 = 0; (fe2 + IJ— 2fe2 = 0.
Разлагаем левую часть на множители: (k2 + I — V2k) (k2 + 1 +
+ Vk) = 0. Отсюда получаем два уравнения:
/г2 — /2/г +1=0 и /г2 + ]/2/г +1=0.
Решая эти уравнения, находим:
Ь _Ll , /2 ^ _ /2/2
На основании A9,16) частными решениями, соответствующими
первым двум корням, будут
Ц* /2 ?* . /2
yt = e2 cos^-д:; у2 = е2 sin^-^
а частными решениями, соответствующими третьему и четвертому
корням:
jqx /г -^ . /г
у3 = е 2 cos-^-д;; у^ = е 2 sin-'y-x
Общее решение:
О, т/2 ^ i/2 -^ 1/2
г/= С2е 2 cos -^- д; + С2е 2 sin-^-^ + C3e 2 cos-^-* +
-- /2
+ С4е 2 sin Y- л:,
или
Во многих прикладных науках (например, в сопротивлении ма-
материалов) принято функции е" и е~х заменять гиперболическими
по формулам A9,18). На основании этих формул:
е^х = ch -^ х + sh lp-jc; e~~2" = ch "Q- x - sh ^ л:.
Поэтому предыдущее решение может быть записано так:
, /г /г , ,1/2.1/2, ,/2 /2 .
г/ = d ch ~ д; cos ~ х + с2 ch ^~ x sin ^ х + с3 sh -^y x cos -^ л: +
, „ _h /2 . /2
+ с4 sn -у л; sin -g- ж,
где с2 = Сх + С3; с2 = С2 + С4; с3 = Сх — С3; с4 = С2 — С4.
886
7) Характеристическое уравнение:
/г6 — 2/г4 — /г2+ 2 = 0.
Легко заметить, что корнями этого уравнения будут: kx = 1
и k2 = —1. Разделив левую часть уравнения на k2—1, получим
&*_?2_2. Поэтому левую часть уравнения можно записать в виде
(k — 1) (k + 1) (/г4 — k2 — 2) = 0.
Решая биквадратное уравнение k4— k2 — 2 = 0, найдем корни:
ks = 1/2; k4 = — У 2; ks,e = ± i.
Частными решениями уравнения будут: е1
г г V2x —V2x
У\ = е , у2 = е , г/3 = е ; yt = e ; г/6 = cos *; г/6 = sin *.
Общее решение:
г/ = de* + Сф-Х + d^2'" + C^e~V2x + d cos * + d sin *.
8) Характеристическое уравнение: k* — 13^2 + 36 = 0. Его кор-
корни: &! = 2; k2 = —2; k3 = 3; /fe4 = — 3.
Частные решения: л^ = e2t; x2 = e~~2t; xa = e3t\ х± = е~ы.
Общее решение:
v* —¦ i л2( I {* 0—2i | {* pot I {* о—3f
9). Характеристическое уравнение: k3 — 6&2 + 12/fe — 8 = 0.
Левая часть уравнения — куб разности k — 2, и уравнение пе-
переписывается так: (k — 2K = 0.
Его корни: kx = 2; k2 = 2; k3 = 2 — вещественны и все равны
между собой. Поэтому на основании A9,15) частными решениями
будут (иметь в виду, что искомая функция — г, независимая пе-
переменная — и):
гv = e2u; z2 = ue2u; z3 = и2е2и.
Общее решение:
z = de2" + С2ие2и + С3и?е2и,
ИЛИ
z = е2" (d + С2и + С3и2).
10) Характеристическое уравнение:
US J Kb* _L 1 ОЬЗ 1 R А2 1_ 1 Ob А П
Очевидным корнем его является 1 (ky = 1). После деления ле-
левой части уравнения на k — 1 получим &4 — 4k3 + 8k2 — 8k + 4.
Левая часть уравнения теперь представится в виде произведения
двух множителей:
(k — 1) (k* — 4k3 + 8/е2 — 8k + 4) = 0,
откуда
k—.1 =0; kx = 1; &* — 4&3 + 8k2 — 8k + 4 = 0.
Представим последнее уравнение в виде
(fe2 — 2kf + 4 (fe2 — 2k) + 4 = 0.
29* 8§7
Левая часть этого уравнения есть полный квадрат суммы
[(k2 — 26)+ 2]2, а потому (k2 — 2k + 2J = 0.
Корнями этого уравнения являются числа:
k2,3 = 1 ± «; К,ь = 1 ± h
т. е. его корни — комплексные и кратные.
Первому корню соответствует решение у1 == е*, остальным че-
четырем корням на основании A9,17) — решения (а=1; [3 = 1):
г/2 = е* cos д:; уа = ех sinx;
t/i — хех cos х; уь = дсе* sin л:.
Общее решение:
г/ =-Cie* + С2ех cos л: -f- Сфх sin л; -f C4A;ev cos x -f С^лге* sin л:,
или
г/ = [Cj + (С, + С4лг) cos jc + (С, + Съх) sin jc] e«.
В заключение решим четыре задачи с граничными (краевыми)
условиями.
Как уже указывалось, в этих задачах искомая функция и ее
производные задаются не при одном и том же значении аргумента,
как это делается в задачах с начальными условиями (в задаче
Коши), а при разных значениях аргумента, соответствующих гра-
границам (краям) некоторого промежутка интегрирования. Поэтому
они и называются граничными (иначе краевыми) задачами.
Учащийся должен иметь в виду, что не всякая граничная за-
задача имеет решение, а если и имеет его, то во многих случаях
оно не является единственным.
Приведем пример граничной задачи, которая не имеет решения.
Найти решение дифференциального уравнения у' + Ау = О,
удовлетворяющее граничным условиям: при хя= 0 искомая функция
у = 2; при х = y искомая функция у = 3.
Здесь заданы значения искомой функции на концах проме-
жутка 10, Y) •
Характеристическое уравнение: k2 + 4 = 0. Его корни: kx — 2i;
k2 — —2t. Частные решения уравнения: ух — cos 2х; у2 = sin 2x.
Общее решение: у = С^о^л: + C2sin 2x. Определим теперь произ-
произвольные постоянные так, чтобы у удовлетворял граничным усло-
условиям. Подставим в общее решение первое граничное условие у @) = 2
и получим, что 2 = Ci. Подстановка же в общее решение второго
граничного условия */(-?Н = 3 дает 3 = —Сх. Система
3 = — I
888
не совместна и, таким образом, нет решения предложенного урав-
уравнения, удовлетворяющего заданным граничным условиям.
На языке геометрии это означает, что через точки @, 2) и
Z-, З] не проходит ни одна интегральная кривая.
Если бы второе граничное условие: у = 3 при х = -? мы заме-
нили, положив у = —2 при * = -S-, то оказалось бы, что —2 =
= — Сь и для определения С] получилась бы уже совместная
система уравнений, а именно:
а решение, удовлетворяющее заданным граничным условиям, запи-
записалось бы так:
у = 2 cos 2х + С2 sin 2л:,
где С2 — произвольная постоянная. Это означает, что существует
бесчисленное множество интегральных кривых заданного уравне-
уравнения, проходящих через точки @,2) и (^-, 2|.
Задача 19,12. Найти решение уравнения
удовлетворяющее граничным условиям:
1) при z = 0 у = 0; 2) при г = 0 ^ = 0;
3)приг = / 3 = 0; 4) при*-/ g = 0. A9>28)
Решение. Это уравнение встречается при решении задачи
о потере устойчивости стержня, находящегося в магнитном поле.
(Здесь EI — жесткость стержня; а — начальное расстояние между
магнитом и стержнем; к — коэффициент пропорциональности; у —
отклонение стержня от положения равновесия).
Из уравнения видно, что искомой функцией является у, а неза-
независимой переменной — г. Разделим обе части уравнения на El
и обозначим
Ak i *
а; "
Уравнение переписывается так:
§-«'* = о
и представляет собой дифференциальное уравнение изогнутой оси
стержня.
889
= e~az = ch az — sh az
yt — sin az.
Характеристическое уравнение: № — а4 = 0. Разлагая его левую
часть на множители, получаем:
(?2 _ а2) (?2 _|_ а8) = о, или (? — а) (^ + а) (^2 + а2) = 0.
Его корни: ki = а; &2 = — а; k3ii = ± а/. Частные решения урав-
уравнения
Ух — еаг = ch az + sh az; г/
(см. формулы A9,18)); ys = cosaz; y
Общее решение:
у — Cx (ch az + sh az) + C2 (ch az — sh az) + C3 cos az + C4 sin аг.
Перепишем его в виде
у = (Ci + С2) ch az + (Ci — С2) sh az + C3 cos az + Q sin az.
Обозначим: Сг -\- C2 = Ax\ Ct — C2 = A2, и для однообразности
обозначений примем С3 — А3; С4 = Д,.
Общее решение запишется теперь так:
у = /li ch az + Л2 sh az + -^з cos az 4- At sin az. A9,29)
Для определения четырех произвольных постоянных используем
четыре заданных граничных условия A9,28) и получим систему
уравнений:
Ах +А3 =0
. А2 +А, =0
Ах ch a/ + А2 sh a/ — Л3 cos a/ — Л4 sin a/ = 0
Л1 sh a/ 4- A2 ch a/ + ^з sin al— At cos a/ = 0
Уравнения A9,30) представляют собой систему линейных одно-
однородных уравнений относительно неизвестных Ах, А2, А3, Л4. Как
и всякая система алгебраических линейных однородных уравне-
уравнений, она имеет тривиальное (самоочевидное) решение:
Л1 = 0; Л2 = 0; А3 = 0; Л4 = 0.
Чтобы система A9,30) имела решение, отличное от нулевого
необходимо и достаточно, чтобы определитель этой системы был
равен нулю:
10 1 0
0 1 0 1
ch al sh a/ — cos al — sin al
sh al ch al sin al — cos al
Вычислим этот определитель. Отнимем от элементов четвертого
столбца соответствующие элементы второго столбца, и уравнение
A9,31) перепишется так:
= 0
890
A9,30)
= 0
A9,31)
ch
sh
1
0
al
al
0
1
sh
ch
al
al
1
0
— cos al
sin al
0
0
— sin
— cos
al —
al-
sh
ch
al
al
Во второй строке все элементы, кроме второго, равны нулю,
а поэтому определитель равен произведению этого неравного
нулю элемента на его алгебраическое дополнение, и теперь урав-
ние A9,31) будет выглядеть так:
1 1 О
ch al — cos al — sin al — sh al
sh al
sin al
¦ cos al — ch al
= 0.
Вычислив определитель третьего порядка по известному пра-
правилу, получим уравнение
cosa/cha/ = —1, A9,32)
которое перепишем в виде
cos al = —
1
char
Построим графики функций cos а/ и — ^-^ (см. чертеж).
Абсциссы точек пересечения этих графиков и будут корнями
уравнения A9,32). Наименьший его
корень, наиболее важный, а/ = 1,873.
Установим теперь, какая зависи-
зависимость существует между произволь-
произвольными постоянным Аи А2, А3, А4.
Первое и второе уравнения си-
системы A9,30) показывают, что
Исключая Л3 и Л4 из третьего и -(О-
четвертого уравнений этой системы,
получим:
0,5
о
¦0,5-
К задаче 19,1-2
A± (ch al -f- cos al) -f- Л2 (sh a/ -f- sin al) = 0
Ax (sh a/ — sin al) -j- Л2 (ch a/ -)- cos a/) = 0
Первое уравнение системы A9,34) дает
I -+" COS al д
+ sin al *¦'
A9,34)
A9,35)
И, таким образом, все произвольные постоянные могут быть
выражены через Av
Подставляя в A9,35) al = 1,873 и учитывая равенства A9,33),
получаем:
Л2 = — 0,734Л1; Аа = —Аи Л4 =
* cos 1,873 = —0,2976;
= 3,3307.
sin 1,873 = 0,9547; sh 1,873 = 3,1771; ch 1,873
891
1 873
а потому, так как ct = -y-, общее решение A9,29) запишется
так:
Окончательно, вынося Ах за скобку, получим уравнение изогну-
изогнутой оси стержня
y = At (ch 1,873 у - 0,734 sh 1,873 у — cos 1,873 у +
+ 0,734 sin 1,873 у),
содержащее единственный неопределенный параметр Аъ харак-
характеризующий масштаб кривой изгиба.
Замечание. Мы указали общий способ решения системы
A9,30). Однако можно было бы и не идти этим общим путем,
а исключить с помощью первого и второго уравнений этой системы
неизвестные А3 и Л4 и тем самым получить систему A9,34), из
которой, приравнивая нулю ее определитель:
ch at + cos al sh al + sin ah _ п
sh at — sin al ch al + cos al '
получили бы
ch2 al + 2 ch al cos al + cos* al — sh* al + sin2 al = 0.
Отсюда
1 + 1 + 2 ch a/ cos a/ = 0, или cos al ch al = —1,
т. е. уравнение A9,32), которое было получено раньше.
Задача 19,13. Найти решение дифференциального уравнения
$: + *? = 0 A9,36)
(s — постоянная величина), удовлетворяющее граничным усло-
условиям:
1) у" = о при г = 0; 2) у"' = 0 при 2 = 0;
3) у = 0 при г = Ь\ 4) у' — 0 при г — Ь.
Решение. К уравнению A9,36) приводит решение задачи
об исследовании искривленной поверхности пластинки, жестко
опертой по одной из ее длинных кромок и свободной вдоль дру-
другой, когда изгиб пластинки обусловлен аэродинамическими нагруз-
нагрузками. Величина s в уравнении зависит от скорости потока и от
параметров пластинки.
892
Характеристическое уравнение: kl -f s3k = 0. Разлагая его
левую часть на множители, получаем k (k3 -f s3) = 0;
k (k + s) (k2 — sk + s2) = 0.
Корни:
kx = 0; k2 = —s; kz, 4 = -j ± *tt si.
Частные . решения уравнения A9,36): #i = l; </2 = е~*г\ #3 =
= e" sin i^- sz; г/4 = e 2 cos ^- sz.
Общее решение:
у = С, + C2e-S2 + (с, sin ^5 sz + C4 cos & sz} /*". A9,37)
Если использовать граничные условия, то для определения
произвольных постоянных получим систему четырех однородных
линейных алгебраических уравнений:
Сг -\—2~ С3 —j С4 = О
С4 = 0
?i + C2e-Sb + (с, sin ^.sb + d cos & sb) e^~ = 0
-C2e~sb + ~ eT Cs (sin ^sb + V3 cos *Q soj -f
¦f -5- e 2 c41 cos ^ so — V 6 sm ^ so I = 0
A9,38)
Для того, чтобы эта система уравнений имела решение, отлич-
отличное от тривиального
С\ = С2 = С3 = С4 = О,
необходимо и достаточно, чтобы определитель этой системы был
равен нулю.
Однако мы не будем составлять этот определитель и вычислять
его, а выразим неизвестные Са и С4 через С2.
Из второго уравнения следует, что
С4 = — С,. A9,39)
Подставляя это значение С4 в первое уравнение A9,38) по-
получим
откуда
A9,40)
893
Теперь эти выражения С4 и С3 через С2 подставим в четвер-
четвертое уравнение:
- С2е~°ь - -^ ** С2 (sin ^-sb + V?> cos ^ sb) -
Вынося — C2 за скобку, получим
- C2 (e-*b + 41* sin ^-sb +13 cos
Так как по предположению С2 ^= 0, то
^Jz Для определения параметра sb по-
получаем уравнение
^==_0>5e~^. (Л)
Графическое решение этого транс-
цендентного уравнения дано на чер-
чертеже. .
Абсциссы точек пересечения этих кривых будут корнями уравне-
уравнения (Л). Наименьший, наиболее важный корень дает
sb= 1,864; s-ifl
К задаче 19,13
(см. чертеж).
Подставляя найденное значение s?> в третье уравнение и ис-
используя соотношение A9,39) и A9,40), выразим Сх через Са:
d = — C2e~sb
sin
С2 cos
( sin ^ s& + cos ^sb) eT] C2;
s& = 1,854, а поэтому
d=1.942C2. A9,41)
Подставляя A9,39), A9,40) и A9,41) в A9,37), получим реше-
решение, удовлетворяющее граничным условиям:
у = [l ,942 + e~sz — (j/1 sin ^~ sz + cos ^ szj eT] C2.
Это решение содержит один произвольный параметр С2.
894
Задача 19,14 (для самостоятельного решения).
Найти решение уравнения
удовлетворяющее граничным условиям: w @) = 0; w (I) = 0.
Указание. К этому уравнению приводит задача о продоль-
продольном изгибе стержня (задача Эйлера). Здесь Р — сила, сжимаю-
сжимающая стержень вдоль его оси.
Обозначить
*2 (л)
Уравнение приводится к виду -^ -f №w = 0. Это дифферен-
дифференциальное уравнение изогнутой оси стержня при продольном изгибе.
Его общее решение: a^C^cos kx+
-\-Сгъткх. Из граничных уело- ^ ?
вий получаем: из первого усло-
условия С^ = 0; из второго условия, .
зная, что Ci = 0, имеем
0 = C2sin?/, /7=-
К задаче 19,14
отсюда или С2 = 0, или sin kl=0.
Если Сг = 0, то w = 0, т. е. решение тривиальное, которое,
собственно, и искать было нечего. Остается рассмотреть sin kl = 0.
Отсюда kl = ш\ k = Y> гДе п — любое целое число, не равное
нулю. Так, если kl = 0, то / = 0, k = 0, а этого не может быть.
Из kl = mt (п ф 0) следует, что /г2/2 = пЧ*, k2 = ~ ; k =
~ V Т' Подставляя эти значения в (А), получим -pj==-jr,
ИЛИ Р = ^— • (В)
Выражение (В) дает так называемое критическое значение
сжимающей силы Р, действующей вдоль стержня, при котором
становится возможным продольный изгиб.
Решение, удовлетворяющее граничным условиям, запишется
так:
„ . /171 (/til Л
= C2sm—x ly = fel.
w
При п = 1 сжимающая сила Р = —^- , уравнение изегнутой оси
стержня
w = С2 sin -т-х.
Это основной случай.
895
Так как наибольшее значение sin у = 1, то wmHe = С2, и та-
таким образом, С2 есть не что иное, как наибольший прогиб стержня.
При п = 2 сила Р = —^—, а уравнение изогнутой оси стержня
„ . 2%
имеет вид до = C2sin-j-x и т. д.
Число п представляет собой число полуволн синусоиды, рас-
располагающихся по длине изогнутого стержня (см. чертеж).
Задача 19,15 (для самостоятельного решения).
Найти решение уравнения
p
niW~ g dz*'
удовлетворяющее граничным условиям:
1) при г = 0 у = 0; 2) при г = 0 у" = 0;
3) при 2 = / у = 0; 4) при г = / у" = 0.
Указание. К предложенному уравнению сводится задача
о статической неустойчивости трубопровода. Здесь EI—жест-
EI—жесткость поперечного сечения трубопровода; q — вес жидкости, при-
приходящейся на единицу длины трубопровода; g — ускорение силы
тяжести; v — скорость потока жидкости; у — прогиб оси трубо-
трубопровода.
Положить
Уравнение приобретает вид
Частные решения: ух = 1; у2 = г; у3 — cos sz; y4 — sin sz.
Общее решение:
у = d + C2z + С3 cos sz + С4 sin sz.
Из граничных условий окажется, что
sin si — 0; si — rnz.
Первое значение si, которое наиболее важно: si = тс; s = у .
Решение, удовлетворяющее граничным условиям:
у — С4 sin sz.
Из (А) следует, что v — sy ^- , и при s = -у получаем так
называемое критическое значение скорости vKP = — 1/ — потока
жидкости, при котором наступает потеря устойчивости прямоли-
прямолинейной формы равновесия трубопровода.
ДВАДЦАТОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Линейные неоднородные дифференциальные уравнения.
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1. Линейное неоднородное дифференциальное уравнение имеет
вид
У(п) + Рх (*) У{п~1) + р2 (х) г/<«-2> + ... + pn-iy' + pny = f (х).
B0,1)
2. Общее решение линейного неоднородного уравнения нахо-
находится так:
а) Найти одно какое-нибудь его частное решение.
б) Найти общее решение соответствующего однородного урав-
уравнения.
в) Сложить эти два решения. Сумма их и будет общим реше-
решением уравнения B0,1).
Так, если частное решение неоднородного уравнения есть Y,
а общее решение соответствующего однородного есть ClyiJt-C2y2-\-
+ .. . -\-СпУп, то общее решение линейного неоднородного урав-
уравнения B0,1):
у = См + С2у2 + СзУз + ... + СпУп + Y. B0,2)
Условия, налагаемые на коэффициенты р,(х) и правую часть
/ (х), изложены в пояснениях к уравнению A9,1).
3. Если правая часть уравнения B0,1) есть сумма двух
функций:
Ум + Рх (х) */<"-» + Рг (х) */<"-2> + . • . + Pn-i (х) У' + Рп (х) у =
= /i (*)+/«(*), B0,3)
следует рассмотреть два уравнения, у которых левые части та-
такие же, как в B0,3), но в одном из них правой частью будет
функция /х (х), а во втором /2 (х), т. е. рассмотреть уравнения
Ум + Рх (х) ^"-»> + р2 (х) у<«-*> + . . . + рп-х (х) у' +
+ рп (х) у = П (х) B0,4)
и
Ум + Рх (х) */<"-" + р2 (*) y[n~2) + ... + pn-i (х) У' +
+ Pn(x)y = f,(x). B0,5)
Если функции Yx и Y2 — соответственно частные решения
уравнений B0,4) и B0,5), то их сумма ^ + ^2 будет частным
решением.. уравнения B0,3). (Это свойство называется наложе-
наложением решений и распространяется на случай, когда правая часть —
сумма п функций).
4. Если известно общее решение однородного линейного урав-
уравнения, соответствующего заданному неоднородному, то его
897
частное решение Y можно найти с помощью квадратур методом,
который указал Лагранж. Этот метод называется методом вариа-
вариации (изменения) произвольных постоянных.
Получив общее решение A9,3)
У = СхУх + С2у2 + ... + Спуп
линейного однородного уравнения A9,2), поступают так: полагают,
что в этом решении величины Съ С2, ... , Сп являются не по-
постоянными, а функциями независимой переменной, х. Записывают
это так:
у = d (л;) yv + С2 (х) уг + ... + Сп {х) уп. B0,6)
Для определения функций Ci(x) (i = 1, 2, ., . , п) состав-
составляется система уравнений:
С[ {х)У1 + С^(х)у2+ ... +С'п (х) уп =
B0,7)
Ух (х)у["~2) + С2 (х)у2п~2) + ... +С'п(х) */<"-2) = 0
-i' (*) У{ГХ) + С; (х) у2п~1) + ... +С'п{х) */<Г" = / (;
Мы рассмотрим подробно этот метод для линейных диффе-
дифференциальных неоднородных уравнений второго порядка:
и" -+- v (х) и' А- о (х) и = / (х) B0 8)
Получив общее решение
B0,9)
соответствующего однородного уравнения, поступают так: пола-
полагают, что в этом решении величины С2 и С2 являются не постоян-
постоянными, а функциями независимой переменной х, и записывают
это так:
Для определения функций Сх (х) и С2 (х) составляется система
уравнений B0,7):
2=f(x)}-
Ci(x)y'+C;(x)y
Определитель этой системы — определитель Вронского. Так как
B0,9) есть общее решение уравнения B0,8), то функции у1 и у2
линейно независимы и их определитель Вронского не равен нулю.
Поэтому система B0,10) всегда имеет решение и притом един-
единственное.
898
Решая эту систему уравнений относительно С[ (х) и С2 (х),
получим:
О у2
fix) Г'
с; (х) =
2 (х) =
W
</i О
У{ fix)
w
W
W
B0,11)
где определитель Вронского .
W =
У1 Уг
У'\ У'г
Из B0,11) интегрированием находим:
B0,12)
Подставляя B0,12) в B0,9), получим
Раскрывая скобки, найдем
У =
съУг + У 2
W
W
¦dx.
Сравнивая с B0,2), замечаем, что первые два слагаемых
+ с2у2 в правой части — общее решение однородного уравнения,
соответствующего B0,8), а последние два слагаемых — частное
решение неоднородного уравнения B0,8). Обозначая эти два^ сла-
слагаемых через Y, получаем формулу частного решения линейного
неоднородного уравнения второго порядка
'yifjx)
W
dx — i
У,Пх)
w
dx.
В более компактной форме частное решение линейного неодно-
неоднородного уравнения второго порядка может быть записано так:
CyJjx) , СушНА
J w dx J w
dx
J/2
B0,13)
Все величины, входящие в эту формулу, известны.
Замечание. Следует иметь в виду, что система B0,10),
так же как и формула B0,13), имеет место тогда, когда коэффи-
коэффициент при старшей производной равен единице. Функция / (х)
есть правая часть уравнения при этом.* предположении.
899
5. Метод вариации произвольных постоянных — универсальный.
Он позволяет при помощи квадратур определить частное решение
линейного неоднородного дифференциального уравнения B0,1),
если известно общее решение соответствующего ему однородного
уравнения.
Ниже будет рассмотрен случай, когда частное решение неодно-
неоднородного уравнения B0,1) может быть найдено без применения
метода вариации произвольных постоянных, и тем самым без вы-
вычисления интегралов.
Приступим к упражнениям, связанным с применением метода
вариации произвольных постоянных.
Задача 20,1. Найти общее решение уравнения
*У — 4ху' + 6у ¦= ж4 — ж2,
зная, что частным решением соответствующего ему однородного
уравнения является функция ух = ж2.
Решение. Прежде всего преобразуем уравнение так, чтобы
коэффициент при старшей производной, т. е. при у", был равен
единице. Для этого обе части уравнения разделим на ж2 и получим
у°-ту' + т>у = х*-1- (л)
Теперь правая часть уравнения /(ж)=ж2—1. Отбросим ее и
найдем общее решение уравнения
у"-тУ' + -уЛ = °> <5)
зная его одно частное"решение. По формуле A9,6) определим второе
частное решение: —щх)йх
4 Г Г 4
У нас р (ж) = ; — p{x)dx— — dx = 4 In ж = In ж4;
>/>(*)</* _ giB»i _ Ж4_ Помня, что г/j = ж2, получаем
i
¦ dx ;= ж2 • ж ^ л^.
Итак, у2 = ж3.. Общее решение у0 уравнения (В) запишется так:
у0 = ClX* + C2xs. (С)
Теперь применим формулу B0,13) для определения частного
решения уравнения (А). Определитель Вронского
Ух У2
Ух Уг
ж ж
2л: Зж2
= Зж4 — 2Ж4 = ж4;
900
Подставляя в B0,13) значения интегралов и частные реше-
решения у1 и у2 уравнения (В), получим
1 X2
х* х3 2
Складывая это частное решение заданного неоднородного
уравнения с общим решением (С) соответствующего ему одно-
однородного, получим общее решение заданного уравнения
+ С2х + + х + х1п\х\.
Это выражение можно упростить, если объединить подчеркну-
подчеркнутые слагаемые и обозначить Сх + 1 через сь а С2 = с2. Тогда
Задача 20,2. Найти общее решение дифференциального урав-
уравнения
Bх + 1) у" + Dх — 2)у' — 8у = 2ех Bх + IK,
зная, что функция у1 = е~гх является частным решением соответ-
соответствующего ему однородного уравнения.
Решение. Преобразуем уравнение (А) так,- чтобы коэффи-
коэффициент при старшей производной у" был равен единице. Разделим
его обе насти на Bх + !)• Получим
Правая часть этого уравнения f (х) = 2ехBх+])*. Отбросим
правую часть и найдем общее решение полученного однородного
уравнения
Здесь опять-таки чтобы найти «/„следует воспользоваться форму-
лой A9,6), в которой р (х) = ггтгт > #i = е~2* (согласно условию):
2 In | 2х + 1 | = — 2х + In Bх + IJ;
Wx)d -2i BХ + IJ;
J
= е~*х J е2' Dл;2 + 4ж + 1) йж = у е~2дг Dж2 + 1) е21 = у Dл;2 + 1);
901
Этот интеграл проще всего вычислить так:
J е^ (Ах2 + Ах + 1) dx = eiK (ax* + bx
c).
Теперь следует продифференцировать обе части этого равен-
равенства, сократить на е2с и сравнить коэффициенты при одинаковых
степенях х в левой и правой частях равенства. Получится, что
Dл;2 + Ах
= e2t Bах* + 2Ьх + 2с + 2ах + Ь).
Отсюда 2а = 4; 26 + 2а = 4; 2с + b = 1;
fl = 2; b = 0; с = у .
Итак, общее решение г/0 уравнения (S) запишется так:
(в последующем множитель -я- во втором слагаемом мы включим
в состав произвольной постоянной С2).
Чтобы воспользоваться формулой B0,13) для определения
частного решения заданного неоднородного уравнения (А), опре-
определим вронскиан:
W =
У\ Уч
У\ У'г
,-гх
—2e-
Ax
IJ
Так как правая часть уравнения (A) f (х) = 2е*Bж+ 1J> вы'
ражения для интегралов, входящих в B0,13), будут такими:
W
'dx =
I
8 i I7
~9X ¦ 27
(Последний интеграл вычислен способом, указанным выше).
Найденные значения интегралов и частные решения ух и г/2
уравнения (В) подставим в B0,13), получим частное решение Y
заданного неоднородного уравнения:
¦у _
1
902
Учитывая общее решение (В) однородного уравнения, соот-
соответствующего уравнению (А), и прибавляя к нему только что
найденное частное решение заданного неоднородного уравнения,
получим общее решение заданного уравнения:
у = Схе-* + С, Dж2 + 1) + 1 (Збж2 + 12х + 5) е*.
Задача 20,3 (для самостоятельного решения). Найти общее
решение неоднородных линейных уравнений, зная одно частное
решение соответствующего однородного уравнения:
1) х*у" — ху' + у = Зж3; yi = x;
2) хгу" — 2ху' + 2у = ж5 In ж; ух = ж2;
1
о\ у2/у" Oij у2- it *
о
Ответ. 1) у = CiX + C2x In [ ж | + -j ж3;
2) ^/ = С1ж2 + С2ж + ^1п|ж|-щЖ5;
МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ ДЛЯ ОПРЕДЕЛЕНИЯ
ЧАСТНОГО РЕШЕНИЯ НЕОДНОРОДНОГО ЛИНЕЙНОГО УРАВНЕНИЯ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Сведения из теории
Пусть в уравнении B0,1) коэффициентами являются не функ-
функции, а вещественные числа, а его правая часть / (х) имеет вид
f (ж) = е« [Р (х) cos р х + Q (х) sin p ж], B0,14)
где Р (х) и Q (ж) — многочлены, которые могут быть одной и
той* же степени, и разных степеней. Если они разной степени,
то пусть п — их наивысшая степень (при п = 0 эти многочлены
попросту постоянные величины).
Величины аир — вещественные числа.
В рассматриваемом случае метод вариации произвольных по-
постоянных для определения частного решения неоднородного урав-
уравнения, конечно, также применим. Однако здесь можно отыскать
частное решение более простым способом, пользуясь которым не
понадобится вычислять интегралы. Интегрирование уравнения
можно провести с помощью только алгебраических операций при
помощи метода, который называется методом неопределенных ко-
коэффициентов.
Если правая часть имеет вид B0,14), то следует рассмотреть
два возможных случая:
903
1. Число а + $i не является корнем характеристического урав-
уравнения соответствующего однородного уравнения.
В этом случае частное решение неоднородного уравнения
ищется в виде
у = e*x[p(x)cos$x + q(x)s\n$x], B0,15)
где р (х) и q (x) — многочлены одной и той же степени, равной
наивысшей степени многочленов Р (х) и Q(x). Коэффициенты
многочленов р (х) и q (x) — числа, подлежащие определению.
В B0,15) только эти коэффициенты и подлежат определению,
числа же а и р — те же, что и в B0,14).
2. Если число а + Щ является корнем Кратности k (k>\)
характеристического уравнения соответствующего однородного
уравнения, то частное решение неоднородного уравнения ищется
в виде
Y = хк [р (х) cos рж + q (x) sin рж], B0,16)
здесь р (х) и q (х) — многочлены, степень которых равна наивыс-
наивысшей степени многочленов Р(х) и Q{x) в B0,14), а коэффициенты
многочленов р (х) и q^x) подлежат определению; показатель сте-
степени k равен кратности корня a 4 Р« характеристического урав-
уравнения. Таким образом, и в этом случае определению подлежат
только коэффициенты многочленов р(х) и q{x), все же остальные
числа а, |3 и k — известны.
Неопределенные коэффициенты многочленов р(х) и q (x) как
в том, так и в другом случае находятся так:
В заданное уравнение подставляется У и сравниваются коэф-
коэффициенты при одинаковых степенях независимой переменной в
левой и правой частях равенства. Ниже на примерах мы укажем,
как это выполняется практически.
Заметим, что рассматриваемый вид неоднор'одных линейных
уравнений (коэффициенты постоянны, а правая часть имеет вид
B0,14)) встречается очень часто, а техника их интегрирования
исключительно проста. Мы рассмотрим различные возможные
случаи сначала для линейных неоднородных уравнений второго
порядка, а потом и порядка выше, чем второй.
Задача 20,4. Найти общее решение уравнения
у"-7у' + 12у = 5. (А)
Решение. Уравнение линейное неоднородное. Прежде всего
отбрасываем правую часть и решаем соответствующее однородное
уравнение
у"-7у' + 12у = 0. (В)
Характеристическое уравнение
№ — 7/г 4- 12 = 0
имеет корни:
kx = 3; k2 = 4. (С)
904
Частные решения уравнения (В):
Ух = е3х; у2 = е*\
Общее решение однородного уравнения
Уо^С^ + С***. (D)
Теперь рассмотрим правую часть уравнения (А) и сравним ее
с B0,14). Так как правая часть не содержит множителя еах, то
надо считать, что a =j0 (еах = е°'х = е° = 1).
Правая часть не содержит также ни синуса, ни косинуса. Это
значит, что р = 0 (sin 0-х = sinO = 0; cos 0-х — cosO = 1). Число 5
в правой части надо рассматривать как многочлен нулевой сте-
степени.
. Составляем число a -f- pi, чтобы решить вопрос, является ли
оно корнем характеристического уравнения. Так как у нас
а = р = 0, то а -|- ^' = 0. Из рассмотрения корней (С) характери-
характеристического уравнения видно, что 0 не является корнем характе-
характеристического уравнения. Значит, имеет место первый случай и
частное решение надо искать в виде B0,15), в котором положить
а = 0, р=0, а многочлены р(х) и q (х) — нулевой степени.
Таким образом, частное решение будем искать в виде
4 Y = А (А — const). (E)
Подставляя (Е) в заданное уравнение (А), получим
12
(-7)
Y = A
Y' = 0 (F)
Y" = 0
Приравниваем сумму левых частей равенств (F) правой части
заданного уравнения (мы вправе это сделать, так как предпола-
предполагается, что Y — частное решение заданного уравнения. Так мы
будем поступать и при решении последующих задач, не делая
этой оговорки).
Учитывая это указание и складывая почленно равенства F,
получаем
5 = Ш,
откуда А = J2 и, следовательно, частное решение неоднородного
уравнения У = -^.
Складывая Y с общим решением (D) однородного уравнения,
находим общее решение заданного уравнения:
у =
1.
Задача 20,5 (для самостоятельного решения). Найти общие
решения уравнений: 1) у" — 6у' -f 8у — 10; 2) у" + fy = 8.
Ответ. 1) у = Схе2х + Сге4х + -|;2)у = Схcos2х + С3sin2x+
4-2.
905
Задача 20,6. Найти общее решение уравнения
у"-Бу' = 7. (Л)
Решение. Соответствующее однородное уравнение имеет
вид
у" — 5у' = 0. (В)
Характеристическое уравнение: № — 5& ~ 0.
Его корни: ky = 0; k2 — 5. Частными решениями уравнения
(В) являются: t)i— 1; Уг = еЬх. Общее решение этого уравнения:
уо = С1 + С2е5\ (С)
Сравним теперь правую часть уравнения (Л) с B0,14).
Правая часть не содержит ни множителя е", ни тригономет-
тригонометрических функций. Значит, а = 0 и C = 0. Поэтому число а.+
+ [3, = 0, а нуль есть простой (однократный) корень характерис-
характеристического уравнения. Поэтому частное решение неоднородного
уравнения (Л) следует искать в виде B0,16), в котором надо
взять &=1;а = 0; [3 = 0, а многочлены р(х) и q(x) должны
быть той же степени, что и многочлен в правой части задан-
заданного уравнения, т. е. нулевой. Итак, Y = Ах.
0
(-5)
Y = Ах
У =А
Y" = 0
7 = — 5Л; А = — |-
Подставляя это значение А в выражение для Y, получим
Y = — -g- х. Общее решение уравнения (Л) будет суммой общего
решения (С) соответствующего однородного уравнения и только
что, найденного частного решения заданного неоднородного. Тогда
у = С1 + С8в5* —-g-jt.
Задача 20,7 (для самостоятельного решения).
Найти общие решения уравнений:
1) у" + 6у' = 8; 2) у"-у' = 3.
Ответ. 1) y = Ci + Caer^ + ±.x; 2) ¦у = С1 + С^г* — Зх.
Задача 20,8 (для самостоятельного решения).
Найти решение уравнения
dt* dt ° ~ "'
удовлетворяющее начальным условиям: ж@)= 1; л:'@) = 0.
Указание. Общее решение имеет вид:
Ответ, х = т= e3t + -r- e~2t —5- •
±.
906
Задача 20,9. Весомая частица массы т брошена вертикально
вверх и при движении испытывает сопротивление, пропорцио-
пропорциональное первой степени скорости. Определить закон движения
частицы, если в начальный момент t = 0 положение точки опре-
определяется координатой х = s0, а начальная скорость v — v0.
Решение. На точку действуют две силы: 1) сила тяжести
Р, (g — ускорение силы тяжести) и 2) сила сопротивления J =
= kamv, где через fe2m обозначен для удобства коэффициент про-
пропорциональности.
Направим ось Ох, по которой происходит движение, верти-
вертикально вниз.
Уравнение движения будет таким:
m5T* =
B0,17)
где Р и f — соответственно модули силы тяжести и силы сопро-
сопротивления.
Следует учесть, что q
сила сопротивления на-
направлена всегда противо-
противоположно направлению дви-
движения, а скорость — в сто-
сторону движения. Модуль
силы сопротивления
dx
(А)
При Движении частицы
вверх проекция
отрицательна
скорости
т. е. -г- <0,
V
dx
dt
f
т
cos(x,fhcos/800=-i
х
К задаче 20,9
а модуль вектора всегда.
положителен. Поэтому в
(А) при движении вверх надо взять знак минус. В этом слу-
случае угол между силой сопротивления J и осью Ох равен 0°,
вследствие чего cos (х, /) = 1, а произведение f cos (x, }) =
При движении частицы вниз проекция скорости -у- > 0. Для
того, чтобы модуль силы f был величиной положительной, надо
в (А) взять знак плюс. В этом случае угол между силой со-
сопротивления / и осью Ох равен 180°, а потому cos(x, f) = — 1. а
произведение / cos (x, f) по-прежнему равно — №tn ~. Учитывая,
что сила тяжести направлена вертикально вниз, ее модуль
907
P = trig, угол между силой тяжести и осью Ох равен 0°, а
cos (л:, Р) = 1, уравнение движения запишем так:
Л*
Сокращаем на т и переписываем уравнение в виде
Мы получили линейное неоднородное уравнение (искомая
функция —х, независимая переменная —t, правая часть равна g).
Отбрасываем правую часть и находим общее решение соот-
соответствующего однородного уравнения
g? + *«g = O. (С)
Его характеристическое уравнение: г2 -f k*r = 0, г (г -\- ka) — 0.
(Конечно, буквой к здесь нельзя обозначать неизвестное ха-
характеристического уравнения, так как эта буква уже занята.
Неизвестное характеристического уравнения мы обозначили'бук-
обозначили'буквой г).
Корни характеристического уравнения:
/¦!=¦(); /•, = — *». (D)
Частные решения уравнения (В):
хх = 1; х2 = е~кН.
Его общее решение
х0 = Сх + С2б-*г'. ^ (?)
Теперь определим частное решение неоднородного уравнения
(В). Сравнивая его правую часть с выражением B0,14), прихо-
приходим к выводу, что а = C = 0, поэтому число а 4- Щ = 0. Среди
корней (D) характеристического уравнения нуль есть. Значит,
число а + Pi — корень характеристического уравнения простой
(или однократный). В "выражении B0,16) число k=\. Так как
g — величина постоянная, многочлен нулевой степени, то и в
B0,16) надо р (х) и q(x) считать многочленами нулевой'степени
и, следовательно, учитывая, что k=l, искать частное решение
неоднородного уравнения в виде X = At:
0
ft2
1
X
X'
X"
= At
= A
= 0
g = Ak\ A = ±
908
Поэтому X — ^t, а общее решение уравнения (В) будет равно
сумме общего решения (Е) уравнения (С) и только что найден-
найденного частного решения неоднородного уравнения
Теперь нам осталось из начальных условий определить про-
произвольные постоянные Ct и С2. Подставляя t = 0 и х —- s0, по-
получим
so = CL + Ca. (G)
- Продифференцируем обе части (F)
и поставим t = О, а -т = v0:
v0 = —
Отсюда
Подставляя это значение в (G), найдем
Найденные значения Ci и С2 подставим в (F) и получим
окончательно решение, удовлетворяющее начальным условиям:
или
Из полученного результата можно сделать интересный вывод:
если бы время t неограниченно возрастало, то е~кЧ -*• 0, и тогда
т. е. движение асимптотически приближается к равномерному
со скоростью -~ = ~.
Положение точки при очень большом t мало отличалось бы
от того, которое бы она занимала, двигаясь равномерно со ско-
скоростью Jj , выйдя из начального положения, абсцисса которого
равна s0 -f- ~ — Jj.
' 909
Задача 20,10. Найти общее решение уравнения
У" + У' +У = Зе2*. (А)
Решение. Отбрасываем правую часть Зе2х и будем искать
общее решение соответствующего однородного уравнения:
У" + У'+У = О. (В)
Его характеристическое уравнение
?2 + k + 1 = 0
имеет корни
•*..2 = -!±^/. (С)
Частные решения уравнения (В):
yi = e 2 cos-^-x; y2 = e 2 sin-^л:,
а его общее решение
Теперь отыщем частное решение неоднородного уравнения
(А). Сравнивая его правую часть с B0,14), заключаем, что
о = 2; р = 0, многочлен Р (х) имеет нулевую степень (множи-
(множитель при е2х—величина постоянная). Число а + Щ = 2 и не яв-
является корнем характеристического уравнения (среди корней (С)
число 2 отсутствует). Частное решение следует искать в виде
B0,15), полагая в нем а = 2; р = 0; многочлены р (х) и q(x) надо
взять нулевой степени. Таким образом, Y = Ае2х:
Y =Ае2х
Y' = 2Ае2х
Y" = 4Ае2*
Зе2* = е2х (А + 2А + АА)\ 3 = 7А;А=~
и, значит Y = y е2х- Общее решение заданного уравнения будет
суммой этого частного решения неоднородного уравнения и об-
общего решения (D) соответствующего однородного:
у = е~х(Сг cos-^* + C2 sinЦ- *) + у е2*.
Задача 20,11 (для самостоятельного решения).
Найти общие решения уравнений:
1) у + 2у' -Зу = 4е-*; 2) %- 5 § + 4^ = 7е«.
Ответ. 1) г/ = Схе* + С2е~3х — е~х; 2) х = Схе* +
~~те •
910
Задача 20,12. Найти общее решение уравнения
fj*_6§ + a* = 3e« (A)
Решение. Находим общее решение соответствующего одно-
однородного уравнения
Корни его характеристического уравнения k2 — 6fe + 8 = 0
равны: ki = 2; k2 = 4. Частные решения: x1 = e2t; х2=е4*. Его
общее решение
х0 = (V + С2е4'. (С)
Теперь приступим к отысканию частного решения неоднород-
неоднородного уравнения (А).
Сравнивая его правую часть с выражением B0,14), заклю-
заключаем, что а = 2; р = 0. Число а + $i = 2. Но 2 есть простой ко-
корень характеристического уравнения. Поэтому частное решение
неоднородного уравнения (А) ищем в виде B0,16), в котором
/г = 1, а независимую переменную х надо заменить на t, много-
многочлены же р (х) и q (x) взять нулевой степени, т. е. такой же,
как и многочлен, стоящий множителем при е21 в правой части
заданного уравнения. Таким образом, ищем частное решение
уравнения (А) в видеХ = Ate2t (члены, содержащие t уничтожились)
—6
1
X = Ate2t
X' = e2f (A + 2At)
X" = e2t D А + 4At)
3e2t = e2i (8At — 6Л — 12Л^ + 4A + 4At).
, Сокращая на e2t, получим уравнение для определения неиз-
неизвестного коэффициента А:
о = 2. А; А = 2",
и поэтому частное решение неоднородного уравнения
а его общее решение будет суммой этого частного решения и
общего решения (С) соответствующего однородного уравнения:
или
9Ц
Задача 20,13 (для самостоятельного решения).
Найти общие решения уравнений:
1) У" — 7у' + 12у = 5е3*; 2) у"-4у' =
Ответ. 1) у = Се3* + C2e** — 5л:еЗЛГ;
2) y = C1+C^*t+^te-t.
Задача 20,14. Найти общее решение уравнения
$g (Л)
Решение. Заданное уравнение — неоднородное линейное.
Искомая функция — г, независимая переменная — ср. Однородное
уравнение, соответствующее ему:
$-.? + *-<». да
Характеристическое уравнение k2 — 6?-f-9 = 0 имеет корни:
ftj = 3; k2 = 3. (Q
Частные решения уравнения (fi):
Общее решение уравнения (В)
г0 = С^3? + Сасре3?. (Е)
Теперь отыщем частное решение неоднородного уравнения (Л).
Сравнивая его правую часть с B0,14), замечаем, что а == 3; |3 =
= 0. Число а + pi = 3.
Среди корней (С) характеристического уравнения оно встре-
встречается дважды. (В таком случае говорят, что 3 — двукратный
корень характеристического уравнения). Частное решение следует
искать в виде B0,16), в котором надо взять k = 2. Учитывая,
что правая часть уравнения (Л) имеет постоянный множитель,
т. е. многочлен нулевой степени, надо и в B0,15) многочлены
р (<?) и q (<p) взять нулевой степени.
Таким образом, частное решение надо искать в виде
R = <р Me3?
(в формуле B0,16) мы заменили независимую переменную х не-
независимой ф):
' R =
—6
1
R' = Ле3? Bср +
R" = Ае^ A2? + V + 2)
= 2Ле3?; 2Л = 4; Л == 2
- Я
912
Складывая это решение с общим решением (Е) однородного
уравнения, получим общее решение заданного уравнения:
г = C^f +
или
г = е3? (d + С2? + 2<р2).
Задача 20,15 (для самостоятельного решения).
Найти общие решения уравнений:
1) у" + V + 4у = бе-2*; 2) у" - 2/ + у = ЗеК
Ответ.
1) ^ = «-^(^ + ^ + 4?»); 2) У =
Задача 20,16. Найти общее решение уравнения
у-.8у'+7у=*Зл* + 7х + 8. ' (А)
Решение. Находим общее решение соответствующего одно-
однородного уравнения
у"-8у' + 7у = 0. (В)
Характеристическое уравнение № — 8k -f- 7 = 0 имеет корни:
А.1==1; ^2 = 7. ¦ (С)
Частные решения уравнения (В):
Ух = е*; г/а = е".
Его общее решение
Переходим к определению частного решения неоднородного
уравнения {А). В его правой части отсутствуют множитель е?х
и тригонометрические функции. Поэтому а = 0; р = 0. Число
а + ^ = 0, а нуль не является корнем характеристического урав-
уравнения (см. (С)). Частное решение следует искать в виде B0,15),
причем многочлены р (х) и q (x) должны иметь вторую степень.
(Очевидно многочлен q (х) не будет участвовать, так как р = 0,
а при многочлене q (x) множитель sin $x = 0. Частное решение
ищем в виде У = Ах2 -f Bx + С:
7
—8
1
У
У
Y"
= Ах*
= 2Ак
= 2Л
+
+
Вх
В
+
С
Зх2 + 7л: + 8 = 7Ахг + (JB — 16Л) х + BЛ — 8В + 7С).
913
Сравнивая коэффициенты при одинаковых степенях буквы х
в левой и правой частях этого равенства, получаем:
7Л = 3; Л = 1;
7Я-16Л = 7; В = |;
2А — 8В + 7С = 8; С = -^,
и, таким образом,
У =ТХ2+ 49-К + -343"-
Общим решением заданного уравнения будет сумма этого ча-
частного решения неоднородного уравнения (А) и общего решения
(D) соответствующего однородного уравнения (В):
Задача 20,17 (для самостоятельного решения).
Найти общие решения уравнений:
2) х" — Зх' — 4х = t2.
Ответ. 1) i, = C1e-* + Cae«*-i-*» + x*1-fJC+T;
2) * = <;!<?-<+ Са<?*'-1 *» + •§¦/-й-
Задача 20,18. Найти общее решение уравнения
у" — 2у' = ха + 2х—1. (А)
Решение. Соответствующее однородное уравнение
у"-2у' = 0. (В)
Его характеристическое уравнение k2 — 2k = 0 имеет корни
^ = 0; k2 = 2. (С)
Частные решения уравнения (В):
У1=1; & = *¦*.
Общее решение уравнения (В)
Теперь приступим к определению частного решения данного
неоднородного уравнения (А). Сравнивая его правую часть с B0,14)
и замечая, что в ней отсутствуют множитель еах и тригонометри-
тригонометрические функции, заключаем, что а = 0 и р = 0. Число а + Щ = 0.
Но нуль есть среди корней (С) характеристического уравнения.
Корень этот простой, однократный, Частное решение будем искать
в виде B0,16), в котором следует взять k — 1, а многочлены р(х)
и q (x) — той же степени, что и многочлен в правой части урав-
уравнения (А), т. е. третьей. Ясно также, что многочлен q (x) будет
отсутствовать, так как множитель при нем sin рх = 0 (р = 0).
Итак, частное решение ищем в виде
Y = х {Ах3 + В*2 + Сх + D) *;
0
—2
1
У = Ах* + Вх3 + Сх2 + Dx
Y' = 4Ах3 + ЗВх2 + 2Cx + D
Y" = 12Ах2 + ЪВх + 2С
хз _|_ 2x — 1 = — 8Ax3 + A2Л — 6B) л;2 + FB — 4C) x + BC — 2D).
Сравнивая коэффициенты при одинаковых степенях буквы х
в левой и правой частях этого равенства, получаем:
6В —4С = 2; С = —~;
О
о
Таким образом, частное решение заданного неоднородного
уравнения
1 1 7 О
V Lv-4 уЗ '__ У2 ± у
о 4 о о
Складывая это частное решение уравнения (А) с общим ре-
решением (D) соответствующего ему однородного уравнения, полу-
получим общее решение заданного уравнения:
у = Сх + С^х -~х* -\х3 -!*• —|х
Задача 20,19 (для самостоятельного решения).
Найти решение уравнения
х" + х' = t* + 2t,
удовлетворяющее начальньГм условиям: jc@) = 4; х' @) = —2.
Ответ. х = 2 + 2е-< + ~t3.
Задача 20,20. Найти общее решение уравнения
у"-2у' + 4у = (х + 2)езх. (А)
Решение. Найдем общее решение соответствующего одно-
однородного уравнения
у"-2у' + 4у = 0. ' {В)
* Такое умножение на х часто называется «усилением».
915
Характеристическое уравнение k2 — 2k -f 4 = 0 имеет корни:
*i,2 = 1 ± КЗг. (С)
Частные решения уравнения (В):
г/i = е* cos Y^x; y2 = ех sin У^Зх.
Его общее решение
г/0 = ех (Сх cos /Зл: + С2 sin J/jc). (D)
Отыскиваем частное решение неоднородного уравнения (А).
Сравнивая его правую часть с B0,14), заключаем, что а = 3,
Р = 0. Многочлен Р (х) имеет первую степень. Число а -f- Щ = 3.
Оно не является корнем характеристического уравнения. Поэтому
частное решение ищем в виде B0,15) (q (x) sin (Зя = 0, так как
р = 0):
¦ Y =езх(Ах + В)
Y' зх (ЗА А
—2
1
Y' = езх (ЗАх + А + SB)
Y" = e3X (9Ax + 6A + 9S)
(л: + 2) е?х = е3* GЛл: + 4Л
Сокращая на е3* и сравнивая коэффициенты при одинаковых
степенях х, получим:
1=7А; А = \-\ .
12.
Поэтому
Общее решение уравнения (А) есть сумма этого его частного
решения и общего решения (Ь) соответствующего однородного
уравнения:
у = е* (Q cos КЗл: + С2 sin УЗх) + ё* (l x + [
Задача 20,21 (для самостоятельного решения).
Найти общие решения уравнений:
§^ = *'('•-5/+ 2);
. 2JР + 5^-14г = е"Bе»-Зе-1).
Указания. 1) Частное решение X неоднородного уравнения
следует искать в виде
X = е* (Л/2 + В/ + С),
916
коэффициенты А, В я С определятся из равенства
*« — 5* + 2 = 8At* + (8S — 8A)t + BА — 4В + 8С).
2) Частное решение R неоднородного уравнения следует искать
в виде
R = бе26 (Л6з + Я62 + С6 + D).
Это удобно переписать так:
R = е26 (Л6* + 593 + С6а + D6),
коэффициенты Л, В, С и D определятся из равенства
2Q3 — 36 — 1 = 36Л63 + A2Л + 27В) 62 + A8С + 6В) 9 + (9D 4- 2С).
Ответ. 1) л: == е3'(С1! cos 2* 4-С2 sin 20 + е'(-^а — ~t— l) ;
2) r — de +C2e ' + е ^g6 gl 4g66 218у1
Задача 20,22. Найти общее решение уравнения
у" 4- у = 5 sin 2x. (Л)
Решение. Рассмотрим соответствующее однородное уравнение
у" + у = 0. (В)
Характеристическое уравнение k2 -\- 1 = 0' имеет корни
К 2 = ± i- (С)
Частные решения уравнения (В): y1 = cosx; y2 = sinx.
Общее решение уравнения (В)
у0 = Ct cos x 4- С2 sin x. (?>)
Теперь обратимся к определению частного решения неоднород-
неоднородного уравнения. Сравнивая правую часть уравнения (Л) с B0,14),
заключаем, что а = 0; C = 2. Число а 4- N = 2i не является кор-
корнем характеристического уравнения. Решение будем отыскивать
в форме. B0,15). В правой части постоянный множитель 5 при
sin 2x должен рассматриваться как многочлен нулевой степени.
Поэтому в B0,15) вместо многочленов р(х) и q(x) надо взять
постоянные величины, которые следует определить.
Учитывая это, а также то, что а = 0, р = 2, частное решение
будем искать в виде
Y = Л cos 2x 4- В sin 2x. (E)
Y = Л cos 2x 4- 5 sin 2x
У = 2S cos 2х — 2Л sin 2д;
Y" = — 4А cos 2х — 4В sin
5 sin 2х = (—4Л 4- Л) cos 2х + (В — Щ sin 2x
30 И. А. Каплан ^ 917
Так как левая часть не содержит cos 2х, то в правой части
коэффициент при cos 2х должен быть равен нулю, т. е. —АА +
+ А = 0; коэффициенты при sin 2x должны быть равны между
собой, т. е. В — 4В = 5. Значит, А = 0; В = — -|.
О
Поэтому частное решение (Е) равно
У = —-|sin2x.
Общее решение уравнения (А) будет суммой только что най-
найденного частного решения заданного неоднородного уравнения
и общего решения (D) -соответствующего однородного уравнения:
у = Ci cos x -\- С2 sin х —я" s'n 2х.
О
Задача 20,23 (для самостоятельного решения).
Найти общее решение уравнения
Частное решение неоднородного уравнения следует искать
в виде
Y = A cos х + В sin х.
Ответ, у = Схек -f C2e6K + ^ cos х + щ sin л:.
Задача 20,24 (для самостоятельного решения).
Найти общие решения уравнений:
1) у" + 2у' + Ьу = 4 sin х + 22 cos л:;
2) #" — V + 29у = 44 sin Зд; + 28 cos Зх.
Указание. В первом примере частное решение неоднород-
неоднородного уравнения искать в виде Y = A cos x -f- В sin x.
Ответ. 1) у = е~х (Сх cos 2х + С2 sin 2x) + 3 sin x + 4 cos x;
2) у = е2х (Сг cos 5х + С2 sin 5х) + sin Зх + 2 cos Зх.
Задача 20,25. Найти общее решение уравнения
y" — 2y' + \0y = xcos2x. (A)
Решение. Соответствующее однородное уравнение
y"-2*/'+10y = 0. (В)
Его характеристическое уравнение
k2 — 2fe + 10 = 0
имеет корни:
К 2 = 1 ± з/. (С)
Частные решения уравнения (В):
У! = ех cos Зх; У2 = е* sin Зх.
Общее решение уравнения (В):.
Уо = ех (Cj cos Зл; + С2 sin Зх). (D)
918
Приступаем к отысканию частного решения неоднородного
уравнения (А). Сравнивая правую часть этого уравнения с B0,14),
заключаем, что а = 0; р = 2; число а + Pi = 2i не является кор-
корнем характеристического уравнения (среди корней (С) число 2i
отсутствует). Решение будем искать в виде B0,15). Нам осталось
решить вопрос о степени многочленов р (х) и q(x) в B0,15). Сле-
Следует помнить, что эти многочлены должны иметь одну и ту же
степень, причем степень эта должна быть равна наибольшей сте-
степени многочленов Р (х) и Q (х) в B0,14).
В нашем случае многочлен Р (х), стоящий множителем перед
cos2x в правой части уравнения (А), имеет первую степень, мно-
многочлен Q (х) равен нулю. Поэтому многочлены р(х) п q(x) в B0,14)
должны иметь первую степень. Учитывая все это (а = 0, р = 2;
степень многочленов р(х) и q(x) — первая), частное решение сле-
следует искать в виде
Y = (Ах + В) cos 2л; + (Сх + D) sin 2л:;
10 У = (Ах + В) cos 2л; + (Сх + D) sin 2x
—2 У = BСл: + A + 2D) cos 2л: + (—2Ах — 2В + С) sin 2x
1 Y" = (—4Ах — 4В + 4С) cos 2л; + (—4Сл; — 4/4 — 4D) sin 2x
х cos 2х = FАх — 4Сх — 2А + 6В + 4С — 4D) cos 2x + DАх
+ QCx — 4A + 4B — 2C + 6D) sin 2x
Перепишем правую часть этого равенства так, чтобы ясно
были видны коэффициенты при х и свободные члены многочленов:
xcos 2х = [фА — 4С) х — 2А + 6fi + 4С — 4D] cos 2x +
+ [DЛ + 6С) х — 4А + 4В — 2С + 6D] sin 2x. (E)
Сравниваем коэффициенты при cos 2x и sin 2x в левой и правой
частях этого равенства, получаем:
при cos 2л;
при sin 2x
х = (<оА — 4С) х — 2А + 6В + 4С — 4D;
0 = DА + 6С) х — 4А + 4В — 2С + 6D
(в последнем равенстве в левой части стоит нуль, так как в ле-
левой части равенства (Е) sin 2л: отсутствует). Сравнивая коэффици-
коэффициенты .при одинаковых степенях буквы х в левой и правой частях
равенств (Г), находим:
6/4 — 4С = 1
4А +6С
= о}
—4/4 + 4В — 2С + 6D = 0 }
Из системы (I) с.
30*
Из системы (I) следует, что А = 4; С = — 4 •
919
Подставляя в систему (II) значения А и С для определения
В и D, получим систему
f
2fi + 3D = 1
из которой следует, что В = ^щ ; D = — jgg .
Таким образом, искомое частное решение будет таким:
OQ \ / 1 1
Л + C0 + I X
(
26 Л + 338
Общее решение заданного уравнения получим, складывая это
частное решение с общим решением (D) соответствующего одно-
однородного уравнения:
у = ех (С, cos3x + C2 sin3x) + (^х + Ц] cos2x +
Задача 20,26 (для самостоятельного решения).
Найти общее решение уравнения
У" — V + Ьу = Dх + 22) sin Зх — B8х + 84) cos Зх.
Ответ.
у = е2Х (С1 cos х + С2 sin х) -\- Bх + 6) sin Зх + (х + 5) cos Зх.
Задача 20,27. Найти, общ ее решение уравнения
у" _(_ 4г/ = 3 sin 2*. (Л)
Решение. Отбрасываем правую часть и решаем соответст-
соответствующее однородное уравнение
у" + 4у = 0. E)
Корнями характеристического уравнения k2 + 4 = 0 являются
числа
*1,я=±а-. • (Q
Частные решения уравнения (S):
г/х = cos 2х; г/2 = sin 2x,
а его общее решение
у0 = Сг cos 2x + С2 sin 2x. (D)
Приступаем к определению частного решения заданного неод-
неоднородного уравнения (А). Сравнивая его правую часть с B0,14),
заключаем, что а = 0; C = 2. Теперь надо определить число а+Р*.
Оно равно 2г. Число 2г является простым (однократным) корнем
характеристического уравнения (k — 1). Частное решение ищем
в виде B0,16), в котором следует взять k = \\ а = 0; р = 2, сте-
степень многочленов р (х) и q (x) равна нулю,
920
Следовательно, надо взять
У = х (A cos 2x + В sin 2x)
1
У" = 2 (—2А sin 2х + 2В cos 2*) + х (—4А cos 2х — 45 sin
3 sin 2х = — 4Л sin 2* + 4Б cos 2x
Учитывая, что в левой части этого равенства cos 2x отсутст-
отсутствует (а, следовательно, коэффициент при нем равен нулю), за-
заключаем:
—4Л = 3;
3 3
Отсюда А = —^-; В = 0 и поэтому У = —^- х cos 2х.
Общее решение:
у = С1 cos 2х + С2 s^n ^ —т х cos 2;c'
Задача 20,28 (для самостоятельного решения).
Найти общее решение уравнения
у" + г/ = xcosx.
Указание. Частное решение следует искать в виде
У = х [(Ах + В) cos х + (Сх + D) sin x].
После подстановки в заданное уравнение окажется, что Л=0;
В=±; С = ~; D = 0.
4 4
Ответ, г/ = Сх cos х + С2 sin х + -j x cos х + -j x* sin x.
Задача 20,29 (для самостоятельного решения).
Найти общее решение уравнения
у" + 9г/ = 18 cos Зх — 30 sin Зх.
Указание. Частное решение искать в виде
У =
, О т в е т. г/ = Сх cos Зх 4- С2 sin Зх + х E cos Зх + 3 sin Зх).
Задача 20,30. Найти закон движения точки, на которую дей-
действуют две силы: 1) сила притяжения к неподвижному центру,
пропорциональная расстоянию точки от этого центра Р = — k2mx
(см. задачу 19,8), и 2) периодическая сила, определяемая форму-
формулой F = Am cos pt.
Решение. Дифференциальное уравнение движения будет
таким:
ш-тгг = — №пгх -\- Am cos pt,
821
Оэкратим уравнение на т и запишем его в виде
|f + k2x = A cos pt. (A)
Уравнение — линейное неоднородное.
Рассмотреть следует два случая: 1) р Ф k; 2) р — k.
Уравнение (А) часто встречается в механике. Оно называется
уравнением вынужденных колебаний при отсутствии сил сопро-
сопротивления. Сила F = Am cos pt называется возмущающей.
Первый случай (k ф р). Отбросим в уравнении (А) правую
часть и найдем общее решение уравнения
§ + k2x = 0 (В)
(уравиение свободных гармонических колебаний). Характеристи-
Характеристическое уравнение г2 -j- k2 = 0 имеет корни:
rlt 2 = ± ki. (С)
Общее его решение:
х0 — Ci cos kt + С2 sin kt. (D)
Частное решение неоднородного уравнения (А) в случае, когда
р Ф k, следует искать в виде B0,15) (а = 0; |3 = р; а + |3г = pi
не является корнем характеристического уравнения):
k2
1
X = В cos pt + С sin pt
К" = — 5р2 cos pt — Ср2 sin pt
A cos pt = (Bk2 — Bp%) cos pt + (Ck2 — Cp2) sin p*
Сравнивая коэффициенты при cosp^ и sinp^, получаем урав-
уравнения для определения неизвестных коэффициентов В и С:
В/г2 — Вр2 =
Ck2 — Ср2 =
Поэтому
4
(так как р Ф k, то &2 — р2 ^ 0).
Общее решение уравнения (А) в этом случае будет таким:
х = С1! cos to + С2 sin to + Л 2 cos рЛ (?)
Второй случай (р = k). В этом случае по-прежнему а = 0;
C = р, но так как р = k, то р == ^, а число а + р/ = to является
корнем характеристического уравнения (см. (С)), поэтому частное
решение надо искать в виде B0,16) (только не упустить из вида,
что независимую переменную х надо заменить на t). Правая
часть заданного уравнения теперь равна AQQskt (р замененд
буквой k),
№
Итак, частное решение в этом случае:
k2 X = t(C cos kt + D sin kt)
1
X" = 2 (—Ck sin kt + Dk cos kt) +
+ t (—Ck2 cos kt — Ш2 sin to)
A cos/W = — 2Ck sin « + 2Dk cos «
Сравнивая коэффициенты при cosfe^ и sin& в левой и правой
частях этого равенства, получаем
П — А. • г — о-
2k' ~ '
частное решение неоднородного уравнения X = * -——, а потому
общее решение уравнения вынужденных колебаний (А) при р = k
(это уравнение полезно запомнить) запишется так:
х = Сх cos W + С2 sin fe^ + t
Рассмотренный второй случай представляет особый интерес.
Наличие множителя t в последнем слагаемом указывает на то,
что с возрастанием времени t абсцисса х точки (т. е. ее размахи)
неограниченно. увеличивается и может достигнуть сколь угодно
большой величины. Это явление называется резонансом. Оно
наступает тогда, когда частота возмущающей силы равна частоте
свободных колебаний точки (р = k). Следует обратить внимание
на то, что при отсутствии возмущающей силы движение описы-
описывалось бы уравнением (В), а закон движения — уравнением (D)
и точка совершала бы свободные гармонические колебания (см. за-
задачу 19,6, п. 9). Уже рассмотрение решения (Е) показывает, что,
когда частоты свободных и вынужденных колебаний (числа р и k)
мало отличаются одна от другой, знаменатель k2 — р2 в послед-
последнем слагаемом мал, а само оно становится большим.
Из сказанного ясно, что при проектировании сооружений,
судов, машин, фундаментов и т. д. надо всячески избегать явления
резонанса, т. е. не допускать совпадения частот собственных
колебаний с частотой накладывающейся возмущающей силы.
Устранение этого явления может быть достигнуто увеличением
разности между этими частотами.
Задача 20,31. Найти общее решение уравнения
У" + У = (Зх + 2) sin 2х + (г* + х + 2) cos 2x.
'Решение. Соответствующее однородное уравнение
у" + у = о.
Его характеристическое уравнение k% -f- I = 0 имеет корни:
923
Частные решения уравнения:
y1 = cos x; y2 = sin x,
а его общее решение
г/о = Ci cos x + C2 sin x.
Приступая к определению частного решения заданного урав-
уравнения, сравним его правую часть с B0,14). Замечаем, что а = 0
(множитель е" отсутствует в правой части), C = 2; число a -f-
+ |3г = 2г не является корнем характеристического уравнения.
Частное решение надо поэтому искать в форме B0,15). Нам
осталось решить вопрос о степени многочленов 'р (х) и q (x)
в B0,15). Так как многочлены при sin2x и cos2x в "правой части
заданного уравнения различны, то степень многочленов р (х)
и q (x) должна быть равна наибольшей из них, т. е. второй,
и частное решение должно иметь вид:
Y = (Ах2 + Вх + С) cos 2х + (Dx2 + Ex + F) sin 2x
Y" = (—ААх2 — АВх + 8Dx + 2А — AC + Щ cos 2x + (—4Dx2 —
— АЕх — 8Ах — 4B + 2D — AF) sin 2x
C* + 2) sin 2x + (х2 + х + 2) cos 2х = (—ЗАх2 — ЗВх + 8Dx + 2A—
— ЗС + Щ cos 2х + (—3Dx2 — ЗЕх — 8Лх — 45 + 2D — 3F) sin 2x
Сравнивая коэффициенты при sin2x и cos2x в левой и правой
частях последнего равенства, получаем:
—3Dx2 + (—ЗЕ — 8А)х + (—45 + 2D — 3F) = Зх + 2;
—ЪАх2 i- (-3B + 8D)x + BA — ЗС + Щ = х2 + х + 2.
Сравнивая коэффициенты при равных степенях, получаем:
—3D = 0; D = 0
при х2
1
—ЗА = 1; А = —я-
при
свободный
член
Значит,
ОС О Л О. OZ7I
"ОС — o/i === Of —O?Z ~т~ ~Т" ==
О D I Q /^ . 1 • Q D 1 • D
2А-ЗС
— •§¦ —ЗС
2\ F = —~
~| = 2; С = -g
924
а общее решение заданного уравнения:
Теперь учитывая, что учащийся приобрел уже прочные навыки
в отыскании частного решения неоднородного линейного урав-
уравнения по виду его правой части, мы предлагаем для самостоятель-
самостоятельного решения несколько дифференциальных неоднородных урав-
уравнений, порядок которых выше второго.
Задача 20,32 (для самостоятельного решения).
Найти решения уравнений, удовлетворяющие начальным уело-
виям: 1) *?- + | = е«; *@) = 0; *' @) = 0; *" @) = 0;
2) Ж + 4F = cos'; х <°> = х' <°) = х" <°) = 0; *'" (°> = 5"'
3) XW + Ах = /•; X @) = х' @) = л:" @) = х1" @) = 0;
^L ^ г @) = /¦' @) = 1; г"@) =
= 1 —2й2; /" @) = —2а2.
Указания. В третьем примере характеристическое урав-
уравнение № + 4 = 0 может быть переписано так: fe4 -j- 4fe2 + 4 —
— 4/г2 = 0, или (k2 + 2J — B/гJ = 0; (/г2— 2fe + 2) (fe2 + 2^ + 2) = 0.
Его корни: &i,2= 1 ± i; ^зл = —1 ± *'• Частное решение неодно-
неоднородного уравнения X = -^-12-
В четвертом примере характеристическое уравнение k* -f-
-f 2a2/e2 + а4 = 0; (fe2 + a2J = 0 имеет кратные корни: k\ — ai;
&2 = —ai; k3 = ai\ kt = —ai. Частные решения соответствую-
соответствующего однородного уравнения: rv — cosa<p; rz = sinacp; r3 = cp cosa<f;
r4 = <p sina'f. Частное решение неоднородного уравнения /? =
= Л cos f + В cos у
12 1 1
Ответ. 1) x = —к- + -g-cos^ sin^ +
3) x = -i- /2 — -j e' sin ^ + -j e~' sin
—i-sin/;
4) г = [l — (fll _|_ 1Jj cos acp + ~ sin acp + i cos ay —
- 2^+1)sin a^ + (arrijf cos ?.
925
Задача 20,33 (для самостоятельного решения).
Решить уравнение
d2y . .3.1
ф 4# = sinxsinTx
при начальных условиях у @) = 1; у' @) = 0.
Указания. Заменить произведение синусов в правой части
разностью косинусов:
sin -j x sin -j x = ~ (cos x — cos 2x).
Рассмотреть два неоднородных уравнения:
4y =
и отыскать для каждого из них частные решения: для первого
в виде
Yl = A cos х -f- Б sin л;,
для второго
F2 = Лх cos 2x -f- 5i sin 2x.
После определения коэффициентов Л, Б, Лх и 5Х образовать
сумму Ух + У2, которая и будет частным решением заданного
уравнения.
Ответ. i, = ^^-pj|-^"-^ ^
ДВАДЦАТЬ ПЕРВОЕ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ
Содержание: Уравнение Эйлера. Системы линейных дифференциаль-
дифференциальных уравнений с постоянными коэффициентами (основные понятия).
I. УРАВНЕНИЯ ЭЙЛЕРА
Основные сведения из теории
Уравнение Эйлера является линейным дифференциальным
уравнением, которое имеет вид
(ах + Ь)п «/<"> + а± (ах + 6)«-у»-« + а2 (ах + Ь)п~2у^'2) +
+ ¦¦¦ +an-1(ax + b)y'+any = f(x), B1,1)
где все а; (i = 1, 2, . ..), а также а и Ь'—вещественные числа,
а правая часть / (х) — функция ' независимой переменной х, и по
этой переменной вычислены все производные в B1,1).
В частном случае, когда а= 1, 6 = 0, уравнение B1,1) при-
принимает вид
_ а^-у»-1) + a2xn~zy(n-2i + • • • + ап-\ху' +
+ any = f(x). B1,2)
926
Уравнения Эйлера B1,1) и B1,2) представляют собой частный
случай линейных дифференциальных уравнений с переменными
коэффициентами.
В приложениях математики уравнение Эйлера встречается
часто.
Если ввести замену независимой переменной по формуле
ax + b = e( (t = \п\ах + Ь\) B1,3)
в случае, если уравнение имеет вид B1,1), или
х = е? {t = \n\x\), B1,4)
если уравнение имеет вид B1,2), то уравнение Эйлера приво-
приводится к линейному уравнению с постоянными коэффициентами.
Из B1,3) следует:
у ~
d?y_ __ dy
<u* W
B1,5)
)
Делая в B1,1) замену переменных по формулам B1,5), это
уравнение преобразуем в линейное дифференциальное уравнение
с постоянными коэффициентами, которое мы умеем интегри-
интегрировать.
Сначала решим несколько однородных уравнений Эйлера, т. е.
таких, в которых правая часть / (х) = 0.
Задача 21,1. Найти общее решение уравнения
х2у" + Ьху' + Зг/ = 0.
Решение. Это уравнение Эйлера типа B1,2).
Произведем замену переменной х — е< по формуле B1,4) на
основании B1,5) при а = 1 и получим
Подставляя эти значения производных в заданное уравнение
и замечая, что'на основании B1,4) х2 = e2t, получаем
f^ 4- 3w - n
dt +6y - 0-
Отсюда следует, что
927
Делая приведение подобных членов, имеем
Сделанная подстановка привела нас к линейному уравнению
с постоянными коэффициентами. Характеристическое уравнение
имеет вид k2 + Ak + 3 = 0. Его корни: кг = —3; k2 = —1.
Частные решения:
г/i = e~3t; у2 = е~{. (А)
Теперь надо возвратиться к старой переменной х. Из B1,4)
следует, что t = In х.
Частные решения запишутся в виде:
__ 1 . _ 1
а общее решение заданного уравнения
или окончательно
Задача 21,2 (для самостоятельного решения).
Найти общие решения уравнений Эйлера:
1) х2у" + ху' — 9у = 0; 2) х2у" + ху' + 9у = 0; 3) х*у' + ху'= 0.
Ответ. \)-у = С^3 + С2х~3; 2) у = Сг cos C In х) + С2 sin C In x)\
3) У = CL + C2 In х.
Задача 21,3 (для самостоятельного решения).
Найти общее решение уравнения
х2у" — ху' + у = 0.
Указание. Рассматриваемое уравнение — уравнение Эйлера
типа B1,2).
Применив подстановку х = е\ получим уравнение
Характеристическое уравнение: k2 — 2k + 1 = 0. Его корни
&! = k2 = 1; частные решения: г/х = е'\ у2 = ^е'.
Ответ, у = Слх -\-С2х\пх, или г/ = х(С1 + С2Inx).
Задача 21,4 (для самостоятельного решения).
Найти общее решение уравнения
Указание. Если обе части уравнения (А) умножить на <р2,
то оно примет вид B1,2): <р2д—2 — 2<р-з 4г = 0. Это и есть урав-
уравнение Эйлера (независимая переменная — <р). Подстановка B1,4)
в данном случае имеет вид <р — е*.
928 •
Используя формулы B1,5а), в которых у надо заменить на г,
получим уравнение--зтг — 3-п— Аг = 0. Его общее решение: г =
= Сув** + С2е~(. Возвращаясь к старой переменной, по формуле
ср = е' получим e4t = ср4; е~* = у-
Ответ, г = С^-\-С^~К
Задача 21,5 (для самостоятельного решения).
Найти общие решения уравнений Эйлера:
,. о d2u „ du . е п оч ,, d2* о, их _ _
') Р ^-3Pd~p + 5M = 0; 2) ' 5?* —3^ — 5^ = 0;
3) л:2г/" — Ъху' + 8г/ = 0.
Указание. Во втором примере искомой функцией является х,
а независимой переменной t. Подстановка B1,4) может быть за-
записана так: t = еи, где и — новая независимая переменная.
Ответ. 1) и = р2 (С1 cos In p -f- C2 sin In p);
2) х = С^ъ + y\ 3) у = С^ + Сгх\
Задача 21,6. Найти общее решение уравнения Эйлера
Cx+l)V-2Cx + l)«/'-12r/ = 0. (Л)
Решение. Сделаем замену независимой переменной по фор-
формуле B1,3), полагая, что
3^+1=^. (В)
На основании B1,5), учитывая, что а — 3, 6 = 1, (Зх + 1J=е2',
получим
9е^-^(g-1)-2 • ЗА-*^-12^ = 0.
Отсюда получаем (после приведения подобных членов и со-
сокращения на 3)
Характеристическое уравнение: 3&2 — 5^ — 4 = 0. Его корни:
, _ 5 , /73 . _ 5 /73
1 ~ 6 "•" ~6~ ' 2 ~~ Т 6 *
Общее решение уравнения (С)
у=е* (Cie 6 +C2e е }.
Из (В) следует, что t — In (Зх + 1), а потому ее =e6"x =
_5 УТз , /73
= (Зх + 1N ; е 6 = (Зх + 1) 6 .
Общее решение заданного уравнения запишется так:
y=Cx+l)S[C1Cx+l) 6 +С2(Зх+1) * 1.
920
Задача 21,7 (для самостоятельного решения).
Проинтегрировать уравнения Эйлера:
2) Bх+1)*у"
3) E + х)*у-
__4_
Ответ. 1) и = С1 + С2(Зг + 2) 3;
2) у = С1Bх+1)' + СаBх + 1)-ъ
3) y = E + xJ[CL + C2lnE + x)].
Задача 21,8 (для самостоятельного решения).
Найти общее решение уравнений Эйлера:
1) х*у"' — 6xY + 18ху' — 24у = 0;
2) *V v — х3у"' + Зх*у" — бху' + 6у = 0.
Указания. 1) После подстановки х = ё на основании фор-
формул B1,5) при а=\ получится уравнение у'" — 9у" + 26у' —
— 24у = 0.
Характеристическое уравнение k3 — 9k2 + 26& — 24 = 0 имеет
корни: h = 2; k2 = 3; А3 = 4.
2) Замена независимой переменной по формуле х = е' дает
такое выражение для четвертой производной:
Оно получается из последней формулы в B1,5) при а = 1, если
обе ее части продифференцировать по я. При этом надо иметь
в виду, что для вычисления в правой части производной по х
надо ее продифференцировать по t, и результат дифференциро-
дифференцирования умножить на -т- или, что то же, разделить на -тт = е*. Но
деление на ё равносильно умножению на е~*. Таким образом,
чтобы найти производную по х правой части этой формулы, надо ее
продифференцировать по t, и результат дифференцирования умно-
умножить на е~*.
После приведения подобных членов получится уравнение
g_7§+17g'-17f+ 6 = 0.
dt* dt3 ' dt2 dt '
Характеристическое уравнение имеет корни:
ftlS=l; fe,= l; Л3 = 2; kt = 3.
Ответ. 1) г/ = С^2 + С2д:3 + С3л;4;
2) г/ == Сух + С2х \пх + С3х2 + С4л:3.
930
Задача 21,9. При изучении предмета «Сопротивление материа-
материалов» приходится решать так называемую задачу Ляме об опре-
определении напряжений в точках толстостенной цилиндрической тру-
трубы по известным равномерно распределенным давлениям, действу-
действующим на ее внутреннюю и наружную поверхности. Решение за-
задачи приводит к дифференциальному уравнению
которое является уравнением Эйлера. ф^
Проинтегрируйте его самостоятельно.
Ответ. « = С]р + С2—.
Теперь проинтегрируем несколько неоднородных уравнений
Эйлера, т. е. таких, у которых правая часть f (х) в B1,1) или
в B1,2) не равна нулю.
Задача 21,10. Найти общее решение уравнения
хгу" + 4ху' + \2у = In х. (А)
Решение. Предложенное уравнение — уравнение Эйлера.
От уравнений, решенных выше, оно отличается наличием правой
части, являющейся функцией той независимой переменной, по
которой вычислены производные.
Как и раньше, это линейное уравнение с переменными коэф-
коэффициентами может быть преобразовано к линейному уравнению
с постоянными коэффициентами с помощью подстановки B1,4):
х = е'\ t = In x.
Применяя формулы B1,5а), получим уравнение
?' + 30+12, = /, . (В)
которое является линейным неоднородным уравнением с постоян-
постоянными коэффициентами. Поступаем так же, как и на предыдущем
практическом занятии: отбрасываем правую часть и ищем общее
решение уравнения
§ + 3f+ 12у = 0. (С)
Его характеристическое уравнение
3
имеет корни: kh 2 = — -j ±
931
Частные решения уравнения (С):
Уг-e-i'co
а его общее решение
Теперь отыщем частное решение уравнения (В). Сравнивая его
правую часть с B0,14), отмечаем, что а = 0; |3 = 0. Число а+
-f- |3i = 0 не является корнем характеристического уравнения
(среди корней (Е) чиата нуль нет).
Частное решение ищем в виде B0,15):
12
3
1
У =
У =
у"
At A
г-Я
Л
0
t = 12At + 12В + ЗА (К)
Сравнивая коэффициенты при одинаковых степенях буквы t
в левой и правой частях равенства (К), получим
1; А = ±; 125+ЗЛ = 0; В = ±.
Подставляя эти значения А и В в (G), найдем
Складывая это частное решение неоднородного уравнения (В)
с общим решением (F) соответствующего однородного уравнения
получим общее решение уравнения (В):
Теперь следует возвратиться к старой переменной х с помощью
равенства B1,4): t = \nx. Имея в виду, Что
з
3 . 3 , , о~ 3
е 2 =е 2 =е , =х 2
получаем окончательно
In x) + C sin (?Ш in x)] + j-2
у = х~ Т [Cl cos (?f In x) + C2 sin (?Ш in x)] + j-2 In x - 4!.
Задача 21,11 (для самостоятельного решения).
Найти общие решения уравнений:
1) х2у" + ху' — у = 9х2;
2) х* у" - ху'+ у = Зх3;
3) xY — Зху' + *у = Ьх\
4) Bх+ \fy"~2Bx
932
Указание. Сделать подстановку
2х + 1 = ё (А)
и воспользоваться формулами B1,5). Из (А) следует:
Ответ. 1) у = dx + CiX'1 + Зх2;
2) г/ == Сгх + С2х\пх + ~х3;
3) у = CLx2 + С2х2 In х + 5х;
4) j, = C1Bx + l)8 + C2Bx
16'
"96*
II. СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ПЕРВОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
а) Нормальной системой дифференциальных уравнений назы-
называется система уравнений вида:
~Д1 = /1 V,
~^ = /2 ('>
dX3'- f U
~?f — /3 \1 >
2> • • • , хп)
2> • • • > Хп)
2> • ¦ ¦ 7 Хп)
~jj In \t,
% Xn)
B1,6)
В этой системе уравнений неизвестными являются п функций
хъ х2, ... , хп, а независимой переменной — t.
Особенности нормальной системы дифференциальных урав-
уравнений:
1) Все входящие в систему уравнения являются уравнениями
первого порядка.
2) Все уравнения системы разрешены относительно производ-
производных искомых функций 3 , -Jj -^р.
Если нормальная система уравнений B1,6) линейна, а коэф-
коэффициенты при неизвестных функциях постоянны, то она имеет
вид:
dx, . . . , ...
-J7 = ЯцХ, + CLioX* + . .. + аЛпх„ 4- <р, (г)
dx
" - - +а22х2+ ... +a2nxn + f2(t)
dt
anix2
?n (t)
B1,7)
933
Все искомые функции хъ х2 хп входят в систему B1,7)
в первой степени, а функции fi(t), <р2 @ ?я @ — функции
независимой неременной /, по которой вычислены производные.
Если все эти функции равны нулю, то система B1,7) назы-
называется однородной, а если хотя бы одна из них не равна нулю,—
неоднородной.
Число произвольных постоянных, входящих в общее решение
нормальной системы уравнений, равно числу неизвестных функ-
функций, входящих в систему. Произвольные постоянные определя-
определяются из начальных или краевых условий.
Способ интегрирования нормальных систем линейных уравне-
уравнений с постоянными коэффициентами мы покажем на примере
однородной системы из трех уравнений.
Задача 21,12. Найти общее решение системы:
их „ ,
37 = 3*— у + г
dz
(Л)
Решение. Неизвестными функциями являются х, у и z, a
независимой переменной t.
Приведем решение этой системы к решению одного уравнения,
порядок которого равен числу уравнений, входящих в систему.
Для этого любое из уравнений системы (А) продифференцируем
по t и заменим в полученном уравнении производные ~, — и
~ их выражениями из системы (А). Поступая так, например,
с первым уравнением, получим
dbc nd? dy .dz
IP ~ di ~ Ш ~т~ Ш '
Заменим в этом уравнении производные ~, ¦— и -?, стоящие
в правой части, их выражениями из второго и третьего уравне-
уравнений заданной системы (А) и получим уравнение
^ = 3 (Зх — у + г) -(- х + Ъу — г) + (х-у + Зг),
dx dy dz
dt dt di
откуда после приведения подобных членов в правой части найдем
а~ = \1х-9у + 7г. - (В)
Это уравнение опять продифференцируем по t и получим
~3& = Ш ~~ dt "*" 'dt '
934
/-* - dx du dz
Снова заменим в правой части производные -тт, —¦ и -т- их
выражениями аз заданной системы (А) и получим уравнение
^ = И {Ъх-у + г) -9(-х + Ъу-г) + 7 (х-у + Зг),
которое после приведения подобных членов в правой части запи-
запишется так:
-т^- = 49л; — 63г/ + 41г. (С)
Рассмотрим систему уравнений, состоящую из первого урав-
уравнения заданной системы (А), т. е. уравнения, обе части которого
мы дифференцировали, и уравнений (В) и (С):
(D)
Чтобы прийти к уравнению, содержащему только одну не-
неизвестную функцию, из первых двух уравнений системы (D)
определим функции у и г. Из этих уравнений следует:
Решая их относительно у я г, получим:
^-g _ 16*+ !&-??
У— 2 ' Z
2
Подставляя эти значения у и z в третье уравнение системы (D),
найдем
/ d2
После упрощений в правой части получаем
^- = 36^-36^+11^. (F)
Уравнение (F) — линейное однородное уравнение третьего по-
порядка с постоянными коэффициентами. Перепишем его так:
d3x ,. d2x . ocdx па л <п\
11+3636а: = 0 (О)
935
и найдем его общее решение по известным правилам. Составляем
характеристическое уравнение
k*—llk* + 36/е — 36 = 0.
Корнями этого уравнения являются числа:
kx = 2; k2 = 3; k3 = 6.
Частными решениями уравнения (G) будут функции:
а его общим решением
х = Cte2t + С2е3' + C3e6t. (К)
Чтобы определить две остальные неизвестные функции у я г,
воспользуемся выражениями (Е). После подстановки в (Е) вы-
dx dH
ражении х, -j и ^ получим:
у = С2е™ — 2C3e6t; z = — Суе» + C2e3t + С3е«К
Задача 21,13 (для самостоятельного решения).
Найти общие решения систем уравнений:
1) х = -Зх + у ) . 2) х = -I-) . 3) х = х + 4у \ .
6 Г ]' 1'
Х~ dt' У ~ dt
Ответ. 1) х = С^* + С2е<; у = ЪС^1 + АС2е(;
2) х = Cj cos / + С2 sin /; г/ = 2СХ sin г1 — 2С2 cos t;
3) х = el Id cos B j/3>) + С2 sin
У = ^?е* [С2 cos B /30 — d sin
Задача 21,14 (для самостоятельного решения).
Найти общее решение системы:
¦? = — х + у + 2 sin t — 3 cos t
4jL = _ 6x + Ay + 7 sin t — 20 cos t
Указание. Обе части первого уравнения продифференциро-
продифференцировать по t. В полученное уравнение подставить вместо производ-
производной — ее значение из второго уравнения, а вместо у — его зна-
значение из первого уравнения;
У.= %[ +х — 2sin/ + 3cos*. (Л)
Получится уравнение
% ~ 3Ш + 2х = 2 sin t ~ 6 cos L
Интегрировать его следует как линейное неоднородное урав-
уравнение.
936
Чтобы определить функцию у, надо в выражение (А) подста-
подставить найденное значение х и его производную -г .
Ответ, х = С^ + C2e2t + 2 sin t\
у = 2Схё +3C2e2t •+5 cos*.
Задача 21,15 (для самостоятельного решения).
Решить системы уравнений при заданных начальных условиях:
1) х' = —2г/ + ЗП лс@) = 2;
y' = 2x + 4 } уф)=3;
х и у — искомые функции, t — независимая переменная.
2) х' + у' = у + ё
2х' + у' = — 20 + cos/
Указание. Разрешить систему относительно х' и г/'. По-
Получится
х'= Sy + cost — e1)
f }
Интегрировать эту систему, как и предыдущую. Искомые функ-
функции и независимая переменная те же.
Ответ. I) x = 1-^cos2t — 3sm2t — -j\
у = 3cos2t + 1-?s,in2t + ^t;
2) x = e<-l±e«-± ^±
2 22
г/ = — -g-e' +gje4
Задача 21,16 (для самостоятельного решения).
Найти решения систем, удостоверяющие заданным условиям:
\)х' = у-г ()
' Уф) = 2;
г@) = 3.
2) х' = 6х — 72г/ + 44г ) х @) = 9;
у' = — 4ж + 40г/ — 22г г/@) = 5;
2' = _6ж + 57г/ —31г] г @) = 7.
(Искомые функции — х, у я г, независимая переменная —t).
Ответ. l)x = 2 — et;y = —2+4et—tet\ z = — 2+5e' — teu,
2) х^-
937
III. СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
С линейными системами дифференциальных уравнений второго
порядка приходится встречаться часто в теоретической механике,
сопротивлении материалов и в других приложениях математики.
Система дифференциальных уравнений, разрешенных относи-
относительно наивысших производных искомых функций, называется
канонической. В случае трех неизвестных функций х, у и г
и независимой переменной / эта система уравнений записывается
так:
<Рх , /, dx dy
x и г
x< y> z. dt, dt. dt
dPz , I. dx dy dz
— tb I г if 11 J _ у
V\1 X У г
B1,8)
Общее решение этой системы содержит шесть произвольных
постоянных, для определения которых задается шесть начальных
условий (в механике это начальное положение и скорость точки
в некоторый момент времени t —10).
Для определения решения канонической системы уравнений
B1,8) применяется такой же прием, как и при решении рассмот-
рассмотренных выше нормальных систем: последовательным дифферен-
дифференцированием одного уравнения системы (или нескольких ее урав-
уравнений) следует исключить все искомые функции, кроме одной.
Сущность этого приема подробно разбирается на примере в сле-
следующей задаче.
Задача 21,17. Найти общее решение системы уравнений:
dt2 — гХ *
— -x — ly
Решение. Продифференцируем первое уравнение два раза
по t и получим
dt* * zdt* qdi* ¦ ' к '
Подставим в (А) вместо — его выражение из второго уравне-
уравнения системы.
Тогда
ИЛИ
g=-2g-4, + 28^. (В)
938
Из первого уравнения системы определим у и подставим его
в уравнение (В):
(С)
С этим значением у уравнение (В) перепишется так:
Раскрывая скобки и перенося все члены уравнения в его левую
часть, получаем
— ЗС2 sin l/it — 6С3 cos Кб^ — 6С4 sin
Характеристическое уравнение
k* + 9k* + 18 = О
имеет корни: k1<2 — ± V3i; кзл = ± |/6i.
Частные решения:
Xi — cos V~3t; хг = sin V~2>t; xs — cos V^bt; xt — sin
Функция
x = d cos Y3t + C2 sin Vbt + C3 cos У^бг1 + C4 sin Кб^. (D)
Теперь из (С) найдем г/. Из (D) находим
gf = _3d*cosl
Подставляя х и ^f в (С), получим
у = -L d cos Y~3t + i- C2 sin Кз7 + C3 cos V^6/ + C4 sin
Задача 21,18. Найти общее решение системы:
у" = 4у — 2г\
(независимая переменная х).
Решение. Продифференцируем по х дважды второе уравне-
уравнение:
гD) _ у" _|_ 2»# Щ
Заменим в (А) у" его значением из первого уравнения.
Тогда
z<4> = Ау — 2г + г". (В)
Чтобы получить уравнение, содержащее одну неизвестную
функцию, исключим из него у с помощью второго уравнения си-
системы. Из него следует, что
y = f — ?. (Q
939
Подставляя это значение у в (В), получим
2D) = 4 (г" — г) — 2г + г",
а после упрощений
2D) _ 52" + 6г = 0.
Характеристическое уравнение k* — 5k2 + 6 = 0. Его корни:
Частные решения:
Функция
г = Cie + С2е + ^з^ + ь4е
или на основании формул A9,18), вводя обозначения:
Ci + С2 = сх; Сх — С2 = с2; С3 + С4 = с3; С3 — С4 = с4,
г = Cj ch j/Зл; + с2 ch |/Зл; + с3 ch |/2л; + с4 sh У~2х.
Подставляя найденное, значение функции г и ее вторую про-
производную г" в выражение (С), получим
у = 2сх ch У~3х + 2с2 sh УЗх + с3 ch Кгл; + с4 sh V2x.
Задача 21,19 (для самостоятельного решения).
Найти общие решения систем (во второй системе найти реше-
решение, удовлетворяющее начальным условиям):
1) хГ @ + ашу = 0\. 2) x"(t) + 6х + 1у = 0
/(*) » OJ f(t) + 3 + 2 2t
д;@) = 2; у@) = 1; дс'@) =
У' @) = 3.
Ответ. 1) *= С, cosl-^i-l-Cosin
2) л: = Сге^ + С2е~< + 7С3 cos Ы + 7С4 sin 3^ + ~t\
у ~ -de* — Сге~1 + ЗС3 cos Ш + ЗС4 sin 3f — -i/.
О
ОПТ 01 О
Из начальных условий: Сх = — щ; С2 = 25; С3 = ^; С4==
135"
940
Задача 21,20. Найти решение системы
dbc _ _ ,dx
dt2 ~ dt
удовлетворяющее начальным условиям: л:@) = у@) = 0; х' @) =
= vOx\ у' @) = voy (k и g—постоянные величины).
Решение. Предложенная система уравнений описывает дви-
движение снаряда с учетом сопротивления среды.
Каждое из уравнений системы содержит только одну неиз-
неизвестную функцию.
Из первого уравнения следует
» + *§-»•
Характеристическое уравнение г2 + kr = 0 имеет корни: ^=0;
г2 = —k. Частные решения уравнения: хк— 1; x2 = e~kt. Его об-
общее решение
х = С, + Сае-*. (Л)
Чтобы определить С\ и С2, найдем х':
х' = — C2ke~kt. (В)
При t = 0 имеем:
из (Л) 0 = d + С2;
из (В) vox = —Cak.
Отсюда С1 = -^; Са = —-^.
Подставляя эти значения С1 и С2 в (Л), получим
x = -^(l-e-«). (I)
Второе уравнение перепишем так:
Уравнение линейное неоднородное. Общее решение соответ-
соответствующего однородного уравнения:
у0 = С3 + С4е-«.
Так как корни характеристического уравнения — числа 0 и — k,
из сравнения с B0,14) а = р = 0, а число а + $i = 0 является
корнем характеристического, то частное решение следует искать
в виде:
941
0
k
1
у
г
Y"
= Л/
= л
= 0
Общее решение уравнения (С);
г/ = С3 + С4е-«-|;. (D)
Для определения С3 и С4 из начальных условий найдем у':
y' = -Ctke-»-%. (E)
Учитывая начальные условия, получаем систему уравнений:
из (D) 0 = С, + С4;
из (Е) voy = —Ctk — f;
Подставляя эти значения С3 и С4 в (D), получим
(II)
Уравнения (I) и (II) являются параметрическими уравнениями
траектории снаряда.
Исключите самостоятельно параметр t из этих уравнений (из (I)
выразить t через х и подставить в (II)). Окажется, что
Из последнего уравнения можно определить горизонтальную
дальность стрельбы, если положить в нем у — 0, и из получен-
полученного уравнения найти х.
СОДЕРЖАНИЕ
Часть I
Практические занятия по аналитической геометрии иа плоскости
и в пространстве
Первое практическое занятие. Координаты точки на плоскости. Рассто-
Расстояние между двумя точками 8
Второе практическое занятие. Деление отрезка в заданном отношении.
Координаты середины отрезка. Определение площади треугольника
по известным координатам его вершин 15
Третье практическое занятие. Различные виды уравнения прямой. Ис-
Исследование общего уравнения прямой. Построение прямой по ее
уравнению 23
Четвертое практическое занятие. Уравнение прямой, проходящей через
данную точку в данном направлении. Уравнение прямой, проходя-
проходящей через две данные точки. Угол между двумя прямыми. Условие
параллельности и перпендикулярности двух прямых. Определение
точки пересечения двух прямых . 35
Пятое практическое занятие. Расстояние от данной точки до данной
прямой 46
Шестое практическое занятие. Уравнение биссектрисы угла между двумя
прямыми. Задачи повышенной трудности : 52
Седьмое практическое занятие. Полярная система координат. Переход
от полярных координат к декартовым и обратно. Построение кри-
кривой, определяемой уравнением в полярных координатах 61
Восьмое практическое занятие. Составление уравнения кривой по ее
геометрическим свойствам 73
Девятое практическое занятие. Продолжение упражнений в составлении
уравнений линий 77
Десятое практическое занятие. Кривые второго порядка: окружность,
эллипс ., 82
Одиннадцатое практическое занятие. Кривые второго порядка: гипер-
гипербола, парабола 89
Двенадцатое практическое занятие. Преобразование прямоугольных ко-
координат. Параллельный перенос координатных осей без изменения
их направления 99
Тринадцатое практическое занятие. Преобразование координат поворо-
поворотом координатных осей без изменения начала координат ...... ПО
Четырнадцатое практическое занятие. Упрощение общего уравнения
кривой второго порядка •. Цб
Пятнадцатое практическое занятие. Определители и системы линейных
алгебраических уравнений 124
Шестнадцатое практическое занятие. Векторная алгебра 139
Семнадцатое практическое щнящие. Основные, задачи на плоскость . . 159
ИЗ
Стр.
Восемнадцатое практическое занятие. Основные задачи на прямую
в пространстве 171
Девятнадцатое практическое занятие. Задачи на прямую н плоскость . 180
Двадцатое практическое занятие. Поверхности второго порядка .... -188
Часть II
Практические занятии по дифференциальному исчислению функций
одной и многих независимых переменных
Первое практическое занятие. Интервал, отрезок, промежуток. Абсо-
Абсолютная величина числа. Свойства абсолютных величин 212
Второе практическое занятие. Величины постоянные и переменные.
Функция. Область существования функции. Основные элементарные
функции 217
Третье практическое занятие. Продолжение упражнений в определении
области существования функции \ . . . . 225
Четвертое практическое занятие. Построение графиков функций .... 229
Пятое практическое занятие. Продолжение упражнений в построении
графиков функций. Графики показательной и логарифмической
функций 239
Шестое практическое занятие. Построение графиков тригонометриче-
тригонометрических и обратных тригонометрических функций '. . 244
Седьмое практическое занятие. Построение графиков функций, заданных
несколькими аналитическими выражениями. Построение графика суммы,
разности и произведения нескольких функций 254
Восьмое практическое занятие. Решение уравнений с помощью графиков.
(Графическое решение уравнений) 259
Девятое практическое занятие. Обратная функция и ее график. Перио-
Периодические функции 263
Десятое практическое занятие. Последовательности 267
Одиннадцатое практическое занятие. Предел последовательности .... 271
Двенадцатое практическое занятие. Дальнейшие упражнения в опреде-
определении предела последовательности 280
Тринадцатое практическое занятие. Определение предела последова-
последовательности (задачи повышенной трудности) 291
Четырнадцатое практическое занятие. Предел функции 300_
Пятнадцатое практическое занятие. Продолжение упражнений на нахо-
нахождение предела функции 308
Шестнадцатое практическое занятие. Определение пределов тригоно-
тригонометрических функций и упражнения на использование предела
ljmSJ??
*-о х
Семнадцатое практическое занятие. Число е 323
Восемнадцатое практическое занятие. Вычисление пределов выражений,
содержащих логарифмы и показательные функции 333
Девятнадцатое практическое занятие? Сравнение бесконечно малых ве-
величин - 338
Двадцатое практическое занятие. Непрерывность функции. Односторон-
Односторонние пределы. Точки разрыва и их классификация 343
Двадцать первое практическое занятие. Задачи, приводящие к вычис-
вычислению производной. Непосредственное вычисление производной из
определения. Геометрический и механический смысл производной . . 358
Двадцать второе практическое занятие. Дифференцирование алгебраи-
алгебраических функций 364
Двадцать третье практическое занятие. Дифференцирование тригоно-
тригонометрических функций 377
944
Стр.
Двадцать четвертое практическое занятие. Дифференцирование обрат-
обратных тригонометрических функций 382 г
Двадцать пятое практическое занятие. Дифференцирование логарифми-
логарифмической и показательной функций. Логарифмическое дифференциро- '
ва"ние 389
Двадцать шестое практическое занятие. Гиперболические функции.
Дифференцирование гиперболических функций. Дифференцирование
¦ неявных функций 397
Двадцать седьмое практическое занятие. Параметрическое представле-
представление функции. Дифференцирование функций, заданных параметрически . 401
Двадцать восьмое практическое занятие. Дифференциал функции . . . 407
Двадцать девятое практическое занятие. Производные высших порядков.
Формула Лейбница • 418
Тридцатое практическое занятие. Предел отношения двух бесконечно
малых и двух бесконечно больших величин (Правило Лопнталя) . . 423
Тридцать первое практическое занятие. Возрастание и убывание функции . 434
Тридцать второе практическое занятие. Определений максимума и ми-
минимума функций. Наибольшее и наименьшее, значение функции.на
отрезке ,. 439
Тридцать третье практическое занятие, Продолжение упражнений на
определение максимума и минйм-ума функций и их наибольшего
и наименьшего значения на отрезке • 449
Тридцат»четвертое практическое заняргйе. Точки перегиба. Асимптоты . 46$
Тридцать пятое практическое занятие. Общее исследование функции . 471
Тридцать шестое практическое занятие. Геометрические приложения
производной: уравнения касательной и нормали к плоской кривой.
Длины касательной и нормали. Подкасательная и поднормаль и "их
длины. Кривизна, радиус кривизны. Цецтр кривизны. Соотношение
между радиусом кривизны и длиной нормали. Эволюта кривой ... 481
Тридцать седьмое практическое занятие. Функции многих независимых
переменных. Область существования. Частные производные. Полное
приращение и полный дифференциал первого порядка функции не-
нескольких независимых переменных 499
Тридцать восьмое практическое занятие. Дифференцирование сложной
функции от одной и нескольких независимых переменных 512
Тридцать девятое практическое занятие. Производные и дифференциалы
высших порядков функций нескольких независимых переменных . . 520
Сороковое практическое занятие. Линии и поверхности уровня. Произ-
Производная функции по заданному направлению. Градиент функции . . . 535
Сорок первое практическое занятие. Дифференцирование неявных функций . 543
Сорок второе практическое занятие. Экстремум функции нескольких
независимых переменных. Наибольшее и наименьшее значения функ-
функции двух независимых переменных 550
Сорок третье практическое занятие. Касательная плоскость и нормаль
к поверхности 568
Часть III
Практические занятия по интегральному исчислению и интегрированию
дифференциальных уравнений
Первое практическое занятие. Первообразная функция и неопределенный
интеграл. Свойства неопределенного интеграла. Непосредственное
интегрирование ? 575
Второе практическое занятие. Интегрирование показательной и триго-
тригонометрических функций 591
Третье практическое занятие. Продолжение упражнений в непосред-
непосредственном интегрировании 600
945
Стр.
Четвертое практическое занятие. Замена переменной в неопределенном
интеграле (метод подстановки). Интегрирование по частям 614
Пятое практическое занятие. Простейшие дроби. Разложение рациональ-
рациональной дроби на простейшие 627
Шестое практическое занятие. Интегрирование простейших рациональ-
рациональных дробей 637
Седьмое практическое занятие. Интегрирование рациональных дробей . 648
Восьмое практическое занятие. Интегрирование выражений, содержащих "
тригонометрические функции . 658
Девятое практическое занятие. Интегрирование алгебраических ирра-
циональностей 685
Десятое практическое заняЪшг. Интегральная сумма. Определенный инте-
интеграл и его основные свойства. Вычисление определенного интеграла
как предела интегральной суммы 716
Одиннадцатое практическое занятие. Задачи механики и физики, приво-
приводящие к определенному интегралу 729
Двенадцатое практическое занятие. Замена переменной в определенном
интеграле. Интегрирование по частям. Теорема о среднем значении . 745
Тринадцатое практическое занятие. Несобственные интегралы по беско-
бесконечному интервалу и от разрывных функций. Принцип сравнения
несобственных интегралов с положительными подынтегральными
функциями : 756
Четырнадцатое практическое занятие. Приближенное вычисление инте-
интегралов: формулы прямоугольников, трапеций и Симпсона (формула
парабол) 770
Пятнадцатое практическое занятие. Приложения определенного инте-
интеграла к геометрии. Определение площадей плоских фигур 777
Шестнадцатое практическое занятие. Приложения определенного инте-
интеграла к геометрии (продолжение): длина дуги плоской кривой, объем
тела вращения, поверхность тела вращения J792 ^
Семнадцатое практическое занятие. Дифференциальные уравнения пер- ~'""' '
вого порядка 812
Восемнадцатое практическое занятие. Дифференциальные уравнения выс-
высших порядков, допускающие понижение порядка 838
Девятнадцатое практическое занятие. Линейные дифференциальные урав-
уравнения высших порядков 865
Двадцатое практическое занятие. Линейные неоднородные дифференци-
дифференциальные уравнения 8Ш...У
Двадцать первое практическое занятие. Уравнение Эйлера. Системы ли-
линейных дифференциальных уравнений с постоянными коэффициентами . 926
Илья Абрамович Каплаи
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Редакторы А. С. Нестеренко и И. Л. Базилянская
Обложка художника А. П. Шулики
Техредактор Л. Т. Момот
Корректоры М. И. Лелюк и Р. Е. Дорф
Сдано в набор 10/1 1967 г. Подписано к печати 25/IV 1967 г. БЦ 45267.
Формат бОхЭО'Дв- Объем 59,25 физ. печ. л., 59,25 усл. печ. л., 52,1 уч. изд. л.
Св. Т. П. Издательств Университетов 1967 г. поз. 13
Зак. 7-45. Тираж 50 000. Цена 1 руб. 61 коп.
Книжная фабрика имени Фрунзе Комитета по печати
при Совете Министров УССР, Харьков, Доиец-Захаржевская, 6/8.