л-С ХРЕНОВ
Ю В ВИЗИРОВ
логарифмическая
линейка

Л. С. ХРЕНОВ, Ю. В. ВИЗИРОВ
ЛОГАРИФМИЧЕСКАЯ
ЛИНЕЙКА
Под общей редакцией
проф. Л. С. Хренова
ИЗДАТЕЛЬСТВО
ВЫСШАЯ ШКОЛА
Москва — 1968
УДК 681.143
X—91
Аннотация
Хренов Л. С., Визиров Ю. В Логарифмическая линейка.
«Высшая школа», 1968 г.
В брошюре дано краткое описание нормальной счетной ло-
гарифмической линейки, счетного логарифмического диска «Спут-
ник» и круговой логарифмической линейки КЛ-1
Здесь в популярном изложении рассмотрены общие правила
алгебраических и тригонометрических действий с помощью всех
трех линеек, а также и решения самых различных задач, встре-
чающихся в практике работы техника.
Приведены некоторые способы выбора оптимальных алгорит-
мов (алгорифмов) при использовании логарифмических линеек
при различных вычислениях и даны способы определения поряд-
ка результатов вычислений.
Основное назначение брошюры — научить учащихся техни-
кумов считать на различных логарифмических линейках и слу-
жить справочным пособием в их дальнейшей работе.
Она может быть использована самым широким кругом чита-
телей, желающих научиться считать на различных логарифми-
ческих линейках
Рис. 24, табл 5, библиограф. 8.
2-2-4
254—68
ПРЕДИСЛОВИЕ
Развитие науки, техники и управления народным хо-
зяйством связано с разнообразными вычислительными
операциями, объем которых все время возрастает. Боль-
шое количество вычислений повседневно выполняют ин-
женеры и техники, экономисты, работники учета и раз-
личные специалисты, занятые в промышленности и других
отраслях хозяйства нашей страны. Стремление облегчить
труд вычислителей привело к развитию вычислительной
техники.
Производительность труда, прежде всего, зависит от
правильно выбранных средств вычислений. В зависимо-
сти от точности исходных данных и характера самих
вычислений пользуются разнообразными средствами —
таблицами, номограммами, счетными приборами и
машинами.
Однако несмотря на быстрое развитие вычислительных
машин, являющихся одним из замечательных достиже-
ний нашего века, счетная логарифмическая линейка
продолжает оставаться самым массовым прибором инди-
видуальных вычислений, не требующих большой скоро-
сти и точности.
В этой брошюре, кроме кратких теоретических обо-
снований и описания устройств, получивших распростра-
нение разных счетных логарифмических линеек, основное
внимание уделено практике работы на них.
При пользовании настоящим пособием необходимо
1*
3
иметь описанные здесь логарифмические линейки для ре-
шения примеров и выполнения приводимых в нем уп-
ражнений.
В этой работе написаны: Ю. В. Визировым §7 и
9—14, Л. С. Хреновым и Г. А. Гафт § 8, а все
остальное — Л. С. Хреновым.
Пользуясь случаем, авторы выражают искреннюю бла-
годарность рецензенту Н. И. Гуревичу за весьма цен-
ные советы и замечания, которые были учтены при под-
готовке рукописи к изданию.
Авторы обращаются ко всем пользующимся этой бро
шюрой с просьбой сообщить свои замечания, направлен-
ные на ее улучшение.
Проф. Л. С. Хренов
ВВЕДЕНИЕ
В практике самых различных вычислений исходными
данными могут быть не только точные, но чаще всего
приближенные величины, определенные с той или
иной степенью точности. При этом, однако, следует учи-
тывать, что и при вычислении с точными величинами
точные результаты могут быть получены лишь при сло-
жении и вычитании и только за некоторым исключением
при умножении и возведении в степень. Результаты
вычислений с приближенными числами будут всегда
лишь приближенными. Поэтому наряду с различными
таблицами1, представляющими совокупность с установ-
ленной точностью численных значений данной функции,
соответствующих определенным, последовательно распо-
ложенным значениям аргумента, широкое применение
имеют различные механические средства вычислений1 2.
Самым простейшим механическим средством будут две
совершенно одинаковые равномерные шкалы, перемеща-
ющиеся относительно друг друга. При помощи такого
прибора можно производить графически действия сложе-
ния и вычитания.
Так например, если иметь две линейки Р и Q с оди-
наковыми делениями (рис. 1, а), то для получения сум-
мы двух чисел 6+8=14 следует поступить так. Линей-
ку Р передвинуть вправо относительно линейки Q так,
чтобы ее нулевой штрих был против штриха 6 (первое
слагаемое), нанесенного на линейке Q (рис. I, б). После
этого против штриха 8 (второе слагаемое) на линейке Р
можно прочитать по шкале линейки Q искомую сумму
14.
1 Рывкин А. А., Рывкин А, 3., Хренов Л. С. Спра-
вочник по математике. Изд. второе. М., «Высшая школа». 1968.
2 Хренов Л. С. Малые вычислительные машины. Изд. четве-
ртое. М., «Наука», 1966.
5
На равномерных шкалах (см. рис. 1) отрезки пропор-
циональны числам, подписанным против соответствую-
щих штрихов на шкале. Уравнение для таких шкал
будет иметь вид
у=т-х>	(1)
где т— модуль или масштаб равномерной шкалы.
Следовательно, равномерная шкала является графиче-
ским изображением функции одного переменного (х),т. е.
=	(2)
а) т
Рис. 1. Линейки с равномерными шкалами:
а — совмещенное положение двух линеек;
б — получение суммы двух чисел
Примечание. Для равномерной шкалы, показанной на
рис. 1, модуль т равняется длине наименьшего отрезка.
Если сложение и вычитание быстрее производить на
русских счетах1, нежели с помощью равномерных шкал,
то для умножения и различных алгебраических и триго-
нометрических действий целесообразно пользоваться гра-
фическими способами. Только в этом случае используют
шкалы неравномерные, т. е. такие, на которых от-
счеты непропорциональны соответствующим отрезкам.
Примером неравномерных функциональных шкал будут
шкалы, построенные, например, для уравнений
r/ = mlgx, # = mlgtgv и т. п.
1 С конца XVIII в. они уже приобрели современный вид.
6
Если построить две логарифмические шкалы, для ко-
торых уравнение будет иметь вид
у = mlgx,	(3)
то, пользуясь такими шкалами, можно графически про-
изводить умножение, деление и различные алгебраичес-
кие действия.
Известно, что Бригговым, иначе, обыкновенным
или десятичным логарифмом числа М называют пока-
затель А степени, в которую надо возвести основание
10, чтобы получить число М. Так, в равенстве 1(М =М
число Л —бриггов логарифм числа /И. Это записывают
так: А — IgM.
При вычислениях пользуются следующими свойствами
логарифмов:
lgMAT = IgM + IgA/,	(4)
1g-у-= IgAl — IgAf,	(5)
lgMn = /ilgM,	(6)
(7)
Если положительное число M представляет целую
положительную или отрицательную степень основания
10к т. е.
М=10±л,
то логарифм этого числа равен положительному или от-
рицательному целому числу.
Например,
1g 1000 = 3, так как 103 = 1000.
1g 100 = 2, так как 102 = 100,
1g 10 =1, так как 101 = 10,
lg 1	=0,	так как 10°= 1,
1g 0,1= — 1, так как 10*1 = 0,1,
1g 0,001 = — 3, так как 10"3 = 0,001 и т. д.
Для любого другого положительного числа, отличного
от нуля, его логарифмом будет число иррациональное,
которое, как известно, можно с любой степенью точности
заменить десятичной дробью. Целую часть такой дроби
7
называют характеристикой логарифма, а дробную -
часть — его мантиссой.
Итак,
1g ЮМ = 1g 10 + IgM = 1 -Ь 1gМ,
1g 100М = lg 100 4- 1g M = 2 4- 1g M,
=	I000 = lgM-3 и т. д.,
т. e. логарифмы чисел M, 10Л1, 100M, 0,1Л4, 0,01Л4 и т. д.
имеют одинаковые мантиссы. Следовательно, мантисса
какого-либо числа не зависит от положения запятой в
этом числе.
Что же касается характеристики логарифма, то для
ее определения пользуются следующими правилами.
1. Для числа М> 1 характеристика его логарифма
положительна и равна числу цифр без одной в целой
части М, т. е. имеем:
1<М<	10 — характеристика логарифма 0,
10<^Л1 <	100 — характеристика логарифма 1,
100<Л4 < 1000—характеристика логарифма 2,
1000 <7И< 10000—характеристика логарифма 3 и т. д.
2. Для положительного числа М < 1 характерис-
тика его логарифма отрицательна и равна числу ну-
лей в М до первой значащей цифры1, включая и нуль
целых, т. е.
1 > М > 0,1	— характеристика
0,1 > М > 0,01 — характеристика
0,01	0,001 —характеристика
0,001 > Л4 > 0,0001 — характеристика
логарифма — 1,
логарифма — 2,
логарифма — 3,
логарифма — 4
и т. д.
Итак, характеристика логарифма есть целое (положи-
тельное или отрицательное) число или нуль, а мантисса
логарифма всегда считается положительной.
При записи логарифма, у которого характеристика
отрицательна, знак «минус» пишут над характеристикой;
этим подчеркивают, что мантисса положительна.
1 Значащими цифрами каждого числа будут все его цифры,
за исключением нулей, стоящих впереди первой цифры, отличной
от нуля. Нули, стоящие впереди числа, позволяют определить раз-
ряд первой, отличной от нуля цифры в данном числе.
8
Например, lg7 = 0.8451; lg23 = 1.3617; lg0.0149 =
= 2.1732; 1g 12 405 = 4.0936; 1g 0.00000694=6.8414;
1g 12 000 000 = 7.0792; lg 0.916 = 1.9619.
Пользуясь свойствами логарифмов, можно построить
логарифмические (неравномерные) шкалы, урав-
н ения которых будут
У = tn Igx,	(8)
0,602	\	
. 0,645	
Рис. 2. Построение логарифмической шкалы
и производить по ним умножение, деление и другие
действия.
Для построения логарифмической шкалы поступают
так. Если некоторый отрезок АВ (рис. 2) считать равным
единице, то, следовательно, его можно (см. выше) при-
нять за 1g 10.
Теперь определим размеры отрезков, соответствующих
логарифмам чисел 1, 2,..., 9 (табл. 1).
Таблица 1
1	2	3	4	5	6	7	8	9	10
0,000	0,301	0,477	0,602	0,699	0,778	0,845	0,903	0,954	1,000
Например, 1g 4 изобразится отрезком
АС = lg 4:1g 10 = 0,602,
a lg 7 — отрезком
AD = lg 7:1g 10 = 0,845 и т. д.
На рис. 3 показана логарифмическая шкала, постро-
енная для уравнения (8) при модуле т = 12,5 см.
Продолжив такую шкалу вправо от штриха 10, мож-
но построить продолжение логарифмической шкалы, по-
лучив второй ее участок. Так можно получить продол-
жение первой шкалы до 100 и т. д.
2 Заказ № 550
9
F
1
2	3 Ь 5
Рис. 3. Логарифмическая шкала
6 7 8 9 Ю
НОРМАЛЬНАЯ СЧЕТНАЯ ЛОГАРИФМИЧЕСКАЯ
ЛИНЕЙКА
§ 1.	ОПИСАНИЕ ЛИНЕЙКИ
Основой устройства логарифмической линейки являет-
ся логарифмическая шкала1 — графическое изо-
бражение логарифмов чисел.
Такая линейка служит для выполнения механи-
ческим путем различных вычислений. Точность вычи-
слений на счетной логарифмической линейке зависит от
длины ее шкал. На нормальной линейке с длиной шкал
в 25 см можно получить результаты с тремя-четырьмя
значащими цифрами с ошибкой не более единицы послед-
него знака.
Нормальная логарифмическая линейка (рис. 4) состо-
ит из трех, покрытых белым целлулоидом частей (ГОСТ
5161—57): корпуса М, имеющего продольный паз,
движка Q, перемещающегося в пазах корпуса, и
бегунка Б.
На корпусе линейки нанесено шесть (F, К, A, D,
L, и Р1 2) различных шкал. (см. § 2) длиной по 25 см каж-
дая.
На движке занесено такой же длины, как и на
корпусе, три (В, R и С) неравномерные шкалы на лице-
вой стороне (см. рис. 4) и т р и (S, S и Т и Т) неравно-
1 Идея устройства логарифмической шкалы принадлежит проф.
Э. Гутнеру (1581—1626), предложившему ее в 1620 г., т. е.
спустя примерно шесть лет шосле опубликования (1614) Д. Непе-
ром (1550—1617) его работы о логарифмах.
2 Измерительная шкала Р, занесенная на вертикальной грани
корпуса линейки (на рис. 4 не видна).
2*	11
^^/f/////f//hf///)/i/H//f//h/i//i/iiii/iiii/iiliiiiiijiiii^liiiiiii^l]liji]liyiiillil^liTI"IHn]lliTfTTn] ГТТ7[ГГП(ТГПр
Г
Б
К |1111||111|||11|1111|1111|1111||111|111|111|11111|1|111|1|1|111|1|11Ш11|||||||1||||Ц||НИ1 &
.........................................................  Ill	I iiinnliii L

plllllllllllll[lllllllll[llll
iiiiiiiiiiiiiiiiiiiiiniiiiiii'iiiiiiiiiiiiiaiiii i
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIBBI
- ... t .... 2....
Q р^щдпгтапт|1|||Щ|Ц111|1|1|1|1|^1 гпг|цц||1|1|1|1|1|тщщ]тт
p1	1<1 9	12	1,3 1A 1,5
12
1.3
1,6
1 3	1	j	5	Б	7	8	9	10
					
1? , 1ft , 1,9 ,	| Р"	'		' 1	3	л
1.8
1.9
iiiiiiaiiiiiiiiniiiiiiiiiiiinuiii
iiiiiiiiiiitiiiiiiiiiiiiiiiiiiHiaiiiniiiiiiiii
1,1 c
1.2
1.5
1.6
L iiiiihiiiiiiiiiiiniiiiihiiiiiiiiiiiiiliiiiiiihliiiiiiiiiiiiiiiiiiiiiiiiliiiitnntniiiiiiiiiiiiiiiiilii
uiiiiiiLiiliiiddiiliuiiiiiihuHi'iiiiiiilrriiiiiniiintnn
M
3 *
c
N

Г

{|l|l|l|ip|!|l|l|)|l|ffll|llll|liy
.	2.0 '	,	3.0 м '.	§.0	'	5.0 '	6.0	7.0 flO . 9p . *00
LiaiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiniiiiiiiaMHilBBaaBaeBBiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiBieaiBHiHiiiiiniiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
(1мтапими11шмш11111111111111111111навв1ааа8118881111П111111111111Н11^11Ш11Ш111Ш11ММ111Ш1Ш11111111а11Н1Г111111Ш1Ш11111№
2'0	1	JO A	'4IO- I  •  ^IO 6'o	'	7»0 ' 8'0 ' 90	100
Рис. 4. Лицевая сторона нормальной логарифмической линейки
noHodoio HOHiudQO wiaHHawauioon ‘доолжиатг э илиании* келэаьикф^елог KBaairB^vdopj g oad
001	06	08	00	09	09	0* г 00	02	*
qi ъг съ гъ \i oz 6v 9v tv 9v sv м cv
XwwXwwXwwNwwXwwXwwXxiwywssXwvvXxwvXvivvXuvvVviit^ntiliiiililillitiiliiithiiiltiiiliiiilifiififiiliiiiJMit
|hniiiiiiiiniiiiiiiniiiiiiiiiiiiiiiiiii>»iiiiiimiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiuiniiiiiniHiiiiiiinii»»Hl
|||||||1и1П11Ш111111ПШ1111Ш1пшп11111П11111111111Ш111111»н1111Н11111111111111»111М1111вн1нйиваммаввмввМна»внвяа1|
ОС V
8v tv 9V $v
<zv
Cv I 2V
рхщтг
cv
iv
Ov I 6	*	9	1 L
1.ЩЦ1 p.|.q 11.LP111ГH1 '111.1ГТ rjЩЩ
OL
tv ' 9V • Sv I *7l
шцшргщг^-------
9
6
9

a
1
s
N


01-	6	9
\ V
W
¥ C
9
^7
Z
9
L
мерные шкалы (см. § 2) на обратной стороне движка
(рис. 5).
Бегунок состоит из прямоугольной металлической
рамки со стеклом, на середине которого нанесена тонкая
черта—указатель (визир). Бегунок удерживается на
линейке соприкасающимися с ее корпусом закраинами
рамки. Между рамкой бегунка и корпусом линейки по-
ставлена пружина, способствующая свободному переме-
щению бегунка и удержанию его на линейке.
И, наконец, на обратной стороне корпуса линейки
приведены некоторые данные справочного характера:
математические и физические постоянные, коэффициен-
ты линейного расширения, модули упругости, удельные
веса некоторых тел и другие данные.
Счетная логарифмическая линейка требует бережного
обращения. Между работами на линейке ее сохраняют в
футляре.
Линейку нельзя ронять; ее запрещается хранить в
горячем или влажном месте. Загрязненные шкалы линей-
ки можно протирать только винным спиртом (водкой).
Поверки .линейки
1.	Верхняя поверхность движка должна лежать в од-
ной плоскости с верхней поверхностью корпуса линейки.
2.	При совмещении начального штриха шкалы А на
корпусе с начальным штрихом шкалы В движка визир
бегунка должен отмечать - начала и концы всех шкал
линейки; шкала D корпуса должна совпадать со шка-
лой С движка, шкала квадратов А корпуса — со шкалой
квадратов В на движке, а, в вырезах обратной стороны
отсчетные черточки должны совпадать с началом и кон-
цом тригонометрических шкал.
3.	Движок и бегунок должны передвигаться в пазах
корпуса достаточно легко и равномерно без проскаль-
зывания и лишнего трения. При тугом перемещении
движка можно тальком, воском или парафином протереть
его боковые ребра, а при слишком легком скольжении
бегунка по линейке следует осторожно подогнуть те его
части, которыми он держится на ней.
4.	Для выборочного контроля шкал следует произ-
вести некоторые вычисления, например >^8= ]/4~
14
= 1 : 0,5=2; >/27=/9=1: 0,333 = 3; ^64 =/16 =
= 1 : 0,25 = 4; sin 30°=0,5;...
Соответствующие штрихи на основной шкале D кор-
пуса и штрихи на шкале обратных чисел (на обратной
стороне движка) должны совпадать (проверять, пользуясь
бегунком).
§ 2.	ШКАЛЫ ЛИНЕЯКИ
На лицевой стороне корпуса (см. рис. 4) верхняя
шкала Д' (кубичная) и ниже ее — шкала А (квадратич-
ная) служат для вычисления соответственно кубов и
квадратов чисел, значения которых отсчитывают по шка-
ле D. Мантиссы логарифмов чисел шкалы D нанесены на
нижней шкале L линейки, которая заменяет собой трех-
значную таблицу мантисс логарифмов чисел и является
единственной из четырех на лицевой стороне равномер-
ной шкалой, разделенной на полумиллиметры; осталь-
ные шкалы логарифмические — неравномерные.
На шкале L наименьшее деление соответствует 0,002,
а метки, обозначенные на ней цифрами 2, 3, 4.. чи-
тают как 0,2, 0,3,. 0,4 и т. д.
Шкала D на корпусе линейки и шкала С на движке,
называемые основными шкалами линейки, каждая
состоит из трех участков, на концах которых стоят 1 и
2, 2 и 4, 4 и 10.. Каждый такой участок является ло-
гарифмической шкалой. На них нанесены отрезки про-
порционально логарифмам (/nlgx) соответствующих чисел,
но уменьшенным в четыре раза, так как длина всей
шкалы равна 0,25 м, а не 1 м (т. е. mlgx = 2501gx при
х от 1 до 10). Поэтому на этих шкалах каждое наимень-
шее деление на участке 1—2 обозначает 0,01 (сотые до-
ли), на участке 2—4 оно равно 0,02, а на участке 4—-
— 10— уже 0,05.
На линейке кубичная шкала К, являясь также лога-
рифмической (/nlga), построена с модулем т = (250: 3)
и для а от 1 до 1000; она состоит из трех участков, на
левых концах которых поставлена цифра 1. На ее первом
участке (левый крайний) наименьшее деление (цена одного
деления) в интервале 1—2 равно 0,02, в интервале 2—5 рав-
но. 0,05 и в интервале 5—1 (10) равно 0,1. На ее втором
участке (среднем) в интервалах 1 (10) —2 (20), 2 (20) —5 (50)
15
и 5 (50)—1 (100) наименьшее деление равно соответ-
ственно 0,2, 0,5 и 1. И, наконец, на ее третьем участке
(правом крайнем) в интервалах 1 (100)—2 (200), 2 (200)—
5 (500) и 5 (500) — 1 (1000) наименьшие деления соот-
ветственно равны 2, 5 и 10.
Квадратичная шкала А на линейке и точно такая же
шкала В (верхняя на движке /nlgc) построены каждая с
модулем т = (250:2) мм для значений с от 1 до 100 и
состоят из двух одинаковых частей, оцифрованных по
концам 1 —10 и 10— 100. На этих шкалах цена одного
деления в интервале 1—2 равна 0,02, в интервале 2—5
равна 0,05 и в интервале 5—10 равна 0,1, а на втором
участке в интервалах 10—20, 20—50 и 50—100 равна
соответственно 0,2, 0,5 и 1.
На лицевой стороне движка между шкалами В и С
нанесена средняя шкала R (см. рис. 4) —шкала об-
ратных значений. Она представляет собой ту же
шкалу С (D), но только в перевернутом виде, т. е. метка
10 поставлена на ее.левом, а метка 1 на правом конце.
На этой шкале отрезок от ее левого конца до любой
метки, например до метки р, равняется 250—250 Igp =
= 250 1g (1 :р).
На обратной стороне движка нанесены три логариф-
мические шкалы (рис. 5), предназначенные для вычисле-
ний с тригонометрическими функциями. Уравнения этих
шкал следующие:
для шкалы Sin r/ = Z’(lgsin-f- 1)	— шкала си-
нусов;
для шкалы ShT <7 = А 1g -у (sin v + tgv) + 2	—
шкала синусов и
тангенсов
для шкалы Tg у = k (1g tg + 1)	— шкала
тангенсов,
где и vz—пометки углов, соответствующие шкалам.
На верхней шкале Sin нанесены от начальной точки
в масштабе основной шкалы логарифмы синусов углов
от 5°43', 77 до 90°, а на нижней шкале Tg — логарифмы
тангенсов углов от 5°43',77 до 45°. На средней шкале
S и Т — щкале синусов и тангенсов от начальной точки
16
(как и на крайних шкалах) нанесены логарифмы этих
функций для значения острых углов от 0°34',38 до
5°43',77.
Для каждой из этих шкал значения углов выбраны
так, что значение функции крайнего правого отсчета в
десять раз больше значения той же функции для началь-
ного левого отсчета.
Действительно
sin 0°34',38 « tg0°34',38 « 0,01 000;
sin 5°43',77 « tg5°43',77 ~ 0,1000;
sin 90° = 1,000, a tg 45° = 1,000.
Следовательно, шкалы Sin и Tg содержат логарифмы
углов, синусы и тангенсы которых меняются в пределах
от 0,1 до 1, а средняя шкала S и Т — логарифмы углов,
синусы (тангенсы) которых меняются в пределах от 0,01
до 0,1.
На шкале Sin на участке от ее начала до 10° наи-
меньшее деление соответствует 5', на участках 10—20° и
.20—90° оно соответственно равно 10' и 20'.
На шкале Tg наименьшие деления 5' и 10' имеют
участки, соответствующие углам в пределах 0—20° и
20—45°.
На средней шкале (S и Т) наименьшее деление на
участке до 3° соответствует 1', а от 3° и дальше 2'.
Такое сочетание шкал, нанесенных на лицевой сто-
роне линейки и на двух сторонах движка, позволяет
выполнять по ним самые различные вычисления.
И, наконец, на некоторых шкалах лицевой стороны
линейки и на одноименных шкалах движка особыми штри-
хами отмечены константы: к (на шкалах А, В, С и D),
М — 1 : те (на шкалах А и В), С — У 4 ; к, Сх = ]/40 ; те,
р°, р', р" и р ==у^о (на шкалах С и D, см. рис. 4).
$ 3. УСТАНОВКА И ЧТЕНИЕ ЧИСЕЛ ПО ШКАЛАМ ЛИНЕЙКИ
Установить заданное число на шкале линейки — это
значит найти его место на этой шкале. И, наоборот,
если на шкале линейки указано место, то для определе-
ния числа, соответствующего этому месту, необходимо
17
PI121ULZ1IL1
уметь на шкале прочиты-
вать это число. При этом
следует помнить, что каж-
дая метка (черточка) на
шкале счетной линейки
соответствует не одному
какому-либо определенно-
му числу, а всякому дру-
гому, которое может быть
получено умножением это-
g	го числа на 10 в любой
S	степени. ’ Так, например,
э	число 19,75 (см. отсчет по
к	визиру бегунка на шкале
8	С, рис. 6) будет на линей-
ке в том же месте, что
§	числа 1975, 1,975, 0,1975,
|	0,01975, 0,001975 и т. п.
н При установке чисел
g	на шкалах счетной ли-
о	нейки не следует обра-
<5	щать внимания ни на
запятые, ни на нули,
£	стоящие в конце уста-
навливаемого числа.
Следовательно, при ус-
тановке чисел на шкалах
надо читать все его циф-
ры в последовательном
порядке и определять ме-
сто 'этого числа на шка-
ле, руководствуясь соот-
ветствующими ее деле-
ниями.
На рис. 6 с помощью
показана .установка:
указателя (визира) бегунка
на шкале А — числа 3,90 (три, девять, ноль);
на шкале R — числа 5,051 (пять, ноль, пять, один);
на шкале С — числа 19,75 (один, девять, семь, пять).
На шкале D по указателю бегунка (см. рис. 6) можно
прочитать число .0,001975, или* 1,975, или 197,5, или 1975.
А на шкале L по тому же указателю читаем 296.
18
На счетной линейке в начале шкал Л, В, /?, С и D
(см. рис. 4) можно устанавливать или прочитывать четы-
ре цифры, а в середине и в конце этих шкал — только
три цифры числа (рис. 7).
Продолжение шкал Айв
9 Ю	.	20	|.	30	>	40 I । 50	60 I 70 8Z) 90 10

3 Ю	20 Г з’о" ' ' 1 " ’ 40	"50	60 | 70	&0 90 Ю
\&8 I 422 , -	I 63Z
Продолжение шкал С и В
?!• с.
С
D л"
piuiiiiiifiintiaitiit iiinituuiiimtiiiiifiiii
346
5
475
577	\909
Рис. 7. Части шкал A, В, С и D нормальной логарифмической
линейки
Если число состоит из большего числа цифр, то при
работе на счетной линейке, остальные цифры отбрасывают,
пользуясь при этом округлением по правилу с поправ-
кой. При таком округлении:
1)	если первая из отбрасываемых цифр равна или
больше пяти (5) единиц, то последнюю оставляемую
цифру в числе увеличивают на единицу;
2)	если первая из отбрасываемых цифр меньше пяти
(5) единиц, то последнюю оставляемую цифру в числе
сохраняют без изменения;
3)	если в точном числе последней цифрой является
цифра пять (5), то предшествующую ей цифру увеличи-
19
вают на единицу только в том случае, когда она нечет-
ная.
Примеры.
Число 131,29853 после округления будет 131,299 или
131,30.
Число 87,8242 после округления будет 87,824 или
87,82.
Если числа 35,965 и 149,875 точные, то после окру-
гления они будут 35,96 и 149,88.
Уменье правильно устанавливать и читать числа по
шкалам линейки — залог успеха в работе на линейке.
§ 4. ПОРЯДОК ЧИСЕЛ
Для определения окончательного результата вычисле-
ний на счетной логарифмической линейке необходимо
иметь понятие о порядке или значности чисел.
Порядком или значностью числа, равного или больше
единицы, называют число цифр, стоящих в его целой
части; такой порядок (значность) называют положитель-
ным.
Порядком или значностью числа, меньшего единицы,
называют число нулей, стоящих после запятой до его
первой значащей цифры; такой порядок (значность) счи-
тают отрицательным.
Примеры
Число	Порядок (значность)	Число	Порядок, (значность)
7	1	о,1	0
29	2	0,19	0
561	3	0,19994	0
561,7	3	0,00750	—2
561,384	3	0,084	—1
281,35	3	0,0001	—3
2,811	1	0,99	0
5133,5133	4	0,00000181	—5
Из приведенных примеров видно, что порядок любого
числа (большего или меньшего единицы) всегда на еди-
ницу больше характеристики его десятичного (бриггова,
см. стр. 7) логарифма (табл. 2).
20
Таблица 2
Число	Л огарифм	Порядок ч	। Число	Логарифм	Порядок
4,131	0.6161	1=0+1	0,012	2.0792	— 1 = —2+ 1
63	1.7993	2=1 + 1	0,137	£.1367	0 = — 1 + 1
127,4	2.1052	3 = 2+1	0,000961	£.9827	_3 = —4+ 1
93,18	1.9693	2=1 + 1	0,00239	3.3784	_2 = —3+ 1
§ 5. АЛГЕБРАИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ
ДЕЙСТВИЯ НА ЛИНЕИКЕ
На счетной логарифмической линейке механическим
путем можно производить умножение, деление, возведе-
ние в степень и извлечение корня, а также определять
натуральные значения тригонометрических функций за-
данных углов и, наоборот, по заданным натуральным
значениям функций находить соответствующие им углы,
определять логарифмы и антилогарифмы чисел и лога-
рифмы тригонометрических функций и производить раз-
личные вычисления (см. § 7).
Так, например, по шкалам лицевой стороны линейки
при помощи только одной установки указателя бегунка
можно получить сразу четыре результата: число на
основной шкале D, его логарифм на нижней шкале L,
а квадрат и куб этого числа соответственно на шкалах
А и К-
На рис. 8 по указателю бегунка, поставленного на
штрих, подписанный на шкале D числом 1,9, можно по
шкале L прочитать 1g 1,9 = 0,279; по шкале Л—квадрат
этого числа, т. е. 1,92 = 3,61, а по шкале К — куб этого
числа, т. е. 1,93 «6,86.
Если же указатель бегунка установить, например, ыа
шкале кубов К или квадратов Л, то по этому указа-
телю можно на соответствующих шкалах прочитать
кубический или квадратный корень этого числа на шка-
ле D, а логарифм этого корня на нижней шкале L кор-
пуса линейки.
Примечание. Если при работе на линейке шкалы движка
ее не используются, то для удобства вычислений его следует выдви-
нуть из пазов линейки (см. рис. 8 ).
21
ггттуттггртттртп
Для приобретения
навыков в работе со
счетной логарифмиче-
ской линейкой следует
на ней проделать рас-
смотренные .ниже при-
меры.
Умножение и деление
Эти действия на ли-
нейках основываются
на известных свойствах
логарифмов (см. стр. 7)
и при умножении сво-
дятся к сложению со-
ответствующих отрез-
ков на логарифмиче-
ских шкалах С и D, а
при делении—к вычи-
танию их.
Пример 1. Тре-
буется вычислить
х= 32,4 х 23.
В этом случае, поль-
зуясь соответствующи-
ми шкалами линейки,
необходимо сложить
два отрезка (32,4 и 23).
Для этого указа-
тель бегунка на шкале
D ставят на деление
32,4, а перемещением
движка вправо подво-
дят левую крайнюю ци-
фру 1 его на шкале С
под указатель. Затем бе-
гунок переводят вправо,
устанавливая его ука-
затель на деление 23
шкалы С, и по указа-
телю прочитывают на
22
основной шкале линейки D ответ: число 745 т. е.
х « 745.
Пример 2. Определить х = 5,65 х 3,17.
В этом случае для вычисления произведения воспо-
льзуемся равенством а + Ь — (10 + а) — (10 — 6), в ко-
тором а и b логарифмы сомножителей. Для этого пра-
вый крайний штрих (10) на шкале С движка, передвигая
последний влево, совмещают с делением 5,65 на основ-
ной шкале D линейки. Затем, установив указатель
бегунка на деление 3,17 шкалы С движка, по указателю
читают на шкале D ответ: х = 17,9.
При умножении чисел можно пользоваться и обратной
шкалой (средняя шкала лицевой стороны движка).
Пример 3. Вычислить х — 42,5 х 12,7.
В этом случае указатель бегунка следует поставить
на штрих 42,5 основной шкалы, а затем переместить
движок влево до совмещения-с указателем числа 127
обратной шкалы /?; на основной шкале О, против коне-
чного штриха обратной шкалы 7?, читают результат
произведения, равный 540.
Пример 4. Требуется вычислить у = 6,44 : 2,19.
Для этого ставят указатель бегунка на деление 6,44
основной шкалы D линейки и перемещают движок вле-
во до совмещения с указателем деления 219 шкалы С
движка. После этого ставят указатель бегунка на левую
крайнюю цифру 1 шкалы С и на основной шкале читают
искомое число, т. е. у ~ 2,94.
Пример 5. Вычислить #=5,24 : 7,76.
В нашем примере делимое меньше делителя, следова-
тельно, указатель бегунка совмещают с делением 524
основной шкалы D и под него подводят деление 776
щкалы С. После этого указатель бегунка совмещают с
правым крайним штрихом (10) на движке и по указате-
лю читают на основной шкале D результат: у = 0,675.
п	до	2,17x3,81
Пример 6. Вычислить z —	—•
Для решения этой задачи поступают так. Указатель
бегунка и левую крайнюю цифру 1 на шкале С совме-
щают с делением 2,17 на шкале D. Затем указатель
бегунка ставят на деление 381 шкалы С и подводят под
указатель деление 4,35 шкалы С. Против левой крайней
цифры 1 шкалы С читают на шкале D ответ; в нашем
примере z= 1,90.
23
Пример 7. Найти произведение числа 17,8 на сле-
дующие множители: 2,41, 4,19, 0,213.
Совмещают указатель (визир) бегунка с отсчетом
17,8 — первым сомножителем на шкале D. Перемещают
движок вправо до совмещения левого крайнего штриха
на шкале с визиром бегунка. После этого перемещают
бегунок по линейке, совмещая его визир последовательно
со штрихами на шкале С с соответствующим вторым
множителем — 2,41, 4,19 и 0,213, и каждый раз на
шкале D прочитывают произведения 42,9 « 17,8 х 2,41;
74,6 « 17,8 х 4,19 и 3,80 « 17,8 X 0,213.
При делении чисел, содержащих десятичные дроби,
необходимо всякий раз определять в частном место за-
пятой, отделяющей целую часть числа от дробной, т. е.
определять количество целых знаков в частном. При этом
можно руководствоваться следующим положением:
1) если первая значащая цифра делимого а меньше
первой значащей цифы делителя ft, то порядок (значность)
частного п равен разности значностей делимого па и де-
лителя пь, т. е.
п = па — пь\	(9)
2) если первая значащая цифра делимого а больше
первой значащей цифры делителя ft, то порядок, (зна-
чность) частного равен разности значностей делимого па
и делителя пь и плюс единица, т. е.
П = (па — Пь)+ 1.	(10)
Примечание. Если первые значащие цифры делимогр и
делителя равны, то определение порядка частного по формулам (1)
и (2) производят по вторым значащим цифрам делимого и делите-
ля, а при равенстве вторых значащих цифр определяют по треть-
им и т. д.
Возведение в степень и извлечение корня
При возведении в степень и извлечении на линейке
квадратного или кубического корня из числа поступают
так.
На шкале D отыскивают штрих, соответствующий
основанию степени М и с ним совмещают визир бегунка.
По этому же визиру на шкалах квадратов А или кубов
/С прочитывают соответственно квадрат или куб числа М.
При этом для установления порядка (значности) опреде-
24
Таблица 3
Действие .	Чтение результата	Порядок результата Р равен
Возведение в квадрат Возведение в квадрат	На левой поло- вине шкалы А На правой по- ловине шкалы А	Удвоенному порядку осно- вания стёпени- р минус 1 (еди- ница), т. е. Р = 2р — 1 Удвоенному порядку осно- вания степени р, т. е. Р=2р
Возведение в куб Возведение в куб Возведение в куб	На левой части шкалы К На средней ча- сти шкалы На правой час- ти шкалы К	Утроенному порядку осно- вания степени р без двух, т. е. Р = Зр — 2 Утроенному порядку осно- вания степени р без единицы, т. е. Р = Зр~ 1 Утроенному порядку осно- вания степени р, т. е. Р=3р
Действие	При установке подкоренного числа	Порядок результата Р равен
Извлечение квадратного корня	На левой поло- вине шкалы А	Половине увеличенного на единицу порядка подкоренно- d Р + * го числа р, т. е. Р —  % '
Извлечение квадратного корня	На правой по- ловине шкалы А	Половине порядка подкорен- п	р него числа р, т. е. Р = —
Извлечение кубического корня	На левой час- ти шкалы К	Одной трети порядка подко- ренного числа р, увеличенно- D го на два, т. е. Р —  
Извлечение кубического корня	На средней части шкалы К	Одной трети порядка подко- ренного числа р, увеличенно- го на единицу, т. е. Р _Е±± У	3
Извлечение кубического корня	На правой час- ти шкалы К	Одной трети порядка подко- ренного числа р, т. е. п__р F ~ 3
3 Заказ № 550
25
ляемой степени или искомого квадратного или кубичес-
кого корней следует пользоваться правилами, приведен-
ными в табл. 3.
Примеры.
1.	0,142 = 0,0196 (результат прочитывают по левой
половине шкалы А; порядок (значность) Р = 2 р — 1 =
= 2x0 — 1= — 1, табл. 3).	•
2.	9002 = 810000 (результат прочитывают на правой
половине шкалы Д; порядок Р = 2р = 2хЗ = 6, табл. 3).
3.	1,633	4,33 (результат прочитывают по левой части
шкалы К; порядок Р = 3р — 2 = 3 х 1 — 2=1, табл. 3).
4.	3,423 » 40,00 (результат прочитывают по средней
части шкалы К; порядок Р = 3р— 1=3x1—1=2,
табл. 3).
5.	703 = 343 000 (результат прочитывают по средней
части шкалы Д'; порядок Р = 3р = 3 х 2 = 6, табл. 3).
В табл. 4 приведены примеры для упражнения в
определении квадратов и кубов чисел.
Таблица 4
п	пг	пя	п	п"	п*
17	289	4913	1,98	3,92	7,762
59	2500	125 000	0,015	225-10-6	3375-10-9
44	1936	85184	22,6	510,8	И 543
1,19	1,416	1,685	384	147 4’56	56 623 104
219	47 961	10 503 459	8,29	68,7	569,7
138	19 044	2 628 072	0,643	0,413	0,266
Так как извлечение корня — действие, обратное воз-
ведению в степень, поэтому на линейке его производят,
пользуясь шкалами К и 4, на которых отыскивают под-
коренное число, а на шкале D прочитывают значение
соответствующего кубического или квадратного корня.
Примеры.
1.	Для извлечения квадратного корня, например
lz264, поступают так. На левой половине шкалы квад-
ратов А отыскивают подкоренное число 264 и с ним
26
совмещают визир бегунка, а на шкале D под визиром
прочитывают искомый корень. Итак,
/264 « 16,25;
порядок корня Р==^4р-=='-Цр- = 2 (табл. 3).
2.	/3085 « 55,5 (результат прочитывают на правой
Р 4
половине шкалы D); порядок Р = -^- = — = 2 (табл. 3).
3.	Для извлечения кубического корня, например
подкоренное число находят на правой части шкалы ку-
бов К, с ним совмещают визир бегунка, а на шкале D
под визиром прочитывают искомый корень. Итак,
^81Г «9,33;
порядок корня Р = -у- = -|1= 1 (табл. 3).
4.	у^76 « 4,24 (результат прочитывают на средней
части шкалы D); порядок Р =	г (таблч3)
5.	-^0,00385 « 0,1567 результат прочитывают на ле-
р । 2	_2 I 2
вой части шкалы О); порядок Р =	= 0 (та-
О	о
бл. 3).
Ниже приведены примеры для упражнения в извле-
чении квадратных и кубических корней.
1. /15Т « 12,288.
2. /389 « 19,723.
3. /бЭГ « 26,287.
4. /935 « 30,578.
5. /4700 « 68,557.
6. /77200 «277,85.
7. /0,000185 «0,0136.
8. /0,000090«0,00949.
9.	^164 « 5;474.
10.	у^287 « 6,596.
11.	j/376 « 7,218.
12.	/590 «8,387.
13.	//7930 « 19,941.
14.	/98 900 « 46,245.
15.	/0^б7Т5^» 0,415.
16.	^248 « 1,355.
3'
27
Нахождение десятичного логарифма и числа
по его логарифму
Для решения этих задач по линейке пользуются ее
шкалой L (см. рис. 4), представляющей графически таб-
лицу мантисс логарифмов.
Чтобы найти десятичный логарифм числа, визир бе-
гунка устанавливают на отсчет заданного числа на шка-
ле D (см. рис. 4) и по визиру на шкале L прочитывают
мантиссу, а спереди приписывают к ней характеристику
(см. стр. 7).
Так, например, на рис. 8 1g 1,90 = 0,280, а
1g 197,5 = 2,296 (см. рис. 4).
Для потенцирования — нахождения числа по его де-
сятичному логарифму — заданную мантиссу логарифма
устанавливают визиром на шкале логарифмов L линей-
ки, а число, ей соответствующее, прочитывают по ви-
зиру на основной шкале D.
Например, для определения числа по заданному де-
сятичному логарифму 1,296 визир бегунка совмещают с
отсчетом 296 на шкале L (рис. 6), соответствующим ман-
тиссе заданного логарифма, и на шкале D по визиру
прочитывают 1975, а с учетом характеристики заданного
логарифма оно соответствует числу 0,1975.
Ниже приведены для упражнения примеры опреде-
ления десятичных логарифмов и чисел по их логариф-
мам.
Примеры.		
1.	351 =2.5453.	5. 4.8306 =	1g 0,000677.
2.	58,6= 1.7679.	6. 2,5502 =	1g 355.
3. 0,964= 1.9841.	7. 1,9499 =	lg0,891.
4. 0,00711 =3.8519.	8. 0,4949 =	Ig3,125.
Вычисление значений тригонометрических функций
Логарифмические шкалы (Sin, ShT и Tg), нанесен-
ные на обратной стороне движка, позволяют произво-
дить самые различные вычисления по формулам, в ко-
торые входят тригонометрические функции. Для опреде-
ления по этим шкалам натуральных значений cos и ctg,
28
отсутствующих на шкалах движка, пользуются обще-
известными формулами:
cos v = sin (90° — v),
ctg v = для v от 0 до 45°,
ctgv = tg(90° — v) для v от 45° до 90°.
Так как начало счета делений на средней шкале движ-
ка (S и Т) начинается от 0°34',38, то для определения sin
и tg углов от 0 до 0°34',38 пользуются соотношениями
sinv« tgv «v'sin Г = -у- = -з^ .
Пример 1. Вычислить /z==stgv, если s = 108 м,
v = 8°35'.
В этом случае движок должен быть вставлен в пазы
линейки так, чтобы шкала Sin совместилась со шкалой
Л, а шкала Tg — со шкалой D.
Для вычисления h = 108 tg 8°35' указатель бегунка
ставят на штрих 108 шкалы D и, перемещая движок
вправо, подводят под указатель начальный штрих шка-
лы Tg движка. Затем совмещают указатель бегунка со
штрихом 8°35' на шкале Tg и по нему на шкале D чи-
тают ответ; в нашем примере h 16,30 м.
Пример 2. Вычислить
Ах = s cos а, если s = 218 ж и а = 41°20'.
Так как
Ах= 218-cos41°20'= 218 • sin48°40',
то указатель бегунка ставят на штрих 218 шкалы D.
Перемещая движок влево, совмещают с ним его конечный
штрих шкалы sin и, пользуясь указателем бегунка, про-
тив штриха 48°40' на шкале Sin читают ответ на шкале
D; -в .нашем примере Ах ^164 ж.
Натуральные значения sin и tg можно находить на
линейке и другим способом, не переставляя движка в па-
зах. С этой целью на обратной стороне линейки сдела-
ны два продолговатых выреза так, что в левом вырезе
видна лишь одна шкала Tg, а в правом — только две
другие шкалы движка — Sin и S и Т. На скошенных стен-
29
ках этих вырезов нанесены штрихи: на «левой один, а
на правой два.
Если* совместить левый штрих на вырезе корпуса с
каким-либо делением шкалы Tg (например, 8°), то на
обратной стороне движка по его шкале С против началь-
ного штриха 1 основной шкалы линейки можно прочи-
тать натуральное значение Ц этого угла; для нашего
примера на шкале С читаем 1405, т. е. tg 8° = 0,1405.
Если же под верхний штрих правого выреза подвести,
например, 35° шкалы Sin движка, то против правого
крайнего штриха, отмеченного на основной шкале линей-
ки числом 10, можно прочитать натуральное значение
sin этого угла; для нашего примера читаем 574, т. е.
sin 35° = 0,574.
По линейке можно не только определять натуральные
значения тригонометрических функций по их углам, но
решать и «о б р а т н ы е» задачи—находить углы по на-
туральным значениям этих функций.
1. Для нахождения угла по натуральному значению
sin или tg на лицевой стороне линейки находят значе-
ние sin или tg на шкале С движка и, перемещая послед-
ний в пазах линейки, совмещают это значение с конеч-
ным штрихом шкалы D и, перевернув линейку обрат-
ной стороной, в правом вырезе ее против черточки про-
читывают ответ соответственно на шкалах Sin или Tg.
2. Для нахождения угла по . натуральному значению
cos v или ctgv сначала находят по линейке, как указано
выше, значения sinv ли ctg v, а потом по формулам
определяют
cosv = sin(90° — v) и ctgv = tg(90°—-у).
Примечания: 1. При определении величины угла по задан-
ному значению тригонометрической функции необходимо учитывать,
что одному и тому же натуральному значению функции будут соот-
ветствовать четыре значения угла, если не принимать во внима-
ние знак этих функций, или два значения, если учитывать эти
знаки. Следовательно, при решении таких задач надо знать,в какой
четверти находится искомый угол.
2. Для решения этих задач необходимо определить цену деле-
ний на всех участках шкал Sin, Зи.Ти Tg обратной стороны дви-
жка.
На стр. 31 для упражнения приведены примеры вы-
числений с тригонометрическими функциями.
30
Примеры.
1.	sin 5°10' = 0,0901.
2.	cos 15° 10= 0,9652.
3.	tg SSW = 1,600.
4.	ctgl9°20' = 2,850.
5.	sin v = 0,355; y=19°35'.
6.	cos y = 0,975; y=12°45'.
7.	tg у = 0,0693; y= 3°58'.
8.	ctgv = 0,135; y=82°20'.
И, наконец, нахождение натуральных значений три-
гонометрических функций можно производить на лицевой
стороне линейки по шкале D. В этом случае вставляют
в линейку движок обратной стороной так, чтобы край-
ние штрихи на движке и корпусе линейки совместились.
Теперь для нахождения значения тригонометрической
функции совмещают визир бегунка с соответствующим
углом заданной функции и под визиром на шкале D,
прочитывают натуральное значение искомой функции.
§ 6. ОСОБЫЕ ЗНАЧКИ НА ШКАЛАХ ЛИНЕЙКИ
Пользуясь штрихами на шкалах линейки, отмечаю-
щих константы т:, Л4, С, р°, р' и р", можно с их помощью
производить различные расчеты. Так, например, можно
производить перевод градусов, минут и секунд в радианы
и обратно по формулам:
где ср и у соответственно значение угла ч в радианной и
градусной мере.
Пример 1. Найти значение угла v=10°32z в ра-
дианной мере.
Вначале выражают заданный угол в минутах (у = 632')
Затем указатель бегунка ставят на деление 632 основнбй
шкалы линейки и подводят под указатель штрих шкалы
С, отмеченный значком р'. После этого против левой край-
ней цифры на движке читают на шкале D ответ: у
^0,1838.
Пример 2. Найти в градусной мере значение угла
ф==0,84, выраженного в радианах.
Согласно формуле (11) решение этой задачи сводят к
перемножению двух чисел фхр; для нашего примера
0,84 х 57,3. Для этого указатель бегунка ставят на де-
ление 84 основной шкалы D. Перемещая движок влево,
31
подводят под его указатель правый крайний штрих шка-
лы С, отмеченный числом 10.
Ставят указатель бегунка на штрих, отмеченный на
шкале С значком р° (57°,3), и против него читают на
шкале D ответ; в нашем случае v = 48°,l.
rd2
Пример 3. Определить площадь круга 3 = —
для d = 23,5 м.
Для решения этой задачи ставят визир бегунка на
отсчет 235 на шкале D корпуса линейки и подводят под
этот визир число 4 шкалы В движка. Перемещают ви-
зир бегунка до совпадения с штрихом, отмеченным на
шкале В движка штрихом к, и по визиру на шкале
квадратов А корпуса линейки прочитывают ответ 433 м2.
§ 7. ПРИМЕНЕНИЕ ЛИНЕЙКИ ПРИ РАСЧЕТАХ
I. Умножение и деление
Пример 1. Уравнение прямой на плоскости имеет
вид у = 24х + 8. Найти значение ординаты у, если
х= + 4.
у = 24 ( + 4)4-8 = 4- 96 + 8= + 104.
Пример 2. Найти площадь прямоугольника 3 со
сторонами а = 63 м и b = 248 м.
S = a • 6 = 63 • 248 ~ 15 620 ж 1,562 (га).
Пример 3. Найти Р — вес 2,3 м3 песка, если его
плотность 7 = 1,65 т/м3.
. Р = 7 . 17=1,65 • 2,3^3,8 (г).
Пример 4. Вычислить среднюю скорость движения
поездов Уср на участке 3 = 2520 км, если пассажирс-
кие поезда тратят на этот путь 35 ч.
1/ср = 3 : t = 2520 : 35 = 72 (км/ч).
Пример 5. Грузоподъемность автомашины 2,5 г,
сколько потребуется рейсов п для перевозки 145 т кир-
пича.
п = Р : р= 145 : 2,5 = 58 рейсов).
32
Пример 6. Площадь параллелограмма 5 = 480 еж2,
высота А=13 см. Найти основание /.
1 = S : h = 480 : 13 — 36,9 (см).
II.	Применение шкал тригонометрических функций
Возможно двоякое применение этих шкал: с поворо-
том движка, что бывает удобно для дальнейшего просто-
го (однократного) умножения или деления функции, и
без поворота его, с прочтением значения функции в од-
ном из вырезов обратной стороны линейки, как обычно
и делают при сложных вычислениях.
Пример 1. Угол прямоугольного треугольника
а = 31° 15', прилежащий к нему катет 6=48 м. Опре-
делить другой катет треугольника а.
а = 6-tg а = 48-tg 31° 15'-29,1 (ж).
Для решения этой задачи без поворота движка сна-
чала по шкале тангенсов находят угол 31° 15', тангенс
которого прочитывают по начальному штриху шкалы D
корпуса на шкале С движка, т. е. 0,605, и умножают
это значение на 48.
* Пример 2. По полярным координатам точки на
плоскости р = 71,3 и ф = 20°35' определить прямо-
угольные (декартовы) координаты этой точки х и у.
х = р• cos ср = 71,3-cos 20° 35' = 71,3• sin 69° 25' с- 66,7;
у = р • sin ф = 71,3 • sin 20° 35'	25,1.
III.	Применение шкал квадратов и кубов
Наряду с основными шкалами D корпуса и С движ-
ка при умножении и делении чисел пользуются шкала-
ми квадратов Л и В и кубов К- Если при этом в ходе
вычислений нужно извлекать корень второй (третьей)
степени, то операции на линейке производят на основ-
ных шкалах С и D и на шкалах Л или В (соответствен-
но К — если в процессе вычислений требуется извлечь
корень третьей степени). Если же среди сомножителей
есть числа, которые должны быть возведены в квадрат,
то все вычисления производят в произвольном порядке
на шкалах Л и В и на шкалах С и D.
зз
Пример 1. Определить диагональ квадрата а, если
его площадь 5 = 37 сж2.
В 'этом примере вычисления производят на шкалах
квадратов Л и В, а ответ прочитывают на шкале кор-
пуса линейки D:
а = Y2S = ]/F37	8,6 (еж.)
Пример 2. Вычислить массу (весовое количество
вещества) Р цинкового кубика со стороной 2,3 см (плот-
ность цинка 7 = 7,14 г/см3).
Р = т.а = 7,14.(2,3)3^86,9 (г).
Пример 3. Вычислить площадь круга 5 при радиу-
се R = 71 см.
5 = к./?2 = т:(71)2^ 15800	1,58 (м2).
Пример 4. Вычислить гипотезу с прямоугольного
треугольника, катеты которого а = 17 см и В = 26 см.
с = У а2 + Ь* = У 172 + 262	31 (см).
IV.	Вычисление выражений вида X =
Для решения подобных задач можно рекомендовать
вначале произвести деление ——, а потом эту величину
умножить на а2. При этом все действия производят соот-
ветственно на шкалах С и D.
Пример 1. Вычислить*из пропорции
2,03
0,51
14
х
X = JttiL « 3.52.
2,03
Г7	о о	17/6
Пример 2. Вычислить у = -—
Вычисления производят на основных шкалах D и
С и на шкале квадратов А:	11,9.
4 92 • т;
Пример 3. Вычислить <=	— ss 9,42.
34
Для этого Следует пользоваться шкалами квадратов
Л и В и шкалой корпуса D.
Пример 4. Вычислить кинетическую энергию
тела массой т = 3,1 кг, движущегося со скоростью
и = 15 м!сек.	9
lv/ mv2 3,1 (15)2 олп ,	2
Wh = ------=  -- --	349 нм!сек2.
к 2	2
V.	Вычисление выражений вида X = —1—
В этом случае визир бегунка следует установить над
числом аг основной шкалы D корпуса, подвести под него
движок числом by шкалы С, передвинуть визир на число
Ь2 шкалы обратных чисел R и под визиром бегунка на
шкале D корпуса прочитать ответ: X ——.
• Ь2
Этими действиями выражение X = —— было пред-
1
ставлено в виде X =----------, а вычисления отличались
от предыдущих лишь применением шкалы обратных чи-
сел /?.
Пример 1. Вычислить X = —; X ~ 0,069.
н н	0,2Ь33
5
Пример 2. Вычислить X —-------; X 0,505; в этом
7 ]/2
случае вычисления производят на шкале D, шкале
квадратов движка В и шкале обратных чисел R.
Пример 3. Вычислить диаметр цилиндра D, если
его высота Л =13,6 м, а площадь боковой поверхности
. S = 200 ж2.
При вычислениях пользуются шкалами С и D и шка-
лой обратных чисел R:	4
Пример 4. Вычислить Х =----------~ 0,202.
F н	3,1-sin 50°
При решении этой задачи следует пользоваться шка-
35
Лой S на обратной стороне движка и верхним штрихом
на правом вырезе обратной стороны корпуса линейки.
п	cd	1,125-43- 1Л0,18 пппо
Пример 5. Вычислить х = —1—6h-=г5—---------=±0,098.
□О-0,0
п	со	6,3143
Пример 6. Вычислить г/ = ——-
Вычисления производят на шкалах квадратов А и В:
г/ 7,35.
Пример 7. Вычислить
 5,4'0,29	 5,4-0,29	~ q ggg
sin36°.3 У~2	0,587-3/2
VI. Вычисление выражений вида Х=а1а2 а3
При наличии на движке шкалы обратных чисел R
это выражение предварительно следует представить в ви-
. де X = -М-.
а3
Пример 1. Вычислить площадь боковой поверхнос-
ти конуса S, радиус основания которого /? = 5 см, а
длина образующей / = 41 см.
S,	=	» 6,45 дм2.
бок. ПОВ	4	|	|	’
т т
Пример 2. Вычислить массу Р ртутного столбика
сечением 3,2 см (а^) на 1,5 см (а2) и высотой h = 16 см,
если плотность ртути 7 =13,6 г!см\
п	1	7^	13,6-16 тле
Р = т a,aJi =---1---= —---------1045 г.
1	1 1	1
щ а.2	3,2 1,5
Пример 3. Вычислить х = —- 12‘^- » 27,1.
/5Г
Пример 4. tg 1°05-2,13-37	1,487.
Следует указать, что в некоторых вычислениях, со-
держащих, например, возведение чисел в квадрат, мож-
36
но действия производить на основных шкалах С и D,
заменив возведение в степень (а2) на умножение а-а.
п	к 2,162
Пример 5. х =----------.
F к	1,74
Вычисления производят на шкалах С и D.
к = 2’16-'2-16 . ~2,68.
1,74
Пример 6.	х = —-— _	~ о,753 (вычисле-
н н	41,1	41,1
ния произведены' на шкалах Л и В с использованием
шкал С и D для* получения числа к2).
VII. Вычисление выражений, содержащих
сомножители вида
Х=ат, причем т не равно двум или трем
Решение подобных примеров производят с использо-
ванием шкалы мантисс логарифмов L.
Пример L
Пример 2.
Пример 3.
5
377 =13,18. •
0,2813-3,6« 0,0000217.
Z2 : tg22° « 12,52.
§ 8. РАЗЛИЧНЫЕ ЛОГАРИФМИЧЕСКИЕ ЛИНЕЙКИ
Кроме обычных (см. рис. 4 и 5), бывают нормальные
счетные линейки с двойными логарифмическими и дру-
гими шкалами и линейки, на шкалах которых нанесены
значения функций, встречающихся, например, в прак-
тике геодезических, электротехнических, гидравлических
и других расчетов.
Счетные линейки с двойными шкалами бывают раз-
личные. На рис. 9, а показана часть шкал, нанесенных
на корпусе и лицевой стороне движка известной линей-
ки «Кейфель и Эссер». На лицевой стороне корпуса
этой линейки нанесены 6’шкал и 4 шкалы на движке.
Здесь логарифмические шкалы С и D и шкала обратных
значений С1 такие же, как и на обычной нормальной
линейке. Дополнительные шкалы DF и CF являются
37
a)
I °	1	2	3	I
L- liinliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiihiiiliiiiliiiiliiiiliiiihiilli/iiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiiliiiilnillillililiilnilk
M 11 iwl ।	।	।	।	0,5	।	।	।	। k02 ।	।
*- L- ' I • i > 11	* i I । t  11 111 1111 । 11111 il 111111111111111111111111111111111111 к 11111111111111111111 ill 111111111 । । i 11 i i 111 11 i 1111111111
—pi|iii>lii»l<iiiliiii|iiii|iin|i»n|nii|iI»11h11|<-HHИ 1<НН<14»-|»Н-НФГН1|1'1ф1|1»||(4|||Ж4Н
Q Jp 111 i 11 I I 11 | l I I 11 I l l I | I I I i | I I I I | I i i I | III i | । I I I | I i I I | I I I I | I I I I 11111 |l II11111111111111111111111111111111111111111 11 11 11 I I I I | I I I I | I l/
Q a I §	2	9	8	7	6	5
c I
hliiiiliiiiliiiiliiiiliiiiliinl
\ I 110 i
llililil ilililililililihlilil
I 3 к
,L1,1,1,1,1.1,1,1.1,T I  .  I	, I . I, I ,I . I ,I , I ,I , I, I , I , I , I i I i I , I i I . I । I > I < I < I i I , I , I , I t I I I . I . I i I < I > I \
-------lj ИИ-[-11н[нн}нп[нн|Нн|шфН1рНф|Н^|фж|иН}Ж<Д И4 t) t H11И 11 [
|^|	11 I I I | I I I l'| HI 11 I 111 [ 111 I|IIII|IIII|IIII|II|I|IIII|IIII|IIII|IIII| I | I I I | I | I | I | I | I | I | l| l| I |l| l|l|l|l|l|l|l| I I I I | I I I I | I I I l| I H ||||ll||ll||llll|llll| I I I I |/
pi I I I | I I 1 I | I I I I | I I I I | I I I I | I I I 11 I I I 11 I I I 11 I H I 1111 1111 111111111111| 1111| 1111| 1111| 11 ll|lll l|llll| I I I I | I I I I j I I I I | I I I I | I I I I | I I I I 111 I I |{
LL2 in	ng	12	1.25	\
• • 11111111 Ijl 11111111 • 111111 Ц
\i 11111 • 11111111 CI
)|Ф|^|||||||||Ф1Ф1 p -
I'I'ITI11 "l"TI , . 4
10000 200000LLJ
2.5 e
Рис. 9. Линейка «Кейфель и Эссер» и «Логарекс»:
а — шкалы на лицевой стороне линейки «Кейфель и Эссер», б — шкалы на лицевой стороне
линейки «Логарекс»
обычными логарифмическими, как и шкалы С и £), но
только сдвинутыми влево так, что любому числу п на
шкале соответствует число ~п.
Особенностью двойных логарифмических шкал LL1,
LL2 и LL3 является то, что они построены как продол-
жение одца другой. Эти шкалы служат для вычислений
с натуральными логарифмами, для определения значе-
ний показательных функций (ех), вычисления степеней с
дробными показателями и для решения показательных
и логарифмических уравнений.
Такие же двойные логарифмические шкалы, в числе
других 10 шкал, нанесены и на обратной стороне кор-
пуса линейки, но в обратном, справа налево направле-
нии. И, наконец, шкала L на лицевой стороне линейки
— равномерная; она служит для определения мантисс
логарифмов1.
На рис. 9, б показана часть лицевой стороны пласт-
массовой линейки «Логарекс», изготовляемой в ЧССР.
Шкалы лицевой стороны корпуса и движка служат для
вычислений значений, указанных слева против каждой
из них.
На обратной стороне движка нанесено три шкалы,
предназначенные для вычислений значений основания
натурального логарифма ех, eQ'Xx и г0,01х.
Уравнения этих шкал следующие:
для шкалы Н: у = lgeo,olx;
для шкалы Р: у = lg^°’lx ;
для шкалы М: y = lgex.
На бегунке нанесено три коротких и один длинный
визирных штриха.
Шкалы Р и М являются продолжением шкалы Н.
Для определения наименьшего значения каждого деле-
ния по участкам этих шкал следует пользоваться табл. 5.
I.	Установка и Чтение заданного числа на шкалах А,
/<, Л, В(х2), С(х) и D и S, ТиХиТ ничем не
отличается от аналогичных действий на нормальной ло-
гарифмической линейке (см. § 3).
1 Подробнее см. Д. Ю. Панов. Счетная линейка. Издание
восемнадцатое. М., «Наука», 1966. Стр. 133—163.
39
Таблица В
Участок	Значение деления	Участок	Значение деления
Шкала И		Шкала М	
1,01—1,02	0,0001	30-50	1,0
1,02—1,05	0,0002	50—100	2,0
1,05—1,1	0,0005	100—200	5,0
Шкала Р	/	200—400	10,0
1,1 —1,2	0,001	400—700	20,0
1,2—1,4	0,002	700—103	50,0
1,4—1,8	0,005	ЮЗ—3-103	100
1,8—2,0	0,01	3.103—5.ЮЗ	200
2,0—3,0	0,02	5-103—104	500
Шкала М			
3,0—6,0	0,05	101—2.104	1000
6,0—10	1	0,1	2-Ю4—5-Ю4	2000
ю—зо •	0,5	5-104—10’	10г
II.	Для определения значений на шкалах /7, Р и М
при неперевернутом движке заданное значение X уста-
навливают на шкале С движка и совмещают его с циф-
рой 1 или числом 10 на шкале корпуса, а ответ прочи-
тывают на обратной стороне движка (пользуясь визиром
для чтения шкал //, Р и Л4).
Пример 1, Определить у = е^^7.
Устанавливают движок цифрой 7 шкалы С против 1
шкалы D и на обратной стороне движка по шкале Н
читают ответ у= 1,0716.
Пример 2. Определить 4/1 = е0’03 и #2 = г2’35.
При определении этих чисел поступают по предыду-
щему, а ответы читают на шкале Р для уг и на шка-
ле М для у2. Ответ: уг = 1,35 и у2= 11.
III.	Для определения значения X при перевернутом
движке вначале следует совместить штрих, соответству-
ющий числу 2,72 на шкале М с 1 на шкале D. Затем
устанавливают визир на штрих, соответствующий задан-
ному значению X на шкале D, а ответ читают на шка-
лах //, Р и Л4 в зависимости от величины X. Так, на-
пример, при определении у1==е°^73и z/2 = e°’137 ответы
читают у = 1,0382 по шкале //, а у2 = 1,147 на шка-
ле Р.
IV.	Такие действия, как умножение, деление, возве-
дение в степень, извлечение корня, нахождение деся-
40
тичного логарифма и числа по его логарифму на этой
линейке, производят так же, как и на нормальной лога-
рифмической линейке (§ 6).
V.	Для вычисления значений с тригонометрическими
функциями поступают так.
Пример 1. Вычислить a=6tga, если 6 = 24,7, а
а = 4°2Г.
Устанавливают визир на штрих, соответствующий
4° 2 Г на шкале SnT, и передвижением движка влево
подводят под визир деление, отмеченное числом 10 на
шкале С. Затем переводят визир на деление 24,7 шка-
лы С движка. На шкале D читают ответ: 188. Так как
тангенс малых углов близок к нулю, окончательно бу-
дет: а = 1,88.
Пример 2. Вычислить p = q cos а, если д = 324, a
а = 37° 24'.
Так как р = 324 cos 37° 24' = 324 sin 52° 36', то уста-
навливают визир на делении 52° 36' шкалы S и перед-
вижением движка влево подводят под визир деление 10
шкалы С. Затем переводят визир на деление 324 шкалы
С движка. На шкале D под визиром читают ответ: чис-
ло 257, т. е. р = 257.
VI.	Вычисление выражений с основанием натураль-
ного логарифма е на этой линейке производят в два
приема: отыскивают число, соответствующее заданному
х, а затем производят указанное действие с этим най-
денным числом.
Пример 1. Вычислить k = тех, если т=1,83, а
х = 0,523.
Передвинув движок влево до совпадения штриха, со-
ответствующего 0,523 на шкале С с 1 на шкале D, чи-
тают на шкале Р значение 4/= e0*523= 1,69. Производя
умножение тх y = k обычным путем, получают ответ:
k= 1,83-1,69 = 3,09.
Пример 2. Вычислить с = -^-, если d = 0,84, а
ех
х=1,23.
Поступая как и в предыдущем примере, на шкале М
находят у = ех ’23 = 3,43. Далее, производя деление
d *
— = с обычным путем, получают
У
С = 0,84 .*3,43 = 0,245.
41
Для вычисления у=-е*, когда х>10, поступают
так.
Показатель степени разбивают на несколько частей,
каждая из которых должна быть меньше 10, т. е. выра-
жение у = ех представляют в виде произведения
у=е^е^ _
где Дх— составная часть показателя степени.
Затем для каждого члена произведения определяют зна-
чение еДх.
Таким образом, выражение ех при х> 10 можно
представить в виде произведения
у = Ау^у2 ... \уп,
где
^Л = е^.
Для примера у = е21 наименьшее количество частей,
на которое разбивают показатель степени, будет 3, т. е.
это выражение можно представить в виде
у = gio+iot? = ею eioe7.
Откуда
\У1 = ei° = 2,2 • 10»; Лу2 = е10 = 2,2 • 104;
\ys = ei= 1,1. Ю3.
Следовательно,
у = 2,2-104-2,2-Ю4-1,1 -103 = 5,32-Ю11.
VII. Вычисление выражений, в которые входит зна-
чение вида 1 — х2 .
Пример 1. Определить у = k У1 — х2 , если k —
= 0,431, а х =0,836.
Устанавливают визир на деление шкалы D, соответ-
ствующее 0,836, и на шкале N читают число 0,549. За-
тем производят обычным способом умножение 0,431 на
0,549. Получают: у = 0,236.
Пример 2. Определить z =-------- а ...-, если а =
У1 — X2
= 231, а х = 0,324.
Визир совмещают с делением 0,324 шкалы D. На
42
шкале N читают число 0,946; обычным способом произ-
водят деление 2,31 на 0,946 и получают z = 2,45.
Основным недостатком шкалы N является то, что при
х<0,1 пользоваться ею нельзя, а достоинством ее явля-
ется получение значения косинуса угла по заданному
синусу.
Пример 3. Определить cos 38°26'.
Устанавливают визир на деление 38° 26' шкалы S, а
на шкале 2V читают ответ: cos 38° 26'= 0,783.
ДИСКОВАЯ СЧЕТНАЯ ЛОГАРИФМИЧЕСКАЯ
ЛИНЕЙКА «СПУТНИК»
§ 9. ОПИСАНИЕ ЛИНЕЙКИ
к
Значительный интерес для вычислителей представля-
ет выпускаемый московским заводом «Калибр» логариф-
мический диск «Спутник», предназначенный, как и нор-
мальная счетная логарифмическая линейка, для различ-
ных вычислений.
Логарифмический диск (рис. 10), шкалы которого по-
строены по принципу непрерывного (замкнутого) лога-
рифмического круга, состоит из установочного кольца /,
корпуса 2, диска-движка 3; он имеет с обеих сторон
два прозрачных визирных диска-бегунка 4. Все части
«Спутника» имеют такое же назначение, как и соответс-
твующие части нормальной линейки (см. § 1).
На корпусе лицевой стороны линейки «Спутник»
(рис. 10, а) нанесены; основная шкала чисел (О) 5, шка-
ла квадратов чисел (Л) 6 и шкала кубов чисел (Д) 7.
На лицевой стороне движка расположены основная шка-
ла чисел (С) 8 и шкала обратных чисел (Д) 9.
На обратной стороне корпуса линейки (рис. 10, б)
нанесены: шкала тангенсов (Г) 10, шкала тангенсов и
синусов малых углов (ShT) 11 и шкала синусов (S) 12,
а на движке — шкала мантисс логарифмов (L) 13 и ос-
новная шкала чисел (£) 14.
На линейке «Спутник» (см. рис. 10, а и б) три оди-
наковые основные шкалы (С, D и Е) являются логариф-
мическими. Каждая из них представляет логарифмичес-
кую шкалу чисел 1, 2, ..., 9,1 (число 1, кроме подписи,
снабжено узкой черточкой). Здесь внутри интервала
(1—2) нанесены числа 1,1; 1,2;	; 1,8; 1,9; 2, проме-
43
Рис. 10. Диск круговой логарифмической линейки «Спутник»:
а — лицевая сторона; б — обратная сторона:
/ — установочное кольцо; 2 — корпус; — диск-движок; 4 — бегунок
Жутки между которыми разделены на пять делений. Це-
на наименьшего деления составляет 0,02 интервала ли-
нейки (1—2). Следующие интервалы шкалы (2—3), (3—4)
и (4—5) разделены каждый на 20 частей с ценой наи-
меньшего деления 0,05. На этой части шкалы каждое
четное деление (0,1 интервала) отмечено несколько бо-
лее длинным штрихом. Промежутки между штрихами,
отмеченные 5, 6, 7, 8, 9, 1, разделены каждый на 10
частей; середина такого промежутка (пятый штрих) вы-
делена удлиненной чертой.
На основных шкалах диска линейки особыми штри-
хами отмечены константы тс = 3,14; с = У4 : тс; р,=3438';
р"=206 265".
При малых габаритах (диаметр 7,2 см, толщина 0,5
см и вес 40 г) логарифмический диск «Спутник» не-
сколько портативнее малых логарифмических линеек дли-
ной 12, 5 см.
Счетная линейка «Спутник» обеспечивает получение
более точных результатов по сравнению с малой линей-
кой, так как шкалы этой линейки, кроме шкал обрат-
ных чисел/? и мантисс логарифмов L, длиннее соответ-
ствующих шкал малой логарифмической линейки.
Поверки линейки
Перед пользованием логарифмической линейкой
«Спутник» необходимо проверить в ней выполнение сле-
дующих условий:
1.	При совмещенных началах движка и корпуса ли-
цевой стороны диска числа обеих шкал должны совпа-
дать.
2.	Движок и корпус линейки должны лежать в од-
ной плоскости.
3.	При совмещенных началах движка и корпуса ви-
зир бегунка должен пересекать начала всех шкал; та-
кую поверку следует делать отдельно для обоих сторон
диска.
4.	Для проверки шкал необходимо произвести неко-
торые вычисления:
1)	по шкалам R и С: 3 = 1 :0,333; 2=1; 0,5;
1,25= 1 : 0,8;
2)	по шкалам £, S и Т: sin 30° =0,5, tg 45° = 0,577;
45
3)	по шкалам С и D: 2 х 3 = б; 3x3 = 9;
4)	по шкалам D и А: 22 = 4 и З2 = 9;
5)	по шкалам К и D: 23 = 8; 33 = 27.
§ 10.	УСТАНОВКА И ЧТЕНИЕ ЧИСЕЛ
ПО ШКАЛАМ ЛИНЕЙКИ
При установке и чтении чисел на рассматриваемой
линейке пользуются теми же правилами, которые ука-
заны для нормальной счетной логарифмической линейки
(см. стр. 14—16).
I.	Для установки, например, на шкале D корпуса
линейки визира бегунка на число 41,5 поступают так:
поскольку число 41,5 находится в интервале (4—5), то,
найдя этот интервал, замечают, что он разделен длин-
ными штрихами на 10 частей, а затем каждая такая
часть поделена пополам. Следовательно, визир бегунка
должен занять положение, показанное на рис. 11,а.
Пример 1. Установить визир бегунка на число
0,0152 по шкале движка С.
Для этого на шкале С в интервале (1 —2) между
числами 1,5 и 1,6 находят число 0,0152 (рис. 11, а).
Пример 2. На рис. 11, а показаны отсчеты 268
и 863 по шкалам С и D на лицевой стороне линейки.
И. Шкала квадратов Л, нанесенная на диске (см.
рис. 10, а), состоит из двух равных частей: первая с чис-
лами 1, 2, . . ., 10 и вторая с числами 10, 20, ... , 90,
1. Первая часть этой шкалы предназначена для извле-
чения квадратных корней из чисел, у которых в первой
грани высшего разряда будет только одна цифра, а вто-
рой частью шкалы пользуются, если в первой грани выс-
шего разряда окажутся две цифры.
Здесь интервалы шкалы (1—2), (2 — 3), (10 — 20) и
(20 — 30) разделены каждый на 20 частей с выделени-
ем десятых долей этих интервалов более длинными
штрихами. Интервалы этой шкалы (3—4), (4—5), (5—6)
и (30—40), (40—50)'и (50—60) разделены каждый на 10
частей, а интервалы (6—7) до (9 — 10) и от (60—70) до
(90—1) на пять частей каждый.
Для установки по этой шкале визира бегунка сле-
дует предварительно это число разбить на грани.
Пример 1. Установить число 43,3.
Так как в грани высшего разряда две цифры (4 и 3),
46
то число устанавливают во второй половине шкалы А
(см. рис. 11, я).
Пример 2. Установить число 189.
В данном случае в грани высшего порядка одна циф-
ра (1), поэтому заданное число надо устанавливать в
первой части шкалы А (см. рис. И, а), т. е. в интерва-
ле (1—2).
Пример 3. Прочитать на рис. И, а по шкале
квадратов число, находящееся под визиром бегунка. По-
рядок этого числа выяснен быть не может из-за недо-
статка данных в условии задачи. Ответ: 67,8 или 0,678.
III.	Шкала кубов X3 (см. рис. 10, а) состоит из трех
совершенно одинаковых частей с нанесенными цифра-
ми 1,2, . . . , 8, 9, 1. Здесь интервалы (1—2) разделе-
ны на 20 частей, причем каждое четное деление отме-
чено длинным штрихом и означает 0,1 интервала (1—2).
Интервалы (2—3) и (3—4) разделены каждый на 10 час-
тей, а остальные интервалы (4—5), (5—6), (6—7), (7—8),
(8—9), (9—1) — на 5 частей каждый. Чтобы установить
на этой шкале число Х‘\ следует предварительно раз-
бить его на грани по три цифры, и если в грани выс-
шего порядка окажется одна цифра, то число X3 сле-
дует отыскивать в первой трети шкалы К- Если же в
грани высшего разряда будут две цифры, то число сле-
дует устанавливать в средней части шкалы К> И, на-
конец, если в грани высшего разряда три цифры, то
число находят в третьей части шкалы /С
Пример 1. Установить на шкале кубов К число
.0,385.
Так как в грани высшего разряда этого' числа три
цифры, то число находят в первой трети шкалы К меж-
ду цифрами 3 и 4 (см. рис. 11, б).
Пример 2. Установить визир бегунка на число
82,2 по шкале кубов.
Для этого, разбив число на грани по три цифры,
имеем в грани старшего порядка две цифры (82) и по-
этому число следует устанавливать в интервале (8—9)
второй трети шкалы кубов К (см. рис. 11, б).
Пример 3. Прочитать на рис. 11, б на шкале К
число под визиром бегунка.
Порядок этого числа неизвестен; ответ: 0,116 или
116 и т. д.
IV.	На шкале обратных чисел R (см. рис. 10, а) под-
47

a — по основным шкалам и по шкале квадратов;
б — по шкале кубов и по шкале обратных чисел
писанные цифры возрастают в направлении против часо-
вой стрелки. Здесь интервал шкалы между 1 и 2 раз-
делен на 50 частей, из них каждое пятое оцифровано.
(1,1; 1,2; . . . ; 1,9); наименьшее деление 0,02.
Следующие интервалы шкалы (2—3), (3 — 4), (4 — 5)
разделены на 20 частей каждый; каждое второе деле-
ние, означающее 0,1 интервала, имеет длинный штрих,
а середины интервалов сверх того подписаны (2,5; 3,5;
4,5). И, наконец, интервалы шкалы от (5—6) до (9—1)
разделены каждый на 10 частей.
Пример 1. Установить на шкале обратных чисел
R визир бегунка на значение 1: X =15,5.
Это число будет находиться в интервале (1 —2) шка-
лы между числами 1,5 и 1,6 (см. рис. 11, б).
Пример 2. Поставить на шкале обратных чисел
R визир бегунка на отсчет 0,813.
Число 813 следует искать в интервале шкалы R
(8—9) (см. рис. 11, б).
Пример 3. Прочитать на рис. 11, б числа, нахо-
дящиеся под визиром бегунка по шкале R.
Ответы: 322 и 212.
V.	На обратной стороне диска на шкале тангенсов Т
в масштабе основной шкалы (см. рис. 10, б) нанесены
логарифмы тангенсов углов от 5°43', 5 до 45°, соответ-
ствующие изменению этой функции от 0,1 до 1. На этой
шкале интервалы градусов: 6, 7, 8 разделены на 12
частей каждый (наименьшее деление равно 5'), интер-
валы, кратные 10°, отмечены удлиненным штрихом. Гра-
дусы 8, 9, . . . , 13, 14, 16, 18, 20 поделены на 6 ча-
стей; наименьшее деление 10'. И, наконец, от 20° до
45° наименьшее деление 20', каждый градус имеет длин-
ный штрих, а подписаны только градусы, кратные пяти.
Пример 1. Установить на шкале тангенсов Т ви-
зир бегунка на штрихи, соответствующие 12°50', 15°00',
38° 10'-и на отсчет 7°34' (рис. 12).
VI.	На шкале синусов S (см. рис. 10, б) от началь-
ной точки в масштабе основной шкалы нанесены лога-
рифмы синусов углов от 5°43',5 до 90°. Эта шкала со-
стоит из пяти участков. На участке от начала ее до 16°
наименьшее деление 10', далее от 16° до 30°—20',
от 30° до 40 —30', от 40° до 60э—1°, от 60° до 80°—
2° и, наконец, на участке 80"—90° помечен только один
штрих (85°).
50
Рис. 12. Чтение чисел по шкалам Т, S цТ и S и по шкале
мантисс логарифмов логарифмической линейки «Спутник»
Пример 1. Установить по шкале синусов S визир
бегунка на отсчеты, соответствующие синусам углов
11° 16z, 32°00z и 68°20z (см. рис. 12).
VII.	На шкале S и Т — шкале синусов и тангенсов
(см. рис. 10, б), как и на шкалах S и Т, от начальной
точки в масштабе основной шкалы нанесены логарифмы
этих функций для значения острых углов от 0° 34',38 до
5°43z,77. Здесь наименьшее деление на участке до l°30z
равно Г, а на участках l°30z—3°00z и 3°00z—5°43',77
соответственно 2Z и 5Z.
Пример 1. Установить визир бегунка на отсчеты
по шкале соответственно на 0°56z,5 и 5°37z (см. рис. 12).
VIII.	Мантиссы логарифмов чисел шкалы Е нане-
сены на движке обратной стороны линейки на шкале L
(см. рис. 10, б). Она одна представляет собой равномер-
ную шкалу. На ней наименьшее деление соответствует
0,05.
Пример 2. На рис. 12 по визиру бегунка, постав-
ленному на штрих, подписанный на шкале Е числом 186,
можно по шкале L прочитать lg 186 ~ 2,268.
§ 11.	ПРИМЕНЕНИЕ ЛИНЕЙКИ
При пользовании линейкой «Спутник» порядок числа
определяют так же, как и при работе с нормальной счет-
ной логарифмической линейкой (см. § 4—5).
I.	Возведение чисел в квадрат
Для возведения числа X в квадрат визир бегунка ус-
танавливают под этим числом на основной шкале корпу-
са D, а искомое число X2 прочитывают под визиром на
шкале квадратов А.
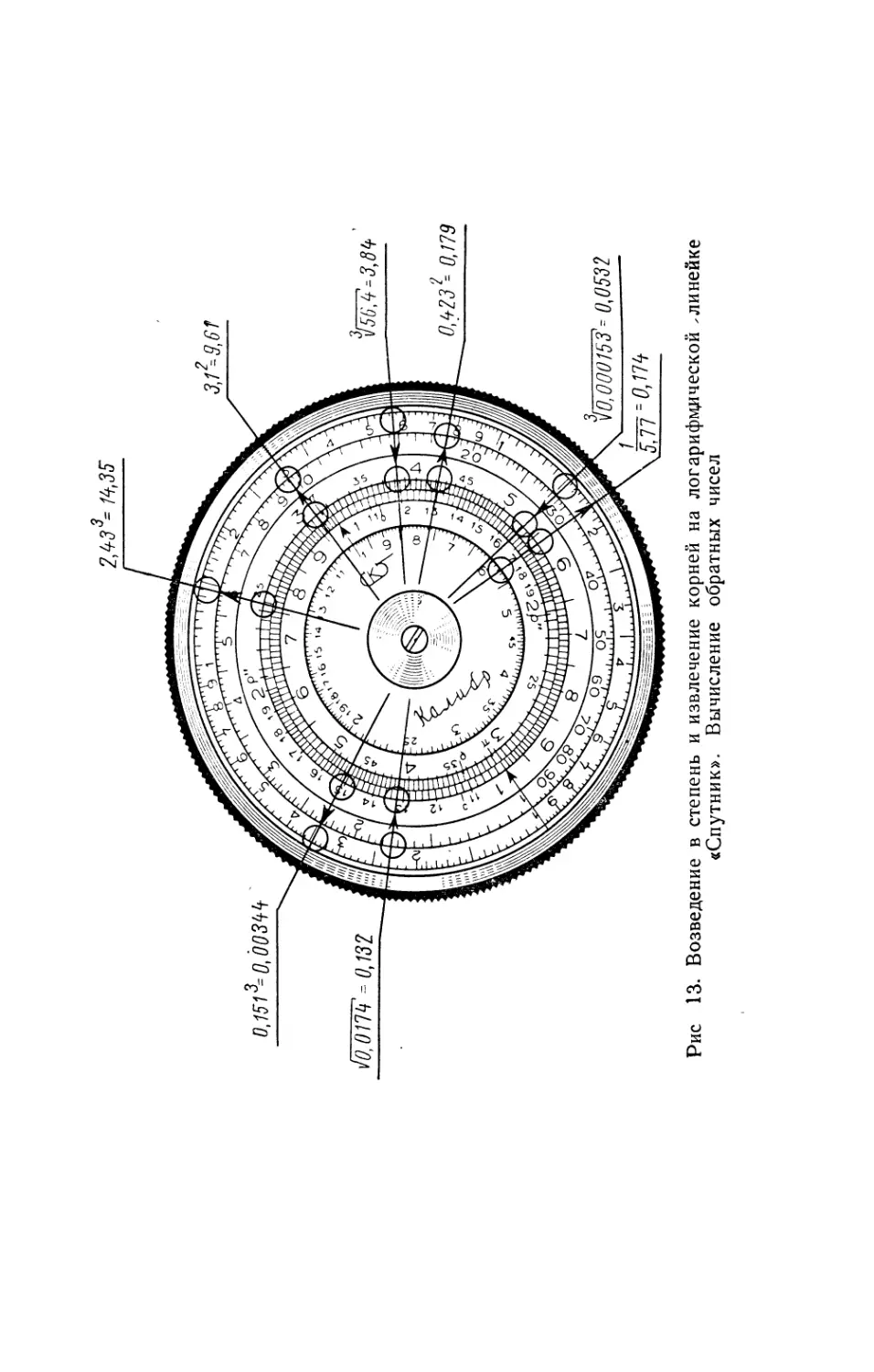
Пример 1. Вычислить х2, если х = 3,1.
Визир бегунка совмещают с числом 31 на основной
шкале D корпуса (рис. 13), а под визиром бегунка на
шкале квадратов А получаем 961. Итак (см. табл. 3),
х2 = 9,61.
Пример 2. Вычислить х2, если х = 0,423.
Совместив визир бегунка с числом 423 на шкале D
(см. рис. 13), на шкале квадратов Л читают: х2^ 0,179.
52

II.	Возведение в куб
Чтобы возвести число X в куб, нужно установить ви-
зир бегунка над числом X по основной шкале корпуса D
и результат прочитать под визиром бегунка на шкале ку-
бов К.
Пример 1. Для возведения 0,151 в куб находят
это число на шкале D корпуса и, совместив с ним визир
бегунка, прочитывают ответ на шкале кубов К по ви-
зиру бегунка (рис. 13).
Итак,
0,1513 ^0,00344.
Пример 2. Вычислить 2,433 » 14,35.
Результат прочитывают по средней части шкалы К (см.
рис. 13).
Пример 3. Вычислить 48,23 » 112 000.
Результат прочитывают по правой части шкалы ку-
бов /С.
III.	Извлечение квадратного корня
Для извлечения квадратного корня на шкале А оты-
скивают подкоренное число, с ним совмещают визир
бегунка и на шкале D под визиром прочитывают иско-
мый корень.
Пример 1. Вычислить J/"0,0174 —0,132.
Подкоренное число разбивают на грани. В старшей
грани имеем одну цифру, поэтому визир бегунка ста-
вят над числом 174 в первой половине шкалы Л и по
основной шкале D корпуса линейки прочитывают под
визиром число 132 (см. рис. 13).
Пример 2. К11 65 — 3,41.
Подкоренное число находят в правой части шкалы Л.
IV.	Извлечение кубического корня
Пример 1. Вычислить 56,4 .
Подкоренное число находят на средней части шкалы
кубов /С, с ним совмещают визир бегунка, а на шкале
D прочитывают искомый результат под визиром:
1^56,4 ^3,84 (см. рис.. 13)
54
Пример 2. Вычислить >/0,0098 ^0,214.
Подкоренное выражение отыскивают в левой части
шкалы кубов /<.
Пример 3. Вычислить уЛ0,000153^0,0532.
Подкоренное выражение устанавливают в правой ча-
сти шкалы кубов К (см. рис. 13).
V.	Пользование шкалой обратных чисел
Для вычисления обратных чисел (1 : X) визир бегун-
ка устанавливают на лицевой стороне диска над числом
X основной шкалы движка С, а результат читают по
визиру на шкале обратных чисел R.
Примеры. 1) —5« 0,174 (см. рис. 13);
5,77
2) —— 0,318; 3) —!—« 0,0625;	4) —~ 3,7;
7 3,14	16,0	0,27
5) —« 0,00962; 6) — » 0,00206.
104	' 486
VI.	Умножение чисел
Умножение чисел производят при помощи основных
шкал корпуса и движка лицевой стороны диска. Это
действие сводят к сложению соответствующих отрезков
на логарифмических шкалах С и D.
Пример 1. Для умножения 82 • 6,6 совмещают на-
чальный штрих движка шкалы С с числом 82 на основ-
ной шкале D корпуса (рис. 14). Визир бегунка уста-
навливают над числом 66 основной шкалы С движка и
под этим визиром на шкале D корпуса прочитывают от-
вет 541.
Пример 2. Вычислить 0,0455-0,166 ^0,00755 (см.
рис. 14).	____
Пример 3. Вычислить 8,6]/3,1	15,2 (рис. 15).
Визир бегунка совмещают с числом 31 в первой по-
ловине шкалы квадратов А. Движок началом основной
шкалы С подводят под визир бегунка. Визир бегунка
совмещают с числом 86 на основной шкале С движка.
Ответ (152) читают под визиром бегунка по основной
шкале D корпуса.
55
03: 35 = 1,228
82*5,5=501
0,0055*0,156
Рис. 14. Умно-
жение и деление
на логарифми-
ческой линейке
«Спутник»
81,5:0,37=220
= 0,00755
Рис. 15. Умножение
Рис. 16. Умножение
и деление на шкалах
• sin 5 9°0-0,858
cos 89 ° 05 '=0,103
Пример 4. Вычислить 0,455 •	0,573 (рис. 16).
Движок ставят штрихом, соответствующим числу 455
на основной шкале С, против начала основной шкалы
D корпуса. Визир бегунка совмещают с числом 2 в ле-
вой части шкалы кубов АГ. Под визиром бегунка чита-
ют ответ (0,573) на основной шкале С движка.
VII.	Деление чисел
Действие, деление, как обратное умножению, сводит-
ся к вычитанию на линейке соответствующих отрезков
на логарифмических шкалах С и D.
Пример 1. Требуется вычислить 43 : 35	1,228.
В этом случае ставят визир бегунка на деление 43
основной шкалы D корпуса линейки (см. рис. 14) и пе-
ремещают движок так, чтобы с визиром совпал штрих,
отмеченный числом 35 на шкале С. Затем против на-
чального штриха шкалы С читают на шкале D ответ
1,228.
Пример 2. Вычислить 81,5 : 0,37 « 220 (см. рис.
14).
Пример 3. Вычислить ]/3” : 7,8 (см. рис. 16).
Визир бегунка совмещают с числом 3 на левой части
шкалы квадратов А на корпусе линейки.
Под визир бегунка подводят штрих, соответствующий
78 на основной шкале С движка. Против начального
штриха шкалы С движка прочитывают на шкале D кор-
пуса искомый результат.
Итак, /3 : 7,8 « 0,223.
Пример 4. Вычислить 0,254 : рТЙГ » 0,0574.
Визир бегунка совмещают с числом 2 во второй час-
ти шкалы кубов /С (см. рис. 15). Под визир бегунка
подводят движок числом 254 основной шкалы движка С.
Ответ (574) прочитывают на шкале С движка против на-
чального штриха шкалы D корпуса.
VIII.	Вычисление тригонометрических функций
При пользовании логарифмическими шкалами Т, $ и
S и Г, нанесенными на обратной стороне корпуса ли-
нейки «Спутник», начальные штрихи этих шкал долж-
ны совпадать с начальным штрихом шкалы Е.
59
Ниже приведены примеры упражнений со шкалами
S, Т и S и Т.
Пример 1. sin 59°,0 « 0,858.
При совмещенном положении начала шкалы Е движ-
ка с началом тригонометрических шкал (рис. 17) визир
бегунка следует подвести к числу 59°,0 на шкале S, а
на шкале Е под визиром прочитать ответ 858.
Пример 2. tg 9° 25' « 0,1658.
Пример 3. cos84°05' « sin5°55' « 0,103.
Пример 4. sin 0° 42',5 « tg 0°42',5 « 0,0123.
Пример 5. tg 3°08'« sin 3°08'« 0,0547.
Примечание. Для вычисления значений ctg, cosec или sec
вначале следует определять соответственно функции tg, sin или cos,
а затем на лицевой стороне движка линейки, пользуясь его основ-
ной шкалой С и шкалой обратных чисел /?, получить значения ис-
комых функций.
Пример 6. Вычислить ctg34°20'.
Пользуясь шкалами Т и Е, определяют tg 34°20' « 0,683
(см. рис. 18), а на лицевой стороне движка по шкалам
R и С получают 1:0,683 «1,46 (рис. 18). Следова-
тельно,
ctg 34° 20' « 1,46.
IX.	Применение шкалы мантисс
Для определения десятичного логарифма числа на
линейке «Спутник» пользуются шкалой мантисс логариф-
мов L и основной шкалой С на лицевой стороне движка.
Для этого визир бегунка совмещают на шкале С со штри-
хом, соответствующим числу, логарифм которого опре-
деляют, а на шкале L по визиру прочитывают мантиссу
логарифма; впереди мантиссы к ней приписывают харак-
теристику (см. стр. 22—23).
Примеры. 1) 1g 190 «2,2_79; 2) 1g47,9«1,680; 3)
lg0,964 « 1,984; 4) 1g 0,00183 « 3,262; 5) 1g 25 300 «4,403;
6) lg 8 010 ООО « 6,904.
Для нахождения числа по его десятичному логари-
фму мантиссу заданного логарифма устанавливают ви-
зиром бегунка на шкале логарифмов L, а число, ей со-
ответствующее, прочитывают по визиру на основной
шкале С движка линейки.
60
Примеры:	1) 3,450 lg 0,00282;	2) 0,382 «
« lg2,41;	3) 2,843 ~lg 697;	4) 1,104 1g 12,7.
Рис. 18. Умножение чисел с помощью шкалы 7? и вычисление
обратных чисел на логарифмической линейке «Спутник»
X.	Комбинированное умножение и деление. Вычисления
с помощью шкалы обратных чисел
Для вычисления выражений вида X = посту-
пают так:
1)	на основной шкале D корпуса линейки визир
бегунка совмещают с штрихом, соответствующим чи-
слу ах\
2)	под визир бегунка подводят движок штрихом,
соответствующим числу Ьг шкалы С;
3)	переставляют визир бегунка на штрих, соответ-
ствующий числу а2 на шкале D;
61
4)	по начальному штриху шкалы С на основной шка-
ле корпуса D прочитывают результат X.
Пример 1. Вычислить х = 166‘87- « 14,6.
Уэ
При вычислении выражений вида X = al-a2-a3-ai
следует пользоваться шкалой обратных чисел R на
движке, представляя это выражение в виде
Х = -^- .
1 . 1
а3
Пример 2. Вычислить х = 4,18-7,68-0,9 (рис. 18).
^ii2^8^28,9.
0?9
КРУГОВАЯ СЧЕТНАЯ ЛОГАРИФМИЧЕСКАЯ
ЛИНЕЙКА КЛ-1
§ 12. ОПИСАНИЕ ЛИНЕЙКИ
Наиболее портативным прибором для вычислений
является круговая логарифмическая линейка, выпуска-
емая под маркой КЛ-1. На этой линейке можно выпол-
нять умножение, деление, возведение в квадрат и из-
влечение квадратного корня и производить вычисления
с тригонометрическими функциями и определять обрат-
ные величины. Выполнение этих действий (кроме умно-
жения и деления)'на линейке КЛ-1 сходно с выполне-
нием аналогичных действий на нормальной логарифми-
ческой линейке (см. § 5). Что же касается умножения
и деления чисел, то эти действия на линейке КЛ-1
производят несколько иначе.
Линейка КЛ-1 состоит из двух циферблатов, заклю-
ченных в металлическую оправу с двумя головками 1
и 2 (рис. 19). Неподвижный циферблат — корпус линей-
ки— наглухо скреплен с оправой. На этом циферблате
нанесены три шкалы: основная шкала —шкала чисел
общей длиной 12 см (D), шкала логарифмов синусов
длиной 11,5 см (S) и шкала логарифмов тангенсов дли-
ной 13,5 см (Т). Второй циферблат — подвижный — дви-
жок. Он вращается при помощи головки с черной точ-
62
a)
t)
Рис. 19 Общий вид круговой логарифмической линейки КЛ-1:
а — вид со стороны корпуса; б — вид со стороны движка:
1 — головка с черной точкой, 2 — головка с красной точкой, J — бегунок^
4 — индекс движка
63
кой — черной головки 1. На движке нанесены две шка-
лы: внутренняя основная шкала чисел (С) и наружная
шкала — шкала квадратов (В); длины этих шкал по
11,5 см.
Над движком против черной головки 1 помещена не-
подвижная маленькая стрелка красного цвета — индекс-
указатель, которым отмечено начало основной шкалы
неподвижного циферблата (корпуса). И, наконец, над
корпусом (неподвижным циферблатом) и над движком
(подвижным циферблатом) одновременно вращается крас-
ная стрелка — бегунок, управляемая головкой 2 с крас-
ной точкой — красной головкой (см. рис. 19).
Поверки линейки КЛ-1
1.	При совмещении индекса и стрелки-бегунка по-
следняя должна быть над началом шкал корпуса D, S,T.
2.	Для поверки шкал С и D стрелку-бегунок уста-
навливают против числа W на шкале D корпуса, затем
движок началом шкалы С подводят под бегунок и смот-
рят, совпадает ли индекс с числом 2V; в этом случае
линейкой работать можно. Такую поверку на шкалах
D и С следует производить равномерно, пользуясь чис-
лами 15, 2, 25, 3, 35, 4, 5, 6, 7, 8, 9.
3.	Для поверки шкал В, S и Т проверяют некоторые
равенства. Например, 2I. 2 = 4, З2 = 9, sin 30° = 0,5, tg
30° —0,577.
§ 13.	УСТАНОВКА И ЧТЕНИЕ ЧИСЕЛ ПО ШКАЛАМ
ЛИНЕЙКИ
I. Основная шкала D корпуса и аналогичная ей основ-
ная шкала С движка представляют собой обычную кру-
говую (сомкнутую логарифмическую шкалу чисел 1, 2,
... ,9,1. Интервал 1—2 разделен на 50 частей, причем
каждая десятая часть этого интервала подписана. Ин-
тервалы 2—3, 3—4, 4—5, 5-^-6 разделены каждый на
20 частей с ценой деления в 0,05 соответствующего
интервала; на этих частях шкалы каждое деление, соот-
ветствующее 0,1 интервала, выделено длинным штри-
хом. И, наконец, интервалы 6 — 7, 7 — 8, 8—-9 и 9 — 1
шкалы разделены каждый на 10 частей.
64

Рис 20. Чтение и установка чисел на круговой логариф-
мической линейке КЛ-1:
а —- положение со стороны корпуса; б—положение со сто-
роны движка
65
На основной шкале движка С нанесены два вспомо-
гательных значка: С = "|/и я = ~ . Кроме того,
число z нанесено еще на основной шкале D корпуса, а
также на шкале квадратов (см. рис. 19).
Пример 1. Чтобы на основной шкале D корпуса
установить стрелку-бегунок на число 0,210, следует, не
обращая внимания на порядок числа, в интервале 2—3
шкалы D найти число 21 и вращением красной головки
2 совместить с ним стрелку-бегунок, как это показано
на рис. 20,а.
Пример 2. На рис. 20,а показана установка на
основной шкале D корпуса стрелки-бегунка на число
1240.
Пример 3. Прочитать число х, находящееся под
стрелкой-бегунком на основной шкале D корпуса (см.
рис. 20,а); х =685.
Пример 4. Найти на движке число 257 и поста-
вить его против индекса.
Это число находится в интервале 2—3 шкалы С дви-
жка. Вращением черной головки его нужно подвести
под индекс (см. рис. 20, б).
Пример 5. Прочитать число х, находящееся на
основной шкале С движка под стрелкой-бегунком (рис.
20, б).
х = 424.
II.	Логарифмическая шкала квадратов чисел В на дви-
жке линейки состоит из двух одинаковых частей (см.
рис. 19, б). Одна часть шкалы, оцифрованная 1, 2......
10, разделена на три участка: 1—2, 2—6 и 6—10 с на-
именьшими делениями каждый соответственно 0,05; 0,1
и 0,5. Вторая часть шкалы от 10 до 1(100) также со-
стоит из трех участков. Здесь на участках 10—20,
20—60 и 60—1(100) наименьшие деления равны соот-
ветственно 0,5; 1 и 5 единиц.
Например, под стрелкой-бегунком на рис. 20, б на-
ходится на шкале квадратов число 41; или, например,
число 13,1 на шкале квадратов будет между числами
10 и 20 (см. рис. 20, б).
III.	На логарифмической шкале синусов 3 (на кор-
пусе линейки) от начальной точки ее в масштабе осно-
вной шкалы нанесены логарифмы синусов углов от
66
5°43',77 до 90°. На участке этой шкалы от начала ее
до 10° каждый градус разделен на шесть частей; наи-
меньшее деление 10'. На участке от 10° до 20° — каж-
дый градус разделен на 3 части; наименьшее деление
20'. На участке от 20° до 30° каждый градус разделен
пополам; наименьшее деление 30'. На участке между
штрихами, соответствующими 30° и 70°, нанесены де-
ления через градус, И, наконец, участок шкалы от 70°
до 90° разделен на четыре части; наименьшее деление
5°. Здесь оцифрованы лишь штрихи, соответствующие
75° и 80°.
Пример 1. На рис. 20,а стрелка-бегунок находит-
ся на шкале синусов S над штрихом, соответствующим
22°25'.
Пр.имер 2. На рис. 20, а на шкале синусов S стрел-
ка-бегунок поставлена на штрих, соответствующий 9°23'.
IV.	Логарифмическая шкала тангенсов Г, представ-
ляющая собой спираль, расположена в центре корпуса
линейки (рис. 20, а). Она состоит из двух частей. На
первой ее части, предназначенной для определения на-
туральных значений тангенсов для углов от 1° до 6°,
наименьшее деление равно 5'. Вторая часть этой шка-
лы, используемая для вычислений натуральных значе-
ний тангенсов углов от 6° до 45°, имеет наименьшее
деление — 10'.
Натуральные значения sina и tga для углов а менее
5°43',77 в пределах трех значащих цифр можно считать
равными, поэтому шкалу тангенсов Т используют и для
определения натуральных значений синусов углов от 0°
до 5°43',77.
Пример. На рис. 20, а стрелка-бегунок совме-
щена на шкале тангенсов Т с штрихами, соответст-
вующими 3040' и 3°18'.
§ 14.	ПРИМЕНЕНИЕ ЛИНЕЙКИ
1.	Возведение в квадрат и извлечение
квадратного корня
Для возведения в квадрат числа X необходимо вра-
щением красной головки поставить стрелку-бегунок над
этим числом X на основной шкале С движка и выше
по стрелке-бегунку на шкале квадратов В прочитать
67
искомый результат. При этом для установления поряд-
ка результата следует руководствоваться указаниями,
приведенными в табл. 3.
Для извлечения квадратного корня из числа X не-
обходимо предварительно разбить это число на грани по
две цифры влево или вправо от запятой (что соответ-
ствует числам больше 1 пли меньше 1), и если в стар-
шей грани будет одна значащая цифра, то стрелку-бе-
гунок следует установить над числом X в первой поло-
вине шкалы квадратов (там, где цифры 1, 2,.. ,9,10), если
же значащих цифр будет две, то бегунок нужно устано-
вить над числом X во второй половине шкалы квадра-
тов (там, где цифры 10,20,...,90,1); в обоих случаях
результат (]/ X ) следует прочитать ниже по нити бе-
гунка на основной шкале.
Пример 1. 0,5062	0,256.
Ставят стрелку-бегунок над числом 506 на основной
шкале движка С (см. рис. 20, б) и выше по шкале ква-
дратов В читают ответ 256.
Пример 2. Вычислить ]/"253 ж 15,9.
Вначале разбивают подкоренное выражение на гра-
ни. В старшей грани будет лишь одна цифра, поэтому
стрелку-бегунок ставят над числом 256 шкалы квад-
ратов В в ее первой половине. Ниже на основной шка-
ле С движка читают: 159 (см. рис. 21). Итак,
1 253 « 15,9.
II.	Вычисление выражений вида 1 : X, 1 : X2 и 1 : ] X
В этом случае предварительно следует поставить
движок в «нормальное положение», т. е. совместить на-
чало движка с индексом (рис. 21). Чтобы вычислить
значение обратной величины (1 : X), следует стрелку-бе-
гунок совместить на основной шкале D корпуса со
штрихом, соответствующим числу X, а на шкале С
движка под стрелкой-бегунком прочитать искомый
результат.
Для вычисления значения 1 : X2 необходимо подвести
стрелку-бегунок к числу X на основной шкале D кор-
пуса линейки (рис. 21) и, повернув к себе диск обратной
стороной, под стрелкой-бегунком прочитать на шкале
квадратов В ответ.
68
Для вычисления выражений вида 1:]/Х стрелку-
бегунок следует поставить над числом X шкалы квад-
ратов В и, повернув к себе диск обратной стороной,
под нитью стрелки-бегунка получить результат на ос-
новной шкале D корпуса.
Рис. 21. Вычисление на круговой логарифмической линейке КЛ-1
обратных чисел
Пример 1. На рис. 21 показано получение значе-
ния 1 : 6,6 = 0,152.
Пример 2. Вычислить N — 1 : 2,852	0,123.
Установив стрелку-бегунок над числом 285 по шкале
D корпуса и приведя движок в «нормальное положение»,
получают под стрелкой-бегунком на шкале квадратов В
ответ 123 (см. рис. 21).
Пример 3. Вычислить /И — 1 : ]/0,00063	39,8.
После приведения диска в «нормальное положе-
ние» устанавливают стрелку-бегунок в первой поло-
вине шкалы квадратов В над числом 63, а результат
398 прочитывают под нитью стрелки-бегунка на
шкале D,
69
III.	Вычисление натуральных значений
тригонометрических функций
Для определения sin X при 5°43',77 < X < 90° стре-
лку-бегунок следует устанавливать над соответствую-
щим штрихом на шкале синусов S, а на основной шка-
ле D корпуса прочитать ответ.
При вычислении натуральных значений cos X поль-
зуются формулой cos Х = sin (90° — X) и по sin (90° — X)
определяют значение cosX.
кой линейке КЛ-1 тригонометрических функций
Для определения натурального значения tgX при
5°43',77 < X < 45°
стрелку-бегунок следует устанавливать на шкале Т над
штрихом, соответствующим заданному значению X, а
по основной шкале D корпуса под стрелкой-бегунком
прочитать ответ.
Вычисление натуральных значений sinX и tgX малых
углов (при 1° <Х < 5°43'77) производят по одной шкале
тангенсов 7, так как в этих случаях можно считать
sinX « tgX. В этих случаях стрелку-бегунок устанавли-
вают над соответствующим штрихом на шкале танген-
сов Т, а ответ прочитывают по основной Щкале D кор-
70
пуса. Для определения натуральных значений sin X и
tg X углов X менее Г можно воспользоваться извест-
ным выражением
sin X ж tg X ж — sin п X ~ — tg п X,
которое для этих углов остается справедливым до четы-
рех значащих цифр.
При вычислении натуральных значений ctg X при
5°43',77 < X < 45°
и cos X при
5°43',77 < X < 90°
следует поступать так. Если нужно вычислить натура-
льное значение ctg X, устанавливают стрелку-бегунок
на шкале тангенсов Т (или, если вычисляют cosec X, то
на шкале S) над штрихом, соответствующим значению
X, и после приведения движка в «нормальное положе-
ние» прочитывают ответ на обратной стороне диска под
стрелкой-бегунком на основной шкале С движка.
При нахождении натурального значения sec X сле-
дует воспользоваться формулой sec Х = cosec (90° — X)
и далее по cosec (90° — X), находить значение sec X так,
как это было изложено ранее.
Для определения натурального значения tg X при
45° < X < 90°
вначале определяют ctg (90° — X), а далее поступают
так, как это указано в § 5.
Н% линейке КЛ-1 можно производить вычисления
значений 1 : sin2 X, 1 :tg2X, а также значений sec2 X,
cosec2 X и ctg2X. В этих случаях стрелку-бегунок необ-
ходимо совместить с соответствующим штрихОхМ на шка-
ле S или Т, движок привести в «нормальное положе-
ние», а ответ прочитать под стрелкой-бегунком на шкале
квадратов В движка.
Для нахождения угла по натуральному значению
тригонометрической функции стрелку-бегунок на шкале
D корпуса совмещают с штрихом, соответствующим за-
данному значению функции, а на шкале. 5 или Т про-
читывают под стрелкой-бегунком искомый угол. В слу-
чае определения значения угла X по заданному нату-
ральному значению ctg X или cosec X стрелку-бегунок
71
Следует, приведя линейку в «нормальное положение»,
совместить с соответствующим штрихом на шкале С
движка, а ответ прочитывать на соответствующих шка-
лах Т или S корпуса линейки.
Пример 1. Определить натуральное значение
sin 53°30z.
Для этого на шкале синусов S отыскивают штрих,
соответствующий 53°30' (см. рис. 22), а на основной
шкале D корпуса линейки читают 804. Итак, sin 53°30z ж
0,804.
Пример 2. Определить натуральное значение
tg8°23z.
В этом случае на шкале тангенсов Т находят штрих,
соответствующий 8°23z (см. рис. 22). Совмещают с этим
штрихом стрелку-бегунок и по ней на шкале D корпуса
читают 1473, т. е. tg 8°23z	0,1473.
Пример 3. Вычислить натуральное значение
tgl°17',5.
Устанавливают стрелку-бегунок на шкале тангенсов
Т над штрихом, соответствующим l°17z,5 (см. рис. 22),
а на основной шкале D корпуса линейки читают 2255.
Итак, tgl°17'5 = 0,02255.
Пример 4. Для определения натурального значения,
например cos 89°28z, следует поступать так. Учитывая,
что cos 89°28z = sin 0°32z	-j- sinl°04z, совмещают по
шкале тангенсов Т стрелку-бегунок с штрихом, соответ-
ствующим l°04z (см. рис. 22), а под стрелкой-бегунком
на шкале D читают 1862.
Итак, cos 89°28z ^ 0,00931.
Пример 5. ctgl0°13z ^5,55, a cosec 68°30z « 1,075.
Пример 6. Натуральное значение tg 54с25' =
= ctg35°35z	1,40.
Пример 7. 1 : sin2 17c30z	11,16.
Пример 8. cosec2 40°15/2,40.
Пример 9. 1 :tg23°16z ^ 307.
Пример 10. sec2 63с02~ 4,86.
Пример 11. cosec2 3°02'~ 357.
Пример 12. ctg2 5°20z	114,7.
Пример 13. Если sin х = 0,505, то для определе-
ния значения угла х следует стрелку-бегунок поста-
вить над числом 505 основной шкалы D корпуса и по
72
стрелке-бегунку на шкале синусов S прочитать значение
угла х ~ 30°2(У.
Пример 14. ctgх = 2,66; х ж 20°36'.
IV.	Умножение и деление чисел
Для умножения чисел стрелку-бегунок следует сов-
местить со штрихом, соответствующим значению пер-
вого сомножителя, на основной шкале D корпуса. За-
тем подвести основную шкалу С движка штрихом, соот-
ветствующим второму сомножителю, и под индексом
движка получается произведение.
Рис. 23. Умножение чисел на круговой логарифмической линейке
КЛ-1
При делении чисел следует поступать следующим
образом. На шкале С движка отыскивают штрих, соот-
ветствующий делимому, и движок этим числом под-
водят под индекс. После этого стрелку бегунок ставят
на шкале С на штрих, соответствующий делителю. И
повернув линейку, на шкале D корпуса под стрелкой-
бегунком прочитывают результат — частное.
Пример 1. Вычислить 16,4-20,7 (рис. 23).
Стрелку-бегунок совмещают со штрихом 164 на ос-
новной шкале D корпуса. На шкале С движка находят
число 207 и подводят его под стрелку-бегунок. Резуль-
тат 339 прочитывают под индексом движка на основной
шкале С.
73
Пример 2. Вычислить 266: 15,2 (рис. 24).
Подводят движок штрихом 266 основной шкалы С
под индекс. Ставят стрелку-бегунок над числом 152 ос-
новной шкалы С движка. Прочитывают ответ 175 под
стрелкой-бегунком на шкале D корпуса.
Итак, 266: 15,2 = 17,5.
Пример 3. Вычислить Р =
Движок штрихом 25 на основной шкале С ставят под
индекс. Стрелку-бегунок подводят к штриху 437 основ-
Рис. 24. Деление чисел на
круговой логаоифмической линейке
КЛ-1
ной шкалы С движка. Под стрелку-бегунок подводят
штрих, отмеченный на шкале С движка значком к. Под
индексом прочитывают на основной шкале С движка
ответ 1,8.
ГТ	Л D	ГУ	0,67 • С
Пример 4. Вычислить Q =	—•
Найдя на шкале	квадратов В	движка	штрих,	соот-
ветствующий числу	86, вращением черной	головки под-
водят этот штрих под индекс. При помощи поворота
красной головки устанавливают стрелку-бегунок над
штрихом, соответствующим числу 67 на основной шка-
ле С движка. Подводят под стрелку-бегунок значок С
на основной шкале С движка. Ответ 257 прочитывают
на шкале С.
Итак, Q = 0,257.
74
ЗАКЛЮЧЕНИЕ
При выборе счетной линейки той или иной конструк-
ции следует учитывать эксплуатационные особенности
каждой из них.
1.	Нормальная логарифмическая линейка и подобные
ей (§ 8) обладают несравнимым преимуществом перед
другими конструкциями линеек, так как эксплуатация
их, выдержавшая испытания «временем», не требует
переучивания.
Их недостатком является наличие съемных бьющих-
ся частей и неустойчивость против воздействия темпе-
ратуры и влажности воздуха.
2.	Дисковая линейка «Спутник», наоборот, весьма
устойчива против механических повреждений. Кроме
того, она позволяет иметь набор дисков с различными
шкалами, смена которых не вызывает затруднений.
Недостатком таких линеек является неустойчивое
положение в них визира, что может привести к ошиб-
кам при вычислениях.
3.	Линейки типа КЛ-1 являются весьма портатив-
ными и устойчивыми против влияния температуры, вла-
жности и пыли. Они так же позволяют легко произво-
дить замену шкал.
Эксплуатационный недостаток такой линейки заклю-
чается в необходимости переворачивания ее при выпо-
лнении на ней умножения и деления.
ПРИЛОЖЕНИЯ
1.	Основные правила приближенных вычислений
1.	В записи приближенного числа с помощью десятичной дроби
оставляют только верные знаки.
2.	При сложении или вычитании приближенных чисел в резуль-
тате (сумме или разности) необходимо оставлять столько десятичных
знаков, сколько их дано в компоненте с наименьшим числом этих
знаков.
3.	При умножении и делении приближенных чисел в результате
необходимо оставлять столько значащих цифр, сколько их имеет
приближенное данное из заданных с наименьшим числом значащих
цифр.
4.	При возведении приближенных чисел в квадрат или в куб в
результате необходимо оставлять столько значащих цифр, сколько
их имеет основание степени; однако при этом последняя цифра, и
особенно при возведении в куб, будет все же менее надежна, чем
последняя цифра основания.
5.	При извлечении квадратного или кубического корня из при-
ближенного числа в результате следует брать столько значащих
цифр, сколько их имеет подкоренное число. При этом последняя
цифра квадратного, и особенно кубического корня, будет получа-
ться более надежной, чем последняя цифра подкоренного числа
6.	Если для получения искомой величины требуется произвести
ряд различных действий, то в этом случае во всех промежуточных
результатах необходимо сохранять лишь на одну цифру больше,
чем это указано в правилах 2—4, отбрасывая эту лишнюю цифру
только в окончательном результате.
7.	Если некоторые данные, участвующие в вычислениях, имеют
десятичных знаков (при сложении и вычитании) или значащих цифр
(при умножении, делении, возведении в степень или извлечении
корня) больше, чем другие, то их предварительно округляют, сох-
раняя лишь одну лишнюю цифру против числа, заданного с на-
именьшим числом значащих цифр.
8.	Выполняя вычисления, необходимо всегда помнить о той
точности, которую можно получить или которая необходима в каж-
дом конкретном случае.
9.	Для получения результата с п цифрами исходные данные
для вычисления необходимо брать с таким числом цифр, какое да-
ют, согласно правилам 2—5, п -ф 1 цифр результата.
76
10.	Вычисления однозначных выражений при помощи логариф-
мов следует производить по таблицам логарифмов с числом десятич-
ных знаков на один больше наименьшего числа значащих цифр,
содержащихся в приближенном данном. В окончательном резуль-
тате последняя значащая цифра отбрасывается.
2.	Памятка вычислителя
1.	Приступая к вычислениям, следует прежде всего подготовить
рабочее место и иметь все необходимые для этого средства.
2.	Так как практически все вычисления производят, главным
образом, по соответствующим формулам, поэтому последние пред-
варительно должны быть преобразованы так, чтобы при данных
средствах вычислений определение искомой величины выполнялось с
минимальной затратой времени.
3.	Числовой материал, используемый при вычислениях, следу-
ет располагать в определенной последовательности. Для этой цели
при вычислениях’ пользуются специально разработанными схемами
(бланками, ведомостями, журналами с соответствующей разграф-
кой), позволяющими каждый результат, участвующий в вычислени-
ях, разместить в отведенном для него месте. В заголовке схем,
ведомостей часто приводят формулы, для которых они составлены.
4.	При вычислениях числа в столбцах следует записывать так,
чтобы цифры соответствующих разрядов были бы под цифрами тех
же разрядов в выше записанном числе. При этом ошибочные резу-
льтаты или ошибочно записанные числа не стирают, а аккуратно
перечеркивают красными чернилами и ими же сверху записывают
верный результат или число.
5.	Вычисления нельзя считать законченными, если не произ-
ведена тем или иным способом их проверка. При этом лучше,
если эту проверку выполнить новым способом, не зависящим от
принятого при первоначальных вычислениях.
Особенно внимательно следует производить вычисления, которые
нельзя проконтролировать.
6.	При вычислениях в числах дробную часть от целой следует
отделять запятой, а в логарифмах — точкой.
7.	Вычисления необходимо вести на одной стороне листа; обра-
тная сторона не должна использоваться.
8.	При вычислениях числа, состоящие из многих цифр, должны
быть записаны с интервалами, например 8 320 000.
9.	При однотипных вычислениях должен быть выработан стан-
дарт в последовательности их выполнения.
10.	Всякая замеченная ошибка в вычислениях должна быть
исправлена немедленно.
11.	Результаты отдельных вычислений должны быть выделены
более крупным шрифтом и подчеркнуты.
ЛИТЕРАТУРА
1.	Березин С. И. Счетная логарифмическая линейка. Изд. 3,
дополненное и переработанное. М., «Машиностроение», 1965.
2.	Ларченко Е. Г, Техника вычислений М., Геодезиздат,
1952.
3.	Лифшиц Ф. Д. Счетная линейка для экономистов. М.,
Госстатиздат, 1954.
4.	Назаров В. Г. Справочник по логарифмической линейке.
Физматгиз, Г959.
5.	П а н о в Ю. Д Счетная линейка Изд. 18. М., «Наука»,
1966.
6.	Р у м ш и н с к и й Л. 3. Счетная линейка М., Физматгиз,
1968.
7.	Рывкин А. А., Рывкин А. 3., Хренов Л. С. Спра-
вочник по математике. Изд. второе. М., «Высшая школа», 1968.
8.	Широких И. И. Логарифмическая линейка и ее приме-
нение. Томское книжное изд-во, 1964.
СОДЕРЖАНИЕ
Стр.
Предисловие ...............................................3
Введение ................................................. 5
Нормальная счетная логарифмическая линейка
§ 1.	Описание линейки.....................................11
§ 2.	Шкалы линейки .......................................15
§ 3.	Установка и чтение чисел по шкалам	линейки .17
§ 4.	Порядок чисел........................................20
§ 5.	Алгебраические и тригонометрические	действия на линейке . 21
§ 6.	Особые значки на шкалах линейки......................31
§ 7.	Применение линейки при расчетах......................32
§ 8.	Различные логарифмические линейки	.....37
Дисковая счетная логарифмическая линейка «Спутник»
§ 9.	Описание линейки «Спутник»...........................43
§ 10,	Установка и чтение чисел по шкалам линейки «Спутник» . 46
§ 11.	Применение линейки «Спутник»........................52
Круговая счетная логарифмическая линейка КЛ-1
§ 12.	Описание линейки КЛ-1...............................62
§ 13.	Установка и чтение чисел по шкалам линейки КЛ-1 . . „64
§ 14.	Применение линейки КЛ-1 . . . .  ...................67
Заключение . , s . . . . ...............................	75
Приложения ...........................................    76
1. Основные правила приближенных вычислений............,	. 76
2. Памятка вычислителя....................................77
Литература , . » tЧ t ( t t 8 » . < . . s . t , t . . 78
79
Леонад Сергеевич Хренов
Юлий Васильевич Визиров
«ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА»
Редактор А. И. Селиверстова
Технический редактор 3. В. Нуждина
Корректор Э. П. Шерман
Т-04805. Сдано в набор 1/II-68 г. Подп. к печати 6/III-68 г.
Формат 84Х108’/з2. Объем 2,5 печ. л. 4,2 усл. п. л. Уч.-изд. л. 3,48.
Изд. № ФМ/391. Тираж 200 000 экз. Цена 9 коп.
Тематический план издательства «Высшая школа» (вузы и тех-
никумы) на 1968 г. Позиция № 254
Москва, К-51, Неглинная ул., д. 29/14,
Издательство «Высшая школа»
Ярославский полиграфкомбинат Главполиграфпрома Комитета
по печати при Совете Министров СССР
Ярославль, ул. Свободы, 97.
Зак. 550

9 коп.
ВЫСШАЯ ШКОЛА
19 6 8