Текст
В.Г.Бс )л тя некий
ТРЕТЬЯ
ПРОБЛЕМА
ГИЛЬБЕРТА
в. г. волтянскии
ТРЕТЬЯ ПРОБЛЕМА
ГИЛЬБЕРТА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕР АТУРЫ
Москва 1977
517.3/6
Б 79
УДК 513.0
Третья проблема Гильберта. Болтянский В. Г. Глав-
ная редакция физико-математической литературы издательства
«Наука», М., 1977, 208 стр.
Среди проблем Гильберта, сформулированных па рубеже XIX
и XX столетий, особое место занимает третья проблема — един-
ственная, связанная с методикой преподавания элементарной мате-
матики. В ней Гильберт ставит вопрос, можно ли отказаться от
предельного перехода в выводе формулы объема треугольной пира-
миды и ограничиться только методом равносоставленности. Проб-
лема эта породила большое число работ (М. Ден, давший отрица-
тельное решение проблемы Гильберта, В. Ф. Каган, математики
швейцарской школы и др.).
Книга знакомит читателя с современным состоянием теории
равносоставленности, которая за последние годы обогатилась рядом
новых результатов. Она предназначена для научных работников,
преподавателей университетов, педвузов, школ, студентов-матема-
тиков и всех читателей, серьезно интересующихся математикой.
Табл. 2, Илл. 108, Библ. 60.
20203—040
Б 053(02)-77
33-77
© Главная редакция
физико-математической литературы
издательства «Наука», 1977
ОГЛАВЛЕНИЕ
Предисловие............................................... 4
Глава I. Измерение площадей и объемов..................... 7
§ 1. Понятие площади................................. 7
§ 2. Аксиомы площади................................ 10
§ 3. Дальнейшие свойства площади.................... 19
§ 4. Независимость аксиом площади................... 24
§ 5. Методы вычисления площади фигур................ 32
§ 6. Измерение объемов и третья проблема Гильберта 41
Глава II. Равносоставленность многоугольников............ 47
§ 7. Теорема Бойяи — Гервина........................ 47
§ 8. Равносоставленность и равнодополняемость в не-
архимедовых и неевклидовых геометриях .... 53
§ 9. Равносоставленность по группе параллельных пе-
реносов н центральных симметрий..................... 65
§ 10. Равносоставленность по группе переносов ... 73
§ 11. Минимальность группы переносов и центральных
симметрий....................................... 81
Глава III. Равносоставленность многогранников............ 87
§ 12. Равносоставленность симметричных многогранни-
ков ................................................ 87
§ 13. Решение третьей проблемы Гильберта............. 93
| 14. Теорема Хадвигера............................. 101
§ 15. Условие Брикара................................ ПО
§ 16. Эквивалентность методов разбиения и дополнения 115
§ 17. Теорема Дена — Сидлера........................ 130
§ 18. Многогранники, равносоставленные с кубом . . . 151
§ 19. Равносоставленность многогранников по группе
параллельных переносов............................. 164
§ 20. Инварианты Дена — Хадвигера и теорема Ессена 177
§ 21. Минимальность группы сохраняющих ориентацию
движений........................................... 189
§ 22. Алгебра многогранников........................ 193
Заключение.............................................. 198
Добавление. О понятии длины............................. 200
Литература.............................................. 205
1*
ПРЕДИСЛОВИЕ
Рис. 1.
На рубеже XIX и XX столетий в Париже состоялся
II Международный конгресс математиков, па одном из
заседаний которого (8 августа 1900 года) Давид Гильберт
прочитал свой знаменитый доклад «Математические проб-
лемы» [33]. В этом замечательном произведении, напи-
санном выдающимся математиком с весьма разносторон-
ними интересами, охвачены все основные направления
математики. Интерес к проблемам Гильберта не ослабевает
в течение всего XX века, и зна-
чение проблем для развития ма-
тематики трудно переоценить.
Из 23-х поставленных Гиль-
бертом проблем подавляющее
большинство относится к но-
вым, быстро развивающимся
разделам математики (в боль-
шую часть которых сам Гиль-
берт внес существенный вклад).
И лишь одна проблема, третья,
связана с вопросами препода-
вания «школьной» геометрии.
Гильберт обращает внимание
на то, что при вычислении объ-
ема треугольной пирамиды еще
со времен Евклида использу-
ется довольно сложный пре-
дельный переход («чертова лестница» — ср. рис. 1, взятый
из учебника геометрии А. II. Киселева [40], стр. 53),
тогда как учение о площадях в планиметрии обходится
без аналогичного предельного перехода. Обосновать ис-
пользование этого «лишнего» (по сравнению с планимет-
рией) предельного перехода, доказать, что без него
теория объемов многогранников не может быть построе-
на,— в этом и состоит существо проблемы.
ПРЕДИСЛОВИЕ
5
Постановка этой проблемы объясняется не только
интересом Гильберта к вопросам преподавания элемен-
тарной геометрии. (Напомним, что доклад «Математи-
ческие проблемы» был сделан через год после выхода
книги «Основания геометрии» [32], в которой Гильберт
изложил свою широко известную систему аксиом евклидо-
вой геометрии.) Очевидно, Гильберт предвидел, что
поставленный вопрос имеет значение не только в узкой
области методики преподавания объемов, но и далеко выхо-
дит за зти рамки и может привести к созданию математи-
чески интересной и богатой результатами теории равно-
составленности многогранников.
Предвидение Гильберта полностью оправдалось. Уже
в том же 1900-м году М. Ден [13] подтвердил высказанную
Гильбертом гипотезу, доказав существование многогран-
ников одинакового объема, которые не являются равно-
составленными. Доказательства Дена, очень сложные и,
надо сказать, довольно путаные, были существенно усо-
вершенствованы В. Ф. Каганом [39]. А середина XX сто-
летия ознаменовалась новыми успехами в зтом направ-
лении: известный швейцарский геометр Г. Хадвигер
вместе со своими учениками внес новые, свежие идеи
в теорию равносоставленности (см. [20]’— [27], [30] и
ряд более поздних работ).
В книге автора [6] приведено наиболее простое дока-
зательство теоремы Дена, основанное на идеях швейцар-
ской школы геометров, а также изложение наиболее важ-
ных результатов, связанных с третьей проблемой Гиль-
берта. Ко времени своего выхода (1956 г.) зта книга
(см. также статью [7]) содержала сравнительно полный
обзор результатов, относящихся к этому направлению.
Однако книга давно уже разошлась, а прошедшие два
десятилетия ознаменовались дальнейшими успехами;
в частности, Ж.-П. Сидлер [54] установил, что найден-
ные Деном инварианты дают не только необходимое, но и
достаточное условие равносоставленности. Сейчас можно
считать, что вопросы, связанные с третьей проблемой
Гильберта, полностью изучены для плоскости и трехмер-
ного пространства и почтиДполпостью для четырехмер-
ного. Это и определило необходимость написания новой
книги, знакомящей читателя с современным состоянием
теории.
ПРЕДИСЛОВИЕ
Книга презназначена для научных работников, пре-
подавателей университетов, пединститутов и школ, сту-
дентов-математиков; материал параграфов 1—3, 5—7,
9—14 доступен также интересующимся математикой стар-
шеклассникам. Автор попытался ввести читателя в курс
современного состояния излагаемых вопросов и, вместе
с тем, сделать изложение максимально популярным.
Пользуюсь случаем выразить искреннюю признатель-
ность Николаю Владимировичу Ефимову, Виктору Абра-
мовичу Залгаллеру и Исааку Моисеевичу Яглому за
дружеское участие и ценные замечания.
В. Болтянский
ГЛАВА I
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ *)
§ 1. Понятие площади
Обычно говорят, что площадь s (F) фигуры F есть чис-
ло, показывающее, из скольких единиц площади «состав-
ляется» эта фигура. При этом в качестве единицы площади
берется квадрат, стороной которого является отрезок,
принятый за единицу длины. Однако такое разъяснение
(принятое в школе) не может служить точным математи-
ческим определением понятия площади. Это —
лишь наглядное пояснение, апелляция к представлениям,
почерпнутым из повседневно-
го опыта. Неясно, например,
как можно определить, из
скольких единиц площади
«составляется» круг заданно-
го радиуса.
Один из способов уточне-
ния понятия площади осно-
вывается на рассмотрении
палетки — разбиения [плос-
кости на конгруэнтные квад-
раты. Пусть, напрпмер, сто-
рона каждого из квадратов,
составляющих палетку, имеет
длину 1. На рис. 2 фигура F содержит фигуру, составлен-
ную из 9 квадратов палетки, и содержится в фигуре,
•) Изложение теории площадей и объемов имеется во многих
источниках; см., например, [28], [46], а также дополнение И. М. Яг-
лома к небольшой интересно написанной книге Дубнова [12]. При
желании читатель может лишь бегло проследить за идейной линией
главы I, уделив несколько большее внимание последним трем ее
параграфам.
8
ИЗМЕРЕНИИ ПЛОЩАДЕЙ И ОБЪЕМОВ
1ГЛ I
составленной из 29 квадратов. Это позволяет написать
двойное неравенство
9 s (/’) < 29.
Для более точной оценки площади можно использовать
палетку, квадраты которой имеют стороны длиной
1/10 (так что в каждом квадрате прежней палетки содер-
жится 100 квадратов новой палетки). Если, скажем, F со-
держит фигуру, составленную из 1716 квадратов новой
палетки, и содержится в фигуре, составленной из 1925
таких квадратов, то
17,16 < s (F) < 19,25.
Еще раз измельчая палетку (т. е. уменьшая в 10 раз длины
сторон квадратов), мы получим оценку площади фигуры
F с еще большей точностью, и т. д.
Для уточнения описанного процесса условимся началь-
ную палетку (у которой длины сторон квадратов равны
1) считать нулевой палеткой. После к измельчений мы
получим к-ю палетку, у которой длины сторон квадратов
равны 1/10*. Пусть F содержит фигуру, составленную из
ак квадратов Ar-й палетки, и содержится в фигуре, состав-
ленной из Ък таких квадратов, к = 0, 1, 2, ... Так как
каждый квадрат /с-й палетки содержит 100 квадратов
(А + 1)-й палетки, то ак квадратов /с-й палетки, содержа-
щихся в фигуре F, дают при измельчении 100flft квадра-
тов (к + 1)-й палетки, содержащихся в F. Кроме того,
в F могут содержаться еще некоторые квадраты (к + 1)-й
палетки (получающиеся при измельчении из тех квадра-
тов А-й палетки, которые не целиком содержались в F).
Следовательно, ак+1 lOOn*. Аналогично, Ьк+1 100Д:.
Разделив эти неравенства на 102(k+1>, получаем
ак < аН-1
IO2* io2(fc+i) ’
Ьк+1 < Ьк .
102(/,’+1) 102ft ’
/с = 0,1,2,...
Таким образом,
л <" а* °2
° IO2 101
102*
102* ‘
_______X Ъл /Л \
Т(Н
§ 1]
ПОНЯТИЕ ПЛОЩАДИ
9
так что существуют пределы
lim—~=s(F), lim—= s (F),
fc-»OO IO21 - ' ’ ft_OO 104ft ' h
(2)
причем s (F)<^$ (F). Если фигура F такова, что эти пре-
делы совпадают, то фигура F называется квадрируемой,
а число s (F) = s (F), т. е. совпадающее значение преде-
лов (2), называется площадью *) фигуры F и обозначается
через s (F). Иными словами, описанный выше процесс
измерения используется не только для оценки площа-
ди (или ее вычисления — с помощью предельного
перехода), но также и для самого определения
понятия площади.
Имеется, впрочем, одна нечеткость в приведенном оп-
ределении. После выбора нулевой палетки первая опреде-
ляется однозначно: стороны каждого квадрата нулевой
палетки делятся на 10 конг-
руэнтных частей и через точ-
ки деления проводятся пря-
мые, параллельные линиям
нулевой палетки. Точно так
же первая палетка однознач-
но определяет вторую (деле-
нием сторон квадратов па 10
частей) и т. д. Таким обра-
зом, если нулевая палетка
фиксирована, то од-
нозначно определены все
Рис. 3.
последующие палетки, а по-
тому (для заданной фигуры F) однозначно определе-
ны числа «л, 6/t и пределы (2). Если же нулевую па-
летку сдвинуть или повернуть, то числа ak, bk могут
измениться. Так, на рис. 3 фигура Ф содержит 5 квадра-
тов первоначальной палетки (изображенной сплошными
линиями) и лишь 3 квадрата смещенной палетки (изобра-
женной штриховыми линиями). Априори неясно, не изме-
нится ли понятие квадрируемости, если сместить нуле-
вую палетку (т. е. не может ли случиться, что фигура,
*) Такое^ионимапие площади связано с работами Жордана,
поэтому s (F) называют иногда жорданоеой площадью (см. [28],
гл. III).
10
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. ]
квадрируемая при одном положении нулевой палетки, не
окажется квадрируемой при ином ее положении); априо-
ри неясно также, совпадает ли площадь фигуры F, вычис-
ленная при одном положении нулевой палетки, с пло-
щадью этой же фигуры, вычисленной при ином положе-
нии нулевой палетки (если в том и в другом случае
фигура F квадрируема).
Эта трудность может быть преодолена, если жестко
фиксировать все палетки. Например, фиксировав прямо-
угольную систему координат х, у, можно считать /с-й
палеткой систему квадратов, па которые плоскость разби-
вается прямыми х = p/10fc, у = q/10k, где р, q пробегают
целые числа. Такого понимания площади мы и будем пока
придерживаться. О том, что происходит при сдвиге или по-
вороте пулевой палетки, речь будет идти ниже.
Заметим, что площадь представляет собой функцию
s, заданную па множестве всех квадрируемых фигур-
каждой фигуре F взятой из этого множества (т. е. квадри.
руемой), она сопоставляет действительное число;? (F):
§ 2- Аксиомы площади
Изложенное в предыдущем параграфе определение
позволяет доказать ряд свойств площади. В этом
параграфе мы рассмотрим лишь следующие четыре перво-
начальные свойства, которые впоследствии будет удобно
принять за аксиомы:
(а) Функция s неотрицательна, т. е. площадь s (F)
любой квадрируемой фигуры F является неотрицательным
числом.
(Р) Функция s аддитивна, т. е. если F' и F" — квадри-
руемые фигуры, не имеющие общих внутренних точек, то
фигура F' (J F" квадрируема и s (р" (J F") = s (F') -|-
+ * (Л-
(т) Функция s инвариантна относительно параллель-
ных переносов, т. е. если F — квадрируемая фигура и
F' — фигура, получающаяся из F с помощью некоторого
параллельного переноса, то фигура F' также квадрируема
и s (F') = s (F).
(6) Функция s нормирована, т. е. единичный квадрат
Q является квадрируемой фигурой и s (Q) — 1.
! 21
АКСИОМЫ ПЛОЩАДИ
11
В свойстве (6) под единичным квадратом понимается
фиксированный квадрат, длина стороны которого равна 1,
а именно один из квадратов нулевой палетки.
В свойстве (0) речь идет о фигурах, не имеющих общих
внутренних точек. В связи с этим условимся о следующем
обозначении: если Flt . . ., FK— фигуры, попарно не име-
ющие общих внутренних точек, то их объединение будем
обозначать через + . . . + Fk. Иначе говоря, запись
F = Fx + . . . + Fk означает, что выполнены следующие
два условия: 1) фигуры Flt . . ., Fk попарно не имеют
общих внутренних точек, 2) F = Fx (J . . . (J Fk. В этих
обозначениях свойство (0) можно выразить следующим
образом: если F = F' + F", то s (F) = s (Fr) + s (F”). Из
этого свойства с помощью очевидной индукции выводится
следующее более общее утверждение: если F = FT + . . .
. . . + то s (F) = s (FJ + . . . + s(Fk).
Доказательство свойства (а). Число
а0 (т. е. число квадратов нулевой палетки, содержащихся
в фигуре F) либо равно нулю, либо является натуральным
числом. Из неравенства а0 0 вытекает, что все числа
as/102,c неотрицательны (см. (1)) и потому, в силу (2),
s (А) > 0. Так как фигура F квадрируема, то s (А) =
= s (F) > 0.
Доказательство свойства (0). Числа
ак и Ьк, построенные для фигуры F’, будем теперь обоз-
начать через а>£ и Ьк. Иначе говоря, F’ содержит фигуру,
составленную из ак квадратов Zc-й палетки, и содержится
в фигуре, составленной из Ьк таких квадратов. Аналогич-
ные числа для фигуры F” обозначим через щ и а обоз-
начения щ, Ьк (без штрихов) сохраним для фигуры
F' + F".
Никакой квадрат не может одновременно содержаться
и в фигуре F', и в фигуре F". Следовательно, взяв все
квадраты Zc-й палетки, содержащиеся в F', и все квад-
раты, содержащиеся в F", мы получаем фигуру, состав-
ленную из ait + «л квадратов этой палетки и содержащую-
ся в F’ + F". Возможно также, что существуют квадраты
fc-й палетки, не содержащиеся ни в одной из фигур F’,
F", но содержащиеся в F’ + F" (рис. 4). Таким образом,
ак>ак + ак и потому > —— + . Нто неравен-
12
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ЕЛ. I
ство справедливо для любого к = 0, 1, 2,... Переходя
к пределу (см. (2)), получаем
s (F' + F") ' s (F') + s (F").
Аналогично, рассматривая числа Ък, Ък, Ьк, находим
s (F’ + F") s (F) + s (F").
Так как, кроме того, s (F' + F") s s (F" + F"), то
рате Q' и ближе всего
s (F' + F") = 8 (F' + F") =
= 8 (F') + 8 (F").
Это и означает, что справед-
ливо свойство (Р).
Доказательство
свойства (у). Пусть
Q' — квадрат, получающий-
ся из единичного квадрата
Q параллельным переносом.
Обозначим через q0 ту из
вершин первой палетки,
которая содержится в квад-
расположена к левой нижней
вершине этого квадрата (рис. 5). Горизонтальная прямая,
Рис. 5.
Рис. 6.
проходящая через q0, отстоит от нижпей стороны квад-
рата Q' (а вертикальная — от левой стороны) менее, чем
на Vxo- Из этого следует, что квадрат со стороной
§ 2]
АКСИОМЫ ПЛОЩАДИ
13
длины и/10, левой нижней вершиной которого служит точ-
ка q0, содержится в Q' (см. рис. 5), т. е. в Q' содержится
фигура, составленная из 81 квадрата’первой палетки. (Воз-
можно, что в Q' содержится и большее число квадратов
первой палетки; это будет, если точка д0 лежит па кон-
туре квадрата Q'.) Окаймляя квадрат со стороной В/]П,
содержащийся в Q', полоской шириной в один квадрат
первой палетки (рис. 6), мы получаем фигуру, составлен-
ную из 121 квадрата первой палетки и содержащую Q'.
Аналогичное рассуждение, примененное к к-й палетке,
показывает, что Q' содержит фигуру, составленную из
(10fc — I)2 квадратов к-й палетки, и содержится в фигуре,
составленной из (10ft + I)2 таких квадратов. Иначе говоря,
числа и Ьк (взятые для квадрата Q') удовлетворяют не-
равенствам ак (ПУ1' — I)2, bk (1(У; + I)2. Следова-
тельно,
ак /. 1 V Ьк - /, 1 \2
__z>h--------— \ < /1 ч—-—) .
102fc ^t\ 10‘ / 102к \ 10ft )
Переходя к пределу (см. (2)), получаем s (Q') 1,
з (Q') 1, т. е. s (Qr) = s (Q') = 1. Таким образом, Q’ —
квадрируемая фигура и s (Q') = 1.
Аналогично, если Р — некоторый квадрат к-й палетки
и Р’ — квадрат, получающийся из Р с помощью парал-
лельного переноса, то Р’ — квадрируемая фигура и
s (Р‘) = l/102ft.
Пусть, далее, G — фигура, составленная из а квадратов
к-й палетки, a G' — t (G) — фигура, получающаяся из G
с помощью параллельного переноса t. Обозначим через
Рг, . . Ра квадраты к-й палетки, из которых составляет-
ся G, так что G = Рл + . . . + Ра. В силу уже доказан-
ного свойства (Р), мы имеем s (G) = s (Рг) + -..+« (Ра) =
= я/102,с. Так как каждый квадрат t (Pt) имеет (как это
доказано выше) площадь I/IO2*, то, аналогично, s (G') =
= 8 (t (G)) = 8 (t (/\)) + . . . + s (i (PJ) = a/102ic. Таким
образом, 8 (G) = 8 (Gz), t. e. если фигура составлена из
нескольких квадратов к-й палетки, то ее площадь при
параллельном переносе не меняется.
Пусть, наконец, F — произвольная квадрируемая фи-
гура. Так как s (F) = s (F), то для любого е _> 0 найдется
такое к, что ак/1()21: _> s (F) — е/2, где ак таково, что
некоторая фигура G, составленная из ак квадратов к-й
14
ИЗМЕРЕНИЕ ПЛ0ЩАДЕЙ И ОБЪЕМОВ
1ГЛ. I
палетки, содержится в F. Иначе говоря, s (G) s (F) —
— е/2, где G CZ F, причем фигура G составлена из квадра-
тов /с-й палетки. Применим теперь некоторый параллель-
ный перенос t. Тогда t (G) CZ t (F), причем в силу дока-
занного выше фигура t (G) квадрируема и s (t (G)) = s(G).
Из квадрируемости фигуры t (G) вытекает существование
такого I, что имеется фигура G*, составленная из квадра-
тов Z-й палетки, удовлетворяющая условиям G* с t (G)
и щ/102* s (t(GJ) — е/2, где а( — число квадратов
Z-й палетки, из которых составляется фигура G*. Мы
имеем
G*CZZ(G)CZZ(F),
(G)) —= s(G) —s (F) — е.
Таким образом, фигура G*, составленная из о( квадратов
Z-й палетки, содержится в t (F), и потому s (Z (F)) >
> fl;/102' з (F) — е. Так как это имеет место для любого
е 0, то з (Z (F)) з (F).
Аналогично доказывается неравенство s (t (F)) s (F).
Так как, кроме того, s (Z (F)) s (Z (F)), то s (Z (F)) ==
= s (t (F)) = s (F).
Доказательство свойства (б) очевидно.
Прежде чем переходить к изложению аксиоматиче-
ской точки зрения па понятие площади, докажем квад-
рируемость произвольного многоугольника. Под много-
угольником мы будем понимать замкнутое ограниченное
множество на плоскости,
граница которого состоит
из конечного числа отрез-
ков. Из этого определения
следует, что к многоуголь-
никам причисляются фи-
гуры, ограниченные одной
или несколькими замкну-
Рис. 7.
тыми ломаными, в том
числе и несвязные фигуры, состоящие из отдель-
ных кусков (рис. 7). Многоугольник можно также опре-
делить как объединение конечного числа треугольни-
ков (это определение равносильно предыдущему).
§ 2]
АКСИОМЫ ПЛОЩАДИ
15
Теорема 1. Всякий многоугольник является квад-
рируемой фигурой.
Доказательство. Обозначим через L лома-
ную (возможно, состоящую из нескольких отдельных кус-
ков), являющуюся границей многоугольника F, и пусть
р — длина ломаной L. Фиксируем некоторое натуральное
число к и построим на пинии L систему точек хг, . . ., х„,
представляющую собой 1/10к-сеть (т. е. такую, что любая
точка х GE L отстоит от какой-либо из точек xt менее,
чем на 1/10*). Нетрудно видеть, что число q можно счи-
тать удовлетворяющим условию q р НУ' + т, где т —
число отрезков (звеньев), из которых состоит L. В самом
деле, пусть . ., Lm — звенья ломаной L, и пусть
Pi — длина звена так что р = рг + . . . + рт. После-
довательно откладывая на отрезке £г (от одного из его
концов) отрезки длиной 1/10’“', мы получим на этом отрез-
ке 1/10к-сеть, состоящую из не более, чем Pi-10ft + 1 точек.
Взяв такие 1/10к-сети на каждом из звеньев Lx, . . ., Lm,
мы получаем 1/10*-сеть на линии L, состоящую из не бо-
лее, чем (Рх + • • + pm)10k + т = р-1бк + т точек.
Итак, пусть на L выбрана 1/10к-сеть {^, . . ., xq},
где + m. Обозначим через Qi объединение де-
вяти квадратов Р-й палетки,
один из которых содержит точ-
ку х^ а остальные восемь при-
мыкают к нему (рис. 8). Все
точки линии L, находящиеся
от хл на расстояниях, меньших
1/10к, содержатся внутри квад-
рата Qi- Поэтому все квадраты
к-a палетки, имеющие общие
точки с линией L, содержатся
в фигуре Qi U • • -U Qu кото-
рая составлена из не более, чем
Qq квадратов Р-й палетки. Та-
Рис. 8,
ким образом, число квадратов
р-й палетки, имеющих общие точки с линией L, не пре-
восходит 9у 9 (р-10к + т).
Пусть теперь ак — число квадратов к-й палетки, со-
держащихся в многоугольнике F, а Ьк — число квадратов
Р-й палетки, имеющих общие точки с F. Ясно, что любой
квадрат, имеющий общие точки с F, но не вошедший
16
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
в число тех квадратов, которые целиком содержатся
в F, имеет общие точки с линией L. Следовательно, 0
9 (p-10R+нг). Таким образом, О &fc/102ft —
— щЛО2* < 9p/10k + 9щ/1Оа5с откуда, переходя к пределу
при к-+ <х>, получаем 0 s (F) — s (F) 0. Это озна-
чает, что s (F) = s (F), т. е. многоугольник F является
квадрируемой фигурой.
Теорема 2. На множестве всех многоугольников
существует одна и только одна функция s, удовлетворяю-
щая условиям (а), (Р), (-у), (б).
Доказательство. Так как каждый многоуголь-
ник F является квадрируемой фигурой (теорема 1), то
определена его площадь s (F). Как мы видели, эта функция
удовлетворяет условиям (а), (Р), (у), (б). Этим доказано
существование. <
Докажем единственность. Пусть s* (F) — некоторая
функция, заданная на множестве всех многоугольников и
удовлетворяющая условиям (а), (Р), (у), (б). В силу
(б), s* (Q) — 1, где Q — единичный квадрат. Далее, рас-
смотрим те сто квадратов первой палетки, которые содер-
жатся в Q-, обозначим их через Рг, . . ., Р100. Так как
любые два из этих квадратов получаются друг из друга
параллельным переносом, то, в силу (у), s* (Р}) =
= s* (Р2) = ... = «* (Р100). Далее, так как Q = 1\ + ...
• • • + Рщо, то, в силу (Р), S* (Pj) 4- . . . + S* (Лоо) =
— s* (Q) = 1, т. е. 100s* (Л) — 1, и потому s* (Рх) =
= Лоо. Но тогда в силу (у), s* (Р) = V^o, где Р — произ-
вольный квадрат первой палетки. Аналогично доказы-
вается, что еслц Р — какой-либо квадрат Zc-й палетки,
то s* (Р) — l/102ft. Следовательно, если G — фигура, со-
ставленная из а квадратов Zc-й палетки, то $* (G) = <z/102/f.
Иными словами, для любой фигуры G, составленной из
квадратов k-й палетки, справедливо равенство s* (G) =
= s (G).
Пусть, наконец, F — произвольный многоугольник.
Обозначим через Gft объединение всех тех квадратов к-й
палетки, которые содержатся в Л и пусть ак — число
квадратов к-й палетки, из которых составлена фигура Gft.
Далее, через Нк обозначим такой многоугольник, что
Л- + Нк — F (т. е. Нк — F\Gk). Мы имеем, в силу
(Р), s* (F) s* (Gfr) -f- s* (Пк), а так как, согласно (а),
s* (Дк) 0, то s* (F) s* (Gfc). Но в силу уже доказан-
§ 2J
АКСИОМЫ ПЛОЩАДИ
17
ного, s* (Gk) = s (Gk) -- ak/i 02ft. Таким образом, s* (F)
a?,/102,c. Переходя к пределу при к —>- оо, получаем
s* (F) s (F), т. е. s* (F) s (F). Аналогично доказы-
вается неравенство s* (F) s (F). Итак, s* (F) = s (F)
для произвольного многоугольника F.
Доказанная теорема означает, что конструктивное
определение площади, изложенное в предыдущем пара-
графе, может быть для многоугольников заменено аксио-
матическим: площадью называется действительная функ-
ция, заданная на множестве всех многоугольников и удов-
летворяющая условиям (а), (Р), (у), (6) (которые при таком
подходе рассматриваются как аксиомы площадп).
Теорема 2 показывает, что эта аксиоматика непротиворе-
чива и полна (поскольку функция s существует и единст-
венна). При аксиоматическом определении площадп рас-
смотрение палеток становится ненужным, но единичный
квадрат Q фиксирован. Вопрос о замене единич-
ного квадрата будет рассмотрен в следующем параграфе-
Излагаемая в этой книге теория, содержащая решение третьей
проблемы Гильберта и развитие содержащихся в ней идей, ограни-
чивается изучением площадей многоугольников *)
(а в пространстве — объемов многогранников). Однако
для полноты мы покажем, каким образом аксиоматическое опреде-
ление площади распространяется на произвольные квадрируемые
фигуры.
Теорема 3. Фигура F в том и только в том случае квадри-
руема, если для любого в > О существуют такие многоугольники
G и Н, что G С F О II и s (Н) — s (G) < в.
Доказательство. Пусть фигура F квадрируема. Тогда
s (F) — S (F) (см. (2)), и потому для любого заданного в > 0 можно
найти такое натуральное к, что существует фигура Gk, составленная
из ак квадратов к-ё палетки, и фигура Нк, составленная из Ьк
квадратов этой палетки, удовлетворяющие условиям Gj С 7 С
С Нк, Ьк/Ю^ — < в. Так как s (Ял) — s (Gft) = bfc/10lft —
— afc/lO2* < в, то многоугольники Gk и Нк — искомые.
Обратно, пусть для любого в > О существуют такие много-
угольники G и Н, что s (Н) — s(G)<e п GC F C1I. Мы можем
(для того же в > 0) выбрать настолько большое к, что существуют
фигуры G£, Ht, составленные из квадратов к-ё палетки и удовлет-
воряющие условиям GecG, Я£ Z) Н, s (G) — s (G£) < в, s (Я£) —
—s (Я) < в. Таким образом, G£ С /' С Я£, причем s (Я£) — s (G£) <
< Зе, т. е. bft/102ft — а/с/102/с < Зв, где ак, Ък — число квадратов
к-ё палетки, составляющих фигуру С£, соответственно Я£. В пре-
*) Теория равносоставленности для произвольных
множеств небогата результатами; см., например, [28], гл. III.
18
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
доказательство.
пусть G', G", FT, Н" — такие
деле (при е —» 0) получаем S (F) — s (F) 0, т. е. Г (F) = £ (F),
и потому фигура F квадрируема.
Теорема 4. Если фигуры F' и F" квадрируемы, то каждая
из фигур F' (J F”, F' П F", F' \ F" также квадрируема.
Выберем произвольное в > 0 и
многоугольники, что G' С F' С Н',
G" С F" С Н" и s (Н')—з (С) < е/4,
s (1Г) — s (G") < е/4 (рис. 9; эти
многоугольники существуют в силу
теоремы 3). Мы можем дополнитель-
но предполагать (несколько увели-
чив, если нужно, многоугольник Н"),
что F" С int Н", где int обознача-
ет внутренность соответствующего
многоугольника. Тогда
G' \ int Н" С F' \ F" С
С Н' \ int G",
т. е. К = G' \ int Я", L = Н' \
Рис. 9. \ int G" представляют собой много-
угольники, удовлетворяющие усло-
вию К С F' \ F" С L. Для доказа-
тельства квадрируемости множества F' \ F" остается убедиться,
что s (L) — s (К) < е.
Из аксиомы (Р) вытекает, что s (Н' \ G') = s (Я') — s (G') <
< е/4. Аналогично, s (Я" \ G") < е/4. Следовательно, при доста-
точно большом к существуют такие фигуры Qlt (?2, составленные из
квадратов к-й палетки, что
Я' \С'С<21, Я"\С"С<22- s«?i)<e/2, s Ш < е/2.
Из легко проверяемого включения
L \ К С Я' \ G' U Н" \ G"
(см. рис. 9) вытекает, что L \ К содержится в фигуре (J Qz,
составленной из квадратов Л-й палетки и удовлетворяющей условию
s (<?i U <?г) С s (<?i) + s (С2) < е. Следовательно, s (L \ К) < е,
т. е. s (L) — s (Я) < е, откуда и вытекает квадрируемость множества
F' \ F".
Пусть теперь М — многоугольник, содержащий обе фигуры
F', F". Из соотношений
F' J F" = М \ (М \ (F' U F")) = М \ ((М \ F') \ F"),
F' П F" = М \(M\{F' П F")) = М \ ({М \ F') (J (М \ F"))
вытекает в силу доказанного, что каждая из фигур F' U F", F' (~|
П F” также квадрируема.
Теорема 5. На множестве веет квадрируемых фигур су-
ществует одна и только одна функция s> удовлетворяющая условиям
(а). (₽). (У), №)•
В 3]
ДАЛЬНЕЙШИЕ СВОЙСТВА ПЛОЩАДИ
19
Доказательство аналогично доказательству теоремы 2. Для
каждой квадрируемой фигуры F определена ее площадь s (F).
Эта функция удовлетворяет условиям (а), (0), (у), (б). Этим доказа-
но существование.
Пусть теперь s* — какая-либо функция, удовлетворяющая ус-
ловиям (а), (0), (у), (6). Возьмем произвольную квадрируемую
фигуру F и произвольное е > 0 и выберем такие многоугольники
G, Н, что G С F С Н и s (Я) — s (G) < е. В силу (а) и (0) мы имеем
(учитывая, что по теореме 4 фигура F \ G квадрируема):
s* (F) = s* (G + (F \ G)) = s* (G) + s* (F \ G) > s* (G).
Точно также s* (F) «С s* (Я). В силу теоремы 2 имеют место соот-
ношения s* (G) = s (G), s* (Н) = s (h), и потому
8 (G) < s* (F) < 8 (Я).
Аналогичное двойное неравенство справедливо и для s (F):
s (G) s (F) s (Я).
Из этих неравенств вытекает, что | s* (F) — s (F) | s (Я) —
— s (G) < e. Ввиду произвольности e > 0 имеем | s* (F) — s (F) | =
= 0, t. e. s* (F) = s (F). Этим доказана единственность.
§ 3. Дальней.ппе свойства площади
Так как аксиомы (а), (0), (у), (б) однозначно определя-
ют понятие площади, то естественно ожидать, что все
дальнейшие свойства площади могут быть выведены
только с помощью этих аксиом. Здесь мы именно
таким, аксиоматическим путем выведем несколько даль-
нейших свойств площади. Два из этих свойств обозначают-
ся через (а*) и (у*), так как они близки по смыслу
к сформулированным выше аксиомам (а) и (у).
(а,*). Если для квадрируемых фигур F и Н справедливо
включение F сН, то s (F) <1 s (77).
Пусть F и Н — многоугольники. Обозначим через
G такой многоугольник, что Н = F + G, т. е. G = Н \ F.
В силу аксиомы (0) мы имеем s(H) = s (F) + s (G). Кроме
того, s (6?) > 0 (аксиома (а)). Следовательно, s (77) >
> з (Л-
Операция замыкания была применена при определении фигуры
G в связи с тем, что мы условились все многоугольники считать
замкнутыми. Для произвольных квадрируемых фигур F,
Н доказательство проще (см. теорему 4):
8 (Я) = 8 (F) + 8 (Я \ F) S (Г).
Доказанное свойство (а*) (монотонность пло-
щади) нередко принимают за аксиому, используемую
20
ИЗМЕРЕНИЕ ПЛОЩАДЕЙИ ОБЪЕМОВ
[ГЛ. I
вместо (а), т. е. строят теорию площадей, исходя из ак-
сиом (а*), (Р), (у), (6). (Действительно, эта аксиоматика
эквивалентна предыдущей, поскольку из аксиом (Р), (у),
(6) и свойства монотонности вытекает справедливость
утверждения (а).)
Теорема 6. Для любых квадрируемых фигур F',
F" справедливо соотношение:
s (F' [J F") = s (F1) + s (F") -s(F' f) F").
Доказательство. Так как F' (J F" — F' +
+ (F" \ F'), то согласно аксиоме (Р) (см. также теорему
4) мы имеем
s (/?' [J F") = s (F') + s (F" \ F').
Далее, так как F" — (F" \ F') -Т (F" (~| F"), то, ана-
логично,
s (F") = s (F" \ F') + s (F' П F").
Из этих соотношений и вытекает справедливость теоремы.
Следствие, s (F' (J F") s (F") -f- s (F") для лю-
бых квадрируемых фигур F', F".
Для установления следующих свойств площади нам
понадобится хорошо известная формула площади прямо-
угольника.
Теорема 7. Площадь прямоугольника F может
быть вычислена по формуле s (F) = ab, где а и Ъ — длины
сторон прямоугольника. F.
Доказательство проведем сначала в слу-
чае, когда стороны прямоугольника F параллельны сторо-
нам единичного квадрата Q. Из справедливости теоремы
7 в этом частном случае мы выведем еще одно свойство
площади, после чего справедливость теоремы 7 в общем
случае станет очевидной.
Итак, пусть стороны прямоугольника F параллельны
сторонам единичного квадрата Q (т. е. линиям палеток).
В силу свойства (у) мы можем, кроме того, предполагать
(применив, если нужно, параллельный перенос), что левая
нижняя вершина q0 прямоугольника F совпадает с одной
из вершин нулевой палетки. Обозначим через р0 ту из вер-
шин Л-й палетки, которая содержится в прямоугольнике
F и ближе всего расположена к правой верхней его вер-
шине (рис. 10). Тогда фигура, составленная из всех квад-
I 31
дальнейшие свойства площади
21
ратов к-й палетки, содержащихся в F, представляет собой
прямоугольник противоположными вершинами которо-
го служат точки рп, qQ. Обозначим через <зк и число
квадратов к-й палетки, укладывающихся в сторонах
прямоугольника тогда
а-10* — 1 < <а-10*,
Ь-10* — 1< р/;< Ь-10*.
Следовательно, число квадра-
тов к-й палетки, из которых
составляется Gk, т. е. число
— “uPfc удовлетворяет не-
равенствам
(а-10* — 1) (Ь-10* — 1) <
а* ab • 102*.
Окаймляя Gk справа и сверху полоской шириной в
один квадрат к-й палетки, мы получаем прямоуголь-
ник ЯЕ- ~) F, составленный из bl: = (as + 1) (₽k + 1)
квадратов к-й палетки. Таким образом,
ab-102* < bk < (а-10* + 1) (Ь-10* + 1).
Из написанных неравенств мы получаем
Переходя к пределу при А’ —> оо (см. (1), (2))^ получаем
отсюда s (F) > ab, s (F) < ab, и потому s (F) = s (F) = ab,
т. е. s (F) = ab.
Итак, если стороны прямоугольника параллельны сто-
ронам единичного квадрата Q, то утверждение теоремы 7
справедливо. Выведем отсюда следующее свойство:
(-у*). Площадь инвариантна относительно движений,
т. е. если F — квадрируемая фигура и F' = g (F) — фигу-
ра, получающаяся из F с помощью движения g, то фигура
F' также квадрируема и s (F') - - s (F).
Доказательство. Пусть Q' = g (Q), где Q —
единичный квадрат, и Р — описанный вокруг Q' квадрат,
стороны которого параллельны сторонам квадрата Q
22
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
1ГЛ. I
(рис. 11, а). Квадрат Р разбивается па квадрат Q' и четыре
конгруэнтных прямоугольных треугольника Тг, Т2, Т3,
длины катетов которых обозначены через а и Ъ. По тео-
реме Пифагора а2 + b2 = 1 (так как гипотенуза треуголь-
ника 7\, т. е. сторона квадрата Q’, имеет длину 1). На
рис. 11, б изоображено разбиение квадрата Р на два
квадрата со сторонами а, Ъ и четыре треугольника
Тг, Т2, Тя, Ttl- В силу аксиомы (Р),
s(P) = s (Qr) + S (Л) + s (Г2) + s (Ts) + 8 (Л),
s(P) = s (&) + s (<?2) + s (TJ + s + s (T3) + s (Л).
Кроме того, s = s (T1,), i = 1, 2, 3, 4, так как Т\
получается из параллельным переносом (аксиома (у)).
Таким образом,
8 (<?') = 8 (&) + 8 (&)•
Но стороны квадратов (21и(?2паРаллельны сторо-
нам единичного квадрата Q, и потому, в силу теоремы 7,
s ((7J = a2, s (Qs) = b2, т. е. s (Q’) = а2 + Ъ2 = 1. Итак,
любой квадрат Q', конгруэнтный единичному квадра-
ту Q, имеет площадь 1.
Положим теперь s* (F) = s (g (F)) для любого много-
угольника F. Ясно, что функция s* удовлетворяет аксио-
ме (а). Далее, если многоугольники F и F' получаются
друг из друга параллельным переносом, то g (F) и g (F')
также получаются друг из друга параллельным перено-
сом, и потому s* (F) = s* (F'), т. е. функция s* удовлет-
§ 3] ДАЛЬНЕЙШИЕ СВОЙСТВА ПЛОЩАДИ 23
воряет и аксиоме (у). Так же просто проверяется и аксио-
ма (Р). Наконец, s* (Q) — s (g (0) = s (Q') = 1 (как до-
казано выше), т. е. s* удовлетворяет аксиоме (6). Итак,
s* удовлетворяет всем аксиомам (а), (Р), (у), (6); по теоре-
ме 2, функция з* совпадает с s, т. е. s* (F) = s (F)
для любого многоугольника F. Иначе говоря, s (g (F)) =
= * (Л-
Таким образом, свойство (у*) доказано для много-
угольников. Отсюда непосредственно вытекает, что тео-
рема 7 справедлива для любых прямоугольников.
Пусть теперь F — произвольпая квадрируемая фигура и в > 0.
Выберем такие многоугольники G, Н, что G С F С Н и s (Н) —
— s (G) < в (теорема 3). Тогда многоугольники G' = g (G), Н' =
= g (Н) удовлетворяют условию G' С g (F) С Н', причем в силу
доказанного выше, s (О') = s (G), s (Н') = s (Н) и потому s (Н‘) —
— s (С) = s (Я) — s (G) < в. Итак, фигура F’ = g (F) квадри-
руема.
Теперь справедливость свойства (у*) для произвольных квад-
рируемых фигур доказывается точно так же, как и для многоуголь-
ников (со ссылкой на теорему 5, а не на теорему 2).
Утверждение (у*) является более общим свойством
площади, чем аксиома (у). Часто его принимают за ак-
сиому вместо (у), т. е. строят теорию площадей, исходя
из свойств (а), (Р), (у*), (б), рассматриваемых как аксио-
мы. Изложенное выше убеждает нас в том, что эта аксио-
матика эквивалентна первоначальной. В дальнейшем мы
нередко будем иметь в виду именно эту аксиоматику
(«), (Р), (V*), (6).
Теорема 8. При замене единичного квадрата
Q конгрузнтным, ему квадратом площади фигур не изме-
няются.
Доказательство. Пусть Q* — квадрат, кон-
груэнтный Q. Обозначим через s площадь, построенную
с помощью Q в качестве единичного квадрата, а
через з*— площадь, построенную с помощью Q*. В си-
лу теоремы 7, з* (0 = s* (Q*) = 1. Следовательно,
функции s и s*, рассматриваемые на множестве всех мно-
гоугольников, удовлетворяют всем аксиомам (ct), (Р), (у),
(б) (с Q в качестве единичного квадрата), и потому, по тео-
реме 2, 8 (F) = з* (F) для любого многоугольника F.4
Теорема 3 показывает теперь, что класс квадрируемых фигур
один и тот же, как для », так и для s*. Но тогда, по теореме 5, «(?’)—
= s* (F) для любой квадрируемой фигуры iF.
24
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ 11 ОБЪЕМОВ
[ГЛ. I
Из теоремы 8 вытекает, что если при конструктивном
определении площади (§ 1) заменить нулевую палетку
любой конгруэнтной ей палеткой, то площади фигур не
изменятся (как и сам класс квадрируемых фигур).
Теорема 9. Пусть / — подобие с коэффициентом
к, т. е. отображение плоскости на ту же плоскость,
увеличивающее расстояния в к раз. Тогда если F — квадри-
руемая фигура, то фигура F' = / (F) также квадрируе-
ма и s (Fr) = k2s (F).
Доказательство. Положим s* (F) — s (f (F)).
Так как / переводит произвольный многоугольник снова
в многоугольник, то функция s* определена на множестве
всех многоугольников. Без труда проверяется, что она
удовлетворяет аксиомам (а), (Р), (у). Далее, если Q —
единичный квадрат, то / (Q) — квадрат, длина стороны
которого равна к. По теореме 7, s (/ (0) — к2, т. е.
$* (0 = —s(/((?)) = 1, т. е. s* удовлетворяет и аксио-
ме (б). Согласно теореме 2, s* (F) = s (F) для любого
многоугольника F, т. е. s (/ (F)) = k2s (F).
Из этого вытекает, что если F — квадрируемая фигура, то
фигура / (/'') также квадрируема (теорема 3). Следовательно, функ-
ция s* определена на множестве всех квадрируемых фигур. Так
как она удовлетворяет аксиомам (а), (Р), (у), (б), то s* (F) = s (F)
для любой квадрируемой фигуры F, т. е. s (f (F)) = k2s(F).
§ 4. Независимость аксиом площади
Здесь устанавливается, что аксиомы (а), (Р), (у), (б)
независимы. Иначе говоря, каждая из аксиом су-
щественна, т. е., отбросив ее, мы сможем построить на
множестве квадрируемых фигур функцию, удовлетворяю-
щую оставшимся аксиомам и отличную от площади.
Проще всего устанавливается независимость аксио-
мы (б): положив ss (F) = 0 для любой квадрируемой фи-
гуры F, мы получаем функцию «в, отличную от площади
s и удовлетворяющую аксиомам (а), (Р), (у). Другим
примером может служить функция «в (F) = Xs(F), где
к 0 — фиксированное число. Она также удовлетворяет
всем аксиомам (а), (Р), (у), по не удовлетворяет (при X #= 1)
аксиоме (б). Можно доказать (тем же приемом, с помощью
которого была доказана теорема 9), что любая функ-
§ 4] НЕЗАВИСИМОСТЬ АКСИОМ ПЛОЩАДИ 25
ция,-удовлетворяющая аксиомам (ос) (Р), (у), имеет вид
Xs (F), где X > 0.
Без труда строится также функция, показывающая не-
зависимость аксиомы (р): достаточно положить sp (F) =
= 1 для любой квадрируемой фигуры F (выполнение ак-
сиом (а), (у), (б) здесь очевидно). Другим примером может
служить функция sp (/’) = (s (F))2 пли sp (F) =
Для построения функции, показывающей независи-
мость аксиомы (у), обозначим через Р± и Р2 две полуплос-
кости, на которые плоскость разбивается фиксированной
прямой I, причем будем предполагать, что единичный квад-
рат Q расположен в полуплоскости Р±. Для любой квад-
рируемой фигуры F положим
sY (F) = s (F П Л) + 2s (F П Рг).
Без труда проверяется, что функция sY удовлетворяет
аксиомам (а), (Р), (б). В то же время, аксиома (у) не вы-
полняется; например, если Q' — квадрат, получающийся
из Q параллельным переносом и расположенный в полу-
плоскости Р2, то sY (Q") = 2, sY (Q) = 1, т. е. sY (Qr) Ф
Ф Sy (Q). Можно определить функцию sY и иначе:
Sy (F) = s (F \ Н) + Xs (F Н), где Н — фиксирован-
ная квадрируемая фигура положительной площади, не
пересекающаяся с Q, а X 1 — фиксированное положи-
тельное число.
Наконец, перейдем к вопросу о независимости аксио-
мы (а). Этот вопрос имеет два аспекта, в зависимости от
того, какую аксиоматику мы рассматриваем: (а), (Р), (у),
(б) или (а), (Р), (у*), (б). Вопрос о независимости аксиомы
(а) от (Р), (у*), (б) является более сложным, но и более
принципиальным. Речь идет о построении функции
sa (F), не удовлетворяющей аксиоме (а), которая удовлет-
воряет аксиомам (Р), (б) и является инвариантной относи-
тельно любых движений плоскости. В частности, эта
функция будет инвариантна относительно параллельных
переносов; таким образом, решение вопроса о независимо-
сти аксиомы (а) от (Р), (у*), (б)включаетв себя ре-
шение вопроса о независимости от аксиом (Р), (у), (б).
Именно этот аспект (независимость от аксиом (р), (у*),
(б)) мы здесь и рассмотрим; более простой вопрос о неза-
висимости аксиомы (а) от (Р), (у), (б) рассматривается
в § Ю.
26
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
Итак, нужно построить функцию sa (F), удовлетворяю-
щую аксиомам (Р), (у*), (6), но не обладающую свойством
(а). Ее построение связано с тонкими вопросами теории
множеств и опирается па аксиому выбора (или какое-ни-
будь эквивалентное ей предложение, например, лемму Цор-
на). Пусть / (z) — некоторая аддитивная функция (опре-
деленная для действительных х и принимающая действи-
тельные значения), т. е. такая функция, что
/ (х' + х") = / (х') + / (х") (3)
для любых х', х". Положив sa (F) = f (s (F)), где s — обыч-
ная площадь, мы получаем функцию sa, определенную на
множестве всех квадрируемых фигур и удовлетворяющую
аксиомам (Р), (у*). Например, если F = F' + F", то,
учитывая аксиому (Р) для площади s п соотношение (3),
мы имеем:
Sa (F’ + F") = / (s (F' + F")) =
= / (s (F') + s (F")) = f (s (F')) + / (s (F")) =
= sa (F') + sa (F"),
т. e. аксиома (P) для функции sa выполняется. Легко про-
веряется и аксиома (у*). Если / (х) удовлетворяет, кроме
того, условию
f (1) = 1, (4)
то функция sa удовлетворяет также аксиоме (6):
sa (Q) = f {s (0) = /(!) = 1.
Таким образом, если удастся построить аддитивную
функцию / (z), удовлетворяющую условию (4) и при-
нимающую для некоторого х 0 отрицательное значение,
то требуемая функция sa (F) = f (s (F)) будет построена.
Например, если / (х) будет принимать при х = 5 зна-
чение /()^5) = —1, то для прямоугольника F, длины
сторон которого равны 1 и |Л5, найдем, в силу теоремы 7:
Sa (F) = / (s (F)) = / (1 ./5) = / (/5) = -1,
так что аксиома (а) не будет выполнена.
Любая линейная функция / (х) = 7.x является адди-
тивной (удовлетворяет условию (3)). Однако если она
удовлетворяет условию (4), то Z.-1 = 1, т. е. А = 1, и по-
НЕЗАВИСИМОСТЬ АКСИОМ ПЛОЩАДИ
27
§ 4]
тому функция / (х) — х принимает для любого х 0 и о-
ложительное значение. Таким образом, требуемая
аддитивная функция не может быть линейной.
Изучим свойства аддитивных функций. Из (3) находим
/ (2ж) = f (х + х) = / (х) + f (х) = 2/ (х),
/ (За:) = f (2х + х) = / (2а:) + / (х) = 2f (х) + f (х) =
= 3/ (а:)
и т. д. Таким образом, для любого натурального г имеем
f (rx) = rf (х). (5)
Далее, для натуральных т, п имеем из (3) и (5):
mf (я) = f (пгх) = / ((т — м) х + пх) =-
= f ((т — п) х) + f (пх) = / ((т — n) х) + nf (х),
т. е. / ((т — п) х) = (т — п) / (а:). Это означает, что
соотношение (5) справедливо также для г — т — и, т. е.
для любых целых чисел г. Наконец, если р и q 0 —
целые числа, то
Р/ (®) = / (РХ) = / (<? • а;)) = qf (-?- а:] ,
и потому /^-^-а:^ =-у-/(а:). Таким образом, соотноше-
ние (5) справедливо для любого рационального г.
Отметим еще вытекающее из (3) и (5) соотношение
f 01 X! + . . . + rkxh) = i\f (а:х) + . . .+ г^(хк), (6)
справедливое для любых рациональных г*, . . ., гк и дей-
ствительных xlt . . хк.
Если аддитивная функция f (х) н е п р е р ы в н а, то
из справедливости соотношения (5) для рациональ-
ных г вытекает «по непрерывности» справедливость его
для любых действительных г. В частности, при
х = 1 получаем: / (г) = rf (1), т. е. f (г) — где
^ = / (!)• Так как это справедливо для любого действи-
тельного г, то функция / (х) линейна. (Можно дока-
зать, что измеримая аддитивная функция также обяза-
тельно линейна.) Таким образом, нужная нам аддитивная
функция не может быть непрерывной (и, более того, долж-
28
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. 1
на быть неизмеримой). Покажем, как такая функция мо-
жет быть построена.
Положим = 1. Согласно (4), / = /(!) = 1.
Возьмем еще какое-либо число £2. Если £2 рационально, то
значение / (g2) однозначно определено: / (£2) = / (£2-1) =
= £2/ (1) = Если же g2 не рационально, скажем,
g2 = /5, то соотношение (5) (или (6)) не позволяет найти
значение / (£2), и можно выбрать его произвольно, на-
пример, / (/5) = —1. Возьмем число £3. Если £3 рацио-
нально выражается через |2, например, |3 = 3/Б-1 —
- 7/5, то, в силу (6), / (В3) = 3/Б/ (1) - 7/ (/5) =
= 3/Б-1 — 7- (—1) = 3,/Б. Если же £3 не представляется
в виде линейной комбинации (с рациональными коэффици-
ентами) чисел £lt £2, то соотношение (6) не позволяет найти
/ (g3) и можно выбрать его произвольно.
Пусть функция f (х) уже задана на некотором (конечном
пли бесконечном) множестве А — {g1? g2, g3, . . .}. Возь-
мем еще одно число |а. Если представляется в виде
линейной комбинации (с рациональными коэффициента-
ми) некоторого конечного множества чисел из Л, то фор-
мула (6) позволит однозначно определить значение / (ga).
Если же не представляется в виде такой комбинации,
то можно выбрать / (£а) произвольно. Таким образом,
функция / (х) окажется определенной в точке х ~ £а,
т. е. эту точку можно присоединить к множеству А, на
котором уже задана функция / (х). Затем можно присо-
единять к А еще и еще точки.
Можно ли, беря новые и новые числа, перебрать
все множество R действительных чисел? Если можно, то
в результате мы получим требуемую функцию / (х). Сов-
ременная математика (точнее, теория множеств, в которой
выполняется аксиома выбора) позволяет рассматривать
конструкции, связанные с «перебором» всех элементов
произвольного множества (в частности, множества R).
Это означает, что (в рамках теории множеств, допускаю-
щей аксиому выбора) требуемая аддитивная функция
/ (я) существует. Этим доказывается существование функ-
ции sa (F) = f (s (F)), подтверждающей независимость ак-
сиомы (а).
Аддитивные функции, не являющиеся непрерывными,
называются функциями Коши — Гамеля (они впервые
§ 4] НЕЗАВИСИМОСТЬ АКСИОМ ПЛОЩАДИ 29
были рассмотрены в работе Гамеля [31]). Рассмотренная
выше идея построения такой функции может быть изложе-
на иначе, с помощью понятия рационального базиса чис-
ловой прямой В. Множество CZ /? называется рациональ-
ным базисом, если оно обладает следующими двумя свой-
ствами:
а) любое число х ЕЕ В представляется в виде линейной
комбинации с рациональными коэффициентами несколь-
ких чисел из В, т. е. существует такое натуральное т, та-
кие числа Ьг, . . ., Ьт 6Е В и такие рациональные числа
И, . . ., гт, что х = r-fiy + - • - + rmbm-,
б) никакое число Ь Е й не может быть представлено в
виде линейной комбинации (с рациональными коэффици-
ентами) нескольких отличных от Ъ чисел, принадлежащих
множеству В.
Изложенное выше рассуждение, связанное с перебором
множества В и поясняющее построение функции Коши —
Гамеля / (ж), содержит в себе построение рационального
базиса числовой прямой. В самом деле, определим множе-
ство В, относя к нему числа = 1, = а также
каждое число которое не представляется в виде ли-
нейной комбинации (с рациональными коэффициентами)
никаких чисел, встретившихся в этом процессе перебора
раньше, чем £а. Легко видеть, что это множество В
является рациональным базисом числовой прямой В.
Описанное выше построение функции Коши — Гаме-
ля может быть осмыслено следующим образом: в точках
базиса В значения функции / (ж) выбираются произ-
вольно, после чего в остальных точках (рационально
выражающихся через элементы базиса) значения / (х)
однозначно определяются соотношением (6). Из этого вид-
но, что существует 2х функций Коши — Гамеля. Для
доказательства независимости аксиомы (а) нужна была
одна функция такого вида. Например, можно было по-
ложить / (1) = 1, / (ж) = —1 для всех остальных элемен-
тов базиса В (в частности, / (]Л5) = —1), после чего про-
должить / (ж) на все множество В в силу (6).
Наконец, приведем полное доказательство существова-
ния рационального базиса В, содержащего числа = 1,
g2 = )Л5 (а значит, и доказательство существования тре-
буемой ^функции Коши — Гамеля). При этом будем ис-
30
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
пользовать не саму аксиому выбора, а эквивалентное ей
(и более употребительное сейчас) утверждение, известное
под названием леммы Цорна [58].
Множество М называется упорядоченным, если указа-
но, для каких пар (а, Ъ) его элементов (а Ь) считается
выполненным соотношение а < Ь; при этом требуется,
чтобы из справедливости соотношений а < b, Ъ <Е с вы-
текало а < с и чтобы ни для каких а, Ь ЕЕ М не были од-
новременно выполнены соотношения а < Ъ, Ъ < а. Если
для элементов а, b ЕЕ М (а Ь) ни одно из соотношений
а < Ь, Ъ < а не имеет места, то а и b называются несрав-
нимыми. Подмножество С ЕЕ М называется цепью, если
оно не содержит двух несравнимых элементов, т. е. для
любых а, Ъ ЕЕ С (а Ь) какое-либо из соотношений а <
< Ъ, Ъ < а имеет место. Цепь С ЕЕ М называется ограни-
ченной, если существует такой элемент q ЕЕ: М (принадле-
жащий или не принадлежащий цепи С), что а q для лю-
бого элемента а ЕС. Элемент т ее М называется макси-
мальным, если не существует элемента а ЕЕ М, удовлетво-
ряющего условию т < а. Ясно, что если упорядоченное
множество М само является цепью, то в нем имеется не
более, чем один максимальный элемент. В произволь-
ном же упорядоченном множестве может существовать бо-
лее одного максимального элемента.
Лемма Цорна. Если все цепи, содержащиеся в
упорядоченном множестве М, ограничены, то М содержит
(хотя бы один) максимальный элемент.
Лемма Цорна представляет собой одну из форм аксио-
мы выбора. Сейчас известно (см., например, [57]), что тео-
рия множеств, включающая аксиому выбора, непроти-
воречива (так же как и теория множеств, отвергаю-
щая эту аксиому, т. е. включающая ее отрицание).
Для доказательства существования рационального ба-
зиса числовой прямой R условимся подмножество В ЕЕ R
называть рационально независимым, если оно удовлетво-
ряет указанному выше условию б) (входящему в определе-
ние рационального базиса). Множество всех рационально
независимых подмножеств В с R, содержащих числа
1 и У5~, обозначим чер ев М. Для двух элементов Blt Bt G
Е= М (т. е. двух рационально независимых подмножеств
Вг с R, В2 С R) условимся считать, что Вг < В2, если
В,. С В2.
6 41 НЕЗАВИСИМОСТЬ АКСИОМ ПЛОЩАДИ 31
Пусть С CZ М — некоторая цепь. Рассмотрим все эле-
менты В ЕЕ С и обозначим через Вс объединение
всех этих В (рассматриваемых как подмножества число-
вой прямой В). Легко видеть, что множество Вс рациональ-
но независимо, т. е. Вс е= М. В самом деле, пусть хг, . . .
. . ., хт — произвольные (различные между собой) числа,
принадлежащие множеству Вс. Для каждого i = 1, . . .
. . т найдется такое В, е С, что xt GE Bt. Так как С —
цепь, то среди конечного числа элементов В±, . . ., Вт
имеется наибольший; пусть, для определенности, Вт —
наибольший элемент, т. е. Bt с: Вт, i = 1, . . ., т. Тогда
Xi GE Bi CZ Вт, т. е. все числа хг, . . хт содержатся в
Вт; так как Вт GE М, то числа ж1, . . ., хт рационально не-
зависимы. Итак, любые числам, . . ., хт Вс рациональ-
но независимы, т. е. Вс ЕЕ М. Так как, по определению,
В < Вс для любого /? £ С, то цепь С ограничена.
Таким образом, каждая цепь С (ЕЕ М ограничена. По
лемме Цорна в М существует максимальный эле-
мент В*. Иначе говоря, В* есть такое рационально неза-
висимое подмножество числовой прямой R, что никакое
большее подмножество не является рационально не-
зависимым. Это оначает, что любое действительное число
х представляется в виде линейной комбинации (с рацио-
нальными коэффициентами) нескольких чисел из В*.
Таким образом, В* удовлетворяет условию а), т. е. яв-
ляется базисом (причем этот базис содержит числа 1 и
У"5). Этим и завершается доказательство.
В заключение сделаем несколько замечаний, связанных
с вопросом о независимости аксиом (а), (0), (у*), (б), оп-
ределяющих понятие площади. Независимость аксиомы
(а) означает, в частности, что формула площади прямо-
угольника не может быть выведена только из аксиом (0),
(у*), (б) без использования аксиомы (а). В самом деле, по-
строенная функция sa (F)=f (s(F)) удовлетворяет аксиомам
(0), (у*), (б), и потому любое рассуждение, использующее
лишь аксиомы (0), (у*), (б), применимо как для площади
з (F), так и для функции sa (F). Следовательно, если бы
формула площади прямоугольника могла быть выведена
только из акспом (0), (у*), (б), то эта формула была бы
справедлива и для функции sa (F). Между тем для прямо-
угольника Р, длины сторон которого равны 1] и
функция sa принимает значение sa (Р) = —1, отлич-
32
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ I
ное от значения s (Р) = 1-^5 = [Лг>, получаемого
по формуле площади прямоугольника.
Далее, в теории множеств, отвергающей аксиому вы-
бора, не существует функции sa (F), удовлетво-
ряющей аксиомам (0), (у*), (б) и отличной от площади.
Действительно, обозначая через Р^ прямоугольник с дли-
нами сторон 1 и х и полагая / (х) = sa (Рх), мы получили
бы функцию Коши — Гамеля, т. е. некоторую неизмери-
мую функцию; но тогда, в силу результатов работы [471,
должна была бы выполняться аксиома выбора. Иначе го-
воря, в теории множеств, отвергающей аксиому выбора,
единственной функцией, удовлетворяющей аксиомам (0),
(у*), (б), является площадь s (F). Однако, если в этой тео-
рии возможен вывод формулы площади прямоугольника
с помощью аксиом (0), (у*), (6), то этот вывод по необ-
ходимости должен опираться на отрицание аксиомы
выбора.
Если мы условимся не считать «элементарно-геометри-
ческими» рассуждения, которые используют факты, зави-
сящие от выполнения или невыполнения аксиомы выбора,
то вынуждены будем признать, что элементарно-гео-
метрическими методами формула площади прямоуголь-
ника не может быть выведена только из аксиом (0),
(у*), (б) беэ использования аксиомы (а) (поскольку такой
вывод мог бы быть проведен как в рамках теории множеств,
включающей аксиому выбора, так и в рамках теории, от-
вергающей эту аксиому). Иными словами, с «элементарно-
геометрической» точки зрения аксиому (а) следует считать
независимой от аксиом (0), (у*), (б).
Еще раэ подчеркнем, что вопрос о независимости ак-
сиомы (а) от аксиом (0), (у), (б) более прост и решается без
использования аксиомы выбора (см. § 10).
§ 5. Методы вычисления площади фигур
Аксиома (а) (или эквивалентное ей свойство моно-
тонности площади) может быть непосредственно ис-
пользована лишь для получения оценок (неравенств).
Однако с помощью предельного перехода из этих нера-
венств могут быть получены равенства (т. е. точ-
ные значения площадей фигур). Схема такого рассуждения,
МЕТОДЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУР
33
§ 5]
содержащего предельный переход, может быть изложена
следующим образом.
Рассматривается квадрируемая фигура F и последо-
вательность Gx. G2, . . . вложенных в нее квадрируемых фи-
гур-, если часть фигуры F, не заполненная фигурой Gk
(т. е. F \ Gfl), имеет площадь, неограниченно уменьшаю-
щуюся при к -> оо, то s (F) = lim s (Gh). Доказательство
/с—»oo
непосредственно вытекает из соотношений s (F) = s (Gft) +
+ s (F \ Gh) и lim s (F \ Gh) = 0. Такой метод вычис-
ft—*oc
ления площади фигуры F называется методом исчерпыва-
ния, поскольку фигуры G,, G2, . . . постепенно «исчерпы-
вают» всю площадь фигуры F. Имеется также модифи-
кация метода исчерпывания, состоящая в том, что, кроме
последовательности Gx, G2, - . . вложенных фигур, рассмат-
ривается последовательность Нх, Н2, . . . объемлющих фи-
гур (содержащих F). Если при этом lim s (Hh \ G\) = 0,
то по-прежнему справедливо соотношение lim s (Gh) =
k—*oo
= s (F). В самом деле, так как F \ Gk Г~ II h \ Gh,
то, в силу аксиомы (а), 0 s (F \ Gh) s (Hh \ Gk),
и потому lim s (F \ Gh) = 0, что и позволяет приме-
fc-»oo
нить метод исчерпывания в его первоначальной форму-
лировке. Объемлющие фигуры II h используются для удоб-
ства оценки площади фигуры F \ G(, (так как может
оказаться, что площадь фигуры \ Gk вычислить про-
ще, чем площадь фигуры F \ Gh). Имеется и еще одна
модификация метода исчерпывания: для проверки равен-
ства lim s (Hh \ Gk) = 0 достаточно убедиться, что
/С-»оо
lim s (Gft) = lim s (FZft) (или даже lim s (Gfe) > lim s (Hk),
*CO >CXj ft—>op fc—*oo
так как обратное неравенство очевидно).
Пример применения метода исчерпывания мы имели
в § 3 при вычислении площади прямоугольника. В этом
случае за Gk, Нк принимались прямоугольники, состав-
ленные из квадратов к-к палетки, причем Gt CZ F CZ II
где F — заданный прямоугольник (см. рис. 10). При этом
фигуры Gk и Hk существенно проще, чем F, так как
они составлены из квадратов А-й палетки и потому их
площадь непосредственно вычисляется. Так как при
2 В. Г. Болтянский
34
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ II ОБЪЕМОВ
[ГЛ. I
ЭТОМ
то lim s (Gh) lim s (/Zft), что и дает соотношения
К-»ос fc—>оо
.s(/'’) linis(G(c) lim s (Hl;) — ab.
k—»-oo R--»oo
Использование аксиомы (а) и предельного перехода (т. е.
«метода исчерпывания») при выводе этой формулы сущест-
венно.
Другим известным из школьного курса примером при-
менения метода исчерпывания является вычисление площа-
ди круга *). В выводе фор-
мулы
h
« U9 = V (J;) dx
а
для площади «криволи-
нейной трапеции», ограни-
ченной осью абсцисс, ор-
динатами х = а, х = b и
графиком положительной
функции у = f (х), также
легко заметить применение метода исчерпывания; здесь Gh
и Н). представляют собой «ступенчатые фигуры» (рис. 12).
Итак, метод исчерпывания связан с применением пре-
дельного перехода и, по-существу, представляет собой ин-
тегрирование в явной или завуалированной форме. По-
нятие предела и связанная с ним «е-техника» относятся к
*) Если Gj- — правильный 2к-угольник, вписанный в круг F,
а Нк — правильный 2л-угольнпк, описанный вокруг F, то, как
показывают несложные подсчеты, «полоска» между и неогра-
ниченно уменьшается по площадп при к —» со, т. е. lim s (ffk\ G/д =
к-»оо
— 0. Следовательно, s (Е) = lim s (G/(). Однако в школе это равен-
к-
ство обычно не доказывается, а принимается в качестве «определе-
ния» площади круга F.
§ 5] МЕТОДЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУР 35
числу наиболее сложных, неэлементарных понятий школь-
ного курса математики. Условимся в связи с этим метод
исчерпывания (или всякое рассуждение, использующее
аксиому (а) и в этом смысле эквивалентное методу исчер-
пывания) относить к числу неэлементарных ме-
тодов вычисления площади. Элементарными же будем
считать рассуждения и методы, основанные лишь на аксио-
мах (0), (у), (6) (или (Р), (у*), (б)) и. разумеется, не свя-
занные с аксиомой выбора. С этой точки зрения теоремы
о площади прямоугольника и круга неэлементар-
ны. Ив самом деле, теоремы эти (с полными и аккурат-
ными доказательствами) являются в школьной теории пло-
щадей наиболее сложными и трудными для понимания.
Прежде чем переходить к характеристике элементар-
ных методов вычисления площади, рассмотрим вопрос о
связи изложенной выше теории площадей со школьным
курсом геометрии. Школьное понимание площади весьма
близко к аксиоматическому ее пониманию (см. § 2). В са-
мом деле, при аксиоматическом понимании определе-
ние площади становится ненужным, т. е., грубо говоря,
под площадью понимается «то, что удовлетворяет аксио-
мам (а), ((3), (у), (6)». В школьном изложении также от-
сутствует определение площади, а все теоремы о площади
фигур доказываются на основании утверждений (а), (0),
(у*), (б) (которые, правда, называются не аксиомами, а
«свойствами» площади и считаются очевидными). Во вся-
ком случае, утверждения (а), (0), (у*), (б) известны каж-
дому школьнику, хотя, может быть, в несколько иной
формулировке; например, аксиома (у*) известна в форму-
лировке «конгруэнтные фигуры имеют одинаковую пло-
щадь».
При аксиоматическом изложении мы имеем теорему
существования и единственности, значительно обогащаю-
щую наше представление о площади. Существование озна-
чает непротиворечивость аксиоматики площади. Не ме-
нее важное значение имеет1 и единственность, ко-
торая является удобным инструментом при доказательстве
теорем о свойствах площади (мы видели это в § 3). Можно
считать, однако, что и у школьника должна быть уверен-
ность в существовании и единственности площади (т. е.
«того, что имеет свойства (а), (0), (у*), (б)»). В самом деле,
площадь представляет собой абстракцию, являющуюся
2*
36
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
1ГЛ. I
отражением некоторого объективного свойства реальных
предметов — свойства, о котором школьники имеют пред-
ставление в результате повседневного опыта, а также пер-
воначального изучения площади на уроках математики в
III и IV классах и на уроках физики. Объективность это-
* го свойства заменяет теорему существования, соз-
дает у школьников представление о том, что они изучают
что-то реальное, существующее. Что же касается единст-
венности, то поскольку на основании свойств (а), (0),
(у*), (6) удается в конце концов однозначно вы-
числить площадь любого многоугольника (а впоследствии
площадь круга), можно это обстоятельство считать (дос-
тигнутым к концу изучения темы о площади) доказатель-
ством единственности.
Наконец, отметим, что для семиклассника, приступаю-
щего к изучению темы о площадях многоугольников,
единственным многоугольником, для которого известна
формула вычисления площади, является прямо-
угольник. Эта формула поясняется в III и IV классах
для прямоугольников, длины сторон которых выражаются
конечными десятичными дробями. И хотя доказательство
справедливости этой формулы для любых прямоуголь-
ников в школе, как правило, не рассматривается, счита-
ется все же, что семиклассник «знает» формулу площади
прямоугольника в общем случае.
Итак, исходная точка, к которой мы пришли, изучая
с позиций современных математических представлений
свойства площади, довольно точно соответствует уровню
знаний семиклассника: известны свойства (а), (0), (у*),
(6) площади и формула площади прямоугольника. Отправ-
ляясь от этой исходной точки, нужно получить эффектив-
ные способы вычисления площади любого мно-
гоугольника.
Это достигается с помощью простого приема, называе-
мого методом разложения и основывающегося на аксио-
мах (0), (у*)- Для уяснения этого метода рассмотрим фи-
гуры F и II, изображенные на рис. 13 (все отрезки, со-
ставляющие фигуру F, конгруэнтны между собой, углы
прямые, сторона квадрата II конгруэнтна отрезку аЪ).
Штриховые линии разбивают эти фигуры на одинаковое
число соответственно конгруэнтных частей (конгруэнт-
ные части отмечены одинаковыми цифрами). О фигурах F
§ 5]
МЕТОДЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУР
37
и Н говорят, что они равпосоставлены. Иначе говоря,
фигуры F и Н называются равносоставленными, если, оп-
ределенным образом разрезав фигуру F на конечное число
частей, можно (располагая эти части иначе, т. е. рассмат-
ривая фигуры, конгруэнтные этим частям) составить из
них фигуру II.
Условимся равносоставленность фигур F нН выражать
знаком а конгруэнтность фигур Рг и IIt — знаком
Таким образом, равносоставленность фигур F и Н (т. е.
F ~ Н) означает, по определению, существование таких
фигур F2, . . ., Fkn Н±, Н2, . . .,Hk, что
F =? Fr + . . . + Fk, Н = Ях + . . . + Hh-
Fr .. ., Fh s Hh\
все фигуры F, Н, Fr, . . ., Fk, Нл, . . ., Hk предполагаются
квадрируемыми.
Из аксиом (Р) и (у*) непосредственно следует, что две
равносоставленпые фигуры равновелики, т. е. имеют оди-
наковую площадь: если F ~ II, то s (F) = s (II). На этом
основан метод разложения (или разбиения), состоящий
в том, что для вычисления площади фигуры пытаются раз-
бить ее на конечное число частей таким образом, чтобы
из этих частей можно было составить более прос-
тую фигуру (площадь которой нам уже известна). Этот
способ вычисления площади был известен еще Евклиду,
жившему свыше 2000 лет назад.
Напомним примеры применения этого метода. Парал-
лелограмм F равносоставлен *) с прямоугольником Н,
•) Заметим, однако, что этот прием (отщепление одного тре-
угольника) применим не всегда (ср. рис. 15).
38
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
имеющим то же основание и ту же высоту (рис. 14). Сле-
довательно, F и Н равновелики, и потому, зная формулу
площади прямоугольника, находим, что площадь парал-
Рис. 14.
лелограмма равна произведению длин его основания и со-
ответствующей высоты.
Треугольник равносоставлен с параллелограммом, ко-
торый имеет то же основание и вдвое меньшую высоту
(рис. 16). Из этого легко выво-
дится формула площади треу-
гольника. Наконец, на рис. 17
изображен прием вычисления
площади трапеции.
После вывода формулы пло-
щади треугольника может быть
вычислена площадь любого
многоугольника: достаточно
разбить его на треугольники и воспользоваться аксио-
мой (Р), т. е. сложить площади этих треугольников.
Рис. 16.
Заметим, что при любом другом способе разбиения на тре-
угольники результат будет тем же самым. Действительно,
результат и того, и другого вычисления дает одно-
§ 5]
МЕТОДЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ ФИГУР
39
з н а ч н о определенное число: площадь s (F) рассматри-
ваемого многоугольника F *).
Существует и другой способ вычисления площади, ос-
нованный на аксиомах ((3) и (у*),— метод дополнения. Он
Рис. 17.
состоит в том, чтобы дополнить две фигуры конгруэнтны-
ми частями так, чтобы получившиеся после такого допол-
нения фигуры были конгруэнтными. Например, чтобы ус-
тановить равенство площадей фигур F и Н, изображенных
на рис. 13, можно было бы добавить ик кресту, и к
квадрату по четыре конгруэнтных треугольника (рис. 18).
Так как в результате такого добавления получаются кон-
груэнтные фигуры, то фигуры F и Н равновелики.
*) Заметим, что имеется и другой путь построения теории пло-
щадей многоугольников. Он состоит в том, чтобы не пользоваться
теоремой существования и единственности, а определить
площадь любого многоугольника F, разбивая его на треугольники
и считая площадь s (F) равной сумме площадей составляющих тре-
угольников (формула площади треугольника при таком подходе
будет аксиомой). Наибольшие затруднения здесь доставляет
доказательство того факта, что площадь s (F) однозначно опре-
делена, т. е., что суммы площадей треугольников, составленные
для различных разбиений многоугольника F на треугольники, бу-
дут одинаковыми (см. [45], стр. 195—204).
40
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
Рис. 19 показывает, что параллелограмм и прямоуголь-
ник с одинаковыми основаниями и одинаковыми высота-
ми могут быть конгруэнтными треугольниками дополне-
ны до конгруэнтных трапеций. Поэтому параллелограмм
Рис. 19.
и прямоугольник равнове-
лики. (Заметим, что этот
прием применим всегда
в отличие от способа дока-
зательства, показанного
на рис. 14.)
Метод дополнения был
применен выше при дока-
зательстве свойства (у*) (рис. 11): фигуры Q' и Qr + Q2
дополнялись конгруэнтными треугольниками до конгру-
энтных квадратов. Если же свойство (у*) принимается в
качестве аксиомы, то этот
прием может быть приме-
нен для доказательства
теоремы Пифагора (такой
способ доказательства из-
вестен под названием
«древнеиндийского»). Для
сравнения приведем чер-
теж к доказательству те-
оремы Пифагора методом
разложения (рис. 20).
Вообще, фигуры F и Н
условимся называть рав-
нодополняемыми, если су-
ществуют такие фигуры
Flt • > Ph Рис. 20.
что Fj ~ Нг, . . ., Fh ~
= Hh и F + Fr + . . .
. . . + Ft эЯ + + . • • + Нк. Из аксиом (0) и
(у*) непосредственно вытекает, что равнодополняемые фи-
гуры равновелики.
Итак, в теории площадей многоугольников аксиома
(а) (и метод исчерпывания) попользуется лишь один
раз — при выводе формулы площади прямоугольника.
Если эта формула уже установлена, то площади любых
многоугольников вычисляются элементарно — с помощью
метода разбиения (или дополнения), основанного лишь
§ В] ОБ'ЬИМЫ И ТРЕТЬЯ ПРОБЛЕМА ГИЛЬБЕРТ X 41
на аксиомах (0) и (у*) (об аксиоме (6) речь не идет, посколь-
ку формула площади прямоугольника содержит утверж-
дение, выражаемое этой аксиомой).
Метод исчерпывания вновь становится необходимым
при вычислении площадей криволинейных фигур, напри-
мер, площади круга и его частей (см. скоску на стр. 34).
Однако в школе общее определение площади не рассмат-
ривается, а площадь круга определяется как
предел площадей вписанных в этот круг правильных мно-
гоугольников при неограниченном удвоении числа их сто-
рон (например, такой способ изложения принят в учеб-
нике [40]). В связи с этим роль «неэлементарной» аксиомы
(а) смазывается. А так как и формула площади прямо-
угольника, как правило, дается в школе без аккуратного
и полного доказательства, то у школьников создается впе-
чатление, что теория площадей основывается только на
аксиомах (0), (у*), (6), а аксиома (а) является ненужной.
Как мы видели в предыдущем параграфе, такая точка зре-
ния неправильна: даже теория площадей многоугольников
существенно нуждается в использовании аксиомы (а).
Впрочем, если условиться считать формулу площади пря-
моугольника аксиомой (по существу, в школе так
и делается), обозначив ее, скажем, как аксиому (а**),
то можно сказать, что теория площадей многоугольников
строится на основе только трех аксиом (а**), (0) и (у*).
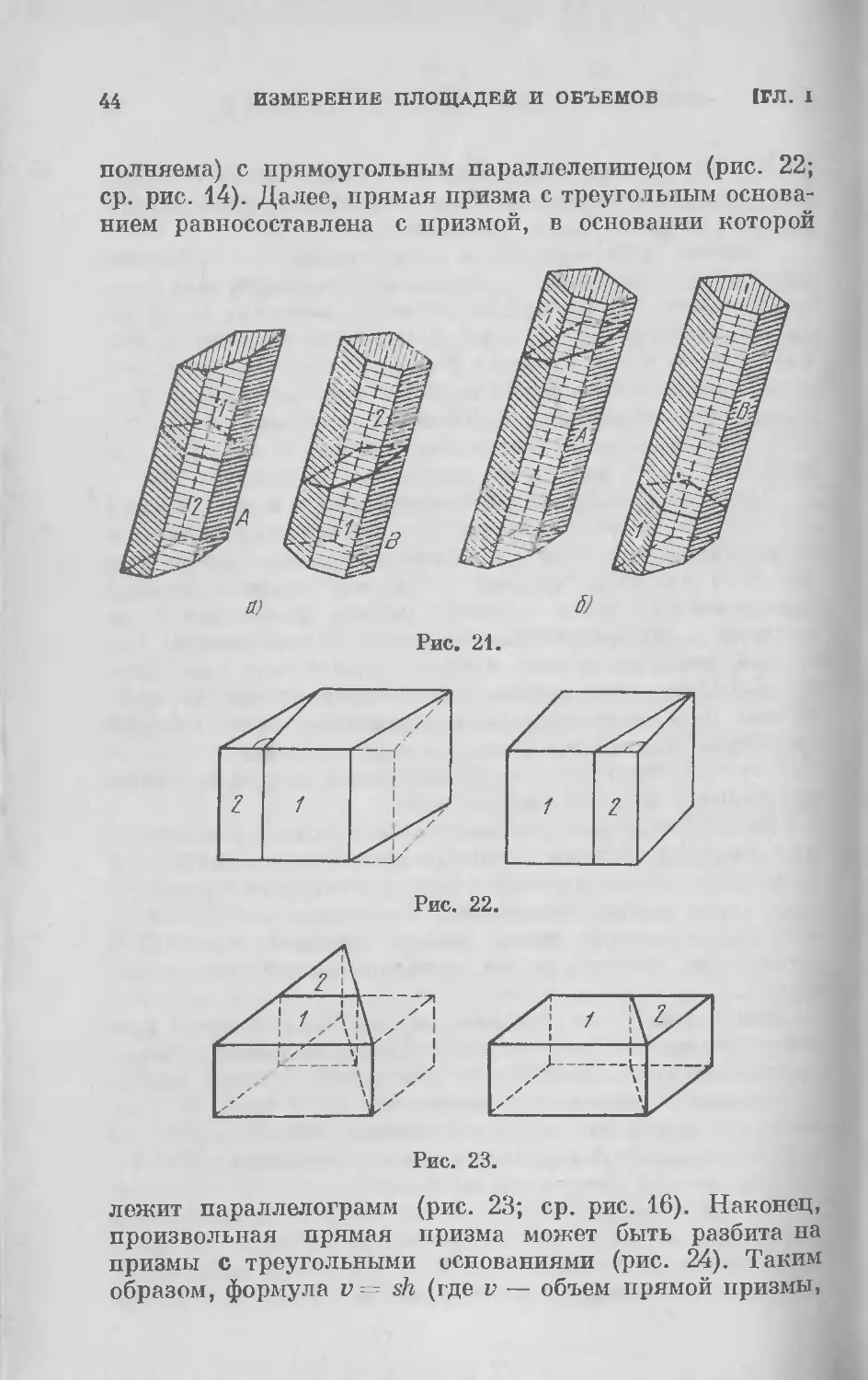
§ 6. Измерение объемов и третья проблема Гильберта
Понятие объема вводится аналогично понятию площа-
ди. При конструктивном определении рассматриваются
кубилъяжи (аналоги палеток), т. е. разбиения пространст-
ва на конгруэнтные кубы. Например, фиксировав прямо-
угольную систему координат х, у, z, можно условиться
считать k-м кубильяжем систему кубов, на которые прост-
ранство разбивается плоскостями х — р/10к, у = «у/Ю*
и z = r/iOk, где р, q, г пробегают целые числа. Это дает
возможность рассмотреть пределы
О, _ Ь,
u(F) — Bin —к-~, v(F) - Вт—|j-,
ft-.-, 10м R-oo 103/l
где ah — число кубов k-vo кубильяжа, содержащихся в
теле F, a bh — число кубов этого кубильяжа, имеющих
42
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. I
с F общие точки. Совпадение пределов у (F) и v (F) означа-
ет, по определению, что тело F кубируемо, а число v (F) =
== v (F) = v (F) называется в этом случае объемом
тела F.
Как и площадь, объем может быть определен аксиома-
тически, причем аксиомы, на которых основывается поня-
тие объема, совершенно аналогичны аксиомам площади.
Вот эти аксиомы:
(а) . Функция v неотрицательна, т. е. объем, v (F)
любого кубируемого тела F является неотрицательным
числом.
(Р). Функция v аддитивна, т. е. если F' и F" — куби-
руемые тела., не имеющие общих внутренних точек, то
v (F" U F") = v (Fr) + v (F").
(у). Функция v инвариантна, относительно параллель-
ных переносов, т. е. если F — кубируемое тело и F' — те-
ло, получающееся на F с помощью некоторого параллель-
ного переноса, то тело F' также кубируемо и и (F') =
= v (/’).
(б) . Функция v нормирована, т. е. единичный куб яв-
ляется кубируемой фигурой и имеет объем 1.
Под единичным кубом понимается фиксированный куб,
длина ребра которого равна 1.
Если в основу положено конструктивное определение
объема (с помощью кубильяжей), то (а), (Р), (у) и (б) до-
казываются как теоремы (доказательства аналогичны из-
ложенным в § 2).
Многогранник можно определить как огра-
ниченное множество, граница которого представляет со-
бой объединение конечного числа плоских многоуголь-
ников (или как объединение конечного числа тетраздров,
т. е. треугольных пирамид). Каждый многогранник являет-
ся кубируемым телом.. Доказательство этого факта анало-
гично доказательству теоремы 1. Вначале доказывается,
что в границе Q многогранника F при любом к можно по-
строить l/lO^'-ceTb, состоящую из не более, чем p-102ft +
4- (/-НД + т точек (где р, q, т — некоторые числа, опре-
деляемые многогранником F и не зависящие от к). Дейст-
вительно, если некоторая грань Г многогранника F по-
мещается в квадрате G со стороной а, то вершины к-й па-
летки, построенной в плоскости этой грани, образуют
ПЮ^-сеть, причем в квадрате G содержится не более
§ 6]
ОБЪЕМЫ И ТРЕТЬЯ ПРОБЛЕМА ГИЛЬБЕРТА
43
(«•10fc +1)2 точек этой 1/10'1-сети. После этого проходит
(с очевидными изменениями) заключительная часть доказа-
тельства теоремы 1.
Теорема существования и единственности, а также не-
обходимое и достаточное условие кубируемости тела уста-
навливаются совершенно аналогично тому, как были до-
казаны теоремы 2, 3, 4, 5 в § 2. Обобщаются и все факты,
изложенные в § 3, включая формулу объема прямоуголь-
ного параллелепипеда и свойство (у*) (инвариантность
объема при движениях). Независимость аксиом (а), (0),
(?*)> (^) доказывается для случая объема так же, как и для
площади.
Аксиома (а) служит основой неэлементарных
методов вычисления объемов (метода исчерпывания, ин-
тегрирования), которые основаны на использовании пре-
дельного перехода. Аксиомы же (0) и (у*) служат основой
элементарных методов (метода разбиения и до-
полнения). Использование аксиомы (а) необходимо для
вывода формулы объема прямоугольного параллелепипе-
да. Впрочем, если длины ребер рациональны, формула
объема прямоугольного параллелепипеда легко устанав-
ливается без использования аксиомы (а). Поэтому к X
классу средней школы (когда изучается теория объемов)
эта формула считается «известной».
Возникает вопрос, можно ли, имея в своем распоряже-
нии формулу объема прямоугольного параллелепипеда,
вычислить объем произвольного многогранника, пользу-
ясь только методами разбиения или дополнения, без при-
менения неэлементарного метода исчерпывания? Ведь
именно так обстояло дело в случае площадей многоуголь-
ников.
Метод разбиения (или дополнения), в самом деле, при-
меняется в некоторых случаях при вычислении объемов
многогранников. Например, наклонная призма равно-
составлена (и равнодополняема, рис. 21) с прямой приз-
мой, у которой основанием является перпендикулярное
сечение наклонной призмы, а длина бокового ребра та-
кая же, как и у наклонной призмы.
В свою очередь объем прямой призмы может быть
вычислен с помощью метода разбиения (или дополнения).
Действительно, прямая призма, в основании которой ле-
жит параллелограмм, равносоставлена (а также равнодо-
44
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
1ГЛ. I
полняема) с прямоугольным параллелепипедом (рис. 22;
ср. рис. 14). Далее, прямая призма с треугольным основа-
нием равносоставлена с призмой, в основании которой
Рис. 23.
лежит параллелограмм (рис. 23; ср. рис. 16). Наконец,
произвольная прямая призма может быть разбита на
призмы с треугольными основаниями (рис. 24). Таким
образом, формула v = sh (где v — объем прямой призмы,
I «1
ОБЪЕМЫ И ТРЕТЬЯ ПРОБЛЕМА ГИЛЬБЕРТА
45
s — площадь ее основания, h — высота) может быть дока
зана без привлечения «неэлементарной» аксиомы (а).
Однако при вычислении объема пирамиды
учебная литература применяет метод исчерпывания: рас-
сматривают «ступенчатые тела»
(см. рис. 1) и переходят к пре-
делу при неограниченном воз-
растании числа ступенек («чер-
това лестница»).
Напомним вкратце, как
обычно выводится формула
объема тетраэдра. Возьмем
Рис. 24.
тетраэдр abed и рассмотрим
наклонную призму с треугольным основанием а.Ъс и бо-
ковым ребром ad (рис. 25). Эту призму можно разбить на
три тетраэдра b\, F2, F3 (рис. 26), первые два из которых,
а также последние два имеют совпадающие основания и
одинаковые высоты. Таким образом, для установления то-
го, что объем пирамиды abed втрое меньше объема рас-
смотренной призмы (т. е. для вывода формулы объема пи-
рамиды), «остается» доказать, что две треугольные пира-
миды, имеющие конгруэнтные основания и конгруэнтные
высоты, равновелики. Именно для этого используется
метод исчерпывания (или интегрирование).
Итак, по сравнению с теорией площадей многоуголь-
ников изложение теории объемов многогранников содер-
46
ИЗМЕРЕНИЕ ПЛОЩАДЕЙ И ОБЪЕМОВ
[ГЛ. !
жит одно «лишнее» применение аксиомы (а): если в плани-
метрии вывод формулы площади треугольника совершенно
элементарен, то пространственный аналог (формула объ-
ема тетраэдра) излагается с использованием аксиомы (а).
По существу ли это? Не объясняется ли такое изложение
лишь тем, что математикам «не посчастливилось» найти
простой вывод формулы объема пирамиды методом разло-
жения или дополнения? Иными словами, любые ли две
треугольные пирамиды с конгруэнтными основаниями и
конгруэнтными высотами равносоставлены (или равнодо-
полпяемы)? Это п есть третья проблема Гиль-
берта; приведем ее оригинальную формулировку [33]
(в русском переводе см. [2], стр. 28).
«Гаусс в двух своих письмах к Герлингу выражает сожа-
ление по поводу того, что некоторые известные положения
стереометрии зависят от метода, исчерпывания, т. е.,
говоря современным языком, от аксиомы непрерывности (или
от аксиомы Архимеда).
Гаусс специально отмечает теорему Евклида, согласно
которой объемы треугольных пирамид, имеющих равные
высоты, относятся как площади их оснований. Аналогич-
ная задача планиметрии ныне полностью решена. Герлин-
гу удалось также доказать равенство объемов симметрич-
ных многогранников при помощи разбиения их на конгру-
энтные части.
Тем не менее, как мне кажется, в общем случае доказа-
тельство упомянутой теоремы Евклида этим способом
провести невозможно и это, по-видимому, может быть
подтверждено строгим доказательством невозможности.
Такое доказательство можно было бы получить, если
бы удалось указать такие два тетраэдра с равными осно-
ваниями и равными высотами, которые никаким способом
не могут быть разложены на кэнгруетные тетраэдры и кото-
рые также не могут быть дополнены конгруэнтными тет-
раэдрами до таких многогранников, для которых разло-
жение на конгруэнтные тетраэдры возможно».
В добавление к этому тексту Гильберт приводит ссыл-
ки на работы Гаусса, на свою книгу [32], а в более поздней
публикации «математических проблем» (вошедшей в его
Собрание сочинений, изданное в 1932—1935 годах в Берли-
не) — ссылку на работу Дена [13].
ГЛАВА II
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
§ 7. Теорема Бойяи — Гервина
Читатель, несомненно, обратил внимание на содержа-
щуюся у Гильберта фразу «.Аналогичная задача планимет-
рии ныне полностью решена». Конечно, Гильберт здесь не
имеет в виду тот простой факт, что формула площади тре-
угольника выводится (в отличие от формулы объема пи-
рамиды) с помощью метода разбиения (или дополнения),—
это было известно еще Евклиду. Смысл гильбертовской
фразы раскрывается сноской, которую он дает к этой фра-
зе и в которой упоминаются «более ранняя литература»
и четвертая глава его «Оснований геометрии» [32] (см. снос-
ку 2 на стр. 28 книги [2]). Содержание главы IV книги [32]
показывает, что Гильберт имеет в виду найденное в прош-
лом столетии полное решение вопроса о взаимосвязи по-
нятий равновеликость, равносоставленность и равнодопол-
няемостъ для многоугольников.
В чем же состоит эта взаимосвязь? Как отмечалось в
§ 5, любые два равносоставленных многоугольника равнове-
лики, т. е. если F ~ Н, то s (F) = s (И). Естественно по-
ставить обратный вопрос: всякие ли два многоугольника,
имеющие одинаковую площадь, равносоставлены, т. е.
всегда ли из s (F) = s (Н) вытекает, что F ~ Н? Утверди-
тельное решение этой проблемы независимо друг от друга
получили венгерский математик Ф. Бойяи *) (1832 г.) и
немецкий офицер и любитель математики П. Гервин
(1833 г.). Иными словами, теорема Бойяи — Гер-
вина состоит в том, что два многоугольника в том и толь-
ко в том случае раеновелики, если они равносоставлены. Из
*) Отец знаменитого Я. Бойяи, который, независимо от Н. И.
Лобачевского, пришел к идеям неевклидовой геометрии.
48
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. I
этой теоремы легко вытекает также, что два многоуголь-
ника в том и только в том случае равновелики, если они
р авн о д о и о л няемы. Таким образом, равновели-
кость, равносоставленность и равнодополняемостъ — эк-
вивалентные свойства многоугольников в евклидовой
планиметрии. Изложению указанных результатов и по-
священ этот параграф.
Лемма 1. Если А~ВиВ~С, то А~С.
Иначе говоря, если каждая из фигур А, С равносостав-
лена с В, то А и С также равносоставлены. В самом деле,
проведем линии, разбивающие фигуру В на части, из кото-
рых можно составить фигуру А (сплошные линии на
Рис. 27.
рис. 27, а); проведем, кроме того, линии, разбивающие фигу-
ру В на части, из которых можно составить С (сплошные ли-
нии на рис. 27, б). Те и другие линии вместе разбивают В
на более мелкие части, из которых можно составить как
А, так и С. Таким образом, А ~ С.
Это доказательство можно формализовать следующим
образом. Пусть
А = А} ~Т . . . -J- Ah, В = Вг -р ... 4- Bh =
= Bv 4- . . . + Bi, С = Сг 4" . . . Сi‘,
пусть, кроме того, справедливы соотношения
А = /1 №), • • ; Д (Bh), С, - gl (BJ, ...
• • • , Ci = gi (Bi),
§ 7J ТЕОРЕМА IJOflHH - ГЕРВИНА /,9
где Д, . . /ft, gl5 . . gj — некоторые движения (так что
Аг — Вг и т. д.). Написанные соотношения и означают,
что каждая из фигур А, С равносоставлена с В. Положим
Fl} = Bt П Bj (где i = 1, . . ., к', j = 1, . . Z; заметим,
что некоторые из фигур Рц могут оказаться пустыми). Яс-
но, что фигуры Fi} попарно не имеют общих внутренних
точек; если, например, i* i, то /'Vp CZ В,», F^ CZ Bt,
а так как Btt и Bt не имеют общих внутренних точек, то
Fi*j* и Ftj их также не имеют. Наконец, мы имеем
и Fij = и (Bi п В-) = Bi n ( и в]) = Bi п в = Bi
j=l j-l j-l
и потому
It к к I к I
А = и Ai= и fi(Bi) = и fi( и Fij) = и и /г(Лз).
г 1 i=l i=l j = l i=l j=l
Аналогично,
С = U и g> (Fa).
г=1 j=l
Остается заметить, что /, (Рц) = gj (Ftj) (движение gjofi1
переводит первую из этих фигур во вторую), и потому
А ~ С.
Из этого доказательства видно, что А, В, С, а также
At, Bi, Bji Cj могут здесь быть произвольными квадрируе-
мыми фигурами; фигуры Fi} также квадрируемы в силу
теоремы 4. В том случае, когда В( и Bj — много-
угольники, пересечение Рц = Bt f) Bj также яв-
ляется многоугольником. В этом случае можно говорить
о «линиях», которые разбивают фигуру В на части Blt. . .
Вh (или Вг, . . ., Вг). В дальнейшем понадобится
лишь случай, когда все рассматриваемые фигуры — мно-
гоугольники.
Лемма 2. Всякий треугольник равносоставлен с не-
которым прямоугольником.
Действительно, в треугольнике abc опустим на его наи-
большую сторону (скажем, аЪ) высоту cd (рис. 28). Точка
d находится между а и Ъ (иначе сторона ab не была бы
наибольшей; см. рис. 29). Проведем среднюю линию тп\\ ab
и перпендикуляры ае и bf к прямой тп. Тогда мы получим
50
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. II
прямоугольник aefb, равносоставленный с треугольником
аЪс. В самом деле, треугольники, отмеченные на рис. 28
одинаковыми цифрами, конгруэнтны между собой. Каж-
Рис. 28.
Рис. 29.
дая же из фигур abc, aefb состоит из заштрихованной тра-
пеции и двух треугольников 1, 2.
Л е м м а 3. Если два прямоугольника равновелики,
то они равносоставлены.
В самом деле, расположим равновеликие прямоуголь-
ники так, чтобы у них был общий прямой угол (прямо-
Рис. 30.
голышки оар и dnb подобны,
угольники oabc и отпр на
рис. 30). Обозначим длины
отрезков ос, оа, ор, от че-
рез lY, hr, l2, h2 соответст-
венно. Тогда = l2h2
(поскольку прямоуголь-
ники равновелики), т. е.
-fr = -V’ откуда сле-
дует, что ар || тс. Далее,
= _ , т. е. треу-
и потому nb || ар. Итак, все
три прямые ар, тс, nb параллельны.
Если при этом отрезок тс пересекается с пря-
моугольником oadp, то равносоставленность прямоуголь-
ников oabc и отпр очевидна: каждый из них состоит из
заштрихованного на рис. 30 пятиугольника, одного из
двух конгруэнтных треугольников, отмеченных цифрой 1,
и одного из двух конгруэнтных треугольников gmn, cfb.
Рассмотрим теперь случай, когда отрезок тс не пере-
секается с прямоугольником oadp (рис. 31). Так как отрез-
S 71
ТЕОРЕМА БОЙЯИ — ГЕРВИНА
51
ни тп, ad и fb копгруэпгны, то в атом случае сумма длин
отрезков ad и fb меньше длины отрезка ab, т. е. 212 <; 1г
(тогда как в случае, изображенном на рис. 30, 212 1г).
Обозначим через е середину отрезка ос. Далее, пусть к —
наименьшее из таких натуральных чисел, что, откладывая
Рис. 31.
на ос отрезки op, pq, . . ., конгруэнтные ор, мы получим
после к откладываний точку t, расположенную вне отрез-
ка ое (т. е. точка t будет лежать внутри отрезка ес). На
рис. 31 мы имеем к = 3. Разобьем теперь прямоугольник
отпр отрезками, параллельными ор, на к конгруэнтных
частей и уложим эти части вдоль отрезка ot. Мы получим
прямоугольник ouvt (очевидно, равносоставленный с
отпр), у которого длина I' основания ot удовлетворяет
условию 21' 1г. В силу доказанного выше, прямоуголь-
ники оаЪс и ouvt равносоставлены, а потому (по лемме 1)
равносоставлены прямоугольники oabc и отпр.
Теорема 10 (теорема Бойяи — Гервина). Два мно-
гоугольника, имеющие равные площади, равносоставлены.
Доказательство. Всякий многоугольник F
может быть разбит на конечное число треугольников.
Каждый из этих треугольников равносоставлен с некото-
рым прямоугольником (лемма 2). Таким образом,
F ~ Рг + . . . + Pk, ipeP1, . . ., Pk — прямоугольники.
Возьмем, далее, произвольный отрезок а0Ь0 и в его концах
восставим перпендикуляры аос и bod (рис. 32). Наконец,
проведем такие отрезки а^, а2Ь2, . . ., akbk, параллель-
ные а0Ь0, что прямоугольник а^а^Ь^ (обозначим его
через Ht) равновелик прямоугольнику Pt, i =
= 1, 2, . . ., к. Так как s (Рг) = s (Ht), то Р, ~ Ht (лем-
ма 3). Следовательно, Рг + . . . + Ph ~ Нг + . . . + Нк.
52
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
(гл. и
Рис. 32.
По лемме 1, многоугольник F равносоставлен с
Hi + ... + Hh, т. е. с прямоугольником аоалЬлЬо-
Итак, каждый многоугольник равносоставлен с неко-
торым прямоугольником. Если теперь F и G — такие мно-
гоугольники, что s (F) = s (G), то
мы можем выбрать равносоставлен-
ные с ними прямоугольники Р и
Q, т. е. F ~ Р, G ~ Q. Прямо-
угольники Р и Q имеют одинако-
вую площадь и, следовательно,
Р ~ Q (лемма 3). Таким образом,
F ~ Р, Р ~ Q, Q ~ G и потому,
в силу леммы 1, многоугольники
F и G равносоставлены.
Теорема 11. Две равносос-
тавленные фигуры равнодополня-
емы.
Доказательство. Пусть
А ~ В. Положим С = А П В
и обозначим через М и N такие фигуры, что А =
= С + М, В — С + N. Далее, пусть Л* и В* — такие
фигуры, что А А*, В = В*, причем A J В, А* и В*
попарно не пересекаются. Так как А В, то Л* ~ В*,
т. е. существуют такие фигуры Рг, . . Phl Qh,
что
Л* = л + - . + Ph, й* = ft + . . . + Qh;
P^Q., . . ., Ph~Qk.
Пусть /, g— такие движения, что Л* = / (Л), В* =
= g (В). Мы имеем
(Л и В) + Л* + В* = (Л + N) + / (Л) + Q1 + . . .
. . . + Qk = Л + А' + (Д + . . . + Qk + / (С) + / (Л7),
(Л [J В) + Л* + В* = (В + М) + Рг + . . . +Pft +
4- g (В) = В + М + Pt + . . . + Pk + g (С) + g (N).
Таким образом,
А + Q! + . + Q, + f (М) + N + f (C)
= В + Гх + . . . + Ph + M + g (A) + g (C),
откуда видно, что Л и Б равнодополняемы.
: si
НЕАРХИМЕДОВЫ И НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
53
Доказанные теоремы 10 и 11 устанавливают эквива-
лентность понятий «равновеликость», «равносоставлен-
ность» и «равнодополняемость» для многоугольников.
Действительно, если многоугольники равновелики, то
они равносоставлены (теорема 10) и потому равнодопол-
няемы (теорема 11). Обратное непосредственно вытекает
из аксиом (0) и (у*). Заметим еще, что можно было бы
понимать равнодополняемость более общим образом:
дополнять конгруэнтными фигурами не до конгруэнтных,
а до равносоставленных фигур (именно так
понимает равнодополняемость Гильберт, как зто видно из
данной им формулировки проблемы). Однако из теоремы
11 следует, что такая «обобщенная равнодополняемость»
эквивалентна обычной равно дополняемости.
§ 8. Равносоставленность и равнодополняемость
в неархимедовых и неевклидовых геометриях
В лемме 3 (составляющей существенную часть доказа-
тельства теоремы Бойяи — Гервина) была использована
аксиома Архимеда: мы предположили, что, откладывая на
ое конгруэнтные отрезки op, pq, . . ., получим после не-
скольких откладываний точку, лежащую вне отрезка
ое. В главе IV книги [32] Гильберт изящным примером
показывает, что при доказательстве этой теоремы приме-
нение аксиомы Архимеда (или какой-либо иной аксиомы
непрерывности) неизбежно. Именно, в так называемых
неархимедовых геометриях эквивалентность по-
нятий равновеликости и равнодополняемости сохраняется
(для многоугольников), тогда как равносоставленность
уже не будет эквивалентна этим понятиям.
Разумеется, при доказательстве теоремы Бойяи —
Гервина использовались и другие аксиомы геометрии,
например, аксиома параллельности (поскольку рассмат-
ривались прямоугольники). Однако, в отличие
от аксиомы Архимеда, применение аксиомы параллельно-
сти не является неизбежным: в неевклидовых геометриях
Лобачевского и Римана теорема Бойяи — Гервина остает-
ся справедливой. Изложению указанных результатов и
посвящен этот параграф.
Будем рассматривать степенные ряды вида
х = tK («п 4- 4- а2/2 + -), а0 #= 0, (7)
54
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. II
где к — некоторое целое число, а степенной ряд, сто-
ящий в скобках, сходится для какого-либо отличного от
нуля значения /(и, следовательно, сходится абсолютно
и равномерно на отрезке [—е, е], где е — некоторое поло-
жительное число). Через £2 обозначим множество, элемен-
тами которого являются все ряды указанного вида, а так-
же нулевой ряд 0. Сумма, разность, произведение и част-
ное двух рядов вида (7), вычисленные по обычным правилам
действий со степенными рядами, снова являются рядами
вида (7). Таким образом, множество £2 является полем.
Условимся писать х 0, если а0 0 (см. (7)); далее,
х у, если х — у > 0. Для любых элементов х, у ЕЕ £2
имеет место одно, и только одно, из соотношений х > у,
х = у, у> х. Ясно, что сумма и произведение положи-
тельных элементов поля £2 положительны, откуда выте-
кают все свойства неравенств. Таким образом, поле £2
является упорядоченным. Это поле неархимедово,
т. е. можно найти такие положительные элементы ж, у ЕЕ
ЕЕ £2, что неравенство пх у ни для какого натурального
п места не имеет: достаточно взять такие положительные
элементы х (см. (7)) и
у = tl (b0 + b^t + b2t2 + ...), Ъо 0,
что I <Z к. Отметим еще, что для любого неотрицательного
элемента х ЕЕ £2, у которого число к (см. (7)) четно, опре-
делен элемент \/ х; иначе говоря, существует и притом
только один неотрицательный элемент z, удовлетворяющий
условию z2 = х. В частности, для любых х, у ее £2 опреде-
лен элемент ^х2 + у2.
С помощью поля £2 можно построить неархимедову
геометрию (ограничимся случаем планиметрии). Именно,
каждую пару (ж0, у0), где ж0, у0 ЕЕ £2, условимся считать
точкой. Прямая есть множество всех точек (ж0, уй),
координаты ж0, г/0 которых удовлетворяют уравнению
вида ах + by + с = 0 (где а, Ь, с ЕЕ £2, причем а2 + Ъ2
Ф 0). Д в и ж е и и е м называется преобразование, пе-
реводящее каждую точку (ж, у) в некоторую точку
(ж', у ) по формулам
ж' -= аж + Ъу + р,
у' = сх + dy + q,
НЕАРХИМЕДОВЫ И НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
55
§ 8]
где а, Ъ, с, d, р, q — элементы поля £2, удовлетворяющие
условиям
а2 + с2 = 1, Ъ2 + d2 = 1, ab + cd = О
(эти условия означают, что матрица преобразования орто-
гональна, т. е. что оно сохраняет скалярное произведение
векторов).
Как обычно, две фигуры называются конгруэнтными,
если одна из них переводится в другую некоторым движе-
нием. Расстояние между точками а = (хг, ub = (х2, у2)
определяется формулой
d (а, Ь) = У(ж2 — жг)2 4- (г/2 — уг)-.
Это расстояние (являющееся элементом поля £2) не меня-
ется при движениях: квадрат этого расстояния есть ска-
лярный квадрат вектора а , а скалярные произведения при
движениях не меняются. Можно также в этой геометрии
говорить о параллельных прямых (векторы, направленные
вдоль прямых, пропорциональны), о перпендикулярных
прямых (векторы, направленные вдоль прямых, ортогональ-
ны, т. е. их скалярное произведение равно нулю), о тре-
угольниках, параллелограммах, прямоугольниках и о
длинах их сторон и высот (эти длины являются положи-
тельными элементами поля £2).
Наконец, перейдем к учению о площадях. Примем,
что площадь прямоугольника выражается формулой
s = аЪ, где а, b — длины его сторон, as — площадь.
Отсюда (ср. рис. 19, 16) выводятся обычные формулы пло-
щади параллелограмма и треугольника. Наконец, любой
многоугольник может быть разбит на треугольники, что
позволяет вычислить его площадь. В результате получа-
ется функция s (F) (площадь), определенная на множестве
всех многоугольников. Можно доказать, что эта функция
удовлетворяет аксиомам (а), (|3), (у*), (6). Однако она не
является единственной функцией, удовлетворя-
ющей этим аксиомам. В самом деле, для элемента ж GE £2
(см. (7)) положим
/ (ж) == Р* (а0 4- агР 4-
Легко видеть, что / (ж) е £2. Далее, без труда проверяется,
что функция / (ж) аддитивна, т. е. удовлетворяет
56
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[гл. II
условию (3). Наконец, ясно, что если х 0, то и / (?) 0.
Таким образом, в отличие от функций Коши — Гамеля,
эта аддитивная функция (не являющаяся линейной)
положительна па всех положительных элементах
поля Q. Заметим еще, что / (1) = 1 (где 1 — единица поля
£2, т. е. ряд t° (1 + 0-t + 0-Z2 + ...)). Положим, наконец,
s* (F) = f (з (F)).
Непосредственно проверяется, что функция s* (F) также
удовлетворяет аксиомам (а), (0), (у*), (6), чем и устанав-
ливается отсутствие единственности. Если же вместо (а),
(6) включить в число аксиом формулу площади пря-
моугольника, то аксиомы (0), (у*) вместе с этой новой ак-
сиомой однозначно определяют площадь (на мно-
жестве многоугольников).
Приведем теперь пример Гильберта, показывающий
неэквивалентность понятий равновеликости
и равносоставленности в неархимедовой геометрии. Пусть
на луче отложены два отрезка аЪ и ad, длины ей/ который
таковы, что ни для какого натурального и не выполняется
а 6 d
Рис. 33.
соотношение пе > I. Пусть, далее, отрезки ас и dq, пер-
пендикулярные прямой ab, имеют длину е (рис. 33). Тогда
равновеликие треугольники аЪс и abq (они имеют общее
основание и одинаковые высоты) не будут равно-
составленными. В самом деле, допустим, что каждый из
них разбит на конечное число треугольников. Каждый из
частичных треугольников, на которые разбит A abc,
имеет периметр, меньший периметра треугольника аЪс,
т. е. подавно меньший, чем 4е (поскольку длпна стороны
Ъс меньше суммы длип двух других сторон треугольника
аЪс). Значит, сумма периметров этих треугольников
меньше 4/сс, где к — число частичных треугольников,
па которые разбит A abc. Так как 4/се < I и, значит, 4/се
меньше длины стороны aq, то сумма периметров частичных
§ 81
НЕАРХИМЕДОВЫ И НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
57
треугольников, па которые разбит Д abq, больше
4/се. Но тогда частичные треугольники, па которые раз-
биты A abc и A abq, не могут быть попарно конгруэнт-
ными.
Итак, в неархимедовой геометрии равновеликие мно-
гоугольники могут не быть равносоставленными. В то же
время равновеликость и равнодополняемостъ остаются,
как мы сейчас увидим, эквивалентными понятиями. При
доказательстве условимся равподополпяемость много-
угольников А и В обозначать записью А ~ В.
Лемма 1с. Если А ~ В и В ~ С, то А ~ С.
В самом деле, пусть
л +/1 (АЛ) + ... + fk (Mk)=f* (В + ЛЛ + . . . + мк),
с + ft (Л\) + . . . + gl (Nt) = g* (В + Л\ + . . . + Nt),
где ft, gj, f*, g* — движения. Положим
Рц = Mi Г) N}, M*i = AA\ (At U • • U A^f).
a; = AA(M> U • • и A4).
Тогда
a + 2 fi (M’i) + 2Л ( A3) + 2 /* (^J) =
= A + 2 Л (m + 2 Л3) + 2 /* W:) =
= ^ + 2/гт+2/* (Nl) =
г i
= /* (B+2 м<) + 2 /* (л/j) = r(B + 2 -Mi + 2 =
= j*(B u2Miu2^Y
\ i i I
Аналогично,
C + 2 (N]) + 2 gt (Pi?) + 2 g* (Mi) =
= g*^U2MiU2^)-
Таким образом, многоугольники
A + 2 /, (M’) + 2/* (^-) + 2 А (Л3)
и i ’ ь’
с + 2 g* (мг‘) +2 gj (Л/J) + 2 gi (Pa)
г j i.j
58
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. IX
конгруэнтны и, следовательно, по теореме И, равнодо-
полнясмы. Из этого непосредственно следует, что А ~ С.
Лемма 2С. Всякий треугольник равнодополняем
с некоторым прямоугольником.
Это вытекает из леммы 2 и теоремы 11 (в доказатель-
ствах которых аксиома Архимеда не использовалась).
Лемм а Зе. Если два прямоугольника равновелики,
то они равнооополняемы.
Мы не можем вывести лемму Зс из леммы 3 и теоремы
11, так как лемма 3 основывалась на аксиоме Архимеда.
Рис. 34.
Доказательство, не исполь-
зующее этой аксиомы, ясно
из рис. 34: из равновелико-
сти прямоугольников F и G
вытекает, что А bmp А cnq
и потому каждый из прямо-
угольников F, G дополняется
треугольниками 1, 2 до кон-
груэнтных фигур (до A abc
и A dmri).
Лемма 4с. Если Мг~
~Л\,. . ., Mk ~ Nk, причем
М±, . . ., Mh попарно не имеют общих внутренних точек
и то же справедливо относительно Nk, . . ., Afe, то
+ ... + + . . . 4-Afc.
Заметим, что аналогичная лемма, относящаяся к слу-
чаю равносоставленности, фактически использовалась при
доказательстве теоремы Бойяи — Гервина, но ввиду оче-
видности не формулировалась.
Доказательство проведем для к = 2 (далее идет оче-
видная индукция). Выберем такое движение /, что все
многоугольники, которые нужны для установления соот-
ношения Мг А\, попарно не имеют общих внутренних
точек с многоугольниками, которые нужны для установ-
ления соотношения / (Л/2) ~ / (-^г), (т- е- движение /
«достаточно далеко» уносит пару многоугольников А/2,
N2 от Мг, А\). Ясно, что
Mt + м2^~ Mt+ N, + N2 A Aj + / (A2); (8)
например, Мг + M2 и Мг + / (М2) дополняются конгру-
энтными фигурами / (М2) и М2 до многоугольника М± (J
НЕАРХИМЕДОВЫ И НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
59
§ 8]
U^U/ С^а)- Далее, из соотношений Мг Д\, / (М2)
/ (N2) вытекает, что
Мг + f (М2) ^Nr + f (М2), N, + / (М2) Nt + / (N2).
(9)
Из (8) и (9) в силу леммы 1С следует, что Мг + М2 Л, Ej +
+ TV2-
Теорема 10с. Два равновеликих многоугольника
равнодополняемы.
Доказательство дословно то же, что и в случае теоре-
мы 10; нужно лишь всюду слово «равносоставлены» заменить
на «равнодополняемы» и использовать леммы 1с — 4с.
Теорема 10с устанавливает эквивалентность понятий
«равновеликость» и «равнодополпяемость» в неархимедовой
геометрии.
Обратимся наконец к выяснению роли аксиомы па-
раллельности. В гиперболической и эллиптической гео-
метриях учение о площадях основывается на четырех ана-
логичных аксиомах (при этом аксиома (6) требует видо-
изменения, поскольку в этих геометриях не существует
квадратов). Как и в евклидовой геометрии, аксиомы
(а), (Р), (у*) определяют функцию s (F) (площадь) с
точностью до положительного мно-
жителя. Поэтому аксиома, аналогия- //
ная (6), нужна, чтобы однозначно /
фиксировать этот множитель. В гео- -----------/
метрии Лобачевского удобна аксиома /
(6ь) Бесконечный «треугольник'», /
ограниченный тремя попарно парал- \ /
лелъными прямыми (рис. 35), име- \ /
ет площадь л. \ I
В геометрии Римана удобна ак- \
сиома
(6е) Вся плоскость имеет пло- Рис. 35.
щадъ 2л.
Для доказательства теоремы существования использу-
ется понятие дефекта (пли, как еще говорят, «углового
дефекта») многоугольника. Если F — многоугольник,
ограниченный простой замкнутой ломаной с п вершинами,
то его дефект D (Е) определяется как число л (и — 2) —
— 2, где £ — сумма величин внутренних углов много-
угольника F (для многоугольников, имеющих более
60
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. п
сложную форму, определение очевидным образом видоиз-
меняется). В гиперболической геометрии дефект любого
многоугольника положителен, в эллиптической геометрии
отрицателен (число —D (F) называется угловым избыт-
ком многоугольника F). Непосредственно проверяется,
что функция s (F) — | D (F) | удовлетворяет аксиомам
(а), (Р), (у*). Несложный предельный переход доказывает,
что функция s (F) удовлетворяет в геометрии Лобачевского
аксиоме (бд) (величина каждого «угла» бесконечного
«треугольника» на рис. 35 равна нулю), а в геометрии
Римана — аксиоме (бе). Это и дает доказательство теоремы
существования. Доказательство единственности мы рас-
смотрим ниже *).
Лемма 5. Два треугольника с общим основанием и
равными дефектами равносоставлены.
В самом деле, пусть тп — средняя линия треугольника
abc (рис. 36). При симметрии относительно точки п точка
а перейдет в некоторую
точку d, а точка т — в
некоторую точку р пря-
мой тп. Ясно, что п —
середина отрезка ad, а
р — середина отрезка bd
(так как точки b, d, р сим-
метричны точкам с, а, т).
Таким образом, пр —
средняя линия треуголь-
ника abd, т. е. средние
линии тп, пр расположе-
ны на одной прямой и кон-
груэнтны. Из конгруэнт-
ности треугольников, отмеченных на рис. 36 одинако-
выми цифрами, вытекает, что Д abc и A abd равпосостав-
лены (и, следовательно, имеют одинаковые дефекты).
Мы можем повторить это построение, произведя сим-
метрию относительно точки р (в результате чего полу-
чится Д аЬе, равпосоставленный с треугольником abc
и имеющий среднюю линию pq, конгруэнтную тп), и т. д.
В силу аксиомы Архимеда, после конечного числа шагов
*) Используемые при доказательстве единственности леммы
5, 6 и теорема 12 следуют идеям изложения теории площадей, содер-
жащегося в книге Успенского [55].
§ 81
НЕЛРХИМЕДОВЫ И НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
61
мы получим треугольник (A abf на рис. 36) с основанием
ab, равносоставленный с треугольником abc, средняя
линия которого имеет общую точку о с перпендикуляром
L к отрезку ab в его середине.
Пусть abf — полученный треугольник. Опустим пер-
пендикуляры аи, bv, fw на его среднюю линию qr. Отрезки
uq и wq симметричны относительно точки q и потому кон-
груэнтны; точно так же конгруэнтны vr и wr. При гомо-
тетии с центром w и коэффициентом точки и, v переходят
в q, г, и потому qr — полови-
н а отрезка uv. Иначе говоря,
отрезок uv имеет длину 21, где
I — длина отрезка qr. В силу сим-
метрии отрезки аи и fw конгру-
энтны, так же как fw и bv. Сле-
довательно, аи и bv конгруэнтны,
и потому четырехугольник abvu
симметричен относительно прямой
L. Отсюда вытекает, что каждая
из точек и, v находится на рас-
стоянии I от точки о. Точки же
/
Рис. 37.
q, г находятся от о на расстоянии,
не превосходящем I (так как точка о принадле-
жит отрезку qr длины Z). Таким образом, обе точки q, г
принадлежат отрезку uv (рис. 37). Из соображений сим-
метрии треугольники, отмеченные на рис. 37 одинаковы-
ми цифрами, конгруэнтны. Следовательно, /\ abf, а потому
и A abc, равносоставлен с четырехугольником abvu.
Заметим теперь, что четырехугольник abvu одно-
значно определяется исходным треугольником abc.
В самом деле, сторона аЪ задана. Далее, каждый из углов
1
а, Ъ четырехугольника abvu имеет величину (л — Д),
где Д — дефект треугольника abc] (так как abc и abvu
равносоставлены и потому имеют одинаковые дефекты);
следовательно, положение прямых аи и bv также известно.
Наконец, прямая uv однозначно определяется как общий
перпендикуляр прямых аи и bv.
Таким образом, если abc' — любой треугольник с тем
же основанием ab и тем же дефектом Д, то A abc' равно-
составлен с тем же четырехугольником abvu, и потому
A abc и А аЬс' равносоставлены.
62
РАВНОСОСТАВЛЕННОСТЬ МН ОГОУГОЛЬНИКОВ
[ГЛ. II
Лемма 6. Два треугольника с равными дефектами
равносоставлены.
Действительно, пусть аЪс и тпр — два треугольника
с дефектом Д. Пусть, для определенности, из шести сторон
этих треугольников отрезок аЬ — наибольший (или один
из наибольших). Если какая-либо из сторон треугольника
тпр, скажем, тп, конгруэнтна аЪ, то A abc и Д тпр
имеют конгруэнтные основания аЪ и тп и равные дефекты;
следовательно, по предыдущей лемме они равносостав-
лены.
Пусть теперь каждая из сторон треугольника тпр
меньше аЪ. Отложим на луче тр отрезок mg, конгру-
энтный ab (рис. 38), и внутри угла ртк, смежного с углом
ртп, проведем дугу окружности с центром т, проходя-
щую через точку q. Пусть точка х пробегает эту дугу от
точки q до точки I, лежащей на луче тк', дефект получа-
ющегося треугольника тпх непрерывно зависит от по-
ложения точки х. Когда точка х близка к I, дефект тре-
угольника тпх близок к нулю (ибо угол хтп близок к л,
а два других угла — к нулю). Если же х = q, то дефект
треугольника тпх (равный сумме дефектов треугольников
тпр и прф) будет, по модулю, больше дефекта треуголь-
ника тпр. Следовательно, найдется положение точки х
на рассматриваемой дуге, при котором дефект треуголь-
ника тпх будет равен Д.
Так как Д аЪс и Д тпх имеют конгруэнтные стороны
ab и тх и равные дефекты, то они равносоставлены (лем-
ма 5). По той же причине равносоставлены Д тпх и Д тпр
(у них общая сторона тп и равные дефекты). Следователь-
но, Д аЪс и Д тпр равносоставлены.
§ Si НЕАРХIIМЕДОВЫ II НЕЕВКЛИДОВЫ ГЕОМЕТРИИ G3
Теорема 12. В эллиптической и гиперболической
геометрии любые ива многоугольника с равными дефектами
равносоставлены.
Доказательство. Пусть F и G — два много-
угольника с равными дефектами. Разобьем каждый из них
на треугольники:
F = + . . . + Тт, G = Т[ + . . . + Т'п.
Пусть, для определенности, из всех треугольников 7г,
Tj наименьший но модулю дефект имеет треугольник Тт.
В частности,
|я (лжт|. сю)
Если здесь выполняется равенство, то, по лемме 6,
Тт Тп, остается доказать равносоставленность много-
угольников
F* = Тг + . . . + Гт_1 и G* = ?; + ... + Тп-Г,
которые разбиты на меньшее, чем m -0 п, число
треугольников. Если же в (10) равенство места не имеет,
т. е. | D (Тт) | < | D (Тп) |, то прямой, проходящей через
вершину, можно Тп разбить на два треугольника Т* и
Тп, первый из которых имеет дефект, равный D (Тт).
Следовательно, по лемме 6, треугольники Тт и Тп равно-
составлены, и остается доказать равносоставленность мно-
гоугольников
F* = Тг + . . . 4- Тт-Х и G** = Т[ + . . . + Т'п., + Тп,
которые разбиты на меньшее, чем m -|- п, число
треугольников.
Этот прием уменьшения числа треугольников позво-
ляет, с помощью очевидной индукции, завершить дока-
зательство.
Следствие (теорема единственности). В гипер-
болической (эллиптической) геометрии существует един-
ственная функция s (F), определенная на множестве всех
многоугольников и удовлетворяющая аксиомам (а), (0),
(у*), (6ъ) (соответственно, (а), (0), (у*), (бе)), а именно
s(F) = \D(F)\.
Приведем доказательство в случае гиперболической
геометрии. Допустим, что существует функция s* (F),
м
РАВНОСОСТАВЛЕННОСТЬ многоугольников
1ГЛ. п
отличная от D (F) и удовлетворяющая аксиомам (а),
(р), (у*), (6h). Выберем многоугольник Fo, для которого
Z) (^о) s* (Л>): пусть, для определенности, D (Fo)
^>s* (Fo). Если многоугольник F удовлетворяет условию
D (F) = — D (Fo), где q—натуральное число, то объединение
q многоугольников, конгруэнтных F, имеет тот же дефект,
что и Fo. По теореме 12 это объединение представляет
собой многоугольник, равносоставленный с Fo, и потому
функция s* (удовлетворяющая аксиомам (Р) и (у*)) при-
нимает па этом объединении и на Fo одинаковые
значения. Отсюда вытекает, что s* (F) — — s* (Fo). Итак,
если D (F) = ~-D (Fo), то s* (F) = (Fo). Из этого
следует,что если D (F)= D (Fo),
то s*(F) = — s* (Fo).
Выберем такое е 0, что
(л — е) D (F0)ls* (Fo) > л (s суще-
ствует, так как D (F0)/s* (Fo) 1).
Выберем, далее, такой треуголь-
ник F, содержащийся в беско-
нечном «треугольнике», что
s*(F) л — е (рис. 39). Мы можем
при этом предполагать (увеличив,
если нужно, треугольник F), что
р, q — натуральные числа. Тогда,
Рис. 39.
D(F) = -^D(F0), где
как доказано выше, s*(F) = -^-s*(F0), и потому
D (F) = D (F„) _ D (Fo) > (л - «) > л,
что невозможно. Полученное противоречие и доказывает
единственность.
Из доказанного следствия вытекает, что в теореме 12
речь идет о многоугольниках с равными площадями,
т. е. в эллиптической и гиперболической геометрии два
равновеликих многоугольника равносоставлены. Итак, рав-
новеликость и равносоставленность — эквивалент-
ные понятия в этих геометриях. Равнодополняемость
§ 91 равносоставленность по ГРУППЕ s 65
также им эквивалентна (теорема 11). Таким образом, в от-
личие от аксиомы Архимеда, аксиома параллельности
не является существенной для справедливости теоремы
Бойяи — Гервина.
§ 9. Равносоставленность по группе
параллельных переносов и центральных симметрий
Изложенное выше (§§ 7, 8) и составляет, в общих чертах,
то, о чем Гильберт сказал «Аналогичная задача планимет-
рии ныне полностью решена». Однако Гильберт был не
совсем прав. В рамках обычного (евклидова) понимания
равновеликости, равносоставленности и равно дополняе-
мости его фраза совершенно правомочна (мы видели это
в § 7). Но при изучении связи между этими понятиями
в различных геометриях (в частности, неархиме-
довых, начало чему положил сам Гильберт) возникают
новые направления исследования. Одно из таких новых
направлений было открыто работами швейцарской школы
геометров, возглавляемой Г. Хадвигером *). О резуль-
татах, полученных в этом направлении, и пойдет речь
дальше.
В связи с теоремой Бойяи — Гервина возникает инте-
ресный вопрос о наложении дополнительных ограничений
на число или расположение частей, из которых составля-
ются равновеликие многоугольники. Для пояснения одно-
го из таких ограничений представим себе плоскость в виде
листа цветной бумаги, у которого одна сторона красная,
а другая (изнаночная) — белая. Если из такой бумаги
вырезаны два равновеликих многоугольника, то возни-
кает вопрос, можно ли один из них разрезать па части,
из которых удастся сложить красный многоуголь-
ник, конгруэнтный второму (т. е. части разрешается пере-
кладывать, пе переворачивая их на белую, изнаночную
сторону). Математически задача состоит в том, чтобы раз-
*) Кстати, в одном из писем Хадвигер писал автору этих строк
об «окончательном» решении планиметрической проблемы равно-
составленности, содержащемся в работе [5] (речь шла о доказывае-
мой ниже теореме 17). По-видимому, все зависит от точки зрения;
в § 7 было изложено решение в рамках евклидовых концепций,
а в этом и двух следующих параграфах та же проблема рассматри-
вается с позиции клейновских идей.
3 В. Г. Болтянский
66
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. II
бить равновеликие многоугольники F, С на части, которые
получаются друг из друга с помощью движений, сохра-
няющих ориентацию (т. е. поворотов или параллельных
переносов):
F = Мг + . . . + Mh, G = /ДЛЛ) + ...+fh (Mh),
где А, - . .,/й — движения, сохраняющие ориентацию.
Частный случай этой задачи был предложен на одной
из московских математических олимпиад в следующей
шуточной форме. Чудак-кондитер испек торт в форме
Рис. 40.
разностороннего
треугольника. Сделали и
коробку к торту, но по
недосмотру склеили ее не-
верно, так что торт и ко-
робка оказались сим-
метричными друг
другу. Нужно (по возмож-
ности экономно) разрезать
торт на части, которые
удалось бы уложить в эту
коробку; разумеется, час-
ти торта нельзя уклады-
вать кремом вниз. На рис. 40 показан способ разрезать
торт на части, каждая из которых обладает осью симмет-
рии, что и позволяет уложить их в коробку.
Теперь ясно, что ответ на поставленный вопрос поло-
жителен: если многоугольники равновелики, то их равно-
составленность может быть установлена при помощи
движений, сохраняющих ориентацию. В самом деле, по
теореме Бойяи — Гервина можно разбить два равновели-
ких многоугольника на соответственно конгруэнтные
части, а потому — на соответственно конгруэнтные тре-
угольники. Но два конгруэнтных треугольника либо
получаются друг пз друга движением, сохраняющим
ориентацию, либо же (как на рис. 40) могут быть разбиты
каждый на три части, получающиеся друг из друга дви-
жениями, сохраняющими ориентацию.
Интересный результат, связанный с наложением до-
полнительных требований на расположение частей, был
получен в 1951 году Хадвигером и Глюром [30]: равно-
составленность двух равновеликих многоугольников может
§ 91 РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ S 67
быть установлена при помощи таких разбиений, что со-
ответствующие части имеют параллельные стороны.
На первый взгляд это кажется даже неправдоподобным:
трудно поверить, что два конгруэнтных треугольника,
повернутых друг отно-
сительно друга на про- /X.
извольный угол (рис.
41), всегда можно раз- г \
бить на конгруэнтные /\
части с соответственно
параллельными сторо- рис
нами.
Прежде чем доказывать теорему Хадвигера — Глюра,
рассмотрим связь наложенных дополнительных ограниче-
ний с группами движений. Множество всех движений
плоскости (как сохраняющих, так и меняющих ориента-
цию) обозначим через D. Напомним, что некоторое непу-
стое подмножество G множества D называется группой
движений, если оно обладает следующими двумя свой-
ствами:
1) вместе с каждыми двумя движениями /, g ЕЕ G
композиция g°f (т. е. результат их последовательного вы-
полнения) также принадлежит множеству G;
2) вместе с каждым движением / GE G множеству G
принадлежит и обратное движение /-1.
Множество D является, очевидно, группой движений.
Множество Do, состоящее из всех движений, сохра-
няющих ориентацию, также представляет
собой группу движений (в самом деле, композиция дви-
жений, сохраняющих ориентацию, также сохраняет ори-
ентацию; если движение / сохраняет ориентацию, то и
сохраняет ориентацию).
Множество Т всех параллельных переносов плоскости
является группой движений. Действительно, композиция
параллельных переносов является параллельным перено-
сом; движение, обратное параллельному переносу, также
является параллельным переносом.
Более сложный пример группы движений представляет
собой множество S, состоящее из всех параллельных пере-
носов и всех центральных симметрий. Чтобы убедиться,
что S — группа движений, возьмем произвольный вектор
а 0. При параллельном переносе он переходит в
3*
68
РАВНОСОСТАВЛЕННОСТЬ многоугольников
[ГЛ. II
вектор, равный а; при центральной симметрии а переходит
в вектор, равный —а. Поэтому при композиции двух дви-
жений /, g ЕЕ S вектор а переходит в вектор, равный либо
а, либо —а. Но движение, сохраняющее ориентацию и
переводящее а в равный ему вектор, представляет собой
параллельный перенос; движение же, сохраняющее ори-
ентацию и переводящее а в вектор, равный —а, представ-
ляет собой центральную симметрию. Это означает, что
композиция движений, принадлежащих множеству S,
также принадлежит множеству S. Далее, при / ЕЕ S
движение /-1 также принадлежит S. Таким образом, S —
группа движений. Заметим, что
Тс SrD„GD.
Напомним теперь основные положения геометрической
концепции Клейна [41]. Пусть G — некоторая группа
движений плоскости *). Фигура А называется G-конгру-
энтной фигуре В, если существует такое движение / ЕЕ
С G, что / (Л) = В, т. е. если А можно «наложить» на В
с помощью некоторого движения / GE G. Легко видеть, что
если фигура А конгруэнтна В, то и фигура В конгруэнт-
на А; в самом деле, если / (Л) = В, / ЕЕ G, то /-1 (В) =
= Л, причем /-1 ЕЕ G в силу свойств группы движений.
Таким образом, если Л В, то В Л, где знак S озпа-
G с G
чает G-конгруэнтпость, т. е. отношение G-конгруэнтности
симметрично. Нетрудно видеть также, что отношение G-
конгруэнтности транзитивно. Действительно, пусть
Л ~ В и В С, т. е. существуют такие движения
G G
f,g ЕЕ G, что / (Л) = В, g (В) = С; тогда
(g°f)(A) = g(f (Л)) = g (В) = С,
т. е. движение gcf (также принадлежащее группе G)
переводит фигуру Л в С, и потому Л С. Наконец, от-
G
ношение G-конгруэнтности рефлексивно. В самом деле,
если / — произвольное движение, принадлежащее группе
*) Можно рассматривать любую группу преобразований G про-
извольного множества М. Для наших целей достаточно ограничить-
ся случаем, когда М — евклидова плоскость, а все преобразования,
входящие в группу G, являются движениями.
§ 9] РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ 8 69
G, то f~l GE G, а потому группа G содержит тождест-
венное движение е — так как е (А) = А для
любой фигуры А, то А А. Итак, отношение G-конгру-
G
эптности рефлексивно, симметрично и транзптпвно, т. е.
является отношением эквивалентности.
Далее, некоторое свойство фигур называется инвари-
антным относительно группы G (или, короче, G-инвариант-
ным), если оно сохраняется при всех движениях, принад-
лежащих группе G (т. е. из того, что фигура А обладает
этим свойством, вытекает, что и любая фигура, G-koh-
груэптная А, также обладает этим свойством). Например,
свойство «быть многоугольником» G-инвариантно: оно
сохраняется при любых движениях и, в частпости,
при движениях, принадлежащих группе G. Можно также
говорить о свойстве пары фигур. Так, равнове-
ликость есть свойство пары фигур; фигуры А, В
обладают этим свойством, если $ (Л) = s (В). Это свойство
также G-инвариантно: равновеликость сохраняется при
любых движениях, а потому и при движениях, при-
надлежащих группе G. Разумеется, группа движений G
может иметь и свои специфические G-инвариантные свой-
ства, которые не сохраняются при любых движениях,
но сохраняются при движениях, принадлежащих группе G.
Согласно Клейну, каждая группа движений G опре-
деляет свою геометрию — назовем ее G-геометри-
ей. Предметом изучения в ней являются всевозможные
G-инвариантные свойства.
Например, евклидова планиметрия (изучающая свой-
ства фигур, сохраняющиеся при любых движениях)
является, согласно Клейну, D-геометрией. Укладывается
в схему Клейна и неархимедова геометрия (надо рассмот-
реть группу G всех движений неархимедовой плоскости
М и изучать G-инвариантные свойства фигур, располо-
женных в М), а также гиперболическая и эллиптическая
геометрии, аффинная и проективная геометрии и многие
другие. В качестве еще одного примера отметим, что Т-
геометрия, по-существу, совпадает с векторной алгеброй:
равенство векторов (направленных отрезков) ab и cd
означает, что, они могут быть совмешепы (учитывая на-
правления) с помощью некоторого параллельного переноса,
т. е. что эти направленные отрезки Т-конгруэнтны.
70
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. II
В дальнейшем мы будем рассматривать лишь группы
движении евклидовой плоскости (оставляя в сто-
роне неархимедову плоскость, гиперболическую плоскость
и т д.).
В каждой G-геометрии имеется свое понятие рав-
носоставленности: многоугольники А и В называются
G-равносоставленными (Л ~ В), если существуют такие
многоугольники Av . . ., Ah и Вг, . . Bh, что
А = А, 4- . . . + Ah, В = Вг + . . . + Bh;
s Blt. . . , Ah s Bb.
G G
Аналогично определяется G-равнодополняемость. Таким
образом, в каждой G-геометрии возникает проблема об
эквивалентности понятий равновеликости, G-равносостав-
ленности и G-равнодополняемости.
Рассмотренные в начале этого параграфа дополни-
тельные ограничения на расположение частей, из которых
составляются равновеликие многоугольники, тесно свя-
заны с понятием G-равносоставленности. Первое ограни-
чение (рассмотрение только движений, сохраняющих
ориентацию) означает, очевидно, что речь идет о
В0-равносоставленности. Таким образом, как установлено
в начале параграфа, справедлива следующая
Теорема 13. Два равновеликих многоугольника
D^-равнос оставлены.
Далее, если два многоугольника получаются друг из
друга с помощью параллельного переноса или централь-
ной симметрии, то их стороны соответственно параллельны.
Обратно, если соответствующие стороны двух конгруэнт-
ных многоугольников параллельны, то эти многоуголь-
ники получаются друг из друга параллельным переносом
или центральной симметрией. Иначе говоря, соответству-
ющие стороны двух конгруэнтных многоугольников в том
и только в том случае параллельны, если эти многоуголь-
ники S-к онгруэнтны. Поэтому теорема Хадвиге-
ра — Глюра, о которой шла речь выше, может быть сфор-
мулирована в следующей эквивалентной форме:
Теорем а 14. Два равновеликих многоугольника
S-равносоставлены.
§ 9J
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ 8
а
В этой форме мы ее и докажем. Как и для доказатель-
ства теоремы Бойяи — Гервина, потребуются несколько
лемм.
Лемма 1g- Если А — В и В — С, то А — С.
G G G
Доказательство — дословно то же, что и в случае
леммы 1; надо лишь предполагать, что движения /1Т . . .
• • •> Ви • • •> gi принадлежат группе G, так что движе-
ния gjo/f1 также принадлежат этой группе.
Доказанная лемма, в частности, справедлива для груп-
пы 5: если А В и В С, то А С.
Лемма 2g. Всякий треугольник S-равносоставлен
с некоторым прямоугольником.
В самом деле, именно зтот факт и был установлен при
доказательстве леммы 2, поскольку треугольники, отме-
ченные одинаковыми цифрами,
центрально симметричны.
Лемма Зу. Два равнове-
ликих прямоугольника Т-равно-
составлены.
Здесь рассуждение, приме-
ненное при доказательстве лем-
мы 3, должно быть уточнено.
В самом деле, первая фраза
этого рассуждения («располо-
жим...») означает применение
поворота (рис. 42). По-
скольку дальнейшая часть рас-
суждения использует лишь па-
раллельные переносы частей,
достаточно доказать, что если
М— произвольный прямоугольник и L — прямая, то суще-
ствует Т’-равносоставленный с М прямоугольник N, одна
сторона которого параллельна L. Проведем через вершину
прямоугольника М прямую, которая параллельна L
и рассекает М на две части. Одна из этих частей является
треугольником (рис. 43). Отрезав этот треугольник и
переместив его в новое положение с помощью параллель-
ного переноса, мы получим параллелограмм, одна из сто-
рон которого параллельна прямой L. Проведем из вершины
тупого угла зтого параллелограмма высоту на сторону,
параллельную L. Если эта высота целиком расположена
72
РАВНО COCTA В ПЕНН ОСТЬ МНОГО УГО ЛЬН ИНОЙ
1ГЛ. II
внутри параллелограмма, то она отсекает треугольник,
переставляя который мы и получаем искомый прямоуголь-
ник (рис. 44). Если же эта высота частично расположена
вне параллелограмма, то, разделив параллелограмм на
несколько конгруэнтных частей прямыми, параллельными
Рис. 43.
L, и переставляя эти части (рис. 45), мы получим парал-
лелограмм, Z-равносоставленный с первоначальным, у ко-
торого высота уже целиком расположена внутри. Этим и
завершается доказательство леммы Зу.
Заметим, что если Н 3) G, то G-равпосоставлепные мно-
гоугольники являются также Я-равносоставленными.
Рис. 44. Рис. 45.
В частности, из ^-равносоставленности двух многоуголь-
ников вытекает их .^-равносоставленность. Поэтому, в си-
лу доказанной леммы, равновеликие прямоугольники
S-равносоставлены.
Теперь теорема 14 доказывается дословно так же, как
и теорема Бойяи — Гервина (надо лишь всюду слово
«равносоставлены» заменить на «G-равносоставлены»).
Заметим, наконец, что теорема 11 сохраняется (вместе
с доказательством) и в G-геометрии: два G-равносоставлен-
§ 10]
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ ПЕРЕНОСОВ 73
ных многоугольника G-равнодополняемы. Поэтому пз тео-
ремы 14 вытекает, что понятия равновеликости, 5-равно-
составленности и 5-равнодополняемости эквива-
лентны (ср. конец § 7).
§ 10. Равносоставленность по группе переносов
Из теорем 10, 13 и 14 теорема 14 является наиболее
сильной, поскольку D ZD Do ZD S. Естественно возникает
вопрос, нельзя ли найти группу движений G, меньшую
чем S, которая все еще обладала бы тем свойством, что
любые равновеликие многоугольники являются G-равно-
составленными? В частности, не является ли такой груп-
пой Т, т. е. нельзя ли разбить любые два равновеликих
многоугольника па части, получающиеся друг из друга
с помощью одних параллельных переносов?
Ответ на этот вопрос отрицателен. Это также
было установлено Хадвигером и Глюром [30]. Более
того, они дали необходимое и достаточное условие
^-равносоставленности многоугольников. Изложению этих
результатов и посвящен настоящий параграф.
Пусть G — некоторая группа движений. Функция
<р (F), заданная на множестве всех многоугольников, на-
зывается аддитивным G-инвариантом, если, во-первых,
она аддитивна, т. е. удовлетворяет аксиоме (р) (ф (/') =
= ф (В) + Ф ПРИ F = F' F"), и, во-вторых, ее
значения инвариантны относительно движений группы G,
т. е. <р (F) — ф (f (F)) для любого многоугольника F и
любого движения / GE G.
Теорема 15. Пусть функция ф (А) является
аддитивным G-инвариантом. Для G-равносоставленности
(а также для G-равнодополняемости) многоугольников А
и В необходимо выполнение равенства <р (Л) = ф (В).
Доказательство. Пусть А В, т. е.
А = Лх + . . . + Ak, В = Вг 4- . . . + Bh\
А1 = Br, . . ., Ak Bk.
G G
В силу аддитивности функции ф (F) мы имеем
ф (Л) = ф (Лх) + . . . + ф (Ль),
Ф (В) = ф (В.) + . . . + ф (Bft).
74
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. IX
Далее, в силу G-инвариантности этой функции,
Ф (4J = ф (BJ,. . ., ф (Ль) = ф (Bh).
Отсюда и вытекает справедливость равенства ф (4)=ф (В).
Для случая равнодополняемости доказательство ана-
логично.
Теперь построим аддитивные Т’-инварианты, которые
позволят получить необходимое и достаточное условие
Т-равносоставленности. Пусть р — некоторая прямая.
Будем называть эту прямую оснащенной, если указано,
какая из двух полуплоскостей, определяемых прямой р,
считается положительной. Пусть F — произвольный мно-
гоугольник и аЪ — некоторая его сторона. Если она не
Рис. 46.
Рис. 47.
параллельна прямой р, то припишем стороне аЪ коэффи-
циент е = 0. Если аЬ || р, причем многоугольник F при-
мыкает каЬс положительной стороны (рис. 46),
то стороне аЪ припишем коэффициент 8=1. Наконец,
если аЪ || р и многоугольник F примыкает к аЪ с отрица-
тельной стороны, то 8 = —1. Весом стороны ab в много-
угольнике F назовем число el, где I — длина стороны ab.
Наконец, через Jp (F) обозначим сумму весов всех сторон
многоугольника F. Таким образом, в сумму Jp (F) входят
(с коэффициентами ±1) лишь длины сторон, параллель-
ных прямой р.
Докажем, что функция Jp (F) является аддитивным
^-инвариантом. В самом деле, пусть F = F’ + F". Рас-
S 10) РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ ПЕРЕНОСОВ
75
смотрим все точки, являющиеся вершинами этих много-
угольников. Они разобьют стороны многоугольников
F, F', F" на более мелкие отрезки, которые условимся
называть звеньями. На рис. 47 сторона аЪ многоугольника
F состоит из трех звеньев am, тп, пЪ.
Ясно, что для вычисления значений Jp (F), Jp (F'),
Jp (F") можно взять сумму (с соответствующими коэф-
фициентами) длин звеньев, а не сторон, так как
длина каждой стороны равна сумме длин составляющих
ее звеньев.
Рассмотрим некоторое звено, целиком (кроме, может
быть, концов) расположенное внутри F (звено cd
на рис. 47). К этому звену примыкают оба многоуголь-
ника F', F", причем с разных сторон. Поэтому при вычис-
лении суммы Jp (F") это звено войдет с одним коэффициен-
том, а при вычислении Jp (F") — с противоположным
коэффициентом, и в общей сумме Jp (F') + Jp (F") эти сла-
гаемые дадут 0. Таким образом, при вычислении суммы
Jp (F') + Jp (F") можно не учитывать звеньев, располо-
женных внутри F.
Возьмем теперь звено, расположенное на границе
многоугольника F и параллельное прямой р (звено
ат на рис. 47). К нему примыкает только один из
многоугольников F', F", причем стой же сто-
роны, что и многоугольник F. Следовательно, в сумму
Jp (Fz) + Jp (F") это звено войдет с тем же знаком, что
и в Jp (F).
Этим доказано равенство
Jp (Р) = Jp (Р') + Jp п
т. е. установлена аддитивность функции Jp.
Ее Z-инвариаптность очевидна. Таким образом, Jp есть
аддитивный 7-инвариант.
С помощью этого инварианта нетрудно доказать, что
существуют равновеликие многоугольники, не являю-
щиеся 7-равносоставленными. В самом деле, пусть А —
треугольник и р — оснащенная прямая, параллельная
одной из его сторон. Пусть, далее, В — параллелограмм,
равновеликий треугольнику А. Ясно, что Jp (Л) Ф 0,
Jp (5) = 0, т. е.
Jp (Л) =# Jp (В).
76
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
1гл. ii
По теореме 15, многоугольники А и В не являются
Г-равносоставленными*).
Естественно возникает вопрос о нахождении усло-
вий, которые (помимо равновеликости) нужно наложить
на многоугольники А и В для того, чтобы они были Т-
равносоставленными. Такие условия содержатся в следую-
щей теореме Хадвигера — Глюра [30].
Теорема 16. Для Т-равносоставленности равнове-
ликих многоугольников А и В необходимо и достаточно,
чтобы для каждой оснащенной прямой р было выполнено
равенство Jf (Л) = Jp (В).
Доказательство. Необходимость вытекает из
теоремы 15 (поскольку JT (F) есть аддитивный Т'-инва-
риант).
Докажем достаточность. Пусть равновеликие много-
угольники А к В обладают тем свойством, что Jp (А) =
= Jp (В) для любой оснащенной
прямой р. Фиксируем некоторую
прямую q и проведем через все
вершины многоугольников в Л и
В прямые, перпендикулярные q.
Тогда Л и В разобьются на час-
ти, каждая из которых представ-
ляет собой либо трапецию, осно-
вания которой перпендикулярны
q (частным случаем трапеции яв-
ляется параллелограмм), либо тре-
угольник, одна из сторон ко-
торого перпендикулярна q (рис. 48). Треугольник можно
заменить суммой двух трапеций (рис. 49). Трапецию же
*) Заметим, что с помощью функции Jp (В) легко установить
независимость аксиомы (а) от аксиом (Р), (у), (6) (для многоуголь-
ников). В самом деле, так как Jp (F) = 0 для любого параллело-
грамма F и, в частности, для единичного квадрата Q, то функция
’а(Л = «(Л + Ш
рассматриваемая на множестве всех многоугольников, удовлетворяет
(при любом выборе оснащенной прямой р) аксиомам (Р), (у), (6).
Однако аксиоме (а) она не удовлетворяет. Если, например, F —
треугольник площади 1/2, у которого имеется сторона длины 1,
параллельная р, причем он примыкает к ней с отрицатель-
ной стороны, то
«а (Л = s (/ ) + Jp (F) = V2 — 1 < 0.
5 101 РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ ПЕРЕНОСОВ
77
можно разбить на несколько прямоугольных
трапеций (для чего, возможно, нужно будет разрезать
ее на более «узкие» трапеции прямыми, параллельными
основаниям; рис. 50). Таким образом,
Л — Лт + . . . Д- Ah, В — Вг 4~ . . . Д- Bt, (11)
т т
где Aj,Bj — прямоугольные трапеции, основания которых
Рис. 50.
Рис. 49.
перпендикулярны q. Иначе говоря, каждая из тра-
пеций Лг, Bj имеет не более, чем одну сторону, непа-
раллельную и не перпендику-
лярную q.
Пусть трапеция не явля-
ется прямоугольником, т. е.
имеет сторону не парал-
лельную и не перпендикулярную
q. Обозначим через рг оснащен-
ную прямую, параллельную
причем положительную по-
луплоскость выберем так, что
JPl (ИД > 0, т. е. А1 примыкает
к с положительной стороны.
Допустим, что JPl (Л2) < 0, т. е.
Л2 имеет сторону а2Ь2, парал-
Рис 51.
лельную рг, и примыкает к ней с отрицательной сто-
роны. Пусть, для определенности, сторона имеет не
меньшую длину, чем аг&2. Отложим на а1Ь1 отрезок ахс,
78
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. II
конгруэнтный агЪг, и через точку с проведем прямую,
перпендикулярную д. Эта прямая разбивает на две
трапеции Ау, Му, первая из которых имеет сторону ОуС,
конгруэнтную а2Ь2 (рис. 51). Приложив и Л2 друг к дру-
гу их параллельными сторонами (с помощью параллель-
ного переноса), мы получим прямоугольник
М2 — А2 + Ау, причем Ау + А2 — Му + М2.
т Т
В результате из двух трапеций Ау, А2, для которых
инвариант Jp, принимал значения разных знаков, мы по-
лучим лишь одну трапецию Му, для которой Jpi при-
нимает отличное от нуля значение, и прямоугольник М2.
Повторяя этот прием, мы получим новое соотношение
А — Му . . . -f- Mh, в котором все отличные от нуля
т
числа JP,(MJ,. . ., JP1 (Mh) имеют одинаковые
знаки, причем многоугольники Му,. . ., Mk по-прежнему
представляет собой трапеции, основания которых пер-
пендикулярны д (частными случаями являются прямо-
угольники). Аналогично, В — + . . . + Nt. Так как
Jp, (А) = Jp, (В), то г
JP1 (MJ + ... + Jp, (MJ = Jv, (A\) + .. - + Jp^)-
от нуля числа Jp, (MJ, Jp, (NJ
имеют одинаковые знаки —
Поэтому все отличные
пусть, для определенности,
все они положительны.
Мы можем предполагать, что
Jp. (MJ > 0, JPt (NJ > 0. Обоз-
начим через Cydy и c2d2 сторо-
ны трапеций Му, Ny, парал-
лельные прямой рх, и пусть,
для определенности, сторона
c2d2 имеет не меньшую длину,
чем Cydy. Отложим на с2б/2 от-
резок с2е, конгруэнтный Cydy,
и через точку е проведем пря-
Рис Б2. мую, перпендикулярную д. Эта
прямая разбивает Ny на две тра-
пеции Ny, Ny, первая из которых имеет сторону с2е, кон-
груэнтную Cydy (рис.52). Пусть, для определенности, тра-
пеция Му имеет соответственно большие основания, чем Ny.
§ 10] РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ ПЕРЕНОСОВ
79
Тогда (рис. 53, а)
71/^^ + П, N^t^HJ,
где П — некоторый прямоугольник, — параллельный
перенос. (Если Мг имеет меньшие основания, то М± = Hlt
= tx (Hj) + П, рис. 53, б; характер дальнейших рас-
суждений от этого не меняется.) Мы получаем
А ~(Я, + П) + Мй + . . . + Mh, B~{tr {HJ + X) +
+ Я2 + . . . + Nt. (12)
Здесь трапеции Нг и (Яа) являются Т-конгруэнтны-
ми, а П — прямоугольник. Число же остальных трапе-
ций М2,. . ., Mh, Ni, N2,. . ., Nh т. е. к + I — 1 стало
меньшим, чем число трапеций в правых частях соотно-
шений (11).
Если теперь X не является прямоугольником, то, пов-
торяя то же построение, мы получим соотношения вида
А ~ Нг + Я2 + П + X + . - . + Mh,
т
В — Ч (Я1) -|- t2 (Я2) II' + Я2 + . . . + Nr
т
и т. д. В конце концов мы придем к соотношениям
А — Hi Яг П2 + . . . + Па,
т
в~ч {Hi) + ... + tr{iir) + X + ... + пр,
т
80
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[ГЛ. (I
где flt. . tr — параллельные переносы, а Пг, Щ—
прямоугольники.
Теперь уже нетрудно завершить доказательство. Так
как А и В равновелики и, кроме того, Яг и tt (Я;) также
равновелики, то равновеликими будут и многоугольники
Пх - . . . -f- Па и Пх + • - . + Пр. Но тогда из леммы Зг
(стр. 71) нетрудно вывести, что
Пх + . . .+ Па~п;+ . . . + Пр.
т
Отсюда и вытекает требуемое соотношение А — В.
т
Заметим, что хотя в доказанной теореме 16 говорится
о выполнении равенства Jp (4) = Jp (В) для любой
оснащенной прямой, в действительности достаточно про-
верить выполнение этого условия для конечного
числа прямых, а именно, для прямых, параллельных сто-
ронам многоугольников А и В (для остальных оснащенных
прямых Jp (Л) = Jp (Z?) = 0). Таким образом, содержа-
щееся в теореме 16 условие вполне эффективно.
В качестве применения теоремы 16 рассмотрим задачу
о нахождении выпуклых многоугольников, которые
Т-равносоставлены с квадратом. Так как для квадрата Q
справедливо равенство Jp (Q) = 0 (для любой оснащенной
прямой р), то, в силу теоремы 16, речь идет о нахождении
выпуклых многоугольников, у которых инвариант Jp
равен нулю для любой прямой р. Пусть многоугольник F
обладает этим свойством и р — оснащенная прямая, па-
раллельная стороне аЪ этого многоугольника. Тогда мно-
гоугольник F должен иметь еще сторону, параллельную
ab, скажем, сторону тп, причем стороны ab и тп должны
быть конгруэнтными (иначе число Jp (F), равное разности
длин сторон аЪ и тп, пе будет равно нулю). Итак, для каж-
дой стороны многоугольника F имеется конгруэнтная и
параллельная ей сторона, откуда легко следует, что мно-
гоугольник F центрально-симметричен. Ясно и обратное:
если F центрально-симметричен, то Jp (F) = 0 для любой
оснащенной прямой р. Таким образом, выпуклый много-
угольник F в том и только в том случае Т-равносоставлен
с квадратом той же площади, если этот многоугольник
центрально-симметричен 130].
§ 11] МИНИМАЛЬНОСТЬ ГРУППЫ 8 81
§ 11. Минимальность группы переносов
и центральных симметрий
Здесь мы дадим ответ на вопрос, поставленный в нача-
ле предыдущего параграфа: докажем, что 5 есть наи-
меньшая группа движений, позволяющая установить
равносоставленность любых равновеликих многоуголь-
ников.
Теорема 17 (см. [5], [6]). Если G — такая группа
движений, что любые равновеликие многоугольники
G-равносоставлены, то Gpj S, т. е. G содержит все парал-
лельные переносы и все центральные симметрии.
Доказательство опирается на несколько лемм; при фор-
мулировке этих лемм мы будем всегда предполагать, что
G есть группа, удовлетворяющая условиям теоремы.
Лемма 7. Группа G транзитивно, т. е. для любых
двух точек р, q плоскости существует в группе G движение,
переводящее р в q.
Пусть, напротив, существуют такие точки р и q, что
никакое движение, принадлежащее группе G, не перево-
дит точку ръ q. Обозначим через IV множество всех точек,
в которые точка р может быть переведена некоторым
движением, принадлежащим группе G; таким образом,
q W. Если F — произвольный многоугольник, то через
Iw (F) обозначим сумму величин тех его углов, вершины
которых принадлежат множеству W. Покажем, что если
F = Ft + ... + Fk, то
7w (F) = Iw (Fj) . . . + Iw (F+ rm, (13)
где n — целое число. Доказать это достаточно при к — 2,
т. е. F = Fj + F2. Всякая вершина а многоугольника F
является либо общей вершиной многоугольников F1 и F2
(рис. 54, а, б), либо вершиной одного из них (скажем, FJ,
причем в этом случае а может быть внутренней
точкой стороны многоугольника Fa (рис. 54, в) или может
совсем не принадлежать F2 (рис. 54, г). В первом случае
(рис. 54, а, б) имеем а — аг + сс2, где а, cq, а2 — величи-
ны углов многоугольников F, Flt F2 при вершине я;
во втором случае а — + л (рис. 54, в) или а =
(рис. 54, г). Складывая эти равенства по всем верпшнам
многоугольника F, принадлежащим множеству W, мы
и получаем соотношение (13).
82 РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ [ГЛ II
Далее, функция Iw является G-инвариаптной, т. е.
Iw (F) = Iw (g (F)) (14)
для любого многоугольника F и любого движения g Ez G.
В самом деле, если а — вершина многоугольника F, то
соответствующая вершина g (а) многоугольника g (F)
в том и только в том случае принадлежит W, если a ЕЕ W,
причем величины углов многоугольников F и g (F) в соот-
ветствующих вершинах а и g (а) одинаковы. Отсюда и вы-
текает (14).
Из (13) и (14) следует, что
IW(M) = Лг(Л’) + 1л при M-^N, (15)
где I — некоторое целое число.
Пусть теперь pqm и pqn — два конгруэнтных равно-
бедренных тупоугольных треугольника, первый из кото-
рых имеет вершину тупого угла в точке р, а второй — в
точке q. Величину острого угла этих треугольников обо-
значим через а. Так как р ЕЕ W, q W, то функция Iw
принимает па kpqm либо значение л — а, либо значение
л — 2а (в зависимости от того, выполнено или нет включе-
ние т ЕЕ И7)- Значение же Iw (A pqn) равно а или 2а.
Поскольку а< л/4, равенство Iw (A pqm)— Iw(& PQn) +
/л не может иметь места ни при каком целом Г,
следовательно, в силу (15), треугольники pqm и pqn не
могут быть G-равпосоставленными. Это однако противо-
речит свойствам группы G (равновеликие, а тем более кон-
груэнтные многоугольники должны быть G-равпосостав-
ленными). Полученное противоречие и доказывает тран-
зитивность группы G.
S 111
минимальность группы s
83
Замечание. Соотношениям (13) и (15) можно при-
дать несколько иной вид. Обозначим через X множество
всех чисел вида 1л, где I — целое. Множество X являет-
ся подгруппой аддитивной группы R всех дейст-
вительных чисел. Обозначим через <р естественный гомо-
морфизм группы R на факторгруппу Rn = R/Х. Тогда
Ф (1л) = 0 для любого целого I, и потому соотношения
(13) — (15) принимают вид1
<Р (tw (Г)) = ф (I^FJ) + . . . + Ф (Iw (Fk)), (13')
Ф(ЛУ(Г)) = cp(Iw(g(F))), (14')
<p(Iw (М)) ~ ф (Iw (А)) ПРИ М — N. (15')
G
Соотношения (13') и (14') показывают, что ф (Iw (F))
является аддитивным G-инвариантом со значениями в Rn.
Соотношение (15') является при такой трактовке следстви-
ем теоремы 15.
Лемма 8. Группа G содержит хотя бы одну цент-
ральную симметрию.
Каждое движение плоскости является (см. [56]) либо
параллельным переносом, либо поворотом, либо скользя-
щей симметрией (т. е. композицией симметрии относи-
тельно некоторой прямой и параллельного переноса вдоль
этой прямой; прямая эта называется осью скользящей
симметрии).
Если G содержит хотя бы одну скользящую симмет-
рию, то фиксируем какую-либо направленную прямую р,
которая перпендикулярна оси некоторой скользящей сим-
метрии /i Е G. Движение h переводит р в противо-
положно направленную прямую. Если же группа G
не содержит скользящих симметрий, то фиксируем про-
извольную направленную прямую р. Далее, нап-
равленную прямую р' условимся считать отмеченной,
если в группе G имеется сохраняющее ориентацию движе-
ние, которое переводит р в направленную прямую, парал-
лельную и одинаково направленную с р'.
Предположим, что из любых двух противоположно на-
правленных прямых не более чем одна является отме-
ченной. Рассмотрим произвольный многоугольник F
и пусть ab — его сторона. На прямой ab выберем такое
направление, что многоугольник F примыкает к стороне
84
РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ
[гл. it
ab слева. Если направленная таким образом прямая
ab является отмеченной, то стороне ab припишем коэф-
фициент е = 1; если противоположно направленная пря-
мая является отмеченной, то припишем стороне ab коэф-
фициент е = —1; наконец, если пи одна из этих прямых
не является отмеченной, то стороне ab поставим в соответ-
ствие коэффициент в = 0. Через Кр (F) обозначим сумму
длин сторон многоугольника F, взятых с указанными
коэффициентами.
Построенная функция Кр (F) является аддитивным
G-инвариантом. Аддитивность доказывается дословно
так же, как и в случае функции Jp (F) (стр. 74). Докажем
G-инвариантиость. Пусть F — произвольный многоуголь-
ник и g €Е G. Пусть, далее, — сторона многоуголь-
ника F, а а2Ь2 — соответствующая сторона многоугольника
g (F), т. е. а2 = g (аД, b2 = g (fcj). Обозначим через pv
прямую направленную так, что многоугольник F
примыкает к стороне щД слева, через р2 — направлен-
ную прямую, в которую переходит р1 при движении g,
а через р2 — прямую р2, взятую с противоположным на-
правлением. Предположим, что стороне а1Ь1 многоуголь-
ника F поставлен в соответствие коэффициент 1, т. е. пря-
мая р2 отмечена. Тогда существует сохраняющее ориента-
цию движение f Е= G, переводящее р в прямую, парал-
лельную и одинаково направленную с рг. Если при этом
движение g сохраняет ориентацию, то g°f есть
сохраняющее ориентацию движение, переводящее р в
прямую, параллельную и одинаково направленную с р2,
т. е. прямая р2 также отмечена. Так как g сохраняет ори-
ентацию, то g (Е) примыкает к отрезку а2Ъ2 направленной
прямой р2 слева (так же, как F примыкает к а^),
т. е. стороне а2Ъ2 многоугольника g (F) приписан коэф-
фициент 1. Если же движение g меняет ориентацию,
то g (F) будет примыкать к стороне а2Ь2 слева, если па
прямой а2Ь2 задать направление р2 (а не р2). Движение
g°f°h сохраняет ориентацию и переводит р в прямую, па-
раллельную и одинаково направленную с р2. Следователь-
но, прямая р2 отмечена, т. е. ив этом случае стороне а2Ь2
многоугольника g (F) приписан коэффициент 1.
Итак, если стороне а1Ь1 многоугольника F поставлен
в соответствие коэффициент 1, то стороне а2Ь2 мпогоуголь-
§ ill
МИНИМАЛЬНОСТЬ ГРУППЫ s
85
ника g (F) также поставлен в соответствие коэффициент 1.
Аналогично устанавливается, что если стороне
поставлен в соответствие коэффициент —1, то и стороне
а2Ь2 поставлен в соответствие коэффициент —1. Наконец,
если стороне а1Ь1 поставлено в соответствие число нуль,
то это же имеет место и для стороны а2Ь2 многоугольника
8 (F) (многоугольник F получается из g (F) с помощью
движения g 1, и если бы стороне а2Ь2 соответствовал коэф-
фициент ± 1, то такой же
коэффициент соответство- С1
вал бы стороне a^bj). Итак, s'?
соответствующие стороны \
многоугольников F и g (F) .s'
берутся в суммах Кр (F) и
Кр (g (F)) с одинаковыми D1
коэффициентами, так что //
Кр (F) = Кр (g (F)). 7 \
Рассмотрим теперь два ™
треугольника с длинами
сторон 1, 1^2, ]/3, распо-
ложенные, как указано па ис‘ 55'
рис. 55. Так как опи кон-
груэнтны (и, значит, равновелики), то они G-равносо-
ставлены и потому, по теореме 15, Кр (Л ахЬхсх) =
= Кр (/у ®2^2^2)> Т. е.
а! •14-Р1-]^2-|-т1-]/3 = а3-1-[-Р2-1^2 +Т2‘УЗ,
где ах, 0Х, ух — коэффициенты, приписанные сторонам
треугольника ахЬхсх, а а2, 02, у2 — сторонам треугольника
а2Ь2с2. Так как все коэффициенты целые (+1, —1 или 0),
то написанное равенство может иметь место лишь при
ах — а2, 0Х = 02, ух = у2. Однако ясно, что ах = 1,
а2 = —1, т. е. ах а2. Итак, предположение о том, что
из любых двух противоположно направленных прямых
не более, чем одна является отмеченной, приводит к про-
тиворечию.
Следовательно, найдутся две противоположно направ-
ленные прямые дг, д2, которые обе отмечены. Обозначим
через gj ЕЕ G (i = 1, 2) такое сохраняющее ориентацию
движение, которое направленную прямую р переводит в
прямую, параллельную и одинаково направленную с д^
86 РАВНОСОСТАВЛЕННОСТЬ МНОГОУГОЛЬНИКОВ [ГЛ. 11
Тогда g2°gi1 GE G есть сохраняющее ориентацию дви-
жение, переводящее в противоположно направленную
прямую, т. е. центральная симметрия.
Доказательство теоремы 17. Пусть г —
центральная симметрия принадлежащая группе G (лемма
8), ох — центр этой симметрии, а о — произвольная точка
плоскости. Пусть, далее, g G — движение, переводящее
точку о в ох (лемма 7). Тогда движение / = g-1 ° (г о g),
принадлежащее группе G, представляет собой централь-
ную симметрию. Так как это движение, как легко видеть,
оставляет точку о на месте, то f — симметрия относитель-
но точки о. Таким образом, центральная симметрия отно-
сительно произвольной точки о принадлежит группе G,
т. е. G содержит все центральные симметрии. Так как
любой параллельный перенос представляется в виде ком-
позиции двух центральных симметрий, то G содержит и
все параллельные переносы. Следовательно, G S.
ГЛАВА III
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
§ 12. Равносоставленность симметричных
многогранников
В тексте Гильберта есть фраза о том, что Герлингу
удалось «доказать равенство объемов симметричных много-
гранников при помощи разбиения их на конгруэнтные ча-
сти». Из этого видно, что симметричные многогранники
Гильберт не считает конгруэнтными. В трехмерном ев-
клидовом пространстве симметрия относительно плоско-
сти (так же, как и центральная симметрия) представляет
собой движение, меняющее ориентацию. Гильберт
же считает конгруэнтными лишь такие многогранники
(или, вообще, фигуры), которые получаются друг из дру-
га с помощью движений, сохраняющих ориен-
тацию.
Смысл теоремы Герлинга (она была установлена им в
1844 году и передоказана в 1896 году Брикаром [9]) удоб-
нее всего пояснить с групповой точки зрения. Будем рас-
сматривать различные группы движений трехмерного ев-
клидова пространства 7?а: группу D всех движений, груп-
пу Do сохраняющих ориентацию движений, группу Т
параллельных переносов и др. Понятия G-конгруэнтности,
G-равносоставленности и G-равнодополняемости (где G —
некоторая группа движений пространства R3) определяют-
ся для многогранников так же, как для многоугольников
на плоскости.
Таким образом, под «конгруэнтностью» Гильберт по-
нимает лишь 2)0-конгруэнтность, и, в соответствии с этим,
когда он говорит о доказательстве равенства объемов при
помощи разбиения на «конгруэнтные части», то имеет в
виду D ^-равносоставленность. Иными словами, теорема
88
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. ш
Герлипга состоит в том, что симметричные многогранники
Вй-равносоставлены. Ясно, что симметричность здесь не
по существу: речь идет о многогранниках, получающихся
друг из друга с помощью движения, меняющего
ориентацию. Если же два многогранника получаются друг
из друга с помощью движения, сохраняющего
ориентацию, то они не только £)0-равносоставлены, но да-
же /)о-конгруэнтны. Итак, теореме Герлинга можно при-
дать следующую формулировку:
Теорема 18. Если два многогранника D-конгру-
энтны, то они D п-равносоставлены.
Доказательство. Если М — многогранник,
симметричный относительно некоторой плоскости a, a N —
многогранник, ZJ-конгруэптный ему, то М и N являются
также £)0-конгруэнтнымп. Действительно, если / — дви-
жение, переводящее М в N, a s — симметрия относитель-
но плоскости а, то движение f°s также переводит М в N,
причем одно из движений /, f°s является сохраняющим
ориентацию, т. е. принадлежит группе Do.
Из этого следует, что если многогранник А можно раз-
бить на части Мг,. . ., Mh, каждая из которых обладает
плоскостью симметрии, то любой многогранник В, кото-
рый £>-конгруэнтеп А, является £>0-равносоставленным
с Л. В самом деле, разбив В на части Л\,—, Nh, соответ-
ственно jD-конгруэптные многогранники М1Т. . М1{,
мы найдем (в силу симметричности многогранника
что Mi и Ni не только /)-конгруэнтны, но и 2)0-конгруэнт-
ны, и потому А и В являются 290-равносоставленными.
Итак, достаточно доказать, что любой многогранник А
можно разбить на части, каждая из которых обладает
плоскостью симметрии. Пусть А — произвольный много-
гранник. Проведем все плоскости, в которых расположе-
ны его грани. Эти плоскости разобьют И наконечное число
выпуклых многогранников. Далее, каждый вы-
пуклый многогранник можно разбить на пирамиды (мно-
гоугольные): достаточно, взяв внутри многогранника точ-
ку q, рассмотреть все пирамиды, имеющие точку q своей
вершиной, а грани многогранника — своими основания-
ми (рпс. 56). Наконец, каждую многоугольную пирамиду
можно разбить на несколько треугольных пирамид
(рис. 57). Итак, многогранник А может быть разбит на
треугольные пирамиды, и остается доказать, что любую
§ 12]
СИММЕТРИЧНЫЕ МНОГОГРАННИКИ
Ь9
треугольную пирамиду можно разбить на части, каждая
из которых обладает плоскостью симметрии.
Пусть abed — треугольная пирамида, о — центр впи-
санного в нее шара и alt blt clt dr — точки касания вписан-
ного шара с гранями пирамиды (точка ах лежит в грани,
Рис. 56.
Рис. 57.
не проходящей через вершину а, точка — в грани, пе
проходящей через Ь, и т. д.). Разобьем пирамиду abed
на шесть многогранников:
oa^cd, oajbcjd, oa^cdy, oab^d, oa^cd^ oabc^dy. (16)
Для завершения доказательства мы установим, что каж-
дый из них обладает плоскостью симметрии.
Точка о равноудалена от плоскостей acd и bed (так как
вписанный шар касается обеих плоскостей), и потому точ-
ка о находится в плоскости |3, которая проходит через
ребро cd и делит пополам двугранный угол пирамиды
90
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ 1ГЛ. lit
abed, имеющий cd своим ребром. Следовательно, точки Ъг
и щ (т. е. проекции точки о на плоскости acd и bed) симмет-
ричны относительно плоскости р, а потому и многогранник
oa^cd симметричен относительно р. Аналогично доказы-
вается симметричность остальных многогранников (16).
Следствие. Понятия D-равносоставленности и
D 0-равносоставленности (для многогранников в В3) экви-
валентны.
В самом деле, пусть А и В являются D-равносостав-
ленными, т. е. А = Мг + . . . 4- Mk, В — . .
...+ N h, где Mt = Nt, i — 1,. . А: (как и раньше, запись
D
вида Рг + . . . + Pk означает объединение многогран-
ников Рг , . . ., Ph, которые предполагаются попарно не
имеющими общих внутренних точек). Из соотношения
Mi Ni вытекает, в силу теоремы 18, что Mt и Nt яв-
D
ляются £)0-равносоставленными. Следовательно, А л В
также Do-равносоставлены.
Обратно, если А л В являются £)0-равносоставленны-
ми, то они также D-равносоставлены (поскольку Do С D).
Установленное следствие показывает, что решение
третьей проблемы Гильберта не зависит от того, будем ли
мы понимать «равносоставленность» в смысле Do-равно-
составленности или D-равносоставленности. Именно пос-
ледний аспект (D-равносоставленность) мы будем иметь
в виду в следующем параграфе, посвященном решению
третьей проблемы Гильберта.
Причина, по которой Гильберт ограничивается при по-
становке проблемы Do-равносоставлепностью, т. е. огра-
ничивается лишь движениями, сохраняющими ориента-
цию, понятна: эти движения осуществляются непре-
рывным перемещением пространства В3
по себе как «твердого целого», тогда как движение,
меняющее ориентацию, может быть осуществлено в виде
результата непрерывного перемещения лишь с выходом
в пространство большего числа измерений. Особенно по-
нятной разница между движениями, сохраняющими и
меняющими ориентацию, становится в случае много-
угольников и многогранников в сферических простран-
ствах. Например, симметричные между собой разносто-
ронние сферические треугольники (рис. 58) не могут быть
совмещены не только в сфере, но и в содержащем эту сфе-
§ 121 СИММЕТРИЧНЫЕ МНОГОГРАННИКИ
91
ру трехмерном пространстве; для их совмещения непре-
рывным перемещением требуется выход в четырехмерное
евклидово пространство (или трехмерное сферическое).
В связи с этим равновели-
кость двух симметричных
фигур на сфере не счита-
ется «очевидной» (т. е. не
аксиоматизируется), а д о-
казывается уста-
новлением их равносостав-
ленности.
Отметим, что приведен-
ное выше доказательство
теоремы Герлинга дослов-
но обобщается на случай
многогранников в сфери-
ческом (или эллиптичес-
ком) пространстве, а также
в пространстве Лобачев-
ского — и притом любого
числа измерений. Именно, многогранник (в п-мерном
пространстве постоянной кривизны — евклидовом, эл-
липтическом или гиперболическом) разбивается на
n-мерные симплексы, а каждый тг-мерный симплекс разби-
вается на + многогранников, обладающих зеркаль-
ной симметрией. Последнее разбиение осуществляется
с помощью шара, вписанного в рассматриваемый симплекс:
если Т — некоторая (п — 2)-мерная грань симплекса,
о — центр вписанного шара и Ьг — точка касания впи-
санного шара с (и — 1)-мерными гранями симплекса,
содержащими Т, то выпуклая оболочка множества Т (J
(J {о, fej} представляет собой зеркально-симметричный
п(п-{-1)
многогранник, причем всего получится —- таких много-
гранников (по числу (п — 2)-мерных граней), которые и
составляют разбиение рассматриваемого n-мерного сим-
плекса. Для п = 3 такое разбиение рассматривалось при
доказательстве теоремы Герлинга, а для п = 2 —при
доказательстве теоремы 13 (см. рис. 40).
Теорема Герлинга, изложенная выше, вместе с содер-
жанием параграфов 7 и 8 дает представление о состоянии
92
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
(ГЛ. III
теории равносоставленности на рубеже XIX и XX веков,
когда Гильберт сформулировал свои проблемы *). Были
также известны отдельные примеры равносоставленных
Рис. 59.
многогранников. Наиболее интересные из них (помимо
тривиальных примеров, вроде равносоставленности пря-
мой и наклонной призм; см. рис. 21) были найдены в
1896 году английским математиком Хиллом [34]. Он ука-
зал примеры тетраэдров, равносоставленных с кубом.
•) В работе Брикара [9], датированной 1896 годом (см. § 15),
содержится доказываемая ниже теорема 20, принадлежащая Дену
и дающая решение третьей проблемы Гильберта. Однако приведен-
ное в [9] доказательство некорректно. Таким образом, работа [9]
фактически не содержит никаких результатов, но она, видимо, ока-
зала определенное влияние на Гильберта и Дена.
§ 131 РЕШЕНИЕ ТРЕТЬЕЙ ПРОБЛЕМЫ ГИЛЬБЕРТА 93
Один из тетраэдров Хилла показан па рис. 59. Здесь
ab, Ъс и cd — взаимно перпендикулярные ребра, имею-
щие одинаковую длину I, а отрезки Ьт и тп имеют длину
Z/3. На рис. 59 показано, каким образом можно разбить
тетраэдр на четыре многогранника, чтобы, перегруппи-
ровав их, получить прямую треугольную призму. В свою
очередь эта призма равносоставлена с прямоугольным
параллелепипедом, а потому и с кубом. (Подробнее о
тетраэдрах, равносоставленных с кубом, будет идти речь
в § 18).
Итак, существуют тетраэдры, объем которых
может быть найден методом разбиения. Гильберт предви-
дел, однако, что теорема Герлинга, тетраэдры Хилла и т. п.
дают лишь частные, удачно подобранные примеры
равносоставленности равновеликих многогранников, ко-
торые следует рассматривать как исключения, а не как
иллюстрацию общей закономерности. Об этом и го-
ворит его фраза: «... как мне кажется, в общем случае до-
казательство упомянутой теоремы Евклида этим спосо-
бом провести невозможно...». Теперь мы выяснили смысл
каждой фразы в данной Гильбертом формулировке его
третьей проблемы.
§ 13. Решение третьей проблемы Гильберта
В том же 1900-м году, когда Гильберт произнес свой
доклад «Математические проблемы», его третья проблема
была решена. Гильберт оказался прав: методы разложе-
ния и дополнения бессильны для вывода формулы
объема пирамиды (в общем случае). Это установил Ден [13],
который показал, что существуют многогранники, имею-
щие равные объемы, но не равносоставлепные. В частно-
сти, куб и правильный тетраэдр одинакового объема не
равносоставлены, не равнодоиолняемы (и не дополняются
конгруэнтными частями до равносоставленных много-
гранников). Существуют также не равпосоставленные тет-
раэдры с конгруэнтными основаниями и одинаковыми вы-
сотами. Тем самым обосновывается необходимость привле-
чения неэлементарных методов в теории объемов много-
гранников.
Работа М. Дена как бы прожила несколько жизней.
Изложение самого Дена было трудным для понимания.
94
равносоставленность многогранников
(ГЛ. III
В 1903 году вышла работа Кагана [39], в которой рассуж-
дения Дена были существенно усовершенствованы, из-
ложены более систематично и популярно. Это было как
бы второе рождение работы Дена. В пятидесятые годы ряд
интересных результатов в теории равносоставленности
был получен швейцарскими геометрами — Г. Хадвигером
и его учениками. Эти работы (в частности, [21], [24], [27])
позволили по-новому взглянуть на работу Дена, получить
основной ее результат на основе прозрачных идей в сов-
ременном изложении. Единственным недостатком их из-
ложения было применение аксиомы выбора (связанное с
использованием рациональных базисов в поле действи-
тельных чисел; ср. стр. 29). Наконец, в [6] было дано
переработанное доказательство Хадвигера, в котором
рассмотрение всей числовой прямой В заменено рассмот-
рением конечных множеств; это позволило избежать
применения аксиомы выбора. Доказательство теоремы
Дена, данное в [6], по-видимому, является наиболее про-
стым. Это доказательство мы здесь и приведем.
Пусть М — некоторое множество действительных чи-
сел. Элементы xlt. . ., xh ЕЕ М будем называть зависимы-
ми, если существуют такие целые числа пи. . ., nft,
не все равные нулю, что
П1Х1 + П^Х2 + • - • + nhxh — 0- (17)
Соотношение (17) будем называть зависимостью *).
Действительную функцию / (ж), заданную на множе-
стве М, будем называть аддитивной, если для каждой
зависимости (17) между элементами множества М зави-
симость с т е м и же коэффициентами имеется и между
соответствующими значениями функции /, т. е.
nJ (^) + nJ (хг) + . . . + nJ (xh) = 0.
Пусть, наконец, А — некоторый многогранник, а1э
а2,. . ., ар — величины его двугранных углов, выражен-
ные в радианах, a Zn 12,. . ., 1Р — длины соответствующих
ребер. Если / — некоторая аддитивная функция, задан-
•) Выше (в § 4) мы рассматривали зависимости с рацио-
нальными коэффициентами, которые принципиально не от-
личаются от зависимостей с целыми коэффициентами (рациональные
коэффициенты могут быть приведены к общему знаменателю).
6 13] РЕШЕНИЕ ТРЕТЬЕЙ ПРОБЛЕМЫ ГИЛЬБЕРТА 95
ная на множестве М, содержащем все числа а15. . ар,
то сумму
lif (»i) + У («2) + . . + lPf (ар)
обозначим через / (Л) и будем называть ее деповским ин-
вариантом многогранника А. (Этих определений у Дена
не было, но идейно они восходят к его работам.)
Следующая теорема представляет собой видоизменение
одного результата Хадвигера [27] и служит ключом для
решения третьей проблемы Гильберта.
Т е о р е м а 19. Пусть а1;. . сер — величины дву-
гранных углов многогранника А, а рх, . . ., — величи-
ны двугранных углов многогранника В. Пусть, далее, М —
некоторое множество действительных чисел, содержащее
числа
л, аъ. . ., ар, рп. . рд. (18)
Если на этом множестве существует такая аддитив-
ная функция /, что / (л) = 0, а соответствующие денов-
ские инварианты многогранников А и В не одинаковы, т. е.
/ (Л) =# / {В), то многогранники А и В не равносостав-
лены (и не равнодополняемы).
Доказательство теоремы 19 мы приведем в следующем
параграфе, а сейчас с помощью этой теоремы изложим ре-
зультаты Дена. В соответствии с формулировкой теоремы
19 мы в дальнейшем всегда будем предполагать, что
рассматриваемые аддитивные функции удовлетворяют ус-
ловию / (л) = 0.
Лемма 9. Для любого натурального п 3 число
1 1
— агссоэ — иррационально.
Доказательство. Допустим, напротив, что
ф/л = Ilk, где k, I — натуральные числа, ф = arccos 1/п.
Так как Ахр = 1л, то cos к<р = ± 1, т. е. cos ktp есть ц е-
л о е число. Это утверждение мы и приведем к противоре-
чию, т. е. покажем, что ни при каком натуральном к
число cos кц> не является целым.
Мы имеем
cos (к 4- 1) <р + cos (к — 1) ф = 2 cos Ахр cos ф,
откуда, учитывая соотношение cos ф = 1/н, получаем
2
cos (А: 4~ 1)<Р = — cos Ахр — cos (Ас — 1)ф. (19)
96 РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Дальнейшую часть доказательства проведем отдельно
для четных и нечетных п. Пусть и нечетно. Покажем, что
в этом случае cos Аф выражается дробью, знаменатель
которой равен пк, а числитель — целое число, взаимно
простое с и; отсюда и будет следовать, что cos к(р ни при
каком натуральном к не является целым. При к = 1 и
к = 2 это утверждение непосредственно проверяется:
1 О о . 2 . 2 — П2
cos ф = —, cos 2ф = 2 cos- ф — 1 = — — 1 =-j—
71 72“ 71^
(число 2 взаимно просто с п, так как п нечетно; поэтому и
число 2 — п2 взаимно просто с п). Предположим, что (прп
некотором к ;> 2) для всех чисел 1,2,..., к наше утвер-
ждение доказано, и установим его справедливость для чис-
ла к + 1. Согласно предположению индукции, имеем
cos/пр—соз(й —1)ср = —,
где а, Ь — целые числа, взаимно простые с и. В силу (19),
, .. 2 а Ъ 2а — brfi
COS (к + 1) <|: = — -у - •
Так как числа а и 2 взаимно просты с п, то число 2а так-
же взаимно просто с и, а потому и числитель 2а — 6п2
взаимно прост с п. Проведенная индукция и доказывает
лемму для случая нечетного п.
Если же п четно, т. е. п = 2т, где т'^ 2 — натураль-
ное число, то cos А'ф выражается дробью, знаменатель ко-
торой равен 2тк, а числитель —
целое число, взаимно простое с
т (это доказывается анало-
гичной индукцией). Следова-
тельно, и в этом случае ни при
каком натуральном к число
cosArp не является целым.
Теорема 20 (см. [13]).
а Правильный тетраэдр не рав-
носоставлен (и не равнодопол-
няем) с кубом того же объема.
рис go Доказательство.
Обозначим через <р величи-
ну двугранного угла правильного тетраэдра Р. Легко
видеть, что ф = arccos — (на рис. 60 точка е — центр тя-
О
§ 13] РЕШЕНИЕ ТРЕТЬЕЙ ПРОБЛЕМЫ ГИЛЬБЕРТА
97
жести грани abc, отрезок de — высота и справедливо соот-
ношение | е/ j = А. (а/1 = | df\).
Применим теперь теорему 19. Величина каждого дву-
гранного угла куба Q равна ; поэтому числа (18), о кото-
рых идет речь в теореме 19, здесь будут следующими:
л, —, <р. За М мы и примем множество, состоящее из этих
трех чисел: М — {л, , ср}. На множестве М зададим дей-
ствительную функцию /, положив
/(«)=», /(4) = °’ = (2°)
Нетрудно показать, что эта функция, заданная на мно-
жестве М, аддитивна. В самом деле, пусть
птл + /г2-А + п3ф = 0 (21)
— некоторая зависимость между элементами множества М
(пъ п2, ns — целые). Допустив п3 0, мы найдем из (21),
что число
1 1 Ф
— arccos
•ГС о JT
I Пг
2
п3
рационально — вопреки лемме 9. Таким образом,
и3 = Ои потому, в силу (20), находим
ni/ (л) + «2/ (4) + пз/ (ф) = 0.
Это и означает, что функция / аддитивна.
Остается вычислить деповские инварианты. Куб Q име-
ет 12 ребер. Обозначим длину его ребра через I. Тогда
/(0 = 12Z/(-A)=O
(см. (20)). Далее, обозначив через т длину ребра правиль-
ного тетраэдра Р, найдем
/ (Р) = 6mf (<р) = 6m 7^ 0.
Таким образом, / (Р) / (0 и потому (по теореме 19)
4 В Г. Болтянский
98
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ill
правильный тетраэдр Р и куб Q не равносоставлены (и не
равнодополняемы)*).
Теорема 20 показывает, что, как и предвидел Гиль-
берт, для многогранников понятие равновеликости (ра-
венства объемов) не эквивалентно равносо-
ставленности (или равнодополняемости).
Приведем еще несколько примеров вычисления депов-
ских инвариантов. Прежде всего покажем, что деповский
инвариант любого параллелепипеда равен нулю (при лю-
бом выборе аддитивной функции). В самом деле, пусть
аЪ и cd — две противоположные стороны некоторой гра-
ни abed параллелепипеда Р. Если а — величина двугран-
ного угла при ребре ab, то величина двугранного угла при
ребре cd равна л — а. Таким образом, множество М, на
котором задана аддитивная функция f (пригодная для вы-
числения деповского инварианта f(P)), должно содержать
числа л, ос, л — а (и, возможно, какие-либо другие чис-
ла). Между этими числами имеется зависимость
— л + ос + (л — а) = 0,
и потому, в силу аддитивности функции /,
—f (л) + / (а) -Г f (л — а) = 0.
Кроме того, / (л) = 0 (это условие всегда накладывается
при рассмотрении деповских инвариантов; ср. теорему 19).
Таким образом, / (а) + / (л — а) — 0. Наконец, так как
ребра ab и cd имеют одинаковую длину Z, то соответствую-
щие этим ребрам слагаемые lj (а) и Z/ (л — ос) дают в сум-
ме нуль. То же справедливо для слагаемых, соответствую-
щих двум другим ребрам, параллельным ab и cd.
Итак, четверка параллельных между собой ребер дает
нуль при вычислении инварианта / (Р). То же справедли-
во для двух других четверок параллельных ребер. Таким
образом, / (Р) = 0.
В качестве второго примера укажем более общий факт:
деповский инвариант любой призмы равен нулю. Действи-
тельно, если abed — боковая грань призмы Q, причем
*) Как показал Лебег [42], никакие два правильных много-
гранника (равновеликих между собой) не являются равносостав-
ленными, т. е. их деновские инварианты попарно различны (при
надлежащем выборе аддитивной функции / (.т), удовлетворяющей
условию / (л) = 0).
§ 13] РЕШЕНИЕ ТРЕТЬЕЙ ПРОБЛЕМЫ ГИЛЬБЕРТА 99
ребра ab и cd принадлежат основаниям, то величины дву-
гранных углов при этих ребрах равны соответственно а
ил — а. Отсюда, кап и выше, следует, что соответствую-
щие этим ребрам слагаемые If (а) и If (л — а) дают в сум-
ме нуль. Таким образом, при вычислении деновского ин-
варианта f (Q) слагаемые, соответствующие ребрам верх-
него и нижнего оснований, дают в сумме нуль. Остаются
боковые ребра. Пусть т — длина бокового ребра призмы
Q. Тогда
/ (0 = mf («Л + mf (а2) + . . . + mf (aj,
где а15 ос2,. . ., ап — величины двугранных углов при бо-
ковых ребрах рассматриваемой и-грапной призмы Q. Но
ах,. . ап — величины внутренних углов п-угольника,
являющегося перпендикулярным сечением призмы Q,
и потому
+ а2 + • . • + — (и — 2) л = 0.
В силу аддитивности функции f отсюда вытекает, что
/ («1) + / (а2) + . • • + / (а,.) - (п - 2) f (л) = 0.
Учитывая равенство / (л) = 0, мы и получаем / (0 = 0.
В рассмотренных примерах было дано прямое вычис-
ление деновских инвариантов. Впрочем, равенство
/ (Q) = 0 для любой призмы (и, в частности, параллеле-
пипеда) Q можно вывести из теоремы 19: так как любая
призма равносоставлена с некоторым прямоугольным па-
раллелепипедом А, то, по теореме 19, соотношение / (Q) Ф
/ (Л) не может иметь места, т. е. / (0 = f (Л) — 0.
Аналогичным образом теорема 19 может быть приме-
нена для вычисления деновского инварианта тетраэдра
Хилла. Так как этот тетраэдр (обозначим его через Я)
равносоставлен с некоторым кубом Л, то, по теореме 19,
соотношение / (Я) f (Л) не может иметь места, т. е.
/ (Я) = / (Л) = 0.
Наконец, приведем еще один пример многогранника,
у которого имеется отличный от нуля деповский инвари-
ант (при надлежащем выборе аддитивной функции /).
Именно, рассмотрим тетраэдр Я, у которого ребра ch, ас.
cd попарно ортогональны и имеют одинаковую длину I
(рис. 61). Если е — середина ребра ab, то длины отрезков
4*
100
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
ab, се и de соответственно равны Zj/2, Z/j/2 и Z|/3/)/2.
Следовательно, обозначая через а величину двугранного
угла при ребре ab, мы найдем из прямоугольного треуголь-
ника cde, что cos а = 1/|Л3. Далее, величины двугранных
углов при ребрах bd и ad также равны
а а, а величины двугранных углов при
А ребрах cb, ас и cd равны л/2.
«> На множестве М = {л, л/2, а} за-
дадим действительную функцию f, по-
, г ложив
/(п) = 0, /(-^) = 0, /(а) = 1.
При любом натуральном к мы имеем
Рис. 61. coska = ак/(\^3)к, где ак — целое число,
взаимно простое с числом 3 (доказа-
тельство этого факта аналогично доказательству леммы 9),
al 1
откуда вытекает, что число — = arccos - иррацио-
нально. Дословно так же, как и при доказательстве
теоремы 20, устанавливается аддитивность рас-
сматриваемой функции /.
Теперь имеем
ЦП) = 31 + 3Z/2 - / (и) = 3Z/2 ф 0.
Так как для куба А мы имеем / (Л) = 0, то, в силу теоремы
19, тетраэдр R не равносо-
ставлен с равновеликим ему
кубом.
Наконец, сравним между
собой рассмотренный тет
раэдр R и тетраэдр Хилла II
(рис. 62). Первый из них не
равносоставлен с равновели-
ким кубом, второй — равно-
составлен. Таким образом, рис 62.
тетраэдры 7? п Н н е рав-
носоставлены (и не равнодополняемы) между
собой. В то же время эти тетраэдры имеют конгруэнтные
основания (равнобедренный прямоугольный треугольник
ТЕОРЕМА ХАДВИГЕРА
101
£ *41
bed, катет которого имеет длину Z) и одинаковую высоту I.
Это и дает тот пример, нахождением которого интересо-
вался Гильберт (см. последний абзац его формулировки).
§ 14. Теорема Хадвпгера
Для обоснования результатов, изложенных в преды-
дущем параграфе, осталось доказать теорему 19. Этому и
посвящен настоящий параграф. В конце его эта теорема
излагается в той форме, которую ей первоначально при-
дал Хадвигер.
Л е м м а 10. Пусть / — аддитивная функция, задан-
ная на множестве М, и у—действительное число, не
принадлежащее этому множеству. Обозначим через М*
множество, получающееся из М добавлением к нему эле-
мента у. Тогда функцию / можно продолжить на множе-
ство М*, т. е. существует аддитивная функция, заданная
на множестве М* и совпадающая с / на множестве М.
Доказательство. Рассмотрим два случая.
Случай 1. Между элементами множества М* не
существует никакой зависимости
п1х1 4- п2х2 + . . . + щхк + пу = 0,
в которой коэффициент п при числе у был бы отличен от
нуля. Иначе говоря, число у ни в одну зависимость не
входит. В этом случае число / (у) никакими условиями не
связано, т. е. за / (у) можно принять любое действитель-
ное число.
Случай 2. Имеется зависимость, в которую входит
число у:
гцх^ -f- п2х2 + . . . + nkxh + пу = 0, п 0. (22)
Фиксируем какую-либо одну зависимость вида (22) и
с ее помощью определим число / (у) из соотношения
их/ (^i) + (х2) + . . . 4- щф (хк) 4- nf (у) = 0, (23)
т. е. положим
/(?)=- - • • • - -^Ж)-
Покажем, что таким путем мы получим аддитивную
функцию на множестве М*. В самом деле, рассмотрим
102
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ш
произвольную зависимость между элементами множест-
ва М*. Если число у в эту зависимость не входит, мы ус-
ловимся считать, что оно входит в эту зависимость с ко-
эффициентом 0. Точно так же, можно считать, что в рас-
сматриваемую зависимость входят все числа х±, . . ., хк
(возможно, с нулевыми коэффициентами). Наконец, в
нее могут входить некоторые числа уг, . . .,J(E М, отлич-
ные от хг, . . ., хк. Таким образом, рассматриваемую за-
висимость можно записать в виде
тгхг + . . . + nifcXfc + р±уг + . . . + piyi + ту = 0.
(24)
Мы должны показать, что зависимость с теми же коэффи-
циентами имеется и между значениями функции, т. е.
(^i) + • • • + mkf (хк) + pj (уг) + -•-• + Pif (yi) +
+ mf(y) = 0. (25)
Покажем это. Умножим соотношение (24) на п и вычтем
из него соотношение (22), умноженное на т:
(трг — mnL) хг + . . . + (ткп — тпк)хк +
+ Р1пУ1 + • • • + Piny 1 = 0. (26)
Это — зависимость между элементами множества М, и
потому
(трг — тт^) f (х^) + . . . + (ткп — тпк) f (хк) +
+ Pinf (У1) + . . • + ptnf (yt) ~ 0
(так как функция /, рассматриваемая на М, аддитивна).
Прибавив к этому соотношению равенство (23), умножен-
ное на т, найдем
(xj) + . . . + mknf (хк) +
+ Pinf (У1) + • • • + р inf (у i) + mnf (у) = 0.
Наконец, сокращая последнее равенство на число п=^ 0,
мы и получаем (25). Таким образом, функция /, рассмат-
риваемая на множестве М*, аддитивна.
Лемма 11. Пусть А = Рг + . . . + Рк и пусть
М — множество, содержащее число л и величины всех
двугранных углов всех многогранников А, Рг, . .., Рк-
Пусть, далее, f — аддитивная функция, заданная на мно-
§ 14]
ТЕОРЕМА ХАДВИГЕРА
103
жестве М и удовлетворяющая условию / (л) = 0. Тогда
деновские инварианты рассматриваемых многогранников
связаны соотношением
= f (PJ + ...+/ (рк). (27)
Доказательство. Рассмотрим все отрезки,
являющиеся ребрами многогранников А, Рг, . . Рк,
и отметим на этих отрезках все точки, являющиеся верши-
нами многогранников А, Рг, . . Рк, а также все точки,
в которых пересекаются ребра между собой. Мы получим
Рис. 63.
Рис. 64.
конечное число более мелких отрезков, которые будем
(следуя В. Ф. Кагану) называть звеньями. На рис. 63
изображено разбиение куба на многогранники (ср. рис.
64); ребро lk состоит из трех звеньев тг, т2, т3. Вообще,
каждое ребро каждого из многогранников А, Рг, . . ., Рк
состоит из одного или нескольких звеньев.
Рассмотрим некоторое звено, лежащее на одном из
ребер многогранника А, и пусть т — длина этого звена,
а а — величина соответствующего двугранного угла
многогранника А. Тогда аЕ А] и потому определено
число f (а). Произведение m-f (а) назовем весом рассмат-
риваемого звена в многограннике А. Так же определяют-
ся веса звеньев в многогранниках 7\, . . ., Рк.
Возьмем теперь все звенья, лежащие на ребрах много-
гранника А, найдем их веса в многограннике А и соста-
вим сумму всех этих весов. Нетрудно видеть, что эта
сумма равна деновскому инварианту f (Л). Действитель-
но, если, например, ребро 1г многогранника А состоит из
104
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ш
трех звеньев, имеющих длины тг, т2, т3 (см. рис. 63),
то каждому звену mlt т2, т3, а также ребру I соответст-
вует в многограннике А один и тот же двугранный угол
ах, и потому сумма весов звеньев т1, т2, т3 равна
mif (“1) + (ai) + msf («i) = (™i + m2 + m3)f (aj =
= У («i).
Точно так же сумма весов всех звеньев, из которых сос-
тоит ребро 12 многогранника А, равна l2f (а2), где а2 —
величина двугранного угла при этом ребре, и т. д. Поэто-
му сумма весов всех звеньев, расположенных на ребрах
многогранника А, равна деповскому инварианту / (Л)
многогранника А.
Аналогично, деповский инвариант каждого из мно-
гогранников Р, равен сумме весов (в многограннике Р,)
всех звеньев, расположенных на его ребрах.
Для вычисления суммы, стоящей в правой части соот-
ношения (27), нужно взять сумму весов всех звеньев, по
всем многогранникам Р1У . . ., Рк. Найдем, с каким коэф-
фициентом будет входить в эту сумму некоторое звено т.
Обозначим величины всех тех двугранных углов мно-
гогранников Р1г . . ., Рк, которые примыкают к звену
т, через ух, . . ., у8(эти числа содержатся в множестве
М). Тогда вес рассматриваемого звена в многограннике
с двугранным углом равен mf (yj); вес его в многогран-
нике с двугранным углом у2 равен тп/ (у2) и т. д. Таким
образом, сумма весов звена тп по всем тем многогранникам
Рг, . . ., Pk, которые примыкают к этому звену, равна
mf (Т1) + mf (Тг) + • • • + mf (ys). (28)
Все звенья можно разбить на три группы.
1. Звенья, которые целиком (кроме, может быть,
концов) расположены внутри многогранника А. Если т
есть такое звено и если каждый из примыкающих к этому
звену многогранников Рг, . . ., Рц содержит звено иг на
одном из своих ребер, то двугранные углы примы-
кающих к звену тп многогранников образуют в сумме
полпый угол (рис. 65; па этом чертеже, как и на следую-
щих, изображено сечение многогранника А и многогран-
ников, примыкающих к отрезку тп, плоскостью, перпен-
дикулярной звену гп; само звено т изображено одной точ-
§ 14]
ТЕОРЕМА ХАДВИГЕРА
105
кой г). Таким образом, в этом случае Ti + . . . + у,
= 2л, т. е.
Vi + • • • + ь — 2л = 0.
Это есть зависимость между элементами множества М,
и потому, в силу аддитивно-
сти функции /, мы имеем
/ (Vi) + • • • + / (у,) -
- 2/ (л) = 0,
т. е. /(Т1) + . . •+/(?.) =0
(в силу равенства / (л) =
= 0). Таким образом, в
этом случае выражение (28)
обращается в нуль.
Если же т есть звено,
расположенноевнутри много-
гранника А, по один *) из
многогранников Ри . . ., Рк,
примыкающих к отрезку т, содержит т внутри ка-
кой-либо своей грани, то двугранные углы остальных
примыкающих к отрезку т многогранников составляют
развернутый угол (рис. 66), т. е. yi + . . . + ys = л.
Отсюда, как и выше, вытекает, что выражение (28) об-
ращается в нуль.
Таким образом, звенья, расположенные внутри
многогранника А, можно при вычислении правой части
равенства (27) не учитывать (для них сумма весов равна
нулю).
2. Звенья, расположенные на гранях многогранника
А, но не на его ребрах. В этом случае у1 + . . . + у8 = л
(рис. 67), и выражение (28), как и в предыдущем случае,
обращается в нуль.
3. Остается рассмотреть звенья, лежащие на ребрах
многогранника А. В этом случае сумма у2 + . . . + у8
*) Если два многогранника, примыкающие к отрезку т,
не содержат гп на своих ребрах, т. е. если отрезок т лежит внутри
граней двух примыкающих друг к другу многогранников, то
только эти два многогранника и примыкают к отрезку т, так что
этот отрезок пе лежит ни на одном ребре многогранников Ръ . . .
. . Рк и потому не является звеном.
106
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
равна а или а — л, где а — величина двугранного угла
многогранника А (рис. 68). В обоих случаях имеем
/(Ti)+ •..+/(?.) =/(а).
и выражение (28) оказывается равным mf (а), т. е. весу
рассматриваемого звена в многограннике А. Итак, сумма,
Рис. 67,
Рис. 66.
Рис. 68.
стоящая в (27) справа, равна сумме весов всех звеньев
многогранника А, т. е. равна деповскому инварианту
/ И).
Доказательство те о’р е м ы 19. Пусть А
и В равносоставлены:
А = л +. . . + Л, В = Qy 4- . . . + <?ft;
Pi == Qii • • 1 Pk == Qk-
ТЕОРЕМА ХАДВИГЕРА
107
§ 141
Согласно лемме 10, аддитивную функцию f, заданную на
множестве М (см. формулировку теоремы 19), можно,
добавляя к множеству М одно за другим новые числа,
продолжить на множество М', содержащее множество М
и величины всех двугранных углов всех многогранников
Р1, . . ., Pk (у конгруэнтных им многогранников Qlt . . .
. . Qk величины двугранных углов те же). В силу
леммы 11 мы имеем теперь
f И) = / (Л) + -..+/ (Рк),
= f (&) + ...+/ (&).
Далее, так как многогранники Pt и Q, конгруэнтны, то
у них длины ребер и величины двугранных углов соответ-
ственно одинаковы, и потому / (Р;) = / (Qi), i = 1, . . ., к.
Таким образом, / (Л) — / (В).
Доказанной теореме можно придать другую форму,
если воспользоваться понятиями, введенными в § 4.
Именно в этой форме было дано изложение теории равно-
составленности в работах Хадвигера ([21], [24], [26], [27]
и др.).
Т е о р е м а 21. Пусть / — аддитивная функция, за-
данная на всей числовой прямой R и удовлетворяющая
условию f (л) = 0. Тогда деновский инвариант f (А) явля-
ется аддитивным D-инвариантом, где D — группа всех
движений пространства R3.
Доказательство. Так как функция / опреде-
лена на множестве всех действительных чисел, то денов-
ский инвариант f (А) определен на множестве всех много-
гранников. Если А = Рг + . . . + Ph, то / (Л) = / (Рг) + - ..
... A- f (Pit) (лемма 11), т. е. функция / (Л) адди-
тивна. Наконец, /^-инвариантность этой функции оче-
видна: если Л = В, то длины ребер и величины двугран-
ных углов у многогранников Л и В соответственно.оди-
наковы, и потому / (Л) = / (В).
Следствие. Пусть / имеет тот же смысл, что
и в теореме 21. Для равносоставленности (а также для
равнодополняемости) многогранников А и В необходимо
выполнение равенства / (Л) = / (В).
Это непосредственно вытекает из предыдущей теоремы
(в силу теоремы 15, которая сохраняется, вместе с дока-
зательством, и для многогранников).
108
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
Покажем теперь, каким образом из этого следствия
может быть выведена теорема 20. Пусть f — какая-либо
функция Коши — Гамеля, которая удовлетворяет усло-
виям / (л) = 0, / (<р) = 1, где ср = arccos 1/а есть величина
двугранного угла правильного тетраэдра * *). Тогда / (л/2) =
= 0, и потому для куба А выполнено соотношение
/ (Л) = 0. В то же время для правильного тетраэдра В
мы имеем / (В) = bmf (q>) 7^ 0 (где т — длина ребра тет-
раэдра). Таким образом, / (Л) / (S) и, в силу приве-
денного выше следствия, многогранники Л и В не равно-
составлены и не равнодополиясмы.
Это доказательство, использующее результаты Хад-
вигера (теорема 21 и следствие из нее), идейно несколько
«чище», чем приведенное в предыдущем параграфе дока-
зательство теоремы 20, основанное на применении тео-
ремы 19. Эта идейная чистота состоит, например, в том,
что вместо деповских инвариантов, которые в предыдущем
параграфе определялись лишь для некоторых многогран-
ников (а именно тех, величины двугранных углов которых
принадлежат множеству М, на котором задана функция /),
здесь рассматриваются аддитивные D-инварианты, оп-
ределенные сразу па множестве всех многогранников.
Обстоятельство это немаловажно: оно позволит рассмат-
ривать деповские инварианты, как гомоморфизмы алгебры
многогранников (см. § 22). В то же время хадвигеровское
изложение, использующее функции Коши — Гамеля, су-
щественно опирается на аксиому выбора. «Конечный»
вариант этого изложения, основанный на применении
теоремы 19, свободен от применения аксиомы выбора (и
потому более элементарен). Таким образом, оба варианта
доказательства отличаются лишь алгебраическим оформ-
лением, а «геометрическое ядро» (в приведенном здесь
изложении) одинаково — оно состоит в применении лем-
мы 11.
Ф
*) Так как отношение — иррационально (лемма 9), то сущест-
вует рациональный базис числовой прямой R, содержащий числа
л и <р (см. стр. 30). Положим / (л) = 0, / (ср) = 1 и определим зна-
чения функции f на остальных элементах взятого базиса произволь-
но. В остальных точках числовой прямой (рационально выражаю-
щихся через элементы базиса) значения функции / однозначно опре-
делятся соотношением (6). Это и дает требуемую функцию.
§ 14] ТЕОРЕМА ХАДВИГЕРА Ю9
В заключение заметим, что в духе хадвигеровских
идей можно изложить решение третьей проблемы Гиль-
берта несколько иначе (не акцентируя внимание на не-
равносоставленности куба и правильного тетраэдра или
на существовании двух неравносоставленных тетраэдров
с конгруэнтными основаниями и одинаковыми высотами).
Рассмотрим ту же, что и выше, функцию Коши — Гамеля
f (х). Соответствующий деновский инвариант / (Л), оп-
ределенный на множестве всех многогранников, является,
согласно теореме 21, аддитивным D-инвариантом. При этом
/ (Р) = 0 для любого параллелепипеда (или призмы)
Р и f (В) 0, если В — правильный тетраэдр. Положим
теперь
v* (Л) = v (Л) + f (Л),
где v — объем. Функция и* (Л), определенная на множе-
стве всех многогранников, является аддитивным D-инва-
риантом. При этом для любого параллелепипеда (или
призмы) Р справедливо равенство v* (Р) = v (Р), тогда
как v* (В) v (В) для правильного тетраэдра В.
Итак, v* (Л) является отличным от v (Л) адди-
тивным D-инвариантом, удовлетворяющим условию
v* (Р) = v (Р) = abc,
где Р — прямоугольный параллелепипед с длинами ре-
бер а, Ъ, с. Иными словами, аксиомы (0), (у*) и формула
объема прямоугольного параллелепипеда не позво-
ляют однозначно построить функцию v (Л) (объем) на
множестве всех многогранников. А так как формула объ-
ема треугольной пирамиды вместе с аксиомами (Р), (у*)
однозначно определяет объем любого многогран-
ника (ср. рис. 56, 57), то формула объема треугольной
пирамиды не может быть выведена на основе формулы
объема прямоугольного параллелепипеда и аксиом (Р), (у*).
Иначе говоря, для вывода формулы объема треугольной
пирамиды необходимо привлечение «неэлементар-
ной» аксиомы (а). В частности, теорема о равенстве объ-
емов двух треугольных пирамид с конгруэнтными основа-
ниями и одинаковыми высотами не может быть
доказана на основе формулы объема прямоуголь-
ного параллелепипеда и аксиом (Р), (у*) (так как это —
единственное место в теории объемов многогранников,
где используется аксиома (а)).
110
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ш
§ 15. Условие Брикара
В 1896 году была опубликована работа Брикара [9],
в которой содержалось следующее утверждение:
Если многогранники А и В равносоставлены, то най-
дутся такие натуральные числа nt, п. и такое целое р, что
п±аЛ + . . . + nqaq = ?ггрг + . . . + «,(\ + рл, (29)
где <хх, . . а() — величины двугранных углов многогран-
ника А, а . . ., 0Г — величины двугранных углов мно-
гогранника В.
Это утверждение назовем условием Брика-
ра. В частности, если В — куб, то правая часть в (29)
имеет вид р'-л/2, где р' — целое (причем р’ 0, так как
левая часть в (29) положительна). Мы получаем (умножая
на 2, если нужно) следующий частный случай условия
Брикара:
Если многогранник А равносоставлен с кубом, то при
некоторых натуральных пг, . . ., nq, р справедливо соот-
ношение
тца^ + . . . + nQa9 = рл, (30)
где а1; . . ., aq — величины двугранных углов многогран-
ника А.
Из соотношения (30) сразу же вытекает теорема 20
(которая и была сформулирована в работе [9]). Таким
образом, работа Брикара, вышедшая за четыре года до
постановки проблемы Гильбертом, содержала формули-
ровку теоремы о неравпосоставленности правильного тет-
раэдра и куба! Однако данное Брикаром доказательство
оказалось ошибочным (видимо, именно в связи с этим
Гильберт эту работу не цитирует).
Проследим за ходом рассуждений Брикара. Допус-
тим, что многогранники А и В равносоставлены:
А = Л + . . . + Pk, B = Q1 + .. . + Qk;
Qi = i = i,. к,
где . . ., fи — некоторые движения. Как и при дока-
зательстве леммы 11, разобьем ребра всех многогранни-
ков на з в е н ь я. Допустим, что (измельчая, если нуж-
но, звенья) нам удалось пайти такое разбиение па звенья,
§ 15]
УСЛОВИЕ БРИКАРА
lit
которое инвариантно относительно движений /г (т. е. /f
переводит звенья многогранника Р, в звенья многогран-
ника Qi). Обозначим через 2 сумму величин двугранных
углов многогранников Plt . . ., Рк по всем звеньям (так
что если в многограннике Pt ребро с двугранным углом
а разбито, скажем, на пять звеньев, то в 2 войдет сла-
гаемое 5а). Если звено т лежит внутри многогранника
А или внутри некоторой его грани, то, как мы видели
при доказательстве леммы 11, сумма величин двугранных
углов многогранников Pt при этом звене равна 2л или л.
Если же звено т лежит на ребре I многогранника А, то
сумма величин двугранных углов многогранников Pt
при этом звене равна а или а — л, где а — величина
двугранного угла многогранника А прп звене т (т. е.
при ребре Z). Следовательно,
2 = пл + п^Пу + . . . + nqaq,
где п — целое, а пг, . . nq — натуральные числа (более
точно, nt есть число звеньев, на которые разбито ребро,
двугранный угол при котором имеет величину аг, так как
слагаемое а; или az — л получится от каждого звена,
лежащего па этом ребре).
Так как при отображении /г звенья многогранника Pt
переходят в звенья многогранника Qt, то сумма величин
двугранных углов многогранников Qlt . Qk по всем
звеньям также равна 2. Поэтому, как и выше,
2 = п'л + HjPj + . . . + HrPr,
где п' — целое, а пг, . . ., пг— натуральные числа.При-
равнивая найденные для 2 значения, мы и получаем
соотношение (29).
Итак, приведенное рассуждение содержит доказатель-
ство соотношения (29) в случае существования инвариант-
ного разбиения на звенья. Брикар ошибочно полагал, что
такое разбиение существует всегда, а это, как мы сейчас
увидим, неверно.
Рассмотрим два равносоставленных многогранника
А = Рг + Р2 + Р3 и В = + Q2 + Q3, изображенных
на рис. 69. Здесь Qt ~ (Р;), i = 1, 2, 3, где /1; /2 —
параллельные переносы, а /3 — винт (композиция пово-
рота на л/2 вокруг прямой ah и параллельного переноса
вдоль этой прямой). Многогранники Plt Р2, Р3 имеют об-
112
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
щее ребро ab, которое движениями /2, /3 переводится
соответственно в отрезки pq, тп, qr. Будем считать, что
длина ребра ab равна 1, а длина отрезка рт (обозначим
ее через £) является иррациональным числом, меньшим
единицы (например, £ = —1). Допустим, что сущест-
вует инвариантное разбиение на звенья, и обозначим
Рис. 69.
через W множество всех точек, являющихся концами
звеньев. Множество W конечно.
Будем обозначать через F (х) дробную часть числа х
(т. е. О F (ж) < 1 и х — F (ж) — целое). Нетрудно
показать, что при любом натуральном к точка тк отрезка
pq, находящаяся на расстоянии F (&£) от р, принадлежит
множеству W. В самом деле, при к = 1 мы имеем F (к%) —
— F (£) = т. е. точка тг совпадает с тп потому при-
надлежит W. Пусть уже доказано, что тк GE W. Тогда
= Д1 (тк) СЕ W и потому п1с — /2 (7г/с) GE W. Точка
пк находится от р на расстоянии F (&£) + £. Если F (к%) 4-
+ £ < 1, то F (Arg) + £ = F ((к + 1) £), т. е. пк совпа-
дает с тк+1 и потому тк+1 GE W. Если же F (&£) + £ > 1,
то точка пк лежит на отрезке qr и находится от q на рас-
стоянии F (kt) + £ — 1 = F ((к -|- 1) £). Но тогда точка
fitfs1 (ify)), принадлежащая И7, находится от р на расстоянии
F ((к + 1) £), т. е. совпадает с тк+1. Следовательно, и в
этом случае тк+1 GE W.
Таким образом, все точки тк, к = 1, 2, . . ., принад-
лежат W. Но ввиду иррациональности числа £ все числа
F (А£), к = 1, 2, . . ., различны, т. е. все точки тк,
$ 15]
УСЛОВИЕ БРИКАРА
113
к = 1, 2, . . ., различны, и потому множество Wдолжно
быть бесконечным. Полученное противоречие и
доказывает, что инвариантного (относительно движений
/1, /г, /з) разбиения на звенья не существует.
Итак, предложенное Брикаром доказательство содер-
жит невосполнимый пробел. Однако, высказанное им
утверждение все же справедливо (это было установлено
еще Деном [13]). Для доказательства положим
М = {ап . . ., а,г, рп . . ., рг, л}.
Каждая зависимость между элементами множества М
имеет вид
+ . . . + гйая + + . . . + srpr = tn,
где rt, Sj, t — рациональные числа, среди которых име-
ются отличные от нуля. Эту зависимость можно записать
в виде уравнения
ГЛ + . . . + rqxq + + . . . + sryr = tn,
имеющего решение xt = at, y} =P>. Система всех таких
уравнений совместна: она имеет решение xt = at, у} = р,.
Из теории линейных уравнений следует, что эту систему
(состоящую из бесконечного числа уравнений) можно
разрешить относительно некоторых неизвестных, т. е.
она эквивалентна системе, которую (изменив, если нужно,
нумерацию неизвестных) можно записать в виде
, g т
Xi = <1цХ] S ^аУ] 4" cin> i = 1,..., X;
j=x+i i=H+i
G r ,
Уг — OijXj -[ 2 ^]У1 4" cint i = 1, . . . , |X,
j=X-H j=44-i
где Gtj, bi}, ct, а'ц, c\ — некоторые рациональные
числа, a a?x+1, . . ., xq, У\>.+1,..., уT — «свободные» неизвест-
ные. Иначе говоря, между элементами множества М име-
ются зависимости
. q т .
«1 = Jj + Ci11’ i = 1, -.., X;
j=x+i J=M-1 (31)
G r ,
Pi = У| dijaj Ч" 3 4~ Cin’ i = 1, • • • ,
j=X+i i-y+l
114
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
причем все остальные зависимости являются следствием
этих.
Отсюда следует, что функция /, заданная на М, в том
и только в том случае аддитивна, если выполняются соот-
ношения
/(ф) = 2 ««/(«;)+ 2 М(Рз) + с;/(л),
3=М-1 3=14-1
г 1 = (32)
/(Pi) = S ау/(а,)+ 2 Ьу/(Р;)+ ci/(n),
з=*+1 з=н-1
i = 1,. .., р.
Предположим теперь, что К < q. Фиксируем некоторое
число v = X + 1, . . д и положим
/ К) = 1;
/ (а7) = 0 при отличных от v индексах / = X + 1, . . q;
/ (Р;) = 0 при / = р + 1, . . ., г; f (л) = 0.
Определив остальные числа / (а(), / (Р,) из (32):
/ (и0 — i = 1, ..X; /(Pi) = fltv, i = 1, • • p,
мы получаем на множестве М аддитивную функцию,
удовлетворяющую условию / (л) = 0. Теперь, обозначая
через Ц длины ребер многогранника А, а через I] — дли-
ны ребер многогранника В, найдем деповские инварианты
/ (Л) и / (5):
/ (Л) = hf (oj) . -f- lqf (aq) = Zitzjv + ... + Zxaxv + Zv,
/ (-®) = Zi/ (pl) -|- lrf (fir) — Zifliv + .. - + Zpa^v
Так как A В, to f (Л) = f (В) (теорема 19), т. e.
X [Л
^1 ^i^iv ’ УI ==— О*
i=i i==i
Это соотношение имеет место для любого v = X + 1, - - •
. . д. Аналогично,
1 р',
— 2 1 Av + S' 9, v — р + 1, ..., г.
i=l i=l
§ lej
ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ
115
Выберем теперь положительные рациональные числа
Ир . тк, т\, . . т~'., настолько близкие к llt . . ., Zx,
Zu . . Zji, что числа
X (Л
2 m — 2 = — mv, v = X + 1, ..q;
i=l
и , (33)
— 2 m Av + 2 Miv = — V == p + 1, . . Г,
i=l i 1
отрицательны. Иначе говоря, все числа wzlt . . т,.,
т'г, . . тг положительны и рациональны. Из (31) и
(33) получаем
<з г
2 — 2 —
i=l i=L
Х а г
= 2 2 fliiai + 3 + —
К-1 3 ^+1 з'=Р+1
<1 ( У' 11
I CCV ( 2 2
v=X+l vi=i i=i
H ,, 4 r , , x
— 2 тЦ 2 ячаз + 3 Mi + c‘n)—
i=i j=x+i M-i
— 3 ₽v( 2 rn^i» — 2 ”&) = ( 2 m<ci — 3 m'iC^n.
V=^+1 xi=l 1=1 xi=l i=l
Так как числа тг, т\ положительны и рациональны
(ачисласг, с\ рациональны), то, освобождаясь от знамена-
телей, мы получаем соотношение вида (29), чем и завер-
шается доказательство условия Брикара.
Из приведенного доказательства видно, что это усло-
вие вытекает из теоремы 19, т. е. является следствием
деновских условий равносоставленности.
§ 16. Эквивалентность методов разбиения и дополнения
В § 7 мы видели, что для многоугольников (в евклидо-
вой плоскости) методы разбиения и дополнения эквива-
лентны, т. е. равносоставленность и равнодополняемость
означают в этом случае одно и то же. Доказательство это-
го факта состояло из двух частей. То, что из равносостав-
116 РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. 111
ленности двух многоугольников вытекает их равнодонол-
няемость (теорема И), как мы видели, сохраняется в
различных G-геометриях; сохраняется этот факт, вместе с
доказательством, и для многогранников в трех-
мерном (или и-мерпом) пространстве. Доказательство об-
ратного утверждения (из равнодополняемости двух мно-
гоугольников вытекает их равносоставленность), приве-
денное в § 7, существенно опиралось на теорему Бойяи —
Гервина о равносоставленности любых двух равнове-
ликих многоугольников.
Таким образом, если аналог теоремы Бойяи—Гервина
(т. е. эквивалентность равновеликости и равносоставлен-
ности) в некоторой геометрии места не имеет, то вопрос
об эквивалентности методов разбиения и дополнения не
решается столь же просто, как в § 7, а требует допол-
нительного исследования *).
Так, в неархимедовой геометрии (§ 8), где нет аналога
теоремы Бойяи—Гервина, методы разбиения и дополне-
ния не эквивалентны (треугольники на рис. 33 равнове-
лики и, следовательно, по теореме 10с, равнодополняемы,
но равносоставленными они не являются). Несколько
похожая ситуация имеет место для многогранников в трех-
*) В работе Хадвигера [25] рассматривается произвольная
кристаллографическая группа G, т. е. дискретная группа движений
пространства Вп, обладающая ограниченной фундаменталь-
ной областью. В этих условиях также доказывается экви-
валентность методов разбиения и дополнения, но. схема рассужде-
ний несколько иная. Именно, Хадвигер строит некоторую систему
аддитивных G-инвариаптов и доказывает, что выполнение равенств
Фа (Л) = фа (В) для всех инвариантов фа построенной системы явля-
ется необходимым и достаточным условием G-
равносоставленности многогранников А и В. Если теперь много-
гранники А и В являются G-равнодополняемыми, то, по теореме 15,
Ф (Л) = ф (В) для любого аддитивного G-ипварианта ф, и по-
тому, в силу сказанного выше, А ~ В.
G
Хадвигеровские инварианты фа для кристаллографической
группы G строятся следующим образом. Если Л — произвольный
многогранник и а е Rn, то через va (Л) обозначается отношение
v (А П S)/v (S), где v — обычный объем, aS- достаточно малый
шар с центром а (это отношение не зависит от радиуса шара, если он
достаточно мал). Далее,
geG
(в этой сумме отлично от нуля лишь конечное число слагаемых).
§ 161 ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ 117
мерном пространстве: изложенное выше решение третьей
проблемы Гильберта показывает, что равновеликость
и равносоставленность — неэквивалентные по-
нятия для многогранников. Однако, в отличие от неар-
химедовой геометрии, равносоставленность и равнодопол-
няемость являются для многогранников эквивалент-
ными понятиями. Этот факт, установленный Сид-
лером [50], и является предметом рассмотрения в этом
параграфе.
Первоначальное доказательство, принадлежащее Сид-
леру, было обобщено Хадвигером па случай тг-мерного
евклидова пространства [22], [28]. Впоследствии совер-
шенно иное доказательство было найдено Зылевым [59].
Оно более формально, но его достоинствами являются
краткость и большая общность получаемого результата.
Это доказательство (в несколько измененной форме) мы
и приведем.
Лемма 12. Пусть v (Л) > v (В), где А, В CZ Вп-
Тогда существует такое разложение А — М + N, что
М ~ В.
т
Доказательство. Положим е = у (у (Л) —
—v (В)). Возьмем некоторый кубильяж и обозначим через
Q объединение всех его кубов, имеющих общие точки с
многогранником В, а через Р — объединение кубов того
же кубильяжа, содержащихся в Л. Если выбранный ку-
бильяж был достаточно мелким, то выполнены неравен-
ства v (0 — v (В) < е, v (Л) — v (Р) < е. Следователь-
но, v (Q) < v (Р), т. е. многогранник Р составлен из
большего числа кубов рассматриваемого кубилья-
жа, чем Q. Пусть К±, . . ., Kt — кубы, составляющие Q,
т. е. Q = К1 + . . . + Kt. Пусть, далее, . . ., Lt —
какие-либо (попарно различные) кубы взятого кубилья-
жа, для которых ТЛ 4- . . . + Lt CZ Р CZ Л. Пусть, на-
конец, ft — параллельный перепое, переводящий куб
Kt в L,. Положив Ut = В Q Kt, Vt = (Ut), M =
= Fj -|- . . . + Vt, мы найдем
В = В п + - - - + Kt) = их + ... + ut ~
т
~ Vi + . . . + Vi = М cz а.
т
118
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
Остается за N принять дополнение многогранника М в
Л, т. е. N = А \ М.
Теорема 22 (см. [22]). Пусть G — группа движе-
ний пространства Rn, содержащая все параллельные пе-
реносы. Два многогранника в R" тогда и только тогда
G-равнодополняемы, когда они G-равносоставлены.
Для доказательства (которое мы изложим, следуя
идеям работы [59]) понадобится следующая
Лемма 13. Пусть А Pi Т" • • « -Ь Рк R 4-
G
+ Vi + • • + Сь причем Pt — Qt, i = 1, . . ., к, и
G
2н {P к) < и (Л). Тогда существуют такие многогранники
ЛЧ Р<1), . . ., Р&, что
Л(1) + рп) + ... + в + С1 + ... + (34)
Л(1) ~ Л, Р<Д ., Ж ~ Qkl. (35)
G G G
Доказательство. Пусть f EEG — такое дви-
жение, что
/(£ + & + ... + <2,) - Л + Рг + . . . + Рк. (36)
Положим / {Qk) Г) Pt = Ui, Vi = Pt \ Up, тогда
Pt = Ui + Vi, i = 1, . . „к. (37)
Мы имеем
и (U, + . . . + Uk) = и (f (Qk) П {Pi + • • - + Pk)) <
< v {f Ш » {Qk) = » {Ph) < V (Л) - v (Pk) =
= V (Л) -v{i (Q,)) < V (Л \ f {Q,.)).
Следовательно, в силу леммы 12, существуют (поскольку
Т CZ G) такие многогранники Wt — Ut, . . ., ~ Uh и
G G
N, что
4 \ f Ш = N + W. + . . . + Wk,
и потому
A = {f {Qk) (]A)+A\f (Qk) =
= (f {Qh) П A) + N + Wk + +
(38)
§ 16]
ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ
119
Мы имеем
/ = / (&) А и + Л + • • - + Р.) =
= (/ «М Г\ A)+ (f (&) п Л) + • • • + (/ (&) A PJ =
= (/ (&) А л) + . + ик,
и потому, в силу (37), (38),
л+Л + --- + Л=(/ША^) + ^ + и/1 + ---
. . . + Wk + иг + . • • + ик + F, + . . . + 7r =
= f (<2r) + N+ Vr + • • • + Ffc + . + Wk.
Таким образом, положив
Л(1)= N + Vk + wk, p?’ = Vx + wlf..., 4°!= v^+w^,
мы получим
Л + Px +... + Pr = /(Cr) + л(1) + P<n + ... + P&,
и потому, согласно (36),
f(B + <21 +... + <2r) = л(1) + р^ + ... + Р& + f(Qk).
Из этого вытекает, что
f(B + Q. + ... + Cr-x) = Л(1) + Pxt. u) + - - - + Р&,
т. e. соотношение (34) справедливо. Далее,
JP^ = ri + Tyi~Fi + ^i = Pi~<2iI 1 = 1, ..., fc-1;
G . G
A = (f (<2r) A A) + N + wr + • • + wk ~
~ tf (&) A A) + N +-ur + . . . +GUk =
= N + а (&)АЛ) + (/ (&)АЛ) + ... + (/ (Cr) APr) =
= N + (/ (&) A (A + Pl + • • • + pfc)) =
= N + f (&) ~ W + Pr =
= N + Uk + П ~ N + + Fr = Ла),
G
t. e. соотношения (35) также выполнены.
Доказательство теоремы 22. Если мно-
гогранники G-равносоставлены, то они G-равнодополня-
емы (ср. теорему 11). Обратно, пусть многогранники А и
120
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ III
В являются G-равнодополняемыми, т. е. существуют та-
кие многогранники Рк, Qi, . . Qk, что Pt Qi и
G
А + Pt + . . . + Рк В + Q. + . . . + Qk.
G
Измельчив, если нудою, многогранники Pt, Qt (и увели-
чив тем самым их число), мы можем добиться выпол-
нения неравенств 2v (Рг) < v (Л) для всех i = 1, . . ., к.
Применяя лемму 13, мы найдем, что существуют мно-
гогранники Л^1)., Р^\ . . P‘k-lf удовлетворяющие соот-
шениям (34), (35). При этом, по-прежнему, 2v (Pfl)) <
< v (ЛО)), i — 1, . . ., к — 1 (поскольку v (Л*1)) = v (Л),
V (Р?>) = V (Рг)).
К соотношению (34) снова применим лемму 13, в ре-
зультате чего получим такие многогранники Л(2), .
. . . , Рк12, что
Л<2) + р(2) + . + р(Д_ В + Q1 + . + Q* 2J
G
М2) ~ <?Ъ • • ~ ^(2) ~ ~ А.
G G G G
Продолжая таким образом, мы получим последова-
тельность соотношений
40) + р^+...+Р^_.+ . .. 4- Q^, А® ~ A(i 1).
G G
(39)
При / = к первое из соотношений (39) принимает вид
Лда В. Таким образом, учитывая второе соотношение
G
(39), находим
Л~Л(1)~Л(2)~...~Л«^Й,
G G G G G
и потому Л В.
G
Доказанная теорема *) имеет теоретико-множествен-
ный характер; единственное «евклидовое» место в приве-
*) Заметим, что доказательство использует неравенства для
объемов 2v (Pi) <; v (Л), которые справедливы лишь постольку,
поскольку объем есть действительное число, а в поле
действительных чисел выполняется аксиома Архимеда. Как показы-
вают результаты § 8, аксиома Архимеда существенна для
справедливости теоремы 22.
§ 16] ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ 121
денном рассуждении — доказательство леммы 12 (на ко-
торую мы опирались). Но лемма 12 — при замене соот-
ношения G ZD Т требованием транзитивности группы G —
остается справедливой (разумеется, с другим доказатель-
ством) в п-мерном эллиптическом и гиперболическом
пространствах, т. е. лемма 12 и теорема 22 справедливы в
следующих модификациях:
Лемма 12'. Пусть G — транзитивная группа дви-
жений в п-мерном (евклидовом, гиперболическом или эллип-
тическом) пространстве и А, В — многогранники, удов-
летворяющие услови'ю v (А) v (В). Тогда существует
такое разложение А = М + N, что М — В.
G
Теорема 22'. Пусть G — транзитивная группа
движений в п-мерном (евклидовом, гиперболическом или
эллиптическом) пространстве. Два многогранника в этом
пространстве тогда и только тогда G-равнодополняемы,
когда они G-равносоставлены.
Более того, требование транзитивности группы G мо-
жет быть ослаблено: достаточно потребовать, чтобы
группа G была почти транзитивной (для любых точек
а, Ь и любого е О существует такое движение / GE G,
что расстояние между точками а и / (Ь) меньше е). Дока-
зательство этих результатов В. Б. Зылева (т. е. доказа-
тельство леммы 12' для почти транзитивной группы G,
поскольку доказательства леммы 13 и теоремы 22 оста-
ются дословно теми же) сравнительно несложно, но мы
его опускаем.
Рассмотрим теперь некоторые леммы, которые состав-
ляют «технику» равносоставленности, развитую Сидле-
ром [50] и Хадвигером [22], [26], [28]. Мы выведем неко-
торые из них с помощью теоремы 22 (хотя первоначально
они были доказаны непосредственно и послужили Сид-
леру и Хадвигеру аппаратом для установления этой тео-
ремы).
Пусть А17 . . ., А— выпуклые множества в Нп.
Через At X ... X Ak будет обозначаться их сумма Мин-
ковского, т. е. множество всех точек вида + . . . + ак,
где aY ЕЕ ak ЕЕ Ak (имеются в виду вектор-
ные суммы «1 + . . . + щ., т. е. flj, . . ., ak рассматри-
ваются как элементы векторного пространства R").
Отметим, что при параллельных переносах миогогран-
122
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ill
ников Alt . . ., A/t сумма Минковского Л1 v . . . X Ак
также подвергается параллельному переносу. Многогран-
ник A CZ Rn будем называть к-призмой, если существует
такое разложение Rn = LY + . . . 4- пространства
Rn в прямую сумму подпространств и такие многогран-
ники Aj GZ Д, . - ., CZ Lk, каждый из которых имеет
положительную размерность, что А = X . - .
. . . X Ак. «Обычные» призмы являются 2-призмами в R3
(рис. 70). Многогранник, представляющий собой п-приз-
му в Rn, называется «-мерным параллелепипедом. Заме-
тим, что если к I, то каждая /с-призма является также
/-призмой.
Через Zfc обозначим множество всех тех «-мерных мно-
гогранников М CZ которые Г-равносоставлены с мно-
гогранниками вида Мг 4- . . . + Ma, где s — какое-либо
натуральное число, а многогранники Mlt . . ., Ms явля-
ются Л-призмами.
Пусть теперь ег, . . .,ек — линейно независимые век-
торы пространства R”. Через [е17 . . ., ек] будем обозна-
чать fc-мерный симплекс с вершинами
бо, ~ + ei, ^2 = Ьо 4- ег + е2, - . .
• • •> Ьк = Ьо . 4- ек (40)
(рис. 71); здесь Ьо — произвольная точка пространства
Rn, которую будем считать начальной вершиной симплек-
са [ех, . . ., efe]. При изменении начальной вершины сим-
плекс [вл, . . ek] подвергается параллельному переносу.
ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ
123
§ 16]
Каждая точка х симплекса [ех, . . ej с начальной
вершиной Ьо (см. (40)) однозначно записывается в виде
х = (1 — Хх — ... — Xj;)b0 + ХхЬх + . . . + Xfcfefc,
где Хх, . . ., Х^ — неотрицательные числа, удовлетворяю-
щие условию Хг + . . . + Хь 1. Иначе говоря,
х = Ьо + + . . . + хкек, (41)
где
=* Xj + . . . + X/f, х2 = Х2 + . . . + Хк, ...
• • •> %к-1 = “F хк = ^к-
Таким образом, каждая точка х (Е= [ех, . . ., e/J однозначно
записывается в виде (41), где координаты т15 . . ., хк свя-
заны неравенствами
1 > ж2 > . . . > > 0.
Пусть теперь Мг, . . ., Мр — попарно не имеющие
общих внутренних точек многогранники, каждый из кото-
рых У-конгруэптен данному многограннику М; в этом
случае многогранник Мг + . . . + Мр условимся обозна-
чать через р-М. Далее, через Х7И (без точки!) будем
обозначать многогранник, гомотетичный многограннику
М с коэффициентом гомотетии X. Очевидно, что X [ех, . . .
. . ., еД = [Хех, . . ., ХеД.
Лемма 14. Для любых положительных X, р спра-
ведливо соотношение
(X + R) [«1, •en] ~Х [ех, ..., еп] +
т
I
+ И [ех, ..., е„] + 2 X [ех, ..., et] X р [е<+1, ..еп].
Доказательство. Симплекс (X + р) [ех, . . .
. . ., еп] состоит из точек
х — Ьо хгег + • • + хпеп, (42)
удовлетворяющих условию X + р > «х > . . . > хп > 0.
Обозначим через Mt (0 i п) многогранник, состоя-
щий из точек (42), для которых
X + р > «1 > • - . > «г > р > »i+1 > . . . > хп > 0.
(43)
124
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ш
Многогранники Мо, Mlt . . Мп попарно не имеют
общих внутренних точек, а их объединение совпадает с
(X + р) ten • • •> enL т- е-
(X + р) [еп . . еп] = Мо + . + Мп.
Многогранник Мо состоит из точек (42), для которых
р «I'l хп О,
он представляет собой симплекс [реп . . ., реп] = р [еп...
. . ., еп] с начальной вершиной Ьо. Многогранник Мп сос-
тоит из точек (42), для которых X + р > . .^хп^
> р; он представляет собой симплекс [Хсц . . Хеп] =
= X [ег, . . ., еп] (с начальной вершиной Ьо + рег + . . .
. . . + реп). Наконец, если 0 < i <Z п, то каждая точка
х £ Mt представляется в виде аг + а2> где
== -|- х^с^ -|- . . . -|- Xi@i, Xi+i€i+i -f- . . . хпеп,
Рис. 72.
ясно, что Mt — Аг X Bt, где At — симплекс [Хег, . . .
. . ., Хег] = X [еп . . ., ег] с начальной вершиной Ьо +
+ pei + . . . + рег, a Bi — симплекс [рег+1, . . ., реп] =
= р [ег+1, . . ., еп] с начальной вершиной о. Это и дает
требуемое разложение. (Для иллюстрации случай п =3
изображен на рис. 72.)
§ 16]
ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ
125
Лемма 15. Для любого многогранника М CZ Вп и
любых положительных Z, ц справедливо соотношение
(X 4- р) М — ХМ + рТИ + Р, где Р GE Z2.
т
Доказательство. Пусть М — произвольный
n-мерный многогранник и пусть М = By 4- • • +
где By, . . ., Bk — симплексы. В силу леммы 14,
(X + р) Bj — XBj + [iBj + Рj,
т
Следовательно,
(X + р) М ~ ХВу + .. . + хвк
т
Ру ЕЕ Z2; j = 1,
. к.
4~ цВу + . . . + +
+ Pl • • 4" Plr — ^М 4" P^f Р'
т
где Р = Ру + ... + Рк е z2.
Лемма 16. Для любого многогранника М CZ Вп и
любого натурального р справедливо соотношение
рМ~р-М + Р, P^Z2.
т
Доказательство. В силу леммы 15, имеем
рМ ~ М 4- (р — 1) М + Р, где Р е Z2. Далее идет
т
очевидная индукция.
Пусть теперь П CZ Вп — бесконечная призма, пред-
ставляющая собой сумму Минковского М X Z, где М —
некоторый (п — 1)-мерный многогранник, а I — пря-
мая, не лежащая в его гиперплоскости. Пусть, далее,
W — полоса, ограниченная в Вп двумя параллельными
гиперплоскостями Г1; Г2, каждая из которых пересекается
с Z в одной точке. Тогда II (4 W есть призма (наклонная)
в R'1, многогранники П (~) Гх и П Г2 — ее основания,
а длина отрезка Z (~| W — ее боковое ребро.
Лемма 17. Пусть П = М X Z — бесконечная приз-
ма и Ау = П Р| Wy, А2 = П П W2 — две призмы, вы-
секаемые из нее полосами Wy, W2. Если эти призмы имеют
одинаковое боковое ребро, то они Т-равносоставлены.
Доказательство. Мы можем предполагать (при-
менив, если нужно, параллельный перенос в направлении
Z), что Ау Р| А2 = 0. Обозначим через В часть бесконеч-
ной призмы П между Ау и А2. Многогранники Ау В
и Л2 4- В являются Т-конгруэнтными (ср. рис. 21), и
126
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
потому Xj и А2 являются У-равнодополняемыми:
Аг + (А2 + В) = А2 + (А, + В).
Доказательство,
параллелепипед. Фиксируем в
Рис. 73.
Следовательно, многогранники Л1 и А2 являются У-равно-
составленными (теорема 22).
Лемма 18. Равновеликие многогранники Л, В Zn
в Выявляются Т-равносоставленными.
Пусть А — произвольный
Вп прямоугольную систему
координат хг ,. . ., хп.
Возьмем какое-либо ребро
/ параллелепипеда А, не
параллельное гиперплос-
кости хг = 0. Согласно
лемме 17 параллелепипед
А является , У-равносос-
тавленным с параллеле-
пипедом Alt у которого
по-прежнему У является
боковым ребром, а основа-
ния параллельны гипер-
плоскости^ = 0 (рис. 73).
При переходе от А к 4,
несущие гиперплоскости
всех (п — 1)-мерных граней, кроме оснований, остаются
неизменными.
Теперь можно заменить Aj параллелепипедом’ А2, ко-
торый У-равносоставлен с Аг (и с А) и имеет не только
грань, параллельную гиперплоскости х± = 0, но и грань,
параллельную гиперплоскости х2 = 0. Продолжая та-
ким образом, мы получим У-равносоставленный с А парал-
лелепипед Ап, у которого все грани параллельны коорди-
натным гиперплоскостям, т. е. ребра параллельны осям
координат.
Пусть 1г 1п — длины ребер параллелепипеда Ап,
параллельных осям хг ,. . ., хп. В силу леммы Зу мы мо-
жем заменить Ап таким У-равносоставленным с ним парал-
лелепипедом, у которого ребра, параллельные осям
х3 ,. . ., хп, имеют по-прежнему длины Zs,. . ., Zn, а реб-
ра, параллельные осям xlt х2, имеют длины 1 и 1г12 (рис. 74).
Затем можно тем же приемом сделать равными одинпце
длины всех ребер, параллельных осям х17 х2, . . ., жп_г
§ 16]
ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ
127
Итак, люоой параллелепипед 7-равносоставлен с прямо
угольным параллелепипедом, основанием которого слу
жит единичный куо, лежа-
щий в гиперплоскости
хп = 0.
Если теперь М Zn,
то М — Мг Мк,
т
где Мг ,. . ., Mk — парал-
лелепипеды. Заменяя их
Т'-равносоставленными с
ними прямоугольными па-
раллелепипедами Рг ,. . .
...,Рк, у которых осно-
Рис. 74.
ваниями являются еди-
ничные кубы гиперплоскости хп — 0, а затем складывая
эти параллелепипеды «стопкой» (рис. 75), мы получаем
параллелепипед Р = Р± 4- . . . 4- Рц, который7-равно-
составлен с М. Основанием
Рис. 75.
Доказательств
М — М1 4- ... 4" Мк, где
т
параллелепипеда Р служит
единичный куб гиперплоско-
сти хп = 0, а высота его рав-
на v (М). Таким образом,
два равновеликих многогран-
ника М, N ЕЕ Zn являются
Т’-равносоставленными с од-
ним и тем же параллелепи-
педом Р, и потому М — N.
т
Л е м м а 19. Равновеликие
многогранники М, N G= Z2 в
Я3 равносоставлены.
о. Пусть М ge Z2, т. е.
Мг ,. . ., Mh — призмы. Каж-
дая призма равносоставлена (в силу леммы 17) с неко-
торой прямой призмой. Прямая призма разбивается
на несколько прямых треугольных призм (рис. 24), а пря-
мая треугольная призма равносоставлена с прямоуголь-
ным параллелепипедом (рис. 76; ср. рис. 28). Таким обра-
зом, М ~ Р, где Р ge Z3. Остается применить лемму 18.
Леммы 16 и 19 были применены Сидлером [50] для до-
казательства того, что равнодополняемые трехмерные
128
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
многогранники равносоставлены. Приведем для сравнения
его доказательство. Пусть А и В равнодополняемы, т. е.
А + С + D, С ~D. (44)
Выберем натуральное число р, удовлетворяющее условию
p2v (4) > v (Л) + v (С). Тогда
v (рА) = p3v (А) > pv (Л) +
+ Pv (Q = v (р-А + р-С). (45)
Кроме того, согласно лемме 16,
рА ~ р-А + Р,
рВ ~ р-В +(?; P,Q^Z2. (46)
Из (45) и (46) вытекает, что
V (Р) > v (р-С), и потому, в силу
леммы 12, существуют многогран-
ники М, N, удовлетворяющие условиям
Р = М + N,
М ~ р-с.
(41)
Далее, из соотношения (46), в силу равенств v (рА) =
= v (рВ), v (р-А) = v (р-В), вытекает, что v (Р) = v (Q).
Таким образом, согласно лемме 19,
Р ~ Q. (48)
Из (44), (46) — (48) получаем
рА р • А -Т Р = р-А 4- М N ~ р• А р-С N —
= р-(А + С) + TV ~ р-(В + D) + N = р-В+
4- p-D -J- N р-В 4- р - С 4- 7V р-В 4~ М 4~
4- N = р-В 4- Р ~ р-В 4- Q ~ рВ.
Итак, рА и рВ равносоставлены, т. е. их можно раз-
бить на соответственно конгруэнтные части. Уменьшая по-
добно в р раз многогранники рА, рВ, а также части, на
которые они разбиты, мы найдем, что А — В.
В заключение рассмотрим вопрос, близкий к теме этого
параграфа и связанный с работой Зылева [60]. Обозначим
через Г группу, состоящую из всех гомотетий с положи-
тельными коэффициентами и всех параллельных переносов
пространства Вп. Пусть далее, G — некоторая группа аф-
финных преобразований пространства Нп, содержащая Г.
S 16] ЭКВИВАЛЕНТНОСТЬ МЕТОДОВ 129
При любых преобразованиях g ZE G многогранники
переходят в многогранники, и потому можно говорить о
G-равносоставленности и G-равнодополняемости много-
гранников в Rn. Теоремы 23, 24 принадлежат Зылеву [60].
Теорема 23. Пусть G — некоторая группа аф-
финных преобразований пространства Rn, содержащая Г.
Два многогранника А, В CZ Rn в том и только в том слу-
чае G-равнодополняемы, если они G-равносоставлены.
Доказательство. Прежде всего докажем ана-
лог леммы 12: для любых двух многогранников А, В CZ
CZ Rn существует такое разбиение А = М 4- N, что
М^В. В самом деле, пусть So, SY — такие шары, что
G
В, CZ А. Тогда существует гомотетия (или парал-
лельный перенос) g (ЕЕ Г CZ G, переводящая шар £0 в S±.
Таким образом, g (В) CZ А и остается положить М =
= g (В), N = А \М.
Теперь без изменений проходят рассуждения, про-
веденные при доказательстве леммы 13 и теоремы 22 (за
исключением того, что неравенства 2v (I*,) < v (Л) ста-
новятся ненужными).
Теорема 24. Обозначим через П группу всех подо-
бий в R3 (т. е. преобразований, представляющихся в виде
композиции гомотетии и движения). Любые два много-
гранника в R3 являются П-равносоставленными.
Доказательство. В силу леммы 16,
М^ЗМ — З-М + Ри М^2М~ 2-М + Q-,Pi,Q
пт пт
Таким образом, 3-717 + Рг — 2-М + Q, т. е. существуют
п
такие многогранники Р2, Р3, Q2, Q3, конгруэнтные М, что
(М + Р2 + Р3) + Р, ~ (Q2 + Q3) 4- Q.
п
Наконец, пусть А — куб. Если X 0 — такое число, что
к (Х0 = v (Л) 4~ v (Pi), toQ — А 4- Pi (лемма 19).
п D
Итак,
М 4- Pi 4- Р3 4- Ps ~ А 4- Рг 4- Q2 4- <23,
п
Р2 s Q2, р3 Qs,
т. е. многогранники М и Л являются П-равнодополняемы-
5 В. Г. Болтянский
130
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
ми, а потому и П-равносоставленпыми (теорема 23). Мы
видим, что любой многогранник П-равносоставлен с ку-
бом, а потому любые два многогранника И-равносостав-
лены.
Заметим, что на плоскости имеет место более сильное
утверждение: любые два многоугольника Г-равносоставле-
ны. Доказательство — то же, только Pt, Qt, Q будут здесь
параллелограммами, и вместо леммы 19 надо
воспользоваться тем фактом, что любые два параллело-
грамма Г-равносоставлепы (подвергая один из них гомо-
тетии, можно сделать их площади равными, после чего
по теореме 16, или по лемме 18, они станут Т’-равносостав-
ленными). Рис. 77 иллюстрирует Г-равносоставленность
треугольника и прямоугольника; одинаковыми цифрами
обозначены Г-конгруэитные многоугольники, а через £
обозначен положительный корень уравнения £а = £ + 1,
т. e.g = | (/5 + 1).
Являются ли Г-равносоставленными любые многогран-
ники в В3, неизвестно. Неизвестно также, справедлива ли
теорема 24 в Rn при п > 3.
§ 17. Теорема Дена — Сидлера
В 1965 году теория равносоставленности обогатилась
новым замечательным результатом: Сидлер [54] доказал, что
необходимое условие Дена (см. теорему 19) является так-
же и достаточным, т. е. для равносоставленности
двух равновеликих многогранников А и В необходимо и
§ 171
ТЕОРЕМА ДЕНА — СИДЛЕРА
131
достаточно равенство / (Л) = / (В) их деновских инвариан-
тов для каждой аддитивной функции f, удовлетворяю-
щей условию f (л) = 0. Этот результат можно назвать
теоремой Дена — Сидлера *).
В 1968 году Ессену [36] (см. также [38]) удалось, со-
хранив основные геометрические леммы Сидлера, су-
щественно упростить алгебраическую часть доказатель-
ства. Изложение доказательства Ессена и приводится в
этом параграфе.
Обозначим через Z* множество всех многогранников,
равносоставленных с кубами. В силу леммы 19, каждый
многогранник М GE Z2 равносоставлен с равновеликим ему
кубом, т. е. Z2 CZ Z*.
Лемма 20. Пусть М — пирамида с основанием
abed и вершиной о. Если ребра Ьс и ad перпендикулярны
плоскости oed, причем ( cd | =
= | od | и | Ьс | = 2 | ad |, то
М е £*
Доказательство.
Пусть k, I — середины ре-
бер оЪ и Ьс (рис. 78), a h —
точка, симметричная I отно-
сительно к. Тогда oh = lb =
—cl=da, т. е. /\hla получает-
ся из A oed параллельным
| ah | = | al | и потому ак | hl. Кроме того, отрезок
ак параллелен плоскости oed, и потому ак [ Ьс, т. е.
ак — перпендикуляр к плоскости оЬс. Таким образом,
при повороте на угол п вокруг прямой ак тетраэдр акЫ
переходит в тетраэдр akoh. Это означает, что пирамида М
равносоставлена спризмой ocdhla, и потому М (= Z*.
Для формулировки следующей леммы рассмотрим
функцию
w (ж) = 1 ---- - (49)
переносом. Следовательно,
•) В работе Николетти [44] имеются необходимые условия рав-
носоставленности многогранников, содержащие деновские условия
и, как полагал автор, ряд дальнейших условии, не сводящихся к де-
новским. Однако, так/как (но теореме Дена — Сидлера) деновские
условия являются также и достаточными, то условия Ни-
колетти эквивален т^н ы деновскпм.
5*
132
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ III
При х, у GE 10, 1[ обозначим через Т (х, у) тетраэдр
abed, у которого ребра ab, be, cd попарно перпендикуляр-
ны и имеют длины jfw (х), ~\fw(x) w (у), (у). В этом
тетраэдре величина двугранного угла при ребре ab равна
величине угла cbd (рис. 79), т. е. равна arctg l/]/rw(x),
а величина двугранного угла при ребре cd_________равна
arctg 1/]Аг (у). Так как векторы (1, 0, (у)) и
(— 1, (х), 0) соответственно ортогональны плоскостям
acd и abd (рис. 80), то величина двугранного угла при
ребре ad равна
arccos r --- г — = arccos у а у =
(ж) У1 4-w (У)
л .1
= -г- - arctg ,г-г-т
z У W (ху)
(см. (49)). Далее,
| ad | — У| ab Р + | Ьс |2 | cd |- =
= ]/ и? (ж) + w (ж) w (у) + w (у) = ]fw (ж?/), (50)
V(T(x, y))=4‘iabi'ibci’icdi=4“w;('7)w;(?y)=
= -|-(IP («г/) — w(x) — w(y)). (51)
S 17]
ТЕОРЕМА ДЕНА - СИДЛЕРА
133
Лемма 21. Для любых х, уг, у2 ЕЕ Ю, If справедливо
соотношение
Т (х, уг) + Т (ху±, у2) ~
Доказательство,
раэдры abc^ = Т (х, уг) и
abc2d2 = Т (х, у2) с общим
ребром ab; здесь Cybdx =
=^c2bd2 (величина этого угла
равна arctg 1/ргы? (х)). Так
как углы djCjd-z и d^d^ пря-
мые, то точки с15 d15 с2, d2
лежат на одной окружности с
центром в середине g отрезка
dxd2. Следовательно, точки
а, clf d±, с2, d2 лежат на одной
сфере S, центр h которой рас-
положен на перпендикуляре
к плоскости bdxd2,
чим через М, Р,
т (z, У2) + Т (ху2, У1). (52)
На рис. 81 изображены тет-
Рис. 81.
проведенном через точку
Q, R многогранники
Обозна-
abd1d2hpip2^
T(x,gd
Рис. 82.
ahp^Cyd^, djip^d^, ahd^ (рис. 82), где р2 — проекции
центра h на плоскости abd± и abd2. Тогда
М = Т (х, У1) + Р + Q + R. (53)
(Заметим, что при ином выборе чисел х, уъ у2 возможна
переброска слагаемых Р, Q в левую часть соотношения
(53); например, если точка g лежит внутри треугольника
134
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Ъс^!, причем отрезки и с232 не пересекаются, то
M + Q = Т (х, ух) + Р + /?;
характер дальнейших рассуждений от этого не меняется.)
Плоскость abc2 пересекает сферу S по окружности К,
имеющей центр рг. Так как точки а, с2, <4 лежат и на сфе-
ре «S', и в плоскости аЪс2, то они принадлежат окружно-
сти К:
Аналогично,
I = | РА | = | Pic2 |.
I Рга | = | Р2С1 | = | РЛ |-
Далее, так как отрезок gh параллелен плоскости abc2,
то g и h находятся на одинаковом расстоянии от этой
плоскости, a d2 — на вдвое большем расстоянии, т. е.
отрезки pji и c2d2 перпендикулярны плоскости abc2 и
| c2d2 | = 2 | pjh |. Аналогично, отрезки p2h и перпен-
дикулярны плоскости аЪсг и | c}dA | = 2|р2Л |. Следова-
тельно, Р GE Z*, Q ЕЕ Z* (лемма 20).
Наконец, займемся многогранником В. Пусть —
точка окружности К, диаметрально противоположная а.
Вписанные углы ае^ и ac2d± конгруэнтны (рис. 83), и
потому величина угла ае^ равна у2 = arctg 1/]/ ш (у2)
(рис. 81). Так как | adx | = (ху^ (см. (50)), то
I ^1 | = | adr | ctg у2 = yW (хУ1)-У^{у2).
Обозначим через q точку, симметричную а относительно
точки h (рис. 84). Тогда | e±q | = 2 | pji | = | c2d2 | =
= (у2). Итак, ребра adz, d1e1, exq попарно перпенди-
кулярны и имеют длины (ху^), Уw^xy-^uty^,
5 1?1
ТЕОРЁМА ДгЛа — СИДЛЕЁА
135
У'г (у?), т. е. тетраэдр ad^q есть Т (хуг, у2). Ясно, что
Т (ХУ1, Уг) = R + N, где N — пирамида djip^q. Так как
I Piei | = | Pi^i | (поскольку pj — центр окружности К),
то N ее Z* (лемма 20). Учитывая (53), получаем теперь
м + и ~ Т (х, У1) + Т (хУ1, у2) + Г; и, V е Z* (54)
(для получения этого соотношения, возможно, придется
переместить многогранники с помощью некоторых дви-
жений, чтобы слагаемые не имели общих внутренних то-
чек) .
Меняя роли индексов х и 2, находим аналогично
М + V ~ Т (х, у2) + Т (ху2, У1) + F'; U', V S Z*.
(55)
Из (54), (55) получаем
Т (х, У1) + Т (хУ1, у2) + V + U' ~ М + U + U' ~
~ Т (х, у2) + Т (ху2, У1) + V' + и. (56)
Заметим теперь, что многогранники, стоящие в левой
и правой частях соотношения (52), равновелики
(см. (51)). Поэтому, в силу (56), v (F + U') = v (V' + U).
Следовательно, многогранники V + U’ ее Z* и V' + U ее
Z* равносоставлены. Это означает, согласно (56), что
многогранники
Т (х, ух) + Т (хуъ у2) и Т (х, у2) + Т (ху2, уг)
равнодополняемы и потому, по теореме 22, равносостав-
лены.
Лемма 22. При z 0, у 0, z 0 справедливо
соотношение
хТ! х + у \ т / * + у у_ \ _
V* + У + z ’ * + у J ' У 4- У + г ’ х-I-у /
_ хт I т + г х 4- zT ( x+z г
+ У + 2 ’ X Z / ' \х -|- у Z ’ X + 3 j
Доказательство. Пусть в тетраэдре oabc реб-
ра оа, ob, ос попарно ортогональны и имеют длины ^yz,
j/zz, У хр. Плоскость, проходящая через ребро ос и
перпендикулярная ab, разбивает его на два тетраэдра
adoc и bdoc (рис. 85). Ребра bd, do, ос попарно перпепдику-
136
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. til
лярны и имеют длины
т/ z -if xyz лг--
х I/ —;— , г —i— , V -ЧЬ
г х+у [ ^+у г
Рис. 85.
откуда легко следует, что тетраэдр bdoc совпадает с
хТ ( ж У—, —v—- Тетраэдр же adoc совпадает с
\Я + У + z X + у )
уТ (—I, г-г-—J - Таким образом, тетраэдр оаЬс равен
левой части доказываемого соотношения. Для получения
правой части нужно тот же
тетраэдр oa.bc разбить на два
тетраэдра плоскостью, которая
проходит через ребро оЪ и пер-
пендикулярна ас.
Лемма 23. Пусть числа
L 1], С Е=Ю> зт/2[ удовлетворяют
условию £ -Т 1] -Т £ = л. Тогда
существует такой прямоуголь-
ный параллелепипед R с диа-
гоналями ab, cd, ef, gh, что ве-
личины двугранных углов при
ребре аЬ тетраэдров 7Ч1',. . . ., T^>, на которые R разби-
вается плоскостями abed, abef, abgh, равный,, т], £, т], £.
Доказательство. Рассмотрим шестиугольник
с' g'fd’h'e', являющийся аффинным образом правильного
шестиугольника и имеющий между диагоналями углы т],
С (рис. 86). Прямоугольный параллелепипед R, ортого-
нальная проекция которого вдоль диагонали ab совпадает
с этим шестиугольником, и является искомым.
£ 17]
ТЕОРЕМА ДЕНА — СИДЛЕРА
137
Перейдем к алгебраическим рассмотрениям Ессена
[36], [38].
Лемма 24. Пусть F (х, у) — действительная функ-
ция, заданная при х, у 6=10, 1[ и удовлетворяющая усло-
виям
F (х, у) = F (у, х),
F (х, у,) + F (хуг, у2) = F (х, у2) + F (ху2, yj.
Тогда существует такая действительная функция / (х),
заданная на интервале ]0, 1[, что F (х, у) = f (х) +
+ f (и) — f ИО-
Д о к а з а т е л ь с т в о. Соотношение Ф (и, v) =
= F (е~и, e~v) задает функцию Ф (и, v) для положи-
тельных и, V, причем эта функция удовлетворяет
условиям
Ф (и, v) = Ф (к, и), Ф (и, vx) + Ф (и + vlt v2) =
= Ф (и, v2) + Ф (и + v2, Vj). (57)
Положим, кроме того,
Ф (0, 0) = Ф (0, v) = Ф (и, 0) = 0.
Наконец, условия
Ф (— и, — v), = — Ф (и, и), (58)
Ф (и, и) = Ф (и, w) = Ф (к, ы) при и v + и> = 0 (59)
однозначно определяют функцию Ф (и, v) для всех дей-
ствительных и, v (так как среди трех отличных от нуля
чисел и, v, w, удовлетворяющих условию и + v + w = 0,
имеются два числа с одинаковыми знаками). Докажем,
что полученная функция Ф (и, v) удовлетворяет условиям
(57) для любых действительных и, v, vr, v2. Первое из
этих соотношений очевидно. Для доказательства второго
положим
G (и, vu v2) =
= Ф (и, 14) + Ф (и + vlt v2) — Ф (и, V2) — Ф (и -г v2, 14).
Тогда
G (и, vx, v2) = —G (и, v2, 14), (60)
G (и, v2) = 0 при и >0, Ki 0, v2 0 (61)
138
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ III
(см. (57)). Далее, согласно (58), (59),
G (и + ^1, — vu v2) = Ф {и + vr, ~Vj) + Ф (и, v2) —
— Ф (и + vu У2) — Ф (и + I?! 4- У2, — У,) =
= Ф (— iz, — 14) + Ф (и, v2) — Ф (и + у17 у2) —
— Ф (— и — v2, — Vj) = — G (и, vlt у2),
и потому
G (и, vlt v2) = — G (и + у1? — vlt v2). (62)
Аналогично устанавливаются соотношения
G (и', v', v") = — G (— if, if + v’, if + v") =
= G (if, — u' — v', if + v") =
= G (if, if + if, — if — v"). (63)
Докажем, например, первое из них:
G (— и', и' + if, и' + у") == ф (— и’, и' + v') +
+ Ф(у', и' + if) — Ф (— и', и' + if) — Ф (v", и' 4- у') ==
= Ф(— и', — у') 4~ Ф (и' + v”i V') — Ф (— и', — if) —
— Ф (и' 4- и’, V") = — G (и', if, v").
Далее, положив о = и’ 4- v> + и", мы аналогичным обра-
зом докажем равенства
G (и', if, v") = — G (cr, — и' — у', — и' — у"), (64)
G (и', if, v“) = G (—о, у', if). (65)
Пусть теперь и, vt, v2 — произвольные действительные
числа. Применяя, если нужно, соотношение (62), мы мо-
жем добиться, чтобы два последних аргумента были
неотрицательными, т. е.
G (и, уь у2) = + G (и1, v', v")-, v' 0, у" > 0.
Если хотя бы одно из чисел и', vr, v" равно нулю, то,
как показывает непосредственная проверка, G (и', v', v")=
= 0. Предположим поэтому, что все числа и', v', if от-
личны от нуля. Если и' ^>0, то G (и', v', v") = 0 со-
гласно (61). Далее, если и' 0, но хотя бы одно из чи-
сел и' 4- V, и' 4* V’ неотрицательно, то G (и', v', v") = 0
в силу (63). Наконец, если оба числа и’ vr, if 4- v" от-
S 171 ТЕОРЕМА ДЕНА — СИДЛЕРА 139
рицательны, то также G (и', v', v") — 0 (это вытекает из
(64) при о > 0 и из (65) при а 0).
Таким образом, в любом случае
G (и, vlt v2) = + (и', v , v") = 0,
т. е. справедливость второго соотношения (57) (для любых
действительных аргументов) доказана.
Определим теперь в множестве R х В всех пар дей-
ствительных чисел операцию сложения, положив
(а, х) + (Ь, у) = (а + Ъ, х + у + Ф (а, &)). (66)
Непосредственно проверяется (в силу (57)), что эта операция
превращает R X R в абелеву группу с нулевым элементом
(0, 0).
Обозначим через л операцию проектирования множест-
ва R X R на первую координату, т. е. л (а, х) = а.
Подгруппу Н CZ R X R условимся называть отмечен-
ной, если она однозначно проектируется (т. е. из
(а, х) ЕЕ Н, (а, х') ЕЕ Н следует х = х'). Множество М всех
отмеченных подгрупп непусто; например, отмеченной яв-
ляется подгруппа, состоящая только из нулевого элемента
(0,0). Множество М упорядочено по включению: Н < Н',
если На Н'. Ясно, что если некоторое множество отме-
ченных подгрупп является цепью (см. стр. 30), то объеди-
нение всех этих подгрупп также является отмечен-
ной подгруппой. Поэтому, в силу леммы Цорна, сущест-
вует хотя бы одна максимальная отмеченная
подгруппа.
Пусть Н* — максимальная отмеченная подгруппа. До-
кажем, что л (Н*) = R. Допустим, напротив, что сущест-
вует число с л (Н*). Если при некотором целом к ^4= 0
справедливо включение кс ЕЕ л (//*), то через q обозначим
наименьшее натуральное число, удовлетворяющее усло-
вию gc Е л (Н*). Тогда существует такое число Ь, что
(qc, b) а Н*. Мы имеем (для любого х a R)
q (с, х) = (qc, qx -f- У, Ф (с, кс) ,
и потому, положив
1 / 1 \
d=~(b- ^Ф(с,кс)),
’ ' fc=l '
140
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
1ГЛ. Ill
получаем q (с, d) = (qc, b) EE H*. Если же ни при каком
целом к =/= 0 включение кс ЕЕ л (Н*) места не имеет,
то положим q = 0, а число d фиксируем произвольно;
в этом случае также q (с, d) ЕЕ Н*.
Обозначим через Н** подгруппу, состоящую из всех
элементов вида (а, х) + п (с, d), где (а, х) GE Н*, п —
целое. Если элемент (а, х) + п (с, d)^H** удовлетво-
ряет условию л ((а, х) + п (с, d)) = 0, т. е. а + пс = 0,
то пс = —а ее л (Н*), и потому п = kq, где к — целое.
Следовательно,
(а, х) + п (с, d) = (а, х) + k-q (с, d) ЕЕ Н*. (67)
Так как подгруппа Н* является отмеченной, то из (67),
в силу соотношения л ((а, х) + п (с, d)) = 0, вытекает,
что (а, х) + п (с, d) = (0, 0). Итак, в точку 0 проектиру-
ется лишь элемент (0, 0) подгруппы Н**, т. е. Н** также
является отмеченной подгруппой. Но это противоречит
максимальности подгруппы Н* (так как Н** ZZ) Н*,
причем (с, d) GE Н**, (с, d) Н*). Получепное противо-
речие и доказывает, что л (Н*) = R.
Соотношение л (Н*) = R означает, что для любого
и GE R определено (однозначно) число ср (и), для кото-
рого (и, ср (и)) ЕЕ Н*. Для любых и, v^R мы имеем
(и, ср (и)) + (р, <р (р)) е II*, т. е.
(и + V, ср (и) + ср (р) + Ф (и, р)) GE Я*.
Это означает, что
ср (и) + Ч> (р) + Ф (“> v) = Ч> (и + р)-
Следовательно, полагая / (е~и) = —ср (и), мы получаем
для любых чисел х = те~и, у = e~~v интервала 10, 1[:
F (х, у) = F (е~и, e~v) = Ф (и, v) --
= ср (и + р) — ср (и) — ср (р) =
= / (е"“) + / (е-г) — / (е-“-®) = / (х) + / (у) — / (ху).
Лемма 25. Пусть Ф (и, р) — действительная функ-
ция, заданная при и 0, v 0 и удовлетворяющая ус-
ловиям
ф {и, р) = Ф (р, и), Ф (ки, kv) = ХФ (и, р), (68)
Ф (и, pj + Ф (и + р17 р2) = Ф (и, р2) + Ф (и + Р2, PJ.
(69)
§ 17] ТЕОРЕМА ДЕНА СПДЛЕРА 141
Тогда существует такая действительная функция g (и),
определенная при и 0 и удовлетворяющая условию
g (и) + g (у) — g (uv) = 0, (70)
что
Ф (и, v) = ug (и) + vg (v) — (и + v) g (и + v). (71)
Доказательство. Функцию Ф (и, v) продолжим
для всех действительных и, v так же, как и при доказа-
тельстве леммы 24 (см. (58), (59)). Теперь Ф (и, v) удов-
летворяет условиям (68), (69) для всех действительных
w, v, l?i, ’2, К.
Определим в R X R сложение и умножение, положив
(а, х) + (&, у) = (а + Ъ, х + у + Ф (а, Ь)),
(а, х) (Ь, у) = (аЪ, Ьх + ау).
Эти операции превращают R X R в коммутативное коль-
цо с нулевым элементом (0, 0) и единицей (1, 0).
Обозначим через л проектирование на первую коорди-
нату, т. е. л (а, х) = а. Подкольцо Н CZ R X R, содер-
жащее единичный элемент (1, 0), условимся называть
отмеченным, если оно однозначно проектируется
(т. е. из (а, х) е Н, (а, х') е Н следует х = х'). Мно-
жество М всех отмеченных подколец непусто; например,
множество Но, состоящее из всех элементов вида п-(1, 0),
где п пробегает целые числа, является отмеченным под-
кольцом (так как л (п-(1, 0)) = п). Множество М упорядо-
чено по включению: И < Н', если Н CZ И'. Ясно, что
если некоторое множество отмеченных подколец является
цепью, то объединение всех этих подколец также являет-
ся о т м е ч е н н ы м подкольцом. Поэтому, в силу лем-
мы Цорна, существует хотя бы одно максимальное отме-
ченное подкольцо.
Пусть Н* — максимальное отмеченное подкольцо. До-
кажем, что л (И*) = R. Допустим, напротив, что суще-
ствует число с л (И*). Изоморфизм л кольца Н* на
л (Н*) продолжается до изоморфизма сг кольца многочле-
нов И* [z] на кольцо многочленов л (Н*) [г].
Рассмотрим сначала случай, когда с является алгеб-
раическим элементом над кольцом л (Н*), и обоз-
начим через <? Е л (77*) [z] многочлен наименьшей
степени, имеющий с своим корнем: q (с) = 0. Так как
142
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
(с, х) = (с, 0) + (0, х), то, по формуле Тейлора, много-
член qr = о 1 (д) GE Я*[г] удовлетворяет условию
9i ((<\ 0) = 91 ((<, 0)) + д[ ((с, 0)) (0, х) (72)
(дальнейшие члены отсутствуют, так как (0, х)2 = (0, 0)).
Далее, так как л (д} ((с, 0))) = д (с) = 0, то дг ((с, 0)) =
= (0, Ь), где Ъ — некоторое число. При этом, так как
многочлен д' имеет меньшую степень, чем q, то q' (с) ф 0
и потому ((с, 0)) = (s, г), где s = q' (с) =/= 0, a t — не-
которое число. Следовательно, в силу (72), при х0 = —-
мы имеем qx ((с, х0)) = (0, 0).
Обозначим через Н** подкольцо кольца R X R, сос-
тоящее из всех элементов вида рг ((с, х0)), где р1еЯ*[г].
Если л (pj ((с, х0))) = 0, то многочлен р — а (рх), при-
надлежащий кольцу л (Я*) [z], удовлетворяет усло-
вию р (с) = 0. Следовательно, ар = qr, где а 0 —
элемент кольца л(Я*) и г СЕ л (Я*)[г]. Так как а СЕ
СЕ л (Я*), то найдется число h, для которого (a, h) СЕ Н*,
и потому (а, h) рг = др\, где гх = о-1 (г). Таким образом,
(a, h) рг ((с, х0)) = (0, 0), и потому рг ((с, х0)) = (0, 0) (так
как а =/= 0). Итак, в точку 0 проектируется лишь элемент
(0, 0) подкольца Н**, т. е. Н** также является отмечен-
ным подкольцом. Но это противоречит максимальности
подкольца Н* (так как Я** ЕЭ Я*, причем (с, х0) ЕЕ Я**,
(с, х0) Ej£ Н*). Полученное противоречие и доказывает, что
л (Я*) - Я.
Пусть теперь с — трансцендентный элемент над коль-
цом л (Я*), т. е. р (с) =/= 0 для любого отличного от нуля
многочлена р ЕЕ л (Я*) [г]. В этом случае число хй фикси-
руем произвольно и обозначим через Я** подкольцо, сос-
тоящее из всех элементов рг ((с, ж0)), где pr СЕ Я* [z].
Если л (рД(с, я0))) = 0, т. е. р (с) = 0, где р = о (рг),
то р = 0 и, следовательно, pL = (0, 0). В частности,
Pi ((с>хо)) — (0, 0). Таким образом, подкольцо Я** являет-
ся отмеченным, и возникает то же противоречие, которое
показывает, что л (Я*) = Я.
Соотношение л (Я*) = R означает, что для любого
u Е Я определено (однозначно) число <р («), для которого
(и, <р (п)) ЕЕ Я*. Для любых и, v СЕ Я мы имеем
(и, <р (п)) 4- (к, <р (п)) Я*, (и, <р («)) (v, <р (к)) е Я*,
§ 17]
ТЕОРЕМА ДЕНА — СИДЛЕРА
143
т. е.
(и + v, ф (и) + <р (е) + Ф (и, 0) S Н*,
(им, шр (v) + vq> (и)) ЕЕ Н*.
Это означает, что
Ф (и) 4- <р (г) + Ф (и, v) = ф (и + v),
U(f (V) + Р<₽ (К) = Ф (№)"
Остается положить
= — (при и>оу
Лемма 26. Пусть F (х, у) — действительная функ-
ция, заданная при х, у €= ] 0, 1[ и удовлетворяющая ус-
лов илм
F (х, у) — F (у, х), F (х, pi) + F (хуг, у2) =
= F (х, у2) + F (ху2, yi), (73)
Тр( х + У1 х > t р ( Ж + У1 У1 \ =
\® + У1 + у2’ x + yj г \х + У1 + у2’ x + yj
= тта) • (74)
Тогда существует такая действительная функция h (х),
заданная на интервале 1 0, 1( и удовлетворяющая условию
xh (х) + yh (у) = 0 при х + у = 1, (75)
что при любых х, у S ] 0, 1[ справедливо соотношение
F (х, у) = h(x) + h (у) — h (ху). (76)
Доказательство. Из (73) следует, согласно
лемме 24, что
F (х, у) = / (ж) + / (у) — / (ху), (77)
где / (.г) задана на интервале ] 0, 1[. Условие (74) принимает
вид
Ш+.-МШ)+(("+’-'М +
+ (»+*+1^)= (г/ (jtis) + ,hl (г+s))+
+ (и + !fe) / (, + ^+и) + (78>
144
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Определим функцию ¥ (и, г) при и > 0, v^> 0, положив
= + (79)
Из (79) непосредственно следует, что
Т (и, v) = V (v, и), V (Хп, Х0 = XT (u, v),
а соотношение (78) переписывается в виде
Т (и, Vj) + Т (и + vlt v2) = Т (к, п2) + Т (и + и2, пг).
В силу леммы 25, существует такая действительная функ-
ция g (и), определенная при и 0 и удовлетворяющая ус-
ловию (70), что
Т (и, V) = ug (и) + Vg (0 — (п + 0 g (и + 0. (80)
Наконец, введем функцию h (х) = / (ж) — g (0, оп-
ределенную на интервале ] 0,1[. Из (77) и (70) следует спра-
ведливость соотношения (76). Далее, из (70) следует, что
g (1) = 0, и потому, согласно (79), (80),
Т (ж, у) = xf (0 + yj (у) = xg (х) + yg (0
при X + у = 1.
Из этого непосредственно вытекает соотношение (75).
Прежде чем формулировать следующую лемму, ус-
ловимся многогранники А, В называть Z^-эквивалентны-
ми (А — В), если существуют такие многогранники Р,
Q GE Z*, что А + Р ~ В + Q. Если А + В — С, то бу-
*
дем также писать А — С — В. Легко видеть, что Z*-
«
эквивалентности можно складывать, т. е. если А — В,
С — D, то Л + С — В D (при этом, возможно, много-
гранники придется переместить, чтобы А и С, а также В
и D, не имели общих внутренних точек). Наконец, в си-
лу лемм 15 и 19 для любых X, р и любого многогранника
А справедливо соотношение
ХЛ + рЛ — (X 4- р) Л
(при наличии отрицательных коэффициентов достаточно
перенести слагаемые из одной части’в другую).
Г” Некоторое множество В = многогранников про-
странства Rs будем называть базисом многогранников,
S 17]
ТЕОРЕМА ДЕНА — СИДЛЕРА
145
если любой многогранник A CZ R3 однозначно представ-
ляется в вйде
А~^^а, (81)
•а
где Ха — действительные числа, лишь конечное число из
которых отлично от нуля.
Лемма 27. Базис многогранников В — {Na} в R3
существует.
Доказательство. Некоторое множество много-
гранников будем называть независимым, если никакой из
них не выражается через остальные (ср. (81)). В силу лем-
мы Цорна существует максимальное независимое
множество В = {7Va}; докажем, что оно является ба-
зисом.
Пусть A CZ R3. Добавляя к множеству В многогранник
А, мы уже не получаем независимое множество много-
гранников (так как В максимально), т. е. существует за-
висимость vA — Здесь v У= 0 (иначе мы имели бы
a
зависимость между элементами множества В). Можно
считать (перенося, если нужно, слагаемые в другую часть),
что v 0. Далее, умножая на 1/v (т. е. производя гомоте-
тию с коэффициентом 1/v), получаем А — где
a
Xa = Xa/v. Таким образом, любой многогранник A CZ R3
выражается через многогранники Na.
Докажем, что это представление единственно. Пусть
имеются два представления:
A~^aNa, A~^aNa. (»2)
а а
Вычитая и приводя подобные члены, находим ^j(Xa —
a
— Ha) — 0. Если бы среди чисел — На имелись отлич-
иые от нуля, то мы получили бы, что какой-либо из много-
гранников множества В выражается через остальные,—
вопреки независимости множества В. Таким образом, пред-
ставления (82) совпадают, т. е. В — базис.
Чтобы сформулировать следующую лемму, фиксируем
некоторый базис многогранников В = {Na} и для любых
х, у е Ю, 1[ выразим симплекс Т (ж, у) через элементы
146
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
базиса:
T(x,y)^Fa[x, y)Na.
а
(83)
Из леммы 21 вытекает (в силу разложения (83)), что для
каждого а функция Fa (х, у) удовлетворяет условию (73),
а в силу леммы 22, она удовлетворяет условию (74). Сле-
довательно, согласно лемме 26, существует такая действи-
тельная функция ha (х), заданная на интервале ]0, 1[
и удовлетворяющая условию
xha (х) + yha (у) = 0 при х + у = 1, (84)
что при любых х, уЕ ]0, 1[ справедливо соотношение
Ра (х, у) = Zla (ж) + Ла (у) — ha (ху).
Введем в рассмотрение функцию <ра (х), положив
tg х • ha (sin2 х), если х ф ~ ,
кп
если х - -г- .
Z
(85)
(86)
Фа И =
О,
Лемма 28. Функция <ра (х) аддитивна.
Доказательство. Заметим прежде всего, что
фи(ж) + фа(?/) = 0 при х + у = кп/2. (87)
В самом деле, если числа х и у не кратны п/2, причем к
нечетно, то sin2y — cos2 х, tg у = ctg х, и потому
фа (я) + Фа (У) = sTnAxss (sin2 Ж • Ла (sin2 z) +
+ cos2z-7ia (cos2 ж)) = О
(см. (84)). Далее, если х и у не кратны л/2, но к четно, то
sin2 у = sin2 х, tg у = —tg х, и из (86) следует, что (87)
справедливо. Наконец, если х и у кратны л/2, соотноше-
ние (87) очевидно.
Введем теперь обозначение
фа (Л) = /1фа (Ti) + . . . 4- 1тЦ>а (уго), (88)
где Zj ,. . ., 1т — длины ребер многогранника А, а ,. . .
. . ., ут — величины соответствующих двугранных углов.
Нетрудно видеть, что
фа (Г (х, у)) = Fa (Х^у). (89)
§ 171
ТЕОРЕМА ДЕЙА — СИДЛЕРА
147
В самом деле, в тетраэдре abed (см. рис. 79) длины ребер
db, cd и ad равны Zr = ]fie(x), le = ]/w (у), l3 = w (xli)
(см. (50)), а соответствующие двугранные углы имеют
значения
Ti = arctg , Та = arctg -L^,
У w (х) У w (у)
Л , 1
Тз = -2--arctg-== .
У w (ху)
Следовательно,
2 1 1
smz 71 = Т—:—г-5 = —т—;-—; = X,
Г l+ctg2?! l+w(x)
sin2 у2 = у, sin2 --= ху.
Таким образом, в силу (86), (87), (85),
Лфа (Т1) + ^фа (Тг) + 4фа (Тэ) =
= 4фа(Т1) + ^Фа(Тг) — ---= Fa(x, у).
Остается заметить, что остальные двугранные углы тетра-
эдра abed — прямые и, согласно (86), <ра (л/2) = 0.
Из соотношения (89) вытекает, в силу (83), что
T(x,y)~%<pa(T(x,y))Na. (90)
а
Пусть теперь числа £,т], £ GE ]0, л/2 [ удовлетворяют ус-
ловию £ + 1] + С = л. Каждый из тетраэдров Тт ,. . .
. . ., ZW, указанных в лемме 23, имеет вид КТ (х, у) (при
некоторых К, х, у), и потому, в силу (90),
— i = 1, . . ., 6. (91)
а
Так как TW + • • .4-7’(в) есть параллелепипед, т. е.
TW + . . . + тт ~ 0, то
Фа (тт) + . . . + фа (Г<в)) = 0 (92)
(см. (91)). При всех ребрах, кроме ае, ag, bf, bh, be, ad,
ab (см. рис. 86) тетраэдры имеют прямые дву-
гранные углы, и потому соответствующие слагаемые
(?i) равны нулю (см. (86)). Далее, к каждому из
148
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
ребер ае, ag, bf, bh, be, ad примыкают два из тетраэдров
TW, причем величины их двугранных углов
при этом ребре дают в сумме л/2, и потому, в силу (87),
сумма соответствующих этому ребру слагаемых /,фа (?/)
равна нулю. Остаются в левой части (92) двугранные углы
при ребре ab, и, в силу леммы 23, соотношение (92) при-
нимает вид 2Z<pa (|) -|- 2Z(pa (Т]) + 2/фа (С) = о, где Z —
длина ребра ab. Итак, <ра (£) + фа (т]) + Фа (0 = 0 при
ё, т), £ ЕЕ ]0, ^ [ , £ + т) + £ = л. В силу равенства
фа (л — £) = — Фа (О (см. (86)), это означает, что
фа (£) + фа (П) = фа (В + Т]) (93)
при g, Т1 е Ю, у[ , £+пе]у,л[. Вейлу (86), (87),
соотношение (93) имеет место также при £, t) Е [О, л/2],
£ + Ц ЕЕ [л/2, л].
Если т) [О, л/2] и | + »] ЕЕ Ю, л/2], то = л/2 —
— |, т)' = л/2 — т] удовлетворяют условиям т)' ЕЕ
ЕЕ [0, л/2], £' + ц' ЕЕ [л/2, л] и, согласно (87), (93)
фа (£) + фа (п) = —(фа (В') + фа ОТ)) =
= —фа (?' +»]') = —фа (Л — | — T]) = фа(£ + Т]).
Таким образом, (93) имеет место при любых £, ц ЕЕ
еЮ, л/2].
Наконец, для любых £, ц ЕЕ R имеем (при некоторых
целых к, т) = кл/2 — sEIO, л/2], tj* = тл/2 —
— т] ЕЕ [0, л/2] и потому, в силу (87),
Фа (В) + Фа СП) = — Фа (Г) ~ фа (П*) =
= — фа(Г + ТГ) = — фа^^-— — В — Т]) = Фа(£ + П)>
что и доказывает лемму.
В силу (86), аддитивная функция <ра (у) удовлетворяет
условию фа (л) = 0, и потому <ра (Л) (см. (88)) представ-
ляет собой некоторый деновский инвариант многогран-
ника А.
Лемма 29. Для любого многогранника A CZ R3
имеем
Л~2фа(Л)Л/а. (94)
а
6 171 *
•ТЕОРЕМА ДЕНА — СИДЛЕРА
149
Мы уже видели (см. (90)), что это соотношение имеет
место для Т (ж, у), а потому и для любого тетраэдра
рТ1 (ж, у). Далее, если А — В, т. е. А + Р ~ В + Q;
Р, Q GE Z*, ТО фа (-4) = фа (В) (поскольку фа (Р) = 0,
фа (0 = 0). Отметим еще, что если А — В ± С, то
фа (Л) = фа (В) ± фа (0. ПоЗТОМу 6СЛИ А ~ В ± С, ПрИ-
чем для В и С соотношение (94) справедливо, то оно спра-
ведливо и для многогранника А:
A ~ в ± С ~ 5Дфа (В) ± фа (С)) Na = 2 фа (A) Na.
а а
Пусть теперь A CZ В3 — произвольный многогранник.
Нетрудно видеть, что справедливо соотношение
(95)
г
В самом деле, А можно разбить на тетраэдры. Далее,
каждый тетраэдр (используя центр его вписанного шара
и точки касания вписанного шара с гранями) можно
разбить на 12 тетраэдров,
у каждого из которых од-
но ребро является высо-
той (рис. 87). Наконец,
если в тетраэдре oarbc
ребро оа1 перпендикуляр-
но грани агЬс, то, опустив
перпендикуляр ath на
прямую Ъс, найдем, что
этот тетраэдр имеет вид
КТ (х', у') + К'Т (х", у")
(поскольку каждый из
тетраэдров oajib, oajic
имеет вид КГ (ж, у); знаки
чисел К, К' зависят отпо-
Рис. 87.
ложения точки h на пря-
мой Ъс; рис. 88). Это и дает соотношение (95), из ко-
торого в силу (90), следует, что справедлива формула (94).
Теорема 25 (см. [13], [54]). Для равносоставлен-
ности равновеликих многогранников А, В CZ В3 необхо-
димо и достаточно равенство их деповских инвариантов
150
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ Ill
/ (Л) = / (В) для каждой аддитивной функции /, удовлет-
воряющей условию / (я) *= 0.
Доказательство. Необходимость устанавли-
вается теоремой 19. Докажем достаточность. Пусть А и
В удовлетворяют указанному условию. Тогда, в частности,
Рис. 88.1
фа (Л) = <ра (В) для любого а и потому, в силу леммы 29,
л ~ 3 Ф« (Л) ZVK = 3 фа (В) Na Л. В.
а а
Иначе говоря, Л + Р ~ В + Q, Р, Q Z*. Так как
v (Л) = v (В), то из соотношения Л + Р ~ В + Q вы-
текает, что v (Р) = v (0, и потому многогранники Р и Q
равносоставлены. Следовательно, Л и В равнодополняемы,
а потому, согласно теореме 22, равносоставлены.
Замечание. Проведенное доказательство теоремы
Дена — Сидлера можно изложить, не опираясь на аксио-
му выбора. В самом деле, обозначим через Y множество,
состоящее из всех чисел х,, у,, участвующих в соотно-
шении (95), и аналогичных чисел для многогранника В.
Через R* обозначим поле, содержащее действительные
числа, получающиеся из чисел множества Y с помощью
четырех арифметических действий и извлечения квадрат-
ных корней. Вместо базиса (лемма 27) выделим из мно-
жества всех тетраэдров вида Т (ж, у), где х, у В*,
максимальное независимое подмножество В* = {lVa}
(это осуществляется без использования леммы Цорна,
так как множество В* счетно). Доказательство леммы
24 достаточно провести в случае, когда функция F(x, у)
задана лишь при х, у 6Е ]0, 1[ р| В*. При этом Ф (н, г)
§ 18] МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 151
определяется, когда и, v пробегают аддитивную группу
R', содержащую лишь счетное множество элементов
(положительными элементами группы /?' являются чис-
ла вида —In х, где х е]0, 1[ Г) /?*). Вместо R X R рас-
сматривается лишь группа R' X R (с тем же сложением
(66)), что позволяет завершить доказательство леммы 24
без использования леммы Цорна. То же относится к лем-
мам 25, 26 (при х, у, 'k€=R*).
Далее, в лемме 28 функции (х) рассматриваются
лишь на множестве S, состоящем из всех х, для которых
sin х е R*. Легко видеть, что 5 является аддитивной груп-
пой. В самом деле, если ж GE 5, т. е. sin х GE R*, то после-
довательно заключаем:
sin2 х GE R*, cos2 x — 1 — sin2 x GE R*,
| cos x | = cos2 x GE R*, cos x = + | cos x | GE R*.
Следовательно, при x, у S имеем
sin z GE/?*, sin у GE R*, cos x GE R*, cos у GE 7?*,
и потому sin (ж + у) GE R*, т. e. x + у GE <S. Ясно также,
что —x GE 5 (при x GE 51), т. e. 5 — группа по сложению.
Заметим, что все симплексы рГ (ж, у), участвующие в
разложении (95) и аналогичном разложении для много-
гранника В, обладают тем свойством, что величины их
двугранных углов принадлежат множеству 5 (в силу соот-
ношений sin2 = ж, sin2 у2 = у, sin2 (л/2 — у3) = ху, по-
лученных при доказательстве формулы (89)). Из этого выте-
кает, что инвариант (88) определен для всех тетраэдров
р?1 (ж, у), где ж, у £ R*, а потому и для многогранников
A, В (см. (95)).
Наконец, соотношение (94) вытекает непосредственно
из (90) и (95) (и аналогично для В), что и позволяет завер-
шить доказательство теоремы 25.
§ 18. Многогранники, равносоставленные с кубом
В 1896 году Хилл [34] дал первые примеры тетраэд-
ров, равносоставленных с кубом. Один из них был приве-
ден выше (см. рис. 59). Сейчас известны и другие примеры
таких тетраэдров. Обзор относящихся сюда результатов
и составляет содержание этого параграфа.
152
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Теоретически теорема Дена — Сидлера дает необходи-
мое и достаточное условие для равносоставленности тетра-
эдра А с кубом: все деновские инварианты такого тетра-
эдра должны быть равны нулю. Однако применение этого
условия к разысканию таких тетраэдров затрудни-
тельно. Значительно более удобным аппаратом является
следующая теорема, доказанная Сидлером [50]:
Теорема 26. Если многогранник, равносоставлен-
ный с кубом, можно разбить на несколько конгруэнтных
между собой многогранников, то каждый из этих много-
гранников также равносоставлен с кубом.
Доказательство. Пусть Р = Лх + . . . + Ар,
где Р — многогранник, равносоставленный с кубом,
а Лх,. . ., Ар — многогранники, каждый из которых кон-
груэнтен А. Иначе говоря, Р ~ р-А. В силу леммы 16
имеем рА ~ р-А + Q, где Qe=Z2. Следовательно, рА ~
~ Р + Q, и потому, в силу леммы 19, многогранник рА
равносоставлен с равновеликим ему кубом. Но тогда и го-
мотетичный ему многогранник А равносоставлен с кубом.
Приведем примеры применения этой теоремы. Пусть
Р — параллелепипед, построенный на трех векторах
р, q, г, которые имеют равные длины и образуют друг
-- > — ->
с другом одинаковые углы (на рис. 89 р = ab, q = bd,
— >
г = de). Три плоскости, каждая из которых проходит че-
рез диагональ ас и еще через две противоположные верши-
ны параллелепипеда, разбивают Р на шесть конгру-
энтных тетраэдров (ср. рис. 86). По теореме 26, каж-
§ i8j МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 153
дый из них (например, тетраэдр abed, рис. 89) равносо-
ставлен с кубом. Это — тетраэдры Хилла первого рода.
В частности, если Р — куб, получается тетраэдр, рас-
смотренный в § 12 (см. рис. 59).
Тетраэдры Хилла первого рода могут быть получены
и иначе. Обозначим через П плоскость, проходящую через
точку а и перпендикулярную прямой ас. Ортогональные
проекции векторов р, q, г на плоскость П имеют одина-
ковые длины. Следовательно, проекция ломаной abdc
на плоскость П представляет собой равносторон-
ний треугольник Т (рис. 90). Если обозначить через I
расстояние точки Ъ от плоскости П, то точка d находится
от этой плоскости на расстоянии 21, а точка с — на расстоя-
нии 31 (поскольку векторы р, q, г имеют одну и ту же
проекцию на прямую ас). Таким образом, построение тетра-
эдров Хилла первого рода может быть изложено следую-
щим образом. Рассмотрим прямую призму, перпендику-
лярным сечением которой служит равносторонний тре-
154
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ 1ГЛ. Ш
угольник Т с вершинами а, т, п, и отложим на ее ребрах
(по одну сторону от плоскости треугольника Т) отрезки
mb, nd, ас, имеющие длины I, 21, 3Z (где I 0 — произ-
вольное число). Тогда а, Ъ, с, d будут вершинами тетра-
эдра Хилла первого рода.
На рис. 90 отложены на ребрах призмы отрезки be
и df длины 3Z. Многогранник Q с вершинами а, b, с, d, е, /
представляет собой треугольную призму (наклонную)
с основанием abd, а каждый из тетраэдров bcde, cdef кон-
груэнтен abed (движение, представляющее собой компо-
зицию поворота на угол 2л/3 вокруг оси призмы и парал-
1 1 ””
лельного переноса на вектор -у (р -f- q -f- г) = — ас, пере-
водит точки a, b, d, с, е соответственно в b, d, с, е, f). Таким
образом, из трех тетраэдров, конгруэнтных тетраэдру
Хилла первого рода, можно составить треугольную приз-
му Q. Это дает (в силу теоремы 26) другое доказательство
того, что этот тетраэдр равносоставлен с кубом.
Заметим теперь, что прямая L, проходящая через се-
редины g, h ребер ас и bd, является осью симметрии тетра-
эдра abed, т. е. поворот на угол я вокруг этой оси совме-
щает тетраэдр abed с самим собой. Поэтому любая плос-
кость, проходящая через прямую L, разбивает тетраэдр
abed на две конгруэнтные части.
Ряс. 91.
Рис. 92.
В частности, если в тетраэдре abed провести плоскость,
проходящую через ребро bd и середину g ребра ас, то полу-
чатся два конгруэнтных тетраэдра (рис. 91). По теореме26,
§ 18] МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 155
каждый из пих равносоставлен с кубом. Это — тетраэдры
Хилла второго рода.
Если провести плоскость, проходящую через ребро ас
и середину h ребра bd, то также получатся два конгру-
энтных тетраэдра (рис. 92), каждый из которых равносо-
ставлен с кубом. Это — тетраэдры Хилла третьего рода.
Обозначая через а величину двугранного угла при
ребре ab, легко вычислить остальные двугранные углы
тетраэдров Хилла Нг (а), Н2 (а), Н3 (а) и длины их ребер.
Эти данные приведены в таблице на стр. 156—159.
Кроме этих трех бесконечных серий, в таб-
лице приведены несколько отдельных тетраэдров, равно-
составленных с кубом.
Тетраэдр То был найден Хиллом. Разумеется, Хилл
непосредственно (разбиением на части) дока-
зывал равносоставленность тетраэдра То с кубом. Для нас
же этот факт очевиден: величины двугранных углов яв-
ляются рациональными кратными числа л, так что все
деновские инварианты / (То) обращаются в нуль, и по
теореме Дена—Сидлера То равносоставлен с кубом. Легко
проверяется, что и для остальных указанных в таблице
тетраэдров все деновские инварианты обращаются в нуль.
Равносоставленность каждого из тетраэдров Т± — Т\
с кубом была доказана в работе Сидлера [52] на основе
теоремы 26. Тетраэдры Тъ, Тъ были найдены в 1958 году
Гольдбергом [14], а в 1962 году Лепхард [43] добавил
к этому списку еще пять тетраэдров Т7 — Т11. Заметим,
что, например, в тетраэдре Тъ имеются ребра {ad и cd),
величины двугранных углов при которых не являются
рациональными кратными числа л. Однако при вычислении
любого деновского инварианта / (Те) эти ребра дают нуль:
-^-/(О1) + -^/(л —ах) =
= f (аг) + /(л) - /(аД = 0.
Так как величины остальных двугранных углов являются
рациональными кратными числа л, то / (Т8) = 0, и по тео-
реме 25 тетраэдр Те равносоставлен с кубом. Тетраэдры
Ленхарда отличаются тем, что в них нет ни одного прямого
двугранного угла.
Ребра H 1(0) Я2(а) я, (а)
ДЛИНЫ двугр. углы длины двугр. углы ДЛИНЫ Двугр. углы
ab sin а а 2 sin а а 2 sin а а
ас У 3 cos а л/З j/Tcos а л/З У12 cos а л/6 л — arccos/_A_cos а\ \ ут /
ad 1 л/2 2 л/2 л — arccos ^А etg а^ У 2 + sin2 а
be 1 л/2 У 5 sin2 а — 1 2 л/2
bd sin а л — 2а 2 sin а л/2 — а arccos ^А. etg а^ sin а л — 2а arccos /—А_ cos а\ \Уз }
cd sin а а У 5 sin2 а — 1 У 2 + sin2 а
Ребра To Ti То Та
ДЛИНЫ двугр. углы ДЛИНЫ двугр. углы ДЛИНЫ двугр. углы ДЛИНЫ Двугр. углы
ab /3 л/З т = (/5 + 1)/2 л/2 Уз 2л/3 уТ Ут л/5
ас У 2" л/2 1/т л/2 л/5 /3 л/З
ad 2 л/4 1 л/2 ^гуг л/5 2 л/2
be 1 л/2 /З л/З 2л/5 К 5/Ут Зл/5
bd Уз л/З уТУ? л/5 у'Т/УТ 2л/5 У~№ л/З
cd /2 л/2 V 5 1 УТ 2л/5 2 л/2 "5/ Ут» 2л/5
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
§ 181 МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 157
двугр. углы Зл/5 со ?г ю LO К" со К" Зл/5
ь
1 длины 1 и ко *'*• 1 н ко У5
двугр. углы | 4 л/5 LO. ко ?г СО К* со *г СМ
ь
| длины 1^ ко [н ко 1 н ко ко *> 1со см
Двугр. углы | 2л/5 СО СО tf 2 л/5 Ю ем см
£ч'
I длины 1 н [ио ко lio сТ
3 к
— двугр. уг. ю к л/3 ел КО 2л/3 Зл/5
длины | /Зт см 1 н loo 1^ ко
trf а о о О <3 о Г-С) 'g
си
Ребра Ti, Ти т„ ти
длины двугр. углы длины двугр. углы ДЛИНЫ двугр. углы ДЛИНЫ двугр. углы
аЪ yT /т Зл/10 /з л/6 V24-T л/5 /2+7 л/5
ас /з л/6 /з л/6 Уб - Зт л/3 2/6 - Зт л/3
ad 1 а4= л — arctg 2т2 / 5/2 а,= л — arccos 2/3 2/т л/2 2/5-2 л/2
be V^7/7 л/10 2 л/4 2/т л/2 У 7+Зт/т2 л — а3
bd 1 а6 = л — arctg 2 /5/2 л — а,/2 У 6 — Зт л/3 У 7+Зт/т2 а2
cd 1 «в = 2л — а4 — а6 / 5/2 л — а7/2 У 18—11т Зл/5 2У 18—11т Зл/10
Ребра Ти Ти Т„ Ти
длины двугр. углы длины Д в угри углы ДЛИНЫ двугр. углы ДЛИНЫ двугр. углы
аЪ 2 /2 + т л/10 /2 + т л/5 У2 + т л/5 /7-4т л/5
ас 2 У 6 - Зт л/3 т/ 3 л/3 т/3 л/3 Уз-т л/5
ad У 10 - Зт л — а3 2т л/2 2 л/2 У6-3т 2л/3
be 2/5-2 л/2 /з 2 л/3 /з л/3 Уб —Зт 2л/3
bd у 10 — Зт аз /2+т 2л/5 У 6 —Зт 2л/3 /З/т2 л/3
cd У18—11т Зл/5 У3-т л/5 /3-т 2 л/5 У 7 - 4т л/5
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. II
6 18] МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 159
| «Л | двугр. углы S СО СО е ««51 к a10 = arctg w, a>=yil 4-16т ’ Зл/10
длины | |со 1со W сч i т ъс *1 2/3-т
1 1 двугр. углы | вл. со ^2, cq со^ СО сЗ Е
длины | 1 Iе0 I'F ,1 ,1 4^ [rC.
1 1 двугр. углы л/10 л/5 л — ав 2 л/3 а9 = arccos v, v=r',2/(2y 5) л/З
длины 2У24-Т 21/3 —т Y loo те + ! €•
Т„ | | двугр, углы л/6 л/5 л — ав 2л/3 ae = arccos и, М=т2/(2 /3) л/5
1 длины | 2/3 (т-1) 2V3-T д-е — oM У10 — 3т + <n
Ребра Л У и <3 <3 «3 U3 ь© со
! *!-ь 1 | двугр. углы STD — g/И а12= arctg/ 3/5 4 л/5 л/2 2л/5 л/З
I ДЛИНЫ j Ice 1те ТI? со X < 1те
« Еч двугр. углы | d 6 со у. Q. | 6 К ? Q К* К сч
| длины у 6 — Зт /3 2/4-2т Гз_, СО 1 CD /7-4т
п1 || Е!Л двугр. углы л/6 л/З л — аи 2 л/5 ац=агссозг, г=1/(2/Зт2) Зл/5
двугр. углы || длины [те. СО 1 CD сч 4? 1 *1 со хЛ 1 /7 - 4т/2
го со *£2. R п <м <м А со
длины | 1те > СО 1 со т со X со 1 CD 4? 1
Ребра rO V чз о 43 с с с л ~
160
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
Тетраэдр Т12 был найден еще в 1923 году Зоммервил-
лем в работе [48], связанной с восемнадцатой
проблемой Гильберта. То, что этот тетраэдр равносостав-
лен с кубом, было замечено в 1969 году Гольдбергом
[15]. Наконец, остальные тетраэдры Г13 — Т2й указаны
в статье Гольдберга [17], где раскрыты также «секреты
кухни». Укажем, следуя этой работе, приемы нахождения
тетраэдров, равносоставленных с кубом.
На рис. 93 изображен сидлеровский тетраэдр Т^,
который разбит плоскостью аЪе, перпендикулярной
плоскости грани acd, на два меньших тетраэдра. У ребер
надписаны величины двугранных углов. Непосредственно
проверяется (по величинам двугранных углов), что аЪсе
есть сидлеровский тетраэдр Т3, тогда как abde — новый
тетраэдр, который принимается за Т19. Таким образом,
Т4 = Т3 + Т13, так как Т3, Т\ равносоставлены с кубом,
то и Т13 равносоставлен с кубом.
Тетраэдр Т13 имеет ось симметрии, проходящую через
середины двух противоположных ребер. Поэтому, как и
тетраэдр Хилла первого рода, его можно разбить на два
конгруэнтных тетраэдра; это дает Tlt. Другой способ раз-
биения тетраэдра Т13 на два конгруэнтных тетраэдра
дает Т1Ъ. Далее, Tlt = Т9 + Т1е и т. д.
Интересно, что для каждого из тетраэдров Th,
к = 0, . . ., 26, условие Брикара (30) выполняется в более
специальной форме: все коэффициенты nt равны между
собой, т. е. с у м м а 2 величин всех шести двугранных
углов есть рациональное кратное числа л. То же справед-
ливо для тетраэдров Хилла первого и второго рода.
I 18] МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 161
Помимо тетраэдров, известны другие многогранники,
равносоставленные с кубом. В работе Сидлера [51] при-
веден пример ортогонального многогранника *) (у кото-
рого любые две грани, имеющие общее ребро, перпендику-
лярны друг другу). Величина каждого двугранного угла
ортогонального многогранника
равна л/2 или Зл/2, и по теореме
25 каждый такой многогранник
равносоставлен с кубом. Ряд ин- -х
тересных примеров центрально- \/
симметричных ортогональных \ / \
многогранников (невыпуклых) \ / \ /
приведен в работе Ессена [35]; \/\——
каждый из них имеет тот же топо- z
логический тип, что и п р а -
вильный икосаэдр. Один / ч/Х
из икосаэдров Ессена показан
на рис. 94; его вершины имеют
(в прямоугольной системе) коор-
динаты (±2; ±1, 0), (0, ±2, ±1), Рис- №
(±1, 0, ±2); восемь граней —
правильные треугольники, остальные — равнобедрен-
ные. Выпуклая оболочка показанного на рис. 94 икоса-
эдра Ессена представляет собой правильный ико-
саэдр.
В заключение — несколько слов о связи с восем-
надцатой проблемой Гильберта. Она состоит в оты-
скании многогранников, конгруэнтными копиями которых
можно заполнить все пространство без перекрытий (см. [2],
стр. 50—51). Пусть G — некоторая группа движений
пространства R3. Заполнение пространства R3 многогран-
никами будем называть G-паркетажем, если каждые два
из этих многограников G-конгруэнтны.
На плоскости любой треугольник дает паркетаж
(рис. 95). В R3 уже не любой тетраэдр позволяет осуще-
ствить паркетаж.
Четыре тетраэдра, дающих £>0-паркетаж, были указаны
в 1923 году Зоммервиллем [48], [49]. Это были (в принятых
выше обозначениях) тетраэдры (я/3), То, Н2 (л/4) и Т12.
♦) Ортогональные многогранники играют важную роль в пер-
воначальном сидлеровском изложении [54] теоремы 25.
6 В. г. Болтянский
162
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Три из них независимо найдены Дэвисом [11]. Несколько
позже Баумгартнер [3], [4] нашел четыре тетраэдра, даю-
щих 7?0-паркетаж, причем три из них — зоммервиллевскпе,
а один — новый (а именно, Н2 (л/3)).
Как мы видели (ср. рис. 89), шесть конгруэнтных тет-
раэдров Хилла Н1 (а) заполняют параллелепипед. Так как
параллелепипед дает паркетаж, то тетраэдры Хилла
Н1 (ос) позволяют осуществить паркетаж. Этот способ дает,
вообще говоря, /Хпаркетаж, а не Р0-паркетаж, так как
среди шести тетраэдров имеются три, получающиеся из
abed движениями, обращающими ориентацию. По-видн-
мому, именно зто обстоятельство направляло усилия ис-
следователей на отыскание среди тетраэдров Хилла
частных случаев, дающих £>0-паркетажи.
В 1974 году Гольдберг [18] заметил, что все тетраэдры
Хилла дают £>0-паркетажи. Его соображения можно из-
ложить следующим образом. Рис. 90 показывает, что три
£>0-копгруэнтных тетраэдра Хилла Н1 (а) позволяют со-
ставить наклонную треугольную призму. Из этих наклон-
ных призм составляется бесконечная призма, перпендику-
лярным сечением которой является равносторонний
треугольник. Из двух таких призм составляется бесконеч-
ная призма, перпендикулярное сечение которой представ-
ляет собой ромб. Наконец, такими ромбическими «бал-
§ 18] МНОГОГРАННИКИ, РАВНОСОСТАВЛЕННЫЕ С КУБОМ 163
ками» можно заполнить все пространство R3. Таким обра-
зом, Н1 (а) дает Dg-паркетаж. Так как из двух Do-koh-
груэнтных между собой тетраэдров Н2 (а) (так же, как
из двух Н3 (а)), составляется тетраэдр Нг (а), то Н2 (а)
и Hs (а) также дают Dp-парцетажи.
Итак, Н1 (а), Я2 (а), Hs (а), То и Т12 позволяют осу-
ществить 1)0-паркетажи; существование двух последних
паркетажей вытекает из соотношений 2- То = Н2 (л/4),
4«7’12 = Нг (л/3) (если abed — одна из граней куба,
q — центр этой грани, а о — центр куба, то oabc есть
Н2 (л/4), а каждый из тетраэдров aboq, bcoq есть То; далее,
если m — центр тяжести тетраэдра Нг (л/3), то каждый
из четырех тетраэдров с общей вершиной т, основаниями
которых служат грани тетраэдра Н} (п/3), представляет
собой Т12). Другие тетраэдры, позволяющие осуществить
Do-паркетаж, неизвестны.
В [16], [19] приводятся примеры пятигранников,
дающих /)0-паркетажи. Укажем лишь два примера. Мы
отмечали, что тетраэдр Хил-
ла Нг (а) имеет ось симме-
трии L. Любая плоскость,
проходящая через прямую L
и не содержащая ни одного
из ребер ас, bd, рассекает
/11 (а) на два Do-конгруэнт-
ных пятигранника (рис. 96),
каждый из которых дает
Do-паркетаж. Для построе-
ния второго примера рассмот-
рим бесконечную призму Р,
перпендикулярное сечение
которой представляет собой
правильный и-угольник, где
п — одно из чисел 3, 4, 6.
Рис. 96.
Через / обозначим композицию поворота вокруг оси этой
призмы на угол 2л/п и некоторого параллельного переноса
вдоль оси. Наконец, пусть П — такая плоскость, не па-
раллельная оси призмы, что n-угольники П ("| Р и
/ (П) [Д Р не имеют общих точек. Тогда многогранник Qlt
представляющий собой часть призмы Р, заключенную
между этими тг-угольниками (рис. 97), позволяет осу-
ществить Do-паркетаж. Это вытекает из того, что
164
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[гл. ш
многогранники
<2п <?2 = / «21), <2з = / (<2г), • -, Qn = / (<2п-1)
составляют наклонную призму, так как n-кратное приме-
нение движения / дает параллельный перенос (из этого,
в силу теоремы 26, вытекает равносоставленность много-
гранника с кубом). Такими наклонными призмами мож-
но заполнить всю бесконечную призму Р, а призмами,
конгруэнтными Р, все пространство. При п = 3 много-
гранник представляет собой пятигранник, дающий
Z) „-паркетаж.
Симплексы, позволяющие осуществить паркетажи в Вп,
рассматривались Баумгартнером [3], [4] и Данцером [10].
Хадвигер показал, что тг-мерные симплексы, являющиеся
обобщением тетраэдров Хилла, равносоставлены с тг-мер-
ным кубом.
§ 19. Равносоставленность многогранников
по группе параллельных переносов
В этом параграфе мы укажем найденное Хадвиге-
ром [29] необходимое и достаточное условие Т’-равносо-
ставленности многогранников в R3.
Пусть П — плоскость в 7?3, а р — содержащаяся
в ней прямая. Одну из двух полуплоскостей, на которые
f 19]
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ Т
165
иащение, р, П
Пусть, далее,
— входящие
М — много-
прямая р разбивает П, назовем положительной полуплос-
костью; одно из двух полупространств, определяемых
плоскостью П, назовем положительным полупростран-
ством. Такую четверку (прямая, плоскость, полуплос-
кость, полупространство) будем называть [-оснащением.
Пусть теперь Р — плоскость в Rs. Одно из двух опре-
деляемых ею полупространств назовем положительным
полупространством. Такую пару (плоскость, полупрост-
ранство) будем называть 2-(
Пусть а — некоторое 1-о
в него прямая и плоскость,
гранник, у которого имеется
грань Г, параллельная плос-
кости П, причем грань Г име-
ет сторону г, параллельную р.
Если грань Г примыкает к
г с положительной стороны
(рис. 98), то ребру г припи-
шем знаке! = 1; в противном
случае = —1. Далее, если
М примыкает к грани Г с
положительной стороны, то
грани Г припишем знак
е2 = 1; в противном случае
(см. рис. 98) е2 = —1. Весом
рассматриваемого ребра в
многограннике М назовем
произведение e^l, где I — длина ребра г. Еслп же ребро г
не параллельно р или если г || р, но в М нет грани, кото-
рая параллельна плоскости П и примыкает к ребру г,
то вес ребра г будем считать равным нулю. Через Ка (М)
обозначим сумму весов всех ребер многогранника М.
Пусть теперь т — некоторое 2-оснащение и Р — вхо-
дящая в него плоскость. Пусть, далее, М — многогран-
ник, у которого имеется грань Г, параллельная Р. Если М
примыкает к грани Г с положительной стороны, то гра-
ни Г припишем знак е2 = 1; в противном случае е2 = —1.
Весом грани Г в многограннике М назовем число e2s,
где s — площадь грани Г. Наконец, через Кх (М)
обозначим сумму весов всех граней многогранника М,
параллельных плоскости Р (если таких граней нет, то
Кх (М) = 0).
Р
'П
Н
Рис. 98.
llifi
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ill
Покажем, что каждая из функций Кв (М), Kz (М) яв-
ляется аддитивным Т-инвариантом. Их Т’-инвариапт-
ность очевидна (при параллельном переносе многогранни-
ка М значения Кв (М), Kz (М) не меняются). Докажем
аддитивность. Пусть А = Рг + Р2, разобьем ребра много-
гранников А, Рг, Р2 на звенья, как при доказательстве
леммы 11. Тогда инварианты Кв (Л), Кв (Рг), Кв (Р2)
можно вычислять не по ребрам, а по звеньям.
Возьмем сумму 2 весов всех звеньев по обоим много-
гранникам Рг, Р2. Если звено т, параллельное р, лежит
внутри многогранника А, то к нему могут примыкать
по^граням, параллельным плоскости П, либо оба много-
гранника Р17 Р2, либо ни один из них (рис. 99; как и на
рис. 65, здесь изображено сечение плоскостью, перпенди-
кулярной т). В любом случае сумма весов звена т равна
нулю. То же справедливо для звеньев, параллельных р.
которые расположены на гранях многогранника А
(рис. 100). Наконец, если звено т лежит на ребре много-
гранника А (рис. 101), то оно дает в сумме 2 слагаемое,
равное весу звена т в многограннике А. Отсюда и выте-
кает справедливость равенства
Кв (Л) = Кв (PJ + Кв (Р2).
Докажем, наконец, аддитивность функции Kz. Пусть,
по-прежнему А = J\ + Р2. Всевозможные двумер-
ные пересечения Г Q Г17 Г |~| Г2, 1\ |~| Г2, где Г, Гц
Г2 — грани многогранников Л, Рг, Р2, будем называть
§ 19]
РАВНОСОСТАВЛЕННОСТЬ НО ГРУППЕ Г
167
ячейками. Каждая грань каждого из многогранников
A, Р1г Р2 представляет собой объединение нескольких
ячеек, попарно не имеющих общих внутренних точек.
Для вычисления Кх (Л), Кх (Р^, Кх (Р2) можно взять
Рис. 101.
сумму (с соответствующими коэффициентами) площадей
ячеек, а не граней.
Если некоторая ячейка, параллельная плоскости Р,
целиком (кроме, может быть, точек контура) расположена
внутри Л, то к ней примыкают оба многогранника
Р1, Р2, причем с разных сторон. Поэтому в Кх (Pj) пло-
щадь этой ячейки войдет с одним знаком, а в Кх (Р2) —
168
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Щ
с противоположным, и в сумме Кх (Рг) 4- К- (Р2) эти два
слагаемых дадут нуль.
Возьмем теперь ячейку, расположенную на границе
многогранника А. К ней примыкает только один из
многогранников Рг, Р2, причем с той же стороны, что и А.
Следовательно, в сумму Кх (Рг) 4- Кх (Р2) площадь этой
ячейки войдет с тем же знаком, что и в Кх (А).
Итак, Кх (Л) = Кх (Pj) + Кх (Р2), т. е. функция Кх
аддитивна.
Лемма 30 (см. [37]). Пусть в В3 заданы многоуголь-
ник М и не параллельный его плоскости отрезок I. Тогда
для любого X 0 существу-
ют такие многогранники Р,
/ \ Q €= Z3, что
/ \г I X ХМ + Р~ XI X M+Q.
/ \ т
Доказательство.
\ , \ Пусть сначала М — тре-
-^4 " \ угольник с вершинами а, Ь, с.
\ Обозначим через d середину
, “J
стороны be и положим е2 —са,
Рис. 102. _ ^а. через обозначим
отрезок I, на котором выб-
рано некоторое направление. Тогда (рис. 102)
М = [е2, е3] 4- [—е2, е3]. (96)
Согласно лемме 14,
(1 + X) [gj, е2, е3] ~ [е1, е2, е3] +
т
4- X [еп е2, е3] 4~ [ег] X X [е2, е3] 4- [е^ е2] X X [е3],
(X 4- 1) [elt е2, е3] ~ X [q, е2, е3] 4-
т
4* [е1? е2, ез1 4" X [еД X [е2, е3] 4“ X Iex, е2] X [е31-
Взяв в каждом из этих соотношений два последних сла-
гаемых, получаем многогранники, которые являются
Т’-равнодополняемыми, а потому и Т’-равносоставленными
(теорема 22):
[ej] X X [е2, е3] 4“ [бц е2] X X [е3] ~
— X [ej X [е2, е3] 4- X [q, е2] X [е3]. (97)
т
« 191
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ Т
169
Рис. 103.
Напишем аналогичное соотношение, заменив ег, е2
на ——е2:
[—ej X X 1—е2, е3] + [—ег, —е2] X X [е3] ~
т
~ X [—X [—е2, е3] + X [—elt —ег1 X [е3]. (98}
Так как
[ег, е2] + [—ег, —е2] ~ W,
т
где W — некоторый параллелограмм, а каждый из одно-
мерных симплексов [ej, [—ег] совпадает с отрезком /,
то, складывая (97), (98), получаем:
I X кМ + W X X [е3] ~ X/ X М 4- kW X [е31
т
(см. (96)). Так как W X к [е3] и kW X [е3] — параллеле-
пипеды, то в случае, когда М — треугольник, лемма
справедлива. Отсюда (разбие-
нием на треугольники) выво-
дим ее справедливость для лю-
бого многоугольника Л/.
Пусть Q — некоторая плос-
кость в R3. Ортогональное про-
ектирование на плоскость Q бу-
дем обозначать через л. Если
М — некоторый многоуголь-
ник, не пересекающий плос-
кость Q, причем плоскость
многоугольника М не парал-
лельна и не перпендикуляр-
на Q, то через W (М) будем
обозначать выпуклую оболочку
множества М (J я (М) (рис.
103).
Лемма 31. Пусть
Мг, . . ., Mh, Nlt . . ., Nt-
такие многоугольники, расположенные по одну сторону
плоскости Q, что их плоскости не параллельны и не
перпендикулярны Q, а проекции л . ., л (Мк),
п C^i)» • • л (Ni) попарно не пересекаются. Тогда если
ко (W (МО) + . . . 4- Ка (Ж(МЬ))=
- Ка (W (NJ) 4- ... 4- кв (W (7V0), (99)
170
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
(W (ЛЛ)) + . . . 4- Кх (W (Mk)) =
= АНИЧ^)) + - • - + Кх (Ж (N,)), (100)
Ь’(1У(ЛЛ)) + ... + р(Ж(>й)) =
= v (IV (NJ) 4- . . . + V (W (Nt)), (101)
то W (MJ + ... + W(Mk) и W (А\) 4- • • • + W (Nt)
являются Т-равносоставленными.
Доказательство. Будем считать, что плоско-
сти многоугольников Мг, . . ., Мг, Nlt . . ., Ng (г к,
q I) параллельны одной плоскости А, а плоскости
остальных многоугольников не параллельны Р. Так как
плоскость Р не параллельна и не перпендикулярна Q,
то мы можем считать (применив, если нужно, параллель-
ные переносы; рис. 104), что Мг, . . ., Mr, Nlt . Nq
лежат в плоскости Р.
Через т* обозначим 2-оснащение, которое задается
плоскостью Р, причем положительное полупространство
выбрано так, что W (Мг), . . ., W (Mr), W (Л\). . - •
. . ., W (Nc,) примыкают к граням Мг, . . ., Мг, Л\, . I
..., Nq с положительной стороны. Тогда
Кх* (Ж (Mj)) = s(Mi) при i = 1, ..., г;
Кх*(W(№>)) = 0 при 7 = г4-1, ..., к;
KX*(W (N^) = s(Ni) при i = 1, ..., q‘,
Kx* (W (N,)) = 0 при у' = q 4- 1, ..., I,
§ 19]
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ Т
171
и потому, в силу (100),
s (Мх) -)-... + s (Mr) = s (А\) + . . . + s (NQ). (102)
Далее, пусть р — прямая, лежащая в плоскости Р.
Через о* обозначим 1-оснащение, которое задается плос-
костью Р и прямой р (при том же выборе положительного
полупространства и некотором выборе положительной
полуплоскости). Тогда
ко.
Ко> = о
к0.(1У(^)) = тр(^)
{W(Nj)) = 0
при i = 1, ..., г;
при у = г + 1, ..., к
при i = 1, ..., g;
при / = q + 1, .. ., I,
где Jp — аддитивный инвариант (в плоскости Р), рассмо-
тренный в § 10. Таким образом, в силу (99),
Jp (Мх)+ . . . + Jp (Mr) = Jp (Ax)+ . . . + Jp (Nq). (103)
Соотношение (f03) справедливо для любой прямой р CZ Р,
и потому, в силу (102), многоугольники Мг + . . . 4- Мг и
7VX + . . . + Nq, лежащие в плоскости Р, являются
Т-равносоставленными (теорема 16). Иначе говоря,
Мх + . . . + Мг = Мх + . . . + Ms, (ла/\
N. + • • - + Nq = X + • • - + X, ( '
где Mt и Vj являются Т-конгруэнтными (i = 1, . . ., s).
В силу (104),
W (Мх) + . . . + W (Mr) = W (М') + . . . + W (М*8),
W (Ах) + . . . + W (Nq) = W (М) + ... 4- W (N's).
(105)
Аналогично, если плоскости многоугольников
Мг+Х, . . ., МГ’, Nq+1, . . ., Nq- параллельны одной плос-
кости Р', а остальные многоугольники лежат в плоскостях,
не параллельных Р', то
W (мг+1) + ... + W (Мг.) = W (М8’+1) + ... + W(M'.),
W (Nq+1) + . . . + W (Nq-) = W (X+1) + • • + w (Nt),
(106)
где Mi и TV, являются Т-конгруэнтными (г = s + 1, . . .
. . ., s').
172
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. III
Продолжая таким образом и складывая получающиеся
соотношения (105), (106), . . ., получим наконец:
W (Мг) + . . . + W (Мк) = W (X) + . . . + W(M‘m),
W(N1) + ...+ W (Nt) = W (Ni) + . . . + W (1Q,
(Ю7)
где 71/i и Nt являются ^-конгруэнтными (i = 1, . . ., m).
Обозначим через параллельный перенос, переводя-
щий 71/i в Ni. Для каждого i = 1, . . ., т справедливы
либо соотношения
W (М?) = Аь W (Ni) = Bt + П; Bi = tt (At)
(рис. 105, а), либо соотношения
W (Mi) = At + П, W (Ni) = Вс, Bt = ti (At)
(рис. 105, б), где П — прямая призма, основания которой
191
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ Т
173
параллельны плоскости Q. Таким образом,
W (Mi) + ... + W (M*m) =
— Ai + • • • + Am 4- Пх 4- ... 4* Па,
w (X) + • • + w (X) =
= 4* . . . + Bm 4- IIj 4- . . . 4- Up,
где П;, П{ — прямые призмы, основания которых парал-
лельны Q.
Призма Пг имеет вид Пг = Хг/ X где Lt CZ Q —
некоторый многоугольник, а I — отрезок длины 1, пер-
пендикулярный Q. В силу леммы 30,
Щ 4- р\ ~ I х KLi + А, A, P\ е Z3.
т
Далее, согласно лемме 18, Pi ~ I X L<, Pi ~ I X Lj,
т т
где Li, LiCZQ—некоторые прямоугольники. Таким образом,
ГЛ 4- I X Li ~ I X ДА 4- I X Li = I X (ДА 4- L-).
т
Так как многогранники в левой и правой частях равнове-
лики, то s (Li) < s (^ iLt + Lt), и потому ДА 4- Lt =
= L\ 4- Li , где Li ~ Li (лемма 12). Теперь получаем
т
П, 4~ I X Li I X Li 4~ I X Li .
т
Так как I X Li ~ I X Д*, то многогранники Ди/ X L*'
т
являются Т-равнодополняемыми, а потому и Т’-равносо-
ставленными (теорема 22), т. е. П; ~ I X Li . Следова-
т
тельно, в силу (108),
W (М*) 4- ... 4- W (М'п) ~ Ai 4- .• . . Am 4- I X L,
LCZQ, (Ю9)
где L = Li 4- . . . 4- L’a • Аналогично,
W (Ni) 4- • • • + W (N'm) ~ Bi 4- . . . 4- Bm 4- I X L',
L'CZQ. (HO)
174
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Щ
Соотношения (101), (107), (109), (110) показывают, что
s (L) = s (L')- Далее, пусть р' CZ Q — некоторая прямая
и Р' — плоскость, содержащая р' и перпендикулярная
плоскости Q. Одно из двух полупространств, определяе-
мых плоскостью Р’, примем за положительное, и получаю-
щееся 2-оснащение обозначим через т'. Легко видеть, что
К-е (IxL) = Jp- (£), К.- (I X L') = (£'),
где Jp- — аддитивный инвариант (в плоскости Q), рассмо-
тренный в § 10. Таким образом, в силу (100), (107), (109),
(110) получаем
JP-(L) =
Это соотношение справедливо для любой прямой р’ CZ Q,
и потому, по теореме 16, L ~ L' (так как s (Z) — s (L )).
т
Следовательно, I X L ~ I X L'. Отсюда, в силу (107),
т
(109), (110) и соотношений = Bt имеем
т
W . 4- W (М.) ~ W (7VJ + . . . + W (TV,).
т
Теорема 27. Для Т-равносоставленности равнове-
ликих многогранников А, В Г~ R3 необходимо и достаточно
выполнение равенств Кв (Л) = К„ (Б), Kz (Л) = 1Д (В)
для всякого i-оснащения о и всякого 2-оснащения т.
Доказательство. Необходимость непосред-
ственно вытекает из теоремы 15. Докажем достаточность.
Пусть v (Л) = v (В) и Ко (Л) = Ко (В), К-. (Л) = Kz (В)
для любых а, т. Представим А и В в виде
Л = Лх 4~ • • 4" Л(л, В = Вх 4- • • • 4~ Bv,
где At и Bj — выпуклые многогранники.
Выберем плоскость Q, не параллельную и не перпен-
дикулярную ни одной грани ни одного из многогранни-
ков Alt Bj. Мы можем считать (применив, если нужно,
параллельные переносы), что все многогранники Л,, Bj
лежат по одну сторону плоскости Q и их ортогональные
проекции л (Лх), . . ., л (Л^), л (7?х), . . ., л (Bv) на плос-
кость Q попарно не пересекаются.
Пусть Г — некоторая грань многогранника Лi и а —
внутренняя точка этой грани. Если отрезок [я, л («)1
пересекается с внутренностью многогранника Л,, то Г
§ 191
РАВНОСОСТАВЛЕННОСТЬ ПО ГРУППЕ Т
175
будем называть верхней гранью (рис. 106, а); в противном
случае (рис. 106, 6) Г — нижняя грань. Аналогично
определяются верхние и нижние грани многогранни-
ков Bj.
Рис. 106.
а
Рис. 107.
Пусть Гх, . . ., Га — все верхние грани всех много-
гранников А1г . . ., а Гх, . . ., Гр — нижние грани.
Тогда (рис. 107)
А + W (Г7) + ... + W (Гр’) = W (Гх) + . . . + ТУ(Га).
Аналогично,
В + W (Д^ + . . . + W (Д^) = W (Дх) + . . . +1У(Д7),
176
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
где Ах, . . ., Ау — верхние, а Д15 . . ., Ag — нижние гра-
ни многогранников Вг, . . В». Из этих равенств полу-
чаем
А + D W (ГО + 3 W (ДО = в + 3 W (А.’) + 2 W (ГО, (111)
2 к0 (iv (ГО) + з ЛО(1¥(Д 0) = з Ka(W (Д0)+ з хо(ИЧГ0),
з кх (IV (ГО) 4- 3 кх (ИЧДО) = 3 ^(ГИ(Д’)) + 2 KJW (ГО),
2 v (ру (гЬ) + 2 v{w (до) = 2 W (до) + 2 к (Ж (го).
Последние три из этих соотношений (справедливые для
любых оснащений о, т) показывают, в силу леммы 31, что
1>(го +W>)~W)+Wi)-
т
Следовательно, в силу (111), многогранники А и В явля-
ются Т-равнодополняемыми, а потому (по теореме 22)
Т-равносостав ленными.
Из теоремы 27 вытекает, в частности, следующий
интересный результат, принадлежащий Хадвигеру [29]:
для того чтобы выпуклый многогранник был Т-равносо-
ставлен с кубом, необходимо и достаточно чтобы каждая
его грань была центрально-симметричным многоугольни-
ком. Этому результату можно, пользуясь одной теоремой
А. Д. Александрова [1], придать более изящную форму.
Для этого заметим, что сумма Минковского нескольких
отрезков может быть: 1) отрезком (если все складываемые
отрезки параллельны одной прямой), 2) выпуклым цен-
трально-симметричным многоугольником (если складывае-
мые отрезки параллельны одной плоскости, но не одной
прямой), 3) выпуклым многогранником (если отрезки не
параллельны одной плоскости). Выпуклые многогранни-
ки, представляющиеся в виде суммы Минковского несколь-
ких отрезков, называются зоноэдрами-, например, призма,
основанием которой служит центрально-симметричный
многоугольник, является зоноэдром. Теорема Александ-
рова (точнее, ее следствие) состоит в том, что выпуклый
многогранник тогда и только тогда является зоноэдром,
когда все его грани центрально-симметричны. Например,
архимедово тело, гранями которого являются правиль-
ные шестиугольники и квадраты, представляет собой зоно-
эдр. Таким образом, результат Хадвигера может быть
5 20] ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА 177
сформулирован следующим образом: для того чтобы
выпуклый многогранник был Т-равносоставлен с кубом,
необходимо и достаточно, чтобы этот многогранник был
зоноэдром (т. е. суммой Минковского нескольких отрез-
ков). Отсюда следует, что два равновеликих зоноэдра
Z-равносоставлены. В частности, два конгруэнтных зоно-
эдра, как бы они ни были повернуты друг относительно
друга, являются 7'-равносоставленными.
§ 20. Инварианты Дена — Хадвпгера п теорема Ессена
Многомерное обобщение деновских инвариантов было
предложено Хадвигером [27]. Для пояснения хадвигеров-
ской идеи условимся через <р0 (В) обозначать р-мер-
ный объем р-мерного многогранника В (для любого
р = 1, 2, . . .). Тогда деповский инвариант многогран-
ника A CZ Rs можно записать в виде
/И)=ЗИЖ) = Зфо(Д)/(щ), (И2)
где Лх, . . ., Ah — ребра (т. е. одномерные грани) много-
гранника А, 1г = гр0 (ИД, . . ., lh = <ро Ил) — их длины,
ах, . . ., ah — величины соответствующих двугранных
углов, а / (х) — некоторая функция Коши—Гамеля, удо-
влетворяющая условию / (л) = 0.
Доказательство аддитивности функции / (А)
(лемма. 11) основывалось на следующих соображениях.
Пусть А = Рх Д- . . . -ф Рц. Ребра (одномерные грани)
многогранников Аг, Plt . . ., Pq можно разбить па звенья
таким образом, чтобы многогранники А, Рг, . . ., Pq при-
мыкали друг к другу целыми звеньями. Далее, <р0 есть
аддитивная функция, т. е. длина lt = tp0 (Л;) ребра At
равна сумме длин составляющих его звеньев. Нако-
нец, сумма Vi + - • • + Vs величин двугранных углов при
звене т по всем многогранникам Рг, которые к этому
звену примыкают, равна 2л или л, если звено т не лежит
ни на одном ребре многогранника А, и равна щ или
at — л, если звено т лежит на ребре многогранника А.
Легко видеть, что все эти соображения непосредственно
применимы к n-мерпым многогранникам при любом и > 3.
Именно, пусть A CZ Rn — некоторый п-мерный много-
гранник и A j,..., A h — все его (п — 2)-мерные грани.
Если П — двумерная плоскость в Rn, ортогональная
7 В. Г. Болтянский
178
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[гл. тц
грани At и проходящая через внутреннюю точку q зтой
грани, то Л П П есть многоугольник в плоскости П,
одной из вершин которого является q. Величина угла
многоугольника A f~) II при вершине q принимается за
величину двугранного угла многогранника А при его
(п — 2)-мерной грани Л,.
Обозначим через alt . . ah величины двугранных
углов многогранника А при его (тг — 2) мерных гранях
Лп . . Ah. Пусть, далее, f (х) — функция Коши-
Гамеля, удовлетворяющая условию / (л) = 0, а <р — не-
который аддитивный Р-ипвариант, заданный для (и — 2)
мерных многогранников. Тогда функция
к
f(A)= 2ф(ЛЭ/(щ), (ИЗ)
1=1
определенная па множестве всех n-мерных многогранни-
ков, очевидно, является Р-инвариантной.
Если Л = Рх + . . . 4- Рг, то, вообще говоря, много-
гранники Л, Рг, . . ., Рг не примыкают друг к другу
целыми (и — 2)-мерными гранями. Однако, взяв все-
возможные (и — 2)-мерные многогранники, являющиеся
пересечениями (п — 2)-мерных граней многогранников
Л, Plt . . ., Рг, мы получим конечное число более мел-
ких многогранников (ячеек), причем многогранники Л,
Рг, . . ., Рг примыкают друг к другу целыми ячейками.
Теперь устанавливается (ср. доказательство леммы И),
что функция (ИЗ) аддитивна. Таким образом, справед-
лива следующая
Теорема 28. Пусть / — функция Коши—Гамеля,
удовлетворяющая условию j (л) = 0, а <р — аддитивный
D-инвариант, заданный для (п — 2)-мсрных многогранни-
ков. Тогда функция (ИЗ) (суммирование по всем (п — 2)-
мерным граням многогранника Л) является аддитивным
D-инвариантом.
В частности, если в (ИЗ) функция <р = <р0 есть
(п — 2)-мерный объем, мы получаем аддитивный P-инва-
риант
< Р1(Л) = Хфо(Л,)/(а;). (114)
При п — 3 эта формула дает деновский инвариант много-
гранника Л CZ R3-
§ 20]
ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА
179
Формула (114) определяет также функцию фх на мно-
жестве всех Zc-м е р н ы х многогранников при 3 к п
(в этом случае суммирование ведется по (к — 2)-мерным
граням, а <р0 означает (к — 2) мерный объем). В частности,
можно рассмотреть фт для (и — 2)-мерных многогранников:
< Р1 И) = Е Фо Иг) /о (аг), (115)
где /0 — функция Коши—Гамеля, удовлетворяющая усло-
вию /0 (л) = 0 (суммирование по (и — 4)-мерным граням
(и — 2)-мерного многогранника Л).
Теперь при п> 5 в (ИЗ) можно в качестве ср взять
функцию фх, в результате чего получаем аддитивный
D-инвариант
фгИ) = Лф1(А)/1(аг),
где фх задается формулой (115), а /х—функция Коши —
Гамеля, удовлетворяющая условию /х (л) = 0 (и, вообще
говоря, отличная от /0).
Инвариант ф2 также можно рассматривать на /с-мерных
многогранниках (5 к и), и потому, приняв в (ИЗ)
за ф инвариант <р2, мы получим аддитивный D-инвариант
Фз И) =Еф2 ИОЛ («О,
где /г — новая функция Коши—Гамеля, и т. д. Вообще,
формула
< Р1 (^) = 3<Pj-l (А) Л-1 («г),
определяет в Нп инварианты ф, (Л), j — 1, . . ., г, где
г — наибольшее целое число, удовлетворяющее условию
2r + 1 п.
Функции <рг, . . ., фг введены в работе Хадвигера [27);
мы будем называть их инвариантами Дена—Хадвигера.
Так как «р^, . . ., <рг являются аддитивными D-инвариан-
тами, то, в силу теоремы 15, для равносоставленности
п-мерных многогранников М, N CZ Rn необходимо выпол-
нение равенств
Ф,- (М) — фу (N), / = 0, 1, . . г, (116)
(первое из них выражает требование равновелик о-
с т и).
/*
180
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. III
С помощью инварианта <ра Хадвигер [27] обобщил тео-
рему 20: при и 3 правильный п-мерный симплекс не
равносоставлен с кубом. В самом деле, двугранный угол
при (и — 2)-мерной грани правильного n-мерного симплек-
са А имеет величину arccos 1/н. В силу леммы 9, сущест-
вует такая функция Коши—Гамеля /, что / (л) = 0,
/ (arccos 1/и) 0. Определяя с помощью этой функции
инвариант фг (см. (114)), находим, что <ра (Л)^= 0. В то же
время для куба В имеем <ра (В) = 0. Таким образом,
А и В не равносоставлены.
В В3 и В4, кроме ф0 (т. е. объема), имеется лишь один
инвариант Дена—Хадвигера фх. Как показывает теорема
Дена — Сидлера, в трехмерном случае необходимое условие
равносоставленности (116) является и достаточным.
Ессен [37] установил, что такой же результат справедлив
в четырехмерном случае:
Теорема 29. Для равносоставленности двух рав-
новеликих четырехмерных многогранников М, N необхо-
димо и достаточно, чтобы их инварианты Дена — Хадви-
гера совпадали, т. с. чтобы для любой функции Коши—
Гамеля / (а;), удовлетворяющей условию f (л) = 0, было
справедливо равенство фх (М) = фх (А7) (см. (114)).
Доказательство использует следующие три леммы
(см. [37]):
Лемма 32. Для любой 2-призмы А X В (X В4 и лю-
бого X 0 существуют такие многогранники Р, Q ЕЕ 23,
что
kA X В + Р ~ А X кВ + С-
т
Доказательство. Мы имеем (ср. (97))
[еД X к [е2, е3, е4] + [ех, е2] X к [е3, е4] +
+ lex, е2, е3] X к [е4] ~ к [еД X [е2, е3, е4] +
т
+ к [ех, е2] X Ге3, е4] Д- к [ех, е2, е3] X [е4]. (И7)
Заменяя ех на —ех и переставив левую и правую части,
получаем (учитывая, что [—ех] = [еД):
т
к [сД X [е2, е3, с4] Д- к [ сх, е21 X [с3, с4] Д-
Д- к [— ех, е2, е3] X [е4] ~ [еД X' к {е2, е3, е4] Д-
т
Д- [—ех, е2] X к [е3, е4] Д- [—ех, е2, е3] X к [еД-
§ 20]
ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА
181
Складывая эти два соотношения и выбрасывая одинаковые
слагаемые в левой и правой частях (на основании теоре-
мы 22), находим
[ej, е2] X X [e8, б4] + 1 [—еп е2] X [е3, б4] +
+ [ех, е2, е8[ X X [е4[ + X [— е15 е2, б3] X [с4[ ~
т
~ X [elt е2] X [е3, е4] + [— е1г е2] X X [в8, е4] +
т
*31 [^4] “|“ I Cj, €21 Cgf X X [e^J.
Заменяя здесь е4 на —е4 и переставив левую и правую ча-
сти, получаем еще одно соотношение; прибавив его к пре-
дыдущему, находим (выбрасывая одинаковые слагаемые
в левой и правой частях)
[en e2] X X [в8, е4] + [— бх, е2] X X [е3, —е4] +
+ [—е1? е2] X [е3, е4] + X [ех, е2] X [е3, —е4] ~
т
~ [—вх, е2] X X [e3, е4] + [е1? е2] X X [е3, —е4] +
т
4- X [ex, е2] X [е3, б4] X [—ех, е2] X [е3,—б4]. (118)
Теперь заметим, что
[—еп е2] + [б! — б2, 2е2] ~ [бп е21 + [бх] X [б2]
т
(рис. 108), и потому
1—61, е2] X X [е3, б4] + [бх — б2, 2е2] X X [с3, б4] ~
’ т
~ 1бх, б2] X X 1б8, б4] + 16j] X [е2] X X 1б3, б41.
т
Аналогично,
[6ц е2] X X [б3, —б4] + [ei] X [б2] X X [б3, —б4] ~
т
~ [— ех, б2] X X [б8, —б4] + [ет — б2, 2е21 X X [б3, —б41,
т
X |бх, е2] X [б8, б4] + X [бх] X X [б2] X [б3, б4] ~
т
1 бх, e2J X [б8, б41 | X [бх б2, 2б21 X [б3, e4J,
у
X [—61, б2] X [е8, — е4] + X [вх — е2, 2ег] X [е8, —е4] ~
т
~ X [ех, е8] X [в3, — е4] + Ц1 X X [б8] X [б3, —с4].
т
1S2
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ III
Прибавляя эти четыре соотношения к (118) и упрощая,
находим
kj — е2, 2ег] X X [е3, е4] + A [q — ег, 2ег] X [е3, —е4] 4-Р' ~
~ A [ej — е2, 2е2] X [е3, с41 +
+ [е4 — е2, 2ег1 X А [е3, —е4] + Q', (119)
Рис. 108.
где Р', Q' GE Z3. Далее, так как
le3, — е4] + [2е3, е4 — е3] ~ [е8, е4] + [e3J X 1е4],
т
то мы имеем
|с4 — а2, 2е21ХА [е3, —е4] ~|“[е4 е2, 2e2] X А [2е3, а4 е31
(е1 — е2, 2е2] X X [е3, е4] + [е2 — е2, 2е2] X X k8] XА[е4],
т
А [е4 — е2, 2е2] X [es, е4] + A [q — в2, 2е2] X [е3] X [е4] ~
А |ех — е2, 2е2] X [е3, —е4] + А [е4 — е2, 2е2] X
X [2вд,
Прибавляя эти соотношения к (119) и упрощая, получаем
Iei — еа> 2е2] X А [2еа, е4 — е3] + Р" ~
~ А [ех — е2, 2e3J X {2еа, е4 — еа] + Q"', Р", Q" 6= Z3.
т
Здесь е4, с2, е3, е4 — любые линейно независимые век-
торы; полагая е4 — сй — а, 2сг = Ь, 2е3 = с, е4 — е3 = d,
S 2oJ ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА 183
находим
[а, Ь] X X [с, cl] + Р" ~ X [а, Ь] X [с, d] + <?"
г
(для любых линейно независимых а, Ь, с, d). В частности,
X кх, е2] X [е3, е4] + Рх ~ [q, e2J X X [е3, е4] 4 (4;
т
P^Qi^Z,. (120)
Прибавляя это соотношение к (117), получаем
1сх] X X [с2, е3, е4] [ех, в2, c3J X [с41 4~ Рх * '
т
~ X [ej X [е2, е3, е4] + X [ех, е2, е3] X [е4] + Q4.
т
Заменив ех на —ех и переставив левую и правую части,
находим
X [ej X [ег, е3, е4] + X [— elt е2, е3] X [е4] + Рх ~
г
[ех] X X [с2, г3, е4] [ сх, е2, е31 X [е4Ц-0 х.
т
Складывая это соотношение с предыдущим, получаем
[q, е2, е3] X X [е4] + X [—ех, е2, е3] X [е4] + Ра ~
т
~ X [е1; е2, е3] X [?4| + [—elt е2, е3] X X [е4] + Q2 (121)
т
(где Р2, Q2 С Z3).
Условимся через {6Х, Ь2, Ь3} обозначать тетраэдр, по-
строенный на векторах Ъ4, Ь2, Ь3, т. е. тетраэдр с верши-
нами Ъо, Ьо + fo,, b0 + Ь2, Ьо + Ъ3 (где Ьо выбирается
произвольно). Несложно проверяется, что
2-{б1, е2, е3) Ч~ [ сх, Ь2, Ь3] ~ {2ех, е2, е3} -р [ех, Ь2, Ь3],
т
где Ъ2=е2—е4, Ь3—е3—е2.
Отсюда получаем (для любых линейно независимых
еы ^3i ei)
2* {гх, с2, е3) X [с4] - | ^х, fe2, £?3] X [е4]
~ {2ет, е2, с3) X [е4] + [ех, Ь2, Ь3] X [е4]. (122)
т
184 РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [Ил. lit
Заменив в этом соотношении е4 на Ае4 и переставляя
левую и правую части, находим
{2^1, е2, е3} X А[е4] 4~ 1ех, Ь2, Ь3] X 1 [е4] ~
т
~ 2- {ех, е2, е3} х X [<?4] -|- [—ех, Ь2, Ь3] х А [е4].
Далее, заменив в (122) ех, с2, еа на Аег, Ас2, Ае3, имеем
2-А {ех, е2, е3} X [е4] А [—ех, Ь2, Ьа] X [е4] ~
т
А {2ех, е2, е3} X [е4] -|- A [сх, Ъ2, 53] X [е4].
Складывая два последних соотношения и учитывая (121),
получаем
{2ci, е2, е3} X А [е4] + 2-А {ех, е2, еа} X [е4] Q2 ~
т
~ 2-{ех, е2, е3} X А [е4] + А {2ех, е2, е3} X [е41+ Р2, (123)
где Р2, Q2 GE Z3. Аналогично,
{2ех, 2е2, еа) X А [е4] + 2-А {2ех, е2, еа} X [е4] + Qz ~
т
~2- {2е1,е2, еа} хА [е4] -J- А {2ех, 2е2, е3} X [е4] + Р2, (124)
{2ех, 2е2, 2е3) X А [е4] -|- 2-А {2ех, 2е2, еа) X [е4] -|- Q3 ~
~ 2- {2е1, 2ег, е3} X А [е4] + А- 2е2, 2е3} х [е4] + Р2-
(125)
Складывая четыре экземпляра соотношения (123), два
экземпляра соотношения (124) и соотношение (125), на-
ходим теперь
8-А {е^ е2, е3} [е4] + {2е1г 2е2, 2е3} X А [е4] + Q*
~ 8-{ех, е2, е3} X А [е4] + А {2ех, 2еа, 2е3} X [е4] + Р*;
Р*, Q* G Z3. (126)
Далее, учитывая соотношение 8-Л/ + Р ~ 2М + 6Л/+^;
т
§ 20]
ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА
185
Р, Q ЕЕ Z2, вытекающее из леммы 16, можем написать
8- {ег, е2, е3} X X [ej + Q[ ~
т
~ {2elt 2е2, 2е3} X X [е4] + {6en 6е2, 6е3} X X [е4] + Р4,
т
"К {2ех, 2es, 2е3} X [е4] + X {6ех, 6е2, 6е3) X [е4] + (?* ~
т
~ 8-Х {е15 е2, е3} X [е4] + Р2,
т
где Pi, ЕЕ Z3. Складывая два последних соотношения
и соотношение (126), получаем, наконец,
X {6ex, 6е2, 6е3} X [е4] + <?** ~
т
~ {6ех, 6е2, 6е3) X X [е4] + Р**; Р**, ()** е Z3. (127)
т
Соотношения (120) и (127) показывают, что утвержде-
ние леммы 32 справедливо в случае, когда А и В — сим-
плексы. Отсюда, с помощью разбиения на симплексы,
мы заключаем, что оно справедливо для любой 2-призмы
А X В Q Л4.
Лемма 33. Любой многогранник A CZ Р4 раеносо-
ставлен с многогранником вида I X W, где I — отрезок
длины 1, ортогональный трехмерному многограннику W.
Доказательство. Прежде всего рассмотрим
произвольный ортогональный симплекс в Ri, т. е. симплекс
[ех, е2, е8, е4], где ех, е2, е3, е± — попарно ортогональные
векторы (произвольной длины). Каждая точка х этого
симплекса однозначно записывается в виде
х = Ьо + х1е1 + х2е2 + х3е3 + х4е4 (128)
(см. (41)), где координаты хг, х2, х3, х4 удовлетворяют
условиям
1 > > х2 > х3 > ж4 > 0. (129)
Обозначим через М множество точек х [ех, е2, е3, е4],
удовлетворяющих дополнительному условию х2 + х3 1,
а через N — множество точек х ЕЕ [q, е2, е3, е4], для ко-
торых ж2 + х3 > 1. Ясно, что
[е1? е2, е3, е4] = М + N.
Далее, через АТЛ обозначим множество точек х ЕЕ Л7, удо-
влетворяющих условию л;2 , а через Т1/2 — множество
186
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. 1Ц
точек х G= М, для которых г2 > у. Тогда М = Мг + М2.
Пусть g — отображение, переводящее точку (128) в точку
b0 + (1 — ’тК + (1 — ж2)с2 + ж8е3 + ж4е4. (130)
В силу ортогональности векторов ег, е2, е3, е4, отображе-
ние g является движением. Многогранник g (М2)
состоит из точек (130), удовлетворяющих условиям (129)
и неравенствам я:2 + х3 1, х2 х/2; иначе говоря,
g (М2) состоит из точек (128), удовлетворяющих условиям
0 -С тх ж2, о а?4 я3 х2 х/2.
Отсюда видно, что М4 g (М2) состоит из точек (128),
удовлетворяющих условиям
о 1, о ж4 ж3 я2 х/2,
т. е. М4 + g (М2) = [еД X V2 [е2, е9, е4].
Аналогично, разбивая N на две части A',, N2 условиями
х3 V2, xs х/2 и применяя движение h, переводящее
точку (128) в точку
4* 4~ х2е2 4~ (1 Хд)вд 4* (1
мы найдем, что h (Л\) + N2 = х/2 [е15 е2, е3] X [е4]. Таким
образом,
ten е2, е3, е4] ~ [ej X х/2 [е2, е3, е4] 4* 1/2 К, еа, е3] X [е4].
(131)
Пусть теперь X — длина вектора ех, т. е. ех = 1а4, где
а4 — вектор длины 1, ортогональный трехмерному про-
странству L CZ /?4, натянутому па векторы е2, е3, е4. В силу
леммы 32,
1 1
[ej X -у- [е2, е3, е4] + Р ~ [щ] х -у- [е2, е3, е4] + Q,
P,Q(= Z9. (132)
Далее, любая 3-призма в IP имеет вид А X В X С, где
А, В — отрезки, a С — некоторый многоугольник; так
как многоугольник С равносоставлен с параллелограммом
(теорема 10), то 3-призма А X В X С равносоставлена
с некоторым четырехмерным параллелепипе-
дом. Следовательно, для многогранников Р, Q (см. (132))
мы имеем
S 20 j
ИНВАРИАНТЫ ДЕНА — ХАДВИГЕРА
187
В силу леммы 18, можно считать, что
Р' = [aj X U, Q' = [aj X V,
где U, V CZ L — параллелепипеды. Соотношение (132)
принимает вид
[ej X VB [е2, е3, е4] Д- [ax] X U ~ [аД X (| [е2, е3, с4] Д- V).
Так как многогранники в левой и правой частях равнове-
лики, то п(С7)<^п [е2, е3, е4] Д- , и потому
4-[е2’ез,е4] +V^U’+W',
где U' ~ U (лемма 12). Таким образом,
т
lex] X % 1«2» e3i е4] Д- [aj X U ~ [яД X U' Д- [«TJ X W,
т. е. многогранники 1ех] X */2 [е2, е3, е4] и [ax] X РИ'рав-
нодополняемы, а потому (по теореме 22) равносоставлены!
lej X V2 le2, е3, е4] — I X W.
Здесь W CZ L — трехмерный многогранник, а I = [аД —
отрезок длины 1, ортогональный подпространству L.
Аналогично,
V2 [ех, е2, е3] X [е4] ~ / X W";
мы можем считать при этом (применив, если нужно, не-
которое движение), что W и W" лежат в одном и том же
подпространстве L и не имеют общих внутренних точек.
Таким образом, в силу (131),
[ех, е2, е3, е4] ~ I X (W Д- W"),
т. е. в случае, когда А — ортогональный симплекс, лем-
ма 33 справедлива.
Далее, если А — произвольный симплекс, то сущест-
вуют такие ортогональные симплексы A,, Aj, что
А Д- Ах Д-. . . . Д- Ак- ~ А4 + . . . + Ai (133)
т
(ср. доказательство леммы 29). Из (133) в силу доказан-
ного выше вытекает, что утверждение леммы 33 справед-
ливо для любого симплекса, а потому и для произ-
вольного многогранника.
188
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Щ
Лемма 34. Пусть W — трехмерный многогранник
расположенный в трехмерном подпространстве L Q Т?6
и I — отрезок длины 1, ортогональный L. Тогда
фх (7 X IV) = ф, (IV), где ф, — инвариант Дена—Хад-
вигера (см. (114)).
Доказательство. Обозначим через а и Ъ кон-
цы отрезка 7. Двумерными гранями многогранника I X W
являются многоугольники вида а X М, b X М, I х К,
где М — произвольная двумерная грань многогранни-
ка W, а К — произвольное его ребро. Двугранные углы
при гранях а X М и Ъ X М — прямые, и потому зти
грани можно не учитывать при вычислении инварианта
Фх (7 X И7). Далее, двугранный угол многогранника
I X W при грани I X равен двугранному углу at-
многогранника IV при ребре Kt. Поэтому, обозначая
через Z, длину ребра Kt, мы имеем
Фо (/ X Ki)f (a;) = s (7 X Kt)f (a.) = (1-/4)/ (a,-) =
= kf («0,
откуда, суммируя по всем ребрам многогранника IV,
получаем требуемое соотношение ф, (7 X Ю = Фх (IV).
Доказательство теоремы 29. Необхо-
димость вытекает из того, что ф, есть аддитивный D-инва-
риант (теорема 28). Докажем достаточность. Пусть
Л, В CZ Z?4 — такие четырехмерные многогранники, что
Фо U) = Фо (В), фх (Л) = фх (В)
(при любом выборе функции Коши—Гамеля /, удовлетво-
ряющей условию / (л) = 0). В силу леммы 33,
А ~ I X IV,, В - I X IV2,
где Wlf IV2 — трехмерные многогранники, расположен-
ные в подпространстве L CZ Ri, а I — отрезок длины 1,
ортогональный L. Мы имеем
г (TV,) = фс (/ X IV,) = ф0 (Л) = ф0 (В) = ф0 (Z X PV2) =
= и (IV2).
Кроме того, согласно лемме 34,
Фх ТО = Ф, (7 X IV,) = ф, (Л) = Ф, (В) = ф, (7 X IV2) =
- Фх ТО-
$ 21J
МИНИМАЛЬНОСТЬ ГРУППЫ П,
189
Таким образом, И\ и W2 — равновеликие многогранники,
имеющие одинаковые деповские инварианты, и потому
WL W2 (теорема 25). Но тогда 7 X И\ ~ I X W2,
и потому А ~ В.
§ 21. Минимальность группы сохраняющих ориентацию
движений
Как мы видели в § 12, понятия Р-равносоставленностп
и 7)0-равпосоставленности эквивалентны. Здесь мы дока-
жем [8], что Do — минимальная группа, об-
ладающая этим свойством, т. е. справедлива следующая
теорема (аналогичная теореме 17 для многоугольников).
Теорема 30. Пусть G — такая группа движений
пространства В3, что любые равносоставленные много-
гранники G-равносоставлены. Тогда G совпадает с одной
из групп D, Do.
Иначе говоря, если G не совпадает ни с одной из групп
D, Do, то найдутся два равносоставленных многогранника,
не являющихся G-равносоставлсппыми.
Доказательство. Обозначим через Т* CZ В'3
тетраэдр, определяемый в прямоугольной системе (ж, у, z)
неравенствами:
х Z>U, у 0, z ^>0;
Через о обозначим начало координат, а через а, Ъ, с —
вершины тетраэдра Т*, лежащие на осях х, у, z. Единич-
ные векторы внешних нормалей к граням тетраэдра Т*
имеют вид
Я1 = (-1, и, 0); а2 = (0, -1, 0); а3 = (0, 0, -1);
Поэтому, обозначая через у2, у3 величины двугранных
углов тетраэдра Т* при ребрах ab, ас, Ъс, мы имеем
190
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. Ш
Так как
Д' 5л , / рТ г__________________
12е" 6 .. У '^-lA-nr
12 г 2 2 I 4
то Тг = Тз = 5л/12, т. е. величины двугранных углов при
ребрах ас и Ьс являются рациональными кратными чис-
ла л. То же имеет место для двугранных углов при ребрах
оа, оЪ, ос (эти углы — прямые). Остается двугранный
угол при ребре ab.
Мы имеем cos 2уг = 2cos2 ух — 1 = j/З — 1. Соотно-
шение
cos 2 (к + 1)ух = 2 cos 2ух cos 2куг — cos 2 (к — 1)ух (134)
позволяет, исходя из значений
cos 2у± — /3 — 1; cos 4ух — 2cos22y1— 1 = —4^3+7,
последовательно вычислять cos 2куг для к = 1, 2, . . .
Мы можем положить
cos 2*Vx = (-1)*-iph /3 + (-iyffft, к = 1, 2, . . .,
(135)
где ph, qk определяются в силу (134) рекуррентными фор-
мулами
f А+1 — %Рк + ^Як — Рк-ii Pi — li Рг = 4,
I Як+i = §Рк 4- 2qk — qk^- qi = 1, q2 = 7.
Записав эти равенства в виде >
Рк+1 — Рк = (Р>: — Рк-i) + 2^; рк+1 — рк 2дк (рк — Рк-1)>
*7fc+l Як = (Як — Як-i) + 6рк> Як+i = $Рк + Як + (Як — Як-1р
находим, что если для некоторого к 2 выполнены соот-
ношения
Pk—Ph-i>0, Як-Як-1>0, Pk>®, Як >0,(136)
то они справедливы и для к + 1. Для к = 2 они верны,
и потому неравенства (136) выполняются для всех к 2.
Отсюда следует, что рк, qh — натуральные числа, причем
Pk 0 при к — 1, 2, . . ., и потому, в силу (135), cos 2кух
есть иррациональное число. В частности,
cos 2куг Ф 1 при к = 1, 2, . . ., т. е. 2ку± 2/л при на-
§ 211 МИНИМАЛЬНОСТЬ ГРУППЫ По 191
туральных к, I. Иначе говоря, число yjn иррацио-
нально. Поэтому, положив
f (я) = / (-J-) = / (5-) = °’ / (Vi) = 1, (137)
мы получаем аддитивную функцию на множестве
{я, л/2, 5л/12, Yj}, содержащем число л и величины дву-
гранных углов тетраэдра Т*. Соответствующий деповский
инвариант / (Т7*) отличен от нуля:
/ (71*) = У (н) = О,
где I — длина ребра аЪ.
Пусть теперь р CZ Z?3 — произвольная прямая. Обо-
значим через Р множество всех прямых, получающихся
из р движениями, принадлежащими группе G. Далее,
пусть / — некоторая аддитивная функция, удовлетворяю-
щая условию / (л) = 0, и М — произвольный много-
гранник. Положим
/р(Л7) = Z1/(a1) + - . +
где Zj, . . ., lk — длины тех ребер многогранника М,
которые лежат на прямых, принадлежащих множеству Р,
а аг, . . ., ак — величины соответствующих двугранных
углов. Дословным повторением рассуждений, проведен-
ных при доказательстве леммы 11 и теоремы 19, устанав-
ливается, что если fp (71/) =/= /р (7V), то М и N не являются
G-равносоставленными.
Допустим теперь, что существует прямая рг, которую
нельзя получить из р никаким движением, принадлежа-
щим группе G. Обозначим через Т (соответственно, Т^)
тетраэдр, конгруэнтный Т*, у которого ребро, конгру-
энтное ab, лежит на прямой р (соответственно, р^. Тогда
для функции /, определяемой соотношениями (137), имеем
/ (П = if (Т1) = Z ф о, / (Л) = О
(поскольку pt Р). Таким образом, конгруэнтные между
собой (и, следовательно, равносоставленные) тетраэдры Т
и rJ\ не являются С!-равносоставленными. Но это проти-
воречит выбору группы G.
Итак, для любых двух прямых р, рг существует дви-
жение g Е fi, удовлетворяющее условию g (р) = рх.
192
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ [ГЛ. ITI
Остается доказать, что группа G, обладающая этим свой-
ством, содержит Do.
Пусть рг, р.2, рэ — три попарно не параллельные пря-
мые и gt, faEG — такие движения, что {р^ = р2,
S-2 (Рг) = Рз- Движение g3 = g2 о удовлетворяет усло-
вию ёз (Р1) = Рз- Так как g3 = g2 ° gt, то хотя бы одно
из движений gj, g2, gs сохраняет ориентацию. Итак, су-
ществует сохраняющее ориентацию движение g* GE G,
которое некоторую прямую переводит в не параллельную
ей прямую и, следовательно, не является параллельным
переносом.
Напомним, что сохраняющее ориентацию движение
пространства В3, не являющееся параллельным переносом,
представляет собой винт, т. е. композицию поворота па
угол а вокруг некоторой направленной прямой I
(О < а <Е 2л; поворот осуществляется против часовой
стрелки, если смотреть вдоль направления прямой Z)
и параллельного переноса на вектор ка, где а — единич-
ный вектор направленной прямой Z; условимся такой винт
обозначать через (Z, а, к). Таким образом, указанное выше
движение g* GE,G имеет вид (Z*, а*, X*).
Пусть теперь р — произвольная прямая и g (Е G —
движение, переводящее прямую Z* в р; на р выберем
такое направление, что направленная прямая I* переходит
в направленную прямую р при этом движении. Легко
видеть, что движение h = g о g* ° g~J GE G представляет
собой винт (p, а*, к*) с теми же а*, к*. Движение h1
представляет собой винт (р', а*, к*), где р — направлен-
ная прямая, получающаяся из р изменением направле-
ния па противоположное. Таким образом, для любой
направленной прямой р в группе G имеется винт
gp = (р, а*, к*).
Пусть теперь р — фиксированная направленная пря-
мая, р' — противоположно направленная прямая, a q —
переменная направленная прямая. Если q совпа-
дает с р, движение gq ° gp представляет собой винт
(р, 2a*, 2Z*) с углом поворота 2a*. Если же q совпадает
ср', движение gq ° gp является тождественным отображе-
нием. Рассматривая движение gq р gp при непрерывном
перемещении направленной прямой q от положения р
до положения р', получаем в силу соображений непрерыв-
ности, что для любого р, 0 < Р 2a*, в группе G содер-
S 22] АЛГЕБРА МНОГОГРАННИКОВ |93
жится некоторый винт с углом р. Из этого в свою очередь
вытекает, что при любом р, 0 <; Р < 2л, в группе G имеет-
ся некоторый винт с углом р. Более того, как показывает
проведенное выше рассуждение, для любой направленной
прямой р п любого р, 0 < р <; 2л, в группе G имеется
(при некотором Я,) винт (р, р, Я,).
Для доказательства включения G ~~) Do остается уста-
новить, что группа G содержит все параллельные пере-
носы; действительно, из этого будет следовать, что вместе
с винтом (р, р, Я) при некотором X группа G содер-
жит винты (р, р, Я) при любом Я.
Пусть pj и р2 — параллельные прямые, не совпадаю-
щие между собой. В силу доказанного, в группе G имеются
при некоторых Я2 винты g, = (р17 л, Ях) и g2 = (р2, л, к2).
Композиция t = g2 ° pj представляет собой параллель-
ный перенос на отличный от нуля вектор.
Итак, в группе G имеется параллельный перенос t
на вектор е, имеющий длину I 0. Пусть е' — любой
вектор, имеющий ту же длину I. Выберем винт g ЕЕ G,
который переводит вектор е в вектор е'. Тогда движение
g о t о g~l ЕЕ G представляет собой параллельный перенос
на вектор е'. Таким образом, параллельный перенос на
любой вектор, имеющий длину I, принадлежит группе G.
Беря композицию одинаковых параллельных переносов,
находим, что параллельный перенос на любой вектор,
имеющий длину kl, где к — натуральное число, принад-
лежит группе G. Но тогда любой параллельный
перенос принадлежит группе G (достаточно рассмотреть
равнобедренный треугольник, у которого основание —
произвольно заданный отрезок, а длина боковой стороны
равна kl).
§ 22. Алгебра многогранников
Во всем предыдущем изложении запись М = Аг .
. . . + Ah означала, что многогранники Ах, . . ., Ah по-
парно не имеют общих внутренних точек и, при этих усло-
виях, М есть объединение многогранников А1г . . ., Ак.
В соответствии с этим, если, например, нужно сложить
соотношения А ~ В и С ~ D, то предварительно следует
позаботиться о том, чтобы в каждой части многогранники
не имели общих внутренних точек, т. е. вместо записи
194
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
Ггл. иг
А + С ~ В + D надо рассматривать соотношение
A -j- С ~ В -}- D', где многогранники С = С, D ' ~ Г)
выбираются так, что суммы А + С и В + D' определены.
Можно, однако, условиться не различать конгруэнтные
между собой многогранники, т. е. в каждой сумме рассма-
тривать слагаемые лишь с точностью до конгруэнтности,
что позволит писать сумму А + С (или В + D), не забо-
тясь о том, имеют ли слагаемые общие внутренние точки.
Условимся также соотношение А ~ В — С понимать
в смысле А + С ~ В (такое понимание разности исполь-
зовалось в предыдущем изложении).
Наконец, уславливаясь считать каждую 2-призму
эквивалентной нулю, мы найдем, в силу леммы 15, что
при любых действительных А, ц многогранники (А, + р)Л/
и ХМ + рМ эквивалентны. Фактически, именно такое от-
ношение эквивалентности составляло основу изложения
в § 17. Формализация этого отношения эквивалентности
приводит к введенному Хадвигером [24] понятию алгебры
многогранников, рассмотрению которого и посвящен этот
параграф.
Обозначим через Рп векторное пространство, элемен-
тами которого являются формальные линейные комбина-
ции ХуМу + . . . + XkMk, где Му, . . ., Мк — произволь-
ные n-мерные многогранники в Вп, Xt — действительные
числа, a к — произвольное натуральное число. Фикси-
руем некоторую группу G движений пространства Вп,
содержащую группу Т всех параллельных переносов.
Отметим четыре случая, в которых формальная линейная
комбинация будет считаться несущественной. Во-первых,
если М s N, то элемент М — N = 1М + (—1)AT (= Р'1
G
будем считать несущественным. Во-вторых, если
4 = Му [J • • • U где Му, . . ., Мк попарно не
имеют общих внутренних точек, то элемент А — Му — .
. . . — Мк ЕЕ Рп будем считать несущественным. В-треть-
их, если многогранник М получается из N некоторой го-
мотетией с коэффициентом X 0, то элемент М — XN ЕЕ Р
будем также считать несущественным. Наконец, в-чет-
вертых, будем считать несущественными все 2-призмы.
Подпространство пространства Рп, порожденное всеми
несущественными элементами, обозначим через Ро (G),
а факторпространство Xn(G) = Рп!Р™ (G) будем называть
я 221
АЛГЕБРА МНОГОГРАННИКОВ
195
п-мерной G-алгеброй многогранников. Через к обозначим
естественный гомоморфизм Рп -+ PnIP^ (G).
Нетрудно показать, используя лемму 15 и теорему 22,
что для многогранников А, В QZ Пп соотношение
х (А — В) = 0 (т. е. включение А — В е Ро (6)) имеет
место в том и только в том случае, если А и В являются
G-равносоставленными по модулю Z2, т. е. существуют
такие многогранники U, V е Z2, что А + U и В ф- V
являются G-равносоставленными. Именно это и определяет
геометрический смысл алгебры многогранников. Заметим,
что при п = 3 равносоставленность по модулю Z2 сов-
па д а е т для равновеликих многогранников с р а в н о-
состав леиностыо (это вытекает из леммы 19
и теоремы 22). Иначе говоря, принимая в качестве G
группу всех движений пространства В3, мы находим,
что многогранники А, В Q2 R3 в том и только в том случае
равносоставлены, если v (Л) = v (В) и х (Л — В) = 0.
Фактически, это и было алгебраической основой прове-
денных в § 17 рассуждений. Заметим также, что если за G
принимается группа D всех движений пространства В4,
то Ро (G) = Р4 (лемма 33), т. е. факторпространство
S4 (Р) = Р4/Ро (D) тривиально. Это послужило алгебраи-
ческой основой рассуждений Ессена (теорема 29). Более
того, как показал Хадвигер [24], если п ч е т н о, а груп-
па G движений пространства Вп содержит все параллель-
ные переносы и все центральные симметрии, то Рп =
= Рп0 (G), т. е. пространство Xn (G) тривиально.
Заметим, что для п — 3 (и других нечетных п) про-
странство Хп (D) = Pn/Pp (D) бесконечномерно
(точнее, имеет размерность $(). Для п — 3 это выте-
кает из того факта (установленного еще Деном [13]), что
среди равновеликих трехмерных многогранников имеется
несчетное множество таких, которые попарно не равносо-
ставлены.
В трехмерном случае деновские инварианты являются
гомоморфизмами алгебры многогранников (т. е. линейными
функционалами на векторном пространстве S3 (Р) —
= P3/Pl (Р)). В самом деле, если f (А) — деповский ин-
вариант (определяемый некоторой функцией Коши—
Гамеля, удовлетворяющей условию /(л)=0), то можно
496
РАВНОСОСТАВЛЕННОСТЬ МНОГОГРАННИКОВ
[ГЛ. Ш
положить
f (МА + • + ЧМк) = М (ЛА) + ... + W (Mh)
для любой формальной линейной комбинации + . . .
. . . + khMk GE Р3. Непосредственно проверяется, что /
обращается в нуль на подпространстве (D) (т. е. на
любом несущественном элементе; в частности, как мы ви-
дели в § 13, / обращается в нуль на призмах). Это и озна-
чает, что деповский инвариант / может рассматриваться
как линейный функционал па факторпространстве
Ps/Pq (Р). Заметим, что при п 3 это уже не так, по-
скольку инварианты Дена — Сидлера не обращаются
в пуль на 2-призмах (ср. доказательство теоремы 29).
Интересную трактовку деповских инвариантов (в трех-
мерном случае) предложил Ессен в работе [361. Именно,
обозначим через 7Д аддитивную группу действительных
чисел, приведенную но модулю л, и рассмотрим тензорное
произведение R 0 7Д. Положим, далее,
Д (Л) = 1А 0 аг + . . . + lk 0 а..,
где Z15 . . ., lk — длины ребер многогранника A CZ R3,
а ап . . ., ak — величины соответствующих двугранных
углов. Функция Д продолжается, по аддитивности, на
векторное пространство Р3. Без труда проверяется, что
получаемый гомоморфизм Д: Р3 R 0 Вг. обращается
в нуль на подпространстве Р,\ (7)), благодаря чему опреде-
ляется гомоморфизм 6 = Д ° х-1 факторпространства
(р) _ рз/р3(/ур Гомоморфизм Д (или 6) фактически
объединяет в себе все деповские инварианты. Более точно,
пусть <р: R 0 Rn В — аддитивный гомоморфизм, ли-
нейный по первому сомножителю (т. е. удовлетворяющий
условию <р (к 0 а) *= Z<p (1 0 а)). Тогда <р ° Д: Р3 -* R
есть некоторый деповский инвариант, причем любой
деповский инвариант может быть получен таким образом.
В этой трактовке теорема Дена — Сидлера формулируется
следующим образом: для равносоставленности многогран-
ников А, В CZ R3 необходимо и достаточно выполнение
равенств v (Л) = v (В), Д (Л) = Д (В).
Отметим в заключение еще один вопрос, связанный
с рассмотрением алгебры многогранников. Из способа
построения векторного пространства (G) = Рп/Ро (Q
§ 221
АЛГЕБРА МНОГОГРАННИКОВ
197
непосредственно вытекает (с использованием леммы Цор-
на) существование в Нп такого множества В = {Na} мно-
гогранников, которые составляют базис векторного
пространства (G) (такой базис для случая п = 3,
G = D мы использовали в § 17). Иначе говоря, для любого
многогранника М CZ Вп однозначно определены действи-
тельные числа ра (Af) (лишь конечное число из которых
отлично от нуля), удовлетворяющие условию
^-Зна(л/)Л^еРоп(б).
а
Функции ра однозначно продолжаются на пространство Рп:
ра (XjAfj + • + ^ЛЦ) — XjPa (Мг) + • . + Kkpa(Mh).
Так как эти функции обращаются в пуль на подпростран-
стве Рп0 (G), то их можно считать заданными на фактор-
пространстве 2n (G) = Рп!Р^ (G). Каждая функция
На (ЛЦ. является аддитивным G-инвариантом и обладает
свойством однородности (т. е. ра (КМ) = Хра (А/)). Иначе
говоря, ра есть линейный функционал на
пространстве S" (G). Ясно, что если ра (М') — ра (А/")
для любого а, т. е. ра (ЛГ — М") = 0, то М’ — М" е
ЕЕ T’o (G) и потому многогранники М' и М" являются
G-равносоставленными по модулю Z2. Таким образом,
справедлива следующая теорема 124): для G-равносостав-
ленности многогранников М', М" CZ Rn по модулю Z2
(где G 2D Т) необходимо и достаточно, чтобы для любого
однородного аддитивного G-инварианта р выполнялось
равенство р (М') = р (М").
Для случая G = Т неопределенность, связанная с рас-
смотрением «всех» однородных аддитивных G-инвариантов,
устраняется: в работе [24] содержится явное перечисление
однородных аддитивных ^-инвариантов. Это дает в эф-
фективной форме необходимое и достаточное условие
^-равносоставленности многогранников по модулю Z2.
Однако лишь при п 3 удалось установить (см. §§ 10 и
19), что эти условия необходимы и достаточны для 7-рав-
носоставленпости (без добавления «по модулю Z2»).
Заметим, что для любого однородного аддитивного
Z-инварианта р и любых выпуклых многогранни-
ков Р, Q имеем р (Р X Q) = р (Р) + р (Q), и потому
многогранники Р X Q и Р + Q являются Т’-равносостав-
лениыми по модулю Z2.
ЗАКЛЮЧЕНИЕ
В приведенной ниже таблице содержится сводка ос-
новных результатов, связанных с третьей проблемой Гиль-
берта. Незаполненные клетки таблицы дают представление
о нерешенных проблемах. Наиболее важными из них, не-
сомненно, являются проблема нахождения необходимого
и достаточного условия D-pавносоставленности
многогранников в Rn (при п 5), а также проблема на-
хождения необходимого и достаточного условия Г-р а в-
носоставленности многогранников в Rn (при
п 4).
Есть также ряд нерешенных проблем, имеющих менее
важное значение (например, нахождение критериев 5-рав-
Равновеликость и рав носостав л е н- ность Р авносостав л е н- ность и равнодо- полняемость D-равносоставлен- ность и De-равно- составленность
Я2 эквивалентны, § 7 эквивалентны, § 7 эквивалентны, §9
R3 не эквивалент- ны, § 13 эквивалентны, § 16 эквивалентны, § 12
R1 не эквивалент- ны, § 20 эквивалентны, § 16 эквивалентны, § 12
\Vto ал не эквивалент- ны, § 20 эквивалентны, § 16 эквивалентны, § 12
ЗАКЛЮЧЕНИЕ
199
носоставленности в пространстве, проблема минимально-
сти группы Do для n-мерных многогранников прп м?>3,
вопросы «минимальности» осуществляющих равносостав-
ленность разбиений и др.)- Ряд излагаемых в книге ре-
зультатов не отмечен в таблице: результаты, относящиеся
к неархимедовым и неевклидовым геометриям (см. § 8),
равносоставленность по группе подобий (конец § 16),
тетраэдры, равносоставленные с кубом (см. § 18) и др.
И этим результатам соответствуют некоторые нерешенные
проблемы (например, проблема равносоставленности п-мер-
ных многогранников по группе подобий при п 3; воп-
рос о существовании несчетных семейств тетраэдров,
отличных от хилловских и равносоставленных с кубом,
и др.).
Сейчас можно сказать, что, несмотря на наличие
пустых мест в таблице (и других нерешенных проблем)
теория равносоставленности (и равнодополняемости)
многогранников, в основных чертах, завершена, и ее кра-
сивое здание является достойным памятником Давиду
Г илъберту.
Условия D-равио- состав л енности Условия Т-равно* составленности Минимальная груп- па, равносоставлен- ность по которой совпадает с D-равно- составлен ноет ь го
необходимое и достаточное, § 7 необходимое и достаточное, §10 § И
необходимое и дос- таточное, §§ 14 и 17 необходимое и достаточное, § 19 § 21
1 необходимое и достаточное, § 20 необхо- димое, § 22
необходи- мое, § 20 необходи- мое, § 22
ДОБАВЛЕНИЕ
О понятии длины
В главе I мы рассмотрели основные положения, свя-
занные с определением площади и объема. Здесь мы обра-
тимся к понятию длины.
Длина отрезка определяется при помощи хорошо
известного процесса измерения, который может быть
описан, например, следующим образом. Фиксируется
некоторый отрезок 10, который принимается за единицу
измерения. Далее, на прямой R фиксируется целочислен-
ная шкала, т. е. совокупность точек, получающихся,
если от некоторой точки а €= R мы будем в обе стороны
последовательно откладывать отрезки, конгруэнтные 10.
Эту шкалу условимся называть нулевой шкалой. Точки
нулевой шкалы разбивают прямую R на счетное число
отрезков, конгруэнтных /0 и попарно не имеющих общих
внутренних точек; мы будем называть их отрезками
нулевой шкалы. Разделив каждый отрезок нулевой шкалы
на 10* конгруэнтных частей, мы получим разбиение
прямой R на счетное число конгруэнтных отрезков, попар-
но не имеющих общих внутренних точек; эти отрезки
будем называть отрезками k-й шкалы (к =1, 2,. . .).
Пусть теперь Q Q R — произвольный отрезок. Обоз-
начим через яй число отрезков fc-й шкалы, целиком содер-
жащихся в отрезке Q, а через Ък — число отрезков fc-й
шкалы, имеющих непустое пересечение с Q. Легко видеть,
что имеют место неравенства
Ч ък
ю Ч---Ч iOk Ч---Ч iOk Ч---Ч ю
Из этих неравенств вытекает, что существуют пределы
lim я^Ю*, liin Ьк/10*, (1)
fr-*oo
О ПОНЯТИИ ДЛИНЫ
201
причем, в силу легко доказываемого соотношения =
= ак 4- 2, эти пределы совпадают. Это общее
значение пределов (1) называется длиной отрезка Q и
обозначается через I (0.
Несложно доказывается (ср. §2), что длина отрезка
(конструктивно введенная при помощи описанного выше
процесса измерения) обладает следующими свойствами,
аналогичными тем, которые мы рассматривали в главе I
для площади и объема:
(а) Функция I неотрицательна, т. е. длина I (Q)
любого отрезка Q является неотрицательным числом.
(0) Функция I аддитивна, т. е. если Q± и Q2 — отрез-
ки, на которые отрезок Q разбивается точкой с (= Q, то
(Qr) + I (Qz).
(у) Функция I инвариантна, т. е. конгруэнтные от-
резки имеют одинаковую длину.
(б) Функция I нормирована, т. е. единица измерения
10 имеет длину 1.
Подобно тому, как площадь фигуры не зависит от
выбора нулевой палетки (или объем — от выбора нулево-
го кубильяжа), длина отрезка не изменяется при переме-
щении нулевой шкалы (или при замене измерения 10
конгруэнтным отрезком 10). Доказательство этого факта
здесь существенно проще, чем в случае площади или
объема. Дело в том, что на прямой любые два конгруэнт-
ных отрезка могут быть получены друг из друга с помощью
параллельного переноса. Поэтому вместо
двух аксиом (у), (у*), которые мы имели в случае
площади (или объема), здесь достаточно одной аксиомы.
Иначе говоря, если некоторая функция (заданная на мно-
жестве всех отрезков прямой R) инвариантна относитель-
но параллельных переносов, то она инвариантна относи-
тельно любых движений прямой R (т. е. инвариантна
и относительно симметрий).
Указанные свойства однозначно определяют длину,
т. е. на множестве всех отрезков существует, и притом
только одна, функция I, обладающая свойствами (а), (0),
(у), (б)- Поэтому конструктивное определение длины
t отрезка может быть заменено аксиоматическим: длиной
называется действительная функция, заданная на множе-
стве всех отрезков и удовлетворяющая условиям (а), (0),
(Y), (6)-
202
ДОЁАВЛЕНиЕ
Вопрос о независимости аксиом («), (0)> (т),
(6) рассматривается аналогично случаю площади (§ 4)
или объема. Однако здесь имеется одна тонкость. Вспом-
ним, что в § 10 (см. сноску на стр. 76) независимость аксио-
мы (а) от аксиом (0), (у), (6) была установлена (в
случае площади) без использования аксиомы
выбора. Иначе говоря, была конструктивно определена ад-
дитивная и нормированная функция sa, инвариантная отно-
сительно параллельных переносов и не удовлетворяющая
аксиоме (а). Поскольку в случае длины речь идет именно об
инвариантности относительно параллельных пе-
реносов, может создаться впечатление, что незави-
симость аксиомы (а) в случае длины отрезка устанав-
ливается без использования аксиомы выбора. В дей-
ствительности это не так, поскольку изложенные в § 10
соображения требуют не менее двух измерений и на
случай прямой R не переносятся.
Рассмотрим этот вопрос подробнее. Именно, мы пока-
жем, что для длины отрезка независимость аксиомы (а)
может быть установлена только с использованием
аксиомы выбора. В самом деле, используя аксиому
выбора, мы можем построить функцию Коши — Гамеля
/(ж), удовлетворяющую условиям /(1) = 1, / (]/Т) —
= —1 (ср. стр. 29), и тогда la (Q) = / (I (Q)) будет
действительной функцией на множестве всех отрезков,
которая удовлетворяет аксиомам (0), (у), (б), но не
удовлетворяет аксиоме (а).
Обратно, допустим, что на множестве всех отрезков
прямой R существует функция la (Q), удовлетворяю-
щая аксиомам (0), (у), (б), но не удовлетворяющая
аксиоме (а). Введем на прямой R координату х, т. е.
фиксируем точку о е Л и направление («вправо — влево»)
на прямой R, после чего определим координату х произ-
вольной точки а ЕЕ R следующими соглашениями:
| х | = I ([о, а]); х 0 в том и только в том случае,
если точка а лежит справа от о. Наконец, определим
функцию / (х), положив
/ (я) = la ([о, dx] ) при X > 0, (2)
/ (—*) = — / (я), (3)
где ах — точка прямой R, имеющая координату х. Легко
о понятии длины
203
видеть, что функция / (х) аддитивна. В самом деле, если
х 0, у > 0, то мы имеем
1 + У) = k (Io> ax+J) = la ([о, aj) + 1а ([ах, ах+у]) =
= k ([о, <U) + la (to, avI) ~ / (х) + / (у)
(здесь мы использовали аксиомы (р), (у) для функции
1а, а также конгруэнтность отрезков [йх, ax+vJ и [о, ау1).
Таким образом, при х 0, у 0 справедливо равенство
/(* + */)=/(*) + / (у);
в силу (3) это равенство справедливо для любых дей-
ствительных х, у. Иначе говоря, функция / (г) а д д и т и в-
н а. Так как, кроме того, 1а не удовлетворяет аксиоме
(а), т. е. существует отрезок Q, для которого la (Q) 0,
то существует, в силу (2), положительное число х0, для
которого / (х0) <" 0. Наконец, / (1) = 1, поскольку 1а
удовлетворяет аксиоме (б). Итак, мы приходим к
существованию аддитивной функции / (х), не являющейся
линейной, а это, как отмечалось на стр. 32, означает
справедливость аксиомы выбора.
Таким образом, в одномерном случае (т. е. при рас-
смотрении длины отрезка) положительное или отрицатель-
ное решение вопроса о независимости аксиомы (а) от
аксиом (Р), (у), (б) связано с принятой аксиоматикой
теории множеств (т. е. с тем, принимается или отвергает-
ся аксиома выбора).
Отметим в заключение, что все изложение книги было
связано с рассмотрением п-мерного объема множеств,
расположенных в п-мерном пространстве Rn (основной
текст книги связан с рассмотрением случаев п 2, а это
добавление посвящено случаю n= 1). Вопрос об измерении
fc-мерного объема множеств в У?" при к п существенно
более сложен. В частности, при к п уже не удается
обойтись (для определения /с-мерного объема в Rn)
аксиомами (а), (р), (у*), (б). Даже в простейшем
случае А = 1, п = 2, т. е. при определении длины линии
на плоскости R2, приходится добавлять еще одну аксиому,
а именно аксиому полунепрерывности снизу. Ограничи-
ваясь определением длины для простых дуг, можно эту
акспому сформулировать следующим образом:
204 ДОБАВЛЕНИЕ
(е) Пусть L — некоторая простая дуга не — поло-
жительное число-, тогда существует такое число 6 О,
что для всякой простой дуги L', удовлетворяющей условию
L CZ иъ (L'), выполнено соотношение I (I/) > I (L) — е.
Аксиомы (а), (Р), (у*), (6), (е) уже позволяют
построить понятие длины для линий (простых дуг) на
плоскости. Именно, условимся называть простую дугу
спрямляемой, если длины вписанных в нее ломаных огра-
ничены сверху. Оказывается, что на множестве всех
спрямляемых простых дуг существует одна и только
одна функция I, удовлетворяющая аксиомам (а), (р),
(?*), (6), (е). При этом каждая из аксиом (Р), (у*),
(6), (е) (а также и аксиома (а) — в случае принятия
аксиомы выбора) независима от остальных аксиом.
В частности, независимой является аксиома (е), т. е. на
множестве всех спрямляемых простых дуг существует
функция Z£, удовлетворяющая аксиомам (а), (Р),
(Т*)> (6), но не удовлетворяющая аксиоме (е). Иначе
говоря, построение теории длин (для линий на плоскости)
только на основе аксиом (а), (Р), (у*) , (б) (без
аксиомы (е)) невозможно. Детали читатель может
найти в статье автора «Длина кривой и площадь поверхно-
сти) (ЭЭМ, т. 5, «Наука», 1966, стр. 88—141).
ЛИТЕРАТУРА
1. Александров А. Д., Одна теорема о выпуклых много-
гранниках, Тр. физ.-матем. ин-та им. Стеклова, 1933, т. 4, 87.
2. Александров П. С. (ред.), Проблемы Гильберта (сбор-
ник), «Наука», 1969.
3. Baumgartner L., Zerlegung des vierdimensionalen Rau-
mes in kongruente Fiinfzelle, Math.-Phys. Semesterber. 15 (1968),
76—86.
4. Baumgartner L., Zerlegung des n-dimensionalen Raumes
in kongruente Simplexe, Math. Nachr. 48 (1971), 213—224.
5. BoltjanskiiV. G., Zerleugungsgleichheit ebener Polygone,
Bui. Inst. Politehnic, Ia?i, IV(VIII), № 1—2 (1953), 33—38.
6. Б о л т я n с к и й В. Г., Равновеликие и равносоставленные
фигуры, Гостехиздат, 1956.
7. Б о л т я н с к и й В. Г., Равносоставленность многоугольни-
ков и многогранников, ЭЭМ, т. V, «Наука», 1966, стр. 142—
180.
8. Болтянский В. Г., Равносоставленность многогранников
и группы движений, ДАН СССР 231, № 4 (1977), 788—790.
9. Bricard R., Sur uu question de geometric relative aux po-
lyedres, Nouv. Ann. Math. 55 (1896), 331—334.
10. D a n z e г L., Zerlegung endlichdimensionaler Raume in kongru-
ente Simplices, Math.-Phys. Semesterber. 15 (1968), 87.
11. D a v i e s H. L., Packings of spherical triangles and tetrahedra,
Proc. Colloquium on Convexity, Copenhagen, 1965, pp. 42—51.
12. Дубнов Я. С., Измерение отрезков, Физматгиз, 1962.
13. D ehn М., Uber den Rauminhalt, Gottingen Nachr. Math. Phys.
(1900), 345—354; Math. Ann. 55(1902), 465—478.
14. Goldberg M., Tetrahedra equivalent to cubes by dissection,
Elem. Math. 13 (1958), 107—108.
15. Goldberg M., Two more tetrahedra equivalent to cubes by
dissection, Elem. Math. 24 (1969), 130—132; correction, 25
(1970), 48.
16. Goldberg M., The space-filling pentahedra, J. Combinato-
rial Theory 13 (1972), 437—443.
17. Gold b erg M., New rectifiable tetrahedra, Elem. Math.
29 (1974), 85—89.
18. G о 1 d b e r g M., Throe infinite families of tetrahedral space-
fillers, J. Combinatorial Theory 16 (1974), 348—354.
19. Goldberg M., The space-filling pentahedra. II, J. Combina-
torial Theory 17 (1974), 375—378.
20. Hadwiger H., Zerlegungsgleichheit uud additive Polyeder-
funktionale, Arch, Math. 1 (1948—1949), 468—472.
206
ЛИТЕРАТУРА
21. HadwigerH., Zum Problem der Zerlegungsgleichiieit der
Polyeder, Arch. Math. 2 (1949—1950), 441—444.
22. HadwigerH., Erganzungsgleichheit A-dimensionaler Poly-
eder, Math. ZeitB. 55 (1952), 292—298.
23. HadwigerH., Mittelpunktspolyeder und translative Zer-
legungsgleichheit, Math. Nachr. 8 (1952), 53—58.
24. Hadwiger H., Lineare additive Polyederfunctionale und
Zerlegungsgleichheit, Math. Zeits. 58 (1953), 4—14.
25. Hadwiger H., Uber Gitter und Polyeder, Monatsh. Math.
57 (1953), 246—254.
26. HadwigerH., Zur Zerlegungstheorie euklidischer Polyeder,
Annali di Matematica, Serie IV, 36 (1954), 315—334.
27. HadwigerH., Zum Problem der Zerlegungsgleichheit k-
dimensionaler Polyeder, Math. Ann. 127 (1954), 170—174.
28. Hadwiger H., Vorlesungen uber Inhalt, Oberflache und
Isoperimetrie, Berlin — Gottingen — Heidelberg, 1957 (рус-
ский перевод: Г. Хадвигер, Лекции об объеме, площади
поверхности и изопериметрии, «Наука», 1966).
29. Hadwiger Н., Translative Zerlegungsgleichheit der Poly-
eder des gewohnlichen Raumes, J. Reine Angew. Math. 233
(1968), 200—212.
30. HadwigerH., GlurP., Zerlegungsgleichheit ebener
Polygone, Elem. Math. 6 (1951), 97—106.
31. Hamel G., Eine Basis aller Zahlen und die unstetigen Losungen
der Fimktionalgleichung: / (x + y) = / (x) + f (y), Math. Ann.
60 (1905), 459—462.
32. Hilbert D., Grundlagen der Geometric, Leipzig, 1899
(русский перевод: Д. Гильберт, Основания геометрии,
Гостехиздат, 1948).
33. Н i 1 Ь е г t D., Mathematische Probleme, Nachr. Gesellschaft
Wiss. Gottingen, Math.-Phys. KI. (1900) (русский перевод
имеется в книге [2]).
34. Hill М. J. М., Determination of the volume of certain species
of tetrahedrons, Proc. London Math. Soc. 27 (1896), 39—52.
35. Jessen B., Orthogonal icosahedra, Nordisk matem. tidskrift
15 (1967), 90—96.
36. J e s s e n B., The algebra of polyhedra and the Dehn — Sydler
theorem, Math. Scand. 22 (1968), 241—256.
37. Jessen B., Zur Algebra der Polytope, Nachr. Akad. Wiss.
Gottingen, Math.-Phys. Kl„ 1972, № 4, 47—53.
38. Jessen B., Karpf J., Thor up A., Some functional
equations in groups and rings, Math. Scand. 22 (1968), 257—
265.
39. Kagan B., Ueber der Transformation der Polyeder, Math.
Ann. 57 (1903), 421—424. См. также В. Ф. К а г а н, О преобра-
зовании многогранников, Mathesis, Одесса, 1913; второе изда-
ние, Гостехиздат, 1933.
40. Киселев А. П., Геометрия, ч. II (стереометрия), «Просве-
щение», 1974.
41. Klein F., Vergleichende Betrich tungen iiber neuere geomet-
rische Forschungen, Erlangen, 1872. См. также Math. Ann. 43
(1893), 63—109.
Литература
207
42. Lebesgue Н., Sur 1’equivalence des polyedres, en particu
Tier des polyedres reguliers, ct sur la dissection des polyedres
n'guliers en polyedres reguliers, Ann. Soc. Polon. Math. 17
(1938), 193—226; 18 (1945), 1—3.
43. L enh aid H.-С., Ober fiinf neue Tetraeder, die einem Wiirfcl
aquiwalent sind, Elem. Math. 17 (1962), 108—109.
44. Nicoletti O., Sulla equivalenza dei poliedri, Rend. Circ.
Mat. Palermo 37 (1914), 47—75; 40 (1915), 194-200.
45. Перепелкин Д. И., Курс элементарной геометрии, ч. I,
Г остехиздат, 1948.
46. Рохлин В. А., Площадь и объем, ЭЭМ, т. V, Наука, 1966,
стр. 7—87.
47. S о 1 о v а у R., A model of set theory in which every set of
reals is Lebesgue measurable, Ann. Math. 92 (1970), 1—56.
48. S о m m e r v i 11 e D. M. Y., Space-filling tetrahedra in eucli-
dean space, Proc. Edinburgh Math. Soc. 41 (1923), 49—57.
49. Sommer v ill e D. M. Y., Division of space by congruent
triangles and tetrahedra, Proc. Royal Soc. 43 (1923), 85—116.
50. S у d 1 e r J.-P., Sur la decomposition des polyedres, Comment,
math. Helvet. 16 (1943/44), 266-273.
51. S у d 1 e r J.-P., Quelques proprietes de la configuration de De-
sargues, Elem. Math. 10 (1955), 32—37.
52. Sydler J.—P., Sur les tetraedres equivalents a un cube,
Elem. Math. 11 (1956), 78—81.
53. Sydler J.-P., Sur quelques polyedres equivalents obtenus
par un procede en chaines, Elem. Math. 14 (1959), 100—109.
54. Sydler J.—P., Conditions necessaires et suffisantes pour
1’equivalence des polyedres de Pespace euclidien a trois dimen-
sions, Comment, math. Helv. 40 (1965), 43—80.
55. Успенский Я., Введение в неевклидову геометрию Лоба-
чевского — Болиаи, «Сеятель», Петроград, 1922.
56. Я г л ом И. М., Геометрические преобразования, ч. I, Гостех-
издат, 1955.
57. Йех Т., Теория множеств и метод форспнга, «Мир», 1973.
58. Zorn М., A remark on method in transfinite algebra, Bull.
Amer. Math. Soc. 41 (1935), 667—670.
59. 3 ы л e в В. Б., О равносоставленности двух равподополняе-
мых многогранников, ДАН СССР 161, JN° 3 (1965), 515—516.
60. 3 ы л е в В. Б., О С-составлснности и G-дополпяемости, ДАН
СССР 179, № 3 (1968), 529—530.
Владимир Григорьевич Болтянский
ТРЕТЬЯ ПРОБЛЕМА ГИЛЬБЕРТА
М., 1977 г., 208 стр. с ипл.
Редактор Ф. И. Дизнер
Техн редактор. Л. В. Лихачева
Корректор Н. Д. Дорохова
Сдано в набор 25. И. 1976 г.
Подписано к печати 15. 02. 1977 г.
Бумага 84х1081/*2 Физ. печ. л. 6,5.
Условн. печ. л. 10,92. Уч.- изд. л. 10,62.
Тираж 13800 экз. Т-03461. Цена книги 64 коп.
Заказ № 1432.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука»
Москва, Г-99, Шубине кий пер., 10