и. м. яглом
Проблема
тринадцати шаров
БИБЛИОТЕКА Г У
МАТЕМАТК^ЖЯ
KC/t/iEAJ
Издательское объединение «Вища школа»
Головное издательство
Киев — 1975

513
Я29
УДК 519.1
Проблема тринадцати шаров. Я г л о м И. М. Изда¬
тельское объединение «Вища школа», 1975, 84 с.
В книге в научно-популярной форме изложен ряд во¬
просов комбинаторной геометрии. Рассматривается про¬
блема тринадцати шаров, интересовавшая еще И. Кеплера
и И. Ньютона, а также многие важные результаты комби¬
наторной геометрии, полученные в последние годы. Об¬
суждаются нерешенные до настоящего времени задачи и
проблемы, которые могут заинтересовать и юных матема¬
тиков.
Рассчитана на учащихся физико-математических школ.
Книгой смогут пользоваться преподаватели математики
и учащиеся старших классов общеобразовательных школ.
Ил. 52. Библиогр. 15.
Редакционная коллегия:	член-кор.
АН УССР А. В. Скороход (ответственный редактор), проф.
Л. А. Калужнин, проф. Н. И. Кованцов, доц. В. И. Коба,
доц. Н. Я. Ляшенко, доц. Ю. М. Рыжов, доц. М. И. Ядрен-
ко (заместитель ответственного редактора), канд. пед. наук
Л. В. Кованцова.
Редакция литературы по математике и физике
Зав. редакцией А. С. Макуха
20201—173
Я М211(04)—75 418“75
(С) Издательское объединение <Вища школа», 1975.

ПРЕДИСЛОВИЕ
Характерные для нашего времени глубокие изменения
в математике, частично связанные с появлением электрон¬
ных цифровых вычислительных машин и с созданием того
направления математической мысли, которое обозначается
собирательным термином «кибернетика», нашли своеобраз¬
нее отражение также и в столь, казалось бы, устоявшейся
области математической науки как элементарная геомет¬
рия. На роль «элементарной геометрии XX века» начинает
претендовать лишь недавно созданная комбинаторная гео¬
метрия изучающая экстремальные геометрические задачи
(т. е. задачи на максимум и минимум), связанные с отыска¬
нием «самых лучших» (или, во всяком случае, «достаточно
хороших») расположений конечного числа точек или фигур.
Интерес к комбинаторной геометрии естественно связать
с общим интересом к задачам на максимум и минимум, по¬
рожденным большим числом чисто прикладных задач,
в которых ищутся оптимальные режимы работы отдельных
механизмов или больших систем.
Зта книга посвящена комбинаторной геометрии, она рас¬
сказывает об одной несложной по формулировке задаче,
у истоков которой стоят Еелнкие имена Иоганна Кен
лера (1571- 1630) и Исаака Ньютона (1643—1727).
Наш рассказ о «проблеме 13 шаров» отнюдь не претен¬
дует на полноту. Основную роль в нем играют 16 задач,
которые тематически связаны одна с другой, но математи¬
чески доеольно независимы, что позволяет читателю просто
опускать те из них, которые покажутся ему трудными или
недостаточно его заинтересуют. Хочется обратить внимание
2--1406
3

читателей иа ряд сформулированных не решенных до сих
пор задач, некоторые из которых вполне могут стать трамп¬
лином для самостоятельной работы в области комбинатор¬
ной геометрии.
Отзывы и пожелания о содержании книги просим по¬
сылать по адресу: 252054, Киев, 54, Гоголевская, 7, Голов¬
ное издательство издательского объединения «Вища шко¬
ла», редакция литературы по математике и физике.
Автор

ГЛАВА I
ЗАДАЧИ О КРУГАХ И ШАРАХ
§ 1. ЗАДАЧА НЬЮТОНА - ГРЕГОРИ
Начнем изложение со слету ющей задачи:
Задача 1. Какое наибольшее число кругов на плоскости
можно приложить к равному им кругу Кр так, чтобы
никакие дви из них не пересекались (но все они соприкасались
с границей круга Кр, не пересекая его)?
Решение. Если круг Кр\ приложен к равному
ему кругу Кр, то он виден из центра О круга Кр под углом
Ф = 60 Другими словами, проведенные из центра О к
кругу Kpi касательные ОМ и ON образуют угол .ИОД' =
= 60 (рис. I, а). Примем радиус г крута Кр за 1. Так как
касательные, проведенные из точки О к любому другому
приложенному к Кр кругу Кр2 радиуса I, не пересекаю¬
щему круга Kpi, будут проходить вне угла MON, то всем
приложенным к Кр непсрессчаннцимт кругам того же ра¬
диуса 1 будут соответствовать псперекрывающпеся утлы
с общей вершимой О, каждый из которых будет равен 60'.
Поэтому к кругу Кр можно приложигь не более, чем
060 : 60 = 6
равных Кр кругов, хдовлегроряющнх условию задачи
(рис. 1,6).
Задаче 1 родственна такая задача:
Задача 2. Какое наибольшее число материальных (непе
ресекающихся) шаров можно приложить к равному им шару
Ш так, чтобы все они своей поверхностью соприкасались
с поверхностью шара 111, не пересекая его?
Попробуем эту задачу решить так же, как и задачу 1.
5

Пусть единичный шар Ш,, т. е. шар, радиус R которого
равен 1, соприкасаемся < равным ему шаром Ш (рис. 2, а);
тогда шар Ш\ виден из центра О шара Ш под «пространст¬
венным углом» (|, измеряемым величиной «сферического
сектора» (или «сферической шапочки») о, гысекаемой из
Рис. 1
а	д
pm 1
есреры шара Ш конусом касательных, проведенных к шару
/J7, из точки О А так как высота АР = h «шапочки» о
*рис. 2, б) рапта:
h--- 1-сьь.Ч.Т 1 - V* 0,134 ...
ь

то отношение поверхности шара Я/ к поверхности «ша¬
почки» о равно
2:0,134	.	14,9	.
Но непересекающимся шарам Я/j, III2, Я/3, ..., приложен¬
ным к шару Я/, должны соответствовать неперскрывающиеся
«шапочки» аь а2, а3,
поэтому ясно, что больше 14
(материальных)	шаров,
равных шару Ш, к этому
шару приложить нельзя.
А сколько же матери¬
альных шаров, равных ша¬
ру Ш, мо ж и о приложить
к нему? Нетрудно сообра¬
зить, что к III можно при¬
ложить 12 равных ему ша¬
ров. В самом деле, пусть
шар III лежит па горизон¬
тальной плоскости; прило¬
жим к нему G равных ему шаров (рис. 3). При этом сверху
и снизу от шара III образуется по шесть выемок. Положим
теперь в три несмежные из шести верхних выемок 3 рав¬
ных шару 111 шара так, чтобы каждый из них касался трех
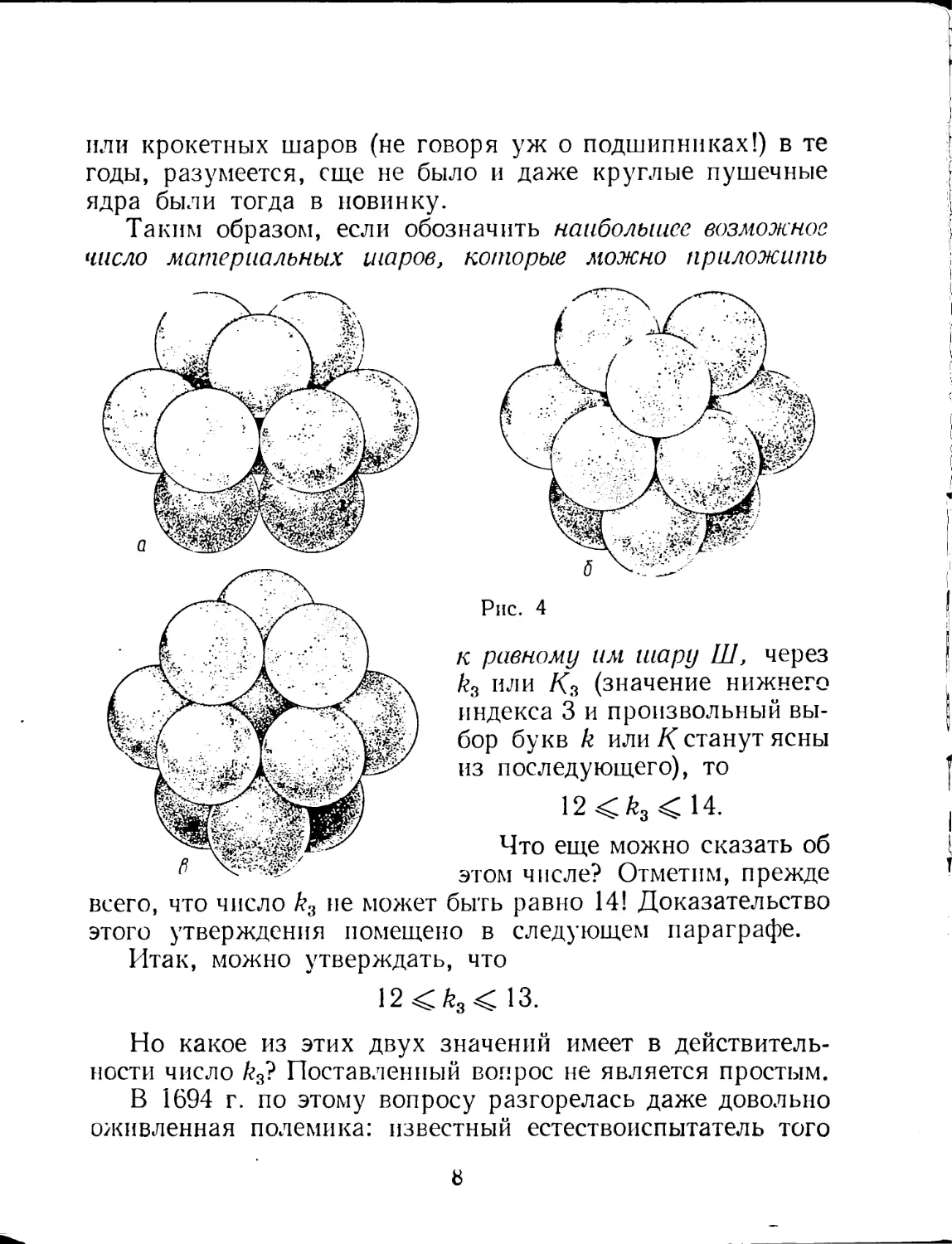
нижних шаров — в том числе и шара Я/ (рис. 4, а). Если,
далее, расположить подобным образом еще 3 шара снизу
от Я/, то 111 окажется окруженным 12 равными ему шарами,
каждый из которых касается Я/; при этом 3 шара снизу от
111 можно даже приложить двумя различными способами:
в выемки, расположенные точно под занятыми верхними
шарами выемками (рис. 4, б), или в три другие выемки
(рис. 4, в). Подобное расположение тринадцати равных
шаров впервые описано в 1611 г. одним из создателей сов¬
ременной астрономии и математики знаменитым Иоганном
Кеплером; однако практически складывали таким
образом одинаковые шары (образовывая из них «пирами¬
ду»), вероятно, и ранее того времени, хотя биллиардных
7
Рис. 3

или крокетных шаров (не говоря уж о подшипниках!) в те
годы, разумеется, еще не было и даже круглые пушечные
ядра были тогда в новинку.
Таким образом, если обозначить наибольшее возможное
число материальных шаров, которые можно приложить
Рис. 4
к равному им шару Ш, через
k3 или К3 (значение нижнего
индекса 3 и произвольный вы¬
бор букв k или К станут ясны
из последующего), то
12 </г3 < 14.
Что еще можно сказать об
этом числе? Отметим, прежде
всего, что число k3 не может быть равно 14! Доказательство
этого утверждения помещено в следующем параграфе.
Итак, можно утверждать, что
12</г3< 13.
Но какое из этих двух значений имеет в действитель¬
ности число &3? Поставленный вопрос не является простым.
В 1694 г. по этому вопросу разгорелась даже довольно
оживленная полемика: известный естествоиспытатель того
ь

Бремени Дэвид Г р е г о р и утверждал, что к шару мож¬
но приложить i3 равных ему материальных шаров, а ге¬
ниальный Исаак Ньютон — что нельзя, но доказать
свою правоту, т. е. точно определить число кя ни одному из
них не удалось. Первым, кому удалось решить эту задачу,
а именно доказать гипотезу Ньютона, утверждающую, что
Лз=12	(1)
был немецкий геометр Рудольф Гоппе; об этом сооб¬
щается в статье его соотечественника К. Бендера, опубли¬
кованной в 1874 г., т. е. через 180 лет после дискуссии
Ньютон — Грегори. Годом позже доказательство Р. Гоппе
усовершенствовал другой немецкий геометр С. Г ю н т е р;
однако оно все еще оставалось очень сложным и запутан¬
ным. Многие специалисты, например, известный венгер¬
ский геометр Ласло Ф е й е ш Тот, считают даже, что
первое безупречное доказательство равенства (1) (первое
решение задачи 2) дали в 1953 г. (через 342 г. после того,
как Н. Кеплер доказал, что кя > 12 и через 259 лет после
дискуссии Ньютона с Грегори) один из крупнейших алгеб¬
раистов XX века голландец Бартель Леенберт ван дер
Варден и выдающийся немецкий логик Карл Ш ю т т е.
Еще более простое доказательство того, что к шару нель¬
зя приложить 13 равных ему материальных шаров предло¬
жил в 1956 г. англичанин Джон J1 и ч — однако и это до¬
казательство является довольно сложным.
С проблемой 13 шаров тесно связана задача о самой
плотной укладке равных кругов на плоскости и равных
шаров в пространстве. Эта задача, открывшая новый боль¬
шой раздел геометрии, называемый дискретной гео¬
метрией, вызывает сегодня очень большой интерес
в силу обнаруженных за последние десятилетия неожидан¬
ных важных приложений ее «многомерного варианта» к вы¬
числительной математике и теории связи.
Предположим, что плоскость заполнена непересекающи-
мися равными кругами; составим отношение суммарной
8

площади тех кругов, которые целиком помещаются внутри
круга 2 большого радиуса R, с центром в произвольной
точке О плоскости) к площади nR2 этого круга. Предел,
к которому стремится это отношение при R оо, называет¬
ся плотностью рассмотренного расположения (ук¬
ладки) равных кругов на плоскости; задача заключается
в том, чтобы найти гну укладку кругов, плотность которой
является самой большой из всех возможных. Аналогично
формулируется и задача о самой плотной укладке равных
шаров в пространстве.
В замечательном тракте «О снежинке, или новогодний
дар», составленном И. Кеплером в качестве подарка
его другу королевскому советнику Вакгеру фон Вакген-
фельсу по случаю наступления нового, 1611 года, были
разобраны две укладки равных кругов на плоскости: в пер¬
вой из них (рис. 5, а) центры кругов образуют сетку рав¬
ных квадратов и каждый круг касается четырех соседних
с ним, а во второй (рис. 5, б) — центры кругов образуют
сетку правильных шестиугольников, и каждый круг ка¬
сается шести соседних с ним. И. Кеплер считал, что вторая
укладка шаров является наиболее плотной из всех воз¬
можных. Действительно, в то время как плотность первой
а
б
Рис. 5
10

укладки ~ « 78,54%, плотность второй укладки больше:
она равна л^3 » 90,69%. Далее, в том же трактате
Кеплер рассматривает вопрос об укладке равных шаров
в пространстве. Самая плотная из таких укладок получает-
3	ся следующим образом: на плоскости по схеме рис. 5, б
|	укладываются равные круги, являющиеся «экваториаль¬
ными кругами» равных шаров; при этом образуется «шести¬
угольный слой» шаров, в котором каждый шар касается
шести соседних. Затем второй, такой же слой шаров, накла¬
дывается сверху на первый так, что шары верхнего слоя
попадают в выемки шаров нижнего слоя, касаясь трех
из нижних шаров (ср. рис. 4, а). Если затем продолжать
накладывать таким же образом подобные слои шаров сверху
и снизу от уже имеющихся, то получим заполнение всего
пространства равными шарами, где каждый шар будет ка¬
саться двенадцати соседних с ним. Заметим, что поскольку
каждый слой можно наложить на уже имеющийся двумя
способами (ср. рис. 4, б и в), то фактически получается
бесконечно много разных систем заполнений пространства
равными шарами; однако, все эти укладки шаров имеют,
очевидно, одинаковую плотность. Эта плотность равна
я» 74,05%.
ь
С тех пор как Кеплер опубликовал свой трактат, прош¬
ло уже более 360 лет. За это время было предложено много
различных укладок равных кругов на плоскости и шаров
в пространстве, и никто никогда не сомневался, что най¬
денные Кеплером укладки являются самыми плотными,—
но доказать это оказалось Еовсе не просто. Считают, что до¬
казательство того, что изображенная на рис. 5, б схема
укладки равных кругов является самой плотной, впер¬
вые дал в 1892 г. выдающийся норвежский математик, один
из основателей геометрических методов в теории чисел
Адольф Т у э. Однако оригинальное доказательство А. Туэ
3—1406
11

не было опубликовано. Краткое резюме доклада на эту
тему, прочитанного А. Туэ в 1892 г. на конгрессе матема¬
тиков скандинавских стран, содержит смцественные и
трудно восполнимые пробелы. Более убедительным является
другое доказательство того же факта, опубликованное
А. Туэ в 1910 г.,— но и это доказательство вряд ли может
удовлетворить современным требованиям математической
строгости. Полные доказательства соответствующего пред¬
ложения (иногда называемого «теоремой Туэ») были даны
в 1940 г. уже упоминавшимся выше Ласло Ф е й е ш е м
Тотом и, независимо от него, в 1944 г.— известными
специалистами по геометрическим методам в теории чисел
итальянским математиком Беньямино С е г р е и немецким
математиком Куртом Малером. Несколько доказа-
тельств этой теоремы приведены в книге Л. Ф е й е ш а
Тота [8] (см. литературу на стр. 84).
Несмотря на всеобщее убеждение о том, что в простран¬
стве не существует укладок равных таро в, плотность
которых превосходила бы -л ^ . доказать это пока не
удалось никому. Не решены также и многомерные аналогии
соответствующей задачи, при этом не найдена даже вели¬
чина плотности самой лучшей укладки (или нескольких
самых лучших укладок) равных (многомерных) шаров.
§ 2. ТЕОРЕМА О ЧЕТЫРНАДЦАТИ ШАРАХ
Докажем следующую теорему:
Теорема 1 (теорема о 14 шарах). К данному ма¬
териальному шару LU нельзя приложить более 13 равных
ему материальных (не пересекающихся между собой и не
пересекающих шар Ш) шаров.
Доказательство. Воспользуемся методом «от
противного». Предположим, что к шару 111 радиуса 1 с
центром О удалось приложить четырнадцать рав¬
ных шару Ш материальных шаров Шг, ZZ/2, ..., Д/14. Центры
12

9тих шаров обозначим через Qlt Q.,, QI4, а точки пере¬
сечения отрезков OQ,, 0Q2, ..., 0QU с ограничивающей
шар Щ сферой Сф (т. е. точки касания шаров Ш и Щ,, Ш
и Щ2  Ш и 1Лц) — через Alt А2, ■ ■■, Л14. Так как точ
ки Q{ и Q/ (номера i и / могут принимать любое из значе-
А.
ний 1, 2,	14; I Ф /) — центры непересекаю¬
щих с я шаров единичного радиуса, то Q£Q;- >• 2; поэтомх
Л£у4/ > 1 и следовательно ^ A{Aj «большой окружности»
сферы Сф, высекаемой из Сф плоскостью, должна быть
больше или равной 60° (ср. рис. 6 с рис. 1, а).
Будем считать, что точки Аъ А2, ..., Аи не принадлежат
одной полусфере сферы Сф (ниже мы покажем, что даже на
полной сфере Сф нельзя расположить четырнадцать точек
так, чтобы расстояние между каждыми двумя из них было
больше пли равно 1). «Натянем» на точки Alt А2, Аи
выпуклый многогранник (рис. 7), т. е. рассмотрим выпук¬
лую оболочку наших четырнадцати точек. Наглядно ее мож¬
но представить себе как тело, ограниченное охватывающей
Аи А2, ..., Аи резиновой пленкой, которая стягивается,
стремясь уменьшить свою поверхность, однако не может
сдвинуть «колышки» Аи А2, ...,	Л14. Разумеется, не все
грани многогранника М будут треугольниками; если это
так, то каждую (выпуклую) грань многогранника М можно
8*
18

разбить на треугольники диагоналями, проходящими
через одну из ее вершин. Тогда получим выпуклый много¬
гранник М, вписанный в сферу Сф, все грани которого
'будут треугольниками (вообще говоря, многогранник М
:является «вырожденным», т. е. некоторые из соседних его
граней лежат в одной плоскости).
Воспользуемся теперь теоремой Эйлера:
для каждого выпуклого многогранники
В-Р\-Г- 2,	(2)
.где В, Р и Г — соответственно число вершин, ребер и гра-
,ней многогранника (доказательство этой теоремы см. на
•стр. 72—73).
В рассматриваемом случае В — 14, а так как каждая
:из Г граней многогранника М имеет по т р и ребра и каж¬
дое ребро при таком счете «по граням» учитывается д в а ж -
д ы (ибо оно разделяет две грани), то
р ~г.
Подставляя эти значения в формулу (2), получаем
3
14	—	Г -г П — 2 пли Г = 24 и, следовательно,
Р 4-г- зе.
Пусть теперь А1А,„Ап (/, т, и - какие-то конкретные
номера; 1 Г /, т, п .	14) — произвольная грань много¬
гранника М. Мы знаем, чго Л1Ат > 1, АтАп > 1, Л„Л( ^
;> 1. Опишем вокруг треугольника AtAmAn окружность
s (рис. 8, а) — эта окр.жность будет линией пересечения
плоскости А1А,пАп со сферой Сф. Хотя бы одна из сторон
треугольника AtAmAn будет стягивать дугу, не большую
120°. Но если — Л;Л,„ < 120°, a AlAm > 1, то обозначая

средину хорды AtAm через Р, а центр и радиус окружности!
s соответственно через Q и р. получим:
: р < AtP: р - Ап /_ A,QP < sin 60° — —2-Э- ,
откуда
P>-L5-	0,577...
Рис. 8
Таким образом, для радиуса р окружности, описанной около
любой из двадцати четырех граней многогранника М, имеем
Р>Р о =	0,577
откуда вытекает, что сферический радиус Г окружности s
сферы Сф равен (рис. 8, б)
Р arcsinp - arcsin Р0 arcsin0,577 . . . =»35° 16'.
Поэтому площадь S ограниченного окружностью s сфери¬
ческого круга о («шапочки» высотой 1 — cos Р) будет
S (l— cos Р) ■	> S0 (1 — cos Р0) •
«(1 - cos 35° 16')-	0,0922,
где 5 = 4л = 12,56 ... - площадь всей сферы Сф.

Опишем теперь около каждой из точек Аъ Л2, • ••, Л14
сферические круги («шапочки») аг, аг, ..., ам одного и то¬
го же сферического радиуса Р0^=35° 16' и одной площади
S0 > 0,0922. Оценим площадь части сферы Сф, покрытую
всеми этими «шапочками». Отме¬
тим, прежде всего, что никакие
три из «шапочек» су, сг2, ...,
о14 не пересекаются. Действитель¬
но, если бы «шапочки» at, от,
ап имели бы общую (внутреннюю)
точку Z, то круг сферического ра¬
диуса Р0 с центром Z покрыл бы
точки Л(, Ат и Ап; следователь¬
но, сферический радиус описан¬
ной вокруг треугольника Л1АтАп
Рис. 9	окружности	был	бы м е и ь ш е
Р0 — что противоречит доказан¬
ному ранее. Поэтому «шапочки» аи сг2, ..., а14 перекры¬
ваются не более, чем по две, и вся покрытая ими площадь
равна
S4 -f- S2 + ••• -f- Sl4 — 5|,2 — Si>3— ••• —5]3j4,
где Slt S2, ...,	S14 — соответственно площади «шапочек»
olt a2, ..., a14, a Sir/- (i и / — какие-то из номеров 1, 2, ...
...,	14)	обозначает	площадь	пересечения	«шапочек» а( и
О/. (Разумеется, что если «шапочки» ai н а,- не пересекаются,
то величина Si,/ равна пулю.)
Так как все величины S( (где 1 = 1,2,..., 14) по усло¬
вию равны S0 > 0,0922, то остается только оценить ве¬
личины Si,,-. Если «шапочки» о{ и а/ пересекаются (рис. 9),
то их пересечение представляет собой некоторую «линзу» L.
Площадь этой линзы будет тем больше, чем меньше рас¬
стояние А;А/. Но А[А/ > 1 (или — AtA/ > 60°); поэтому
площадь каждой линзы L не больше площади изображенной
на рис. 9 линзы L0 с хордой UV, для которой
АА = 1-

Линза L0 состоит из двух равных сферических сегмен¬
тов, отсекаемых от сферических кругов о,, о; сферической
хордой UV (т. е. дугой UV большой окружности сферы Сф,
образуемой при пересечении Сф плоскостью OUV). Уандем
площадь каждого из этих сегментов. Обозначим че^с'*
радианную меру сферического центрального угла UАЛ/
сектора AtUV круга сг,, т. е. угол между дугами Л,7/ и Л,Т
больших окружностей, образуемых при пересечении сферы
Сф плоскостями ОАси и ОД, Т (точнее — угол между ка
сагельными к этим окружностям в точке Д,-). Тогда плп
щадь сектора ALUV равна	так	как	отношение пло
щади этого сектора к площади S,, «шапочки» о( равно огно
шеппю сс : 2л (центрального угла ос сектора к полному у г
лу 2л). С другой стороны, площадь сферического треуголь¬
ника Л,ОТ, ограниченного дугами AJJ, Л,Т, ОТ больших
окружностей, равна
ил. Л,ОТ = Z. Л,- -[- Z. О + Z. Т — л,
где Z. Л,, /_ О, Z. Т — сферические углы этого треуголь
пика, измеренные в радианной мере (ср. стр. 68). Но Z О =
= -2-, поскольку точку О можно принять за центр окруж¬
ности, описанной около равностороннего сфери¬
ческого треугольника A-AjB со стороной Д,ЛУ (напомним,
чго радиус окружности, описанной около равностороннего
сферического треугольника со стороной — ЛfЛ,- = 60° =
= — равен 1’0 = — AtU = ~ A,U). Далее,
Z. AJUAi = Z. AtUB = z. BUAt (=	•
Точно так же и
Z.T- <LU
а так как Z. Л,- = а, то
Л I 11 7	I	■	Л	Л
пл. AJUV = & -\—g—Т -д—- л = а
LJ

и
пл еегм. = пл. сект AJUV — пл Д A}JV ~
(X л	/	ЗХ \
п ~[а	г) '
Следовательно,
пл линзы Lu = 2 пл сегм. == Sn — ^2а	.
Теперь определим величину угла а. Из рис. 9 следует,
что
а = Z. U At V = 2д UAtAj = Z. В АД-.
Другими словами, а — это угол равностороннего сфери¬
ческого треугольника AtAjB со сторонами — AtAj =
~ — AtB = - AjB = Так как Z. AfiA, = Z. АсОВ —
= Z_ AjOB = -2-, то четыре точки At, Aj, В и О являются
вершинами правильного тетраэдра с ребром, равным 1
(т. е. треугольной пирамиды, все ребра которой имеют
одну и ту же длину, равную 1). Но BALAj = а — это
угол между касательными к дугам AtB и AtAj в точке At,
т. е. угол между перпендикулярами Аф и Afl, к ребру
ОА, правильного тетраэдра AtAjBO, проведенными в точ¬
ке At и лежащими в плоскостях ОА{В и OALAj, или двугран¬
ный угол правильного тетраэдра — угол между его граня¬
ми OAlB и OAtAh Отсюда следует, что
sin X = НГ = °’577
(см. стр. 73), и, следовательно,
~ < 35° 16', а <70° 32'< 1,227 (рад) (но а > 1,226).
Таким образом, имеем:
пл. S(j = пл. линзы L < пл. линзы L0 =
18

= -^S0-2a + ~n<	0,0922	-2-1,226	+
+ -i- 2 < 0,0052,
где 2 = 4л обозначает поверхность сферы Сф.
Отметим теперь, что число попарных пересечений «шапо¬
чек» а„ а2, ..., а14 не превосходит числа пар «соседнпх>
точек среди вершин /4,, А2, ■■■, Аи многогранника /14, т. е.
не превосходит числа Р = 36 ребер этого многогранника
Поэтому общая площадь, покрытая кругами а,, а2, ..., ст14
должна быть не меньше, чем
14S0— 36 пл. L0> 14 0,0922-30 0,0052 > 1,12,
т. е. эта площадь оказалась больше площади 2 всей сфе¬
ры! Полученное противоречие и доказывает справедли¬
вость теоремы, т. е. неравенство
*3<14
§ 3. ЗАДАЧА О ШАРАХ В л-МЕРНОМ ПРОСТРАНСТВЕ
Рассмотренные задачи 1 и 2 допускают целый ряд ва¬
риантов и обобщений. Одно из первых обобщений связано
с очень важным понятием п -мерного евклидова
пространства". Хорошо известно, что содержание
школьной планиметрии, следуя идеям Рене Декарта
(1596—1650) и Пьера Ферма (1601 —1665), можно оха¬
рактеризовать так:
условимся сопоставлять каждой точке А плоскости ее
дакартовы прямоугольные координаты (х, у)\ при этом
множество точек плоскости можно будет отождествить с
множеством пар вещественных чисел (х, у). Р а с стоя-
" См.: Б. А. Р о з е н ф е л ь д, Н. М. Я г л о м. Многомерные
пространства. Энциклопедия элементарной математики (ЭЭМ), кн. V,
«Геометрия», М., «Наука». I960, с 344—393.
4-1406
19

н И е АВ между точками А (х, у) и В (лг,, //,), очевидно,
равно (рис 10):
АВ =	1	— xf	+ (у, — yf .	(3)
Фигуры	(множества	точек — в	используемом нами	здесь
языке аналитической геометрии под множеством точек по¬
нимается	множество	пар чисел)	F и F' называются	р а в -
н ы м и,	если между	их точками можно установить	взаим¬
но однозначное соответствие так. что расстояния между
соответствующими парами точек равны: пусть точкам А
и В фигуры F отвечают точки А' и В' фигуры F', тогда
АВ — А'В'. Предмет геометрии можно теперь описать как
изучение свойств фигур плоскости, где равные фигуры счи¬
таются «одинаковыми», т. е. обладающими одинаковыми
геометрическими свойствами, пли как еще говорят, плани¬
метрия изучает свойства плоских фигур, «заданных с точ¬
ностью до замены фигуры равной ей».
Аналогично определению декартовых прямоугольных
координат на плоскости можно ввести и координаты (х, у, г)
точки А пространства, при этом расстояние А В
между точками А (х, у, г) и В (хь уи г,) пространства будет
равно (рис. 10):
АВ - Г (дг, - *>а f (Ус ~ У)2 t (*, - г)2	(4)

Равенство фигур в пространство определяется те¬
перь так же, как в случае плоских фигур; содержание же-
стереометрии составляет изучение геометрических свойств
фигур в пространстве.
Отметим также, что аналогично можно описать предмет
«геометрии прямой»; для этого достаточно сопоставить точ¬
кам прямой их к о о р д п н а г ы (т. е. числа) х и опреде¬
лить расстояние АВ межд\ точками .1 (л) и В (аД
прямой по формуле, аналогичной формулам (3) и (4) (рис. 10)
АВ 1 (V, — х)2 - | чу х|.	(5)
Та к как каждая фигура имеет на прямой единст¬
венное намерение (длину а), на плоскости — два из¬
мерения (длину а и ширину Ь), в пространстве — три
измерения (длину а, ширину b и высоту с), то геометрию
на прямой часто называют «одномерной геометрией», гео¬
метрию на плоскости (планиметрию) — «двумерной гео¬
метрией», а геометрию в пространстве (стереометрию) —
«трехмерной геометрией». Естественным обобщением всех
этих понятий является понятие п - мерного прост¬
ранства, точки которого понимаются как упорядочен¬
ные наборы п чисел (.г,, х.>, ..., хп) — координат этих
точек. Таким образом, каждый раз, когда мы имеем мно¬
жество каких-либо объектов, характеризуемых заданием
п чисел, то можно говорить об ««-мерном пространстве» этих,
объектов. Так, например, физики часто говорят о четырех¬
мерном «множестве (мире) собьипшЪ, или (четырехмерном)
«пространстве-времени», элементы которого, называемые
с о б ы г и я м и, характеризуются четырьмя числами*
(х, у, z, /), где первые три числа (v, у, г) указывают место
события, а координата I — его время. Другим примером
многомерного пространства, постоянно используемого фи¬
зиками, является так называемое фазовое прост¬
ранство, отвечающее движущимся материальным точ¬
кам: точка шестимерного фазового пространства характе¬
ризуется шестью числами (х, у, г, а', у', г’), где х, у, z —
4*
21

это координаты движущейся материальной точки,
а х', //, г — се с к о р о с т и (в направлениях осей Ох,
О у и Ог соответственно). Аналогично этому геометры гово¬
рят о четырехмерном «пространстве сфер», каждая «точ¬
ка» 5 которого (сфера) характеризуется четырьмя коорди¬
натами (х, у, г, р), где Q (х, у, г) центр сферы S, ар — ее ра¬
диус или о (четырехмерном) «пространстве прямых», где за
координаты (х, у, уи г) прямой АВ можно принять коорди¬
наты точек А (х, у) и В (ylt г) ее пересечения с плоскостями
хОу и уОг (координаты прямых, параллельных одной из
этих плоскостей, здесь приходится вводить особо).
Введем теперь в я-мерном пространстве «метрику», опре¬
делив расстояние АВ между точками А (ду, х2, ...
..., хп) и В hju у,, ..., уп) формулой
А В = 1 (у, — А',)2 + (уг — х2у А +(Уп — хп)2-	(6)
Это определение имеет тот смысл, что равенство нулю рас¬
стояния АВ здесь означает, что у1 = хг, у2 = х2, ..., уп =
= хп, т. е. что А и В — одна и та же точка; малость
же расстояния А В означает, что все разности г/, — лу,
у, — х2, ..., уп — хп по абсолютной величине малы, т. е.
«точки» А (лу, лу, ..., хп) и В {уи у2, ..., уп) «близки» в
том смысле, что им отвечают близкие значения всех коорди¬
нат ч. я-мерное пространство с определенным по формуле
(6) расстоянием между точками называется евклидо¬
вым пространством (я-мерным). Две фигуры F
и F' евклидового и л-мерного пространства — т. е. два мно¬
жества «точек» или упорядоченных наборов я чисел — на¬
зываются равными, если между точками фигур F и F'
можно установить такое взаимно однозначное соответст¬
вие, что расстояния между соответствующими парами то¬
чек этих фигур будут одинаковы: если точкам А к В фигу-
** Так, например, «близость» в четырехмерном пространстве сфер
.двух сферS (х, у, г, р,) и Sx (хи уи гх, р^ означает, что центры Q (х, у, г)
и Q, (х,, у„ г,) близки друг к другу в пространстве и радиусы р н р, сфер
мало отличаются друг от друга.
22

ры F соответствуют точки Л' и В' фигуры F', то А В =*
= А'В'. Наконец, предметом евклидовой геометрии /i-мер¬
ного пространства (или «-мерной евклидовой
геометрии) является изучение геометрических (одних
Рис. 11
и тех же у любых двух равных фигур) свойств фигур п-мерно-
ео евклидового пространства.
Отметим еще, что в числе основных геометрических об¬
разов «-мерной евклидовой геометрии входит п-мерный шар
с центром Q и радиусом г, т. е. множество всех
таких точек «-мерного пространства, для которых
QA < г.
Ясно, что «одномерный шар» представляет собой не что
иное как отрезок со срединой Q (рис. 11, а), «двумер¬
ный шар» - это круг (рис. 11, б), а «трехмерный шар» —
обыкновенный шар (рис. 11, е). «Граница» «-мерного
щара, т, е. множество таких точек В, что
QB = г,
23

называется ((п — 1)-мерной) сферой; так «одномерной сфе¬
рой» является о к р у ж н о с I ь, а «двумерной» — обык¬
новенная сфера, т. е. поверхность трехмерного шара; роль
вестно то н-мерпын симплекс С = Л1А., ... ЛпАп11 мож¬
но определить как множество всех отрезков, соединяющих
точку Л„ , 1 сточками (и - I )-мернигасимплекса С =э ALA.,...
... Ап (па рис. 12 взят случай, когда п = 3).
Примечание. Понятие о т р е з к а (т. е. 1-мерного симплекса)
n-мерного пространства не нуждается в специальном определении: отре¬
зок длины d можно описать как фигуру, равную отрезку 0D оси 0xlt
т. е. множеству всех точек (л:,, 0, 0	0) оси Олу, где 0 xl ^ d.
Нетрудно понять, что одномерный симплекс АВ — это
просто отрезок (рис. 13, «); двумерный симплекс —
это треугольник ABC (рис. 13, б); наконец, трех¬
мерный симплекс — этот тетраэдр (рис. 13, в). Роль
параллелограмма в «-мерной геометрии играет параллело-
11 См. например, И. С. С о м и н с к и й, Л. И. Головина,
И. М. Я г л о м. О математической индукции. М., «Наука», 1967,
с. 97—100, 120—121, 124, где в определении n-мерного симплекса не рас¬
сматривается одно дополнительное условие, заключающееся в том, что
точка Ап 1.| должна лежать вне мпоскостн», в которой расположен сим¬
плекс С-
же «0-мерной сферы» — грани¬
цы «одномерного шара», т. е.
отрезка — играет просто па¬
ра точек.
Простейшим ««-мерным
многогранником» (многомер-
Рнс. 12
ные многогранники часто на¬
зывают политопами) является
так называемый «-мерный
симплекс с п + 1 вершиной
Аи Л о, ..., Ап 11. Если считать,
что содержант* понятия «(/г —
— 1)-мерпын симплекс» уже из-
24

топ. Если считать понятия (п — 1)-мерного параллелотопа
уже известным (см. сноску на стр. 24), то «-мерный парал¬
лелотоп Пар == АгА2 ...	А2п-\	В1В2	...	В2„_| можно опре¬
делить как множество всех отрезков, соединяющих точки
(п — \)-мерного параллелотопа Пар, = А1А2 ...	Л2„_],
А	В
все точки которого имеют координату хп = 0, и точки
равного ему параллелотопа Пар2 = В,В2 ••• B2n-i, полу¬
ченного из параллелогопа Пар, параллельным переносом
на вектора = (су, а2, ..., ап), где ап Ф 0, т. е. такого па¬
раллелотопа Пар2, координаты вершины Bt которого (где
1 < t < 2"~‘) имеют вид (лу + аи хг -f- а2,	...,	+
+ ап—1, ап), где (лу, х», .... хп-ь 0) — координата верши¬
ны Л,- параллелотопа Пар, (на рис. 13, г взят случай, ког¬
да п = 3). Ясно, что одномерный параллелотоп — это
просто отрезок. (Таким образом, «одномерный шар»,
а
Рис. 13
25
к

Рис. 14
«одномерный симплекс» и «одномерный параллелотоп» — это
одна и та же фигура.) «Двумерный параллелотоп» — это п а -
раллелограмм, а «трехмерный параллелотоп» —
параллелепипед.
Укажем еще (эю нам понадобится в дальнейшем), что в
известном смысле самым «симметричным» из всех л-мерных
симплексов является так назы¬
ваемый правильный симплекс
А2А2, ..., Ап+1, все «ребра» АСА/
которого (где i, j= 1,	2, ...,
п + 1) равны между собой.
Частным случаем правильного
симплекса есть правиль¬
ный треугольник на
плоскости и правильный тетраэдр в прост¬
ранстве. Частным случаем параллелотопа является так на¬
зываемый прямоугольный параллелотоп, полностью харак¬
теризуемый своими «измерениями» («размерами») аи а..., ап:
прямоугольный параллелогоп с размерами аи а2, ..., ап
можно охарактеризовать как множество всех таких точек
(*i, х2, ..., хп) п-мерного пространства, что
О < х( < а{, где 1 < i < п
(ср. рис. 14, где п = 2). Прямоугольный параллелотоп, все
размеры которого одинаковы, называется л-мерным кубом;
л-мерный куб со стороной а можно охарактеризовать как
множество всех тиках точек (хи х2, ..., х„), что
О < хг < а.
Ясно, что при л = 1 л-мерный куб обращается в отре¬
зок, при п = 2 — в квадрат, и при п — 3 — в обыч¬
ный куб.
Сказанное выше естественно связывается с интересным вопросом
о правильных политопах л-мерного пространства, характеризуемых
!)авенством (в смысле я-мерной геометрии) всех «граней» и всех «вершин»
точнее — всех «многогранных углов») политопа; частными случаями
правильных почнтопов являются правильный симплекс и куб. Ясно,
26

что при п = 1 мы имеем единственный «правильный политоп»
(и вообще единственный политоп!) — отрезок; при п -2 — беско¬
нечное семейство правильных многоугольников, а при п - 3 —
пять известных типов правильных многогранников (тетраэдр, куб,
октаэдр, икосаэдр и додекаэдр). Оказывается, что число типов правиль¬
ных политопов в четырехмерном пространстве равно ш е с т и, а в лю¬
бом гс-мерном пространстве, где п>5 — трем (два из которых — эти
и-мерный куб и правильный симплекс):
Число изме¬
рений прост¬
ранства
Число ти¬
пов пра¬
вильных
политопов
1
1
2
оо
3
5
4
6
п >5
3
По этому вопросу см., например, указанн\ю в сноске на стр 24 статью
и названную там литерат\ру
Рассмотрим теперь задачу о шарах уже в л-мерном про¬
странстве.
Задача 3. Каково наибольшее число kn материальных
п-мсрных шаров, которые можно приложить к равному
им шару Ш так, чтобы ни	в А
один из них не пересекал Ш,  ь . ... ^
но граница каждого из та-	-	0 ft
рое соприкасалась бы < грани-	Рнс )5
цей U1?
Кроме равенств к., — 6 (рнс 1, б), к3 = 12 (рис. 4, б, е)
и тривиального равенства кг = 2 (рис. 15) в этом отноше¬
нии пока известно не очень много. Правда, удалось дока¬
зать, что
24 < kt < 26; 40 < къ < 48; 72 < ke < 85;
126 С /г7 С 146; 240 < kb < 244.
Однако дальнейшего решения вопроса (хогя бы точного
определения величины /г,) ожидать в ближайшие годы,
5- 1406
27

видимо, не приходится. Но так как уже переход от задачи 1
к задаче 2 (г. е. от размерности п = 2 к размерности п = 3)
приводит, как мы видели выше, к весьма резкому скачку
сложности рассматриваемой задачи, то здесь скорее надо
удивляться точности оценки величины ks, а не тому, что
истинные значения всех величин kn, где п > 3, остаются
до сих пор неизвестными. И в самом деле, при переходе
через значение н = 8 имеющаяся информация о границах,
в которых может заключаться величина, резко падает:
так для следующей за к8 величины к,, мы пока имеем лишь
следующие весьма грубые оценки
272 <	<	440,
улучшить которые пока никому не удалось.
§ 4. ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ
И ВИДОИЗМЕНЕНИЯ ОСНОВНОЙ ЗАДАЧИ
Задачи 1—3 допускают целый ряд вариантов. В сле¬
дующей глаье будет рассмотрен вопрос о замене кругов и
шаров другими фигурами; здесь же остановимся на иных
постановках задач о прикладывании материальных кругов
(шаров) к равному им кругу (шару).
Известные венгерские геометры Л. Фейеш Тот
иАладар Хеппеш дали следующее обобщение за¬
дачи 1—3.
Рассмотрим, ианрпмер, круг Кр, радиус которого можно
принять за 1 (рис. 16). Приложенные к нему непересекаю-
щиеся круги того же радиуса назовем соседями, или первыми
соседями, круга Кр- Совокупность как всех этих кругов,
так и всех касающихся их (непересекающихся) кругов
того же радиуса назовем вторыми соседями Кр; совокуп¬
ность всех вторых соседей Кр и всех касающихся их (непе¬
ресекающихся) кругов того же радиуса — третьими со¬
седями Кр и т. д. Аналогично определяются и первые,
вторые, третьи ... соседи материального шара Ш.
28

Имеет смысл следующая задача:
Задача 4. Определить наибольшее возможное число к2 (О
i-x соседей круга Кр и наибольшее возможное число■ k3 (i)
i-x соседей обыкновенного шара Ш, а также наибольшее воз¬
можное число kn (0 i-x соседей п-мерного шара Я/.
Ясно, что kn (1) = kn (поэтому задача 4 обобщает задачи
1—3) и, следовательно,
k2(\)=k, 6, Ml) = *a=12, 24 <**(!>< *5
и т. д. Нетрудно установить также, что
М2)	18
(рис. 16, 17). Предлагаем читателю самостоятельно доказать
это равенство.
Однако ни одна из величины kn (/), где п ;> 2‘>, от¬
личная от k2 (i), ко (2) и k:t (1), до сих пор точно не определена
'* Случай п= 1, как Есегда, не представляет интереса: очевидно,
что k2 (i) = = 2i (почему?).

Л Ф е и е ш Тот и А. X е п п е ш установили, что
56 .< k3 (2) С 63 п 168 < 64 (2) .< 232;
что же. касается Еелнчпн кп (t), где i > 2, то имеющиеся
для них оценки относятся лишь к случаю, ког .а п — 2.
Рис. 17
Вот еще одна задача, родственная рассматриваемым ра¬
нее:
Задача 5. Чему равно наименьшее возможное число к2 пе¬
не ресекающихся одинаковых кругов, которыми можно пол¬
ностью «окружить» равный им круг Кр, т. е. расположить
их на плоскости так, что любой проведенный из центра
круга Кр луч пересечет один из этих кругов?
Решить тот же вопрос для наименьшего возможного
числа \ материальных одинаковых шаров, которыми можно
■юкружиты> равный им шар Ш, а также для числа kn п-мер-

ных шаров, которыми можно «окружить» ti-мерный шар Ш
тоги же радиуса.
Ясно, что изображенное на рис. 1, б расположение шести
кругов Kpi, .... К Ре, «окружающих» крут Кр, является
«самым выгодным», т. е. /?2 = 6. Однако изображенные на
рнс. 4, б, в расположения шаров задачу 5 уже не решают,
ибо фигурирующие на них 12 шаров, очевидно, не «окру¬
жают» центральный шар 111. Наиболее экономное из извест
ных к настоящему моменту расположений шаров, «окру¬
жающих» шар Ш, предложил известный немецкий геометр
Людвиг Д а н ц е р; у Данцера шар Ш «окружают» 42 рав
ных Ш непересекающпхся шаров, откуда следует, что /л,
. 42. Кроме того, Л. Ф е и с ш Тот доказал, что ^ 19.
а А. Хеппеш - что 1;:.	1:4; таким образом, имеем
24 < Ъ3 <. 42.
Для величин же Ъп, где и 3, нет до сих пор никаких со
держательных оценок.
Разумеется, что задачи 4 и 5, так же как и задачи 1 —3,
можно обобщать и видоизменять далее. Например, можно
заменить круги и шары произвольными выпуклыми фигу¬
рами (причем, здесь возможны два подхода к этим «обобщен¬
ным» задачам, родственные задачам 6 и 7 из гл. II); однако
сложность самих исходных задач 4 и Б делает поиьпкн их
обобщения достаточно мало перснекгнвными.
31

ГЛАВА II
ЗАДАЧИ О МНОГОУГОЛЬНИКАХ,
МНОГОГРАННИКАХ И ПРОИЗВОЛЬНЫХ ФИГУРАХ
§ 5. ТЕОРЕМА ХАДВИГЕРА
Естественным обобщением задач 1—3 является следую¬
щая задача:
Задача 6. Пусть F — произвольная фигура (рис. 18).
Чему равно наибольшее возможное число К (F) равных F
■непересекающихся фигур /у, /’2, ..., которые можно прило¬
жить к F (т. е. расположить так, чтобы ни одна из них
не пересекалась с F, но граница каждой из фигур F\, Г'2, ...
соприкасалась с границей фигуры F)?
Из сказанного в гл. 1 вытекает, что задача эта — особен¬
но в том случае, когда фигура F является не плоской,
.а пространственной (трехмерной или даже п-мерной) —
(слишком трудна для того, чтобы по виду фигуры F можно
(было сразу определить отвечающее ей число К (F). Поэтому
упростим сначала эту задачу, заменив ее следующей:
Задача 7. Пусть F—произвольная фигура (рис. 19).
Чему равно наибольшее возможное число k (F), равных F и
параллельно F расположенных нспере-
секающихся фигур F2, ■■■, которые можно приложить
к F?
Задача 7 проще задачи 6 потому, что здесь фигуры
Flt F2, ... должны быть расположены параллельно
F, т. е. получаться из F не произвольным движением б,
а параллельным переносом л.
Примечание. Это обстоятельство важно еще и потому, что оно
позволяет отнести задачу 7 не к евклидовой геометрии, а к более простой
афинной геометрии, в то время как задача 6 бесспорно относится соб¬
ственно к евклидовой геометрии. По этому поводу см., например,
И. М. Я г л о м, Л. С. А т а н а с я н. Геометрические преобразования.
32

Энциклопедия элементарной математики (ЭЭМ), кн. IV', Геометрия. М.,
Физматгиз, 1963, с. 98—108 или И. М. Я г л о м и В. Г. А ш к и н у -
те. Иден и методы афиннон н проективной геометрии. Ч. I, Лфинная
геометрии. Л!.. «Просвещение' 1962.
Рис. 18	Рис. 19
Задачи 6 и 7 допускают следующую обшу ю формулировку (служа¬
щую, одновременно, их обобщением):
Пусть G — какая-то совокупность («группа») движений плоскости;
обозначим через k (F, G) наибольшее число фигур, получаемых из F дви¬
жениями из G, которые можно «приложить» к F с соблюдением условий
задач 6 и 7. Чему равно число k (F, С)? Ясно, что если G — это совокуп¬
ность D всех движений плоскости, то k (F, D) = k {F), а если G — это
совокупность Т параллельных переносов, то k (F, 71 =
k (F); «промежуточной» между задачами 6 и 7 является, например,
задача оценки чисел k (F, S), где 8 — совокупность всех параллельных
переносов и всех центральных симметрий (ср., например, В. Г Б о л -
т я н с к в и. Равновеликие и равносоставленные фигуры М., Гостех-
тдат, 1956, 1} Г)
Ясно, что произвольность размещения фигур Fu F2, ...
в задаче 7 значительно меньшая, чем в задаче 6; поэтому
k(F)^K[F).	(7)
Заметим, что в рассматриваемых в задаче 5 располо
женнях фигур F,, F2 ... разобраться гораздо легче, чем в
тех расположениях, анализ которых предусматривает за
дача 6. Кроме юго, как тадача 7, так и задача 6, могу'
•й

рассматриваться как обобщение задач 1—3, поскольку любые
два равные круга Кр и Кри как и два одинаковые шара Ш
и Шх, всегда расположены параллельно (т. е. мо¬
гут быть переведены один в другой параллельным пе¬
реносом); поэтому в условиях гл. 1 задачи 6 и 7 полностью
совпадают:
К = К (Кр) - К2 (Кр), k, = k, (Ш) = К3 (Ш), ...
, kn= К(Ш) = Кп(Ш), ...
(здесь и дальше нижний индекс возле букв k и К указывает
размерность фигуры F и вмещающего ее пространства).'
Поскольку общее понятие «фигуры» является настолько
сложным, что его и к геометрии-то относить рискованно 1>,
мы впоследствии ограничимся рассмотрением одних лишь
выпуклых фигур. Выпуклую фигуру F (плос¬
кую, трехмерную или даже n-мерную) можно опреде¬
лить как такую, что фигуре F принадлежит каждый
отрезок АВ, соединяющий две произвольно выбранные
точки А и В этой фигуры. Выпуклую фигуру F можно
описать еще как фигуру, которую ограничивает «выпук¬
лая», т. е. не имеющая «вмятин», замкнутая линия L;
последнее означает, что через каждую точку линии L
можно провести прямую I (называемую опорной пря¬
мой выпуклой фигуры), не пересекающую F, т. е. такую,
что F целиком лежит по одну сторону от /. Это описание
выпуклых фигур родствен,ю известному из средней школы
описанию выпуклых многоугольников как
таких, которые распоюжсны по одну сторону от каждой
своей стороны. Заметьте, что через каждую вершину вы¬
пуклого многоугольника прохо-ш м н о г о опорных пря¬
мых .
Переходя теперь к рассмотрению задачи 7, начнем с
простых примеров:
Ол о,,пя лп попят! ско[ хе относят к хтнчантичена ш/ анаииу
(к теории множеов) или 1 топологии, чем к геометрии-
■Я

Задача 8, Чему равно число
а) k2 (Тру,
б) k2 (Кв),
где Тр означает равносторонний треугольник, а Кв —
квадрат?
Рис. 20.
Решение, а) Ясно, что сторонй А В треугольника
(Тр) ABC во внутренней точке этой стороны может ка¬
саться лишь один не пересекающий его равный и па-
Рис. 21
раллельно Тр расположенный треугольник Трх, ибо два
таких треугольника Трх и Тр2 обязательно пересекутся
(рис. 20, а). При этом, когда имеется такой Три соприка¬
6—140-j	35

сающийся со стороной АВ, то к вершине Л (и к вершине В)
треугольника Тр может прилегать не более чем один,
не пересекающий ни Тр, ни Трг, треугольник Тр', равный
и параллельно Тр расположенный, в то время как при от¬
сутствии такого треугольника Трг к вершине А могут при¬
легать два равных и параллельно Тр расположенных
Рис. 22
треугольника Тр' и Тр", не пересекающих ни Тр, ни друг
друга (рис. 20, б). Так как это рассуждение справедливо
и для любой другой стороны треугольника Тр, то из него
вытекает, что k2 (Тр) < 6. Из рис. 21, а, б следует равен¬
ство	и	/'Г	\	с
К (Тр) = 6.	(8)
б) К стороне АВ квадрата (Кв) ABCD можно прило¬
жить один, два (рис. 22, а) или три (рис. 22, б) рав¬
ных и параллельно Кв расположенных квадрата, не пере¬
секающих Кв и не пересекающихся между собой. При этом,
если к стороне АВ квадрата Кв приложено два квадрата
/(в, и Квп или три квадрата Кви Ква и Кв3, то к сторонам
ВС и AD квадрата Кв можно дополнительно приложить еще
только по д в а квадрата, а к стороне CD после — лишь

один новый квадрат. Это рассуждение (которое в целях
полной строгости надо еще несколько дополнить, что мы
предоставляем сделать читателю) и убеждает нас в том,
что (рис. 22, б)
к% (Кв) = 8.	(8а)
Примечание. Решение задачи 8 нисколько не изменится (ве¬
личина k2 будет иметь те же значения 6 и 8), если мы под фигурой Тр
будем понимать ие обязательно равносторонний, а произвольный тре
угольник, а под Кв — произвольный параллелограмм Пр
Заметим, что полученные при решении задачи 8 резуль¬
таты (8) и (8а) имеют, по существу, общий характер.
В 1957	г.	выдающийся швейцарский	математик	Гуго	X	ад-
си	г е р	доказал,	что справедлива	следующая	теорема:
Теорема Г. Хадвигера. Для любой плоской выпуклой ''
фигуры
6 < fc2 (F) < 8.	(9)
Г. Хадвигер предположил также, что ft2 (/•) = 8 лишь
в том случае, когда Т — параллелограмм, но доказать это
ему не удалось. Однако интуиция не обманула Хадвигера:
его предположение ьсе же оказалось верным; это доказа¬
ли в 1961 г. (всего через 4 года после того, как Г. Хадвигер
выдвинул свою гипотезу) немецкий геометр Гельмут Г р ё -
мер и Бранко Г рюнбаум. Последний дал также
полное решение задачи 5 для случая плоских (выпуклых)
фигур, показав, что
(6, если F — не параллелограмм;
К (F) = 1о	п
(8, если г — параллелограмм
§ 6. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ХАДВИГЕРА
Доказательство неравенства (9)	сводится	к	проверке,
того, что для любой плоской (выпуклой)	фигуры	F
	 кг (F) > 6 и кг (F)	< 8.
!) В 1959 г. американские математики К. Дж. Хальберг-
младший, Е. Левин, Е. Г. Страус показали, что (F) > 6 также
и для невыпукшх (плоских) фигур F.
6*
37

Таким образом, нас здесь, по существу, интересует следую¬
щая задача:
Задача 9. Чему равно
а) наибольшее возможное значение kmax\
б) наименьшее возможное значение km\n
чисел k2 (F), определяемых для всевозможных плос¬
ких выпуклых фигур F?
Решение. Основную роль в решении этой задачи
играет следующая лемма:
Лемма. Для каждой (плоской, выпуклой) фигуры F
существует такая центрально симметрич¬
ная фигура F*, что
k2 (F*) = k2 (F).
Доказательство леммы является сравнительно неслож¬
ным; однако по своему характеру оно отличается от осталь¬
ных используемых в решении задачи 9 рассуждений, ибо
опирается на одну общую конструкцию (а именно на с и м -
метризацию М и н к о в с к о г о), специфическую
для теории выпуклых тел. Поэтому мы доказательство лем¬
мы дадим в приложении (стр. 80—83); здесь же ограни¬
чимся решением задачи 9 для одних лишь центрально сим¬
метричных выпуклых фигур.
Решение задачи 9, а). Пусть F — произволь¬
ная центрально симметричная фигура с центром О, а
Flt F.2 ... Fk — k выпуклых фигур, равных фигуре F и
параллельно ей расположенных, причем каждая из этих
фигур имеет с фигурой F общие (внутренние или гранич¬
ные) точки (рис. 23, а). Условимся сопоставлять каждой
точке М плоскости вектор гм = ОМ —радиус-век¬
тор этой точки (рис. 23, б); при этом, если М и N — две про¬
извольные точки, то га/ = гм + MN, т. е. MN = ON —
- ОМ = га/ — гм, а если точки М и Мх симметричны от¬
носительно центра О фигуры F, то гм, = — Гм-
Пусть В — произвольная точка фигуры Fu получа¬
емой из F параллельным переносом на вектор alt а А —
38

общая точка фигур F и Fv Так как точки А' и В', из ко¬
торых А и В получаются переносом на вектор а1г принад¬
лежат фигуре F, то, очевидно,
га =	га- + а„ г в = гв■ + аи
Гв= ГА +	АВ =	Га + (Гв — Га) = га + I {г в-	+	«i)	—
— (г А- +	ах)] =	гА + (г В — ГА-) = Га + Гв-	—	га-	=
= Га + Г в- + rAl,
где гА, = — г At т. е. Ах — точка, симметричная точке А’
фигуры F относительно точки О (в силу центральной сим¬
метрии фигуры F эта точка также принадлежит фигуре F).

Рассмотрим теперь полностью принадлежащий фигуре
F (согласно ее выпуклости) треугольник АВ'Av. Радиус-
вектор средины N стороны В'А1 запишется формулой
гм = \ (г в- + rAl),
а центр тяжести треугольника (точка пересечения медиан)
М, делящая отрезок AN в отношении AM : MN = 2:1,
находится по формуле '>
rA + 2rN	, Г	1
Гм = з   = -д-1 ГА + 2 • (гВ' + Га,)
= -^-{га + Г В- + Г л,).
Из сравнения формул
Гв = Га + г в- + ГА, и гм = ~ (гА + гв- гА.)
следует, что точка В гомотетична точке М фигуры F
с центром гомотетии О и коэффициентом 3; иными слоьа-
ми, В принадлежит лучу ОМ и ОВ = 3ОМ, т. е. В принад¬
лежит фигуре 3F, гомотетичной фигуре F с центром гомо¬
тетии О и коэффициентом 3. Таким образом, каждая
точка В фигуры Fx (и, аналогично, каждая точка каждой
из фигур Fu F\, Fk) принадлежит фигуре 3F.
Предположим теперь, что никакие две из фигур F,
Flt F2, ..., Fk не имеют общих внутренних точек. Тогда
площадь, покрываемая всеми этими фигурами, равна сумме
площадей всех фигур, т. е. равна (k + 1)-кратной площади
фигуры F, поскольку все k + 1 фигуры равны. Но так как
все эти фигуры расположены внутри фигуры 3F, подобной
фигуре F с коэффициентом подобия 3 и потому имеющей
площадь, равную девятикратной площади фигуры
F, то
k + 1 <9, т. е. k <8.
** См. ЭЭМ, ки. IV, с. 317 (статья «Векторы и их применения в гео¬
метрии»).
40

Доказанное неравенство к.г (F) <. 8 и равенство k2 (Кв) =
= 8 (см. задачу 8, б) показывают, что для центрально сим¬
метричных выпуклых фигур (а согласно лемме и для любых
плоских выпуклых фигур!)
Решение задачи 9,б) несколько сложнее. Они
шем вокруг центрально симметричной фигуры F централь¬
но симметричный шестиугольник
(Шк) Л,Л2Л3Л4Л5Лв н а и м е н ь -
жит границе фигуры F. В самом а4
деле, пусть это утверждение не- L	^
верно, т. е. пусть отрезок Л,К,
I	Аи
где АгК > AXZX = -j- Л,Л2, сто-	Рис.	24
роны Л4Л2 шестиугольника Шк
полностью свободен от точек границы F (рис 24). Так как
фигура F центрально симметрична, это же будет справед¬
ливо и для отрезка Л4Т= АгК (Л4£ £ Л4Л9), где Л4Т
симметричен АХК относительно центра О шестиугольника
и фигуры F. Повернем теперь слегка отрезки А,А., и Л4Л5
вокруг точек К и L, соответственно в таком направлении,
чтобы точка Ах сместилась по направлению к точке Лв,
а точка Л4 — к точке Л3, и чтобы полученные поворотом
из Л4Ла и Л4Л5 новые прямые А\А-, и Л4Лз остались по-
прежнему параллельными. Образованный четырьмя преж¬
ними сторонами шестиугольника и повернутыми прямыми
Л|Лг и Л4Л5 шестиугольник л1Л2Л3Л4Л5Лв обозначим че¬
рез Шкх. Ясно, что этот шестиугольник будет центрально
симметричным и если Z. АХКА\ = а настолько мал, что
прямая Л1Л2 не пересекает F, то Шкх по-прежнему заклю¬
k,
шах
= 8
шей возможной пло¬
щади. Докажем, что средина
Z,, например, стороны А}А2 это¬
го шестиугольника, принадм-
41

чает F внутри себя. Кроме того, если
А\К > А\Аъ> КА2,
что наверное будет иметь место при достаточно малом угле а,
то
V w: = 4- кАкА sina>4 sin а = SbA*A,
11 аналогично
с , \ с
ДД.ДЛ	A л, la,'
Поэтому
SWK, = SujK+	+ SA LAtAt~ SbKA,A— 5 A LAX
что противоречит предположению о том, что площадь шес¬
тиугольника Шк — наименьшая из возможных.
Этим и доказано, что средина стороны A4A2 (как и средины
всех остальных сторон шестиугольника Шк) действитель¬
но принадлежит F.
Наконец, отразим шестиугольник Шк вместе со впи¬
санной в него фигурой F от средин Zj, Z2, ..., Z„ всех его
сторон. Мы получим конфигурацию из 7 шестиугольников,
аналогичную изображенному на рис. 1, б расположению 7
кругов. На рис. 25, например, AXU || А3А2 [| АьАй,
A2V II А4А3 || АвАг и т. д. При этом шестиугольник Шк
окажется «окруженным» шестью другими, равными ему
шестиугольниками Шки Шк2, ..., Шке, а фигура F —
шестью другими непересекающимися и равными ей фигу¬
рами Flt F2, ..., Fe, вписанными в эти шестиугольники и
соприкасающимися с фигурой F в срединах сторон шести¬
угольника Шк.
Заметим теперь, что фигуры Flt F2, ..., Fe не только
равны фигуре F, ноипараллельно ей рас¬
положены (могут быть получены из F параллельным
переносом). В самом деле, фигура рг получается из фигуры
F симметрией относительно средины Zx стороны АгА2 шес-
42

Рис. 25
тиугольника Шк (поворотом на 180° вокруг точки Z}).
А так как фигура F — центрально симметрич-
н а, то от нее к Fx можно перейти с помощью двух последо¬
вательно осуществленных центральных симметрий — сим¬
метрии относительно
центра О фигуры F (эта
симметрия переводит F в
себя) и последующей сим¬
метрии относительно точ¬
ки Zx (эта симметрия пе¬
реводит F в Fx).
Примечание. После¬
довательность двух централь¬
ных симметрий представляет
собой параллельный перенос.
Действительно, если М —
Рис. 26
произвольная точка плоскости, М' — точка, симметричная М
относительно О, а Мх — точка, симметричная М' относительно Z,
(рис. 26), то так как OZx — средняя линия треугольника ММ'Ми то
ozx = ~^-ммх,
43

или
MMi «= 20Z„
т. e. точка M , получается из точки /И параллельным пере¬
нос о м на вектор 20 Z±. Отсюда следует, что фигура Ft, которую можно
получить из F двумя последовательными симметриями относительно то¬
чек О и Zlt может быть также получена из F параллельным переносом
на вектор 20Z,. Точно так же доказывается, что и фигуры F2, .... Fe по¬
лучаются из F параллельными переносами (на векторы 20 Z2, .... 20Ze
соответственно).
Таким образом, изображенные на рис. 25 фигуры Flt
F.,, ..., Fe удовлетворяют всем условиям задачи 7, откуда
следует, что для любой плоской выпуклой центрально сим¬
метричной фигуры F
л, (О >6.
Это неравенство и равенство k2 (Тр) = 6 (см. задачу 8, а)
и доказывают, что для центрально симметричных выпук¬
лых фигур
^min “ 5.
§ 7. ЗАДАЧИ О ПРИКЛАДЫВАНИИ КВАДРАТОВ
И ТРЕУГОЛЬНИКОВ
До сих пор мы рассматривали лишь задачу 7 из § 5;
перейдем теперь к более сложной задаче 6. Начнем с при¬
меров:
Задача 10, Чему равно число
а) К2 (Кв)-,
б) К2 (Тр),
где символы Тр и Кв имеют тот же смысл, что и в задаче 8.
Решение задачи а). Из результата задачи 8, б)
(рис. 22, б) и из неравенства (7) следует, что К2 (Кв) > 8.
Докажем, что имеет место равенство
К2(Кв) = 8.	(10)
Рассмотрим замкнутую линию L, образованную про¬
ходящими вне квадрата Кв, со стороной 1, прямыми, па¬
44

раллельными сторонами квадрата Кв и удаленными от них
на расстояние эта линия представляет собой квадрат
со стороной 2 и периметром 8 (рис. 27, а). Докажем, что дли¬
на части ломаной L, отсекаемой от L приложенным к Кв
квадратом Квх, равным Кв, всегда > 1; отсюда и будет
следовать, что к Кв нельзя приложить более, чем 8:1=8
равных Кв непересекающихся квадратов.
Разберем все возможные случаи взаимного расположе¬
ния квадрата Кв и равного ему квадрата Квх, не пересе¬
кающего Кв, но соприкасающегося с ним.
I.	Пусть одна из ее р шин квадрата А^фИфдх, напри¬
мер, Ах лежит на стороне квадрата ABCD. При этом
может быть, что:
1°. Квадрат Квх отсекает из линии Lom резок, при¬
надлежащий одной из четырех сторон квадрата ABCD = L.
Если при этом ни одна вершина квадрата Кви отличная
от вершины Аъ не попадает внутрь линии L и сторона АХВУ
образует с проходящей через точку А} стороной квадрата
Кв угол	а, то
ab =* аР 4- РЬ = АХР ctg а +	АгР tg а = -i- (ctg а 4- tg а) =
1 /	sin а	cos а  	1	sin'2 а + cos2 а
2 I	cos а	sin а	I	2	sin а cos а
2 sin а cos а sin 2а
(равенство имеет место при а = 45°). Если же внутрь линии
L попадут две вершины Аг и Вх квадрата Кв1г то проводя че¬
рез точку ах пересечения отрезка AXDX с линией L прямую
аф[ |i АгВи получим
афj > афI = AxBx = 1
(равенство имеет место, когда сторона АХВХ квадрата Кву
примыкает к стороне квадрата Кв).
45

5
Рис. 27

2е. Кв'драт Кв, отсекает от линии L ломаную,
т. е. одна из вершин квадрата ABCD =э L, например А,
попадает внутрь квадрата Кв,. Перенесем теперь квадрат
Кв, параллельно в положение Кв, (AB\C[D'\). Так как угол
Р < Z. £71.1 = 45°, то
ЬгЬ2 = b'2Q • tgp = АА1 - tgр = ага2 ■ tg р <а2а2,
поэтому а2АЬ2 < а2АЬ2. Но так как, очевидно, A Aa2F =
= Л 'АЬ2Е, ибо AF = АЕ и А FAa2 = Z. ЕАЬ2 = р, то
a^F — Ь2Е и, следовательно,
a2Ab2 - а2А -f Ab'2 = (a2F -)- FA) (АЕ — b2E) =
= £Л + Л£ = 4-+4-=1-
Таким образом, и в этом случае имеем
a2Ab2 > a2Ab2 = 1
(равенство имеет место при а2а2 = Ьф'2 = 0 и квадрат Кв,
совпадает с Кв,).
II.	Пусть на одной из сторон квадрата
например, на стороне А,В,, лежит вершина квадрата
Кв (рис. 27, б). Здесь имеем те же два случая, что и выше.
1°. Если квадрат Кв, отсекает от линии L отре¬
зок, то мы имеем условия, близкие к тем, которые были
в случае I. Так:
ab = аР + РЪ = А,Р ctg а -f- А,Р tg а > 2А,Р >• 1,
ибо А,Р > или
a,b, > a,b, — BtA, = 1.
2°. Если квадрат Кв, отсекает от линии L лома¬
ную а2СЬ2 идее вершины А, и В, этого квадрата лежат
47

внутри линии L то, проведя через точку а2 прямую а.,Ь'2 ||
■ ВхАх, получим:
а2СЬ2 у> аф2 > а2^2 = BXAX = I ■
Если же квадрат КвЛ отсекает от линии L ломаную
aJDbz и внутри L находится лишь одна вершина А1
этого квадрата, то переместив /Се, параллельно в направ¬
лении A1D1 в положение DB\C\D\ = Кв\, убедимся, что
квадрат Квх отсекает от/-большую часть L, чем квад¬
рат Кв\, в то время как квадрат Кв\ отсекает от L ломаную
длины 1 или отрезок длины больше или равной 1 (ср. со слу¬
чаем 1). Поэтому и здесь
a:iDbt > 1,
(равенство может иметь место лишь в случае, когда квад¬
рат Квх совпадает с Кв\).
Эти рассуждения и завершают доказательство равенст-
ва (10)	’
11 При разборе всевозможных вариантов взаимного расположения
квадратов Кв и /(в, мы не рассматривали случая, когда сторона А1В1
квадрата Ке1 соприкасается с вершиной квадрата Кв и обе вершины Ах
и В[ находятся в н е L. Почему мы так посту тин?
48

Решение задачи 10,6. Как видно из рис. 28, а,
К2 (Тр) > 12. Рассмотрим описанную вокруг правильно¬
го треугольника Тр == ABC со стороной 1, шес¬
тиугольную замкнутую ломаную L = А1А2В1В2С1С2
(рис. 28, б), натянутую на такие точки Аг и В2, Вг и С2,
Сг и А2 сторон АВ, ВС и СА треугольника Тр, что ААг =
= АА2 — ВВг — ВВ2 = CCt = СС2 = Как и при ре¬
шении задачи а), можно установить, что при любом поло¬
жении «приложенного» к треугольнику Тр равного ему
треугольника Тр1 (несколько возможных вариантов рас¬
положения треугольника Трг изображены на рис. 28, б),
он отсекает от L часть длины, большую или равную -у
(докажите это самостоятельно). А так как общая длина
ломаной L, очевидно, равна 6 (ибо А,А2 = В, В2 — С1С2 =
= а А2Вг = В2С1 - С2Аг = ~), то отсюда следует
что к Тр нельзя приложить более чем 6 : у = 12 не-
пересекающихся равносторонних треугольников, равных
Тр, т. е.
К2 (Тр) = 12.	(11)
Равенство (11) впервые (без доказательства) встречается
в работе Л. Фейеша Тота, опубликованной в 1967 г.;
еще раньше задача определения величины Кг (Тр) была по¬
ставлена автором настоящих строк перед учащимися мос¬
ковских математических школ и была решена несколькими
школьниками. В той же работе Л. Фейеш Тот высказал
предположение, что величина К2 (Мнп), где Мнп правиль¬
ный п-угольник, равна 12 при п = 3, равна 8 при п =* 4
и равна 6 при п> 4. Для всех пфЪ это предположение
в 1971 г. доказал венгерский геометр К- Б ё р ё ц к и.
Таким образом, из всех относящихся к правильным
многоугольникам задач определения величины k2 и К2
49

у////:// '///;,
т
? Ъ/ш/шъ
Рис. 29
открытой пока остается лишь задача нахождения числа
К2 [Пт), где Пт — правильный пятиугольник. Однако мы
не советуем читателям заняться этой не особенно интерес¬
ной задачей. Дело в том, что если полученные в процессе
решения задачи 8 формулы (8)
и (9) в известном смысле ха¬
рактеризуют общую ситуацию,
то формулы (10) и (11), и
любые подобные им, не могут
претендовать на большее, чем
только служить достаточно
частными иллюстрациями за¬
дачи 6. Конечно, очевидное
по самому смыслу величин
k (F) и К (F), где буква F обозначает одну и ту же
фигуру и поэтому нижний индекс у букв k и К опущен
(он одинаков, т. к. соответствует размерности F) неравенст¬
во (7) совместно с неравенством Хадвигера и равенством
k2 = k2(Kp) = K2(Kp) = 6
(рис. 1, б) доказывает, что для любой плоской выпуклой фи¬
гуры F
К2 (F) > 6	(12)
(где наименьшее возможное значение /(2 = 6 достигается,
например, для круга); однако никакой «верхней оценки»
для числа дать нельзя: выпуклую фигуру F можно выбрать
так, что число К2 (F) будет сколь угодно вели¬
ко. В самом деле, легко видеть, что если F ;=з Прт есть
.прямоугольник с целочисленными сторонами 1 и т, то
К2 (Прт) > 2т + 6
см. рис. 29, гдет = 9 и 2т + 6 = 24. А может быть вы су¬
меете доказать, что К2 (Прт) = 2т + 6?
Таким образом, неравенством (12) в некотором смысле
исчерпывается все, что мы можем сказать о величине К2 (F).
Дальнейшие же содержательные задачи могут возникнуть
50

лишь в том случае, если выбрать фиксированную
фигуру F или как-нибудь ограничить класс рассматривае¬
мых фигур.
Представление о задачах, связанных с фиксированным
выбором фигуры F может дать, например, такая задача:
Рис. 30
Задача 11. Чему равна величина
а) К2(Тр(а, Ь, с)), где Тр(а, Ь, с) — треуголь¬
ник со сторонами а, b и с (а < b с);
б) К2 (*5 (а, Ь)), где Э (а, Ь) — эллипс *> с полуосями
а и b (а >■ Ь).
Ясно, что форма треугольника Тр (а, Ь, с) полностью
определяется отношениями —■ = х и	гДе У ^ I.
х <. у,	X + у > 1 (ибо X + у =	а а + b > с);
поэтому величину /<■> (Тр (а, Ь, с)) можно также обозначить
через	(х, у) — это есть функция двух переменных х и у,
удовлетворяющих неравенствам
//<1; х < £/; х + г/ > 1.
Эти неравенства опрезеляют на плоскости (х, у) треуголь¬
ник UVW (рис. 30. а), являющийся областью определения
искомой функции /<., (х, у). Из результата задачи 10, б)
следует, что в точке U (1, 1) (эта точка соответствует рав¬
носторонним треугольникам) функция К2(х, у) принимает
значение 12; кроме того, она неограниченно возрастает при
11 См., например, ЭЭМ, кп. V (геометрия). М., «Наука», 1966,
С 579—585 (статья «Конические сечения»).
51

приближении точки к стороне VW. Однако никаких мето¬
дов патного определения функции /<., (х, у), т. е. никаких
способов решения задачи 11, а) указать сегодня, видимо,
нельзя.
Аналогично, форма эллипса Э (а, Ь) с полуосями а и b
Ь
определяется одним числом — = г; поэтому величину
Кг (Э (а, Ь)) можно также обозначить через /\2 (г), где 0 <
< z 1 — функция одного аргумента г, определенная на
отрезке 0 «с г < 1 (отрезке ОЕ, рис. 30, б). Из § 1 следует,
что в конце Е отрезка ОЕ функция /<., (г) принимает значе¬
ние 6, ибо точка Е соответствует обращению эллипса в
окружность; также и в точках отрезка ОЕ, достаточ¬
но близких к точке Е, \. е. для эллипсов Э (а, Ь), мало от¬
личающихся or окружности, /<2 (г) = 6, а при приближе¬
нии точки z к концу О отрезка ОЕ функция /<, (г) стремится
к бесконечности. Однако полная картина зависимости ве¬
личины Кг (г) от z остается пока достаточно неясной.
§ 8. ОБОБЩЕНИЯ И ВАРИАНТЫ
Рассмотрим один из возможных способов, позволяющих
выделить определенный класс выпуклых фигур F, для ко¬
торых величина /<., (Г) остается ограниченной.
Условимся называть ширину Д само й узко й по¬
лосы, ограниченной параллельными прямыми 1г и /2 и та¬
кой, что внутри этой полосы можно поместить (плоскую,
выпуклую) фигуру F (рнс. 31, а) просто ш и р и н о й фи¬
гуры. Таким образом, ширина \ фигуры F равна расстоя¬
нию между наиболее близкими друг к другу па¬
раллельными опорными прямыми этой фигуры. А ширину D
самой широкой полосы, внутри которой можно
поместить фигуру F так, чтобы эта фигура «упиралась»
в ограничивающие полосу параллельные прямые ;//, и пи
(рис. 31, б), назовем диаметром фигуры. Таким об¬
разом, диаметр — это расстояние между наиболее
52

удаленными друг пт друга параллельными опорными
прямыми фигуры F. Так, например, ширина треуголь-
и и к а, очевидно, равна его наименьшей высоте, а диа¬
метр — наибольшей стороне: ширина п р я м о у г о л ь -
:о
1м
Рис. 31
ника равна его менынен стороне, а диаметр — диагона¬
ли; ширина э л л и п с а равна его меньшей оси, а диа¬
метр - большей оси. Для к руга диаметр и ширина сов¬
падают — оба они равны диаметру круга в элементарно-
геометрическом понимании этого слова.
Нетрудно видеть, что диаметр D (плоской, выпуклой)
фигуры равен наибольшему расстоянию между ее точками.
В самом деле, пусть А В - наибольший
из отрезков, соединяющих точки фигу- т<
ры F (рис. 32). В этом случае, очевид¬
но, А и В — граничные точки F — ведь
иначе отрезок АВ можно было бы уве¬
личить, продолжив его за один из кон¬
цов. Проведем теперь прямые /;/, и///2,
перпендикулярные к отрезку АВ и
проходящие через его концы. Ясно,
что nii и пи — опорные прямые
фигуры F: в самом деле, если бы,
скажем, существовала точка М фигуры /’, расположен¬
ная по другую сторону от пи, чем точка В, то тогда
было бы AM > АВ — что противоречит нашему допущению
об отрезке АВ. Далее, если бы существовали параллельные
опорные прямые /г, и п., фигуры F, расстояние между
которыми было бы больше расстояния АВ, то отрезок KL,
Рис 32
53

соединяющий точки соприкосновения /(, и п., с границей F,
был бы больше отрезка АВ, чю опять протнЕоречит тому,
что расстояние между точками А и В фигуры F — наиболь¬
шее.
Отсюда и следует, что отрезок АВ раьен расстоянию D
между наиболее удаленными друг от друга параллельными
опорными прямыми пц и т2 фигуры F.
Таким образом, ширина А фигуры F — это как бы ее
«наименьшая ширина», а диаметр D — «наибольшая ши¬
рина».
При м е ч а и и е. Сказанное имеет следующий точный смысл:
каждая выпуклая фигура F имеет только две опорные прямые lt и 12,
параллельные любой произвольно фиксированной прямой I (которую
можно характеризовать, например, задав ^c.NOx = а между прямой
0N_\_ I и положительным направлением оси Ох); расстояние Д (а) между
этими прямыми /, и /2 называется шириной фигуры F в направ¬
лении ON. При этом наибольшее значение функции Л (а) (ко¬
торую можно считать определенной, например, при 0	^ 180', при¬
чем Д (0) = Д (180е)) совпадает, очевидно, с диаметром D (F) фигуры F,
а наименьшее — с ее шириной Д (F).
Отношение ~ принимают за «меру вытянутости» фи¬
гуры F. Условимся теперь рассматривать только те фигуры,
D
для которых эта «мера вытянутости» -д- не превосходит не¬
которого фиксированного значения с (очевидно, что с >• 1).
При этом величина К2 (/•’) уже не сможет быть слишком
большой. Таким образом, можно поставить следующую
задачу:
Задача 12. В каких пределах может меняться величина
К-г (F), если известно, что отношение ~ диаметра фигуры
F к ее ширине меньше или равно с, где с >- 1?
Эта задача состоит в определении некоторого мно¬
жества чисел К-г (F), отвечающих всевозможным фигурам
F, таким, что
64

^то множество чисел можно обозначить, например, через
К2 (с) или просто через К (с), ибо мы здесь рассматриваем
только плоские фигуры. Ясно, что при любом с и а и
меньшим числом множества К (с) (его можно обоз па
чить, скажем, через /(min (с)) Есегда будет число 6, ибо на-
Рнс. 33
гу	D(Kp)	,
пример, для круга Кр, у которого д (др) = • имеем
К (F) = 6. Таким образом, основная трудность заключает¬
ся в определении наибольшего числа К шах (с) мно¬
жества К. (с).
Л. Ф е й е ш Тот установил, что
Ктах (с)	(2я -f- 4) С -)	  р	2.	(13)
Для некоторых значений с эта оценка числа является точ¬
ной, в том смысле, что Д',пах (с) = [(2я + 4) с -р -j- + 2],
где квадратные скобки означают целую часть числа;
однако она справедлива далеко не для всех значений с.
Так, например, предположив, что с=1, мы придем к
«максимально округлым» или «наименее вытянутым» фигу¬
рам, имеющим во всех направлениях одну и ту же
ширину (рис. 33); такие фигуры называются фигурами
постоянной ширины б. Из неравенства (13) следует, что для
б О фигурах постоянной кривизны см., например, § 7 книги. [15].
65

новой фигуры F постоянной ширины
K{F)< |2л4-71	113, 28...1	13,
в то время как в той же работе J1. Фейеш Тот показал, что
для всех таких фигур К (F) < 8 н предположил, что
tfnu*(l)“7, т. е. /С(1) = {6, 7),
другими словами, что характеристики К2 (F) плоских и вы¬
пуклых фигур постоянной ширины могут иметь лишь два
значения: 6 и 7. Первое из них достигается, например, для
круга (рис. 1, б), а второе — для изображенного, например,
на рис. 33, в так называемого треугольника Рел-
л о, ограниченного тремя дугами АВ, ВС и АС окружно¬
стей радиуса 1 с центрами в Еершинах равностороннего
треугольника ABC со стороной 1. В 1970 г. это предполо¬
жение J1. Фейеша Тота доказал венгр И. Ш о п, что, впро¬
чем, доставило немного новой информации о всем комп¬
лексе связанных с задачей 12 вопросов. Так, до сих пор
остается открытой проблема полного описания того се¬
мейства фигур постоянной ширины, для которых К (F) = 6
и тех фигур, для которых /< (/•’) - 7, к решению которой
пока не видно никаких подходов, или проблема оценки
D
того наименьшего значения отношения с == —, для которо¬
го множество К (с) превосходит множество К_ (1), т. е.
для которого существует выпуклая фигура F, такая, что
~ с н чт0 к F можно «приложить» 8 равных F фигур.
Новые вопросы возникают при переходе ктрехмер-
н о м у или многомерному пространству. Так,
Г. Хадвигер установил «верхнюю оценку» для чисел
kn (F), показав, что при ыооом п
kn(F)< 3»-1,	(14)
в частности, что
k3 (F) < З3 — 1 =26
56

для всякого пространственного выпуклого тела F. Он пред¬
положил также, что kn (F) = 3"	1	в	том	и	только в том
случае, когда F- параллелотоп. например
k3 (F) = ‘26, если F параллелепипед (куб). Это
предположение было позже доказано Г. Грёмером и
Б. Грюнбаумом. Последний установил также «ниж¬
нюю оценку» величины kn (F), доказав, что для каждого
п-мерного выпуклого тела F
п2 | п 4,kn(F) < 3" — 1,	(15)
причем здесь оба крайние значения величины kn (F) до¬
стигаются:
kn (/’) — а’ + п, если / «-мерный симплекс;
kn (F) -= Зп — 1, если F /i-мерный параллелотоп.
При п = 1 неравенство (15) означает лишь, что для лю¬
бой «одномерной» выпуклой фигуры F (о т резка)
I2 + 1 < ft, (F) < 3 — 1, т. е. ft, (F) = 2,
а при п = 2 это неравенство обращается в уже известное
неравенство Хадвигера: для любой плоской выпуклой фи
гуры
22 + 2 < k2 (F) < З2 — 1 или 6 ^ ft, (F) <. 8.
Однако уже при п = 3 неравенство (15) содержит новую и
нетривиальную информацию: из него следует, что для лю¬
бого выпуклого тела F обыкновенного трехмерного простран¬
ства
3*- 3	12 Cft-^A) <26	3:i — 1,	(16)
причем, оба крайних значения достигаются:
ft, (Г)	12,	ft,	(Кб)-26,
где Т — треугольная пирамида (тетраэдр), а 1{б — куб.
Аналогично, при п = 4 имеем
20 - 42 1- 4 < k, (F) < З4 - 1 = 80.
57

Рассмотрим теперь трехмерный и многомерный вариан¬
ты более трудной задачи.
6. Ясно, что неравенство Грюибаума (16) совместно с
равенством
к3 = к3(Ш) КАШ)- 12	(17)
(равенством Ньютона—Г'оппе-ван дер Вардена—Шютте —
Лича) доказывают, что
Д':,(/7)>12,	(18)
причем, эта оценка величины Д., (F) является точно й:
равенство К3 (F) = 12 достигается, например, для шара
Ш. Более общее неравенство (15) доказывает, что для лю¬
бой п-мерной фигуры F
K,l(F)>ni + п,	(19
где однако уже нельзя утверждать, что полученная оцен¬
ка является точной, т. е., что существуют такие «мерные
фигуры F, что Кп (/’) = гг + п. Задачи определения вели¬
чины К (F) для конкретных (трехмерных или даже «-мер¬
ных) тел весьма трудны и, видимо, никогда не ставились.
Задачи 1—3 могут быть обобщены и в ряде других на¬
правлений.
Примечание. Естественным является, скажем, перенос всей
проблематики настоящей книги в область разного рода «неевклидовых»
геометрий, вроде геометрии на поверхности сферы — сферической гео¬
метрии или неевклидовой геометрии Лобачевского (см. ЭЭМ, кн. V, статья
«Неевклидовы геометрии»)
Ясно, что также и задачи 4 и 5 могут быть сформулиро¬
ваны и с заменой кругов и шаров произвольными, но ф и к -
сированными выпуклыми фигурами F. При этом
возможны два варианта таких «обобщенных» задач, возни¬
кающих в зависимости от того, будем ли мы требовать от
рассматриваемых в обобщении задачи 4 «соседей» фигуры F
или от фигурирующих в обобщении задачи 5 фигур, «окру¬
жающих» F, лишь их равенства исходной фигуре
F или также их параллельного F располо-
Б8

жени я. Числа, определяемые в эти* Дву* вариайтйЗс
обобщения задачи 4 естественно обозначить через К (i, F)
и k (/, F), а те числа, определения которых требует обобще¬
ние задачи 5 —■ через К (F) и k (F). По поводу этик обобщё*
ний задач 4 и 5 неизвестно пока почти ничего; можно только
указать на полученное Л. Фейешем Тотом нера¬
венство:
если	то К (г, F)<2 (л/2 + 4t) с + 4" + 2*>
обобщающее неравенство (13), стр. 55.
Далее, в задачах 1—3 мы оценивали наибольшее число
непересекающихся кругов или шаров, которые можно при¬
ложить к равному им кругу
или шару; в обобщении этой
постановки вопроса мы уже
рассматривали вопрос о числе
«копий» произвольно заданной
(выпуклой) фигуры F, кото¬
рые можно приложить к фи¬
гуре/7. Но можно, разумеется,
ставить вопрос и о числе, на¬
пример, единичных кругов или
шаров, которые можно прило¬
жить к заданной фигуре F с
соблюдением всех требуемых
условий:
Задача 13. Чему равно наи-	р	34
большее возможное число %п (F)
непересекающихся кругов или шаров диаметра 1, которые
можно приложить к данной выпуклой фигуре F так,	чтобы
никакой	из них не пересекал F, но все они имели	с	F	общщ
граничные точки (рис. 34)?
Ясно, что
h {КР) = *2 = 6, Хд (Ш) = fc) = 12,
/С4 (Ш) — kit ,, . ,
59

где Кр — круг; Ш — шар диаметра I; номер или «индекс»
п внизу, как всегда, указывает размерность фигуры F и вме¬
щающего ее пространства, а также прикладываемых к F
шаров, где «двумерный шар» — это круг. Таким образом,
задачи 1—3 являются частными случаями задачи 13. По¬
нятно, однако, что для «больших» в том или ином смысле
фигур F число х (F) будет весьма велико; поэтому задача
оценки чисел X (F), отвечающих тому или иному семей¬
ству фигур F, имеет смысл лишь тогда, когда мы
тем или иным способом ограничиваем размеры F (или фик¬
сируем F). Представление о возникающих при этом во¬
просах может дать следующая задача:
Задача 14. Какие значения могут иметь величины Ха (F),
отвечающие всевозможным (плоским, выпуклым) фигурам F
диаметра 1?
Решение. Эта задача состоит в определении неко¬
торого множества чисел X (F), которое можно обозна¬
чить, например, через X. Докажем, что интересующее нас
множество чисел
Х= {4, 5, 6},
т. е. число X (F), отвечающее плоской фигуре F диаметра 1,
может иметь лишь одно из трех значений: 4, 5 или 6.
Для этого установим, что:
1°. Наименьшее число Xmin множества X не мо¬
жет быть меньше 4:
Xmin ^ 4;
другими словами, к каждой плоской выпук.юй фигуре F
диаметра 1 можно приложить четыре круга Kpt, Кр»,
Кр3, Kpi единичного диаметра с соблюдением условий зада¬
чи. Действительно, фигуру F диаметра 1 можно заключить
в полосу шириной 1, ограниченную двумя параллельными
опорными прямыми тг и т2 этой фигуры, касающимися гра¬
ницы фигуры в некоторых точках Л и Б (рис. 35). Рассмот¬
рим два круга Крг и Кр2, расположенные вне этой полосы и
60

касающиеся mt и т, соответственно в точках А и В; они
будут соприкасаться в то же время и с контуром фигуры F.
Возьмем еще два круга Кр'3 и Кр'4, расположенные внутри
ограниченной т1 и т2 полосы и вне F, по разные стороны
от /^-Перемещая эти круги по направлению к F вплоть до их
соприкосновения с границей F, мы получим требуемые 4
круга Кри Кр2, КРз и Кр*.
2°. Наибольшее число %тах множества X не может быть
больше 6;
У-mas 6;
другими словами, ни к какой плоской, выпуклой фигуре F
диаметра 1 нельзя приложить более 6 кругов единичного
диаметра с соблюдением условий задачи. Действительно,
предположим, что к фигуре F диаметра 1 приложено 7 еди¬
ничных непересекающихся кругов Кр*, Кр2, Кр7, каса¬
ющихся контура фигуры в точках А1г Аг, А7 (рис. 36, а).
Проведем опорные прямые а,, а2, ..., а7 фигуры F, проходя¬
щие через точки Аи А2, ..., Л7; они образуют описанный
вокруг F выпуклый семиугольник.
61

Примечание. Здесь мы считаем, что точки At, Аг, ..., Л, ИЗ'
столько «равномерно» распределены вдоль контура F, что прямые oti
0|i ...* сf образуют описанный вокруг F выпуклый многоугольник. Пред¬
лагаем читателю самостоятельно рассмотреть иной случай.
Воспользуемся теперь тек называемой теоремой
Юнга (стр. 74), По которой каждую фигуру диаметра 1
i/Г
можно заключить в круд радиуса Пусть Окр — окруж-
Рис. 36
ность радиуса , заключающая F внутри себя. Переме¬
стим все круги Kplt ■ ■■, Кр7, не касающиеся Окр, в направ¬
лении, перпендикулярном к Сторонам аъ ..., а7 семиуголь¬
ника, до их соприкосновения с Окр. При этом круги
КРъ Кр7, равные между собой, только «разойдутся»,
т. е. они по-прежнему не будут пересекаться. Однако, круг
1/3
Кр диаметра 1, касающийся окружности Окр радиуса
62

(рис. 36, б), виден ич центра О этой окружности под таким
утлом «, что
3
V
%
2)3 + 3
т. е.
-у-да27° 40' и а ■
2 1 3 — 3 «0,464;
<55° 20',
— откуда и следует, что к Окр нельзя приложить 7 непере-
2л
секающихся кругов единичного диаметра, так как да
360° СС/7
~ 55° 20' ~
Полученное противоречие и доказывает ошибочность
сделанного предположения о возможности приложить к фи¬
гуре F семь единичных кру¬
гов.
Нетрудно видеть, что су¬
ществуют фигуры F единично¬
го диаметра, для которых X (F)
принимает как значение 4,
так и значение 5 или 6; это де¬
лает содержательной (видимо,
достаточно трудную) задачу
об описании тех фигур F,
для которых, например, X (/г)—
= 4 (или 5, или 6). Так, эл¬
липс Э диаметра 1 — это эллипс с осями I и 2Ь, где 0 <
< 2b < 1; при этом эллипсам с очень малым b соответст¬
вуют значения X (5) = 4 (рис. 37), в то время, как при
2Ь = 1 эллипс переходит в круг, для которого X = 6.
Однако, даже задача полного описания функции X (b) =
= Х (5(-|-, Ь)), где Э (-^-, Ь) — эллипс с осями 1 и 26, яв¬
ляется, видимо, совсем не простой.
Разумеется, задачи 13 и 14 могут быть перенесены в
трехмерное или в «-мерное пространства. Возможны также
иные варианты задач о характеристике X (F) фигур F.
63

Для иллюстрации сложности задач рассматриваемого
здесь типа остановимся еще на одной задаче, в некотором
смысле близкой к задаче 10:
Задача 15. Чему равно наибольшее возможно„ число
Рис. 38
а) параллелограммов (например, квадратов);
б) треугольников,
которые можно расположить на плоскости так, чтобы
каждые два из них соприкасались по некоторому участку
границы (соприкосновение многоугольников лишь своими
вершинами здесь не учитывается)?
Ответ: а) 3 (рис 38, «); б) 4 (рис. 38, б). Предла¬
гаем читателям самостоятельно решить эту задачу.
Рассмотрим теперь следующий «трехмерный вариант»
задачи 15.
Задача 16. Чему равно наибольшее возможное число
а) параллелепипедов (кубов);
б) треугольных пирами) (тетраэдров),
которые можно расположить в пространстве так, чтобы
каждые два из них соприкасались по некоторому плоскому
(или «двумерному») участку границы (не по части ребра,
и тем более, не в одной лишь вершине)?
Обозначим числа, искомые в задачах 15, а), б) и 16, а),,
б)	соответственно через Р., (Кв), Р.г (Тр), Р.3 (Кб), Рз (Т)~
64

Тогда, как уже указывалось,
Р2 (Кв) - 3 и Р2 (Тр) = 4.	(20)
Нетрудно	видеть, что в пространстве	можно	располо¬
жить 6	кубов	или 8 тетраэдров с соблюдением	условий за¬
дачи 16, так что
Р3(Кб)>Ь и Р3(7)>8	(21)
/
/
/
Рис. 39
Действительно, считая плоскость листа бумаги гори¬
зонтальной, «поставим на плоскость» три куба, основания
которых изображены на рис. 39, а сплошными линиями;
затем «приложим к этой плоскости снизу» еще три куба,
образующих аналогичную конфигурацию кубов, но повер¬
нутую по отношению к системе первых трех кубов (на ри¬
сунке основания этих кубов изображены пунктиром). При
этой мы получим 6 кубов, расположенных в пространстве
так, что каждые два из них соприкасаются по некоторой
части границы. Аналогично, можно «поставить на плос¬
кость» четыре тетраэдра с общей вершиной, основания ко¬
торых изображены на рис. 39, б сплошными линиями; если
затем «приложить к этой плоскости снизу» еще четыре тет¬
раэдра с общей вершиной (основания их изображены пунк¬
тиром), то мы получим конфигурацию из 8 тетраэдров, удов¬
летворяющих условиям задачи 16, б).
65

Но равны ли числа Р3 (Кб) и Р3 (Т) соответственно 6 и 8,
или они больше этих значений? Ответ здесь дать, видимо,
совсем не просто. Предположение о том, что
Р,(Т) - 8
впервые высказал американский математик Ф. Б е й д-
ж е м и л, но он не сумел доказать свою гипотезу. Впо¬
следствии задачей 16 занимался английский геометр
В. Д ж. Д. Б е с т о н, посвятивший этой проблеме свою
диссертацию. В. Бестон заявил, что он может доказать
равенство
Р3(Щ = 6.
Развив специальный алгебраический аппарат, он доказал,
что
Р3(Т)< 9,
но доказать, что Р3 (Т) = 8, Бестон так и не сумел. Таким
образом, на сегодняшний день вся имеющаяся у нас по пово¬
ду задачи 16, б) информация ограничивается, видимо, двой¬
ным неравенством
8<Р3(7)<9	(22)
(хотя В. Бестон уверен, что Р3 (Т) = 8).
Задачи 14 и 15 возникли в связи со знаменитой «проблемой
четырех красок», требующей доказать, что любую географиче¬
скую карту на плоскости можно закрасить четырьмя красками так,
что никакие две страны, имеющие общий участок границы, не будут за¬
крашены одной краской '*. На плоскости невозможно расположить 5 об-
0 Эта проблема, имеющая более чем вековую историю, до сих пор
еще не решена. См.:
Г. Радемахер, О. Теплиц. Числа и фигуры. М., «Наука»,
1966, тема 13;
Д. Гильберт, С. Кон-Фоссе н. Наглядная геометрия.
М.— Л., Гостехиздат, 1951, п. 51;
Р. Курант, Г. Роббиис. Что такое математика? М., «Просве¬
щение», 1967, § 3, гл. V;
Е. Б. Д ы и к и и, В. А. У с п е и с к и й. Математические беседы.
М.— Л., Гостехиздат, 1952, раздел I.
И. С. С о м и и с к и и, Л II. Г о л о в и н а, И. М Я г л о м.
О математической индукции. М., «Наука», 1967, § 2 части II.
66

ластей так, чтобы каждая из них граничила со всеми четырьмя другими
(образованную подобными пятью «странами» карту, разумеется, нельзя
было бы закрасить четырьмя красками с соблюдением требуемых усло¬
вий); таким образом, ответ на вопрос задачи 15, б) парадоксальным об¬
разом не изменитея при замене треугольников совершенно произ¬
вольными (даже не обязательно выпуклыми) многоуголь¬
никам и: в понятных обозначениях
Р2 (Мн) = 4,	(23)
где Мн обозначает произвольный (скажем, выпуклый, хотя на самом
деле это условие здесь несущественно) многоугольник. Напротив,
в пространстве можно так расположить любое, сколь угодно большое,
число выпуклых многограиииков, что каждые два из
них будут иметь общий плоский участок границы. Таким образом,
Р3(Мнгр) =оо,	(24)
где Мнгр обозначает произвольный выпуклый многогранник. Сравнение
второго из равенств (20) с равенством (23), а также результатов (22) и
(24), показывает, кстати сказать, опасность бездумного переноса на про¬
странство результатов, относящихся к плоскости: если в планиметри¬
ческих вариантах рассматриваемых здесь задач переход от треугольников
к произвольным, даже не обязательно выпуклым, многоугольникам не
сказывается на результатах, то в стереометрических вариантах тех же
задач замена тетраэдров произвольными выпуклыми многогранниками
резко меняет картину.
Символическое «равенство» (24), из которого вытекает бессодержа¬
тельность пространственного варианта «задачи о красках» — отсутствие
такого, сколько угодно большого, «универсального» числа N, что любую
«пространственную географическую карту» можно раскрасить N крас¬
ками,— впервые установил еще в 1905 г. известный немецкий геометр
Генрих Т и т ц е; в 1947 г. этот результат был доказан видным англий¬
ским математиком Александром Б е з и к о в и ч е м, видимо не знакомым
с работой Титце.

ПРИЛОЖЕНИЕ
I.	Несколько теорем из элементарной геометрии
При доказательстве теоремы о 14 шарах нам понадобились несколько
предложений, которые можно считать относящимися к области сфериче¬
ский геометрии. Роль прямых в сферической геометрии играют так назы¬
ваемые большие окружности — линии пересечения сферы с плоскостью,
проходящей через центр О сферы (рис. 40, о), а роль треугольников -
сферические треугольники (рис. 40, б), ограниченные тремя дугами АВ,
ВС и СА больших окружностей и представляющие собой пересечение
(общую часть) трех ограниченных соответствующими большими окруж¬
ностями полусфер Длины сторон сферического 1рсугольннка изме¬
ряются соответствующими этим сторонам центральными утлнми ЛОВ,
ВОС и СОА сферы, а величины углов — двугранными углами между
соответствующими сторонам треугольника плоскостям (и те и другие
удобно измерять, например, в радианах, что мы и будем делать в даль¬
нейшем). Место сбычных п-угольников в сферической геометрии зани¬
мают сферические ti-угольники (рис. 40, е), ограниченные п дугами боль¬
ших окружностей; здесь п 3 — произвольное целое число. Радиус
сферы Сф, являющейся «полем действия» сферической геометрии, мы
дальше будем считать равным 1.
Теорема 1 (теорема о площади сферического треугольника). Пло¬
щадь сферического треугольника ABC рс&на
А 4 В + С -IX,
где А, В и С — углы треугольника (из этой теоремы, в частности, сле¬
дует, что сумма углов любого сферического треугольника б о л ь ш е л).
Доказательство. Прежде всего покажем, что площадь AAt
сферического двуугольника («ломтя») с углами А = Ах (рис. 41, о)
НСр.: Б. А. Р о з е и ф е л ь д. Основные понятия сферической гео¬
метрии и тршонометрпп. ЭЭМ, кн. IV, с. 518- -557;
Ж. А д а м а р. Элементарная геометрия, ч. II. М., «Просвещение»,
1958, гл. VIII пятой книги:
Д. И. Перепелки н. Курс элементарной геометрии, ч. 2.
М.— Л., Гостехнздат, 1949, гл. XVI.
68

равна 2i4. Для этого предположим, что угол А двуугольника с о и з м е -
оим с я:
р
л А =■ — я, р, q — целые числа.
Я
Рис. 40
Разделим всю сферу на 2q «элементарных ломтиков» с помощью q про¬
ходящих через вершины А и Ах двуугольника больших окружностей
(«меридианов»). Так как поверхность всей сферы радиуса 1 равна 4я,
1	2я
то площадь каждого «ломтика» будет равна ■=— • 4я — ——, а площадь
zq	q
двуугольника AAlt составленного из р таких ломтиков, равна
2я	р
пл. ААх = р ■ 	=	2	—я - 2А,	(1)
Я	Я
— что и требовалось доказать. Отсюда обычным способом с помощью
предельного перехода можно убедиться в справедливости этого утверж¬
дения и для двуугольников, -угол которых несоизмерим с л
/

Рассмотрим теперь сферический треугольник ABC (рис. 41, б) и со¬
ставим сумму площадей: пл. А А1 пл. ВВ, пл. CCj + пл. АгА +
+ пл. В,В 1 пл. CjC шести двуугольников с углами А, В, С, а так¬
же с углами, вертикальными этим углам. Эти 6 двуугольников полностью
покрывают сферу Сф, причем треугольник ABC и симметричный ему
относительно центра О сферы треугольник ЛХВА покрываются трех¬
кратно, а остальная часть сферы — однократно. Отсюда, ис¬
пользуя формулу (1), получаем
4,4 + АВ -|- 4С = пл. Сф + 2 пл. ,4 ВС + 2 пл. АВ А- (2)
Но площадь всей сферы равна 4л, а площади треугольников ЛВС
и ,41В1С1 (сим етричных, т. е. одинаковых) равны1* между собой; поэтому
имеем
4Л + 4В + 4С = 4л + 4 пл. ЛВС,
откуда
пл. ABC—А А-ВС—л,	(3)
- что и требовалось доказать.
Теорема 2 (теорема о площади сферического я-> гольника). Пло¬
щадь сферического многоугольника Л А ... Л„ равна
А + А + ■ • ■ f Л„ — (я — 2) л.	(4)
Доказател ьство. Покажем, прежде всего, что каждый сфе¬
рический п-угольник можно разбить на п — 2 неперекрывающихся сфе¬
рических треугольника с теми же вершинами, что и у исходного много¬
угольника. Доказательство будем вести методом математи¬
ческой индукции.
Для п = 3 это утверждение бессодержательно («каждый сфериче¬
ский треугольник можно разбить на 3 — 2 = 1 сферический треуголь-
Для того, чтобы строго доказать это утверждение, достаточно за¬
метить, что если треугольник ЛВС — равнобедренный, то тре¬
угольник Л1В1С1 будет также равнобедренным и равным ЛВС; по¬
этому площади этих треугольников не могут быть различными. Если же
треугольлик ЛВС разносторонний,™ достаточно найти внутри
него точку Q, равноудаленную от всех вершин ЛВС — центр описан¬
ной вокруг ABC окружности (нахождение этой точки не отличается от
решения соответствующей планиметрической задачи) и соединить ее
дугами больших окружностей со всеми вершинами треугольника. При
этом треугольник ЛВС разобьется на три равнобедренных треугольника
.4 QB, BQC и CQA\ аналогично, треугольник А,В1С1 разобьется на три
равных им равнобедренных треугольника Л, QiB,, B,Q,C, и САА,
где Qj — точка, диаметрально противоположная Q — центр описан¬
ной вокруг Л,В1С, окружности,— откуда и вытекает, что пл. Л,В,С, =
= пл. ЛВС.
70

ник»); однако оно, разумеется, верно. Предположим, теперь, что нйше
утверждение доказано для всех m-угольников, где т < и, и рассмотрим
п-уголъник Мн = А,А2...Ап. Проведем всевозможные дуги больших
окружностей, исходящие из вершины ^п-угольника и заключенные внут¬
ри Мн (рис. 42, о). Если среди этих дуг имеется диагональ А,А, сфериче¬
ского многоугольника, то А,А, делит Мн на два меньших многоуголь¬
ника, Мн, и Мн2\ пусть Мн, = А,А2 ... Л; имеет ft, (п,= i) вер¬
шин, а Мн2 = Л;Л,-+1, ..., АпА, имеет (n2 = п — ( + 2) вер
Рис. 42
шин. Ясно, что п, + п2 =- п + 2 (ибо сложив п, вершин многоугольника
Мн, и я2 вершин многоугольника Мн% мы получим п вершин Мн, при¬
чем, вершины А, и Л,- в этой сумме будут фигурировать дважды); кроме
того, по предположению Мн, можно разбить на п, — 2 треугольника,
а Мн2 — на л.2 — 2 треугольника. При этом весь многоугольник Мн
разобьется на
(п, — 2) г («2 — 2) = (п, -f- п2) — 4 =. (п -1- 2) — 4 = п — 2
треугольников, что и требовалось доказать. Если же среди исходящих
из вершины А, дуг больших окружностей нет диагоналей многоутоль-
ника Мн, то все эти дуги «упираются» своими концами в одну (в опреде¬
ленном смысле — «противоположную вершине Л,у,) сторону многоуголь¬
ника (рис. 42, б). Но в этом случае диагональ Л„Л2 отсекает от Мн тре¬
угольник А,А.,Ап н является стороной (и — 1)-угольннка Л2Л3 ... Л„,
который, по предположению можно разбить на (я — 1) — 2 — п — 3
треугольников. Прибавив сюда треугольник А„А,А2, мы снова получим
разбиение многоугольника Мн на
(я — 3) + 1 = п — 2
треугольников, которое и требовалось отыскать.
Обозначим теперь углы п — 2 треугольников, на которые разби¬
вается в соответствии со сказанным выше n-угольник Мн = А,А2 ... Ап,
71

череза,, Pj, Yi;a2. Р2. V2l —! «,,_2< Pn_2* Yn—2. Так как площадь много¬
угольника Мн равна сумме площадей тех п — 2 треугольников, на ко¬
торые он разбивается, то, применяя формулу (3), получаем:
пл. Мн a (ax + Pi + Yi — я) + (aa + P8 + Ys — я) + - • • +
+ (an—2 + Pn—2+Vn-I — n)=*^i + 4i+ "• -Мл — (n — 2)31,
что и требовалось доказать (здесь мы используем то, что сумма углов
всех п — 2 треугольников равна сумме Ах + At + ... + Ап углов
л-угольника Мн).
Следствием теоремы о площади сфе¬
рического многоугольника является такая
теорема:
ТеоремаЗ (теоремаЭйлера). Пусть
В — число вершин произвольного выпуклого
I многогранника, Р — число его ребер и Г —
| число граней. Тогда
В — Р + Гш= 2.	(Э)
Доказательство. Опишем во¬
круг многогранника М какую-то сферу Сф,
радиус которой примем за 1, и спроекти¬
руем из центра О сферы вершины и грани
многогранника М на поверхность Сф
(рис. 43). При этом Сф разобьется на Г
сферических многоугольников мнх, мн2, ..., мнг, являющихся проек¬
циями граней многогранника М. По формуле (4)
Рис. 43
пл. мнх = Ki + се, + • • • + a„t — (пх — 2) л
пл. лна«= р, -f-	-|- ••• + РП1 - (иа— 2)л
пл. мНр X] -f-	-}-	*	•	■	-{-	—	(пр	—— 2) л
(б)
где «!, «а, ..., пг — числа вершин многоугольников мни мн^ мнг,
а аи аа, ..., ап\ рь ра, ...,РП>;	>.„г—	углы этих многоуголь¬
ников. Сложим теперь почленно все равенства (5). Тогда в левой части
равенства получим:
пл. мн1~\- пл. мн2 -{-	-J-	пл.	мнр	*=	пл. Сф — 4л,
7S

Я в правой
выражение
сумму углов всех многоугопытнков, уменьшенную на
(Н)	2)	Л	+-	(^2	2)	Л	■	•	-|~	(П[	2)	Л -	(о|	-|- AIj -|-
•'	+ п/-) л 2Гл.
Заметим теперь, что сумма
(«1 + 0-2 +	+	«и,)	+ (Pi + Р- + • • • + P„s) + • • +
+ (Г. -* Vi + ■ Тпг)
углов всех многоугольников разбиения равна, очевидно, 2Вл, нбо
вокруг каждой из В вершин ра 1бнення сф( ры на многоугольники ipvnmi-
руются углы, сумма которых равна 2л. С дру	g
гон стороны,
2 Я,
П1 + «2 +
Ь «/
ибо «1 + «2 + -■- + пгесть не что иное как
сумма чисел сторон сферических многоуголь¬
ников мни мн2, ..., мнг, а в этой сумме про¬
екция каждого из Р ребер многогранника
фигурирует дважды — в соответствии с темп
двумя сферическими многоугольниками, кото¬
рые разделяет проекция этого ребра. Таким
образом, окончательно получаем
4л = 2Вл — (2Ял — 2/’л) - 2Вл - 2Ял + 2/'л,
откуда и следует равенство
В —Я+ /'«=2.
В § 2, гл. I используется следующая теорема:
Теорема 4 (теорема о двугранном угле правильною тетраэдра).
Двугранный угол а между гранями правильного тетраэдра танов, что
sin —г- =
I 3
(6)
Доказательство. Проведем высоты АЕ и BE граней A CD
и BCD правильного тетраэдра ABCD (рис. 44). Общее основание Е
этих высот совпадает, очевидно, со срединой ребра CD тетраэдра. Ясно,
что ^ ЛЕВ = а. Так как АЕ - BE =
уз
(это высоты равносторонних
треугольников со стороной 1), а АВ — 1, то из прямоугольного тре¬
угольника AEF, где Я — средина ребра АВ, а следовательно, EF —
73

высота li биссектриса равнобедренного треугольника AFB, получаем
. а	)^3
sin ^ AEF = sin -5- = —5— •
Z	о
При решении задачи 14 используется следующая важная теорема:
Теорема 5 (теорема Юнга). Каждую плоскую фигуру F диамет¬
ра t можно заключить в круг радиуса
1/3
/? = -^(«=* 0,577).
Круг наименьшего возможного радиуса, заключающий фи¬
гуру внутри себя, называется описанным кругом этой фигуры.
Так как диаметр описанного круга фигуры, содержащей такие две точ¬
ки Л и б, что А В = 1, не может быть меньше 1, то из теоремы Юнга вы¬
текает, что радиус г описанного круга фигуры F диаметра 1 всегда заклю¬
чен в пределах
0,5 = -L < г < -^-= 0,577 . . .
Например, г — если F — квадрат диаметра 1, г = -У—, если
а	<5
F — равносторонний треугольник диаметра 1.
Доказательство теоремы. Пусть F — плоская выпук¬
лая фигура диаметра 1, а Окр — объемлющая ее окружность. Ясно, что
если Окр вообще не содержит граничных точек фигуры F, то существует
окружность меньшего радиуса, содержащая F внутри себя; чтобы
получить такую окружность, достаточно уменьшить радиус Окр не меняя
ее центра, причем это «сжатие» Окр можно производить до тех пор, пока
уменьшенная окружность не коснется границы F в какой-либо точке А
(рис. 45, с).
74

Далее, если заключающая F окружность Окр содержит един¬
ственную точку А границы F, то также существует окружность
меньшего радиуса, заключающая F внутри себя. Для того, чтобы
убедиться в этом, достаточно переместить Окр в направлении радиуса
ОА (О — центр Окр) так, чтобы точка А оказалась внутри Окр и фигура F
все еще не вышла за ее пределы (рис. 45, й). При этом мы получим равную
Окр окружность Окр,, уже не содержащую граничных точек F, которую,
как показано выше, можно уменьшить с тем, чтобы фигура Г все еще
оставалась внутри уменьшенной окружности.
Наконец, если окружность Окр, заключающая Г внутри себя, со¬
держит две граничные точки А н В фигуры F, не являющиеся диамет¬
рально противоположными точками Окр и большая полуокружности
kjAB окружности Окр не содержит более никакие граничных точек F,
то также существует м е н ь ш а я, чем Окр окружность, заключающая F
внутри себя. Для того, чтобы убедиться в этом, достаточно переместить
Окр в направлении OS, где S — средина хорды А В, так, чтобы точки А
и В оказались внутри окружности, a F не вышла за ее пределы (рис.45, б).
При этом мы снова приходим к равной Окр окружности Окр,, заключаю¬
щей F внутри себя и не содержащей ни одной точки F; эту окружность
мы можем уменьшить так, чтобы F все еще заключалась внутри умень¬
шенной окружности.
Итак, если Окр есть наименьшая из всех заключающих F
окружностей, то Окр либо содержит две граничные точки А и В фигуры F,
являющиеся диаметрально противоположными точками Окр (рис. 46, а),
либо содержит три граничные точки А, В и С фигуры, такие, что они
разбивают Окр на три дуги, меньшие, чем полуокружность (эти три точ¬
ки являются вершинами остроугольного треугольника ABC,
рис. 46, б).
Как видно из рисунка 46, а,	_
1	13
2г = АВ < I, следовательно, г , т. е, г < —5— i
Z	о
75

где г — радиус окружности Окр.
Далее в остроугольном треугольнике ABC (рис. 46, б) хотя бы один
из углов будет больше или равен 60° (ибо сумма всех трех его углов равна
180° = 3 ■ 60°); пусть, например, ^ С > 60°. Тогда, применяя к тре¬
угольнику ABC теорему синусов и принимая во внимание, что АВ ^ 1,
получаем
В теории выпуклых тел широко используются преобразования,
переводящие выпуклые фигуры в новые фигуры, являющиеся более
симметричными, чем исходные — такие преобразования выпуклых фи¬
гур называются симметризациями. Относительная трудность
задач, связанных с выпуклыми фигурами, по сравнению, скажем, с зада¬
чами школьного курса геометрии, объясняется в первую очередь тем,
что в теории выпуклых фигур изучаются фигуры довольно общего вида,
так что здесь нет возможности использовать какие-либо индивидуальные
особенности формы этих фигур. Именно поэтому чрезвычайно ценной
является всякая возможность замены изучаемой фигуры новой фигурой,
более симметричной, чем первая (здесь мы пока не уточняем смысл тер¬
мина более симметричная фигура, который можно по¬
нимать по-разному). В связи с этим в теории выпуклых фигур значитель¬
ное место занимает метод симметризаций, смысл которого
как раз и заключается в подобной замене.
Существует целый ряд различных способов симметризации выпук¬
лых фигур и тел. В теории плоских выпуклых фигур, в частности,
основную роль играют два типа симметризации: симметризация отно¬
сительно прямой (или симметризация Штейнера), переводящая вся¬
кую фигуру в фигуру, имеющую ось симметрии, и симметриза¬
ция относительно точки (или симметризация Минковскоео), переводя¬
щая каждую фигуру в фигуру, имеющую центр симметрии.
Симметризация относительно прямой I заключается в том, что все пер¬
пендикулярные к I хорды фигуры F перемещаются вдоль содержащих эти
хорды прямых в такое новое положение, что I делит новую хорду по¬
полам, т. е. является осью симметрии этой хорды; образованная таким
образом фигура F', для которой, очевидно, прямая I является осью сим¬
метрии (рис. 47) и называется образом/7 при симметризации относи¬
тельно I.
П р и м е ч а н и е. Рекомендуем читателю самостоятельно доказать
следующие свойства симметризации Штейнера;
sin С sin 60° ““ /з/а =
Vs
2
что и требовалось доказать.
II.	О симметризации Минковского
76

1°. Если F — выпуклая, то F' — тоже выпуклая.
2е. Площадь F' равна площади F.
3°. Периметр / ' не больше периметра F.
Из этих свойств, в частности, можно вывести знаменитую и з о -
периметрическую теорему, утверждающую, что из всех
плоских выпуклых фигур фикси-	i	L
рованной площади наименьший
периметр имеет круг, который
обладает осями симметрии всех
возможных направлений и по¬
этому не может быть «улучшен»
симметризацией ни относительно
какой прямой (см.: Д. А. Кры-
жановский. Изопериметры,
М., Физматгиз, 1959, § 14).
Аналогично симметризацию
относительно точки О можно бы¬
ло бы определить так: все проходящие через точку О хорды фигуры F пе¬
ремещаются вдоль содержащих эти хорды прямых в такое новое положе¬
ние, что Оделит новую хорду пополам (рис. 48). Однако, такое преобра¬
зование может перевести выпуклую фигуру F в невыпуклую фн-
гуру А; поэтому это определение приходится заменять другим.
В определении симметризации Минковского выпуклая фигура F
рассматривается как образованная при пересечении бесконечного числа
полос, ограниченных всевозможными нарами
параллельных опорных прямых фигуры. Затем
все эти полосы перемещаются в перпендикуляр¬
ном им направлении в новое положение, при ко¬
тором точка О оказывается принадлежащей сред¬
ней линии полосы (т. е. является центром симмет¬
рии новой полосы). Образованная таким образом
фигура F*, для	которой, очевидно, точка О яв¬
ляется центром	симметрии (рис. 49, а, б) и на¬
зывается образом фигуры F при симметри¬
зации относительно точки О.
Рис. 48	Можно	доказать	следующие	свойства	симмет¬
ризации Минковского, переводящей выпуклую
фигуру F в новую фигуру F*:
1 .	Для	любой	выпуклой фигуры F	фигура F* тоже будет выпуклой.
2°.	Диаметр	и	ширина фигуры F*	равны диаметру и ширине фи¬
гуры F.
3°. Периметр фигуры F* равен периметру фигуры F.
4е. Площадь фигуры F* не меньше площади фигуры F.
Эти свойства используются для доказательства ряда связанных с выпук¬
лыми фигурами теорем.
77

Примечание. Так, например, из свойств 2° и 4" симметриза¬
ции Минковского следует, что каждую выпуклую фигуру F диаметра D
можно заменить центрально симметричной фигурой F* т о г о же диа¬
метра ине меньшей площади, откуда вытекает, что из всех фигур
диаметра D наибольшую площадь может иметь лишь центрально сим¬
метричная фигура. А так как каждая фигура диаметра D с центром сим-
а	б
Рис. 49
четрнн О шключается, очевидно, внутри круга с центром О и радиусом
то отсюда имеем, что из всех (выпуклых) фигур фиксированного диа¬
метра наибольшую площадь имеет круг.
Нам, однако, нужно здесь лишь свойство 1 симметризации Минков¬
ского, которое мы и докажем, заменив предварительно данное выше
определение симметризации относительно точки другим, более удобным.
Пусть F — произвольная плоская выпуклая фигура, F' — фигура,
симметрична я F относительно некоторой точки О, a F* фигура,
образованная срединами А3 всевозможных отрезков А А', где A f-
а А' £ F' (рис. 50). Полученную таким образом фигуру Г* можно также
описать следующим образом: если принять точку О за начало отсчета
ра дчус< в векторов, сопоставляя каждой точке N плоскости ее радиус-
вектор гN = ON, то F* есть множество всех таких точек А*, что
г А, =— (гА + гА.), 1де А А' £ F'	(7)
78

или
г ,» = -i- (г , - г 4|) у А, А. где А, /1, Р F
ибо на рис. 50 гд^ = —где А’£ F', AX^F, ОА* = уЛгЛ.
Фигуру F* и будем называть образом фигуры F при симметри¬
зации относительно точки О. Предлагаем читателю установить, что та¬
кое определение симметризации Минковского равносильно данному вы¬
ше А теперь докажем, что полученная фигура Г'
1) центрально симметрична;
2) вытук гая.
]) Гак как центратьпая симметрия игноентелыю О (поворот BOKpyi
О на 15а I лишь MciiHci местами фнг\ры Г и F', то ли преобразование
переводит множ1 'тво /•' срепы нее\ отргтков, соединяющих точки / с
■ очками Г', само в себя: таким обрн i ль точка О является центром
С II М М С Т р И И ф|| \ р,,| /■'
2) П\сп> 1 и В'	те	и; он (вольные тчкн фигуры F . Нам надо
пока а ь, чю i /;/,> як	'	В	. ипыо причин ‘ -чти I По определс
11 сто фиг>ры I точки /' и В яр..1якч1 я среди, амп некоторых отрезков
Л 1' и ВВ . 1.1 А. В ■	I	и Г, В	I По так как фигуры F и F' вы-
ьук.ше, то к а ж тая	точка	’!	(предка 1В i рнга.межиг Г, а к а ж
да я гт чка ЛГ ттрыка А'В' при. адлежщ F' Но-ному F' принадлежит
определяемая равенствам
1
Г,И* ^~^Г.МЛ r\l)
средина М- к а ж ч о г о из отрешов Л1ЛГ.
79

Заметим теперь, что
ГМ = ГА + АМ и rМ’ ~ r/1' "Ь ^ 'АЛ',
где
AM I АВ, А'М' = /' • А'В'\ 0<I,
Отложим от точки А* векторы
А*В1 = ~ АВ, Л*В2=-^-А'В', А*М1 = -^-АМ,
А*М2 = — А’М’,
2
тогда
гм* =	+	г	и-)	=	I*	(гЛ'	+	')] =
= 4*(Гл'!'г'>'н'ТАЛ : 4"а,л,’ = Гд* Л*Л| + Л*Л1,=
А*М*,
где А*М* диагональ параллели! рамма А*М, М*Мг. построенного
на векторах А*МХ и А М2.
Когда I и /' пробегают все значения между нулем и единицей, то вер¬
шины М* параллелограммов А* МгМ* Мг «заметают» параллелограмм
А*В1В~А2, построенный на векторах Л' В, и А*Вг. Вершиной этого па¬
раллелограмма является точка В*, так как при I V =1 точки М и
М’ совпадают с точками В и В', а следогательно, точка Д1Е совпадает
сточкой В*. Таким образом, параллелограмм A*BiB1rВ., полностью при¬
надлежит фигуре В6, поскольку F" принадлежит каждая его точка
М*. В частности, F5 принадлежит п от ре ши /ГВ!‘ диагональ рас¬
сматриваемого параллелограмма,— что и доказывает выпуклость
F*
Покажем теперь, чго пли фигура F' получается ил фигуры F сим мет¬
ризацией Минковского, то
k(F*)-.-k{F)	(8)
(см. лемму на стр. 38). Рассмотрим две фигуры Fa и Fb, получаемые
из фигуры F параллельными переносами на векторы а и В, а также фи¬
гуры F а и F ь, получаемые таким же образом из фигуры F* (рис. 51).
Докажем, что если фигуры Г а и Fb соприкасаются (имеют общие гра¬
ничные точки) или пересекаются (имеют общие внутренние точки), то и
фигуры Fа и / (| соответственно соприкасаются или пересекаются и об-
80

ратпо, если фигуры F* и f'b соприкасаются (пересекаются), то и фигуры
Fа и Гь соприкасаются (пересекаются).
Действительно, если фигуры Fa и Гьимеют общую точку С, получа¬
емую переносом на вектор а из точки Ct фигуры F и переносом на вектор
b из точки С2 той же фигуры, то (за начало отсчета радиусов-векторов
точек мы по-прежнему принимаем точку О)
''с,-: «-= rCt + ь = гс,
т. е.
= *>-«•
Заметим теперь, что по формуле (7) точки С' и С", где
1	I
rc -g-l'c.-'c.) и ГС'’ ^гс>~гс)
принадлежат фигуре F* (эти точки симметричны друг другу относитель¬
но центра О фигуры F*). А так как
I	1
гс- - г с- = — (rCi - rcJ - — (rCa - rCt) = rCt -rCa = b-a,
то
rc. + a = ra, + b.
81

Обозначим точку плоскости г ралнлсом вектором гс. а, а также
/-£.< + Ь через С*. Ясно, что эта точка принадлежит фигуре F*a, так как
она получается параллельным переносом на вектор а из точки С' фигуры
F*,— и в то же время принадлежит фигуре Fb, ибо она получается пе¬
реносом на вектор Ь из точки С" фигуры F*. Отсюда следует, что фигуры
!*а и F'b имеют общую точку С". Белее того, если все точки, достаточно
близкие к точке С, являются общими для фигур 1и и />, т. е. если эти
фигуры пересекаются, то все точки, блн жне к точке С', являют¬
ся общими для фигур F и Fь, т. с эти фигуры тоже пересека¬
ются.
Обратно, предположим, что фигуры f 'n и I ь имеют общую точку С*,
г. е. что
гс,	гл,	-i я	гв,	; Ь,
где
1 1
га* = ~2-1га~га^ гв- --£&в-гву,
точки A, Alt В, Bt £ F и, следовательно Л*. В* £ F* (рис. 52). Тогда
имеем
1 1
-у(''л-'Ч) + «=-^-(гв-гв1Н Ь,
82

2	-	.	■	о,-	.	2
Но, очевидно,
1 1
— с А + ГВ.) = rs> -£-(гв+гА1)=гт,
где S и Т — средины отрезков АВг и ВАЪ принадлежащие выпуклой"
фигуре F. Следовательно,
rs + o = гг-Ь Ь,
т. е. точка U фигуры Fai получаемая из точки S фигуры Г переносом на
вектор а, совпадает с точкой фигуры Fb, получаемой из точки Т фигуры F
переносом на вектор Ь. Таким образом, фигуры Fa н Fb имеют общую
точку U; при этом, в точности как и выше, легко установить, что если
С* — внутренняя точка фигур Fa и Fb, то V — внутрен¬
няя точка фигур Fa и Fb.
Теперь мы можем уже непосредственно доказать справедливость
формулы (8). Предположим, что характеристика k (F) фигуры F равна
некоторому числу k, т. е., что можно найти k непересекающихся фигур
Flt f2, .... Fit, получаемых из фигуры F параллельными переносами но
векторы аг, а2, .. ., а* таких, что ни одна из них не пересекает фигуры F,
но все они соприкасаются cF и что нельзя найти более k фигур, обладаю¬
щих этими свойствами. Пусть F* — центрально симметричная фигура,
получаемая из F симметризацией Минковского; тогда:
1) центрально симметричные фигуры F\, F2, ..., F*k, получаемые из
фигуры F* параллельными переносами на векторы aif «2,	а*,,	также
не пересекаются между собой, не пересекают фигуры F*, но имеют с F*
общие граничные точки;
2) если бы к F* можно было бы «приложить» k \- I непересекающихся
фигур F\, f2* получаемых из F* параллельными переносами на век¬
торы Ь1г Ь2, bk+ ], то к F можно было бы приложить к + 1 непере¬
секающихся равных F и параллельно F расположенных фигур Fu
F2, ...,	полученных	из F параллельными переносами на векторы
bi, ft2, ...,	—что, однако, противоречит сделанному предположению.
Таким образом,
k(F*)=k(F) (*■= k),
что и завершает доказательство леммы.

ЛИТЕРАТУРА
1. В. Г. Болтянский, И. Ц. Гохберг. Разбиение фигур
на меньшие части. М., «Наука», 1971.
2. В. Г. Б олтянский И. М. Яглом. Выпуклые фигуры и тела.
ЭЭМ, кн. V (геометрия). М., «Наука», 1966, с. 181—269.
3. В. Г. Б о л т я н с к и й, И. М. Яглом. Геометрические задачи
на максимум и минимум, ЭЭМ, кн. V, с. 270—348.
4. Н. Б. Васильев, С. А. Молчанов, А. Л. Розенталь,
А. П. Сави н. Математические соревнования (геометрия). М.,
«Наука», 1974.
5. Л. Д а н ц е р, Б. Г р ю н б а у м, В. К л и. Теорема Хелли.
М., «Мир», 1969.
6. Л. А. Л ю с т е р н и к. Выпуклые фигуры и многогранники. М.,
Гостехиздат, 1956.
7. К. А. Роджерс. Укладки и покрытия. М., «Мир», 1968.
8. Л. Ф е й е ш Тот. Расположения на плоскости, на сфере и в
пространстве. М., Физматгиз, 1958.
9. Г. Хадвигер, Г. Дебруннер. Комбинаторная геомет¬
рия плоскости. М., «Наука», 1965.
Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в, И. М. Яглом.
: Геометрические неравенства и задачи на максимум и минимум. М.,
«Наука», 1970.
11. Д. О. Ш к л я р с к и й, Н. Н. Ченцов, И. М. Яглом. Гео¬
метрические оценки и задачи из комбинаторной геометрии. М.,
«Наука», 1974.
32. Д. О. III к л я р с к и й, Н. Н. Ченцов, И. М. Яглом Избран¬
ные задачи и теоремы планиметрии. М., «Наука», 1967.
13. И. М. Яглом. О комбинаторной геометрии. М., «Знание», 1971.
14. И. М. Яглом. Элементарная геометрия прежде и теперь М.,
«Знание», 1972.
1-5. И. М. Яглом, В. Г. Болтянский Выпуклые фи| уры.
М.— Л., Гостехиздат, 1951.

ОГЛАВЛЕНИЕ
Предисловие	3
Глава I- Задачи о кругах и шарах
§ 1. Задача Ньютона — Грегори	5
§ 2. Задача о четырнадцати шарах .	.	.12
§ 3. Задача о шарах в n-мерном пространстве 19
§ 4. Дальнейшие обобщения и видоизменения ос¬
новной задачи ...	 28
Глава II. Задачи о многоугольниках, многогран¬
никах и произвольных фигурах
§ 5. Теорема Хадвигера ......	32
§ 6. Доказательство теоремы Хадвигера	.	37
§ 7. Задачи о прикладывании квадратов и тре¬
угольников 	44
§ 8. Обобщения и варианты	52
Приложение
I. Несколько	теорем	из	элементарной геометрии 68
II.	О симметризации	Минковского	76
Литература	84
Яглом Исаак Моисеевич
Проблема тринадцати шаров
Пособие для учащихся физико-математических школ
Издательское объединение «Вища школа»
Головное издательство
Редактор Г. Ф. Трофимчук. Обложка художника Е. В. П о-
лова. Художественный редактор И. Р. О й х м а н. Техничес¬
кий редактор А. Д. Новик. Корректор Н. В. Косачева.
Сдано в набор 14.11. 1974 г. Подписано к печати 25.07. 1975 г.
Формат бумаги 70Х1087з2. Бумага книжио-журнальиая. Физ.-печ.
л. 2,625. Условн. печ. л. 3,67. Уч.-изд. л. 3,53. Тираж 40 000.
Изд. № 1605. БФ 08139. Цена 12 коп. Зак. № 1406.
Головное издательство издательского объединения сВища школа»
252054, Киев. 54. Гоголевская, 7.
Отпечатано с матриц Головного предприятия республиканского
производственного объединения «Полиграфкиига» Госкомиздата
УССР, г. Киев, ул. Довженко, 3, в Киевской типографии JVe 1,
ул. Волошская, 55.