CM.I ’.КОЛЬСКИЙ
M. К. 1.(ЛАЛОВ
Н.Н. РЕШЕ! Л И КОВ
А. В. ШЕВКИН
АРИФМЕТИКА
L—L___
С. М. НИКОЛЬСКИЙ
м. К. ПОТАПОВ
Н. И РЕШЕТНИКОВ
А. В. ШЕВКИН
АРИФМЕТИКА
МОСКВА «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 8
1
ББК 22.130
Н64
УДК 511.1(075.4)
Никольский С. М., Потапов М. К., Решетни-
ков Н. Н.» Шевкин А« В» Арифметика. Пособие для самообра-
зования.— М.2 Наука. Гл. ред. физ,-мат. лит,, 1988.—384 с.
ISBN 5-02-013764-2
Школьный арифметический материал излагается в книге систе-
матически, поэтому последовательность изложения отличается от при-
нятой в известных учебниках по математике для 5—6 классов.
Приведены основные упражнения и задачи.
Для преподавателей математики и самообразования. Доступна
школьникам 5—6 классов.
Ил. 115. Табл. 12.
Рецензенты
доктор физико-математических наук В, А. Скворцов
доктор физико-математических наук профессор А. Б» Шидловский
„ 1702030000—087
Н...053(02)-88~~ 8°-88
ISBN 5-02-013764-2
2
© Издательство «Наука».
Главная редакция
физико-математической
литературы, 1988
ОГЛАВЛЕНИЕ
Введение . ....... . . ; . . ;........................г	♦	1
Глава I. Натуральные числа и нуль...................  •	11
§	1.	Натуральный ряд ...................................................................... 11
§ 2.	Строение натурального числа в десятичной системе
счисления...........................................  12
§	3.	Сравнение натуральных чисел ............................... 15
§	4.	Законы сложения . 18
§	5.	Вычитание............................................................................. 21
|	‘6	.	Умножение. Законы умножения........................................................  23
§	7.	Распределительный закон............................................................... 27
§	8.	Сложение и вычитание чисел столбиком ......	30
§ 9.	Вычисление произведений целых неотрицательных
чисел ................................... .........	33
§ 10.	Степень с натуральным показателем .................................................... 36
§ 11.	Деление.........(	•	38
§ 12.	Свойства делимости ........•	40
§ 13.	Признаки делимости...................................................................  42
§ 14.	Деление с остатком ...... . , . . • • . . . .	47
§ 15.	Числовые выражения...................................................................  50
§ 16.	Вычисления с помощью микрокалькулятора ....	53
§ 17.	Представление натуральных чисел на координатной
полуоси.............................................. 57
§ 18.	Исторические сведения................................................................. 59
Вопросы для повторения по материалу главы I ...... .	62
Глава II. Метрическая система мер .............................................................. 65
§ 19.	Измерение отрезков........................  .	65
§ 20.	Величины. Исторические сведения......................................................  67
§ 21.	Метр.................................................................................. 68
§ 22.	Метрические единицы длины.................  .	70
§ 23.	Прямоугольник  ......................................................................  72
3
§ 24.	Единицы площади ................	75
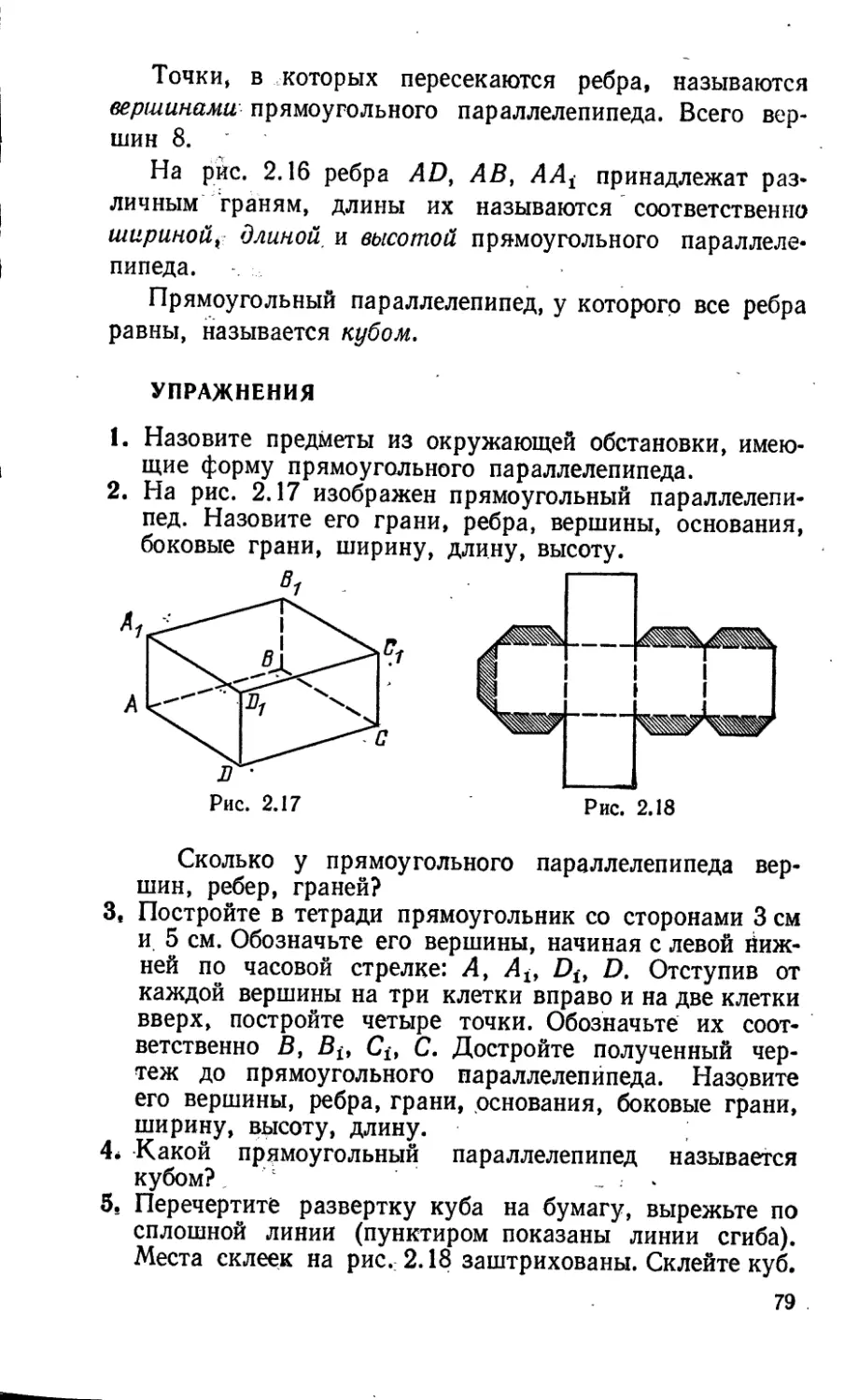
§ 25.	Прямоугольный параллелепипед . ...... 78
§ 26.	Единицы объема....................... 80
§ 27.	Единицы массы .....................   82
.• § 28. Единицы времени...................... 83
Вопросы для повторения по материалу главы II	•	86
Глава III. Целые числа	89
§ 29.	Отрицательные целые числа......................... 89
§ 30.	Правила знаков. Модуль-числа...................... 91
§ 31.	Сравнение целых чисел............................. 93
§ 32.	Сложение целых чисел ............................. 94
§ 33.	Законы сложения целых чисел....................... 97
§ 34.	Разность целых чисел.......................... 99
§ 35.	Произведение и частное целых чисел. ............. 101
§ 36.	Распределительный закон.......................... 104
§ 37.	Раскрытие скобок и заключение	в скобки........	107
§ 38.	Действия с суммами нескольких	слагаемых.......	110
§ 39.	Представление целых чисел на координатной оси . .	111
§ 40.	Исторические сведения............................ 113
Вопросы для повторения по материалу главы III	115
Глава IV. Обыкновенные дроби............................  116
§ 41.	Простые и составные числа...................... 116
§ 42.	Делители натурального числа.................... 118
§ 43.	Наибольший общий делитель...................... 123
§ 44.	Наименьшее общее кратное....................... 125
§ 45.	Понятие дроби.................................. 128
§ 46.	Равенство дробей............................... 133
§ 47.	Приведение дробей к общему знаменателю .....	139
§ 48.	Сравнение дробей............................... 143
§ 49.	Сложение дробей ............................... 149
§ 50.	Законы сложения ............................... 154
§ 51.	Вычитание дробей............................... 158
§ 52.	Смешанные дроби................................ 162
§ 53.	Сложение и вычитание смешанных дробей ♦ . . . .	166
§ 54.	Умножение дробей............................... 169
§ 55.	Деление дробей................................. 174
§ 56.	Законы умножения............................... 178
§ 57.	Решение задач.................................. 183
§ 58.	Площадь прямоугольника. Объем прямоугольного па-
раллелепипеда ................................ .....	188
§ 59.	Единицы измерения скорости	192
4
§ 60.	Представление положительных дробей на координат-
ной оси ..................................... .......	195
§ 61.	Исторические сведения........................... 199
Вопросы для повторения по материалу главы IV.............  202
Глава V. Рациональные числа . ............................ 203
§ 62.	Отрицательные дроби. ........................... 203
§ 63.	Рациональные числа..................... . .	206
§ 64.	Сравнение дробей ..............................  211
§ 65.	Сложение и вычитание дробей..................... 213
§ 66.	Произведение и частное дробей................... 216
§ 67.	Переместительный и сочетательный законы сложения.
Распределительный закон............................... 221
§ 68.	Переместительный и сочетательный законы умноже-
ния .................................................. 225
§ 69.	Представление рациональных чисел на координатной
оси ... .............................................. 230
Вопросы для повторения по материалу главы V .............. 234
Глава VI. Пропорции* . .................................   238
§ 70.	Буквенные выражения............................. 238
§ 71.	Подобные слагаемые.............................. 244
§ 72.	Уравнения.................................... . .	248
§ 73.	Решение задач с помощью уравнений............... 251
§ 74.	Отношение и пропорция........................... 256
§ 75.	Прямая и обратная пропорциональность.............	262
§ 76.	Масштаб......................................... 268
Вопросы для повторения по материалу главы VI.........., .	273
Глава VII. Десятичные дробя .............................	275
§ 77.	Понятие десятичной дроби.......................  275
§ 78.	Сравнение положительных десятичных дробей . . .	280
§ 79.	Перенос запятой в десятичной дроби...........	284
§ 80.	Сложение и вычитание положительных десятичных
дробей................................................ 287
§ 81.	Умножение десятичных	дробей..................... 293
§ 82.	Деление	десятичных	дробей......................  298
§ 83.	Понятие	о проценте............................   304
§ 84.	Решение задачи на проценты..................  .	309
§ 85.	Десятичные дроби произвольного знака .......	313
§ 86.	Исторические сведения.......................  .	316
Вопросы для повторения по материалу главы VII ............ 319
5
Глава VIII. Обыкновенные и десятичные дроби........... 320
§ 87.	Разложение обыкновенной дроби в конечную десятич-
ную дробь *.......................................	320
§ 88.	Понятие периодической десятичной дроби ......	324
§ 89*	Периодичность десятичного разложения обыкновенной
дроби ............................................ 328
§ 90.	Непериодические десятичные бесконечные дроби* Ир-
рациональные числа................................ 332
§ 91.	Сравнение действительных чисел. Приближение числа 337
§ 92.	Вычисления с помощью микрокалькулятора .... 345
§ 93.	Округление при умножении и делении чисел ....	349
§ 94.	Основные свойства действительных чисел ...... 352
Глава IX. Система координат........................... 356
§ 95.	Длина отрезка ............................   356
§ 96.	Координатная ось............................ 360
§ 97.	Декартова система координат на плоскости .....	365
§ 98.	Графики..................................    372
§ 99.	Исторические сведения ...............	377
Приложение..........................................   383
6
ВВЕДЕНИЕ
Данная книга представляет собой попытку системати-
чески изложить арифметику в пределах программы V и
VI классов. Таким образом, предполагается, что наш
читатель знает математику в пределах начальной школы:
умеет производить арифметические действия с натураль-
ными числами и даже имеет некоторое представление о
дробях.
Дроби изучаются практически с самого начала, но
тот факт, что школьник имеет некоторое представление
о дробях, освобождает нас от необходимости вводить мно-
го примеров, приводящих к понятию дроби. Мы имеем в
виду такие важнейшие «физические» примеры, как, на-
пример: 1) три яблока разделить между пятью мальчи-
ками; 2) убедиться в том, что две третьих части торта и
и четыре шестых _его части—это физически одно и то же.
Первая задача приводит не только к понятию дроби
3
у, но и к тому, что ее надо рассматривать как частное
3:5. Вторая задача приводит к естественности формаль-
2	4
ного равенства -д- = у.
Перед авторами стояла задача все эти вещи формали-
зовать, изложить компактно и доступно, но так, чтобы
было видно, где в них логическое начало и где конец,
где здесь «физика» и где логика. Логику тоже нельзя
замазывать— она как раз дает основу для умения правиль-
но вычислять.
Арифметика—логическая наука, на ней можно учить-
ся логически мыслить—конечно, если излагать ее не
«вверх ногами», как это иногда случается. Счастливым
образом формализм арифметики имеет прикладное значе-
ние, потому что он дает правила вычислений. Но при-
7
кладной части тоже надо уделять внимание. Умножить
у на у— это значит вычислить дробь уу; это надо твер-
до знать. Но также необходимо знать, что при этом мы
решили и физическую задачу—взяли две третьих части
от пяти седьмых (например, яблока) или вычислили пло-
2	5
щадь прямоугольника со сторонами у и у.
Мы старались систематически изложить обе стороны
указанных явлений—формальную и прикладную—их объ-
единить и в некоторых случаях разъединить, потому что
формализм арифметики необходим для практики вычисле-
ний. Конечно, должна быть еще и общая идея. Такой идеей
яляется формирование понятия числа как длины отрезка,
а еще точнее—как координаты произвольной точки пря-
мой. В этом втором смысле понятие «число» объединяет
в себе положительные и отрицательные числа.
Наконец, большую роль в этих вопросах играет и пе-
дагогика—надо изложить вопрос доходчиво и компактно.
Мы очень часто слышим, что школьники доходят до стар-
ших классов и не знают арифметики. В старших классах
это положение исправляют тем, что заставляют отстающих
выполнять упражнения на повторение арифметики. Но
это плохой выход. Прежде всего надо подумать об улуч-
шении преподавания арифметики в то время, когда она
изучается. Это возможно, если арифметику проходить в ло-
гическом порядке или, как мы говорим, систематически.
Опыт такого систематического изложения мы предлагаем
в этой книге. Избран следующий порядок изложения:
I.	Натуральные числа и нуль.
II.	Метрическая система мер.
III.	Целые числа.
IV.	Обыкновенные дроби.
V.	Рациональные числа.
VI.	Пропорции.
VII.	Десятичные дроби.
VIII.	Обыкновенные и десятичные дроби.
IX.	Система координат.
8
От натуральных чисел мы переходим к целым. Наб-
людения показывают, что на главе «Натуральные числа»
не надо долго задерживаться, потому что школьники и
даже учителя считают, что все это уже проходилось в
младших классах, и неохотно работают с этим материалом.
Но на самом деле натренированность учеников в вычисле-
ниях с натуральными числами в это время еще недостаточна.
Мы вводим целые числа так рано потому, что идею
отрицательного числа легче всего усвоить на целых числах,
которые могут при этом служить новым интересным мате-
риалом для продолжения отработки навыков работы с на-
туральными числами. Получается экономия времени и сил.
В следующей главе («Обыкновенные дроби») отрица-
тельные числа не нужны, но в упражнениях для повто-
рения они рассматриваются. Свойства чисел любого знака
(глава «Рациональные числа») сводятся к соответствую-
щим свойствам целых чисел.
При желании главы III и IV можно переставить.
Впрочем, в этом случае выражения типа 1.—2 + 3 при-
дется разъяснять после дробей—мы считаем это по край-
ней мере странным.
Десятичные дроби стоят у нас после обыкновенных
дробей. Мы прямо скажем, что не можем согласиться с
порядком изложения этих вопросов, предлагаемом в «Те-
матическом планировании» программы по математике для
средней школы. По этому плану десятичным дробям пред-
шествует малосущественный кусочек из обыкновенных
дробей. Из него можно почерпнуть только понятие обык-
новенной дроби, а также сравнение, сложение и вычи-
тание дробей с одинаковыми знаменателями. Основное
свойство дроби, неизменность ее при сокращении (см.
пример с тортом), предлагается рассматривать только
через год. Но приведенных фактов о дробях недостаточно
даже, чтобы обосновать, например, что 0,5 = 0,50.
Нельзя также согласиться с методом введения дробей
любого знака (рациональных чисел), культивируемым в
наших учебниках при полной поддержке методистов. Есть
более простой способ—перспективный как с научной, так
9
и о педагогической точки зрения. Идея отрицательного
числа вводится на целых числах, в дробном же случае
она сводится к целым числам.^ йо естественно. Непонятно
почему этот путь не используется. Наши читатели-учите-
ля могут проверить этот вопрос на деле.
Мы употребляем ‘буквы, но очень осторожно—только
в той мере, когда кажется, что буква легче поясняет
вопрос, чем пример с числом. В большей части рассуж-
дений доказательства ведутся на характерных числовых
примерах. Все же примеров,’ когда выгодно использова-
ние буквенных выражений, достаточно много, и, таким
образом, книга вносит определенный алгебраический эле-
мент в образование читателя.
Отметим, что вопросы, излагаемые в главах VIII и
IX этой книги, предусмотрены школьной программой 7-го
и следующих классов. Мы думаем, что при соответствую-
щем элементарном изложений место этих вопросов долж-
но находится на стыке 6-го и 7-го классов. Это даст ис-
пинную опору при изучении алгебры и геометрии. Кроме
того, систематическое изложение арифметики предпола-
гает определенную завершенность курса.
Мы выражаем благодарность учителю средней школы
№ 75 пос. Черноголовка Московской области Е. А. Ве-
денеевой, обучавшей школьников по этой книге.
Высказанные выше идеи на практике проверены также
одним из авторов книги А. В. Шевкиным при работе в
школе № 679 г. Москвы.
Мы благодарны методической комиссии Математичес-
кого Института АН СССР, которая положительно оценила
материалы рукописи нашей книги, а также В. А. Сквор-
цову и А. Б. Шидловскому за полезные советы.
Отметим, что данная книга может быть полезна тому,
кто желает привести в порядок свои знания по арифме-
тике, в частности при подготовке к вступительным экза-
менам в техникумы и высшие учебные заведения.
Ю
Глава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
§ 1. Натуральный ряд
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ... назы-
ваются натуральными или целыми положительными чис-
лами.
Мы записали натуральные числа в порядке их воз-
растания. В таком виде они образуют натуральный ряд
или ряд натуральных чисел.
Число 0 не считается натуральным.
Для записи натуральных чисел пользуются десятич-
ной системой счисления, в основе которой лежат знаки
0,	1,	2 3,	4,	5,	6,	7,	8,	9,
называемые цифрами.
Натуральные числа записываются при помощи цифр.
Например, число 37 записано цифрами 3 и 7, число 108 —
цифрами 1, 0 и 8, а число 5—цифрой 5.
На первом месте в натуральном ряду стоит число 1,
за ним следует 2, далее 3 и так до 9; после 9, согласно
правилам десятичного счисления, следует 10, а за 10 сле-
дует 11 и так далее.
В натуральном ряду нет последнего числа—за каж-
дым натуральным числом следует еще одно натуральное
число, за которым следует другое натуральное число и
так далее. Все натуральные числа записать невозможно.
Поэтому при записи натурального ряда выписывают не-
сколько первых натуральных чисел, после которых ставят
многоточие.
11
Важную роль в десятичной системе счисления играет
число 10. Десять единиц называются десятком, десять
десятков—сотней, десять сотен—тысячей и так далее.
Эти названия используются при чтении натуральных чи-
сел в десятичной системе счисления:
1—единица
10—десять
100—сто
1 000—тысяча
10000—десять тысяч
100000—сто тысяч
1000 000—миллион
10 000 000—десять миллионов
100000000—сто миллионов
1000 000 000—миллиард
10000000000—десять миллиардов
100000000000—сто миллиардов
УПРАЖНЕНИЯ
I.	Назовите первые десять натуральных чисел.
2.	Сколько различных цифр используется для записи на-
туральных чисел в десятичной системе счисления?
3.	Является ли число 0 натуральным числом?
4.	Прочитайте следующие числа:
100,	10000, 1000000, 10, 10000000, 100000, 1000.
5.	Как называется запись натуральных чисел, располо-
женных в порядке возрастания (начиная с 1)?
8. Запишите следующие числа:
сто тысяч, миллион, сто, десять миллионов, десять ты-
сяч, миллиард, тысяча, десять миллиардов, десять, сто
миллиардов, сто миллионов.
§ 2. Строение натурального числа
в десятичной системе счисления
В десятичной системе счисления один и тот же знак
(цифра) имеет различные значения в зависимости оттого
места (позиции), где он расположен.
12
В связи с этим для записи любых натуральных чисел
необходимо только десять цифр для обозначения нуля и
первых девяти натуральных чисел.
Если натуральное число записано одной цифрой, то
оно называется однозначным, двумя цифрами—двузначным,
тремя цифрами—трехзначным и так далее. Например,
1,	7, 9—однозначные числа,
11, 27, 99—двузначные числа,
320, 589	—трехзначные числа,
56321	—пятизначное число.
Нуль считается однозначным числом.
Первая цифра справа в десятичной записи натураль-
ного числа называется цифрой первого разряда или разряда
единиц, вторая цифра справа—цифрой второго разряда
или разряда десятков, третья—цифрой третьего разряда
или разряда сотен.
Как определяются натуральные числа по их записи,
видно из следующих примеров:
Число 99 состоит из 9 десятков и 9 единиц:
99 = 9 десятков-ф 9 единиц.
Это можно записать так:
99 = 9.104-9-1.
Число 3 278 состоит из 3 тысяч, 2 сотен, 7 десятков,
8 единиц: 3 278 = 3 тысячи 4- 2 сотни 4- 7 десятков + 8 еди-
ниц или
3 278 = 3 • 1000 4-2-100 4-7-10-4-8-1.
Вот еще примеры:
5 031=5 тысяч 4-0 сотен 4-3 десятка+1 единица =
= 5 тысяч 4- 3 десятка 4-1 единица
или
5031 =5-10004-0-1004-3-10+1-1 = 5-1000 4-3-10-}-1-1.
20012=2 десятка тысяч 4-1 десяток 4-2 единицы =
= 2-100004-1-104-2.1.
13
УПРАЖНЕНИЯ
1.	Приведите примеры:
1)	двузначного числа; 2) трехзначного числа;
3)	пятизначного числа; 4) семизначного числа.
2.	В следующих числах укажите цифры разрядов еди-
ниц, десятков, сотен, тысяч, десятков тысяч и так
далее:
1)123;	2)102;	3) 4 387;
4) 12530; 5) 13 287 905; 6) 2000000006.
3.	Является ли нуль однозначным числом?
4.	Запишите число, состоящее из
1)	одной тысячи, двух сотен, трех десятков и пяти
единиц;
2)	пяти десятков тысяч, девяти тысяч, семи сотен и
четырех единиц;
3)	восьми сотен, пяти десятков;
4)	шести сотен тысяч и трех десятков.
5.	Прочитайте следующие числа, запишите их в виде
суммы разрядных слагаемых. Например, 325 == 300 +
+ 20 + 5.
1)	12 638; 2) 138536; 3) 3 174 643.
6.	Прочитайте следующие числа, запишите их в виде
суммы произведений цифр разрядов на один, десять,
сто и так далее. Например, 325 = 3-100 + 2-10 + 5-1.
1) 725; 2) 53 306; 3) 803 120.
7,	Запишите числа:
1)	восемьсот двадцать три тысячи триста семьдесят
четыре;
2)	семнадцать миллионов четыреста восемьдесят три
тысячи пятьсот семь;	v
3)	двести восемь тысяч пять;
4)	тридцать две тысячи десять;
5)	семьсот два миллиона семьдесят два.
8,	Сколько цифр использовано для записи числа 18917?
Сколько из них различных цифр?
9.	Составьте все трехзначные числа, в записи которых
используются цифры 0, 1, 2, без повторения одина-
ковых цифр в одном числе.
10,	Какие цифры могут стоять в каждом разряде числа?
Какие цифры могут стоять в высшем (наибольшем)
разряде числа?
11,	Сколько всего однозначных, двузначных, трехзначных
натуральных чисел?
12,	В книге пронумерованы все страницы с 1 по 148.
Сколько всего цифр потребовалось напечатать для
нумерации страниц?
13.	Для нумерации страниц в книге потребовалось напе-
чатать 1989 цифр. Сколько страниц в книге?
14.	Ученик токаря сделал 120.деталей за смену, а то-
карь на 36 деталей больше. Сколько деталей за сме-
ну изготовили токарь и ученик вместе?
15.	Мальчик прочитал 42 страницы книги, и ему осталось
прочитать на 2 страницы больше. Сколько страниц в
книге?
§ 3. Сравнение натуральных чисел
Пусть а и b—натуральные числа. Число Ь считается
большим числа а, если оно находится в ряду натураль-
ных чисел
1,	2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...
правее, чем число а. При этом пишут b > а и говорят
<tb больше а» или пишут а < b и говорят «а меньше Ь».
А Л В
ГТ—1--1  t""T" т—।—1—
О123ЬВ67^
Рис. 1.1
Пример. На рис. 1.1 изображен отрезок АВ длиной
5 см и отрезок AD длиной 3 см.
Отрезок AD есть часть отрезка АВ, поэтому мы го-
ворим, что длина АВ больше длины AD. Это соответст-
вует тому, что 5 > 3, т. е. что в натуральном ряду число
5 находится правее числа 3.
Если а, b и с—натуральные числа и & в ряду нату-
ральных чисел находится правее а, а с находится правее
Ь, то из этого следует, что с находится правее а. То есть
из b > а и с > b следует, что с > а.
Пишут также это в виде двойного неравенства
а<Ь<с, говорят «5 больше а, но меньше с».
Но натуральные числа можно сравнивать и по их за-
писи. Правила сравнения заключаются в следующем:
1.	Числа равны, если у них одинаковое число разрядов
и цифры соответствующих разрядов одинаковые. .
15
Пример. 12345678 и 12345 678 равны. В этом лег-
ко убедиться, записав одно число под другим.
2.	Из двух чисел больше то, у которого число разрядов
больше.
Пример. 3 456 > 987, потому что число 3 456 содер-
жит на один разряд больше числа 987.
3.	Из двух чисел с одинаковым числом разрядов боль-
ше то, у которого цифра высшего разряда больше.
Пример. 2801 <3322, потому что оба числа четы-
рехзначные и цифра высшего (четвертого) разряда перво-
го числа меньше цифры высшего (четвертого) разряда
второго числа (2 < 3).
4.	Если цифры высшего разряда двух чисел (с одинако-
вым числом разрядов) одинаковые, то для сравнения этих
чисел надо обратиться к наибольшему разряду, для кото-
рого цифры данных чисел различны. То из чисел больше,
у которого цифра этого разряда больше.
Пример. 2817<2821, потому что оба числа четы-
рехзначные, цифры их четвертых и третьих разрядов
соответственно равны, а цифры второго разряда разные—
у первого числа эта цифра меньше, чем у второго.
Каждое натуральное число а больше нуля. Это запи-
сывают так:
а > 0.
Натуральные числа называют еще целыми положитель-
ными числами. Число 0 тоже целое, но не положитель-
ное число.
Числа 0, 1, 2, 3, 4, 5, ... называют целыми неотри-
цательными числами. Это название оправдано тем, что
кроме неотрицательных чисел есть еще и отрицательные
числа, с которыми мы познакомимся позднее (в главе JII).
Заметим, что выражение «цифра 2 меньше цифры 3»
употреблялось нами для упрощения речи. На самом деле
имелось в виду «число 2 меньше числа 3».
УПРАЖНЕНИЯ
1.	Назовите число, которое следует в натуральном ряду
за числом:
13, 276, 3590, 305 899, 999999999.
?6
2.	Назовите число, которое предшествует в натуральном
ряду числу:
2, 74, 100, 3050, 438109, 1000 000000,
3.	У каждого ли натурального числа есть в натуральном
ряду последующее и предшествующее (предыдущее) на-
туральные числа?
4.	Запишите наименьшее однозначное, двузначное, трех-
значное, четырехзначное натуральное число.
5.	Запишите наибольшее однозначное, двузначное, трех-
значное, четырехзначное натуральное число.
6.	Существует ли наименьшее натуральное число?
Существует ли наибольшее натуральное число?
7.	Прочитайте запись:
1)	1 < 2;	2) 7 <10;	3) 11 < 25;
4)	12 > 4;	5) 26 > 23;	6) 123 < 132.
8.	Верно ли использованы знаки сравнения:
1)	123765 >	123675;	2)	153 335 < 156 654;
3)	177642 <	177042;	4)	10000 000=100000;
5)	377 551 <	37 751;	6)	756 453 > 756 543?
9.	Поставьте между следующими числами знак сравнения
(=, < »:
1)	123 и	123;	2)	123 и 124;
3)	123 и	121;	4)	12345 и 12346;
5)	75315	и 75515;	6)	1001001 и 1000	101.
10.	Сравните натуральные числа, заменяя знак «?» одним
из знаков сравнения (=, <, >):
1)	7 892? 654;	2) 3598? 3589;
3)	75497? 7549;	4) 450? 4500.
11.	Прочитайте двойные неравенства:
1)	2 < а < 7;	2) 3 < а < 5;
3)	10<а< 15.
Назовите все натуральные числа а, удовлетворяющие
каждому из этих неравенств.
12.	Запишите в виде двойного неравенства условия:
1)	3<а, а<7;	2) 4 < а, 8 > а-,
3)	10 > а, 5 < а;	4) 25 > а, а > 22.
13.	Существует ли целое число, меньшее любого нату-
рального числа?
14.	Запишите в виде равенства или неравенства следую-
щие предложения:
1)	число 12988 больше 129;
2)	число 33005 меньше числа 33 066;
3)	число 7 больше числа 0;
4)	числа 15 и 15 равны.
2 С. М. Никольский и др.	17
15.	Поставьте знак сравнения:
1)	20 к. и 15 к.;	2) 1 р. и 90 к.;
3)	120 к. и 1 р.;	4) 5 р. 25 к. и 526 к.
16.	Книга стоит 45 к., а авторучка на 50 к. больше.
Сколько стоят книга и авторучка вместе?
17.	В магазине купили пакет молока за 32 к., батон
хлеба за 18 к. и пачку масла, которая на 40 к. дороже
пакета молока. Сколько стоит вся покупка?
18.	Принимая участие в операции «Миллион—Родине»,
пионеры 4 «А» класса собрали 220 кг макулатуры,
пионеры 4 «Б»—на 60 кг больше, а пионеры 4 «В» —
на 10 кг меньше, чем пионеры 4 «А» и 4 «Б» вместе.
Сколько килограммов макулатуры собрали пионеры
трех классов вместе?
19.	Старшеклассники помогали совхозу. За первый день
они собрали 312 ящиков огурцов, за второй—на 120
ящиков больше, чем за первый. За третий день они
собрали на 18 ящиков меньше, чем за первый и вто-
рой вместе. Сколько ящиков огурцов собрали старше-
классники за три дня?
§ 4. Законы сложения
Чтобы сложить числа 5 и 3, можно рассуждать сле-
дующим образом. Рассмотрим ряд натуральных чисел.
Отметим в этом1 ряду число 5, отсчитаем от него вправо
три числа. Получится число 8, называемое суммой чисел
5 и 3: 8 = 5 + 3.
।	।---------1
1,	2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...
t I_______________t
Но можно отметить в натуральном ряду сначала число 3,
а затем от него отсчитать вправо пять чисел. Получится
снова число 8, называемое суммой чисел 3 и 5:
8 = 3 + 5.
Таким образом, сумма не изменяется от перестановки
слагаемых:
5 + 3 = 3 + 5.
Точно так же для любых натуральных чисел а и Ь
справедливо равенство
a + b = b + a,
18
выражающее переместительный или коммутативный закон
сложения:
От перестановки слагаемых сумма не изменяется.
Сложим теперь три числа 3, 2, 4. Для этого, приме-
няя уже известный способ, отметим в натуральном ряду
число 3, затем отсчитаем от него вправо 2 числа и 4 числа.
Получится число 9.
1 П ।-----------I
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, И, ...
t I-------------i
Следовательно,
(34-2)4-4 = 9.
Отметим теперь в натуральном ряду число 3, отсчи-
таем от него 2-}-4 = 6 чисел. Получится тоже 9: 3 4-
4-(24-4) = 9.
Таким образом, мы получили равенство
(34-2)4-4 = 34-(24-4),
показывающее, что вместо того, чтобы к (34-2) приба-
вить 4, можно к 3 прибавить (2 4- 4), а результат будет
тот же.
Точно так же для любых натуральных чисел а, b и с
справедливо равенство
(а 4-&) 4-с=а 4- (& 4-с),
выражающее сочетательный или ассоциативный закон сло-
жения:
Чтобы к сумме двух чисел прибавить третье, можно
к первому числу прибавить сумму второго и третьего.
Отметим, что сумму трех слагаемых можно записать
и без скобок:
3 4-2 4-4 = (3 4-2) 4-4 = 3 4-(2 4-4).
Для любого натурального числа а справедливы ра-
венства
а 4- 0 = а,
04-а = а,
04-0 = 0.
2»
19
В сумме нескольких слагаемых можно переставлять
слагаемые и заключать их в скобки любым образом.
Например, верны равенства
1 + 24-3 = 3 + 2+ 1,
1 + 2 + 3 + 4 = (1 + 2) + (3 + 4).
Докажем эти равенства, применяя на каждом этапе
рассуждений переместительный или сочетательный закон
сложения:
1 + 2 + 3 =» 1 + (2 + 3) = 1 +(3 + 2) = (3 + 2)+ 1 = 3 + 2+ 1,
1 + 2 + 3 + 4 = (1 + 2 + 3) + 4 = (1 + 2) + (3 + 4).
Рассмотренные законы сложения широко используют
для упрощения вычислений.
Пример. 23+ 118+ 17 = (23+ 17)+ 118 = 40+ 118 =
= 158.
УПРАЖНЕНИЯ
1.	Поясните, как можно найти сумму чисел 4 и 3 с по-
мощью натурального ряда.
2.	Запишите переместительный закон сложения для чисел
5 и 8, 124 и 39, а и Ь.
3.	Устно выполните действия:
1)	200 + 300;	2) 5000 + 8000;
3)	170+ 130;	4) 250 + 50;
5)	33 + 367;	6) 55 + 4145;
7)	98 + 922;	8) 26 + 8164.
4.	Определите порядок выполнения действий при вычис-
лении суммы:
1)	(725+ 48)+ 809;	2) 725 +(48 + 809).
Получатся ли в заданиях 1) и 2) одинаковые резуль-
таты? Почему?
5.	Запишите сочетательный закон сложения для чисел
2, 3, 5 и а, Ь, с.
6.	Примените законы сложения для упрощения вычисле-
ний и выполните сложение:
1) 38+43 + 7;	2) 19 + 56+14;
3) 138 + 35 + 22;	4) 456+68 + 32;
5) 664+12 + 88;	6) 156 + 44 + 97.
7. Найдите сумму:
1) 571 + 324 + 129;	2) 44 + 459 + 356;
20
3) 4344-237 + 66;	4) 183 + 56 + 217;
5) 522 + 73 + 127;	6) 157 + 143 + 357.
8. При устном сложении натуральных чисел часто ис-
пользуют следующий прием: 474+ 109 = 474+ (100 +
+ 9) = (474+ 100) + 9 = 574 + 9 = 583 или 497 + 228 =
= 497 + (3 + 225) = (497 + 3) + 225 = 500 + 225 = 725.
Используя этот прием, выполните сложение чисел:
1) 399 + 425; 2) 819+ 156; 3) 256 + 98;	4) 748+ 197;
5) 305 + 238; 6) 999 + 578; 7) 7499 + 325; 8) 893+198.
9. Вычислите сумму натуральных чисел от 1 до 100:
1 + 2 + 3 + 4+ ... + 97 + 98 + 99+ 100.
Постарайтесь выполнить задание устно.
10*. Можно ли среди первых ста натуральных чисел вы-
брать 50 чисел так, чтобы среди них не было двух
чисел, дающих в сумме 100? Можно ли выбрать
52 числа с теми же условиями?
§ 5. Вычитание
Пусть а и Ь—неотрицательные целые числа и а больше
или равно Ъ (пишут а^Ь).
Разностью чисел а и Ь называется такое число, обозна-
чаемое а—Ь, которое при сложении с b дает а, т. е.
(а—b) + b = a или а—Ь + Ь — а.
Число а называется уменьшаемым, b—вычитаемым.
Пример. Из 9 вычесть 6.
Очевидно, что 9—6 = 3, так как 3 + 6 = 9.
Покажем это с помощью натурального ряда.
Отметим в натуральном ряду число 9 и отсчитаем от
него влево 6 чисел. Получится число 3: 9—6 = 3.
5-------------1 |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ...
Если к 3 прибавить 6, т. е. отсчитать от числа 3 вправо
6 чисел, то получится число 9:
3 + 6 = 9 или (9—6) + 6 = 9.
УПРАЖНЕНИЯ
1. 1) Какое число называется разностью чисел 5 и 3,
8 и 7, а и 2, аяЬ? Запишите в каждом случае
разность, назовите уменьшаемое и вычитаемое.
2) Докажите, что 12—8 = 4.
21
2. Как называется неизвестное число х в следующих при-
мерах? Объясните, как его найти.
1) 62 + 45 = х;	2)	62—20 = х;
3) 56 4-х = 66;	4)	58—х=32;
5) х + 28 = 98;	6)	х—48 = 60.
3.	Туристы планировали за три дня пройти 65 км. За
первый день они прошли 24 км, за второй день —
22 км. Сколько километров им оставалось пройти после
первого дня? Сколько километров им осталось пройти
в третий день?
4.	В вазе стоят гвоздики двух цветов—розовые и крас-
ные. Розовых 12, а красных на 3 меньше. Сколько
всего гвоздик стоит в вазе?
5.	В магазине заплатили за сыр 78 к., за молоко—на
6 к. меньше, чем за сыр, а за сахар на 26 к. ббльше,
чем за сыр. Сколько стоит вся покупка?
6.	В трех классах 44 девочки—это на 8 человек меньше,
чем мальчиков. Сколько в трех классах мальчиков?
Сколько всего учащихся в трех классах?
7.	Мальчику 10 лет. Он на два года старше своего
брата, а их отец в 5 раз старше младшего из маль-
чиков. Сколько лет отцу? z
8.	Доярки надоили за июль 300 тысяч литров молока,
что на 4 тысячи литров больше, чем они надоили
в июне, и на 6 тысяч литров меньше, чем надоили
в августе. Сколько литров молока доярки надоили за
летние месяцы?
9.	Устно найдите разность чисел 46 и 22, прибавьте
к уменьшаемому и вычитаемому по 1, по 2, по 3 и
в каждом случае найдите разность. Сравните полу-
ченные результаты.
10.	Докажите, что от прибавления к уменьшаемому и вы-
читаемому одного и того же числа разность не изме-
няется, т. е. если а—Ь = с, то (а + о)—(6-f-n) = c.
11.	Объясните способ вычитания, использованный в упраж-
нениях 1)—3):
1)	38—9 = 39—10 = 29;
2)	725—96 = 729—100 = 629;
3)	4 325 — 190 = 4 335 — 200 = 4135;
примените этот способ для вычисления разности:
4)	72—9;	5) 98—9;	6) 64—8;
7) 102—8;	8) 146—18;	9) 132—29.
12.	Устно вычислите разность:
1)	62 и 8;	2) 53 и 9;	3) 71 и 7;
4)	172 и 9;	5) 382 и 8;	6) 591 и 99.
22
§ 6« Умножение, Законы умножения
Умножить натуральное число 3 на натуральное чис-
ло 4—это означает найти сумму трех слагаемых, каждое
из которых есть 4. Таким образом,
3-4 = 4 + 4 + 4.
Числа 3 и 4 называются множителями а число 3-4 —
их произведением.
Для любого числа а верно равенство 1-а = а.
Вот еще примеры:
5-3 = 3 + 3 + 3 + 3 + 3=15,
3-1 = 1+1 + 1 = 3,
1-7 = 7.
Для любых натуральных чисел а и Ъ верно равенство
а-Ь = Ь-а,
выражающее переместительный или коммутативный закон
умножения'.
От перестановки множителей произведение не изме-
няется.
Переместительный закон умножения легко проверяется
при подсчете двумя способами числа квадратов на рис. 1.2.
Все квадраты можно расположить в 3 ряда по 4 квад-
рата— всего 3-4 квадрата (рис. 1.3). Но можно располо-
жить все квадраты в 4 столбца по 3 квадрата—всего 4-3
квадрата. Так как число квадратов в обоих случаях
одно и то же, то
3-4 = 4-3.
Для любых натуральных чисел а, b и с верно ра-
венство
[ab]-c=a[bc),
23
выражающее сочетательный или ассоциативный закон
умножения'.
Чтобы произведение двух чисел умножить на третье
число, можно первое число умножить на произведение с
второго и третьего чисел.
Сочетательный закон легко проверяется при подсчете
числа кубиков на рис. 1.4. Все кубики можно располо-
жить в два слоя—нижний и верхний—по 3-4 кубика
в каждом—всего 2-(3-4) кубика (рис. 1.5).
Рис. 1.5
Но можно расположить все кубики в 4 слоя по 2 3
кубика в каждом—всего 4-(2-3) = (2-3)-4 кубика.
Так как число кубиков в обоих случаях одно и то же, то
(2-3)-4 = 2-(3-4).
Этим примером мы проиллюстрировали сочетательный
закон умножения для натуральных чисел.
Отметим, что произведение трех (и более) чисел можно
записать и без скобок:
(2-3)-4 = 2(3-4) = 2-3-4.
Изученные нами законы умножения применяются для
упрощения вычислений.
Пример. Вычислить произведение (5 -48) -2.
Пользуясь принятым порядком действий, мы должны
сначала умножить 5 на 48, а полученный результат умно-
жить на 2.
24
Для упрощения вычислений применим переместитель-
ный и сочетательный законы умножения:
(5-48).2г=(48.5).2 = 48-(5.2) = 48.10 = 480.
В произведении нескольких множителей можно пере-
ставлять множители и заключать их в скобки любым
способом.
Пример. 3-4-5-6 = 6-5.4-3, 3-4.5.6 = (3-4).(5.6).
По определению считают, что для любого неотрица-
тельного числа а
а-0 = 0,
0-а = 0.
Тогда равенства а-Ь=Ь-а и (а-6)-сео-(6-с) верны и для
неотрицательных чисел.
Например, 5-0 = 0-5, (5-3)-0 = 5-(3-0).
УПРАЖНЕНИЯ
1.	Наташа купила 3 пакета молока по 32 к.» а Коля
купил 2 пирожных по 22 к. Какими двумя способами
можно подсчитать стоимость каждой покупки?
2.	Замените сумму произведением:
1)	75 + 75 + 75;	2) 701+701+701+701+701;
3)	82 + 82 + 82 + 82;	4) 603 + 603 + 603 + 603;
5)	101+101+101 + 101; 6)909 + 909 + 909;
7)	80 + 80 + 80 + 80;	8) 0 + 0 + 0 + 0 + 0 + 0 + 0.
3.	Вычислите сумму:
1)	7 + 7 + 7 + 7+7 + 7 + 7;
2)	5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5;
3)	8 + 8 + 8 + 8 + 8 + 8 + 8 + 8;
4)	9 + 9 + 9 + 9 + 9 + 9 + 9 + Э.
4.	Запишите сумму в виде произведения:
1)	а + а + а + а;
2)	&+& + & + & + &;
3)	х+х+х+х+х + х+х+х;
4)	У + У + У+У + У + У + У-
5.	Устно выполните умножение:
1)	30-20;	2)	80-4000;	3)	700-90;
4)	70-800;	5)	800-900;	6)	120-30;
7)	300-70;	8)	900-30;	9)	500-80;
10)	150-20;	11)	40-90;	12)	140-50.
6.	Запишите число в виде произведения двух множи-
телей:
25
1) 48 = 8-...;	2)42 = 6-...;
3)72 = 8-...;	4)81=9-...;
5)36 = 6....;	6)63 = 7-...;
7)35 = 5-...;	8)49=7....;
9)56 = 7-...;	10)54 = 6-...
7.	Запишите число в виде произведения двух равных
множителей:
1)1;	2)0;	3)9;	4)16;
5) 25;	6) 4;	7) 64;	8) 49;
9) 36;	10) 81;	И) 100;	12) 121.
8.	Запишите числа 15, 24, 36, 18, 27, 16, 20, 30, 40,
13, 14, 17 в виде произведения двух множителей всеми
возможными способами.
9.	В школьную библиотеку привезли 20 пачек книг по
16 штук в каждой пачке. Сколько книг привезли
в библиотеку? Нужно ли развязывать все пачки, чтобы
пересчитать книги?
10.	На овощную базу привезли помидоры на 6' машинах
по 120 ящиков в каждой и _еще на 8 машинах по
140 ящиков в каждой. Сформулируйте вопрос задачи
и решите ее.
Замечание. В выражениях а + (Ь-с), а—(Ъ-с),
а + (Ь:с), а—(Ь-.с) принято опускать скобки, но под-
разумевать их и сначала выполнять умножение и де-
ление. Таким образом, а + (b-c) — a + b-c, а—(Ь-с) =
— а—Ъ-с, a + (b'c)=a + b'.c, а—(Ь‘.с) = а—Ь:с. На-
пример, 24-3.5 = 2+15 = 17, 12—8:2—12—4 = 8.
11.	В следующих примерах на вычисление определите
порядок действий. Какое действие выполняется по-
следним? Как называется результат последнего дей-
ствия?
1)	3-2 + 5-7; ...	2) 3 (2 + 5);
3) 3-2 + 3-5;	4) 4-2 + 6-(7 + 8).
12.	Какое действие в следующих выражениях выполняется
последним? Как прочитать данные выражения?
1)	а-2 + 7-Ь;	2) п-(2 + 5);
3)	х-З + у-5;	4) а-(Ь + с);
5)	a-b + a-с;	6)а + «-(5 + х).
13.	Для упрощения вычислений полезно помнить, что
2-5=10,	4-25 = 100,	8-125=1000.
Устно вычислите произведение:
1)13-2-5;	2)7-8-125; -
3)	2-17-5;	4) 8-19-125;
5)4-9-25;	6)125-12-8;
7)7-25-4;	8)8-2-4-125.
26
14.	Выполните умножение:
1)	16-25 = 4-4-25 = 4-(4-25)= ...;
2)	16-125 = 2-8-125 = 2-(8-125)=...;
3)	28-25;	4) 25-24;	5) 125-24;
6)64-5;	7)48-25;	8)64-125.
15.	Вычислите произведение:
1)56-25;	2)88-125;
3)5-48-25;	4)25-32-125;
5)	13-16-25;	6) 17-6-5.
16.	Вычислите произведение:
1)	2-4-6-8-0;	2) (108-2 + 5-13)-0.
17.	Какой цифрой оканчивается произведение
1-2-3-...-14-15?
18г Мастер за час обрабатывает 12 заготовок, а его уче-
ник—8 заготовок. Над выполнением порученного им
задания сначала работал мастер 2 часа, а потом мас-
тер и ученик вместе в течение 3 часов. Сколько за- ,
готовок они обработали вместе за 5 часов?
§ 7, Распределительный закон
Для любых натуральных чисел а, b и с верно ра-
венство
а-(& + с) = а-& + а-с,
выражающее распределительный закон:
Чтобы число умножить на сумму двух чисел, можно
это число умножить на каждое слагаемое и полученные
произведения сложить.
Поясним это на примере. Подсчитаем двумя способами
число квадратов на рис. 1.6.
сшнишн
МИННЕ
ставши
Рис. 1.6
I способ. В каждом ряду расположено 3 белых и
5 черных квадратов, а всего в каждом ряду (3 + 5) квад-
ратов. В четырех же рядах всего 4-(3 + 5) квадратов.
27
II способ. Белые квадраты расположены в четырех
рядах по 3 квадрата в каждом, т. е. белых квадратов 4-3.
Аналогично, черных квадратов 4-5, а всего квадратов
4-3 + 4-5.
Одно и то же число квадратов подсчитано двумя спо-
собами, поэтому
4-(3 + 5) = 4-3 + 4-5.
Отметим, что распределительный закон верен не только
для двух, а для любого числа слагаемых. Например,
верны равенства
(a + b + c)-d = a-d+b-d + c-tf,
(a + f»+c+d)-n=a-n + &-n + c«n+d-/i.
Докажем первое из этих равенств, сводя рассуждения
к уже известным нам сочетательному и распределитель-
ному законам для двух слагаемых:
(а + b + с) • d = ((а + Ь) + с) • d — (а + Ь) • d + с • d —
= a-d + b-d-\-c-d.
Замечание. Любое из чисел в этих равенствах
может быть нулем, поэтому можно сказать, что эти ра-
венства верны для неотрицательных целых чисел.
Кроме того, если а > Ь, то верно также равенство
с-(а—Ь)=>с-а—С’Ь.
Например, верно равенство
7(5—3) = 7-5—7-3,
потому что на основании распределительного закона для
неотрицательных целых чисел
7-(5—3) + 7-3 = 7-[(5—3) + 3] = 7-5.
Переход от а-Ь+а-с к a-(& + c) и от а-Ь—а-с к
а-(Ь—с)называют вынесением общего множителя за скобки.
Вынесение общего множителя за скобки позволяет
упрощать вычисления. Например,
95 • 43 + 95 • 57 = 95 • (43 + 57) = 95 • 100 = 9500.
28
УПРАЖНЕНИЯ
I. Примените распределительный закон для раскрытия
скобок:
I) 7-(3 + 8); 3) 10.(15 + 6); 2. Раскройте скобки: 1) (12 + 3)-10; 3) (54+ 81)-92; 3. Раскройте скобки: 1) 5-(8 +с); 3) 12-(а+ 5);	2) 5.(10+12); 4) 6.(12 +4). 2) (15+ 7). 17; 4) (93 + 28)-79. 2) 7-(х+ 9): 4) (х+10-15.
4. Используя распределительный закон, запишите сле-
дующие суммы в виде произведения:
1) 7-3 + 7-2;	2) 5»3 + 5-8;
3) 8-9 + Э-7;	4) 10-5 + 3-5.
5. Используя распределительный закон, вынесите мно-
житель за скобки:
1) 5-7 + 6-5;	2)17-5+17.1;
3)9-2 + 2.11;	4)8-12 + 20.12.
6. Раскройте скобки:
1) 8-(18—10);	2) (22—14)-5;
3) (42—23).6;	4) 45-(10—1).
7. Представьте следующие суммы и разности в виде про-
изведения:
1)	12 + 34 = 2-6 + 2.17 = 2-(6+17) = 2-23;
2)	45—20 = 5.9—5.4=...;
3)	100 + 75; 4) 48—36; 5) 128—96; 6) 58 + 87.
8.	Вычислите сумму, используя распределительный закон:
1)	37-12 + 37-88;	2)3-15 + 3-25;
3)12-7 + 7.8;	4)6-13+17-6.
9.	Вычислите разность:
1)	52-12—12-51;	2) 54.11—49.11}
3)	126-5—96-5;	4) 256.17—17-46.
10.	Вычислите суммы и разности, записав предварительно
их в виде произведения:
1)	7-5+15;	2) 35 + 5-3;
3)	6-8 + 6;	4) 8-5—16.
И. В швейной мастерской было 12 кусков материи по
40 м в каждом и 8 кусков материи по 30 м в каждом
куске. Сколько метров материи осталось после того,
как израсходовали 340 м?
12.	Вычислите:
1) 7-55 + 7.45 + 3-55 + 3.45;
2) 8-2 + 2-92 + 8-Э8 + 92-98;
С9
3)	37-594-41-37 +63-59+41-63;
4)	356-73 + 644-27 + 73-644 + 27-356.
13.	Выполните действия:
1)	(5486 + 3578)+1422;
2)	4 523+ (3788+1477);
3)	(357 + 768 + 589) + (332 + 211 + 643).
14.	Представьте числа в виде суммы разрядных слагаемых
и найдите их сумму:
1)	1337 и 2551;	2) 3216 и 3483.
15.	От Ленинграда до Петрозаводска 401 км, а от Петро-
заводска до Мурманска на 643 км больше. Сколько
километров от Ленинграда до Мурманска через Петро-
заводск?
16.	Длина прямоугольника 246 мм, а ширина прямоуголь-
ника на 95 мм меньше. Определите периметр (сумму
длин всех сторон) прямоугольника.
17.	Ширина прямоугольника 16 м, а его длина на 350 см
больше. Определите.периметр прямоугольника.
§ 8. Сложение и вычитание чисел столбиком
При сложении и вычитании однозначных чисел надо
помнить таблицы сложения и вычитания. Сложение и
вычитание многозначных чисел выполняют по разрядам,
используя переместительный, сочетательный и распреде-
лительный законы. Обычно сложение и вычитание прово-
дят столбиком, записывая числа одно под другим так,
чтобы цифры одинаковых разрядов были написаны друг
под другом, и начинают действия с единиц.
Пример 1. 35+21 = 3-10+5+2-10+1 = (3+2)-10+
+ (5 + 1) = 50 + 6 = 56.
.35
+35
। Пишут обычно короче: 21
56	56
Пример 2. 68— 43=6-10+8— 4-10— 3=(6—4)-10+
+(8—3) = 20 + 5 = 25.
68
43	_ 68
I Пишут обычно короче: J3
2!Г	25
30
Если сложение в каком-либо разряде дает в результате
число, большее 10, то десять единиц этого разряда заме-
няют единицей следующего разряда.
Пример 3. 45+79 = 4-10+5+7-10+9 = (4+7). 10+
+(5 + 9) = 11 • 10+ 14 = 1Ь 10+10.1+ 4=(11 +1)10+4=
= 120+4=124.
45 Пишут обычно короче, запоминая, что в разряд
—гг десятков добавляется один десяток:
+_цо	+ g
124	ТгГ
Если в каком-либо разряде цифра уменьшаемого меньше
цифры вычитаемого, то нужно «занять» одну единицу
в следующем разряде уменьшаемого.
Пример 4. 72—9=7-10 + 2—9=6-10+10 + 2—9^
=6-10 +(12—9) = 60 +3 = 63.
Это записывают, отмечая точкой разряд, в котором
«занята» единица:
72
'~_9
Пишут обычно короче:
63-
72
9
63
УПРАЖНЕНИЯ
1. Выполните сложение:
П .	375	2)	,3 156
' + 48 324	’ +2231
3) ,15 386	4)	,39 584
' + 2 809	+75 986
2. 1) 325 и 806;	2)	6292 и	4 596;
3) 2099 и	8 520;	4)	9128 и	7357;
5) 6 312 и	1599;	6)	4890 и	1716.
3. Прибавьте:
1) к	4890 число 1716;	2)	к	5 617	число	9861;
3) к	399 число 1523;	4)	к	9091	число	909;
5) к	999 число 3001;	6)	к	7831	число	2169;
7) к	8 435 число 6 890;	8)	к	376 число 9	734.
4. Увеличьте:
1) 756 на 234;	2) 582 на 343;
3) 2592 на 375;	4) 709 на 2570;
5) 983 на 215;	6) 1708 на 2425.
31
Вычислите:
5.1)	784 + 296;	2)	365 + 645;
3)	999 + 854;	4)	351 + 999.
6.	1) 52338 + 4691;	2) 6 856 + 77 281;
3)	757664 + 15 979;	4)	18635 + 574985.
7.	1)	100004 + 57806;	2)	3000008 + 799992;
3)	3847569+2409001; 4) 15 999996 + 708 000004.
Выполните вычитание:
8.	1)	728	2)	1358	3)	92507
’ "~325	7 ~~ 246	'	2 400
9.	1) 6 778—5 513;	2) 3 956—2 165;
3)	4238—2119;	. 4) 5789—2899.
10.	Найдите разность чисел:
1)	721 и 209;	2) 2538 и 283;
3)	1453 и 820;	4) 10021 и 8 096.
11.	Вычтите:
1)	из 925 число	296;	2)	из 623 число 284;
3)	389 из числа	850;	4)	727 из числа 2 300.
12.	Найдите неизвестное число х:
1)	х + 209 = 700;	2)	296 + х = 925;
3)	х—283 = 79;	4)	х+ 8096= 10951;
5)	756—х=236;	6) 839—х= 125.
13.	На доске были записаны верно выполненные примеры
на сложение, потом некоторые цифры стерли и заме-
нили их. буквами. Перепишите примеры, заменяя
буквы цифрами так» чтобы опять получились верные
записи:
1)	л. 72И	2) , Д52	3) . 5ИН
' + 1РЗ ' + 6В4	1 + Д79
Т98	78А	0381
14*. Восстановите вычисления, считая, что одинаковые
буквы обозначают одинаковые цифры, а разные
буквы—разные цифры:
1) д_ БЗБ 1 + 76Б A300		2) . А4А ’ + ЗЗА Б0 8 4	
3)	. УДАР + УДАР	4)	, ДЕТАЛЬ + ДЕТАЛЬ
	ДРАКА		ИЗДЕЛИЕ
Выполните действия:
15.	1) (5 486+ 3578)+1422;
2)	4 523+ (3 788+ 1477);
3)	(357 + 768 + 589) + (332 + 211 + 643).
16.	1) 375 026 + 408724— 49 678;
2)	700000—(50345+ 168724);
82
3)	700 000—(125 480 + 89 256);
4)	1 700 000—(836 724 + 64048).
17.	Самые высокие горы на территории СССР—Пик Ком-
мунизма, Пик Победы и Пик Ленина. Пик Победы
имеет высоту 7439 м, что на 305 м выше Пика Ленина
и на 56 м ниже Пика Коммунизма. Определите высоту
Пика Ленина и Пика Коммунизма.
18.	На XXII Олимпийских Играх (Москва, 1980год) совет-
ские спортсмены завоевали 195 медалей, из них
126 золотых и бронзовых, 149 золотых и серебряных.
Сколько золотых, серебряных и бронзовых медалей
в отдельности завоевали наши спортсмены?
§ 9. Вычисление произведений целых неотрицательных
чисел
Произведения однозначных чисел составляют таблицу
умножения. Вычисление же произведения однозначного
числа на многозначное, тем более многозначного числа на
многозначное, требует применения не только таблицы
умножения, но и законов сложения и умножения целых
неотрицательных чисел.
Надо помнить, что для любого неотрицательного числа
а+0 = а, а-1=а,	а-0 = 0.
Пример. Вычислить произведение 327-8.
Решение. 327 = 300 + 20 + 7, поэтому 327 • 8 =
= (300+ 20+ 7)-8 = 300-8+20-8+7.8 ==2 400+160+56=
= 2 616.
Записать умножение столбиком можно подробно:
х 327
х 8
56	X 327
+ ««о или кратко: ______1
2400	2616
2616
Сложение выполняют устно; при этом запоминают, сколько
единиц нужно прибавить к следующему разряду.
Пример. Вычислить произведение 329-24.
Решение. 329-24 = 329-(20 + 4) = 329-20 + 329 4 =
= 6580+1316 = 7896.
2 С. М. Никольский и др.	33
Эти вычисления можно записать столбиком подробно:
v 329	329	'
х 24	х 24
- ИЛИ кРатко- 4* £я6
boot)	* ооо
’7896’	"7896’
Пример. Вычислить произведение 382-729.
Решение. 382-729=382-(7004-204-9)=382-7004-
4-382 -20 4- 382 • 9 = 267 400 4- 7 640 + 3 438 = 278 478.
То есть при умножении столбиком нужно 9 единиц
умножить на 382—получится 3438 единиц, 2 десятка умно-
жить на 382—получится 764 десятка, 7 сотен умножить
на 382—получится 2674 сотни.
Полученные результаты записываем один под другим
с учетом разрядов:
v 382
х 729
3438
’	764
2674
278478
Пример. Вычислить произведение 324-203.
Решение. В этом примере при умножении 0 десят-
ков на 324 получается 0 десятков. Поэтому вторую строку
(второе слагаемое) не пишут.
* 324
х 203
972
 648
65772
Пример. Вычислить произведение 460-48.
Решение. Так как 460-48=46-10-48, то можно вы-
полнить умножение 46 на 48 и умножить полученный
результат на 10, т. е. приписать к нему справа 0.
* 460
х 48
₽	368
4- 184
22080
34
Аналогично поступают и в других возможных случаях:
432
х 650
, 2160 '
+ 2592
280800'
7530
х 2600
, 4518
+ 1506
19578000
В последнем примере выполнено умножение 753 на 26
и к полученному результату справа приписано три нуля
(10-100=1000).
УПРАЖНЕНИЯ
1. Объясните—как получены результаты в следующих
упражнениях: 1)	748 4 X 6		2)	X	973 50	3)	X	7050 7
4)	4488 у 926 х 38	5)		48650 у 326 х 502	6)		49350 У 4830 х 4900
	, 7408 + 2778		+	652 1630		+	4347 1932
	35188			163652			23667000
Вычислите произведение:
2.	1) 12-10; 4) 20-100;		2) 32-100; 5) 300-1000;	3) 65-1000; 6) 1500-1000.
3.	1)	24-2;	2) 31-3;	3) 52-4;
	4)	7-338;	5) 106-4;	6) 401-8.
4.	1)	4381-2;	2) 7713-8;	3) 7-6204;
	4)	9-5007;	5) 6-5769;	6) члт.
5.	1)	1320-5;	2) 6-3054;	3) 7-8080.
6.	1)	23-11;	2) 43-12;	3) 22-33;
	4)	73-542;	5) 85-206;	6) 807-16.
7.	1)	101-332;	2) 302-648;	3) 321-562;
	4)	955-317;	5) 861-242;	6) 999-732.
8.	Вычислите наиболее простым способом:
1)	24-98 + 48;	2) 305-199+305;
3)	51-18—18;	4) 173-596 + 692.
9.	Вычислите:
1)	7668-24 + 968;	2) 3522 + 4583-26;
3)	5 306-42—536-82; 4) 1654-32—68-95.
10.	Выполните действия:
1)	325-40;	2) 3508-250;	3) 7380-420;
4)	3 800-550;	5) 973-101;	6) 789-1020.
11.	Мальчик заметил, что удар грома послышался через
12 с после того, как блеснула молния. Определите,
2*	35
на каком расстоянии от мальчика происходила гроза,
если известно, что скорость звука в воздухе 330 м
в секунду.
12.	Пульс здорового человека примерно 75 ударов в ми-
нуту. Сколько ударов пульса произойдет за 1 час?
13*. Произведение четырех последовательных натураль-
ных чисел равно 3024. Найдите эти числа.
14*. На доске записали несколько примеров на умноже-
ние натуральных чисел, потом некоторые цифры
стерли и вместо них поставили звездочки. Восстано-
вите стертые 1) X72	цифры: 2) х_£	3) х 52
,217 *г **	** 135	** 2*8
***	**-1»0	****
10. Степень	с натуральным	показателем
Мы уже знаем, что сумму одинаковых слагаемых при-
нято записывать короче—в виде произведения:
5 + 54-5 + 5 = 4 • 5, л + л + ц + ц==4*д.
Произведение одинаковых чисел также записывают
короче:.
5-5-5-5 = 54, а-а-а — а*
и называют степенью. Читают «пять в степени 4», «а в
степени 3».
Например, запись 2®—«два в степени три»—означает
2-2-2. При этом число 2 называют основанием степени,
3—показателем степени. Число 3 показывает, сколько
раз нужно взять множителем основание—число 2:
23 = 2-2-2 = 8.
Таким образом, степенью числа а с натуральным пока-
зателем п (п> 1) называется произведение п множителей,
каждый из которых равен а.
ап~а-а-а- ... -а, п > 1.
--——пиит- , 7
П
Пример. Вычислить 24.
24 = 2-2-2-2= 16.
т
36
Пример. Вычислить З7.
37 = 3-3-3-3-3-33 = 2187.
7
Таким образом можно вычислить любую степень с на-
туральным показателем, большим единицы. Нам остается
выяснить—что означает запись вида 2\ т. е. степень
с показателем, равным единице. Ведь не имеет смысла
говорить о произведении одного множителя.
Принято считать, что 2l = 2, 5* = 5, 1001 = 100, т. е.
первая степень любого числа равна самому числу:
а1=а.
Вторая степень числа называется также квадратом
числа. Читают: 52—«пять в квадрате», а2—«а в квадрате».
Третья степень числа называется кубом числа. Читают:
53—«пять в кубе», а8—«а в кубе».
О происхождении этих названий мы расскажем в сле-
дующей главе.
УПРАЖНЕНИЯ
1. Запишите в виде произведения:
1)54-5 + 5 + 5;	2) 2 + 2 + 2 + 2 + 2;
3) 3 + 3;	4) а + а + а\
5) b + b + b + b + b + b + b + Ь.
2. Запишите в виде степени, назовите основание степени
и ее показатель:
1)5-5.5-5;	2) 2-2-2.2.2;
3) 3-3;	4) а-а-а;
5)	b-b-b-b-b-b-b-b.
3.	Прочитайте следующие записи, назовите основание и
показатель степени: 10\ 8*, 7е, 25, 8е, 5W, 2И0.
4,	Используя специальные названия второй и третьей
степеней, прочитайте следующие записи: 22, 23, З2, З3,
4s, 52.
5.	Вычислите:
1)	З2;	2)	3-2;	3)	52;	4)	5-2;
5)	92;	6)	9-2;	7)	23;	8)	2-3.
6.	Вычислите:
1)	З3;	2)	58;	3)	42;	4)	82.
7.	Составьте таблицу квадратов чисел от 0 до 15.
8.	Составьте таблицу кубов чисел от 0 до 10.
37
9.	Вычислите:
1)	I2;	2) О2;	3) 3l;	4) 51;
5)	1ОО1;	6) 1’;	7) l1;	8) О10.
10.	Вычислите степени числа 2 с показателями от 1 до 10.
11.	Вычислите:
1)	З4;	2) 3?;	3) 43;	4) 44;
5)	53;	6) 54;	7) 62;	8) б3.
12.	Запишите в виде степени с основанием 10 числа:
1)	100;	2)	10000;	3)	1000;
4)	10;	5)	100 000;	6)	10000000;
7)	100000000;	8)	1000000.
13.	Запишите	следующие	числа в	виде	степени:
1)	4;	2) 100;	3) 16;	4)	49;
5)	25;	6) 81;	7) 64;	8)	36.
§ 11. Деление
Пусть а и b—натуральные числа и а больше или
равно b (а^Ь). Говорят, что а делится на b нацело,
если существует натуральное число с, произведение
которого на b равно а:
а = с-Ь.
При этом пишут а:Ь = с и называют а делимым,
b—делителем, с—частным. Таким образом, (сг.Ь)-Ь = а,
т. е. если а разделить на & и результат умножить на Ь,
то получится а.
Любое натуральное число а делится на 1 и само на
себя:
а: 1 — а, а:а= 1,
.так как а-1 — а, 1-а = а.
Например, 15 делится на 1 и 15, а также на 3 и 5,
а 19 делится только на 1 и само на себя. Считают также,
что 0ib — 0 для любого натурального числа Ь, так как
0.J=0.
Но делить на 0 нельзя. Для любого натурального
числа а не существует такого числа с, чтобы выполнялось
равенство а:0 = с, так как с-0 = 0.
При делении 0 на 0 можно было бы считать, что
0:0 = с, потому что с-0=0. Но в этом случае частным
S8
могло бы быть любое число с. Поэтому считают, что и
О нельзя делить на 0.
Отметим, что частное неотрицательных чисел а и &
(Z> #= 0)—единственное число.
Отметим важное свойство частного: делимое и дели-
тель можно умножить или разделить на одно и то же
натуральное число—частное от этого не изменится.
Например, 48:24 = 2 и (48-2): (24-2) = 96:48 = 2.
Это свойство часто используют для упрощения вы-
числений: 168:42=(168:3):(42:3)=56:14=(56:7):(14:7) =
= 8:2 = 4.
Таким образом, верны формулы
а:Ь = (а-п):(/ьп), а:& = (а:п):(&:п),
где п—натуральное число и во второй формуле а и b
делятся на п.
Докажем первую из них. Пусть а:Ь<=с, тогдас-Ь = а,
но тогда (а-п):(b-ri) также равно с, потому что с•(&•«)=
= (с-Ь)-п=ап.
УПРАЖНЕНИЯ
"*• * *
1.	Какое число называют частным чисел 8 и 2, 20 и 4,
а и 4?
2.	Докажите, что: 8:2 = 4, 12:4 = 3, 0:5 = 0.
3.	Запишите следующие числа в виде произведения двух
множителей различными способами и укажите, на
какие числа они делятся нацело:
1)	12;	2) 15;	3) 25;	4) 20;
5) 17;	6) 0;	7) 48;	8) 96.
4.	Как называется неизвестное число х в следующих
равенствах? Объясните, как его найти.
1)	62-2 = х;	2) 88:2 = х;
3) 31-х = 93;	4) 120:х=40;
5)	х-4=168;	6)	х:42 = 2.
5.	Устно найдите частное:
1)	40 и 8;	2)	72 и 9;	3)	64 и 8;
4)	560 и 7;	5)	140 и 7;	6)	360 и 6;
7)	606 и 2;	8)	808 и 4;	9)	909 и 9.
6,	Вычислите частное:
1)	400:80=(400:10):(80:10) = 40:8= ...;
2)	800:400;	3) 16 000:800;
39
4) 300:50;	5) 6 400:1 600;
6)	20000:4 000;	7) 2000:500.
7,	При делении на 5 и 50 иногда бывает удобно умно-
жить делимое и делитель на 2 и выполнить деление на
10 и 100.
Вычислить частное:
1)	95:5 = (95-2):(5-2)= 190:10= ...;
2)	2400:50 = (2400-2):(50-2) = 4800:100= ...;
3)	3200:5;	4) 1320:5;
5)	4 320:5;	6) 23300:50.
8.	Устно разделите:
1)	120:5;	2) 320:5;	3) 440:5;
4) 2 100:50;	5) 2020:5;	6)2130:5.
9.	На руках одного человека 10 пальцев. Сколько паль-
цев на 10 руках?
10.	Число 12 увеличили в 3 раза, потом еще в 2 раза.
Во сколько раз увеличили число 12 за два раза?
Решите задачу двумя способами. Сделайте вывод.
11.	Задумали число, увеличили его в 5 раз, потом в 6
раз. Во сколько раз увеличилось в итоге задуманное
число?
12.	Число 48 уменьшили в 4 раза, потом еще в 2 раза.
Во сколько раз уменьшилось первоначальное число?
Рещите задачу двумя способами.
13.	Перелетная саранча может пролететь без посадки
2200 км, а летучая мышь—в 2 раза меньше. На
сколько километров меньше может пролететь без
посадки летучая мышь по сравнению с саранчой?
14.	Ученик умножил число а на наибольшее трехзначное
число и получил наибольшее шестизначное число.
Найдите число а.
15.	Число 297 243 равно произведению трех чисел, два
из которых 27 и 109. Найдите третье число.
16.	Число 522 500 равно произведению трех чисел, из
которых первое 25, а второе на 75 больше первого.
Найдите третье число.
17.	Число 92610 равно произведению трех чисел, из
которых’ первое 147, а второе в 7 раз меньше первого.
Найдите сумму этих трех чисел.
§ 12. Свойства делимости
Свойство 1. Если одно число делится на второе,
а второе делится на третье, то первое число делится
на третье.
40
Например, 777 делится на 111, потому что 777 =а
= 7-111, а 111 делится на 3, потому что 111=37-3. Из
этого следует, что 777 делится на 3, потому что
777 = 7-111 = 7-(37-3) = (7-37)-3 = 259-3.
Свойство 2. Если каждое из двух чисел а и b де-
лится на число с, то сумма а-\-Ь и разность а—b де-
лятся на с.
Например, 100 делится на 4, потому что 100 = 25-4;
36 тоже делится на 4, потому что 36 = 9-4. Тогда 136
делится на 4, потому что 136=100 + 36 = 25-4 + 9-4 =
= (25+9)-4 = 34-4.
Можно также заключить, что число 64 делится на 4,
потому что 64=100—36 = 25-4—9-4 = (25—9)-4=16-4.
Свойство 3. Если одно из двух чисел а и Ь делится
на с, а другое не делится на с, то сумма а-\-Ь и
разность а—b не делятся на с.
Например, 148 делится на 37, потому что 148 = 4-37,
а 11 не делится на 37.
Рассмотрим равенство (148+ 11) —148=11. Справа в
нем находится число, не делящееся на 37. Если допу-
стить, что сумма (148+И) делится на 37, то левая часть
делится на 37 как разность чисел, делящихся на 37.
Тогда и правая часть должна делиться на 37, а это не-
верно. Поэтому (148+11) не делится на 37.
Также можно доказать, что и разность (148—11) не
делится на 37.
УПРАЖНЕНИЯ
1,	Покажите, что любое число, делящееся на 2, можно
записать в виде 2-й (где k — натуральное число):
1) 12 = 2-6;	2) 14;
3) 6;	4) 8.
2. Покажите, что любое из следующих чисел: 15, 20,
25, 10, 5 можно записать в виде 5-й.
3, Объясните, почему
1) 6-й делится на 2;	2) 15-й делится на 3;
3) 36-й делится на 18;	4) 18-й делится на 9?
4. Запишите в виде произведения натуральное число,
которое
41
1) делится на 2;	2) делится на 5;
3)	делится на 20;	4) делится на 7.
5.	Докажите, что если каждое из двух слагаемых делится
на 2, то и сумма делится на 2.
6.	Докажите, что если каждое из двух слагаемых делится
на 5, то и сумма делится на 5.
7.	Докажите, что если уменьшаемое и вычитаемое де-
лятся на 3, то и разность делится на 3.
8,	Объясните, почему
1)	454-36 делится на 9;	2) 994-88 делится на 11;
3)	13-а4-13-е делится на 13;
4)	12-а4- 15-&4-9«с делится на 3?
9.	Докажите, что
1)	(3 • а 4- 3 • Ь): 3 = а 4- Ь, где а и b—натуральные числа;
2)	(c-a + c-b):c—a + b, где а, b и с—натуральные
числа.
10.	Вычислите:
1)	(484-36):2 = 48:24-36:2= ..
2)	(164-20): 4;	3) (504-120): 5;
4)	(484 4-426): 2;	5) (840—488): 4;
6)	(963—690): 3;	8) (990 4-99): 9.
И. У двух мальчиков одинаковое число монет—у одного
десятикопеечных, а у другого пятнадцатикопеечных.
Всего же у них 1 р. 75 к. По скольку монет у каж-
дого?
12.	В кассе выдали 35 р. банкнотами по 3 р. и 5 р.,
причем трехрублевых было на 1 больше, чем пяти-
рублевых. Сколько выдали банкнот по 3 р. и 5 р.?
13.	Задача-шутка. У мальчика две монеты общей стои-
мостью 15 к. Одна из них не пятак. Что это за
монеты?
14,	Первый рабочий за 1 ч делает 32 детали, а второй
за 4 ч делает столько, сколько первой делает за 5 ч.
За сколько часов, работая вместе, они сделают 216
деталей
15,	Одна машинистка печатает 10 страниц за час, а вто-
рая за 5 ч отпечатывает столько же, сколько первая
за 4 ч. Сколько страниц отпечатают обе машинистки
за 3 ч совместной работы?
§ 13, Признаки делимости
Если число оканчивается цифрой 0, то оно делится
на 10.
Например, 4560 делится на 10, потому что 4560 =
42
= 456-10. Число 4561 не делится на 10, потому что
4561 = 4560+ 1—сумма числа 4560, делящегося на 10, и
числа 1, не делящегося на 10 (свойство 3).
Если число оканчивается на 0 или 5, то оно делится
на 5.
Например, число 2300 делится на 5, потому что
2300 = 230-10, а 10 делится на 5 (свойство 1), Число
2305 тоже делится на 5, потому что 2305 = 2300 + 5 —
сумма чисел, делящихся на 5 (свойство 2). Число 2327
не делится на 5, потому что 2327 = 2320 + 7—сумма
чисел 2320, делящегося на 5, и 7, не делящегося на 5
(свойство 3).
Если число оканчивается на цифры 0, 2, 4, 6, 8, то
оно делится на 2.
Если число оканчивается на цифры 1, 3, 5, 7, 9, то
оно не делится на 2.
Например, число 130 делится на 2, потому что
130=13-10, а 10 делится на 2 (свойство 1). Число 136
тоже делится на 2, потому что 136= 130 + 6—сумма
чисел, делящихся на 2.
Число 137 не делится на 2, потому что 137 = 130 + 7 —
сумма числа 130, делящегося на 2, и числа 7, не деля-
щегося на 2 (свойство 3).
Если две последние цифры числа образуют число,
делящееся на 4, то и само число делится на 4.
Например, число 3700 делится на 4, потому что
3700 = 37-100, а 100 делится на 4 (свойство 1). Число
3732 делится на 4, потому что 3732 = 3700 + 32—сумма
чисел 3700 и 32, делящихся на 4 (свойство 2). Число
3730 не делится на 4, потому что 3730 = 3700 + 30 —
сумма чисел 3700, делящегося на 4, и 30, не делящегося
на 4 (свойство 3).
Если сумма цифр числа делится на 9, то и само число
делится на 9.
Например, сумма цифр числа 7245 делится на 9:
7 + 2 + 4+5=18. Число 7245 делится на 9, потому что
его можно представить в виде 7 • 1000 + 2 • 100 + 4 • 10 + 5 =
= 7.(999+1) + 2-(99+ 1) + 4-(9+ 1) + 5 = (7-999+ 2-99+
43
+4-9) +(7+2+4+5), где сумма в первой скобке де-
лится на 9, так как каждое слагаемое делится на 9.
А во второй скобке стоит сумма цифр данного числа,
делящаяся на 9.
Число 375 не делится на 9, так как сумма его цифр
3+7+5=15 не делится на 9. Это можно доказать сле-
дующим образом: 375=3-(99+1)+7-(9+1)+5=
= (3-99+7-9) + (3+7+5), где сумма в первой скобке
делится на 9, а во второй скобке стоит сумма цифр
числа 375, не делящаяся на 9.
Если сумма цифр числа делится на 3, то и само чис-
ло делится на 3.	-	.
Например, у числа 375 сумма цифр делится на 3
(3+7+5=15) и оно само делится на 3, потому что
375= (3-99+7-9) + (3+7+5), где сумма в первой скобке
делится на 3, а во второй скобке стоит сумма цифр
числа 375, тоже делящаяся на 3.
Число 679 не делится на 3, так как сумма цифр
6+7+9=22 не делится на 3. Это можно доказать так:
679 = 6 (99+1)+7 (9+1)+9 = (699+7-9) + (6+7+9),
где сумма в первой скобке делится на 3, а во второй
скобке стоит сумма цифр числа 679, не делящаяся на 3.
УПРАЖНЕНИЯ
1. Из следующих чисел выпишите те, которые делятся
на 2, на 5, на 10, на 2 и 5:				
1) 128;	2) 325;	3)	500;	4) 506;
5) 725;	6) 905;	7)	830;	8) 962;
9) 750;	10) 1000;	И)	1262;	12) 2440.
2. Запишите	любые шесть	чисел,	, которые	делятся на:
1) 2;	2) 5;	3)	10;	4) 2 и	5.	'
3.	Запишите все числа от 15 до 95, которые делятся на 10.
4.	Запишите все числа от 23 до 46, которые делятся на 5.
5.	Запишите все числа от 51 до 73, которые делятся на 2.
6.	С помощью цифр 2, 7,5,3 (без повторения) запишите
все четырехзначные числа, которые делятся на 2;
делятся на 5.
7.	Можно ли с помощью цифр 1, 2, 5, 6 составить
трехзначное число, которое делилось бы па 2; на 5;
на 10?
44
8.	Натуральное число, которое делится на 2, называется
четным. Назовите любые шесть четных чисел.
9.	Покажите, что четные числа 18, 20, 48, 96 можно
записать в виде 2 k,	k—натуральное число.
10.	Натуральное число, которое не делится на 2, назы-
вается нечетным. Назовите любые шесть нечетных
чисел.
11.	Покажите, что нечетные числа 7, 9, Б, 13 можно
записать в виде 2-k-\- 1, где k — натуральное число.
12.	Докажите, что произведение четного числа на любое
натуральное число есть число четное.
13.	Докажите, что сумма двух четных чисел является
четным числом.
14*. Докажите, что сумма двух нечетных чисел является
четным числом.
15*. Докажите, что сумма четного числа нечетных сла-
гаемых является четным числом.
16.	Можно ли разменять 25 рублей десятью банкно-
тами по 1 р.; 3 р.; 5 р.? А десятью любыми банкно-
тами?
17.	Ученик выполнял решение примеров:
3 548 + 7256 + 8 108= 18911
и
9756 + 8 322 + 6565 = 24 642.
Не проверяя промежуточных вычислений, учитель
сразу сказал, что ученик ошибся при выполнении
каждого примера. Как была обнаружена ошибка?
18.	Саша купил в магазине 20 тетрадей, 2 альбома для
рисования, авторучку за 90 к., несколько каранда-
шей по 4 к. и несколько обложек для книг по 20 к.
Продавец сказал, что нужно уплатить в кассу 3 р. 57 к.
Саша попросил пересчитать стоимость покупки, и
ошибка была исправлена. Как он определил, что
была допущена ошибка?
19.	Какие из следующих чисел делятся на 4:
1)	7928;	2) 3553;	3). 1985; 4) 1796;
5)	7 568 936; 6) 42217766;
7)	100000000; 8) 13500?
20.	Из следующих чисел выпишите те, которые делятся
на 3; на 2; на 6; на 9:
1)	726; 2) 549; 3) 321;	4) 568;
5) 738; 6) 600; 7)1818; 8) 134 466.
21,	С помощью цифр 1, 2, 3 запишите шесть различных
трехзначных чисел (без повторения цифр в одном
45
числе). Будут ли полученные числа делиться на 3;
на 6; на 9?
22,	Как, не выполняя деления, определить, делится ли
число
111 111 111 111 111 111 111
на 3; на 9?
23,	Какую цифру нужно поставить вместо звездочки,
чтобы число делилось на 9:
1)	738*; 2) 85*; 3) 4*;	4) 5*;
5) 6*7;	6) 7*2; 7) 25«0; 8) 2090*?
24,	Известно, что число 12345*6789’0 делится на 9.
Какую цифру заменили звездочкой?
25,	Не вычисляя суммы цифр, докажите, что число
369999633 делится на 3, а число 963366992 не де-
лится на 3.
26,	Обязательно ли вычислять сумму всех цифр, чтобы
доказать, что число:
1)	390962700 делится на 3;
2)	909369927 делится на 9;
3)	360993300 не делится на 9;
4)	123123123123 делится на 3?
27,	Назовите наибольшее и наименьшее шестизначные
числа, которые делятся на
1)	2; 2) 3; 3) 5; 4) 9; 5) 10.
28*. Сколько чисел от 1 до 1000 не делятся ни на 2, ни
на 3?
29*, Какими	двумя	цифрами	оканчивается	число
1-2-3-...•13?
30*. Какими	тремя	цифрами	оканчивается	число
1-2-3-...-15?
31*, На сколько нулей оканчивается число 1-2-3-... • 100?
32, Разгадайте секрет фокуса. Если в одной руке кто-
нибудь спрячет трехкопеечную монету, а в другой —
двухкопеечную, то я могу легко определить, в какой
руке спрятана двухкопеечная монета. Для этого я
попрошу умножить число копеек в правой руке на
4, а в левой—на 5 и результаты сложить. Не на-
зывая мне сумму, нужно лишь сказать—четная она
или нет. Если получилась четная - сумма, то двух-
копеечная монета в левой руке, а если нечетная,
то в правой.
33, Если задача № 32 вызвала затруднение, то можно
добавить, что для фокуса подойдут и другие монеты:
1 к. и 2 к.; 10 к. и 15 к., но не подойдут монеты
10 к. и 20 к.
46
Умножать можно на 2 и 3, на 3 и 4, но нельзя
на 3 и 5. Научитесь выполнять этот фокус с различ-1
ными монетами.
§ 14. Деление с остатком
Число 14 не делится нацело на 3, так как нет на-
турального числа, произведение которого на 3 равно 14.,
В самом деле, будем перемножать последовательно
числа натурального ряда, на 3. Получим числа, распо-
ложенные в возрастающем порядке:’ 1-3 = 3, 2-3 = 6,
3.3 = 9, 4-3=12, 5-3=15, ...
Первое из этих чисел есть 3, второе больше первого
на 3, третье больше второго тоже на Зит. д. Среди
этих чисел нет числа 14. Однако среди них есть наи-
большее число, меньшее 14, это число 12 = 4-3. Чтобы
получить 14, надо прибавить к 12 число 2, которое
меньше 3.
Итак, справедливо равенство 14 = 4-3 + 2, где 4 —
наибольшее число, произведение которого на 3 меньше 14.
Это число называют неполном частным от деления 14
на 3, а число 2—остатком. Остаток меньше делителя.
Результат деления 14 на 3 записывают так:
14:3 = 4 (ост. 2).
Вот еще пример: 37 = 7-5 + 2, где 2 <5. Здесь 7 —
неполное частное от деления 37 на 5, а 2—остаток.
Поэтому можно записать: 37:5 = 7 (ост. 2).
Если одно число делится нацело на другое, то иногда
считают, что оно делится с остатком, равным нулю.
Разделить число а на число b—это значит найти
частное а-.Ъ, если а делится нацело на Ь, или найти не-
полное частное и остаток, если а не делится нацело на Ь.
Для малых чисел деление производят в уме,, а для
больших—уголком. Рассмотрим несколько примеров.
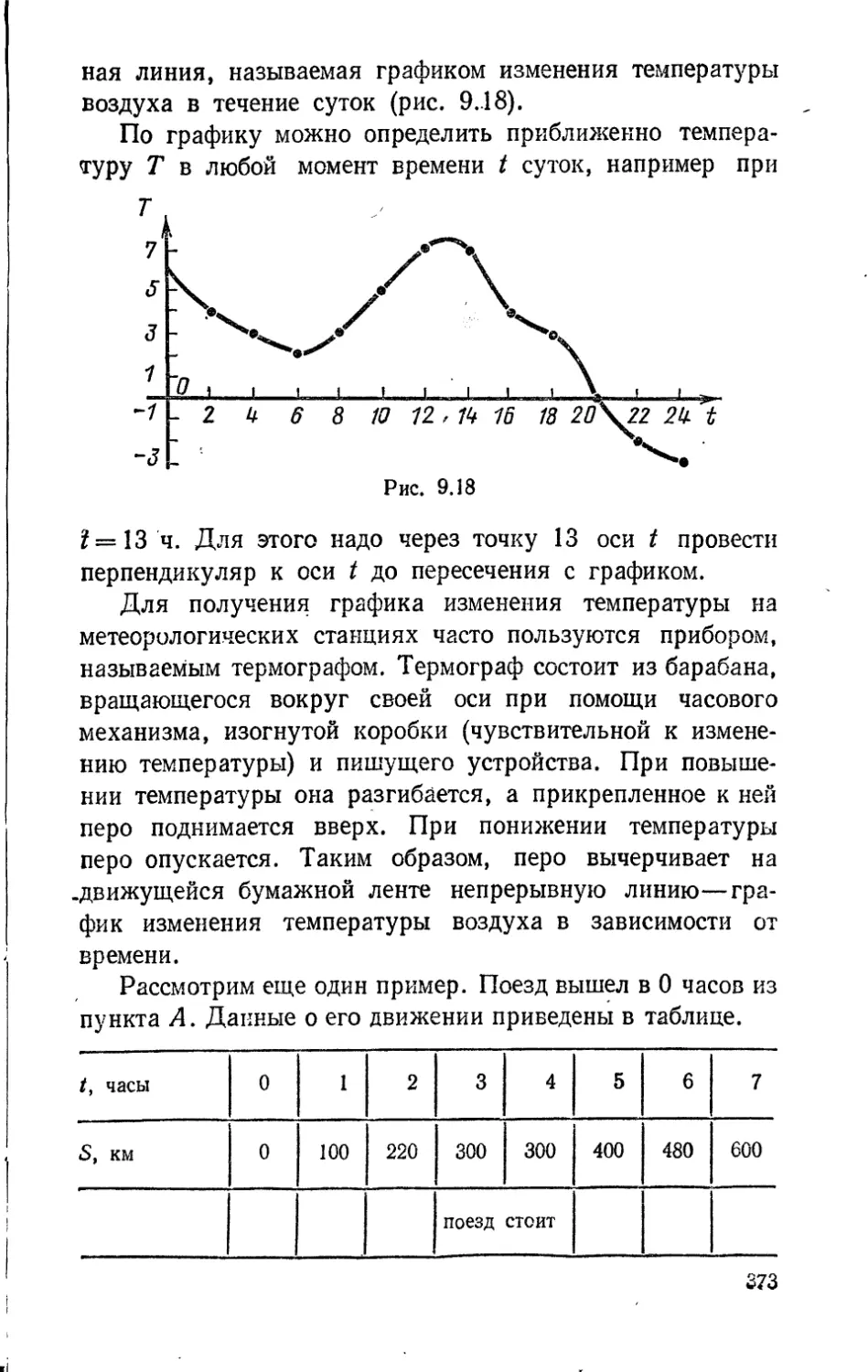
Пример. Разделить 42 на 3.
42:3 = (30+ 12):3 = 30:3+ 12:3 = 10 + 4 = 14.
Пример. Разделить 356 на 4.
356:4 = (320 + 36):4 = 320:4 + 36:4 = 80 + 9 = 89.
47
Такое деление записывают обычно коротко—уголком:
42 I	3	356 I	4
I	14	9L	89
12 1 * *	36 1
*~12	~~36
о	о
Аналогично выполняют деление уголком на двузнач-
ное, трехзначное и т. д. числа.
Пример. Разделить 14688 на 36.
14688 I 36
!44.- 408
28 1
—00
288
~'288
0
14 тысяч не делится на 36 нацело. Будем делить на 36
число сотен—146 сотен. 146:36 = 4 (ост. 2). Теперь не-
обходимо разделить остаток от деления сотен—2 сотни и
8 десятков, т. е. 28 десятков, на 36. 28:36 = 0 (ост. 28).
Остается разделить остаток от деления десятков—28
десятков и 8 единиц, т. е. 288 единиц, на 36. 288:36 = 8.
Таким образом, 14 688:36 = 408.
Пример. Разделить 1409 на 7.
_ 1409 | 7_
I4— 201	>-
0
•~0
9
~~7
2—остаток
Делим на 7 число сотен—14 сотен. 14:7 = 2 (ост. 0).
Делим на 7 число десятков—0 десятков. 0:7 = 0.
Делим на 7 число единиц—9 единиц. 9:7=1 (ост. 2).
Таким образом, 1409:7 = 201 (ост. 2).
УПРАЖНЕНИЯ
Выполните деление с остатком:
1) 49:8;
4) 118:23;
7) 453:6;
2) 73:8;
5) 400:57;
8) 368:5;
3) 58:7;
6) 487:17;
9) 588:13.
48
2.	Какой остаток может получиться при делении на-
турального числа на 2; на 3; на 4; на 7?
3,	Ученик выполнил деление: 148:15 = 8 (ост. 24).
. В чем заключается его ошибка? Выполните деление
верно.
4.	На доске написано несколько примеров на деление
с остатком. Делимые стерли и вместо них написали
буквы. Как найти делимые?
1)	а: 12 = 3 (ост. 1);	2) &:26 = 7 (ост. 4);
3)	с: 18 = 5 (ост. 2);	4) А:48 = 5 (ост. 47).
5.	Определите делители:
1)	56:а = 11 (ост. 1); 2) 93:Ь = 2 (ост. 3);
3)	146 :с = 12 (ост. 2); 4) 228:d = 3 (ост. 3)'.
6.	Определите неполное частное:
1)	76:12 = а (ост. 4);	2) 156:16 = & (ост. 12);
3)	808:35= Л (ост. 3); 4) 442:29 = d (ост. 7).
7,	Какой остаток получится от деления числа
L2-3-4-5-6.7-8-910+ 1
на 2; на 3; на 4; на 5; на 6; на 7; на 8; на 9; на 10?
Какой остаток получится при делении этого числа
на 100?
8.	В вазе лежат яблоки. Их надо разделить поровну
между двумя, тремя, четырьмя детьми, дав каждому
наибольшее возможное число яблок. Сколько яблок
может остаться в вазе в каждом случае?
9.	Какой наибольший остаток может получиться, если
число разделить на 2, 3, 4, 5?
Какой наименьший остаток может получиться во
всех случаях?
10.	Выполните действия:
1)	6324:102+ 11285:305;
2)	2628:36 + 972:36.
11*, Семь девочек играли в прятки. Они решили, что
первой будет водить та из них, которая окажется
25-й при счете по кругу. Вера начала счет от себя:
1, 2, 3, ... Катя, не дожидаясь окончания счета,
сказала: «Я вожу». Как она догадалась? Какой
номер был у Кати в начале счета?
12*, Найдите наименьшее число, которое при делении на
3, 5 и 7 дает в остатке:
1) 1;	2) 2;	3) 0.
13*. Найдите наименьшее число, которое при делении на
3, 4, 5, 6, 7 дает в остатке 1.
4 С. М, Никольский и др.
49
2)
14,	Объясните, как выполнено деление:
2187 I 26
208 - 84
107 1
104
3 (ост.)
3222 | 9
~45
72
*~72
0
15.	Выполните деление:
1)	861:7;	2) 1872:8;	3) 2144:6;
4)1742:13; 5)3685:15; 6)12363:13.
16.	Вычислите:
1) 18147:23; 2) 18600:24; 3) 9576:21;
4) 560:80;	5) 900:30;	6) 7200:900;
7) 24000:800;	8) 5400:600;	9) 6300:700.
17. Вычислите частное:
1)	5180:140;	2) 28600:520; 3) 129600:320;
4)	263 900:1300;	5) 54 720:90;	6) 192 290:670.
18.	1)	12 423:123;	2)	98532:322;	3)	140751:351;
4)	17 145:135;	5)	67176:311;	6)	80772:381;
• 7)	56 088:456;	8)	114 103:943;	9)	101952:236.
19.	Произведение четырех чисел равно 23625. Три пер-
вых числа равны друг другу, и их сумма равна 45.
Найдите четвертое число.
20.	Вычислите:
1)	1470:21:7-20;	2) 1 470: (21:7) - 20;
3)	336:7 + 5—4;	4) 336:(7 + 5) —4;
5)	336:(7 + 5 —4);	6) 336:7 + (5 —4).
§	15. Числовые выражения
Число 4 можно записать в виде суммы (3+1), разно-
сти (9—5), произведения (2-2), частного (12:3), степени
(22) или более сложными способами:
12:2—2,	3-(12—11)+1,	4а—36:(5а—11-2)
и т. д.
Запись, в которой используются только числа, знаки
арифметических действий и скобки, называется числовым
выражением. Числовые выражения могут быть довольно
сложными. Их упрощение, т. е. постепенное выполнение
действий и приведение числового выражения к наибо-
лее простой форме—числу, нередко требует серьезных
усилий.
со
Для правильного упрощения числовых выражений мало
знать правила вычисления результатов отдельных дейст-
вий. Нужно еще знать порядок выполнения этих действий.
Если в числовом выражении требуется выполнить только
сложение и вычитание или только умножение и деление,
то эти действия выполняют по порядку слева направо:
1	2	3	1 2 3 4
8—3 + 5+10;	7-8:2:45.
Если в числовом выражении требуется выполнить умно-
жение и деление, а также сложение и вычитание, то сна-
чала выполняются умножение и деление, а потом—сложе-
ние и вычитание, так как при записи умножения и деле-
ния скобки не пишут, но подразумевают их (см. заме-
чание на с. 26):
4	1 5 2 3	6
15 + 48:6-3-52:26 + 3;
1 4	2 5	3
7-9—12:3+ 12:12.
Если в числовом выражении есть степень с натураль-
ным показателем, то сначала требуется вычислить ее и
только после этого приступать к выполнению действий:
62 + 52—10:5 = 36 + 25—10:5.
Если в числовом выражении есть скобки, то сначала
выполняются все действия в скобках, а потом за скобками:
5	3	6	4	1	2
15 + 48:6—3-(52:26 + 3).
Изменять принятый порядок действий можно только
в тех случаях, когда это позволяют законы сложения и
умножения:
1	3	2	2	1
48-26 + 52-26 = 26.(48+52).
Мы уже знаем, почему нельзя число делить на нуль.
Про числовые выражения, которые содержат деление на
куль, говорят, что они не имеют смысла, например,
3: (4-5—20)=3: (20—20) = 3:0. Выражения3:0, 3:(20—20),
3: (4-5— 20) не имеют смысла.
4*	51
УПРАЖНЕНИЯ
1. Упростите выражение:
1) 117 + 73—50—90+ 12;	2) 3-15-4:9:20.8.
2. Определите порядок действий и упростите числовое
выражение:
1) 28-2 + 4;	2) 28-(2 + 4);
3) 100:4 + 6;	4) 100:(4 + 6);
5)	320—64:8+ 16;	6) (320—64):8+ 16.
3.	Упростите числовое выражение:
1)	320—(64:8+16);	2) 45+ 24-5 —(59—9);
3)	98-72:9—(35 + 55) :3;
4)	200:(333:3 —И) + 48.
4.	Вычислите:
1)	848 + 6—756: (45—45:5);
2)	48:4+1200:(75—75:5);
3)	9 + 252:(108:18—6);
4)	1 + 654—324: (48:12—4).
5.	Прочитайте выражения, используя названия «сумма»,
«разность», «произведение», «частное», «квадрат {числа,
суммы, разности и т. д.)»:
1)3+15;	2)15—3;	3)15-3;
4)	15:3;	5) (3 + 5)а;	6) (15—З)2;
7)	(15-3)’;	8) (15:3)а;	9) 32 + 152;
10)	82 + 92;	11) 92—7”;	12) 102—92.
6.	Прочитайте выражение:
1)	а + 5;	2)	а—Ь\	3)	а-.Ь-,
4)	а-Ь;	5)	(а + Ь)2;	6)	(а—Ь)2;
7)	(а-ЬУ;	8)	(а:Ь)2;	9)	(а + д)3;
10)	а2 + Ь2;	И)	а2—52;	12)	а3 + &3.
7,	Запишите и вычислите:
1)	сумму чисел 49 и 54; сумму чисел 145 и 73;
2)	разность чисел: а) 59 и 44; б) 145 и 73;
3)	сумму квадратов чисел: а) 5 и 4; б) 7 и 3;
4)	квадрат суммы чисел: а) 5 и 4; б) 10 и 6;
5)	разность квадратов чисел: а) 5 и 3; б) 10 и 6;
6)	квадрат разности чисел: а) 5 и 3; б) 10 и 6;
7)	сумму кубов чисел: а) 4 и 3; б) 5 и 4;
8)	куб суммы чисел: а) 4 и 3; б) 5 и 4;
9)	разность кубов чисел: а) 5 и 4; б) 4 и 2;
10)	куб разности чисел: а) 5 и 4; б) 4 и 2.
8,	Вычислите:
1)	(714:7—100)*;	2) (824:8—102)*;
3)	(954:9—636:6)”;	4) (758—658)2:(38 +62)2.
9,	В двух комнатах было 56 человек. Когда в первую
пришли еще 12 человек, а во вторую—8 человек, то
Б2
в комнатах стало поровну человек. Сколько человек
было в комнатах первоначально?
10,	В двух комнатах было 56 человек. Когда из первой
вышли 8 человек, а из второй—12, то в комнатах
осталось одинаковое число человек. Сколько человек
было в каждой комнате первоначально?
11,	На двух полках 48 книг. Когда с первой полки сняли
10 книг, а на вторую поставили 12 книг, то на пол-
ках оказалось одинаковое число книг. Сколько книг
стояло на полках первоначально?
12,	В трех вазах стояло 36 гвоздик. Когда из первой
вазы во вторую переставили 3 цветка, то во всех ва-
зах гвоздик стало поровну. Сколько гвоздик было
в каждой вазе первоначально?
§ 16. Вычисления с помощью микрокалькулятора
В настоящее время широкое распространение для руч-
ных вычислений получили микрокалькуляторы. Они по-
зволяют практически мгновенно выполнять арифметиче-
ские операции.
Ввод данных и команд в микрокалькулятор осуществ-
ляется нажатием клавиш. Мы будем пользоваться кла-
вишами
1	2	3	4	5
6	7	8
для ввода чисел,
— X . 4- для ввода знаков действия,
для вывода на экран результата действия,
для сброса (очистки экрана).
Заметим, что вывести результат операции на экран
можно нажатием любой клавиши
вместо клавиши в . Этим пользуются при вычислении
с несколькими числами. В случае ошибки нажмите кла-
вишу с и повторите все действия сначала.
53
О назначении некоторых других клавиш мы расска-
жем позже.
1. Вычислим сумму 12345 + 67890.
Нажмите клавиши в следующем порядке:
2
На экране по мере нажатия клавиш мы увидим первое
слагаемое 1 2 3 4 5, потом второе слагаемое 67890,
потом сумму 8 0 2 3 5.
Итак, 12345 + 67890 = 80235.
Аналогично выполняются и другие арифметические
операции. Запишем их кратко.
2. 7549—825
7549	—	825	=
От вет. 6 7 2 4.
3. 48x571
4	8X5
7	1	=
Ответ. 27408.
4. 10148:236
10	14
8	4-236
Ответ. 43.
При выполнении нужных операций клавишу = на-
жимают в конце, а промежуточные результаты вычисле-
ний выводятся на экран после нажатия клавиш +
— х
5. 139 + 256 + 354
1	3
4	=
9	+	256	+	35
Ответ. 749.
54
6. 99999—12345—54321
9
9
9	9	—
2	3	4
9
5	—	5	4	3	2
1
Ответ. 33333.
7. (7236—945): 9
 7	2	3
9	4	5:9
6
Ответ. 699.
Заметим, что микрокалькулятор выполняет и действия,
невыполнимые для натуральных чисел.
8. 7—9
7	—	9	=
Ответ —2.
При этом рядом с числом 2 на экране появляется
минус. Смысл этой операции мы объясним в главе III.
9. 6:4
6	+	4	=
Ответ. 1,5.
На экране появляется запись 1.5, показывающая, что
при делении с остатком неполное частное равно 1. Зна-
чение цифры 5 и запятой мы поясним позже.
УПРАЖНЕНИЯ
1.	Проверьте с помощью микрокалькулятора, что
1)	9735 + 7427 = 17162;
2)	808404—789789= 18615;
3)	951x753 = 716103;
4)	273429:369 = 741.
2.	Вычислите сумму. Сделайте проверку вычитанием:
1)	784 + 239;	2)	1917 + 69;
3)	928+1075;	4)	2509 + 7001.
3.	Вычислите разность. Сделайте проверку сложением:
1)	1111 — 987;	2)	2509—798;
3)	4000—3871;	4)	58976—6795.
55
4.	Вычислите произведение. Сделайте проверку делением:
1)	123x321;	2)	509x703;
3)	999x999;	4)	755x755.
б. Вычислите частное. Сделайте проверку умножением:
1)	153117:159;	2)	88825:209;
3)	252525:25;	4)	808707:101.
6.	С помощью микрокалькулятора проверьте равенства
0х9+1 = 1
1X9+2=11
12x9 + 3=111
123x9+4=1111
1234X9 + 5=11111
12345x9 + 6=111111
123456 x9 +7=1111111
1234567 x9 + 8=11111111
1Х8+1=9
12x8 + 2 = 98
123x8+3^=987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
123456 x 8 + 7 = 9876543
1234567 Х8 + 8 = 98765432
7.	Вычислите степень с помощью микрокалькулятора:
1) 752 = 75x75 = 5625.
7	5x75
2) 31Р; 3) 252;	4) 53;	5) 123.
8.	У многих микрокалькуляторов предусмотрено упро-
щение вычислений при возведении в степень. Напри-
мер, «Электроника БЗ-ЗО» позволяет вычислять степень
числа 2 так: 22 = 2х2.
2 X
Для получения 23 надо еще раз нажать клавишу
Получите таким способом
22; 23; 24; 26; 2е; 27; 28; 2е; 210.
9.	Вычислите З10; ЗЗ5.
10.	Вычислите с помощью микрокалькулятора неполное
частное и остаток от деления:
1) 48 на 5. Решен и е. 4
8
5
На экране получим 9,6—неполное частное 9. Вычис-
лим остаток: 48—5x9 = 48—45 = 3.
45:5 = 9 (ост. 3).
2) 3596 на 47; 3) 2958 на 328; 4) 7253 на 259.
56
§ 17, Представление натуральных чисел
на координатной полуоси
Отрезок, длину которого принимают за единицу, на-
зывают единичным отрезком. При помощи данного еди-
ничного отрезка измеряют длины других отрезков.
Зададим луч, выходящий из точки О в направлении,
отмеченном стрелкой, и единичный отрезок. На луче от
начальной точки О отложим один за другим несколько
отрезков единичной длины. Полученные точки обозначим
числами	0,	1,	2,	3,	4,	5,	...	(рис.	1.7).
О	1	2	3	4	5	6
।_____i_____t_।___i_____i____।__
Рис. 1.7
Мы построили координатную полуось. С помощью ко-
ординатной полуоси натуральные числа и нуль изобра-
жаются точками.
Начальную точку О называют еще нулевой точкой или
точкой 0 (нуль). Говорят еще, что точка О имеет коор-
динату 0 (пишут: 0(0)). Следующие точки называют со-
ответственно: точка 1, точка 2, и т. д.
Координатная полуось напоминает* нам линейку, на
которой отмечены числа 0, 1, 2, 3, 4 и т. д., с той лишь
разницей, что любая линейка ограничена (конечна), а
координатная полуось неограничена (бесконечна).
Мы не можем полностью изобразить бесконечную ко-
ординатную полуось, но можем себе ее представить (во-
образить).
Произвольное натуральное число п изображается на
координатной полуоси точкой, расстояние от которой
до нулевой точки равно п. Эту точку называют точкой
п или точкой с координатой п.
Например, на рис. 1.7. отмечена точка А с коорди-
натой 5. Пишут: Л (5). Длина отрезка ОА равна 5. Пи-
шут: О Л —5.
57
Обычно координатную полуось изображают слева на-
право. В этом случае точка, имеющая большую коорди-
нату на координатной полуоси, расположена правее.
УПРАЖНЕНИЯ
1,	Дана координатная полуось. Некоторые ее точки обо-
значили буквами (рис. 1.8). Укажите координаты точек
А, В, С, D, Е. Найдите расстояние от этих точек до
нулевой точки. Например, А (2), О А = 2.
0^	1	2	3	6.	5	6
I----1----1---1----1----1---(-*-
О	Е .	А	С	В	D
Рис. 1.8
2,	Постройте координатную полуось с единичным отрез-
ком 1 см (2 клетки тетради). Отметьте точки 0, 1, 2,
3, 4, 5, 6, 7. Обозначьте некоторые точки буквами
так, чтобы получилось Л (5), В(3), С(1).
3,	Какая из точек Л (7), В (100), С (56) расположена на
координатной полуоси правее других?
4.	Назовите три точки, расположенные левее, и три точ-
ки, расположенные правее точки:
1)	7;	2) 13;	3) 100;	4) 998.
5,	Сколько точек на координатной полуоси отмечено
между точками:
1)	0 и 9;	2) 4 и 14;	3) 90 и 120?
6,	На координатной полуоси отметьте точки 0, 1, 2,
3, ..., 12. Выделите цветом точки, соответствующие
четным числам. Какие точки не выделены цветом?
7.	Кузнечик прыгает вдоль координатной полуоси попе-
ременно на 5 единичных отрезков вправо и на 3 еди-
ничных отрезка влево. Сможет ли он за несколько
прыжков из точки 0 попасть в точку 6?
—I--1---1—н—।---------1--1—
198В 1987 ,	- а а+1
Рис. 1.9
8,	На рис. 1.9 изображена часть координатной полуоси.
Назовите изображенные на ней точки.
58
9.	Улитка за день поднимается на 4 м, а за ночь опу-
скается на 2 м. За сколько дней она поднимется на
вершину столба высотой 8 м?
§ 18. Исторические сведения
Способ обозначения чисел называется системой счис-
ления. Исторически у разных народов в разное время
употреблялись различные системы счисления. У перво-
бытных народов не существовало развитой системы счис-
ления. Еще в 19-м веке у многих племен Австралии и
Полинезии было только два обозначения—для числа
«один» и числа «два». Зти обозначения они комбинировали
в пределах шести. Число «три» они называли два да
один, число «четыре»—два да два, число «пять»—два,
два и один, число «шесть»—два, два и еще два. А числа,
большие шести, они не различали и называли словом
«много».
Египтяне за 3000 лет до нашей эры применяли, в
сущности, десятичную систему счисления. Число 345 за-
писывалось так:
s s SA Л Л Л1 I 11 I,
где I-единицы, !\—десятнц, сотни
Десятичная система, которой широко пользуются в
настоящее время во всем мире, более совершенна. Вме-
сто палочек (|), взятых от одной до девяти, используют
цифры 1, 2, 3, 4, 5, 6, 7, 8, 9. Для обозначения десят-
ков, сотен и т. д. не нужны новые значки, так как те
же цифры используют и для записи десятков, сотен и
т. д. Одна и та же цифра имеет различные значения в
зависимости от места (позиции), где она записана. Бла.
годаря этому свойству современную десятичную систему
счисления называют позиционной. Десятичная позицион-
ная система счисления позволяет записывать сколь угодно
большие натуральные числа.
Народы пришли к этой системе постепенно. Она за-
родилась в Индии в 5-м веке. В 9-м веке ею уже вла-
59
дели арабы, в 10-м веке она дошла до Испании, а в 12-м
веке появилась и в других странах Европы, но широкое
распространение получила лишь в 16-м веке.
Долгое время развитие позиционной системы тормози-
лось отсутствием в ней числа и цифры нуль. Только
после введения в математику нуля система стала совер-
шенной.
В России десятичная система счисления начала рас-
пространяться в 17-м веке. До этого времени числа за-
писывались буквами славянского алфавита. Числа от 1
до 9 записывали так:
"А’,'Б, Т, Д, Т, 5, '%, и, -ё-
Для чисел ставили особый знак (титло), чтобы
отличать их от слов:
1-10, А 1-11, Б 1-12,.. , К-20, К А-21,...,
Л-30, М-40	О -100 , ОА-101,...
1 (•> I
Интересно, что числа от 11 (один—на десять) до 19 (де-
вять— на десять) записывали так же, как и говорили,
т. е. «цифру» единиц ставили до «цифры» десятков. Если
число не содержало десятков, то «цифру» десятков не
писали.
В других странах имелись системы счисления с дру-
гими основаниями — 5, 12, 20, 60. Например, древнева-
вилонская система счисления была шестидесятиричная.
Следы этой системы сохранились и сейчас в единицах
измерения времени и величины угла (1 ч = 60 мин,
1 мин = 60 с).
Примером непозиционной системы счисления без нуля
может служить римская система. В ней числа от 1 до 20
обозначают так: I, II, III, IV, V, VI, VII, VIII, IX, X,
XI, XII, XIII, XIV, XV, XVI, XVII, XVIII, XIX, XX.
Однако для записи больших чисел требуются новые обо-
значения:
50—L, 100—С, 500—D, 1000—М.
60
Запишем в римской системе число 1917: MCMXV1I или
MDCCCCXVII.
Если меньшая цифра стоит после большей, то она
прибавляется к большей: MD=1500, XVII = 17; если
меньшая цифра стоит перед большей, то она вычитается:
СМ—900, IV—4. Римскую запись чисел используют и
сейчас для обозначения веков, глав в книгах и т. д.
Современные электронно-вычислительные машины при-
способлены к вычислению в двоичной системе счисления,
основанной на обозначении чисел двумя цифрами 0 и 1.
Для примера запишем в двух системах числа от 1 до 9:
Двоичная система
0
1
10
11
100
101
ПО
111
1000
1001
Десятичная система
0
1
2 = 2
3 = 2+1
4 = 2*
5 = 2* + 1
6 = 22+2
7 = 22 + 2+1
8 = 23
9 = 23 + 1
Таблицы сложения и умножения однозначных чисел
в двоичной системе очень просты:
0 + 0 = 0;	1 + 0=1
0x0 = 0;	1x0 = 0:
1 + 1 = 10;
1Х1«1.
Поэтому и выполнение действий с числами, записанными
в двоичной системе счисления, не представляет больших
трудностей:
1)	, 101 + 110 1011	2) ,111 + 101 1100	3)	111 + 111 1110	4)	1111 101 1010	В) 101 ” 11 13
6)	101 х 11 , 101 + 101	7)	1.11 х 101 . 111 + 111			
	1111	100011			
УПРАЖНЕНИЯ
1.	Используя древнеегипетскую систему счисления:
1)	прочитайте запись числа
V VA Л A i 11 ПН.
61
2)	запишите номер этой страницы.	I
2,	Используя римскую систему счисления:
а)	прочитайте: первый печатный учебник по матема- ;
тике (Арифметика Л. Ф. Магницкого) был выпущен ;
в России в начале XVIII века;	<
б)	запишите год своего рождения и текущий год.
8,	Запишите числа от 11 до 29 в старой русской системе ¥
счисления. Чем объясняется различный порядок напи- f
сания «цифр» в числах 23 и 13?	£
4« В двоичной системе счисления запишите числа' от 10 j
до 20.	|
5, Выполните действия в двоичной системе счисления: |
1)1101+1;	2)1101 + 11;	3)1101 — 1;	I
4) 1101 — 11;	5) 1101x11;	6) 1101x101.
На одной из старых улиц Москвы стоят два дома, на |
фасаде которых обозначена дата их постройки:	I
1) MDCCCCV; 2) MDCCCLXXXXIX.
В каком году построен каждый дом?	|
7, Упростите запись чисел в римской системе счисления |
(упр. 6), учитывая, что четыре одинаковые цифры f
подряд обычно не пишут.	|
9 ВОПРОСЫ для ПОВТОРЕНИЯ	|
• ПО МАТЕРИАЛУ ГЛАВЫ I	f
-lr
1.	Какие числа называются натуральными? Является ли нуль I
натуральным числом?	?
2.	Существует ли наименьшее натуральное число? Существует |
ди наибольшее натуральное число?	|
3.	Почему известная нам десятичная система счисления назы- |
вается позиционной?	|
4.	Скольких цифр достаточно для записи любого натурального |
числа в десятичной системе счисления?	|
5.	Сформулируйте правила сравнения натуральных чисел. 1
6.	Какие числа называются целыми неотрицательными?	|
7.	Сформулируйте переместительный закон сложения, запишите |
его для чисел а и Ь,	1
8.	Сформулируйте сочетательный закон сложения, запишите его I
для чисел а, Ъ и с.	|
9.	Что значит из числа а вычесть число’6?	|
10.	Как найти неизвестное слагаемое?	|
11.	Как	найти	неизвестное	уменьшаемое?	I
12.	Как	найти	неизвестное	вычитаемое?	i
13.	Сформулируйте переместительный закон умножения, запиши- j
те его для чисел а	и Ь.	|
62	I
14.	Сформулируйте сочетательный закон умножения, запишите его
для чисел а,Ьпс.
15.	Сформулируйте распределительный закон, запишите его для
чисел а, b и с.
16.	Что значит число а разделить на число
17.	Как найти неизвестный множитель?
18.	Как найти неизвестное делимое?
19.	Как найти неизвестный делитель?
20.	Сформулируйте признаки делимости на 2, 3, 4, 5, 9, 10.
21.	Сформулируйте определение степени с натуральным показа-
телем.
22.	Сформулируйте правила порядка действий.
УПРАЖНЕНИЯ
1.	Вычислите:
1)	53-2+44;	2)48:16+13-4;
3)	320 — 56-2+120:6;	4) 53.(2 + 44);
5) 320—(56-2+120:6); 6) (48:6+13)-4,
2.	Вычислите:
1)	26—(53—48)-4—4;	2) 48— (31 — 15).2— 2;
3) 66—(65—47):6 + 3;	4) 54;(13—10)-2+36.
3.	Сколько раз используется цифра 9 в записи первых ста нату-
ральных чисел?
4*. В строку записали числа 1, 2, 3, 4, 5, >.., 97, 98, 99. Потом
запятые стерли и получили огромное число. Сколько в нем цифр?
Сколько раз в его записи используется цифра 3? Найдите сумму
цифр этого числа?
5, Вычислите:
1) (5+2)2;	2) (9—8)3;	3) 5 + 22;
4) 52+22;	5) 92—8; -	6) 92-82.
6.	Запишите число 4 двумя двойками (3 способами).
7.	Запишите двумя одинаковыми цифрами число:
1)	4; 2) 1; 3) 27; 4) 256.
8.	Вычислите степени числа 10 с показателями от 1 до 6. Запиши-
те без вычислений степени числа 10 с показателями от 7 до 10.
9.	Используя четыре цифры 3, знаки арифметических действий и
скобки, можно получить любое число от 0 до 10. Например,
3+3—(3+3) = 0,	(3+3):(3+3) = 1 и т. д.
Найдите другие решения для 0 и 1, а также решения для
остальных чисел от 2 до 10.
10.	Используя четыре цифры 8, составьте числовое выражение, рав-
ное:
1)	1; 2) 2; 3) 3; 4) 4; 5) 6; 6) 7; 7) 8.
11.	С помощью четырех восьмерок составьте числовое выражение
равное; 1) 9; 2) 10.
63
12.	Вычислите:
1)	б2—52 + 32—22;	2) 13-f-22-{-З1 — 23;
3)	(82:16 — 2)2 + 23;	4) (92:27—2)-52.
13.	Запишите следующие числа в виде степени: 27; 125; 243.
14.	Сколько чисел в натуральном ряду от 1 до 125; от 1 до 99; от
100 до 125? Сколько чисел в натуральном ряду между числами
294 и 451?
15.	У колхозника было несколько поросят и несколько ягнят оди-
накового веса. Пионер спросил, сколько весит один поросенок
и один ягненок. Колхозник сказал, что три поросенка и два
ягненка весят 22 кг, а два поросенка и три ягненка весят 23 кг.
Сколько весит один поросенок и один ягненок отдельно?
16.	(Старинная задача.) Крестьянин принес лукошко яиц. Его спро-
сили: «Много ли яиц у тебя в. лукошке?» И крестьянин отве-
тил: «Когда я перекладывал яйца в лукошко парами, то одно
яйцо было в остатке. Когда я перекладывал их по три, по че-
тыре, по пять, по шесть — всегда оставалось одно яйцо. А когда
я перекладывал по семь яиц, то остатка не было.» Сколько яиц
было в лукошке?
17.	Четвероклассник увидел в тетради старшего брата число 51
— Что означает восклицательный знак?—спросил он.
— Это не восклицательный знак. Запись п! (читается: эн — фак-
ториал) означает произведение натуральных чисел от 1 до п.
Например, 51 = 1 •2*3«4‘5= 120.
Вычислите 21, 31, 4!, 61, 71.
18.	С помощью микрокалькулятора вычислите
81, 91, 101, 111, 121, 131.
19.	Старший брат выписал из справочника число 151, но случайно
поставил кляксу на одну цифру.
151= 130|674568000.
Какая эта цифра? Обязательно ли для поиска ответа вычислять
произведение 1»2*3'.*.«14«15? А если бы клякса закрыла две
цифры?
20*. Докажите признак делимости на 4:
Если сумма последней цифры и удвоенной предпоследней цифры
числа делится на 4, то и число делится на 4.
64
Глава II. МЕТРИЧЕСКАЯ СИСТЕМА МЕР
§ 19. Измерение отрезков
Ученик IV класса и его сестра—десятиклассница ре-
шили подсчитать число шагов от дома до школы. Полу-
чилось, что одно и то же расстояние равно 300 шагам
брата и 200 шагам сестры. Очевидно, что разные резуль-
таты получились из-за того, что сестра измеряла рассто-
яние большими шагами, чем брат.
В таких случаях говорят, что были использованы
различные единицы измерения.
Возьмем в качестве единичного отрезок длины 1 см.
Тогда измерение удобно производить при помощи санти-
метровой линейки.
Пусть задан отрезок АВ, который надо измерить.
Приложим к нему шкалу сантиметровой линейки, сов-
местив ее нулевую точку О с точкой А отрезка. Если
при этом окажется, что точка В совпадает с некоторым
делением шкалы, например, с отметкой 5, то говорят,
что длина отрезка АВ равна 5 см, и пишут АВ = 5 см
АВА	В
Г”Т."I	I	1 1 " Т-1-1-—	г-!-1-1	।	।	-1-----1-
0	1 2	3	5	В	7	О	1	2	3 If	S 3'7	8	_
Рис. 2.1	Рис. 2.2
(рис. 2.1). Если нет, то можно указать два деления,
между которыми находится точка В, например, 5 и 6
(рис. 2.2).
Точная длина АВ нам осталась неизвестной. Однако
мы видим, что величины 5 см и 6 см отличаются от длины
С. М. Никольский и др.	65
АВ не более чем на 1см. Их называют «приближениями»
или «приближенными значениями длины АВ с точностью
до 1 см», записывают	i д
АВ т 5 см, ЛВ«6см г
и говорят, что длина АВ приближенно равйа 5 см или
6 см с точностью до 1 см.
Так как 5 см < АВ < 6 см, то еще говорят, что 5 см
и 6 см приближают АВ с точностью до 1 см соответст-
венно с «недостатком» и «избытком».
На практике широко пользуются также понятием при-
ближения с «округлением». Поясним его на данном при-
мере.
То из делений шкалы 5 см и 6 см, которое располо-
жено ближе к В, называется «приближением длины АВ
с точностью до 1 см с округлением», а если В находится
посредине между этими делениями, то приближением
длины АВ с точностью до 1 см с округлением принято
называть большее из указанных делений, т. е. 6 см. На-
пример, на рис. 2.2 ЛВ«6 см с округлением, а на
рис. 2.3 ЛВ«5 см с округлением.
А	В
« 1 I 1 I-1-1—г*—г
0. 1 2 3 U 5 6
Рис. 2.3
Пример 1. Длина отрезка АВ равна 275 см. Найти
его приближение с точностью до 1 дм (10 см) с недостат-
ком, избытком и округлением.
Решение. АВ = 275, см « 27 дм с недостатком;
АВ = 275 см « 28 дм с избытком и округ-
лением.
Пример 2. Расстояние между двумя городами равно
628 км. Найти его приближение с точностью до ста ки-
лометров с недостатком, избытком и округлением.
Решение. 628 км«600 км с недостатком, и округ-
лением;
628 км« 700 км с избытком.
66
УПРАЖНЕНИЯ
1.	С помощью сантиметровой линейки измерьте (рис. 2.4)
длины отрезков АВ, CD, КР с недостатком и избыт-
ком с точностью до 1 см. Определите для каждого
отрезка его длцну (с точностью до 1 см) приближенно.
А	ВС	В К	Р
н----—--------1 I-------1 I--------------1
Рис. 2.4
2.	Начертите в тетради три произвольных отрезка. С по-
мощью сантиметровой линейки определите приближен-
но их длину (с точностью до 1 см).
3.	Расстояние, от Москвы до Владивостока 9302 км. Най-
дите его приближение с точностью “до 1000 км с не-
достатком, избытком и округлением.
§ 20. Величины. Исторические сведения
Такие понятия, как длина, площадь, объем, вес, на-
зываются величинами. Величина есть результат измерения,
она определяется числом, выраженным в определенных
единицах. Для обозначения величины пишут это число,
а рядом—название единицы. Например,
5 см, 10 кг, 12 км, 4 т, 5 мин.
Одна и та же величина в разных единицах выража-
ется разными числами. Например,
5 см = 50 мм, 1 ч = 60 мин, 2 кг = 2000 г.
В древней Руси пользовались такими единицами
длины:
пядь—расстояние между вытянутыми большим и ука-
зательным пальцами руки; это расстояние колеблется от
18 до 23 см;
локоть—расстояние от конца среднего пальца руки
До локтя; это расстояние колеблется от 38 до 46 см;
сажень—различали «простую» (примерно 152 см или
4 локтя), «маховую» (примерно 176 см) и «косую» (при-
мерно 213 см) сажени.
S*	67
г Д XVI—XVII веках появились новые яшнипы дли-
ны: верста, аршин, четверть и вершок;,
.1 верста «в 500 саженям» 1067 м, . го
1 сажень — 3 аршинам » 2 м,
. 1 аршин = 4 четвертям»71 см,	£
1 четверть = 4 вершкам» 18 см.
§ 21. Метр
В СССР и в большинстве стран мира за основную
единицу длины принимается метр.
В городе Севре (Франция) в Международном бюро
мер и весов в специальном помещении, где поддерживав
ется постоянно температура 0°С, на специальных под-
ставках лежит стержень, сделанный из весьма твердого
сплава платины и иридия. На нем имеются две отметки.
Расстояние между ними по международному соглашению
и принято считать основной единицей измерения длин и
называть метром. Зтот стержень и считается эталоном
(образцом) метра.
Во многих странах мирз в соответствующих помеще-
ниях находятся тщательно изготовленные копии указан-
ного эталона. У нас в стране эта копия хранится во
Всесоюзном исследовательском институте метрологии
имени Д. И. Менделеева.
История метра такова. В 1792 году Парижская ака-
демия наук решила по возможности точно измерить длину
земного меридиана, проходящего через Париж; Отдель-
ные части этого меридиана были фактически измерены, а
длина других частей была вычислена на основе этих из-
мерений теоретически. В результате большой работы,
которая продолжалась 7 лет, была найдена длина Па-
рижского меридиана в существовавших тогда француз-
ских мерах длины—туазах.
Парижской академией наук было решено ввести новую
единицу длины—метр, равную одной десятимиллионной
доли четверти Парижского меридиана, найденного ука-
занным путем. Решено было также изготовить эталон
С8
метра, который п хранится теперь в городе Севре. Была
введена также так называемая метрическая система мер,
в основу которой положен метр. Она оказалась очень
удобной, хорошо приспособленной к десятичной системе
счисления. В дальнейшем и другие страны мира стали
использовать метр и вообще метрическую систему мер.
Наша Советская страна перешла на метрическую си-
стему сразу же после Октябрьской революции. Старые
аршины, версты, сажени окончательно забыты и пред-
ставляют тёперь только исторический интерес.
Итак, метр есть одна десятимиллионная часть четвер-
ти Парижского меридиана. Это не совсем точно—на са-
мом деле метр есть одна десятимиллионная часть приб-
лиженной длины, которая получилась как результат из-
мерений четверти Парижского меридиана, проведенных
Парижской академией наук в конце XVIII века.
В настоящее время существуют и другие эталоны
длины, более надежные, чем металлический стержень.
Об этих эталонах вы узнаете в старших классах на уро-
ках физики.
УПРАЖНЕНИЯ
1.	Веревку разрезали на части. При этом сделали 6
разрезов. Сколько частей получилось?
2.	Вдоль дорожки парка через равные промежутки по-
сажены деревья. Володя насчитал от первого, до вто-
рого дерева ровно 5 шагов. Сколько шагов от пер-
вого до третьего дерева; от второго до четвертого;
от третьего до десятого?
3.	Вдоль дороги от дома до школы посажено 20 де-
ревьев. Расстояние между деревьями по 2 м. Миша
вычислил расстояние от первого до последнего де-
рева так: 20-2 = 40 (м). В чем ошибка? Решите за-
дачу правильно.
4.	От первого этажа до второго 18 ступеней. Сколько
ступеней от первого до пятого этажа?
б*. Имеются бревна длиной 4 м и 5 м. Сколько бревен
по 4 м и по 5 м надо распилить, чтобы получить
42 бревна по 1 м и сделать наименьшее число рас-
пилов?
69
§ 22. Метрические единицы длины
Метр состоит из 10 дециметров, т. е. 1 дециметр есть
одна десятая часть метра.
Дециметр состоит из 10 сантиметров, т.- е. 1 санти-
метр есть одна десятая часть дециметра или одна сотая
часть метра.	\ .
Сантиметр состоит из 10 миллиметров, т. е. 1 мил-
лиметр есть одна десятая часть сантиметра, одна сотая
часть дециметра и одна тысячная часть метра.
Записывают: 1 м=10 дм, 1 дм =10 см, 1 см=10мм,
1 м = 10 дм =100 см=1000 мм.
Пример.
2358 мм = 2м Здм 5 см 8 мм = 2 м 35 см 8 мм,
15 м 48 см 4 мм= 15 м 4 дм 8 см 4 мм= 15484 мм.
Для измерения больших длин введена единица длины
1 километр, равная 1000 метрам. Пишут: 1 км = 1000 м.
Очень большие расстояния—астрономические—выра-
жают в виде степеней 10 или в виде произведения неко-
торого числа, большего 1, но меньшего 10 на определен-
ную степень 10. Например,
20000000000000000000 м = 2-101# м = 210“ км,
так как 1 км= 10* м.
Очень малые длины измеряют микронами и микроми-
кронами’.
1 мм = 1000 микронов,
1 микрон =1000 микромикронов.
В науке приходится иметь дело с еще меньшими рас-
стояниями. Чтобы выразить их, указывают, какую часть
микрона они составляют.
УПРАЖНЕНИЯ		
1. Заполните пропуски:	мм; 3) 1 дм= .	
1) 1м=...дм; 2) 1см=...		.. см;
4) 3 м = ... дм; 5) 12 см = ..	. мм; 6) 24 дм =	..см.
2. 1) 40 см= ... дм; 2) 620дм = .	.. м; 3) 50 мм = ..	. см;
4) 6 м = ... см; 5) 8 дм = ...	мм; 6) 900 мм = .	.. дм.
70
1 км = ... см; 2) 1 км = ... мм; 3) 12 км =
1 км 300 м= ... м; 5) 12 км 312 м= ... м;
6 км! 60 м = ... м.
1000 м = ... км; 2) 12000 м = ... км;
4252 м = ... км;
6900 м км ... м;
7506 м = ... км ... м;
12350 м = ... км ... м;
100000 м = ... км ... м.
12 дм = ... м ... дм;
62 см= ... дм ... см;
263 дм == ... м ... дм;
255 мм = ... дм ... см ... мм.
м;
6. Выполните действия с величинами:
6 см 3 мм 2) । 7 дм 8 см
3 см 2 мм 1 дм 2 см
3) ,5м 60см
"^5 м 54 см
4)	4 км 250 м 5)	7 км 250 м 6) _12км 425 м
Зкм 100 м Зкм 550 м	560 м
7.	Одна сторона треугольника равна 5 см, вторая в 2 раза
больше, а третья на 3 см больше первой. Найдите пери-
метр (сумму длин сторон) треугольника.
8.	Одна сторона треугольника равна 18 см, вторая в 3 раза
меньше, а третья на 5 см меньше, чем первая. Най-
дите периметр треугольника.
9.	Две стороны треугольника имеют длины 6 ди и 8 дм.
Найдите третью сторону, если известно, что периметр
этого треугольника равен 24 дм.
10.	Периметр треугольника равен 46 м. Одна сторона тре-
угольника равна 11 м, вторая на 4 м больше. Найдите
третью сторону треугольника.
11,	После того как велосипедист проехал 5 км 360 м, ему
осталось проехать на 3 км 420 м больше, чем он уже
проехал. Какой путь проедет велосипедист?
12.	Найдите периметр треугольника АВС, у которого
1)	АВ =12 см 4 мм, ВС на 2 см Эмм больше АВ,
а АС на 1 см 8 мм меньше АВ;
2)	АВ = 3 дм, ВС на 12 см меньше АВ, а АС на ПО мм
больше АВ.
13.	Из города в противоположных направлениях выехали
велосипедист и легковая машина. Какое расстояние
будет между ними, если
1)	велосипедист проехал 12 км, а машина—64 км;
2)	велосипедист проехал 15 км 600 м, а машина —
70 км 800 м?
71
§23. Прямоугольник	’ i
Четырехугольник, у которого все углы прямые, назы-
вается прямоугольником.
На рис. 2.5 изображен прямоугольник ABCD. Верх-
няя и нижняя его стороны называются основаниями. Они
равны между собой.
Принято считать, что слово «основание» обозначает не
только отрезок, но и его длину.
Боковые стороны прямоугольника называют высотами.
Они равны между собой. Длины их также называются
высотами. Стороны прямоугольника называют еще длиной
и шириной прямоугольника.
Точки, в которых пересекаются стороны прямоуголь-
ника, называются вершинами.
Если все стороны прямоугольника равны между собой,
то такой четырехугольник называется квадратом. Квад-
рат называется единичным, если длина его стороны равна
единице. Про единичный квадрат говорят, что он имеет
площадь, равную одной квадратной единице. Например,
квадрат со стороной 1 см имеет площадь 1 кв. см или 1 см*.
Читается: «один квадратный сантиметр».
Если прямоугольник можно разрезать на S единичных
квадратов, то говорят, что он имеет площадь, равную S
квадратным единицам.
Например, на рис. 2.6 изображен прямоугольник с ос-
нованием а = 3 см и высотой & = 5 см. Его можно разре-
зать на 3-5=15 единичных квадратов со стороной 1 см.
Следовательно, его площадь S = 3 см-5 см= 15 см*. Пишут
72
еще: S=3-5 = 15 (см2) и читают: «15 квадратных, санти-
метров». „
Площадь прямоугольника равна произведению основа-
ния на высоту.
S=a-b (кв. единиц),
где а и b—длины сторон, выраженные натуральными
числами.
Замечание. Вторую степень числа называют квад-
ратом числа. Это название связывают с тем, что площадь
квадрата есть вторая степень длины его стороны.
УПРАЖНЕНИЯ
1.	С помощью чертежного треугольника проверьте, яв-
ляется ли угол прямым (рис. 2.7).
Рис. 2.7
2,	С помощью чертежного треугольника постройте пря-
моугольник, стороны которого равны 3 см и 2 см.
3.	Какой из* четырехугольников, изображенных на
рис. 2.8, является прямоугольником; квадратом?
4.	Какой четырехугольник называется прямоугольником?
Какой прямоугольник называется квадратом?
5.	Постройте прямоугольник ABCD со сторонами:
ЛВ = Зсм, AD — 4cm. Какова длина CD? Какова
длина ВС? Определите площадь ABCD.
6.	На рис. 2.9 изображено 9 прямоугольников, из них
5 квадратов. Сколько прямоугольников изображено
на рис. 2.10? Сколько из них квадратов?
73
7,	Девочка начертила на асфальте прямоугольник для
Игры в «классики» и разбила его на 8 квадратов
(рис. 2.11). На самом деле квадратов получилось не-
сколько больше. Сколько всего получилось квадратов?
Сколько всего получилось прямоугольников?
	
	
Рис. 2.9
4	5
<У,	: 6
2	7
1	Со '
Рис. 2.11
8.	Какой квадрат называется единичным? Чему равна
площадь квадрата со стороной 1 км; 1 см?
9.	Определите площадь прямоугольника ABCD, если
1) АВ = 6 см, ВС = 5 см; 2) ВС — Зм, CD— 12 м;
3)	ЛР = 8мм, В А = 4 мм; 4) СВ == 10 км, CD = 5 км.
10.	Найдите площадь квадрата со сторонами:
1)	1 см; 2) 2 см; 3) 3 см; 4) 5 см; 5) 10 см.
11,	Найдите площади фигур, изображенных на рис. 2.12.
12.	Расстояние между городами равно 36 км. Два пут-
ника вышли из этих городов навстречу друг другу.
Какое расстояние будет между ними, если
1) первый прошел 12 км, а второй—15 км;
2)	первый прошел 16 км, а второй—20 км;
3)	первый прошел 20 км, а второй—25 км?
13, Три села А, В и С связывает грунтовая дорога
(рис. 2.13). Расстояние между А и В равно 6 км,
I f п
л в	с
Рис. 2.13
74
а между В и С—20 км. Из сел А и В вышли пут-
ники? и отправились в село С. Какое расстояние будет
между' ними, если
1)	первый путник (идущий из А) прошел 5 км, а вто-
, рой путник (идущий из В) прошел 3 км;
2)	первый прошел 10 км, а второй—6 км;
3)	первый прошел 15 км, а второй—9 км?
§ 24. Единицы площади
Площадь Квадрата равна второй степени длины его
стороны. Площади различных фигур измеряют в квад-
ратных единицах.
Мы знаем следующие единицы длины—их еще назы-
вают линейными единицами: 1 мм, 1 см, 1 дм, 1 м, 1 км.
Рассматривая квадраты, стороны которых имеют пере-
численные длины, мы получим следующие единицы пло-
щади:
1 мм2—квадратный миллиметр,
1 см2—квадратный сантиметр,
1 дм2—квадратный дециметр,
1 м2—квадратный метр,
1 км2—квадратный километр.
Так как 1см=10мм, то 1 см2 = 10 мм-10 мм—100 мм2.
Аналогично,
1 дм2 = 10 см -10 см= 100 см2,
1м2 = 10 дм-10 дм = 100 дм2,
1 км2 = 1000 м • 1000 м = 1000 000 м2.
Используя степень числа 10, квадратный километр
можно записать так:
1 км2 = 10* м2.
Для измерения небольших земельных участков оказа-
лось удобным ввести специальную квадратную единицу —
1 ар. Пишут: 1 а. Это площадь квадрата со стороной
10 м. Так как 10 м-10м=100 м2, то эту единицу пло-
щади часто называют соткой.
Для измерения более крупных земельных участков
ввели еще одну квадратную единицу— 1 гектар. Пишут:
75
1 га. Это площадь квадрата со стороной КЮм,; т..е, 1 га=
= 100 м- 100 м = 10000 м2= 104 м2; 1 га« 100 а. <
На практике, измеряя площади, мы чаще всёго поль-
зуемся приближенными значениями величин. Например,
пусть требуется найти площадь S
прямоугольника ABCD (рис. 2,14).
Измерив его стороны АВ и AD,
мы получили АВ ж 22 см, AD «
« 34 см с недостатком (с точно-
стью до 1 см).
Так как длины сторон изме-
рены с недостатком, значит, пло-
Рис. 2.14
щадь S прямоугольника ABCD больше, чем 22-34 =
= 748 (см2), т. е. S > 748 см2.
Если мы возьмем длины сторон с избытком: А В «23 см,
AD « 35 см, то площадь S прямоугольника ABCD будет
меньше, чем 23-35 = 805 (см2), т. е. S<805 см2.
Получается, что площадь S прямоугольника ABCD
больше 748 см2 и меньше 805 см2. Это можно записать
так:
748 см2 < S < 805 см2.
Точность измерения площади в нашем случае: 805 —
— 748 = 57 (см2).
УПРАЖНЕНИЯ
1.	Чему равна площадь квадрата со стороной:
1)	1 см; 2) 1 м; 3) 10 м; 4) 100 м?
2.	Сколько квадратов со стороной 1 см содержится в квад-
рате со стороной:
1)	1 дм; 2) 1 м; 3) 10 м; 4) 1 км?
3.	Во сколько раз
1)	1	см2 больше, чем 1 мм2;	2)	1 дм2 больше, чем 1 см2;
3)	1	м2 больше, чем 1 дм2;	4)	1 а больше, чем 1 м2?
4.	Во сколько раз
1)	1	дм2 больше, чем 1 мм2;	2)	1 м2 больше, чем 1 см2;
3)	1	а больше, чем 1 дм2;	.4)	1 га больше, чем 1 м2?
5.	Сколько квадратных сантиметров содержится в
1)	1 дм2; 2) 1 м2; 3) 1а; 4) 1 га; 5) 1 км2?
6,	Во сколько раз увеличится площадь прямоугольника,
если одну его сторону увеличить в два раза; в три
раза?	г
7.	Во сколько раз увеличится площадь прямоугольника,
если .одну его сторону увеличить в два раза, а дру-
гую—в три раза?
8.	Во сколько раз увеличится площадь квадрата, если
его ЙЪрону увеличить в два; в три; в пять раз?
9.	Во сколько раз
1)	1 м2 меньше, чем 1а; 2) 1 см2 меньше, чем 1 дм2;
3)	1 а меньше, чем 1 га; 4) 1 га меньше, чем 1 км2?
10.	Заполните пропуски:
1)	1м2=...см2; 2) 1дм2=...см2;
3)	7 м2 =... дм2; 4) 8 см2 = ... мм2.
11.	1) 100дм2=...м2;	2) 200 мм2 = ... см2;
3)	16 дм2 = ... см2; 4) 25 га = ... м2.
12.	Сколько квадратных метров содержит 1 ар? Как
по-другому называется 1 ар?
Сколько квадратных метров содержат 2 гектара? Сколь-
ко аров содержит 1 квадратный километр?
13.	Колхозный сад имеет форму прямоугольника со сто-
ронами 1500 м и 400 м. Выразите площадь сада в квад-
ратных метрах; в арах; в гектарах.
14.	Сложите величины:
I)	Зга 12а 48м2	2) , 7 га 82а 26м2
‘6га18а22м2	+2га11а94м2
3)	, 17 га 48 а 56 м2	4) , 12 га 88 а 15 м2
+ 8га 64а 24м2	+ 17га 23а 88м2
15.	Каждая клетка шахматной доски является квадратом
со стороной 3 см. Определите площадь всех клеток
шахматной доски. Какую площадь занимают все чер-
ные клетки шахматной доски?
16.	Найдите периметр и площадь прямоугольника со сто-
ронами:
1)	5 дм и 60 см;	2) 7 см и 3 дм;
3)	8 дм и 1м;	4) 62 дм и 2 м.
17.	Составьте выражение для вычисления периметра пря-
моугольника со сторонами:
1)	35 см и 12 см; 2) 1 км 200 м и -750 м;
3)	а дм и 4 дм; 4) а м и & м.
18.	Прямоугольник имеет стороны Зсм и 5 см. Найдите
сторону квадрата, периметр которого равен пери-
метру данного прямоугольника.
19.	Прямоугольник имеет стороны 5 дм и 7 дм. Найдите
площадь квадрата, периметр которого равен пери-
метру данного прямоугольника.
77
20.	Даны прямоугольник со сторонами 24 см и' 18 см и
квадрат со стороной 12 см. Во сколько рая площадь
квадрата меньше площади прямоугольника?
21.	Колхозное поле имеет площадь 18 га, а огород около
дома колхозника—8 соток. Во сколько раз колхозное
поле больше огорода?
22.	Основание прямоугольника равно 8 см, а высота на
2 см больше. Найдите периметр и площадь прямо-
угольника.
23.	Даны площадь прямоугольника и одна из его сторон.
Нгйдите другую сторону:
-1) 48 см2 и 6 см; 2) 6 см2 и 60 мм;.
3) 120 дм2 и 150 см; 4) 5 га и 200 м.
доп	6м саО. 20м
о город	
12м	20м
Рис. 2.15
24, На плане земельного участка показаны дом, огород
и сад (рис. 2.15). Подсчитайте двумя способами пло-
щадь, занятую под сад и огород вместе.
§ 25.	Прямоугольный параллелепипед
Обычная комната, коробка конфет или кирпич могут
дать представление о прямоугольном параллелепипеде.
На рис. 2.16 изображен прямоугольный параллеле-
пипед ABCDA1B1C1DV Снизу, сверху и с боков он огра-
ничен гранями. Каждая грань есть часть плоскости —
прямоугольник. Нижняя и верхняя грани называются
основаниями прямоугольного параллелепипеда, остальные

Рис. 2.16
четыре грани называются боковыми
гранями. Всего граней 6.
Грани пересекаются по отрез-
кам—ребрам прямоугольного па-
раллелепипеда. Всего 12 ребер. Их
можно разделить на три группы.
В каждую группу входят четыре
ребра, равные между собой.
78
Точки, в которых пересекаются ребра, называются
вершинами прямоугольного параллелепипеда. Всего вер-
шин 8.
На рис. 2.16 ребра AD, АВ, AAt принадлежат раз-
личным граням, длины их называются соответственно
шириной^ длиной, и высотой прямоугольного параллеле-
пипеда.
Прямоугольный параллелепипед, у которого все ребра
равны, называется кубом.
УПРАЖНЕНИЯ
1.	Назовите предметы из окружающей обстановки, имею-
щие форму прямоугольного параллелепипеда.
2.	На рис. 2.17 изображен прямоугольный параллелепи-
пед. Назовите его грани, ребра, вершины, основания,
боковые грани, ширину, длину, высоту.
Сколько у прямоугольного параллелепипеда вер-
шин, ребер, граней?
3,	Постройте в тетради прямоугольник со сторонами 3 см
и 5 см. Обозначьте его вершины, начиная с левой йиж-
ней по часовой стрелке: A, Alt Dit D. Отступив от
каждой вершины на три клетки вправо и на две клетки
вверх, постройте четыре точки. Обозначьте их соот-
ветственно В, Bit С^, С. Достройте полученный чер-
теж до прямоугольного параллелепипеда. Назовите
его вершины, ребра, грани, основания, боковые грани,
ширину, высоту, длину.
4,	Какой прямоугольный параллелепипед называется
кубом? ‘	-	-
5,	Перечертите развертку куба на бумагу, вырежьте по
сплошной линии (пунктиром показаны линии сгиба).
Места склеек на рис.: 2.18 заштрихованы. Склейте куб.
79
§ 26.	Единицы объема “	'
Куб с ребром, имеющим единицу длины, называется
единичным кубом.	; ;
За единицу объема принимается объем единичного
куба.
Если прямоугольный параллелепипед можно разрезать
на К единичных кубов, то говорят, что его объем равен
К кубическим единицам.
На рис. 2.19 изображен прямоугольный параллеле-
пипед, у которого ширина 3, длина 4, а высота 2 ли-
нейные единицы. Мы видим, что прямоугольный паралле-
лепипед можно разрезать на 2 слоя, в каждом из кото-
рых 3-4=12 единичных кубов. Всего прямоугольный
параллелепипед содержит
(3-4)-2= 12-2 = 24 .
единичных кубов.
Заметим, что если ширина а, длина b и высота с пря-
моугольного параллелепипеда выражены натуральными
числами в одной единице измерения, то вычисление объема
сводится к нахождению их произведения:
V=a-&-c (куб. единиц).
Но а-b есть площадь основания, поэтому объем прямо-
угольного параллелепипеда может быть вычислен как
произведение площади основания на высоту:
V=S-c,
где S—площадь основания.
60
Объем куба с ребром 1 см называется кубическим сан-
тиметром л обозначается так: 1 см8.
АналбгтйУйо определяются другие кубические единицы:
1 см8 = 10 мм-10 мм-10 мм = 1000 мм®,
1 дм8 =	см'-1© см- ТО см =1000 см8,
1 м8 = 10 дм-10 дм-10 дм= 1000 дм8
или ' ' fч;!"
1 м8 = 100 см'• 100 см • 100 см = 1000 000 см*,
1 км8= 1000 м- 1000м-1000 м= 1000000000м8= 10е м8.
1 дм8 называют еще литром’. 1 л = Г дм8.
3 а меча н и е. Так как объем единичного куба, по
существу, есть произведение трех одинаковых множите-
лей, то слово «куб» стали использовать для обозначения
третьей степени числа.
УПРАЖНЕНИЯ
1.	На рис. 2.20 изображена кладка кирпичей. Подсчи-
тайте число кирпичей в кладке.
2.	На сколько единичных кубов может быть разделен
прямоугольный параллелепипед, изображенный на
рис. 2.21? Каков его объем?
3.	Вычислите объем прямоугольного параллелепипеда,
длина, ширина и высота которого соответственно
равны:
1)	1 м, 2 м, 3 м; 2) 20 дм, 3 м, 100 см;
3) 15 см, 2 дм, 1 м; 4) 16 дм, 3 м, 20 см.
4.	Аквариум имеет форму прямоугольного параллелепи-
педа, ширина которого 30 см, длина 45 см, высота
25 см. Сколько раз придется наполнять водой трех-
литровую банку, чтобы с ее помощью наполнить ак-
вариум на 20 см в высоту?
5,	Сколько кубических сантиметров содержится в 1 дм8;
в 1 м8; в 1 км8?
С. М. Никольский и др.	81
6.	Во сколько раз увеличивается объем куба при уве-
личении его ребра: в два раза; в три раза; в десять раз?
7.	Заполните пропуски:
1)	1м8®... дм8;	2)	1м*®... л;.,
3)	1дм8=...см8;	4)	1л=...см8;
5)	1см8=...мм3;	6)	1м8=...см8.
8.	Площадь пола в комнате_ 14 м8, а высота комнаты 3 м.
Какой объем занимает комната?
9.	Комната занимает объем 45 м8 и имеет площадь пола
15 м8. Какова высота комнаты?
10.	Комната занимает объем 48 м8, а ее высота равна 3 м.
Какую площадь имеет пол в комнате? Какова длина
и ширина комнаты, если пол имеет форму квадрата?
11,	Вычислите объемы фигур, изображенных на рис. 2.22.
Размеры указаны в сантиметрах.
•25
Рис. 2.22
12.	Окрашенный куб с ребром в 10 см распилили на ку-
бики с ребром в 1 см. Сколько среди них окажется
кубиков: с одной окрашенной гранью; с двумя окра-
шенными гранями, с тремя окрашенными гранями?
§ 27.	Единицы массы
Основная единица массы*)—грамм. По предложению
Парижской академии наук за 1 грамм принята масса 1 см*
воды при температуре 4 °C.
Тысяча граммов называется килограммом!
1 кг® 1000 г.
Таким образом, масса 1дм8 воды (1000 см8) составля-
ет 1 кг.
*) В обиходе массу называют весом и говорят, например, «вес
1 грамм» вместо «масса 1 грамм».
82
Тысяча Килограммов называется тонной'.
1 т = 1000 кг.
Масса 1 м8 воды составляет 1 т.
На практике часто используют еще одну единицу
массы—центнер'.
1ц=100кг.
Парижская академия наук организовала взвешивание
1 дм8 воды при 4 °C. Была изготовлена из металла гиря,
имеющая массу, весьма точно равную массе 1 дм8 воды.
Эта гиря хранится вместе с эталоном метра в г. Севре.
По ней, как по эталону, изготовлены точные ее копии,
которые хранятся во всех странах мира. У нас эта копия
вместе с другими эталонами-хранится в Институте метро-
логии имени Д. И. Менделеева.
УПРАЖНЕНИЯ
1.	Сколько кубических дециметров содержит 1л; 3 л?
2.	Какой объем воды при температуре 4 °C надо взять,
чтобы получить 1 кг воды; Зкг воды?
3.	Какой объем занимает 10 кг воды? Сколько килограм-
мов воды можно поместить в бак объемом 1 м8?
4.	Какой объем занимает 1 т воды при температуре 4 °C?
5.	Перепишите, заполняя пропуски:
1)	1	кг = ... г;	2) 2 т 525 кг = ... кг;
3)	1	т = ... кг;	4) 3 т 700 кг = ... г;
5)	3	т= ... г;	6) 12 т 50 кг= ... кг.
6.	Во сколько раз
1)	2	ц больше,	чем	2 кг; 2) 2 кг больше,	чем	4 г;
3)	5	т больше,	чем	500 кг; 4) 750 ц больше, чем	15 г?
7.	Известно, что 1 г—масса 1 см3 воды, 1 кг—масса 1 дм8
воды, 1 т—масса 1 м8 воды. Объясните, почему 1 т=
= 1000 кг, 1 кг= 1000 г?
8.	Что тяжелее—1 кг железа или 1 кг ваты?
§ 28.	Единицы времени
Любые процессы и движения происходят во времени.
Время одного движения можно измерять при помощи
времени другого движения, например, вращения Земли
вокруг ее оси.
6*	83
Время, в течение которого Земля совё'рЬаетполный
оборот вокруг своей оси, называется сутками. Сутки —
единица времени. Одни сутки содержат 24 Часа:
1 сутки = 24 ч.
Один час равен 60 минутам, а минута равна 60 се-
кундам'.
1 ч = 60 мин, 1 мин = 60 с, 1ч = 3б00с.
В науке основной единицей времени считается секунда.
Даже очень большие промежутки времени выражаются
в секундах с помощью степени числа 10.
Приходится иметь дело и с долями секунды. В совре-
менных спортивных соревнованиях различные достижения
(например, в беге, плавании и т. д.) измеряются в деся-
тых и даже в сотых долях секунды.
В обыденной жизни, в том числе в хозяйственной дея-
тельности наших государственных предприятий и учреж-
дений, пользуются такими единицами времени, как год,
месяц, неделя (эти названия вам знакомы) и еще квартал
и декада.
Год есть время обращения Земли вокруг Солнца с точ-
ностью до 5—6 минут. 1 год—365 суток и 6 часов.
По действующему во всем мире календарю считается,
что если номер года делится на 4 (например, 1988), то
этот год содержит 366 суток. Такие годы называются ви-
сокосными. А невисокосные годы содержат по 365 суток.
Указанная выше прибавка в 6 ч за четыре года состав-
ляет 24 часа, т. е. целые сутки, которые и приписывают
к високосному году.
Год делится на 12 месяцев. Так как 365 и 366 не де.
лится на 12, то пришлось распределить дни года между
месяцами неравномерно:
по 31 дню—январь, март, май, июль, август, октябрь,
декабрь;
по 30 дней—апрель, июнь, сентябрь, ноябрь; февраль
в зависимости от года содержит 28 или 29 дней.
Квартал содержит 3 месяца, декада—10 дней, неделя —
7 суток.
84
УПРАЖНЕНИЯ
1.	Сколько., минут содержат:
1)	2 ч; 2) 3 ч; 3) 5 ч; 4)' сутки?
2.	Сколько секунд содержат:
1)	2 ч; , 2) 3 ч; 3) сутки; 4) неделя?
3.	Вычислите сумму величин:
1)	3 ч 15 мин и 2 ч 12 мин;
2)	Зч20мин и 1 ч 40 мин;
3)	7 ч 43 мин и 2 ч 25 мин;
4)	2 ч 53 мин и 3 ч 48 мин.
4.	1) 3 мин 12 с и 1 мин 3 с;
2)	2 мин 10 с и 50 с;
3)	4 мин 42 с и 7 мин 53 с;
4)	8 мин 42 с и 6 мин 49 с.
Вычислите разность величин:
5.	1) 6 мин 20 с и 3 мин 15 с; 2) 9 мин 15 с и 4 мин 45 с;
6.	1) 6 мин и 3 мин 18 с; 2) 4 мин 28 с и 2 мин 56 с.
7.	Самолет поднялся в воздух в 12 ч 35 мин и нахо-
дился в полете 2 ч 40 мин. Когда приземлился са-
молет?
8.	Самолет поднялся в воздух в 14 ч 45 мин, а при-
землился в другом городе в 17 ч 10 мин. Сколько
времени продолжался полет?
9.	Сколько месяцев в году имеют по 30 дней?
Может ли в феврале быть 5 понедельников? Может
ли в феврале быть 5 понедельников и 5 вторников?
А в январе?
10.	Увеличьте:
1)	3	ч	15	мин	в	3	раза;	2)	1	ч	20	мин	в	4	раза;
3)	5	ч	24	мин	в	3	раза;	4)	2	ч	12	мин	в	7	раз.
11.	Уменьшите:
1)	3	ч	15	мин	в	3	раза;	2)	4	ч	48	мин	в	4	раза;
3)	6	ч	56	мин	в	2	раза;	4)	5	ч	55	мин	в	5	раз.
12.	Требуется распилить бревно на 6 частей. Каждый рас-
пил занимает 1 мин 30 с. Сколько потребуется вре-
мени на работу?
13.	Комбинат бумажных изделий установил новую машину,
которая за 1 мин выпускает 1050 м бумаги. На сколь-
ко метров бумаги в час новая машина выпускает
больше, чем старая, которая выпускала 750 м в ми-
нуту?
14.	Лифт поднимает с первого этажа на третий за 6 с.
За сколько секунд он поднимет с первого этажа на
пятый этаж?
85
О ВОПРОСЫ для ПОВТОРЕНИЯ
* ПО МАТЕРИАЛУ ГЛАВЫ II
1.	Объясните на примере, что называется приближенным значе-
нием длины отрезка с недостатком; с избытком; с округлением.
2.	Какую часть метра называют дециметром; сантиметром; мил-
лиметром? Что такое километр?
3.	Какой четырехугольник называется прямоугольником?
4.	Какой прямоугольник называется квадратом?
5.	Какой квадрат называется единичным? Что такое ар; гектар;
сотка; квадратный километр?
6.	Какой прямоугольный параллелепипед называется кубом? Какой
куб называется единичным?
7.	Как вычислить объем прямоугольного параллелепипеда, если
известны его ширина, высота и длина? Как вычислить объем прямо-
угольного параллелепипеда, если известны площадь его основания
и высота?
8.	Назовите единицы измерения длины в порядке их возрастания.
9.	Назовите единицы измерения площади в порядке их возрастания.
10.	Назовите единицы измерения объема и массы в порядке их
возрастания.
1L Что такое центнер; литр?
12. Назовите единицы измерения времени. Сколько секунд содер-
жит минута? Сколько минут содержит час? Сколько часов содержат
сутки? Сколько суток содержит год?
УПРАЖНЕНИЯ
1.	Измерьте длины сторон треугольников на рис. 2.23. Найдите
периметры треугольников.
2.	На прямой отметьте точки А, В и С так, чтобы
1)	AS = 2 см, SC==3 см; сколько решений имеет задача?
2)	АВ = 2 см, АС=1 см; сколько решений имеет задача?
3.	Отрезки AS, AC, AD, А/С имеют общую точку А. Постройте эти
отрезки. Сколько решений имеет задача?
86
4.	Измерьте длины отрезков на рис. 2.24 с недостатком; с избытком;
с округлением (с точностью до 1 см).
|----------1	I----------------4	I----------------------1
А	В	С	Я	К.	Р
Рис. 2.24
5.	Запишите вое отрезки, изображенные на рис* 2.254 Сколько отрез-
ков изображено на рис. 2.26?
А	В	CD
I---Н—---1--—{
Рис. 2.25
6.	На глаз разделите отрезки АВ и CD (рис. 2.27) на две равные
части. Проверьте свой глазомер с помощью линейки.
А	ВС	И
1---------1 I-------------------1
Рис. 2.27
7.	Постройте в тетради три произвольных отрезка. Разделите каж-
дый из них на три равные части. Проверьте свой глазомер
с помощью линейки.
8.	Число 48 увеличили в 4 раза. На сколько увеличили это число?
9.	Число 48 уменьшили в 4 раза. На сколько уменьшили это число?
10.	Число 48 увеличили в 2 раза, потом увеличили на 2. Полученное
число уменьшили в 2 раза, потом уменьшили на 2. Получится ли
в результате этих изменений число 48? Какое число получится?
11.	Проверьте, верно ли равенство:
1)	З34-43 + 53х=63; 2) 113+123+138+143 = 203;
3)	412+432+453 = 5555?
12.	В 12 одинаковых коробках лежат 144 карандаша. Сколько каран-
дашей в 13 таких же коробках?
13.	За 3 ч автомат на кондитерской фабрике заворачивает 345 кон-
фет. Сколько конфет завернет тот же автомат за 5 ч?
14.	За 3 кг сахарного песку заплатили 2 р. 70 к. Сколько нужно
заплатить за 2 кг сахарного песку?
15.	Токарь может обточить 72 заготовки за 3 ч, а его ученику на
выполнение этой работы требуется в два раза больше времени.
За сколько часов они обточат 72 заготовки при совместной работе?
16.	На первом станке можно отштамповать 480 деталей за 4 ч, а на
втором станке на это потребуется в 3 раза больше времени. За
какое время можно отштамповать 480 деталей при совместной
работе двух станков?
87
17.	Вычислите:
1)	723.36 +77616:99; 2) 46585:77+52866:66.
18.	Может ли сумме цифр натурального числа быть равной сумме
цифр квадрата этого числа?
19.	Может ли сумма цифр натурального числа быть больше суммы
цифр квадрата этого числа?
20.	Какие цифры можно поставить вместо звездочек, если известно,
что число:
1)	7*8* делится на 9; 2) 7*8* делится на 18?
21.	Какие цифры можно поставить вместо звездочек, если известно,
что число 52*2* делится на 36?
22.	Докажите, что нельзя подобрать пять нечетных чисел, сумма кото-
рых равна 100*
23.	Из двух портов навстречу друг другу вышли два теплохода. При
встрече оказалось, что один из них прошел 512 км, а второй на
74 км больше. Каково расстояние между портами? В задаче не
сказано, что движение начато одновременно—влияет ли это усло-
вие на результат?
24.	Из села в противоположных направлениях выехали велосипедист
и мотоциклист. Через некоторое время велосипедист был на рас-
стоянии 18 км от села, а мотоциклист—35 км. На каком рас-
стоянии друг от друга были они в этот момент? В задаче не ска-
зано, что движение начато одновременно—влияет ли это условие
на результат?
25.	Какие величины нужно знать, чтобы найти:
I)	пройденный путь; 2) скорость движения?
26.	Найдите неизвестные величины:
№	Путь	Скорость	Время
1		200 км в час	6 мин
2		4 м в секунду	12 с
3	120 км		2 ч
4	18 км		3 мин
5	200 м		10 с
6	15 км	15 км в час	
7	3000 м	500 м в минуту	
8	480 м	12 м в секунду	
27. Из пунктов А и В одновременно навстречу друг другу вышли
два поезда. Поезд, идущий из А, имеет скорость 70 км в час,
а поезд, идущий из В, имеет скорость 80 км в час. Поезда встре-
тились в пункте С через 2 ч после начала движения. Найдите
расстояние от А до С, от В до С, от Л до В через С.
88
Глава Ш. ЦЕЛЫЕ ЧИСЛА
Рио. 3.1
§ 29.	Отрицательные целые числа
Термометр, изображенный на рис. 3.1, показывает тем-
пературу 7° тепла. Если температура понизится на 4°, то
термометр будет показывать 3° тепла. Уменьшению тем-
пературы соответствует действие с натуральны-
ми числами: 7—4 = 3.
Если температура понизится на 7°, то тер-
мометр покажет 0°: 7—7 = 0.
Если же температура понизится на 9°, то
термометр покажет —2° (2° мороза). Но ре-
зультат вычитания 7—9 не выражается целым
неотрицательным числом, хотя он имеет ре-
альный смысл.
Проиллюстрируем вычитание на ряде це-
лых неотрицательных чисел.
1)	От числа 7 отсчитаем влево 4 числа и
получим 3:
0, 1, 2, 3, 4„ 5, 6, 7, 8, 9, ...
Т I t
7—4 = 3.
2)	От числа 7 отсчитаем влево 7 чисел и получим 0:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ...
т l t	.
7—7 = 0.
Отсчитать же в ряду неотрицательных чисел от числа 7
влево 9 чисел нельзя. Чтобы действие 7—9 стало выпол-
89
нимым,. расширим ряд неотрицательных чисел. Для этого
запишем влево от нуля по порядку числа 2, 3..........
добавляя к каждому из них знак минус (—), который
будет показывать, что число стоит слева от нуля. Эти
числа читаются так: «минус один», «минус два»,- «минус
три» и т. д.:
.... —5, —4, —3, —2, —1, 0, 1, 2, 3, 4, 5, ...
Справа от числа 0 расположены натуральные числа,
которые еще называют целыми положительными числами.
Слева от числа 0 расположены целые отрицательные
числа.
Число 0 не является ни положительным, ни отрица-
тельным числом. Оно разделяет положительные и отрица-
тельные числа.
Полученный нами ряд чисел называется рядом целых
чисел. Таким образом, натуральные, целые отрицательные
числа и нуль образуют ряд целых чисел. Вправо й влево
этот ряд можно продолжать неограниченно.
УПРАЖНЕНИЯ
1.	Что означает запись: 5°, 0°, —4°, —7°?
2.	Используя знак минус (—), запишите:
1)	3° мороза; 2) 6° мороза;
2)	4° ниже нуля; 4) 15° ниже нуля.
3.	Установите на модели термометра: 5°, 6°, 0°, —1°, —7°.
4.	С помощью модели термометра определите, какая тем-
пература получится, если она увеличится:
1)	с 3° на 7°; 2) с 0° на 5°; 3) с 5° на 7°.
S.	С помощью модели термометра определите, какая тем-
пература получится, если она уменьшится:
1)	с 10° на 5°;	2) с 4° на 3°; 3) с 5° на 5°;
4) с 18° на 18°; 5) с 6° на 7°; 6) с 8° на 10°.’
6.	Устно определите, какая температура получится, если
она:
1)	повысится с 2° на 8°;	2) понизится с 5° на 6°;
3) уменьшится с 4° на 9°; 4) понизится с 0° на 3°.
7, Какое число в ряду целых чисел стоит ближе к числу 0:
1) 1 или 5;	2) 12 или 3; 3) —3 или —1;
4) —5 или —2; 5) —4 или 5; 6) 10 или —18?
8. Какие числа расположены в ряду целых чисел справа
от нуля?
90
Какие числа расположены в ряду целых чисел слева
от нуля? Являются ли число 0 положительным числом;
отрицательным числом? Является ли число 0 целым
числом?
9. Существует ли наибольшее целое число? Существует
ли наименьшее целое число? Какие числа называют
целыми?
§ 30. Правила знаков. Модуль числа
Считают, что если перед целым числом поставить знак
плюс (+), то это не изменяет самого числа. Например;
5 = +5, —5 = +(—5).
Ряд целых чисел можно записать так:
..., —4, —3, —2, —1, 0, +1, 4-2, +3, 4-4, ...
Целые числа, которые отличаются только знаком, на-
зываются противоположными. Например, 1 и -—1, —5 и 5,
10 и-—10 являются противоположными числами.
Если перед целым числом поставить знак минус (—),
то получается число, ему противоположное: —(4-1) =—1,
-(-2) = 4-2.
Единственным числом, которое не изменяется, если
перед ним поставить знак «—», является число 0:
0 = —0 = 4-0. Нуль считается противоположным самому
себе.
Число, противоположное числу а, обозначается —а.
Заметим, что —а может быть положительным, отрицатель-
ным числом и нулем. Например, если а = 4-2, то —а=—2, :
так как—(4-2) = —2; если а = —3, то—а = 4-3, так как
— (—3) = 4-3; если а = 0, то—а = 0, так как —0 = 0.
Введем новое понятие—модуль числа.
Модулем положительного числа называется само это
число. Например, модулем числа 4-3 является 4-3. Пишут: >
|4-3| = 4-3.
Модулем числа 0 является число 0. Пишут:
|0| = 0.
Модулем отрицательного числа называется противо-
положное ему число. Например, модулем числа —4
91
является число 4-4. Пишут:	nt--.
|_41 = 4-4.
Таким образом, модуль целого числа—положительное
число или нуль.
Модуль положительного или отрицательного числа по-
казывает, на каком месте от нуля (справа или слева)
стоит это число в ряду целых чисел. Противоположные
числа имеют одинаковый модуль'.
|4-3| = |-3| = 3, |-5| = |4-5| = 5,
|а| = | —а|.
УПРАЖНЕНИЯ
1.	Прочитайте числа —5,4-6,4-8, —10,0, 4-4, —0. Какие
из них являются целыми; целыми положительными;
целыми отрицательными числами?
Перепишите эти числа, изменяя перед каждым из них
знак на противоположный. Прочитайте полученные
числа. Как изменились числа? Все ли числа измени-
лись?
2.	С 8 часов утра до 12 часов дня температура увели-
чилась на 5°. Определите температуру в 12 часов,
если в 8 часов термометр показывал:
1) 20°;	2) 15°;	3) 10°;	4) 5°;	5) 0°;
6)	—5°; 7) —10°; 8) —15°; 9) —20°; 10) —25°.
3.	С 12 часов до 16 часов температура понизилась на 5°.
Определите температуру в 16 часов, если в 12 часов
термометр показывал:
1)	25°; 2) 20°;	3) 15°;	4) 10°;	5) 5°;
6) 0°;	7)	—5°;	8) —10°; 9) —15°; 10) —20°.
4.	Найдите модули чисел
4-2, —2, 4-5, —5, 4-8, —10, 4-Ю0, 4-0, —3.
5,	Найдите два различных числа, модули которых равны.
Для следующих чисел: 2, 5, —3, 10, —17 укажите
числа, имеющие те же модули.
6,	Назовите противоположные числа, модули которых
равны:
1) 2; 2) 7; 3) 0; 4) 8.
7,	Заполните пропуски:
1)	|4-1|=...; 2) |-61
3)	|01 =...; 4)|—13|=... '
92
8.	Вычислите:	-
1)	|-0|+|-6|; 2) |- 5}4-|4-3|;
3)	|-201-|-61; 4) |-17|-|-8|.
9.	Вычислите сумму:.
1)	I- 7| + |+5| + |+8| + |-10|;
2)	|-12| + |-12j+|4-10| + |-2°|.
10.	Всегда ли модуль числа равен самому числу, т. е.
|а| = а? Для каких чисел это равенство справедливо?
11.	Всегда ли модуль числа равен противоположному ему
числу, т. е. | а | = — а? Для каких чисел это верно?
12.	Для какого числа выполняются оба условия |а| = а
и |а| = —а?
§ 31. Сравнение целых чисел
Из двух целых чисел больше то, которое в ряду целых
чисел
.... -4, -3, -2, -1,0, +1, 4-2, +3, 4-4, ...
стоит правее.
Например,
1 > —1, —2 > —6, 0 > —5, —6 < —3, —10 < —2.
Отсюда следует, что любое положительное число больше 0,
а любое отрицательное число меньше 0; любое положи-
тельное число больше любого отрицательного.
Отрицательные числа удобно сравнивать с помощью
их модулей. Так как в ряду целых чисел отрицательное
число с большим модулем стоит левее, то из двух отри-
цательных чисел больше то, у которого модуль меньше-.
| —21 < | —61, значит, —2 > —6.
УПРАЖНЕНИЯ .
1.	Сравните числа:
1)	5 и 0;	2) —5 и 0; 3) 7 и 0;
4)	—7 и 0; 5) 8 и —7; 6) —3 и 100.
2.	Сформулируйте правила сравнения:
1)	целых чисел с нулем;
2)	положительных и отрицательных чисел;
3)	отрицательных чисел.
3.	Сравните числа и запишите сравнение с помощью
знаков >, < и =:
1)	—9 и —6;	2) —3 и —20;	3) —7 и —15;
93
4) —25 и —1; 5) —20 и 0;	6) 0 и —40;
7) —8 и 13;	8) 128 и —300; 9) —5 и —6.
4.	Для каких чисел верно утверждение: если а > Ь, то
|а| > |6|? Приведите примеры.
5.	Для каких чисел верно утверждением если а < Ь, то
|а| > |6|? Приведите примеры.
6.	Может ли быть так, чтобы а^Ь, но |а| = |6|?
Приведите примеры.-Как называются числа а и 6?
7.	Какая может получиться температура (положительная
или отрицательная), если она:
1)	с 5° увеличится на несколько градусов;
2)	с 10° уменьшится на несколько градусов?
Для каждого возможного случая приведите примеры.
8.	Найдите разность:
1)	+51-|-51; 2) 1—51-|+5|;
3)	+3|—I—3|; 4) |—3|—1+3|.
9.	Для какого числа —а = а?
10.	Маша по ошибке считает, что —а означает запись
отрицательного числа. Приведите примеры такого
числа а, чтобы —а было: 1) положительным числом;
2) отрицательным числом; 3) нулем. -
§ 32. Сложение целых чисел
Сумма целых чисел а и Ь есть число с, отстоящее
в ряду целых чисел от а на |&| чисел вправо, если b > 0,
и влево, если b < 0.
Пример. Определить сумму 3 + 8. Так как 8 > 0,
то от числа 3 в ряду целых чисел отсчитаем 8 чисел вправо:
2,— 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
t t t
+ 8
Таким образом, 3 + 8=11.
Пример. Определить сумму (—3) + (—8).- Так как
—8 < 0 и | —81 = 8, то от числа! —3 в ряду целых чисел
отсчитаем 8 чисел влево:
...» —11—Ю,—9,—8,—7,—6,—5,—4,—3,—2, ...
1_________________________ »
-8
Таким образом, (—3) + (—8) = — (3 + 8) =—11.
Рассмотренные примеры подтверждают правило;
14
Чтобы сложить числа одинаковых знаков, надо вы
числить сумму их модулей и поставить перед суммой
знак слагаемых.
Например, на основании указанного правила
::	7+ 9=+(7 + 9) = + 16= 16,
(-6) +(-8) = -(6 +8)------14.
При ме р. Определить сумму 5+(—2). Так как —2 < О
и | —21 = 2, то от числа 5 в ряду целых чисел отсчитаем
влево 2 числа:
.... —1, О, Г, 2, 3, 4, 5, 6, 7, ...
t___________________! t
-2
Таким образом, 5 + (—2) = + (5—2) = +3 = 3.
Пример. Определить сумму 5+(—8). Так как —8 < О
и |—81 = 8, то от числа 5 в ряду целых чисел отсчитаем
влево 8 чисел:
..., —4, —3, —2, — 1, 0, 1, 2, 3, 4, 5, 6, ...
t! t
-8
Заметим, что | —81 > 15 | и сумма получилась меньше нуля:
5 + (—8) = — (8—5) = —3.
Пример. Определить сумму (—7) + 3. Так как 3 > О,
то от числа —7 в ряду целых чисел отсчитаем -вправо
3 числа:
.... —7, —6, —5, —4, —3, —2, —1, ..;
т I t
+з
Таким образом,- (—7) + 3 = — (7—3) = —4. Заметим, что
|—7|>|3| и сумма получилась меньше нуля.
Рассмотренные примеры подтверждают правило:
Чтобы сложить два числа разных знаков, надо из боль-
шего модуля вычесть меньший модуль и перед разностью
поставить знак слагаемого, имеющего больший модуль.
Например, 17 +(—20) = — (20—17) = —3, так как
|-20| >|17|,
(—2)+ 1 = — (2 —1) =—1, так как |—2| > ] 11.
95
Сумма противоположных чисел равна нулю: а4-(— а)=0.
Например, 5 + (—5) = 0.
Для любого целого числа а: а4-0 = 04-а = а.
Например, 0 + (—3) = (—3)4-0 = —3.
6.
7.
8.
УПРАЖНЕНИЯ
1.	С помощью ряда целых чисел определите сумму:
1)	34-2; 2) 04-4; 3) (-3)4-(-2); 4) (-2)4- (-3).
2.	Используя правило сложения, вычислите:
1)	(+7)4-(+9)=4-(74-9) =-...;
2)	(-4)4-(-6)=-(4 + 6)=...;	;
3)	(-5) 4-(-6); 4) (-5) +(-9);
5)	(~б)4-(-1); 6) (- 1) + (-б).
3.	Устно найдите сумму:
1)	(-1)4-(-2); 2)(-2) + (-1);
3)	(—2)4-(—4); 4) (—5)4-(—1);
5)(-3) + (-8); 6) (-4) 4-(-Н).
4.	Упростите числовое выражение:
1)	(-102)4-(—98); 2) (—33) 4-(—167);
3) (—128) 4-(—12); 4) 6884-957;
5)	(—172) 4-(—118); 6) 694 4-738.
Например,
(—755) 4- (—983) = — (755 4- 983) =—1738. ,755
+983
1738
S. С помощью ряда целых чисел определите сумму:
1)	34-(-2); .2) 24-(-3); 3) (-4) 4-(+2);
4)	(-2)+ 4; 5) (-5)+ 7; 6) (-5)4-3.
Используя правило сложения, вычислите:
1)	7.4-(—6) = +(7—6) =+ 1 = 1, так как |7|>|—6|;
2)	(-18)4-12=—(18—12)=—6, так как 1—181>| 121;
3)	(-8)4-9;	4) 84-(-9);	5) 124-(-15);
6) (—13) 4-18; 7) (—2) 4-18; 8) 25 4- (—32).
Устно найдите сумму:
1) (-1) 4- 2; 2) 5 + (-2); 3) (-4) 4-1;	'
4) (-8)4-2; 5) 7 4-(-9); 6) (-10)4-4.
Вычислите:
1) 3594-(—483); 2) (—703)4- 117; 3) (—14)Н-864;
4) 151 4-(—87);	5) 17 4-(—256); 6) 476 4-(—253).
Например,
(—986) 4- 754 = — (986 — 754) = —232.	986
—754
232
f
I
96
§ 33.	Законы сложения целых чисел
Для любых целых чисел а, Ь, с выполняются пере-
местительный (коммутативный) и сочетательный (ассоциа-
тивный) законы сложения:
a+b — b + a, a + b + c = a + (b-\-c).
Переместительный закон сложения следует из правил
сложения. Ведь эти правила не зависят от порядка сла-
гаемых в сумме.
Например:
1)	-3 + (-5) = -(3 + 5) = -(5 + 3) = -5 + (-3);
2)	—7 + 2 = —(7—2) = 2 + (—7);
3)	—5 + 5 = —(5—5) = 5 + (—5).
Что же касается сочетательного закона, то его можно
вывести из определения суммы при помощи ряда целых
чисел. Например,
(2 4-5) 4-(—-3) — 4
и
2+ [5 + (-3)]=4,
следовательно,
(2 + 5) + (-3) = 2 + [5-Ь(-3)].
С помощью переместительного и сочетательного зако-
нов можно показать, что в сумме нескольких целых чисел
можно переставлять слагаемые и заключать их. в скобки
любым образом.
Например, верно равенство
а + & + с + ^ + п = (& + п) + (а + &4-с).
Докажем это:
а 4- Ь 4" с 4" k 4“ п (а 4- Ъ 4- с 4- &) 4- н ==
= п 4- (а 4- b 4- с 4- k) = п 4- [(а 4- Ъ 4- с) -f- =«
«= п 4- [fe 4- (а 4- b 4- с)] = (п 4- k) 4- (а 4- b 4- с) ж
«= (& 4- п) 4- (а 4- b 4- с).
4 С. М. Никольский и др.
УПРАЖНЕНИЯ
1.	Вычислите сумму:
1)	8+(-5)=+(8-5)=...; 2) -9 + 3=-(9-3)=...j
3)	40 + (—20);	4) —80 + 50;
5)	100 + (—99);	6) —70 + 65.
2.	1) 23+(—25) = —(25 — 23) = —2;
2)	—47—52;	3) 78 + (—96);	4)—95+117;
5)	13+ (—191); 6) 88+ (—105); 7) —102+220.
3.	Запишите и вычислите:
1)	сумму 17 и —23; 2) сумму —20 и 4;
3)	сумму числа, противоположного—13, и числа —25;
4)	сумму числа —26 и числа, противоположного —12.
4.	Заполните пропуски:
1)	3 +5+(—8) = [3 +(—8)1 + ...;
2)	6+... + (-1) = (-1) + Тб + (-2)];
3)	(-4) + ... + (—7).=2 +[...+ (-4)];
4)	(— 1)+... + ... — [3 + (—7)] + ...
5.	Упростите числовое выражение:
1)	(-1) + 2 + (-3) + 5 = 2 + 5 + (-1) + (-3) =
_=(2 + 5) + [(-1) + (-3)]=...;
2)	(—2) + (—4) + 2 + 5 + (—3) + 1 + (—3);
3)	10 + (—8)+ 2 + 5 +(—1)+ (—!) + (—3);
4)	(-4) + (-1) + 3 (-2) + (-3) + 9.
6.	Можно ли выписать в строчку три числа так, чтобы
сумма любых двух соседних чисел была положительна,
а сумма всех чисел была отрицательна?
7.	Можно ли выписать в строчку четыре числа так,
чтобы сумма любых двух соседних чисел была поло-
жительна, а сумма всех четырех чисел была отрица-
тельна?
8.	Можно ли выписать в строчку пять чисел так, чтобы
сумма любых двух соседних была положительна, а
сумма всех пяти чисел была отрицательна?
9.	Можно ли расставить в клетках таблицы, состоящей
из четырех строк и семи столбцов, целые числа так,
чтобы сумма чисел:
1)	в каждой строке была равной —14, а в каждом
столбце—равной —8;
2)	в каждой строке была равной —14, а в каждом
столбце—равной 8?
10.	Не вычисляя, прикиньте (с точностью до 1000)
результат. Проверьте прикидку вычислением:
1') 8520 + 3910 — 9535 ; 2) 1573 — 9050 + 708.
11.	1) Как изменится сумма, если одно из слагаемых
увеличить на 17?
98
2)	Как изменится сумма, если одно из слагаемых
уменьшить на 80?
3)	Как изменится разность, если уменьшаемое увели-
чить на 7?
4)	Как изменится разность, если вычитаемое умень-
шить на 5?
5)	Как изменится сумма, если одно слагаемое умень-
шить на 3, а другое увеличить на 7?
6)	Как изменится сумма, если одно слагаемое, уве-
личить на 10, а другое увеличить на '5?
7)	Как изменится разность, если уменьшаемое и вы-
читаемое уменьшить на 9?
8)	Как изменится разность, если уменьшаемое и вы-
читаемое уменьшить на 50?
9)	Как изменится разность, если уменьшаемое уве-
личить на 6, а вычитаемое уменьшить на 10?
12.	В булочную привезли 654 кг ржаного и белого хлеба.
После того как продали 215 кг ржаного и 287 кг
белого хлеба, того и другого сорта хлеба осталось
поровну. Сколько было привезено в булочную белого
и сколько ржаного хлеба?
13.	В двух магазинах было 452 холодильника. После
того как- оба магазина продали поровну холодиль-
ников, в одном осталось 72, а в другом—84 холо-
дильника. Сколько холодильников было в каждом
магазине?
14.	Сумма двух чисел равна 304, одно из чисел больше
другого на 50. Найти оба числа.
§ 34. Разность целых чисел
Разностью целых чисел а и Ь называется такое число
а—Ь, сумма которого с Ь равна а:
(а—b) + b — a.
Покажем, что разность а—b есть сумма числа а и числа,
противоположного Ь.
Чтобы доказать это, надок a-f-(—b) прибавить числоЬ;
а -|- (— &) -}- b — а -|- ((— Ь) + Ь) — а 4- 0 = а.
Таким образом, чтобы из одного числа вычесть другое,
надо к уменьшаемому прибавить число, противоположное
вычитаемому:
а—Ь = а + {—Ь).
4*
99
Например,
(-3) _ (-5) = (-3) + 5 = +(5-3) = 2,
2—7 = 2+ (—7) = — (7—2) = —5,
(—7)—2 = (-7) + (-2) = - (7 + 2) = -9,
О—О = О + (—О) = О + О = О.
УПРАЖНЕНИЯ
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Верно ли равенство:
1)22—9=14;	2) 7—12 = —5;
3) (—2)—(—3) = 1; 4) (—12)—! = —11?
Заполните пропуски:
1)	5-8= 5 +(-8)----(.. .);
2)	(_4)—3 = (-4) + (-3)  -(4 + 3) = ...;
3)	7—13 = 7 + (—13)=...;
4)	(—2)—7 = (—2) +(—7)= ...;
5)	(—1)—(—2) = (—1) +2= ...;
6)'(-8)-(-4) = ...
Вычислите разность:
1)9—10; 2)6—8;	3)4—10;
4)5—20; 5)6—11; 6)8—13.
1) 24—48;	2) 35— 47;	3) 64—71;
4) 91 — 119; 5) 102—89; 6) 67—105.
1) (—3)—7;	2) (—4)—8;	3) (-5)-2;
4) (—8)— 1+ 5)_(—10)—10; 6) (—20)—60.
6) (—200)—400.
3) 4—10;
2) 35— 47f 3) 64—71;_
3) (—5)—2;
1.) (-3)-?;
1) (—28)—17;
Используя равенство а—Ь=а+(—Ь), упростите запись:
1) 5 +(-2) = 5-2; 2) (-1) + (-3) = (-1)-3;
3) 15 +(-12);	4) (-6)+ (-14);
5) 100+ (—200);	6) (—30)+ (—6000).
Здесь и далее скобки у первого слагаемого можно
2) (—4)—8;
2) (—5)—91; 3) (—92)—18;
4)/(—240)—14; 5) 50—105;	--
опускать.
1) (-1)-(-1)-----1 + 1; 2) 2—(—2); 3)(—3)—(—4);
4) (-5)-(-2);	5) 8—(—6); 6) 10-(-5).
Вычислите:
1) (—824)+ (—642);	2)	(—498)—(—402);
3) (—864)—(—164);	4)	(—1240)—200;
5) (—1000)—(—2500); 6) 80—(—10800).
1)	Разность числа 245 и числа, противоположного
числу —18;
2)	разность числа —14 и числа, противоположного
числу +15;
3)	разность числа 17 и числа —23;
4)	разность числа —24 и числа —25.
100
11,	Не вычисляя, прикиньте (с точностью до 100) резуль-
тат.' Проверьте прикидку вычислением:
1)	854—956 + 254; 2) 786 + 392—607.
12.	Можно ли выписать в строчку шесть чисел так,
чтобы сумма любых трех соседних чисел была поло-
жительной, а сумма всех чисел была отрицательной?
13.	Если а и b—натуральные числа, то можно ли
утверждать, что их сумма и разность также являются
натуральными числами?
14.	Если а и b—целые числа, то можно ли утверждать,
что их сумма и разность также являются целыми
числами?
15.	Какие из четырех арифметических действий не всегда
выполняются для натуральных чисел а и Ь?
16.	1) Представьте в виде суммы следующие числовые
выражения:
2—3; —2—3; —4—(—5).
2)	Представьте в виде разности следующие числовые
выражения:
2 + 5; —2 + 3; —4 +(—5).
17.	Найдите неизвестное число х, если
1)	х+8=8;	2)5 + х=5;	3)	12—х=12;
4)	х— 7=0;	5)6—х=0;	6)	12 + х = 0;
7)	х + 8=3;	8)5 + х=2;	9)	—7 + х =—10;
10) —7 + х=10; 11)8—х=—13; 12) 17—х = 28.
§ 35. Произведение и частное целых чисел
Произведением двух целых чисел называется произведе-
ние их модулей, взятое со знаком плюс (+), если эти
числа одинаковых знаков, и со знаком минус (—), если они
разных знаков.
Например,	7-(—3) = —(7-3) = —21;
—5-10 = —(5-10) = —50;
-5-(—10) = 5-10 = 50;
8-6 = 48.
Произведение целого числа а и нуля равно нулю,
а-0=0-а = 0.
Например,	7.0 = 0- 7 = 0;
—10.0 = 0.(—10) =0; -
0-0 = 0.
101
Из определения произведения целых чисел и выпол-
нимости переместительного и сочетательного законов умно-
жения для натуральных чисел следует, что эти законы вы-
полняются и для целых чисел:
a-b — b-a, (а-Ь)-с = а-(Ь-с).
Покажем это на примерах:
5-(—3) = — (5-3) = — (3-5) = (—3)5;
(5 • (-3)) • (-4) = - (5 • 3) • (-4) = (5 • 3) • 4 = -
= 5.(34) = 5((-3).(-4)).
Если |а| делится на |Ь| нацело, то частное целых
чисел а и Ь равно частному их модулей, взятому со зна-
ком плюс (+), если эти числа одинаковых знаков, и со
знаком минус (—), если они разных знаков.
Например,
40:8 = 5;
(—20): (—5) = +(20:5) = 4-4 = 4;
8:(—2) = —(8:2) = —4;
(—12):3 = —(12:3) = —4.
Если частное а'.Ь умножить на Ь, то получится а\
(a:b)-b = a.
Например,
(8: (-2)) • (-2) = (-4) • (-2) = 4-8 = 8.
УПРАЖНЕНИЯ
1.
2.
Устно выполните действия:
1) (-2).(4-3);
4)	(-7)-4;
7) (-7)-(-9);
10) 0-(—5);
Определите знак
2) (4-8)-(-3);
5)	(—2)(—1);
8) 9-(-8);
П) 3 0;
произведения:
3) 6-(-5);
6)	(-8).(-8);
9) (—10).77;
12) (—6)-0.
2) (—!)•(—1)-(—!)•(—1)-с—1);
з.
4) (-3).(-2).(-1)-4;
5) (_2).3.(-4).5.(-6)-7.
1)	Сколько отрицательных множителей должно со-
держать произведение, чтобы оно было положи-
тельно?
102
2)	Сколько отрицательных множителей должно содер-
жать произведение, чтобы оно было отрицательно?
4.	Вычислите:
1)	2 (—3)-(—10); 2) (-4)-17-25;
3)	8-(-25)-(-3); 4) (-6)-(-5)-(-7);
5) 8-(—17)-125;	6) (—3)-16-(—125).
Например,
(—16)-(—7)-(—25) = —(16-25-7) = —(4-4-25-7) =
= —100-4-7 = —100-28 = —2800.
5.	Верно ли, что если
1)	а > 0, Ь>0, то а-&>0;
2)	а < 0, b < 0, то а-b < 0;
3)	а-b > 0, то а > 0 и b > 0;
4)	а-6<0, то а>0 и ft<0?
Объясните, почему данное утверждение верно, или
приведите хотя бы один пример, показывающий, что
утверждение неверно.
6.	Произведение трех чисел положительно. Можно ли
утверждать, что все три числа положительные? При-
ведите примеры.
7.	Произведение двух чисел равно нулю. Докажите, что
среди этих чисел есть хотя бы один нуль.
Устно выполните деление:
8.	1) (+60):(—10) = —(60:10) = —6;
2)	(—20):5;	3)	(—50): 10; 4)	(—80):(—20);
5)	(—100):(—25);	6)	30:(—15); 7)	64:(—8).
9.	1) 200:(—40);	2)	(—500): 100;	3) 720:(—90);
4)	(—810): (—9);	5)	(—560): (—70);	6) (—480): 60.
10.	Сформулируйте свойства деления, которые выра-
жаются следующими равенствами:
1)	(a-b)'.c = (a:c)-b = a-(b:c);
2)	a:(b-c) = a:b:c,
3)	сг.Ь = (а-с):(Ь-с).
11. Вычислите:
1) 576-13—846-15;	2).849-18 —783-28;
3) 136-13—(8416+12319); 4) 3712:4—8445:5.
Например
13-15—28-15 = 195—420= —(420-195) = —225.
1)	' “ ‘
X15 х 13	2)	28 х 15	3)	420 “ 195
45	. 140	225
15	+ 28 ’	
195	420	
12.	Вычислите:
1)	(-1)’;	2) (-1)’;	3) (-1)*;	4) (-1)5;
103
5) (—З)2;	6) (—2)2;	7) (-4)?;	8) (-5)2;
9) (—2)3; 10) (—3)3; 11) (—4)’; 12) (—5)3.
13.	Какое число больше:
1)	—2? или (—2)2;	2) —3? или —23;
3)	(—3)? или (—2)3; 4) (—4)3 или —З4?
14.	Вычислите:
1)	(—1)и—(—О11; 2) (-1)4-(-1)2-(-1)2;
3)	(_2)5-(_З)3;	4) (-!)?+ (-1)’ + (-1)4.
15.	Запишите:
1)	квадрат числа —2;	2) произведение чисел —4
и 7;
3)	сумму чисел —7 и 7; 4) куб числа —10;
5)	четвертую степень чис- 6) разность —4 и —12.
ла —5;
16.	Вычислите, предварительно указав порядок действий:
1)	3 (—2)2; 2) —4-(—З)3;
3) —(—З)4; 4) —(—2)3;
5)	—(—5)а; 6) —4-(—З)2.
17,	Поезд проехал 240 км за 4 ч. Сколько времени он
потратил бы на тот же путь, если его скорость:
1)	увеличить на 20 км в ч; 2) уменьшить на 20 км в ч?
18.	Первый покупатель купил 1 кг конфет и 1 кг пе-
ченья и заплатил за покупку 4 р. 80 к., а второй
покупатель за 1 кг таких же конфет и 2 кг такого
же печенья заплатил 6 р. Сколько стоит 1 кг кон-
фет и сколько стоит 2 кг печенья?
19.	Мальчик купил 3 общие тетради и 10 карандашей,
а девочка купила 3 такие же тетради и 5 каранда-
шей. Мальчик заплатил 69 к., а девочка—54 к.
Сколько стоит тетрадь и сколько стоит карандаш?
20.	Мастер делает в час 18 деталей, а его ученик—на 6 де-
талей меньше. Сколько деталей сделают мастер и
ученик вместе за 5 ч?
Что показывают выражения:
1)5-18;	2)5-12;	3)5-18+5-12;
4)18+12; 5)5(18+12)?
§ 36. распределительный закон
Для любых целых чисел а, Ь, с выполняется распре-
делительный закон:
(а + Ь)-с = а-с + Ь‘С.
Доказательство его сводится к распределительному
закону для натуральных чисел. Например, [(—3)+(—2)]х
104
X 7 = (—3) • 7 + (—2)  7. Докажем это: [(—3) + (—2)] • 7 =
= [— (3 + 2)]-7 = — [(3 + 2)-7] = -(3-7 + 2-7)=—3-7 —
— 2-7 = (—3)-7 + (—2)-7.
Распределительный закон верен и для нескольких сла-
гаемых. Например, [(—3) + 5 + (—7)] • (—1) = (—3) • (—1)+
+5-(—1) + (—7) •(—!) = 3—5 + 7 = 10—5 = 5.
Переход от (а-\-Ь)-с к а-c+b-c называют ракрытием
скобок, а переход от а-с + Ь-с к (a-Vty-c называют выне-
сением общего множителя за скобки.
Пример. Раскрыть скобки: (—48 + 35) • (—2).
Каждое слагаемое умножим на (—2) и полученные
результаты сложим:
(_48 + 35) • (-2) = (-48) • (-2) + 35 • (-2).
Пример. Раскрыть скобки и вычислить сумму
(—2)-(—95+ 39)+ 78.
Решение.	(—2) • (—95+39) + 78 = (— 2) • (— 95)+
+(—2) • 39 + 78 = 190—78 + 78 = 190.
Пример. Вынести общий множитель за скобки: 3-35+
+3-(—65).
Решение. 3-35 + 3• (—65) = 3• [35+(—65)].
УПРАЖНЕНИЯ
1.	Запищите распределительный закон для чисел а, Ь, с.
Убедитесь, что закон верен при
1)	а = — 5, Ь = 3,	с = —10;
2)	а — —5, Ь ——3, с = 6.
2.	Верно ли равенство:
1)	(—2) (5 + 7) = —10—14;
2)	(7—8).(—3) = —21 + 24;
3)	6-[(—4) + (—12)] = —24—72;
4)	(—7 + 5—8)-(—2) = 14—10 + .16?
3.	Раскройте скобки, определяя устно знак прозведения:
1) 3 (2—7);	2) —5-(—6—7);
3)	(-2).(6 + 9); 4) -2(6-9).
4.	Упростите числовое выражение:
1)	—8-(—7 + 5)—5-(—8);	2) 3-(—98 + 2) + 3-98;
3)	(—8)-(—47+125)—47-8;
4)	(—25)-(45—100)+ 25-45;
5)	83 (—98— 1)—98-83;
6)	(_15). (—7+15)—7-15.
105
б. 1) (12—27)-(—1);	2) (—1)-(35— 88);
3) (—1).(56—74);	4) (—!)•(—28—112).
6. 1) 4 (—25 + 76+24);	2) (25 — 62 — 38)-(—4);
3) (7—125+13)-(—8); 4) 8-(—8+100—22 +25).
7, 1) 58-64 + 58-36;	2) 72-128—72-228;
3)	63-356—556-63;	4) (-99)-12—99-88;
5) (—67)-85 —67-115; 6) 41-91—91-51.
8.	Докажите, что:
1)	43-15—55-15 + 34-15 делится на 22;
2)	12-17—16-17+13-17 делится на 9;
3)	99-51—99-91 + 11-99 делится на 29;
4)	63-23—32-63 + 22-63 делится на 13.
9.	Вычислите:
1)	42-53—32-53—42-63 + 32-63;
2)	79-45 + 79-55 — 89-45 —89-55;
3)	88-75—12-45+ 12-75—88-45;
4)	392-23—492-23 + 392-77—492-77.
•10. Устно решите задачу: Мальчик заметил, что на путь
по течению реки они с папой затратили меньше вре-
мени, чем на путь против течения. Чем это объяс-
нить, если учесть, что мотор лодки работал одина-
ково хорошо в течение , всей поездки?
11.	Устно решите задачу: На путь по реке из пункта А
в пункт В теплоход тратит 1 ч 40 мин, а на обрат-
ный путь—2 ч. В каком направлении течет река?
12.	Скорость катера по озеру (в стоячей воде) равна
18 км в ч. Какой путь пройдет катер за 3 ч?
13.	Скорость течения реки равна 2 км в ч. На сколько
колометров река относит любой предмет (щепку, плот,
лодку) за 1 ч; 5 ч?
14.	Скорость катера в стоячей воде равна 18 км в ч.
Скорость течения реки 2 км в ч. С какой скоростью
будет двигаться катер по течению реки? С какой ско-
ростью будет двигаться катер против течения реки?
15,	Скорость катера в стоячей воде (ее обычно называют
собственной скоростью) равна 12 км в ч, а скорость
течения реки равна 3 км в ч.
1)	Определите скорость катера по течению реки.
2)	Определите скорость катера против течения реки.
3)	Определите расстояние, которое пройдет катер за
Зч, двигаясь против течения реки.
4)	Определите расстояние, которое пройдет катер
за 5 ч, двигаясь по течению реки.
16,	Сколько времени затратит теплоход на путь по тече-
нию реки между двумя причалами, если расстояние
106
между ними равно 90 км, собственная скорость тепло-
хода 27 км в ч, скорость течения реки 3 км в ч.
17,	Собственная скорость моторной лодки 20 км в ч,
а скорость течения реки 2 км в ч. Сколько времени по-
требуется для того, чтобы на этой лодке проплыть 72 км
против течения?
18.	Катер, имеющий собственную скорость 15 км в ч,
проплыл 2 ч по течению реки и 3 ч против течения.
Какое расстояние проплыл катер, если скорость течения
реки 2 км в ч?
19,	Расстояние между двумя причалами 24 км. Сколько
времени потратит моторная лодка на путь от одного
причала до другого и обратно, если собственная
скорость моторной лодки 10 км в ч, а скорость тече-
ния реки 2 км в ч?
20,	Расстояние между двумя причалами 36 км. Сколько
времени потратит на путь от одного причала до дру-
гого и обратно катер, если его собственная скорость
15 км в ч, а скорость течения реки Зкм в ч?
§. 37. Раскрытие скобок и заключение в скобки
Такое выражение/ как —34-6—1, называют суммой,
потому что его можно записать в виде суммы (—3) +
+ (+6) 4- (—!)•
Мы знаем, что — Таким образом, например,
+5 = 5,
+(-5) = -5,
+ (3 + 5) = 3 + 5,
+ (5—2) = 5—2,
+ (—34-6—1) = —3 + 6—1.
Эти же результаты можно получить, используя ра-
венство
+а=4-1а.
Например, + (—3 4-6— 1) = +1 • (—3 4-6—1) =
= 4-1(—3)+Ь64-1(—1) = —3 + 6—1.
Таким образом, верно равенство -
+(— 34-6—1) = — 34-6— 1.
Говорят, что в левой части этого равенства слагаемые
заключены в скобки, а в правой—скобки раскрыты.
107
Если сумма заключена в скобки, перед которыми стоит
знак плюс (+), то при раскрытии скобок знаки слагаемых
оставляют без изменений.
Например, + (—7 + 3—4) =—7 + 3—4.
Обратно, если сумма заключается в скобки, перед ко-
торыми ставят знак плюс (+), то знаки слагаемых,
•заключаемых в скобки, оставляют без изменений.
Например, —3 + 8—7—12= + (—3 + 8—7—12).
Отметим, что верно равенство
— а ——1-а.
Например, —5 = —1-5; — (—2) = (—!)• (—2) = 2.
Используя распределительный закон и равенство
—а — —1-а, можно раскрывать скобки, перед которы-
ми стоит знак минус (—).
Например, — (—5 + 2) = (— 1) • (—5 + 2) = (—1) • (—5)+
+ (—1) - 2 = 5-2; — (6—4) = (-1)-(6-4) = (-1)-6-
— (—1).4 = — 6+4.
Если сумма заключена в скобки, перед которыми стоит
знак минус (—), то при раскрытии скобок знаки слагае-
мых меняют на противоположные.
Например, —(—8 + 3—11) = +8—3+11.
Обратно, если сумма заключается в скобки, перед ко-
торыми ставят знак минус (—), то знаки слагаемых,
заключаемых в скобки, меняют на противоположные.
Например, 9—17+ 18—4 = — (—9+ 17—18 + 4).
УПРАЖНЕНИЯ
1.	Раскройте скобки, объясняя свои действия с помощью
правил:
1)	+(5 + 7);
3)	+ (—3 + 8,+ 7);
2.	1) -(5 + 7);
3)	-(-3+8 + 7);
3.	1) + (а—Ь—су,
3)	+ (— а + Ъ + с);
4.	Раскройте скобки:
1)	+(56 + 42);
3)	+ (56 + 6-7);
5.	1) — (45—35);
3) -(9-5-53);
2) +(3-8 + 7);
4) +(—10—12+1).
2) -(3-8 + 7);
4) —(—Ю—12+1).
2) —(а—Ь—с);
4) — (— а + Ь + с).
2) +(7-8 + 42);
4) +(7-8 +6-7).
2) -(45—7-5);
4) -(9.5-7-51.
108
6.	Раскройте скобки:
1)	+(48—93)—8;	2) —(96—35)—6;
3)	— (7-8—20) + 7-8;	4) + (99—5 + 8)—17.
7.	1) —(-75+ 48)+ 23;	2) -(-32—74)-74;
3)	+ (—120—3-3)—91;	4) + (120—3») + 91.
8.	Раскройте скобки и вычислите сумму:
1)	—(—72 + 39)+ 39 = +72— 39 + 39 =72;
2)	+ (398—700) + 700;	3) — (754—1200) —1200;
4)	+(—32—491)+ 32;	5) —(—129 + 59)—129.
9.	1) (7-95—900)—7-95;	2) — (795 — 9-99)—99-9;
3)	(-48+ 101—29)—101+29;
4)	— (—79—39 + 81) + 81—39.
10.	Перепишите, заполняя пропуски:
1)	45-36=+(...);	2)	45—36 = — (...);
3)	-79+11 = +(...);	4)	—79+11 = —(...).
11.	1) 38 + 59 = +(...);	2)	38 + 59 = —(...);
3)	—17—81 = + (...);	4)	-17—81 = — (...).
12.	Заключите два первых слагаемых в скобки, перед
скобками проставьте знак плюс (+):
1)	79- 48 + 15 - 8;	2) -56 + 38— 12 + 100;
3) 43 + 50-35—11;	4) -43—59 + 35+11.
13.	В упр. 12 перед скобками поставьте знак минус (—).
14.	У мамы было 20 р. Она купила младшему сыну ко-
стюм за Юр. и ботинки за Зр. Сколько денег оста-
лось у мамы после покупки? Решите задачу двумя
способами.
15. У мальчика было 90 к. Он купил в магазине цветные
карандаши за 69 к. и клей за 12 к. Сколько денег
осталось у мальчика? Решите задачу двумя способами.
16. Вычислите:
17.
18.
19.
1) 345:15—7а;	2) 28-11 — 128;
3) 82 — 560:8;	4) 221:17—23.
1)	9152:352-(10296:264)—1000;
2)	23085:513-(5894:421) + 70.
1) -48:6+ 95:(—5);	2) -35-204 +36-125;
3)	—39:(—13)+ (128—49:(—7));
4)	81:(—27) —(154—56:(—8)).
Найдите неизвестное число х, если
1) х-7 = 0;
3) х-7 = —21;
5) х-(—8) =16;
7) х:(—3) = 3;
9) 12:х=—6;
И) (—25):х=—5;
2) х-7 = —7;
4) х-(—3) = 3;
6) х:2 = —8;
8) х:(—4) = 5;
10) (—48):х=6;
12) (—24):х=—1

109
§ 38.	Действия с суммами нескольких слагаемых
В предыдущем параграфе мы научились раскрывать
скобки, перед которыми стоит знак плюс (+) или ми-
нус (—). Но встречаются числовые выражения, в кото-
рых стоящие перед скобками знаки плюс (+) и минус (—)
обозначают действия сложения и вычитания. Оказывает-
ся, что и в этом случае применимы изученные нами пра-
вила, т. е.
а+ (Ь—с) = а + Ь—с,
а—(Ь—с) = а—Ь + с.
Второе равенство доказывается так:
а—(Ь—с) = а + [— (Ь—с)] = а + [— b + с] = а—b +с.
Например, (7—9)+(8 + 3) = 7—9+8 + 3;
(7—9)_(8 + 3) = 7—9—8—3.
Рассмотрим сумму нескольких слагаемых: 78—89 +
+ 32—11. Обычно складывают сначала положительные,
потом отрицательные слагаемые и находят сумму полу-
ченных чисел. При этом используют законы сложения:
78—89 + 32— 11 = (78 + 32) + (—89— 11) =
== 110—(89 + 11) = 110—100 = 10.
УПРАЖНЕНИЯ
1.	Раскройте скобки:
1)	49—(38—5);	2) —32+ (78—9);
3)	72+ (—32+ 9);	4) — 63—(63+1).
2.	1) (79—39)—(79—48); 2) (37 — 49) —(87 — 59);
3)	— (45—64)+(38—24); 4) — (—35 + 2) + (—35—8).
3.	Раскройте скобки и вычислите:
1)	108—(108—5);	2) —49—(—49 + 2);
3)	—56 +(—98+56);	4) 100—(—5 + 100).
4.	1) (79—81)—(39—81);	2) (—78 + 23) + (27 + 78);
3)	(—39+15)—(5—39); 4) (105—48)—(62+105).
5.	Вычислите, раскрывая скобки только в тех случаях,
когда это облегчает вычисления:
2) 43+ (23+ 77);
4) 43+(77—43).
2) 102—(102—5):
4) —72—(99+1)
1) 79—(63 + 7);
3) 79—(79—7);
6. 1) 102—(56 + 44);
3) 93—(68+93);
НО

7. 1) 48—(11 + 19);
3) —56+ (96+ 9)
8. 1) 52—(32—41);
2) 48—(18+19);
4) 59+ (96+ 4).
2) 73—(68—8);
3) —25 — (—45+19);	4) —49—(И—68).
9. Заключите два последних слагаемых в скобки двумя
способами—со знаком плюс (+) и со знаком ми»
2) 45—2—12;
4) 76 + 38—52.
2) 84—(44 + 26);
4) 728—(328—179).
2) 83—21—29;
4) 236—108— 92.
НУС (—) перед скобками:
1) 37 + 12+13;
3)	75—28 + 22;
10.	Вычислите двумя способами:
1)	48—19 — 1;	2) 93—12—13;
, 3) 48—(27+ 13);	4) 48—(18—10).
11.	Вычислите, выбирая удобный способ:
1)	84—(44 + 28);
3)	826—(231 + 269);
12.	1) 83—23—29;
3)	236—136—92;
13.	1) —(398 + 49) —(102—49)';
2)	(723—254) —(623—354);
3)	(749 + 237) —(137 + 249);
4)	—(395+ 105) — (398—98).
14.	1) (—34—47):41 —15;	2) (48—59)-(—3)—55;
3)	—64:4—42:3;	4) —120: (—4) + 15-(—4)’.
§ 39.	Представление целых чисел на координатной оси
Зададим прямую, на которой определим (стрелкой)
направление, называемое положительным, и еще точку 0,
называемую начальной. Зададим единичный отрезок.
-4 -3 -2 -1 0 1,23 4 5
----1 1---1--1-----1----1—I-1-Н-
во-------------------------А
Рис. 3.2
Этим задана координатная ось (рис. 3.2).
Обычно координатную ось рисуют в виде прямой,
идущей слева направо.
Но бывает удобным направить ее иначе, например,
снизу вверх.
Координатная ось делится точкой 0 на два луча. Один
из них—положительный, идущий от 0 в положительном
направлении (на рис. 3.2—вправо); его называют поло-
111
жительной координатной полуосью. Другой—отрицатель-
ный (на рис. 3.2 слева от 0), называемый отрицательной
координатной полуосью. С помощью координатной оси
целые числа изображаются точками. Произвольное целое
число п изображается точкой, расстояние которой до
точки 0 равно модулю этого числа |л|; она находится на
положительной полуоси, если п > 0, и на отрицательной,
если п < 0. Эту точку называют точкой п или точкой
с координатой п.
Например, на рис. 3. отмечена точка А с координатой
4: А (4) и точка В с координатой —2: В (—2).
ОЛ = |4| = 4, ОВ = |— 2| = 2.
Если т и п—целые числа и т>п, то
1) точка т расположена на координатной оси правее
точки п;
2) расстояние между точками тип равно т—п.
Например, на координатной оси отмечены точки А (7)
и В(—4), 7 > — 4, значит, А правее В, и
АВ = 7—(—4) = 7 + 4=11.
Противоположные числа находятся на одинаковом
расстоянии от начальной точки, но на разных полуосях.
УПРАЖНЕНИЯ
1.	Дана координатная ось (рис. 3.3), некоторые точки
обозначены буквами А, В, С, D, Ё. Укажите коорди-
наты этих точек.
-5 -U -3 -2 -1 0 7 2 3 U 5 6
Н---1-1--1-1-1-1--1—I--1—I—н>-
Л В	ОСА Е
Рис. 3.3
2.	Найдите длину отрезка (рис. 3.3), соединяющего точки:
1)	О и Л; 2) О и В; 3) О и С; 4) О и D.
3.	Вычислите длину отрезка (рис. 3.3):
1)	ЛС; 2) ЛЕ; 3) ОЕ; 4) СВ; 5) DA.
4.	Изобразите координатную ось с единичным отрез-
ком 1 см (2 клетки тетради). Отметьте на ней точки
Л (—5), В (7), С (4), D(—4). Вычислите длину отрезка:
112
1)	ОЛ; 2) ОВ\ 3) ВС-, 4) BD- 5) AD.
Результаты проверьте с помощью сантиметровой
линейки.
5,	Даны точки Л (7), В(3), С (12) на координатной оси.
Какая из этих точек расположена правее других;
левее других? Найдите длину отрезков:
1)	ОД; 2) ОВ\ 3) ОС; 4) ЛВ; 5) ВС.
6,	Кузнечик прыгает вдоль координатной оси на 6 еди-
ничных отрезков вправо и на 4 единичных отрезка
влево. Постройте координатную ось и отметьте цветом
все точки, в которые может попасть кузнечик из точки 0.
Сможет ли он попасть за несколько прыжков из точки О
в точку 5? Сможет ли он за несколько прыжков из
точки 1 попасть в точку 5?
7.	На координатной оси отметили две точки (рис. 3.4).
Назовите остальные точки.
8.	Определите расстояние между точками т и п на ко-
ординатной оси, если
1)	/п = 7; п = —3;	2) т = 3, п = —7;
3) /п = —8, п = — 2;	4) т = —8, и = 8.
§ 40. Исторические сведения
Впервые отрицательные числа встречаются в одной из
книг древнекитайского трактата «Математика в девяти
главах» (Джан Цань—I век до нашей эры). Отрицательное
число понималось как долг, а положительное—как
имущество. Сложение и вычитание отрицательных чисел
производились на основе рассуждений о долге. Например,
правило сложения формулировалось так: «Если к одному
долгу прибавить другой долг, то в результате получится
долг, а не имущество». Знака минус тогда не было,
а чтобы отличать положительные и отрицательные числа,
Джан Цань писал их разными по цвету чернилами.
С. М, Никольский И др.	ИЗ
Идея отрицательных чисел с трудом завоевывала себе
место в математике. Эти числа казались математикам
древности непонятными и даже ложными, действия с ними—
неясными и не имеющими реального смысла.
В VI—VII веках нашей эры индийские математики
уже систематически пользовались отрицательными числами,
по-прежнему понимая их как долг. Впервые все четыре
арифметических действия с отрицательными числами при-
ведены индийским математиком и астрономом Брахмагуп-
той (598—660 гг.). Например, правило деления он форму-
лировал так: «Положительное, деленное на положительное,
или отрицательное, деленное на отрицательное, становится
положительным. Но положительное, деленное на отрица-
тельное, и отрицательное, деленное на положительное/
остается отрицательным».
Независимо от индийцев к пониманию отрицательных
чисел как противоположности положительных пришел
итальянский математик Леонардо Фибоначчи Пизанский
(XIII в.). Но понадобилось еще около 400 лет, прежде
чем «абсурдные» (бессмысленные) отрицательные числа
получили полное признание математиков, а отрицательные
решения в задачах перестали отбрасываться как невоз-
можные.
В 1544 году немецкий математик М. Штифель впервые
рассматривает отрицательные числа как числа, меньшие
нуля (т. е. «меньшие, чем ничто»). С этого момента отри-
цательные числа рассматриваются уже не как долг,
а совсем по-новому.
Современное истолкование отрицательных чисел, осно-
ванное на откладывании единичных отрезков на числовой
оси влево от нуля, было дано в XVII веке, в основном в
работах голландского математика Жирара (1595—1634 гг.)
и знаменитого французского математика и философа
Р. Декарта (1596—1650 гг.).
Для того чтобы разработать этот понятный и естест-
венный сейчас для нас подход, понадобились усилия
многих ученых на протяжении восемнадцати веков от
Джан Цаня до Декарта.
Ш
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
• ПО МАТЕРИАЛУ ГЛАВЫ III
1.	Назовите несколько целых положительных чисел. Как еще
называют эти числа?
2.	Назовите несколько целых отрицательных чисел.
3.	Является ли нуль целым числом; положительным числом;
отрицательным числом?
4.	Какие числа называются противоположными? Приведите при-
меры.
5.	Сформулируйте правило знаков и примените это правило
к числам +(+1), +(-2), —(+3), -(-4).
6.	Назовите такое значение а, при котором число — а является
положительным; отрицательным числом; нулем.
7.	Что называется модулем числа?
8.	Сформулируйте правила сравнения целых чисел.
9.	Сформулируйте правила сложения целых чисел.
10.	Всегда ли сумма целых чисел больше каждого слагаемого?
В каких случаях это верно, в каких — нет? Приведите примеры.
11.	Запишите для чисел a, b, с переместительный и сочетатель-
ный законы, сложения целых чисел.
12.	Что называется разностью целых чисел? Чему равна разность
целых чисел?
13.	Что называется произведением целых чисел?
14.	Запишите для целых чисел a, bt с переместительный и соче-
тательный законы умножения.
15.	Запишите для чисел а, Ь, с распределительный закон.
16.	Сформулируйте правила раскрытия скобок, перед которыми
стоит знак плюс; знак минус.
17.	Сформулируйте правила заключения в скобки.
18.	Как вычислить расстояние между точками /пип координат-,
ной оси? Поясните свой ответ примерами.
115
i
Глава IV. ОБЫКНОВЕННЫЕ ДРОБИ
§ 41. Простые и составные числа
Если при делении одного натурального числа на дру-
гое в частном получается натуральное число, то говорят,
что первое число делится нацело на второе или что пер-
вое число кратно второму.
Например, 6 делится нацело на 3, т. е. 6 кратно 3;
7 не делится нацело на 3, т. е. 7 не кратно 3.
Каждое натуральное число делится на 1 и само на
себя:
р:1=р, р:р=1,
где р—произвольное натуральное число.
Простым числом называется такое натуральное число,
которое больше единицы и делится только на 1 и само
на себя.
Вот первые десять простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Не простые натуральные числа, большие единицы,
называются составными. Каждое составное число делится
на 1, само на себя и еще хотя бы на одно натуральное
число.
Вот все составные числа, меньшие 20:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18.
Принято считать, что единица не является ни простым,
ни составным числом.
Таким образом, множество всех натуральных чисел
состоит из простых чисел, составных чисел и единицы.
116
УПРАЖНЕНИЯ
Ответьте на вопросы:
I.	1) Является ли число 0 натуральным числом?
2)	Каким числом является сумма натуральных чисел?
3)	Как называются компоненты и результат сложения?
4)	С помощью координатной прямой покажите, что
34-5 = 8.
2.	1) Что значит умножить 4 на 5?
2)	Какие числа получаются при умножении нату-
ральных чисел?
3)	Как называются компоненты и результат умноже-
ния?
3.	1) Что значит разделить 20 на 4?
2)	Как называются компоненты и результат деления?
4,	1) Всегда ли выполнимо деление нацело одного на-
турального числа на другое? Приведите примеры.
На какие натуральные числа делится нацело произ-
вольное натуральное число?
2)	Делятся ли нацело на 7 числа 12, 27, 42, 126?
3)	Кратны ли числу 15 числа 30, 105, 215, 360?
4)	Назовите пять чисел, которые делятся нацело на 9.
5)	Назовите пять чисел, кратных 12.
5.	Верно ли, что
. 1) Все четные числа кратны 2?
-2	) Все нечетные числа кратны 3? Приведите пример
нечетного числа, кратного 3; не кратного 3.
3)	Все числа, оканчивающиеся на 5, делятся наце-
ло на 5?
4)	Все числа, сумма цифр которых кратна 3, делятся
нацело на 3?
5)	Все числа, сумма цифр которых кратна 9, делятся
нацело на 9?
6.	1) Какие числа называют простыми? Приведите при-
меры.
2)	Являются ли числа 9, 12, 14, 17, 28, 37 простыми?
3)	Назовите все простые числа, ббльшие 30, но мень-
шие 50.
7.	1) Какие числа называют составными? Приведите
примеры.
2)	Назовите составные числа, ббльшие 10, но мень-
шие 40.
3)	Является ли единица простым числом? Является
ли единица составным числом?
4)	Существует ли, кроме 2, четное простое число?
8.	С помощью таблицы простых чисел (с. 383) опреде-
117
лите, является ли простым число: 47, 69, 127,
301, 447, 517, 673, 879?
9.	С помощью таблицы простых чисел выпишите те из
них, разность между которыми равна 2. Сколько
таких пар простых чисел встречается от 1 до 1000?
10.	Как проверить, является ли натуральное число про-
стым? Являются ли простыми числа 998, 999, 1000?
11.	Выполните деление:
1)	37600:4;	2) 9840:60;
3)	864800:800;	4) 3246:21.
12.	Вычислите:
1)	28728:63;	2)	50904:72;
3)	10489:17;	4)	51414:66.
13.	Определите частное чисел:
1)	598424 и 76; 2) 18952 и 412;
3)	51211 и 617; 4) 41702 и 719.
14.	Ученик купил пять общих тетрадей и тридцать те-
традей по 3 к. Всего он уплатил за покупку 1 р. 60 к.
Сколько стоит одна общая тетрадь?
15.	За 5 кг конфет и 4 кг печенья уплатили 27 р. 80 к.
Сколько стоит 1 кг конфет, если 1 кг печенья стоит
1 р. 20 к.?
16.	В автобусе было 25 пассажиров. На первой остановке
вышло .8 и вошло 12 пассажиров, на второй вышло 7
и вошло 5 пассажиров. Сколько пассажиров стало
в автобусе после второй остановки?
17.	В автобусе было несколько пассажиров. На первой
остановке вышло 7 и вошло 4, а на второй вышло 6
и вошло 13 пассажиров. Сколько пассажиров было
в автобусе до первой остановки, если после второй
остановки в автобусе находилось 38 пассажиров?
§ 42. Делители натурального числа
Делителем натурального числа называется натураль-
ное число, на которое данное число делится нацело.
Из этого следует, что каждое простое число имеет
только два делителя—единицу и само себя, а каждое
составное число, кроме единицы и себя, имеет и другие
делители.
Например, делителями числа 13 являются числа 1 и
13, делителями числа 4 являются числа 1, 2, 4, а де-
лителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
118
Если делитель—простое число, то он называется
простым делителем.
Например, число 13 имеет один простой делитель—13,
число 4—один простой делитель—2, а число 12—два
простых делителя—2 и 3.
Каждое составное число можно представить в виде
произведения его простых делителей или их степеней.
Например,	28 = 2-2-7 = 2»-7;
22 = 2-11;
81 = 3-3-3-3 = 3*;
100 = 2.2-5-5 = 2».5».
Правые части полученных равенств называются разло-
жениями на простые множители чисел 28, 22, 81 и 100.
Разложить данное натуральное число на простые множи-
тели—это значит представить число в виде произведения
различных его простых делителей или их степеней. Можно
доказать, что такое разложение единственно для каждого
натурального числа, т. е. что у этого числа нет других
простых делителей, и что его простые делители нельзя
записать в других степенях.
Например, покажем, как разлагают на простые мно-
жители 90.
1)	90 делится на простое число 2, поэтому 90=2-45.
2)	45 не делится на 2, но делится на простое число 3,
поэтому 45 = 3-15.
3)	15 делится на 3, поэтому 15 = 3-5. Так как 5 —
простое число, то процесс отыскания простых делителей
закончен.
Итак, получаем равенство
90 = 2-3-3-5 = 2-3»-5.
УПРАЖНЕНИЯ
1, 1) Что называется делителем натурального числа?
2) Что называется простым делителем натурального
числа?
3) Что значит разложить число на простые множи-
тели?
119
2. Сформулируйте признаки делимости чисел на 2, 6,
10, 3, 9, 4. •
3. Укажите все делители числа:
1) 2;	2)	6;	3)	12;	4)	18;	5)	16;
6) 20;	7)	28;	8)	7;	9)	1;	10)	48;
11) 100;	12)	104;	13)	121;	14)	256.
4. 1) Приведите примеры натуральных чисел, имеющих
делителями:
а) 2; б) 2 и 5; в) 3 и 4; г) 5 и 10.
2) Какие еще делители имеют выбранные числа,
кроме указанных?
5. 1) Приведите примеры натуральных чисел, имеющих
простыми делителями только числа:
а) 2; б) 3; в) 2 и 5; г) 2 и 3.
2)	Запишите пять натуральных чисел, не имеющих
других простых делителей, кроме 2 и 5.
6.	Определите все простые делители числа:
1)	4;	2)	9;	3)	15;	4)	10;	5)	24;
6)	46;	7)	50;	8)	58;	9)	99;	10)	128;
11)	196;	12)	254;	13)	400;	14)	625.
Указание. При разложении числа на простые мно-
жители обычно пользуются одним из двух способов
нахождения простых делителей.
I способ. Устно проверяется кратность числа прос-
тым числам 2, 3, 5, 7, ... й решение записывается
«в строчку». Например, 56=2-28=2-2- 14=2-2-2-7 =
= 23-7.
II способ. Устно выполняют деление числа на под-
ходящее простое число, записывая промежуточные
результаты «в столбик». Например,
56	2)
28	2 1 28
14	2J
7	7 — простое число,
так что 56 = 28-7.
7.	Разложите на простые множители число:
1)	16;	2) 18;	3) 26;	4) 35;
5)48;	6)72;	7)144;	8)210;
9)	800;	10)216;	11) 343;	12) 1024;
13)	1728; 14) 1575; 15) 9225; 16) 1001.
8.	Представьте числовое выражение в виде произведе-
ния возможно большего числа множителей, отличных
от 1:
1) 40-24;	2) 12-25;	3) 164-10;	4) 8-125;
5)125-64; 6)112-147; 7)1001-37; 8)47-201.
120
9.	Запишите в порядке возрастания все делители числа:
1) 12; 2) 15; 3) 18; 4) 24.
10.	Запишите число в виде произведения двух его дели-
телей всеми возможными способами:
1)	32; 2) 62; 3) 51; 4) 100.
11.	Запишите следующие числа сначала в виде степени
числа 10, а затем в виде произведения степеней чи-
сел 2 и 5:
1)	10; 2) 100; 3) 1000; 4) 10000;
5) 1000000; 6) 1000000000000 000;
7) число, записанное единицей с тридцатью нулями.
12. Запишите следующие числа в виде степени или про-
изведения степеней простых чисел:
1) 64;	2) 200;	3) 144;	4) 256;
5) 333;	6) 346;	7) 512;	8) 100000;
9) 4096; 10) 250000; 11) 75000000;
12) 120000000000.
13,	Ученик заметил, что делители числа 12 обладают
интересным свойством:
Это наблюдение позволило ему сократить «перебор»
делителей. После того, как найдены делители 1, 2,
3, остальные делители можно найти делением: 12:3,
12:2, 12:1. Примените этот способ поиска делителей
для числа:
1)	32; 2) 48; 3) 56; 4) 36; 5) 98.
14.	Если при поиске делителей какого-нибудь числа пос-
ледовательно перебирать натуральные числа (начиная
с 1), то на каком делителе можно остановить-
ся (учитывая, что остальные можно получить деле-
нием):
1)	128; 2) 256; 3) 398; 4) 500; 5) 625?
15.	Определите, является ли число простым или состав-
ным:
1)	89;	2)	123;	3)	279;	4) 335;	5) 642;
6)	601;	7)	729;	8)	835;	9) 1571;	10) 2563.
16.	Определите порядок действий, прочитайте выражение,
найдите его значение:
1)	(23)а; 2) (22)8; 3) (3?—23)6; 4) (З3—22)2.
121
17.	Проверьте справедливость равенства:
1)	102+ 112+ 122= 132+ 142;
2)	33 + 43 + 5’ = 6s.
18.	Используя равенства из упр. 17, вычислите:
1)	(102+И2+ 122+ 132+ 142):365;
2)	(33 + 48 + 53 + 68):216.
19.	Проверьте справедливость равенства:
1)	13+ 63 + 83 = 93;
2)	1082 + 1092 4- 1102 = 1ЗЗ3 + 1342;
3)	113+ 123+ 138+ 143 = 203.
20.	Используя равенства из упр. 19, вычислите:
1)	(1082 + 1092 + ПО2—1332—1342):365;
2)	(113+ 128+ 133+ 143 + 208):1000.
21.	Сколько раз используется цифра 9 в записи нату-
ральных чисел от 1 до 100?
22,	1) Какой цифрой не может оканчиваться квадрат на-
турального числа?
2)	В каких случаях квадрат натурального числа яв-
ляется четным числом?
. 3) Какими цифрами оканчиваются кубы натуральных
чисел? В каком порядке повторяются эти цифры
(если рассматривать кубы последовательных нату-
ральных чисел)?
23.	Запишите какое-нибудь четырехзначное число, которое
делится на 9. Переставьте в нем цифры произволь-
ным образом. Будет ли новое число делиться на 9?
Почему?
24.	Замените звездочку (*) цифрой в записи чисел 375*
и 2737* так, чтобы полученное число делилось на
1) 3; 2) 9; 3) 2; 4) 5; 5) 4; 6) 25. Всегда ли это
возможно?
25.	Два ученика по очереди пишут цифры 20-значного
числа. Может ли второй ученик добиться того, чтобы
это число делилось на 9, если первый ученик стара-
ется ему помешать? Может ли первый ученик добить-
ся того, чтобы полученное число делилось на 9, если
второй ученик старается ему помешать?
26,	Решите задачу:
Прилетели галки, Если же на каждой палке
сядут по две галки,
то одна из палок
будет без галок.
Сколько было галок?
Сколько было палок?
сели на палки.
Если на каждой палке
сядет по одной галке,
то для одной галки
не хватит палки.
122
§ 43. Наибольший общий делитель
Число 12 имеет делители 1, 2, 3, 4, 6, 12. Число 54
имеет делители 1, 2, 3, 6, 9, 18, 27, 54. Мы видим, что
числа 12 и 54 имеют общие делители 1, 2, 3, 6.
Если рассмотреть разложения чисел 12 и 54 на прос-
тые множители: 12 = 2-2^3, 54 = 2-3-3-3, можно заме.
тить, что в эти разложения входит одинаковая группа
множителей 2-3. С помощью этих множителей легко
определить общие делители чисел 12 и 54: 1, 2, 3, 6
(6 = 2-3).
Наибольшим общим делителем чисел 12 и 54 является
число б—произведение общих простых делителей этих
чисел.
Наибольший общий делитель чисел а и b обозначается
НОД (а, 6). Например, НОД (12, 54) = 6.
Рассмотрим примеры нахождения наибольшего общего
делителя/
1) Найдем НОД(180, 336). Решение.
180
90
45
15
5
1
2
2
3
3
5
336
168
84
42
21
7
1
2
2
2
2
3
7
180 = 2-2-3.3-5;
336 = 2-2.2-2.3.7.
НОД(180, 336) = 2-2-3 = 12.
Ответ. 12.
2) Найдем НОД(56, 45). Решение.
56
28
14
7
1
2
45 3	56 = 2.2-2-7;
15 3
5 5	45 = 3-3-5.
56 и 45 не имеют общих простых делителей, поэтому
НОД(56, 45)= 1.	Ответ. 1.
Числа, не имеющие общих простых делителей, назы-
ваются взаимно простыми числами. Наибольший общий
делитель взаимно простых чисел равен 1.
Два простых числа (например, 17 и 23), а также два
соседних натуральных числа (например, 24, 25) являются
взаимно простыми (докажите).
123
Найдем НОД (12, 4). Решение.
12 2 4 2 12 = 2-2-3:
6-222
3 3 1	4 = 2-2.
1	НОД(12, 4) = 2-2 = 4.
Ответ. 4.
Но можно выполнить это задание короче, если заме-
тить, что 12 делится нацело на 4. Очевидно, что
НОД (12, 4) = 4.
Таким образом, если одно из чисел делится нацело
на другое, то наибольший общий делитель этих чисел
равен меньшему из них.
УПРАЖНЕНИЯ
1.	Найдите все делители числа 45 и числа 60. Найдите
все общие делители этих чисел, их наибольший об-
щий делитель.
2.	Найдите:
-	1) НОД (30, 36);	2) НОД (50, 45); 3) НОД (42, 48);
4) НОД (120, 150); 5) НОД (124, 93); 6) НОД (46, 69).
3.	1) НОД (24, 48); 2) НОД (62, 31); 3) НОД (132, И);
4)	НОД (256, 32); 5) НОД (45, 15); 6) НОД (63, 21).
4.	Число 12321 делится на 111. Найдите НОД (12321, 111),
не выполняя разложения данных чисел на простые
множители.
5.	Число а делится на Ь. Найдите НОД (а, Ь).
6.	Найдите устно:
1)	НОД (14, 7); 2) НОД (26, 13); 3) НОД (48, 8);
4)	НОД (64, 16); 5) НОД (9, 45); 6) НОД(11, 66).
7,	С помощью разложения чисел на простые множители
докажите, что числа:
1)	24 и 35; 2) 56 и 99; 3) 63 и 88;
4) 11 и 17; 5) 32 и 33; 6) 48 и 49
являются взаимно простыми.
8. Какие числа называются взаимно простыми? Чему
равен наибольший общий делитель взаимно простых
чисел?
9. Найдите устно:
1) НОД(5, 13); 2) НОД(3, И); 3) НОД(29, 19);
4) НОД (54, 55); 5) НОД(62, 63); 6) НОД (98, 99).
10,	В каких случаях, не выполняя разложения чисел на
124
простые множители, можно утверждать, что они вза-
имно простые? Приведите примеры.
11.	Что можно сказать про числа а и Ь, если НОД (а,
Ь)=1? Придумайте пять пар таких чисел.
12.	В каком случае НОД (а, 6) = а?
Найдите:
13.	1) НОД(1,48);	2) НОД (15, 55); 3) НОД (182,82);
4)	НОД (1000, 125); 5) НОД(ЮО, 25); 6)НОД(121,11).
14.	1) НОД (320, 40); 2) НОД (233, 79); 3) НОД (278, 279);
4)	НОД (484, 44); 5) НОД (84, 96); 6) НОД (100, 175).
15.	Ученик вычислял НОД (33, 198) и получил 66. Не
проверяя вычислений, учитель сказал, что допущена
ошибка. Как он это определил?
16.	Объясните, почему наибольший общий делитель двух
чисел не может быть больше любого из этих чисел.
17.	Для участия в эстафете нужно разделить 36 девочек
и 24 мальчика на равные (по числу участников) ко-
манды, состоящие только из мальчиков или только
из девочек. Какое наибольшее число человек может
быть в каждой команде? Сколько команд получится
в этом случае?
18.	Для новогодних подарков приготовили 184 мандари-
на, 138 яблок и различные сладости. Какое наиболь-
шее число подарков можно подготовить, чтобы в них
было поровну мандаринов и поровну яблок?
§ 44. Наименьшее общее кратное
Числу 12 кратны числа 12, 24, 36, 48, 60, 72, 84 и
т. д. Числу 18 кратны числа 18, 36, 54, 72, 90, 108, 126
и т. д. Мы видим, что есть числа, кратные одновременно
и 12, и 18. Эти числа называются общими кратными 12
и 18. Таких чисел сколько угодно. Все они имеют вид
36-п, где п—какое-либо натуральное число.
Среди чисел 36-п есть наименьшее—при п«=1. Это
число 36. Его называют наименьшим общим кратным чи-
сел 12 и 18.
Вообще наименьшим общим кратным натуральных
чисел а и b называется наименьшее число, делящееся
нацело и на а, и на Ь. Это число обозначается
НОК (а, &). Аналогично определяется наименьшее общее
кратное трех чисел.
125
Нахождение НОК (а, Ь) обычно выполняют одним из
двух способов. Рассмотрим их. Найдем НОК (12, 18).
I способ. Будем выписывать числа, кратные 12,
проверяя каждое из них—делится ли оно на 18:
12-1 ==12—не делится на 18,
12*2 = 24—не делится на 18,
12*3 = 36—делится на 18.
НОК (12, 18) = 36.
II способ. Разложим числа 12 и 18 на простые
множители:
12 = 2*2*3, 18 = 2*3*3.
НОК (12, 18) должно делиться и на 12, и на 18. По-
этому это число содержит все простые множители 12
(т. е. числа 2, 2, 3) и еще недостающие множители из
разложения 18 (т. е. еще одно число 3). Поэтому
НОК (12, 18) = 2*2*3*3 = 36.
Заметим, что взаимно простые числа не имеют общих
простых делителей, поэтому их наименьшее общее кратное
равно их произведению. Например, 24 и 25—взаимно
простые числа, поэтому НОК (24, 25) = 2*2*2*3*5*5 =
= 24*25 = 600.
Если одно из двух чисел делится нацело на второе,
то наименьшее, общее кратное этих чисел равно большему
из них. Например, 120 делится нацело на 24, следова-
тельно, НОК (120, 24)= 120.
УПРАЖНЕНИЯ
1, Найдите несколько кратных числа 10 и несколько
кратных числа 15. Найдите несколько общих кратных
этих чисел. Найдите наименьшее общее кратное этих
чисел.
Найдите:
2, 1)	НОК (6, 8);	2) НОК (15, 25);	3)	НОК (16,	12);
4)	НОК (48,	42); 5) НОК (35, 20);	6)	НОК (56,	63).
8, 1)	НОК (12,	6);	2) НОК (40, 8);	3)	НОК	(51,	17);
4)	НОК (23,	3);	5) НОК (34, 2);	6)	НОК (16,	48).
4,	Число 123454321 делится на 11111. Найдите наимень-
шее общее кратное этих чисел, не выполняя разложе-
ния на простые множители.
126
5,	Известно, что число а делится на число Ь, Найдите
НОК (а, Ь).
6,	Найдите устно:
1)	НОК	(135,	5); 2) НОК (120,	10); 3)	НОК (432,-2);
4)	НОК	(234,	9); 5) НОК (123,	3); 6)	НОК (16,	64).
7,	Являются ли числа:
1)	12 и	25;	2) 39 и 40; 3) 42	и 55;
4)	22 и	51;	5) 48 и 49; 6) 39	и 50
взаимно простыми? Найдите наименьшее общее крат-
ное и произведение данных чисел в каждом случае.
Сделайте вывод.
8.	Найдите устно:
1)	НОК (5, 4); 2) НОК (И, 3); 3) НОК (7, 8); .
4)	НОК (9, 10); 5) НОК (13, 5); 6) НОК (17, 3).
9,	Придумайте пять пар таких чисел а и Ь, чтобы
НОК (а, Ь) = а-Ь. Являются ли эти числа взаимно
простыми?
10.	В каком случае НОК (а, Ь) — а?
Найдите:
11.	1)	НОК (36,	48);	2)	НОК (49,	50);	3)	НОК	(14,	15);
4)	НОК (99,	100);	5)	НОК (28,	21);	6)	НОК	(24,	25).
12.	1)	НОК (19,	20);	2)	НОК(Н,	НО);	3)	НОК	(26,	52);
4)	НОК (И,	13);	5)	НОК (66,	88);	6)	НОК	(198, 9).
13,	Ученица вычисляла НОК (33, 198) и получила 99-
Не проверяя вычислений, учитель сказал, что допу-
щена ошибка. Как он это определил?
14.	Объясните, почему наименьшее общее кратное данных
чисел не может быть меньше любого из них.
15.	Даны разложения чисел а и Ь. Найдите НОД (а, Ь)
и НОК (а, Ь). Для решения задачи достаточно соста-
вить произведение множителей и не вычислять его:
1) а = 23-34-5, Ь = 24-35-52;
2)	а = 22-33-72, Ь = 32-53;
3)	а = 22 53.-11, 6 = 34-72;
4)	а = 33-74-13, & = 34-74-134.
16.	Убедитесь, что НОД(36, 48)-НОК(36, 48) = 36-48.
Выполняется ли это свойство и для других чисел?
17,	Докажите, что НОД(а, &)-НОК(а, b) = a-b
1)	для взаимно простых чисел;
2*) для любых чисел.
18.	Какой наименьшей длины должна быть веревка, что-
бы ее можно было разрезать на куски:
1)	по 4 или по 5 м; 2) по 4 или по 6 м?
19,	Мальчик хочет купить несколько мороженых по 20 к.
У него есть только монеты по 15 к, а у продавца
127
нет сдачи. Какое наименьшее число мороженых смо-
жет купить мальчик?
20.	Из двух сцепленных шестерен одна имеет 16, а дру-
гая—28 зубцов. До начала движения мелом отметили
два соприкасающихся зубца. Через сколько оборотов
каждой шестерни будет повторяться совпадение меток?
§ 45. Понятие дроби
Нам уже встречались дробные числа или дроби. На-
1 -
пример, число у есть дробь.
Если отрезок длиной 1 см разделить на две равные
части, то каждая из них будет иметь длину -у см (рис. 4.1).
1см
% CM	IjCH
Рис. 4.1
Если 1 кг сахара рассыпать поровну в два пакета, то
каждый из них будет иметь массу у кг. Число у выра-
жает половину некоторой единицы (миллиметра, килог-
рамма, часа и т. д.). Число у—треть или одна третья —
выражает третью часть единицы.
„ 1111
Такой же смысл имеют числа т, -г, т, •=
Если q—натуральное число, то выражение
ет дробь, которая читается так: «одна кутая».
Например, если 1 км разделить на q равных частей,
то каждая часть будет иметь длину — км.
2
Рассмотрим примеры более сложных дробей: у—две
3	5	7
трети, у—три четверти, у—пять восьмых, -jy—семь
6	5
одиннадцатых, у—шесть шестых, у—пять четвертых.
128
И т. д.
1
— означа-
ч
Например, если буханку хлеба массой 1 кг разрезать
на 3 равные части—каждая по у кг, то две такие час-
2
ти будут иметь массу у кг. Если же эту буханку разре-
зать на 4 равные части, то 3 такие части будут весить
I-
Еще один пример: если на отрезке АВ ровно три ра-
за укладывается отрезок длины у дм (четверть децимет-
з
ра), то длина АВ равна у дм (трем четвертым деци-
метра).
Число, которое можно записать в виде у (читается
«пэ кутых»), где р и q—натуральные числа, называется
положительной дробью или положительным дробным
числом.
В этой главе для простоты положительные дроби мы
будем коротко называть дробями.
Число р, находящееся над чертой, называется числи-
телем дроби.
Число q, находящееся под чертой, называется знаме-
нателем дроби.
Чтобы получить число у из единицы, надо разделить
единицу на q равных частей и взять р таких частей.
Любое натуральное число р считается дробью со зна-
менателем 1:
t_T	С ®	*7	1 I
Например, 5=—, 7 =—, 1=у-
УПРАЖНЕНИЯ
ls 1) Сколько минут в половине часа?
2)	Сколько граммов в половине килограмма?
3)	Сколько часов в одной трети суток?
4)	Сколько килограммов в четверти тонны?
5 С. М. Никольский и др.	129
2. 1) Сколько минут составляет у ч?
2) Сколько миллиметров составляет у см?
3) Сколько граммов составляет т?
8.	1) Какую часть часа составляет минута?
2)	Какую часть сантиметра составляет миллиметр?
3)	Какую часть 1 см* 1 2 составляет 1 мм2?
4)	Какую часть 1 м3 составляет 1 см3?
4.	В магазине купили 100 м рыболовной лески. Поло-
вину намотали на катушку удочки. Сколько метров
лески осталось?
5.	От мотка телефонного провода длины 12 м отрезали
его четвертую часть. Сколько метров провода оста-
лось в мотке?
6.	Сколько копеек составляет:
1)	уРм 2)-g-p.; 3)j^p.; 4)^р.?
7.	Прочитайте дробь, назовите числитель, знаменатель:
1)4; 2)1; 3)1; 4) А; 5)1; 6)1.
8.	Нарисуйте в тетради циферблат часов — окружность
радиуса 3 ’ см. Отметьте положение каждого часа, от
1 до 12, на окружности.
1)	На сколько частей разделилась окружность?
часть окружности отделяют стрелки часов
(если считать от минутной стрел-
ки к часовой по их ходу) в
6 ч 00 мин; в 3 ч 00 мин?
3) Какую часть окружности пройдет
конец минутной стрелки за 30 мин;
за 15 мин; за 20 мин; за 45 мин; за
40 мин?
4) Какую часть 1 ч составляет: 10 мин;
5 мин; 25 мин; 55 мин?
9. На рис. 4.2 изображена окружность, разделенная на
8 равных частей отрезками, проходящими через центр
окружности.
1) Покажите на рисунке у круга. Сколько полови-
нок в круге?
2) Покажите на рисунке круга. Сколько четвер-
тей в круге? Сколько четвертей в половине
круга?
130
3)	Покажите на рисунке у круга. Сколько восьмых
в круге? Сколько восьмых в половине круга?
Сколько восьмых в четверти круга?
10.	Постройте в тетради отрезок длиной 8 см. Разделите
О	„ ~	12	3	4
отрезок на 8 равных частей. Отметьте: у, у, у, у»
5 6 7 8
Т’ Т’ Т- -8 отрезка.
11.	Постройте отрезок Л В = 6 см. Постройте отрезок
CD = у АВ. Постройте отрезок КР — у АВ. Определи-
те длины CD и К.Р.
12,	Постройте отрезок АВ длиной 15 см. Отметьте точки
С, D, М, К. так, чтобы ЛС = уЛВ, AD=^r АВ,
AM =—АВ, АК=±АВ.
2	О
13.	Какую часть отрезка АВ на рис. 4.3 составляет от-
резок AD?
А	ИВА	В В
3)	I—I—I—1—I—I—I	4) I—I—I—I—I—Ы
Рис. 4.3
14, Вычислите:
1) у от 120;	2) у от 50;	3) у от 45;
4)	1 от 10;	5) ± от 300; 6) от 400.
15.	Какую часть 12 см составляет:
1)	6 см; 2) 4 см; 3) 3 см; 4) 1 см?
16.	Отрез ткани длины 5 м разделили на 5 равных час-
тей. Запишите в виде дроби, какую часть отреза сос-
тавляет: одна часть; две части; три части; четыре
части. Запишите длины получаемых при этом частей
отреза.
17.	Из пакета с картошкой, вес которого 3 кг, отсыпали
1 кг. Запишите в виде дроби, какая часть картошки
осталась в пакете.
18.	Запишите в виде дроби:
1)	две трети; 2) три четверти;
5*
131
3)	четыре пятых; 4) семь десятых;
5)	восемь восьмых; 6) двенадцать десятых.
19.	Прочитайте дроби:
п 2. 2 4 £ 17 9ч 2. А 3 5 р х
^2’ 5’ 7’ 3’ 17’ 30’	3’ 2* р' a' q’ у'
20.	1) Что называется дробью?
2)	Как называются числа р и q в записи дроби у?
21.	Назовите три дроби с числителем 3; три дроби со
знаменателем 10.
22.	1) Запишите две дроби, у которых числитель на
2 больше знаменателя.
2)	Запишите две дроби, у которых знаменатель на
4 больше числителя.
23.	От каната длиной 100 м отрезали его длины.
Сколько метров каната отрезали? Сколько метров
каната осталось?
24.	Сколько копеек составляет:
!) ^р.; 2) ^р.; 3) ’р, 4) ip.f
25.	Вычислите:
1)	1 от 40;	2) ± от 96; 3) от 12;
4)	от 45?	5) у от 140; 6) у от 96;
7)	от 176; 8) -у от 6;	9) у от 49.
26.	Длина автобусного маршрута 24 км. Расстояние от
начала маршрута до первой остановки составляет:
1)	всего маршрута. Определите это расстояние.
§
2)	gy всего маршрута. Определите длину остальной
части маршрута.
3)	у всего маршрута. Определите длину остальной
части маршрута.
27.	Два класса 5 «А» и 5 «Б» собрали вместе 768 кг ма-
кулатуры. 5 «А» собрал всей макулатуры. Какой
класс собрал больше макулатуры и на сколько ки-
лограммов?
28.	Найдите число, если у этого числа равны 30.
29.	Для компота купили 900 г сухофруктов. Яблоки со-
ставляют 4 части, груши — 3 части, сливы — 2 части
132
общего веса Сухофруктов. Сколько граммов яблок,
груш и слив было в отдельности?
30.	Яблоки составляют 7 частей, груши — 4 части, сли-
вы — 5 частей веса сухофруктов для компота. Сколь-
ко граммов яблок, груш и слив в отдельности содер-
жится в 800 г сухофруктов?
31.	Для варенья из китайских яблок рекомендуется брать
на 2 части яблок 3 части сахара. Сколько сахара
следует взять на 2 кг 600 г яблок?
32.	Для варенья из малины на 2 части ягод берут 3 части
сахара. Сколько килограммов ягод было у мамы, если
она взяла 4 кг 500 г сахара?
§ 46. Равенство дробей
Для любой дроби можно указать сколько угодно ей
равных дробей.
„	1	2	3	4	1	2	3
Например,	==‘8==г ‘ ‘ * или ж 9" в
““12
Это можно объяснить так: если отрезок разделить по-
полам, а половину также пополам, то ясно, что половина
1	2 ~
отрезка равна двум его четвертям, т. е. у — у. 1акже
можно показать, что половина 	।	, ।	.
равна трем шестым и т. д. ’ 1'
(рис. 4.4). '	[	J	—<
Можно еще сказать, что дро- ______1
1	2	J
би -у и -у определяют одно и у
z 	а
то же число; записанное в раз-	рис
ных формах. Дроби | и ~ так-
же определяют одно и то же число, записанное в разных
формах, и т. д.
Если числитель и знаменатель дроби умножить на
одно и то же натуральное число, то получится дробь,
равная данной, т. е. выполняется равенство
(I)
q q*n	v '
133
Это свойство называют основным, свойством дроби.
С его помощью можно получать дроби, равные данной
дроби.
„	3	3-10 30 2	2-4	8
Например, 5 —5.10 — 50;. 3 —3.4—12;
. 1 _ 1-3_ 3 _ 4 _ 100,
1 - 1 “ 1-3~ 3 ~ 4 — 100’
с_£_	12
1 — Ь2“ 2 *
Равенство (1) можно записать и в обратном порядке'.
=	(2)
q-n q	' '
В таком виде левая часть равенства есть дробь, чис-
литель и знаменатель которой имеют общий множитель п.
Если n> 1, то говорят, что можно дробь сократить
на п и получить дробь Д. Говорят еще, что можно раз-
делить числитель и знаменатель на общий множитель п.
Поэтому основное свойство дробей можно сформули-
ровать по-другому:
Если числитель и знаменатель дроби имеют общий
множитель, отличный от 1, то дробь можно сократить
на этот множитель. При втом получится дробь, равная
данной.
гт	6	8	15 16
Пример. Сократить дроби у, у, у, -у.
Решение. i	г
6	_ 3	8	ЗГ-4: .4 15
8 ~ Я-4 4	6 •«•3.“ з'з’
’ Л 1
5 _ 5 _ g 16	7 1 =1 =
1	’ 13	**
Если р—натуральное число, то справедливо равенство
Действительно, X = Х1А = X =1.'
Р -Pi1 1 э
Дробь называется несократимой, если ее числитель и
знаменатель не имеют общих простых делителей.
134
гт	-13511
Например, дроби у » у > у» у — несократимые дро-
би, так как числа 1 и 2, 3 и 4, 5 и 7, 11 и 8 не имеют
общих простых делителей.
Для каждой дроби существует единственная равная
ей несократимая дробь.
„	82 12	4 21	333
Например, 12— 3 , 15— 5 » 14— 2 » 5	5 •
Левые части равенств—данные дроби, а правые—рав-
ные им несократимые дроби.
Чтобы получить несократимую дробь, равную данной
дроби, надо сократить данную дробь на наибольший общий
делитель ее числителя и знаменателя. Часто наибольший
общий делитель числителя и знаменателя указать трудно.
В этом случае сокращение дроби выполняют постепенно.
Пример. Сократить дробь
Решение.
1 1,11
192 _	.2г'-96	^-48	б-Л'	^3	3
250	Z'128	;2Г-б4	8 •Л'	ЛГ-4	4	'
11 11
УПРАЖНЕНИЯ
12	3
1.	Объясните с помощью рис. 4.5, почему -у = —= — =
4
£= - .
8
2.	В коробке лежат 16 кубиков.
1)	Если взять 2 кубика, то какими дробями можно
записать взятую часть кубиков?
2)	Если взять 4 кубика, то какими дробями можно
записать взятую часть кубиков?
3)	Если взять 8 кубиков, то какими дробями можно
записать оставшуюся часть-кубиков?
3.	Яблоко разрезали на 6 равных частей и поделили
ломтики поровну между тремя девочками. Какими
135
дробями можно записать часть яблока, полученную
каждой девочкой?
4.	Получится ли дробь, равная данной дроби, если ее
числитель и знаменатель умножить на одно и то же
натуральное число? Как называется это свойство
дроби? Приведите пример на использование этого
свойства дроби.
5.	Докажите с помощью основного свойства дроби, что
п	1-1- 21	1-1- 31	1-1- 41	1-Л-
'	2 ” 10 ’	5 — 10 ’ '	4 — 20 ’ >	4 ” 100 ’
К1	3 — 60 •	R1 3	60 . 7ч 3 _ 375 .	я\ 3 __	24
°'	5“ 100’	10 ” 200’	' 8 ” 1000’	°7 125 ”	1000*
6.	Что значит сократить дробь? Приведите пример дро-
би, которую можно сократить на какое-нибудь число,
назовите общий делитель числителя и знаменателя,
сократите дробь.
7.	Докажите с помощью основного свойства дроби, что
В 10 -1- 91 32-1 • 41 22.-1. 41 12.-1.
> 100” 10’ ’ 80” 4 ’ ’ 100” 5 ’ ’ 600 ”30’
ri 22-1 • Ri 22—1- 71 20 L- 222—1
°) 42 7 > 48 — з ’ ’ 8000 “ 400 ’ °! 480 “ 4 ’
8.	Сократите дробь:
til 2 1 1-911 1 22 Л
8 ’ 36 ’ 28 ’ 35 ’	8 ’ 24  8 ’ 100 ’
1	1 * 111 1
Например, — =	И'2. = JL
г г 36	,2/18	.20 9 Л'-З	3
111
9. Равна ли натуральному числу дробь:
1) у; 2) у ; 3) у; 4) у; 5) j|?
10. Запишите натуральные числа 1, 2, 5 в виде дробей,
знаменатели которых равны: 1) 1; 2) 2; 3) 3; 4) 10;
5) 100.
II. Запишите равенство, заменив букву х так, чтобы ра-
венство было верным:
п 18 * . «I 5 60. х 20 .. 49	7
,)27 = у. 2) у = 7; 3) ^ = 25; 4) у =
12. 1) Замените дробь у равной ей дробью со знамена-
телем 18.
2) Замените у равной ей дробью с числителем 17.
3) Можно ли заменить дробь у равной ей дробью со
знаменателем 121?
136
4)	Можно ли заменить дробь равной ей дробью ео
знаменателем 144?
13.	Сократите дробь:
п 75 42 56 8£.	72 75 35 36.
100 ’ 63 ’ 60 ’ 720 ’	24 ’ 25 ’ 45 ’ 32 ’
42 32	75 48.	.. 75	108 600 800
°' 49 ’ 60’ 100 ’ 56’	125’ 144 ’ 720’ 1000’
14.	Какую часть отрезка длиной 12 см составляет отре-
зок длиной:
1)	1 см; 2) 4 см; 3) 6 см; 4) 8 см?
15.	Найдите от 12 см:
п 1 1 1 1.	1 1 1 1
' 2 ’ 3 ’ 6 ’ 12’	’ 3 ’ 6 ’ 12 ’ 12’
16.	Определите, сколько минут составляет:
1)	1	2) 1ч; 3)1 ч; 4) 1 ч.
17.	Какую часть часа составляет:
1)	1 мин; 2) 2 мин; 3) 4 мин; 4) 6 мин;
5)	20 мин; 6) 22 мин; 7) 35 мин; 8) 55 мин?
18.	Укажите все общие делители и НОД чисел:
1)	12	и	18;	2)	30	и	20;	3)	6	и	12;
4)	14	и	21;	5)	12	и	16;	6)	15	и	30.
19.	Определите НОД чисел:
1)	54	и	72;	2)	18	и	64;	3)	56	и	68;
4)	81	и	54;	5)	24	и	36;	6)	56	и	49.
Например; определите НОД (18, 81).
Решение. 18 = 2^9 = 2-3-3,
81 = 9-9 = 3-3«3-3. НОД (18, 81) = 3-3 = 9.
пл п	, 1Ч 84 .	468. оч 420. .. 780
20.	Сократите дробь: 1) Тоб; 2) 54б; 3) 455 ’ 4) 2730’
21.	Определите, равны ли дроби, результат запишите с
помощью знака равенства (=) или неравенства (#=).
1». 3	18	20	„	4	.	о.	2	15	.
0 ~4	и	24 ’	2)	35	И	7	’	3)	5	И	25	’
.. 18	9	е.	5	36	7	72
4)	22	И	11 ’	б)	§	И	56	’	6)	8	и	Ю8	*
22.	Сколько сантиметров доставляет:
1)	у м; 2) ^м; 3) удм; 4) удди; 5) yggM?
23.	Какую часть метра составляет:
1)	1 см; 2) 2 см; 3) 4 см; 4) 10 см; 5) 50 см?
137

24.	Устно определите, какую часть составляет:
1)	2 от 4; 2) 3 от 9; 3) 4 от 16; 4) 6 от 36.
25.	Какую часть составляет:
1)	1	мин от 1 ч;	2)	1 ч от 1 суток;
3)	2	с от 1 мин;	4)	6 мин от 1 ч;
5)	4	ч от 1 суток;	6)	36 с от 1 мин?
26.	Устно определите длину отрезка, составляющего:
	100 0Т .. 3 4> 100 0Т	1	3 1 м; 2) от 1 дм; 3) j^ot 1 см;	
		1 км; 5) 4- от 1 О	23 1 дм; 6) уэд от 1 км.
27.	Выразите:		
	1) дм	в сантиметрах;	' 3 2) -£• дм в миллиметрах;
	3) 1 кг	в граммах;	4) -g- км в дециметрах;
	2 5) у т в	килограммах;	/чч 2 6) Too т в килогРаммах*
28.	100 т	в килограммах;	2) удо кг в граммах;
	3) у я в	секундах;	4) у ч в секундах;
5)-jr мин в секундах; 6) у суток в минутах.
29.	В классе 36 учеников. Во время субботника шестая
часть всех учащихся занималась уборкой кабинета,
четвертая часть работала на территории школы, а
остальные ребята помогали подшефному детскому
саду. Сколько учащихся работало в кабинете? Сколько
учащихся работало на территории школы? Сколько
учащихся помогало детскому саду?
30.	Из 36 учеников одного класса контрольную работу по
математике на «5» выполнили 6 человек, на «4» —
18 человек, на «2» не написал работу ни один чело-
век. Какую часть класса составляют ученики, полу-
чившие отметку «5»? Какую часть составляют те, кто
получил «4» или «5»? Сколько человек получили «3»
и какую часть класса они составляют?
31.	Из 1200 т овощей, собранных в совхозе за месяц,
800 т собрали старшеклассники. Какую часть рабо-
ты на сборе овощей за этот месяц выполнили стар-
шеклассники?
32.	Урок длится 45 мин, а перемена—15 мин. Какую
часть часа составляет продолжительность урока и
продолжительность перемены?
138
33.	Купили 60 тетрадей, причем в клетку тетрадей было
в 2 раза больше, чем в линейку. Сколько купили
тетрадей в клетку, а сколько в линейку?
34.	Ученик купил тетрадей в клетку на 15 больше, чем тет-
радей в линейку. Сколько всего тетрадей он купил, если
тетрадей в клетку было в 4 раза больше, чем в ли-
нейку?
35.	При помоле ржи на каждые две части муки полу-
чается одна часть отходов. Сколько смололи ржи,
если муки получилось на 35 ц больше, чем отходов?
36.	Сплав содержит одну часть свинца и две части олова
по массе. Сколько олова и сколько свинца содержит
сплав, если его масса 1 кг 800 г? Во сколько раз
олова больше, чем свинца?
37.	В сплаве массой 3 кг 540 г олова в два раза боль-
ше, чем свинца. Сколько олова и сколько свинца в
сплаве?
38.	1) Представьте число 8 в виде произведения несколь-
ких чисел так, чтобы сумма этих множителей была
равна 8.
2) Представьте число 35 в виде произведения не-
скольких чисел так, чтобы сумма этих множите-
лей была равна 35.
§ 47. Приведение дробей к общему знаменателю
7	13
Дроби от Их? имеют одинаковые знаменатели. Говорят,
что они имеют общий знаменатель 25. Дроби -4 и v имеют
- О О
разные знаменатели, но их можно привести к общему зна-
менателю с помощью основного свойства дробей. Для
этого найдем число, которое делится на 8 и на 3, напри-
мер, 24. Приведем дроби к знаменателю 24, для этого
умножим числитель и знаменатель дроби у на дополни-
тельный множитель 3. Дополнительный множитель обыч-
но пишут слева над числителем:
s,7 __ 3-7 _21
8 — 3-8 — 24*
Умножим числитель и знаменатель дроби у на допол-
нительный множитель 8:
8> 1 _ 8-1 _ 8
3	8-3 — 24*
139
3	5
Приведем дроби -g и 12 к °^щемУ знаменателю. Чаще
всего дроби приводят к наименьшему общему знамена-
телю, который является наименьшим общим кратным зна-
менателей данных дробей. Так как НОК (8, 12) = 24, то
дроби можно привести к знаменателю 24. Найдем допол-
нительные множители дробей: 24:8 = 3, 24:12 = 2. Тогда
®3 _ 3*3 _ 9	®>5	2-5	10
8	3-8	24’ 12 —2.12-24’
К общему знаменателю можно приводить несколько
дробей.
2	3	1
Пример. Приведем дроби 25>7ои-ё к общему
знаменателю. Так как 25 = 52, 10 = 2*5, 6 = 2*3, то
НОК (25, 10, 6) = 2*3*52= 150.
Найдем дополнительные множители дробей и приведем
их к знаменателю 150:
0)
2	6-2	12 .
25	6-25 ~~ 150*
,6,3 _ 15-3 _ 45 .
10 “15-10“ 150’
2б>
1 _25,1_ 25 '
6	25-6 “150’
150:25 = 6,
150:10= 15,
150:6 = 25,
УПРАЖНЕНИЯ
1.	С помощью рис. 4.6 покажите, что 1=-|==А = А>
2.	Постройте прямоугольник со сторонами 3 см и 4 см.
С его помощью покажите, что 4-=тт> и 4 = Л*
4	о 12
Рис* 4.6
3.	Сформулируйте основное свойство дробей.
4.	Замените следующие дроби равными им дробями со
знаменателем 12: 1) X; 2) 4*; 3) %?; 4) 4*. б) 4;
О	О	4	О
б)|.
140
13	5	7
5.	1) Дроби у, у, у» 12 приведите к знаменателю 24.
112	5
2)	Дроби -я-» Т • 'o’ > Тя приведите к знаменателю 36.
£ О У 1 о
6.	1) Сколько четвертых содержится в у?
2)	Сколько двадцатых содержится в у?
3)	Сколько тридцатых содержится в у?
7.	Приведите дроби к общему знаменателю:
..	1	1	„ч	1	1	11	1	..	1	1
1)	2	и	3	;	2)	2	и	5	;	3)	2 и	7 ;	4)	2 И	9.
о	IV	1	1	™	з	5	1	1	..	3	11
8.	1)	7	и	8	;	2)	7	и	8	;	3)	10	и 13, 4)	10	и 13.
9.	Назовите три числа, кратные 2 и 3; 2 и 5; 3 и 4.
10.	Назовите три числа, кратные 2 и 4. Назовите наи-
меньшее общее кратное чисел 2 и 4.
11.	Назовите три числа, кратные 6 и 8. Назовите наи-
меньшее общее кратное чисел 6 и 8.
12.	Найдите наименьшее общее кратное чисел:
1)	4 и 6; 2) 4 и 12; 3) 4 и 22; 4) 4 -и 34; 5) 10 и 15;
6)	10 и 25; 7) 10 и 8; 8) 10 и 45.
13.	Приведите дроби к наименьшему общему знаменателю:
IX	1	1	О\	1	1	04	1	1	Л4 1	1
1)	2	и	4 ’’	2)	з	и	в ’	3)	4	и 12 ’	5	и	30 *
14.	1)	у	и	у;	2)	у	и	J6;	3)	и	;	4)	и	.
15.	1)	у	и	42 *»	2)	у	и	j^2; 3) у	и	;	4) у	и	.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
16.	Выполните действия (устно):
1)	48—48:(17—9) + 40;	2) 54—(48—39)-5—5;
3)	67—(62—38):6—4;	4) 48:(31 —19):2 + 2.
17.	Вычислите:
1)	468—396:(42—42:7) + 8;
2)	342—297: (36—36:4)4-5;
3)	3221—294:(98:14—7);
4)	2864 — 792:(72:9—8) + 1001.
18.	1) 1985—2000;	2) —452 + 899;
3) —4325 + 452;	4) —256—337;
5)	673—(—227);	6)—7352+(—436).
19.	Однажды из порта вышли три теплохода. Известно,
что первый теплоход совершает свой рейс один раз
141
в два дня, второй—один раз в три дня, третий — один
раз в четыре дня. Через сколько дней эти теплоходы
опять выйдут в рейс в один день?
20.	Два пешехода вышли из двух населенных пунктов
навстречу друг другу. Первый шел со скоростью 4 км
в ч и через 3 ч встретил второго. Второй пешеход
шел до встречи 2 ч. Какова скорость второго пеше-
хода, если расстояние между населенными пунктами
22 км?
21.	Сократите дробь:
П 25~12 • 26+13. 7 + 28. .. 45+5
> 12-13 ’ > 13-26 ’ Т28“ ’ V 5-45 ’
22 п (17-12).8 . ~ (25 - 9)-25 .	17.8-12-8
'	15-16	’	75.(38 — 22) ’	80
23.	Коробка из под конфет имеет форму прямоугольного
параллелепипеда. Ее длина равна 28 см, ширина со-
ставляет у длины, а высота—ширины. Найдите
объем коробки.
24.	Длина строительного кирпича 250 мм, а ширина со-
ставляет У длины. Высота составляет длины. Най-
дите объем кирпича в кубических сантиметрах.
25.	Для городского парка привезли 684 саженца, причем
4
•д’этого числа составляли липы и березы, а осталь-
ную часть—тополя. Сколько лип, берез и тополей
привезли, если лип и берез было поровну?
26.	При изготовлении кофейного напитка «Ячменный» на
4 части ячменя приходится 1 часть цикория. Сколько
пачек напитка изготовлено, если каждая пачка весит
250 г, и на изготовление этой партии напитка затра-
чено ячменя на 36 кг больше, чем цикория?
27.	При изготовлении кофейного напитка «Наша марка»
на 7 частей кофе берут 6 частей цикория, 5 частей
желудей и 2 части каштанов. Сколько пачек напитка
изготовлено, если каждая пачка весит 200 г, и кофе
и цикория вместе израсходовано 26 кг?
28.	При печатании фотографий количество проявителя
берут из расчета площади фотобумаги, которая будет
проявлена. Сколько листов фотобумаги размером
10x15 см можно проявить в проявителе, которого
хватает на 50 листов фотобумаги размером 9 X 12 см?
29.	Приготовленного раствора фиксажа (его еще назы-
вают закрепителем) хватит для обработки 130 листов
фотобумаги размером 9x12 см. Сколько листов фо-
142
тобумаги размером 13 х 18 см можно обработать в этом
растворе?
30.	Два пешехода идут навстречу друг другу со скоро-
стями 5 км в ч и 4 км в ч. Сейчас расстояние между
ними 18 км. Покажите на схеме, где будут пешеходы
через 1 ч; 2 ч; 3 ч. Какова скорость сближения пе-
шеходов до встречи? Какова скорость удаления пе-
шеходов после встречи?
31. Два поезда идут навстречу друг другу со скоростями
60 км в ч, 70 км в ч. С какой скоростью поезда
сближаются?
32.	Две автомашины едут в противоположных направле-
ниях. Скорости автомашин 65 км в ч и 68 км в ч.
С какой скоростью удаляются друг от друга авто-
машины?
33.	Как с помощью нескольких гирь в 1 кг и 200 г за
одно взвешивание на чашечных весах отвесить
2 кг 800 г муки?
34.	Как с помощью гири в 1 кг и гири в 200 г отве-
сить на чашечных весах 3 кг 400 г? Можно ли это
сделать за одно взвешивание?
35.	Как с помощью одной гири в 100 г отвесить на ча-
шечных весах 1 кг 500 г муки за 4 взвешивания?
36.	Сократите дробь:
n ZZ- 21 Z2Z- 31	41-^-
*' 88’ > 808’ ' 888’ > 1212 ’
о7 п 45-56-1-45.14	38-53 — 38-25 ,
б/>	70772	’	19-42
395-43 + 5-43 ,	.. 359-23— 59-23
695-86+105-86’	758-69—158-69 ’
§ 48. Сравнение дробей
На рис. 4.7 изображен отрезок АВ длины 1. Он раз-
4
делен на 7 равных частей. Отрезок АС имеет длину у,
а отрезок AD имеет длину у.
Длина отрезка AD больше длицы отрезка АС, т. е.
Дробь у больше дроби у (у>у ).
143
Из двух дробей с общим знаменателем больше та,
у которой числитель больше, т. е.
.	р . г
если р > г, то — > —.
<7	9
Рис. 4.7
и	2.1	6.4 13 .2	1.24^,
Например, 3 > 3, 7 > у» П > ТТ или 3 < 3 ’ 7 <
. _6 2^13
^7’ 11 < 1Г
Чтобы сравнить любые две дроби, их приводят к об-
щему знаменателю, а затем применяют правило сравне-
ния дробей с общим знаменателем.
3	5
Пример. Сравнить дроби у и -jy
Решение. НОК (8, 14) = 56. Тогда -5- = 5-7 —II.
4)	4	'	О 0*7 DO
5	5*4	20 т	от ч сл 3.5
14 = ТГ4 = 56• ТаК КаК 21 >20’ т0Т>14-.
Если первая дробь меньше второй, а вторая меньше
третьей, то первая меньше третьей.
Доказательство. Пусть даны три дроби. Приве-
дем их к общему знаменателю. Пусть после этого они
Г 8 t
будут иметь вид —, Так как первая дробь меньше
второй, то г < s. Так как вторая дробь меньше третьей,
то s < t. Из полученных неравенств для натуральных
чисел следует, что г < t, тогда первая дробь меньше
третьей.
Дробь называется правильной, если ее числитель
меньше знаменателя.
Дробь называется неправильной, если ее числитель
больше знаменателя или равен ему.
1	2	3	17
Например, дроби у, у, у,	—правильные, а дроби
2 3 5 24 8
—, "2’ У’ 17’ "8—неправильные.
Правильная дробь меньше 1, а неправильная дробь
больше или равна 1.
144
УПРАЖНЕНИЯ
3	1
1.	С помощью рис. 4.8 объясните, почему -£>-4,
£ 2
2 < 4*
Рис. 4.8
2.	Сравните дроби и запишите результат сравнения
с помощью знаков-> или <:
1 \ 1	4л\2	1	7	8
~5 и Т ’	7 и 7 ’ 3) 15 и 15’
.. 7	6 . м 27	33 . R4 1700	1800
81 И 81 ’ °' 100 И 100 ’	1986 И 1986'
„о	-35142768	11
3.	Запишите дроби у, у, у, у, у, у, р р в по-
рядке возрастания.
л о	х37	1	5	249 17 25
4.	Запишите дроои	75, jo» Тб в по*
рядке убывания.
5.	Найдите дробь, которая больше одной из данных
дробей, но меньше другой. Полученные три дроби
запишите с помощью двойного неравенства:
п 3	9 . о\	5 И .	3	99 ...	5	201
17 10	И 10’ Z'	12	И 12*	100	И 100’	125	И 125'
6.	Сравните дроби:
Т	и	з" ’	2)	"5й	7 ’	3) ТТ и П ’ 4) 'д’ и Тб ’
_	,.9	14	оч	2	7	оч 9	7 . ,ч 13 „ 17
7'	1) 10	И	15 ’	2)	12 И	18 ’	3) 40	И 30 ’ 4) 24 И 36'
8.	Запишите дроби у,	у	и у	в порядке возрастания.
9.	Запишите дроби , у и у в порядке убывания.
10.	у > у и у < т. Можно ли утверждать (без вычис-
4	4
лений), что у > у ?
11.	Запишите дроби в порядке возрастания:
п 3 7_1_ 2_ ±. 9\ 1 J. If Д £
" 4 ’ 8 ’ 2 ’ 5 ’ 20 ’	5 ’ 2 ’ 20’ 4 ’ 8 '
С. М. Никольский и др.
145
2 5	6
Например, у, -g-, &. Решение. НОК (3, 6, 12) =
,O ~	4)2 2-4 8 a5 5-2 10 T c .
— 12. Тогда 3—3.4 — 12» e — 6-2 —12 • Так как
< 8 < 10, to 72 < T2
12 И 12	3	6
12.	Запишите дроби в порядке убывания:
.. j_ j_ £ 7_ 16. m 5 1 з 5 7
И 3’ 5» 5’ 10* 20’	8’ 2’ 4’ 9’ 18'
13.	Существуют ли дроби, для которых верно двойное
2 о 3
неравенство у < ^ < у ? Если существуют, то при-
ведите примеры.
14.	Можно ли назвать 10 дробей, больших одной из
данных дробей, но меньших другой:
1	39	1 з_
!) 40 И 40’ 2) 4 И 4 ?
Можно ли назвать 100, 1000, 10000 таких дробей?
15.	Найдите дробь, которая больше одной из данных
дробей и меньше другой:
1\ 1	1 m 5	2 о. 3	3
) 5	И 3	’ 2) 6	И 3	’ 3) 8	и 4	’
.х 3	7	3	2 4) 20 И 30 ’	7 И 9 ’ Например, 4- и 4-. Р 8)	Z	О 1	1-8	8	„ Т=3^=24- ПоДхоДит 10 __ 2-5 _ 5 24 2-12“ 12’	10	2 б) 11 и 5 • 12>1		Ы2 _	_12
	10 24, так как	8 24	2-12 . 10 <24*	24 ’ 12 ^24’
16. Какие из следующих дробей являются правильными,
1	35673	1	8-.
а какие неправильными: у, -$> ~q> у» 17 
17. Среди дробей со знаменателем 10, 20, 30 назовите:
1) наименьшую правильную дробь;
2) наибольшую правильную дробь.
18. Можно ли среди дробей со знаменателем 10, 20, 30
назвать:
1)	наименьшую неправильную дробь;
2)	наибольшую неправильную дробь?
19.	Можно ли указать:
1)	все правильные дроби со знаменателем 7;
2)	все неправильные дроби со знаменателем 13?
20*. Докажите, что
1)	все правильные дроби меньше 1;
2)	все неправильные дроби больше или равны 1.
21. С помощью знаков — или Ф сравните числа:
146
3	6	о. 2	16	оч 7	27
5	И 10 ’	2) з	И 21 '	3) 5	И 20 ’
л\ 1	50 .	кч 1	25	сч 3	75
4)	2	И 100’	5) 4	И 100’	6) 4	И 100*
3	7
22. 1) Купили у кг конфет и кг печенья. Чего ку-
пили больше?
2) За тетради заплатили р., а за карандаши —
р. За что заплатили меньше?
23. Сравните дроби, не приводя их к общему знамена-
телю:
1Ч	1	1	1	1	2	2
1)	2	и	3	’	2)	7	и	4	’	3)	з	и	5 ;
..	7	7	3	3	с.	8	8
4)	16	И	15’	5)	5	И	7	’	11	И	7’
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
24.	Четным или нечетным является число: 1) 25; 2) З5; 3) 4’; 4) 21’8?; 5) З1’8’?
25.	Четной или нечетной является сумма: 1) 7956 + 8524;	2) 17353+ 18795; 3) 198198+ 197197;	4) 21,88+1; 5) 31988+ 1;	6) 2100+ 220’; 7) 37?® + З*®3;	8) 2М + 3,М?
26.	Для сравнения дробей не обязательно вычислять знаменатель. Например, сравним дроби 35 и jy: 171	35) _2_М7	34	1 _ 1-35	35_	3. .35 35 ~ 35-17 - 35-17’ 17 — 17-35“ 17-35’ ТаК КЯК м<’30’ 34	35 Т0 35-17 < 35-17 И 35^ 17' Сравните дроби: 48 И 55 ’ 2) 53 И 55’	39 И 19’ ..2	1 .	е. 1	3 -	m 1	1 99 и	49 ’	300	И 1000 ’	°' 1985	И 1986*
27*. Докажите, что из двух дробей с равными числите-
лями больше та, у которой знаменатель меньше.
28. При сравнении дробей бывает удобно сравнивать
не сами дроби, а их «дополнения» до единицы. На-
пример, сравним дроби -£ и —. Так как до еди-
147
I 8	1
ницы дополняет -g-, a g- до единицы дополняет -д ,
1^1	7	8
И 8 > 9 ’ Т0 8 < 9 '
Сравните дроби:
п 41	„	42.	53	„	54.	100	101
) 42	И	43’	54	и	55-	3) 10J И	102;
.. 25	24.	109	108.	д. 1986	1987
26	И	25’ °' НО И	109’	°' 1987	И 1988'
39. Устно решите задачи:
1)	Собственная скорость моторной лодки 12 км в ч,
а скорость течения реки 2 км в ч. Найдите ско-
рость моторной лодки по течению реки и против
течения реки.
2)	Скорость моторной лодки по течению реки 18 км в ч,
а скорость течения реки 2 км в ч. Найдите соб-
ственную скорость моторной лодки и ее скорость
против течения реки.
3)	Пловец плывет против течения реки со скоростью
2 км в ч. Скорость течения реки 1 км в ч. Какова
собственная скорость пловца и скорость пловца
по течению реки?
4)	Скорость катера по течению реки 36 км в ч. Ско-
рость течения реки 3 км в ч. Какова скорость
катера против течения реки?
5)	Скорость теплохода против течения реки 48 км в ч.
Скорость течения реки 3 км в ч. Какова скорость
теплохода по течению реки?
6)	Скорость теплохода по течению реки 48 км в ч,
а против течения реки 44 км в ч. Найдите ско-
рость течения реки и собственную скорость тепло-
хода.
30. 1) Расстояние между двумя городами по реке тепло-
ход прошел в одном направлении за 7 ч, а в обрат-
ном—за 6 ч. Какова собственная скорость тепло-
хода и скорость течения реки, если расстояние
между городами по реке равно 336 км?
2) Расстояние между двумя пристанями 72 км. От
одной из них отправился катер, собственная ско-
рость которого 24 км в ч. От другой пристани
одновременно с ним отправили плот, Скорость
течения реки 3 км в ч.
Через сколько часов катер встретит плот при
движении навстречу?
Через сколько часов катер догонит плот при
движении в одну сторону?
148
31*. Двенадцать солдат построили в колонну по 4 чело-
века в ряду и 3 человека в шеренге. В каждом
ряду выбрали самого высокого и из них выбрали
самого низкого. В каждой шеренге выбрали самого
низкого и из них выбрали самого высокого.
Кто выше ростом—самый низкий из высоких или
самый высокий из низких?
Решите задачу в случаях, когда
1)	оба солдата стоят в одном ряду;
2)	оба солдата стоят в одной шеренге;
3)	оба солдата стоят в разных рядах и шеренгах.
Зависит ли ответ в задаче от числа солдат?
§ 49. Сложение дробей
Единичный отрезок АВ разделен на 9 равных частей
(рис. 4.9), причем AC — i-, CD = -^, ЛЭ —-5-. Длина ЛО
У	У	У
2
равна сумме длин АС и CD: AD = AC + CD, т. е. -^- +
, _3 _ _5
+ 9	9*
Рис. 4.9
Сумма дробей с общим знаменателем есть дробь с тем
же знаменателем и числителем, равным сумме числителей
данных дробей:
P.+L = P±L,	И)
я я я	'
„	2,9	112,4	6'	.
Например, 7+7 = -- -g + g- = -g-= !.
Чтобы сложить две дроби с разными знаменателями,
надо привести их к общему знаменателю и полученные
дроби сложить.
Например:
п	В2	?>3_2.5	,	3-3_ 10	9 _ 1°+9_ 19.
Э	3	+	5 — 3-5	'	3-5 — 1515 — 15 ~15’
9.1Й3	,	4>1 __ 3-3	,	4.1 _ 9	,	4 _ 94-4 _ 13.
8	6 — 3-8‘t'4-6 — 24	‘24	24	24’
НОК (8, 6) = 24.
149
Дроби с разными знаменателями можно складывать
по формуле
Р_ । т_р-з+r-g
q ' s q-s '	' '
Например, сложим дроби 1 и по формуле (2)1
7	13 _ 7‘ 96+ 13-48 _ 672 + 624 _ 1296
48 + 96 “	48-96	48-96	48-96 “
- -^324 __j£81_ = Ад-3-3 _ _9_
~ /Г-12-96 "/Г-3-96	лгз'-зг зг *
1 1 11
Однако, найдя наименьший общий знаменатель этих дро-
бей, можно намного упростить вычисления:
У <	1
7 I 13	_ 2-7	13	14	13	14 + 13	27	Х-9	9
48	96	2-48 Т 96	96	96	~ 96 “	96 ~Л'-32 = 32'
1.3 I
почему
УПРАЖНЕНИЯ
1. С помощью рис. 4.10 объясните,
Рис. 4.10
2. Вычислите:
О Тобм + тоом’ з'ч-1_з’4’
о\ 3	3 .	.. 1	,47
3) Тос + Тос:	4) 60мин + 60МИН.
О п 127	, 123	17	, 983
‘ ) 1000 км +юоо км; 2) юоо т"^Тбоот’
3)	юо га +юоГа; 4) юа + 1оа*
4.	Устно вычислите:
1)| + |; 2)4+4; 3)1+4;
4) yl'T’ 5) Тб + Тб’	2б"*'20‘
150
- 11 Ил.-• 91	• 41 Ед.!2-
o. ij 27-г27> зб^зб’	' 60^60’
..	36 , 23	-.5,8	c. 12 ,	12
4)	55+55’	5>зз + зз;	6) 43+48'
„	..	1 , 1 ,	1	-.2,1,3	-.3,2,1
6.	1)	3 + 3 +	3 ; 2)5 +	5 + 51	3)	7 +	7 +	7 ’
7.	Может ли сумма двух правильных дробей с общим
знаменателем быть правильной дробью; неправильной
дробью? Приведите примеры.
8.	Сложите дроби, полученную дробь сократите:
п 5 j_ 2 । 2 •	01 1 , 1 _i_ 1 _i_ 1 -
') з’+з’+'з ’ 2' т+"2+‘2 + l ’
-. 7 . 11 , 2 . 6 .	..1 ,15 .17 /9
3)	13 +13 +13 +13’ 4) 42 + 42 + 42 + 42'
q 11 17 ,15	101	123. - 5 _1_ 31 И
и' V 128 + 128 "г 128 ‘г’ 128’	’ 96 96 "г96 96*
Вычислите:
10.	1) усм + ^см; 2)^м + ^м;
-.7	, 3	.. 256	, 34
3)тодм + удм; ^j^KM + iooKM.
11-	О 6ОЧ+§6Ч’	2) эд мин + -g- мин,
3) ^сут-Цсут; 4)1с+^с.
12. 1)± + т; 2) 4+4; 8)1+4: 4> 4+4-
u	8>1 , 5	3 . 5	8	2-4	4
Например, 2+б — б + 6 ~ 6 “г-з 3’
14 ц 3  7 . п\ ^1 I 1 . ох 17 I 17 .
М io^lOO’ 100^10’ °> 1000^100’
.. 53 , и . -х fllj.^ \22-
юо + юоо’ °' \бо"*'зо; ’20’
R\ 3 Л-(7 J_9V 71 f7J-nk13
b) 2S + ^3o + 5Oj’ 'Ц4о + 7б;+зб'
14	11	l7	। 3 •	91 3 I 2 •	щ	13 1 7 .
*7	125	150’	' 625 * 75 ’	'	1200 ^	360’
41	3	J_ 9	•	RI-IL-lJ9-.	R1	51 ] 31
1600 + 2400’ °' 32002800 ’ °' 4900"I”6300’
15. Устно определите, какие две дроби нужно сложить,
чтобы получить: 1) 2; 2)	; 3) 2; 4) А.
16, Подберите дробь так, чтобы ее сумма о данной
дробью была равна 1:
i\ 1 • о\ 1 . ох 2 . .. 12.	13. д. 29
0 5 ’ 2) 3 » 3) 7 » 4) 17, 5) 28, 6) 30 •
151
17# Два ученика решили пример на сложение дробей
разными способами.
.	,	”’з , 1	3.2 , 1	6 , 1	7
I способ.	5 +10 — 5.2 + 10"“	ю+10“10-
тт	-	3.1	3.104-5.1	304-5 35 i.7	7
II способ. -§-+10 =...5.Ю = —= 5(+ЪгГр’
1
Какой способ проще?
18,	Ученик не понял и не выучил правила сложения
дробей, и сложил две дроби так: 4-+ 4 = 1^5=4 •
В чем ошибка? Вычислите правильно.
19.	1) За завтраком съели у торта, а за обедом—-|-
торта. Весь ли торт съели за завтраком и обе-
дом?
у
2)	За первый день машинистка перепечатала yg ру-
кописи, а на следующий день —у рукописи. За-
кончила ли она перепечатку рукописи?
20.	1) Рабочий до обеда выполнил задания, а после
обеда—^задания. Выполнил ли он задание?
2)	За первую неделю бригада выполнила у плано-
4
вого задания, а за вторую неделю—у планового
задания. Был ли выполнен план за прошедшие
две недели?
21.	За первый час велосипедист проехал половину, а за
второй час—третью часть пути. Какую часть пути
он проехал за первые два часа?
22.	1) Какова длина троса, если от него отрезали три
7	13	9
куска, длины которых км, jggg км, км, и
еще осталось ygg км?
3	1
2)	Урок продолжается у ч, а перемена—g- ч. Ка-
кую часть часа продолжаются урок и перемена?
23.	Найдите число, которое на
8	3	2	1	1	9
1)	yg больше f 1 2) ioi больше у; 3) у больше .
152
3	I
24.	1) Длина прямоугольника м, ширина на у м
больше длины. Найдите периметр прямоугольника.
25.	Какую часть составляют сутки от продолжитель-
ности января; февраля; марта; июля?
26.	Некоторое задание можно выполнить за 1) 2 ч;
2) 3 ч; 3) 5 ч. Какую часть задания можно вы-
полнить за 1 ч?
27.	Расстояние между двумя городами можно проехать
на легковой автомашине за 2 ч, а на грузовой—за
3 ч. Какую часть этого расстояния можно проехать
за 1 ч на грузовой машине и какую часть—на лег-
ковой машине?
28.	Заготовленного корма хватит корове на 60 дней,
а овцам—на 90 дней. Какую часть корма съедает
в день корова? Какую часть заготовленного корма
съедают в день овцы?
29.	Один рабочий может выполнить задание за 4 ч,
а второй—за 6 ч. Какую часть задания выполнит
за 1 ч каждый рабочий? Какую часть задания вы-
полнят за 1 ч оба рабочих, если будут работать
одновременно?
20.	Первый пешеход может пройти расстояние между
селами за 4 ч, а второй—за 3 ч. На какую часть
этого расстояния сблизятся пешеходы за 1 ч, если
одновременно выйдут из этих сел навстречу друг
другу?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
31. Сформулируйте правило приведения дробей к обще-
му знаменателю, если знаменатели дробей—взаимно
простые числа.
32. Найдите десять чисел, которые больше -g-, но меньше
2
5 ’
33*. Найдите все дроби со знаменателем 10, которые
,	5
больше у, но меньше -§•.
„. -	л 12	16	л
с4. Сравните дроби и не приводя их к общему
знаменателю.
35.	Сумма длины и ширины прямоугольника 25 см.
Длина на 5 см больше ширины. Найдите площадь
прямоугольника.
153
36.	Периметр прямоугольника равен 46 см. Длина на
5 см больше ширины. Найдите площадь прямоуголь-
ника.
37.	Сумма длины и ширины прямоугольника 24 см.
Длина в 3 раза больше ширины. Найдите длину и
ширину прямоугольника. Найдите площадь прямо-
угольника.
38.	Периметр прямоугольника равен 36 см. Длина в
2 раза больше ширины. Найдите площадь прямо-
угольника.
39.	Первый цех завода железобетонных изделий расхо-
дует в день 25 т цемента. Сколько цемента расхо-
дует в день второй цех завода, если’ привезенных
870 т цемента хватит на 15 дней работы двум
цехам?
§ 50, Законы сложения
2	4	4	2
Докажем, что у+у = у4-у. Действительно,
2	4 _2+4_4+2_ 4,2
7+7	7 — 7	7'7*
При доказательстве мы использовали переместительный
закон сложения натуральных чисел.
Переместительный закон сложения справедлив и для
любых дробей:
Сумма дробей не изменяется от перестановки слагае-
мых.
Пусть даны две дроби у и р Мы рассматриваем дро-
би с общим знаменателем, так как любые две дроби можно
привести к общему знаменателю. Докажем, что — 4-— =
.	Q Q
~ 4 + Q *
а_ , b  a-J- Ь b-f-a Ь , а
4	4 — 4	4	.7 ' Т'
Для дробей справедлив и сочетательный закон сложе-
ния:
Сумма нескольких дробей не изменится, если любые
рядом стоящие слагаемые заменить их суммой:
154
Докажем это:
fo+Z>)4.g _ q + (ь 4- с) _
Q	Q ~~
a . b-]-c a f b . c \
~~r”	( ““ | **” ) •
q q q \q q J
Сочетательный, закон сложения позволяет записывать
сумму трех и более дробей без скобок:
(а . b \ . с а . / b с \ а . b . с
7 + 7; + 7==7 + k7+7j==7 + 7 + 7-
На основании указанных свойств в сумме нескольких
слагаемых можно переставлять местами и заключать в
скобки слагаемые любым образом.
Этим пользуются для упрощения вычислений.
Например,
Л + А+^ = р4А?|4..з. = ^ + _з__
25 + 7 + 25	^25 + 25/ + 7	2? + 7
.7?	5/	•	5
_ 1	3 7-1	5-3 _ 7	15 7+15 22
" 5 J 7	7 • 5 Г 5 • 7	35 + 55 " 35	35
УПРАЖНЕНИЯ
1, На рис. 4.11 изображен отрезок АВ =12 см; АС=
~±АВ.
1) Найдите длины отрезков АС и СВ.
Рис. 4.11
1	3
2) С помощью рис. 4.11 покажите, что
=Л+1.
4'4
Вычислите, используя законы сложения:
2 n Н-4-13 17. 2. 19 18	12.
1> 48+48 + 48’ ^* 55 ' 55 ' 55’
64^64'64’ ^70^70^70*
28 , 52 ,19.	17	11	23
5) 43+43+43* 6) 45+45+45*
3’ i) 4+i+r5; 2)|+й+1
Q4 3 , 5 . 4	.. 7 , 2 , 11
3' 49+7+49* + ю + 15 + 30'
з> п+(ге+1т); «НН)-
5*, Для трех дробей	запишите перемести-
тельный и сочетательный законы сложения. Дока-
жите справедливость этих законов, используя зако-
ны сложения натуральных чисел.
в, Устно сократите Дробь:
D Г! 2)^; 3)§; 4)§;
к\ 48 с. 18	32 ох 99
7» Сократите дробь:
1)	2)	31	41
1) 56’	64’	> 375’	256 •
Л 35*8 лх 2*27	72*3 дд 25*3
8* ’) 4Г5» 2)	3)	4)
9, Вычислите:
27+9"’ 2) 4§+15 5 3) й+ТЗ’ 4) 17+19’’
5) А+А; 6) &+& 7) А+А’’ 8>и+й-
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
10. 80 деталей можно обработать на старом станке за
8 ч, а на новом станке—за 4 ч. Сколько деталей
можно обработать на двух станках за 1 ч; за 2 ч?
I
I----->-
J 5^
I------>-
ь-1-i-l 6 I I 1 +1-1 1-1 I 1-1-1 I I I 1 1 1-1-1 I-I-1I-1 Т
А В
Рис. 4.12
Расстояние между двумя селами 4 км. Два пешехода
вышли одновременно из этих сел в одном направле-
нии (рис. 4.12). Через сколько часов второй догонит
первого?
156
12.	Две бригады убрали картофель с площади 12 га за
4 дня. Первая бригада могла бы выполнить эту ра-
боту за 6 дней. За сколько дней вторая бригада
могла бы выполнить эту работу?
13,	В рукописи 42 страницы. Одна машинистка перепеча-
тает рукопись за 3 ч, а вторая—за 6 ч. За сколь-
ко часов машинистки могут перепечатать 42 страницы
при совместной работе? Сколько страниц при этом
перепечатает вторая машинистка?
14.	Бак вмещает 600 л воды. Через первый кран его
можно заполнить за 10 мин, а через второй—за
15 мин. За сколько минут можно заполнить бак
через оба крана?
15.	Прямоугольник разделили на 8 равных частей. За.
I	1
красили сначала у прямоугольника, потом у, по-
том у. Весь ли прямоугольник закрасили?
16.	Круг разделили на 6 равных частей. Закрасили сна-
1	1	1 D
чала у, потом у, потом у. Весь ли круг закра-
сили?
17.	Мальчик отпил у чашки черного кофе и долил мо-
1
лока, отпил -j- чашки—долил молока, отпил еще
и
1	U
у чашки—долил молока. Наконец, мальчик допил
кофе с молоком. Чего мальчик выпил больше—кофе
или молока?
18.	Можно ли разрезать квадрат на две части так, что-
бы эти части составляли по площади:
,.3	5
1)	у и у площади квадрата;
о. 4	5
2)	у и у площади квадрата;
1	3
3)	у и у площади квадрата?
28. Двум ученикам было поручено подклеить в библио-
теке 30 книг. Когда работа была закончена, один
3
из них сказал, что он выполнил у задания, а вто-
2
рой сказал, что он выполнил у задания. Библиоте-
карь сразу заметил, что они ошиблись в подсчете.
Как он догадался?
157
20* На первой полке стояло в три раза больше книг,
чем на второй. На двух полках вместе стояли 72
книги. Сколько книг стояло на каждой полке?
21* На первой полке стояло в четыре раза больше книг,
чем на второй. Это на 12 книг больше, чем на второй
полке. Сколько книг стояло на каждой полке?
22* В книге 276 страниц. Девочка прочитала в 3 раза
меньше страниц, чем ей осталось прочитать. Сколь-
ко страниц прочитала девочка?
§ 51, Вычитание дробей
Разностью двух дробей называется дробь, которая
в сумме с вычитанием дает уменьшаемое.
3	12	2	13
Например, у—у=у, так как у4-у=у (рис. 4.13).
Рис. 4.13
Пока мы будем рассматривать случай, когда умень-
шаемое больше вычитаемого.
Разность двух дробей о общим знаменателем есть
дробь с тем оке знаменателем и числителем, равным раз-
ности числителей уменьшаемого и вычитаемого'.
q q Я	' '
Чтобы найти разность двух дробей с разными зна-
менателями, надо сначала привести их к общему знаме-
нателю и найти разность полученных дробей.
”1 _21	8 _21-8_13
3 ““24	24	24 “24'
?>7 _ 15	14_ 15—14_ 1
18 “ 36 3636 “36‘
Например,
®5
12
158
Дроби с разными знаменателями можно вычитать по
формуле
Р г . рч-r-g
q	s q-s	' '
7	13
Например, вычтем из дроби дробьпо формуле (2):
7	13	7-96—13.48 — 672— 624 — 48_1_
48 96“	48-96	— 48-96	48«96	96'
Однако, найдя наименьший общий знаменатель этих
дробей (равный 96), можно намного упростить вычисления:
g,7	13	2-7	13	14	13—14—13 _1
48	96 — 2-48 96 ~96 96	96 “"Эб*
Принято считать число 0 равным дроби вида где q —
натуральное число.
Например, 0 = у = у —у ==...’
Если уменьшаемое равно вычитаемому, то разность
равна нулю.
„	2	2	2—2 О п
Например, у—у = -у-=у = 0.
УПРАЖНЕНИЯ
Выполните вычитание:
„	п	3	1	.	о\	7	3	.	12	3 .	18	11
*•	5	5	’	20	20’	16	16’	25	25*
«	14	1	I	ох	5	1	.	Q1	7	3 .	их	16	1
2,	1)	у—4	>	2)	9	з	«	.3)	ю	б »	4)	27	9	.
q п 1 1 . 24 3_ 1. з: 1—-• 44 -~
3* 1) ~2~~3 ’	"5 Т ’ Т 3 ’	4 7 *
4.	1) 1-4-; 2) 1—4; 3) 1—i.
5,	Устно вычислите:
1)	1-1; 2) 1-Ь 3)	4) 1-4.
6,	Найдите неизвестное число х:
1)	= т + *=12;	Х~ 2б=5'5
4)	х—y = 2i”> 5) у—x=-g-; 6) у—х=у.
159
9
7.	Тракторист должен за день вспахать -=- поля. До
обеда он вспахал поля. Какую часть поля ему
осталось вспахать?
8.	За два часа турист прошел у намеченного пути,
з
Причем за первый час он прошел уд пути. Какую
часть пути он прошел за второй час?
9,	За самостоятельную работу -у- класса получила «3»,
а остальные «4» и «5». Какая часть класса получила
«4» и «5»?
10.	Придумайте две дроби, разность которых равна:
Dll 2)Ь 3)4; 4)|.
11.	Площадь поверхности Земли составляет 510 млн. км2.
этой площади занимает Мировой океан. Составь-
те задачу по приведенным данным и решите ее.
12,	Рабочий выполнил некоторое задание за 5 ч. Исполь-
зуя усовершенствованное оборудование, он стал вы-
полнять это же задание за 4 ч; На какую часть за-
дания в час рабочий стал выполнять больше?
13.	Сон взрослого человека примерно у суток. Какую
часть суток человек бодрствует?
14.	Купили уд кг печенья и конфет. Печенья было уд кг.
Сколько было конфет?
16	,. 1) Собственная скорость моторной лодки -у км в мин,
а скорость течения реки ддкм в мин. Найдите ско-
рость лодки по течению и против течения.
з
2)	Скорость моторной лодки по течению уд км в мин,
а скорость течения реки км в мин. Найдите
собственную скорость моторной лодки и ее ско-
рость против течения реки.
16.	Устно решите задачу:
1)	Рабочий выполнил -у сменного задания. Все ли
задание он выполнил? Какую часть задания оста-
лось выполнить?
160
2)	Рабочий выполнил сменного задания. Все ли
задание он выполнил?
7
3)	Завод перевыполнил задание на части плана.
Какую часть плана выполнил завод?
4)	Водители автобазы выполнили уд месячного плана.
Какую часть плана составило его перевыполнение?
7
5)	Передовой рабочий выполнил за смену у смен-
ной нормы. Какую часть сменной нормы состав-
ляет перевыполнение?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
17.	Вычислите:
1)	6954:1159—16255:3251;
2)	43127:6161—9930:1986.
18.	Устно вычислите:
1)	5—6;	2) -8-3;	3) 72:(—8); 4) (—4)+(—6);
5)	8—12; 6) —7+5; 7) —18—2;	8) —7-(—2).
19.	Для приготовления грузинских пряностей «Хмели
сунели» берут 1 часть шафрана, 2 части сельдерея,
3 части фенхеля, по 4 части кориандра и петрушки
и 6 частей пажитника голубого.
1)	Сколько граммов каждого компонента нужно взять
для приготовления 600 пачек пряностей по 100 г
в каждой пачке?
2)	Сколько граммов каждого компонента нужно взять
для приготовления пряностей, если сельдерея и
петрушки взяли вместе 3 кг?
3)	Сколько граммов каждого компонента нужно взять
для приготовления пряностей, если петрушки взя-
ли на 3 кг больше, чем сельдерея?
20.	В совхозе для производства 1 ц молока расходуют
' кормов на 10 р., что составляет половину всех рас-
ходов на производство молока. Определите себестои-
мость (т. е. стоимость всех расходов совхоза на про-
изводство 1 кг молока) молока в совхозе.
21,	Мама дала брату с сестрой деньги на обед и завтрак
2
в школе. Брат дал сестре ур., и у них денег стало
поровну. На сколько рублей у брата денег ,было
больше первоначально?
6 С. М. Никольский и др.	161
22*. Можно ли написать 45 различных двузначных чисел
так, чтобы среди них не было двух чисел, дающих
в сумме 100?
23*. Можно ли написать 55 различных двузначных чисел
так, чтобы среди них не было двух чисел, дающих в
сумме 100? Какое наибольшее число таких чисел
можно выписать?
§ 52. Смешанные дроби'
Сложение и вычитание неправильных дробей можно
упростить. Как это делается, будет показано в следую-
щем параграфе, а здесь мы подготовимся к его изучению.
Заметим, что если числитель неправильной дроби де-
лится нацело на знаменатель, то такая дробь равна нату-
ральному числу.
з
Рис. 4.14
Если числитель неправильной дроби не делится нацело
на знаменатель, то неправильную дробь можно записать
в виде суммы натурального числа и правильной дроби.
Для этого в числителе выделим наибольшее натуральное
число, делящееся нацело на знаменатель.
U	17	164-1	16 . 1	0,1
Например, у = —у-= у + у-= 8 + у.
Сумму натурального числа и правильной дроби записы-
вают сокращенно без знака плюс (4-) и называют смешан-
ной дробью.
Например, 8+у=8у—смешанная дробь; читают:
7	7
«восемь целых одна вторая»; 2 + у =2 у—смешанная
дробь; читают: «две целых семь восьмых».
162
Если смешанная дробь получена сложением натураль-
ного числа и правильной дроби, то натуральное число
называют целой частью, а правильную дробь—дробной
частью смешанной дроби.
Чтобы записать неправильную дробь в виде смешанной,
надо ее числитель разделить на знаменатель. Если деле-
ние выполняется нацело, то неправильная дробь равна
натуральному числу. Чаще деление выполняется с остат-
ком. Тогда неполное частное будет целой частью смешан-
ной дроби, остаток—числителем, делитель—знаменателем
дробной части.
Например, у=8у;
1 — остаток
Чтобы записать смешанную дробь в виде неправильной
дроби, надо знаменатель дробной части умножить на це-
лую часть, прибавить числитель и полученное число записать
в числитель, а знаменатель оставить без изменений.
Например, =	=
<5	о	О
УПРАЖНЕНИЯ
1. Используя рис. 4.15,
1) 2=|; 2) 2=|;
3) 2=|; 4) 2=f.
восстановите равенство:
Рис. 4.15
2. Запишите дробь в виде целого числа:
4	<1 f ’
I
3.
4.
2) 7; 3) у; 4)f; 5)2.
Можно ли записать дробь в виде целого числа (ответ
объясните): 1) -у*, 2)	3)	4) у?
Устно найдите целое число, равное дроби:
12. 9 40. о. 100. .. 75. 5. 1000. ~ 625
3 ’ 2) 20 ’ 3) 25 ’	3 ’	' 8 ’ ' 25'
6*
163
5.	Запишите числа 3, 7, 11 в виде дробей, знаменатели которых равны числам 3, 7, 11.
6,	Разделите с остатком: 1) 3 на 2;	2)	4 на 3;	3)	5 на 4; 4) 9 на 2;	5)	28 на 3;	6)	19 на 6; 7) 17 на 5;	8)	38 на 13;	9)	42 на 15.
7.	Запишите неправильную дробь в виде смешанной дроби: 1)|; 2) А; 3)1; 4)|; 5)1; 6) Г> 7> 4; 8) Г’ 9> Тб’’ 10) 7’ 11)	12) g; 13)	14) f; 15) ™
8.	Запишите сумму в виде смешанной дроби: 1) 5 + 1; 2) 13 + у; 3) 2 + 1; 4) 17 + g.
е.	Запишите смешанную дробь в виде суммы целого числа и дроби: ')	2) 715; 3) 14+ 4) 1015.
10.	Упростите: 1) 1 + 1; 2) 3 + 1; 3) 2 + g; 4) 10 + 1 Сравните числа:
п.	1) 1 и 1;	2) 11	и 11;	3) 21	и 1|;4)	]1и24. &	О	&	О	£	0
12.	.. 2	1 о. 9 2	л 1	. 2	01	.. „ 2	.1 0 5	И 2 ’ 2) 8 5	и 3 2	; 3) 4 5	и Зу; 4) 3 5	И 4у.
13.	1\2	3 О\ П 2	О3 О\ О 2	Л3	Е 2	еЗ 1) з	и 4 » 2) 9g	и 8р 3) 8-у	и и, 4) 5g и 5^	,
14.	Преобразуйте смешанную дробь, уменьшив натураль- ное слагаемое на 1: 1) +=4+у=3+ 14-у = 34-у + у=3 + +, 2) 5{; 3) 4|; 4) 7^; 5) 2±; 6) 8^ Вычислите сумму:
15.	1) 9+51; 2) 131+5; 3) 8^ + 7; 4) 13 + 21 О	ДО	17
16.	1) 13+281; 2)481+13; 3) 12+231; 4) 39+421. 	9	9	^\)
164
17.	Запишите сумму в виде смешанной дроби, найдите
целую и дробную части смешанной дроби:
1)	7 + у = 7 + 2-|-= 9у,^9—целая,-|-—дробная часть;
2)	8+.1; 3) 9 + ^; 4) 7 + ^; 5) 3 + ^
Вычислите:
18.	1) 2| + 4; 2) 3^ + 1; 3) з} + |; 4) 7|+7.
19.	1)	2) 17-pg-j-yg, 3) у+2-g-; 4) jg + jg-
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
Вычислите:
20.	1) (4+4+S)* 177:118;
2)	129-(4 + 4 + J+ 5):86;
3)	(4+4 + 4+3)*119:68;
4)	3456:(| + 4 + А+7):16.
21.	1) (4+й+т+1) • (-5) + (~756):(-36)>
2)	(4о+4+4+т)-(-123)-(-5О92>:76-
22.	Две работницы фасуют сахарный песок в пакеты по
1 кг. Первая фасует 4 пакета за минуту, а вторая —
3 пакета за минуту. За сколько минут совместной
работы они расфасуют 140 кг сахарного песку?
23.	Два автомата на кондитерской фабрике выпустили
за 24 мин. совместной работы 24 000 карамелей. Пер-
вый автомат выпустил бы это количество карамелей
за 40 мин. За сколько минут второй автомат смог бы
выпустить 24000 карамелей?
24.	Книга дороже общей тетради в два раза. Кйига
с тетрадью стоят 1 р. 32 к. Сколько стоит книга?
25.	Книга дороже общей тетради в три раза или на 28 к.
Сколько стоит книга?
26.	Скорость течения реки 2 км в ч. На сколько ско-
рость лодки по течению больше скорости лодки про-
тив течения? Зависит ли ответ на вопрос задачи от
скорости лодкой?
27.	Скорость лодки по течению реки больше скорости
165
лодки против течения на 6 км в ч. Какова скорость
течения?
28,	Два поезда движутся навстречу друг другу. Один
идет со скоростью 80 км в ч, а другой—60 км в ч.
На каком расстоянии друг от друга они будут за 1 ч
до встречи? На каком расстоянии друг от друга они
будут через 1 ч после встречи?
29*. Дано число 12345678910111213.. .979899. Делится ли
это число на 3; на 9?
§ 53. Сложение и вычитание смешанных дробей
Сложение смешанных дробей выполняют с помощью
законов сложения.
Например, 2-^-4- 3-у = ^2 4-	^3 4-	= (2 4~ 3) 4*
, (1+1}-5 4-1-51
Однако на практике запись сложения упрощают:
91 , ,2	р-1-4-2 гЗ
2т+35 = 5—=5Т'
Чтобы сложить смешанные дроби, надо отдельно сло-
жить целые, затем дробные части и полученные резуль-
таты сложить:
37+l7=44-f-=44-7=47;
514- 21= 74-1±1= 74-1 = 8;
4	4	‘4	1 4	*
о 7 , q 9 к I	к ।	• к * 8	д 3
3Тб+ 2То= 5 + -Го-= 5+ю= 5 + т = 5+ ’у = 6Т:
8)	2)
4 4+24=4*4- 2* = 6^1=61.
Вычитание смешанных дробей также выполняют с по-
шью законов сложения и вычитания. При этом следует
различать случаи:
1)	дробная часть уменьшаемого больше дробной части
вычитаемого, например, ?1—31=44-11= 44-1 = 4I;
2)	дробная часть уменьшаемого меньше дробной части
вычитаемого, например, 7^— 3-1. В этом случае «зани-
166
мают единицу» у целой части уменьшаемого:
-3	«9	.3	9 о , 10+3—9	„ . 4	,2
7Io-3io=4io-io= 3+—io—= 3+i0=35;
3)	дробная часть уменьшаемого равна дробной части вы-
читаемого, например, 7у—5-у = 2.
УПРАЖНЕНИЯ
1.	Вычислите сумму:
1)	ly+Sy, 2) Зу+ 5-g-i	3)7у+3у,
2.	1) 3^ + 11; 2) 91+ 11;
3)71+21; 4)71+71.
3.	1)8^+61; 2)912+21;
з)	42га-'	4>
4.	Устно вычислите сумму:
1)	|1+ 21; 2)71+21;
3)61+31; 4)21+11;
5)41+1“; 6)21+11.
5.	Вычислите:
1)21+1; 2)31+!; 3) 4+1; 4) 71+1.
6.	1)121+31; 2) 51+3^;
3)821+436;	4) 9зд+ Ijg.
7.	По стволу упавшего дерева навстречу друг другу пол-
зут две улитки. Скорость одной из них 7 см в мин,
второй—б см в мин. Через сколько минут они встре-
тятся, если сейчас между ними: 1) 39 см; 2) 52 см?
8,	Навстречу друг другу со скоростями 10у м в мин
и м в мин ползут две черепахи. Через сколько
минут они встретятся, если сейчас расстояние между
ними: 1) 38 м; 2) 95 м?
167
9.	Отрезок АВ разделен точкой С на два отрезка. При-
чем отрезок АС равен 4у см, а ВС на 1-|- см больше,
чем АС. Найдите длину АВ.
10.	Отрезок АВ разделен точкой С на два отрезка. Причем
3	1
отрезок АС = 7-j^ дм, а ВС на 2^ дм больше, чем АС.
Найдите длину АВ.
11.	Даны три числа. Первое , второе на 5 больше, чем
первое, а третье на Зу больше, чем первое. Найдите
их сумму.
12.	Отрезок АВ разделили на 3 части точками С и D;
АС = Зу дм, CD = 5-j- дм, DB — дм. Найдите длину
отрезка АВ.
13.	Отрезок АВ разделили на 3 части точками С и D;
11	2
АС = 2^- дм, CD на дм больше AC, DB на З-g- дм
больше АС. Найдите длину отрезка АВ.
14.	Сократите дробь:
12	15. л. 25. .. „128.	-208	.750
о 36’ 2) 25’ 3) 75 ’ 4)	5) 7256 ’ 6) 4Т000-
15.	Устно выполните действия:
П Z-1- 21 1—1- 31
12	12’	15	15’	'36 36’
4)4-4; 5)4-3; 6) 4~1;
7) 7'5~Т ’ 8) ^7“'27’	939—139‘
16. Вычислите:	<
1) 99~у'»	2) Sjg—•-§-;	3)	;
4)31-2|; 5) 8-1-4Ь 6) 2*-1^.
17.1)1-4;	Ъ'-к’	3)l-g;
4)127—1; 5)251—4; 6)301—1
IS. 1) 1-1-4; 2) 11-4; 3) 11-1;
.. , 2	7 Л	1 с. . 7	2
4) Ц	9 > 3) 513 2 ; 6) 4J5	з.
IC8
, ч Л 1 Q 1	Л\ Q 9	| 7	Qv I Л 1	-J 1 1 в
19, 1) 4зо~	2) З25—ljQ, 3) 224““ 118’
4)9°_2А; 5) 74 + 24 ; 6)31+2*.
20- К 4-2|++	2) 4-2 + ]1;
q\ q 7 q 3	1	. v д 14 .7 3
3) 3-8-2Т“У ’	4) 445“1l5—5;
c. o13 7.1,14 o8 .3,2
3) 2зо ^10+5)’ 6) 2i5 ho+s*
21. Подберите дробь, которая в сумме с данной дробью
дает 1:
1) 4; 2)-J ; 3) 4 ; 4) А ;
§54. Умножение дробей
Произведение двух дробей равно дроби, числитель ко-
торой равен произведению числителей, а знаменатель —
произведению знаменателей этих дробей:
р г =Р‘Г
q s q-s'
TI	2 5	2-5	10
Например,-3. у = ^ = 5I.
Так как любое натуральное число можно представить
в виде дроби, то справедливо равенство
п • — = —
q q
тт	р п р П-р п-р
Доказательство, п • ~ =	• -~=
Чтобы умножить натуральное число на дробь, надо
числитель дроби умножить на это натуральное число, а
знаменатель оставить без изменения.
о 2	3-2	6
Например, 3 • у = — = у.
Можно считать, что произведение натурального числа
п на дробь у* есть сумма п слагаемых, каждое из кото-
р
рых равно
169
тт	о 2	3-2	2+24-2	2,2,2
Например, 3 - у = —=-^-=т + т + т.
Дробь -у называется обратной для дроби —.
У	Р
Дроби ~ и называются взаимно обратными числами;
здесь р и q—натуральные числа.
Произведение взаимно обратных чисел равно 1.
2	5
Например, у и у—взаимно обратные числа;
5 * 2 ~ 5-2“ 10“ b
При умножении смешанных дробей удобно сначала
записать их в виде неправильных дробей.
Например,
« 2.,. в и з _ ц-ж = н =	1
** 3 * 1 2 И 3 " 2 ”	.2 = 2. Э 2 ’
УПРАЖНЕНИЯ
1	. Сократите дробь:
.. 7-8 . 9 6-15 .	35-42
4-15’	30-18’	30-49’
2	. Вычислите произведение:
В — . — - 21— • — • 31—.—
М3 7’^5 11 ’ 8 5’
3	11 —• —• 21—• —• 31—• —•
И 12 8 > z) 7 9 »	1з з »
.. _4 27. еч £4 100. ~ 39 1000
9'16’	25 ' 49 ’	100' 13 *
4	nl.l. 1. 21 1-A.12
**• м -2 5 6 *	8 35 9 ’
- п А А ±- 9\ 1? 16 15
°’ ^16 ’ 15 * 3 ’	56 * 5 * 36’
Вычислите:
«• 1)4-2--1-4=...;2)|-2;
3)4-2; 4) Л.Б; 5) g-3.
7.	1)А-2; 2)1.3; 3)1-5; 4)6-1.
J70
8.	Запишите произведение в виде суммы:
1)3-4; 2) 5-1; 3)1.7; 4)1.6.
9.	Запишите сумму в виде произведения:
о\ 2 д. 2.4- 2 . 2 . 2 . 4ч 7	7	7	7	7 7
3> Т + 5 +т+т+т’ 4) з’+’з + Т + "з +з’+’з •
10.	Упростите числовое выражение:
!)2:(4 + 4); 2)6:(4 + 4 + 4 + 4);
з)(М+1)-4-.4)(4+|+4+4)-^
11.	Для следующих чисел укажите им обратные числа:
1)4, 1,1.1; 2) 2. з, 1, ю.
12.	Числааиб—взаимно обратные, а = 3. Определите Ь.
Являются ли числа у и 18 взаимно обратными?
Ответ поясните.
13.	1) Найдите произведение числа -j и числа, обрат-
ного 3.
2)	Найдите произведение числа 7 и числа, обрат-
ного -у.
3)	Найдите произведение числа, обратного 5, и квад-
рата числа 3.
4)	Найдите произведение числа, обратного 4, н числа,
обратного у.
14.	Вычислите произведение: ,
1)	1 2-. 10=-|-. 10= ...;
2)	2у. 12; 3) 8-3-Ь 4)Зу-28; 5) 2-5|.
15.	1)14-14; 2) 21-11; 3)71.21; 4) 51.11.
112	4
16.	Для чисел 1 у, 2-у, 2-g-, 1у укажите обратные им
числа.
2
17.	Найдите число, обратное у; запишите его в виде
смешанной дроби.
18.	1) Увеличьте |м в два раза;
171
2)	увеличьте -у км в 5 раз;
3)	умножьте уд дм на 10;
2
4)	умножьте у мм на 14;
5
5)	умножьте 3 на у см;
з
6)	умножьте 100 на у м.
19.	Вычислите:
О -4 кг • -3 » 2) 10 Т ’ 14 ’ 3) *5 Г ’ 27‘
20.	1) (lp.+4-p. + lp.)‘3;
„ /23	,17	, 83	\ 1Л
\ 100 Рф 100 Р' + 100 Р' ) ’
3)	4-^км + уКм); 4) 6‘(4 ч+1 у ч).
21-	пЦ+А-гб’ 2)4+4-Гб’
о\ 3JL.A_— • 417__2—• —
6 5 8	13’	1 Z 7 40*
22.	1)7*з“П 51*38’	2) З-3 • 52+1 у • 3;
3)	_ . 5 --1	1 у, 4) l-.I-_l-.2-g-.
23.	1) Число 2 умножили на некоторую правильную
дробь. Какое число получится в результате —
больше 2 или меньше?
2)	Может ли при умножении числа 3 на правильную
дробь получиться число, меньшее 1? Приведите
два примера.
3)	Может ли при умножении числа 4 на правиль-
ную дробь получиться число, больше 1? Приве-
дите два примера.
4)	Верно ли, что при умножении натурального числа
на правильную дробь получается меньшее число?
Приведите два примера.
Вычислите:
24.	0	2> (4У; 3) (т)'; 4)	5>	;
25.	1) (2 у— 1 у) • (з у—g-) • 1 у;
2) (40га-291; -21-87-4-г
172
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
26.	Работница магазина фасует конфеты по у кг в один
пакет. Сколько килограммов конфет она расфасует:
1) в 2 пакета;	2) в 5 пакетов;
3)	в 24 пакета;	4) в 35 пакетов?
з
27.	1 кг яблок стоит у р. Сколько нужно заплатить за
2 кг; 3 кг; 4 кг; 5 кг?
28.	Сторона квадрата равна а. Вычислите периметр
квадрата, если а равно:
1)	у мм; 2) | м; 3) см; 4) дм.
29.	На изготовление одной детали рабочий затрачивает
у ч. Сколько времени рабочий затрачивает на изго-
товление:
1)	2 деталей;	2) 3 деталей;
3)	8 деталей;	4) 12 деталей?
3
30.	Скорость грузовой машины у км в мин. Сколько
километров проедет машина за 1 мин; 2 мин; 4 мин;
8 мин; 10 мин?
31.	Скорость легковой машины 1 у км в мин. Сколько
километров проедет машина за 1 мин; 3 мин; 5 мин;
7 мин?
32.	Сторона квадрата имеет длину а. Найдите периметр
квадрата, если а равно:
1)	2 у м; 2) 5 у дм; 3) Зу дм; 4) 1у см.
33.	В бочке было 40 ведер воды. Когда несколько ведер
отлили из бочки, то осталось в 7 раз больше воды,
чем отлили. Сколько ведер отлили?
34.	Банка меда стоит 1 р. 40 к. Стоимость меда в 13 раз
больше стоимости банки. Сколько стоит мед?
35.	Поезд проходит путь от А до В за 12 ч. Какую
часть пути ему останется пройти через 7 ч после
начала движения от Л?
36.	Ученик токаря может выполнить задание за 5 ч, а
токарь—за 3 ч. Какую часть задания им останется
выполнить через 1 ч совместной работы?
37.	Путь от Л до В скорый поезд может пройти за 12 ч,
а пассажирский—за 16 ч. Какую часть пути им
останется пройти до встречи через 1 ч после того,
как поезда выйдут одновременно из А и В навстречу
друг другу?
173
§ 55. Деление дробей
Частное двух дробей равно дроби, которая при умно-
жении на делитель дает делимое.
Частное двух дробей вычисляется по формуле
q‘s q-r'
„	p-s r	p-s-r p
В самом деле, т-т-—--- ----- -•
’ q-r s	q^r-s	q
Заметим, чт0 ^7 = •у • у > где у—Дробь, обратная де-
лителю, т. е.
Чтобы разделить дробь на дробь, надо делимое умно-
жить на дробь, обратную делителю.
Например:
D 2. • А = 7 . 8 _ 7'8 = 56 .
9 ' 8	9 ‘ 5 " 9 • 5	45’
2) 8:^=8-4 = 8-2 =16 ;
2	1
2
5 ’ 4	5 ’ 1 “ 5 * 2	5
1
При делении смешанных дробей удобно сначала запи-
сать их в виде неправильной дроби.
Например•
1 4
? 1 . 5 _ 5 . 5 _ 5 8	Х-Х __ 4 Л ,
4 2 ’ 8	2 ‘ 8	2 * 5	1 4 9
1 1 о
1	3
9Л	= А- А = А. 9 = АА = 3 .
1 3 ‘ 1 9 = 3 ’ 9	3 * 16 &МГ 4
1 4
Частное любых двух натуральных чисел равно дроби,
числитель которой равен делимому, а знаменатель—де-
лителю.
тт	о о 2 3	2	1	2-1	2
Например, 2:3 = -:т =т •-3=^=3-.
Таким образом, можно считать, что 2 делится на 3,
.	2
но частное равно не натуральному числу, а дробному у.
Черту в записи дроби можно рассматривать как знак
деления числителя на знаминатель.
Например, -у = 7:3, 2:9 =-|-.
174
УПРАЖНЕНИЯ
1. Устно найдите частное и проверьте решение умно-
жением:
1) 8:4;	2) 100:25; 3) 1000:8; 3) 625:25;
5) 144:12; 6) 121:11; 7) 196:14; 8) 169:13.
2. Вычислите частное и проверьте решение умножением:
1)44; 2>44’ 3>44: 4>т4- •
П £.±. 9\ *6.24.	52.26. .. 100 75
о. 1) 9 -21 , I) 25'35’	81'27’	123J82'
4. Назовите делимое и делитель; определите дробь,
обратную делителю; замените деление умножением на
число, обратное делителю; вычислите полученное
произведение:
21—• —• 31—• 41—' —
И 6'2 ’	3'6 ’	7'7 ’	9'3'
- П 15.12- 9\ 12.25 •	и\38. 19
Э* *) 16*24’	17'34’ 6> 75*25’	75:ПЙ*
6.	I) 1:2; 2) 1:2; 3) 1:3; 4) 1:9.
7.	1)44; 2)3:1; 3)5:1; 4)8:1.
о 14 1 1 1 о\ о 1 1 04 О 4 3 ,ч 1 7 32
8.	1) 1 g : 2 ; 2) 2 3 : 6 , 3) 3 5.10, 4) 1 9 .45-
9.	l)y:l-g-; 2)^-:2у; 3)-g-:l^; 4)у:3^.
10.	1)21:31; 2) 11:21; 3)71:51; 4) sl-.iol
11.	Найдите неизвестное число х:
14	3	4	оч	2	4	оч 1	1
О *•у	— т§;	2)	3	х—	7	;	3) х: 2 — 2 ,
..	2	7	7	7	лх 12	3
4)	х:	7	—12;	5)	9	:х—	18;	6) 25'.х — 5 •
12.	Отрезок, длина которого равна 1 м, надо разделить
на равные части длиной м. Сколько частей полу-
чится?
13.	1 кг кофе рассыпали в несколько пакетов по
1)	у кг в каждом пакете; 2) по кг в каждом па-
кете. Сколько пакетов получилось?
14,	Квадрат площадью 1 м2 разрезали на несколько
квадратов равной площади. Сколько получилось
квадратов, если площадь каждого из них составляет:
1) т 2) 1 «; 3) 1 м-; 4) 1, м=?
175
15.	Веревку, длина которой равна 20 м, разрезали на i
3 равные части. Найдите длину каждой части.
16.	Рыболовную леску длиной 11 м разрезали на 4 рав« i
ные части. Найдите длину каждой части.
17.	Автомат фасует сливочное масло в пачки по у кг.
Сколько пачек получится*
1)	из 4 кг масла;	2) из 12 кг масла;
3)	из 8 кг масла;	4) из 15 кг масла?
18.	Периметр квадрата равен: 1) 16 см; 2) 14 см; 3) 13 см;'
4)	17 см. Найдите длину стороны квадрата.
19.	Ленту нужно разрезать на части так, чтобы длина
каждой части равнялась у м. Сколько таких частей
получится из ленты, длина которой: 1) 1 м; 2) 3 м;
3)	2-J м; 4) 51 м?
20.	Уменьшите:
1) 48 р. в 2 раза;
3) 13 кг в 10 раз;
5) у т в 3 раза;
2) 5 м в 2 раза;
4) 25 ч в 4 раза;
6) 1 мин в 3 раза
21.	1)’Разделите числа 40, 50, 60 на 2; на 1.
13	1	1
2)	Разделите числа т, 1-» на 3; на -5-
У о	л	□
22.	Запишите в виде дроби:
1)	1:2; 2) 2:5; 3) 7:10; 4) 23:100.
23.	1) 2 м:5; 2) 4 дм: 10; 3) 3 кг: 1000; 4) 7 т:1000.
Вычислите:
24.	1) 15:3; 2) 17:4; 3) 23:5; 4) 31:6.
25 nfl.A_J.Yl. 911.1-1.1.
zo- 2 ' 4	9 / 5 ’	2 • 8	9'5’
4\l.fl—11Y 41 1-1—1 1
й' 5 ' \ 10	5'9;’	> 5 ’ 10	5*9'
26.	1)	2) l^j-l 4):3|;
3>	4> (Ц'4-з1):2т-
27.	Решите устно. Токарь вытачивает за 1 ч 6 деталей.
За сколько часов он выточит 72 детали?
28.	Рабочий выполняет в день у задания. За сколько
дней он выполнит все задание?
29.	Машина за 1 ч проезжает 1 расстояния между двумя
176	i
!
городами. За сколько часов машина проедет все рас-
стояние?
30,	Плот за 1 ч проплывает расстояния между двумя
пристанями, а катер—у этого расстояния. За сколько
часов проплывает все расстояние между пристанями:
1) плот; 2) катер?
31.	Вычислите:
nfAj.1 7 А ^0___9.9— I 9 ' •
lf <1515; 103	4 32	3 ’
2>(7-Г2Т-1244);6+34+57-
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
32.	Скорость теплохода по течению реки 1з|м в с, а
2
против течения—12 у м в с. Найдите скорость тече-
ния реки и собственную скорость теплохода.
33.	Один ученик может убрать класс за 20 мин, а вто-
рой—за 30 мин. За сколько минут уберут класс оба
ученика?
34.	Мама может почистить картофель для обеда за 8 мин,
а сын затратит на эту работу в 3 раза больше вре-
мени. За сколько минут мама с сыном почистят кар-
тофель вместе?
35.	На птицеферму привезли корм, которого хватило бы
уткам на 30 дней, а гусям—на 45 дней. Рассчитай-
те, на сколько дней хватит этого корма и уткам, и
гусям.
36.	Сколько всего существует различных двузначных
чисел, все цифры которых нечетные? А сколько та-
ких трехзначных чисел?
37.	Каких чисел больше среди первой тысячи (от 0 до
999): тех, в записи которых встречается единица,
или тех, в записи которых ее нет?
38.	Задача-шутка. Из верхнего угла комнаты вниз по
стене поползли две мухи. Спустившись до пола, они
поползли обратно. Первая муха ползла вниз и вверх
с одинаковой скоростью, а вторая хоть и подни-
малась в два раза медленнее первой, но зато спус-
калась вдвое быстрее ее. Какая из мух раньше при-
ползет обратно?
39.	В свободные клетки впишите числа 23, 41, 47, 65,
71 так, чтобы по всем строкам, столбцам и двум диа-
 С. М, Никольский и др.	177
гоналям (отрезки, соединяющие углы прямоуголь-
ника) в сумме получалось одно и то же число.
35		17
		59
	11	
40.	Задача-шутка. Крышка стола имеет четыре угла.
Если один из углов отпилить, сколько углов будет
у крышки?
41.	Сколькими способами можно уплатить 78 р., имея
банкноты 3- и 5-рублевого достоинства?
42.	На сколько частей можно разбить плоскость четырь-
мя прямыми? Рассмотрите все возможные случаи и
для каждого случая сделайте чертеж.
§ 56. Законы умножения
Докажем, что 4 • 4- = 4-• 4- Действительно,
2 5 _2-5 5-2 5 £
3 ’ 7 — 3-7“7-3 — 7*3*
При доказательстве использовался переместительный
закон умножения натуральных чисел. Таким, образом, этот
закон справедлив и для дробей:
От перестановки множителей произведение дробей не
изменяется.
Для дробей справедлив и сочетательный закон умно-
жения:
Произведение дробей не изменяется, если любые рядом
стоящие множители заменить их произведением.
(a>b)-c=a-(b-c), где а=-у, Ь=^-, с=±.
На основании переместительного и сочетательного за-
конов умножения в произведении нескольких дробей
178
можно переставлять множители и заключить их в скобки
любым образом.
Например,
1	9
2 . S . 27 = / 2_ . 27_\ . 5 = ЖДГ , = А . А = 8-5 =	.
3 ' 7 " 8	\ 3 ’ 8 / ’ 7 = ЖЖ ' 7 4 ’ 7 = 4- 7 = 28 ’
1 4
Для дробей а, Ь, с справедлив и распределительный
закон умножения для суммы и разности.
a-(b + c) = ck-b + a-c, где а = 4« & = Т> С=27Г>
Ц	о	U
a-(b—c) = a-b—a-c, где а = “, & = Д, С==Т'
Чтобы сумму дробей умножить на дробь, можно каж-
дое слагаемое умножить на эту дробь и полученные про-
изведения сложить.
Чтобы разность двух дробей умножить на дробь,
можно уменьшаемое и вычитаемое умножить на эту дробь
и из первого произведения вычесть второе.
Например:
•fl 2../А+ 15\ A..9.	11
1 з \ 10	14 / -3 10	3 ' 14 °°
13	1	5 7/	5/
^ЖЖ Ж.Ж jj/5 21 + 25	46.
1 ¥ 3 7	33	35 ’
2^—5 И 5	7 _
7 7 415	45/= 7 ’ 15 “ 7 45 "
1	2	1 1 31
ЖХ ЖЖ \ 1 <6 j_ 5_
3 9 9 9 ~ 9
13	19
Докажем распределительный закон:
Р_. 1г , М _ р r-j-t _ rp-(r+i)  p-r+p-t
q \ s ”•* s J q ’ s q-s	q-s
P'r t P,f _P r \ P f
q*s ' q*s q s q * s 9
УПРАЖНЕНИЯ
Вычислите:
1 n A Z A	1? A 1	Z 34
b 9 ’ 15 * 4 ’ 25 * 11 * 4 ;	15 ‘ 17 ‘ 39 ‘
2, 1)	2) Sl.li.8.
179
q i\ кЕЗ. 141	nx q3 1
^7* 9‘19’	J8" *T’16’
Q\ ₽‘.5	5 К 1	6,1 1 ,	4\ 3	< 1 « 1 4Л 1 w 1
S)	бу.^.Э^.уИу; 4) T.lT.7r12T:7-2 .
4 1)	15е——-4—	•	2)	—. 1~‘А . IL5.L •
’ 1,	10-i8*t>8^’27 *5	9	99 55’15 2O’°2’
ЗА	1?. lA*A 4 A. 9*	4A	85 ^6 «5.0 n 2
3>	95 14’5 4 4 2'	91 517’7’8’25“-
5.	Объясните, как выполнено вычисление:
^.2 = (з+1).2-3.2+1.2=6+4 = б4.
6.	Докажите, что для любых натуральных чисел верно
равенство (a + b):c — a:c+b’.c.
7.	Вычислите:
1)	(888+ 444):4;	2) (999 + 666): 111;
3)	(2774+ 304): 38—304:38;
4)	(3538 + 671):61—3538:61;
5)	(397 + 794):37—494:37.
8.	Магазин получил 450 т яблок, которые будут про-
даны по у р. за 1 кг. Какую сумму выручит магазин
от продажи яблок?
9.	Магазин получил 320 кг лимонов, которые будут
проданы по 2-у р. за 1 кг. Какую сумму выручит
магазин от продажи лимонов?
10.	Стороны прямоугольника имеют длины 2-j дм и 3^- дм.
Найдите периметр прямоугольника двумя способами.
з
11.	Сторона квадрата равна 3^- дм. Найдите его периметр
двумя способами.
4
12.	1 пакет печенья стоит -у р. В каждую коробку пакуют
по 24 пакета печенья. Сколько стоит печенье в пяти
таких коробках? Решите задачу двумя способами.
13.	Вычислите:
1 \ к 1	1 к 1	1 о 5 . 2 q 5
О 7-54	7,54» 2) з'37+з”3Т’
з)	44-44; 4) 1-4+44-
14.	1)	2) (б + ^)-7;	3) (100 + 4)-4;
4)	(4 + 4).4; 5) (17 + {).10; 6) (12 + ^‘9-

180
15.	1)	(8-±)-3;	2)	(24-А).5;	3) (27-1)-5;
4)	(120-1)-25; 5)	(49-^). 100; 6) (з5-§)-9.
16.	1)	11-2;	2)	4-3;	3) 4^-3;	4) 7^2;
5)	17^-5; 6)	24,1.3; 7) 291-5;	8) 481-4.
17.	1) f:2^ + 14 + (10-22:2i).23;
2> (6-44)<7+'4)+(5t-4)-
«О 14 1 7 Л10 О 1 О17. I19.
18.	1) 148'4ц-Зб-225.148,
л\ 9
/ °"9 * 64 * 29’1 3 ’
19,	1)	200^-17;	2)	1986-^-100;
3)	327^-11;	4)	259^-16.
20.	1)	753^-25;	2)	638^-100;
3)	457^-49;	4)	257^-36.
21.	Вычислите устно:
1) 11.4; 2) 3-1.3; 3) 4^-7;
4)	21’7; 5) 7-1-3; 6) 5-1.4.
22.	Объясните и выполните действия:
1)	48-1 = 48:4 = 48:2 = 24;
2)	55-1; 3)172.1; 4) 64-1.
23.	Сформулируйте правило умножения числа на дробь,
числитель которой равен единице.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
24, Вычислите произведение:
1)	35.±; 2) 13.1; 3) 70-1;
4)	246.1; 5) 484-1; 6) 125-1.
181
25. Вычислите:
п 1-А 1-1	1 -З-з'-Н ' 3
4 5 *25* 10—5 ‘ 6 " 10 J|72-|-2-% = T;
9\ 1 2АЛ А 1-1
9 25’81 ’	> 7 ’ 15‘27‘
9ft П 1-1 А-	9\ 1®.^ 38.
4	' 17*23 ” 23’	' 19*37 ’ 81 ’
1 А.А. А- 4Л 1-1-1 А
й' 2 ‘ 3 * 3 * 4 ’	8 * 8 * 6 ’ б ’
27.	Старинная задача. Один муж может выпить кадь
питья в 14 дней, а с женою—в 10 дней. Спраши-
вается, в сколько дней жена его отдельно выпьет
ту же кадь?
28.	Мама дала сыну деньги на школьные завтраки
на 24 учебных дня. Мальчик подсчитал, что этих
денег ему хватило бы на школьные обеды на 12 дней.
На сколько дней этих денег хватит мальчику, если
он будет и завтракать, и обедать в школе?
29.	Из села в город вышел пешеход. Одновременно е ним
из города в село выехал велосипедист. Пешеход при-
шел в город через 6 ч, а велосипедист приехал в село
через 3 ч. Через сколько часов после начала движения
они встретились?
30.	Легковая машина может проехать расстояние от А
до В за 2 ч, а грузовая машина может проехать
расстояние от В до А за 3 ч. Через сколько часов
машины встретятся, если выедут одновременно на-
встречу друг другу из А и В?
31.	Легковая машина может проехать расстояние от А.
до В за 6 ч, а грузовая машина может проехать рас-
стояние от В до А за 9 ч. Через сколько часов машины
встретятся, если одновременно выедут навстречу друг
другу из Л и В?
32.	Имеющихся материалов хватит для бесперебойной
работы первого цеха на 30 дней или второго цеха
на 42 дня. Хватит ли этих материалов для беспере-
бойной работы двух цехов в течение 18 дней?
33,	Передовая бригада решила выполнить пятилетнее за-
дание за 4 года. Сколько годовых заданий выполнит
бригада за пятилетку, если считать, что производи-
тельность труда бригады будет неизменной?
34,	Имеются 9 палочек разной длины, от 1 см до 9 см.
Квадраты с какими сторонами и сколькими способами
можно составить из этих палочек? Способы составле-
182
ния квадрата считаются различными, если использо-
ваны разные палочки и не обязательно все.
Можно ли составить квадраты, длины сторон ко-
торых равны 1 см; 2 см; ...; 6 см? Почему? Можно ли
составить квадрат, длина стороны которого равна 7 см?
Как это сделать? Сколькими различными способами
его можно составить? Рассмотрите дальше все возмож-
ные случаи. Можно ли составить квадрат, длина
стороны которого равна 12 см и более? Почему?
35.	Старинная задача. Двенадцать человек несут 12 хлебов.
Каждый мужчина несет по 2 хлеба, женщина—по
половине хлеба, а ребенок—по четверти хлеба, причем
в переносе участвуют все 12 человек. Сколько было
мужчин, сколько женщин и сколько детей?
36.	Можно ли поместить все население Земли на квад-
ратной площадке со стороной 10 км; 100 км? Произ-
ведите расчеты при условии, что на одном квадратном
метре могут поместиться 4 человека, а численность
населения Земли для простоты расчетов примем
5000000000 человек.
§ 57. Решение задач
Задача 1. Нахождение дроби данного числа.
Найдем, например, две трети числа 60. Будем считать,
что число 60 состоит из трех третьих долей. Тогда одна
60 п
треть в три раза меньше: . Две же трети в два раза
больше: ^^ = 40. Мы видим, что для решения задачи
2 СЛ	2-60	2 СЛ
надо умножить у на 60, так как
2
Примеры. 1) Найдем у числа 10.
Решение. Так как у числа 10 равна у, тоу числа 10
2-10 20 п6
равны -у-=у = 2у, т. е. для решения задачи надо ум-
2 1Л	2,10	2 1Л
ножить у на 10, так как -у-=у • 10.
Ответ. 2у.
2) Найдем у числа 120.
183
Решение. Так как числа 120 равна у = 24, то
6	,ОЛ	6-120	...	6 ,	' 6-120	...
= числа 120 равны —=—=144, или • 120 = - . - = 144.
О	ООО
Ответ. 144.
3) Увеличим число 12 на у этого числа.
Решение. Если число увеличить на 4- этого числа,
О
-	а	.,14
то полученный результат будет составлять 1-|-у.= у дан-
4	4	4*12
ного числа. Найдем -$ числа 12: -% -12 =—г— = 16.
О	о	о
Ответ. 16.
4) Уменьшим число 7у на этого числа.
Решение. Если число уменьшить на -Г этого числа,
1	5
то полученный результат будет составлять 1—у==у дан-
тт «	5	«1	5 м 1	5*36	«
ного числа. Найдем числа т--7-?- = -^~г = 6.
О	ООО 6*0
Ответ. 6.
Задача 2. Нахождение числа по его дроби.
Найдем, например, число, две трети которого равны 40.
Будем считать, что искомое число состоит из трех третьих
долей. По условию его две трети равны 40. Но тогда
40
одна треть в два раза меньше: у, а три трети в три
раза больше: у 3 = 60. Мы видим, что для решения за-
дачи надо 40 разделить на -f-5 40:-|- = 40-4=^^ = 60.
Ответ. 60.
УПРАЖНЕНИЯ
1.	Найдите от числа 360:
1)	одну вторую; 2) одну пятую;
3)	одну десятую; ' 4) одну тысячную.
2.	Найдите от числа 25:
1)	две пятых;	2) три десятых;
3)	четыре седьмых; 4) семь пятидесятых.
184
3.	Найдите от числа gg:
l)j; 2)|; 3) {А; 4) 1|.
4.	Космический корабль «Прогресс» при общей массе 7 т
доставил на орбиту грузы, масса которых составляла
23
общей массы корабля. Сколько килограммов грузов
доставил на орбиту космический корабль?
5.	1) Что	больше:	4-	от	60	или	Л	от	60?
1	D	10
2)	Что	больше:	4	от	60	или	Д	от	600?
'	О	10
3	4
3)	Что больше: от 60 или -гр от 135?
'	О	1О
6.	Выразите:
1)	в квадратных метрах -g- га;
з
2)	в квадратных метрах км2;
оч	17
3)	в арах га.
7.	Выразите:
1)	в кубических сантиметрах gg м8;
з
2)	в кубических дециметрах м3;
з
3)	в кубических метрах км8.
8.	Найдите число, -g- которого равна:
1)	6;	2) 4;	3) 27;	4) 5;
5)	6) 1|; 7) 2|; 8) з|.
4
9.	Найдите число, у которого равны:
1)	4; 2) 12; 3) 28; 4) 1-А-.
10.	Найдите число, для которого 100 составляет:
1)	1; 2)}; 3) 1|; 4) 2±
11.	Реактивный самолет может подниматься на высоту
2
•до 40 км, что составляет jg высоты, на которую
обычно запускают искусственные спутники Земли.
На какой высоте летают искусственные спутники
Земли?
185
5
12, 1) Найдите число, если известно, что у этого числа
равны 155.
2)	Найдите число, если известно, что числа
равны 354.
31
3)	Найдите число, jqoq которого равна 6510.
13.	На овощную базу доставили 2870 т помидоров, что
составляет плана. Сколько тонн помидоров было
запланировано доставить на базу?
14.	На приготовление домашнего задания по математике
ученик затратил 35 мин, что составляет всего вре-
мени, затраченного учеником на приготовление домаш-
них заданий по всем предметам. Сколько минут ученик
готовил все домашние задания?
15,	1) Ширина прямоугольника 8 см, что составляет
у длины. Найдите периметр и площадь прямо-
угольника.
з
2) Сторона треугольника 12 см, что составляет у одной
4
и у другой стороны этого треугольника. Найдите
периметр треугольника.
16.	Рабочий получил в середине месяца 102 р., что соста-
вило у его зарплаты за месяц. Какую часть зарплаты
он получил в конце месяца? Какова зарплата рабо-
чего за этот месяц?
з
17,	1 кг яблок стоит у р. Сколько нужно заплатить за
1) 4- кг; 2) 4- кг;	3) 2 кг;
4)	у кг; 5) 1у кг; 6) 2у кг?
18.	1 кг лимонов стоит 34- р. Сколько нужно заплатить за
£
о 4кг;	2) 4кг;	3> 4кг;
4) 1у кг; 5) 1^ кг; 6) 2-| кг?
19, Число 75 увеличьте:
1) в 3 раза; 2) в у раза; 3) в 2у раза.
186
20, 1) В баке помещается 30 л воды. Его можно напол-
нить через кран за 6 мин. Сколько литров вода
нальется в бак за 5 мин?
2)	Бак можно наполнить водой через кран за 6 мин.
Какая часть бака наполнится за 5 мин?
21* Некоторое задание можно выполнить на старом станке
за 8 ч, а на новом станке—за б ч. Какую часть за-
дания можно выполнить на двух станках вместе
за 1 ч; за 2 ч; за 3 ч?
22,	Ванну можно наполнить или из одного крана за 15 мин,
или из другого крана за 10 мин. Какую часть ванны
можно наполнить из двух кранов за 1 мин; за 5 мин?
Наполнится ли ванна за 6 мин?
23,	Одна машинистка может перепечатать некоторую
рукопись за 6 ч, а другая—за 7 ч. Успеют ли маши-
нистки вместе перепечатать рукопись за 3 ч; за 4 ч?
24,	Использование 1 т макулатуры позволяет получить
т бумаги. На производство 1 т бумаги идет при-
мерно 16 деревьев, которые росли 60—80 лет. Какое
количество деревьев заменяют 20 т макулатуры,
собранные учащимися вашей школы за год?
25.	Число 45 увеличили:
1)	на у этого числа; 2) на у этого числа;
2	4
3)	на у этого числа; 4) на -у этого числа.
Найдите полученное число двумя способами.
26.	Число увеличили:
1)	на у этого числа; 2) на у этого числа;
1	3
3)	на у этого числа; 4) на у этого числа.
Во сколько раз увеличилось число?
27.	Число увеличили:
1)	в Ijg раза; 2) в | раза;
3) в у раза;	4) в у раза.
На какую часть увеличилось число?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
28, За один день в нашей стране добывалось в 1970 г.
540 тыс. т железной руды, а в 1984 г. на у этого
187
количества больше. Сколько руды добывалось за один
день в 1984 г.?
29. Сравните дроби:
1Ч	2323	23	о.	71
6464	И	64 ’	%)	98	и
80.	Укажите все дроби	со
-	4	7
больше тх, но меньше
7171
9898-	I
знаменателем 10, которые |
I
81, Как изменится произведение двух чисел, если один
1
множитель увеличить на -=- его часть, а другой мно-
О
1
житель уменьшить на у его часть?
32. Делимое уменьшили на его часть, а делитель уве-
личили на pj его часть. Как изменилось частное?
§ 58. Площадь прямоугольника, Объем прямоугольного
параллелепипеда
Если длина и ширина прямоугольника выражены в
какой-либо одной единице длины натуральными числами
а и Ь, то его площадь вычисляется как произведение а-Ь,
Формула S = a-b верна и при дробных а и Ь.
На рис. 4.16 изображен прямоугольник со сторонами
а=-|-дм и й = -|-дм. Покажем, что его площадь равна
q 9	Я 9	1
5=^да.-|дм = -5--уДмг = уДМа.
Достроим прямоугольник до квадрата со стороной 1 дм.
Одну сторону квадрата разделим на 4 равные части; три
из них составляют длину прямоугольника. Другую сто-
рону квадрата разделим на 3 равные части; две из них
составляют ширину прямоугольника.
Квадрат разделен на 4-3 равных частей, площадь
каждой из которых равна ^дм?.
Прямоугольник состоит из 3-2 равных частей, по-
1	3»2	3
этому его площадь равна (3-2) • дм^^дм^удмх
2
Ху ДМ.
Итак, S—дм • у дм =	| дм? = дм2.
188
Площадь прямоугольника со сторонами а и b вычис-
ляется по формуле
S—a-b, где а — — , Ь=—.
q s
Если длина, ширина и высота прямоугольного парал-
лелепипеда выражены в какой-либо одной единице длины
натуральными числами а, b и с, то его объем вычисля-
ется как произведение а-Ь-с.
Формула V = a-b-c верна и при дробных а, Ь, с.
На рис. 4.17 изображен прямоугольный параллелепи-
2	12
пед с ребрами а = -&дм, & = удм, с=у дм. Покажем, что
его объем равен
у=4дм4дм4дм=^да1’=:йда13-
Достроим параллелепипед до куба с ребром 1 дм.
Одно его ребро разделим на 5 равных частей; две из
них составляют ширину параллелепипеда. Другое ребро ку-
ба разделим на 2 равные части; одна из них составляет
длину параллелепипеда. Третье ребро разделим на 3 рав-
ные части; две из них составляют высоту параллелепипеда.
Куб разделен на 5-2-3 = 30 равных частей, объем каж-
1
ДОИ ИЗ КОТОРЫХ равен е-я-я дм8.
Прямоугольный параллелепипед состоит из 2-1-2 = 4
таких частей. Поэтому его объем равен
1	9.19	1	9
(21>2). 537зДмЗЕ=б^зда18=-бда1,7да-Зда,<
189
.'1
Итак, V = yдм-удм-уда = |^удм3 = ^да8.	5
Объем прямоугольного параллелепипеда с ребрами а, Ь, %
с вычисляется по формуле	--	|
V = a-b-c> где	^=7't с==~и*	|
9	£
Примеры. 1) Стороны прямоугольника равны 4-^см и
б	9	5	49*5
у см. Его площадь равна 5 = 4-^ см -у см = |уусм8 ~
7» 1 а л 1 П
= Н“Т СМ2 = 3-х- см2.
Л * 4	&
2)	Ребра прямоугольного параллелепипеда равны Зу дм,
4	3 с ,	,/о143	10.4-3	1 .
jg дм, у дм. Его объем равен V = Зу ‘io'8’=зПоТ8==‘2 (дм )•
УПРАЖНЕНИЯ
1,	Вычислите площадь прямоугольника, длина и шири-
на которого равны:
1)	у м и ум;	2) ^дм и уда;
3)	1уМ и 1ум; 4) 3-|дм и 2удм.
2.	Площадь прямоугольника равна 4 дм2. Вычислите
длину прямоугольника, если его ширина равна:
1) у дм; 2) у дм; 3) 1-|-дм; 4) 1удм.
3,	Вычислите площадь и периметр прямоугольника, дли-
на и ширина которого равны:
2	3	11
1)	1уМ и Зум; 2) 4эдМ и Зум.-
4,	Вычислите площадь и периметр квадрата, сторона ко-
торого равна:
1)	у см; 2) у дм; 3) ^м; 4) 1удм.
5,	Сколько потребуется банок краски, чтобы покрасить
крышу дома, если крыша имеет размеры, указанные
на рис. 4.18, и содержимого одной банки хватает на
окраску Юм2 поверхности?
6,	Требуется покрыть кафельной плиткой пол, имеющий
форму прямоугольника со сторонами 4 м и 2 м 50 см.
Плитки имеют форму квадрата, сторона которого
180
я
равна 12 см. Сколько ящиков плитки потребуется,
если в каждом ящике 50 плиток?
7,	Вычислите объем куба, ребро которого равно:
1)	ум; 2)|м; 3) 1усм; 4) 2-|-дм.
8,	Вычислите объем прямоугольного параллелепипеда,
ребра которого равны:
1)	|м, ум,-|-м; 2)дм, у дм, — дм;
3)	50 мм, 2 см, ioqM; 4) у^дм, у^м, 2 дм.
9,	Вычислите площадь всех граней куба, ребро кото-
рого равно:
1} -3 см; 2) -g-дм.
10.	Вычислите площадь всех граней прямоугольного па-
раллелепипеда, ребра которого равны:
1)	1-удм, 2^-дм, 4удм;
2)	2-|-дм, 1-у-дм, 1-§-дм.
11.	Вычислите объем классной комнаты, если ее ширина
6 м, длина 8 м, высота 3-|-м. Сколько литров возду-
ха приходится на каждого ученика класса, в кото-
ром 40 человек?
Составьте и решите задачу, учитывая размеры
своей классной комнаты и количество учеников в
своем классе.
12.	В магазине продаются два аквариума. Размеры одного
из них 42 см, |м, 2удм, а другого 54 см,-у-м,-|-м.
Объем какого аквариума больше?
Рис. 4.18	Рис. 4.19
13.	Вычислите объем, который занимает пачка сахара-
рафинада. Размеры в сантиметрах указаны на рис. 4.19.
15,	3 кг конфет и 1у кг печенья стоят 10у р., а 5 кг тех
191
•i
же конфет и 1укг того же печенья стоят 15-у р. Сколь-
ко стоит 1 кг конфет и сколько стоит 1 кг печенья? .
16.	Чтобы узнать, является ли число 2503 простым, его
стали делить на 2, 3, 5, 7, 11, 13, ... На каком
простом числе можно прекратить испытание?
17.	Разность двух нечетных чисел равна 8. Докажите,
что эти числа взаимно простые.
18.	Докажите, что если в трехзначном числе средняя
цифра равна сумме крайних, то число кратно 11.
19.	Может ли наибольший общий делитель двух чисел
быть больше их разности?
§ 59. Единицы измерения скорости
При решении задач на равномерное движение поль-
зуются формулой
s = v-t,
где s—путь, v—скорость, t—время движения.
Единицами измерения длины (пройденного пути) яв-
ляются: 1 мм, 1 см, 1 дм, 1 м, 1 км.
Единицами измерения времени являются: 1 с, 1 мин,
1 ч.
Единицами измерения скорости являются: 1 мм вс,
1 мм в мин, 1 мм в ч, 1 см в с, ... На практике часто
используют для измерения скорости следующие единицы:
1 м в с, 1 км в ч.
Чтобы определить скорость равномерного движения, надо
путь разделить на время движения:
V = S'.t.
Так как s:i = у, то для единиц скорости приняты обо-
значения: 1 м в с=1 —, 1 км в ч=1—.
Чтобы определить время равномерного движения, надо
путь разделить на скорость движения;
t=S'.V.
При решении задач на движение необходимо согласо-
вывать единицы измерения пути и времени с единицами
измерения скорости.
192
Пример. Найдем скорость о, взяв за единицу изме-
рения 1 ™, если путь s равен 6 м, а время t равно 3 с.
Решение.
1)	Так как 1м=^-км, то 6м-6-^км-
3
₽ 40№КМ	500 KNf’
500
2)	Так как 1с==~-мин, а 1мин«-~-ч,
би	60	’
ТО 3 с == 3 • — • — ч ~ ——— ч « —ч
00	60 JKT- 60	1200 Д •
3)	v-s:t, поэтому
/	nuaivmy V 500-1200	5	'з\Ч/
fi	rj 1 км
Отв ет. 7-=-*—.
о ч
УПРАЖНЕНИЯ
1.	Найдите пройденный путь, если известны скорость
движения и время движения:
1)	с’=2-^, f = 3c; 2) v = 2y, / = ^мин.
2.	Найдите скорость движения о, если известны прой-
денный путь s и время движения 1\
1)	$ = 6 м, / = 3с; 2) s=6 м, <=^ч.
3.	Скорость пешехода . Найдите путь, пройденный
пешеходом:
1)	за 2 ч; 2) за 1уч;
3)	за 45 мин; 4) за 125 мин.
4.	Расстояние в1у км пешеход прошел за 20 мин.
Найдите скорость движения пешехода. Ответ запиши-
те в следующих единицах:
1)	2)2^; 3) —; 4); 5) Д
' ч ’ ' мин * 1 ч * ' мин ' с
5, Скорость легковой автомашины 72—. Какой путь,
.она пройдет:
1)	за ч; 2) за 45 мин; 3) за 50 мин; 4) за 165 мин? <
7 С. М. Никольский и до.	193
6, Скорость легковой автомашины 1200^. За сколько
часов машина пройдет:
1) 144 км; 2) 36 км; 3) 8 км; 4) 54 км?
7, Найдите скорость автомашины, если 80 км она про-
езжает:
4	4	Я
1) за 1 ч; 2) за -g-ч; 3) за у ч; 4) за уч;
5) за 50 мин; 6) за 65 мин; 7) за 90 мин; 8) за 100 мин.
8. Два конькобежца стартовали на дистанцию 10000 м
по замкнутой дорожке, длина которой равна 400 м.
Скорость одного из них 20 ™, а скорость второго —
22™. Обгонит ли второй конькобежец первого на
круг до конца дистанции? А на два круга?
9. 15 июля 1923 г. из Москвы в Нижний Новгород
(г. Горький) вылетел аэроплан «Ультиматум». Так
была открыта первая трасса Аэрофлота длиной 420 км.
Аэроплан шел на высоте 250 м и преодолел все рас-
стояние за 3 ч. 30 мин. Найдите скорость аэропла-
на. Какое условие в задаче является лишним?
10*, 1) Поезд проходит мимо столба за 2 мин. За сколь-
ко минут он проедет через мост, длина . которого
в 2 раза больше длины поезда?
2)	Поезд проходит мимо столба за 40 с. За сколько
секунД он проедет туннель длиной 1 км, если дли-
на поезда 800 м?
11.	Замечательные русские изобретатели-самоучки отец
и сын Черепановы построили первый паровоз в 1834 г.
Он проезжал 500 м за 2 мин. Какова скорость па-
ровоза в метрах в минуту и километрах в час?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
12.	Вычислите:
1)14:3+15:6; 2)17:10—7:5;
58:7+ 45:14.	.. 56:13—100:26
45:7—48:14 ’	100:13 +56:26'
13.	Сложите 4- числа 2-|- и %. числа 3-1-.
4-5	3	6
«л тл о3	«1	о 1	16
14.	Из 2-=- числа 1-т- вычтите 2-$ числа р=.
/о	о	1/
15,	Найдите число, три четверти которого равны четы-
рем пятым числа 80.
16,	Из пункта А в пункт В по реке отправили плот.
Одновременно с ним из В в А вышел катер, который
194
прибыл в А через 5 ч. Через сколько часов катер
встретил плот, если плот прибыл. в 5 через 20 ч.
после начала движения?
17.	Токарь и его ученик выполнили задание за 1 ч 40 мин.
Токарь мог бы выполнить это задание за 2 ч 30 мин.
Сколько времени затратил бы ученик на выполнение
этого же задания?
18.	Два тракториста вспахали поле за 2 ч. Первый трак-
торист выполнил бы эту работу за 3 ч 20 мин. За
сколько часов второй тракторист мог бы вспахать
это поле?
19,	Из пункта А в пункт- В выехала грузовая машина.
Одновременно с ней из В в Л выехала легковая ма-
шина. Грузовая машина через 1 ч встретила легко-
вую и еще через 1 ч 30 мин прибыла в пункт В.
Сколько времени потратила легковая машина на путь
из В в Л?
20,	Из пункта Л в пункт В вышел катер. Одновременно
с ним из В в Л отправили плот. Катер встретил
плот через 3 ч 20 мин, а еще через 20 мин. прибыл
в пункт В. Сколько времени плыл из В в Л плот?
§ 60. Представление положительных дробей
на координатной оси
На координатной оси (рис. 4.20) можно изобразить
любые положительные дроби у. Для этого надо у часть
единичного отрезка отложить р раз на координатной оси
от точки О в положительном .направлении.
Рис. 4.20
Точку, изображающую на координатной оси дробь у,
называют точкой -у или точкой с координатой 2-.
195
t д	в с	л
Ч----1------1—1---1-
Ч	р	1i
Рис. 4.21
Например, точка А (рис. 4.21) имеет координату -L
о
Пишут:	говорят: точка Л с координатой у или
точка у.
—точка 4’ ^(1)—точка Г, D^l-~)—точка 1-^-.
Положительные дроби называют еще положительными
рациональными числами, а точки, изображающие их на
оси, называют рациональными точками.
а+ъ
а ~Т~ Ъ
4-------1------
Рис. 4.22
Если а и Ь—два положительных рациональных числа
и Ь > а, то
: 1) точка b на координатной оси находится правее точ-
ки а;
2)	расстояние между точками а и & равно Ь—а\
3)	точка является серединой отрезка, соединяю^
щего точки а я b (рис., 4.22).
В самом деле, чтобы вычислить координату точки С—
середины отрезка АВ, надо к числу а прибавить поло-
вину. длины отрезка АВ'.
.Ь—а_2а,Ь-ча_2аЦ-Ь—а_аЦ-Ь\
	’	2 ”" 2 ' 2 “	2	~ 2 '
Пример. Найдем длину отрезка, соединяющего точки
з
п«®у и Ь«=1, и координату середины этого отрезка. Оче-
видно, что у < 1, поэтому точка 1 находится на коорди-
3
соединяю-
Середина
натнои оси правее точки у, а длина отрезка,
щего точки у и 1, равна о—а—1—у = у.
этого отрезка имеет координату
4
л+ Ь 1	„	1/. . 3\ 1 8 .1'-B'
1 1
196
Таким, образом, можно вычислить координату середи-
ны отрезка, соединяющего любые две рациональные точки.
Отсюда следует, что между любыми двумя рациональными
точками находится еще хотя бы одна рациональная точка.
Число называется средним арифметическим чисел
а и. Ь.
Например, среднее арифметическое чисел 3 и 5 равно
3+5	,	.	21
—=4, а среднее арифметическое чисел у и у равно
в)
( 2. + lY2-f± + lkl = £.-L=5
\ 3	6 г к 6 '6/2	6 2	12‘
Вообще, средним арифметическим нескольких чисел на-
зывается частное от деления суммы этих чисел на число
слагаемых.
Например, для чисел 1, 3, 7 среднее арифметическое
равно
1+3+7. _ И q2.
з ~з“'>3’
для чисел 1, 2, 3, 4 среднее арифметическое равно
1+2+3+4 ю .О1
4	4 “ 2 ’
УПРАЖНЕНИЯ
>1, Изобразите на координатной оси (ед. отр. 6 см) точки
n 1	2 3 4 5	6	7 8 9 10 L1 12 г
°* 6 ’ 6’ 6’ 6’ 6’ 6’ 6’ 6’6’6’ 6’ 6 ’ А
„	1 1 2 , . 1 . 1 т
на этой оси находятся точки у, у, у, 1, 1у, 1у,2?
2.	Выберите удобный единичный отрезок и отметьте на
координатной оси точки:
1)	0, 1, 2, 3,	1|;
2)0,4,4,1,2,21,21,24.^
3,	Изобразите на координатной оси точки А (у), В (2),
Найдите длину отрезков А В, ВС, АС.
4,	Найдите координату середины отрезка, соединяющего
точки:
1) 4-и±;2)|и±; 3)21и|;4)з1 и з|.
197
5.	Даны точки А (2) и В • Найдите координаты
точки С—середины отрезка АВ, точки D—середины
отрезка СВ, точки Е—середины отрезка CD. Изо-
бразите эти точки на координатной оси.
6.	Найдите координату точки В по координатам точки
А и точки С—середины отрезка АВ:
1) А (2), С (5); 2) А (1), С (3); 3) л(±), с(|).
7.	Найдите координаты точек, делящих отрезок АВ на
три равные части:
1) А (5), В (4); 2) А
8.	Найдите среднее арифметическое чисел:
1)	4 и 6; 2) 1 и 3; 3) 1 и 1|; 4) 2| и
9. На рис. 4.23 указаны координаты точек Л и В, най-
дите координаты остальных точек.
Рис. 4.23
10.	Найдите среднее арифметическое чисел:
1)	3, 5, 7;	2) 12, 15, 18; 3) 100, 200, 300;
4)	1, 2, 10; 5) 1, 2, 5, 12; 6) 3, 4, 5, 6, 7.
11.	Среднее арифметическое двух чисел равно пяти. Най-
дите сумму этих чисел.
12.	Среднее арифметическое пяти чисел равно двум. Най-
дите сумму этих чисел.
13.	Средний возраст 11 игроков футбольной команды
21 год. Во время матча один из игроков получил
травму и ушел с поля. Средний возраст оставшихся
4
игроков стал равен 20-g- года. Сколько лет игроку,
получившему травму?
14.	Дети спросили своего учителя математики:
— Сколько Вам лет?
— Если подсчитать средний возраст 32 учеников
нашего класса, то получится 10у года; если же при
этом учесть и мой возраст, то получится 11 лет.
Сколько лет учителю?
198
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
15,	1) (—156):(—12)—238-3 + 3859;
2) (—8277): 267 — 459: (—9) +7348.
16,	Выразите в ™:
1)	10СшЬ; 1 4 = 60 мин. значит, 10°^=-П^- =
, 60» 100 м 6000 м 6 км g км е
60-1 мин 60 мин 1 ч ~ ’
2)	1080 — ; 3) 480-^-; 4) 720 — ; 5) 120—,
7 мин ’ 7 мин * 7 мин * 7 мин
17,	Выразите в —:
мин
1)	48- = 4#^ = ^J = 800-^-;
7 ч 1ч 60 мин мин
2)	180™; 3) 120™; 4) 54™; 5) 36™.
18.	Плот плывет от А до В 40 ч, а катер—4. Сколько
часов плывет катер от В до Д?
19.	Плот плывет из Д в В. 24 ч, а моторная лодка—3 ч.
Сколько часов моторная лодка плывет из В в Д?
20,	Кто проедет большее расстояние—велосипедист со
1 м 5
скоростью 3 -у — за-g-мин или автомобиль со ско-
t 1 КМ о ~
ростью 1 у— за 3 с?
§ 61. Исторические сведения
Люди в своей практической деятельности пришли
к понятию дробного числа очень давно, в связи с потреб-
ностью измерять различные величины. Сохранились еги-
петские папирусы со времени 2000—1600 лет до нашей
эры с записями арифметических действий над дробями.
Древние вавилоняне тоже оставили после себя памят-
ники с письменами, содержащими вычисления с дробями.
Сначала для вычислений употребляли только дроби с чис-
лителем, равным 1	, у, gg»• • •) • Например, в египет-
ском папирусе, написанном около 1600 лет до нашей эры,
записано решение такой задачи: «Если прибавить к не-
которой величине ее седьмую часть, то получится 19.
19Э
Найдите эту величину». После сложных вычислений там
записан ответ, который в современных обозначениях можно
записать так: 16 4-+4-. Из этого примера видно, что
египтяне в то время еще не умели выразить одной
5	11
дробью -g- сумму у 4" у, и это затрудняло вычисления.
-Индийцы записывали дроби так, как мы это делаем
сейчас: числитель писали над знаменателем, но черту
дроби не писали. Дроби отделяли друг от друга верти-
кальными и горизонтальными линиями. Например, дробь
1
у записывалась так:
I
:	'	2
Знака плюс (+) для записи суммы не существовало,
12	4
и сумму у + у + у записывали так:
1 2 2 3	4 5
В Древнем Вавилоне (2000 лет до н. э.) основу си-
стемы мер веса и денег составлял 1 талант; его делили
на 60 мин, а 1 мину—на 60 шекелей.
В соответствии с этим основные расчеты производи-
лись с дробями, знаменатель которых равен степени
шестидесяти:
1 1_______1_ 1 1
60 ’ 602 — 3600’ 60s — 216 000
и т. д. Для упрощения громоздких записей применялись
специальные обозначения и названия:
I =бо—минута,
секУВДЗ,
1'"=-6^—терция
' 200
и т. д. Это позволяло записывать дроби без знаменателя, на-
пример, запись 2’54'38"'37/" означала	.
OU O0UU ZlOvvU
Следы этой системы счисления дробей сохранились до
наших дней в единицах измерения времени и углов. Так,
1 мин=1ч, 1 с=1мин=115-ч,
1'=1.Г 1"=Д. l'=-L. 1°.
1	60 1 ’	1	60	3600
Одним из примеров практического применения дробей
может служить нотная запись в музыке. Здесь факти-
чески используется понятие дроби и даже сложение дро-
бей. Так, длительности половинные, четвертные, восьмые
соответствуют дробям 1, Л, 1, а схема длительностей
а 4 О
(рис. 4.24) соответствует суммам =="4'+"4’>	•
Схема, длительностейi
J — полоВинная	J
J — четвертная	J
— восьмые
Рис. 4.24
Обозначение J. (нота с точкой) используется для увели-
чения длительности на половину. Например, J.=J+Jr,
1,1	3
что соответствует сумме у+,4’=Т'
Дробью фактически обозначается и размер, так как ниж-
няя цифра обозначает длительность доли—на рис. 4.25 —
Рис. 4.25
четвертная, а верхняя цифра—количество долей в такте—
две доли. Отличие заключается в том, что черту дроби
не пишут и дробь не сокращают. Хотя две четвертные
длительности составляют одну половинную.
Д01
ВОПРОСЫ для ПОВТОРЕНИЯ
• ПО МАТЕРИАЛУ ГЛАВЫ IV
1.	Какое натуральное число называется простым, состав-
ным? Является ли Г простым или составным числом?
2.	Какое число называется кратным данного числа?
3.	Какое число называется делителем данного числа?
4.	Что называется положительной дробью? Приведите
примеры. Назовите числитель и знаменатель каждой
дроби.
5.	Сформулируйте основное свойство дробей. Приведите
примеры равных дробей.
6.	Какая дробь называется несократимой? Приведите
примеры.
7.	Сформулируйте правила сравнения дробей.
8.	Какая дробь называется правильной, неправильной?
9.	Сформулируйте правило сложения дробей.
10.	Сформулируйте переместительный и сочетательный
законы сложения.
11.	Сформулируйте правило вычитания дробей.
12.	Сформулируйте правило умножения дробей.
13.	Какие дроби называются взаимно обратными? Приве-
дите примеры.
14.	Сформулируйте правило деления дробей.
15.	Сформулируйте законы умножения.
16.	Как вычислить расстояние между двумя рациональными
точками на координатной оси?
17.	Как вычислить координату середины отрезка?
18.	Что называют средним арифметическим чисел а и Ь?
19.	Что называют средним арифметическим нескольких
чисел?

Глава V. РАЦИОНАЛЬНЫЕ ЧИСЛА
§ 62.	Отрицательные дроби
До сих пор мы изучали положительные дробные чи-
сла—их еще называют положительными дробями.
..	1 2	3	8	6	7
Например, числа . т, -г.	-т-, т есть положи-
г г	2’0	4	/	0,1
тельные дроби.
Если перед положительной дробью поставить знак плюс
(+), то получится то же самое число, т. е.:
1	, 1	8	,87	,7
2	~ "Г 2 ’ 7 “ "** 7 ’ 1	+ 1 '
Если перед положительной дробью поставить знак ми-
нус (—), то получится новое число, которое называется
отрицательным дробным числом или отрицательной дробью.
Например, числа —у, —у,—-р— отрицательные
дроби.
Дроби, отличающиеся только знаком, называются про-
тивоположными.
Например, дроби + у и ——противоположные.
Одно из двух противоположных чисел положительно,
другое отрицательно. Исключением является число нуль —
g п , О о
нуль противоположен самому себе: 0 = + р- =— у, где
п — любое натуральное число.
Введем понятие абсолютной величины или модуля дроби.
Модулем положительной дроби называется сама эта
5	5
дробь. Например, модуль g- равен р что записывают
| 5 |	5
так: -б- =-0 •
203
Модулем отрицательной дроби называется противопо-
ложная ей (положительная) дробь. Например, модуль
5	5	15 15
— -х- равен -я-, что записывают так: —s- =-г.
0*0	I о | о
Модуль нуля равен нулю: |0| = 0.
Модули противоположных чисел равны. Например,
|5| I 5|__5
I 8	I	8 | 8 *
Иногда знак минус (—), стоящий перед дробью,
удобно записывать в числителе дроби. Например, верны
равенства:
1 _	— 1	.	5 _	—5 .	—13	13.	о —о
2 ~	2	’	7 “	7 ’	16 ~	16’	2	- 2	*
УПРАЖНЕНИЯ
1.	Приведите три примера отрицательной дроби.
2.	Какие из следующих дробей являются положитель-
ными, какие отрицательными:
3.	Для следующих дробей назовите противоположные им
дроби:
О 2)	3) -1; 4) -А; 5) •=* ; 6)0.
4.	Существует ли число, противоположное самому себе?
5.	Что называется модулем:
1)	положительной дроби;
2)	отрицательной дроби; -
3)	нуля?
6.	Упростите записы
1)	|2|;	2)	|-3|;	3)	||;	4) |—1|;
5)	||;	6)	-| ;	7)	-||;	8) |0|.
7.1)	|||;	2)	-j ;	3)	-|-|| ;	4) -|-||;
5)	1 -4|;	б>	4-41; 7)	14-41;	з) ||-(4)’|.
204
8.	Запишите:
1)	три положительные дроби и дроби им противопо-
' ложные; 2) три отрицательные дробй, как можно
записать эти дроби по-другому?
9.	Равны ли дроби:
1)	з и з ; 2) 8 и g ;
3)	"9 И “Э-’ 4) у И у?
10.	Запишите дроби: —-I-, —4, — X так, чтобы знак
г	О	У	1 и
(—) стоял в числителе дроби.
11.	Запишите дроби:	> -jy-l уу так, чтобы знак (—)
стоял перед дробью.
12.	Упростите запись:
» |+|; 2> |тЬ 3) Н1; 41 Нг|-
13.	Найдите модуль числа:
1)	-1; 2)	3)	4) X; 5) 0; 6) -А.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
Я ЧЧ 449 7fil 709
14.	Сократите дроби: А.; ww.
15.	Приведите дроби к знаменателю 48:
Г. 2.. 3  ,5 • _7. • А
2’3’4’6’8’12'
16.	Вычислите:
1)	2—3+5—2—4—7;	2)—3—5—1+8+4-2;
3)—2—74+28—14+74; 4) 29—39—29—31—7.
17.	1)зА.з1:(1±-§);
2) (2-1-: 10+ 10:4-4)' +
3)4;[(4га“3я)4+(3й+2й)-1н]- '
18.	Велотурист в течение 10 дней проезжал по 36 км.
Сколько километров в день ему необходимо проезжать,
чтобы вернуться обратно за 9 дней?
19.	Велотурист в течение 10 дней проезжал по 21 км. За
сколько дней он сможет вернуться обратно, если будет
проезжать в день по 35 км?
205
20,	На 2 р. 40 к. купили тетради—поровну, стоимостью
2 к. и 3 к. Сколько было куплено тетрадей каждого
вида?
21,	Купили одинаковое число карандашей стоимостью
10 к. и 3 к. Сколько купили карандашей каждого
вида, если карандаши за 10 к. вместе стоили на 91 к.
больше, чем карандаши за 3 к.?
22,	Два поезда вышли одновременно навстречу друг другу
из городов, расстояние между которыми 420 км.
Через какое время расстояние между поездами будет
60 км, если скорость одного поезда 33 км/ч, а вто-
рого 27 км/ч?
23,	Два поезда, расстояние между которыми 884 км,
движутся навстречу друг другу. Скорость первого
поезда 54 км/ч, а второго 46 км/ч. Через какое время
расстояние между поездами будет равно 84 км?
§ 63. Рациональные числа
Число, которое может быть записано в виде Д, где
р и 4'—целые числа и q=£0, называется рациональным
числом или дробью.
Например, числа
2—6	8	—7
3 ’ 5 ’ —И ’ —7
есть рациональные числа.
Число р называется числителем, а число q—знамена-
телем дроби Д.
Некоторые дроби считают равными. Равенство дробей
устанавливают при помощи основного свойства дробей:
если числитель и знаменатель дроби умножить на одно
и то же целое число п 0), то получится равная ей
дробы
(1)
q q*n 9	' >
где р, q, п—целые числа, q^0, «У=0.
206
Например:
з _ 3.(-2) _ -6 . 9Х—5 _ (—5)>3 _ -15 .
4 4 “ 4>(—2)	—8 ’	> 2 ~ 2-3 “ 6 ’
ох 2 _ 2.(-П _ -2
—3	(—3).(— 1)	3 *
Переход от дроби к дроби ££ в равенстве (1) на-
зывают приведением дроби к новому знаменателю, а обрат-
ный переход называют сокращением дроби'.
__ д	(2)
q-n q '	'
Равенство (2) означает, что если числитель и знамена-
тель дроби имеют общий множитель п, то дробь можно
сократить на п. При этом получится дробь, равная
данной.
Например! -п ~12	• -а .
' 14	7 -я 7 ’
1
9\ -15 _	5	5 ;
^-9	"3 •
1
Рациональное число есть:
а)	положительная дробь, если р и q одного знака;
б)	отрицательная дробь, если р и q разных знаков;
в)	число нуль, если р = 0.
Покажем это на примерах!
. з	.
a)	-g—положительная дробь, так как ее числитель и
знаменатель—натуральные числа;
__7	/ j\tf п	у	_7
—о	тг = “г> т. е.—г-—положительная дробь;
“ О	(—0)’(—1)	о	—б
__3	3	_3
б)	-5- — — -5 , т. е. —-отрицательная дробь;
з з.(—1) —зз	3
=	— - —т- е- Tie-отрицатель-,
ная дробь;
207,
Для любого целого числа р верно равенство» '
Оно означает, что любое целое число является рациональ-
ным числом.
Эго равенство для положительных дробей было опреде-
лено в главе IV. Если р отрицательное число, например,
—3, то =^-=—|=- 3.
Пользуясь основным свойством дроби, можно любую
дробь привести к положительному знаменателю.
5	(—1).5	5 m —6 —64—I) 6
Например» 1) _3— (_^ц_3) — 3 ; 2) _7—7 •
УПРАЖНЕНИЯ
1. Что называется рациональным числом? Приведите
пример рационального числа.
2/Являются ли рациональными числами»
1) натуральные числа; 2) положительные дроби;
3)	целые отрицательные числа?
3.	Сформулируйте основное свойство дроби. Приведите
пример использования основного свойства дроби для
приведения дроби к новому знаменателю.
4.	В каком случае дробь можно сократить? На основа*
нии какого свойства сокращают дробь?
5.	Приведите дробь к положительному знаменателю»
1) Eb 2)	3)	4) =?.
6.	Сократите дробь; результат запишите в виде дроби
q положительным знаменателем:
l\	"—*35 qv 36	45
О 2)	3) 33g; 4)
7.	Запишите дробь в виде целого числа»
i\ ® о\	б •	“44
О 2> ~г; 3)	4> ~-
8,	Равны ли рациональные числа»
«. 1	**-8	—75	—3	—
О -4 И =^’	=400 И =4’
24 и -27. .. —Tf	63 з
3) —40 И‘ 45 ’ 4) —88 И 72?
208 х
9. Упростите запись рационального числа:
П Г4!* 9) =^* 3) =^- 4) -144-
*' 56 ’	—60’ d' 72 ’ 4' 96 ’
—55. ~ —125.	1000.	.32
—75’ °' 625 ’	—8 ’ °’ —1024*
10. Найдите три дроби с положительным знаменателем,
равные числу:
1)5; 2) —2; 3) —12; 4)0.
11. Упростите выражение:
.. —56:(—8)4-8	7+8  15 5*3 «.
" 19* (—5) + 100 “ —95 +100 ~ ~ "б" = й’
-45-56 . „ 75- 45. . -48:6+8	1
‘ 49— 251 ’	’ 45—65’	1 45-7— 400*	V i .
12. Какие из следующих рациональных чисел равны
целым числам, какие—натуральным числам»
1) 5гJ 2)	3) =£; 4) А;
6)=^; 6) ^; 7)=g; 8)=§?
13, Выпишите рациональные числа, равные между собой:
1) V’ 2) =п>* 3>	4> -й;
17 • 7\ 0 • О\ 100
5)	Too* 6' 34"’ 7' =7’	—300*
14.	Упростите:
п 12—3*8 ~ 72:4-5-8
‘ " 3—45:5*	16*3—в-в’
15,	Найдите число xi
о 44;2) з) 44 =
л\ 5 х.	4 —20. fi. —3	18
<$.“-6=30* 5> ’"Т“ПГ* 6) V==12-
16,	Приведите дроби j и к знаменателю:
1)	8; 2) 28; 3) —8; 4) —28; 5) —40; 6) —100.
17,	Приведите к знаменателю 60 дроби:
1)	-4; 2) Ц; 3)
41 =й-> 5) =15; 6) ±ЯР
18,	Сравните с нулем дробь:
I) 4'* 2) =5? 3)	4)	5): ——6) “3-
209
19.	При каких тип верно равенство:
jx I m I_____n-j I w I_______
' |~| n ’ ' ~ n
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
20.	Вычислите:
1)	7—(8—15);	" 2) 21 —(38—43);
3)	178—(24—196)—257; 4) 281 —(484—795) —1254.
21.	!) 31.21.
2)(>|!2т)!(8Т!1т)-22т:
ох ( 3 _L 5 _i_ 7W 5 J_ 1 -47\ (а 1	Ч2\
3' \ 4	9 ’^12/Д12‘т' lo'f'go; * \ 15 33/’
22.	1) Известно, что число а делится на 9. Простым или
составным является это число? Ответ обосновать.
2)	Верно ли утверждение: любое натуральное число
является простым или составным? Ответ обосновать.
3)	Сколько существует простых четных чисел? Ответ
обосновать.
4)	Простым или составным числом является произве-
дение двух простых чисел? Ответ обосновать.
23.	1) На координатном луче отмечены числа 1 и а.
Отметьте на координатном луче точкой число а 4-3
(рис. 5.1).
О „ 1 а	а ° а Ь.
|	[	।__________i	|----1-------S-
Рис. 5.1
Рис. 5.2
2) На координатном луче отмечены числа а и 4.
Отметьте на координатном луче число а 4- 4 (рис.5.2).
24. I) Известно, что 9—х—у. Отметьте на координатном
луче точкой число х+у (рис. 5.3).
0 1	х О	1	Ъ	х
i I--1-------1---------
Рис. 5.3	Рис. 5.4
2) Для чисел а и b выполняется равенство а—3*=Ь.
На координатном луче отмечено точкой число Ь.
Отметьте точкой число а (рис. 5.4).
210
§ 64.	Сравнение дробей
Любые две дроби можно привести к общему положи-
тельному знаменателю.
2	3
Например, приведем дроби и — у к общему по-
ложительному знаменателю
-5)	7)
2_ -5-2	10	3 —3 7-(—3)	—21
—7~—5-(—7)~ 35 ’	5“ 5	7-5	35 '
Для сравнения двух дробей их надо привести к общему
положительному знаменателю и сравнить их числители.
Из двух дробей с общим положительным знаменателем
больше та, у которой числитель больше.
Таким образом, сравнение дробей сводится к сравне-
нию целых чисел.
3	5
Пример. Сравним дроби —-g- и •
-	2)
3	“-3	——6	5	—5 л е»
Решение. -т=-г=-у;-6<-5,
—6^—5	3	5
значит, nyC-je H-g-<=Tg.
Из общего правила следует, что положительная дробь
больше отрицательной и больше нуля, отрицательная
дробь меньше нуля.
Например, у>— у, потому что -у =	—4=17» .
. п 4.-9
4 >	9 и 12 > 12 .
УПРАЖНЕНИЯ
1. Приведите дроби к наименьшему общему положитель-
ному знаменателю:
0 У и —12’ 2) 16 и —12’
ох =3	J_	J_.	.. ^7	_1£	-9
°) 24 ’	—30 ’	—9 ’	' 25	’ —30	’ —20 ’
2. Сравните дроби:
IX 3	.	7	. ОХ	—5 „	-,7.	QX —25	„	17	.
20	И 60’ 2)	12 и	36 ’	3) —36	и	24	’
х 7	— 4	0	5	сх	°	.. 1
4) _15	и 7 *»	5) 32	И _24 >	б)	_7	И 4	.
211
'3. Сравните дроби с нулем:
JU: 2)^ 3)^; 4)	5) &•
4. Сравните дроби:
п	2	5	оч	1	13
)	7	И	99’	2)	2	и 25’
2	2	.	..	7.8
3) . 5 и 5 » 4)	1()0 И 99.
5, Вычислите:
1) 313125:625;	2)	248363:(-809);
3) 2008609:(—401);	4)	—818176:272;
5) —841161: (—3273);	6)	—200043: (—7409).
6.	1) Делитель равен 12,	частное	8, остаток 5. Найдите
делимое.
2)	Делитель равен 27, частное 15, остаток 10. Най-
дите делимое.
7.	1) Делимое равно 576, частное 62. Найдите де-
литель.
2)	Частное равно 301, делимое 1204. Найдите де-
литель.
8.	Вычислите:
,1'\/о^.л21Л2.о^\л^.
(3^’^з4-4у.3yj-4y,
\ 4 " 6 J’Ufr 4 А 6 ‘*9 ] '
2
9.	1) Найдите число, уу которого равны 5.
2)	Найдите число, которого равны 6. ‘
10.	Решите устно:
3
Г) Рабочий выполнил -у работы за 1 ч 15 мин. За
сколько часов он выполнит оставшуюся часть
работы?
2)	За Г ч 20 мин поезд прошел 4- расстояния между
двумя станциями. За какое время Он пройдет все
расстояние, если все время будет двигаться с одной
и той же скоростью?
11,	Найдите число, у которого, уменьшенная на его у,
о2 .
равна 2у.
212
9	3
12.	Если к jg числа прибавить у этого же числа, то
получится 7у. Найдите это число.
13.	В состав Московского городского совета народных
депутатов в 1985 г. избрано 1000 человек.
1)	числа избранных депутатов имеют возраст свыше
30 лет, а ’ имеют возраст до 24 лет. Сколько
депутатов моложе 24 лет, сколько имеют возраст
от 24 лет до 30 лет и сколько старше 30 лет?
127
2)	часть депутатов имеют высшее образование,
13 человек—неполное среднее образование. Сколько
человек в составе городского совета имеют высшее
образование и сколько законченное среднее обра-
зование?
§ 65. Сложение и вычитание дробей
Сумма дробей, имеющих общий знаменатель, равна дроби
с тем же знаменателем и с числителем, равным сумме
числителей.
ы	п -2 , 3	-2+3	1 .
Например: 1)	=	— = у;
91 ~2  ~3 - -2+(~3) -5
И "г 11	11	11 *
Отметим, что сумма противоположных дробей равна
нулю.
U	з . ( з\ з , —3 3-Н-З) о Л
Например, у + (-•у) -^4-5-=-^-^=у=°.
Разность двух дробей, имеющих общий знаменатель,
равна дроби с тем же знаменателем и с числителем, равным
разности числителей уменьшаемого и вычитаемого.
..3	4	3-4 —1	1
Например: 1)	--g-----г = -у;
91	3 —4 —3—(—4)	34-4	1
5	5 ~	5	5	-Т*
Чтобы вычислить сумму или разность произвольных
дробей, их приводят к общему положительному знамена-
телю, а затем применяют правило сложения или вычи-
тания дробей.	>•
213
Например:
7)	5)
n 3,2	-3 -2 —21 , —10_—21+(-10) —31.
5 + —7	5'7	35	35 “	35	— 35 ’
3	11_9	11_9— П_— 2_	2.
5	15 15 15	15	15	15*
3)	2)
„х__L_zz?— zzl_z^ —
°'	30	45 “ 30	45 ~ 90	90 3
3—(—4)_-3+4_ 1
“	90	— 90 —90‘
Разность дробей a и b равна сумме уменьшаемого и
числа, противоположного вычитаемому.
а—Ь=а-\-(—Ь).
В самом деле, приведем дроби к общему знаменателю:
а=?-, Ь=£-. тогда а-Ь=Р—=
я я	я я я я я
+ vef+(—
Этими правилами пользуются для упрощения вычи-
слений.
„	3 [	2\	3 , 2 21 , 10 31
Например, 5	7 ) — 5	7 —35“^35 — 35 '
Можно еще сказать, что разность дробей а и b есть
такое число а—Ь, которое в сумме с в,.читаемым дает
уменьшаемое', (а—Ь) + Ь=а.
Доказательство. В самом деле, приведем дроби
к общему знаменателю: а=-у, Ь — .Тогда (а—b)+b=?
_(Р	г'\\г^р~г\ г ^~г + г - р а
\я я Уг я я "г я я я
УПРАЖНЕНИЯ
1.	Вычислите:
2)то + 1б’ 3) Тб'+б’’
.. 5 , -11. ех -7, 13 . д. -29 ,9
4) —12 + 24 ’ 5) 48+—36 ’ 6) 75 "^25
2,.1-1 + К М-4)+^ 3)g+(-y
214
4>(-4) + (-r8y 5) (-з)+Й-,6>(-я)+^-
3.	1) (-4) + (-4); 2) (_71) + (_11);
3) (-4)+1Т’ 4> 4+(~2т);
5) 4+(-51); 6) (-б|) + 4.
4.	') 1-4; 2> Нт)=
..	_Z_A- ЧЧ	2 — 11 •	R\	:L—(z^\
4'	15 45 ’	28 35 ’	°'	40	\ 24) '
К П	3	f 5У	91 1Z-13-
О. 1)	7	7) >	2) 25	25’	*'27 9 ’
..	1	t	3\ . к.	9	Г 16\ .	25 (	ИХ
4)	2	\	8 / 4 *'	10	15/’6'26 \	13/'
в- 1) 4-4: 2)	(-4) ; 3) -<4-(-4):
4)	?4-4: 5) 44-3j: 6)-4-(-4)-
7.	Найдите х из равенства:
1)	*+|=4: 2) i+x=i •>
3)	х+у =	4) Тб + Х= s’-	-
8.	1) х—у = у;	2)х—у=—
31V-1Z--12.	4ix_15=Z
°' х 18 —	9 ’ f 22 II *
л	lx	2	3	оч	8	17.
9.	1)	5 —х— 5	;	2)	у	х—18,
о.	4	1	Л.	7	13
3)	15	Х~ 5	’	4)	9Х	18*
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
10.	Вычислите:
1)	161784:(—321);	2) —2164320:432;
3)	—4101630:(—507);	4) —1936980: (—918).
11.	Существует ли несократимая дробь, числитель кото-
рой в три раза меньше знаменателя?
12,	1) Как разменять 59 к. пятнадцатью монетами
по 3 к. и 5 к.? 2) Можно ли разменять 59 к. шест-
надцатью монетами по 3 к. и 5 к.?
215
13.	Скорый поезд проходит расстояние между двумя го-
родами за 8 ч 15 мин, а пассажирский—за б ч 36 мин.
Через сколько часов встретятся эти поезда, если они
выйдут из обоих городов одновременно навстречу друг
другу?
14.	Пароход проходит некоторое расстояние по течению
за 10 ч, а против течения—за 20 ч. За какое время
проплывет это расстояние плот?
15.	Расстояние между двумя пешеходами, движущимися
равномерно в одном направлении, равно 2 км 500 м.
Первый пешеход проходит за 2 ч 8 км, а второй про-
ходит 1км за 12 мин. Через сколько часов второй
пешеход догонит первого?
16,	Чтобы определить глубину подземной полости в пе-
щере, спелеолог бросил вниз камень. Найдите глубину
полости, если известно, что в первую секунду камень
пролетает 4^м, а в каждую следующую на 9-|-м
больше, чем в предыдущую, и известно, что камень
коснулся дна полости через Зс.
17.	Расстояние между двумя городами 400 км. Из этих
городов навстречу друг другу одновременно выехали
две машины и через 5 ч встретились. Определите
скорости машин, если одна из них проезжала в час
на 12 км больше второй.
18.	От Москвы до Курска 537 км. Из Москвы в Курск
вышел поезд со скоростью 60	. Через 6 ч, в 20ч 55мин,
на промежуточной станции первый поезд встретился
с поездом, вышедшим из Курска в Москву в 17 ч 55 мин.
Определите, с какой скоростью двигался до встречи
второй поезд.
19,	Пассажир, едущий в железнодорожном вагоне, заме-
тил, что встречный состав прошел мимо окна за 9 с.
Определите длину встречного состава, если оба поезда
г“/\ КМ
двигались со скоростью 50 — .
§ 66. Произведение и частное дробей
Произвольные дроби перемножаются и делятся по сле-
дующим правилам:
Р г _р-г р ,r	p-s
q s q-s ’ q в	q-r ’
т. е. по тем же правилам, что и положительные дроби.
'216
Например:		.
г
•<\'А 4	(-з)-4	И)’3'4 г- 3'^ г- 6 .
2 ’-5	2-(-5)	(-1)-2-5	«'•5	5’
V _L = JL. -L = <-5.)А- _ W.A. - 12-;
' 5' -3	1-3	1-(-3)	3
-3 . .4	(-3)-5	-15 .
°' 2 ‘ 5	2-4	8 ’
3	7-1_________7 ,
1 “ (-8)-(*-3) ~ 24
Отметим равенство, которое легко получается на ос-
новании правила деления:
p:g=f.
Др а	р>1	р
оказательство. Р‘.а = -!г'.-т — ‘т— = -т-.
г ’ 1-1	l-q q
Таким образом, дробь — можно рассматривать как
частное от деления ее числителя на знаменатель.
Например: 1) -|-=2:3; 2) -2:5=-^.
Чтобы умножить дробь на целое число, надо ее числи-
тель умножить на это число, оставив без изменения зна-
менатель.
п	Р Р г	Р‘ С Р'С
Доказательство, ~г • -р == •£у-.
Например: 1)• 3 = у • т=т;
2) (_7).l=zzt ,1 = ±=ZH =1ZL.
1 .4 4	1	4	1-4	4
Эти вычисления обычно записывают короче:
и £.3-^-1- 21 ( 71 1 _(-7Н_ -7
Чтобы разделить дробь на целое число (не равное нулю),
надо умножить ее знаменатель на это число, оставив
без изменения числитель.
n	Р Р Г Р‘\ Р
Доказательство. —:	=-г~г.
я q I Я’Г Я‘Г
„	—7 о —7 3	-7-1	—7
Например, —:3=—:Т=ТГ=:ЛГ’
или, короче, —-:3=-=£=-=£.
217

Дроби — и ~, где р и q не равны нулю, называются
взаимно обратными. Их произведение равно единице. |
Доказательство. — • —= -т-^-=-г= 1.
я Р я-р 1
и	,	2	3	—7	8	1	—5
Например, дроби у и -j, -у- и —у, —у и —।----
взаимно обратны.
Чтобы разделить одно число на другое, надо делимое
умножить на дробь, обратную делителю.
Например, у:-у-_— 7.(_2)=у ”zy-
Докажем, что для любой дроби о=у верно равенство
(— 1)-а = — а.
Доказательство. В самом деле,так как=^-= ——,
<7 я
то
(_1).а==(_1).Д = ±2±£ = Г1£ = _Д = _о.
v k ’ я я я я
УПРАЖНЕНИЯ
1,
2,
3,
4.
5.
6.
7,
8,
Вычислите:
п ~3	5 .	~3 ~4 • чч —9 —1 л\ —7	4
Ч 7 ‘ —9 ’	8 * 5 ’°' 10  — 2 ’	' = 35
—5 3 t 0. 2 —7 в л. —7	4	.< 18	—4
Ч 6 * 10’ Z' 3 ‘ 16 ’	32 ’ =2Г ’	=5 ‘ "8Г‘
0 2у * =75’ ’ 2) ly ’ Тб" ’ 3) Зу • _юо • 4) ~9“ ’ 4У
1 \ "‘""‘3 , 5 .	~~~3 * —-5 в л\ 9	“~1 , л \ 2 6
0 7 -_9 > 2) 8’4’3) _10-—, 4) у.—.
п 3 . 5 .	16	8 . ох —9 —18 . .. 45 —15
И 7 : _б ’ Ч —25 * —15 ’ Ч 20 ‘ 75 ’	4б: 69 ’
п о!.— И .	8. 16 . оч -7.nl и\ —9 J3
О 12 ’ 2) 15’—25 ’ 3) 9 -23 , 4) _16-132.
Используя равенства — у=, выполните
умножение:
о -44; 2> -4-4’3>4> 4-4-
«> -Н-4); => -4-(-4)= з)
218
9.	D 2> -4-24-; 3) з4(—g);
озН-Ю-
10.	Докажите, что у = р:(/.
11.	Запишите частное в виде дроби с положительным
знаменателем;
1)	—17:(—18); 2) 15:(—25); 3) —19:(—5); 4) 29:(—15).
12.	Назовите и запишите число, обратное данной дроби:
2'Г з)т^;
5)	4; 6) -4 7)-4; 8)—=1.
13.	1) Могут ли взаимно обратные числа быть: а) поло-
жительными; б) отрйцательнымщ в) разных знаков?
Приведите примеры.
2)	Имеет ли 0 обратное число?
3)	Докажите свойство взаимно обратных чисел.
14.	Представьте смешанную дробь в виде —-у-:
1)	—2у= —(24) = ~(4) = “4 * или’ коРоче’
________2.
2	2 ’
2)	-11; 3) -71; 4) -121; 5) -171.
15.	Выполните деление:
1)	_21-z3-=-1-A=_4.
2 8	\ 2 5/	1
16.	Вычислите:
1)	-2-1; 2) -5.^.; 3) -11-(-4);
4) -9.(-11).
17.	1) 4:(-4) ; 2) (-2-1):10; 3) -6:31;
4) —2у:(—38).
•в-»4:(“4)- 2) -4i2l: 3> - ‘4:(-4)•
“2's':(—-Зп)'
219
19. Упростите:
О 2) (-1)• ef-; з)(-1).|;
4) (-1)-^; 5)	•(-1); 6) ^-(-1).
20. 1) -1. (-1); 2) -I-—; 3) -l.(-ll);
4) ~з|.(-1); 5) - 1-j; 6) - b(-4).
первое число означает: 4-1—<<мне нравится», —1 —
«мне. не нравится»; второе число означает: 4-1—«хо-
роший поступок», —1—«плохой поступок»; третье
число означает: 4-1—«это хорошо», —1—«это плохо».
Мальчик прочитал первое, предложение так: «Мне
нравится хороший поступок—это хорошо». Прочи-
тайте остальные предложения.
. УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
22. Вычислите:
1) -520-370;	2) —1200-1200;
3)	60 (—9800);	4) —8500-(—640).
23.	1)-60-(—15000); 2) —800-1200; 3)—7000 (—1420).
24.	1) —700:25;	2) 5600:(—25);
3)	—2500:25;	4) —625:(—25). к.
25.	1) 2525: (—25); 2) —750:(—25);
3)	19625: (—25); 4) —28050: (—25).
2) (10:21+7±: К>).
27. При делении числа а на 14 ученик получил в ос-
татке 15. Правильно ли он выполнил деление? Ответ
обосновать.
28, При делении числа на 7 ученик получил остаток 7,
а приближенное частное 87. Правильно ли выпол-
нено деление? Ответ обосновать. Можно ли определить
делимое?
[ 29, При делении числа а на 7 получили остаток 3, а при-
; ближенное частное Ю. Какое это число? Ответ обо-
| • сновать.
[яэо
30,	Остаток от деления числа а на 5 равен 4. Делится
ли число а + 1 на 5?	;
31.	Остаток от деления числа а на 5 равен 1. Делится
ли число а—1 на 5?	:
О	а	Ъ	а>	О	Ъ	а	а
F-------1----1--------£•.	Н------1----
Рис. 5.5	Рис. 5.6
32.	На координатном луче отмечены точками числа а
и Ь. Отметьте на координатном луче, число а+Ь
(рис. 5.5).
33.	На координатном луче отмечены точками числа а и Ь.
Отметьте на координатном луче число а—b (рис. 5.6).
§ 67. Переместительный и сочетательный законы
сложения. Распределительный закон
Дроби а, Ь, с подчиняются законам:
a + b~b + a,	(1)
(a + b) + c=a + (b + c),	(2)
(a + b)-c=d-c + b-c.	(3)
Доказательство. Докажем законы (1), (2),. (3),
опираясь на соответствующие законы для целых чисел.
Пусть а=Д, 6—у, с=="^—данные дроби, имеющие
общий положительный знаменатель, Тогда:
2) (o+4+,=(z+4.)+|-.e±.'+i-fca±*>;
-=£±^)-f+'-±-s-f+(7+f) = «+.«’+^
,3) (a + 6).c-7i+^.i-£±i-i-^±±i =
' *	’ \q q 1 q	q q q-q
=	=£2 +	= £ . ±+L .
q-q	q-q q-q q q q q
Так как разность можно рассматривать как сумму
уменьшаемого и числа, противоположного вычитаемому,
то распределительный закон верен и для разности.
221
Например: 1)1.	=	+ (~т)) =
1 2,1 (____i_\ 1	*
= 2 ’ 5 ' 2 \	5/2*5	2*5’
или, короче,
1	/3,___И—I 2.___L ±.
2	’ \ 5	5	2*5	2*5’
2Y 2— • 7——2—.	— 2— ( 7—_8—\ =
29 41 29 б11—Z9V11 °11J
= 21 .(-I)— 21.
Так же, как для целых чисел, для дробей с помощью
указанных законов можно доказать правило:
В сумме любого числа слагаемых можно слагаемые пере-
ставлять и заключать в скобки любым образом.
Верны также следующие правила:
Если перед скобками стоит знак плюс (4-), то скобки
можно опустить, не меняя знаки слагаемых, заключенных
в скобках.
Если перед скобками стоит знак минус (—), то скобки
можно опустить, изменив знаки слагаемых, заключенных
в скобках, на противоположные.
Например: 1) + (1-1) = 1-1;
2Y -(2_П_______
\10 з)~ 1(И 3‘
В самом деле,.если заменить знак плюс (4-) на мно-
житель 4-1, а знак минус (—) на множитель —1 и при-
менить распределительный закон, то справедливость правил
становится очевидной:
~(+о^-(+о4=й-Г’
~~	=у)=
= (— О-уо~(— О- з’ = ~То+"з •
Эти правила позволяют упрощать выражения.
222
Например: 1) 4-.7-|+4-{=4+|_
-4Ч-4+(-4)=4+(-4)-
=-(s|—•)—4;
2> 4-4-(4-4)=4-4-4+4=
-(4-4)+(4-т)=0+4“4-
УПРАЖНЕНИЯ
1.	Вычислите удобным способом:
1)	4 + 21+4;	2)4+72+14;
’)2й+т+т' 4> 4+4+4-
2.	Запишите выражение в виде суммы:
J) 7У—в7Т'^( 21з)+т»
2) 3-g-—2-jj—1у;	3) — 4-g~ 2y + j0.
3.	Назовите каждое слагаемое суммы; вычислите:
п1 1 4.1-21-	2^ 1-1-4-31-1
4.	Вычислите удобным способом:
1)	-4i+4+4-=57-+4~4=
=4-4“8-4-4:
2)	-1 + 4+4;	3) з1-71+2|;
4)-4+4+4; 5)1-2-!.
5,	Упростите выражение:
о 4+(4-4)=4+4-4“5+4=4--
=20-4-14-4-14;
223
6.	Примените для вычислений распределительный закон:
n 1 ‘2—2 2—2 72—2^ —2 ±—Ц_2-
'2*9 2*9. 2*\9 9	2 * 9 -’2.9“ 9 ’’
21 2. is ; ® , X. 31 12 . g * 1 1 1 1 ,
12 15 12 15 ’ ' 3 Z 5 13* 1~5 ’
4)	72.82-72.62;
с\ л I q35 . I
5)	1247 • 41об’“847 • 4Т00
7.	Вычислите:
« 4-4+4-2>4-4-4-4-
з>(-4)-4+(-4)-(-4>
4> (-4)-<-5)+4-(-4)-
8.	Найдите х из равенства:
I)	ж+4-51; 2) х + 51 = 1;
. ’>4+J*4= 4> 4+*“4-
9,	1) 2-i— х-1-j;	2) х-44 = -11;
3)х-4-- 41; 4)-б1-х = 21.
10.	1) 4+*“4"’4+4-
. 2)4-*+4=-4+4-
11.	Вычислите:
/51+1± 1±+2\ 2-2
n I 2^ 7	7^21 |-9	19
' 152-12’12-1 )tTTTi
7	7 21 / 9 '19
4+4	.
\4“4 14+4/ 4~(44)
12.	1) Найдите число, у которого равны 35.
2)	Найдите число, 1у которого равна 22.
3	4
13.	1) Из числа , -g- которого равны 1, вычтите число, у
которого равны 2.

2)	К числу, 1у которого равна -р прибавьте число,
3	2
которого равны 3-j-.
14.	За 12 тетрадей и несколько альбомов^ число которых
составляло у числа тетрадей, заплатили 1 р. 44 к.
Сколько стоит тетрадь и сколько стоит альбом, если
тетрадь дешевле альбома на 28 к.?
15.	Для школы-интерната купили 425 комплектов уче-
нической формы для мальчиков и 376 комплектов для
з
девочек на сумму 18491у р. Сколько стоил один
комплект формы для мальчиков и сколько для дево-
чек, если комплект для мальчиков на 2 р. 80 к.
дороже, чем для девочек?
16.	Докажите, что (а + 6):с = а:с + 6:с, где а, Ь, с —
произвольные рациональные числа (с^О).
17.	Докажите, что (а—Ь):с=а:с—Ь:с, где а, Ь, с —
произвольные рациональные числа (с=/=0).
18.	От автобусной станции в 7 ч утра по разным марш-
рутам выходят три автобуса. Первый возвращается
на станцию через 3 ч, второй—через 4 ч, а третий —
через 6 ч. В котором часу все три автобуса встре-
тятся на станции, если движение будет выполняться
строго по графику?
19.	По дорожке стадиона бегут четыре спортсмена. Один
из них пробегает ее за 20 мин, второй—за 15 мин,
третий—за 12 мин, а четвертый—за 10 мин. Если
бы они стартовали одновременно, то через сколько
минут они снова одноврёменно пробежали бы мимо
линии старта? Сколько раз пробежал бы всю дорожку
стадиона каждый из них за это время?
§ 68.	Переместительный и сочетательный законы
умножения
Произведение дробей подчиняется переместительному
или коммутативному закону умножения:
а-Ъ—Ь-а,
а также сочетательному или ассоциативному закону
умножения:
(a-b)-c=a-(bc).
8 С. М. Никольский и др.
225
Доказательство. Пусть даны дроби а
Ч	s
t	1- Р т Р*г Г*Р т Р t
с = -; тогда	= |. т = ^=^=-. | = &.а и
(Й.&).С₽(Д.^.1=£ДЛ=^=^ =
v '	\ q s ] и q*s и (q»s)»u	q»(s*u)
= p.LL = JL. ±.l\=a.(b.c).
q s-и . q \ s и /	'	'
Выполнимость переместительного и сочетательного
законов умножения для дробей следует из выполнимости
этих законов для целых чисел (любых знаков).
На основании переместительного и сочетательного
законов можно заключить, что в произведении несколь-
ких дробей можно переставлять множители и заключать
их в скобки любым образом. Этими законами широко
пользуются для упрощения вычислений.
Например: 1) ( -|) • ( -~) = (-1) (-1) • у < у=;
2)	_n.J..JL—__Л.
\	7 J 5 V	7	5 —	35’
*'7	К 5 ;—'	1 ‘	7	5“	35 •
Знак произведения зависит от знаков множителей и
определяется по тем же правилам, как и для целых чисел:
(+1).(+1) = + 1,	(+!)•(-1) = -1,
Модуль произведения, как и для целых чисел, нахо-
дится умножением модулей множителей. Таким образом,
рациональные числа можно умножать по следующим
правилам:
Произведение двух чисел одинаковых знаков есть число
положительное, равное произведению их модулей.
Произведение двух чисел разных знаков есть число от-
рицательное, противоположное произведению их модулей.
Например: 1)
9.	/_2\	3 __	2-3 _	6	.
V	7 )	’Т“	7-5 ~	35’
оч	2	f	3\	2-3	6
----7-5--35*
226
Произведение нескольких множителей вычисляют так
же: сначала определяют знак произведения, потом пере-
множают модули множителей.
Например: 1)	( “т) =	* 2" * т) =4б ’
7__з\ (____1_\ /___1 _L\_ _£
V 5/‘\ 2 J * V 4	\ 5 ’ 2 * 4 J ~ 40 •
УПРАЖНЕНИЯ
1, Устно выполните действия:
4>п-Н); М4Н; М-тНЧ)-
2. Определите знак произведения:
й);
2) (-4)-4-<-» (-4);
м-^н-^м-я.
4)	_П.2>
' \	—5 / \	4 j 5 \ 7 J
3. Определите знак произведения. Вычислите произведе-
ние:
1>НН4Н; 2>НМ-4Н-Я
4. 1) Сколько отрицательных множителей должно со-
держать произведение, чтобы оно было положительным?
2) Сколько отрицательных множителей должно со-
держать произведение, чтобы оно было отрицательным?
Вычислите:
5-	1)	2) НМ^М-ЦН-я)-
6.	1) (-5)4; 2) 7-(-4); 3)
7.	I) (-2|) • (- 4) ; 2) (- 4)  2}; 3) 4  (-51).
8,	1) Произведение пяти множителей положительно.
1 Можно ли утверждать, что все множители положи-
тельны?
2) Произведение четырех множителей положительно.
Можно ли "утверждать, что все множители поло-
жительны?
8*
227
9, Сформулируйте свойства деления, которые выра-
жаются следующими равенствами:
1)	с:6 = (а-п):(Ь-п); 2) а:& = (а:п):(й:п).
10.	Вычислите степень, предварительно назвав основание
и показатель степени:
1)	(!)•; 2) (-4)’; 3) (-!); 4) (-!)•.
11.	Запишите:
2	I
1)	квадрат числа —у; 2) куб числа — 1у;
3)	произведение чисел —2-г и 3-i-;
4)	четвертую степень числа —2-у;
5)	квадрат суммы чисел —3-|- и 2у.
12.	Вычислите, предварительно указав порядок действий:
2)	НН4-(-4))4-.
з)	4-
<>(з1.2±).((-4)4).
13.	Вычислите:
»Ч-4Н)> Ч-4Н-Н);
з)21.Н)4; о(-4Ы-Н)-
^•(-4)-(-4)= <> 4-(4-(-Ж
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
15,	Вычислите:
1) —90000:360;	2) —1651200: (—3200);
3)	2128000:(—7600);	4) —18777600:(—4800)’.
16,	1) Какое число надо разделить на —12, чтобы полу-
чить 14?
2)	Какое число надо разделить на 18, чтобы полу-
чить —15?
17,	1) На какое число надо разделить —798, чтобы по-
лучить 19?
228
2)	На какое число надо разделить 1081, . чтобы полу-
чить —23?
18,	1) Какое число надо умножить на —18, чтобы полу-
чить —1134?
2)	На какое число надо умножить 29, чтобы полу-
чить —2639?
19.	Вычислите:
2)	2:| + 4.:2+1±:6 + 6:4.
20.	1) 21:(4-4) + (4+4.):Ц.;
21.	1) Пешеход проходит 1 км за 12-i- мин. За сколько
А
2
минут он пройдет у км?
з
2)	Часы отстают за сутки на Зу мин. На сколько
2	-ч
они отстанут за у суток?
22.	1) 1 м ткани стоит 12-|-р. Сколько метров ткани можно
купить за а) 10 р.; б) 16 р.; в) 20 р.?
2)	Пешеход проходит в час 4у км. За сколько часов
2
он может пройти 32у км?
3
23.	1) Для выполнения у работы необходим 1 ч. Сколько
времени нужно для выполнения всей работы?
2)	Геолог прошел маршрута, а осталось ему пройти
2у км. Какова длина маршрута?
24.	Трое рабочих взяли обязательство изготовить опре-
деленное число деталей. Первый рабочий изготовил
Уо всех деталей, второй—у остатка, а третий —
остальные 84 детали. Сколько деталей изготовил пер-
вый рабочий и сколько второй?
25.	Три завода получили заказ на изготовление моторов
для лифтов нового жилого массива. Первый завод
13	«5
выполнил gg всего заказа, второй—у остатка, а тре-
229
тий—остальные 180 моторов. Сколько моторов изго-
товили первый , и второй заводы отдельно?
26.	На кормление 300 голов молодняка и коров, число
которых составляет общего числа, ежедневно рас-
ходуют 5950 кг сена. Сколько сена расходуют в день
на одну корову и на одну голову молодняка, если
на корову расходуют на 9у кг больше, чем на одну
голову молодняка?
27.	За 25 столов и 40 стульев заплатили вместе 504 р.
Сколько стоят все столы и сколько все стулья, если
стол дороже стула на 10 р. 15 к.?
28.	Представить в виде произведения степеней простых
чисел-1-2-3-4-5-...•14-15.
§ 69. Представление рациональных чисел
на координатной оси
На координатной оси можно изображать не только
целые числа и положительные дроби, но и отрицательные
дроби.
Для того чтобы изобразить на координатной оси от-
рицательную дробь—(р > 0, Я > 0), надо отложить-^-
часть единичного отрезка р раз влево от нулевой точ-
ки — в отрицательном направлении.
. ~ii -1	-i ~l	о к	i	% 1	?£
—I—4-----1----1—I---1—H---1---1—I----1—>
Рис. 5.7
На рис. 5.7 изображена координатная ось, на которой
12	1*	3	4	,
отмечены точки —у, —-j-= —-g, —Т» —Т = —1 и
другие точки.
Таким образом, отрицательные дроби изображаются
точками на отрицательной полуоси, а положительные дро-
би— на положительной полуоси.
Точка, изображающая на координатной оси рацио-
нальное число а, называется точкой а или точкой с ко-
ординатой а.
230
Если а и b—рациональные числа и а <_Ь, то
1)	точка b находится на координатной оси правее
точки а;
2)	расстояние между точками а и b равно b—а;
3)	точка -у- есть середина отрезка, соединяющего
точки а и b (рис. 5.8).
В
середины отрезка АВ, надо
вину длины отрезка АВ:
. b—а 2а . Ь—а
а+—=т+—=	
—а __ а 4-6
2
Например, для точек
А (-4') и В (44):
\	5 J \ 5 /
2	4
1)	—г <4-г-, значит,
' о о
самом деле, чтобы вычислить координату точки С —•
к числу а прибавить поло-
Рис. 5.8
точка В находится правее
точки А на координатной оси.
л о а 4	(	2 \ л4 2 л 6 г 1
2)	А В = 4“е— ( —— ) = 4“Р" -j—г* = 4 -р т" — 5-=-«
'	5	\	5 у 5*5	‘5	5
3)	Середина отрозка АВ имеет координату:
4±+(,_2> а
5)_ 45 _д2.9_91 s
2	“2 Т,z-z5 *
Точка, изображающая на координатной оси раци-
ональное число, называется рациональной точкой.
Так как для любых рациональных чисел а и b число
Hi* тоже рациональное, то между любыми рациональными
точками на оси существует еще хотя бы одна рациональ-
ная точка.
Число называется средним арифметическим чисел а
и Ь. Вообще, средним арифметическим п чисел называется
число, равное сумме этих чисел, деленной на п.
В дальнейшем мы узнаем, что кроме рациональных
точек на координатной оси есть и другие точки.
231
УПРАЖНЕНИЯ
1, Изобразите на координатной оси с единичным отрез-
ком, равным 4 см, точки:
пл.	!• 1 •	— •	— •	— • — •	1— • — •	— •
V.	*. у.	4л	4 »	у. 4 »	14 . 8 >	8 ’
01	1-	1 •	2- — 1-	—2- —2-	--
~1> ~~	2 ’	2	’	4	’	4 ’	4 »	.4	‘
2.	Выберите удобный для работы единичный отрезок и
изобразите на координатной оси точки:
1)	-1|: -4; -31; -41;
91 L- _2- 11-  12- _ 2—'  2—
з• з ’	* з *	1з’ Z3 ’ Z3 •
3.	На координатной оси изобразите точки:
I)	а (-21); 2) в(-4): 3> с(-4);
4)D(-1o1).
4.	Определите расстояние между точками:
1)	л(-Зу) и В (2);	2) Л (—4) и в(-21);
3)	Л (-31) и В (-41);
4)	л(-4|) и B(-61).
5.	Найдите среднее арифметическое чисел:
1)31„_21;	2) -21» -11;
3)	-101»-1°1;	4) -211 и -2|1.
6.	Определите координату середины отрезка АВ, если
1)	Л (-4), В(—1);	2) Л (-8), В(3);
3) л(-га). fl(-ii>): 4> л(-'4)’ в(-4)-
7. Точка С—середина отрезка АВ. Определите коорди-
нату точки В, если
1) Л(-2), С(41);	2) Л(-31), с(-1);
3) Л(~21), С(-1); 4) л(-4-|), с(-б1)ч
8. Найдите среднее арифметическое чисел:
1) _3, —2, —1, 5;	2) —7, —3, 1, 5;
232
9, Определите координаты точек, делящих- отрезок АВ
на четыре равные части:
1) А (-3), В (б|); 2) А (~б|) , В (-2±).
10, 1) Среднее арифметическое 4 у и числа а равно 2у.
Найдите число а.
2)	Среднее арифметическое числа а и —у равно у.
Найдите число а.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
11.	Вычислите:
2.5 _17\ 18
18 36/65
1)
1	1	2
2;3|+3|:13:|-
3	1
12.	1) Число 4у увеличили в 2у раза. На сколько уве-
л3 .
ЛИЧИЛИ ЧИСЛО 4у?
7	1
2) Число увеличили на 11^. Во сколько раз
- 7 -
увеличили число 5jg?
5	'	1
13.	1) Число 17у уменьшили в 4j§ раза. На сколько
§
уменьшили число 17у?
1	4	х
2)	Число 13у уменьшили на бу. Во сколько раз
уменьшили число 13у?
14.	Найдите два числа, сумма которых равна 4, а раз-
2
НОСТЬ у.
15,	Найдите два числа, сумма которых равна 5у , а раз-
. 1
НОСТЬ 1 у .
16,	1) Одно число в 2 раза больше другого, а их сумма
3
равна 6jg. Найдите эти числа.
233
2)	Одно число в 3 раза больше другого, а их разность
равна Зу. Найдите эти числа.
17,	1) Найдите три числа, из которых второе больше пер-
вого в 2 раза, а третье больше первого в 3 раза.
Сумма трех чисел равна 7-§-.
2)	Найдите три числа, из которых второе больше пер-
вого в 2 раза, а третье больше второго в 3 раза.
Сумма трех чисел равна 7-|-.
18.	Найдите х из равенства:
1)	Зх=—5;	2) —Зх=16;
3)-4*=—4*=1т:
5>	6)-8|х=-7|. .
19.	Устно сравните число с нулем, а затем упростите:
4)	5)(—i):(-7):(-3); 6) (-j)’;
(-4)’ 8>	« (-4У-
20.	Определите, какое из выражений больше (постарайтесь
выполнить задание, не выполняя вычислений):
.If	7 \	/	3	\	-7/	4 \	8
)42Д	5	)	А	197	ИЛИ	& 9	А	177:13:
~	[ 1	\	[	1 \	[	1	\	(	1 \	1 [	1	\
2)	( 2	)	А	з )'	\	4	)	ИЛИ	V	4 ):	3 А	2	) ’
з)	м"
_LV(____!_>
V 2 J \ ю J \ loo у •
2 ВОПРОСЫ для ПОВТОРЕНИЯ
• ПО МАТЕРИАЛУ ГЛАВЫ V
1.	Сформулируйте основное свойство дроби.
2.	Являются ли целые числа рациональными?
3.	Являются ли натуральные числа и число нуль рациональными?
4.	Любое ли рациональное число является целым?
5.	Какие дроби называются положительными?
6.	Какие дроби называются отрицательными?
7.	Имеются ли дроби не положительные и не отрицательные?
8.	Какие дроби называются противоположными?
234
9.	Какая дробь противоположна сама себе?
10.	Что называется модулем дроби?
11.	Сформулируйте правило сравнения двух дробей с общим знаме-
нателем. Какое ограничение накладывается на знаменатель в этом
правиле?
12.	Объясните, как сложить, вычесть дроби с равными знаменателями.
13.	Объясните, как сложить, вычесть дроби с разными знаменате/ями.
14.	По какому правилу умножают дроби?
15.	Как умножить дробь на целое число?
16.	По какому правилу делят дроби?
17.	Как разделить дробь на целое число?
18.	Какие дроби называются взаимно обратными? Каким свойством
обладают взаимно обратные дроби?
19.	Сформулируйте правило деления дробей.
20.	Запишите переместительный, сочетательный законы сложения и
распределительный закон для дробей а, b и с.
21.	Сформулируйте переместительный и сочетательный законы умно-
жения и запишите их для дробей а, b и с.
22.	Как определить расстояние между рациональными точками на
координатной оси, если координаты точек известны?
23.	Как вычислить координату середины отрезка, если известны коор-
динаты концов отрезка?
24.	Сколько на координатной оси существует рациональных точек,
расположенных между любыми двумя рациональными точками?
25.	Что называется средним арифметическим двух чисел? Приведите
примеры.	i
26.	Что называется средним арифметическим п чисел? Приведите
примеры для п = 3, л=4.
УПРАЖНЕНИЯ
1.	7 1) Какое число надо умножить на —-§> чтобы получить 28? 3 2) Какое число надо умножить на 28, чтобы получить -*-g-?
2.	6 1) Какое число надо разделить на jj, чтобы получить *—12?
	2) Какое число надо разделить на —12, чтобы получить —--у?
3.	1) Какое число надо умножить на — 2-i-, чтобы получить 3-~-?
	2) Какое число надо разделить на —7^rt чтобы получить
	-4’
4.	Докажите, что
235
f 1 \ —8 , 3
0	7	4 >
5.
6.
7.
8.
9.
10.
11.
/ £\ . /—25\ 5 —1
12 18/V 7 J < V 36 J •’ —12* 11 •
Вычислите:
7—3.8 14
9* 14 +15:—5 :
/ ]8\ Z	9\ J5 14
V 25 A 10/ 49*25;
Наибольшее количество соли/ которое растворяется в воде,
9	п
составляет веса воды. Сколько килограммов соли растворится
в -у ведра воды, если ведро воды весит 12 кг?
3
Рабочий за час выполнил у порученной работы. За сколько
часов он может выполнить всю работу?
5
Бассейн наполняется за час до jy объема. За какое время он
наполнится весь?
2
Окружность колеса 14 — дм, а его диаметр (отрезок, соединяю-
о
щий две точки окружности и проходящий через ее центр) равен
2
4-я- дм. Во сколько раз окружность длиннее диаметра?
о
В 1975 г. всеми видами городского транспорта г. Москвы за
1 день перевозилось 14у млн. пассажиров, а в 1984 г. за 1 день
в l^g раза больше. Сколько пассажиров перевозил городской
транспорт г. Москвы за 1 день в 1984 г.?
12*. Три швейные мастерские получили ткань одинакового качества.
Первая мастерская получила -5- всего количества ткани, отпу-
о
о	1 1
щенного трем мастерским. Вторая мастерская получила в 1-g- раза
больше ткани, чем третья мастерская. Первая мастерская полу-
чила на 20 м ткани больше, чем третья. Первая мастерская
сшила из полученной ткани 14 рубашек и 28 платьев. На одно
4
платье пошло на — м больше, чем на одну рубашку. Сколько
и
метров ткани пошло на 1 рубашку и 1 платье в отдельности?
236
13*. Производительность самоходной косилки при работе на первой
7	3
скорости 3 га в час, на второй 4jg га в час, на третьей 6— га
в час. Определите площадь, скошенную косилкой за 10 ч. работы,
.	ч	4
если время ее работы на второй скорости составило времени
о
работы на первой, а на третьей того, что на второй.
14.	Головоломка. Вырежьте из цветной бумаги четырех цветов
по 4 равных квадрата каждого цвета. Сложите из этих квадратов
квадрат 4x4 так, чтобы одинаковый цвет не повторялся:
1) ни в строчках, ни в столбцах;
2)	ни в строчках, ни в столбцах, ни в диагоналях.
15.	Пронумеруйте квадраты каждого цвета (упр. 14) числами 1, 2, 3,
4. Сложите квадрат 4x4 так, чтобы и цифры, и цвета не повто-
рялись ни в строчках, ни в столбцах, ни в диагоналях.
16.	В коробке лежат пять пилоток—две синие и три красные. Учи-
тель вызывает к доске трех учеников, которые становятся лицом
к классу и закрывают глаза. Учитель надевает каждому на го-
лову одну пилотку, а остальные убирает в коробку. Ученики
открывают глаза, каждый видит пилотки своих товарищей, но не
видит своей. Может ли кто-нибудь из них верно определить цвет
своей пилотки? Рассмотрите три случая:
1)	надеты 2 синие и 1 красная пилотка;
2)	надеты 1 синяя и 2 красные пилотки;
3)	надеты 3 красные пилотки.
17.	В первенстве по футболу принимают участие 8 команд, каждая
с каждой играют по одному разу. За выигрыш присуждают 2 очка,
за ничью 1 очко, за проигрыш 0 очков. Места определяются по
числу очков. Какая может быть наименьшая разница очков между
первым и последним местом, если первое место заняла одна
команда и последнее место заняла одна команда?
18; Четыре ученика: Витя, Петя, Юра и Сергей заняли на матема-
тической олимпиаде четыре первых места. На вопрос, какие
места они заняли, были даны ответы: а) Петя—второе, Витя —
третье; б) Сергей—второе, Петя —первое; в) Юра—второе, Витя —
четвертое. Указать, кто какое место занял, если в каждом ответе
правильна лишь одна часть.
237
Глава VI. ПРОПОРЦИИ
§ 70. Буквенные выражения
Если в числовом выражении некоторые (или все) числа
заменить буквами (разные числа—разными буквами), то
получится буквенное выражение.
Мы уже пользовались буквенными выражениями. Про-
извольные натуральные числа мы обозначали буквами
а, Ь,.произвольное рациональное число мы обозначали
у, где р и q—целые числа (<7=Н=0).
Приведем примеры других буквенных выражений:
1) любое четное положительное число можно записать
в виде буквенного выражения 2-п, где п—натуральное
число;
2) любое нечетное положительное число можно записать
в виде буквенного выражения 2 и—1, где п—натуральное
число.
Если в буквенном выражении 3-я—7 вместо а подста-
вить число, например, 3, то получится числовое выраже-
ние 3-3—7, равное числу 2. Это число называется зна-
чением буквенного выражения 3-а—7 при а — 3.
Пример. Найдем значение буквенного выражения
7-Х+2-Л: при х =— 2.
Решение. 7-(—2)4-2-(—2) = —14—4 = — (144-4)=
= — 18.
В буквенных выражениях обычно не пишут знак умно-
жения (•) между числами и буквами. Поэтому считают,
например, что 8-у=8у.
238
Буквенные выражения широко применяют для записи
формул. Формула—это запись математических и других
законов с помощью чисел, букв и специальных знаков.
Некоторыми формулами мы уже пользовались. Например:
1)	Р = 2(а+Ь)—формула периметра прямоугольника,!
где а и b—стороны прямоугольника;
2)	S = ab—формула площади прямоугольника, где а
и b—стороны прямоугольника;
3)	V = abc—формула объема прямоугольного паралле-
лепипеда, где а, b и с—его стороны (длина, ширина,
высота);
4)	s = vt—формула пути равномерного движения по
прямой, где v—скорость, t—время движения;
5)	S-a? и Р=4а—формулы площади и периметра!
квадрата, где а—сторона квадрата.
УПРАЖНЕНИЯ
1.	Найдите число, равное числовому выражению:
1)Ц-6п+^);
3)	6.(-14) + (-4):(-1|);
4)	(Ц.24-5|:18).5.
2.	В числовом выражении ~7<5_| замените число 5 бук-,
вой а. Запишите полученное буквенное выражение.
3.	Приведите два примера буквенных выражений.
4.	Подставьте вместо буквы а в буквенное выражение
а + 3 числа:
1)	5; 2) 3; 3) 1; 4) 0; 5) —1; 6) -3.
5.	Устно найдите значение буквенного выражения 7 + х
при х, равном:
1)	0; 2) 3; 3) -1; 4) -6; 5) —7; 6) -10.
6.	Выражение а + 2 представляет собой сумму чисел а
и 2, выражение 3—х—разность чисел 3 и х.
Прочитайте буквенное выражение:
1)	5 +а;	2)	7—а;	3) 4—х;
4) а + 12;	5)	2а;	6) 7Ь\
7) —За;	8)	— х;	9)а+(—3).
7. В произведении Зх число 3 называют числовым мно-
жителем или коэффициентом, а число х—буквенным
239
множителем. Назовите коэффициент и буквенный
множитель в произведении:
1)	7а; 2) 4у; 3) —26; 4) ~х.
8,	Вычислите значение буквенного выражения. При*
мер. 10—4х при х——5. Решение. 10—4х =
= 10—4 •(—5) = 10 4- 4 • 5 = 10 + 20=30.
1)	2х+Г при х=5;
2)	6-f-8x при х= — 1;
3)	5—4а при а=2;
4)	3—7b при Ь=—2.
9.	1) а4-6 при а>1, 6=3;
2)	а—Ь	при а==—2,6=4;
3)	2х—у при х=2, у=5;
4)	Зх—2у при х=—1, t/=—5.
3	4
10.	1) аб при а=у, 6=1у;
2)	2 (а4-6) приа=уд, 6=1у;
3)	хуг при х=—2, у=-|, z=lyj
4)	ху—4г при х=6, у=—2, z=—*у,
11.	Не перенося в тетрадь таблицу, найдите значение каж-
дого буквенного выражения при всех х, ‘ указанных
в первой строке таблицы:
240
13# При каких а и b верно равенство:
1) а + 6=0;	2) а-6=1; 3) a-b^cr, 4) a b=—1?
14, Что означает запись 2х и х2? Как можно записать
Эти буквенные выражения по-другому? Как можно
назвать (прочитать) эти буквенные выражения?
15. Вычислите значение хг при х, равном:
1) 2; 2) 5; 3) —1; 4) —2; 5) —5; 6) 7.
17, Вычислите объем куба, ребро которого равно:
1) 1 см;	2) 10 см;	3)	см;	4) см;
5)	у м;	6) у дм;	7)	км;	8)	1у мм.
18.	Стороны прямоугольника а и Ь. Запишите формулу
периметра прямоугольника. Вычислите периметр при
1) о = 2 см, 6 = 3 см;
2)	а — 1 см, 6=9 см; v
3)	o = l-g- см, 6 = 3у см;
I	о
4)	а = 2-=- см, 6 = 3-=- см.
О	о
19.	Стороны прямоугольника а и 6. Запишите формулу
площади прямоугольника. Вычислите площадь при
1) а—1 см, 6=13 см;
2)	а = 2у см, 6=4 см;
1	9
3)	О = 3у дм, 6 = ^ дм;
4)а=6удм, 6=2-^ дм.
20, Длина, ширина и высота прямоугольного параллеле-
пипеда а, 6 и с. Запишите формулу объема прямо-
угольного параллелепипеда. Вычислите объем при
1) а=7 см, 6 = 8 см, с=5 см;
2
2)	а=у см, 6=10 см, с=4 см;
241
'М';
1	3
3)	а = 2-g- см, Ь —15 см,	с = jg см;
4)	а—2^- см, Ь = зД- см, с=зЛ см,
Z	О	1U
21.	Сторона квадрата а. Запишите формулу периметра
квадрата, формулу площади квадрата. Вычислите пе- -
риметр и площадь при
1)	а = 9 см; 2) а=1у дм;
3)а=2^дм; 4) а = з| м.
Составьте буквенное выражение по условию задачи
(№ 22—29):
22.	На одной полке х книг, на другой на 15 книг боль-
ше. Каким буквенным выражением можно обозначить
число книг на второй полке? Каким буквенным вы-
ражением можно обозначить число книг на двух
полках вместе?
23.	В одной пачке х тетрадей, а в другой на 11 тетра-
дей меньше. Сколько тетрадей в двух пачках вместе
(каким буквенным выражением можно обозначить это
число)?
24.	Сестра нашла х белых грибов, а брат в 3 раза боль-
ше. Сколько белых грибов нашел брат? Сколько белых
грибов нашли брат и сестра вместе?
25.	Одно число в четыре раза больше другого. Обозначив
одно из чисел (какое лучше?) буквой и выразив с
помощью этой буквы другое число, найдите сумму и
разность этих чисел.
26.	В вазе лежало 15 яблок. Маша угостила трех под-
ружек, дав каждой одинаковое число яблок (будем
считать по х яблок). Сколько яблок осталось в вазе?
27.	Одна сторона прямоугольника равна 5 см, а другая
неизвестна. Запишите формулу для вычисления:
1) периметра прямоугольника;
2)	площади прямоугольника.
28.	Пешеход идет со скоростью 4 ™. Какой путь он
пройдет за х часов? Вычислите путь при х, равном
29,	Расстояние между селами 15 км. Пешеход идет со
скоростью 4 Сколько километров ему останется
пройти через х часов? Вычислите значение получен-
ного выражения при х, равном 1, 2, 3.
242
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
30.	Вычислите:
и 4+34-(-6й-1в)+5г.
У (318~7п+	1 10“4;
3)	( — 615— *	5"б	2“Т'
«п+пЧ3^-7^1?)-
31, 1) Может ли дробь, у которой числитель меньше
знаменателя, быть равной дроби, у которой чис-
литель больше знаменателя?
2)	Может ли дробь, у которой числитель больше зна-
менателя, быть меньше 1?
32.	Задача-шутка (решите устно).
1)	Почтовая карета, запряженная тройкой лошадей,
проехала 30 верст. Сколько верст проскакала каж-
дая лошадь?
2)	Каждое колесо четырехколесного автомобиля
. проехало 200 км. Какой путь проехал автомо-
биль?
33.	Автотурист отправился в путешествие на четырех-
колесном автомобиле с одним запасным колесом. По
дороге он менял колеса с таким расчетом, чтобы они
изнашивались равномерно. В итоге каждое колесо
проехало один и тот же путь.
Определите:
1)	сколько километров проехало каждое колесо, если
автомобиль проехал 4000 км;
2)	сколько километров проехал автомобиль, если
каждое из пяти колес проехало 4000 км?
34.	Один автолюбитель рассказывал: «Я отправился пу-
тешествовать на «Москвиче», имея одно запасное ко-
лесо. Время от времени я заменял колеса, и оказа-
лось, что 1-е колесо проехало 1000 км, 2-е—900 км,
3-е—800 км, 4-е—700 км и 5-е (запасное)—600 км».
7 Сколько километров проехал автомобилист?
35.	Может ли автомобилист так проводить замену колес,
чтобы после поездки оказалось, что 1-е колесо про-
ехало 600 км, 2-е—800 км, 3-е—1000 км, 4-е—1200 км
и 5-е (запасное)—1400 км?
243
§ 71. Подобные слагаемые
В буквенных выражениях буквы обозначают числа.
Поэтому для буквенных выражений справедливы равенства:
1)	a + b=b + a\ 2) (а + Ь) + с=а + (& + с);
3) ab = ba;	4) (ab)c=a(bc)‘,
5) а (Ьс) = ab + ас, 6) а + 0 = а;
7) а4-(—а) = 0;	8) а—Ь = а + (—&);
9) а=1-а;	10) —а =— 1-а; 11) а-0 = 0.
С помощью этих равенств можно упрощать буквенные
выражения. Например, 7х4- Зх—5х= (74- 3—5) х = 5х.
Слагаемые 7х, Зх, —5х отличаются только числовыми
множителями. Такие слагаемые называются подобными.
Пользуясь распределительным законом, можно упрощать
выражения, содержащие подобные слагаемые. Например,
упростим выражения:
1)	5а—4а = (5—4)а= 1-а = а;
2)	9а—13а4-а = 9 а—13-а4- 1-а = (9—134- 1)а =
==—За;
3)	7а—а—6а=7-а—1-а—6-а—(7— 1—6)а = 0-а =0;
4)	х—6х=1-х—6-х=(1—6)х =—5х.
Такое упрощение выражений называется приведением
подобных слагаемых.
В простых случаях промежуточные вычисления опус-
кают, например, пишут:	'
- 1) 5 а—4а = а; 2) 9а— 13а 4-а = — За.
При приведении нескольких (больше двух) подобных
слагаемых полезно сначала сгруппировать отдельно те,
перед которыми стоит знак плюс (4-), и отдельно те,
перед которыми стоит знак минус (—). Например, упрос-
тим выражение 2а—4а—а 4-На—6а—8а 4-За:
2а—4а—а 4- На—6а—8а 4- За =
= (2а4- На4-За)4-(—4а—а—6а—8а) =
«=(24-11 4-3) а—(44-14-6 4-8) а = 16а—19а=(16—19) а=
«= —За.
244
УПРАЖНЕНИЯ
1.	Запишите все произведения, которые получаются из-
менением порядка множителей:
1)	хб; 2) аб-2; 3) х6у; 4) а-у
2.	Упростите запись буквенного выражения:
1)	1а;	2) + х; 3) (— 1)с;	4) 0-у;
5)	5-2а; 6) 2x3; 7) За4;	8) 6-2-3.
3.	Запишите число, противоположное:
1)	а; 2) 2х; 3) 0; 4) —Ь; 5) —2с; 6) —^у.
4.	Запишите сумму в виде произведения:
1)	х+х; 2) а + а; 3) 6 + 6+6;
4)	у + у+у+у; 5) z+z + z + z + z + z+z;
6) с + с+с+с + с+с+с+с.
б. Запишите произведение в виде степени; назовите ос-
нование и показатель степени:
1) аа; 2) ххх; 3) bbbb; 4) kkkkkk.
6.	Устно укажите коэффициенты в произведении:
1)	12х; 2) 7аЬ; 3) —4у, 4) а; 5) —с; 6) -|-а.
7.	Запишите:
1)	произведение чисел а и 3;
2)	произведение чисел х и у,
3)	квадрат числа /; 4) удвоенное число Ь.
8.	Укажите слагаемые, отличающиеся только коэффици-
ентом. Как называются такие слагаемые?
1)	2а + 7 + За—1; 2) Зх—у + 4х+х+2у.
9.	Укажите подобные слагаемые и приведите их. Нап-
ример, 7х—8+ 4х—2=(7х+4х)+(—8—2) = (7+4) х—
— (8 + 2) = 11х—10.
1)	2а + 3а;	2) Зх+5х;
3)	12# + 7у; 4)3/+ 4/.
10.	1) т—8т;	2) а—16а;
3)—х—6х; 4) —Ь—126. .
11.	1) 2а—За; 2) —46 + 76;
3)	— 12//—15г/; 4) —27с+13с.
12,	1) 56 -1* 26 + k; 2) х + 2х + Зх; .
3) 7п—6п + л; 4) 4d—2d—3d.
13.	1) Зх—2 + 5х; 2) 8у—12— 10//;
3)	4—8а—13; 4)—3+156—7.
245
14.	1) З/п + п + 5/п + п; 2) 4k—За + а—2k;
3)	6x—2++—4x + 2r/;
4)	9x + 4—3x—5r/ + 5—8y.
15.	Упростите буквенное выражение и найдите его зна-
чение:
1)	х+4х—1 при х =—2;
2)	а—6а + 4 при а=—3.
16.	Упростите буквенное выражение:
1)	4х:4; 2) 5х:5; 3) 6а:2.
17.	1) 6/п:3; 2) 25z/:5; 3) 326:4.
18.	1) —8х:4; 2) 18а:(—3); 3) — 28у.{—7).
19.	Приведите подобные слагаемые:
1)	ух + ух; 2) j/n+y/n; 3) lya + ya.
20.	I) ±k-±k; 2) b—|-6; 3)2^х-1±х.
21.	1) За + 46—5а +36—76 + 6а—86; -
2)	х—4у—у + 7х-\-2у—8х—х + 5у.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
22.	Вычислите:
1)	5 + 6-9 + 21 + 7—2~6;
2)	17+24—48+21 у—24 +48—211;
3)	— 72 + 46 + 72—351 + 351 —146;
4)	125 — 157 + 391+57—25—1.
23.	В классе х мальчиков. Запишите буквенное выраже-
ние, показывающее, что в классе девочек на 7 боль-
ше, чем мальчиков.
24.	Миша прочитал несколько страниц книги. Ему оста-
лось прочитать в три раза больше, чем он уже
прочитал. Запишите с помощью буквенного выраже-
ния, сколько страниц в книге, если число прочитанных
страниц обозначить буквой х.
25.	Одна сторона прямоугольника на 3 см больше дру-
гой. Обозначив одну из сторон буквой, выразите
периметр прямоугольника буквенным выражением.
26.	Одна сторона прямоугольника в 3 раза больше дру-
гой. Обозначив одну из сторон буквой (какую лучше?),
246
выразите периметр прямоугольника буквенным выра-
жением.
27,	Одно число в 5 раз меньше другого. На сколько это
число меньше другого? Какова сумма этих чисел?
В качестве ответа на вопрос задачи приведите бук-
венные выражения, в которых буквой обозначено
одно из чисел (какое удобнее?).
28.	Ученик задумал число—обозначим его буквой х,
увеличил задуманное число на 5, результат увеличил
в 4 раза. Каким буквенным выражением можно за-
писать полученное число?
29.	Если любое число умножить на 5, прибавить к ре-
зультату 3, полученное число увеличить в 2 раза и
из результата вычесть 6, то полученное число в 10
раз больше первоначального. Разгадайте секрет этого
числового фокуса.
30.	Старинная задача. Купец купил ПО фунтов табака.
50 фунтов оказались подмоченными и купец продал
их на 2 рубля дешевле за 1 фунт, чем заплатил сам.
Остальной табак он продал на 3 рубля дороже за 1
фунт, чем уплатил сам. Подсчитайте прибыль купца.
31.	Скорость моторной лодки 15 Скорость течения ре-
ки 3 На сколько скорость лодки по течению реки
больше скорости лодки против течения реки? Какое
условие в задаче лишнее?
32.	Докажите, что
1)	+ Ь)а; 2) (<*+&) —(а—
33.	Докажите, что
^по теч 4" у пр. теч_,.	. о\ °по теч ^пр. теч_..
1)	2	°собств > *•)	2 '	итс ч •
34.	Докажите, что сумма двух четных чисел есть число
четное. Для доказательства используйте формулу чет-
ного числа..
35.	1) Докажите, что сумма двух нечетных чисел есть
число четное.
2) Докажите, что сумма четного и нечетного числа
есть число нечетное.
36, Записано четыре числа: 0, 0, 0, 1. За один ход раз-
решается прибавить 1 к любым двум из этих чисел.
Можно ли за несколько ходов получить 4 одинако-
вых числа?
247
37, Можно ли представить единицу в виде суммы
—+-J, где а, о, с, а—нечетные натуральные
числа?
§ 72, Уравнения
Если известно, что х+5 равно 8, и требуется узнать,
какое число обозначено буквой х, то говорят, что надо
решить уравнение х + 5 = 8.
Неизвестное число, обращающее уравнение в числовое
равенство, называется корнем уравнения. Решить уравне-
ние—значит найти его корни. Поэтому корень уравнения
иногда называют решением уравнения.
Решим уравнение х+5 = 8. Слева записано число
х+5, а справа—равное ему число 8. Чтобы равенство
не изменилось, уменьшим на 5 не только левую, но и
правую часть уравнения, тогда х=8—5, т. е. х=3.
Обычно, вместо того чтобы говорить «уменьшим обе
части уравнения на число», говорят «перенесем число с
противоположным знаком в другую часть уравнения».
Пример. Решить уравнение х—2 = 5.
Решение. Перенесем —2 с противоположным зна-
ком в правую часть уравнения: х=5 + 2, х=7.
Ответ. 7.
Этим приемом пользуются, когда в какой-либо части
уравнения есть сумма или разность числа и буквы (бук-
венного выражения). Можно сформулировать этот прием
так: «перенесем слагаемые, содержащие гнеизвестное чис-
ло, в одну часть уравнения, а все известные числа —
в другую часть уравнения»..
Пример. Решить уравнение Зх=4.
Решение. Произведение 3 и х равно 4, значит,
х=4:3=-|«1у.
Ответ. 1у.
Это рассуждение помогает решать уравнения, в одной
части которых произведение числа и буквы (буквенного
множителя), а в другой части уравнений известные числа.
248
В сложных случаях, когда в частях уравнения много
слагаемых, следует сначала перенести слагаемые с неиз-
вестным числом в одну часть, а известные числа—в дру-
гую. После этого останется упростить обе части и решить
получившееся уже несложное уравнение.
Пример. Решить уравнение 3—4-х=5.
Решение.
1) Перенесем 3 с проти-
воположным знаком в
другую часть уравне-
ния:
2) Так как произведение
1	п
—у и х равно 2, то
—1-х=5—3, —ух=2.
х=2: ( —) = — 2 • 2 =4.
Ответ. —4.
УПРАЖНЕНИЯ
1.	Что называется корнем уравнения?
2.	Является ли число 2 корнем уравнения:
1)	х—2 = 0; 2) х+4 = 0;	3) 2х=4;
4)	Зх—4 = х; 5) х+3 = 2х+1; 6) Зх+4 = 6х—2?
3.	Решите уравнение:
1)	х—2 = 0; 2) х+4 = 0; 3) 100 + х = 0.
4.	1)	х—5 = 6;	2) х+2 = 5; 3) х—11	= — 7;
4)	12 + х=17;	5) х+7 = 7; 6) х—6 = 6.
5.	1)	5 + х = 3;	2) —7 + х=—2; 3)	х+3 = —6;
4)	12 + х=— 8; 5) х+18=18;	6)	—13 + х=—5.
6.	1) х—1 = 2; 2) х—2 = |; 3) х— 4=1 у;
4)	X—--2=у; 5) X з’—6)	18+х~Т2’
7.	1) х—1 = —2) у+х=П;
3)	1у + х = 3;	4) х—-6у=—Зу;
5)	-д-4-х = 2у; 6) х 2у=	1 у.
8.	Решите уравнение. Пример. -— 72х = 44.
Л	11
Ответ. —jg.
249
1)	2х = 4;	2) 6х = 24;	3) 7х=—14;
4)	—5х=100; 5) —2х=—8; 6) 17х=—5.
9.	1) Зх = 2; 2) 6х=—7; 3) —2х= —13;
4)	2х=0; 5) —5х = 0; 6) — х = 2.
10.	1) —х = 0; 2) —х=—5; 3) — х=1;
4)	2х=1; 5)Зх=-|; 6) -2х=|.
11.	1) ух = 3;	2)|х=1;	3) — |х= — 3;
4)	—|х = О; 5) — 4х==; 6) 2х= 1
-Г	I	О
12.	Решите уравнение. Пример. Зх+4 = 5х—7.
Решение. Зх—5х =—7—4; (3—5)х =—(74 4);
—2х= —11; х = ^у = у=5|.
гч	к 1
Ответ. 5у.
1) 2х—6 = 0;	2) 12 + Зх = 0; 3) —х + 7 = 0;
4) 15—Зх = 0; 5) Зх+1=7;, 6) 5—2х=1.
13. 1) Зх + 2х=10;	2) 5х + х = 6; 3) 4х + 2х—7 = 5;
4) 7х + х+3 = 19; 5) 5 = 4х—Зх; 6) 8 = 3х—х.
14. 1) Зх—1=2х;	2) Зх—6 = х;
3) х + 3 = Зх—7;	4)	3—х = 1 + х;
5) 7х + 2 = 3х—10; 6) 5х—8 = 3х—8.
'15, 1)1х—3=2—ух; 2) 5х—2± = ±х;
о; 2	,3	13
3)	1 —-4 х—20;
4) 2х—|х = -|х—у—-|-х+2.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
16. Вычислите:
2	3^4	5*6*
2) 4-4+4-4+'|;
3) 1_.L + ±_ 1 + ±.
2	4^8	12^ 16’
о. 4-4+4-4+14
17,	Подряд записаны 6 натуральных чисел так, что лю-
бые 3 соседних числа имеют четную сумму. Докажите,
что сумма 6 чисел тоже четная.
250
18.	Докажите, что если взять 7 натуральных чисел таких, i
что любые 3 соседних числа имеют сумму четную, то I
сумма всех 7 чисел может быть как четным, так и '
нечетным числом.
19.	Сколькими различными способами могут чередоваться
четные и нечетные числа в задаче № 17? Для кратко-
сти записи можно обозначить четные числа буквой «ч»,
а нечетные—буквой «н».
§ 73.	Решение задач с помощью уравнений
С помощью уравнений можно решать многие задачи. !
Для этого нужно:
1)	неизвестную величину обозначить буквой;
2)	используя условия задачи, составить уравнение;
3)	решить полученное уравнение, т. е. найти неизвест-1
ную величину;
4)	ответить на вопрос задачи.	,
Пример. Ученик задумал число, увеличил его в;
2 раза, прибавил 3 и получил 7. Какое число задумал
ученик?
Решение. Пусть ученик задумал число х. -Тогда;
2-х4-3 = 7, 2х = 7—3, 2х = 4, х = 4:2, х — 2. Ученик за-j
думал число 2.	;
Ответ. 2.1
Пример. В классе 37 учеников, причем мальчиков '
на 5 больше, чем девочек. Сколько девочек в классе?
Решение. Пусть в классе х девочек. Тогда маль- i
чиков х+5. Так как в классе 37 учеников, тох-Ь(*+5)=37, '
х-|-х4-5 = 37, 2х = 37—5, 2х = 32, х = 32:2= 16. В классе '
16 девочек.
Ответ. 16.
Пример. Петя и Таня имели поровну денег на по-
купку ручек. Петя купил 2 ручки, и у него осталось 18 к.,
а Таня купила 3 ручки, и у нее осталось 3 к. Сколько
стоит одна ручка?
Решение. Пусть стоимость ручки х копеек. Тогда
у Пети было 2х + 18 копеек, а у Тани Зх + З копеек. Так
как у ребят по условию задачи было поровну денег, можно
251
составить уравнение: 2х + 18 Зх+3, 2*-—Зх =« 3 —18,
— х=—15, х=15. Ручка стоит 15 к.
Ответ. 15 к.
Пример. Найти число, у которого равны 5.
Решение. Пусть неизвестное число*. Тогда у-х—5,
е 4	- 7	5-7	35	о3	и	о3
х— 5:-=-=5-т=-т- = т = 8-т. Неизвестное число 8т-.
7	4	4	4	4	4
Ответ. 8-|-.
УПРАЖНЕНИЯ
1.	Обозначив неизвестное число буквой, составьте урав-
нение по условию задачи:
1)	Задумали число, прибавили к нему 8 и получили 33.
2)	Задумали число, умножили его на 4 и получили 52.
3)	Задумали число, умножили его на 7, прибавили
к произведению 12 и получили 26.
4)	Задумали число, вычли из него 4, умножили раз-
ность на 5 и получили 15.
2.	1) Одно число на 6 больше другого, а их сумма рав-
на 18. Составьте по условию задачи уравнение,
обозначив буквой:
а) первое число; б) второе число.
2)	Одно число на 4 меньше другого, а их сумма равна 12.
Составьте уравнение по условию задачи, обозначив
буквой:
а) первое число; б) второе число.
3.	Составьте уравнение по условию задачи и решите его:
1)	Одно число в 5 раз меньше другого, а их сумма
равна 42. Какое число, первое или второе, удобнее
обозначить буквой? Почему?
2)	Одно число в 3 раза больше другого, а их сумма
равна 28. Какое число, первое или второе, удобнее
обозначить буквой? Почему?
4,	1) Одно число в 4 раза больше другого, а их раз-
ность равна 39. Найдите эти числа.
2)	Одно число в 8 раз меньше другого, а их разность
равна 54. Найдите эти числа.
5,	1) На двух полках стоят 93 книги, причем на одной
в два раза меньше книг, чем на другой. Сколько
книг на каждой полке?
2)	Брат нашел в 3 раза больше белых грибов, чем
сестра. Всего они нашли 24 белых гриба. Сколько
нашел каждый?
252
6,	1) В одной пачке тетрадей на 11 тетрадей больше, чем
во второй, а всего в двух пачках 73 тетради. Сколько
тетрадей в каждой пачке?
2)	Одна автомашина за рейс перевезла на 1у т груза
меньше, чем другая. Обе машины за рейс перевезли
7 т груза. Сколько тонн груза перевезла каждая
«автомашина за рейс?
7.	Отрезок длиной 12 см разделили на 2 части так, что
один из получившихся отрезков больше другого:
1) в 2 раза; 2) в 3 раза.
Найдите длину каждого из получившихся отрезков,
8.-Второе звено собрало в 3 раза больше макулатуры,
чем первое. Всего оба звена собрали 72 кг макула-
туры. Сколько собрало каждое звено?
9.	Первая глава книги содержит в 3 раза меньше стра-
ниц, чем две другие вместе. Всего в книге 276 стра-
ниц. Сколько страниц содержит первая глава?
10,	Ученик задумал число, увеличил его в 2 раза, к ре-
зультату прибавил 7 и получил 121. Какое число он
Задумал?
11.	Одно число в 4 раза больше другого. Найдите эти
числа, если
1)	их сумма равна 45;
2)	их разность равна 45.
12.	Число увеличили в 3 раза; при этом оно увеличилось
на 30. Найдите это число.
13.	В бидоне было 3 л кваса. Из него отлили в 5 раз
' меньше, чем осталось. Сколько литров кваса отлили
и сколько осталось в бидоне?
14.	На трех полках было 87 книг. На первой полке на
5 книг больше, чем на второй, а на третьей на 13 книг
больше, чем на второй. Сколько книг было на каж-
дой полке?
15.	За кресло, стул и диван заплатили 390 руб. Сколько
стоит каждая вещь, если кресло вчетверо дешевле
дивана, а стул в пять раз дешевле кресла?
16.	В двух пробирках налито по 45 см" уксусной кислоты.
Необходимо распределить эту кислоту так, чтобы
в одной пробирке было в 2 раза меньше кислоты,
чем в другой. Сколько кислоты нужно перелить для
этого из одной пробирки в другую?
17,	Мост длиной 324 м имеет четыре пролета, из которых
два в два раза короче двух других, равных между
собой. Определите длины пролетов моста.
253
18.	В кассе магазина оказалось 100 трехрублевых и пяти-
рублевых банкнот—всего на сумму 445 р. Сколько
было трехрублевых банкнот в кассе?
19.	Натуралист собрал в коробку пауков и жуков—всего
8 штук. Если пересчитать, сколько всего ног в ко-
робке, то окажется 54 ноги. Сколько в коробке пауков
и сколько жуков? (У жука 6 ног, у паука 8 ног.)
20.	Вычислите устно:
1)	480:160— 48:16 = 48:16 — 48:16 = 0, так как 
46:16 = 48:16;
2)	2448:12—1224:6; 3) (209:И):(418:22);
4)(1212:101): (3636:303) + 5.
21.	Найдите наименьшее число, которое делится на
1)	2 и 3;	2) 2, 3 и 4;
3)	2, 3, 4 и 5; 4) 2, 3, 4, 5 и 6.
22.	Найдите наименьшее число, которое при делении
1)	на 2 и 3 дает в остатке 1;
2)	на 2, 3 и 4 дает в остатке 1;
3)	на 2, 3, 4 и 5 дает в остатке 1;
4)	на 2, 3, 4, 5 и 6 дает в остатке 1.
23.	Найдите наименьшее число, которое при делении на 2
дает в остатке 1, а при делении на 3 дает в остатке 2.
Найдите 5 таких чисел.
24.	Определите по рис. 6.1 массу 1 пакета муки.
Рис. 6.1
25. Кирпич весит столько же, сколько весят полкирпича
и гиря в 1 кг. Сколько весит кирпич (рис. 6.2)?
Рис. 6.2
26.	Рыба весит 5 кг и еще полрыбы. Сколько весит рыба?
27,	Книга стоит 1 р. и еще половину стоимости книги.
Сколько стоит книга?
28,	За выполненную работу члены бригады получили
поровну—по 120 р. Если бы в бригаде было на 2 че-
254
ловека меньше, то каждый получил бы на 40 р. больше.
Сколько человек в бригаде?
29,	Пешеход прошел расстояние между двумя селами со
скоростью 4 км/ч. Если бы он проходил в час на 1 км
больше, то ему потребовалось бы на тот же путь на
1 ч меньше. Сколько времени шел пешеход и какой
путь он прошел?
30.	Поезд проехал расстояние между двумя городами со
скоростью 80 км/ч. Если бы скорость была на 20 км/ч
меньше, то потребовалось бы на эту поездку на 1 ч
больше. Найдите расстояние между городами.
31.	Головку сыра требуется разрезать на 8 равных частей.
Какое самое маленькое число прямых разрезов необ-
ходимо сделать для этого, если перекладывать части
между разрезами не разрешается (рис. 6.3)?
Рве. 6.3
Рис. 6.4
32.	Если распилить куб с ребром 1 м на кубики с реб-
ром 1 дм и сложить их в ряд, то какой длины будет
этот ряд?
33.	Если распилить куб с ребром 1 м на кубики с реб-
ром 1 см и сложить их в ряд, то какой длины будет
этот ряд?
34.	На рис. 6.4 изображены треугольники и четырех-
угольники—всего 15. У них 53 угла. Сколько тре-
угольников и сколько четырехугольников на рисунке?
35.	Один человек спросил своего приятеля:
— Сколько лет твоему сыну?
— Если к возрасту моего сына прибавить столько же,
да еще половину, то будет 10 лет.
Сколько лег сыну?
36,	Одного человека спросили:
— Сколько Вам лет?
На что он ответил!
— Когда я проживу еще половину, да треть, да чет-
верть моих теперешних лет, тогда мне будет 100 лет.
Сколько лет этому человеку?
255
87, Старинная задача. Летит стая гусей и навстречу ей
один гусь.
— Здравствуйте, сто гусей!—сказал гусь.
— Нас не сто,— ответил вожак стаи.—Вот если бы
нас было еще столько, да полстолько, да четверть.
столько, да еще один гусь—вот тогда бы нас было
сто гусей.
Сколько гусей было в стае?
§ 74. Отношение и пропорция
Частное двух не равных нулю чисел а и Ь называют
еще отношением а к Ь. Числа а и b называют членами
отношения. Например, 8:2 или -я- есть отношение
8 к 2.
Равенство двух отношений называется пропорцией. Про-
порцию
f < ас
cr.b — c'.d или =
о а
читают так: «отношение а к b равно отношению с к d»
или «а относится к Ь, как с относится к cb>.
Числа and называют крайними членами пропорции
(рис. 6.5), а числа b и с—средними членами пропорции:
Средние /
члены
а
а: Ъ -с-, а
Крайние члены
Рис. 6.5
Эти названия условны—достаточно записать пропорцию
по-другому (справа налево): c:d=a:b, и крайние члены
станут средними, а средние — крайними.
Основное свойство пропорции:
Произведение крайних членов пропорции равно произве-
дению^ ее средних членов:
а с	«	«
то a*d^b*c.
256
В самом деле, умножим равенство ~ = на по-
лучим
1
—1г—— или а-а — Ь-с.
1	г
Верно и обратное рассуждение: если разделить ра-
венство
a-d = b-c на b-d (b=£0, d=£0),
то получим равенство
Если один из членов пропорции неизвестен и необхо-
димо его определить, то говорят, что нужно решить про-
порцию.
Пример. Решить пропорцию =
Решение. Умножим равенство на 12; получим
3
7 •

№21.
Ответ. 21.
Пример. Решить пропорцию у = -|-
Решение. Заменим пропорцию у = на пропорцию
^ = -|- .* *) Умножим равенство на 30; получим
1 в
=	х = 48.
-б'
1 1
Ответ. 48.
ас	Ь d
*) Из пропорции —=— следует пропорция —=—потому что
если две дроби равны, то и обратные им дроби равны.
9 С. М. Никольский и др.	257
УПРАЖНЕНИЯ
1.	Используя слово «отношение», прочитайте запись:
1)7:2; 2)	3) 1:5; 4)1.
2.	Запишите отношение:
1)	7 к 3; 2) 5 к 9); 3) 12 к 4; 4) 10 к 1000.
3.	Найдите отношение:
МО 1 оч к	оч~7 21 .	12 „ 48
1)	3 к у; 2) 5 к уд; 3) 8 к 32, 4) 17 к 5]
4.	Запишите в виде пропорции:
1)	2 относится к 3, как 10 относится к 15;
2)	у относится к 6, как 1 относится к 18;
3)	3 во столько же раз больше 2, во сколько раз
6 больше 4;
4)	7 во столько же раз больше Зу, во сколько раз
21 больше 10у.
5.	Можно ли составить пропорцию из отношений:
• 1) 6:3 и 24:12; 2) 1:5 и 17:85;
. 3) 2:5 и 10:4;	4) 20:8 и 35:14?
6.	Верно ли равенство:
1)4 = ё> 2)7:5 = g;3)l|=14:21?
7.	Можно ли составить пропорцию из следующих чисел:
1)	1, 2, 4, 8;	2) 3, 4, 9, 12;
3)	5, 9, 45, 81; 4) 3, 50, 5, 90?
8.	К данной тройке чисел подберите такое четвертое число,
чтобы эти числа могли образовать пропорцию. Сколько
решений имеет задача?
1)	1, 2, 3; 2) 3, 5, 7; 3) 10, 14, 15.
9.	Останется ли верной пропорция, если
1)	оба крайних члена умножить на одно и то же число;
2)	оба средних члена умножить на одно и то же число;
3)	оба крайних члена разделить на одно и то же число,
а оба средних члена умножить на одно и то же число?
10.	Замените отношение дробных чисел равным ему отно-
шением целых чисел:
п 1-1 • 21	• 31 —• 11
2 ’ 3 ’	3  7 ’	17‘1 2'
11.	Равенство произведений замените пропорцией:
1)	12-2 = 6-4;	2) 15-6 = 9-10;
3)	42-4 = 84-2; 4) 24-10 = 2-120.
£58
12.	Из данной пропорции получите новую, поменяв
местами крайние члены; средние члены:
!)§ = §; 2) 28:25 = 84:75.
13. Решите пропорцию:
	2)	со| к II •м| to
3)п=А	4)	х 	 9 В “32е
	2)	13	x~t 15 “ 10;
" 311? —А* 21 ~ 14 ’	4)	48 _ х 5Т“34‘
15- 1)7=4’	2)	24 __ 8 , х “ 7 ;
•2? * 1 го Сл|	4)	25 _ 5 х “ 7е
	2)	8—15. 7 “ х *
'3)7=4	4)	8 = |.
*<	1 v 1	8 17. 1) х'-2=-§;	2)	2	3 Х: 3 “ 4 ’
3)у = 74’	4)	* 	 1 , Q 6 “ 3 Ле
18. 1) {| = 3:х;	2)	12_ 1 ф 29“ 58:Х’
•>) 25	15'*’	4)	144	, 1 . 125 — 1 2 ,Х'
19. Докажите, что	а с если —	, то о	а 1	
1) £ — . > ь а'		а b
20. Докажите, что	а с . если -г- = т, то о а ’	
п а~^е— с • о\ а
d ’ b ~ b-j-d*
21. Решите пропорцию:
п А — А- 91—— А*
3 “ 9 ;	5 “ 10 ’
их 8 ' 6х '	л\ 12__18*
^Т5“Т;	Тз—^Г
22.	1)^--2:3л,	2) |=’;
3^А = &-	4)1-32:38*.
9*
259
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
23.	Вычислите наиболее простым способом:
1)	239-324—156-315+ 156-315;
2)	31905:45+571-33—33-571;
3)	22 796:41 + 505-707—22 796:41;
4)	896-127+9906:78—127-896.
24.	Сумма и произведение четырех натуральных чисел
равны 8. Что это за числа?
25.	Можно ли число 203 представить в виде суммы не-
скольких натуральных чисел так, чтобы произведение
этих чисел тоже было равно 203?
26.	Не отрывая карандаша от бумаги и не проводя им
дважды по одной и той же линии, нарисуйте изобра-
женную на рис. 6.6 фигуру.
Рис. 6.6
27.	В, совхозе под картофель занята площадь, в 4 раза
большая, чем под капусту. Под капусту занято на
36 га меньше, чем под картофель. Какая площадь за-
нята под картофель?
28.	Длина реки в 3 раза больше, чем длина ее притока.
Приток короче реки на 178 км. Какова длина при-
тока и реки?
29.	Слон в 5 раз тяжелее белого медведя. Белый медведь
на 3 т 600 кг легче слона. Сколько весит каждое
животное?
2
30.	Известно, что скорость белого медведя составляет у
скорости слона. Слон может бежать со скоростью, на
25 — большей, чем белый медведь. С какой скоро-
стью может бежать белый медведь и с какой скоростью
может бежать слон?
31.	Чтобы выполнить план, цех должен был ежедневно
изготовлять 30 приборов. Повысив производительность
труда, рабочие цеха стали изготовлять по 34 прибора
ежедневно и поэтому выполнили план на 2 дня раньше
срока. Сколько приборов нужно было изготовить по
плану и за сколько дней?
260
32.	Проехав половину всего пути, пассажир заснул. Когда
он проснулся, то оказал,ось, что ему осталось проехать
половину того расстояния, которое он проехал спящим.
Какую часть всего пути пассажир проехал спящим?
33.	Стороны прямоугольника 3 см и 5 см. Увеличим их
в 2 раза—площадь увеличится в 4 раза: S = 3-5 =
= 15 (см2), $! = (2-3)-(2-5)=4-(3-5)=4S. Верно ли для
любого прямоугольника, что если стороны его увели-
чить в 2 раза, то площадь увеличится в 4 раза?
34.	Папа решил выложить на кухне часть стены (на рис. 6.7
она отмечена штриховкой) керамической плиткой. Вни-
мательно рассмотрите рисунок и определите, сколько
Рис. 6.7
понадобится плиток, если они имеют форму квадрата
со стороной 15 см.
35.	Завод получил заказ на изготовление некоторого числа
машин к определенному сроку. Если завод будет вы-
пускать ежедневно по 250 машин, то к сроку будет
изготовлено на 1000 машин меньше, чем заказано.
Если же завод будет ежедневно выпускать по 320 ма-
шин, то к сроку будет изготовлено на 400 машин
больше, чем заказано. Сколько заказано машин и каков
срок выполнения заказа?
36.	Поезд выходит из города А и через 10 ч 40 мин при-
ходит в город В. Если бы поезд проходил в час на
10 км меньше, то прибыл бы в город В на 2ч 8 мин
позже. Определите расстояние между городами А и В
и скорость поезда.
37.	Переднее колесо кареты в одном из залов музея имеет
в окружности 35 дм, а заднее—44 дм. На расстоянии
в некоторое число километров переднее колесо кареты
261
сделало бы на 387 оборотов больше, чем заднее. На
каком именно расстоянии?
38.	Мальчику через 2 года будет вдвое больше лет, чем
ему было два года назад. Девочка через три года будет
втрое старше, чем три года назад. Кто из них старше?
39.	В квадрате, состоящем из 9 клеток, расставьте числа
от 1 до 9 так, чтобы суммы чисел, стоящих в каждом -
вертикальном столбце, в каждом горизонтальном ряду,
а также по двум диагоналям (отрезкам, соединяющим
вершины квадрата, не принадлежащие одной стороне),
были равны.
§ 75.	Прямая и обратная пропорциональность
Частное двух величин также называется отношением.
Отношение величин одного наименования (длин, скоростей,
стоимостей и т. д.) есть число.
,,	5 км 5-1 км 5	2 дм 20-1 см 20 ОЛ
Например, s— = •5-:— = -5- или г-=- = —;-= -т- = 20-
г г’3км 3-1 км 3	1 см 1 см 1
Отношение величин разных наименований (путь и ско-
рость, стоимость и количество товара и т. доопределяет
новую величину.
т.	5 км 5 км
Например, — = у—.
Величины называются прямо пропорциональными, если
при увеличении одной из них в несколько раз другая уве-
личивается во столько же раз.
Пример. Пройденный путь и время движения прямо
пропорциональны при постоянной скорости движения. Если
машина, двигаясь равномерно, за 2 ч проедет 120 км, то
за 6 ч она проедет 360 км—6 ч во столько раз больше
2 ч, во сколько раз 360 км больше 120 км. Поэтому можно
записать пропорцию:
360
2 '”’120*
Величины называются обратно пропорциональными,
если при увеличении одной из них в несколько раз другая
уменьшается во столько же раз.
Пример. Скорость и время равномерного движения
обратно пропорциональны на одном участке пути. Если
262
участок пути машина проедет со скоростью 50 за 4 ч,
то со скоростью 25	— за 8 ч, так как уменьшение ско-
рости в два раза влечет увеличение времени прохождения
пути в два раза.
Задача 1. Какой путь проедет поезд, двигаясь рав-
номерно, за 15 с, если 60 м он проехал за 2 с?
Решение. 1) Пусть х—путь, который проехал поезд
за 15 с. Тогда
| х м—15 с I
। 60 м — 2 с |
2) Составим и решим пропорцию:
1 зо
2L = 15_, х • «г _ 15 £& х = 450-
60	2	^
Ответ. 450 м.
Одинаково направленными стрелками мы отметили, что
величины прямо пропорциональны: чем больше время дви-
жения, тем больше пройденный путь.
Задача 2. За 7 ч работы токарь изготовил 252 де-
тали. Сколько деталей изготавливал токарь за 15 мин,
если производительность его труда была постоянной?
Решение. 1) Выразим время работы в одних едини-
цах измерения:
1К	15 Г1
15 МИН = ?7Г Ч = -т- ч.
60	4
2) Пусть х—количество деталей, которые токарь изго-
тавливал каждые 15 мин. Тогда
7 ч —252 детали
1
ч—х деталей
3) Составим и решим пропорцию: 7:-|- = ^. Так как
7:Т = 7-4-28, W 28 = --—;
х 28	252
28	г.	п
1	1	Ответ. 9 деталей.
263
При решении мы выразили величины одного наимено-
вания— время с помощью одной единицы измерения—часа.
В ответе записано число деталей, которое изготавливал
токарь каждые 15 мин.
Задача !3. Пассажирский поезд, скорость которого
45	, затратил на некоторый участок пути 4 ч. За сколько
часов пройдет этот же участок пути товарный поезд, если
it\ КМ -ч
его скорость 40 — ?
Решение. 1) Пусть х ч—время, за которое товарный
поезд пройдет участок пути. Тогда
.с КМ .	"
45-----4 ч
ч
.. км
40-----х ч
V Ч
1 1
2) Составим и решим пропорцию: я
10	1
45	9 л 1
Х~~ 10 — 2 — 42‘
Ответ. 4у ч.
Записывая коротко условия задачи, противоположно
направленными стрелками мы отметили, что величины
обратно пропорциональны: чем меньше скорость, тем больше
время движения.
УПРАЖНЕНИЯ
1, 1) Объясните, почему при равномерном движении со
с км
скоростью 5 — путь и время движения прямо про-
порциональны.
2) Объясните, почему при движении на определенном
участке пути скорость и время равномерного дви-
жения обратно пропорциональны.
2.	Какая зависимость существует между скоростью и рас-
стоянием, если время движения постоянно?
3.	При равномерном движении поезд за 2 с проехал 60 м.
1)	За какое время поезд проедет 100 м?
2)	Сколько метров проедет поезд за 15 с?
264
4.	За 4 м ткани заплатили 18 р.
1)	Сколько стоят 14 м этой ткани?
2)	Сколько метров ткани можно купить на 27 р.?
5.	Из 5 кг яблок получается 4 кг яблочного пюре.
1)	Сколько пюре получится из 13 кг яблок?
2)	Сколько килограммов яблок следует взять для по-
лучения 15 кг пюре?
6.	Чтобы покрасить стены дома за 2 дня, требуется
20 маляров.
1)	За сколько дней эту работу выполнят 4 маляра?
2)	Сколько маляров потребуется, чтобы покрасить
стены дома за 5 дней?
7.	Ширина прямоугольника 15 см, а его площадь 300 см2.
Какова длина прямоугольника?
Какова ширина второго прямоугольника, имеющего
ту же длину, но площадь которого равна 400 см2?
8.	Два прямоугольника имеют одинаковую площадь.
Длина первого 20 см, а второго 25 см. Ширина пер-
вого 10 см. Найдите ширину второго прямоугольника.
9,	При равномерном движении поезд прошел 200 км за
3 ч.
1)	За сколько часов поезд пройдет 300 км?
2)	Какой путь пройдет поезд за 5 ч?
10.	Поезд прошел участок пути со скоростью 80 за
3 ч. За сколько часов поезд пройдет этот же участок
пути, если будет двигаться со скоростью 100 -^?
11.	1) 8 м ткани стоят 42 р. 40 к. Сколько стоят 9 м
ткани?
2)	3 м ткани стоят 25 р. 20 к. Сколько стоят 7 м ткани?
12.	1) Годовая подписка на газету «Пионерская правда»
стоит 1 р. 68 к. Сколько стоит подписка на 10 ме-
сяцев?
2)	Годовая подписка на журнал «Моделист—конструк-
тор» стоит 4 р. 20 к. Сколько стоит подписка на
4 месяца?
13.	Находятся ли в прямой пропорциональной зависимости
следующие величины? Если ответ положительный, то
(введя необходимые буквы) запишите эти зависимости
с помощью формул.
1)	Количество проданных в автобусе билетов и вы-
ручка кассы.
2)	Количество оборотов колеса и скорость автомашины.
3)	Количество оборотов колеса и пройденный ею путь.
265
4)	Число книг в библиотеке и количество читателей
библиотеки.
5)	Норма выработки деталей за смену и время изго-
товления детали.
14.	1) Известно, что норма выработки деталей за смену—
80 штук. Определите норму выработки за месяц
(25 смен).
2)	Самолет поднялся на высоту 8 км за 20 мин. Можно
ли указать высоту, на которую поднимется само-
лет за 4 ч?
15.	1) Мальчик за 2 ч поймал 6 карасей. Сколько кара-
сей он поймает за 4 ч?
2)	Два петуха разбудили 5 человек. Сколько человек
могут разбудить 4 петуха?
16.	1) 1 кг металлолома заменяет 2-|- кг богатой желез-
ной руды. Ученики V класса собрали 4 т металло-
лома. Сколько руды сберегли ученики?
2)	В 1 кг морской воды содержится 40 г соли. Сколько
соли содержится в 650 г морской воды?
17.	Число 40 представьте в виде двух слагаемых, отноше-
ние которых равно: 1) 1:3. Решение. х+Зх = 40,
4х=40, х= 10, Зх=ЗО.
Ответ. 10 и 30.
2)	3:5; 3) 1:4; 4) 7:3.
18.	Число 100 представьте в виде суммы двух слагаемых,
отношение которых равно:
1)	4:1;	2) 37:13;	3) 71:29.
19.	Отрезок длиной 60 см разделили на две части. Найдите
длины полученных отрезков, если их отношение равно:
1) 3, т. е. 3:1; 2) 2; 3) 1; 4) 6; 5) 12.
з
20.	Суточное потребление топлива на заводе составило Зу т,
а годовой расход на топливо—6000 р. После прове-
денной реконструкции суточный расход топлива сни-
з
зился на -у т. На сколько снизился годовой расход
на топливо?
21.	За 1 ч бригада маляров покрасила половину стены
дома. Оставшуюся часть стены покрасил 1 человек
за 4 ч. Сколько маляров в бригаде?
4
22.	Бригада за полдня выполнила -g- своего задания.
Оставшуюся часть задания выполнил 1 человек за
полдня. Сколько человек в бригаде?
266
23.	Бригада плотников выполнила задания за полдня,
половина бригады работала еще полдня. Оставшуюся
часть задания выполнил один плотник задень. Сколько
плотников в бригаде?
24.	Задача Л. Н. Толстого. Косцы должны выкосить два
луга. Начав с утра косить большой луг, они после
полудня разделились: одна половина осталась на пер-
вом луге и к вечеру его докосила, а другая—перешла
косить на второй луг,' площадью вдвое меньше пер-
вого. Сколько было косцов, если известно, что в тече-
ние .следующего дня оставшуюся часть работы выпол-
нил один косец?
25.	Мальчик катается на велосипеде, переднее колесо
которого за один оборот проезжает 1 м, а два задних —
по 60 см.
1)	Сколько метров проехал мальчик, если задние ко-
леса сделали по 25 оборотов?
2)	Сколько метров проехал мальчик, если переднее
колесо сделало 25 оборотов?
3)	Сколько оборотов сделает переднее колесо, если
задние колеса сделают по 35 оборотов?
4)	Сколько оборотов сделает каждое колесо, если маль-
чик проедет по прямой 12 м? Какое колесо сделает
меньше оборотов и почему? Важно ли, что движе-
ние совершалось по прямой?
5)	Сколько метров проехал мальчик, если первое ко-
лесо сделало на 20 оборотов больше, чем задние?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
26.	Вычислите:
1)	35 + 33 4-31 + 29 + 27 + 25;
2)	36-35 —35-34 + 34-33 —33-32 + 32-31—31-30 +
+ 30-29—29-28+28-27—27-26 + 26-25—25-24.
27.	Найдите шесть натуральных чисел, имеющих нечетное
число делителей.
28.	Является ли простым числом число:
1)	111111111;	2) 123456789;
3)	111111111111;	4) 123456789123456789?
29.	Докажите, что если а + с = b + d, то abed делится на 11.
30.	Найдите число abed, для которого а + <?+=& + d, но
оно делится на 11.
31,	Сколькими нулями оканчивается произведение нату-
ральных чисел от 1 до 35?
267
32.	Сколько необходимо сделать разрезов, чтобы разделить
куб на 27 кубиков?
33.	Один мальчик на гранях куба написал натуральные
числа от 1 до 6. Другой мальчик этот куб не видел,
но утверждает, что у него имеются две соседние грани,
на которых написаны два соседних в натуральном ряду
числа. Прав ли он?
84.	Кузнечик прыгает по прямой большими прыжками по
12 см и малыми прыжками по 7 см. Сможет ли куз-
нечик из одной точки прямой попасть в другую, если
расстояние между точками 3 см?
35.	В двадцатиэтажном доме испорчен лифт: он может либо
подняться на 13 этажей вверх, либо спуститься на
8 этажей вниз. Докажите, что, пользуясь таким лиф-
том, нельзя попасть с 4-го этажа на 5-й этаж.
36.	В одной коробке лежат два белых шара, в другой —
два черных, в третьей—один белый и один черный.
На каждой коробке висела табличка, указывающая
ее состав: бб, бч, чч. Какой-то шутник перевесил все
таблички так, что каждая из них указывает состав
неправильно. Из какой коробки, не глядя, надо вынуть
один шар, чтобы можно было определить содержимое
каждой коробки?
87.	Определите на глаз, во сколько раз длина отрезка ВС
больше длины отрезка АВ. Результат сравнения про-
верьте с помощью линейки (рис. 6.8).
Во сколько раз длина отрезка АС больше длины от-
резка ЛВ?
§ 76. Масштаб
Рисуя на бумаге изображения различных предметов,
'мы вынуждены изменять их настоящие размеры. Чтобы
изображения поместились на листе бумаги, большие пред-
меты приходится изображать в уменьшенном виде, а ма-
268

ленькие—увеличивать. Но рисунок, а особенно чертеж.'
или план (географическая карта), должен давать представ*
ления о настоящих размерах предметов. На рисунках,
можно изображать какой-нибудь предмет, размеры кото-
рого хорошо известны. На чертежах и планах приходится
поступать по-другому—делать специальную запись, пока-
зывающую отношение длины какого-нибудь отрезка на
чертеже к его настоящей длине.
Пример. На плане комнаты отрезком в 2 см изобра-
жается отрезок, настоящая длина которого 1 м. В этом
случае пишут: 1 м в 2 см, или 2 см:1 м, или 2 см ЛОО см,
ел	2 см
или «уменьшено в 50 раз», или -р-^.
Отношение длины линии на чертеже или плане к длине
соответствующей линии в натуре называется масштабом.
При одинаковых единицах измерения предметов и их
изображений масштаб выражается числом.
тт	' 2 см 2 см 2	1
Например, _ = ^_== —=
Рис. 6.9
Масштаб, выраженный числом, называется числовым
масштабом. Для географических карт числовой масштаб
выражают дробью, числитель которой равен 1, а знаме-
натель есть число, показывающее, во сколько раз любое
269
расстояние на карте меньше соответствующего расстояния
на местности.
Пример. Запись -п> nA	или 1:25 000 000 означает,
11	ZD иии иии
что 1 см на карте соответствует 25 000 000 см на мест-
ности.
На картах используют еще и линейный масштаб. Ли-
нейный масштаб—это отрезок, разделенный на равные
части, причем у каждой точки деления записывается
число, указывающее длины соответствующих им отрезков
в натуре (рис. 6.9).
УПРАЖНЕНИЯ
1.	Определите числовой масштаб, если извесно, что 1 см
на плане изображает отрезок в натуре длиной:
1)	10 см; 2) 50 см; 3) 6 дм; 4) 10 м.
2.	Определите числовой масштаб, если известно, что 1 см
на плане (географической карте) изображает отрезок
в натуре длиной:
1)	100 м; 2) 1 км; 3) 6 км; 4) 10 км.
3.	Расстояние между двумя городами равно 200 км.
Определите расстояние между изображениями этих
городов на карте, если числовой масштаб карты
равен:
1)	1:1000000; 2) 1:200000;
3) 5 000 000 ’	2 000 000'
4.	Числовой масштаб карты равен . Определите
расстояние на местности, если на карте оно равно:
1)	1 см;	2) 5 см;	3) 22 см;
4)	37 мм;	5) lj дм;	6) 1 дм 4 см 6 мм.
5,	План комнаты имеет вид прямоугольника со сторонами
4 см и 31 мм. Определите размеры (длину и ширину)
, 1
комнаты, если числовой масштаб плана ™-ч.
ZUv
6.	Огород имеет вид прямоугольника, длина которого
340 м, а ширина 220 м. Какие размеры будет иметь
изображение этого огорода на плане, выполненном
в масштабе 1:500?
7,	Прямоугольник со сторонами 1 дм 2 см и 60 мм изо-
бражает на плане угодий колхоза поле, занятое под
270
овес. Определите масштаб плана, если большая сто-
рона поля имеет длину 480 м. Определите меньшую
сторону поля.
8.	Используя план местности, определите:
1)	расстояние от А до В;
2)	расстояние от Л и от В до моста через реку;
3)	расстояние от В до леса;
4)	площадь поля (рис. 6.10).
9.	За сколько часов туристы преодолеют расстояние от
А до В, если будут двигаться со скоростью 4
(рис. 6.11)?
10.	Прямоугольник со сторонами 18 см и 54 см изобра-
жает на плане строительную площадку. Определите
масштаб плана, если известно, что площадь строитель-
ной площадки 97 200 ма.
11.	Определите масштаб плана, если поле площадью 32 га
изображено на этом плане в виде прямоугольника со
сторонами 32 см и 16 см.
12.	Начертите план класса в масштабе 1:100.
13.	Начертите план своей комнаты в масштабе 1:50.
14.	Начертите план школьного здания в масштабе 1:250.
15.	Можно ли начертить план здания (прямоугольной
формы в основании) длиной 50 м и шириной 20 м на
странице тетради, если использовать масштаб 1:50?
Какой масштаб следует использовать, чтобы план по-
местился на странице тетради?
271
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
15. Решите уравнения:			
1) х+ 24 = 51;	2)51 + х=24; 3) х—7 = 42;	4) х— 42 = 7; 5)	70 + х=28;	6) 128 +х = 9. 17.	1) 48 + х = 73;	2) 26 + х = 11; 3)	—2 + х = —7;	4) —15 + х = —18; 5)	—50 + х = — 26;	6) х+290=170. 18.	1) 15—х=12;	2) 48—х = 27; 3)	—23—х=24;	4) —27—х = —24; 5)	—29—х = — 51;	6) —120—х = —94. 19.	1) 2х = 8;	2) 4х=16; 3)	8х = 32;	4) — 4х = —16; 5)	—х =—5;	6) —х = 8. 20.	Заполните пропуски: 1)	1 см =10 мм; 1 см2 =	мм2; 1 см’ =			мм3;
2)	1 дм =	см;	1 дм2= см2; 1 дм3 =	см3;
3)	1 м = дм;	1 м2 = дм2; 1 м3 =	ДМ3.
21. 1)	1 дм = мм;	1 дм2= мм2; 1 дм3 =	мм3;
2)	1 м = см;	1 м2 = см2; 1 м3 =	см3.
22. 1)	1 см = мм;	1 дм = см; 1 м =	дм;
2)	1 см2 = мм2;	1 дм2 = см2; Г м2 =	Дм2;
3)	1 см3 = мм3;	1 дм3= см3; 1 м3 =	ДМ3.
23. 1)	1 а= м2;	1 га= а; 1 км2 =	га;
2)	1 а= дм2;	1 га= м2; 1 км2 =	а.
24. Во сколько раз происходит увеличение величин в каж-
дой строке таблицы при чтении слева направо?
— а	1 мм	1 см	1 Дм	1 м	10 м	100 м	1 км
□ а2	1 мм2	1 см2	1 Дм2	1 м2	1 a	1 га	1 км2
0 а3	1 мм3	1 см3	1 ДМ3	1 м3	103 м3	10е м3	1 км3
25.	Заполните пропуски:
1)	1 мм — см; 1 см = дм; 1 дм = м;
272
2)	1	мм* =	см2;	1 см2 =	дм2;	1 дм2=	м2;
3)	1	мм3 =	см3;	t см3=	дм3;	1 дм3=	м3.
26.	1)	1	см =	м;	1 мм =	дм;	1 м =	км;
2)	1	см2=	м2;	1 дм2=	а;	1 м2=	га.
27.	ЛАама дала дочери и сыну всего 65 к.— дочери на 15 к.
больше, чем сыну. Сколько денег она дала каждому?
28.	Саша собрал на 5 кг меньше макулатуры, чем Коля,
а вместе они собрали 23 кг макулатуры. Сколько со-
брал каждый?
29.	Одно число в 3 раза больше другого, а их сумма
равна 348. Найдите эти числа.
30.	Одно число в 4 раза меньше другого, а их разность
равна 800. Найдите эти числа.
31.	За уборку 60 кг моркови совхоз платит 3 р. 15 к.
Старшеклассники за день убрали 1т 140 кг моркови.
Сколько денег они заработали?
32.	Старинная задача. За аршина сукна заплатили
3 алтына. Сколько надо заплатить за 100 аршин та-
кого же сукна? Учтите, что 1 алтын = 6 денег » 3 ко-
пейки.
33.	Один прохожий догнал другого и спросил;
— Как далеко до деревни, которая у нас впереди?
— Расстояние от той деревни, от которой ты идешь,
равно третьей части всего расстояния между де-
ревнями. А если ты пройдешь еще два километра, то
будешь ровно посередине между деревнями.
Сколько километров осталось пройти до деревни пер-
вому прохожему?
84.	Два поля имеют форму прямоугольника. Один прямо-
угольник со сторонами 200 м и 400 м, а другой —
400 м и 800 м. Во сколько раз больше удобрений (при
одинаковом расходе на единицу площади) нужно внести
на второе поле, чем на первое?
ВОПРОСЫ для ПОВТОРЕНИЯ
• ПО МАТЕРИАЛУ ГЛАВЫ VI
1.	Приведите примеры подобных слагаемых.
2.	Что называется корнем уравнения?
3.	Что называется отношением двух чисел а и 6?
4.	Что называется пропорцией?
Б. Сформулируйте основное свойство пропорции.
6.	Какие величины называются прямо пропорциональными?
7.	Какие величины называются обратно пропорциональными?
8.	Что называется масштабом? Для чего применяется масштаб?
273
УПРАЖНЕНИЯ
1.	Сумма числителя и знаменателя дроби равна 32, а числитель на
2 меньше знаменателя. Найдите эту дробь.
2.	Числитель на 8 больше знаменателя, а сумма числителя и зна-
менателя равна 34. Найдите эту дробь.
3.	Знаменатель дроби на 17 больше числителя, а их сумма равна
15. Найдите эту дробь.
4.	Числитель на 13 больше знаменателя, а их сумма равна —3.
Найдите эту дробь.
5.	Дедушка говорит своим внукам: «Вот вам 130 орехов. Раздели-
те их на две части так, чтобы меньшая часть, увеличенная в 4
раза, равнялась большей части, уменьшенной в 3 раза». Как
нужно разделить орехи?
6.	Два мальчика ели сливы. Один сказал другому: «Дай мне две сли-
вы, тогда у нас будет поровну слив»,— на что другой ответил:
«Нет, лучше ты дай мне две сливы, тогда у меня будет в 2 ра-
за больше, чем у тебя». Сколько слив было у каждого?
7.	В трех пачках 99 тетрадей. В первой пачке на 6 тетрадей боль-
ше, чем в третьей, а во второй на 3 тетради больше, чем в
третьей. Сколько тетрадей в каждой пачке?
8.	В трех классах 102 ученика. В I классе на 1 ученика меньше,
чем во II классе, а в III классе на 4 ученика больше, чем во
II классе. Сколько учеников в каждом классе?
9.	Два велосипедиста выехали одновременно из двух деревень на-
встречу друг другу. Один из них может проехать все расстоя-
ние между деревнями за 6 ч, а другой—за 4 ч. Через сколько
часов после выезда встретятся велосипедисты? Каково расстоя-
ние между деревнями, если скорость одного из велосипедистов
к	'	n КМ _
больше скорости второго на 3 —— ?
10.	Из двух поселков навстречу друг другу выехали два велосипе-
ш I км	км _
диета. Скорость первого 13-д——, второго 12— . Первый ве-
2	,
лосипедист проехал расстояние между поселками на —ч бы-
о
стрее второго. Определите расстояние между поселками.
II*. Из города А в город В вышли два поезда. Первый вышел в
8 ч 2 мин и идет со скоростью 63	, а второй вышел на I ч
позже и идет со скоростью 55	» Когда первый поезд при-
шел в город В, второй находился от него на расстоянии 165 км.
В каком часу первый поезд пришел в В и каково расстояние
между А и В? В каком часу второй поезд пришел в В?
274
Глава VII. ДЕСЯТИЧНЫЕ ДРОБИ
§ 77, Понятие десятичной дроби
Дроби, у которых знаменатель является степенью
числа 10, часто записывают в более простой форме, без
знаменателя, отделяя целую и дробные части друг от
друга запятой (считают при этом, что целая часть пра-
вильной дроби равна 0).
и	27 О7 0-7.	1717	1-7 17	1-7 1-7.	111
Например, 10 —210 —2,7, 100 — 17100— 17,17, ]000 —
— 0,111.
Записанные в такой форме дроби называются деся-
7
тичными дробями. Так что 2-^ и 2,7—разные формы
записи одного и того же числа: первая — в виде обык-
новенной дроби, вторая — в виде десятичной дроби. Пока
мы будем рассматривать только положительные десятич-
ные дроби.
Десятичная форма записи дробей позволяет записы-
вать их, сравнивать и выполнять с ними арифметические
действия по правилам, очень похожим на правила запи-
си, сравнения и действий с натуральными числами.
Напомним, что в десятичной системе счисления зна-
чение каждой цифры зависит от разряда (позиции), в ко-
тором она записана. При этом единицы соседних разря-
дов отличаются в 10 раз. Например, десяток в 10 раз
меньше сотни, единица в 10 раз меньше десятка.
Первый разряд после запятой называют разрядом де-
сятых.
275
Например, число 2,7 состоит из 2 целых и семи де-
сятых—читают «две целых семь десятых».
Второй разряд после запятой называют разрядом сотых.
Например, число 0,35 состоит из 0 целых, 3 десятых
и 5 сотых—читают «нуль целых тридцать пять сотых».
Чтобы лучше понять правила записи и чтения деся-
тичных дробей, рассмотрим таблицу разрядов и приве-
денные в ней примеры записи чисел.
7	8	5 , 4	2	7
7fi5427
7851000
39
100
19
10000
Ю-701.....
10 000 000
0,39
0,00	1	9
0	0	0	0	7	0	1
Для записи числа в десятичной форме нужно
19 _ 10+9	10	9	1 I 9
учесть, что юооо-юооо ю ооо + ю ооо — юоо + юооо*
Так что запись числа JoTJqo содержит 1 тысячную и 9
десятитысячных и не содержит целых единиц, десятых,
сотых — в десятичной дроби в соответствующих разрядах
пишут нули.
Нужно помнить, что после запятой в записи десятич-
ной дроби должно быть столько цифр, сколько нулей со-
держит знаменатель этой дроби.
276
Например:
1) -Л_=
> 1 0000
4 нуля
0,0135;
4 цифры
2> 1!ТИ®" 12’™3-
/—5 цифр
Б нулей
УПРАЖНЕНИЯ
1.	Запишите обыкновенные дроби в виде десятичных и
прочитайте полученную запись:
11 3—• 9—. 15—* — • — •
1> 40’ 10’ 10’ 10’ 10’
91	72® . fi2L. Л- Л-
100’	100’	100’ 100’ 100’
, 135 . 17 399 . о 999 . 777 , 123 .
°1000 ’ *4000’ 4000’ 1000’ 1000’
д. 4 8899 . . 5678 . 1234 . 6969
4 0 000’ 40 000’ 10 000 ’ 10 000’
2.	Прочитайте дроби:
1)	3,2; 7,3; 3,5; 0,1; 0,9;
2)	7,12; 9,23; 10,34; 0,45; 0,56;
3)	12,333; 16,596; 0,887; 0,379; 0,111;
4)	2,1111; 5,1986; 4,1987; 0,1988; 0,1989.
3.	Запишите десятичные дроби, приведенные в упр. 2,
в виде обыкновенных дробей.
4.	Запишите обыкновенные дроби в виде десятичных и
прочитайте полученную запись:
В 4-L. 215—Л • JL- JL-
Ч ‘‘юо’ ^11400’ 100’ 100’
91 Ч 1 • 7-2-. _8_. Л_.
*4000’ 4000’ 1000’ 1000’
g 5	9 13 . 356 . 679 .
40000 ’ 40 000’ 10 000’ 10 000’
7 7 1ПП 46 .	627 . НИ
" ' 100 000’ 1ии100 000’ 100 000’ 100 000’
5.	Прочитайте дроби:
1)	5,05; 7,01; 12,07; 0,01; 0,09;
2)	19,004; 6,016; 8,008; 0,001; 0,022;
3)	13,0007; 2,0089; 16,0999; 0,0001; 0,0022;
4)	31,00009; 7,00099; 0,00001; 0,00666.
6,	Прочитайте дроби. Сколько целых, десятых, сотых,
тысячных и т. д. содержат данные дроби:
1)	16,789; 0,1234; 100,56789;
2)	0,023; 7,00526; 0,00017?
277
7,	Запишите в виде десятичной дроби:
.. 18_____ 3-6 _ 6 _
Ч зо~зИо~То —и,&:
~ 27. 24 . 24. 48.
90’ 120 ’ 40 ’ 60’
™ 15 . 160 . 36 . £40.
500’ 4000’ 900 ’ 700 ’
.V 11 . 81 .	144 .	8888
11 000 ’ 3000 ’ 40 000 ’ 400 ООО ‘
8.	Запишите в виде десятичной дроби:
П А —	25 _Q gr.
' 4 4-25 — 100-и’20’
1-	I- 1. 1- ±-
2 ’ 5 ’ 5 ’ 5 ’ 5 ’
ох 2- 1. Л - L.
41 I- 1- 2Л- 1- Л
' 20 ’ 50 ’ 50 ’ 40 ’ 200*
9. Запишите в виде десятичной дроби:
1)	16. 324. 99. 1234. 10’ 100’ 10’ 1000’
2)	168. 328. 9999ф 1648. 40 ’ 80 ’ 900 ’ 160 ’
3)	3 . 6 . 17. 39. 2 ’ 5 ’ 4 ’ 25 ’
4)	13. 14. 14 . 35 . 36 20’ 20’ 700’ 500’ 500
10.	Запишите величины, используя десятичные дроби:
1)	23 см 2 мм = 23^ см = 23,2 см;
2)	5 м 6 дм;	3) 7 м 54 см;
4)	8 м 4 см;	5) 11 р. 52 к.;
6)	11 р. 50 к.; 7) 11 р. 5 к.
11.	Запишите в виде неправильной дроби:
1)	12,3;	2)	1,23;	3)	10,123;
4)	987,6;	5)	98,76;	6)	9,876;
7)	2,2222;	8)	22,222;	9)	222,22.
12.	Выполните действия, предварительно записав деся-
тичные дроби в виде обыкновенных дробей:
1)	7,35 + 2,28--9,63;
2)	8,23 + 3,56; 3) 7,39—6,27;
4)	0,3-0,2;	5) 1,3-0,02;
6)	4,62:2;	7) 4,62:0,2.
278
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
13.	Устно вычислите:
и 2 ~3 j_ 7 —18 •
' 3 ’ 2 + 9 ' 7 ’
™ 3 —10	16 7
' 5 * 3	7*8’
ох 15 17	—99	5.
17 ’ 3 ' 50 * 99 ’
’ 10 10^—33*
14.	Решите уравнение:
1)	—5х = 30;	2) х:(—2) = 16;
3)	8х:2=12;	4) 3х:3 = 4;
5)2x4-5=11; 6) Зх—7 = 5.
15.	1) 154-2х = 27;	2) 2х—5 = —7;
3)	х4-24-х = 4;	4) —х 4-2x4-7=1;
5)	х—2 4-Зх=10; 6) 2х4-4х—8=4.
16.	1) Два землекопа выкапывают 2 м канавы за 2 ч.
Сколько землекопов за 5 ч выкопают 5 м канавы?
2)	10 насосов за 10 мин выкачивают 10 т воды. За
сколько минут 25 насосов выкачают 25 т воды?
17.	Старинная задача. Послан человек из Москвы в Во-
логду, и велено ему в хождении своем совершать во
всякий день по 40 верст. На следующий день вслед
ему послан второй человек, и приказано ему прохо-
дить в день по 45 верст. На какой день второй че-
ловек догонит первого?
18.	Расстояние от Земли до Солнца 150 млн. км. Ско-
рость света 300 тыс. . За сколько минут луч Солн-
ца достигает Земли?
19.	В кастрюлю налили 5 л воды, отлили 1 л и налили
1 л сока. Тщательно перемешали и отлили 1 л сме-
си, еще раз долили 1 л сока. Какую часть воды от-
ливали каждый раз? Какая часть воды остается?
Сколько воды осталось в кастрюле?
20.	Пять карандашей и две тетради стоят 16 к., а один
карандаш и 4 тетради стоят 14 к. Сколько стоят 6
карандашей и 6 тетрадей? Сколько стоят 1 карандаш
и 1 тетрадь вместе? Сколько стоит карандаш?
21.	В трех маленьких и четырех больших коробках 150
цветных карандашей, а в четырех маленьких и трех
больших 144 цветных карандаша. Сколько каранда-
279
шей в семи больших и семи маленьких коробках
вместе? Сколько карандашей в одной большой и од-
ной маленькой коробке вместе? 'Сколько карандашей
в большой коробке?
§ 78. Сравнение положительных десятичных дробей
Натуральное число можно представить в виде деся-
тичной дроби.
Например, 27 = 27-^ или 27 = 27,000.
К любой десятичной дроби можно приписать справа
нули (в дробной части)—получится дробь, равная данной.
Например, 24,2 = 24,200, потому что 24,2 = 24-^ =
= 24р^. Кроме того, 0 = 0,0 = 0,00 = 0,000 = ...
luUU 1
Если у десятичной дроби имеются справа нули (в дроб-
ной части), то их можно отбросить—получится дробь,
равная данной.
Например, 0,368000 = 0,368, так как
П ЧйЯ ЛПА и 368000 _ 308 • 1ООО- _ 368 _ _
0,368000 юооооо юоо «юво- юоо 0’36®*
.1
На практике нули справа приписывают в тех случаях,
когда нужно подчеркнуть точность, с которой произво-
дились измерения.
Например, если в результате вычисления, которые
производились с точностью до копейки, получилось 3 р.,
то пишут 3,00 р.
Из двух десятичных положительных дробей больше
та, у которой целая часть больше-, при равенстве целых
частей—та дробь больше, у которой цифра разряда де-
сятых больше-, при равенстве целых частей и цифр раз-
ряда десятых—та дробь больше, у которой цифра раз-
ряда сотых больше и т. д.
Например: 1) 3,5 > 2,5, так как целая часть первой
дроби больше целой части второй дроби;
2) 0,5 > 0,38, так как 0,5 = 0,50 и
280
3) 2,841 <2,85, так как 2,85 = 2,850 и 2^4 <
IvvU
о 850
пооо •
УПРАЖНЕНИЯ
1.	Уравняйте число цифр после запятой у следующих
дробей:
1)	1,2;	3,51;	0,123;
2)	0,6;	3,02;	7,125;	0,48000;
3)	6,23;	7,5;	8,2000;	9,00000.
2.	Сколько десятых, сотых, тысячных содержит дробь:
1)	1,235; 2) 1,27; 3) 3,51; 4) 0,5?
3.	Какая из дробей содержит больше целых, десятых,
сотых:
1)	6,35 и 5,19; 2) 7,48 и 7,51;
3)	2,52 и 2,53; 4) 17,49 и 17,5?
4.	Используя знаки = и =#, сравните дроби:
1)	7,5 и 7,50;	2) 8,5 и 9,1;
3)	0,48 и 0,4;	4) 0,25 и 0,2500;
5)	7,48 и 7,481;	6) 3,1 и 2,99.
5.	Используя знаки > и <, сравните дроби:
1)	3,59 и 7,1;	2) 6,28 и 6,9;
3) 0,4 и 0,51;	4) 72,7 и 7,27;
5)	4,1234 и 4,1231;	6) 12,39 и 1,2399.
6.	1)	2,078 и 2,780;	2)	3,205 и 3,025;
3)	7,250 и 7,205;	4)	4,290 и 4,295;
5)	12,4 и 12,41;	6)	15,129 и 15,1.
7.	1) 6,92 и 6,9;	2) 72,39 и 7,2399;
3)	. 1,2 и 1,1999;	4) 0,48 и 0,471111.
8.	Укажите одно число, расположенное между числами
(т. е. большее одного из данных чисел, но меньшее
другого):
1)	4000 и 5000;	2) 4200 и 4300;
3)	4250 и 4260;	4) 4290 и 4300.
9.	1) 0,600 и 0,700;	2) 0,650 и 0,660;
3)	0,650 и 0,655;	' 4) 0,655 и 0,660.
10.	1) 0,6 и 0,7;	2) 0,65 и 0.66;
3)	0,48 и 0,49;	4) 0,325 и 0,326.
11.	Расположите дроби в порядке возрастания:
1)	0,8; 1,17; 0,789; 1,7;
2)	3,5; 0,35; 3,35;	0,335.
12.	Расположите дроби в порядке убывания:
1)	7,4;	6,98; 7,199; 6,899;
2)	0,449; 0,49; 0,5;	0,499.
281
13.	Изобразите на координатной прямой числа:
1)	0,1;	0,2;	0,3;	0,4;	0,5;
0,6;	0,7;	0,8;	0,9;	1,0;
2)	0,2;	0,4;	0,6;	0,8;	1,0;
1,2;	1,4;	1,6;	1,8;	2,0.
14.	В каком порядке (слева направо) на координатной
прямой расположены точки:
1)	Л (1,2);	В (0,2);	С (1,13);
2)	М (7,48);	IV (4,78); /<(7,8)?
15.	Запишите величины с помощью десятичных дробей и
сравните их:
1) 7 кг 485 г
2) 5 м 48 см
и 6 кг 90 г;
и 5 м 40 см;
3)	7 км 740 м
4)	8 т 5 кг
16.	Запишите в
1)	6,79 р.;	12,48
2)	19,01 р.;	7,40
17.	Запишите в тоннах
1)	3,569 т; 6,760 т;
2)	6,007 т; 4,480 т;
и 7 км 74 м;
и 8 т 500 кг.
рублях и копейках:
р.; 16,06 р.; 16,60 р
р.; 7,4 р.;	8,1 р.
и килограммах:
6,700 т; 6,070 т;
4,48 т; 9,4 т.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
18.	Вычислите:
1	\ е 3 . —7 . 3 —40 в
' “‘ 2О,—о-’
2	) 18-А-24. -^ + (-^4;
3)274“14:тг+16'^
4)25.1-254 + (-4рЛ.
19.	Решите уравнение:
1)	х:(—3) = 15;	2)	6х + 2 = —16;
3)	12—Зх = 6;	4)	5х—2х=18;
5)	—18х:9 = 10;	6)	12 4-Зх = 6;
7)	—9 4-7х = —23;	8)	Зх4-4х = 56.
20.	Определите на глаз, во сколько раз угол АОВ боль-
ше угла ВОС (рис. 7.1). Результаты сравнения про-
верьте с помощью транспортира. Во сколько раз
угол АОС больше угла ВОС?
21.	Внутри угла в 90° провели луч так, что он разделил
угол на два угла, один из которых на 15° больше
другого. Найдите величины полученных углов.
282
22.	Из вершины угла в 54° провели луч, делящий его на
два угла, один из которых на 16° меньше другого.
Найдите величины получившихся углов.
23.	Внутри прямого угла провели луч, делящий его на
два угла, один из которых в 5 раз больше другого.
Найдите величины получившихся углов.
24.	Из вершины угла в 1.20° провели луч, делящий его на
два угла, один из которых в 3 раза меньше другого.
Найдите величины получившихся углов.
25.	Запись трехзначного числа оканчивается нулем. Если
этот нуль отбросить, то число уменьшится на 432.
Найдите это число.
26.	Сумма двух натуральных чисел 352. Если к мень-
шему приписать справа нуль, то получится большее
число. Найдите эти числа.
27.	Велотуристы пользовались картой, числовой масштаб
которой 1:1000000. Сколько потребуется времени,
чтобы проехать на велосипеде из одного города в
другой со скоростью 12-^-, если на карте расстоя-
ние между этими городами равно 0,6 дм?
28,	Старинная задача. Хозяин нанял работника на год
и обещал ему дать за работу 12 р. и кафтан. Но ра-
ботник, проработав 7 месяцев, захотел уйти. При
расчете он получил кафтан и 5 р. Сколько стоит
кафтан?
29.	Два человека вышли одновременно в одном направ-
лении из одного Места и пошли вокруг леса. Один
из них идет со скоростью о——, а второй—
Длина дороги вокруг леса 15 км. Через сколько ча-
сов первый догонит второго? Сколько каждому при-
дется пройти?
283
§ 79. Перенос запятой в десятичной дроби
Если в десятичной дроби перенести запятую вправо
на k цифр (приписав при необходимости нули спра-
ва), то получится десятичная дробь, большая данной
в 10* раз.
Например: 1) Перенесем запятую в дроби 35,783 на
одну цифру вправо—получим дробь 357,83. Так как
а. 7ОО 35783 ОЕ7 оо 35783
35,783 = -1000 , а 357,83 =	, мы видим, что пере-
нос запятой на одну цифру вправо увеличил дробь
в 101 раз.
2) Перенесем запятую в дроби 35,783 на две цифры
вправо—получим дробь 3578,3. Эта дробь в 100 раз
(100= 102) больше данной дроби 35,783, так как 35,783 =
35783 о-7о о 35783
^Тооб-’ а 3578,3 ==—То-•
3) Если учесть, что 35,783 = 35,78300, можно пере-
нести запятую в дроби 35,783 на пять цифр вправо —
получим число 3578300, которое в 105 раз больше данной
дроби.
Таким образом, перенося запятую в записи дроби на
одну, две и т. д. цифры вправо, мы увеличиваем эту
дробь в 10, 100 и т. д. раз.
Если в десятичной дроби перенести запятую на k цифр
влево (приписав при необходимости нули слева), то полу-
чится десятичная дробь, в 10* раз меньшая данной.
Например: 1) Перенесем запятую в дроби 35,783 на
одну цифру влево—получим дробь 3,5783. Эта дробь в
10 раз меньше данной (покажите самостоятельно).
2) Если в данной дроби 35,783 приписать слева нуль
(получим равную ей дробь), то можно перенести запятую
на две цифры влево—получим дробь 0,35783. Эта дробь
в 100 раз (100= 102) меньше данной (покажите самостоя-
тельно).
Таким образом, перенося запятую в записи десятичной
дроби на одну, две и т. д. цифры влево, мы уменьшаем
эту дробь в 10, 100 и т. д. раз.
284
УПРАЖНЕНИЯ
1.	1) Как изменится дробь, если в ее десятичной запи-
си запятую перенести на 3 цифры вправо?
2)	Как изменится дробь, если в ее десятичной записи
запятую перенести на 3 цифры влево?
2.	Как изменится дробь, если
1)	запятую в ее десятичной записи перенести сначала
на 2 цифры вправо, а затем на 3 цифры влево;
2)	запятую в ее десятичной записи перенести сна-
чала на 3 цифры влево, а затем на 2 цифры
вправо?
3.	Как изменится десятичная запись дроби, если эту дробь
1)	сначала увеличить	в 10 раз,	потом	в 1000	раз;
2)	сначала увеличить	в 10 раз,	а потом уменьшить в
100 раз;
3)	уменьшить в 10 и	еще в 100	раз;
4)	уменьшить в 10 и	увеличить	в 100	раз?
4.	Какое число больше и во сколько раз:
1)	32,549 и 325,49;	2) 2,7543 и 2754,3;
3)	47,58 и 4,758;	3) 123,45 и 1,2345?
5.	Какое число меньше и во сколько раз:
1)	0,4853 и 4853;	2) 0,296 и 0,00296;
3)	480 и 0,48;	4) 200 и 0,02?
6.	Увеличьте следующие дроби в 10, 100, 1000 раз:
1)	7,3459; 2) 8,279; 3) 9,13; 4) 7,2.
7.	Выразите в сантиметрах:
1)	4,25 дм; 4,25 дм = 4,25-1 дм = 4,25-10 см = 42,5 см;
2)	4,2 мм; 4,2 мм = 4,2-1 мм = 4,2 • -^см= (4,2:10) см =
= 0,42 см;
3)	5,21 дм; 4) 3,2 дм; 5) 13,2 мм; 6) 2,1 мм.
8.	Выразите в дециметрах:
1)	4,84 м; 2) 3,5 м; 3) 396,7 см; 4) 2,5 см.
9.	Выразите в метрах:
1)	15,6 дм; 2) 3,4 дм; 3) 0,5265 км; 4) 1,4356 км.
10.	Выразите в килограммах:
1)	1,246 ц; 2) 12,46 ц; 3) 124,6 ц; 4) 15 ц.
11.	1) 1,5245 т; 2) 15,245 т; 3) 152,45 т; 4) 0,0485 т.
12.	1) 7548 г; 2) 238 г; 3) 45 г; 4) 5 г.
13.	Выразите в км2:
1)	1256 га; 2) 125 га; 3) 1256 а; 4) 125 а.
14.	Выразите в см2:
1)	3,548 дм2; 2) 3,9 дм2; 3) 635 мм2; 4) 23 мм2.
285
15.	Выразите в м3:
1)	4754 дм3; 2) 723 дм3; 3) 35 дм3; 4) 7 дм3.
16.	Выразите в мм3:
1)	0,3574 см3; 2) 2,3915 см3; 3) 7,29 см3; 4) 4,325 см3.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
17.	Устно вычислите:
1)	123-1001; 124-1001; 123-124124—124-123123;
2)	1986-19871987—1987-19861986.
18.	Вычислите:
i)	100 ' ( з):(3100:32
2П + (1Н:1|-4)4;^;
\	о z у <5 1 ии
3)б1 + 24-:(14:24-з);
4> (hHI+'W-A-
3	9	7
19.	Приведите дроби	5-^ к знаменателям!
2) 2х+(4х + 11) = 3;
4) 4х—(х+2) = 7;
6) 3—(4х+1) = — 2.
2) 6 + (3—х) = 10;
4) —2х—(5+х) = 13;
6) (х + 2) + (х+3)=11.
а) 100; б) 1000; в) 10000. Запишите полученные дро-
би в виде десятичных дробей.
20.	Масса 1 семени рапса составляет 0,0041 г. Опреде-
лите массу 1000 семян.
21.	Решите уравнение:
1)	2х + (3х—1) = 4;
3)	Зх—(х—1) = 7;
5)	7 + (Зх—8) = 8; ;
22.	1) 9—(5+х) = 6;
3)	8х+(2х—1) = —11;
5)	(1+7х) —(5х—3)==4:
23.	Лев, олень и верблюд весят вместе 1100 кг. Олень и
верблюд весят вместе 875 кг, а верблюд и лев вместе
весят 390 кг. Сколько весит каждое животное?
24.	Пассажирский самолет летит со скоростью 450 ™.
Выразите его скорость в —; —.
г	г	мин’ с
25.	Скорость разгона лыжников при прыжках с трампли-
на достигает 35 . Выразите эту скорость в .
26.	Лыжник движется со скоростью 18-^. Выразите эту
м м
скорость в ----: —.
г	МИН ’ С
286
27.	Спринтер (бегун на короткие дистанции) пробежал
100 м за 10 с. Какова его скорость в -у. ?
28.	Конькобежец пробежал 500 м за 40 с. Какова его
КМ
скорость в —.
29.	В прямоугольнике ABCD сторона АВ равна 4 см, а
сторона AD равна 7 см. Как изменится площадь
прямоугольника, если сторону АВ увеличить в 6 раз?
30.	В прямоугольнике ABCD сторона АВ равна 66 см, а
сторона AD равна 3 см. Как изменится площадь
. прямоугольника, если сторону АВ уменьшить в 7 раз?
31.	Стороны прямоугольника равны см и см. Одну из
сторон увеличили в 2 раза. Как изменится площадь
прямоугольника? Сколько решений имеет задача?
32.	Стороны прямоугольника равны у дм н-|- да!. Одну
из сторон уменьшили в 3 раза. Как изменится пло-
щадь прямоугольника?
33.	Лист тетради, разлинованной в клетку, дает нам пред-
ставление о том, как может быть покрыта плоскость
равными квадратами. Как по-другому могут быть
расположены равные квадраты, чтобы ими можно
было покрыть плоскость?
34.	Придумайте несколько способов покрытия плоскости
равными прямоугольниками. Приведите примеры, где
используются такие разбиения плоскости.
§ 80. Сложение и вычитание положительных
десятичных дробей
Сложение положительных десятичных дробей произ-
водится так же, как и сложение натуральных чисел. По-
кажем это на примерах.
Пример 1. Сложим числа 2,35 и 7,561.
Решение. Учитывая, что 2,35 = 2,350, сложим дан-
ные числа столбиком, подписывая цифры соответствующих
разрядов друг под другом:
. 2,550
+ 7,561
9,911 '
Рассуждаем следующим образом: 0 тысячных-)-1 ты-
сячная = 1 тысячная. Пишем (под чертой) в разряде ты-
сячных цифру 1.
187
5 сотых4-6 сотых=11 сотых =1 десятая 4-1. сотая.
Пишем в разряде сотых цифру 1 и запоминаем 1 десятую.
-1 десятая 4- 3 десятых 4- 5 десятых — 9 десятых.
Пишем в разряде десятых цифру 9.
2 единицы 4-7 единиц = 9 единиц. Пишем в разряде
единиц цифру 9.
Вычитание десятичных дробей производится так же,
как и вычитание натуральных чисел. Пока мы рассмат-
риваем вычитание из большего положительного числа
меньшего.
Пример 2. Вычислим разность 3,51 —2,987.	л;•
Решение. 3,51—2,987 = 3,510—2,987.	- £987
0,523
Из 0 тысячных вычесть 7 тысячных (чтобы получить
положительное число) нельзя. Занимаем в уменьшаемом
одну сотую и раздробляем ее в 10 тысячных. Тогда
10 тысячных—7 тысячных = 3 тысячных. Пишем в раз-
ряде тысячных цифру 3.
Из 0 сотых вычесть 8 сотых (чтобы получилось поло-
жительное число) нельзя. Занимаем в уменьшаемом одну
десятую и раздробляем ее в 10 сотых. Тогда 10 со-
тых— 8 сотых = 2 сотых. Пишем в разряде сотых цифру 2.
Из 4 десятых вычесть 9 десятых (чтобы получить по-
ложительное число) нельзя. Занимаем в уменьшаемом
одну единицу и раздробляем ее в 10 десятых. Тогда
14 десятых—9 десятых = 5 десятых. Пишем в разряде
десятых цифру 5.
2 единицы—2 единицы = 0 единиц. Пишем в разряде
единиц цифру 0.
УПРАЖНЕНИЯ
1. Вычислите:
1) 1,54-2,3;
3) 12,3 4-1,23;
5) 125,344- 12,534;
2. 1) 6,48—2,35;
3) 2,528—1,9;
5) 6,98—3,99;
8. 1) 384-0,56;
3) 9,736 4-25;
5) 7,2—1,899;
4. Вычислите, используя
1) 7,48 4-3,194-1,12 4-
2) 6,24-7,494-1,84-1,
2) 3,74- 1,4;
4) 7,844-8,9;
6) 7,534-8,624.
2) 7,26—3,19;
4) 7,2—3,148;
6) 7,25—3,261.
2) 7,394-11;
4) 8,248 — 6;
6) 5—3,78.
группировку слагаемых:
6,81;
288
3)	16,28 + 5,395—1,18 — 4,305;
4)	7,358 + 8,24—6,458—2,84. .
5.	1) 5,236+ (4,664—2,6);
2)	4,756—(2,395—1,244);
3)	14,529+ (2,461 —1,8);
4)	9,75—(3,65 + 1,999).
6.	Заменив десятичную дробь обыкновенной, вычислите:
1)2,5+31;	2)7——2,25;
3)	0,2-3;	4)	4,8:4;
5)	6:0,6;	6)	12:0,3.
7.	Заменив обыкновенную дробь десятичной, вычислите:
1)	++2.5;	2)	7^-2,15;
3)4,12-14-;	4)	9,1 + 3-4;
5)17,3—91;	6)6,09 + 21.
8.	Вычислите периметр прямоугольника, если ,
1)	ширина прямоугольника равна 2,3 см, а длина
на 1,9 см больше;
2)	ширина прямоугольника равна 2,48 дм, а длина
на 1,6 дм больше;
3)	длина прямоугольника равна 12,1 см, а его ширина на
4,8 см меньше;
4)	длина прямоугольника равна 18 дм, а его ширина
на 4,7 дм меньше.
9.	Вычислите:
1)	1,2 дм+ 1,2 см = 1,2 дм + 0,12 дм= 1,32 дм;
2)	16 см+ 4,35 дм;	3) 7,35 м + 4,9 дм;
4)	2-4,8 дм;	5) 4,8 дм:2;
6)	12,3 дм—42 см;	7) 34 дм—34 см.
10.	Вычислите периметр треугольника, имеющего стороны:
1)	490 мм,	48 см,	4,7	дм;
2)	23 мм,	3,4 см,	0,48	дм;
3)	3,5 см,	0,38 дм,	0,041	м.
11.	В квартире две жилые комнаты. Одна комната имеет
площадь 16,3 м2, а вторая на 1,9 м2 меньше. Какова
площадь двух комнат?
12.	В квартире 3 комнаты общей площадью 44,8 м2. Одна
комната имеет площадь 11,3 м2, вторая на 3,5 м2
больше. Найдите площадь третьей комнаты.
13.	Вычислите наиболее простым способом:
1)	23,28—(17,41 —16,13)—4,03 + 7,41;
2)	7,39+ (6,52—4,59)—6,52+1,41;
10 С. М. Никольский и др.	289
3)	13,125 — 2,751 —(4,025 — 2,729) —1,729;
4)	49,5 + 2,738— 6,856—(2,638—7,956).
14.	Троллейбусный парк нашей страны увеличился с
1960 г. на 20,7 тыс. троллейбусов и насчитывал
к концу 1984 г. 26,1 тыс. троллейбусов. Сколько трол-
лейбусов было у нас в 1960 г.?
15.	В таблице приведены расходы нашего государства на
образование и здравоохранение (в млрд, р.) по годам.
Перечертите таблицу в тетрадь и заполните ее.
	1980 г.	1981 г.	1982 г.	1983 г.
Образование Здравоохранение и физи- ческая культура Итого	31,6 17,2	32,5 17,8	34,0 18,6	34,7 19,2
16.	В таблице приведены сведения о производстве важ-
нейших видов пищевых продуктов. На сколько уве-
личилось производство мяса, молока, яиц, колбасных
изделий и животного масла за отмеченные в таблице
годы?
	1970 г.	1984 г.	Прирост
Мясо (млн. т)	12,3	16,7	
Молоко (млн. т)	83,0	п 97,6	
Яйца (млрд, шт.)	40,7	76,0	
Колбасные изделия (млн. т)	2,28	3,3	
Животное масло (млн. т)	0,9	1,5	
17.	Численность рабочих, служащих и колхозников в
СССР составляла в 1970 г. 106,8 млн. чел. Это на
23 млн. чел. больше, чем в 1960 г., и на 22,7 млн.
чел. меньше, чем в 1984 г. Какова была численность
рабочих, служащих и колхозников в нашей стране
в 1960 и 1984 гг.?
18.	Решите уравнение:
1)	х— 2,3=1,8;	2) х+ 3,1 = 17,49;
3)	х+ 1,9=11,15;	4) х—1,95 = 6,3.
280
19.	1) Зх— 2,18 = 2x4-4,9; 2) 10x4-3,54 = 9x4-8,3.
20.	1) 5,2х—3,2х=14;	2) 3,6х+1,4х= 155;
3)	9,57х—0,57х = 450; 4) 0,39x4-12,61х= 13.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
21.	Решите уравнение:
1)	13(х—2) = 26;	2) 6-(х—4) = 12;
3)	2(х— !)—5=15;	4) 2(х—3)4- 1=63;
5)|(х-4)=1;	6) |(х4-1) = 2.
22.	1) 3(х—2) = 8;	2) 4(х4-2) = 7;
3)	11 =5(х—3)—9;	4) (2x4-1)-94-5 = 23.
23.	Скорость лодки в стоячей воде 6,2 а скорость
течения реки 1,7—. С какой скоростью лодка может
плыть по течению реки и с какой против течения реки?
24.	У брата было в 3 раза больше денег, чем у сестры.
Когда они купили по мороженому стоимостью по
20 к., у брата стало в 4 раза больше денег, чем у
сестры. Сколько денег было у каждого?
25.	В одной коробке в 4 раза больше цветных каранда-
шей, чем в другой. Когда из каждой коробки выну-
ли по 3 карандаша, то в первой стало в 5 раз боль-
ше, чем во второй. Сколько карандашей было в
каждой коробке?
26.	Велосипедист за первые два часа проехал 25 км, а
за следующие три часа—30 км. С какой постоянной
скоростью велосипедист мог бы проехать тот же путь
за то же время (5 ч)?
Рис. 7.2
27.	Можно ли покрыть фигуры (рис. 7.2) костями доми-
но, если каждая кость покрывает точно две клетки?
Ответ обосновать.
ю*
291
28.	Докажите, что нельзя обойти все клетки доски с от-
резанными углами (рис. 7.3) шахматным конем, по-
бывав на каждой клетке только один раз.
29.	Одну и ту же работу первая бригада выполняет за
6 дней, а вторая—за 8 дней. Какую часть работы вы-
полняет каждая бригада ежедневно? Какую часть ра-
боты выполняют за день обе бригады, работая вместе?
30.	Один рабочий обрабатывает деталь за 2 ч, а второй —
за 3 ч. Какую часть работы выполняет каждый ра-
бочий в час? Сколько деталей они изготовят за 6 ч?
31.	Расстояние между двумя городами мотоциклист про-
езжает за 2 ч, а велосипедист—за 6 ч. Через сколь-
ко часов они встретятся, если выедут из этих городов
одновременно навстречу друг другу?
32.	Путешественник идет из одного города в другой 10 ч,
а второй путешественник тот же путь проходит за
15 ч. Через сколько часов они встретятся, если вый-
дут одновременно навстречу друг другу из этих го-
родов?
33.	Если на разных участках пути происходит движение
с разными скоростями, то средней скоростью на всем
участке называют скорость, с которой можно тот же
путь пройти за то же время. Какова средняя ско-
рость велосипедиста в задаче 26? Вычислите среднюю
скорость поезда, если он двигался:
1)	1 ч со скоростью 80™ и 4 ч со скоростью 60™;
2)	1 ч со скоростью 60™и 4 ч со скоростью 80™;
3)	как объяснить, что во втором случае средняя ско-
рость выше?
34.	Расстояние между двумя городами равно 70 км. Из
этих городов навстречу друг другу одновременно вы-
ПЛ КМ
ехал мотоциклист, скорость которого 30	, и вышел
пешеход, скорость которого 5 —. Через сколько часов
они встретятся?
35.	Из пункта А в пункт В одновременно вышли два
СКМ .КМ п
пешехода со скоростями 5-^- и 4—. Первый пришел
в В, повернул назад и пошел с той же скоростью
навстречу второму. Пешеходы встретились через 2 ч
после выхода из Д. Какое расстояние они прошли до
встречи? Какое расстояние между Д и В?
292
36.	Из пункта А в пункт В вышли два пешехода со ско-
ростами 5 — и 4 —. Первый пришел в В, повернул
назад и пошел с той же скоростью навстречу второму.
Через сколько часов они встретятся, если расстояние
АВ равно 18 км?
37.	Расстояние между пунктами А и В равно 17 км. Из
А в В выехал велосипедист со скоростью 12™. Одно-
временно с ним из Л в В вышел пешеход со ско-
ростью 5 ™  Велосипедист доехал до В, повернул и
поехал назад с той же скоростью. Через сколько
часов после начала движения они встретятся?
§ 81. Умножение десятичных дробей
Десятичная форма записи позволяет выполнять умно-
жение дробей практически по тем же правилам, по кото-
рым умножают натуральные числа. Отличие заключается
в том, что необходимо определять место запятой в полу-
ченном произведении. Поясним сказанное на примере;
вычислим произведение 2,5-1,02.
Перенесем запятую в первом множителе на одну цифру
вправо, а во втором—на две цифры вправо. Тем самым
первый множитель увеличится в 10 раз, второй—в 102 =
= 100 раз, а произведение—в 10-100= 1000 раз.
Определим произведение натуральных чисел 25 и 102:
25-102 = 2550.
Это число в 1000 раз больше, чем требуемое произ-
ведение. Поэтому необходимо число 2550 уменьшить в
1000= 10s раз, т. е. перенести в этом числе запятую влево
на 3 цифры. Таким образом,
2,5-1,02 = 2,550 = 2,55.
Можно рассуждать по-другому:
9 к 1 м__25 Ю2____25-102 _ 2550_п сел__о кс
2,0 • 1,02 — 1() 1(ю - 10110() — 1(Х)0 — 2,00U — 2,00.
Таким образом, чтобы перемножить две десятичные
дроби, достаточно, не обращая внимания на запятые,
перемножить их как натуральные числа, а затем в
полученном произведении справа отделить запятой столько
цифр, сколько их было после запятых в обоих множите-
лях вместе.
293
Например,
х 2’5
х1,02
,	50
+25
2,550
= 2,55
УПРАЖНЕНИЯ
Вычислите произведение:
I. 1) 1,25-10; 4) 0,002-10;		2) 3,29-100; 5) 3,2-100; 8) 0,041 -100;	3) 0,32-100; 6) 0,3-1000; 9) 0,0005-1000.
	7) 2,39-1000;		
2.	1) 2,4-2; 4) 2,5-4; 7) 5,2-0,4;	2) 3,1-3; 5) 1,25-8; 8) 7,1-0,9;	3) 0,5-2; • 6) 0,072-2; 9) 0,08-0,13.
3.	1) 6,5-0,004; 4) 0,048-0,09;	2) 0,09-0,18; 5) 0,7-0,0085;	3) 7,6-0,005; 6) 0,009-0,78;
	7) 80,8-0,7;	8) 0,09-5,007;	9) 0,6-3,054.
4.	1) 3,59-0,1; 4) 63,2-0,01; 7) 723,1-0,001;	2) 2,3-0,1; 5) 3,5-0,01; 8) 79,4-0,001;	3) 0,0235-0,1; 6) 2,32-0,01; 9) 3,8-0,001.
5.	1) 4,381-0,2; 4) 0,2569-0,6; 7) 42,25-0,4;	2) 7,713-0,8; 5) 0,3-2,451; 8) 362,5-0,8;	3) 0,07-620,4; 6) 67,19-0,05; 9) 512,5-0,08.
6.	1) 2,3-1,1; 4) 53-0,31; 7) 4,35-2,2;	2) 4,3-1,2; 5) 0,68-61; 8) 3,2-0,25;	3) 0,22-3,3; 6) 0,72-0,015; 9) 0,084-0,55.
7.	Вычислите наиболее простым способом: 1)	0,25-0,3-4;	2}	0,2-Q,13-5,0; 3)	0,8-0,11-1,25;	4)	0,125-3-0,8; 5)	0,5-7,3-2,2;	6)	0,25-1,7-1,6.		
8. Вычислите:
1) 2,4-4,8 +2,6-4,8;
3) 5,1-1,8—1,8;
9. 1) 0,1-0,1;
3) 0,3 0,3-0,3 0,3;
5) 0,6 0,6 0,6;
7) (0,5 + 0,2)2;
9) (0,9—0,4)3;
И) (1,2)?—1,2;
10. 1)9,51-18;
3) 8,47 0,64;
5) 0,85-2,06;
2) 30,5-20,3—30,5-0,3:
4) 4,9-6,2 +6,2.
2) 0,2-0,2-0,2;
4) 0,05-0,05;
6) 0,08-0,08;
8) (0,7+О,З)3;
10) 0,8 + (1,1)2;
12) 1,5?—0,25.
2) 66,3-26;
4) 7,3-5,42;
6) 8,07-0,016.
294
2) 3,02-6,48;
4) 95,5-3,17;
6) 0,999-0,732.
11. 1) 3,32-0,101;
3) 3,21 -0,562;
5) 0,861-0,242;
12.	1) 7,668-24 — 9,68;	2) 35,224-45,83-2,6;
3)	5,306-42 + 5,36-82; 4) 1,654-3,4 + 6,4-9,5;
6) 35,4-1,99 + 35,4;
8) 1,22-97+3,66;
5) 2,4-98 + 4,8;
7) 3,2-103—9,6;
9)	10,2-0,5 + 5,1.
13.	Известно, что 8-125= 1000. Вычислите:
1)	8-12,5;	2) 0,08-125; 3) 0,8-12,5;
4)8-0,125; 5)0,8-1,25; 6)0,08-12,5.
14.	Стоимость перевозки 1 т груза от Москвы до Ленин-
града по железной дороге 1,5 р., от Москвы до
Ростова-на-Дону 2,8 р. Вычислите стоимость пере-
возки 40 т груза в обоих случаях.
15.	Пешеход идет со скоростью 4,4^-. Какой путь он
пройдет:
1)	за 2 ч; 2) за 0,5 ч; 3) за 1,5 ч?
16.	Собственная скорость моторной лодки 12,6	, а ско-
рость течения реки 1,8	. Какой путь пройдет лодка
по течению и против течения:
1)	за 3 ч; 2) за 2,5 ч; 3) за 0,5 ч?
17.	Вычислите площадь прямоугольника со сторонами
а и Ь:
1)	а = 3,6см, 6 = 4 см;	2) а = 5дм, 6 = 3,13 дм;
3)	а = 3,12 дм, 6 = 3,5 дм;	4) а = 6,25 м, 6= 1,6 м.
18.	Вычислите объем прямоугольного параллелепипеда,
длина, ширина, высота которого а, 6, с:
1)а = 4,5см, 6 = 2,Зсм, с=10см;
2)	а = 3,2 дм, 6=1,5 дм, с = 2,5дм.
19.	1 м3 воздуха весит 1,29 кг. Определите вес воздуха
в вашем классе.
20.	1 см3 алюминия весит 2,7 г, 1 см3 свинца весит 11,3 г.
Какой кубик больше весит—алюминиевый с ребром
3 см или свинцовый с ребром 2 см?
21.	Использование 1 т макулатуры позволяет получить
0,7 т бумаги и заменить при этом 4,4 м3 древесины,
Сколько бумаги можно получить из 7,5 т макулатуры?
Сколько при этом экономится древесины?
22.	За один день в нашей стране производилось в 1960 г.
6,4 тыс. т бумаги. В 1984 г. производство бумаги
возросло по сравнению с 1960 г. в 2,5 раза. Сколько
бумаги производилось за один день в 1984 г.?
23.	Сумма нескольких чисел равна 1. Мржет ли сумма
их квадратов быть меньше 0,1; меньше 0,01?
24.	Две трети расходов на содержание жилого фонда наше
государство берет на себя. Определите расходы госу-
дарства за год на содержание одной квартиры пло-
щадью 50 м2, если плата за 1 м2 в месяц составляет
16,5 к.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
25.	Вычислите устно:
1)48-10;	2)48-100;	3)48-1000;
4)	5000:10; 5) 5000:100; 6) 5000:1000.
26.	1) 0,74-0,2; 2) 0,74-2; 3) 1,44-2,8; 4) 9,9 + 0,1;
5)	7,2—0,2; 6) 7,2—2; 7) 1,3—0,7; 8) 10—0,6.
27.	Решите уравнение:
1)	3(х—5) = 2х + 1; 2) 5(х+2) = 4х+5;
3)	х+2 = 4(х—1);	4) 3—х = 2(х—3).
28.	Решите уравнение:
1)	3(2х— 1) = х+2;	2) 4(Зх-Ь 2)= 10х—6;
3)	9х+ 10 = 2(4x4-7);	4) 7—Зх = 2(Зх + 8).
29.	Длина прямоугольника на 7 см больше ширины, а пе-
риметр равен 50 см. Найдите стороны прямоугольника.
30.	Ширина прямоугольника на 9 см меньше длины, а пе-
риметр равен 66 см. Найдите стороны и площадь
прямоугольника.
Рис. 7.4
31.	Одна сторона прямоугольника в 3 раза больше дру-
гой, а периметр равен 1 м 6 дм 8 см. Найдите стороны
и площадь прямоугольника.
296.
32,	Одна сторона прямоугольника в 2 раза меньше дру-
гой, а периметр равен 1 м 44 см. Найдите площадь
прямоугольника.
33.	Нарисуйте, не отрывая карандаша от бумаги и не
проводя по одной линии дважды, фигуры (рис. 7.4).
34.	В упр. 33 некоторые фигуры построить не удалось.
Обратите внимание в каждом случае на число «нечет-
ных» узлов, в которых сходится нечетное число
отрезков. В каком случае можно построить фигуру,
а в каком—нельзя?
35.	Можно ли нарисовать фигуру, у которой имеются три
таких «нечетных» узла? Почему?
36.	Какие из фигур, изображенных на рис. 7.5, можно
нарисовать, не отрывая карандаша от бумаги и не
проводя по одной линии дважды?
Рис. 7.5
37.	В шести коробочках лежат деньги. В первой—1 к.,
во второй—2 к., в третьей—3 к. и т. д., в шестой —
6 к. За один ход разрешается в любые две коробочки
добавить по 1 к. Можно ли за несколько ходов урав-
нять суммы в коробочках?
38.	Найдите:
1)	от 1 см;	2) от 1 дм;	3) ± от 1 м;
4)	.Тббо от 1 км; 5) КЙЮ от 1 кг;	6) 1^6 от 1 т;
7)	Ж от 1	8) от 1 а.
39.	Старинная русская денежная единица 1 деньга содер-
жала 2 полушки. Какую часть копейки составляли
1 деньга и 1 полушка отдельно, если 10 денег и
8 полушек составляли 7 копеек?
40,	Собственная скорость моторной лодки 15	, скорость
течения реки 3	. Лодка проходит расстояние между
двумя пристанями по течению на 1 ч быстрее, чем
против течения. Каково расстояние между пристанями?
297
41.	Пионерский отряд шел 3 ч со скоростью 5 ™ ,
Л	л КМ	Л	. 1 КМ
2 ч со скоростью 4 — и еще 2 ч со скоростью 4у “ .
На привалы был затрачен 1 ч. С какой средней ско-
ростью отряд прошел весь маршрут?
42.	У Светы и Наташи было 8 яблок. Света дала Наташе
столько яблок, сколько было у Наташи. Потом Наташа
дала Свете столько яблок, сколько было у Светы.
После этого у девочек оказалось равное число яблок.
Сколько яблок первоначально было у каждой девочки?
43.	Имеются три монеты, из которых две настоящие —
одинакового веса и одна фальшивая—легче настоящих.
Как одним взвешиванием на весах без гирь определить
фальшивую монету?
44.	Можно ли решить задачу № 43, если неизвестно,
какая из монет легче — настоящая или фальшивая?
45.	Как изменится площадь прямоугольника, если одну
сторону увеличить в 4 раза?
46.	Как изменится площадь прямоугольника, если одну
сторону уменьшить в 8 раз?
47.	Первая бригада может выполнить задание за 28 ч,
а вторая — за 56 ч. Мастер рассчитал, что работу
можно организовать так, чтобы сначала первая бри-
гада работала несколько полных дней (по 8 ч), а затем
вторая бригада. При этом задание будет выполнено
за 4 дня. Сколько дней должна работать каждая
бригада?
§ 82. Деление десятичных дробей
Рассмотрим пример деления десятичной дроби на на-
туральное число.
Пример. Вычислить 46,8:2.	46 8 2
Решение. 4 десятка делим на 2—по-	* ""^4
лучаем цифру частного 2 (2 десятка).	_|
6 единиц делим на 2 —получаем цифру	—щ
частного 3 (3 единицы).	"~8
Деление целой части закончено—отде- 0
ляем в частном целую часть запятой.
8 десятых делим на 2 — получаем цифру частного 4
(4 десятых). Остаток равен 0—деление закончено.
298
Деление десятичной дроби на десятичную дробь сво-
дится к делению на натуральное число переносом запятых
в делимом и делителе на столько цифр вправо, чтобы
делитель стал натуральным числом.
Пример. Вычислить 4,42:0,2.
Решение. Так как в делителе одна цифра после
запятой, то достаточно перенести запятые в делимом и
делителе на 1 цифру вправо. Тем самым делимое и дели»
тель увеличиваются в 10 раз, поэтому частное не изме-
нится. При этом делитель будет натуральным числом.
Итак,
4,42:0,2 = 44,2:2.
Дальше деление выполняется так, как показано в преды-
дущем примере.
Можно рассуждать и таким образом:
4 42‘0 2 — 4’42 — 4’42 10 — 44’2 — 44 2*2
— Q 2	0,2-10	2
Но не всегда получается точный результат при деле-
нии десятичных дробей. Чаще приходится довольство-
ваться приближенным* частным. Пример. Найти частное 1,723:0,03. Решение. Освободимся от запятой в делителе: 1,723:0,03= 172,3:3. Вы- полним деление. Начиная с разряда сотых, цифра 3 в частном повторяется без конца, по- тому что остаток, начиная с третьего этапа процесса деления, все время ра- вен одному и тому же числу 1.	_172,30 3 -12	57-433--’ ““21 13 “12 10 ““ 9 10 ~ 9 10...
В следующих параграфах мы подробно изучим это
явление, а сейчас отметим лишь, что для практических
целей деление в таком случае на некотором этапе обры-
вают и частное записывают приближенно.
Если оставить у частного первые две цифры после
запятой, то получится приближенное равенство:
172,3:3 «57,43.
299
УПРАЖНЕНИЯ
1( Вычислите:
1) 12,5:10;	2) 72,6:100;	3) 173,56:100;
4) 9,3:100;	5) 0,73:1000; 6) 1,664:10000.
2*	1)	783:10;	2) 988:100;	3) 54000:10000;
4)	7800:1000;	5) 3:1000;	6) 5:100000.
3.	1)	3,6:3;	2)	75,5:5;	3)	1,24:4;
4)	2,53:11;	5)	7,81:11; 6)	13,2:24.
4.	1) 0,48:8;	2) 0,84:21-;	3) 0,001:5;
4) 0,002:4; 5) 0,125:25; 6) 0,0625:25.
5.	Выполните действие и проверьте полученный результат:
1)	3,1:0,1;	2) 7,21:0,01; 3) 6,3571:0,01;
4) 4,729:0,001; 5) 4,29:0,1;	6) 7,1:0,001.
6, Вычислите:
1) 6:0,1;	2) 7:0,01;	3) 8:0,001;
4)	35:0,1; 5) 49:0,01; 6) 56:0,001.
7.	1) 1:0,2; 2) 1:0,25; 3) 1:0,125;
4)	1:0,4; 5) 1:0,8;	6) 1:0,5.
8.	Как изменится частное, если
1)	делимое увеличить в несколько раз;
2)	делитель увеличить в несколько раз;
3)	делимое и делитель увеличить в одинаковое число
раз?
9.	Вычислите:
1)	48:4,8;	2) 536:5,36; 3) 921:92,1;
4)	39:0,39; 5) 4:0,4;	6) 999:99,9.
10.	1) 53,6:5,36;	2) 5,36:0,01;	3) 72,34:7,234;
4)	7,234:0,01; 5) 372,9:3,729; 6) 3,729:0,1.
11.	Выполните действие и проверьте полученный результат:
1)	4:0,5;	2) 3:0,2;	3) 2:0,02;
4)	14:0,07; 5) 12:0,004; 6) 10:0,005.
12.	1) 7,6:0,2;	2) 6,3:0,3;	3) 0,64:3,2;
4)	0,49:0,7; 5) 0,01:0,05; 6) 0,004:0,8.
13.	Вычислите:
1)0,21:0,84; 2) 0,19:0,095; 3)3,76:0,4;
4)	7,05:1,4;	5) 3,5:0,4;	6) 25,9:3,7.
14.	1) 1,75:1,4;	2) 18,4:7,36;	3) 16,92:4,23;
4)	86,1:2,46; 5) 21,875:3,125; 6) 183,96:5,256.
15.	1) 0,25:4+15,3:5+12,4:8+0,15:3;
2)	96,7:10 + 0,045:5+140,4:12+ 1,53:15.
16.	1) 4,912:16 +(18,305:7+0,0368:4);
2)	72,492:12 + 78,156:36—120,03:15.
1)	1У,00-1УС,/ и
2)	19,87-1,988 и
3)	198,8-198,9 и
4)	1,989-199,0 и
19. Вычислите устно:
п 12,3-3,21 .	с
1,23-32,1’
о-. 0,123-321.	z
1 OQ.O О1 »
17.	1) 1,35:2,7 + 6,02 — 5,9 + 0,4:2,5-(4,2 — 0,075);
2) 4,3—3,5+ 1,44:3,6+ 3,6:1,44-(0,1—0,02).
18.	Не выполняя вычислений, сравните произведения:
1,986-1987;
198,7-19,88;
1,988-1,989; .
1,989-1990.
12,3-3,21.
1,23-3,21 ’
0,123-0,321
1,23-3,21 *
20.	На прямолинейном участке железнодорожного пути
должны быть уложены рельсы длиной 12,5 м. Сколько
рельсов будет укладываться на 1 км пути?
21.	В таблице приведена грузоподъемность некоторых
советских самосвалов:
Марка самосвала	Г рузоподъемность
ГАЗ	3,5 т
ЗИЛ	4,5 т
КАМАЗ	7,0 т
МАЗ	8,0 т
КрАЗ	11,0 т
Во сколько раз грузоподъемность МАЗа больше грузо-
подъемности других самосвалов?
22.	От продажи одной коробки яиц магазин получает
31,5 р. Сколько яиц в одной коробке, если десяток
яиц стоит 1,05 р.?
23.	Слон тяжелее бегемота на 0,7 т, а их общий вес 8,3 т.
Сколько весит каждое животное?
24.	Вычислите скорость движения пешехода, который
1)	за 2,4 ч прошел 10,8 км;
2)	за 1,8 ч прошел 9,9 км.
25.	На производство 1 т бумаги расходуется 250 т воды.
Это в 12,5 раза больше, чем расходуется на произ-
водство 1 т стали, и в 6 раз меньше, чем на произ-
водство 1 т аммиака. Сколько тонн воды расходуется
на производство 1 т стали и 1 т аммиака?
301
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
26.	Вычислите:
1)	1у—3-|”0,2;	2) 1-|: 1,6-1-0,125;
3)	2-1-0,4:0,125-1-|;	4) 1,7-0,3+19:0,5-1.
27.	1) (1,545:1,5—1)-2-| + 0,5-1;
2)	(2,678:1,3-2)-31 + 0,3-14.
28.	Решите уравнение:
1)	5х = 4 (х + 0,2);	2) 0,2х = 0,3(х—5);
3)	3х = 3,2(х—0,4);	4) 1,2х = 3(х—0,3);
5)	3,2х+1,2х=33;	6) 3,5х—0,1х = 51.
29.	Купили конфет по 3 р. за 1 кг. Если бы купили
конфеты на 0,6 р. за 1 кг дороже, то их было бы
на 0,5 кг меньше. Сколько килограммов конфет
купили?
30.	На имеющуюся сумму денег можно купить 4 кг кон-
фет одного сорта или 3 кг конфет другого сорта,
стоимость которого за 1 кг на 1,5 р. больше. Сколько
стоит 1 кг конфет каждого сорта? Какая сумма денег
имеется?
31.	Тракторист должен вспахать поле за 5 дней. Увеличив
выработку на 2,5 га в день, он выполнил работу
за 4 дня. Какова площадь поля?
32.	Найдите:
1)	0,2 от 500;	2) 0,5 от 42;
3)	0,25 от 600;	4) 0,43 от 200;
5)	0,3 от 6;	6) 0,7 от 5.
33.	Найдите число, 0,2 которого равны:
1)	70; 2) 10; 3) 100.
34.	Найдите число, 0,15 которого равны:
1)	15; 2) 90; 3) 330.
35_. Решите уравнение:
1) V + |x=10;	2) |х + 4х=18;
з)	ix+ix==—3'> 4) tx~jx==4-
36,	1) х + 4-х = 8;	2) х—тх = 5;
О	о
3)х + -1х=10;	4) х—1х=15.
£02
37.	Длина прямоугольника составляет ширины, а пе-
риметр равен 72 см. Найдите длину и ширину прямо-
угольника.
2
38.	Одно число составляет у другого, а их сумма равна 20.
Найдите эти числа.
2
39,	Даны два числа. Одно составляет у второго, а их
сумма равна 99. Найдите эти числа.
40.	Если ученица будет только завтракать в школе, то
имеющихся у нее денег хватит на 30 дней, а если
она будет только обедать, то-денег хватит на 15 дней.
На сколько дней хватит денег, если ученица будет
и завтракать, и обедать в школе?
41.	Сережа шел 1 ч со скоростью 4 — и 3 ч со скоростью
5	. Андрей шел 1 ч со скоростью 5 и 3 ч со
скоростью 4 Jy. Какой путь прошел каждый маль-
чик? С какой средней скоростью шел каждый из них?
Почему средняя скорость Сергея была выше?
42.	Лошадь съедает воз сена за месяц, коза—за два ме-
сяца, овца — за три месяца. Какое время потребуется
лошади, козе и овце, чтобы съесть вместе воз сена?
43.	Смешали 12 кг чернослива по 2 р. за 1 кг, 10 кг су-
шеных яблок по 1,7 р. за 1 кг и 7 кг сушеных груш
по 1,6 р. за 1 кг. Определите стоимость 1 кг смеси.
44.	Смешали 6 кг чернослива по 2 р. за 1 кг, 6,6 кг су-
шеных яблок по 1,7 р. за 1 кг и 7,8 кг сушеных
груш по 1,6 р. за 1 кг. Сколько стоит 1 кг полу-
ченной смеси?
45.	Одна бригада может выполнить задание за 9 дней,
а вторая—за 12 дней. Первая бригада работала над
выполнением задания 3 дня, потом вторая бригада
закончила работу. За сколько дней было выполнено
задание?
46.	Один экскаватор может вырыть траншею за 30 ч,
другой—за 20 ч. Первый проработал 9 ч, а второй
закончил работу. За сколько часов была выполнена
работа?
47,	К числителю и знаменателю дроби у прибавили
одно и то же число и получили дробь, равную 0,5.
Какое число прибавили к числителю и знаменателю
дроби?
303
48.	Имеются три монеты, из которых' одна фальшивая,
о которой неизвестно—легче или тяжелее эта монета,
чем настоящая. Как за два взвешивания на рычажных
весах определить фальшивую монету?
49.	Из шести монет одна фальшивая, она легче остальных.
Как за два взвешивания на рычажных весах без гирь
определить фальшивую монету?
50.	Решите задачу № 48 для 9 монет и трех взвешиваний.
51.	Решите задачу № 48 для 27 монет и четырех взве-
шиваний.
§ 83. Понятие о проценте
В метрической системе мер, и вообще в десятичной
системе счисления, широко используются сотые части.
Сотая часть называется процентом (от латинского
pro cento—на сотню, из сотни, с сотни) и обозначается %.
Поэтому пишут 1 % =0,01.
Например: 1) 1 % рубля = 0,01 рубля =1 копейке;
2) 1 % метра = 0,01 метра = 1 сантиметру.
Запись «2 %» читается «два процента» или «две сотые».
Вместо того чтобы говорить «тридцать девять сотых», гово-
рят «тридцать девять процентов» и пишут «39 %».
Задача 1. Найти 25 % от 36.
Решение. I способ. 1) Найдем 1 % от 36:
36:100=
2) Найдем 25 % от 36. Это в 25 раз больше:
36	25-36	36 А
100 ~ 100 — 4 “У'
II способ. Так как 25 % = 0,25, то задача сводится
к нахождению 0,25 числа 36: 0,25-36 = ^|^-=-^- = 9.
Ответ. 9.
Задача 2. Найти число, 30 % которого равны 7.
Решение. I способ. 1) Если 30 % числа равны 7,
7
то 1 % числа равен 7:30 = -^-.
7
2) Если 1 % .числа равен то само число в 100 раз
-	7 1ПП 7-100	70 оо 1
больше:	• 100— 30 — g —23
304
II способ. Обозначим неизвестное число через х;
тогда 0,30-х = 7,
— х— 7 х — 7*— 7-— — — — 23 —
10 х-1, л-t. 10 — / 3 — 3-2б3.
УПРАЖНЕНИЯ	Ответ. 23-j.
1.1)	Что называется процентом?
2) Запишите в виде обыкновенной и десятичной дро-
бей: 1%; 5%; 70%; 100%; 120%; 200%; 1020%.
2.	Прочитайте предложение, выразите число процентов
дробью и еще раз прочитайте предложение, которое
получилось:
1)	25 составляет 25% от 100;
2)	20 составляет 50% от 40;
3)	найдите 10% от 200;
4)	число 500 увеличили на 10% и получили 550.
Выразите в процентах:
3.	1) 0,12; 0,25; 0,48; 0,99; 0,10;
2) 0,1; 0,2; 0,9; 1; 1,20; 1,3; 3.
4 п 1	2 3 4	5 * * * *	10 J_. JL.
" 100 ’ 100 ’ 100 ’ 100 ’ 10 ’ 20 ’
2) — • — • — • — • 2' 1
50 ’ 5 ’ 2 ’ 4 ’	1 100 •
2) 1% от 300;
4) 7% от 200.
2) 25% от 48;
4) 120% от 250.
7. Члены профсоюза ежемесячно платят членские взносы
в размере 1% месячного заработка. Сколько должен
заплатить рабочий в профсоюз, если его зарплата за
месяц составляет:
1) 200 р.; 2) 240 р.; 3) 195 р.?
8. Сравните 35% от 40 и 40% от 35.
9. В бригаде 12 человек. 75% членов бригады состав-
ляют комсомольцы. Сколько комсомольцев в бригаде?
10. Сберегательные кассы в СССР не только хранят вклады
трудящихся, но и выплачивают им ежегодно доходы
в виде процентов от вклада. В конце каждого года
к имеющемуся вкладу прибавляются 2% этого вклада
(для простоты будем считать, что вклад в течение
года не изменялся). Какой доход начислит кассир
в конце года по вкладу:
1) 100 р.; 2) 269 р.; *2) 1000 р.; 4) 555 р.?
5. Найдите:
1) 1% от 100;
3) 5% от 40;
6. 1) 20% от 15;
3) 100% от 49;
805
II.	При хранении денег в сберегательной кассе на сроч-
ном вкладе начисляются 3% годовых. Какой доход
начислит кассир в конце года по срочному вкладу:
1) 100 р.; 2) 890 р.; 3) 1987 р.; 4) 2563 р.?
12.	Какую часть числа составляет его
1)	1%;	2) 5%;	3) 10%; 4) 20%;
5)	25%; 6) 50%; 7) 75%; 8) 100%?
13.	Устно вычислите:
1)	50% от 400;	2) 10% от 20;	3) 25% от 16.
14.	Из сахарной свеклы получают сахар, вес которого
составляет 18% веса свеклы. Сколько сахара полу-
чится при переработке:
1)	40 т свеклы; 2) 30 т свеклы; 3) 500 т свеклы?
15.	Из семян конопли получают масло, вес которого состав-
ляет 15% веса семян. Сколько масла получается из
1) 44 кг семян; 2) 58 кг семян; 3) 80 кг семян?
16.	Бригада шахтеров за сутки должна добывать на од-
ном месторождении 500 т угля. План был выполнен
на 130%. На сколько процентов перевыполнено зада-
ние? Сколько тонн угля добыто за сутки сверх плана?
17.	Стоимость путевки в санаторий 180 р. Рабочий опла-
тил только 30% ее стоимости, остальную часть стои-
мости путевки оплатил профсоюз. Сколько рублей
заплатил рабочий за путевку, а сколько профсоюз?
13. Увеличьте число:
1) 60 на 10%;	2) 80 на 25%;	3) 40 на 50%.
19.	Уменьшите число:
1)	60 на 10%;	2) 80 на 25%;	3) 90 на 50%.
20.	1) Число 200 увеличили на 25%. Во сколько раз уве-
личилось число?
2)	Число 300 увеличили на 13%. Во сколько раз
увеличили число?
3)	Число а увеличили на 35%. Во сколько раз уве-
личили число?
21.	1) Число 200 увеличили в 1,3 раза. На сколько про-
центов увеличили число?
2)	Число 400 увеличили в 1,4 раза. На сколько про-
центов увеличили число?
3)	Число а увеличили в 2,5 раза. На сколько про-
центов увеличили число?
22.	Найдите число:
1)	1% которого равен 3; 2) 10% которого равны 40;
3) 15% которого равны 30; 4) 50% которого равны 250.
23.	Магнитный железняк содержит 70% чистого железа.
Сколько железа в 13 т железняка?
306
24.	Сплав содержит 62% олова и 38% свинца. Сколько
олова и сколько свинца в 40 г сплава?
25.	Припой содержит 40% олова, 2% сурьмы, остальную
часть составляет свинец. Сколько олова, свинца и
сурьмы в 30 г припоя?
26.	Завтрак детей и подростков должен составлять 25%
дневного рациона, второй завтрак—15%, обед—40%.
, Сколько процентов дневного рациона должен состав-
лять ужин?
27.	Экономия 1 % горючих и смазочных материалов в сель-
ском хозяйстве страны сберегает за год 1,5 млн. т
горючего и 150 тыс. т смазочных материалов. Опреде-
лите годовой расход горючего й смазочных материалов
в сельском хозяйстве нашей страны.
28.	Токарь до обеденного перерыва обработал 24 детали,
что составляет 60% сменной нормы. Сколько деталей
должен обработать токарь за смену?_
29.	Туристы прошли 75% маршрута, и им осталось
пройти еще 5 км. Какова длина маршрута?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
Вычислите:
30.	1)	0,64-0,24;	2)	0,79-0,23;	3)	0,042-0,68;
4)	0,86-0,049;	5)9,6-0,0016;	6)	0,72-0,25.
31.	1)	1,356 + 25,12;	2)	73,12—6,999;	3)	15,12 + 603,3;
4)	7,549 + 27,24;	5)	16,13 — 7,222;	6)	9—4,11.
32.	Oj+l; 2)1+1; 3)1-1; 4) 1+4.
33.	Найдите 1,2 числа: 1) 200; 2) 350; 3) 45; 4) 5.
34.	Найдите 0,12 числа: 1) 300; 2) 250; 3) 25; 4) 1,5.
35.	7,2 числа составляет: 1) 0,36; 2) 0,18; 3) 0,9
неизвестного числа. Найдите это число.
36.	Сейчас отец в 4 раза старше сына. Через сколько лет
он будет старше сына в 2 раза, если сейчас сыну 8 лет?
37.	Сестре 6 лет, а брат в 2 раза старше. Через сколько
лет он будет в 3 раза старше сестры? Как объясйить
полученный результат?
38.	Туристы наметили пройти маршрут за 3 дня. В пер-
вый день они проедут поездом 0,5 маршрута, во вто-
рой день—автобусом 0,5 оставшейся части маршрута,
а в третий день они пройдут пешком оставшиеся 12 км.
Какова длина маршрута?
39.	Туристы наметили за три дня пройти и проехать
маршрут длиной 198 км. В первый день они проедут
307
поездом некоторую часть маршрута, во второй—поло-
вину того пути, что проехали поездом, а в третий
день пройдут оставшиеся 18 км пешком. Сколько кило-
метров туристы проедут поездом?
40.	Расстояние от А до В первый пешеход пройдет за 2 ч,
а второй—за 3 ч. Через сколько часов первый дого-
нит второго, если они одновременно выйдут из А
и В в одном направлении (рис. 7.6)?
I	Л
--------------।----------------j------------
А	В
Рис. 7.6
41.	Бак наполняется через первую трубу за 6 мин и опо-
рожняется через вторую трубу за 9 мин. За сколько
минут наполняется бак через первую трубу, если
вторую трубу оставить открытой?
42.	У хозяйки спросили: «Хорошо ли несутся Ваши куры?»
«Считайте сами,— был ответ,— полторы курицы за
полтора дня несут полтора яйца, а всего у меня
12 кур». Сколько яиц несут куры в день?
43.	На одном и том же расстоянии одно колесо делает
80 оборотов, а другое—70 оборотов. Длина окружно-
сти одного из колес на 2 см больше. -Определите длины
окружностей колес.
44.	Шутка. Летели утки: одна впереди, две позади, одна
позади и две впереди, одна между двумя и три в ряд.
Сколько всего уток? -
45.	Из пунктов А и В одновременно навстречу друг другу
вышли два пешехода и встретились через 1 ч. Первый
из них пришел в В через 1 ч 50 мин после начала
движения. Сколько времени второй шел из В в Л?
46.	Из пунктов А и В одновременно навстречу друг другу
вышли два пешехода и встретились через 35 мин.
Через 25 мин после встречи первый пришел в В.
Через сколько минут после встречи второй пришел в Л?
47.	На рис. 7.7 показано, как можно покрыть плоскость
равными шестиугольниками. Можно ли покрыть
Рис. 7.7
308
плоскость равными пятиугольниками? Если можно, то
как? Можно ли покрыть плоскость равными семи-
угольниками?
48,. Требуется закрасить прямоугольники (рис. 7.8) так,
чтобы каждый из них был одного цвета и чтобы пря-
моугольники, имеющие один цвет, не касались друг
друга сторонами. Почему в случаях 2)—6) нельзя
обойтись двумя цветами? Какое наименьшее количество
цветов потребуется для закрашивания всей плоскости?
Выполните такое закрашивание.
§ 84. Решение задач на проценты
С процентами связаны задачи трех основных типов:
— нахождение процентов данного числа;
— нахождение числа по его процентам;
— нахождение процентного отношения чисел.
Задачи первых двух типов уже рассмотрены в преды-
дущем параграфе. Для их решения достаточно знать, что
процент—сотая часть. Задачи третьего типа связаны с вы-
ражением в процентах отношения двух чисел.
Пример. Из 300 учеников IV и V классов школы
в различных кружках занимается 138. Сколько процен-
тов учащихся IV и V классов занимается в кружках?
Решение. I способ. Вопрос задачи сводится к
определению числа процентов, которое составляет 138
от 300. Примем 300 человек за 100%. Тогда 3 человека
составляют 1 %, так как 300:100 = 3.
309
Определим, сколько процентов составляют 138 учеников:
138:3=46 (%).
II способ. Отношение 138 к 300 равно
138	138-100	1 _ 138-100 0/ _ 4fi 0/
300 ~ 300 ‘ 100 ~ 300 /0“ ™ Л"
Решение обычно записывают короче:
138	138-100 л/ .с 0,
300 =-300“ %=46 %-
Ответ. 46 %.
Чтобы найти процентное отношение двух чисел, надо
их отношение умножить на 100.
Все три типа задач на проценты можно решать е по-
мощью одного приема как задачи на прямую пропорцио-
нальную зависимость.
Примеры. 1) Найдем 7 % от 35.
Решение. Пусть х—искомое число; тогда
х—7 %	х _ 7	_ 35-7 _ 7-7 _ 49 _ „ 9
35 — 100 %	35 — 100’ Х~ 100 — 20 —
V	V
Ответ. 2-^-.
2) Найдем число, 12 % которого равны 3.
Решение. Пусть х—искомое число; тогда
X - 100 %	100	_ лмоо = —
П 3 - 12% I а 12
Ответ. 25.
3) Найдем процентное отношение чисел 8 и 35.
Решение. Пусть х—искомое число процентов; тогда
8— Х% [	8	_ Х_	ЗДГ-8	_ 160 _ „„	6.
35 -100% |	35	100	’ ж	~ 1 ~	7	’
Ответ. 22у %.
УПРАЖНЕНИЯ
1.	1) Найдите 18 % числа 50.
2)	Найдите число, 18 % которого равны 9.
3)	Сколько процентов числа 50 составляет число 9?
310
2.	1) Найдите 15% числа 36.
2)	Найдите число, 15% которого равны 36.
3)	Сколько процентов числа 36 составляет число 27?
3.	Какую часть от числа 100 составляет число:
1)	5;	2) 7;	3) 15;	4) 75?
Ответ выразите в процентах и дробью.
4.	Сколько процентов от 200 составляет число:
1)	28;	2) 12;	3) 100;	4) 188?
5.	В начале XX века в России из каждых 100 человек,
занятых в хозяйстве, 9 человек работали в промыш-
ленности, 75 работали в сельском хозяйстве, 9 человек
работали в торговле. Выразите в процентах долю
работников, занятых в промышленности, сельском
хозяйстве и в торговле, от общего числа занятых
в хозяйстве.
6.	Из 40 учеников класса 25 человек занимается в раз-
личных кружках. Сколько процентов учащихся класса
занимается в кружках?
’ 7. Сколько процентов составляет число:
1)	50 от 40;	2) 40 от 50?
8.	На сколько процентов
1)	50 больше, чем 40;	2) 40 меньше, чем 50?
Почему получились разные ответы в заданиях 1) и 2)?
Поясните.
9.	Увеличьте число 60 на 1) 5%; 2) 15%; 3) 50%.
10.	Выразите дробь (отношение) в процентах:
п 20)3	3-20	60	дп0/.
5 = 5^0=Ю0 =QQ%>
9Y 100)5	5-100	500	1	1СС2О/
3“ 3-100 — 3 ’ 100 “ 1663
3)|; 4) А; 5) 6:8; 6) 8:6.
11.	Уменьшите число 60 на
1)	15%;	2) 20%;	3) 25%;	4) 75%.
12.	Мясо при варке теряет 40% своего веса.
1)	Сколько вареного мяса получится из 6 кг свежего?
2) Сколько свежего мяса нужно взять, чтобы полу-
чить 6 кг вареного?
13.	Цену товара уменьшили на 10%, затем еще на 10%.
На сколько процентов уменьшили цену за 2 раза?
14.	Цену товара сначала повысили на 10%, а затем пони-
зили на 10%. Как изменилась цена в результате?
15.	Цену товара сначала понизили на 10%, а затем повы-
сили на 10%. Как изменилась цена товара в резуль-
тате?
311
16.	Одну сторону прямоугольника увеличили на 10%,
а другую—на 20%. На сколько процентов увеличи-
лась площадь прямоугольника?
17.	Бригада шахтеров решила ежегодно увеличивать
добычу угля на 5%. На сколько процентов за пяти-
летку увеличится добыча угля?
18.	На сколько процентов увеличится вклад в 1000 р.,
при 3% годовых, за 1 год; за 2 года; за 3 года?
19.	На сколько процентов 64 больше, чем 50?
20.	Число 200 увеличили на 20%, полученный результат
уменьшили на 20%. Получится ли число 200 в ре-
зультате? Какое число получится? '
21.	Число а увеличили на 20%, потом еще на 20%. Во
сколько раз увеличилось число а? На сколько про-
центов увеличилось число а за два раза?
22.	В одном килограмме сыра содержится, в зависимости
от сорта, от 200 до 250 г высокопитательного белка.
Сколько процентов белка содержится в сыре?
23.	Кофейный напиток «Дружба» состоит из кофе (20%),
цикория (30%), ячменя (35%) и сои (15%). На изго-
товление напитка использовали на 3,5 кг ячменя
больше, чем цикория. Сколько кофе использовали для
изготовления напитка?
24.	Сплав содержит 62% олова и 38% свинца. В куске
такого сплава содержится олова на 7,2 г больше, чем
свинца. Сколько граммов свинца в этом куске?
25.	Припой содержит 40% олова, 2% сурьмы, остальную
часть припоя составляет свинец. В куске такого при-
поя свинца на 3,2 г больше, чем олова. Определите
вес куска припоя.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
26.	Три доярки обслуживают на ферме 125 коров. Сколько
доярок потребуется для обслуживания 625 коров?
27.	Мама купила 200 г конфет и заплатила за них на 18 к.
меньше, чем в прошлый раз, когда она купила 250 г
таких же конфет. Сколько стоит 1 кг таких конфет?
28.	Для приготовления кофе с молоком в кафетерии на 8
частей кофе берут 75 частей молока, 25 частей сахара
и 92 части воды. Сколько граммов каждого компо-
нента (молока, сахара, воды и кофе) взяли для при-
готовления 12,8 кг напитка?
29.	Для узбекского плова на 10 частей баранины берут
7 частей жира, 15 частей риса, 5 частей лука, 1 часть
моркови, а также соль и специи по вкусу. Сколько
312
лука и моркови надо взять для плова, если риса
берут на 750 г больше, чем баранины?
30.	Первую половину времени, затраченного на всю
поездку, машина ехала со скоростью 55 вторую —
со скоростью 66-^-. Какова средняя скорость движе-
ния?
31.	Первую половину пути машина ехала со скоростью
55-^-, вторую—со скоростью 66-^-. Какова средняя
скорость движения машины на всем участке пути?
32.	Докажите, что на рычажных весах можно взвесить
любой груз весом в целое число граммов, большее
шести, имея гири по 3 и 4 г. Гири разрешается ста-
вить только на одну чашу весов.
33.	Можно ли любой груз весом в целое число граммов,
большее семи, взвесить с помощью гирь по 4 и 5 г,
если при этом разрешается ставить гири лишь на
одну чашу весов?
34.	Докажите, что любую сумму в целое число рублей,
большую семи, можно уплатить трехрублевыми и пяти-
рублевыми банкнотами. При этом расчет можно произ-
вести без сдачи.
§ 85. Десятичные дроби произвольного знака
При работе с десятичными дробями надо помнить, что
десятичная дробь—другая форма записи обыкновенных
дробей.
Любое свойство обыкновенных дробей переносится на
десятичные дроби.
В частности, если перед положительной десятичной
дробью поставить знак плюс (+), то дробь не изменится,
потому что если поставить знак плюс (+) перед равной
ей обыкновенной дробью, то это не изменяет ее.
Например, 2,78 = 4-2,78; 3,99 = 4-3,99.
Если перед положительной десятичной дробью поста-
вить знак минус (—), то получим другую—отрицательную
дробь (меньшую нуля).
Например, 0,9 = -^, -0,9 = -^; 2,71 = 2^, -2,71 =
— Z100‘
313
УПРАЖНЕНИЯ
1. Вычислите:
1) 2,1+(—3,5); 2) (-4,9)+ (-1,3); 3) 4,8—9,9;
4) 6,2—(—1,7); 5)—7,9—(—1,8);	6)—1,2—3,5.
2.	1) 1,56 + (—8,28); 2) —7,53—6,48; 3) —13,75—5;
4)	12,51 — 17,23;	5) 12,285—13,999; 6) 13,4—17,48.
3.	1) (—1,2) 5;	2) (—4,9):7;	3) (—6,4):(—0,8);
4)	72:(—0,6);	5) (— 4,8):0,16; 6) (—1,25)-(-6,4).
4.	1) 4,16-5,1-3,2;	2) 7,39—1,21:1,1;
3)	(— 44,4): 4 + 1,1;	4) (— 6,25): 2,5 + 2,5;
5)0,48:1,6—4,8;	6) 12,5-(— 4):(— 2).
5.	1) 44:(— 25)—6-(4,3 0,8—3,7);
2)	(—11,2: (— 2,8)—3,6 + 2,4):(— 0,4);
3)	—3,6-(—0,5)—(—3,2+ 0,8)-1,05;
4)	21,96:(— 4,5—2,7)—4,5-0,2,
6.	1) (4,28 + 3,6-(—0,85)):(—0,4);
2)	7,68—6,4: (—1,2—0,4);
3)	(— 4,7 + 2,3)-(— 3,5)—8,7 +0,3;
4)	(—14,4):(4,8—4,8-(—1,5))*(—0,3).
7.	1) (0,5—1,2+ 0,3): 1,8+ 0,4; '
2) 0,2-(0,4—1,08+ 0,15)+ 0,2;
3) (0,04 • 0,01 —0,01): 0,25—0,231;
4) —0,8 + 4,2.(0,002:0,04—4,1).
8. Решите уравнение:
1) 0,4х = 3;	2)2х=1,8;
3) 0,Зх = —2,7;	4) 1,5х= —10,5;
5) —0,002х = 25;	6) —1,4х = 2,842.
9. Вычислите:
1)	(654,84:32,1—35,568-.3,42): 2,5;
2)	(3,17 + 25,9632:4,32):(74,358:24,3);
3)	(2763,36:30,4 + 70,7): (714,07:7,07).
10.	Вес розового масла составляет 0,1% от веса перера-
ботанных розовых лепестков.
1)	Сколько масла получится из 1 кг розовых лепестков?
2) Сколько масла получится из 1 т розовых лепестков?
3)	Сколько килограммов розовых лепестков собрали
школьники на плантации, если после переработки
получили 8 кг масла?
11.	Средневолокнистый хлопчатник сорта «Чимбай ЗОЮ»
дает урожай хлопка-сырца до 40 ц с гектара. Выход
волокна составляет до 37,5%. Урожайность сорта
«Фархад» составляет 47 ц с гектара. Выход волокна
из хлопка-сырца этого сорта достигает 32,8%. Какой
сорт хлопчатника дает больше волокна с одного
гектара?
314
12,	Имеется 700 г молока жирности 6%. Сколько воды
надо добавить в это молоко, чтобы получить молоко
жирности 3,5%?
13,	Кусок сплава весом Зкг, содержащий 80% олова
и 20% свинца, сплавили с куском олова весом 7 кг. i
Каким стало процентное содержание олова в сплаве?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
14.	Некоторое число и 0,23 этого же числа в сумме дают:
24,6. Найдите это число.
15.	Некоторое число больше 0,42 этого же числа на 2,9.
Найдите это число.
16.	Число и 25 % этого же числа в сумме равны 625. Най-
дите число.
17Г Число и 20% этого же числа в сумме равны 36. Най-
дите число.
18.	Число больше 25% этого же числа на 60. Найдите
число.
19.	25% числа больше 12% этого же числа на 78. Най-
дите число.
20.	40% числа в сумме с числом 6 равны 66. Найдите
число.
21.	-g- числа и его 15% дают в сумме 90. Найдите число.
22.	В первой бочке 48 ведер воды, а во второй 22 ведра.
Из первой отлили в 2 раза больше ведер воды, чем
из второй. По сколько ведер воды отлили из каждой
бочки, если в первой осталось в 3 раза больше воды,
чем во второй?
23.	Даны три числа. Первое на 5 больше второго, а тре-
тье составляет -у второго. Их сумма равна 54. Най-
дите эти числа.
з
24.	Даны три числа. Первое составляет второго, а тре-
тье в 2 раза больше первого. Сумма трех чисел рав-
на 91. Найдите эти числа.
з
25.	30% класса и еще 5 человек пошли в кино, a v
О
класса и оставшиеся 8 человек—на экскурсию. Сколь-
ко человек в классе?
26.	Смешали сорокапроцентный и десятипроцентный раст-
воры кислоты и получили 600 г пятнадцатипроцент-
ного раствора кислоты. Сколько граммов каждого
раствора взяли?
315
27.	Имеется молоко двух сортов—с жирностью 8% и 5%.
Сколько килограммов молока каждого сорта нужно
взять, чтобы при смешивании получить 60 кг молока
с жирностью 6%?
28.	В квадрате, состоящем из 9 клеток, расставьте три
единицы, три двойки и три тройки так, чтобы в каж-
дом горизонтальном ряду (строке) и в каждом вер-
тикальном ряду (столбце) любая из цифр 1, 2, 3 встре-
чалась только один раз.
29.	В каждой из 9 клеток квадрата поставьте одно из
чисел 1, 2, 3 так, чтобы сумма чисел, стоящих в каж-
дом вертикальном ряду, в каждом горизонтальном
ряду, а также по диагонали, равнялось 6. Сколько
решений имеет задача?
§ 86. Исторические сведения
Мы уже познакомились с вавилонским способом записи
дробей без знаменателей. Например, запись 15°12'36"54'"
соответствует сумме 15 + gg + gg?+go?' Несмотря на гро-
моздкие знаменатели, такая запись позволяла довольно
быстро выполнять действия с дробями. Так, сумма
(5 + бб+збОб; + ^6 + бо+зббб) может быть вычислена
коротко:
, 5°38'54* ,
^6°12'14ff
11°5Г08"
11 , 51 .	8
и равна 11 + эд+зеоо. '
По аналогии с шестидесятеричными дробями позднее
стали записывать и дроби со знаменателями 10, 100,
1000, ...:
6»=6+п+пб+»-5°1,2"з'"-
Потом такую запись упростили, стали отделять целую
и дробную части друг от друга не кружком сверху, а
запятой снизу; цифры десятых, сотых, тысячных и т. д.
стали писать слитно:
5°1'2"3'" = 5,123.
316
В 1427 году самаркандский математик и астроном
Джемшид ибн-Масуд аль-Каши впервые подробно описал
систему десятичных дробей и действий над ними. В Европе
десятичные дроби стали известны через 100 с лишним лет
после этого, благодаря главным образом трудам фламанд-
ского инженера и ученого С. Стевина.
В русской литературе учение о десятичных дробях
было впервые изложено в «Арифметике» Л. Ф. Маг-
ницкого—первом русском печатном учебнике по мате-
матике (1703 г.). Л. Ф. Магницкий был преподавателем
математики в московской школе математических и
навигационных наук. Его книга сыграла большую роль
в распространении математических знаний в России,
по ней учился гениальный русский ученый М. В. Ломо-
носов.
Десятичные дроби, благодаря простой записи и сход-
ным с натуральными числами правилам действий, полу-
чили широкое распространение в практических расчетах.
В некоторых странах, например в США, целую и дроб-
ную части десятичной дроби отделяют не запятой, а точ-
кой. Вместо 1,2; 35,48; 2,008 пишут: 1.2; 35.48; 2.008.
УПРАЖНЕНИЯ
1.	Запишите в виде обыкновенной дроби шестидесяте-
ричную дообь:
1)	3°12'; 2) 5°30'30"; 3) 2°5'45".,
2.	Запишите в виде шестидесятеричной дроби дробь:
» 6?; 2> 2п; 3> Зи-
3.	Запишите в часах и минутах:
1)	97 мин; 2) 125 мин; 3) 357 мин.
4.	Выразите в часах, минутах и секундах:
1)	68 сек;	2) 315 сек;	3) 423 сек.
5.	1) 4000 сек; 2) 4500 сек; 3) 5555 сек.
6.	Выразите в градусах и минутах:
1)	69';	2) 225';	3) 458'.
7.	Выразите в минутах и секундах:
1)	73";	2) 340";	3) 521".
8.	Выразите в rpaflycaxs минутах и секундах:
- 1) 3999";	2) 4222";	3) 8000".
3J7
4
9.	Длину прямоугольника увеличили в у раза. На какую
дробь нужно умножить ширину прямоугольника, что-
бы его площадь не изменилась?
10.	Одну сторону прямоугольника уменьшили на 0,1 ее
длины. Во сколько раз надо увеличить другую сто-
рону, чтобы площадь прямоугольника не изменилась?
11.	Длину прямоугольника уменьшили на 20 %. На сколько
процентов надо увеличить ширину прямоугольника,
чтобы его площадь не изменилась?
12.	На некотором участке пути шофер уменьшил скорость
автомашины на 25%. На сколько процентов увели-
чится время движения?
13.	На некотором участке пути машинист увеличил ско-
рость поезда на 25%. На сколько процентов умень-
шится время движения на этом участке?
14.	На клетчатой бумаге нарисовали квадрат 4x4. Его
надо разрезать на две равные части, которые совпа-
дают при наложении. Но резать разрешается только по
горизонтальным и вертикальным линиям. Знайка на-
шел три решения этой задачи (рис. 7.9). Помогите
Незнайке найти остальные три решения.
Рив. 7.9
15.	Разделите по тем же правилам на две равные части
прямоугольник 3x4. Сколько решений имеет эта
задача?
16.	Велосипедист проехал от села до города со ско-
ростью 15 — , а возвращался со скоростью 10 —.
Какова средняя скорость движения велосипедиста?
Решение. Пусть расстояние от села до города х км.
318
гг	-	х . х 2х , Зх 5л
Тогда велосипедист был в пути ^-)-То=зо+зб=зб
= часов и проехал х+х = 2х км. Вычислим сред-
нюю скорость:

Ответ. 12 —.
ч
17.	Велосипедист ехал со скоростью 15™, потом точке
такое же время—со скоростью 10 Какова сред-
няя скорость движения велосипедиста?
18.	Легковой автомобиль проехал расстояние от А до В
по скоростной трассе со скоростью НО ™, а обрат-
но—со скоростью 90 ™. Определите среднюю ско-
рость автомобиля на всем участке.
19.	Автомобиль ехал со скоростью 110 ™, потом такое же
время—со скоростью 90 ™. Какова средняя скорость
автомобиля?
ВОПРОСЫ для ПОВТОРЕНИЯ
• ПО МАТЕРИАЛУ-ГЛАВЫ VII
1.	Какие дроби называются десятинными?
2.	Как из данной десятичной дроби получить равную ей деся-
тичную дробь? Приведите примеры.
3.	Как сравнить две десятичные дроби?
4.	Как изменится десятичная дробь, если запятую перенести
на k цифр вправо; влево? Приведите примеры.
5.	Покажите на примере, как сложить, вычесть две десятичные
дроби. Приведите примеры.
" 6. Сформулируйте правило умножения десятичных дробей.
7.	Объясните на примере, как разделить десятичную дробь на
натуральное число.
8.	Как разделить одну десятичную дробь на другую?
9.	Что называется процентом?
10.	Как найти несколько процентов числа?
319
Глава VIII. ОБЫКНОВЕННЫЕ И ДЕСЯТИЧНЫЕ
ДРОБИ
§ 87. Разложение обыкновенной дроби
в конечную десятичную дробь
До сих пор мы рассматривали десятичные дроби, на-
зываемые конечными десятичными дробями. Их называют
конечными, потому что после запятой у них стоит конеч-
ное число цифр.
В дальнейшем мы рассмотрим и бесконечные десятич-
ные дроби. У них после запятой бесконечно много цифр.
Рассмотрим примеры:
л Q7C _ 'Ж*	8	3 .
0,375— 1000 — 8	= 2з,
R 79 _ 672	. 168  168 .
0,/Z “ 100 — 25	5а ’
О псе	65	13	13 .
V,UOO 1(Х)О —	2д 53 ,
17 п	170	17
17,0
Из этих примеров видно, что если конечную десятич-
ную дробь записать в виде обыкновенной несократимой
дроби то ее знаменатель q не имеет других простых
делителей, кроме 2 и 5.
Это утверждение можно доказать в общем случае.
Верно и обратное утверждение:
Если знаменатель q несократимой дроби £ не имеет
других простых делителей, кроме 2 и 5, то эта дробь
разлагается в конечную десятичную дробь.
230
Например, | = ±| = -1 = о,8.
В этом примере мы умножили знаменатель дроби на 2,
в результате он превратился в степень числа 10. Чтобы
дробь не изменилась, надо и числитель умножить на 2.
Так же поступаем и в следующих примерах:
501 _ 501 _ 50Ь2 _ 1002	,
500	22.5» “ 23-53-2 — 1000 “1|UUZ-
Для разложения в конечную десятичную дробь обык-
новенной несократимой дроби, знаменатель которой не
имеет других простых делителей, кроме 2 и 5, сущест-
вуют два способа.
Один из них мы уже рассмотрели, он сводится к умно-
жению числителя и знаменателя дроби у на степень 2
или на степень 5, чтобы в знаменателе получилось число 10
в некоторой степени.
Вторым способом является способ деления числителя
на знаменатель уголком. Например, обратим этим спо-
з
собом дробь в десятичную дробь:
3	| 40
30	|0,075
300
~ 280
200
~~ 200
0
з
Следовательно, —0,075.
УПРАЖНЕНИЯ
1.	Может ли иметь простые делители, отличные от 2
и 5, знаменатель обыкновенной несократимой дро-
би, равной конечной десятичной дроби?
2.	Каким свойством должен обладать знаменатель обык-
новенной несократимой дроби, чтобы она разлагалась
в конечную десятичную дробь?
3.	Какими способами можно разложить обыкновенную
дробь в десятичную дробь? Приведите пример.
11 С. М. Никольский и др.	321
4.	Какие простые множители содержит знаменатель дроби:
О	“64” ’	2)	*48” 5	3)	-gg—;	4)	 24 ;
128 ’	6)	"78*'»	7)	—256“;	8)	-62б »
9)	ИГ’	1°)	Too’	И)	Тобо’’	12)	Юооо 7
5. Найдите несократимые дроби, равные данным:
1)	24 60 ’	21 X. • О 20 ’	3)	JL. 100 ’	4) 94 • q> 100 ’
5)	21 . 30 ’	16 - 6) 400 ’	7)	х. 100 •	8) Тбоо •
б.	Запишите в виде обыкновенных несократимых дробей:
1)	0,4;	2) 0,12; 3) 0,125; 4) 1,2;
5) 0,45; 6) 0,04; 7) 1,008; 8) 0,0018.
7.	Запишите дроби в виде дробей, у которых знамена-
тель является степенью 10:
1)	4-i 2) 4: 3) Ь 4) 4-; 5) 4; 6) | .
8.	Разложите обыкновенные дроби в десятичные двумя
способами:
1)Ь, 2)1; 3)£; 4)4.
10.
11.
12.
Разложите обыкновенные дроби в десятичные спосо-
бом деления уголком:
i)-h 2)4= 3> -ЙН 4)Ж =
5) 4;	6)	7)	4’	8>4--'
о 4’	2)	4-;	з)	4-j	4) 4-5
3	.	12	.	7\	17	-	123
5)	25	’ 6) 75	’	7)	200	’3)	20	*
п	783	.	324	.	625	.	„	860	.
*'	40	’	25	’	125	’	400	’
с. 33	с.	1024	804 .	624
5) 60 ’	6)	256	5	7)	400 :	°) 120 ‘
Возможно ли разложение данных обыкновенных дро-
бей в конечные десятичные дроби:
1) 7 ’ 2) 48 ’> 3) 352 ; 4)	;
120 сч 12 . ~ 21 оч 7
3) 38 5 3) 96 ’ 7) 75 5 зоо ?
322
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
13. Представьте числовые выражения в виде произведе-
ния возможно большего числа множителей (отличных
от 1):
1) 40-24;	2) 12-25;
3)	164-125;	4) 112-47.
14.	Определите, является ли данное число простом или
составным:
1)	89; 2) 123; 3) 279; 4) 335;
5)	642; 6) 601; 7) 101; 8) 111.
15.	Определите порядок действий; прочитайте данные
выражения; найдите их значения:
1)	(23)2; 2) (22)3; 3) (З2—23)3; 4) (З2—22)3.
16.	Проверьте справедливость равенства:
1)	1,02+ 1,12+ 1,22= 1,32+ 1,42;
2)	0,33 + 0,43 + 0,53 = 0,63.
17.	Используя равенства упр. 16, вычислите:
1)	(1,02 + 1,12+ 1,22+ 1,32+ 1,42):3,65;
2)	(0,334-0,43 + 0,53 + 0,6s) :2,16.
18.	Проверьте справедливость равенства:
1)	0,13 + 0,63 + 0,83 = 0,93;
2)	10,82 + 10,92 + 11,О2= 13,32+ 13,43;
3)	1,13Ч- 1,23+ 1,33+ 1,43 = 23.
19.	Используя равенства упр. 18, вычислите:
1)	(10,82+ 10,92+ 11,02—13,32—13,42):365;
2)	(1,13+ 1,23+ 1,33+ 1,43 + 23): 1000.
20.	Запишите в виде степени 10:
1)	10; 2) 100; 3) 1000; 4) 1000000;
5)	число, записанное единицей с тридцатью нулями.
21.	Запишите числа в виде произведения простых чисел:
1)	64;	2) 128; 3) 200;	4) 144;
5)	256;	6) 333; 7) 346;	8) 125.
22.	1) 512;	2) 1728; 3) 10000;	4) 4096;
5)	250000;	. -	6) 75000000;
7)	120000000;	8) 3000000000.
23.	Какой цифрой не может оканчиваться квадрат нату-
рального числа?
24.	В каких случаях квадрат натурального числа явля-
ется четным числом?
25.	Какими цифрами оканчиваются кубы последователь-
ных натуральных чисел? В какой последовательности
повторяются эти цифры?
11»^	323
§ 88. Понятие периодической десятичной дроби
Если знаменатель несократимой дроби имеет про-
стой делитель, отличный от 2 и 5, то эта дробь не
разлагается в конечную десятичную дробь. Применив к ней
правило деления уголком, мы не сможем получить конеч-
ную десятичную дробь.
у
Разложим в десятичную дробь число •=. Это несокра-
тимая дробь, и ее знаменатель имеет простой делитель 3,
7
отличный от 2 и 5. Поэтому число у заведомо не раз-
лагается в конечную десятичную дробь. Применим все же
к этой дроби способ деления уголком числителя на зна-
менатель:
7	19
70	0,777...
~~63
70
~63___
70
*~63
70
• • •
На каждом этапе вычислений получается один и тот
же остаток 7, а в частном—одна и та же цифра 7.
Процесс этот бесконечен (не имеет конца). Он привел
нас к выражению
0,777...,
где точки означают, что цифра 7 периодически повторя-
ется бесконечно много раз.
Выражение 0,777... называют бесконечной периоди-
ческой десятичной дробью или просто периодической
дробью и записывают:
0,(7).
Читают это выражение так: «нуль целых и семь в пери-
оде».
Т'	7
Говорят, что число д- представлено в виде периоди-
324
1
ческой дроби 0,(7) или что число -д- разложено в перио-
дическую дробь 0,(7). При этом пишут:
i = 0,777... =0,(7).
У
Выражения -д- и 0,(7) являются разными обозначени-
ями одного и того же числа—в виде обыкновенной дро-
би и в виде бесконечной периодической дроби 0,(7).
2
Пример. Дробь gg несократимая, и ее знаменатель
имеет простые делители, отличные от 2 и 5. Поэтому ее
десятичное разложение не может быть конечным. В самом
деле,
2,00... I 99
2 0 I 0,0202...
2 00
“1 98
20
200
~~ 198
2
• • •
Процесс деления здесь бесконечный, он приводит
к выражению
0,0202...,
где точки означают, что группа цифр (02) периодически
повторяется бесконечно много раз. Это выражение также
называют периодической дробью и записывают: 0,(62).
Читают это выражение так: «нуль целых и нуль два в пе-
риоде»;
Говорят, что число gg представлено в виде периодиче-
ской дроби или разложено в периодическую дробь. При
этом пишут:
^ = 0,0202... =0,(02).
Пример, = 3,1777. .. = 3,1(7).
Правая часть этого равенства читается так: «три це-
лых, одна десятая и семь в периоде».
325
Приписывая к целому числу или к конечной десятич-
ной дроби бесконечно много нулей, мы также превра-
щаем их в бесконечные периодические десятичные дроби
с периодом 0. Например,
27=27,000... =27,(0);
0,354 = 0,354000... =0,354(0).
Следовательно^ любое целое число и любую конечную
десятичную дробь можно считать частным случаем беско-
нечной периодической дроби.
УПРАЖНЕНИЯ
1.	В каком случае несократимая обыкновенная дробь
не разлагается в конечную десятичную дробь?
2.	Каким способом разлагается любая обыкновенная
дробь в десятичную?
3.	Какие десятичные дроби могут получиться при деле-
нии уголком числителя обыкновенной дроби на ее
знаменатель?
4.	Как узнать, в какую десятичную дробь разлагается
обыкновенная дробь—в конечную или бесконечную?
Приведите три примера.
5.	Разложите обыкновенную дробь в десятичную деле-
нием числителя на знаменатель уголком:
1)1; 2)|; 3)1; 4)
Не выполняя деления, разложите обыкновенную дробь
в десятичную:
- 5)|; 6)	7)1; 8)
6.	Разложите обыкновенную дробь в десятичную деле-
нием числителя на знаменатель уголком:
1А — • 91 — •' 3} — • 41 —
*'99’	’ 99 ’	' 99’	' 99 ’
Не выполняя деления, разложите обыкновенную дробь
в десятичную:
56 . R4 67 . ~ 78 . „ 89
5)	99 ’ °) 99 * *' 99 ’ °' 99 ‘
7.	Используя предыдущие задания, запишите периоди-
ческую дробь в виде обыкновенной дроби:
1)	0,(1);	2) 0,(3);	3) 0,(5);	4) 0,(7);
5) 0,(25); 6) 0,(37); 7) 0,(10); 8) 0,(05).
8.	Решите уравнение:
1)	5х+2х = 28;	2) 6х—2х = 36;
326
3)	8х4-х = 72;	4) 9х—х = 72;
5)	5х = 35—2х;	6) бх = 2x4-93;
7)	7х = 78—х;	8) 4х = х4-42;
9)	7х = 2(х4-5);	10) 6х = 4(х—13);
11)	5х = 3(х—10); 12) 9х = 5(х4-16).
9.	Одно из двух равных чисел увеличили на 48, а дру-
гое—в 5 раз. И снова получили равные числа. Най-
дите данные числа.
10,	Число увеличили на 44. При этом оно увеличилось
в 5 раз. Найдите это число.
11,	Одно число в 6 раз больше другого, а их сумма
равна 357. Найдите эти числа.
12.	Одно число в 10 раз больше другого, а их разность
равна 144. Найдите большее число.
13,	В треугольнике АВС АВ= 18 см, ВС на 3,5 см мень-
ше АВ, АС в 1,2 раза больше АВ. Найдите периметр
треугольника АВС.
14.	В треугольнике АВС АВ= 18 см. Это на 3,5 см мень-
ше ВС и в 1,2 раза больше АС. Найдите периметр
треугольника АВС.
15.	Вычислите:
1)	0,424- 1,3;	2)0,42-1,5;	3)0,52:1,3;
4) 3,52—1,002;	5) 3,28:0,16;	6) 5,25-1,04;
7)4,2:0,07;	8)0,8-12,5;	9)0,0164-1,4;
10)	12—3,59;	11) 6,25-3,2;	12) 5,1:0,17.
16.	Как можно записать конечную десятичную дробь или
натуральное число в виде бесконечной десятичной
дроби? Приведите два примера.
17.	Запишите периодические дроби, равные следующим
обыкновенным дробям:
1)|; 2) |; 3)^; 4)12.
«8- Dg; 2)g; 3) A; 4)g.
19.1)|; 2)|; 3)|; 4) |.
20	.1)|?; 2)g; 3)*; 4)g.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
21.	Числа 6, 18, 30, 42 представьте в виде суммы степе-
ней числа 2.
22.	Запишите числовые выражения в виде квадрата не-
которого числа:
1)	32-2;	2) 8-2;	3) 4«-4;	4) 3*-4«.
327
23,	Почему при возведении в квадрат несократимой дроби
(со знаменателем, отличным от 1) не может полу-
читься целое число?
24.	Почему при возведении в квадрат несократимой дроби
не может получиться сократимая дробь?
§ 89. Периодичность десятичного разложения
обыкновенной дроби
Покажем, что если к несократимой дроби Д применить
способ деления уголком, то в частном получим либо ко-
нечное, либо бесконечное периодическое ее десятичное
разложение.
Мы уже знаем, когда может получиться конечное де-
сятичное разложение. Для этого q не должно иметь дру-
гих простых делителей, кроме 2 и 5. В остальных случаях
может быть только бесконечное десятичное разложение.
Наша цель показать, что оно периодическое.
Рассмотрим сначала пример; найдем десятичное разло-
g
жение дроби у. Будем делить 8 на 7 по правилу уголка:
8	17
*“ 7 I 1,14285714...
* гп°
“	7
3 О
2 а
1 4
Tlo
’56.
3 5
“"4 9
—
1 0
2 8
328
Получаемые при делении остатки заключены в квадра-
тики. Мы видим, что остатки, отмеченные одной и двумя
звездочками, равны между собой. Это показывает, что
процесс деления носит периодический характер и приво-
дит к бесконечной периодической дроби, т. е.
4=1,(142857).
То, что десятичное разложение дроби у должно быть
бесконечным периодическим, можно объяснить и без вы-
числений.
Данная дробь у несократимая, ее знаменатель содер-
жит простой делитель, отличный от 2 и 5. Следовательно,
8	л
десятичное разложение числа у не может быть конеч-
ным—возникающие при делении остатки положительны
(не равны нулю) на любом этапе деления. В то же время
каждый остаток меньше 7, т. е. он равен одному из чисел
1, 2, 3, 4, 5, 6. Но тогда, если мы будем рассматривать
подряд остатки, начиная с отмеченного одной звездочкой,
то среди первых 7 из них обязательно должны найтись
два равных между собой, что и показывает, что мы должны
получить в частном периодическую дробь.
Эти рассуждения проводятся для любой несократимой
у, знаменатель которой q имеет хотя бы один про-
стой делитель, отличный от 2 и 5. Если делить р на q
по правилу уголка, то наступит такой этап, когда все
цифры делимого будут снесены. Если рассмотреть подряд
все возникающие (начиная с этого момента) остатки, то
среди первых q из них всегда окажутся два равных между
собой. А это и показывает, что процесс деления беско-
нечный и периодический.
Итак, показано, что любое положительное рациональ-
ное число у разлагается в бесконечную периодическую
дробь.
Напомним, что конечную десятичную дробь мы тоже
называем периодической дробью (с периодом 0).
329
Любая периодическая дробь есть десятичное разложе-
ние некоторого положительного рационального числа.
Рассмотрим на примерах, как можно находить это число.
Пример 1*. Запишем периодическую дробь 0,(8)
в виде обыкновенной дроби. Для этого обозначим иско-
мую дробь через х. Тогда справедливо равенство
х = 0, (8).
Умножая это равенство на 10, получим верное равенство
10х=8, (8) или 10х=8 + 0, (8).
Вычитая первое равенство из второго, находим, что
10х—х = 8, 9х=8,
8
откуда х=-^.
Применив к дроби способ деления уголком, полу-
чим, что эта дробь действительно равна периодической
дроби 0, (8).
Пример 2*. Запишем периодическую дробь 2,35 (7) •
в виде обыкновенной дроби. Для этого обозначим иско-
мую дробь через х. Тогда справедливо равенство х=2,35 (7).
Умножая это равенство на 100 и на 1000, получим,
что верны равенства 100 х = 235, (7) и 1000х = 2357, (7).
Вычитая второе равенство из третьего, находим, что
ЮООх— 100%=2357—235,
откуда
_ 2357 — 235 _ 2122
Х~ 900	900 * 1! ’
2122
Применив, к дроби способ деления уголком, полу-
чим, что эта дробь действительно равна периодической
дроби 2,35 (7).
Можно заметить, что
2,4(0)=^-4 = 2,4,
2,3(9) = ^=^=2,4.
Следовательно,
2,4 = 2,4(0) = 2,3 (9).
330
Также показывается, что любую периодическую дробь
с периодом 9 всегда можно заменить соответствующей
конечной десятичной дробью.
Замечание. Отметим, что при делении уголком де-
сятичное разложение с периодом 9 не возникает. Поэтому
в дальнейшем нет необходимости рассматривать перио-
дические дроби с периодом 9.
УПРАЖНЕНИЯ
1.	Сколько цифр может быть в периоде десятичного раз-
ложения обыкновенной несократимой дроби со знаме-
нателем 13?
2.	Какие обыкновенные несократимые дроби разлагаются
в периодические с периодом О?
3.	Можно ли произвольную периодическую дробь рас-
сматривать как десятичное разложение некоторой
обыкновенной дроби?
4.	В каком случае разложение обыкновенной дроби в
десятичную является конечным?
5.	В каком случае десятичное разложение несократимой
дроби будет бесконечным и периодическим?
6.	Сформулируйте правило записи периодической дроби
в виде обыкновенной. Приведите пример.
7.	Покажите на примере, как периодическая дробь с пе-
риодом 9 превращается в конечную десятичную дробь.
8.	Какое условие должно обязательно выполняться, чтобы
обыкновенная дробь разлагалась в периодическую
с периодом, отличным от О?
9.	Чем объясняется периодичность десятичного разложе-
ния обыкновенной дроби?	'
* 10. Следующие периодические дроби запишите в виде
обыкновенных дробей:
1) 1, (0);	2) 0, (3);	3) 0, (7).
11.1)0,1(2); 2)1,12(3); 3) 7,5(4).
12	.1)0,(12); 2)1,0(12); 3)8,7(21).
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
13.	Укажите на координатной оси числа:
п 9 1 1 1 А- 21 1 1 1 1
Ч	2 ’ 4 ’ 8 ’ 8 ’ ’ 5 ’ 10 ’ 20 ’ 40*
14.	Вычислите:
1)	5,01-7,3 — 26,184:8;
2)	0,5.(7,523 — 3,893):0,11;
331
3) 35,49-7,5—23,31-7,5;
4) 47,53-8,7 + 52,47-8,7.
15.	Найдите значение выражения:
1) 5х+ 8—2х	при	х—7;,
2) 13х+7—15х	при	х = 8;
3) —15х—7+8х—3	при	х — —3;
4) 19х+5—28х—7	при	х=—4.
16.	Решите уравнение:
1)	Зх—±-х=8; 2) х—^-х=12;
а	о
3)	уХ + уХ=10; 4) х + уХ=16.
17.	Решите пропорцию:
i х •*-_8 ф лх 3___х_,
'Т-Т’ >~5~ 10’
ox __ ® • д\ 7 ____ X
д'Ц~~ Тб* ^25 — 7‘
18.	Запишите частное в виде обыкновенной дроби. Выра-
зите эту дробь в виде конечной десятичной дроби (где
это возможно):
1)	1:2;	2) 1:3;	3) 1:4;	4) 1:5.
19.	1) 7:8;	2) 8:7;	3) 5:8;	4) 8:5.
20.	Одно число на 34 больше другого. В то же время
первое число в 3 раза больше второго. Найдите мень-
шее число.
21.	Одно число больше другого на 39 и в 4 раза. Най-
дите большее число.
22.	Сумма двух чисел равна 484. Если к одному из этих
чисел приписать справа нуль, то получится второе
число. Найдите эти числа.
23.	Сумма двух чисел равна 473. Одно из них оканчи-
вается нулем. Если этот нуль зачеркнуть, то полу-
чится второе число. Найдите эти числа.
.24. Несколько ложек стоят 2 р., а столько же вилок
стоят 1 р. 76 к. Сколько стоит 1 ложка, если она
дешевле 50 к.?
§ 90. Непериодические десятичные бесконечные дроби.
Иррациональные числа	~
До сих пор мы рассматривали периодические десятич-
ные дроби, но возможны и бесконечные непериодические
десятичные дроби. Выражение 0,10110111011110111110...,
где после запятой стоят единица, нуль, две единицы, нуль,
три единицы, нуль и т. д., может служить примером по-
332
ложительной бесконечной непериодической дроби. В ней
никакая группа цифр не является периодом (нет периода
сразу после запятой и после любой из цифр). Это пока-
зывает, что данная десятичная дробь не является деся-
тичным разложением какого-либо рационального числа.
Эту бесконечную десятичную дробь принято считать
десятичным разложением положительного иррационального
(нерационального) числа.
Число, которое можно записать в виде бесконечной
непериодической десятичной дроби, называют иррацио-
нальным (нерациональным) числом.
Вот примеры иррациональных чисел:
0,01001000100001...;
17,12345678910111213...;
3,012345678910111213...
У первого числа после запятой стоят нуль, единица, два
нуля, единица, три нуля, единица и т. д.
У второго числа после запятой записаны в возрастаю-
щем порядке числа натурального ряда.
Если обозначить иррациональное число буквой, на-
пример,
а = 0,10110111011110...,
то говорят, что правая часть этого равенства есть деся-
тичное разложение числа а.
Рациональные и иррациональные числа называются
действительными числами.
Любое действительное число представляется в виде
бесконечной десятичной дроби. Если число рациональное,
то дробь периодическая; если число иррациональное, то
дробь непериодическая.
Число до запятой у положительной бесконечной деся-
тичной дроби мы будем называть целой частью этой дроби.
Первую цифру после запятой у бесконечной десятич-
ной дроби называют цифрой первого разряда после запятой,
вторую цифру—цифрой второго разряда после запятой,
третью—цифрой третьего разряда после запятой и т. д.
Для записи произвольной бесконечной десятичной дроби
часто пользуются буквами. Положительная бесконечная
333
десятичная дробь может быть записана при помощи букв
следующим образом:
...
Здесь а0—целая часть дроби. Таким образом, а0 есть нуль
или натуральное число, cq—цифра первого разряда после
запятой, аа—цифра второго разряда после запятой и т. д.
При этом число а0 или хотя бы одно из чисел а,,
а2, ... отлично от нуля. Иначе число было бы нулем.
Поставив перед положительной десятичной дробью знак
минус, получим отрицательную десятичную дробь
OCQjOCyOCgOtgOS^ • • •
Числа (дроби) a0,aia2as ... и —	... назы-
ваются противоположными числами. Если одно из проти-
воположных чисел обозначить буквой а, то другое обо-
значают через —а. .
Если а—положительное число, то —а—отрицательное
число; если же а—отрицательное число, то —а—поло-
жительное число; если а=0, то —а=0.
Модуль (абсолютная величина) действительного числа а
обозначается |о| и определяется следующим образом:
|a[==a,	если а положительно,
|а| = 0,	если а=0,
|а| = — а, если а отрицательно.
Мы определили действительные числа пока формально.
Полное их определение получится, если дать правила их
сравнения, а также правила их сложения, вычитания,
умножения и деления.
УПРАЖНЕНИЯ
1.	Какое число называется рациональным, иррациональ-
ным, действительным числом?
2.	Что называется целой частью бесконечной десятичной
дроби?
3.	Что называется цифрой третьего разряда бесконечной
десятичной дроби? Приведите пример.
4,	Какие числа называются противоположными? Приве-
дите пример.
334
5.	Как обозначается число, противоположное числу о?
6.	Если число обозначено через —а, значит ли это, что
оно отрицательно? Приведите пример.
7.	Что называется модулем (абсолютной величиной)’ дей-
ствительного числа? Приведите три примера.
8.	Как при помощи букв записать положительную (от-
рицательную) бесконечную десятичную дробь?
9.	В каком случае справедливо равенство:
1)	|а| = а; 2) |а| =— а?
10.	Найдите модуль (абсолютную величину) чисел:
1)	—2,(3); 2) —0,5777; 3) —12,0(12); 4) 3,0(13).
II.	Придумайте какие-нибудь пять бесконечных неперио-
дических дробей (иррациональных чисел).
12.	Найдите число, противоположное:
1)	2,5(3); 2) —1,(72);
3)3,1(12); 4) —0,12(37).
13.	Приведите примеры конечных десятичных дробей. За-
пишите их в виде несократимых обыкновенных дробей.
Каким свойством обладают знаменатели полученных
обыкновенных дробей?
14.	Какие из следующих чисел являются рациональными
и какие иррациональными:
1)	0,275;	2)0, (2); 3) 1,32323232...;
4) 1,15(45); 5) 3,10110111011110...; 6) 0,1234567...?
; 15. Запишите четыре числа, являющиеся:
’ 1) натуральными;	2)	положительными;
3) отрицательными;	4)	целыми;
5) рациональными;	6)	иррациональными;
7) четными;	8)	простыми;
9) нечетными;	10)	составными;
11)	кратными 3;	12)	кратными 2 и 5. 4
16.	Запишите два числа, одновременно являющиеся:
1)	рациональными и отрицательными;
2)	целыми и кратными 5;
3)	целыми и положительными;
4)	простыми и большими 30;
5)	составными и четными;
6)	нечетными и кратными 7.
17.	Любое ли иррациональное число является действи-
тельным?
18.	Каждое ли действительное число является иррацио-
нальным? Приведите пример.
19,	Существует ли рациональное число, обращающееся
в бесконечную непериодическую дробь?
S31
20.	Сравните по модулю действительные числа; поставьте
между ними знак > или <; изобразите эти числа на
координатной оси (в произвольном масштабе):
1)	5 и 5,001;	2) 2,6 и 2,596;
3) 2,3 и 2|;	4) 4,7 и 4,(7).
21.	1) у и 0, (142857);	2) | и 0,(12);
3)	—2-| и —2, (67);	4) —0,001 и —0,002.
22.	Верно ли, что каждому рациональному числу соответ-
ствует некоторая точка координатной оси? Верно ли
обратное утверждение, что каждой точке координат-
ной оси соответствует некоторое рациональное число?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
23.	Изобразите на координатной оси числа:
n 1- 1-£• -! _!• _!• 1- -1- 11- -i±-
’	2	’	4 »	4 ’	2 ’	4 »	4 ’	’ *’	4 ’	4	’
9.	1	.	j_.	JL.	£. £•_L-_L-	__1.	__2
2	’	6 »	3 ’	3 ’ 6 »	2 ’	6 ’	3 ’	3	’	6	•
24, Вычислите:
1)	4=1,2+3±.3±;
2)	6,25:-|—(25:154-71-81);
3)	4:34-5:7—2:21;
4)	3,5:41—5,4:7,2.
25. Найдите значение выражения:
1) 4,5*—7,34-5,5* при х= 1,13;
2)4,2*4-13—8,1* при *=1,2;
3)	15*—42,3— 23,6* при *=—0,5;
4)	12,3*—(45—12,3*) при *₽1у.
26, Решите уравнение:
1)	5*—74-1 *=15;
2)	*4-2—31*=—3;
3)	1х-17+ 11*=—4;
4)	1*4-*—11* = —1.
336
27.	За одно и то же время токарь делает 6 деталей, а
а его ученик—4 детали. Сколько деталей сделает
ученик за то же время, за которое токарь сделает
27 деталей?
28.	За одно и то же время мастер делает 6 деталей, а
его ученик—4 детали. Сколько времени потратит
ученик на задание, которое мастер выполняет за 1 ч?
29.	За одно и то же время пешеход прошел 6 км, а ве-
лосипедист проехал 18 км. Сколько километров про-
едет велосипедист за то же время, за которое пеше-
ход пройдет 10 км (если их скорости будут неиз-
менными)?
30,	За одно и то же время пешеход прошел 6 км, а ве-
лосипедист проехал 18 км. Сколько времени потратит
велосипедист на тот путь, который пешеход пройдет
за 2 ч?
31.	Пассажир поезда, идущего со скоростью 60™, за-
метил, что он проехал мост через реку за 0,4 мин.
На обратном пути он проехал мост за 0,3 мин. Опре-
делите скорость поезда на обратном пути.
32,	Автомобилист заметил, что на скорости 60™ он про-
ехал тоннель за 1 мин. За сколько минут он про-
ехал бы этот тоннель на скорости 50™?
33,	Брат с сестрой принесли из леса 23 белых гриба.
Брат помнит, что он нашел на 5 белых грибов боль-
ше, чем сестра. Сколько белых грибов нашел каждый
из них?
34,	В классе 36 учеников, причем девочек на 4 больше,
чем мальчиков. Сколько в классе девочек и сколько
мальчиков?
§ 91. Сравнение действительных чисел.
Приближение числа
Бесконечные десятичные дроби (не имеющие периода 9)'
сравниваются по тем же правилам, как конечные деся-
тичные дроби, на основе сравнения их модулей по циф-
рам разрядов.
Пример. Сравним числа —3,1 и —3,(1).
Так как |—3,11 = 3,1 =3,1000..., |-3,(1)| = 3,(1) =
= 3,1111... и 3,1 < 3,(1), то
-3,1 >-3,(1).
337
С
Действительно, модули этих чисел имеют одинаковые
целые части и одинаковые цифры первого разряда после
запятой, но цифра второго разряда после запятой пер-
вой дроби меньше цифры второго разряда второй дроби.
Поэтому модуль первой дроби меньше модуля второй. Тог-
да по правилу сравнения отрицательных чисел получаем
-3,1 >-3,(1).
Если число мало отличается от числа а, то пишут:
ata at
и говорят, что число а приближенно равно числу а или
что Of есть приближение числа а. Знак « есть знак
приближенного равенства.
Если при этом Of < а, то Of называют приближением а
с недостатком (или снизу). Если же at > а, то Of назы-
вают приближением а с избытком (или сверху).
Если случится, что а1 = о, то Of можно назвать как
приближением а снизу, так и сверху.
Действительные числа, задаваемые бесконечными де-
сятичными дробями или конечными с большим числом
знаков, приближают конечными десятичными дробями.
Сама конструкция десятичной дроби подсказывает, как
эти приближения подбирать. Рассмотрим пример.
Пусть 0 = 2,3(28).
Оборвем эту дробь на цифре второго разряда после
запятой. Получим число 2,32, меньшее, чем а.
Если у числа 2,32 увеличить цифру второго разряда
после запятой на единицу, то получим число 2,33, уже
большее, чем а. Таким образом,
• 2,32 < а < 2,33,
поэтому 2,32 есть приближение числа а снизу, а 2,33
есть его же приближение сверху. Пишут при этом:
a & 2,32, а ж 2,33
и говорят «2,32 есть приближение числа а с точностью
до одной сотой с недостатком (снизу); 2,33 есть прибли-
338
жение числа а с точностью до одной сотой с избытком
(сверху)».
Вместо слов «с точностью до одной сотой» говорят еще
«с точностью до единицы второго разряда после запятой».
Так как третья цифра после запятой у числа больше 5,
то оно ближе к 2,33, чем к 2,32. Поэтому говорят, что
2,33 есть приближение а с точностью до сотой с округ-
лением.
Рассуждая аналогично, получим, что ’
2,328 < а < 2,329, f
а «2,328, а» 2,329,' ч
где 2,328 есгь приближение а с точностью до одной ты-
сячной снизу и в то же время с округлением. Это сле-
дует из того, что цифра четвертого разряда после запя-
той меньше 5, поэтому а ближе к 2,328, чем к 2,329.
2,329 есть приближение а с точностью до 0,001 сверху.
Подобным образом для числа Ь = — 2,3(28) имеют
место неравенства — 2,33 < b <—2,32, откуда	—2,33,
bfst—2,32, и при этом —2,33 есть приближение а с точ-
ностью до 0,01 снизу и в то же время с округлением;
— 2,32 есть приближение с точностью до 0,01 сверху.
Сумма (разность, произведение, частное) двух чисел
считается приближенно равной сумме (разности, произ-
ведению, частному) их приближенных значений.
Отметим, что чем с большим числом разрядов мы бу-
*дем брать приближенные значения двух чисел, тем ближе
будет сумма (разность, произведение, частное) этих при-
ближенных значений к истинной сумме (разности, произ-
ведению, частному) этих чисел.
Пример. Даны числа
а = 3,1834567...,
6 = 1,23(75).
Округлить их с точностью- до десятых и вычислить
приближенно а+ 6, а—Ъ, а-b, округлив результат
до десятых.	j-,
339
Решение.
а «3,2,	6 «1,2;
а + &« 3,2+1,2 = 4,4;
а—&«3,2—1,2 = 2,0;
а-Ь& 3,2-1,2 = 3,84 «3,8;
— ~ — — — — — — 2 666 «27
УПРАЖНЕНИЯ
1.	В каком случае два действительных числа (не имею-
щие периода 9) равны между собой?
2.	Когда не равны два действительных числа?
3.	Как сравнить два действительных числа? Когда одно
действительное число меньше другого? Приведите два
примера.
4.	Если |а[< |&|, то всегда ли верно неравенство а < ft?
5.	Пусть |a| = |ft|. В каких случаях а = Ь и в каких
случаях a#=ft?
6.	Поясните, как надо понимать записи:
1)	а С Ь\	2) а<Ь<с;
3)	а^,Ь<с,	4) а<_Ь^с;
5)	а^Ь^с.
7.	Сравните действительные числа:
1)	2,424242... и —2,424242...;
2)	5,44444... и 5,54444...;
3)	0 и -10,(4);	4) 0,(1) и 0,(2).
8.	1)|и 0,(1); -
2)	0,333333 и |;
3)	—4,313131... и —4,31311311131...;
4)	0,(27) и 1.
9.	Запишите в убывающем порядке следующие действи-
тельные числа:
1)	0,(3);	2) 0,33;	3) 0,3;
4) 0,25;	5) 0,(25);	6)
10.	Запишите в возрастающем порядке следующие дейст-
вительные числа:
1)1;	2)0,2;	3) 0,26; т
4) 0,(2);	5) 0,(26);	6) 0,2626.
340
11.	Покажите справедливость неравенств:
1)	106,727272 < 106,(72) < 106,727273;
2)	—0,34 <— 0,(3) <—0,33.
12.	Расположите числа в порядке возрастания:
1)	—0,142536; —2,(7);	0,125;	0,1(25);
2)	1,(5);	0,(12); —2,778; —2,(778).
13.	Расположите числа в порядке убывания:
Ь —4,7(5); 0,1115; —4,7556;	0,124.
14.	Покажите справедливость неравенств:
1)	5 < 5,(1);	2)	0,(23) < 0,234;
3)	1,2456 < 1,24563;	4)	1,2456 < 1,(3);
5)	0,545454 < 0,(54);	6)	0,(4) < 0,(45).
15.	Верны ли неравенства:
1)	—0,313131 <—0,(3) < 0,313132;
2)	—0,353535 <— 0,(35) <— 0,353534?
16.	Для чисел 2,(1) и 2,111 укажите хотя бы одно такое
число, которое было бы больше одного из них и
меньше другого.
17.	Сравните модули чисел; поставьте между ними знак
>, — или <; изобразите эти числа на координат-
ной оси:
1)	5,1 и 5,001;	2) 12,6 и 12,596;
3)	— 2,3 и 2у;	4) 4,7 и 4,(7).
18.	1) —у и -|;	2) —2,5 и —2,6;
3)	—1,3 и —1,33;	4) —3,(2) и —3,2.
19,	1) Что показывает знак «? Как читается выраже-
ние а « а,?
2)	Какими числами приближают действительные
числа?
3)	Что называется приближением действительного
числа? Приведите пример.
4)	Как получить лучшие приближения действитель-
ного числа?
5)	Как найти приближенно сумму, разность, произ-
ведение и частное двух действительных чисел? По-
кажите на примерах.
20,	1) Что называется приближением с недостатком
(снизу)?
2) Что называется приближением с избытком (сверху)?
3) Что называется приближением с округлением?
Приведите пример.
341
21.	Найдите приближенное значение числа а с недостат- ком: 1)	а = 0,(2) с точностью до 0,001; 2)	л= 1,234567891011... с точностью до 0,01; 3)	а= 12,0(1) с точностью до 0,1.
22.	Найдите приближение числа а с избытком: 1)	а ——0,(3) с точностью до единицы третьего раз- ряда; 2)	а = —1,2777... с точностью до единицы второго разряда; 3)	а =—12,0(01) с точностью до единицы первого разряда.
23.	Найдите приближение числа с точностью до одной сотой: 1) 127,(023);	2) 0,1(27); 3) —1,34(8);	4) —0,56789101112...
24.	Округлите числа с точностью до 0,001: 1) 0,345678; .	2) 0,765432;	3) 0,(42); 4) 0,(26);	5) 0,(62);	6) 0,(500).
25.	Пусть а = 2,14(56), & = 0,78788788878888. Найдите приближенно а + Ь, а—Ь.
26.	Пусть а = 2,13(1), Ь = 0,9(2). Найдите приближенно а-b, -р
27.	Округлите числа с точностью до 0,01 и вычислите их сумму: 1)3+ 0,(1);	2) 1,256 + 2,(5); 3) 0,010010... + 0,2;	4) 2,7(2) + 3,(42)'.
28. Округлите числа с точностью до 0,01 и вычислите их
	разность: 1) 7—0,(3);	2) 1,(45)—1,2; 3) 2,1264—3,(1);	4) 5,(7)—2,(5).
29.	Округлите числа с точностью до 0,1 и вычислите их произведение с точностью до 0,1: 1)3-2,(1);	2) 0,56 0,(3); 3) 0,(1)-0,(2);	4) 12,(45). 10,(1)’.
30.	Округлите числа с точностью до 0,1 и вычислите их частное с точностью до 0,1: 1) 12:0,(1);	2)	0,(2):2; 3) 4,(2): 1,(1);	4)	45,6(12):	10^2)’.
31.	Найдите приближенно сумму чисел, ограничившись двумя знаками после запятой: 1) 3,5+ 3,(5);	2) 1,359 + 3,2(6); 3) 12,351 + 0,(3);	4) 7,(41)+ 5,(36).
342
32. Найдите приближенно разность чисел, ограничив-
шись тремя знаками после запятой!
1) Ц,(4)—7,3;	2) 12,(15)—3,7236;
3) 7,(93)—2,(39);	4) 3,3297—6,(8).
33. Найдите приближенно произведение чисел, ограничив-
шись одним знаком после запятой:
1) 1,3-2,(1);	2) 0,56 0,(3);
3) 9,(1)-6,(2);	4) 12,(45)-10,(1).
34, Найдите приближенно частное чисел, ограничившись
одним знаком после запятой:
1) 3,2:0,(2);	2) 0,(5):2;
3)	3,(82):2,(3);	4) 35,0(8) :4;'(02).
35.	Изобразите на координатной оси (удобно взять еди-
ничный отрезок длиной 10 см) несколько прибли-
женных значений числа 0,(5), т. е. числа 0,5; 0,55;
0,555 и т. д.
36.	Какими свойствами арифметических действий вос-
пользовались при решении следующих примеров:
1) 25-7-3-4 = 25-4-7-3= 100-21=2100;
2)	1,5-7= 1-7 +0,5-7 = 7+3,5=10,5;
з)	64+4=6+4+8+т=6+8+т+4=14?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
37.	Устно вычислите:
1)	0,3:0,5;	2)	0,5:0,3;
3)	0,25:0,75;	4)	0,75:0,25;
5)	0,4:0,05;	6)	0,05:04.
Вычислите:
38,	1) | + 0,5;	2) | + 0,3;
3) -|—0,4;	4) |-0,25;
5)	^ + 0,13;	6)^-0,02.
39.	1) 0,44:0,03—0,21:0,35;
2)	0,45:0,2+3,5:0,03;
3)	12,1:1,1—4,2:0,9;
4)	95: (7,2-0,3:1,44).
40.	Найдите значение выражения:
_	1	2
1)	5х—х	при х=-^-;
3	'	1
2)	х—уХ+5	при ж= —g-;
343
3)'^х--|х+ 1,1 при х=^;
4) 3,2—3,2x4-1уХ при х=-3,
4h Решите уравнение:
1)	2-1 х—6,1 — 1,2х = 0,4;
А
2)	5,2х-|-1-I-X4-6=19-^;
3)	1±Х—3 = 0,7x4-1;
4)	0,3x4-7,3 = — 1-|-х4-1,4.
42,	Решите пропорцию:
1)	х:1| = 5:7;	2) 2,5:х=9:1|;
х — Ь5 .	д\ 1,4__0,35
2,3~0,69’	х ~ 3 '
43.	1) Какие виды десятичных дробей известны?
2)	Приведите примеры конечных десятичных дробей.
Запишите их в виде обыкновенных несократимых
дробей. Каким свойством обладают знаменатели
этих дробей?
3)	Приведите примеры бесконечных периодических
дробей. -
4)	Приведите примеры бесконечных непериодических
дробей. Как называют такие числа?
5)	Как называют числа, которые могут быть записаны
в виде у, где р и q— целые, q^Of
6)	Какие числа называют действительными?
44.	1) Сумма двух чисел равна 432, а их разность
равна 18. Найдите эти числа.
2)	Сумма двух чисел равна 537, а разность—131.
Найдите эти числа.
45.	Одна колхозная бригада собрала на 29 т винограда
больше, чем другая, а вместе они собрали 523 т ви-
нограда. Сколько винограда собрала каждая бригада
в отдельности?
46,	1) Собственная скорость теплохода 40,5™. Скорость
течения реки 3,2™. Найдите скорость теплохода
по течению и против течения реки.
2) Скорость катера против течения реки 20,4™, ско-
344
рость течения реки 2,8™. Найдите скорость ка-
тера по течению.
474 Скорость катера по течению 24,9™, скорость тече-
ния 2,7 ™ . Найдите скорость катера против течения.
Выразите эту скорость в
48.	Скорость лодки по течению 12,1 ™, против течения
2 м
161 у	Найдите собственную скорость лодки и
скорость течения, выразив их в метрах в минуту.
49.	Опытный рабочий может выполнить задание за 12
дней, его ученик—за 24 дня.
1)	Какую часть задания выполнит каждый из них
за 1 день?
2)	Какую часть задания они выполнят при совмест-
ной работе за 1 день?
3)	За сколько дней они выполнят совместно все за-
дание?
4)	Какую часть всего задания при совместном его
выполнении выполнит ученик?
50.	Из двух городов одновременно навстречу друг другу
выехали легковая и грузовая машины. Легковая про-
езжает расстояние между городами за 1 ч 5 мин,
грузовая—за 1 ч 44 мин. Через сколько минут после
начала движения произойдет их встреча?
§ 92. Вычисления с помощью микрокалькулятора
С помощью микрокалькулятора можно выполнять вы-
числения и с десятичными дробями. Для ввода запятой
используют клавишу • . Например, дробь 3,15 вводят
так:	  ___________ ____
3	• ’ 1	5
1	3
1	3	5
0
Дробь 0,135 можно ввести так:
5 , или, короче,
При этом с нажатием клавиши
часть дроби (0).
Действия с десятичными дробями выполняются так же,
как действия с натуральными числами.
вводится и целая
345
Пример 1. Вычислим сумму 3,15 + 2,488.
3
1	5	+	2
4	8	8	=
Ответ. 5,638.
Пример 2. Вычислим разность 0,135—0,048.
Ответ. 0,087.
Пример 3. Вычислим произведение 0,24 х 1,5.
•2 4 х 1 | 5	=
Ответ. 0,36.
Пример 4. Вычислим частное 48,96:0,12.
4	8-9	6	4--	12
Ответ. 408.
561
Пример 5. Выразим дробь в виде десятичной
дроби.
561
Так как дробь равна частному 561:374, то выпол-
ним вычисления по схеме:
5	6______1 +	3 7 4	=
О т в е т. 1,5.
Пример 6. Выразим дробь у в -виде десятичной
дроби.
“1 ~ V “
На экране получится лишь приближенный результат
0,3333333.
Ответ. 0,3333333.
УПРАЖНЕНИЯ
1, Вычислите с помощью микрокалькулятора
1) 3,56 + 7,031;
3) 3,25-4,8;
2, 1) 6,325+1,5031;
3) 6,25-1,92;
2) 4,27— 2,999;
4) 8,8:0,55.
2) 7,1—6,3456;
4) 14,4:0,048.
346
3.	1) 4,295 + 7,35;	2) 7,2391—3,957;
3)	9,58-0,45;	4) 7,896:0,48.
4.	1)	5,728-4,25—20,134;	2)	87,162:4,38+13,78;
3)	6,236-12,5:0,625;	4)	0,729:0,027-3,126;
5)	14,9445:4,05—5,69;	6)	0,016-0,3125—0,05.
5.	С помощью микрокалькулятора найдите приближения
периодических дробей, равных обыкновенным дробям:
1)|; 2)-|; 3)4; 4)
А 1) 13. о\ 25. л» 79	.. 5
6* ’) jjg» 2) gg, 3) gg, 4)
7.	Используя результат упр. 5 и 6, не вычисляя, запи-
шите периодические дроби, равные обыкновенным
дробям:
I)	+ 2)|; 3) g; 4)g.
8.	Вычислите с помощью микрокалькулятора и без него:
1) 1:9-9;	2) 4:7-7.
9.	Вычислите с помощью микрокалькулятора:
1)	891:297;	2) 297:891;
3)	999,9999-9;	4) 7777,7777:1,4.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
10.	Вычислите:
1)	4,526+121—(4у. 1-1 + 4,526);
2) 3-1:2,4 + 9,888—(1+7,888^;
О	\ 1о	у
3) 4>51-31-71-(-5,49-31-10-1);
. 4) 4,573 + 21. з1-(2,073—11-31\.
/ о \	/о у
11.	Найдите значение выражения:
1)	З.(х—11) —1,5х
2)	5,2-(х-1)-(4,2х+-1)
3)	4,8(х + 3) + 2,4-(х—6)
4)	3,5-(2х— 1) — 1,4(5х + 2)
12.	Решите уравнение:
1)	5-(х+ 1,2) = 0,5х— 7,5;
2)	2«(х+з1) = 11х-1;
при х=0,4;
при х——1;
при х=0,5;
ю 13
при х=13^=.
347'
3)	1|.(2х-3) = 4ух+7;
4)	-3-(I= 2*4-3.
13.	Решите пропорцию:
ъ 5,5_ 3 2 .	.. 0,2 _ 2 3
а' X ~~ л 2 ’	х ~ - 1 •
4 —	о —
3	4
14.	Запишите бесконечную периодическую десятичную
дробь в виде обыкновенной дроби:
I)	0,(2); 2) 0,(4); 3) 0,(28); 4) 0,(15).
15.	При изготовлении креветочного масла для бутербродов
на 2 части пасты «Океан» берут 3 части сливочно-
го масла. Сколько пасты и сливочного масла взяли,
если
1)	получилось 250 г креветочного масла;
2)	сливочного масла взяли на 60 г больше, чем пасты
«Океан»?
16.	Для компота взяли 6 частей яблок, 5 частей груш
и 3 части слив. Оказалось, что груш и слив взяли
800 г. Сколько килограммов яблок было взято для
компота? Сколько килограммов фруктов взяли для
компота?
17.	Одна бригада может выполнить задание за 12 дней,
а вместе с другой бригадой—за 9 дней. За сколько
дней вторая бригада может выполнить задание?
18.	Привезенного на ферму корма хватит коровам на 8
дней, а коровам и телятам—на 7 дней. На сколько
дней хватило бы этого корма телятам?
19.	Если раздать детям по 3 яблока, то одного яблока не
хватит. Если раздать по 2 яблока, то 8 яблок оста-
нутся лишними. Сколько было детей? Сколько было
яблок?
20.	Участники математического кружка сели по 2 чело-
века за каждую парту, и 9 парт остались свободны-
ми. Если же они сядут по одному за каждую парту,
то одному человеку не хватит парты. Сколько было
участников кружка?
848
§ 93.	Округление при умножении и делении чисел
Умножение и деление чисел связано с громоздкими
вычислениями. На практике не всегда требуется точный
результат—обычно достаточно вести расчеты приближен-
но. Поэтому при округлении чисел нужно следить за тем,
чтобы не оперировать с цифрами, не влияющими на ре-
зультат. С другой стороны, может оказаться, что отбро-
шенная при округлении цифра как раз существенно вли-
яет на результат.
Надо знать, какие цифры следует оставлять и какие
отбрасывать, чтобы получить оптимальный (наилучший)
результат, т. е. такой, чтобы приближение было по воз-
можности точнее и вычисления были экономными. Точность
вычисления находится в противоречии с простотой вычи-
сления. Большая точность связана с употреблением боль-
шего количества цифр, меньшая требует употребления
меньшего количества цифр, если вычисление производится
правильно.
Чтобы правильно приближенно умножать и делить
числа, надо правильно округлять их. Как это делать, мы
поясним на примерах.
Введем понятие значащей цифры или значащего знака
в десятичной дроби.
Значащей цифрой в десятичной дроби называется ее
первая отличная от нуля, а также все следующие за ней
цифры.
Например, в числе 235000 все цифры значащие, в
числе 0,302 цифры, стоящие после запятой, значащие,
в числе 0,003004 цифры, начиная с цифры 3, значащие.
Округлить число с точностью до третьей значащей
цифры—это значит округлить его с точностью до того
знака, где находится третья значащая цифра. '
Например,
235678 « 236000;
235000 « 235000;
3,7523 «3,75;
0,010278 «0,0103.
349
Сформулируем правило приближенного умножения и
деления положительных чисел, заданных десятичными
дробями.
Чтобы вычислить приближенно произведение или част-
ное положительных чисел с точностью до третьей знача-
щей цифры, надо округлить эти числа с указанной точ-
ностью, перемножить или разделить полученные прибли-
жения и результат округлить с точностью до третьей
значащей цифры.
Пример. Пусть а== 135,78(6), Ь = 0,0068751.
Вычислить приближенно а-b, -у, ~ о точностью до
третьей значащей цифры.
Решение, а «136, 6 «0,00688.
С помощью калькулятора вычислим
а • Ь & 136 • 0,00688 = 0,93568 « 0,936;
f «о»“19767.4--« 19800» 1,98. Ю-;
- &	=0 0000505 *)...« 0,0000506.
а loo	'
Ответ. а-Ьы 0,936; у«1,98104;	«0,0000506.
УПРАЖНЕНИЯ
1.	Укажите значащие цифры для следующих чисел:
1)3,52; 2) 0,352; 3) 0,03520; 4) 7,405.
2.	1) 4,203; 2) 0,005; 3) 0,0420; 4) 7,0003.
3.	1) 10,0050; 2) 6,7000; 3) 0,00067; 4) 0,0100.
4.	Сформулируйте правило приближенного умножения
положительных чисел, заданных десятичными дробями,
с точностью до второй значащей цифры.
5.	Сформулируйте правило приближенного деления по-
ложительных чисел, заданных десятичными дробями,
с точностью до четвертой значащей цифры.
6.	Пусть а = 2,4(3), 6=1,929229222...
Вычислите приближенно а-b с точностью до
1)	второй значащей цифры; 2) третьей значащей цифры.
*) Для определения следующих цифр можно разделить 688 на
136: 688:136 = 5,05882... и в этом числе перенести запятую на 5
цифр влево.
350
7.	Вычислите:
1)	у с точностью до второй значащей цифры',
2)	у с точностью до второй значащей цифры.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
8.	Вычислите:
1)	Г2,75:3|-21:4,375).2А;
2)	(з,244-з|:1±):0,9;
3)	(—4,5)«5-у + (—5,5)-5-|-;
4)	Зу • 7,425 + (—6,425) • 3 у.
9.	Найдите значение выражения:
1)	4у* + 5ух— 2-|-х4- 1 у	при х = у;
2)	5,3х—4,82x4-3,52x4-1	при х—— у",
3)	—(2х—7,2)4-(3,1х—6,3)—1,9 при
4)	5^х—2у) — З(х4-1у)—при х= —у.
10.	Решите уравнение:
1)	(х— 6,2)—(8,54-Зх)= 1,7;
2)	(Зх4-7у) — (бх—2у) = 1;
3)	5(х—7)—3(х—4) = 11;
4)	7(ж+4)_4(х+4)__1.
11.	Старинная русская мера веса золотник составляет
примерно 4,265542 г. Выразите золотник в граммах
с точностью:
1)	до	единиц;	2)	до	десятых;
3) до	сотых;	4)	до	тысячных;
5) до	десятитысячных;	6)	до	стотысячных.
12. На монете 1 р. 1921 г. коллекционер прочитал:
«чистого серебра 4 золотника 21 доля».
1) Определите, сколько граммов серебра содержит
монета, если 1 доля=золотника. Считайте, что
1 золотник «4,27 г.
Ответ округлите до десятых.
2) Определите вес монеты, если серебра в ней 90%.
351
ТЗ. Двигатель автомобиля ЗИЛ-130 мощностью 150 л. с.
расходует 29 л бензина на каждые 100 км пути. Спе-
циальное электронное устройство, подсоединенное к
двигателю, позволяет экономить 6% топлива. Сколь-
ко литров топлива расходует двигатель с электрон-
ным устройством на каждые 100 км пути?
14. На ЗИЛе создан новый двигатель мощностью 185 л. с.,
который расходует на каждые 100 км пути 19 л де-
шевого дизельного топлива. Электронное устройство
позволяет снизить расход топлива до 14 л. На сколь-
ко процентов снижает расход топлива электронное
устройство?
§ 94. Основные свойства действительных чисел
1) Для любых двух действительных чисел а и Ь имеет
место, и притом только одно из соотношений:
а — Ь, а<Ь, а>Ь.
' 2) Для любых действительных чисел а и Ъ таких, что
а < Ь, найдется такое действительное число с, что а < с
и с <Ь, т. е. а < с <Ь.
3) Если а <Ъ и Ъ < с, то а < с—свойство транзитив-
ности неравенств.
4) Если а<Ь, тоа + с<Ы-с для любого действитель-
ного числа с.
5) Если а<& и с—положительное число, то о-с<
< Ь-с.
Для любых действительных чисел а, b и с справедливы
равенства	а -|- b — Ь + а,	(1)
	(а + 6)4-с = а+(й + с),	(2)
	a-b — b-a,	(3)
	(а-Ъ)-с = а(Ь-с),	(4)
	a-(b + c) = a-b + ac,	(5)
	а4-0 = а,	(6)
	а + (—а)=0,	(7)
	а—Ь=а+(—Ь),	(8)
	а! —а,	(9)
	а-0 = 0,	(Ю)
	—а — (—1)-а,	(П)
352
(12)
a.| = |(^°).	(13)
Подчеркнем еще раз, что делить на нуль нельзя, по-
этому запись у бессмысленна для любого действительно-
го числа а, в том числе и для а = 0.
Замечание. Мы знаем, что эти свойства могут
быть обоснованы для рациональных чисел а, Ь, с на осно-
вании соответствующих свойств целых чисел. Подобное
обоснование можно выполнить и для действительных
чисел а, &, с, пользуясь тем, что они приближаются де-
сятичными дробями.
УПРАЖНЕНИЯ
1.	1) В чем заключено свойство (транзитивности нера-
венств?
2)	Что получится с неравенством, если к обеим его
частям прибавить действительное число?
3)	Что получится с неравенством, если обе его части
умножить на положительное число?
4)	Сохранится ли неравенство, если обе его части
умножить на нуль или отрицательное число? При-
ведите примеры.
2.	Сформулируйте:
1)	переместительный закон сложения;^
2)	переместительный закон умножения;
3)	сочетательный закон сложения;
4)	сочетательный закон умножения;
5)	распределительный закон.
‘3. 1) Что получится, если к числу прибавить О?
2)	Чему равна сумма противоположных чисел?
3)	Можно ли разность а—b записать в виде суммы?
4)	Что получится, если число умножить на 1?
5)	Что получится, если число умножить на О?
4.	1) Какое число называется обратным к числу а (а 0)?
2)	Какие числа называются взаимно обратными? При-
ведите примеры.
3)	Чему равно произведение двух взаимно обратных
чисел?
5.	Докажите, пользуясь свойствами действительных чи-
сел, что если
12 С, М, Никольский и др.	353
1)	a < b и с—отрицательное число, то а-с>Ь-с;
2)	0 < а < Ъ, то а* < Ь2;
3)	а < b < 0, то а2 > Ьг.
6. Какими свойствами арифметических действий восполь-
зовались при решении следующих примеров:
1)	125-7-8-3= 125.8.7.3= 1000-21 =21000;
2)	4+4+2++ = 4(74 + 4)-
= ф,0..1131»_^4б4;
4-1 713 ±_22 5 7,3-1 713 —713> '
’5 * ' 19'22 ~ 5 * 22 ’ ' 19 — 1 ’ ' W- ' 19 '
7.	Известно, что если а < Ь, то а + с < b + с для любого
действительного числа с. Проиллюстрируйте это свой-
ство действительных чисел на примере, взяв
а = 4, 7; & = 5, 25; с = 2,
8.	Устно вычислите:
1)	68.48 + 68-52;
3)	87-29 + 87-71;
5)	382-400—500-382;
9.	1) 352-18:9;
3)	126-96:32;
10.	1) 25-7-8;
a) 2++3-+,
5) 78:3-(-1~2-1);
11.	1) 12,5(67)—12,5(67);
3) 4,51(2):!;
3.
2) 59-37 +59-63;
4) 17-73—63-17;
6) 756-350 + 756-650.
2) 748-36:18;
4) 172-256:128.
2) 13-12-25;
4)+7-4-6;
6) (75—100--1)-0,04.
2) 6,7(89)-0;
4) 0:0,0(654).
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
12.	Каково наибольшее действительное число, меньшее
0,9, в запись которого не входит цифра 8?
13,	Существует ли наименьшее число, большее 3,6, в
десятичную запись которого не входят цифры 0, 1,2?
14.	Определите порядок действий, прочитайте выражения
и найдите их значения:
1)	(2,5—5,2)-0,4;
2)	(36,5-5,4+ 0,6):0,1;
3)	(3,5-24,8+ 1,2):0,1;
4)	3,6:(68,l:7,5-8g + 21) + 4A.g.
15.	Расположите в порядке возрастания числа
354
ly; —0,21212121...; 1,112; —0,(2); ly,; —0,(21);
—0,2.
16.	Вычислите, предварительно указав порядок действий:
1) 3-(—2)а;	2) — 4-(—З)3;
3)	— (-3)4;	4) — (—2)3.
17.	Вычислите:
1)	_(_0,3)2;	2)	— (—0,5)3;
3)	—у-С—4)2;	4)	-|.(-3)3;
5)	(-5)8-(—I);	6)	(—З3)2;
7)	(—З2)3;	8)	(—l)ft, k—четное.
18.	При выпечке хлеба из пшеничной муки получается
припек, составляющий массы взятой муки.
1)	Сколько хлеба получится из 2,5 т муки?
2)	Сколько муки надо взять, чтобы получить 2,5 т
хлеба?
19.	При выпечке ржаного хлеба получается припек, состав-
ляющий 30% массы взятой муки.
1)	Сколько хлеба получится из 3,9 т муки?
2)	Сколько муки надо взять, чтобы получить 3,9 т
хлеба?
20.	Старинная задача (Франция, XVII в.). Трое хотят
купить дом за 24000 ливров. Они условились, что
первый даст половину, второй—треть, а третий —
оставшуюся часть. Сколько даст каждый?
21.	Бассейн можно наполнить через одну трубу за 70 мин
или через другую—за 2 ч 6 мин. За сколько минут
можно наполнить бассейн через обе трубы?
22.	Латунь представляет собой сплав меди—3 части и
цинка—2 части.
1)	Определите процентное содержание каждого металла
в сплаве.
2)	Сколько меди и цинка содержит кусок латуни,
в котором меди на 80 г больше, чем цинка? Сколько
весит этот кусок?
23.	Мельхиор представляет собой сплав меди — 80% и ни-
келя—20%.
1)	Определите, сколько частей меди приходится на
одну часть никеля.
2)	Сколько граммов каждого металла содержится
в куске мельхиора, в котором меди на 360 г больше,
чем никеля? Сколько весит этот кусок?
12»
355
Глава IX. СИСТЕМА КООРДИНАТ
§ 95. Длина отрезка
Рассмотрим несколько примеров измерения длины от-
резка. За единичный отрезок (единицу длины) возьмем
1дм (рис. 9.1).
1 ди
|-------------(	]------------1------------1 кв=2 дм
Macuunaffl- 4 Л
Рис. 9.1	Рис. 9.2
Пример 1. Отрезок АВ, изображенный на рис. 9.2,
имеет длину 2 дм, т. е. в отрезке АВ укладывается точно
2 дм.
Пример 2. На рис. 9.3 в отрезке АВ укладывается
2 дм с некоторым остатком, меньшим 1 дм. В этом случае
говорят, что длина АВ приближенно равна 2 дм с точ-
ностью до 1 дм с недостатком, и пишут: АВ « 2 дм.
Рис. 9.3
Пример 3. На рис. 9.4 в отрезке АВ укладывается
2 дм с остатком, в котором укладывается точно 3 см.
В этом случае АВ = 2,3 дм.
1-------------1------------Ч-+-М АВ=2,Здп
А	18
Рис. 9.4
Пример 4. На рис. 9.5 в отрезке АВ укладывается
2 дм с остатком, в котором укладывается 3 см с остатком,
меньшим 1 см. В этом случае длина отрезка АВ прибли-
зь
женно равна 2,3 дм с точностью до 0,1 дм с недостатком:
А В ж 2,3 дм.
।------------|—---------4-Н-Н
д	- 5	.
Рис. 9.5
Пример 5. Если в примере 4 во втором остатке
укладывается, точно 4мм, то ЛВ = 2,34дм.
Пример 6. Если в примере 4 во втором остатке
укладывается 4 мм с остатком, меньшим 1 мм, то говорят,
что длина АВ приближенно равна 2,34 дм с точностью
до 0,01дм с недостатком: АВ «'2,34 дм.
Так же, как в примерах 1—6, можно измерять длины
отрезков любой другой единицей длины: 1 см, 1 м, 1 км, ...
Пример 7. Если АВ = 0,2305, то это значит, что
длина отрезка АВ меньше длины единичного отрезка
(единицы длины); в АВ укладывается 0,2 единицы с остат-
ком, в котором укладывается 0,03 единицы с остатком,
в котором укладывается точно 0,0005 единицы.
Пример 8. Если при измерении АВ при помощи
заданной единицы длины на любом этапе измерения воз-
никает остаток, то длина АВ при помощи конечной десятич-
ной дроби может быть выражена только приближенно.
Точно же длина АВ выражается бесконечной десятичной
дробью: ЛВ = ав,а1а2а8а4 ...
Здесь а0—приближенная длина АВ с точностью до
1 с недостатком,
ae»ai — приближенная длина АВ с точностью до 0,1
с недостатком,
а0.«гаа—приближенная длина АВ с точностью до 0,01
с недостатком и т. д.
Пример 9. Если А В = 3,(07) = 3,070707..., то
3—приближенная длина АВ с точностью до 1 с недо-
статком,
3,0—приближенная длина АВ с точностью до 0,1
с недостатком,
3,07 —приближенная длина АВ с точностью до 0,01
с недостатком,
357
3,070—приближенная длина АВ с точностью до 0,001
с недостатком и т. д.
7
Отметим, что 3,(07) = 3-^. Поэтому это число можно
.рассматривать как длину отрезка, в котором укладывается
7
3 единицы (три единичных отрезка) и еще единицы.
На практике, чтобы начертить отрезок АВ, восполь-
зовались бы его приближенной длиной, заданной деся-
тичной дробью. Например, приняли бы, что АВ а? 3,07.
Ведь обычные измерительные приборы (линейка и др.)
приспособлены к десятичной системе счисления—единица
длины делится на 10, 100, ... равных частей.
Замечание. Ранее вводилось уже понятие длины
отрезка, но только в том случае, когда его длина выра-
жается рациональным числом. В этом параграфе дано
понятие длины произвольного отрезка, которая может
выражаться как рациональным, так и иррациональным
числом.
УПРАЖНЕНИЯ
1.	На рис. 9.6 изображены отрезки ВС, AD, КР.
Определите на глаз длину каждого отрезка в санти-
метрах. Проверьте свой глазомер с помощью линейки.
* с
J) 1
Рис. 9.6
2.	Постройте в тетради три произвольных отрезка и пов-
торите упр. 1.
3.	Определите на глаз расстояние от своей парты до
классной доски (в шагах), а на перемене проверьте
верность прикидки.
4.	Постройте в тетради отрезок длиной в 7, 10 и 13
клеток. Разделите на глаз каждый отрезок на 3 равные
части. Проверьте свой глазомер с помощью линейки.
5.	Постройте отрезок длиной в 17 клеток. Разделите
этот отрезок на 5 равных частей; на 6 равных частей.
6.	Определите на глаз длину и ширину страницы тетради
(в сантиметрах). Найдите при помощи линейки приб-
£58
лиженные значения длины и ширины страницы тетради
(с недостатком) с точностью до 1; с точностью до 0,1,
принимая за единицу измерения 1 см.
7.	Можно ли измерить длину улицы, на которой распо-
ложена школа, с точностью до 0,001; 0,01; 0,1; 1; 10,
принимая за единицу измерения 1 м?
8.	Определите на глаз размеры крышки парты (стола)
- в сантиметрах. Проверьте свой глазомер, определив
при помощи линейки приближенное значение (с недо-
статком) длины и ширины крышки парты (стола)
с точностью до 1, приняв за единицу измерения 1 см.
С 1 Л
।----------1
Рис. 9.7
9.	На рис. 9.7 изображены отрезки АВ и CD,
Приняв за единицу измерения отрезок CD, измерьте
на глаз отрезок АВ с точностью до 1 с недостатком.
Проверьте свой глазомер с помощью циркуля.
10.	Длина отрезка АВ выражена числом 5,375. Запишите
приближенную длину отрезка АВ с точностью до 1;
до 0,1; до 0,01 с недостатком.
11.	Длина отрезка КР равна:
!) 31; 2) 2^; 3) 3^.; 4) 4^-.
Выразите длину отрезка десятичной дробью и найдите
приближенную длину отрезка АВ с точностью до 1;
до 0,1; до 0,01 с недостатком.
12.	Выразите длину отрезка АВ ( АВ— 3^-1 десятичной
дробью и найдите приближенную длину отрезка АВ
с точностью до
1)	0,1;	2) 0,01;	3) 0,001;	4) 0,0001
с недостатком.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
13.	Вычислите:
1)	(111-0,411^:0,59;
2)	(бА-1,35): (24 + 0,2);
359
3)	12,8-0,25: (4—0.125 у,
4)	3-£.(з-§—3,125):4.
14.	Упростите выражение:
1)	Зх—4x4-5х—6;	2) 9—8х 4- 1х—6х;
3)	1,2x4-1,3x4“ 1.7х-}-1,8х;
4)	2,4х4-5,17х—1,9x4-2,83х.
15.	Решите уравнение:
1)	х:5=1,2; 2) х:21 = 3,2;
3)	18:х = 0,3;
4)	4|:х = 2.
16.	Из двух пунктов одновременно навстречу друг другу
выехали всадник и велосипедист и встретились через
1,5 ч. Всадник на весь путь затратил 2 ч 20 мин.
Сколько времени затратил на весь путь велосипедист?
17.	Два пешехода вышли одновременно из двух сел
навстречу друг другу; Один прошел все расстояние
за 220 мин, другой—за 264 мин. Через сколько часов
после начала движения они встретились?
18.	Из двух городов одновременно навстречу друг другу
выехали две автомашины. Одна проехала весь путь
за 4 ч, другая—за 336 мин. Через сколько минут
после начала движения они встретились?
19.	Старинная задача. Летела стая тетеревов, села на
рощу деревьев: подвое на дерево сядут—одно дерево
лишнее, по одному сядут—один тетерев лишний.
Сколько тетеревов в стае?
20.	Задача из трактата «Математика в девяти книгах»
(Джан Цань, Китай, I в.). Сообща покупают вещь. Если
каждый человек внесет по 8, то избыток равен 3. Если
каждый человек внесет по 7, то недостаток равен
4. Спрашивается количество людей и стоимость вещи.
§ 96. Координатная ось
Зададим прямую, на которой выбрано направление,
называемое положительным, и выбрана точка О, называе-
мая начальной точкой. Зададим еще отрезок, длину кото-
рого примем за единицу—единичный отрезок.
Прямую, на которой выбрана начальная точка, поло-
жительное направление и единичный отрезок, называют
координатной осью.
360
На рис. 9.8 координатная ось нарисована горизон.
тально с положительным направлением, идущим вправо
о 1
_____—।-----------------------------
Рис. 9.8
/
от точки О. Но, вообще говоря, координатная ось может
быть расположена вертикально или еще как-нибудь и
положительное направление на ней может быть выбрано
так, как это может оказаться удобным.
Начальная точка О делит координатную ось на два
луча. Один из них, идущий от точки О в положительном
направлении, называется положительным, другой—отри-
цательным.
Каждой точке координатной оси поставим в соответ-
ствие действительное число х по следующему правилу:
начальной точке О поставим в соответствие число нуль
(х = 0); точке А, если она находится на положительном
луче, поставим в соответствие число х, равное длине от-
резка О А (х = ОА);
точке А, если она находится на отрицательном луче,
поставим в соответствие отрицательное число х, равное
длине отрезка ОА, взятой с отрицательным знаком
(х = — ОА).
Определенную таким образом координатную ось назы-
вают координатной осью х, или, коротко, осью х.
Число х, согласно указанному правилу соответствую-
щее произвольной точке оси х, называют координатой
этой точки.
Впрочем, в этих названиях буква х может быть заме-
нена любой другой буквой, например буквами y,z,t.
и тогда говорят об оси у, оси z и т. д.
Согласно указанному правилу:
1)	Каждой точке оси х соответствует действительное
число—координата этой точки.
2)	Две различные точки А, В оси х имеют разные
координаты xt и х2. При этом, если точка В расположена
правее точки А, то Xi < ха.
361
3)	Каждое действительное число есть координата неко-
торой точки оси х.
Иначе говоря, установлено взаимно однозначное соот-
ветствие между точками оси х и действительными чис-
лами.
Точку О называют началом координатной оси х.
Положительный луч называется положительной коор-
динатной полуосью х, а отрицательный луч называется
отрицательной координатной полуосью х.
Для краткости точку, имеющую координату х, назы-
вают точкой х.
Замечание. Ранее вводилось понятие координатной
оси. Но там рассматривались только рациональные точки
числовой прямой, т. е. точки, имеющие рациональные
координаты х, и прямая была «дырявая»— без ирра-
циональных точек. Однако координата х произвольной
точки координатной оси есть, вообще говоря, действитель-
ное число, т. е. оно может быть рациональным или ирра-
циональным. Этот вопрос и был выяснен нами на осно-
вании общего понятия длины отрезка, введенного в § 95.
Теперь координатная ось перестала быть «дырявой» —
каждой ее точке соответствует действительное число.
УПРАЖНЕНИЯ
1.	Что называется координатной осью?
2,	Что называется координатой точки на координатной
оси?
3,	Отметьте на координатной оси х числа:
1)	2; 3; 4; 5;
2)	—1; —2; —3; —4.
4,	Отметьте на координатной оси х точки:
1)	0;	1; —1;	2; —2; 3;	—3;	4; —4; 5;	—5;
2)	0;	1; —2;	3; —4; 5;	—6;	7; —8; 9;	—10.
5,	Как надо понимать утверждение: множество всех
точек координатной оси находится во взаимно одно-
значном соответствии с множеством всех действитель-
ных чисел?
6.	Начертите в тетради координатную ось, взяв единич-
ный отрезок длиной в 2 клетки. Укажите на этой
оси числа:
S62
n	j_. _2_.	A- A-	A-	A- L-
l'	2	’ 2	’	2 ’ 2	’	2 ’	2	’ 2	’
ox	1	2.	3.	4.	5.	6.	7
2 ’	2 ’	2 ’	2 ’	2	’	2	’	2 •
7.	Начертите в тетради координатную ось с единичным
отрезком 5 см.
Укажите на оси числа:
1)	0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9;
2)	—0,1; —0,2; —0,3; —0,4; —0,5; —0,6; —0,7;
—0,8; —0,9.
8.	Начертите координатную ось и укажите на ней еле-,
дующие числа, выбрав удобный для работы единичный
отрезок и положение начальной точки (начала коор-
динатной оси):
___1_. _3 .	_4_. _5	.	_6 .	7_.	___3	.
2 ’ 4 ’	4 ’ 4	’	4 ’	4 ’	4	’
__2 . А-	—А-	А- _1. _1±
5’5’	5 ’	5	’	1;	1	5 :
1)	А- _1. А-
Ч 4 >	4’2’
2)	Г’ -Т’ 4’
-ф.
з)
4.	5 . 9. 7 . 8. о. 10. 11 .
О » О > ^9 О > О J Ф О 9	> 4;
4)	0,5; —0,5; —1; 1,5; —1,5; —2; —2,5; —3; —3,5.
9.	Что такое точка х—5, точка х =— 3?
10.	Что называется рациональной и иррациональной точ-
ками координатной оси?
11.	Как изобразить на координатной оси точки с боль-
шими координатами (по абсолютной величине)? Напри-
мер, укажите на координатной оси точки:
1)	10, И, 12, 13;	2) —25, —24, —23, —22;
3)	100, 101, 102, 103; 4) —257, —256, —255, —254;
5)	60, 70, 80, 90, 100; 6) —30, —20, —10, 0, 10.
• 12. Как изобразить на координатной оси точки с мало
различающимися координатами (или малыми по абсо-
лютной величине)? Например, укажите на координат-
ной оси точки:
1) 2; 2,1; 2,2; 2,3; 2,4; 2) —3,2; —3,1; —3; —2,9; —2,8;
3) 0,01; 0,02; 0,03;	4) —0,04; —0,05; —0,06;
5) 4,053; 4,054; 4,055; 6) —10,01; —10,02; —10,03.
13. Выделите на координатной оси числа, удовлетворяю-
щие следующим условиям:
1) большие 3;	2) х>4;
3) меньшие —2;	4) х<—3;
5)	большие 1,5;	6) —1 <х<0;
7)	меньшие 7,2;	8) —2^х<:5.
363
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
14.	Вычислите:
1)	42,51 — 73,6—4,2-(—1,6);
о\ о4 г 2	. 1	, 2
2)	37-5-2Г- MIT
о, — 4,84:(—0,044)-0,1
3,24-0,375)4-0,1 ’
—6,25:12,54-0,6
4' —10,24:(—6,4):0,08 *
15.	Упростите выражение:
1)	(5х—3)—(Зх—5);
2)	—(8х— 4) + (10х+1);
3)	3-(2х—1)—2-(Зх—1);
4)	5-(Зх—6)—6-(2,5х—5)’.
16.	Вычислите значение выражения:
1)	(2х—7)—(7х—3)	при	х = 0,1;
2)	—(4х—1) — (5—Зх)	при	х — — 0,2;
3)	4(5х—7)—7 (Зх—4)	при	х = —200;
4)	—8 (6х—5) + 4-(12х—10) при	х= 100,001.
17.	Решите уравнение:
! л 2 \	о 4
Х‘\ 4 7 )	и 15 ’
2)	х:0,05 = — 4у;
о\	1С 8	О 4
3)	1627 :х—	827 I
4)	—3j:x=l,5.
18.	Решите пропорцию:
i\ 2L—L. •	9^ — — — •
4 400	50 ’	' 333“ 111 ’
100 __ 25	.. .16 __ 48
~ 51 ’ х “ 5 ‘
19.	Кофе при жарении теряет 12% своего веса.
1)	Сколько жареного кофе получится из 2,5 кг све-
жего кофе?
2)	Сколько свежего кофе надо взять, чтобы получить
2,2 кг жареного?
20.	Яблоки при сушке теряют 80% своего веса.
1)	Сколько сухих яблок получится из 250 т свежих
яблок?
2)	Сколько свежих яблок надо взять, чтобы получить
250 т сухих яблок?
21.	Тракторист должен за 7 дней вспахать поле. Но он
364
вспахивал в день на 2 га больше, чем было заплани-
ровано, и вспахал поле за 6 дней. Сколько гектаров
в день должен был вспахивать тракторист? Какова
площадь поля?
22.	Механизатор должен за 7 дней посеять лен на кол-
хозном поле. Но он засевал в день на 3 га больше,
чем было запланировано, и закончил работу на 1 день
раньше. Сколько гектаров в день засевал механизатор?
23.	Лодка проплыла некоторое расстояние по озеру за 4 ч.
Такое же расстояние плот проплывает по реке за 12 ч.
Сколько времени затратит лодка на тот же путь:
1)	по течению реки; 2) против течения реки?
24.	Катер проплывает некоторое расстояние по озеру за
6 ч, а по течению реки—за 5 ч. Сколько времени по-
требуется плоту на такое же расстояние?
25.	Расстояние между двумя пристанями по течению катер
проходит за 8 ч, а плот—за 72 ч. Сколько времени
потратит катер на тот же путь по озеру?
26.	В старом учебнике математики .расстояние между
Москвой и Петербургом (Ленинград) в одной задаче
выражено в верстах: 609 верст. Выразите это расстоя-
ние в километрах, учитывая, что 1 верста «1,067 км.
Ответ округлите до единиц.
§ 97. Декартова система координат на плоскости
Зададим на плоскости две оси координат, расположив
их под прямым углом друг к другу (такие прямые назы-
ваются взаимно перпендикулярными),—юсь х и ось у —
.с точкой пересечения О, являющейся начальной точкой
каждой из этих осей. Единичные отрезки осей возьмем
равными друг другу.
Говорят, что этим на плоскости определена прямо-
угольная система координат хОу. Ее называют еще де-
~картовой системой координат по имени французского
математика и философа Декарта, введшего в математику
это важное понятие.
Ось х называют еще осью абсцисс, а ось у—осью ор-
динат. Точку О пересечения осей координат называют
началом системы координат. Плоскость, на которой задана
декартова система координат, называют координатной
плоскостью.
365
Обычно ось абсцисс рисуют в виде горизонтальной
прямой, направленной вправо, а ось ординат—в виде вер-
тикальной прямой, направленной вверх (рис. 9.9).
Буквы х, у мы иногда будем заменять другими бук-
вами Z, t, S, и, .. .
Пусть Л — произвольная точка координатной плоскости.
Проведем через точку А прямые, параллельные осям
координат.
Ул
3 -
2 -
1 -
J__i__i__i__i__i__^ 	।	।	।__i_
-5 -4 -3 -2 -1	1	2	3	Lt	5	х
-	1 -
-	2 -
•	Jl-
Рис. 9.9
Прямая, параллельная оси у, пересечет ось х в точке
А*, а прямая, параллельная оси х, пересечет ось у в точке
А2. Координата точки At на оси х называется абсциссой
точки А. Координата точки Аг на оси у называется ор-
динатой точки А. Абсцисса х и ордината у точки А
называются координатами точки А.
Координаты точки записывают в скобках рядом с
буквой, обозначающей эту точку: А (х; у), причем на
первом месте пишется абсцисса, а на втором месте—ор-
дината. Например, точка А, изображенная на рис. 9.10,
366
имеет абсциссу х = 4 и ординату у — 3, поэтому пишут:
Л (4; 3).
На рис. 9.11 изображены прямоугольная система ко-
ординат хОу и точки 0(0; 0), Л (2; 3), В(—1; 1),
С(—3; —2), D(l; 0), Е (2; —2), F (0; 4).
Прямоугольная система координат хОу разделяет пло-
скость на четыре части, называемые координатными
углами или координатными четвертями.
Мы обозначим их римскими цифрами I, II, III, IV
(рис. 9.12).
Если исключить точки, лежащие на осях координат,
то можно сказать, что
точки угла I имеют координаты (х; у) такие,
х > 0, у > 0;
Ул
F -
что
Рис. 9.11	Рис. 9.12
точки угла II имеют координаты (х; у) такие, что
х < 0, у > 0;
точки угла III имеют координаты (х; у) такие, что
х < 0, у < 0;
точки угла IV имеют координаты (х; у} такие, что
х> 0, у < 0.
Например, точка В(—1; 1) на рис. 9.11 принадлежит
углу II; точка Е (2; —2) принадлежит углу IV. Легко
видеть, что абсцисса точки равна нулю тогда и только
тогда, когда эта точка лежит на оси у; ордината точки
равна нулю тогда и только тогда, когда эта точка ле-
жит на оси х.
867
Например, на рис. 9.13 точка Е лежит на оси у и
имеет абсциссу х = 0; точка F лежит на оси х и имеет
ординату у = 0.
Напомним еще, что точка О—начало координат.
Она имеет обе координаты, равные нулю.
у	Важно отметить, что если на пло-
скости задана прямоугольная система
координат, то каждой точке А пло-
р 1 -	скости приводится в соответствие пара
чисел (х; у) — пара координат точки Л,
и в то же время произвольную пару
чисел (х; у) можно рассматривать как
Рис. 9.13 пару координат некоторой точки А
плоскости.
Нужно иметь в виду, что если пара состоит из
разных чисел, то, поменяв эти числа местами, мы
получим другую пару, определяющую другую точку
плоскости.
Поэтому пару координат (х; у) точки А называют
упорядоченной парой чисел. Абсциссу х точки А назы-
вают еще первой координатой, а ординату у—второй ко-
ординатой.
Итак, если на плоскости задана прямоугольная си-
стема координат хОу, то
1)	каждой точке плоскости поставлена в соответствие
упорядоченная пара чисел (пара координат точки);
2)	разным течкам плоскости поставлены в соответствие
разные упорядоченные пары чисел;
3)	каждая упорядоченная пара чисел соответствует
некоторой (одной в силу пункта 2) точке плоскости.
Замечание. Точки (х; у), где х и у—рациональ-
ные числа, называют рациональными точками координат-
ной плоскости.
Рациональные точки полностью не заполняют пло-
скость, между рациональными точками на плоскости
располагаются еще и точки с иррациональными коорди-
натами.
c6S
УПРАЖНЕНИЯ
Is 1) Что означают слова «на плоскости задана декарто-
ва система координат»?
2)	Что называется координатной плоскостью?
3)	Что называется началом системы координат?
4)	Что называется абсциссой, ординатой и координа-
тами точки на координатной плоскости?
5)	Как записывают координаты точки?
6)	Что называется координатными углами?
7)	Для каких точек абсцисса равна нулю?
8)	Для каких точек ордината равна нулю?
9)	Для каких точек абсцисса положительна?
10)	Для каких точек ордината положительна?
11)	Каким свойством обладают координаты точек I,
II, III, IV четвертей?
12)	Как надо понимать утверждение «между точками
координатной плоскости и упорядоченными парами
чисел имеет место взаимно однозначное соответ-
ствие»?
2. Определите координаты точек, изображенных на
рис. 9.14.
Рис. 9.14
3.	Постройте систему координат и отметьте в ней точки:
1)	Л (4; 3); 2) В (2; 4);
3)	С (—5; 2); 4) D(4; —3);
5)	£(—1; 3); 6) М(1; 3);
7)	ЛЦЗ; 0); 8) К(0; —4).
4.	1) А (5; 1); 2) В (—4; 2);
3)	S(—3; —2); 4) Q(l; —4);
5) С (—5; —1); 6) В (4; —2);
7)	L{—3; 0); 8) Р (0; 4).
369
5.	Назовите абсциссу и ординату точки; постройте точку
в системе координат:
1)	А (—3; 4); 2) В (4; —2);
3)С(—2; — 4); 4) D(5; 2);
5) £ (0; 4); 6) £(0; —4);
7) Л4(3; 0); 8) ЛЦ—3; 0)’.
6.	Постройте в системе координат точки (2; 1), (2; 5),
(6; 5), (5; 4), (6; 3), (2; 3). Соедините отрезками
первую точку со второй, вторую с третьей и т. д.
Какая фигура получилась?
7.	Постройте по данным точкам в системе координат
фигуры, соединяя точки, как в упр. 6:
1)	(0; 4), (—2; —2), (3; 2), (—3; 2), (2; —2), (0; 4);
2)	(2; 3), (—2; 3), (—2; 5), (3; 5), (5; 3), (2; 3),
(2; —5), (0; —5), (0; 3);
3)	(0; —4), (0; 0), (3; 3), (6; 0), (6; —4), (0; —4),
(6; 0), (0; 0), (6; —4).
8.	На рис. 9.15 изображены фигуры пентамино (об этой
игре мы рассказывали в IV классе). Для фигуры 1
Рис. 9.15
указаны координаты точек, по которым ее можно
построить:
(—10; 5), (—8; 5), (—8; 4), (—9; 4),
(—9; 1), (—10; 1), (—10; 5).
Укажите координаты точек для остальных фигур.
9.	Постройте фигуру по точкам:
(4; -3), (2; -3), (2; -2), (4; -2), (4; -1), (3; 1),
(2; 1), (1; 2), (0; 0), (—3; 2), (—4; 5), (0; 8), (2; 7),
(6; 7), (8;-8), (10; 6), (10; 2), (7; 0), (6; 2), (6; —2),
(5; -3), (4; -3), (4; -5), (3; -9), (0; -8), (1; -5),
, (1; -4), (0; -4), (0; -9), (-3; -9), (-3; -3),
370
(-7; —3), (-7; -7), (-8; —7), (-8; —8),
(—11; —8), (—10; —4), (—11; —1), (—14; —3),
(-12; -1), (-11; 2), (-8; 4), (-4; 5).
Постройте отдельно две точки: (2; 4), (6; 4).
50. Постройте отрезки АВ и CD, если А (—3; 4),
В (2; —1), С(—2; 0), £>(4; 3). Найдите координаты
точки пересечения отрезков АВ и CD.
11.	Постройте прямые АВ и CD, если А (—1; 1), В(1; 2),
С(—3; 0), D(2; 1). Найдите координаты точки пере-
сечения прямых АВ и CD.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
12.	Вычислите:
1)	49-68+51-68+49-12 + 51-12;
2)	87-52—17-52+87-38—17-38;
3)	77-99 + 23-99 — 77-29 — 23-29;
4)	108-86 — 86-18—108-56+18-56.
13.	Найдите значение выражения:
1)	25х—50 + 44х—88, при х = 2;
2)	13х +39 +21х+63 при х =—3;
3)	128—7%+356—8х	при х — 7;
4)	121 — 11х+456—10х при х=11.'
14.	Решите уравнение:
1)	6(х—3) +2(х + 2) = 10;
2)	5(х— 1)—4(х—2) =10;
3)	2(2х— 1)—3(х—2) = 6 +4(3—2х);
4)	2(х+2)—3(х—2) = 5—4(3х— 1). .
15.	Разрежьте произвольный прямоугольник на две части,
из которых можно сложить треугольник. Сколько
решений имеет задача, если разрез провести по пря-
мой линии?
16.	Разрежьте четырехугольник на две части так, чтобы
из них можно было сложить прямоугольник (рис. 9.16).
Рис. 9,16
371
17.	Разрежьте прямоугольник со сторонами 9 см и 4 см
на две части так, чтобы из них можно было сложить
квадрат.
18.	Старинная задача (Древний Египет, папирус Райнда).
Найти число, если известно, что от прибавления к
2
нему у его и вычитания от полученной суммы ее
трети получается 10.
19.	Старинная задала («Всеобщая арифметика» Ньютона).
Некто желает распределить между бедными деньги.
Если бы у него было на 8 динариев больше, то он
мог бы дать каждому по три, но он раздает лишь
по два и у него остается три. Сколько было
бедных?
20.	Старинная задача (предложена Эйлером). Можно ли
поочередно обойти все семь мостов города Кенигсберга
(ныне г. Калининград), соединяющих районы этого
города с островами на реке Прегель, проходя по
каждому только один раз (рис. 9.17)?
§ 98. Графики
В таблице указаны изменения температуры воздуха в
течение суток.
Время, часы	0	2	4	6.	8	10	12	14	16	18	20	22	24
Температу- ра, градусы	6	4	3	2	3	5	1	7	4	3	0	—2	—3
В системе координат ЮТ отмечены точки (/; Т), а
затем соединены плавной кривой. Получилась непрерыв-
372
ная линия, называемая графиком изменения температуры
воздуха в течение суток (рис. 9.18).
По графику можно определить приближенно темпера-
туру Т в любой момент времени t суток, например при
Z = 13 ч. Для этого надо через точку 13 оси t провести
перпендикуляр к оси t до пересечения с графиком.
Для получения графика изменения температуры на
метеорологических станциях часто пользуются прибором,
называемым термографом. Термограф состоит из барабана,
вращающегося вокруг своей оси при помощи часового
механизма, изогнутой коробки (чувствительной к измене-
нию температуры) и пишущего устройства. При повыше-
нии температуры она разгибается, а прикрепленное к ней
перо поднимается вверх. При понижении температуры
перо опускается. Таким образом, перо вычерчивает на
.движущейся бумажной ленте непрерывную линию—гра-
фик изменения температуры воздуха в зависимости от
времени.
Рассмотрим еще один пример. Поезд вышел в 0 часов из
пункта А. Данные о его движении приведены в таблице.
часы	0	1	2	3	4	5	6	7
S, км	0	100	220	300	300	400	480	600
				поезд стоит				
373
Здесь S—расстояние в километрах от поезда до
пункта А в момент времени t.
Нанесем точки (/; S) на координатную плоскость и
соединим их отрезками, считая, что единица длины на
оси t соответствует часу, а единица длины на оси 5 со-
ответствует 100 км (рис. 9.19).
Полученная ломаная есть график движения поезда.
С его помощью можно приближенно определить, где на-
, 1
ходился поезд .в момент времени, например г=уЧ,
1	1	О1	о 1	.1
1-2 ч. 2ТЧ, Sy ч, 4уч.
Так, в момент / = уЧ поезд находился на расстоянии
50 км от пункта А, так как точка графика, имеющая
абсциссу t=-2> имеет ординату 5 = 50.
Расстояния поезда от пункта А в другие моменты вре-
мени определите самостоятельно.
УПРАЖНЕНИЯ '
1.	В 6 ч утра из поселка на озеро, находящееся в 3 км
от поселка, отправились рыбачить отец и сын. Туда
они шли пешком, а обратно ехали на попутной ма-
шине. На рис. 9.20 изображен график их движения.
Определите с помощью графика:
1)	В какое время рыболовы пришли к озеру?
2)	Что они делали с 7 ч до 8 ч 45 мин?
374
3)	Сколько времени занял у них обратный путь?
4)	С какой скоростью они шли пешком?
5)	С какой скоростью ехала машина?
2.	1) Постройте систему координат (для выполнения за-
дания достаточно рассмотреть первую четверть).
2)	Постройте точки с координатами (1; 4), (2; 7),
(3; 10). Эти точки лежат на одной прямой. Про-
ведите эту прямую.
3)	Отметьте на этой прямой еще две точки, обозначьте
их буквами А и В и запишите их координаты.
4)	Точка С (2,3; 7,9) также лежит на этой прямой.
Покажите ее примерное положение.
5)	Постройте точку D (1,5; 5,3).
6)	Сколько точек отмечено на прямой?
7)	Точка Е (6; у) лежит на этой прямой. Чему ра-
вен у}
8)	Точка К. (х; 16) лежит на этой прямой. Чему ра-
вен х?
3.	На рис. 9.21 приведен график изменения температу-
ры воздуха в течение месяца. Измерения проводились
1)	Какая температура была 4, 8, 12, 21, 27 числа?
2)	В какие дни температура была выше 0°?
375
3) В какие дки температура была ниже 0°?
4.	По данным, приведенным в таблице, постройте гра-
фик изменений температуры воздуха в течение двух
недель. Т—температура воздуха в градусах по Цель-
сию, t—дни.
1)	Сколько дней температура была выше 0°?
2)	Сколько дней температура была ниже 0°?
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
5.	Вычислите:
1)	4,6-7,3 + 5,4-8,5 + 4,6-8,5 + 5,4 7,3;
2)	9,8-17,42 +9,8-5,58—1,8-17,42—1,8-5,58;
3)	15,37-7,88—9,37-7,88—15,37-2,12 + 9,37-2,12;
4)	4,54-77,7—4,54.7,77 + 7,46-77,7—7,46-7,77.
6.	Упростите выражение:
1)	3-(х—5) + 5(х+1) + 10;	'
2)	5 (%— 1)—2(х+3) — Зх;
3)	1,2-(2х— 1) + 3,5-(х—2)+ 10,2;
4)	2,5(х—0,2)—5(2х—0,4) + 0,5х.
7.	Найдите значение выражения:
1) 4,2%—84 + 2,3%—46 + %	при	% = 20;
2) 2,1% +6,3—2,4х—6,2—5	при	х =—3;
3) 3,2-(%—3,2)+ 5,5(%— 2,2)	при	х = 3,2;
4) 6,3-(%+2,4)—9,1-(%+ 1,4)	при	х = —1,4.
8. Решите уравнение:
1)	4-1 %=9,9; 2) 5,5х = — 66;
£
3) —3,6х= 14-|;	4) —2,2% = —4,84.
9. Решите пропорцию:
1) х:7 = 5:8;	2) х:3 = 4:5;
3) 2:х = 3:4;	4) Г.х = 7:8.
376
10,	Прямоугольник задан его вершинами: (—2; —2),
(—2; 2), (7; 2), (7; —2). Разрежьте прямоугольник
на две части так, чтобы из них можно было сложить
квадрат.
11,	Четырехугольник задан своими вершинами: (—4; 1),
(—2; 5), (7; 5), (5; 1). Разрежьте четырехугольник
на две части так, чтобы из них можно было сложить
прямоугольник.
12.	Прямоугольник ABCD задан вершинами: А (—3; 2),
В.(—3; 5), С(5; 5), D(5; 2). Как разрезать прямо-
угольник на две части так, чтобы из них можно было
сложить треугольник? Найдите два способа решения
задачи.
13.	Старинная задача (Китай). В клетке находятся кро-
лики и фазаны. У всех у них 100 ног и 36 голов.
Сколько фазанов и сколько кроликов в клетке?
14.	Старинная задача (Индия). Из четырех жертвовате-
лей второй дал вдвое больше первого, третий—втрое
больше второго, четвертый—вчетверо больше третьего,
а все вместе дали 132. Сколько дал первый?
§ 99. Исторические сведения
Мы уже знаем, что за несколько тысяч лет до нашей
эры натуральными числами пользовались для счета пред-
метов и грубых измерений. Необходимость уточнения из-
мерений привела к открытию дробных чисел.
Еще древние греки рассматривали число как длину
отрезка, знали, что такое отрезок рациональной длины.
Но, занимаясь геометрией, они обнаружили также от-
резки, длины которых не выражаются рациональными
числами. Например, длину диагонали квадрата (отрезка,
соединяющего две его вершины, не принадлежащие одной
стороне) нельзя выразить рациональным числом, если
длина стороны квадрата равна 1. Об этом будет подробно
рассказано в курсе алгебры средней школы.
Таким образом, при решении математических задач
стали появляться иррациональные (нерациональные) числа.
Такими, например, являются числа, квадраты которых
равны соответственно 2; 3; 17. Такие числа знал, а мо-
жет быть, впервые их открыл знаменитый греческий ма-
377
тематик VI века до н. э. Пифагор. Выдающийся италь-
янский математик Д. Кардано в XVI веке пользовался
в своих исследованиях иррациональными числами, кубы
которых равны целым числам.
Важную роль в математике играет число, равное от-
ношению длины Окружности к ее диаметру. Обозначение
этого числа греческой буквой л (пи) получило широкое
распространение после работ Леонарда Эйлера — акаде-
мика Российской академии наук в XVIII веке. Ученые
вычисляли значение л с разной точностью. Так, великий
греческий математик и механик Архимед (III в. до н. э.)
доказал, что л больше 3~, но меньше 3— :
qlO о 1
Оуу ЯС \ О-у •
Самаркандский математик Д. аль-Каши. (XV в.) вы-
разил приближенное значение числа л шестидесятиричной
дробью: л« 3°8'29"44"'. Только в XVIII веке было до-
казано, что число л—иррациональное.
Список отдельных иррациональных чисел, которые
возникали в исследованиях математиков более раннего
времени, можно было бы продолжить, однако к точному
определению действительного числа, выражающего длину
произвольного отрезка, математики пришли сравнительно
недавно—в прошлом столетии.
Это понятие вводится в нашей книге с помощью де-
сятичных дробей. Длина отрезка выражается десятичной
дробью, вообще говоря, бесконечной. Обратно, любая де-
сятичная дробь есть длина некоторого отрезка. Длина
отрезка тесно связана с понятием координатной оси и
системы координат.
Мы знаем, что еще во II — I веках до н. э. китайские
ученые использовали отрицательные числа для обозначе-
ния противоположных состояний: наличие—долг, при-
ход— расход. Они сформулировали и правила действий
с отрицательными числами, но широкое применение от-
рицательные числа получили лишь после того, как их
использовали наряду с положительными числами для
378
обозначения противоположных направлений на прямой.
Французский математик и философ Рене Декарт
(1596—1659 гг.) первым применил систему координат
для решения геометрических задач. В его честь прямо-
угольную систему координат называют декартовой систе-
мой координат.
УПРАЖНЕНИЯ
1.	Выразите десятичной дробью с точностью до тысячных
значения числа л с недостатком и с избытком (по
Архимеду).
2.	Выразите десятичной дробью приближенное значение
числа л по аль-Каши. Результат округлите до седь-
мого знака после запятой и сравните с полученным
позднее значением л « 3,1415926535897932...
3.	Отношение длины окружности (С) к ее диаметру (d)
обозначается буквой л:
Вычислите длину окружности, диаметр которой равен:
1)	Зсм; 2) 5 см; 3) 10 см; 4) 21дм, считая л «3,14.
4.	С помощью нитки и линейки ученица измерила длину
окружности и ее диаметр. Результаты нескольких из-
мерений занесены в таблицу:
С	31,5 см	41 мм	88 мм	14 см
d	10 см	13 мм	28 мм	4,5 см
я				
1)	Вычислите приближенные значения числа л с точ-
ностью до сотых.
2)	Найдите среднее арифметическое четырех прибли-
женных значений числа л.
3)	Проделайте такие же измерения, используя ободок
стакана, банки и т. п.
5.	Диаметр окружности (d) равен двум радиусам (7?):
d = 2/?. Выразите с помощью формулы длину окруж-
ности:	~
1)	через диаметр d; 2) через радиус /?.
379
6.	Вычислите длину окружности радиуса R, если:
1)	#=10 см; 2) # = 5дм; 3) # = 2,5 см; 4) # = 3,5 м.
7.	Площадь круга радиуса R выражается формулой
S = n#2. Вычислите площадь круга, если:
1)	# = 2дм; 2) # = 5см; 3) # = 3м; 4) # = 4см.
8.	Выразите площадь круга через его диаметр d.
9.	В Древнем Египте считали, что площадь круга равна
8
площади квадрата, сторона которого равна у диаметра
круга. Найдите по этим данным приближенное значе-
ние числа я с точностью до сотых.
10.	Старинная задача (из «Арифметики» Л. Ф. Магниц-
кого). Вокруг некоторого города вырыт водный ров,
имеющий внешнее окружение 440 аршин и ширину
14 аршин. Требуется узнать, сколько аршин имеет
этот ров по внутреннему окружению.
11.	Задача-шутка. Земной шар стянули по экватору обру-
чем. Потом длину обруча увеличили на 1 м. По всему
экватору образовался зазор. Пролезет ли в него кошка?
12.	Кордовая авиамодель сделала в воздухе 10 кругов
радиуса 16 м за 25 секунд. Определите скорость кор-
«	км
довои авиамодели в —. Ответ округлите до десятых.
УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
13.	Вычислите*);
(6,25—3,75)-0,8	(2,54-0,75):3,25 .
(4—2,7о):6,25 +	(40 —38,8)-5 ’
14.	Чтобы приготовить стекло, берут 10 частей поташу,
31 часть песку и 2 части мелу. Сколько нужно этих
материалов на 86 пудов стекла?
15.	Число 34 разделите на три таких части, чтобы первая
относилась ко второй как 1:2, а вторая относилась
к третьей как 3:4.
16.	Число 72 разделите на три части так, чтобы первая
, относилась ко второй как 3:5, а вторая относилась
к третьей как 7:8.
17.	Сколько делителей имеет число:
1)	2-2-2-5-5-7; 2) 150; 3) 4000?
18,	Для перевозки 25 зеркал нанят извозчик с условием
заплатить ему по 1р. 50 к. за доставку каждого зер-
*) Задания 13—20—из «Собрания арифметических задач для гим-
назии», изд. 9-е, М., 1874; задачи 21—29—из математических руко-
писей, «Арифметики» Л, Ф. Магницкого и «Курса чистой математики»
Е. Войтяховского.
380
кала в целости и вычесть с него по 5 р. за каждое
разбитое им зеркало. На дороге извозчик действи-
тельно разбил несколько зеркал и за перевозку полу-
чил только 18 р. Сколько зеркал он доставил в целости?
19.	Одна артель плотников, состоящая из 28 человек,
может построить дом в 54 дня, а другая из 30 чело-
век в 45 дней. Какая артель работает лучше?
20.	Десять работников должны кончить работу в 8 дней.
Когда они проработали 2 дня, то оказалось необхо-
димым кончить работу через 3 дня. Сколько нужно
еще нанять работников?
21.	Четверо купцов имеют некоторую сумму денег. Из-
вестно, что, сложившись без первого, они соберут
90 рублей; сложившись без второго,— 85 рублей; сло-
жившись без третьего,— 80 рублей; сложившись без
четвертого,— 75 рублей. Сколько у кого денег?
22.	В жаркий день 6 косцов выпили бочонок кваса за
8 часов. Нужно узнать, сколько косцов за 3 часа
выпьют такой же бочонок кваса?
23.	Лошадь съедает воз сена за месяц, коза—за два ме-
сяца, овца—за три месяца. За какое время лошадь,
коза и овца вместе съедят такой же воз сена?
24.	Четыре плотника хотят построить дом. Первый плот-
ник может построить дом за год, второй—за два года,
третий—за три года, четвертый—за четыре года. Спра-
шивается, за сколько лет они построят дом при сов-
местной работе?
25.	Некий человек покупал масло. Когда он давал деньги
за 8 бочек масла, то у него осталось 20 алтын. Когда
же стал давать за 10 бочек, то не хватило денег пол-
тора рубля с гривною. Сколько денег было у этого
человека?
Примечание: 1 рубль—100 коп., 1 гривна —
10 коп., 1 алтын—3 коп.
26.	Купил полторажды полтора аршина, дал полтретьяжды
полтретьи гривны. Сколько следует уплатить за пол-
девятажды полдевята аршина?
Примечание: в этой задаче «полторажды пол-
тора» означает 1у • 1у, «полтретьяжды полтретьи» —
2у • 2у , «полдевятажды полдевята»—8у • 8у.
27,	Спросил некто учителя: «Скажи, сколько у тебя в классе
учеников, так как хочу отдать к тебе в учение своего
сына». Учитель ответил: «Если придет еще столько
381
учеников, сколько имею, и полстолько и четверть
столько и твой сын, тогда будет у меня учеников 100».
Спрашивается, сколько учеников в классе?
28.	На вопрос «Который час?» ответствовано: «-§- прошед-
ших часов от полуночи до сего времени равны у ос-
тальных до полудня». Спрашивается число часов до
того времени.
29.	Капитан на вопрос «Сколько имеет в команде своей
2
людей?» ответствовал, что -=- его команды в карауле,
2	1	”
У в работе, у в лазарете, да 27 человек налицо.
Спрашивается число людей его команда.
80.	Пекарня получила заказ на выпечку 1,4 т ржаного
хлеба и 1,08 т пшеничного хлеба. Известно, что ржа-
ная мука дает 40 % припека, пшеничная—35 %. Какое
количество муки каждого сорта потребуется для вы-
полнения заказа?
81,	Ученик рассчитал, что стоимость одной книги состав-
ляет 70 % имеющихся у него денег, стоимость дру-
гой—60%. Если бы он имел еще 90 к., то смог бы
купить обе книги. Сколько стоит каждая книга? Сколько
денег было у ученика?
82.	Лист бумаги разрезали на 3 части. Некоторые из. них
снова разрезали на 3 части и т. д. несколько раз.
Может ли в результате получиться 1987; 1988; 1989
кусочков?
33.	Решите задачу 32 при условии, что каждый лист раз-
резали на 5 частей.
84,	Квадрат 3x3 (рис. 9.22) надо разрезать на 9 равных
квадратов. При этом разрешается делать прямые раз-
резы без накладывания частей квадрата друг на друга.
Какое число разрезов придется сделать? Можно ли
его уменьшить?
382
35.	Доказать, что найдется натуральное число п такое,
что запись числа 3" будет оканчиваться цифрами 01.
36,	На дороге, соединяющей два аула, нет ровных участ-
ков. Автобус едет в гору со скоростью 15-^-, а под
гору—со скоростью 30^-. Найти расстояние между
аулами, если путь туда и обратно без остановок авто-
бус проезжает за 4 часа.
37.	Вычислите
].2.3+2.4.6-1-4.8.12+7.14-21
1.3.5 + 2-6.10+ 4.12-20+ 7.21.35'
38.	Дано число А ==1-2-3-4...99-100-101. Докажите, что
числа А + 2, А + 3, А + 4, ..., А + 101—составные.
383
П р иложение
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ (ДО SS7)
2	3	5	7	11	13	17	19
23	29	31	37	41	43	47	53
59	61	67	71	73	79	83	89
97	101	103	107	109	113	127	131
137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223
227	229	233	239	241	251	257	263
269	271	277	281	283	293	307	311
313	317	331	337	347	349	353	359
367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457
461	463	467	479	487	491	499	503
509	521	523	541	547	557	563	569
571	577	587	593	599	601	607	613
617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719
727	733	739	743	751	757	761	769
773	787	797	809	811	821	823	827
829	839	853	857	859	863	877	881
883	887	907	911	919	929	937	941
947	953	967	971	. 977	983	991	997
Никольский Сергей Михайлович, Потапов Михаил Константинович,
Решетников Николай Николаевич, Шевкка Александр Владимирович
АРИФМЕТИКА
Редактор В. В. Абгарян. Художественный редактор Т. И. Кольченко.
Технический редактор С. Я. Шкляр. Корректоры Н. Б. Румянцева, Н. Д. Храпка
ИВ № 32378
Сдано в набор 12.06.87. Подписано к печати 22.02.88. Формат 84 х 108/32.
Бумага тип. № 2 Гарнитура литературная. Печать высокая. Усл. печ. л. 20,16.
Усл. кр.-отт. 20,48. Уч.-изд. л. 20,42. Тираж 400 000 экз. (1-й завод
1—200 000 экз.). Заказ № 8244. Цена 80 коп.
Ордена Трудового Красного Знамени издательство «Паука». Главная ре-
дакция физико-математической литературы, 117071, Москва В-71, Ленинский
проспект, 15
Ордена Октябрьской Революции и ордена Трудового Красного Знамени МПО
«-Первая Образцовая типография» имени А. А. Жданова Союзполиграфпро- /
ма при Государственном комитезе СССР/ по делам издательств, полиграфии
и книжной торговли, 113054, Москва. Валовая, 28
Отпечатано в типографии издательства «Коммуна», г. Воронеж, пр. Рево-
люции, 39.	х

80 коп.