А. Г. ГУРЕВИЧ
МАГНИТНЫЙ РЕЗОНАНС
В ФЕРРИТАХ
И АНТИФЕРРОМАГНЕТИКАХ
ИЗДАТЕЛЬСТВО «наука»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1973
537
Г 95
УДК 538.27
Магнитный резонанс в ферритах и антиферромагнетиках, А. Г. Г у р е в и ч, монография, М., Главная редакция физико-математической литературы изд-ва «Наука», 1973.
Книга представляет собой введение в теорию магнитных колебаний (или магнитного резонанса) в магнитоупорядоченных средах: ферро-, ферри-и антиферромагнетиках. В ней излагаются основные экспериментальные факты, физические представления, модели и методы исследования магнитных колебаний в неметаллических магпитоупоря-дочепных веществах. Рассматриваются процессы, происходящие при достаточно малых амплитудах колебаний — линейные явления.
В книге излагается макроскопическая теория малых магнитных колебаний: однородных (ферромагнитный и антиферромагнитный резонансы) и неоднородных (магнитостатические колебания и спиновые волны). Излагаются также основы электродинамики систем, содержащих намагниченные (гиротропные) среды. Рассматривается и микроскопическая теория магнитных колебаний. Сравнительно подробно исследуются процессы релаксации, ответственные за диссипацию энергии магнитных колебаний.
Табл. 8, библ. 573, рис. 229.
© Издательство «Наука», 1973.
г 0236-1828 042(02)-73
ОГЛАВЛЕНИЕ
Предисловие....................................................... 5
Глава 1. Намагниченный до насыщения изотропный ферромагнетик 9
§ 1.1. Ферромагнетизм. Уравнение движения намагниченности .	9
§ 1.2. Прецессия намагниченности и тензор восприимчивости.
Ферромагнитный резонанс . ;........................ 29
§.1.3.	Учет диссипации.................................. 39
§ 1.4.	Однородные колебания намагниченности малого эллипсоида ....................................................... 48
Глава 2. Анизотропный ферромагнетик........................ 63
§ 2.1.	Обобщение уравнения движения намагниченности	....	63
§ 2.2.	Ферромагнитный резонанс в монокристаллах......... 79
§ 2.3.	Ферромагнитный резонанс в поликристаллах......... 100
Глава 3. Колебания намагниченности при наличии доменои	.	.	110
§ 3.1.	Доменная структура и усредненные параметры ненасыщенного ферромагнетика .'.................................... НО
§ 3.2.	Ферромагнитный резонанс при наличии доменной структуры ....................................................... 125
§ 3.3.	Колебания границ доменов.............................. 136
Глава	4. Антиферромагнетики и ферримагнетики................ 145
§ 4.1.	Антиферромагнетизм. Уравнения движения намагниченностей подрешеток............................................. 145
§ 4.2.	Антиферромагнетики с легкой	осью	анизотропии.......... 160
§ 4.3.	Антиферромагнетики с легкой плоскостью анизотропии.
Слабые ферромагнетики................................... 181
§ 4.4.	Ферримагнетики........................................ 199
Глава 5. Основы электродинамики гиротропных сред.................224
§ 5.1.	Уравнения............................................. 224
§ 5.2.	Однородные плоские волны.............................. 235
§ 5.3.	Квадратичные соотношения. Метод возмущений ....	253
Глава 6. Волноводы и резонаторы с гиротропными средами . .	268
§ 6.1.	Волновод с продольно намагниченной гиротропной средой 268
§ 6.2.	Прямоугольный волновод с поперечно намагниченной гиротропной средой.............................................. 278
§ 6.3.	Резонаторы, содержащие гиротропную среду.......... 294
§ 6.4.	Гиротропный эллипсоид в волноводе................. 310
Глава 7. Магнитостатические колебания и волны................... 322
§ 7.1.	Магнитостатические волны в неограниченной	среде	.	.	322
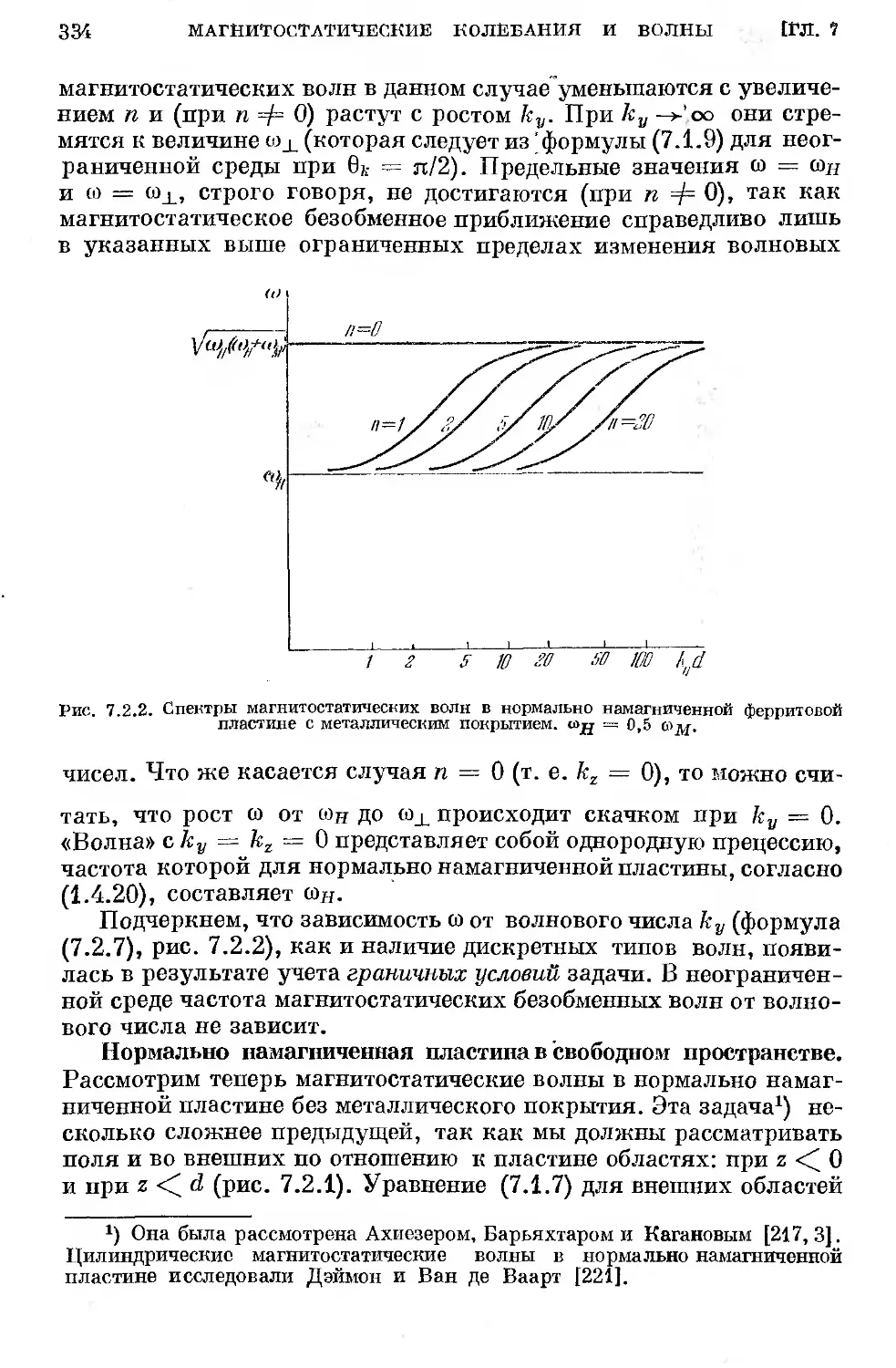
§ 7.2.	Магнитостатические волны в пластинах и стержнях	.	.	.	332
§ 7.3.	Неоднородные магнитостатические колебания......... 351
1*
4
ОГЛАВЛЕНИЕ
Глава 8. Спиновые волны....................................	374
§ 8.1.	Спиновые волны в неограниченном ферромагнетике . .	374
§ 8.2.	Спиновые волны в антиферромагнетиках и ферримагнетиках ..................................................... 388
§ 8.3.	Спиновые волны в ограниченных телах и неоднородных средах................................................... 403
§ 8.4.	Магноны........................................... 424
§ 8.5.	Микроскопическая теория магнонов.................. 436
Глава	9. Процессы релаксации............................. 454
§ 9.1.	Диссипация энергии магнитных колебаний и процессы релаксации в магнитоупорядоченных веществах ....	454
§ 9.2.	Спин-спиновая релаксация в идеальном магнитоупорядоченном кристалле......................................... 465
§ 9.3.	Двухмагнонные процессы............................ 487
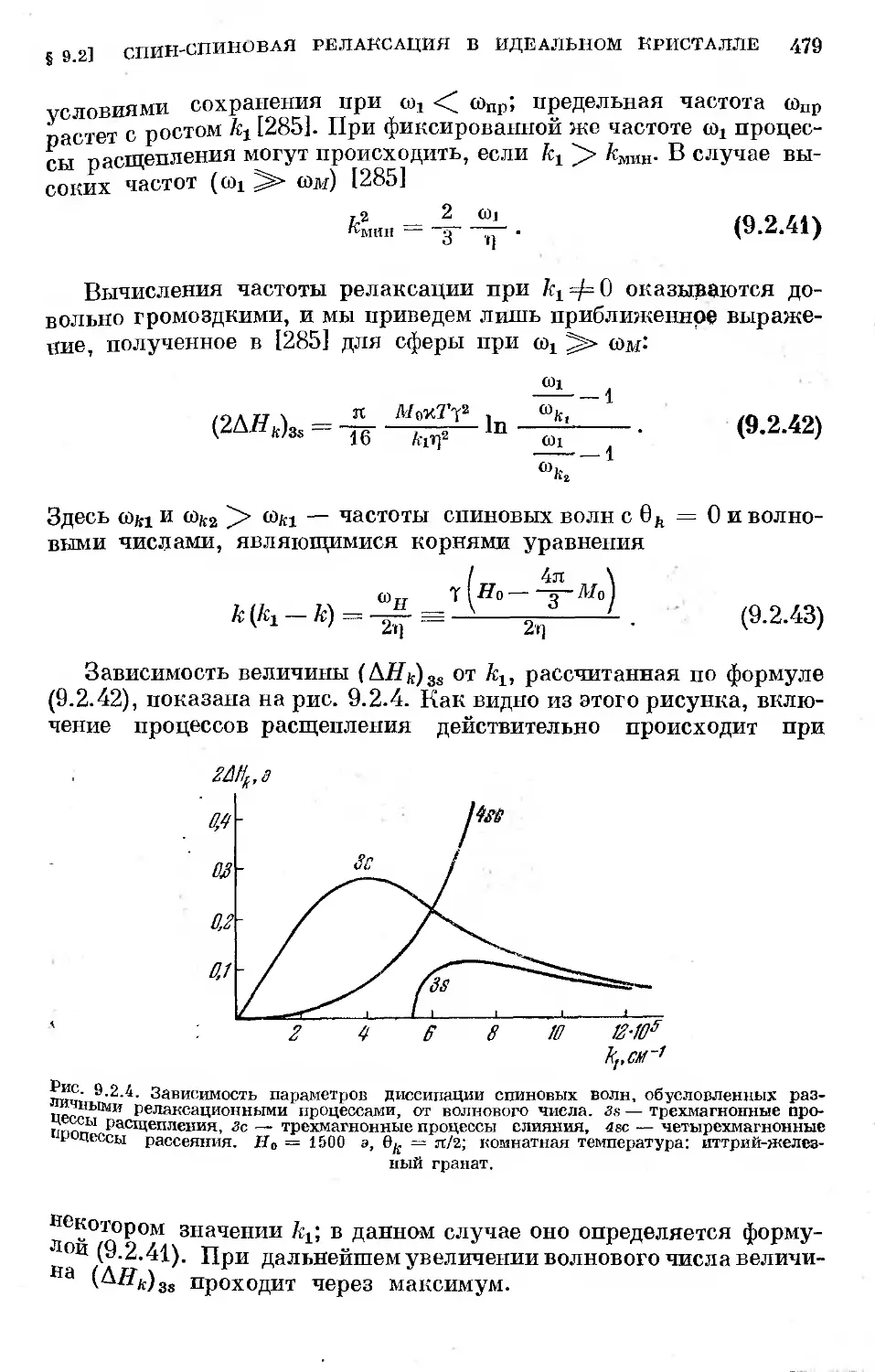
§ 9.4.	Спин-решеточная релаксация........................ 509
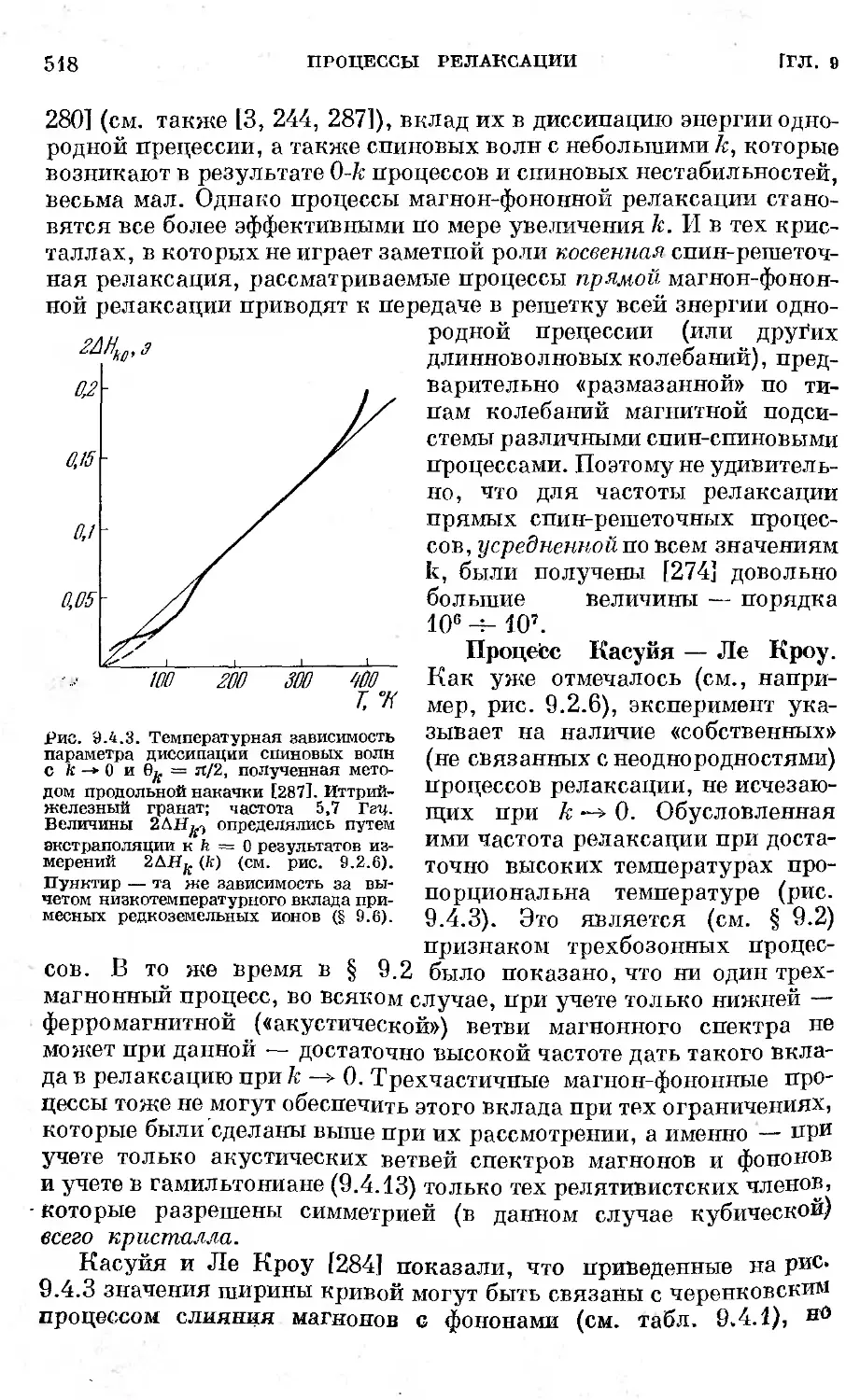
§ 9.5.	Релаксация с участием носителей	тока.............. 519
§ 9.6.	Ионная релаксация................................. 533
Приложение 1. Связь между единицами и значения постоянных 567
Приложение 2. Размагничивающие факторы эллипсоида . .	571
Литература.................................................. 574
ПРЕДИСЛОВИЕ
В этой книге рассматриваются магнитные колебания или магнитный (электронный спиновый) резонанс в веществах, обладающих спонтанным магнитным упорядочением, т. е. в ферро-, ферри-и антиферомагнетиках.
Магнитный резонанс в магпитоупорядоченных веществах существенно отличается от резонанса в неупорядоченных (в магнитном отношении) веществах — парамагнетиках. При магнитном резонансе в парамагнетиках кванты электромагнитного поля вызывают переходы между энергетическими уровнями отдельных атомов. В магнитоупорядоченных же веществах поглощение квантов поля при магнитном резонансе приводит к возникновению коллективных возбуждений всей магнитной системы. Это различие приводит к ряду особенностей магнитного резонанса в магнитоупорядоченных веществах, изучение которых и является предметом книги. В частности, интенсивность резонанса в магнитоупорядоченных веществах с большим спонтанным магнитным моментом — ферромагнетиках и ферримагнетиках — на много порядков превышает интенсивность парамагнитного резонанса.
Изучение магнитного резонанса в магнитоупорядоченных средах представляет интерес по крайней мере с трех точек зрения. Во-первых, эта задача является частью общей проблемы магнитного резонанса и еще более фундаментальной проблемы взаимодействия излучения с веществом.
Во-вторых, исследование магнитного резонанса, т. е. магнитных колебаний, динамики магнитоупорядоченных систем является эффективным средством изучения важных для физики и техники веществ. Путем исследования магнитного резонанса могут быть получены сведения о магнитной структуре ферро-, антифер-ро- и ферримагнетиков, о природе взаимодействий в них, могут быть измерены их основные параметры: обменные константы, константы анизотропии и пр.
В-третьих, магнитный резонанс, в неметаллических ферримагнетиках — ферритах, лежит в основе многочисленных применений ферритов в диапазоне сверхвысоких частот. Этот диапазон (дециметровые, сантиметровые и миллиметровые волны) используется,
6
ПРЕДИСЛОВИЕ
как известно, в радиолокации, космической связи и экспериментальной физике (радиотелескопы, ускорители элементарных частиц, диагностика плазмы). Применение поликристаллических ферритов произвело в середине 50-х годов переворот в технике сверхвысоких частот, открыв возможности создания невзаимных и быстроуправляемых устройств. В настоящее время, в связи с получением высококачественных монокристаллов ферритов и рядом успехов в исследовании магнитного резонанса, открываются возможности создания новых устройств, например ограничителей мощности, управляемых линий задержки и др.
В этой книге будут охвачены далеко не все вопросы магнитного резонанса в магнитоупорядоченных веществах. Во-первых, мы ограничимся рассмотрением малых колебаний, т. е. линейных процессов. За пределами книги останутся нелинейные явления х), в частности спиновые нестабильности (они лишь слегка будут затронуты в § 9.2).
Далее, мы будем рассматривать, в основном, процессы, происходящие внутри магнитоупорядоченной системы. Не будут исследоваться связанные колебания магнитной системы и кристаллической решетки * 2), связанные колебания электронной и ядерной магнитных систем 3) и другие «смешанные» колебания, обусловленные взаимодействиями магнитной системы и других систем магнитоупорядоченного вещества. Однако влияние некоторых из этих взаимодействий на процессы релаксации (которыми определяется диссипация энергии магнитных колебаний) будет подробно исследовано.
И, наконец, мы ограничимся рассмотрением слабо проводящих, неметаллических ферро-, ферри- и антиферромагнетиков. Конечно, и для металлов будет справедливо очень многое из приведенного в книге. Но специфика магнитного резонанса в металлах 4) почти полностью останется за ее рамками.
Эта книга является, по существу, введением в теорию магнитного резонанса (малых магнитных колебаний) в магнитоупорядоченных средах. В соответствии с таким ее назначением в ней рассматриваются главным образом физические представления, 'модели, теории явлений. Экспериментальные результаты приводятся и обсуждаются лишь в очень ограниченном количестве,"как правило, в тех случаях, когда они дают нечто принципиально новое, не следующее из рассмотренной теории, или когда предпосылки теории нуждаются в экспериментальной проверке. Исключение сделано
*) Нелинейные явления при ферромагнитном резонансе рассмотрены, например, в [15, 537].
2) См., например, обзоры [347, 355], а также соответствующие главы в [3, 244].
8) См. монографию [22].
. 4) См. ,Пнапример, [363].
ПРЕДИСЛОВИЙ
1
лишь для нескольких экспериментов, сыгравших особо важную роль в истории исследования магнитного резонанса. Описание аппаратуры и техники эксперимента не входит в задачу книги.
Эта книга является прежде всего учебным пособием, а не справочной монографией, хотя, по-видимому, в какой-то мере будет выполнять и функции последней. Книга рассчитана на студентов, аспирантов, научных работников и инженеров — радистов или технологов, приступающих к изучению данной, как нам кажется, довольно интересной области физики. Цель книги — ввести читателя в круг представлений этой области, познакомить с методами, которые в ней используются, подготовить к чтению оригинальной литературы.
Такой целью определяются отбор материала и характер изложения. Автор старался ограничиться сравнительно небольшим числом вопросов, но разобрать их подробно, с обоснованием принятых методов исследования и допущений, подробными выкладками и анализом результатов. Конечно, выбор таких вопросов не может не быть субъективным, но автор стремился остановиться на задачах, наиболее простых и в то же время важных в принципиальном и, по возможности, в практическом отношении. Лишь в отдельных случаях, ради полноты освещения важных вопросов, затрагиваются задачи, подробное решение которых оказалось бы слишком громоздким. Тогда, без попыток дать сокращенный вывод, приводятся основные предпосылки и окончательные результаты.
Предполагается, что читатель изучал математику, электродинамику, квантовую механику и физику твердого тела в пределах курсов вузов физического или радиотехнического профиля. Сведения из теории магнетизма *), необходимые для понимания рассматриваемых в книге вопросов, приводятся кратко по ходу изложения. Первые параграфы глав 1,2,3 и 4 в значительной части посвящены этому.
Изложение носит индуктивный характер, с наращиванием сложности. Поэтому рекомендуется не нарушать последовательности проработки глав, лишь пропуская в случае нехватки времени некоторые, менее актуальные для данного читателя разделы (например, главу 3, параграфы 4.2 и 4.3 или главу 6). В книге не приводится перечня задач. Но читателю настоятельно рекомендуется проделывать подробно все выводы, проводить численные оценки, сопоставлять различные результаты. Автор надеется, что в большинстве случаев читатель найдет в тексте все необходимые советы и данные.
х) Для первого знакомства с основами магнетизма можно рекомендовать, например, соответствующие главы [19] или [32]. Подробное изложение теории магнетизма дается в [5] (см. также [12, 13, 17, 18, 21, 23, 244]).
8
ПРЕДИСЛОВИЕ
В книге используется исключительно гауссова система единиц. И во многих случаях размерности численных величин опускаются. Связь единиц гауссовой системы с единицами системы СИ дана в Приложении 1. В этом же приложении даются значения некоторых фундаментальных постоянных, а также величины «специальных» единиц энергии (электрон-вольт, обратный сантиметр и т. п.). В Приложении 2 приводятся графики размагничивающих факторов эллипсоида.
В список литературы включены, во-первых, источники, на которые имеются ссылки в тексте; во-вторых,— работы, с которыми, по мнению автора, полезно познакомиться при изучении затронутых в книге вопросов; в-третьих,— некоторые работы по вопросам, которые не рассматриваются в книге, но входят или близко примыкают к проблеме магнитного резонанса в магнитоупорядоченных веществах. Более подробная характеристика списка литературы приведена в введении к нему (стр. 574).
Во время работы над книгой очень многие коллеги и товарищи автора прочли рукопись или отдельные ее главы или приняли участие в обсуждении рассмотренных в книге вопросов. Их замечания и советы позволили устранить ряд ошибок и улучшить изложение. Не имея возможности перечислить здесь всех, кто способствовал таким образом улучшению этой книги, автор выражает им свою глубокую благодарность.
Автор отчетливо понимает, что книга содержит множество недостатков, и будет благодарен за все замечания.
ГЛАВА 1
НАМАГНИЧЕННЫЙ до насыщения изотропный
ФЕРРОМАГНЕТИК
§. 1. Ферромагнетизм. Уравнение движения намагниченности
В этой книге будут рассматриваться малые колебания магнитной системы магнитоупорядоченных сред. К таким средам относятся прежде всего ферромагнетики. Для них характерна спонтанная (возникающая и в отсутствие внешнего магнитного поля) параллельная ориентация элементарных магнитных моментов, приводящая к большой намагниченности. Ферромагнитны, как известно, некоторые металлы: железо, никель, кобальт, гадолиний и ряд сплавов, как этих, так и других металлов. Ферромагнетизм наблюдается также в некоторых неметаллических соединениях: окислах (например, ЕпО, СгО2), галогенидах (СгВг3) и более сложных соединениях (например, CdCrgSeJ.
К магнитоупорядоченным веществам относятся также анти ферромагнетики. Они не обладают, как правило, спонтанной намагниченностью х), магнитная восприимчивость их невелика. Но весь комплекс свойств антиферромагнетиков свидетельствует о наличии порядка в расположении их элементарных магнитных моментов. В простейшем случае это может быть «шахматное» упорядочение, когда каждый магнитный момент окружен моментами, антипарал-лельными ему. Возможны и более сложные антиферромагнитные структуры. Антиферромагнитны некоторые металлы (например, Сг, Мп, Се, Pr, Nd, Ей) и сплавы. Однако этот вид магнитного упорядочения особенно характерен для неметаллических соединений. В настоящее время известно огромное количество антиферромагнитных диэлектриков и полупроводников: окислов, фторидов, хал-когенидов и др.
Интересный и очень важный с практической точки зрения класс магнитоупорядоченных веществ составляют ферримагнетики. В них упорядочение элементарных магнитных моментов носит антиферромагнитный характер, например, соседние моменты анти-параллельны. Но из-за различия чисел или величин моментов, направленных в разные стороны, имеет место большой спонтанный момент. Ферримагнетизм характерен для неметаллических соеди-
*) В некоторых антиферромагнетиках (см. главу 4) возникает небольшая спонтанная намагниченность, обусловленная силами, более слабыми, чем те, которые ответственны за антиферромагнитное упорядочение.
10
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
нений. Многие неметаллические ферримагнетики х) нашли очень широкое применение в технике. Благодаря малой электропроводности они успешно применяются в системах, в которых происходят быстропротекающие импульсные процессы или колебательные процессы высоких и сверхвысоких частот. Последнее обстоятельство делает изучение динамики магнитной системы ферримагнетиков особенно актуальным.
Следует подчеркнуть, что различные виды магнитного упорядочения существуют лишь в определенных пределах изменения температуры, давления и внешнего магнитного поля. В простейшем случае ферромагнитный или антиферромагнитный порядок имеет место (при отсутствии внешнего поля) в интервале температур от О °К до некоторой критической, характерной для данного вещества температуры, называемой температурой Кюри (для ферромагнетиков) или Нееля (для антиферромагнетиков); при этой температуре тепловое движение разрушает магнитный порядок, и выше нее вещество становится парамагнитным. Однако иногда происходят и более сложные магнитные превращения. Например, вещество может быть ферромагнитным в одном температурном интервале и антиферромагнитным — в другом; при достаточно высоких температурах оно, конечно, всегда переходит в парамагнитное состояние.
Как уже отмечалось в предисловии, мы будем рассматривать в этой книге магнитные колебания главным образом в неметаллических магнитоупорядоченных веществах. И в то же время мы начнем изучение их с колебаний в ферромагнетиках (главы 1,2 и 3), хотя неметаллических ферромагнетиков не так уж много. Имеются два оправдания такой «непоследовательности». Во-первых, целесообразно из методических соображений начать изучение с более простой системы, которой (во всяком случае, с точки зрения динамики) является ферромагнетик. Во-вторых, колебания в ферримагнетиках при тех частотах и полях, при которых они наиболее широко исследуются и используются в технике, в достаточно хорошем приближении описываются при помощи ферромагнитной модели * 2).
В главах 1 и 2 будет подробно исследовано поведение ферромагнетика, намагниченного до насыщения, когда постоянная намагниченность однородна по всему образцу3). Такая однородная
х) Их называют иногда ферритами — в широком смысле этого слова. В'узком смысле слова, ферриты — это соединения MFe3O4 (где М — двухвалентный переходный металл, например, Мн, Ni, Со); большинство их являются ферримагнетиками.
2) Обоснование этого, а также обсуждение особенностей магнитных колебаний в ферримагнетиках будет дано в § 4.4.
®) Следует заметить, что для колебаний, рассматриваемых в главах 1 и 2, переменная намагниченность также однородна.
§ 1.1]
ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЙ
11
намагниченность имеет место при достаточно сильных внешних магнитных полях, а также (при любых полях) для очень мелких частиц. Если эти условия не выполняются, то ферромагнитное тело разбивается на области — домены, намагниченные в разных направлениях. Магнитные колебания при наличии доменов будут исследованы в главе 3.
В главе 1 рассматривается идеализированный случай изотропного непроводящего и однородно намагниченного ферромагнетика. Многие ферримагнетики, используемые в исследованиях магнитного резонанса и в технике сверхвысоких частот (например, иттриевый феррит со структурой граната YsFe5O12), имеют малую анизотропию; теория магнитных колебаний, развиваемая в главе 1, является для них неплохим первым приближением.
Изучение магнитных колебаний на протяжении почти всей книги будет основываться на решении уравнений движения намагниченности. Получение такого уравнения для случая изотропного ферромагнетика является главной задачей этого параграфа. Однако прежде чем перейти к записи уравнения движения намагниченности, целесообразно напомнить некоторые представления теории магнетизма, определить ряд величин и привести формулы, которые нам в дальнейшем понадобятся. Это будет сделано предельно кратко, обоснования и подробности читатель найдет в монографиях по магнетизму [5,8, 12, 13, 18, 231.
Механические и магнитные моменты электрона. Начнем с самого начала — с моментов количества движения и магнитных моментов элементарных частиц. Согласно представлениям квантовой механики (см., например, [30]) эти величины следует рассматривать как векторные операторы, которые действуют на волновые функции частицы. Частица, в частности электрон, обладает прежде всего собственным (спиновым) моментом количества движения. Собственные значения проекции оператора спинового момента количества движения s на некоторую ось — ось квантования — составляют [30, 13]
s' = hs, Гг (g — 1), ..., (— ftg);	(1.1.1)
здесь h~h /2л (где h — постоянная Планка), as — спиновое квантовое число (спин) данной частицы. Моменты количества движения (или механические моменты) принято измерять в единицах Ti. Тогда
$* = $,($—!),...,(—$).	(1.1.1')
Для электрона s = */2 и
s* = +-L.	(1.1.2)
12
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
Собственное значение квадрата оператора s (в единицах Й* 2) составляет [30]
s2 = s (s + 1).	(1.1.3)
С оператором: спинового механического момента электрона связан оператор магнитного момента х)
= — TsSs,	(1.1.4)
где магнитомеханическое отношение для спина электрона 2)
здесь е — заряд электрона, — его масса покоя, с — скорость света, a gs — фактор спектроскопического расщепления (фактор Ланде или g-фактор) для спина электрона. Из квантовой электродинамики [41] следует, что
gs-= 2(1-4-^-------) = 2,0023.	(1.1.6)
С учетом этого
ys = 1,7608-107.
Согласно (1.1.2) и (1.1.4.) собственные значения проекции спинового магнитного момента электрона на ось квантования, в частности на направление магнитного поля, составляют ч
=	(1.1.7)
где
р.в = -^4 = 0,9274-10'20	(1.1.8)
— магнетон Бора.
Кроме спинового момента, электрон, находящийся на орбите с азимутальным квантовым числом Z, обладает механическим орбитальным моментом. Проекция оператора этого момента 1 на ось квантования может принимать значения
lz = I, (I - 1), ..., (-Z),	(1.1.9)
а квадрат оператора 1, аналогично (1.1.3), имеет собственные значения
F = Z(Z-|-1).	(1.1.10)
J) В дальнейшем механические моменты будут всегда измеряться в единицах Й, а магнитные — в абсолютных единицах.
2) Номера наиболее важных формул выделяются жирным шрифтом.
§1.1]	ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЯ	13
С орбитальным механическим моментом электрона связан маг-
нитный момент	Ж; = — ТьМ,		(1.1.11)
где, аналогично (1.1.5),	Ti =	g;lel 2rn с ’	(1.1.12)
но	gi =	1.	(1.1.13)
Из (1.1.9), (1.1.11) и (1.1.12) следует, что проекция орбитального магнитного момента электрона на ось квантования может принимать значения
nV = Zub, (Z — 1) рв,...,(— Zpb)-	(1.1.14)
Полный механический момент электрона j является векторной суммой спинового и орбитального моментов:
j = s + 1,	(1.1.15)
а полный магнитный момент
№ =	+	(1.1.16)
Проекция полного механического момента на ось квантования {предполагается, что направление этих осей одинаково для s и 1, а следовательно, и для j) имеет собственные значения
7Z = /,(/ —1), ..., (—/),	(1.1.17)
где квантовое число /, в свою очередь, при данных s и Z может принимать значения
j=(l +S), (Z + s - 1), ...,(Z —s).	(1.1.18)
Проекция полного магнитного момента принимает значения tnz = j'Xh, (j — 1)гЛ, • ••,(— fth).	(1.1.19)
Магнитомеханическое отношение, связанное с g-фактором обычной формулой
будет зависеть теперь от квантовых чисел s, I и /. Если пренебречь отличием gs (см. (1.1.6)) от 2, то для g-фактора получится выражение
^4+-+w+(1)+1)-	(1л-21)
14
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
Легко видеть, что если отсутствует орбитальный момент (I = О, / = s), то g — 2 ж gs- если бы отсутствовал спин (s = 0, / = Z), то g == 1 = gt.
Моменты атомов и ионов. Мы будем изучать магнитные явления, которые происходят в кристаллах, построенных из атомов или ионов. Металлы, в которых, кроме локализованных в пространстве ионов, имеется «газ» (или, правильнее, «жидкость») коллективизированных электронов проводимости, почти не будут нас интересовать. Поэтому, не затрагивая г агнитных свойств коллективизированных электронов, перейдем к магнитным свойствам атомов или ионов * 2). Сначала рассмотрим свободные, не взаимодействующие друг с другом атомы в отсутствие внешних полей.
Магнитный момент атома складывается из результирующего магнитного момента электронов и магнитного момента ядра. Механические моменты ядер (если они не равны нулю) — одного порядка с механическими моментами электронов. Однако магнитные моменты ядер малы, так как магнитомеханические отношения для тяжелых частиц (с массой — тр), входящих в состав ядра, в тр/те раз меньше, чем для электронов. Поэтому влияние магнитных моментов ядер на магнитные колебания в магпитоупорядочен-ных кристаллах, как правило, мало 2), и мы не будем его рассматривать.
Электронные моменты атома, механический и магнитный, являются векторными суммами соответствующих полных моментов всех электронов атома. Эти моменты являются, в свою очередь, суммами спиновых и орбитальных моментов электронов. Порядок суммирования моментов в принципе безразличен. Однако взаимодействие электронов в большинстве атомов и, в частности, в интересующих нас атомах переходных и редкоземельных элементов носит такой характер (связь Рассела — Саундерса [30]), что удобнее сначала суммировать спиновые моменты всех электронов атома:
2	= S	(1.1.22)
п
и все орбитальные моменты:
S t = L,	(1.1.23)
п
х) Для краткости будем говорить в дальнейшем об атомах, имея в виду как нейтральные атомы, так и ионы.
2) Наличие магнитных моментов ядер приводит тем не менее к таким важным явлениям, как, например, ядерный магнитный резонанс [5, 22]. Их взаимодействие с моментами электронов (так называемое сверхтонкое взаимодействие) оказывается также в некоторых случаях весьма существенным (см., например, [22]).
§ 1.11	ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЯ	15
а затем уже складывать S и L:
S + L = J.	(1.1.24)
Вследствие принципа Паули (30] как спиновые, так и орбитальные моменты электронов каждой целиком заполненной оболочки компенсируют друг друга. Поэтому электроны внутренних заполненных оболочек атомов не участвуют в образовании моментов. Что касается наружных s-'лектронов, то в ионных кристаллах они переходят с катионов на анионы, в результате чего образуются заполненные оболочки. В металлах наружные электроны коллективизируются, и образующаяся электронная «жидкость» играет, по-видимому, заметную роль в магнитных явлениях [5, 13]. В этом случае нельзя говорить о локализованных атомных моментах; в величины же средних моментов, приходящихся на атом, «-электроны вносят существенный вклад. В неметаллических соединениях с преобладанием ионной связи, которые нас интересуют в первую очередь, магнитные моменты атомов образуются электронами внутренних незаполненных оболочек. Ими являются З^-оболоч-ка.— для переходных элементов группы железа, 4й-и 5d-o6o-лочки — для переходных элементов групп палладия и платины и 4/-оболочка — в случае редкоземельных элементов.
Допустимые значения проекций результирующего спинового S и результирующего орбитального L моментов атома, а также квадратов этих векторов зависят от квантовых чисел атома SuL точно так же, как соответствующие величины для одного электрона — ьт квантовых чисел« и I (выражения (1.1.1), (1.1.3), (1.1.9) и (1.1.10)). Значения же квантовых чисел S и Lb основных состояниях атомов и ионов определяются эмпирическими правилами [30] (в первую очередь, правилами Хунда) и известны для всех интересующих нас атомов.
При данных L и S квантовое число J атома может, аналогично (1.1.18), принимать значения
J = (L +S), (L + S - 1), ..., \L - 5|.	(1.1.25)
Количество этих значений составляет (2L\-1) или (2 .S'4- 1), в зависимости от того, что больше, L или S. Энергия свободного атома при данных L и S зависит от J вследствие спин-орбитального взаимодействия.
Для проекций полных моментов атома, механического и магнитного, на некоторое направление z справедливы выражения (1.1.17) и (1.1.19)—(1.1.21), в которых нужно лишь заменить квантовые числа s, I, и / на квантовые числа атома S, L и J. В частности, проекции полного магнитного момента атома
W = JgPB, (/ —l)gpB,...,(—JgH^),
(1.1.26)
16
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
3	5(5 Н)-Ь(Ы-1)	(1127)
g- — +-------2JV + 1)-----	(1.1.2/)
Для свободного атома — в отсутствие внешних полей состояния, отличающиеся лишь величинами проекций J или 9)? на некоторое направление, являются, конечно, вырожденными.
Парамагнетизм. Рассмотрим теперь поведение атомов (или ионов) во внешнем магнитном поле. Заметим прежде всего, что, независимо от наличия собственных магнитных моментов атомов, орбитальное движение электронов в магнитном поле приводит к появлению диамагнитной намагниченности, пропорциональной полю и противоположной ему по направлению. Эта намагниченность очень мала (восприимчивость имеет порядок 10-в) и существенна лишь для веществ (диамагнетиков), атомы которых не имеют собственных магнитных моментов.
Если же атомы обладают собственными магнитными моментами, то возникает парамагнитная намагниченность, обусловленная частичной ориентацией моментов в магнитном поле (полной ориентации препятствует тепловое движение). Такая намагниченность в не очень сильных полях также пропорциональна полю, но восприимчивость, в отличие от диамагнитной, положительна и обычно значительно больше ее по величине. Парамагнитная восприимчивость была впервые вычислена Ланжевеном для классических магнитных моментов, проекции которых на направление поля могут принимать любые значения.
В действительности проекции магнитных моментов атомов квантуются согласно (1.1.26). При наложении магнитного поля Н появляется потенциальная энергия моментов в этом поле (зеемановская энергия)
ен = - 50?Н = -	(1.1.28)
и вырождение состояний, соответствующих разным значениям J2, снимается: возникают 2J -|- 1 эквидистантных уровня, разделенных интервалами
Де = р РвН-	(1.1.29)
Переходы между этими уровнями с поглощением квантов электромагнитного поля Гил представляют собой явление электронного парамагнитного резонанса [11. Условие резонанса с учетом (1.1.20) имеет вид
<1л-зо>
Различие населенностей уровней с разными приводит к появлению среднего магнитного момента, направленного по полю, т. е. парамагнитной намагниченности. Вычисление ее обычными ме
§ 1.1]	ферромагнетизм, уравнение движения	17
тодами статистической физики [361 приводит [5, 18] к следующему выражению для намагниченности (среднего момента единицы объема):
Mz=Jg^BNB^x),	(1.1.31)
где
х =---~,
х7
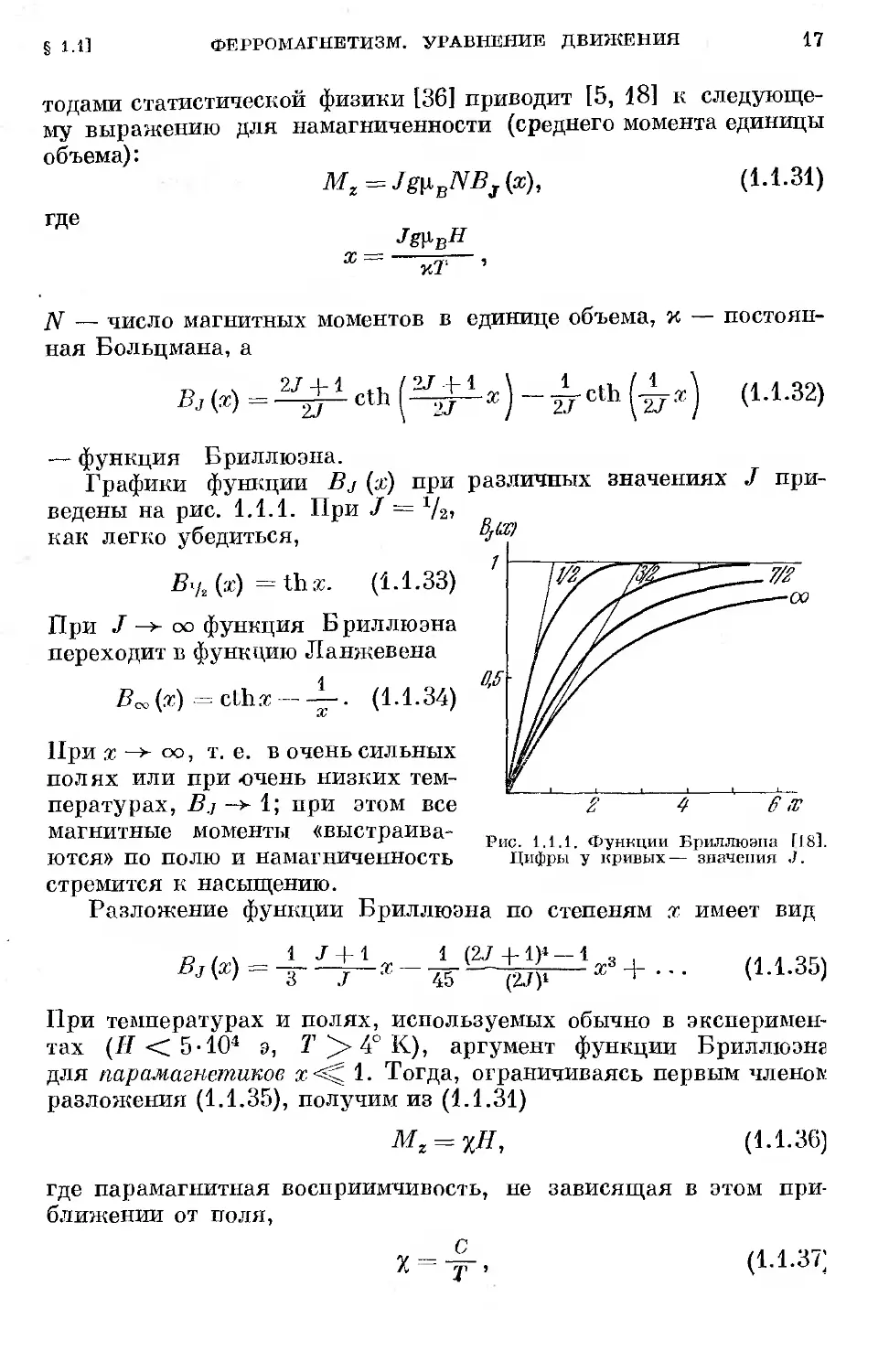
Рис. 1.1.1. Функции Бриллюэна 118]. Цифры у кривых— значения J.
N — число магнитных моментов в единице объема, х — постоянная Больцмана, а
Bj(») = ^+leth (^>1 и)	fa) (1-1-32)
•— функция Бриллюэна.
Графики функции Bj (х) при различных значениях J приведены на рис. 1.1.1. При J = х/2, как легко убедиться,
Я/2 (х) = th sc. (1.1.33)
При J -у оо функция Бриллюэна переходит в функцию Ланжевена
(т) = clh х--. (1.1.34)
При х оо, т. е. в очень сильных полях или при очень низких температурах, В.]	1; при этом все
магнитные моменты «выстраиваются» по полю и намагниченность стремится к насыщению.
Разложение функции Бриллюэна по степеням х имеет вид
к / \	1 J + l 1 (2J4-1)* — 1 „ ,	.. . „с.
=	т__Г^_жз+...	(1.1.35)
При температурах и полях, используемых обычно в экспериментах (Я < 5-Ю4 э, Т )> 4° К), аргумент функции Бриллюэна для парамагнетиков 1. Тогда, ограничиваясь первым членов разложения (1.1.35), получим из (1.1.31)
MZ = %H,	(1.1.36)
где парамагнитная восприимчивость, не зависящая в этом приближении от поля,
х = ^,	(1-1-37;
18
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
а
с = 4- -(4+1)g^7V.	(1.1.38)
Выражение (1.1.37) представляет собой закон Кюри, а величина С носит название постоянной Кюри.
До сих пор мы считали атомы свободными (идеальный парамагнитный газ). В твердых телах имеет место взаимодействие атомов друг с другом: электростатическое (кулоновское) и магнитное. Электростатическое взаимодействие является более сильным, энергия его е2/а — 10-11 (где а — расстояние между атомами), в то время как энергия магнитного (диполь-дипольного) взаимодействия рв/я3 — 10-1в. Электростатическое взаимодействие может быть частично учтено при помощи эффективного электрического поля — так называемого кристаллического поля, симметрия которого совпадает с локальной симметрией окружения иона. Кристаллическое поле приводит к изменению энергетических уровней иона; характер этого изменения определяется симметрией поля, т. е. симметрией окружения. В частности, происходит расщепление некоторых из уровней, которые были вырождены для свободного иона (эффект Штарка).
Для элементов группы железа кристаллическое поле приводит к подавлению (или «замораживанию») орбитального момента [5]. Оно проявляется, в частности, в том, что величины J, вычисленные из экспериментальных значений постоянной Кюри (1.1.38), для парамагнитных соединений этих элементов лежат значительно ближе к спиновым моментам свободных ионов, чем к их полным моментам. Для редкоземельных элементов, в которых незаполненная 4/-оболочка экранирована от окружающих атомов 5й-обо-лочкой, эффективное кристаллическое поле гораздо слабее, и подавления им орбитального момента почти не происходит.
Обменное взаимодействие и магнитное упорядочение. Роль электростатического взаимодействия в магнетизме отнюдь не исчерпывается теми, упомянутыми выше эффектами, которые описываются при помощи кристаллического поля. Электростатическое по своей природе, так называемое обменное взаимодействие является причиной магнитного упорядочения.
Энергия электростатического (кулоновского) взаимодействия заряженных частиц зависит непосредственно только от расстояний между ними, т. е. для микрочастиц, в частности электронов, определяется координатными волновыми функциями и не зависит от спинов. Но, как показывается в квантовой механике, вид координатных волновых функций системы электронов’’зависит от взаимной ориентации их спиновых моментов. Поэтому в энергии кулоновского взаимодействия системы электронов можно выделить часть, зависящую от взаимной ориентации спинов. Эта часть ку-
§ i.l]
ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЙ ДВИЖЕНИЯ
19
ооновской энергии и носит название энергии обменного взаимодействия или обменной энергии.
Как показал Дирак [48], оператор энергии обменного взаимодействия двух частиц может быть представлен в виде
X=-2//rS/Sr,	(1.1.39)
где Sy и S/< — операторы спинов этих частиц, а Iff — так называемый обменный интеграл, зависящий от расстояния между частицами и обычно быстро убывающий при увеличении этого расстояния. Поскольку S/ и S/, (измеряемые в единицах К) представляют собой безразмерные величины, то Z//-имеет размерность энергии.
Энергия обменного взаимодействия электронов, принадлежащих разным атомам, чаще всего минимальна при антипараллель-ной ориентации спинов, т. е. величина отрицательна. Так обстоит дело, например, в молекуле водорода [30]. Но может иметь место и такое положение, когда обменная энергия минимальна при параллельной ориентации спинов всех атомов вещества (Z//- Д-Д> 0); в этом случае осуществляется ферромагнитное упорядоче--ние 1). Поскольку ферромагнитный порядок разрушается при температуре Кюри Тс, то ясно, что энергия обменного взаимодействия, отнесенная к одному атому, должна быть порядка мТс, т. е. для обычных ферромагнетиков — порядка 10~13. Но как уже отмечалось, полная кулоновская энергия, отнесенная к одному атому, имеет порядок 10~и, и поэтому обменная энергия, являющаяся сравнительно небольшой частью ее, вполне может иметь требуемую величину. Отсюда ясно, между прочим, что магнитное взаимодействие (с энергией — 10-1в) не может явиться причиной магнитного упорядочения.
В дальнейшем в этом параграфе, а также в §§ 4.1 и 8.5 мы рассмотрим более подробно природу и способы описания обменного взаимодействия. Теперь же остановимся на феноменологической теории ферромагнетизма, которая была создана Вейссом [451 на основе теории парамагнетизма Ланжевена (см. [5]). Заменим лишь, следуя, например, [18], классические представления Ланжевена квантовыми. Основным предположением скорректированной таким образом теории Вейсса является следующее: для намагниченности ферромагнетика справедливо то же выражение (1.1.31), что и для парамагнетика, но с заменой внешнего поля Н на эффективное поле, которое равно сумме Н и некоторого внутреннего («молекулярного») поля На, пропорционального намагниченности
Нд=ЛМ	(1.1.40) В *
В Такое объяснение природы ферромагнетизма было выдвинуто Френ-
келем [46] и Гейзенбергом [47].
20
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[гл. 1
(А — константа молекулярного поля). Предположим для простоты, что Н и М совпадают по направлению, и опустим в (1.1.31) индекс z у Мг. Тогда
где
М° = JgpBN
(1.1.41)
(1.1.42)
— намагниченность насыщения.
Выражение (1.1.41) представляет собой трансцендентное уравнение относительно М. Графическое решение его при Н = 0 иллюстрирует рис. 1.1.2. Из этого рисунка видно, что при опреде-
ленном соотношении между параметрами может возникать спон-тайная намагниченность М =j= 0. Условие возникновения ее заключается в том, чтобы прямая NxT
Л (Ai'or~х шла менее КРУТО> чем касательная к Bj (ж) в точке х =0. Это условие, как легко убедиться, принимая во внимание (1.1.35), выполняется, если
Рис. 1.1.2. Графическос решение урав-непия (1.1.41) для спонтанной намагниченности.
7<ГС,	(1.1.43)
где
Тс = С А, (1.1.44)
а постоянная С определяется выражением (1.1.38). Критическая температура Тс носит название температуры Кюри. В соответствии со сделанным выше замечанием о «замораживании» орбитальных моментов, под величиной J в (1.1.38), для Зй-ионов следует понимать скорее спиновый момент атома, чем полный момент.
Если Т Тс, то спонтанная намагниченность равна нулю, а намагниченность при II 0 мала. Тогда, ограничиваясь в (1.1.35) первым членом, получаем, что
где восприимчивость
М ==
С т^тс •
(1.1.45)
(1.1.46)
Выражение (1.1.46) представляет собой закон Кюри—Вейсса. Зависимости обратной восприимчивости от температуры для парамагнетика (закон Кюри (1.1.37)) и ферромагнетика (закон Кюри— Вейсса (1.1.46)) приведены на рис. 1.1.3.
§ 1.11	ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЙ
21
Теория Вейсса позволяет найти закон, по которому спонтанная намагниченность стремится к нулю при Т Тс. При этом можно по-прежнему считать М малым, но следует учесть два первых члена в разложении (1.1.35). В результате получим
= А (1-	(1.1.47)
Рис. 1.1.3. Температурные зависимости обратной магнитной восприимчивости. 1-— парамагнетик (закон Кюри); 2— ферромагнетик (закон Кюри — Вейсса); •?— антиферромагнетик, 4 — ферримагнетик.
где А — коэффициент порядка 1. Соотношение (1.1.47) не подтверждается экспериментально вблизи Т(— намагниченность оказывается пропорциональной (1 — Т1ТсУ\ где обычно (см., например, [69]) 0 ~ 0,33 - 0,37. Закон (1.1.46), который, как правило, довольно хорошо выполняется вдали от точки Кюри, вблизи ее переходит в выражение х = С' (Т — Тс)~\ где у 1,3	1,4. Таким обра-
зом, феноменологическая теория Вейсса, «объясняя» качественно поведение ферромагнетика выше и ниже Тс, не может дать количественного описания его характеристик в области фазового перехода (в критической области).
В теории Вейсса наличие эффективного поля, пропорционального намагниченности, постулировалось и постоянная Л в выражении (1.1.40) являлась феноменологической константой. Как следует из (1.1.44) и (1.1.38), эта константа для обычных ферромагнетиков по порядку величины равна 103, т. е. молекулярное поле II — 10е э. Энергия элементарного магнитного момента в таком поле (рассматриваемом как внешнее магнитное поле), согласно (1.1.28), составит 10“13. Таким образом, источником молекулярного поля, которое, согласно феноменологической теории Вейсса, приводит к ферромагнитному упорядочению, действительно может явиться обменное взаимодействие.
Гейзенберговская модель. Ферромагнетик, как и любое конденсированное вещество, представляет собой сложную систему, построенную из элементов—атомов, ионов, имеющих, в свою очередь, сложную структуру (в металлах в состав этой системы входят, кроме того, еще коллективизированные электроны проводимости). Такая система, построенная из микрообъектов, подчиняется законам квантовой механики и квантовой статистики. Неочевидно, что строгое описание ее, исходя из этих общих законов,
22
НАМАГНИЧЕННЫЙ изотропный ферромагнетик
(ГЛ. 1
неимоверно сложно. Как остроумно заметил Кеффер [244], «единственной счетной машиной, которая сумела бы строго вывести из общих законов квантовой механики все следствия для данного магнитного материала, является сам образец из этого материала». Поэтому «в теории магнетизма рассматриваются более простые системы, которые моделируют только наиболее важные или считающиеся таковыми черты реальных магнетиков» (Тябликов [23]).
Рис. 1.1.4. Классические интерпретаций гейзенберговской модели, а— прецессирующие (в основном состоянии) спины, б-— ориентированные спины.
Моделью, которая наиболее широко используется в теории магнитоупорядоченных веществ, является модель Гейзенберга — Дирака — Ван-Флека или, как ее обычно называют, гейзенберговская модель. Эта модель представляет собой систему спиновых моментов S, расположенных в узлах магнитной решетки (в тех точках пространства, где находятся центры «магнитных атомов») и связанных друг с другом обменным взаимодействием. Согласно (1.1.39) оператор энергии (гамильтониан) этого взаимодействия может быть записан в виде
(1.1.48) t г
(f+n
где — номера узлов магнитной решетки.
Как указали Хеллер и Крамере (см. [244],) гейзенберговская модель допускает классическую интерпретацию, при которой спины рассматриваются как «обычные» классические векторы. При этом возникает, однако, трудность, связанная с тем, что собственное значение длины вектора S с максимальными собственными значениями проекций | S |, согласно (1.1.3), составляет / >8' (>8'	1),
в то время как длина классического вектора с теми же проекциями должна быть S. Возможны два варианта преодоления этой трудности (рис. 1.1.4). В первом варианте спины считаются классиче-
§ 1.1]
ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЯ
23
сними векторами с длинами у S (S + 1), которые всегда (даже в основном состоянии системы) прецессируют вокруг оси z, так что проекции их на эту ось не могут быть больше S. В основном состоянии фазы прецессии случайны, и поперечные проекции момента любого макроскопического объема равны нулю. В другом варианте спины заменяются классическими векторами с длинами S, в основном состоянии они направлены по оси z. Такая простая модель удобна для наглядного качественного описания ряда процессов в ферромагнетиках, и мы будем ее в дальнейшем использовать.
При классической трактовке спинов (1.1.48) представляет собой часть потенциальной энергии ферромагнетика, обусловленную обменным взаимодействием. Если обменные интегралы 0, то минимум этой энергии соответствует параллельной ориентации всех спинов. При температуре Т = О ° К такое полностью упорядоченное состояние является равновесным. При Т О условием термодинамического равновесия является [36] минимум некоторого термодинамического потенциала (например, магнитной свободной энергии, см. подробнее § 2.1), содержащего член (—TS), где S — энтропия системы. Поэтому в равновесном состоянии при Т ~^> 0 параллельная ориентация всех спинов не будет иметь места. Можно полагать, в соответствии с опытом и с феноменологической теорией Вейсса, что дальний магнитный порядок, несмотря на частичное разупорядочение, сохранится при температурах Т < Тс. Однако получить строго этот результат с помощью гейзенберговской модели пока не удалось ввиду математических трудностей.
Несмотря на то, что гейзенберговская модель не позволяет пока получить строго фазовый переход от беспорядка к ферромагнитному порядку в точке Тс, она с успехом применяется для решения многих других вопросов г). Представляет поэтому интерес обобщить ее, учтя, кроме обменного, и другие взаимодействия в ферромагнитном кристалле. В первую очередь следует учесть взаимодействие магнитных моментов с внешним магнитным полем Н (зеемановское взаимодействие) и магнитное (диполь-дипольное) вза-модействие их друг с другом. По аналогии с классическим выражением (1.1.28) гамильтониан зеемановского взаимодействия, учитывая (1.1.4), можно записать в виде
f	f
(1.1.49)
(внешнее магнитное поле Н направлено по оси z). Гамильтониан диполь-днпольного взаимодействия может быть записан [3,23] по
*) В § 8.5 гейзенберговская модель будет использована для исследования спиновых волн.
24
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
аналогии с классическим выражением для потенциальной энергии взаимодействия магнитных диполей [431:
= 4- W22 [4-S/Sr------------V	(Sr rr) 1, (1.1.50)
f r L rff'	rtf'	J
(МГ) где
rff = г/ — i'f,
a i'f и if — радиусы-векторы, соответственно, /-го и /'-го узлов. Полный гамильтониан для обобщенной гейзенберговской модели является суммой гамильтонианов (1.1.48), (1.1.49) и (1.1.50).
Одним из допущений, принятых в гейзенберговской модели, является полная локализация магнитных моментов в узлах магнитной решетки. Прямые эксперименты по рассеянию нейтронов (см., например, [66]) показывают, что для ферромагнитных металлов это допущение выполняется плохо — магнитный момент «размазан» по всему кристаллу. Для таких веществ более подходящей является зонная модель ферромагнетизма [13]. Однако для ферромагнитных (а также антиферромагнитных и ферримагнитных) диэлектриков или полупроводников с небольшой проводимостью, которые нас интересуют в первую очередь, магнитные моменты в хорошем приближении можно считать локализованными и использовать гейзенберговскую модель. Правда, в таких веществах магнитные ионы разделены, как правило, немагнитными, и обменное взаимодействие носит более сложный, косвенный характер, (см. § 4.1). Но это влияет на величины обменных интегралов и их зависимости от rff, само же выражение (1.1.48) для магнитоупорядоченных веществ с небольшой проводимостью можно считать справедливым [58].
Вторым важным допущением гейзенберговской модели является иеучет орбитальных магнитных моментов. Можно попытаться учесть их влияние в рамках этой модели, полагая, что коэффициент у в (1.1.49) и (1.1.50) отличается от его значения для электронных спинов, а также вводя в гамильтониан дополнительные члены, учитывающие влияние магнитной кристаллографической анизотропии, которая (см. главу 2) обычно связана с наличием орбитальных моментов. Аналогичный путь используется и в теории парамагнитного резонанса [1], где он получил название метода спин-гамильтониана. Ясно, что он применим тем лучше, чем сильнее «заморожены» орбитальные моменты в соединениях элементов 3d-и других переходных групп. С другой стороны, для редкоземельных соединений, где «замораживания» орбитальных моментов почти нет, гейзенберговская модель, по-видимому, тоже может быть применена, но с заменой спиновых моментов S па полные моменты J.
I l.lj
ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЯ
25
В гейзенберговской модели часто используют так называемое приближение ближайших соседей. Обменный интеграл If быстро убывает с увеличением расстояния между атомами. Учитывая это, в сумме (1.1.48) ограничиваются лишь членами, в которые входят спины атомов ближайших соседей. Тогда гамильтониан (1.1.48) принимает вид
z
< = -2^2/^,	(1.1.51)
t g=i
где Z — число ближайших соседей.
Иногда гейзенберговская модель применяется в (довольно грубом) приближении молекулярного поля [18]. При этом оператор S/ в (1.1.48) заменяется его средним значением (Sy)1) и гамильтониан (1.1.48) записывается в виде
= (1Л-52)
г где
(1Л-53>
г
— так называемое молекулярное поле. Это поле является внутренним, оно действует на спины и в то же время вызвано ими; поэтому в выражение (1.1.52) введен множитель 1/2.
Континуальный подход. Наличие обменного взаимодействия, сильно связывающего между собой элементарные магнитные мо^ менты в магнитоупорядоченных веществах, приводит к тому, что для описания процессов в этих веществах часто с успехом используется континуальный (или макроскопический или квазиклас-сический) подход. При таком подходе мы отвлекаемся от микроскопического строения магшггоупорядоченного кристалла, например ферромагнетика. Величиной, полностью характеризующей магнитное состояние ферромагнетика, является теперь макроскопическая намагниченность
ДУ ’
(1.1.54)
где A§R — магнитный момент малого, но макроскопического объема АУ. Заметим, что именно такой континуальный подход был применен в теории Вейсса.
х) Здесь и в дальнейшем угловые скобки <> обозначают квантовомеханические средние значения стоящих в них операторов. Статистические средние значения (как операторов, так н численных величин), полученные в результате усреднения по некоторым ансамблям, будут в дальнейшем обозначаться чертой над соответствующими величинами.
26	НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК [ГЛ. 1
Если может быть использована гейзенберговская модель, то
ДЗИ = _	<S/>,	(1.1.55)
f
где суммирование производится по объему АЕ. Если, к тому же <S/> изменяется в пространстве достаточно медленно, то объем AF можно выбрать таким, чтобы <S) было в нем постоянным. Тогда из (1.1.54) и (1.1.55) следует
М = - yhN<S')t	(1.1.56)
где N — 1/а3 — число элементарных моментов в единице объема (а — среднее расстояние между моментами).
С учетом (1.1.56) выражение (1.1.53) можно записать в виде
H-'=[w«S7dM-	(1-'г'7)
Таким образом, поле обменного происхождения Нм/, действующее на элементарные моменты гейзенберговской модели, в приближении молекулярного поля оказывается пропорциональным макроскопической намагниченности и, таким образом, может быть отождествлено с молекулярным полем (1.1.40) в теории Вейсса. Феноменологическая константа А этой теории выражается через параметры гейзенберговской модели следующим образом:
л-дагЗ7»-’ <1Л-58>
или в приближении ближайших соседей (1.1.51) (считая Ig не зависящим от g)
А = тдаг	(1.1.5»)
Из (1.1.44) и (1.1.59) следует
%TC = ^-J(J + 1)ZI,	(1.1.60)
откуда видно, что кТс по порядку величины совпадает с отнесенной к одному атому энергией обменного взаимодействия. Более точные расчеты (см., например, [244] ) показывают, что в соотношение (1.1.60) должен входить множитель порядка 1, зависящий от структуры кристалла.
Величина М, характеризующая ферромагнетик приТконтину-альном подходе, есть именно та намагниченность, которая входит в уравнения макроскопической электродинамики (см. главу 5) и, в частности, в соотношение.
В = Н|- 4лМ,	(1.1.61)
§ 1.11
ФЕРРОМАГНЕТИЗМ. УРАВНЕНИЕ ДВИЖЕНИЯ
27
где Н — магнитное поле, а В — магнитная индукция. Намагниченность является функцией координат и времени, и отыскание этой функции М (г, t) при определенных условиях (например, при заданных внешних полях и температуре) является задачей теории ферромагнетизма в ее континуальной трактовке.
Подчеркнем еще раз, что в континуальной теории наличие обменного взаимодействия, приводящего к появлению спонтанной намагниченности или молекулярного поля ДМ, постулируется. Величина Л и спонтанная намагниченность при 0° К в рамках этой теории являются феноменологическими постоянными. Несмотря на это, континуальный подход оказывается очень эффективным при решении многих вопросов теории ферромагнетизма. К ним относятся, в частности, следующие проблемы: отыскание равновесных конфигураций намагниченности (например, доменных структур), исследование переходных процессов (процессов перемагничивания) и, наконец, проблема малых магнитных колебаний, составляющая основное содержание этой книги. На протяжении почти всей книги мы будем использовать, в основном, континуальный подход, привлекая микроскопические соображения лишь в отдельных случаях — главным образом, для пояснения физической картины явлений и оценки величин констант. И лишь в § 8.5 мы вернемся к гейзенберговской модели.
Уравнение движения намагниченности. При континуальном рассмотрении ферромагнетика возможно и обычно наиболее целесообразно использовать классическую теорию1). В этом случае намагниченность М (г, t) может быть найдена путем интегрирования классического уравнения движения намагниченности, т. е дифференциального уравнения, связывающего М (г, t) с магнитным полем Н (г, t), которое рассматривается как заданное. Такое уравнение было впервые записано и использовано Ландау и Лифшицем [111]. Для рассматриваемых в этой главе однородных колебаний намагниченности в идеализированном изотропном ферромагнетике и пока без учета диссипации энергии уравнение движения намагниченности имеет вид 2)
-^ = -тМхН,	(1.1.62)
л
где у — магнитомеханическое отношение, рассматриваемое в рамках континуального подхода как феноменологический параметр.
J) При рассмотрении микроскопических моделей использование квантовой теории является, конечно, необходимым. Но и при континуальном подходе квантовомеханические методы в некоторых случаях, в частности, при исследовании термодинамических вопросов (§ 8.4) и, в особенности, процессов релаксации (глава 9) могут оказаться полезными.
2) Обобщение этого уравнения будет проведено в §§1.3 (учет диссипации) и 2.1 (учет анизотропии среды и неоднородности намагниченности).
28
НАМАГНИЧЕННЫЙ изотропный ферромагнетик
[ГЛ. 1
Строгое обоснование уравнения Ландау—Лифшица возможно, по-видимому, лишь на основе микроскопической квантовой теории (см., например, [288]), в рамках классической континуальной теории его следует рассматривать как постулат. Мы дадим сейчас нестрогий, но наглядный «вывод» этого уравнения, исходя из упомянутой выше квазиклассической модели (или, точнее, интерпретации гейзенберговской модели) Хеллера—Крамерса. Рассмотрим систему классических элементарных волчков, моменты количества движения которых J связаны, однако, квантовомеханическим соотношением
= - yj	(1.1.63)
с элементарными магнитными моментами (здесь J в абсолютных единицах). Уравнение движения волчка—твердого тела, закрепленного в одной точке, имеет вид
с1-1-64)
где Т — момент сил. Для магнитного момента находящегося в поле Н [41],
Т = SR X И.	(1.1.65)
Из (1.1.63), (1.1.64) и (1.1.65) следует уравнение движения элементарного момента J. Умножая его на (—yN), где N— число моментов в единице объема, получаем уравнение движения намагниченности (1.1.62).
В связи с этим уравнением необходимо сделать два замечания. Во-первых, при «выводе» его мы не учитывали обменного взаимодействия. Но очевидно, что молекулярное поле (1.1.40), источником которого является это взаимодействие, не дает вклада в уравнение (1.1.62). Как мы увидим в дальнейшем, учет обменного взаимодействия, в континуальной теории не исчерпывается, вообще говоря, введением молекулярного поля. Если намагниченность зависит от координат, появляется еще одно обменное эффективное поле, которое уже входит в уравнение движения намагниченности. Оно оказывается тем большим, чем резче намагниченность изменяется в пространстве. Таким образом, уравнение (1.1.62) справедливо, кроме всего прочего, лишь в случае достаточно "'медленных изменений намагниченности в пространстве. -	'	"
Второе замечание касается величины у в уравнении движения. Отметим прежде всего, что эта величина является характеристикой коллективного движения магнитных моментов ферромагнетика, сильно взаимодействующих друг с другом. Поэтому связанная с у соотношением (1.1.20) величина g-фактора, конечно, не совпадает с величинами g-факторов тех же ионов, как в свободном состоянии (формула (1.1.27)), так и в парамагнитных кристаллах. Не совпадает она и с величиной g-фактора (g'), которая получается
§ 1.21
ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ И ВОСПРИИМЧИВОСТЬ
29
из гиромагнитных опытов, например Барнета или Эйнштейна — де Гааза [37, 40]. Причина этого несовпадения, согласно Киттелю [114] и Ван-Флеку [115], связана с тем, что величина g' представляет собой отношение (в единицах | е | /(2 те с)) полного магнитного момента электронов Й? к их полному механическому моменту J (конечно, с учетом упомянутого выше эффекта «замораживания»). В то же время величина g в первом приближении есть отношение
к спиновому механическому моменту S. Отсюда, как нетрудно убедиться, следует соотношение
A. + _L = i.	(1.1.66)
Эксперимент по дает точного подтверждения этого соотношения. Но качественно оно имеет место (см. [114]) — значения g превышают 2, а значения g' оказываются меньше 2, вообще говоря, тем сильнее, чем больше вклад орбитального момента в J. Если же орбитальный момент отсутствует (как, например, для ионов Fes+, Мп2+), то значения g и g' очень мало отличаются от 2.
§ 1.2. Прецессия намагниченности и тензор восприимчивости. Ферромагнитный резонанс
Приступим теперь к решению уравнения движения намагниченности для изотропного ферромагнетика. Сначала, в этом и следующем параграфах, мы остановимся на задаче о колебаниях намагниченности в некоторой точке тела под воздействием заданных постоянного и переменного магнитных полей в той же точке. В результате решения такой задачи будет найдена динамическая (или высокочастотная) магнитная восприимчивость ферромагнетика по отношению к внутреннему переменному полю. Ясно, что для неограниченной среды такая постановка задачи является единственно возможной. Для тел конечных размеров эта задача представляет собой лишь часть полной (самосогласованной) задачи, ибо внутреннее поле, в свою очередь, зависит от намагниченности.
Как уже отмечалось, в главах 1 и 2 мы будем иметь дело с ферромагнетиком, намагниченным постоянным магнитным полем до насыщения. Для идеализированного бесконечного изотропного ферромагнетика это не является дополнительным ограничением, потому что такой ферромагнетик будет намагничиваться до насыщения сколь угодно малым постоянным магнитным полем. Но для тел конечных размеров и анизотропных сред насыщение будет достигаться лишь при определенных значениях приложенного постоянного магнитного поля. Заметим, что мы ограничиваемся пока изучением однородных колебаний намагниченности, т. е. предполагаем, что не только постоянная, но и переменная составляющая намагниченности не зависит от координат.
30
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
ГЛ. 1
В этом параграфе будет исследован идеализированный случай отсутствия диссипации, т. е. будет решаться уравнение движения (1.1.62).
Собственные колебания намагниченности. Рассмотрим сначала свободные колебания намагниченности—без вынуждающего переменного поля. В отсутствие диссипации они будут незатухающими. Такие незатухающие свободные колебания называют обычно собственными колебаниями. Итак, примем в уравнении (1.1.62)
Н = Н0 = гоЯ0,	(1.2.1)
где Но — заданная величина постоянного магнитного поля в данной точке, a z0 — единичный вектор, направленный по этому полю.
В равновесии 5M/5Z = 0, и равновесная намагниченность Мо, как видно из (1.1.62), параллельна ЕГ0:
Мо = z0Mn,	(1.2.2)
где Мо — намагниченность насыщения (при данной температуре), которую мы считаем не зависящей от Но и известной. Наша задача заключается в исследовании собственных колебаний намагниченности около этого равновесного состояния.
Отметим, прежде всего важное свойство уравнения (1.1.62). Умножив обе его части скалярно на М, получим
4-М2 = 0.	(1.2.3)
dt	' 7
Таким образом, при любых изменениях вектора М, допускаемых уравнением, длина этого вектора М остается неизменной. Ясно, что
М = Мо.	(1.2.3')
Сохранение длины вектора М при колебаниях дает право говорить об этих колебаниях, как о прецессии намагниченности.
Характер собственной прецессии намагниченности может быть получен непосредственно из уравнения (1.1.62). Обратимся к рис. 1.2.1. Для того чтобы вектор ffMJdt был, согласно (1.1.62), всегда антипараллелен вектору М X Но, конец вектора М должен двигаться по окружности в плоскости, перпендикулярной оси z. Учтя это, приравняем величины векторов dNiJdt и уМ X Но:
М sin 0	=
где 6 и <р — полярный и азимутальный углы вектора М. Отсюда следует, что угловая скорость (круговая частота) движения вектора М
^ = а) = ГЯ0.	(1.2.4)
§ 1.2] ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ И ВОСПРИИМЧИВОСТЬ
31
z
Рис. 1.2.1. Собственная прецессия намагниченности ферромагнетика.
Определяется и направление прецессии вектора М — прецессия является правой1) относительно оси z (рис. 1.2.1).
Получим теперь те же результаты более формальным путем. Предполагая колебания гармоническими и учитывая их однородность, запишем с использованием метода комплексных амплитуд (см., например, [29])
M(t) = М= -j- me'“f,	(1.2.5)
где М= —постоянная составляющая намагниченности, m — комплексная амплитуда переменной намагниченности, а © — неиЗ' вестная пока частота. Подставим (1.2.5) с учетом (1.2.1) в (1.1.62) и спроектируем полученное уравнение на оси координат. В результате получим
М=х = М=!У = 0,	(1.2.6)
iamx + xHjnv = О, — ЧН^Пк + i®mv = 0,	(1.2.7)
mz = 0.	(1.2.8)
.Из (1.2.8) видно, что конец вектора М движется в плоскости, перпендикулярной оси ‘z, т. е. вектор переменной намагниченности m лежит в плоскости ху. Условие совместности системы (1.2.7)— равенство нулю ее определителя, дает
выражение (1.2.4). Подставляя его в любое из уравнений (1.2.7), получим
ту = — imx.	(1.2.9)
Это и означает, что конец вектора m движется по окружности в правом направлении 2), т. е. вектор m имеет круговую поляризацию с правым вращением.
Итак, собственным однородным колебанием намагниченности в изотропном ферромагнетике является правая круговая прецессия
х) Под правым вращением тела относительно некоторого заданного направления мы будем понимать такое вращение, когда точки тела движутся по кратчайшему пути от положительного направления оси х к положительному направлению оси у в правой системе координат, в которой положительное направление оси z совпадает с заданным направлением. Иными словами, тело вращается как головка правого винта при поступательном перемещении винта в заданном направлении.
*) Для того чтобы убедиться в этом, достаточно, в соответствии с требованиями метода комплексных амплитуд [29], умножить (1.2.9) на ewt и записать вещественную часть полученного выражения.
32 Намагниченный изотропный ферромагнетик Ггл. 1 вектора намагниченности относительно направления постоянного поля с частотой, определяемой формулой (1.2.4). Амплитуда переменной намагниченности т (радиус прецессии или значение угла 6) остается при этом (как всегда при рассмотрении собственных колебаний) неопределенной. Заметим, что никаких предположений о малости т при этом не делается. Единственным ограничением является т sC ЛГ0, что следует из (1.2.3).
Линеаризация уравнения движения. Перейдем к рассмотрению вынужденных колебаний намагниченности, пренебрегая по-прежнему диссипацией. Пусть, кроме постоянного поля По, будет приложено однородное переменное магнитное поле, так что
И (t) = Но + heiu(,	(1.2.10)
где h — комплексная амплитуда, а © — частота переменного поля. Установившуюся намагниченность будем по-прежнему искать в виде (1.2.5), но © теперь — заданная частота вынуждающего поля.
При рассмотрении вынужденных колебаний нам придется сделать предположение о малости переменных составляющих поля и намагниченности х):
т<7И0, Л<Я0.	(1.2.11)
Подставим (1.2.10) и (1.2.5) в уравнение движения (1.1.62). Предположение (1.2.11) дает право использовать метод последовательных приближений. В нулевом приближении
М=х но 0,	(1.2.12)
т. е. постоянная составляющая намагниченности направлена по постоянному полю. Эта постоянная намагниченность в данном случае совпадает с равновесной намагниченностью:
М= = Мо.	(1.2.13)
В первом приближении, учитывая (1.2.12) и сохраняя в уравнении только члены первого порядка малости, получим так называемое линеаризированное уравнение движения, которое связывает переменные составляющие намагниченности и поля;
iojm + -ym X Но = — yMoXh.	(1.2.14)
Последующих приближений мы, оставаясь в рамках линейной теории, не рассматриваем.
Тензор высокочастотной магнитной восприимчивости. Неизвестный вектор ш теперь (при рассмотрении вынужденных колебаний) определяется однозначно. Для этого можно использовать два пути. Первый путь основан на решении линеаризированного
х) Это предположение будет сохраняться на протяжении всей книги, посвящеппой изучению линейных процессов — малых магнитных колебаний.
§ 1.21 ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ И ВОСПРИИМЧИВОСТЬ
33
уравнения д координат, в	вижения в проекциях. Проектируя (1.2.14) на оси олучим штх -[- анту = rfMohv, — ынтх 4- iconiy = —	(1.2.15) iwnz — 0,
где обозначес	до = ЧН0.	(1.2.16)
Решая (1.2.1	5), находим ТЛ/0йн	. уМоСО т, тх ~	2	9	+ 1	2 (£>Н — СО2	(£>н — СО2 . ТЛ/о'<0 .	. ТЛ^о«>н 7	/1 9 17! т}, = — г —5	hx 4	5	5- h,,,	(1.2.1 /) У	со?. —со2	со2 —со2	х Jtl mz = 0.
Выражени гут быть заш	я (1.2.17), впервые полученные Полдером [113], мо-асаны в тензорной форме: ш 'уД-	(1.2.18)
Магнитная вс (или высоко* тензор второ!	юприимчивость по отношению к переменному полю [астотная восприимчивость) % представляет собой "о ранга [35] следующего вида: % «Ха 0 7*= ~«Ха X 0 ,	(1.2.19) ООО
где	ТЛ/оОтт х =	о-2-20) ИН — 0)2 Ха--ГС\-	(1.2.21) CDjj — О2
Зависимости % и %а от частоты и величины постоянного поля показаны на рис. 1.2.2.
Другой путь получения выражений (1.2.18)—(1.2.21) основан па решении уравнения (1.2.14) в векторной форме. Перепишем это уравнение следующим образом:
iam + coHm xz0 = YMohj_ X z0,	(1.2.22)
где lix = h — z0 (hz0) — проекция вектора h на плоскость xy. Будем искать решение в виде суммы трех взаимно перпендикулярных векторов:
m = ahjL 4- х z0 + cz0.	(1.2.23)
2 А. Г. Гуревич
34
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
Подставляя (1.2.23) в (1.2.22), находим, что с = 0, а для а и Ь справедлива система линейных уравнений, решая которую получаем
m = XhjL + iXahjL X z0,	(1.2.24)
где % и Xo имеют тот же вид (1.2.20), (1.2.21). Выражение (1.2.24), которое эквивалентно (1.2.18) и (1.2.19), можно переписать следующим образом:
m = Xh_L + ihjL X gm	(1.2.24')
и вектор
gm = ХаА,	(1.2.25)
назвать магнитным вектором гирации.
Заметим, что продольная составляющая переменного поля в данном случае (намагниченного до насыщения ферромагнетика) не вызывает переменной намагниченности. Поперечное же переменное поле вызывает переменную намагниченность, не только
Рис. 1.2.2. Зависимости компонент тензора высокочастотной магнитной восприимчивости от ы (при Но = const) и от Но (при ы = const).
параллельную полю, но и перпендикулярную ему. Такое свойство среды называется еиротропией, оно и приводит к тому, что восприимчивость для переменных составляющих становится несимметричным тензором, имеющим не только диагональные компоненты X, но и антисимметричные (гиротропные) компоненты iXa и (— i%a)-
Существенной особенностью полученного решения является резонансная зависимость как диагональных, так и гиротропных компонент тензора восприимчивости от частоты переменного поля о и величины постоянного поля Но (ем. (1.2.20) и (1.2.21) и рис. 1.2.2). Такая зависимость приводит, как мы в дальнейшем убедимся на целом ряде примеров, к резонансному поглощению
§ 1.2] ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ И ВОСПРИИМЧИВОСТЬ 35 энергии электромагнитного поля ферромагнетиком. Это явление носит название ферромагнитного резонанса. Оно было предсказано, исходя из классических соображений, Аркадьевым (см. [27]) и, исходя из квантовых соображений, Дорфманом [1101. Поскольку обе эти работы были выполнены не только до открытия природы ферромагнетизма, но и до открытия спина электрона, объяснение резонанса в них не могло соответствовать современной точке зрения. Первая теория ферромагнитного резонанса, близкая к современному пониманию природы магнетизма, была развита Ландау и Лифшицем в работе [111]. Экспериментально ферромагнитное резонансное поглощение было обнаружено Гриффитсом [127] и, независимо, Завойским [128] 2).
Поскольку мы не учитывали пока диссипации энергии в среде, величины X и оказались чисто вещественными и имеющими полюсы в точке резонанса (о> = уН0). Это означает, что поглощение энергии электромагнитного поля веществом в предельном случае отсутствия диссипации происходит только строго при резонансе, т. е. ширина резонансной кривой является бесконечно малой.
Резонансную частоту (1.2.4), казалось бы, можно получить из следующих простых соображений. Квант электромагнитного поля, поглощаясь при резонансе, приводит к изменению на yh ~ == gpiB (.см. выражение (1.1.26)) z-проекции элементарного момента, вследствие чего зеемановская энергия (1.1.28) увеличивается на уТгН0. Отсюда непосредственно следует (1.2.4). Однако такие соображения, которые в предыдущем параграфе были использованы для получения частоты парамагнитного резонанса, неприменимы к ферромагнитному резонансу. Элементарные магнитные моменты в ферромагнетике образуют сильно связанную систему многих частиц. В такой системе не может происходить независимых изменений проекций элементарных моментов отдельных частиц. Под действием квантов поля в ней изменяется z-проекция полного момента всего образца, т. е. — на другом языке — рождаются элементарные коллективные возбуждения всей системы — магноны. Однако при всех принятых выше допущениях расстояния между зеемановскими уровнями энергии’всего образца (либо энергии элементарных коллективных возбуждений) составляют'как раз ЛуН0.
Представляет интерес выяснить, в какой мере вид (1.2.19) тензора % обусловлен конкретной моделью и в какой — он свойствен вообще изотропной среде в присутствии внешнего магнитного поля.
1) Завойский еще раньше [126] обнаружил резонансное поглощение в парамагнетике, что явилось .Вообще первым наблюдением магнитного резонанса в вещество,
2*
36
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
ГГЛ. 1
В самом общем случае тензор X может быть записан в виде
Х =
Хи	Х12	Хи
Хи	Х22	Хзз
Хя	Хз2	Хзз
(1.2.26)
Для того чтобы найти условия, накладываемые на его компоненты, необходимо учесть, что в изотропной среде существует только одна выделенная ось — направление постоянного поля. Совместим ее с третьей осью. При любом повороте системы координат вокруг этой оси компоненты тензора не должны изменяться. Формулы преобразования компонент X при произвольном повороте системы координат имеют вид [35] гз з
Xp's' = 2 S «pp'«ss'Xps (р > £ —	2, 3),	(1.2.27)
Р=1 s=i
где аРр' и agg- — косинусы углов между старыми (р, s) и новыми (р', s') осями. При повороте на угол ф вокруг третьей оси
«11- = «22- = COS ф, a33' = 1,
«21- = — «12- = sin ф,	(1.2.28)
«ЭИ ” «32' — «13' ~ «23' ~ 0.
Достаточно учесть инвариантность, например, трех следующих компонент: %ц, '/дя и %81. Выражая их в новой (штрихованной) системе через компоненты в старой системе по формулам (1.2.27) и учитывая (1.2.28), получим
sin2<p (х22 — Хи) + sin ср cos ф (%12 + х21) = О, (cos Ф — 1) %13 + sin фХаз = О, (cos ф — 1) xsl — sin ф %32 = 0.
Поскольку угол ф — произвольный, отсюда следует
Хи — Х22, Х21 “ — Xi2i Х1з — Х23 — Xsi — Хзг = 0.
Обозначая
Хи — Х22 = X, Х12 =	Х21 = ^Ха> Хзз = 5С||т
мы получаем, что тензор магнитной восприимчивости изотропной среды в присутствии постоянного магнитного поля в самом общем
случае имеет вид
« X
х= -%
О
^Ха X о
(1.2.29)
Тензор (1.2.19) для намагниченного до насыщения ферромагнетика отличается от (1.2.29) лишь тем, что Хц- = 0.
§ 1.2] ПРЕЦЕССИЯ НАМАГНИЧЕННОСТИ И ВОСПРИИМЧИВОСТЬ
37
Ясно, что вид, аналогичный (1.2.29), будет иметь любой тензорный параметр среды (магнитная проницаемость, электропроводность и пр.) при наличии лишь одного выделенного (совпадающего с третьей осью) направления.
Высокочастотная магнитная проницаемость. В электродинамике широко используется вектор магнитной индукции (1.1.61). Комплексная амплитуда его переменной составляющей
b = h + 4лш, (1.2.30)
где h и т — комплексные амплитуды переменного поля и переменной намагниченности. Подставляя (1.2.18) в (1.2.30), получим
b = ph, (1.2.31)
где тензор высокочастотной магнитной проницаемости *)
р = 1 -+- 4л%.	(1.2.32)
Рис. 1.2.3. Зависимости компонент тензора высокочастотной магнитной проницаемости от Но (при о = const).
Учитывая (1.2.19)—(1.2.21), Проницаемости
получим для тензора магнитной
р	гра 0
Р = Ч1а Р о о
(1.2.33)
о
1
где
ц=1 + 4л%=
to?, —и2
(1.2.34)
На = 4л%а = —--------- .
<0^ — to2
Здесь введено обозначение
= г4лЛ/0,
(L2.35)
(1.2.36)
которое будет часто использоваться и в дальнейшем. Зависимости р и ра от Но показаны на рис. 1.2.3.
Следует отметить, что диагональная компонента р отрицательна в некоторой области постоянных полей от Нг до резонансного поля (рис. 1.2.3). Это значит, что составляющая переменной индукции, совпадающая по направлению с переменным полем h, в этой области отличается от него по фазе на л (кроме того, при всех постоянных полях имеется, конечно, гиротропная составляющая
х) Строго говоря, в (1,2,32) вместо 1 следует писать единичный тензор [35].
38
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
индукции, перпендикулярная h и сдвинутая по фазе на л/2). Легко получить, что поле, при котором ц. = О,
Я2 = ]/(у? 4- (2л7И0)2 - 2л7И0,	(1.2.37)
а поле (см. рис. 1.2.3), при котором ц = |	|,
/Д = у - 4лЛ0.	(1.2.38)
Иногда оказывается целесообразным ввести в рассмотрение циркулярные поперечные составляющие векторов h, m и Ь:
h+ ~ hx 4~ ihy, h__ = hx — ihu	(1.2.39)
и аналогично и fe±. Тогда, как легко убедиться, справедливы следующие соотношения:
(1.2.40)
Ъ+ = рчДь',	(1.2.41)
где
Z^Z+b-^,	(1.2.42)
63 гт -l- оз it г нр- 63
- И ± На = 1 +	•	<L2-43)
Таким образом, в новых переменных тензоры восприимчивости и проницаемости диагонализируются: составляющая поля h+ вызывает только составляющие т+ и Ь+, а составляющая h_ — только т_ и Ь_.
Составляющая h+ соответствует полю с Крутовой поляризацией и правым вращением. Действительно, если имеется только поле h+, a h_ — 0, то, согласно (1.2.39), hy = —ihx. Это соотношение (аналогичное соотношению (1.2.9)) и характеризует поле с круговой поляризацией и правым вращением. Составляющая h_ соответствует полю с круговой поляризацией и левым вращением. Такие же поляризации имеют, конечно, намагниченности и индукции, вызванные этими полями.
Зависимости величин и %_ от Но показаны на рис. 1.2.4. Из рис. 1.2.4 и из выражения (1.2.42) видно, что только %+ (воспри
Рис. 1.2.4. Зависимости циркулярных к ом-понент тензора высокочастотной магнитной восприимчивости от Но.
j 1,з1	Учёт дйсоШаЦйй	зй
имчивость для поля с правым вращением) изменяется по резонансному закону, величина же %_ не проходит через резонанс и остается малой во всей области изменения 7/0 (или <о). Этот фундаментальный факт имеет очень простое объяснение: собственным движением намагниченности в ферромагнетике является правая прецессия, и поэтому только поле с правым вращением может вызывать ферромагнитный резонанс.
§ 1.3. Учет диссипации
В предыдущем параграфе были исследованы колебания намагниченности (или магнитный резонанс) в идеализированном ферромагнетике, в котором отсутствует диссипация энергии. Однако в действительности колебания магнитной системы, по-видимому, неизбежно связаны с диссипацией энергии, т. е. с передачей ее другим системам, в конечном счете — кристаллической решетке. Наличие диссипации приводит к тому, что свободные колебания намагниченности затухают, а вынужденные — имеют конечную амплитуду при резонансе и конечную ширину резонансной кривой.
Физические процессы, приводящие к диссипации энергии магнитных колебаний, будут рассмотрены в главе 9. Однако феноменологический учет диссипации может быть проведен уже сейчас. Это позволит описать особенности колебаний намагниченности в реальных средах, которые были упомянуты выше.
Диссипативные члены в уравнении движения. Одним из путей феноменологического учета диссипации может явиться соответствующая коррекция окончательных выражений для компонент тензора %. Но предпочтительнее другой-путь, основанный на внесении поправок в исходное уравнение движения намагниченности. При этом основной член в правой части уравнения (1.1.62) можно оставить без изменения и добавить сравнительно малый член, учитывающий диссипацию энергии. Уравнение приобретает тогда вид
~ = - ГМ X И 4- R.	(1.3.1)
Перейдем к обсуждению различных форм записи диссипативного члена R. Наиболее простым является допущение о том, что на намагниченность действует дополнительное эффективное поле, пропорциональное по величине и обратное по знаку скорости изменения М («трение», пропорциональное скорости). Тогда, введя безразмерный параметр а, получим уравнение
f =-rMxH + ^Mxf ,	(1.3.2)
известное как уравнение Гильберта.
40	НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК [ГЛ. 1
Если в правой части (1.3.2) заменить, используя для этого уравнение без диссипативного члена, dM/dt на (— уМ X И) и вместо а ввести параметр диссипации <Dd — ауМ, то получится уравнение движения в форме Ландау — Лифшица [111] 2):
®=-ТМхН-^Мх(МхН). (1.3.3)
Уравнения (1.3.2) и (1.3.3) эквивалентны не только приближенно, но и точно — при некоторой перенормировке коэффициента у при главном члене. Действительно, как легко убедиться, (1.3.3) превращается в (1.3.2) при замене
Диссипативные члены в (1.3.2) и (1.3.3) перпендикулярны М и, следовательно, не препятствуют выполнению условия (1.2.3), т. е. постоянству длины вектора М. Заметим, что некоторые процессы, приводящие к диссипации (см. главу 9), не обеспечивают такого постоянства. При наличии этих процессов уравнения (1.3.2) и (1.3.3) не являются вполне пригодными (но тем не менее часто используются).
Оба рассмотренных уравнения характеризуются одним параметром диссипации. Было много попыток записать уравнения движения намагниченности с большим числом таких параметров, которые обеспечивали бы, в частности, возможность изменения длины вектора М. Можно, например, следуя Каллену [279], разложить вектор dM/dt по трем взаимно перпендикулярным векторам
= Ш1м - rM X Н - М х (М х Н).	(1.3.5)
Это уравнение отличается от (1.3.3) только наличием члена о^М, который и «препятствует» сохранению длины М. Разложение (1.3.5) является совершенно общим. Но параметры и tod могут являться функциями ЛГ0, 7/0 и скорости изменения М, т. е. для гармонических процессов — частоты. Предполагая же их постоянство, мы приходим к определенному частному виду уравнения движения.
Также два, но других параметра диссипации входят в уравнение Блоха [275]
^=-уМх И- —(1.3.6) д£	'	Т2	Ti	'	'
Здесь М_£ = М — z0M2 — поперечная составляющая вектора М, а г0 — единичный вектор, направленный вдоль оси z, которая, как обычно, совпадает с направлением равновесной намагничен-
*) В работе [111] был введен параметр диссипации X = <od/y.
§ 1.31
УЧЕТ ДИССИПАЦИИ
41
ности Мо. Это уравнение было предложено для описания магнитного резонанса в магнитно неупорядоченных системах: ядерного магнитного резонанса и электронного парамагнитного резонанса. Иногда его используют и в случае ферромагнитного резонанса. В (1.3.6) параметры диссипации различны для поперечной и продольной составляющих намагниченности. Для каждой из них скорость диссипации пропорциональна разности мгновенного и статического значений соответствующей составляющей (для поперечной статическое значение равно нулю).
Однако с термодинамической точки зрения (см., например, [120]) правильнее считать, что скорость диссипации в каждый момент пропорциональна разности мгновенной намагниченности и той величины ее, которая установилась бы, если бы было «заморожено» мгновенное значение поля. Если сделать такое предположение и считать, кроме того, что параметры диссипации для поперечных и продольной составляющих намагниченности одинаковы, т. е. тх = т2 = тг (для ферромагнетиков это допущение является, по-видимому, обоснованным), то можно прийти к следующему уравнению [277]:
^=-ТМхН-сог(М-ХоН)’	(1.3.7)
где = 1/тг — частота релаксации, а
(1-3.8)
— статическая магнитная восприимчивость. Уравнение (1.3.7) (которое называют иногда модифицированным уравнением Блоха), так же как и уравнение Блоха (1.3.6), не дает постоянства длины М и может подойти для описания тех процессов диссипации, при которых это постоянство не имеет места.
Процессы диссипации при ферромагнитном резонансе (см. главу 9) многообразны и сложны, и точно описать реальную ситуацию при помощи уравнения с одним или даже двумя постоянными параметрами диссипации, конечно, нельзя. Однако для приближенного описания явлений, связанных с диссипацией, обычно можно пользоваться приведенными выше уравнениями (1.3.2), (1.3.3) или (1.3.7), считая входящие в них параметры не зависящими от (о,^Н0 и Мо в определенных пределах изменения этих величия.
’’Линеаризированные уравнения движения с учетом диссипации. Запишем теперь уравнения движения с диссипативными членами для малых амплитуд переменных составляющих поля и намагниченности. Рассмотрим сначала уравнение (1.3.2). Подставив в него (1.2.5) и (1.2.10) и учтя условия малости (1.2.11), и следствие их (1.2.13), получим для комплексных амплитуд переменных намагниченности и поля линеаризированное уравнение
йот -]-утх Но + ’-^т х Мо = — уМ0 х h. (1.3.9)
42
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
Оно является обобщением уравнения (1.2.14). Наличие диссипации не может, конечно, повлиять на равновесную ориентацию намагниченности, которая по-прежнему остается параллельной Но. С учетом этого уравнение (1.3.9) можно переписать следующим образом:
гот Ч- (он + txa) m X z0 = уЛ70й х z0,	(1.3.9')
где о>н = а zo — единичный вектор, параллельный Но и Мо. Отсюда видно, что (1.3.9) отличается от уравнения без диссипации (1.2.14) только заменой
(Он —> (Он 4- into.	(1.3.10)
Линеаризируя таким же образом уравнение (1.3.3), получим
йот + (Опт х z0 4- — т = yMoh X z0 + wdh. (1.3.11)
Линеаризация (1.3.7) приводит к уравнению, совпадающему с (1.3.11) при условии
(1.3.12)
Уравнения (1.3.9) и (1.3.11) на первый взгляд заметно отличаются друг от друга. Однако (1.3.11), как нетрудно проверить, приводится к виду (1.3.9) при помощи замены (1.3.4), которая переводит одно в другое и полные уравнения (1.3.2) и (1.3.3). Отсюда ясно, что в случае малой диссипации, когда
а2 < 1,	(1.3.13)
все три уравнения, получающиеся в результате линеаризации (1.3.2), (1.3.3) и (1.3.7), эквивалентны. В этом случае между параметрами диссипации существует связь:
aTMo = (od.	(1.3.14)
Подчеркнем, что соотношение (1.3.14) справедливо при любых амплитудах переменной намагниченности, в то время как соотношение (1.3.12) справедливо только при лялыж амплитудах, но произвольной диссипации. Таким образом соотношение
аан = (ог,	(1.3.15)
которое является следствием (1.3.12) и (1.3.14), имеет место при малых амплитудах и малой диссипации. Следует заметить, что все сказанное справедливо в том случае, если параметры диссипации a, (£>d и (£>г определены уравнениями, соответственно, (1.3.2), (1.3.3) и (1.3.7). Конечно, в любом случае можно формально переходить от одних параметров к другим, пользуясь соотношениями (1.3.12), (1.3.14) или (1.3.15), но если не будут выполняться указанные условия (малость амплитуд или диссипации), введенные
§ 1.3]
УЧЕТ ДИССИПАЦИИ
43
таким образом параметры будут иметь несколько иной смысл, чем в уравнениях (1.3.2), (1.3.3) или (1.3.7).
Затухающие свободные колебания. Перейдем теперь к решению полученных линеаризированных уравнений. Рассмотрим сначала свободные колебания, т. е. примем h = 0. Заметим, что в этом случае уравнение (1.3.11) отличается от уравнения (1.2.14) заменой
СО —> СО — Й)г.	(1.3.16)
Частота и затухание свободных колебаний при наличии диссипации могут быть получены из условий существования решений
Рис. 1.3.1. Затухающая прецессия намагниченности, а— согласно линеаризированному уравнению (1.3.9); б— согласно уравнениям (1.3.2) или (1.3.3), обеспечивающим сохранение длины вектора намагниченности.
однородных (при h = 0) уравнений (1.3.9) или (1.3.11). Для того чтобы записать эти условия, достаточно произвести замену (1.3.10) или (1.3.16) в условии (1.2.4) существования решений однородного уравнения без диссипации. Для уравнения (1.3.9) получим таким
путем
со =
5 “ Г j~,---3 = w +	,
1 — icc 1 а2 1 + а2
(1.3.17)
а для уравнения (1.3.11)
со = 0/; -f- i = a' -j- 1л".
(1.3.18)
Как и следовало ожидать, частота свободных колебаний оказалась комплексной; ее вещественная часть есть действительная частота колебаний, а мнимая, как обычно, характеризует затухание колебаний, в данном случае — затухание прецессии намагниченности. Величина т — 1/со" является временем, за которое амплитуда прецессии убывает в е раз. Затухающая прецессия намагниченности показана на рис. 1.3.1.
44	намагниченный ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК [ГЛ. 1
Согласно выражению (1,3.18), полученному из уравнения (1.3.11), вещественная частота свободных колебаний не изменилась при наличии диссипации. В то же время, согласно выражению (1.3.17), полученному из уравнения (1.3.9), она уменьшилась в (1 + а2) раз. Очевидно, что это различие связано с перенормировкой (1.3.4) постоянной у при переходе от одного из этих уравнений к другому. Изменится же или не изменится (и как изменится) в действительности частота прецессии при наличии диссипации, будет зависеть от конкретных особенностей процессов релаксации в системе. Ими будет определяться, какое из уравнений (1.3.9) или (1.3.11) является более подходящим и, следовательно, какое из выражений (1.3.17) или (1.3.18) лучше выполняется. Сейчас, не выходя за рамки феноменологического описания диссипации, мы не можем ответить на этот вопрос. Следует, однако, заметить, что при условии малой диссипации (1.3.13), которое часто хорошо выполняется, рассмотренное различие несущественно.
Компоненты тензора восприимчивости. Решение уравнений (1.3.9) или (1.3.11) для вынужденных колебаний (h =£ 0) может быть проведено одним из способов, использованных при решении уравнения (1.2.14). Однако в случае уравнения (1.3.9) в этом нет необходимости; компоненты тензора % могут быть получены при помощи замены (1.3.10) прямо из выражений (1.2.20) и (1.2.21):
ТМо (со„ + iaw) 7 — —----------S-------------
<o2j — (ip-a2)co2 p-2/а<1Хои
у = _________________________
a — (Ip- a2) co2 p- 2iacocoH
Для уравнения (1.3.11) такой путь не может быть использован, так как замена (1.3.16) справедлива лишь при h = 0. Решение уравнения (1.3.11) приводит к восприимчивости вида (1.2.29), где
ын 4" ыг — со2 р- 2сыгсо ’
Ха = -*~1	~ ’	(1-3’22)
ЫН +	— 0)2 + 2гыга>
__ Мо ссог
ЭД ~ JJц со — jcor ’
(1.3.23)
Таким образом, учет диссипации привел к тому, что поперечные компоненты / и тензора восприимчивости стали комплексными величинами. Кроме того, при использовании уравнения (1.3.11) появилась малая (если мал параметр диссипации) и не изменяющаяся резонансным образом продольная компонента % и.
§ 1.31
УЧЕТ ДИССИПАЦИИ
45
Заметим,что параметры диссипации а и сог в (1.3.19) — (1.3.23) могут являться функциями частоты и счн (т. е. постоянного поля). Однако в дальнейшем, рассматривая частотные и полевые зависимости компонент тензора %, мы будем для простоты считать параметры диссипации постоянными.
Вещественные и мнимые части компонент тензора восприимчивости принято вводить следующим образом:
% = / — %а = Ха~ i%a и т- п- (1.3.24)
Как будет показано в § 5.3, обмен энергией между электромагнитным полем и веществом определяется величинами %", %а и т. д., причем поглощению энергии поля веществом соответствуют положительные значения этих величин.
В случае малой диссипации приближенные выражения для компонент тензора %, полученные из уравнений (1.3.9) и (1.3.11), эквивалентны. Запишем эти выражения, используя, например, параметр диссипации сог (переход к другим параметрам может быть осуществлен при помощи соотношений (1.3.12) или (1.3.15)):
X'= D-WoCOh И, - со2), /'=	(со^ + со2), (1.3.25)
Ха = £>-1ТМосо (со2, - со2),	= D~^M02^,	(1.3.26)
где
D = (со2; — со2)2 -j- 4со2со2.
Зависимости вещественных и мнимых частей X и ха от Но показаны на рис. 1.3.2.
Максимальные значения х” и Х« в случае малой диссипации имеют место при со = сон и составляют
у'	(1.3.27)
Лрез рез 2сог	'
Величины их тем больше, чем меньше параметр диссипации. Иными словами, поглощение энергии при резонансе увеличивается при уменьшении параметра диссипации. Как легко видеть из (1.3.25) и (1.3.26), вдали от резонанса (| со — сон | сог) имеет место обратная зависимость. Вещественные части компонент тензора восприимчивости при резонансе, как следует из (1.3.19) и (1.3.20) или (1.3.21) и (1.3.22), составляют
(1.3.28)
Для характеристики диссипации в различных резонансных системах часто используется полуширина резонансной кривой. В данном случае этот параметр следует определить как половину
46
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ.1
интервала между значениями и (при Но = const) или Но (при со = const), при которых
х"=тх;ез и™ х>|х;рез-
Можно убедиться, что в случае малой диссипации (1.3.13) оба определения приводят к одинаковым выражениям для полуширины
мнимых частей компонент тензора х от Но. Расчет по формулам (1.3.25) и (1.3.26) при Мо — 160 ее, ь>/2л = 9,4 Ггц и ь>г = 3-10“ (2АН - 170 э).
резонансных кривых
Дсо = со,.,	(1.3.29)
ДЯ =	.	(1.3.30)
Таким образом, в данном случае
Дсо = у ЛН. (1.3.31) Вообще говоря, конечно,
Дсо=~ДЯ. (1.3.32)
Если определить ДЯ как было указано выше, то выражение (1.3.30) точно лишь при постоянных и малых параметрах диссипации. Однако это выражение можно считать определением ДН, справедливым независимо от постоянства и величины со,.. Полуширина кривой является в этом случае просто параметром диссипации, выраженным в единицах поля. Она совпадает с полушириной
кривой %" (Но) или Ха (Но), определенной не точно на середине
высоты этой кривой, но — при не очень больших сог — достаточно близко к ней.
Сравнивая формулы (1.3.27) и (1.3.30), мы получаем важное соотношение
2ДПХрез = М0.	(1.3.33)
Для полей или частот, близких к резонансным
(| со — сон |	), выражения (1.3.25) и (1.3.26) можно прибли-
женно записать в форме
= 3
Хрез Хрез. 1 "Ь 3
X" Xg 1 х",ез	хрез	i + p'
(1.3.34)
S 1.3]
УЧЕТ ДИССИПАЦИИ
47
Здесь
Но— —
или
г ДН	1 сог
—.относительные расстройки, соответственно, при <о = const или Но = const. Формулы (1.3.34) представляют собой выражения для лоренцевой резонансной кривой. Таким образом, при малой диссипации и малых расстройках форма кривой ферромагнитного резонансного поглощения является лоренцовой.
Интегрируя %" в (1.3.34) по Но, получим с учетом (1.3.33)
со	со
$ Ж = $ x'W0 = -f- Мо.	(1.3.35)
о	о
Эта величина, как и произведение Хрез A# (формула (1.3.33)), остается конечной при АН -> 0. Отсюда следует, что в предельном случае отсутствия диссипации мнимые части компонент тензора восприимчивости не просто обращаются в нуль, а переходят в дельта-функции. Действительно, дельта-функция Дирака *) определяется следующим образом:
6 (ж) = 0 при х =Д 0,	(1.3.36)
хл
6 (ж) dx = 1, если интервал хг~х2 х,	содержит точку х = 0.
Сравнивая (1.3.35) с (1.3.36), мы видим, что
(х")дн-ч> = ООдн-ч) = т М» 6 (Яо - у) •	(1-3.37)
В § 1.2 было показано, что в циркулярных переменных тензор восприимчивости диагонализируется, т. е. для полей с круговой поляризацией и различными направлениями вращения имеют место скалярные восприимчивости Х+ ; т 7. ± Za- Это, конечно, остается в силе и при учете диссипации. Выражения для х+ и х_ легко получить из (1.3.19) и (1.3.20) или из (1.3.21) и (1.3.22). В частности, в случае малой диссипации
Х+ - Т^о	. •	(1-3’38)
Отсюда при резонансе
4М.-Т=24«.-	<13-39>
х) Свойства дельта-функции см., например, в [30].
48
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
В то же время вещественная и мнимая части не испытывают резонансного изменения и остаются малыми. График зависимостей вещественных и мнимых частей %+ и %_ от Но приведен на рис. 1.3.3.
Компоненты тензора магнитной проницаемости р при нали-
Рис. 1.3.3. Зависимости вещественных и мнимых частей циркулярных компонент
тензора % от Но. Значения параметров — те же, что и на рис. 1.3.2.

определены согласно (1.2.32).
В заключение этого параграфа остановимся на вопросе об интегральных соотношениях между вещественными и мнимыми частями компонент тензора %. Для скалярных восприимчи-востей такие соотношения были установлены Кронигом и Кра-мерсом, исходя из самых общих предпосылок — линейности системы и принципа причинности (см. например, [1, 17]). Как показал Гурари [278] (этот вопрос подробно рассмотрен в [120]), соотношения Кронига — Крамерса справедливы для всех компонент %ps (р, s = х, у, z) тензора восприимчивости:
, . .	2 f 'V (v) , .	.
7 (и) =-----\ -Д---Г + const,
Aps V ' Л J V2 — CO2
0
(1.3.40)
„ . .	2 C ®X^(v)
7 (co) =------\ —2—-dv.
Aps \ /	Jt J V2 — CO2
0
(1.3.41)
Соотношения (1.3.40) и (1.3.41) позволяют вычислить вещественную (или мнимую) часть любой компоненты у при любой заданной частоте, если известна вся частотная зависимость мнимой (или вещественной) части этой компоненты.
§ 1.4. Однородные колебания намагниченности малого эллипсоида
Тензор магнитной восприимчивости, который мы вычисляли в предыдущих параграфах, связывал переменную намагниченность с внутренним (локальным) переменным магнитным полем. Это поле рассматривалось как заданное. Однако заданным обычно
I 1.4]
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
49
является не внутреннее, а так называемое внешнее поле, например, поле на достаточном удалении от образца. Внутренее же поле зависит от намагниченности, и характер этой зависимости определяется формой образца. Задача заключается, таким образом, в определении переменной намагниченности и, одновременно, переменного внутреннего поля при заданном внешнем поле. Для решения такой задачи необходимо использовать уже не только уравнение движения намагниченности, но и уравнения электромагнитного поля (уравнения Максвелла), а также граничные условия на поверхности образца.
Уравнения Максвелла для ферромагнитной среды будут рассмотрены в главе 5, затем в главах 6 и 7 будут разбираться различные граничные задачи. Однако простейшую из граничных задач, основанных на совместном решении уравнения движения и уравнений поля, можно и целесообразно рассмотреть уже сейчас — перед дальнейшим обобщением уравнений движения, которое будет проведено в главе 2. Такой - граничной задачей является задача об однородных колебаниях намагниченности (или однородном магнитном резонансе) в изотропном ферромагнитном эллипсоиде с размерами, малыми по сравнению с длиной электромагнитной волны. Задача об однородном магнитном ре-• зонансе в малом эллипсоиде была решена Киттелем [112], и это явилось следующим после работы Ландау и Лифшица [111] фун-даментальным вкладом в теорию ферромагнитного резонанса.
Большинство экспериментальных работ по ферромагнитному, резонансу проводится на малых образцах — сферах или тонких пластинках, являющихся частными случаями эллипсоида. Рассмотрение киттелевской граничной задачи даст нам возможность при изучении влияния кристаллографической анизотропии и доменной структуры (в главах 2 и 3) сравнивать теоретические результаты с экспериментом. Это является первым доводом в пользу такого «непоследовательного» рассмотрения теории ферромагнитного резонанса. Есть и еще один довод: метод учета влияния формы (или, как можно сказать, «анизотропии формы»), предложенный Киттелем, может быть использован, как мы убедимся в дальнейшем, при учете и других видов анизотропии.
Итак, сформулируем следующую задачу: в однородном внешнем постоянном поле Но и слабом однородном внешнем переменном поле h0 находится малый эллипсоид из изотропного *), непроводящего, намагниченного до насыщения ферромагнетика. Необходимо найти его переменную намагниченность в зависимости от величины постоянного поля, частоты, формы эллипсоида и
х) Имеется в виду, как и в предыдущих параграфах, изотропия в отсутствие внешнего постоянного поля. При его наличии свойства вещества по отношению к переменному полю будут, конечно, существенно анизотропны — гттптппптгкт
50
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
ГГЛ. 1
параметров вещества (у, Мо и параметров диссипации). При этом под заданными внешними полями понимаются поля, строго говоря, на бесконечном удалении от образца, а практически — на расстояниях от него, во много раз превышающих его размеры.
Условие равновесия и уравнение движения. Размеры эллипсоида предполагаются во много раз меньшими, чем длина электромагнитной волны в веществе. Это дает право использовать не полные уравнения Максвелла, а уравнения или непосредственно результаты магнитостатики. Как известно из магнитостатики (см., например, [43]), магнитное поле Нг внутри непроводящего магнитного эллипсоида, расположенного в однородном внешнем (в указанном выше смысле) поле Н, является "также однородным. Для него справедливо выражение
Hj = Н - NM,	(1.4.1)
где М — намагниченность, являющаяся, вообще говоря, функцией Н;, a N — тензор размагничивающих факторов эллипсоида (см. Приложение 2). Поле
Нм = - NM	(1.4.2)
называется размагничивающим полем.
При выводе выражения (1.4.1) обычно предполагается, что поле Н не зависит от времени. Однако при определенных условиях это выражение будет справедливо и для зависящих от времени величин. Одно из условий (оно уже упоминалось выше) заключается в том, чтобы размеры эллипсоида были малы по сравнению с длиной электромагнитной волны в веществе. При этом условии членами уравнений Максвелла с производными по времени (см. § 5.1), которые учитывают эффект запаздывания при распространении электромагнитных волн, можно пренебречь, и задача превращается в квазистатическую: в каждый момент времени мгновенные значения Н, Нг и М связаны теми же уравнениями и граничными условиями, что и статические величины. Второе условие заключается в том, чтобы в эллипсоиде возбуждалась однородная прецессия намагниченности1).
Р*’’’Пусть внешнее поле Н, а следовательно, и внутреннее поле Нг и намагниченность имеют постоянные и переменные составляющие а):
Н = Но + hoe*“(, Нг =!Hi0 + he™, M =гМ0'+'теш. (1-4.3) ________________	“	“	”<1ИВ
*) Малый намагниченный эллипсоид (см. главу 7) имеет бесконечное множество собственных типов прецессии намагниченности. Лишь для одного из них — однородной прецессии — намагниченность не зависит от координат, и соотношение (1.4.1) справедливо.
2) Вводимые обозначения могут показаться не совсем логичными, по они позволят избежать в дальнейшем записи лишних индексов.
§ 1.41
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
51
Тогда если выполняются указанные выше условия и выражение (1.4.1) имеет место, то в силу его линейности
HjQ = Но — NM0,	(1.4.4)
h = h0 — Nm.	(1.4.5)
Метод рассмотрения однородного ферромагнитного резонанса в малом эллипсоиде, предложенный Киттелем [112], состоит в том, что с помощью выражений (1.4.4) и (1.4.5) из уравнения движения исключается неизвестное внутреннее поле и намагниченность связывается с заданным внешним полем. Этим методом мы и воспользуемся.
Будем исходить, например, из уравнения (1.3.2). Входящая в него величина Н является теперь внутренним магнитным полем Hf. Представим Нг и М в виде сумм (1.4.3) и используем выражения (1.4.4) и (1.4.5). Будем считать переменные составляющие малыми и воспользуемся методом последовательных приближений.
В нулевом приближении получим
MoxHiosMox(Ho-NMo) = 0.	(1.4.6)
Условие (1.4.6) (равновесная намагниченность параллельна внутреннему статическому полю, зависящему, в свою очередь, от намагниченности) может быть использовано для определения равновесной ориентации Мо. Длину этого вектора можно считать заданной, так как образец намагничен до насыщения. Не останавливаясь на решении статической задачи, будем считать вектор Мо, а следовательно, и внутреннее статическое поле Hi0 известными.
В первом приближении мы найдем линеаризованное уравнение движения для комплексных амплитуд m и h0:
irom 4- ym X Н,о x T (Nm) X Mo+ '^mxM0 = — rM0 X h0. (1.4.7) Это уравнение можно, конечно, получить и из линеаризованного уравнения (1.3.9), если заменить входящую в него величину Но на внутреннее поле Hi0 и выразить h через внешнее поле h0 согласно (1.4.5). Уравнение (1.4.7) можно, аналогично (1.3.9'), записать в форме
icom + (соя 4- icuo) m х zo Д- r(M0 (Nm) х Zq = T-A-/0h0 х z0, (1.4.7') где теперь, в отличие от (1.2.16) х),
______________ыН =	(1.4.8)
х) Такое определение Од будет использоваться на протяжении всей книги.
52
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
а ось z (рис. 1.4.1) направлена параллельно векторам Нго и Мо (при этом она в общем случае не совпадает с Но или с какой-либо, из главных осей эллипсоида).
Таким же образом, но исходя из (1.3.11), можно прийти к уравнениям с параметрами диссипации cod или оу, например,
йот + ушу Hi0 + У (Nm) х Мо 4- ю,. (1 4- %0N) m =
== — yMoyho4-corxoho, (1.4.9)
где теперь
го
При малой диссипации уравнения (1.4.7) и (1.4.9) эквивалентны
и между параметрами диссипации существуют соотношения (1.3.12), (1.3.14) и (1.3.15) (соотно-
Рис. 1.4.1. Системы координат при рассмотрении колебаний намагви-
ченности эллипсоида. Оси у', z' совпадают с осями эллипсоида.
шение (1.3.12) справедливо при любой диссипации), в которых о>п и %0 определяются согласно (1.4.8) и (1.4.10).
Собственные частоты. Приступая к решению уравнений (1.4.7) или (1.4.9), рассмотрим прежде всего свободные колебания без диссипации (собственные колебания), т. е. положим h0 == 0 и а = 0 или а>г = 0. Тогда (1.4.7) или Ц .4.9) перейдет в однородное уравнение
йот + ушу Нго + 7 (Nm) у Мо = 0.
(1.4.11)
Спроектируем уравнение (1.4.11) на оси декартовой системы координат с осью z, параллельной векторам Мо и Hi0 (рис. 1.4.1). Пусть в этой системе координат симметричный тензор N имеет вид
Агн N12 N13
TV]2 N22 N%3
А5з Nss
(1.4.12)
Тогда в результате проектирования с учетом правила умножения тензора на вектор [35] получим
(йо -I- yZV- 12^0) тх 4“ (®н +	22470) ту — 0,
— (Он 4- тАГцМо) тх 4- (in — lNl2M0) ту = 0, mz — 0.
(1.4.13)
§ 1.4]
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
53
Равенство нулю определителя системы (1.4.13) дает выражение для собственной частоты однородной прецессии намагниченности малого эллипсоида
= (сон + pVnMo) (сон + rW) -	(1.4.14)
Проектируя (1.4.4) на ось z, получим
Hi0 = H0z-NssM0.	(1.4.15)
Подставляя (1.4.15) в (1.4.14), найдем окончательно
(у)2 = [HOz + (2Vu - Nss) Mo] [HOz + (Дг22 - 2V33) Mo] - N^M*.
(1.4.16)
Подчеркнем, что вычисление coo по формуле (1.4.16) требует предварительного решения статической задачи, т. е. определения ориентации вектора Мо относительно осей, эллипсоида. Зная ее, можно получить значения компонент N в системе координат, в которой ось z совпадает с Мо, и вычислить проекцию Но на эту ось.
Подставляя (1.4.16) в одно из уравнений 0.4.13), можно убедиться, что собственная прецессия в этом случае не является круговой — конец вектора М движется в плоскости, перпендикулярной оси z (см. рис. 1.4.1), т. е. перпендикулярной Мо х) по некоторой эллиптической орбите.
Проведенный расчет является обобщением теории Киттеля [112], который рассмотрел частный случай, когда внешнее поле Но направлено по одной из осей эллипсоида. Постоянная намагниченность Мо в этом случае (для намагниченного до насыщения изотропного образца) будет совпадать по направлению с Но. Тогда Nlz = О, Nu = Nx, Д\2 = Ny, N3S = Nz и
Hi0 = H0-NzM0.	(1.4.17)
Выражение (1.4.16) переходит в этом случае в известную формулу Киттеля
(у)2 = 1Н0 + (Nx - Nz) Мо] i#o + (Ny ~ Nz) Mo\. (1.4.18)
Предельные случаи формулы (1.4.18) приведены в табл. 1.4.1, а соответствующие формы образцов показаны на рис. 1.4.2.
Заметим, что формулы (1.4.19) и (1.4.20) (в табл. 1.4.1) справедливы, строго говоря, только для бесконечно тонкой пластины. Они очень хорошо выполняются для тонких пленок, как непроводящих так и металлических. Эти формулы используются иногда
!) Движение в плоскости, перпендикулярной Мо, является, конечно, следствием предположения о малости колебаний.
54
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
и для ферромагнитного резонанса в массивных металлических образцах; наличие сильного поверхностного эффекта приводит к тому, что играет роль лишь тонкая поверхностная пленка. Именно для этого случая формула (1.4.19), которая может быть записана в виде
®о - Y (W,	(1.4.19')
была впервые применена Киттелем (см. [112]). Используя эту формулу, он объяснил результаты опытов Гриффитса [127] по
ферромагнитному резонансу в металле. Однако по поводу применения этой формулы и вообще формулы Киттеля (1.4.18) к массивным металлическим образцам необходимо сделать два замечания. Во-первых, следует помнить, что входящая в (1.4.18) величина
Таблица 1.4.1
Предельные случаи формулы Киттеля
Образец	Направление намагничения	Обоз-наче-ние на рис. 1.4.2	Размагничивающие факторы			top Т	Ki формулы
			Nx	У	Кг		
Пластина	Касательное	а	0	4л	0	[Но(Но+4лЛ-/о)Г'2	(1.4.19)
	Нормальное	б	0	0	4л	Но — 4лЛ/о	(1.4.20)
Цилиндр	Продольноэ	е	2л	2л	0	Но + 2лЛ/о	(1.4.21)
	Поперечное	г	2л	0	2л	[Нс(Но—2лМ„)]^	(1.4.22)
Сфера		д	4л "З	4л ~з	4л "3	Но	(1.4.23)
§ 1.4]
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
55
Nz представляет собой статический размагничивающий фактор, который может, конечно, отличаться от 0 или 4л для образца, намагниченного, соответственно, касательно или нормально к его поверхности. Величины же N х и Nv представляют собой размагничивающие факторы для высокочастотного поля; для них благодаря сильному скин-эффекту могут быть приняты значения О или 4л, как для тонкой пластинки. Во-вторых, даже при внесении этой поправки использование формулы (1.4.18) и ее частных случаев для массивных металлических образцов не может дать точных результатов, поскольку при выводе формулы (1.4.18) предполагалась однородность внутреннего переменного поля, а при наличий"скин-эффекта она, конечно, не имеет места х).
Для эллипсоида вращения вокруг оси z (Nx = Ny =s. выражение (1.4.18) с учетом (1.4.2) запишется в виде
®о = Т(^о + (3N±- 4л.) Мо].	(1.4.24)
Частными случаями (1.4.24) являются формулы (1.4.20), (1.4.21) и (1.4.23).
В случае сферы выражение для собственной частоты однородных колебаний намагниченности имеет особенно простой вид, и, самое главное, в него не входит статическая намагниченность. Благодаря этому сферические образцы использовались в подавляющем большинстве опытов по ферромагнитному резонансу в слабо проводящих (неметаллических) веществах 1 2).
Подчеркнем, что киттелевская формула (1.4.18) и ее частные случаи (1.4.19) — (1.4.24) справедливы при следующих допущениях. Во-первых, внешнее постоянное магнитное поле дожно быть направлено по одной из осей эллипсоида. Во-вторых, это поле должно быть достаточно велико (или размеры образца — достаточно малы), чтобы образец был намагничен до насыщения, т. е. чтобы в нем отсутствовала доменная структура. Для идеализированного изотропного ферромагнетика, который мы пока рассматриваем, это условие выполняется для образцов любых размеров, если внутреннее прстоянное поле, вычисленное по формуле (1.4.17), оказывается положительным. И в-третьих, вектор Мо должен по направлению совпадать с Но. Для изотропного ферромагнетика это условие всегда выполняется при выполнении первых двух условий.
Зависимости собственных частот однородных колебаний намагниченности от вычисленные по формулам (1.4.19) — (1.4.23), показаны на рис. 1.4.3.
1) Этого вопроса мы коснемся в § 9.5.
2) Этому способствовало и то, что сферические образцы весьма малых размеров могут быть с большой точностью изготовлены, например, методом обкатки сжатым воздухом [500].
56	НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК [ГЛ. 1
Общая, формула (1.4.16) справедлива при произвольном направлении Но, но, конечно, по-прежнему при величинах Но, достаточных для того, чтобы доменная структура отсутствовала. При
этом направление Мо, вообще
Рис. 1.4.3. Зависимости собственных частот ы0 однородных магнитных колебаний от внешнего постоянного магнитного ноля Но для предельных случаев изотропного эллипсоида. Расчет по формулам (1.4.19)— (1.4.23). Буквы у кривых соответствуют рис. 1.4.2 и табл. 1.4.1. Пунктир— расчет несправедлив из-за наличия доменной структуры.
при помощи такой же замены из
говоря, не совпадает с на прав-лением Но, и расчет собственной частоты может быть проведен лишь -после того, как будет решена статическая задача о равновесной ориентации вектора Мо.
Затухающие свободные колебания. Рассмотрим теперь свободные колебания намагниченности эллипсоида при наличии диссипации, т. е. положим в уравнениях (1.4.7) или (1.4.9) h = 0, но а =f= О или о>г =(=0. Уравнение (1.4.7)
при этом будет отличаться от уравнения без диссипации (1.4.11) лишь заменой(1.3.10), и уравнение для комплексной частоты свободных колебаний может быть получено выражения (1.4.14). Это урав-
нение будет иметь вид
®2 (1 ф- а2) —	— 2йщлн® = О,
где
/?-(! + хЛи) (I + /<№) ~ s Ч (т0 — собственная частота (1.4.14)), а
? == 1 Н- ~2 Хо G^ii + N22)-
Подставляя в (1.4.25) ы = го' ф~ ia", находим „ “шн?
“	1 ф- а2 ’
. “о “М/?2
) — 1 + a2 (1 + а2)2 • 
(1.4.25)
(1.4.26)
(1.4.27)
(1.4.28)
(1.4.29)
Решая уравнение (1.4.9) при h0= 0 1), мы придем к уравнению для комплексной частоты, которое будет отличаться от (1.4.25)
Ц Замена (1.3.16) не пепевопит это гпавнение в (1.4.11).
§ 1.41
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
57
на величины второго порядка малости относительно параметров диссипации. Решение его даст
G)" = (org,	(1.4.30)
(со')2 = ^ + «2(р2-д2).	(1.4.31)
Таким образом, учет диссипации привел к появлению мнимой части частоты (характеризующей затухание свободной прецессии эллипсоида), пропорциональной или (в первом приближении) а. Изменение же действительной части частоты, как для всех колебательных систем, оказалось второго порядка малости относительно параметра диссипации.
Для характеристики затухания в колебательных системах часто вводится величина
Со — ,	(1-4.32)
называемая добротностью системы. Это определение равносильно следующему:
Со=~,	(1-4.33)
где W — энергия системы, а Р — мощность потерь. Таким образом, добротность есть умноженное на 2л отношение энергии, запасенной в системе, к потерям энергии за период колебаний.
В нашем случае в первом приближении с учетом соотношений (1.3.12) и (1.3.14)
2иг7 Ztodl ^аЯ ’
(1.4.34)
где р и q определяются согласно (1.4.26) и (1.4.27). При совпадении внешнего поля с одной из осей эллипсоида, когда справедливо (1.4.17), множитель p/q выражается явно через Но, Мо и размагничивающие факторы. Для эллипсоида вращения этот множитель, как легко убедиться, обращается в 1, и
О .	_ Н’Ио £
2<вг 2a>d 2а *
(1.4.35)
Из (1.4.35) видно, что если постоянным является параметр диссипации а, то и добротность Qo постоянна; если постоянно a>d, то <?0 зависит только от намагниченности; если же постоянно со„ то добротность зависит также от частоты (через Но) и формы образца. Какой параметр диссипации, в каких случаях с большим правом можно считать постоянным, на этот вопрос может ответить только эксперимент или микроскопические теории релаксации (которые будут рассмотрены в главе 9).
Мы учли выше поглощение энергии только в веществе эллипсоида и не учитывали потерь энергии вследствие излучения
58
Намагниченный изотропный ферромагнетик
[гл. i
электромагнитной энергии образцом. Поэтому введенную добротность следует назвать собственной добротностью.
Пользуясь результатами магнитостатики, мы считаем размеры эллипсоида малыми по сравнению с длиной электромагнитной волны. При этом излучение будет, конечно, мало. Однако и собственная диссипация в образцах из совершенных монокристаллов ферритов весьма мала — собственная добротность Qo может достигать значений ~ 104. При этом излучение может быть заметным уже для образцов сравнительно малых размеров, например для сфер с диаметром 1—2 мм в трехсантиметровом диапазоне длин волн 4).
Внешний тензор восприимчивости. Перейдем теперь к рассмотрению вынужденных колебаний намагниченности малого эллипсоида под воздействием заданного внешнего переменного поля. Как и в предыдущем параграфе, ограничимся рассмотрением установившихся гармонических колебаний; тогда задача будет заключаться в нахождении комплексной амплитуды переменной намагниченности m при заданной комплексной амплитуде внешнего переменного поля Ьо. В силу линейности задачи искомая зависимость может быть записана в виде
m = xeh0,	(1.4.36)
где Xе — так называемый внешний тензор восприимчивости эллипсоида, и подлежит определению.
Решать эту задачу можно, вообще говоря, двумя путями. Первый путь основывается на использовании уже известной связи ш с внутренним полем 1:
m = %’h.	(1.4.37)
Внутренний тензор X’ — это, по существу, тот же тензор X, который был определен в § 1.3; необходимо лишь в выражениях для его компонент заменить постоянное поле Нй на внутреннее постоянное поле Hi0. Исключая 1), из (1.4.5) и (1.4.37), мы получим, что тензор Xе связан с тензорами X’ и N соотношением * 2)
(Xе)’1 = (хТ1 + N,	(1.4.38)
где (Xе)-1 и (Х’)-1 — обратные тензоры 135].
В Вопросы излучения электромагнитной энергии малым ферромагнитным образцом будут затронуты в 6.4 и 7.3. Мы увидим, в частности (§ 7.3), что излучение приводит не только к дополнительному затуханию, но и к изменению собственных частот колебаний.
2) Следуя Аркадьеву [27], можно '/е назвать восприимчивостью тела, %* — восприимчивостью вещества, a (N)-1 — «восприимчивостью формы».
§ 1.41
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
59
Если образец является эллипсоидом вращения (7VX = Ny hs = N±), то тензоры X’ и Xе диагонализируются при переходе к циркулярным переменным (1.2.39). Из формулы (1.4.38) вытекает тогда простое выражение, связывающее циркулярные компоненты этих тензоров, т. е. восприимчивости по отношению к полям с круговой поляризацией
(xyWxvr+W	(1-4-39)
В общем случае вычисление компонент тензора Xе с помощью (1.4.38) оказывается трудоемким, и выгоднее выбрать другой путь решения этой задачи. Он заключается в непосредственном решении уравнения (1.4.7) или (1.4.9) — без использования внутреннего тензора восприимчивости.
Пренебрегая сначала диссипацией, найдем
	Хех	Xes+iXea	0	
Xе =	X Д’ >2	0	(1.4.40)
	0	0	0	
Здесь
Х« = IT Wo (Hi0 + 2VMM0),	(1.4.41)
xl = Л-Wo (Hi0 + AW0),	(1.4.42)
X: = -D-W12M02,	(1.4.43)
; £ =	(1.4.44)
D = coo2 — (D2,
где Hl0 - внутреннее постоянное магнитное поле (1.4.15), a <d0 — собственная частота (1.4.16).
Из полученных выражений видно, что компоненты внешнего тензора восприимчивости эллипсоида сильно зависят от формы образца и существенно отличаются от компонент внутреннего тензора восприимчивости X7. Резонансной частотой тензора Xе (при которой его компоненты имеют полюсы) является собственная частота однородных колебаний намагниченности эллипсоида соо, в то время как резонансной частотой тензора X* является а>н = = yHi0. Недиагональные компоненты тензора Xе, в отличие от тензора X7, содержат, вообще говоря, не только антисимметричные составляюгцие.± i%ai но и симметричные составляющие %в. Однако они обращаются в нуль в «киттелевском» случае, когда направления Но и Мо совпадают с одной из осей эллипсоида.
Интересно отметить, что для сферы компоненты тензора Xе (без диссипации) совпадают с компонентами (1.2.20), (1.2.21)
60
НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 1
тензора Хг для неограниченной среды (но не с компонентами тензора %* для сферы, в которые вместо Но войдет Hi0 = я0-4?-м0).
Вычисление компонент тензора Xе с учетом диссипации не представляет трудностей. В случае уравнения (1.4.7) для этого достаточно произвести замену (1.3.10) в выражениях (1.4.41) — (1.4.44). Уравнение же (1.4.9) следует спроектировать на оси координат и решить полученную систему. Мы не будем приводить здесь выражений для компонент Xе, которые получаются таким образом. Отметим лишь, что они, конечно, оказываются комплексными; мнимые части величин %ех, и '/J, т. е. (см. § 5.3) ан-тиэрмитовы составляющие тензора Xе, характеризуют поглощение энергии внешнего переменного поля эллипсоидом. В случае уравнения (1.4.9) учет диссипации приводит также к появлению малой (при сог <<г со) продольной компоненты уд3- Условие резонанса поперечных компонент комплексного тензора Xе (при выполнении которого мнимые части их проходят через максимумы) в случае уравнения (1.4.7) имеет вид
2_ “О “ — 1 + & ’
а в случае уравнения (1.4.9)
со2 = соо2 -|- р2сог2.	(1.4.46)
Резонансные частоты, определяемые выражениями (1.4.45) или (1.4.46), отличаются от соответствующих частот со' свободных затухающих колебаний (формулы (1.4.29) и (1.4.32)), но это отличие — так же как и отличие резонансных частот от соо — второго порядка малости относительно параметра диссипации.
Приведем выражения для вещественных и мнимых частей компонент тензора при резонансе (мнимые части — в первом приближении при малой диссипации):]
(Хх)рез = (Х^)рез = 2Н°а ’ (%“)l>e3= (Xs)pes =,0,	(1.4.47)
/„в."	_ тМо! +Z<№2
Uxjpes — 2c|^ и
Wpes -	,
(1.4.45)
i^\" _ Тл/» i + xoMi клз/урез —
2cor pq ’ zvef __	ТМо ХЛ12 (1-4.48)
'Xsjpes —	2(i>r pq ’
где y0 определяется выражением (1.4.10), а р и q — выражениями (1.4.26) и (1.4.27)!).
l) Формулы (1,4.47) и (1.4.48) интересно сравнить С (1.3.27) и (1,3.28),
§ 1.41
ОДНОРОДНЫЕ КОЛЕБАНИЯ МАЛОГО ЭЛЛИПСОИДА
61
Для эллипсоида вращения с осью, совпадающей с направлением постоянного поля (2VU = 2V22, 2V12 = 0):
„	„ н.
(Хх)рез = (Ху)рсз = (Ха)рез = 2(ow Хрез> ^s)pe3 =	(1-^-49)
Г
С учетом (1.4.49) формула (1.4.35) для собственной добротности эллипсоида вращения может быть записана в виде
(1А50)
Ширина резонансной кривой. Рассмотрим теперь вопрос о ширине резонансной кривой малого эллипсоида. Аналогично § 1.3 определим эту величину 2(ДЯ)£. как разность постоянных полей, при которых мнимая часть одной из поперечных компонент тензора ув составляет половину ее значения при резонансе. Можно показать, что в первом приближении при малой диссипации определения (АЯД с помощью компонент (yj)", (/у)" или (/„)" эквивалентны и приводят к следующему выражению:
(ДЯ)е = (ДЯ)0—,	(1.4.51)
4	10
где (ДЯ)0 — <ат1у — ширина резонансной кривой тензора % (формула (1.3.30)). Принимая во внимание выражение (1.4.35) для собственной добротности эллипсоида вращения, формулу (1.4.51) можно записать в виде
2(ДЯ)е = ^.	(1.4.52)
Если предположить, что (ДЯ)0 постоянно, то выражение (1.4.51) дает зависимость (ДЯ)е от формы образца. Для эллипсоида вращения из (1.4.51) с учетом (1.4.24) следует
(1.4.53)
Из (1.4.53) видно, что если при изменении формы эллипсоида вращения частота поддерживается постоянной (а Яо соответственно изменяется), то ширина кривой минимальна для нормально намагниченного диска и максимальна для продольно намагниченного цилиндра. Существенно, однако, подчеркнуть, что полученная зависимость является следствием определенного допущения о характере диссипации (<вг не зависит от формы образца). Действительно, с учетом (1.3.12) выражение (1.4.51) может быть
62	НАМАГНИЧЕННЫЙ ИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК [ГЛ. 1
записано следующим образом;
(ДЯ)е =
<0 .СО d
Т2А/о '
(1.4.54)
Отсюда видно, что при wd = const ширина резонансной кривой эллипсоида не зависит от его формы, В действительности различные механизмы релаксации могут приводить к существенным зависимостям как cod, так и (АЯ)0 от формы образца.
Сравнивая выражения (1.4.49) и (1.4.51), мы видим, что для эллипсоида вращения с постоянным полем, направленным по его оси, имеет место соотношение
2(ДЯ)(,Хрез = М0,	(1.4.55)
аналогичное соотношению (1.3.33) для внутреннего тензора восприимчивости х).
*) В дальнейшем индекс е у компонент внешнего тензора и ширины р<£ зонансной кривой эллипсоида мы будем часто опускать.	--ел 
ГЛАВА 2
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
§ 2.1. Обобщение уравнения движения намагниченности
Задачей этой главы является изучение анизотропии, в первую очередь кристаллографической, малых однородных магнитных колебаний ферромагнетика.
Анизотропия — это зависимость свойств тела от углов между направлениями, в которых проявляются (или измеряются) эти свойства, и некоторыми фиксированными направлениями. В предыдущей главе мы имели дело с идеализированным изотропным ферромагнетиком, в котором в отсутствие внешнего постоянного магнитного поля не было каких-либо выделенных направлений, и свойства которого поэтому не могли зависеть от углов. Параметры такого вещества, например магнитная восприимчивость, являлись скалярными. Однако при наложении постоянного магнитного поля (или при наличии остаточной намагниченности) в таком изотропном веществе появлялось выделенное направление — направление постоянного поля (или намагниченности) и, как мы видели, возникал особый вид анизотропии высокочастотных свойств — гиротропия. Магнитная проницаемость вещества (по отношению к слабому переменному полю) становилась несимметричным тензором. Когда же в § 1.4 мы перешли от изучения свойств вещества к изучению свойств тела, а именно, малого эллипсоида, появились новые выделенные направления — оси эллипсоида и возникла зависимость свойств (тела) от углов по отношению к этим направлениям — так называемая анизотропия формы. Тензор магнитной восприимчивости эллипсоида по отношению к внешнему переменному полю 7/' усложнился по сравнению с тензором вещества 7, стал зависеть от формы эллипсоида и от углов между направлением внешнего постоянного поля и осями эллипсоида.
Как правило, ферромагнетики (а также и другие магнитоупорядоченные вещества) являются кристаллами *). В них имеются выделенные направления — кристаллографические оси, и их свойства зависят от углов по отношению к этим осям. Известно
*) Недавно были обнаружены аморфные ферромагнетики [68], предсказанные Губаповым [56].
64	АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК	[ГЛ. 2
(см., например, [43]), что все параметры кристаллов, в том числе и магнитная восприимчивость, в отсутствие внешнего постоянного поля и остаточной намагниченности, представляют собой симметричные тензоры. При наличии внешнего постоянного поля магнитная восприимчивость ферромагнитного кристалла становится тензором, имеющим как симметричные, так и антисимметричные составляющие. Этот тензор зависит от параметров, характеризующих кристаллографическую анизотропию вещества, и от углов между постоянным полем и осями кристалла. Если же мы будем и в этом случае интересоваться свойствами тела, например, малого эллипсоида, то заметим, что тензор его магнитной восприимчивости (по отношению к внешнему переменному полю) будет определяться как кристаллографической анизотропией, так и формой образца. В выражения для его компонент будут входить углы, которые образует постоянная намагниченность как с кристаллографическими осями, так и с осями образца. Наша задача будет заключаться в определении этого тензора. Общие методы ее решения, основанные на введении в уравнение движения эффективных полей анизотропии, будут развиты в этом параграфе. Затем в § 2.2 эти методы будут применены к исследованию двух широко распространенных кристаллов — одноосного и кубического, а также к специальному случаю анизотропии, обусловленной сближениями энергетических уровней ионов.
На практике, а также и в физических исследованиях применяются часто поликристаллические ферро- и ферримагнитные материалы, состоящие из небольших кристалликов (зерен), обычно произвольно ориентированных друг относительно друга. Макроскопические параметры такой среды (усредненные по объему, значительно превышающему размеры зерен) изотропны. Но они существенно отличаются от параметров однородной изотропной среды. Магнитные колебания в таком поликристаллическом ферромагнетике будут рассмотрены в § 2.3 х).
Кроме кристаллографической анизотропии, в ферромагнитных кристаллах может иметь место анизотропия магнитных свойств, вызванная внешними упругими напряжениями. Выделенными направлениями в данном случае являются направления, по которым приложены напряжения. Причиной возникновения такой анизотропии является магнитоупругое взаимодействие, взаимосвязь упругого и магнитного состояния магнитоупорядоченных кристаллов [5]. Мы не будем рассматривать магнитоупругой анизотропии, но заметим, что общие методы, которые будут развиты ниже, применимы и в этом случае (см., например, [116]).
Исследуя магнитные колебания в анизотропных средах, мы будем по-прежнему использовать континуальный, феноменологи-
г) К этому вопросу мы вернемся в § 9.3.
§ 2.1] ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ 65
ческий подход1). Исходными будут являться выражения для макроскопической энергии (или некоторого термодинамического потенциала) того взаимодействия, которое является причиной рассматриваемого вида анизотропии. Эти выражения всегда можно записать как функции намагниченности из общих, симметрий-ных соображений, а входящие в них постоянные рассматривать как феноменологические константы.
Энергия и термодинамические потенциалы ферромагнетика. Рассмотрим сначала ферромагнетик при 0°К. Он будет характе-ризоваться^плотностью магнитной энергии, которая является функцией намагниченности. Одним из членов этой плотности энергии2) является энергия магнитных моментов ферромагнетика во внешнем поле Н или зеемановская, энергия
UB = - МН,	(2.1.1)
которая получается в результате суммирования энергий (1.1.28) по всем магнитным моментам в единице объема.
В предыдущем параграфе мы ввели в рассмотрение размагничивающее поле Нм. С ним связана внутренняя магнитная энергия
UM =-----МНм	(2.1.2)
(множитель 1/2 введен в это выражение потому, что поле Нм является функцией, причем линейной, намагниченности). Для малого эллипсоида, согласно (1.4.2),
С7м =MNM	(2.1.3)
или в координатных осях, совпадающих с осями эллипсоида,
UM = - j- (7VXM + N^M2v + A'ZMZ). (2.1.3')
Микроскопическим источником этой энергии является магнитное (диполь-дипольное) взаимодействие элементарных магнитных моментов.
Обменное взаимодействие при континуальном подходе приводит, прежде всего, к появлению внутренней энергии моментов в «молекулярном» поле Нд (1.1.40). Поскольку поле Нд
г) В данном случае это не только целесообразно, но и необходимо, потому что создание модельных (микроскопических) теорий кристаллографической анизотропий и магнитоупругого взаимодействия встречает большие трудности.
2) Не интересуясь поверхностными явлениями, мы будем рассматривать пока исключительно объемные плотности различных видов энергии, обозначая их буквой U с различными индексами. При этом слово «плотность» мы будем часто для краткости опускать.
3 А. г. Гуревич
66
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
пропорционально намагниченности, то (в изотропной среде)
t/д =---|-МНл = -	(2.1.4)
Для анизотропной среды выражение (2.1.4) необходимо обобщить следующим образом:
С7л=-4-МЛМ,	(2.1.5)
Хи
где обменная константа Л — тензор второго ранга, вид которо-
го, как и всех параметров вещества, определяется симметрией кристалла.
Однако выражения (2.1.5) недостаточно для полного учета обменного взаимодействия. Энергия ферромагнетика, обусловленная этим
Рис. 2.1.1. Линейная цепочка спинов.
взаимодействием, должна возрастать при непараллельности соседних моментов, которая будет иметь место при быстром изменении М в пространстве. Это обстоятельство может быть учтено, если принять, что энергия обменного взаимодействия
ие = ик + uq,
(2.1.6)
где энергия неоднородного обменного взаимодействия
3	3
р=1 s=l	Р s
Здесь хр и xs — координаты х, у и z, a — компоненты тензора неоднородного обменного взаимодействия q. Для изотропной
среды q скалярно и
(2.1.8)
Заметим, что выражения (2.1.4) и (2.1.8) можно получить, переходя от дискретных моделей с дираковским гамильтонианом (1.1.48) к континууму. Убедимся в этом на простейшей модели линейной цепочки спинов (рис. 2.1.1), рассматриваемых как классические векторы. Обменная энергия /-го спина в приближении ближайших соседей запишется для такой модели в виде
Разложим S/+1 и S/_1 в ряды около точки, где находится /-й спин:
ч _ Q , asf о2 &sf S/±1 - Sz + a + -y--^
§ 2.1] ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ &7
Учитывая, что S/ = const, получим, опуская индекс /,
ее = 2IS* 2 + /а2	.
Умножая это выражение на число спинов в единице объема N, получим сумму энергий (2.1.4) и (2.1.8); при этом Л имеет вид (1.1.59) (в данном случае Z = 2), а
q = а2Л.	(2.1.9)
Мы записали члены магнитной энергии, соответствующие тем видам взаимодействия, которые были уже рассмотрены выше. Энергии других видов взаимодействия в ферромагнетике также могут быть записаны как функции вектора намагниченности, точнее говоря, его ориентации, как так длина этого вектора при 0°К считается известной. В частности, энергия взаимодействий, которыми определяется кристаллографическая анизотропия, или энергия магнитной кристаллографической анизотропии Uа может быть записана в виде некоторого разложения по степеням проекций вектора М (или его направляющих косинусов). В следующем параграфе будут приведены примеры таких разложений.
В случае магнитоупругой энергии Uma, которой определяется анизотропия по отношению к направлениям внешних упругих напряжений, разложение может вестись по проекциям намагниченности и компонентам тензора деформаций (см. § 9.4). Подчеркнем, что коэффициенты в этих разложениях, как и величины Л и q в выражениях (2.1.5) и (2.1.7), являются феноменологическими константами, которые могут быть определены экспериментально или, в принципе, из микроскопических теорий.
Величину
и, = UM + и, + иа + ита	(2.1.10)
можно считать внутренней энергией г) ферромагнетика. Величину же
UE = Ui + UH = UM 4- Ue 4- Ua 4- Uma - МН (2.1.11) с термодинамической точки зрения (см., например, [36]) следует называть магнитной энтальпией. Ее минимум является условием равновесия ферромагнетика при заданном поле Н (и, конечно, при (ГК).
Если температура Т > 0 °К, то условием равновесия при заданных Т и Н является [36] минимум магнитного потенциала Гиббса (или магнитной свободной энергии) 2)
-Up = UE - ST = Ui - МН - ST,	(2.1.12)
х) См. сноску а на стр. 65.
2) Величину Up мы будем называть в дальнейшем просто свободно-! перепей.
3*
68
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
где S — плотность энтропии ферромагнетика. Заметим, что энтропийный член (— S Т) в этом выражении становится очень существенным при высоких температурах. Именно из-за него при Т > Тс (где Тс — температура Кюри) более выгодным становится магнитно-неупорядоченное состояние, обладающее большей энтропией. Однако для тех задач, которые нас будут интересовать (определение равновесных конфигураций намагниченности, исследование магнитных колебаний), можно будет обойтись без явной записи этого члена и, следовательно, без вычисления энтропии. Мы будем по-прежнему использовать выражения (2.1.1), (2.1.2), (2.1.5), (2.1.7) и разложения Ua и Uma такие же по форме, как и при Т = О °К, и не писать вовсе члена (—ST). Но проекции М, входящие во все эти выражения, будут теперь проекциями намагниченности при данной температуре. При этом член (—ST) распределится по остальным членам свободной энергии Up 1) • Величины же A, q и другие феноменологические константы, входящие в различные члены Up, будут, конечно, функциями температуры.
Уравнение Ландау — Лифшица и эффективное поле. Теперь можно перейти к центральной задаче этого параграфа — получению уравнения движения намагниченности в анизотропном ферромагнетике. Это уравнение было впервые записано Ландау и Лифшицем [Ш], а затем, в более общем виде, Макдональдом [116]. Оно имеет следующий вид:
“=-ГМхНй, + К,
где эффективное поле 2)
Неи =
dU
ам
(2.1.13)
(2.1.14)
а. U — плотность энергии или (при Т > 0) свободной энергии ферромагнетика. Уравнение (2.1.13) не может быть строго выведено в рамках континуального феноменологического рассмотрения ферромагнетика, и цель приводимых ниже рассуждений сос
3) В дальнейшем мы будем часто для краткости называть выражения (2.1.1), (2.1.2), (2.1.5), . . . и при Т > 0 соответствующими членами магнитной энергии, хотя на самом деле это — члены плотности свободной энергии или, точнее, плотности магнитной свободной энергии (или магнитного потенциала Гиббса).
2) Производная от скаляра по вектору определяется как вектор, проекции которого суть производные от этого скаляра по соответствующим проекциям вектора. Например,
dV dU dU dU
sm ~ хо амя + Уо дМу + zo дМt *
§ 2.1] ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ
69
тоит в том, чтобы показать, что оно является естественным обобщением уравнения (1.3.1) (которое, впрочем, тоже не было строго выведено).
Будем исходить из того, что условием равновесия является стационарность (в действительности, конечно, минимум) свободной энергии, т. е. равенство нулю ее вариации:
4^W==0	(2.1.15)
J	I	с):с2 cteg I	'
при дополнительном	условии	(1.2.3) постоянства длины	вектора
М.	Как	известно из вариационного исчисления	(см., например,
[38]), необходимое условие этого может быть записано в виде
-^[П + Ш2] =0,	(2.1.16)
где б/бМ обозначает вариационную производную
а ^ — постоянный множитель Лагранжа. Сравнивая /2.1.17^ и (2.1.14), мы видим, что эффективное поле
н.„	(2.1.18)
Тогда из условия (2.1.16) следует
Неи - 2Ш = 0,
т. е.
МхНе„ = 0.	(2.1.19)
Итак, условие (2.1.19) — параллельность М и Нен — является необходимым условием равновесия.
Но для изотропного ферромагнетика в заданном магнитном поле Н условием равновесия (см. § 1.2) было
М X Н = 0,
а уравнение движения (строго говоря — для однородных колебаний, а практически — для достаточно медленных изменений М в пространстве) имело вид (1.3.1). Поэтому естественно предположить, что для анизотропного ферромагнетика и произвольных изменений намагниченности, когда условие равновесия (как было строго показано) имеет вид (2.1.19), уравнение движения следует записать в виде (2.1.13).
70
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
ГГЛ. 2
Применяя формулу (2.1.14) к различным членам магнитной энергиих) ферромагнетика, можно получить соответствующие составляющие эффективного поля. Зеемановская энергия (2.1.1) даст, естественно, внешнее поле II. Магнитная энергия для случая малого эллипсоида (2.1.3) даст размагничивающее поле (—NM) (в этом легко убедиться, проводя, например, вычисления в проекциях). Применяя же формулу (2.1.14) к обменной энергии (2.1.6), получим эффективное поле обменного взаимодействия
3	3
Не = ДМ + 2 2 qps = Нл + Н,.	(2.1.20)
р=1 ‘~1 Р S
Величина Нд представляет собой молекулярное поле, а НГ; — эффективное поле неоднородного обменного взаимодействия. В частности, для изотропной среды (qPs = q)
з
Ие = ДМ+ q 2 ~^ДМ+ qV* 2M. (2.1.21) Р=1 дхр
Диссипативные члены в обобщенном таким образом уравнении движения могут быть записаны в формах, аналогичных приведенным в § 1.3. При этом диссипативный член в уравнении (1.3.2) останется без изменения и уравнение с таким членом будет иметь вид
— = - гм х Не„ 4- _ м х -	(2.1.22)
В диссипативных членах в (1.3.3) и (1.3.7), по-видимому, целесообразно заменить Н на Не«, так что соответствующие уравнения запишутся в виде 2)
~=-ТМх Ней
|MX(M X Hetf),
- - ТМ х Не„ - ЮГ(М - ХоНей).
(2.1.23)
(2.1.24)
Величина у0, входящая в уравнение (2.1.24) и в соотношение (1.3.12) между параметрами диссипации, представляет собой теперь статическую восприимчивость по отношению к аффективному полю
Хо = #-,	(2Л.25)
х) См. примечание1 на стр. G8.
2) Уравнение движения в форме, почти не отличающейся от (2.1.23) (см. примечание па стр. 40), было использовано Ландау и Лифшицем [111].
§ 2.1] ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ 71
а величина а>н, входящая в соотношение (1.3.15), заменяется на
(IJH eft = T-^eHo-	(2.1.26)
Преимущество уравнения (2.1.22) перед уравнениями (2.1.23) и (2.1.24) заключается именно в том, что для него эффективное поле (которое может быть довольно сложной функцией намагниченности) не входит в диссипативный член.
Необходимо заметить, что в рассмотренных уравнениях движения анизотропия среды учтена еще не полностью. Вообще говоря, и параметр у (т. е. g-фактор) для анизотропного ферромагнетика необходимо считать тензором, на что было указано Власовым и Ипгмухаметовым [121]. Вопрос об уравнениях движения намагниченности ферромагнетика с анизотропным g-фактором еще не вполне ясен, и мы ограничимся краткими замечаниями.
Рассмотрим для простоты случай, когда в энергии U отсутствует неоднородный член Uq, т. е. примем U = U (М). Уравнение (2.1.13) тогда примет вид
^- = TMx-^+R.	(2.1.27)
.Для изотропного (скалярного) g-фактора это уравнение может быть записано также в виде
# = -1 X -Я- + R'-	(2.1.28)
где J = — у-1М — плотность механического момента. Уравнения (2.1.27) и (2.1.28) обеспечивают (во всяком случае, при отсутствии диссипации) постоянство длин векторов J и М. Если энергия U не зависит явно от времени (т. е. отсутствуют вынуждающие силы) и R = 0, то эти уравнения обеспечивают также, как легко убедиться, постоянство U, что и должно иметь место при отсутствии вынуждающих сил и диссипации.
Если g-фактор является тензором и векторы J и
- М = -7j	(2.1.29)
не параллельны, то уравнения (2.1.27) и (2.1.28) не эквивалентны. Уравнение (2.1.27) в этом случае не обеспечивает постоянства энергии (при отсутствии вынуждающих сил и диссипации) и поэтому не может являться уравнением движения. Что же касается уравнения (2.1.28), (то оно обеспечивает (при упомянутых условиях) как постоянство энергии, так и постоянство длины вектора J и, по-видимому, может быть использовано в качестве уравнения Движения, если только постоянство J не противоречит каким-либо свойствам системы. В этом случае, конечно, все члены энергии Должны быть представлены как функции составляющих J. Заметим,
72
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
!ГЛ. 1
что тензор у при этом войдет, во всяком случае, в зеемановскую энергию (2.1.1) и будет таким образом присутствовать в уравнении движения.
Результаты экспериментов по ферромагнитному резонансу интерпретируются обычно на основании уравнения движения (2.1.13) — в предположении скалярной .величины у ’), а вся анизотропия учитывается при помощи составляющих эффективного поля. И хотя имеются экспериментальные данные [144], которые -свидетельствуют в пользу необходимости учета в некоторых случаях тензорного характера g-фактора, мы в дальнейшем, следуя традиции и для простоты, будем считать у скалярной величиной.
Линеаризованное уравнение движения. Представим теперь величины, входящие в уравнение движения намагниченности, в виде сумм постоянных и переменных величин. Переменные величины будем считать, как и раньше, зависящими от времени по гармоническому закону и воспользуемся методом комплексных амплитуд:
М = Мо + те'“',	(2.1.30)
Heff = Heffo + hefQe1"* = Heffo + heffe’“( + he’“(
При этом мы выделили из переменного эффективного поля hetfIei“' заданное переменное поле he’“( (заданное внешнее постоянное поле входит в Heff0). Заметим, что he’“( может представлять собой внутреннее или внешнее поле, в зависимости от того, для вычисления какой восприимчивости, %* или у/ (см. § 1.4), будет использоваться уравнение движения.
Суммы (2.1.30) следует подставить в одно из уравнений (2.1.22), (2.1.23) или (2.1.24). Будем считать переменные величины малыми по сравнению с постоянными. Тогда в нулевом приближении найдем условие равновесия (2.1.19). В первом приближении получим уравнения движения для комплексных амплитуд намагниченности. В случае исходного уравнения (2.1.22) такое линеаризированное уравнение будет иметь вид
icom + rm У НеИо + гМ0 X heft + ^mxM0 = - YM0 X h. (2.1.31)
Легко видеть, что линеаризованные уравнения (1.3.9) и (1.4.7) следуют из этого уравнения.
Интегрированию уравнения (2.1.31), т. е. решению задачи о малых колебаниях намагниченности, должно предшествовать определение равновесной намагниченности Мо. Вообще говоря, она является функцией координат. Но в этой главе, как и в предыду-
J) При интерпретации результатов измерений парамагнитного резонанса g-фактор обычно считается тензором [1].
§ 2.1J ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ 73
щей, мы рассматриваем ферромагнетик, однородно намагниченный до насыщения. Задача о равновесии заключается тогда в определении ориентации вектора Мо (длина его предполагается известной функцией температуры). Для этого может быть использовано уравнение (2.1.19) либо другие, эквивалентные ему условия стационарности плотности энергии (или свободной энергии) U', например,
dU _ „	dU_
эе : и’ "ёф
(2.1.32)
где 6 и <р — углы, определяющие ориентацию вектора М. Необходимо, конечно, убедиться, что найденная ориентация соответствует действительно минимуму энергии. В дальнейшем в качестве примеров будут решены некоторые задачи об определении равновесных ориентаций намагниченности. Но в большинстве случаев, исследуя малые колебания, мы будем просто использовать результаты решения таких статических задач.
Метод эффективных размагничивающих факторов. Перейдем теперь к рассмотрению методов решения линеаризированных уравнений движения намагниченности анизотропного ферромагнетика. Будем предполагать, что постоянное внешнее поле Но, равновесная намагниченность Мо и переменное поле h (внешнее или внутреннее) заданы, а анизотропия определена посредством задания зависимости U (М). При этом мы ограничимся случаем, когда не только постоянная, но и переменная намагниченность не зависит от координат (однородные колебания) и, следовательно, в выражении (2.1.14) будем учитывать только первый член.
Первый метод решения линеаризованного уравнения движения, известный как метод эффективных размагничивающих факторов, был предложен еще Киттелем [112] и подробно разработан Макдональдом [116]. Он основан на том, что эффективное поле представляется в форме
Heff = Н - NeffM,	(2.1.33)
где Neff — тензор эффективных размагничивающих факторов, компоненты которого -являются функциями Мо.
Запись (2.1.33) всегда возможна, если переменные составляющие намагниченности малы по сравнению с постоянными. В этом случае проекции h и m связаны линейными соотношениями. Как видно, например, из (2.1.31), составляющие heft при этом также линейно зависят от составляющих ш, и можно записать
heffl = h - NeIf (Мо) m.	(2.1.34)
Выберем в качестве системы координат декартову систему с осью z, направленной вдоль векторов Мо и Негг„ (которые, согласно (2.1.19), параллельны). В этом случае heff и m будут иметь только
74
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
ГГЛ. 2
поперечные составляющие и в (2.1.34) войдут только поперечные (Nil, N^, и A|-f) компоненты тензора Neff. Произвольную же зависимость Hetfo от Мо можно записать в виде
НеВо = HOZ~	(Мо) Мо.	(2.1.35)
Выражения (2.1.34) и (2.1.35) эквивалентны (2.1.33).
Подставляя (2.1.34) и (2.1.35) в линеаризованное уравнение движения, например в (2.1.31), можно получить уравнение для ия. В него войдут компоненты тензора Neff, которые всегда можно найти, зная зависимость U (М). Примеры вычисления этих компонент будут приведены в следующем параграфе.
Однако нет необходимости производить указанную подстановку и решать полученное уравнение для ш. Выражение (2.1.33) при замене Neff на N приобретает такой же вид, как и (1.4.1), а уравнение (2.1.31) совпадает с уравнением (1.4.7), решения которого были получены в § 1.4. Поэтому можно просто воспользоваться этими решениями, заменив в них компоненты тензора размагничивающих факторов N на соответствующие компоненты тензора Netf.
Тензор Netf является, вообще говоря, суммой тензоров, соответствующих всем учитываемым членам энергии U, кроме зеемановской энергии (2.1.1). Но в случае изотропной обменной константы А эффективное поле однородного обменного взаимодействия («молекулярное» поле) не войдет в уравнение движения. Анизотропную же часть однородной обменной энергии С7Л обычно относят к энергии анизотропии. Неоднородного члена Uq обменной энергии мы пока не рассматриваем. Таким образом, в нашем случае в Neff входят только тензор размагничивающих факторов (формы) N х) и тензор эффективных размагничивающих факторов анизотропии Na. Если мы подставим в формулы § 1.4 вместо компонент N компоненты №, то получим решение задачи о тензоре восприимчивости анизотропного ферромагнетика; компоненты его будут функциями внутреннего постоянного поля Н;о. Если же подставить в эти формулы вместо компонент N компоненты N + Na, то будет найден внешний тензор восприимчивости эллипсоида из анизотропного ферромагнетика; параметром при этом будет внешнее постоянное поле Но. Возможна, конечно, и такая постановка задачи: найти внутренний тензор восприимчивости
!) Заметим, что тензор N может быть введен для тел любой формы, но только в случае эллипсоида он оказывается не зависящим от координат.
| 2.1] ОБОБЩЕНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ НАМАГНИЧЕННОСТИ 75
движения намагниченности
Рис. 2.1.2. Намагниченность в декартовых и сферических координатах.
эллипсоида, т. е. зависимость переменной намагниченности от внутреннего переменного поля, но с внешним постоянным полем в качестве параметра. Для решения такой задачи следует в выражение (2.1.34) поставить только тензор Na, а в выражение (2.1.35) — сумму Nss + NsS.
' Решение уравнения движения в сферических координатах. Другой метод решения уравнений с учетом анизотропных (зависящих от углов вектора М) взаимодействий был предложен Смитом и Бельерсом [117] и Сулом [118] и распространен на случай наличия диссипации Скроц-ким и Курбатовым [120]. Этот метод основан на использовании уравнений движения, в которые непосредственно введена, согласно соотношению (2.1.14), энергия соответствующих взаимодействий. Такие уравнения будут иметь особенно простой вид, если перейти от декартовой системы координат к сферической.
Будем исходить, например, из уравнения (2.1.23), а в формуле (2.1.14) учитывать только первый
член в правой части, не рассматривая таких взаимодействий (например, неоднородного обменного взаимодействия), энергия которых зависит от пространственных производных намагниченности.
Вместо декартовых составляющих намагниченности Мх, Му и Мг введем переменные М, 6 и <р (см. рис. 2.1.2). Очевидно, что
Мх = М sin 6 cos (f, Му — М sin A sin <р, Mz = М cos 6,
е.
М	Л1у
6 = arccos	<р = arctg .
(2.1.36)
(2.1.36')
Так как используется уравнение (2.1.23), то можно считать
М = const.	(2.1.37)
По формуле (2.1.14) (без неоднородного члена) с учетом (2.1.36') и (2.1.37) вычислим декартовы составляющие эффективного поля (индексы eff у низ опускаем)
ГТ _ &U ____ dU dQ dU 5<р sin <р dU
Лх^дИГ^ де дмх ~ "адГ дм~х ~ м sin е 'ёф' ’
(2.1.38)
• тт	cosip dU „	1 dU
\	• Hv— м sin е й([1 »	— A/si;) Q-00- •
76
AilH зоТропный ФЕРРОМАГНЕТИК
if л. а
Подставляя теперь (2.1.36) и (2.1.38) в проекции уравнения (2.1.23) на оси х, у и z, мы убеждаемся, что три полученных уравнения удовлетворяются тождественно, если справедливы следующие два уравнения:
ае	(ил
(2.1.39)
Эф _______Т ТТ , ^d ff
at ~ sine 8 л/sine *’
(2.1.40)
где
1 dU тт	1 dU	. ...
nn 7 Нtp —-	. 'A г .	(2.1.41)
М 30 ’ ф М sin 0 d(p	х 7
Легко убедиться, что Н$ и II tf — не просто обозначения, а действительно представляют собой проекции эффективного поля на оси локальной системы координат, орты которой касательны к координатным линиям 0 и <р (третья составляющая, параллельная М, в уравнение (2.1.23), а следовательно, и в уравнения (2.1.39) и (2.1.40) не входит).
Если бы мы исходили из уравнения (2.1.22), для которого тоже справедливо условие (2.1.37), то пришли бы к уравнениям, отличающимся от (2.1.39) и (2.1.40) только заменой (1.3.4). Аналогичным образом можно записать в сферической системе координат и уравнение (2.1.24), для которого М =£= const. В этом случае все величины будут зависеть от трех переменных 0, <р и М, и мы придем к трем уравнениям. Два из них совпадут с (2.1.39) и (2.1.40) при учете соотношения (1.3.12), а третье запишется следующим образом:
=	(2.1.42)
где
(2.1.43)
Уравнения (2.1.39), (2.1.40) и (2.1.42) справедливы для произвольных движений вектора намагниченности М. Теперь рассмотрим случай малых отклонений М от равновесной намагниченности Мо, ориентация которой характеризуется углами 0о и <р0 (рис. 2.1.2). Уравнение (2.1.42) в этом случае будет содержать только малые величины второго порядка, и мы его не будем рассматривать, а уравнения (2.1.39) и (2.1.40) линеаризуем — сохраним в них члены только первого порядка малости.
Предположим сначала, что переменное поле отсутствует, т. е. рассмотрим малые свободные колебания намагниченности. Разложим dU/д® и dUldy в ряды по малым величинам ДО = 0 — 0о и Д<р = <р — <Ро и ограничимся первыми членами этих рядов.
§ 2.1] ОБОБЩЕЙИЕ УРАВЙЁЙЙЯ ДВИЖЕНИЯ НЛМАГ НИЙЕНЙОСТИ	??
Учитывая, что в положении равновесия	«	<
IdU \	= fdU_\ = 0
\ 50 /е=е„,<р=<р0	\ 5<р /0=0с,ф=фо	’
получим из (2.1.39) и (2.1.40) линеаризированные уравнения движения
^+(и^-л*’+ЭЧАе+	" 
+ (м sLo;Uw + Ue*)Л(₽^ °’
(2.1.44) д (Дф)_/ Т tj__________tod тт \ до _
Si ^Л7ойп0.ее ^sin20„ J
— f -7 -д-	---„Ю(г2  С/фф) Аср = 0.
^ДМО8Ш0О * л/а sin2 Оо )
Здесь обозначено
TJ = (^SL\ е<₽ \S0S<p /е=е0,ф=ф0 ’ аналогичный смысл имеют L’M и ?7ф(р.
Предположим, что собственные колебания являются гармоническими:
Д0 = (A0)j е’“(, А<р = (Аф)х eiMf, где со — комплексная собственная частота колебаний, которую и нужно определить. Для комплексных амплитуд (А0)х и (Аф)х из (2.1.44) получается система алгебраических уравнений. Определитель ее '	. - '
•4 /’
ICO ,С0 I	4	\	'
о 1	‘
- -л74 1 27	= °'	(2Л-45)
Лг* sinz0Q
Без учета диссипации (cod = 0) отсюда следует важная формула [117, 118]
<2-1л6)
При наличии диссипации, подставляя в (2.1.45) со = со' + гео", можно найти со' и jco". В частности, [120]
<2Л-47>
В Нервом приближении (cod <7: уЛД>) частота со' совпадает с соо-
1я
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
(ГЛ. 2
Заметим, что в формулы (2.1.44) — (2.1.47) входят множители (sin 0О)-1 и, таким образом, эти формулы, казалось бы, теряют смысл при 0о = 0. Практически, в этом случае обычно возникают неопределенности, которые могут быть устранены. Тем не менее, если мы хотим «без раздумий» пользоваться методом Смита — Сула, то следует так выбирать полярную ось, чтобы 0о =/= 0. Это всегда возможно, потому что, в отличие от метода эффективных размагничивающих факторов (где обязательно 0о == 0), в методе Смита — Сула никаких ограничений на выбор оси не накладывается.
Величина U в формулах (2.1.46) и (2.1.47) может включать в себя все виды плотности энергии ферромагнетика. Если же мы учтем в U только зеемановскую энергию и энергию размагничивающих полей, то найдем собственную частоту и добротность малого эллипсоида, полученные другим методом в § 1.4.
Рассмотрим теперь вынужденные колебания намагниченности под воздействием заданного переменного поля h_. Уравнения (2.1.39) и (2.1.40) будут в этом случае, конечно, справедливы, но входящая в них плотность энергии должна включать теперь дополнительно зеемановскую энергию в переменном поле
ГЛ = -МЬ_.	(2.1.48)
Обозначим суммарную плотность энергии через U1} а под U будем понимать ту же величину, что и раньше:
иг = U + Uh.	(2.1.49)
Будем снова считать колебания малыми и разложим теперь уже OUJdQ и dUJdq в ряды вблизи положения равновесия:
dUi I dU \ . гт «о । тг л t । (dUfr \ .
~дГ = \~де)0 +г7ееЛе + С7°фЛф + • • • +	)0 + • • •’
~д^~ =	+ г7вфА0 +	+ • • • + Х'д^'/о + • • •
В положении равновесия
IdU \ __ fdU \ __ „ \ 00 )о \ /о ’
Рассматривая малые колебания, можно ограничиться этими нулевыми членами разложения dUhldQ и dUhldq.
Выражение (2.1.48) в полярных координатах запишется следующим образом:
Uh — ~ Mh~ [sin 0 sin 0n cos (<р — <рй) + cos 0 cos 0h], (2.1.51)
где 6Й и <рд— полярный и азимутальный углы вектора h~, a h„ — его длина. Для получения уравнений движения достаточно про
*
§ 2.21 ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ	79
дифференцировать (2.1.51) по 6 и <р, заменить в производных 6 и <р на их равновесные значения 0О и <р0, подставить эти выражения в (2.1.50), а полученные выражения для dUJdft и dU-Jdq подставить вместо dU/dQ и dUldq в уравнения (2.1.39) и (2.1.40). Получающиеся таким образом уравнения несколько громоздки, и мы запишем их только для случая отсутствия диссипации
+ лГЧ,Г(Г <f7e-A0 +	= T^~sineft sin(<p0 — <рл),
t/t	ru Q вш Un
(2.1.52)
= — [ctg е0 sin 0,t cos (<р0 — <pft) —cos Oft].
Величины 7г~, Ой и <рй являются заданными функциями времени; в частности, для переменного поля с линейной поляризацией углы Оп и <fft постоянны. Углы же О0 и <р0 (входящие также в величины Um, UV} и U^) должны быть известны из решения задачи об определении равновесной намагниченности.
В заключение заметим, что выше было сделано существенное допущение. Предполагалось, что выражение для энергиих) U, которое первоначально записывалось как равновесное, сохраняет свой вид и для переменных намагниченностей и полей, и из этого выражения соответствующими дифференцированиями могут быть получены как постоянные, так и переменные составляющие эффективных полей. Очевидно, что это справедливо, если характерные времена тех процессов, которыми определяется анизотропия, много меньше, чем период колебаний. В § 9.5 будет рассмотрен случай, когда это допущение не выполняется.
§ 2.2. Ферромагнитный резонанс в монокристаллах
Перейдем к исследованию конкретного вида анизотропии в ферромагнетике — кристаллографической магнитной анизотропии. Наиболее отчетливо ее влияние проявляется, конечно, в монокристаллах. Все процессы в них протекают в более чистом виде, чем в поликристаллических веществах, и поэтому монокристаллы широко применяются в различных физических исследованиях, в том числе и ферромагнитного резонанса. Монокристаллы ферримагнетиков применяются и в технике [11].
Источники кристаллографической магнитной анизотропии. Как уже отмечалось в § 1.1, причиной магнитного упорядочения является зависящее от спинов электростатическое взаимодействие электронов, которое может трактоваться как сильное обменное взаимодействие их спиновых моментов. Причиной же магнитной кристаллографической анизотропии являются значительно более
х) См. примечание 1 на стр. 68.
80
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
слабые — магнитные (или, как их иногда называют, релятивистские) взаимодействия спиновых и орбитальных моментов электронов, участвующих в магнитном упорядочении. Можно отметить следующие механизмы кристаллографической анизотропии ферромагнетиков (подробнее см., например, [59]).
1) Магнитное':, (диполь - дипольное) взаимодействие магнитных моментов ионов. Энергия такого взаимодействия какого-либо иона со всеми остальными может быть разбита на две суммы: по ионам, которые находятся вне малой сферы, окружающей данный
Рис. 2.2.1. Схема, иллюстрирующая механизм анизотропного обмена 159].
ион,ипоионам, которые находятся внутри нее. Первая сумма дает обычную энергию размагничивающего поля. Вторая же существенно зависит от структуры кристалла и углов между его осями и направлениями моментов ионов. Это может, в принципе, явиться источником магнит
ной кристаллографической анизотропии. Однако в случае ферромагнетиков диполь-дипольное взаимодействие обычно не вносит заметного вклада в анизотропию1).
2) Анизотропное обменное взаимодействие. Спин-орбитальная связь приводит к тому, что обменное взаимодействие начинает
зависеть от углов между направлением намагниченности М, т. е. направлением спинов, и осями кристаллической решетки * 2). Поясним это следующим образом [591: в силу спин-орбнтальной
связи поворот спинов относительно решетки приводит к некоторому изменению электронных оболочек ионов (рис. 2.2.1). Следовательно, должно измениться и обменное взаимодействие, являющееся по своей природе электростатическим взаимодействием электронных оболочек. Таким образом, энергия обменного взаимодействия при наличии спин-орбитальной связи зависит от ориентации спинов относительно линий, соединяющих точки их расположения, т. е. относительно кристаллической решетки. Это справедливо как для прямого обмена (который играет, видимо, определенную роль в металлах), так и для косвенного обмена — через отрицательные ионы, — играющего главную роль в ионных кристаллах ®). Подчеркнем, что механизм анизотропного обмена существенно связан со спин-орбитальным взаимодействием. Он
!) Для антиферромагнитиков вклад этого механизма является в некоторых случаях существенным (см. § 4.1).
2) Такая анизотропия обменного взаимодействия была учтена при записи выражений (2.1.5) и (2.1.7). Как уже отмечалось выше, анизотропную часть энергии 17д принято включать в энергию кристаллографической анизотропии.
з) См, подробнее в § 4.1,
§ 2.2]
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
81
не может иметь места в тех случаях, когда ионы, как например, ионы Fe3+ или Мп3+, не обладают орбитальным моментом.
3) Одноионная анизотропия. Энергетические уровни магнитных ионов в магнитоупорядоченном кристалле, как отмечалось в § 1.1, образуются в результате расщепления уровней изолированных ионов в эффективном поле обменного взаимодействия и локальном электрическом (кристаллическом) поле. И в этом случае спин-орбитальное взаимодействие играет важную роль. Оно приводит к тому, что энергетические уровни ионов оказываются зависящими от углов между вектором М и осями решетки и вносят таким образом вклад в зависящую от этих углов энергию кристалла, т. е. в энергию магнитной кристаллографической анизотропии. Ниже будет подробно рассмотрен интересный специальный случай такой одноионной анизотропии — влияние примесных ионов с «пересекающимися» энергетическими уровнями.
В предыдущем параграфе отмечалось, что в магнитоупорядо-ченпых кристаллах имеется также анизотропия, обусловленная магнитоупругим взаимодействием. И если речь идет о внешних механических напряжениях, то учет этой анизотропии, как правило, не является необходимым, поскольку внешние механические напряжения в образцах, используемых для наблюдения магнитного резонанса или применяемых в устройствах СВЧ диапазона, обычно малы ’). Однако намагничивание ферромагнетика в силу магнитоупругого взаимодействия сопровождается спонтанными магнитострикционными напряжениями и деформациями [5J. Их энергия, так же как и энергия рассмотренной выше «естественной» (не учитывающей спонтанных деформаций) кристаллографической анизотропии, зависит от углов между вектором М и осями кристалла. Эта энергия может быть объединена с энергией естественной кристаллографической анизотропии [5]. И мы в дальнейшем под энергией и эффективными полями кристаллографической анизотропии будем всегда понимать суммарные величины, включающие вклады магнитоупругой энергии, обусловленной спонтанными деформациями.
Феноменологические выражения энергии' кристаллографической анизотропии. Независимо от физической природы кристаллографической анизотропии, можно, как показал Акулов (см. [5J), для каждого типа кристаллической решетки записать выражение для энергии магнитной кристаллографической анизотропии в виде степенных рядов по составляющим (или направляющим косинусам) намагниченности. Коэффициенты при членах этих рядов
1) Магнитоупругая анизотропия ферро-и аптиферроманитного резонанса, возникающая под воздействием специально приложенных внешних упругих напряжений, изучалась в ряде работ (например, в [343—345, 510]). Измерение этой анизотропии позволяет определить феноменологические константы магнитоупругого взаимодействия.
82
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
являются феноменологическими константами, характеризующими магнитную кристаллографическую анизотропию вещества. При записи таких рядов сохраняются л нить те члены, которые удовлетворяют условиям симметрии данной кристаллической решетки, т. е. инвариантны относительно всех преобразований симметрии, свойственных ей.
Заметим прежде всего, что в этих разложениях будут присутствовать лишь члены четных степеней относительно составляющих намагниченности. Тогда энергия кристалла не будет изменяться, как это и должно быть, при изменении направления намагниченности на обратное.
Приведем теперь выражения для энергии магнитной кристаллографической анизотропии некоторых кристаллов. Для кристаллов тетрагональной сингонии ’)
Uа = Кг sin2 6 + К2 sin46 + К2 siii46 cos2<p	(2.2.1)
где 0 — угол между намагниченностью М и осью четвертого порядка, а ф — азимутальный угол М в плоскости, перпендикулярной этой оси. Для кристаллов гексагональной сингонии
Ua = Кх sin20 К2 sin46 + Ks sine0 + K3r sin® 0 cos 6<p+ . . .
(2.2.2)
Для кубических кристаллов выражение энергии анизотропии обыч-' но записывается в виде
Ua~ (ct2ct2 + С11<Хз 4" Ct2Ct|) "Ь ^2а1а2й3 4~ • • •,	(2.2.3)
где а1>2,з — косинусы углов, образуемых вектором М с осями четвертого порядка. Константы Кг, К2 и т. д. в этих выражениях, имеющие размерность плотности энергии, называются константами анизотропии. Они являются функциями температуры. Обычно, во всяком случае при не очень низких температурах, первая константа анизотропии Кг превышает все остальные.
Минимизация выражений типа (2.2.1), (2.2.2) и (2.2.3) позволяет найти направления равновесной намагниченности при отсутствии внешнего поля и при условии, что форма образца не оказывает влияния на зти направления (например, образец — сфера). Такие направления называются осями легкого намагничения (или, просто, легкими осями). Направления, для которых Ua максимальна, называются трудными осями. При Кг > 0 и |Т^2|, |А'2' |, |А'31 <4 |.&41 в гексагональных, тетрагональных или тригональных кристаллах легкими осями будут выделенные оси (соответственно, шестого, четвертого или третьего порядка), а при
х) Описание структур кристаллов см., например, в [28].
§ 2.2]
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
83
Кг < 0 легкие оси в таких кристаллах будут лежать в базисной (перпендикулярной выделенной оси) плоскости. В кубическом 9
кристалле при	|/<х| направления легких и трудных
осей определяются знаком Кр. при Кг > 0 легкими будут оси
четвертого порядка, а трудными — оси третьего порядка, при Кл < 0 эти направления поменяются местами.
С учетом энергии размагничивающих полей (2.1.2) и при наличии внешнего поля, т. е. с учетом зеемановской энергии (2.1.1) направления равновесной намагниченности определяются в результате минимизации суммарной
энергии, включающей члены (2.1.1), (2.1.2) и энергию анизотропии Ua. Некоторые примеры решения таких задач будут рассмотрены ниже, в других случаях будут использоваться готовые результаты их решения.
Одноосные кристаллы. В магнитных кристаллах с одной выделенной осью или так называемых одноосных кристаллах (гексагональных, тетрагональных и тригональных) анизотропия в базисной плоскости, характеризуемая константами К2' или К3', обычно мала по сравнению с анизот-
Рис. 2.2.2. Оси координат в одноос-ном ферромагнетике.
ропией в плоскостях, содержащих
выделенную ось. Для таких кристаллов членами с Кл' или К3 в выражениях (2.2.1) и (2.2.2) можно пренебречь, т. е. считать, что кристаллы обладают цилиндрической симметрией. Мы исследуем сейчас в таком приближении ферромагнитный резонанс в
одноосных кристаллах.
Воспользуемся сначала методом эффективных размагничивающих факторов. Введем две системы координат (рис. 2.2.2): систему х' у’ z', в которой ось z' совпадает с выделенной осью кристалла — осью анизотропии, и систему xyz, в которой ось z совпадает с направлением, равновесной намагниченности. Именно в этой последней системе мы знаем решение уравнений движения, содержащее компоненты тензора N (§ 1.4). Не теряя общности, две оси, например х и х', этих систем можно совместить.
Выражения (2.2.1) или (2.2.2) с учетом только первых двух членов можно записать в виде
/ Af® \	/ М* V
иа = К. 1-------г- + К2 1-------М .	(2.2.4)
По формуле (2.1.14) нахрдим составляющие эффективного поля
84
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
trJT. 2
анизотропии в системе x'y'z'-.
К,	I м,- М* \
Haz. = 2 — Mz> + 4К2 ~------------z- ,
az	2	\ ДУ2 Л74 s
О	4 О	О I
Нах.= Нау^0. (2.2.5)
Для перехода к системе координат xyz воспользуемся обычными формулами преобразования проекций векторов [35]. Учитывая, что в данном случае (рис. 2.2.2) косинусы углов между соответствующими осями составляют
Pxz' 65 Pyz' sin 6g, Pzz' COS 6g,
получим проекции эффективного поля анизотропии
Нах = ®, Яад = —Gsiii90, ffaz=G cosQ0,
(2.2.6)
где
G = (Mz cos 0o Mv sin 0O) +	Г Mz cos 0o — Mv sin 0o —
Mo	Mo L
— ~^(MZ cos3 Go — 3MlMv cos2 0o sin 0o)
Мы рассматриваем малые колебания намагниченности (Мх, Mv <<: Mz х Мо), поэтому в выражении для G можем заменить Ml на М02. Тогда зависимости проекций На от проекций М линеаризируются и могут быть представлены, согласно (2.1.33), в виде
Но = — №М.
(2.2.7)
В данном случае
№ = № = О,
Naw = - sin2 60 + ~- (2 sin2 е0 - 3 sin4 е0),	(2.2.8)
Ч	Л/о
Мзз = — cos2 е0 — (cos2 е0 — cos4 е0).
Ч	Л/2
Этим задача о ферромагнитном резонансе в одноосном кристалле (без учета анизотропии в базисной плоскости), по существу, решается. Подставляя полученные компоненты тензора N° соответствующим образом (вместо компонент тензора N или в сумме с ними) в формулы § 1.4, можно вычислить, как указывалось выше, компоненты внутреннего тензора восприимчивости одноосного ферромагнетика или резонансные частоты и компоненты внешнего тензора восприимчивости эллипсоида из такого ферромагнетика.
i 2.21 ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ	85
Определим, например, собственную частоту однородных магнитных колебаний сферы из одноосного ферромагнитного монокристалла. Для зтого достаточно подставить выражения (2.2.8) для компонент тензора анизотропии вместо компонент тензора N в формулу (1.4.16). В результате получим (опуская индекс Оу собственной частоты)
(v)2=^oz	cos2 е°—Has sin2 20°'х
>< (HOz + 2Hai cos 20о + 4Яа2 sin2 0о(1 + 2 cos 20о)]. (2.2.9) Здесь
^=ТвЬ	(2.2.10)
а HOz, как и в (1.4.16),— проекция Но на направление Мо. Обычно |//л2| l#Ail- Величину 2НAl называют часто полем анизотропии ’).
Для вычисления резонансной частоты по формуле (2.2.9), как и для проведения всех других расчетов, связанных с учетом анизотропии и формы образца, необходимо предварительно решить статическую задачу об определении ориентации вектора Мо по заданным ориентации и величине внешнего постоянного поля Но. Рассмотрим зту задачу, предполагая, что образец однородно намагничен. Пусть направление вектора Но характеризуется известными углами Он и <рн (см. рис. 2.2.2), а направление вектора М — углами 0 и <р, равновесные значения которых 0О и ф0 и должны быть определены. Для определения углов 0О и ф0 необходимо минимизировать суммарную магнитную знергию, которая включает зеемановскую энергию (2.1.1), знергию анизотропии (2.2.4) и энергию размагничивания (2.1.3). В сферической системе координат суммарная энергия для эллипсоида, как нетрудно убедиться, запишется следующим образом:
U = — М0Н0 [sin 0 sin 0H cos (ф — фн) + cos 0 cos Он] + К± sin2 0 Ц-+ К2 sin3 4 0 4- ...
... + Ml (Nx sin2 0 cos2 ф + Nv sin2 0 sin2 ф + Nz cos2 0)	(2.2.11)
(при этом предполагается, что одна из осей эллипсоида совпадает с осью анизотропии).
Для простоты будем учитывать только первую константу анизотропии и рассмотрим случай сферы. Тогда
U = — М0Н0 [sin 0 sin Он cos (ф — фн) cos 0 cos 0Н] 4~
+ Ki sin2 0 +	М20.	(2.2.12)
3) Постоянную скалярную величину НА1 не следует путать с аффектив-
ным полем анизотропии На, которое зависит от ориентации Мо и имеет постоянную и переменную составляющие.
86
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Необходимыми условиями равновесия являются
= °’	= °-	(2.2.13)
\	/е=Р„, ф=ч>0	\<этр /е=е„. <₽==<₽»	'
Дифференцируя (2.2.12), получим
MqH0 [cos 6о sin ()н cos (<р0 — <Рн) — sin 60 cos 6Н] — Кг sin 26О = О,
(2.2.14)
A/0770sin Onsin sin (<р0— <р«) = 0.	(2.2.15)
Из (2.2.15) следует
Фо = фн-	’	(2-2.16)
Таким образом, векторы Мо и Но лежат в одной плоскости, проходящей через ось анизотропии, что, впрочем, ясно и из симметрии задачи. Тогда из (2.2.14) вытекает уравнение, определяющее угол 0о: sin 20о = sin (0Н - 0О),	(2.2.17)
иА1
где НА1 определяется выражением (2.2.10).
Примем сначала, что Кг > 0 (легкая ось). Тогда, как нетрудно убедиться, в частных случаях уравнение (2.2.17) имеет сле-
дующие решения: при
ея = о
при
малых 0j
е0 = о,
__
~	Н Al '
j+2 НГ
. Яо ’ = arcsin
е0
(2.2.18)
при
Он = -у- и
6о
Но>2НА1 значениях 0
«о
__ л
уравнение (2.2.17) может быть
При произвольных
легко решено относительно 0н. Аналогичным образом может быть рассмотрен и случай Кг < 0 (легкая плоскость анизотропии). Полученные таким образом зависимости 0о от 0ц при различных значениях Н0ША1 показаны на рис. 2.2.3 (пунктир на рпсупке соответствует ориентациям, которые не осуществляются, так как в образце возникает доменная структура). Как видно из рис. 2.2.3, вектор Мо совпадает по направлению с полем Цо, если последнее направлено по легкой оси или лежит в легкой плоскости. Если Но направлено вдоль трудной оси или лежит в трудной плоскости, совпадение направлений Мо и Но имеет место при Яо > 2
Для других направлений Но вектор Мо приближается к Но асимптотически по мере роста Яо, причем в сильных полях, превышающих в несколько раз поле анизотропии, разность 0О — 0н невелика.
2Яат
§ 2.21
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
87
Рис. 2.2.3. Равновесные ориентации намагниченности в сфере из одноосного ферромагнетика в зависимости от ориентации Но. Цифры у кривых™ значения Но/Н^д.
(принято 4rtMo —
Следует заметить, что полученное решение справедливо не при всех значениях Но и Од. В самом начале, записывая выражение (2.2.11), мы предположили, что образец однородно намагничен. В действительности же в образце (если его размеры превышают определенные критические величины) в некоторых интервалах значений Но и 0Н энергетически более выгодным будет существование доменной структуры.
Решения, которые не осуществляются из-за возникновения доменной структуры, на рис. 2.2.3 показаны пунктиром.
Используем теперь результаты решения статической задачи для вычисления резонансной частоты сферы по формуле (2.2.9). Если принять во внима
ние (2.2.16), то формула (2.2.9) (без учета К2) запишется следующим образом:
(v)2='11,1 cos	~+ 2Н Ai cos2 °"1 '
X [Но cos (0о — Од) -р 2НА1 cos 20о]. (2.2.19)
Легко показать, что если 0о=ДО (т. е. 0Н=ДО), то формула (2.2.19) с учетом условия равновесия (2.2.17) может быть также записана в виде
(-у)2 - Но [ //0 cos (0О - ел)+2ЯА1 cos 20о]. (2.2.19')
Применим теперь к той же задаче второй из упомянутых в §2.1 методов учета анизотропии при ферромагнитном резонансе — метод Смита — Сула. Ограничимся по-прежнему исследованием свободных незатухающих колебаний — определим их собственную частоту по формуле (2.1.46). Для этого необходимо вычислить вторые производные магнитной энергии образца по углам 6 и ф. Рассмотрим случай сферы и учтем только первую константу анизотропии. Тогда, дифференцируя (2.2.12), получим
Uw = М0Н0 [sin 0 sin 6Л cos (ф — фн) + cos 0 cos Он] Д- 2.К1 cos 20, Uw = М0Н0 sin 0 sin Од cos (ф — <ри),	(2.2.20)
U69 — МйНь cos 0 sin 0H sin (ф — фН).
88
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2 . •
Подставляя значения этих производных при равновесии в формулу (2.1.46), мы придем к выражению (2.2.19). Таким образом, на примере сферы из одноосного кристалла мы убедились, что оба метода описания ферромагнитного резонанса в анизотропной среде — метод эффективных размагничивающих факторов и^метод Смита — Сула, совершенно эквивалентны.
Рис. 2.2.4. Собственные частоты однородных магнитных колебаний сферы из одноосного ферромагнетика. Расчет по формулам (2.2.21) и (2.2.22)—в пределах их применимости — и с учетом несовпадения направления Мо и Но— при малых полях для трудных направлений. Пунктир— расчет несправедлив, так как принятое основное состояние не является равновесным (4лМ0 — Нд1).
Остановимся теперь па некоторых частных случаях формулы (2.2.19). Примем сначала Кг > 0. Если при этом 0н = 0 (поле направлено по легкой оси),то, согласно (2.2.18), 0о = 0 и из (2.2.19) следует
ю = т(Я0 + 2^а1).	(2.2.21)
Эта формула была впервые получена Киттелем [112]. Если поле лежит в трудной плоскости и Но > 2//ai> т°, согласно (2.2.18), 0О — л/2 и
со2 = Г*Н0 (Но - 2HaJ.	(2.2.22)
Для случая < 0 и поля, направленного по трудной оси или лежащего в легкой плоскости, получаются те же формулы (2.2.21) и (2.2.22). Но теперь НА1 < 0, и формула (2.2.21) имеет место только при Но > 2|#aiI, а формула (2.2.22) — при любых значениях Но. Результаты расчета по формулам (2.2.21) и (2.2.22) приведены на рис. 2.2.4. Заметим, что формулы (2.2.21) и (2.2.22), так же как и выражение (2.2.19), несправедливы при таких зна-
§ 2.21
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
89
чениях постоянного поля, при которых однородная намагниченность не является равновесным состоянием и в образце возникает доменная структура (см. рис. 2.2.4). Резонанс при наличии доменной структуры будет исследоваться в главе 3.
В предельном случае больших полей (Но |//лг1), пренебрегая раличием углов Од и 0о и отбрасывая члены с IIА1 и HAz в степенях выше первой, получим из (2.2.9)
— — Но НА1	—g- cos 20н j +
+ НА2 ----cos 26д-------— cos .
(2.2.23) Эта формула справедлива только при очень высоких частотах, так как поля |jEQx | для одноосных ферро- (и ферри-) магнетиков обычно велики — измеряются десятками килоэрстед.
Для произвольных 0д и Но зависимость g>(H0, Qh) нельзя записать в замкнутом виде, но ее легко рассчитать численно, используя резонансные формулы (2.2.9) или (2.2.19) и условие равновесия (2.2.17). Результаты такого расчета и соответствующие экспериментальные данные приведены на рис. 2.2.5. Из рисунка видно, что расчет дает довольно хорошее совпадение с экспериментом * 2).
Кубический кристалл. В качестве второго примера рассмотрим монокристаллы кубической сингонии. Этот случай представляет очень большой практический интерес, так как к кубическим
кристаллам принадлежит большинство ферритов2), используемых при исследованиях ферромагнитного резонанса и в технике сверхвысоких частот. Кубическими являются ферриты со структурами шпинели и граната, в частности иттрий-железный гранат, который нашел очень широкое применение в физических исследованиях и в технике.
Рис. 2.2.5. Зависимость резонансного поля от угла между Но и трудной осью для сферы из ферромагнетика с легкой плоскостью анизотропии [141J. Точки— эксперимент для кристалла RbNiFa при частоте 31,4 Ггц. Сплошная линия — численный расчет с учетом резонансного условия (2.2.9) и уравнения для 60, являющегося обобщением (2.2.17), при g = =2,24, Нд1 = — 8,3 кэ и Нда = =0,9 кэ. Пунктир— расчет по формуле (2.2.23) при тех же значениях параметров.
х) Совпадение может быть еще улучшено [141], если в уравнении движения учесть анизотропию (тензорный характер) ^-фактора (см. стр. 71).
2) Эти вещества, являющиеся ферримагнетиками (см. § 4.4), могут рассматриваться как ферромагнетики при описании их свойств в диапазоне сверхвысоких частот в не очень сильных магнитных полях.
60
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Воспользуемся методом эффективных размагничивающих факторов. Выражение (2.2.3) для энергии анизотропии кубического
Рис. 2.2.6. Кристаллографические оси и плоскости и оси координат в кубическом ферромагнетике.
кристалла можно записать следующим образом (учитывая, что а'( а| + аз= — 1, и отбрасывая член, не зависящий от ориентации М):
Ua= -4-^1(aJ + at +
+ аз) Я- ^2al°-2a3	• • •
(2.2.24)
Оси штрихованной системы координат, в которой первоначально записываются выражения для энергии и эффективного поля анизотропии, совместим с осями [100], [010] и [001]’) (рис. 2.2.6). Тогда выражение (2.2.24) для
энергии анизотропии перепишется следующим образом:
Ua = - —Г (М1'+	+ М3') +	Ml. (2.2.24')
По формуле (2.1.14) найдем проекции эффективного поля анизотропии
Нар- =	(2.2.25)
/Пр	/Пр
где р', s', v' = 1,2,3 и р' =(= s' =/= v'.
Перейдем теперь к новой — нештрихованной системе координат, в которой третья ось совпадает с направлением равновесной намагниченности, а затем линеаризируем зависимости проекций На от проекций М в этой системе, учитывая малость и М2 по сравнению с М3 Мо. Тогда эти зависимости примут вид (2.2.7), а выражения для компонент тензора размагничивающих факторов анизотропии (с учетом только первой константы анизотропии) окажутся следующими [116]:
з
- -В- 2	(Р, * = 1, 2),
0 р'^1	(2.2.26)
<-=-^23^
_____________ О Р'=1
г) Для обозначения осей и плоскостей в кристалле эдесь используются, как обычно, индексы Миллера [28] (см. также [32]).
§ 2.21
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
91
Если направить оси нештрихованной системы так, как показано на рис. 2.2.6 (ось 1 лежит в плоскости Г 2'), то для косинусов Ррр' будут иметь место значения, приведенные в табл. 2.2.1. Подставляя эти значения в (2.2.26), получим
= — 3 sin2 60 sin2 2ф0,
A'12 = — 3 sin2 60 cos 60 sin 4ф0, 7И2
к	/	1	\	(2-2.27)
Na22 = _ 3 sin2 260 1 - ~ sin2 2<р0 , Л/2	\	4	/
^зз - -	(1 + cos2 260 - sin4 60 sin2 2ф0).
Ат
Теперь, решив предварительно статическую задачу об определении углов 60 и <р0, можно будет определить резонансную частоту эллипсоида из кубического кристалла и вычислить компоненты тензоров восприимчивости, внутреннего или внешнего.
Таблица 2.2.1
Косинусы углов между осями для кубического кристалла (см. рис. 2.2.6)
р	р'	г	2'	3'
	1	sin фо	— COS фо	0
	2	COS ();. COS фо	cos Оо sin фо	— sin 00
	3	sin 6о cos фо	sin 0о sin фо	cos 0о
Мы не будем останавливаться на решении упомянутой статической задачи, которая совершенно аналогична рассмотренной выше задаче для одноосного кристалла. Приведем лишь некоторые результаты для случая сферы с учетом только первой константы анизотропии. Если постоянное поле Но направлено по одной из легких осей «100) х) для Кг > 0 и (111) в случае Кг < 0), то вектор Мо направлен по этой же оси. Для Но, направленного по другим осям симметрии кристалла, направления Но и Мо совпадают, если значения Но превышают величины Нг, приведенные
х) Как обычно, < > обозначает одну из эквивалентных осей, например, <100> — любую из осей четвертого порядка [100], [010] или [001], а <111> — любую из осей третьего порядка [111], [Ill], [111] или [111].
82
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Таблица 2.2.2
.Характерные поля Hi для кубического кристалла
	я»	
Направление постоянного ПОЛЯ	К, > 0	К, < 0
<100>		о 1^1 1 Z Но
<111>	1 -,= 		
<110>	К1 2 Л/о	1 Ki 1 Л/о
в табл. 2.2.2. Для других направлениг Мо приближается по направлению к Г		постоянного поля вектор Ео асимптотически по мере
роста Нй, причем отклонения становятся очень малыми, если Но превышает в несколько раз величину }К1}/Л/0.
Эти результаты получены в предположении однородной намагниченности образца (т. е. отсутствия доменов). Как и для одноосного кристалла, домены отсутствуют, если поле Но, направленное по легкой оси, превышает по величине размагничивающее поле. Если Но направлено по другой оси симметрии кристалла, то Но должно превышать сумму размагничивающего поля и поля Hi, приведенного в табл. 2.2.2. Таким образом, если постоянное поле направлено по любой оси симметрии кубического кристалла, то в случае однородной, намагниченности направления Мо и Но будут совпадать.
Определим теперь резонансную частоту для сферы из кубического кристалла, когда направления Мо и Но можно считать совпадающими. В этом случае последний член в (1.4.16) можно отбросить. Действительно, для осей (100), (110) и (111) (и, вообще, для плоскостей {100} и {110} х), в которых лежат эти оси), как следует из (2.2.27), Дц2 = 0. В случае же Но +> |А\ |/М0 последним членом в (1.4.16) можно пренебречь, как малым членом второго порядка. Величина HOz в формуле (1.4.16) в рассматриваемом случае совпадает с Но, а углы 0О и <р0 в (2.2.27) — с углами 6Я и и’фд вектора Но. В результате получим (опуская индексы у углов) (= {Яо’+ Hai [ 1 + cos1 2 20 — (sin4 0 + 3 sin2 0) sin2 2<p}} X
X |я0 + Hai |^2 — 4 sin2 20 + sin2 20 — sin4 oj sin2 2<p, (2.2-28)
1) { } обозначает одну из эквивалентных плоскостей, например, {100}—
одну из плоскостей симметрии (100), (010) или (001).
§ 2.2)
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
9.'
где НА1 определено согласно (2.2.10). Подчеркнем еще раз, что формула (2.2.28) справедлива:
а)	точно — для Но, направленного по одной из осей симметрии, и величин Яо, при которых отсутствует доменная структура;
б)	приближенно — для любых направлений Но, но при Но ->\Наг |.
При экспериментальном исследовании ферромагнитного резонанса в кубических монокристаллах сферические образцы ориентируются обычно так, чтобы ось вращения, перепендикулярная магнитному полю, совпадала с осью <110>. Тогда Но лежит в плоскости {110} (рис. 2.2.6) и при вращении образца (или магнита) совпадает поочередно со всеми осями симметрии кристалла.
Резонансная формула для этого случая получается из (2.2.28), если положить ф = л/4. Запишем ее [132] с учетом второй константы анизотропии К2 (в (2.2.27) и (2.2.28) члены с К2 были для простоты опущены):
= [но + НА1 (-	+ 2 cos 20 + -J- cos 4о) +
4- нА2 4 4+4cos 2е)sin2 2е ]х
X [н0 Hai	cos 20 + 4 cos 40 j +
+ На2 (----4 cos 20 + 4 cos 40^ sin2 ol ,
\	о 4	о	j	J
(2.2.29)
где Нах и НА2 определяются согласно (2.2.10). Частные случаи формулы (2.2.29) приведены в табл. 2.2.3. Заметим, что отличие формулы (2.2.32) (в этой таблице), содержащей два различных множителя, от формул [2.2.30) и (2.2.31) связано с тем, что в направлениях < 100> и < И1 > энергия анизотропии имеет минимум или максимум, а направление <110> является точкой седла для поверхности Ua (0, ф).
Таблица 2.2.3
Частоты ферромагнитного резонанса в сфере из кубического кристалла
Направление Но	6	ы 7	№ формулы
<100>	0	Яо4 2На1	(2.2.30)
<111>	54°44'	н0-~нА1-^нА2	(2.2.31)
<110>	90’	[(Но — 2HAi) (Но 4 НА1 + 4^/,	(2.2.32)
94
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Зависимость со/у от Но для различных направлений постоянного поля показана на рис. 2.2.7. В тех пределах, в которых формулы (2.2.30)— (2.2.32) справедливы, кривые на рис. 2.2.7 построены по этим формулам (с учетом только первой константы анизотропии). При малых же полях для трудных и промежуточного направлений, когда Мо не совпадает по направлению с Но, на рис. 2.2.7 приведены зависимости, рассчитанные в [119] на основании решения статической задачи в предположении однородной
Рис. 2.2.7. Частоты однородных магнитных колебаний сферы из кубического ферромагнетика [119]. Постоянное поле Но направлено вдоль осей, обозначенных у соответствующих кривых. Расчет с учетом несовпадения направлений Мо и Но. Пунктир— расчет несправедлив, так как принятое основное состояние не является равновесным.
намагниченности. Однако эти зависимости (показанные на рисунке пунктиром) не реализуются, так как в образце образуются домены. Действительные условия резонанса при наличии доменов будут найдены в главе 3.
Для произвольных 6 и <р формула (2.2.28), как уже отмечалось, справедлива только при Но |Ялг I- Поэтому целесообразно упростить ее при том же условии. В результате получим
4 = Но + НА1 [2 - 4- sin2 26 -4 sin4 6 sin2 2qA . (2.2.33) I	\ Л	&	/
Легко видеть, что для осей (100> и <111> формула (2.2.33) дает точные величины (2.2.30) и (2.2.31), а для осей <110) результат вычисления по ней совпадает с (2.2.32) лишь приближенно с точностью до квадратичных членов по Ядр Зависимость Яо от 0 при о = const и ф = 45° (плоскость (110)), рассчитанная по формуле (2.2.33), показана на рис. 2.2.8. На рис. 2.2.9 приведена рассчитанная по той же формуле зависимость резонансного поля
§ 2.21	ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ 95
от угла <р в плоскости (001) (0 = л/2). Очевидно, что она совпадает с зависимостью от 0 при <р = 0 или <р = л/2.
Как видно, например, из (2.2.33), имеются углы, для которых (о/у = Но. В частности, в плоскости {110} это имеет место при 0 = 29°20' (рис. 2.2.8), а в плоскости {100} — при <р = 31°45' (рис. 2.2.9). Для сферы из монокристалла, ориентированной таким образом, резонансное поле Но не будет зависеть от температуры (с точностью до К2 и более высоких констант анизотропии).
Рис. 2.2.8. Зависимость резонансного поля от угла между Но и осью <100> в плоскости {110) кубического кристалла для случая | П/ц | «С С и/у и Ki < 0. Линия— расчет по формуле (2.2.33). Точки— эксперимент для иттрий-железного граната при частоте 9,3 Ггч и комнатной температуре [136] (g — 2,00; | НА11 = 36 е).
Рис. 2.2.9. Зависимость резонансного поля от угла между Но и осью <100> в плоскости {1001 Для |На^|-<ы/уи Kt < 0. Расчет по формуле (2.2.33).
Предельный случай | Hai | #о (и I Haz I I Hai I ) имеет большое практическое значение, так как многие ферриты (см. [19]), в том числе те, которые благодаря узкой резонансной кривой наиболее широко' применяются в технике и в физических исследованиях, имеют малую анизотропию. На рис. 2.2.8 приведены результаты эксперимента для иттрий-железного граната при частоте ~ 9 Ггц‘, теоретическая кривая совмещена с ними подбором значений у и Hai- Как видно из рисунка, точки очень хорошо ложатся на теоретическую кривую. Этого и следовало ожидать, так как в данном случае Но/\ Hai | ~ 40.
Однако при более низких частотах или для ферритов с большей анизотропией формула (2.2.33), а также — при произвольных углах — формулы (2.2.28) и (2.2.29) не являются точными.
96
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Рис. 2.2.10. Зависимость резонансного поля от угла между Но и осью <100> в плоскости{ 110/1119]. Пунктир— расчет по приближенной формуле (2.2.33). Сплошная линия — расчет с учетом несовпадения направлений Мо и Но. Точки— эксперимент для марганец-цинкового феррита при частоте 9,2 Ггц и температуре 77°К.
Это иллюстрирует рис. 2.2.10. Напомним, что аналогичное положение имело место для одноосных кристаллов (рис. 2.2.5).
Мы не будем останавливаться на применении к кубическому кристаллу методики Смита — Сула. Ход вычислений в этом случае совершенно аналогичен рассмотренному выше на примере одноосного кристалла, необходимо лишь исходить из плотности энергии анизотропии для кубического кристалла (2.2.3), которая в сферических координатах, как легко убедиться, запишется следующим образом:
TJa =-^~ Кх (sin2 20 4- sin4 0 sin2 2tp) + + -^K2 sin2 20 sin2 0 sin2 2<p. (2.2.34) Результаты же, полученные обоими методами, конечно, будут совпадать.
«Аномалии» анизотропии, обусловленные сближениями энергетических уровней ионов. До сих пор мы исходили из выражений для энергии анизотропии (2.2.2) или (2.2.3) и учитывали в этих выражениях один или, максимум, два члена. Однако могут быть случаи, когда кристаллографическая анизотропия магнитных свойств не может быть описана при помощи энергии вида (2.2.2) или (2.2.3)
даже с большим числом членов. Такая «аномальная» анизотропия имеет место, в частности, в иттрий-железном гранате с примесями некоторых редкоземельных ионов при низких температурах. На рис. 2.2.11 приведены в качестве примера низкотемпературные угловые зависимости резонансного поля в иттрийжелезном гранате с небольшой примесью ионов ТЬ3+. Из рис. 2.2.11 видно, что ионы тербия приводят к появлению пиков резонансного поля при некоторых углах между направлением постоянного поля и осями кристалла. Ясно, что описание этих пиков, исходя из энергии вида (2.2.3), во-первых, потребовало бы учета очень большого числа членов, а во-вторых, оставило бы в стороне причину появления пиков.
Аналогичные пики, но при других углах наблюдаются в иттрий-железном гранате с другими редкоземельными ионами (см., например, [409]). При повышении температуры зти пики, практически не сдвигаясь, расширяются, уменьшаются по высоте и исчезают при температурах порядка 10—20 °К. Аномалии резонансного поля в таких веществах сопровождаются сложными и
§ 2.21	ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ 97
Рис. 2.2.11. Зависимость резонансного поля от угла между Но и осью <100> в плоскости (110) для иттрий-железного граната с 0,015 мол. % ионов ТЬ3+[409]. Температура 4,2 °К, частота 8,2 Гец.
интересными особенностями ширины резонансной кривой. Этот вопрос будет подробно рассматриваться в § 9.6. Здесь мы ограничимся объяснением причины возникновения указанных «аномалий» резонансного поля. Это объяснение, предложенное Киттелем [383], основано на рассмотрении энергии отдельных примесных ионов (например, тербия), т. е. на упоминавшемся выше одноион-ном механизме анизотропии.
Зависимость энергетических уровней иона ТЬ3+ в иттрий-железном гранате от угла между постоянным полем и одной из осей кристалла показана на рис. 2.2.12. Отвлекаясь от конкретных особенностей и природы этих уровней (они будут в некоторой степени рассмотрены в §9.6), отметим лишь одну характерную черту их — наличие при некоторых углах довольно резких сближений нижних уровней. Можно предполагать, что эти сближения возникли в результате воздействия некоторых возмущений на уровни, пересекающиеся при данных углах. Эти сближения (near-cros-уровней и являются причиной появления пиков резонансного поля х).
Как видно из формулы (2.1.46), пики резонансной частоты, а следовательно, и резонансного поля — при постоянной частоте — должны иметь место в тех точках, где производные плотности свободной энергии U по углам достигают больших величин. Частью величины U является в, нашем случае свободная энергия Ut примесных ионов. При вычислении ее ограничимся учетом только двух нижних, наиболее населенных уровней. Энергии их (до наложения возмущения, которое приводит к расталкиванию пересекающихся уровней) можно аппроксимировать (рис. 2.2.13)
*) В гранате ионы ТЬ3'*’ могут занимать различные кристаллографически неэквивалентные положения (см. § 4.4). На рис. 2.2.12 показаны энергетические уровни для некоторых из этих положений. Они имеют сближения (нижних уровней) при углах 36° и 78°, которым соответствуют два из трех пиков, показанных на рис. 2.2.11. Третий пик обусловлен пересечением Уровней ионов в других неэквивалентных положениях.
4 А. Г. Гуревич
98
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
(ГЛ. 2
следующим образом:
(si,s)o — Pl, 2®,
(2.2.35)
Рис. 2.2.12. Энергетические уровни иона ТЬ8+ в иттрий-железном гранате в зависимости от угла между постоянной намагниченностью и осью <100> в плоскости {110} [3871. Расчет для одного из незквивалентных кристаллографических положений иона То3 г в гранате (см. § 4.4), исходя из вьсперимен-тальных зависимостей Лрез от
ен-
где 0 — полярный угол намагниченности, практически совпадающий с полярным углом постоянного внешнего поля, а /ц и р2 — постоянные коэффициенты, положительные или отрицательные. При наличии возмущения энергии этих уровней будут определяться уравнением
(Лр \ 2 = о,
(2.2.36)
где Демин — параметр, который имеет (рис. 2.2.13) смысл минимального расстояния между уровнями.
Плотность свободной энергии ионов (см., например, £36]) может быть определена следующим образом:
Ui = - xZWlu^e хГ, (2.2.37) j
где N — концентрация ионов, а суммирование производится по всем энергетическим уровням иона. Учитывая только два нижних (сближающихся) уровня, получим
Ui=- xTN In 4- е~(2.2.38)
где Ej и е2 — корни уравнения (2.2.36).
Выясняя влияние рассматриваемых ионов на условие ферромагнитного резонанса, мы не будем усложнять эту задачу учетом каких-либо других факторов. Тогда в плотность свободной энергии U необходимо будет включить только зеемановскую энергию основной
спиновой системы (— МН0) и свободную энергию ионов Ui-Из выражений (2.2.20), полученных при вычислении резонансной частоты в одноосном кристалле по методу Смита — Сула, видно, что в случае совпадения направлений Мо и Но зеемановская энергия дает слагаемые: Н0М0 в d2Uid№ и Н0Мй sin2 0 в d2Uidq2. Производная же d2Ui!dQ2 может быть вычислена из (2.2.38) с учетом (2.2.36). В частности, в точке сближения уровней (0 = 0)
(2 2 39)
МИН
§ 2.21
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В МОНОКРИСТАЛЛАХ
99
Мы ввели в рассмотрение зависимость 2 только от одного угла 0. Но, конечно, эти энергии зависят также от угла <р. Для качественной оценки можно принять
дЧЦ	d2Ui	94J.
я „	~	aQ	Sin2 0О,	aQ *	= 0.
Оф2	90	и’	96д<р
(2.2.40)
С учетом всего этого из (2.1.46) получим окончательно, что в точке сближения
,_©	, N (Pl--Р2)2 , , Аемин
— Т ! -2ЛЛЛ1.М1|11
(2.2.41)
Из выражения (2.2.41) видно, что в точках сближения нижних энергетических уровней примесных ионов действительно должны наблюдаться пики резо-
нансного поля, высота которых пропорциональна концентрации этих ионов и зависит от степени сближения уровней и температуры. При низких температурах (иТ Демин) высота пиков
л иг__ тт ®________М (pi Р2)2
₽е3 т ~ 2Л/0Лемин
(2.2.42)
не зависит от температуры и обратно пропорциональна мини-
Рис. 2.2.13. Сближение энергетических уровней. Пунктир—- невозмущенные уровни, сплошные линии— с учетом возмущений.
мальному расстоянию между уровнями. При повышении температуры, когда -иТ становится
порядка Д емин, величина пика, согласно (2.2.41), начинает
уменьшаться и при х7 Д^мин
я тт _____ N (pi f’a)8
(2.2.43)
При высоких температурах дН будет убывать еще резче с ростом температуры из-за того, что начнут заселяться более высокие энергетические уровни иона. Таким образом, рассмотренная теория дает качественное объяснение всех особенностей пиков резонансного поля, обусловленных примесями редкоземельных ионов в иттрий-железном гранате.
Оценим теперь величину пиков ЬН, основываясь на структуре энергетических уровней, показанной на рис. 2.2.12. Согласно этому рисунку пр имем
|pi —рг|*_ 100 ок _Ле = 5 оК
Я	’ X
4*
100
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
Учте 1, что в кристаллографических положениях, которым соответствуют уровни рис. 2.2.12, находится 1/3 всех ионов ТЬ3+ [387]. Тогда при полной молярной концентрации этих ионов 0,015% концентрация «активных» ионов N = 3-1018 *). Учитывая также, что Мо = 195 гс, а Т = 4,2 °К, получим по формуле (2.2.41)
6Я ж 10? э.
Экспериментальная же высота пиков при 0 = 36° и 0 = 78°, которые определяются рассмотренными ионами, составляет (рис. 2.2.11) ~ 200 э. Полученному согласию не следует, однако, придавать слишком большого значения, так как угловые зависимости энергетических уровней (рис. 2.2.12), использованные при оценке, не были получены из независимых расчетов 2) или экспериментов, а были вычислены Диллоном и Уокером [387] на основе угловых зависимостей Hve3, аналогичных тем, которые показаны на рис. 2.2.11. Таким образом, можно говорить пока лишь об отсутствии противоречий в понимании этого явления, а не о количественной экспериментальной проверке теории.
§ 2.3. Ферромагнитный резонанс в поликристаллах
Несмотря на широкое применение монокристаллов, поликри-сталлические ферриты являются основными магнитными материалами, применяемыми в технике сверхвысоких частот. Кроме того, многие монокристаллы еще не удается вырастить, и ряд исследований ферромагнитного резонанса также приходится проводить на поликристаллах. Поэтому нам необходимо выяснить особенности ферромагнитного резонанса в поликристаллических веществах.
Поликристаллические материалы представляют собой конгломераты маленьких кристалликов (зерен или кристаллитов) с размерами порядка 10-4	1(Г3 см. Эти кристаллики имеют раз-
личную, обычно неправильную форму, между ними находятся пустоты (поры) также различной формы, занимающие часто значительную долю (до 20%, а иногда и более) всего объема. В плотных, «хорошо испеченных» образцах эта доля (относительная пористость) уменьшается до единиц процентов.
*) В этом легко убедиться, учитывая, что постоянная кристаллической решетки граната (см. § 4.4) составляет ж 12,5 А, а в элементарной ячейке находится 8 формульных единиц Y3Fe50i2.
2) Характер энергетических уровней ионов ТЬ3+ в иттрий-железном гра-
нате и, в частности, точки «пересечения» нижних уровней были найдены [396] из независимых теоретических соображений. Но важная для оценки величина j pj — Ра 1 из этой теории не может быть получена.
§ 2.3J	ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В ПОЛИКРИСТАЛЛАХ	101
Обычно кристаллографические оси зерен произвольным образом ориентированы друг относительно друга, отсутствует какая-либо преимущественная ориентация и геометрических осей кристалликов. В этом случае в поликристалле отсутствуют какие-либо выделенные направления, и оп обладает свойствами изотропной среды. Если же при синтезе поликристаллических образцов принимаются специальные меры, например, прессование или термообработка производится в магнитном поле, то равномерность углового распределения кристаллографических или геометрических осей зерен нарушается, и такой текстурованный поликристалл приближается по своим свойствам к монокристаллу. Мы будем рассматривать обычные (нетекстурованные) поликристаллы. Тензор восприимчивости для них имеет вид (1.2.29). В достаточно сильных постоянных магнитных полях, когда имеет место магнитное насыщение, величина %33 для каждого кристаллика, а следовательно, и для всего поликристалла либо равна нулю, либо (при определенном виде диссипативного члена в уравнении движения) имеет малую величину (см. (1.3.23)). Таким образом, сверхвысокочастотные свойства нетекстурованного поликристалла в сильных полях определяются, в основном, двумя комплексными параметрами % и %а.
Однако, как следует уже из сделанных выше кратких замечаний о структуре поликристалла, он представляет собой чрезвычайно сложную систему. И его усредненные параметры % и %а, конечно, существенно отличаются как от аналогичных параметров изотропной среды, так и от компонент тензора воприимчивости монокристалла того же вещества.Это различие, как мы увидим дальше, проявляется в увеличении ширины резонансной кривой, смещении ее максимума и искажении формы. Расширение резонансных кривых поликристалла впервые обсуждалось Ван-Флеком [115], а сдвиг максимумов этих кривых был отмечен в работе Окамура, Торицука и Койима [133].
Строгое решение задачи об определении % и %а поликристалла должно основываться на определении переменных намагниченностей отдельных зерен.. При этом нужно учесть, что, кроме внешних полей и эффективных полей кристаллографической анизотропии,. зависящих от ориентации осей зерен, на них действуют сложные размагничивающие поля, постоянные и переменные, обусловленные скачками намагниченности на границах зерен и порами. Наличие переменных размагничивающих полей приводит к связи переменных намагниченностей зерен. Вследствие неэллипсоидальной формы зерен и близости соседних зерен намагниченность внутри каждого зерна, конечно, не является однородной. Если бы мы могли решить задачу об определении неоднородных связанных колебаний намагниченности большого числа зерен, то параметры X и Ха поликристалла мЪгли бы быть затем найдены усреднением
102
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
по всем зернам. Но совершенно очевидно, что такая задача не может быть решена и для определения параметров поликристаллов нужно вводить те или иные модели.
Модель независимых зерен. Не будем учитывать внутренних размагничивающих полей, возникающих на границах зерен, примем во внимание лишь различие ориентаций кристаллографических осей зерен по отношению к внешнему полю. Условием справедливости такой модели будет
|Ял|>4л7И0,	(2.3.1)
где | На I — некоторое поле анизотропии, например, |Ял1| (см. (2.2.10)) для одноосного или кубического кристалла с преобладанием первой константы анизотропии. При выполнении условия (2.3.1) учет формы зерен является также несущественным. Таким образом, можно считать, что модель независимых зерен — это набор не взаимодействующих друг с другом сферических монокристаллов, ориентации осей которых определенным образом (для обычного, нетекстуровапного поликристалла — равномерно) распределены по углам.
Задача определения восприимчивости каждого зерна в этой модели полностью сводится к рассмотренной в предыдущем параграфе задаче о монокристалле. Полученные восприимчивости Хп (со, Но, 0„, <р„) (где п — номер зерна, а 0Л и <рл — углы между направлением поля и кристаллографическими осями n-го зерна) нужно затем усреднить по всем значениям 0Л и <рл. При этом, конечно, суммирование можно заменить интегрированием. Тогда, например, диагональная компонента восприимчивости поликристалла запишется в виде
Х(®, Яо) =	(», Яо, 0, <р) /(9, ср) sin 0 d4 dip, (2.3.2)
где (со, Но, 0, ср) — диагональная компонента восприимчивости зерна, / (0, ср) — функция распределения зерен по ориентациям (для нетекстурованного поликристалла /=4), а интегрирование производится по сфере. Аналогичное выражение будет справедливо и для Ха (со, Яо). Заметим, что восприимчивости зерен мы первоначально получаем в различных системах координат (см. § 2.2), в которых оси z совпадают с равновесными намагниченностями. Перед подстановкой же в (2.3.2) мы должны преобразовать их в одну и ту ясе систему координат, а именно в такую, в которой ось z совпадает с направлением постоянного поля. Лишь при условии Но ^>На, когда равновесные намагниченности зерен практически совпадают по направлению с Но, в таком преобразовании нет необходимости.
Однако даже в последнем случае определение / ихо поликристалла на модели независимых зерен связано с большими мате-
§ 2.3J' ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В ПОЛИКРИСТАЛЛАХ	ЮЗ
магическими трудностями. Поэтому целесообразно, следуя Шлё-манну [3081, рассмотреть предельный случай, когда ширина резонансной кривой монокристаллических зерен (ДЯ)П -> 0, и ограничиться вычислением только мнимых частей % (со, На) и %а (со, Но). Тогда, аналогично (1.3.37), восприимчивость под интегралом в (2.2.2) будет пропорциональна дельта-функции. Примем, например, что со = const. Тогда аргументом этой функции будет величина
7/рез (со, 6, ср),
где Дрез (со, 6, ср) — резонансные поля для монокристалла, которые вычислялись в § 2.2. С учетом этого для нетекстурованпого поликристалла
%"(со, Яо)= -^Мо 6 [Яо — Ярез(со, 0, ср)] sin0 dOdcp. (2.3.3)
Величина %" в данном случае пропорциональна функции распределения wa (Но) зерен поликристалла по величинам резонансного поля; задача заключается, таким образом, в нахождении этой функции.
Рассмотрим в качестве примера кубический кристалл, ограничимся учетом только первой константы анизотропии и примем К1 < 0. Основываясь на результатах, полученных в § 2.2, рассмотрим характер функции распределения wa (Но). Эта функция (см. рис. 2.2.8) не равна нулю в интервале полей от
-Имин = —	(2.3.4)
I °
соответствующего легким осям <111), до
Нмвкс = -~+ 2|ЯЛ1|,	(2.3.5)
соответствующего трудным осям <100); ширина этого интервала 10
составляет — |77ai|- Наличие экстремумов Ярез (0, ф) при совпадении Но с осями <111) и <100) должно привести к «ступенькам» функции wa (Но) на границах интервала. В направлениях <110) находятся точки седла поверхности Нрез (0, ср). Вблизи этих направлений имеются «сгущения» в распределении зерен, и мы вправе ожидать, что при значении /70, соответствующем оси <П0), будет находиться пик функции распределения. Это значение определяется выражением (2.2.32) и при \Hai со/у составляет
Я<110> =	(2.3.6)
(см. рис. 2.2.8). Анализ функции распределения [3081 подтверждает эти предположения: максимумам и минимумам Нрез (0, ф)
104
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИКА	'[ГЛ. 2
соответствуют разрывы функции распределения, а седлу Нрез (6» ф) — логарифмическая особенность этой функции.
Основываясь на указанных свойствах функции wa (Но), Шлё-
манн рассчитал зависимости %" (Но) при различных значениях | Hai |; результаты расчета приведены на рис. 2.3.1 (пунктиром). Из рисунка видно, что при малой анизотропии функция %" (Но)
имеет один пик при поле (2.3.6) и ступеньки — на границах интервала. Центр тяжести ее сов-
Рис. 2.3.1. Резонансные кривые кубического поликристалла с К, < 0 в приближении независимых зерен [308]. Пунктир— функция распределения wa (Но), сплошные линии—с учетом конечной ширины кривой монокристалла.
падает с «изотропной точкой» co/у. При увеличении анизотропии удельный вес направлений, прилегающих к легкой оси, возрастает и центр тяжести %" (Но) смещается к малым Но. Ступенька на нижнем краю интервала увеличивается и при | НЛ1 | ^0,1 (co/у) переходит во второй пик.
Приведенные па рис. 2.3.1 пунктиром зависимости дают форму резонансной кривой поликристалла при бесконечно малой ширине кривой монокристалла (А//)г. Учет конечной величины (ДЬ’)П приведет к «размазыванию» резонансных кривых поликристалла, как это показано на рис. 2.3.1 (сплошными линиями). Однако и после
будет резко отличаться по форме
этого, если только (Д/Цп не будет много больше, чем | Hai |, резонансная кривая поликристалла (в приближении независимых зерен) От «обычной» — близкой к
лоренцевой — кривой для изотропной среды или монокристалла. Она будет несимметричной, будет иметь Ступеньки (правда, сглаженные) на обоих склонах, а при большой анизотропии будет иметь два максимума. Максимум кривой будет смещен относительно co/у в сторону меньших полей (при Кх < 0)
на величину
(6Я)	И11
v ,а 2 Мо
(2.3.7)
§ 2.3]
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В ПОЛИКРИСТАЛЛАХ
105
Как видно из рис. 2.3.1, расширение резонансной кривой
(2ДЯ)О —(2.3.8)
Заметим, что условие (2.3.1) применимости модели независимых зерен хорошо выполняется вблизи точек компенсации в ферритах (см. § 4.4). При этом резонансные кривые, близкие по форме к кривым, показанным на рис. 2.3.1, наблюдались экспериментально [3091. Характерные нелоренцевы кривые наблюдались [313] и в поликристаллических одноосных ферритах с большой анизотропией, для которых условие (2.3.1) также выполняется.
Рис. 2.3.2. Резонансные кривые поликристаллических ферритов Ni1_xCoxMn0 02Fe1>9O4 с различными знаками первой константы анизотропии [306].
Для большинства же ферритов, в особенности кубических ферритов с небольшой анизотропией, применяемых в диапазоне сверх-в >1 со к их частот, условие (2.3.1) не выполняется. Резонансные кривые поликристаллических образцов таких ферритов не обнаруживают характерных ступенек, которые следуют из теории независимых зерен. Тем не менее некоторые выводы этой теории качественно подтверждаются и для таких поликристаллов. Смещение максимума и расширение резонансной кривой в тех случаях, когда не преобладают другие факторы, например пористость (см. ниже), по порядку величины определяются формулами (2.3.7) и (2.3.8) (см., например, [306]). Иногда наблюдается и несимметрия резонансных кривых, предсказываемая теорией независимых зерен. Дак следует из рис. '2-3.1, при К, < 0 более крутым должен
<06
АНИЗОТРОПНЫЙ ФЕРРОМАГНЕТИК
[ГЛ. 2
являться склон кривой в сторону малых полей. Ясно, что при Кл 0 картина будет обратная. На рис. 2.3.2 приведены экспериментальные резонансные кривые для поликристаллических ферритов с различными величинами константы анизотропии. Как видно из этого рисунка, несимметрия кривых качественно соответствует выводам теории независимых зерен.
Модель сильно связанных зерен. Другой моделью поликристалла, допускающей сравнительно простую математическую трактовку, является модель сильно связанных зерен. Связь предполагается настолько сильной, что поликристалл может рассматриваться как однородная среда, на которую накладывается некоторое постоянное во времени неоднородное возмущающее магнитное поле На (г). Это возмущающее поле и моделирует наличие зерен. Его амплитуда пропорциональна полю анизотропии | На |, а средний пространственный период близок к среднему размеру зерен. Поскольку связь между колебаниями зерен осуществляется магнитными силами, пропорциональными Мо, то ясно, что условие применимости модели сильно связанных зерен будет обратно условию (2.3.1):
|Нл|<4лМ0.	(2.3.9)
Наличие поля Ия (г) приводит к тому, что основной — однородный тип колебаний намагниченности (который мы до сих пор рассматривали) будет связываться с другими—неоднородными типами колебаний и передавать им энергию. Это приведет к увеличению параметра диссипации и; следовательно, к расширению резонансной кривой. Теория такого процесса будет рассмотрена в § 9.3 после изучения неоднородных типов прецессии намагниченности, а также общих принципов исследования диссипативных процессов. Приведем здесь лишь основной результат этой теории: расширение резонансной кривой
Н2
(2.3.10)
где F — множитель порядка единицы, который является функцией <в, Мо и формы образца и зависит, главным образом, от того, насколько частота однородной прецессии вырождена с неоднородными типами прецессии; если этого вырождения нет, то F =0.
Сравнивая формулы (2.3.10) и (2.3.8), мы видим, что теория сильно связанных зерен приводит к появлению в выражении для ширины резонансной кривой множителя
Id
!яа1
4пМ0'
(2.3.11)
При условии (2.3.9) применимости модели сильно связанных зерен
Id 1- Появление этого множителя является следствием так ца-
§ 2.31
ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В ПОЛИКРИСТАЛЛАХ
107
Рис. 2.3.3. Модель Шлё-маннадля расчета ширины резонансной кривой, обусловленной порами.
зываемого дипольного сужения, которое возникает в результате связи между колебаниями намагниченности в отдельных зернах, обусловленной магнитным (диполь-дипольным) взаимодействием. Эта связь учитывается теорией сильно связанных зерен, но никак не принимается во внимание в модели независимых зерен.
Для многих ферритов не выполняются ни условие (2.3.1), пи условие (2.3.9), величины На и Мо оказываются одного порядка-При этом ни одна из рассмотренных моделей (независимых зерен и сильно связанных зерен) не описывает достаточно хорошо сложных явлений, происходящих при магнитных колебаниях в поликристалле.
Влияние пор и включений. Положение еще усложняется наличием в поликрист алличе-ских материалах пустот (пор) и включений других, в частности, немагнитных фаз. Одним из методов учета их влияния является метод независимых областей, аналогичный рассмотренному выше методу независимых зерен при учете влияния «поликристалличности». В зтом приближении влияние пор и включений заключается в том, что они создают неоднородные размагничивающие поля Пл( (г),
. дят к разбросу резонансных частот в разных точках образца. При грубой оценке можно принять, что ширина резонансной кривой, обусловленная этим разбросом, равна средней квадратичной величине размагничивающих полей в образце и составляет
которые приво-
(2АЯ)/, — Нм (г)	4лЛ/0 -у,
(2.3.12)
где v — суммарный объем всех пустот и немагнитных включений, а V — объем образца.
Для того чтобы получить в приближении независимых областей более точные р эзультаты, необходимо сделать какие-то предположения о форме пор. Шлёманн (см., например, [285]) предложил модель— сферическую полость в центре сферического образца (рис 2.3.3) и провел для нее расчет, аналогичный расчету влияния поликристалличности на модели независимых зерен. Форма резонансной кривой совпадает при этом с функцией распределения wp элементов объема образца по значениям резонансного поля. Она оказывается резко нелоренцевой, с острым пиком, сдвинутым по отношению к со/у на величину
(8Н)Р =^М0^г,	(2.3.13)
где = 4/3 л/?® — объем сферической полосуй. Аппроксимируя
108	ЛНЙЙО'ГРОПНЬТЙ ФЁРРОМЛГНЕТ’ИЙ	ir.1I. 2
резонансную кривую лоренцевой кривой, Шлёманн получил (2ДЯ)Р = -1=4лМ0_£..	(2.3.14)
Предполагая далее, что формулы (2.3.13) и (2.3.14) справедливы и для пор, смещенных относительно центра образца, и что вклады всех пор аддитивны, можно заменить в этих формулах v1 на суммарный объем v всех пор. Тогда выражение для (2ДЯ)Р будет отличаться от оценки (2.3.12) множителем 1,5.
В действительности колебания отдельных областей образца с неоднородным внутренним полем нельзя считать независимыми. Они связаны между собой магнитным взаимодействием, и должно иметь место дипольное сужение. Это было особенно наглядно показано Гешвипдом и Клогстоном [305], которые наблюдали ферромагнитный резонанс в полусфере- Внутреннее постоянное магнитное поле Hi0 при этом изменяется по образцу в очень широких пределах — приблизительно на 2л7И0. Ширина же резонансной кривой оказалась гораздо меньшей, и форма ее отнюдь не совпадала с функцией распределения wr (Я;о).
Для случая пор в множитель который должен появиться в выражении для (2Д//)Р в результате дипольного сужения, вместо поля анизотропии (формула (2.3.11)) войдет некоторое среднее размагничивающее поле, пропорциональное Мо. Поэтому будет теперь просто численным множителем порядка 1.
Другой подход к «геометрическим» неоднородностям1), автоматически учитывающий дипольное сужение, будет подробно рассмотрен в § 9.3. В этом случае вариации размагничивающего поля неоднородностей, аналогично вариациям поля анизотропии в модели сильно связанных зерен, рассматриваются как возмущение, вызывающее переход энергии от однородного типа колебаний к другим — неоднородным типам. Такие расчеты, в согласии с приведенным выше замечанием о характере дипольного сужения, приводят (см. § 9.3) по-прежнему к пропорциональности (2А/7)Р намагниченности Мо (а также отношению v)V), но с другим множителем, чем в (2.3.14). В выражении для (2ДЯ)Р, аналогично (2.3.10), появляется теперь множитель, зависящий от степени вырождения однородного и неоднородных типов колебаний.
Экспериментальное исследование вопроса о влиянии пористости на ферромагнитный резонанс в поликристаллических ферритах осложняется еще и тем обстоятельством, что величина и характер пористости влияют на условия применимости к поликристаллу той или иной модели (независимых зерен или сильно связанных
х) К «геометрическим» неоднородностям, кроме пор в поликристаллах, относятся шероховатости поверхности, которые имеют место как в поликристаллах, так и в монокристаллах.
i 2.51	ФЕРРОМАГНИТНЫЙ РЕЗОНАНС В ПОЛИКРИСТАЛЛАХ
109
зерен), учитывающей влияние анизотропии. А именно, к поликристаллу с большой пористостью лучше применима модель независимых зерен, а к плотному поликристаллу — модель сильно связанных зерен. Таким образом, два рассмотренных источника
расширения и сдвига резонансных (анизотропия и поры) нельзя считать независимыми и аддитивными.
Тем не менее оценки (2.3.13) и (2.3.12) или (2.3.14) оказываются справедливыми по порядку величины, а качественный вывод, который из них вытекает — об очень большом влиянии пористости на резонанс в поликристаллических	ферритах,—
полностью подтверждается экспериментально. Это иллюстрирует рис. 2.3.4, на котором показаны зави- 200 симости ширины резонансной кривой от пористости. Из этого рисунка видно, что вклад пористости в данном случае оказывается, в среднем, близким к оценке (2.3.12). Ширина же кривой, экстраполированная к нулевой пористости, (2Д//)0 ~ 40 э оказывается меньшей, чем величина 2 \Кг \1М0 (в данном случае ~ 90 э1), которую дает теория независимых зерен. Этого и следовало ожидать, так как при 2 |/<j | /Мо и Мо одного
в поликристалле
W,
кривых 2 ЛИ, з ООО
Рис. 2.3.4. Зависимость ширины резонансной кривой поликристаллических ферритов от относительной пористости р — v/V [314]. Различные кружки— образцы иттрийжелезного граната, синтезированные различными способами; треугольники — лютеций-железный гранат.
,_________1_
0,1 Т 0,2	0,3	0,0
(2ЛН)в+0ЛМар
порядка (в данном случае Мо = 140 э), тем более для плотного по-
ликристалла, теория независимых зерен не должна быть справедливой и должно сказываться дипольное сужение. Заметим, что разброс точек на рис. 2.3.4 обусловлен различием размеров и формы зерен и пор в различных образцах.
Еще одним источником расширения и смещения резонансных кривых в поликристаллах является анизотропия, обусловленная
внутренними механическими напряжениями, возникшими при синтезе материала. Однако обычно этот источник не очень существен.
х) Ширина резонансной кривой монокристалла в этом случае'весьма мала (~ 1 э).
ГЛАЁА S
КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ
ДОМЕНОВ
§ 3.1. Доменная структура и усредненные параметры ненасыщенного ферромагнетика
До сих пор предполагалось, что основным состоянием ферромагнетика, около которого происходят колебания намагниченности, является однородная намагниченность всего образца. Но это состояние является равновесным лишь при достаточно больших внешних магнитных полях, или для достаточно малых тел. При меньших полях (в частности, при поле, равном нулю) ферромагнитное тело не очень малых размеров разбивается на области — домены, намагниченные в различных направлениях. В этой главе мы рассмотрим колебания намагниченности, происходящие при наличии в образце доменов. Тем самым теория ферромагнитного резонанса будет распространена на область малых постоянных магнитных полей.
Остановимся прежде всего на основных физических представлениях, связанных с ферромагнитными доменами (подробнее сц., например, [5, 52]). Предположим сначала, что внешнее магнитное поле отсутствует и образец явлется монокристаллом. Основными видами энергии ферромагнитного образца при отсутствии внешнего поля являются (см. § 2.1): обменная энергия, энергия кристаллографической анизотропии, упругая и магнитоупругая энергии (если имеются внешние напряжения) и магнитостатическая энергия, связанная с размагничивающими полями. При однородной намагниченности всего образца в направлении одной из легких осей обменная энергия и энергия анизотропии минимальны. Однако магнитостатическая энергия достигает при этом большой величины. Эта энергия может трактоваться как энергия поля, создаваемого поверхностными «магнитными зарядами», пропорциональными скачку нормальной составляющей намагниченности Мп на границе образца. При возникновении в образце доменов, намагниченных в противоположных направлениях, эта энергия существенно уменьшится. Так, например, можно показать [52], что отнесенная к единице поверхности магнитостатическая энергия системы доменов-слоев, показанных па рис. 3.1.1,
WM^Mld.	(3.1.1)
§ 3.1]
ДОМЕННАЯ СТРУКТУРА И УСРЕДНЕННЫЕ ПАРАМЕТРЫ
111
где Мй—намагниченность насыщения. Эта энергия уменьшается при уменьшении толщины доменов d, и, таким образом, разбиение на домены является энергетически выгодным (если, конечно, оно не приводит к значительному увеличению других видов энергии).
Для того чтобы при разбиении образца на домены не происходило увеличения магнитостатической энергии за счет образования магнитных зарядов на границах между ними, должно выполняться условие на границе
АМп = М1п— М2п = 0.	(3.1.2)
В частности, намагниченности соседних доменов Мх и М2 могут
быть параллельны границе раздела, как на рис. 3.1.1.
Границы между доменами. Выясним теперь, что представляет собой граница между доменами. При этом мы должны будем принять во внимание обменную энергию и энергию кристаллографической анизотропии. На достаточных удалениях от грани
цы направления намагниченности в -»-)
соседних домепах Мг и М2 совпадают Рис злл Слоистая доменная с направлениями легкого намагниче-	структура.
ния. Энергия анизотропии была бы
минимальна, если бы поворот намагниченности от Мх к М2 совершался скачком. Но при этом резко возросла бы обменная энергия. Легко показать [52], что обменная энергия будет тем меньше, чем более плавно совершается поворот. Что же касается магни-
тостатической энергии, то она не возникает, если при повороте Мп остается постоянной. Обычно именно этот случай соответствует минимуму полной энергии. Тогда закон изменения угла поворота намагниченности 6 в граничном слое определяется компромиссом между энергией анизотропии и обменной энергией и может быть найден в результате решения вариационной задачи о минимизации их суммы. Такая задача была решена Ландау и Лифшицем [111]
для случая одноосного кристалла в предположении, что толщина доменов d (рис. 3.1.1) весьма велика х). Полученный ими закон изменения 6 имеет следующий вид (рис. 3.1.2):
Ki
sin2 6,
(3.1.3)
х) Учет конечных размеров доменов был проведен Широбоковым [50], при этом характер измерения М в граничном слое и оценки толщины границы Ц ее энергии не изменились.
112 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
или после интегрирования:
cos 6 = — thl -^х, V ЧМ1
(3.1.3')
где Ку — первая константа анизотропии одноосного кристалла, a q — постоянная неоднородного обмена (см. выражение (2.1.8)).
Рис. 3.1.2. Поворот векторов намагниченности на границе между доменами.
Величину:
Ь = лМ0)/~£	(3.1.4)
можно назвать толщиной границы, опа представляет собой расстояние, на котором совершается в основном (на 75%) поворот вектора М. Для минимизирующего распределения (3.1.3') обменная энергия и энергия анизотропии границы оказываются равными, и суммарная энергия, отнесенная к единице площади границы,— так называемая энергия границы
Wrp = 2nM0V qKy = 2ЪКу. (3.1.5)
Аналогичные расчеты были проведены и для кубического кристалла [52], при этом для толщины и энергии границы получились выражения того же порядка, что и (3.1.4) и (3.1.5), в которых Ку — теперь уже первая константа анизотропии кубического кристалла (по абсолютной величине). Если, имея в виду иттрий-железный гранат при комнатной температуре, принять J Ку J = 5,5-103, Мо = 140 гс и q = 4-10-11, то
Ъ = 5-10“® см, Wrp = 0,5 эрг/см2.
Доменные структуры. Перейдем теперь к рассмотрению формы и размеров доменов. В отличие от толщины границ, они существенно зависят от размеров и формы образца. Рассмотрим, например, образец в виде бесконечной плоскопараллельной пластины, поверхности которой перпендикулярны легкой оси, и предположим, что домены представляют собой слои, параллельные легкой оси (рис. 3.1.1). При этом магнитная энергия кристалла (отнесенная к единице его поверхности) состоит из магнитостатической энергии(3.1.1)магнитных «зарядов»на обеих поверхностях и энергии доменных границ (отнесенной теперь к единице поверхности образца)
W 1
ПЕ, ,	(3.1.6)
§ 3.1]
ДОМЕННАЯ СТРУКТУРА И УСРЕДНЕННЫЕ ПАРАМЕТРЫ
ИЗ
где d — толщина доменов, а I — размер образца (рис. 3.1.1). Минимизация суммы этих энергий дает

fz.
d
м0
(3.1.7)
Домены-слои, параллельные осям легкого намагничения (рис. 3.1.1), в большинстве случаев реализуются в объеме образца. Однако вблизи его поверхности могут иметь место разнообразные и иногда довольно сложные структуры. Очень часто происходит
замыкание у поверхности магнитных потоков доменов, так что «магнитных зарядов» на поверхности вообще не образуется и связанная с ними магнитостатическая энергия обращается в нуль. При этом, однако, неизбежно возрастают другие виды энергии (анизотропии, магнитоупругая) и размеры доменов определяются компромиссом между ними и энергией границ.
Простейшая из поверхностных
Рис. 3.1.3. Слоистая доменная структура с замыкающими доменами [111].
доменных структур показана на
рис. 3.1.3. В случае такой структуры для одноосного кристалла ' толщина доменов d определяется компромиссом между энергией
границ, которая в первом приближении (d/Z^l) имеет вид (3.1.6) , и энергией анизотропии в поверхностных замыкающих доменах-призмах
Wa = -^-Kld.	(3.1.8)
Ci
Это приводит к толщине доменов

(3.1.9)
Такая структура, предсказанная Ландау и Лифшицем [111], реализуется в одноосных кристаллах в определенном интервале значений I. Для очень малых I (пленок) более выгодна простая структура рис. 3.1.1, а для больших I — возникает более сложная поверхностная структура [51]., Структура рис. 3.1.3 может реализоваться и в кубических кристаллах. Если в таком кристалле Кг 0, то направление намагниченности в замыкающих призмах является легким направлением и энергия анизотропии не участвует в определении размеров доменов. Они определяются тогда [52] компромиссом между энергией границ и магнитоупругой энергией. В случае Кг < 0 роль играет по-прежнему энергия анизотропии и размер доменов но порядку величины определяется
144 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМВНОВ [ГЛ. 3
формулой (3.1.9). Для иттрий-железного граната d^w-ут.
Таким образом, размер доменов существенно зависит от размеров образца и вида поверхностной структуры, который, в свою очередь, определяется размерами и формой образца и параметрами вещества.
Локальные доменные структуры, похожие на поверхностные, возникают и внутри образца на различных неоднородностях: пустотах, границах между зернами поликристалла, участках с внутренними упругими напряжениями и т. д. Эти структуры играют большую роль в низкочастотных процессах перемагничивания [5, 52]. Однако их роль, как и роль поверхностной доменной структуры, в высокочастотных колебаниях намагниченности, по-видимому, не столь существенна (во всяком случае она совершенно не исследована). Поэтому мы в дальнейшем при рассмотрении высокочастотных колебаний намагниченности в кристалле с до-менпой структурой будем всегда принимать, что домепы представляют собой плоскопараллельные слои.
Как видно из формул (3.1.7) и (3.1.9), размер доменов d пропорционален Z, и при достаточно малом I = 10 образец с размерами ~ 10 во всех трех измерениях (например, сфера) не будет разбиваться па домены. При малых размерах образца можно использовать формулу (3.1.7), из которой следует
/0^.	(3.1.10)
о
Для иттрий-железного граната Zo ~ 10-s см. Таким образом, достаточно маленькие частицы ферромагнетика являются однодоменными х). Это фундаментальное для теории ферромагнетизма обстоятельство было впервые отмечено Френкелем и Дорфманом [49]. Последующие более точные расчеты [52] показали, что оценка (3.1.10) справедлива по порядку величины.
Квазистатические процессы перемагничивания и динамические колебания. При наложении внешнего магнитного поля II в энергии ферромагнитного образца появляется дополнительный член — зеемановская энергия (2.1.1). Равновесное состояние наступает в этом случае при наличии некоторой средней намагниченности образца в направлении, близком к направлению внешнего поля. Переход в повое равновесное состояние может происходить [5] двумя путями:
г) Ферромагнитный резонанс в однодоменйой частице исследовал^ Мцхай-довский, Поллак и Соколов [124].
§ 3.1i
Доменная структура и усредненные параметры Н5
1) перемещением границ доменов, ведущим к росту тех доменов, в которых намагниченность М составляет острый угол с Н (процессы смещения);
2) поворотом векторов М внутри доменов (процессы вращения) .
Процессы смещения преобладают при малых полях и, практически, заканчиваются с исчезновением основной доменной структуры (когда в образце могут оставаться лишь отдельные домены — «зародыши перемагничивания»). Процессы вращения, начинаясь также при малых полях, продолжаются и после исчезновения (в результате смещения границ) доменной структуры и заканчиваются лишь после того, как намагниченность будет направлена по внешнему полю. Такая схема процессов намагничения усложняется в некоторых случаях качественным преобразованием доменной структуры при определенных значениях поля Н. Так например, в пленках с достаточно большой одноосной анизотропией (с легкой осью, перпендикулярной поверхности пленки) в некотором интервале значений поля (приложенного перпендикулярно поверхности) возникают изолированные цилиндрические домены — так называемые «пузырьки» (bubbles).
При наложении переменного магнитного поля достаточно низкой частоты (меньшей, чем собственные частоты и частоты релаксации магнитной системы) процессы перемагничивания происходят квазистатически. Это означает, что в каждый данный момент доменная структура и ориентации намагниченностей, а следовательно, и результирующая средняя намагниченность определяются мгновенным значением внешнего поля с учетом, конечно, магнитной предыстории данного образца, но независимо от скорости из-менепия поля. Однако при увеличении частоты такой квазиста-тичесчий подход становится совершенно неприменимым. Процессы перемагничивания можно рассматривать теперь как динамические колебания около основного — равновесного состояния, которое (при достаточно малых амплитудах высокочастотного поля) определяется постоянной составляющей магнитного поля.
Таким основным состоянием в этой главе будет являться определенная доменная структура. Ее наличие внесет следующие усложнения в теорию малых колебаний намагниченности, по сравнению с теорией ферромагнитного резонанса в насыщенном ферромагнетике, рассмотренной в предыдущих главах.
1)	Рассматривая процесс вращения (прецессию) намагниченности внутри каждого домена, необходимо учитывать переменные размагничивающие поля, связанные с непостоянством нормальной составляющей переменной намагниченности на границах доменов.
2)	Полученные значения переменной намагниченности или компонент тензора восприимчивости доменов следует затем усреднить по всем доменам.
116 НОЛЕЙАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
3)	Должны быть рассмотрены высокочастотные (динамические) процессы смещения границ доменов.
4)	Следует учесть вклад самих границ доменов в переменную намагниченность.
Усреднение но доменам. Рассмотрим прежде всего усреднение по доменам (второй из перечисленных факторов) без учета остальных, в частности, не принимая пока во внимание переменных размагничивающих полей на границах доменов. Тогда для каждого домена будет полностью справедлива теория, рассмотренная в предыдущих главах и, в частности, будет иметь место уравнение (2.1.31).
Заменим в уравнении (2.1.31) внешнее переменное поле h на внутренее поле h, = h — Nm. Тогда в этом уравнении herr будет представлять собой hra = — N'Tn, где N“ — тензор размагничивающих факторов анизотропии (см. § 2.1). Величина же Неио в уравнении (2.1.31) будет включать в себя внешнее постоянное поле, размагничивающее поле и эффективное поле Но0 = = — N°M0.
Усреднение решений уравнения (2.1.31) по доменам с учетом тензора Na представляет собой сложную задачу даже в случае монокристалла. Для поликристалла она дополнительно усложняется необходимостью усреднения по зернам. Поэтому, следуя Радо [153], рассмотрим прежде всего простой предельный случай, когда
Яе«о<-у,	(3.1.11)
т. е.
Яо<—, Яао<—,	4лМ0<—.
Эти условия выполняются в коротковолновой части диапазона сверхвысоких частот для небольших внешних полей (намного меньших, чем резонансное) и веществ с небольшой анизотропией. Например, для иттрий-железного граната они удовлетворительно выполняются при частотах, больших ~ 10 Ггц, и внешних полях, не превышающих, приблизительно, 1 кэ.
Условие (3.1.11) позволяет пренебречь вторым и третьим членами в левой части уравнения (2.1.31). Для простоты не будем также учитывать диссипативного члена. Тогда из (2.1.31) получим
m = -J-Mo х 1ц.	(3.1.12)
В выражение (3.1.12) величина N не входит, и его легко усреднить по доменам. И если учесть, что направления Мо и 11г в доменах не коррелируют друг с другом, то в результате усреднения
§ 3.1J ДоМйнйай с/груктура и усредиеййНе Параметры in
получится [153]
in = 4гМо х 11[-
(3.1.13)
Здесь Мо — средняя («техническая») намагниченность, а 11г — усредненное по доменам внутреннее переменное поле ’).
Проектируя (3.1.13) на оси координатной системы, в которой ось z совпадает с Мо, найдем усредненный тензор восприимчи
вости ненасыщенного ферромагне
тика
О
-iXa О
О О
(3.1.14)
О
О
О
где
—	(3.1Л5)
Простые выражения (3.1.14) и (3.1.15) при выполнении условия (3.1.11) справедливы как для монокристалла, так и для поликристалла. Тензор восприимчивости имеет в этом предельном случае только антисимметричные компоненты, пропорциональные средней намагниченности.
Многочисленные эксперимен
Рис. 3.1.4. Зависимость компонент тензора ц поликристаллического магниймарганцевого феррита от Но. Частота 9,3 Ггц. Пунктир— расчет ра по формуле (3.1.15) на основании экспериментальной кривой намагничения Мо (Но).
ты показывают, что полученные соотношения приближенно выполняются в коротковолновой части диапазона сверхвысоких частот. Это иллюстрирует рис. 3.1.4, на котором представлены экспериментальные данные для компо
нент тензора р = 1|- 4 л/ поликристаллического феррита в трехсантиметровом диапазоне. Как видно из рис. 3.1.4, выражения (3.1.14) и (3.1.15) передают в самом грубом приближении ха
рактер зависимости вещественных частей компонент р от постоянного поля при малых полях. На более высокой частоте или для феррита с меньшей намагниченностью совпадение было бы лучшим, так как лучше выполнялось бы условие (3.1.11).
Очевидно, что условием справедливости рассмотренного усреднения является также малость размеров доменов и зерен по сравнению с длиной электромагнитной волны в веществе.
118 КОЛЕБАНИЙ ЙАМАГЙИЙЁЙЙОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ (ГЛ. 3
структурой, показанной (при
Рис» 3.1.5. Доменная структура водноосном монокристалле при небольшом постоянном поле Но, приложенном вдоль легкой оси. Пунктиром показана структура при Но = 0.
Если условия (3.1.11) не выполняются, компоненты %, конечно, существенно различаются для монокристалла и поликристалла и могут быть найдены лишь в результате усреднения переменных намагниченностей для конкретной доменной структуры. Если по-прежпему не учитывать переменных магнитных зарядов на границах доменов, то такое усреднение в некоторых случаях можно провести очень просто.
Рассмотрим, например, одноосный монокристалл с доменной отсутствии постоянного поля) на рис. 3.1.3. Небольшое внешнее поле Но, направленное по легкой оси, приведет к некоторому смещению границ доменов (рис. 3.1.5). Определим усредненные значения компонент тензора восприимчивости для такого кристалла. При этом не будем принимать во внимание замыкающих доменов-призм, считая, что занимаемый ими объем мал по сравнению с объемом доменов-слоев. Не будем для простоты учитывать и размагничивающего действия поверхности кристалла, интересуясь внутренним тензором X или же предполагая, что образец — сфера (в первом случае нужно считать, конечно, что Но — внутреннее постоянное поле).
Такая задача будет являться обобщением задачи, рассмотренной (для Но = 0) еще Ландау и Лифшицем [111].
Для определения тензора % внутри доменов можно воспользоваться общими результатами, полученными выше методом эффективных размагничивающих факторов (хотя, конечно, не представляло бы труда найти его и непосредственным решением уравнения Ландау — Лифшица). Тензор Netf включает в себя в данном случае только тензор размагничивающих факторов анизотропии, который для одноосного кристалла определяется выражениями (2.2.8). В нашем случае углы 6 между намагниченностями и осью анизотропии составляют 0 или л и, согласно (2.2.8), не обращается в нуль компонента NS3. С учетом только первой константы анизотропии
/V33 “
27G
Л/* ’
3.1]
ДОМЕННАЯ СТРУКТУРА И УСРЕДНЕННЫЕ ПАРАМЕТРЫ
119
При использовании метода эффективных размагничивающих факторов оси координат должны быть выбраны таким образом, чтобы ось z совпадала с постоянной намагниченностью. Таким образом, для разных доменов оси координат будут направлены по-разному, как показано на рис. 3.1.5. С учетом этого по формуле (1.4.16) найдем собственные частоты
“о± = т|^±^о|,	(3.1.16)
где знаки плюс соответствуют большим доменам, для которых направления Но и Мо совпадают, а знаки минус — малым.
Для простоты не будем учитывать диссипации. Тогда необ-ращающиеся в пуль компоненты тензора у запишутся, согласно (1.4.40) — (1.4.44), следующим образом:
1шо+Л7<)	ТсоЛ/о -о . .....
=	Xat = —--------r. (3.1.17)
Для усреднения компонент % нужно перейти к общей для обоих доменов системе координат, например, системе х+, у+, z+ (больших доменов). Очевидно, что при этом для малых доменов компонента х останется без изменения, а изменит знак. В результате усреднения с учетом толщин доменов получим
(3.1.18)
(3.1.19)
где d = d+ d_.
Если Но — 0 и d+ = d_, то (3.1.18) и (3.1.19) переходят в выражения, полученные Ландау и Лифшицем [111]:
w.i z
к м6 )
Ха =0.
(3.1.20)
Таким образом, при отсутствии внешнего магнитного поля (и, конечно, остаточного намагничения) антисимметричная компонента тензора х обращается в нуль, а симметричная — зависит от частоты по резонансному закону. Оба эти утверждения являются весьма общими, они справедливы независимо от рассматриваемой модели и сделанных допущений. Резонанс при отсутствии внешнего постоянного поля называется обычно естественным ферромагнитным резонансом. В рассмотренном случае (для одноосного монокристалла) и для принятых допущений (важнейшее из которых — цеучет переменных магнитных зарядов на границах доменов)
120 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
его частота оказалась равной 2 у | Кг | /Мо. В других случаях она будет выражаться, конечно, по-другому. В реальных образцах, в особенности в поликристаллах, доменная структура будет сложной, неоднородной по объему образца. При этом будет иметься целое распределение — полоса частот естественного ферромагнитного резонанса.
Заметим, что в рассмотренном случае при отсутствии постоянного поля Хх = Xv = X, но Xz = 0- Таким образом, тензор X является (при Но = 0) диагональным, но не обращается в скаляр. Ясно, что это будет иметь место для любых монокристаллов г). В случае же поликристалла в результате двойного усреднения по доменам и зернам тензор X при Но = 0 обратится в скаляр. При учете диссипации все компоненты рассматриваемого усредненного тензора восприимчивости будут, конечно, комплексными. В частности, поликристалл при Но = 0 характеризуется двумя комплексными параметрами и Y'. Зависимости их от частоты изучались еще Аркадьевым [27] и были названы им магнитными спектрами * 2).
Переменные размагничивающие поля доменов. Перейдем теперь к рассмотрению размагничивающих полей, связанных со скач ками намагниченности па границах доменов. Одно из граничных условий на поверхности раздела любых сред заключается (см. § 5.1) в непрерывности нормальной составляющей магнитной индукции. Из этого условия следует, что
IIjBo — Н2и0 = — 4л (M]i>0 — М2ио),	(3.1.21)
где индексы 1 и 2 соответствуют двум средам, а п0 — единичный вектор нормали к поверхности раздела. Таким образом, нормальная составляющая магнитного поля испытывает на границе скачок, равный умноженному на 4л скачку нормальной составляющей намагниченности. Так как внешнее поле не имеет особенности на границе, то должно возникнуть размагничивающей поле, испытывающее на границе указанный скачок.
Рассмотрим, например, систему бесконечных плоскопараллельных доменов-слоев (рис. 3.1.6). Предположим, что нормальные составляющие намагниченности испытывают на границах скачки + АЛ/„. Легко видеть, что размагничивающие поля, направленные перпендикулярно границам и равные
^Mi,2 =+2л | ДЛ/П|,	(3.1.22)
х) При отсутствии внешнего магнитного поля и остаточного намагничения тензор % должен быть симметричны и, следовательно, в самом общем случае становится диагональным при соответствующем выборе осей,
2) К магнитным спектрам мы вернемся в § 3.3,
§ 3.1] ДОМЕННАЯ СТРУКТУРА Й УСРЕДНЕННЫЕ ПАРАМЕТРЫ
121
обеспечивают выполнение граничных условий (3.1.21). Такие поля удовлетворяют, как нетрудно убедиться, и уравнениям магнитостатики (§ 5.1), т. е. представляют собой решение рассматриваемой задачи.
Часто, особенно при качественных рассуждениях, оказывается удобным вводить фиктивную поверхностную плотность магнитных зарядов
б =	= М]П0 — М2п0
(3.1.23)
и считать ее источником размагничивающих полей. Так, в рассмот-
ренном выше примере «магнитные заряды» с плотностями п+ = = | &Мп | и п_ = — |Д Мп | будут
равномерно распределены на границах.
Как уже указывалось выше, равновесная намагниченность обычно не имеет скачков нормальной составляющей на границах доменов. Но при достаточно высокой частоте переменного поля, когда процессы уже не происходят квазистатически, нормальные составляющие переменной намагниченности могут иметь скачки на границах доменов. Это приведет к возникновению переменных «магнитных зарядов» на границах доме
Рис. 3.1.6. Размагничивающие поля доменов и «магнитные заряды» на их границах.
нов и переменных размагничивающих
полей, зависящих от намагниченностей не только данного домена, но и соседних.
Интересно отметить (это будет проиллюстрировано на конкретном примере в следующем параграфе), что переменные размагничивающие поля, обусловленные скачками намагниченности на поверхностях образца, будут также зависеть от намагниченностей доменов. Наличие как тех, так и других размагничивающих полей приведет к связи между колебаниями намагниченности соседних доменов. Частоты этих связанных колебаний и значения усредненных компонент тензора восприимчивости будут существенно отличаться от величин, полученных выше без учета взаимодействия
между переменными намагниченностями доменов.
Задача о ферромагнитном резонансе с учетом переменных размагничивающих полей, вызванных скачками намагниченности на границах, будет рассмотрена в следующем параграфе. Здесь мы остановимся на нестрогом (полукачественном) учете влияния этих полей па усредненные параметры ферромагнетика.
Вернемся к рассмотренному выше одноосному кристаллу с доменами-слоями, параллельными оси z. Ограничимся случаем Но = 0. Проекции переменной намагниченности доменов на оси
122 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ ГГЛ. 3
общей для обоих доменов системы запишутся в виде
ту+ Ь ^Ха^х Ч~ X^yi И12± = 0.
(3.1.24)
Величины % и %а определяются формулами (3.1.17), где <в0+ = = 2у | Кг | 1Мп. Отсюда видно, что если hy = 0, то
ту- ~ ту+ = ^ХаАх, а при hx = 0
= ту+ = хйу.
Таким образом, переменное поле hx, параллельное границе, приводит к появлению скачка нормальной к границе составляющей
Рис. 3.1.7. Образование переменных «магнитных зарядов» па границах доменов и на поверхности эллипсоида [152J. а— прецессия намагниченности в доменах при переменном поле, параллельном или перпендикулярном границам (векторы намагниченностей в некоторый момент времени показаны сплошными линиями, и через 1/4 периода— пунктиром); б— мгновенное распределение переменных «магнитных зарядов» на границах доменов и на поверхности эллипсоида.
переменной намагниченности, т. е. к появлению переменной плотности «магнитного заряда»
о = &mv = i	- hx.	(3.1.25)
. \ Me ]
Переменное же поле, перпендикулярное границе, переменных магнитных зарядов на границе не вызывает. Это иллюстрирует рис. 3.1.7, а, на котором показана прецессия намагниченности в со
§ 3.1]. ДОМЕННАЯ СТРУКТУРА И УСРЕДНЕННЫЕ ПАРАМЕТРЫ 123
седних доменах под воздействием переменных магнитных полей: параллельного и перпендикулярного границе.
Формулы Полдера — Смита. Рассмотрим теперь, следуя Полдеру и Смиту-[152], эллипсоид из монокристалла, разбитый на домены так, как показано на рис. 3.1.7, б. Примем, что толщина доменов d много меньше размеров эллипсоида. Выясним, какие поверхностные заряды будут возникать на границах доменов и на поверхности эллипсоида, и попытаемся учесть их влияние.
Рассмотрим сначала случай, когда переменное поле hx параллельно границам доменов. Тогда на границах будут возникать поверхностные заряды, обусловленные скачками ту. Переменные магнитные заряды на поверхности эллипсоида будут вызываться, вообще говоря, проекциями как тх, так и ту на нормаль к поверхности. Но в случае поля, параллельного границам, величины ту будут иметь разный знак в соседних доменах и вызываемые ими магнитные заряды на поверхности будут знакопеременными. Связанные с ними размагничивающие поля будут сосредоточены лишь в узком слое вблизи поверхности. Величины же тх будут иметь одинаковый знак во всех доменах. Вызываемые ими магнитные заряды будут такими же, как если бы доменов вообще не было. Размагничивающее поле, связанное с этими зарядами, может быть учтено введением обычного размагничивающего фактора эллипсоида Nx эл. Размагничивающий же фактор Ny эл, обусловленный зарядами на поверхности эллипсоида, должен быть принят равным нулю. Однако должен быть введен размагничивающий фактор, учитывающий переменные заряды на границах доменов Ny д. Поскольку мы считаем, что толщина доменов много меньше размеров эллипсоида, можно принять Nvn ~ 4 л. Рассуждая таким же образом, нетрудно убедиться, что в случае переменного поля hy, перпендикулярного границам, Nx = 0, a Ny = Ny эл. Что же касается эффективного размагничивающего фактора в направлении оси z, обусловленного постоянными размагничивающими полями, то он должен быть принят равным нулю, так как постоянные магнитные заряды на поверхности будут знакопеременными.
Для того чтобы определить собственную частоту колебаний намагниченности рассматриваемого эллипсоида, достаточно подставить приведенные значения размагничивающих факторов в формулу Киттеля (1.4.18). При этом можно учесть также приближенно влияние кристаллографической анизотропии, вводя эффективное поле анизотропии (—Мо) = 2Нл^2\К1 | / Мо. Тогда для колебания, которое возбуждается переменным полем, параллельным границам доменов, получим
со — Т [(2Яа + Nx влМ0) (2На + Nv ДМО)]*'«,	(3.1.26)
а для колебания, которое возбуждается полем, перпендикулярным
124 КОЛЕБАНЙЙ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ Д0МЁЙОВ [ГЛ. 3
границам,
со = г [2Яа (2Яа + Nv ЭЛМО)Г\	(3.1.27)
Подчеркнем, что сумма размагничивающих факторов по разным осям, входящих в эти формулы, не должна быть равна 4л, как для однородно намагниченного эллипсоида.
Перейдем теперь к рассмотрению естественного резонанса в поликристалле. Предположим, что его зерна представляют собой эллипсоиды различной формы с показанной на рис. 3.1.7 доменной структурой; они не взаимодействуют между собой и различным образом ориентированы относительно переменного поля. Резонансные частоты этих эллипсоидов будут лежать в широкой полосе от
сомин^2ГЯа	(3.1.28)
(^311 = 0 в формуле (3.1.27)) до
Омане ~ 7 (2Яа + 4лМ0)	(3.1.29)
(Яд-эл = 4л и Ny д = 4 л *) в формуле (3.1.26)).
Несмотря на весьма нестрогий характер приведенных рас-суждений, оценки (3.1.28) и (3.1.29) довольно хорошо подтверждаются экспериментально. Особенно большой интерес представляет величина (Омаке, которая является граничной частотой так называемых «начальных потерь». На частотах, меньших соМакс, при Яо = 0 (а также при малых постоянных полях, когда еще сохраняется доменная структура) имеют место резонансные магнитные потери, которые препятствуют применению данного феррита в устройствах, работающих при малых полях. Например, для магний-марганцевого феррита, который широко применяется в таких устройствах (Мо = 160 гс, | Кг |	104), граничная ча-
стота <£>макс/2л = ЬГгц (длина волны 5 см).
Для устройств, работающих при малых постоянных полях на более длинных волнах, нужны ферриты с меньшей намагниченностью и с достаточно малой анизотропией. Очевидно, что требованием к таким ферритам является также малая ширина резонансной кривой. Был разработан целый ряд материалов, удовлетворяющих в той или иной мере этим требованиям: магниевые ферриты-алюминаты [473] и магниевые ферриты-хромиты со структурой шпинели, иттриевые ферриты-алюминаты и ферриты-галлаты [102], а также другие — более сложные ферриты со струк-
х) Эффективный размагничивающий фактор доменов Nv , может, конечно, несколько отличаться от 4л. Это отличие несущественно для оценочной формулы (3.1.29). Однако оно, как показали Ле Кроу и Спенсер [156] (см. также [6]) может явиться причиной интересной «аномалии»— возникновения в некоторой области постоянных полей отрицательных значений %а (рис. 3.1.4).
§ 3.2] ФЕРРОМАГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 125
турой граната [100] (см. [9]). Их использование позволило продвинуть границу применимости СВЧ ферритовых устройств, работающих при малых полях — в области существования доменной структуры, приблизительно до длин волп 10—20 с.и1).
В заключение заметим, чго формулы Полдера — Смита (3.1.28) и (3.1.29) позволяют оценить лишь границы полосы частот естественного ферромагнитного резонанса в поликристаллах. Зависимости X' и %" от со в этой полосе и, в частности, положение максимума х" определяются многими факторами, прежде всего — размерами и формой зерен и пор и особенностями доменной структуры.
§ 3.2. Ферромагнитный резонанс при наличии доменной структуры
Строгий расчет ферромагнитного резонанса в ненасыщенных образцах возможен практически лишь при достаточно простых предположениях об их доменной структуре. Такой расчет впервые провел Нагамийя [151] для случая диска из тетрагонального
кристалла. Для эллипсоида вращения из магнитно-одноосного кристалла этот расчет был проведен Смитом и Бельерсом [117], а для сферы из кубического кристалла — Артмапом [119]. В этих работах предполагалась простейшая доменная структура, состоящая из плоскопараллельных слоев равной толщины 2). Такая структура сохраняй ется при наложении постоянно-
Рис. 3.2.1. Доменная структура, сохраняющаяся при наложении постоянного поля. Пунктир™ намагниченности доменов при Но = 0, сплошные линии™ при Но 0.
го поля, если выполняется следующее условие: равновесные (при отсутствии поля) намагниченности обеих групп доменов образуют с полем одинаковые
углы Ад (рис. 3.2.1); угол же <ря, образованный полем страницами доменов, может быть любым. В этом случае обе группы до
менов остаются «равноправными» в энергетическом отношении и
х) СВЧ ферритовые устройства созданы и для гораздо более длинных: дециметровых и метровых волн [11]. Однако в этих устройствах используются постоянные поля, при которых доменная структура практически отсутствует. Для ферритов, работающих в таких устройствах, требование малой намагниченности не является обязательным.
2) Нагамийя [151] рассматривал также случай доменов-слоев неравной толщины.
126 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРП НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
при наложении поля, и смещения границ не происходит. Намагничение достигается путем процессов вращения, т. е. поворотами векторов намагниченности по направлению к полю.
Связанные уравнения движения для двух групп доченов. В работах [117] и [119] использовался метод расчета ферромагнитного резонанса в сферических координатах (§ 2.1), обобщенный на случай двух «магнитных фаз» — двух групп доменов. Остановимся прежде всего на этом обобщении. Следуя, в основном, Смиту и Бельерсу [117], рассмотрим вынужденные колебания и для простоты не будем учитывать диссипации.
Уравнения (2.1.39) — (2.1.41) справедливы для каждой фазы при условии, что входящая в них плотность энергии отнесена к единице объема соответствующей фазы. Мы же хотим по-прежнему иметь дело с плотностью энергии, отнесенной к единице объема всего кристалла. И если объемы обеих фаз равны, то в результате такой «перенормировки» плотности энергии получаются (без учета диссипации) следующие уравнения [117]:
981,2	2у______дЦ'	„ ? ..
“	Ма sin 01>2 9<р12	’	' ‘ ‘ '
dq>j,2	2т dU’
dt	=	Л/с sin81)2 S01|2 »	(3.2.2)
где U' — плотность энергии, отнесенная к единице объема всего образца, а 6112 и <pli2, соответственно, полярные и азимутальные углы векторов намагниченностей фаз Mj и М2. Как и при рассмотрении вынужденных колебаний в однофазной системе (см. (2.1.49)), величина U' включает в себя плотность зеемановской энергии в переменном магнитном поле.
Плотность магнитной энергии U (без зеемановской энергии в переменном поле) будет зависеть теперь от направлений намагниченностей обеих фаз, т. е. от 61; 62, (|Д и<р2 *). Разложим производные dU/dQ^2 и 8К/8(р1>2 в ряды вблизи равновесного положения 610, е20, <Рю, <Р20; например,
дщ" = Ke, -р Kti/ijAt.'] -р Ко1Ф1Д(р1 -р /7о,02Д92 -р £701Ч>2Дф2	, (3.2.3)
где [701, П0102, [701<р, и т. д. по-прежнему означают соответствующие первые и вторые производные в равновесном положении. При
х) Плотность магнитной энергии зависит, вообще говоря, и от относительных размеров доменов [159]. Но мы не принимаем во внимание этой зависимости, пренебрегая как возможностью равновесного смещения границ (вследствие упомянутого выше специального выбора направлепия постоянного поля), так и динамическими их колебаниями, Колебания границ доменов будут рассмотрены в следующем параграфе. В работе Власова и Оноприенко [159] дается трактовка вращательных колебаний намагниченности в доменах и колебаний границ в единой вычислительной схеме. В общем случае эти колебания оказываются связанными.
§ 3.2] ФЕрРдЙ&ГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 127
равновесии
Е\ = U., = С7Ф1 = и^г = 0.	(3.2.4)
Зеемановская энергия в переменном поле, согласно (2.1.51), запишется следующим образом:
Utl ----2 [SH10jSin6hCOs((pj — <Ph) + COS 0; cos 9h], ,
3=1, 2
(3.2.5)
где 6h и cph — полярный и азимутальный углы переменного поля. Подставим в уравнения (3.2.1) и (3.2.2) выражение (3.2.3) и аналогичные выражения для других производных от U с учетом (3.2.4), а также первые производные от (3.2.5) в равновесном положении. В результате получим линеаризированные уравнения движения для двухфазной системы
>0 sin 61 о	+ ^о^Дфх + С/е,вгЛ92 + СЛ^Лфг) =
= — [ctg 0i 0 sin Qh cos (^ 0 — cph) — cos 0J,
'	~ 1 Л/oshi6io	+ ^Т1тЛф1 + ^<Pie2^O2 + П^^Дфо) =
= sin eh sin (ф10 — фЛ),
(3.2.6)
Qt )----Л/0 sin 62 o' (^ei°2^®l+ Uф102Лф1 4" ^0262^62+^02ср2Лф2) =
= — [ctg 92 0 sin 9fc cos (<p2 0 — cph) — cos 9h ],
^dt + Ma sin 62 о	"Ь ^Ф1Ф^ф1 +	Пф^Дфг) =
= ф/г~ sin 9h sin (q>2 0 — q>h).
Уравнения (3.2.6) являются связанными, если хотя бы одна из «межфазных» вторых производных l/(!1d2, UW1, U0i№2 и не обращается в нуль.
В нашем случае
U = Uh + Um пов + Um гр + Ua.	(3.2.7)
Здесь Uh — плотность зеемановской энергии в постоянном магнитном поле, Umhob — плотность энергии размагничивающих полей, обусловленных скачками намагниченности на поверхности образца, Пмгр — плотность энергии размагничивающих полей, возникающих вследствие скачков намагниченности на границах доменов, a, Ua — плотность энергии анизотропии.
128 КОЛЕБАНИЙ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЁНОВ [ГЛ. 3
Энергия Uh, аналогично (3.2.5), запишется:
UH = -—5- М0Н0 2 tsin 6; siii 9н cos (<р, — <рй) + cos 9; cos Он].
3=1. 2
(3.2.8)
Примем, что толщина доменов много меньше размеров образца. Тогда для энергии размагничивающих полей, обусловленных поверхностью, будет справедливо выражение (2.1.3'), в котором под Мх, Му и Mz следует понимать усредненные по доменам значения соответствующих составляющих намагниченности, а под Nx, Nv и N- — «обычные» размагничивающие факторы, такие же как для однородно намагниченного эллипсоида ’). В нашем случае равных толщин доменов
Um пов =	3/q [Nx (sin 91cos Ti + si1162 cos (р2)2 +
+ Nv (sin 9i sin rpL -]- sin 92 sin cp2)2 Nz (cos Oi -f- cos 02)2]. (3.2.9)
Размагничивающие поля, связанные co скачками намагниченности на границах доменов, определятся согласно (3.1.22). Плотность их энергии
?7Л/гр--^-|ЯМ1,2|2 = 4(7И1?1-М2и)2,	(3.2.10)
где М1п и М2.г — проекции намагниченностей доменов на нормаль к границе.
Сфера из одноосного ферромагнетика. Рассмотрим одноосный кристалл. Тогда плотность энергии анизотропии каждой фазы запишется в виде (2.2.4). С учетом только первой константы анизотропии
Ua = Ki (sin2 0! ф- sin2 02).	(3.2.11)
Дальнейшие вычисления проведем на конкретном примере сферического образца (Nx = Nv ~ Nz ~ 4п/3) с Kj )> 0. Постоянное магнитное поле направим перпендикулярно оси анизотропии (рис. 3.2.2). Очевидно, что тогда будет выполняться сформулированное в начале этого параграфа условие и принятая доменная структура будет сохраняться в определенном интервале значений //(1. Предположим также, что постоянное поле перпендикулярно границам доменов. Переменное магнитное поле пусть
х) Нетрудно убедиться, что введенные в предыдущем параграфе при выводе формул (3.1.26) и (3.1.27) эффективные размагничивающие факторы находятся в согласии с этим утверждением. В частности, эффективные размагничивающие факторы обращались в нуль, когда соответствующие составляющие намагниченности имели противоположные знаки в соседних доменах, т. е. когда их среднее значение было равно нулю.
§ 3.2J ФЕРРОМАГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 129
лежит в плоскости, перепендикулярной оси анизотропии. Направим оси координат так, как показано на рис. 3.2.2. Тогда
фп = -^-, eh = ~	(3.2.12)
и плотность энергии (3.2.7) с учетом (3.2.8) — (3.2.11) запишется следующим образом:
1
U =-----%-М0Н0 (sin 0! sin q?! -|- sin 02 sin <р2) 4-
+ ~ Ki (sin2 0х 4- sin2 02) Ц- Afo[sin ()х sin 02 cos (фх — ф2) + Z	О
+ cos 6Х cos 02 4- 1] 4-	M^sin©! sin (fr— sin 02 sin ср2)2. (3.2.13)
Найдем прежде всего равновесные ориентации векторов намагниченности. Из симметрии задачи очевидно, что
Ф1 о — Фа о — фн — ~2~ j	91 о — л — 02 о = 0о- (3.2.14)
Это можно было бы получить и строго из условий равновесия (3.2.4). С учетом (3.2.14) выражение (3.2.13) примет вид
sin 0О =
Uo = —Mo#osin0o4-
4- (к! 4- 4^- М$\ sin2 0О. (3.2.15)
Условием равновесия будет
ае.>
Отсюда при Но 2 Нл1+4лЛ/0/3
Но
2иЛ1+4«;
Рис. 3.2.2. Доменная структура и направления полей, принятые при расчете ферромагнитного резонанса в сфере из одноосного кристалла.
где, как и прежде, Hai определяется согласно (2.2.10). При Но 2 Нах лМп/3
9о
л
2“’
т. е. доменная структура исчезает.
5 А. Г. Гуревич
130 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ ГРЛ. 5
3
Вычисляя вторые производные U и подставляя в них равновесные значения (3.2.14), получим *)
1
U6101= 02^2^Aifi = ~2“ А/qH0 sin Gq -(- Ki cos 20o -f-
+ -J- Ml cos 29O + MM% cos2 0o,
К<р1Ф, =	== Uw = ~ M0Hо sill 0O------Mg sin2 0O,
л ,»	,	(3.2.17)
£7е,ея —----3- Ml cos 260 + "Ml cos2 0O,
KW2 = ^M?sin20o,
- U<p2fl2	 ^7<₽102	6*
Таким образом, из упомянутых выше межфазных производных, обеспечивающих связь колебаний намагниченности двух групп доменов, в данном случае не обращаются в нуль U^e, и f/<p1<P2. Как видно из выражений для этих производных, связь вызывается пе только размагничивающими полями, обусловленными границами доменов (член лЛТу cos260 в U^), но и размагничивающими полями, связанными с поверхностью образца.
Будем считать переменное поле линейно поляризованным и гармоническим:
tph = const, h~ = heiwt.
Тогда Д01<2 и Acplj2 будут зависеть от времени также по гармоническому закону:
АО] =	А62 = ч2е‘“', Aipj = Pje™*, Аср2 = р2е';“(.
Если в уравнениях (3.2.6) принять во внимание (3.2.17), а также учесть условия (3.2.12) и (3.2.14), то для комплексных амплитуд °i,2 и Pi,2 получится следующая система алгебраических уравнений:
2KMjai — igoiPi + 2К(„(!гп2 = hM0 cos 0о sin <pft, igcoo! + 2KwPi + 2К<р1<й1Р2 = hM0 sin 90 cos cph, 2KMct2 — igtt»p2 + 2К61(!гП1 = — hM0 cos 60 sin tpft, igcoa2	2UфсрРг + 2Кф^Р! == hM0 sin 0O cos <р^,
(3.2.18)
где | = Mo sin 0o/y.
Если в (3.2.18) перейти к новым переменным
1	1
« ± = — («К + а2),	Р± = (Pi ± ₽г),
’) Величины Но и sin Оо в (3.2.17) связаны соотношением (3.2118).
§ 3.2] ФЕРРОМАГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 131
то для них получатся две независимые системы, соответствующие двум разным типам колебаний,
2 (U ео + U о,о2) п+ — iJ;cop+ = 0,	(3.2.19)
igwa+ + 2	₽+ = hM0 sin 0О cos <рл,
2 (Z7oe — U 61Bl) ct_ — i£u)₽_ = hM0 cos Go sin <p,„	(3.2.20)
i|coa_ + 2 (?7W — t/<pltP2) P_ = 0.
Колебания первого типа (система (3.2.19)) возбуждаются составляющей переменного поля, перепендикулярной постоянному полю, а колебания второго типа (система (3.2.20)) — составляющей, параллельной постоянному полю. Собственные частоты этих колебаний о>д_ и co || получаются в результате приравнивания нулю определителей систем (3.2.19) и (3.2.20):
<ог,» = мгтаг/(^о±ад(^±г^),	(3.2.21)
где верхние знаки соответствуют частоте а нижние — частоте (0 || .
Подставляя в (3.2.21) производные (3.2.17) и учитывая (3.2.16), получим
((О \
= #1,11-Щ., о	(3.2.22)
где
8л
I	7-п	Ал "0 “5— Мо
Hl = [2НА1 + М\ {2НА1 + 4лмо), гц. =---------------±----
'	1	2НА1 + — Мо
Н\ = 2Ял1 (2ЯА1 + ЛД мД п || =----------------•
'	'	'	2НА1 + —Мо
На рис. 3.2.3 показаны вычисленные по формулам (3.2.22) зависимости сод_ и co || от Но. На тот же график перенесена с рис. 2.2.4 зависимость со от Но, полученная ранее без учета доменной структуры. Как видно из рис. 3.2.3, учет доменной структуры привел, во-первых, к существенному увеличению частоты (ох колебания, возбуждаемого поперечным переменным полем ’). Эта частота уже ни при каких полях не обращается в нуль, ее наименьшее значение составляет
(Ох мин = ГМ° (2Я^ + пгмо)- (3.2.23)
*) Рост собственной частоты вследствие учета влияния доменной структуры следовал и из приближенной модели Полдера — Смита (см. предыдущий параграф).
5*
132 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ £ГЛ. 3
ченных зависимостей и соц
О)
Во-вторых (как и следовало ожидать для рассматриваемой системы с двумя степенями свободы), появился второй тип колебаний — с частотой со и, который возбуждается переменным полем, параллельным постоянному.
Смит и Бельерс [117] рассмотрели несколько более общий случай: произвольного эллипсоида вращения и произвольного угла между постоянным полем и границами доменов; характер полу-от Но оказался таким же, как и в рассмотренном выше частном случае. Эти зависимости были подтверждены экспериментально [1171 для тонкого диска.
Сфера из кубического ферромагнетика. Расчеты ферромагнитного резонанса в ненасыщенных образцах из кубического кристалла в тех частных случаях, когда реализуется простая слоистая структура, могут быть проведены так же, как и для одноосного кристалла. Один из таких случаев был подробно исследован Артманом [119]. Им был рассмотрен сферический образец с учетом только первой константы анизотропии. Постоянное магнитное поле Но было приложено в направлении <110>. Легко видеть, что сформулированное в начале этого параграфа условие сохранения при Но =/= 0 слоистой
структуры с доменами равной толщины может выполняться в этом случае как при Кг 0, так и при Кл 0. При К± 0 намагниченности доменов, направленные при Но = 0 по легким осям [100] и [010] (рис. 3.2.4), с ростом Но приближаются к направлению поля, находясь все время в плоскости (001). При Кл О намагниченности доменов с ростом поля поворачиваются в плоскости (110).
Как и в рассмотренном выше случае одноосного кристалла, угол между Но и границами доменов в работе Артмана 1119] был принят равным л/2 (рис. 3.2.4). Анализ условий равновесия показал, что минимум энергии (при Кл 0) соответствует такой структуре в интервале полей
О<Яо<2ЯА1 + -^-Мо	(3.2.24)
Я	"о
рис. 3.2.3. Частбты ферромагнитного резонанса в сфере из одноосного кристалла при наличии доменной структуры, показанной на рис. 3.2.2 [117].
> 0, остальные константы анизотропии не учитываются. Постоянное поле перпендикулярно оси и границам доменов. Пунктир— резонансная частота без учета доменной структуры (рис. 2.2.4). При расчете принято
4
НА1
(величина Hai по-прежнему определяется согласно (2.2.10)).
§ 3.2] ФЕРРОМАГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 133
При Н0=2НД1 + 4 л М0/3 углы <р0 становятся равными л/4 и доменная структура исчезает. В случае же Кл 0 принятая структура
Рис. 3.2.5. Частбты ферромагнитного резонанса в сфере из кубического кристалла с доменными структурами, показанными на рис. 3.2,4 [119]. Постоянное поле направлено по оси [110]. Пунктир— резонансные частоты без учета доменной структуры (рис. 2.2.7).
4	1
При расчете принято	= — Л1ИО при К, > 0 и |	| = — Мо при Kt < 0.
(при 4л Мп/3 > 21 Hai |) обеспечивает минимум энергии лишь при Условии
j/Tp (^-	“ -Г 1 На* |)	4г <0 .Tf-1НА11, (3,2.25)
134 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
чему соответствуют следующие пределы изменения угла 60:
arcsin
Расчет условий ферромагнитного резонанса в кубическом кристалле с доменной структурой [119] аналогичен рассмотренному выше расчету в случае одноосного кристалла с тем единственным отличием, что энергия анизотропии (в каждом домене) записывается теперь согласно (2.2.34). Поэтому мы приведем лишь окончательные результаты этого расчета. В интервалах (3.2.24) и (3.2.25)
CD Ж 24 -
20
16
l^/i
Рис. 3.2.6. Экспериментальная проверка условий ферромагнитного резонанса в сфере из кубического кристалла [160]. Точки— экспериментальные данные для иттрий-железного граната при постоянном поле, направленном по оси <110>. Кривые— расчет согласно [119].
существуют, как и в случае одноосного кристалла, два типа колебаний. Один из них (с частотой (OjJ возуждается переменным полем, перепендикулярным постоянному, а другой (с частотой со л) переменным полем, параллельным постоянному. Зависимости частот coj_ и со ц от Яо показаны на рис. 3.2.5. Как и в случае одноосного кристалла, эти зависимости обладают следующими особенностями:
1) при поперечном возбуждении (h ± Но) в некотором интервале частот наблюдаются резонансы при двух ((а в случае К± 0 — даже при трех) полях, большем — без доменной структуры и меньшем (или меньших)— при наличии доменной струк-
туры;
2) при частотах, меньших некоторой предельной, резонанс при поперечном возбуждении вообще не наблюдается;
3) при более низких частотах должны наблюдаться два резонанса при продольном возбуждении (h || Но).
Первые две особенности были подтверждены еще в ранних опытах Танненвальда [155] и в ряде последующих работ [160, 163, 164]. На рис. 3.2.6 приведены, например, экспериментальные данные Мануйловой и Богдановой [160] для случая /<-, <^0, а также соответствующая теоретическая кривая. Как видно из этого
рисунка, совпадение экспериментальных частот с расчетными оказывается хорошим в некотором интервале полей, правда, несколько более узком, чем теоретический интервал (3.2.25). Отсюда можно сделать вывод, что в этом интервале полей доменная структура действительно близка к принятой при расчете. Интерес-
§ 3.21 ФЕРРОМАГНИТНЫЙ РЕЗОНАНС ПРИ ДОМЕННОЙ СТРУКТУРЕ 135
но отметить, что в той области, где имеет место хорошее совпадение экспериментальных частот с теоретическими, резонансная кривая при наличии доменной структуры является почти такой же узкой, как и в насыщенном образце. Это иллюстрируется кривыми рис. 3.2.7, взятыми из той же работы [160].
Зависимости, аналогичные тем, которые были рассчитаны и наблюдались экспериментально при Но, параллельном оси (НО), были получены также [119] (для Кл < 0) и при Но, направленном

Рис. 3.2.7. Экспериментальные кривые ферромагнитного резонансного поглощения в сфере из иттрий-железного граната [160]. Но направлено по оси <110>. Частоты “1234 показаны на рис. 3.2.6. D — коэффициент прохождения волны через резонатор с исследуемой сферой.
по трудной оси (100). И в этом случае возможны простые слоистые структуры, для которых намагничение осуществляется поворотом векторов намагниченнссти и доменная структура сохраняется в сравнительно больших полях.
Если же в образце имеет место сложная доменная структура с границами, ориентированными различным образом (относительно кристаллографических осей и поля) в различных участках образца, то резонансные условия также будут различны в этих участках, и наличие доменной структуры приведет к существенному расширению резонансной кривой. -Это, в частности, всегда имеет место в поликристаллах и явлется одной из причин того, что область «естественного» ферромагнитного резонанса в поликристалле является обычно очень широкой 1).
*) В предыдущем параграфе рассматривался метод приближенного опрй деления границ этой области, предложенной- Полдером и Смитом.
136 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧЙИ ДОМЕНОВ 1гЛ. S
§ 3.3. Колебания границ доменов
В этом параграфе будут рассмотрены колебания границ доменов под воздействием переменного магнитного поля достаточно высокой частоты — такой, что смещение границ не происходит квазистатически. Постоянное поле может либо отсутствовать, либо иметь величину и направление, при которых сохраняется доменная структура. Переменное же поле должно быть приложено таким образом, чтобы смещение границы приводило к изменению зеемановской энергии в переменном поле. Для этого переменное поле не должно образовывать равных углов с намагниченностями доменов. Например, оно может быть параллельно намагниченности одного из соседних доменов.
Уравнение движения границы. Смещение границы между доменами происходит в результате поворотов векторов намагниченности. Поэтому теоретическое рассмотрение смещения границы должно основываться на решении уравнения движения намагниченности в граничном слое. Учет диссипации теперь необходим, так как иначе скорость смещения границы оказалась бы бесконечно большой. Можно использовать, например, уравнение (2.1.23). Эффективное поле, входящее в (2.1.23), должно включать внешнее переменное поле, постоянное внешнее поле (если оно приложено), эффективное поле анизотропии, эффективное поле обменного взаимодействия и размагничивающее поле. Намагниченность в граничном слое изменяется в пространстве очень быстро. Поэтому в эффективном поле обменного взаимодействия (2.1.21)' нужно учесть второй член (первый в уравнение движения намагниченности ферромагнетика не входит). Для определения размагничивающего поля, обусловленного изменением намагниченности в граничном слое, нужно исходить из уравнений Максвелла (см. § 5.1). Размагничиающими же полями, вызванными границами образца, можно для простоты пренебречь.
Такой расчет был проведен Ландау и Лифшицем [111] для одноосного кристалла (доменная структура, которая имеет место в этом случае, показана на рис. 3.1.3). При расчете предполагалось, что поле Н приложено параллельно оси анизотропии (так же, как постоянное поле на рис. 3.1.5), вклад замыкающих доменов не учитывался. Мы не будет рассматривать здесь этого расчета, приведем лишь его основной результат. Оказалось, что уравнение движения намагниченности имеет решение, зависящее от координаты х в направлении нормали к границе и от времени t в комбинации (х — vf), где
п =	(3.3.1)
Это решение соответствует смещению границы, как одного целого,
§ 3.31
КОЛЕБАНИЯ ГРАНИЦ ДОМЕНОВ
137
со скоростью v. Здесь
р =
1/И11 Т2л/о V q '
(3.3.2)
a coj — параметр диссипации в уравнении движения (2.1.23), связанный с другими параметрами соотношениями (1.3.12) и (1.3.14).
Выражение (3.1) можно переписать в виде
(3.3.3)
и рассматривать как уравнение (3.3.3) есть «сила трения», а правая — «давление», вызывающее смещение границы.
Кроме этих сил, как указал Беккер [150], на границу действует некоторая упругая сила (— t,x). Ее появление объясняется тем, что в реальном кристалле с различными неоднородностями граница занимает всегда некоторое равновесное положение — находится в «потенциальной яме». При отклонении границы от положения равнове-
движения границы. Левая часть
г
Рис. 3.3.1. Движение доменной границы.
сия на нее начинает действовать упругая сила, стремящаяся вернуть ее в это положение.
Исследуя детально движение границы между доменами, Дёринг [148] показал, что в энергии границы, кроме (3.1.5), имеется дополнительный член, пропорциональный квадрату скорости движения. Он может быть записан в форме
ИДрг, = 4-тгр1Л	(3.3.4)
где тгр — эффективная масса движущейся границы, отнесенная, как и РЕГр i>, к единице ее поверхности. Из следующих простых, но нестрогих соображений [150] можно наглядно представить себе причину появления дополнительной энергии и оценить величину П1гр-
Рассмотрим границу, для которой намагниченность лежит все время в плоскости границы — плоскости yz (рис. 3.3.1). Предположим, что повороты намагниченности, в результате которых граница движется со скоростью г, происходят под действием некоторого поля Н15 направленного по оси х. Тогда уравнение движения намагниченности может быть записано следующим образом (потери здесь учитывать не обязательно, так как скорость движения
438 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
границы рассматривается как заданная):
Но 1-gJ-l = M0-g- = а | -ТМХ xHJ Отсюда
H± = —	.	(3.3.5)
Дополнительную энергию движущейся границы можно рассматривать как энергию этого поля:
4- ОО
и7гР1>=-^ 5 H*dx-	(3-3-6)
Подставляя (3.3.5) в (3.3.6) и принимая во внимание (3.3.4), получим
-1-00
1 С / S6 \2 Л
//ipl) ~9 ’ \ I о I р 4лт2 J \ дх ) •—ос
или с учетом (3.1.3)
+°°
тгр =	sin20<7a;,	(3.3.7)
где Ь — толщина границы (3.1.4). Интеграл в (3.3.7) по порядку величины равен Ь, и окончательно
тогр~-^7>
(3.3.8)
что с точностью до множителя порядка 1 совпадает с выражением полученным Дёрингом (148]. Формула (3.3.8) по порядку величины справедлива и для кубических кристаллов. Для иттрийжелезного граната (Ь 5 • 10“б с.и.)
т,,р ~ 0,5 • 10'10 г]см2,
а для кобальтового феррита с большой анизотропией (й ~10 6 см) mTV ~ 2,5 -10"10 г/см?'.
Добавляя в (3.3.3) упругую силу и инерционный член, получим окончательно уравнение движения границы [150]
+о =м°я’ <3-3-9)
совпадающее по форме с классическим уравнением гармонического осциллятора.
§ 3.31
КоЛебайиЯ границ доменов
439
Восприимчивость, обусловленная смещением границ. Найдем теперь восприимчивость, связанную со смещением границ доменов под действием поля Н. Соседние границы смещаются в противоположные стороны (см. рис. 3.1.5), и намагниченность
(3.3.10)
где d — толщина доменов.
В статическом случае (Я = Но, х — х0, М = Л/=) из уравнения (3.3.9) получим
----g п Q.
Отсюда с учетом (3.3.10) следует, что упругий коэффициент £ связан со статической восприимчивостью X п о = М-__ГН0 соотношением
2/И2
S = v-T-	(3-3-11)
Л II 0°
Решая уравнение (3.3.9) в случае гармонического переменного поля Я = переходя затем от ж к переменной намагниченности М — тё^, согласно (3.3.10), и принимая во внимание (3.3.11), получим выражение для высокочастотной восприимчивости, обусловленной колебаниями границ,
— v____________Х110______
h -ЛИ «2	(3.3.12)
<02 + 1 too Q
Здесь собственная частота
(ЗЛ.13) а добротность
(),	.	(3.3.14)
Р
Нет необходимости проводить подробный анализ выражения (3.3.12), совпадающего с известным из механики или радиотехники (см. также [17]) решением для вынужденных колебаний гармонического осциллятора. Однако некоторые замечания полезно все-таки сделать. При Q 1 спектр носит резонансный характер (рис. 3.3.2, а) : вещественная часть восприимчивости %ц имеет максимум и минимум, лежащие недалеко от точки со = ®0; максимум мнимой части % ц лежит вблизи этой точки (при Q 1 практические ней совпадает). При() = 1 максимум %ц пропадает. При дальнейшем уменьшении Q минимум % ц, быстро уменьшаясь
140 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
по величине, смещается в сторону больших частот. Максимум же
% И, медленно уменьшаясь, смещается в сторону низких частот порядка и0<2, где происходит и основной спад %’ц. Спектр приобретает релаксационный характер (рис. 3.3.2, б). При Q 1 для
Рио. 3.3.2. Магнитные спектры, обусловленные колебаниями границ [17]. а— резонансный спектр (Q >1); б— релаксационный спектр (Q< 1).
области частот й<^соо вторым членом в знаменателе (3.3.12) можно пренебречь, тогда
со
		^ || 0	5С ц о	шрел ®0	(3.3.15)
	л|| -	°	со	со2	со2 ’	
где		1 + 1 а. 1 + 2 1 + 2 Рел	шрел	шрел Г ®рел = ®oQ ~ “ •	(3.3.16)
Согласно (3.3.15) максимум %ц лежит при со = соре.п, в этой точке 1
%11 = %И = — % II 0-
Попытаемся теперь оценить величины (»0 и Q для колебаний доменных границ. Из (3.3.13) с учетом (3.3.11) получаем
(0в = тМвтЛ-^-	(3.3.17)
или, используя (3.1.4), (3.1.9) и (3.1.5),
сов (-£)1/s I* (X 1,0)-V«.	(3.3.18)
Для поликристаллических ферритов под I в формуле (3.3.18) следует понимать размер зерен (10~2	10-4 см), а для монокрис-
таллов — размер образцов. Тогда, например, для поликристал-
§ 3.SJ	коЛеёанйя границ ДоМёйой	141
лического иттрий-железного граната (х ц 0 ~ Ю, остальные величины были приведены в § 3.1)
^ = 25 — 75 Мгц.
Для поликристаллического кобальтового феррита (Х||о~0>3) -g- = 250-4- 850 Мгц.
Для монокристаллов, как следует из (3.3.18), величины со0 будут в несколько раз больше. Из приведенных оценок следует, что собственные частоты колебаний доменных границ должны лежать в диапазоне десятков и сотен мегагерц.
Для величины со" = со0/2@ из (3.3.13) и (3.3.14) с учетом (3.3.2), (3.3.8) и (3.1.4) получаем простое выражение
co" = ^-cod,	(3.3.19)
т. е. со" с точностью до множителя порядка 1 совпадает с параметром диссипации cod. Однако оценка cod для интересующих нас процессов встречает определенные трудности. Надежные значения параметров диссипации для ферритов получены из экспериментов по ферромагнитному резонансу в монокристаллах. Например, в диапазоне длин волн 3 -4- 10 см для иттрий-железного граната и некоторых других совершенных кристаллов cod — 106 (АН — 1 э), для менее совершенных кристаллов cod — — 107 (АН — 10 э). Трудность заключается прежде всего в том, что неясно, в какой мере (и для какого из параметров в большей степени) значения параметров диссипации являются независимыми от частоты и величины постоянного поля. Кроме того, значения их в случае быстро меняющейся в граничном слое намагниченности могут отличаться от значений для однородной намагниченности при ферромагнитном резонансе. Если все же принять, что приведенные значения сохраняются при движении доменных стенок, то для со" получим оценку
= 1-4-10 Мгц.
Предположение о независимости от частоты и поля параметра диссипации сог = уА/f приводит к величинам со" на порядок большим.
Скорость движения доменной границы была непосредственно измерена Голтом [154] в монокристаллах магнетита Fe2+ Fel+O4 и железо-никелевого феррита Ni0>75Feo^aFe2+04. Из этих измерений, в частности, следует, что для железо-никелевого феррита
= 35 Мгц.
142 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛИЧИИ ДОМЕНОВ [ГЛ. 3
Оценка ю0 по формуле (3.3.18) для такого феррита (поликристал-лического) дает
-^- = 280 Мгц.
Из приведенных оценок следует, что, по-видимому, в большинстве случаев движение доменных стенок характеризуется значениями Q, большими 1, т. е. зависимость % ц от частоты должна носить резонансный характер.
Магнитные спектры. На рис.
3.3.3 приведены полученные Перекалиной, Аскочинским и Санниковым [158] зависимости р, || и р,ц от частоты для монокристалла кобальтового феррита. Эти зависимости безусловно связаны с колебаниями доменных границ, так как естественный ферромагнитный резонанс в кобальтовом феррите(А\=4-106)
должен иметь место при значительно более высоких частотах. Зависимости, показанные на рис. 3.3.3, носят четко выраженный резонансный характер: ®0/2п = 360 Мгц, ю"/2п = 25 Мгц. Величины (о(| и ю" находятся в разумном соответствии с приведенными выше оценками.
Подавляющее большинство весьма многочисленных измерений магнитных спектров (см., например, [19, 157]) выполнено на поликристаллах. В этом случае никогда не удается наблюдать узкого резонанса, обусловленного колебаниями доменных границ. Основной причиной, вызывающей «размазывание» резонанса доменных границ в магнитных спектрах поликристаллов, является сложность доменной структуры, разнообразие форм, размеров и ориентаций доменов. Заметим, что эта причина сказывается и в монокристаллических образцах, если только не приняты специальные меры для упрощения доменной структуры, как, например, в упомянутых работах [154] и [158].
В результате обусловленная колебаниями границ область магнитных спектров ферритов представляет собой растянутый на широкую полосу частот спад р/ и соответствующий ему «горб» р". Эта область спектра обычно «налезает'» на область, обусловленную естественным ферромагнитным резонансом (рис. 3.3.4, а), а иногда совершенно сливается в ней (рис. 3.3.5). И несмотря на то, что собственные частоты колебаний доменных границ, вообще говоря, ниже собственных частот естественного резонанса, высокочастотный «хвост» области спектра, обусловленной колебаниями
§ 3.3J
КОЛЕБАНИЯ ГРАНИЦ ДОМЕНОВ
143
границ, может достичь частот даже более высоких, чем максимальная частота естественного резонанса, которая определяется формулой Полдера — Смита (3.1.29).
На характер магнитных спектров ферритов оказывают также влияние различные процессы, которые сопутствуют смещению
Рис. 3.3.4. Магнитные спектры поликристаллического никелевого феррита [157J. I — область, обусловленная колебаниями границ доменов {Г— участок, где проявляются релаксационные процессы, сопутствующие колебаниям границ); II — область естественного ферромагнитного резонанса.
границ доменов и в силу своей инерционности тормозят его. К числу таких процессов принадлежат диффузия ионов, различные
электронные процессы, например, переходы электронов между ионами Fe2+ и Fe3+ (см. § 9.5) и др. Эти процессы приводят к спадам р' и максимумам р" при частотах, совпадающих с их частотами релаксации 1/т. Если величина 1/т близка к собственной частоте колебаний доменных границ ©0, то сопутствующие процессы приводят к расширению резонанса, обусловленного колебаниями границ. Если же 1/т	©0, то релакса-
ционный максимум р" и соответствующий спад р', связанные с
Рис. 3.3.5. Магнитный спектр поликристаллического никель-цинкового феррита Ni0,6Zn0,6Fe2O4 [19].
рассматриваемыми процессами, образуют отдельную область
магнитного спектра, которая отчетливо видна, например, на рис. 3.3.4,б.
До сих пор мы рассматривали высокочастотные колебания границ доменов при отсутствии постоянного магнитного поля. Предположим теперь, что такое поле приложено, но величина
144 КОЛЕБАНИЯ НАМАГНИЧЕННОСТИ ПРИ НАЛ ИЧИИ ДОМЕНОВ [ГЛ. 3
его недостаточна для полного исчезновения доменной структуры. Тогда колебания границ доменов около новых положений равновесия будут происходить качественно так же, как и при отсутствии постоянного поля. Колебания границ (во всяком случае для поликристаллического феррита) внесут одинаковый вклад во все диагональные компоненты тензора восприимчивости, и этот тензор запишется следующим образом1):
7=Хвр + %||,	(3-3.20)
где Хвр — тензор, обусловленный процессами вращения намагниченности внутри доменов (именно он рассматривался в предыдущих параграфах), а — восприимчивость, обусловленная колебаниями границ.
1 Строго говоря, величину х II в (3.3.20) следует умножить на единичный тензор.
ГЛАВА 4
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
§ 4.1. Антиферромагнетизм. Уравнения движения намагниченностей подрешеток
В предыдущих главах мы рассматривали магнитные колебания в ферромагнетиках — веществах, в которых обменное взаимодействие вызывает параллельную ориентацию элементарных магнитных моментов. Однако существуют магнито упорядоченные вещества и с другими магнитными структурами. Они могут быть коллинеарными (когда элементарные магнитные моменты параллельны или антипараллельны) и неколлинеарными, могут иметь или не иметь средний макроскопический спонтанный магнитный момент. Малые магнитные колебания в некоторых из таких веществ будут рассмотрены в этой главе.
Важным классом магнитоупорядоченных веществ являются антиферромагнетики — вещества, в которых при наличии магнитного упорядочения спонтанный (без внешнего магнитного поля) магнитный момент элементарной магнитной ячейки и, следовательно, любой макроскопической области равен нулю или же имеет небольшую, по сравнению с суммой элементарных моментов, величину х). К таким веществам относятся некоторые переходные и редкоземельные металлы и очень многие их окислы и соли. В качестве характерных примеров можно привести окислы МпО, NiO, Сг2О3, ct-Fe2O32); галогениды MnF2, NiF2, CuC12-2H2O; карбонаты МпСО3, СоСО3 и многие соединения состава Me+Me2+F3 или В3+Ме3+О3 (где Ме+ — ион щелочного металла, Ве3+ — редкоземельный ион, Ме2+ и Ме3+ — ионы переходных металлов).
Выше некоторой температуры — температуры Нееля, все эти вещества являются парамагнетиками, и их статическая
х) Введение в это определение величины области связано с тем, что и для ферромагнетиков средний момент достаточно большой области может быть равен нулю из-за наличия доменов. Замечание же о возможности наличия небольшого момента обусловлено тем, что обладающие таким моментом так называемые слабые ферромагнетики разумно отнести к антиферромагнетикам. Можно антиферромагнетики определить как вещества, в которых обменное взаимодействие «стремится» так сориентировать элементарные магнитные моменты, чтобы магнитный момент любой макроскопической области был равен пулю.
2) Окись железа имеет и другую — ферримагнитную модификацию T-Fe2O3.
146
АНТИФЕРРОМАГНЕТИКП И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
восприимчивость, как и восприимчивость ферромагнетиков выше температуры Кюри (см. § 1.1), удовлетворяет закону Кюри — Вейсса. Но, в отличие от ферромагнетиков, парамагнитная температура Кюри Тр для антиферромагнетиков отрицательна (см.  рис. 1.1.3). При температуре Tn имеют место «аномалии» теплоемкости и некоторых других величин, характерные для фазового перехода второго рода [36]. Ниже температуры Zjv восприимчивость антиферромагнетиков, в отличие от ферромагнетиков, остается небольшой, но обнаруживает (в монокристаллах) резкую анизотропию — быстро уменьшается с понижением температуры для одних направлений приложенного поля (хц на рис. 1.1.3) и остается постоянной или уменьшается медленно — для других ('/.[)• Величины Tn изменяются в широких пределах — от единиц градусов (например, 4,3 °К для СпС12-2Н2О) до сотен градусов (647 °К для NiO, 950 °К для a-Fe2O3).
Магнитные структуры. «Аномальное» (по сравнению с парамагнетиками) поведение восприимчивости антиферромагнетиков
Рис. 4.1.1. Магнитные структуры тетрагональных антиферромагнетиков (74]. Черные кружки— ионы Мп2+ или Ni2+, светлые кружки— ионы F~. Штрих-пуиктиром показаны оси (винтовые) четвертого порядка. Моменты ионов Ni2^ в слабом ферромагнетике NiF2 (см. § 4.3) слегка пеколлипеарны.
ниже температуры Нееля свидетельствует о магнитном упорядочении, которое имеет место при Т Tn- Идея такого магнитного упорядочения, не приводящего к появлению спонтанного момента, была выдвинута Неелем и Ландау [70]. Неель предположил существование «шахматной» структуры, в которой каждый элементарный магнитный момент, направленный в какую-либо сторону («вверх»), имеет в качестве всех ближайших соседей моменты, направленные в противоположную сторону («вниз»). Ландау же предложил модель, в которой слои моментов, направленных «вверх», чередуются со слоями моментов, направленных «вниз». Возможны, конечно, и более сложные магнитные структуры.
До проведения опытов по дифракции медленных нейтронов в антиферромагнетиках наличие тех или иных магнитных структур
§ 4.11
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЯ ДВИЖЕНИЯ
147
Рис. 4.1.2. Магнитная структура МпО [87]. Черные кружки— ионы Мп2+, светлые кружки— ионы О2-. Магнитные моменты лежат в плоскости (111). Приведена одна кристаллографическая элементарная ячейка, элементарная ячейка магнитной структуры имеет в два раза бблыпие линейные размеры. Небольшое сжатие по оси [111], имеющее место в магнитоупорядоченном состоянии, не показано.
оставалось удобной гипотезой, исходя из которой пытались объяснять магнитные свойства этих веществ. Опыты по дифракции нейтронов (см. [10]) подтвердили наличие магнитного упорядочения в антиферромагнетиках и позволили определить магнитные структуры для многих веществ. Так, например, выяснилось, что в тетрагональном кристалле MnF2, в котором (рис. 4.1.1) «магнитные» (обладающие магнитным моментом) ионы Мп2+ образуют объемно-центрированную решетку, моменты ионов, расположенных в вершинах и в центре призмы, направлены в разные стороны.
Такое «шахматное» упорядочение (по Неелю) возможно также в простых кубической, тетрагональной или орторомбической решетках магнитных ионов. Очевидно, что при этом будет происходить удвоение периода магнитной решетки по отношению к периоду кристаллографической (или, как говорят, кристаллохимической) решетки. Однако в гранецентрированной решетке магнитных ионов этот вид упорядочения невозможен. Такую решетку имеет, например, кубический ‘) кристалл МпО. Магнитное упорядочение в нем происходит так, как показано на рис. 4.1.2, и соответствует ело-’ истой модели Ландау.
Очень много антиферромагнетиков имеют кристаллографические структуры, принадлежащие к одноосным сингониям: тригональной, тетрагональной и гексагональной. Главная ось симметрии (третьего, четвертого или шестого порядка) этих кристаллов является осью магнитной анизотропии, и, в зависимости от знаков констант анизотропии, элементарные магнитные моменты направлены вдоль или перпендикулярно главной оси. Один из таких кристаллов — тетрагональный MnF2 был рассмотрен выше, магнитная структура тригональных антиферромагнетиков: Сг2О3 и др. показана на рис. 4.1.3. Мы ограничимся приведенными примерами, магнитные структуры антиферромагнетиков более подробно рассмотрены в [81, 10].
-1) С небольшими тригональными искажениями вдже точки Нееля.
148
АНТИФЁРРОМАГНЕТ'ИКИ Й ФЕРРЙМАГНЁТИЙИ
[ГЛ. 4
Косвенное обменное взаимодействие. Высокая температура Tn перехода в упорядоченное состояние, сравнимая по величине с температурой Кюри в ферромагнетиках, говорит о том, что за упорядочение в антиферромагнетиках ответственно обменное
Рис. 4.1.3. Магнитные структуры тригональных антиферромагнетиков [86, 81J. Черные кружки — ионы Сг3+, Fe3+ и Mns+; анионы не показаны. Тм— точка Морина; Tn~ тем' Пература Нееля. Моменты катионов в слабых ферромагнетиках (см. § 4.3) a-Fe2O3 (при Т > Tpj) и МпСО3 слегка неколлинеарны.
взаимодействие. То обстоятельство, что оно стимулирует анти-параллельную ориентацию спинов, заставляет полагать, что интегралы обмена (см. § 1.1) в случае антиферромагнетиков отрицательны. Это хорошо согласуется с отрицательной величиной Тр в законе Кюри — Вейсса.
Обсудим вопрос о природе обменного взаимодействия в антиферромагнетиках. Ограничимся рассмотрением ионных кристаллов, к которым принадлежит подавляющее большинство антиферромагнетиков. В этих кристаллах магнитные ионы находятся на таких больших расстояниях друг от друга, что прямым обменным взаимодействием между их спинами можно пренебречь. Магнитные ионы разделены «диамагнитными» — не обладающими магнитными моментами — анионами. Крамере (см. [58]) выдвинул идею косвенного обменного взаимодействия через анионы — так называемого сверхобменного (superexchange) взаимодействия. Рассмотрим механизм такого взаимодействия на сильно идеализированной модели [58] двух металлических ионов, например, Мп2+ с одним анионом О2” между ними (рис. 4.1.4).
Предположим, что моменты ионов ориентированы вдоль некоторой оси, пока в любом направлении. Предположим далее, что ион кислорода может передать электрон одному из ионов марганца, например левому на рис. 4.1.4, и что переход электрона на
§ 4.1]
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЯ ДВИЖЕНИЯ
149
3<7-оболочку иона марганца происходит без переворота его спина. В соответствии с правилом Хунда (см., например, [30]) перейдет тот электрон, который будет иметь спин, обратный спинам электронов левого иона марганца. В результате перехода ион кислорода (теперь О") приобретет магнитный момент, направленный параллельно моменту левого иона марганца (теперь Мп+). Ион 0“ будет
Рис. 4.1.4. Модель, иллюстрирующая механизм сверхобменного взаимодействия. Пунктиром показана 2р-алектронная орбита иона О-.
обменно взаимодействовать с правым ионом марганца. Предположим, что интеграл обмена является отрицательным; тогда обменное взаимодействие приведет к антипараллельной ориентации спинов этих ионов, как показано па рис. 4.1.4. Таким образом, магнитные моменты ионов марганца оказались сориентированными антипараллельно.
Конечно, оба рассматриваемые в этой модели иона Мп2+ равноправны, и электрон с равными вероятностями может перейти на любой из них. Кроме того, правильнее говорить не о полном переходе электрона с иона на ион, а о смешивании (гибридизации) электронных состояний 3d и 2-р, характерном для ковалентной связи. Таким образом, рассмотренная схема механизма сверхобменного взаимодействия является лишь грубой иллюстрацией. В реальных кристаллических решетках анион имеет всегда более двух соседвй-катионов (например, шесть в МпО, см. рис. 4.1.2), и все они, вообще говоря, участвуют в косвенном обмене друг с другом через анион. Но интенсивности взаимодействия для разных пар катионов не одинаковы. Как известно, 2р-оболочка имеет гантелевидную форму (см. рис. 4.1.4). Можно ожидать, что перекрытие ее с ЗсТоболочкой иона марганца и, следовательно, интенсивность сверхобмена будут тем сильнее, чем ближе будет к 180° угол, который образован векторами, проведенными из центра иона кислорода в центры двух катионов. Это находится в согласии с существующими магнитными структурами. Например, в случае МпО (рис. 4.1.2) все пары катионов, для которых указанные выше векторы образуют угол 180°, имеют антипараллельные моменты, в то время как моменты пар с векторами, образующими 90°, параллельны и антипараллельны в равных количествах, хотя они расположены на меньшем расстоянии друг от друга.
Теория косвенного обменного взаимодействия рассмотренного типа (сверхобменного взаимодействия), разработанная Андерсоном и другими (см. [58]), подтвердила приведенные выше грубые
150
АЙТиФЁРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
качественные соображения. Оказалось, что гамильтониан сверхобменного ваимодействия, аналогично гамильтониану прямого обмена (1.1.48), может быть записан в виде
<№е косв = ' ' 2 2 А/'косвБ/S/,,	(4.1.1)
где Sy и S/' — спины двух взаимодействующих катионов, а 1//-К0Св — некоторый эффективный «интеграл косвенного обмена», существенно зависящий от свойств аниона и взаимного расположения (углов и расстояний) трех ионов.
Косвенный обмен через анионы может иметь место и в соединениях переходных металлов других групп, и в соединениях редкоземельных (4/-) элементов. Косвенное обменное взаимодействие может осуществляться и коллективизированными электронами проводимости. Этот механизм (s-d или «-/-обмен) играет большую роль в металлах [5]. Он может иметь место и в сильно легированных полупроводниках, как антиферромагнитных, так и ферромагнитных (см., например, [377]).
Проблема квантового основного состояния. Обменное взаимодействие, если оно является, независимо от его природы, отрицательным (интегралы обмена Iff КОсв <С 0), стимулирует анти-параллельную ориентацию соседних магнитных моментов. Но отсюда нельзя делать вывода о том, что полностью упорядоченная антипараллельная структура, такая, например, как на рис. 4.1.1, 4.1.2 и 4.1.3, является основным состоянием данной системы. Более того, такая структура вообще не является собственным состоянием системы с гамильтонианом вида (4.1.1). Не приводя здесь строгих соображений по этому поводу (см. [5, 27]), заметим лишь, что обменный гамильтониан должен быть инвариантен относительно перестановок соседних спинов. Этому условию удовлетворяет ферромагнитная структура, но, конечно, не удовлетворяет идеально упорядоченная антиферромагнитная.
Проблеме основного состояния антиферромагнетика было посвящено большое число работ (см. [2]). И хотя эта проблема до сих пор не решена, ряд важных результатов удалось получить. В частности, Андерсон [72] оценил пределы, в которых должна лежать энергия U основного состояния антиферромагнетика:
-Б0>Б>-(1 + ^-Ш0.	(4.1.2)
Здесь
- U0	-yAZ|I|S2
— энергия полностью упорядоченного антиферромагнитного со
§ 4.1]
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЯ ДВИЖЕНИЯ
151
стояния (которое, как уже отметалось, не может являться основным состоянием) в приближении ближайших соседей, 5 — величина спина (в единицах Й), I — обменный интеграл, N — число магнитных ионов, Z — число ближайших соседей. Пределы, определяемые неравенствами (4.1.2), довольно узки, особенно для больших S. Например, для MnF2 (Z = 8, S = 5/2) интервал составляет всего 5% от Uo. Таким образом, энергия неизвестного и, видимо, достаточно сложного основного состояния мало отличается от энергии (—Uo) полностью упорядоченной антипа-раллельной структуры.
Однако энергия наинизшего состояния, не обладающего дальним магнитным порядком, также весьма близка к (—77О) [2]. Отсюда ясно, что задача отыскания основного состояния является сложной; по-видимому, ее нельзя решить без учета обменного взаимодействия с дальними соседями, и, возможно, без учета анизотропии. С другой стороны, многочисленные экспериментальные результаты, полученные с помощью дифракции нейтронов, убеждают нас в том, что основное состояние с дальним порядком существует. Оно представляет собой, по-видимому, некоторую неизвестную пока комбинацию различных упорядоченных конфигураций. Но с точки зрения ее энергии и даже пространственного распределения (о чем говорят нейтронные эксперименты) это основное состояние может быть в хорошем приближении заменено простой антиферромагнитной структурой типа показанных на рис. 4.1.1, 4.1.2 и 4.1.3.
Следует отметить, что мы рассматривали до сих пор основное состояние при О °К. При конечных температурах конфигурация, соответствующая основному состоянию при 0 °К, будет, конечно, нарушаться тепловым движением. Эти нарушения, в особенности при низких температурах, можно описывать, как и в ферромагнетиках, с помощью элементарных возбуждений — спиновых волн (см. главу 8). Свойства антиферромагнетиков при более высоких' температурах, включая области вблизи и выше температуры Нееля, могут быть, во всяком случае качественно, описаны в приближении молекулярного поля. Сущность этого приближения (см. § 1.1) заключается в том, что обменное взаимодействие спина с его соседями заменяется взаимодействием его с некоторыми эффективными полями, пропорциональными средним значениям спинов. Такое приближение, как отмечалось в § 1.1, используется иногда и при микроскопическом подходе к теории ферро- и антиферромагнетиков. Однако наиболее естественно оно входит в макроскопическую, континуальную теорию, в которой переменными величинами являются не элементарные магнитные моменты, а макроскопические намагниченности. Такая теория для случая антиферромагнетиков была развита Неелем [92]. Ван-Флеком [71] и другими (см. [2]).
152
АНТИФЕРРОМАГНЕТИКИ II ФЕРРИМАГНЕТИКИ
ГГЛ. 4
Континуальное рассмотрение. Отвлечемся от конкретного расположения элементарных магнитных моментов в пространстве и объединим моменты, находящиеся в эквивалентных местах кристаллической решетки и одинаково направленные, в так называемые магнитные подрегиетки. Введем намагниченности этих подрешеток
М/>
(4.1.3)
где — средние значения элементарных магнитных моментов, входящих в /-ую подрешетку, а суммирование производится по всем таким моментам, находящимся в малом макроскопическом объеме AV. Векторы М7- являются независимыми переменными при континуальном рассмотрении антиферромагнетиков.
Число подрешеток в общем случае должно быть равно числу магнитных ионов в элементарной магнитной ячейке. Однако в сложных магнитных структурах некоторые подрешетки иногда могут быть объединены (см. § 4.4). Что же касается сравнительно простых антиферромагнетиков с магнитными ионами одного сорта, к которым принадлежат, например, упомянутые выше MnF2, NiF2, МпО и Сг2Оа, то для описания большинства (а в случае' MnF2 и NiF2 — и всех) их свойств достаточно ввести дее подрешетки, каждая из которых объединяет все моменты, направленные в одну сторону.
Континуальная теория антиферромагнетиков и вообще магнитных систем с несколькими подрешетками строится аналогично континуальной классической теории ферромагнетиков (§ 2.1). Исходным является выражение для плотности энергии (при Т — — О °К) или магнитной свободной энергии (при T^> G)*,U как функции векторов М7-. Эффективные поля, действующие на каждую нодрешетку, могут быть найдены по формуле
з
ц________ди I у д ".
еИ 3	9М; дх
1	Р=1 р
dU
(4.1.4)
д
р
которая является обобщением формулы (2.1.14). Здесь / = = 1,2, . . ., п, где п — число подрешеток.
Естественно предположить, что для векторов М; справедливы такие же уравнения движения Ландау — Лифшица
дМ.
Т = ~ ГД,- х Ие„ 3- + Rj,	(4.1.5)
как и для намагниченности ферромагнетика. Здесь Г; — магнитомеханические отношения, вообще говоря, не одинаковые для
§ 4.П
Антиферромагнетизм. уравнения движения
153
разных подрешеток, a R, — диссипативные члены. Они, по-ви-димому, могут быть записаны в одной из форм, обсуждавшихся в § 1.3. Как и в случае ферромагнетика, предпочтение той или иной форме записи этих членов можно отдать, только исходя из характера процессов диссипации.
Составляющие энергии и эффективные поля. Остановимся кратко на основных видах энергии (или при Т '^> 0 — свободной энергии) антиферромагнетиков. К ним относятся: энергия обменного взаимодействия Ue, энергия магнитной кристаллографической анизотропии Ua, зеемановская энергия UH и энергия размагничивающих полей Um- Кроме того, в выражение для полной энергии могут войти члены, характеризующие взаимодействия рассматриваемой электронной магнитной системы антиферромагнетика с другими системами, например, ядерной магнитной системой и упругими колебаниями решетки. Но мы их пока не будем учитывать и полную плотность энергии запишем в виде
U = Ue + Ua + Ua + UM.	(4.1.6)
Обменная энергия антиферромагнетика, как и в случае ферромагнетика, является суммой однородной и неоднородной частей. Однородную часть для системы с несколькими подрешетками обычно записывают в виде
п п
= - 4- 2 2 АЖ',	(4.1.7)
>=1 ;’=1
где Ajj- — константы, характеризующие обменное взаимодействие между спинами /-й и /'-й подрешеток. Эти константы являются скалярными (как и в выражении (2.1.4) для ферромагнетика), т. е. обменное взаимодействие предполагается изотропным. В действительности обменное взаимодействие в антиферромагнетике, как и в ферромагнетике, не является изотропным. Но анизотропную часть обменной энергии можно отнести к энергии Ua магнитной кристаллографической анизотропии.
Если величины А}}-	0, то обменное взаимодействие поло-
жительно, т. е. носит ферромагнитный характер; если Л7у О, то обменное взаимодействие является отрицательным, антиферромагнитным. В системе с несколькими подрешетками величины Ajj- могут иметь разные знаки, но ясно, что в антиферромагнетике по крайней мере одна из этих величин должна быть отрицательной. Заметим, что в выражение (4.1.7) должны были войти_также изотропные (зависящие лишь от взаимной ориентации векторов М;) члены четвертого и более высоких порядков [21]. Однако мы ограничимся в (4.1.7) записанными — квадратичными и билинейными членами, так как в большинстве случаев их достаточно для описания основых свойств антиферромагнетиков. Тогда
154
АНТИФЁРРОМАГНЕТИНИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
эффективные поля однородного обменного взаимодействия (с учетом того, что Лл- = Лг;) будут иметь вид
п
Ял/ = 2i	(4.1.8)
}'~i
Эти поля называют обычно молекулярными полями, а обменные константы Ajj- — константами молекулярного поля. В отличие от ферромагнетика, в системах с несколькими подрешетками только один член молекулярного поля AWM; не войдет в уравнение движения для /-й подрешетки, а все остальные члены войдут, обеспечивая связь между изменениями намагниченностей подрешеток.
Для антиферромагнетика с двумя подрешетками
UА	~ -ТЛ22М* ~	(4.1.9)
Нлц= AUMT + Л12М2, НЛ2 = Л22М2	Л12М1.	(4.1.10)
Для идентичных подрешеток, конечно, Ли = Л22.
Неоднородную часть обменной энергии системы с п подрешетками, обобщая выражение (2.1.7), можно записать следующим образом:
п п 3	3
4 ЧП №1 VI	aVI • О Лх - /
=	2 2 2	~&Г 	(4.1.11)
?=11'=1Р=1 S=1	Р *
В этой главе мы не будем рассматривать неоднородных распреде лений статической намагниченности (которые имеют место, на пример, в доменных стенках) и неоднородных колебаний. Тогда необходимо будет принимать во внимание только однородную обменную энергию U
Энергия кристаллографической магнитной анизотропии антиферромагнетика U а записывается обычно в виде ряда по степеням MjXp, допускаемого симметрией данной кристаллической решетки. Выражения для эффективных полей Haj находятся дифференцированием Ua по составляющим намагниченностей в соответствии с первым членом формулы (4.1.4). Конкретные примеры таких вычислений для случая одноосной анизотропии будут рассмотрены в следующих параграфах. Физические источники анизотропии в антиферромагнетиках [59], вообще говоря, те же, что и в ферромагнетиках (§ 2.2). Но если в ферромагнетиках магнитное (дипольное) взаимодействие обычно не вносит заметного вклада в анизотропию, то в некоторых антиферромагнетиках (например, в MnF2) вклад этот является существенным.
Следует отметить еще два обстоятельства, касающихся кристаллографической анизотропии в антиферромагнетиках. Во-пер
§ 4.1J
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЯ ДВИЖЕНИЯ
155
вых, роль ее гораздо важнее, чем кристаллографической анизотропии в ферромагнетиках. В этом мы убедимся на конкретном примере в следующем параграфе. Во-вторых, симметрия некоторых кристаллов допускает появление в разложении энергии по М?Жр, кроме «обычных» анизотропных членов, приводящих к ориентации векторов М; в определенных кристаллографических направлениях, также членов, приводящих к небольшому нарушению коллинеарности векторов М,-. В антиферромагнетиках этот, вообще говоря, малый эффект приводит к очень серьезным последствиям — к появлению спонтанного момента, так называемому слабому ферромагнетизму (§ 4.3).
Энергия зеемановского взаимодействия антиферромагнетика с внешним полем Н
UH = - МН,	(4.1.12)
где
М=2М1	(4.1.13)
Г=1
— суммарная намагниченность. Она не равна, вообще говоря, нулю даже для антиферромагнетика без слабого ферромагнетизма— как вследствие влияния постоянного внешнего поля, так и из-за наличия колебаний. Ясно, что эффективное поле зеемановского взаимодействия представляет собой внешнее поле Н.
Так как магнитные подрешетки антиферромагнетика «перемешаны», «вставлены друг в друга», то энергия размагничивающих полей Um, являющаяся результатом дальнодействующих дипольных взаимодействий, будет зависеть только от результирующей намагниченности М. Для малого эллипсоида с тензором размагничивающих факторов N будет справедливо выражение (2.1.3). С помощью формулы (4.1.4), учитывая симметрию тензора N, легко убедиться, что эффективные поля этого взаимодействия одинаковы, как и следовало ожидать, для всех подрешеток и равны
Им = - NM.	(4.1.14)
Основное состояние в континуальной трактовке. Рассмотрению малых колебаний в антиферромагнетиках, как и в ферромагнетиках и вообще в любых колебательных системах, должно предшествовать отыскание * равновесных — основных состояний, около которых совершаются малые колебания. В рамках континуального подхода при этом'пе возникает той принципиальной трудности определения квантового основного состояния антиферромагнетика, о которой упоминалось выше. Она, ^конечно, не разрешается, но обходится путем задания магнитной структуры,
156
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
ГГЛ. 4
т. е. числа подрешеток и их намагниченностей при О °К в отсутствие внешнего поля. Задачей же континуальной теории является определение равновесных длин векторов М и их ориентаций в зависимости от величины и направления приложенного поля и температуры.
При О °К длины равновесных векторов М; постоянны и заданы, и задача об отыскании основного состояния сводится к определению ориентации этих векторов по отношению к кристаллографическим осям при заданной ориентации и величине постоянного магнитного поля Но с учетом кристаллографической анизотропии и формы образцов. Последний фактор, однако, несуществен для антиферромагнетиков в сравнительно слабых внешних полях, когда суммарный момент М мал. Решение этой задачи, как и для ферромагнетика (§ 2.1), может быть начато двумя, с первого взгляда, различными способами. Первый заключается в том, что следует приравнять нулю производные от плотности энергии антиферромагнетика (4.1.6) по 2п независимым переменным, например полярным и азимутальным углам п векторов MJ. Другой путь заключается в том, чтобы использовать выражения
М;0Х Heffj0 = 0,	(4-1.15)
которые непосредственно следуют из уравнений движения (4.1.5) и означают, что равновесные намагниченности подрешеток параллельны эффективным полям. Оба пути, конечно, совершенно эквивалентны, так как производные от энергии по углам представляют собой соответствующие проекции вращающего момента (4.1.15). После получения всех решений упомянутых 2п уравнений необходимо путем исследования вторых производных или непосредственным сравнением величин плотности энергии выяснить, какие из них соответствуютминимуму энергии, т. е. равновесной конфигурации. Заметим, что решение задачи об основном состоянии часто существенно облегчается тем, что удается из соображений симметрии предугадать некоторые особенности равновесной конфигурации и тем уменьшить число переменных. Примеры отыскания основных состояний в некоторых частных случаях будут рассмотрены в следующих параграфах этой главы перед рассмотрением колебательных задач.
г При Т О °К уравнения движения (4.1.5), формула (4.1.4) для эффективного поля и 'выражения, например (4.1.7)и (4.1.11), для различных членов U остаются справедливыми, но под U следует понимать плотность магнитной свободной энергии, а под Му — термодинамические средние намагниченности подрешеток при данной температуре. Эти векторы не будут теперь иметь постоянную длину, и для отыскания основного состояния нужны дополнительные условия. Можно, например, предположить, что зависимости равновесных намагниченностей подрешеток от.со
§ 4.11
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЯ ДВИЖЕНИЯ
157
ответствующих эффективных полей и температуры имеют такой же вид, как и зависимость (1.1.41) для ферромагнетика:
Mj = М°}В,. неа; ) ,	(4.1.16)
где
М? =	(4.1.17)
— намагниченность j-й подрешетки при О °К, Bj - — функция Бриллюэна (1.1.32), J j — механический момент ионов j-й подрешетки (в единицах Л), gj — их фактор спектроскопического расщепления, Nj — число этих ионов в единице объема, — магнетон Бора, ах — постоянная Больцмана. Результаты прямых измерений температурных зависимостей методами ядерного магнитного резонанса [5, 22] и резонансной гамма-спектроскопии (эффекта Мессбауэра) ]5] показывают, что выражение (4.1.16) справедливо для не очень низких температур.
Совместное решение уравнений (4.1.16), уравнений, связывающих эффективные поля Heft; с намагниченностями подрешеток М;, и условий равновесия (4.1.15), позволяет, в принципе, найти равновесные намагниченности М7 0 при заданных температуре и внешнем поле. Таким путем можно найти, в частности, температуру Нееля Tn как ту температуру, при которой возникают ненулевые решения указанной системы уравнений при Но = 0. Может быть вычислена и восприимчивость при температурах выше Tn- Причем вблизи или выше точки Нееля при не очень больших внешних полях аргументы функций Бриллюэна можно считать малыми и использовать разложение (1.1.35).
Рассмотрим в качестве примера систему с двумя неодинаковыми коллинеарными подрешетками. Ограничимся областью температур Т Tn, когда можно пренебречь влиянием анизотропии и размагничивающих полей и сохранить в разложении (1.1.35) только первый член. Эффективные поля в этом случае будут включать внешнее поле Но и обменные поля (4.1.10), которые будут коллинеарны с Но. Тогда уравнения (4.1.16) приведут к следующей системе:
it \
---Ail) Mi о Л12Л/3 о — 7/о,
Х	ir	(4.1.18)
— Л12Л/1 о +	— A22j Ms 0 — Но,
где
+	(4.1.19)
Равенство нулю определителя системы (4.1.10) дает температуру Нееля. В частности, для антиферромагнетика с двумя
158
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
идентичными подрешетками, обозначая
All = А22 -	А,,	Л12 = — Л, Cl = С% == С,
получим
TN=C (А -АО-	(4.1.20)
Решая систему (4.1.18) при Но =f= 0, можно найти выражение для статической парамагнитной восприимчивости. Для антиферромагнетика с идентичными подрешетками из этого выражения следует закон Кюри — Вейсса
=	(4.1.21)
р
с отрицательной парамагнитной температурой
-С(Л + Л5)	(4.1.22)
(см. рис. 1.1.3). Если обменным взаимодействием внутри подрешеток можно пренебречь (|Лг| <С Л), то Тр = —Ты. Закон (4.1.21) довольно хорошо подтверждается на опыте вне критической области (т. е. для температур, не очень близких к Ты). Однако соотношение |.7’р| = Ты обычно не имеет места.
Вычисление намагниченностей подрешеток при Т Ты, естественно, не может быть проведено с помощью уравнений (4.1.18), основанных на приближенном представлении функций Бриллюэна, а требует решения полных уравнений (4.1.16) совместно с другими уравнениями сформулированной выше самосогласованной задачи1).
Малые колебания. Малые магнитные колебания в антиферромагнетиках могут быть рассмотрены на континуальной модели двумя способами: путем отыскания собственных значений (диагонализации) феноменологического континуальпого гамильтониана [21] и путем решения уравнений движения [169]. Оба пути, конечно, эквивалентны, но второй, по-видимому, удобнее для рассмотрения когерентных однородных колебаний, особенно, если нас интересуют не только собственные частоты, но и амплитуды вынужденных колебаний под действием заданного переменного поля. Путь решения уравнений движения был использован в предыдущих главах при рассмотрении ферромагнитного резонанса, мы воспользуемся им и в этой главе.
Задача заключается прежде всего в том, чтобы записать для системы с несколькими подрешетками линеаризированные уравнения движения, которым удовлетворяют амплитуды малых колебаний. Очевидно, что малые колебания окажутся
9 В следующем параграфе будет приведена фазовая диаграмма (рис.
4.2.11), которая следует из решения такой задачи для антиферромагнетика с двумя идентичными подрешетками.
§ 4.1]
АНТИФЕРРОМАГНЕТИЗМ. УРАВНЕНИЙ ДВИЖЕНИЙ
159
гармоническими, и можно записать
Му (г, t) = Му о (г) 4- mj (г) е'ш/,	(4.1.23)
где Му0 (г) — постоянные составляющие намагниченностей подрешеток, в случае малых колебаний совпадающие с их равновесными значениями, а ту (г) — комплексные амплитуды переменных составляющих намагниченностей подрешеток. В линейном приближении эффективные поля можно представить в виде
Ией j = Ней io + heff ;ег“г ф- 11е1И(,	(4.1.24)
где Ней у о — постоянные эффективные поля (включающие и эффективное поле зеемановского взаимодействия — внешнее постоянное поле Но), heff у — комплексные амплитуды переменных составляющих эффективных полей (без внешнего переменного поля), a h — комплексная амплитуда внешнего переменного поля. В линейном приближении (|тпу | Мj 0) поле Неп j о совпадает с равновесным эффективным полем. Оно зависит в общем случае от всех М710 (k = 1, 2, . . ., и), а йсй1 зависит, и притом линейно, от всех шк.
Подставим (4.1.23) и (4.1.24) в уравнение движения (4.1.5) с диссипативным членом, например, в форме (1.3.2) и учтем малость переменных составляющих по сравнению с постоянными. Тогда в нулевом приближении получим условия (4.1.15), а в первом приближении — линеаризированные уравнения движения /юту ф- туту X Ней/о + Ъ'Муо X ЬеЯуф-
ШдСО
+ 'ТТ—ту х Му0 = — ТуМуо X h, (4.1.25) з о
совпадающие по форме с уравнением (2.1.31). Уравнения (4.1.25) для комплексных амплитуд ту являются связанными, так как hefty зависит не только от my, но и от других ink(k = 1, 2, . . ,,н). Они образуют систему п линейных векторных уравнений, т. е. Зп уравнений в проекциях.
Положив в (4.1.25) h = 0, мы придем к однородной линейной системе уравнений для амплитуд свободных колебаний. Приравнивая нулю ее определитель, получим характеристическое уравнение для частот свободных колебаний. Если пренебречь диссипацией (положить ау = 0), то это уравнение окажется вещественным и его решения дадут вещественные собственные частоты. Характеристическое уравнение будет степени Зп, но оно будет иметь всегда (в чем мы убедимся в дальнейшем на ряде примеров) лишь п положительных корней, соответствующих частотам собственных колебаний рассматриваемой системы с п степенями свободы. С учетом диссипации корни характеристического уравнения окажутся комплексными, их мнимые части будут характеризовать затухание свободных колебаний.
460	АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ	ГГЛ. 4
При наличии внешнего переменного поля система уравнений, полученных в результате проектирования (4.1.25) на оси координат, будет иметь однозначные решения т7-, соответствующие амплитудам вынужденных колебаний. Все проекции т7- будут линейно зависеть от проекций Ь,и суммарную намагниченность можно будет представить в виде
п
2m;^m=%h,	(4.1.26)
j=i
где % — тензор магнитной восприимчивости анэиферромагнетика Резонансные частоты тензора % будут, конечно, в первом приближении (тем точнее, чем меньше диссипация) совпадать с собственными частотами колебаний. Если в эффективные поля включить размагничивающие поля (дляслучая эллипсоида), то мы получим, как и для ферромагнетика, внешний тензор восприимчивости, если эти поля не будут включены, получим внутренний тензор (см. § 1.4). Конечно, для антифферромагпетиков в не очень сильных постоянных полях разница между внутренним и внешним тензорами восприимчивости не будет большой.
Подчеркнем еще раз, что в уравнения (4.1.25) входят постоянные составляющие намагниченностей подрешеток: как явно, так и в величины НеГг;0; и поэтому конкретное исследование колебаний возможно лишь после того, как определены все Мхо, т. е. решена задача об основном состоянии.
§ 4.2. Антиферромагнетики с легкой осью анизотропии
Намеченные в предыдущем параграфе пути решения задачи о малых однородных магнитных колебаниях антиферромагнетиков в этом и следующем параграфах будут реализованы на простом, но очень важном примере антиферромагнетика с двумя идентичными подрешетками и одноосной анизотропией.
Предположим, что энергии анизотропии подрешеток аддитивны; это, в частности, должно иметь место, если источник анизотропии — одиоионный (см. § 2.2). Для простоты учтем только первую константу осевой анизотропии и пренебрежем пока анизотропией в перпендикулярной оси (базисной) плоскости. Тогда плотность энергии анизотропии можно будет записать аналогично (2.1.1)
Ua = -i- К (sin2 0Х + sin'2 02),	(4.2.1)
где 0| и 02 — углы, которые образуют векторы намагниченностей подрешеток Мх и М2 с осью анизотропии.
§ 4.21
АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 161
Энергия антиферромагнетика *) в рассматриваемом случае состоит из обменной энергии (4.1.9), зеемановской энергии (4.1.12) и энергии анизотропии (4.2.1); энергии размагничивающих полей мы пока не учитываем. Совмещая ось z с осью анизотропии и отбрасывая члены, не зависящие от ориентации векторов М2 и М2, запишем энергию в виде
и = ДМ2М2 - Н (М2 + М2) - -^[(M1ZoV + (M2z0)2], (4.2.2)
где Л = —Л12 — константа межподрешеточного обменного взаимодействия (Л 0), z0 — единичный вектор по оси z, а Мо — длина векторов М2 и М2 (возможным различием их длин пока
пренебрегаем). Если бы мы отказались от предположения об аддитивности энергии анизотропии подрешеток, то в выражение (4.2.2) добавился бы «перекрестный» член Д'(М1г0)(М2я0). Для простоты не будем его учитывать.
Заметим, что от переменных Мх и М2 можно перейти [21] к переменным
М = Мх + М2 и L = Мх — М2
(L — вектор антиферромагнетизма). Тогда выражение (4.2.2) с точностью до членов, не зависящих от ориентации Мх и М2, примет вид
и = 4- ЛМ2 - НМ-------[(Mz0)2 +
2	4Л/2 v '
+ (Lz0)2j. (4.2.2')
Рис. 4.2.1. Равновесные нама1-ниченности подрешеток одноосного антиферромагнетика.
В этом параграфе мы рассмотрим случай положительной анизотропии (К ^>0), когда легким направлением векторов Мх и М2 является ось анизотропии.
Равновесные состояния. Определим прежде всего ориентации равновесных векторов намагниченностей подрешеток Мх 0 и М2 0 при заданных величине и ориентации внешнего постоянного поля Но. Из цилиндрической симметрии задачи (связанной с неучетом анизотропии в базисной плоскости) следует, что векторы Но, М10 и М20 лежат в одной плоскости, проходящей через ось z. Направим оси х и у так, чтобы эта плоскость была плоскостью yz (рис. 4.2.1). Для определения равновесных значений углов 0Х и е2 в этой плоскости воспользуемся сначала условиями минимума энергии. В данном случае выражение (4.2.2) можно записать
J) См. примечание 2) па стр. 65.
& А. г. Гуревич
162
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
в виде
U = — Н0М0 [cos (0Л — 01) cos (6Л — 0s)] +
+ AMg cos (01 — e2) + -L К (sin2 01 + sill3 02).	(4.2.3)
Необходимыми условиями минимума являются
= — Н0М0 sin (Од — 0j) — AAfo sbi 0i — 62)	К sin 01 cos 0i — 0,
(4.2.4)
= — H0M (l sill (0Я — 02) + AJIo sill (91 — 1'2) + К sin 02 cos02 = 0.
Второй путь нахождения равновесных ориентаций намагниченностей подрешеток заключается в использовании условия (4.1.15). Эффективные поля могут быть вычислены, исходя из энергии (4.2.2), по общей формуле (4.1.4):
Нен 1,2 = Но - ДМ2>1 + z0 (M1>2Zo).	(4.2.5)
Проектируя (4.1.15) с учетом (4.2.5) на ось х, получим те же уравнения (4.2.4). Таким образом, оба пути отыскания основного состояния совершенно эквивалентны, что уже отмечалось выше для случая ферромагнетика.
Переходя к анализу условий равновесия, отметим прежде всего, что если Но = 0, то энергия минимальна при 6j = 0 и 02 = л (или при 01 = л и 02 = 0). При Но =}= 0 мы ограничимся двумя частными случаями.
1.	Постоянное поле направлено по оси анизотропии (H0||z0, т. е. 0д = 0). В этом случае из цилиндрической симметрии задачи следует, что может осуществиться одна из трех конфигураций (рис. 4.2.2):
1)	0J = 0, 02 = л (или наоборот),
2)	01= — 02=0д,
3)	01 = 02 = 0.
Первая и третья конфигурации удовлетворяют условиям (4.2.4).
Для второй из (4.2.4) можно получить
#osin0|| — (2/74, — НА) sin 0 у cos 0 ц =0,	(4.2.6)
где обозначено
НЕ = ЛМо,	(4.2.7)
Из (4.2.6) следует, что для второй конфигураций cos6« - (4Л9)
5 4.21 АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 161
Таким образом, в случае 0Н = 0 могут иметь место три равновесных состояния, приведенных в табл. 4.2.1 и показанных на рис. 4.2.2. Вычисляя по формуле (4.2.3) энергии этих состояний, можно убедиться, что они будут наименьшими в пределах изменения Но, приведенных в табл. 4.2.1.
Детальный анализ [21] показывает, что в интервале полей
Hci \ + Н° Г (2Яе + Ял) На //сз
(4.2.16)
устойчивы первое и второе состояния. Отсюда следует, что переход из первого состояния во второе при возрастании поля происходит скачком при Но = IIс3- Этот переход называют опрокидыванием подрешеток антиферромагнетика (spin-flop), а второе состояние — опрокинутым состоянием. Обратный переход
Рис. 4.2.2. Разновесные состояния одноосного аптиферромагпетика (К > 0) при внешнем поле, направленном по оси. а— аптипараллельное состояние; б— неколлинеарно-(опрокинутое) состояние; в— захлопнутое состояние.
иэ второго состояния в первое также происходит скачком, но при Но =-- Нср, таким образом, имеет место гистерезис. Переход же из второго состояния в третье, как видно из (4.2.9), происходит «плавно» при Но = Hei- Этот переход называют захлопыванием подрешеток, а третье состояние — захлопнутым. При Но = Hei антиферромагнетик переходит, по существу, в ферромагнитное состояние.
Оценим величины полей, при которых происходят рассмотренные переходы. Величина НЕ связана с температурой Нееля соотношением, которое следует из формул (4.1.20), (4.1.19) и (4.1.17):
ИвЯк = Вх7\,	(4.2.17)
где £ — коэффициент порядка 1. Для большинства антиферро-, магнетиков Тц —10	100 °К и НЕ — 103 ~ 106 э. Поля
6*
от
Таблица 4.2.1
Равновесные состояния и собственные частоты однородных колебаний одноосного антпферромагнетика (К>0)
Направление постоянного поля	Состояние	Углы равновесных намагниченностей	Пределы изменения поля	Собственные частоты		№№ формул
				Выражения >)		
По II z0	1 (антипарал-лельное)	01=0, 02 = л	О<Яо< </(2Яв-ЯА)ЯА=ЯС2	-у- = /'(2Яе + ЯА) НА ± Яо		(4.2.10)
	2 (опрокинутое)	01 = —05 = 0| | (выражение (4.2.9))	ЯСа<ЯР<2ЯЕ-ЯА = = НЕ1	[со	_ 2Яе(2Яе+Яа) _	(2ЯВ—ЯА)= на — ^пЕаА 1 = 0]	(4.2.11)
	3 (захлопнутое)	01 = 02 — 0	НЕ1<НО	у- = Яо+ЯА [у-=Яо + ЯА-2Я^		(4.2.12)
Ho-Lzo	1	0г=л —03=О± (выражение (4.2.20))	0<H0<2HE + HA=HEi	1 СО) \ 1 / / CDS \ т	2=(2Яе+Яа)Яа+2^_^//о2 2= (2Я„+ Ял ) Н д —		п-2 ( Е~Г А> А	2Не + Нао	(4.2.13) (4.2.14)
	2 (захлопнутое)	Л 01 = 02 =	нЕ2<н0	1 (01 \ т [а	\ =Н0(Н0-НА) 12=0]	(4.2.15)
’) В квадратных скобках — частоты колебаний, которые не возбуждаются однородным переменным полем.
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ	[ГЛ.
§ 4.2] АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 165
анизотропии антиферромагнетиков составляют обычно 10 г-104 э. Таким образом, как правило, На <С Не. Тогда шириной интервала (4.2.16) можно пренебречь и считать
IIС1 ~ IIсг	Hcs= Нс	V2НеНа.	(4.2.18)
Как следует из приведенных оценок, поля опрокидывания Нс
Рис. 4.2.3. Равновесные состояния одноосного антиферромагнетика (К > 0) при внешнем поле, перпендикулярном оси. а— неколлинеарное состояние; б— захлопнутое состояние.
имеют обычно порядок 104	10s э. Например, для Сг2О3 Нс =
= 59 кэ [176], а для MnF2 Нс = 93 кэ [168]. Однако для антиферромагнетиков с малой анизотропией и низкой температурой Нееля они могут быть значительно меньше.
2. Постоянное поле лежит в базисной плоскости (H0±Zo, т. е. Од = л/2). В этом случае симметрия системы (см. рис. 4.2.3) требует, чтобы
6, = л — 02 - 0Х.
Из условий (4.2.4) теперь можно получить
Но cos 0jl — (2ЯВ + НА) sin cos 0р = 0.	(4.2.19)
Как видно из (4.2.19), возможны два состояния. Для первого
Для второго (захлопнутого) состояния
cos0x = O, т. е. 01==02 = -J-.	(4.2.21)
Эти состояния показаны на рис. 4.2.3. Легко убедиться, что они соответствуют минимальной энергии в пределах изменения Но, приведенных в табл. 4.2.1. Практически обычно можно считать
НЕ1^НЕ2^2НЕ.
16В
АНТНФЕРРОМАГНЕТИКИ II ФЕРРИМАГНЕТИКИ
1ГЛ. 4
Зная равновесные ориентации векторов М2 и М2, можно найти при любом Но статическую намагниченность
М= =	0 + м20.
Для рассмотренных выше частных случаев вектор М= параллелен Но, и можно ввести скалярную статическую восприимчивость
Zo =
В случае Но || z0 для первого
Рис. 4.2.4. Статические намагниченности и восприимчивости одноосного антиферромагнетика (К > 0). Индексы || соответствуют случаю H0||z0 (рис. 4.2.2.), а индексы X — случаю Но I zo (рис. 4.2.3). Масштаб по оси абсцисс искажен, чтобы сделать заметными малые интервалы Щу Щ;2 и Ищ + ^Е2
Все полученные к температуре
состояния статическая восприимчивость
Хоц =0,
а для второго (опрокинутого) состояния, как легко убедиться,
Хо|| =	—
7 (4.2.22)
В случае Но J z0 для первого состояния
,	/ Н. \
Хо1 = Л(4+	—
Е (4.2.23)
Зависимости 7И= и /0 от Но показаны на рис. 4.2.4. Отметим, что зависимость Л/= от Но для антиферромагнетика является, в целом, существенно нелинейной и сильно
анизотропной.
выше результаты относятся, строго говоря, Т = 0 °К. Для многих антиферромагнетиков они
хорошо совпадают с экспериментальными данными при низких температурах (см., например, [81, 172]). Случай Т 0 будет кратко рассмотрен ниже.
Колебания в первом состоянии в случае продольного поля: собственные частоты и затухание. Перейдем теперь к исследованию малых однородных магнитных колебаний (антиферромагнитного резонанса) в одноосном двухподрешеточном антиферромагнетике. Воспользуемся линеаризованными уравнениями движения (4.1.25) (7 = 1, 2). Не будем пока учитывать размагничивающих полей (ниже будет показано, что влияние их невелико). Тогда эффектив
i 4.21 АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 167
ное поле будет иметь вид (4.2.5). Так как подрешетин в данном случае идентичны, примем = у2 = у и ах = а2 = «•
Рассмотрим случай Но || z0 и остановимся сначала на первом состоянии (Яо < Нс)- В этом случае (см. табл. 4.2.1)
Но = т.оН0, Му 0 = z0/W0,	М20 =	%0Мй.	(4.2.24)
С учетом (4.2.24) и (4.2.5) получим из (4.1.25) связанные уравнения
i ошу h [т(Я0 + НЕ + НА) + itro] иц х z0 + уЯЕт2 X z0 =-=
=	:< z0,	(4.2.25)
i®m2 + |Y (Яо — Не—На) — itroj т2 х z0 — гЯЕту X zu = = — r?-/oh >' Zo.
Проектируя их на ось z, найдем
mlz = miz — 0;
проекции же на оси х и у дадут систему четырех уравнений для неизвестных т1х, т1у, т2х и т2У. В силу цилиндрической симметрии рассматриваемого состояния целесообразно перейти к циркулярным переменным (см. § 1.2). Для этого достаточно умножить на (Д i) проекции уравнений (4.2.25) на ось х и сложить их с проекциями соответствующих уравнений па ось у. Тогда для пар переменных т2, и /Щ-., т2 _ получатся независимые (в этом и проявилась симметрия состояния) системы уравнений
1± <о — ш о - у (Яо !- Нц -р НА)1	— уН Ет., (. = — уЛДД 4.,
(4.2.26)
%HEmr t + _|Д 4- ю 4- ictto—у (Яо — НЕ ~НА)] m2.z
Исследуем сначала свободные колебания, т. е. примем h± = 0. Тогда, приравнивая нулю определитель системы (4.2.26), получим Р t == <о2 (1 -Д (?) -р 2тЯ0 о — 2iA.or {НЕ + НА) —
-Г2(2ЯЕЯА-рЯ1-Я®)=0.	(4.2.27)
Выражение (4.2.27) представляет собой уравнение для комплексной частоты со = to' -р in" свободных колебаний. Не представляет труда записать его точное решение. Однако обычно а 1 и можно воспользоваться методом последовательных приближений.
В нулевом приближении (без учета диссипации), накладывая условие о р> 0, получим две частоты ((4.2.10) в табл. 4.2.1), показанные на рис. 4.2.5. Они соответствуют двум ветвям колебаний данной системы, имеющей две степени свободы. При отсутствии внешнего поля эти ветви оказываются вырожденными и частота «естественного» антиферромагнитного резонанса
•°о = г f (2Яе + ЯА) НА = ТЯСз ГЯС. (4.2.28)
168
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
Таким образом, эффективным внутренним полем, определяющим частоту антиферромагнитного резонанса, является среднее геометрическое обменного поля и поля анизотропии, равное полю опрокидывания.
В первом приближении (по а) получаем для со' то же выражение (4.2.10), а для со" — формулу
со" = поз
<0.)
аю'
(4.2.29)
Сравнивая (4.2.29) с выражением (1.3.17) для ферромагнетика, мы видим, что при одинаковых параметрах диссипации и одинако-
Рис. 4.2.5. Собственные частбты однородных колебаний (частоты антиферромагнитного резонанса) одноосного антиферромагнетика ЦО > 0) при Но, параллельном оси. Масштаб по оси абсцисс искажен, как и на рис. 4.2.4. Пунктир— колебания, для которых суммарная переменная намагниченность равна нулю.
вых собственных частотах (последнего можно добиться соответствующим подбором внешних полей) затухание свободных колебаний в антиферромагнетике в (НЕ[Нс} = = УНе!2На раз больше. Отсюда, однако, не следует, что со" и (см. ниже) ширина резонансной кривой антиферромагнетиков будет обязательно больше, чем соответствующие величины для ферромагнетиков, так как параметры
диссипации а для них могут существенно различаться.
Характер собственных колебаний. Из соображений симметрии ясно, что собственные колебания векторов Мт и М2 в рассматриваемом слу-направле-
чае представляют собой круговую прецессию. Найдем
ния вращения и отношения амплитуд прецессии Мг и М2 для обеих ветвей колебаний. Рассмотрим, например, верхнюю ветвь с частотой со+ = соо + тН0. При этом значении частоты обращается в пуль определитель системы (4.2.26) для т1+ и т2+ (с верхними знаками перед со) и не обращается в нуль определитель D_ системы для т2_ и т2_ (нижние знаки перед со). Следова-
тельно, эта последняя система имеет при со = со+ только тривиальное решение
Ш-1- = т2- = 0.
Отсюда
(4.2.30)

= — гт^,
Ш-2у —
§ 4.2] АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 169
т. е. рассмотренный «верхний» тип колебаний с собственной час-totoii <»+ представляет собой (см. выражение (1.2.9)) круговую прецессию с правым вращением. Таким же образом легко убедиться, что нижняя ветвь с частотой и_ = (й0 — соответствует круговой прецессии векторов М2 и М2 с левым вращением.
Для того чтобы найти отношение амплитуд собственной прецессии тц- и ш24-, достаточно подставить значения собственных
Рис. 4.2.6. Прецессия векторов намагниченностей подрешеток одноосного антиферромагнетика для первого основного состояния при Но, параллельном оси. а— верхняя ветвь (с частотой w^.); б— нижняя ветвь (с частотой ы_). Различие амплитуд прецессии векторов М, и М2 утрировано.
частот в уравнения (4.2.26) (при = 0 и а = 0). В результате получим
U С "|~ Д “}- НСо	/	Нг \
= ~	- и-	- <4-2-31)
1±	Г.	\	аЕ /
Таким образом, отношение амплитуд прецессии намагниченностей подрешеток не зависит от Но и мало отличается от (—1); для верхней и нижней ветвей это отличие имеет разный знак. Характер прецессии показан на рис. 4.2.6.
Вынужденные колебания. Наибольший интерес представляет суммарная переменная намагниченность ш = иц -ф- ш2, которая определяет все наблюдаемые эффекты в опытах по антиферромагнитному резонансу. Решая систему (4.2.26), получаем т)
2
т± = т1+ + Тп2+ = — ТМО (чНа + гхсо) h± == %+h^, (4.2.32)
*) Тензор восприимчивости антиферромагнетика в данном случае имеет вид (1.2.19), а циркулярные восприимчивости у_+ и связаны с его компонентами соотношениями = X it Ха- Условием справедливости этих соотношений, так же как и (1.2.19), является лишь цилиндрическая симметрия системы.
170
АНТИФЕРРОМАГНЕТИКИ II ФЕРРИМАГНЕТИКИ
[ГЛ. 4
На
(4.2.35)
где D j. имеет вид (4.2.27). При малой диссипации (а <§1) из (4.2.32) следует
~ (® t — ф) (®+ + ф) +- 2ia<or (ЯЕ + Ял) ’	(4.2.33)
где частоты со t определяются формулой (4.2.10) (в табл. 4.2.1). Таким образом, восприимчивость антиферромагнетика по отношению к переменному полю в рассматриваемом состоянии пропорциональна константе анизотропии. При резонансе
% t Рез =	J"'	(4-2’34)
Сравним эту величину с восприимчивостью (у !рез)ф.м; (1.3.39) при ферромагнитном резонансе. Их отношение при равных резонансных частотах и одинаковых параметрах диссипации с учетом (1.3.15) будет равно
__% ,.<.з раз) ф. м
! Как следует из приведенных выше оценок, это отношение обычно составляет 10 :! -г-10~4.
Ширину резонансной кривей антиферромагнетика (по частоте) 2Дсо определим как разность частот, при которых
1
X Т — ~л~ X Р рез*
Из (4.2.33) следует
~ (НЕ + ЯА),	(4.2.36)
что совпадает с мнимой частью частоты свободных затухающих колебаний (4.2.29). Полуширина резонансной кривой по полю в случае достаточно узких резонансных кривых может быть определена из соотношения (1.3.32). В данном случае | да>!дН01 = г и
ДЯ± = a “ (ЯЕ + ЯА).	(4.2.37)
Произведение восприимчивости при резонансе на ширину резонансной кривой, согласно (4.2.34) и (4.2.37), составляет
27/.
Х^рез-ЗДЯр^-уАЛ/о.	(4.2.38)
11С
Оно отличается от аналогичной величины для ферромагнетиков (1.3.33) малым множителем (2ЯЯЯс) -- У2На/Не.
§ 4.21
АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 171
Колебания в опрокинутом состоянии. Рассмотрим теперь антиферромагнитный резонанс в поле Но, по-прежнему направленном по оси анизотропии, но по величине превосходящем Нса, когда основным состоянием является опрокинутое (рис. 4.2.2, б). Теперь
о М4 cos 0 л	уо.ц о siw ь и,	? q 39)
М2 о = zoM0 сок 9 и “Ь Уо-^Л) siu ® 11»
где угол 61| определяется выражением (4.2.9).
Заметим, что иногда задачу об антиферромагнитном резонансе целесообразно решать в «локальных» системах координат, в которых оси Zj совпадают с направлениями равновесных намагниченностей соответствующих подрешеток. Тогда при рассмотрении малых колебаний для каждой подрешетки останутся всего два уравнения — проекции (4.1.25) на оси, перпендикулярные осям Zj. Метод решения этих уравнений, основанный на введении эффективных размагничивающих факторов (см. § 2.1), может быть обобщен на систему с несколькими подрешетками. Может быть обобщен на такую систему и метод решения уравнений движения намагниченности в сферических координатах (§ 2.1). Согласно этому методу уравнения движения для системы с п подрешетками сведутся к 2п уравнениям для угловых отклонений векторов М7- от их равновесных ориентаций. Однако для рассматриваемой сравнительно простой системы нет необходимости использовать эти методы. Как мы убедимся, задача решается очень просто в общей для обеих подрешеток декартовой системе координат. Но при этом окончательная система уравнений будет содержать проекции (4.1.25) на все три оси.
Ограничимся рассмотрением свободных незатухающих колебаний. Используя выражение для эффективного поля (4.2.5) и учитывая (4.2.39) и (4.2.9), запишем проекции уравнения (4.1.25) для первой подрешетки
~у- '«ы + НЕ cos 91| mly + (IIЕ — IIА) sin 0 ц mlz	IIЕ cos 0gт2у ф-
ф- IIЕ sin 91| /га3г = О,
-у-mly — НЕ cos О 0 т1х — IIЕ cos 0 „	= 0,	(4.2.40)
— НК sib ° II ™1х — НЕ sin 6 и ТПъх = °-
Проекции уравнения (4.1.25) для второй подрешетки будут отличаться от (4.2.40) заменой индексов 1	2 и изменением знака
перед sin 0 ц .
Складывая и вычитая соответствующие уравнения полученной системы шести уравнении, мы приходим к двум независимым
172	АНТИФЕТФОМАГНЕТПКИ И ФЕРРИМАГНЕТИКИ	[ГЛ. 4
(4.2.42)
системам
тх + 2/7 д cos 61| ту — IIА sin 6 и Zz = О, ^-mv-2HECose^mx = 0, ^-lz~ 2НВ sin 6 и тх = О,
^-lx + (2НЕ - НА) sin е „ т2 = О, ico « А	ico А
-уЛ = 0,	— тг = 0.
Здесь m = mx Д- ш2 и I = nij — m2 — переменные составляющие введенных выше векторов М и L 1).
Равенство нулю определителя системы (4.2.41) с учетом условия равновесия (4.2.9) дает выражение (4.2.11) для одной из собственных частот (($!), приведенное в табл. 4.2.1. Зависимость со1 от Но показана на рис. 4.2.5. Приравнивая нулю определитель системы (4.2.42), получаем со2 = 0.
Для того чтобы выяснить характер собственных колебании, будем рассуждать так же, как и в случае первого основного состояния. Для колебаний с частотой со1 система (4.2.42) имеет только тривиальные — нулевые решения, т. е. для этого типа колебаний
= П?2зс,	~	^z “ mlz 4“ Hl2z - 0.
Удовлетворяющая этим условиям прецессия векторов Mj и М2, а также прецессия вектора М показаны на рис. 4.2.7. Отношение осей эллипсов прецессии векторов Мх и М2, как следует из (4.2.41) и (4.2.11), много больше 1 при Но порядка поля опрокидывания и стремится к 1 при/Д, стремящемся к полю захлопывания НЕ1. Отношение осей эллипса прецессии вектора М
(4.2.41)
У Я®-Я?,'
Для типа колебаний с частотой со2, как видно из (4.2.41), тх = ти = lz = 0. Но при со2 = 0 из первого уравнения (4.2.42) следует, что mz = 0. Таким образом, для этого типа колебаний обращаются в нуль все составляющие суммарной переменной
’) Уравнения (4.2.41) и (4.2.42) можно получить и несколько иным путем. Для этого с самого начала в выражении для энергии антиферромагнетика следует перейти к переменным М и L. Эффективные поля, действующие на векторы М и L, можно найти затем по формулам, аналогичным (4.1.4), а уравнения движения переменных векторов m и 1 записать в виде, аналогичном (4.1.25). Проекции этих уравнений на оси координат и дадут (4.2.41) и (4.2.42).
g 4.21 АНТИФЕРРОМАГНЕФИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 173
намагниченности, и следовательно, он не возбуждается однородным переменным полем. Нетрудно убедиться, что этот тип колебаний представляет собой круговую прецессию векворов Мх и М2 вокруг оси z.
Наличие собственного колебания с частотой, равной нулю, связано о особым характером симметрии системы. Действительно, постоянное магнитное поле направлено в данном случае по оси z, анизотропия в базисной (перпендикулярной оси z) плоскости не учитывается, и следовательно, энергия (или при Т 0 — свободная энергия) имеет цилиндрическую симметрию, т. е.
Рис. 4.2.7. Прецессия векторов намагниченности одноосного антиферромагнетика в опрокинутом состоянии. Цифрами обозначены положения концов различных векторов в одинаковые последовательные моменты времени.
инвариантна относительно поворота на произвольный угол ср вокруг оси z. Но в то же время векторы Мх и М2 для рассматриваемого состояния лежат в некоторой плоскости (zy на рис. 4.2.2, б). Таким образом, основное состояние нарушает симметрию энергии системы. Поскольку вращение плоскости, в которой лежат векторы Мх и М2, вокруг оси z происходит без изменения энергии системы, частота, соответствующая такому вращению, должна обращаться в нуль.
Здесь проявляется некоторое общее свойство колебательных систем с нарушенной (broken) симметрией, которое известно, как теорема Голдстоуна. Колебание с нулевой собственной частотой называется голдстоуновским колебанием, а нормальная координата (в данном случае угол ф), которая изменяется при этом колебании,— голдстоуновской координатой. Следует заметить, что в реальных системах различные, не учитываемые в первом приближении взаимодействия (например, в нашем случае — анизотропия в базисной плоскости) приведут к понижению симметрии
174
АНТИФЕРРОМАГНЁТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
энергии системы. Теорема Голдстоуна не будет уже иметь места, и <о2 будет отличаться от нуля. Однако эта частота будет значительно ниже других собственных частот системы. Типы колебаний с такими частотами называют иногда мягкими модами.
Решение уравнений (4.1.25) для опрокинутого состояния с учетом диссипации и внешнего переменного поля (т. е. рассмотрение вынужденных колебаний) не представляет трудностей, и мы не будем его приводить. Отметим лишь (это ясно и из характера собственных колебаний), что колебания с частотой возбуждаются переменным полем, перпендикулярным Но, и восприимчивость растет с ростом Но, приближаясь к значению для ферромагнетика при Но —> Hei-
Не будем останавливаться подробно на колебаниях в третьем (захлопнутом) состоянии. Решение системы, следующей из (4.1.25), дает в этом случае две собственные частоты, которые приведены в табл. 4.2.1. Однако для второго типа колебаний m = 0. Первый же тип колебаний полностью совпадает с колебаниями в ферромагнетике с намагниченностью 27ИО и константой анизотропии К.
Колебания при поперечно й поле. Рассмотрим теперь случай, когда постоянное поле направлено перпендикулярно оси анизотропии и по величине меньше, чем поле захлопывания НЁц (табл. 4.2.1). Тогда (см. рис. 4.2.3)
Н0 = уоЯ0, M10 = z0470co3 01 + y0A/0sine1,
М2о = — zoMocos0x + yoMoSinOjL,	'	’ ’
где угол 6j_ определяется выражением (4.2.20). Поступая так же, как в предыдущем случае, мы придем к системе шести уравнений для проекций векторов ш1 и т2; она распадется на две независимые системы для составляющих векторов га и 1: одну систему — для тх, 1У и т, и другую — для lx, ту и 12. Равенство нулю определителей этих систем даст выражения для собственных частот (4.2.13) и (4.2.14), приведенные в табл. 4.2.1. Зависимости этих частот от Но показаны па рис. 4.2.8.
Так же как и в рассмотренных выше случаях, можно убедиться, что для первого типа колебаний (с частотой {ог)
т1х = т2х, т1г •= ш2г, ту т1у + т2у = 0, а для второго (с частотой <о2)
= т2у, тх = т1х Ц- т2х = 0, mz = mlz ф- т<>, — 0.
Таким образом, для первого типа колебаний вектор m лежит в плоскости, перпендикулярной Но. Отношение осей его эллипса поляризации (или эллипса прецессии вектора М) lwJ _ ТЯ-,
(4.2.45)
<01
§ 4.2J АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ П5
Оно мало при малых полях и стремится, как и следовало ожидать, к 1 по мере приближения //0 к полю захлопывания. Для второго типа колебаний вектор m линейно поляризован по оси у — в
Рис. 4.2.8. Частбты однородных колебаний одноосного антиферромагнетика при Но, ,	перпендикулярном оси.
направлении постоянного поля. Характер прецессии векторов Мп М2 и М для обоих типов колебаний показан на рис. 4.2.9.
Из характера собственных колебаний ясно, что первый тип колебаний возбуждается переменным полем, перпендикулярным постоянному, и интенсивность возбуждения (восприимчивость) возрастает по мере увеличения Но. Второй тип колебаний возбуждается переменным полем, параллельным постоянному, и восприимчивость для пего уменьшается с ростом Но, стремясь к нулю при захлопывании. Конечно, эти результаты могут быть получены строго, если рассмотреть задачу о вынужденных колебаниях.
При Но = Не-2 первый тип колебаний переходит в обычный ферромагнитный тип прецессии «захлопнутого» аптиферромагне-тика. Частота его (4.2.15) (см. табл. 4.2.1) совпадает с (2.2.22).
Произвольная ориентация поля. Мы рассмотрели сравнительно подробно равновесные состояния и малые однородные колебания магнитной системы двухподрешеточпого одноосного антиферромагнетика в двух частных случаях: когда Но параллельно оси анизотропии и когда оно перпендикулярно этой оси. В общем случае, когда Но направлено под произвольным углом 0# к оси анизотропии, вычисления становятся громоздкими, и мы приведем лишь (рис. 4.2.10) графики зависимости собственных частот от Но.
Как видно из рис. 4.2.10 и как следует из рассмотренных выше частных случаев, ориентация постоянного магцитного цоля
176
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
оказывает очень сильное влияние на частоты антиферромагнитного резонанса и характер колебаний. Это влияние особенно велико при полях порядка Нс- В частности (см. рис. 4.2.10), даже небольшие отклонения угла от значения 6Я — 0 (например, из-за погрешности в ориентировке образца) приводят к тому, что резонанс может наблюдаться уже не при сколь угодно малых частотах (как при Он = 0), а только при частотах, превышающих некоторые предельные значения.
Гис. 4.2.9. Прецессия векторов намагниченности одноосного антиферромагнетика при Но, перпендикулярном оси. а— колебания с частотой (рис. 4.2.8); б— колебания с частотой со2. Цифры— как на рис. 4.2.7.
Значение спектра однородных колебаний в антиферромагнитных монокристаллах позволяет сделать некоторые заключения и о резонансе в поликристаллических антиферромагнетиках. Задача эта проще, чем в случае ферромагнетика, так как в антиферромагнетике (если, конечно, исключить из рассмотрения область очень сильных полей, сравнимых с 2Не) результирующая намагниченность мала и приближение независимых зерен довольно хорошо выполняется. И если мы определим компоненты тензора восприимчивости для монокристалла при произвольном бц
§ 4.21 АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 177
(что связано, конечно, с некоторыми вычислительными трудностями), то затем сможем, в принципе, усреднить их с учетом функции распределения (см. § 2.3), т. е. найти компоненты тензора восприимчивости поликристалла. Качественные заключения о резонансе в поликристаллическом одноосном антиферромагнетике могут быть сделаны и без этих вычислений, на основании графиков рис. 4.2.10. Например, при частоте со, меньшей
Рис. 4.2.10. Частоты колебаний одноосного антиферромагнетика (К > 0) при различных ориентациях постоянного поля [172]. Цифры у кривых— значения угла Од между Но и осью. Принято, что Нд Не и интервал Hqi 4- (в отличие от рис. 4.2.5) не показан.
уНс, в поликристалле будет наблюдаться полоса поглощения с резкой (тем более резкой, чем меньше диссипация) нижней границей при поле Но = Нс — <о/у и размазанной верхней границей.
Влияние размагничивающих полей. Рассмотрим теперь влияние формы образцов на антиферромагнитный резонанс. Ограничимся, как и для ферромагнетика (см. § 1-4), случаем эллипсоида малых по сравнению с длиной электромагнитной волны в веществе х) размеров. Тогда для учета формы образцов достаточно добавить в эффективные поля, входящие в уравнения движения (4.1.25), постоянные и переменные составляющие размагни-
J) Для рассматриваемых в этом параграфе одноосных антиферромагнетиков резонансные частоты (кроме области полей вблизи опрокидывания) высоки. Указанное условие — магнитостатического приближения — выполняется для них лишь при очень малых размерах образцов (например, для тонких пленок).
178
ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ	[ГЛ. 4
чивающего поля (4.1.14). Для двухподрешеточного антиферромагнетика
Нмо = — N (Мх 0 + М2 0),	(4.2.46)
= — N (nij -J- m2).	(4.2.47)
Переменное размагничивающее поле (4.2.47) приведет к дополнительной (кроме обусловленной обменными полями) связи колебаний подрешеток. Заметим, что это поле будет существовать даже при Но = 0, когда М10 + М20 -= 0.
Из условия совместности получешшх таким образом уравнений в отсутствие внешнего переменного поля h можно найти собственные частоты колебаний антиферромагнитных образцов, а решая их при наличии h, можно вычислить внешний тензор восприимчивости. Не останавливаясь па этих вычислениях, приведем лишь выражение для собственных частот в случае H0||z0 и Н0<Нс, когда в уравнения движения войдут лишь переменные размагничивающие поля. Если принять, что одна из осей эллипсоида совпадает с осью анизотропии — осью z, то выражение для собственных частот будет иметь вид
~ Я2Сз + Яо + НАМ0 (Nx + Nv) ±
± {4Я2 [Я^3 + НАМо (Nx + Ny)] + (Nx ~ Ny)^, (4.2.48)
где Nx и Ny — размагничивающие факторы образца, а Яр3 определяется выражением (4.2.16). В частности, для эллипсоида вращения (Nx = Ny = Nj_)c учетом того, что Мо <^Нск НА <С Не,
-^-=нс 1 + -—i)±H0.	(4.2.49)
При Яо = 0 из (4.2.48) следует наличие двух частот колебаний
Яс [1 +	(4.2.50)
(по-прежнему принято НА Яр). Колебания с частотами <лх и <ду возбуждаются переменными полями, направленными соответственно по оси жи по оси у. Таким образом, размагничивающее поле снимает вырождение двух типов колебаний антифер-ромагиетика нои Яо = 0. Как видно из (4.2.50) и (4.2.49), расщепление частот приЯо=0 и, вообще, влияние размагничивающих полей на частоты антиферромагнитного резонанса для рассматриваемого основного состояния весьма мало (кроме случая низких частот па нижней ветви колебаний, когда Яо ~ Нс)-Во всех других случаях относительное изменение частоты под
S 4.2] АНТИФЕРРОМАГНЕТИКИ С ЛЕГКОЙ ОСЬЮ АНИЗОТРОПИИ 179
действием размагничивающих полей будет порядка MJHe, что для большинства антиферромагнетиков составляет 10~3 ~ 10-4. Однако этот малый эффект, как мы увидим в § 8.2, оказывает значительное влияние на вырождение однородных колебаний со спиновыми волнами в антиферромагнетике.
Влияние размагничивающих полей становится еще более существенным при очень больших внешних полях в других основных
состояниях, когда статическая намагниченность |МХ 0 + М2 01 становится сравнимойсЛ/0.
Температурные зависимости. Теория малых колебаний в антиферромагнетиках, которая была на конкретном примере рассмотрена выше, справедлива и при Т 0. Но под Мг 0 и М2 0 теперь следует понимать термодинамические средние значения намагниченностей подрешеток при данной температуре, а значения всех параметров^, Л,К) брать также при этой температуре. При этом некоторые параметры (у, Л) зависят от температуры слабо, а, например, константа анизотропии К — очень сильно. Наибольшая трудность заключается
Рис. 4.2.11. Фазовые диаграммы антиферромагнетика с легкой осью анизотропии [89J. а и б— вид диаграмм при Но, направленном по оси (а) и перпендикулярно оси (6); в и г — области диаграмм, исследованные экспериментально для случая МпГ2 (точкам соответствуют максимумы поглощения упругих воли).
в определении основного
состояния при Т>0, т. е. ориентаций и величин равновесных намагниченностей подрешеток при заданной температуре и заданных величине и ориентации постоянного магнитного поля. Не останавливаясь на решении этой задачи, приведем лишь для рассматриваемого случая двухподрешеточного аитиферромагне-тика с легкой осью анизотропии фазовые диаграммы (рис. 4.2.11), т. е. области существования различных основных состояний на плоскости //0, Т. Очевидно, что состояния на оси ординат этих диаграмм совпадают (в предельном случае НА Не, для которого построены диаграммы) с найденными выше при Т = 0
180
АНТИФЕРГОМАГНЕТИКН И ФЕРРОМАГНЕТИКИ
[ГЛ. 4
основными состояниями (табл. 4.2.1, рис. 4.2.2 и 4.2.3). Существенно, что при Т 0, т. е. везде, кроме осей ординат фазовых диаграмм, величины намагниченностей подрешеток Мг 0 и М2 0 отличаются друг от друга и от Мп.
Считая величины Мг 0 и влияние окажет их различие
Рис. 4.2.12. Влияние параметра [3 = = Хо || /Хо_р на спектр частот антиферромагнитного резонанса в антипарал-лельном основном состоянии. Величина р = 0 при Т = 0 и растет с ростом температуры.
окончательную формулу для собственной
М2 о известными, выясним, какое на частоты антиферромагнитного резонанса. Ограничился случаем, когда Но направлено по оси анизотропии и по величине не превышает (зависящего теперь от температуры) поля опрокидывания. Основное состояние при этом будет коллинеарным (область 0 НсН'сТн на диаграмме рис. 4.2.11, а). Решение уравнений движения в этом случае аналогично проведенному выше для первого основного состояния при Т— 0, с тем лишь отличием, Ито теперь о 4= М 2 0. Мы не будем приводить здесь этого решения, потому что в§ 4.4 будет подробно рассматриваться более общий случай, когда не только равновесные намагниченности, но и все другие параметры подрешеток отличаются друг от друга. Приведем лишь частоты [172]:
4
-- = )/ 2НеНа + Н2а + Н20^±Н0
(4.2.51)
Здесь Не и На по-прежнему определяются выражениями (4.2.7) и (4.2.8), но Мо заменяется на Мот = ]AZ1/1O М20 , а
(Л11о-Мъо>(НЕ+НА) МоТ^о
(4.2.52)
Очевидно, что при Т — 0 параметр р обращается в нуль и (4.2.51) переходит в (4.2.10).
Можно ввести продольную статическую восприимчивость
ЛГ1 О	0	//О
Ь ||=-----д;-------	(4.2.53)
(при Г = 0 она была равна нулю, см. рис. 4.2.4). Тогда с учетом (4.2-23) (при НА <^Не)
₽ =	.	(4.2.54)
лот.
§ 4.3]
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
181
Влияние величины [3 на зависимости со от Но, в соответствии с формулой (4.2.51), иллюстрирует рис. 4.2.12. Фактические температурные зависимости резонансных частот определяются в основном температурными зависимостями Нд и ХоЛ •
В заключение заметим, что результаты, полученные в этом параграфе на простой модели двухподрешеточного одноосного антифеоромагнетика без учета высших констант анизотропии и анизотропии в базисной плоскости, довольно хорошо согласуются с экспериментальными данными для Cr2Os [176], MnF2 и ряда других антиферромагнетиков (см. [81, 172]).
§ 4.3. Антиферромагнетики с легкой плоскостью анизотропии. Слабые ферромагнетики
В зтом параграфе будут исследоваться однородные магнитные колебания в антиферромагнетике, также двухподрешеточном и одноосном, но с отрицательной первой константой анизотропии. Легкие направления намагниченностей подрешеток такого антиферромагнетика лежат в базисной (перпендикулярной оси анизотропии) плоскости, и в некоторых случаях возникает небольшой спонтанный момент, вызванный непараллельностью намагниченностей подрешеток. В дальнейшем мы уделим значительное внимание резонансу в таком не полностью скомпенсированном аптиферромагнетике. Но сначала рассмотрим «простой» скомпенсированный антиферромагнетик с легкой плоскостью анизотропии.
Основное состояние и резонанс в антиферромагнетике с легкой плоскостью анизотропии. Как и в предыдущем параграфе, будем принимать во внимание только первую константу анизотропии и сначала пренебрежем анизотропией в базисной плоскости. Тогда для плотности энергии будет по-прежнему справедливо выражение (4.2.2), но с К 0. Так же как и в предыдущем параграфе, рассмотрим два частных случая: Но || z0 и Но | z0.
Из выражения (4.2.2') следует, что при К 0 равновесный вектор антиферромагнетизма Lo = М10 — М2о лежит в базисной плоскости ху. Из соображений симметрии ясно, что в частных случаях Но || z0 и H0JLz0 векторы М10иМ20 направлены так, как показано па рис. 4.3.1. В обоих случаях вектор М = Мх 0 + М2 0 параллелен Но.
При Но||z0 (рис. 4.3.1, а) равновесное значение угла 6 легко находится из условия минимума плотности энергии или из условия (4.1.15). Оказывается, что при Но 2Hi
о	ТО
C0Se" - 2Не+\На\ ’
где НЕ и На по-прежнему определяются согласно (4.2.7) и (4.2.8)-При Но = 2Не + \НА\ происходит захлопывание.
(4.3.1)
182
ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
Рассмотрение свободных колебаний может быть проведено, как и в предыдущем параграфе, путем проектирования уравнения (4.1.25) на оси координат с учетом выражения (4.2.5) для эффективного поля. Полученная система уравнений распадается на две независимые системы для переменных тх, ту, 1г и 1Х, 1у, mz. Условие совместности первой системы (без учета диссипации) дает’)
[ ел \з ,	2НГ,(2НР — I//, I) „
(—) ^2НЕ\НА\	VHI (4.3.2)
Определитель же второй системы обращается в нуль при со2 = 0. При этом обращаются в нуль все составляющие вектора т, так же как и для ветви с со2 = 0 в опрокинутом состоянии при К 0
Рис. 4.3.1. Равновесные состояния одноосного антиферромагнетика с К < 0 (с легкой
плоскостью анизотропии).
(см. предыдущий параграф). Характер прецессии векторов М, и М2 для первого типа колебаний (с частотой со,) при К 0 также не отличается от прецессии для первого типа колебаний в опрокинутом состоянии при К 0 (рис. 4.2.7).
В случае H0[zo (рис. 4.3.1, б) условие равновесия при Но 2НЕ дает
Но
(4.3.3)
*) Выражение (4.3.2) совпадает с (4.2.11) (поскольку теперь Н А = — | НА)). Этого, конечно, и следовало ожидать, так как рассматриваемое основное состояние не отличается от опрокинутого состояния при К )> 0, для которого было получено выражение (4.2.11).
§ 4.31
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
183
При Но = 2ЯЕ, когда зеемановская энергия достигает обменной, происходит «захлопывание».
Три уравнения системы, полученной проектированием (4.1.25), будут иметь в этом случае следующий вид:
•у- тп1х + [(ЯЕ — | НА |) sin ф L — Яо] m12 — НЕ sin фХт2г = О,
(4.3.4)
у- т1у + (НЕ + I На |) cos ф±ти + НЕ cos <pxm2z = О,
-у- ™12 — (НЕ sin ФХ — Яо) т1х — НЕ cos q>±mlv Т НЕ sin <р_цт2х — — НЕ cos фдпг2!/ = 0.
Три другие уравнения будут отличаться от (4.3.4) заменой индексов 1	2 и изменением знака перед cos(pj_. Эта система распадается
на две независимые системы:
~ тх — (Яо + | НА | sin фХ) mz = 0,
~~ т2 + Нотх = 0,	(4.3.5)
•у- lv + (2ЯЕ + | НА |) cos ф_]Нг2 = 0,
-у 1Х — | НА | sin фд/2 = 0,
у- lz ~ 2Не cos q>±mv = 0,	(4.3.6)
у- mv + | Нл | cos ;p_LZz = 0,
где mXtVtz и ZXi !h г, каки раньше,— проекции векторов m =	+
+ т2 и 1 = т1 — т2. При записи системы (4.3.6) учтено условие равновесия (4.3.3).
, Условие совместности системы (4.3.5) дает частоту первого типа колебаний
=	+	(4.3.7)
а системы (4.3.6) — частоту второго типа колебаний
= 2Не IНА | - Щ Я02.	(4.3.8)
Зависимости, частот (4.3.7) и (4.3.8), а также частоты (4.3.2)
184
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
от Но приведены на рис. 4.3.2. Из этого рисунка видны две интересные особенности спектра частот антиферромагнитного резонанса при К <Z 0, т. е. в антиферромагнетике с легкой плоскостью анизотропии. Первая особенность — наличие низкочастотной (при малых Яо) ветви (4.3.7) при H0J_zo. Ее называют бесщелееой или безактивациоиной ветвью, понимая под щелью (или энергией активации) энергию элементарного возбуждения TicDj при й0 = 0. Вторая особенность — совпадение частот (вырождение) двух ветвей в случае H0J_zo при Но Нс- Вырождение же при Но = 0, которое имело место при К £> 0, в этом случае отсутствует.
Характер прецессии для обоих типов колебаний при Но £z0 показан на рис. 4.3.3. Он напоминает характер прецессии при К £> 0 и такой же ориентации постоянного ПОЛЯ (см. рис. 4.2.9) с тем, конечно, отличием, что равновесные векторы Mi о и М20 лежат теперь в базисной плоскости. Ясно, что первый тип колебаний — с частотой со. (рис. 4.3.3, а) возбуждается переменным
полем, поперечным по отношению к Но, а второй — с частотой со2 (рис. 4.3.3,6) —продольным.
Учет анизотропии в базисной плоскости. До сих пор мы не учитывали анизотропии в базисной плоскости ху, которая для реальных одноосных кристаллов всегда имеет место. Если принять для простоты (как и при записи выражения (4.2.1), что энергии анизотропии подрешеток аддитивны, то анизотропия в базисной плоскости может быть учтена дополнительными членами в энергии анизотропии каждой подрешетки, аналогичными таким членам для ферромагнетика (см. выражения (2.2.1) и (2.2.2)). Решение уравнений движения при наличии этих членов связано с довольно громоздкими вычислениями. Поскольку нашей целью является лишь выяснение качественного влияния анизотропии в базисной плоскости, рассмотрим, следуя [82], случай, когда выделенная ось является осью второго порядках).
у\/гн^А\
Ц>г
Частоты однородных колебаний ан-
Рис. 4.3.2. .	.....
тиферромапхетика с легкой плоскостью анизотропии. Для колебания с нулевой частотой (пунктир) суммарная переменная намагниченность равна нулю.



4
х) Это соответствует случаю орторомбического кристалла.
§ 4.3J
СЛАБЫЕ ФЁРРОМАГНЁТИКЙ
185
Плотность энергии анизотропии в базисной плоскости ту в случае оси второго порядка можно записать в виде
Ua± = —-^-К± (cos 2Ф1 + cos 2сра) =
= -	+ «х - Мл, (4.3.9)
/И о
где индексы 1 и 2 соответствуют, как обычно, двум подрешеткам,
Рис. 4.3.3. Прецессия векторов намагниченности антиферромагнетика с легкой плоскостью анизотропии при Но, лежащем в легкой плоскости (H„£z0). а—колебание с частотой со,; б — колебание с частотой со2 (рис. 4.3.2). Цифры обозначают’ положения концов векторов в одинаковые моменты времени.
а ’Pi,2 — азимутальные углы векторов М1>2. Эффективные' поля, Учитывающие анизотропию в плоскости ту, будут иметь вид
(/=1,2).	(4.3.10)
iV1 о	iV1 о
186
АН'ГИФЕРРОМАГНЕ*ГИКИ И ФЕРЙИМАГНЕТИЙИ
11’Л. 4
Я± =7 К±/Мо << ПЕ, угол (f'j
Рис. 4.3.4. Равновесное состояние анти-ферромагнетика при Но, лежащем в базисной плоскости, и Яо> я । ,
Эти эффективные поля следует добавить в уравнения движения намагниченностей подрешеток.
Прежде всего необходимо обсудить влияние анизотропии в базисной плоскости на основное состояние. Примем	тогда
при Но = 0 равновесные векторы Мх 0 и М2 0, как следует из (4.3,9), будут направлены по оси х. Если поле Но приложено по оси у, то векторы М< 0 и М2 0 по мере роста Но будут отклоняться на равные углы <pj_ от оси х 11 равновесная конфигурация намагниченностей качественно не будет отличаться от принятой выше при К I =0. Более того, так как поле анизотропии в плоскости будет практически по-прежнему определяться выражением (4.3.3). Таким образом, в случае H0|jyo достаточно добавить соответствующие проекции эффективного поля (4.3.10) в уравнения (4.3.4).
Если Нй приложено в плоскости ху под произвольным углом <ри (рис. 4.3.4), то при малых полях (/f0 ~ Ну) равновесные направления намагниченностей подрешеток определяются компромиссом между энергией анизотропии, стремящейся направить векторы М. 0 и М2 0 (практически аптипараллельные) по оси ж, и зеемановской энергией, стремящейся повернуть их таким образом, чтобы вектор М= — Mj 0 -|- М2 0 был направлен по полю. При больших полях {Нй^>Ну) равновесная конфигурация намагниченностей почти пе зависит от Н±. И если перейти к осям х'у' (см. рис.4.3.4), то она будет совпадать сполучепной ранее без учета анизотропии в плоскости (рис. 4.3.1, б) и использованной при записи уравнений (4.3.4). Угол <pj_ будет иметь прежнее значение, определяемое формулой (4.3.3). Теперь для учета влияния анизотропии в базисной плоскости на антиферромагнитный резонанс, так же каки в случае Н0||у0 достаточно добавить в уравнения движения (4.3.4) соответствующие проекции эффективного поля (4.3.10) на оси х' и у . В результате для собственной частоты первой ветви колебаний получится следующее приближенное выражение:
2	„
~ /(о - М1ВНх cos 2<рн.
(4.3.11)
§ 4.31
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
187
М=
Рис. 4.3.5. Возникновение слабого спонтанного момента из-за неколлинеарности намагниченностей подрешеток.
Оно справедливо при На <^Не, Па Не, Но Не и, в общем случае, при Но 5> Последнее условие не обязательно, когда Но направлено по оси у (т. е. <рд = л/2).
Таким образом, учет анизотропии в безисной плоскости привел к появлению щели для той ветви, которая была бесщелевой при отсутствии зтой анизотропии. Величина щели определяется средним геометрическим из поля анизотропии и обменного поля и зависит от угла <рд. В частности, опа положительна, если поле Но приложено в легком (с точки зрения анизотропии в базисной плоскости) направлении — по оси у, и отрицательна, если оно приложено в трудном направлении. В этом отношении имеется полная аналогия с осевой анизот
ропией: формулы (4.2.11) и (4.2.13) аналогичны (4.3.11) при <рн, равном соответственно 0 и л/2. Заметим, что выражение (4.3.11) теряет смысл при <рд < л/4 и 7/0 4ЯЬ Я±| cos2(pn|; в зтом случае основное состояние отличается от принятого при выводе (4.3.11).
Если ось z является осью не второго порядка, как было принято для простоты, а осью v-ro порядка (v = 3, 4, 6), то все сделанные выше качественные выводы останутся в силе, а в выражении (4.3.11) cos2<pH заменится, соответственно, Hacosvtpn (или cos 2т<рд при v = 3).
Мы не рассматриваем влияния анизотропии в базисной плоскости на частоту второй ветви колебаний при Но, лежащем в плоскости, а также на частоту антиферромагнитного резонанса при Но || z0, так как это влияние при малой анизотропии в базисной плоскости (/ZL НА) несущественно.
Слабый ферромагнетизм. В антиферромагнетиках часто имеет место интересное явление, которое было подробно исследовано в последние годы и получило (не совсем удачное) название слабого ферромагнетизма. Оно состоит в том, что при наличии обменного взаимодействия, стремящегося установить антиферромагнитное упорядочение, возникает небольшой спонтанный момент, обусловленный более слабыми взаимодействиями. Наиболее распространенный механизм возникновения спонтанного момента заключается в том, что равновесные намагниченности подрешеток двухподрешеточного антиферромагнетика оказываются не строго антипараллельными, а образуют некоторый, близкий к 180° угол. В результате этого возникает момент М= = Мх 0 + М2 0 (рис. 4.3.5), перпендикулярный вектору антиферромагнетизма Lo = =	0 — М 2 0. Такое «сламывание» векторов М10 и М20 связано
€ отклонениями от антипар аллельной ориентации соседних
188
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
элементарных магнитных моментов, принадлежащих к разным подрешеткам. Природа сил, приводящих к указанным отклонениям, та же, что и сил, обусловливающих магнитную анизотропию в ферро- и аптиферромагнетиках. Соответствующие этим силам эффективные поля одного порядка с эффективными полями анизотропии, т. е. составляют обычно 103	104 а. И так как на-
рушению антипараллельности элементарных моментов препятствует обменное взаимодействие с эффективными полями порядка 106 э, то углы между векторами М, 0 и М2 0 составляют обычно доли, редко — единицы градусов, т. е. слабый ферромагнетизм является действительно слабым эффектом. Однако возникающий спонтанный момент (которого не было в скомпенсированном антиферромагнетике), существенно влияет на все статические магнитные свойства. Как мы увидим ниже, он оказывает сильное влияние и на некоторые ветви магнитных колебаний.
Слабый ферромагнетизм фактически наблюдался еще в 1916 г. в а = Fe2O3 ’). Его происхождение связывалось тогда с нарушениями идеальной структуры этого кристалла. Затем, ‘когда слабый ферромагнетизм обнаружили Маттарес и Стаут [75] в NiF2 и Боровик-Романов и Орлова [77] в весьма совершенных кристаллах карбонатов МпСО3 и СоСО3, была выдвинута [77] "гипотеза о том, что он связан с неточной антипараллельностью1’ (некол-линеарностью) намагниченностей подрешеток. Дзялошинский [781 показал, что слабая неколлинеарность является органическим свойством определенных антиферромагнетиков, вытекающим из их кристаллографической и магнитной структуры. Этот вопрос был подробно исследован Туровым [79, 21] с феноменологической и Мория [82] — с микроскопической точек зрения. Не ставя своей целью сколько-нибудь подробное изложение проблемы слабого ферромагнетизма (см. [21, 81, 82]), приведем здесь некоторые факты, которые понадобятся нам при рассмотрении резонансных явлений в антиферромагнетиках со слабым моментом.
Отметим прежде всего, что спонтанная намагниченность (в отсутствие внешнего поля) может возникнуть в антиферромагнетике, если его энергия будет содержать члены вида
Uc=ApsL^Ms,	(4.3.12)
где L = Мг — М2, М = М, + М2; р, s = х, у, z, а п = 1, 3, ... Действительно, легко проверить, что сумма членов вида (4.3.12) j
и обменного члена	(см. (4.2.2')) может иметь минимум при
^«-модификация окиси железа — гематит (см. рис. 4.1.3) является ап- • тиферромагнетиком с легкой осью анизотропии (К > 0) при Т < Тм ~ ж 250 °К и антиферромагнетиком с легкой плоскостью анизотропии (К •< О) со слабым моментом при Тм < Т < ТN яг 950 °К.
§ 4.3]
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
189
М =f= 0, в то время как учитываемые нами до сих пор члены энергии анизотропии такого минимума дать не могут.
Возникает вопрос, в каких кристаллах и для каких антиферромагнитных структур могут существовать члепы вида (4.3.12) и какую конкретную форму они имеют. Для того чтобы ответить на него, оказывается достаточным последовательно учесть, что члены (4.3.12), как и другие члены разложения энергии,по составляющим L и М, должны быть инвариантны по отношению ко всем преобразованиям симметрии кристалла. Такой анализ был проведен Туровым [21]. Некоторые из полученных им результатов мы здесь приведем.
Введем прежде всего понятие о четности данной магнитной структуры по отношению к определенной операции симметрии кристалла: трансляции, повороту и т. д. Структура является четной, если при этой операции меняются местами атомы одной и той же подрешетки, и нечетной — если атомы одной подрешетки заменяются на атомы другой. Первое правило, установленное в [21], заключается в том, что спонтанный момент может возникать лишь в структурах, четных относительно трансляций на период кристаллохимической (не магнитной!) элементарной ячейки. Иными словами, слабый Ферромагнетизм невозможен для магнитных структур, элементарная ячейка которых содержит несколько кристаллохимических элементарных ячеек. Примером таких структур является показанная на рис. 4.1.2 структура МпО- Далее, слабый ферромагнетизм невозможен для магнитных структур, нечетных относительно центра симметрии. К ним принадлежит показанная на рис. 4.1.3 структура Сг2О3.
Учитывая затем требования инвариантности относительно всех других операций симметрии различных кристаллов, можно получить все возможные для них инварианты вида (4.3.12), приводящие к слабому ферромагнетизму (табл. 4.3.1).
Приведем некоторые выводы из табл. 4.3.1.
1)	Слабый ферромагнетизм возможен в кристаллах всех сингоний, кроме триклинной (в кубической — только за счет инвариантов высших порядков), но для высших сингоний — от тетрагональной до кубической, только в некоторых пространственных группах.
2)	В тригональной сингонии слабый ферромагнетизм возможен только для структур, четных относительно гласной оси. Это справедливо и для гексагональных кристаллов, если ограничиться только низшими инвариантами, приведенными в таблице.
3)	Во всех одноосных кристаллах отсутствуют инварианты второго порядка, содержащие Lz. Поэтому слабый ферромагнетизм, обусловленный этими инвариантами, невозможен в таких кристаллах, если осью антиферромагнетизма (по которой направлен вектор Lo) является главная ось.
190
АПТИФЕРРОМАГНЕТИКИ II ФЕРРИМАГНЕТИКИ
[ГЛ. 4
Таблица 4.3.1
Инварианты второго порядка, приводящие к слабому ферромагнетизму в антиферромагнитных кристаллах [21]
Сингония	Номера пространств, групп «)	Четность магнита, структуры относит. элементов симметрии г)	Инварианты	
			в переменных 1^,	в переменных Afjp. M%$
Моноклинная	3—15	2г"	М x^z » y^z» ^Z^Xi	(М1ХМ3)Ж, (MiXM-a)^, Л/1^47 iz — Л/2v47 22, MiyNhz
Орторомбическая	16—74	2z+, 2a	1 М у^х	(MrXMsk, M1XM iv — Al 2XA12V
		22“, 2Ж+	L MyLz, Mzia’v	(MiXMzJoc, MiyMiz MiyM^z
		2г~, 2Ж'	MXLZ, M ZLX	(МхХМг)),, AlixAf\z — MzxMi,z
Тетрагональная	81—92, 101—142		MXLV + ^y^xi ^X^X My^y	AlixMiy — А1гхМч,у, <-^~Л/2х + +
			M^Ly 4~ ^yLx	
		<z . 2(j	MXLX MyLy	М2Л —Al2 — Л7? 1 + M22V
		V, 2d-	(Mxl)z	(MiXM2)z
Тригональная	147—159, 162—167	3/, 2Ж-		
		’z1, 2^		
Гексагональная	168—173, 178, 179, 190	6z"	-3)	-3)
§ 4.3]
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
491
Таблица 4.3.1 (продолжение)
Сингония	Номера пространств, групп J)	Четность магнитя, структуры относит, элементов симметрии 2)	Инварианты	
			в переменных Ь„, Л Г о	в переменных М1р, M2s
Гексагональная	174—177, 180—189, 191—194	62+, 2Х_	(MXL)Z	(М1ХМг)г
		62~, 2Ж+ » ^у	-3)	~3)
Кубическая	207—230	4", 3+		
Примечания.
1) Номера пространственных групп соответствуют [28]. Там же см. описание их и другие сведения по симметрии кристаллов.
2) Vp (у ~ 2, 3, 4, 6; р = х, у, z) обозначает ось симметрии v-ro порядка, параллельную оси р. Ось z в одноосных кристаллах направлена вдоль главней оси. Оси х и у в тетрагональном кристалле направлены вдоль сторон базисного квадрата, в тригональном и гексагональном кристаллах — вдоль диагоналей базисного ромба. 2d обозначает ось второго порядка, параллельную диагонали базисного квадрата. Индексы плюс и минус указывают, соответственно, на четность или нечетисСхЬ антиферромагнитной структуры относительно данной оси.
3) Возможны инварианты более высоких порядков.
Таким образом, в одноосных кристаллах с положительной анизотропией, рассмотренных в § 4.2, слабый ферромагнетизм (во всяком случае, связанный с инвариантами второго порядка) невозможен. К числу таких кристаллов относятся MnF2 и Cr2O3 J), магнитные структуры которых приведены на рис. 4.1.1 и 4.1.3. Для рассматриваемых же в этом параграфе одноосных кристаллов с К •< 0, в которых равновесные векторы М10, М20 и, следовательно, вектор Lo лежат в базисной плоскости, слабый ферромагнетизм возможен. К числу таких кристаллов принадлежат уже упоминавшиеся выше тригональные ce=Fe2O3 и МпСО3итетрагональный NiFa. Их магнитные структуры также приведены на рис. 4.1.1 и 4.1.3.
Как видно из табл. 4.3.1, все инварианты второго порядка делятся на две группы. В первую входят проекции векторного произведения Мх X М2 на различные оси. Для одноосных кристаллов входит проекция только на ось z, и соответствующий член энергии может быть записан в виде
Ud=- Dz0 (Mj X M2).	(4.3.13)
Как следует из табл. 4.3.1, инварианты такого вида соответствуют
*) Слабый ферромагнетизм в Сг2О3 невозможен, как отмечалось выше, и по другой причине — из-за нечетности магнитной структуры относительно центра симметрии.
192
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
структурам, четным относительно главной оси. Для тригональных и гексагональных кристаллов они являются единственно возможными инвариантами второго порядка.
Во вторую группу входят суммы «несмешанных» произведений вида MjpMjS (j = 1,2; р, s = х, у, Из одноосных кристаллов инварианты этой группы могут быть только в кристаллах тетрагональной сингонии для магнитных структур, нечетных относительно главной оси. Легко убедиться, что два таких инварианта переходят один в другой при повороте системы координат на 45° вокруг оси z, так что при рассмотрении всех свойств этих кристаллов можно использовать любой из них. Запишем соответствующий член энергии в виде
Uf - - F {M1XM1V - М2ХМ2У).	(4.3.14)
Инвариантом такого вида определяется слабый ферромагнетизм в NiF2) так как его магнитная структура является нечетной относительно оси четвертого порядка (см. рис. 4.1.1).
Таким образом, из соображений симметрии следует, что слабый ферромагнетизм в одноосных кристаллах (если учитывать только инварианты второго порядка) описывается, в зависимости от структуры кристалла, членами энергии [4.3.13) или [4.3.14), причем члены (4.3.14) возможны только для тетрагональных кристаллов. Что же касается коэффициентов D и F при этих членах, то их величины могут быть получены только из микроскопической теории, рассматривающей конкретные модели антиферромагнетика. Такая теория была разработана Мория (см. [82]). Он показал, что член вида (4.3.14) возникает в результате действия одпоионного механизма анизотропии (§ 2.2), а член вида (4.3.13) обязан своим происхождением механизму анизотропного косвенного обмена между подрешетками.
После приведенных кратких замечаний об особенностях и природе слабого ферромагнетизма перейдем к исследованию малых однородных колебаний в антиферромагнетиках со слабым моментом. Рассмотрим последовательно оба случая, которым соответствуют энергии (4.3.13) и (4.3.14).
Колебания в антиферромагнетике со слабым моментом, обусловленным взаимодействием между подрешетками. Рассмотрим снова антиферромагнетик с легкой плоскостью антизотропии (К < 0), но учтем в его энергии член (4.3.13). Заметим прежде всего, что выражение [4.3.13) инвариантно относительно поворотов вокруг оси z, вследствие чего имеет место изотропия в базисной плоскости — в отсутствие внешнего постоянного поля направление спонтанного момента в этой плоскости не определено. В действительности, конечно, всегда имеется какая-то анизотропия в базисной плоскости, связанная с другими членами энергии, но мы ею пока пренебрегаем.
§ 4.31
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
193
Применяя общую формулу (4.1.4) к выражению (4.3.13), получим эффективные поля, действующие, соответственно, на первую и вторую подрешетки:
Hdi = D (х0М2у	Hd2 = D (—+ y0Mix). (4.3.15)
Все дальнейшие вычисления можно вести по той же схеме, которой мы неоднократно пользовались выше, но в условия равновесия (4.1.15) и уравнения движения (4.1.25) следует добавить постоянные и переменные составляющие эффективных полей (4.3.15).
Остановимся на наиболее интересном случае, когда постоянное поле Но приложено в базисной плоскости. Так как взаимодействие, учитываемое эффективными полями (4.3.15), изотропно в этой плоскости, можно без ограничения общности направить Но, как и раньше, по оси у. Тогда статические намагниченности подрешеток будут лежать в базисной плоскости и образовывать с осью х равные углы Фх(см. рис. 4.3.1, б). С помощью (4.1.15) или из условия минимума суммарной энергии приходим к условию равновесия
Но cos <рх — Hesih 2<pj_ + HDcos 2<рх = 0»	(4.3.16)
где
Hd=DM0.	(4.3.17)
Заметим, что поле осевой анизотропии в (4.3.16) не вошло.
При Фх 1, т. е. при Н0<§^НЕ (условие Не<^:Не обычно выполняется), из (4.3.16) следует
я.,-рлГ)
sin (рх <рх ~	.	(4.3.18)
E
Статическая намагниченность Мл — М10 + М20 направлена по оси ?/, и при фх 1
М= = Мп + %охЯ0,	(4.3.19)
где спонтанная намагниченность
MD=M0^-,	(4.3.20)
а статическая восприимчивость
Zox^i-	(4.3.21)
(как и в случае антиферромагнетика без слабого момента).
Перейдем к исследованию собственных колебаний. В три Уравнения движения первой подрешетки (4.3.4) добавятся, соответственно, члены (—Нг> cos ф । ),1Гп sin ф|7И1? и ЯпС08ф,т1а: —
7 А. г Гуревич
194
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
(ГЛ. 4
— HD sin ф_1_7И1У — HD cos т2х — HD sin (p±m2y Уравнения движения второй подрешетки будут отличаться заменой (как и раньше) индексов 1	2, cos фх -> —cos фх и, кроме того, как
это следует из (4.3.15), заменой знака перед HD. Складывая и вычитая соответствующие уравнения полученной системы, мы придем к независимым системам
— (Яо 4-1ЯА| sirups 4- HDcos фх) mz = О,
-у mz 4- Нйтх = 0, (4.3.22)
•у- 1У 4- (2Яесоз фх 4 | Нд\ cos фх 4" ЯBsin фх) mz = О,
-у 1Х — (| НА| sinфх 4 HDsm ф± tg ф±) lz = О,
у- lz 4 HDsec (p±lx — (2ЯЕсо« фх 4 2ЯВ8й1 фх) ту = 0,	(4.3.23)
-у- ту 4 (| НА| cos фх 4 Hvsitiфх) 12 = О,
которые являются обобщением систем (4.3.5) и (4.3.6) для антиферромагнетика без слабого момента. При записи (4.3.23), так же как и (4.3.6), учтено условие равновесия, в данном случае — (4.3.16).
Условие совместности системы (4.3.22) дает
(тТ =	4 | НА| sin фх 4 HDcos ф±),	(4.3.24)
или при малых фх
(у-У = Я0(Я04Яо).	(4.3.25)
Из условия совместности системы (4.3.23) при фх 1
(-у)2 = 2Не\На\ 4 HD(H0 4 HD). (4.3.26)
Как видно из (4.3.24), первая ветвь колебаний осталась бесщеле-вой, но зависимость ее частоты от постоянного поля изменилась (рис. 4.3.6).
Характер собственных колебаний в данном случае остается качественно таким же, как и для коллинеарного антиферромагнетика (рис. 4.3.3).
Для того чтобы рассмотреть вынужденные колебания с учетом диссипации, следует исходить из полных уравнений (4.1.25). Не приводя промежуточных выкладок, запишем лишь одну из независимых систем, к которым мы придем в этом случае, вместо
§ 4.3]
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
195
систем (4.3.22) и (4.3.23):
— [н0 + | HA\sin <р_ц 4- HDcos фх + sin фх^ ™z =
= —27WO sin фх^г, (4.3.27) cos фх^г/ = 27l/0 sin фх^д ,
1(й
— т. т
ia>
V
~ by + (2Не cos <р_1_ + | Яа.| cos фх + HDsin Фх 4 —
т
ict(O .	\__
— sinquJm,
Заметим, что в правые части уравнений системы (4.3.27) не вошла составляющая переменного поля hy. Наоборот, в правые части второй независимой системы — для переменных lx, lz и mv (которую мы не выписываем) войдет только hy.
Практический интерес представляют, конечно, составляющие суммарной переменной намагниченности ш. Можно записать
m = %h,
(4.3.28)
причем из отмеченных особенностей системы (4.3.27) и системы для Zx, lz и ту вытекает, что тензор восприимчивости имеет вид
X. о
% =
У.2Х
О
Хуу о
У-xz о

(4.3.29)
cos фх I mz =
Рис. 4.3.6. Частбты нижней ветви колебаний антиферромагнетика с легкой плоскостью анизотропии при внешнем поле Но, лежащем в базисной плоскости. 1 — без слабого момента (формула (4.3.7), рис. 4.3.2); 2— со слабым моментом, обусловленным взаимодействием между подрешетками (формула (4.3.2»)); 3— со слабым моментом одноионного происхождения (формула (4.3.38)).
Компоненты %хх, %Х2, %2Х и %22 тензора % определяются в результате решения системы (4.3.27); в случае Ф_ц<^ 1 (т. е, HD Не и Но	Не) , а также
НА^НЕ и а 1 они запишутся
^ = -^4-Г2(Я0 + Яи)2,	=
Мо 1
%zx %xz — ^'Ха, где
следующим образом:
“ (®i	2i® Асо),
(4.3.30)
Ха ~ С~	^п)’
Е
1
С — <£>1 ~— w2 И- 2io»Aw,
196
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
сох — собственная частота (4.3.25) первого типа колебаний, а
А® = ауНЕ.	(4.3.31)
Величина А со — пока просто обозначение. Но легко убедиться, что А со есть полуширина резонансной кривой, определяемая обычным образом как расстройка частоты, при которой мнимая часть компонент у^хх, хо и приближенно xzz составляет половину значений этих величии при резонансе (при со = сщ). Полуширина резонансной кривой по полю определится из соотношения (1.3.32) и при <рх 1
АЯ = оЯе
V Ho<Ho + Hd)
1
11 о + 2 HD
(4.3.32)
Компонента %уу тензора (4.3.29) определится в результате решения системы для lx, lz и ту. В том же приближении, в котором были записаны другие компоненты этого тензора (HD, На, Н0<^Не и а 1),
2
V’	(4.3.33)
пЕ cog — со Ц-2i(oAo)
где резонансная частота со2 есть собственная частота (4.3.26) второго типа колебаний.
Влияние анизотропии в базисной плоскости на резонанс в слабом ферромагнетике можно учесть так же, как и в антиферромагнетике без слабого момента. В результате, аналогично (4.3.11), получим
ж Но (Но + HD) - ЬНЕНЕ cos vq>H, (4.3.34)
где v = 2 для орторомбического слабого ферромагнетика, v = 4 для тетрагонального и v = 6 для тригонального и гексагонального.
При рассмотрении колебаний в слабом ферромагнетике все время предполагалось, что постоянное поле Но лежит в базисной плоскости. Если Но будет направлено по оси z, то эффективное поле (4.3.15), вызывающее слабый момент, не приведет к сколько-нибудь существенным отличиям от рассмотренного в начале этого параграфа случая коллинеарного антиферромагнетика с отрицательной константой анизотропии.
Колебания в антиферромагнетике со слабым моментом одно-ионного происхождения. Рассмотрим теперь антиферромагнетик с отрицательной одноосной анизотропией, энергия которого со
§ 4.31
СЛАБЫЕ ФЕРРОМАГНЕТИКИ
197
держит член (4.3.14), также приводящий к слабому ферромагнетизму. В отличие от (4.3.13), этот член не инвариантен относительно поворотов вокруг оси z и стимулирует не только определенную взаимную ориентацию векторов Мт 0 иМ20 в базисной плоскости, но и определенную ориентацию их относительно осей х и у, жестко связанных с осями кристалла. Иными словами, этот член, наряду со спонтанным моментом, обусловливает и анизотропию в базисной плоскости.
Очевидно, что энергия (4.3.14) минимальна, если векторы М1СиМ20 направлены так, как показано пунктиром на рис. 4.3.7.
Такой их ориентации препятствует, конечно, обменное взаимодействие, и минимуму суммарной энергии в отсутствие постоянного поля соответствует конфигурация, показанная на том же рисунке сплошными линиями. Рассмотрим наиболее интересный случай, когда постоянное поле Но лежит в базисной плоскости. В случае слабого ферромагнетика с инвариантом (4.3.14), как и для коллинеарного антиферромагнетика (или слабого ферромагнетика с инвариантом (4.3.14)) при дополнительном учете анизотропии в базисной плоскости, не безразлично, как будет направлено Нп в этой плоскости. Для простоты направим его по оси у. Тогда углы (см. рис. 4.3.7), образуемые векторами Mi 0и М2 0, соответственно с положительным и от-
Рис. 4.3.7. Равновесное состояние антиферромагнетика со слабым моментом одноионного происхождения. Пунктир — под влиянием только энергии (4.3.14), сплошные линии— с учетом и обменной энергии.
рицательным направлениями оси х, будут по-прежнему равны друг другу.
Энергии (4.3.14) соответствуют эффективные поля
Ид = F (хо/Иху-)- уо(И 1ж),	.,
Н/2 - - F (х0М2у + у0М2ж).
Легко убедиться, подставляя, например, постоянные составляющие этих полей, а также внешнее поле и эффективное поле обменного взаимодействия в проекции (4.1.15) на ось z, что условие равновесия совпадает с (4.3.16) при замене Нг> на
HF = FM0.	(4.3.36)
Выражение (4.3.18) и формула для спонтанного момента (4.3.20) будут, конечно, также справедливы при такой замене.
Для исследования свободных колебаний поступим так же, как мы неоднократно поступали ранее. Тогда мы снова придем к двум независимым системам уравнений. Первая из них запишется
198
АНТИФЕРРОМАГНЕТИКИ И ФЕРРОМАГНЕТИКИ
(ГЛ. А
в виде
-у- тх — (Яо + I Ял| sin <р± + Яр cos фх) mz = °»
-у- mz + (Яо + 2Ярсок гр±) тх — 2HFs\x\ q>±lv = 0, (4.3.37)
-у- Z,, 4- (2Яесоз <p_l + | Я^| cos фх + HFsin фх) тг = 0.
Эта система, в отличие от условия равновесия, не переходит в систему (4.3.22) при замене HF на Яр. Приравнивая нулю определитель системы (4.3.37) при ф± 1 с учетом условия равновесия, получим
(~)2 (Яо + HF) (Но + 4Яр),	(4.3.38)
что существенно отличается от (4.3.25). Вторая же система — для переменных lx, lz и ть, при указанной замене совпадает с (4.3.23). Следовательно, выражение для собственной частоты второй ветви получится из (4.3.26) заменой HF на Нр.
Как видно из рис. 4.3.6, частоты магнитных колебаний в слабых ферромагнетиках двух типов значительно отличаются друг от друга. Если в слабых ферромагнетиках с инвариантом (4.3.13) (например, в a-Fe2O3 или МпСО3) низкочастотная ветвь остается (без учета анизотропии в базисной плоскости, которая обычно мала) бесщелевой, то в слабом ферромагнетике с инвариантом одноионной природы (4.3.14) (например, в NiF2) она имеет щель, равную 2yHF.
Мы все время предполагали, что магнитомеханические отношения у,, связывающие магнитные моменты подрешеток с механическими, являются величинами скалярными и одинаковыми для обеих подрешеток. Однако эти величины (или связанные с ними g-факторы подрешеток) могут быть тензорами, причем не одинаковыми для двух подрешеток. Проведенный Туровым [211 анализ, основанный на соображениях симметрии, показывает, что для ряда кристаллов, а именно, для всех тех, для которых существуют инварианты второго порядка, приведенные в табл.4.3.1, тензоры g-факторов подрешеток содержат антисимметричные компоненты. А это, в свою очередь, приводит к неколлинеарности магнитных моментов подрешеток и к появлению слабого ферромагнетизма даже в том случае, если векторы механических моментов подрешеток равны по величине и строго антипараллельны.
Расчет резонансных частот с учетом анизотропии g-фактора [21] показывает, что в одноосных кристаллах с инвариантом (4.3.13) наличие этой анизотропии не изменяет характера спектра, приводя лишь к некоторой перенормировке константы Нр. Для кристаллов же тетрагональной сингонии с. инвариантом (4.3.14)
g	ФЙРРЙМАГНЁ’ЙГКЙ'
вклад анизотропии g-фактора в частоты антиферромагнитного резонанса не сводится к перенормировке константы Hf- В таких кристаллах анизотропию g-фактора можно обнаружить экспериментально,-
Это же справедливо и для орторомбических кристаллов, в которых могут иметь место (см. табл. 4.3.1) оба инварианта: типа (4.3.13) и типа (4.3.14). Экспериментальные данные по антиферромагнитному резонансу в орторомбическом кристалле NaNiF3 [181] свидетельствуют о том, что в данном случае все три источника: взаимодействие между подрешетками, связанное с инвариантом (4.3.13), внутриподрешеточное взаимодействие, связанное с инвариантом (4.3.14), и анизотропия g-факторов, вносят вклад в слабый ферромагнетизм.
В заключение заметим, что известно много антиферромагнетиков со сложными магнитными структурами. Среди них значительное место занимают неколлинеарные структуры, в которых, в отличие от слабых ферромагнетиков, неколлинеарность обусловлена обменным взаимодействием и достигает иногда большой величины. Спектры частот и характер колебаний в кристаллах с такими магнитными структурами разнообразны и сложны. Однако к ним примененимы методы рассмотрения, использованные выше для простых структур. Более того, многие из отмеченных особенностей антиферромагнитного резонанса имеют лесто и для сложных многоподрешеточных и неколлинеарных антиферромагнетиков.
§ 4.4. Ферримагнетики
В ферримагнетиках, так же как и в антиферромагнетиках, обменное взаимодействие вызывает антипараллельную ориентацию моментов, принадлежащих к разным подрешеткам. Но вследствие различия абсолютных величин намагниченностей подрешеток возникает сравнительно большой спонтанный момент. Различие величин намагниченностей подрешеток может быть вызвано разным количеством ионов в подрешетках или различием моментов этих ионов или одновременно и тем и другим.
Большинство известных в настоящее время ферримагнетиков является неметаллическими соединениями. С другой стороны, большинство неметаллических веществ с большими спонтанными моментами принадлежит к ферримагнетикам1). И поскольку применение металлических магнитных материалов в технике высоких и сверхвысоких частот затруднено поверхностным эффектом, ферримагнетики представляют особый интерес для этих областей техники. Многие ферримагнетики (например, иттрий-железный
]) Исключения имеются (ЕиО, СгВгз, CdCr2Se4 и ряд других), но они все же редки.
200	ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ	[ГЛ. 4
гранат Y3Fe60i2) обладают узкой резонансной кривой и малой анизотропией и являются поэтому удобным объектом для исследования многих вопросов магнитного резонанса.
В этом параграфе мы рассмотрим особенности магнитного резонанса в ферримагнетиках, выясним, в частности, в какой мере к ним применима теория, развитая в главах 1, 2 и 3. Прежде всего мы остановимся очень кратко на некоторых вопросах структуры и статических магнитных свойств ферримагнетиков [19, 97].
Кристаллические и магнитные структуры. Большинство ферримагнетиков представляет собой ионные кристаллы. Основой их кристаллических структур, как и структур неметаллических аптиферромагнетиков (§ 4.1), является решетка анионов, например кислорода О2’, серы S2- или фтора F~, соответствующая достаточно плотной (но не всегда плотнейшей) их упаковке. Катионы в некоторых случаях, если их размеры, как, например, ионов Ва2+, достаточно велики, замещают анионы, однако обычно размещаются в пространствах между ними, несколько искажая их решетку.
Места в кристалле, где располагаются катионы (катионные позиции), отличаются числом ближайших соседей-анионов. Если этих соседей четыре, т. е. они образуют более или менее правильный тетраэдр, позиции называются тетраэдрическими, при наличии шести ближайших соседей — октаэдрическими, при наличии восьми соседей — додекаэдрическими. Как правило, структуры ферримагнетиков характеризуются наличием двух или более различных катионных позиций. Эти позиции могут быть заняты как «магнитивши» (парамагнитными) ионами переходных или редкоземельных элементов, так и «немагнитными» (диамагнитными) ионами, не обладающими магнитными моментами. При этом одинаковые ионы могут находится в разных позициях и, наоборот, по одинаковым позициям могут быть распределены, беспорядочно или упорядоченно, различные ионы. Занятие ионами тех или иных позиций зависит от их размеров и структуры их электронных оболочек. Расположение же ионов в решетке, а именно, расстояния между ними и углы, наряду со строением электронных оболочек ионов, определяют характер и силу косвенных обменных взаимодействий между ними (см. § 4.1). Это, в свою очередь, определяет взаимную ориентацию магнитных моментов ионов, т. е. магнитную структуру.
Наиболее хорошо изучены и нашли широкое применение в технике кислородные ферримагнетики с двумя кубическими структурами: типа шпинели и типа граната, и некоторыми гексагональными.
Структуру минерала шпинели (MgAl204) имеют ферримагнитные соединения MeFe|+04, где Me — двухвалентный металл, например Ni, Со, Fe, Мп, Mg, или комбинация одно- и трехвалент-
§ 4.4]
ФЕРРИМАГНЕТИКИ
201
кого металлов, например Li0>5 Fe^t. Эти кристаллы и представляют собой ферриты в узком смысле слова, с исследования которых началось изучение ферримагнетизма. Часть ионов Fe3+ в них может быть- замещена другими трехвалентными ионами: А13+, Сг3+ и т. д.
Ионы О2 ' в структуре шпинели образуют кубическую гранецентрированную плотно упакованную решетку. В ней [19] имеются пустоты двух типов: тетраэдрические и октаэдрические в количествах, соответственно, по две и по одной на один ион кислорода. Часть их, а именно, 1/8 тетраэдрических и 1/2 октаэдрических занята катионами, так что число занятых октаэдрических позиций, т. е. октаэдрических катионных узлов, в два раза больше, чем тетраэдрических. В результате образуется довольно сложная структура кубической сингонии, в элементарную ячейку которой с ребром около 8 А входят 8 формульных единиц MeFe2O4. Следует заметить, что локальная симметрия окружения катионов в тетраэдрических узлах — кубическая, а в октаэдрических — тригональная. Причем имеется четыре типа неэквивалентных октаэдрических узлов, отличающихся направлением локальных осей — локальные оси третьего порядка направлены вдоль четырех осей <111> кристалла.
Распределение катионов по узлам в ферритах со структурой шпинели может быть записано в виде
(MeyFe4_y) [Me1_1/Fe1+y] О4,
где 0 у «С 1, а скобки соответствуют разным узлам: круглые — тетраэдрическим, а квадратные — октаэдрическим. Если у = 1, шпинель называется нормальной, если у = 0 — обращенной. Все ферримагнитные шпинели — полностью или частично обращенные х). Например, для никелевого феррита у = 0, для марганцевого у ~ 0,8.
Характер магнитного упорядочения в кислородных ферримагнетиках со структурой шпинели определяется тем, что наиболее сильным косвенным обменным взаимодействием является взаимодействие между ионами, находящимися в октаэдрических и тетраэдрических узлах. Действительно (см., например, [19]), для таких пар ионов длины отрезков, соединяющих их центры с центром иона кислорода, являются наименьшими, а углы, образованные этими отрезками, наиболее близки к 180°, что (см. § 4.1) благоприятно для косвенного обмена. Обменное взаимодействие является в данном случае антиферромагнитным, и моменты ионов в тетра- и окта-узлах ориентируются антипараллельно друг
*) Нормальные кислородные шпинели (Me) [Fc2]O4 (где Me — немагнитный ион Cd2+ или Zn2+) антиферромагнитны, а нормальные халкогенидные шпинели (Me) [Сг8]Х4 (где Me — Cd2+ или Hg2+, а X — S2- или Se2-) — ферромагнитны.
202
ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
другу, образуя две антипараллельные магнитные подрешетки. Косвенные обменные взаимодействия между ионами внутри каждой подрешетки являются обычно также антиферромагнитны ш, но значительно более слабыми и не могут воспрепятствовать параллельной ориентации моментов ионов каждой подрешетки. Такие представления, впервые выдвинутые Неелем [92], хорошо подтверждаются величинами намагниченностей насыщения ферритов со структурой шпинели [19]. Например, для полностью обращенной шпинели результирующий магнитный момент должен быть близок к моменту ионов Ме2+, что и имеет место, в частности, для никелевого феррита.
Структуру типа граната (например, минерала Ca3Al2Si3O12) имеет соединение Y3Fe6O12 — иттрий-железный гранат. Этот ферримагнетик, открытый Бертой Форра [93], является, как уже отмечалось, прекрасным объектом для изучения ферромагнитного резонанса и важным материалом в технике сверхвысоких частот.
Структура граната, относящаяся к кубической сингонии, является весьма сложной [96]. В элементарную ячейку входит восемь приведенных выше формульных единиц, ребро элементарной ячейки (постоянная решетки) превышает 12 А. В структуре граната имеются катионные позиции трех типов: тетраэдрические, октаэдрические и додекаэдрические; локальная симметрия во всех этих позициях не является кубической. Как и в случае шпинелей, имеется четыре типа неэквивалентных октаэдрических узлов с тригональной локальной симметрией. Локальная симметрия додекаэдрических узлов является орторомбической, имеется шесть типов узлов, отличающихся направлением локальных осей. В отличие от шпинели, все, катионные позиции в структуре граната заняты катионами, что обусловливает большую стабильность этой структуры. Распределение катионов по узлам в иттрийжелезном гранате имеет вид
{Y33+} (FeD [Fen О12,
где фигурные скобки обозначают додекаэдрические узлы, а круглые и квадратные, как и раньше,— тетраэдрические и октаэдрические.
Ионы Y3+ в гранате могут быть замещены трехвалентными редкоземельными ионами R3+. Если В —- тяжелый редкоземельный элемент от Sm до Yb или Lu, это замещение может быть полным. Ионы Fe3+ могут быть замещены частично или полностью другими трехвалентными ионами, например А13т или Ga3+. Возможны и более сложные соединения (аналогичные в этом отношении естественным гранатам), когда ионы Y3+ замещаются двухвалентными ионами, а часть ионов Fe3+ для сохранения электрической нейтральности — ионами более высокой валентности.
§ 4.4]
ФЕРРИМАГНЕТИКИ
203
Среди таких кристаллов следует отметить совсем не содержащие иттрия или редкоземельных элементов ферримагнитные гранаты Са» Bifla-Fe3+ х V 'V О12, которые существуют при 1,5^ж	3 [100].
Расположение ионов в кристаллической решетке граната таково, что наиболее сильным является косвенное обменное взаимодействие между ионами в тетра-узлах и ионами в окта-узлах, например взаимодействие (Fe)— О — [Fel. Оно является антиферромагнитным, и магнитные моменты тетраэдрической и октаэдрической подрешеток ориентируются всегда антипараллельно друг ДРУГУ' Следующим по силе является антиферромагнитное косвенное обменное взаимодействие {R} —О —- (Fe), в силу которого моменты додекаэдрической и тетраэдрической подрешеток в редкоземельных гранатах ориентируются антипараллельно. Остальные взаимодействия — более слабые, самым слабым является взаимодействие {R} — О — {R}.
Изложенные соображения, как и в случае шпинелей, находятся в согласии с величинами намагниченностей насыщения (см., например, [97]). В частности, магнитный момент на формульную единицу иттрий-железного граната должен быть равен разности моментов трех ионов Fe3+ в тетра-узлах и двух — в окта-узлах, т. е. составлять 5p.g. Экспериментальное же значение (при 4,2 °К) составляет 4,96 Цв [96]. В случае редкоземельных гранатов необходимо, однако, иметь в виду, что эффективные магнитные моменты редкоземельных ионов в кристалле существенно отличаются как от их спиновых моментов, так и от полных моментов изолированных ионов.
Гексагональные структуры имеют ферримагнетики состава BaFe12Olu и целого ряда более сложных соединений, например Ba2Me2Fe12O22, BaMe2FeieO27, Ba3Me2Fe24O41 [19]. Здесь Me — ионы двухвалентных металлов — тех же, которые входят в ферриты со структурой шпинели, а ионы Ва могут быть замещены ионами Са, Sr, Pb. Кристаллические решетки указанных соединений состоят из блоков со шпинельной структурой, не содержащих ионов Ва, которые чередуются в направлении главной оси с блоками, содержащими эти ионы. Размеры элементарных ячеек таких кристаллов в направлении главной оси достигают 50 А и более, а в поперечных направлениях составляют ~ 5 А. Среди гексагональных ферримагнетиков имеются кристаллы как с положительной анизотропией (моменты направлены вдоль гексагональной оси), так и с отрицательной (моменты лежат в базисной плоскости).
Все упомянутые выше ферримагнетики представляют собой кислородные соединения. Однако известны ферримагнитные кристаллы, в которых анионами являются сера, фтор и др. Можно отметить, например, гексагональный (с отрицательной анизотропией) ферримагнетик RbNiF3 [101] и халкогенидные шпинели
204	АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ	[ГЛ. 4
МеСг|+Х4, где Me — двухвалентный ион, а X — ион S2-, Se2-или Те2- [95] х).
Подрешеточная модель и точки компенсации по составу. Как следует из приведенных выше примеров, величины намагниченности насыщения ферримагнетиков при низких температурах находят хорошее объяснение на основе подрешеточной модели. Эта модель была введена в § 4.1 и использовалась в §§ 4.2 и 4.3 для частного случая двух идентичных подрешеток. Напомним, что число подрешеток, вообще говоря, равно числу ионов в элементарной ячейке, но во многих случаях ионы, имеющие параллельные моменты, могут быть объединены в одну подрешетку. Тогда для коллинеарных структур мы приходим к модели двух подрешеток с антипараллельными моментами.
Особенностью ферримагнетиков является неидентичностъ подрешеток. Как уже указывалось, подрешетки могут отличаться числом ионов, их моментами, а также окружением в кристалле. В результате при континуальной трактовке различными оказываются намагниченности подрешеток Mj0, величины магнитомеханического отношения у;, обменные константы и другие параметры, входящие в уравнения движения (4.1.25).
Неидентичностъ подрешеток ферримагнетика приводится тому, что результирующий механический момент и результирующая намагниченность, вообще говоря, отличны от нуля. Однако при некоторых температурах или определенных составах они могут обращаться в нуль. Такие температуры или составы называются точками компенсации. В этих точках ферримагнетик приближается по своим свойствам к антиферромагнетику. Однако подрешетки ферримагнетика и в точках компенсации остаются неидентичными. Различие g-факторов подрешеток приводит к тому, что точки компенсации магнитного момента М = JVL и механического мо-
з
мента J =	не совпадают друг с другом. Их называют,
з
соответственно, магнитной и механической точками компенсации.
Ограничиваясь пока случаем низких температур, остановимся несколько подробнее на точках компенсации по составу. Пусть имеются две антипараллельные подрешетки, и момент одной из них \Мг | превышает момент другой | AJ2 |. Будем замещать ионы первой подрешетки немагнитными ионами. В качестве примера остановимся на замещении железа галлием в гранатах. Рассмотрим сначала иттрий-железный гранат. Ионы Ga3+ предпочитают тетраэдрическое окружение [102]. Если бы такое предпочтение было абсолютным, гранат {Y3} (Feg-xGa^) [Fe2]O12 имел бы точку компенсации при х = 1. Экспериментальная зависимость
J) Среди них, как уже отмечалось, имеются и ферромагнетики.
§ 4.4]
ФЕРРИМАГНЕТИКИ
205
Рис. 4.4.1. Намагниченности гранатов YsFeg-xGa^O,, [102]. М в магнетонах Бора на формульную единицу. При х ~ 1,3— точка компенсации по составу. Пунктир— за положительное направление принято направление намагниченности тетраэдрической подрешетки;сплош-ная линия — за положительное направление принято направление Но.
намагниченности рассматриваемых твердых растворов от х приведена на рис. 4.4.1. Из этого рисунка видно, что компенсация магнитного момента в действительности происходит при х 1,3, что, конечно, объясняется некоторым «проникновением» ионов Ga в октаэдрическую подрешетку. В данном случае g-факторы обеих подрешеток, состоящих из одинаковых магнитных ионов, очень близки, и механическая точка компенсации почти совпадает с магнитной.
Иначе дело обстоит при введении Ga3+ в европий-железный гранат, в результате чего образуется кристалл состава Eu3Ga3CFeg_3CO12 [195]. Тетраэдрическую и октаэдрическую подрешетки теперь можно рассматривать как одну железную подрешетку с g-фактором, очень близким к 2. Намагниченность этой подрешетки совпадает с намагниченностью иттриевого граната с галлием (рис. 4.4.1), при х < 1,3 она уменьшается с ростом х. Второй подрешеткой является додекаэдрическая, состоящая из ионов европия. Эта подрешетка в первом приближении совсем не имеет механического момента, так как ион Еп3+ в свободном состоянии имеет полный механический момент J = 0. Для свободного иона в основном состоянии равен нулю и магнитный момент, нов кристалле ионы европия будут иметь некоторый магнитный момент, наведенный эффективным полем. Таким образом, g-фактор подрешетки европия оказывается очень большим. При хм х 0,7 намагниченность железной подрешетки (рис. 4.4.2) становится равной по величине намагниченности подрешетки европия, т. е. наступает магнитная компенсация. Механическая же точка компенсации лежит, как и для иттриевого граната с галлием, при xj 1,3, как так механический момент подрешетки европия отсутствует.
Основные состояния в сильных полях. Остановимся теперь на вопросе о равновесных состояниях ферримагнетика при наличии постоянного поля произвольной величины *). Рассмотрим двухподрешеточный ферримагнетик и пренебрежем для простоты
г) Этот вопрос был впервые исследован Тябликовым [94] с квантовой точки зрения. Приведенный ниже вывод принадлежит Шлёманну [192],
206
ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
кристаллографической анизотропией и влиянием формы образца. Тогда для плотности магнитной энергии и эффективных полей будут справедливы выражения
U = - Но (МХ + М2) - ЛцМ? - 4“ Л2»М2 ~ Л12М1М2> С4’4’4) не„ 1 = Но 4- ЛцМх -j- Л12М2, Hetf 2 = но 4- Л22М2 4* Л12М1. (4.4.2)
В общем случае равновесные векторы 0 и М2 0 будут направлены, как показано на рис. 4.4.3 (из соображений симметрии ясно,
Рис. 4.4.2. Моменты подрешеток и точки компенсации в гранате Eu3Feg_JCGaa.O12 (схематически).
Рис. 4.4.3. Равновесные векторы намагниченностей подрешеток ферримагнетика.
что Но, М10 и М20 лежат в одной плоскости). Равновесные значения углов 0j и 02 могут быть определены из условий минимума выражения (4.4.1); отбрасывая члены, не зависящие от 0Х и 02, его можно записать в виде
U = — Но (Mi cos 0j 4~ 4f2cos 02) 4- AAfjA/gCos' (0х — 02),
(4.4.3)
где Л == —Л12. Приравнивая нулю производные от (4.4.3) по 0Х и 02 и решая полученные уравнения, находим, что либо sin 0Х — sin 02 = 0, либо
COS0 - .^+Л2(Мх20-^0)	„^02-л2(^0-л/220:
01	гЛЯоЛУю ’	02 2ЛЯоЛГ2'о
. (4.4.4)
При этом выполняется условие
Мг 0 sin 0Х = —М2 0 sin 02.	(4.4.5)
Легко убедиться, что решение (4.4.4) существует при Но < Н2, где
= Л(М1о-ЛГ2о), Я2 = Л(М10 +АГ20),	(4.4.6)
§ 4.4]
ФЕРРИМАГНЕТИКИ
207
и соответствует во всем интервале полей минимальной энергии. Для интервала 0 Но Н1 минимальная энергия будет при 0! = 0 и 02 = л, а для Но > Н2 — при 0Х = 02 = 0. Зависимости углов 0Х и 02 от Но, рассчитанные по формулам (4.4.4), показаны

JW нв
Рис. 4.4.4. Зависимости равновесных углов и 02 (рис. 4.4.3)), результирующей намагниченности и статической восприимчивости двухподрешеточного ферримагнетика от постоянного поля. Зависимости 6, и 62 от Но рассчитаны по формулам (4.4.5). Принято Mi о — 2 М2 0.
на рис. 4.4.4. Таким образом, в зависимости от величины постоянного поля Но реализуются три равновесные конфигурации:
1)	антипараллельная при 0 Но Нг,
2)	неколлинеарная при Нг < Но < Н2,
3)	параллельная («захлопнутая») при Яо >= Н2.
Заметим, что в отличие от антиферромагнетика, резкого «опрокидывания» подрешеток здесь не происходит, а отклонение от антипараллельности начинается плавно при «первом обменном поле» Нг. В обычных ферритах Н1 ~ 105 э. Захлопывание же при «втором обменном поле» Н2 происходит совершенно аналогично случаю антиферромагнетика.
Как следует из (4.4.5), вектор постоянной намагниченности М==М10 4- М2 о всегда направлен параллельно Но; в антипарал-
208
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
лельном и захлопнутом состояниях 7W, не зависит от II0, а в не-коллинеарном состоянии, как легко убедиться,
^=_l#o	(4-4-7)
(см. рис. 4.4.4).
Учет кристаллографической анизотропии и размагничивающих полей, обусловленных формой образца, существенно изменит основное состояние при малых полях — меньше или порядка полей анизотропии и размагничивающих полей (т. е. значительно меньших, чем первое обменное поле). Будет возникать доменная структура, направления векторов Мх 0 и М2 0 будут отличаться от направления Но. Однако при этом поведение ферримагнетика будет совершенно аналогично поведению ферромагнетика с намагниченностью (Мг 0—М2 0). В сильных же полях влияние анизотропии и формы на полученные выше основные состояния будет несущественным.
Магнитные свойства при Т 0. Равновесные состояния ферримагнетиков при Т 0 могут быть также найдены на основе континуальной подрешеточной модели. Для области температур вблизи или выше температуры упорядочения этот вопрос уже рассматривался в § 4.1. Было показано, что температура упорядочения (температура Кюри или температура Нееля) двухпод-решеточного антиферро- или ферримагнетика может быть получена из условия равенства нулю определителя системы (4.1.18). Если внутриподрешеточные обменные взаимодействия намного слабее, чем взаимодействие между подрешетками (|ЛЦ|, |А22|
—Л12 eh Л), то из этого условия с учетом (4.1.19) следует
Тс / СгС2К = 4г	V NxN2\,	(4.4.8)
где

величины элементарных магнитных моментов, образующих подрешетки, a Nj — числа их в 1 см3 (остальные обозначения см. в § 4.1).
Решение системы (4.1.18) дает выражение для статической восприимчивости двухподрешет очного ферримагнетика выше точки Кюри. В случае малого внутриподрешеточного обменного взаимодействия с учетом (4.4.8)
-^т(с1 + с2)-тсус1с2 Хо *
(4.4.9)
г2 _
Из Выражения (4.4.9) видно, что зависимость от Т для фер
§ 4.4]
ФЕРРИМАГНЕТИКИ
209
римагнетика является, в отличие от ферромагнетика и антиферромагнетика с идентичными подрешетками (когда Су = С2), нелинейной (см. рис. 1.1.3).
Для определения зависимостей 7И1О(7’, Но) и Л/2 0 (Т, Но) при Т <Z Тс необходимо, как уже отмечалось в § 4.1, решить уравнения (4.1.16) совместно с выражениями, дающими связь Heft с Му 0 и М20 (в простейшем случае — выражениями (4.4.2)) и уравнениями, вытекающими из условий равновесия, т. е. минимума магнитной свободной энергии. Даже при Но = 0 эта задача может быть решена только численными методами. При различных
соотношениях между величинами Л12, Ли и Л22 и различных намагниченностях подрешеток при Т = 0 (которые мы обозначим Му 0 (0) и М2 0 (0)), могут иметь место качественно различные температурные зависимости суммарной намагниченности [92].
Наиболее интересным является случай, когда, например, Му 0 (0) > М20 (0), но спад Му 0 с ростом температуры является более резким. Тогда при некоторой температуре TvM будет иметь место равенство Му 0 = М2 0, а при другой температуре TK,j будет Му о/?1 ~ М2 0/у2. Эти температуры называются точками компенсации по температуре, соответственно, магнитной и механической. Примером ферримагнетиков с такими точками компенсации являются
Рис. 4.4.5. Температурные зависимости намагниченностей подрешеток и результирующей намагниченности граната {Gd3) (Fe3)[Fe2]O12.
— намагниченность додекаэдрической подрешетки, А1р(> — намагниченность объединенной подрешетки железа, М — результирующая намагниченность (в магнетонах Бора на формульную единицу). Пунктир и сплошные линии— аналогично рис. 4.4.1 (но с заменой тетраэдрической подрешетки на додеказдри-ческую).
редкоземельные ферриты со структурой граната (см., например, [4, 19, 97]). На рис. 4.4.5 приведены температурные зависи-
мости намагниченностей подрешеток и суммарной намагничен-
ности одного из таких веществ — гадолиний-железного граната Gd3Fe6O12. Тетраэдрическая и октаэдрическая подрешетки, состоящие из ионов Fe3+ и сильно связанные между собой, могут быть, как и в рассмотренном выше случае европиевого граната, объединены в одну подрешетку. Вторая подрешетка — додекаэд-рическая, состоит из ионов Gd3+. Как видно из рис. 4.4.5, в этом случае магнитная точка компенсации Ткм 13 ° С. Другие редкоземельные гранаты имеют точки компенсации при более
210
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
низких температурах. Точки компенсации по температуре наблюдаются и в некоторых ферритах со структурой шпинели, например в Li0,5Cr1<26Fe1,25O4 (см. 119]).
Основные состояния ферримагнетика при произвольных внешних полях и температурах исследовали Кларк и Каллен [103].
Рис. 4.4.6. Фазовые диаграммы изотропного двухподрешеточпого ферримагнетика [103]. а — при отсутствии точки компенсации по температуре; б — при наличии точки компенсации.
На рис. 4.4.6 приведены полученные ими фазовые диаграммы двухподрешеточного ферримагнетика.
Собственные колебания в антппараллельном основном состоянии. Теперь, после краткого описания структур и статических магнитных свойств ферримагнетиков, можно перейти к рассмотрению малых магнитных колебаний в них (ферримагнитного резонанса). Теорию этих колебаний, как и в случае антиферромагнетиков, можно строить на основе континуальной подрешеточной модели, исходя из линеаризированных уравнений движения намагниченностей подрешеток (4.1.25). В отличие от антиферромагнетиков (§§ 4.2 и 4.3), величины Mj() и теперь различны для разных подрешеток. Эффективные поля в уравнениях (4.1.25) по-прежнему определяются формулами (4.1.4) и имеют, вообще говоря, те же составляющие. Так же как и для антиферромагнетиков, из составляющих «молекулярных» полей в уравнения движения войдут лишь те, которые соответствуют межподрешеточным обменным взаимодействиям. Наличие большой спонтанной намагниченности ферримагнетика приводит к значительно большей роли размагничивающих полей и, следовательно, к более сильному влиянию формы образцов, чем в антиферромагнетиках.
Исследуя колебания в ферримагнетиках, мы будем пользоваться деухподрешеточной моделью. При этом в подрешетки объединяются обычно ионы, занимающие одинаковые узлы и имеющие
Ферримагнетики
211
§ 4.4]
одинаково направленные моменты, как, например, ионы железа в тетра- или в окта-узлах в иттрий-железном гранате или в шпинелях. Однако в некоторых случаях в одну подрешетку могут быть объединены ионы, находящиеся в разных узлах и имеющие противоположно направленные моменты, но сильно связанные обменным взаимодействием, как, например, все ионы железа — в тетра- и окта-узлах — в редкоземельных гранатах (вторую подрешетку в последнем случае образуют редкоземельные ионы в додекаэдрических узлах).
Число подрешеток, как уже указывалось выше, строго говоря, должно быть равно числу магнитных ионов в элементарной ячейке; для ферримагнетиков оно обычно велико. Число же типов магнитных колебаний (т. е. ветвей спектра) равно числу подрешеток. Поэтому использование двухподрешеточной модели приводит к «потере» некоторых типов колебаний.
Мы ограничимся рассмотрением колебаний (ферримагнитного резонанса) в первом — антипараллелъном основном состоянии ферримагнетика. Резонанс во втором — неколлинеарном состоянии пока экспериментально не исследован, так как оно реализуется в довольно сильных постоянных полях. Анализ колебаний в этом состоянии может быть проведен по использованной выше (§§ 4.2 и 4.3) схеме. Свойства же ферримагнетика в третьем — захлопнутом основном состоянии не отличаются от свойств ферромагнетика.
Пренебрежем сначала для простоты размагничивающими полями и кристаллографической анизотропией. Тогда вклад в уравнения движения будут вносить следующие эффективные поля (см. выражения (4.4.2)):
НеИ12 = Н-ДМ1>2,	(4.4.10)
где Л = Л12	0. Направив ось z по постоянному полю Но и при"
няв, как и раньше, что М± 0 М2 0, запишем
Mio = zo^io> М, 0=	z0Tl/2().	(4.4.11)
Спроектируем уравнения (4.1.25) для обеих подрешеток на оси координат, учтем (4.4.10) и (4.4.11) и перейдем, так же как и при исследовании колебаний в первом основном состоянии антиферромагнетика в § 4.2, к циркулярным переменным mlt 2t = = mi, гж +	в результате получим следующие системы
уравнений:
[± со — тх (Яо + AM 2 0) — iXito] mx t — ТхДЛ/х 0т2 ь = — чхМ±
(4.4.12)
Т2ЛМ2 ОШ1± + [± СО — у2 (Яо — AMх 0) + ix2co] m2±. = у2М2 oh±.
212
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
Рис. 4.4.7. Частбты однородных колебаний двухподрешеточного ферримагнетика в анти-параллельном основном состоянии.
Здесь, так же как и в (4.2.21), верхние и нижние знаки соответствуют двум типам движения, одному — с нормальными переменными т1+ и т2+, и другому — с переменными тх_ и т2_. Ясно (см. § 4.2), что первый тип колебаний соответствует правой прецессии векторов Мх и М2 и возбуждается переменным полем h+ с круговой поляризацией и правым вращением, а второй — соответствует левой прецессии и возбуждается полем с левым вращением.
Как обычно, рассмотрим сначала собственные колебания (свободные колебания без диссипации). Приравнивая нулю определитель системы (4.4.12) при ах = = ссг = 0, получим уравнение для собственных частот
со2 ± со [А (т2М 1 0 — Т1М2 0) — — (Тх + Т2) Но] —
Т1Т2 [Л (ЛГХ 0	М2 о)
-Яо] яо = 0, (4.4.13) где знак плюс перед вторым членом соответствует типу движения с правой поляризацией, а знак минус — с левой. При исследовании уравнения (4.4.13) удобно для второго типа колебаний заменить со на (—со). Тогда знак ± перед вторым членом заменится на -{-.Таким образом, частота первого типа колебаний (со+) и наком (—со_) являются кор
нями одного и того же уравнения. Нетрудно убедиться, что оно представляет собой уравнение гипербол, проходящих через точки (со = О, Яо = 0) и (со = О, Яо = Л (Мх 0 - М2 0) = Ях). Вид этих гипербол существенно зависит от знака разности ух — у2 (рис. 4.4.7); при ух = у2 гипербола вырождается в две параллельные прямые.
Поскольку собственные частоты колебаний должны быть положительными (мы, пользуясь методом комплексных амплитуд, приняли зависимость от времени e+i“f), отрезки гипербол с со {> 0 соответствуют частотам со+, а отрезки с со < 0 дают частоты (— со_). Физический смысл имеют, конечно, только участки гипербол в пределах 0 Но Ях, в которых существует принятое при этом расчете основное состояние. Как видно из рис. 4.4.7, частота со+ равна нулю при Яо = 0 и растет с ростом поля, при малых полях — приблизительно пропорционально ему; коэффициент про-
частота второго типа с обратным
§ 4.41
ФЕРРИМАГНЕТИКИ
213
порциональности (эффективный g-фактор) засисит от ух и у2-Частота же со_ при Но = 0 имеет большую величину — порядка уН1г и уменьшается с ростом поля, обращаясь в нуль при Но =НГ.
Не выписывая в общем случае решения квадратного уравнения (4.4.13), рассмотрим область малых полей
	Яо < ЕН Л (7ИХ 0 - М2 0).	(4.4.14)
Для	нее, как легко убедиться,	
где	CD+ Ж Тэфф-Н'о, Л/io -—	о	(4.4.15) (4.4.16)
	Тэфф М1°_' Т1	Т2	
Для	той же области полей (4.4.14)	
где	<0_	|?эфф вНд,	(4.4.17)
а	Ое == Л (Тг^ ю Т1^2 о)» тГМго	(4.4.18) (4.4.19)
	Тафф в	Д/ip	Мур * 71	Та	
Таким образом, один из типов колебаний — с правой поляризацией имеет при малых полях собственную частоту, которая выражается такой же формулой (4.4.15), как для ферромагнетика, но с заменой у на уЭфф- Этот тип колебаний называют низкочастотным, ферромагнитным или СВЧ типом колебаний, его частота при обычно используемых полях лежит в диапазоне сверхвысоких частот. Частота второго — левополяризоеанного типа колебаний (4.4.17) при малых полях лежит в инфракрасном диапазоне, этот тип колебаний называют высокочастотным, инфракрасным или обменным.
Подставляя значения собственных частот в уравнения (4.4.12) (с hф-=0 и ах = а2 = 0), мы можем, как и для антиферромагнетиков (§§ 4.2 и 4.3), исследовать характер прецессии векторов Мх и М2 для обоих типов колебаний. Для первого типа при условии (4.4.14) можно пренебречь членами с со и Но в (4.4.12) по сравнению с обменными членами, тогда

т2± Мго
(4.4.20)
Соотношение (4.4.20) означает (рис. 4.4.8* а), что векторы Мх и М2, прецессируя, остаются все время антипараллелъными
214
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
ДРуг другу. При этом не совершается работы против обменных сил, вследствие чего обменная константа и не входит в выражение (4.4.15) для частоты первого типа колебаний.
Для второго типа колебаний, подставляя (4.4.17) в (4.4.12), мы убеждаемся, что при том же условии (4.4.14)
т2-
Т1
Т2 ‘
(4.4.21)
Теперь (рис. 4.4.8, б) векторы Мх и М2 уже не антипараллельны.
Из (4.4.21) видно, что суммарная переменная намагниченность
Рис. 4.4.8. Прецессия векторов намагниченности подрешеток ферримагнетика в анти-параллельном основном состоянии, а— низкочастотный (ферромагнитный) тип колебаний; б— высокочастотный (обменный) тип колебаний. Малое (при I Т2 I Ti) различие амплитуд mi~ и mz- не показано.
для второго типа колебаний возникает только при Xi =1= Тг- Другим «источником» суммарной переменной намагниченности для этого типа колебаний может явиться анизотропия (которой мы пока не учитываем). В антиферромагнетике (когда = Тг) именно она являлась, как видно, например, из формулы (4.2.33), причиной возникновения суммарной переменной намагниченности.
Подчеркнем еще раз, что выражения (4.4.15) — (4.4.21) справедливы приближенно — при выполнении условия (4.4.14). Это условие перестает выполняться при больших полях. Например, для иттрий-железного граната (Л ~ 104) погрешность выражений (4.4.15) — (4.4.19) достигает 1% при Но ~ 50 кэ. Условие (4.4.14) также не выполняется и формулы (4.4.15) — (4.4.21) перестают быть справедливыми (даже в малых полях) при подходе к точкам компенсации.
Согласно (4.4.16) Гафф обращается в нуль в магнитной точке компенсации и в бесконечность — в механической. Хотя формула
§ 4.41
ФЕРРИМАГНЕТИКИ
215
(4.4.16) перестает выполняться при подходе к точкам компенсации, указанная тенденция имеет место. Это подтверждается экспериментально (рис. 4.1.9 и 4.1.10). Частота же второго — обменного типа колебаний, как следует из (4.4.17) и (4.4.18), должна пони
жаться при подходе к точкам компенсации и может попасть в диа-
пазон СВЧ, что также наблюдалось на опыте [191]1).
Не представляет особого труда рассмотреть решения уравнения(4.4.12)вблизи точек компенсации без ограничения (4.4.14). Однако это не имеет смысла, так как основным состоянием вблизи точек компенсации (без учета анизотропии!) уже в самых малых полях будет не анти-параллельное состояние, принятое при выводе (4.4.12), а неколлинеарное. С учетом анизотропии (он становится теперь совершенно необходимым) критическое поле, при котором возникает неколли-
Рис. 4.4.9. Эффективный ^-фактор и аффективное поле анизотропии граната YsFes_xGraxO12 с точками компенсации по составу [196]. Кружки— экспериментальные значения при частоте 9,1 Ггц и температуре 77 °К.	—
g-фантор тетраэдрической подрешетки, рассчитанный в предположении, что g-фантор октаэдрической подрешетки g2 не зависит от х.
неарность, уже не стремится к нулю при Мг 0 —> М2 о-Поведение ферримагнетика вблизи точки компенсации становится аналогичным поведению антиферромагнетика, рассмотренного в § 4.2, одна-
ко более сложным, так как g-факторы и поля анизотропии подрешеток теперь не одинаковы. Строгое рассмотрение резонанса в ферримагнетике вблизи точек компенсации проведено, например, Гешвиндом и Уокером [191].
Учет диссипации. Следуя обычной программе изучения колебаний, перейдем к рассмотрению затухающих свободных колебаний двухподрешеточного ферримагнетика в первом основном состоянии. Приравнивая нулю определитель системы (4.4.12),
9 Трактовка одного из двух резонансных пиков, наблюдавшихся в ряде работ при подходе к точкам компенсации в поликристаллах, как обменного была подвергнута критике Шлёманном и Зиндером [309]. Они указали, что второй пик может возникнуть благодаря усреднению в поликристалле в соответствии с теорией независимых зерен (см. § 2.5). Но к наблюдению двух резонансов вблизи точек компенсации в монокристалле [191] эта критика не относится.
216
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
получим вместо (4.4.13)
со2 (1 + а±а2) ± “ [Л (г2Мх 0 — TvW2 0) — (П + Тг) Яо]—
— Y1Y2 [Л (ЛД о — Л/2о) — Яо] Но — ito [а^г (ЛАД о — Но) +
Ч~ a2Ti (ЛМ2 0 -j- Но)] 4- is2 (а2 — ах) = 0, (4.4.22)
где верхние и нижние знаки перед вторым и последним членами соответствуют двум типам колебаний — с правой и левой поляризацией. Корни этого уравнения со = со' + гео" с положительными
Рис. 4.4.10. Эффективный g-фактор и ширина резонансной кривой граната Gd3Fe6O,2 с точками компенсации по температуре [193]. Частота 9,5 Гец. Величина 2 АН — для направления < 111 >.
вещественными частями представляют собой комплексные частоты обоих типов колебаний. Рассмотрим эти типы колебаний по отдельности, ограничиваясь для простоты случаем малых полей и достаточного удаления от точек компенсации (условие (4.4.14)). Примем также1), что аь 2 меньше или порядка 1.
Для низкочастотного (правополяризованного) типа колебаний в (4.4.22) можно пренебречь членами с со2, а в остальных членах — пренебречь слагаемыми с Но. В результате получим
где Тэфф выражается формулой (4.4.16), а эффективный параметр
При этом мы оставляем в стороне случай так называемой «быстрой релаксации» (см. § 9.6), когда параметр затухания одной из подрешеток а2 >> 1.
§ 4.41
ФЕРРИМАГНЕТИКИ
217
диссипации
М1 о	7И 2 О
а1~+а2^г эфф	Л/ip _ ТИзо
Т1 ~ Т2
(4.4.24)
Разделяя вещественную и мнимую части (4.4.23), находим
(4.4.25)
1 + аэфф
со" = „аэффТ2эфф но.	(4.4.26)
1 + аэфф
Выражение (4.4.26) имеет максимум при аэфф = 1. При а112	1
(4.4.25) переходит в (4.4.15), a
со та ОэФфТэфф^о-	(4.4.27)
Как видно из (4.4.24), эффективный параметр диссипации двухпод-решеточного ферримагнетика аЭфф оо при подходе к механической точке компенсации (но, как уже неоднократно отмечалось, вблизи точек компенсации это приближенное рассмотрение становится несправедливым).
Для высокочастотного (левополяризованного) типа колебаний, рассматривая по-прежнему случай, когда выполняется условие (4.4.14), получим из (4.4.22)
со' = А
TzMio
1+«|
ТхЛЛо \
1 + ’
(4.4.28)
со" = Л
CteTaMi о
1+af
(4.4.29)
, CfiTjTWa о \
1+< J'
Аналогично низкочастотному типу колебаний можно и для высокочастотного ввести в рассмотрение эффективный параметр диссипации аэфф в, определив его следующим образом:
со =s сх^фф всо .	(4.4.30)
Величина аэффВ отличается от (4.4.24), но как и аЭфф, растет при подходе к механической точке компенсации.
Вынужденные колебания. Решая систему (4.4.12) при тех же допущениях, что и выше (условие (4.4.14) и «умеренная» диссипация, т. е. а1( 2 меньше или порядка 1), но при наличии переменного поля (с правой поляризацией), найдем
m+ = m1+ + mi+ = %+Л+,
218
АаТИФЁРРОМЛГИЕТИЬЙ Й ФЁЕГЙЙЛГЙЕ'ГЙЙЙ
(М. 4
где
_ ТэффС^10— М20) Тэфф Но ~ “ + Чфф“
(4.4.31)
причем для Тэфф и <х8фф справедливы прежние формулы (4.4.16) и (4.4.24). Полученный результат является очень важным. Выражение (4.4.31) отличается от аналогичного выражения для ферромагнетика х) только заменой намагниченности Мо на результирующую намагниченность ферримагнетика (7ИХ 0 — М2 0), а величин Т и а — на их эффективные значения Т;>фф и аЭфф.
Не выписывая вещественной и мнимой частей (4.4.31), приведем выражение для восприимчивости при резонансе
(4.4.32)
^реэ
Тэфф (М10 — М2 о)
авфф“
Ширину резонансной кривой ДЯ определим, как обычно,
как разность	|Ях/2 — Ярез1, где Н12 — поле, при котором у" — —5— у" . Л	2 Лрез
Из (4.4.31) и	(4.4.32) следует, что ДЯ =	,	(4;4.33) Тэфф 1
или с учетом	(4.4.16) и (4.4.24) М1 о	М2 о Я1 ~	+ Я2 „ • <4-4-34)
В отличие от а8фф и ширины резонансной кривой по частоте Дсо — со", которые возрастают (при постоянных параметрах диссипации подрешеток) при подходе к механической точке компенсации, ширина резонансной кривой по полю, как видно из (4.4.34), возрастает при подходе к магнитной точке компенсации. Заметим, что это возрастание, как и возрастание Дсо при подходе к механической точке компенсации, не связано с появлением какого-то нового механизма релаксации, а определяется феноменологическими особенностями рассматриваемой двухподрешеточ-ной системы. Это — явление такого же типа, как отмечавшееся в § 4.2 увеличение ширины кривой антиферромагнетика по сравнению с шириной кривой ферромагнетика с тем же параметром диссипации.
J) Чтобы получить такое выражение, достаточно произвести замену (1.3.10) в (1.2.42).
§ 4.4]
ФЕРРИМАГНЕТИКИ
219
Обычно g-факторы подрешеток ферримагнетика мало различаются и точки компенсации — механическая и магнитная — очень близки друг к другу. В этом случае ДЯ, как и Д<о, растет при подходе к точкам компенсации (см., например, рис. 4.4.10).
Рассмотрим теперь специальный случай, когда g-факторы подрешеток существенно отличаются друг от друга и, следовательно, механическая и магнитная точки компенсации далеко разнесены. Тогда вблизи механической точки компенсации можно получить большие значения 'р;)фф при сравнительно небольшой Д Я. Таким ферримагнетиком с далеко разнесенными точками компенсации является европиевый железо-галиевый гранат Eu3Fe8_xGaxO12 (см. рис. 4.4.2). В этом веществе вблизи механической точки компенсации Ле Кроу, Ремейка и Меттьюс [195] действительно наблюдали большие значения g-фактора (—4) при довольно узкой (2ДЯ = 9 э при низких температурах) резонансной кривой.
Для левополяризованного переменного поля, принимая по-прежнему условие(4.4.14)и ограничиваясь (в отличие от правой поляризации) случаем «1,2^ 1, находим
лг_ = тх_ ш2_ — %_Л_, где
Ml 0Л/2 о
=	.	(4.4.35)
иЕ-м + гяэффв<оЕ	v
Из формулы (4.4.35) видно, что восприимчивость для обменного типа колебаний уменьшается с уменьшением различия g-факторов подрешеток (это обстоятельство уже отмечалось при анализе левополяризованного типа собственных колебаний).
Мы рассмотрели возбуждение малых однородных магнитных колебаний в ферримагнетике поперечным (по отношению к Но) переменным полем с круговой поляризацией и правым или левым вращением. Произвольное поперечное переменное поле может быть разложено на два поля с круговой поляризацией и разными направлениями вращения. Каждое из них будет возбуждать намагниченности с круговой поляризацией и соответствующим направлением вращения. Определив их амплитуды с помощью формул (4.4.31) и (4.4.35), можно затем записать, если это необходимо, поперечные компоненты тензора % в декартовой системе координат. Что же касается продольной (по отношению к Но) составляющей переменного поля, то она для рассматриваемого основного состояния не будет- возбуждать в линейном приближении переменной намагниченности.
При малых Но две собственные частоты ферримагнетика очень сильно отливаются друг, от друга. И если-только диссипация не
220
ЛНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
[ГЛ. 4
очень велика, то составляющие намагниченности т+ и т_ практически не возбуждаются одновременно: при частотах, близких к Тэфф^о! возбуждается ш+, а при частотах, близких к п>£, возбуждается т_.
Заметим, что рассматриваемая теория магнитного резонанса в ферримагнетиках, так же как и теория антиферромагнитного резонанса (§§ 4.2 и 4.3), справедлива и при температуре Т 0, если для всех параметров, входящих в уравнения движения, принять их значения при этой температуре. В частности, под Mi 0 и М2 о следует понимать равновесные намагниченности подрешеток при данной температуре. Существенно, что они зависят не только от температуры, но и от Но. Эту зависимость следует учитывать при выяснении влияния постоянного поля Но на различные резонансные характеристики при Т > 0.
Учет анизотропии и формы образцов. До сих пор мы не учитывали размагничивающих полей. Поэтому полученные выше величины х+ ц X- представляют собой внутренние восприимчивости (по отношению к внутреннему переменному полю, см. § 1.4), а частоты (4.4.15) и (4.4.17) являются резонансными частотами этих восприимчивостей. Как было показано в § 1.4, для малых по сравнению с длиной электромагнитной волны эллипсоидальных образцов может быть введена внешняя восприимчивость — по отношению к заданному внешнему переменному полю. Ее резонансные частоты являются собственными частотами колебаний соответствующих образцов. Переход от внутренней восприимчивости к внешней представляет собой магнитостатическую задачу. Решение ее дается формулой (1.4.38), которая справедлива для любых сред. Поэтому сделанный выше вывод о приближенной эквивалентности ферримагнетика для низкочастотного типа колебаний ферромагнетику с параметрами Мо = М10 — Л/20, Т = Тэфф и а = а»ФФ, несомненно, будет справедлив и для собственных частот и компонент внешнего тензора восприимчивости малого эллипсоида. Тем не менее поучительно убедиться в этом непосредственно для какого-либо простого случая.
Рассмотрим, например, собственные колебания малого ферримагнитного эллипсоида. Одновременно учтем и кристаллографическую анизотропию. Будем считать ее для простоты одноосной и совместим ось анизотропии с осью z. Примем, как и ранее, что энергии анизотропии подрешеток аддитивны. Тогда с учетом. (4.2.5) эффективные поля вместо (4.4.10) запишутся следующим образом:
нэфф1,2 = Н - ЛМ211 +	(M112Zo) z0 — N (М2 + M2), (4.4.36)
M 1,2 О
где К1л — первые константы анизотропии двух подрешеток (мы
§ 4.4]
ФЕРРИМАГНЕТИКИ
221
ограничиваемся учетом только этих констант), a N — тензор размагничивающих факторов.
Предположим, что образец представляет собой эллипсоид вращения вокруг оси z. Направим постоянное поле также по оси z. Если она является легкой осью или если Но превышает поле анизотропии (но меньше первого обменного поля Ну), то равновесные намагниченности подрешеток будут направлены по оси z, т. е. будут справедливы выражения (4.4.11). Тогда, проектируя уравнения (4.1.25) при аЬ2 = 0 и h = О на оси а? и у и переходя к циркулярным переменным, получим вместо (4.4.12)
[+ со — Г1Н0 — XiHai — Т1 (Л + Nz) М2 0 —
— Т1 (Nj. — Nz) Мг 0] т1± — Ti (Л + 7V±) Му 0^2+ = О,
Тг (Л + TV J.) -^2 omi± + (zb ю — ТгЯ0 +	+	(4.4.37)
+ Гг (Л + Я) Му 0 + Тг (Wj. — Nz) М20] т2± = О,
где Nz и Л’х — размагничивающие факторы образца, а
ЯА1,2 =	(4.4.38)
— поля анизотропии подрешеток.
Приравняем нулю определитель системы (4.4.37), предполагая, что Но Л {Му о — М2 0), и ограничиваясь рассмотрением только первого, низкочастотного типа колебаний, для которого при этом условии со Ti,2A (Му 0 — М2 0)- Тогда для собственной частоты колебаний анизотропного ферримагнитного эллипсоида вращения получим выражение
СО = Тэфф ГЯ0 + На Эфф + (7V± - 7VZ) (Му 0 - М2 „)], (4.4.39)
где ТВфф по-прежнему определяется формулой (4.4.16), а эффективное поле анизотропии
ТТ _____ оЯа1 + о^Аг
J' А вфф —
(4.4.40)
Му о — М2 о
Заметим, что На эфф —> 00 при подходе к магнитной точке компенсации. Но в непосредственной близости от нее, как уже неоднократно отмечалось, все это рассмотрение и, в частности, формулы (4.4.39) и (4.4.40) делаются несправедливыми. Рост На эфф при подходе к точке компенсации иллюстрирует рис. 4.4.9.
По аналогии с (4.4.38) можно записать
НА эфф = м ks^M ,	(4.4.41)
введя таким образом эффективную константу анизотропии. Из (4.4.40), (4.4.41) и (4.4.39) видно, что в данном случае (энергиц
222
АНТИФЕРРОМАГНЕТИКИ И ФЕРРИМАГНЕТИКИ
(ГЛ. 4
анизотропии подрешеток аддитивны)
^эфф 3=3	К%.	(4.4.42)
Выражение (4.4.39), как и следовало ожидать, совпадает с аналогичным выражением для ферромагнетика. Мы убедились на простом примере, что при сделанных выше допущениях (низкочастотный тин колебаний, постоянное поле значительно меньше, чем первое обменное поле) эллипсоид вращения из анизотропного ферримагнетика приближенно эквивалентен такому же образцу из ферромагнетика с намагниченностью, равной результирующей намагниченности ферримагнетика, с g-фактором, равным эффективному g-фактору (4.4.16), и некоторой эффективной константой анизотропии. В случае аддитивной (например, одноион-ной) анизотропии она просто равна сумме констант анизотропии подрешеток. Можно убедиться на других примерах и, вероятно, доказать в общем виде, что этот вывод справедлив и для других ориентаций постоянного поля, других кристаллических симметрий, с учетом большего числа констант анизотропии, с учетом диссипации и т. д. В последнем случае должен быть введен, согласно (4.4.24), эффективный параметр диссипации. Этот вывод будет, конечно, справедлив и для произвольного эллипсоида, что следует из наличия уже отмечавшейся общей связи между внешней и внутренней восприимчивостями.
Приближенная эквивалентность ферримагнетика с эффективными параметрами для низкочастотного типа колебаний ферромагнетику будет оставаться в силе и для веществ с более сложными магнитными структурами. В частности, Туровым [21J было показано, что в коллинеарных магнитоупорядоченных кристаллах с любым числом подрешеток при наличии спонтанного момента М = SMj обменной природы (т. е. ферримагнетизма) среди ветвей спектра магнитных колебаний всегда будет одна низкочастотная или «ферромагнитная» ветвь. Очевидно, что такая ветвь колебаний будет иметься и в неколлинеарных ферримагнетиках. Для нее весь «пучок» векторов намагниченностей подрешеток Mj будет двигаться как одно целое (без изменения углов между МД, и это движение будет происходитьтак’же, как движение вектора М с эффективными параметрами 7"эфф, аэфф и т. д.
Вывод об эквивалентности (в указанном выше смысле) ферримагнетика ферромагнетику имеет большое практическое значение. Ферримагнетики являются важнейшим объектом для исследования магнитных колебаний в магнитоупорядоченных средах и единственным классом магнитных материалов, широко применяемым в настоящее время в технике сверхвысоких частот. В большинстве исследовательских работ и во всех применениях используется низкочастотный тип колебаний ферримагнетиков в сравнительно слабых -постоянных полях. То обстоятельство, что
§ 4.4]	ФЕРРИМАГНЕТИКИ	2'28
ферримагнетик ведет себя при этом, практически, как ферромагнетик, существенно упрощает все расчеты и, в частности, позволяет полностью применить теорию, которая была развита в предыдущих главах.
Однако не следует забывать и об особенностях магнитных колебаний в ферримагнетиках. Во-первых, кроме ферромагнитного типа колебаний, в них существуют п — 1 (где п — число подрешеток) высокочастотных, обменных колебаний. Их собственные частоты при малых постоянных полях лежат в «далекой» (длинноволновой) части инфракрасного диапазона. Максимумы поглощения, соответствующие этим колебаниям, обнаружены в некоторых редкоземельных ферритах со структурой граната [194J. Однако ряд обстоятельств, в первую очередь, слабая освоенность далекого инфракрасного диапазона и малая интенсивность колебаний (как мы видели, для изотропного ферримагнетика она пропорциональна (Yi — Т2)2), приводит к тому, что обменные типы колебаний в ферримагнетиках еще очень плохо изучены.
Во-вторых, вывод об эквивалентности ферримагнетика для одного из типов колебаний ферромагнетику несправедлив даже в слабых постоянных полях вблизи точек компенсации. В этой области частоты двух типов колебаний (для двухподрешеточного ферримагнетика) сближаются и обе зависят от константы обменного взаимодействия. Теоретическое рассмотрение колебаний вблизи точек компенсации встречает, как уже отмечалось, определенные трудности, связанные прежде всего с отысканием основных состояний с учетом анизотропии. В тех немногих случаях, когда такие расчеты были проведены, сравнение с ними экспериментальных результатов дало весьма ценную информацию (см., например, [191]).
В-третьих, специфика ферримагнетиков проявляется в сильных постоянных нолях, меньших, чем первое обменное поле 1Ц, но сравнимых с ним. При этом частоты обоих типов колебаний, как видно, например, из рис. 4.4.7, становятся сравнимыми по величине и зависят от обменной константы. В частности, при постоянном поле — Н^/2 происходит вырождение двух типов колебаний.
И, наконец, в-четвертых, при постоянном поле, лежащем в интервале между первым и вторым обменными полями, основное состояние ферримагнетика является неколлинеарным и магнитные колебания имеют много общего с колебаниями антиферромагнетиков в неколлинеарных основных состояниях.
ГЛАВА 5
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
§ 5.1. Уравнения
В предыдущих главах изучалось, в основном, поведение ферро-, антиферро- и ферримагнетиков в заданном переменном магнитном поле (при наличии постоянного магнитного поля). Это поведение определялось тензором магнитной восприимчивости, компоненты которого мы находили, решая уравнение движения намагниченности или систему уравнений движения намагниченностей подрешеток. Однако уже в § 1.4 отмечалось, что переменное магнитное полей, действующее на вещество в реальных системах, не может рассматриваться как заданное. Заданными являются поля или потоки энергии в каких-либо, обычно удаленных от ферромагнитных образцов частях системы. И для того чтобы полностью описать электромагнитные процессы в таких системах (найти как намагниченности, так и переменные поля), необходимо, кроме уравнений движения намагниченности, использовать уравнения электромагнитного поля, а также граничные условия на поверхностях раздела различных сред.
Простейшая задача такого типа рассматривалась в § 1.4; исследуемая система представляла собой малый (по сравнению с длиной электромагнитной волны) ферромагнитный эллипсоид в неограниченном пространстве; на больших расстояниях от эллипсоида имело место однородное переменное магнитное поле. В этом случае применимы уравнения магнитостатики, и мы (следуя Киттелю) воспользовались известным решением их для эллипсоида в однородном поле. Если образец — не эллипсоид или внешнее поле не однородно, это решение, конечно, неприменимо. Если же размеры образца сравнимы с длиной электромагнитной волны, то необходимо использовать уже не уравнения магнитостатики, а общие уравнения электродинамики.
Уравнения Максвелла. Макроскопическая электродинамика неподвижных сред основывается на уравнениях Максвелла [40,43]
rot Е-ф-= 0, divB = 0, с ot
rotH ——	= — J, divD=4n7?,
с dt с
(5.1.1)
§ 5.1]
УРАВНЕНИЯ
225
где Е и Н — векторы электрического и магнитного поля, a D и В — электрической и магнитной индукции, J — плотность свободного тока, Л — плотность свободного заряда. Напомним, что входящие в уравнения (5.1.1) величины являются [43] усредненными в пространстве и во времени значениями следующих микроскопических величин: вектор Е — электрического поля Ек, вектор D — величины Ем + 4лР (где Р — электрическая поляризация), вектор В — магнитного поля Нм, а вектор Н — величины Нм — 4лМ (где М — намагниченность).
В настоящее время нет сомнения в справедливости уравнений Максвелла (5.1.1). Эта уверенность основывается па том. что все их следствия полностью подтверждаются опытом. Кроме того, они следуют из уравнений Максвелла — Лоренца для полей Ем и Нм в вакууме, все следствия которых также находятся в полном согласии с опытом.
Граничные условия. Граничные условия, т. е. соотношения, которым удовлетворяют векторы Е, Н, D и В на границе раздела двух сред, являются следствиями уравнений Максвелла. Если обозначить индексом 1 величины в одной из сред, а индексом 2 — в другой и ввести единичный вектор нормали к граничной поверхности п0 (направленный из первой среды во вторую), то граничные условия запишутся следующим образом [41, 26]:
Ех X п0 — Е2 х п0 = О,
D^o— D2no = 4лц, Нгхио-Щхио = BjHo — В2п0 = О, где г) и I — поверхностные плотности свободных заряда и тока. Они равны нулю для реальных сред, но часто вводятся при приближенном рассмотрении границы очень плохо проводящей среды (диэлектрика) с хорошо проводящей (металлом). В этом случае в первом приближении *) можно считать, что поле в металле (второй среде) отсутствует и
Е1Хио = 0, Н1Хпо = ^-1,
В|П0 = 0, D1n0 = 4nT).	(5.1.3)
Тогда в диэлектрике электрическое поле нормально, а магнитная индукция (но, вообще говоря, не магнитное поле!) касательна к поверхности раздела с металлом.
(5.1.2)
J) В следующем приближении на границе металла, буду? иметь место граничные условия Леонтовича (см., например, [37]).
8 А. г. Гуревич
226
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Материальные соотношения. Для того чтобы получить полную систему уравнений, к уравнениям Максвелла (5.1.1) следует добавить так называемые материальные соотношения, дающие связь R, J, D и В с векторами Е и Н. Величины R и J связаны между собой уравнением сохранения заряда
divJ + # = 0’	(5-1.4)
которое, как легко убедиться, является следствием третьего и четвертого уравнений Максвелла (5.1.1). Поэтому достаточно дополнить уравнения Максвелла соотношениями, связывающими J, D и В с Е и Н. Они должны] явиться результатом микроскопической теории, рассматривающей конкретные свойства вещества, или следовать из эксперимента.
Разделение микроскопической задачи об определении материальных соотношений и макроскопической задачи об интегрировании уравнений Максвелла не всегда возможно. Часто эти задачи должны решаться совместно. Такое положение имеет место, например, в случае металлов при достаточно высоких частотах, когда глубина проникновения поля в металл («толщина скин-слоя») делается сравнимой или меньшей, чем характерные размеры, определяющие свойства вещества, например, размер доменов или длина свободного пробега носителей тока. Но для интересующих нас веществ — неметаллических ферро-, антиферро-и ферримагнетиков, толщина скин-слоя достаточно велика, и указанные задачи могут быть рассмотрены последовательно.
При достаточно больших (но легко достижимых на практике) величинах Е и Н материальные соотношения становятся нелинейными, что приводит к нелинейности всей задачи, несмотря на строгую линейность уравнений Максвелла. В ферро- и ферримагнетиках зависимость В от Н существенно нелинейна уже при довольно малых полях.
Уравнения для комплексных амплитуд. Нас интересуют процессы, при которых магнитное поле является суммой постоянного (или сравнительно медленно изменяющегося) и быстропеременного полей:
H = H0 + h~.	(5.1.5)
Для общности примем, что и электрическое поле
Е = Е0 + е~.	(5.1.6)
Тогда и остальные электродинамические величины представятся в виде таких же сумм:
D = D„ + d~, B = Bo + b~, J = Jo + j , R — R0 + p~- (5.1.7)
Если переменные поляЬ~ и е~ достаточно малы, то связь d~> и j~ и и 1ь~ можно считать линейной. При этом все перемен"
УРАВНЕНИЯ
227
§ 5.1]
ные составляющие будут изменяться во времени по гармоническому закону, если по такому закону изменяются заданные — «возбуждающие» переменные поля или токи. Воспользуемся, как и в предыдущих главах, методом комплексных амплитуд: запишем переменные составляющие в виде
е (г, t) — Re [е (г) е’и<],	(г, t) — Re fh(r) e’"f], - -(5.1.8)
где e (r), h (г) и т. д.— комплексные амплитуды соответствующих величин.
Подставив суммы (5.1.5), (5.1.6) и (5.1.7) в уравнения (5.1.1) и приняв во внимание (5.1.8), получим две независимые системы: одну — для постоянных (или медленно меняющихся) величин Ео, Но, Do, . . • и другую — для комплексных амплитуд быстропеременных величин. Первой системой, которая по форме будет совпадать с (5.1.1), мы интересоваться в дальнейшем не будем, считая, что решения ее известны. Заметим лишь, что при достаточно медленном изменении Ео, Но и т. д. во времени она распадется на две независимые системы; систему уравнений электростатики для Ео, Do и 7?о и систему уравнений магнитостатики для Но, Во и Jo-
div Во = 0, rotH0 = -у-Jo-	(5.1.9)
Система уравнений Максвелла для комплексных амплитуд переменных величин запишется следующим образом:
rote-}-—Ь = 0,	(5.1.10)
divb = 0,	(5.1.11)
roth-^d = ^j,	(5.1.12)
divd = 4np.	(5.1.13)
Заметим, что уравнение (5.1.11) является непосредственным следствием (5.1.10), а (5.1.13) следует из (5.1.12) с учетом соотношения
div j + trap = 0,	(5.1.14)
вытекающего из уравнения сохранения заряда (5.1.4). Граничные условия для комплексных амплитуд не отличаются от (5.1.2) или (5.1.3).
Остановимся теперь на форме материальных соотношений, связывающих комплексные амплитуды j, d и b с комплексными амплитудами ей h х). Плотность тока может быть записана
*) В дальнейшем, как и в предыдущих главах, мы будем опускать слова «комплексные амплитуды», подразумевая под всеми переменными величинами их комплексные амплитуды.
8*
228
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
следующим образом:
j — ое jcT»
(5.1.15)
где о — проводимость (j = ое — закон Ома), a jCT — сторонний ток; в этот ток, который при решении уравнений Максвелла обычно считается заданным, входят токи, имеющие неэлектромагнитное происхождение, а также токи, вызванные электромагнитными полями, не рассматриваемыми в данной задаче.
Будем считать, что электрическая индукция d не зависит от h, а магнитная b — не зависит от е х). Тогда для малых амплитуд
d = е1е,	(5.1.16)
b = ph,
(5.1.17)
где г.( — диэлектрическая проницаемость, ар — магнитная проницаемость. Величины о, ех и р в общем случае являются тензорами второго ранга с комплексными компонентами.
Для того чтобы исключить векторы d и b из уравнений (5.1.10) — (5.1.13), подставим в эти уравнения выражения (5.1.15), (5.1.16) и (5.1.17) и примем во внимание (5.1.14); тогда получим
rot е 4- ph = 0,	(5.1.18)
div (ph) = 0,	(5.1.19)
rot h - Ге = jCT,	(5.1.20)
div (ее) = 4лрст.	(5.1.21)
Здесь обозначено
8 = 8!— б,	(5.1.22)
рст= ~divjCT.	(5.1.23)
Комплексный тензор 8 мы будем называть электрической проницаемостью среды (в отличие от диэлектрической проницаемости Sj). Под электрической индукцией будем в дальнейшем понимать вектор
d — ее.
х) При этом исключаются из рассмотрела» сяавЫв:иапйИО8лектрические эффекты (см., например, [81]).
5 5.1]	УРАВНЕНИЯ	229
Очевидно, что уравнения (5.1.19) и (5.1.21) являются следствиями (5.1.18) и’ (5.1.20) с учетом (5.1.23).
Из уравнений (5.1.18) и (5.1.20) нетрудно исключить е или h и получить дифференциальные уравнения второго порядка для каждого из этих векторов:
rot(u-irote)--^7e = -^jCT, (5.1.24)
rot (е-1 rot h) — ph = rot (E-ljcT), (5.1.25)
где p-1 и е-1 — тензоры, обратные тензорам р и е [35].
Большое практическое значение имеет случай, когда в рассматриваемом объеме Jct = 0. Тогда из (5.1.20) и (5.1.21) получим
rot h —ее = 0,	(5.1.26)
div (ее) = 0.	(5.1.27)
Уравнения (5.1.18) и (5.1.26), а также (5.1.19) и (5.1.27) переходят одно в другое при замене
e^h, —р.	(5.1.28)
Отсюда вытекает, что и все следствия этих уравнений инвариантны относительно замены (5.1.28) (если, конечно, соответствующим образом заменить граничные условия). Это обстоятельство известно как принцип перестановочной двойственности [331.
Введем теперь обозначения компонент тензоров р и е. Представим р в виде суммы симметричного и антисиммет/ ичного тензоров [35]. Обозначим компоненты симметричного тензора
(Pc)ps = (Pc)sp = P'ps “ 9ps фрз,	(5.1.29)
(где p, s = 1, 2, 3 = x, y, z), а компоненты антисимметричного тензора
(P'ac)sp — (Pac)sp = фа sp ~ I (Haps фар®) (5.1.30)
(для антисимметричного тензора р =1= s). Здесь pps, pps, Paps и Haps — вещественные величины. Целесообразность введения именно таких обозначений будет ясна ниже. Три величины paps можно считать проекциями вектора 4ngm, где gm — магнитный вектор гирации, являющийся обобщением (1.2.25). Как легко убедиться,
b = pch ф- i4nhxgm.
(5.1.31)
230
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 6
Тензор ц может быть представлен также в виде суммы эрмито-еого (рв) и антиэрмитового (paB) тензоров. Их компонентыJ):
(Ps)ps P'ps Д' ф aps,	(Paa)ps — Ра ps фрз
(5.1.32)
(при р = з компоненты paps и paPs равны нулю). Соотношения, аналогичные (5.1.29) — (5.1.32), можно записать и для тензора е.
Тензоры рис являются функциями частоты, параметров вещества (намагниченности, констант анизотропии и пр.), а также величин и направлений постоянных полей Но и Ео. Наиболее существенно, конечно, влияние Но, которое и приводит к тиротропин среды — появлению антисимметричных компонент тензоров р и е, и магнитным резонансам — резонансным зависимостям компонент р от и и Но. Влияния Ео мы не убудем рассматривать, для интересующих нас сред оно мало.
Уравнения для изотропной среды. Остановимся на частном случае среды, изотропной в отсутствие поля Но. Для такой среды, как было показано выше, любые тензорные параметры имеют вид (1.2.29), если направление Но (единственное выделенное направление) совпадает с осью z. В частности,
			0
9 =		и	0
	0	0	И|
	е	ге а	0
Е =	— ie а	Е	0
	0	0	6II
(5.1.33)
(5.1.34)
’Строго говоря, р и е любых изотропных (в отсутствие постоянного лоля) сред приобретают в присутствии магнитного поля вид (5.1.33) и (5.1.34). Однако лишь для некоторых сред гиротропные (антисимметричные) компоненты ря и еа имеют значительную величину. К таким средам относятся прежде всего подробно рассмотренные в предыдущих главах ферро- и ферримагнетики. Для них (в диапазоне сверхвысоких ^частот) большую величину имеет
х) Соотношения (5.1.32) являются определениями эрмитового и антиэрмитового тензоров. Иными словами, эрмитовым называется тензор, у которого вещественные части компонент образуют симметричный тензор, а мнимые — антисимметричный; для антиэрмитового тензора — наоборот.
§ 5.1]
УРАВНЕНИЯ
231
|ia, а еа практически равно нулю. Примером среды с большой Еа (и р,а = 0) является плазма в магнитном поле [446]. Малыми, но все же заметными величинами р,а обладают намагниченные парамагнетики и антиферромагнетики, а небольшими величинами еа — ряд кристаллов и жидкостей (в которых наблюдается, в частности, эффект Фарадея) [43].
Таким образом, при изучении явлений в гиротропных средах можно обычно’одну из’величин, р,£или е, считать скалярной. Однако мы будем в этой главе рассматривать так называемую биги-ротропную среду, одновременно обладающую параметрами (5.1.33) и (5.1.34). Это даст определенные методические преимущества (симметрия получаемых уравнений, использование при их выводе принципа перестановочной двойственности).
Ограничение же средами, изотропными в отсутствие внешнего магнитного поля, т. е. имеющими параметры (5.1.33) и (5.1.34), позволит изучить электродинамические эффекты в системах с гиротропными средами в наиболее простой форме.
После этих предварительных замечаний рассмотрим некоторые пути решения уравнений электродинамики для среды с параметрами (5.1.33) и (5.1.34). Первым этапом решения должно быть получение уравнений для векторов е и h в отдельности. Один вариант таких уравнений — (5.1.24) и (5.1.25) был уже приведен выше. В данном случае входящий в (5.1.24) тензор (ц)-1 имеет вид
(5.1.35)
где
и,2
=	(5-1.36)
Г
(тензор е-1 выражается аналогичным образом).
Уравнения (5.1.24) и (5.1.25) неудобны тем, что при проектировании их на оси любой, в том числе и декартовой, системы координат получаются уравнения, в каждое из которых входят все
три составляющие е или h. Уравнения для отдельных декарто-
вых составляющих е и h проще всего получить, исключая остальные составляющие из проекций уравнений Максвелла (5.1.18) — (5.1.21). Ограничимся случаем, когда jCI = 0. Тогда, исключая
232
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПЙЫХ СРЕД [гл. 6
поперечные составляющие, получим для продольных уравнения 1)
(vi + "Г-	+ Аое И Н±) ez + к0'х к + у-) hz = 0,	4
(v± +	иеЛhz — Аоеи f-y- 4-j ez = О,
где
&<> = -?-,	(5.1.38)
a Vj_ — оператор Гамильтона («набла») в поперечной плоскости:
Г7	9 ,	9	r?2	S2 I S2
Vi = хоуг~ + У о -а~» т. е. V|=—— 4-——.
-1- цдх ду	-1-	дх% 1 ду2
Если среда не обладает гиротропией (еа = ц„ = 0), то система (5.1.37) распадается на независимые уравнения для ez и hz. Отсюда следует хорошо известный факт существования в такой среде поперечно-электрических ТЕ (с ez = 0) и поперечно-магнитных ТМ (с hz—G) электромагнитных полей (см., например, [29]). Для гиротропных сред, как видно из (5.1.37), поля ТЕ и ТМ могут существовать только, если они не зависят от z.
Исключая из уравнений (5.1.37) одну из величины, ez или /г~, и используя принцип перестановочной двойственности, мы убеждаемся, что ez и hz удовлетворяют одинаковым уравнениям
Ж(ег) = 0,	#(Лг) = 0,	(5.1.39)
где X — линейный дифференциальный оператор четвертого порядка
х = V1+ 4J4 £- + (4- + ) Vi	+ к> («,	иШ V1 +
4-2/соеир,и ^1 4-	4- ^оЕцР-иЕхР-л- (5.1.40)
Можно показать (см. [439,6]), что уравнениям (5.1.39) удовлетворяют и поперечные составляющие векторов е и h, а следовательно, и сами эти векторы:
5?(е) = 0, 5?(h) = 0.	(5.1.41)
Подчеркнем, что, в отличие от уравнений второго порядка (5.1.24) и (5.1.25), при проектировании уравнений четвертого порядка (5.1.41) на оси декартовой системы координат получаются независимые (и одинаковые) уравнения для каждой составляющей е и h. Если мы найдем решения этих уравнений для какой-нибудь
*) Достаточно получить исключением поперечных составляющих одно из уравнений (5.1.37), второе можно написать сразу, пользуясь принципом перестановочной двойственности (5.1.28).
§ 5.1]
УРАВНЕНИЯ
233
составляющей (что, конечно, но просто и может быть выполнено строго лишь в немногих частных случаях), то остальные составляющие можно будет получить с помощью уравнений Максвелла. Однако при этом снова придется решать дифференциальные уравнения. Поэтому целесообразно попытаться ввести некоторые скалярные функции (потенциалы), для которых были бы справедливы уравнения, аналогичные (5.1.39), и через которые все составляющие поля выражались бы простыми дифференцированиями.
Такой путь широко применяется в электродинамике сред со скалярными |1 и е [29. 331, где потенциальные функции, удовлетворяющие дифференциальным уравнениям второго порядка, вводятся отдельно для полей ТЕ и ТМ. Для гиротропных сред, как мы видели, полей ТЕ и ТМ в общем случае не существует. Однако для сред с параметрами (5.1.33) и (5.1.34) может быть введена скалярная функция ф *), которая удовлетворяет, как и декартовы составляющие поля, уравнению четвертого порядка
X (ф) = 0	(5.1.42)
и через которую все составляющие поля выражаются при помощи операций дифференцирования.
Очень хотелось бы представить дифференциальный оператор X в виде произведения двух операторов второго порядка, сведя тем самым уравнения четвертого порядка для функции ф или составляющих поля к дифференциальным уравнениям второго порядка. К сожалению, при произвольной зависимости полей от z это возможно только при ра = Еа = 0, т. е. если среда не обладает гиротропией.
Частный случай гармонической зависимости от г. Рассмотрим теперь частный случай, когда составляющие поля, а следовательно, и скалярная функция ф зависят от z — координаты в направлении постоянного магнитного поля по гармоническому закону. Тогда
Ф (х, у, z) = Z (z) ф± (ж, у),	(5.1.43)
где Z (z) — гармоническая функция (et,/f2\ cos kz z, sin kzz или их линейные комбинации). Этот случай включает в себя и любые поля, не зависящие от z (kz= 0). Для гармонической зависимо-сти от z оператор X, как легко убедиться, примет вид
^ = V4l + pV2±+?,	(5Д.44)
где р и q — некоторые функции компонент тензоров (5.1.33) и (5.1.34), к0 и kz. Оператор (5.1.44), в отличие от общего случая произвольной зависимости от z, может быть представлен в виде
*) Для магнитно-гиротропной среды — со скалярной е — это было показано Эпщтейном [449], Случай бигиротропной среды рассмотрен в [6].
234
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
произведения двух операторов второго порядка:
^=(V2J.+ «21)(V2±+x2),	(5.1.44')
где хх и х2 — корни квадратного уравнения
х4 — рх2 + q = 0.	(5.1.45)
Из (5.1.42) и (5.1.44') следует, что поперечная функция ф^и полная функция ф удовлетворяют теперь уравнениям ’Гельмгольца
?2±Ф± + <2ФХ=О.	(5.1.46)
Корни уравнения (5.1.45) имеют вид
и2,2 = ~g~| $ (Е ||	+ Р II Е±) —	&2] ±
+ \ f -у to (Е и Р1 ~~ РII Ех) ““ (-/• —jr)^l "+ №IIРII ("7" + *77')’
(5.1.47)
В случае изотропной среды (ео = ра = 0, ец = е, рц = р) отсюда следует, что Xi = х2 = х2 и имеет место известное соотношение [29]
Тс? = &о Ер ~ *2-
Для гиротропных сред оно не выполняется, и постоянная распространения kz связана с собстственными значениями хх и х2, характеризующими распределение поля в поперечных плоскостях, более сложным образом.
При гармонической зависимости от z векторы поля выражаются через функцию ф следующим образом:
е = Пуф, h = V уф.	(5.1.48)
Компоненты тензоров U и V [6] являются функциями компонент тензоров р и е, величин к0 и kz и корней хЬ2 уравнения (5.1.45). Существенно, что соотношения (5.1.48) справедливы не только в декартовых координатах, но и в любых ортогональных криволинейных координатах, для которых выполняются следующие условия:
1) зависимость от z является гармонической (или отсутствует),
2) направление постоянного намагничения совпадает с направлением координатных линий z.
На полученных соотношениях основывается довольно общий метод решения граничных электродинамических задач для гиротропных среде параметрами (5.1.33), (5.1.34). Он заключается в следующем. В системе координат, выбранной исходя из граничных условий задачи (и, конечно, удовлетворяющей приведенным
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
235
выше требованиям), записываются два решения уравнения (5.1.46), соответствующие величинам и х2 (которые определяются по формуле (5.1.47)). Для каждого решения по формулам (5.1.48) определяются составляющие поля. Эти «элементарные решения» должны быть затем сгруппированы в удовлетворяющие граничным условиям задачи собственные типы колебаний или волн. Учет граничных условий позволяет определить характеристики рассматриваемых колебаний или волн, например, собственные частоты полого резонатора, содержащего гиротропную среду, или постоянную распространения в волноводе с такой средой. При этом, однако, кроме приведенных выше условий, ограничивающих выбор систем координат, возникают и другие ограничения, которых мы коснемся ниже (§ 6.1).
§ 5.2.	Однородные плоские волны
Рис. 5.2.1. Оси координат при рассмотрении плоской волны в гиротропной среде.
В качестве первой, наиболее простой задачи электродинамики гиротропных сред рассмотрим распространение однородных плоских волн в неограниченной среде г). Эта задача представляет интерес не только как пример использования уравнений электродинамики гиротропных сред, но и как модель волноводных систем, содержащих гиротроп-ные среды.
Плоские волны в неограниченной гиротропной среде. Рассмотрим однородную плоскую волну, которая распространяется в среде с параметрами (5.1.33) и (5.1.34) под произвольным углом 6 к направлению постоянного намагничивания — оси z. Задача заключается прежде всего в определении постоянной распространения этой волны в зависимости от параметров среды и угла 6.
Поскольку среда не обладает анизотропией в плоскости ху, оси х и у можно направить
произвольным образом, например, так, чтобы волновой вектор (см. рис. 5.2.1) лежал в плоскости yz. Тогда функция ф (см. предыдущий параграф) для этой волны запишется следующим образом:
ф = фое-to = фое-' (^г+кг/),	(5.2.1)
где
kz — к cos 6, х = к sin 6.	(5.2.2)
*) Для однородной волны составляющие поля зависят только от одной координаты — в направлении распространения. Для плоских волн координата qs декартова, т. е. поверхности равной фазы qs = const представляют собой плоскости.
236
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЁД
[г Ji. fe
Очевидно, что х в (5.2.1) совпадает с собственным значением х в общей теории, рассмотренной в предыдущем параграфе. Зависимость от координаты z является в данном случае гармонической, и справедливо уравнение (5.1.45). Подставляя в (5.1.45) значения (5.2.2) величин kz и х, получим уравнение для волнового числа к:
№ / sin* 2 * 0 cos2 0 \ / sin2 0 . cos2 0 \
е11 +	6	+ И J
к2 Г / Е . Д । \	/	8 Ц \]
- — sin2 е Ui +	+ 2 cos2 0 1 + -gL +	= 0, (5.2.3)
Ag L	\ у r || /	\	/ j
где kB =alc, a (и аналогично EjJ определяется согласно (5.1.36).
Уравнение (5.2.3) можно получить и не прибегая к общей теории, рассмотренной в § 5.1, а исходя непосредственно [6] из уравнений Максвелла (5.1.18) и (5.1.26). Для однородной плоской волны, когда
е = eoe~ikr, h = hoe~ikr	(5.2.4)
(е0 и h0 — постоянные векторы), эти уравнения запишутся в виде
к х е0 + /copho = О, к X h0 — /соеео = 0.
(5.2.5)
Двум корням квадратного (относительно к2) уравнения (5.2.3) соответствуют две волны с различными волновыми числами '). Используя уравнения (5.2.5), можно определить поляризацию каждой из этих волн, т. е. найти направления векторов е0 и h0 и соотношения между их амплитудами и фазами. Это будет проделано ниже для некоторых частных случаев.
Для среды со скалярной е (поликристаллический ферро-, ферри-или антиферромагнетик) решение уравнения (5.2.3) запишется следующим образом 2):
/ Hj. \	/	/ р,	\2	р2
2 + sin20(— — 1 ±1/ sin4 0 [	— 1) + 4 cos2 0-775-
к2 = кдЁ-------------------  „Z.--------------------------==
и	« / S1H2 6 COS2 0
2 J----- । ----- i
X hi H /
= /СоЕрэфф (6).	(5.2.6)
*) Это обстоятельство не является специфическим для гиротропной среды а имеет место для любых сред с тензорными е или р.
2) Формула (5.2.6) была получена Поддером [113] для случая р ц = 1,
т. е. среды, намагниченной до насыщения.
। 6 2]	ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ	237
Заметим, что решение уравнения (5,2.3) при произвольных параметрах среды и произвольном направлении распространения не может быть представлено в виде
/с2 = /соСэффР-эфф,	(5.2*7)
где еЭфф зависело бы только от 6 и компонент тензора е, а рЭфф — от 6 и компонент р. Однако такое представление возможно, как мы убедимся ниже, для некоторых направлений распространения.
Компоненты тензора р, входящие в (5.2.3) и (5.2.6), зависят от частоты (а также от Но и параметров вещества). Эти зависимости были подробно исследованы в предыдущих главах. Зависят, вообще говоря, от частоты и компоненты е. Если частотные зависимости компонент р и е подставить в выражения (5.2.3) или (5.2.6), то получатся уравнения, связывающие частоту колебаний и с волновым числом к. Эти уравнения называются дисперсионными соотношениями. Зависимость и от к называют также (не особенно удачно) спектром волны.
С учетом диссипации компоненты р и е будут комплексными. Волновое число к, которое определяется уравнениями (5.2.3) или (5.2.6), окажется при этом также комплексным х):
к = к' - ik”.	(5.2.8)
Дисперсионными соотношениями теперь будут зависимости к' (и) и к" (и). Если возможна запись (5.2.7), то, как легко убедится, справедливы формулы Аркадьева [27]
/с = -к0 | Еэфф 11 Рэфф | -р бвффЦэфф ЕэффРвфф,	(5.2.9)
& =	| Еэфф | | Рафф | — ЕэффРвфф "4“ ЕэффРвфф. (5.2.10)
Продольно-намагниченная среда. Эффект Фарадея. Рассмотрим частный случай 0 = 0] (продольное намагничение). В этом случае решения уравнения (5.2.3) будут иметь вид
F=/с02(б±Еа)(р±ра).	(5.2.11) •*)
•*) Отрицательный знак перед ik" взят Для того, чтобы (для принятой зависимости от времени в*"1) волна затухала при положительном к".
238
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Подставляя (5.2.11) в проекции уравнений (5.2.5) (при 6 = 0), получим
е, h
ez = h2 = O,	(5.2.12)
(5.2.13)
Верхние знаки в (5.2.11), (5.2.12) и (5.2.13) соответствуют одной волне, а нижние — другой. Из (5.2.12) следует, что обе волны являются поперечными (ТЕМ) и имеют круговую поляризацию. Верхним знакам в (5.2.11), (5.2.12) и (5.2.13) соответствует волна с правым вращением, а нижним — с левым вращением векторов поля'). Этим волнам мы будем в дальнейшем приписывать индексы, соответственно пил. Величину £ можно назвать волновым сопротивлением продольно намагниченной среды для волн с правым и левым вращением.
Рассматривая случай 6 — л, мы нолучим те же выражения (5.2.11) и (5.2.12), а в (5.2.13) — обратные знаки перед радикалом. Заметим, что изменение знака волнового сопротивления при изменении направления распространения имеет место и для сред со скалярными параметрами. Из (5.2.11) и (5.2.12) следует, что при 6 = 0 или 6 = л могут быть введены эффективные скалярные параметры среды
®эфф п, л = ® Hz 8<м Р-вфф п, и = Р Ч~ Ца.
Это находится в соответствии с тем обстоятельством (см. §1.2), что [1+ = р ± рп является магнитной восприимчивостью для поперечного поля с круговой поляризацией и правым или левым вращением.
При исследовании поперечных волн, в частности, в продольно намагниченной гиротропной среде очень удобно использовать метод двух комплексных плоскостей. Сущность его заключается в том, что вместо векторов поля, лежащих в плоскости ху, вводятся комплексные числа. Их вещественные части являются проекциями соответствующих векторов на ось х, а мнимые — на ось у. Чтобы отличить эту пространственную комплексную плоскость от временной, введенной в связи с использованием комплексных амплитуд, мы будем мнимую единицу в пространственной плоскости обозначать через j.
Тогда комплексная амплитуда поперечного поля, например, электрического, линейного поляризованного в направлении, составляющем угол а с осью х, запишется в форме
елин = (cos а 4- j sin а) = е^а,
х) См. примечание 1 на стр. 31.
§ 5 2]	ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ	239
а комплексная амплитуда поля с круговой поляризацией — в форме
₽кр = еп, л (1 + ij), где еп, л = | е„, л | е,<₽п-л.
Пользуясь методом двух комплексных плоскостей, можно очень просто получить необходимые нам в дальнейшем соотношения, характеризующие произвольное (эллиптически поляризованное) поперечное поле. Такое поле является суммой двух полей с круговой поляризацией;
с = |en|ei<₽n(l - ij) + |сл|е^(1 + ij). (5.2.14)
Выражение (5.2.14) можно записать в виде
е = [(| еп| + кл |)+ ij(|₽п| - клI)е^(<₽п+<₽л) , (5.2.14') где
Отсюда видно, что произвольное поперечное поле может быть представлено в виде суммы двух полей с амплитудами (| еп | + + кл I) и (кп | — | ел |), линейно поляризованных в пространстве в двух взаимно перпендикулярных направлениях и сдвинутых по фазе во времени на л/2.
Нетрудно убедиться, переходя от комплексных амплитуд к мгновенным значениям ех и еу, что конец вектора е движется в плоскости ху по эллипсу с полуосями (| еп |	| ел |) и (| еп | —
— | ел |). Большая полуось эллипса составляет с осью х угол ft. Мы будем называть его углом поляризации поля, а отношение полуосей
I еп I I ел I — эллиптичностью поля.
Рассмотрим изменение угла поляризации и эллиптичности произвольно поляризованной волны в продольно намагниченной гиротропной среде. Пусть волна распространяется в положительном направлении оси z и при z = 0 комплексные амплитуды ее составляющих с круговой поляризацией имеют вид
еп о = К о| ег<,,по,	ел о = к* о | ег<₽л °.
При z = I комплексные амплитуды будут следующими:
еа = | еП о | ё~кп1,е1 * * * (фп<г*пО ел = | ел 01 e"V е5	(5 2.17)
Используя (5.2.15), найдем угол поляризации при z — I
0	+ ДО,	(5.2.18)
240 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД [ГЛ. 5
где начальный угол (при z = 0)
= -тгОРчо — Фло),	(5.2.19)
а угол поворота поляризации на пути длиной I ^^~{кя-кя)1.	(5.2.20)
Эллиптичность при z = I, согласно (5.2.16), выразится так:
Э = cth | -g- (т]п 0 — т]л 0) 2~ (кГ[ — кп) 11 ,	(5.2.21)
где углы т]по и цл0 определяются выражениями |еп0| = е4110, |ело| = е1'л0.
Поворот поляризации волны в продольно намагниченной гиротропной среде на угол Ай, определяемый выражением (5.2.20), представляет собой эффект Фарадея. Важно подчеркнуть, что направление поворота не зависит от направления распространения волны. Действительно, для волны, распространяющейся от плоскости z = 0 в отрицательном направлении оси z, при z = — I будут справедливы те же выражения (5.2.17), и следовательно, угол поляризации и эллиптичность будут такими же, как для волны, распространяющейся в положительном направлении, при z — I. В частности, при прохождении волной отрезка I в прямом и обратном направлениях угол поворота поляризации удваивается х). Из выражения (5.2.20) видно, что угол поворота поляризации изменяет свой знак при изменении направления постоянного намагничения, так как при этом правая и левая волны меняются местами.
В частном случае при z = 0 может быть | еп | = | ея |, тогда, согласно (5.2.14), волна при z - 0 будет линейно поляризована в направлении, составляющем с осью х угол (5.2.19) (эллиптичность ее Эо = оо). На пути I ее поляризация повернется на угол (5.2.20), а эллиптичность, согласно (5.2.21), составит
3-cth(4-|^-^|z).	(5.2.22)
Таким образом, волны с эллиптической, в частности, линейной (при некотором z) поляризацией распространяются в продольно намагниченной гиротропной среде с преобразованием поляризации — угол поляризации и эллиптичность изменяются по мере распространения. Только волны с круговой поляризацией распространяются без изменения поляризации, изменяется лишь их амплитуда и фаза. Такие волны являются нормальными волнами данной системы.
*) При этом не учитывается отражение волн на границах отрезка.
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
241
Рассмотрим теперь в качестве примера распространение элект-тромагнитных волн в продольно намагниченном ферромагнетике. При этом е можно считать скалярной величиной, а для компонент р принять зависимости, полученные в главах 1 и 3. Остановимся на случае достаточно сильных постоянных полей, когда вещество
Рис. 5.2.2. Дисперсионные соотношения для электромагнитных волн в непроводящем, намагниченном до насыщения ферромагнетике (без учета диссипации). О— угол между направлением распространения и направлением намагничения.
намагничено до насыщения (доменная структура отсутствует), и пренебрежем диссипацией. Тогда для (р, ± р,а) будет справедливо выражение (1.2.43). Подставляя его в (5.2.11), получим с учетом (5.1.38) дисперсионное соотношение
С0м
ощ + со +	= 0.	(5.2.23)
Здесь, как и в (5.2.11), верхний знак соответствуют волне с правым вращением, а нижний — с левым.
Зависимости со от к, которые следуют из уравнения (5.2.23) для волн с правым и левым вращением, приведены на рис. 5.2.2. Из этого рисунка видно, что для волны с левым вращением (для которой р и ра не проходят через резонанс) дисперсионное соотношение мало отличается от линейной зависимости со (/с), которая имела бы место для среды с не зависящими от со параметрами. Для волны с правым вращением спектр имеет две ветви1). Дляод-
!) Аналогичные ветви возникают, как мы увидим, и для других направлений распространения. Волны, соответствующие магнитостатическим ветвям (с ограниченной частотой), будут подробно рассмотрены в главе 7. В главе 8 мы убедимся, что учет обменного взаимодействия для этих волн приводит к тому, что компоненты р начинают зависеть не только от частоты, но и от волнового вектора, что приводит к дальнейшему усложнению дисперсионных соотношений.
242
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
ной из них (ее можно назвать электромагнитной) со неограниченно
растет с ростом к, стремясь к с
Рис. 5.2.3. Зависимости параметров, характеризующих распространение волн в продольно намагниченном феррите, от постоянного магнитного поля. О,— угол поворота поляризации на пути в 1 cat; Sl — эллиптичность в конце пути в 1 с.« волны, линейно поляризованной в начале. Для Но > 1000 э принимались значения р и цо, полученные по формулам § 1.3 при М„-=160 гс, <о/2я= 9,4 Ггц и о>г = З-Ю8. Для Н < 1000 э использовались экспериментальные зависимости рис. 3.1.4. Было принято е = 9. Горизонтальная штрих-пунктирная прямая— расчет по формуле (5.2.24).
высоких частотах^ сипацией, получим
]/е к. Для другой — магнитостатической или спиновой ветви со при больших к стремится к постоянной величине сод.
С учетом диссипации волновое число к, как уже отмечалось, становится комплексным. Величины к' и к" для правой и левой волн определятся при этом в результате подстановки в (5.2.9) и (5.2.10) (при скалярном е) вещественных и мнимых частей рЭфф = р ± ра. Результаты такого расчета, а также расчета угла поворота поляризации и эллиптичности по формулам (5.2.20) и (5.2.22) приведены на рис. 5.2.3.
Как видно из рис. 5.2.3, изменение параметров правой волны носит резонансный характер; в области резонанса имеет место интенсивный максимум поглощения, а угол поворота поляризации изменяет знак. Изменение параметров левой волны, как и следовало ожидать, не является резонансным.
Рассмотрим теперь частный случай постоянных полей, малых по сравнению с резонансным полем, однако достаточно больших, чтобы ферромагнетик можно было считать намагниченным до насыщения и использовать результаты теории, рассмотренной в главе 1. Очевидно, что этот случай может осуществиться лишь при достаточно со/у и пренебрегая дис-
Учитывая, что Но
ф =	(5.2.24)
В таком приближении угол поворота поляризации не зависит
$ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ волны
243
ни от частоты, ни от Но, а определяется только е и намагниченностью вещества.
Учитывая результаты, полученные в § 3.1, формулу (5.2.24) можно использовать и при полях, недостаточных для насыщения,
если Мо заменить на «техническую» намагниченность при данном поле. Как следует из формулы (5.2.24) и рис. 5.2.3, угол поворота поляризации в ферритах может иметь значительную величину в сравнительно слабых постоянных полях при малых потерях и небольшом снижении эллиптичности. Это позволило широко использовать эффект Фарадея в намагниченных ферритах в технике сверхвысоких частот [11].
Отражение от границы раздела. Перейдем теперь к изучению одно
Рис. 5.2.4. Прохождение волны через границу раздела продольно намагниченных сред.
родных плоских волн при наличии границ раздела между различными гиротропными средами. Ограничимся по-прежнему случаем продольно намагниченных сред (0 = 0 или 0 = л) и рассмотрим для простоты бесконечные плоские поверхности разде
ла, перпендикулярные направлению распространения и намагничения. Остановимся прежде всего на простейшей задаче такого типа — об отражении от границы раздела.
Пусть на плоскую поверхность раздела падает волна из среды I (рис. 5.2.4), а в среде II отсутствуют волны, распространяющиеся по направлению к границе, т. е. выполняется так называемое условие излучения. В качестве падающей волны примем сначала волну с круговой поляризацией и правым или левым вращением. Комплексные амплитуды этой волны запишем в форме
e1+n,n=^(l=Fi7-)e4/Cln-<
^П, Л =	(1 + ii) e’ifcl п- Л
п, л
(5.2.25)
где А — заданная величина. Предположим, что отраженная волна в области I и проходящая в области II будут волнами также с круговой поляризацией и тем же направлением вращения (относительно фиксированного направления — оси z), что и падающая волна. Тогда их комплексные амплитуды запишутся следующим образом:
ein, л = В (l=pi7)eikin,nzt
К п. л = -	(1 =F И) elfei". <
ЧП, Л
(5.2.26)
244
осйовЫ г6Лек'гроДинамикй ГПРОТРОПНЫХ сред
1гЛ. 5
и
4п.л = С (l + i/)e-ik2n.«z,	(5.2-27)
п, л =	(1 + ij) e~ik*п- д2.
^2 П, Л
Знак минус перед выражением для ЛГП,Л записан на том основа-нии, что для волны, распространяющейся в отрицательном направлении оси z (6 = л), волновое сопротивление имеет обратный знак.
Для определения неизвестных величин В и С в (5.2.26) и (5.2.27) воспользуемся граничными условиями (5.1.2), которые в данном случае дадут
4п,л + еГи,л = 4п,л,	(522g)
h\ п, Л “F П, Л — ^2 П, Л •
Если подставить (5.2.26) и (5.2.27) в (5.2.28), то множители (1 н2 ij) сократятся и амплитуды В и С выразятся через А:
В = Гп, ЛА, С = D„t ЛА, где коэффициент отражения
Гп, л =	,	(5.2.29)
=2 п, л "Г =1 п, л
а коэффициент прохождения
2t
Яп.л = т------------	(5.2.30)
»2п, Л ' ^1 п. л
Таким образом, граничные условия на поверхности раздела двух продольно намагниченных гиротропных сред удовлетворяются при наличии падающей, отраженной и проходящей волн с круговой поляризацией и одним каким-либо направлением вращения. Иными словами, волны с круговой поляризацией — нормальные волны в таких средах — проходят через границу раздела без изменения их поляризации.
Заметим, что выражения (5.2.29) и (5.2.30) имеют такой же вид, как выражения для Г и D на стыке двух линий передачи с характеристическими сопротивлениями и £2 (см., например, [29]). И мы могли бы записать эти выражения сразу, если бы учли, что комплексные амплитуды еп.л и /гп,л волн с круговой поляризацией удовлетворяют всем условиям, которые предъявляются к переменным обобщенной теории линий передачи [29]. В дальнейшем мы используем это обстоятельство, применяя ап-
§ 5.21
ОДНОРОДНЫЕ ПЛОЙКИЕ воЛйы
245
Рис. 5.2.5. Прохождение волны через слой продольно намагниченной среды.
парат теории линий передачи к волнам с круговой поляризацией в продольно намагниченных гиротропных средах, как это было предложено Поливановым, Колли и Хасиной [444].
Если падающая на границу раздела волна имеет произвольную поляризацию, то ее можно разложить на две волны с круговой поляризацией и, рассмотрев прохождение каждой из этих волн, сложить затем амплитуды отраженных и проходящих волн. Углы поляризации и эллиптичности отраженной и проходящей воли определятся тогда по формулам (5.2.15) и (5.2.16).
Рассмотрим частный случай падения линейно поляризованной волны из изотропной среды (например, вакуума) на границу с гиротропной средой. Эллиптичности отраженной и проходящей волн в этом случае будут иметь вид
|дп| + |рл| 1°п|-|рл| ’
(5.2.31)
а углы поляризации (при f)na„ = 0) запишутся следующим образом:
&отр = -у targ arg
(5.2.32),
1
'в'прох [arg (Пп) — arg (£)л)].
Подчеркнем, что параметры (5.2.31), (5.2.32) относятся к гра-ницр раздала сред (z = 0). При дальнейшем распространении в гиротропной среде параметры проходящей волны будут преобразовываться так, как было рассмотрено выше. Поворот поляризации при отражении от гиротропной среды носит название магнитооптического эффекта Керра. Из формул (5.2.32) следует, что этот эффект отсутствует, так же как и поворот поляризации проходящей волны (при z = 0), если параметры среды р, ра и е являются вещественными.
Прохождение через слой. Перейдем теперь к рассмотрению несколько более сложной задачи о прохождении плоской волны через плоскопараллельный слой продольно намагниченной гиротропной среды ^>ис. 5.2.5). Параметры остального пространства примем скалярными и равными е = р = 1.
246
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Комплексную амплитуду падающей волны в области I можно записать в виде
4 = [etn (1 — if} + et л (1 + if}} е~;/‘°2,	(5.2.33)
ГД® etn и etл— заданные комплексные величины. Примем, что в области III имеет место только проходящая волна, распространяющаяся от слоя II. Задача заключается в определении амплитуды этой волны и амплитуды отраженной волны в области I. Как отмечалось выше, для решения подобных задач можно использовать аппарат теории линий передачи, применяя его к двум нормальным волнам с круговой поляризацией и суммируя затем полученные амплитуды этих волн.
Не останавливаясь на несложном решении задачи теории линий для данного случая, приведем лишь ответ. Амплитуды отраженных волн в I области (при z — 0)
е1 И, Л = ^П, Ле1 П. Л »	(5.2.34)
где коэффициенты отражения
>	_ _____цп, л_______
П,П - г’п, n~ictgftn. лг
(5.2.35)
Амплитуды проходящих волн в области III (при z = Г} е3+п.л = £>в.л^п,л,	(5.2.36)
где коэффициенты прохождения
Рп ч =-----г——г 	(5.2.37)
cos/cn. лг +W’n, л81Г1 кп,л1	4	’
Здесь &п, л — постоянные распространения во II области, которые определяются выражением (5.2.11),
,,	1 / £п, Л	£<) И, Л \	т, __ 1 / £п, Л ] £о И, Л
™п, л о \ 7*	7* I > л ~ ' 2 17*	t
* \ Чп, л »п. л /	4 \Ц п, л ^п, л
где tn, л — волновые сопротивления во II области, которые определяются формулой (5.2.13), а £0 п. л— + 1 — волновые сопротивления в областях I и III.
Окончательное решение задачи будет иметь вид
е? = [Рп(1 — if} etn + Рл(1 + ij) etn] eifc»z,
(5.2.38) e3 = [Рп (1 ~ ij) etn + Рл (1 + ij) et«] e^« W.
Углы поляризации и эллиптичности отраженной и проходящей волн определятся по общим формулам (5.2.15) и (5.2.16). Легко могут быть вычислены и коэффициенты отражения и прохожде
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
247
ния «по мощности», которые можно определить как отношения мощностей некоторых составляющих отраженной и проходящей волн к мощности падающей волны. Поскольку параметры I и IIII областей одинаковы, эти коэффициенты равны отношениям квадратов модулей соответствующих комплексных амплитуд.
Остановимся несколько подробнее на частном случае линейной поляризации падающей волны *) (ej п = Щ ; ej, когда для углов поворота поляризации и эллиптичностей справедливы формулы (5.2.31) и (5.2.32). Коэффициенты прохождения по мощности запишутся в этом случае, как нетрудно убедиться, следующим образом: для составляющих, поляризованных так же, как падающая волна, и перпендикулярно ей
Tx=~\Dn+ Dit\\ 7’v = ^|Dn-DJI|2;	(5.2.39)
для составляющих, поляризованных, соответственно, по большой и малой осям эллипса поляризации,
Т’макс = 4(IЯп| + ||)2, 7’мин = 4(1£>п|-|Рл|)2. (5.2.40)
Отношение полной мощности проходящей волны к мощности падающей волны
Т = Тх + Ту = Тматаз Ц- Тмпн = -g- (| Dn |2	1 Da |2) (5.2.41)
можно назвать полным коэффициентом прохождения по мощности. Аналогичным образом могут быть определены и коэффициенты отражения по мощности, например,
^X=4-Irn + Z\|2.	(5.2.42)
Рассмотрим предельный случай малой толщины слоя (| &п. al |	!)• Принимая, что еа = 0, получим в первом при-
ближении
1
'б'прох = ~2~ ^О^а,	(5.2.43)
Т’макс = 1 - V (|Х" + е").	(5.2.45)
Обращает на себя внимание, что в этом предельном случае угол поворота поляризации зависит только от р,'(, а эллиптичность только от ра-
г) Этот случай был рассмотрен Гинцбургом и Сулом и Уокером [446]. Аналогичная задача, но f металлической плоскостью в области III решалась в уже упоминавшейся работе [444].
248
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
ГЛ. 5
Для произвольной толщины слоя все вычисления по приведенным выше формулам существенно упрощаются, если можно пренебречь диссипацией, т. е. считать р, ра, е и ей вещественными. Тогда, например,
ФпрОХ -
arctg
' 1 \ /1
— tg кл1\ — arctg I—tg kJ.
(5.2.46)
Результаты расчета зависимости Опрох от толщины слоя приведены на рис. 5.2.6.
Рассмотренная одномерная система — неограниченный плоскопараллельный слой гиротропной среды, представляет интерес как простейшая модель так называемых фарадеевых или поляризационных ферритовых устройств диапазона СВЧ [11]. В этих устройствах продольно намагниченный ферритовый образец имеет огра
Рис. 5.2.6. Зависимость угла поворота поляризации волны, прошедшей через слой продольно намагниченного феррита, от толщины слоя 1.1 — расчет по формуле (5.2.46) — без учета диссипации— при ц = 0,9; |ift = 0,5 и е = 9; 2— расчет по общей формуле (5.2.32) при техже значениях вещественных частей компонент ji и е и ц," = 0,7; 8— по формуле (5.2.43)— для тонкого слоя (Хо— длина волны в свободном пространстве).
ниченные размеры и иногда довольно сложную форму и находится внутри волновода. Электромагнитные поля в таких устройствах, конечно, значительно сложнее, чем в рассмотренной одномерной системе. Однако многие особенности поведения продольно намагниченных ферритовых образцов в волноводах, как, например, нелинейная
волны от длины образца, находят
зависимость угла поворота поляризации проходящей качественное объяснение на
модели гиротропного слоя.
Плоские волны в поперечно намагниченной среде. Вернемся к задаче о распространении волн в неограниченной среде и остановимся на другом частном случае — поперечного намагничивания (6 = л/2). Направление распространения волн совпадает теперь с осью у (рис. 5.2.1).
При 6 = л/2 уравнение (5.2.3) имеет два решения:
fci = ^оУвиНд.,
к9 = к0 Ур и
(5.2.47)
(5.2.48)
§ 5.21
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
249
а система уравнений — проекций (5.2.5) распадаотОД на две независимые системы:
е2 + phx 4- iVahy = О, ipa/ix 1 9, ® и 4 hx ~ О,
~h2 — яех — isaey = О, г’еаел. — ееу — О, Р|Л--^л. = °.
(5.2.49)
(5.2.50)
Нетрудно убедиться, что (5.2.47) является условием совместности системы (5.2.49). Система (5.2.50) при к = кх имеет только нулевые решения. Следовательно, для первой волны
hz = ех = еу = 0.	(5.2.51)
Для этой волны электрическое поле линейно поляризовано в направлении постоянного намагничивания. Как видно из (5.2.49),
Рис. 5.2.7. Векторы поля и индукции для волн в поперечно намагниченной гиротропной среде, а— волна ТЕ; б— волна ТМ (относительно направления распространения).
для нее Ьу = 0 и вектор переменной магнитной индукции линейно поляризован по оси х (рис. 5.2.7, а). Магнитное же поле эллиптически поляризовано в плоскости, перпендикулярной оси z, эллиптичность его
= р/ра.
(5.2.52)
Итак, первая волна является поперечно-электрической (ТЕ) относительно направления распространения и поперечно-магнитной (ТМ) относительно направления постоянного поля — оси z.
246
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Комплексную амплитуду падающей волны в области I можно записать в виде
= [еГп (1 - V) + ejл (1 + */)] е~*°г,	(5.2.33)
где Ci п и ex л—заданные комплексные величины. Примем, что в области III имеет место только проходящая волна, распространяющаяся от слоя II. Задача заключается в определении амплитуды этой волны и амплитуды отраженной волны в области I. Как отмечалось выше, для решения подобных задач можно использовать аппарат теории линий передачи, применяя его к двум нормальным волнам с круговой поляризацией и суммируя затем полученные амплитуды этих волн.
Не останавливаясь на несложном решении задачи теории линий для данного случая, приведем лишь ответ. Амплитуды отраженных волн в I области (при z = 0)
ei п, л = Гп> лех п, л >	(5.2.34)
где коэффициенты отражения
I ____ ______цп, л_______
П,Л - г’п,л-гс18/сп.л/
(5.2.35)
Амплитуды проходящих волн в области III (при z — I) еЗП, 31 — Ин, яе1 п, л>	(5.2.36)
где коэффициенты прохождения
Рп Л =------;----------------г •	(5.2.37)
cos/cn. лг+»’п, л81П Лп,лг	'
Здесь Ап, л — постоянные распространения во II области, которые определяются выражением (5.2.11),
1 / £п, Л	£о П, Л \	__ 1 / £п, л | ^оп, л
^п, и ~~~ о । $•	I » ^п, л “ 2 ( Г I	I »
\ »0п, л	»п, л /	4 \ =о п, л =п, л /
где ^п, л — волновые сопротивления во II области, которые определяются формулой (5.2.13), а £0 п, л= + I — волновые сопротивления в областях I и III.
Окончательное решение задачи будет иметь вид
е? = [Гп (1 - 0)	+ Гл (1 + ij) е}л] е«Ч
(5.2.38)
ез = [Оп (1 - ij) etn + £>л (1 + ij) et л]
Углы поляризации и эллиптичности отраженной и проходящей волн определятся по общим формулам (5.2.15) и (5.2.16). Легко могут быть вычислены и коэффициенты отражения и прохожде
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
247
ния «по мощности», которые можно определить как отношения мощностей некоторых составляющих отраженной и проходящей волн к мощности падающей волны. Поскольку параметры I и III областей одинаковы, эти коэффициенты равны отношениям квадратов модулей соответствующих комплексных амплитуд.
Остановимся несколько подробнее на частном случае линейной поляризации падающей волны *) (ein— etn^Cj), когда для углов поворота поляризации и эллиптичностей справедливы формулы (5.2.31) и (5.2.32). Коэффициенты прохождения по мощности запишутся в этом случае, как нетрудно убедиться, следующим образом: для составляющих, поляризованных так же, как падающая волна, и перпендикулярно ей
=	«ч|2, Ту = 4-1 Dn - Лл |2;	(5.2.39)
для составляющих, поляризованных, соответственно, по большой и малой осям эллипса поляризации,
Умакс = 4 (I	| + I Da |)2, Т’мин = 4 (I Пп I - I I)2. (5.2.40)
Отношение полной мощности проходящей волны к мощности падающей волны
Т = ТХ+ТУ = Гмакс + Гмин = 4 (I Du |2 + | D.n I2) (5.2.41) можно назвать полным коэффициентом прохождения по мощности. Аналогичным образом могут быть определены и коэффициенты отражения по мощности, например,
Px=4lrn + ^|2-	(5.2.42)
Рассмотрим предельный случай малой толщины слоя (| кп, Я11 <<: 1). Принимая, что еа = 0, получим в первом приближении
^прох = ^o^ai	(5.2.43)
Э = —,	(5.
Гмакс = 1 - к01 (и" + е").	(5.2.45)
Обращает на себя внимание, что в этом предельном случае угол поворота поляризации зависит только от р„, а эллиптичность только от |Ха.
х) Этот случай был рассмотрен Гинцбургом п Сулом и Уокером [446]. Аналогичная задача, но с металлической плоскостью в области III решалась в уже упоминавшейся работе [444].
248
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
ГЛ. 5
Для произвольной толщины слоя все вычисления по приведенным выше формулам существенно упрощаются, если можно пренебречь диссипацией, т. е. считать р,, ра, е и еа вещественными. Тогда, например,
^прох — 2
arctg
’ 1 \
— tg kJ) — arctg I
tg kjX\ \ vn	/]
(5.2.46)
Результаты расчета зависимости Опрох от толщины слоя приведены на рис. 5.2.6.
Рассмотренная одномерная система — неограниченный плоскопараллельный слой гиротропной среды, представляет интерес как простейшая модель так называемых фарадеевых или поляризационных ферритовых устройств диапазона СВЧ [11]. В этих устройствах продольно намагниченный ферритовый образец имеет огра
Рис. 5.2.6. Зависимость угла поворота поляризации волны, прошедшей через слой продольно намагниченного феррита, от толщины слоя 1.1 — расчет по формуле (5.2.46) •— без учета диссипации— при р. = 0,9; ц([ = 0,5 и е = 9; 2— расчет по общей формуле (5.2.32) при тех же значениях вещественных частей компонент р и е и р," = 0,7; з— по формуле (5.2.43)— для тонкого слоя (Хо— длина волны в свободном пространстве).
ниченные размеры и иногда довольно сложную форму и находится внутри волновода. Электромагнитные поля в таких устройствах, конечно, значительно сложнее, чем в рассмотренной одномерной системе. Однако многие особенности поведения продольно намагниченных ферритовых образцов в волноводах, как, например, нелинейная
волны от длины образца, находят
зависимость угла поворота поляризации проходящей качественное объяснение на
модели гиротропного слоя.
Плоские волны в поперечно намагниченной среде. Вернемся к задаче о распространении волн в неограниченной среде и остановимся на другом частном случае — поперечного намагничивания (6 = л/2). Направление распространения волн совпадает теперь с осью у (рис. 5.2.1).
При 6 = л/2 уравнение (5.2.3) имеет два решения:

^2 — &0 У 1| еЛ»
(5.2.47)
(5.2.48)
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ волны
249
а система уравнений — проекций (5.2.5) распадается на две независимые системы:
к	+ Wahy = 0, ' гца/гж —	= 0, & II ^z 4	^х = 0,
к kt)	-hz — чех—ieaey = 0,
	ieaeT — eev = 0,
	нА — -^-ех = о.
(5.2.49)
(5.2.50)
Нетрудно убедиться, что (5.2.47) является условием совместности системы (5.2.49). Система (5.2.50) при к = кг имеет только нулевые решения. Следовательно, для первой волны
/iz = ех = еу = 0.	(5.2.51)
Для этой волны электрическое поле линейно поляризовано в направлении постоянного намагничивания. Как видно из (5.2.49),
Рис. 5.2.7. Векторы поля и индукции для волн в поперечно намагниченной гиротропной среде, а— волна ТЕ; б — волна ТМ (относительно направления распространения).
для нее bv = 0 и вектор переменной магнитной индукции линейно поляризован по оси х (рис. 5.2.7, а). Магнитное же поле эллиптически поляризовано в плоскости, перпендикулярной оси z, эллиптичность его
= ц/ца.
(5.2.52)
Итак, первая волна является поперечно-электрической (ТЕ) относительно направления распространения и поперечно-магнитной (ТМ) относительно направления постоянного поля — оси z.
250 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД [ГЛ. 5
Таким же образом легко убедиться, что для второй волны — с постоянной распространения (5.2.48) векторы поля направлены так, как показано на рис. 5.2.7, б, т. е. эта волна является волной ТМ относительно направления распространения и волной ТЕ относительно оси z.	1
Если р скалярно (случай, обычно рассматриваемый в оптике), то первая волна превращается в волну ТЕМ. Если же, как для
Рис. 5.2.8. Частотные зависимости компонент тензора ц и эффективнх проницаемостей намагниченного до насыщения ферромагнетика (без учета диссипации).
ферро-, ферри- или антиферромагнетиков в СВЧ диапазоне, е скалярно, то вторая волна превращается в «обыкновенную» ТЕМ волну с постоянной распространения
/с2 = к0 ]Лец ||,	(5.2.53)
а первая —«необыкновенная» ТЕ волна имеет постоянную распространения
кг = к0 ерх.
(5.2.54)
§ 5.2]
ОДНОРОДНЫЕ ПЛОСКИЕ ВОЛНЫ
251
Рассмотрим распространение волны при 6 = л/2 в намагниченном до насыщения ферромагнетике. Тогда р ц — 1 и
^2 = ^оТЛё’-	(5.2.55)
Если пренебречь диссипацией, то для р и ра будут справедливы выражения (1.2.34) и (1.2.35), и
__ (ин + 0)м)2 — 0)2
(Од (Од -4- <ом) — ©2
Эта величина проходит через резонанс (рис. 5.2.8) при частоте
o)_l — V(1,н (о)д -j- (им) = у УHi0 (tfi0 -р 4л7И)	(5.2.57)
(при которой р обращается в нуль). Ее иногда называют частотой поперечного ферромагнитного резонанса. Она совпадает (так
Рис. 5.2.9. Зависимости вещественной и мнимой частей от постоянного магнитного
поля. Расчет проводился при тех же значениях параметров, что и на рис. 5.2.3. Для сравнения показана кривая р/ (Яо), рассчитанная при этих же значениях параметров.
как при этом Hio = №о) с резонансной частотой (1.4.19) в тонкой пластине, намагниченной касательно к ее плоскости. Как видно из (5.2.56), рд. (без учета диссипации) обращается в нуль при оз = ын +	== у (Яо + ^пМ).	(5.2.58)
Интересно, что при этом же условии обращается в нуль (см. рис. 5.2.8) и величина р+ = р + р„ хотя резонансные частоты Рх и Р+ существенно различаются.
252
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[гл. 5
С учетом (5.2.56) из (5.2.54) следует дисперсионное соотношение для необыкновенной волны в поперечно намагниченной (до насыщения) среде:
fc2 = ®2 - (^ + “м)2~<°2 2 .	(5.2.59)
е	<Од (сод ч>м)2 — <о
Зависимость со {к), которая определяется этим соотношением, приведена на рис. 5.2.2 наряду с линейным спектром обыкновенной волны и спектрами волн с круговой поляризацией для 6 = 0.
При учете затухания выражение (5.1.36) для fij становится комплексным. Зависимости вещественной и мнимой частей от постоянного магнитного поля приведены на рис. 5.2.9. На
Рис. 5.2Л0. Волновое число ht' и коэффициент затухания h," волны ТЕ в поперечно иа-магниченном феррите. Расчет по формуле (5.2.54) при значениях и приведенных на рис. 5.2.9, е = 9 и о>/2 Л = 9,4 Ггц.
рис. 5.2.10 показаны вещественная и мнимая части постоянной распространения кг, рассчитанные на основании данных рис. 5.2.9.
Произвольная однородная плоская волна, распространяющаяся перпендикулярно направлению постоянного намагничения, может быть представлена в виде суммы рассмотренных нормальных волн. Различие постоянных распространения этих волн приведет к тому, что поляризация суммарной волны будет преобразовываться по мере распространения.
Рассмотрим, например, «ферромагнитный» случай (е скалярно) и предположим, что при у = 0 вектор е суммарной волны линейно поляризован в направлении, составляющем 45° с осью х в плоскости xz (рис. 5.2.11). Эта волна может быть разложена на две нормальные волны с равными амплитудами и фазами электрического поля (при у = 0): необыкновенную (ТЕ) волну с век-
{ 5.3]
КВАДРАТНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ
253
тором ej (рис. 5.2.11) и обыкновенную (ТЕМ) — с вектором е2. Если величина постоянного магнитного поля далека от резонансной для волны ТЕ, то коэффициенты затухания обеих волн kL и Л2 будут невелики. Различие же и к2 приведет к преобразованию поляризации суммарной волны. При у = 1г, где
1	2 | Л/— Л/1 ’
электрическое поле волны будет иметь круговую поляризацию (если пренебречь различием и Л2), а при у = 21А — снова линейную, но в перпендикулярном направлении (рис. 5.2.11).
Следует подчеркнуть, что преобразование поляризации в поперечно намагниченной среде (в отличие от продольно намагниченной среды) является взаимным.
Оно не зависит от знака постоянного намагничения и при изменении направления распространения пойдет «в обратном порядке». Взаимность распространения волн в поперечно намагниченной среде связана с тем, что р,., и е(1 входят в выражения для
Рис. 5.2.11. Преобразование поляризации волны в поперечно намагниченном феррите.
постоянных распространения 41И Л2 этих волн
только в четных степенях.
Рассмотренные выше эффекты — резонансные зависимости к/ и к{' от со или Но и преобразование поляризации — имеют место (правда, в более сложной форме) и в волноводах, содержащих намагниченные ферритовые образцы. Эти эффекты используются для создания некоторых ферритовых устройств диапазона СВЧ: взаимных аттенюаторов и так называемых устройств с двойным лучепреломлением [478, 11] ’).
§ 5.3. Квадратичные соотношения. Метод возмущений
В электродинамике широко используются (см., например, [43, 33]) квадратичные соотношения, которые содержат произведения составляющих Е и Н и являются следствиями уравнений Максвелла. К числу их принадлежат, в частности, энергетические соотношения [41, 43]. Мы рассмотрим квадратичные соотношения, связывающие комплексные амплитуды переменных состав-
х) В волноводах, содержащих поперечно намагниченные гиротропные образцы, возникают и новые, невзаимные явления, существенно связанные с граничными условиями и не имеющие аналогий в неограниченной среде. Некоторые из них будут рассмотрены в главе 6.
254
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
ляющих электрического и магнитного полей для сред с тензорными параметрами е и р.
Основные квадратичные леммы. Выведем прежде всего основные леммы, из которых в дальнейшем будут получены все квадратичные соотношения. Для этого запишем уравнения Максвелла (5.1.18) и (5.1.20) для двух электромагнитных процессов с различными частотами, различными сторонними токами и различными параметрами среды:
rot С] i ~ ji Jij = 0,	(5.3.1)
rot hx — i-y- e^i = — jCT i,	(5.3.2)
rote2-j-i-^p2h2 = 0,	(5.3.3)
rot h2 — i i-2e2 = jCT 2.	(5.3.4)
Умножим скалярно (5.3.1) на h2, (5.3.2) на (-p е^), (5.3.3) на (+ hj) и (5.3.4) на (— ej. Сложив все эти равенства и использовав формулу для дивергенции векторного произведения [35], получим соотношения
div (Cj х h2 + Сг х hi) + — (wili^bi + w2hip2h2 + Wie^i +
4- w2eie2e2) + jCT 2в! ± jCT xe2 = 0.	(5.3.5)
Таким же образом, но исходя из (5.3.1), (5.3.2) и уравнений, комплексно-сопряженных с (5.3.3) и (5.3.4), получим
~ div (ех х h2 + е2 X h,) -ф (ицб^цЬ! =j= юАрХ ±
zb	o)2eie2e2) -j- Jct 2®i zb |ст d*2 = 0. (5.3.6)
Четыре выражения (5.3.5) и (5.3.6) и представляют собой основные квадратичные леммы для комплексных амплитуд ')
Обобщенная лемма Лоренца. Предположим, что параметры среды и частоты для обоих процессов одинаковы (рх =. р2 ~ р, 61 = е2=е, <»! = со2 = со). Тогда (5.3.5) (с нижними знаками) перейдет в следующее соотношение:	|
di\(ei|x h2’-re2|xjhi)|+ [(Kphi - li!pli2) -
— (e2eei — ei8e2)} -f- jCT 2Ci — jCT je2 = 0. (5.3.7)
J) Они являются обобщением квадратичных лемм, которые для случая изотропной среды сформулировал Кисунько [33].
§ 5.31 КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ 255
Оно является формулировкой леммы Лоренца для случая сред с произвольными тензорными параметрами.
Рассмотрим соотношение (5.3.7) более подробно. Представим р, и е в виде сумм симметричных (рс и ес) и антисимметричных (р,ас и еас) тензоров (см. § 5.1). Тогда, как легко, убедиться,
baPchj = 1ццс112, h2p,achi — — 1цр,ас112.
С учетом этих соотношений и аналогичных — для электрических полей и тензоров ес и еас — выражение (5.3.7) запишется в виде ~ div (е2 х h2 — е2 X hi) +
+ (h2pachi — е2еасе!) + jCT 2et — jCT = 0 (5.3.7')
или (если ввести векторы гирации gm и gf, см. § 5.1) в виде
div (ej х h2 — е2 х 1ц) +
+ 2» [gTO (hr х 1ц) — ge (ex X e2)J + jCT 2ej — j^.	= 0. (5.3.7")
Если fi и e являются симметричными тензорами (ftac = = eac = 0), в частности скалярными величинами, то (5.3.7') переходит в обычную лемму Лоренца [33]
div (ех х 1ц — е2 X 1ц) + jCT2ег — jCT= 0.	(5.3.8)
Эта лемма является дифференциальной формулировкой теоремы взаимности (см. [37]), которая широко используется в электротехнике и радиотехнике. Как видно из (5.3.7'), эта теорема (в дифференциальной форме) справедлива только для сред, параметры которых являются симметричными тензорами (в частности, скалярами), т. е. для сред, не обладающих гиротропией.
Интегрирование (5.3.8) по некоторому объему V дает интегральную формулировку теоремы взаимности для системы, заключенной в этом объеме:
~ (е, х h2 — е2 х 1ц) nodS + (jCT 2ej — jCT 2е2) dV = 0.	(5.3.9)
8	V
Здесь S — поверхность, ограничивающая объем V, а п0 — единичный вектор нормали к этой поверхности.
Интегрируя по тому же объему V выражение (5.3.7"), мы видим, что условием справедливости интегральной теоремы взаимности (5.3.9) для системы, заключенной в объеме V, является
$[gm(hi X 112) —ge(ei х е2)]б/И = 0.	(5.3.10)
256
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Системы, для которых выполняется это условие, можно назвать взаимными в интегральном смысле. Очевидно, что при определенной симметрии системы условие (5.3.10) может выполняться и при gm =/= 0 и ge =j= 0, т. е. системы, невзаимные в дифференциальном смысле, могут быть взаимными в интегральном. В качестве примера таких систем можно назвать прямоугольный волновод с поперечно намагниченным гиротропным (например, ферритовым) образцом, расположенным симметрично относительно плоскости, в которой лежит ось волновода и постоянное магнитное поле (см. § 6.2). При смещении образца из симметричного положения относительно этой плоскости система становится невзаимной и в интегральном смысле: ее характеристики (фазовый сдвиг, затухание) начинают зависеть от направления распространения энергии или направления постоянного магнитного поля.
Для среды с параметрами (5.1.33) и (5.1.34), изотропной в отсутствие постоянного намагничения, для которой
ц J	е
gm=zo^-',	(5.3.11)
(z0 — единичный вектор в направлении постоянного намагничения), выражение (5.3.7") примет вид
div (ej X h2 — е2 X 1ц) ф-
+ А> [(hj х h2)	— (Oi X еа) еа] + jCT — jCT ге2 = 0. (5.3.12)
Теорема Умова — Пойнтинга. В качестве второго следствия основных квадратичных лемм рассмотрим комплексную теорему Умова — Пойнтинга — уравнение баланса энергии гармонического (стационарного) электромагнитного поля. Чтобы получить это уравнение, сложим соотношения (5.3.6) с верхними и нижними знаками, положив в них
Р2 —— Р? ^'1	^'2 === OJj ~~ ^2
== о2 = о, hi = h2 = h, jCT i = jCT 2 = jCT.
Это приведет к выражению
div (е х h*) + (h’jih — ее*е*) + j^e = 0.	(5.3.13)
Равенство нулю вещественной части (5.3.13У можно записать в виде
div П + Р + Рст = 0,	(5.3.14
§ 5.31
КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ 257
где
а
П = ^-Re(e х h’),
Per = -|- Re (jcTe), P---^-Im(hph-ePe*).
(5.3.15)
(5.3.16)
(5.3.17)
Как известно [41], П представляет собой среднее по времени значение плотности потока электромагнитной энергии — вектора Пойнтинга, а РС1 — среднее значение мощности сторонних токов в единице объема. Отсюда ясно, что (5.3.14) является дифференциальной формулировкой уравнения баланса средней энергии, а величина Р представляет собой среднее значение мощности потерь в единице объема, т. е. энергии, передаваемой в единицу времени электромагнитным полем единице объема вещества и диссипируемой им — переходящей в другие виды энергии. Интегрируя (5.3.13) и (5.3.14) по некоторому объему V, можно получить, соответственно, интегральную запись комплексной теоремы Умова — Пойнтинга и уравнение баланса средней электромагнитной энергии для гармонических колебаний в объеме V.
Рассмотрим более подробно величину Р, выясним, с какими компонентами тензоров р и е связана диссипация электромагнитной энергии. Представим р и е в виде сумм эрмитовых (рэ и еэ) и антиэрмитовых (раэ и Еаэ) тензоров (см. § 5.1). Легко убедиться, что эрмитовы тензоры не дают вклада в Р, и
Р = - (h*R0h + е*еаае).	(5.3.17')
Таким образом, диссипация электромагнитной энергии в среде связана только с антиэрмитовыми составляющими р и е, т. е. с мнимыми частями симметричных компонент и вещественными частями антисимметричных компонент этих тензоров [43]. Среда без диссипации должна была бы иметь вещественные симметричные компоненты и чисто мнимые антисимметричные компоненты х) тензоров р и е.
х) Это обстоятельство было учтено в §§ 1.3 и 5.1 при введении обозначений компонент тензоров р и е — они были введены таким образом, чтобы диссипация всегда определялась компонентами с двумя штрихами.
9 А. г. Гуревич
258
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
Остановимся на частном случае среды с параметрами (5.1.33) и (5.1.34). Обозначим, как и раньше,
|Л = р'-ф", Ри = |/ц — ф'у, ра = Ра—ipo,
(5.3.18) е = е' — ie", е || = е II — IE и,	еа = е'а — ie„.
Тогда для произвольного электромагнитного поля с составляющими
hp hp —|— ihp, €р €р -j- ъ€р (jp = ж, у, z) выражение (5.3.17х) запишется следующим образом:
р = (I I2 + I hv I2) + ИII \hz |2 + 2р,а {h'yhx - hxh"y) +
+ е" (I ех |2 + | еу |2) + е'[| I ez I2 + 2еа' (е'е" — ехеу)]. (5.3.19)
Отсюда видно прежде всего, что потери определяются мнимыми частями ц, р у, рп, е, е ц и еп, т. е. антиэрмитовыми компонентами тензоров (5.1.33) и (5.1.34).
Из выражения (5.3.19) следует также, что диссипация энергии («положительные потери») связана всегда с положительными значениями р", р ц, е" и е ц, если знаки перед ними выбраны так, как в (5.3.18). В отношении ра и ео такого вывода нельзя сделать, так как стоящие при этих величинах множители (hvhx — — hxh^j и (еуех — ехеу) могут иметь различные знаки в зависимости от поляризации поля. Легко убедиться, что они положительны для полей с круговой поляризацией и правым вращением (относительно положительного направления оси z, которое задано направлением постоянного намагничения), отрицательны для полей с круговой поляризацией и левым вращением и обращаются в нуль для линейно поляризованных полей. Таким образом, одни и те же положительные величины ро и еа вносят для полей с круговой поляризацией и правым вращением положительные потери, а для полей с левым вращением —«вносят отрицательные потери», т. е. приводят к уменьшению диссипации, обусловленной другими компонентами ц и е; для линейно поляризованных полей компоненты р,н и еа не участвуют в диссипации.
Для пассивной среды при любой поляризации поля должно быть Р 0. Отсюда следует
ц" >0, ц || > 0, е" > 0,	$[| О,
(5.3.20)
IRI < Р-", IС | < е".
§ 5.3
КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ 259
Знаки же величин и еа могут быть, вообще говоря, любыми 2).
Формулы возмущений. Трудности, возникающие при решении граничных электродинамических задач, существенно возрастают (как мы убедимся, в частности, в следующей главе) при переходе к гиротропным средам. Это заставляет в случае таких сред обращать особо серьезное внимание на разработку приближенных методов решения граничных задач. Наиболее простым и универсальным является метод возмущений. Согласно этому методу исследуемая система рассматривается как результат малого изменения (возмущения) другой, более простой системы, для которой решение задачи известно. В нашем случае начальной (невозмущенной) системой будет система, не содержащая гиротропных сред, а возмущение будет представлять собой введение в нее образца из гиротропного вещества.
При выводе формул электродинамического метода возмущений можно исходить из основных квадратичных лемм (5.3.5) и (5.3.6). Будем считать, что электромагнитный процесс, характеризующийся индексами 2, соответствует начальному состоянию системы, а процесс с индексами 1 — возмущенному состоянию. Предположим, что в начальном состоянии параметры среды являются скалярными и вещественными:
р2 = р0, с2 = е0.	(5.3.21)
Предположим также, что сторонние токи отсутствуют как в начальном, так и в возмущенном состоянии. Тогда, переходя к новым обозначениям
Ц1 - > Ц, Ех —> е, вх е, 11 ]"- > h, «х —> ю, ©г—>ео, h2—> ho,
из основных квадратичных лемм (5.3.5) и (5.3.6) получим div (е х h0 — ео X h) +
+ — [whoph — wopohoh — (<ое0Ее — <вОЕоеое)] = 0, (5.3.22)
div (е х ho + во X h) +
-ф- -i- [cohoph — cooPohoh -|- совоЕе — coo^e^e] = 0. (5.3.23)
Выражения (5.3.22) и (5.3.23) можно назвать леммами возмущений. Применим их] к трем фундаментальным граничным
2) Как было показано в главе 1, в намагниченном до насыщения ферро-Сили ферри-) магнетике ра > 0. Однако в слабых постоянных полях при наличии доменной структуры может быть и р” •< 0 (см. примечание на стр. 124).
9*
260
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
задачам: о постоянной распространения регулярного волновода, об отражении волны от нерегулярности в волноводе и о собственных частотах полого резонатора. Во всех этих задачах металлические поверхности, ограничивающие полые системы, будем считать идеально проводящими.
Рассмотрим первую из перечисленных задач. Регулярный волновод с произвольным поперечным сечением 6’0 (рис. 5.3.1) в невозмущенном состоянии заполнен средой с параметрами р0 и е0, и в нем имеется поле бегущей волны
е0 = ^oe~ikz'°z'.
Рис. 5.3.1. Регулярное гиротропное возмущение волновода.
h0 = 5^oe“ikz'oZ',
(5.3.24)
где kZ’O — постоянная распространения невозмущенного волновода, 1s0 и .То — его собственные функции [29], а ось z' направлена вдоль оси волновода (в отличие от оси z, которая совпадает с направлением J постоянного поля).
Возмущение заключается в том, что внутрь волновода вводится бесконечный цилиндр с произвольным сечением Sx (рис. 5.3.1), с параметрами р и е и осью, параллельной оси z'. В возмущенном волноводе имеет место поле
в = Сб
h = 3fe~ikz'z',
(5.3.25)
где /cZ', S и Ж — постоянная распространения и собственные функции возмущенного волновода.
Для вывода формулы, связывающей величины kz- и /с2'о с параметрами среды и собственными функциями 80, <о, .То и Т, воспользуемся леммой (5.3.23). Подставляя в нее (5.3.24) и (5.3.25) и принимая во внимание, что в данном случае <о = <о0, получим после несложных преобразований
divjj (g х X + X Ж) - i {kz- - kz-0) (gj.' х Ж'о1_- +
+ Cl' X ад х0 + ~ (ЖоМ + ^Де£) = 0. (5.3.26)
Здесь divX' — двухмерная дивергенция в плоскости поперечного сечения волновода,
Др = р — р0, Де = е — е0,	(5.3.27)
индексом _[_' обозначены поперечные (перпендикулярные оси волновода) составляющие собственных векторных функций, а Zo — единичный вектор в направлении оси волновода.
§ 5.3] КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ 261;
Интегрируя (5.3.26) по сечению волновода, учитывая граничные условия
х п0 = О, «’о X п0 = О	(5.3.28)
(где ио — перпендикулярный оси волновода единичный вектор нормали к кривой, ограничивающей поперечное сечение волновода) и принимая во внимание, что тензоры Др и Де не обращаются в нуль только в области St, по-
лучим окончательно х)
/cZ' — kz’o -
\ (^Ap^+^Aeg)^’
<i> s,_______________________
~~c 5 (%l' X 4- X as
So
(5.3.29)
Перейдем теперь ко второй за-	I'
даче - о гиротропной нерегуляр- Рис 5 3 2 Гиротропная нерегуляр. ности. Рассмотрим ВОЛНОВОД, за- ность в волноводе.
полненный в начальном состоянии
средой с р0 ие0; возмущение заключается в том, что в него вводится тело конечных размеров с объемом и параметрами вир (рис. 5.3.2). Будем исходить теперь из леммы (5.3.22). Интегрируя '(5.3.22) по объему Vo (см. рис. 5.3.2), ограниченному боковой поверхностью волновода 11 двумя поперечными сечениями S^ (z' = 0) и S2 (z' = I), получим
(e X h0 + eo X Ь)пой5 — § (е±, z hOJ/ + еэ±' x hjJ z'odS +
S6	St
4- \ (e_i_' x h0JL' еох- X hj_') zodS + — (Ь0ДрБ -j- е0Дзе) dV — 0, 8,	Vt
(5.3.30)
где индексом как и раньше, обозначены поперечные (относительно оси волновода) составляющие соответствующих векторов.
f Предположим, что в невозмущенном волноводе может распространяться волна только одного типа, а сечения «Sj и S2 находятся на таких больших расстояниях от У2, что ближние поля, вызванные возмущением, имеют на SL и Sz пренебрежимо малые амплитуды. Тогда возмущение приведет к появлению отраженной
4 Формула (5.3.29), а также формулы (5.3.35) и (5.3.36) были выведены Никольским [452, 457, 496).
262
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
волны в сечении 6^ и изменению комплексной амплитуды проходящей волны в сечении S2. При этом, учитывая некоторые свойства волноводов [29], можно записать: в сечении 5]
eoj_- =	eJ_' =	(1 + Г),
(5-3.31)
hod.' = zo X &o±', h_L' = zo X <ooj/ (1 — П);
в сечении Sz
eoj_' -	,	e_L' = ^o±'D,
(5.3.32)
hoj_' = -у— А) X <oo_L'e i0 , h_L' ~ ~r~ zo X
Здесь <^0±- — поперечная собственная функция певозмущепного волновода, £0 — его волновое сопротивление, а Г и D — коэффициенты отражения и прохождения, которые необходимо определить.
Интеграл по До в (5.3.30) равен нулю в силу граничных условий (5.3.28). Подставляя (5.3.31) и (5.3.32) в остальные интегралы в (5.3.30), нетрудно убедиться, что все члены с коэффициентом прохождения D уничтожаются, а для коэффициента отражения Г получается следующая формула:
Г = "Йг S (hoAHh + е0Дее) dV, (5.3.33) где
= |^-|2^	(5.3.34)
s0
— константа нормировки поперечных собственных функций волновода (интегрирование в (5.3.34) производится по поперечному сечению волновода).
Формула для коэффициента прохождения
1 _ De^ot =	(lhAnh + еоДее) dV (5.3.35)
Vi
может быть получена таким же образом, исходя из второй леммы возмущений (5.3.23).
Рассмотрим теперь последнюю из перечисленных выше задач — о гиротропном возмущении полого резонатора. Воспользуемся для этого снова леммой (5.3.23). Пусть поле е0, h0 в (5.3.23) соответствует одному из собственных колебаний (с частотой соо) полого резонатора, заполненного средой с щ и е0. Поле е, h пусть соответствует одному из собственных колебаний того же резонатора, но возмущенного введением в него образца с объемом Vt
§ 5.31 КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ
263
и параметрами р и в (рис. 5.3.3). Частота этого типа колебаний со и подлежит определению.
Интегрируя (5.3.23) по объему резонатора Fo и учитывая граничные условия (5.3.28), получим формулу гиротропного возмущения резонатора
(h*A|ih + е*Дее) dV
= __ 	(5.3.36)
“	(|iF*h + еое*е) dV
V»
Для среды с параметрами (5.1.33) и (5.1.34) входящая в формулу (5.3.29) величина 7/о/Хр Ж запишется следующим образом:
З^ДиЗ^ = ДнЖ^^ + ipozo (Ж*о± X Ж Г) + Др II Ж*тЖг,	(5.3.37)
где, согласно (5.3.27),
Др — Р — Ро, Др || — Р и — Ро,
осв z совпадает с направлением постоянного намагничения, а индексы | (в отличие от _]_') обозначают составляющие векторов, перпендикулярные этой оси. Таким же образом запишется для среды с параметрами (5.1.33) и (5.1.34) величина и аналогичные выражения, входящие в формулы (5.3.33), (5.3.35) и (5.3.36).
Формулы возмущений (5.3.29), (5.3.33), (5.3.35) и (5.3.36), как и леммы (5.3.22) и (5.3.23), из которых они получены, явля
ются строгими. Однако входящее в них возмущенное поле е, h неизвестно, и при практическом исполвзовании формул возмущений приходится подставлять вместо него некоторые другие поля. Это делает результаты расчета по формулам возмущений приближенными. Заметим прежде всего, что в знаменателях формул (5.3.29) и (5.3.36) можно заменить возмущенные поля известными невозмущенными, если <Х: So (для волновода) или Fi Fo (для резонатора). Тогда эти формулы запишутся следующим образом:
к*' ~	~	+ goAeg) dS, (5.3.38)
s,
~ - WT $ (h«^h + <*Д~е)dV’	(5.3.39)
v,
Рис. 5.3.3. Гиротропное возмущение полого резонатора.
264
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
где
К0
£0 — волновое сопротивление определяется согласно (5.3.34)
невозмущенного а
волновода,
Wo = е01 е0 j2 dV = § р01 ho |2 dV Vo	V„
(5.3.40)
есть умноженная на 8л полная энергии невоэмущенного резонатора.
Квазистатическая^ аппроксимация возмущенного поля. Наиболее простым и универсальным методом аппроксимации возмущенного поля в числителях формул возмущений является квази-статический метод. Он заключается в том, что связь между возмущенными полями е, h в образце и невозмущенными полями е0, h0 принимается такой же, как связь между статическими полями в образце той же формы с теми же е и р, и внешними однородными статическими полями.
Статические задачи об определении электрического и магнитного полей в образце независимы, и при отсутствии токов и свободных зарядов (что имеет место в нашем случае) решения их совпадают при замене Е И и е ц. Эти задачи, как отмечалось в § 1.4, могут быть решены строго, если образец является эллипсоидом, бесконечной плоскопараллельной пластиной или бесконечным эллиптическим цилиндром; для таких образцов в случае магнитостатической задачи внутреннее поле h и намагниченность m однородны, и имеет место соотношение (1.4.5). Заметим, что внешняя среда при этом предполагается немагнитной (р0 = 1).
Постановка магнитостатической задачи и использование ее решения будут теперь несколько отличаться от § 1.4. Во-первых, мы будем рассматривать более общую задачу об образце, помещенном в среду с магнитной проницаемостью ц0. Как следует из уравнений и граничных условий магнитостатики, решение магнитостатической задачи не изменится, если проницаемости всех сред разделить на одну и ту же скалярную величину. Используя зто, заменим задачу об эллипсоиде с проницаемостью р, в среде с проницаемостью р0 на задачу об эллипсоиде с проницаемостью ц/ц0 в немагнитной среде. Решение ее дается выражением (1.4.5) (в которое проницаемость явно не входит), a m и h связаны теперь соотношением
h 4лш — — h.	(5.3.41)
Ро
Во-вторых, в § 1.4 мы исключали внутреннее переменное поле и, решая уравнение движения, находили связь намагниченности с внешним полем. Теперь же мы должны исключить намагниченность и найти связь внутреннего (возмущенного) поля с внешним.
5 5.3] КВАДРАТИЧНЫЕ СООТНОШЕНИЯ. МЕТОД ВОЗМУЩЕНИЙ 265
Исключая ш из (1.4.5) и (5.3.41), получим
h = ТЬ0,	(5.3.42)
где тензор
М1+,5-3-43)
Рассмотрим, например, случай среды с параметрами (5.1.33) и (5.1.34) и предположим, что ось z (направление постоянного намагничения) совпадает с одной из осей эллипсоида. Оси х и у можно совместить с осями эллипсоида без дальнейшего ограничения общности. Тогда тензор N будет диагональным с компонентами Nx, Nv и Nz. Тензор Т в этом случае запишется следующим образом:
J_h , ЛР\	ра	О
£ \	' 4л р0 /	£ 4л р0
<-►	,• Л’.,, р	1 / N л.. \	,
1__V	1 11-1_х I	О
Е,	4л	р«о	£ \	‘	4л	р-э /
АН и V1
4 л [х > /
(5.3.44) где Др, = р, — р0, Др и = рц — ро, а
Nx Ар\ Л	Ар \	a;tv7< pg .
4л p.i / \ ' 4л рэ ) 16ла
в = (1 +
Подставляя в (5.3.44) значения размагничивающих факторов (см. § 1.4), можно вычислить компоненты тензора Т и, подставляя их затем в проекции (5.3.42), найти связь между внутренним и внешним полями. Для касательно намагниченной пластины (рис. 1.4.2, а) получаем таким образом
hx = hox, hv —-~-hOx--—hOy, hz -- hOz. (;>.3.45) P	P
Для нормально намагниченной пластины (рис. 1.4.2, б) hj. = hoj_i hz — ~— hOz.	(5.3.46)
Для цилиндра, намагниченного вдоль его оси (рис. 1.4.2, в),
h± =	hol+ -...---у-,- «о X hox, hz = Ло, (5.3.47)
(p + pop-pg	(P + P‘)2~Pg
Для цилиндра, намагниченного перпендикулярно оси (рис. 1.4.2, г),
/г = Л-------------Л = h h _ —hOz. (5.3.48)
V р + р0 °* Р + Ро у V V	Р (I I Р°
266
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ ГИРОТРОПНЫХ СРЕД
[ГЛ. 5
И, наконец, для сферы
(р Ч~ 2р«) h_____________ЗЩора________
(р + 2|1>)2 —	°’L (И + 2р0)2  |й
_ ЗрП ,
ZoXhoj_,
(5.3.49)
Для того чтобы получить формулы, связывающие внутреннее и внешнее электрические поля, достаточно в выражениях (5.3.42) — (5.3.49) заменить компоненты р, на соответствующие компоненты е. Для нас представляет наибольший интерес случай скалярной электрической проницаемости. Тогда для пластины (ось у перпендикулярна ее плоскости)
сх срл-, Су £ eQy, ez cqx,	(5.3.оО)
для цилиндра (ось z направлена вдоль его оси)
2eq	2еэ	®	/1" о г' а \
р i" г	р j ^Oyj ez “		(5.3.51)
b “Т" Г'Э	«* ~Т' Ь()
для сферы
e = rrke°-	(5.3.52)
Необходимым условием применимости квазистатической аппроксимации внутреннего поля является малость размеров образца по сравнению с длиной электромагнитной волны в веществе. Если учесть, что поперечные диагональные компоненты тензоров р, и е во всяком случае не меньше по модулю, чем другие их компоненты, то это условие может быть записано следующим образом:]
с ' 1 1 * 1 о
(5.3.53)
Под величиной d следует понимать диаметр сферы, диаметр цилиндра или толщину пластины. Что же касается других размеров пластины и длины цилиндра, то их малости не требуется. Наоборот, чем больше эти размеры по сравнению с d, тем точнее будут формулы (5.3.45) — (4.3.48) и (5.3.50), (5.3.51). При этом, конечно, внутреннее переменное поле будет приблизительно однородно только по толщине пластины и в поперечном сечении цилиндра. В плоскости пластины и по длине цилиндра это поле будет изменяться по такому же закону, как и невозмущенное поле, так что связывающие их формулы (5.3.45)	(5.3.48),
(5.3.50) и (5.3.51) останутся справедливыми.
§ S.3J КВАДРАТИЧНЫЕ СООТНОШЕНИЙ. МЕТОД ВОЗМУЩЕНИЙ 267
Условие малости размеров образца не является, однако, достаточным для применения рассмотренной квазистатической аппроксимации внутреннего поля. Формулы (5.3.43) — (5.3.49) предполагают однородность внутреннего поля и намагниченности. Она имеет место для того (однородного) типа прецессии, рассмотрением которого мы до сих пор ограничивались. Но, как мы увидим в главе 7, даже в сколь угодно малых гиротропных образцах могут существовать и другие — неоднородные типы прецессии. Для них уравнения магнитостатики по-прежнему применимы, но решения (5.3.41) — (5.3.49) несправедливы. Таким образом, вторым условием применимости рассмотренного метода квазистатической аппроксимации внутреннего поля является наличие однородного типа прецессии.
ГЛ A 13 Л 6
ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ
СРЕДАМИ
§6.1. Волновод с продольно намагниченной гиротропной средой
Рис. 6.1.1. Регулярный волновод, заполненный продольно намагниченной гиротропной [средой.
В этой главе мы рассмотрим несколько примеров решения граничных задач для полых электромагнитных систем (волноводов и резонаторов), содержащих гиротропные среды. Такие задачи представляют большой практический интерес, поскольку полые системы с гиротропными средами, прежде всего — с намагниченными ферритами, широко применяются в технике сверхвысоких частот. Теории и экспериментальному исследованию полых систем с ферритами было посвящено огромное количество работ (см., например, обзоры и монографии [6,11, 446, 449]). Задача этой главы— проиллюстрировать особенности постановки и решения граничных задач для гиротропных сред и рассмотреть физические процессы, происходящие в некоторых простейших системах, представляющих в то же время интерес для практических применений или для измерений параметров вещества.
•'Для простоты мы ограничимся средами с параметрами (5.1.33) и (5.1.34), а в ряде случаев будем считать е скалярной величиной (изотропный феррит).
Прежде всего в первых двух параграфах мы рассмотрим регулярный (бесконечный, с постоянным сечением) волновод, заполненный целиком или частично гиротропной средой. Волноводные ферритовые устройства, в которых используются такие волноводы с различным поперечным сечением (круглые, прямоугольные, коаксиальные), широко применяются в технике. В них используются ферритовые образцы конечной длины, но поскольку обычно принимаются меры для их согласования (уменьшения отражений от их концов), модель регулярного волновода • позволяет понять принцип действия таких устройств и даже дать в ряде случаев их количественное описание.
§ 6.11	' ЁОЛНОВОД С ПРОДОЛЬНО НАМАГНИЧЕННОЙ СРЕДОЙ
269
Рассмотрим сначала волновод с гиротропной средой, намагниченной вдоль оси волновода (случай продольного намагничения). В этом случае можно будет сделать некоторые общие заключения, не конкретизируя формы поперечного сечения волновода.
Произвольный регулярный волновод. Рассмотрим полую цилиндрическую трубу произвольного сечения (рис. 6.1.1) с идеально проводящими стенками. Внутренний объем трубы заполнен средой с параметрами (5.1.33) и (5.1.34). Зависимость комплексных амплитуд составляющих электромагнитного поля от координаты z (в направлении постоянного намагничения и оси волновода) примем в виде , где kz — постоянная распространения, которая подлежит определению. Эта зависимость соответствует бегущим волнам, распространяющимся в волноводе в положительном (если Re (/cz)	0) или отрицательном
(при Re (к-)	0) направлениях оси z.
Для продольных составляющих поля из (5.1.37) в данном случае следуют уравнения
(СТ	& II ст	ст	\	Р1 \
Vl-^-fe2+	+ hz = 0, (6.1.1)
---ii e±j hz — ikzk0E ц -y-j ez = 0, (6.1.2)
(где kQ = o/c). Так как ось z является одновременно направлением постоянного намагничения, то гармоническая зависимость от z позволяет использовать выражения (5.1.44) — (5.1.48).
Уравнения (6.1.1) и (6.1.2) или уравнения (5.1.46) для скалярной функции ф должны быть дополнены граничными условиями, учет которых и позволит найти составляющие поля (с точностью, конечно, до общих амплитудных множителей) и значения постоянной распространения для нормальных волн рассматриваемого волновода. Граничные условия запишутся следующим образом:
ez = 0 на L,	(6.1.3)
e_L X и0 = 0 на L,	(6.1.4)
где L — контур, ограничивающий поперечное сечение волновода, а п0 — единичный’ вектор нормали к этому контуру, лежащий в плоскости поперечного сечения волновода (рис. 6.1.1).
Из уравнений (6.1.1) и (6.1.2) следует, что если hz = 0, то и ez = 0, и наоборот. Таким образом, типы волн в волноводе с продольно намагниченной гиротропной средой имеют в общем случае hz =f= 0 и ez =/= 0, т. е. не являются волнами ТЕ или ТМ. Однако, как видно из (6.1.1) и (6.1.2), они становятся волнами
270 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
ТЕ и ТМ в предельном случае «отсечки» г), когда kz -> 0, т. е. длина волны в волноводе Хв—>оо.
При kz — 0 (6.1.1) и (6.1.2) переходят в следующие уравнения:
^1+^иИ±)е2 = 0,	(6.1.5)
(Vl+^„8±)fez = 0,	(6.1.6)
которые совпадают с аналогичными уравнениями для изотропной среды с параметрами ец и р± (волны ТМ) или р,ц и е± (волны ТЕ). Для волн ТМ граничное условие (6.1.3) также совпадает с условием для изотропной среды. Поэтому собственные значения
/СоБ || Хо	(6.1.7)
уравнения (6.1.5) будут такими же, как для изотропной среды. Но, как известно [29], эти собственные значения связаны следующим образом с предельной длиной волны пустого волновода:
Ио = -Лг-	(6.1.8)
Из (6.1.7) и (6.1.8) с учетом (5.1.38) следует, что предельные длины волн волновода с гиротропной средой для типов волн, превращающихся при отсечке (а также при 0 и -+ 0) в волны ТМ,
^прТМ ~ (^-прТм)о Б || Рх-	(6.1.9)
Для волн ТЕ (при kz = 0) из (6.1.4) следует граничное условие [61
=	(6.1.10)
дп е дт:	1	х '
где д!дп— производная по направлению нормали п0, а д]дх— производная по направлению касательной т0 к контуру L (рис. (6.1.1). Условие (6.1.10) не совпадает, вообще говоря, с условием
dhz  „ дп
для изотропной среды. Но для магнитно-гиротропных сред (ферриты, антиферромагнетики) с еа = 0 эти условия совпадают, и рассуждая так же, как и выше, получим
^пр те = (^пр те)о Р^ер и.	(6.1.11)
Таким образом, для произвольного волновода, заполненного продольно намагниченной магнитно-гиротропной средой, спра
1) Этот случай осуществим, строго говоря, только при отсутствии диссипации.
§ 6.1]
ВОЛНОВОД С ПРОДОЛЬНО НАМАГНИЧЕННОЙ СРЕДОЙ
271
ведливы простые выражения (6.1.9) и (6.1.11) для предельных длин волн. Следует, однако, подчеркнуть, что, в отличие от волновода с изотропной средой, знание этих предельных длин волн отнюдь не дает возможности определить по известным [29] простым формулам длины волн в волноводе при X < Хпр.
Для определения постоянной распространения и структуры поля в волноводе с продольно намагниченной гиротропной средой можно использовать метод скалярных функций., рассмотренный в § 5.1 (подробнее см. [449, 61). Скалярные функции фх и ф2 являются решениями уравнений (5.1.46), где хг и х2 определяются выражением (5.1.47). Функциям фг и ф'2 соответствуют два поля, до наложения граничных условий они независимы.
Граничные условия (6.1.3) и (6.1.4) с учетом (5.1.48) приведут [6] к следующим условиям для функций и ф2:
Xi, 2ф1,2 = 0 на L,	(6.1.12)
(Ui,2Vj.i]?i,2) х По = 0 на L.	(6.1.13)
Можно убедиться, что эти условия не совместны, т. е. поля, определяемые функциями Tpj и ф2 по отдельности, не удовлетворяют граничным условиям. В качестве функции ф следует принять линейную комбинацию
ф = АФх + Л2ф2.	(6.1.14)
Тогда граничные условия (6.1.12) и (6.1.13) приведут к соотношениям
Л^фх + Л2я2ф2 = 0	на L,
«	«	(6.1.15)
-41 (UiVjJh) X п0 + Л2 (UjjVjjh) X По на L.
Соотношения (6.1.15) сведутся к системе двух однородных линейных алгебраических уравнений относительно Аг и А2, если будут выполнены следующие условия [6]:
1)	контур L, ограничивающий поперечное сечение волновода, должен состоять из отрезков линий дц = const и q2 = const, где и q2 — координаты в плоскости поперечного сечения;
2)	переменные qr и qz в уравнении (5.1.46) должны разделяться;
3)	на линии = const зависимость ф от q2 должна быть экспоненциальной, и наоборот.
Первое и второе условия должны выполняться и для сред со скалярными параметрами, а третье специфично для гиротропных сред. Причем зависимость ф от qt или q2 должна быть не любой гармонической, а именно экспоненциальной.
Если все приведенные условия выполняются, то, приравнивая нулю определитель получающейся алгебраической системы, мы получим уравнение, которое совместно с двумя уравнениями
272 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
(5.1.47) позволит найти х2 и kz. Затем может быть найдено отношение A-JA2 и определены (с точностью до постоянного множителя) все составляющие поля. К сожалению, ограничения, накладываемые упомянутыми условиями на выбор координат
Рис. 6.1.2. Круглый волновод, заполненный продольно намагниченной гиротропной средой.
в плоскости поперечного сечения, приводят к тому, что эта программа может быть выполнена лишь для круглого или коаксиального [волноводов.
Круглый волновод. Рассмотрим идеально проводящую круглую трубу радиуса R (рис. 6.1.2), заполненную гиротропной средой, намагниченной вдоль оси трубы. В цилиндрической системе координат, в которой необходимо решать эту задачу (чтобы
иметь возможность удовлетворить граничным условиям на поверхности трубы), уравнение (5.1.46) для функции запишется следующим образом (см., например, [291):
д* 2Ф± £ дФ-1_ , 1
Sp2 ""Г р др р2
+ х2г.2Ф± = О,
(6.1.16)
Частным решением уравнения (6.1.16), конечным при р = О, является [38]
= Jm (xi,2p) eim<₽,	(6.1.17)
где Jm — функция Бесселя, а | т | = 0, 1, 2, ... из условия периодичности (т. е. сохранения величины ф± при изменении ф на 2л). Принятая в (6.1.17) зависимость от <р соответствует волнам с круговой поляризацией т) или волнам, бегущим по азимуту. В случае гиротропной среды только такие волны удовлетворяют всем упомянутым выше условиям, т. е. могут обеспечить выполнение граничных условий.
Для вычисления составляющих поля следует подставить ф = ф±е“^г	(6.1.18)
в проекции выражений (5.1.48) на направления единичных векторов р0, фо и zo цилиндрической системы координат. Полученные таким образом поля будут соответствовать при данном | т | Д= О четырем элементарным решениям или «парциальным волнам» 2);
') Следует различать поляризацию волны, определяемую видом зависимости (*р), п поляризацию поля этой волны, которая будет различной в разных точках сечения волновода.
2) Для краткости мы говорим о волнах, но это могут быть как распространяющиеся волны, так и ближнре поля, в зависимости от знака Re (А:2).
6.1]	ВОЛНОВОД С ПРОДОЛЬНО НАМАГНИЧЕННОЙ СРЕДОЙ 273
с Xj и е’1т|ф, с хг и е“’1’',1<₽, с х2 и е’1;,11'-₽ и, наконец, с х2 и е ’! До наложения граничных условий эти волны независимы.
Граничные условия будут следующими:
е2 = 0 и = 0 при р = R.	(6.1.19)
Эти граничные условия, в соответствии с высказанными выше общими соображениями, не удовлетворяются для парциальных волн по отдельности. Сумма же двух парциальных волн с различными х и любыми, но одинаковыми знаками т будет удовлетворять граничным условиям. Ей соответствует функция
Ф = [4j/m(xip) + Л21т (х2р)] ег<тч>”М.	(6.1.20)
Подставляя в граничные условия (6.1.19) составляющие е2 и вычисленные исходя из функции (6.1.20), получим систему линейных однородных уравнений для Аг и Л2. Равенство нулю ее определителя даст трансцендентное уравнение, которое в интересующем нас случае магнитно-гиротропной среды (еа =0, ец = е) запишется следующим образом:
/А-2ер.±—fc2 \ /'n(zi77)	к* \ Jm(x2R) ,
\ Xi	Jm(xiR) \ х^ Х2/	(хз«) 1
Уравнение (6.1.21)х) совместно с двумя выражениями (5.1.47) дает возможность определить хх, х2 и постоянную распространения kz.
Заметим прежде всего, что kz входит в уравнение (6.1.21), как и в выражения (5.1.47), только в квадрате. Поэтому знак кг, т. е. направление распространения не влияет на величины | kz |, хг и х2. Изменение направления распространения не влияет в данном случае и на конфигурацию поля.
Величины р0 и т входят в уравнение (6.1.21) и в первых степенях. Поэтому направление постоянного намагничения и направление вращения поляризации волны оказывают влияние на | kz |, хх и х2. Поскольку и т входят в первых степенях только в виде произведения рат, то определяющим, как и в случае неограниченной среды (§ 5.2), является направление вращения поляризации волны относительно направления постоянного намагничения. Волны с правым и левым вращением относительно этого направления имеют разные постоянные распространения kzn и к2Л. Исключение представляет лишь случай т — 0, т. е.
т) Опо было независимо и почти одновременно получено Сулом и Уикером [446], Кейдзом [442], Гинцбургом [445] и Гамо,
274 ВОЛНОВОДЫ И РЕЗОНАТОРЫ с ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
волн с осевой симметрией, для них направление постоянного намагничения не влияет на | /с2 |.
Различие постоянных распространения к:Т1 и kzSl (при т 0) приводит в волноводе с продольно намагниченной средой, так же как и в неограниченной среде (§ 5.2), к преобразованию поляризации эллиптически поляризованной волны ’). В частности, имеет место поворот оси эллипса поляризации волны — эффект Фарадея. При | т | = 1 формулы § 5.2, связывающие параметры эллиптически поляризованной волны с постоянными распространения к2П и к2Л, будут справедливы и для волновода. При | т | > 1 формула (5.2.20) для угла поворота поляризации заменится [446] на
к п — Аг
(б-1-22)
Уравнение (6.1.21) имеет при каждом значении т бесконечное количество корней, соответствующих типам волн (или ближних полей) с различной радиальной структурой поля. При произвольных параметрах среды уравнение (6.1.21) совместно с (5.1.47) может быть решено лишь численными методами. В случае малых
(так называемое слабо-гиротропное приближение) может быть применен метод возмущений, при котором невозмущенной системой является волновод, заполненный средой с теми же е и р,, но с рй = 0. Подробное исследование корней уравнения (6.1.21) с учетом зависимости компонент р, от частоты проведено в [446].
Круглый волновод с гиротропным стержнем. Рассмотренная выше задача представляет принципиальный интерес, но на практике круглый волновод, целиком заполненный ферритом, редко применяется в устройствах, использующих эффект фарадея. Причина этого заключается в следующем: если размеры сечения волновода с ферритом оставить такими же, как и пустого волновода, то в нем будут существовать, кроме рабочего типа волны, несколько паразитных высших типов волн; уменьшение же размеров сечения волновода в месте расположения феррита усложнит согласование устройства. Кроме того, добротность (отношение угла поворота поляризации к потерям) таких устройств оказывается невысокой. Указанные трудности могут быть устранены при частичном заполнении волновода ферритом. При этом целесообразно, во-первых, сохранить осевую симметрию системы, а, во-вторых, разместить феррит в той области, где при круговой
х) Роль вектора, поляризация которого рассматривается, в случае волновода играет некоторый вектор, лежащий в плоскости поперечного сечения и жестко связанный с мгновенной структурой поля. Этот вектор можно назвать вектором поляризации волны. Поляризация же поля будет, конечно, различной в разных точках сечения волновода.
§ 6.1] ВОЛНОВОД С ПРОДОЛЬНО НАМАГНИЧЕННОЙ СРЕДОЙ	275
поляризации волны поляризация поля также будет приближаться к круговой. Этим требованиям удовлетворяет круглый волновод с коаксиальным круглым ферритовым стержнем (рис. 6.1.3). Такой волновод нашел широкое применение в технике сверхвысоких частот в устройствах, использующих эффект Фарадея (см., например, [11]).
Задача о круглом волноводе с круглым коаксиальным стерж-
нем из продольно намагниченного гиротропного вещества может быть решена строго. Необходимо записать выражения для состав-
ляющих поля в обеих областях (см. рис. 6.1.3): гиротропной среде (р <С Ро) и изотропной (р0 < р<С R), и наложить на них граничные условия. Составляющие поля в гиротропной среде запишутся так же, как в предыдущей задаче. Поле в изотропной среде будет являться суммой полей ТЕ и ТМ и, поскольку точка
р = 0 не принадлежит данной обла- Рис. 6.1.3. Круглый волновод с прости, будет содержать не только функ- д“	гиротроп'
ции Бесселя Jm (хор), но и функции
Бесселя второго рода (функции Неймана) Nm (хор) [38, 44]. В ре-
зультате в выражения для составляющих этого поля войдет
четыре константы.
Граничные условия будут заключаться в равенстве нулю касательных составляющих электрического поля на стенках вол
новода:
е02 = 0 и Соф = 0 при р = R	(6.1.23)
и непрерывности касательных составляющих электрического и магнитного полей на поверхности раздела сред:
е02 = ez, е<№ = е<₽, hoz = hz и	при р = р0. (6.1.24)
Шесть условий (6.1.23) и (6.1.24) дадут систему однородных линейных уравнений для шести констант, входящих в выражения для составляющих поля в обеих средах. Приравнивая нулю определитель этой системы, мы получим трансцендентное уравнение для неизвестных величин: kz, хп х2 и х0. Решая его совместно с двумя уравнениями (5.1.47) и простым соотношением
= ^оеоИо — ^z,	(6.1.25)
для изотропной среды можно найти все четыре неизвестные величины, т. е. определить постоянную распространения и структуру поля в волноводе.
2?6 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГЙРОТРОПНЫМН СРЕДАМИ |ГЛ. В
Не выписывая указанного трансцендентного уравнения, отметим лишь, что в него, как и в уравнение (6.1.21), kz войдет только в четных степенях, а и т — ив первой степени в виде произведения р.ат. Отсюда следует, что в волноводе с продольно намагниченным гиротропным стержнем, так же как и в неограниченной среде и в целиком заполненном волноводе, | kz | не зависит от направления распространения и зависит от направления вращения поляризации относительно направления намагничения. Преобразование поляризации, в частности поворот осей эллипса поляризации (эффект Фарадея), будет происходить в волноводе со стержнем качественно так же, как и в целиком заполненном волноводе. В частности, будет справедлива формула (6.1.22).
Осуществление намеченной выше программы приводит к громоздким вычислениям и практически осуществимо только с использованием электронных вычислительных машин. И поскольку эта задача представляет большой практический интерес, целесообразно остановиться на методах ее приближенного решения. Если радиус стержня достаточно мал, может быть применен метод возмущений (§ 5.3) с квазистатической аппроксимацией внутреннего поля. Рассмотрим кратко применение этого метода к нашей задаче 1).
Будем исходить из формулы (5.3.38). Используя соотношение (5.3.37) и выражая составляющие внутреннего поля через составляющие невозмущенного поля по формулам (5.3.47) и (5.3.51), получим для магнитно-гиротропного (например, ферритового) стержня
,, к	t Го.. Н2-Н2о~^	,
2No J L (Р + Р-^-р2
Ф Ра	*	»
+ 4 , , 42	2 zo (х ЗГо±) + (И II - Ро) + 1 ’
(и + р(1)2—Ра
+ 2+ (8 - 80) dS, (6.1.26) С  |— o;j	J
где все обозначения такие же, как в § 5.3.
Входящие в (6.1.26) собственные векторные функции невозмущенного волновода целесообразно выразить через его скалярную функцию ф0. Для нее в данном случае следует принять выражение;
[фо = Лп(хор)е1т!р,	(6.1.27)
соответствующее волнам с круговой поляризацией и правым или левым, в зависимости от знака т, вращением, так как именно эти
г) Более подробное решение приведено в [6].
§ e.ij полповод с продольно намагниченной средой 271
волны являются нормальными волнами для возмущенного волновода.
Предположим, что в невозмущенном волноводе имеет место волна ТЕ. Тогда составляющие собственных векторных функций невозмущенного волновода и выразятся через скалярную функцию следующим образом [291:
и2
<o_L = ^'Фо> «^Ог = £"7“ Фо,
20	(6.1.28)
8>o_l — ^о'‘'Фп X г.(|, Йо? = 0.
Подставим эти выражения с учетом (6.1.27) в формулу (6.1.26) и заменим в ней интеграл по сечению стержня на произведение подынтегральной функции в центре волновода на площадь сечения. Такая замена допустима, если радиус стержня р0 много меньше длины волны в веществе, что совпадает с условием применимости квазистатической аппроксимации внутреннего поля.
После сравнительно несложных вычислений, при которых используются некоторые общие формулы теории волноводов [29], мы придем к окончательному выражению для представляющей наибольший практический интерес волны ТЕП:
2	? 2
{kz - Mteu = 2,1/с20 М	. (6.1.29)
\ и 1 Zt Иа + Е» ZrJ S + Во /
Здесь знаки плюс перед соответствуют волне с правым вращением, а знаки минус — волне с левым вращением относительно направления постоянного намагничения. Зная постоянные распространения этих волн, можно затем по общим формулам (5.2.20) и (5.2.22) найти угол поворота поляризации и изменение эллиптичности линейно поляризованной волны. Например, угол поворота поляризации на единицу длины
4,2Д0(£)2
_____________
(р + цо)2—р2
4 Qn\
I О. X .0X7 1
Оценим пределы применимости проведенного расчета. Величина d в выражении (5.3.53) представляет собой в данном случае диаметр стержня 2р0. Принимая, например, 7?Д0 = 1/(2 ]/2), | 8 | = 9 и | р. | = 1, получим
£<0,04.
На практике в поляризационных (фарадеевых) ферритовых устройствах [11] используются значительно большие отношения р0/Я, и метод возмущений с квазистатической аппроксимацией становится неприменимым для количественных расчетов. Однако
27g ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
полученные этим методом выражения, в частности (6.1.29) и (6.1.30), правильно отражают зависимости характеристик вол-
новода от параметров вещества.
При небольших величинах р„ (слабо-гиротропное приближение) для более точного расчета постоянной распространения в волноводе с продольно намагниченным стержнем может быть использован другой вариант метода возмущений. В качестве невозму-
Рис. 6.1.4. Зависимости угла поворота поляризации в круглом волноводе с ферритовым стержнем (рис. 6.1.3) от отношения радиусов стержня и волновода при различных значениях е феррита [455]. #]—угол поворота поляризации на Длине 1 см. Сплошные линии расчет при ц = ц ц =1 ицй = 0,2. Пунктир— расчет по формуле (6.1.30) при тех же значениях параметров.
щенной системы принимается в этом случае волновод со стержнем тех же размеров и с теми же р и е, но с ра = 0. Разумеется, задача об определении его постоянной распространения должна быть предварительно решена. Параметром малости является теперь р.й/р, а радиус стержня Ро может быть произвольным. На рис. 6.1.4 приведены полученные Моносовым [455] таким методом зависимости угла поворота поляризации от р0. При малых р0 (в соответствии с приведенной выше оценкой) они совпадают с (6.1.30). Затем рост происходит гораздо быстрее и при некотором значении р0, тем меньшем, чем больше е, достигается максимум. Такой характер зависимости от р0 подтверждается экспериментально. Резкое возрастание в некотором интервале значений
радиуса стержня качественно может быть объяснено эффектом
концентрации энергии в стержне, а дальнейшее немонотонное изменение flj — изменением структуры электромагнитного поля.
§ 6.2. Прямоугольный волновод
с попертчно намагниченной гиротропной средой
Рассмотрим теперь регулярный волновод с гиротропной средой, намагниченной в направлении, перпендикулярном оси волновода (поперечное намагничивание). В этом случае, в отличие от продольного намагничения, вряд ли можно получить какие-либо определенные результаты при произвольной форме поперечного сечения волновода. Поэтому мы разберем конкретный пример прямоугольного волновода с постоянным полем, перпенди
§ 6.2]	ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ	279
кулярным его широкой стенке. Такие волноводы с ферритом широко используются в технике сверхвысоких частот. Важным их преимуществом является сравнительно небольшой магнитный зазор.
Прямоугольный волновод, заполненный гиротропной средой. Остановимся прежде всего на задаче о регулярном прямоугольном волноводе, целиком заполненном поперечно намагниченной средой (рис. 6.2.1). Рассмотрим простейшие типы волн в таком
волноводе, характеризующиеся независимостью поля от координаты z (ось z, как всегда, совпадает с направлением постоянного намагничения).
В случае dldz — 0 общая методика расчета, развитая в конце §5.1 для гармонической зависимости от z, в принципе применима. Функция ф удовлетворяет уравнению (5.1.46), а для х1)2 из (5.1.47) следует
Рис. 6.2.1. Прямоугольный волновод, заполненный поперечно намагниченной гиротропной средой.
х‘( =	и Н_ц,	Х2 = /СоеДР|)  (6.2.1)”
Однако для вычисления составляющих поля в данном случае более простым является путь, основанный на непосредственном проектировании уравнений Максвелла на оси прямоугольной системы координат (рис. 6.2.1).
Запишем
комплексные амплитуды поля (не зависящего от z)
в виде
e = ev(a;)e-iV, h = hv(®)e4V	(6.2.2)
и подставим их составляющие *) в проекции уравнений (5.1.18) и (5.1.20) при jCT = 0. Для тензоров ii и е примем выражения (5.1.33) и (5.1.34). В рассматриваемом случае, когда d/dz = 0, полученная система шести уравнений распадается на две независимые системы:
kyez — koyhx — ik0'iahy = 0, — k0'iahx — ikouhy — 0,	(6.2.3)
- Л е2 + ikbbx + — = 0
и систему для составляющих hz, ех и еу, которую мы не выписываем.
х) Индекс v при этих составляющих опускаем.
280 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
Граничное условие
Cv у п0 =	0 на	стейках	волновода
(п0 — единичный	вектор	нормали к	поверхности волновода)
в данном случае дает
еу = 0	при х	= 0,	х = a,	z = 0, z = b,
ех = 0	при	z = 0, z = Ь,	(6.2.4)
ez = 0 при х = 0, х = а.
Так как граничные условия для составляющих поля независимы, то две упомянутые выше системы уравнений должны соответствовать двум независимым классам полей: ТЕпо1) (система (6.2.3)) и ТМПО (система для hz, ех и еу). Однако, как видно из (6.2.4), все составляющие вектора ev для полей ТМГ10 равны нулю при z = 0 и z = Ь, а следовательно, в силу независимости от z — и везде. Таким образом, полей ТМ„0 в прямоугольном волноводе не может существовать.
Для полей ТЕ,м из системы (6.2.3) легко выразить составляющие магнитного поля через е2:
<6-2 *-5)
а для ег получить следующее уравнение:
•^- + >^ = 0.	(6.2.6)
Здесь
=	(6.2.7)
а как и раньше, определяется выражением (5.1.36). Ясно, что
Хх + /Су = X2,
где х — величина, входящая в уравнение (5.1.46); значения ее, следующие из общей теории, были приведены выше — выражения (6.2.1). Сравнивая (6.2.1) и (6.2.7), мы видим, что значение хх соответствует полям ТЕ„0 (полей с х2 не существует).
Решение уравнения (6.2.6), удовлетворяющее граничным условиям (6.2.4), запишется в виде
ez = A sin хус,	(6.2.8)
причем
Хх = (и = 1, 2, 3, . . -).	(6.2.9)
2) Индексы п и 0, как обычно, укалывают на число вариаций ноля по осям
гс и ? в плоскости поперечного сечения волновода.
§ 6.21
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ
281
С учетом (6.2.9) из (6.2.7) следует окончательное выражение для постоянной распространения в прямоугольном волноводе, заполненном поперечно намагниченной гиротропной средой,
ку =	(6.2.10)
Полагая в (6.2.10) ку = 0 (параметры ец, р и ра при этом считаются вещественными), получим выражение для предельных длин волн
Ьпр =	(6.2.11)
Таким образом, в рассматриваемом случае предельная длина волны в волноводе, а следовательно и фазовая и групповая скорости, определяются по тем же формулам, как и для волновода с изотропной средой [29] с заменой е->ец и р.pj_.
Структура электрического поля (выражение (6.2.8)) также не отличается от случая изотропной среды. Можно убедиться, что
Рис. 6.2.2. Силовые линии магнитного поля волны ТЕ1С в прямоугольном волноводе, заполненном ферритом, для двух направлений распространения, е — 9; р = 0,9;
Ка= 0,6, длина волны в свободном пространстве — V‘2 а.
не отличается от случая изотропной среды и магнитная индукция b — цЛ. Однако структура магнитного поля, как следует из (6.2.5), существенно отличается отлизотропного случая.
Как видно из (6.2.5), структура магнитного поля изменяется при изменении знака ку, т. е. направления распространения, и знака ца, т. е. направления постоянного намагничения (рис. 6.2.2). В этом проявляется невзаимность (в дифференциальном смысле, см. § 5.3) данной системы. Очевидно, что одновременное изменение знаков ку и ра не изменит конфигурации магнитного поля.
282 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [гл. 6
Зависимость структуры магнитного поля от направления распространения приводит, между прочим, к тому, что условия на плоской, перпендикулярной оси волновода границе двух сред, из которых хотя бы одна является гиротропной, не удовлетворяются, в отличие от случая изотропных сред, при наличии только падающей, отраженной и проходящей воли одного типа. На такой границе при падении одной из волн ТЕИО будут возникать бесконечные ряды отраженных и проходящих волн ТЕп0 с разными п.
Мы не будем останавливаться подробно на исследованных Микаэляном [447] и другими [453] типах волн в прямоугольном волноводе с гиротропной средой, для которых составляющие поля зависят от обеих координат х и z. Заметим лишь, что в этом случае «парциальные» волны с x.j и х2 не удовлетворяют граничным условиям, а нормальные волны волновода, как и в случае волновода с продольно намагниченной средой (§ 6.1), являются их суммами. Эти волны не являются волнами ТЕ или ТМ. Наличие двух парциальных волн с разными зависимостями от х приводит к тому, что граничные условия при х = 0 и х = а могут удовлетворяться не только при синусоидальных, но и при экспоненциальных зависимостях от х, т. е. при x2x1i2 <С 0. Отсюда, в свою очередь, следует возможность существования распространяющихся волн (fcy 0) при сколь угодно больших значениях хж и х2, т. е. при сколь угодно малых поперечных размерах волновода. Наличие таких волн, исследованных Сэйделом [453] и другими, является одним из наиболее интересных следствий гиротропности заполняющей волновод среды ’). При достаточно малых размерах сечения волновода эти волны являются магнитостатическими (см. главу 7).
Волновод с поперечно намагниченной фгрритовой пластиной. Перейдем теперь к исследованию регулярного волновода, частично заполненного поперечно намагниченной гиротропной средой. При частичном заполнении волновода гиротропной средой не только устраняются недостатки, свойственные целиком заполненному волноводу (возникновение высших типов волн, трудности согласования), но и возникают, как мы убедимся, новые интересные невзаимные эффекты.
Остановимся на наиболее простом случае волновода с поперечно намагниченной пластиной, параллельной его узкой стенке (рис. 6.2.3). Эту задачу рассматривали Кейлз, Чет и Саки-отис [443] и многие другие (см., например, [448, 460]). Для тензора магнитной проницаемости пластины примем по-прежнему выражение (5.1.33), а электрическую проницаемость ее и пара-
*) Распространение волн в волноводах малого сечения (отсутствие отсечки) имеет место и в волноводе с продольно намагниченной гиротропной средой [446, 453].
§ 6.2]
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ
283
метры остального волновода (ж < g и g + h < х < а) будем считать скалярными. Составляющие поля и другие величины, относящиеся к изотропной среде, будем писать с индексами 0, а величины для гиротропной среды (будем называть ее для простоты ферритом) — без дополнительных индексов.
Ограничимся рассмотрением полей с dldz = 0, комплексные амплитуды их будем записывать в виде (6.2.2), опуская, как и
раньше, индексы v у составляющих этих амплитуд. Электрическое поле в феррите удовлетворяет уравнению (6.2.6), а величина х, входящая в это уравнение, определяется выражением (6.2.7). В дальнейшем индексы х у величин хх и хож мы будем опускать. Электрическое поле в изотропной среде удовлетворяет уравнению
rf26'	о
_^+х^02 = 0, (6.2.12) где
х"2 — &о8о|Го — Zc®. (6.2.13)
Рис. 6.2.3. Прямоугольный волновод с поперечно намагниченной ферритовой пластиной.
Составляющие магнитного поля в феррите связаны с ег соотношениями (6.2.5), а в изотропной среде — соотношениями
h - v е h -	1	02
" А-оро °2’	°!' ~ ~	’
(6.2.14)
Граничные условия будут следующими:
eoz = 0	при ж = О и х ~ а, (6.2.15)
е02 = ег и hOy = hu при х = g и х = g A h. (6.2.16)
Электрические поля, удовлетворяющие уравнениям (6.2.6) и (6.2.12) и граничным условиям (6.2.15), можно записать следующим образом:
при при при
0<ж<д £<£<g+h h<A х<А а
eOz = A sin хож,
е2 = С зтх(ж — g) -|~ D cos х (ж — g), eoz = 2?sinx0(a — ж).	(6.2.17)
Четыре условия непрерывности касательных составляющих поля (6.2.16) с учетом (6.2.5) дадут систему линейных однородных уравнений для коэффициентов А, В, С и D. Приравнивая нулю определитель этой системы, получим уравнение
р ctg х.Л (tg xog + tg x0Z) — —2--g2 tg xog tg x0Z 4- p0 +
+ g (tg — tg x0Z) = 0/ (6.2.18)
284 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРО тропными СРЕДАМИ [ГЛ. 6
где
Р ”	’ Р° ~~	’
r_L	г ’
Иа' у о == ------,
PPj_
(6.2.19)
а I = а — g — h (рис. 6.2.3).
Из уравнения (6.2.18) совместно с (6.2.7) и (6.2.13) могут быть определены постоянная распространения ку и величины х и х0, характеризующие распределение поля в поперечном сечении. Уравнение (6.2.18) имеет бесконечное множество корней, соответствующих различным типам полей в рассматриваемом волноводе. Эти типы полей можно обозначать ТЕП 0, где п — номер корня уравнения (6.2.18). При толщине пластины h -> 0 они переходят в обычные поля ТЕп0 в волноводе с однородной изотропной средой. Те из полей, для которых (при вещественных параметрах среды) окажется ку 0, будут иметь характер распространяющихся волн, а остальные — ближних полей с экспоненциально убывающей амплитудой. Предельные длины волн, размеры или значения параметров, при которых происходит переход распространяющейся волны в ближнее поле, могут быть определены с помощью уравнения, которое получится из (6.2.18), если положить в нем ку = 0. Интересно отметить, что в этом случае величина войдет в уравнение только в квадрате, т. е. предельные величины не зависят от направления постоянного намагничения.
В общем же случае уравнение (6.2.18) содержит последний член, в который ц,, а также ку входят в первой степени. Следовательно, корни этого уравнения, т. е. постоянные распространения волн или коэффициенты ослабления ближних полей, будут различными для разных направлений намагничения и разных направлений распространения. При одновременном изменении обоих направлений корни уравнения (6.2.18) останутся прежними. Как видно из уравнения (6.2.18), замена g I, т. е. перенос пластины к другой стенке волновода приводит к такому же изменению корней уравнения, как и изменение знака р.г или ку.
Последний член уравнения (6.2.18) обращается в нуль и, следовательно, величина постоянной распространения не зависит от знака ра или ку при g = I, т. е. при симметричном расположении пластины в волноводе.
Зависимость | ку | от направления распространения, направления намагничения или положения пластины в волноводе представляет собой принципиально новый невзаимный эффект, который связан с граничными условиями и не имеет аналога в неограниченной поперечно намагниченной среде. Этот эффект находит очень широкое применение в технике сверхвысоких частот. Зависимость вещественной части постоянной распространения kv вдали от ферромагнитного резонанса от направления
§ 6.2]
ВОЛНОВОД С ПОПЕРЕЧНО НА МАГНИЧЕННОЙ СРЕДОЙ
285
распространения используется для создания невзаимных фазовращателей, а невзаимность мнимой части kv в области резонанса— для создания резонансных вентилей [11].
Случай тонкой пластины. Большой принципиальный и практический интерес, который представляет рассматриваемая задача, делает целесообразным более подробный анализ решений уравнения (6.2.18). Остановимся сначала на предельном случае малой толщины пластины.
Уравнение (6.2.18) можно привести к виду
sinx0(a— h) ф- h^±u0—tg-?— — 0,	(6.2.20)
*	X(j хл
где
л
F (kv) = у (Ро + Р2 + tf2)cos хо (а — К) +
+ у (Р20 — Р2 — <72) cos х0 (g — I) + poq sin х0 (g — /). (6.2.21)
В нулевом приближении (й -> 0)
(*о)о=~ (и = 1, 2,3, ...).	(6.2.22)
При этом первый член (6.2.20) стремится к 0, а множитель F (ку)/х0 остается конечным. Поэтому, решая уравнение (6.2.20) в первом приближении, можно для этого множителя принять нулевое приближение F (ку0)/(и0)0, где, согласно (6.2.13),
Руо — ^оеоро — (ио)о •	(6.2.23)
Первый член (6.2.20) может быть в первом приближении записан в виде
sin х0 (а — h) = пп — (а — h).
Здесь (xq)j — значение х0 в первом приближении, которое, согласно (6.2.13), имеет вид
(ХО)5 = (х0)0 [ 1 - Ьку] ,	(6.2.24)
где &ку = ку — ку0. Итак, уравнение (6.2.20) в первом прибли жении сводится к следующему:
пл - (ХоХ (а - h) + F{(kw) = 0-	(6-2.25)
^О/О
Интересуясь основной волной ТЕ10, примем п = 1. Тогда с учетом (6.2.22), (6.2.23) и (6.2.24) получим из (6.2.25) формулу для приращения постоянной распространения при введении в
286 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ.
волновод тонкой ферритовой пластины
д^ = - (м+Я 	(6,2’26)
Вычисляя величину F (ку0) согласно (6.2.21), придем к окончательному выражению . , h Г Л2 ! Р- L	. \	9 Л . ,2	! r . \	„ л
А/ц, = ~7  —г~ —-----1 COS2 — F + &о'-оео---1 8Ш — g +
v akw L а2 \ Ио У а	\ R; / а
+ 4.(1	(6.2.27)
Выражение (6.2.27), полученное в первом приближении из строгого уравнения (6.2.18), в точности совпадает с выражением, которое может быть найдено [452] методом возмущений с использованием формулы (5.3.38) при квазистатической аппроксимации внутреннего поля. Однако метод возмущений может быть применен и для пластины, высота которой меньше высоты волновода, и для других конфигураций гиротропных образцов в волноводе (рис. 6.2.4), для которых строгое решение не может быть проведено.
Воспользуемся теперь формулой (6.2.27) для вычисления так называемой неезаим-
ной разности постоянных распространения
&ку = ку+ — ку~,	(6.2.28)
где ки+ и ку_ соответствуют разным направлениям распространения или разным направлениям постоянного намагничения или положениям пластины у противоположных стенок волновода. Как следует из (6.2.27),
^2n-^sin^g.	(6.2.29)
Зависимости $ку от g, вычисленные по формуле (6.2.29), показаны (пунктиром) на рис. 6.2.5. Как и следовало ожидать, дку = О при g = а/2, что при Л -► 0 соответствует симметричному расположению пластины в волноводе.
В качестве второго примера использования формулы (6.2.27) определим зависимость Аку = ку — ку0 от pio при g = а/^. Тогда
Рис. 6.2.4. Поперечно намагниченные пластины в прямоугольном волноводе, используемые в ферритовых устройствах диапазона СВЧ.
§ 6.2]
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ
287
из (6.2.27), как нетрудно убедиться, следует
AA-'j, —	~ Мо +
(6.2.30)
где Л о, и А2 зависят от р, р0, е, е0 и а. Зависимость Аку от р„ показана (пунктиром на рис. 6.2.6. Эта зависимость представляет интерес для области малых постоянных полей, где (при достаточновысоких частотах) р мало зависит от поля (см. рис. 3.1.4). При этом ра в первом приб
лижении пропорционально намагниченности Мо и, следовательно, зависимость Аку от Мо носит такой же характер, как и зависимость, показанная на рис. 6.2.6.
В качестве критерия справедливости формулы (6.2.27) можно принять выражение (5.3.53),из которого для обычных ферритов вдали от ферромагнитного резонанса следует условие
— ^0,04. а 7
Это условие обычно не выполняется в применяемых на практике ферритовых устройствах. Поэтому рассмотренное первое приближение, правильно отражая некоторые тенденции (например, отмеченные в приведенных выше примерах), не может быть ис
Рис. 6.2.5. Зависимость невзаимной разности фазовых постоянных от толщины и положения поперечно намагниченной пластины в прямоугольном волноводе (см. рис. 6.2.3). Пунктир— расчет по формуле (6.2.29). Сплошные линии— точный расчет [460]. Цифры-у кривых— значения Л/а; е = 9; р, = 0.9; р. = 0,5 = 1,39 а.
пользовано для расчетов.
Пластина произвольной толщины. При произвольных значениях толщины пластины уравнение (6.2.18) может быть решено лишь численными методами. Рассмотрим в качестве примера некоторые результаты таких расчетов [454, 460], проведенных с помощью электронной вычислительной машины.
Вдали от области ферромагнитного резонанса, когда мнимые части р" и ца, так же как и е", малы по сравнению с вещественными (не превышают -~0,1), расчет вещественной части постоянной распространения к',, можно вести, пренебрегая этими мнимыми частями. На рис. 6.2.5, 6.2.6 и 6.2.7 приведены результаты таких расчетов. Как видно из рис. 6.2.5, при малой толщине пластины
288 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6

h зависимость невзаимных фазовых сдвигов от положения пластины довольно близка к той, которая получается в первом приближении по формуле (6.2.29). Однако по мере увеличения h максимум Ьку быстро смещается к стенке волновода, а величина его резко возрастает. Это возрастание качественно можно объяснить концентрацией энергии в пластине (так называемым «эффектом диэлектрического волновода»). Оно происходит тем резче, чем больше е пластины. Из рис. 6.2.5 видно также, что при большой толщине пластины заметный невзаимный фазовый сдвиг имеет место уже при g = 0, т. е. когда пластина прилегает к стенке волновода. При дальнейшем увеличении толщины пластины и увеличении е этот сдвиг резко возрастает (рис. 6.2.7).
Как видно из рис. 6.2.6, характер зависимости приращения постоянной распространения Аку к'у — —куо от ра при промежуточных (g =/= 0 и g -4= (а — h)/2) положениях пластины передается приближенной формулой (6.2.30). Однако зависимость !\кут: p,t оказывается в действительности значительно более сильной вследствие уже упоминавшегося эффекта концентрации энергии в пластине.
по сравнению с веществен-
Рис. 6.2.6. Зависимость приращения фазовой постоянной, вызванного поперечно намагниченной ферритовой пластиной в прямоугольном волноводе, от при различных положениях пластины. Пунктир— расчет по формуле (6.2.30). Сплошные линии--' точный расчет 14601 h = 0,08 а (при этом максимум 6k имеет место яри g = = 0.07 а), е =- 9; д —0,9; л0 — 1,39 а.
Если мнимые части р, ра и е малы
ными, то для вычисления мнимой части постоянной распространения к,,, характеризующей затухание волн в волноводе с гиротропной средой, может быть использована приближенная формула
к'у =	+	.	(6.2.31)
v де'	ф' f ф- ‘ а	’
С помощью этой формулы был проведен [460] расчет добротности ферритового невзаимного фазовращателя
Q = -г „
2 (S/++
(6.2.32)
§ 6.2]
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ 289
поле, которое в
Рис. 6.2.7. Зависимости невзаимной разности фазовых постоянных от толщины поперечно намагниченной ферритовой пластины, расположенной у стенки волновода, при различных е феррита [454]. ц = 0,9;
ца = 0,5: Ло= 1,39 а.
(индексы плюс и минус соответствуют двум направлениям распространения). Результаты этого расчета приведены на рис. 6.2.8.
В области ферромагнитного резонанса, где величины р" и ря одного порядка или больше, чем р' и ря, формула (6.2.31), конечно, не справедлива и необходимо искать комплексные корни уравнения (6.2.18). При этом разумно вести расчет, не задавая р и рл независимо, а определяя их по формулам § 1.3 через независимые параметры: to, Мо, Hi0 (внутреннее § 1.3 обозначалось Hq) и параметр диссипации. Результаты такого расчета приведены на рис. 6.2.9 в зависимости от внешнего поля Но. Из рис. 6.2.9 видно прежде всего, что резонанс (максимум к", резкое изменение к’у) в волноводе с пластиной происходит отнюдь не при поле Но = 5490 э, при котором в данном случае имеет место резонанс параметров вещества р и ра, а при поле Но — 2340 э. Эта величина совпадает с полем киттелевского резонанса в касательно намагниченной пластине (формула (1.4.19)). Поскольку толщина пластины была при расчете принята настолько малой, что условие справедливости квазистатического приближения хорошо выполнялось, указанное совпадение совершенно естественно.
Из рис. 6.2.9 видно далее, что невзаимность потерь наиболее силь
на при положении пластины с g = 0,185а, которое, как следует из рис. 6.2.5, является оптимальным для данного hla и с точки зрения дку. При расположении пластины у стенки невзаимность kv и ку невелика (пластина довольно тонкая), а при симметричном положении пластины в волноводе (g = (а — h)/2 — — 0,49а) невзаимность, как и следовало ожидать, совершенно исчезает.
Волновод с двумя пластинами. Уравнения для постоянной распространения, аналогичные уравнению (6.2.18), могут быть получены, в принципе, для волн ТЕ с д/dz — 0 в прямоугольном волноводе с любым числом поперечно намагниченных гиротропных и изотропных пластин, параллельных узким стенкам волновода. Мы рассмотрим наиболее простые случаи двух пластин одинаковой
10 А. Г. Гуревич
Л290 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМЙ СРЕДАМИ [Ел. 6
Рис. 6.2.8. Зависимость добротности (6.2.32) невзаимного ферритового фазовращателя от толщины ферритовой пластины и положения ее в волноводе [460].» е = 9—10,02; р=0,9—i 0,01; да = 0,5— г 0,005. Кружки соответствуют максимумам невзаимной разности фазовых сдвигов (см. рис. 6.2.5).
Рис. 6.2.9. Резонансные кривые при различных положениях поперечно намагниченной ферритовой пластины в волноводе [460]. Л = 0,02 а; цифры у кривых — значения g/a. ы/2л = 9,4 Геи; Мо = 170 гс; = 2-10в; е — 9. Величины |1 и на определялись согласно (1.3.21) и (1.3.22); предполагалось, что зти формулы остаются справедливыми и
при малых полях, если заменить в них Мо на «техническую» намагниченность Мо.
§ 6.2]
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ
291
толщины, симметрично расположенных в волноводе и намагниченных в противоположных направлениях (рис. 6.2.10, а) или одинаково (рис. 6.2.10, б). Еще до решения этих задач можно сделать качественные заключения о невзаимных эффектах, которые должны при этом наблюдаться. В первом приближении (параметр малости — толщина пластин h) приращения kv, обусловленные обеими пластинами, аддитивны. Тогда из формулы (6.2.29) следует, что в первом случае (противоположно намагниченных пластин) невзаимная разность постоянных распространения Ьку удваивается по сравнению с одной пластиной, а во втором случае (одинакового намагничения) обращается в нуль. Для пластин произвольной толщины аддитивность, конечно, не имеет места, однако и здесь в случае встречного намагничения можно ожидать увеличения 6/с,7 по сравнению с одной пластиной (по крайней мере для не очень толстых пластин). В случае же одинакового намагничения система обладает симметрией относительно плоскости, проходящей через ось волновода и параллельной направлению намагничения, и невзаимность ку должна полностью отсутствовать при любой толщине пластин.
.^Приступим теперь к выводу уравнений для постоянных распространения волн ТЕ с dldz = 0 в волноводе с двумя пластинами. Так же как и в случае одной пластины, следует записать выражения"'для"'составляющих'гполя'"во'гвсех областях и, наложив на^них'граничньиГусловия, получить” систему однородных уравнений для входящих'в’”эти’гвыражения”коэффициентов. Равенство
выми пластинами.
нулю определителя этой системы даст искомое уравнение. Граничные условия заключаются в равенстве нулю ez на стенках волновода и непрерывности ez и hv на всех границах раздела сред.
Будем обозначать индексами 1 и 2 величины для первой (g х g + h, рис. 6.2.10) и второй (g-\-h-\-2l<^x<^g + + 2h -|- 21) пластин, а индексом 0, как и раньше,— величины
10*
292 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
для изотропной среды. Решения уравнений (6.2.6) и (6.2.12) с учетом граничных условий при х = 0 и х = а можно записать,5 например, в следующем виде:
при 0 < х < g	е02	=	A sin хох,
при а — g<Zx<Za	е02	=	В sin х0 (а — х),
при g 4- h <4 х <g + h 4- 21 eoz = Csin x0 — x\ 4~
4- D cos x0 — xj, (6.2.33)
для первой пластины elz = F sin и (x — g) + G cos и (x — g),	. 4
для второй пластины e22 = К sin х (а — g — х)	М cos х(а—g—х)а
Магнитное поле в первой пластине будет определяться выра-w жением
hiv = -Д- (ку elz -	,	(6.2.34>,‘
аналогичным (6.2.5), а во второй пластине
h -	1	1~Г7г е zz I
Лсрх \+Kv р 2Z dx ) ’
(6.2.35)
где верхний знак соответствует случаю противоположно намагниченных пластин (рис. 6.2.10, а), а нижний — одинаково намагниченных (рис. 6.2.10, б). Это единственное различие приведет, как мы увидим, к существенному различию результатов.
Наложение граничных условий на поверхностях пластин с учетом (6.2.34) и (6.2.35) приводит к системе линейных однородных уравнений для восьми коэффициентов в (6.2.33). Для противоположно намагниченных пластин (рис. 6.2.10, а) из полученной системы вытекает
CD = 0.
Таким образом, эта система оказывается совместной в двух случаях:
1) С = 0, откуда следует А = В, F = К и G = М,
2) D = 0, откуда следует А = —В, F = —К и G = —М. Из выражений для составляющих поля можно видеть, что первый случай соответствует полям ТЕ,, 0 с нечетными п (к которым принадлежит и основная волна ТЕ10), а второй случай — полям ТЕпв с четными п.
В первом случае (нечетных п) равенство нулю определителя системы для оставшихся независимыми коэффициентов дает
§ 6-21
ВОЛНОВОД С ПОПЕРЕЧНО НАМАГНИЧЕННОЙ СРЕДОЙ
293
уравнение
р ctguh (tg xog- — ctgXoO + - tg xog ctg x0Z 4- p0 +
+ q (tg xog + ctg uol) = O. (6.2.36)
Оно отличается от уравнения (6.2.18) для одной пластины лишь заменой tg x0Z -> —ctg x0Z. Так же как уравнение (6.2.18), оно содержит «невзаимный» член, изменяющий знак при изменении направления распространения или направления намагничения обеих пластин (т. е. при замене их местами). Во втором случае (п четное) равенство нулю определителя системы для независимых коэффициентов приводит к уравнению, полностью совпадающему с (6.2.18). В этом нет ничего удивительного, так как структура поля в половине волновода с двумя пластинами для полей с четными п совпадает со структурой поля в волноводе с одной пластиной.
Рассмотренная задача о волноводе с двумя симметрично расположенными и противоположно намагниченными пластинами представляет интерес как модель так называемых «дискретных» фазовращателей, используемых в технике сверхвысоких частот в системах управления диаграммами направленности антенн [493]. В таких фазовращателях используются образцы с замкнутой магнитной цепью в состояниях остаточного намагничения [481]. Перемагничивание их производится импульсами тока; при этом вследствие невзаимности постоянной распространения фазовый сдвиг изменяется на некоторую (дискретную) величину.
В случае одинаково намагниченных пластин (рис. 6.2.10, б, нижний знак в (6.2.35)) все коэффициенты в выражениях (6.2.33) остаются независимыми и равенство нулю определителя системы для этих коэффициентов приводит к довольно громоздкому уравнению. Мы запишем его в частном случае пластин, прилегающих к узким стенкам волновода (g = 0):
tg 2x0Z [(ро + q2) tg2Kh — p2] — 2pop tg uh = 0.	(6.2.37)
В это уравнение (как и в уравнение при g =/= 0) величины kv и |ia входят только в квадратах. Следовательно, постоянная распространения в волноводе с двумя симметрично расположенными и одинаково намагниченными пластинами будет взаимна в соответствии с заключениями, которые были сделаны выше, исходя из анализа в первом приближении, а также из соображений симметрии.
Найдя решения уравнений (6.2.18), (6.2.36) или (6.2.37) совместно с выражениями (6.2.7) и (6.2.13), т. е. зная величины ку, х и х0, можно затем определить из соответствующих систем уравнений коэффициенты А, В, С, ... (конечно, с точностью до постоянного множителя), т. е. найти структуру поля в волноводе. Не
294 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
останавливаясь на этих вычислениях, приведем лишь в качестве примера структуры электрического поля в волноводах с одной и с двумя противоположно и одинаково намагниченными пластинами (рис. 6.2.11). Заметим, что структура поля является невзаимной даже в тех случаях (пластина в середине волновода, две симметрично расположенные и одинаково намагниченные
рис. 6.2.11. Электрическое поле в волноводах с поперечно намагниченными ферритовыми пластинами. Сплошные линии и пунктир — разные направления распространения.
пластины), когда постоянная распространения взаимна. Невзаимность структуры поля используется для создания ферритовых вентилей «со смещением поля» [477, 11]. В одном из таких вентилей поглощающая пленка помещается в том месте волновода (см. рис. 6.2.11), где для одного из направлений распространения электрическое поле мало, а для другого — имеет значительную величину.
§ 6.3. Резонаторы, содержащие гиротропную среду
Перейдем теперь ко второй фундаментальной задаче электродинамики полых систем с гиротропными средами — задаче о колебаниях полого электромагнитного резонатора, заполненного целиком или частично гиротропной средой. Теория таких резонаторов является обобщением теории полых резонаторов, заполненных однородной изотропной средой (см., например, [29]), которая была развита Кисунько [33] с использованием введенных Френкелем [43] собственных функций полого электромагнитного резонатора.
§ 6.3]
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
295
Собственные колебания. Рассмотрим замкнутый объем V (рис. 6.3.1), ограниченный металлическими стенками и содержа
щий среду, тензорные параметры которой р и е являются функциями координат. Пренебрежем диссипацией энергии в резона-
торе, т. е. будем считать тензоры р и е эрмитовыми (см. § 5.3), а проводимость стенок резонатора бесконечной, и рассмотрим свободные колебания, которые будут в этом случае незатухающими,— собственные колебания резонатора.
Комплексные амплитуды поля в резонаторе удовлетворяют уравнениям Максвелла (5.1.18) и (5.1.20) при jra = 0 и граничным условиям
е х По = 0 и ph  п0 = 0 на S, (6.3.1)
Рис. 6.3.1. Полый ^'резонатор, содержащий среду с тензорными парамет-|рами.
где щ — единичный вектор нормали к поверхности стенок резонатора S (см. рис. 6.3.1). Представим векоры е и h в виде
е (г) = ёет (г), h (г) = Жт (г),	(6.3.2)
где $ и Ж — комплексные амплитуды, связанные между собой соотношением
Ж = 1ё.	(6.3.3)
Подставляя (6.3.2) в уравнения Максвелла и учитывая (6.3.3), получим, что векторы ет (г) и hm (г) удовлетворяют уравнениям
rot hm = eem, rot em = ^2- phm. (6.3.4)
Граничные условия для них
ет X По = 0 и phm • п0 = 0 на S	(6.3.5)
непосредственно следуют из (6.3.1). Векторы ет (г) и hm (г) представляют собой собственные функции резонатора. В (6.3.4) to заменено на сот, чтобы подчеркнуть, что речь идет о частотах колебаний, соответствующих собственным функциям ет и hm.
Решения системы (6.3.4) при граничных условиях (6.3.5) существуют лишь при определенных значениях tom, образующих бесконечное дискретное множество собственных частот резонатора. Как правило, каждой паре функций ет и hm соответствует своя’собственная частота сот, и индекс т имеет смысл номера типа колебаний. В частных случаях, конечно, может иметь место вырождение — несколько разных типов колебаний могут иметь одинаковые частоты.
296 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
Исключая ет или hm из (6.3.4), получим, что эти векторы удов-
§ G.31
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
297
Получим теперь условия ортогональности и нормировки собственных функций. Запишем уравнение, комплексно-сопряженное с (6.3.6), для другого собственного колебания:
rot (р rot е„) = — е е„.
(6.3.9)
При этом, не принимая во внимание частотной зависимости компонент е и ц, считаем их в обоих случаях одинаковыми. Такое допущение является оправданным, если учесть, что непосредственный интерес представляют вынужденные колебания, происходящие с частотой <в возбуждающих токов или полей. Рассмотрение свободных колебаний имеет смысл построения системы функций, по которым будет проводиться разложение поля вынужденных колебаний. Эти функции можно строить для резонатора, заполненного гипотетической средой, для которой компоненты е и р при всех собственных частотах ат, <вп, ... имеют одинаковые значения — те же, что и реальная среда при частоте <в.
Умножим скалярно уравнение (6.3.6) на еп, а уравнение (6.3.9) — на ет, вычтем полученные выражения и проинтегрируем по объему резонатора. Учитывая эрмитовость тензоров ц (тензор рГ1 при этом тоже будет эрмитовым) и е и принимая во внимание граничные условия, придем к соотношению
(oim — и,?) e„eemdF = 0.	(6.3.10)
v
В отсутствие вырождения (<вт =/= со„) из (6.3.10) непосредственно следует условие ортогональности электрических собственных функций
е„еетс/У = 0	п).	(6.3.11)
v
При наличии вырождения из (6.3.10) еще не следует (6.3.11). Но если вырожденные собственные функции окажутся не ортогональными, всегда можно (см., например. [38]) перейти к их ортогональным линейным комбинациям.
Таким же образом, исходя из уравнения (6.3.7), можно показать, что магнитные собственные функции удовлетворяют условию ортогональности
й^цй^дС^У;	0 {т
(6.3.12)
298 ВОЛНОВОДЫ И РЕЗОНАТОРЫ с гиротропными СРЕДАМИ [ГЛ. 6
Если т = п, то интегралы в (6.3.11) и (6.3.12), конечно, не обращаются в нуль и их можно приравнять константам нормировки соответствующих функций. Из формул (6.3.8) с учетом (6.3.4) и эрмитовости тензоров р, и е легко получить, что константы нормировки электрических и магнитных собственных функций одинаковы. Принимая их равными 1, запишем окончательно условия ортогональности и нормировки в виде
en&emdV = hnphmdy = К у	у.
Здесь дельта-символ Кронекера
(6.3.13)
1 при
О при
т = п, m=j=n.
(6.3.14)
Остановимся теперь кратко на учете диссипации в среде, находящейся в резонаторе. Для собственных частот в этом случае будут по-прежнему справедливы формулы (6.3.8), при выводе которых не делалось предположения об эрмитовости тензоров ц и е. Но собственные функции, если определить их так, как было сделано выше для среды без диссипации, не только изменятся, но и перестанут удовлетворять условию ортогональности (при выводе которого был учтен эрмитов характер р и е). Однако если диссипация в среде мала, то в первом приближении можно подставить в (6.3.8) собственные функции резонатора со средой, которая имеет те же эрмитовы компоненты р, и е, но равные нулю антиэрмитовы компоненты. Собственные частоты при этом окажутся комплексными (®m =	+ г'®,„), и в соответствии с об-
щим определением (1.4.33) может быть введена добротность резонатора для пг-го типа колебаний, обусловленная потерями в среде
Вынужденные колебания. Предположим, что возбуждение колебаний в резонаторе производится сторонними токами, зарядами и магнитными моментами в резонаторе и полями на отверстиях в его стенках. Будем считать их заданными величинами. В действительности они, конечно, в свою очередь, зависят от поля в резонаторе. Но задача о возбуждении резонатора заданными источниками может служить первым приближением при рассмотрении вынужденных колебаний.
Пусть возбуждающие токи, заряды, моменты и поля зависят от времени по гармоническому закону с частотой <в. Если ампли-
§ 6.з1
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
299
Риз. 6.3.2. Возбуждение колебаний резонатора.
туды колебаний достаточно малы, то поле в резонаторе будет также гармоническим. Его комплексные амплитуды е и h удовлетворяют уравнениям Максвелла (5.1.10) — (5.1.13). Для того чтобы учесть возможность возбуждения сторонними магнитными моментами, примем]
b = p,h + 4лтст.	(6.3.15)
Тогда Первые два уравнения запишутся^ виде
rote + -^-pJi= — i mcT) (6.3.16)
div (p,h) = — 4л div mCT. (6.3.17)
Два других уравнения совпадут с (5.1.20) и (5.1.21).
Для того чтобы учесть возможность возбуждения резонатора полями на отверстиях, необходимо задать касательную составляющую злектрического поля Э и нормальную составляющую магнитной индукции Б на отверстиях. Тогда граничные условия запишутся следующим образом (рис. 6.3.2):
по X (в X ^о)----
Э на So (на отверстиях), 0 на S — So (на остальной поверхности резонатора),
(6.3.18)
ph  и0
на So, на S — So.
(6.3.19)
В этих уравнениях и граничных условиях ц, е, mCT, jcr, Э и Б— заданные функции координат, а рст = (i/и) div jCT.
Комплексные амплитуды поля вынужденных колебаний будем искать в видех)
е= 2$пеп —Гфе, п
(6.3.20)
h — 2 п
(6.3.21)
где еп и hn — введенные выше собственные функции резонатора, удовлетворяющие уравнениям (6.3.4) или (6.3.6), (6.3.7) и
*) Различие знаков в (6.3.20) и (6.3.21) связано только с традицией.
300 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
граничным условиям (6.3.5). Коэффициенты <Sn и 3fn, а также «градиентные» функции ф(. и ф/, подлежат определению. Необходимость введения этих функций обусловлена тем, что hn и еп, а следовательно, и их суммы удовлетворяют уравнениям (5.1.18), (5.1.19) и (5.1.27), в то время как h и е должны удовлетворять уравнениям с правыми частями (6.3.16), (6.3.17) и (5.1.21).
Подстановка (6.3.20) в (5.1.21) дает уравнение
div(eVi[\,) = — 4лрст.	(6.3.22)
Граничное условие для ф(, может быть принято следующим:
фе = 0 на S.	(6.3.23)
Подстановка (6.3.21) в (6.3.17) дает уравнение для функции ф/,
div (рТфь) = — 4л div mCT.	(6.3.24)
Граничное условие для нее следует из (6.3.19):
«-»	(Б на So,
(pWJiio = j	(6.3.25)
V lid О ---- О().
С помощью выражений (6.3.4), (6.3.5) и (6.3.23), учитывая эрмитовость тензоров е и ц, легко найти условия ортогональности векторных и градиентных функций
е;пеГфейУ = 0.	(6.3.26)
V
= 0.	(6.3.27)
v
** *
Умножая (6.3.20) на е и затем скалярно на ет, интегрируя по объему резонатора и принимая во внимание условия ортогональности (6.3.11) и (6.3.26), получим важную формулу
<$т = emsedV.	(6.3.28)
v
Аналогично можно получить
Жп = § IwhdF.	(6.3.29)
v
Найдем теперь окончательные выражения для искомых коэффициентов ёт и через заданные функции, характеризующие источники возбуждения. Умножим (6.3.16) скалярно на h™, а
§ 6.3]
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
301
(5.1.20) — на вт и проинтегрируем по объему резонатора. После некоторых преобразований, в ходе которых используются формулы (6.3.28) и (6.3.29) и граничные условия и учитывается эрмитов характер тензоров р и е, мы придем к системе уравнений
где
ат$т +	— F т — iy>G.rn,
' I mi
(6.3.30)
(6.3.31)
(6.3.32)
(6.3.33)
Im — 4 л emjCTdV, V
Gm = 4л hmmCTdV, v
nodV.
Выражения (6.3.30) — (6.3.33) имеют такой же вид, как и для резонатора, заполненного однородной изотропной средой [29]. Ио, в отличие от этого частного случая, для тензорных параметров они справедливы строго только при отсутствии диссипации, когда тензоры р и е эрмитовы.
Однако если диссипация мала, то ее можно учесть приближенно, заменив в (6.3.30) вещественные собственные частоты на комплексные частоты сот +шиг. Тогда, решая уравнения (6.3.30) получим (принимая во внимание (1.4.32) и опуская [штрихи У ®,„)
Т	^esmGm	^0	34)
4~	-|- <£>%Gm	35)
Vm
При этом в выражения (6.3.31) — (6.3.33), так же как и в формулы (6.3.8), используемые для расчета комплексных собственных частот, можно подставлять собственные функции резонатора без диссипации. Из (6.3.34) и (6.3.35) видно, что если частота со достаточно близка к собственной частоте сот одного из типов колебаний резонатора, то в разложениях (6.3.20) и (6.3.21) можно ограничиться только членами, соответствующими этому типу колебаний.
Итак, поле вынужденных колебаний в резонаторе, содержащем гиротропную среду с не очень большой диссипацией, может быть
302 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
сравнительно легко вычислено, если известны собственные функции и собственные частоты такого резонатора. Однако их определение представляет значительные трудности.
Волноводные резонаторы. Строгий расчет электромагнитных систем с гиротропными средами возможен, как уже отмечалось выше, лишь в весьма ограниченном числе случаев. К ним принадлежат задачи о регулярных волноводах, рассмотренные в §§ 6.1 и 6.2. Поэтому интересно выяснить, можно ли полученные для этих волноводов результаты применить к расчету резонаторов.
В случае изотропных сред, зная поле и постоянную распространения в регулярном волноводе, легко получить собственные функции и собственные частоты так называемого волноводного резонатора. Волноводный резонатор — это отрезок регулярного волновода, ограниченный двумя металлическими плоскостями, перпендикулярными оси волновода. Собственные функции такого резонатора представляют собой (в случае изотропной среды) стоячие волны, которые образуются в результате суперпозиции двух волн одинакового типа, распространяющихся в волноводе в противоположных направлениях. Собственные частоты определяются из условия
М“т)=т>	(б.з.зб)
где I — длина резонатора, р — целое число, a kz- (<в) — постоянная распространенная в волноводе, которую мы считаем известной функцией частоты.
Граничные условия на торцевых металлических плоскостях волноводного резонатора заключаются в равенстве нулю поперечных (касательных к этим плоскостям) составляющих электрического поля. Поэтому необходимым условием образования поля стоячей волны в резонаторе в результате суперпозиции двух распространяющихся в противоположных направлениях волн в волноводе является взаимность структуры поперечного электрического поля е± в плоскости поперечного сечения волновода:
ej_+ = ej_-.	(6.3.37)
(знаки плюс и минус соответствуют двум направлениям распространения). Условие (6.3.37) всегда выполняется для изотропных сред и, вообще говоря, не выполняется для волновода, содержащего сиротропную среду. В таком волноводе двух волн, падающей и отраженной, недостаточно для выполнения граничного условия ejL = 0 на торцевых поверхностях резонатора. Это условие может быть выполнено лишь при наличии бесконечного количества волн и ближних полей в волноводе, образующих в результате поле собственного колебания в резонаторе. Формула (6.3.36) в этом случае теряет смысл.
§ 6.3]
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
303
Взаимность же постоянной распространения, т. е. выполнение равенства
kZ'+ = kZ'_	(6.3.38)
не является необходимым условием образования стоячей волны в резонаторе в результате суперпозиции двух волн, распространяющихся в противоположных направлениях. Если равенство (6.3.38) не выполняется, то условие (6.3.36) заменяется следующим: *
fcz4((oro) + ^_(G)m) = ^.	(6.3.39)
Условие (6.3.37) выполняется и для гиротропных сред в некоторых частных случаях, например в случае круглого волновода, заполненного продольно намагниченной средой или содержащего коаксиально расположенный стержень из такой среды (см. § 6.1), а также в случае прямоугольного волновода с волной ТЕ„0, целиком заполненного поперечно намагниченной средой (§ 6.2). В обоих этих случаях постоянная распространения тоже взаимна, и собственные частоты соответствующих волноводных резонаторов могут быть определены по формуле (6.3.36).
Что же касается прямоугольных волноводных резонаторов с поперечно намагниченными пластинами, то для них формулы (6.3.36) и (6.3.39) неприменимы, так как распределение электрического поля в прямоугольном волноводе с такими пластинами невзаимно (см. рис. 6.2.11), независимо от того, взаимна или нет постоянная распространения.
Расчет резонаторов методом возмущений. Сложность строгого расчета резонаторов с гиротропной средой заставляет уделять большое внимание приближенным методам. Наиболее простым из них является метод возмущений с квазистатической аппроксимацией внутреннего поля (§ 5.3). Рассмотрим несколько примеров применения этого метода к расчету собственных частот резонаторов, содержащих гиротропные образцы.
Пусть, например, образец представляет собой тонкую ферритовую пластину, намагниченную касательно к ее плоскости (плоскости xz). Подставля выражения (5.3.45) и (5.3.50) для внутреннего поля в такой пластине в формулу (5.3.39), получим выражение для собственной частоты резонатора с пластиной
S — h*oxh°x + ? — h*wh°v +
Vi
+	+ (0II - Ро) h*0zh02 +
+ 7- (е ~ Ео) е^е01/ + (с — e0)|(e^e0J+ eJ2e02)] dV, (6.3.40)
ЗС4 ВОЛНОВОДЫ Ц РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. G
Рис. 6.3.3. Прямоугольный резонатор с ферритовой пластиной.
где |1_l определяется согласно (5.1.36), а интегрирование производится по объему пластины.
Предположим теперь, что пластина находится в прямоугольном резонаторе (рис. 6.3.3) с пепозмущенным полем типа TMmn0. Составляющие этого поля можно записать в виде [29] <?02 = sin кхх sin kvy, Г()х :==: Оои —— 6,	(6.3.41)
hOx =-jp siii кх:с cos куу, hOy = cos kxx sin kvy, hoz ~ 0» где
, Лт , Лп ко =	= Vkl + k*y.
Подставляя выражения (6.3.41) в формулу (6.3.40),
мы замечаем, что третий член подынтегрального выражения, про-порциональный гр,а, обращается в нуль. Причина этого заключается в линейной поляризации певозмущеиного поля. Вычисляя величину Wo по формуле (5.3.40) и учитывая, что толщина пластины h мала, получим окончательно
(О — (Оо
<о
/ 2
= - 4	“ Но) р c°s2 + [но
sin2 kygj .
(6.3.42)
В этом приближении сдвиг частоты пропорционален отношению объема пластины к объему резонатора и состоит из трех членов, пропорциональных приращениям величин цх, 1/ц и е.
В качестве второго примера рассмотрим резонатор с тонким ферритовым цилиндром, намагниченным вдоль его оси. Подстановка выражений (5.3.47) и (5.3.51) в (5.3.39) дает
Vi
И2-Ц20-Ц2	.
°	;—w—г hoj_no_L .
щ + Цо)2 — H2
zo (ho_L X h0 j_) ф- (ц || p.o) hozhoz +
(Ц + p0)2 — Ц2
+.2eo|rSeo±e^ + <e - e*0^]dV, (6.3.43)
§ 6.31
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
305
где индексом J_ обозначены, как обычно, векторы, перпендикулярные оси z.
Если цилиндр расположен на оси кругового цилиндрического резонатора и длина его совпадает с длиной резонатора, то строгий расчет такого — волноводного резонатора сводится к расчету круглого волновода с гиротропным стержнем (§ 6.1). Собственные функции резонатора явятся суперпозицией нормальных волн в таком волноводе и, следовательно, так же как и зти волны, будут-иметь круговую поляризацию. Собственные частоты определятся из условия (6.3.36). Для тех типов полей, для которых
Рис. 6.3.4.’Резонатор ТМ12 о квадратного сечения с ферритовым цилиндром. Индексы типа колебаний 1,2, 0, относятся, соответственно, к осям х, у z. Приращение собственных частоты зависит: а — от р и р ; б —от е; в — от р ц .
волны с правой и левой поляризацией имеют разные постоянные распространения, собственные частоты колебаний с правой и левой поляризацией будут также различны. Мы не будем останавливаться на расчете такого резонатора методом возмущений (аналогичные вычисления для волновода были проведены в § 6.1). Отметим лишь, что метод возмущений может быть применен при любой длине гиротропного цилиндра и, вообще говоря, при любом расположении его в волноводе. В качестве невозмущенных колебаний необходпмо принимать колебания с такой же поляризацией, какая должна быть у возмущенного колебания. Для случая расположения гиротропного цилиндра на оси резонатора это будет круговая поляризация.
Поместим теперь тонкий продольно намагниченный ферритовый цилиндр на оси резонатора квадратного сечения (рис. 6.3.4, а) с колебаниями TMmn0- Наряду с ними в резонаторе могут существовать и колебания ТМ?,т0’> ферритовый образец связывает эти колебания. По аналогии с круговым цилиндрическим резонатором следует предположить, что собственные колебания резонатора с образцом будут иметь круговую'поляризацию. Это заставляет
306 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [Г Л. 6
принять в качестве невозмущенных полей следующие комбинации полей ТМт„0 и TMnm0:
е0 -j- ienm0, h0 = h?nno '4 ^nmo* (6.3.44)
Записывая составляющие e„r„n, e„m0, и hnm0 аналогично (6.3.41), подставляя их в формулу (6.3.43) и учитывая, что радиус цилиндра р0 мал, получим после некоторых преобразований (для определенности т принято нечетным, а п — четным)
to ‘ «0   лр2о	р ра ро	.g 45^
со	я3 т1 ~Ь w2 Р i Ра + Ро ’	'	'
В это выражение не входит е, так как ферритовый цилиндр находится в узле электрического поля, а р и входят в комбинации Ц + Цо, так как цилиндр находится в магнитном поле с круговой поляризацией.
Если ферритовый цилиндр смещен относительно оси резонатора, то собственные колебания будут иметь уже не круговую, а некоторую эллиптическую поляризацию. Если цилиндр находится в пучности электрического поля и узле магнитного (рис. 6.3.4, б), то поляризация будут линейной. Такую же поляризацию следует принять в этом случае и для невозмущенного колебания. Тогда из (6.3.43) получим
9Т._ 2
~ =----------(6.3.46)
Если цилиндр, намагниченный по-прежнему вдоль его оси, расположен, как показано на рис. 6.3.4, в, то поляризацию невозмущенного колебания также следует принять линейной. Для этого случая из (6.3.43) следует
2	F
р.3.47)
В качестве третьего примера рассмотрим малую ферритовую сферу. Подставляя (5.3.49) и (5.3.52) в (5.3.39), мы можем получить формулу для приращения частоты произвольного резонатора с такой сферой, аналогичную выражениям (6.3.40) п (6.3.43)
Пусть сфера находится на оси кругового цилиндрического  резонатора с колебанием TEmnp (рис. 6.3.5) и намагничена вдоль оси резонатора. Так же как и в случае ферритового цилиндра на оси резонатора с круглым или квадратным сечением, в качестве невозмущенного колебания следует принять колебание с круговой поляризацией. Составляющие поля можно тогда записать в виде (29]
е = ех = p0fc0Zz0 х Гф, Кь = “ Vij‘, hz — и27ф, (6.3.48)
§ 6.3]
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
307
где
Z — sin kzz, ф = Jm (xp) einVf, kz = -p-, причем kR — n~i't корень уравнения J' (xp) = 0 (здесь Jm — функция Бесселя т-го порядка, а размеры показаны на рис. 6.3.5). Подставляя поля (6.3.48) в формулу для приращения частоты резонатора со сферой, мы получим в частном случае т = п = р = 1 и р.о = е0 = 1
03 ~~ 0)0 __«а го Г(Qo\2 Н d: На ~ 1 к „ I 6 ~ ^:п2 ь „1 /со ло\
<о	6,4IR* 1^2])	р.±Ра+2С0	+е+2 z J'
Здесь Zo = 2л/к0 — длина волны в свободном пространстве, а г о — радиус сферы. Если сфера будет намагничена постоянным
полем перпендикулярно оси резонатора — в направлении переменного магнитного поля, то в (6.3.49) множитель (р. ± щ, — 1)/(ц ±	+ 2) заменит-
ся на (ри — 1)/(рц + 2).
Мы проиллюстрировали на ряде примеров технику применения метода возмущений с квазистатической аппроксимацией внутреннего поля к расчету резонаторов с малыми гиротропными образцами. В качестве критерия применимости этого метода может быть принято условие (5.3.53), где d представляет собой толщину пластины, диаметр цилиндра или диаметр сферы.
В формулы (6.3.40), (6.3.43), (6.3.49) и др. входят комплексные параметры р., р а, р || и ей комплексная частота ®. Разделяя вещественные и мнимые части, можно получить выражения для изменения вещественной собственной частоты А®' и добротности резонатора (), обусловленной потерями в образце *).
Z
Рис. 6.3.5. Круговой цилиндрический резонатор ТЕ,,, с ферритовой сферой. Электрическое поле на оси z направлено по оси у. Приращение собственной частоты зависит: 1 —от ц иц(, (сфера намагничена по оси z) или от ц || (сфера намагничена по оси х); 2 и з — от е; 4—от ц ц (сфера намагничена по оси z).
Резонаторы, содержащие образцы из гиротропной среды, могут
быть использованы для измерения параметров среды — компо-
нент тензоров р и е. Если размеры образцов малы (в указанном выше смысле), то могут быть использованы формулы, полученные методом возмущений, в частности, для изотропного (в отсутствие
х) Добротность (?р резонатора с образцом связана с Q соотношением (?р1= (J-1 4- ^~х0, где <2р 0 — добротность резонатора без образца.
308 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ. ЕГЛ. 6 постоянного поля) поликристаллического феррита — приведенные выше формулы. Измеряя приращения собственных частот и изменения добротностей резонаторов в четырех опытах, можно определить все четыре комплексных параметра, которыми характеризуется такой феррит. Эти четыре опыта могут отличаться формой резонатора, типом колебаний в нем [445], формой образца, расположением его в резонаторе [496] и направлением постоянного поля. Они должны быть так выбраны, чтобы привести к четырем независимым выражениям, в которые входили бы все четыре параметра. Желательно, конечно, чтобы в каждое выражение входило бы минимальное число параметров.
Этим требованиям удовлетворяют, в частности, цилиндрические резонаторы квадратного или круглого сечения с цилиндрическими или сферическими образцами [496], рассмотренные выше (второй и третий примеры). Например, два выражения (6.3.45) и выражения (6.3.46) и (6.3.47) представляют собой соотношения для определения всех параметров феррита. В случае прямоугольного резонатора с пластиной (первый пример) мы можем получить только три независимых уравнения для параметров. Однако и такой резонатор можно использовать для измерения параметров феррита, если предположить, что е не зависит от магнитного поля. В этом случае е определяется из измерения при достаточно большом постоянном магнитном поле, когда можно считать ц = 1.
Связь собственных частот с компонентами внешнего тензора восприимчивости. До сих пор мы выражали приращения собственных частот резонаторов с гиротропными образцами через компоненты тензора магнитной проницаемости вещества р, = = 1 + 4л %, где % (см. § 1.4) есть тензор восприимчивости по отношению к внутреннему переменному магнитному полю h или так называемый внутренний тензор восприимчивости. Но, как было показано в § 1.4, в случае однородных колебаний малого эллипсоида может быть введен также внешний тензор восприимчивости
по отношению к внешнему переменному магнитному полю h0. Его резонансные частоты (или при со = const — резонансные поля) не совпадают с резонансными частотами (или полями) тензоров % и ц. Разумно ожидать, что собственная частота резонатора с гиротропным образцом — малым эллипсоидом — будет испытывать резонансное изменение (со" будет проходить через максимум, а со'— быстро изменяться) не при резонансном поле внутреннего тензора %, а при резонансном поле внешнего тензора В этом нетрудно убедиться непосредственно с помощью приведенных выше формул: приращения частоты имеют особенности (при отсутствии диссипации (со — <оо) —> со) при значениях внешнего постоянного поля Но, удовлетворяющих резонансным уело-
§ 6.3]
РЕЗОНАТОРЫ, СОДЕРЖАЩИЕ ГИРОТРОПНУЮ СРЕДУ
309
виям (1.4.19) — (1.4.23) для образцов соответствующей формы.
Эти условия являются условиями резонанса тензора
Из сказанного ясно, что приведенные выше формулы, которые связывают приращение частоты резонатора с компонентами тензора ц вещества, неудобны для расчетов (хотя, конечно, справедливы) вблизи резонансных частот (или полей) как этого тензора, так и внешнего тензора %е. Поэтому целесообразно, используя по-прежнему метод возмущений, выразить приращение собственной частоты резонатора через компоненты внешнего тензора восприимчивости малого гиротропного эллипсоида. При этом отпадет необходимость учета связи между внутренним и внешним полями и окончательные выражения будут гораздо проще.
Ограничимся случаем магнитно-гиротропной среды (ферро-, ферри- или антпферромагнетика). Будем рассматривать только магнитную часть приращения собственной частоты (первый член под интегралом в (5.3.39)), либо считая, что образец находится в узле электрического поля, либо просто не интересуясь небольшой и не зависящей от постоянного магнитного поля электрической частью приращения частоты. Примем также ц0 = 1 и учтем очевидное соотношение
%h = ш = %Ъ0.	(6.3.50)
Тогда для малого образца получим из (5.3.39)
—— = -	hoX bo,	(6.3.51)
где Vj — объем образца. Принимая во внимание соотношение дляй0%еЬ0, аналогичное (5.3.37), запишем (6.3.51) следующим образом:
=	1%е | Ло± |2 + lXZo (h^ х hoJ +	|	)2Ь	(6.з.52)
Формула (6.3.52) может быть использована для определения компонент тензора из опытов по ферромагнитному или антиферромагнитному резонансу. При этом приращение частоты обычно мало и в знаменателе левой части (6.3.52) со можно заменить на ®0. При исследовании ферромагнитного (и ферримагнитного, но не всегда антиферромагнитного) резонанса величиной %jl можно пренебречь. И если (как это обычно бывает в опытах по магнитному резонансу) образец находится в переменном магнитном поле с линейной поляризацией, второй член в правой части (6.3.52) обращается в нуль. Тогда, разделяя вещественную и мнцмую части приращения частотАг и принимая во внимание
310 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТОРПНЫМЙ СРЕДАМИ [гл. 6
формулу (5.3.40), получим1)		i.
,	2лсО(^Р1 .	, ®	с°о~	Го (Xе),		(6.3.53)
1 1	1	(6.3.54)
Q QP	Qpo	Н> (х)’	
где По — объем резонатора, а		
g =	ML ^h%dV	(6.3.55)
	Vo	
— множитель порядка единицы, который легко вычислить для обычно используемых резонаторов простой формы.
Для ветвей колебаний в антиферромагнетиках-, которые возбуждаются переменным магнитным полем, параллельным постоянному полю (см. §§ 4.2 и 4.3), х*| существенно. Но тогда ж 0 и в формулах (6.3.53) и (6.3.54) следует просто заменить (%е)' на (Х||)' и (хс)" на (хп)"-
При практическом использовании формул (6.3.53) и (6.3.54) для измерений ферромагнитного резонанса в веществах с узкой резонансной кривой часто в качестве со0 и Quo принимают значения соответствующих величин для резонатора с образцом, но вдали от резонанса.
§ 6.4. Гиротропный эллипсоид в волноводе
Выше были рассмотрены две фундаментальные задачи электродинамики полых систем с гиротропными средами — задача о регулярном волноводе (§§ 6.1 и 6.2) и о резонаторе (§ 6.3). В этом параграфе мы остановимся на третьей фундаментальной задаче — о гиротропной нерегулярности в волноводе. Постановка такой задачи уже рассматривалась в § 5.3 в связи с применением к ней метода возмущений. Она заключается в следующем: в некотором участке регулярного волновода (см. рис. 5.3.2) находится среда с параметрами р и е, являющимися заданными функциями координат, в частности образец из среды с однородными параметрами. Задана амплитуда волны какого-либо типа, «падающей» на нерегулярность. Требуется найти электромагнитное поле в волноводе по обе стороны от нерегулярности.
Строгое решение таких граничных задач весьма сложно и практически может быть проведено лишь численными методами с применением электронных вычислительных машин. Достаточно указать, что даже задача о прохождении волны через участок волновода со средой, ограниченный перпендикулярными оси вол-
г) См. примечание на стр. 307.
§ 6.4]
ГИРОТРОПНЫЙ ЭЛЛИПСОИД В ВОЛНОВОДЕ
311
повода плоскостями, которая для изотропной среды решается элементарно [29], в случае гиротропной среды оказывается сложной.
Если гиротропный образец, помещенный в волновод, представляет собой малый эллипсоид, то для решения сформулированной выше задачи можно попытаться использовать метод возмущений с квазистатической аппроксимацией внутреннего поля. Для определения коэффициентов отражения и прохождения волны того же типа, что и падающая (предполагается, что только такая волна распространяется в волноводе), могут быть использованы формулы (5.3.33) и (5.3.35). Внутреннее (возмущенное) поле h, е в этих формулах может быть выражено через невозмущенное поле h0, е0 в квазистатическом приближении либо по формулам (5.3.45) — (5.3.52) с использованием компонент внутренних тензоров ц и е, либо простым способом, рассмотренным в конце § 6.3,— с помощью соотношения (6.3.10).
Под невозмущенным полем h0, е0 приходится понимать заданное поле в волноводе без образца. В результате этого расчет по формулам возмущений (5.3.33) и (5.3.35) становится очень грубым. В частности, по мере увеличения размера образца или увеличения его %рез (т. е. уменьшения ширины резонансной кривой) величины | Г | и | D (, вычисленные по формулам (5.3.33) и (5.3.35), неограниченно растут и могут превысить 1, что противоречит закону сохранения энергии. Для монокристаллов с узкой (~ 1 э) резонансной кривой это наступает при таких размерах образцов, когда еще применимо квазистатическое приближение.
Метод самосогласованного поля. Парадоксальный результат, к которому приводит использование формул (5.3.33) и (5.3.35), связан с допущением, что намагниченность образца определяется невозмущенным полем в волноводе. Для того чтобы получить более точное решение задачи, необходимо учесть «обратную реакцию» образца, т. е. принять, что его намагниченность m определяется суммарным — самосогласованным полем, включающим невозмущенное поле h0 и поле излучения образца в волновод Ьи. Если образец представляет собой эллипсоид и выполняется условие (5.3.53) применимости квазистатического приближения, то вместо (6.3.50) можно записать
m = % (К + К.),	(6.4.1)
где %е — внешний тензор восприимчивости образца. Поле излучения, в свою очередь, можно представить в виде
Ьи=— iwm,	(6.4.2)
где w — некий тензор, который зависят» од размеров и формы
312 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ 1ГЛ. 6
волновода и образца и от частоты; его можно найти в результате решения задачи о возбуждении волновода заданной намагниченностью. Для вычисления коэффициентов прохождения и отражения теперь не нужно прибегать к формулам (5.3.33) и (5.3.35), достаточно исключить намагниченность ш из выражений (6.4.1) и (6.4.2). Тогда мы получим связь между Ьи и Ьо, которая и определит эти коэффициенты.
Намеченный путь решения задачи о гиротропном эллипсоиде в волноводе может быть, в принципе (в рамках, конечно, квази-статического приближения), строгим. Но тогда необходимо найти строгое выражение для поля излучения Ьи. Поле излучения (вне образца) может быть разложено по нормальным волнам и ближним полям волновода [29]. Нахождение большого числа коэффициентов этого ряда связано с громоздкими вычислениями и, кроме того, приводит к принципиальной трудности, которую мы сейчас обсудим. В соответствии с определением внешнего тензора поля h0 и Ьи в (6.4.1) должны быть взяты на некотором удалении от образца, где они предполагаются однородными. Это не вносит практических затруднений при условии, что поля меняются медленно на расстояниях, сравнимых с размерами образца. Такое условие выполняется для поля h0 и нескольких первых членов разложения Ьи по нормальным волнам и полям. Однако для последующих членов, которые соответствуют полям, очень быстро убывающим при удалении от места возбуждения, предположение об однородности не выполняется и учет их теряет смысл. Если в волноводе распространяется волна только одного типа, то для простоты можно учесть в Ьи только один член, соответствующий этой волне, и значение его взять, например, в точке, где находится центр образца. Полученное таким образом решение будет, конечно, приближенным, но значительно более точным, чем полученное без учета влияния поля излучения на образец. В частности, как мы увидим, величины | Г | и | D | с увеличением объема образца или с уменьшением его LH будут стремиться теперь к разумным значениям.
Излучение эллипсоида в волновод и добротность связи. Рассмотрим для определенности следующую задачу [466]. На оси прямоугольного волновода (рис. 6.4.1), в котором может распространяться волна ТЕ10, находится малый ферритовый эллипсоид, намагниченный до насыщения в направлении, перпендикулярном широкой стенке волновода. Требуется определить коэффициенты отражения и прохождения в этом волноводе.
Не приводя здесь решения задачи о возбуждении поля в таком волноводе переменной намагниченностью in эллипсоида х), запи_
1) Эта задача может быть решена на основе теории возбуждения волне-вода заданными источниками, изложенной, например, в [29].
§ 6.4]
ГИРОТРОПНЫЙ ЭЛЛИПСОИД В ВОЛНОВОДЕ
313
шем окончательное выражение для комплексной амплитуды поперечной составляющей магнитного поля основной волны ТЕ10:
,	. 4лК1,	. -нс iy-y'i	„
— i—g-kymxsmnxe у .	(6.4.3)
Здесь ку — постоянная распространения в волноводе, х = п/а — собственное значение для волны ТЕ10, 5 — площадь поперечного сечения волновода, Уг — объем образца, а тх — комплексная амплитуда поперечной составляющей переменной намаг
ниченности эллипсоида; штрихом обозначена координата точки, где находится образец. Это поле мы и примем приближенно в качестве поля излучения (6.4.2) образца в волновод. Как видно из (6.4.3), оно является полем волны, «разбегающейся» в обе стороны от образца.
Вычислим мощность, излучаемую образцом в волновод. Мощность, переносимая найдена по формуле [29]
Рис. 6.4.1. Намагниченный ферритовый эллипсоид на оси прямоугольного волновода.
в каждую сторону, может (быть
Рг = ^SkyV?A\	(6.4.4)
где А — амплитуда волны, определенная таким образом, что ь = -аде^114'’1,
а ф — нормированная собственная функция волновода, а в нашем случае
ф = р2 cos их.
Найдя А из сравнения (6.4.4) с (6.4.3), получим окончательно полную мощность излучения (в обе стороны от образца)
Ри = 2Рг =
2л<и7г,,Р?
_____L-L ,и2
S * В * * * * *
(6.4.5)
В дальнейшем нам окажутся полезными две величины, характе-
ризующие эллипсоид — его собственная добротность Qo и доброт-
ность связи его с волноводом Qc. Первая величина была уже вве-
дена в § 1.4, ее определением являлось соотношение (1.4.33), а
окончательным выражением для эллипсоида вращения — фор-
мула (1.4.49). Аналогично (1.4’,33) может быть определена и
314 волноводы и Резонаторы с гиротропными средами [гл. в
добротность связи
Qc = ^W/PB,	(6.4.6)
где Ри — мощность излучения (6.4.5), a W — колебательная магнитная энергия эллипсоида. При вычислении ее, следует учесть переменные члены в зеемановской энергии (2.1.1) и энергии размагничивающих полей (2.1.3). Примем для простоты, что образец представляет собой эллипсоид вращения и постоянное магнитное поле направлено вдоль его оси. Тогда, если пренебречь малыми членами второго порядка — произведениями переменных величин, а также ограничиться областью вблизи ферромагнитного резонанса и считать диссипацию малой, то для энергии W получится следующее выражение [466]:
W	(6.4.7)
где т — комплексная амплитуда переменной намагниченности, имеющей при сделанных допущениях круговую поляризацию.
Подставляя (6.4.5) и (6.4.7) в (6.4.6) и учитывая, что в данном случае | тх | ~ | т |, получим добротность связи ферритового эллипсоида вращения, расположенного на оси бесконечного прямоугольного волновода
<6-4-8)
1 lly
где введено уже неоднократно использованное обозначение (1.2.36). Из (6.4.8) видно, что добротность связи тем меньше (т. е. связь образца с волноводом тем сильнее), чем больше намагниченность образца и его объем.
Коэффициенты прохождения и отражения в бесконечном прямоугольном волноводе. Перейдем теперь непосредственно к интересующей нас задаче — вычислению коэффициентов прохождения и отражения в прямоугольном волноводе, на оси которого находится намагниченный ферритовый эллипсоид вращения. Будем исходить из соотношения (6.4.1). Проектируя его на ось х, получим
тх = % (hox + hax).	(6.4.9)
Здесь % = %' —	— диагональная поперечная компонента внеш-
него тензора восприимчивости образца х), hox — проекция заданного поля в волноводе в точке, где находится образец, а /гиж — проекция поля излучения образца в той же точке. В рассматривав мом случае (образец на оси бесконечного волновода) hox совпадает с заданной амплитудой падающей волны h+. Величина hax-
х) В этом параграфе мы будем опускать индекс е у компонент %е.
§ 6.4]	ГИРОТРОПНЫИ ЭЛЛИПСОИД В ВОЛНОВОДЕ	315
получается из выражения (6.4.3), если принять в нем ж = а/2 и У = у’-
hax = — iwmx,	(6.4.10)
где
w =	.	(6.4.11)
Л
Принимая во внимание (1.4.49) и (6.4.8), замечаем, что
w = д/х'рез,	(6.4.12)
где
q =	(6-4.13)
Коэффициент отражения, отнесеный к сечению волновода, в котором лежит центр образца,
r = h-~.	(6.4.14)
Исключая тх из (6.4.9) и (6.4.10) и учитывая (6.4.12), получим!
Г —	—________ 'УУ- /Хрез /Хрез	/с 4 1 г.\
1+-Х - 1 + 9х"/х;ез+ад7%рез •	’
Коэффициент прохождения, отнесенный к тому же сечению волновода, h-m- + h,	4
D = их, - - + = 1 + Г = .-Д—.	(6.4.16)
h+	1	1 -|- iw%	'	'
Подставляя в (6.4.15) и (6.4.16) выражения для %' и %" (см. § 1.4), можно найти зависимости Г и D от частоты и постоянного магнитного поля. Мощность, поглощенная образцом, отнесенная к мощности падающей волны, может быть определена следующим образом:
Т= 1 — |ГТ — |£>|2.	(6.4.17)
В точке ферромагнитного резонанса (%' ^ 0, %" = %рез)
ГРез=14^’ В^3=:Г+д^ Т^а = (1 -Д)2 	(6-4-18)
Зависимости этих величин от q приведены на рис. 6.4.2. Из выражений (6.4.18) с учетом (6.4.13), (1.4.49) и (6.4.8) следует, что при увеличении объема образца или сужении его резонансной кривой величины Г, D и Т остаются конечными: | Грез| —> 1, £>рез ->0 и Урез —> 0, и закон сохранения энергии выполняется.
Эллипсоид в закороченном волноводе. Аналогичным образом можно рассмотреть и ферритовый эллипсоид, расположенный на оси прямоугольного волновода на некотором расстоянии d от ко
316 ВОЛНОВОДЫ И ^РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ Ггл. 6
роткого замыкания (рис. 6.4.3). Заданной является по-прежнему амплитуда h+ падающей волны. Однако теперь hox не совпадает' с Л+. Наряду с падающей волной в волноводе существует волна, отраженная от короткого замыкания:
hOx = h+e~ikyv + fc.eV	(6.4.19)
Амплитуду h_ можно определить из граничного условия — равенства нулю электрического поля ez на коротком замыкании (при у = 0). Учитывая, что [29]
, . 1
П+х ~ ~Т~ £- e±Z
(где £ — волновое сопротивление волновода), мы получаем ив
Рис. 6.4.2. Зависимости резонансных значений коэффициента отражения Г, коэффициента прохождения D и относительной поглощенной мощности т в прямоуголь-ном волноводе с ферритовым эллипсоидом от отношения добротностей q = Qc/Q0.
граничного условия: h_ = /г+ при у — 0. Следовательно, в точке у = — d, где расположен образец,
hQx = 2h+ cos kvd.	(6.4.20)
Поле излучения образца в общем случае может быть записано в виде [29]
Лих = hlx + C^~ikvv + cj куу,	(6-4.21)
где hlx — частное решение задачи о возбуждении, для которого справедливо выражение (6.4.3). В случае бесконечного волновода из условия излучения (т. е. отсутствия волн, бегущих из бесконечности к месту возбуждения) следовало С+ = CL = 0.
§ 6.4]
ГИРОТРОПНЫЙ ЭЛЛИПСОИД В ВОЛНОВОДЕ
317
Для закороченного волновода С+ = 0, а С_ может быть определено, аналогично амплитуде /?_, из граничного условия: ez = 0 на коротком замыкании. В результате получим в точке, где расположен образец,
Лих=—2iwmxcos kyd (6.4.22) (величина w определяется по-прежнему выражением (6.4.11)).
Коэффициент отражения, отнесенный к сечению волновода, где находится образец (?/ = — d), определится теперь следующим образом:
Г =	; Л -• (6-4.23)
Л.е v
Рис. 6.4.3. Ферритовый эллипсоид в закороченном прямоугольном волноводе.
Подставляя (6.4.20) в (6.4.9), исключая тх из получецного соотношения и (6.4.22) и используя (6.4.23), найдем
1 — 2q 2— — i (tg kyd -j- 2q -2— _______^рез______’______ %рез '
1 + 27 4- -b i (tg kyd -j- 2q2*L' А>ез *	^Срез ‘
(6.4.24)
где q определяется по-прежнему выражением (6.4.13). В частности, при ку&.=рл (р=0, 1, 2, . . .), например, для образца вблизи короткозамыкающей стенки и при ферромагнитном резонансе
	(М.25)
Эта величина стремится к (—1) при увеличении размера или сужении резонансной кривой образца.
Связь скрещенных волноводов. Перейдем теперь к несколько более сложной задаче о ферритовом эллипсоиде, расположенном в отверстии, которое соединяет два волновода. Наибольший интерес представляет случай, когда в отсутствие образца (или при наличии его, но вдали от ферромагнитного резонанса) связи между волноводами нет. Для этого магнитные поля их нормальных волн (мы по-прежнему предполагаем, что в каждом волноводе может распространяться волна только одного типа) вцентре отверстия должны быть перпендикулярны. Рассмотрим для определенности два скрещенных прямоугольных волновода (рис. 6.4.4) с отверстием в середине широких стенок обоих волноводов и ферритовым образцом, расположенным в центре отверстия. Предположим, что
318 ВОЛНОВОДЫ И РЕЗОНАТОРЫ с ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
в объеме образца магнитные поля обоих волноводов однородны и совпадают с магнитными полями волн ТЕ10 в этих волноводах у их общей стенки в отсутствие отверстия. Конечно, такое предположение не выполняется точно, но оно дает возможность просто решить рассматриваемую задачу. Сложный учет действительной конфигурации полей в отверстии не изменит основных качественных результатов этого решения.
В случае скрещенных волноводов можно записать следующие очевидные соотношения, заменяющие выражение (6.4.9) для оттого волновода:
тх ~	+ &их1) + tya (^0у2 + ^твд),	f /о z OP
+ l( • • )
Рис. 6.4.4. Намагниченный ферритовый эллипсоид, связывающий два скрещенных волновода.
поля,* соответственно, в первом и втором волноводах, ahIixl и feII;,2—поля излучения образца в эти волноводы1).
Остановимся сначала на случае, когда оба волновода — бесконечные, а __ энергия поступает из одно-у го плеча, например, первого волновода. Тогда /?Ох — —fe+, hOy = 0, а для полей излучения справедливо выражение (6.4.10) и анало-
гичное ему
йиу = — twmy. (6.4.27)
Исключая тх и mv из системы уравнений (6.4.26), (6.4.10) и (6.4.27), мы можем выразить hax и h^y через /?+и найти все интересующие нас величины: коэффициент отражения (6.4.14), коэффициент прохождения в противоположное плечо первого волновода Dr, который определится аналогично (6.4.16), и коэффициенты передачи в плечи второго волновода
— hiyyjhy.
(6.4.28)
Так, например, для Г получается следующее выражение:
г^Х + и? — X2)
1 + 2iwx + (X2 — х2)
 (6.4.29)
х) В дальнейшем индексы 1 и 2 мы будем опускать.
§ 6.4]
ГИРОТРОПНЫЙ ЭЛЛИПСОИД В ВОЛНОВОДЕ
319
Используя формулы для х и Ха, приведенные в § 1.4, нетрудно убедиться, нто при небольших расстройках относительно ферромагнитного резонанса членами с (х^ — х2) можно пренебречь. В точке резонанса
Гр№ = 1	, А рез = 1 + 2q ’ D2pe3 = r^’ С6*4'30)
В этом случае при увеличении объема образца или сужении его резонансной кривой величины | ГРез|2, | рез|2 и |А рез |2 стремятся к 1/4, т. е. падающая мощность поровну делится между всеми четырьмя плечами волноводов.
[Рис. 6.4.5. Ферритовые фильтры.
Аналогичным образом может быть решена задача об эллипсоиде, связывающем два скрещенных закороченных волновода (рис. 6.4.5, а). Случай, показанный на рис. 6.4.5, б, сводится к ней при = <72 = 0. Теперь, так же как и для одного закороченного волновода, мы должны принять
hQx = 2h+ cos kdlf	(6.4.31)
hKX, у = — 2iwmXty cos /сй1>2е-гМ1,2,	(6.4.32)
где к — постоянная распространения, одинаковая в обоих волноводах. Исключая с учетом (6.4.31) и (6.4.32) тх и mv из системы (6.4.26), (6.4.10) и (6.4.27), можно найти коэффициенты прохождения и отражения. Приведем лишь выражение для коэффициента прохождения при резонансе (при dr = d2 d):
4iq cos2 kd e 2,f:d
1 -|- kq cos kd e-ikd
(6.4.33)
320 ВОЛНОВОДЫ И РЕЗОНАТОРЫ С ГИРОТРОПНЫМИ СРЕДАМИ [ГЛ. 6
Зависимость коэффициента прохождения при резонансе при kd = = рп (р = 0, 1, 2, ...) от отношения добротностей показана па рис. 6.4.6. Как видно из рис. 6.4.6 или из формулы (6.4.33), с увеличением объема образца или его %рез коэффициент прохождения I Dpes | —» 1, т. е. ферритовый образец достаточно больших размеров и с достаточно узкой резонансной кривой переизлучает почти всю мощность во второй волновод. Это используется для создания ферритовых фильтров, перестраиваемых в широких пределах
/ г 5 ю д
Рис. 6.4.6. Зависимость коэффициента прохождения ферритового фильтра при резонансе от отношения добротностей Q = Qc/Qo-
путем изменения внешнего посте-явного поля (см., например, [486]).
Полученные выражения для коэффициентов отражения и прохождения качественно подтверждаются на опыте. Вследствие ряда упрощающих предположений количественное совпадение получается при значениях добротности связи Qc, несколько отличающихся от величин, рассчитанных по формуле (6.4.8).
Приведенные соотношения могут быть использованы при измерениях ширины резонансной кривой (или собственной добротности)
ферритовых образцов. Для этого, вообще говоря, можно применить все рассмотренные выше случаи: бесконечного (согласован-
ного) волновода, закороченного волновода и скрещенных волноводов. Измерение | D | или | Г | в точке ферромагнитного резонанса в любом из этих случаев позволяет определить величину q = QJQc- Но так как добротность связи Qc не может быть вычислена точно, необходимы дополнительные измерения при некоторых расстройках частоты или постоянного поля.
Проще всего поступить следующим образом: найти для данного 1 "
q значения | Г | или | D |, при которых %" = vXpes, и определить £
ширину резонансной кривой как интервал частот или полей между этими значениями (обозначим их | Г |i/„ и | /)|у2). Определив затем по формуле (1.4.52) Qo и зная q, можно, если это необходимо, найти и экспериментальное значение добротности связи Qc. Такой метод измерения представляет интерес для ферритов с узкой резонансной кривой. Поэтому при выводе формул для |Г |,/2 и | D h/2 можно считать (см. § 1.4), что %' ~ Х*-
Мы предположили для определенности, что ферритовые образцы находятся в прямоугольном волноводе при х = а/2, где магнитное поле волны ТЕ10 линейно поляризовано и поперечно. Метод самосогласованного поля может быть распространен, конечно, и
§ 6.41
ГИРОТРОПНЫЙ ЭЛЛИПСОИД В ВОЛНОВОДЕ
321
на другие положения образца. Особый интерес представляет расположение образца в топке с круговой поляризацией магнитного поля, когда можно ожидать наиболее яркого проявления различных невзаимных эффектов. Не останавливаясь подробно на зтом вопросе, приведем лишь два примера такой невзаимности.
Если намагниченный ферритовый эллипсоид находится в бесконечном волноводе в точке с круговой поляризацией магнитного поля, то он, естественно, будет оказывать заметное влияние на
распространение энергии по волноводу лишь для того направления распространения, для которого магнитное поле в месте расположения образца будет иметь правое вращение. Коэффициент отражения будет практически равен нулю, так как для отраженной волны магнитное поле будет иметь левое вращение, и эта волна не будет возбуждаться намагниченностью образца с правым вращением.
В качестве второго примера рассмотрим случай, когда образец расположен в отверстии, соединяющем два скрещенных волновода, в точках с круговой поляризацией магнитного поля основной волны обоих волноводов (рис. 6.4.7). Пусть падающая
М
1 2,3 ©-----
Рис. 6.4.7. Ферритовый фильтр-циркулятор.
волна распространяется из плеча 1 нижнего волновода. В точке расположения образца ее магнитное поле будет иметь круговую поля-
ризацию с правым вращением (относительно направления Но), и при выполнении условия резонанса эта волна будет эффективно возбуждать переменную намагниченность образца. Очевидно, что образец будет излучать в верхний волновод (рис. 6.4.7) лишь в том направлении (в плечо 2), для которого магнитное поле основной волны будет иметь в точке расположения образца правое вращение. По причине, которая отмечалась выше, отраженной волны в плече 1 не будет. При выполнении определенных условий не будет и прохождения энергии в плечо 4, т. е. вся энергия из плеча 1 будет проходить в плечо 2. Легко убедиться, что энергия, поступающая из плеча 2, будет проходить в плечо 3, из плеча 3 — в плечо 4, а из
плеча 4 — в плечо 1. Таким образом, рассматриваемая система является циркулятором 3). Существенно, что она обладает одновременно свойствами фильтра, перестраиваемого при помощи внеш-
него магнитного поля.
’) Циркулятор является одним из наиболее распространенных СВЧ ферритовых устройств (см., например, [482, 483, 490], а также [И]). Применяются циркуляторы с четырьмя п — чаще всего — с тремя плечамп. В них используются поликристаллические ферритовые образцы и постоянные поля, отличающиеся от резонансного.
11 А. Г. Гуревич
ГЛАВА 1
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
§ 7.1. Магнитостатические волны в неограниченной среде
Решая в главах 5 и 6 электродинамические задачи для систем с гиротропными средами, мы учитывали главным образом наличие тех или иных компонент тензоров р. и е таких сред. Конкретный же вид этих компонент и* в частности, их частотные зависимости почти не принимались нами во внимание. Зависимости компонент р от частоты и других параметров, которые определяются уравнениями движения намагниченности (или намагниченностей подрешеток), были подробно исследованы в главах 1—4. Ясно, что только учет этих зависимостей (которые носят резонансный характер) позволит полностью проанализировать поведение систем с гиротропными средами, найти все возможные в них типы колебаний или волн, определить собственные частоты колебаний и дисперсионные соотношения для волн.
Одним из важных следствий учета частотной зависимости компонент тензора р в магнитно-гиротропных средах является возможность существования в таких средах (см. § 5.2) «медленных» волн с очень малыми (по сравнению с «обычными» электромагнитными волнами) длинами волн. В ограниченных образцах могут иметь место собственные колебания с частотами, значительно более низкими, чем частоты «обыкновенных» электромагнитных колебаний в образцах таких размеров. Примером этих колебаний является однородная прецессия намагниченности эллипсоида, подробно рассмотренная в § 1.4.
Малость длины волны (или размеров образца) по сравнению с длиной обычной электромагнитной волны дает возможность при исследовании медленных волн или низкочастотных колебаний пренебречь «запаздывающими» членами
Догео ** — цп и — ее с	с
в уравнениях Максвелла, т. е. использовать уравнения магнитостатики. Это дает основание называть такие волны и колебания магнитостатическими. Использование уравнений магнитостатики вместо полных уравнений Максвелла существенно упрощает рас-
§ 7.1] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ СРЕДЕ 323 смотрение граничных задач. В этой главе, после исследования в магнитостатическом приближении волн в неограниченной среде, будет проведено решение ряда таких задач. Мы почти не будем учитывать диссипации, интересуясь, в основном, типами нормальных волн и колебаний, их дисперсионными соотношениями и собственными частотами.
Основное внимание будет уделено рассмотрению магнитостатических волн и колебаний для случая ферромагнетика, намагниченного до насыщения. Как следует из § 4.4, полученные результаты будут справедливы и для ферримагнетиков (ферритов).
При укорочении длины волны возникает, вообще говоря, необходимость учета неоднородного члена обменной энергии (см. § 2.1). Однако, как мы убедимся ниже, существует довольно широкий интервал значений волнового числа к, в котором, с одной стороны, уже можно пользоваться уравнениями магнитостатики, а с другой стороны — еще можно не учитывать неоднородного обменного взаимодействия. В этой главе мы ограничимся такими значениями к.
Неограниченная изотропная среда. Дисперсионные соотношения для электромагнитных волн в неограниченном изотропном намагниченном до насыщения ферромагнетике могут быть получены, как уже отмечалось в § 5.2, в результате подстановки в формулу (5.2.6) выражений для компонент тензора ц. Полученные таким образом зависимости со (к) были приведены для двух направлений распространения на рис. 5.2.2. Из этого рисунка видно, что в намагниченном ферромагнетике действительно могут иметь место волны, частоты которых остаются ограниченными с ростом волнового числа к и для достаточно больших к практически от к не зависят *).
Считая е скалярным и приняв (для медленных волн)
к^каУ	(7.1.1)
мы получим из (5.2.3) выражение 2)
В = - Ctg2 eft,	(7.1.2)
определяющее (так как pi зависит от ®) частоту медленных волн.
Неравенство (7.1.1) является условием справедливости уравнений магнитостатики, и рассматриваемые волны можно назвать магнитостатическими. Убедимся непосредственно, что выражение
х) Последнее справедливо только, если пренебречь неоднородным членом в энергии обменного взаимодействия. Учет его (глава 8) приведет к увеличению частоты с ростом к.
а) Угол между направлением распространения волны и осью z (совпадающей с направлением постоянной намагниченности) мы будем теперь обозначать 0*.
11*
324	МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ [ГЛ. 7
(7.1.2) следует из уравнений магнитостатики. Для переменного поля при отсутствии сторонних токов эти уравнения (5.1.9) будут иметь вид
rot h = О,	(7.1.3)
div (p. h) = 0.	(7-1.4)
Из (7.1.3) следует, что может быть введен магнитостатический потенциал ф, так что
h = Гф.	(7.1.5)
Подставляя (7.1.5) в (7.1.4), получим уравнение для потенциала
div (|л?ф) = 0.	(7.1.6)
Для изотропной среды, намагниченной до насыщения в направлении оси z, тензор [л имеет вид (1.2.33). Тогда из (7.1.6) следует уравнение
+	=	(7.1.7)
1 (да2 от/2/ 1 oz2	'	'
Оно носит название уравнения Уокера, который впервые записал его в работе [200J. Интересно отметить, что в это уравнение входит только диагональная компонента тензора ц.
Для плоской волны в неограниченной среде решение уравнения (7.1.7) мы должны искать в виде
=	(7.1.8)
причем
Л/Г / 4- /с2 /4 + 4 + k2 = k\ у = tg efc.
Подставляя (7.1.8) в уравнение (7.1.7), получим (7.1.2).
Решая уравнение (7.1.2) с учетом (1.2.34) относительно со, находим
со2 = сон («я +'®м sin2 0J.	(7.1.9)
Таким образом, частота магнитостатических волн в неограниченной среде не зависит от волнового числа к, а определяется только значениями постоянного поля и намагниченности и углом между волновым вектором (направлением распространения) и направлением постоянного намагничения. Эти волны, как видно из (7.1.2), существуют лишь в области отрицательных значений pi. Отсюда, так же как и из формулы (7.1.9), следует, что их частоты (при заданном значении постоянного поля) лежат в пределах
ЮН <0 Ид. =	(®н + ®м)«
(7.1.10)
§ 7.1] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ СРЕДЕ 325
При фиксированной же частоте величины постоянного поля изменяются в зависимости от угла 0(;, в пределах от Н2 (см. формулу (1.2.37) и рис. 1.2.3) до со/у.
В дальнейшем мы будем рассматривать магнитостатические волны и колебания в ограниченных телах, учитывая граничные условия на поверхностях раздела сред. Однако при достаточно больших к этот учет становится несущественным и для многих целей (например, при рассмотрении процессов релаксации или нелинейных явлений) волны или колебания в таких тела в достаточно хорошем приближении можно заменить однородными плоскими волнами, для которых справедливо соотношение (7.1.9). При этом необходимо лишь под н>н понимать величину
СОн = ХНгО,
где Hi0 — внутреннее постоянное поле. В частности, если образец представляет собой малый эллипсоид, то
сон = Г(НОг-7У33Л/о).	(7.1.11)
Интересно отметить1), что частота однородной прецессии эллипсоида (1.4.18) может лежать как в пределах (7.1.10) («внутри спектра» однородных плоских магнитостатических волн), так и выходить за верхнюю границу этого спектра. Сравнивая (1.4.18) с (7.1.9) с учетом (7.1.11), нетрудно получить условие того, чтобы частота однородной прецессии эллипсоида (намагниченного вдоль одной из главных осей — оси z) лежала выше верхней границы спектра плоских магнитостатических волн:
Яо<(^ + ~^)мо.	(7.1.12)
Для продольно намагниченного тонкого цилиндра {Nz ~ 0) условие (7.1.12) всегда выполняется. Для нормально намагниченного тонкого диска оно не может быть выполнено, так как одновременно должно иметь место: Но — 4лЛ/0	0; в этом случае частота
однородной прецессии совпадает с нижней границей (0fc = 0) спектра магнитостатических волн. Для сферы из (7.1.12) следует
2
G) (Ojf = ®пр о*	(7.1.13)
Для иттрий-железного граната при комнатной температуре определяемая таким образом предельная частота составляет 3,16 Ггц.
Пределы применимости магнитостатического приближения. Обсудим теперь пределы справедливости используемого в этой главе приближения. Снизу йнтервал допустимых значений к
х) Это обстоятельство играет существенную роль в процессах релакеа-ции (глава 9).
326
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
ограничивается условием (7.1.1). Для обычных ферритов и сантиметрового диапазона волн (е 10, со 2л-1010) из условия (7.1.1) следует
к > 10.
Для оценки верхней границы учтем, что в линеаризованное уравнение движения намагниченности *) должны, вообще говоря, войти члены
ТМ0 X hs и ym X Неи о,
где Мо — постоянная намагниченность, hQ — эффективное переменное поле неоднородного обменного взаимодействия, m — переменная намагниченность, а Непо — постоянное эффективное поле, включающее внешнее поле, размагничивающее поле и поле анизотропии. Условие, определяющее верхнюю границу значений к, заключается в том, чтобы первый из этих членов был пренебрежимо мал по сравнению со вторым:
<^<тЯеио.	(7.1.14)
Для плоской волны, согласно (2.1.21), hq = ql^m.
С учетом этого из (7.1.14) следует
(7.1.15)
Далее можно либо учесть приближенное соотношение (2.1.9), либо использовать непосредственно экспериментальные значения q. В первом случае, принимая а = 3-10-8, ЛМ0 = 107 и Hett0 = == 103, получим
к <3-105 см-1.
Используя экспериментальное значение q = т]/(Т7И0) = 4-10'11 (иттрий-железный гранат при комнатной температуре), мы придем к той же оценке.
Таким образом, существует довольно широкий интервал значений волновых чисел: от, приблизительно, 10* 2до 104 н- 105, в котором справедливо магнитостатическое приближение без необходимости учета неоднородного члена в энергии обменного взаимодействия 2). Эта оценка, проведенная для одиородпых^'плоских волн
х) Подробнее см. § 8.1.
2) В дальнейшем мы будем называть это приближение магнитостатическим безобманным приближением. Следуя традиции, будем называть волны, для которых справедливо магнитостатическое безобменное приближение, магнитостатическими волнами, а волны, для которых по-прежнему (и даже с большим правом) можно пользоваться уравнениями магнитостатики, но необходимо учитывать неоднородное обменное взаимодействие, —спиновыми волнами. Такие волны будут рассмотрены в главе 8. На самом деле и те и другие волны являются спиновыми и магнитостатическими.
§ 7.11 МАГНИТОСТАТИЧЕСКИЕаВОЛНЫ В НЕОГРАНИЧЕННОЙ СРЕДЕ 327
в неограниченной среде, остается справедливой и для более сложных волновых или колебательных процессов, в том числе и в ограниченных телах. Тогда под к следует понимать величину, обратную расстоянию, на котором амплитуда или фаза переменной намагниченности существенно изменяется.
Анизотропный ферромагнетик. При исследовании магнитостатических волн в анизотропной среде можно по-прежнему исходить из уравнения (7.1.6) и (рассматривая плоские волны в неограниченной среде) использовать выражение (7.1.8). Но для компонент тензора ц теперь необходимо принять выражения, справедливые для анизотропной среды.
Как было показано в § 2.2, выражения для компонент внутреннего тензора восприимчивости анизотропной среды получаются из выражений (1.4.39) — (1.4.43) для внешнего тензора восприимчивости изотропного эллипсоида заменой поперечных компонент тензора N на соответствующие компоненты тензора эффективных размагничивающих факторов анизотропии N“, а величины N33 — на сумму N33 + /V33. Тогда, как нетрудно убедиться, тензор магнитной проницаемости намагниченного до насыщения антизотроп-ного ферромагнетика (без учета диссипации) запишется так:
	Р-х	Р-в + Фа °	
ц =	Не — Ща	Н1/	0	,	(7.1.16)
	0	0	1	
где		
		
Гх	2	9 ’	2 .	W*-W2	СО*-		~“2	(7.1.17)
	С0м<04	COj	и °’
а	™	©2-W2 ’	со*-		-со2 ’
	= СО^ — со2.	(7.1.18)
Здесь		
сож = сод-j-Т(А22 — М33)М0,	(£>у — Y (Ап — NS3)M0,
со, = тМ2Т1/о,	(7ЛЛ9)
а Ын по-прежнему определяется выражением (7.1.11).
Если магнитная проницаемость имеет вид (7.1.16), то из (7.1.6) следует уравнение
, й2ф ,	й2с1) , й2ф п
Их	7Г5 + Л—г- + ЛТ = 0>	(7.1.20)
‘  ох2, у оу2, ох оу OZ2,	'	'
которое является обобщением уравнения Уокера (7.1.7). Заметим, что антисимметричная компонента ца в (7.1.20), так же как и (7.1.7), не входит.
§28 Магнитостатический колебаний Й ВОЛНЫ frjl. 7
Для плоских волн общее уравнение (7.1.6) переходит в соотношение з з
kpks 2 2РрЛЛ = 0	(1, 2, 3 ==х, у, z). (7.1.21)
P=»l S=1
Для тензора р вида (7.1.16) из (7.1.21) (или из (7.1.20) с учетом (7.1.8)) следует
рХ- +	4- ИЛЧ + $ = 0.	(7.1.22)
После деления на (к* + к%) получаем
Их cos2 фК + pySin2 (pft + у ps sin 2cpfe + ctg2 6fc = 0, (7.1.22')
где и фк — полярный и азимутальный углы волнового вектора к. Выражение (7.1.22') является обобщением выражения (7.1.2).
Подставляя компоненты (7.1.17) в (7.1.22), мы получим формулу для частоты магнитостатических волн, являющуюся обобщением формулы (7.1.9),
• И2 —	°4м [ (|)х 4'	+
f + (®х — ©u)сок 2(pfe— cos siii2cp/£]sin2 6fc.
(7.1.23)
Из (7.1.23) видно, что частота волны, распространяющейся в направлении постоянного намагничения ' (6ft = 0), совпадает с резонансной
частотой со 0 тензоров восприимчивости и проницаемости среды. Для других направлений распространения такого совпадения нет.
Следует подчеркнуть, что углы 0^ и срк в (7.1.23) отсчитываются от осей системы координат, в которой ось z совпадает с направлением постоянной намагниченности Мо. Поэтому для проведения расчетов по формуле (7.1.23) необходимо предварительно решить статическую задачу об определении ориентации вектора Мо. Такое же положение имело место и для однородного резонанса (глава 2). Так же как и при однородном резонансе, расчеты существенно облегчаются, если направление Мо совпадает с заданным направлением Но («киттелевский» случай).
Разберем теперь некоторые примеры использования формулы (7.1.23). При этом для простоты ограничимся случаем достаточно больших величин /70 по сравнению с размагничивающими полями и полями анизотропии, когда направления Но и Мо можно считать совпадающими.
§ 7.1] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В НЕОГРАНИЧЕННОЙ СРЕДЕ 329
Рассмотрим сначала одноосный кристалл (рис. 7.1.1). Для него из (7.1.23) и (7.1.19), используя выражения (2.2.8) для эффективных размагничивающих факторов, получим (с учетом только первой константы анизотропии)
(w/y)2 =	+ 2/7А) cos 26) (7Д0 + 2/7cos- 6) + 4лЛ/п x
X [Hi0 + Hai (3 cos2 6 — 1 — sin2 6 cos2 <pfc)] sin2 6te. (7.1.24)
Здесь, согласно (2.2.10), НА1 = KJMO, a 0 — угол между Mo (а так
же и Но) и осью анизотропии. Заметим, что в (7.1.24) не входит угол ф, поскольку мы не учитываем анизотропии в базисной плоскости, но входит угол ф/;. Он отсчитывается (см. рис. 7.1.1) от перпендикуляра к плоскости, проходящей через ось анизотропии и вектор Мо. Для 6k = 0 (7.1.24) переходит при замене Hi0 —> Но в формулу (2.2.19) для резонансной частоты сферы из одноосного ферромагнетика. Если же 6 = 0, т. е. постоянное поле направлено следует
Рис. 7.1.2. Магнитостатическая волна в кубическом кристалле.
по оси кристалла, то из (7.1.24)
(»/ Y)2 = (Hi0 + 2НА1) (//i0 + 2НА1 + 4лМо sin2 6fc). (7.1.25)
Для кубического кристалла (рис. 7.1.2) мы ограничимся частным случаем, когда Но (и Мо) лежат в плоскости {110}. Тогда, используя выражения (2.2.27) для эффективных размагничивающих факторов, получим (с учетом только первой константы, анизотропии) (уУ = [/До + НА1 (------1- + 2 cos 26 + 4 cos 4е)] х
X ГHi0 + НА1 (4 cos 26 + 4 cos	+
L	\	I
+ 4лЛД {/До + НА1 [—jg- —— cos 26 + -jg-cos 46 +
+ [4------|~cos 20 + 4 cos 4 cos sin2 9к. (7.1.26)
При 6k = 0 эта формула переходит с заменой Hi0 —» //0 в выражение (2.2.29) для частоты ферромагнитного резонанса в сфере. Если постоянное поле (предполагается все время, что направления Мо и Но совпадают) направлено по одной из осей симметрии куби
330
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
ческого кристалла, то из (7.1.26) следует: для осей <100) (0 = 0)— формула (7.1.25), для осей <111> (0 = arccos (17)^3) == 54°44')
(<о/т)2 = (Hi0----(Я1О------------IIА1 + 4лМ0 sin2 0fe) , (7.1.27)
и для осей <110) (0 = л/2)
(co/y)2 = (Hi0 + II ai) (7?io	%Hai) +
+ 4лМ0 + НЛ1 (------------Г + cos sin2 6/с’ (7-^-28)
Сравнивая (7.1.25) и (7.1.27) с формулой (7.1.9), мы видим, что выражения для спектра магнитостатических волн в одноосном и кубическом кристаллах для этих направлений не содержат угла (pit и отличаются от спектра в изотропной среде лишь заменой
Hi0^Hi0 + Ha-,	(7.1.29)
поле На принимает (при учете только первой константы анизотропии) значения, приведенные в табл. 7.1.1.
Таблица 7.1.1
Значения поля На
Кристалл	Одноосный	Кубический	
Направление Мо	Ось	<100>	<111>
На	27С1		4 Ki
			3 м0
Заметим, что и в случае однородного резонанса (§ 2.2) собственные частоты для приведенных в табл. 7.1.1 направлений Мо отличались от частот изотропных образцов заменой (7.1.29). Очевидно, что это связано с общим свойством решений электродинамических задач. Действительно, если для анизотропной среды с магнитной проницаемостью вида (7.1.16) окажется
Их = Ир и ps = 0,	(7.1.30)
то все уравнения электродинамики (в частности, магнитостатическое уравнение (7.1.20)) будут иметь такой же вид, как и для изотропной среды. Из (7.1.17) и (7.1.19) видно, что (7.1.30) имеет место, когда
=	и Я“2 = 0.	(7.1.31)
При выполнении условий (7.1.31) выражения (7.1.17) для рж =
§ 7.1] МАГНИТОСТАТИЧЕСКИЕ ВОЙНЫ В НЕОГРАНИЧЕННОЙ СРЕДЕ &И
и р,а отличаются от выражений для р и р.а изотропной среды только заменой (7.1.29), где
Я“ = (Д^-2У“3)МО.	(7.1.32)
Следовательно, при выполнении условий (7.1.31) решения любых магнитостатических задач, полученные для изотропной среды, будут справедливы и для кристалла при замене (7.1.29), (7.1.32).
Легко убедиться с помощью выражений (2.2.8) и (2.2.27), что для приведенных в табл. 7.1.1 направлений и только для них условия (7.1.31) выполняются, а значения № в этой таблице, следуют из (7.1.32). Для всех других направлений намагничения, в том
Рис. 7.1.3. Зависимости частоты магнитостатических волн от направления постоянной намагниченности для разных направлений распространения волны в кубическом кристалле. 0 — угол между Мо и осью <100> в плоскости (110}. Мо = 140 гс, Kt = —6-10г (иттрий-железный гранат при комнатной температуре); — 2500 », что соответствует частоте однородной прецессии в сфере ы/2л = 8,65 Ггц.
числе и для лежащих в базисной плоскости одноосного кристалла и направлений < 110> в кубическом кристалле, спектр магнитостатических волн зависит от угла (рл и не может быть получен заменой (7.1.29) из спектра (7.1.9) для изотропной среды.
На рис. 7.1.3 приведены в качестве примера зависимости частоты магнитостатических волн в кубическом кристалле от направления намагничения для разных направлений распространения волны. Как видно из рис. 7.1.3, даже в таком кристалле с малой константой анизотропии, как иттрий-железный гранат, анизотропия спектра магнитостатических волн, в том числе и зависимость от угла (pt, весьма существенна. Эта зависимость, как уже отме
332
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛЙЫ
Ггл. 1
чалось, отсутствует для направлений намагничения ( 100) и (111) и оказывается максимальной (см. рис. 7.1.3) для направлений <110).
Остановимся теперь на вопросе о совпадении частот (вырождении) плоских магнитостатических волн и однородной прецессии намагниченности эллипсоида для случая анизотропной среды. При выполнении (7.1.31), т. е. для направлений, приведенных в табл. 7.1.1, условие перехода частоты однородной прецессии соо через верхнюю границу спектра магнитостатических волн ; получится из «изотропного» условия (7.1.12) при замене
Яо Яо 4- на,	(7.1.33)
а условие (7.1.13) для сферы будет по-прежнему справедливо. Для других направлений намагниченности это уже не будет иметь места, и условия перехода <а0 через верхнюю границу спектра магнитостатических волн должны быть получены путем сравнения частоты со 0 и максимальной частоты магнитостатических волн, которая будет зависеть теперь от углов и ф». Так, например, нетрудно убедиться, что для направлений (110) в сфере из кубического кристалла (с учетом только первой контанты анизотропии) условия того, чтобы соо лежала выше верхней границы спектра плоских магнитостатических волн, будут иметь следующий вид:
при	Ях>0	Яо <^-|-4лЛ70 — 4ЯА1,	(7.1.34)
при	Ях<0	Я0<-|-4лМ0-5|Яа1|.	(7.1.35)
§ 7.2. Магнитостатические волны в пластинах и стержнях
Перейдем теперь к изучению магнитостатических волн в более сложных системах, содержащих поверхности раздела разных сред. При этом для простоты мы ограничимся случаем изотропного (в отсутствие постоянного поля) намагниченного до насыщения ферромагнетика. Простейшей из таких систем является неограниченная в двух измерениях плоскопараллельная ферромагнитная пластина.
Нормально намагниченная пластина с металлическим покрытием. Остановимся прежде всего на случае пластины, намагниченной постоянным полем перпендикулярно ее плоскости (рис. 7.2.1). Пусть сначала пластина будет ограничена с обеих сторон идеально проводящими металлическими стенками. Тогда необходимо рассмотреть лишь поле в области 0< z < d (рис. 7.2.1). Это поле определяется уравнениями (7.1.5) и (7.1.7) и граничным условием, которое, согласно (5.1.3) и (7.1.5), запишется в виде
(р?ф)по = 0,	(7.2.1)
§ 7.21 МАГНИТОСТАТИЧЕСКИЙ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ ЗЗЗ
Где п0 — единичный вектор нормали к границе с металлом. В данном случае эта граница перпендикулярна направлению постоянного намагничения (n0 = z0) и из (7.2.1) следует
= 0 при z = О и z = d.	(7.2.2)
Нас интересуют волны, распространяющиеся вдоль пластины. Совместив с направлением распространения ось у и рассматривая волны, не зависящие от х, запишем решение уравнения (7.1.7)
в виде
ф = (4 cos kzz -J- В sin kzz) e~'kvJ .	(7.2.3)
Наложение граничных условий (7.2.2) дает А = Ои
7^ = ^-	(« = 0,1,2,...). (7.2.4)
Подставляя решение (7.2.3) в уравнение (7.1.7), получим
— рку = kt
ъ г Рис. 7.2.1. Нормально намагниченная пластина.
Поскольку граничные условия требуют вещественности kz, распространяющиеся волны (ку 0) возможны (так же как и в неограниченной среде) только при таких частотах—лежащих в интервале (7.1.10)—при которых ц < 0. При этом в пластине может существовать бесконечное количество типов волн, различающихся значениями п.
Выражения (7.2.4) и (7.2.5) с учетом частотной зависимости р, (1.2.34) определяют дисперсионное соотношение со (ку) для исследуемой волны. Его можно записать в виде
<о2. - <о2	АГ2
-Н(«)= W2_W2 = 7^ ’
BL	а
(7.2.6)
где в данном случае нормально намагниченной пластины со# = =*	— Юм, а
ПЛ
(величина определяется формулой (5.2.57)).
Уравнение (7.2.6) можно решить относительно <о:
со2 = сон
, шм
J-------------
1 -I- —
М (kyd)*
(7.2.7)
результаты расчета зависимостей и (ку) по формуле (7.2.7) приведены на рис. 7.2.2. Как видно из (7.2.7) и из рис. 7.2.2, частоты
334
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. ?
магнитостатических волн в данном случае уменьшаются с увеличением п и (при п =/= 0) растут с ростом ку. При ку —>’оо они стремятся к величине wj_ (которая следует из 'формулы (7.1.9) для неограниченной среды при б;,- = л/2). Предельные значения со = сод и со = coj^, строго говоря, не достигаются (при п =1= 0), так как магнитостатическое безобменное приближение справедливо лишь в указанных выше ограниченных пределах изменения волновых
Рис. 7.2.2. Спектры магнитостатических волн в нормально намагниченной ферритовой пластине с металлическим покрытием. = 0,5 &>д/.
чисел. Что же касается случая п = 0 (т. е. кг = 0), то можно считать, что рост со от сон до со± происходит скачком при ку — 0. «Волна» с к у = kz = 0 представляет собой однородную прецессию, частота которой для нормально намагниченной пластины, согласно (1.4.20), составляет сод.
Подчеркнем, что зависимость со от волнового числа ку (формула (7.2.7), рис. 7.2.2), как и наличие дискретных типов волн, появилась в результате учета граничных условий задачи. В неограниченной среде частота магнитостатических безобменных волн от волнового числа не зависит.
Нормально намагниченная пластина в свободном пространстве. Рассмотрим теперь магнитостатические волны в нормально намагниченной пластине без металлического покрытия. Эта задача1) несколько сложнее предыдущей, так как мы должны рассматривать поля и во внешних по отношению к пластине областях: при z 0 и при z d (рис. 7.2.1). Уравнение (7.1.7) для внешних областей
х) Она была рассмотрена Ахиезером, Барьяхтаром и Кагановым [217, 3]. Цилиндрические магнитостатические волны в нормально намагниченной пластине исследовали Дэймон и Ван де Ваарт [221].
§ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 335
переходит в уравнение Лапласа
Г72чЬ - I д2Ч'0 [	р	/7 п ох
V Фо =	- О-	(/.2.8)
Интересуясь по-прежнему волнами, распространяющимися в плоскости пластины — по оси у, мы можем записать решения для пластины (0 < z <; d) в форме (7,2.3). Решения для внешних областей можно представить в виде
фо = Ge^VV при z<0,	(729)
фо = С2е-,Сго2е_1/с1/1' при z d.
Поскольку для пластины уравнение и вид решения остались без изменения, соотношение (7.2.5) также останется справедливым. Подстановка же решений (7.2.9) в уравнение (7.2.8) даст
kl = к*.
И так как к„ 0 по условию задачи (рассматриваются волны, бегущие вдоль пластины), то к20	0. Тогда из условия конечности
решения при z оо и z -> — оо вытекает, что kz0 0. Таким образом (принимая ку 0),
kz0 = ky.	(7.2.10)
Граничные условия заключаются в непрерывности касательных составляющих магнитного поля и нормальной составляющей магнитной индукции на поверхностях раздела сред: z = 0 и z = d. Нетрудно убедиться, что из непрерывности hx и hy следует
ф = ф0 при z = 0 и z = d.	(7.2.11)
Из условия же непрерывности нормальной составляющей магнитной индукции (pi ¥ф)п0 в данном случае вытекает
4z"= ПРИ z = 0 и z = d. (7.2.12)
Накладывая граничные условия (7.2.11) и (7.2.12) на решения (7.2.3) и (7.2.9), мы получим для коэффициентов А, В, Сг и С2 систему однородных уравнений. Условие совместности этой системы даст
tg k2d = 2к*20 .	(7.2.13)
С учетом (7.2.5) и (7.2.10) уравнение (7.2.13) запишется в виде 2_1_
tg g = т-т4г------F & кУ	(7-2-14)
(v)-1 
336
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
где

(7.2.15)
Выражение (7.2.14) совместно с (7.2.15) и частотной зависимостью р, (1.2.34) определяет закон дисперсии рассматриваемых волн. При вещественных Г—ц уравнение (7.2.14), если задаться kvd, может быть решено графически (рис. 7.2.3). Оно имеет бесконечное количество корней, соответствующих различным типам волн. Обозначая эти корни через Xn(kyd) (п = 1, 2, 3, ...), получим из (7.2.15)
Рис. 7.2.3. Графическое решение уравнения (7.2.14), определяющего спектр магнитостатических воли в нормально намагниченной пластине, kyd — к. Черные кружки — значения Хп для пластины с металлическим покрытием.
Это выражение совпадает по форме с (7.2.6) и, таким образом, закон дисперсии может быть по-прежнему за писан в виде (7.2.7), но теперь Хп является функцией kyd. Как видно из рис. 7.2.3, отличие корней Хп (kyd) уравнения (7.2.14) от корней Хп = пл для пластины с металлическим покрытием уменьшается с ростом п, а характер зависимости частот от kyd л п
остается для пластины без покрытия таким же, как для пластины с металлическим покрытием (рис. 7.2.2).
При мнимом В уравнение (7.2.14), как легко убедиться, не имеет решений. Таким образом, магнитостатические волны в нормально намагниченной пластине, так же как и в свободном пространстве, могут существовать только при ц < 0, т. е. в области частот (7.1.10).
Касательно намагниченная пластина. Пусть теперь постоянное магнитное поле лежит в плоскости пластины (рис. 7.2.4). Отличие этой задачи от предыдущей заключается, во-первых, в том, что теперь направление распространения нельзя совместить с одной из осей координат, а необходимо рассматривать волну, распространяющуюся в плоскости пластины под произвольным углом 6/с к оси z (направленной, как всегда, по постоянному полю). Решение уравнения (7.1.7) для потенциала в пластине должно быть теперь записано в виде
ф = (Л cos кхх В sin к^х) е-1(М+к*2),	(7.2,17)
§ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 337
Во-вторых, изменение направления постоянного намагничения приведет к изменению граничных условий. Остановимся на случае пластины с металлическим покрытием. Из общего условия (7.2.1) теперь будет следовать
0 при ж = 0 и x = d- (7-2.18)
Наложение условий (7.2.18) на решение (7.2.17) приводит к системе уравнений для А и В; равенство нулю ее определителя дает
(р2/^ + sin kxd = 0.
Подставляя (7.2.17) в (7.1.7),
— Н (кх -}- ку) = kz.
Рис. 7.2.4. Касательно намагниченная пластина.
(7.2.19) получим (7.2.20)
Заметим, что выражение (7.2.20) совпадает с (7.1.2), если обозначить г~...............ctg efc.
V% +
Но определенный таким образом угол 0к отличается от угла 0/; между осью z и направлением распространения волны.
Уравнения (7.2.19) и (7.2.20) с учетом зависимостей р и ро от частоты со (или постоянного поля Но) определяют закон дисперсии для рассматриваемых волн, т. е. зависимость со (или Но) от ку и kz.
Если р лежит в пределах
к2, -ctg2efc^-_£ kv
то, как видно из (7.2.20), кх вещественно. Тогда из (7.Х..19) следует
kxd = пл ~ Хп.	(7.2.22)
С учетом (7.2.22) из (7.2.20) и (1.2.34) вытекает дисперсионное соотношение
о,
(7.2.21)
со^ — со2 (АуО2
“ И = со2 —со^ ~ (kvdy + ЛГ2 ’
Решая (7,2.23) относительно со2, получим, аналогично (7.2.7),
со2 = СОд
(7.2.23)
(7.2.24)
Н +	(kd)*
1+(W)2 + *2
Результаты расчета по формуле (7.2.24) приведены на рис. 7.2,5,
338
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
Как видно из (7.2.24) и рис. 7.2.5, частоты в этом случае увеличиваются с ростом п (в отличие от нормально намагниченной пластины) и увеличиваются с ростом угла 0fc. При = л/2 (т. е. kz = 0) со — со± независимо от п и ку. При 0л = 0 (т. е. ку = 0) со убывает
Рис. 7.2.5. Спектры магнитостатических волн в касательно намагниченной ферритовой пластине с металлическим покрытием, шд = 0,5 Сплошные линии — две объемные волны, пунктир — поверхностная волна.
с ростом kz от Юх до (он- Таким образом, при распространении волны в направлении Но зависимость со от волнового числа оказывается обратной по сравнению со случаем распространения в направлении, нормальном к Но (рис. 7.2.2).
Поверхностные волны. Исследуем теперь возможность существования решений с мнимыми кх. Подставляя кх = в уравнение (7.2.19), мы видим, что это уравнение может удовлетворяться при условии
р2х2 - рХ = 0,	(7.2.25)
откуда с учетом (7.2.20)
|l'2
р -	= - -I- - ctg* efc. (7.2.26)
Выражение (7.2.26) совместно с частотной зависимостью р± (формула (5.2.56), рис. 5.2.8) определяет закон дисперсии волны с мнимым кх. Ее частота зависит только от угла и изменяется (рис. 7.2.5) в пределах
(°± = Vюн (®н + юм) ®	(°н + (Ом- (7.2.27)
Этот интервал частот примыкает к интервалу (7.1.10), в котором лежат частоты волн с вещественными кх.
§7.21 МАГНИТОС'ГАТИЧеСЩЙЁ ЁОЛЙЬГ fe ПЛАСДЙЙАХ Й СТЕЙЖНЯХ 339
При мнимом кх потенциал ф запишется в виде ф = (Сеххж _|_ De~**x) е~^у-кг2\
(7.2.28)
Учитывая граничное условие (7.2.18), легко убедиться, что либо
либо
С = 0	и	их = — к,,,
D = О	и	хз; = - — к„.
х	|Х V
Очевидно, что обе эти возможности соответствуют одной и той же зависимостипотенциала от координаты х. Потенциал, а следователь-
но, и составляющие поля убывают экспоненциально при удалении от одной из плоскостей пластины (рис. 7.2.6). От какой именно — зависит от знака ку (т. е. направления распространения волны) и знака ро (т. е. направления постоянного поля). В этом свойстве волны с мнимым кх проявляется невзаимность рассматриваемой системы.
Как видно из (7.2.25), хж растет с ростом ку, для больших ку (т. е. коротких волн) поле убывает очень быстро при удалении от поверхности пластины. Это дает основание назвать волну с мнимым кх поверхностной
Рис. 7.2.6. Распределение поля по толщине касательно намагниченной пластины для поверхностной волны.
магнитостатической волной.
Итак, в ферромагнитной пластине, намагниченной касательно к
ее плоскости, может существовать бесконечное количество объемных (с синусоидальной зависимостью от х) магнитостатических волн и одна поверхностная (с экспоненциальной зависимостью от х) волна с невзаимным распределением поля. Их частотные интервалы соприкасаются и вместе занимают область
(7.2.29)
Мы не будем приводить решения задачи о магнитостатических волнах в касательно намагниченной пластине без металлического покрытия, которое получили Дэймон и Эшбах [220] (см. также [11]). Заметим лишь, что существенным отличием результатов для пластины в свободном пространстве от пластины с металлическим покрытием является сужение интервала частот поверхностных типов волн. Их частоты изменяются теперь в пределах
/ , . 1
®_L	® <^®д + — ®м-
340
магнитостатические колебания и волны
[гл. 7
Интервал частот (7.1.10) объемных волн остается без изменения, и таким образом вся область частот магнитостатических волн в касательно намагниченной пластине без металлического покрытия составляет
®н м ®н Н—g-	(7.2.30)
Круглый стержень. Перейдем теперь к рассмотрению магнитостатических волн в волноводах х). Заметим, что легко может быть решена [223] задача о магнитостатических волнах в прямоугольном стержне с металлическим покрытием (прямоугольном волноводе), намагниченном перпендикулярно одной из его стенок * 2 3). Задача о таком стержне без металлических стенок уже не имеет элементарного решения. Не может быть просто решена и задача о продольно (параллельно оси) намагниченном прямоугольном стержне, даже с металлическим покрытием. Причина зтого заключается в следующем: наложение граничного условия (7.2.1) на поверхностях, параллельных оси z, только тогда приводит к простому аналитическому решению, когда зависимость составляющих поля хотя бы от одной из поперечных координат является экспоненциальной 3). В случае же продольно намагниченного прямоугольного стержня зависимости от обеих поперечных координат должны быть синусоидальными.
Рассмотрим магнитостатические волны в продольно намагниченном круглом стержне. При этом координатой, зависимость от которой является экспоненциальной, будет полярный угол ср, и задача может быть решена как при наличии, таки в отсутствие металлических стенок.
Рассмотрим стержень с металлическим покрытием, т. е. круглую трубу с идеально проводящими стенками, заполненную непроводящим ферромагнетиком, намагниченным до насыщения в направлении оси трубы 4).
Необходимость наложения граничного условия на цилиндрической поверхности р = R (рис. 7.2.7) требует перехода к цилиндрическим координатам р, tp, z. В этих координатах уравнение Уокера
х) Волноводы — это такие системы, в которых граничные условия накладываются в двух измерениях, а направление распространения волны (в третьем измерении) является, с точностью до знака, определенным.
2) Однако при решении этой задачи приходится предположить, что внутреннее постоянное поле 1Ц0 однородно, что, конечно, не реализуется при помещении прямоугольного стержня в однородное внешнее поле.
3) Это находится в согласии с общим замечанием (см. § 6.1) об ограничении класса граничных электродинамических задач, которые могут быть аналитически решены в случае гиротропных сред.
4) В отличие от § 6.1, где рассматривалась такая же система, мы теперь учитываем конкретный вид компонент тензора |х, но зато ограничиваемся магнитостатическим приближением.
§ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 341
(7-1.7)
запишется следующим образом:
/ д2ф 1	<h|) . 1	Э2ф \	.	д2ф
\ Эр2	' р	др "Г” р2	скр2 у	'	3z2
(7.2.31)
Граничное условие (7.2.1) в данном случае (п0 = р0) примет вид
н| + ^7¥ = 0 при р = 7?-	<7-2-32)
Используем для решения уравнения (7.2.31) обычный метод разделения переменных (см., например [38]) и учтем соображения
о виде зависимости от угла ф, приведенные при решении уравнения^.1.16). Тогда мы убедимся, что решение уравнения (7.2.31),
которое соответствует волне, бегущей вдоль оси z, и остается конечным при р = 0, можно записать в виде
ф = Jm (хр) e^e-’V, (7.2.33), где Jm — функция Бесселя, т = О ±1, ±2, ..., а х = /с2/К— И- Подставив решение (7.2.33) в граничное условие (7.2.32), найдем х)
+ k*R
(7.2.34)
Рис. 7.2.7. Продольно намагниченный стержень.
где штрих, как всегда, обозначает дифференцирование по аргументу. Уравнение (7.2.34) совместно с частотными зависимостями р и ро (1.2.34) и (1.2.35) определяет дисперсионное соотношение (спектр) магнитостатических волн в стержне.
Перепишем уравнение (7.2.34) следующим образом: ц (со)
(7.2.349
где
(вид этой функции не зависит от со и кг), а
Графики функций Fm (£) приведены на рис. 7.2.8. Задаваясь параметрами сод и и угловым индексом волны т, мы можем для
х) Уравнение (7.2.34) может быть получено в магнитостатическом приближении (kz кп) из (6.1.21) с учетом (5.1.47).
342	МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ Й ЙОЙЙЫ fM. ?
каждого значения частоты найти графически корни £ *= Хтп уравнения (7.2.34) (п — номер корня). Подставляя их в (7.2.35), получим уравнение для нахождения зависимости со (kz). Его можно записать в виде
со - СО2 __ (fc27?)2
СО2-^	^,2тг(С0) ‘
(7.2.36)
Уравнение (7.2.36) похоже на (7.2.23) при/с^ = 0, т. е. для волн в пластине, распространяющихся (так же как и рассматриваемые волны в стержне) в направлении постоянного намагничения. Однако теперь, в отличие от случая пластины, величины Хтп зависят,
Рис. 7.2.8. Графическое решение уравнения (7.2.34*), определяющего спектр магнитостатических волн в продольно намагниченном стержне с металлическим покрытием I Ва/Ц| = 2,5.
вообще говоря, от частоты, и (7.2.36) не может быть решено в явном виде относительно со.
Остановимся сначала на случае р < 0, которому, согласно (7.2.35), соответствуют вещественные значения £. Уравнение (7.2.34') имеет в этом случае (рис. 7.2.8) бесконечное количество корней. Номера их п указывают на число вариаций поля по радиусу.
При т = 0 корни ХОп уравнения (7.2.34') не зависят от со и представляют собой корни функции Бесселя первого порядка А (ё) • Уравнение (7.2.36) тогда может быть решено относительно со; получающаяся формула, если в ней заменить R —>- d и ХОп -> Хп, совпадает с (7.2.24) при ку = 0. Рассчитанные по этой формуле зависимости со (Zcz) приведены на рис. 7.2.9.
§ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 343
Рис. 7.2.9. Спектры магнитостатических волн в продольно намагниченном ферритовом стержне с металлическим покрытием, од = 0,5 п>др Пунктир — расчет по приближенным формулам(7.2.38) и (7.2.39) для объемной волны ст = 0ип=1.
При т =/= О величины Хтп должны быть определены путем графического решения уравнения (7.2.34'). Они будут зависеть от отношения | р<, |/| р |, т. е. от частоты, и будут различны для разных знаков величины тр„/р (рис. 7.2.8). Знак этой величины определяется направлением вращения поляризации волны относительно направления постоянного намагничения. Действительно, положительным т соответствует правое вращение вокруг оси z. Значения же р„ при ц < 0 (рис. 5.2.8) отрицательны для среды, намагниченной в положительном направлении оси z (именно для этого случая построен график рис. 5.2.8), и наоборот-Таким образом, положительным значениям шри/ц соответствует правое вращение, а отрицательным — левое вращение вокруг направления постоянного намагничения. Зависимости со (kz) при т =f= 0 качественно не отличаются от приведенных на рис. 7.2.9 для т = 0; характер дисперсии (спад со с ростом волнового числа) совпадает с характером дисперсии при ку — 0 в касательно намагниченной пластине (рис. 7.2.5). В этом нет ничего удивительного, так как в обоих случаях волны распространяются в направлении постоянного намагничения.
При больших и малых kz можно получить приближенные дисперсионные соотношения для магнитостатических волн в стержне. Нетрудно убедиться, что при (со — сод) <СГ сон (т. е. для больших kz)
~ ± Ц-
Тогда (7.2.34') переходит в следующее уравнение:
Fm {I) = ±т.
(7.2.37)
С учетом рекуррентных формул для бесселевых функций [42] оно эквивалентно уравнению
(ё) — 0,
где знаки минус и плюс соответствуют правому и левому вращению вокруг направления постоянного намагничения. Корни этого
344
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
1ГЛ. 7
уравнения Хтп не зависят от частоты, и из (7.2.36) следует
со - ®н+ —
(7.2.38)
В случае малых kz, когда
(со_£ — со)	можно получить
СО = C')j_ —
1 юмюн <М?)2
2	«п)2 ’
(7.2.39)
где Хтп — корни уравнения
jm (В) = 0.
Значения kz ограничены условиями (7.1.1) и (7.1.15) применимости магнитостатического безобменного приближения. Сравнивая эти условия с условиями справедливости приближенных формул (7.2.38) и (7.2.39), можно убедиться, что для обычных значений R ~ (0,1	0,5) см формула (7.2.38) справедлива в довольно
широких пределах изменения волновых чисел: от ~ 102 -и 108 до уже упоминавшихся выше предельных значений ~ 105. Формула же (7.2.39) может быть использована лишь в узких пределах изменения kz для стержней, радиус которых много меньше длины электромагнитной волны. На рис. 7.2.9 результаты вычислений по формулам (7.2.38) и (7.2.39) сравниваются с результатами точного расчета.
Рассмотрим теперь случай р 0, т. е. мнимых Как видно из рис. 7.2.8, уравнение (7.2.34') для мнимых £ имеет один корень iXm при условии, что
%- т > Fm (0),	(7.2.40)
Г
или, поскольку Fm (0) = | т | (см. рис. 7.2.8),— при условии
Р'а т
|1 |т|
(7.2.40')
Учитывая частотные зависимости р иро (рис. 5.2.8), легко видеть, что (7.2.40'), совместно с условием р 0, выполняется для волны с левым вращением относительно направления постоянного намагничения в том же интервале частот (7.2.27), в котором существуют поверхностные волны в касательно намагниченной пластине с металлическим покрытием.
При р^> 0 выражение для потенциала, конечное при р = 0, запишется следующим образом:
Ф = 1т
Г — I “	“	* rt
(7.2.41)
$ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 345
где Im (х) = (i)~m Jm (ix) — функция Бесселя мнимого аргумента [42]. Эта функция быстро возрастает с ростом аргумента 1). Следовательно, при достаточно больших kz потенциал и все составляющие поля очень быстро убывают при удалении от поверхности стержня. Это дает основание, так же как и в случае касательно намагниченной пластины, называть волны в стержне при р > О (при мнимых £) поверхностными волнами. Зависимости со (kz) для этих волн показаны на рис. 7.2.9.
Итак, в продольно намагниченном непроводящем ферромагнитном стержне с металлическим покрытием может существовать (при заданном т =/= 0) бесконечное количество объемных типов волн с правым и левым вращением с частотами, лежащими в интервале < со < coj_, и один поверхностный тип волны с левым вращением (относительно направления постоянного намагничения) с частотой, лежащей в интервале со± <; со <; сод -|- соЛ1.
Распространение магнитостатических волн в продольно намагниченном стержне без металлического покрытия рассматривалось Флетчером и Киттелем [216] и затем было подробно исследовано Джозефом и Шлёманном [219]. Мы не будем приводить здесь полностью решения этой задачи, ограничимся лишь следующими замечаниями. Потенциалф в стержне по-прежнему может быть записан в виде (7.2.33). Решение уравнения Лапласа для потенциала ф0 в наружной области (р R) можно представить в виде
фо = /ММе^е"Ч
(7.2.42)
где Кт(х) — функция Бесселя мнимого аргумента 2 * * *). Граничные условия заключаются в непрерывности h?, hz и (p.h)₽ на границе раздела р = R. Первые два условия сводятся к непрерывности ф при р = R, а последнее условие дает
(-5г+*«-М|- = тг при р = л- <7'2-43)
Учет граничных условий приводит к уравнению
Z ( k*R \
1Г ~	-1-	= о. J7.2.44]
Оно отличается от уравнения (7.2.34) для стержня с металлическим покрытием наличием дополнительного — второго члена.
р) Асимптотическая формула для нее 1т (х) са (2ла?)_'4еж.
2) К-т (х) и введенная выше функция 1т (М представляют собой фунда-
ментальные решения уравнения Бесселя с отрицательным знаком при ж2
и целым индексом [42]. Из асимптотической формулы Кт ~
~ (—1)тл‘^ (2ж)^ е~х видно, что Кт (х) —» 0 при х —» оо.
' К
346
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
При достаточно больших kzR для объемных волн (когда — сон ия) этот член мал по сравнению с остальными членами уравнения (7.2.44). Таким образом, при больших kzR дисперсионные соотношения для продольно намагниченного стержня в свободном пространстве должны мало отличаться от соотношений для стержня с металлическим покрытием. В частности, по-прежнему будет справедлива приближенная формула (7.2.38). Заметим, что аналогичная ситуация имела место и для пластин.
Анализ уравнения (7.2.44) и результаты численных расчетов зависимостей со (kz) приводы гы в [219]. Из этих результатов следует, что для объемных волн дисперсионные соотношения во всем интервале изменения кг носят такой же характер, как и в стержне с металлическим покрытием. В частности, остаются прежними пределы изменения частот и характер их зависимости от индексов т и п и от kz (см. рис. 7.2.9). Однако для поверхностных волн пределы изменения частоты становятся другими, они совпадают с пределами изменения частоты поверхностных волн в касательно намагниченной пластине без металлического покрытия. Максимальнрй частотой является теперь не ан -J- ым, как в стержне (а также пластине) с металлическим покрытием, а	/2.
Задача о распространении магнитостатических волн в поперечно намагниченном круглом стержне не имеет простого аналитического решения, потому что направление постоянного намагничения не совпадает с направлением координатных линий круговой цилиндрической системы координат (в которой необходимо решать задачу, чтобы иметь возможность наложить граничные условия). Однако, принимая во внимание неоднократно отмечавшуюся аналогию между распространением магнитостатических волн в продольно намагниченном стержне и касательно намагниченной пластине, мы вправе ожидать, что характер дисперсионных соотношений в поперечно намагниченном стержне будет таким же, как в нормально намагниченной пластине (рис. 7.2.2).
Групповая скорость и время распространения сигнала. Интерес к магнитостатическим волнам особенно возрос в начале 60-х годов, когда началась разработка управляемых линий задержки в диапазоне сверхвысоких частот [487]. Малая скорость распространения магнитостатических волн и резкая зависимость этой скорости от постоянного магнитного поля дают возможность использовать их, наряду с магнито упругими волнами [347], для создания таких линий.
Сигналы, которые используются в линиях задержки, обычно представляют собой импульсы длительностью в единицы или доли микросекунд. Скорость распространения максимумов их амплитуды близка к групповой скорости
=	(7.2.45)
§ 7.2] МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 347
где 7с< — проекция волнового вектора на направление распространения, например, kz — для продольно намагниченного и ку — для поперечно намагниченного стержня; производная в (7.2.45) должна вычисляться при центральной частоте спектра импульса, т. е. при несущей частоте.
Отметим прежде всего, что групповая скорость магнитостатических волн может быть как положительной, так и отрицательной х). Положительной является frp для нормально намагниченной пластины (формула (7.2.7) и рис. 7.2.2) и для поперечного намагниченного стержня. Отрицательная vrpимеет место в тех случаях, когда направление распространения совпадает с направлением постоянного намагничения: для касательно намагниченной пластины при ку = 0 (формула (7.2.24), рис. 7.2.5) и для продольно намагниченного стержня (уравнение (7.2.36), приближенные формулы (7.2.38) и (7.2.39), рис. 7.2.9). Во всех случаях |кгр|, как видно, например, из рис. 7.2.2 и рис. 7.2.9, стремится к нулю при k-Q -> 0 и к^ -> оо и имеет максимум при промежуточных значениях k-Q.
Вычисление групповой скорости не представляет труда для всех рассмотренных выше систем, для которых закон дисперсии со (fc^) может быть выражен аналитически (как для пластины или круглого стержня при т = 0) или рассчитан численно. Мы ограничимся лишь одним примером — касательно намагниченной пластины (при ку = 0) или продольно намагниченного стержня (при т = 0). В этих случаях закон дисперсии, согласно (7.2.24) и (7.2.36), имеет вид
о WrrCOiyr
®2 = <^+	(7.2.46)
где для пластины Хп = пл, ad — толщина; для стержня Хп — корни функции Бесселя J\ (g), a d — радиус. Дифференцируя (7.2.46) по kz, получим
____ ШНШМ	1 Ггр = й	у
\+^Г/
Исключая из (7.2.46) и (7.2.47) kz или со, можно представить кГр как функцию частоты или волнового числа. Например, исключая kz, найдем
_________d (а2 — Л2 [сон (сон +	— со211/г Ггр~ Хп	<™мин
х) Отрицательная групповая скорость означает, что направление изменения фазы волны противоположно направлению перемещения максимума амплитуды.
(7.2.48)
348
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
Из (7.2.48) видна зависимость групповой скорости от постоянного поля Hi0 = <йя/т, которая используется для создания управляемых линий задержки. Эта зависимость показана на рис. 7.2.10.
При больших kz (когда со — а>н а>н) из (7.2.48) следует
пгр - 2’М'2 (и -	(7.2.49)
Очевидно, что выражение (7.2.49) можно получить и дифференцированием (7.2.38). Формула (7.2.47) несправедлива для стержня при т =/= 0, так как величины Хтп в дисперсионном уравнении (7.2.36) зависят теперь от частоты. Однако в предельном случае
Рис. 7.2.10. Зависимости волнового числа и групповой скорости магнитостатической волны (т ~ 0, п = 1) в продольно намагниченном ферритовом стержне от постоянного магнитного поля. ш/2л = 9,35 Гг-ц, MQ = 190 ас, К = 0,15 см. Пунктир — не выполняется условие магнитостатического приближения.
больших kz этой зависимостью, как уже отмечалось, можно пренебречь, и приближенная формула (7.2.49) может быть использована и при т =/= 0.
Теория, которая была развита в этом параграфе, непосредственно относится к распространению магнитостатических волн в бесконечной пластине и бесконечно длинном цилиндре. Экспериментально же исследуется распространение магнитостатических волн в образцах конечных размеров: дисках [221] или стержнях [222, 228] из монокристаллов ферритов. При этом магнитостатические волны обычно возбуждаются переменным магнитным полем на торцевой поверхности стержня или боковой поверхности диска (рис. 7.2.11) и, в свою очередь, возбуждают электромагнитное поле на той же или противоположной (в случае стержня) поверхности. Сравнение «принятого» электромагнитного сигнала с сигналом,
§ 7.21 МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНАХ И СТЕРЖНЯХ 349
возбудившим магнитостатическую волну, позволяет найти время запаздывания сигнала ’).
Если параметры среды можно считать постоянными во всем образце, то время запаздывания первого задержанного импульса * 2) Тх = ,L]vrv,	(7.2.50)
где L — путь, проходимый волной, например, длина стержня I, когда возбуждение и прием производятся на противоположных его торцах, или 21, если возбуждение и прием производятся на одном
и том же торце с отражением волны от противоположного торца.
Однако если образец не является эллипсоидом (например, представляет собой стержень или диск с конечным отношением размеров), то внутреннее постоянное поле Hi0 не будет
однородным при од-
ггптгп Рис.	Схемы экспериментов по ^возбужде-
но р ОДНОМ внешнем поле. нию магнитостатических волн в диске (а) и стер-Параметры среды ц и ра	жне (б>-
будут являться теперь
функциями координат.Строгое рассмотрение магнитостатических волн в таких образцах представляет, конечно, очень большие трудности. В первом приближении можно пренебречь изменением параметров в поперечном направлении (по сечению стержня или по высоте диска), а изменение в направлении распространения считать медленным 3). Тогда время запаздывания
угр (?)
(7.2.51)
Зная распределенйе внутреннего поля Hi0 (£), можно найти кгр (Но, <о,£) и определить (Но, со). Результат такого вычисления и сравнение его с экспериментом для случая продольно намагни
*) Может быть измерено и ослабление сигнала, которое определяется затуханием волны при ее распространении и потерями энергии при возбуждении и при «приеме».
2) В результате многократных отражений от поверхностей стержня или диска образуется последовательность («цуг») импульсов с временами задержки ip = тг + (р — l)2Z/rrp (р = 1, 2, 3, ...).
®) Это предположение делается в геометрической оптике (см., например, [43]) или при рассмотрении волновых процессов методом ВКБ (Вентцеля — Крамерса — Бриллюэна) [38].
350
магнитостатические колебания и волны
[ГЛ. 7
ченного стержня приведены на рис. 7.2.12. Обращает на себя внимание очень резкая зависимость тх (Яо), которая возникает при таких Но, когда в образце появляется область с нгр->0 (т. е. с Hi0-+ <о/т).
В заключение остановимся кратко па вопросе о затухании магнитостатических волн вследствие диссипации в ферромагнитной среде ’). Учет диссипации не связан с принципиальными трудностями — необходимо лишь вместо выражений (1.2.34) и (1.2.35) для параметров среды принять комплексные выражения, например,
Рис. 7.2.12. Результаты исследования магнитостатических волн в продольно намагниченном стержне из иттрий-железного граната [222]. а —- размеры стержня (в миллиметрах) и распределение внутреннего постоянного магнитного поля на оси; б — осциллограммы принятых задержанных импульсов (возбуждение и прием — см. рис. 7.2.11, б — производились на одном и том же торце стержня); в — зависимость времени задержки от внешнего постоянного поля; кривая рассчитана по формуле (7.2.51) с учетом (7.2.48) при тех же параметрах, что и на рис. 7.2.10.
являющиеся следствием (1.3.19) и (1.3.20). В результате уравнения, например, (7.2.6), (7.2.23) или(7.2.36), определяющие спектры магнитостатических волн, станут комплексными. При вещественной частоте со (т. е. для стационарных волн) эти уравнения будут удовлетворяться при комплексных кг = к? — ikr. Здесь к^ (£ — координата в направлении распространения) представляет собой волновое число, определяющее, в частности, групповую скорость кгр = ды/дк^, а к^ — коэффициент затухания волны.
J) Влияние диссипации будет рассмотрено более подробно в следующей главе для случая волн в неограниченной среде, но с учетом неоднородного обменного взаимодействия.
§ 7.3] НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
351
§ 7.3. Неоднородные магнитостатические колебания
Перейдем теперь к изучению, по-прежнему в магнитостатическом безобменном приближении, колебаний намагниченности в ограниченных телах. Один из типов таких колебаний — однородная прецессия намагниченности малого эллипсоида — был рассмотрен в § 1.4. Однако из наличия бегущих магнитостатических волн в неограниченных системах (§§ 7.1 и 7.2) следует, что в ограниченных телах должны существовать и неоднородные магнитостатические колебания. Такие колебания возникали еще, как впоследствии стало ясно, в ранних опытах по ферромагнитному резонансу и проявлялись в дополнительных максимумах, накладывающихся на основную резонансную кривую (см. [114]). Уайт и Солт [199], применив.неоднородное возбуждающее поле, отчетливо разрешили эти дополнительные максимумы и объяснили их возбуждением неоднородных типов колебаний намагниченности. Теорию таких колебаний для случая ферромагнитного эллипсоида вращения (сфероида) разработал Уокер [200] (см. также [201, 240]). Ниже мы познакомимся с этой теорией, но сначала рассмотрим на более простых примерах некоторые характерные черты неоднородных магнитостатических колебаний.
Рассматриваемая задача аналогична исследованной в § 6.3 задаче о колебаниях резонатора с гиротропной средой. В отличие от § 6.3, мы теперь ограничимся магнитостатическим приближением, но зато учтем конкретный вид компонент тензора магнитной проницаемости. Для простоты будем сначала иметь дело с изотропным (в отсутствие внешнего поля) ферромагнетиком и пренебрежем диссипацией, т. е. примем для компонент тензора ц полдеровские выражения (1.2.34) и (1.2.35).
Как уже отмечалось (§§ 6.1 и 7.2), для гиротропных сред класс граничных задач, которые решаются аналитически, существенно ограничивается тем обстоятельством, что зависимость потенциалов и полей от одной из поперечных координат должна быть экспоненциальной. Вследствие этого ограничения задачи о магнитостатических колебаниях могут быть строго решены только для тел вращения относительно оси z (совпадающей с направлением постоянного намагничения). К таким телам принадлежит сфероид, для которого задача о магнитостатических колебаниях была решена Уокером. Мы остановимся сначала на случае кругового цилиндра.
Цилиндр между металлическими плоскостями. Задача о магнитостатических колебаниях кругового цилиндра конечной длины, намагниченного в направлении его оси, может быть просто решена при двух условиях. Во-первых, цилиндр, как показано на рис. 7.3.1, должен быть расположен между двумя бесконечными металлическими плоскостями (z = 0 и z = Z). Во-вторых, внутреннее постоянное магнитное поле в цилиндре должно быть одно-
352
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
Рис. 7.3.1. Продольно намагниченный цилиндр между металлическими плоскостями.
родно х). При выполнении этих условий исследуемый резонатор является волноводным резонатором (см. § 6.3), образованным из волновода — продольно намагниченного стержня, магнитостатические волны в котором были рассмотрены в § 7.2. Как было показано в § 6.3, собственные частоты волноводного резонатора могут быть определены, исходя из частотной зависимости постоянной распространения, по формулам (6.3.36) или (6.3.39) при условии, что распределение поля в волноводе взаимно. Это условие выполняется для объемных магнитостатических волч в стержне и, конечно, не выполняется для поверхностных, которые являются однонаправленными. Для объемных волн постоянная распространения также взаимна, и собственные частоты могут быть определены из выражения (6.3.36).
Зависимость kz (и) для продольно намагниченного стержня определяется уравнением (7.2.36), где Хтп (а) для стержня с металлическим покрытием представляет собой корень уравнения (7.2.34'), а для стержня без покрытия — корень уравнения, которое получится из (7.2.44), если обозначить в нем	—р = Хтп. Под
ставляя, согласно (6.3.36), kz (ы)=л,р/ в (7.2.36), получим трансцендентное собственных частот:
уравнение для определения
О)2 =	-|--------
1 +
сонсом
Г Лр I2
(7.3.1)
\11
Решениями уравнения (7.3.1) будут дискретные частоты атпр; индексы т, пир характеризуют тип колебаний. Как видно из (7.3.1), частоты ®mrip зависят только от отношения размеров R и I, т. е. от формы образца. Этого, конечно, и следовало ожидать, поскольку уравнения магнитостатики не содержат параметра с размерностью длины.
Если т = 0 (аксиально-симметричные типы колебаний), то, как было показано в § 7.2, величины Хо„ не зависят от ми представляют собой корни функции Бесселя (£). В этом случае (как и при р = 0) уравнение (7.3.1) дает в явном виде частоты колебаний. Они могут быть записаны явно также в предельном
х)Это условие, конечно, пе выполняется при помещении цилиндра в однородное внешнее поле.
§ 7.3] НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ 353
случае
лр R
когда справедливо приближенное выражение (7.2.38).
Суперпозиция двух «волноводных» решений (7.2.33) ckz = \kz\ и kz = — \к z | даст потенциал для рассматриваемого резонатора. С учетом граничных условий
== 0 при 7, = 0 и z = I
он запишется в виде
г], = CJm (хр) cos kzz е'”'*.	(7.3.2)
Здесь kz = лр]1, x = kz — |i, а С — постоянный множитель, который остается неопределенным, поскольку мы рассматриваем свободные колебания и не нормируем собственные функции. Конечно, к выражениям (7.3.2) и (7.3.1) можно было бы прийти без всяких ссылок на задачу о волноводе — путем решения уравнения Уокера (7.2.31) и учета граничных условий на боковой поверхности и на торцевых металлических плоскостях.
Из выражения (7.3.2) можно непосредственно получить составляющие магнитного поля собственных колебаний в цилиндриче-г ской системе координат:
Ap = -JL,	hz = ^-.	' (7.3.3)
н op ’	* р оср ’ z oz	'	'
Для магнитостатических колебаний и волн наибольший интерес представляет переменная намагниченность m = %h. Для вычисления составляющих m можно записать составляющие поля в декартовой системе координат и затем, используя «обычный» тензор % (1.2.19), получить тх и mv (mz = 0). Но проще воспользоваться записью тензора % в цилиндрической системе и получить выражения для тр и непосредственно из hp и В нашем случае, когда ось цилиндрической системы совпадает с направлением постоянного намагничения, тензор % имеет в цилиндрической системе такой же вид, как и в декартовой. Для составляющих намагниченности получаются тогда следующие выражения:
Шр = С [%х7^ («р) + Ха у- Jm (ир)] cos kzz
т^= — iC J%ax7^ (хр) + %-y- 7m (xp)] cos kzz
Простейшими типами колебаний являются такие, для которых р = 0 или т = 0, а остальные индексы равны 1. Нетрудно убе-
12 А. Г. Гуревич
354
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
Рис. 7..3.2. Намагниченная сфера.
диться, что при р == 0 и т = 1 возможен только один тип колебаний (п = 1), для него тх и ту не зависят от координат и ту — = — imx. Этот тип колебаний представляет собой однородную прецессию намагниченности.
Рассмотренная задача не только представляет интерес как простой пример магнитостатических колебаний, но и имеет определенное практическое значение — магнитостатический цилиндрический резонатор было предложено [505] использовать для измерения параметров ферритов.
Сфера. Как уже неоднократно отмечалось, для исследований резонанса в неметаллических ферро- и ферри- (а в последнее время и антиферро-) магнетиках наиболее широко используются сферические образцы. Сферы из монокристаллов ферритов применяются и в ферритовых устройствах диапазона СВЧ (см., например, [486, 489]). Естественно, что изучению магнитостатических колебаний в сферах было уделено наибольшее внимание. Сфера является частным случаем эллипсоида вращения, магнитостатические колебания которого были теоретически исследованы Уокером [200]. Однако мы рассмотрим случай сферы непосредственно, следуя в основном работе Флетчера и Бэлла [204].
Рассмотрим ферромагнитную непроводящую сферу (рис. 7.3.2), намагниченную до насыщения внешним однородным полем. Пренебрегая диссипацией и анизотропией, примем для компонент
тензора магнитной проницаемости вещества сферы выражения (1.2.34) и (1.2.35). Ограничимся случаем сферы в свободном пространстве (без металлического покрытия), который представляет наибольший практический интерес.
Если удовлетворяются условия (7.1.1) и (7.1.15) справедливости магнитостатического безобменного приближения, то задача сводится к нахождению магнитостатического потенциала ф, удовлетворяющего уравнению Уокера (7.1.7) внутри сферы, уравнению ^Лапласа (7.2.8) — вне ее и граничным условиям на поверхности сферы. Граничные условия заключаются, как обычно, в непрерывности касательных составляющих магнитного поля и нормальных составляющих магнитной индукции. Из первого условия, также как и в рассмотренных ранее задачах, следует
а из второго—
ф = фо ПРИ г = П, МР-УФ) = §7 при г R.
(7.3.5)
(7.3.6)
§ 7.3] НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ 355
Здесь го — единичный вектор, направленный по радиусу, а индексы 0 соответствуют внешней области (г^>Я); величины, относящиеся к внутренней области (г < R), мы пишем без индексов.
- Необходимость наложения граничных условий требует, чтобы поверхность сферы (г = R) была координатной поверхностью в той системе координат, в которой мы собираемся решать задачу. Ясно, что этому условию удовлетворяет сферическая система координат г, 6, <р. Решения уравнения Лапласа (для внешней области) в сферической системе координат, конечные при г—> со, имеют следующий вид [38]:
ф0 = Сг^п~Ч>[п] (cos 6) e-imtp,	(7.3.7)
где — присоединенные полиномы Лежандра [42], п = 1, 2, 3,... ..., т - 0, ±1, ±2, . . ., ±н, С — постоянная величина.
К сожалению, уравнение (7.1.7) не может быть решено в сферической системе координат. Но оно переходит в уравнение Лапласа при замене
z-^z7/p".	(7.3.8)
Поэтому наша задача была бы решена, если бы мы нашли координаты, удовлетворяющие следующим условиям:
а)	при замене (7.3.8) они должны переходить в какие-либо координаты, для которых решение уравнения Лапласа известно',
б)	поверхность г = R должна быть для них (как и для сферической системы) координатной поверхностью.
Этим условиям удовлетворяют координаты £, tj, <р, связанные с х, у, z соотношениями
х = У р — 1 R ф'72 — 1 sin 1] cos <р,
у = р, — IT?)/^2 — 1 sin 1] sin <p,	(7.3.9)
z = |/(p — 1 )/p 77E. cos Т].
Действительно, при замене (7.3.8) они переходят в сфероидальные координаты, для которых решение уравнения Лапласа известно [38]. С другой стороны, как легко убедиться, при г == /ж2 ± у2 ± z2 ~ R
=	и (л)г=н = е, (7.3.10)
т. е. поверхность сферы является поверхностью | = const.
Итак, решение уравнения (7.1.7) в координатах 5, т), <р будет иметь такой же вид, как решение уравнения Лапласа в сфероидальных координатах. Учитывая условие конечности при г = 0 и опуская нормировочную константу, можно записать
ф = Р'п1 (В) Р1™' (cos л) е-^'Л	(7.3.11)
356	МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ [ГЛ. 7
Здесь, как и в (7.3.7),	— присоединенные полиномы Лежанд-
ра, fi — 1, 2, 3, . . ., гл - - 0, 4-1. ±2, . . ., Ч~л.
Наложим теперь на решения (7.3.11) и (7.3.7) граничные условия. Из условия (7.3.5) с учетом (7.3.10) следует, что значения п и т в (7.3.7) и (7.3.11) одинаковы, а постоянная
С==	(7.3.12)
Выражение в левой части условия (7.3.6) можно вычислить следующим образом:
го (pV'M’) =sin 6 cos Ч’ (и "S’ + "S") + 1	• а •	/	• дф дф \	„ дф
+ SH1 6 81Н(Ц-	4-р. -£-) + COS 6-^- .
Производные ф по х, у и z определяются из выражения
и аналогичных выражений для у и z, а производные £, ц и <р по х, у и z легко вычислить, дифференцируя, например, соотношения
—И----------6?—-(.и-1)— =lg<p,
непосредственно следующие из (7.3.9). Правая часть условия (7.3.6) определяется прямым дифференцированием (7.3.7). Учитывая затем (7.3.10) и принимая во внимание (7.1.12), мы, после некоторых преобразований, придем к «неожиданно» простому уравнению 2)
± На I ml + n + 1 — 0,	(7.3.13)
гДе определяется согласно (7.3.10), а штрих обозначает, как обычно, дифференцирование по аргументу. Знаки плюс и минус перед вторым членом (7.3.13) соответствуют положительному и отрицательному знаку т, т. е. разным (соответственно, правому и левому) направлениям изменения фазы ф (а следовательно и поля, и намагниченности) при изменении азимутального угла. При этом предполагается, что ось z всегда совпадает с направлением постоянного намагничения и, таким образом, для р.„ всегда принимается выражение (1.2.35).
х) Простота его связана, конечно, с высокой степенью симметрии сферы
§ 7.3]
НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
357
Выражение (7.3.13) с учетом зависимостей (1.2.34) и (1.2.35) и от частоты представляет собой уравнение для определения собственных частот магнитостатических колебаний сферы. Принимая во внимание известную формулу [42]
/ d
W
Р«© = (1
РП®,
где Рн (£) — полиномы Лежандра, уравнение (7.3.13) можно преобразовать к виду
где
Gkm| (Ь) ч- (и ± На) Iт I + п + 1 = О,
(7.3.13')
,к^т|+1М)
(7.3.14)
Анализ уравнения (7.3.13) в общем случае произвольных т и п довольно сложен, но некоторые общие заключения могут быть легко сделаны. Прежде всего следует отметить, что в это уравнение радиус сферы R не входит, т. е. собственные частоты магнитостатических колебаний, как и следовало ожидать, от размера образца не зависят. Они зависят от параметров сад и сам, входящих в выражения для р. и (т. е. от постоянного поля Но и постоянной намагниченности Мо) и от трех индексов, характеризующих тип колебаний: п = 1, 2, 3, . . .; т = 0, +1, +2, . . ., ± п и третьего индекса г, определяющего номер корня уравнения (7.3.13) при данных п и т.
Следуя Уокеру [200], введем число г = 0, 1, 2, . . ., р таким образом, чтобы порядковый номер корня был г + 1 при т Ч> 0 и г при т <4 0 (значению г = 0 при т 0 не соответствует корня). Тогда число корней будет равно р + 1 при т 0 и р при т 0. Анализ уравнения (7.3.13) (на котором мы здесь не останавливаемся) показывает, что при такой нумерации корней
Р = Г4"(И~ । т
(7.3.15)
где квадратные скобки обозначают целую часть числа, стоящего в них.
Зная потенциалы (7.3.7) и (7.3.11), можно вычислит^ составляющие поля собственных колебаний внутри (h = /ф) и вне (Ьй = Фф0) сферы и составляющие «собственной» намагниченности m = %h. В выражения для этих составляющих войдут явно только индексы пит. Однако на самом деле поле и намагниченность будут зависеть и от третьего индекса г, от которого зависит собственная частота, а следовательно и параметры вещества ц и цо, входящие в выражения для поля и намагниченности.
358
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
Рассмотрим теперь некоторые частные случаи. Пусть сначала п = | т |. Тогда, как легко убедиться, G$\ = 0 и (7.3.13') сводится к уравнению
Принимая во внимание (1.2.43), мы видим, что уравнение (7.3.16) удовлетворяется только при положительном т (знак плюс в его левой части) и имеет при этом (в согласии с (7.3.15!)) один корень
вт, т, о = °’Н +	(7.3.17)
Для сферы а>н == yHi0 = уН0 — сом/3 и
(,)т, т, о =	4---з~ 2т | 1 ®м'	(7.3.17')
Потенциал (7.3.11) в случае п = т запишется следующим образом:
ф = (х — iy)m ==	(7.3.18)
где р = ]/~ х2 + у2. Вычисляя, как указывалось выше, составляющие намагниченности, получим с точностью до постоянного множителя
тх = imv — {х — iy)m-1 = р™	(7.3.19)
Как видно из (7.3.19), переменная намагниченность в этом случае имеет круговую поляризацию с правым вращением, амплитуда ее растет как рт-1 при удалении от оси, а фаза изменяется по закону волны, бегущей по азимуту с угловой скоростью а>Кт — 1) х).
Для колебания типа (1, 1, 0) намагниченность, как видно из (7.3.19), не зависит от координат, а частота, согласно (7.3.17') составляет
®ы,о —
Этот тип колебаний представляет собой однородную прецессию намагниченности, которая подробно рассматривалась в § 1.4 и последующих главах.
В другом частном случае п = \т | + 1 уравнение (7.3.13') дает
(7-3-20)
*) Чтобы убедиться в этом, достаточно записать мгновенное значение любой составляющей намагниченности и определить угловую скорость волны как dty/dt при постоянстве фазы.
f 7 51 НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
359
И в этом случае т может быть только положительным (знак плюс в левой части (7.3.20)). Уравнение (7.3.20) имеет один корень
<Om+i, т, о ==	4“	[ 3	~ ЧНо 4 з 2т 4- 3	(7.3.21)
Интересно отметить, что типы колебаний (т, т, 0) и (3m + 1, 3m, 0), как видно из (7.3.17) и (7.3.21), являются вырожденными. В частности, однородная прецессия вырождена с типом (4,3,0).
В случае п = т 4~ 1 потенциал внутри сферы
ф = z(x-iy)m,	(7.3.22)
а составляющие намагниченности (с точностью до постоянного множителя) имеют вид
тх = imv = z (ж — iy)™''1 = zpm-1 e~i<m~P'₽.	(7.3.23)
В этом случае, так же как и для колебаний (т, т, 0), намагниченность имеет круговую поляризацию, носит характер волны, бегущей по азимуту, и растет как рт-1 при удалении от оси. Но, в отличие от колебаний (т, т, 0), амплитуда намагниченности тедерь линейно зависит от z. При m = 1, т. е. для колебаний (2, 1, 0) зависимость от р и ф отсутствует, амплитуда переменной намагниченности зависит только от z, а фаза как и для однородной процессии, постоянна во всем образце х).
Из формул (7.3.17) и (7.3.21) следует, что разности о> — ощ для колебаний (т, т, 0) и (т + 1, т, 0) пропорциональны Мо и не зависят от Но. Распределения потенциала, поля и намагниченности этих типов колебаний не зависят ни от сон, ни oi*o>M. Указанные особенности, так же как и круговая поляризация поля и намагниченности, характерны для серий (т, т, 0) и (т 4~ 1, т, 0) и не имеют места для других типов колебаний. Проиллюстрируем это на примере колебаний с т = 0, для которых частоты и распределения намагниченности также могут быть, сравнительно, легко рассчитаны.
При m = 0 (7.3.13') сводится к уравнению
ь44гг“-<"+1’-	<7Л24>
Если п = 1, то [42] 1\ (£) = £ и (7.3.24) решения не имеет. Если
*) Точнее, фазы постоянны в верхней и нижней полусферах, но отличаются на л из-за изменения знака амплитуды при z = 0.
дао
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И 'ВОЛНЫ
ТТЛ. «
п = 2, то Р2 (£) = (ЗЕ,2 — 1)/2 и (7.3.24) имеет единственный корень^ = 175, откуда следует1)
®2, о, 1 = юн	j •	(7.3.25')
Составляющие намагниченности для колебаний (2, 0, 1) имеют вид
7П₽ = хр, = — iXaP,	(7.3.26)
где X и Х« — компоненты тензора восприимчивости, зависящие от
<£>м и со (которая, в свою очередь, зависит, согласно (7.3.25), от ®н и сом).
Рис. 7.3.3. Распределения переменной намагниченности для простейших типов магнитостатических колебаний сферы. Показаны векторы переменной намагниченности в трех плоскостях z = const в некоторый момент времени t, (сплошные стрелки) и в момент t, = tt + я/(2и) (пунктирные стрелки). Для типа колебаний (2, 0, 1) намагниченность имеет эллиптическую поляризацию, а для остальных — круговую.
Используя выражения для полиномов Лежандра [42], легко с помощью (7.3.24) рассчитать частоты колебаний с т — 0 и п = 3, 4, 5. Не приводя выражений для этих частот, заметим, что в согласии с (7.3.15) при п = 3 будет один корень (с г = 1), при п = 4 и тг = 5 — по'два корня и т. д.
г) В работе [204], в отличие от [200], принято, что г = 0, 1, 2, .... при т = 0. Например, тип колебаний (2, 0, 1) в [204] обозначается как (2, 0, 0). Заметим, что имеется еще одно отличие в нумерации корней в этих работах: в [200] числа г возрастают при уменьшении, а в [204] — при увеличении разности о — ыи.
S 7.3]
НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
361
Для других типов колебаний расчеты собственных частот тре-'буют применения численных или графических методов. Не останав-.ливаясь на них, отметим лишь, что во всех случаях, кроме рассмотренных выше серий (m, т, 0), (т + 1, т, 0) и (п, 0, г), возможны колебания с т > 0 и т < 0, причем, как минимум, три типа колебаний при данных п и | т\ |: два'с т > 0 и один с т < 0. Например, при п = 3 и | т | = 1 возможны типы колебаний (3, 1, 0), (3, 1, 1) и (3, —1, 0).
Результаты расчета частот, полей и намагниченностей для всех магнитостатических колебаний сферы с п 5 приведены в [204]. На рис. 7.3.3 показаны распределения намагниченности для
Гис. 7.3.4. Зависимости частот магнитостатических колебаний сферы от постоянного магнитного поля [200, 204]. Пунктиром показаны границы спектра магнитостатических колебаний.
некоторых простейших типов колебаний. Для построения этих распределений достаточно перейти в выражениях (7.3.19), (7.3.23) и (7.3.26) от комплексных амплитуд составляющих намагниченности к их вещественным мгновенным значениям.
Частоты некоторых магнитостатических колебаний сферы показаны на рис. 7.3.4 . Из рис. 7.3.4 видно, в частности, что только для серий (т, т, 0) и (т + 1, т, 0), разности [ю — уН0) не зависят от Но. Частоты всех колебаний лежат в пределах (7.2.30). Отсюда следует, что при постоянной частоте резонансные значения постоянного поля всех магнитостатических типов колебаний сферы
362
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
лежат в пределах
2	« + 4	(7.3.27)
Г °	Го
Ширина этого интервала полей составляет 2л7И0.
Как видно из рис. 7.3.4, кроме упоминавшегося выше вырождения типов (т, т, 0) и (3m 4- 1, 3m, 0), в спектре магнитостатических колебаний имеет место целый ряд «случайных» вырождений — совпадений частот различных типов при определенных значениях параметров.
Заметим, что при повышении температуры интервал (7.3.27) в целом и расстояния между резонансными полями отдельных типов колебаний уменьшаются вследствие уменьшения намагниченности. Для колебаний (т, т, 0) и (т + 1, т, 0) уменьшение расстояний между резонансными полями происходит пропорционально Мо. Измерение интервала по частоте или полю между какой либо парой колебаний этих серий представляет собой один из наиболее простых и точных методов измерения температурной зависимости намагниченности [205, 505].
Эллипсоид вращения. Приведем теперь кратко некоторые результаты решения [200] (см. также [201, 2401) более общей задачи о магнитостатических колебаниях эллипсоида вращения (сфероида), намагниченного в направлении оси вращения. Все допущения и математическая формулировка этой задачи аналогичны рассмотренному выше случаю сферы. Необходимо найти решения уравнения Лапласа (7.2.8) для магнитостатического потенциала вне и уравнения (7.1.7) для потенциала внутри сфероида и обеспечить выполнение на поверхности сфероида граничных условий, которые заключаются в непрерывности касательных составляющих магнитного поля и нормальной составляющей магнитной индукции. Выполнение этой программы приводит к следующему уравнению для частот собственных колебаний намагниченности сфероида1):
ьва  r~i--------В u„ /п а? — ga —г-;---=	(7.3.28)
Здесь (g) и (£) — присоединенные полиномы Лежандра первого и второго рода [42], а = da (рис. 7.3.5),
t . 1/	t	“
В уравнение (7.3.28) входит параметр а, характеризующий форму сфероида. Он может изменяться в пределах от 0 до оо. Значение а = 1 соответствует сфере, при этом переходит в а
х) Для удобства сравнения с (7.3.13) уравнение (7.3.28) записано в обозначениях, несколько отличающихся от [200].
§ 7.3]
НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЙ ЗбЗ
Рис. 7.3.5. Намагниченный эллипсоид вращения.
-+ оо. Можно убедиться, используя асимптотические свойства полиномов Qlnl (£) [42], что уравнение (7.3.28) при а -+ 1 переходит в (7.3.13).
Детальный анализ уравнения (7.3.28), проведенный Уокером [200], показал, что многие свойства магнитостатических колебаний, которые были отмечены выше для случая сферы, имеют место и для произвольного сфероида. В частности, и для сфероида типы колебаний могут характеризоваться индексами п, т и г, где г определяет номер корня уравнения (7.3.28) для данных п и т. Число этих корней, т. е. различных типов колебаний с данными п и т, составляет, как и для сферы, р + 1 при т 0 и р при т 0, где р определяется выражением (7.3.15).
Серии колебаний с р = 0, т. е. (т, т, 0) и (m г 1, иг, 0), и в случае сфероида характеризуются круговой поляризацией поля и намагниченности, независимостью распределения поля и намагниченности от Но и Мо и независимостью разности (со — сон) от Но. Собственные частоты колебаний этих серий в зависимости от отношения осей сфероида а показаны на рис. 7.3.6. Тип колебаний (1, 1,0) и в случае произвольного сфероида представляет собой однородную (киттелевскую) прецессию намагниченности.
Для магнитостатических колебаний сфероида по-прежнему справедливы неравенства (7.2.30), где теперь сан = у(Нй — N2M0).
При а —> 0 (тонкий нормально намагниченный диск) спектр магнитостатических колебаний сфероида «сжимается» в точку
со = со// == у (Но — 4л7И0),
а при </. -> оо (тонкий продольно намагниченный цилиндр) — в точку
(О = (Он + -g- юм = т (Но + 2л7И0).
Это свойство спектра магнитостатических колебаний сфероида иллюстрирует рис. 7.3.6.
Затухающие и вынужденные колебания. Следуя общей схеме изучения колебательных процессов (см. §§ 1.3, 1.4, 6.3), мы должны перейти теперь к рассмотрению свободных затухающих магнитостатических колебаний. Для этого достаточно в характеристические уравнения (7.3.1), (7.3.13), (7.3.28) подставить выражения ц и [i,t с учетом диссипации (§ 1.3). Решения характеристических уравнений окажутся комплексными, их мнимые части со" будут
364
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
1гл. i
характеризовать затухание свободных колебаний. Вычисления, к которым это приводит, достаточно громоздки, а результаты не являются особенно интересными: добротности неоднородных магнитостатических колебаний оказываются одного порядка с добротностью однородной прецессии, что подтверждается и экспериментально (см., например, [2021).
Рис. 7.3.6. Зависимости частот магнитостатических колебаний (m, т, 0) и («4-1, т, 0) от формы эллипсоида вращения [200].
Переходя к рассмотрению вынужденных колебаний, отметим прежде всего, что магнитостатические колебания удовлетворяют соотношениям ортогональности [209, 240], которые являются следствиями уравнения Уокера (7.1.7) и граничных условий на поверхности образца. Приведем одно из этих соотношений:
mv ;< mu-dr = 0 при v=/=v'.	(7.3.29)
v
Здесь интегрирование производится до объему образца, а т и v' означают совокупности индексов, характеризующих тип колебаний, например, для сфероида (сферы) — индексов п, т и г. Намагниченности собственных магнитостатических колебаний, удовлетворяющие условиям ортогональности, образуют (в рамках магнитостатического приближения) полную систему функций, по которой можно вести разложение произвольной переменной намагниченности.
Ортогональность и полнота (в рамках магнитостатического приближения) системы собственных функций — намагниченностей магнитостатических колебаний — позволяет построить теорию вынужденных колебаний, аналогичную теории вынужденных электромагнитных колебаний полых резонаторов (§ 6.3). Простейшей задачей такой теории является задача о возбуждении магнито-
§ 7.3] НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ Зб5 статических колебаний заданным внешним переменным полем (h (г) — его комплексная амплитуда, а со—частота). Комплексную амплитуду намагниченности образца можно искать в виде ряда по намагниченностям собственных колебаний, определенным образом нормированным:
m(r) = 2Cvmv (г).	(7.3.30)
Для коэффициентов этого ряда получатся формулы вида
Cv = Со/2
f h (г) ш* (г) <П’
V__________________
со2 — со2 + 2rav<B2
(7.3.31)
где cov и а„ — собственные частоты и параметры диссипации магнитостатических колебаний, а С — константа, зависящая от нормировки собственных функций; интегрирование в (7.3.31) производится по объему образца.
Если параметры av достаточно малы (что имеет место для полированных образцов из хороших монокристаллов, например иттрий-железного граната), то, как правило, будет происходить поочередное возбуждение различных типов прецессии при изменении частоты возбуждающего поля со или величины внешнего постоянного поля (влияющего на собственные частоты ок). Это и имело место в опытах по возбуждению магнитостатических колебаний в сферах [199, 202], дисках и цилиндрах [207]. Некоторые из полученных в таких опытах серий резонансных кривых приведены на рис. 7.3.7 и рис. 7.3.8.
Условием возбуждения данного магнитостатического типа ко-  лебаний является неравенство нулю интеграла возбуждения, стоящего в числителе формулы (7.3.31). При однородном внешнем поле h интеграл возбуждения не обращается в нуль только для однородной прецессии (1,1,0). Для возбуждения других —неоднородных типов колебаний необходимо неоднородное переменное поле, и интенсивность их будет тем больше, чем ближе структура переменного поля к структуре намагниченности данного типа. Этот вопрос исследовался экспериментально (см., например, [202]), и было получено удовлетворительное совпадение с теорией. В частности, тип колебаний (2, 1, 0), характеризующийся, как видно из (7.3.23), линейной зависимостью намагниченности от z, возбуждается (см. рис. 7.3.7) только в том случае, когда имеет место нечетная зависимость поперечного магнитного поля от z.
Правда, магнитостатические типы колебаний возбуждаются часто и тогда, когда интеграл в (7.3.31), казалось бы, должен обращаться в нуль, например при помещении образца в область
Зеб “ТаАГНИТОСТАТИЧЁСКИЕ КОЛЁВАНИЙ it ВОЛНЫ (ГЛ. 9
//,/./?
Рис. 7.3.7. Кривые резонансного поглощения при расположении ферритовой сферы 'в переменных магнитных полях с различной симметрией [202]. Частота 9 Гец. Сфера диаметром 1,1 мм из монокристалла иттрий-железного граната помещалась в различных точках прямоугольного резонатора ТЕ22о. Начала отсчета на осях абсцисс смещены таким образом, чтобы линии однородной прецессии (которые расположены при различных полях из-за разных ориентаций сферы) оказались на одной вертикали. Пунктиром показаны силовые линии переменного магнитного поля.
§ 7.3]
НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
367
однородного поля резонатора. Это бывает связано с неточностью расположения образца, искажениями поля в резонаторе неоднородностью внутреннего поля вследствие неэллипсоидальной формы образца (рис. 7.3.8), а также с влиянием анизотропии и размеров образца, па котором мы остановимся несколько ниже.
Задача о возбуждении магнитостатических типов колебаний может быть поставлена и по-другому, с учетом свойств той полой
системы, в которой находится ферромагнитный образец. Пусть, например, такой системой является полый резонатор. Тогда может быть сформулирована задача об определении поля в резонаторе и намагниченности образца при заданных возбуждающих токах и полях на отверстиях резонатора. Это, по существу, та же задача, которая рассматривалась в § 6.3. Градиентная функция
в (6.3.21) совпадает с магнитостатическим потенциалом главы 7, И ее можно искать в- виде ряда по собственным магнитостатическим типам колебаний образца.
Влияние кристаллографической анизотропии. До сих
Рис. 7.3.8. Кривые резонансного поглощения в диске (верхняя кривая) и в диске с закругленными краями, мало отличающемся от эллипсоида вращения (нижняя кривая) в однородном внешнем переменном поле [207].г, Частота 9 Ггц. Размеры образцов — в миллиметрах, величины внешнего постоянного поля — в эрстедах.
пор, рассматривая магнитостатические колебания, мы принимали для тензора магнитной проницаемости выражение (1.2.33), т. е. считали, что среда (в отсутствие посто-
янного намагничения) изот-
ропна. Но эксперименты проводятся обычно на монокристаллах. Поэтому интересно выяснить, какое влияние оказывает на маг
нитостатические колебания кристаллографическая анизотропия
вещества.
В § 7.1 было показано, что решения магнитостатических задач, полученные для изотропной среды, справедливы для монокристалла при замене (7.1.29), если выполняются условия (7.1.31). Отсюда следует, что резонансные частоты всех магнитостатических колебаний при выполнении этих условий будут сдвинуты относительно резонансных частот в изотропных образцах той же
368
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
формы па одну и ту же величину
6 о = %1Г,
(7.3.32)
ВН(е)-ВН(О),з
Рис. 7.3.9. Зависимость интервалов между резонансными полями разных типов колебаний от ориентации постоянной намагниченности относительно кристаллографических осей [206J. Сферы из иттрий-железного граната. Частота 8,3 Ггц, температура 77 “К; 6Н =	^(2,2,0)’	® угол
между Мо и осью <100) в плоскости 010). Сплошные линии — теоретические кривые.
а резонансные поля (при со = const) — сдвинуты на одну и ту же величину *)
6Ярез=-Я“.	(7.3.33)
Напомним, что условия (7.1.31) выполняются, если постоянная намагниченность направлена по оси одноосного кристалла или по осям <100) или <111) кубического кристалла. Соответствующие величины На приведены в табл. 7.1.1.
При других ориентациях Мо, когда условия (7.1.31) не выполняются, решение задачи о магнитостатических колебаниях в монокристаллах сводится к интегрированию уравнения (7.1.20) при соответствующих граничных условиях, что представляет значительные трудности. Солт и Флетчер [206] получили решение этой задачи для нескольких простейших типов колебаний сферы. Более общую теорию развили Кривченков и Пильщиков [208]. Оказалось, что интервалы между резонансными полями различных типов колебаний в монокристалле (кроме упомянутых выше направлений Мо), как и следовало ожидать, отличаются от изотропного случая. При изменении ориентации Мо они изменяются на величину порядка (К^МдУ/^/у), что, например, для
иттрий-железного граната при комнатной температуре в трехсантиметровом диапазоне составляет —1 э. Зависимости некоторых из этих интервалов от ориентации Мо в сфере из кубического монокристалла приведены на рис. 7.3.9. Эти интервалы, действительно, одинаковы для осей <100) и <111) и наиболее сильно изменяются при переходе к оси <110).
Влияние размеров образца. Как уже неоднократно отмечалось, в рамках магнитостатического приближения влияния размеров
г) Сдвиги (7.3.32) и (7.3.33) при выполнении условий (7.1.31) имеют место, конечно, и для однородной прецессии (см. § 2.2).
§ 7.31
НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ
369
образцов на магнитные колебания не должно быть. Для того, чтобы получить зависимости частот, затуханий, структуры полей и других характеристик магнитных колебаний от размеров образцов, мы должны учесть «эффект запаздывания», т. е. принять во внимание членыее и	в уравнениях Максвелла. Эти
члены, которые отбрасываются в магнитостатическом приближении, содержат параметр с размерностью длины — длину электромагнитной волны А.о = 2nd л, и поэтому учет их дает зависимость от размеров. Поскольку отношение размеров образцов к Хо в интересующем нас случае мало, эффект запаздывания можно учесть методом возмущений. Такие расчеты провели для случая однородной прецессии эллипсоида Хард [459] и другие, а для типов колебаний (т, т, 0) и (т + 1, т, 0) в сфере Сюй Янь-шен [463] и Плюмье [209].
Собственная частота магнитных колебаний сферы с такой «электродинамической» поправкой оказывается равной
= mv0 — сом (Л0Я)2 А,	(7.3.34)
где е\0 — собственная частота в магнитостатическом приближении, <»м = 4лу Мо, R — радиус сферы, к0 — ю/с = 2я/А.о, а функция /v, учитывающая тип колебаний, имеет вид
,	1	/ тф1 . m -И \
А = чо—гч55 s "о—4-5 + -з----т- для (т, т, U),
1	(2т -р I)2 \ 2m 4-3 1 2m —1 / м	п ~
,	1	1 т + ‘3 . т+ 2 \	.	, .
h~-7^--575 8 о---Т-к+ч5---Ôà ДЛЯ (т + 1, 7П, 0).
'	(2т 4- З)2 ( 2m 4- 5 2m 1 /	'	'
Как и следовало ожидать, поправка пропорциональна квадрату отношения размера образца к длине электромагнитной волны и растет с ростом е. Из (7.3.35) видно, что поправка уменьшается с ростом т. Качественно это можно объяснить следующим образом: в критерий справедливости магнитостатического приближения входит некоторое эффективное расстояние («длина волны» магнитостатических колебаний), на котором происходит существенное изменение внутреннего поля и намагниченности; с ростом т такое расстояние уменьшается.
Для типов колебаний (т, т, 0) и (т 4- 1, т, 0) разность ®о — У как уже отмечалось, не зависит от Но, и из (7.3.34) следует, что резонансное поле с «электродинамической» поправкой
^рез = (Ярез)0 + 4лмо (к0 R)* fv.	(7.3.36)
В частности, для однородной прецессии
Ярез = (Ярез)0 4~ ~^яМ0 (е 4- 5) (k0R)2.	(7.3.37)
Для иттрий-железного граната рассмотренная поправка составляет —10 э для сферы с диаметром 1 мм в трехсантиметровом
370
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
[ГЛ. 7
диапазоне волн. Таким образом, даже при таком малом отношении размеров к длине волны эту поправку необходимо учитывать при исследовании спектра магнитостатических колебаний, при точном измерении g-фактора и т. д.
Влияние кристаллографической анизотропии и эффект запаздывания приводят не только к сдвигу резонансных частот собственных колебаний, но и к изменению структуры их полей и намагниченностей. Если анизотропия и размеры образца не очень велики, то часто оказывается целесообразным раскладывать поле и намагниченность в ряды не по собственным колебаниям, а по хорошо известным и сравнительно простым уокеровским типам колебаний изотропного малого образца. Однако теперь — при учете анизотропии и конечных размеров образца — эти типы колебаний оказываются связанными ’).
Как показано в [208], анизотропия в кубическом кристалле приводит к связи всех уокеровских типов колебаний, для которых как п, так и т имеют одинаковые четности. Например, связанными будут типы (2,2,0) с (2,0,1); (1,1,0) с (3,1,0), (3,1,1), (3,—1,0). Связь Исчезает при ориентации Мо по осям <100) и <111). Эффект распространения, согласно [203,463, 209], приводит к связи типов колебаний, для которых п имеют одинаковую четность, ат — одинаковы. Например, из перечисленных выше типов колебаний связанными будут только (1,1,0) с (3,1, 0) и(3,1,1).
Наличие связи между типами колебаний означает, что не обращается в нуль интеграл
hxm2dV, v
(где hx — поле одного из связанных типов колебаний, а ш2 — намагниченность другого), аналогичный интегралу возбуждения в формуле (7.3.31). Иными словами, поле одного из этих типов колебаний возбуждает другой; возбуждение одного из них внешним полем сопровождается появлением, в принципе, всех других связанных с ним типов. Однако при заметном различии собственных частот связанных колебаний эффект связи весьма мал. Он проявляется лишь вблизи точек вырождения, т. е. тех точек, где собственные частоты связанных колебаний (без учета связи) совпадают. Наличие связи приводит тогда к «отталкиванию» резонансных частот или полей связанных типов. Это явление неоднократно наблюдалось экспериментально [203, 213] (рис. 7.3.10).
х) Такой метод рассмотрения в теории колебаний носит название метода связанных колебаний, в отличие от метода нормальных колебаний, когда разложение ведется по собственным (нормальным) типам колебаний, являющимся несвязанными, ортогональными,
§ 7.з} Неоднородные магнитостатические нолейания 371
Заметим, что источниками связи между магнитостатическими типами колебаний могут являться также «геометрические» дефекты образца (поры, дефекты поверхности) [203], магнитные дефекты (включения вещества с другой намагниченностью), а также
0,1
_J__________________I------------------L_
z '	г	з
Но/0!ГМо
Рис. 7.3.10. «Отталкивание» частот связанных магнитостатических колебаний сферы [203]. Типы колебаний обозначены согласно Уокеру [200], в отличие от [203], где обозначения совпадают с [204] (см. примечание на стр. 360).
держатель образца [202] и металлические стенки резонатора или волновода. Конечно, во всех случаях, наряду со связью, возникает и смещение собственных частот колебаний.
Магнитостатические колебания в антиферромагнетиках. Неоднородные магнитостатические колебания и магнитостатические волны возможны и в антиферромагнетиках. Наличие постоянной намагниченности М= не является необходимым условием их существования; они возможны и для тех основных состояний антиферромагнетиков, для которых М= = 0. Если тензор магнитной проницаемости антиферромагнетика имеет «полдеровский» вид (1.2.33) (независимо от конкретных выражений для его компонент), то вся рассмотренная выше общая теория магнитостатических волн и колебаний в телах различной формы, включая и характеристические уравнения, содержащие компоненты р, например, (7.3.13) или (7.3.28), будет применима к антиферромагнетикам. Изменятся лишь результаты анализа этих уравнений с учетом конкретных зависимостей компонент р от частоты и Но.
Как было показано в § 4.2, тензор магнитной проницаемости имеет вид (1.2.33) для одноосного антиферромагнетика с положительной анизотропией, если постоянное поле направлено вдоль оси
372
МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ Й ВОЛНЫ
[ГЛ. 1
и по величине не превышает поля опрокидывания Нс ~ V2НеН д (здесь Не — обменное поле (4.2.7), а На — поле анизотропии (4.2.8)). Для этого состояния из (4.2.33) (в отсутствие диссипации) следует
W± На = 1 + ~г	,	(7-3.38)
<0£ - (<£>-р YHc,)2
где К = М0На — константа анизотропии (Мо — постоянная намагниченность подрешетки), a юс = ЧНс- Определяемые формулой (7.3.38) величины р, и должны быть подставлены в характеристические уравнения и выражения для потенциалов и полей магнитостатических колебаний.
Следуя Бимену [2111, ограничимся случаем сферы и рассмотрим простейшие колебания (ш, т, 0) и (т + 1, т, 0), для которых характеристическое уравнение (7.3.13) сводится, соответственно, к (7.3.16) и (7.3.20). Подставляя в (7.3.16) или (7.3.20) р 4- ра из (7.3.38), получим (в обоих случаях)
(05 + гЯ0)2 = ®2С + К ,	(7.3.39)
или при 7И0 Не
со сос (1 + 2л	± TZZ0. (7.3.40)
\	JJ ja АП "~Т~ 1 j
Заметим, что при п — |сл| = 1 (однородная прецессия) (7.3.39), как легко убедиться, эквивалентно выражению для собственной частоты антиферромагнитной сферы с учетом размагничивающих полей, которое следует (при Nх = Пу = из (4.2.48).
Из (7.3.40) видно, что диапазон, в котором лежат частоты рассмотренных типов колебаний антиферромагнитной сферы, составляет Ь,?>-2л'(М{>Нс.1Не, в то время как аналогичный диапазон для ферромагнетика составляет (см. формулы (7.3.17) п (7.3.21)) 0,3-2л7Мо. Отсюда, не проводя анализа уравнений (7.3.13) и (7.3.28) для других типов колебаний, можно, по-видимому, сделать вывод, что и полный диапазон, в котором лежат частоты магнитостатических колебаний антиферромагнитного сфероида, уменьшится, по сравнению с ферромагнетиком, в том же отношении, т. е. будет
6» = 2лтМ0Нс/Не = 2лТМ0 ]Г2На!Не- (7.3.41)
Поскольку в данном случае дл/дН = -4- -у, то диапазон постоянных полей, в котором лежат магнитостатические типы колебаний одноосного антиферромагнетика для первого основного состояния,
&Н0^2лМ0У2На1Не-	(7.3.42)
g 7.3] НЕОДНОРОДНЫЕ МАГНИТОСТАТИЧЕСКИЕ КОЛЕБАНИЯ 373
Оценка для антиферромагнетика Сг2О3 (Л/о = 286 ее; IIА	700 э;
НЕ ~ 2,5-10е э 1176]) дает
677() ж 40 э.
Как было показано на некоторых примерах в главе 4, тензор р, для других основных состояний одноосного антиферромагнетика и для антиферромагнетиков другого типа имеет вид, отличный от полдеровского. Для расчетов частот и полей магнитостатических колебаний в этих случаях требуется обобщение теории, аналогичное тому, которое необходимо для учета кристаллографической анизотропии в ферромагнетике. Выражения для 8Н0, к которым мы придем в результате таких расчетов, будут, конечно, отличаться от (7.3.42), но порядок величины, видимо, останется таким же. Это подтверждается экспериментами, в которых наблюдались неоднородные магнитостатические колебания в антиферромагнетиках [211, 330].	. '
СПИНОВЫЕ ВОЛНЫ
§ 8.1. Спиновые волны в неограниченном ферромагнетике
Перейдем к изучению неоднородных магнитных колебаний с более быстрыми вариациями переменной намагниченности в пространстве, чем те, которые рассматривались в предыдущей главе. Теперь уже необходимо будет учитывать возрастание энергии обменного взаимодействия вследствие непараллельности соседних элементарных магнитных моментов. В первых четырех параграфах этой главы мы будем по-прежнему использовать континуальную модель, в которой состояние магнитоупорядоченной среды описывается классическими векторами намагниченностей подрешеток М; (для ферромагнетика — одним вектором М), являющимися непрерывными функциями координат. В этой модели возрастание обменной энергии из-за непараллельности соседних магнитных моментов описывается при помощи неоднородных членов обменной энергии, зависящих от производных М, по координатам. Для случая ферромагнетика такие неоднородные члены можно записать в виде (2.1.7).
Намагниченность в (2.1.7) является суммой постоянной и переменной составляющих:
M(r,i) = М0(г) Д-m~(r,f)	(8.1.1)
(по-прежнему	|М0|).Мы будем рассматривать в этой гла-
ве намагниченный до насыщения ферромагнетик (без доменной структуры). При этом постоянная намагниченность Мо не будет быстро изменяться в пространстве и в (2.1.7) войдет только переменная намагниченность
3	3
ГТ 1 V V дт~ 9т~
2 Z Z Qps дх дх •
Р=1 s=l	Р «
(8.1.2)
С помощью формулы (2.1.14) может быть найдено соответствующее эффективное поле
з з
2 2 4ps
Р=1 S=1
d2m~
дхдх р s
(8.1.3)
§ 8.1] СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 375
Переменную намагниченность пщ (г, t) можно представить в виде суперпозиции плоских волн (фурье-гармоник)
mK = т	(8.1.4)
с различными частотами 0) и волновыми векторами к. Задача будет заключаться прежде всего в определении закона дисперсии этих волн, т. е. зависимости со от к1). Для волновой зависимости (8.1.4) из выражения (8.1.3) следует
he= -—(kqk)m, (8.1.5) ' р S	‘
где hQ — амплитуда волны эффективного поля, a q — тензор с компонентами qps.
Как отмечалось в предыдущей главе, в неметаллических ферро-, ферри- и антиферромагнетиках имеется широкая область значений к, в которой можно не учитывать неоднородного обмена и в то же время при нахождении спектра колебаний не принимать во внимание запаздывания при распространении электромагнитных волн. Отсюда следует, что, рассматривая обменные спиновые волны в неметаллах, во всяком случае можно пользоваться магнитостатическим приближением2). Для того чтобы получить спектр этих волн, необходимо решить совместно уравнение движения намагниченности (для антиферромагнетика — уравнения движения намагниченностей подрешеток) и уравнения магнитостатики с учетом, вообще говоря, граничных условий.
Однако учет граничных условий при нахождении спектра колебаний или волн важен лишь тогда, когда размеры тел сравнимы с длиной волны в среде. Мы убедились в этом, в частности, в § 7.2 при рассмотрении дисперсионных соотношений для магнитостатических волн в пластинах и стержнях. Отсюда ясно, что по мере перехода к спиновым волнам с большими к (для которых необходим учет неоднородного обмена) роль граничных условий уменьшается, их учет становится существенным лишь для очень тонких пленок, очень мелких частиц и т. п.3). Таким образом,
г) Для безобменных магнитостатических голи в неограниченной среде (§ 7.1) и зависело только от направления вектора к. Но теперь, когда в (8.1.2) входят производные по координатам и параметры qps с размерностью квадрата длины, мы вправе ожидать зависимости о и от величины к.
2) В металлах длина электромагнитных волн существенно укорачивается из-за влияния проводимости, и область магнитостатических безобменных голи обычно отсутствует. При рассмотрении спиновых волн с не очень большими к в металлах нужно использовать полные уравнения Максвелла.
3) Речь идет о граничных условиях для переменных величин. Граничные условпя для постоянных величин должны, конечно, всегда приниматься во внимание при определении внутреннего постоянного магнитного поля, которое является параметром при рассмотрении колебательных процессов.
СПИНОВЫЕ ВОЛНЫ
большое значение, не только принципиальное, но и практическое, приобретают задачи о спектре волн в неограниченной среде. В этом и следующем параграфах мы будем рассматривать такие задачи. Учет граничных условий будет проведен в § 8.3.
Изотропный ферромагнетик. Рассмотрим сначала изотропный ферромагнетик, намагниченный до насыщения постоянным полем Но. Для плоской волны (8.1.4) в такой среде справедливо магнитостатическое уравнение (7.1.2), в котором 0;. — угол между направлением распространения волны и осью z, направленной, как всегда, параллельно Мо. Задача об определении спектра волн свелась, таким образом, к определению магнитной проницаемости р с учетом (в отличие от § 7.1) неоднородного члена энергии обменного взаимодействия. Для того чтобы найти компоненты р, достаточно решить линеаризированное уравнение движения (2.1.31). Входящая в него величина h есть внутреннее переменное магнитное поле, которое при вычислении р, должно рассматриваться как заданное. Величины m и h зависят от координат и времени по закону (8.1.4). Эффективные поля должны учитывать обменное взаимодействие и зеемановское взаимодействие с постоянным полем. Таким образом, в данном случае
Heft о = Н»о,
где Нго — внутреннее постоянное магнитное поле, a heft определяется выражением (8.1.5). Для изотропной среды
hQ = — qk2m.	(8.1.6)
Подставляя (8.1.6) в (2.1.31) и учитывая, что Неи0 = Hi0 = = z0 Hi0, а Мо = z0M(), получим окончательно уравнение движения для амплитуд волн m и h:
i am + (j>j; + цЛ2 ia o) m x z0 = уМ0Ь x z0,	(8.1.7)
где, как всегда, ед, — тЯго, а
П = УЯМ0.	(8.1.8)
Проектируя уравнение (8.1.7) на оси х и у и решая полученную систему, можно было бы получить компоненты тензоров X и р. Однако нет необходимости проводить такое решение, поскольку (8.1.7) отличается от уравнения движения без учета неоднородного обмена (1.3.9'). только заменой
он—> (Од -|- т]/с2,	(8.1.9)
и мы можем провести эту замену в окончательных выражениях
з 8.11 СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 377
(1.3.19)	и (1.3.20) для компонент х- В частности, теперь
(О)// -I + М («7Г + vlk2 +	— “2 /о 4 „и
 1‘------------4-^+1»)’	--------- <8ЛЛО»
где, как обычно, = т4л7И0.
Компоненты тензора ji ферромагнетика с учетом неоднородного обменного взаимодействия зависят, таким образом, не только от частоты, но и от волнового вектора к. Такая зависимость носит название пространственной дисперсии. Предполагая в выражении (8.1.2) qps = q, мы получили, что компоненты р зависят только от к2, в общем случае они зависели бы от составляющих вектора к.
Для того чтобы найти дисперсионное соотношение (спектр) спиновых волн в изотропном ферромагнетике, достаточно подставить выражение (8.1.10) в уравнение (7.1.2). В результате получим ®2 — (мд + ч\к2 4- iao) (лн + i]k2 Ц- w/л Ц- ым sin2 ОД = 0,	(8.1.11)
где 0fc — угол между направлением распространения и осью z, совпадающей в данном случае с направлением постоянного поля Но.
Выражение (8.1.11) дает (в магнитостатическом приближении) связь между частотой а и волновым вектором к для плоской волны (8.1.4) в изотропном ферромагнетике. Параметрами в (8.1.11) являются внутреннее постоянное поле Hi0 = «щ/р и постоянная намагниченность Мо = ым/^лу.
Заметим, что к дисперсионному соотношению (8.1.11) можно прийти и, на первый взгляд, несколько иным путем. Этот путь, использованный Херрингом и Киттелем [232], заключается в интегрировании уравнения движения, в котором предварительно учитывается связь h с т, следующая из уравнений магнитостатики. Легко убедиться, что для плоских волн (8.1.4) такая связь имеет вид
h=—^-k(mk).	(8.1.12)
И так как рассматриваются собственные (нормальные) волны при отсутствии внешнего переменного поля, то (8.1.12) представляет собой полное переменное поле. Подставляя его в уравнение движения (8.1.7), мы приходим к однородному уравнению
iwm -[- (юя J-ч|/,;2 lay) щ < zo 4- ам (тЮ = 0. (8.1.13)
/С"
Из условия совместности системы, которая получается в результате проектирования (8.1.13) на оси координат, следует дисперсионное соотношение (8.1.11). Таким образом, рассмотренные два
378
СПИНОВЫЕ ВОЛНЫ
[гл. 8
пути вывода этого соотношения отличаются лишь последовательностью учета уравнений магнитостатики и уравнений движения.
Незатухающие спиновые волны. Переходя к анализу дисперсионного соотношения, пренебрежем сначала дисссипацией — примем а = 0. Тогда из (8.1.11)1 получится известное выражение для спектра незатухающих спиновых волн *):
<о2 = (<£>н + г]/са) (<£>н + г|/с2 + (ом sin2 0fc).	(8.1.14)
Если П/с2< <оя, то (8.1.14) переходит в соотношение (7.1.9) для безобменных магнитостатических волн. Как видно из (8.1.14), учет обменного взаимодействия приводит к росту <о при увеличении к. При очень больших к имеет место квадратичный закон дисперсии:
<о т\к2.
Для используемой континуальной модели рост к и, следовательно, частоты « спиновых волн ничем не ограничен. Однако эта модель перестает быть применимой, когда 1/к становится сравнимым с межатомными расстояниями — 1СГ8 см.
При Gfc = 0, т. е. для спиновых волн, распространяющихся в направлении постоянного намагничения, (8.1.14) переходит в
со = сод + т\к2.	(8.1.15)
В этом (и только в этом) случае собственная частота спиновых волн совпадает с резонансной частотой внутренних тензоров % и р с учетом пространственной дисперсии (см., например, выражение (8.1.10)).
Если (Ом < (Он + т]А:а, то может быть использовано приближенное выражение
<о (он + 1]Л2 + (Ом sin2	(8.1.16)
Зависимости ю от к при <оя = const и юя от к при <о = const показаны на рис. 8.1.1 для 6fc = 0 и 6Й = л/2. Дисперсионные кривые для промежуточных значений углов G/- лежат между ними, образуя непрерывные полосы спектра спиновых волн в неограниченной среде. Из рис. 8.1.1, б видно, что при данной частоте спиновые волны могут существовать только при величинах постоянного внутреннего поля, не превышающих определенных, зависящих от угла 6/; значений Ямакс (0/с); для этих предельных полей к =
х) Это выражение получили впервые квантово-механическим путем Холыптейн и Примаков [231] (см. § 8.5).
§ 8.1] СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 379
= 0 *). При увеличении к значения постоянного поля уменьшаются и обращаются в нуль при некоторых значениях /сМакс (0л). В частности, при 0/; = О
Ямакс(0) = О)/Г,	/смакс(О)-]/-у.	(8.1.17)
Для, иттрий-железного граната при комнатной температуре
Рис. 8.1.1. Спектры незатухающих спиновых волн в изотропном ферромагнетике. М„ ~ 140 гс, ц = 0,1 (иттрий-железный гранат при комнатной температуре), а —	= 0,5 wjj (Hio = 870 а): б — <о == 0,75 од
(а>/2 я = 365 Мгц).
т] = 0,1 и для (о/2л = 1010 гц (длина электромагнитной волны в свободном пространстве 3 см)
Ямакс (0) = 3500 Э, ЙмаКС (0) = 8  10е СЛГ1.
0 При к —> 0 излагаемая теория и, в частности, выражение (8.1.14), строго говоря, несправедливы: для больших образцов (с размерами, сравнимыми с длиной электромагнитной волны) — вследствие неучета «запаздывающих» членов в уравнениях Максвелла, а для малых образцов — вследствие неучета граничных условий. Однако как уже неоднократно отмечалось, при таких малых к нет необходимости учета обменного взаимодействия, и соответствующие задачи уже рассматривались в главах 6 и 7.
380
СПИНОВЫЕ волны
(ГЛ. 8
Групповая скорость спиновых волн ггр = д<л!дк может быть легко определена дифференцированием (8.1.14) ио к\
1
®Н +	+ ~2~ WM sin2
рГр = 2х\к----------------------
(8.1.18)
Рис. 8.1.2. Поляризация спиновой волны.
Дробь в (8.1.18) представляет собой отношение среднего арифметического величин (сод + ц/с2) и (т>н + т]7«2 + sin2 0Л) к их среднему геометрическому и мало отличается от 1 при со^ < ын 4--f- t]kz, когда справедливо приближенное выражение (8.1.16). При этом
Ргр ж 2т]7с.
Таким образом, групповая скорость обменных спиновых волн в неограниченной среде, в отличие от безобменных магнитостатических волн в волноводах (§ 7.2)х), всегда положительна и растет приблизительно пропорционально волновому числу. При максимальном для данной частоты значении к = /смакс (0) она достигает величины
(PrpUKc-2/^. (8.1.19)
Для иттрий-железного граната в трехсантиметровом диапазоне волн (гГр)макс —1,6-105 см/сек.
Эта величина меньше скорости упругих волн («звука») в том же кристалле и значительно меньше групповой скорости магнитостатических волн в большей части диапазона изменения последней (см., например, рис. 7.2.10). Малая величина групповой скорости спиновых волн позволяет получать большие времена задержки передаваемых с помощью этих волн сигналов, что используется при создании линий задержки [487, 355] (см. несколько подробнее в § 8.3).
Для определения поляризации спиновых волн воспользуемся уравнением (8.1.13). Не теряя общности, для рассматриваемой изотропной среды оси координат можно выбрать так (рис. 8.1.2), чтобы, например, ку = 0. Проектируя (8.1.13) при а = 0 на эти оси и принимая во внимание (8.1.14), получим
- i 1 /14------ sin2 0/£.	(8.1.20)
тх [/ <oH4-W
При 6fc = 0 отсюда следует ту = — imx, т. е. спиновые волны, распространяющиеся в направлении постоянного намагничения,
х) Групповая скорость безобменных магнитостатических волн в неограниченной среде равна нулю, так как частота этих волн не зависит от к.
§ 8.U СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 381
имеют круговую поляризацию с правым вращением. Для углов (),. =f= 0 поляризация становится эллиптической, по она мало отличается от круговой при сом < ан Ц- ц/г2 и приближается к ней с ростом к.
Затухание спиновых волн. При учете диссипации (a =f= 0) дисперсионное уравнение, естественно, не может удовлетворяться при вещественных и и к. Возможны две простейшие постановки задачи. В первом случае рассматриваются стационарные волны (<) вещественно), которые при наличии диссипации затухают в пространстве (к комплексно). Во втором случае мы предполагаем, что к вещественно, и рассматриваем затухание во времени (со комплексно) волны с постоянной в пространстве амплитудой. Осуществление той или иной ситуации (или промежуточной, когда и со, и к комплексны) зависит, конечно, от условий возбуждения волн.
Рассмотрим первую задачу, т. е. примем, что в (8.1.11) ® вещественно, а
к = к' - ik".
Предположим, что направление распространения и направление затухания волны совпадают1), т. е. векторы к' и к" параллельны. В этом случае
(^ + ку)/к2 = sin2 0^,
где 6ft — угол между направлением векторов к' и к" и осью z, который мы считаем заданным. Тогда два вещественных уравнения, эквивалентных (8.1.11), дают связь к' лк" с «и 6fc.
Остановимся сначала на случае малого затухания, т. е. примем а <<; 1 и
к"<^к'.	(8.1.21)
Пренебрегая в (8.1.11) малыми величинами порядка выше первого, получим для к' («) прежнее выражение (8.1.14), а для к" — соотношение
=	(8-1.22)
Согласно (8.1.22) при очень больших к', когда ® » цк'2,
к" = -^-к'.
При малых же к', когда со почти не зависит от к' (либо в том случае, когда частота является заданной, а к' регулируется изме-
) Это предположение не является, вообще говоря, обязательным. Электро-магпитнью волны с несовпадающими направлениями распространения и затухания были рассмотрены Френкелем [43].
382
СПИНОВЫЕ волны
[ГЛ. 8
нением постоянного поля или угла 0(£), к" обратно пропорционально к'. Однако, как только к" становится сравнимым с к', рассматриваемое приближение перестает быть справедливым. Подставляя (8.1.22) в (8.1.21), получим условие его справедливости:
к > V = V -Г (°)s fenp-
(8.1.23)
Если условие (8.1.23) не выполняется, то величины к' и к" должны быть найдены путем точного решения уравнения (8.1.11). Подставляя к = к' — ik" в (8.1.11) и приравнивая нулю вещественные и мнимые части, получим
о2 — [®н + 1] (к'2 — к"2)] [<£>н + ц (к'2 — к"2) + ым sin2 0k] +
-j- (а« — 2т\к'к")2 = 0,	(8.1.24)
(сио — 2г\к'к") [2®н Ц- 2ц (к’2 — к”2) + sin2 0fe] = 0. (8.1.25)
Выражение в квадратных скобках в (8.1.25) не может обращаться в нуль, так как тогда при к" —> 0 для к' получилось бы выражение, которое ничего общего не имеет с (8.1.14) и в которое вообще не входит частота ®. Следовательно, в (8.1.25) обращается в нуль первая скобка. Таким образом, соотношение (8.1.22), которое было получено раньше для случая к'^>к", справедливо и в общем случае. Уравнение (8.1.24) тогда отличается от (8.1.14) лишь заменой к2 на к'2 — к"2. Оно может быть легко решено совместно с (8.1.22) относительно к’ и к". Введем обозначения:
к’ = -£-, к" = -^-, 0 = J_r-]/w2+ / 1 ю sin2e V__ fcnp	апр ““ L '	2 Л’ У
— ®н----®м sin2 е/£] ,	(8.1.26)
где /сПр определяется согласно (8.1.23). Тогда решение запишется в форме
к' = pVFPT +₽, к" =	-₽ (8.1.27)
(соотношение (8.1.22) в обозначениях (8.1.26) примет вид к'к" = = 1).
Зависимости к' и к" от 0 показаны на рис. 8.1.3. На том же рисунке приведены результаты расчета в первом приближении, когда к’ вычисляется без учета диссипации, а к" — из соотношения (8.1.22). Из рис. 8.1.3 видно, что приближенное решение, как и следовало ожидать, практически совпадает с точным при 0 ^>1, когда к'^>к". Однако как только 0 приближается к 1 (т. е. к" — к к'), точный спектр начинает существенно отличаться от приближенного. Приближенный спектр существует только при
§ 8.11 СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 383
0 > 0 (и затухание неограниченно возрастает при 0 -> 0), точный же спектр «заходит» в область отрицательных 0 (например, для 6 =0 — в область ®н Д’ но’ конечно, затухание при этом воз
растает.
Представление о распространяющихся спиновых волнах справедливо только в том случае, если к' к", т. е. с учетом (8.1.22) и (8.1.23) — если к' Д> knv. Для монокристаллов иттрий-железного граната осю/у == Д/Д — 1 э и
~ 104;
в веществах' с большей диссипацией /сПр будет еще больше. Спектр спиновых волн (зависимости к' и к" от <о) иттрий-железного граната в области к' Д> к” показан для двух крайних значений угла 0/; на рис. 8.1.4.
Остановимся теперь кратко на второй возможной постановке за
Р
Рис. 8.1.3. К расчету спектра] затухающих спиновых волн в ферромагнетике. Величины 7?, Tt" и р определяются выражениями (8.1.26). Пунктир — первое приближение	сплошные
линии — по точным формулам (8.1.27).
дачи о затухающих спиновых вол-
нах — рассмотрим затухание во времени волны с вещественным к. Положим в (8.1.11) со = н>' -j-г®" и примем, что а <Д 1, а
<о" <Д а'.
(8.1.28)
Тогда для <£>' получим прежнее выражение (8.1.14), а для ®" — выражение
®" = а ((он + т]А"2 + <ом sin2 .	(8.1.29)
При <ом < «>н, когда справедливо (8.1.16),
(о" ~ ала'.	(8.1.30)
Из (8.1.30) или в общем случае из (8.1.29) видно, что условие (8.1.28) (в отличие от (8.1.21)) всегда выполняется, если только а <С 1.
Как видно из (8.1.29), затухание спиновых волн во времени при небольших к сравнительно слабо зависит от к1). Затухание же в пространстве, характеризуемое к", как мы видели, зависит от к' очень сильно. Такое различие связано с сильной дисперсией спиновых волн. Действительно, в первом приближении для группо-
х) От к (а также, конечно, и от о) может зависеть и параметр а, но на этих зависимостях мы пока не оставливаемся, они будут обсуждаться в главе 9.
384
вой скорости, которую можно при наличии диссипации определить как да>'1дк', будет справедливо выражение (8.1.17) с заменой к на к'. Сопоставляя его с (8.1.22) и (8.1.29), получим
®" = кгр7Л	(8.1.31)
Отсюда видно, что при (ом (когда игр пропорционально к') и т]/с'2 << (когда к" пропорционально 1///) величина и", в согласии с (8.1.30), не зависит от к’.
Рис. 8.1.4. Спектр затухающих спиновых волн (при k’ > li") в изотропном ферромагнетике. АН^ = 0,5Js; остальные параметры — такие же, как па рис. 8.1.1, а (иттрийжелезный гранат).
При рассмотрении затухающих спиновых волн часто вводят величину
^ = 1/2(0",	(8.1.32)
которую называют временем жизни спиновой волны. Очевидно, что квадрат амплитуды переменной намагниченности затухающей во времени спиновой волны убывает как e-//T/f, т. е. тц есть время релаксации квадрата этой амплитуды. Аналогичным образом может быть введена величина
Zft = 1/2/с",	(8.1.33)
которую можно назвать длиной пробега затухающей в пространстве спиновой волны. Она представляет собой расстояние, на котором квадрат амплитуды переменной намагниченности спиновой волны убывает в е раз. Выражение (8.1.31) можно записать в виде
h = ^rpTfc.	(8.1.34)
Анизотропный ферромагнетик. До сих пор мы рассматривали спиновые волны в изотропной среде. Однако затухание спиновых волн, вообще говоря, велико, и наибольший практический инте
S, 8.11 СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 385
рес представляет исследование их в монокристаллах, обладающих малой диссипацией. Кроме того, для коротковолновых спиновых волн и поликристаллы (размеры зерен которых превышают 1/7с) нельзя рассматривать, как изотропную среду с усредненными параметрами (см., например, [320, 323]).
Переходя к рассмотрению спиновых волн в анизотропной среде, пренебрежем для простоты диссипацией. Для а =/= 0, но при выполнении условия (8.1.23) полученные таким образом зависимости /с (т>) будут в первом' приближении соответствовать зависимостям к' (со), а к" или со" смогут быть определены по формулам (8.1.22) или (8.1.29).
Для вычисления спектра спиновых волн в анизотропном ферромагнетике используем тот же путь, который был применен выше для изотропной среды: вычислим сначала магнитную проницаемость с учетом неоднородного члена энергии обменного взаимодействия, а затем воспользуемся уравнениями магнитостатики.
Линеаризированное уравнение движения намагниченности анизотропного ферромагнетика имеет вид (2.1.31). Теперь следует принять
heff = — N“m + h?,	(8.1.35)
где he — переменное эффективное поле неоднородного обменного взаимодействия (8.1.3), a N“ — тензор эффективных размагничивающих факторов анизотропии. Тензор размагничивающих факторов формы в (8.1.35) не входит (см. § 2.1), поскольку мы ищем проницаемость вещества и, соответственно, h в правой части (2.1.31) представляет собой внутреннее магнитное поле. Постоянное же эффективное поле в этом уравнении должно включать размагничивающее поле
Heff0 = Hi0-N°M0 = H0-NM0-NaM0. (8.1.36)
Направим ось z, как обычно, параллельно векторам Мо и Heff 0 и будем искать решение (2.1.31) в виде бегущей волны (8.1.4). Тогда для ha будет справедливо выражение (8.1.5), и амплитуда волны будет удовлетворять уравнению
icom + yH'ett om X z()yM0 (kqk) m X z0 +
+ YM0(Nam) X z0 -j- ia»m X z0 = rMoh x z0.	(8.1.37)
Проектируя (8.1.37) на оси x и у и решая полученную систему относительно тх и ту, можно определить компоненты тензоров % и р анизотропного ферромагнетика с учетом пространственной дисперсии.
1 3 А. Г, Гуревич
386	СПИНОВЫЕ ВОЛНЫ	[ГЛ. 8
Заметим, что антисимметричные компоненты тензора q не дают вклада в эффективное поле (8.1.5) неоднородного обменного взаимодействия. Для простоты пренебрежем вовсе анизотропией этого взаимодействия, т. е. будем считать q скалярной величиной. Оправданием такого допущения может служить то обстоятельство, что релятивистские взаимодействия, ответственные за магнитную анизотропию (см. § 2.2), вообще говоря, слабее, чем обменное взаимодействие. Не будем учитывать также диссипации. Тогда уравнение (8.1.37) запишется следующим образом:
i«m + ®нш X z0 q/An X z0 — у7Иот X (Naz0) -j-
+ Л (N“in) X z0 = TMoh X z0,	(8.1.38)
где г| определяется выражением (8.1.8), а од для случая эллипсоида — выражением (7.1.11).
Как видно из (8.1.38), учет неоднородного обменного взаимодействия и в случае анизотропной среды (но в предположении изотропии этого взаимодействия) сводится к замене (8.1.9). Поэтому мы можем, не решая уравнения (8.1.38), произвести замену (8.1.9) во всех формулах, которые были получены в § 7.1 для анизотропного ферромагнетика без учета неоднородного обмена. Тогда для компонент тензора р. будут по-прежнему справедливы выражения (7.1.16) — (7.1.18), а для спектра волны — (7.1.23). Но во всех этих выражениях вместо (7.1.19) следует принять
= <£>н + Т « - ТУзз) Мо + xtf,	(8-1-39)
®г/ = ®н + Т (Nи — Nзз) +	ms =
(выражение для сщ осталось без изменения).
Мы не будем записывать формулы для спектра спиновых волн в различных частных случаях; все они получаются из соответствующих выражений, приведенных в § 7.1, при замене (8.1.9), т. е.
Hi0-^Hi0 + Dk*,	(8.1.40)
где
D=^ = qM0.	(8.1.41)
Все соображения, высказанные в § 7.1 о характере анизотропии спектра магнитостатических волн, остаются в силе и для обменных спиновых волн. В частности, для приведенных в табл. 7.1.1 направлений (и только для них) формулы для спектра спиновых волн получаются заменой (7.1.29) из формулы (8.1.14) для изотропной среды. Например, для одноосного кристалла при 6 = 0 такая замена дает
(®/т)2 = (Я40 + 2НА1 + £>F) (Hi0 + 2НЛ1 + Dk* + 4лМ0 sin2 6ft).
Г8.1.42)
§ 8.1] СПИНОВЫЕ ВОЛНЫ В НЕОГРАНИЧЕННОМ ФЕРРОМАГНЕТИКЕ 387
Вырождение спиновых волн с однородной прецессией. При исследовании процессов релаксации (см. главу 9) оказывается очень существенным взаимное расположение частоты однородной прецессии (или другого типа колебаний, релаксация которого рассматривается) и спектра спиновых волн. Этого вопроса мы уже касались в главе 7 при рассмотрении длинноволновых (безобмен-ных) магнитостатических волн. Мы видели, что частота однородной прецессии эллипсоида соо лежит всегда выше нижней границы (0/г = 0) спектра безобменных волн (совпадает с ней в предельном
Рис. 8.1.5. вырождение однородной прецессии со спиновыми волнами в изотропной ферромагнитной сфере. Мо = 140 гс, ц = 0,1 (иттрий-железный гранат). Кружки — частоты однородной прецессии.
случае нормально намагниченного тонкого диска), но может лежать выше или ниже верхней границы спектра этих волн в зависимости от выполнения приведенных в § 7.1 условий.
В случае коротковолновых спиновых волн, т. е. с учетом неоднородного обменного взаимодействия, однородная прецессия (как и любой магнитостатический тип колебаний) всегда будет вырождена (рис. 8.1.5) с определенной группой волн. Если выполняются условия типа (7.1.12), т. е. частота однородной прецессии (оо лежит выше верхней границы безобменного спектра, то вырождение будет иметь место в некотором интервале к2 н- кг волновых чисел (рис. 8.1.5, а). Если же о>0 лежит ниже верхней границы безобменного спектра, то вырождение имеет место в интервале волновых чисел от 0 до kt (рис. 8.1.5, б). Интересно отметить, что для эллипсоида вращения величина кг — максимальное волновое число спиновых волн, вырожденных с однородной прецессией, не зависит от Но и имеет вид
N±M0.
(8.1.43)
388
СПИНОВЫЕ волны
[ГЛ. 8
§ 8.2. Спиновые волны в антиферромагнетиках и ферримагнетиках
Рассмотренную в предыдущем параграфе классическую феноменологическую теорию спиновых волн в ферромагнетике можно без особых трудностей обобщить на случай магнитных систем с несколькими подрешетками. При этом следует исходить из линеаризированных уравнений движения намагниченностей подрешеток (4.1.25) и уравнений магнитостатики, например в форме (7.1.21). Вид уравнений магнитостатики не зависит, конечно, от того, какую среду мы рассматриваем, а входящий в них тензор р для системы с несколькими подрешетками определяется следующим образом (см. главу 4):
т~ = 2 т~; = %Ь, р = 1 + 4л%.
В уравнениях движения (4.1.25) необходимо теперь учесть эффективное поле неоднородного обменного взаимодействия. Если предположить, аналогично предыдущему параграфу, что постоянные намагниченности подрешеток не испытывают быстрых изменений в пространстве, то энергию этого взаимодействия, обобщая (8.1.2), можно записать в виде [21, 3]
п п з з
=	2 3 2	’	(8.2.1)
3=1 j'=l Р=1 s=l	Р S
где п — число подрешеток.
Остановимся на случае двух идентичных подрешеток. Тогда
Д JL г 1	/ dm . 9m , 9m . dm „ \	, 9m dm „ 1
q jZisZlL 2 V dXP dXs dXP dXs '	дХР J
(8.2.2)
Эффективные поля неоднородного обменного взаимодействия определятся по формуле (4.1.4):
3	3
hgi,2 = 2 2 (яps q'x дх~ + qps дх~дх~) *	(8.2.3)
Р=1 в=1 '	Р S	Г S '
Для плоских волн
Щ—1.2 = т112ег<0>/"кг\
и из (8.2.3) следует (аналогично (8.1.5))
зз	зз
hgl.2 ~	(22 Qps^P^sj m1.2 ‘ (22 <1Р*крК] ®2,1 =
'р=1 s=l	'	s=l	'
— (kqk) mli2 — (kq'k) ш2Д. (8.2.4)
§8.2] ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТ ИКАХ 389
Дисперсионное соотношение для спиновых волн в антиферромагнетике, как и в случае ферромагнетика (§ 8.1), может быть получено (в рамках рассматриваемой классической теории) двумя путями; они отличаются последовательностью учета уравнений движения и уравнений магнитостатики. Как мы увидим ниже, учет уравнений магнитостатики, т. е. учет магнитного взаимодействия (который дает зависимость закона дисперсии от формы образца и направления распространения волны), для антиферромагнетиков приводит к малым поправкам. Это имело место и для однородного антиферромагнитного резонанса (§ 4.2) и связано с малыми величинами суммарных намагниченностей антиферромагнетиков, как постоянной (в не очень сильных магнитных полях), так и переменной.
В этом параграфе, так же как и в главе 4, мы ограничимся исследованием одноосных антиферромагнетиков. Спектры спиновых волн в них получили на континуальной модели методом решения уравнений движения Каганов и Цукерник [235] и с учетом магнитного взаимодействия — Лудон и Пинкус [241]. Квантовый расчет на континуальной модели был проведен Туровым и Ирхиным [21].
Одноосный антиферромагнетик в поле, параллельном оси. Как было показано в § 4.2, в одноосном антиферромагнетике с двумя идентичными подрешетками при положительной анизотропии (легкая ось) и постоянном поле Но, приложенном вдоль оси, возможны (см. рис. 4.2.2 и табл. 4.2.1) три основных состояния. При Н^НС~	а (первое состояние) равновесные векторы
намагниченностей подрешеток направлены по оси (рис. 4.2.2, а). Уравнения движения для этого состояния без учета неоднородного обменного взаимодействия имели вид (4.2.25). Теперь необходимо добавить в них эффективные поля (8.2.4). Тогда, решив эти уравнения, мы найдем тензор восприимчивости % с учетом пространственной дисперсии. Следуя первому пути получения дисперсионного соотношения для спиновых волн, мы должны подставить компоненты тензора % в магнитостатическое уравнение (7.1.21).
Добавляя в (4.2.25) члены уМ1>20 X 112, приходим к уравнениям ‘
ifomi 4- [у (Яо 4- НЕ + НА + Нк) 4- iaco| иц х z0 4-
+ Ч(НЕ 4- Нк) 1Н2 х Zo = уЛГ0Ь х Zo, (8.2.5)
icom2 4- [у (Яо — НЕ — НА — Я/г) — icta] m2 х z0 —
— Т (НЕ 4- Нк) nii X z0 = — yMoh X z0,
390
СПИНОВЫЕ волны
(ГЛ. 8
(8.2.6)
где введены обозначения:
Нк — Мо 2 2 р S
Нк = Мо 3 2 QpJcpk, р S
(величины Не и На определяются по-прежнему согласно (4.2.7) и (4.2.8), а Мо есть длина векторовМ10 и М20). Сравнивая полученные уравнения с (4.2.25), мы видим, что уравнения (4.2.25) переходят в (8.2.5) при замене
ЯЕ->ЯЕ + Нк,
НА-+НА + Нк-Нк
(8.2.7)
Следовательно, можно произвести эту замену в окончательных выражениях для компонент тензора %, который по-прежнему
будет иметь вид	~1Г(х+ + %_)	0	
Х =	i	1 — ~2~ (Х+— Х_) -2-(%+ + %_)	0	(8.2.8)
	0	0	0	
.2.7) в выражении (4.2.33) и пренебрегая
(<о — со±) (со + со^)
(8.2.9)
Производя замену (8 диссипацией, получим
%+= -
где, согласно (4.2.10),
-у- = /(2Яе +Яа) На +2Не (Як~Я;.)+2ЯаЯк+ Як - Я?± Яо.
(8.2.10)
Магнитостатическое уравнение (7.1.21) для тензора вида (8.2.8) запишется следующим образом:
1 + 2л (Х+ + Х_) sin2 0(. = 0.	(8.2.11)
Выражение (8.2.11) с учетом (8.2.9), (8.2.10) и (8.2.6) представляет собой дисперсионное соотношение для спиновых волн в рассматриваемом антиферромагнетике. Оно дает зависимость частоты этих волн ю (входящей в уд) от составляющих вектора к (которые входят В Як, Як И 81П26к = (й + fcy)/^2).
В рассматриваемом случае в кристалле имеется только одно выделенное направление — ось z. Поэтому тензоры q и д' долж
§ 8.2] ВОЛНЫ В АНТИФЕРХЮМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 391
ны иметь вид (1.2.29). Как и в случае ферромагнетика, антисимметричные компоненты тензоров q и q ' пе войдут в (8.2.6), и эти выражения примут вид
Нк = Мок2 (q и cos2 + q± sin2 0fc),	2
= M0k2 (g'u cos20/; +’g±sin2e/c).
Таким образом, в дисперсионное соотношение, как и следует ожи
дать, исходя из симметрии задачи,войдет только длина вектора к и угол вц между ним и осью z.
Так же как и для ферромагнетика (§ 8.1), пренебрежем различием продольных и поперечных компонент q и q т. е. примем
дх==9в ql = я и д'-
Тогда, обозначая
M0(q-.q') = D, (8.2.13)
Рис. 8.2.1. Спектры спиновых волн в антиферромагнетике с легкой осью анизотропии при постоянном поле, параллельном оси и меньшем поля опрокидывания, без учета магнитного взаимодействия (или при 0;г = 0). НЕ = 2,5-10» э, НА = 700 э, М, = 300 гс, Л = 10-“ (приблизительно соответствует Сг203 при низких температурах); Н, = 28 кэ. Кружки — частоты однородного антиферромагнитного резонанса.
запишем (8.2.11) с учетом (8.2.9) в виде
1
где
(СО2 — (О2) (СО2 — СО2)
sin2 6fc = О,
(8.2.14)
&2т = 8лг2 Мо (НА + D№).
Для резонансных частот со+ и ох_, учитывая, что На, Hk, Нк < Не, получим из (8.2.10) следующее приближенное выражен'
(8.2.15\ ii
ti>+ = yV2HE(HA+Dk2)±rH0^a0±^H0.	(8.2.1 „
’НЫИ
При 6/; = 0 корни дисперсионного уравнения (8.2.14) совий? в дают с со, и ю_, т. е. частоты спиновых волн, распространяющий^ ся в направлении оси z, определяются выражениями (8.2.10) ил,аг_ приближенно (8.2.16), полученными без учета магнитного взаимсеть действия. Зависимости частот ох+ и со_ от волнового числа к приьге ведены на рис. 8.2.1. При к -> 0 эти частоты совпадают с собст-а’ венными частотами однородного антиферромагнитного резонанса
392
СПИНОВЫЕ ВОЛНЫ
(4.2.10), полученными без учета влияния размагничивающих полей.
При малых к (когда
со± « ТЯС±ТЯ0 + Г VНЕ !2На№,
(8.2.17.)
а при больших к (когда Dk2 !>> НА) j
ы+~чУ2НЕБк±'хН0.
(8.2.18)
Таким образом, закон дисперсии спиновых волн рассматриваемого антиферромагнетика является приближенно квадратичным при малых к и линейным — при больших.
При Ок =/= 0 корни уравнения (8.2.14) — частоты спиновых волн не свпадают с ю+ и ю_; учет магнитного взаимодействия приводит к зависимости частот спиновых волн от угла 0)с. Решения уравнения (8.2.14) имеют вид
®+т — ~2~ (®+ '	"4”	8Й12 Ок) zb
+	V(ю2 — cd2)2 + 2t0m (cd+ — CD-)2 sin2 0/r + CO™ sin4 0fc , (8.2.19)
где <om определяется выражением (8.2.15). Величина <om обычно мала по сравнению с со+ и со_ (кроме случая, когда Но близко к Нс и со_ становится малым)., но не обязательно мала по сравнению с (со+ — «_) = 2Я0.
Рассмотрим случай Яо = 0. Тогда из (8.2.19) следует
<O_W — (Oq, K>+m — ’ CD0	tomsin2 0 к	CDg
Л/ sin2 6,. V_______п
НЕ
(8.2.20)
где w0 — частота спиновых волн при 0t = 0 и Яо = 0 — определяется выражением (8.2.16). Таким образом, с учетом магнитного взаимодействия частоты двух ветвей сшш-волнового спектра при Яо = 0 не являются (при 0j; =£= 0) вырожденными. Частота одной из ветвей совпадает с частотой со0 (которая получается без 3 учет а магнитного взаимодействия), а частота другой — отличает-ч от нее и зависит от 0fc. Зависимости частот обеих ветвей (второй— /и ©к = л/2) от к показаны на рис. 8.2.2 (средняя пара кривых).
Вь, При достаточно больших полях, когда ат уЯ0, из (8.2.19) сгледует
л (О2
®+т =	4*' ~т—~~ sin2 ©к.	(8.2.21)
—	4 <uo
В этом случае магнитное взаимодействие приводит к увеличению f- частот обеих ветвей спектра спиновых волн на одинаковую, зависящую от угла 6 k величину. Зависимости частот спиновых волн
§ 8.2] ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 393
от к при промежуточном значении Но, рассчитанные по общей формуле (8.2.19), приведены на рис. 8.2.2.
Как видно из формул (8.2.20) и (8.2.21) (с учетом того, что Мо<^ <С Не) и из Рис- 8.2.2, «расщепление» спектра спиновых волн антиферромагнетика, . обусловленное магнитным взаимодействием весьма невелико. Это, конечно, будет справедливо и для “других основных состояний и для других антиферромагнетиков.
Для процессов релаксации и нелинейных явлений в антиферромагнетиках, так же как и в случае ферромагнетиков, большой
интерес представляет исследование вопроса о вырождении (совпадении частот) однородного резонанса со спиновыми волнами. С этой 'точки зрения влияние магнитного взаимодействия на спектры спиновых волн оказывается довольно существенным. Без учета магнитного взаимодействия, как видно из сравнения формул (8.2.16) и (4.2.10) или из рис. 8.2.1, имеет место лишь вырождение (при Нп =j= 0) верхней ветви однородного резонанса cdq+ с нижней ветвью спиновых волн со_. При учете же магнитного взаимодействия, которое приводит к зависимости частот спиновых волн от 0/;, а частот однородного резо-
Рис. 8.2.2. Спектры спиновых волн в одноосд ном антиферромагнетике с учетом магнитного взаимодействия. Основное состояние и значения параметров — те же, что и на рис. 8.2.1; Н2 = 300 э. Кружки — частоты однородного резонанса сферы.
нанса — от формы образца
(§ 4.2) *), вырождение имеет место и при Но — 0, а также между «одноименными» ветвями спектра (соо+ с со+ и wo_ с со_). Это иллюстрирует рис. 8.2.2, на котором, наряду со спектрами спиновых волн, показаны и частоты однородного резонанса антиферромагнитной сферы.
Э Для рассмотренного основного состояния постоянный магнитный момент равен нулю, и поэтому поле Но, входящее в приведенные выше в этом параграфе формулы (вообще говоря, оно должно, было бы являться внутренним постоянным полем), совпадает’с внешним полем. Для других основных состояний необходимо было бы учитывать в II п постоянное размагничивающее поле, вследствие чего частоты спиновых волн стали бы зависеть от формы образца. Очевидно, что эта поправка, как и другие связанные с учетом магнитного взаимодействия в антиферромагнетиках, невелика, кроме случая очень больших внешних полей, сравнимых с НЕ.
394
СПИНОВЫЕ волны
Антиферромагнетик в поле, перпендикулярном оси. Рассмотрим теперь антиферромагнетик с легкой осью анизотропии в случае, когда постоянное поле приложено перпендикулярно оси. Основное состояние для этого случая и частоты однородных колебаний (без учета магнитного взаимодействия) были получены в § 4.2. Вычисляя спектр спиновых волн, будем также пренебрегать магнитным взаимодействием. Тогда, как ясно из предыдущего примера, частоты спиновых волн совпадут с полюсами тензора %, определенного для плоской волны с учетом неоднородного обменного взаимодействия. Однако вычислять компоненты этого тензора, т. е. решать уравнения движения с правой частью, нет необходимости. Частоты спиновых волн могут быть найдены из условия обращения в нуль определителя системы однородных уравнений движения, в которые войдут эффективные поля обменного взаимодействия (8.2.4).
С учетом обозначений (8.2.6) эффективные поля (8.2.4) запишутся в виде
К 1.2 = ть2 л/7т2.1‘	(8.2.22)
Добавим в однородные уравнения движения (4.1.25) (без диссипации) члены tMi.20 X h,t, 2 и спроектируем эти уравнения на оси координат с учетом (4.2.44). Складывая и вычитая соответствующие уравнения полученной системы, мы (так же, как и для однородного резонанса) придем к двум независимым системам для проекций векторов m = mx -ф- ш2 и 1 = пц — т2. Приравнивая нулю определители этих систем, можно найти частоты соответствующих ветвей спектра спиновых волн. Учитывая, что На Не и Н1;, Нк Не х), и пренебрегая, как и раньше, различием qк и в (8.2.12), получим
^2Не(На+ Dk2) + Hl, (-у) ^2HE(HA+Dk*)
(8.2.23)
(8.2.24)
где величина D по-прежнему определяется согласно (8.2.13). Заметим, что условие Но НЕ при этом не использовано, т. е. выражения (8.2.23) и (8.2.24) справедливы, так же как и выражения (4.2.13) и (4.2.14), при любых значениях постоянного поля
J) Первое условие {НА НЕ),кяк уже неоднократно отмечалось, хорошо’ выполняется для большинства антиферромагнетиков. Второе условие также хорошо выполняется при длинах спиновых волн, много больших, чем постоянная решетки, что является условием применимости рассматриваемой континуальной теории.
§ 8.2] ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 395
(О Но < 2Не), при которых имеет место данное основное состояние.
Частоты спиновых волн для опрокинутого основного состоя' ния (Яс Яо 2Не) при Но fl z0 могут быть получены таким же способом, как и выражения (8.2.23) и (8.2.24), Приведем лишь окончательные формулы в том же приближении На, Н^, Нц<^. < НЕ-
=Я§-2ЯЕЯА+П/г2(2ЯЕ-^-),	(8.2.25)
W = Dk* (2НЕ- -ДЦ •	(8.2.26)
\ I /	\	Z77E /
При к -> 0 они переходят (с учетом того, что На <С 77е) в выражения (4.2.11) для частот однородного резонанса в опрокинутом основном состоянии.
Слабый ферромагнетик с легкой плоскостью анизотропии. Остановимся теперь на случае отрицательной анизотропии {На < 0), когда равновесные намагниченности подрешеток в отсутствие внешнего поля (а также при поле, перпендикулярном оси) лежат в базисной — перпендикулярной оси плоскости. Такой антиферромагнетик был подробно рассмотрен в § 4.3. Он интересен тем, что для него возможен слабый ферромагнетизм, и тем, что одна из ветвей спектра однородных колебаний в нем является «бесщелевой». Как указывалось в § 4.3, неколлинеар-ность векторов намагниченностей подрешеток, приводящая к слабому ферромагнетизму, может быть связана с двумя типами инвариантов в выражении для энергии кристалла: (4.3.13) и (4.3.14). Мы рассмотрим спектр спиновых волн для инварианта (4.3.13), который возможен в кристаллах всех одноосных сингоний (табл. 4.3.1).
Для вычисления спектра спиновых волн с учетом магнитного взаимодействия используем тот же метод, который был применен выше. Найдем прежде всего тензор восприимчивости % с учетом пространственной дисперсии, обусловленной неоднородным обменным взаимодействием. Тензор % без учета этого взаимодействия вычислялся в § 4.3. Уравнения движения свелись тогда к двум независимым системам: (4.3.27) для переменных тх, 1У, mz и системе для переменных 1Х, ту, 12 (которая не была приведена в § 4.3). Теперь мы должны добавить в эти уравнения проекции членов тМ1>20 X hQ 12, где эффективные поля неоднородного обменного взаимодействия hg li2 по-прежнему имеют вид (8.2.22).
Для сокращения выкладок ограничимся сразу приближением и’ в отличие от предыдущего примера,  0 Н.Е- Тогда уравнения движения (без учета диссипации)
39й
СПИНОВЫЕ волны
[ГЛ. 8
примут ВИД
~ тх — (Яо + IID) т г - — 2М0 sin <p±7iz,) ^ly + 2HEmz = 2Mohz, I
у- mz— (Нк — Нк) 1У 4- Нотх = 2M0 sin <рхЛх,
-у ту + (На + Ядзш <[. | у II к — IIft) 1г — О, l^-l2~2HEmv = ~2MJiv,
(8.2.27)
(8.2.28)
где угол <p_L определяется согласно (4.3.18). Решая системы (8.2.27) и (8.2.28), мы получим для компонент тензора % (который по-прежнему будет иметь вид (4.3.29)) выражения, совпадающие по форме с (4.3.30) и (4.3.33) при Ди = 0. Но резонансные частоты компонент х будут теперь другими. В частности, при малых вместо (4.3.25) и (4.3.26)
(у-)2 = Яо (Я0 + Яр) у 211Е (IIк - ЯД,	(8.2.29)
(-у)2 = 211ЕНА + ЯС(ЯО + Яр) у 2Яе (II к - Нк). (8.2.30)
Без учета магнитного взаимодействия резонансные частоты (8.2.29) и (8.2.30) являлись бы собственными частотами спиновых волн. Для получения дисперсионных соотношений с учетом этого взаимодействия необходимо подставить компоненты тензора % в магнитостатическое уравнение (7.1.21). Для тензора (4.3.29) уравнение (7.1.21) примет вид
1 + 4л (%хх sin2 Qk cos2 <pft+ %т sin2 sin2 <pfc+ %zz cos2 6Д = 0, (8.2.31)
где 0R и ерь — полярный и азимутальный углы вектора к.
Частоты coj и <о2, кроме случая вырождения при Яо Нс (см.
§ 4.3), очень сильно отличаются друг от друга. Поправки же к этим частотам, обусловленные магнитным взаимодействием, будут, конечно, невелики. Поэтому, вычисляя с помощью (8.2.31) частоту первой ветви спиновых волн, можно пренебречь величиной %уУ, а вычисляя частоту второй ветви,— наоборот, пренебречь % хх И %zz.
Для полного учета магнитного взаимодействия необходимо *) в выражениях для компонент тензора % заменить Яо на внутреннее постоянное поле Яго. Если образец представляет собой эллип-
х) См. примечание на стр. 393.
s 8.21 ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 397
соид, а постоянное поле (направленное по оси у) совпадает по направлению с одной из его осей, то
Hio = Н 0
В данном случае согласно (4.3.19) и (4.3.21)
M===-^(Hi0 Яр).	(8.2.32)
Используя выражения (4.3.30) для и %гг (при Ао> = 0), получим для первой ветви спектра спиновых волн с точностью до малых величин первого порядка относительно MJHe
(^у = (^)’_^(Яо + нп) +
+[(я°+я")2 sin2 °*cos2 +(тГcos2 М ’ (8-2-33)
где со1 — частота спиновых волн без учета магнитного взаимодействия, которая определяется выражением (8.2.29). Второй член в правой части (8.2.33) представляет собой «статическую» поправку — обусловленную статическим размагничивающим полем, а третий член — «динамическую» поправку, связанную с переменным магнитным полем волны.
Для второй ветви таким же образом получим
(\	/ 0)2 \	у Л/ о ,, . j, .	. 4 л Л/ о/о)а\ • on  о
_ Яд(Я°+	+	sm2efcsin2 <pR,
(8.2.34)
где о)2 имеет вид (8.2.30). Выражения (8.2.33) и (8.2.34) содержат зависимости частот спиновых волн от величины постоянного поля, волнового числа к, направления распространения волны и формы образца — эллипсоида. Две последние зависимости, обусловленные магнитным взаимодействием, являются слабыми. Следует отметить, -что, в отличие от выражений (8.2.29) и (8.2.30), не учитывающих магнитного взаимодействия, формулы (8.2.33) и (8.2.34) при к 0 не дают частот однородного антиферромагнитного резонанса.
При = п/2 и ерь = л/2, т. е. для спиновой волны, распространяющейся в направлении постоянного поля, в выражении (8.2.33) для первой ветви (для второй ветви это не справедливо) остается лишь статическая поправка. Заметим, что динамическая поправка обращалась в нуль для волн, распространяющихся вдоль постоянного поля, и в случае ферромагнетика (см. § 8.1), и в случае антиферромагнетика с легкой осью анизотропии для рассмотренного выше антипараллельного основного состояния.
398
СПИНОВЫЕ волны
В последнем случае статическая поправка обращалась в пуль при всех направлениях распространения, так как М= = 0.
Зависимости частот и а>2 от волнового числа — спектры спиновых волн без учета магнитного взаимодействия, показаны на рис. 8.2.3. Из рис. 8.2.3 и из формул (8.2.33) и (8.2.34) видно, что спектры, как и в рассмотренных ранее примерах, являются квадратичными при малых к (для первой ветви — при к<^
]/Я0 (Яо + Яр) / (2ЯЕЯ)) и линейными — при достаточно больших к. Для первой ветви в отсутствие внешнего поля
Рис. 8.2.3. Спектр спиновых волн в антиферромагнетике с легкой плоскостью анизотропии и слабым моментом при постоянном поле, лежащем в легкой плоскости (без учета магнитного взаимодействия).
НЕ = 9-10е э, НА = Ю4 a, HD = 2-Ю4
D — 10~® (приблизительно соответствует а - Fe2O3 при комнатной температуре):
Но=3-104 э.
дней. В монокристаллах ферритов щие спиновые волны х), которые
спектр (без учета магнитного взаимодействия и анизотропии в базисной плоскости) является линейным при любых к. Заметим также, что наличие слабого момента (как видно из (8.2.33) и (8.2.34)) не меняет характера спектра спиновых волн по сравнению со случаем коллинеарного (Яр = 0) антиферромагнетика с легкой плоскостью анизотропии.
Ферримагнетик. Рассмотрение спиновых волн в ферримагнетиках представляет первостепенный интерес, так как из всех известных в настоящее время магнитоупорядоченпых веществ именно ферримагнетики — в первую очередь ферриты со структурой граната (см. §4.4)— обладают наименьшей диссипа-удается поэтому возбудить бегу-используются и в практических
целях — для создания сверхвысокочастотных линий задержки [487]. Процессы релаксации (см. главу 9) и нелинейные явления [15, 537] при магнитном резонансе в магнитоупорядоченных кристаллах, в которых определяющую роль играют спиновые волны, исследуются также наиболее интенсивно в ферримагнетиках * 2).
]) Механизмы этого возбуждения будут рассмотрены в следующем, параграфе.
2) Отсюда, конечно, ни в какой мере не следует вывод о том, что спиновые волны в антиферромагнетиках или ферромагнитных металлах являются малоинтересными. В частности, изучению стоячих спиновых воли в металлических ферромагнитных пленках (см. следующий параграф) было уделено огромное внимание.
§ 8.2] ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 399
Однородные магнитные колебания в ферримагнетиках были рассмотрены в § 4.4. Было показано, что в области достаточно низких частот (много меньших, чем резонансная частота в эффективном поле обменного взаимодействия) и достаточно слабых постоянных полей (много меньших, чем это эффективное поле) и вдали от точек компенсации возбуждается практически только низкочастотный («ферромагнитный») тип колебаний, для которого ферримагнетик эквивалентен ферромагнетику с эффективными g-фактором и полем анизотропии. Кроме этого типа колебаний существует еще п — 1 (где п — число подрешеток) высокочастотных или «обменных» типов колебаний, возбуждение которых становится существенным (в области полей, меньших обменного, и вдали от точек компенсации) лишь при высоких частотах.
Очевидно, что аналогичные ветвиЧйщут иметь место и с учетом неоднородного обменного взаимодействия, т. е. для спиновых волн в ферримагнетике. Мы рассмотрим сейчас спектры этих волн. В частности, мы убедимся, что для низкочастотной ветви спиновых волн при выполнении указанных выше условий ферримагнетик практически эквивалентен ферромагнетику с эффективными параметрами.
Остановимся па двухподрешеточном ферримагнетике. Как отмечалось в § 4.4, эта модель позволяет описать наиболее важные свойства магнитных колебаний в ферримагнетиках. Для двухподрешеточного ферримагнетика выражение (8.2.1) для энергий неоднородного обменного взаимодействия примет вид
з з
j-r _ V V /	SmjSini .	1 dmaЭта ’ dmidm2\
9	\ 2 51 ?>s дхр dxs '	2 52 ?>s дхр dxs ' дхр dxs j ’
(8.2.35) а эффективные поля в случае волновой зависимости от координат запишутся следующим образом:
3	3	3	3
К 1.2 = — ( 2 2 51.2PS ) т1.2 —(22	) т2,1-	(8.2.36)
8^1	p=ls=l
Для того чтобы получить частоты магнитных колебаний двухподрешеточного ферримагнетика с учетом неоднородного обменного взаимодействия, необходимо в уравнения движения намагниченностей подрешеток добавить члены ylj2 Mlj2j 0 X hQ Ь2. Тогда, аналогично рассмотренным выше случаям ферромагнетика и антиферромагнетика, условие совместности однородных уравнений^ даст частоты без учета магнитного взаимодействия, а тен-30Р X, полученный в результате решения уравнений с правой частью, будучи подставлен в магнитостатическое уравнение
400
СПИНОВЫЕ волны
(7.1.21), позволит определить эти частоты с учетом магнитного взаимо действия.
Ограничимся рассмотрением первого — коллинеарного основного состояния ферримагнетика, которое, как было показано в § 4.4, имеет место при Но Л {М± 0 — М2 0) (здесь Л — константа однородного обменного взаимодействия между подрешетками, Мг 0 и М2 0 — статические намагниченности подрешеток) -Уравнения движения в этом состоянии с учетом эффективных полей одноосной кристаллографической анизотропии и эффективных полей (8.2.36) в циркулярных переменных т112 + = лг1>2 х + ±	как нетрудно убедиться, примут вид1)
[+— Ti {Hio -|- Не, 4“ Нах 4- Нм)] mi+ —
~~ Ti {Hei 4- Hfcl) -ь = —	<Л±,	(8.2.37)
|+— Та (77io — НЕ1 — На, — 77К2)] лг2 + 4-
4- Та {Не, 4“ 77А2) тг + =	oh±.
Здесь Hi0 — внутреннее постоянное поле; На 1,2 — эффективные поля одноосной кристаллографической анизотропии (в предположении аддитивности энергий анизотропии подрешеток и с учетом только первых констант они имеют вид (4.4.38)); величины /7(|. Ь2 и 77fci,2> аналогично (8.2.6), обозначают
з з
77fci,2 = 7171,20 2 2 ?i,2ps^pT:s,
Р=1 s=l
(8.2.38)
з з
77^1,2 = 71712о 2 2 4ps^p^s-
P=>1 S=1
Из уравнений (8.2.37) видно, что учет неоднородного обменного взаимодействия свелся к замене, аналогичной (8.2.7),
Не 1,2 —> НЕ 1,2 4~ Нк 112,
(8.2.39)
На 1,2 Нагл + 77 1>2 — Н к 112.
Воспользовавшись этим, можно сразу же получить выражения для частот спиновых волн и компонент тензора % с учетом неод-
4 Аналогичные уравнения (4.4.37) были записаны для собственных однородных колебаний. Теперь, поскольку мы рассматриваем колебания под действием заданного внутреннего переменного поля (ищем внутренний тензор восприимчивости), из уравнений следует исключить члены	0
(но оставить члены у	о ~ М2 0), учитывающие постоянные размаг-
ничивающие поля).
§ 8.2] ВОЛНЫ В АНТИФЕРРОМАГНЕТИКАХ И ФЕРРИМАГНЕТИКАХ 401
породного обменного взаимодействия из соответствующих выражений для однородных колебаний (§ 4.4).
Произведя замену (8.2.39) в выражении (4.4.39) (без члена ZVj_ (Л/г о —М2 о)), мы получим частоту первой (низкочастотной) ветви спектра спиновых волн ферримагнетика без учета магнитного взаимодействия
(□1 = “Гафф (/Go “1“ Нд 8фф -|- Нк йфф)-	(8.2.40)
Здесь 7Г)фф и Нд ;,фф определяются выражениями (4.4.16) и (4.4.40), а
1Г +
"'-"И1	Mi о—Мао
(8.2.41)
Если учесть вид тензоров дг, q2 и q', определяемый одноосной симметрией задачи, и пренебречь, как и раньше, различием продольных и поперечных компонент этих тензоров, то
Н*= - m10-mL -к2 <8-2-42)
И, наконец, если принять (хотя трудно привести какие-либо доводы в пользу этого) q± == q2 = q' ~ q, то
Нк Эфф = (М} 0 - М2 0)qk*.	(8.2.43)
Сравним выражения (8.2.40) с выражением (8.1.42) для частоты спиновых волн в одноосном ферромагнетике при постоянном поле, направленном, как и для ферримагнетика, вдоль оси х). Если в (8.1.42) положить 6Jt == 0 (что равносильно неучету магнитного взаимодействия), то указанные выражения совпадают при
-4/10	'^2 0=^0,	/^А1 = /?Аэфф, Y = /эфф И D = Пэфф.
Таким образом, в рассматриваемом частном случае (низкочастотная ветвь спиновых волн, одноосная анизотропия и другие оговоренные выше условия) ферримагнетик эквивалентен ферромагнетику с эффективными параметрами. Легко убедиться, что такая эквивалентность, имеет, место и без предположения о равенстве продольных и поперечных компонент тензоров qb 2 и д'. Имеет она место, конечно, и для других ориентаций постоянного поля, и для кристаллов с другой (не одноосной) симметрией.
’) В выражении (8.1.42) (как и в главах 2 и 7) индекс 1 указывает на связь "А1 с первой константой анизотропии. В этом параграфе (как и в главе 4) учитывается только первая константа анизотропии, а индексы 1 и 2 обозначают номера подрешеток.
402
СПИНОВЫЕ ВОЛНЫ
Производя замену (8.2.39) в выражениях компонент тензора X для низкочастотных однородных колебаний ’) или же непосредственно решая систему (8.2.37) при На.1Л, Нк1,2,Нк 12*^ <g£(I[Kv — 77в2) и-Но (Янх — Яе2), получим для низкочастотной области (ю <С ше Т2 НЕ1 — Yi77e2)
'll эфф (^1 ° ~	о)
— ол^со
(8.2.44)
где определяется выражением (8.2.40). Как видно из (8.2.44), тензор восприимчивости ферримагнетика с учетом неоднородного обменного взаимодействия в низкочастотной области совпадает с тензором восприимчивости ферромагнетика с эффективными параметрами. Отсюда ясно, что для низкочастотной («ферромагнитной») ветви спектра спиновых волн при достаточно малых внешних полях (Но Hei — Не%) закон дисперсии и с учетом магнитного взаимодействия будет таким же, как для ферромагнетика.
Исследуем теперь вторую (высокочастотную) ветвь спектра спиновых волн. При этом рассмотрим для простоты изотропный ферримагнетик (JIai — На^ = 0). Тогда, приравнивая нулю определитель системы (8.2.37) по-прежнему в предположении, что Но, Нк 1,2, Нк 1,2 <С Hei — Не2, но не для низкочастотной области, а, наоборот, для высоких частот (® ;>> 7:,фф//0), получим
и2 =	— ГэффН{0 4~ ^эффЯ/с Офф.	(8.2.45)
Здесь соЕ и уофф определяются соответственно формулами (4.4.18) и (4.4.19), а величина
«а fe «« - »в) + (у	- «й) (8 2 46)
--.-"и
Если принять qr = q2 = q' = q, то
эфф —
(Т1 — Та)2 Л/i оМ% О
Т2ЛПо —
(8.2.47)
Выражение (8.2.45) получено без учета магнитного взаимодействия. Для учета его следовало бы подставить восприимчивость для второй ветви спиновых волн, полученную в результате решения системы (8.2.37), в магнитостатическое уравнение (7.1.2). Но восприимчивость эта, как отмечалось в § 4.4, имеет малый числитель — пропорциональный (^ — т^)2. Частота же второй ветви (мы рассматриваем область небольших //0) велика. Поэтому по-
') Эти выражения с учетом кристаллографической анизотропии не были приведены в § 4.4, но их нетрудно получить, решая уравнения (4.4.37) без членов с N ,.
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 403
правка к частоте, обусловленная магнитным взаимодействием, оказывается пренебрежимо малой.
В заключение заметим, что кристаллические и магнитные структуры антиферромагнетиков и ферримагнетиков отличаются большим разнообразием. Столь же разнообразны и спектры спиновых волн в них. Небольшое число рассмотренных выше простых примеров могло лишь дать представление о некоторых особенностях этих спектров и познакомить с методом их расчета, основанным на решении уравнений овижения намагниченностей ’). Результаты расчета спектров для различных антиферромагнетиков приведены в [21] и [244].
§ 8.3. Спиновые волны в ограниченных телах и неоднородных средах
В двух предыдущих нарагр^ах рассматривались плоские спиновые волны в неограниченных однородных средах. Экспериментально же приходится иметь дело с телами конечных размеров, граничащими с другими, обычно — немагнитными средами. В этом параграфе мы рассмотрим некоторые ситуации, когда существенным становится учет конечных размеров тел, в которых распространяются спиновые волны, а также учет неоднородности параметров среды. Неоднородность параметров может быть обусловлена, в частности, неоднородностью постоянного магнитного поля.
Задачи о распространении электромагнитных волн в ограниченных телах рассматривались в главах 6 и 7. Но в главе 6 это рассмотрение велось без учета зависимости параметров среды от частоты и волнового вектора. В главе 7 зависимость магнитной проницаемости от частоты принимались во внимание, но зависимость от волнового вектора (пространственная дисперсия), обусловленная неоднородным обменным взаимодействием, не учитывалась. Как уже отмечалось в главе 7, совместный учет неоднородного обменного взаимодействия и граничных условий необходим только в тех случаях, когда размер тела (в каком-либо одном измерении) становится сравнимым или меньшим, чем величина
, 1
— —г~ /ci
(8.3.1)
(&i — такое волновое число, при котором вклад неоднородного обменного взаимодействия в частоту спиновых волн становится существенным). Оценка для иттрий-железного граната (ц = 0,1) и сантиметрового диапазона волн дает
d^lO-s^-lO-6 см.
0 Других методов расчета спектров спиновых волн в ферро*'И антифер-ро-магнетиках мы коснемся в § 8.5.
404
СПИНОВЫЕ волны
Таким образом, учет граничных условий (в слабо проводящих средах) становится необходимым лишь в случае мелких частиц, а также тонких стержней (нитей) и тонких пленок, поперечные размеры которых измеряются долями микрона *). Следует подчеркнуть, что это относится лишь к влиянию граничных условий на спектр спиновых волн. Что же касается таких задач, как, например, задача о прохождении и отражении спиновых волн через границы раздела, то для них, конечно, учет граничных условий на поверхности раздела необходим независимо от размеров тел.
Аналогичное положение имеет место и для сред с плавно изменяющимися параметрами, в частности, для случая неоднородного постоянного магнитного поля. Если изменение параметров — достаточно медленное, т. е. расстояния, на которых они заметно изменяются, гораздо больше, чем 1//с (где к — волновое число рассматриваемых волн), то спектр волн в каждой точке определяется значениями параметров в этой точке. Задачи о распространении спиновых волн в такой среде с медленно изменяющимися параметрами аналогичны задачам геометрической оптики. Если же расстояния, на которых происходят заметные изменения параметров, сравнимы или меньше, чем 1//с, то магнитные колебания не являются плоскими волнами, и зависимость m (г, t) может быть найдена лишь путем совместного решения уравнений движения намагниченности и уравнений поля (обычно — в магнитостатическом приближении) при заданной зависимости параметров от координат.
Возбуждение спиновых волн. Исследование распространения спиновых волн в неоднородных средах тесно связано с проблемой возбуждения спиновых волн. Некогерентные (тепловые) спиновые волны возбуждаются под воздействием тепловых колебаний кристаллической решетки. При этом возникает некоторое равновесное распределение таких спиновых волн с различными щ и к. Когерентные спиновые волны, которые нас больше всего интересуют, мо-могут возбуждаться в результате нелинейных процессов под воздействием однородных колебаний намагниченности [522] или непосредственно переменного магнитного поля [528] достаточно большой амплитуды (см. также [537, 15]). Рассмотрение такого возбуждения выходит за пределы этой книги, посвященной линейным проблемам 1 2). lie будем мы рассматривать и возбуждения спиновых волп упругими колебаниями, которое происходит благодаря связи между магнитной системой и решеткой в магнитоупорядоченных кристаллах [347, 3]. Остановимся лишь на линей
1) В металлах, в которых глубина проникновения поля (толщина скин-слоя) сравнима с l/Azi, учет граничных условий в задачах о спиновых волнах необходим для образцов любых размеров.
2) Вопрос о нелинейном возбуждении спиновых волн (спиновых нестабильностях) будет лишь слегка затронут в § 9.2.
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 405
ном (имеющем место при сколь угодно малых амплитудах) воз
У7Кдотург 1'1 когерентных спиновых волн	моепитпым/
полем.
Не проводя строгого исследования задачи о возбуждении спиновых волн, отметим лишь, что ее решение в случае дискретного спектра спиновых волн ’) можно искать, так же как и для магнитостатических (безобменных) волн, в виде ряда (7.3.30). Величины mv (г) в (7.3.30) будут теперь комплексными амплитудами спиновых колебаний с собственными частотами о v, а для коэффициентов при соответствующей нормировке собственных функций пц (г) будет справедлива формула (7.3.31).
Если же спектр спиновых волн — непрерывный, как например, в неограниченной среде или волноводе 2), то ряд v7.3.30) должен быть заменен интегралом. И если собственными функциями задачи являются плоские волны пц. (г), то интегрирование может вестись по волновым векторам к этиз^волн:
m(г) = ( ci- (к) иц (г) d3k.	(8.3.2)
Величина сА (к) характеризует интенсивность возбуждения нормальной волны с волновым вектором к. Для нее справедлива формула, аналогичная (7.3.31),
ci: = Ссо2
^h(r)m* (r)dE со2 — со£ + 2ia(|.<i)2
(8.3.3)
где со — заданная частота возбуждающего поля, а — параметр диссипации; интегрирование в (8.3.3) производится по всему пространству, где h (г) ф 0 и нц (г) ф 0.
Рассмотрим в качестве самого простого примера возбуждение бегущей спиновой волны в однородной неограниченной среде. Тогда
пц(г) = пмпгкг,	(8.3.4)
a cojc собственная частота, связанная с к дисперсионными соотношениями, которые подробно исследовались выше. В этом случае возбуждение происходило бы наиболее интенсивно, если бы возбуждающее поле представляло собой бегущую волну с тем же волновым вектором, что и спиновая волна, для которой ю/г =ю-Наибольший практический интерес мог бы представить случай, когда возбуждающее переменное поле однородно. Однако тогда интеграл в (8.3.3) обращается в нуль. Действительно, в случае
’) Дискретный спектр спиновых волн, как и в случае безобменных магнитостатических волн (§ 7.3), электромагнитных волн (§ 6.3) и других волновых ^процессов, имеет место для ограниченных тел.
) См. примечание 1 на стр. 340.
406
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
однородного поля h (г) может быть вынесено на знак интеграла и интеграл m* (г) dV, который представляет собой величину, v
сопряженную с суммарным магнитным моментом, обращается в нуль для однородной плоской волны. Таким образом, возбуждение спиновых волн в однородной неограниченной среде однородным переменным полем (если не касаться нелинейных процессов) невозможно.
Положение существенно изменится, если мы перейдем к возбуждению спиновых волн в ограниченных телах достаточно малых размеров или в средах с неоднородными параметрами. Тогда собственные функции намагниченности спиновых волн не будут являться плоскими волнами (8.3.4) и интеграл от произведения однородного переменного магнитного поля на эти функции может не обратиться в нуль. Ниже мы рассмотрим два характерных примера такого возбуждения спиновых волн: в тонкой пленке и в неоднородном постоянном магнитном поле.
Граничные условия для намагниченности. Учет неоднородного обменного взаимодействия приводит, как мы видели, к появлению в уравнениях движения производных от намагниченности по координатам. Порядок дифференциальных уравнений, которые получаются при совместном решении уравнений движения и уравнений электромагнитного поля, повышается, и обычных электродинамических граничных условий становится недостаточно для однозначного решения граничных задач. Электродинамические граничные условия (непрерывность касательных составляющих магнитного и электрического полей и нормальных составляющих магнитной и электрической индукции, см. § 5.1) должны быть дополнены теперь некоторыми условиями, накладываемыми на намагниченностьнаграницераздела. Они должны быть следствиями уравнений движения, так как уравнения поля уже использованы при выводе электродинамических граничных условий. Поскольку в уравнения движения входят теперь (см., например, выражения (8.1.3) и (8.2.3)) вторые производные переменной намагниченности по координатам, то можно полагать, что искомые граничные условия будут содержать составляющие намагниченности и их первые производные.
Переходя к выводу граничных условий для намагниченности, рассмотрим наиболее важный случай, когда магнитная среда представляет собой ферромагнетик г) и граничит с немагнитной (р,0 = = 1) средой. Следуя Радо и Уиртмену [256], мы получим дополнительные граничные условия путем интегрирования уравнения
х) Очевидно, что граничные условия, которые мы получим, будут справедливы и для низкочастотной («ферромагнитной») ветви магнитных колебаний в ферримагнетике.
§ 8.3]	ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 407 движения аналогично тому, как электродинамические граничные условия получаются интегрированием уравнений Максвелла (см., например, [29]).
Считая для простоты неоднородное обменное взаимодействие изотропным, т. е. тензор q в (2.1.7) скалярной величиной (qps = = q), запишем исходное уравнение движения в виде
— х	х V2M + M х Hs= 0. (8.3.5)
Здесь Heff включает в себя внешнее поле, размагничивающее поле и все эффективные поля (поле объемной анизотропии, эффективное поле, учитывающее диссипацию), не зависящие или слабо зависящие от координат; поле Hg есть эффективное поле поверхностной анизотропии, которое очень сильно зависит от координаты в направлении, перпендикулярном к граничной поверхности.
Поле Hg существует тот$>ко в поверхностном слое толщиной d. Оно учитывает особые условия, в которых находятся магнитные моменты вблизи границы ферромагнетика. Не обсуждая подробно природу поверхностной анизотропии, заметим лишь, что источником ее, согласно Неелю (см., например, [244]), может явиться то, что ионы у поверхности находятся в другом окружении, чем внутри ферромагнетика. Поверхностная анизотропия может возникать также из-за наличия на поверхности топкой пленки другого химического состава, чем внутри, например, антиферромагнитной окисной пленки на границе ферромагнитного металла. Существенно, что интеграл от поля Hg по объему поверхностного слоя не является, вообще говоря, малым, несмотря на малую толщину слоя.
Поверхностная анизотропия может являться либо одноосной с осью — легкой или трудной, совпадающей с нормалью к поверхности, либо однонаправленной (когда, в отличие от одноосной анизотропии, направления к поверхности и от нее не эквивалентны). Рассмотрим для определенности первый случай. Тогда, согласно (2.2.5), ограничиваясь первой константой анизотропии, можно записать
Hs = ii()^(Mn0),	(8.3.6)
где п0 — единичный вектор внешней нормали к граничной поверхности S (рис. 8.3.1). Величина Hs зависит — причем, как уже отмечалось, сильно — от координаты z' в направлении, перпендикулярном поверхности, и обращается в нуль вне поверхностного слоя.
Проинтегрируем уравнение (8.3.5) по объему V (рис. 8.3.1)— тонкому диску с площадью а и толщиной 2d± (где d±, хотя и ма
408
СПИНОВЫЕ волны
[ГЛ. 8
ло, но больше, чем толщина поверхностного слоя d), «разрезанному пополам» граничной поверхностью S. При достаточно малом первые два члена (8.3.5) дадут пренебрежимо малые вклады и результат интегрирования можно будет записать в виде
1Х + 12 = О,
(8.3.7)
где
= х V2Md7, v
I2 = J М х HsdV.
V
(8.3.8)
(8.3.9)
Применяя вторую формулу Грина [35] к проекциям (8.3.8) на
Рис. 8.3.1. К выводу граничных условий для намагниченности. 8 — граница между ферромагнетиком (г' < 0) и немагнитной средой.
оси декартовой системы координат, нетрудно преобразовать' в интеграл по поверхности >2, ограничивающей объем диска V:
1Х = q М X (iioeV) М d2.	(8.3.10)
Здесь пое — единичный вектор внешней нормали к 2, а (поЕ\/)М = = дМ/дп-£, — производная М по направлению этой нормали. Интегралом по боковой поверхности диска в (8.3.10) можно пренебречь. На внешнем (лежащем вне ферромагнетика) основании диска М = 0, а на внутреннем поЕ = —п0. Тог
да, считая площадь основания о малой (хотя и большей, чем боковая поверхность диска), получим окончательно
11 = — б9М х (n0V) М,	(8.3.11)
где (nov)M — производная М по направлению нормали к граничной поверхности «S’. Подчеркнем, что в (8.3.11) входит величина М внутри ферромагнетика — на расстоянии от границы, превышающем толщину поверхностного слоя.
Займемся теперь интегралом (8.3.9). Учтем, что П% существует лишь в поверхностном слое и изменяется быстро только в направлении z', а площадь основания диска о является малой. Тогда, принимая для Hs выражение (8.3.6), получим
d
12 = б М х По(Mn0) dz'.	(&3.12)
о
t 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ II НЕОДНОРОДНЫХ СРЕДАХ 409
В (8.3.12) от z' может зависеть не только Hs, но и вектор М — его направление и длина. Если изменением М в поверхностном слое можно пренебречь, то (8.3.12) примет вид
2зА'ч
12 = -^М хпо(Мпо),	(8.3.13)
где
d
о
(8.3.14)
— поверхностная плотность энергии взаимодействий, учитываемых эффективным полем Hg.
Можно рассмотреть и более общий случай, когда М изменяется в поверхностном слое, однако таким «симметричным» образом, что направления вектора Г2 и вектора М X п0 (вне поверхностного слоя) совпадают. В этом случае выражение (8.3.13) можно по-прежнему считать справс^ивым, принимая в нем, как и в (8.3.11), величину М вне поверхностного слоя. Но теперь определением поверхностной энергии Ks будет уже не формула (8.3.14), а равенство выражений (8.3.12) и (8.3.13).
Подставляя (8.3.11) и (8.3.13) в (8.3.7), получим граничное условие
2АЧ
X (n0V)M + п0 X М(п0М) = 0.	(8.3.15)
Это условие накладывается на вектор М вблизи границы, но вне поверхностного слоя, а свойства поверхности учитываются единственным параметром Kg.
Рассмотрим теперь случай малых колебаний намагниченности:
М = Мо -'г те’®', т Мо	(8.3.16)
и получим граничное условие для комплексной амплитуды переменной намагниченности т. Подставляя (8.3.16) в (8.3.15) и приравнивая нулю линейные по m члены, найдем в случае Мо = const, т. е. отсутствия доменной структуры,
gz0 X (nov) m 4- no X Zo (nom) + (nozo) n0 x Ш =,P, (8.3.17) где z0 — единичный вектор в направлении Мо, а
2KS-
(8.3.18)
Выражение (8.3.17) эквивалентно двум скалярным условиям для составляющих вектора ш. Направив оси координат, как показано на рис. 8.3.1 (ось х касательна к граничной поверхности),
410
СПИНОВЫЕ волны
[ГЛ. 8
и проектируя /8.3.17) на эти оси, получим
^+^c°s2e = °, ^ + ^cos2e = 0, (8.3.19)
где 6 — угол между постоянной намагниченностью и нормалью к граничной поверхности.
В важном частном случае, когда постоянная намагниченность перпендикулярна'поверхности (6 = 0), из (8.3.17) или (8.3.19) следует х)
^ + т = 0.	(8.3.20)
Для плоских спиновых волн
где кг- — составляющая волнового вектора в направлении нормали к поверхности. Поэтому относительная роль первого и второго членов в (8.3.17) или (8.3.20) изменяется в зависимости от величин £ и kZ’. В частности, в случае 6 = 0 условие (8.3.20) при Zcz-£J>1 (т. е. для слабой поверхностной анизотропии и коротких спиновых волн) переходит в условие
^ = 0,	(8.3.21)
которое было получено Аментом и Радо [253]. В другом предельном случае /с2;£	1 (т. е. достаточно сильной поверхностной ани-
зотропии) из (8.3.20) следует
ш = 0.	(8.3.22)
Этот случай, впервые рассмотренный Киттелем [254], получил название закрепления (pinning) магнитных моментов на поверхности.
Стоячие спиновые волны в нормально намагниченной пленке. В качестве примера граничных задач для спиновых волн рассмотрим стоячие спиновые волны в тонкой ферромагнитной пленке. Возможность возбуждения таких волн переменным магнитным полем была предсказана Киттелем [254] и экспериментально подтверждена Сиви и Танненвальдом [255]. Мы ограничимся наиболее простым случаем пленки, намагниченной перпендикулярно ее поверхности. Исследуем сначала собственные колебания намагниченности в такой пленке.
^Граничное условие, эквивалентное (8.3.20), было получено Киттелем [254] на простой модели — линейной цепочке спинов, рассматриваемых как классические векторы.
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 411
Итак, рассмотрим неограниченную плоскопараллельную пластину (рис. 7.2.1) из изотропного ферромагнетика х), намагниченного до насыщения внешним полем Но, направленным по нормали к пластине. Уравнение движения намагниченности в пластине (8.1.7), переходя к циркулярным переменным (1.2.39) и опуская диссипативный член, можно записать следующим образом:
<лт+ — ыЕт+ 4- T]V2m+ = — ^Muh+.	(8.3.23)
Здесь ®н = уЯго = у (Яо — 4я7И0), a h+ — внутреннее (размагничивающее) переменное поле. При этом исключаются из рассмотрения тонкие поверхностные слои, влияние которых будет учтено при помощи граничных условий. Поскольку эти условия накладываются только на поверхностях z = const, решение уравнения (8.3.23) можно искать в виде волны, стоячей по z и бегущей в плоскости ху,
т+ = (A cos kzz В sin /czz)e“‘!(fcxX+^).	(8.3.24)
Аналогично запишутся /г+ и магнитостатический потенциал ф. Подставляя выражения вида (8.3.24) в (8.3.23) или же производя замену (8.1.9) в (1.2.42), мы найдем восприимчивость для волны (8.3.24)
v =--------------- (8.3.25)
л+ мн +	—w	'	'
— такую же как и для бегущих (по всем трем координатам) волн, которые рассматривались в § 8.1.
Переход к волне, стоячей по z, не повлияет и на дисперсионное соотношение, которое по-прежнему будет иметь вид (8.1.14). Каи видно из (8.3.25) и (8.1.14) (это обстоятельство неоднократно отмечалось выше), собственная частота спиновой волны, вообще говоря, не совпадает с резонансной частотой восприимчивости Однако такое совпадение имеет место при
е _ arcsin 1	+ kv __ Q
= di СЫН 1/  ^2  — и,
т. е. при отсутствии зависимости от координат хну. Мы ограничимся рассмотрением именно этого простого случая.
При 0fc = 0 из (8.3.25) и (8.1.15) следует, что %+ = оо, и так как т+ должно быть конечно, то h+ = 0. Это же непосредственно видно из выражения (8.1.12). Снаружи пластины, как следует из
*) Мы не учитываем проводимости вещества пластины, хотя большинство экспериментов выполнялось с металлическими пленками. Но поскольку толщина пленки в этих экспериментах обычно меньше глубины проникновения поля в металл (толщины скин-слоя), учет проводимости не является особенно существенным.
412
СПИНОВЫЕ ВОЛНЫ
ГЛ. 8
(7.2.9) и (7.2.10), ф0 = const и h0+ = 0. Таким образом, в рассматриваемом случае переменное магнитное поле (для собственных колебаний) обращается в нуль как снаружи пластины, так и внутри. Тогда независимо от вида намагниченности т+ удовлетворяются оба электродинамических граничных условия и остается лишь учесть дополнительные граничные условия (8.3.20), В данном случае они будут иметь следующий вид:
— £	+ т+ == 0 при 2 = 0,
п	.	(8.3.26)
т+ = 0 при z = d.
Здесь учтено, что направление внешней нормали к граничной поверхности (см. рис. 7.2.1) при z = d совпадает, а при z = 0 — противоположно положительному направлению оси z.
Подставляя решение (8.3.24) при kx = kv = 0 в условия (8.3.26), получим соотношение между постоянными:
А = %kzB	(8.3.27)
и трансцендентное уравнение для кг = к:
lgkd=~^r'	(8.3.28)
Уравнение (8.3.28) можно, конечно, непосредственно решить графически, но удобнее заменить его двумя более простыми уравнениями х):
-tg^- = gA:,	(8.3.28')
с^!^- = 1к.	(8.3.28")
Графическое решение этих уравнений показано на рис. 8.3.2. Как видно из рис. 8.3.2, корни kd = Хп уравнения (8.3.28) (н = = 0, 1, 2,...) являются поочередно корнями (8.3.28') и (8.3.28"): четным п соответствуют корни (8.3.28'), а нечетным—корни'(8.3.28"). Нетрудно убедиться, что в первом случае решения будут антисимметричны относительно центра пластины (z = d/2), а во втором случае — симметричны. При достаточно больших п и g =f= 0
Хп^(п — 1)л.
При | = 0, т. е. при закреплении магнитных моментов
Хп = пл.	(8.3.29)
Поскольку (8.3.28) следует как из (8.3.28'), так и из (8.3.28"), его корни включают в себя корни обоих этих уравнений.
§ 8.31 ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 413
В этом случае на толщине пластины укладывается целое число полуволн, что непосредственно следует и из граничного условия (8.3.22).
Подставляя значения кп = X ,Jd в выражение для спектра (8.1.15), получим собственные частоты стоячих спиновых волн в пластине
®п = сон + т] (Xn/d)2.	(8.3.30)
В частности, при закреплении магнитных моментов
+ П №№	(8.3.31)
В этом случае резонансные частоты зависят от номера типа колебаний по квадратичному закону. По такому же закону зависят от и и резонансные поля при to — const.
Рассмотрим теперь возбуждение стоячих спиновых волн в пластине однородным внешним переменным полем. Согласно выражению (7.3.31) (которое, как уже отмечалось, справедливо и в данном случае) амплитуда намагниченности и-го типа колебаний Сп пропорциональна величине
Рис. 8.3.2. Графическое решение уравнений (8.3.28') и (8.3.28"), определяющих спектр стоячих спиновых волн в нормально намагниченной пленке. Цифры у точек пересечения — значения номера корня и.
-d
^^m^zjdz. (8.3.32)
о
Эта величина представляет собой собственный магнитный момент для данного типа колебаний, отнесенный к единице площади пластипы. Подставляя в (8.3.32) собственную функцию
тп+ = A cos knz + В sin knz	(8.3.33)
и учитывая соотношение (8.3.27) и уравнения (8.3.28') или (8.3.28"), получим
Жг = 2В]кп для нечетных п,
(8.3.34) Жг — 0 для четных п.
Таким образом, однородное переменное поле возбуждает только стоячие волны, соответствующие нечетным п (которые, как уже отмечалось выше, симметричны относительно центра пластины).
414
СПИНОВЫЕ волны
[ГЛ. 8
Выясним влияние граничных условий на возбуждение стоячих волн в пленке. При этом следует так нормировать собственную функцию (8.3.33), чтобы амплитуда ее была постоянной, например,
+ £2 = 1.
Тогда для нечетных п (для четных Сп =0), принимая во внимание (8.3.34) и (8.3.27), получим (со-знак процорциональности)
£n~(^/r+W*r.	(8.3.35)
Отсюда видно, что амплитуда стоячей волны возрастает с уменьшением £ и максимальна при £ = 0, т. е. при закреплении магнитных моментов.
Величиной, которая может быть непосредственно измерена, является переменный магнитный момент пленки
d
ЭД = \m+dz.	(8.3.36)
о
Если можно считать, что возбуждается только один тип колебаний, то
d
ЭД = Сп mn+dz = С„ЭД„. lb 1	lb lb
О
С учетом (8.3.34) и (8.3.35) получим
ЭД~[*п(1 + ^Г1-	(8.3.37)
Для случая закрепления (£ = 0) с учетом (8.3.29)
ЭД ccl/n2 .	(8.3.38)
Как видно из выражения (7.3.31), амплитуды возбуждаемых стоячих спиновых волн, а следовательно, и переменные моменты пленки содержат «резонансные знаменатели» сг — соп + шп<0п-И если частота переменного поля со или величина постоянного поля Но (входящая в соп) изменяется, то будут возбуждаться поочередно те типы колебаний, для которых Сп =/= 0. Амплитуда каждого из них будет изменяться по резонансному закону, и для того чтобы эти типы колебаний были различимы («разрешались»), должно выполняться условие
Ж > (ДЯ)П.	(8.3.39)
Здесь 8Н0 = (Н0)п —	— расстояние по полю между со-
седними типами, а (АЯ)П — полуширина резонансной кривой, связанная с параметром релаксации ап в (7.3.31) соотношением
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 415
7(ЫГ)п = an<f>n- В частности, для случая закрепления из (8.3.39) с учетом (8.3.31) получим
2д}тг>(ДЯ)п.	(8.3.40)
оптимистической оценкой для ме-
П 10	9 8 7 8 5 9 3
I "1 I I !	I—I—I
Рис. 8.3.3. Кривая резонансного поглощения электромагнитной энергии стоячими спиновы ми волнами в нормально намагниченной плег ке кобальта [257]. Частота 8,8 Ггц. Толщи на пленки d = 2940 А. Цифры у максиму мов — значения постоянного поля в эрстедах.
Отсюда видно, что стоячие спиновые волны можно наблюдать лишь в достаточно тонких пленках. Принимая, например, (&Н)п = = 10э (что является довольно таллов) и D = 1(Г;', получим (при п = 5) d < 10-4 см.
Экспериментальному исследованию стоячих спиновых волн в тонких ферромагнитных пленках было посвящено огромное количество работ (см., например, [257, 265, 270]). Интерес к этому явлению обусловлен в значительной степени тем, что оно является, пожалуй, наиболее прямым доказательством реальности существования спиновых волн и дает возможность, в принципе, очень просто измерять основную характеристику спектра спи
новых волн — константу неоднородного обменного взаимодействия.
Эксперименты показали, что в ряде случаев, особенно, когда принимались меры для получения однородных по толщине пленок, неплохо выполнялись предсказания рассмотренной выше теории. К числу их относятся: преимущественное возбуждение волн с нечетными п, а также (при £ = 0) убывание интенсивностей этих волн как 1/п2 и квадратичная зависимость резонансных полей от п. Поскольку две последние зависимости справедливы только при £ = 0, их экспериментальное подтверждение, когда оно имело место, говорило в пользу закрепления магнитных моментов на поверхности (кс, 1). Результаты двух работ, в которых наблюдались указанные зависимости, приведены на рис. 8.3.3 и рис. 8.3.4.
Однако в других случаях имели место «аномальные» зависимости Ярез (и). Они не могли быть объяснены неполным закреплением. Для их объяснения Портис (см. [262]) выдвинул предположение, что постоянная намагниченность Мо может быть неоднородна не только в поверхностном слое (что учитывается граничными условиями), но и во всей пленке. Собственные колебания
416
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
Рис. 8.3.4. Зависимости резонансного поля от номера колебания для стоячих спиновых волн в двух нормально намагниченных пленках пермаллоя (82% Ni, 18% Ре) [265]. Пленки были приготовлены способом, обеспечивающим их однородность. Частота 12,3 Ггц.
намагниченности в такой пластине с Мо (z') отличаются от синусоидальных стоячих волн (8.3.33), что приводит к другим зависимостям резонансных полей и интенсивностей возбуждения от п. Если принять зависимость Мо (z') параболической, то задача может быть сравнительно легко решена [262], и полученный закон Ярез(п), близкий к линейному при малых п и квадратичному при больших, хорошо соответствует результатам некоторых экспериментов.	B-ti
Мы пе будем останавливаться подробно на других граничных задачах для спиновых волн (касательно намагниченная пластина [263], цилиндр и пр.). Путь их решения, в принципе, такой же, как для поперечно намагниченной пластины. Он сводится к наложению электродинамических граничных условий и дополнительного условия (8.3.17) на решения уравнений магнитостатики при восприимчивости х» полученной с учетом неоднородного обмена. Однако вычисления, к которым это приводит, оказываются значительно более громоздкими, чем в рассмотренном выше простом случае Мо || п01| к, когда х (без учета дис
сипации) обращалась в бесконечность. Ясно, что при D —> 0 решения граничных задач для спиновых волн должны переходить в решения соответствующих задач, полученные в § 7.2 без учета неоднородного обмена.
В § 7.2, в частности, была рассмотрена задача о распространении волн в продольно намагниченном круглом ферромагнитном стержне. Полученное дисперсионное соотношение при больших kz имело вид (7.2.38). Учет неоднородного обменного взаимодействия приводит к тому, что в этом соотношении появляется дополнительный член, пропорциональный квадрату волнового числа [216]:
« ~ 4-1 ымтЙВ- +	(8.3.41)
Заметим, что при наличии неоднородного обменного взаимодействия, так же как и без него (§ 7.2), могут существовать поверхностные спиновые волны [215, 264]. Они распространяются вдоль поверхности раздела (например, ферромагнетика с немагнитной средой), и амплитуды их переменной намагниченности
§ 8.3J ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 417
Рис. 8.3.5. Возбуждение спиновых волн в неоднородном постоянном поле, а — зависимость постоянного поля от координаты z (пунктир — зависимость, принятая при расчете); б — зависимость волнового числа от х\ в — мгновенное значение переменной намагниченности (схематически).
убывают по экспоненциальному закону по мере удаления от этой поверхности.
Возбуждение спиновых волн в неоднородном постоянном поле. Перейдем теперь ко второму классу задач, составляющих содержание этого параграфа,— спиновым волнам в средах с параметрами, зависящими от координат. Рассмотрим распространение спиновых волн в неоднородном постоянном магнитном поле. В таком поле, как показал Шлёманн, бегущие спиновые волны могут весьма эффективно возбуждаться однородным переменным полем.
Рассмотрим, следуя Шлё-манну [260, 261], неограниченный ферромагнетик, находящийся в неоднородном постоянном внутреннем магнитном поле Нг0 = z0 Яго(х), направленном по оси z и зависящем только от z. Предположим, что все остальные параметры вещества, включая и постоянную намагниченность Мо — z0 2И0, не зависят от координат. Пусть
Hi0 (— оо) = Яъ
#io( + °°) = Н 2, и изменение Яо происходит плавно, в основном,, в- некотором интервале Zj z2 (рис. 8.3.5, а). Предположим далее, что Нг и/у Н2, так что Hi0 = co/у в некоторой точке z0, лежащей в интервале zx z2. По причинам, которые будут ясны ниже, эту точку называют точкой поворота.
Будем рассматривать спиновые волны, распространяющиеся вдоль оси z. Для них дисперсионное соотношение имеет вид (8.1.15), откуда
= (8-3-42)
Из (8.3.42) следует (см. рис. 8.3.5, б), что 0 при z z0 (справа от точки поворота) и к2 <; 0 при z < z0. Иными словами, справа от точки поворота имеют место бегущие волны с волновым
14 А. Г. Гуревич
418
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
числом, возрастающим при увеличении £, а слева от этой точки — колебания с экспоненциально убывающей амплитудой. В точке поворота, согласно (8.3.42), волновое число к обращается в нуль.
Однако следует помнить, что соотношение (8.3.42) и, вообще, представление решения в виде синусоидальной волны приближенно справедливы лишь при условии, что Яго изменяется достаточно медленно на расстояниях, сравнимых с i/jkl. Это условие, которое может быть записано в виде
Idf/ I
<|7c]ZTi0,	(8.3.43)
выполняется лишь вдали от точки поворота. Вид решения в окрестности точки поворота нам пока неизвестен; он, конечно, зависит от конкретного закона Hi0 (z). Однако можно предполагать, что при плавном изменении Hi0 (рис. 8.3.5, а) характер зависимости переменной намагниченности от z будет примерно таким, как показано на рис. 8.3.5, в. Вблизи точки поворота возникнет не обращающийся в нуль суммарный собственный переменный магнитный момент, который и обеспечивает возможность возбуждения бегущей спиновой волны справа от точки поворота однородным переменным магнитным полем, приложенным вблизи этой точки.
Перейдем теперь к количественному рассмотрению задачи о возбуждении спиновых волн в неоднородном постоянном поле. Следуя Шлёманну [2601, зададимся простым законом изменения Hi0:
Hi0 (z) - Я2 + 4/z\	(8.3.44)
который позволит, как мы увидим, легко довести до конца все вычисления! Зависимость (8.3.44) показана (пунктиром) на рис. 8.3.5, а. Опа довольно хорошо аппроксимирует зависимость Hi0(z), принятую при качественном рассмотрении, (сплошная линия на рис. 8.3.5, а) справа и в окрестности точки поворота. Что же касается существенного различия их слева от z0, то оно не сыграет большой роли, так как в этой области амплитуды колебаний малы.
Уравнение движения намагниченности после перехода к циркулярным переменным будет иметь вид
т+ ~
или с учетом (8.3.44)
(8.3.45)
(8.3.46)
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 419
Здесь
к
2 __ 1 w _______ IT
2
(8.3.47)
— асимптотическое значение квадрата волнового числа при z_+oot a z0 — координата точки поворота, которая, как следует из (8.3'42), (8.3.44) и (8.3.47), связана с константой А соотношением
k2z0 = VAjD.	(8.3.48)
Рассмотрим сначала уравнение (8.3.46) без правой части. Подстановкой m+= z у оно сводится, как нетрудно убедиться, к уравнению Бесселя порядка
р = V k22zl + 1/4.	(8.3.49)
Отсюда следует, что в качестве фундаментальных решений (8.3.46) могут быть приняты
mi = z (k2z), т2 =	Н<$> (k2z), (8.3.50)
где (k2z) и (k2z) — функции Ханкеля первого и второго рода [42]. Учитывая асимптотическое поведение функций Ханкеля при больших значениях аргумента, легко убедиться, что фундаментальные решения (8.3.50) при z—>-оо принимают вид
(™1,2)ос
+ i(klZ_^_2L) е- V 2	4'
(8.3.51)
т. е. превращаются в бегущие синусоидальные волны.
Решение уравнения (8.3.46) с правой частью, согласно методу вариации постоянных (см., например, [39]), можно искать в виде
т+ =	(z)	+ С2 (z) т2.	(8.3.52)
Для функций Сг (z) и С2 (z) имеет место система уравнений
dCx dC%
откуда
dmi dCi dm2 dC? dz dz dz dz
(8.3.53)
dCi Mo , dC2 Mo 7 dz ~ ~DW	17 “ ~ "W
(8.3.54)
Здесь W — определитель системы (8.3.53) — определитель Врон-f-° исходного уравнения (8.3.46). Согласно формуле Лиувилля в.датшом случае (когда уравнение не содержит первой произ-днои) определителя Вронского це зависит от Оц может быть,
420
СПИНОВЫЕ ВОЛНЫ
ГГЛ. 8
таким образом, вычислен при z—>оо, когда и т2 имеют вид (8.3.51). Это дает
W = — 2 ik2.	(8.3.55)
Предположим, что переменное поле h+ не обращается в нуль в некотором интервале z3 -ь zt (рис. 8.3.5, а), содержащем точку поворота. Тогда из (8.3.54) с учетом (8.3.55) следует
Z
С1,2 = + 4^ Ц rn2ilh+dz 4-	(8.3.56)
«3
(если z z4, то интегрирование производится фактически до z4)-Общее решение (8.3.52) уравнения (8.3.46) запишется теперь в виде
Z	Z
т+ =	m2h+dz — т2 mji^dz + ф- B2m2j .	(8.3.57)
Для определения постоянных Вг и В2 на решение (8.3.57) необходимо наложить следующие граничные условия.
1) При z —оо решение т+ должно быть пропорционально т2, так как должна отсутствовать волна, распространяющаяся из (+°о). Это условие, как видно из (8.3.57), дает
Вх = — \ m2h+dz.	(8.3.58)
Zs
2) При z -> 0 решение должно быть ограничено, т. е. т+ должно быть пропорционально тх + т2, так как
mi +	== 2	z Л> (^2Z)	(8.3.59)
— единственная линейная комбинация фундаментальных решений, ограниченная при z = 0 (Jp (k2z) — функция Бесселя). Из этого условия следует
В± = В2	(8.3.60)
(интегралы в (8.3.57) обращаются в нуль при z = 0, так как точка z = 0 лежит вне интервала z3 -г- z4, в котором^ =f= 0).
Окончательно с учетом (8.3.60) и (8.3.58)
'z	z	z4
^m2k+dz — т2 ^mxh+dz — (тх 4- т2) ^m2/i+dzj .
2g	Z3	Zg
(8.3.61)
Нас интересует решение при2-> оо. Предположим, что h+ постоянно в интервале z3 f- z4. Тогда; из (8.3.61) с учетом (8.3,51)
§ 8.3] ВОЛНЫ В ОГРАНИЧЕННЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ 421
и (8.3.59) получим
, . Mfh I
= -^Ге
(8.3.62)
где
I = УZ Jv (k2z) dz.	(8.3.63)
г8*
Таким образом, решение при больших z действительно представляет собой волну с волновым вектором /с2, бегущую от области возбуждения. Амплитуда этой волны пропорциональна величине I, которую можно назвать длиной области взаимодействия (электромагнитного поля со спиновой волной).
Оценка (см. ниже) показывает, что величина k2z0, а следовательно, и. порядок (8.3.49) функции Бесселя в (8.3.63) много больше 1. Характер зависимости функции Бесселя большого порядка р от аргумента х иллюстрирует рис. 8.3.6; первый максимум этой функции находится вблизи х = р, т. е. как раз
около точки поворота. Отсюда следует, что интеграл в (8.3.63) может быть приближенно замене11 интегралом от 0 до оо. Вычисление его [261] дает	___
(8.3.64) Т 4^2
Поток энергии спиновой волны с круговой поляризацией может быть вычислен по формуле [260]
П = т*к.	(8.3.65)
Подставляя сюда (8.3.62) и учитывая (8.3.64), получим
/Г=	h\.	(8.3.66)
2 Dk*
Выражение (8.3.66) представляет собой результат решения рассматриваемой задачи. Однако входящая в зто выражение величина zo не является «хорошем» параметром, поскольку она связана в
422
СПИНОВЫЕ ВОЛНЫ
принятым конкретным законом (8.3.44) изменения поля, в то время как результат должен, по-видимому, зависеть лишь от поведения поля вблизи точки поворота. Поэтому мы перейдем от z0 к градиенту поля dll.-Jdz в точке z0. Дифференцирование (8.3.44) дает
I dHin |	2Dkl
=-----2.	(8.3.67)
dz L zo	4	'
I	1 Zn
С учетом (8.3.67) окончательно
ntoMo
hl
(8.3.68)
Как показано в [261], к выражению (8.3.69) можно прийти, не задаваясь конкретным законом Но (z), а предполагая лишь общий ход поля, показанный на рис. 8.3.5, а, и линейное изменение поля вблизи точки поворота. Из (8.3.68) видно, что эффективность преобразования электромагнитной энергии в энергию спиновой волны увеличивается с уменьшением градиента постоянного поля в точке поворота. Из параметров вещества эффективность преобразования зависит только от постоянной намагниченности.
Наличие диссипации (которая не учитывалась выше) приведет к тому (см. § 8.1), что возбуждаемая спиновая волна будет довольно быстро затухать. Поэтому практическая реализация рассмотренного метода возбуждения спиновых волн возможна лишь в веществах с достаточно малой диссипацией, например, в монокристаллах иттрий-железного граната. Вторым усложняющим обстоятельством является наличие магнитоупругого взаимодействия. При значениях лишь не намного меньших величины поля в точке поворота, имеет место [332—334] пересечение спектров спиновых и упругих волн (см. § 9.4). В этой области магнитоупругое взаимодействие приводит, как показали Шлёманн и Джозеф [338], к весьма эффективному преобразованию спиновой волны в упругую. Таким образом, волной, которая в рассмотренной выше задаче уходит на (+ оо), будет фактически упругая волна. Отсюда ясно, что вещество, в котором может наблюдаться возбуждение спиновых волн в неоднородном постоянном поле, должно обладать также очень малыми упругими потерями. Иттрий-железный гранат хорошо удовлетворяет и этому требованию.
Неоднородность внутреннего постоянного поля, необходимая для возбуждения спиновых волн рассмотренным способом, может быть проще всего реализована при помещении ферромагнитных образцов неэллипсоидальной формы в однородное внешнее поле. Так, например, внутреннее поле в ферромагнитном цилиндре, находящемся в однородном внешнем поле Но, параллельном его оси, имеет вид, показанный на рис. 8.3.7. Как видно из рис. 8.3,7, ве-
J S.S1 Е6ЙПЫ fi бГрАЙЙЧЕЙНЫХ ТЕЛАХ И НЕОДНОРОДНЫХ СРЕДАХ
Рис. 8.3.7. Внутреннее поле на оси ферромагнитного цилиндра, находящегося во внешнем поле И 0, параллельном оси.
личина Но может быть выбрана такой, чтобы внутри образца имели место «точки» поворота (в действительности из-за неоднородности поля в радиальном направлении это будут некоторые криволинейные поверхности). В них приложенное к образцу переменное магнитное поле будет возбуждать спиновую волну, распространяющуюся по направлению к ближайшему торцу образца.
Такое возбуждение спиновых волн в неоднородном внутреннем постоянном поле наблюдалось в цилиндрах из монокристаллов иттрий-железного граната и некоторых других ферритов и было подвергнуто подробному экспериментальному исследованию (см., [347]). Заметим, что при этом имели место градиенты постоянного поля порядка 103 дкм. Принимая, например, [dHi0/dz\ = 3-103 и к2 = 105, получим, что порядок функции Бесселя в (8.3.63) р = = 400; таким образом, сделанное выше предположение (р 1) хорошо оправдывается.
Заметим, что наличие магнитоупругого взаимодействия, т. е. связи магнитной системы с колебаниями кристаллической решетки, приведет к тому, что спиновые волны, возбужденные пере
менным магнитным полем в ферритовом цилиндре (см., например [339, 342, 351]), будут преобразовываться в упругие волны1). Это преобразование, как уже отмечалось выше, происходит, в основном, в «точках» пересечения спектров магнитных и упругих волнгх и zu которые лежат вблизи точек поворота z0 и г0(рис. 8.3.7). В результате распространения упругих волн по цилиндру, отражения их от торцов и обратного преобразования в спиновые волны будут образовываться последовательности задержанных сигналов. Скорость распространения спиновых волн, а также положения точек поворота и точек пересечения спектров зависят от со и Но. Таким образом, рассматриваемая система может быть использована для создания дисперсионной и управляемой линии задержки. 1акая — магнитоупругая линия задержки конструктивно не отличается от магнитостатической линии задержки (§ 7.2), отличие заключается лишь в величине постоянного магнитного поля.
вармл“^РаВИЛЬиее ГОВОРИТЬ ° возбуждении и распространении в рассматри-слгч»И сястеме смешанных магнито упругих волн [340, 341], предельными у ями которых являются спиновые и упругие волны.
424
СПЙЙОВЫЕ ВОЛНЫ
[гл. 8
Аналогичное возбуждение спиновых волн (с последующим преобразованием их в упругие) наблюдалось в нормально намагниченном диске Эшбахом [259]. Поверхностью поворота в этом случае являлась цилиндрическая поверхность So (рис. 8.3.8) и возбуждаемая волна представляла собой цилиндрическую волну, распро-
страняющуюся в радиальном направлении.
В рассмотренной выше теории возбуждения спиновых волн в
неоднородном постоянном поле использовалась одномерная мо-
Рис. 8.3.8. Возбуждение спи-
дель — система предполагалась неограниченной и однородной в поперечных (перпендикулярных оси z) направлениях. Эксперименты же проводились в стержнях и дисках с поперечными размерами, измеряемыми единицами миллиметров. Для спиновых волн с большими к (при которых уже необходимо принимать во внимание неоднородный обмен) учет неодномерности задачи, т. е. граничных условий на боковой
новых волн в нормально на- поверхности стержня или торцевых поверх-магниченном диске 1259J.	J	л
пунктиром показана цилин- иостях диска, как уже отмечалось выше, дрическая^рПоверхность по- несуществен. Но вблизи поверхностей поворота, где возбуждаемые волны имеют к ~ 0, учет граничных условий становится необходимым. Волны,которые возбуждаются в этих областях, представляют собой в действительности безобменные магнитостатические волны со спектром, зависящим от поперечных размеров (см. §7.2), но, конечно, с переменным к. При дальнейшем распространении волн, по мере увеличения к, влияние граничных условий на их спектр становится все меньшим, и при к ~ 102 -i- 103 этим влиянием можно уже пренебречь.
§ 8.4. Магноны
Во всех предыдущих главах и предыдущих параграфах этой главы высокочастотные процессы в магнитоупорядоченных веществах трактовались как колебания или волны намагниченности М (г, t) (в антиферро- и ферримагнетиках — как связанные колебания или волны намагниченностей подрешеток М7- (г, /)). При описании таких процессов мы исходили из уравнений движения намагниченностей М или М; — уравнений Ландау — Лифшица, которые, по существу, постулировались. Принимались также во внимание уравнения макроскопической электродинамики, в силу которых изменения намагниченности связывались с изменениями электромагнитного (в магнитостатическом приближении — магнитного) поля в веществе. Таким образом, рассмотренная выше теория высокочастотных процессов в ферро- и антиферромагне
МАГНОНЫ
425
§ 8.4]
тиках основывалась на континуальной модели и была классической При этом "она обязана была быть феноменологической, поскольку невозможно понять природу взаимодействий, вычислить величины констант, входящих в выражения для энергии и уравнения движения, и даже обосновать сколько-нибудь строго вид уравнений движения, оставаясь в рамках классической, макроскопической теории.
В следующем параграфе мы рассмотрим высокочастотные процессы в магнитоупорядоченных веществах, исходя из микроскопической модели и пользуясь, естественно, методами квантовой механики. Но предварительно отметим, что, используя общий принцип корпускулярно-волнового дуализма — один из фундаментальных принципов физики, можно перевести на корпускулярный язык («проквантовать») все полученные выше результаты. Принцип корпускулярно-волнового дуализма заключается в том, что любые колебания или волны можно рассматривать также как скопления или потоки частиц, энергия которых пропорциональна частоте колебаний, а импульс — волновому вектору. Электромагнитным волнам соответствуют в этом смысле частицы — фотоны, а таким «материальным» (обладающим, в отличие от фотонов, массой покоя) частицам, как электроны, протоны и пр.,— волновые функции, с которыми имеет дело квантовая механика.
Различного рода возбуждения в твердом теле — упругие, магнитные и др., также можно рассматривать двояко: либо как колебательные процессы, происходящие в среде, либо как некоторые частицы. Например, в случае механических колебаний — тепловых или когерентных, такими частицами будут фононы. И если среду, в которой происходят колебания, считать состоящей из дискретных частиц (а, строго говоря, мы должны поступать именно гак), то частицы или, как их обычно называют, квазичастицы — аналоги колебаний (например, фононы) будут принципиально отличаться от частиц (атомов, ионов), образующих среду. Наиболее существенными отличиями их от «настоящих» частиц являются не-сохранение их числа и отсутствие локализации в пространстве.
Квантование спиновых волн. Из сказанного ясно, что можно проквантовать и исследованные выше на континуальной модели магнитные колебания и волны (спиновые волны в широком смысле слова), т. е. сопоставить этим волнам некоторые квазичастицы. Энергия каждой из них
е = tie>,	(8.4.1)
где о — частота магнитных колебаний или волн, а импульс
р = Лк,	(8.4.2)
где к —- волновой вектор магнитной волны. Такие квазичастицы носят название маенонов.
426
СПИНОВЫЕ ВОЛНЫ
ГГЛ. 8
Зависимость го(к), вычислением которой для разных случаев мы подробно занимались выше, выражает в то же время, как видно из (8.4.1) и (8.4.2), зависимость в (р), т. е. закон дисперсии магнонов.
В частном случае однородной прецессии импульс магнонов р = 0, а энергия
е0 = Йк>о,’	(8.4.3)
где соо — частота однородного ферромагнитного или антиферромагнитного резонанса. В другом крайнем случае больших к, когда в выражении (8.1.14) для частоты спиновых волн ферромагнетика можно пренебречь всеми членами кроме обменного,
еЦр2-	(8.4.4)
Сравнивая это выражение с соотношением между энергией и импульсом свободной нерелятивистской частицы е = р2/(2т0), мы видим, что в данном случае (при больших к) магнон в ферромагнетике является свободной частицей с эффективной массой
т0 = Й/2тр	(8.4.5)
Оценка для иттрий-железного граната (ц = 0,1) показывает, что т0 превышает приблизительно в 5 раз массу покоя электрона.
На корпускулярном языке высокочастотная магнитная энергия ферро- или антиферромагнетика запишется следующим образом:
W = 2 «Л + 2 nftefc,	(8.4.6)
V	к
где tb — числа магнонов, соответствующих различным типам прецессии, а Пь — числа магнонов, соответствующих спиновым волнам с достаточно большими волновыми векторами к. При этом предполагается, что допустимые значения к дискретны.
Дискретность спектра собственных магнитных колебаний должна иметь место — вследствие влияния граничных условий — для любых образцов конечных размеров. Однако для коротковолновых спиновых волн, как отмечалось выше, конкретный вид граничных условий и форма граничных поверхностей несущественны (они влияют только на величину внутреннего постоянного поля); эти типы колебаний во многих случаях можно считать плоскими волнами и характеризовать вектором k. II для того чтобы наиболее простым путем получить дискретность значений к, можно ввести, как это часто делается в физике твердого тела (см., например, [32]), периодические граничные условия Борна — Кармана. При этом следует считать, что М; (г) — периодические функции координат х, у и z с периодами, соответственно, 12
МАГНОНЫ
427
§ 8.4]
и I Тогда допустимыми значениями проекций волнового вектора будут
,	2«V1	, 2лу2 , 2луз
^=-ТГ' к^~'
(8.4.7)
где vx, v2 и v3 — целые числа. Пока используется континуальная модель, значения этих чисел не ограничены.
Запись энергии в виде (8.4.6) предполагает также, что взаимодействие между типами колебаний с разными к отсутствует, т. е. «газ магнонов» является идеальным. Пока мы находимся в рамках линейного приближения (рассматриваем малые колебания), а диссипацию учитываем только феноменологически (не интересуясь теми процессами, которые к ней приводят), это предположение выполняется.
Связь между составляющими намагниченности и числами магнонов. Рассмотрим теперь связь между величинами М; (г) и числами магнонов щ и щ. Как известно, квантовая механика (нерелятивистская) частиц с нулевым спином имеет дело со скалярной волновой функцией ф (г). Величина |ф (r)|2 dV пропорциональна (при соответствующей нормировке волновой функции — равна) вероятности обнаружения частицы в объеме dV. При достаточно большом числе частиц величины | ф (г)|а пропорциональны числам частиц в соответствующих точках пространства. В нашем случае квантуются векторные поля М7 (г), и вопрос о связи чисел магнонов с составляющими векторов М, (г) требует специального обсуждения.
Для того чтобы найти число магнонов, соответствующее колебанию или волне с заданной амплитудой переменной намагниченности, достаточно приравнять классическую высокочастотную магнитную энергию, выраженную через эту амплитуду, величине щщ или nfceif. Здесь ev или — энергия одного магнона, которая определяется соотношением (8.4.1).
Ограничимся для простоты ферромагнетиком и рассмотрим сначала частный случай однородной прецессии малого эллипсоида. Энергия его будет состоять из зеемановской энергии (2.1.1) и энергии размагничивающих полей (2.1.3), в последнюю формально с помощью эффективных размагничивающих факторов (см. § 2.1) может быть включена и энергия анизотропии. Будем интересоваться только колебательными членами энергии и учтем соотношение 2)
~	- 23Г,	(8.4.8)
*) Величины т~х и — мгновенные значения, в отличие от комплексных амплитуд тх и mv.
428
СПИНОВЫЕ волны
1ГЛ. 8
вытекающее в случае малых колебаний из условия сохранения длины вектора М. Тогда плотность энергии однородной прецессии эллипсоида запишется в виде
II	Л	d
U°= W	+ 2 m~x - Л'2) + 4 (Nv - Nz).
Приравняв ее величине
и о = Ь&дПо,
где <оо — частота однородной прецессии, можно определить число магнонов однородной прецессии (в единице объема) п0. Выражение для него получается особенно простым, если образец представляет собой эллипсоид вращения относительно оси z, а ось анизотропии (в случае кубического кристалла — ось <100} или <111» совпадает с осью z. Тогда Nx — Nv ss А'_ц и, как легко убедиться,
0 2л7оТЙ
~х
(8.4.9)
В этом частном случае прецессия является круговой с амплитудой т = У т^х	и (8.4.9) может быть переписано в виде
пгг
Пп — -----т •
0 2'ИоТЙ
(8.4.9')
Для спиновых волн применим тот же путь определения чисел магнонов; необходимо лишь включить в выражение для энергии энергию неоднородного обменного взаимодействия и объемных размагничивающих полей и не включать энергию поверхностных размагничивающих полей. Как и в случае однородной прецессии, результат оказывается простым, когда прецессия намагниченности является круговой, т. е. для волн, распространяющихся вдоль оси z. В этом случае, аналогично (8.4.9) и (8.4.9'),
2МщН 2мщК'
(8.4.10)
Выражение (8.4.10) остается приближенно справедливым и для волн, распространяющихся в произвольном направлении, если выполняется условие
Но 4- Dk2 4лМ0,	(8.4.11)
при котором (см. § 8.1), поляризация спиновой волны близка к круговой. Выражение (8.4.9) приближенно справедливо для произвольного эллипсоида при аналогичном условии
Но > 4лМ0.
§ 8.4]
МАГНОНЫ
429
Если же прецессия намагниченности не будет близка к круговой, то "простые выражения (8.4.9) и (8.4.10) будут справедливы лишь по порядку величины.
Используя соотношение (8.4.8), можно переписать (8.4.9) и (8.4.10) в виде
Мо — Mz = nyh,	(8.4.12)
где п — число магнонов однородной прецессии (и0) или спиновых волн («ь) в единице объема. Иными словами, каждый магнон однородной прецессии или спиновых волн уменьшает z-составляю-щую намагниченности на величину yh = ррн (где — магнетон Бора).
Для неоднородных длинноволновых (уокеровских) типов прецессии, в отличие от однородной прецессии и бегущих коротковолновых спиновых волн, имеет смысл говорить лишь о числах магнонов ш во всем образце. Эти числа можно определить, приравнивая высокочастотную магнитную энергию образца при данном типе прецессии величине п,Л(о... При тех же условиях, что и выше (малые колебания; прецессия, близкая к круговой), получим
1 с
(8А13>
V
И если в образце существуют одновременно однородная прецессия, различные уокеровские типы колебаний и спиновые волны с различными к, то полное изменение z-составляющей магнитного момента образца 2)
M0V — ЭЛ2 = пуП,	(ЪЛЛЬ)
где в = п0 + 2	+ 2 пк — полное число магнонов в образце,
v	к
Заметим теперь, что для всех неоднородных типов колебаний (как уокеровских типов прецессии, так и спиновых волн ) поперечные составляющие полного магнитного момента -ЭК образца обращаются в нуль. Следовательно,
ЭЛХ = VmOx, gnv = VmOy,
где тОх и тоу — составляющие намагниченности однородной прецессии. Тогда, вычисляя ®2 =	с учетом
(8.4.14) и (8.4.9) и принимая во внимание, что для малых колебаний ну M0V, найдем
ЭЛ = M0V — (п — п0) ун.	(8.4.15)
]) Важное соотношение (8.4.14) может быть выведено более строго, чем это было сделано выше (см., например., [20]).
430
СПИЙОВЫЕ ВОЛНЫ
1гл. 8
Таким образом, уменьшение длины вектора магнитного момента образца определяется магнонами всех типов, кроме магнонов однородной прецессии. Следует подчеркнуть, что формула (8.4.15) справедлива только для образца (малого эллипсоида) в целом, аналогичное соотношение для намагниченностей, вообще говоря, не имеет места. Однако если отсутствуют уокеровские типы колебаний (вклад которых в 3Jix и обращается в нуль только при усреднении по всему образцу), то соотношение (8.4.15) может быть записано и для любой области, размеры которой значительно превышают длины спиновых волн.
Магноны при наличии диссипации. Рассмотрим теперь, как повлияет на квантовую (корпускулярную) картину спиновых волн диссипация, которую мы до сих пор не принимали во внимание. Заметим прежде всего, что учет диссипации не изменит энергии и импульса магнонов. Иными словами, <о и к в выражениях (8.4.1) и (8.4.2) — это всегда вещественные величины, не зависящие от диссипации. Учет диссипации приведет лишь к тому, что время жизни магнонов и длина их пробега станут конечными. Среднее время жизни магнонов с учетом (8.4.9) и (8.4.10) будет равно времени релаксации квадрата амплитуды соответствующих колебаний или волн, т. е. совпадет с введенным в § 8.1 временем жизни спиновой волны (8.1.32). Средняя длина пробега магнонов lh совпадает с длиной пробега спиновой волны (8.1.33).
Уменьшению амплитуд переменной намагниченности при свободных затухающих магнитных колебаниях или волнах соответствует, таким образом, уменьшение чисел магнонов. Оно происходит в результате элементарных процессов столкновений магнонов между собой и другими квазичастицами. Феноменологический учет этих процессов и приводит к появлению диссипативных членов в уравнениях движения намагниченности. При вынужденных незатухающих колебаниях постоянство чисел магнонов поддерживается процессами рождения магнонов, например, за счет уничтожения фотонов возбуждающего электромагнитного поля.
Заметим, что говорить о магнонах, как и о других квазичастицах, имеет смысл, если
Tfc^>l/tofc и lh>ilk.	(8.4.16)
Аналогия^ с уравнением Шредингера. Число магнонов (в случае круговой прецессии), как видно из (8.4.10), пропорционально квадрату амплитуды прецессии т, аналогично тому, как в квантовой механике электронов число их пропорционально квадрату модуля волновой функции ф. Можно полагать, исходя из этого, что уравнение движения для т должно быть аналогично уравнению Шредингера для функции ф 2). Действительно, в простейшем
*) Такую аналогию впервые отметил Шлёманн. В случае произвольной (не круговой) прецессии она рассмотрена Цукерником [249].
S 8.41
МАГНОНЫ
431
случае спиновой волны, распространяющейся по оси ? в изотропном ферромагнетике без диссипации, уравнение движения может быть записано в виде
(8.4.17)
где D — константа неоднородного обменного взаимодействия (8.1.41) (уравнение (8.4.17) можно получить проектированием (2.1.31) с учетом (8.1.3)). Уравнение же Шредингера (см., например, [30]) для принятой нами зависимости от времени г) е’“г будет иметь вид
! .f. д , ft? (ft тт \ , п	/о г ло\
нт +	—77 ф = 0,	(8.4.18)
\ dt 2mo5z2 у т »	'	'
где тп0 — масса частицы, a U — ее потенциальная энергия. Уравнения (8.4.17) и (8.4.18) совпадают, если
=	Йа/2ш0	(8.4.19)
И	=	U.	(8.4.20)
Из	(8.4.19)	следует,	что	эффективная	масса	квазичастиц,
соответствующих	«волновой функции»	т,	т.	е.	магнонов,	опреде-
ляется по-прежнему выражением (8.4.5), которое было получено ранее для «свободных» магнонов (при Но = 0). Из (8.4.20) видно, что потенциальная энергия магнона во внешнем поле Но составляет уЛН0, т. е. магнон имеет магнитный момент ш, равный по абсолютной величине уЛ и направленный в рассматриваемом частном случае антипараллельно внешнему постоянному полю. В общем случае он будет антипараллелен оси z, совпадающей с направлением постоянной намагниченности, так что
m = — гоуЛ = — zogp,B.	(8.4.21)
Очевидно, что это же следует из выражений (8.4.14) или (8.4.15).
Спин и статистика магнонов. Магноны являются элементарными возбуждениями магнитной системы, образованной 3d- или 4/-электронами. Поэтому естественно предположить (конечно, это рассуждение не строго), что и магнитомеханическое отношение для квазичастиц — магнонов будет таким же, как и для действительных частиц — электронов, образующих рассматриваемую магнитную систему, т. е. будет равно (— у). Тогда, согласно (8.4.21), магнон будет обладать механическим моментом (спином), равным Л или в единицах Л — спином, равным 1. Поскольку магнитный момент магнона антипараллелен оси z, механический момент будет направлен по оси z.
*) В квантовой механике принимается обычно зависимость е-г“\ вследствие чего знак перед первым членом в (8,4,18) изменяется на обратный.
432
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 9
Как известно [30], частицы с нулевым или целым (в единицах К) спином подчиняются статистике Бозе—Эйнштейна; число таких частиц (бозе-частиц или бозонов) в данном состоянии не ограничено. Функция распределения бозе-частиц по энергиям в случае «идеального газа» (когда взаимодействием частиц между собой можно пренебречь) и непостоянного числа частиц в системе имеет вид [36]
1 7? —Z ______
’	(8-4-22)
е — 1
Здесь п — среднее число частиц в каждом состоянии с энергией е, а х — постоянная Больпмана.
Поскольку магнонам, как отмечалось выше, может быть приписан (во всяком случае — приближенно) спин 1, их можно считать бозе-частицами. Для магнонов (так же как и для фотонов и фононов) число частиц нс фиксировано и п определяется формулой (8.4.22).
Тепловые магноны и термодинамика ферромагнетика. До сих пор мы рассматривали когерентные магнитные колебания и волны, возбуждаемые, например, переменным электромагнитным полем. Им соответствуют магноны, которые также можно назвать когерентными. Число типов таких магнонов, одновременно существующих в реальных условиях, как правило, невелико. Очень часто это магноны одного какого-либо типа: например, магноны однородной прецессии с к = 0 в опытах по однородному ферромагнитному или антиферромагнитному резонансу или магноны с определенным значением к в опытах по возбуждению стоячих спиновых волн (§ 8.3). Энергия таких магнонов (если ограничиваться рассмотрением линейных процессов) всегда соответствует частоте возбуждающего поля. Числа же их могут быть весьма велики (выше была установлена связь этих чисел с амплитудами составляющих намагниченности). Таким образом, распределение когерентных магнонов в k-пространстве характеризуется несколькими (чаще всего — одной) дискретными «линиями». Ясно, что такое распределение является неравновесным и поддерживается только за счет непрерывного рождения магнонов электромагнитным полем. После прекращения действия возбуждающего поля это неравновесное распределение релаксирует с характерным временем, равным времени жизни данных магнонов.
В отличие от таких неравновесных, когерентных магнонов в магнитоупорядоченном кристалле при любой температуре Т 0 имеются некогерентные магноны, находящиеся в статистическом равновесии с другими квазичастицами, существующими в кристалле, в первую очередь с фононами. Распределение равновесных магнонов по энергиям и в k-пространстве определяется статистикой
§ 8.4]
МАГНОНЫ
433
магнонов (она является приближенно бозевской) и их спектром. Это распределение зависит от температуры и внешних параметров, в первую очередь — постоянного магнитного поля. В отличие от распределения неравновесных магнонов, оно является достаточно широким (особенно при высоких температурах) — занимает, строго говоря, всю область допустимых, исходя из закона дисперсии, значений е и к.
Равновесные или, как их иногда называют, тепловые (термические) магноны существенно влияют на термодинамические характеристики магнитоупорядоченных веществ. К числу таких характеристик относятся температурные зависимости статической намагниченности Мо (Т) и магнитного вклада в теплоемкость сит (.?) Наццем, следуя Кефферу [244], эти зависимости для случая ферромагнетика.
Для вычисления намагниченности воспользуемся формулой (8.4.12), в которой теперь Мо М (0) — намагниченность при отсутствии магнонов, т. е. при 0 °К, Mz = М (Г) — искомая намагниченность при температуре Т, а п — полное число всех равновесных магнонов в единице объема при этой температуре. Величина п может быть определена следующим образом:
* п = — у п d3k,	(8.4.23)
где V — объем (в координатном пространстве), / — плотность состояний магнонов в k-пространстве, п — среднее число магнонов в каждом состоянии, а интегрирование производится по всему к-пространству.
Для определения плотности состояний / примем периодические граничные условия на параллелепипеде с ребрами Z1} Z2 и Z3 (объем его Z,Z2Z3 = V). Тогда из (8.4.7) следует,^ что точки в к-простран-стве, соответствующие разрешенным состояниям, образуют прямоугольную решетку, ячейки которой имеют ребра 2nUr, 2n/Z2 и 2n/Z3, т. е. объем (2л)3/К. Отсюда плотность состояний
/ = У/(2л)3.	(8.4.24)
Величина п определяется формулой (8.4.22), в которой е есть функция к, определяемая законом дисперсии магнонов. Таким образом,
М (0) — М (Т) =	——— .
' '	) (2я), е	(8.4.25)
— 1
В качестве закона дисперсии примем
е = Гщк2,	(8.4.26)
пренебрегая для простоты влиянием постоянного магнитного поля, кристаллографической анизотропии, магнитного взаимодей
434
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
ствия, а также особенностями спектра длинноволновых магнонов (однородной прецессии^ уокеровских типов колебаний). Все эти пренебрежения не исказят особенно существенно результата, потому что мы будем интегрировать по всему k-пространству, и вклад коротких спиновых волн, для которых закон дисперсии приближается к (8.4.26), будет преобладать. Подставляя (8.4.26) в (8.4.25), получим
Рис. 8.4.1. Температурная зависимость намагниченности насыщения иттрий-железного граната в области низких температур. Кружки — эксперимент [105], прямая — расчет по формуле (8.4.28) при значении т]—0,1, полученном из измерений теплоемкости (см. рис. 8.4.2).
М(0) — М(Т) = —	/,„™ №dk
(2л)8 \
J хТ , о е — 1
(8.4.27)
Интеграл в (8.4.27) легко приводится к интегралу [42]
со
V V -—- J. о
при о = 3/2. Здесь £ (о) — дзета-функция Римана, а Г (о) — гамма-функция. С учетом того, что [44] £ (3/2) = = 2,61, а Г (3/2) = /л/2, получим окончательно
М (0) - М (Т7) = 5,9 • 1б-* 2тй X
х	5 •
(8.4.28)
Выражение (8.4.28) представляет собой известный закон трех вторых, впервые полученный (на микроскопической модели) Блохом [230]*).
На рис. 8.4.1 приведена экспериментальная температурная зависимость намагниченности насыщения иттрий-железного граната и показаны результаты вычисления по формуле (8.4.28) 2). Как видно из рис. 8.4.1, рассмотренная выше спин-
*) В работе Блоха [230] было впервые введено представление о магнонах.
2) Иттрий-железный гранат выбран для сравнения с проведенным расчетом потому, что для него хорошо известна по результатам независимых измерений константа неоднородного обменного взаимодействия в. То обстоятельство, что он является не ферро-, а ферримагнетиком и имеет по меньшей мере две ветви спин-волнового спектра, не является здесь особенно существенным, так как при низких температурах, когда справедлива рассмотренная теория, верхние ветви почти не возбуждаются.
§ 8.41
МАГНОНЫ
435
волновая теория справедлива при низких температурах. При более высоких температурах действительная зависимость М (Т) является более сильной.
При рассмотрении когерентных (неравновесных) магнитных колебаний и волн в области температур Т > 0 обычно считают, что длина вектора намагниченности Мо определяется всеми остальными — равновесными спиновыми волнами и зависит, таким образом, от температуры, например, по закону (8.4.28). Это справед-
ливо, однако, лишь при том условии, что время релаксации величины 7И0 (Т) к его равновесному значению меньше времени релаксации тех когерентных колебаний, которые мы рассматриваем. Как показали расчеты (см. [3]), такое соотношение между временами релаксации действительно имеет место — во всяком случае, если волновое
Рис. 8.4.2. Температурная зависимость теплоемкости ттрий-железного граната [43].
число к рассматриваемых когерентных волн* много меньше, чем среднее значение к в равновесном распределении магнонов. Для исследуемых в настоя-
щее время сравнительно длинноволновых когерентных спиновых волн последнее условие выполняется кроме, может быть, области очень низких температур (где отличие Мо (Т) от Мо (0) вообще мало).
Расчет магнонного вклада в теплоемкость может быть произведен аналогично расчету намагниченности:
(dU\	1 д ( , -
свт = 5ЧГ “Т/дтЛМ6 “К • rm	v t V dJ’ У
в результате получим
£ (5/2) Г (5/2) -2^-	тГ’'Т*.
ол	(]Ц]) /г
(8.4.29)
(8.4.30)
Для того чтобы отделить магнонную теплоемкость точного (фононного) вклада, пропорционального Т3 образно построить результаты измерения cv (Т) в
и cvT~s\	~	"

от реше-[32], целесо-координатах как показано на рис. 8.4.2. Из данных, приведенных на рис. 8.4.2, следует, что для иттрий-железного грана-та Ц = Одо. Эта величина и была использована нами во всех оценках.
436
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
Представление о магнонах как о частицах с энергией Йи и импульсом 7гк не только используется в термодинамических расчетах, подобных приведенным выше, но и оказывается очень полезным при трактовке процессов релаксации в магнитоупорядоченных кристаллах (глава 9). Оно используется также при анализе различных процессов взаимодействия фотонов, нейтронов и др. частиц с магнитной системой магнитоупорядоченных кристаллов (см., например, 1101). Такие процессы можно трактовать как столкновения фотонов или нейтронов с магнонами.
§ 8.5. Микроскопическая теория магнонов
В предыдущем параграфе было показано, что квантование колебаний намагниченности в непрерывной магнитоупорядоченной среде (в качестве примера был рассмотрен ферромагнетик) приводит к представлению о квазичастицах — магнонах. Однако в действительности магнитоупорядоченное вещество — не непрерывная среда, а система, построенная из дискретных микроскопических объектов — атомов, ионов, электронов проводимости. Нашей задачей является теперь выяснение влияния дискретности структуры магнитоупорядоченных веществ на свойства магнонов.
Как отмечалось в § 1.1, микроскопическое рассмотрение магнитоупорядоченных веществ приходится проводить на некоторых — достаточно простых моделях. Для неметаллических кристаллов наиболее подходящей является гейзенберговская модель, которая представляет собой систему локализованных спинов, расположенных в узлах магнитной решетки и связанных обменным взаимодействием. Гейзенберговская модель рассматривалась в § 1.1, но затем была оставлена в связи с переходом к континуальной модели и классическому описанию. Теперь вернемся к ней и посмотрим, как в этой модели «получаются» магноны. При этом мы а) дадим более строгое обоснование результатов, найденных выше на континуальной модели;
б) найдем условия, ограничивающие область применимости континуальной модели;
в) обсудим пути построения теории в той области, где континуальная модель неприменима; можно полагать, забегая вперед, что это будет область коротковолновых возбуждений, для которых к сравнимо с На, где а — расстояние между магнитными ионами или расстояние между спинами в гейзенберговской модели.
Гамильтониан гейзенберговского ферромагнетика. В квантовомеханической теории, которой необходимо пользоваться, рассматривая микроскопическую гейзенберговскую модель, исходным является выражение для оператора энергии — гамильтониана системы. В этом параграфе основное внимание будет уделено ферромагнетику. Выражения для операторов энергии обменного,
§ 8.51
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ
437
зеемановского и диполь-дипольного взаимодействия в гейзенберговской модели ферромагнетика были приведены в § 1.1. Сначала мы не будем учитывать диполь-дипольного взаимодействия. Тогда гамильтониан, согласно (1.1.48) и (1.1.49), запишется следующим образом х);
^=-22 Л/'S/ Sr + тй 2	(8.5.1)
1 г	/
Напомним, что здесь
Q Q	г»Х пХ I фУрУ 1 nZrrZ
Of Of' = Of О f' -f- Of Of'	О p/«,
a z — операторы проекций спинов (как всегда — в единицах п), находящихся в узлах / и /'. Ось z совпадает в данном случае с направлением внешнего магнитного поля Н. Операторы S^f’’z, как все операторы проекций момента количества движения, удовлетворяют перестановочным соотношениям [30, 13]
[5?, 57-] = iAfrSZf (8.5.2)
и двум другим, получающимся из (8.5.2) циклической заменой индексов х, у и е. Здесь Д/у. — дельта-символ Кронекера (6.3.14). Собственные значения операторов и (S,)2 выражаются согласно (1.1.1') и (1.1.3).
В основном состоянии системы, описываемой гамильтонианом (8.5.1), собственные значения z-проекций всех спинов равны (— S). Заметим, что отсюда не следует равенства нулю собственных значений 5/ и б’/) более того, эти операторы не коммутируют с Sf и, вообще, не могут иметь определенных значений в состояниях с определенными значениями Szt. Однако средние значения поперечных проекций спинов, которыми, согласно (1.1.55), определяются поперечные проекции момента любого макроскопического объема ферромагнетика, будут в основном состоянии, конечно, равны нулю.
Перейдем теперь к исследованию возбужденных состояний ферромагнетика с гамильтонианом (8.5.1). Заметим прежде всего, что состояние с одним локализованным спиновым отклонением (z-составляющая определенного спина увеличена на 1), в частности, для спина х/2 — состояние с одним «перевернутым» спином, не есть собственное состояние этого гамильтониана. Как показал Плох [230], действительные возбужденные состояния могут рассматриваться как синусоидальные волны спиновых отклонений, распространяющиеся по всему криталлу. Более строгая теория
1) Как и в § 1.1,	— оператор плотности энергии.
438
СПИНОВЫЕ волны
[ГЛ. 8
была развита в работе Холыптейна и Примакова [231] х), которой мы будем в дальнейшем, в основном, следовать.
Допустим, что гамильтониан (8.5.1) удастся привести к виду
$ = Uo + 2 «А»	(8.5.3)
к
где Uo — энергия основного состояния, — оператор, собственные значения которого представляют собой целые числа п,с = О, 1, 2, ..., а суммирование производится по всем допустимым значениям к. Это будет означать, что энергия (отсчитанная от Uo) является суммой энергий элементарных возбуждений, которые можно рассматривать как квазичастицы — магноны. Зависимость ел от к даст закон дисперсии квазичастиц, а возбужденное состояние системы будет однозначно характеризоваться числами пк — числами заполнений возбужденных состояний или числами магнонов. Преобразование гейзенберговского гамильтониана к виду (8.5.3) и было приближенно осуществлено в работе [231] рядом последовательных переходов от одних операторов к другим — знаменитых преобразований Хольштейна — Примакова.
Переход к операторам рождения и уничтожения спиновых отклонений. Прежде всего перейдем от поперечных проекций спинов к их циклическим комбинациям
Sr = S* + iSvf.	(8.5.4)
Тройки операторов Sf, Sf и Sz или S/, S/ и S/ связаны условием сохранения длины вектора Sf:
(S/)2 + (S/)2 + (S/z)2 = I (S/+S7 + S/S/) + (Sff == S (S + 1). (8.5.5)
Поэтому целесообразно попытаться выразить их через пары операторов й/ и й/. Потребуем, чтобы эрмитово-сопряженные операторы й/ и а/ удовлетворяли перестановочным соотношениям
[й/, df-] = Aff, [dj, df'] = 0,	[й/, й/»] = 0,	(8.5.6)
где Д//', как и в (8.5.2),— символ Кронекера. Иными словами,
[й/, й/J = 1,	(8.5.6')
а все остальные пары этих операторов коммутируют. Потребуем далее, чтобы
Sf == — Sdfdf.	(8.5.7)
х) В работе [231] было также впервые учтено влияние магнитного (диполь-дипольного) взаимодействия на возбужденные состояния гейзенберговского ферромагнетика.
g 8.5]	МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ	439
Тогда, как можно убедиться, операторы й/ и df должны быть связаны с поперечными проекциями спинов соотношениями
S^y'2S (1-	S7 = V2S й+(1 -	\ (8.5.8)
Выражения (8.5.7) и (8.5.8) представляют собой первое преобразование Холыптейна — Примакова.
Как известно из . квантовой механики (см., например, [30]), операторы й/ и df, удовлетворяющие перестановочным соотношениям (8.5.6'), являются операторами, соответственно, уничтожения и рождения некоторых квазичастиц, подчиняющихся статистике Бозе — Эйнштейна. Действуя на волновые функции системы в представлении вторичного квантования (в котором волновые функции представляют собой совокупности чисел частиц в различ ных состояниях), оператор df увеличивает на 1 число частиц в состоянии /, а оператор af — уменьшает это число на 1. Оператор
dfdf^=nf	(8.5.9)
есть оператор числа частиц в состоянии /. Его собственные значения nf — 0,1,2, ... представляют собой числа частиц в данном состоянии. Для бозе-частиц числа nt не ограничены.
Из выражения (8.5.7) видно, что квазичастицами, операторами рождения и уничтожения которых служат операторы й/ и й/, являются спиновые отклонения на /-м узле, т. е. увеличения z-проекции спина в этом узле на 1. В представлении, к которому мы перешли, введя операторы й/ и af, состояние ферромагнетика характеризуется числами отклонений nf на всех узлах. Поскольку собственные значения z-проекций спинов не могут превышать величины S, числа спиновых отклонений
nf < 2S.	(8.5.10)
Условие (8.5.10) отличает спиновые отклонения от обычных бозе-частиц. Оно выделяет из всего пространства чисел отклонений разрешенную или, как говорят, «физическую» область. Заметим, что выполнение условия (8.5.10) автоматически обеспечивается выражениями (8.5.8), так как эти выражения имеют смысл только при выполнении (8.5.10).
Однако операторные соотношения (8.5.8) весьма сложны. По-°™му Разл°жим входящие в них радикалы в ряды по степеням af af I (2S) и ограничимся первыми членами этих рядов, т.е. вместо (8.5.8) примем
V2Sdf, Sf ж V2Sa^.	(8.5.11)
440
СПИНОВЫЕ волны
[ГЛ. 8
Основное предположение теории Холыптейна — Примакова состоит в том, что указанная замена допустима при достаточно низких температурах, когда средние значения чисел спиновых отклонений
(8.5.12)
Оправдание этого предположения содержится лишь в более строгих теориях, например в теории Дайсона [233].
Пользуясь формулами (8.5.4), (8.5.11) и (8.5.7), введем новые операторы й/ и af в гамильтониан (8.5.1). Учитывая соотношения коммутации (8.5.6), получим
$=С70 + $2 + $4,	(8.5.13)
где энергия основного состояния
и0 = - S2 3 2 Iff' - rfSNH0,	(8.5.14)
f г (W)
(N — число спинов в единице объема), квадратичные члены
= — 2|?23^/' (й/й/- — &f&{) + ^hH0^afaf, (8.5.15)
а члены четвертого порядка
Ж, = - 2 2 Iff’&fafa^ar.	(8.5.16)
/ /-(МП
При низких температурах, когда выполняется условие (8.5.12), членами .^4 можно пренебречь с не меньшим основанием, чем высшими членами в разложениях (8.5.8). Однако гамильтониан (8.5.15) не имеет диагонального вида (8.5.3) (этому мешают «смешанные» члены а/ af-), т. е. состояния с локализованными на узлах спиновыми отклонениями не являются (как уже отмечалось выше) собственными состояниями гейзенберговского гамильтониана.
Переход к операторам"! рождения и уничтожения магнонов. Для того чтобы привести гамильтониан (8.5.15) к диагональному виду (8.5.3), т. е. найти собственные возбужденные состояния гейзенберговского ферромагнетика, необходимо перейти от локализованных на узлах операторов к коллективизированным — «размазанным» по всему кристаллу. Этот переход можно осуществить при помощи фурье-преобразования операторов й/ и at — второго преобразования Хольштейна — Примакова:
"Ч, й? = S <^4,	(8.5.17)
J 8.51
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ
441
Обратное преобразование имеет вид 1 vi	-+	1 о il<r/,+
/ N f 1	V N f
(8.5.18)
Здесь if — радиусы-векторы узлов решетки ферромагнетика, а к — волновые векторы, т. е. радиусы-векторы в к-пространстве.
Как известно, решетке с узлами г? соответствует в к-пространстве обратная решетка х) с узлами kn, так что
ек«г/ = 1.	(8.5.19)
Вследствие соотношений (8.5.19) волновые векторы к в (8.5.17) и ,(8.5.18) определяются лишь с точностью до прибавления векторов обратной решетки kn. Для того чтобы избавиться от этой неоднозначности, следует при суммировании в (8.5.17) ограничиться одной элементарной ячейкой обратной решетки. В качестве ее обычно выбирают первую зону Бриллюэна [30].1
Как и при рассмотрении магнонов в континуальной модели, примем периодические граничные условия на поверхностях параллелепипеда с объемом V = 1^1... Тогда допустимые значения к будут по-прежнему определяться условиями (8.4.7), т. е. образовывать в k-пространстве решетку с периодами 2л112 и 2nlls (рис. 8.5.1). Однако теперь, в отличие от континуальной модели, при суммировании по узлам этой решетки мы должны ограничиться объемом первой зоны Бриллюэна. Число узлов решетки допустимых значений к в элементарной ячейке обратной решетки, в частности, в первой зоне Бриллюэна равно числу узлов прямой решетки в объеме периодичности V [30]. И если выбрать параллелепипед периодичности так, чтобы его объем был равен объему рассматриваемого кристалла, то число членов в (8.5.17) будет равно числу N узлов в кристалле. В частности, если прямая решетка — простая кубическая с постоянной а, то
2V = i.	(8.5.20)
В дальнейшем (как и раньше) мы будем считать W оператором плотности энергии, так что объем периодичности будет кубом с ребром 1 см, a N — числом спинов в 1 см3 (N — 1/а3).
Легко проверить, что выражения (8.5.17) и (8.5.18) являются следствием Друг друга с учетом соотношения «ортогональности»
^2ei<k-k')r/=A(k-k'),	(8.5.21)
/
(8-5.22)
к
также *|34])СТВа °^атно” Решетки хорошо изложены, например, в [32] (см.
442
СПИЙОВЫЁ ЙОЛЙЫ
(гл. g
которые вытекают из периодических Здесь, аиалогично (6.3.14),
граничных условий [34].
Д(х) =
при при
х = О, х 0.
(8.5.23)
Операторы ак и ак удовлетворяют перестановочным соотношениям
[йк, ак-] = А (к — к'), [aft, ак-] = 0,	[й£, й£-] = 0, (8.5.24)
если a,f и а/ удовлетворяют соотношениям (8.5.6). В этом можно убедиться непосредственно, используя (8.5.18) и (8.5.21). Таким
Рис. 8.5.1. Решетка допустимых значений к (исходя из периодических граничных условий на параллелепипеде с ребрами 12 и (s) в первой зоне Бриллюэна для простой кубической решетки.
образом, преобразования (8.5.17) и (8.5.18) сохраняют неизменными перестановочные соотношения; такие преобразования называются унитарными.
Операторы йк и ак, поскольку они удовлетворяют бозевским перестановочным соотношениям (8.5.24), можно считать операторами рождения и уничтожения некоторых квазичастиц, подчиняющихся статистике Бозе — Эйнштейна. Оператор
= акак	(8.5.25)
§ 8.5]
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ
443
является оператором числа этих частиц в состоянии, характеризующемся волновым вектором к. Его собственные значения пк = — о 1, 2, ... Очевидно, что квазичастицы, о которых здесь идет речь, и являются магнонами. В отличие от спиновых отклонений (операторами рождения и уничтожения которых являлись af и &f ), они не локализованы на определенных узлах, а «размазаны» по всему кристаллу.
Вследствие дискретности решетки ферромагнетика в принятой гейзенберговской модели волновой вектор к, как уже отмечалось, определен неоднозначно — с точностью до векторов обратной решетки kn. Поэтому импульс, или, как его называют, квази-импульс магнонов в дискретной модели также определяется неоднозначно. Следует заметить, однако, что векторы обратной решетки — это большие величины, наименьший из них kr х 2л/а ~ —108. При низких температурах, когда справедлива рассматриваемая теория, возбуждаются, в основном, спиновые волны с гораздо меньшими к. Такие же спиновые волны представляют интерес и при когерентном возбуждении. Процессы, при которых сказывается неоднозначность квазиимпульса магнонов, становятся тогда маловероятными, и магноны можно рассматривать просто как частицы с определенным импульсом р = Йк.
Подставляя (8.5.17) в (8.5.8) или в (8.5.11) и в (8.5.7), можно выразить проекции спинов непосредственно через операторы рождения и уничтожения магнонов. В частности,
St = - S +	2 2 е’ (V’k) 'Ч&к-.	(8.5.26)
к к'
Если выражения (8.5.26) просуммировать по всем узлам и учесть (8.5.21), то получится
2 = - SN + 2 пк.	(8.5.27)
f	к
Нетрудно видеть, что из этого соотношения следует формула (8.4.14). Заметим, что формула (8.4.15) также может быть получена [20], исходя из гейзенберговской модели ферромагнетика.
Подставив (8.5.17) в гамильтониан (8.5.15) и заменив порядок суммирования, получим
= - 4 2 3	2 21е	- е "-4 -') 1„. +
к к'	f Г
+ ^22^2®*“"'”'- (8.5.28) к к'	/
Введем вектор расстояния между спинами
- г/	(8.5.29)
444
СПИНОВЫЕ волны
Ггл. 8
тожения ак магнонов,
Рис. 8.5.2. Ближайшее окружение спина в простой кубической решетке.
и перейдем в первом члене (8.5.28) от суммирования по / и f к суммированию по / и g. Ясно, что интеграл обмена Iff = Ig зависит только от ге. Суммирования по / и по g не являются независимыми у поверхности кристалла. Считая образец достаточно большим, можно этим пренебречь и поменять порядок суммирования по f и g. Тогда с учетом (8.5.21) и (8.5.25) гамильтониан (8.5.28) примет вид
^2= 25 2nfc2(l-ekrg)/g4-T^02nft. (8.5.30) kg	k
Напомним, что суммирование здесь производится по всем допустимым значениям к в первой зоне Бриллюэна.
Таким образом, перейдя к операторам рождения ак и унич-мы привели гейзенберговский гамильтониан (8.5.1) (без членов четвертого и более высоких порядков по операторам ак и а%) к диагональному виду (8.5.3), где
efe = 2S 2 (1 - eikrz<) Ig + yhH0. (8.5.31) g
Иными словами, состояния, характеризующиеся возбуждением квазичастиц — магнонов с законом дисперсии (8.5.31), являются приближенно собственными состояниями гейзенберговского ферромагнетика.
Спектр магнонов. Сравним (8.5.31) с классическим выражением (8.1.15), которое, так же как и (8.5.31), не учитывает
диполь-дипольного взаимодействия. В обоих случаях энергия магнонов является суммой зеемановского члена	и обменного члена.
Однако для обменного члена теперь, в отличие от (8.1.15), получено выражение, в которое входят микроскопические — модельные параметры Ig и которое явным образом зависит от магнитной структуры ферромагнетика.
Обменные интегралы Ig, как известно, быстро убывают по мере увеличения расстояния rg между спинами. Поэтому при вычислении суммы в (8.5.31) можно ограничиться сравнительно небольшим числом близко расположенных спинов, а при грубых расчетах — суммировать лишь по наиболее близко расположенным спинам — по первой координационной сфере (приближение ближайших соседей). В качестве примера рассмотрим в таком приближении простую кубическую решетку спинов (рис. 8.5.2). Непосредственное вычисление обменного члена в (8,5,31) дает в этом
§ 8.5]
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ
445
eft = 45/(3 — cos k:fa — cos kva — cos kza) -f-	(8.5.32)
где j___обменный интеграл, который теперь не зависит от g.
В случае длинноволновых возбуждений, когда
/са<1,	(8.5.33)
из (8.5.32) следует
Ек = 2SI (ка)* 2 + тйЯ0.	(8.5.34)
Это выражение совпадает с (8.1.15), если феноменологическая константа неоднородного обменного взаимодействия ;
n =	(8.5.35)
Оценим величину ц для иттрий-железного граната *). Для него S =5/2 (ионы Fe8+), а среднее расстояние между ионами а — 3,5 X X10~8 см. Для оценки величины обменного интеграла используем формулу (1.1.60), в которой примем Тс = 558 °К, J = S = =5/2 и Z=6. Тогда из (8.5.35) получим ц=0,015. Экспериментальное же значение т] = 0,1. Совпадение следует считать довольно хорошим, так как принятые оценки для атз.1 справедливы лишь по порядку величины.
Подчеркнем, что выражение (8.5.34), совпадающее с результатом классической континуальной теории, в микроскопической теории получается лишь при выполнении условия (8.5.33). Этого и следовало ожидать, так как континуальная модель применима лишь в тех случаях, когда длина волны спиновых волн много больше, чем постоянная решетки 2).
С другой стороны, в приведенном выше микроскопическом расчете мы игнорировали влияние поверхности образца, и, таким образом, его результаты справедливы лишь для магнонов с
Ы>1,	(8.5.36)
где d — наименьший размер образца. Иными словами, однородная прецессия и неоднородные длинноволновые (уокеровские) типы колебаний при этом расчете выпадают из рассмотрения. Ограничение (8.5.36) не является принципиальным, и квантовая микроскопическая теория длинноволновых типэв колебаний может быть построена 3 *). При построении такой теории, конечно, нельзя пренебрегать влиянием поверхности и необходимо учитывать диполь-
*) См. примечание 2) на стр. 434.
2) Аналогичное положение имеет место и для фононов (см., например, [32, 34В.
3) Для однородной прецессии это было показано еще на заре развития
теории ферромагнитного резонанса Полдером [113], Ван-Флеком [115] и др.
446
СПИНОВЫЕ волны
[ГЛ. 8
дипольное взаимодействие. Мы не будем рассматривать этого вопроса (см. [23, 3, 244]), так как очевидно, что результаты квантовой теории длинноволновых магнитных колебаний должны полностью совпасть с результатами, полученными макроскопическим путем в предыдущих главах.
Учет диполь-дипольного взаимодействия и анизотропии. Оста-новимсяТкратко на вопросе об учете диполь-дипольного взаимодействия и анизотропии в микроскопической теории в том случае, когда условие (8.5.36) выполняется и влияние поверхности образца несущественно. Прежде всего члены, учитывающие соответствующие взаимодействия, должны быть введены в гамильтониан. Гамильтониан диполь-дипольного взаимодействия имеет вид (1.1.50). Магнитная кристаллографическая анизотропия в ферромагнетике, как отмечалось в главе 2, связана со спин-орбитальным взаимодействием, и поэтому в гейзенберговской модели, имеющей дело только со спиновыми операторами, может быть учтена лишь феноменологически. Так, например, для магнитно-одноосного кристалла гамильтониан магнитной анизотропии, ограничиваясь наинизшими членами и предполагая, что ось анизотропии совпадает с осью z, можно записать в виде [23]
(8-5.37) f Г
где Ia/f’ — некоторые феноменологические параметры, зависящие от расстояний между спинами и ориентации спинов относительно вектора (17- — 17). Следует заметить, что при этом, в отличие от обменного гамильтониана, члены с / = /' не исключаются из суммирования, они могут быть ответственными за так называемый одноионный источник анизотропии (см. главу 2).
Добавляя диполь-дипольный гамильтониан 3fA в виде (1.1.50 и Ж, например, в виде (8.5.37) к гамильтониану (8.5.1), мы получим полный гамильтониан, который необходимо привести к диагональному виду (8.5.3) путем перехода от спиновых операторов Sf’y,z к новым переменным. Не будем приводить здесь этих преобразований. Для случая, когда учитывается только 3f,d, они проведены в [231] (см. также [3, 13, 20]). Отметим лишь, что после перехода к операторам а+к и а*, согласно (8.5.11), (8.5.7) и (8.5.17), квадратичные члены полного гамильтониана примут вид
•Ж = 3	+ у (вАа-к + 15*0^)],	(8.5.38)
где Ак и Вк — некоторые функции параметров исходного гамильтониана ц составляющих вектора к, При учет? тодьцо обменного
4	ЙИКРОСЙОПИЙЕСЙАЙ ТЕОРИЙ Магноной	447
§ 8.51
И диполь-дипольного взаимодействий (для изотропной среды [231])
Ак = 2S 3 С1 — е*кг*) Ц +	+ YЙ 2лМ0 sin2 Qk,
g	(8.5.39)
Вк = тЛ2лЛ/(| sin2 0/;е“г2ф\
где Мо = NyhS — намагниченность при 0°К, а 0|; и <р^ — полярный и азимутальный углы вектора к.
Как видно из (8.5.38), при учете диполь-дипольного взаимодействия или анизотропии переход к операторам ак и ак (при 0ft =£= =1= 0) еще не приводит квадратичные члены гамильтониана к диагональному виду (8.5.3): члены с ВкъВк связывают между собой операторы ак и ак. Необходим еще один переход к некоторым операторам ск и ск — третье преобразование Хольштейна — Примакова, которое уже приведет гамильтониан (8.5.38) к диагональному видух).
Пусть новые операторы ск и ск будут связаны с операторами ак и ак линейными соотношениями [231, 3]
ак = икск + vkc-k, а,к = икск -|- vkc~k,	(8.5.40)
в которых ик и vk — неизвестные пока функции к и параметров гамильтониана. Для их определения имеются следующие условия.
1) Операторы ск и ск должны удовлетворять таким же перестановочным соотношениям, как соотношения (8.5.24) для операторов ак и ак . Только при этом условии операторы и ск можно будет считать операторами рождения и уничтожения магнонов. Иными словами, преобразование (8.5.40) должно быть унитарным.
2) В новых операторах гамильтониан (8.5.38) должен стать диагональным:
3^2 = Uo 4- 2 екскск-	(8.5.41)
к
Можно убедиться, что преобразование (8.5.40) является унитарным, если
К|2~Ы2 = 1-	(8-5-42)
Для того чтобы учесть требования, накладываемые на коэффициенты ик и ик видом гамильтонианов (8.5.38) и (8.5.41), можно поступить, например, следующим образом [3]. Запишем квантовомеха-вическое уравнение движения [30] оператора ак (не зависящего
Общая теория преобразований, диагонализирующих квадратичные мильтонианы, была развита Боголюбовым (см. [23]).
448
СПИНОВЫЕ волны
[ГЛ. 8
явно от времени):
<8^з>
где квадратные скобки, как и в (8.5.24), обозначают коммутатор стоящих в них операторов. Вычисляя этот коммутатор с гамильтонианом (8.5.38) с учетом перестановочных соотношений (8.5.24) и переходя затем к операторам ск и cljc согласно (8.5.40), получим
+ vk = Ак (икск + vkclk) + Вк (ukctk + г‘;с(,).(8.5.44)
Запишем теперь уравнения движения операторов cf; и cljt, принимая гамильтониан в виде (8.5.41) и учитывая перестановочные соотношения для этих операторов. Принимая также во внимание, что ек = e_fe, получим
dCj. j л de ы	/
(8-5’45)
Подставляя (8.5.45) в (8.5.44) и приравнивая коэффициенты при операторах ск и ск в левой и правой частях полученного равенства, мы придем к системе однородных линейных уравнений для ик и vk- Равенство нулю ее определителя дает
е.к = /^-|2?fc|2.	(8.5.46)
Коэффициенты ик и vk, а следовательно, и операторы ск и ск могут быть легко определены из этой системы при дополнительном условии (8.5.42).
Найденные таким образом операторы ск и ск (а не ак и ак) являются теперь операторами рождения и уничтожения магнонов. Величины Лк и Вк, как видно, например, из (8.5.39), являются функциями волнового вектора к, и выражение (8.5.46) представляет собой дисперсионное соотношение для магнонов. Оператором числа магнонов является теперь
пк = Скск.	(8.5.47)
Без учета диполь-дипольного взаимодействия и анизотропии или для волн, распространяющихся вдоль постоянной намагниченности, Вк — 0 и выражение (8.5.46) переходит в (8.5.31). В этом случае ик = 1, ик = 0 и операторы ск и ск совпадают с операторами ак и ак. Если же ограничиться длинноволновым приближением (8.5.33), то (при учете только диполь-дипольного взаимодействия)
Ак =	+ t]^/c2 + ТЙ2л:М0 sin2 0fc
(8.5.48)
f 8.5J
МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ
449
(^ определяется согласно (8.5.39)) и выражение (8.5.46), как и следовало ожидать, совпадает с формулой (8.1.14), полученной классическим путем на континуальной модели.
Заметим, что если
|Ь\|<Л,	(8.5.49)
то операторы Q и ?1£ мало отличаются от операторов а£ и ац [20]. В этом случае, согласно (8.1.20), поляризация спиновых волн приближается к круговой. Тогда приближенно выполняются простые соотношения (8.4.9) — (8.4.15), дающие связь чисел магнонов с составляющими намагниченности и магнитного момента образца. Легко убедиться, что для обычных ферромагнетиков энергия | Вк | ~ 0,1 °К. Поэтому для тепловых магнонов, энергии которых при температуре Т будут, в основном, порядка кТ, величиной Bh можно всегда пренебречь при температурах, больших ~ 1 °К. Одпако для когерентных спиновых волн с не очень большими к пренебрежение Biz допустимо лишь при достаточно сильных постоянных магнитных полях.
Термодинамика ферромагнетика с учетом дискретности его структуры. Выясним теперь, как повлияет дискретность структуры ферромагнетика на его термодинамические свойства, в частности, на температурную зависимость намагниченности, которая была рассчитана выше на континуальной модели (формула (8.4.28)). Результаты такого расчета зависят от трех факторов:
1)	статистики, которой подчиняются элементарные возбуждения,
2)	спектра элементарных возбуждений и
3)	области k-пространства, по которой производится суммирование состояний.
Посмотрим, как изменится влияние этих факторов при переходе от континуальной модели к дискретной. Как мы видели, магноны в дискретной — гейзенберговской модели в пределах применимости спин-волновой теории являются (первый фактор), как и магноны в континуальной модели, бозе-частицами. Суммирование состояний (третий фактор), т. е. интегрирование в (8.4.25) должно теперь производиться, строго говоря, только по первой зоне Бриллюэна. Однако при достаточно низких температурах роль магнонов с большими к мала, и интегрирование в (8.4.25) можно по-прежнему производить по всему k-пространству (что, конечно, упрощает вычисления).
Что же касается второго фактора, то спектр магнонов для дискретной модели, как мы видели, существенно отличается (кроме области малых ка) от спектра для континуальной модели. Рассмотрим, к какому изменению термодинамических характеристик ферромагнетика это приведет. Пренебрежем по-прежнему влиянием постоянного магнитного поля, диполь-дипольного взаимодействия
’5 А. Г. Гуревич
450
СПИНОВЫЕ ВОЛНЫ
и анизотропии, рассмотрим для определенности простую кубическую решетку и ограничимся приближением ближайших соседей. Тогда спектр магнонов будет иметь вид (8.5.32). Подставив его вместо спектра (8.4.26) в формулу (8.4.25), можно получить искомую зависимость М (Т) для дискретной модели. Вычисления оказываются при этом довольно громоздкими, и мы приведем окончательный результат (см., например, [244]):
М (0) - Л/ (Г) = С,,г + а!2Т‘,г + C,/f/2 + ...	(8.5.50)
Здесь коэффициент Сз/г совпадает с коэффициентом в формуле (8.4.28). В последующие коэффициенты, в отличие от Су,, войдет в возрастающих степенях (во второй — в Q., в четвертой — в Суг и т. д.) постоянная решетки а. Таким образом, учет дискретности структуры ферромагнетика приводит к появлению членов с Т‘1-, и т. д. в температурной зависимости спонтанной намагниченности. Аналогичные члены появятся и в температурной зависимости теплоемкости. Оценка показывает, что вклад зтих членов мал при тех температурах, при которых еще справедливы основные допущения спин-волновой теории.
Взаимодействие магнонов. Теперь следует остановиться на вопросе о принципиальных трудностях и ограничениях рассмотренной спин-волновой теории Холыптейна — Примакова. Как уже отмечалось, основными допущениями этой теории (кроме выбора модели) являются:
1) возможность замены радикалов в выражениях (8.5.8) на их разложения в ряды по степеням aj at/ (25);
2) возможность пренебрежения всеми членами третьей и более высоких степеней по операторам и dt в гамильтониане (к числу их относятся как члены (8.5.16), так и члены, которые появятся в результате учета более высоких степеней в разложениях (8.5.8)).
Второе допущение представляется довольно обоснованным при достаточно низких температурах. Действительно, высокие члены гамильтониана учитывают столкновения магнонов; при низких температурах, когда средние значения чисел магнонов малы, столкновения маловероятны и их влиянием на спектр можно пренебречь х). Конечно, эти рассуждения не являются строгими.
Первое допущение вызывает серьезные сомнения, в особенности при небольших значениях спина, когда собственные значения операторов df ciff (2S) = nf! (25) отнюдь не являются малыми. Выше уже отмечалось, что наличие радикалов в выражениях (8.5.8) обеспечивает то, что числа спиновых отклонений на каждом узле
х) Как мы увидим в следующей главе, столкновения магнонов, учитываемые высшими членами гамильтониана, ответственны за процессы релаксации.
\	МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ	451
§ 8.51
не превышают величин 2S. Замена радикалов на ряды (даже если не ограничиваться, как в (8.5.11), только первыми их членами) ликвидирует такую возможность. ~
Вследствие указанных трудностей вопрос о справедливости теории Холыптейна — Примакова и, вообще, о правомерности представлений о магнонах, как элементарных возбуждениях ферромагнетика, подвергался всестороннему изучению. Этот вопрос подробно обсуждается во многих монографиях по магнетизму (см., например [3, 13, 23, 244]), мы ограничимся здесь лишь краткими качественными замечаниями.
Фундаментальный вклад в выяснение этого вопроса был сделан Дайсоном [233]. Им было показано, что учет действительных свойств спиновых операторов, приводящих к ограничению чисел спиновых отклонений на каждом узле, эквивалентен некоторому дополнительному взаимодействию (Дайсон назвал его кинематическим) между магнонами, которое носит характер отталкивания. Однако влияние кинематического взаимодействия мало и может практически не приниматься во внимание при низких температурах (вплоть до температур порядка половины температуры Кюри), когда выполняется условие (8.5.12).
Наряду с кинематическим взаимодействием, согласно Дайсону, имеет место динамическое взаимодействие между магнонами, связанное с отбрасываемыми в теории Холыптейна — Примакова высшими членами в гамильтониане. Динамическое взаимодействие носит характер притяжения и дает поправку к спектру магнонов более существенную, чем кинематическое взаимодействие, но все же малую при низких температурах. Эта поправка приводит, в частности, к появлению в температурной зависимости намагниченности дополнительного члена, пропорционального 7'4. Однако вклад его в намагниченность при низких температурах (приблизительно, до половины температуры Кюри) невелик, так же как и членов, пропорциональных Т*/г, Т'2, ..., обусловленных дискретностью структуры ферромагнетика.
Исследование Дайсона показало, что хотя магноны в смысле квазичастиц, подчиняющихся статистике Бозе — Эйнштейна и имеющих приведенные выше спектры, и не являются строго элементарными возбуждениями гейзенберговского Гферромагнетика, они могут приближенно считаться таковыми при сравнительно низких уровнях возбуждения спиновой системы, т. е. для равновесных (тепловых) магнонов — при достаточно низких температурах.
Из того, что при более высоких уровнях возбуждения (высоких температурах) элементарные возбуждения ферромагнетика ие являются рассмотренными выше (блоховскими или холшьтейп-примаковскими) магнонами, отнюдь не следут, что само понятие квазичастиц — элементарных возбуждений теряет смысл при этих
15*
452
СПИНОВЫЕ ВОЛНЫ
[ГЛ. 8
условиях. Представление о таких квазичастицах (их по-прежнему можно называть магнонами) может быть использовано и при высоких температурах, например, при описании процессов релаксации в спиновой системе, различных процессов взаимодействия спиновой системы с другими системами и т. д. Условием для использования этого представления является, пожалуй, лишь следующее соотношение:
^<4,	(8.5.51)
где Tfe — время жизни квазичастицы, а е!г — ее энергия. Более мощные теоретические методы, применимые в широком диапазоне температур, позволяют найти спектры и другие свойства таких квазичастиц. Среди этих методов следует упомянуть метод функций Грина, примененный к ферромагнетикам Боголюбовым и Тябликовым (см. [23]), и диаграмный метод Вакса и Ларкина [247]. В последней работе, в частности, показано, что представление о магнонах, правда, лишь с достаточно малыми к, имеет смысл почти до самой точки Кюри.
О магнонах в антиферромагнетиках. Свойства магнонов были исследованы выше на примере ферромагнетиков. Но ясно, что представление'’о квазичастицах — магнонах, соответствующих элементарным возбуждениям магнитоупорядоченного кристалла, может быть распространено и на многоподрешеточные системы — антиферромагнетики и ферримагнетики. Прежде всего очевидно, что квантование магнитных колебаний и волн в этих веществах, трактуемых как непрерывные среды (см. главу 4 и § 8.2), приведет, так же как и в случае ферромагнетика, к представлению о магнонах. Отличие будет заключаться лишь в том, что в многоподреше-точных системах будет несколько ветвей колебаний или волн (по числу подрешеток) и каждой будет соответствовать определенный сорт магнонов со своим законом дисперсии.
Теория магнонов для дискретной, например, гейзенберговской модели антиферро- и ферримагнетиков может быть построена аналогично рассмотренной выше теории Хольштейна — Примакова для ферромагнетика (см. [23, 34, 20, 244]). Мы ограничимся здесь лишь очень краткими замечаниями. Отметим прежде всего, что незнание точного основного состояния антиферромагнетика (см. § 4.1) не препятствует построению такой теории.
В простейшем случае одноосного двухподрешеточного антиферромагнетика в первом основном состоянии, когда постоянное поле направлено по оси анизотропии и меньше поля опрокидывания, можно, например, исходить из гамильтониана
z
1 = 2 2 r8sflsg и - (Но + НА) 2 - тй (Но - НА) S sfa
*	'	1	(8.5.52)
,	МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ МАГНОНОВ	453
§ 8.5J
где индексы I и II соответствуют двум подрешеткам. При записи пепвого"__обменного члена гамильтониана мы ограничились приб-
лижением ближайших соседей и предположили, что ближайшими соседями спинов одной подрешетки являются спины другой (Z — число ближайших соседей). Знак перед обменным членом изменен по сравнению с (8.5.1), так как взаимодействие носит теперь антиферромагнитный характер, а обменный интеграл Ig по-прежнему считается положительным. Анизотропия учтена феноменологически при помощи эффективного поля анизотропии, оно имеет (см. § 4.2) различный знак для разных подрешеток.
Переход к операторам а* и «/, а затем к их фурье-компонен-там — операторам dg и ак производится аналогично преобразованиям Холылтейна — Примакова для ферромагнетика, но отдельно для каждой подрешетки (см. [34, 20]). Очевидно, что в операторах d/a, dhi, di;li и d/ai гамильтониан антиферромагнетика не будет диагональным, так как не может существовать спиновых волн или колебаний в подрешетках по отдельности. Необходимо еще одно унитарное преобразование, которое уже диагонализирует гамильтониан — приведет его квадратичную часть к виду
-^2 = 2 efclcirlc«l + 2	(8.5.53)
к	к
Здесь операторы с индексами 1 и 2 являются операторами рождения и уничтожения магнонов, соответствующих двум ветвям спиновых волн в антиферромагнетике. Зависимости (к) и е^2 (к) представляют собой дисперсионные соотношения для этих ветвей.
В длинноволновом приближении (8.5.33) дисперсионные соотношения, как и следовало ожидать, совпадут со спе ктрами, полученными на континуальной модели путем классических расчетов, проведенных в главе 4 и § 8.2. Такое совпадение, конечно, будет иметь место и для ферримагнетиков и для более сложных магнитных структур.
ГЛАВА 9
ПРОЦЕССЫ РЕЛАКСАЦИИ
§ 9.1. Диссипация энергии магнитных колебаний
и процессы релаксации в магнитоупорядоченных веществах
В предыдущих главах нам приходилось в ряде случаев учитывать диссипацию энергии магнитных колебаний. Однако учет ее производился лишь феноменологически, чаще всего — путем добавления в уравнения движения намагниченности диссипативных членов. Эти члены записывались, без достаточно строгого обоснования, таким образом, чтобы они приводили к желаемому результату: затуханию свободных колебаний и конечной ширине резонансной кривой — для вынужденных колебаний. Теперь мы перейдем к рассмотрению тех физических процессов — процессов релаксации, которыми определяется диссипация энергии магнитных колебаний в магнитоупорядоченных кристаллах. Их изучение позволит понять наблюдаемые зависимости диссипативных характеристик вещества от его состава, структуры, а также температуры, величины постоянного магнитного поля и других параметров. Мы сможем выяснить, насколько хорошо соответствуют действительности в тех или иных условиях различные варианты феноменологического описания диссипации, сможем оценить теоретически величины параметров диссипации.
Роль процессов релаксации. Процессами релаксации называются те физические процессы, посредством которых система приближается к состоянию термодинамического равновесия. Если внешние силы, которые вывели систему из этого состояния, например, возбудили в ней некоторые типы колебаний, прекратили затем свое действие, процессы релаксации приведут систему к равновесному состоянию. Энергия, которая была передана системе внешними силами, перераспределится между всеми собственными типами колебаний, амплитуды которых примут значения, соответствующие термодинамическому равновесию. Процессы релаксации будут определять в этом случае скорость приближения системы к состоянию равновесия, в частности — скорость убывания амплитуд колебаний, возбужденных внешними силами.
Если же система находится под воздействием периодических внешних сил, непрерывно возбуждающих некоторые (в частности, какой-либо один) типы колебаний, то, несмотря на наличие про-
§ g fl	ДИССИПАЦИЯ ЭНЕРГИИ МАГНИТНЫХ КОЛЕБАНИЙ	455
нелаксации, термодинамическое равновесие, конечно, не будет достигаться. Система будет находиться в стационарном неравновесном состоянии, в котором амплитуды первичных — возбуждаемых внешними силами колебаний (а также ряда других, наиболее сильно с ними связанных) будут значительно превышать равновесные значения. Процессы релаксации осуществляют теперь непрерывный отток энергии от первичных типов колебаний и обеспечивают тем самым возможность непрерывного поглощения системой энергии внешних сил. Процессы релаксации будут определять в этом случае такие диссипативные характеристики системы, как ширину резонансной кривой и антиэрмитовы части компонент тензора восприимчивости.
Заметим, что диссипативные свойства системы тесно связаны с флуктуациями, которые имеют место в ней в состоянии термодинамического равновесия. Эта связь, установленная первоначально Найквистом [272] для случая электрических цепей, была обобщена затем Калленом и Уэлтоном [276] и Кубо [286] на весьма широкий класс систем с многими степенями свободы. Она была сформулирована в виде флуктуационно-диссипационной теоремы [276, 286], устанавливающей зависимость среднего квадрата флуктуаций некоторой величины (например, намагниченности) с мнимыми частями компонент соответствующей (в данном случае — магнитной) восприимчивости системы. Таким образом, процессы релаксации, которые, как отмечалось выше, определяют мнимые части восприимчивости, связаны с флуктуациями в системе.
Процессы релаксации играют определяющую роль в поведении системы при больших уровнях возбуждения, когда существенным становится учет нелинейности системы. Они определяют, в частности, пороги нестабильностей, которые возникают в системе при учете нелинейности [15, 537] (см. § 9.2). Если бы не было процессов релаксации, эти пороги были бы бесконечно малы, т. е. строго говоря, вообще не существовало бы области применимости линейной теории (которая рассматривается на протяжении всей этой книги).
Спин-спиновая и снин-решеточная релаксация. Системой, которая нас интересует, является магнитная система магнитоупорядоченного кристалла: ферро-, антиферро- или ферримагнетика. Собственные типы колебаний такой системы — зто подробно исследованные в предыдущих главах однородная прецессия намагниченности, неоднородные типы прецессии и спиновые волны. Эти колебания возбуждаются обычно электромагнитным полем. С корпускулярной точки зрения собственным колебаниям магнитной системы соответствуют квазичастицы — магноны, а возбуждение их происходит в результате протекания элементарных процессов, при которых уничтожаются кванты поля и рождаются магноны (рис. 9.1.1, а).
45В
ПРОЦЕССЫ РЕЛАКСАЦИИ
ТТЛ. %
Рис. 0.1.1. Примеры элементарных процессов. 1 — при возбуждении магнитных колебаний; б — при спин-спиновой релаксации; в — при спин-решеточной релаксации (р — фотон, к — магноны, ч — фопон).
Корпускулярный подход оказывается очень полезным при изучении процессов релаксации. Процессам релаксации, происходящим внутри магнитной системы, соответствуют элементарные процессы, при которых происходит уничтожение одних магнонов и рождение других. Некоторые из этих процессов показаны в качестве примера на рис. 9.1.1, б.
Однако при исследовании процессов релаксации в магнитоупорядоченных кристаллах мы не можем, вообще говоря, считать магнитную систему кристалла изолированной, а должны рассматривать сложную систему, включающую в себя, кроме магнитной подсистемы, другие, связанные с ней подсистемы кристалла. В их число входит прежде всего кристаллическая решетка (точнее — ее упругие степени свободы), а также электроны проводимости, подсистема локализованных электронных степеней свободы входящих в решетку ионов (мы будем называть ее в даль
нейшем ионной подсистемой) и ядерная магнитная подсистема. Всем этим подсистемам соответствуют свои элементарные возбуждения или, на корпускулярном языке, квазичастицы. Процессы релаксации, посредством которых осуществляется приближение к равновесию всей этой сложной системы, должны включать в себя, наряду с упомянутыми выше процессами, происходящими внутри магнитной (спиновой) подсистемы, также процессы, происходящие внутри других подсистем, и процессы взаимодействия между подсистемами. С корпускулярной точки зрения эти процессы могут трактоваться как элементарные процессы столкновения и взаимного превращения соответствующих квазичастиц. Один из таких процессов показан на рис. 9.1.1, в.
Процессы релаксации, происходящие внутри магнитной подсистемы, называют часто процессами спин-спиновой или магнон-магнонной релаксации, а процессы, связанные с взаимодействием магнитной подсистемы с решеткой,— процессами спин-решеточной или магнон-фононной релаксации. Иногда спин-решеточную релаксацию понимают в более широком смысле, включая в нее все процессы, ведущие к установлению равновесия между магнитной подсистемой и решеткой, в том числе и те из них, в которых участвуют другие подсистемы, например электроны проводимости, ионы и пр. В этом смысле все процессы релаксации, связанные с
S 9.11
ДИССИПАЦИЯ ЭНЕРГИИ МАГНИТНЫХ КОЛЕБАНИЙ
457
магнитной подсистемой, делятся на спин-спиновые и спин-реше-точные.
Заметим, что понятия спин-спиповои и спин-решеточнои релаксации были введены впервые в теории релаксации в парамагнетиках (см., например, [2891). Однако явления в парамагнетиках (существенно отличаются от коллективных магнитных колебаний в магнитоупорядоченном состоянии. Поэтому содержания понятий спин-спиновой и спин-решеточной релаксации в магнитоупо-.рядоченных веществах и в парамагнетиках могут значительно различаться. Например, в разбавленных (в магнитном отношении) ^парамагнетиках релаксация продольной (относительно направления постоянной намагниченности) составляющей магнитного момента определяется только процессами спин-решеточной релаксации и является часто значительно более медленной, чем релаксация поперечных: составляющих. В магнитоупорядоченных же кристаллах релаксация как поперечных, так и продольных составляющих намагниченности определяется, вообще говоря, и спин-спиновыми, и спин-решеточными процессами, и скорости релаксации поперечных и продольных составляющих обычно близки. Это обстоятельство и дает возможность феноменологического '(конечно, приближенного) описания диссипации при ферромагнитном резонансе при помощи одного параметра (§ 1.3).
Как уже отмечалось, процессы релаксации обеспечивают перераспределение энергии между собственными типами колебаний системы.
Рассмотрим этот вопрос несколько подробнее для случая стационарного режима. Пусть, например, электромагнитное поле возбуждает некоторый тип колебаний магнитной подсистемы (в частности, однородную прецессию), а система, кроме магнитной подсистемы и решетки, содержит подсистему носителей тока и подсистему примесных ионов. Потоки энергии, возникающие в этом случае внутри магнитной подсистемы и между подсистемами в результате действия процессов релаксации, показаны на рис. 9.1.2. Если режим является и в тепловом отношении стационарным, то энергия, поступающая от электромагнитного поля, полностью передается окружающим образец телам — тепловому резервуару. При этом температуры резервуара, образца (т. е. его кристаллической решетки) и эффективные температуры различных подсистем (если они могут быть введены) будут постоянны во времени, но могут отличаться друг от друга. Заметим, что эффективные температуры подсистем могут быть введены в том случае, если скорости релаксации внутри подсистем много больше, чем между подсистемами. Если же тепловой режим еще не установился, часть энергии, передаваемой системе электромагнитным полем (а в случае адиабатического режима — вся энергия), «оседает» в различных подсистемах, приводя к повышению их температур.
458
ПРОЦЕССЫ РЕЛАКСАЦИИ
1ГЛ. 9
Следует подчеркнуть, что постановка задачи о релаксации, отраженная на рис. 9.1.2, отнюдь не является единственно возможной. Можно было бы рассмотреть, например, случай, когда
Рис. 9.1.2. Потоки энергии между подсистемами в магнитоупорядочепном веществе при возбуждении однородной прецессии электромагнитным полем.
энергия в стационарном режиме вносится в систему «со стороны» решетки, т. е. внешние силы возбуждают один из упругих типов колебаний образца. Можно было бы исследовать нестационарный режим, т. е. установление равновесия в системе при тех или иных начальных условиях J). Однако задача о диссипации энергии в стационарном режиме при возбуждении определенного типа магнитных колебаний электромагнитным полем представляет для нас наибольший интерес, так как она реализуется обычно при экспериментальном исследовании магнитных колебаний в магнитоупорядоченных кристаллах и при практическом использовании их в ферритовых устройствах диапазона СВЧ. И мы в дальнейшем для определенности всегда будем иметь в виду именно такой случай. Однако во всех случаях релаксация определяется одними и теми же элементарными процессами. Их изучение будет являться основной целью этой главы.	>]
О методах теоретического исследования процессов релаксации. Релаксационные процессы в ферромагнетике впервые теоретически исследовал Ахиезер (274]. С тех пор теории процессов релаксации в магнитоупорядоченных кристаллах было посвящено” огромное количество работ (обзоры их см., например, в (20, 3, 282, 287]). В этих работах наиболее широко использовались два метода: связанных уравнений движения и вероятностей переходов.
*) Эту задачу исследовали Ахиезер, Барьяхтар и Пелетмпнский [3].
( е 1]	ДИССИПАЦИЯ!ЭНЕРГИИ МАГНИТНЫХ КОЛЕБАНИЙ	459
Первый метод основан на том, что процессы релаксации обусловлены взаимодействием различных типов колебаний системы и их описание возможно в результате решения связанных уравнений движения для соответствующих типов колебаний. Это могут быть например, уравнения движения для разных типов колебаний магнитной подсистемы — если рассматриваются процессы спин-спиновой релаксации, или уравнения движения для магнитной подсистемы и механические уравнения движения решетки при рассмотрении прямой спин-решеточной релаксации. Для упомянутых подсистем могут быть использованы, конечно, классические уравнения движения — уравнения Ландау — Лифшица и уравнения теории упругости. Для неколлективизированных подсистем, например ионной, должны использоваться квантовомеханические уравнения.
В нулевом приближении (которым мы интересовались для случая магнитной подсистемы в предыдущих главах) уравнения движения не связаны и их решения дают соответствующие собственные колебания. Учет — в первом приближении — различных взаимодействий приводит к тому, что уравнения движения для разных подсистем или разных типов колебаний одной подсистемы становятся связанными. В результате возникает возможность передачи энергии от одних типов другим, т. е. протекания процессов релаксации. Анализ процессов релаксации методом связанных уравнений движения приводит обычно к довольно громоздким вычислениям, но тем не менее этим методом были получены впервые многие важные результаты для различных процессов.
Второй метод — вероятностей переходов J) основан на том, что, элементарные процессы релаксации (см., например, рис. 9.1.1, б и в) представляют собой переходы системы из одного состояния в другое. Вычисляются вероятности таких переходов в первом приближении квантовомеханической нестационарной теории возмущений [30]. В духе этой теории метод вероятностей переходов не учитывает влияния возмущения на собственные состояния, т. е. на характер и спектры собственных колебаний. Но для вероятностей переходов между состояниями, которыми определяются параметры диссипации, этот метод дает правильные результаты. Как было неоднократно проверено, они совпадают с результатами, которые получаются методом связанных уравнений движения.
Для анализа релаксационных процессов использовались, конечно, и более мощные теоретические методы, разработанные в последние годы, например метод функций Грина [23], метод Кубо [286] и др. Однако мы ограничимся двумя упомянутыми выше методами, так как именно ими были получены почти все интере-
пп Мет°Д вероятностей переходов впервые применил для исследования Р Цессов релаксации в ферромагнетиках Ахиезер [27-4].
460
ПРОЦЕССЫ РЕЛАКСАЦИЙ
(.ГЛ.
сующие нас результаты. Особенно широко мы будем использовать метод вероятностей переходов, который характеризуется наглядностью и сравнительной простотой вычислений.
Метод вероятностей переходов.. Квантовомеханическая нестационарная теория возмущений [30], как известно, позволяет вычислить вероятность перехода системы из одного стационарного состояния в другое под действием некоторого возмущения, зависящего, вообще говоря, от времени. В частности, число переходов в единицу времени под действием постоянного возмущения
2тг
. wim = ^|<7n|^|Z>r26(Ei-em),	(9.1.1)
где |7Z7J |Z> — матричный элемент оператора анергии возмущения Жр для перехода между состояниями Z и т, е; и ет — собственные значения энергии системы в этих состояниях, а б (ж) — дельта-функция Дирака (1.3.36). Из формулы (9.1.1) видно, что wlm =h 0 только для переходов между вырожденными состояниями.
При изучении процессов релаксации очень удобно использовать представление вторичного квантования (см. § 8.5), в котором состояние системы характеризуется числами заполнения различных собственных состояний, т. е. в данном случае — числами квазичастиц. Волновые функции в представлении вторичного квантования являются наборами чисел квазичастиц для всех допустимых значений kg волнового вектора- На эти волновые функции действуют операторы рождения а* и уничтожения akg квазичастиц. Преобразования Холыптейна — Примакова (§ 8.5) и осуществляли переход к представлению вторичного квантования для гейзенберговской модели ферромагнетика. Свойства операторов a1Cg и рассматривались в § 8.5. Напомним лишь, что оператор «й, , действуя на волновую функцию nSl, пЛг, ..., nkg..., увеличивает на 1 число пкп, оставляя все остальные числа без изменения. Оператор °уменъшает число nk на 1. Формула (9.1.1) нестационарной теории возмущений в представлении вторичного квантования дает скорость изменения числа квазичастиц, которые возникают или уничтожаются при рассматриваемом переходе.
В §§ 9.2 и 9.4 мы будем исследовать процессы релаксации, которые могут происходить в идеальном магнитоупорядоченном кристалле. Под идеальным кристаллом понимается кристалл, не содержащий неупорядоченных примесей, дислокаций, пор и других нарушений периодичности. Строго говоря, такой кристалл должен быть неограниченным, но влиянием нарушения периодичности кристалла на поверхности образца можно пренебречь, если раз-
§ e i“J диссипация ЭнёрГий магнитных колебаний 461 мер образца не очень мал и поверхность — достаточно гладкая J). В идеальном кристалле оператор энергии любого возмущения в представлении вторичного квантования будет иметь следующий вид (см., например, [3, 244]):
-- 222 + ’>	(ki — k2 — k3) +
ki кг кз
+2222T, ,	(ki k2 k3 k4) •
ki ks кз k^
+2222 +ы,	(ki + k2 - k8- k4)+-.. + Э. c. (9.1.2)
kt кг кз кд
Здесь Ч+гз, +1,234 и +12,34 — некоторые комплексные амплитуды, а А (х) — дельта-символ Кропекера (8.5.23). Символ а. с. в (9.1.2) обозначает члены, эрмитово-сопряженные с записанными, причем оператором, эрмитово-сопряженным с ак, является ак и наоборот. Например, члены, эрмитово-сопряженные с членами первой суммы в (9.1.2), будут иметь вид 2)
222 +I, i3altsaltiaki-ki кг кз
В выражении (9.1.2) записаны лишь низшие члены — третьего и четвертого порядков по операторам ак и ак- Членов второго порядка в (9.1.2) нет: при кх — к2 эти члены войдут в основной — невозмущенный гамильтониан системы (см., например, выражение (8.5.30)), членов же второго порядка с кх =/= к2 в гамильтониане идеального кристалла не будет, так, для них А (к4 — k2) = 0. По той же причине не будет членов, содержащих только операторы рождения или только уничтожения.
Появление дельта-символов во всех членах гамильтониана связано с тем, что кристалл и при наличии возмущения остается идеально периодическим. Когда мы переходим от операторов в координатном представлении к их фурье-компонентам — операторам ai; и «ft, у членов гамильтониана, содержащих произведения этих операторов (например, dR1 akz af3), появляются множители вида 2 егЧ </с‘ /с-"/£з), где суммирование производится по всем узлам решетки кристалла. Как отмечалось в предыдущем параграфе (формула (8.5.21)), эти множители в идеальном бесконечном кристалле отличаются от нуля только в том случае, когда
Влияние шероховатости поверхпо сти образцов будет рассмотрено ® о 9.3.
в^Если некоторый оператор р = а Ьс, то сопряженный с ним оператор Р* = с*Ь*а*.
462	ПРОЦЕССЫ РЕЛАКСАЦИИ	[ГЛ. 8
равен нулю множитель при rf в- показателе, например кх — k2 — к3 = 0.
Учитывая свойства (8.5.24) и (8.5.25) операторов а1; и|ай, можно убедиться, что каждый член гамильтониана (9.1.2) вносит вклад только в один матричный элемент; при переходе, соответствующем этому элементу, увеличиваются на 1 числа тех квазичастиц, операторы рождения которых входят в данный член гамильтониана, и уменьшаются на 1 числа квазичастиц, операторы уничтожения которых входят в этот член. Так, например, член с амплитудой Т^д дает матричный элемент перехода, при котором увеличиваются на 1 числа пкг и пк, и уменьшается на 1 число nhl. Из свойств операторов ак и ак следует, что этот матричный элемент [30]
О/я — 1, пк2 -I- 1, n,f3 + 11 I nkt, пкг, nka> =
- рЧ. (nfc, + 1) (?Т-3 + 1) Т1; 23Д (Iq - k2 - k3).	(9.1.3)
Член гамильтониана, эрмитово-сопряженный с рассмотренным, дает матричный элемент
<пк1 + 1, n;f2 — 1, пй, — 11ЗСРIН/С1, пкг, пк,> =
= К(п/С1 + 1)ад/£з 'Г1‘,23Д (к, - к2 - к3).	(9.1.4)
Аналогичным образом запишутся матричные элементы, соответствующие членам более высоких порядков.
Выше отмечалось, что процессы релаксации часто трактуются с корпускулярной точки зрения; при этом считается, что в основе их лежат элементарные процессы превращения квазичастиц (см., например, рис. 9.1.1). Рассматриваемый сейчас подход к релаксации с точки зрения теории возмущений в представлении вторичного квантования дает обоснование возможности такой трактовки. Каждому элементарному процессу соответствует свой член в гамильтониане возмущения и относящийся к нему матричный элемент. Так, например, процесс, показанный на рис. 9.1.1, б, описывается матричным элементом (9.1.3), а матричный элемент (9.1.4) соответствует обратному процессу — уничтожения двух магнонов с к2 и к3 и рождения магнона с кх.
Наличие реяътл-функции в формуле (9.1.1) указывает на то, что при каждом элементарном процессе сохраняется энергия. Например, для процессов, которым соответствуют матричные элементы (9.1.3) и (9.1.4),
= Пыкг + 7w/C3.	(9.1.5)
Наличие же дельта-символов во всех членах гамильтониана при
§ 9.11
ДИССИПАЦИЯ ЭНЕРГИИ МАГНИТНЫХ КОЛЕБАНИЙ
463
водит к сохранению импульса х) при каждом элементарном процессе, например
7гкх = 7гк2 + 7гк3.	(9.1.6)
Подчеркнем, что, в отличие от сохранения энергии, сохранение импульса при элементарных процессах превращения квазичастиц имеет место только в идеальном кристалле, т. е. для таких возмущений, которые не нарушают периодичности кристалла. Процессы релаксации, существенно связанные с нарушениями периодичности, для которых не имеет места сохранение импульса при элементарных процессах превращения квазичастиц, будут рассмотрены в § 9.3.
Подставляя матричные элементы, соответствующие определенным процессам, в формулу теории возмущений (9.1.1), мы получим числа таких процессов в единицу времени. Однако нас интересуют не эти числа, а полные скорости изменения чисел квазичастиц определенного сорта, например, dnkJdt. Для того чтобы получить их, следует просуммировать (с учетом знаков) числа всех элементарных процессов, при которых рождаются или уничтожаются квазичастицы данного сорта. При этом получаются выражения такого типа:
4г {2 21 </га' I I *' > П (8и - М -
I' т'
- 2 21 <т" 117"> J2 6 (er - е^)} L (пк„ пкг,. ..), (9.1.7) I" т”
где V и т' обозначают, соответственно, начальное и конечное состояния для тех элементарных процессов, при которых рождаются квазичастицы с kx, а 7" и т" — начальное и конечное состояния для тех процессов, при которых они уничтожаются. Выражение (9.1.7) носит название кинетического уравнения для числа пк1, а величина L, представляющая собой правую часть этого уравнения, называется часто интегралом (в данном случае лучше было бы сказать — суммой) столкновений.
При исследовании релаксационных явлений целесообразно проводить суммирование в (9.1.7) не по всем возможным элементарным процессам, при которых изменяется число nki, а по
х) Как уже указывалось в § 8.5, импульс (или, точнее, квазиимпульс) квазичастиц с учетом дискретности среды определяется с точностью до слагаемых Ак,,, где кп — векторы обратной решетки. Поэтому слагаемое «кп может войти и в условие сохранения импульса при элементарном процессе, например в (9.1.6). Однако в интересующем пас круге проблем, где главную роль играют квазичастицы со сравнительно малыми k (ка 1, т- е. к /ь-п), процессы, для которых это слагаемое нс равно нулю,— так называемые процессы переброса (см., например, [3]), маловероятны.
464
ПРОЦЕССЫ РЕЛАКСАЦИИ
ГЛ. 9
элементарным процессам определенного типа, с тем чтобы выявить особенности данного типа процессов. Практически суммирование производится обычно по волновым векторам (или импульсам) квазичастиц, участвующих в процессах. Например, при вычислении производной dn^Jdt, обусловленной трехчастичными процессами типа (9.1.3) и (9.1.4), суммирование ведется по всем допустимым значениям к2 и к3.
Наличие условий сохранения импульса и энергии ограничивает области k-пространств, по которым фактически должно проводиться суммирование. В рассматриваемом примере трехчастичных процессов наличие векторного условия (9.1.6) приводит к тому, что суммирование должно проводиться только по одному из пространств к2 или к3. Наличие же скалярного условия (9.1.5) приводит к дальнейшему ограничению области суммирования некоторой поверхностью в этом пространстве. Приведенные общие соображения будут проиллюстрированы на примерах в следующих параграфах.
В правую часть уравнения (9.1.7) для числа квазичастиц с кх войдут (из множителей перед амплитудами Т в матричных элементах, например, в (9.1.3) и (9.1.4)) числа не только этих квазичастиц но и всех других пк, щ3, ..., участвующих совместно с квазичастицами с кх в элементарных процессах. Числа nkt, пкг, в свою очередь, зависят от скоростей протекания всех процессов, в которых участвуют соответствующие квазичастицы; для них могут быть записаны кинетические уравнения, аналогичные (9.1.7). Задача сводится, таким образом, к интегрированию системы связанных уравнений и является очень сложной. Опа существенно упрощается, однако, если предположить,что все числа квазичастиц (щ2, пкз, ...), кроме того, числа (пк1), скорость изменения которого вычисляется, мало отличаются от равновесных значений п1;.г, nks, ... Равновесные значения могут быть легко определены, если известна статистика квазичастиц. Для магнонов, а также фононов она является бозевской; полное число этих квазичастиц не сохраняется, и для их равновесных значений справедлива формула (8.4.22). Если для чисел пкг, пк„ ... принять равновесные значения, то правая часть уравнения (9.1.7) будет содержать только неизвестное nkt и это уравнение, как мы убедимся на ряде примеров, сможет быть представлено в виде
dn,.	—	— —	„
-рр- = — (nkt —nfel) 2«г1 (Пкг, nk„.. .).	(9.1.8)
Величину 2(ог> можно назвать частотой релаксации числа квазичастиц в результате протекания всех тех элементарных процессов, которые учитывались при суммировании в (9.1.7). Обратную величину тх = х/(2юГ1) называют временем релаксации данных квазичастиц в результате протекания тех же процессов.
§ 9.2]
СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 465
Поскольку числа магнонов (см. § 8.4) пропорциональны квадратам амплитуд переменной намагниченности, эти амплитуды убывают, стремясь к равновесным значениям, по закону e~“rlf. Величина w,i, определенная выражением (9.1.8), является, таким образом, частотой релаксации амплитуды колебаний. Она представляет собой вклад в феноменологический параметр сог (см. § 1.3), обусловленный всеми процессами, которые были учтены при суммировании в кинетическом уравнении (9.1.7).
Итак, метод вероятностей переходов, основанный на нестационарной теории возмущений, позволяет вычислить параметры диссипации, обусловленной определенными процессами взаимодействия данного типа колебаний магнитной системы с другими типами колебаний. При атом, кроме спектра и статистики всех участвующих во взаимодействии квазичастиц, должна быть, конечно, известна энергия взаимодействия, которое является возмущением. В следующих параграфах метод вероятностей переходов будет применен к анализу ряда процессов релаксации.
Мы ограничимся в дальнейшем рассмотрением неметаллических (но не обязательно непроводящих) кристаллов. Главное внимание будет уделепо процессам релаксации в ферромагнетиках или ферримагнетиках (ферритах) — для низкочастотного («ферромагнитного») типа колебаний.
§ 9.2. Спин-спиновая релаксация в идеальном магнитоупорядоченном кристалле
Перейдем теперь к рассмотрению процессов релаксации, происходящих в магнитной (спиновой) подсистеме магнитоупорядо,-ченных кристаллов. Квазичастицами, о которых шла речь в предыдущем параграфе, будут теперь исключительно магноны. В атом параграфе мы будем исследовать так называемые собственные процессы релаксации, которые могут происходить и в идеальном кристалле. Возмущениями, вызывающими такие процессы, будут все те виды взаимодействий, которые приводят к высшим: трех-, четырех- и более — магнонным членам в выражениях типа (9.1.2) Для гамильтониана идеального магнитоупорядоченного кристалла.
Источники и типы процессов релаксации в идеальном ферромагнетике. В § 8.5, исследуя гейзенберговскую модель ферромагнитного кристалла, мы видели, что обменное взаимодействие приводит к появлению в гамильтониане членов (8.5.16) четвертого порядка по операторам рождения и уничтожения спиновых отклонений. Переходя от этих операторов к операторам рождения и уничтожения магнонов, можно получить [3, 244] члены
466
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
четвертого порядка вида х) (ср. с выражением (9.1.2))
^4е = 222'^ 12< 34	A (ki -ф- к2 — к3— к4),	(9.2.1)
12 3 4
где для длинноволновых магнонов (ка 1) [244]
Т12,34 ~ да 12 (к2 - к4)2 - kl - klj.	(9.2.2)
Заметим, что обменное взаимодействие не дает членов третьего порядка, а также членов четвертого порядка с аг й2 йф (см. выражение (9.1.2)). Причина этого заключается в том, что для процессов, описываемых такими членами, число магнонов не сохраняется и, следовательно (см. § 8.4), пе сохраняется Mz. Оператор же энергии обменного взаимодействия коммутирует с оператором Mz, и поэтому величина Mz, являющаяся средним значением оператора Mz, должна сохраняться при процессах, обусловленных обменным взаимодействием.
Диполъ-диполъное взаимодействие, которое не требует сохранения числа магнонов, приводит к появлению в гамильтониане членов третьего порядка и членов четвертого порядка типа &з а\. Как показал Ахиезер [274], переход в гамильтониане диполь-дипольного взаимодействия (1.1.50) к операторам а* и (которые в пренебрежении третьим преобразованием Холь-штейна — Примакова — см. § 8.5 — являются операторами рождения и уничтожения магнонов) дает члены третьего порядка
222 2зй1а2язА (kj — k2 k3) -ф- э. с., (9.2.3) 12 3
где при ка <Д' 1
Т1.23 ~----у--]т-’ (Т^)3'2 (sin 292e“it(’! -|- sin 203е"’%). (9.2.4)
Здесь 02>3 и <р213 — соответственно, полярные и азимутальные углы векторов к2 и к3 (ось z, как обычно, направлена по постоянной намагниченности). Заметим, что, поскольку формулы (9.2.2) и (9.2.4) справедливы при ка <<! 1, они могут быть получены также [285], исходя из континуальной модели ферромагнетика.
Процессы с участием метшего числа частиц, вообще говоря, более вероятны, но обменное взаимодействие гораздо сильнее диполь-дипольного. Поэтому необходимо учитывать как трехмаг-нониые члены (9.2.3), так и четырехмагнонные члены (9.2.1),
х) В дальнейшем вместо индексов кг, &2, . . . мы будем писать индексы 1, 2, ..., так что в (9.2.1) суммирование производится по к,, к2, к3 и ki, я операторы Oj, аг, ... суть операторы cfti, а^, ...
§ 9 21 сИИН-СпИНОЙАН релаксаций в идеальном КРИСТАЛЛЕ №1
Таблица 9.2.1
Элементарные процессы, лежащие в основе трехмагнонных процессов релаксации (рассматривается релаксация магиоиов с волновым вектором ki)
Процессы релаксации
Элементарные процессы
прямые
обратные
но можно пренебречь всеми остальными членами, обусловленными диполь-дипольным и обменным взаимодействиями.
Перейдем теперь к подробному рассмотрению трехмагнонных процессов. Их впервые исследовал Ахиезер в уже неоднократно упоминавшейся работе [274]. Затем их изучали Каганов и Цукер-ник [292], Ахиезер, Барьяхтар и Пелетминский [293], Спаркс, Лудон и Киттель [285], Шлёманн [296] и др.
Следует различать два вида трехмагнонных процессов: так называемые процессы расщепления и процессы слияния (табл. 9.2.1). В основе их лежат одни и те же элементарные тройные процессы, но они различаются по характеру суммирования элементарных процессов и вследствие этого, как мы увидим, существуют в различных областях частот и волновых чисел и приводят к различным температурным и иным зависимостям параметров диссипации. Процессами расщепления принято называть такие процессы релаксации, для которых прямые элементарные процессы (ведущие к уменьшению неравновесного числа щ рассматриваемых магнонов) суть процессы расщепления этих магнонов на любые (но, конечно, удовлетворяющие законам сохранения) пары магнонов. Обратными процессами при этом являются элементарные процессы слияния (табл. 9.2.1). Процессами же слияния называют такие процессы релаксации, для которых прямые элементарные процессы суть процессы слияния рассматриваемых магнонов с любыми другими, а обратными элементарными процессами являются процессы расщепления.
Трехмагнонные процессы расщепления. Рассмотрим сначала обусловленные диполь-дипольным взаимодействием процессы расцепления. Для них матричный элемент гамильтониана возмуще
4(58
ГШОЦЁССЫ РЁЙАКСАДЙЙ
ГЛ. 9
ния (9.2.3), соответствующий прямому элементарному процессу (табл. 9.2.1), согласно формуле 19.1.3), запишется в виде
— 1, n2 + 1, ns + 11 W:id I nlf п2, п3> =
= /n^ + lHns+l) (Tli23 + Tli32) A (^ - k2 - k3).	(9.2.5)
Наличие в этом выражении суммы амплитуд Ч^аз и Ч^^ связано с тем, что в матричный элемент рассматриваемого перехода вносят вклад два члена гамильтониана (9.2.3): с операторами a^dg и d^gdg. Матричный элемент для обратного элементарного процесса (табл. 9.2.1), согласно (9.1.4), будет иметь вид
+ 1,п2 — 1,^з— 1 l^sdl'A, п2, п3> =
= (пх ф- 1) п2п3 (44,23 4~ Т1>32) A (kj — k2 — k3).	(9.2.6)
Полная скорость изменения числа интересующих пас магнонов запишется, согласно (9.1.7), следующим образом:
-^Г = 4г4~ 221- 1<771~ 1,772 + 1,пз + l|^3d|«i, п2, п3>|2 + lit)	ГС Сл £• *
2 3
+ I <«i + 1, и2 — 1, п.А — 11 IП1, n2, n3> |2] 6 (//«!— Л'ю2— /мо3),
(9.2.7)
где <oJj2;3— частоты соответствующих магнонов. Множитель 1/2 перед суммой в (9.2.7) введен потому, что одинаковые в действительности состояния системы |/ц, п2, л3> и Ittj, ??3, п2У при суммировании 22 считаются дважды. Подставляя (9.2.5) и (9.2.6)
2 з
в (9.2.7) и учитывая, что Ч^,^ = Чг1>32, получим
4? = if 2 21Ti,2s I21772773 — 771 (772 + пз + 1)1 X 2 3
X A (kr — k2 — k3) 6 (ЙЙ! — /гсо2 — ha3). (9.2.8)
Примем теперь, в соответствии с общим замечанием, сделанным в § 9.1, что числа п2 и /г3не отличаются от их равновесных значений п2 и п3. Формула (9.2.8) будет справедлива и при /ц = пг, но в этом случае, конечно, dn-Jdt = 0. Учитывая это, мы убеждаемся, что формулу (9.2.8) можно записать в виде(9.1.8) и частота релаксации (амплитуды колебаний)
~	2 21'1**1’2з12(гггФ и34~ 1) A (kj— k2— k3) 6 (toj— /гм2—fls>3).
2 з
(9.2.9)
Наличие в выражении (9.2.9) множителя A (ki — k2 — k3) означает, что k3 однозначно (kx задано) связано с к2, и следовательно,
§ 9.21 СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 4Й9 суммирование фактически должно производиться только по значениям одного из этих векторов. Таким образом,
21	12 («2 + п3 + 1) 6 (Дод - Д®2 - Дсо3). (9.2.10)
2
Условие !<! — к2 — к3 = 0 должно теперь учитываться при записи амплитуды и дельта-функции.
Для вычисления частоты релаксации целесообразно перейти в (9.2.10) от суммирования по состоянии к интегрированию по к2- пространству, аналогично тому, как это было сделано при вычислении намагниченности и теплоемкости в § 8.4. При этом, как мы видели,
2-?Ия>-
2	1<2
Интегрирование будем производить в сферических координатах. И поскольку в данном случае будут играть роль лишь малые, по сравнению с 1/а, значения волнового вектора, верхний предел при интегрировании по /г2 можно принять равным ос. Тогда вместо (9.2.10) получим
со п 2л
= (2лй)2 J J J I ^”1,23 I2 (П2 + ns + 1) X fc2=0 02=0 <02=0
X 6 («1 — со2 — со3) A^sin O2d/c2d02d<[2. (9.2.11)
При записи (9.2.11) было учтено свойство дельта-фупкции (С — постоянная величина) [301:
6(Сж) = -^-6(х).	(9.2.12)
Выражение (9.2.11) справедливо для любых трехчастичных процессов расщепления в идеальном кристалле. Для магнонов числа п2 и п3могут быть определены по формуле (8.4.22), а зависимости частот магнонов (входящих в эту формулу и в дельта-функцию) от волновых векторов определяются дисперсионным соотношением для спиновых волн, которое подробно рассматривалось выше.
Высокотемпературное приближение. Рассмотрим случай достаточно высоких температур, когда
м7’^>Йго1, /ио2,	(9.2.13)
Для процессов расщепления заданная частота ец является наибольшей из трех частот ©j, а>2 и ю3, и (9.2.13) сводится к условию
нТ > Тищ.	(9.2.14)
470
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Для диапазона сверхвысоких частот это условие выполняется уже при температурах, измеряемых единицами °К.
Выражая равновесные числа магнонов в (9.2.11) по формуле (8.4.22) и принимая во внимание (9.2.13), а также условие сохранения энергии йц = со2 + (о3, получим
оо л 2п
ООО
X 6(а>1— »2 — а>3)sin 02<й2й92йф2. (9.2.15)
В высокотемпературном приближении частота релаксации оказалась пропорциональной температуре. Как мы увидим ниже, это имеет место и для процессов слияния и, вообще, является свойством трехбозонных процессов.
Подстановка в (9.2.11) или в (9.2.15) выражения (9.2.4) приводит к формулам для частоты релаксации, обусловленной диполъ-диполъными процессами расщепления. В высокотемпературном приближении
(orl = rfiM0'K.T(Ох | sin 202ei4’2 ф- sin 203ei4’312 X
ООО
X <02 (<о	<о2)	(Ю1 — 0)2 — Sltl	(9.2.16)
Наличие в выражении (9.2.16) дельта-функции приводит к тому, что интегрирование фактически производится по некоторой поверхности, вид которой, как и пределы интегрирования, определяется спектром спиновых волн и законами сохранения. При вычислениях оказывается полезным от дельта-функции разности частот перейти при помощи формулы1)
(9.2.17)
к дельта-функции одной из координат в к2-пространстве, а затем исключить интегрирование по этой координате, используя следующее соотношение [301:
/ (ж) б (х — ж0) dx = / (ж0)	(ж0 лежит в интервале хг ч-ж2).
(9.2.18)
Вычисления частоты релаксации могут быть, однако, доведены до конца лишь в некоторых частных случаях и при определенных упрощающих предположениях.
х) Частным случаем формулы (9.2.17) является (9.2.12).
g 9.21 СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 471
Процессы расщепления для случая однородной прецессии. Пусть кг = 0, a (Oj = соо (где ®0 — частота однородной прецессии). Тогда из условия сохранения импульса к2 = — к3 = к с учетом условия сохранения энергии получим
(о2 — <о3 — (Од. = ®0/2.
(9.2.19)
Выражение (9.2.16) в этом случае примет вид
оо тс
(0ГО =	sin2 20ft sin 0А б (Юо _ 2^) kWcd^. (9.2.20)
о о
Очевидно, что условие сохранения энергии может выполняться
теперь только в том случае, если прецессии лежит выше нижней границы спектра спиновых волн. Легко убедиться, что условием этого для эллипсоида вращения является
H0C(Nz + Nr)M0. (9.2.21)
Таким образом, релаксация однородной прецессии путем трехмагнонных процессов расщепления может происходить только при малых магнитных полях, т. е. при достаточно низких частотах.
Ограничимся случаем сферы, тогда из (9.2.21) следует (7.1.13), что является одновременно
половина частоты однородной
Рис. 9.2.1, Пределы интегрирования по для процессов расщепления однородной прецессии и магнонов с fc О и — п/2.	о •— частота однородной
прецессии, — частота магнонов.
условием перехода соо через
верхнюю границу спектра безобменных магнитостатических волн. Если условие (7.1.13) выполняется, то допустимые законами сохранения значения к (рис. 9.2.1) лежат в пределах от 0 до кт, где
,2 “пр 0 — “°
Кт “ 2rj
(9.2.22)
С целью упрощения дальнейших расчетов примем для спектра спиновых волн приближенное выражение (8.1.16). Это выражение получается (см. § 8.5), если пренебречь третьим преобразованием Холыптейна — Примакова, что является также условием справедливости принятого нами выше выражения (9.2.4). Но (8.1.16) выполняется лишь при Hi0 2л Мо, что, казалось бы, резко противоречит условию (7.1.13). В действительности, однако, (8.1.16) приближенно справедливо и при не очень больших полях; как показано в [296J, использование выражения (8.1.16) не вносит
472
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
особенно большой ошибки, если только (и0 не очень близко к ®пр о-
При выполнении условия (9.2.19) каждому значению к в пределах от 0 до кт соответствует некоторый угол 0fl- = 0^. Приняв для спектра выражение (8.1.16), получим
=	(9-2.23)
В частности, «начальное» значение (при к = 0) угла определится следующим образом:
sin2 60 = 4- (1 -	.	(9.2.24)
3 \ “про/	k 7
Таким образом, интегрирование в (9.2.20) должно производиться (см. рис. 9.2.1) по к от 0 до кт и по 0ft от 0о до 0. Наличие в (9.2.20) дельта-функции позволяет исключить интегрирование по одной из переменных. Исключим, например, интегрирование по 0к. Для этого перейдем с помощью формулы (9.2.17) к дельта-функции разности углов 0^:
б (ю0 - 2шй) = б (6k - е;.),	(9.2.25)
где 0/ определяется выражением (9.2.23). Вычисляя 0ю/0Ок дифференцированием (8.1.16) и используя затем формулу (9.2.18), получим
о 'V
(ог0 =	A-2sin2 0ft cos OfcdA.	(9.2.26)
о
Поскольку значения угла 6^ <; 0О невелики (см. рис. 9.2.1), а расчет все равно приближенный, можно принять cos 0^ = 1. Тогда интеграл в (9.2.26) с учетом (9.2.23) берется элементарно и
д яГд/.-;'
“г0 = 15л" л/оЯо ’	(9.2.27)
Окончательно с учетом (9.2.22) г)
(2ДНк =	= .g.	. - «.Л	(9.2.28)
Как и следовало ожидать, вклад процессов расщепления в ширину
х) Полученная величина (2AZ/)3s представляет собой ширину резонансной кривой внутреннего тензора восприимчивости. Согласно (1.4.48) ширина резонансной кривой сферы будет содержать дополнительно множитель
5 9 21 СПИН-СПЙИ0ВАЯ1РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 473 резонансной кривой равен нулю при Но = (оПро/т и возрастает при уменьшении Но. Однако область применимости формулы (9.2.28) невелика, так как по мере приближения Но к	=
4пМ0,во-первых,резко возрастает ошибка,связанная с использованием приближенного выражения (8.1.16), а, во-вторых, образец становится ненасыщенным, возникает доменная структура и расчет, игнорирующий это обстоятельство, теряет смысл.
Для оценки примем: Т = 300 °К; Мо = 140 гс, ц = 0,1 (иттрийжелезный гранат) и Н0 = 800 э. Тогда по формуле (9.2.28) получим
(2ДЯ)38 = 0,08 э,
что составляет заметную часть полной ширины резонансной кривой (— 0,3 э) лучших образцов иттрий-железного граната. Таким образом, трехмагнонпые процессы расщепления могут вносить вклад в диссипацию однородной прецессии, конечно, при тех условиях (достаточно низкая частота), когда они разрешены законами сохранения. Однако прямого экспериментального подтверждения их вклада в диссипацию однородной прецессии пока не имеется. Одна из причин этого заключается в следующем: в сферах (с которыми обычно проводятся эксперименты) одновременно с переходом ®0/2 через нижнюю границу спектра происходит переход ю0 через верхнюю границу спектра безобменных спиновых волн. Выход ю0 из пределов (безобменного) спектра приводит, как мы увидим в следующем параграфе, к «выключению» механизмов релаксации, связанных с рассеянием магнонов однородной прецессии на неоднородностях кристалла, которое может маскировать более слабый эффект «включения» трехмагнонных процессов расщепления. Поэтому было бы очень интересно экспериментально исследовать процессы релаксации в таких условиях, когда рассеяние на неоднородностях не играет существенной роли. Оказывается, это возможно, если интересоваться не шириной резонансной кривой однородной прецессии или какого-либо другого типа колебаний, а нелинейными процессами — порогами нестабильности определенных групп спиновых волн.
Спиновые нестабильности. При достаточно больших уровнях возбуждения, например, при больших величинах переменного магнитного поля, в магнитной системе магнитоупорядоченных кристаллов возникают разнообразные нелинейные явления. Некоторые из них (например, появление второй гармоники и др.) могут быть объяснены нелинейностью уравнения движения намагниченности Для одного — возбуждаемого полем, типа колебаний. Наряду с такими нелинейными явлениями [516, 6] возникают (причем, как правило, при меньших амплитудах переменного поля) другие нелинейные явления, связанные с взаимодействием различных типов
474
ПРОЦЕССЫ РЕЛАКСАЦИИ
(ГЛ. 9
колебаний. Эти явления носят пороговый характер, т. е. возникают при определенных — критических амплитудах переменного поля. Они проявляются в насыщении ферромагнитного резонанса, появлении нелинейного нерезонансного поглощения и в ряде сопутствующих явлений (искажение формы резонансных кривых, низкочастотные осцилляции и пр.).
Такие нелинейные явления впервые четко наблюдали Блом-берген, Дэймон и Уанг (см. [520]). Андерсон и Сул [522], развивая предположение Бломбергена и Уанга, объяснили их, исходя из того, что некоторые типы колебаний магнитной системы (спиновые волны) становятся «нестабильными» , т. е. быстро растут в результате взаимодействия с первичным типом колебаний (который возбуждается переменным полем) при определенной — пороговой его амплитуде. Заметим, что взаимодействия, приводящие при больших уровнях возбуждения к такой нестабильности,— это те самые взаимодействия которые приводят (при любых уровнях возбуждения) к процессам релаксации. Отсюда ясно, что теория нелинейных явлений может быть развита теми же двумя путями, которые упоминались в связи с релаксационными процессами в § 9.1. Первоначально такая теория была создана Сулом [522] на основе исследования связанных уравнений движения, затем она была развита также методом анализа кинетических уравнений для чисел соответствующих квазичастиц Калленом и Уайтом и Спарксом [539].
Изучение спиновых нестабильностей, как и вообще нелинейных явлений, не входит в задачу этой книги *). Но поскольку экспериментальное исследование их является важным источником информации о релаксационных процессах, мы приведем некоторые сведения, необходимые для понимания рассматриваемых ниже экспериментов.
Наиболее важным видом нестабильности является нестабильность пары магнитных колебаний (например, спиновых волн с волновыми векторами kj и к2 и частотами, соответственно, и со2) под воздействием некоторого колебания (накачки) с частотой &р-Колебанием накачки может быть спиновая волна с волновым вектором кр или один из длинноволновых типов колебаний магнитной системы, например однородная прецессия, или, непосредственно, переменное магнитное поле. Для рассматриваемого вида нестабильности выполняются условия сохранения:
vkp = кг + к2,	(9.2.29)
Тор = од ф- к>2,	(9.2.30)
х) Нелинейные колебательные процессы в магнитоупорядоченных веществах, кроме упомянутых выше работ, рассматриваются в монографиях и обзорах [6, 15, 537, 20, 244].
СПИН-СПИПОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 475
£ 9.2]
ГдС v = 1, 2, 3, ... Отсюда видно, что с корпускулярной точки зрения в основе рассматриваемых нестабильностей лежат элементарные процессы расщепления одного или нескольких магнонов или фотонов накачки на два магнона потенциально нестабильных колебаний.
Наиболее низкий порог (т. е. наименьшую амплитуду колебания накачки, при которой нестабильность возникает) имеют, вообще говоря, если они допускаются условиями сохранения, нестабильности первого порядка — с v = 1. Мы ограничимся случаем, когда накачкой является однородная прецессия или переменное магнитное поле, т. е. примем кг = 0. Тогда Iq = — к2 == к и для процессов первого порядка
(Oj = ю2 = а>к =	.	(9.2.31)
В случае, когда накачкой является однородная прецессия, пороговая амплитуда линейно поляризованного переменного магнитного поля для нестабильности первого порядка [522]
(1) _ 4шрДНл[(шр-(ооР+(тДЯо)2]’/' ''-пор--------------------------------
01 Al S*n	+ шн + 11^2
где ю0 — частота однородной прецессии, = у4п7И0, а>н = =7 (#о —	\Н0 — параметр диссипации однородной пре-
цессии, а 6к и Д/Д — соответственно, полярный угол волнового вектора и параметр диссипации потенциально нестабильных спиновых волн. Из выражения (9.2.32) видно прежде всего, что пороговое поле пропорционально Д/Д. Заметим, что это имеет место для всех вырожденных (eq = п>2) процессов первого порядка; для невырожденных /?пор пропорционально Y	.
Как следует из (9.2.32), пороговое поле должно быть минимально при (Ир = соо, т. е. при резонансе однородной прецессии на частоте накачки. Но условие сохранения в этом случае, как мы видели выше, может быть выполнено только при достаточно низких частотах, когда имеет место неравенство (9.2.21), или для сферы (7.1.13). Если это неравенство будет едва только выполнено, то угол 0fc будет мал и /?пор5 согласно (9.2.32), будет велико. Но при дальнейшем снижении частоты 0к будет расти и значения ^„ор бУДут резко уменьшаться, достигая весьма малых величин
кй) , Д/ДД/Д’	zq о зз\
Лпор 2лЛ7ц •	(9.2,Л1)
гл
0 по Сулу [522] — случай «совпадения дополнительного по-лощения с основным резонансом». Нестабильными здесь стано-ТСя спиновые волны с малыми к.
476
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ 9
При более высоких частотах накачки, когда условие (9.2.21) не выполняется, порог оказывается паинизшим при значениях постоянного поля, меньших чем резонансное поле для однородной прецессии. Значения постоянного поля и величины 0ft и к нестабильных волн могут быть найдены минимизацией выражения (9.2.32). Это — случай так называемого «дополнительного поглощения».
Для процессов второго порядка (v = 2) при накачке однородной прецессией условие (9.2.30) сводится к сог = ю0, т. е. нестабильными становятся спиновые волны, вырожденные с однородной прецессией. Такие волны всегда имеют место, и нестабильность второго порядка при резонансе всегда наступает, если только (на низких частотах) при меньших переменных полях не достигается порог нестабильности первого порядка. Порог нестабильности второго порядка оказывается минимальным для спиновых волн с 0к = 0, и следовательно, волновое число их к определяется формулой (8.1.43). Для сферы из иттрий-железного граната
к	3 • 10Б см"1.
Пороговая амплитуда переменного магнитного поля (с линейной поляризацией) в этом случае
/&>р^2ДЯ0У -v-^.	(9.2.34)
Пропорциональность порогового поля параметру диссипации потенциально нестабильных колебаний в степени 1/2 характерна для нестабильности второго порядка.
Остановимся теперь на нестабильности спиновых волн, которая возникает под воздействием, непосредственно, переменного магнитного поля, приложенного параллельно постоянной намагниченности {продольная или параллельная накачка). Исследование нелинейных явлений при продольной накачке, в первую очередь измерение порога этой нестабильности, является в настоящее время одним из наиболее распространенных методов экспериментального исследования процессов релаксации.
Для пороговой амплитуды переменного поля продольной накачки Шлёманн, Грин и Милано [528] получили, в случае нестабильности первого порядка, следующее выражение:
Отсюда видно, что нестабильными становятся, в первую очередь, магноны с 6к = л/2. Их волновое число, как легко убедиться, определяется следующим образом:
/?-Х(Яс-Я0),	(9.2.36)
•I
СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 477
§ У
Где для изотропного эллипсоида
1 f [ СО \ 2
=У Ш + (2я7И«)2 - <2я - м«- <9-2-37)
\ /
Рис. 9.2.2. Зависимость пороговой амплитуды переменного поля при продольной накачке от постоянного поля [537]. Частота накачки 9,4 Гец. Сфера иттрий-железного граната при комнатной температуре. Постоянное поле направлено вдоль оси <111>.
Величина Нс, как видно из (9.2.37), приблизительно в два раза меньше, чем резонансное поле для однородной прецессии с частотой ©р. При изменении внешнего поля II0 от II с до некоторой минимальной величины, при которой образец еще насыщен, к возрастает от нуля до величин порядка 105 (для частоты лежащей в сантиметровом диапазоне). Зависимость	от II0 по-
казана на рис. 9.2.2. Вид пологой левой ветви этой кривой определяется зависимостью Д/Zjc от к. Крутая правая ветвь (7/0 Яс) связана с нестабильностью магнитостатических (безобманных) типов колебаний.
Измерение пороговых величии переменного поля для различных нестабильностей позволяет определять параметр диссипации №1% тех спиновых волн, которые становятся нестабильными. Существенно, что процессы релаксации, обусловленные неоднородностями, обычно почти не вносят вклада в определенную таким образом величину ДЯК (этот вопрос будет подробно разбираться в следующем параграфе). Измерение Д7Д позволяет, таким образом, исследовать процессы релаксации, не связанные с неоднородностями, т. е. присущие идеальному кристаллу.
Процессы расщепления при продольной накачке. Вычисление частоты релаксации, обусловленной трехмагнонными
процессами расщепления для магнонов с 6;£=л/2, проводили Шлё7 манн [296]и Спаркс, Лудой и Киттель [285]. Рассмотрим сначала предельный случай Но—>НС, когда волновое число нестабильных магнонов к± —> 0. Условием существования процессов расщепления в этом случае будет
4-“л(*-»0,ел = -^-)>©й(А:->0,ел)= 0.	(9.2.38)
Для сферы это условие приводит к неравенству, аналогичному
— ®з>/2 <^©про?
478
ПРОЦЕССЫ РЕЛАКСАЦИИ
1ГЛ. 9
где a>fc0 — частота магиоиов, релаксация которых рассматривается, а (Ор — частота иакачки. Б результате процессов расщепления будут образовываться магноны с | k2 | = | ks | ~ к и со2 = — <£>з= <0fc0/2 = ®р/4. Значения к лежат теперь в пределах от 0 до кт (см. рис. 9.2.1), а величина кт определяется из условия
1
Ти*
^->0,efc =-^ = QA(k== ^А = 0).	(9.2.39)
Расчет частоты релаксации магнонов с 6fc = л/2 и к —> 0 ана-
логичен приведенному выше расчету для
Рис. 9.2.3. Частотная зависимость параметра диссипации спиновых волн с /с —> О и = л/2, полученная методом продольной накачки [244]. Сфера из иттрий-железного граната; комнатная температура.
однородной прецессии. Представляет интерес рассмотреть частный случай, когда <о^0 мало отличается от предельного значения <апр 0 и, следовательно, кт мало, но зато исходить из точного спектра (8.1.14). Формула (9.2.27) будет справедлива в этом случае, если заменить в пей кт на кт-, для кт из условия (9.2.39) получится следующее выражение:
кт = 101] (®пр° ико). (9.2.40)
Сравнивая его с (9.2.22), мы видим, что окончательная форму ла для 2М1к будет отличаться от (9.2.28) лишь множителем (0,6)’/»Ж 0,3.
Итак, трехмагнониые процессы расщепления «включаются» в релаксацию магиоиов с 6;; = п/2 и к —> 0, когда частота их становится меньше, чем 2/3	; вклад таких процессов в при ком-
натной температуре и достаточном удалении от предельной частоты должен быть порядка нескольких сотых эрстеда. Эти заключения
могут быть проверены экспериментально с использованием продольной накачки. На рис. 9.2.3 приведена частотная зависимость параметра диссипации, определенного по формуле (9.2.35) из измерений пороговой амплитуды переменного поля при Но = Ht-Как видно из рис. 9.2.3, при = шпг 0 действительно начинается рост Д-Щ, который может быть обусловлен «включением» процес
сов расщепления.
Если Но Нс и, следовательно, кг =/= 0, то положение усложняется, поскольку теперь магноны, образующиеся в результате процессов расщепления, будут иметь	и п>2 ¥= ®з- Если
кг задано, то процессы расщепления оказываются разрешенными
§9 2] СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 479
условиями сохранения при оц < ©пр; предельная частота ©пр пастет с ростом kt [285]. При фиксированной же частоте «ц процессы расщепления могут происходить, если ку /смян. В случае высоких частот (о>1 <ом) [285]
/См«н = 4 V '	(9.2.41)
Вычисления частоты релаксации при /q^O оказываются довольно громоздкими, и мы приведем лишь приближенно® выражение, полученное в [285] для сферы при <в1
(2АЯ,)35 = -A- 1П	.	(9.2.42)
---— 1
<4
Здесь (Ofc! и (0fc2 (Ofc! — частоты спиновых волн с 6Ь = 0 и волновыми числами, являющимися корнями уравнения
к(к±-к)
_ шн __т(яо—-у-ЛГо) 2t]	2i]
(9.2.43)
Зависимость величины (A//\)3S от кг, рассчитанная по формуле (9.2.42), показана на рис. 9.2.4. Как видно из этого рисунка, включение процессов расщепления действительно происходит при
личг Зависимость параметров диссипации спиновых волн, обусловленных раз-пррр 1МИ Релаксационными процессами, от волнового числа. 3s — трехмагнонные про-Пооп РасЩепления, Зс — трехмагнонные процессы слияния, 4sc — четырехмагнонные Р цессы рассеяния. Но = 1500 э, 0ft = л/2; комнатная температура: иттрий-железный гранат.
некотором значении J,\] в данном случае оно определяется формулой (9.2.41). При дальнейшем увеличении волнового числа величи-(A2Zft)3s проходит через максимум.
480
ПРОЦЕССЫ РЕЛАКСАЦИИ
(ГЛ. 9
Трехмагпонные процессы слияния. Для процессов слияния (см. табл. 9.2.1) кинетическое уравнение имеет вид
2 2 [ । ^П1	1’112 ~ пз + 11	| пъ и2> пз> |2 +
+ |	+ 1> п2 + 1, пз — 11	1 nii n2i пз> |21- (9.2.44)
В этом выражении отсутствует множитель 1/2, имеющийся в (9.2.7), так как состояния | пх, п2, п3У и | ??1т п3, п2у теперь не эквивалентны. Записывая матричные элементы, входящие в (9.2.44), аналогично (9.2.5) и (9.2.6) и заменяя затем числа п2 и п3 на их равновесные значения, получим
cori = —2 2 । ^?3’12	(к1' г — кз)$ (^Qi+ ^q2— Йсо3).
2 3
(9.2.45)
Из-за наличия множителя Д (Iq ф k2 — k3) суммирование в (9.2.45), как и в (9.2.9), должно фактически проводиться только по к2 или к3. Переходя затем к интегрированию по к2-простраист-ву, получим аналогично (9.2.11)

со л 2Л
J | ^3,12 I2 (»2 — П3) 6 (ЮХ + С02 — С03) ООО
к2 sin e2dk2dd2dq>2.
(9.2.46)
Формула (9.2.46) справедлива для любых трехчастичпых процессов слияния.
Если все квазичастицы являются бозонами, то в высокотемпературном приближении (9.2.13) формула (9.2.46) дает
со л 2л
Wrl== 5 5 I ^3,12 |2 (o’ piYlp Ш2)	С02 — й3)/^8Шб2Й/с2ЙЭ2Йф2-
ООО
(9.2.47)
Таким образом, в высокотемпературном приближении частота релаксации для процессов слияния также оказывается пропорциональной температуре. Но в случае процессов слияния условие справедливости этого приближения (9.2.13) выполняется хуЖе, чем для процессов расщепления. Теперь со3 всегда больше, а также может быть больше, чем сщ, и условие (9.2.13), даже если оно выполняется для рассматриваемых квазичастиц с заданной частотой со1, может не выполняться для других квазичастиц, участвующих в процессе. Однако числа этих квазичастиц, обладающих
§9 2] СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 481
большими энергиями, невелики; поэтому формула (9.2.47) будет приближенно справедлива, если хорошо выполняется неравенство (9.2.14).
В ДРУГ0М предельном случае очень низких температур, когда имеют место неравенства, обратные (9.2.13), зависимость п»г1 для
процессов слияния от температуры становится, как следует из (9.2.46), экспоненциальной. Частота же релаксации для процессов расщепления в этом случае, как видно из (9.2.11), перестает зависеть от температуры (рис. 9.2.5). Это различие объясняется тем, что для процессов слияния необходимы термические магноны (с к2), число которых при низких температурах экспоненциально убывает с понижением температуры. Мы не будем более подробно останавливаться на этом случае, ибо, как уже отмечалось, для диапазона сверхвысоких частот Лсо/х составляет доли градуса.
Подставляя в формулу (9.2.47) амплитуду возмущения (9.2.4), получим частоту релаксации для трехмагнониых процессов слия-
Рис. 9.2.5. Температурные зависимости параметров диссипации, обусловленных трехмагнон-ными процессами расщепления (5s) и слияния (5с) при низких температурах.
ния, обусловленных диполъ-диполъным взаимодействием, в вы-
сокотемпер атуриом приближении:
оо я 2я'
“н = 4	I sin 2e2ei(₽« + sin 26iei<₽1 |2	X
0 0 0
X 6((i>i + <i)2 — co3) /c|sin62d/c2d02d(p2. (9.2.48)
Условия сохранения для процессов слияния имеют вид kt + k2 = k3,	(9.2.49)
сэр -f- <o2 = <£>3.	(9.2.50)
Легко убедиться, что эти условия, в отличие от условий сохранения (9.1.5) и (9.1.6) для процессов расщепления, могут выполняться при любых частотах исходных магнонов. Однако они пе могут выполняться при к, = 0. Таким образом, процессы слияния для однородной прецессии невозможны; они вносят вклад в релаксацию любых магнонов с =/= 0. Но при /q/= 0 расчеты по формуле (9.2.48), как и по формуле (9.2.15) для процессов расщепления, становятся громоздкими. Поэтому мы ограничимся тем, что при-?2QeM ыекотоРые результаты этих расчетов [285, 296] (см. также
16 А. Г. Гуревич
482
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Для малых ку (когда т] ®i) было получено следующее выражение [2851:
(здя^ =	(i+-¥"sil12 е1 —т-sil14 61) • <9-2-51)
Из (9.2.51) видно, что параметр диссипации, обусловленный процессами слияния, как и следовало ожидать, обращается в нуль при ку = 0. Для магнонов с 6г = л/2, которые возбуждаются при продольной накачке, из (9.2.51) следует
(2ДЯЙ)ЗС = -J-	.	(9.2.52)
На рис. 9.2.6 показана экспериментальная зависимость ДЯК от ку, полученная Касуя и Ле Кроу [284]. При ку^_ 1,6-105 эта
Рис. 9.2.6. Зависимость параметра диссипации спиновых ВОЛН с = л/2, возбуждаемых при продольной накачке, от волнового числа [284]. сод/гл — = С0у/4л — 9,7 Ггц. Сфера из иттрийжелезного граната; комнатная температура.
зависимость может быть аппроксимирована прямой
2ДЯК = гДЯ^ + Аку. (9.2.53)
Экспериментальное значение коэффициента А составляет 1,1-10”®, в то время как из формулы (9.2.52) следует А = 0,8-10“®. Таким образом, трехмагнонные процессы слияния вносят существенный вклад в зависящую от Д часть 2ДЯ/£. Что же касается величины 2ДЯ^0 (см. рис. 9.2.6), то ее интерпретация вызвала в свое время оживленную дискуссию. Прежде всего яс-
ио, что эта величина не может быть связана с процессами расщепления, которые при данной частоте и ку = 0 невозможны. Как мы увидим ниже, в нее не вносят замет
ного вклада и четырехмагнонные процессы. Авторы работы [284] предположили, что величина 2ДЯ/;о обусловлена, в основном, трехбозонными процессами слияния магнонов с фононами. Они принадлежат к процессам спин-решеточной релаксации и будут рассматриваться в § 9.4. При высоких температурах некоторую роль могут играть и трехмагнонные процессы слияния. Законы сохранения запрещают, как мы видели, такие процессы в ферромагнетиках при ку = 0. Однако в ферримагнетиках, каким является иттрий-железный гранат, эти процессы могут происходить с участием обменных ветвей спектра. Возмущением, которое может обеспечить заметный вклад таких процессов в 2ДЯ;.О, явля-
g 9 2] СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ 483 ется согласно [284], локальная энергия анизотропии магнитных ионов.
Для магнонов с = л/2 расчет частоты релаксации был проведен [285] и без предположения с малости к17 но по-прежнему в высокотемпературном приближении (9.2.13). При этом для спектра спиновых волн было принято приближенное выражение (8.1.16), а угловой множитель | 81п262ег<₽2 + sin261ei4>1 | 2 под интегралом в (9.2.48) был заменен постоянной величиной В результате было получено выражение
In [1 +------------------—--------1. (9.2.54)
,;7а	Ч2/<1 L их — I]k[ 1 + (СО! — T]fc2)/4i]к[ J	’
При ц/ci й! оно переходит в (9.2.52), если принять £ = 1/8. Зависимость (2ДЯк)3с от кг, рассчитанная по формуле (9.2.54), приведена на рис. 9.2.4. Как видно из этого рисунка и как следует из формул (9.2.42) и (9.2.54), при очень больших кг (когда ц/с2 а>н)
(2A//k)3s = (2ДЯ/;)3с,
и результирующий параметр диссипации магнонов с 6r = л/2, обусловленный трехмагнонными диполь-дипольиыми процессами,
= ' <9-2'55>
Важной особенностью трехмагнонных процессов релаксации является то, что они приводят к изменению полного числа магнонов; при процессах расщепления число магнонов увеличивается, а при процессах слияния — уменьшается. Но полное число магнонов, согласно (8.4.12), определяет величину Mz. Поэтому трехмаг-ноиные процессы могут быть ответственными за релаксацию Мг — приближение этой величины к ее равновесному значению при данной температуре. Мы не будем останавливаться на вопросе о релаксации намагниченности; он рассмотрен подробно в работах Ахиезера, Барьяхтара и Пелетминского [293, 280] (см. также [3]), Спаркса и Киттеля [295] и других.
В § 8.4 отмечалось также (формула (8.4.15)), что число всех магнонов, кроме магнонов однородной прецессии, определяет длину вектора магнитного момента образца. Поэтому все трехмаг-Нонные процессы: процессы расщепления магнонов однородной прецессии (процессы слияния, как мы видели, для однородной прецессии запрещены) и процессы, в которых однородная прецессия не Участвует, связаны с изменением длины вектора магнитного момента. И, строго говоря, описание этих процессов при помощи Уравнений движения (1.3.2) или (1.3.3) невозможно. Однако в » 1.3 показано, что при малых амплитудах и малой диссипации (и
16*
484
ПРОЦЕССЫ РЕЛАКСАЦИИ
Рис. 9.2.7. .Элементарные процессы (прямые), лежащие в основе четырехмагнонных процессов релаксации, s — процессы расщепления; sc — рассеяния; с — слияния. Рассматривается релаксация магнонов с волновым вектором
если интересоваться только поперечными составляющими намагниченности) различные формы записи диссипативного члена приближенно эквивалентны. При этих условиях уравнения (1.3.2) или (1.3.3) можно использовать и в том случае, когда трехмагнонные процессы вносят вклад в диссипацию.
Четырехмагнонные процессы. Четырехмагиоиные процессы релаксации были исследованы Касуя (см., например, [20, 287]), Кагановым и Цукерником [292] и другими. Роль этих процессов в диссипации энергии при ферромагнитном резонансе рассмотрели Пинкус, Спаркс и ЛеКроу [298]. Элементарные четырехмагнонные процессы, при помощи которых может происходить релаксация магнонов с волновым вектором к17 показаны на рис. 9.2.7. Процессы релаксации, для которых элементарные процессы х или с (рис. 9.2.7) являются прямыми, можно назвать, соответственно, процессами расщепления и слияния. Процессы sc (рис. 9.2.7) можно назвать процессами рассеяния магнона на магноне. Процессы расщепления и слияния (при которых изменяется полное число магнонов) ие могут быть обусловлены обменным взаимодействием. Возмущением, вызывающим эти процессы, может быть диполь-дипольное взаимодействие или различные взаимодействия, связанные с магнитной анизотропией. И можно полагать (расчеты [298] подтверждают это), что и клад четырехмагпонных процессов расщепления и слияния пе является существенным. Мы ограничимся рассмотрением процессов рассеяния, которые могут быть вызваны обменным взаимодействием. Члены гамильтониана, ответственные за эти процессы, имеют вид (9.2.1).
Используя метод вероятностей переходов, для четырехчастичных процессов рассеяния получим
~2 221 Ч’хг.м + Т'21>31 ф- Т\2,43 + F2i,43 |2 X 1	2 3 4
X [(Hi + 1) («2 + 1) и3н4 — прг2 (п3 + 1) (и4 + 1)1 X
X А (к, -[- к2 — к3 — к4) 6 (Йац ф- Йюа — 7м>)3 — /гсо4)1. (9.2.56)
Множитель 1/2 перед суммой, аналогично (9.2.7), учитывает неразличимость конечных состояний | пг, п2, п3, nt) и | n4, п2, nit п3у. Принимая для п2, п3 и н4 их равновесные значения, можно привести (9.2.56) к виду (9.1.8); для частоты релаксации получится
9.21
СПИН-СПИНОВАЯ РЕЛАКСАЦИЯ В ИДЕАЛЬНОМ КРИСТАЛЛЕ
выражение
2 о
’	1„ W’
12,43 “1 л 21,43
X 1«2 (пз + ^4 + 1) — н3и4] 6 (Й«! 4- Лсоа — Йсо3 — Й'О4). (9.2.57)
Если учесть (9.2.2) и условие сохранения импульса, то легко полу-| 'f 12,34 4" Р 2i>31 “Н 412,43 “X 21,13|2 = (Й/Ор) (^1^2 г k3k4)“. (9.2.58)
Примем снова приближенное выражение (8.1.16) для спектра спиновых воли. Тогда из условий сохранения энергии и импульса будет следовать, что
kxk2 == k3k4.	(9.2.59)
Подставляя (9.2.58) с учетом (9.2.59) в (9.2.57) и переходя к интегрированию по к2- и к3-прострапствам, получим формулу для частоты релаксации магнонов с волновым вектором к, за счет четырехмагнонных процессов рассеяния:
«ы = лТГГ1 J J [”2	+ "4 + 1) — «з’?41 х
(кг) (ks)
X 6 (с£>1 + со2 — ы>3 — !£>4) /с2 сэз2 a12dJk2i3A3. (9.2.60)
Здесь а12 — угол между векторами к4 и к2. Из выражения (9.2.60) видно, что о;г1 —» 0 при kj —> 0. Этого и следовало ожидать, так как при к4 = 0 не сохраняется число магнонов с к =j= 0 и поэтому не сохраняется длина вектора магнитного момента образца 91?. Но оператор энергии обменного взаимодействия коммутирует с оператором ЭД2, и при процессах, обусловленных обмен; ым взаимодействием, ЭД (как и ЭД2) должно сохраняться.
Из примеров, которые были рассмотрены выше, ясно, что расчеты по формуле (9.2.60) окажутся очень громоздкими, и мы не будем на них останавливаться. Заметим лишь, что в высокотемпературном приближении «статистический» множитель в квадратных скобках в (9.2.60) примет вид
-- /— 1 — I л \-------------W)1 <01 п, («о 4- п. 4- 1) — п3п. -----------------
"V 4 1	41	'	3 4	Й2С02<0з®4
(9.2.61)
и частота релаксации окажется пропорциональной 7’2. Это является общим свойством четырехбозонных процессов в высокотемпературном приближении. Однако, так же как и в случае трехмаг-нонных процессов слияния (см. выше), высокотемпературное приближение плохо выполняется для четырехмагнонных процессов рассеяния; условие (9.2.14) является, конечно, недостаточным.
Расчет частоты релаксации, обусловленной четырехмагнонны-ми процессами рассеяния, с более строгим учетом свойств спино
486
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
вых воли был проведен Дайсоном [2331; полученный им результат *) можно записать в виде
{2MIk)isc = ----------к„ (9.2.62)
V h,isc 2	(4л)‘/Е й‘Ад/2 tfh 1?	'	>
где £ (5/2) = 1,34 (см. § 8.4). Выражение (9.2.62) должно быть справедливо в широком интервале температур от сколь угодно низких до температур порядка половины температуры Кюри.
Если сравнить (9.2.62) с формулами (9.2.42), (9.2.51) и др. для трехмагнонных процессов, то окажется, что при низких температурах и малых /с, доля четырехмагнонных процессов спин-спиновой релаксации мала. Однако вклад их возрастает с увеличением и температуры. Так, например, нетрудно убедиться, что для магнонов 0 0! = л/2 и кг = 5-105 при Но = 1500 э в иттрий-железном гранате вклад четырехмагнонных процессов сравнивается с вкладом трехмагнонных процессов слияния (трехмагнонные процессы расщепления в данном случае невозможны) при Т = 450 °К. Зависимость (2Д/Д)4с8 от къ рассчитанная по формуле (9.2.62), показана, наряду с вкладами трехмагнонных процессов, на рис. 9.2.4. Из этого рисунка видно, в частности, что при тех значениях /г15 при которых происходит «включение» трехмагнонных процессов расщепления, вклад четырехмагнонных процессов рассеяния оказывается уже весьма существенным.
До сих пор речь шла о релаксации когерентных магнонов, которые возникали непосредственно в результате линейного возбуждения поперечным переменным электромагнитным полем или в результате нелинейного, параметрического возбуждения. Но следует иметь в виду, что при релаксации этих — «первичных» магнонов возникают магноны следующих «поколений». И по мере того, как среди них появляются магноны с все большими значениями к, в релаксации все возрастающую роль начинают играть четырех-магнонные процессы. При этом, конечно, четырехмагнонные процессы, обусловленные обменным взаимодействием, будут ответственны за такое перераспределение энергии в магнитной системе, которое происходит без изменения М2 и Мг. В релаксации же величин М2 и участвуют трехмагнонные процессы (небольшой вклад вносят четырехмагнонные процессы расщепления и слияния и процессы более высоких порядков), а также процессы, которые будут рассматриваться в §§ 9.4, 9.5 и 9.6.
Интересно отметить, что в основе упоминавшейся выше нестабильности второго порядка лежат элементарные четырехмагнонные процессы, при которых уничтожаются два магнона одно
*) С небольшой поправкой Кеффера 1244].
§ 9.3]
ДВУХМАГНОННЫЕ ПРОЦЕССЫ
487
водной прецессии (с kj = 0) и возникают два вырожденных с ними магнона с к2 = —к3. Ясно, что обменное взаимодействие не может вызывать этот процесс. Он может быть обусловлен, в согласии с теорией Сула [522], диполь-дипольным взаимодействием.
§ 9.3. Двухмагнонные процессы
Вклад рассмотренных в предыдущем параграфе собственных процессов спин-спиновой релаксации в ширину резонансной кривой однородной прецессии и других длинноволновых типов магнитных колебаний ферро- и ферримагнетиков не превышает величин порядка 0,1 э. Как будет показано в § 9.4, вклад собственных (обусловленных прямым магнон-фононным взаимодействием) процессов спин-решеточной релаксации в диссипацию этих типов колебаний пренебрежимо мал. В то же время экспериментальные значения A/Z в ферритах, а также ферромагнитных металлах измеряются часто десятками, сотнями, а иногда даже тысячами эрстед. Кроме того, все собственные процессы релаксации, как мы видели, приводят к росту АН с увеличением температуры, в то время как экспериментальные значения АН часто уменьшаются с увеличением температуры в некоторых интервалах ее изменения. Эти противоречия были отмечены еще в самом начале экспериментального исследования ферромагнитного резонанса и составили содержание проблемы ферромагнитной релаксации.
Проблема ферромагнитной релаксации была, в основном, решена в конце 50-х — начале 60-х годов. Стало ясно, что наблюдавшиеся большие значения АН и «аномальные» (с точки зрения собственных процессов) температурные зависимости обусловлены наличием двух дополнительных (не собственных) каналов релаксации:
1) спин-спиновой релаксации, связанной с неоднородностями кристалла, и
2) косвенной спин-решеточной релаксации, связанной с наличием в кристалле электронов проводимости или ионов с сильной спин-орбитальной связью.
В этом параграфе, оставаясь пока в пределах магнитной подсистемы, мы рассмотрим первый из упомянутых каналов. Неод-* породностями, которые приводят к его появлению, являются, вообще говоря, любые нарушения периодичности кристалла. Наибольшую роль в процессах релаксации магнитных колебаний игра-К)Т» по-видимому, следующие неоднородности:
а)	нарушения порядка в расположении магнитных ионов в Узлах решетки, неоднородности химического состава образцов;
б)	нарушения постоянства направлений осей кристалла: поли-кристалличность и блочность;
588
ПРОЦЕССЫ РЕЛАКСАЦИЙ
1гЛ. 9
в)	неоднородные упругие напряжения, в частности, вызванные дислокациями;
г)	«геометрические» неоднородности: поры, трещины, шероховатости поверхности образцов.
Методы учета влияния неоднородностей на диссипацию энергии магнитных колебаний. Еще Ван-Флек [115] отметил, что одной из причин расширения резонансных кривых при ферромагнитном резонансе в поликристаллах является разброс резонансных частот (или резонансных полей — при постоянной частоте) в различных кристалликах (зернах) вследствие разной ориентации их кристаллографических осей. Такой подход к магнитному резонансу в неоднородных средах получил название приближения независимых областей Фм. § 2.3). Следует подчеркнуть, что в приближении независимых областей расширение резонансных кривых является результатом не какого-то дополнительного механизма релаксации, а, просто, различия условий резонанса в разных точках образца. С этим связано то обстоятельство, что форма резонансной кривой (как мы убедились на примере поликристалла в § 2.3) не является лоренцевой, а определяется законом распределения резонансных полей по объему образца.
Однако приближение независимых областей является очень грубым, поскольку оно полностью игнорирует свя'зь между магнитными колебаниями в различных точках образца. Даже при резонансе в магнитно неупорядоченных кристаллах обменная связь между магнитными моментами приводит, как известно [11, к заметному сужению резонансных линий, расширенных из-за неоднородности поля. В случае же магнитоупорядоченных кристаллов взаимодействие между магнитными колебаниями в разных точках образца, обменное или диполь-дипольное (в зависимости от размера неоднородностей), должно быть решающим фактором. И действительно, в случае поликристаллов приближение независимых зерен справедливо лишь при условии(2.3.1), которое редко выполняется. В приближении независимых областей для образца резко неэллипсоидальной формы ширина резонансной кривой должна быть очень большой — порядка 2лМ0, ибо именно такого порядка будет разброс внутренних постоянных полей в образце. В действительности же в таком образце могут возбуждаться неоднородные типы колебаний, но значения 2ДЯ для каждого из них, как уже отмечалось в § 2.3, не очень сильно отличаются от ширины резонансной кривой эллипсоидального образца с однородным внутренним полем.
Наличие сильной связи — обменной и диполь-дипольной — между переменными намагниченностями в различных точках образца приводит к тому, что нельзя рассматривать, даже в качестве нулевого приближения, независимые колебания (со своими резонансными условиями) в различных точках, а следует говорить о
е.з]
ДВУХМАГНОННЫЕ ПРОЦЕССЫ
489
Рис. 9.3.1. Часть спектра собственных частот магнитных колебаний ферромагнитного образца. 1 — однородный образец; 2 — при наличии неоднородностей.
собственных типах колебаний всего неоднородного образца. Эти колебания, конечно, отличаются от собственных колебаний однородных образцов, которые подробно рассматривались в предыдущих главах. Задача об определении структуры полей колебаний неоднородных образцов и их собственных частот является, вообще говоря, очень сложной. Она может быть решена строго лишь в том случае, если неоднородность носит регулярный характер, так что возможно ее точное математическое описание. Задача о магнитных колебаниях при наличии простой слоистой доменной структуры, которая была рассмотрена в § 3.2, представляет собой пример таких задач.
Неоднородности, которыми мы интересуемся сейчас (шероховатости поверхности, поры, зернистая структура поликристаллов), являются нерегулярными — их математическое описание возможно лишь статистически, на языке теории случайных величин. При этом задача об определении спектра и структуры полей собственных колебаний, конечно, не может иметь , точного решения. Однако мы можем ожидать, что частоты возмущенных типов колебаний неоднородного образца будут группироваться около частот невозмущенных типов (рис. 9.3.1). Нерегулярный характер неоднородностей приведет к тому, что в каждой такой группе будет иметься, практически, непрерывное распределение собственных возмущенных частот. В частности, группа частот неоднородного образна будет расположена вблизи частоты <оо однородной прецессии. Однородное переменное поле будет возбуждать всю эту группу колебаний, и ширина резонансной кривой увеличится на величину порядка ширины области их частот. Очевидно, что одновременно частота, соответствующая максимуму поглощения (резонансная частота), может сместиться относительно невозмущенной частоты однородной прецессии.
При такой (наиболее строгой) трактовке влияния неоднородностей обусловленное неоднородностями расширение резонансных кривых носит, как и в приближении независимых областей, «пе-Диссипативный» характер в том смысле, что оно не связано с возникновением нового механизма релаксации. Но, в отличие от приближения независимых зерен, расширение резонансной кривой и сдвиг резонансной частоты задаются теперь распределением собственных частот не разных участков образца, а разных типов колебаний всего образца в целом,
490
ПРОЦЕССЫ РЕЛАКСАЦИИ
ГГЛ. 9
Собственные типы колебании неоднородного образца можно искать в виде рядов по собственным типам колебаний однородного образца. Такой путь, конечно, особенно целесообразен, когда неоднородность мала и может рассматриваться как возмущение. Тогда коэффициенты этих рядов и собственные частоты неоднородного образца можно определить, используя методы теории возмущений.
Но в случае малой неоднородности, вообще, не обязательно переходить к возмущенным типам колебаний — нормальным колебаниям неоднородного образца. Можно вести рассмотрение всей задачи «в терминах» невозмущенных колебаний — колебаний однородного образца. При наличии возмущения (неоднородности) они становятся связанными. Связь приводит к перекачке энергии от одного из типов колебаний к другим, а также к сдвигу резонансных частот колебаний.
В классической теории эти эффекты могут быть учтены путем рассмотрения уравнений движения для амплитуд колебаний однородного образца, которые оказываются связанными благодаря наличию неоднородности. Многие важные результаты, касающиеся влияния различных неоднородностей на ферромагнитный резонанс, были*&олучены этим способом, т. е. методом связанных уравнений движения (§ 9.1).
В квантовой теории следует прежде всего выразить оператор энергии, связанной с неоднородностями, через операторы рождения и уничтожения магнонов. Этот оператор, наряду с членами более высоких порядков, будет содержать члены вида
Жч = 2 zEj 'fi,»01!01»-	(9.3.1)
1 2
Такие члены (см. § 9.2) обращаются в нуль в идеальном (бесконечном, строго периодическом) кристалле, но не обращаются'в нуль при наличии неоднородностей. Операторы рождения и уничтожения квазичастиц, соответствующих колебаниям неоднородного образца, и собственные частоты колебаний могут быть найдены в результате диагонализации гамильтониана, являющегося суммой билинейного гамильтониана, например, (8.5.38) однородного образца и гамильтониана (9.3.1).
Если неоднородности малы и могут рассматриваться как возмущение и если нас не интересует обусловленное ими изменение резонансной частоты, то для вычисления ширины резонансной кривой может быть применен метод вероятностей переходов (§ 9.1). При этом энергия неоднородностей рассматривается как возмущение, вызывающее переход энергии от невозмущенных колебаний (т. е. колебаний однородного образца) одного типа к невозмущенным колебаниям других типов. Такой переход можно считать происходящим в результате протекания различных элементарных
ДВУХМАГНОННЫЁ ПРОЦЕССЫ
491
§ 9.3]
процессов. Причем, как всегда, наибольшую роль будут играть процессы с участием наименьшего числа частиц. Ими в данном случае будут двухмагнонные процессы, обусловленные членами гамильтониана возмущения (9.3.1) (в идеальном кристалле они запрещены законом сохранения импульса). Метод вероятностей переходов приводит, как правило, к более простым вычислениям, чем другие методы учета влияния неоднородностей.
Элементарные двухмагнонные процессы, при помощи которых мы теперь интерпретируем расширение резонансных кривых, обусловленное неоднородностями, можно назвать процессами рассеяния магнонов на неоднородностях. В частном случае, когда типом колебаний, релаксация которого рассматривается, является однородная прецессия, эти процессы часто называют 0-к процессами. Интересно заметить, что при такой трактовке, в отличие от упомянутой выше трактовки на языке нормальных колебаний, неоднородности приводят к возникновению нового механизма релаксации. Отсюда ясно, что разделение механизмов расширения резонансных кривых на диссипативные и недиссипативные в данном случае — сильно связанной системы, является условным.
Общая теория рассеяния магнонов на неоднородностях. Исследуем прежде всего (методом вероятностей переходов) некс эрые общие свойства двухмашинных процессов релаксации. Рассмотрим релаксацию магнонов с волновым вектором кх, обусловленную гамильтонианом возмущений (9.3.1). Матричные элементы его, соответствующие прямым переходам, запишутся следующим образом:
(Hi -— 1, п2 -|- 11	п2У — Пу (п2 -|- 1)Р\)2.	(9.3.2)
Аналогично запишутся матричные элементы для обратных переходов. Кинетическое уравнение (9.1.7) примет вид
2 I ^1.2 I2 («2 - "1) 6 * *	 * *С9’3'3)
2
Отсюда с учетом (9.1.8) легко получить
“г =	21 ^1,212 6 («“1 - й«2)	(9.3.4)
2
или, переходя к интегрированию по к2~пространству,
“г = (2^2 I ^1,212 6 (“1 — “2) sin 62й/с2йЭ2йф2. (9.3.5) (fc)
Итак, для двухмагнонных процессов имеет место сохранение энергии, т. е. образующиеся магноны вырождены с исходными. Импульс же для этих процессов не сохраняется.
492	ПРОЦЕССЫ РЕЛАКСАЦИИ	, [ГЛ. 6
Предположим сначала, что | Ч'1) 2 | ~ ] Т ] не Зависит от к2. Допустим также, что спектр спиновых волн, как это имеет место для изотропной среды, не зависит от ср*. Тогда интегрирование в (9.3.5) по <р2 даст множитель 2л. От интегрирования по одной из оставшихся переменных легко избавиться используя свойства дельта-функции (см. § 9.2). Избавляясь, например, от интегрирования по к2, получим
== ।т I2 $ (tXL sin <9-3-6) о	в
где кв (02) определяется из условия вырождения (рис. 9.3.2)
Рис. 9.3.2. Вырождение спиновой волны (<о,, к,) с другими спиновыми волнами.
m-fe, е2) =©!,	(9.3.7)
а 60 — из условия
©к (к = О, 0О) = (Оу (9.3.8) Формулу (9.3.6) можно записать в виде [30]
0)г = -Йгт2Рв(®1).	(9.3.9)
Величина pB(<oi), которая в данном случае равна
V г / cto,. \-1 о
Рв(“1) = J \^)k=kB/rBSin02^02’
(9.3.10)
является плотностью вырожденных состояний, отнесенной к единичному интервалу частот.
Рассмотрим частный случай O-Zc процессов, т. е. предположим, что Л^ = 0, а(о1=(оо — частота однородной прецессии. Примем для простоты приближенное выражение (8.1.16) для спектра магнонов и ограничимся случаем сферы. Тогда
= 2т]/с, 0О = arcsin -|- , к2в = (sin2 0о — sin2 02), и вычисление по формуле (9.3.6) дает
®г0= 1,2-10“2——£-1 Т I2.	(9.3.11)
В действительности амплитуда возмущения Т, конечно, зависит от волнового вектора 1<2 и эта зависимость определяется характером зависимости неоднородности от координат. По-види
j g 3]	ДвухмаГнойньтё процессы	493
мому, чем «мельче» неоднородность, тем больше те значения к%, при которых лежит максимум | Т (й2) |. Чтобы убедиться в этом, воспользуемся гейзенберговской моделью ферромагнетика. Предположим, что возмущение может быть описано некоторым эффективным полем Н (г), так что энергия возмущения может рассматриваться как зеемановская энергия спинов в этом поле. Тогда, согласно (8.5.1), принимая для простоты, что поле Н(г) направлено по оси z (которая, как всегда, совпадаете направлением равновесной ориентации спинов), запишем оператор энергии возмущения в виде
N
=	(9.3.12)
f=i
Перейдем в .(9.3.12), согласно (8.5.7), к операторам af и й):
N
f=i
Интересуясь только билинейной частью этого гамильтониана, выразим ее, согласно (8.5.17), через операторы и а+к. Одновременно разложим Н (г/) в ряд Фурье:
N
—L- 2 с"к2Г'«2 2 ~7= 2	~Л- 2	•
‘	Й VN £	1 ГJV	Н
(9.3.13) Здесь
^•н = -у^2^(0)^кнГ/	(9-3-14)
—кн-я гармоника z-составляющей эффективного поля.
Поскольку неоднородное возмущение было учтено при помощи эффективного, как бы внешнего поля, мы можем теперь считать кристалл периодическим, для которого справедливо соотношение 8.5.21). С учетом этого соотношения имеет место формула
2Wf) = 2l-tfJ2	(9.3.15)
f	к
(аналогичная формуле Парсевалля [38]), а гамильтониан возмущения (9.3.13) принимает вид
=v^222 %ЯкнД(к1-к2 + кн). (9.3.16) Г п ki к2 кн
Сравнивая полученное выражение для гамильтониана возмущения
494
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
с (9.3.1), мы видим, что
Т1>2 = -^Я(к2_к1).	(9.3.17)
Таким образом, двухмагнонные (кх к2) процессы будут идти, если среди пространственных гармоник эффективного поля., моделирующего неоднородность, имеется гармоника (к2 — ку); интенсивность их будет тем больше, чем больше эта гармоника. Как следует из (9.3.16), можно считать, что при двухмагнонных процессах импульс «сохраняется», но с учетом импульса Tikg = /z (k2—ly), который передается кристаллу в целом. С этой точки зрения понятно, что анергия кристаллу (обладающему очень большой, по сравнению с магнонами, массой) при процессе рассеяния на неоднородностях не передается, т. е. имеет место вырождение исходных и рассеянных магнонов.
Подставляя (9.3.17) в формулу (9.3.5), получим
§ Я(к2_к,)6 (wi — ®2)/«2sin02dM02^<₽2- (9.3.18)
Это выражение можно переписать следующим образом:
= 75^ "7Г Я(к2-к,)	6 (®i ~ ®2) sin 02^M92dcp2, (9.3.18')
I L t xV
(k2)
где Ярй-к,) есть величина Я(к2-к), усредненная по всей разрешенной законом сохранения энергии (условием вырождения) части к2-пространства.
В случае рассеяния однородной прецессии (кх = 0) интеграл, входящий в (9.3.18'), был уже вычислен (для приближенного спектра (8.1.16)) при выводе выражения (9.3.11). В этом случае (заменяя индекс к2 на к) найдем
<огО = 1,2-10-® -L Н%.	(9.3.19)
Введем, согласно (4.2.7), (2.1.9) и (8.1.8), обменное поле
ЯЕ = -^,	(9.3.20)
где a = (V/N)113 — среднее расстояние между элементарными магнитными моментами. Тогда (9.3.19) можно будет записать в форме
(2Л#и «= 0,024 Hl (9.3.21)
Как показывает оценка по формуле (9.3.21), величины V Н%, необходимые для того, чтобы 0-к процесс вносил заметный вклад
„ „	ДВУХМАГНОННЫЕ ПРОЦЕССЫ	495
S у-йз
в релаксацию, оказываются большими. Так, например, при (2ДЯ)0-й — 1з для иттрий-железного граната	105 э.
Если эффективное поле неоднородностей Н (г) носит характер совершенно случайных флуктуаций («белый шум»), то амплитуды его фурье-гармоник можно считать не зависящими от к. Тогда из формулы (9.3.15) следует, что
я1 = ^^^2№(Г/)	(9.3.22)
(Нр — среднее квадратичное эффективное поле неоднородностей). Таким образом, в этом случае необходимо очень сильное неоднородное поле, чтобы 0-к процесс был эффективен. Однако, как мы убедимся ниже, положение существенно изменяется, если неоднородности носят более «упорядоченный» характер, так что спектральная плотность Нк их эффективного поля имеет заметную величину лишь в некоторой, сравнительно узкой полосе спектра.
Как видно из полученных выражений, частота релаксации, определяемая двухмагнонными процессами, явно от температуры не зависит. Ее температурная зависимость связана лишь с температурными зависимостями входящих в эти выражения параметров.
Отметим еще две особенности двухмагнонных процессов. Первая заключается в том, что при этих процессах не изменяется число магнонов, и следовательно, двухмагнонные процессы (так же как четырехмагнонные процессы рассеяния) не могут участвовать в релаксации Mz. Что же касается длины вектора М, то она сохраняется для двухмагнонных процессов без участия однородной прецессии и не сохраняется для 0-к процессов.
Второй важной особенностью двухмагнонных процессов является то,’что они не вносят непосредственного вклада в параметры релаксации, которыми определяются пороги спиновых нестабильностей. В частности, 0-к процессы почти не вносят вклада в величину ДЯИ, которая определяется (см. § 9.2) путем экстраполяции к к = 0 зависимости Д7/;; (fc), измеренной методом продольной накачки. Действительно, влияние неоднородностей, как отмечалось выше, приводит к тому, что типы колебаний однородных образцов (одним из которых является однородная прецессия) заменяются другими типами нормальных колебаний — неоднородных образцов. На языке квантовой теории это означает, что двухмагнонные члены энергии возмущения, связанной с неоднородностями, и двухмагнонные члены основной энергии совместно диагонализируются. При наличии накачки один из этих «новых» нормальных типов колебаний неоднородного образца становится нестабильным, и порог нестабильности определяется параметром диссипации этого типа колебаний. Конечно, он может отличаться от параметра диссипации «старого» типа колебаний — однородного образца.
496
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Но ясно, что двухмагнонные процессы непосредственного вклада в него вносить не будут.
Рассмотрим теперь влияние различных неоднородностей на диссипацию, главным образом — однородной прецессии.
Беспорядок в распределении ионов по узлам. Первой теоретической работой, в которой подробно исследовалось влияние неоднородностей на диссипацию энергии при ферромагнитном резонансе, была работа [304] четырех авторов: Клогстона, Сула, Уокера и Андерсона. В ней рассматри
Рис. 9.3.3. Функция I (NjJ в формуле (9.3.23) [304]. Цифры у кривых - значения Но/(4ЛМ о).
валось влияние микроскопических неоднородностей — беспорядка в распределении различных магнитных ионов по узлам решетки. Такой беспорядок (см. § 4.4) имеет место обычно в ферритах со структурой шпинели; некоторые из них, как, например, литиевый феррит, могут быть как в неупорядоченном, так и в упорядоченном состоянии [19]. В ферритах со структурой граната беспорядок возникает при частичном замещении ионов Fe3+ другими ионами.
В работе [304] был использован метод связанных уравнений
движения для операторов рождения и уничтожения магнонов однородной прецессии и вырожденных с ними магнонов с к 0. Для частоты релаксации в случае эллипсоида вращения было получено следующее выражение:
= ~ i[n
Т	ДЩ	Д7г	\ -
(9.3.23)
4лМ0 / ’
где Нр — средний квадрат эффективного поля неоднородностей, а I — функция, учитывающая степень вырождения однородной прецессии со спиновыми волнами с k 0, графики ее приведены на рис. 9.3.3. Из этого рисунка видно, что, как и следовало ожидать, / -> 0 при l > 0. Для сферы в предельном случае высоких частот (Яо 4лМ0) I 1.
Частоту релаксации, обусловленную беспорядочным распределением ионов по узлам, как показал Каллен [279], можно рассчитать и методом вероятностей переходов. В данном случае неоднородность носит хаотический характер, и мы можем считать, что величина Нк постоянна. Тогда, как отмечалось выше, эта величина
5 9.3]	ДВУХМАГНОННЫЕ ПРОЦЕССЫ	497
совпадает со среднеквадратичным эффективным полем неоднородностей Нр. Подставляя Нр вместо//2 в формулу (9.3.21) (которая справедлива в случае сферы иЯ0> 4л/1/0), мы придем к выражению, отличающемуся от (9.3.23) лишь множителем порядка 1.
В работе [304] было затем сделано предположение, что рассматриваемая неоднородность представляет собой вариацию псев-додиполъного взаимодействия *). Если бы вся магнитная анизотропия таких ферритов, как, например, никелевый, была связана с этим взаимодействием, то его эффективное поле должно было быть порядка 108 э. Пусть беспорядок в распределении ионов является «очень сильным», т. е. магнитные и немагнитные ионы в приблизительно равных количествах статистически распределены по узлам решетки (как в неупорядоченной полностью обращенной шпинели). В этом случае можно считать, что среднеквадратичное поле флуктуаций псевдодипольного взаимодействия Нр совпадает с самим эффективным полем этого взаимодействия. Тогда оценка обусловленной неоднородностями ширины кривой дает величину — 40 э [304]. Именно такую величину имели минимальные экспериментальные значения 2А/7 ферритов со структурой шпинели (см., например, [132, 134]) в то время, когда выполнялась работа [304]. Это совпадение, казалось бы, свидетельствует о том, что беспорядок в распределении ионов по узлам вносит существенный вклад в 2А/7 таких ферритов, а теория, учитывающая псевдодипольное взаимодействие, правильно этот вклад описывает.
Однако в дальнейшем два обстоятельства поставили под сомнение этив ыводы. Во-первых, по мере улучшения качества монокристаллов значения 2 А// в ферритах со структурой шпинели все уменьшались. Так, например, для никелевого феррита было достигнуто 2А/7 = 1,2 э [329]. Во-вторых, были получены данные [54], говорящие в пользу большего вклада в анизотропию ферритов не анизотропных межионных сил (учитываемых псевдодипольным взаимодействием), а внутриионных («одноионных») взаимодействий (см. § 2.2).
Последнее обстоятельство заставило Каллена и Питтели [315], а затем Хааза и Каллена [317] провести расчеты частоты релаксации, связанной с ионным беспорядком, считая возмущением вариацию от иона к иону внутриионного спин-орбитального взаимодействия.
В работе [315] был рассмотрен случай ионов (например, Fe2+ и Ni2+), нижний энергетический уровень которых в тригональном кристаллическом поле (имеющем место в октаэдрических узлах
J) Псевдодипольное взаимодействие было введено Ван-Флеком, как «источник» магнитной кристаллографической анизотропии (см. [59]). Гамильтониан этого взаимодействия по форме совпадает с гамильтонианом дпполь-Дппольного взаимодействия (1.1.50), по содержит дополнительный постоянный мнощитедь порядка 100, введенный для согласия с экспериментом,
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
шпинели) не вырожден. Было принято, что два сорта ионов — А и В, отличающиеся величиной константы спин-орбитального взаимодействия G, в количествах NA = cN и Nb = (1 — с) N беспорядочно распределены по всем четырем неэквивалентным положениям, которые имеются среди октаэдрических узлов шпинели. Для этой модели расчет частоты релаксации методом вероятностей перехода привел к выражению вида
<ог = (о<о) +	(9.3.24)
где F =	+ с^ссз -(- с^ссз — угловая функция, характеризую-
щая анизотропию кубических кристаллов (см. § 2.2),
«?> = 0,1	(1 - с) (Сл - Grf-	/, (д'±,	, (9.3.25)
а <0г0) со^. В выражении (9.3.25) 5 — среднее значение спинов ионов А и В 2), а 1Г — функция, почти не отличающаяся от функции I (рис. 9.3.3).
Как видно из (9.3.25), частота релаксации <о,. —> 0 при с->0и с —» 1, когда остаются ионы одного сорта, и максимальна при с = = 1/2, когда имеет место наибольший беспорядок. Рассмотрение конкретной модели ионов, распределенных по октаэдрическим узлам кристалла со структурой шпинели, привело в данном случае к существенной анизотропии <о,. Частота релаксации мала, когда Мо параллельно оси <100>, и максимальна при Мо, параллельном оси <111 )>, когда F = 1/3. В последнем случае для сферы при достаточно высоких частотах и при с = 1/2 ширину резонансной кривой можно представить в виде (9.3.21), где эффективное поле беспорядка	____
Нр = VhI	.	(9.3.26)
Если принять S = 2, GA = 2-10"15 (что соответствует ионам Fe2+), a Gb = 0 (ионы Fe3+, Мп2+ и т. п.), то, согласно (9.3.26), Нр = — 2-10Ч 5 э, что приводит к 2А77	10 а.
Аналогичный расчет был проведен в [317] для ионов (например, Со2+), для которых нижний уровень вырожден и спин-орби-тальное взаимодействие является гораздо более сильным. В этом случае вклад механизма рассеяния на неоднородностях в ширину резонансной кривой оказывается практически изотропным и сос
Ч Различие спинов ионов, как и любых других их параметров (например, обменных интегралов), может явиться возмущением, приводящим к расширению резонансной кривой при беспорядочном распределении ионов в решетке. Но вклады всех этих возмущений малы по сравнению с вкладом
различия констант спин-орбитального взаимодействия [315].
g s 3j	ДВУХМАГНОННЫЕ ПРОЦЕССЫ	499
тавляет 204-30 э на 1% Со2+, т. е. превышает на два порядка вклад этого механизма в случае ионов Fe2+.
Экспериментальная проверка теорий рассеяния магнонов на микроскопических неоднородностях затрудняется сложностью выделения вклада этого механизма. Надежды возлагались на литиевый феррит, который может быть как в упорядоченном, так и в неупорядоченном состоянии; исследованию процессов релаксации в нем было посвящено очень много работ (например, [316, 321]). Но в стехиометрическом литиевом феррите присутствуют лишь магнитные ионы Fe3+, не обладающие орбитальным моментом. Роль неоднородностей в этом случае могут играть лишь вариации спинов и интегралов обмена, которые, как уже отмечалось, вносят малый вклад. И не удивительно, что в литиевом феррите вклада механизма рассеяния на микроскопических неоднородностях в &Н не удалось экспериментально обнаружить *).
В никелевом феррите, как это следует из приведенного выше значения 2 А//, вклад рассеяния на микроскопических неоднородностях не превышает — 1 э. Это находится в согласии с теорией [315], поскольку спин-орбитальное взаимодействие в Ni2+ слабее, чем в Fe2+. Механизм рассеяния на ионном беспорядке может быть существенным лишь в кристаллах, содержащих в достаточном количестве такие ионы, как Fe2+, Со2+, или редкоземельные ионы. Но при этом он будет, как правило, маскироваться более эффективным механизмом ионной релаксации (см. § 9.6), который обусловлен теми же самыми ионами. Для случая ионов Со2+ это убедительно показали Тиль и Кларк [393].
Итак, несмотря на то, что рассеяние на атомном беспорядке явилось первым теоретически исследованным двухмагнонньтм процессом, зкспериментально наличие этого механизма релаксации до сих пор не продемонстрировано.
Вариации поля анизотропии в поликристаллах. Рассмотрим теперь неоднородности, которые имеют место в поликристаллах (а также блочных монокристаллах) вследствие того, что кристаллографические оси в зернах (или блоках) повернуты друг относительно друга. В отличие от предыдущего случая ионного беспорядка, когда отсутствовала какая-либо корреляция в расположении ионов, в данном случае существуют макроскопические области, в которых кристалл является упорядоченным. Размеры их в поликристаллах обычно лежат в пределах 14-100 мкм.
) Величины ЛЯ в неупорядоченном литиевом феррите не больше, чем в Упорядоченном. Тем не менее анизотропная часть АЯ в неупорядоченном кристалле первоначально [316] связывалась с рассеянием на неоднородностях сравнивалась с теорией [315]. Однако в дальнейшем выяснилось, что эта низотропная часть обусловлена ионным механизмом релаксации (§ 9.6), язанным с примесными ионами Fe2+.
Boo
ПРОЦЕССЫ релаксации •
Влияние таких неоднородностей было исследовано в § 2.3 в приближении независимых областей. В этом приближении расширение резонансных кривых имеет порядок поля анизотропии На, например, для одноосного или кубического кристалла близко к 2| Hai I ='2|Z<! | /Мо. Но, как уже неоднократно отмечалось, условие применимости приближения независимых областей (2.3.1) обычно не выполняется, и взаимодействие между колебаниями намагниченности разных зерен приводит к сужению резонансной кривой.
В рассмотренном выше случае хаотического распределения ионов по узлам, когда средний размер неоднородностей был порядка атомных размеров, к сужению резонансной кривой приводило обменное взаимодействие. Оно давало в формуле (9.3.23) множитель
1В----(9.3.27)
порядка 10-3 -4- 10-4. Если же размеры неоднородностей — макроскопические, то сужение резонансной кривой должно быть обусловлено диполъ-диполъным взаимодействием. Тогда в (9.3.27) величина Не заменится на 4лЛ70, т. е. вместо мы получим множитель
^~Яр/4лЯ0.	(9.3.28)
Для поликристаллов Нр — На, и множитель, учитывающий дипольное сужение, имеет вид (2.3.11). Для ферритов с малой анизотропией порядок величины этого множителя 10"1 -ч- 10-2. Итак, при На <С 4лЛ7(|, когда существенно взаимодействие между зернами, вклад различия ориентации зерен в ширину резонансной кривой в поликристалле должен быть
(2АЯ)я~Яа/4лМ0.	(9.3.29)
Теория резонанса в поликристалле в соответствии с замечаниями, сделанными в начале этого параграфа, может строиться методом возмущений с использованием колебаний однородного образца в качестве невозмущенных типов колебаний. Возмущением, которое приводит к сеязи этих колебаний, является изменяющееся от зерна к зерну эффективное поле анизотропии. Такая теория автоматически будет учитывать дипольное сужение. Как и в случае микроскопических неоднородностей, можно идти по двум путям: рассматривать связанные уравнения движения для амплитуд колебаний или использовать метод вероятностей переходов. В работе Шлёманна [307], в которой резонанс в поликристаллах был исследован наиболее подробно, использовался первый путь. Однако мы применим более простой второй метод.
ig 9.3]
ДВУХМаТЙОННЙЁ ПРОЦЕССЫ
501
Будем исходить из формулы (9.3.18). Рассмотрим релаксацию однородной прецессии, т. е. примем = 0 и = ю0. Величина J/(i<2-k.) == Нь является в данном случае к-й пространственной гармоникой z-составляющей эффективного поля анизотропии Но.
Теперь уже нельзя, как в случае микроскопических неоднородностей, считать Нк = const; величина Н!: должна существенно изменяться вблизи к = Ml (рис. 9.3.4), где I — средний размер зерен
Для упрощения вычислений примем
С2
О
при при
к > 1~\
Величину С легко найти с помощью формулы (9.3.15). Учитывая, что 2 На (1'0 = ПН а, и переходя в правой части (9.3.15) к интегрированию в k-пространстве, получим
(9.3.30)
С’2^6л2П2-~,	(9.3.31)
к
МАКС
3_____ Рис. 9.3,4. Вырождение однород-
где а = У V/N — среднее расстоя- uoii прецессии ^со спиновыми вол-ние между магнитными моментами.
Из (9.3.31) следует, что величины Пк возрастают при увеличении размеров неоднородностей. Поэтому в случае макроскопических неоднородностей для получения данных значений частоты релаксации требуются уже меньшие величины средних эффективных
полей неоднородностей, чем в рассмотренном выше случае ионного беспорядка.
Для кубического ферромагнетика с учетом только первой кон-
станты анизотропии усреднение поля анизотропии по всем ориентациям дает [&7]
„2 _ 16 гг2
а 21
(9.3.32)
где//А1 == KJMg. Подставляя (9.3.30) с учетом (9.3.31) и (9.3.32) в формулу (9.3.18) для случая релаксации однородной прецессии, получим (опуская индексы 2)
1/1 п 2п
<or = ~x213Hai /с2 sin 0ft6 (<i)0 — ак) dk dQkd(pk. (9.3.33)
000
Примем приближенное выражение (8.1.16) для спектра спиновых В0/лН’ т' е" ограничимся случаем высоких частот. Тогда, переходя в (9.3.33) к дельта-функции разности углов 0i; и избавляясь таким
502
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. S
образом от интегрирования по 0t, получим
,,2 и/
16л ,3 11 Al V А2
7 ' 4лЛ1 о J cos 0в
dk,
(9.3.34)
где угол 6В (к) определяется из условия вырождения. В данном случае, когда 1/Z Амакс (рис. 9.3.4), можно заменить cos 6В на его значение при к = 0, которое для эллипсоида вращения и приближенного спектра (8.1.16) составляет
cos 0о = У NJfat.	(9.3.35)
Тогда окончательно
(2дя)а = —г =	   1	.
1	т 21 у 1^Мп
(9.3.36)
Сравнивая выражение (9.3.36) с оценкой (9.3.29), полученной исходя из представления о дипольном сужении, мы видим, что, например, для сферы они различаются лишь численным множителем порядка 1. Однако формула (9.3.36) содержит множитель 1/f/ Nz, учитывающий приближенно «степень вырождения» однородной прецессии со спиновыми волнами, которые могут возникать в результате процесса рассеяния на рассматриваемых неоднородностях, т. е. плотность состояний этих спиновых волн. При уменьшении Nz частота однородной прецессии поднимается относительно спектра спиновых волн, углы 6,г вырожденных спиновых волн возрастают и плотность вырожденных состояний увеличивается. Подчеркнем, что формула (9.3.36) справедлива при следующих допущениях: замена точного спектра на (8.1.16) (т. е. высокие частоты) и пренебрежение обменным членом в спектре (к этому сводится, как легко видеть, замена 0В (А) на 60).
Для произвольных частот (т. е. исходя из точного выражения для безобменного спектра спиновых волн) Шлёманн [307] в случае сферы получил следующую формулу:
(9.3.37)
где функция
т (1Л у2 — у/3 Ч~ 19/300 2{У) V(у-1/3)2(у-2/3) ’
График этой функции представлен на рис. 9.3.5. Для высоких частот 12 —> 1, и (9.3.37) переходит в (9.3.36). При соо 2/3 сом функция /2 —> °°, пРи этом частота однородной прецессии стремится к верхней границе безобменного спектра и плотность вырожденных с однородной прецессией состояний стремится к оо. При й0 < 2/3 о)дг формула (9.3.37) теряет смысл, частота однородной про
ДВУХМАГНОННЫЕ ПРОЦЕССЫ
503
§ 9.3]
цессии переходит через верхнюю границу безобменного спектра, в рамках принятых допущений отсутствуют вырожденные с однородной прецессией спиновые волны и процессы рассеяния однородной прецессии на крупных неоднородностях не могут происходить.
Выражения, аналогичные (9.3.37), получили при произвольных частотах для эллипсоида Гешвинд и Клогстон [305] и Клогстон [3101. Так же как и для сферы, ширина резонансной кривой в случае эллипсоида стремится к оо при подходе частоты однородной прецессии <о0 к верхней границе безобменного спектра спиновых волн и обращается в нуль при переходе этой границы. Условие перехода имеет вид (7.1.12).
Существенно подчеркнуть, что сингулярность величины (2ДЯ)О в точке перехода частоты ы0 через верхнюю границу безобменного спектра имеет место только при следующих предположениях:
1)	пренебрежение обменным членом цк2 в спектре спиновых волн;
2)	пренебрежение диссипацией спиновых волн;
3)	пренебрежение влиянием неоднородностей на спектр спиновых волн.
Если отказаться хотя бы от одного из этих предположений, сингу
лярность. ширины резонансной кривой при переходе частоты однородной прецессии через верхнюю границу безобменного спектра будет сглажена (см. рис. 9.3.5). Влияние первых двух факторов было исследовано в [307]; было показано, что учет обменного члена приводит к максимальной величине ширины кривой
Рис. 9.3.5. Зависимость множителя в выражении для (2ДН)а, учитывающего плотность вырожденных состояний, от у —	f 307].
Сплошная линия — функция (у) в формуле (9.3.37), пунктир — с учетом обменных членов в спектре спиновых волн или диссипации этих волн.
<9-3-38»
Отсюда видно, в частности, что особенность в точке перехода о>0 через верхнюю границу безобменного спектра тем резче, чем крупнее неоднородности. Роль третьего фактора отмечалась в работах [320, 323]. Влияние второго и третьего факторов было подробно исследовано Шлёманном [325] на модели, учитывающей не только первичные 0 — к процессы, но и вторичные к — к' процессы рассеяния образующихся спиновых волн на неоднородностях.
Оценим вклад рассмотренного механизма релаксации в ширину Резонансной кривой поликристаллических ферритов. Для марган
504
ПРОЦЕССЫ РЕЛАКСАЦИЙ
1ГЛ. 8
цевого феррита при комнатной температуре (К± = 2,8-104; Мо — =320) по формуле (9.3.36) получаем (2А/7)„ — 16 э, а для иттрийжелезного граната (2ДЯ)О = 6 э.
В реальных кристаллах, как монокристаллах, так и поликри-сталлических образцах, всегда имеются дислокации. Обусловленные ими неоднородные упругие напряжения приводят к расширению резонансных кривых, механизм которого очень близок к рассмотренному выше механизму влияния неоднородных полей анизотропии. Теория такого расширения кривых ферромагнитного резонанса была развита Барьяхтаром, Савченко и Тарасенко [324]. Оценки, а также экспериментальные данные говорят о том, что роль этого механизма релаксации обычно невелика.
Поры и шероховатости поверхности. Перейдем теперь к рассмотрению «геометрических» макроскопических неоднородностей, к которым относятся поры между зернами поликристаллов, трещины и шероховатости поверхности образцов.
В приближении независимых областей влияние таких неоднородностей было рассмотрено в § 2.3. В частности, для ширины резонансной кривой были приведены оценка (2.3.12) и формула (2.3.14), полученная Шлёманном на модели сферической полости (рис. 2.3.3). В § 2.3 было отмечено также, что дипольное сужение в случае геометрических неоднородностей дает множитель, близкий к 1.
Теория процессов релаксации, связанных с геометрическими неоднородностями, может быть развита методом возмущений с использованием невозмущенных типов колебаний однородного (сплошного) образца. Но параметром малости будет не отношение эффективного поля неоднородностей к 4лМ(| (оно теперь порядка 1), а отношение объема области возмущения (который одного порядка с объемом пор v) к объему образца. Такая теория может быть построена как методом связанных уравнений движения, так и методом вероятностей переходов.
Метод вероятностей переходов был использован в работе Спаркса, Лудона и Киттеля [285] (см. также [20]). В ней была принята та же модель сферической полости, которую использовал Шлёманн при расчете методом независимых областей. Магнитостатическая энергия для этой модели, выраженная через операторы ак и ак, содержит члены вида (9.3.1); амплитуды их в случае релаксации однородной прецессии (см. [287])
То, k л27??	(3 cos2 6& - 1)	,	(9.3.39)
’	О	т	Hill
где
. , .	1 Г л т ,	1 /sin х	\
М*) = V 2xJ^X^^	~ cos Xj
§ 9.3]
ДВУХМАГНОННЫЕ ПРОЦЕССЫ
505
— сферическая функция Бесселя [38]. Зависимость величины д (kR^/tkRj) от к показана на рис. 9.3.6. Поскольку 1/7?! — 103-н --104 значительно меньше, чем /емакс (см. рис. 9.3.4), мы можем, так же как и при учете неоднородных полей анизотропии, пренебречь зависимостью cos 6fe от к. Тогда приведенный на рис. 9.3.6 множитель будет практически полностью характеризовать зависимость от к амплитуд т. е., согласно (9.3.17), фурье-компонент Як эффективного поля рассматриваемой неоднородности.
Подставим в формулу (9.3.18) (при = 0) величину Як, связанную соотношением (9.3.17) с амплитудой 4%,;., ограничимся случаем высоких частот (т. е. при-
мем приближенный спектр (8.1.16)) [/дХ/Я
и заменим cos 6ft на его значение J
при к = 0. После вычислений,
аналогичных проведенным при выводе выражения (9.3.36), получим [287]
^21 ZnM (3COS2QU-1)2 -27 V ° созбо
(9.3.40)
Рис. 9.3.6. Зависимость от К величины Ji (^Н1)/(ЛН1) в формуле (9.3.89), пропорциональной фурье-компоненте поля сферической полости.
Предполагая далее, что в образце имеется некоторое количество сферических пор (не обязательно одинаковых) и что вклады их аддитивны, найдем окончательно
(2ДЯ)Р = ^-Н-4лМ0-^, '	9 1 u cosOo ’
(9.3.41)
где v — суммарный объем пор, а
G = (3 cos2 е0 - I)2.	(9.3.42)
Рассмотренная теория была первоначально развита в [285] для учета поверхностных неоднородностей. При этом было сделано предположение, что неоднородности представляют собой полусферические ямки радиуса Rt, полностью покрывающие поверхность образца и вносящие тем не менее независимые аддитивные вклады в 2ДЯ. Амплитуда рассеяния (9.3.39) при переходе к поверхностным полусферам должна быть, согласно [285], уменьшена в 4 раза: в 2 раза для учета уменьшения эффективности центра рассеяния и еще в 2 раза — для учета уменьшения объема, по которому интегрируется возмущение. Число же полусфер легко получается из условия полного покрытия ими поверхности сферического образца (радиус его Яо). Тогда, как легко убедиться,
(2ДЯ)г =	.	(9.3.43)
' 's 9 Ко и cos 0О	'	'
506
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Формулы (9.3.41) и (9.3.43) содержат множитель 4лЛ/0, обусловленный, как уже отмечалось, тем, что возмущением в данном случае служит неоднородное размагничивающее поле, т. е. диполь-дипольное взаимодействие, а сужение является тоже дипольным. Множители vIV в формуле (9.3.41) и RJRq в (9.3.43) связаны с объемным в первом случае и поверхностным — во втором характером неоднородностей. Множитель 1/cos 60 учитывает приближенно плотность вырожденных состояний и является характерным для двухмагнонных процессов. Он обращается в оо при подходе частоты однородной прецессии ю0 к верхней границе безобменного спектра спиновых волн. Если бы вычисления были проведены с использованием точного спектра спиновых волн, этот множитель заменился бы на более сложное выражение (аналогичное множителю /3/2 (co0/coM) в формуле (9.3.37)), но также обращающееся в оо при подходе <оо к верхней границе спектра.
Все упомянутые множители в формулах (9.3.41) и (9.3.43) не зависят от формы неоднородностей. Необходимо лишь, чтобы фурье-спектр неоднородностей носил такой характер, как показано на рис. 9.3.6, т. е. чтобы критическое волновое число, вблизи которого происходит спад спектральной плотности, было много больше обратных размеров образца, но лежало в практически безобменной части спектра спиновых волн. В отличие от остальных множителей, вид (9.3.42) множителя G обусловлен принятой моделью.
Переходя к рассмотрению экспериментальных данных по процессам релаксации, связанным с геометрическими неоднородностями, остановимся сначала на случае пор в поликристаллах. В § 2.3 отмечалось уже, что пропорциональность 2\НР относительному объему пор vIV хорошо подтверждается экспериментально (см. рис. 2.3.4). Величина коэффициента пропорциональности находится в качественном согласии с формулой (9.3.41); о количественном совпадении говорить не приходится, так как точное значение множителя G неизвестно.
Вклад пористости в ширину резонансной кривой поликристаллических ферритов, как видно, например, из рис. 2.3.4, велик. В ферритах с небольшой анизотропией он, как правило, превышает вклад различия ориентаций кристаллографических осей. Однако вклад пористости может быть существенно уменьшен, если использовать «сверхплотные» поликристаллы (с относительной пористостью р 0,01). Уменьшая одновременно кристаллографическую анизотропию, можно получить поликристаллические образцы ферритов с очень узкой резонансной кривой. Величина 2ЛН = 2 э была получена таким образом в поликристалличес-ком Y-Ca-Ge-In-Fe-гранате (330]. Вклад пористости в эту величину составлял 0,9 э, а вклад разориентации зерен — всего » 0,2 э. Вклад собственных процессов релаксации (§ 9.2) оцени
§ 9,3]
ДВУХМАГНОННЫЕ ПРОЦЕССЫ
507
вался как 0,4 э, а остальные 0,5 а составлял вклад ионных процессов, которые будут рассматриваться в § 9.6.
При экспериментальном исследовании ферромагнитного резонанса в поликристаллах очень большое внимание было уделено (см., например, [312, 318, 320]) изучению характерных для двух-магнонных (0-/с) процессов особенностей АЯ, возникающих при переходе частоты однородной прецессии через верхнюю границу безобменного спектра спиновых волн. Параметром, изменение
г&н,з
Рис. 9.3.7. Частотные и температурные зависимости ширины резонансной кривой по-ликристаллического иттрий-гадопиний-железного граната [312].
которого вызывает такой переход, может явиться частота, температура .(влияющая на Мо) или форма образца. Эти особенности впервые наблюдал Баффлер [312] (рис. 9.3.7). Как видно из рис. 9.3.7 (последующие эксперименты подтвердили это), особенности сильно сглажены и положения максимумов 2 А// не совпадают с теми, которые получились бы в предположении безобменного, не-диссипативного спектра спиновых волн в однородной изотропной среде. Это может явиться следствием отмеченных выше (см. стр. 503) факторов.
Роль поверхностных неоднородностей в процессах релаксации Б ферромагнетиках была впервые четко зафиксирована Ле Кроу, Спенсером и Портером [311] для монокристаллов иттрий-железного граната, для которых вклады других процессов релаксации малы. Дальнейшие исследования (см., например, [283]) показали, что Бклад поверхностных неоднородностей в 2А77, в соответствии с Формулой (9.3.43), приблизительно (так как множитель G зависит ??D^o) пропорционален Мо (рис. 9.3.8)_и строго^пропорционален
(рис. 9.3.9). Оказалось, что оценка по формуле (9.3.43) дает
508
ПРОЦЕССЫ РЕЛАКСАЦИИ
1ГЛ. 6
правильный порядок величины, если для множителя G принять значения — 1, а в качестве подставить величину, несколько меньшую, чем средний размер зерна образива.
Как и для поликристаллов, большое внимание было уделено (см., например, [318]) измерениям ширины резонансной кривой в образцах из монокристаллов с шероховатой поверхностью в области перехода ю0 через верхнюю границу безобменного спектра спиновых волн. Иногда в точке перехода к»0 через верхнюю границу спектра имел место небольшой максимум 2 АД. Однако интенсивность его очень слабо возрастала с увеличением шероховатости поверхности. Кроме того, не наблюдалось уменьшения 2 АД при «выходе» соо
Рис. 9.3.9. Зависимость ширины резолая* сных кривых от радиуса сферы и степени шероховатости поверхности (экспериментальные данные). Иттрий-железный гранат; частота 9,1 Ггц. Цифры у кривых — средние размеры (в микронах) зерна абразива, на котором производилось окончательное шлифование или полировка сфер. Подъем кривых при больших объясняется возбуждением неоднородных типов колебаний при невыполнении условия справедливости магнитостатического приближения.
Рис. 9.3.8. Зависимость вклада поверхностных неоднородностей в 2АН от намагниченности (283]. Монокристаллические сферы с диаметрами —'0,5 лш. Частота 9,1 Ггц.. Намагниченность изменялась путем изменения температуры. Величины (2AH)S— разности значений 2АН грубо обработанных и хорошо полированных сфер.
из спектра (для поликристаллов такое уменьшение обычно имеет место, см. рис. 9.3.7). Эти «аномалии» могут быть частично объяснены, если предположить, что в случае шероховатостей поверхности фурье-спектр неоднородностей является более широким, чем для пор и вариацйй поля анизотропии в поликристаллах, простираясь как в область малых к (уокеровских типов колебаний), так и в обменную часть спектра.
Мы уже отмечали, что вид множителя G в формулах (9.3.41) и (9.3.43) обусловлен конкретной моделью — сферических облас-
§ g 4]	СПИН-РЕШЕТОЧНАЯ РЕЛАКСАЦИЯ	509
тей. Эта модель, конечно, не соответствует реальным, нерегулярным неоднородностям — шероховатостям поверхности и порам, которые, видимо, вообще нельзя трактовать как независимые центры рассеяния. Поэтому следствия из формул (9.3.41) и (9.3.43), связанные с конкретным видом (9.3.42) множителя G, не должны подтверждаться экспериментально. К числу таких следствий принадлежит, например, стремление 2А77 к нулю с ростом отношения а>о/<ом для сферического образца. И действительно, эксперименты, проведенные для монокристаллов с шероховатой поверхностью и для поликристаллов (см. [287]), показали, что с ростом частоты вклад макроскопических неоднородностей в ширину кривой отнюдь не стремится к нулю. Был сделан ряд попыток заменить выражение (9.3.42) для множителя G некоторым другим — эмпирическим выражением с тем, чтобы получить соответствующий эксперименту частотный ход 2А77. Но, пожалуй, больший интерес представляет работа [322], в которой был разработан метод измерения фурье-компонент эффективного поля поверхностных неоднородностей, а теория рассеяния на этих неоднородностях была сформулирована таким образом, что в нее непосредственна входили эти компоненты. При этом было получено удовлетворительное совпадение теории с экспериментом.
§ 9.4. Спин-решеточная релаксация
В двух предыдущих параграфах рассматривались процессы релаксации, происходящие внутри магнитной подсистемы магнитоупорядоченного кристалла. Теперь мы должны перейти к изучению процессов релаксации, в которых принимают участие и другие подсистемы. В этом параграфе будут рассмотрены процессы, в которых участвуют только две подсистемы: магнитная подсистема и решетка. Такие процессы можно назвать процессами прямой (в отличие от косвенной, с участием других подсистем) спин-решеточной релаксации или (см. § 9.1) спин-решеточной релаксации в узком смысле слова.
Упругие Свойства кристалла и фононы. Упругое состояние кристаллической решетки *) характеризуется смещениями
Аг, = гу — г/0
ионов, находящихся в узлах решетки, относительно их равновесных положений г/0. Для низкочастотных колебаний, как и в случае магнитной подсистемы, допустим континуальный подход, при котором вектор смещений Аг считается непрерывной функцией координат. С этим вектором связан симметричный тензор деформаций _______________
У т) Мы приведем лишь некоторые необходимые в дальнейшем определения, а н^гие свойства кристаллов рассматриваются во всех руководствах по фи-
Ке твердого тела (см., например [32]).
510	ПРОЦЕССЫ РЕЛАКСАЦИИ	[ГЛ. 9
и с компонентами
=	+	(р, $ = 1, 2, 3),	(9.4.1)
где — составляющие вектора Аг. Сила f, действующая на единицу объема, связана с тензором напряжений "о;
з (е-4-2) 8=1
Для малых — упругих деформаций имеет место закон Гука ^pslm^lmi	(9.4.3)
I m
где cpslTn — компоненты тензора четвертого ранга — тензора уп-ругих постоянных (или модулей упругости). Плотность свободной энергии, связанной с упругими деформациями,
Пупр — ~2~ 2 S °psMps “ ~2~ 2	2 2 cpslmupsulm- (9.4.4)
р s	р s I т
Из того, что тензор и является симметричным, следует, что имеется, вообще говоря, 21 независимая компонента cpslm. Однако для кристаллов всех сингоний, кроме триклинной, это число уменьшается. Так, например, для кубических кристаллов имеются только 3 независимые постоянные:
Срррр — О1> сррЦ = Ог И cpsps == ^44*
Для изотропной среды
с12 = сл 2с44,	(9.4.5)
так что остаются лишь 2 независимые упругие постоянные: модуль сжатия сп и модуль сдвига с44.
Уравнения движения упругой среды с учетом (9.4.2), (9.4.3) и (9.4.1) можно записать в виде
а2(Д.ту) = у у у &(Ьхт)	,9 , 6)
Р Qti ~-!р~ Z12j2jcpsi™	>
где р — плотность. Решение уравнений движения для случая однородных плоских волн показывает, что могут существовать три типа волн с различными скоростями распространения, т. е.
= ^14 (j = 1,2, 3),	(9.4.7)
где Oj — частоты этих волн, a q — волновое число. Для изотропной среды две волны являются поперечными и имеют одинаковые
СПИН-РЕШЕТОЧНАЯ РЕЛАКСАЦИЯ
§ 9.4]
скорости г?! — ^2 Ул» а третья волна с v3 = г?,, является продольной.
Упругие волны в непрерывной среде, как и магнитные волны /е g 4^ могут быть проквантованы, им соответствуют квазичастицы ' фононы с законом дисперсии (9.4.7). Вектор смещения Ar (г, I) можно выразить [335, 34] через операторы и bqj рожде
ния и уничтожения магнонов.
Задача об упругих колебаниях кристалла может быть рассмотрена и на дискретной модели — материальных точек с массами
ионов, расположенных в узлах кристалла. Ее решение приводит (см., например, [32, 34]) к трем отличиям от континуальной трактовки:
1)	волновой вектор фононов, как и в случае магнонов (§ 8.5), определяется теперь с точностью до векторов обратной решетки, и для устранения неоднозначности следует ограничить область q-пространства первой зоной Бриллюэна;
2)	закон дисперсии (9.4.7) заменяется более сложным законом (рис. 9.4.1), переходящим в (9.4.7) при aq 1 (где а — постоянная решетки);
3)	кроме акустических ветвей, законы дисперсии которых при aq 1 имеют вид (9.4.7), возникает 3 (и — 1)
Рис. 9.4.1. Спектр упругих волн в кристалле (схематически). Показаны только одна акустическая и одна оптическая ветви. Пунктир — спектр в непрерывной среде.
новых ветвей колебаний,
где п — число различных ионов в элементарной ячейке. Для зтих — оптических ветвей (см. рис. 9.4.1) частота не стремится к нулю при <; —> 0. Всем ветвям колебаний соответствуют свои квазичастицы — фононы, акустические или оптические. Заметим, что
оптические ветви фононов аналогичны высокочастотным — обменным ветвям магнитных колебаний в многоподрешеточных магнитоупорядоченных кристаллах (которые содержат несколько различных в магнитном отношении ионов в магнитной элементарной ячейке).
Переход к операторам рождения и уничтожения фононов в дискретной модели производится [274] следующим образом: оператор смещения иона в узле / из состояния равновесия
+V	(9.4.8)
' q i
гДе Pq/ — единичный вектор поляризации фононов у-й ветви с волновым вектором <j; суммирование по q производится в пределах первой зоны Бриллюэна, а по у, вообще говоря, — по всем Зп Ветвям фононов.
512
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Взаимодействие магнитных и упругих колебаний. До сих пор магнитная подсистема и подсистема упругих степеней свободы кристалла («решетка») рассматривались независимо. В действительности же они связаны. Эта связь приводит, в частности, к явлению магнитострикции [5, 348]. Она же является, как уже отмечалось в § 9.1, причиной спин-решеточной релаксации.
Один из механизмов магнитоупругой связи заключается в том, что обменная .энергия и энергия магнитного (диполь-дипольного) взаимодействия зависят от расстояний между ионами и, таким образом, изменяются при деформациях кристалла. Этот механизм, как источник релаксации, был исследован в уже неоднократно упоминавшейся работе Ахиезера [274].
Исходным в [274] являлось выражение для гейзенберговского гамильтониана (8.5.1) с добавлением диполь-дипольной энергии (1.1.50). Входящее в (8.5.1) и (1.1.50) расстояние между ионами может быть представлено в виде
rfi- = *7/'п + Агг — Аг/,	(9.4.9)
и гамильтониан может быть разложен по степеням Агу. Считая деформации малыми, можно ограничиться нулевым и первым членами этого разложения. Если затем выразить Aiy, согласно (9.4.8), через операторы рождения и уничтожения фононов, а от спиновых операторов перейти к операторам рождения и уничтожения магнонов, то гамильтониан примет вид
W//-) = ^(гщо) + <м. у. + <М. у. + - -	(9.4.10)
где Ж (гщо) — не возмущенный колебаниями решетки гейзенберговский гамильтониан, который использовался в §§ 8.5 и 9.2. Остальные члены в (9.4.10) описывают магнитоупругую связь и имеют вид
24М. у. - 2 2 2+ э. с.) A (k — q), (9.4.11) к q i
24 м. у. = 222 2 R 'Ь, qj&icfiiiibqi + э. с.) A (kj — к2 — q) + к, кг q j
+ (14л, <1! a^aklbqj + э. с.) А (kj + к2 — q)].	(9.4.12)
Аналогично рассмотренным в § 9.2 процессам внутри магнитной подсистемы различные члены в (9.4.11) и (9.4.12) соответствуют элементарным процессам взаимодействия между магнонами и фононами. Билинейные члены, входящие в (9.4.11), описывают двухчастичные процессы взаимного превращения магнонов и фононов. Как видно из (9.4.11), эти процессы протекают при равенстве импульсов квазичастиц. В первом порядке теории возмущений условием их протекания является совпадение и энергий частиц
§ 9.4]
СПИН-РЕШЕТОЧНАЯ РЕЛАКСАЦИЯ
513
(«&);• —hv>njY Таким образом, двухчастичные процессы превращения магнонов в фононы и обратно в этом приближении происходят лишь в точках пересечения их спектров (рис. 9.4.2).
Как отметили Туров и Ирхин [332], более строгим является рассмотрение вещества как единой системы, состоящей из связанных друг с другом магнитной и упругой подсистем. Для того чтобы найти элементарные возбуждения такой системы, следует прибавить к гамильтониану (9.4.10) оператор упругой энергии (9.4.4), выразив его через операторы bqj- и bqj. Затем необходимо провести диагонализацию суммы всех билинейных членов: магнитных, упругих и ш	/ У
членов связи (9.4.11). В результате	/ /
мы получим новые операторы яв-ляющиеся линейными комбинацн-	//
ями операторов рождения и уничто-	/'/
жения магнонов и фононов. Они явля-	/ /
ются операторами рождения и унич-	/ /
тожения новых — смешанных квази-	/у'
частиц, соответствующих нормальным колебаниям системы. Спектр этих ква- л' зичастиц показан схематически на |/ ____________________ ~
рис. 9.4.2. Как видно из рис. 9.4.2,	к
ОТЛИЧИе его ОТ невозмущенных спект- Рис. 9.4.2. Спектр магнитоупругих ров магнонов И фононов существенно волн (без учета затухания). Пунк-1	, л	тир — невозмущенные спектры маг-
лишь вблизи точек пересечения невоз-	нитных и упругих волн,
мущенных спектров.
Высшие смешанные члены в гамильтониане (9.4.10) — л^зм.у. пт. д., аналогично высшим членам спинового гамильтониана, соответствуют элементарным процессам расщепления, слияния и рассеяния, но с участием не только магнонов, но и фононов. Эти члены о'тветственны за процессы спин-решеточной релаксации.
Однако рассмотренный выше механизм — изменение обменной и диполь-дипольной энергий вследствие смещений ионов при деформации решетки, не является единственным источником магнито-упругой связи. Другим ее источником является спин-орбитальное взаимодействие', т. е. взаимодействие спиновых моментов электронов, ответственных за магнетизм, с их орбитальными моментами, которые, в свою очередь, связаны с решеткой. Как отмечалось в § 2.2, спин-орбитальное взаимодействие является основным источником кристаллографической магнитной анизотропии. Оно же является важнейшим источником магнитострикции (см., напри-К1еР, [348]). Очевидно, что спин-орбитальное взаимодействие пе может быть строго учтено в гейзенберговской модели, в которой Кообщё не фигурируют орбитальные моменты. Современное состояние микроскопической теории спин-орбитального взаимодейст-
17 А. г. Гуревич
514
ПРОЦЕССЫ РЕЛАКСАЦИИ
1ГЛ. 9
вия не дает возможности надежно учесть его вклад в магнитоупругую связь. Поэтому остается единственная возможность — построить феноменологическую теорию, которая связала бы амплитуды 4rf; qj и др. в смешанных — магнитоупругих членах гамильтониана с некоторыми постоянными, которые могли бы быть, например, определены экспериментально. Этот путь был предложен Абрахамсом и Киттелем [3311. Его использовали Ахиезер, Барьяхтар и Пе-летминский [333], которые исследовали смешанные магпитоупру-гие волны (обусловленные членами второго порядка ^2м.у.), и Каганов и Цукерник [335], изучавшие процессы спин-решеточной релаксации (связанные с членами третьего порядка
При таком феноменологическом рассмотрении исходным является выражение для магнитоупругой свободной энергии, которое записывается в виде, допускаемом симметрией данного кристалла, т. е. инвариантном относительно операций, входящих в его группу симметрии. Если ограничиться членами, линейными относительно компонент тензора деформаций J) и квадратичными по составляющим намагниченности * 2), то это выражение в общем случае можно записать следующим образом:
Км. у. —	2 2 2 S sulm Ц-
™ 0 р s I т
+ 2222224slmnr иПг, (9.+13) р s I т п г	I
где р, s, I, т, п, г = 1, 2, 3. Постоянные bpslm обусловлены релятивистскими взаимодействиями: спиновым диполь-дипольным и спин-орбитальным (последнее, как уже отмечалось, играет главную роль), а постоянные bJlSlmnr — обменным взаимодействием.
Рассмотрим кубический кристалл, но при записи обменных членов будем для простоты считать его изотропным; тогда выражение (9.4.13) примет вид [335]
км. у.=~ 2	+ 422 mpmsups +
^0 Р	Р 8
+ ъ 22 2^^+х222 2	V™. (9-+14)
р I т I т	р I т ' I 1
т) Строго говоря [3], свободную энергию следует раскладывать не по компонентам симметричного тензора деформаций ups, а по компонентам тензора д (^хр)/дхе. Однако это не приводит, по-видимому, к существенным качественным отлпчиям, и мы, следуя традиции [331—335], используем разложение свободной энергии по компонентам тензора деформаций.
2) Как уже отмечалось в § 2.2, членов, линейных по намагниченности, в энергии кристалла не может быть.
§ 9.4J
СПИН-РЕШЕТОЧНАЯ РЕЛАКСАЦИЯ
515
Л СЛучая изотропной среды в этом выражении /ц- Ь2 = Ъ. Если, считая магнитные колебания малыми (М=М0 + m и | т\ М0), ограничиться членами до второго порядка малости по составляющим ш, то переменные члены в (9.4.14) запишутся в виде
Un. у.—	м0 v^x^xz Ч-	—- mxmvuxy -J-
+ 7^ К + mvuvv “	иЛ т-
7'о
+ К 22^^22^»... (9.4.15) р S 1 S	Р S V р
(Р^в)
Здесь т^- = тх + imy, а ось z направлена, как обычно, по Мо. Выражая в (9.4.15) составляющие намагниченности через операторы Зл и «*, а компоненты тензора деформаций — через операторы bgj и bqj, можно прийти снова к выражениям вида (9.4.10)— (9.4.12). В амплитуды У войдут теперь феноменологические константы fcli2 и Ль2.
Спектр смешанных магнитоупругих колебаний может быть найден путем диагонализации билинейных членов полученного гамильтониана совместно с квадратичными членами магнитного и упругого гамильтонианов. Однако теперь — при феноменологическом подходе — весьма целесообразно использовать метод решения уравнений движения намагниченности и упругих смещений. Наличие смешанных членов (9.4.13) в свободной энергии приведет к тому, что уравнения окажутся связанными. В уравнение Ландау — Лифшица для составляющих m войдет эффективное поле магнитоупругого взаимодействия, которое может быть получено из выражения для магнитоупругой свободной энергии с помощью общей формулы (2.1.14) и будет содержать составляющие вектора смещения Аг. В уравнение движения упругой среды войдут составляющие намагниченности. Совместное решение этих уравнений, например, для бегущих волн позволит не только найти их спектр (который был показан схематически на рис. 9.4.2), но и исследовать структуру волн: поляризацию, соотношения между амплитудами намагниченности и упругого смещения.
Магнитоупругие волны, а также колебания ограниченных образцов представляют очень большой интерес как одно из проявлении магнитоупругого взаимодействия. Изучение этих колебаний и волн имеет и практическое значение в связи с задачей создания магнитоакустических сверхвысокочастотных устройств, например Управляемых линий задержки х). Однако рассмотрение магнито-
*) Как указывалось в § 8.3, для этой цели могут быть использованы и чисто магнитные волны.
17*
516
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
упругих колебаний и волн (см., например, [3, 347, 355]) выходит за рамки данной книги.
Процессы спии-решеточной релаксации. Элементарные процессы взаимного превращения магнонов и фононов, лежащие в основе спин-решеточной релаксации, определяются членами (9.4.12), а также магнитоупругими членами более высоких порядков в гамильтониане (9.4.10). Члены с амплитудами /-2(Н- в (9.4.12) соответствуют (см. табл. 9.4.1) элементарным процессам расщепления магнона на магнон и фонон и слияния магнона и фопона с образованием магнона. Их называют иногда черепковскими процессами, так как рождение фонона при таких процессах аналогично черепковскому излучению света при торможении электрона в среде [37]. Ясно, что условие черепковского излучения, в данном случае ум г’у (где — групповая скорость магнонов, a vM — скорость упругой волны), как видно, например, из рис. 9.4.2, может выполняться. Члены с амплитудами	соответствуют (табл.
9.4.1)	элементарным процессам слияния двух магнонов в фонон и обратным процессам расщепления фонона на два магнона.
В случае изотропной среды выражения для амплитуд трехчастичных процессов будут следующими [335]:
(9’4Л6)
ад = Ъ	(Ря+ + Рш- д+ - Р<&д2) —
— i2rwo	(РвА1-Чк2 + РтД'2-фч) + %2kika qp« ],
(9.4.17)
где pQji- = pqjx + i'Pqjy, a q±. = qx + iqv. Из выражений (9.4.16) и (9.4.17) видно, что, как и следовало ожидать, в амплитуду процессов слияния магнонов (для которых число магнонов не сохраняется) вносят вклад только релятивистские взаимодействия. В амплитуду же черепковских процессов вносит вклад и обменное взаимодействие. Поэтому, в отличие от чисто магнонных процессов, можно совсем не рассматривать четырехчастичные магнон-фонон-ные процессы.
Сравним теперь вклады релятивистских членов в (9.4.16) и (9.4.17) и обменного члена в (9.4.17). Как показано в [335],
^1,2 — <1 ==
_2L
T.Wo ’
(9.4.18)
где q — константа неоднородного обменного взаимодействия (см.
§ 2.1). Таким образом, отношение этих вкладов составит
Трел/ ТоСм —	.	(9.4.19)
СПИН-РЕШЕТОЧНАЯ РЕЛАКСАЦИЯ
517
§ 9.4]
Таблица 9.4.1
ентарные процессы, ответственные за трехчастичные процессы с,лем .	спин-решеточной релаксации
(рассматривается релаксация магиоиов с волновым вектором ki)
Процессы	релаксации	Amii.'i итуда	Элементарн прямые	ые процессы обратные
Черепковские	Расщепления	V	к.	4
	Слияния	/о. к2(13	74	74
Слияния магнонов в фоноп		•пг	"2	АЛ
Например, для иттрий-железного граната (b2 = 3-10® [347]) это отношение больше единицы при к 10®. Таким образом, релятивистские взаимодействия (в первую очередь, конечно, спин-орбиталь-ное) играют главную роль в трехчастичных процессах спин-решеточной релаксации при не очень больших к. При увеличении к вклад обменного взаимодействия увеличивается, одновременно, возрастает роль прямых процессов спин-решеточной релаксации.
К расчету частот релаксации, обусловленных трехчастичными магнон-фононнымн процессами, полностью применима теория трехбозонных процессов, развитая в § 9.2. Рассмотрим, например, черепковские процессы. Так же как и в трехмагнонном случае, следует различать два типа таких процессов — процессы слияния и расщепления (см. табл. 9.4.1). Частота релаксации, обусловленная черепковскими процессами расщепления, запишется аналогично
“н = S 2 2 21 W I2	+ 1) A (kt - k2 - q) X
кг q j
X 6 (<oftl —	— 03ад). (9.4.20)
гДе TVqj — равновесное число фононов с волновым вектором q и вектором поляризации рг/,. Таким же образом могут быть записаны частоты релаксации двух других процессов.
Мы не будем вычислять частоты релаксации для рассмотренных °Роцессов. Отметим лишь, что, как показывают расчеты [335, 293,
518
ПРОЦЕССЫ РЕЛАКСАЦИИ
ГГЛ. 9
Рис. 9.4.3. Температурная зависимость параметра диссипации спиновых волн с fc -> в и = л/2, полученная методом продольной накачки [287]. Иттрийжелезный гранат; частота 5,7 Ггц. Величины 2AIfyf l определялись путем экстраполяции к к — 0 результатов измерений 2AHfc (к) (см. рис. 9.2.6). Пунктир — та же зависимость за вычетом низкотемпературного вклада примесных редкоземельных ионов (§ 9.6).
2801 (см. также [3, 244, 2871), вклад их в диссипацию энергии однородной прецессии, а также спиновых волн с небольшими к, которые возникают в результате 0-к процессов и спиновых нестабильностей, весьма мал. Однако процессы магнон-фононной релаксации становятся все более эффективными по мере увеличения к. И в тех кристаллах, в которых не играет заметной роли косвенная спин-решеточ-ная релаксация, рассматриваемые процессы прямой магнон-фононной релаксации приводят к передаче в решетку всей энергии однородной прецессии (или других длинноволновых колебаний), предварительно «размазанной» по типам колебаний магнитной подсистемы различными спин-спиновыми процессами. Поэтому не удивительно, что для частоты релаксации прямых спин-решеточных процессов, усредненной по всем значениям к, были получены [274] довольно большие величины — порядка 10е -1- 10’.
Процесс Касуйя — Ле Кроу. Как уже отмечалось (см., например, рис. 9.2.6), эксперимент указывает на наличие «собственных» (не связанных с неоднородностями) процессов релаксации, не исчезающих при к 0. Обусловленная ими частота релаксации при достаточно высоких температурах пропорциональна температуре (рис. 9.4.3). Это является (см. § 9.2) признаком трехбозонных процес-было показано, что ни один трех-
сов. В то же время в § 9.2
магнонный процесс, во всяком случае, при учете только нижней — ферромагнитной («акустической») ветви магнонного спектра не может при данной — достаточно высокой частоте дать такого вклада в релаксацию при к —> 0. Трехчастичные магнон-фо но иные процессы тоже не могут обеспечить этого вклада при тех ограничениях, которые были сделаны выше при их рассмотрении, а именно — при учете только акустических ветвей спектров магнонов и фононов и учете в гамильтониане (9.4.13) только тех релятивистских членов, - которые разрешены симметрией (в данном случае кубической) всего кристалла.
Касуйя и Ле Кроу [284] показали, что приведенные на рис. 9.4.3 значения ширины кривой могут быть связаны с черепковским процессом слияния магнонов с фононами (см. табл. 9.4.1), н°
РЕЛАКСАЦИЯ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОКА
51S)
I 0.51
лько при следующих условиях: а) при учете верхней — обменной ветви магнонного спектра, б) при учете верхней — оптической ветви спектра фононов, в) при условии, что возмущением, обусловливающим связь магнонов и фононов, является изменение при деформациях кристалла локальной энергии анизотропии ионов. Эта энергия может в кубических кристаллах во много раз превышать среднюю «кубическую» энергию анизотропии.
Интересно заметить, что процесс Касуйя — Ле Кроу и, вообще, черепковские процессы слияния осуществляют передачу энергии не от магнитной подсистемы решетке (как остальные спин-решеточ-ные процессы), а, наоборот, от решетки магнитной системе. Эта энергия, конечно, передается обратно в решетку другими спин-решеточными процессами, прямыми или косвенными.
§ 9.5. Релаксация с участием носителей тока
Передача энергии от магнитной подсистемы решетке может идти не только прямым путем, который был рассмотрен в предыдущем параграфе, но и через другие подсистемы кристалла, связанные достаточно сильно как с магнитной подсистемой, так и с решеткой. К числу таких подсистем относятся (см. рис. 9.1.2) носители тока (злектроны проводимости), парамагнитные ионы с достаточно сильной спин-орбитальной связью (точнее — подсистема локализованных электронных степеней свободы этих ионов) и, вообще говоря, ядерная магнитная подсистема. Однако роль ядерной магнитной подсистемы в интересующих нас процессах релаксации обычно мала. Процессы же, происходящие с участием первых двух подсистем — носителей тока и локализованных ионов, могут быть очень эффективны. Они будут рассмотрены в этом и следующем параграфах.
Джоулевы потери в случае малой проводимости. Рассмотрим сначала простейший механизм косвенной спин-решеточной релаксации, связанной с носителями тока. Он заключается в том, что переменная намагниченность вследствие электромагнитной индукции наводит электрическое поле, которое вызывает в образце вихревые токи. Джоулевы потери этих токов приводят к передаче энергии, затраченной магнитной подсистемой на их возбуждение, в решетку. Ограничимся случаем малой проводимости. Тогда можно пренебречь обратной реакцией токов на намагниченность, т. е. считать, в духе первого приближения теории возмущений, что магнитные колебания имеют такую же структуру, как и в непроводящем образце.
Для определенности рассмотрим однородную прецессию в изотропной ферромагнитной сфере, намагниченной до насыщения в на-пРавлении оси z (рис. 9.5.1). В этом случае переменная намагниченность будет иметь круговую поляризацию, и ее комплексная
ЙО
процессы релаксаций
1гл. 6
амплитуда
m = т (х0 — гу0),
(9.5.1)
где х0 и у о — единичные векторы, направленные по осям х и у. Вычислим частоту релаксации, обусловленную джоулевыми потерями электрических токов, наводимых в сфере ’). Мощность этих потерь
po=4-c$ieiw’	(9-5-2)
V
где а — проводимость вещества сферы, а е — комплексная амплитуда электрического поля. Частота релаксации может быть вычислена по формуле
Рис. 9.5.1. Однородная прецессия намагниченности в слабопроводящей ферромагнитной сфере с узкой резонансной кривой.
ной магнитной индукции b
со,. = РО/21Ф,	(9.5.3)
где W — энергия однородной прецессии, для которой справедливо выражение (6.4.7).
Задача сводится, таким образом, к вычислению электрического поля в сфере. Оно определяется уравнением Максвелла (5.1.10) или в интегральной форме:
$) etdl = \bndS, (9.5.4)
где I — линия, ограничивающая поверхность S, et — проекция е на эту линию, а Ьп — проекция комплексной амплитуды переменна нормаль к S. В свою очередь,
b = h -ф 4лт = h0 — Nm 4лш,
(9.5.5)
где h — внутреннее, a h0 — внешнее поле. Вблизи ферромагнитного резонанса в случае узкой резонансной кривой | т |	| hn |,
и для сферы
(9.5.6)
Поскольку т, а следовательно, приближенно и b лежат в плоскости ху, то е = ez (в этом легко убедиться, применяя (9.5.4) к контуру, лежащему в плоскости ху). Тогда применяя (9.5.4) к показанному на рис. 9.5.1 малому контуру со сторонами г (М в
х) Аналогичная задача для случая цилиндрического образования Рас' смотрена в [20].
n	РЕЛАКСАЦИЯ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОКА	521
§
Г sinO dtp, получим
г sin0 dtp = — Ь,г2 sin0d3d<p.	(9.5.7)
С учетом (9.5.6) и (9.5.1)
&r = ^msinfie-i<₽.	(9.5.8)
Подставляя (9.5.8) в (9.5.7) и учитывая, что должно зависеть от ф по тому же закону е~гч>, найдем
ez — ~ mr sinO е~'’'.	(9.5.9)
(9.5.10)
Подставляя эту величину в (9.5.2) и производя интегрирование, получим затем по формуле (9.5.3) с учетом (6.4.7)
(2ДЯ)П = y-r = J 4лМ0е" (М)2
Здесь к0 = ®/с — волновое число электромагнитных волн в свободном пространстве, а е" — 4лц/о. Заметим, что в ионных кристаллах, в частности в ферритах, величина о, учитывающая различные виды электрических потерь, сильно зависит от частоты и значительно превышает статическую проводимость.
Как и следовало ожидать, параметр диссипации оказался пропорциональным (k0R)2, поскольку он связан с учетом «эффекта запаздывания», т. е. с использованием полного (а не магнитостатического) уравнения Максвелла. Интересно сравнить полученную формулу (9.5.10) с выражением (7.3.37) для сдвига резонансного поля, обусловленного учетом того же эффекта. Можно ожидать, что (Д-Н)а будет представлять собой мнимую часть выражения, которое получится в результате подстановки комплексной электрической проницаемости е = е' — it,” в (7.3.37). Действительно, выражение для (Д27)О, к которому мы приходим таким образом, отличается от (9.5.10) лишь множителем порядка 1.
Оценим величину (2Д27)О. Для стехиометрических монокристаллов ферритов с узкой резонансной кривой, например; для иттрий-железного граната в сантиметровом диапазоне волн при комнатной температуре е" ~ 0,001 [314, 371]. Тогда, как легко видеть, для малых образцов, используемых обычно при резонансных измерениях (/с02? < 0,1), вклад рассмотренного механизма пренебрежимо мал. Однако для тех же кристаллов, но с небольшим содержанием Fe2+, когда е" может быть, например, 0,05 1371], и длЯ несколько больших образцов (2Д//)0 может достигать 1 э. Что же касается многих ферритов со структурой шпинели, особенно нестехиометрических, то для них джоулевы потери вихревых токов являются существенным источником расширения
522
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
резонансной кривой. Проводимость ферритов носит полупроводниковый характер, и е" быстро растет с ростом температуры. Это приводит к росту 2 А// при увеличении температуры, тем более резкому, чем больше размер образца (см., например, рис. 9.5.2).
Если проводимость достаточно велика, обратной реакцией вихревых токов на намагниченность пренебречь нельзя, и приведенный расчет становится несправедливым. При этом, как известно, действие вихревых токов приводит к поверхностному эффекту
Рис. 9.5.2. Температурная зависимость 2ДН сфер из монокристалла феррита Ni0j75FeQi25re|+O1 [360]. Частота 24 Ггц. Цифры у кривых — диаметры сфер в миллиметрах. Сплошные линии — Н„ направлено по оси	пунктир— по оси <100>.
(скин-эффекту) — переменное электромагнитное поле в среде убывает по мере удаления от поверхности образца по закону Величину 6 = Мк” называют глубиной проникновения поля в среду или толщиной скин-слоя. Ясно, что условием справедливости принятого выше допущения о неискаженной токами однородной прецессии в сфере, т. е. условием справедливости приведенного расчета (2АЯ)О, является
6>Я.	(9.5.11)
Для оценки величины 6 можно использовать формулу (5.2.10), понимая под цЭфф', например, диагональную поперечную компоненту тензора [г. При этом следует учесть (см. § 1.4), что для всех образцов, кроме предельного случая бесконечно тонкого нормально намагниченного диска, вблизи ферромагнитного резо-
релаксация с участием носителей тока
523
9.51
*нанса магнитная проницаемость вещества не проходит через резонанс. Поэтому при не очень широких резонансных кривых можно принять / ж 1 и р" <С р'. Тогда для ферритов (е' ~ 10) даже с большой проводимостью (е" — 1) условие (9.5.11) хорошо выполняется и приведенный выше расчет (2Д//)„ справедлив.
О роли электронов проводимости в процессах релаксации в металлах. Для металлов *) е" г? 4л о/в е'. В этом случае (если по-прежнему р/ ;Э> р") из (5.2.10) следует известная формула
б = ~^== .	(9.5.12)
у 2лр'о<о
Для металлов, в отличие от ферритов, можно считать, что о мало зависит от частоты. Тогда оценка по формуле (9.5.12) показывает, что на сверхвысоких частотах 6 ~ 10~4 см, т. е. 6 (кроме случая тонких пленок) во много раз меньше размеров образца. При этом в образце, естественно, не может быть однородной прецессии. Внешнее однородное поле будет возбуждать в нем спиновые волны, распространяющиеся от поверхности вглубь образца и затухающие вследствие различных механизмов релаксации, в том числе и джоулевых потерь электрических токов, связанных со спиновыми волнами.
Задача о возбуждении таких спиновых волн имеет много общего с задачей о возбуждении стоячих спиновых волн в тонкой пленке, которая рассматривалась в § 8.3. Однако теперь необходимо использовать не магнитостатические уравнения, а полные уравнения Максвелла. Граничное условие (8.3.16) накладывается теперь только на одной поверхности, вследствие чего спектр возбуждаемых спиновых волн является не дискретным, а непрерывным, с максимумом, лежащим в области к = 1/6. Это приводит к дополнительному расширению резонансной кривой.
В качестве величины, которая характеризует ферромагнитный резонанс в металле, удобно рассматривать импеданс поверхности металла, т. е. отношение амплитуд переменных электрического и магнитного полей на поверхности. Амент и Радо [253] вычислили поверхностный импеданс, приняв граничные условия (8.3.21). Сравнение с экспериментами, выполненными на пермаллое в малых постоянных полях [256], показало, что упомянутое расширение кривой, связанное с возбуждением спиновых волн, является в данном случае существенным вкладом в АГ/.
Новые особенности ферромагнитного резонанса в металлах возникают [361], когда имеет место так называемый аномальный
*) Магнитный резонанс в магнитоупорядоченных металлах имеет интересные особенности (см., например, [3, 363]), рассмотрение которых выходит за рамки этой книги. И мы остановимся очень кратко лишь па некоторых вопросах, связанных с этой проблемой.
524
ПРОЦЕССЫ РЕЛАКСАЦИИ
ГГЛ. 9
скин-эффект, т. е. когда длина свободного пробега электронов проводимости превышает толщину скин слоя (это осуществляется в чистых металлах при низких температурах).
В основе механизма передачи энергии из магнитной подсистемы металла в решетку в виде джоулева тепла вихревых токов лежит взаимодействие образующих магнитную подсистему 3d- или 4/-электронов с орбитальным движением s-электронов проводимости. Но в металлах может сказываться и взаимодействие (в первую очередь, обменное) магнитных моментов Зй-или 4/-элект-ронов со спинами s-электронов. Как отмечалось в § 1.1, такое s — d (или s = /) обменное взаимодействие (см. [51) играет, по-видимому, существенную роль в магнитном упорядочении в металлах. Его роль в процессах релаксации также может быть существенной [362, 363].
Релаксация, связанная с Перескоковы л характеро м проводимости. Для механизма релаксации, обусловленного джоулевыми потерями, важна была только величина проводимости, а природа ее не была существенна. Однако в ферритах имеется и другой механизм релаксации, к рассмотрению которого мы сейчас перейдем, также обусловленный проводимостью, но связанный с определенным ее характером.
Большинство ферритов являются полупроводниками с малой подвижностью носителей тока. Проводимость их часто бывав связана с наличием в кристалле одноименных ионов с разной валентностью, например ионов Fe3+ и Fe2+. Для качественного описания такой проводимости обычно используется модель, которую предложили Вервей и де Бур (см., например, [19]). Согласно этой модели заряд переносится в результате переходов («перескоков») электрона с иона Fe2+ на ион Fe3+. При каждом переходе ионы меняются местами, в результате чего происходит как бы диффузия иона Fe2+. В отсутствие внешнего электрического поля процесс носит хаотический характер; при наличии поля переходы происходят преимущественно в направлении, противоположном полю, и возникает ток.
Преимущественные направления переходов электронов могут быть вызваны также прецессией намагниченности. Для этого одноименные разновалентные ионы должны занимать кристаллографически неэквивалентные положения в решетке. В ферритах со структурой шпинели имеется, например, четыре типа таких неэквивалентных октаэдрических узлов (см. § 4.4), в которых находятся ионы Fe3+ и Fe2+. Их локальные оси образуют с намагниченностью разные углы, и энергия системы зависит от того, на каком из неэквивалентных узлов находится «лишний» электрон, т. е. ион Fe2+. Во время прецессии намагниченности углы, образуемые вектором М с локальными осями, все время изменяются, причем по-разному для неэквивалентных узлов. Изменяются
9.51
РЕЛАКСАЦИЙ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОЙА
525
и энергетические уровни системы, соответствующие нахождению иона Fe2+ на разных неэквивалентных узлах. В результате возникают преимущественные направления переходов электронов, также изменяющиеся с частотой прецессии. И если, к тому же, переходы электронов запаздывают по отношению к изменению энергий, т. е. по отношению к прецессии М, то можно ожидать,
что будет происходить диссипация энергии прецессии. Энергия будет передаваться от магнитной подсистемы подсистеме ионов с переменной валентностью, а от нее — решетке, с которой ионы сильно связаны. Таким образом, рассматриваемый процесс может явиться каналом косвенной спин-решеточной релаксации.
Убедимся теперь, что при наличии запаздывания переходов действительно происходит упомянутая передача энергии, приводящая к диссипации магнитных колебаний. Рассмотрим для простоты случай двух ионов, находящихся в неэквивалентных узлах (рис. 9.5.3, а). Пусть Ci и еп будут энергии двух состояний этой пары ионов, отличающихся тем, что «лишний» электрон находится на одном или на другом ионе. Предположим для определенности, что щ и ёц изменяются так, как по-
t
Рис. 9.5.3. Переходы между уровнями энергии системы, которая состоит из пар ионов железа в неэквивалентных узлах. а — состояния (I и II) пары ионов; б — переходы между уровнями энергии при их модуляции в отсутствие запаздывания; в — переходы при наличии запаздывания. Переходы осуществляются в результате перескоков электронов между узлами.
казано на рис. 9.5.3., б и в.
Внутренняя энергия подсистемы, состоящей из таких пар ионов,
и- 2
1=1, п

(9.5.13)
где N} — число пар, находящихся в состоянии /, т. е. населенность соответствующего уровня энергии ионной подсистемы. Изменение энергии подсистемы
dU - V TV- де> 4- У dNj ₽
-df - 21 IF + 21 Er
i .	’
(9.5.14)
526
Процессы релаксаций
1ГЛ. 9
Первый член в правой части (9.5.14) есть работа, совершаемая над системой, т. е. в нашем случае — энергия, передаваемая подсистеме ионов от магнитной подсистемы. Второй член в правой части (9.5.14) — это тепловая энергия, поступающая в систему в данном случае — из решетки. Пусть сначала запаздывание отсутствует. Тогда, как легко видеть из рис. 9.5.3, б, средние значения обоих членов равны нулю.
Если же рассматриваемая ионная подсистема имеет конечное время релаксации, то восстановление равновесных населенностей будет запаздывать по отношению к изменению энергий ецп, и преимущественные переходы будут происходить так, как показано на рис. 9.5.3, в. Тогда, как нетрудно убедиться, среднее значение первого члена в правой части (9.5.14) будет положительно, а второго — отрицательно (среднее значение dUI.it для рассматриваемого стационарного режима равно нулю). Таким образом, запаздывание переходов привело к передаче энергии от магнитной подсистемы ионам, а от них — решетке. В предельном случае бесконечно большого времени релаксации ионов переходы, вообще, «не будут успевать» происходить и передачи энергии не будет (как и при отсутствии запаздывания, т. е. нулевом времени релаксации). Можно полагать, что максимальная передача энергии будет иметь место при он — 1, где т — время релаксации ионов, а и — частота магнитных колебаний.
Заметим, что рассмотренный механизм релаксации, связанный с запаздыванием установления равновесия в системе, имеет много общего с дебаевской релаксацией полярных молекул (см., например, (43]) и с продольной — гортеровской релаксацией в парамагнетиках (см. [289]). Для случая, когда переходы системы из одного состояния в другое связаны с диффузией примесных атомов, аналогичный механизм был предложен Неелем. Для случая же электронных переходов между разновалентными ионами такой механизм был предложен Голтом [154, 360], как источник диссипации при ферромагнитном резонансе и торможения при движении границ доменов в ферритах. Теорию этого механизма развил Клогстон [359].
Теория Клогстона. Рассмотрим ’) систему, состоящую из двух связанных подсистем: магнитоупорядоченной, для простоты — ферромагнитной подсистемы и подсистемы, которую мы назовем ионной. Первая характеризуется вектором намагниченности М, для которого справедливо уравнение Ландау — Лифшица. Вторая состоит из N микрообъектов и характеризуется своими энергетическими уровнями ё; и их населенностями Nj, так что
2 TVj = 2V. з
Вывод, который приводится ниже, несколько отличается от [3591‘
РЕЛАКСАЦИЯ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОКА
527
§ 9.51
В силу связи, существующей между подсистемами (которая в теории Клогстона не конкретизируется), уровни ej зависят от состояния первой подсистемы и, в частности, модулируются с частотой ю при ее колебаниях. Одновременно происходит модуляция с той же частотой равновесных населенностей Njx. Они определяются статистическим распределением (для простоты будем считать его больцмановским) при мгновенных значениях энергий е,-. Будут изменяться с частотой '•> и мгновенные значения населенностей Nj. Эта модель описывает систему, в которой происходят переходы электронов между разновалентными ионами, но является значительно более общей.
В силу запаздывания, о котором шла речь выше, мгновенные населенности Nj (t) не совпадают с равновесными Njx. (t). Основным предположением теории является
dNj _ Nj^ ~ -%-dt	Т
(9.5.15)
Это означает, что все населенности релаксируют к равновесным населенностям с общим для всей системы временем релаксации т *).
Предположим, что колебания намагниченности и обусловленную ими модуляцию населенностей и Nj можно считать малыми. Тогда населенности будут изменяться по гармоническому закону:
Njao = (N]ail)0 + иуоое™',	(9.5.16)
AG = (AG)o + ni eiat.	(9.5.17)
.Подставляя (9.5.16) и (9.5.17) в уравнение (9.5.15), найдем стационарное решение
п-
^ = ^)о + г^.е-
(9.5.18)
Ограничимся рассмотрением однородных колебаний намагниченности и пренебрежем влиянием формы образца (полученные результаты будут справедливы для сферы). Пренебрежем также кристаллографической анизотропией, возникающей в магнитной подсистеме (анизотропия, обусловленная влиянием ионной подсистемы, будет учтена теорией). Тогда свободная энергия
*) Как мы увидим в следующем параграфе, это предположение справедливо лишь для двухуровневой системы,
528
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
системы ')
и =-МН+ 2^-57,
(9.5.19)
где энтропия системы .8’ = — n^Njln (Nj/N) [36].
3
Линеаризованное уравнение движения магнитной
подсистемы
запишется в виде
но и = — ут х Hcff 0 — тМ0 х кеЯ,
(9.5.20)
где Heff 0 и heff — постоянная и переменная составляющие эффективного поля, которое, согласно (2.1.14), определяется следующим образом:
Рис. 9.5.4. Система координат в теории Клогстона.
Не„ =
(9.5.21)
Существенно, что производная в (9.5.21) должна вычисляться при постоянных населенностях. Это следует из того, что правая часть уравнения (9.5.20) представляет собой момент внешних сил, действующих на систему. При вычислении его, а следовательно, при определении НеЯ необходимо принимать во внимание лишь первый член в правой части (9.5.14), т. е. учитывать лишь изменения е,- при Nj = const.
Воспользуемся декартовой системой координат с осью z, направленной вдоль постоянной намагниченности (рис. 9.5.4). Предположим для простоты, что это направление совпадает с направлением постоянного внешнего поля. Рассмотрим свободные колебания — при отсутствии внешнего переменного поля. Введем углы 6 и 0 (см. рис. 9.5.4), такие что
Мх = Л/о sin А0 Мо Д9, Mv = Мо sin А 6 М0А 5 (9.5.22)
(6 — это полярный угол, а ф — sin 0, где — азимутальный угол в сферической системе координат). Тогда проекции эффективного поля (9.5.21) запишутся в виде
\ X/ J	.
I r)TT \	-I „ С>В;
Hetty = “~’
\ У/ J	j
Hett z ~
(9.5.23)
х) См. сноску 2 на стр. 67. Индекс F мы теперь опускаем.
§ 9.51
РЕЛАКСАЦИЯ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОКА
529
где величины Nj определяются согласно (9.5.18). Разлагая Njx в ряд около равновесной точки 60, <р0 и ограничиваясь первыми членами этого ряда, нетрудно получить
Д4 = (А^)о +
т-А— • (9.5.24)
1 -Ргсот '	'
де- Эе-
Производные и также разложим в ряды около равновесного положения 0О, ф0 и ограничимся их первыми членами г). Тогда, подставляя постоянные и переменные составляющие Heff в проекции (9.5.20) и учитывая выражения (9.5.22) и (9.5.24), получим уравнения движения
—мод9 + л/ояоД0 2 Ап + М й-1-гА-
7	°	1	11 °	1	\ 50	1 дф т} дф \ ф пот
• \
де дф А® + дф* / = 0’
(9.5.25)
~ М0Ьф - М0Н0№ + 2 (AfT А0 + М Аг FV— + т и '	и 1	\ 56	1 дф 50 1 + гсот 1
з , /5%;	<Ж;	\
I Zj Л[-ggr А0 + dQd.p = 0.
Здесь опущены индексы 0 у Nи производных; все эти величины определяются при равновесных углах 60 и <р0.
Условие совместности системы (9.5.25) дает комплексную частоту со = со' is>" свободных колебаний. Предположим, что третьи и четвертые члены уравнений (9.5.25) малы по сравнению с первыми двумя, т. е. что (<о' — ТЯО) и а" малы по сравнению с уН0. Это предположение будет всегда выполняться, если концентрация N достаточно мала. В таком приближении, приравнивая нулю определитель системы (9.5.25), получим
(У V	2сиА 11 <О2Т2 1 2rt/()2(ae2	(9-5-26)
со" Т где	ААцА* ’	<9-5-27) Р - _ у & А 4-	/9 ч 50 ' дф дф}-	(9.5.28)
4 См. вывод уравнений/Движения в сферических координата? в § 2.1,
530
ПРОЦЕССЫ РЕЛАКСАЦИИ
[гл. е
При выводе выражений (9.5.26) и (9.5.27) было учтено соотношение
'dNjx 8с- dN^ dej \ < дф о© де дф /
(9.5.29)
которое легко получить, принимая во внимание, что величины Nj-O зависят только от всех е,-.
Из (9.5.27) следует, что ширина резонансной кривой, обусловленная рассматриваемым механизмом релаксации,
Рис. 9.5.5. Частотные зависимости ширины резонансной кривой и динамических сдвигов резонансного поля согласно теории Клогстона.
(9.5.26), запишется следующим
(9.5.30)
Как и следовало ожидать, исходя из приведенных выше качественных соображений, (2ДЯ)Т -> 0 при сот -> 0 и при сот -* оо (рис. 9.5.5). Сдвиг резонансного поля, согласно приведенному выше выражению образом:
Ш РТ^
1
2л/о4Чд02 ' дф*
^(6Я)ИО + (6Я)ТС. (9.5.31)

Это выражение можно привести к виду
,Д/П ________L п ю2т2___________1_
2Л/о 1 + о!т® 2М«
' де, \ э I де А)
+ дф (Л’00 дфУг'
^(6Я)ЫЦ-(6Я)О. (9.5.3Г)
Как видно из (9.5.3Г), (6Я)„,-► 0 при сот-> 0, и следовательно, не зависящая от со величина (6Я)О представляет собой статический сдвиг резонансного поля. В этом случае переходы между энергетическими уровнями системы происходят безынерционно. В другом предельном случае сот-*- оо, как видно из (9.5.31), обращается в нуль величина (6Я)ЫО. Переходы в этом случае «не успевают» происходить. Постоянная величина (бЯ)оо, к которой при этом стремится (6Я)-, может быть названа адиабатически» сдвигом резонансного поля.
Интересно, что величины (6Я)О и (6Я)^ получаются в результате двукратного дифференцирования члена свободной энергии
§ 0.5j	РЕЛАКСАЦИЯ С УЧАСТИЕМ НОСИТЕЛЕЙ ТОКА	531
yNjEj по углам. Первое дифференцирование (при вычислении Heff) производится всегда при Nj = const. Второе же производится при Nj = const, если переходов не происходит (т. е. при вычислении (677)^), и с учетом изменения Nj, если переходы происходят свободно, безынерционно (при вычислении (677)О). Изложенная выше теория позволяет найти (677)Т (а также и (2Д77)Т) и в промежуточных случаях.
Заметим, что теория Клогстона близка к изложенному в § 2.1 общему методу вычисления частоты ферромагнитного резонанса, исходя из свободной энергии системы,— методу Смита — Сула. Она отличается от расчета, проведенного в § 2.1 (кроме несущественного различия систем координат) тем, что в ней рассматривается частный вид системы (описываемый свободной энергией (9.5.19)), но учитывается конечное время релаксации. В конце § 2.2 методом Смита — Сула была рассмотрена, по существу, та же задача, что и в данном параграфе,— о влиянии примесных ионов на резонанс в магнитной подсистеме, но без учета запаздывания. Можно убедиться, что полученный в § 2.2 сдвиг резонансного поля совпадает именно с (677)О.
Возвратимся к наиболее интересной для нас величине (Д77)-(индекс т в дальнейшем будем опускать). Поскольку множитель Р в (9.5.30) не зависит от частоты, ширина кривой, как функция частоты при Т = const, имеет максимум при а = 1/т (рис. 9.5.5). Зависимость же Д/7 от температуры (при ® = const) определяется температурными зависимостями как времени релаксации т, так и равновесных населенностей Nj<x>, которые входят в Р. Производные от TV,,» по углам, а следовательно и величина Р (Т), стремятся к нулю при Т -> 0 (когда населен лишь один — нижний уровень) и при Т —>- оо (когда все уровни населены равномерно). Величина Р (71) будет иметь максимум при температуре порядка Де/и, где Де — некоторое среднее расстояние между уровнями.
Время релаксации т обычно быстро уменьшается с ростом температуры, например, по закону w
т = тоек7'.	(9.5.32)
(где W — некоторая постоянная величина — энергия активации). Множитель Q в (9.5.30), как функция температуры, проходит через максимум, когда т (?') достигает величины 1/со. Результирующая кривая Д/7 (Т) может иметь, таким образом, два максимума или один, если максимумы Р (Т) и Q (Т) сливаются. Наличие температурных максимумов \Н отличает данный механизм релаксации от всех рассмотренных ранее механизмов, приводивших к монотонным температурным зависимостям ширины резонансной кривой.
532
Процессы релаксации
[ГЛ. 8
2&Н, з
Рис. 9.5.6. Температурные зависимости шщшны резонансной кривой в монокристаллах граната А’зГе4в,481о,ов012, содержащих ионы Fe2+ 1366]. Частота 13,4 Ггц. Обозначения у кривых — направления постоянного поля.
Для ферритов со структурой шпинели в выражении (9.5.32) т0 ~ 10-14 и W ~ 0,25 ав [19]. Тогда т достигает 1'' о для сантиметрового диапазона волн при температурах порядка 300 -н н-400 °К. И поскольку зависимость (9.5.32) величины т от температуры является сильной, максимум должен лежать в этой же области температур.
Формула (9.5.30) с учетом (9.5.28) определяет и анизотропию Д/Д т. е. зависимость Д/Т от углов, которые постоянная намагниченность Мо образует с осями кристалла. Для получения конкретного вида этой зависимости нужна информация об угловых зависимостях е,. Энергетические уровни С; зависят от углов между Мо и локальными осями ионов. Структура шпинели (см. § 4.4) содержит 4 неэквивалентных октаэдрических узла с тригональной локальной симметрией и осями, направленными вдоль разных осей Клогстоном было сделано предположение, что имеется 4 уровня энергии
i'j = 80 cos2 Д, (9.5.33) где 6; — углы между Мо и различными осями (111/, а е0 —постоянная величина. При этом предположении расчет приводит к «кубической» анизотропии Д/Д т. е. от углов, какая получается для
резонансного поля в кубическом кристалле (§ 2.2) при учете только первой константы анизотропии. Знак этой анизотропии оказывается таким, что максимумы Д// лежат при Мо |[<100>, а минимумы — при Мо || (111>.
Рассмотренная теория была создана Клогстоном в связи с экспериментами Ягера, Голтаи Мерритта [360]. Теория должна была объяснить температурный максимум Д// (см. рис. 9.5.2) при Т = 160 °К и анизотропию Д/Д Но как видно из рис. 9.5.2, анизотропия Д// имеет обратный знак по отношению к результату расчета на основании модели (9.5.33). Для устранения этого противоречия Клогстону пришлось выдвинуть другую модель — с тремя уровнями энергии, не имеющую никакого физического обоснования, но дающую необходимый знак анизотропии Д/Д Кроме того, из приведенной выше оценки следует, что максимум Д// должен иметь место при более высокой температуре. В дальнейшем в ферритах со структурой граната [366] и шпи
к такой же зависимости ее
§ fl.61
ИОННАЯ РЕЛАКСАЦИЯ
533
нели [369], содержащих ионы Fe2+, были обнаружены максимумы АТ/, которые лежали при более высоких температурах, согласующихся с приведенной оценкой (см., например, рис. 9.5.6). Анизотропия АН при этом имела «правильный» знак в согласии с первой — четырехуровневой моделью Клогстона. Есть все основания полагать, что именно эти максимумы обусловлены рассмотренным выше механизмом релаксации, который связан с межионными электронными переходами, ответственными за перенос заряда.
Что же касается максимумов АН на рис. 9.5.2, то они, как теперь ясно, обусловлены иным механизмом релаксации, не связанным с проводимостью. Этот механизм релаксации будет подробно рассмотрен в следующем параграфе.
§ 9.6. Ионная релаксация
Перейдем к рассмотрению процессов релаксации, которые обусловлены наличием в кристалле определенных ионов, таких как Fe8+, Со2+ или редкоземельные ионы, и (в отличие от процессов, исследованных в предыдущем параграфе) не связаны с переносом заряда. Упомянутые ионы имеют спиновый и орбитальный моменты и характеризуются сильной спин-орбитальной связью. Частоты релаксации их возбужденных состояний велики, т. е. ионы очень быстро передают энергию решетке, а в некоторых случаях, как мы увидим, и магнитоупорядоченной (магнитной) подсистеме. С другой стороны, ионы, сильно связанные обменным взаимодействием с магнитной подсистемой, могут легко возбуждаться под воздействием ее колебаний. Отсюда ясно, что эти ионы и при отсутствии каких-либо механизмов переноса заряда могут выполнять роль промежуточного звена в передаче энергии от колебаний магнитной подсистемы решетке (или другим типам магнитных колебаний). Такие процессы косвенной спин-решеточ-пой или спин-спиповой релаксации мы будем называть ионными процессами релаксации.
Вклад ионной релаксации в ширину резонансной кривой при низких температурах наблюдался, как теперь ясно, еще в середине 50-х годов, в частности, в работе [3601 (рис. 9.5.2). Однако то, что речь идет о механизме, не связанном с проводимостью, было четко понято лишь через несколько лет, когда Диллон и Нильсен [379] и Спенсер, Ле Кроу и Клогстон [380] обнаружили низкотемпературные максимумы АН в монокристаллах иттрийжелезного граната с редкоземельными примесями (рис. 9.6.1) *). Эти максимумы были первоначально объяснены Киттелем, де Жанном и Портисом [381, 382], исходя из развитой ими теории,
J) Одновременно были обнаружены обусловленные темп же ионами «аномалии» анизотропии резонансного поля (см. § 2.2).
634
Процессы ёёЛайсаИий
[Mi. S
которая затем получила название теории быстрой релаксации. Основным предположением теории быстрой релаксации является следующее: частота релаксации редкоземельных ионов настолько велика, что при некоторой температуре она становится равной обменной частоте = '{Не (где Не — эффективное поле обменного взаимодействия ионов с магнитной подсистемой). Вблизи этой температуры и лежит максимум Д/Л
Однако в дальнейшем выяснилось, что предсказания теории быстрой релаксации не подтверждаются экспериментально. Кроме
того, маловероятно, чтобы частоты релаксации ионов были так велики (1012 '1013 гц) при тех сравнительно низких температурах (~ 50 °К), при которых лежат обычно максимумы Д/Л Скорее, они имеют порядок Ю10	10й,
что ближе не к а к частоте колебаний а. Исходя из этого, Тил и Туидэйл [391] и Диллон [392] выдвинули предположение, что релаксация в иттрий-железном гранате с редкоземельными примесями обусловлена запаздыванием переходов между энергетическими уровнями ионов. Тогда максимум Д// должен иметь место при такой
Рис. В.6.1. Температурные зависимости ширины резонансной кривой в иттрийжелезном гранате с редкоземельными примесями, а — с добавкой ТЬа+ [376]; частота 24 Гец-, цифры у кривых — количества ТЬ в мол.%. ,б — с неопределенными примесями [380J (верхняя кривая); нижняя кривая — не более 10“в% примесей; частота 9,3 Ггц.
температуре, когда частота релаксации ионов близка к и. Этот механизм был назван механизмом медленной релаксации. Теория его уже была к тому времени разработана Клогстоном [359] (см. предыдущий параграф). Несколько
иной подход к теории медленной релаксации был развит в работах Ван-Флека [394] и Арман-Бутрон [395]. Многочисленные эксперименты, выполненные на ферритах со структурами как
граната, так и шпинели с различными примесными ионами, свидетельствует о том, что механизм «медленной релаксации» в большинстве случаев преобладает.
Парамагнитные ионы в магнитоупорядоченном кристалле. Остановимся прежде всего на некоторых особенностях энергетических уровней рассматриваемой группы ионов. К ней относятся ионы переходных металлов (3d и других) и редкоземельные (4/) ионы, обладающие в основном состоянии как спиновым моментом S, так и орбитальным моментом L. Как видно из табл. 9.6.1 и 9.6.2, этим условиям удовлетворяют ионы переходных элементов
ИОННАЯ РЕЛАКСАЦИЯ
535
Таблица 9.6.1
Свойства некоторых ионов переходных металлов группы железа
Ион		Crs+	Сг*+ Мп»+ Fe4+	Mti«+ Fes+	Fe2+ Cos+	Co** Ni»+	Ni2+
Число Зс?-электронов		3	4	5	6	7	8
Основное состояние свободного иона	Спиновый момент S	3 2	2	_5 2	2	3 2	1
	Орбитальный момент L	3	2	0	2	3	3
	Полный момент J	3 2	0		4	9 2	4
	Обозначение терма	tF-;.	;7Л,	6‘4	5Di	iF^	3Ft
Таблица 9.6.2
Свойства трехвалентных ионов редкоземельных элементов
Элемент		Се	Рг	Nd	Pm	Srn	Eu	Gd	Tb	Dy	Ho	Er	Tu	Yb
Число ^-электронов		1	2	3	4	5	6	7	8	9	10	11	12	13
1 Основное состояние | свободного иона	S	У	1	3 2	2	~2	3	7 2	3	5 2	2	3_ 2	1	1 2
	L	3	5	6	6	5	3	0	3	5	6	6	5	3
	J	5 2	4	9 2	4	5 2	0	7 2	6	15 2	8	15 2	6	7 2
	Обозначение герма	2Г , «А	sHt	J°/z	5Jt		7Fo	SS,.	’Fe	0^/2	®/8		3Я6	2Fi:
группы железа, кроме Fe3+ и Мп2+, и все трехвалентные редкоземельные ионы, кроме La3+, Cd3+ и Lus+.
Энергетические уровни ионов в свободном состоянии без учета спин-орбитальной связи характеризуются (см. § 1.1) значениями £ и L и вырождены с кратностью (2S	1)(2Л -f- 1). Спин-орби-
536
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
тальная связь приводит к расщеплению этих уровней на уровни (в действительности — мультиплеты), соответствующие различным значениям полного момента J и имеющие кратность вырождения (2/	1). Нижним является уровень с J = |£ — 5|, если
3d- или 4/-оболочка заполнена менее чем наполовину, и с J = = L S, если она заполнена более чем наполовину. Значения S, L и J и соответствующие обозначения нижних (основных) мультиплетов приведены в табл. 9.6.1 и 9.6.2.
Наложение внешнего магнитного поля Но, как уже отмечалось в § 1.1, снимает вырождение мультиплетов (эффект Зеемана). Между соседними их уровнями возникают интервалы (1.1.29), где фактор спектроскопического расщепления g имеет вид (1.1.27).
Внешнее электрическое поле также снимает вырождение мультиплетов (эффект Штарка). Поле орторомбической или более низкой симметрии полностью расщепляет мультиплет, если J целое (т. е. число 3d- или ^-электронов четное). Если же J
полуцелое (число электронов нечетное), то это поле расщепляет мультиплетна (J Ц-*/2) крамерсовых дублетов. Электрические поля более высокой симметрии приводят к частичному расщеплению мультиплетов.
В кристалле ионы находятся под воздействием электростатического взаимодействия с соседями и (также по своей природе электростатического) обменного взаимодействия с магнитной подсистемой (обменным взаимодействием парамагнитных ионов между собой мы пренебрегаем, ограничиваясь случаем малой их концентрации). Обменное взаимодействие может быть приближенно описано эффективным полем, которое приводит к такому же по характеру, но, конечно, более сильному расщеплению уровней мультиплета, как и внешнее магнитное поле. Электростатическое взаимодействие с соседями может быть приближенно описано при помощи эффективного электрического — так называемого кристаллического поля с симметрией, соответствующей локальной симметрии узла, в котором находится ион.
§ ».e1
ИОННАЯ РЕЛАКСАЦИЯ
537
Для ЗгРиопов незаполненная электронная оболочка, которая определяет интересующие нас уровни энергии, является внешней, и эффективное кристаллическое поле весьма велико. Вызываемое им расщепление уровней значительно превышает (см., например, рис. 9.6.2) расщепления, обусловленные спин-орби-тальной связью и обменным взаимодействием. Для 4/-ионов незаполненная электронная оболочка экранирована 5s- и 5/?-элект-ронами, и эффективное кристаллическое поле гораздо слабее. Вызываемое им расщепление значительно меньше, чем спин-орбитальное, и оказывается
Рис. 9.6.3. Расщепление энергетических уровней иона Ybs+ в кристаллическом и обменном полях [422]. Величины интервалов между уровнями (в СЛ1"1) для граната YsFe,Otl с малой добавкой Yb в додека эдрических узлах.
часто близким к обменному (рис. 9.6.3).
Энергетические спектры рассматриваемых ионов в кристалле очень сильно зависят от углов, которые образует направление намагниченности магнитно й подсистемы М (при достаточно сильных магнитных полях оно мало отличается от направления внешнего поля) с осями кристалла. Эту зависимость можно качественно объяснить следующим образом: поворот намагниченности вызывает в силу обменного взаимодействия поворот спинового момента иона S. Вследствие спин-орбиталыюй связи поворачивается и орбитальный момент L; изменение его ориентации по отношению к окружению иона, т. е. его локальным осям, приводит к изменению расщепления в кристаллическом поле. Положение усложняется из-за того, что обменная энергия и энергия иона в кристаллическом поле (для 4/-ионов) сравнимы, и поэтому L и S занимают некоторые промежуточные положения (рис. .9.6.4), определяющиеся минимизацией суммарной энергии. Дополнительное усложнение связано с тем, что само обменное взаимодействие не изотропно, т. е. не стремится сделать направления М и S параллельными.
Результирующие угловые зависимости разных энергетических Уровней будут, конечно, различными. Поэтому, особенно в случае близости кристаллических и обменных расщеплений, возможны пересечения уровней при некоторых направлениях намагниченности. Различные не учтенные пока взаимодействия при
538
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. S
Оометк ВзшшАттбие
СосЛисшы
Kpucffla/uwagoe лол с
Сшн-орбшпшыюе ВлишоВеИапеш;
Рис. 9.6.4. Модель, поясняющая установление равновесных ориентаций моментов иона в кристаллическом и обменном полях [403].
водят к тому, что эти пересечения заменяются сближениями уровней. Пики резонансного поля, возникающие в точках х) таких сближений, рассматривались в § 2.2. Ниже мы увидим, что вблизи этих точек имеют место интересные особенности ширины резонансной кривой, обусловленные ионным механизмом релаксации.
Взаимодействие ионов с магнитной подсиётемой. Ионы, энергетические спектры которых были рассмотрены выше, образуют одну из подсистем (ионную) исследуемой нами системы. Другой подсистемой является магнитоупорядоченная (магнитная) подсистема. В иттрий-железном гранате она образована спиновыми моментами ионов Fe3+. Элементарными возбуждениями этой, сильно связанной подсистемы являются коллек тивные возбуждения — магноны. Поведение ее может быть описано классическими уравнениями движения намагниченностей подрешеток.
Ионная подсистема может рассматриваться, как подрешетка лишь при очень больших концентрациях ионов. Если же концентрация ионов мала, как, например, в случае примеси редкоземельных ионов в иттриевом гранате, то ионная подсистема должна рассматриваться как набор (ансамбль) индивидуальных парамагнитных ионов. Характеристикой этого ансамбля является энергетический спектр индивидуального иона (который был рассмотрен выше). В состоянии термо динамического равновесия экземпляры ансамбля (ионы) статистически распределены по энергетическим уровням спектра. Нарушения равновесного распределения релаксируют с характерной для данных ионов большой частотой релаксации, которая определяется сильной связью их с кристаллической решеткой — третьей подсистемой рассматриваемой системы, а также с магнитной подсистемой. Мы будем в дальнейшем интересоваться именно этим случаем малых концентраций.
Между спиновыми моментами ионов и спинами магнитной подсистемы имеет место обменное взаимодействие. Оно уже принималось во внимание при рассмотрении спектров ионов, когда предполагалось, что на ионы действует эффективное обменное поле, вызванное магнитной подсистемой. Одновременно на маг-
т) Имеются в виду точки на сфере, на которой лежит конец вектора М
ИОННАЯ РЕЛАКСАЦИЯ
5С9
§ 9.61
нитную подсистему будет действовать эффективное обменное поле, вызванное ионами. Мы приходим, таким образом, к задаче о связанных колебаниях коллективизированных намагниченностей подрешеток магнитной подсистемы и индивидуальных магнитных моментов ионов. По существу, та же задача решалась Клогстоном (см. § 9.5), но в несколько иной, более термодинамической постановке. В той постановке, которая была приведена выше, эта задача впервые рассматривалась — без учета процессов релаксации — Диллоном и Уокером [387] (см. также (3891) и подробно, с учетом этих процессов — Арман-Бутрон [395].
Перейдем к математической формулировке задачи о связанных колебаниях намагниченностей магнитной подсистемы и магнитных моментов ионов. При этом, следуя [395], сделаем ряд упрощающих предположений:
1)	магнитную подсистему будем считать ферпомагнитной;
2)	пренебрежем собственной диссипацией магнитной подсистемы г);
3)	не будем учитывать всех видов анизотропии, кроме той, которая обусловлена рассматриваемыми ионами;
4)	примем, что образец — малая сфера, намагниченная до насыщения;
5)	ограничимся рассмотрением однородных колебаний намагниченности;
6)	рассмотрим свободные колебания — в отсутствие внешнего переменного поля.
Плотность энергии обменного взаимодействия ионов с магнитной подсистемой может быть записана следующим образом:
£7е = — АШАМ,	(9.6.1)
где N — концентрация ионов, ЗЯ — их средний магнитный момент, М — намагниченность магнитной подсистемы, а А — постоянная обменного взаимодействия, тензорный ее характер учитывает анизотропию этого взаимодействия. Выражение (9.6.1) можно также представить в виде
/7е=—АМАтШ,	(9.6.1')
где Ат — тензор, транспонированный по отношению к А (так что ATJ9S = Asp).
х) Такое предположение находится в соответствии с обычной практикой Исследования процессов релаксации, когда эти процессы рассматриваются <<по одиночке» (а затем считается, что их вклады аддитивны)»
540
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. д
Эффективное поле, действующее на магнитную подсистему, при сделанных предположениях включает в себя только внешнее постоянное поле Но и эффективное поле обменного взаимодействия, которое может быть получено из (9.6.1') по общей формуле (2.1.14). Таким образом,
Неп т = И» 4* NАТ1И.	(9.6.2)
Эффективное поле, действующее на ионы, состоит, вообще говоря, из тех же двух частей, но внешним полем в этом случае можно пренебречь по сравнению с большим эффективным полем обменного взаимодействия:
Heff i ш ЛМ = ЛМ0 ф- Am eic>/.	(9.6.3)
Здесь Мо, как обычно,— постоянная составляющая, ат — комплексная амплитуда переменной составляющей намагниченности.
Предположим, что по своему воздействию на ионы эффективное поле (9.6.3) эквивалентно обычному магнитному полю. Тогда его постоянная составляющая вызовет постоянный магнитный момент
(9-6-4)
а переменная составляющая — переменный момент
m =	(9.6.5)
Здесь — статическая магнитная восприимчивость ионной подсистемы, а х — восприимчивость ее по отношению к переменному полю. Соотношение (9.6.5) связывает комплексные амплитуды ш и ш, величина у является комплексной и зависит от частоты.
Линеаризованное уравнение движения намагниченности магнитной подсистемы имеет вид
i®m + rm X He(f mо + TMo X heff т = 0,	(9.6.6)
где Heff „г о и heffm — постоянная составляющая и комплексная амплитуда переменной составляющей эффективного поля (9.6.2). Подставляя в (9.6.2)
Ш = Шо + те’в1
с учетом (9.6.4) и (9.6.5), запишем уравнение движения (9.6.6) в виде
-у-m + т х Нв ф- т X Е>М0+ Me xlm = 0.	(9.6.7)
§ 9.6'1
ИОННАЯ РЕЛАКСАЦИЯ
541
Здесь введены тензоры
= ^тХоЛ,
(9.6.8)
1 = лт%д.
(9.6.9)
Проектируя уравнение (9.6.7) на оси х и у координатной системы, в которой ось z совпадает с направлением постоянной намагниченности Мо, и пренебрегая различием ориентаций Но и Мо, получим
tnx 4* {Но 4- Л/(1?П22	Л7(|?!;!/) гПу — О,
(Яо + M0g0zz — М0|.та) тх —	+ 7И0^ rnv = 0.
(9.6.10)
Приравняем нулю определитель этой системы и учтем, что для малых концентраций ионов компоненты тензоров с() и с много меньше 1. Тогда в первом приближении получим следующее уравнение для комплексной собственной частоты:
(т)2 ~ * Т м° ~ я« “ н°м° ~ = °-
(9.6.11)
Здесь компоненты тензора £ — комплексные величины, например, ёхх = хх — ^хх ит. д.; величина £022, конечно, вещественная.
Решение уравнения (9.6.11) будем искать в виде
со = со' 4- гео" = ^Но би' 4- ги",	(9.6.12)
причем для достаточно малых концентраций ионов бсо' уН0 и со"	Тогда из (9.6.11) следует в первом приближении
у- = Моиг - Ф (U 4- Ivv - U + Q, (9.6.13)
(U 4- Bw + 1хУ - U).	(9.6.14)
В этих выражениях содержится общее решение рассматриваемой задачи. Но на пути практического вычисления входящих в них компонент тензоров (9.6.8) и (9.6.9) стоят большие трудности. Компоненты тензора Л определяют энергетические уровни ионов и могут быть найдены, например, из их оптических спектров в соответствующих кристаллах, как это было сделано для ионов Yb3k Виккерсхеймом [422]. Однако экспериментальных данных по таким спектрам еще очень мало, а их интерпретация не является
542
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. э
простой задачей. Для вычисления восприимчивостей ионов /() и Х(а>) необходимо знание энергетических уровней и волновых функций этих ионов, а также, конечно, тех процессов взаимодействия их с решеткой и магнитной подсистемой, которыми определяются времена релаксации ионов. К краткому рассмотрению этих процессов мы сейчас и перейдем. Предварительно заметим, что тензоры А и Ат являются эрмитовыми, и антиэрмитовы ком поненты входящие в (9.6.14) и определяющие диссипацию, связаны исключительно с антиэрмитовой частью тензора %, которая, в свою очередь, определяется упомянутыми процессами релаксации ионов.
Релаксация ионов. Процессы релаксации, посредством которых рассматриваемый ансамбль ионов стремится к равновесному распределению по своим энергетическим уровням, во многом аналогичны процессам релаксации в парамагнетиках [1, 289]. Однако имеются и различия, связанные с тем, что ионы в данном случае сильно обменно взаимодействуют с магнитоупорядоченной подсистемой. Спин-спиновая (ион-ионная) релаксация не играет здесь, в отличие от парамагнетиков, существенной роли, так как взаимодействие ионов между собой (особенно, при малых их концентрациях) гораздо слабее, чем взаимодействия с магнитной подсистемой и с решеткой. Далее, на характер процессов релаксации ионов влияет то обстоятельство, что обменное расщепление их энергетических уровней гораздо больше, чем расщепление во внешнем поле для парамагнетиков. И наконец, в нашем случае, наряду с элементарными процессами релаксации, в которых участвуют фононы решетки, могут идти аналогичные им процессы с участием элементарных возбуждений магнитной подсистемы — магнонов. В отличие от первых процессов, которые можно назвать спин-фононными (под спином при этом понимается момент иона), вторые процессы получили название спин-магнонных [400].
Как спин-фононные, так и спин-магнонные процессы могут происходить с участием одной, двух и, вообще говоря, большего количества квазичастиц — фононов или магнонов. Однако процессы с участием более чем двух квазичастиц, по-видимому, несущественны. Одночастичные, или прямые, процессы (рис. 9.6.5, а) заключаются в поглощении или испускании фонона или магнона с переходом иона с одного энергетического уровня на другой. К двухчастичным относятся прежде всего рамановские процессы (рис. 9.6.5, б) — комбинационное рассеяние фонона или магнона на ионе. Могут быть и иные двухчастичные — так называемые орбаховские [385] процессы (рис. 9.6.5, в), которые как бы состоят из двух стадий (двух прямых процессов): поглощения фонона или магнона с переходом иона на некоторый более высо*
§ 8.6]
ИОННАЯ РЕЛАКСАЦИЯ
543
кий уровень и испускания другого фонона или магнона с переходом иона на другой, отличающийся от исходного уровень. Рамановские и орбаховские процессы не отличаются по своему конечному результату, но для эффективности вторых необходимо, чтобы имелись в достаточном количестве квазичастицы с энергией е2 (рис. 9.6.5, в). Поэтому вероятности обоих процессов могут существенно различаться. Заметим, что при всех упомянутых процессах сохраняются энергия и импульс; начальное и конечное состояния иона различаются не только энергией, но и моментом.
Фононы и магноны являются бозонами. Поэтому температурные зависимости для каждого типа процессов, прямых, рамановских или орбаховских, одинаковы, независимо от того, участвуют
Рис. 9.6.5. Элементарные процессы релаксации ионов, а — прямые; б—рамановские; в — орбаховские.
в них фононы или магноны. Однако благодаря различию возмущений, которыми вызываются эти процессы в случае разных квазичастиц, а также различию спектров квазичастиц другие характеристики процессов, в частности, зависимости от расстояния Де между начальным и конечным уровнями иона, оказываются разными.
Для прямых процессов, как показал Орбах [385], частота релаксации ионов
t
= — cth .
То
(9.6.15)
Для прямых спин-фононных процессов возмущением может явиться энергия иона в кристаллическом поле (энергия орбитально-решеточного взаимодействия) или энергия обменного взаимодействия. Наибольшую роль играет орбитально-решеточное взаимодействие. В этом случае, согласно Хюберу [400], частота Релаксаций 1/тс.ф_, обусловленная прямыми спин-фононными процессами, увеличивается с увеличением Де. При ke.l(Tic) 20 см"1 (что характерно, например, для иона Yb3+ в додекаэдрических Узлах иттрий-железного граната [422]) 1/тс.ф. при не очень высоких температурах оказывается порядка 109 гц.
Для прямых спин-магнонных процессов основным возмущением является обменное взаимодействие. Для таких процессов характер
544
ПРОЦЕССЫЖРЕЛАКСАЦИИ
[ГЛ. <
Рис. 9.6.6. Температурные зависимости частот релаксации ионов для различных процессов (схематически).
зависимости частоты релаксации 1/тс.ы. от Ае оказывается различным для разных ионов. Например, для ионов Ybs+ в додек аэдрических узлах иттрий-железного граната 1/тс.н. растет с ростом Ае и имеет тот же порядок, что и 1/тс.ф. Для ионов Tb3t в таких же узлах вблизи точек сближения нижних энергетических уровней частота релаксации 1/тс.м. растет при уменьшении Ае [400]. При этом 1/тс м.	1/тс.ф., и, таким образом, суммарная
частота релаксации, обусловленная прямыми процессами, растет при подходе к точке сближения уровней. Как мы увидим ниже, это обстоятельство оказывается очень существенным для объяснения экспериментальных угловых зависимостей АН в иттрийжелезном гранате с примесью тербия.
Для рамановских и орбахов-ских процессов, в отличие от прямых процессов, частота релаксации ионов очень быстро растет с ростом температуры [385]. Для рамановских процессов 1/т приблизительно пропорционально Т® или 71’ в случае ионов, соответственно, с нечетным или четным числом 4/-электронов. Для орбаховских процессов 1/т растет с ростом температуры по экспоненциальному закону. Температурные зависимости частот релаксации для всех рассмотренных процессов показаны схематически на рис. 9.6.6. Очевидно, что прямые процессы преобладают при низких температурах, а двухбозонные — рамановские или орбаховские — при высоких.
Несмотря на то, что процессы с участием фононов и магнонов играют, как мы видели, аналогичную роль в релаксации ионной подсистемы, рассматриваемой изолированно, роли их в релаксации всей системы оказываются существенно различными. В случае спин-фононной релаксации ионов ионный механизм в целом является, согласно классификации § 9.1, спин-ре’неточным, им осуществляется передача энергии от магнитной подсистемы решетке (рис. 9.6.7). В случае же спин-магнонной релаксации ионов ионный механизм релаксации является спин-спиновым. Он, как 0 рассмотренные в § 9.3 процессы рассеяния па неоднородностях, осуществляет передачу энергии от одних типов колебаний магнитной подсистемы другим.
Поперечная, в частности, быстрая релаксация. Выше ун{® отмечалось, что для объяснения температурных максимумов А#
§ 9.6]
ИОННАЯ РЕЛАКСАЦИЯ
545
Рис. 9.6.7. Потоки энергии между подсистемами при ионном механизме релаксации однородной прецессии и различных (спин-магнон-ных и спин-фоцонных) процессах релаксации ионов.
в иттрий-железном гранате с редкоземельными примесями сначала была выдвинута гипотеза «быстрой релаксации» [381, 382]. Согласно этой гипотезе максимум А// имеет место, когда частота релаксации ионов 1/т становится порядка уНк, где Не — эффективное поле обменного взаимодействия ионов с магнитной подсистемой. Кроме окрестностей точек сближения уровней, '(Не обычно одного порядка с Де/т, где Де — расстояние между нижними уровнями. Для редкоземельных ионов, как мы видели, Ае/(Ас) ~ 10 -н 100 см *. Чтобы при этом имела место быстрая релаксация, частота релаксации ионов 1/т в максимуме А// должна быть порядка 1013. Как было показано выше, оценки 1/т приводят для тех температур, где лежат максимумы АН (см., например, рис. 9.6.6), к значительно меньшим величинам — порядка 1011. Тем не менее мы остановимся на механизме быстрой релаксации — не только потому, что он представляет исторический инте
рес, но и потому, что отнюдь не исключены ситуации (высокие температуры, малые величины Де), когда он может оказаться существенным.
Общая теория, приводящая к формулам (9.6.13) и (9.6.14), конечно, содержит в себе предельный случай быстрой релаксации. В этом случае, как мы увидим, учет анизотропии обменного взаимодействия, т. е. тензорного характера Л, не является обязательным. Но и при таком упрощении вычисление восприимчивости ионов встречает трудности, и теория быстрой релаксации была первоначально развита [381, 382] иным путем. Прежде всего существование этого механизма было продемонстрировано [381] на модели, в которой иОнпая подсистема рассматривалась как подрешетка с намагниченностью М2 = ИЯЯ.
Двухподрешеточная модель ферримагнетика подробно исследовалась в § 4.4. Но теперь, в отличие от рассмотренных в § 4.4 случаев,- предположим, что диссипация ионной подрешетки очень велика — безразмерный параметр а2 1 или частота релаксации юГ2 со. В случае такой большой диссипации очень существенным становится выбор вида диссипативного члена; примем его в форме Ландау — Лифшица (1.3.3). Тогда, считая, что обменное взаимодействие изотропно, не учитывая других видов анизотропии и пренебрегая параметром диссипации первой (магнитной) СоДрешетки, запишем уравнения движения для случая
А. г. Гуревич
546
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
собственных колебаний следующим образом:
^ = - y-2m2 X (Но - ЛМО - X [М2 X (Но - ЛМ01 ч'
(индексы 1 соответствуют магнитной, а индексы 2 — ионной подрешеткам, у величины соj индекс 2 опущен).
Линеаризируем уравнения (9.6.16), учтем, что Л(М10 — 0) Х> ^>HD, но не будем накладывать, в отличие от § 4.4, никаких ограничений на величину со,.;. Тогда из условия совместности системы, которая получится при проектировании (9.6.16) на оси координат, найдем
	Т1ГЯ (Ah O-Ah «) (та - * ТГ~) со-		(9-6.17) ТгЛДо-ТОАо-гш.— а « 2 0
Отсюда	6Я Но -	—1— но,	(9.6.18) ДЯ = —	^1—Н0,	(9.6.19) Яфф ТМКо ф сфа	1	г
гДе Тэфф и	а>Е определяются формулами (4.4.16) и (4.4.18), а (ад
Рассмотренная макроскопическая («подрешеточная») теория справедлива только при достаточно больших концентрациях ионов. Но в [381] было сделано предположение, что формулы (9.6.18) и (9.6.19) остаются справедливыми и при малых концентрациях, а величина 1/т не зависит от концентрации, являясь действительно частотой релаксации ионов. Справедливость этого предположения подтверждается микроскопической теорией, развитой [382] для частного случая малых концентраций и достаточно высоких температур. Если температура при этом все же намного ниже точки Кюри, так что некогерентным (флуктуационным) вкладом в АД можно пренебречь, то результатом микроскопической теории является;
ДЯ = пЛЛ/г отгЯо,	(9.6.21)
где тг — время релаксации ионов. Лег о видеть, что (9.6.21) совпадает с предельным случаем выражения (9.6.19) для малых
л '	ИОННАЯ РЕЛАКСАЦИЯ	547
§ 9.6J
концентраций (Ме 0 •< Мг 0) и высоких температур (когда можно считать <йеТ 1), если т^ т.
Температурные зависимости оН и &Н, согласно (9.6.18) и (9.6.19), определяются зависимостями от температуры величин /Н2 0, 7И10 и т. Для малых концентраций, когда (вопреки модели, использованной при выводе (9.6.18) и (9.6.19)) ионную подсистему следует рассматривать как ансамбль парамагнитных ионов в эффективном поле обменного взаимодействия ЛМП можно принять
=	,	(9.6.22)
где 501 =	— магнитный момент иона, в В^_ (ж) — функция
Ланжевена (1.1.34). При низких температурах и вдали от точек сближения энергетических уровней ионов аргумент этой функции 5ЩД/1/-|/(хТ) фу> 1, и зависимость М2 0 от температуры слабая. Кроме того, она частично компенсируется зависимостью М±д от Т. Решающую роль играет температурная зависимость частоты релаксации ионов. Как мы видели, для всех механизмов релаксации 1/т растет с увеличением температуры (рис. 9.6.6). И когда она достигает величины &>е, имеет место максимум ДЛ.
Из рассмотренной теории вытекают следующие особенности быстрой релаксации:
1)	положение температурного максимума кН пе зависит от частоты колебаний;
2)	величина (ДЯ)маКс приблизительно пропорциональна частоте;
3)	величина (ДЯ)Макс пропорциональна механическому моменту иона;
4)	сдвиг резонансного поля 6Я положителен и изменяется монотонно с изменением температуры.
Сравнивая экспериментальные результаты с этими предсказаниями теории, можно выяснить, вносит ли механизм быстрой релаксации вклад в релаксацию в данном конкретном случае. Как мы увидим, в большинстве случаев такое сравнение говорит не в пользу быстрой релаксации.
Подчеркнем, что в рассмотренной теории обменное взаимодействие считалось изотропным, а орбитально-решеточное взаимодействие не учитывалось. При таких допущениях постоянные составляющие М], и S? параллельны, и переменное эффективное поле Л1къ действующее на ионы, является поперечным по отношению к постоянной составляющей момента иона. Это дает основание считать рассмотренный механизм механизмом поперечной релаксации.
Поперечная релаксация не обязательно является быстрой. Но и исследованном выше случае Де Ji to условием эффективности поперечной релаксации была ее «быстрота» (1/т со). Чтобы
18*
548
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
проиллюстрировать это, обратимся к квантовой модели, представляющей собой два нижних уровня иона, разделенных интервалом Ае (рис. 9.6.8). Поперечное эффективное поле Am, с частотой <в может вызывать прямые переходы между этими уровнями с поглощением или испусканием магнонов магнитной подсистемы'). Однако если Ае fun, а ширина уровней мала (рис. 9.6.8, а), то переходы практически происходить не будут. Увеличение частоты
Рис. 9.6.8. Квантовая модель поперечной релаксации, а — h/i Ае, й™ Ае (вероятность переходов пренебрежимо мала); б — й.'т — Де, йа> С Ае (быстрая релаксация); в — й/т Ае, йю — Де (резонансная релаксация).
релаксации ионов можно трактовать как расширение их энерге-тических уровней. И когда расширение, которое будет порядка /г/т, станет сравнимым с Ае (при этом 1/т :^> со), переходы станут возможными — см. рис. 9.6.8, б.
Рассмотрим случай, когда Ае сравнимо с Ил. Теперь (рис.9.6.8, в) переходы могут происходить и при невыполнении условия 1/т	<в. Эти переходы являются резонансными, но если 1/т
сравнимо с Ае/Л, то резонанс будет широким. Такой случай — поперечной, но не быстрой, а резонансной релаксации может осуществляться при высоких частотах и вблизи сближений энергетических уровней ионов.
Теория поперечной релаксации была разработана Ван-Флеком [394] с использованием рассмотренного выше метода восприим-чивостей ионов в эффективном обменном поле. Обменное взаимодействие, как и в теории Киттеля и др. [381, 382], предполагалось изотропным и учитывались только два нижних уровня иона, разделенных интервалом Ае. В результате была получена следующая
’) Могут происходить, конечно, переходы п с поглощением непосредственно квантов электромагнитного поля (как при парамагнитном резонансе) Однако в ферромагнетике с достаточно узкой резонансной кривой при ус ловии близости со к частоте ферромагнитного резонанса число таких переходов гораздо меньше, чем переходов с поглощением магнонов.
§ 9.61
ИОННАЯ РЕЛАКСАЦИЯ
549
формула для комплексного сдвига частоты:
<в — Т#о = ^(>>' + йз" =
1	Ле Г I .	1 I ,. Де
= -гг (1,с Т- --л-----=--Ь ----*----—
2	К Де i 1 Де i 2мГ «'--/Г-— а +	—
(9.6.23)
где с == Na3 — относительная концентрация ионов (а — расстояние между магнитивши моментами магнитоупорядоченной подсистемы). Легко убедиться, что в частном случае АеТ^Лю из (9.6.23) приближенно следуют выражения (9.6.18) и (9.6.19) теории быстрой релаксации. При этом необходимо принять
(Л/2о)у—о Ti Де
с~ мГо*
и учесть, что функции th (х/2) и Ва (ж) мало отличаются друг от друга. Случай резонансной поперечной релаксации, как легко видеть, также содержится в формуле (9.6.23).
Медленная (продольная) релаксация. Если частота релаксации ионов 1/т •=<; &е/П- и частота колебаний <в << Ьъ/Н, то рассмотренный выше механизм поперечной релаксации, как мы видели, не будет эффективен. Но если при этом 1/т будет близко к со, то станет играть роль другой механизм релаксации, связанный с модуляцией энергетических уровней иопов и запаздывающими переходами между зтими уровнями. Действительно, если мы обратимся к качественным рассуждениям, которые приводились в § 9.5 для пояснения аналогичного механизма, и к рассмотренной там же теории Клогстона, то заметим, что факт переходов электронов с одного иона па другой не был существен ни для тех рассуждений, ни для теории. Они полностью останутся в силе, если уровнями, о которых там шла речь, будут энергетические уровни изолированного иона. Необходимо лишь, чтобы эти уровни модулировались с частотой <в при колебаниях магнитной подсистемы и чтобы изменение их населенностей в силу конечного времени релаксации т запаздывало по отношению к изменению уровней. Тогда, как было показано в § 9.5, данный механизм релаксации будет эффективен, если 1/т будет порядка <в. В отличие от механизма быстрой релаксации (который эффективен при 1/т '^> <в), он получил название механизма медленной релаксации. Как мы увидим, условием существования этого механизма является наличие составляющей переменного эффективного поля, действующего на ион, параллельной постоянному моменту иона. Поэтому такой механизм называют также механизмом продольной релаксации.
В теории Клогстона было сделано, однако, существенное предположение (9.5.15). При этом было принято, что, во-первых,
550
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
населенность каждого уровня релаксирует к своему мгновенному равновесному значению с некоторым временем релаксации и, во-вторых, что эти времена одинаковы для всех уровней. От второго допущения можно было бы отказаться, обобщив теорию Клогстона на случай различных времен релаксации для разных уровней. Но первое допущение остается необоснованным. Прежде всего релаксация ионов, как мы видели, может определяться несколькими механизмами. Но даже в случае преобладания какого-либо одного механизма отнюдь не очевидно, что релаксация населенностей в многоуровневой системе происходит таким образом, что населенность каждого уровня изменяется по закону (9.5.15). Поэтому возникла необходимость более строгого рассмотрения релаксации ионной подсистемы. Эта задача была выполнена Арман-Бутрон в уже упоминавшейся работе [395] J).
Оказалось, что в случае медленной релаксации (когда частоты релаксации ионов много меньше расстояний между их энергетическими уровнями) населенности уровней удовлетворяют следующим уравнениям:
^==_(/V._/V.cc) 2 Т~+ 2]	(9.6.24)
где j и f — номера уровней ионов, а и Т;<}	— некоторые
величины (в первом приближении не зависящие от времени), которые определяются взаимодействием ионов с решеткой (оно в этой теории пе конкретизируется). Учет взаимодействия ионов с магнитной подсистемой, т. е. спин-магнонных процессов релаксации ионов, вряд ли изменит этот результат.
Соотношение (9.6.24) допускает наглядную трактовку: первый член в его правой часта представляет собой число ионов, покидающих в едини .у времени j-й уровень; оно пропорционально отличию населенности этого уровня от равновесной. Второй член в правой части (9.6.24) есть сумма чисел ионов, приходящих с других уровней на у-й; зти числа пропорциональны отличиям населенностей соответствующих уровней от равновесных. Заметим, что, когда в §§ 9.2, 9.3 и 9.4 мы рассматривали релаксацию в системе квазичастиц — магнонов и фононов, мы всегда отбрасывали «обратные» члены, аналогичные второму члену в (9.6.24), предполагая, что числа всех других квазичастиц (т. е. населенности всех других уровней системы), кроме тех, релаксация которых исследуется, не отличаются от равновесных. Там для этого были серьезные основания — мы интересовались случаем, когда внешнее поле интенсивно возбуждало именно данный сорт квазичастиц
*) Первая часть этой работы заключалась в выводе соотношений, аналогичных (9.6.13) и (9.6.14).
§ S.61
ИОННАЯ РЕЛАКСАЦИЯ
551
(т. е. населяло данный уровень). Теперь же таких оснований нет’ влияние магнитной подсистемы приводит к модуляции (и тем самым делает неравновесными населенности), вообще говоря, всех уровней ионов и уж во всяком случае не какого-то одного.
Итак, уравнения (9.5.15) в общем случае несправедливы и должны быть заменены уравнениями (9.6.24). Однако в случае двухуровневой системы уравнения (9.6.24) сводятся к уравнениям (9.5.15) с одинаковой для обоих уровней частотой релаксации
— =	+ _L .	(9.6.25)
17 171 о. 17oi	'	7
В этом легко убедиться, учитывая, что N,2 = 7V100 TV2CO — = N. Таким образом, для двухуровневой системы теория Клогстона оказывается строго справедливой. Поэтому естественно, что выражения (9.5.30) и (9.5.31), являющиеся результатом этой теории, были получены' в [395] в результате подстановки в формулы (9.6.13) и (9.6.14) восприимчивостей, рассчитанных для двухуровневой системы.
Случай двухуровневой системы представляет большой интерес. Населенности уровней убывают по мере увеличения их энергий, и при достаточно низких температурах рассмотрение только двух нижних уровней может явиться неплохим приближением. Это становится особенно справедливым в двух важных частных случаях. Во-первых, когда нижняя пара уровней представляет собой крамерсов дублет, а расщепление в кристаллическом поле много больше обменного, как это имеет место, например, для ионов Yb31' в додекаэдрических узлах иттрий-железного граната (рис. 9.6.3). Во-вторых, когда мы интересуемся окрестностями точек сближения нижних энергетических уровней, которые имеют место, например, для ионов Рг3+, ТЬ3+ и Но3+ в тех же узлах. Остановимся поэтому на случае двух уровней несколько подробнее.
Входящие (9.5.28) и (9.5.31) равновесные населенности можно выразить через энергии Гу, приняв, в частности, больцма-новское распределение. Для случая двух уровней
М.2ОО = N
и, как нетрудно убедиться,
г/дДе\2 , /аде\2 1 1	,2 Де
—Г -аа- + -ДХ" sech2 -75-^ , 4 [Д 00 /	\ дф ] J я/ 2хГ
(9.6.26)
(9.6.27)
где Де = ег — е2. Величина Р в этом случае зависит от температуры, как показано на рис. 9.6.9, максимум ее имеет место при Т = ZpsO,65-^- .	(9.6.28)
552
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Формулы для ширины резонансной кривой (9.5.30) и зависящего от частоты (динамического) сдвига резонансного поля (см. выражение (9.5.31')) запишутся для двухуровневой системы следующим образом:
2MI
N	, p(Ae)V 1 1	Ае ш _ 1
W(,L\ 36 / "Г \ 30 I \иТ	2v.T 14-0)42 — ЛДК ’
(9.6.29)
N Г (д (Де.)'.2	р (Де)\21 1	} 2 Ае соЧ*
Ж |ДАГI + \~дф~ j J кГ 2кГ 1 + 0)42 •
(6Я)„
(9.6.30)
Зависимости 2ДЯ и (6Я)М от температуры определяются температурной зависимостью множителя Р (рис. 9.6.9) и температур-
ной зависимостью времени релаксаиии ионов т. Как мы видели, т всегда уменьшается с ростом Т. При этом релаксационный множитель Q = = <нт/(1	(Й2Т2), входящий
в (9.6.30), проходит через максимум при такой температуре Тп, когда (»т1, а множитель ю¥/(1 4~ оА2) в (9.6.31) изменяется монотонно. Характер результирующей температурной зависимости ДЯ определяется главным образом соотношением величин Т<, и Тр, а также зави-
симостью т(Т’). Зависимость ДЯ (Т), как уже отмечалось в § 9.5, может иметь два максимума, но чаще имеет один, лежащий между Тр, и Тр. Температурная зависимость (6Я)(1, имеет один минимум, лежащий вблизи ТР.
В основе механизма медленной релаксации лежит модуляция энергетических уровней ионов с частотой колебаний магнитной подсистемы, т. е. зависимость зтих уровней от углов 0 и О вектора намагниченности. Природа этой зависимости была исследована Ван-Флеком и Орбахом (см. [394]). При этом не учитывалось расщепление в кристаллическом поле и рассматривалась двухуровневая система. Для нее величиной, которая модулируется, является расстояние Де между уровнями. Эта величина выражается следующим образом [422]:
Де = у2Гг (А^ 4- Аа7И2, + А3^)’б (9-6.31)
где Л^з — диагональные компоненты тензора обменного взаимодействия Л (см. выражение (9.6.1)) в его главных осях х', у' и z , причем ось z' совпадает с постоянной составляющей момента
§ g_6]	ИОННАЯ РЕЛАКСАЦИЯ	553
иона J. Если бы обменное взаимодействие было изотропным (т. с. Л — скаляром), то направление постоянной составляющей J (ось z) совпало бы с направлением постоянной составляющей намагниченности магнитоупорядоченной подсистемы М (осью z). Поперечные относительно оси z малые переменные, составляющие М вызвали бы в этом случае поперечные относительно z' малые составляющие эффективного поля Атх- и Лиг,/. Из (9.6.31) следует, что эти составляющие в линейном приближении не приводят к модуляции величины Ае. Если же Л будет тензором, то поперечные относительно оси z переменные составляющие М приведут к появлению не только поперечных, но и продольной относительно г' составляющей эффективного поля. Наличие этой составляющей, как видно из (9.6.31), вызовет и в линейном приближении модуляцию Де, т. е. приведет к медленной релаксации.
Как показано в [394], для рассмотренной модели входящая в (9.6.29) и (9.6.30) величина
(ЧгТ+(4^)2=(Ae)2jF (9-6-з2>
где безразмерная функция F{Q, ф) оказывается порядка 0,1. Тогда, подставляя (9.6.32) в (9.6.29) и производя оценку для случая, например, ионов Ybs+ в иттрий-железном гранате (Де/(Лс)
20 см~1) при концентрации (по отношению к количеству ионов Y31) 5 % и температуре 50 ° К, получим
2 ЛЯ = 200 э.
Экспериментальное значение при тех же условиях составляет 150 s [398]. Таким образом, анизотропия обменного взаимодействия действительно приводит к модуляции уровней энергии иона, необходимой для осуществления механизма медленной (продольной) релаксации, и может обеспечить наблюдаемый порядок величины параметра диссипации.
Для принятой выше модели (не учитывающей кристаллического поля) анизотропия обменного взаимодействия является необходимым условием осуществления механизма медленной релаксации. Однако при наличии достаточно сильного (сравнимого с обменным) кристаллического поля направления постоянного момента иона (ось z') и постоянной намагниченности (ось z) не будут совпадать (см. рис. 9.6.4) и в случае изотропного обмена. А это, как мы видели, приведет к модуляции уровней энергии иона под воздействием малых переменных составляющих намагниченности.
В заключение перечислим некоторые выводы из теории медленной релаксации Д, которые можно использовать при сравнении
J) Аналогичные выводы из теории быстрой релаксации были приведены; На стр. 547.
-554
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
этой теории с экспериментом. Для определенности ограничимся •случаем, когда имеет место один температурный максимум АН, образованный в результате «совместного действия» множителей Р и Q в формуле (9.6.29). Тогда
1)	температурный максимум АН сдвигается с ростом частоты в область более высоких температур;
2)	величина (Д/Г)макс мало зависит от частоты (сказывается лишь смещение максимумов Р и Q друг относительно друга), во всяком случае пропорциональность (Д/Г)М)КС частоте, характерная для быстрой релаксации, здесь не имеет места;
3)	угловые зависимости АН имеют минимумы при тех значениях углов, для которых б(Де)/бО = 0 и д{Аъ)!дф = 0, т. е. в точках сближения энергетических уровней;
4)	динамический сдвиг (б//)„, отрицателен и имеет минимум;
5)	отношение динамического сдвига к ширине кривой
АН ~~
(9.6.33)
пропорционально частоте и монотонно уменьшается с ростом температуры.
Редкоземельные ионы в гранате; случай низколежащего дублета. Остановимся теперь на некоторых характерных результатах экспериментального исследования процессов релаксации, обусловленных наличием в кристалле ионов с сильной сшш-орбитальной связью. При их обсуждении необходимо будет учесть, что ионы распределяются обычно по нескольким неэквивалентным узлам решетки, для которых (вследствие различной ориентации локальных осей ионов по отношению к намагниченности) энергетические уровни, а следовательно, и населенности, и величины т будут различны. Поэтому полученные выше выражения для АН и (ЬН)а как в случае быстрой, так и медленной релаксации должны быть заменены соответствующими суммами по всем неэквивалентным узлам. Например, для медленной релаксации, ограничиваясь случаем двух уровней и предполагая равномерное распределение ионов по неэквивалентным узлам, получим вместо (9.6.29)
оЧ* '
(9.6.34)
Для ионов в додекаэдрических положениях в гранате п = 6, для октаэдрических положений п = 4.
Наибольшее внимание в .экспериментах было уделено иттрии-железному гранату, в котором небольшое количество (от сотых долей % до нескольких %) ионов иттрия замещено редкоземельными ионами. Причем наиболее подробно были исследованы два
'<4 _____®
2’Л1' 1
2АЯ =
§ 9.6J
ИОННАЯ РЕЛАКСАЦИЯ
555
упомянутых выше случая: крамерсова дублета, расположенного значительно ниже остальных уровней (Yb3+) и четко выраженных
сближений нижних уровней (Рг3^, ТЬ3+ и Но3+).
Ферромагнитный резонанс в иттриевом гранате с примесью иттербия, наблюдался впервые Диллоном и Нильсеном [384] и был подробно исследован Тилем, Пирсоном, Туидейлом, Кларком и др. [391, 398]. Если отвлечься пока от «аномалий», которые наблюдаются в некоторых направлениях J) при низких температурах и о которых речь пойдет ниже, экспериментальные данные для Yb3+ в иттрий-железном гранате находятся в согласии с «двухуровневой» теорией медленной релаксации.
На рис. 9.6.10 приведены экспериментальные результаты, полученные в [398]. Величины ДЯ были измерены 'непосредственно и представляют собой, практически, вклад одного только ионного процесса релаксации, так как вклады других процессов в этом
Рис. 9.6.10. Температурные зависимости ширины резонансной кривой и динамического сдвига резонансного поля в монокристалле иттрий-железного граната с 5,1 мол. % УЪ®+ Г398]. Кружки — направление треугольники— <100>. Светлые значки— частота 9,3 Ггц, черные— 16,8 Гец.

случае (хорошо полированные монокристаллы, сравнительно низкие температуры) значительно меньше. Величины же (6П)(Л были получены следующим образом:
(6Я)И = Ярез (бЯ)ан - (6Я)О - (6Я)Э.Д„
где (бЯ)ан — сдвиг, вызванный анизотропией, не связанной с
Речь идет, как обычно, о направлениях постоянной намагниченности магнитной подсистемы по отношению к осям кристалла. При достаточно высоких частотах и не очень больших концентрациях ионов они практически ие отличаются от направлений постоянного внешнего поля.
556
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
ионами Yb3+,	— статический вклад ионов Ybs+ (см. выра-
жение (9.5.31')), а (6//)3.д — «электродинамический» сдвиг. Он рассчитывался по формуле (7.3.37), а величина (6Я)ан Д- (6Я)0, не зависящая от частоты, определялась на основании статических измерений вращающих моментов. Кривые кН(Т) (рис. 9.6.10) имеют широкие максимумы, определяемые, в основном, множителями = сот„/(1 4
1 л/ -?’раО/сек
W12 -
W
10
ООО 250 Т.'К
Рис. 9.6.11. Температурные зависимости частот релаксации ионов УЬ“+, найденных из результатов рис. 9.6.10 [398]. Обозначения точек соответствуют рис. 9.6.10. Сплошные линии— теоретические кривые: суммы частот релаксации, обусловленных прямыми и рамановскими процессами. Пунктир — только прямые процессы.
в (9.6.34), и горбы (ступеньки), которые связаны с влиянием множителей Р„. Им, как и должно быть, соответствуют минимумы (б//)(1. Знак (ЬН)ь> и смещение максимумов А// с частотой также находятся в согласии с предсказаниями теории медленной релаксации (стр. 554).
Детальный анализ приведенных на рис. 9.6.10 данных [398] позволил определить компоненты тензора А и время релаксации ионов т. Диаго-ТМо 7 нальные компоненты тензора А оказались . равными: 31,9 слГ1; 22,4 слГ1 и 8,5 слТ1, что подтверждает использованное выше при оценках значение (20сл«-1) обменного расщепления нижнего дублета иона Yb3+. Полученные температурные зависимости 1/т приведены на рис. 9.6.11. Заметим, что для направления <100 > из шести, вообще говоря, неэквивалентных додекаэдрических узлов в
гранате четыре узла эквивалентны, а для двух других Р = 0. Для этого направления единственное время релаксации может быть легко определено с помощью соотношения (9.6.33). Для направления же <111> имеются две группы неэквивалентных узлов с разными tv, и приведенные на рис. 9.6.11 для этого направления величины 1/т, найденные по-прежнему из соотношения (9.6.33), представляют собой некоторые средние значения.
Как видно из рис. 9.6.11, прямые процессы релаксации ионов вносят преобладающий вклад в 1/т при температурах ниже 50 °К. В соответствии с приведенными выше оценками это могут быть как спин-магнонные, так и спин-фононные процессы; авторы [398] полагают, что главную роль играют спин-магнонные процессы. При более высоких температурах начинают играть роль, а затем и становятся преобладающими двухбозонные процессы-рамановские или орбаховские. Сравнение их расчетных темпе-
S 9.61
ИОННАЯ РЕЛАКСАЦИЯ
557
во
во
so° в
20
60
Рис. 9.6.12. Угловые зависимости резонапсног поля и ширины резонансной кривой в иттри! железном гранате с 0,1 мол. % Но3+ [406]. Частота 8,9 Гач, температура 4,2 °К. 0— угол между внешним постоянным полем и осью <100> в плоскости {1101.
2AH.S
ратурных ходов с экспериментом позволяет установить, что большую роль играют рамановские процессы.
Для других редкоземельных ионов с сильной спин-орбиталь-ной связью, не имеющих резких сближений энергетических уровней в додекаэдрических узлах граната (Nd3t, Sm3+, Dy3+, Er3+), экспериментальные данные [392, 399] также свидетельствуют в пользу механизма медленной релаксации. Однако отсутствие у этих ионов низко расположенного дублета не дает возможности такого простой, как в случае УЬ3+, описания результатов.
Редкоземельные ионы в гранате; случай сближающихся уровней. Рассмотрим теперь некоторые результаты экспериментального исследования ферромагнитного резонанса в иттрий-железном гранате, содержащем редкоземельные ионы (ТЬ3+, Но3+ и Рг3+), для которых имеют место резкие сближения энергетических уровней. В окрестностях сближений малым изменениям углов соответствуют большие относительные изменения расстояйия между уровнями. В этих областях наряду с пиками резонансного поля (§ 2.2) можно ожидать появления резких особенностей ширины резонансной кривой. Заметим, что пики Z7pe3 в точках сближения уровней ионов, которые были рассмотрены в § 2.2, представляют собой статические изменения резонансного поля (6Д)О (см. выражение (9.5.31')). Они не зависят от частоты, их можно наблюдать и при измерении статических вращающих моментов 1390]. Одновременно в окрестностях точек сближения уровней, конечно, имеют место и динамические сдвиги резонансного поля (6Я)И, но их в этом случае трудно выделить на фоне мощных «статических» пиков.
Максимумы поглощения, которыми сопровождались пики Нрез в иттрий-железном гранате с примесью ТЬ3+, были обнаружены
558
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
Диллоном и Нильсеном [379]. Температурные и угловые зависимости А/7 в гранатах с различными редкоземельными ионами, имеющими сближения уровней, изучали подробно Гуревич, Соловьев и Агеев [397, 406, 409].
Рассмотрим, например, результаты, полученные в [406] для иттрий-железного граната с примесью ионов Но3+. Как видно из рис. 9.6.12, для направлений намагниченности (100) и (110) имеют место пики /7рез и полосы поглощения, обусловленные сближениями энергетических уровней ионов Но3+. Пики Hve3 и максимумы поглощения для направлений (100) приблизительно
Рис. S.6.13. Направления локальных осей в шести невввивалентных доденаэдри-чсских узлах в решетке граната.
в раза больше, чем для направлений (110). Это можно объяс-i.n ь, если Припять, что сближения уровней имеют место, когда намагниченность Мо (см. рис. 9.6.13) лежит в одной из локальных координатных плоскостей ху. Тогда, как видно из рис. 9.6.13, положению намагниченности в любой плоскости {100} кристалла соответствуют сближения уровней ионов в двух пз шести неэквивалентных узлов. Таким образом, для направлений (НО) сближения имеют место для 1/3 всех редкоземельных ионов, а для направлений (100) (лежащих одно времен та в двух плоскостях {100} — для 2/3 ионов.
Угловые полосы поглощения имеют (см. рис. 9.6.12) «тонкую структуру» — в центре полосы находится минимум ДП. Он связан с обращением в нуль производных д(Де„)/сЮ и д(Де„)/д0 в формуле (9.6.34) в точке сближения уровней. Наличие этого минимума, как уже отмечалось, является характерным признаком механизма медленной релаксации..
§ a.Gl
ИОННАЯ РЕЛАКСАЦИЯ
550
Температурные зависимости ширины резонансной кривой для. того же кристалла (рис. 9.6.14) имеют, вообще говоря, два максимума.
Положение и величина низкотемпературного максимума существенно зависят от направления Мо, при достаточном удалении от точек сближения он исчезает. Приведенные на рис. 9.6.12 угловые зависимости характеризуют именно этот максимум, обусловленный двумя сближающимися уровнями. Второй — высокотемпературный максимум мало зависит от направления Мо; он обусловлен вкладом всех несблпжающихся уровней. Низкотемпературный максимум хорошо описывается формулой (9.6.29) в.
Рис. 9.6.14. Температурные зависимости ширины резонансной кривой в иттрий-железном гранате с 0,1 мои.% Но3+ 1406J. Тот же образеп, что на рис. 9.6.12. Частота 8,9 1гц. Обозначения у кривых— направления постоянного поля.
предположении прямых процессов релаксации ионов при расстояниях между уровнями в направлениях <100> и <110> соответственно 8 см"1 и 5 слГ1.
Итак, приведенные экспериментальные данные для иттрийжелезного граната с ионами Но8+ находят полное описание в рамках теории медленной (продольной) релаксации. Теория медленной релаксации хорошо объясняет также температурные и угловые зависимости ширины резонансной кривой в иттрий-железном гранате с ионами ТЬ3+ [392, 397]. Эти зависимости во многом аналогичны приведенным выше зависимостям для случая Но8+. Отличаются лишь положения точек сближения; для ТЬ3+, как показал Хюбер [396], сближения уровней происходят тогдй, когда направления намагниченности лежат на конической поверхности с осью, направленной по одной из локальных осей иона, и углом при вершине 142°. В результате пики Нрез и полосы поглощения наблюдаются в плоскости {110} при трех направлениях намаг
560
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
ниченности (см. рис. 2.2.11), не совпадающих, в отличие от Но3+, с осями симметрии кристалла.
При исследовании ферромагнитного резонанса в иттрий-железном гранате с ионами Yb3+, наряду с рассмотренными выше зависимостями, как уже отмечалось, наблюдались «аномалии» 1392, 404]. Они заключались в том, что при низких температурах для некоторых направлений намагниченности (в плоскости {110}— для 0 т 30° и 0 = 90°) имели место острые угловые пики 2Лрез, а величины АН для этих направлений монотонно росли с понижением температуры, во всяком случае, до 1,5 °К. Эти аномалии в течение ряда лет оставались необъясненными. Их можно было бы понять, если бы для указанных направлений имели место сближения уровней Yb3+, причем с очень малыми (Ае)мин. Однако таких сближений нет для той структуры уровней иона Yb3+ в додекаэдрических узлах граната, которая соответствует всем остальным результатам для резонанса в иттрий-железном гранате с примесью иттербия (см. рис. 9.6.10) и, кроме того, подтверждается независимыми оптическими измерениями [422]. Объяснение [404] оказалось неожиданно простым: ионы Yb3+ в гранате могут занимать в небольших количествах и октаэдрические положения, и их энергетические уровни в этих положениях имеют резкие сближения при тех углах, при которых наблюдаются «аномалии».
Монотонные температурные зависимости А// в точках сближения энергетических уровней наблюдались также [409] в иттрий-железном гранате с ионами Рг3+ в додекаэдрических положениях (рис. 9.6.15). В обоих случаях—Yb3+в октаэдрических положениях и Рг3+ — минимальные расстояния между уровнями (-~1 см~1) сравнимы с Л®, и возможны прямые переходы между уровнями ионов с поглощением магнонов, характерные для поперечного механизма релаксации.
Если 1/т окажется при этом порядка (А₽)мин/Л, т0 переходы не будут носить остро резонансного характера. Однако можно •ожидать некоторого максимума поглощения при Ае = Л®. Это должно привести к двугорбым угловым зависимостям А// при Л® > (Ае)мин. Такие двугорбые кривые наблюдались в случае Yb3+ при достаточно высоких частотах [404]. Наличие их, а также характер температурных зависимостей А// в случае Рг3+ [409] говорят в пользу механизма поперечной релаксации. Однако если 1/т будет порядка (Ае)мин/Л, т. е. порядка ®, то и механизм продольной релаксации может быть эффективен. Таким образом, в случаях, когда минимальное расстояние между сближающимися уровнями оказывается одного порядка с Л®, возникает интересная и сложная ситуация, когда оба механизма, поперечной и продольной (медленной) релаксации, могут действовать юдиов ременно.
5 9.61
ИОННАЯ РЕЛАКСАЦИЯ
561
Мы до сих пор интересовались иттрий-железным гранатом с малыми примесями редкоземельных ионов. Но рассмотренные механизмы ионной релаксации действуют и в случае редкоземельных гранатов, когда ионы с сильной спин-орбитальной связью
Ж
2ДН, з
60 -
Рис. 9.6.15. Угловая и температурные ависимости ширины резонансной кривой в иттрий-железном гранате с 0,03 мол. % Рг3+ [4091. Частота S Ггц. О— угол между направлением постоянного поля и осью <100> в плоскости {110}. Угловая зависимость— при температуре 4,2 °К. Температурные зависимости— при углах, отмеченных соответствующими точками па угловой зависимости.
занимают все додекаэдрические узлы. И понятно, что редкоземельные железные гранаты (кроме гранатов Gd, Ен и Lu) имеют колоссальные величины AZZ [193]. Явления в этом случае существенно усложняются взаимодействием между ионами. Подсистему редкоземельных ионов теперь, по-видимому, можно рассматривать как подрешетку.
Ионы Зй-группы. Роль ионов, переносящих энергию от магнитной подсистемы решетке (или другим типам колебаний магнитной подсистемы — в случае спин-магнонной релаксации ионов), могут выполнять, как уже отмечалось, и ионы переходных элементов, например, Зй-группы, обладающие спиновым и орбитальным моментом. Расщепление энергетических уровней этих ионов в кристалле отличается от расщепления уровней 4/-ионов. В связи с этим процессы релаксации Зй-ионов могут иметь ряд особенностей по сравнению с процессами релаксации редкозе-
19 А. Г. Гуревич
562
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9

Рис. 9.6.16. Температурные зависимости ширины резонансной кривой в иттрий-железном гранате с 0,69 мол. % Мп’+ [4021. Постоянное поле направлено по оси <111>. Измерения при 56 Ггц— на неполированной сфере.
мельных ионов. Однако рассмотренные выше механизмы релаксации всей системы и описывающие их теории, в которых положения уровней ij и времена реласации рассматриваются как независимые параметры, должны остаться без изменения.
Ионы Зй-группы, обладающие орбитальным моментом (см. табл. 9.6.1), могут играть роль в релаксации в ферритах как со структурой шпинели, так и граната. В гранатах они могут замещать ионы Fe3+. Причем если замещающие ионы — двух- или четырехвалентные, то для получения бездефектного кристалла приходится вводить какие-либо другие ионы (например, немагнитные) с валентностью, соответственно, большей или меньшей чем 3, в количестве, необходимом для сохранения электрической нейтральности кристалла. Ионы Fe2+ возникают в гранате в октаэдрических узлах при добавлении ионов с валентностью, большей чем 3, например, ионов Si4+, замещающих Fe3+. Ионы Fe4+ возникают в тетраэдрических узлах граната при введении двухвалентных ионов, например, ионов Са2+, замещающих Y3+.
Влияние ионов Fe2+ на ферромагнитный резонанс в иттрий-железном гранате было замечено еще в [386] и [388]. Именно этими" ионами был обусловлен небольшой (~ 0,2 э) низкотемпературный максимум 2\Н в монокристаллах, выращенных из очень чистой окиси иттрия, но без принятия специальных мер по избавлению от малых примесей кремния [386]. В поликристаллическом же иттрий-железном гранате, если не принимать мер по уменьшению содержания Fe2+, максимум 2ДЯ может достигать 2000 э [388]. Дальнейшее изучение ферромагнитного резонанса в иттрий-железном гранате с ионами Fe2+ [408] подтвердило, что наряду с высокотемпературным максимумом ДЯ, который свя
зан с переходами электронов между ионами (см. § 9.5), действительно наблюдается низкотемпературный максимум ДЯ, обусловленный енутриионными переходами. Этот максимум хорошо объясняется теорией медленной релаксации.
Ионы Fe4+ [405], а также ионы Мп3+ [402] в иттрий-железном гранате также приводят к появлению типичных для механизма
5 9.6]
ИОННАЯ РЕЛАКСАЦИЯ
563
медленной релаксации температурных зависимостей ДЯ (см., например, рис. 9.6.16).
Очевидно, что поведение ионов Fe2+, Мп3+ и др. в октаэдрических и тетраэдрических узлах шпинелей не должно принципиально отличаться от поведения тех же ионов в аналогичных узлах в гранате. Но количественные отличия, связанные с различием величин кристаллических и обменных полей и времен релаксации ионов, будут, конечно, иметь место. Например, максимум 2ДЯ на рис. 9.5.2, обусловленный, как сейчас совершенно ясно, внутриионной медленной релаксацией Fe2+в никельжелезном феррите со структурой шпинели, лежит при температуре ;г;150 °К, в то время как в иттрий-железном гранате аналогичный максимум имеет место при температуре 30 °К.
Наибольшее внимание при исследовании ионной релаксации в шпинелях было уделено марганцевому ферриту. Для различных образцов этого феррита разными авторами наблюдался либо один температурный максимум ДЯ при 15—20 °К, либо наряду с ним и второй максимум — при 200 °К (рис. 9.6.17). Делалась
/; -Y
Рис. 9.6.17. Температурные зависимости ширины резонансной кривой в двух марганцевых ферритах со структурой шпинели [401]. Частота 9,3 Ггц. Постоянное поле направлено по оси <111>.
попытка объяснить эти максимумы, соответственно, медленной и быстрой релаксацией ионов Fe2+. Однако, как было убедительно показано Кларком [401], низкотемпературный максимум обусловлен медленной релаксацией ионов Мн3+, а высокотемпературный — также медленной релаксацией, но ионов Fe2+.
Введение в различные ферриты ионов Со2+ приводит к резкому увеличению ширины резонансной кривой (см. например [393, 4071). В §9.3 рассматривался один из механизмов такого расширения — рассеяние магнонов на вариациях спин-орбитального взаимодействия, возникающих при беспорядочном замещении
19*
564
ПРОЦЕССЫ РЕЛАКСАЦИИ
[ГЛ. 9
ионами Со2+других ионов — с меньшей спин-орбитальной связью. Однако величина обусловленной ионами кобальта ширины кривой и ее температурные и угловые зависимости, как уже отмечалось в § 9.3, не находятся в согласии с таким механизмом. Эти зависимости являются типичными для механизма медленной ионной релаксации [393].
Мы рассмотрели несколько примеров проявления ионного механизма релаксации в ферритах. Из этих примеров видно, что рассматриваемый механизм является очень эффективным, обеспечивая при низких температурах большие вклады в ширину резонансной кривой даже при сравнительно малых концентрациях ионов. Характерными для этого механизма релаксации являются немонотонная температурная зависимость и сильная анизотропия ширины резонансной кривой. Можно полагать, что ионный механизм релаксации имеет место и в антиферромагнетиках, а также в металлах.
Заключительные замечания по процессам релаксации. В этой главе мы исследовали основные типы процессов релаксации в магнито упорядоченных кристаллах. Посредством таких процессов осуществляется, в частности, диссипация энергии магнитных колебаний. Ради простоты и учитывая практическую важность и степень разработанности вопроса в настоящее время, мы рассматривали главным образом (но не исключительно) релаксацию малых однородных колебаний намагниченности в слабо проводящих ферро- (или ферри- для низкочастотного типа колебаний) магнетиках. Однако исследованными элементарными процессами будут определяться релаксационные и диссипативные явления и в других — не рассмотренных нами случаях.
Теоретические и экспериментальные результаты, изложенные в этой главе, должны были наполнить конкретным содержанием ту схему диссипации энергии магнитных колебаний, возбуждаемых внешним переменным полем, которая была приведена на рис. 9.1.2. Заметим, что показанные на этой схеме и подробно рассмотренные в дальнейшем каналы диссипации действуют одновременно, внося, вообще говоря, сравнимые вклады в параметры диссипации, например в ширину резонансной кривой. Различные каналы характеризуются различными зависимостями параметра диссипации от температуры, частоты, постоянного поля и углов между ним и осями кристалла. И поэтому относительные вклады различных каналов диссипации изменяются при изменении указанных параметров. Лишь в некоторых случаях, как правило, в специально созданных экспериментально ситуациях, и то лишь в сравнительно узких пределах изменения параметров, вклад какого-либо одного 'канала релаксации существенно преобладает. В других случаях разделение вкладов различных каналов требует тщательного анализа температурных и дру
§ 9.61
ИОННАЯ РЕЛАКСАЦИЯ
565
гих зависимостей параметра диссипации. В настоящее время такое разделение далеко не всегда возможно.
Рис. 9.6.18. Вклады различных процессов релаксации в ширину резонансной кривой сфер из монокристаллов иттрий-железного граната. Сплошные линии— монокристалл выращен из окиси иттрия с 0,001 мол.% редкоземельных примесей и поверхность сферы обработана на абразиве со средним размером зерна 3 лж.и; пунктир— монокристалл выращен из очень чистой окиси иттрия (сказываются лишь малые примеси Fe2+) и поверхность сферы тщательно полирована, а— суммарные ^величины ширины резонансной кривой (усредненные данные по результатам различных экспериментов); б— процессы релаксации идеального кристалла, по-видимому, в основном, процессы Касуйя— Ле Кроу (см. рис. 9.4.3); в— двухмагнонные процессы рассеяния на шероховатостях поверхности и внутренних макроскопических неоднородностях; г— ионные процессы релаксации (медленная продольная релаксация); 0— некогерентные (флуктуационные) вклады различных процессов.
Разделение вкладов различных процессов релаксации в ширину резонансной кривой оказывается возможным с определенной степенью достоверности в случае монокристаллов ферритов. В качестве примера на рис. 9.6.18, проведено такое разделение
566	ПРОЦЕССЫ РЕЛАКСАЦИИ	[ГЛ.
для двух сферических образцов иттрий-железного граната. При построении вкладов отдельных процессов релаксации использованы теоретические и экспериментальные температурные зависимости и оценки, которые были приведены в этой главе. Некогерентный (флуктуационный) вклад, который становится существенным при подходе к температуре Кюри, дан совместно для всех процессов.
Такое же разделение можно провести в некоторых случаях и для поликристаллических ферритов (см., например, стр. 506— 507). Для других магнитоупорядоченных веществ: ферромагнитных металлов, антиферромагнетиков, надежное разделение вкладов различных процессов релаксации в параметры диссипации станет возможным только после дальнейшего изучения этих процессов.
ПРИЛОЖЕНИЕ 1
СВЯЗЬ МЕЖДУ ЕДИНИЦАМИ И ЗНАЧЕНИЯ ПОСТОЯННЫХ
В книге используется гауссова система единиц. Соотношения между единицами этой системы и единицами системы СИ даны в табл. П.1.1. В ней приведены за немногими исключениями лишь те величины, которые встречаются в книге. В квадратных скобках даны сокращенные названия, использованные в тексте.
Если аг и оси — единицы, соответственно, гауссовой системы и системы СИ, Лг и Лси— значения некоторой величины, измеренной в этих единицах, а К — множители, приведенные в табл. П.1.1, то
Яси = Кар,
,	(П.1.1)
В табл. П.1.2 даны значения некоторых фундаментальных постоянных, которые встречаются в тексте книги или же необходимы для проведения расчетов по затронутым в книге вопросам.
В атомной физике и физике твердого тела энергия частиц (или квазичастиц — возбуждений) измеряется часто в специальных единицах, которые определяются следующим образом. Электрон-вольт есть энергия электрона, прошедшего разность потенциалов 1 в. Обратный сантиметр есть энергия кванта электромагнитного излучения с длиной волны 1 см. Градус Кельвина — это средняя энергия, приходящаяся на две степени свободы атома идеального газа при температуре 1 °К. И наконец, эрстед (как единица энергии) — это величина зеемановского расщепления уровней при g-факторе электронного спина в магнитном поле 1 э. Величины этих единиц в эргах и соотношения между некоторыми из них приведены в следующей таблице.
Соотношения между единицами энергии
Единица
Связь с другими единицами
Электрон-вольт Обратный сантиметр Градус Кельвина Эрстед
1 зв — 1,6022-Ю 12 арг^	К 8100 CJW 1:	11 600 °К
1 сзг* = 1,9865-10-» эрг?	к1,44 =Кг	; 10 700 а
1° К = 1,3806-10-» эрг я	а 0,7 слг”1 д	г 7 400 а
1 а = 1,8570-IO'20 эрг		
1Й>ИЙОЖЁ'НЙЁ ‘1
Таблица П.1.1
Единицы гауссовой системы и системы СИ [31]
Величина	Обозначение в книге	Размерность в гауссовой системе	Единица в гауссовой системе	Отношение единиц К	Единица в системе СИ
Длина	ZII др.	1	сантиметр	102	метр
Время	t	t	секунда	1	секунда
Угол	9 и др.	е	радиан	1	радиан
Угловая	скорость (круговая частота)	СО	ег1	радиан в сек.	1	радиан в сек.
Частота	ю/2л	Г1	герц	1	герц
Масса	т	т	грамм	103	килограмм
Сила	f	mlt~2	дина	10®	ньютон
Работа, энергия1)	W, е	ml2t~2	эрг	10’	джоуль
Мощность	Р	ml2t~3		10’	ватт
Плотность потока энергии (вектор Пойнтинга)	П	* mt~3		103	ватт н? кв. метр
Количество электричества [заряд]				2,9979-10®	ккулон
Электрический потенциал	<р, А	gl-^		3,3356-10-3	вольт
Напряженность электрического поля [электрическое поле]	Е	gl~2	ч	3,3356-10-®	вольт на метр
Емкость		I	сантиметр	0,8988-1012	фарада
’) Энергия, особенно тепловая, измеряется часто в калориях: 1 калория равна 1,1868 джоуля.
») Эрстед принято считать единицей магнитного поля, а гаусс — единицей магнитной индукции. Однако в гауссовой системе единиц все величины Е, Н, I), М и В имеют одинаковую размерность и могут быть измерены в одинаковых единицах, например, в эрстедах.
СВЯЗЬ МЕЖДУ ЕДИНИЦАМИ И ЗНАЧЕНИЯ ПОСТОЯННЫХ
569
Таблица П.1.1 (продолжение)
Величина	Обозначение в книге	Размерность в гауссовой системе	Единица в гауссовой системе	Отношение единиц К	Единица в системе СИ
Диэлектрическая [электрическая] проницаемость	Е	1		O,8988-l()io	фарада на метр
Электрическая индукция	D	gZ~2	Ч	2,9979-106	кулон на кв. метр
Сила электрического тока [ток]		gt-i		2,9979-10»	ампер
Плотность тока	j	g/-2Z~i		2,9979-106	ампер на кв. метр
Электрическое сопротивление		1~Ч		1,1126-10-12	ом
Электрическая проводимость		It"1		0,8988-1012	сименс
Удельная электрическая проводимость [проводимость]	<5	fl		0,8988-1010	сименс на метр
Магнитный потенциал	ф	Ql~l		3,7673-Юю	ампер
Напряженность маг* нитвого поля [маг* нитное поле]	н	ql~2	эрстед	1,2566-10-2	ампер на метр
Индуктивность		ГЧ*		10»	генри
Магнитная проницаемость	н	1		10’	генри па метр
Магнитная индукция Намагниченность	в м	ql~2	гаусс')	101	тесла
Магнитный поток		q		10»	вебер
Термодинамическая температура [температура]	т	T	градус Кельвина	1	градус Кельвина
•) См. примечание !) на стр. 568.
570
ПРИЛОЖЕНИЕ 1
Таблица П.1.1 (продолжение)
Величина	Обозначение в книге	Размерность в гауссовой системе	Единица в гауссовой системе	Отношение единиц К	Единица в системе СИ
Теплоемкость системы Энтропия системы		т1Ч~*Т~1	эрг на градус	10’	джоуль на градус
Объемная удельная теплоемкость [теплоемкость] Плотность энтропии [энтропия]	с S			10	джоуль на куб. метр- градус
Таблица П.1.2
Значения некоторых постоянных (в гауссовой системе единиц) [41]
Постоянная	Обозначение и связь с другими постоянными	Величина
Скорость света в вакууме	с	2,9979-IO10
Заряд электрона	е	4,8032 -10~i!
Масса покоя электрона	те ’	9,1095-10~28
Масса покоя протона		1,6727-IO'24
Атомная единица массы	т0	1,6606-10'24
(1/12 массы атома 42С)		
Число Авогадро	Na = 1/m.i	6,0220-IO83
Постоянная Планка	h = /г/(2л)	1,0546-Ю-27
Магнетон Бора	Рв = еП/(2тес)	9,2741-IO-21
Ядерпый магнетон	Р„ = eh/(2mvc)	5,0508-IO'24
g-фактор электронного спина	gs	2,0023
Магнитомеханйческое отноше-	~ __ gse _	1,7608-IO7
кие для электронного спина	2mec	h	-
Постоянная Больцмана	x	1,3806-10-1’
ПРИЛОЖЕНИЕ 2
РАЗМАГНИЧИВАЮЩИЕ ФАКТОРЫ ЭЛЛИПСОИДА
Для непроводящего эллипсоида, помещенного в однородное внешнее постоянное магнитное поле Н, граничная магнитостатическая задача имеет строгое решение: намагниченность эллипсоида М и внутреннее поле И, оказываются однородными, и размагничивающее поле
Нм =Н{ —Н = —NM,	(П.2.1)
где N — тензор размагничивающих факторов эллипсоида. Если внешняя
Рис. П.2.1. Размагничивающий фактор эллипсоида в направлении большой оси в зависимости от отношений полуосей [441].
среда является немагнитной (ее магнитная проницаемость р0 = 1), то тензор N зависит только от формы эллипсоида. Оси эллипсоида являются глав-
572
приложение 2
ними осями симметричного тензора N, и его диагональные компоненты в этих осях называются размагничивающими факторами эллипсоида. Для них справедливы следующие выражения (см., например, [43]):

dt
J (а2+0'К(а2+0(Ь2 + П(с2 + г)
(П.2.2)
И аналогичные — для А';, и Nc, где а, b и с — полуоси эллипсоида.
Рис. П.2.2. Размагничивающий фактор вллипсоида в направлении средней оси в зависимости от отношений осей [441].
Расчет величин 1Уа,ь,<с в зависимости от отношений Ь/а тц da был проведен Осборном [441]. Построенные им графики приведены на рис. П.2.1 — П.2.3.
Сумма размагничивающих факторов эллипсоида
A'a + A-\+A-\=^4n. в> ’ о 1 с
(П.2.3)
РАЗМАГНИЧИВАЮЩИЕ ФАКТОРЫ ЭЛЛИПСОИДА
573
Рис. П.2.3. Размагничивающий фактор эллипсоида в симости от отношений осей
направлении малой 14411 ,
оси в зави-
[43, 17]: при а >• b = с (вытянутый сфероид)
N = 4л Lr Т-2 /. 1 [а 1 + у _ -j'j ° т2 \ 27	1 — 7	/ ’
при а = b > с (сплющенный сфероид) , 1 — Т2 /	1	\
Nc = 4л —р— — — arctg 71 ,
(П.2.4)
(П.2.5)
где в обоих случаях
а
эксцентриситет сфероида.
ЛИТЕРАТУРА
В приведенный ниже список литературы входят работы, на которые имеются ссылки в тексте, а также ряд других статей, которые рекомендуется прочесть при изучении затронутых в книге вопросов. В список включены некоторые работы по статическим магнитным свойствам ферро-, антиферро-и ферримагнетиков, рассмотрение их не является задачей книги, но они кратко напоминаются в некоторых главах. Включен ряд работ по тем динамическим проблемам, которым в книге почти не уделяется внимания, например, по магнитоупругим волнам, нелинейным явлениям и СВЧ ферритовым устройствам. Приведено также несколько работ по оптическим свойствам магнитоупорядоченных кристаллов.
При отборе работ для списка литературы автор исходил из методических соображений. При наличии нескольких работ по одному и тому же или близким вопросам включалась, как правило, более подробная (обычно — более поздняя) статья. Как правило, не включались оригинальные статьи, результаты которых изложены в монографиях и обзорах тех же авторов, входящих в список литературы. При этом не преследовалось никаких целей приоритетного или библиографического характера. Исключения были сделаны лишь для некоторых «классических» публикаций, явившихся важными этапами в развитии наших представлений о процессах в магнитоупорядоченных веществах. Ясно, что отбор работ, исходя из таких принципов, не может не явиться субъективным, хотя автор и старался избежать этого.
Для удобства пользования списком литературы он разбит на тематические части и разделы. Эта разбивка не носит характера строго научной или библиографической классификации. Отнесение статей к тому или иному разделу является иногда условным. Некоторые работы явно могут быть отнесены к двум или более разделам, в таких случаях обычно даются соответствующие примечания. В некоторые разделы включены работы, примыкающие, хотя, строго говоря, и не относящиеся к тематике данного раздела.
Монографии и сборники статей вынесены в отдельную часть, и в обоих разделах этой части расположены по алфавиту. В остальных разделах принята хронологическая последовательность работ.
I.	Монографии и сборники
1.1.	Магнетизм и магнитный резонанс
1.	С. А. Альтшулер, Б. М. Козырев, Электронный парамагнитный резонанс, «Наука», 1972.
2.	Антиферромагнетизм, Сб. переводов, Ред. С. В. Вонсовский, ИЛ, 1957.
3.	А. И. Ахиезер, В. Г. Барьяхтар, С. В. Пелетминский, Спиновые волны, «Наука», 1967.
4.	К. П. Белов, М. А. Белянчикова, Р. 3. Левитин, С. А. Никитин, Редкоземельные ферро- и антиферромагнетики, «Наука», 1965.
ЛИТЕРАТУРА
575
5.	С. В. Вонсовский, Магнетизм, «Наука», 1971.
6.	А. Г. Гуревич, Ферриты на сверхвысоких частотах, Физматгиз, 1960.
7.	Handbuch der Physik, Bd. XVIII/1, Magaetismus, Springer Verlag, 1968.
8.	Handbuch der Physik, Bd. XVIII/2, Ferromagnetismus, Springer Verlag, 1966.
9.	Handbook of Microwave Ferrite Materials, Ed. W. H. von Aulock, Acad. Press, 1965.
10.	Ю. А. Изюмов, Р.П. Озеров, Магнитная нейтронография, «Наука», 1966.
11.	Б. Лакс, К. Баттон. Сверхвысокочастотпые ферриты и ферримагнетики, «Мир», 1965.
12.	Magnetism, A Tretise on Modern Theory and Materials, Ed. G. T. Rado, H. Suhl, vol. I—IV, Acad. Press, 1963—1966.
13.	Д. Маттис, Теория магнетизма, «Мир», 1967.
14.	3. Метфессель, Д. Маттис, Магнитные полупроводники, «Мир», 1972.
15.	Я. А. Моносов, Нелинейный ферромагнитный резонанс, «Наука», 1971. »
16.	Нелинейные свойства ферритов в полях СВЧ, Сб. переводов, Ред.
А. Л. Микаэлян, ИЛ, 1963.
17.	К. М. Поливанов, Ферромагнетики, Госэнергоиздат, 1957.
18.	Дж. Смарт, Эффективное поле в теории магнетизма, «Мир», 1968.
19.	Я. Смит, X. Вейн, Ферриты, ИЛ, 1962.
20.	М. Sparks, Ferromagnetic Relaxation Theory, McGraw Hill, 1964.
21.	E. А. Туров, Физические свойства магнитоупорядоченных кристаллов, Изд. АН СССР, 1963.
22.	Е. А. Туров, М. П. Петров, Ядерный магнитный резонанс в ферро-и антиферромагнетиках, «Наука», 1969.
23.	С. В. Тябликов, Методы квантовой теории магнетизма, «Наука», 1965.
24.	Ферриты в нелинейных сверхвысокочастотных устройствах, Сб. переводов, Ред. А. Г. Гуревич, ИЛ, 1961.
25.	Ферромагнитный резонанс, Ред. С. В. Вонсовский, Физматгиз, 1961.
26.	Ферромагнитный резонанс и поведение ферромагнетиков в переменных магнитных полях, Сб. переводов, Ред. С. В. Вонсовский, ИЛ, 1952.
1.2.	Руководства по математике и физике
27.	В. К. Аркадьев, Электромагнитные процессы в металлах, ОНТИ, ч. I, 1935; ч. II, 1936.
28.	Г. Б. Бокий, Кристаллохимия, «Наука», 1971.
29.	А. Г. Гуревич, Полые резонаторы и волноводы, «Сов. радио», 1952.
30.	А. С. Давыдов, Квантовая механика, «Наука», 1973.
31.	Единицы измерения и обозначения физико-технических величин, «Недра», 1966.
32.	Дж. Займан, Принципы теории твердого тела, «Мир», 1966.
33.	Г. В. Кисунъко, Электродинамика полых систем, Изд. ВКАС, 1949.
34.	Ч. Киттель, Квантовая теория твердых тел, «Наука», 1967.
35.	И. Е. Почин, Векторное исчисление и начала тензорного исчисления, «Наука», 1965.
36.	Л. Д. Ландау, Е. М. Лифшиц, Статистическая физика, «Наука», 1964.
37.	Л. Д. Ландау, Е. М. Лифшиц, Электродинамика сплошных сред, Физматгиз, 1959.
38.	Ф. М. Морс, Г. Фешбах, Методы теоретической физики, ИЛ, т. 1, 1958; т. 2, 1960.
39.	В. В. Степанов, Курс дифференциальных уравнений, Гостехиздат, 1953.
40.	И. Е. Тамм, Основы теории электричества, «Наука», 1966.
41.	Б. Тейлор, В. Паркер, Д. Лангенберг, Фундаментальные константы и квантовая электродинамика, Атомиздат, 1972,
576
ЛИТЕРАТУРА
42.	Э. Т. Уиттекер, Дж. Н. Ватсон, Курс современного анализа, ФизМат-гиз, ч. I, 1962; ч. II, 1963.
43.	Я. II. Френкель, Электродинамика, ОНТИ, т. I, 1934; т. II, 1935.
44.	Е. Янке, Ф. Эмде, Ф. Лёш, Специальные функции. Формулы, графики, таблицы, «Наука», 1968.
II.	Магннтоупорядоченные вещества: структуры
и статические магнитные св'эйетва
II.1	. Общие проблемы магнитоупорядоченного состояния; ферромагнетизм1)
45.	Р. Weiss, J. de phys. et rad. 4, 661 (1907).
46.	Я. И. Френкель, Zs. fur Phys. 49, № 1—2, 31 (1928).
47.	W. Heisenberg, Zs. fur Phys. 49, № 9—10, 619 (1928).
48.	P. A. M. Dirac, Proc. Roy. Soc. A123, № 792, 714 (1929).
49.	Я. II. Френкель, Я. Г. Дорфман, Nature 126, № 3173, 274 (1930).
50.	М. Я. Широбоков, ЖЭТФ 15, № 1—2, 57 (1945).
51.	Е. М. Лифшиц, ЖЭТФ 15, № 3, 97 (1945).
52.	С. Killel, Rev. Mod. Phys. 21, № 4, 541 (1949). (Перевод в Сб. «Физика ферромагнитных областей», Ред. С. В. Вонсовский, ИЛ, 1951).
53.	W. Р. Wolf, Phys. Rev. 108, № 5, 1152 (1957).
54.	К. Yosida, М. Tachiki, Progr. Thcor. Phys. 17, № 3, 331 (1957).
55.	J. C. Slonczewski, Phys. Rev. 110, № 6, 1341 (1958).
56.	A. T. Губанов, ФТТ 2, № 3, 502 (1960).
57.	В. T. Matthias, R. M. Bozorth, J. H. van Vleck, Phys. Rev. Lett. 7, № 5, 160 (1961).
58.	P. W. Anderson, [12], vol. I, ch. 2.
59.	J. Kanamori, [12], vol. I, ch. 4.
60.	J. B. Goodenough, [12], vol. Ill, ch. 1.
61.	I. S. Jacobs, С. P. Bean, [12], vol. Ill, ch. 6.
62.	S. Shlrikman, D. Treves, [12], vol. Ill, ch. 8.
63.	J. F. Dillon, Jr., [12], vol. Ill, ch. 9.
64.	R. Brout, [12], vol. IIA, ch. 2.
65.	P. K. Baltzer, H. W. Lehmann, M. Robbins, Phys. Rev. Lett. 15, № 11, 493 (1965).
66.	C. G. Shull, H.A. Mook, Phys. Rev. Lett. 16, № 5, 184 (1966).
67.	N. D. Mermin, H. Wagner, Phys. Rev. Lett. 17, № 22, 1133 (1966). (Перевод в [13]).
68.	К. Tamura, H. Endo, Phys. Lett. A29, № 2, 52 (1969).
69.	TV. Menyuk, K. Dwight, T. B. Reed, Phys. Rev. B3, № 5, 1689 (1971).
II.2.	Антиферромагнетизм2)
70.	Л. Д. Ландау, Phys. Zs. der Sowjetuiiion 4, № 4, 675 (1933).
71.	J. H. van Vleck, J. Cheiu. Phys. 9, № 1, 85 (1941). (Перевод в [2].)
72.	P. W. Anderson, Phys. Rev. 83, № 6, 1260 (1951). (Перевод в [2].)
73.	C. G. Shull, W. A. Strauser, E.O. Wollan, Phys. Rev. 83, № 2, 333
(1951). (Перевод в [2].)
74.	R. A. Erickson, Phys. Rev. 90, № 5, 779 (1953). (Перевод в [2].)
75.	L. M. Mattarese, J. W. Stout, Phys. Rev. 94, № 6, 1792 (1954).
76.	T. Nagamiya, K. Yosida, R. Kubo, Adv. in Phys. 4, № 13, 1 (1955).
77.	A. С. Боровик-Романов, M. II. Орлова, ЖЭТФ 31, № 4, 579 (1956).
78.	И. E. ДзялошинскиИ, ЖЭТФ 23, № 6, 1547 (1957).
J) См. также [111, 230, 231, 233, 234].
2) См. также [92] и ряд работ в разделе IIL4.
ЛИТЕРАТУРА
577
79.	Е. А. Туров, ЖЭТФ 36, № 4, 1254 (1959).
80.	I. S. Jacobs, J. Appl. Phys. 32, Suppl. № 3, 61S (1961).
81.	А. С. Боровик-Романов, Итоги науки. Физ.-матем. науки, вып. 4, Изд. АН СССР, 1962.
82.	Т. Moriya, [12], vol. I, ch. 3.
83.	A. Tasaci, S. lida, J. Phys. Soc. Japan 18, № 8, 1148 (1963).
84.	K. Lee, A.M. Portis, G. L. Witt, Phys. Rev. 132, № 1, 144 (1963).
85.	M. M. Ф арзтдинов, УФН 84, № 4, 611 (1964).
86.	L. M. Corliss, J. M. Hastings, R. Nathans, J. Appl. Phys. 36, № 3, pdrt 2, 1099 (1965).
87.	I. A. Blech, B. L. Averbach, Phys. Rev. 142, № 2, 287 (1966).
88.	Г. К. Чепурных, ФТТ 10, № 6, 1917 (1968).
89.	Y. Shapira, S. Foner, Phys. Rev. Bl, № 7, 3083 (1970).
90.	M. II. Каганов, A. H. Омелъянчук, ФТТ 13, № 10, 2993 (1971).
II.3.	Ферримагнетики1)
91.	iS. Hilpert, Ber. deutsch. chem. Geselsch. 42, № 7, 2248 (1909).
92.	L. Neel, Ann. de phys. 3, 137 (1948). (Переводов [2].)
93.	F. Bertaut, F. Forrat, Compt. rend. 242, № 3, 382 (1956).
94.	С. В. Tобликов, ФММ 3, № 1, 3 (1956).
95.	F. K. Lotgering, Philips Res. Rep. 11, № 3, 190; № 4, 337 (1956). (Перевод в УФН 64, № 2, 247 (1958).)
96.	S. Geller, M.A. Gilleo, J. Phys. Chem. Solids 3, № 1/2, 30 (1957). (Перевод в [24].)
97.	W. P. Wolf, Rep. on Progr. in Phys., vol. 24, 1961, p. 212.
98.	C. J. Kriessman, N. Goldberg, [12], vol. Ill, ch. 12.
99.	А. С. Пахомов, А. А. Гусев, ФММ 18, № 1, 156 (1964).
100.	S. Geller, G. P. Espinosa, II. J. Williams, R. C. Sherwood, E.A. Nesbitt, J. Appl. Phys. 35, № 3, part 1, 570 (1964).
101.	Г. А. Смоленский, В. M. Юдин, П.П. Сырников, А. Б. Шерман, ФТТ 8, № 10, 2965 (1966).
102.	S. Geller, J. A. Cape, G. Р. Espinosa, D. Н. Leslie, Phys. Rev. 148, Ks 2, 522 (1966).
103.	A. E. Clark, E. Callen, J. Appl. Phys. 39, № 13, 5972 (1968).
104.	J. Chappert, R. B. Frankel, Phys. Rew Lett. 19, № 10, 570 (1967).
105.	T. Д. Зотов, M. M. Сукровцева, ФТТ 11, № 3, 649 (1969).
106.	R. A Iben, Phys. Rev. B2, № 7, 2767 (1970).
107.	К. П. Белов, Л. А. Черникова, E. В. Талалаева, P. 3. Левитин-, T. В. Кудрявцева, С. Амадези, В. II. Ивановский, ЖЭТФ 58, № '6, 1923 (1970).
108.	J. Bernasconi, D. Kuse, Phys. Rev. B3, № 3, 811 (1971).
109.	А. К. Звездин, В. M. Матвеев, ЖЭТФ 62, № 1, 260 (1972).
III. Однородный резонанс
III.1. Теория ферромагнитного резонанса
110.	Я. Г. Дорфман, Zs. fur Phys. 17, № 2, 98 (1923).
111.	Л. Д. Ландау, Е. М. Лифшиц, Phys. Zs. der Sowjetunion 8, № 2, 153 (1935). (На русском яз. см. Л. Д. Ландау, Сб. трудов, т. 1, «Наука», (1969).)
112.	С. Kittel, Phys. Rev. 73, № 2, 155 (1948). (Перевод в [26].)
ИЗ. D. Polder, Philos. Mag. 40, № 300, 99 (1949). (Перевод в [26].)
г) См. также [192, 429].
578
ЛИТЕРАТУРА
114. С. Kittel, J. de phys. et rad. 12, № 3, 291 (1951). (Перевод в [26].) 115. J. H. van Vleck, Physica 17, № 3—4, 234 (1951). (Перевод в [26].) 116. J. R. Macdonald, Proc. Phys. Soc. A64, 383, 968 (1951). (Перевод в [26].) 117. J. Smit, H. G. Belfers, Philips Res. Rep. 10, № 2, 113 (1955).
118.	H. Suhl, Phys. Rev. 97, № 2, 555 (1955).
119.	J. O. Artman, Phys. Rev. 105, № 1, 62 (1957).
120.	Г. В. Скроцкий, Л. В. Курбатов, [25], гл. 2.
121.	К. Б. Власов, Б. X. Ишмухаметов, ФММ 11, № 1, 3 (1961).
122.	G. F. Herrmann, J. Phys. Chem. Solids 25, № 3, 347 (1964).
123.	A. M. Родичев, ЖЭТФ 48, № 3, 860 (1965).
124.	Л. К. Михайловский, Б. П. Поллак, О. А. Соколов, ФММ 21, № 4, 524 (1966).
125.	G. Е. Everett, R. S. Huges, J. Appl. Phys. 41, № 3, 1120 (1970).
III.2.	Экспериментальное исследование ферромагнитного резонанса1)
126.	Е. К. Завойский, J. Phys. USSR 9, № 3, 245 (1945).
127.	J. Н. К. Griffiths, Nature 158, № 4019, 670 (1946). (Перевод в ]26].)
128.	Е. К. Завойский, ЖЭТФ 17, № 10, 883 (1947).
129.	W. Н. Hewitt, Phys. Rev. 73, № 9, 1118 (1948). (Перевод в [26].)
130.	L. R. Bickford, Jr., Phys. Rev. 78, № 4, 449 (1950). (Перевод в [26].)
131.	N. Bloembergen, Phys. Rev. 78, № 5, 572 (1950). (Перевод в [26].)
132.	D. W. Healy, Phys. Rev. 86, № 6, 1009 (1952).
133.	T. Okamura, Y. Torizuka, Y. Kojima, Phys. Rev. 88, № 6, 1425 (1952).
134.	J. F. Dillon, Jr., S. Geschwind, V. Jaccarino, Phys. Rev. 100, № 2, 750 (1955).
135.	J. F. Dillon, Jr., Phys. Rev. 105, № 2, 759 (1957).
136.	А. Г. Гуревич, II. E. Гублер, ФТТ 1, .№ 12, 1847 (1959).
137.	A. П. Александров, Я. II. Ханин, Э. Г. Ящин, ЖЭТФ 38, № 4, 1334 (1960).
138.	J. Overmeyer, J. Appl. Phys. 32, Suppl. № 3, 142S (1961).
139.	J. F. Dillon, Jr., J. Appl. Phys. 33, Suppl. № 3, 1191 (1962).
140.	C. R. Buffler, J. Appl. Phys. 33, Suppl. № 3, 1360 (1962).
141.	E. II. Головенчиц, В. А. Санина, А. Г. Гуревич, ФТТ 10, № 10, 2956, (1968).
142.	10. М. Яковлев, Ю. Р. Шильников, II. Н. Агапова, ФТТ 10, № 3, 942
(1968).
143.	S. Kurtin, S. Foner, В. Lax, J. Appl. Phys. 40,	2, 818 (1969).
144.	А. Г. Гуревич, В. А. Санина, E. И. Головенчиц, С. С. Старобинец,
J. Appl. Phys. 40, № 3, 1512 (1969).
145.	J. С. Wesley, A. Rich, Phys. Rev. Lett. 24, № 23, 1320 (1970).
146.	R. C. Le Craw, R. Wolfe, A. II. Bobeck, R. D. Pierce, L. G. van Uitert, J. Appl. Phys. 42, № 4, 1641 (1971).
147.	А. Г. Гуревич, Ю. M. Яковлев, В. II. Карпович, A. H. Агеев, Е. В. Рубалъская, Phys. Lett. А40, № 1, 69 (1972). 36, № 7, 1552 (1972).
!) См. также [124]. В этот раздел включены работы по ферромагнитному резонансу в намагниченных до насыщения, главным образом, неметаллических веществах, причем те работы, в которых основное внимание уделяется исследованию резонансных условий, анизотропии. Включены также работы по магнитному резонансу в магнитно неупорядоченных веществах (парамагнетиках), на которые имеются ссылки. Работы, целью которых являлось изучение ширины кривой ферромагнитного резонанса, процессов релаксации, приведены в соответствующих разделах частей V и VI.
ЛИТЕРАТУРА
579
Ш.З. Магнитные колебания и резонанс
в ненасыщенных ферромагнетиках1)
148.	W. Doring, Zs. fiir Naturforsch. За, № 7, 373 (1948). (Перевод в [26].)
149.	G. Т. Rado, R. TV. Wright, ТУ. И. Emerson, Phys. Rev. 80, № 2, 273 (1950). (Перевод в [26].)
150.	R. Becker, J. de phys. et rad. 12, № 3, 332 (1951). (Перевод в [26].)
151.	T. Nagamiya, Progr. Theor. Phys. 10, № 1, 72 (1953).	‘
152.	D. Polder, J. Smit, Rev. Mod. Phys. 25, № 1, 89 (1953).
153.	G. T. Rado, Phys. Rev. 89, № 2, 529 (1953).
154.	J. K. Galt, Bell System Tech. J. 33, № 5, 1023 (1954).
155.	P. E. Tannenwald, Phys. Rev. 99, № 2, 463 (1955).
156.	R. C. Le Craw, E. G. Spencer, J. Appl. Phys. 28, № 4, 399 (1957).
157.	P. A. Miles, W. B. Westphal, A. von Hippel, Rev. Mod. Phys. 29, № 3, 279^(1957). (Перевод в Сб. «Диэлектрическая спектроскопия», ИЛ, 158. Т. М. Перекалииа, А. А. Аскочснский, Д. Г. Санников, ЖЭТФ 40, № 2, 441 (1961).
159.	К. Б. Власов, Л. Г. Оноприенко, ФММ 15, А” 1, 45 (1963).
160.	А. А. Мануйлова, Л. П. Богданова, ФТТ 6, № 9, 2703 (1964).
161.	Б. М. Лебедь, С. Г. Абаренкова, ФТТ 6, № 1, 297 (1964).
162.	R. С. Le Craw, Е. М. Gyorgy, L. С. van Uitert, Appl. Phys. Lett. 9 № 2, 90 (1966).
163.	В. И. Дудкин, А. И. Пильщиков, ЖЭТФ 52, № 3, 677 (1967).
164.	А. И. Пильщиков, Н. Е. Сыръев, ЖЭТФ 57, № 6, 1940 (1969).
Ш.4. Антиферромагнитный резонанс2)
165.	С. Kittel, Phys. Rev. 82. № 4, 565 (1951). (Перевод в [26].)
166.	F. Keffer, С. Kittel, Phys. Rev. 85, № 2, 329 (1952). (Перевод в [2].) 167. J. V. Ubbink, N. J. Poulis, H. J. Gerritsen, C. J. Garter, Physica 18, № 6—7, 361 (1952).
168.	M. Johnson, A. H. Л'ether cot, Jr., Phys. Rev. 114, № 3, 705 (1959).
169.	M. И. Каганов, В. M. Цукерник, ЖЭТФ 41, № 1, 267 (1961).
170.	М. Date, J. Phys. Soc. Japan 16, № 7, 1337 (1961).
171.	D. T. Teaney, M. J. Freiser, R. W. H. Stevenson, Phys. Rev. Lett. 9, № 5, 212 (1962).
172.	iS. Foner, [12], vol. I, ch. 9.
173.	A. J. S ievers, III, M. Tinkham, Phys. Rev. 129, № 4, 1566 (1963).
174.	А. С. Боровик-Романов, H. M. Крейнес, Л. А. Прозорова, ЖЭТФ 45, № 2, 64 (1963).
175.	П. J. Fink, D. Shaltiel, Phys. Rev. 130, № 2, 627 (1963).
176.	S. Foner, Phys. Rev. 130, № 1, 183 (1963).
177.	G. F. Herrmann, J. Phys. Chem. Solids 24, № 5, 597 (1963).
178.	P. L. Richards, J. Appl. Phys. 35, № 3, part 2, 850 (1964).
179.	В. И. Ожогин, В. Г. Шапиро, ЖЭТФ 54, № 1, 96 (1968).
180.	Л. А. Прозорова, А. С. Боровик-Романов, ЖЭТФ 55, № 5, 1727 (1968).
181.	Е. И. Головенчиц, В. А. Санина, А. Г. Гуревич, ФТТ 11, К» 3, 642 (1969).
182.	А. С. Боровик-Романов, Б. Я. Котюжанский, Л. А. Прозорова, ЖЭТФ 58, № 6, 1911 (1970).
г) См. также [117, 119].
2) См. также [83, 144, 211, 235, 241] и работы по процессам релаксации и нелинейным явлениям при антиферромагнитном резонансе — в соответствующих разделах.
580
ЛИТЕРАТУРА
183.	В. А. Санина, Е. И. Головенчиц, Т. А. Фомина, А. Г. Гуревич, Phys. Lett. АЗЗ, № 5, 291 (1970).
184.	J. W. Battles, G. Е. Everett, Phys. Rev. Bl, № 7, 3021 (1970).
185.	IO. M. Гуфан, ЖЭТФ 60, № 4, 1537 (1971).
186.	В. С. Мандель, В. Д. Воронков, Д. Е. Громзин, ЖЭТФ 63, № 3, 993 (1972).
III.5.	Особенности резонанса в ферримагнетиках
187.	R. К. Wangsness, Phys. Rev. 91, № 5, 1085 (1953).
188.	R. К. Wangsness, Phys. Rev. 95, № 2, 339 (1954).
189.	B. A. Calhoun, W. V. Smith, J. Overmeyer, J. Appl. Phys. 29, № 3, 427 (1958).
190.	R. K. Wangsness, Phys. Rev. 113, № 3, 771 (1959).
191.	S. Geschwind, L. R. Walker, J. Appl. Phys. 30, Suppl. № 4, 163S (1959).
192.	E. Schlomann, Solid State Phys, in Electron, and Telecom., vol. 3, Acad. Press, 1960, p. 332.
193.	G. T. Rodrigue, H. Meyer, R. V. Jones, J. Appl. Phys. 31, Suppl. № 5, 376S (1960).
194.	A. J. Sievers, III, M. Tinkham, Phys. Rev. 129, № 5, 1995 (1963).
195.	R. C. Le Craw, J. P. Remeika, H. Matthews, J. Appl. Phys. 36, № 3, part 2, 901 (1965).
196.	Б. E. Рубинштейн, А. Г. Титова, Б. Л. Лаповок, ФТТ 7, № 6, 1639 (1965).
197.	Б. II. Кулиев, Г. М. Недлин, ФТТ 9, № 9, 2678 (1967).
198.	G. A. Gehring, J. Appl. Phys. 41, № 5, 2072 (1970).
IV. Неоднородные магнитные колебания и спиновые волны
IV.1. Магнитостатические (уокеровские) колебания1)
199.	R. L. White, I. Н. Salt, Phys. Rev. 104, № 1, 56 (1956). (Перевод в [24].)
200.	L. R. Walker, Phys. Rev. 105, № 2, 390 (1957). (Перевод в [24].)
201.	L. R. Walker, J. Appl. Phys. 29, № 3, 318 (1958). (Перевод в [24].)
202.	J. F. Dillon, Jr., Phys. Rev. 112, № 1, 59 (1958). (Перевод в [24].)
203.	P. C. Fletcher, I. H. Salt, J. Appl. Phys. 30, Suppl. A? 4, 181S (1959). (Перевод в [24].)
204.	P. C. Fletcher, R. O. Bell, J. Appl. Phys. 30, № 5, 687 (1959). (Перевод в [24].)
205.	R. L. White, J. Appl. Phys. 31, Suppl. № 5, 86S (1960).
206.	I. II. Salt, P. C. Fletcher, J. Appl. Phys. 31, Suppl. № 5, 100S (1960). (Перевод в [16].)
207.	J. F. Dillon, Jr., J. Appl. Phys. 31, № 9, 1605 (1960).
208.	В. Д. Кривченков, A. If. Пильщиков, ЖЭТФ 43, № 2, 573 (1962).
209.	R. Plumier, Physica 28, № 4, 423 (1962).
210.	J. F. Dillon, Jr., J. P. Remeika, Appl. Phys. Lett. 2, № 2, 38 (1963).
211.	D. E. Beeman, J. Appl. Phys. 37, № 3, 1136 (1966).
212.	IO. M. Яковлев, Ю. H. Бурдин, ФТТ 10, № 6, 1622 (1968).
213.	А. И. Пильщиков, H. С. Седлецкая, ФТТ 10, № 5, 1298 (1968).
IV.2. Магнитостатические (безобменные) волны2,
214.	В. В. Никольский, РЭ 5, № 1, 39 (1960).
215.	J. R. Eschbach, R. W. Damon, Phys. Rev. 118, № 5, 1208 (1960).
i) См. также [240, 505].
2) См. также [430].
ЛИТЕРАТУРА
581
216.	Р. С. Fletcher, С. Kittel, Phys. Rev. 120, № 6, 2004 (1960).
217.	В. Г. Баръяхтар, М. И. Каганов, [25], гл. 7.
218.	A. W. Trivelpiece, A. Ignatus, Р. С. Holsher, J. Appl. Phys. 32, № 2, 259 (1961).
219.	R. I. Joseph, E. Schlomann, J. Appl. Phys. 32, № 6, 1001 (1961).
220.	R. W. Damon, J. R. Eshbach, J. Phys. Chem. Solids 19, № 3—4, 308 (1961).
221.	R. IV. Damon, H. van de Vaart, J. Appl. Phys. 36, № 11, 3453 (1965).
222.	R. W. Damon, II. van de Vaart, J. Appl. Phys. 37, № 6, 2445 (1966).
223.	B. A. Auld, К. B. Mehta, J. Appl. Phys. 38, № 10, 4081 (1967).
224.	S. M. Resende, F. R. Morgenthaler, Appl. Phys. Lett. 10, № 6, 184 (1967).
225.	C. F. Vasile, R. La Rosa, J. Appl. Phys. 39, № 5, 2380 (1968).
226.	Г. M. Недлин, P. X. Шапиро, ФТТ 10, № 12, 3740 (1968).
227.	В. A. Auld, Appl. Solid State Science, vol. 1, Acad. Press, 1971, p. 1.
228.	Б. M. Лебедь, В. П. Лопатин, ФТТ 13, № 5, 1397 (1971).
229.	Л. В. Михайловская, Р. X. Хлебопрос ФТТ 13, № 9, 2786 (1971).
IV.3. Спиновые волны в неограниченных средах1)
230.	F. Bloch, Zs. fur Phys. 61, № 3—4, 206 (1930).
231.	T. Holstein, H. Prinutkoff, Phys. Rev. 58, № 12, 1098 (1940).
232.	C. Herring, C. Kittel, Phys. Rev. 81, № 5, 869 (1951). (Перевод в Сб. «Проблемы соврем, физ.», № 5, 6 (1962).)
233.	F. J. Dyson, Phys. Rev. 102, № 5, 1217 (1956). (Перевод в Сб. «Проблемы соврем, физ.», № 2, 101 (1958).)
234.	F. J. Dyson, Phys. Rev. 102, № 5, 1230 (1956). (Перевод в Сб. «Проблемы соврем, физ.», № 2, 129 (1958).)
235.	М. И. Каганов, В. М. Цукерник, ЖЭТФ 34, № 1, 106 (1958).
236.	J. van Kranendonk, J. Н. van Vleck, Rev,. Mod. Phys. 30, №1,1 (1958).
237.	M. A. Гинцбург, ФТТ 2, № 5, 913 (1960).
238.	R. C. Le Craw, R. L. Walker, J. Appl. Phys. 32, Suppl. № 3, 167S (1961).
239.	E. А. Туров, [25], гл. 3.
240.	L. R. Walker, [12], vol. I, ch. 8.
241.	R. Loudon, P. Pincus, Phys. Rev. 132, № 2, 673 (1963).
242.	R. L. Douglas, Phys. Rev. 129, № 3, 1132 (1963).
243.	R. D. Lowde, J. Appl. Phys. 36, № 3, part 2, 884 (1965).
244.	F. Keffer, [8], p. 1.
245.	G. A. Ferguson, Jr., A. W. Saenz, S. Podger, J. Appl. Phys. 37, № 3, 1050 (1966).
246.	В. Г. Вакс, A. II. Ларкин, С. А. Пикин, ЖЭТФ 53, № 1, 281 (1967).
247.	В. Г. Вакс, А. II. Ларкин, С. А. Пикин, ЖЭТФ 53, № 3, 1089 (1967).
248.	С. А. Пикин, ЖЭТФ 54, № 6, 1851 (1968).
249.	В. М. Цукерник, ФТТ 10, № 4, 1006 (1968).
250.	Е. J. Samuelsen, G. Shirane, Phys. stat, solidi 42, № 1, 241 (1970).
251	E. J. Samuelsen, R. Silberglitt, G. Shirane, J. P. Remeika, Phys. Rev.
B3, № 1, 157 (1971).
252.	C. Manohar, G. Venkataraman, Phys. Rev. B5, № 5, 1993 (1972).
IV.4. Влияние границ и возбуждение спиновых волн2)
253.	W. S. Ament, G. Т. Rado, Phys. Rev. 97, № 6, 1558 (1955).
254.	С. Kittel, Phys. Rev. 110, № 6, 1295 (1958). (Перевод в [24].)
255.	M. Н. Seavey, Р. Е. Tannenwald, Phys. Rev. Lett. 1, № 5, 168 (1958). (Перевод в [24].)
J) См. также [105, 318, 440].
2) См. также [215—217].
582
ЛИТЕРАТУРА
256.	G. Т. Rado, J. R. Weertman, J. Phys. Chem. Solids 11, № 3—4, 315 (1959).
257.	P. E. Tannenwald, R. Weber, Phys. Rev. 121, № 3, 715 (1961).
258.	Z.	Frait, Phys. stat, solidi 2,	№	11,	1417 (1962).
259.	J.	R. Eshbach,	J.	Appl. Phys.	34,	№	4, 1298 (1963).
260.	E.	Schlomann,	J.	Appl. Phys.	35,	№	1, 159 (1964).
261.	E.	Schlomann,	R.	I. Joseph, J.	Appl. Phys. 35, № 1, 167 (1964).
262.	J. T. Davies, J. Appl. Phys. 35, № 3, part 2, 804 (1964).
263.	В. В. Ганн, ФТТ 8, № И, 3167 (1966).
264.	Б. И. Филиппов, ФТТ 9, № 5, 1339 (1967).
265.	G. I. Lykken, Phys. Rev. Lett. 19, № 25, 1431 (1967).
266.	M. Sparks, Phys. Rev. Bl, № 9, 3831; 3856; 3869 (1970).
267.	R. E. De Wames, T. Wolfram, J. Appl. Phys. 41, № 3, 987 (1970).
268.	E. Sawado, J. Appl. Phys. 41, № 6, 2521 (1970).
269.	F. Goedsche, Phys. stat, solidi 39, № 1, K29 (1970).
270.	С. H. Bajorek, С. H. Wills, J. Appl. Phys. 42, № 11, 4324 (1971).
271.	T. Wolfram, R. E. De Wames, Phys. Rev. B4 № 9, 3125 (1971).
V. Процессы релаксации в магнитной системе
V.I. Общие вопросы релаксации1)
272.	П. Nyquist, Phys. Rev. 32, № 1, 110 (1928).
273.	Н. В. G. Casimir, F. К. du Pre, Physica 5, № 6, 507 (1938).
274.	А. И. Ахиезер, J. Phys. USSR 10, № 3, 217 (1946).
275.	F. Bloch, Phys. Rev. 70, № 7—8, 460 (1946).
276.	H. B. Callen, T.A. Welton, Phys. Rev. 83, № 1, 34 (1950).
277.	R. K. Wangsness, Phys. Rev. 98, № 4, 927 (1955).
278.	B. S. Gourary, J. Appl. Phys. 28, № 3, 283 (1957).
279.	H. B. Callen, J. Phys. Chem. Solids 4, Ks 4, 256 (1958).
280.	В. Г. Баръяхтар, ЖЭТФ 37, № 3, 690 (1959).
281.	R. C. Fletcher, R. C. Le Craw, E. G. Spencer, Phys. Rev. 117, № 4, 955 (1960).
282.	E. А. Туров, [25], гл. 6.
283.	А. Г. Гуревич, И. Е. Гублер, А. Г. Титова, ФТТ 3, № 1,	19
(1961).
284.	Т. Kasuya, R. С. Le Craw, Phys. Rev. Lett. 6, № 5, 223 (1961).
285.	M. Sparks, R. Loudon, C. Kittel, Phys. Rev. 122, № 3, 791 (1961).
286.	R. Kubo, Сб. «Термодинамика необратимых процессов», Ред. Д. Н. Зубарев, ИЛ, 1962, стр. 345.
287.	С. W. Haas, Н. В. Callen, [12], vol. I, ch. 10.
288.	О. А. Ольхов, Б. Н. Провоторов, Phys. Rev. 140, № 4А, А1296 (1965).
289.	J. C. Verstelle, D.A. Curtis, [7], p. 1.
290.	D. E. Eastman, Phys. Lett. A28, № 2, 136 (1968).
291.	J. P. Kotthaus, V. Jaccarino, Phys. Rev. Lett. 28, № 25, 1649 (1972).
J) См. также [20, 244]. В этот раздел, кроме общих вопросов теории релаксации и обзоров, включены работы, в которых уделяется, приблизительно, одинаковое внимание различным процессам релаксации, а также работы, в которых исследуются процессы, не затронутые в последующих разделах части V ив части VI.
ЛИТЕРАТУРА
583
V.2. Спин-спиновая релаксация в идеальных кристаллах1)
292.	М. И. Каганов, В. М. Цукерник, ЖЭТФ 34, № 6, 1610 (1958).
293.	А. II. Ахиезер, В. Г. Баръяхтар, С. В. Пелетминский, ЖЭТФ 36, № 1, 216 (1959).
294.	М. II. Каганов, В. М. Цукерник, ЖЭТФ 37, № 3, 823 (1959).
295.	М. Sparks, С. Kittel, Phys. Rev. Lett. 4, № 5, 232 (поправка № 6. 320) (1960).
296.	E. Schlomann, Phys. I’ev. 121, № 5, 1312 (1961).
297.	В. H. Генкин, В. M. Файн, ЖЭТФ 41, № 5, 1522 (1961).
298.	Р. Pincus, М. Sparks, R. С. Le Craw, Phys. Rev. 124, № 4, 1015 (1961).
299.	В. II. Ожогин, ЖЭТФ 46, № 2, 531 (1964).
300.	R. L. Comstock, Appl. Phys. Lett. 6, № 2, 29 (1965).
301.	Б. M. Лебедь, К. В. Шевлягин, ФТТ 7, № 5, 1519 (1965).
302.	М. Sparks, Phys. Rev. 160, № 2, 364 (1967).
303.	R. R. Bartkowski, J. Appl. Phys. 41, № 10, 4087 (1970).
V.3. Нлияние неоднородностей, двухмагнонные процессы2)
304.	А. М. Clogston, Н. Suhl, L. R. Walker, Р. W. Anderson, J. Phys. Chem.
Solids 1, № 3, 129 (1956). (Перевод в [24].)
305.	S. Geschwind, A. M. Clogston, Phys. Rev. 108, № 1, 49 (1957).
306.	J. E. Pippin, C. L. Hogan, Trans. IRE MMT-6, № 1, 77 (1958). . .
307.	E. Schlomann, J. Phys. Chem. Solids 6, № 2—3, 242 (1958).
308.	E. Schlomann, J. Phys. Chem. Solids 6, № 2—3, 257 (1958).
309.	E. Schlomann, J. R. Zeender, J. Appl. Phys. 29, № 3, 341 (1958).
310.	A. M. Clogston, J. Appl. Phys. 29, № 3, 334 (1958).
311.	R. C. Le Craw, E. G. Spencer, C. S. Porter, Phys. Rev. 110, № 6, 1311
(1958). (Перевод в [24].)
312.	C. R. Buffler, J. Appl. Phys. 30, Suppl. № 4, 172S (1959). (Перевод в [24].)
313.	E. Schlomann, R. V. Jones, J. Appl. Phys. 30, Suppl. № 4, 177S (1959).
314.	А. Г. Гуревич, II. E. Гублер, А. П. Сафантъевский, ФТТ 1, № 12,
1962 (1959).
315.	H. В. Callen, Е. Pittelli, Phys. Rev. 119, № 5, 1523 (1960).
316.	A. D. Schnitzler, V. J. Folen,9 G. T. Rado, J. Appl. Phys. 31, Suppl. № 5, 348S (1960).
317.	C. W. Haas, H. B. Callen, Phys. Rev. 122, № 1, 59 (1961).
318.	M. W. Muller, C. R. Buffler, J. Appl. Phys. 32, Suppl. № 3, 153S (1961).
319.	К. M. Поливанов, Б. П. Поллак, Изв. АН СССР, сер. физ. 28, № 3, 470 (19 >4).
320.	А. А. Мануйлова, А. Г. Гуревич, ФТТ 6, № 11, 3475 (1964).
321.	J. Р. Remeika, R. L. Comstock, J. Appl. Phys. 35, № 11, 3320 (1964).
322.	G. R. Jones, Phys. Rev. 137,	1A, A182 (1965).
323.	K. Motizuki, M. Sparks, P.E. 'Seiden, Phys. Rev. 140, № ЗА, A972 (1965).
324.	В. Г. Баръяхтар, М. А. Савченко, В. В. Тарасенко, ЖЭТФ 54, № 5, 1603 (1968).
325.	Е. Schlomann, Phys. Rev. 182, № 2, 632 (1969).
J) См. также [233, 274, 280, 284, 285, 328].
2) См. также [115, 266, 283, 285, 546J.
584
ЛИТЕРАТУРА
326.	С. Е. Patton, Phys. Rev. 179, № 2, 352 (1969).
327.	С. Е. Patton, J. Appl. Phys. 41, № 4, 1637 (1970).
328.	R. R. Bartkowski, J. Appl. Phys. 41, № 10, 4087 (1970).
329.	Ю. M. Яковлев, Э. В. Рубалъская, Л. Г. Годес, Б. Л. Лаповок, Т. Я. Бушуева, ФТТ 13, № 4, 1151 (1971).
330.	С. Е. Patton, Я. J. van Hook, J. Appl. Phys. 43, № 6, 2872 (1972).
VI. Взаимодействие магнитной системы с другими системами и процессы релаксации
VI.1. Магнитоупругое взаимодействие
и спин-решеточная релаксация1)
331.	Е. Abrahams, С. Kittel, Phys. Rev. 88, № 5, 1200 (1952). '
332.	Е.А. Туров, Ю. Я. Ирхин, ФММ 3, № 1, 5 (1956).
333.	А. И. Ахиезер, В. Г. Баръяхтар, С. В. Пелетмииский, ЖЭТФ 35, № 1, 228 (1958).
334.	С. Kittel, Phys. Rev. 110, № 4, 836 (1958).
335.	М. Я. Каганов, В. М. Цукерник, ЖЭТФ 36, № 1, 224 (1959).
336.	Я. Matthews, R. С. Le Craw, Phys. Rev. Lett. 8, № 10, 397 (1962).
337.	Г. M. Генкин, Я. Г. Голубева, В. М. Цукерник, ФТТ 6, № 3, 818 (1964)
338.	Е. Schlomann, R. I. Joseph, J. Appl. Phys. 35, № 8, 2382 (1964) (поправка 36, № 3, part 1, 875 (1965)).
339.	W. Strauss, J.	Appl. Phys. 36,	№ 1, 118 (1965).
340.	R. C. Addison,	B. A. Auld, H.	J. Shaw, D. K.	Winslow,	Appl.	Phys.
Lett. 6, № 10, 196 (1965).
341.	Г. M. Недлин,	P. X. Шапиро, ЖЭТФ 51, № 3,	349 (1966).
342.	А. Г. Гуревич,	Б. М.Лебедъ,	С. А. Миронов,	С. С.	Старобинец,
А. Г. Титова, К. В. Шевлягин, Изв. АН СССР, сер. физ. 30, № 6, 1002 (1966).
343.	D. Е. Eastman, R. J. Joenk, D. Т. Teaney, Phys. Rev. Lett. 17, № 6, 300 (1966).
344.	Ю. Я. Котюков, ФТТ 9, № 4, 1149 (1967).
345.	Г. А. Петраковский, Э. М. Смокотин, А. Г. Титова, ФТТ 9, № 8, 2324 (1967).
346.	А. Г. Гуревич, Б. М. Лебедь, С. А. Миронов, К. В. Шевлягин, ФТТ 9, № 4, 1209 (1967).
347.	R. С. Le Craw, R. L. Comstock, Физическая акустика, Ред. У. Мэзон, т. III, ч. Б, «Мир», 1968, гл. 4.
348.	Е. Callen, J. Appl. Phys. 39, № 2, 519 (1968).
349.	R. C. Addison, В. A. Auld, J. H. Collins, J. Appl. Phys. 39, № 3, 1828 (1968).
350.	В. Г. Баръяхтар, В. В. Ганн, ФТТ 10, № 8, 2327 (1968).
351.	В. A. Auld, J. Я. Collins, D. С. Webb, J. Appl. Phys. 39, № 3, 1598 (1968).
352.	S. M. Rezende, F. R. Morgenthaler, J. Appl. Phys. 40, № 2, 524; 537 (1969).
353.	В. В. Леманов, А. В. Павленко, А. Я. Гришмановский, ЖЭТФ 59, № 3, 712 (1970).
354.	H. L. Hu, S. M. Rezende, F. R. Mor gen thaler,	J. Appl. Phys.
41, № 3, 1417 (1970).
*) См. также [227, 274, 280, 284, 293, 417, 431, 487, 491] и работы по нелинейному магнитоупругому взаимодействию в разделе VIII.3.
Литература
585
355.	W. Strauss, Физическая акустика, Ред. У. Мэзон, т. IV, ч. В, «Мир», 1970, гл. 5.
356.	К. Р. Sinha, R. С. Le Craw, J. Phys. Chem. Solids 32, № 2, 373 (1971).
357.	M. Boiteux, P. Doussineau, B. Ferry, A. Levelut, Phys. Rev. B4, № 9, 3077 (1971).
358.	B. A. Huberman, E. Burstein, R. Ito, Phys. Rev. B5, № 1, 168 (1972).
VI.2. Взаимодействие магнитной системы сносителями тока, особенности резонанса в металлах1)
359.	А. М. Clogston, Bell System Tech. J. 34, № 4, 739 (1955).
360.	W. A. Yager, J. K. Galt, F. R. Merritt, Phys. Rev. 99, № 4, 1203 (1955).‘
361.	В. Л. Гуревич, ЖЭТФ 33, № 6, 1497 (1957).
362.	A. H. Mitchel, Phys. Rev. 105, № 5, 1439 (1957).
363.	E. А. Туров, [25], гл. 5.
364.	W. G. Egan, H. J. Juretschke, J. Appl. Phys. 34, № 5, 1477 (1963).
365.	B. Vural, J. Appl. Phys. 37, №<3, 1030 (1966).
366.	D. J. Epstein, L. Tocci, Appl. Phys. Lett. 11, № 2, 55 (1967).
367.	А. Я. Бланк, M. II. Каганов, УФН 92, № 4, 583 (1967).
368.	G. 11. Larson, A. W. Slight, Phys. Lett. A28, № 3, 203 (1968).
369.	A. K. Goswami, M. Rosenbloom, R. W. Teale, J. Appl. Phys. 39, № 2, part 1, 828 (1968).
370.	M.A. Кривоглаз, А. А. Трущенко, ФТТ 11, № 11, 3119 (1969).
371.	А. А. Самохвалов, С. А. Исмаилов, A. M. Котельникова, ФТТ 11, № 2, 392 (1969).
372.	Б. Гейнрих, В. Ф. Мещеряков, ЖЭТФ 59, № 2, 424 (1970).
373.	О. Horan, G. С. Alexandrakis, С. N. Manicopoulos, Phys. Rev. Lett.
25, № 4, 246 (1970).
374.	I. G. Austin, D. Elwell, Contemp. Phys. 11, № 5, 455 (1970). (Перевод в УФН 106, № 2, 337 (1972).)
375.	M. Toda, Appl. Phys. Lett. 17, № 1, 1 (1970).
376.	W. A. Thompson, F. Holzberg, T. R. McGuire, Phys. Rev. Lett. 26, № 21, 1308 (1971).
377.	А. А. Самохвалов, >. А. Гижевский, M. И. Симонова, H. И. Солин, ФТТ 14, № 1, 279 (1972).
378.	I. Balberg, H. L. Pinch, Phys. Rev. Lett. 28, № 14, 909 (1972).
VI.3. Анизотропия и релаксация, обусловленные примесными ионами2)
379.	J. F. Dillon, Jr., J. TV. Nielsen, Phys. Rev. Lett. 3, № 1, 30 (1959). (Перевод в [24].)
380.	E. G. Spencer, R. C. Le Craw, A. M. Clogston, Phys. Rev. Lett. 3, № 1,
32 (1959). (Перевод в [24].)
381.	C. Kittel, Phys. Rev. 115, № 6, 1587 (1959).
382.	P. G. de Gennes, C. Kittel, A. M. Portis, Phys. Rev. 116, № 2, 323 (1959).
383.	C. Kittel, Phys. Rev. 117, № 3, 681 (1960).
384.	J. F. Dillon, Jr., J. W. Nielsen, Phys. Rev. 120, № 1, 105 (1960).
385.	R. Orbach, Proc. Roy. Soc. A264, № 1319, 458 (1961).
386.	E. G. Spencer, R. C. Le Craw, R. C. Linares, Phys. Rev. 123, № 6, 1937 (1961).
i) См. также [14, 154, 253, 256, 258, 560, 568].
2) См. также [359, 528].
586
ЛИТЕРАТУРА
387.	J. F. Dillon, Jr., L. R. Walker, Phys. Rev. 124, № 5, 1401 (1961).
388.	А. Г. Гуревич, А. П. Сафантъевский, В. И. Соловьев, Е. С. Шер, Изв. АН СССР, сер. физ. 25, № 11, 1361 (1961).
389.	L. R. Walker, J. Appl. Phys. 33, Suppl. № 3, 1243 (1962).
390.	R. F. Pearson, J. Appl. Phys. 33, Suppl. № 3, 1236 (1962).
391.	R. W. Teale, K. Tweedale, Phys. Lett. 1, № 7, 298 (1962). „
392.	J. F. Dillon, Jr., Phys. Rev. 127, № 5, 1495 (1962).
393.	R. W. Teale, В. H. Clarke, J. Appl. Phys. 34, № 4, part 2, 1248 (1963).
394.	J. H. van Vleck, J. Appl. Phys. 35, № 3, part 2, 882 (1964).
395.	F. Hartman-Boutran, Phys, kondeus. Materie 2, 80 (1964).
396.	D. L. Huber, J. Appl. Phys. 36, № 3, part 2, 1009 (1965).
397.	В. И. Соловьев, А. Г. Гуревич, ФТТ 7, № 6, 1761 (1965).
398.	В. H. Clarke, К. Tweedale, R. W. Teale, Phys. Rev. 139, № 6A, A1933 (1965).
399.	В. H.	Clarke,	Phys. Rev. 139, № 6A, A1944	(1965).
400.	D. L.	Huber,	Solid State Com. 4, № 9, 435	(1966).
401.	В. H.	Clarke,	J. Phys. Chem. Solids 27, №	2, 353 (1966).
402.	E. M.	Gyorgy,	R. C. Le Craw, M. D. Srurge,	J. Appl.	Phys. 37, № 3,
1303 (1966).
403.	M. Sparks, J. Appl. Phys. 38, № 3, 1031 (1967).
404.	J. F. Dillon, Jr., J. P. Remeika, L. R. Walker, J. Appl. Phys. 38, № 5, 2235 (1967).
405.	D. I. Tchernev, J. Appl. Phys. 39, № 2, 826 (1968).
406.	A. H. Агеев, А. Г. Гуревич, ФТТ 11, № 8, 2122 (1969).
407.	M. D. Sturge, F. R. Merritt, J. C. Hensel, J. P. Remeika, E. M. Gyorgy, R. C. Le Craw, Phys. Rev. 180, № 2, 413 (1969).
408.	T. S. Hartwick, J. Smit, J. Appl. Phys. 40, № 10, 3995 (1969).
409.	А. Г. Гуревич, A. H. Агеев, M. И. Клингер, J. Appl. Phys. 41, № 3, 1295 (1970).
VI.4. Взаимодействие электронной
и ядерной магнитных систем1)
410.	II. Suhl, Phys. Rev. 109, № 2, 606 (1958).
411.	Т. Nakamura, Progr. Theor. Phys. 20, № 4, 542 (1958).
412.	P. G. de Gennes, P. A. Pincus, F. Hartman-Boutran, J. M. Winter, Phys. Rev. 129, № 3, 1105 (1963).
413.	G. L. Witt, A. M. Portis, Phys. Rev. 136, № 5A, A1316 (1964).
414.	A. J. Heeger, T. W. Houston, Phys. Rev. 135, № ЗА, A661 (1964).
415.	Л. Г. Оноприенко, ФММ 19, № 4, 481 (1965).
416.	В. А. Тулин, ЖЭТФ 55, № 3, 831 (1968).
417.	А. И. Тимофеев, Е. А. Туров, ФТТ 10, № 11, 3322 (1968).
418.	В. D. Guenter, С. R. Christensen, А. С. Daniel, Phys. Lett. АЗО, № 7, 391 (1969).
419.	W. J. Ince, J. Appl. Phys. 40, № 3, 1595 (1969).
420.	M. П. Петров, Г. А. Смоленский, А. П. Паугурт, В. Ф. Пашин, ЖЭТФ 61, № 1, 301 (1971).
VI.5. Магнитооптика2)
421.	Г. С. Кринчик, М. В. Четкий, ЖЭТФ 40, № 3, 729 (1961). 422. К. A. Wickersheim, Phys. Rev. 122, № 5, 1376 (1961). , 423. К. A. Wickersheim, [12], vol. I, ch. 7.
i) См. также [22, 572].
2) См. также [570].
ЛИТЕРАТУРА
587
424.	R. С. Le Craw, D. L. Wood, J. F. Dillon, Jr., J. P. Remeika, Appl. Phys. Lett. 7, № 1, 27 (1965).
425.	Y. R. Shen, N. Bloembergen, Phys. Rev. 143, № 1, 371 (1966).
426.	B. A. Auld, D.A. Wilson, J. Appl. Phys. 38, № 8, 3331 (1967).
427.	P. A. Fleury, S. P. S. Porto, J. Appl. Phys. 39, № 2, 1035 (1968). (Перевод в УФН 98, № 1, 71 (1969).)
428.	T. Moriya, J. Appl. Phys. 39, № 2, 1042 (1968). (Перевод в УФН 98, № 1, 81 (1969).)
429.	H. Ф. Харченко, В. В. Еременко, Л. И. Белый. ЖЭТФ, 55, № 2, 419 (1968).
430.	J. Н. Collins, D. A. Wilson, Appl. Phys. Lett. 12, № 10, 331 (1968).
431.	A. W. Smith, Phys. Rev. Lett. 20, № 7, 334 (1968).
432.	Г. С. Кринчик, M. В. Четкий, УФН 98, № 1, 3 (1969).
433.	R. Wolfe, A. J. Kurtzig, R. C. Le Craw, J. Appl. Phys. 41, № 3, 1218 (1970).
434.	J. F. Dillon, Jr., E. M. Gyorgy, J. P. Remeika, J. Appl. Phys. 41, № 3, 1211 (1970).	‘	‘
435.	L. F. Johnson, J. F. Dillon, Jr., J. P. Remeika, Phys. Rev. Bl, № 5, 1935 (1970).
436.	R. S. Caird, W. B. Gam, С. M. Fowler, D. B. Thompson, J. Appl. Phys. 42, № 4, 1651 (1971).
437.	H. L. Hu, F. R. Morgenthaler, Appl. Phys. Lett. 18, № 7, 307 (1971).
438.	P. В. Писарев, И. Г. Синий, Н. Н. Колпакова, Ю. М. Яковлев, ЖЭТФ 60, № 6, 2188 (1971).
439.	S. R. Chinn, Н. J. Zeiger, J. R. O'Connor, Phys. Rev. ВЗ, № 5, 1709 (1971).
440.	А. И. Беляева, В. С. Кулешов, В. И. Силаев, Н. В. Гапон, ЖЭТФ 61, № 4, 1492 (1971).
VII. Электродинамика и устройства
• VII.1. Электродинамика гиротропных сред1) •
441.	J. A. Osborn, Phys. Rev. 67, № 11—12, 351 (1945).
< 442. М. L. Kales, J. Appl. Phys. 24, № 5, 604 (1953).
443.	M. L. Kales, H. M. Chait, N. G. Sakiotis, J. Appl. Phys. 24, № 6, 816 (поправка № 12, 1529) (1953).
444.	К. M. Поливанов, Я. М. Колли, М. Б. Хасина, Изв. АН СССР, сер. физ. 18, № 3, 350 (1954).
445.	М. А. Гинцбург, ДАН СССР 95, № 3, 489 (1954).
446.	Н. Suhl, L. R. Walker, Bell System Tech. J. 33, № 3, 579; № 4, 939; № 5, 1131 (1954). (Перевод Г. Сул, Л. Уокер, Вопросы волноводного распространения электромагнитных волн в гиротропных средах, ИЛ, 1955).
447.	А. Л. Микаэлян, ДАН СССР 98, № 6, 941 (1954).
448.	В. Lax, К. J. Button, L. М. Roth, J. Appl. Phys. 25, № 11, 1413 л (1954).
449.	Р. S. Epstein, Rev. Mod Phys. 28, № 1, 3 (1956). (Перевод в УФН 65, № 2, 283 (1958).)
450.	A. D. Berk, Trans. IRE AP-4, № 2, 104 (1956).
451.	G. S. Heller, Proc. IRE 44, № 10, 1386 (1956).
J) См. также [6, 113, 237]. Приводятся работы по электродинамике систем, содержащих неметаллические гиротропные среды. Некоторые работы по электродинамическим процессам в ферромагнитных металлах см. в разделе VI.2.
588
ЛИТЕРАТУРА
452.	В. В. Никольский, РЭ 2, № 2, 157 (1957).
453.	II. Seidel, Bell System Tech. J. 36, № 2, 409 (1957).
454.	А. В. Воронова, А. Г. Гуревич, РЭ 2, № 4, 401 (1957).
455.	Я. А. Моносов, РЭ 2, № 5, 547 (1957).
456.	II. E. Bussey, L.A. Steinert, Proc. IRE 45, № 5, 693 (1957).
457.	В. В.	Никольский, РЭ	2, № 7, 937 (1957).
458.	А. Г.	Гуревич, РЭ 2,	№ 8, 960	(1957).
459.	В. A.	Hurd, Canad. J.	Phys. 36,	№ 8, 1072	(1958).
460.	А. Г.	Гуревич, A. II. Богомаз, РЭ	3, № 9, 1113	(1958).
461.	А. В. Гапонов, Г. И. Фрейдман, ЖЭТФ, 36, № 3, 957 (1959).
462.	Н. Seidel, В. С. Fletcher, Bell System Tech. J. 38, № 6, 1427 (1959).
463.	Сюй Янъ-шен, РЭ 5, № 12, 1951 (1960).
464.	I. Body, G. McCall, J. Appl. Phys. 32, Suppl. № 3, 146S (1961).
465.	А. Л. Микаелян, В. Я. Антонъянц, 10. Г. Турков. РЭ 6, № 7, 1184 (1961).
466.	А. Г. Гуревич, РЭ 8, № 5, 780 (1963).
467.	В. A. Auld, J. Appl. Phys. 34, № 6, 1629 (1963).
468.	М. И. Каганов, Р. П. Янкелевич, ФТТ 10, № 9, 2771 (1968).
469.	С. F. Vasile, L. В. Felsen, J. Appl. Phys. 41, № 6, 2387 (1970).
470.	R. S. Mueller, J. Appl. Phys. 42, № 6, 2264 (1971).
471.	M. Weiner, J. Appl. Phys. 43, № 3, 1246 (1972).
VII.2. Экспериментальное исследование электродинамических эффектов; ферритовые СВЧ устройства1)
472.	C.L. Hogan, Bell System Tech. J. 31, № 1, 1 (1952).
473.	L. G. van Uitert, J. P. Schafer, C. L. Hogan, J. Appl. Phys. 25, № 7 925*(1954).
474.	B. Lax, J. Appl. Phys. 26, № 7, 919 (1955).
475.	J. L. Melchor, W. R. Ayres, P. H. Vartanian, J. Appl. Phys. 27, № 1, 72 (1956).
476.	M. T. Weiss, Trans. IRE MTT-4, № 4, 240 (1956).
477.	8. Weisbaum, H. Seidel, Bell System Tech. J. 35, № 4, 877 (1956).
; 478. N. Karayianis, J. C. Cacheris, Proc. IRE 44, № 10, 1414 (1956).
479.	B. J. Duncan, L. Swern, Proc. IRE 45, № 5, 647 (1957).
480.	F. Reggia, E. G. Spencer, Proc. IRE 45, № 11, 1510 (1957).
481.	M. A. Treuhaft, L. M. Silber, Proc. IRE 46, № 8, 1538 (1958).
482.	B. A. Auld, Trans. IRE MTT-7, № 2, 298 (1959).
483.	II. N. Chait, T. R. Curry, J. Appl. Phys. 30, SuppL № 4, 152S (1959).
484.	R. W. de Grasse, J. Appl. Phys. 30, Suppl. № 4, 155S (1959).
485.	G. S. Heller, J. J. Stickler, J. B. Traxter, J. Appl. Phys. 32, Suppl. № 3, 307S (1961).
486.	P. S. Carter, Trans. IRE MTT-9, № 3, 252 (1961).
487.	F. A. Olson, J. R. Yaeger, Trans. IEEE MTT-13, № 1, 63 (1965).
488.	Л. К. Михайловский, Б. П. Поллак, В. Ф. Балаков, А. Е. Хантемиров, РЭ 10, № 10, 4739 (1965).
489.	D. II. Hornbostel, Proc. IEEE 53, № И, 1751 (1965).
490.	В. Maher, D. Mitchell, A. Reeves, Trans. IEEE MTT-14, № 1, 42 (1966).
491.	II. van de Vaart, Proc. IEEE 54. № 7, 1007 (1966).
492.	К. K. Chow, M. E. Hines, J. Appl. Phys. 37, № 13, 5000 (1966).
493.	G. P. Rodrigue, J. Appl. Phys. 40, № 3, 929 (1969).
J) См. также [11, 535].